Текст
Алгебра
ОБЛАСТЬ ОПРЕДЕЛЕНИЯ
И УСЛОВИЕ РАВЕНСТВА ДРОБИ
НУЛЮ
А в С D
1 2х-2 5х-20 25 8х+2 20х -5 12 12Х-8 Эх+12
2 2а-0,б 0,За+6 0,12а+2,4 60 100 а-0,5
1,5а-45 0,01а+4 72 а
3 Зх+1 (х+10)(х-5) (5х -I)2 (5х+2)3
х(х-З) 5х-1 х(2х+3) (5х-1)(х+5)
4 2у+1 у2-100 4у2-1 25у2+0,1 ^y^ у2-0,25
у2+4 9у2-4
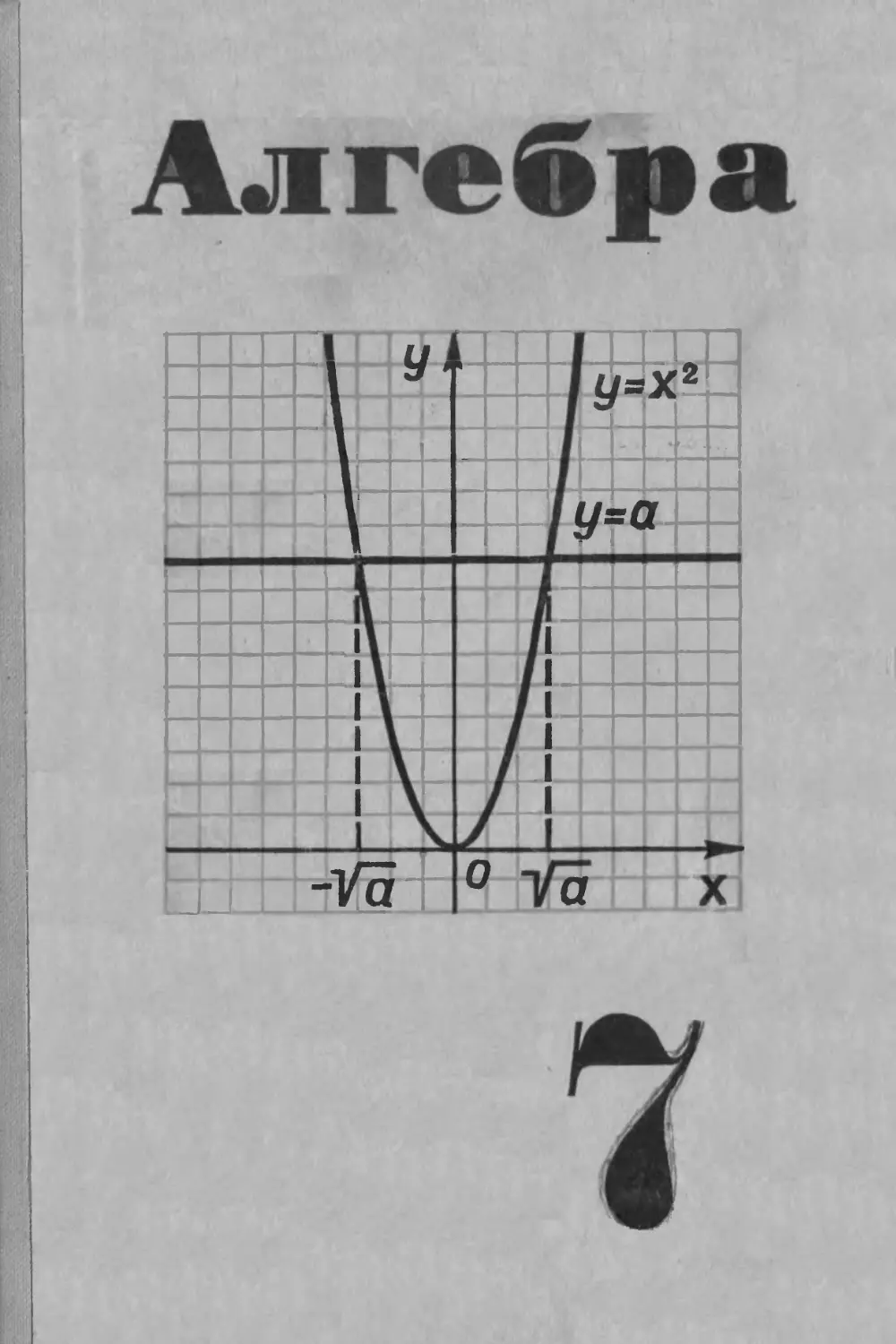
ГРАФИЧЕСКОЕ РЕШЕНИЕ
НЕРАВЕНСТВА
f(x)>g(х)
АЛГЕБРА
УЧЕБНОЕ ПОСОБИЕ
ДЛЯ 7-го КЛАССА
СРЕДНЕЙ ШКОЛЫ
Под редакцией А. И. МАРКУШЕВИЧА
Утверждено Министерством просвещения СССР
ИЗДАНИЕ Б-е
МОСКВА • ♦ПРОСВЕЩЕНИЕ» 197G
612 (075)
A 45
IO. H. МАКАРЫЧЕВ, H. Г. МИНДЮК,
К. С. МУ РАВИН, С. Б. СУВОРОВА
•*75
т- ннф. письмо
6
Глава Г.
ДРОБИ
§ 1. ПОНЯТИЕ ДРОБИ
1. Целые выражения
Числовые выражения, а также выражения с переменными,
в которых используются операции сложения, вычитания, умно-
жения, деления и возведения в степень, называются рацио-
нальными.
В VI классе мы изучали целые рациональные выражения —
это все числовые выражения, а также такие рациональные вы-
ражения с переменными, которые не содержат операции деления
на выражение с переменными.
Было показано, что всякое целое выражение можно пре-
образовать в тождественный ему многочлен стандартного вида.
Например, выполнив преобразование а (а2 4- 4а — 12) —
—(2а—3)2=а34~4а2—12а—4а24-12а—9== а3—9, мы целое выра-
жение а (а2+4а—12)—(2а—З)2 представили в виде многочлена
а3—9 стандартного вида.
Было показано также, что некоторые многочлены можно
преобразовать в произведение, т. е. разложить на множители.
При этом использовались различные способы.
Например, многочлен х3—5х24-30х можно разложить на
множители путем вынесения общего множителя за скобки:
х3—5х24~30х=х (х2—5x4-30).
Многочлен аЪ—25 4-5а—10 можно разложить на множите-
ли, применяя способ группировки:
аЪ— 2&4-5а— 10=(аЬ— 2Ь)4-(5а—10)-
= & (а—2)4-5 (а—2) = (а—2) (&4-5).
При разложении на множители двучлена у3—64 использует-
ся тождество сокращенного умножения (разность кубов двух
выражений):
у3—64=у’—4’=(у—4) (ys +4у+16).
8
При разложении некоторых многочленов на множители ис-
пользуется несколько способов:
Зу6-243у =Зу (у3 4—81)=3у (у2-9) (у2+9) =
=3у (у—3) (у+3) (у2+9).
Существуют многочлены, которые нельзя представить в
виде произведения двух многочленов не нулевой степени.
К числу таких многочленов относится, например, двучлен i
хг+1.
Если бы такое разложение было возможно, то многочлен х2 + 1 можно
было бы представить в виде произведения двух многочленов первой степени,
каждый из которых при некотором значении х обращался бы в нуль. Но тогда
при том же значении х обратился бы в нуль и тождественно равный произведе-
нию двучлен х2 + 1, а это невозможно, так как при всех х значение х* неотри-
цательно, а значенпе х2 + 1 положительно.
1. Преобразуйте выражение в многочлен стандартного вида:
а) х (х+3);
б) 2у (у -5);
в) За (а2—2а —5);
г) 5b (1—ЗЬ — Ь2);
д) 2р2 (Зр2—у2)+2р2у2;
е) бу3—у (4р2-3у);
ж) 2 (m—3n)+3 (т—2л);
з) а2 (а2 + Ь2)—Ъ1 (а2— Ь2).
2. Представьте в виде многочлена стандартного вида:
а) (х—2) (х+5); в) (а +4) (а-4); д) fp Н 1) (р + 1);
б) (у+8) (у-7); г) (Ь—3)(Ы-3); е) (9-у) (у-9).
3. Замените выражение тождественно равным многочленам
стандартного вида:
а) (у—55) (у+55); г) (р2 -1) (1 -р2); ж) (-у + 5)2;
б) (2а+3) (3—2а); д) (х+7)2; з) (-Зр-у)2.
в) (3b— 1) (ЗЬ—1); е) (а—2х)2;
4. Решите уравнение:
а) —5х=16; д) 2 (х—5)— 3 (8—х)=1;
б) 2х=1; е) 18-15 (у-3) =5 (9-у);
б ж) х (х—8)—х (х—9) =25;
В) а> 5*/-12 (8-У) ~9;
73 ’ и) (х+3) (х-5)=(х+1)(х+6);
г) 0,01у = —1; к) (у +3) (у—4)=(у—2) (у +6).
5. Представьте выражение в виде произведения:
а) ax-j-ay;
б) 5b—5с;
в) 6 m—18;
г) Юл+15;
д) 15ах—2Оау;
е) 8а5+125с;
ж) х2—ху;
в) ху—у2;
и) Зху’-гбху2 — 18ху;
к) 15а35+10а25—20а252.
4
6. Разложите на множители:
а) Б (у^-гЗ) —х (у—^3):
б) ту—тх+пу—пх;
в) аЬ+8а4*96+72;
г) 6m—12—2n+mn;
Д) pq—4р4*12 — 3?;
е) а2+а6+ах+Ьх;
ж) х2—ху—5х+5у;
з) а+Ь—аг—ab.
7.
Представьте многочлен
в виде произведения:
а) а2—9; в) х2—4у2;
б) 16—с2; г) 25а2—tr;
д) Xs—4х; ж) а2—6а+9;
е) 4Sps—р\ з) 16х2+8x4-1.
8. Решите уравнение:
а) (х—2) (х+5)=0; г) х2— 12х=0;
б) (у + 8) (2у— 3) = 0; д) х2 + 21х=0;
в) 4 (х—3)=0; е) у2—64=0;
ж) х2+9=0;
з) 25х2—4=0.
0. Представьте в виде произведения:
а) а3—8; в) 1—8ys; д) т"-1;
б) 2763 + 1; г) у'—64b3; е) ря — q\
10. Постройте график функции:
а) у = - х; б)у = 2х —3; в) у = — -Х4*2; г) у = 0-х+4.
2 4
Укажите множество значений х, при которых
У=0; у >0; у <0.
11. Постройте графики функций у—х и у = |х|.
Пользуясь графиком функции у = |xj, решите уравнение:
а) |х|=2; б) |х| = 0; в) |х| = —3.
12. Проходит ли график функции у = 5х2 через точку А (2; 20),
В (—2; 20), С (2;
—20), -Ofi; 1,25'‘, е(—
\ 2 / \ 2
-1,25,?
13. Длина прямоугольника втрое больше его ширины. Если
длину и ширину этого прямоугольника увеличить на 5 см,
то его площадь увеличится на 140 см2. Найдите длины
сторон данного прямоугольника.
14. Длина прямоугольника на 10 см больше его ширины.
Если длину уменьшить на 15 см, а ширину увеличить
&
на 5 см, то площадь прямоугольника уменьшится на 106 с№.
Найдите площадь данного прямоугольника.
15. Из двух Городов, расстояние между которыми 180 км,
навстречу друг другу выехали одновременно мотоциклист
и велосипедист и встретились через 2 часа. Найдите ско-
рость велосипедиста, если известно, что мотоциклист про-
езжает за час на 60 км больше, чем велосипедист.
16. Из натурального ряда выбрали три последовательных чис-
ла так, что произведение второго и третьего числа оказа-
лось больше произведения первого и второго числа на 80.
Найдите среднее число.
2. Дробь. Область определения дроби
Выражение вида —, где буквами а и Ъ обозначены вырьже-
ь
ния числовые или содержащие переменные, называют дробью.
Выражение а называют числителем дроби, выражение Ъ —
ее знаменателем.
4 2
Лпоби 3 164-3-7 7 3
роии _ ,—, —_— являются числовыми выражениями,
1 _1
- 8 х’ — 5x4-7 а b
а дроби —, ----------, ---- — выражениями, содержащими t
а у — 2 10
переменные.
Для отыскания значения числового выражения, представ-
ленного в виде дроби, обычно находят значение ее числителя и
знаменателя и первый результат делят на второй. Если знаме-
натель дроби равен нулю, то такая дробь не имеет значения,
так как делить на нуль нельзя. В таких случаях говорят, что
дробь не имеет смысла.
Значение дроби, содержащей переменные, зависит от значе-
ний входящих в нее переменных. Например, дробь ?-i3 При
а — б
2
а-8 принимает значение, равное 3-, при а~4 ее значение
равно —7.
При а=5 дробь — 3 не имеет смысла. Число 5 —един-
а — б
ственное значение переменной а, при котором рассматриваемая
дробь не имеет смысла. При всех остальных значениях а эта
дробь имеет смысл.
0
—_ в ~i 3
Говорят, что область определения выражения --------- есть
а — о
множество всех чисел, кроме 5.
Определение. Областью определения выражения с
одной переменной называется множество значений переменной,
при которых это выражение имеет смысл.
Целое выражение имеет смысл при всех значениях входя-
щих в него переменных. Например, многочлен f/3-8i/:14-3y—17
имеет числовое значение при любом значении у, так как для
нахождения значения этого многочлена придется над числами
выполнять действия: возведение в степень, умножение, сложе-
ние и вычитание, которые всегда возможны. Поэтому область
определения целого выражения есть множество всех чисел.
Чтобы найти область определения дроби, числитель и зна-
менатель которой — целые выражения, причем знаменатель —
выражение с переменной, нужно найти значения переменной,
обращающие знаменатель этой дроби в нуль, и исключить их
из множества всех чисел.
Приведем примеры.
у — 4
1. Найдем область определения дроби •
Числитель и знаменатель этой дроби имеют смысл при лю-
бых значениях х.
Выясним, при каких значениях х знаменатель дроби обра-
щается в нуль. Для этого решим уравнение:
2x4-6 =0.
2т = —6,
х = —3.
Дробь —^6 имеет смысл при хф —3, т. е. область определе-
ния данной дроби (обозначим ее буквой X) состоит из всех чи-
сел, кроме —3.
Это можно записать так: X = ]—оо; —3[(J ] —3; 4-се[.
2. Знаменатель дроби —°— при любых значениях а от-
личен от нуля (уравнение пл4~1=0 не имеет корней). Поэтому
область определения этой дроби есть множество всех чисел:
]—
3. Знаменатель дроби —— при любом х равен нулю. По-
X — X
этому область определения выражения —— есть пустое мно-
X — X
жество. Такие дроби мы в дальнейшем рассматривать не будем.
7
Область определения дроби, содержащей две переменные,
- 1
например дроби ----, состоит из множества пар чисел вида
х — у
(х; у), которые не обращают знаменатель х—у в нуль (т. е.
не являются решением уравнения х—у=0). Пары чисел (2; 2),
(—2,3; -2,3), '
ние х равно значению у, не входят в область определения дро-
би ---. Если же значение х не равно значению у, то х—у не
х У
равно нулю и в этом случае дробь —— имеет смысл.
Х~У
Условие, при котором дробь ---- имеет смысл, можно за-
Х—У
писать кратко: х—у =/= 0 или х =# у.
2 2 \
31yj Sly! и вообще все те, у которых значе-
17. Какие выражения являются дробями:
-Ь, —, 5- + 1, Л, 2-, - • -?
6 5 х-у 2с 1 7 5 Ь
18. Составьте дробь:
а) числитель которой — произведение переменных х и у,
а знаменатель — их сумма;
6)1 числитель которой — разность переменных а и 6, а
знаменатель — их произведение;
в) числитель которой — разность квадратов переменных
х и у, а знаменатель — сумма квадратов этих перемен-
ных;
г) числитель — удвоенное произведение переменных а и
Ь, а знаменатель — сумма кубов этих переменных.
19. Найдите значение дроби:
0,75-0,4—5,7 .
1,86:0,31 *
1,95:1,34-2,5 .
3,4-0,84-3,28 ’
1L92 — 712
_ •
2532—47а
300
20. Найдите значение дроби -—- при у—3; 1; —5; —; —1,6.
У 2
о у । g
21. Найдите множество значений дроби ——, зная множест-
ве — з
во значений переменной х:
7; 1; 0; - 5; Ц; -13; -0.2; 21.
о
8
22. Найдите значение дроби - ---— при:
аа + ta
а) а — — 3, Ъ — — 1; б) а=1—; Ь — —-0,5.
2
23. При каком значении переменной значение дроби:
\ х — з -
а) —— равно 1;
б) —5— равно—1;
б' + в
Р — 7 к
—— равно 5;
—— равно 9?
24. Найдите
область определения дроби:
б)
2х
_ •
х + б’
в) —!—'
1 — 2х
Д)
2уа-9 .
8(40-1)’
яс)
х — 5
лг;
г)
У .
7^+2*
ч 48
е) ----------
7 5 (9 4-100)
В)
02 ~ 20 — 3
25
25. Найдите область определения выражения:
а) х2 — 8х 4- 4;
б) у3 - 2у* 4- Зу — 6;
ч 16
в) ;
(х-1)(х-4)
у 5 а 3
Г а (а — 4) ’
2х2— 8х*
е) —;
^4-1
5
Ж) ^-5
41
lj-l+2'
3)
26. Функция f задана формулой. Найдите
ния функции f:
ч 1 лч 12 ч 9
а)!/=-; 6) у = -—в) I/= ———;
х х — 3 х2 4- эх
область определе-
v 6
г) У^-ТУа
х2 4- 4
27. Напишите дробь, которая не имеет смысла при:
а) х==7;
б) а = —9;
в) У =6 или {/=13;
г) или Ь = —2.
28. При каком условии дробь не имеет смысла:
ч 8 Лч 15 ч 1 Ч 3 ч 1. лч 19 9
а>-----б> в) "ТГГа; г) Т^Г; д) е) . 9??
а — b а 4" Ь са4-Ьа fi3—Ь2 ab а(Ь — 2)
§ 2. СВОЙСТВА ДРОБЕЙ
3. Условие равенства дроби нулю
Если числитель дроби равен нулю, то дробь либо равна
нулю, либо не имеет смысла.
тт е. О о 0 - О
Например, дроби —,-----, — равны нулю, а дробь — не
б —0,7 3 О
2п
имеет смысла.
Если дробь равна нулю, то ее числитель равен нулю, а
внаменатель отличен от нуля (иначе дробь не имела бы смысла).
Итак:
Дробь —равна нулю тогда и только тогда, когда a=0ub-M).
ь
Покажем, как условие равенства дроби нулю можно исполь-
зовать при решении уравнений.
Рассмотрим примеры.
2___5
1. Решить уравнение----- = 0.
8 +л
2х__5
Дробь ----обращается в нуль при тех и только тех вна-
8 4-х
чениях х, при которых 2х—5=0 и 34-х^-О, т. е. при тех значе-
ниях х, которые являются решениями системы:
2х —5 =0,
34-л-^О.
Уравнение 2х—5=0 имеет корень, равный 2,5. При этом
значении х выражение 3 отлично от нуля: высказывание
34-2,5^0 истинно. Следовательно, число 2,5 — корень уравне-
Решение можно записать так:
^ = 0;
34-*
2х — 5 = 0,
3 + х 0;
2х — 5 = 0,
2х = 5,
х = 2.5.
Высказывание 3 + 2,5 =/ 0 истинно.
Ответ: 2,5.
.’0
2. Решить уравнение * —— — о.
Дробь
ха — 5х
10—2х
обращается в нуль тогда
и только тогда, когда
х2 — 5х = О и 10 — 2х Ф О, т. е.
х2 — 5х — О,
10 — 2х ¥= 0.
Решим уравнение
х2 — 5х — О;
х (х — 5) =0,
х — О или х = 5.
Проверим, обращается ли при этих значениях х предложе-
ние 10 — 2х 0 в истинное высказывание.
Пусть х — 0. Высказывание 10 — 2 • 0 =/= 0 истинно.
Пусть х — 5. Высказывание 10 — 2-5 =/= 0 ложно.
Данное уравнения имеет единственный корень 0.
Ответ: 0.
29. Известно, что числитель дроби равен нулю. Следует ли
отсюда, что дробь равна нулю?
30. Известно, что дробь равна нулю. Следует ли отсюда, что
ее числитель равен нулю?
31. Докажите, что значение дроби равно нулю:
32. Какая из дробей не имеет смысла:
8.3 1,2 + 4,2 5.6- 2.1 — 11,76
-----!-----------ИЛИ ----------------
(81, 2 / 2 \
3 -2 1-5 — 7— 5 — 3- 6-7,9
б 15/ 8 \ »/
33. Какая из дробей равна нулю:
11 2 2
8’в Лб - 2,5 или — 8 : к 2— -9 5 9 9 *
« 1 to м -о 40 1 | со 15 •’Тб 8 *7 4 5 ' 5 ' 7
11
34.
Докажите, что значение дроби равно нулю:
х(х — 5) — 0,5х(2х — 10) t _
1 -------------- при всех х^2;
х — 2
6)
х2 — 4
при всех Хф~ 2 и х=^2.
35.
Напишите дробь, которая содержит переменную у и обра-
щается в нуль при:
а) У = 8;
б) у = -1.
36.
При каких
значениях
У,
5’
<7 — 1.
у-12.
значение дроби равно нулю:
О
у-1'
б)—’
У
У
37. Существуют ли значения переменной х, при которых дробь
равна нулю:
ч 7
х— 2
б> 7
х — 2*
88.
Решите уравнение:
б)
х — 8
125
5х — 12 _
—— VZa
37
^? = 0;
X
= 0;
Д)
39.
= 0;
х — 2
= 0;
•— = 0-,
X
формулой. При
Функция задана
ние функции равно нулю:
X
п= б)г/ =
ж)
=0;
2х
^ = 0.
X
каком значении х значе-
X —4 х +
---• в){/=—I-
X
X — 5
5 — х
8
40.
Функция f задана формулой у — —
х— 2
Найдите: а) / (0), f (—3), f (3), f (12); б) область опре-
деления X функции; в) множество значений переменной х,
при которых f (х) = 0; г) координаты точки пересечения
графика функции с осью у. Проходит ли график функции
через точку А (7; 2), В (—6; 9)?
12
4. Основное свойство дроби. Сокращение дробей
л о Зх3 Зх
Сравним соответственные значения дробей — и —.
Зх3
При х = 0 дробь — не имеет значения (не имеет смысла).
8х
Поэтому в этом случае нельзя указать пару соответственных
Эх2 Зх
значений выражений — и — . Для всех остальных значений х
8х 8
соответственные значения этих выражений существуют.
При х=2 соответственные значения этих дробей равны:
?х2 _ 3 22 2 Зх 3 • 2 3
8х ~ 8 • 2 ~ 4 ’ 8 ~ 8 ~~ 4 *
Соответственные значения рассматриваемых дробей равны
и при любых других значениях переменной х, где х #= 0. Это
следует из свойства частного: если делимое и делитель умно-
жить или разделить на одно и то же число, отличное от нуля,
то значение частного не изменится. Следовательно, можно
утверждать, что все соответственные значения рассматривав-
Зх2 Зх
мых дробей равны. Это значит, что дроби — и — являются
тождественно равными, а равенство
Зх3 _ 8х_
8х “ 8
тождеством.
Рассмотрим дроби — и —. На основании свойства частно-
Ьс Ъ
го при Ь #= 0 и с #= 0 все соответственные значения этих дро-
бей равны. (При b = 0 или с = 0 одна дробь или обе дроби не
имеют значений.)
Поэтому дроби — и — являются тождественно равными, а
Ъс ъ
равенство
ас ._________________________ a fl)
Ъс Ъ
тождеством.
Тождество (1) выражает основное свойство дроби. Оно
„ас
позволяет заменять дробь вида — тождественно равной дро-
Ъс
бью — или, как говорят в таких случаях, сокращать дробь
ъ
— на общий множитель с числителя и знаменателя.
Ъс
13
Рассмотрим примеры сокращения дробей.
Пример 1 Числитель и знаменатель дроби — —
содержат общий множитель х — 2. Сократив данную дробь на
общий множитель, мы выполним тождественное преобразова-
ние:
2х(х—2) _ 2х
Ъ(х — 2) “ 5*
Заметим, что области определения дробей -* и
различны. Область определения первой дроби есть множество
всех чисел, отличных от 2, а область определения второй дро-
би — множество всех чисел. В результате сокращения мы по-
лучили дробь, область определения которой шире, чем область
определения исходной дроби.
Пример 2. Для упрощения дроби — ~9 разложим на
ah 4* 3b
множители ее числитель и знаменатель и выполним сокраще-
ние:
и» —9 _ Jr — 3) (а + 3) _ а—3
аЬ4-ЗЬ Ь(а-|-3) — Ь
Пример 3, Пусть требуется сократить дробь .
а5 д1
Выполнив преобразование, получим:
(— а2Ь)3 _ — дяЬз _ —а
аъЬ* а6Ьл Ъ
Выражение — тождественно выражению — —,
ь ь
Действи-
тельно, при любых значениях а и Ъ (Ь ф 0) значение каждого из
этих выражений есть число, противоположное значению дроби
—. Поэтому все соответственные значения выражений---и
— равны и равенство
ь
есть тождество.
Если числитель и знаменатель дроби — умножить на —1,
ъ
то получим дробь, тождественно равную первой:
—д _ — д (—1) _ _д_
ь ъ (-1) — ъ
Поэтому равенство
а а
—ъ ~~ ъ
(3)
также является тождеством.
14
Тождества (2) и (3) применяются в тождественных преобра-
зованиях выражений, содержащих дроби. В частности, когда
выполняют сокращение дробей, то дроби вида или —
принято представлять так: — —. Поэтому, выполнив преобра-
ь
зование дроби » окончательный ответ следует записать
в виде —
Мы знаем, что деление можно заменить умножением делимого на число,
обратное делителю. Поэтому все соответственные значения
а
выражений
— и
Ъ
1
а • — равны и равенство
а 1
— = а - —
Ь b
есть тождество.
Из втого тожлествт следует:
—а 1 1 / 1\ а
2. — = —а-— = (—1 • а)-— = —1-а-—=——.
b Ь Ъ \ Ь} Ь
Мы показали, что равенства
а —а а
— • b = а и — = ——
ъ ъ ь
являются тождествами.
41. Какими числами (равными, противоположными, обратны-
ми) являются соответственные значения выражений:
ч 1 - v —у
а) х и —; в) — и —;
х 5 5
Л а Ъ . у в
б) - и г) и —
Ъ а 5 5
ч —У У
Д) И —А
О —5
е) — и ~-уЧ
Б —5
42. Сравните соответственные значения дробей
а 4 с
Ь + с
и у при:
а) а =- 8, Ь = 5, с - 7; б) а = —, b — i, с = — .
2 3 о
де
43. Сравните
„ ос
соответственные значения выражений —
Ьс
и
а
Ь
44.
45.
46.
47.
при:
а) а = 3,
Найдите
6 = 5, с = 7; б) а= 1, 6 = 1, с = —-
2 з’ 6
общий множитель
сократите дробь:
. ?х бу .
а) —; б) —; в)
Зх ' 24р 7
Сократите дробь:
. 10х
*4’
6)-;
9Ь
числителя и знаменателя
и
5а.
а3’
. ьз
г) —;
' 7Ь3’
. —2р . —51m
д) ---—; е)--------
—Юр3 1 —17т3
\ 20
в)=г;
г) =5?;
-2?
. аЬ
д) —;
. —аб
е> Т";
Ьс
. ах1
ж) —;
*У
. тп
3) ---,
п3с
Упростите выражение:
ч Зах
ач.;;
в) —;
15ао
. 4с'!
г)^;
а3Ь3
asbs’
е)^;
х1у*
эк) 7р х3 ;
бЗхз^з.
42х6у4
Представьте выражение в
ч —° .
а) —;
—10х
б) —;
- 10х
в)
виде
а
—10х
дроби со знаменателем 10х:
—а
10х ’
г)
48Л Упростите
. — 2а3Ь
За» *
б)1К;
—20х«
выражение:
в)<=^;
(—8bs)a
г) (-Зхз)з.
1Ъх*у3 ’
™ (-6а3у3)3
е)
(—4а3)‘
49,
Найдите
81В
а) — ;
’ 16»
значение выражения:
2733
50.
Сократите дробь:
о (Ь - 2). 3(.г + 4), 15g* (а-Ь).
’ 5 (Ь — 2)’ с (х + 4) ’ f 20b (а — Ь) ’
г)
35у (х + 2у)
42х (х + 2у)
51.
Ня рисунках 1 и 2 изображены
= (х + 2)(х-2) (.г--1) (х- 2)
У *4-2 у “ х — 1
Р ( 2; —4) не принадлежит графику
точка (? (1; - 1) — графику второй функции?
графики функций
Почему точка
первой функции, а
16
Рис 1
Рис. 2
52. Докажите, что следующие
дроби не являются то жд< ст-
венно равными:
. х -|- 3 х —. п 4- 1 1
а) —— и б) ---------------------------- и -
6 2 а а
53
Разложите на множители
би и выпол нт е ее сокращение:
За + 12&
6а Ь
15b — 20с
10b
3-1
9х — 67 ’
а)
б)
в)
числитель или знаменатель дро-
г)
Д)
е)
1т
1т + kin
а2 — 6а
За2 ’
5 >2
8ху — 3i/2'
ж)
з)
и)
3(a-S)
5.г(у + 3),
6h- 4 18 *
а — 3t>
а* — ЗаЪ *
к)-^-
3^4 15 у
54. Напишите выражение, противоположное данному:
„ ч ч а — ь
а) х; в) а — 6; д) —; ж) ——;
О о
б) -2р; г) 2х -у, е)-^; з) —
5 С— р
55. Известно, что при некоторых значениях а и & значение
дроби — равно 5. Найдите при тех же значени: х а и b
а — Ъ
значение выражения:
а) —1- ; б) а — Ь; в) &—а; г) -—
Ь — а 3
17
56.
Докажите тождество
х а — Ъ
' Ь — а
б)
* —У
57
Упростите
8 (Ь — а)
выражение:
г) 22 (а - Зс)
7 33а (Зс—а)
ж)
ху — 3?/
а (3 — х)
5cd—15d
30 — 10с
58.
59
60.
б)
а (х — 2у).
b (2у — х)*
5х (х — у)
*8 (У — х)
Сократите
)2 — д2
Р
Р (Р — 9)
Упростите
а — 1
(1 - а)2
д)
—45Ь(2Ь —7) ,
1862 (7 — 2Ь)
8 (а —12),
lib — ab
дробь:
б) ..Л+3У
х2 — 9у3
выражение:
б)
(Ь - 2)3.
2 — b
з)
И)
Найдите область
ч У' — 16
7 Зу + 12
15г2— 9z
б) ---------
' 25г3 —9
В)
—6pq 4- 20ре
~3д —13 ’
2а — 8Ь
12b — За
ч 4а2—9Ь2
В) --------
2а1 4- ЪаЬ
55г2 — 66Ьх
25х2 - 36b2
В)
4х2 — 4у
25а2 - 25b2
(5а - 5Ь)2
определения дроби и
д2 юд + 25 .
а2 — 25
У2-9
<72 — бу Н
61. Преобразуйте дробь в целое выражение:
ч 25 — а2
a)-7ZT-;
б) + 1
7 1 — X
а* —
а4 — а3
д)
сократите дробь
ь7 — ь10
Ь6 — Ь2 ’
62. ’ Упростите выражение:
а)
ах + Ьх — ау — by е
7х — 7у
б)
8а + 4Ь
2ас + Ъс — 2ad—bd*
ув-1 .
у«4-р2 + 1’
Ж)
В)
ху — X 4- у —
х2-у2
уа4-2у -Г 4.
у» —8
18
63. Найдите значение выражения:
15да — ЮоЬ
3ab — 2Ь3
9с» — 4с?
18c2d — 12сс?
при а = —2
2
при с = —,
Ъ = -0,1;
d = —
2
64. Докажите, что значение выражения не зависит от с (с^2):
ср» —2p»t
2рс — 4р *
б)
сх — 2х-\-су — %у
сх — су — 2х +2у
65. Решите уравнение:
2х — х2
х2 — 4
= 0;
Ру-14 _
У2 — 7У
б)
х3 — 2х» + х — 2
х3 4-х
= 0;
9у3~У = Q
15у + 5
§ 3. ТОЖДЕСТВЕННОЕ ПРЕОБРАЗОВАНИЕ В ДРОБЬ
ПРОИЗВЕДЕНИЯ И ЧАСТНОГО ДВУХ ДРОБЕЙ
S. Произведение дробей
Рассмотрим выражения а 4-—, -—2:р, а-(1 4~—При
ъ х 4- у \ с)
составлении каждого из них использована операция деления
на выражение, содержащее переменные. Такие рациональные
выражения называют дробными.
Одна из основных задач тождественных преобразований
дробных выражений состоит в том, чтобы данное выражение
представить в виде дроби, числитель и знаменатель которой —
целые выражения. Мы увидим в дальнейшем, что такое пре-
образование всегда возможно.
В этом параграфе мы рассмотрим преобразование в дробь
произведения и частного двух дробей, а также натуральной
степени дроби.
Рассмотрим произведение двух дробей — • —.
Ь d
Если переменные a, bt с и d принимают натуральные зна-
чения, то по определению умножения обыкновенных дро-
бей имеем верное равенство:
О С ОС qv
Ь ~d ₽ bd
19
Например, при а =3, Ь — 1, с = 15, d = 13 получим:
15 з 1
7 13 7 13*
Равенство (1) будет верным и при любых других значениях
g
переменных а, Ь, с и d, где Ь=^=0 и d^=0. Например, если а = —,
Ь с — 5,1 и d — 1,2, то
8
3 з
Jl _С_£^Й=2 БД 10 _ 12 61 _ 61 _ 7 2.
Ь ’ 7 “ 7 1,2 7 1,2 • 10 — 7 12 7 7 ’
— — • 8
8 8
ас 3 7-6,1 3 — • 6,1 8-10 2 12 • 61 _ 7 2
bd 7 7 7-12 7 ’
— • 1,2 — • 1,2 • 8 • 19
8 8
_ „ а с
Поэтому все соответственные значения выражении — — и
b d
— равны и равенство (1) е< ть тождество.
bd
Доказать это можно следующим образом,
ос
Дробь — мож1 о рассматривать как частное, где ас — делимое, bd —
bd
ас ас
делитель. В таком случае выражение — • — есть значение частного —. мы
b d ba
знаем, что делимое равно „елителю, умноженному на частное. Поэтому равенство
аг а с
bd~ b ' d
будет верным в том и только том случае, когда верно равенство
— . — I bd = ас.
b d /
Проверка показывает, что при
b ф 0 и d =/ 0 это равенство верно:
В преобразовании мы во'пользовались ранее доказанным тождеством
а- а с
Следовательно, равенсл вс — = — • — верное.
bd b d
20
Произведение двух дробей тождественно равно дроби, у ко-
торой числитель ра*ен произведению числителей данных дро-
бей, а знаменатель — произведению их знаменателей.
Приведем примеры преобразования в дробь произведения
дробей.
1 6а» 10у» _ 6а2. Igy» 4д
бу® 21аЬ бу» • 21ab ~ 7Ь *
2 х» — 2ху_____у _ х(х — 2у) у _ хи
8 ’ л»—4у» “ 3 (х - 2у) (х + 2у) ~ Зх+6у *
66
Представьте произведение
ёсли это возможно:
а) -
з
б) -•
4
В) - •
' 10
в виде дроби и
сократите ее,
х
2’
8#
9’
ъ’
г) -
а
ъ__
7 ’
Зп.
т
Нах х
- . _
3 а
. Ъ Ь3
Ж) - • т?
У У2
з> 4-—:
5»
. За»
и) -хг
р’
а» ,
16х«'
к)
бпг3 2па
п» 25 т3
ч тп
” i.
67. Представьте одночленный множитель в виде дроби со зна-
менателем 1 и выполните преобразование:
а) х • —; в)/а —; д)| — 1 —. ж) х® • —;
Ъ а Ъ ’ х4
б) • у; Г) -Ъ е) • (-6); з) (-ЗаЬ1П).
б 2 у - п*
68. Упростите выражение:
а) 15р4 16у\ 25р3’ 0 5xV - ( °* \. 10х»1 » /
б) 4!м?3 14л " С 49х4 ’ 18а5 ‘ ’ д) 2а ба2 3i 7ba О3 аТ;
в) 7pV ш» # ply4’ е) 15х» 12i,8 8у» 25х4 X
69. Замените выражение гождес венно равной дробью:
. х» — ах а
' а3 х3
. ?Р_.
Ц 27 у» ’
В)
о —Ь 8Ь1
4ЬЭ а3 — ab ’
. т’- Вл’ 2тп
т3п3 т + Зп
21
х9 — х9у х^у 4- ху\
X2 + у2 Х*у
(а 4- Ь)2 . 25аЬ
50а2 * а2 —б2’
х9 — 4у9_________28х2
35ху х2 — 4ху 4- 4у2 ’
4а2 —Ь2
а2 — аЪ
а3 —8
а — Ъ е
2аЬ4^’
_______ 7a 4 21 ,
ба + 15 а2 4 2а + 4 *
л3 4 27 . 12x4 9
8х 46 х2 — Зх 4 9 *
70. Упростите выражение:
а)
ах 4 ау 4 2х 4 2у
2а 44
8а —16
ах 4 оу — 2х — 2у ’
б)
ab — ЬЪх 4 За — 15х
463 _ сзб
а —2\
а — бх*
в) (2—а)2 •
ab — 2Ь
• (х2 — 9).
71. 'Решите уравнение:
4ха — 25 4
8х 4 24 2х 4 5
6h
х2 — 2х
30
6х + 18
х
4x3 _ збх
72. Докажите, что соответственные значения выражений — и
d
d R
— являются взаимно обратными числами,
с
i
6. Частное двух дробей
Мы знаем, что деление одного числа на другое можно заме-
нить умножением делимого на число, обратное делителю. Так
- „ с d
как соответственные значения дробей — и — являются взаим-
d с
но обратными числами, то частное — : — равно произведению
b d
— • — при любых значениях а, Ъ, с и dt кроме 6, с и d, равных
ь с
нулю:
i
a t е _ a d
Т ’~d~~ “с*
22
Это тождество дает возможность представить частное двух
дробей в виде произведения, а следовательно, и в виде дроби.
Частное двух дробей тождественно равно произведению де-
лимого на дробь, обратную делителю.
Приведем примеры преобразования в дробь частного двух
дробей.
1 5x3 . 15* 5х® ба 2а9 6а 2а9 5х3 • 2а9 ах3 15х — ба • 15х “ 9
2 а 4- 2Ь , а3 4" 2аЬ с9 — 9Ь9 * а —ЗЬ а 4- 2Ь а —ЗЬ _ (а 4- 2Ь) (а — 36) а9 — 96я а94- 2а6 (а 4- 36)(а—ЗЬ) • а (а4-26)
1 1
а (а 4- 36) а9 + ЗаЪ ‘
73. Представьте частное в виде дроби:
2 т Зт
а) - : • в)
У 3 2п п
г) 6а Ь • о • >
9 3 b 12а
а9 а®
—: —;
6я 63
х1 t Хб
!/в у* *
ч За9 ба1
эк) — . •
7 Ь9
3) 12р . 8р9
’ 35с9 * 213
74. Упростите выражение:
а) Ь : —; г) : 5х;
a Sy
б) — : у; д) : 14лг3п2;
х 7
. о 12а ч 1 к о, 1 35а4Ь2
в) За : —; е) 15а3&4:------;
7 ь 2
81уя . ( 18г/4\
7рЗ * 35р2/’
45m3 , 27m1
28n3 ’ 42ne *
75. Замените выражение дробью:
х — 2 # Зя — 6,
"зТ” ‘ ’
10а1 . 15а35 .
а2 — Заб а — 36*
т9 — 4п9 , (т 4- 2п)2е
Зтп 9т2
1— 4а 4-4а9 . 4а2 —1
15а9 ’ 5а3 ’
а9 — За я , Эх2 — ах t
12х * 36а ’
ч 5х9 — Ьх 6я —55х
е) --------:--------;
ЗОЬу бОху
ж) (2х-у): Утг—;
*4-У
. 21b — la t о,ч
3) -------; (д _ 3ft);
Ь — а
и) (а4-5&) : (а2—25&2);
к) (х2 —бху 9{/2) : (я2 —9у2).
23
76. Найдите пначекие выражения:
а) : *1±^±2 при х = -0,25;
' OvS бха
б)
а + 3
9а3 4- 72
2
при а = —.
7. Степень дроби
/ а \б - а
Выиаженио — является степенью дроби —.
“ \ъ/ ь.
что это выражение можно представить в виде дроби.
По определению степени имеем:
Покажем,
(а \б а а а а а
Ь / ~ ъ ’ ~ь ' ~ъ ' ~ь ~ъ'
По свойству произведения дробей:
а а а а а _ааааа
Ъ Ъ Ъ Ъ ’ Ь ~ bbbbb *
По определению степени с натуральным показателем:
ааааа _ аь
bbbbb ~ t5 *
/ л \б а5
Итак, I— | =» -гг •
\ ь ) ьь
Вообще, для любого натурального п, большего 1, и b ф О
имеем:
п раз
(а \« а а а аа . . . а _ jcH
ь' ~~ ъ V ‘ ~ь ~ ъь. ..ь ~ ъп ’
п Раз п раз
Степень дроби тождественно равна дроби, у которой числи-
тель есть ст^пень числителя, а знаменатель — степень знаме-
нателя.
Рассмотрим пример преобразования степени дроби в дробь:
2а2Ь \4_ (2а2Ь)4 _ 16а&М
\ Зху ) (Зху)4 81х4//4
24
78.
79.
80.
Представьте
а) (г);
\2»/
м 160 V.
6) (т)!
—ЗрУ
в / ’
степень в виде дроби:
2
т
lnt
а2& V
ч ( 2т* \9
к)--------;
\ Р4?3 /
ч / aW V
В)---------)
’ х8 \4 ч
V7 1 ; и)
.у2*3 /
Представьте дробь в виде степени:
ч 4а2Ьв
а)-^:
Упростите
ч / 2о» \б /
а) ---- * I
\ с’ / I
в)
б)
64а°
выражение:
с9
4а10
Зх’ \« / 9x6 \з
^);
27&з \2
16а4 /
а12
8а3 \з
9Ь2 J
Докажите тождество:
,х2 — ху
—8ав
_______•
(а—Ь)з *
Ь2
а —2 г
3— ь)
ab2 — b*
К)
-(*-4)8
32х10
М
2а — а2
9 —Ь2 ’
< [ Ъ —а \з
। ’ \а2 + 2аЬ 4-Ь2/
4
3
(5 — Х)3 • (25 — х2)3
81.
Решите уравнение:
- <*~5>а =0;
х2 — 7х \з
х2
§ 4. ТОЖДЕСТВЕННОЕ ПРЕОБРАЗОВАНИЕ В ДРОБЬ
СУММЫ И РАЗНОСТИ ДВУХ ДРОБЕЙ
8. Сумма и разность дробей, имеющих равные знаменатели
Выражение — -(- — есть сумма двух дробей с равными вна-
с с
менателями. Покажем, что эту сумму можно представить в
- а 4 Ь
виде дроои —!—.
с
Если переменные at b и с принимают натуральные значения,
то равенство
о I о а 4
с с с
(1)
25
верно на основании правила сложения обыкновенных дробей
с одинаковыми знаменателями. Например, если а =2, b =3 и
с=7, то
2 . 3 2+3
7+F=~*
Это равенство будет верным и при любых целых и дробных
значениях а, b и с, где с=/=0.
2
Например, если а = 1,5, b — —5, с = —, то
3
а . Ь _ 1,5 . —5 _ 2 —5 _ £___15 _ __21 _ _
7”с — 2 + 2 ~ 2 + 2 ~ 4 2 4 4*
7 з з з
1
—з -
а -|-Ь _ 1,5 — 5 ___2_____7 _ _ 21 = 5 1
~ 2 2 2 2 4 4*
3 "з
„ « а . о а+о
Все соответственные значения выражении — !— и ------------
С С с
равны, и равенство (1) есть тождество.
Докажем это.
а 1 b 1
Воспользовавшись тождествами — = а • — и — = Ь • —, получим:
с с с с
£
с
1 а + ь
-fa + Ъ)------
с с
Разность дробей с равными знаменателями можно заменить
суммой и представить в виде дроби:
а Ь а . —Ь а — Ъ
--------------1 ,
с с с с с
Сумму дробей можно представить в виде дроби и в том слу-
чае, когда число слагаемых больше двух.
Например:
a b , d (а , Ъ\
---1-----1----------1---
с с с \с с /
а + Ь । d а + t> -| d
с ' с с
26
Сумма дробей с равными знаменателями тождественно рав-
на дроби с тем же знаменателем и числителем, равным сумме
числителей данных дробей.
Приведем примеры преобразования суммы и разности дро-
бей.
ад»
1 g2fe —6 । 2 +bad 4 6 + 2 |- 5дЬ + 4 д»Ь -г Бад _
ад» ад» ад» ад-
ад (а -f- 5)____а + 5
ад» д
2. 6х — у х + 4у _ вх — у — (х + 4у) вх — y — x — iy
Ьу Ьу 5у бу
_ 5х — 5у _ 5(х —1) х — у
&У бу У
3. За + 2х _ За , 2х - (—1) За L —2х За—2х
х — а а — х х — а (а — х) (—1) х — а х — а х — а
В примере 3 знамена гели х — а и а — х — противоположные
выражения. В подобных случаях, чтобы внаменатели дробей
сделать равными, умножают числитель и знаменатель одной
из дробей на —1.
82. Представьте
сумму или разность дробей в виде дроби:
а)| + Ъ_. 5* Г) 5д» _ 8 Зд» . 3 ’ Ж) х + 3 У 2— х.
> У
6)1- У_. з’ Д) х + у 9 "э’ в) 2с + 1 а 7 а
в) у + 2а. е) — - п — тл
7 7 12 12 ’
83. Преобразуйте выражение в дробь:
х + 5 х ] 2.
*9 9 ’
б)
14 14
. 5m 2n 5m —8п
' 8л 8л
5ft -j- 2г — 7 д +3.
2D 2д ’
0 — 2 20 -f-б 3 — с
----Я~;
ООО
Зх- 2 м . 5х— Зу х - 4у
2* 2х 2х
27
84. Являются ли тождественно равными выражения:
а) б) 5 5 . и — ; а— Ъ Ь — а Зх — 1 1 — Зх и ; 2 2 X 8 n 1 ТГ - - - о- X О’ И * 00 | |
(X — у)2 (у г) —-— и X2 — у4 у2
85. Представьте выражение в виде дроби:
а) 1 н 1 w 'С • Г) Зр _ 2р е р — Q <1~р' \ У — 3 । 3 -|- у ж) -—- +, ; у—1 7—у
б) а 6 С — 3 3 — с’ д) а 4- 1 t а —2 . 2а —1 1 —2а* ч b — 12 8 4- 2Ъ 3) !—. 10 — b b — 10
В) т 2п ф 1 » т — п п — т е) х4-9 8 — 2 г. 1 — Зх Зх — 1’
86. Упростите выражение:
а)
__Р_______5_
р — 2 2 — р
2р .
Р — 2*
а2 а 1
а3 — 1 1 — а^ а3 — 1
6)J
2а
а — b
4.а — 1
Зс4-2 _ 4г —2 2с —5 .
Д\с - I)2 (1 - с)2 + (1 — с)2 ’
. 2х . 1 х
е) -------{------------------•
(Х — 1)3 (1— х)3 (1-Х)3
87. Докажите, что множество значений выражения содержит
лишь один элемент:
(а — Е)а , (д + Ь)2
О2_|_&2 *“ О2 + Ь2*
В) <* + У)2 (х — у)2.
7 ху ху
88. Найдите значение выражения:
при р = -8. в = -0,25.
р-25 р-2у
89. Постройте график функции, заданной формулой:
б)
У =
х2 . 4
х —2 ' 2 —х*
90. Решите уравнение:
а)
Зг —12
17
=0
17
х2 __ 6%
X—6 6—X
б)
Ну + 29
41
8у =0
41
Г)
28
9. Сумма и разность дробей, имеющих различные знаменатели
Пусть поставлена задача: сумму дробей — и — представить
Ь d
в виде дроби.
Умножим числитель и знаменатель первой дроби на dt а
числитель и знаменатель второй дроби на Ь. Получим:
а с _____ad . Ьс
7 bd ' bd ’
Выражение d называют дополнительным множителем к чис-
лителю и знаменателю дроби —, выражение Ъ — дополнитель-
ъ
ным множителем к числителю и знаменателю дроби Мы
-ас _ ad
заменили дроби — и — тождественно равными им дробями —
b d bd
Ьс — .. а
и —, имеющими равные знаменатели. Говорят, что дроби —
bd Ь
и — привели к общему знаменателю. Выражение bd — их об-
d
щий знаменатель.
Теперь можно сумму дробей — и — представить в виде
b d
дроби:
а . с _ ad . be _ad -\-bc
b d ~ bd bd ~ bd
Выполняя преобразование суммы или разности дробей в
дробь, часто удается найти более простой общий знаменатель
дробей слагаемых, чем произведение их знаменателей.
Рассмотрим примеры.
Д 4 1 , д — 1 3 (а 4- 1) 4- 2 (а — 1) _ За 4-3 4~ 2а — 2_ 5а 4- 1
4 6 12 ~ 12 12
а 4- 3 ____ b — 3 ______ а 4- 3
а2 4- а& ab Ь* а (а 4~ 6)
6 — 3 6 (а 4- 3) — а (6 — 3)
b (а 4- b) ab (а 4- Ь)
ab + 3b — ab + За _ 3 (а 4- Ь) _ 3
ab (а 4~ 6) ab (а 4-6) ab
91. Представьте сумму или разность дробей в виде дроби:
18’
29
92
93
д) -
а
5
b
8 7
У
ч 2 , 3
ж) —------
' За 2а
ч 5 3
3)----------
6х 4л
8х Зх
— *
15 10
б?/ , 7у
й + ю
Представьте выражение в виде дроби
х I з_г д) а 3 и)
бу 2у b2 2Ъ
ь 5 э е) п . т к)
За 2а 4р3 Зр
1 ж) Ьу — 3 । Зу — 2*
15ах 9а 3 5
3 5 2х — 5 х — 4
7т — * 28тпп* 3) 6 5 ’
еа — 3d2
4аа ЗЬа 2а2—Ь2
10
15
2с2 — d2
12
8
Преобразуйте
сумму
или разность
дробей в дробь
а2
а — Ъ
ab
ч 2а — ЗЪ , 4а — 5Ь
Д)—----
б)
х — у
х — т
ху
ip2 — 5q2
хт
2р — 3q
PQ Р
2с с — 2Ь
ж)
х — 2у____ 2х — у .
ху2 х2у
За2 — 5а + 1 . 5а — 3
а2у
Ьс
Ь3х
ау
ха — 1
Ъх3
94. Представьте выражение в виде дроби:
.1,1,1 Ч 5 1 1 1
а) —|---4 - —* в)----------J---1
ab be ас 14х3 21x2y 4хуа
1 । 1 1 ч 2 । 3 5
б) —-------; г)-------------------.
' вх 5х 15х За2Ь 5аЬ2 4&3
95. Преобразуйте выражение в дробь:
. х — 2 , 2x4-3 5х — 3
7 2 4 6
2а — Ь а — 4b, 2а — 15b
б)--------------------------;
9 6 2 8
х2 — 2 Зх2 — 7
5х
Зх
ха 4-1.
10х ’
5аа — 12аЬ 4- 4Ь2
2аЬ
а
а—5Ь
b
80
96. Замените сумму или разность тождественно равной дро-
бью:
а — Ъ
а + Ь
а)
а
ъ'
3 а —3
_ , •
2а а + 3*
97. Целое выражение х—5у представьте в виде дроби со зна-
менателем, равным:
а) 1; б) 2; в) а; г) я-1-5у.
98. Представьте выражение в виде отношения двух много-
членов:
а) х 4- i; г) ———h 4; ж) — 4- а — Ъ;
а х — 2у ' ЗаЪ
б)
с 2а Зху
. а4-2Ь о ч (x-|-2y)2 о
в)—I-----3; е)------------— 21/;
b 4х
99. Решите уравнение:
2х — 3 х 4- 6
5 4
Ч * —12 Л
Г) X-----— = 0;
ч 5х— 8 , 2х— 7 ~
д) — -----1--—— — х = 0;
о У
100. Замените дробью
сумму или разность дробей;
2а_______1_.
2а —1 2а 4-1’
3x4-2___2 — Зх,
2 — Зх Зх 4- 2*
X 1 & I г
и) п 4-------- 4*
а — Ь
У 4-3.
у-З’
д)
-4-+—;
*4-У У —х
ч ха 4- 4iy2 , о
к)х~1^+2у
б)^+А
х — у у
31
101. Упростите выражение
з 2
ъ (Ь + 1) ъ (Ь — 1)
3
б) —
х (х — 2)
*_______*2+* 4- 1
х + 1 (х — 1) (х 4-1) х — 1*
к т — 3,m4-3 2m
m 4- 3 т — 3 (m 4 3) (m - 3)
102. Решите уравнение:
--------1_ = о
4-1 х — 1
Зх — 1 х — 3
Зх 4-1 х 4- 3
в)
х — Ь
х— 4
2х — 5 . Зх 4~ 4_1 _q
х4-5 х4-2
103. Знаменатель каждой дроби разложите на множители и
полученное выражение представьте в виде дроби:
3 I 5 .
2t — 2у Зх — Зу *
1 . 1
4а4-4Ь 6а 4-6?/
Ьу __ Чу .
4у-2 6z/-3*
ЗЬ________b_t
5b 4-15 2b 4- 6*
а —1_________5
о2 4- 2a 6a 4- 12 *
ч 1 — 3x , 8
e)-----------------;
x2 —3x 3x —9
. 1 , 1
ж)----------1-------;
x2 — xy xy 4- y2
3________3
a2 4- — b2 ’
m . 1
1— m2 1 4- m *
4n_______2
n2 — 9 n — 3
3)
и)
K)
104. Упростите выражение и найдите его значение:
а)
a 4- 1 a 4- 2
a2 — a a2 — 1
при a = —2;
6)
У 4-2
У8 + Зу
5 —У
у8—9
при у == 1,5.
= 0;
105. Докажите, что выражение принимает положительные зна-
чения при всех значениях а, при которых выражение
имеет смысл:"
ч а2 4- а 4-1 1
с3 4- а а
ч а3 За3 4- 81
г)---------------------.
а — 3 а2 — 9
32
106. Упростите выражение:
а) _4____8_ 12 .
' х 4- 2 х — 2 х2 — 4’
6)f-^— + — + —;
V-9 у-З У+3
е)
ж)
з)
26 _____б 4&2 4~ 9
2Ь + 3 Г 3 — 26 462 — 9 '
з
2х3 + 2х
а — 1
2а 4- 2
4т
4т- — 1
. л ла + о
и) _L—
' '2а2— ab
2х —1 _2#
х» — 1 х ’
а 4- 1
3— За
Га—1
, •
За’ —3 ’
2m 4-1 । 2т — 1 t
6m — 3 4т 4- - ’
16а
4а2— 6»
2а — Ъ
2а2 4* «Ь ’
ч 10 . V 5
К1 _______— I - - - е
х2 — 25у2 Ьуг — ху ха 4" Ъ*У
107. Замените выражение дробью:
. х — 2 х — 2
а)------------------------;
ха 4- 2х 4-1 X2 — 1
б)
а4-3б
а2 — 2аЪ 4-62
а —ЗЬ
а3 — Ь3 ’
в)----------—-----------4- —---------;
(а — З)1 а2 — 9 (а 4- З)2
х — У_________2х х4-у
х2 4- 2ху 4- j/2 х2 — у2 х2 — 2ху 4- *
Д)
2а2 4- 7а 4- 3
а3 — 1
1 — 2а 3
-... - _ •
а2 а 4- 1 а — 1’
е) —----------; ж)
p — q pi — q3
. 6а3 4- 48а За2
3) ---------------------------,
а3 4- 64 а2 — 4а 4~ 1в
108. Между двумя пристанями А и В, расположенными по реке
на расстоянии а км (рис. 3), курсирует катер, имеющий
собственную скорость b км/ч. Сколько времени потребует-
ся катеру на путь от А до В и обратно, если известно,
что скорость течения реки
равна 5 км/ч*!
Составьте выражение и
найдите его значение при:
1) а = 50, b = 25;
2) а =105, д=40.
Объясните физический
смысл значения скорости
при 5 = 5.
Рис. 8
2 Алгебра, 7 кл.
33
109. Чтобы купить т кг слив, нужно заплатить с руб., а на
покупку (тп — 5) кг апельсинов необходимо затратить на
3 руб. больше. На сколько выше цена 1 кг апельсинов по
сравнению с ценой 1 кг слив?
С вставьте выражение и найдите его значение при т — 10,
с — 4.
10. Представление дроби в виде суммы нескольких слагаемых
Мы янаем, что сумму дробей всегда можно представить в виде дроби. На-
пример:
ж—5 2 Зх (х — 5) 2 Зх2 — 15х + 2
х Зх’ Зх’ Ь Зх’ “ Зх2
„ _ „ Зх’- 15х 4- 2
Чтобы решить обратную задачу — представить дробь -----------в виде
Зх2
суммы двух дробей, можно все преобразования выполнить в обратном
порядке:
Зх’ — 15х + 2 Зх (х — 5) 2 х — 5 2
--------------- ----- -- L----- — ------ 4---.
За’ Зх’ Зх’ х Зх’
„ , Зх’ - 15х + 2
Дробь -----——------г можно представить в виде суммы нескольких слага-
Зх-
емых иначе:
З^2 — 15х г 2 Зх’ Их 2 5 2
----- ———- =---------- —---1------1 _ — J-------.
Зх’ Зх2 Зх’ Зх2 х Зх’
Некоторые задачи удается реши.ь проще, если данную дробь представить
в аиле суммы нескольких слагаемых. Приведем пример.
_ „ „ 5л’ |-20
Задача. При каких натуральных значениях и дробь ------------ прини-
п
мает натуральные значения?
Решение. Представим данную дробь в виде суммы двух слагаемых
(целого выражения и дроби):
5л’ + 20 5л2 20 20
----------- - -|-- = 5л 4
л--------л л п
Целое выражение 5л при любом и f N принима< т натуральные значения.
20
Дробь — обращается в натуральное число при тех и только тех значениях л,
л
которые являются нат тральными делитечями 20 т. е. при л, равном 1, 2, 4, 5,
10. 20.
84
Нам удалось решить задачу довольно просто, представив дробь в виде сум-
мы целого выражения и некотсрой правильной дроби, т. е. дроби, у которой
степень числителя меньше степени знаменателя. Такое преобразование дроби
всегда возможно, если только степень многочлена числителя не меньше степени
многочлена знаменателя.
110. Представьте дробь в виде суммы двух дробей:
ч х + 3 а) ——; X2 3(д-34-7 б) 2 А а3 — 4
111. Представьте дробь в виде суммы трех слагаемых:
х» + 6х-|-1 а) я ; а2 _ 1 4. За б> а + 1 ’
112. Представьте дробь в виде суммы целого выражения и дроби:
ч УН 1 а) ; У 2а2 — а — 3 б) -3 1 а3 р2_2р + 7 В) „ о р —2 ха4-5х —9 г) “ • х-4-3
х1_р7х_ 25
113. Учащимся была поставлена задача1 «Представить дробь ----— —•
в виде суммы целого выражения и дроби». Были получены четыре ответа!
7х
1) *4-5 I------
х — 5
12т - 25
2) Х4-------—;
х — 5
2х — 25
8) х2 — х 4 ----—I
х — 5
35
4) х + 12 4------
х —*5
Все ли ответы верные?
114- При ка«их натуральных значениях п дробь принимает натур 1льные зна-
чения:
5п2 4- 8п 12
а) ------1----------1
(и — З)2
б) --------
п
п
115- Докажите тожлество:
Ъх 18
а) = 6 —--------:
х -I 3 *43
ах
б) —— =а
х Ь
аЪ
7+5
2*
85
11G. При каком значении а тожде< твенпо равны выражения:
о)
2х
х + 3
24
п х 4
в)
2х
8 — х
х
б) ----- и
х — 5
а
х — 5’
г)
х-Ь 2
5 — х
а
и —1 -I- ----------?
О - X
1 +
117* Представьте дробь в виде
—2х
6) ----
а)
суммы целого выраэке! ня и дроби:
2х х — 3
в) ------; г) ---------.
5—х 2-х
118* При каком целом п значение дроби есть целое число:
а)
8п
n-J-2'
7п
б) -----?
п — 4
119. Найдите такие значения о и б, чтобы выполнялось тождество:
5х а ’ Ь
а)--------------— ------— —;
(х — 2)(«4-3) х — 2 х + 3
5х 4- 31 а Ь
б)------------—-=------- ------.
(x-5)(x-f-2) х —5 х + 2
11. Тождественные преобразования дробных выражений
7Лы выяснили, что сумму, разность, произведение и частное
дробей всегда можно представить в виде дроби, числитель и
знаменатель которой — целые выражения. Следовательно, лю-
бое дробное выражение также можно представить в виде дроби.
Если при этом нужно выполнить несколько преобразований, то
предварительно следует определить порядок их выполнения.
Приведем пример.
Пусть нужно представить в виде дроби выражение
1 х2___4
------------|- 2х. Это выражение представляет собой сумму
х + 2 Зх
произведения дробей —-— и х ~ 4 и целого выражения 2х. По-
х -{- 2 Зх
этому скачала нужно произведение указанных дробей заменить
дробью, а зятем сумму представить в виде дроби:
1 \ 1 4 (х4-2)(х —2) X —2 е
X 4- 2 Зх (х 1-2) Зх “ Зх ’
х—2 . _ х —2 . 2х • Зх 6х2-| v —2
-----к 2х —--------1------------!----•
Зх Зх Зх Зх
Данное выражение мы представили в виде дроНи
6Х2 4- X — 2
Зх
8«
120. Определите порядок выполнения преобразований и упро-
стите выражение:
4х8 — 1
6а 4-1 , 6а —1
,а2 — 6а
a8 —86
1
у8 — у 4~ 1 ,
у2_2у4-1’
В) аЬ 5s За д а 4-6.
3
L3
Ъ
. / as 4- Ъ2
е) а — —!—
\ а4Ь
\ / 4в
ж) I-----а
' \2 — а
2
а —6,
а» 4- 4
а —2
Г)
4У
8у8
х2 — ху
3
24 4х— х8 —4
(х-2)8‘ 3(х4~6)
121. Упростите выражение:
ь
а —(>'
а
4х8
2х~—1
2 Г
4в2 — ра
Зу
2х — у у2 — 4л1
5х 4 у 5х - - у
2 — 5ху х2 4- 5ху
х8 — 25р8.
х2 4- у2 *
. 9а8 — 16&8
е)
7а
Ж)
3)
4д у
у2 — X2
а —2
36—4а ЗЬ-Ца
,46s — Заб 46» 4- ЗаЬ
1
У
1
а
а2 — 2а
х2 4- 2ху -4- у1,
а8 4 4
а3 — 4a а* -{- 2а
122. Найдите значение
выражения:
х — 5
50
2х — 10 2х 4-10 25 — Xs
х— 5
--- при X=
1
I1
х* — 2ху + у8 ф
2ху
V2 — Xs
_ л 3
при X 8,4« У — —-•
О
У 1
У—Х,
87
123
Используя
ние:
основное свойство дроби, упростите вираже-
124
125.
а
2 ——
а — b
х
а
6) —
2х — 5
----_ 1
У
а2
а
с
У
а — -~
а?
Докажите
одного элемента:
2
а
\2
а
Выполните
ние:
что множество значений выражения состоит из
(а ~ 1)»’
б) д.~2
/а —2\2
с8 — 8 2а
fl—2*
подстановку
и упростите
полученное выраже-
ab
X =-----
х — а
-----, где
х — b
а
— — х
ь
б) -----, где
О
а — Ъ
X = -----
а
126. а) Смешали 6 кг кофе по цене 4 руб. 50 коп. за килограмм
и х кг кофе по цене 4 руб. за килограмм. Какова цена
1 кг смеси?
Составьте выражение и найдите его значение при х = 4,
х = 19.
б) Имеется чай двух сортов: первый сорт по цене 10 руб.
за килограмм и второй сорт по цене 8 руб. за килограмм.
Сколько килограммов чая первого сорта нужно взять,
чтобы его смесь с 20 кг чая второго сорта стоила 8 руб.
75 коп. за 1 хг?
в) Для изготовления сдобы идет мука двух сортов: пер-
вого сорта по цене 45 коп. за килограмм и второго сорта
по цене 36 коп. за килограмм. Муки первого сорта взяли
100 кг. Сколько нужно взять килограммов муки второго
сорта, чтобы 1 кг смеси стоил 42 коп.?
§ 5. СТЕПЕНЬ С ЦЕЛЫМ ПОКАЗАТЕЛЕМ
12. Определение степени с отрицательным целым показателем
В технических книгах и справочниках можно встретить за-
писи вида 6 - 10гз или 10“ 4. Мы знаем, что выражение 1023 означа-
ет произведение двадцати трех множителей, каждый из кото-
рых равен десяти. А какой смысл приписывается записи 10“4?
38
Чтобы разобраться в этом, рассмотрим последовательность
натуральных степеней десяти:
10*, 102, 10’, ... (1)
Эту последовательность можно представить в другом виде:
10, 100, 1000, ... (2)
Попробуем последовательность (2) продолжить влево. Так
как каждый ее член меньше последующего в 10 раз, то перед
числом 10 следует поставить 1, перед числом 1 — число — ,
1 1
перед числом------число — и т. д.:
10 100
- • 10’ 100> - <3)
100 10
В последовательности (1) показатель каждого члена на 1
больше показателя степени предыдущего члена. Продолжая
по этому закону последовательность (1) влево, мы должны перед
членом 101 записать член 10°, перед членом 10° — член 10"1,
перед членом 10"1 — член 10"3 и т. д.:
..., 10-2, 10-1, 10°, 101, 102, ... (4)
Сопоставляя последовательности (3) и (4), естественно при-
нять, что 10“1 равно —, 10~3 равно —Такое соглашение и
10 100
принято в математике не только для степени числа 10, но и для
степени любого, не равного нулю числа.
Определение. а~п — —, где а =/= 0 и п £ N,
ап
Выражение О-3 (и вообще нуль в отрицательной степени)
считается выражением, не имеющим смысла.
После того как мы определили степень с целым отрицатель-
ным показателем, такие выражения, как 10-4,(—
обрели вполне определенный смысл:
8,3“\ при-
2
10"4 = —, (_Д 8= ——, з-8 == —.
10« \ 2) 7 1\« З8
\*~ 2 J
127. Представьте выражение в виде дроби:
а) 10-3; б) 2 8; в) 5-а; г) 7"1; д) а"4; е)
128. Представьте выражение в виде степени с отрицательным
показателем:
То»’ В) Т*’ Г) Тооо’ е) 81’ 27р»’ 16а»‘
39
129. Каждое из чисел 16, 8, 4, 2, 1, —, i, -i представьте
2 4В
в виде степени с основанием 2.
130. Дана последовательность:
—, -1, -, 1, 5, 25, 125, 625.
125 25 5
Запишите эту последовательность, представив каждый ее
член в виде степени с основанием 5.
131. Докажите, что значения следующих выражений являются
взаимно обратными числами:
а) А и 22; в) 58 и 5~8;
6) З-2 и З2; г) 10-20 и 10’";
132. Докажите, что:
где и £ N.
133. Используя отрицательный показатель, запишите выраже-
ние, значение которого обратно значению выражения:
а) 87; б) 15’°; в) (—2,7)“; г) 2525.
134. Найдите значение выражения:
а) 5-2; в) (-25)-’; д)(-Г’; ж)3~2+4-’;
6)1(0,34)"; г)|(—0,5)-4; е) '£'| з)/2-8 —2~4.
135. Узнайте, какое из чисел больше:
а) 2~6 или 3“6; в) 5~7 или 5~6; д) (—2)8 или 2~а;
б) (0,2)-3 или (0,5) 3; г) (0,4) 3 или (0,4)'4; е) 3~4 или ( —3)4.
138. Сравните с нулем:
а) (—I)6; 6) (-2)-3; в) (-0.1)4; г) I- If*.
40
187. Представьте выражение:
а) — в виде степени с основанием 3;
/1’3
6} — в виде степени с основанием 7;
в) 25-2 в виде степени с основанием 5;
г) 8-3 в виде степени с основанием 2.
13. Свойства степени с целым показателем
Нам известны следующие свойства степени с натуральным
показателем:
1. = ат1-'!.
2. а" : а" = а “~п, где тп > п.
3. (ат)" = о™'1.
4. (аЬ)" =- апЪп.
_ / а \" а"
и. — | — —•
\b j ъп
Буквами тип здесь обозначены натуральные числа.
Покажем на отдельных примерах, что эти свойства, устансв-
леннъ е для степенен с натуральными пс казателями, справед-
ливы и для степеней с любыми целыми показателями. При этом
основание степей и будем считать отличным от нуля.
Пример 1. Докажем, что 5-3 • 55 — 5-3+®.
По определению степени с отрицательным целым показате-
лем 5-3 — — . Поэтому 5-3. 5е = — -5® — — — 5®~3 — 5" 3+®.
5-' 53 5г
Основное свойство степени ряспрост раняется и на степей и
с цел ым показателем: произведение < тепеней с одинаковыми ос-
нованиями равно степени с тем лее основанием и показателем,
равным сумме показателей этих ст> пеней.
Для того чтоб ы свойство ап‘аП = а"‘+п выпол гялось для лк-бого целого
показателя степей и, мы обязательно должны б или прим гь, что а~п = —
(a^O.nf JV).
Дей< твительпо, потребовав, чтобы < охра аялосъ основное свойство степегп,
получим для любого n С JV и а 0:
а"а п — ап~п — а1 — i
Отсюьа а~" необходимо должно быть равным — .
а'1
41
Пример 2. Докажем, что 3° : З2 — 3°“2:
3° : 32= -
= 3«- — = з°. з-2
Зл За
= 3°“а
Свойство частного степеней с равными основаниями сохра-
няет силу и для целых показателей, но при этом снимается огра-
ничение, согласно которому показатель степени делимого дол-
жен быть больше показателя степени делителя.
Пример 3. Покажем, что равенство (а5)-6= аб(“с) явля-
ется тождеством:
(а5)“° = — = — = а“3« = а5<“с>.
4 1 (аБ)г‘ а30
Выполняя преобразование, мы дважды опирались на опре-
деление степени с отрицательным целым показателем.
138. Найдите значение выражения двумя способами (первый —
с использованием определений степени с целым показате-
лем, второй — с использованием свойств степени):
а) 8» • 82; в) (2-’)=; д) (3 • 4)~2;
б) 2»: 2Г’; г) (З-1)-2; е) (*.
139. Найдите значение выражения:
а) З-4 • 3е; в) 210 : 212;
б) 16 • 2~3; г) 5~3 : 5~5;
4*
£
9
140. Вычислите:
9-21
а) 8~2 • 4s; д) ----------;
4~ь. 4~|}
б) 9-« • 27г>; е) — ;
в) 10° : 10~3; Ж) 3~10 9d в
г) 125~4:25~6; v
з)
(— 5)~Б-25«\
1258
42
141. Используя отрицательный показатель, представьте дробь
в виде произведения:
\3 х 2а х 1 v а 4-2 а) ; в) -; д) - — ; Ж)
Ь“ с х2у3 (а—2)2
Х . „X 8аБ ч 1 ч (Ь—б)3 б) - ; г) — ; е) — ГГ7 » 3) TTV*
у Ь3 Ъ*с2 Ь 4- 5
142. Представьте произведение в виде дроби:
а) Зх-Б; в) а°д-2; д) с(а4~д)-1;
б) 2z/-3; г) 5а-3д3; е) 2х(х— 3z/)-2.
143. Представьте степень в виде произведения:
а) (а-1Ь-1)-2;
б) («у1)2;
в) (О,5а-3дБ)-2;
г) (—2тпБп-3)2;
ч /1 _2 2\-3
д) -р V ;
\ о ]
е) (—О,5х-3г/4)3.
144. Найдите значение выражения:
а ) 0,2с-254-5а3д-3 при а — —0,125, b = 8;
б )---—— при х = —, у = — 8
7 —2x-6z/“2 4
145. Представьте выражение в виде дроби:
а) а-24-&-2; д) (п + д-1) (а-1—5);
б) 2х-1— ху~2; е) (х—2j/-1) (x-1+2i/);
в) а3х-6-|-а"2х3—2а-4х-3; ж) (а-14- Ь-1) (а4- Ь)-1;
г) 5fc-6c4—3fec-3—2Ь2с; з) (а—6)-2(а-2—д-2).
п 6 7 8 9 10 11 12 13 14 15 16
2п
48
147. С помощью таблицы (см. № 146) выполните умножение.
Сначала по таблице представьте каждый множитель в
виде степени с основанием 2, затем замените произведение
степеней степенью и снова воспользуйтесь таблицей:
а) 32 • 1024; в) 8192 • —; д) 4096 •
' 512 64
б) — • 1024; г) 512 -8; е) -
256 ' 16 8
14. Стандартный вид числа
В технике, физике, астрономии имеют дело с очень боль-
шими и очень малыми (положительными) числами. Например,
расстояние от Земли до Солнца 149 000 000 км\ свет проходит
через оконное стекло за 0,00000000001 сек. Гораздо удобнее
как для запоминания, так и для выполнения некоторых вы-
числений такие числа записывать иначе:
149 000 000 = 1,49 10\
0,00000000001 =ю- и.
Любое положительное число представляют в виде произве-
дения числа а, где 1 <10, и целой степени 10:
а-10*.
При этом если число а дробное, то его представляют в виде
десятичной дроби, выполняя, если это необходимо, округле-
ние.
Такую запись называют стандартным видом числа. Число
п называют порядком числа.
Например, время продолжительности урока (в секундах)
в стандартном виде запишется так: 2,7 • 103. В этой записи
а=2,7; п=3.
Масса одного атома водорода 0,0000000000000000000000017г.
Запишем это число в стандартном виде: 1,7-10~24. Здесь а = 1,7;
п ——24.
Числа, записанные в стандартном виде, легко умножать
и делить, так как легко умножать и делить целые степени де-
сяти. В результате может получиться число нестандартного
вида. При необходимости его легко привести к стандартному
виду.
44
Приведем примеры:
1) (3,l-10s)-(2,3-104)=(3,1-2,3)-107 = 7,13-10’;
2) -’8 - — = • 10-“ = 3,2 • 10-c;
3) (8 • 10я) • (4,5 • 104) =36 • 107 =3,6 • 10*.
118. Записано ли число в стандартном виде? Если нет, то за-
пишите его в стандартном виде и назовите его порядок:
а) 3,4-Ш; в) 10,6 109; д) 19 10"в;
б) 7,51 105; г) 5,2 10"4; е) 4-Ю-8.
149. Запишите в стандартном виде число:
а) 7 000 000 000; г) 1 001 000; ж) 0,00000572;
б) 2 860 000 000; д) 0,02; з) 0,01006.
. в) 30 920 000 000; е) 0,0013;
150. Между какими последовательными целыми степенями чис-
ла 10 расположено число (запишите в виде двойного нера-
венства):
а) 365; б) 24,08; в) 0,0057; г) 0,0001002?
151. Выразите время в секундах и запишите полученное число
в стандартном виде:
а) 1 час; б) 1 сутки; в) 30 суток; г) 1 год.
152. Выразите массу в граммах и полученное число запишите
в стандартном виде:
а) 37 ц; б) 78 мг; в) 43,2 т; г) 969,54 кг.
153. Число, о котором говорится в предложении, запишите в
стандартном виде:
а) масса Земли равна 6 000 000 000 000 000 000 000 т;
б) в одном грамме водорода содержится
600 000 000 000 000 000 000 000 атомов;
в) радиус атома водорода равен 0,0000000001 еле;
г) расстояние 1 км свет проходит за ------- сек.
300 000
154. Сколько секунд длится один футбольный матч? Ответ за-
пишите в виде числа в стандартном виде:
155. Выполните действия:
а) (1,25 10е)-(4 1012); в) (4,2-Ю'2)-(4,2-107);
б) (6/2 10-2) : (3.1104); г) 105 : (8 10~2).
156. Свет проходит 3 108 м в секунду. Какое расстояние (в мет-
рах) пройдет свет за 1000 сек? за 0,01 сек? за 1 ч?
157. Колесо делает один оборот за 3 10~2 сек. Сколько оборо-
тов сделает колесо за 1 ч?
158. Расстояние от Земли до звезды Альфа Центавра состав-
ляет приблизительно 2,06-105 астрономических единиц
(астрономической единицей называется расстояние от
Земли до Солнца). Сколько километров от Земли до звез-
ды Альфа Центавра, если известно, что от Земли до Солн-
ца 1,5-10е км?
15. Степенная функция с целым показателем
В курсе алгебры VI класса мы рассматривали функции,
которые задавались формулами у—ах, у—ах2, у—ах3, где х и
у—переменные, а—число, не равное нулю. Такие функции
называют степенными' функциями с целым показателем.
Функция, которую можно задать формулой вида у — ахп, где
х и у—переменные, а и п— заданные числа, причем а=/=0 и
n£Z, называется степенной с целым показателем.
Здесь мы познакомимся со степенной функцией с отрица-
тельным показателем, равным —1 и —2.
Функция у=ах~1 представляет собой обратную пропорцио-
нальность, так как по определению степени с отрицательным
показателем ах~1 — — , где а#=0. Следовательно, графиком функ-
х
ции у=ах~1 является гипербола, которая при а >0 расположе-
на в первом и третьем координатных углах (рис. 4), при а<0—
во втором и четвертом координатных углах (рис. 5).
Рис. 4
Рис. 5
46
Рассмотрим функцию, заданную формулой у=ах2 (а^О).
При а=1 формула у=ах~2 принимает вид у—х~2. Построим
график функции у =х~2.
При х=0 выражение х~2 не имеет смысла. Значит, число О
не принадлежит области определения функции. При любых
других значениях х выражение х~2 имеет смысл. Значит, область
определения функции есть множество: ]—о©; 0[ (J 1 0? 4"°°[«
Переменную х, значения которой составляют область оп-
ределения функции, обычно называют аргументом функции.
Для рассматриваемой функции только число О не является
значением аргумента.
Составим таблицу:
X —3 —2,5 _9 —1,5 —1 —0,5 0,5 1 1 Х’5 1 2 2,5 8
У 0,11 0,16 0,25 0,44 1 4 4 1 0.44 0,25 0,16 0,11
Построим точки, координаты которых помещены в таблицу
(рис. 6). Можно предположить, что график функции располо-
жен выше оси х. Действительно, значение выражения хг2
при всех значениях аргумента (х#=0) положительно. Следова-
тельно, график функции не содержит ни одной точки с непо-
ложительной ординатой.
Противоположным значениям артумента х соответствуют
равные значения функции. Значит, график функции симметри-
чен относительно оси у.
Так как функция не определена при х=0, то график функции
не пересекает оси у.
График функции у=х~2 состоит из двух ветвей (рис. 7).
Рассмотрим функцию у=х~2 на множестве отрицательных
чисел. Если х = —2, то у =0,25; если х =—0,5, то у =4; если
х — —0,1, то у=100. Мы замечаем, что с возрастанием значений
аргумента х значения функции возрастают. Говорят, что функ-
ция у=х~2 является возрастающей на множестве ]—©о; 0[. Вооб-
ще, функция f называется возрастающей на множестве А, если
любому большему значению аргумента, принадлежащему множе-
ству А, соответствует большее значение функции, т. е.
если х2 >хп и xt,x2 С А, то f (х2) > f (xj.
Рассмотрим функцию у=х~2 на множестве положительных
чисел. Если х=0,5, то у =4; если х=2, то у =0,25; если х=10,
то у =0,01. Мы видим, что с возрастанием значений аргумента х
значения функции убывают. Говорят, что функция у=хг2 яв-
ляется убывающей на множестве ]0; +©o[.
Вообще, функция f называется убывающей на множестве
В, если любому большему значению аргумента, принадлежащему
47
Рис. 6
Рис 7
множеству В, соответствует
меньшее значение функции, т е.
если х2 >Х, И X,, х2 С В, то
f (х2) </ (X,).
Функцию, возрастающую
на данном множестве или
убывающую на нем, называ-
ют монотонной функцией на
этом множестве.
На рисунке 8 построен
трафик функции у=ах~2 при
п =—1. График этой функции
симметричен графику функ-
ции у=х~2 относительно оси
х, так как при одинаковых
значениях аргумент а х зна-
чения этих функций являют-
ся противоположными чис-
лами.
График функции у—ах 2 при а>0 расположен в верхней
полуплоскости, при а < 0 — в нижней полуплоскости.
159. Используя график функции у ~х 2 (см. рис. 7), найдите:
а) значения функции, соответствующие следующим значе-
ниям аргумента; 0,7; —0,7; 1,4;
б) значения аргумента х, которым соответствует значение
функции, равное 3.
160. Используя график функции у ——х~2 (см. рис. 8), выясни-
те, возрастает или убывает функция у =—х~2 на множе-
стве:
а) ]—°°; 0[; б) ]0; |-оо[.
161. Постройте график функции у = —4х-2 и, пользуясь им,
выясните, на какое множество отображается промежу-
ток;
а) [-4; -2]; б) [2; 4]; в) [1; 2]; г) [-2; -1].
162. Принадлежит
а) А (0,1; 1);
б) В (10; 1);
ли графику функции у=0,01х-а точка:
1 \,
25/ ’
г) D (0,5; 0,04);
. г. I 1
в) С-----------
\ 2
д) Е(—0,01; 100);
е) F (0,01; —100)?
163. Найдите значение о, при котором график функции у - ах 2
проходит через точку:
а) В (—0,1; 1000); б) С (50; 0,05).
49
164. Функция задана формулой у=3,86х-2. Не выполняя по-
строения графика этой функции, ответьте на вопросы:
а) При каких значениях х функция принимает положи-
тельные значения?
б) Существует ли значение аргумента х, при котором
значение функции равно 0? равно —5?
в) На каком множестве функция возрастает?
г) На каком множестве функция убывает?
165. Функция задана формулой у = —4,51х”2. Выясните:
а) При каких значениях х функция принимает отрица-
тельные значения?
б) Существует ли значение х, при котором функция при-
нимает значение, равное 1; 0; —100000?
в) На каком множестве функция убывает?
г) На каком множестве функция возрастает?
166. Используя графики функций у — — х-1 и у =—4Х-1 (см.
•4
рис. 4 и 5), найдите множество значений аргумента, на
котором каждая из функций монотонна, и укажите харак-
тер монотонности (возрастание или убывание).
167. Постройте график функции у=6х~1. Выясни! е, возрастает
или убывает функция: а) на множестве положительных
чисел; б) на множестве отрицательных чисел.
§ 6. УРАВНЕНИЯ, СОДЕРЖАЩИЕ ПЕРЕМЕННУЮ
В ЗНАМЕНАТЕЛЕ
16. Решение уравнении с переменной в знаменателе
Пусть требуется решить уравнение
6х __2х +1 .
Зх—1 1Г’ ' '
Представим уравнение (1) в виде
—------?1±1 = 0 (2)
Зх — 1 х
2х -+- 1
(перенесли выражение —--- из правой части уравнения (1)
в левую с противоположным знаком).
Решим уравнение (2). Для этого выражение в левой его ча-
сти представим в виде дроби:
СХ2 _ (2х 4-1) (Зх — 1) _
х(3х—1) “
60
Используя условие равенства дроби нулю, имеем:
6х2—(2x4-1) (Зх—1) = О,
х (Зх—1) #= О,
6х2— 6х2— х4-1 = О,
х=1.
Высказывание 1(3 1—1)=/=0 истинно.
Ответ: 1.
Уравнение (1) можно решить иначе.
Приведем выражения в левой и правой частях его к общему
знаменателю:
6х2
х(3х —1)
(2х 4- 1) (Зх — 1)
х (Зх — 1)
(3)
Так как знаменатели этих дробей равны, то дроби будут
равны при тех и только тех значениях х, при которых равны
числители и знаменатель отличен от нуля, т. е. равенство (3)
верно тогда и только тогда, когда выполняется условие:
6х2 =(2x4-1) (Зх—1),
х (Зх—1) 0.
Решая уравнение, получим:
6х2=6х2 4- х—1,
х —1=0,
х = 1.
Высказывание 1 (3 • 1—1) 0 истинно.
О т в е т: 1. *
Рассмотрим другие примеры.
1. Решить уравнение:
3x4-1 х —5
х — 3 х
Решение. Представим уравнение в виде
Зх-j-l.x — 5 . Л
------1------4 = 0
х — 3 х
и заменим выражение в левой части дробью:
(Зх 4- 1) X 4- (г — 5) (г — 3) — 4х (х — 3)
х (х — 3)
Воспользовавшись условием равенства дроби нулю, имеем:
Б1
/(3r t l)x I (г—5) (x — 3)— Ax(x—3) = 0,
[x (x — 3) /= 0,
3x2 4-x +x2—8x 4-15 -4x? +12x - 0,
5x4-15 = 0,
x = —3.
Высказывание —3(—3—3)7 0 истинно.
Ответ: —3.
• 2. Решить уравнение:
У — 3 у 4-1 (у — 3)(</ + 1)
Решение. Приведем выражение в левой и правой ча-
стях данного уравнения к общему знаменателю:
у 4-14-4 (у - 3)
(у - 3) (у 4-1)
4
(У - 3) (у 4- 1) ’
у 4-1 "Ь4{/ —12 — 4,
0/-3) (//4-1)70,
5у = 15,
0=3.
Высказывание (3—3) (3 4-1)7=0 ложно.
Ответ: уравнение не имеет корней.
168. Решите уравнение:
а)
х — 2____х -Ь 5
3 4
Д)
2х -Ь 3 _ х — 5.
2х — 1 ’ ’ х + 3 ’
1 3 г 5 — 2 г.
1 — 3 г “ 1 4- 2х
ж)
1 1
10у — 1 ~~ 2 — Ъу
5
7у — 2*
169. Найдите корни уравнения:
5 4 1
------------------ _ ;
У — 2 у — 3 у
3_ 7 _ 10.
у — 2 у 4- 2 у ’
х 3 , 7 4 — 20.2
в)--------------=----------;
2у — 1 2у41 1-47
У 4- 5 У — 5
у2 — 5у 2у2 — 10у
У 4-26
2у2 _ 50 *
52
170. Решите уравнение:
а) —= Л-;
х + 5 х + 5
б)-^- = 3х
2х— 3 2% —3
2x2
------— X
Зх —5
1 4- х — 6ха
Зх + 1
= X.
171. Числитель дроби на 2 меньше знаменателя. Если числи-
тель этой дроби уменьшить на 1, а знаменатель увели-
чить на 3, то значение дроби будет равно 0,25. Найдите
дробь.
172.
Знаменатель дроби на 5 больше ее числителя. Если числи-
тель этой дроби увеличить на 1, а знаменатель оставить
без изменения, то значение дроби будет равно — . Найдите
3
дробь.
173. Моторная лодка прошла против течения реки 16 км и
вернулась обратно, затратив на обратный путь на
40 мин меньше, чем на путь против течения. Найдите
собственную скорость лодки, зная, что скорость течения
реки 2 км;ч.
174. Турист проплыл на байдарке по течению реки 24 км и за-
тем вернулся обратно. На весь путь он затратил 7 ч. Ка-
кова скорость течения реки, если собственная скорость
байдарки была 7 огч?
175. Две землечерпалки могут при совместной работе углубить
дно реки за 12 дней. За сколько дней выполнила бы ту же
работу каждая землечерпалка, работая одна, если извест-
но, что производительность одной из них в 1,5 раза выше
производительности другой?
176. Производительность самоходной косилки в 5 раз выше, чем
производительность бригады косцов. Сколько дней потре-
буется бригаде косцов, чтобы скосить луг, если известно,
что самоходная косилка и бригада косцов, работая сов-
местно, смогут закончить сенокос за 3 дня?
177. Из города А в город В вышел поезд. Первые 450 км из-за
задержки в пути он шел медленнее, чем требовалось по
расписанию, на 10 км'ч. На оставшемся участке пути про-
тяженностью 750 км поезд увеличил скорость, с которой
должен был идти по расписанию, на 8 км!ч, в результате
чего он в город В прибыл вовремя. Какую скорость дол-
жен был иметь поезд по расписанию?
178. От деревни Дубки до села Боровково а км. Мальчик на
путь в Боровково обычно тратил столько же времени,
сколько и на обратный путь. На этот раз туда он шел со
53
скоростью, на 1,5 км!ч большей, чем обычно, а обратно со
скоростью, на 1 км'ч меньшей обычного. В результате
время, затраченное на путь туда и обратно, оказалось
такое же, как и всегда. С какой скоростью ходил обычно
мальчик от деревни Дубки до села Боровково и обратно?
Покажите, что ответ задачи не зависит от расстояния а
между деревнями.
179. На перелет от Москвы до Новосибирска самолет тратит но
расписанию столько же времени, сколько и на обратный
путь. Из-за встречного ветра в Новосибирск самолет летел
со скоростью, на 60 км.ч меньшей, чем полагалось. В Мо-
скву же он летел со скоростью, на 70 км/ч большей, чем
сбычно. В результате на оба рейса он затратил столько
времени, сколько требовалось по расписанию. Какова
скорость самолета по расписанию?
17. Уравнение с параметром
Рассмотрим задачу: «‘Теплоход, имевший собственную ско-
рость 26 км/ч, отошел от пристани и проплыл против течения
реки 80 км. Сколько времени затратил теплоход на весь путь,
если известно, что скорость течения реки равна Ь км/ч!*
Обозначим время (в часах), затраченное теплоходом на весь
путь, буквой х.
Скорость (в км, ч) теплохода против течения реки равна 26—Ъ.
Имеем уравнение:
(26—&)х=80.
(1)
В это уравнение относительно х входит переменная Ъ, обо-
значающая скорость течения реки в км ч. Такую переменную,
которая в пределах рассматриваемой задачи сохраняет одно и
то же значение, называют параметром.
По смыслу задачи параметр Ъ может принимать значения,
меньшие 26 и большие 0, т. е. 0 < b < 26.
Если д=6, то уравнение (1) принимает вид: 20л:=80. Ес-
ли д=10, то уравнение (1) примет вид: 16л:=80. Каждому значе-
нию параметра д, где 0<д<26, соответствует определенное
уравнение. Эти уравнения одно от другого отличаются лишь
коэффициентом при х. В выражении (26—Ъ)х—левой час-
ти уравнения (1) — множитель (26 — Ъ) выполняет роль коэф-
фициента.
Выразим переменную х через параметр Ь:
64
Так как 0<Ь<26, то уравнение (1) имеет корень, который
- ' „ , 80
может быть найден по формуле х = ----.
Итак, время, затраченное теплоходом на весь путь, равно
80
---и.
2G — b
С понятием параметра мы встречались и раньше, не употреб-
ляя этого термина. Например, когда определяли линейную фун-
кцию как функцию, которую можно задать формулой вида
у — kx 4- &, буквами к и Ъ обозначались параметры. При рассмот-
рении линейного уравнения с двумя переменными как урав-
нения вида ах + Ъу=с буквами а, & и с обозначались парамет-
ры — коэффициенты линейного уравнения.
Рассмотрим примеры решения уравнения с одним пара-
метром.
Пример 1. Дано уравнение относительно х:
тх—8=х.
Решить его.
Решение. Приведем данное уравнение к виду ах = Ь'.
тх—х=8,
(т—1) х=8.
Если т—1=0, то уравнение примет вид: Ох = 8. Очевидно,
что это уравнение не имеет корней.
Если т—1=7^0, то мы можем переменную х выразить через т:
Ответ: уравнение имеет единственный корень--------,
т— 1
если тп=/-1; уравнение не имеет корней, если т = к.
Пример 2. Дано уравнение относительно х:
пх=5ц.
Решить его.
Решение. Если п/0, то х = — , х = 5.
Если п=0, то уравнение примет вид: 0х=0. Очевидно, что
этому уравнению удовлетворяет любое значение х.
Ответ: уравнение имеет единственный корень 5, если
уравнение имеет бесконечное множество корней (любое
число — корень уравнения), если п = 0.
55
Пример 3. Решить уравнение с параметром а:
а
2-^=3’
Решение, Приведем данное уравнение к виду — Л 0:
Q
а
---— 3^0,
2-V
а-3(2-у) _о
2-у
2-У
= 0.
2 — у^О
6 — а
Мы выразили переменную у через а. Теперь нам нужно проверить, при
6 — о
каких значениях а предложение 2 —----- #= 0 обращается в истинное выска-
3
зыванме, говоря иначе, нужно выяснить, при каких
6 — а
2 — —-— = 0 обращается в ложное высказывание.
Решим уравнение:
значениях а предложение
— = °
а
3 ~ °'
а — 0.
6 — а
Итак, предложение 2 — ------ #= 0 обращается
3
при всех значениях параметра а, не равных нулю.
Ответ: уравнение имеет единственный корень
не имеет корней, если а = 0.
в истинное высказывание
6—о
—-— , если а ф 0; урав-
О
невие
180. Дано уравнение с параметром а*.
ах- 2с + 3.
Напишите уравнение, которое получится при указанном
значении с, и решите его:
а) а = 10; б) «=1; в) а — —1,5; г) а=0.
181. При каких значениях параметра а уравнение ах = 5 не
имеет решений? При каких значениях а данное уравнение
имеет корень, равный:
а) 1; б) -1; в) -2; г) -3,5?
182. Существуют ли такие значения параметра 6, при которых
уравнение %х — Ъ не имеет решений?
183. Решиге уравнение с параметром а:
а) ах=8; б) 5х=а; в) (а—2)х=20; г) —— х = 1— а,
2
184. Уравнение относительно х приведите к виду ах = Ь и реши-
те его:
а) сх-}-2==5; б) 6х—ex —1; в) сх—5 — х; г) сх4-7х—0.
185. Выразите переменную х через а:
а) х 4-2—ах, а=£1; в) — 4- — = 2, а О; а =/= i;
ха 2
х ® 1 i к \ 3 /о
б) --- = 1, а ^=5; г) а = — а=^2.
а — 5 х — 4
136. Выразите переменную у через а и 6:
а) а = ; ъ) — =-----1—•, с О и b О, а -Ь 0;
2 у а ь
г) - = ^- + - , а^О и 5=^0, а— Ъ 0.
2 — у b а у Ъ
Ь 0, а + b Ф 0;
ДОПОЛНИТЕЛЬНЫЕ
К ГЛАВЕ I
УПРАЖНЕНИЯ
К пункту 1
187. Преобразуйте выражение в
а) 5х2 (г2—2x4-3);
б) —8/2 (у2—5у —1);
в) Зх2(—5х24-4х—1) Мбх4;
г) 8у’ — 2у3(1 —Ъу —у2 4-41/3);
д) (а2-5а4-4)(2а+3);
многочлен стандартного вида:
е) (36—2) (61—76-5);
ж) (у— 1) (i/34-i/2 4-1/-1-1);
з) (х4-1)(*4—х3 4-х2—х4-1);
и) (а2 |-7а4-3)(а2—4а 4-2);
к) (62—36—5) (624-36—5).
67
188. Представьтэ выражение в виде многочлена стандартного
вида:
а) (— 4х+7а)(7а+4х); е) (х+1)3;
б) —(а—7Ь) (7Ь +л); ж) (у-2У;
в) (Зс2— 8) (Зе2 4-8); з) (х+у)3- (х+у) (х^ху+у^
г) (2л:—5z/)2; и) (т — п)3 — (т— п) (m24~mn 4-и2);
д) — 2(у- 1)24“(2—р)2; к) х(у— х)2 —у (у— х)24“ (у— х)3.
189. Найдите значение выражение:
а) х2—(х—у)2 при х =—3, у — —1;
б) 9х2—(Зх-\-уУ при х = —3, у — —1;
(5\2 / 3\2
х—4 — ] —[г/—6 — | при х = 10, у = 9;
8 / \ 8 /
Г) (X -I- у)2— (х—у)2 при X = i, у = —5.
4
190. Разложите на множители:
a) a2b-\-ab2\ в) тъп2
б) х3у — ху3- г) pV1—р4<?8;
191. Представьте в виде произведения:
д) 2с8—250с2;
е) 8129 +323.
а) 7х—14ху4 21ах;
б) Эху—Зхр4-15ау;
в) — 48a5&-t-36a6fr5 — 12oW;
г) 8а&2—6а2&2—2а&4-2а3Ь2;
д) 35ах—49 Ьх—5а4-7&;
192. Решите уравнение:
а) 8х—5 (х4-2)=1;
б) 6 (х—9)-|-25=4х—31;
в) 15p2-25i/=0;
е) 16с/?4-6&—40с—15;
ж) х1—х34-х2—х;
з) с4—2с3—с2 4“2с;
и) 36 (а — 2)2 — 25а2;
к) 100 (2t/24-l)2—121р
г) 15уг+251/=0;
д) 36i/a-25=0;
е) 36i/2+25=0.
193. Докажите тождество:
(х4-а) (х -Ь&)=х2-|-(а4-&)х4-а&.
194. Приведите многочлен к виду (х4~а)(х4 Ь):
a) x2-F5x-}-6; б) х2—5x4-6; в) х24-7х4-12; г) х2 43x4-2.
195. Приведите уравнение к виду (х4-а) (х4~6) =0 и найдите
его корни:
а) х24-8x4-15=0; - в) х2— 6х | 8=0;
б) хл—8x4-15=0; г) х24-6х4~8=0.
58
196. Докажите тождество:
fl4c2H=(fl2+c-H) (а2— а 4-1).
Почему при любом значении а верно неравенство:
а) а4+а2-И > 0;
б) а2-Ьа-Ь1 > 0;
в) а2— а +1 > 0?
197. Разложите на множители:
а) х6—1; г) р8+р4-|“1; эк)
б) / + 1; д) &12—1;
в) а8—1; е) ав+2а3— а2+1;
Ъ* — Ь4+2&3 + 1.
198. Постройте график
а) !/ = —0,5х4~3;
б) i/^0,5x+2;
в) z/=l,5x—1;
функции:
г) у ——1,5х—2;
д) j/=0,5x2;
е) у = —0,бх2;
ж) у=*х3;
з) у = — х3.
Используя график, выясните, при каких значениях х:
1) У =0, у > 0, у < 0; 2) переменная у возрастает с возра-
станием х; убывает с возрастанием х.
199. Решите уравнение:
а) х =3; в) х—2| = 1; д) |х =х;
б) х = —5; г) х4-2|=5; е) |х — —х.
200. Сумма двух чисел равна 25, а их разность равна 1. Найдите
эти числа.
201. Одно число в 5 раз больше другого. Сумма этих чисел
равна 54. Найдите меньшее число.
202. Одно число на 1 больше другого, а квадрат первого числа
больше квадрата другого на 21. Найдите эти числа.
К пункту 2
203. Найдите значение дроби:
2
2,25 : 1,5 4-3 : 1—
3
15
,-I •
(5,56 — 4,06) : 3*
37» + 111
40
б)
22,5
9
10
3 1
14— . — 4. 2,17
20 5
895-}-79»
84
58
204.
Найдите значение
2__5
выражения при:
205.
206
а) х ——1;
б)
х = 0,5;
в) х — 2—; г) х=3-.
4 ' 8
Найди е область
х —3
10х Ь 50
а)
б)
в)
Г)
Д)
82
16х — 64
а+ 5
2а2 — 98
____1 _
х3 — 4х
ж)
При каком
а) x24-j/8
б) —
x2f/2
определения дроби;
5
16./ -1
1
-4-2
2
— --8
а
3
9——
а
условии дробь
в)
(*-у)8
ab
г)
(а—Ь)2—1
не
з)
10
и)
К)
30
а2 4-Х
|а|— а
им< ет смысла:
д)-------V
(х+1)2+(у-1)2
®) Г
6
- - 3
207. Соста вьте дробь, которая не имеет смысла при:
а) у =0 или у=2;
б) у = 2 или у= i-;
в) а = 0 или & = 0;
г) а = 0 и Ъ — 0.
208. Какие натуральные значения х и у удовлетворяют уравне-
нию:
а)ж^ = А
7 7
б) —— = 1?
209. Запишите в виде дроби частное от деления числа 273 на
двузначное число вида 10а 4-1. Укажите множество значе-
ний переменной а. При каких значениях а составленное
выражение принимает целые значения?
210. В бассейн объемом 400 мя проведены три трубы. Через
одну из них вода поступает, через две другие вытекает.
60
Через первую трубу по< тупает 15 л 4 в час, а через каждую
из двух других вытекает х м'л в час. Если открыть веэ
три трубы, то пустой бассейн через некоторое время на -
полнится. Через сколько времен и наполнится водой п у-
м ой бассей н, если открыть все трубь:? Составы е выражс
ние. Найдит множество значений переменной х.
211. Первый поезд вышел из А в Ви проходил в час по 60 км.
Второй поезд вышел из В в Л на 3 часа позже, чем первый
из А. Поезда встретились через у часов после выхода пер-
вого поезда. Расстоя еие от А до В ра вно 700 кл. На каком
расстоянии от В произошла их встреча? Какс вл скорость
второго поезд а?
Составьте выражения и найд ите их значения, если:
а) у= 8; б) у= 6.
212. Найдите область определения функпии:
а) 1 г) 2с + 3 Ж) 1/ = 1
у — х — 2* У л2 — 4 ’ |х I — X ’
б) X д) 1 0 У = 1
У Х-1 з’ У |х|- 2 ’ 1*1 +« ’
Е) 1 е) X
У ~ л2 — 5 с У |х| +3 ’
К пункту 3
213. Какая из дробей равна нулю:
2 J5\ с 1
А 1 ' 11
41
7,3“ - 2,7“
„ 1 22 Ч 2 • 1,2 l.f I 1,Е2 — 9 „
Г) -------------——------------------ I
214. Придумайте дробь, которая содержит переменную х и
обращается в нуль при:
а) х 1 5; в) х=0 или х -2;
2
б) х=---—; г) х =— 5 hj и х — 5.
61
215. При каких значениях а значение дро5и равно нулю:
а) в\ 9 ’ г) (2а 4-Ъ2 — 81 . а» 125 . |а —3 ж) -—L ; 10
б) fa { 1)а . 117 ’ д) (а-2)(а-М(а24-1) , а з) lfl|-.fl-? 25
в) а2 (а 4- 5) . а2 — 5а * е) (2а 4- 5) (а — 0,1) (а2 |-1). а 4-Ю
216. Реп иге уравнение:
a) 15A±^ X = 0; Г) ^1 = 0; X- 9 ч |х| —7 ж) J 1 х2 — 40 = 0;
6>^=a ' 14x 4 21 = 0; Д) —У _ Q. У »> -L»l~2 Уа4-4 = 0.
B) H».-8) V = 0; e) 4,3.T25 =o- 2y 4-5
217. Найците если: множество зна тений х. при которых Г(х)-О,
a) f(x) = x —3, в) /(х) = ; о д) f (*) = 6-И .
X 6 4- х '
б) Г(х) = -^Ц^-; г)Нх)=НШ; е) Г(ж) = 1в=£1.
2 5 6 4-х
К пункту 4
218. Сократите дробь:
. 40'ах
в) — ;
45а 7
. 18аЬс
г) —;
108ас
И)
2166:
б)------;
180а:
. 35а6'4 . (—-'(F)’ t
28а4у» ’ (—сМ';)А ’
е) _W_. з)
14х.4ь“ ' (—aSj/1)»
219. Упростите выражение:
а) 7.^ + И;
7 (ху4 14)
8(а—12).
' Ра- 12 ’
(За-Зср
da1 — Ос2
г) £^-Ч8. (°8-9)8 . к)
(6х— ба)2 ’ # (3 — а)» ’
(2а-2Ь)2 . (5?-2р)' .
' 2Ь* — 2аа ' f (4рв —25?»р’
. (4х - 4«)з . х2 - 100
е) -------—; и) ---------------;
(2у - 2х)4 *э р i.Kjy
62
220. Докажите тождество:
. Юаб — 156» 106» — 1Ба6
а) ----------=------------—;
4а» — баб 4а6 — 6а8
g. 2х8 -Юху 2х8 — Юху
} х» —25у» х« —10ху+25у» ’
. а» — 4а -J- 4 а» — ab 4- ?6 — 4
а» + аЬ — 2а — 2‘ а» 4- 2а + 26 — 6»
. (2х — 8у)» + 2х — 8у _ 4х» — 12ху + 0уг
Г' 4х2 — 9у2 + 2х4-3у “ 4х» —9у»
221. Сократите дробь:
ум _ Ь’ +1
а)---------------
6»Ч-1
хЭЭ__ 1
б) — -—
' х»з 4- X82 4- Х«
в) *(У~z)—у(* —») .
' х(у — г)8 — у (х — z)2 ’
аГ6 + 1)2-6(а I- I)2 .
' а8 (6-f-1) — 6» (а 4- 1)'
222. 1) Если у дроби-------- - переменные х и у заменить
Зу» — 5ху
соответственно через kx и ky (k — не равное нулю число),
то получится дробь, тождественно равная первоначаль-
ной. Докажите это.
2) Проверьте, какие из следующих дог бей обладают ука-
занным йыше свойством:
а) ; 6)^; .) ; г)е±й
4ху» -7у» ' x-f-Зу8 (х (-2у) (Зх — у? (х — Зу)в
.223.
Докажите, что значение дроби
Зх8 + у»
Зх» - у2
2 8
при X = - И у=* -
равно значению этой дроби при х ~= 2 и у — 3.
224. Найдите значение дроби:
1.
б’
6=1.
2
„ а»4-8а6 1 .
а) --при а — - - и о —
' аг — аЪ 3
... а8 — аЬ 8
б) ------- при а = —
аг 4- Ьг 4
и
225. Докажите, что при всех значениях переменных а и х, при
которых дробь имеет смысл» ее значение не зависит от xt
а2 2ах 4- 6х — 9 , (а.4 Зх)»—(Зх-1)»
' <а (- 8)» — 2ах - 6х ’ } 6х — бах (а — I)8 *
68
226. Докажите, что если вместо переменной х подставить нату-
2х
ральное число, то получится несократимая дробь ----- .
К пункту 5
а) у-
77а5
8Ь5с®
б) - •
227. Представьте произведение в виде дроби:
22аБхБ . -га3 _ 5Ь» 18а2 _ 18А2
----; в)------------------------;
8 L(/° 12а +12А а» + а&4-Ь«
55с2х3 . х2 — 2ху х' — 16./
126' ’ х2 4- V ' (* — 2у)2 ’
228. Решите уравнение:
а) (х + 5) = 0; г) *±--0;
х —2 х 4- 1 2х
г-х Z -IX х п \ х*—4х Зх к 1 „
6) 0; д)__.—= 0;
в> (« + 2>-!-=^ = °; е)^Ц-(»-!)= 0.
5x4 10 х1 — 1
К пункту 6
229. Предс гавьте частное
144a'V 6x’a»u7
а) — : -—
С5Ь’гЗ 1^3,6
192men" 36nens
б) :---------------;
77р 55р2
в виде дроби:
. 2!ae Юа’А
в) : —-------------------------
6а« _ 6Ь» 9а’ 4 9ab 4- 9Ь2
5хяу . 10х,в</2
' a* — 2ab F 4А2 ’ а2 4 81»
230. Упростите выражение:
. а2 — 10сх f 10ах — ас
а)---------------!----------
х2 — ах
а2 — 100г2 .
а2 — ах
и2 — 10рЛ — 2рп 4- р2-—6pfc .
6/ п — рп и2 -— 25Л2’
х4 —у* . 2х J- у
4v — 2х — у — у2 х3Н • х2у 4 ху2 |- у3’
аа —Ь»________________a -3f-
а2 4 а - ЗА — 9Ь» (а* + А2)2 — аг:>г '
Д)
бху Ь 6 — 4х — 01 .
х2 — 12х |- 36
_ 9У* -Д2>/ + 4
Зху— 18у — 2x4 12’
1! ah - 15 4 9а - 25Ь
(а2 — ЗСа1» -к 25д2
9а2 _ 30а 4 25
15а —25Ь4-9а2 25Ь2‘
64
К пункту 9
231. Замените выражение дробью:
а) * + з х 10 Г) 2j-8 —* —Ю х .
X X — 3 х2 — Зх 4х2 — 25 5 — 2х*
б) — h 2х — 1 _2^ п)1?2+го + 2 1--2а .
2х2+2х X2 — 1 X а3 — 1 а2 4- а т-1 *
®) + 3& + 6 Р — 8й . Зо2 — 12 ’ еч 2 Зхо_ 1 х2+ху + у» хЗ—у» X —у'
232. Упростите выражение:
а) 1 — + —
(а — Ь) (Ь — с) (с — а) (а — 6) (Ь — с) (с — а) *
а(а—Ъ)(а — с) ' 6(fr —с)(& —а) с(с —а)(с —Ь)‘
233. Докажите, что множество значений выражения состоит из
одного элемента:
fe + 1 с + 1 _ с.
b с Ъс *
б) ±+ +
У X ху
Ъс — а* , ас — Р , ah — с2
Ъс
в) ,
аЬ
ас
Г) ± + * + У _ 'х (х + у)
У х — У У(х — у)‘
234. Докажите тождество:
. + _______________lx —ay _ д2 + Р .
(а — Ь) (х -1- у) (а { Ь) (х + у) а2 — Р ’
б) * т~ Л'* _| У — Ь: -| г* _ j . (Р +'*д)2 .
' (Л + *)! 1 (Ь — х)* ’’"(Р-х2?’
v2 j/2 72
в)------------------1--------------- |----------------—
(X — У) (X — г) (у — х) (у — z) (г — х) (г — у)
235. Решите уравнение:
ч 3 а) 7— — = 0; г) + у-=^ =. 2;
2х—1 5х—6 Зу 1 у i 3
б) -4- - 0; д) = 2;
Зх 5 4j 3 2x^5 3x 2
в)^Ч -^=-5 = 0; е)9-^1-^-5 = 1.
у- 1 у - 3 Зх - 2 2х — 3
3 Алгебра, 7 к л
65
236. При каких значениях а п b тождественно равны выраже-
ния:
х —5
ах + b
«4-ю
2х 4- 20
Зх —5
2 (х 4- 10)’
И
б)
5г—2 _ сх4-Ь
Зх — 9 5х 4- 2
4x2 -|_ 45х 4- 5Q
15х2 — 39х — 18
К пункту 10
237.
Представьте дробь в
виде суммы двух дробей:
а 4- 5
а2 — 9’
б)
Ъ
Ъг— 1’
;зх4-1
* •
x(x4-l)t
7х |- 14
(х-2)(х4-5)
238. При каком целом п значение дроби есть целое число:
6) —— ?
2— п
239. Написанные равенства — тождества. В них буквами а, Ъ
и с обозначены некоторые числа. Найдите их:
к 4х2 4-Зх — 25 __ а Ъ ; с
' (х — 1) (X 4- 2) (X — 3) “ х —1 + х4-2 х —з’
X2— 2 а Ь . с
о) -----—------4“--------4~--------»
(X— 1)3 х —1 (X—I)2 (X — 1)3 ’
ч 1Эх2 — 1 ах — 3 , Ъ , с
в)-------------—-------- 4“-----"4“----•
(х — 1) (х 4- 2)а (х 4- 2)2 X 4- 2 х — 1
240. Представьте дробь 181 если это возможно, в виде
х2 — 9
суммы двух дробей —— и ——, где а и Ъ—целые числа.
х4-з х —з
К пункту 11
241. Представьте выражение в виде дроби:
66
242. Докажите, что при любых натуральных значениях п зна-
чение выражения
/9
ла
п2 п
— натуральное число
243. Докажите, что при любом целом а и дробном х значение
выражения
2а
4а
— четное число
л
7
3
3
а —
х а — х
244. Докажите, что при любом значении х, большем 2, значение
выражения
4- —-----2') :
—отрицательное число
2х
245
Упростите выражение:
а — 3
а2— За 4*9
б)
6а —18\ . 5а —15 .
а3-f-27 / ’ 4а34-103’
Ъ
5а
5а2 — oab
{2а—Ъ)2
____2
4а2 — Ъ1
(2аЧ-Ь)2
16а
д)
4с2
(с - 2) ‘
(с - 2)а
са — 4
2*4*У
У~**У
3
а — 2Ъ
а2—2аЬ
1 — 6ab3
2аЪ
4л3 4r2v
а — Ъ
2
х — у
246. Представьте в виде целого выражения:
' 25 2а а34"25аа\ / с , 15а
---------------------------------- а — 5 4--------
а2 4- 5а 4- 25 5 — а а3 — 125 / \ а — 5
(1 - а) (1 - Ь) _ '2 (1 - а2) (1 - b~).
14~чЬ / (14* аЬ)"
247. Преобразуйте выражение в дробь:
а . 4а2Ь — ab2 . ____Ьа____\______За& е
а — Ь Ь3 — а3 ~аа 4- аЬ 4- da / (а — Ь)3*
{ а—х 1 \ /2х 4* а । 2а 4- л\
б)---------------------- ------- + ----- •
\аа 4* о-х 4* х2 а — X] \ а х J
3*
67
248. Докажите тождество:
а2 а Ъ2 Ъ
1 _JL _J__
б) ' д3-^ ~г’ fo+fe)3 _ 1
' (a+b)3+2(c3—ь2)+(а—b)2 ~ (а2 — 6*)» ‘
249. Выполните подстановку и упростите полученное выраже-
ние:
. ах
а) ~
Ъх
аЬ
где х
а — b
х — b
б) ,
х2 — у2
где
2аЬ
--------. У =
а2 — Ь2 *
2аЪ
X =
К пункту 12
250. Представьте выражение в виде
л ем:
степени с целым показате-
) 1G4’ Г) —8’ а »’ К) (0.0001) *’
б)_1_; Д)1; 3)?“.2;
100000 ' 81 б) 7 * * tr*’
в) е) и) ——;
(—5)’ ’ X»’ ’ 125а*
251. Докажите, что следующие выражения взаимно обратны:
и 5 в) ЮОО- и (0.001)—;
о \ о /
б) и (0,6)-*; г) 2,5“ и I7-.’1.
\5/ \5j
252. Сравните выражения:
а) 5-3 и 7-3; в) (2,9)-10 и (3,1)-,0;
г) (0,43) 10 и (0,52)-10.
68
К пункту 13
253. Найдите значение выражения:
„X (— 27)“ (— 9)“ Ф / (8° + 2-S) 6 »
а> (—3, 7---’ б) (-----------------
0,1-»-1.
24
254. Представьте выражение в виде дроби:
а) - а-136~6 — - а-66-1г;
' 24 18
в) (х2+ху)(х2—. у2)-г(ху—у2);
г) (а4-1) (а2—1)-‘а3;
д) тп (п—т)~2—п (т—п)-1;
е) (2а+1) (2а—1) ' — (2а— 1) (2а+1)’1.
255. Представьте дробь в виде целого выражения:
. X6 4 X1» к С6 4“ °® + °7
а) ——; в) -----------;
х'5 4-х 11 a's 4- о*® 4- аг1
б) у°9 ~ V2' • Г) 63 + ьа + ь + 1
} у-ы—уМ ’ ’ Ъ-» 4- Ь'2 4- &-* 4-Г
256. Упростите выражение:
a) (х-1+у-1)-2:(х+у)-2;
б) (а-162—a2b-1):(a-3—5-3);
в) (a~l + b~l)ab (^-а2)-1;
г) (&4-б~2) ((б24-1)б-2-б-1)-1;
д) (х~2— а~2) (а-1— х-1)-1;
е) (ab~l—a~lb) (а-1—&-1)-1.
257. Решите уравнение:
а) бх-1-6 0; г) 6 (у—З)"1—4 (у—2)~1=0;
б) 34-Юх-1=0; д) (5—х-’Г^З 2;
в)9х-2—8(2х + 1)-1=0; е) (9—х-^-^З 3.
К пункту 14
258. Запишите в стандартном виде число, о котором говорится
в предложении:
а) один карат равен 0,0002 кг;
69
б) скорость электрона
равна 59 450 000 см сек\
в) одна миллисекунда
(м/сек) равна 0,000278 ч;
г) одна верста равна
1066,8 м.
259. Выполните действия над
числами, записанными
в стандартном виде:
а) 3,44 1015-71012;
б) 8,1 10-23-2 1021;
в) 4,2-1011-5,1-10-’;
г) 9,6 10-12:(3,2 10-15).
К пункту 15
260. Постройте график функ-
ции |/=12ж ’. Найдите:
Рпс. 9 а) область определения
функции; б) множество
значений функции; в) мно-
жество значений аргумента, на котором функция принимает
положительные значения; отрицательные значения; г) проме-
ж> тки, на которых функция возрастает.
Рис, 1о
70
261. Функция f задана графиком (рис. 9) на отрезке [—4; 3].
Пользуясь графиком, найдите:
а) множество значений функции /; б) множество значений
х, при которых f(x) O, f(x)<0, f (х) >0; в) множество
значений аргумента, на котором функция f возрастает,
убывает.
262. Функция g задана графиком (рис. 10) на отрезке [—3; 5].
Укажите промежуток, на котором функция g:
а) возрастает; б) убывает.
263. В одной и той же системе координат постройте графики
функций f (х)= —х2 и g (х)—\2хг2.
4
Используя построенные графики, решите уравнение или
неравенство:
a) f (х) ^g (х); в) f (х) >g (х); д) / (х) <-;
4
q
б) f (х) < g (X); г) f (г) = —; е) g (х) > 3.
264. Известно, что точка (а; Ь) принадлежит графику функ-
ции f. Принадлежит ли этому графику точка (—а; &),
если:
а) /(х)-81х2; в) f(x)—2х'; д> f (х)= 5х;
б) f(x)=^6x~2-, г) Г(х) = —Зх-‘; е) /(х)=5|х|?
265. Симметричен ли относительно оси у график функции, за-
данной формулой:
а) у = —37х~2; б) у=16х-3; в) у—х3; г) у —|х ?
266. Чем отличаются друг от
если.
a) f(x)=x, g(x) = |x|;
б) f(x)=x2, g(x) = |x|2;
в) Дх)=х3, g(x) = |x|3;
К пункту 16
267. Решите уравнение:
а) — 1 - — 28 •
а' 1- х г 1 + х 1 —Xs’
5 3 20.
х — 2 х -1-2 Xs — 1
друга графики функций f и g.
Г) /(х)=х-1, g(x) = |x|-1;
д) Дх)=х-2, g(x) = |x| 2;
е) Дх) = х~3, g(x) = | «| ?
х + 2 _ х + 1 = _ 4
В 14-3 х 1 (х<3)(х—1)’
г)*и+^—1 = _L_.
х + 1 х - 2 х2—х— 2
71
268. Турист проехал на велосипеде 28 км по шоссе и 25 км по
проселочной дороге, затратив на весь путь 3 ч 36 мин. С
какой скоростью ехал турист по шоссе, если известно, что
по шоссе он ехал в 1,4 раза быстрее, чем по проселочной
дороге?
269. Мотоциклист рассчитывал проехать 120 км за определен-
ное время. Через час после отправления ему пришлось
сделать пятнадцатиминутную остановку. Чтобы прибыть
на место назначения вовремя, мотоциклист увеличил
первоначальную скорость в 1,2 раза. С какой скоростью
ехал мотоциклист в начале пути?
270. Мотоциклист выехал из города А в город В. Если он бу-
дет ехать со скоростью 50 км /ч, то опоздает на 1 ч, если
нее он будет ехать со скоростью 70 км ч, то приедет в В
на час раньше срока. Каково расстояние между городами
А и В?
271. Турист выехал на мотороллере из А в В со скоростью
50 км. ч. Через 24 мин после отправления из А он снизил
скорость на 10 км.'ч и поэтому прибыл в В на 18 мин поз-
же, чем предполагал. Сколько километров от А до В?
272. Моторная лодка, имевшая собственную скорость 16 км'ч,
отошла от пристани А одновременно с плотом вниз по те-
чению. У пристани В лодка развернулась и на обратном
пути встретила плот в 20 км от приста ни А. Каково рас-
стояние между пристанями А и В, если и?вес’гно, что ско-
рость течения реки равна 4 км/ч!
273. Поезд должен был пройти расстояние АВ со скоростью
56 км ч. Однако через полтора часа после выхода из А он
был задержан на 30 мин и, чтобы прийти в В по расписа-
нию, должен был остальной путь проходить со скоростью
63 км/ч. Чему равно расстояние АВ?
274. Пройдя путь ив М в К, равный 360 км, автомобиль по-
вернул назад и через час после выхода из К увеличил
1 - « „ „
скорость на — первоначальной. В результате на обратный
3
путь он затратил на 1 ч 15 мин меньше, чем на путь из М
в К. Какова первоначальная скорость автомобиля?
275. В хоккейном матче команда «А* в каждом периоде за-
бросила одинаковое количество шайб, а команда «В»
в каждом следующем забивала на одну шайбу больше,
ч м в предыдущем. В чью пользу и с каким счетом за-
кончился матч, если известно, что третий период закон-
чил”'! гничью и одна из команд заброс ила шайб в 2 раза
больше другой?
72
276. Два подъемных крана, из которых второй начинает работу
на 5 ч позже первого, разгрузили баржу за 11 ч. За сколь-
ко часов может разгрузить баржу каждый кран, если
производительность второго крана на 10% больше, чем
производительность первого крана?
277. Из М в N вышел товарный поезд, а через 10 мин навстречу
ему из N в М отправился пассажирский поезд, который
шел со скоростью, в 1,5 раза большей, чем скорость то-
варного поезда. Пассажирский поезд, пройдя 210 км,
встретился с товарным поездом. Найдите скорость каж-
дого поезда, зная, что расстояние MN равно 360 км.
278. От станции А к станции В отправился поезд. Пройдя 48 км,
поезд был задержан у семафора на 15 мин и поэтому, что-
бы прийти в В по расписанию, последующий путь прохо-
дил со скоростью, в 1,2 раза большей. Зная, что расстоя-
ние АВ равно 168 км, найдите первоначальную скорость
поезда.
279.
Числитель правильной дроби на 2 меньше знаменателя.
Если числитель дроби увеличить на 2, а знаменатель уве-
личить в 2 раза, то получится
—. Найдите дробь.
К пункту 17
Зй л
280. Равенство----= а7 — а — уравнение относительно х. На-
х-1
пишите уравнение, которое получится при указанном
значении параметра а, и решите его:
а) а——5; б) а=0; в) а — 1; г) а = —2.
281. Дано уравнение относительно х:
Покажите, что:
а) уравнение не имеет корней, если Ь=0;
б) уравнение имеет единственный корень Ь~ , если 5=^0.
282. Покажите, что уравнение
_ Зх
в —3 о-З
при любом значении параметра а, где а^З, имеет беско-
нечное множество корней.
283. Дано уравнение относительно х. Решите его:
а) Ъх — ЗЬ -2х — Ъ; в) - - а;
х — 3
б) ах — 42 = 7х — 6а; г) 1 + г = а>
1 — X
284. Дано уравнение относительно х. Решите его:
а) -
6
х — 2а
10
= 2;
г) ^ + 8=Ь
X X
б)
— За
2
+ — = 3,5а;
3
3.
»
X
в) °— 4 =
X
. а-х 4- 8 , _ . .
е) -----'- - = а- — 2х 4 4.
а + 2
285. При каком значении параметра а уравнение ——— =0
х + а
имеет:
а) два корня; б) один корень?
286.
о t \ Зх — 4
Зная, что 5 (х) =------, найдите:
5
а) 5(2);
б) «(--У;
В) 5(C);
г) 5 (-а);
д) 5 -;
\ а /
е) q (а + 2).
287.
Известно, что f(х) —
——-. Докажите, что:
а)/(с) /(—а); б)/(-а) |-/
288.
Пус ть f (х) —
----. Д( кажите, что:
а) /(х)-/(-х). = 1; в) /(х) = — 1;
г)/(1) /(-x)--i.
289. Известно, что равенство
1 ! 1 _ 1 1
X р(х) X р (х)
есть тождес гво (р(х) — выражение, содержащее перемен-
ную х). Найдите р (х).
74
290. Выясните условие, при котором равны дроби:
.54-е 5 1 ° ч ° ь
а) —!— и —; б) — и —; в) — и —
' 84-е 8 a 4 'ba
Г)г
и —
d
291. Докажите, что:
а) если (г— у)2 —4 и (у 2) (2у -х)¥0, то дроби
х у — 2
--- и ------ равны;
И2 2у — х
б) если |х —у| =2 и (Зх+2) (2x4- у) ¥0,
4х — у 3“ — 2
--- и ------ равны.
Зх 4- 2 2х 4- у
то дроби
с
292. Докажите, что равенство:
я2 4. м «а а
а) -—- — — верно при условии, что — =
a?J_2—ь _ J_ верно прп условии, что - 4“=
' _2м с2 а Ъ
a2bJ
1 4.1 J Л = -----------верно при условии, что
1 а ' Ъ с а-\ Ь-\-с
(в 4 Ь) (Ь + с) = 0 и аЪс ¥ 0.
Глава II
НЕРАВЕНСТВА И ИХ ПРИМЕНЕНИЕ
К ПРИБЛИЖЕННЫМ ВЫЧИСЛЕНИЯМ
§ 7. НЕРАВЕНСТВА II ИХ СВОЙСТВА
18. Понятия «меньше» и «больше»
По известному нам определению из двух чисел л и Ь мень-
шим считается то, которому соответствует на числовой прямой
точка, лежащая левее, и большим считается то, которому соот-
ветствует на числовой прямой точка, лежащая правее (рис. 11).
b а
а>Ь
• •
а b
а< b
Рис. 11
Например:
—16 меньше 0 (неравенство —16 <0 верно), так как точка
с координатой —16 лежит на числовой прямой левее точки с ко-
ординатой 0.
12 12
, так как точка с ко-
ординатой — лежит на числовой прямой правее точки с коорди-
12
5
натои —.
12
Пусть а и Ъ — некоторые числа, причем а больше Ъ. Тогда
точка с координатой а лежит на числовой прямой правее точки
с координатой Ь. Перемещению по числовой прямой вправо от
точки b соответствует прибавление к числу b положительного
числа (рис. 12).
-4-
ь
Рис. 12
76
Значит, а = Ы-с, где с — положительное число. Отсюда сле-
дует, что а—Ь=с. Итак, если а больше &, то разность а—Ъ
есть число положительное.
Допустим теперь обратное: разность а—b равна положи-
тельному числу с. Какое из чисел больше: а или Ъ? Так как
а—Ъ=с, то а = Ъ-{-с. Но прибавление к Ь положительного числа
соответствует передвижению от точки с координатой Ъ вправо
по числовой прямой.
Значит, точка с координатой а лежит правее точки с коор-
динатой Ь, т. е. а больше Ъ.
Аналогично можно показать, что если а меньше Ь, то раз-
ность а—b отрицательна, и, наоборот, если разность а—b от-
рицательна, то а меньше Ъ.
Итак, справедлива теорема:
а >» Ъ тогда и только тогда, когда разность а — Ъ положительна;
a <Z Ъ тогда и только тогда, когда разность а —Ъ отрицательна.
Очевидно, что а = Ъ в том и только в том случае, если раз-
ность а—Ъ равна нулю.
Замечание. а^Ь (а не меньше Ь, т. е. а больше Ъ или
а равно Ь) тогда и только тогда, когда разность а—Ъ равна по-
ложительному числу или нулю (неотрицательна).
а^Ъ (а не больше Ь, т. е. а меньше b или а равно Ъ) тогда
и только тогда, когда разность а—Ъ равна отрицательному
числу или нулю (неположительна).
Неравенства, составленные с помощью знаков > или <,
называют строгими*, неравенства, составленные с помощью
знаков или называют нестрогими.
Покажем, как сформулированную выше теорему можно ис-
пользовать при решении задач.
1. Сравнить числа и 0,33.
Нам известны различные способы сравнения дробей. Рас-
смотрим еще один. Вычислим разность дробей:
1 _ о зз — £ _ 33 _ 100 ~ " 1
3 ’ ~ 3 100 “ 300 “ 300*
Так как разность чисели 0,33 положительна, то —
0,33, т. е. неравенство i
больше
0,33 верно.
2. Доказать, что при любом значении переменной а верно,
неравенство
с2+7а— 34 <а(а+7).
77
Составим разность левой и правой частей неравенства и
преобразуем ее:
а2 4- 7 а—34 — а(а+7) = а2 + 7 а —34 —а2 —7а = —34.
При любом значении а эта разность отрицательна. Следова-
тельно, при любом значении а верно неравенство
а2+7а—34 <а(а+7).
3. Доказать, что при любом значении переменной Ъ верно
неравенство
Ь(&—1)>&—1.
Как и в предыдущем случае, составим разность левой и пра-
вой частей неравенства и преобразуем ее:
&(&—!)— (&—!)=(& — 1)(&—1) =(Ь—I)2.
Преобразовав разность, мы получили не число, как в при-
мере 2, а выражение с переменной Ъ. Особенность этого выраже-
ния состоит в том, что при любом значении b его значение не-
отрицательно: при Ъ—1 оно равно нулю, а при Ъ^=1—положи-
тельно. Значит, при любых значениях Ъ рассматриваемая раз-
ность неотрицательна (положительна или равна нулю). Отсюда
можно сделать вывод, что при любых значениях Ъ верно нера-
венство, причем Ь(Ъ—1) — Ъ—1 при &=1 и &(&— 1) > Ь—1 при
&^1.
293. Верно ли неравенство:
а) _ 5 < 0; г) 15 < 15; ж) < 0,35;
б) — < —; д)0< —1; з)—— 0,075?
в) -7>-11; е)^->0,17;
294. Поставьте знак >, < или так,
высказывание было истинным:
чтобы получившееся
б) -3-.х,-у;
' 7 7
в) 0,04 . . . —;
53
г) 3,0001 . . . 3,001;
д) —0,0018. . .—0,0016;
е) — — ... - 0,925«.
7 625
295. Сравните числа а и &, если разность а—Ъ равна:
а) -2,7; б) 8; в) •; г) (-1)”; д) 5~2.
78
296. Пусть а, b и с — некоторые числа. Сравните числа а и Ъ9
если разность а—Ь равна:
a) kl;
б) —с2;
д) с2 + 1;
е) —5—с2.
297. Известно, что а<Ъ. Может ли разность а—Ь выражаться
числом 3,7; —5; (—0,1)5; |— 0,71; 2~7; — |—3|?
298. Как расположены на числовой прямой точки, изображаю-
щие числа а и Ь, если известно, что:
а) а—Ь — —7; в) Ъ—а = —1,3;
б) а—&=30,6; г) b—а=0?
299. Объясните, почему можно утверждать, что неравенство
верно при всех значениях переменной:
а) х2+5> 0;
б) 14-а2 > 0;
в) (о—3)2^0;
г) — р2—2<0.
300. Существует ли
такое значение х, при котором неверно
неравенство:
а) 2х2+7>0;
б) х2 > 0;
в) Зх-|-1 < х4-1;
г) (х—4)2>0?
301. Докажите, что при любом значении а верно неравенство:
а) 3(о4-1)4-а-4 (24-о)<0;
б) (а— 2)2— а (о—4)>0.
302. Докажите, что при любом значении т верно неравенство:
а) тп24-15тп4-56 >т (т4-15);
б) (7т— 1) (7m 4-1) <49or;
в) (2m 4-3) (2m 4-1) >4m (т4-2);
г) 3m (т4-6) < (3m 4-6) (т4-4).
303. Докажите, что при любых значениях переменных верно
неравенство:
а) а (а4-Ь)>аЬ; в) 2Ьс<Ь24-с2;
б) т2—тгг\-п2^тгг, г) а (о—Ь)>5 (о—Ъ).
304. Докажите, что при любом значении переменной а верно
неравенство
2
79
305. Сравните сумму квадратов двух неравных чисел а и b
с их удвоенным произведением
306. К каждому из чисел 0, 1, 2, 3 прибавили одно и то же
число k. Сравните произведение крайних членов получив-
шейся последовательности с произведением средних ее
членов.
19. Свойства неравенств
Рассмотрим некоторые свойства неравенств.
1. Если а>Ь, тоb <Z а, и, наоборот, если a. <Zb, тоЪ > а.
Геометрически это очевидно: если точка с координатой а
лежит на числовой прямой правее точки с координатой Ь, то
точка с координатой Ъ лежит левее точки с координатой а, и
наоборот (рис. 13).
Ь
а а Ь
Рис. 13
2. Если а>Ьи Ь> с, то а> с.
В самом деле, если точка с
точки с координатой Ь, а точка
точки с координатой с, то точка
точки с координатой с (рис. 14).
координатой а лежит правее
с координатой Ъ лежит правее
с координатой а лежит правее
С
Ь а
Рис. 14
Эго свойство неравенств называют транзитивностью со-
отношения неравенства.
3. Каково бы ни было число с, если а> Ъ, то а + О Ь -f- с.
На числовой прямей хорошо видно, что это свойство спра-
ведливо для положительного с (рис. 15) и для отрицательною с
(рис. 16), для с = 0 оно очевидно.
G+C
Рис. 15
Ь + с
b
а + с
Рис. 18
а
Докажем это свойство, не обращаясь к числовой прямой.
Рассмотрим разность
(а с)—(&4с)=а—&.
Так как а>Ь, то разность а—Ъ положительна, значит, и
разность (а 4 с)—(&+с) положительна. Следовательно,
а4с>6 с.
Итак, если к обеим частям верного неравенства прибавить
одно и то же число, то получится верное неравенство.
Используя это свойство, получаем, что если а-\-Ъ>с, то
а 4 Ь+(—&)> с -(—6), т. е. а>с—Ъ.
Если из одной части верного неравенства перенести в другую
какое-либо слагаемое, изменив его знак на противоположный,
то получится верное неравенство.
4. Каково бы ни было положительное число с, если а>Ь, то
ас>Ьс. Каково бы ни было отрицательное число с, если а~>Ь,
то ас<.Ьс.
Для доказательства преобразуем разность ас—Ъс в произ-
ведение:
ас—Ъс с (а—&).
Так как а > Ъ, то а Ъ — положительное число. При поло-
жительном с произведение с {а—Ъ) положительно, а следова-
тельно, положительна и разность ас—Ъс, т. е. ас >Ъс. При отри
цательном с произведение с (а—&) отрицательно, а значит, от-
рицательна и разность ас — Ъс, т. е. ас < Ъс.
Итак, если обе части верного неравенства умножить на одно
и то же положительное число, то получится верное неравенство.
Если обе части верного неравенства умножить на одно и то
же отрицательное число и заменить знак неравенства на проти-
воположный, то получится верное неравенство.
При с - —1 полу-гаем, что если а >Ь, то а (— 1) <& (—1), т. е.
—а<—Ъ.
Если у обеих частей верного неравенства изменить знак на
противоположный и знак неравенства также изменить на про-
тивоположный, то получится верное неравенство.
Например, из верного неравенства —103 <—87 получаем
верное неравенство 103 >87.
Так как деление можно заменить умножением на число,
обратное делителю, то очевидно, что если обе части верного
81
неравенства разделить на одно и то же положительное число,
то получится верное неравенство, а если разделить на отрица-
тельное число и поменять знак неравенства на противополож-
ный, то также получится верное неравенство.
Например, разделив обе части неравенства 120 >80 на 10,
получим верное неравенство 12 >8. Разделив обе части неравен-
ства 120 >80 на —40 и поменяв знак неравенства на противо-
положный, также получим верное неравенство —3 <—2.
307. Запишите верное неравенство, которое получится, если
к обеим частям неравенства 18 >—7 прибавить по:
а) —5; б) 2,7; в) —18; г) 7.
308. Запишите верное неравенство, которое получится, если
обе части неравенства —9 < 21 умножить на:
309. Запишите верное неравенство, которое получится, если
из обеих частей неравенства 5 >—3 вычесть по:
а) 2; 6)12; в)-5; г) f-AV.
310. Запишите верное неравенство, которое получится, если
обе части неравенства —15 <—3 разделить на:
а) 3; 6) -3; в) -1; г) -1.
311. Покажите на числовой прямой, что если а <Ъ, то —а >—Ъ.
Рассмотрите случаи, когда числа а и Ь оба положительны;
оба отрицательны; b положительно и а отрицательно;
а=0 и Ъ положительно; а отрицательно и Ъ=0.
312. Каков знак числа а, если:
а) 5а<2а;
б) 7а>3а;
в) —За<8а;
г) —12а > —2а;
д) 7а=2а;
е) —а>3;
ж) —а <—0,01?
313. Известно, что а> Ь. Объясните, на основании каких свойств
неравенств можно утверждать, что верно неравенство:
а) — 7а<— 7Ь; г) 0,01а—0,7 >0,016—0,7;
6) Д)1-а<1-6;
о о
в) 2а +11 > 2Ь +11; е) 2 — - < 2 — Д.
2 2
82
314. Докажите, что:
1) если а^Ъ, то Ъ^а\
2) если а^.Ъ и Ь^с, то а^.с\
3) если а^Ь и с—произвольное число, то аЧ-с^&Н-с;
4) если а^Ь и с — положительное число, то ас^Ъс.
5) если а<& и с—отрицательное число, то ас^Ьс.
315. Какие из неравенств верны при любых значениях перемен-
ной х:
а) х (х + 5) > 5х—3; в) Зх (х + 1) >3х2;
б) х (х — 2) > —2х — 4; г) (1 + х)2 4х?
316. Известно, что а<Ъ. Сравните полусумму чисел а и Ъ с
числом а; с числом Ь,
3
317. а) Как изменится дробь у, если к ее числителю и знаме-
нателю прибавить одно и то же положительное число?
13
б) Как изменится дробь —, если к ее числителю и зна-
4
менателю прибавить одно и то же положительное число?
318. Докажите, что с + — ^2 при с > 0. Сформулируйте свой-
с
ство суммы двух взаимно обратных положительных чисел.
Проиллюстрируйте его числовыми примерами.
319. Докажите, что верно неравенство:
а) 9а 4- — > 6 при а > 0; в) & 4~ 2 i при k < 0;
a k
б) 25а < Ю при а < 0; г) — + — — 2 при х < 0.
а 5 х
20. Понятие логического следования
Рассмотрим два предложения с переменной а:
«сумма цифр числа а делится на 9» и «число а кратно 3».
Каждое из них при одних значениях а обращается в истин-
ное высказывание, а при других — в ложное. Например,
при а=39 первое предложение выражает ложь, а второе —
истину; при а = 72 каждое из предложений истинно; при а=67
оба предложения ложны.
Из свойств делимости чисел вытекает: если при некотором
значении а первое из предложений истинно, то истинно и вто-
рое. В таких случаях говорят, что второе предложение следует
из первого. Эту мысль записывают с помощью знака логическо-
го следования г=>:
(сумма цифр числа а делится на 9) с=ф (число а кратно 3).
83
Приведенную запись можно прочитать по-разному, напри-
мер:
а) если сумма цифр числа а делится на 9, то число а крат-
но 3;
б) из того, что сумма цифр числа а делится на 9, следует,
что число а кратно 3.
Эту запись можно прочитать также, используя понятия необходимое усло-
вие и достаточное условие;
в) условие, <jto сумма цифр числа а делится на 9, достаточно для того, чтобы
число а было кратно 3;
г) условие, что число а кратно 3, необходимо для того, чтобы сумма цифр числа а
делилась на 9.
Из предложения «число а кратно 3» не следует предложе-
ние «сумма цифр числа а делится на 9», В самом деле, можно
указать такое значение а, например 12, при котором предложе-
ние «число а кратно 3» обращается в истинное высказывание, а
предложение «сумма цифр числа а делится на 9» — в ложное.
Приведем еще примеры следования одного предложения из
другого.
Пример 1. Каждое из уравнений
х2—8х = 0 и (х2—8х) (х+5) = О
представляет собой предложение с переменной х. Из первого
предложения следует второе:
(х2—8х = 0) :=> ((х2—8х) (х+5) = 0).
В самом деле, если при некотором значении х множитель
х2—8х равен нулю, то и произведение (х2—8х) (х+5) равно
нулю. Значит, если при некотором значении х первое уравнение
обращается в истинное высказывание, т. е. в верное равенство,
то и второе обращается в истинное высказывание.
Пример 2. Неравенства
У >8 и у >4
представляют собой предложения с переменной у. Из первого
неравенства следует второе:
(у>8)==>(у>4).
В самом деле, каждое значение у, обращающее в истинное
высказывание (в верное числовое неравенство) предложение
у >8, обращает в истинное высказывание и предложение у >4.
Пример
ство х>0,2:
3. Из неравенства 17х>3,4 следует неравен-
(17х > 3,4) (х > 0,2).
Р4
Действительно, если обе части верного неравенства разде-
лить на одно и то же положительное число, то получится вер-
ное неравенство. Значит, если при некотором значении х не-
равенство 17х > 3,4 обращается в истинное высказывание, то и
неравенство х > 0,2 обращается в истинное высказывание.
320. Прочитайте запись:
a) (Z.A и Z_B—вертикальные углы) (Z.A ZB);
б) (Z_A, Z_B, Z-C —углы треугольника) (А+В+С —
= 180);
в) ([АС] и [ВВ]—диагонали прямоугольника) =$>(|АС| =а
= !ВВ|);
г) ([АС] и [BJD] — диагонали ромба) t=>((AC) | (BZ>)).
321. Докажите, что из предложения «число а кратно 5» следует
предложение «сумма а 4-15 кратна 5». Запишите вывод,
пользуясь знаком логического следования.
322. Докажите, что:
а) из того, что \а | >3, не следует, что а > 3;
б) из того, что а2 = 16, не следует, что а =4.
323. Приведите пример предложения, которое следует из пред-
ложения «четырехугольник ABCD — квадрат».
324. Следует ли второе уравнение из первого:
а) Зх = 12, х=4; в) x4-v = 12, 5х4-5у=60;
б) 5х—17=0, 5х=17; г) 14х4-7у=4,9, 2х4~у=0,7?
325. Следует ли второе неравенство из первого (при положи-
тельном ответе используйте в записи знак логического
следования):
а) а >12, а >5; в) а>3, а >6; д) а <4, |а| <12;
б) & <17, b <2; г) Ъ<— 4, & <—1; е) |&| <8, &<8?
326. Среди данных неравенств укажите такое, из которого сле-
дуют все остальные:
а)!х>9, х>4, х>1, х>11;
б)|у<10, у <5, у <2, у <12;
в) х >1—, х^ 1,2, х> 1 х>1;
г) а <—2,5, а<—3,5, а <—3, а<— 2.
327. Докажите, что второе
а) Зх>24, х>8;
б) —7х <—28, х >4;
неравенство следует из первого;
в) 5х—1 >0, 5х >1;
г) 4х—3 <5, 4х <8.
85
328. Следует ли первое предложение из второго, следует ли
второе предложение из первого:
а) число а кратно 8; число а четное;
6) число т меньше 1; число т отрицательное;
в) 1,3 (х—1)=0; х—1=0;
г) &>12; &<5?
329. Прочитайте запись, пользуясь словаму! «если ..., то ...».
Докажите:
а) (а и Ъ — положительные числа и а >> d)t=> f — < — У
\ а b )
б) (а и Ъ — положительные числа и a <z b)=$>( — > —У
\ a Ъ J
330. Докажите, что:
а) (а >5) (5а—4 >55 — 4);
6) (а>5)=> (—6а+2 < —65 + 2).
331. Следует лн второе предложение из первого:
a)iTlL2SgO; х —12 = 0; в) -—?<0; 2х — 5<0;
30 4
6 ) х" - 4 = 0;-—S=0; г) 35 —ж>0; —— >0?
7 17 10
332. Приведите пример уравнения, которое следует из уравне-
ния —5х= —12. Приведите пример неравенства, ко-
торое следует из неравенства —13х<—26.
21. Равносильные предложения
Г
Рассмотрим два предложения:
«Ь— положительное число» и «—Ъ — отрицательное число».
Из первого предложения следует второе и, наоборот, из второго
предложения следует первое:
(д — положительное число) =>(—Ь — отрицательное число);
(—Ъ — отрицательное число) =>(Ь — положительное число).
Если из первого предложения следует второе и из второго
следует первое, то эти предложения называются равносильными.
Предложения «Ь — положительное число» и ♦—b — отрица-
тельное число» равносильны. Эту мысль записывают с помощью
знака
(Ь — положительное число) Ф=> (—Ъ — отрицательное число).
Приведенную запись можно прочитать по-разному:
а) если Ь — положительное число, то —Ъ — отрицательное
число, и, наоборот, если —Ъ — отрицательное число, то & —
положительное число;
б) предложение — положительное число» равносильно пред-
ложению <—b — отрицательное число»;
R6
в) —Ъ является отрицательным числом тогда и только тогда,
когда b — положительное число;
г) для то^о чтобы число Ь было ’положительным, необходимо и достаточно,
чтобы число — Ь было отрицательным.
Предложения «сумма цифр числа а делится на 9» и «число а
кратно 3» не являются равносильными, так как из второго пред-
ложения не следует первое.
Приведем примеры равносильных предложений.
Пример 1. Уравнения 27х=0,81 и х=О,ОЗ, представляю-
щие собой предложения с переменной х, равносильны:
(27х=0,81) <=> (х=0,03).
Докажем это. Если обе части верного равенства разделить на
одно и то же число, то получится верное равенство. Значит,
если при некотором х первое уравнение обращается в верное
равенство, то и второе обращается в верное равенство, т. е.
из первого уравнения следует второе. Если обе части верного
равенства умножить на одно и то же число, то получится вер-
ное равенство, поэтому из второго уравнения следует первое.
Пример 2. Неравенства 12х—25 <0 и 12х<25 представ-
ляют собой предложения с переменной х.
Если из одной части верного неравенства перенести слагае-
мое с противоположным знаком в другую часть, то получится
верное неравенство. Значит, из первого неравенства следует
второе и из второго — первое, т. е. рассматриваемые неравен-
ства равносильны:
(12х—25 <0)<=>(12х <25).
Нам известно, что значение переменной, обращающее урав-
нение (неравенство) с одной переменной в истинное высказыва-
ние, называется его решением. Очевидно, что из одного уравне-
ния следует другое, если каждое решение первого является ре-
шением второго. Аналогично из одного неравенства следует
другое, если каждое решение первого является решением вто-
рого. Подобным же образом формулируется условие следования
для уравнений (неравенств) с двумя переменными и для систем
уравнений (неравенств).
Нетрудно понять, что равносильны те и только те уравнения
или неравенства^ множества решений которых совпадают.
Замечание. Уравнения или неравенства, содержащие
одни и те же переменные и не имеющие решений, также счита-
ются равносильными.
333. Прочитайте запись:
а) (а >&)<=> (а—Ъ — положительное число);
б) (а <&)«=> (а—Ь — отрицательное число);
87
в) (ab — О) <=> (а = О или Ь — О);
г) ; - = О; <=>(с - О и Ь^О).
834. Докажите, что предложения х=3 и |х| = 3 не являются
равносил ьными.
335. Докажите, что если число а четное, то число а 4-1 нечет-
ное, и, наоборот, если число а + 1 нечетное, то число а
четное. Запишите вывод, пользуясь знаком равносильно-
сти.
836. Равносильны ли предложения:
а) а и Ь —четные числа, сумма а-\-Ъ —четное число;
б) число а кратно 3, сумма а +6 кратна 3;
в) натуральное число а оканчивается цифрой 0; нату-
ральное число а кратно 10?
837. Равносильны ли уравнения:
а) 8х - 24 и (х—3)(х—15) = О; в) 2х—7=0 и |х-=^7 = 0;
б) 10х=50и (х2+1)(х—5) 0; г) х2—16-0 и ^^-0?
х — 4
838. Составьте уравнение, равносильное данному:
а) 2x4-3 =5; б) Зу —1=8.
839. Докажите, что равносильны неравенства:
а) 26х >52 и х>2; в) 2х4-16<0 и 2х<—16;
б) х—14 >0 и х>14; г) — Зх <3 и х>—1.
340. Составьте неравенство, равносильное данному:
а) 14х <28; б) х > 3.
§ 8. НЕРАВЕНСТВА С ОДНОЙ ПЕРЕМЕННОЙ
22. Графическое решение неравенств с одной переменной
Пусть требуется решить неравенство 0,5х—1,5>0, т. е. най-
ти множество значений переменной х, при которых это неравен-
ство верно. Сделаем это с помощью графика функции у - 0,5х —
—1,5 (рис. 17). Мы видим, что график расположен выше оси х
при значениях х, принадлежащих промежутку ]3; 4-°°[. Зна-
чит, при указанных значениях х, и только при них, значение
выражения 0,5х—1,5 положительно, т. е. неравенство 0,5х—
—1,5 > 0 обращается в верное числовое неравенство. Числовой
промежуток J3; 4-°°[ — множество решений неравенства 0,5х—
- 1.5 > 0.
88
На рисунке 18 построен график функции y—f (х). С помощью
графика можно решить неравенство f (х) <0. Из рисунка видно,
что график расположен ниже оси х при значениях х. принадле-
жащих промежутку ]—8; 2| или промежутку J6; Ч- оо[. Значит,
множество решений неравенства
/(х)<0 есть объединение двух
множеств: ]- 8; 2[ (J ]6; -|-ос[.
Рассмотрим еще пример.
Пусть требуется решить нера-
венство х2 >2х. Для этого по-
строим в одной системе коор-
динат графики функций у=х2 и
у=2х (рис 19). Неравенство
х2 >2х верно при тех и только
тех значениях х, при которых
график функции у~х2 располо-
жен выше графика функции
у = 2х, т. е. при значениях х,
принадлежащих множеству
]— оо; О Г или множеству ]2; + ос [.
Множество решений неравенст-
ва х2 > 2х: ]— со; 0[ (J ]2; F °°[-
80
Рис. 20
341. Решите графически неравенство:
а) х — 2 < 0; б) 7 — 2х > 0.
342. На рисунке 20 построен график функции у = g (х).
С помощью графика решите уравнение g(x)=0 и неравен-
ство g (х) > 0.
343. В одной системе координат построены графики функций
12
У = — и у = х + 1 (рис. 21). Найдите с помощью графиков,
при каких значениях х обращается в истинное высказы-
вание предложение:
90
344. Решите графически уравнение х2=4 и неравенства х2 <4;
х2 >4.
345. Покажите с помощью графиков, что неравенство х2 >х—1
верно при любом значении х.
346. Покажите с помощью графиков, что множество решений
неравенства х2 <х—2 пусто.
23. Решение линейных неравенств с одной переменной
Рассмотрим решение неравенств вида ах-\-Ъ >0 или ax-f-b <0,
где а и b — некоторые числа. Такие неравенства называются
линейными.
Начнем с примера. Решим неравенство
12 — Зх > 0. (1)
Нам известно, что если из одной части верного неравенства
перенести слагаемое в другую часть с противоположным зна-
ком, то получится верное неравенство. Поэтому из неравенства
(1) следует неравенство
—Зх > —12. (2)
Если обе части верного неравенства разделить на одно и то
же отрицательное число и поменять знак неравенства на проти-
воположный, то получится верное неравенство. Значит, из
неравенства (2) следует неравенство
х < 4. (3)
Из свойств неравенств вытекает справедливость обратного:
из неравенства (3) следует неравенство (2), а из неравенства (2)
следует неравенство (1).
Итак, мы можем сделать вывод, что
(12—Зх >0)=ф(х <4)
и (х<4)=>(12—Зх>0),
т. е. что неравенства (1) и (3) равносильны:
(12—Зх >0) <=> (х <4).
Множество решений неравенства х<4, а значит, и равно-
сильного ему неравенства 12—Зх>0 есть числовой промежуток
] — оо; 4[ (рис. 22).
ШШШШ ... » .
4
Рис. 22
91
Таким образом, решая неравенство вида ах 4* b >0 или ах 4>
-£&<0 при а=/=0, мы находим равносильное ему простейшее не-
равенство вида х >с или х <с (с — некоторое число), множество
решений которого очевидно.
Приведем еще пример решения линейных неравенств.
Пример 1. Решить неравенство 4 (6—х)^3 (х—13).
24— 4х<3х—39,
—4х—Зх<—39—24,
—7х<—63,
х>9.
Ответ: [9; 4- оо[.
Множество решений неравенства показано на числовой пря-
мой на рисунке 23.
9
Рис. 23
При решении линейных неравенств могут представиться
особые случаи, когда множество решений неравенства пусто или
когда решением неравенства служит любое_число. Рассмотрим
примеры.
Пример 2. Решить неравенство 2 (х+8)—5х <4—Зх.
2x4-16—5х <4—Зх,
2х—5х4-3х<—12,
О х < —12.
Неравенство О х < —12 не имеет решений, так как ни при i
каких значениях х оно не обращается в верное числовое нера-
венство. Значит, и неравенство 2 (х-f-8)—5х<4—Зх не имеет
решений, т. е. множество его решений пусто.
Ответ: 0.
Пример 3. Решить неравенство 5 (х—12) <12_(х—1)—7х.
5х—60 <12х—12—7х,
5х—12х+7х <—124-60,
, О х <48.
Неравенство 0-х <48 верно при любом значении х. Значит,
и неравенство 5(х—12) <12(х—1)—7х верно при любом значении *
х, т. е. множеством его решений служит вся числовая прямая.
Ответ: ] — оо; 4-°°[.
92
347. Найдите множество решений неравенства и покажите его
на числовой прямой:
а) х<3; б) х>5; в) г) xj>—1.
348. Найдите множество решений неравенства 5x41 >11. На-
зовите несколько значений переменной х, принадлежа-
щих этому множеству.
349. Решите неравенство Зх—2 <6. Принадлежит ли множест-
а 4
ву решений неравенства число 4; 2—; 2у?
350. Решите неравенство и покажите на числовой прямой мно-
жество его решений:
а) 12х>18; д) 7х—24 <4; ] jn) 0>124-5х;
б) 6х<15; е) 18— 5х<12; к) 17— х>6— 6х;
в) —Зх<108; ж) 14^6—х; л) 12х4 0,5^13х—1;
г) —5х>6,4; з) 17<3±4х; м) 8х>5+12х.
351. Решите неравенство:
а) 5(х—1)4-7<1— 3(х + 2); г) 1,7— 3(1— т) <—(т—1,9);
б) 4 (а4 8)—7(а—1) <12; д) а(а— 4)— а2 >12— 6а;
в) 4 (&—1,5)—1,2 >6&— 1; е) (2х—1) 2х—5х<4х2—х;
ж) (а—I)2—(а—7)(а—3)<2а-|-0,8;
з) (Зх—I)2— Зх(1,2Н-Зх)>8х+177.
352. Решите неравенство:
б)
В)
2 Зх
18
12—5х
42
З^х
4
0;
0;
г) i—5х>0;
5
д)
2х —1
х — 3
5
х-1-3
2 —х
3
X —
353. При каких значениях у:
а) значения дроби
дроби
Зу-7.
б) значения
дроби
-—— больше соответствующих значений
6
4,5~_jy меньше соответствующих значе-
5
ний дроби
3 — Зуу
10
93
354. Найдите, при каких значениях х значения функции f по-
ложительны (ответ проверьте графически):
a) f (х)=3х—6; б) f (х) = —2х—5.
355. Найдиге, при каких значениях х значения функции f
отрицательны (ответ проверьте графически):
a) f (х)=х—8; б) f (х) = 3 — 1,5х.
356. Постройте график функции у = | х 4- 2 и найдите, при
каких значениях х значения функции больше 4. Проверь-
те ответ, решив соответствующее неравенство алгебраи-
чески.
357. Найдите множество значений переменной х, при которых
значения функции, заданной формулой у = —х4-2, боль-
ше —3. Ответ проверьте графически.
358. Пользуясь графиками функций у=х+1 и z/=O,5x 4-2
(рис. 24), найдите, при каких значениях х верно неравен-
ство х+1>0,5х+2. Проверьте правильность ответа, ре-
шив это неравенство алгебраически.
359. Найдите множество решений неравенства:
а) 15 (х+4) — 5х<10х; в) 3x4-7 > (х+2)+(2x4-1);
б) 31 (2x4-1)— 12х>50х; г) 12х—1 < 3 (4х—3).
360. При каких значениях х значение дроби больше
соответствующего значения дроби х- —-? Ответ проил-
2
v 2х 1 3
люстрируйте с помощью графиков функций у =---------— и
361. Найдите наибольшее целое число, удовлетворяющее не-
равенству
1,6—(3,2—0,2i/) <5,1.
362. Найдите наименьшее целое число, удовлетворяющее не-
равенству
1 8 (0,6—i/) <24,2—71/.
363. При каких натуральных значениях п разность
(2—1,2и) —(0,5п —6,5) положительна?
364. При каких натуральных значениях п сумма
( —27,1 + Зп) 4-(7,14-5 и) отрицательна?
365. При каких положительных значениях х верно нера-
венство
0,75—х<1,5—0,5х?
366. Найдите множество отрицательных значений у, удовлетво-
ряющих неравенству
1,2(17-5) <0,5z/4-0,l.
367. Выделите из числового промежутка ]—1; 5[ подмножест-
во значений переменной х, при которых значения выра-
жения х—4 меньше соответствующих значений выраже-
ния 2—2х.
368. Выделите из числового промежутка [ —1; 6] подмножество
значений переменной х, при которых значения выраже-
ния 124-Зх больше соответствующих значений выражения
32—2х.
369. При каких значениях а верно равенство:
а) |а|=а; в) |а—2|=а—2; д) |3а—1[=3а—1;
б) |а| = —а; г) \а—5|=5—а; е) |2а4-5| = —2а—5?
370. Сторона прямоугольника 6 см. Какой должна быть другая
сторона, чтобы периметр прямоугольника был меньше
периметра квадрата со стороной 4 см?
95
371. Длина прямоугольного параллелепипеда 12 дм, ширина
5 дм. Какой должна быть высота параллелепипеда, чтобы
его объем был меньше объема куба с ребром 9 дм1
372. На соревнованиях каждый стрелок делал 10 выстрелов.
За каждое попадание он получал 5 очков, а за каждый
промах снималось 1 очко. Победителем считался тот, кто
наберет не меньше 30 очков. Сколько раз стрелок должен
был попасть в мишень, чтобы оказаться в числе победите-
лей?
373. Туристы отправились на моторной лодке по течению реки
и должны возвратиться обратно к стоянке. Скорость тече-
ния реки 2 км ч, а собственная скорость лодки 18 км. ч.
На какое расстояние могут отъехать туристы, чтобы про-
гулка продолжалась не более 3 ч?
§ 9. СИСТЕМЫ НЕРАВЕНСТВ С ОДНОЙ ПЕРЕМЕННОЙ
24. Решение систем линейных неравенств с одной переменной
Рис. 25
На рисунке 25 построены графики функций у=х4-1 и
у =—2х .-8. С помощью графиков нетрудно решить задачу:
♦Найти множество значений переменной х, при которых обе
функции принимают положительные значения».
Искомое множество — число-
вой промежуток ]—1; 4[.
Решим ту же задачу, не
обращаясь к графикам. Най-
дем множество значений х,
при которых верно как не-
равенство х 1 > 0, так и не-
равенство —2х+8>0, т. е. най-
дем множество общих реше-
ний этих неравенств.
Если стави гея задача найти
множество общих решений двух
или нескольких неравенс гв,
то говорят, что надо решить
систему неравенств.
Значение переменной, гри
котором каждое из нера-
венств системы обращается в
верное числовое неравенство,
называется решением системы..
Множество решений систе-
мы есть пересечение множеств
решений входящих в нее нера-
венств.
96
__________--......................'т ' ___J
4
Рис. 26
Итак, надо решить систему неравенств
jx + 1 >0, (1)
[—2х 4> 8 > 0.
Заменив каждое неравенство простейшим, ему равносиль-
ным, получим систему, равносильную данной:
(X > -1, (2)
(х < 4.
Множество решений неравенства х > —1 — числовой проме-
жуток ]—1; +°о[, неравенства х < 4 — числовой промежуток
]—оо; 4[. С помощью числовой прямой найдем пересечение
этих множеств (рис. 26). Получаем, что числовой промежуток
]—1; 4[ — множество решений системы (2), а значит, и равно-
сильной ей системы (1).
Мы получили тот же ответ, что и при графическом способе
решения системы неравенств.
Приведем еще примеры решения систем линейных неравенств.
Пример 1. Решить систему неравенств;
(Зх >27,
(4 — х < 0.
Получаем:
13х > 27, [х > 9,
t—х < —4; [х > 4.
Множество решений неравенства х > 9 — числовой проме-
жуток J9; оо [, неравенства х > 4 — числовой промежуток
]4; -£оо[. Пользуясь числовой прямой, находим, что пересече-
нием этих множеств служит числовой промежуток ]9; -|гоо[
(рис. 27).
Ответ: ]9; + оо[.
Рис. 27
Пример 2. Решить систему неравенств:
7 > х,
2х — 1 < 0.
4 Алгебра, 7 кл.
97
МИНИН
2
Рис. 28
Получаем:
- 7\ (х 7,
12х<1; .1
I 2
Найдем пересечение множеств решений неравенств х 7
. 1
и —» т. е. найдем пересечение числовых промежутков
]—°о; 7] и ]—со; —] (рис. 28).
2
Числовой промежуток ]—со;
ной системы неравенств.
1.
2
]—множество решений задан-
Ответ: 1—со; —1.
2
Пример 3. Решить систему неравенств:
Получаем:
(2х — 9 < О,
(— Зх < —18.
х < 4,5,
х > 6.
Множество решений неравенства х <4,5 — числовой проме-
жуток ]—оо; 4,5[, а множество решений неравенства х>6—
числовой промежуток jG; 4~оо[. Пересечение этих множеств
пусто (рис. 29).
Ответ: 0.
4,5
Рис. 29
Пример 4. Решить двойное неравенство:
—1 <3— 2х< 3.
Данное двойное неравенство представляет собой иную
запись системы неравенств:
/3 — 2х > —1,
3 — 2х < 3.
98
Заменяя каждое из неравенств системы равносильным, получим:
(х < 2,
|х > 0.
Пересечение множеств решений неравенств х < 2 и х > 0 — чис-
ловой промежуток ]0; 2[.
Запись решения двойного неравенства можно вести иначе:
—1<3— 2х<3,
—4 < —2х < О,
2>х>0.
Ответ: ]0; 2[.
Пример 5. Решить систему неравенств:
Зх — 6 > О,
18 < 5х,
1,7х — 13,6 <0.
Получаем:
(Зх> 6,
х> 3,6,
1,7х<13,6;
х> 2,
х > 3,6,
х < 8.
Так как неравенство х >2 следует из неравенства х >3,6, то
решение полученной системы сводится к решению системы двух
неравенств:
(х > 3,6,
х < 8.
Числовой промежуток 33,6; 8[ — пересечение множеств реше-
ний неравенств х > 3,6 и х <8.
Ответ: ]3,6; 8[.
374. Решите систему неравенств:
а) х > 17, в) х >0,
х > 12; х<6;
б) |х<1, г) 1 х <—3,5,
х < 5; х >8;
е) |х>8,
х<20.
375. Найдите множество решений
системы неравенств:
2х—12> О,
Зх > 9;
4х<—4,
5—х> 0;
Зх—10 < О,
2х > 0;
/6х> 42,
4х4-12<0.
99
876. Найдите множество решений системы нераренств и ука-
жите несколько чисел, принадлежащих этому множеству:
а) (х—0,8 > О, в) (1 > Зх,
( —5х<10; ]5х—1 > 0;
6) |2-х<0, г) ,10х<2,
(ж— 4<0; (х>0,1.
377. Решите систему неравенств:
а) 5 (х—2)—х>2,
1-3 (х—1)<—2;
б) 2х—(х—4) < 6,
|ж>3 (2х—
в) 7х (3^ 5х—19,
14х+1 < 22—Зх;
г) .3(2- -Зх) —2 (3 —2х) >х,
6 <х2—х (х -8).
378. Найдите целые решения системы неравенств:
а) 1У> 0, в) (6—4&>0,
17,2—//>4; 36 1 > 0;
б) (12а— 37 > 0, г) (3— 18х<0,
(6а <42; |0,2—0,1х>0.
379. Объясните, почему данная система неравенств не имеет
решения:
а) х-]-7<х4-1, в) 1х—3>О,
2- х>0; |3—х>0;
б) Г(х—2)2<0, г) Г|х|<3,
(ж <1; [ж >12.
380. Найдите множество значений переменной а, удовлетворяю-
щих системе неравенств:
а) (2,5а— 0,5 (8—а) < а 4-1,6,
1,5(2а—1)— 2а < а 4-2,9;
б) 0,7(5а 4 1) —0,5 (14-а) < За,
(2а—(а—1,7) > 6,7.
381. Найдите целые решения системы неравенств:
а)
2х— -—i>"x,
3
X-1<3_L±J;
2
б)
-—'— -—->2х —1,
2 3
2х- —> х—3;
3
в) 17х—5 (х (0,6) < Зх,
2 (3,5—х) 4-5 (2х—2,4) >х—26;
г) х < 39 4-3,6(5х -1)—2 (2х—1,8),
(6х (2,5х— 1)— Зх > х (15х 4-2)—11.
100
382. а) На рисунке 30 построе-
ны графики функций
у-х\ 3 и у— 0,5г— {.Поль-
зуясь графикам и, найди-
те множество значений пе-
ременной х, при которых
обе функции приним ают
положительные значения.
Прове рьте правильное ть
ответ а. составив сист ему
неравенств и решив ее ал-
гебраически.
б) Составив систему нера-
венств, найдите, при каких
значениях переменной х
обе функции у ——х[6 и
у = 3х—9 принимают поло-
жительные значения. Про-
верьте правильность ответа с помощью графиков.
383. Решите двойное неравенство:
а) —3<2х- 1 <3;
б) —12 <5— х<12.
384. С помощью числовой прямой найдите множество решений
системы неравенств:
а) [3^х«^5,
[х<4,2;
б) J— 1<х<3,
|х>2,5.
385. Решите систему неравенств;
а)
х > 8,
х> 7,
х > —4;
б)
У < —1,
У < —5,
У <4;
В)
(т > 9,
т > 10,
\т < 12;
г)
7< 6,
Q< 5.
«>11.
386. Решите систему неравенств:
а)
х— I <8,
2x4 5 <13,
13—х >1;
в) (2х—1<хН 3,
5х—1 >6—2х,
1х—3 <0;
б)
(3 2ц < 7,
7у >7,
12у > 141,
1-УС1;
5х— 4 < 4х—2,
1—2х >2-4х,
Зх— 3 < 5х—5,
17х > 0.
387. а) Ня идите все двузначные числа, большие 40, но мень-
шие 80, у которых цифра единиц на 4 меньше цифры де-
сятков.
1<Ч
б) В двузначном числе цифра единиц на 1 меньше цифры
десятков. Если к этому числу прибавить 7, то полученная
сумма будет больше 19, но меньше 51. Найдите это дву-
значное число.
388. Если турист увеличит скорость на 1 км/ч, то за 4 ч он прой-
дет расстояние, большее 20 км. Если же он уменьшит
скорость на 1 км ч, то за 5 ч он пройдет расстояние, мень-
шее 20 км. Какова скорость туриста?
25. Примеры решения нелинейных неравенств
Решение некоторых нелинейных неравенств сводится к ре-
шению линейных неравенств и их систем. Приведем примеры.
Пример 1. Решить неравенство (х—2)(3—х) >0.
Значение произведения двух множителей положительно в
том и только в том случае, когда значения множителей одного
знака, т. е. оба положительны или оба отрицательны. Значит,
данное неравенство обретается в верное числовое неравенство
при тех и только тех значениях переменной х, которые удовлет-
воряют хотя бы одной из систем неравенств
х—2 >0,
3—х>0 или
х- 2 < 0,
3—х С 0.
Так как каждое решение первой системы является решени-
ем заданного неравенства и каждое решение второй является
решением заданного неравенства, причем других решений не-
равенство не имеет, то множество решений неравенства
(х — 2) (3—х)>0есть объединение множеств решений этих си-
стем неравенств.
Заменяя каждую систему неравенств равносильной, получим:
(х>2, |х <2,
‘х< 3 или > 3.
Множество решений первой системы — числовой промежуток
]2; 3[.
Множество решений второй системы пусто.
Множеством решений заданного неравенства служит объе-
динение числового промежутка ]2; 3[ и пустого множества, т. е.
числовой промежуток J2; 3[.
Ответ: ]2; 3 [.
На рисунке 31 построены графики функций у =х—2 и у 3—х.
Нетрудно заметить, что при значениях х, принадлежащих про-
102
межутку ]2; 32, и только при
этих значениях, функции
принимают значения одинако-
вого знака (обе положитель-
ны), а значит, положительно
и произведение (х—2)(3—х).
Пример 2. Решить не-
_____________з
равенство -__< 0.
Значение дроби отрица-
тельно, если числитель и зна-
менатель имеют значения
противоположных знаков.
Значит, данное неравенство
верно в том и только в том
случае, когда верна хотя бы
одна из систем неравенств
Рис. 31
2х 3>0,
1 —х < 0 пли
2х-3<0,
1—х>0.
Отсюда
х >1,5,
х>1 или
х< 1,5,
х<1.
Множество решений первой системы неравенства — число-
вой промежуток ]1,5; второй —числовой промежуток
]—оо; 1[. Множество решений заданного неравенства — объеди-
нение этих двух множеств.
Ответ: ] — оо; 1 [ IJ ] 1,5; + оо [.
Пример 3. Решить неравенство
— 4>о.
2 — х
Значение дроби положительно, если числитель и знамена-
тель имеют значения одинаковых знаков. Значение дроби равно
нулю, если числитель равен нулю, а знаменатель отличен от
нуля. Значит, данное неравенство верно при тех и только тех
значениях х, при которых верна хотя бы одна из систем нера-
венств
5х— 4>0,
2- г ^0
или
5х—4<0,
2—х<0.
Отсюда
х>0,8,
х< 2
или
хС0,8,
х>2.
юз
Множество решений первой системы — числовой промежуток
[9,8; 2[, множество решений второй систеьйд пусто. Объедине-
ние этих двух множеств — числовой промежуток [0,8; 2[.
Ответ: [0,8; 2[.
тт > . Ол. _
Пример 4. Решить неравенство ------------ > 3.
х — 2
Данное неравенство легко свести к неравенству такого вида, которь й рас-
смотрен в примере 2. Для этого перенесем 3 в левую часть неравенства и преобра-
зуем порученную разность в дробь:
Зх - 2
х —2
0,
— 3 >
Зх — 2 — Зх 6
“ -------7---- > 0
Так как числитель дроби положителен, то значение дроби будет положи-
тельно при положительных значениях знаменателя, т. е, тогда и только тогда,
когда верно неравен 'тво
х — 2 > 0.
Множество решений неравенства х — 2 > 0, а значит, и заданного нера-
венства — числовой промежуток ]2; + со[.
Ответ: ]2;
389. Найдите множество решений неравенства (х—2) (х—5) <0.
Укажите несколько значений переменной х, принадлежа-
щих этому множеству. Вычислите cool ветствующис им зна-
чения произведения (х—2) (х—5) и сравните их с нулем.
390. Найдите множество решений неравенства
(У -5) (2у—3)>0.
Прина алежит ли этому множеству число —8; 0; 1,5; 10;
1000?
391. При каких значениях переменной у:
а) значение произведший (у—1) (у—3) отрицательно;
б) значение произведения у (у—1) положительно?
392. Решите неравенство:
а) х(х—5)> 0; в) (2х—1) (х 1) > 0;
б) (х —1) (х—2) <0; г) (6-*-х)х<0.
393. Решите неравенство, разложив на множители многочлен,
записанный в левой част и:
а) о2 1 6а > 0; в) х2- 64 > 0;
б) Ьг-7,56 < 0; г) у2- 0,25 < 0.
104
394. При каких значениях у верно неравенство:
а) (у -8) (у2 +6) > 0: в) (у-2)2(у-3) > 0;
б) (12— Зу) (1 + 7у2) < 0; г) (у-2,7)(5-у)2 > 0?
395. а) При каких значениях переменной а дробь 8 поло-
fl -+-4
жител ьна?
__2 г
б) При каких значениях переменной b дробь --- отри-
15 — Ь
цательна0
396. При каких значениях переменной верно неравенство:
1
а) —>0; б)----------<0; в) —>0; г) <0?
х —7,2 5- а 5 — 37 у —13
397. Найдите множество решений неравенства
0.
X- 8
Укажите несколько значений переменной х, принадле-
жа щих этому множеству. Вычислите соответствующие им
значения дроби и сравните их с нулем.
398. Найдите множество решении неравенства
— < 0.
5х-|-10
Выбрав произвольное значение переменной х, не принад-
лежащее найденному множеству, покажите, что соответ-
ствующее ему значение дроби неотрицательно.
399, Решите неравенство:
а)---->0; б) --------<0; ь) — ->0; г) — <<0.
9 — х х Зх г 6 х—1
400. При каких значениях переменной х значения функции
у — х положительны; отрицательны?
401. Найдите целые решения неравенства:
V
в)-------------
5л — 11
. 3 — 2х \ л
Г) ------ , 0.
' 4х — 1
105
402. Найдите множество решений неравенства:
а) х2>0,7х; б) 2у<у2; в) х2<16; г) х2>25.
403. Решите неравенство сначала графически, а затем алгебра-
ически: /
а) х2>3х; б) х2<3х.
404. Решите неравенство:
а) — >0; г) —— >0; ж) ^±*<0;
1 + X X X
б)—<0; Д) -Ц<0; з)1=^>0.
х х — 2 х
в) —— < 0; е) -— > 0;
4х 1 —х
§ 10. ПРИМЕНЕНИЕ НЕРАВЕНСТВ К ОЦЕНКЕ ТОЧНОСТИ
ПРИБЛИЖЕННЫХ ВЫЧИСЛЕНИЙ
26. Точные и приближенные значения величин
В практической деятельности люди постоянно имеют дело
со значениями различных величин: длин, площадей, объемов,
масс, температур и др.
Истинное значение величины удается определить лишь в
некоторых случаях. Можно, например, точно указать число ваго-
нов железнодорожного состава, точно подсчитать, сколько уче-
ников находится одновременно в классе. Но в большинстве слу-
чаев приходится иметь дело лишь с приближенными значениями
величин.
Приближенные значения нередко получаются в результате
счета большого числа предметов. Лишь приблизительно оце-
нивают количество зрителей телепередачи, число перелетных
пгиц, число деревьев в лесу.
Приближенные значения получаются в результате измере-
ний. Невозможно, например, точно измерить длину стержня.
Ведь измерения мы ведем с помощью какого-либо прибора (ли-
нейки, штангенциркуля, микрометра, оптиметра* и др.), а точ-
• Оптиметр — оптико-мехяиичрский измерительный прибор.
106
ность измерения прибором всегда ограничена. Кроме того, из-
готовляя прибор в заводских условиях, гарантируют лишь ту
или иную степень точности его изготовления. Наконец, произво-
дя измерения, мы вносим ошибки, связанные с нашим опытом
работы и с нашими личными качествами.
Невозможно точно измерить площадь земельного участка,
температуру воздуха, скорость полета самолета и т. д.
Приближенные значения получаются при округлении истин-
ных значений величин. Так, число 2,19563 в расчете, не требую-
щем высокой точности, можно округлить, заменив его числом
2,196 или даже 2,20, которые являются приближенными зна-
чениями числа 2,19563 с избытком.
405. Укажите, какие числа являются точными значениями ве-
личин, а какие приближенными:
а) число жителей города составляет 7061 тыс. человек;
б) станок состоит из 82 деталей;
в) масса станка 1230 кг;
г) пассажирский самолет находился в полете 2 ч;
д) в самолете 86 пассажиров;
е) скорость звука 332 —;
сек
ж) отношение длины окружности к диаметру равно 3,14;
з) время конькобежца на дистанции 500 м, установленное
с помощью фотофиниша, равно 40,21 сек.
406. Округлите число до десятых и укажите характер получен-
ного приближения (является ли оно приближением дан-
ного числа с недостатком или с избытком):
а) 12,41; в) 3,45; д) 121,03;
б) 8,493; г) 11,75; е) 1,98.
407. Округлите до сотых число:
а) 6,113; в) 1,407; д) 2,5013;
б) 0,318; г) 10,275; е) 11,096.
408. Округлите число 1976,102 до сотых, до десятых, до еди-
ниц, до десятков, до сотен. Какие из полученных чисел
являются приближениями данного числа с недостатком?
409. Округлите число л = 3,11159... до десятитысячных, до
тысячных, до сотых. В каждом случае укажите характер
приближения.
107
Рис. 32
27. Границы значения
величины
Рассмотрим процесс опре-
деления массы детали с по-
мощью рычажных весов и на-
бора разновесков, наиболее
мелкий из которых имеет мас-
су 1 г.
С помощью ДВ5 х взвеши-
ваний установим, что масса
детали больше 20 г, но меньше
30 г (рис. 32, I, II). Обоз-
начим массу детали в грам-
мах через т, тогда резуль-
тат взвешивания можно за-
писать в виде двойного нера-
венства:
20 < тп < 30.
Заменив затем разновесок
в 10 г разно веском в 5 г, убе-
димся, что масса детали боль-
ше 25 г (рис. 32, III), т. е.
25 < т < 30.
Добавив на чашку весов с
разновесками разновесок в 2 г,
установим, что масса детали
меньше 27 г (рис. 32, IV):
25 <т < 27.
Заменив разновесок в 2 г
разновеском в 1 г, выясним,
что масса детали больше 26 г
(рис. 32, V):
26 < т < 27.
Так как более мелких
разновесков у нас нет, то
процесс определения массы на
этом этапе закончим.
В результате взвешивания
мы нашли приближенные зна-
чения массы детали в граммах:
26 — приближение с недостат-
ком, 27 — приближение с из-
бытком. Другими словами, мы установили границы значения
массы в граммах. Число 26 — нижняя граница, число 27 —
верхняя граница.
Заметим, что если бы наиболее мелким был разновесок в 2 г,
то границами значения массы детали в граммах были бы числа
25 и 27, т. е. масса была бы определена менее точно. Еще более
грубую оценку массы мы получили бы, ограничившись резуль-
татами 3-го или 2-го взвешивания (см. рис. 32).
Зная границы значения некоторой величины, можно оце-
нить значение другой величины, зависящей от первой. Пусть,
например, известны приближенные значения (в см) с недостат-
ком и с избытком длины а стороны равностороннего треуголь-
ника:
6,4 <а <5,5.
Нужно найти границы периметра Р.
Периметр равностороннего треугольника вычисляется по
формуле Р=3а. Из условия а ^>5,4 следует, что За ^>16,2; из
условия а<5,5 следует, что За<16,5. Числа 16,2 и 16,5—при-
ближенные значения периметра треугольника (в см) с недостат-
ком и с избытком:
16,2<Р<16,5.
Заметим, что запись решения можно вести с помощью двой-
ного неравенства:
5,4 <а <5,5,
6,4-3<3а<5,5 3, т. е.
16,2<Р<16,5.
Рассмотрим еще один пример. Пусть известны границы неко-
торого числа х:
m 1
Требуется оценить значение выражения — .
Из условия задачи следует, что х — число положительное.
Так как х>3. то — <— ; так как х<6, то
х 3
— > —. Значит,
х 6
6 х 3
„ 1
Заменим границы значения выражения — десятич ными дро-
х
бями. При этом число можно заменить только меньшим числом
(любым приближением с недостатком), а число — — только боль-
3
шим приближением с избытком). Так как
- = 0,166... и -1 =0,333...,
6 3
3Q9
—I 1 I I I I t *...1 t. | .1 .1..I-L.UI I I i |..l t I i i i I I |. I I 4-
₽» QJ Ц2 Ф ) Wt (Lr
6 1
Рис. 33
то в качестве границ значения выражения — можно взять деся-
X
тичные дроби ОД и 0,4:
0,1 < - < 0,4.
X
Заменив нижнюю границу числом 0,1, а верхнюю — числом
0,4, мы расширили промежуток, которому принадлежит значе-
ние выражения — (рис. -33). Если бы мы поступили иначе, округ-
X
лив бесконечные десятичные дроби 0,166... и 0,333... по извест-
ным правилам округления, то получили бы, что 0,2< — <0,3.
X
Но тогда неизвестное нам истинное значение выражения — мог-
X
ло оказаться за пределами полученных границ (см. рис. 33).
410. Укажите границы:
а) средней скорости пешехода;
б) роста учащегося вашего класса;
в) температуры воздуха в вашей области.
411. Можно ли из куска ткани длиной I м. где 2,6 •£^•£^2,8,
сшить платье, на которое при данной ширине требуется
не менее:
а) 2,4 м‘, б) 2,7 л; в) 2.9 м?
412. Можно ли из квадратной пластины со стороной а мм выре-
зать круг диаметром d мм, если:
а) 53<а<55; б) 53^а<55,
49<d<51; 52^d<54?
413. а) Найдите границы периметра квадрат л со стороной
а см, где 5,1 >а-<5,2.
б) Определите границы длины стороны квадрата, зная,
что периметр квадрата равен Р см, где 15,6 ' {Р s^15,8.
414. Дано, что 3^а^4. Оцените значение выражения:
а) 5 а; . 1 г) а; ' 5 ж) 5 — а; к) -. а
б) 0,3 а; Д) а + 2; з) 2а J-5;
в) - а; е) а —3; и) 0,1а 0,1;
но
415. Известно, что 8,4 <6 < 9,2.
Верно ли, что:
а) 8,1 < Ь < 9,4;
б) 8,6 < Ь < 9,3;
в) 8<Ь <9;
г) 7 <Ь < 10?
416. Пусть 11,39 <у <11,53. Укажите другие границы числа
у так, чтобы соответствующее двойное неравенство было
верным. Приведите несколько примеров.
417. Укажите два последовательных целых числа, две после-
дова гельные десятичные дроби с одним знаком после
запятой, две последовательные десятичные дроби с двумя
знаками после запятой, между которыми заключено число:
О
а) 18,243; 6)1-^; в) —0,591.
Ответы запишите в виде двойных неравенств.
418. Известно, что 7 <Ь < 8. Оцените значение выражения — .
ь
Замените найденные границы десятичными дробями с
двумя знаками после запятой.
28. Теоремы о почленном сложении и умножении
верных числовых неравенств
Зная границы некоторого числа а, мы можем, используя
изве стные свойства неравенств, оценить значения таких выра-
жений, как За, —5а, а+10, 2а 4 и т. д.
А как оценить сумму чисел а+Ь, разность а—Ь, произведе-
ние аЬ, частное — , если известны границы а и Ь? Для того чтобы
ъ
решить эту задачу, нам придется рассмотреть некоторые новые
свойства неравенств.
Сложим почленно левые и правые части верных неравенств
6>—3 и 12 >5, каждое из которых составлено с помощью зна-
ка >. Легко видеть, что сумма 6-V12 больше суммы —3+5,
т. е. верно неравенство 6 +12 >—3 + 5.
Если сложить почленно левые и правые части неравенств
2 <6 и —12 <—4, то сумма 2 (—12) будет меньше суммы
64 (—4), т. е. верным является неравенство 2 + (—12) <6+(- 4).
Теорема 1. Если а > Ъ и C>d, то а 4 с > Ь \-d (а, Ь, с и d—
любые числа).
Доказательство. Так как а >Ь, то а-|с>Ь4с.
Аналогично, так как r>d, то Ь4с>Ь У d. По свойству транзи-
тивности из неравенств а4с>Ь1с и b [c^b-\-d следует нера-
венство a+c>fe + d.
ill
Таким образом, при почленном сложении верных неравенств
одного знака верным будет неравенство того же знака.
Теорема верна и в том случае, если число рассматриваемых
неравенств больше двух. Например, складывая почленно ле-
вые и правые части неравенств 3<5,—1<7, —10 <—9, полу-
чим верное неравенство 3 + (— 1) f (—10) <5 г 7- К - 9), т. е.
—8<3.
Если и >Ъ и с <d, то нельзя заранее сказать, в каком соот-
ношении будут находиться суммы a-f-c и b d. Например,
складывая почленно верные неравенства 12 >8 и —10 < —5,
мы будем иметь верное неравенство 2 <3, составленное с помо-
щью знака <. А при почленном сложении неравенств 6 >1
и —8<—7 верным оказывается неравенство —2>—6, состав-
ленное с помощью знака >.
Рассмотрим вопрос о почленном умножении неравенств.
Теорема 2. Если а~>Ь и с> d, где а, Ь, с и d—положитель-
ные числа, то ас':> bd.
Доказательство. Так как а ~>Ь и с — положитель-
ное число, то ас>Ьс. Так как c>d и Ъ — положительное число,
то bc~>bd. По свойству транзитивности из неравенств ас>Ъс и
bc>bd следует неравенство ac>bd.
Итак, при почленном умножении верных неравенств одного
знака с положительными членами верным будет неравенство то-
го же знака.
Например, при почленном умножении неравенств 4 >3 и
— > — получим верное неравенство 4 — > Зу — , т. е. 1>—.
Из верных неравенств 0,1 <0,5 и 9 <10 следует неравенство
0,1 9 <0,5 • 10, т. е. 0,9 <5.
Теорема верна и в том случае, если число рассматриваемых
неравенств больше двух.
Следствие. Если числа а и Ь положительны и а >6, то
а2>Ь2.
Действич ельно, перемножив почленно два верных неравен-
ства а>Ь и а >Ь с положительными членами, получим верное
неравенство а2>Ь2.
Верно и обратное: если а2>Ь2, причем а и Ъ — числа поло-
жительные, то а~>Ъ.
Действительно, из неравенства а2 >Ь2, где а>0 и Ь>0, не
могут следовать соотношения а <5 или а Ь.
Если бы было верно неравенство а<?Ь (а и Ь — числа поло-
жительные), то было бы верно и неравенство а2 <&8, что проти-
воречит условию теоремы.
иг
Из равенства а—Ъ следовало бы, что а* —Ь“, что также про-
тиворечит условию теоремы.
Значит, из неравенства а2>Ь8, где а>0 и Ь>0, следует
неравенство а>Ъ.
Справедливы и более общие утверждения: если а>Ь>0 и
n£N, то а" >ЬГ1\ обратно, если ап>Ьп, где а > О, Ь>0 и n£N,
то а>Ь.
419. Примените к данным неравенствам теорему о почленном
сложении неравенств:
а) 12 >—5, 9 >7;
в) - 2,5 <—О,7, —6.5 <-1,3;
б) — 28 < 0, —10 <— 6;
г) 11 >7,4, 0>—8.
420. Примените к данным неравенствам теорему о почленном
умножении неравенств:
а) 5 >2, 4 > 3; в)3>1,
3 5
б) 1<7, 10«5; г) 8<10,
421. Покажите на примерах, что при почленном умножении не-
равенств одного знака с отрицательными членами нера-
венство, составленное с помощью того же знака, может
быть неверным.
422- Примените к двум данным неравенствам теорему о почлен-
ном сложении неравенств:
а) а>—10, Ь>2;
б) х<5, у<—8;
в) т^7, л^>—7;
г) с<12, 4.
423. Примените к двум данным неравенствам теорему о почлен-
ном умножении неравенств:
а) 012, Ь>~; б) 0<а<0,5, 0<Ь<2.
3
424. Верно ли, что:
а) (т > 2 и п >5) =» (т+ п > 7);
б) (т>2 и п >5) => (т п > 6);
в) (т>2 и п>5)=>(«4 л >10);
г) (т > 4 и п >3)=» (тп >12);
д) (т>4 и и >3)=» (лгл>9);
е) (т>4 и п >3)=ф (тп >22)?
425* Верно ли, что:
а) (а<Ь)=>(а"<Ь2);
б) (а2 <6 )=» (а <Ь)?
из
29. Применение метода границ для оценки значения суммы,
разности, произведения и частного
Пусть известны приближенные значения чисел а и Ъ с недо-
статком и с избытком: 2,8<а<3 и 1,5<&<1,7. Каковы грани-
цы суммы a~h&, разности а—Ъ, произведения аЬ и частного — ?
ь
Решить поставленную задачу мы можем с помощью теорем,
рассмотренных в предыдущем пункте.
Для оценки суммы воспользуемся теоремой о почленном сло-
жении числовых неравенств. По условию а >2,8 и b >1,5.
Сложив почленно неравенства а >2,8 и & >1,5, каждое из ко-
торых составлено с помощью знака >, получим:
а + &>4,3.
Аналогично, применяя теорему о почленном сложении нера-
венств к неравенствам а< 3 и Ъ < 1,7, получим:
а + Ь<4,7.
Итак, мы нашли границы суммы чисел а и &:
4,3 < a-f-b < 4,7.
Заметим, что запись решения удобнее вести с помощью двой-
ных неравенств:
2,8 < а < 3,
1,5 < Ъ <1,7
4,3 <а4~&<4,7.
А как найти приближения с недостатком и с избытком разно-
сти а—Ь?
Так как а—Ь=а-\-(—&), то, для того чтобы найти границы
разности а—Ъ, следует сначала оценить выражение —&, а за-
тем, воспользовавшись теоремой о почленном сложении нера-
венств, оценить сумму а-|-(—&).
Известно, что 1,5 <Ь <1,7. Значит, —1,5>—Ъ>—1,7. За-
пишем последнее соотношение с помощью знака <:
—1,7 <—&<—1,5.
Применим к двойным неравенствам
2,8 < а < 3 и —1,7 <—&<—!,5
теорему о почленном сложении неравенств:
2,8 < а <3,
—1,7 < — Ъ < — 1,5
2,84-(-1,7)< а+(-&) < 34 (-1,5).
Таким образом, 1,1 < а—Ь < 1,5.
114
Для того чтобы найти границы произведения aby восполь-
зуемся теоремой о почленном умножении неравенств (все члены
неравенств — числа положительные):
2,84,5<а6<31,7, т. е. 4,2< аЬ
5,1.
Для нахождения границ частного чисел а и Ъ представим
- а а 1
дробь — в виде произведения: — = а —.
ь ъ ь
1 гп
Найдем сначала границы значения выражения —. 1ак как
1,5 <& <1,7, то или, иначе, -1-<1<2-. ТепеРь
к неравенствам 2,8< с<3 и можно применить тео-
рему о почленном умножении неравенств:
т.е.
2,8 о .. 3
1J 1,5*
Верхняя граница частного — равна 2. Заменим нижнюю гра-
ъ
2 8
ницу^ десятичной дробью с одним знаком после запятой. Раз-
делив числитель на знаменатель, получим бесконечную десятич-
ную дробь 1,64... . Значение нижней границы необходимо взять
с недостатком. Так как 1,6 < то 1,6<~<2.
Для оценки значения выражения мы воспользовались ме-
тодом, который заключается в том, что приближенное значение
выражения находится дважды: один раз получается число, за-
ведомо меньшее искомого результата, другой раз — заведомо
большее. Этот метод называют методом границ.
426. Пусть 3<а<4 и 4<&<5. Найдите границы значения
выражения:
а) а + Ь; б) а—Ъ\ в) ab\ г) — .
115
427. Пусть 6< х<7 и 10< у<12. Оцените значение выражения:
a) x+jG б) ху, в) у—х; г) ху- д) - ; е) .
У X
428. Пусть 5<т<6 и 1 <п <2. Докажите, что 11<2/п-Ьп<14
и 1 <т—2п <4.
429. Пусть 6<с<7 и 2<d<3. Докажите, что24<с (d ]-2)<35
и 0<~ — 2< 1,5.
d
430. Найдите границы значения выражения:
а) Зс+7Ь, если 1,2 <а <1,4 и 0,2 <Ь <0,4;
б) ~ 4 0,6b, если —3<а< — 2 к 0,5<;Ь<;1;
в) Ь2 — аЬ, если 3 <4 и 5 <; b < 6;
г) — + —» если 0,1 < а < 0,2 и 0,4 < Ъ < 0,5.
а Ъ
431. Известны длины а и b основания и боковой стороны рав-
нобедренного треугольника, выраженные в мм: 26<а<28
и 41<&<43. Оцените периметр треугольника.
432. Найдите границы длины средней линии трапеции, если
известны приближенные значения (в сантиметрах) с недос-
татком и с избытком длин а и с ее оснований:
3,4 <а <3,5 и 6,2<с<6,3.
433. Можно ли перевезти на трехтонном грузовике за один
рейс 14 плит, каждая массой т кг, где
260 <т<270,
если не допускается перегрузка свыше 500 кг?
434. Можно ли за один рейс перевезти на пятитонном грузови-
ке 3 плиты, каждая массой т1 кг, и 8 плит, каждая массой
т2 кг, где
970 </nx < 1030, 245 <лгг <255,
если не допускается перегрузка свыше 800 кг?
435. У подножия Останкинской телевизионной башни и вбли-
зи ее вершины расположены барометры. Показание ниж-
него барометра в мм рт. ст. равно р1г где 755<р,<756,
а показание верхнего барометра в льи рт. ст. равно р2,
где 713<р2<711. Определите, на какой высоте располо-
жен второй барометр. (Считайте, что на каждые 12 м вы-
соты давление понижается на 1 мм рт. ст.)
436. В треугольнике АВС известны величины двух углов:
58° <АВС <59 ’ и 102' <ВСА<103\
Определите границы величины угла САВ.
116
30. Погрешность приближения
Имея некоторое приближенное значение величины, полезно
знать, на сколько оно отличается от истинного значения, т. е.
какова его погрешность.
Определение. Погрешностью приближенного значения ве-
личины называется разность между истинным и приближенным
значениями этой величины.
Например, заменяя число х — 3,283 приближенным значе-
нием а = 3,2 с недостатком, мы допускаем погрешность х — а —
= 0,083. Если в качестве приближенного значения числа х взять
приближение b = 3,3 с избытком, то погрешность этого прибли-
жения будет х—b = — 0,017. Легко понять, что погрешность при-
ближения с недостатком всегда положительна, а погрешность
приближения с избытком отрицательна.
Однако, как правило, важнее знать не характер приближе-
ния, а то, как близко оно к истинному значению.
Выясним, к примеру, какое из двух приближений числа х
является лучшим. Для этого сравним модули погрешностей.
Модуль погрешности приближения с избытком (|с—b| =0,017)
меньше, чем модуль погрешности приближения с недостатком
(|х—а|—0,083). Следовательно, приближенное значение с из-
бытком, равное 3,3, лучше, оно меньше отличается от заданного
числа х- 3,283.
O.OSJ 0.017
т---------*-------Л-i-x А
т_^1 _Л, ' I I I I 1 IУ ! 1”
4 2 43
Рис. 34
Если мы изобразим на числовой прямой точки с координата-
ми х, а и Ь, то расстояние между точками с координатами х и Ъ
будет меньше, чем расстояние между точками с координатами х
и а (рис. 34).
437. Пусть х — некоторое число и а — его приближенное зна-
чение. Найдите погрешность приближения и модуль по-
грешности, если:
а) х-9,7иа = 10; в) х — 0,84 и а =0,8}
б) х=0,8 и а=1; г) х = 3,62 и а=3,6.
438. Известны приближенное значение а некоторого числа х
и погрешность приближения. Найдите х, если:
а) а —12 и х—а =0,3; в) а—21 и х—а-—0,2;
б) а=3,2 и х—а =0,07; г) а =0,4 и х—а = -0,03.
117
439. Пусть а — приближенное значение числа хи |х — а| —
модуль погрешности. Найдите х, если;
а) а=10 и |х — а\- 1; в) а=7,5 и |х—а|=0,1;
б) а—2 и |х—а|=0,3; г) а = 3,6 и |х — а|=0,02.
440. Обратите число у в десятичную дробь и округлите эту
дробь последовательно до десятых, до сотых, до тысяч-
ных. Найдите в каждом случае погрешность приближения
числа десятичной дробью, если:
а) У = |; б) у= 1.
о У
441. Проверьте, что число 0,66 является приближенным зна-
2
чением числа — с недостатком, а число 0,67 — с избытком.
Какое из этих двух приближений лучше?
442. Какое из двух приближений числа — лучше: 0,16 или 0,17?
6
443. Известны границы д тины а и ширины Ъ (в метрах) ком-
наты прямоугольной формы: 7,5<а<7,6 и 5,4<д<5,5.
Подойдет ли это помещение для школьной библиотеки,
если для этого требуется комната площадью не менее
40 №?
444. Вычислите границы длины окружности, диаметр которой
равен d си, где 4,5 <d <4,6. Считайте, что 3,14 <л < 3,15.
445. Длина воздушной трассы между двумя пунктами равна
s км. Самолет преодолевает ее за время t ч. Определите
границы средней скорости самолета, если
4950 <s <5050, 5,9 < t < 6,1.
31. Точность приближения
Рассмотрим пример. Пусть известны границы мас'ы т
(в граммах) металлической пластинки:
4<т<5.
Приближенным значением массы (в граммах) может служить
и число 4, и число 5, а также любое другое число между ни-
ми, например 4,1; 4,3; 4,5; 4,65, 4,85; 4,9.
Возьмем в качестве приближенного значения массы число 4.
Не зная точного значения массы т, мы не можем определить
и погрешность приближения. Однако легко понять, что модуль
118
погрешности не может превосхо- т
дить 1. Действительно, рассмот- рев рисунок 35,а, мы видим, что, где бы в промежутке [4; 5 ] ни находилась точка с коорди- натой т, она удалена от точки с координатой 4 не более чем на 1. Значит, \т— 4|^1. Говорят, что число 4 явля- ется приближенным значением массы т в граммах с точностью до 1. Выберем теперь в качестве приближенного значения массы в граммах число 4,2 и оценим g) 1 1 1 1 1 1 1' 1 1 4 а т б) -j—।—i—i—।—।—।—i—i—— J 4 4,2 5 т г * РА -J—i—।—I—।—1—1—1—1—Ш— ' Ь 45 5 Рис. 35 значение выражения jm—4,2 .
Из рисунка 35,6 видно, что, где бы ни находилась точка с коор-
динатой т в промежутке [4; 5 ], она удалена от точки с коорди-
натой 4, 2 не более чем на 0,8, т. е. \т—4,2[^0,8.
Число 4,2—приближенное значение массы т в граммах с
точностью до 0,8.
Аналогично число 4,7 — приближенное значение массы т
в граммах с точностью до 0,7.
Возьмем в качестве приближенного значения массы т в
граммах среднее арифметическое границ, т. е. число 4,5. С по-
мощью рисунка 35,в легко увидеть, что значение выражения
\т—4,51 не превышает половины расстояния между точками
с координатами 4 и 5, т. е. не превышает 0,5. Число 4,5—при-
ближенное значение массы пластинки в граммах с точностью
до 0,5.
Последнее приближение оказалось наиболее выгодным, так
как модуль погрешности мы оценили меньшим числом, чем в
предыдущих случаях.
Вообще, если в качестве приближенного значения числа х
взято число а и известно, что модуль погрешности такого при-
ближения не превосходит некоторого числа h, т. е. |х—а|^Л,
то говорят, что число а является приближением числа х с точ-
ностью до h-
Записывают это так:
х — a±h.
Приведем примеры.
1. Известно, что 2,6 ^х^2,9. Вычислить приближенное зна-
чение х, равное среднему арифметическому границ, и опреде-
лить точность этого приближения.
2.9 + 2,6 5.5 = 2 75
2 2
119
Модуль погрешности приближения числа х числом 2,75 не
превышает полуразности чисел 2,9 и 2,6. Так как 2,9~ 2,6 = ——
—0,15, то х=2,75±0,15.
2. Найти границы, в которых заключено число и, если
J/=12,7zbO,5.
Так как 12,7 есть приближенное значение числа у с точно-
стью до 0,5, то у отличается от 12,7 не более чем на 0,5. Значит,
12,7-0,5<1/<12,7+0,5, т. е.
12,2<1/<13,2.
3. Доказать, что число 0,14 является приближенным значе-
нием числа у с точностью до 0,01.
Найдем модуль погрешности приближения числа — числом
0,14:
- —0,14
7
£ _ 14 _ 1 _ 7 | 50 — 49 1
7 100 7 60 | 350 ~ 350*
- —0,14
7
Так как меньше 0,01, то верно неравенство
<0,01. Значит, число 0,14 является приближенным значением
числа у с точностью до 0,01.
Эту задачу можно решить и другим способом.
Разделив числитель дроби у на знаменатель, получим беско-
нечную десятичную дробь:
- = 0,14 ... .
7
Значит, 0,14< — <0,15. Отсюда ясно, что модуль погрешно-
сти приближения числа — числом 0,14 не превышает 0,01. Дей-
ствительно,
— — 0,14
7
следовательно, верно неравенство
I - —0,14
7
0,15—0,14 , но 0,15 — 0,14 = 0,01,
0,01.
4. Найти множество приближенных значений числа 3,7 с точностью до 0,1.
В качестве приближенного значения числа 3,7 с точностью до 0,1 можно
взять любое число с, отличающееся от числа 3,7 не более чем на 0,1. Значит,
120
приближенным значением числа 3,7 с точностью до 0,1 является любое число,
принадлежащее промежутку [3,7—0,1; 3,7 + 0,1], т. е. промежутку [3,6; 3,8].
Е частности, приближенным значением числа 3,7 с точностью до 0,1 является
В'само число 3,7. Вообще, всякое число является своим приближением с любой
степенью точности.
5. Электроплитка рассчитана на напряжение 220±10 в.
Найти сопротивление спирали электроплитки, если известно,
что через нее должен идти ток 5±0,1а.
Известны приближенные значения с недостатком и с избыт-
ком напряжения U (в вольтах) и силы тока I (в амперах):
210<П<230 и 4,9<7<5,1.
Для определения сопротивления R спирали плитки (в омах)
воспользуемся законом Ома: R =
Оценим вначале значение выражения -у, а затем произве-
тт 1
дения U • —.
Так как 4,9</<5,1, тот. е.-<7<-.
Применим к неравенствам
210<t7<230 и
111
5,1 I 4,9
теорему о почленном умножении неравенств:
210- — < U - < 230 • — , т. е.
5,1^ 1 4,9
210 ' и < 230
5Д 7 4,9’
Значение нижней границы следует взять с недостатком, а верх-
ней — с избытком.
Так как
210 л 230 л л л
— = 41,1 ... и — = 46,9 ... , то
5,1 4,9
41<Я<47.
В качестве приближенного значения сопротивления R возь-
мем среднее арифметическое границ: 41 — 44. Модуль по-
грешности этого приближения не превышает полу разности
границ: 47 ^4— = 3. Итак, R — 44 ± 3.
Ответ: 44±3 ом.
121
446. Вычислите приближенное значение х, равное среднему
арифметическому границ, и укажите точность этого при-
ближения:
а) 6^х^8; в) 4,5 ^х^4,8;
б) 2 < х < 3; г) 2,81 <х<2,83.
447. В каких границах заключено число у, если:
а) у=3±Т; в) у=6,5±0,6;
б) у=3,9±0,2; г) у=0,4±0,15?
448. а) Докажите, что число 1,4 является приближенным зна-
чением числа 1,361 с точностью до 0,05.
б) Докажите, что число 0,3 является приближенным зна-
2
чением числа — с точностью до 0,05.
449. а) Округлите до десятых дроби: 1,487; 0,35; 2,714.
Убедитесь в каждом случае, что модуль погрешности при-
ближения, полученного в результате округления, не пре-
восходит половины от 0,1, т. е. 0,05.
б) Приведите несколько примеров округления десятич-
ных дробей до сотых. Убедитесь в каждом случае, что по-
лученный результат является приближением с точно-
стью до половины от 0,01, т. е. до 0,005.
450. Является ли число 0,2 приближенным значением числа
0,1981 с точностью до 0,5; 0,1; 0,01; 0,001?
451. Пусть — <х< —. Докажите, что числа — и — являются
31 30 31 30
приближенными значениями числа х с точностью до 0,01.
452. Известно, что — <х< —. Являются ли числа — и —
100 99 100 99
приближенными значениями числа х с точностью до 0,05;
0,01; 0,001? I»
453. При измерении длины а и ширины Ь прямоугольника по-
лучили, что а = 5,4 ± 0,1 см и b — 3,7±0,1 см. Найдите
приближенные значения периметра и площади прямо-
угольника.
454. Найдите приближенное значение площади фигуры, изо-
браженной на рисунке 36, если
а=1,2±0,1 см, с=2,2±0,1 см,
Ъ— 2,4±0,1 см, d=l,4±0,l см.
455. Вычислите приближенное значение площади заштрихо-
ванной части фигуры, изображенной на рисунке 37, если
а=8,2±0,2 см, с=2,6±0,1 см,
Ь=6,4±0,2 см, d=l,7±0,l см.
122
Рис. 37
b
a
456. Требуется уложить 1000+20 лг3 бетона. В кузов самосва-
ла заливают 2,25+0,02 лг3 бетона. Сколько рейсов само-
свала потребуется для этой работы?
457. Брусок имеет объем V м9 и массу т кг. Вычислите плот-
ность материала, если 0,0064^1^4^0,0065 и 17,3^ттг ^17,5.
Определите по таблице плотностей, из какого материала
сделан брусок.
/ К2\
Наименование Плотность
медь 8900
сталь 7800
чугун 7000
алюминий 2700
458. Можно ли включить в цепь прибор, имеющий сопротивле-
ние 44+0,5 оле, чтобы при напряжении 215±15 в сила то-
ка не превысила 6 а?
459. Требуется оклеить обоями стены комнаты общей площадью
30+0,2 Л12. Сколько необходимо иметь рулонов обоев,
если в одном рулоне содержится 7+0,03 м обоев при ши-
рине 0,75+0,03 м?
ДОПОЛНИТЕЛЬНЫЕ УПРАЖНЕНИЯ К ГЛАВЕ II
К пункту 18
460. Докажите, что при любых значениях у:
$) значение выражения (6г/—1) (z/4-2) меньше соответ-
ствующего значения выражения (Зу +4) (2г/4-1);
123
б) значение выражения (Зу—1) (2у + 1) больше соответ-
ствующего значения выражения (2у—1) (2+Зу).
461. Составьте двучлен с переменной х:
а) принимающий положительные значения при любых
значениях х;
б) принимающий отрицательные значения при любых зна-
чениях х;
в) принимающий при одних значениях х положительные
значения, при других — отрицательные и обращающий-
ся в нуль при х, равном 5.
462. Какие из неравенств верны при любом значении перемен-
ной а:
а) (а—8)2>0; в) 4— а2<0; д) (а-9)2+26>0;
б) (5-2а)2>0; г) —18—а2 <0; е) (а—5)2+(а-3)2 >0?
463. Докажите, что при любом значении Ъ верно неравенство:
а) (5+4) (6—4)—Ь2 <0; в) (Ь—7)(6+6) +(Ь+50)>0;
б) (2Ь + 1)2— 2(26— 1) >0; г) 5(5— 2) —(&—!)(Ь-г6) <0.
464. Докажите, что при всех значениях переменной а выраже-
ние принимает положительные значения:
а) (а2+2а4 1)+8; в) а2 4 2а +6;
б) (а2—2а \ 1) + 4а2; г) а2—4а М2.
465. Докажите, что при любых значениях переменной а значе-
ние дроби неотрицательно:
а) ' 10 в) Эд2—6д + 1, д2 +1 ’ д) д2 + 6д 4- 10. 12
б) д2 + 4Д Ь 4 . г) 49д2 + 14д -j- 1 д3_+ 9 е) 4д* — 4д + 8 5
466. Какие из неравенств верны при любых значениях перемен-
ной х:
а) 4х(х4 4) >(2хЦ 3) (2х—3)—16х;
б) х2<(3х— 1) (Зх + 1)—4 (2х2—1);
в) (5х—1) (5х I 1)<25х2 — (х4 1);
г) (х+4) (х—4) + 12 <х (х+4)—4х?
467. Как изменяется произведение чисел а и b при увеличении
множителя b на 1?
468. Выясните, при каком условии значения произведения
(а+1) (6 4-1) больше соответствующих значений произве-
дения аЬ. Проиллюстрируйте ответ примерами.
124
469. Докажите, чз о полупериметр треугольника больше длины
каждой из его сторон.
470. Катер прошел 20 км по течению реки и 20 км против тече-
ния реки. Затратит ли он на весь путь больше времени,
чем ему требуется на прохождение 40 км в стоячей воде,
меньше или столько же?
471. Сравните площадь квадрата со стороной 10 см с площадью
произвольного прямоугольника, имеющего тот же пери-
метр.
К пункту 19
472. Запишите верное неравенство, которое получится, если:
а) к обеим частям неравенства прибавить число, записан-
ное в скобках:
18 > - 5 (104); 2 > 2 (0.1); 2 > 2 (- Д;
б) обе части неравенства умножить на число, записанное
в скобках:
4-1 >4-1 (6); 0,34<0,37 (-2); Д < _| (—1);
в) обе части неравенства разделить на число, записанное
в скобках:
; 0,06 <0,21 (—0,03); 10,2 > 8,1 (—1).
473. Какое из соотношений <а больше 6», «о меньше Ъ>, <а рав-
но Ъ» имеет место, если верно неравенство:
а) 0,3а > 0,ЗЬ; в) 17а <176; д) 0.25а > 1 6;
б) — 5а<— 5Ь; г) —1,2а >—1,26; е) —0,02а<—1-М
_3 > _5 'Г.
4 8 \4/
474. При каких значениях а и b верно неравенство:
a) ab > 0; г) - < 0; ’ ь \ °2 ж)- = СО;
б) ab < 0; д) а?6>0; з) -: >0;
о Л Ч | -О "йГ е) а62<0; 3 °-1 Л с о?
475. Докажите, что если а > Ь. , то:
а) а+5>6+3; б) 1—а<2-&.
325
476. Докажите, что если а >Ь >0, то:
а) 5а>4&; в) —4а<—26;
б) 17а>12Ь; г) — 5а < —1,2&.
477. Верно ли, что если а >Ь, то:
а) а+1>64-1; в) 1— а<1—Ь;
б) а—1>Ь—1; г) ->-?
з з
478. Верно ли, что если а>Ь, то:
а) (а + 1)Ь <аЬЬа; в) а2>Ь2;
б) (а+1) (ft— 1) <ab; г) а34-&2>2а6?
479. а) Как изменяется правильная дробь — а> 0, Ь>0, — <11
Ь \ Ъ /
при прибавлении к ее числителю и знаменателю одного
и того же положительного числа?
б) Как изменяется неправильная дробь — (а > 0, Ь>0,
при прибавлении к ее числителю и знаменателю
одного и того же положительного числа?
480. Докажите, что при всех значениях переменной с верно не-
равенство:
а)
с» 4-1
2
> с;
б)
481. Докажите, что при всех значениях переменных а, b и с
верно неравенство
а2 + Ь3-^с3-ЬЗ>2 (airb+c).
482. Докажите, что при любых значениях а, Ь и с верно нера-
венство
a3 41 &3 -^с3>аЬ -Нс-Ь Ьс.
Указание. Умножьте обе части неравенства на 2.
483. Докажите, что при всех значениях а и Ъ верно неравенство
a2+a& + b2>0.
Указание. Используйте тождество ab = 2• а• — Ъ.
484. Докажите, что при любых положительных значениях х
и у верно неравенство:
а) х54-у®^х4у4-ху*; б) х4+у4^х3у+ху3.
126
485. Докажите, что при указанных значениях переменных вер-
но неравенство:
а) п3+1>п2-+п при п >1;
б) п341<п2+п при n <—1.
486. У продавца были весы с различными по длине плечами.
Один килограмм товара он положил на левую чашку, а
другой тому же покупателю — на правую. Получил ли
покупатель 2 кг товара, больше 2 кг или меньше?
487. Дс кажите, что при а >0 и b >0 верно неравенство:
a) - + б) (а + Ь)(- + Д>4.
Ъ2 а2 а Ъ \а о /
488. Докажите, что если а >|д:, то а >Ъ.
К пункту 20
489. При каких значениях а из неравенства 17 >14 следует
неравенство 17а >14а? из неравенства 4 < 10 следует не-
равенство 4а >10а?
490. Докажите, что:
а) из того, что ас = Ьс, не следует, что а = &;
б) из того, что а — отрицательное число, не следует, что
а-|-0,1 — отрицательное число.
491. Найдите среди неравенств такое, из которого следуют все
остальные:
а) х >8, х >5, х >1, х >12;
б) х<4, х<2, х<1,5, х<18;
в) х>1,2, х>1 —, х>1 — , х>1 —;
г) х<1,2, х <1,02, х <1,002, х <1.
492. а) При каких значениях а из неравенства х >а следует
неравенство х >12?
б) При каких значениях b из неравенства х <Ь следует
неравенство х<9?
493. а) Следует ли из предложения х > 3 предложение
х (х2 + 1) >3 (х2 + 1)?
б) Следует ли из предложения у < 5 предложение
!/(-!/2-2)>5(-1/2-2)?
494. При каких значениях а:
д
а) из неравенства ах>3 следует неравенство х> —;
а
2
б) из неравенства ах<2 следует неравенство х>—?
а
127
495. Пусть С — пересечение множеств А и В. Верно ли:
а) (а С (а С С); б) (а € С)=$>(а € А)?
496. Докажите, что:
а) функция, заданная формулой /(х)=Зх+0,5, возраста-
ет на всей области определения;
б) функция, заданная формулой f (х) = —2х—2, убывает на
всей области определения.
497. Докажите, что функция, заданная формулой f(x) —, убы-
X
вает на множестве положительных чисел, убывает на мно-
жестве отрицательных чисел. Проиллюстрируйте вывод на
графике.
498. Докажите, что функция, заданная формулой f (х) = ~1'J,
X
возрастает на множестве положительных чисел, возраста-
ет на множестве отрицательных чисел. Проиллюстрируйте
вывод на графике.
К пункту 21
499. Равносильны ли предложения:
а) число а кратно 5; число 7а кратно 5;
б) число Ь кратно 7; число 35 Ъ кратно 7;
в) число а кратно 4 и 6; число а кратно 12;
г) натуральное число а оканчивается цифрой 5; натураль-
ное число а кратно 5;
д) а и b — нечетные числа; сумма a-j-b — нечетное число?
500. Равносильны ли предложения:
а) х>3; х + — >3+—;
X X
б) х>—3; х + — >—3+-?
X X
501. Равносильны ли предложения:
а) «множество А есть подмножество множества В» и «пе-
ресечение множеств Ли В есть множество А»;
б) «множество А есть подмножество множества В« и «объ-
единение множеств А и В есть множество В»?
502. Равносильны ли уравнения:
а) х - 1 и х“ -- г; г) х2 — 4х и х2 — 4 — 4х — 4;
б) хг = х и х3 = х2; д) * ~-2- — 0 и х2 — 25 О;
х — 10
в) хг 4х и х 4; е) г — 2 и - —— ?
' х —2 х—2
128
503. а) При каком значении а уравнение ах -4-1 = 11 равносильно
уравнению 5х — 4— 21?
б) При каком значении b уравнение Ьх—24=0 равно-
сильно уравнению 8—Зх =—10?
504 а) При каких значениях р уравнение
iLz* « 0
х — р
равносильно уравнению х*—16-0?
б) При каких значениях Ъ уравнение
О
Ъ — х
равносильно уравнению 25 -х3-0?
505. Докажите, что:
а) (х>17)<=>(х+2>19); в) (х >2) <=> (12,5х >25);
б) (х-}2<11) =>(х<11—2); г) (х <-— 3)^( -7х>21).
506. Равносил ьны ли неравенства:
а) 25х <125 и х <5; в) |х| <10 и х<10;
б) х- <25 и х<5; г) — х>—1,4 и х<1,4?
К пункту 22
507. Найдите с помощью графиков;
а) множество значений переменной х, при которых функ-
ция у— Зх—6 принимает положительные значения, от-
рицательные значения:
б) множество значений переменной х, при которых функ-
ция у—х- 4 принимает значения, большие 1.
508. Построив в одной системе координат графики функций
у х' и у х®, решите, используя их, уравнение х® -ха
и неравенства х® >х2 и хэ <ха.
509. Решите графически неравенство:
а) х41<3: в) Зх-4>2х;
б) 0,6- 2х>3,6; г) 5х 1 <х -3.
510. а) Решите графически уравнение х2=1,5х и неравенства
х2>1,5х, х2<1,5х.
б) Решите графически уравнение 0,5хя=2х и неравенства
0,5х3>2х, 0,5х® <2х.
g АлгеЛп к I кл.
J20
g
611. а) С помощью графиков функций у = — и у = 3 решите
х
6 „
неравенство — < 3.
X
о
б) С помощью графиков функций у=х2 и у= - решите
X
о. 8
неравенство х‘>
X
К пункту 23
512. Наймите множество решений неравенства и покажите его
на числовой прямой:
а) xj>4; в) х^5; Д) *>0;
б) х<3; г) х>—1; е) х<7.
513. Решите неравенство:
а) 0,01 (1—Зх) >0,02x4-3,01;
б) 12(1- 12х)+100х>36- 49х;
в) (0,6х—1)—0,2(3x4-1) <5х -4;
г) | (6х Н)— -* (12х—5)<4—6х;
д) (Зх 1)(х-1)—Зх2 >6х 4-7;
е) 15х2—(5х—2) (Зх 4-1) <7х—8.
514. Найдите множество решений неравенства:
а) —1 —1 > -4 1 4 8; в) —2< —
’ 4 3 4 8
За — 1 а —1„ .5а За — 1 . 2а — 1 1
б) ---------->0; г)----------------------<1.
2 4 6 3 2
515. Решите неравенство:
х —0,5 х—0,25 . х — 0,125 е 5 — х 1 — х. ,
а)—-— 4------------------<_0; б)--------------->1.
4 4 8 ' 3 2
516. Найдите множество натуральных значений х, удовлетво-
ряющих неравенству:
а) 3(5—4х) 4(284 2х) >0; б) (х-Ь1)(х—1)—(х2—Зх)<14.
517. Составьте неравенство с одной переменной, множеством
решений которого служит:
а) множество положительных чисел;
б) множество отрицательных чисел,
130
518. Составьте какой-либо двучлен с переменной хг
а) принимающий отрицательные значения тогда и i олько
тогда, когда значение х меньше 17;
б) принимающий положительные значения тогда и толь-
ко тогда, когда значение х бол ьше 1,2.
619. Составьте какой-либо двучлен с переменной у:
а) принимающий отрицательные значения тогда и толь-
ко тогда, когда у больше 6;
б) принимающий положительные значени я тогда и только
1
тогда, когда у меньше — .
520. Существует ли такое значение 1г, при котором верно не-
равенство:
a) 0-fe<-1,7; г) lfr|>—1; ж) (й—l)2+(fe—2)2<0;
б) k-8>k-, pj ]fe| <—1; з) (A—I)2—k(k-2) <0?
в) |fe|<0; е) (й—7)2СО;
521. При каких значениях xi
__g
а) значение дроби —- — больше соответ ствующего значе-
с х —
ния дроби -----;
4
/г 2x4- 4 *
б) значение дроби----— больше соответс гвующего значе-
6
ния /роби —-1?
3
522. Решите неравенство:
а) 2(4у -1)-5у<Зу+5;
б) 6(1—-у)—8(3у4 1)- 30у:-5.
523. Сравните квадрат числа а с квадратом числа, на 1 меиыпе-
го, чем а.
524. Найдите, при каких значениях а уравнение имеет поло-
жите." ьный корень:
а) Зх = 9а; в) х—8=За+1;
б) х 1 2—а; г) 2х—3=аЧ 4.
525. Найдите, при каких значениях Ь уравнение имеет отрица-
тельный корень:
а) 10х=3&; в) 2х-1 М2;
б' X 4- Ь; г) Зх 3-55 2-
526. При каких значениях т верно равенство:
a ) 12m—161 = 2т —16: в) |m|6|=— m—6;
б ) 112-6п,1 - 1- Г) 351 ; _i?
7 12 6»n ’ * Ют — 35
5»
131
527. а) При каком значении а множеством решений неравен-
ства х > — служит числовой промежуток ] —; - • оо [ ?
а 6
б) При каком значении b множеством решений неравен-
ства х< — служит числовой промежуток ]—оо; —2[?
ь
528. При каких значениях а равносильны неравенства:
о 4
а) 5х— а>0 и х> — ; в) ах — 4^ 0 и х>—;
5 а
б) Зх + а <0 и х<-----------— ,
3
г) ах — 4>0 и х<—?
а
529. При кат их значениях k функция y = kx—2 принимает по-
ложительные значения при значениях х, больших и
только при этих значениях?
530. При калих значениях Ъ функция у= i-x b принимает от-
рицательные значения при значениях х, меньших 4, и
только при этих значениях?
531. Для премирования 12 пионеров надо кз пить краски и ка-
рандаши. Набор красок стоит 50 коп., а набор карандашей
стоит 20 коп. Сколько наборов красок следует купить,
чтобы стоимость покупки не пре^ ышала 4 руб.9
532. С турбазы в город, отстоящий на расстоянии 24 км, вышел
турист со скоростью 4 клг/ч. Спустя 2 ч вслер, за ним от-
правился второй турист. С какой скоростью должен идти
второй турист, чтобы догнать первого до его прихода в
город?
533. От деревни до совхоза 20 км, а от совхоза до станнин
40 км (рис. 38). Из совхоза по направлению к станции вы-
ехал велосипедист со скоростью 12 км, ч. Одновременно
и > деревни на станцию через совхоз по той же дороге от-
правился мотоциклист. С какой скоростью должен ехать
мотоциклист, чтобы догнать велосипедис га до его приезда
на станцию?
534. Расст аяние между пунктами А и В равно 28 км. Из пункта
А в пункт В вышел турист со скоростью 4 км ч. Спустя
30 мин навстречу ему из пункта В вышел друюй турист.
С какой скоростью должен идти второй турист, чтоб! I
встреча произошла в точке, расположенной ближе к пунк-
ту А, чем к пункту В?
20 км
4-0 км
Деревня
Совхоз
Станция
Рис. 38
132
535. Между поселками А и В, расположенными на расстоянии
62 км, находится станция С, удаленная от А на 30 км.
Из А в С вы ехал велосипедист со скоростью 12 км, ч Спу-
стя 30 мин из В в С выехал мотоциклист. С какой ско-
ростью должен ехать мотоциклист, чтобы успеть приехать
в С раньше велосипедиста?
К пункту 24
536. Решите систему неравенств:
а) х>8, б) i/<5,
в)
х > 6,5,
г)
1
з
х> 2;
8/<3;
х > 6,05;
1_
4
537. Найдите множество решений системы неравенств:
а) [х>6, б) х< —1,7, в) IX <—5,7, г) Гх> -2,1,
(х <9,3; х> —2,8; х>4; (х < :—2,01.
538. При каких значениях а система неравенств
lx >3,
|х <а
не имеет решения?
539. Решите систему неравенств:
а) х >4, б) х <1, в) х>3,5, г) х<—3,
х >8, х <5, х >6, х<— 2,
х>9, х<2, х <1, х <—б,
х >3; х<0: х<0; х>8.
540. Объясните,
почему не имеет решения система неравенств:
а) [х2+1<0,
Зх -1 >0;
б) [2х—4>2х-1,
(бх >0;
541. Решите систему неравенств:
а) |0,Зх—1 <x-L0,4,
2—Зх< 5х 4-1;
б) 2,5х—0.12 > 0,6х 4- 0,07,
11 —2х> —х -4;
в) '6х<0,
Зх>0;
г) Зх*5<0,
|Зха + 5<0.
2x4- 1,4<*~7“б) 7»
О
2х>8- -;
Б
183
г) 3(х—2)(х -2)—Зхг<.х,
5х—4>4—5х;
Д) (х4)(5х— 1)—5х’>х4-1,
[Зх—0,4<2х-0,6;
е)
1 I- 1 + *> 2х~1
' 3 6
Зх -->4.
4
542. Найдите целые решения системы неравенств:
а) 6х(х—1)—(2х—1)3х < х,
0,5х—3,7 < 0,2х—0,7;
б) (0,7х—3 (0,2х+1)<0,5х+1,
[0,3 (1—х)+0,8х^хН 5,3;
в)
1 (Зх - 2) + 1 (12х + 1) > 0,
О о
1 2
I (14х - 21) + ± (9х - 6) < 0;
г)
0,2(5х —1)+ - (Зх + 1) < х + 5,8,
3
8х— 7—-i (6х — 2) > х.
543. Решите двойное неравенство:
а) - 9<3х<18; в) 3<5х—1<4;
б)1<^-1<2; г) 0< —-<1.
’ 2 ' 3
544. а) При каких значениях х значения выражения 2х—4 при-
надлежат числовому промежутку 1—1; 5[?
х__5
б) При каких значениях х значения дроби - принадле-
2
жат числовому промежутку [0; 5]?
545. Найдите множество положительных значений переменной
у, удовлетворяющих системе неравенств:
а) |3у—(уЧ 6)<5у4-9, б) у-1 , у
[12у—2(3 -у)<2(у—2); / з " 6 ’
2у3 (-у(1—2у)4-5 +у>0.
546. Найди е множество отрица<'ельных значений переменной
у, удовлетворяющих системе неравенств;
а)
5у —1 2у- 1>0
6 2
l_L±i<0;
3
б) ((у+6)(5—у)Ч-у(у 1)>о,
L0,3y(10y+20)- -Зуа+30>0.
134
547. Смешали 12 кг ириса и 10 кг карамели. Килограмм ириса
стоит 1 руб. 60 коп., а стоимость 1 кг смеси больше 1 руб.
40 коп., но меньше 1 руб. 80 коп. Какова стоимость 1 кг
карамели?
548. Если туристы будут проходить в день на 5 км больше, то
они пройдут за 6 дней расстояние, большее 90 км. Если же
они будут проходить в день на 5 км меньше, то за 8 дней
они пройдут расстояние, меньшее 90 км. Сколько кило-
метров в день проходят туристы?
549. Числитель и знаменатель дроби — целые положительные
числа, причем числитель на 3 меньше знаменателя. Если
к числителю и знаменателю прибавить по 1, то получится
а з
дробь, меньшая —; если же из числителя и знаменателя
вычесть го 1, то получится дробь, большая —. Найдите
5
все такие дроби.
К пункту 25
550. Решите неравенство:
а) (Зх—1) (ж-1)^0; г) (х+1) (5+2х)>0;
б) (22—х)х>0; д) (1,8— ж) (34 х2) >0;
в) (1 —Зх) (1- 2х) >0; е) (15—2х) (4ха4-1) <0.
551. Найдите множество решений неравенства:
а) (х I 5) (х—1) >х—1; б) (х—2)х>2 (х— 2).
552. При каких значениях у верно неравенство:
а) (у+5)2(2у 12) <0; в) (у2 - бу-9)( 15 -у) <0;
б) (у-3,5) (у—5)2 >0; г) (у- -6)2(у- -2)а(3у- 15) >0?
553. а) При каких значениях и произведение
(и—2) (и—5) [и—7) положительно?
б) При каких значениях г произведение
г (2—3) (2—4) отрицательно?
554. Решите неравенство:
а) 0,5х2 >х; в) х24 И <0;
б) 0,5х2 <х, г) (х 4-2)х >2х -9.
555. Равносильны ли неравенства ж >1 и ха >х?
556. Решите неравенство:
а) - — >0;
X
б) 3 — <0;
х + 1
. 5 — 5х п
в) ---- г>0;
4x4-4
. 17,3 —х
г) —ГТ 05
1 1 X
Д)
е)
(х4-5)а<°5
14 —2х
-Я----
(8-х)»
>0.
136
557. Найдите целые решения неравенства:
— 5 ezx 8 — 2х \ л ч Зх — 8 Л ч 12—5х _ п
а) ---- <0; б) ------ > 0; в) ------ < 0; г) —— > 0.
х — 2 х — 7 5х — 1 6х
558. Решите неравенство:
559. При каких значениях х значения функции у = — больше 4?
X
Решите задачу графически и алгебраически.
560. При каких значениях переменной а верно неравенство:
a) > о; б) < 0?
а — 5 а — 2
К пункту 26
561. Округлите число:
а) 0,478 до сотых; в) 141,28 до единиц;
б) 12,05 до десятых; г) 1253,41 до десятков.
562. Округлите до сотых число:
а) 1,205; б) 13,096; в) 24,997; г) 49,995.
563. Округлите число 69,9998 до тысячных, до сотых, до деся-
тых, до единиц, до десятков.
К пункту 27
564. Укажите границы:
а) температуры воздуха на территории СССР;
б) барометрического давления в вашей местности;
в) роста взрослого мужчины;
г) скорости легкового автомобиля.
565. В доме 60 квартир. Все квартиры заселены, причем число
жителей в одной квартире не превышает 5 человек. Ука-
жите границы числа жителей дома.
566. Чтобы изготовить деталь, нужно а кг металла. Имеется
р кг металла. Можно ли сделать деталь, если:
а) 23,9 <а <24,7, б) 23,9 <а <24,7, в) 23,9 <а <24,7,
24,8 <р <25,4; 23,4 <р <23,9; 24,3 <р <24,9?
567. Можно ли из прямоугольной пластины длиной а мм и
шириной Ъ мм вырезать круг диаметром d мм, если:
а) 84<а<86,
65 <Ъ <67,
62 <d <64;
б) 84<а<86,
65 <5 <67,
71 <d <73;
в) 84 <а <86,
65 <Ъ <67,
66 <d <68?
136
568. Масса алюминиевой пластины, определенная на аналити-
ческих весах с ценой деления 0,0002 г, составляет 2,9062 г.
Какие приближенные значения массы с недостатком и с
избытком были бы получены при взвешивании пластины
на школьных весах с набором разновесов, где масса само-
го мелкого разновеса 10 лгг? 100 лгг? 1 г?
569. Часы с секундной стрелкой показывают 8 ч 28 мин 15 сек.
Какие приближенные значения времени с недостатком и с
избытком можно прочитать по циферблатам часов, не имею-
щих секундной стрелки, при цепе деления, равной:
а) 1 мин\ б) 5 минЧ
570. Оцените длину средней линии треугольника АВС, парал-
лельной стороне АВ, если 10,4 см < |АВ | <10,5 см.
571. Дано, что 5<Сх^6. Найдите границы значения выражения:
а) 0,2х; в) х 4- 3; д) Зх 4-4; ж) — 4-2;
X
б) —0,5х; г) 10—х; е) 2х—5; з) ——.
х 4- 2
572. В каких границах заключено число с. если:
а) —1,6 <4с <0,4; в) 0,4 <2с4~1< 1,2;
б) — 9 <— Зе <1,8; г) 1,8 >0,3—с >1,6?
573. С помощью графика функции у ==3x4-2 найдите множество
значений выражения 3x4-2, если хС[0,5; 1]. Ответ про-
верьте вычислением.
574. С помощью графика функции у—1—х найдите множество
значений выражения 1—х, если х£]—1,5; 0[. Ответ про-
верьте вычислением.
К пункту 23
575. Примените к данным неравенствам теорему о почленном
сложении неравенств:
а) 13,4 >12,3, б) —1,8 <-0,5,
—11,6 >—11,9; 0,3 <0,5.
576. Примените к данным неравенствам теорему о почленном
умножении неравенств:
а) 15 <23, 0,1 <0,2; б) 100 >50, - >
577. Примените к трем данным неравенствам сначала теорему
о почленном сложении неравенств, а потом теорему о по-
членном умножении:
а) 5>4, 3>2, !>-; б) 0,1<0,5, 1<3, 7<ЗО.
3 4
137
678. Докажите, что если а >Ь и c>d, где а. Ъ и с — положи-
тельные числа, a d—отрицательное, то ac>bd. Проил-
люстрируйте эту теорему на примере.
579. Докажите теоремы:
а) (а>Ь и c^»d)=^(a-J-c^b+d);
б) (а>Ь>0 и c>d>O)=>(ac>bd).
580. Докажите, что если а^2 и Ь^5, то:
а) 5а + 2Ь>20; б) аЫ 4 >14.
581. Докажите, что если с>3, то с2+6 >15.
53Л. Какой числовой промежуток образуют значения выраже-
ния а + Ь, если:
а) а£[3; -|-те[ и Ь£[—3; -J-те[;
б) а С—t»; 5[ и Ь€]—те; —8[?
583. Какой числовой промежуток образуют значения выраже-
ния ab, если:
а) а €[12; + те [ и Ь £[-^-; + те Г;
б) aEJO; 0,5] и Ь£]0;2]?
684. Пусть х£ 2; 4-те[ и у С [4; +те[. Найдите множество
значений выражения:
а) 5х-]-2у: б) —4(х+у); в) х(у—1); г) - +
х у
К пункту 29
585. Найдите границы значения выражения:
а) а+2&, если 0<а<1 и —3<&<—2;
б) - а—Ь, если 7<а<10 и 14<Ь<15;
в) 5а |- 7Ь, если 2,5 <а <3,2 и —i<b<0;
8о
г) -—5а, если 1,2<а<1,3 и 2<Ь<3.
4
586. Оцените значение выражения:
а) тп—1, если 2<тп^3 и 11^п^12;
б) т(п—1), если 0,1^т^0,2 и 5,1<п<5,2;
в) — -|-п, если 5с /и<10 и 12<п<15;
т
г) —— , если 7?Ct?Z-<s8 и 13< п<14.
гг \ п
587. Зная, что З^аС^Ю и 1<х<4, найдите границы значения
разности ах—2х и произведения х(а- 2). Сравните резуль-
таты.
138
588. Пусть 3<х<.4 и 1<у<2. Определите границы значения
произведения (х+у)(х—у) и разности х2— у”. Сравните
результаты.
589. Найдите методом границ приближенные значения суммы
разности -— i, обращая каждую из дробей
— и — в десятичную с тремя знаками
тт 11
Д. ' Я проверки выразите сумму ~ -г — и
в виде обыкновенны к дробей и обратите
после запяий.
1 1
разнос гь ------
их в десятичные
590.
591.
с четырьмя знаками после запятой.
Пусть А, В и С — три а очки, не лежашие на одной прямой,
причем 29 мм <|АВ| <31 мм и 39 мм < [ВС I <41 мм. Мо-
жет ли ЛС| быть равным:
а) 30 мм\ б) 60 ммЧ
Найдите границы значения вы ражения:
а) т-\-п—k, если 3,7 <т< 3,9, 2,6 <п <2,7 и
1,2<fe<l,3;
б) — -| 6, если 3,25<;а< 3,26,
2,51<с<2,52;
в) —— , если 3,04<а<;3,05,
Ь — с
0,14<с<0,15.
6,13<Ь<;6,14 и
1,15<Ь<1,16 и
К пункту 30
592. Найдите погрешность приближения числа у числом Ъ,
если:
а) у — 2,8 и Ь=3; в) у = - 2,8 и Ь — — 3;
б) у = 2,8 и b =2,5; г) у = —2,8 и Ь = — 2,5.
593. Какое приближеннее значение числа х = 35,84 имеет по-
грешность, равную: а) 0,04; б) —0,16?
594. Пусть а — приближенное значение с недостатком некото-
рого числа х и (х—а\—модуль погрешности. Найдита х,
если:
а) а- 12 и |х—al—0,3:
б) а =—8 и [х— al = 0,4.
595. Пусть Ъ — приближенное значение с избы тком нексTopoi о
числа х и |х—Ы — модуль погрешности. Найдите х, если:
а) Ъ~ 6 и |х— Ы=0,1;
б) Ь~ — 9 и |х—Ь,= 0,2.
596. Какое из двух приближений числа п лучше: 0,55 или 0,56?
139
597. Какое из четырех приближений числа п =3,14159... лучше:
3,141, 3,142, 3- или 3-?
7 71
598. В практике вычислений значение выражения (1+тп)2
при значениях тп, близких к нулю, находят по приближен-
ной формуле: (14-тп)2^ l-f-2/n. Какова погрешность это-
го приближения? Найдите этим способом приближенное
значение выражения (14-/л)2 и погрешность приближения,
если:
а) тп =0,1; б) тп=О,О5; в)т = —0,1; г)/и = —0,01.
599. При вычислении значений выражения (14-М3 при значе-
ниях тп, близких к нулю, пользуются приближенной фор-
мулой (14-М3~14-Зтп. Найдите приближенное значе-
ние выражения (14~тп)3, если:
а) т =0,001; б) т = —0,001.
600. Найдите приближенное значение выражения (14-тп)(1 +п)
при 7/1=0,03 и п=0,01, пользуясь формулой (1+ тп)(14~тг^
«14- т + п. Какова погрешность приближения? Каков
точный результат?
Решите эту же задачу, считая, что т =0,02 и п = —0,01.
601. Вычислите значение выражения —— при т = 0,002.
14* ттг
Найдите приближенное значение этого же выражения,
, 1
пользуясь формулой-----« 1 — Шк
1-f- т
Решите задачу, считая, что т =—0,001.
К пункту 31
602. Пусть а^.х^Ъ. Какова точность приближения числа х
a -I- b п
числом —-—?
2
603. Покажите на числовой прямой множество приближенных
значений числа:
а) 2,5 с точностью до 1; в) —2,4 с точностью до 1;
б) 0,7 с точностью до 0,5; г) —2,6 с точностью до 0,5.
604. Найдите множество приближенных значений числа —
с точностью до 0,01. Какие из чисел 0,14; 0,15; 0,16; 0,17;
17
0,162; 0,164; —; — принадлежат найденному интервалу?
6 45
Относительно какого из данных чисел можно утверждать,
что оно является приближенным значением числа — с
13
точностью до 0,01?
140
605. Какие из чисел 1,44; 1,45; 1,46;
1,47; 1,463; 1,468 являются прибли-
7
женными значениями числа 1 — с
15
точностью до 0,01?
606. Можно ли на полке длиной 6+0,01 м
и шириной 1,1+0,01 м разместить в
один ряд 8 ящиков, длина которых
1±0,005 м и ширина 0,75+0,005 м?
607. Какова будет сила тока в гирлянде
из 18 последовательно соединенных
лампочек, если сопротивление каж-
дой лампочки 24+2,4 ом, а напряжение в сети 215+15 в?
608. Площадь большого поршня гидравлического пресса
S2 =240+1 см2, а малого 8^ = 12+0,02 см2 (рис. 39). До-
статочно ли силы в 470+5 н на малом поршне, чтобы полу-
чить на большом не менее 9000 н? (Силу трения не учиты-
вать.)
609. Определите, какую мощность разовьет двигательная уста-
новка первой ступени многоступенчатой ракеты в конце
ее работы, если скорость полета к этому моменту равна
3000+10 м!сек при тяге двигателя 106+ 104 н. (Ответ дать
в млн. киловатт.)
610. Достаточно ли 40 кафельных плиток, чтобы облицевать
прямоугольный участок стены длиной 1+0,005 м и шири-
ной 0,8+0,005 м, если кафельная плитка имеет форму
квадрата со стороной 15+0,2 см?
611. Хватит ли одного рулона линолеума, чтобы покрыть пол
площадью 40+0,2 м2, если в рулоне 20db0,05 м при ши-
рине полотнища 2+0,01 м?
Глава III
КВАДРАТНЫЕ КОРНИ
§11. ПОНЯТИЕ КВАДРАТНОГО КОРНЯ
32. Рациональные числа
В курсе математики мы встречаемся с различными числами.
Натуральные числа (целые положительные числа) исполь-
вуются при счете. В множестве N натуральных чисел есть на-
именьшее число — число 1 и нет наибольшего.
Натуральные числа, числа, им противоположные, и нуль сос-
тавляют множество Z целых чисел. В множестве целых чисел
нет ни наименьшего числа, ни наибольшего.
Любое натуральное число является числом целым. Поэтому
множество натуральных чисел есть подмножество множества
целых чисел:
N-Z.
Это можно проиллюстрировать с помощью специальных
схем, носящих название «кругов Эйлера».
На рисунке 40 большой крут изображает множество Z це-
лых чисел, а малый (заштрихованный) — множество N на-
туральных чисел. Всякая точка малого круга принадлежит
большому кругу.
Незаштрихованной части большого круга соответствует мно-
жество целых чисел, не являющихся натуральными, т. е. мно-
жество целых неположительных чисел. Говорят, что множество
целых неположительных чисел яв чяется дополнением множества
до множества целых чисел.
натуральных чисел
Вообще, пусть имеются два множества
А и U, причем А является подмножест-
вом U.
Тогда множество, состоящее из всех
тех элементов U, которые не принадле-
жат А, называется дополнением множества
А до множества U.
Кроме целых чисел, мы изучали так-
же дробные числа (положительные и от-
рицательные).
Целые и дробные числа составляют
множество рациональных чисел.
142
Рациональные числа — это все числа,
которые нам известны. Например,
29, —41, 0, -, — -, 27 — —
5 3 5
рациональные числа.
Множество рациональных чисел обоз-
начают буквой Q.
Так как любое целое число является
в то же время числом рациональным, то
множество целых чисел есть подмножест-
во множества рациональных чисел'.
ZazQ.
Это соотношение между множествами Z и Q показано с по-
мощью «кругов Эйлера» на рисунке 41. Дополнением множества
целых чисел до множества рациональных чисел служит множе-
ство дробных чисел.
Термин «рациональное число» произошел от латинского
слова ratio, что в переводе на русский язык означает отноше-
ние. Любое рациональное число может быть представлено в
виде отношения — , где т — целое число, ап — натураль-
п
ное, причем одно и то же число может быть представлено в ви-
де такого отношения многими способами. Например:
1 — — L -
2 4 10 80*
3 _ —3 —6 —12 —30,
Т ‘ ’ 4 8 24 40*
—9 —18 _ —180,
5 10 100 ’
7 14 21 _ 105,
Т Т'З 15 *
0 _ 0 _ 0
1 8 20'
Заметим, что среди дробей, изображающих данное рацио-
нальное число, всегда имеется одна и только одна дробь, яв-
ляющаяся несократимой. Д1Я целых чисел это дробь со зна-
менателем, равным 1.
612. Какие элементы множества X, где
9
Х = {-100; —14,5; — 2; — — ; 0; 10, 15; 2О±- ,
' з в J
являются:
а) натуральными числами; б) целыми числами ;
143
в) дробными числами;
г) рациональными числами;
д) отрицательными числами;
е) неотрицательными числами?
613. Составьте такое подмножество множества С, где
С={—4—; -3; 0; 6; 8,3; 9; 12},
элементами которого являются:
а) натуральные числа; г) четные числа;
б) целые числа; д) числа, кратные 3;
в) нецелые числа; е) положительные числа.
614. Назовите несколько значений х, при которых истинно
высказывание:
a) x£N; б) x£Z; в) x£Q.
615. Верно ли:
а) (хСУ)—>(х CZ); в) (xCZ)=>(x€Q);
б) (xCZ)=>(x€W); г) (x€y)=>(x^Z)?
616. Даны множества А и U. Убедитесь в том, что Ac. U. Вы-
пишите множество, которое является дополнением мно-
жества А до множества U:
а) А ={—30; —10; 10), П={0; 10; 20; —10; —20; —30};
б) А={—3; 0; 1}, U={- 3; —2; —1; 0; 1; 2; 3}.
617. Пусть Л — множество натуральных чисел, a Q — мно-
жество рациональных чисел.
а) Изобразите с помощью «кругов Эйлера» соотношение
включения для множеств N и Q.
б) Покажите на вашем рисунке штриховкой множество,
которое явл яется дополнением множества N до множе-
ства Q. Назовите неско лько элементов этого множества,
в) Верно ли высказывание: всякое натуральное число
является рациональным?
г) Верно ли высказывание: всякое рациональное число
является натуральным?
618. Какое множество является дополнением:
а) множества четных чисел до множества целых чисел;
б) множества нечетных чисел до множества целых чисел;
в) множества дробных чисел до множества рациональ-
ных чисел;
г) множества положительных чисел до множества рацио-
нальных чисел;
д) множества неположительных чисел до множества ра-
циональных чисел?
144
619. Найдите объединение и пересечение множеств:
a) N и Z; б) Z и Q; в) Q и N.
620. Представьте в виде отношения целого числа к натураль-
ному следующие числа:
а) 4; 25; 0; —27; —100;
б) 0,3; —10,7; -; 2- ; —з1.
’ 5 8 4
621. Представьте число в виде несократимой дроби —, где
п
т — целое число, ап — нат уральное:
а) 36; в) 4,6; д) 15-; ж)
б) —45; г) —10,2; е) —11|; з) —^.
622. Пусть a £N nb(N. Верно ли, что;
а) а + bCN; б) а—b(.N; в) abCN-, г) — CN?
ь
623. Пусть cr CZ и b £Z. Верно ли, что:
а) сМ HZ; б) a—&CZ; в) ab^Z-, г) — С Z?
ь
624. Пусть aCQ и bCQ- Верно ли, что:
а)а-Ь€3; б) а—bCQ; в)аЬ€б; r)-CQ(b^O)?
ъ
625. Выполните действия с рациональными числами:
а) (3,2-5,9).(-2^
\ 1О о <? /
б) (0,18 : (—0,3)—10.2) : (—0,01).
33. Арифметический квадратный корень
Пусть площадь некоторого квадрата 64 см2. Чему равна его
сторона?
Обозначим длину стороны квадрата в сантиметрах через х.
Тогда площадь квадрата в квадратных сантиметрах будет х2.
По условию площадь равна 64 см2. Следовательно, для того
чтобы найти сторону квадрата, нужно решить уравнение
№=64.
145
Существуют два чис на, квадраты которых равны 64; это 8 и
—8. Так как длина стороны квадрата выражается положитель-
ным числом, то она равна 8 см.
Числа 8 и —8 называют квадратными корнями (или корня-
ми второй степени) из числа 64.
Вообще, квадратным корнем из числа а называется число,
квадрат которого равен а.
тт 1 1 ! I ,»
Число — является квадратным корнем из —, так как । — ] =
1 тт 1 - 1
= —. Число — — также ква/i ра’ныи корень из —, так как
. 1 \2 1
\ з; — э*
Квадратный корень из 0 равен 0, так как О2 =0. Этот корень
из 0 единственный.
Квадратный корень из —16 не существует, так как не су-
ществует числа, квадрат которого был бы равен отрицатель-
ному числу.
В рассмотренной задаче условию удовлетворял лишь един
квадратный корень из 64—число 8. Положительный квадрат-
ный корень из 64 называют арифметическим.
Точно так же число —-----арифметический квадратный ко-
3
рень из -i-, число 0,1 — арифметический квадратный корень
из 0,01. Число 0 будем считать арифметическим квадратным
корнем из 0.
Определение. Арифметическим квадратным корнем из
числа а называется неотрицательное число, квадрат которого ра-
вен а.
Для арифме гического квадратного корня из числа а при-
нято обозначение: Знак У называется знаком корня, а
число а — подкоренным числом.
Например, запись ]/4 означает арифметический квадрат-
ный корень из 4. Причем У4=2, так как 22=4 и 2 —неотрица-
тельное число. Отрицательный квадратный корень из 4 есть
число, противоположное У 4. Его обозначают так: —]/Т. Оче-
видно, что —У 4 =—2.
Запись У 1,21 означает арифметический квадр» гный корень
из 1,21; У 1,21 =1,1, так как 1,1®= 1,21 и 1,1 —неотрицатель-
ное число.
Запись ]/(Г означает арифметический квадратный корень
из 0; уо— 0, так как О2 =~0 и 0 — число неотрицательное.
146
Из определения арифметического квадратного корня сле-
дует:
1) Выражение У~а при отрицательных значениях а не имеет
смысла. Например, не имеет смысла выражение /—25, так
как не существует числа, квадрат которого был бы равен отри-
цательному числу.
2) Если выражение У~а имеет смысл, то его значение не-
отрицательно.
626,
Проверьте, что:
а)
и 3 являются квадратными корнями из чис-
б)
в)
г)
числа —3
ла 9;
3
числа — и
7
9
ла —;
49
числа 0,05 и —0,05 являются квадратными корнями
из числа 0,0025;
2 2
числа 1— и —1— являются квадратными корнями из
3 3
л7
числа 2—.
9
3
— — являются квадратными корнями из чис-
627. Докажите, что:
а) число 5 есть арифметический корень из 25;
б) число —7 не является арифметическим корнем из 49;
в) число 0,3 — арифметический корень из 0,09;
г) число 2— — арифметический корень из 5 -;
4 16
д) число 0,6 не является арифметическим корнем из 3,6;
е) число —0,4 не является арифметическим корнем из 1,6.
628. Докажите, что верно равенство:
а) /121 = 11; б) /400 = 20; в) /0^5 = 0,5; г) /0^9=0,3.
629. Какие из данных выражений имеют смысл:
а) /100, /-100 , —/100;
б) УТ, /“У; —У4'; —/(=4р?
630. Найдите значение корня:
а) У 49; 1)/оЖ; ж) и) 1/1g.
б) I 10000; д) /0.16;
в) /2500; е) /6764; 3> / 1 -9 ;
147
631. Найдите значение выражения:
а) 3/9;
б) — 7/6дТ1;
в) 0,1 /400;
. I о?зб
О -з
. /900
д) —
е) /Збио + р 1600;
Ж) Ив + /J;
») /| + /100;
-) /F-F4>
«>/^-/й-
632. Составьте таблицу квадратов натуральных
до 20. Пользуясь этой таблицей, найдите:
чисел от 11
а) /289; в) /169; д) 1 144 + /256;
б) /225; г) /361; е) /400 — ]/ 321.
€33. Решите уравнение:
а) / х — 10; в)/у = 1; д) 8 /6 — 8;
б) /а = 9; г) }т — у; е) 5/с = 0;
.634 Почему уравнение не имеет корней:
ж) 3/х— 1;
з) 2/а = 5.
а) / х = — 5;
б) /х 1-1 = 0;
в) — /х = 2;
г) 5/х =—15?
34. У равнение х2 = а
Рассмотрим решение уравнения х2 =а, где а — некоторое
число. В зависимое ги от значения а возможны 3 случая.
1) При а<0 уравнение х2=а не имеет корней, так как не
существует числа, квадрат которого равен отрицательному
числу.
На рисунке 42 построены парабола у = х2 и прямая у=а.
Рассматривая графическое решение уравнения х2 =а, где а <0,
мы видим, что парабола и прямая не имеют общих точек.
2) При а = 0 уравнение имеет единственный корень, рав-
ный О.
На рисунке 43 показано графическое решение уравнения
х1—а, где а-0. Парабола у— х“ и прямая у—а (при а -0 она
совпадает с осью х) имеют одну общую точку, абсцисса кото-
рой равна нулю.
3) Рассмотрим теперь случай, когда а>0.
Пусть а—9. Решениями уравнения х2 = 9 служат числа 3
и —3, которые являются ква,'ратными корнями из 9. Исполь-
148
зуя знак арифметического корня, их можно обозначить так:
}/9 и —1/9.
На рисунке 44 построены парабола у=х! и прямая у =9.
Прямая пересекает параболу в двух точках, абсциссы которых
3 и —3.
Рассмотрим уравнение х2=2.
Никакое целое число не является его решением. Действи-
тельно, 1а=1, т. е. I2 меньше 2; 22=4, т. е. 22 больше 2. А меж-
ду 1 и 2 целых чисел нет.
Не существует и дробного числа, квадрат которого равен 2.
Доказательство. Допустим, что существует такое дробное число,
квадрат которого равен 2. Тогда это число можно представить в виде несократи-
т
мгй дроби —, где т — целое число, ап — натуральное,
л
/ т \2 т2
Если I — 1=2, то —- = 2 и т- — 2п2.
\п ) п2
Так как число 2п2 четное, то и равное ему число тоже четное. Но если
четным является число пг2, то и число т также четное.
Представим четное число т в виде 2k и подставим выражение 2k вместо т
в равенство иг2 = 2и3. Получим:
(2Л)г = 2па,
4А2 = 2п2,
2Л2 = п2.
Число 2А’ четное, значит, н ра зное ему число п2 такж< четное. Но если четным
является число п2, то чети >е также и число п.
140
Рис. 45
Мы пришли к выводу, что числа тип четные. Но это протш о] ечит предпо-
т
ложевию о том, что дробь —несократима. Значит, не существует дробноги числа,
п
квадрат которого равен 2.
Таким образом, уравнение х2=2 не имеет рациональных
корней.
Однако, построив график функции у — х2 и прямую у *=2,
мы видим, что, так же как и в предыдущем случае, прямая пе-
ресекает параболу в двух точках (рис. 45). Поэтому естествен-
но считать, что уравнение х" —а и в э гом случае имеет два ре-
шения. Но эти решения не являются рациональными числами.
Корни уравнения х2 =2—числа новой природы; их называют
ирра циональными.
Обозначим корни уравнения х2—2, являющиеся иррацио-
нальными числами, так: У 2 и — ]/2 (У~2 — положительное ир-
рациональное число, квадрат которого равен 2; —2 — чис-
ло, ему противоположное). С помощью графика (см. рис. 45)
1о0
числа У2 и —J/2 мы мо-
жем приближенно выразить ра-
циональными числами:
2» 1,4 и —/2 а?—1,4.
Можно доказать, что кор-
ни таких уравнений, как
х2=3, х2=5, х2=6,5, также
не являются рациона л ьными
числами. Их обозначают соот-
ветственно УЗ и —УЗ, У 5
и —У5, и —Г 6,"5. Чис-
ла_/3, -УЗ, У 5, —У 5,
]/б,5, —у 6,5 иррациональ-
ные. Замет им, что к ирра-
ционшьным числам относится
Рис. 46
также число л, выражающее отношение длины окружности к
диаметру.
Итак, уравнение хг =а при а > 0 имеет два решения: Уа
и —У а, которые могут быть рациональными ил и иррациональ-
ными числами (рис. 46).
Мы знаем, что всякому рациональному числу соответствует
точка числовой прямой. Однако обратное предложение невер-
но: не всякой точке числовой прямой можно поставить в соот-
ветст вие рациона, [ьнсе число.
Например, решая графически уравнение х2 — 2, мы указали
на оси х точки, абсциссы которых (У2 и —У 2) не являются
рациональными числами. Вообще, на числовой прямой беско-
нечно много точек, абсциссы которых — ирраиис нальные
чис п а.
Рациональные числа и иррациональные составляют множе-
ство действительных чисел. Каждому действительному числу
соответст вует точка числовой прямой. Сг раведливо и обратное:
каждой точке числовой прямей соответствует некоторое дей-
ствительное число. Таким образом, введя в рассмотрение мно-
жество действительных чисел, мы можем каждой точке числовой
прямой поставит ь в соот ве гствие ее координат у.
Множество действительных чисел принято обозначать бук-
вой R. Так как каждое рациональное число является действи-
тельным, то множество рациональных чисел Q есть подмноже-
ство множества действительных чисел В: QczR. Множество
иррациональных чисел является дополнением множества ра-
циональны к чисел до множества действительных чисел.
Подробнее о понятии действительного числа будет расска-
зано в старших классах.
151
€35. Постройте на миллиметровой бумаге график функции
у — х~ и прямую у =7. Отметьте на оси х точки, абсциссы
которых равны /7 и —У1.
Найдите цля каждого из чисел ]/ 7 и —j/7:
а) два последовательных целых числа, между которыми
закл ючено это число;
б) две последовательные десятичные дроби с одним зна
ком после запя гой, между которыми заключено это число.
636. Используя график функции у=х2, отметьте на оси х точ-
ки абсциссы которых равны У 5, —J/5, ]/4, —/4, ]/з,5 ,
—]/ Tfi.
637. Запишите с помощью знака У корни уравнени я и, ис-
пользуя график функции у=х2, найдите приближенные
значения этих корней:
а) х2=3; б) х2-6,5.
638. Решите уравнение:
а) х2 = 12; г) х2 — 0,04 = 0;
б) х2 =16; д) х2 — ;
в) х2 + 8 = 0; е) | — х2 = 0;
ж) 2хг = -;
8
з) 2-х2 —.10 = 0;
3
и) 5х2 —23 = 0.
636. С помощью рисунка 45 найдите множество решений не •
равенства:
а) х2<2; б) х2 >2.
640. Имеет ли смысл выражение:
а) /11; б) /83,1, В) — ]/186; г) ]Л=36?
641. При каких значениях пере.™°нной имеет смысл выраже-
ние:
а) / х; в) У —25х; д) / х ,
б) У—х; г) /17г; е) У—8х ?
642. Найдите область определения выражения:
а) /х=1; г) /8~+4с; ж)
«> л /S Жт
в) 1/26-1;
1‘,2
35. Тождество (/a)2 = а
Рассмотрим выражение /а, где а^О. По определению
арифметического кгадратного корня значение этого выраже-
ния есть число неотрицательное, и квадрат его равен а. Значит,
при любом неотрицател ьном а верно равенство
(/а)2 = а. (1)
Равенство (1) являе гея тождеством. Действительно, при всех
значениях а, при которых каждое из выражений (/а)2 и а
имеет смысл, их соответственные значения равны.
Пользуясь тождеством (1), любое неотрицательное число
можно представить в виде квадрат а некоторого числа. Например,
2= (/2)1 5=(/5)2, 1 =
Приведем примеры применения тождества (1) в преобразова-
ниях.
Пример 1. Найти значение выражения (0,1 /18?.
По свойству степени произведения
(0,1 /18)2 = (0,1)2 • (/18'".
Так как (/18)2 = 18, то
(0,1)2 • (Г W =0,0118= 0,18.
х2__3
Пример 2. Сократить дробь----------/Г *
„ „ Xs — 3
Представим числитель дроби ------т= в виде разности квад-
х+УЗ
ратов:
х=— Л-х2— (/3):.
Тогда
х°-3 = х» - (/3)2 = С 4 /3)0 ] F) = х _ -3
х + /3 х -f- р 3 х } 3
643. Найдите кгадраты чисел:
/25, /«Г, ]/2, /3, —/4, рЬ, — /б, —/1,3.
644. Найдите значение выражения:
а) (/7)2; в) (—]/ 2б)г; д) 10 /2 . /2; ж) (0,5 /в/
б)/7 /7; г) -/26' /26; е) (3 |/б)’; з) (—2/15)2:
1ЬЗ
И) (£yi3)!;
ч IVз V /i з V
к) 1 V ] ; л) [ Ь? ; м)
\ 2 / \У6 /
645. Представьте данное выражение в виде квадра а:
а) 9; в) 6; д) 2,5; ж) а, где а>0;
б) 64; г) 10; е) 0,25; з) 45, где Ь>0.
646. Сократите дробь:
а)----; б)---------L; в) — г)________________— .
/2 J 5 ' 3’ 3] а
647. Разложите выражение на множители, вынося общий мно-
житель за скобки:
а) З + рТ; в) 3/11—11; д) а—5Уа;
б) 6-/6; г) 2/7/7; е) Ь-ЗуТ.
648. Сократите дробь:
а)К1 + 8; б) в)^П + 12; г)
8 ) 2 7/12 5/7
649. Докажите, что значение выражения есть число рацио-
нал ьное:
а) (1 + V2 ) (1 — V 2 ); г) (/3 / /б’ )(/б — /3);
б) (] 5 - 2) (/б + 2); д) (2 /3 - 1) (2 /3 / 1);
в) (У ‘7 + /2 )(/7 — V2 ); е) (/5 4 2 /10)(/5 —2/10)-
650. Представьте выражение в виде разности квадратов двух
выражений и разложите его на множители:
а) х‘ 9; в) 4а2—7;
б) а2—3; г) 16b2-11;
д) с—1, где ОО;
е) 5—а, где а >0-
651. Сократите дробь:
. — 4
а)------;
аЧ-2
б)
+—а
с — /6 *
в) ——— ;
/л 4 /2'
а — Ь
У а — уb‘
652. Ренгите неравенство:
а) X*—3<0;
б) х2 >7.
154
36. Приближенные значения квадратных корней
из положительных чисел
Мы знаем, что квадратный корень из положительного числа
может быть числом иррациональным, и в этом случае его нель-
зя представить ни в виде целого, ни в виде дробного числа При-
мером могут служить такие числа, как ]/5, У10, ]/30. На
практике иррациональные числа обычно заменяют их прибли-
женными значениями, выраженными десятичными дробями.
Рассмотрим прием, с помощью которого можно найти при-
ближения /5 с любой степенью точности.
Так как
22<5<32, то
2 <|z5 <3 (рис. 47, а).
Число 2 — приближенное значение ]/ 5 с недостатком, а
число 3 — с избытком, причем эти числа являются приближен-
ными значениями ]/5 с точностью до 1. Действительно,
|]/5— 2|<3—2, т. е. Ц/5—2| <1, и
11/5-31 <3-2, т. е. 11/5--3|<1.
Разделим отрезок [2; 3], длина которого равна 1, на 10 рав-
ных частей. Получим отрезки:
[2; 2,1], [2,1; 2,2], [2,2: 2,3]. [2.9. 3].
Будем последовательно возводить в квадрат числа 2; 2,1; 2,2;
2,3; 2,4; ... , пока не получим числа, большего 5.
Из таблицы видно, что
2,22< 5< 2,32,
следовательно,
2,2<]/5<2,3 (рис. 47,6).
X 2 2,1 2,2 2,3
2 X2 4 4,41 4,84 5,29
X
3
№
У5
A) I I ' '__________________I ,, I , I ..„,1, , I,-------1 ...... 1.
' 2 2,1 2,2 23 22, 2,5 25 Г "в 29 3
Ь} Ji ни,, ........iln/jindHMjiiiXiiiiiiiiliiiiiiiiiliiiiiiixili^iwjli.iiiitiiili.....nil
' 2 2,7 2/ J
2,23 2.24
Рис. 47
1Ь5
Число 2,2 — приближенное значение /J> с недостатком, чис-
ло 2,3—с избытком, причем каждое из этих чисел является при-
ближением V 5 с точностью до 0,1. Действительно,
1} 5—2,21 <2,3—2,2, т е. |/5—2,2| <0,1, и
|]/5—2,3| <2,3—2,2, т. е. || 5—2,31 <0,1.
Чтобы найти приближенные значения /5 с точностью до
0,01, нужно отрезок [2,2; 2,3] длиной 0,1 снова разделить на
10 р 1вных частей и выделить отрезок длиной 0,01, который со-
держит точку с координатой /5.
Из таблицы видно, что 2,232<.5 < 2,24\ следовательно,
2,23 </5 <2,24 (рис. 47, в).
х 2,2 2,21 2,22 2,23
2,24
х214,84 4,8841 4,9284 4,9729
5,0176
Число 2,23 — приближенное значение /5 с недостатком, а
число 2,24 — с избытком, причем каждое из этих чисел являет-
ся приближением /5 с точностью до 0,01.
Анало] ично найдем отрезок плиной 0,001, который содержит
точку с координатой /5:
2,236 < /5 < 2,237.
Числа 2,236 и 2,237 — приближенные значения /5 с точное гью
до 0,001; 2,236 — приближение с недос гатком, а 2,237 — при-
ближение с избытком.
Точно так же находят приближенные значения 1^5 с недо-
статком и с избытком с точностью до 0,0001, до 0,00001 и т. д.
653. Докажите, что:
а) 3< /12 <4;
654. Сравните числа:
б) 7.1 < ] 51 < 7,2.
а) /7 и 3;
б) 7 и /50;
в) /5 и 2,2:
г) 3,3 и /11;
д) J 6,25 и 2,5;
е) /4721 и 2,1.
655. Найдите два
последовательных целых числа, между ко-
торыми заключено число:
а) /27; б) /9,2; в)/0,1; г) / 35,4; д) /120; е) /148.
1бв
656. Найдию две последовательные десятичные дроби с одним
знаком после запятой, между которыми заключено число:
а) |/3; б) —1'3; в) 1/18; г) — ^18.
657. С помощью рисунка 47 выя< ните, какое из двух чисел яв-
ляется лучш им прибл ижением ]/5:
а) 2 или 3; б) 2,2 или 2,3?
658. Не Идите две последовательные дес ятичные дроби с одним
знаком после запятой, между которыми заключено число
] 2. Какая из найденных дробей является лучшим при-
ближением ]/ 2?
659. Что больше:
а)1'29 или 1/10 + 1/19; б) 1^27 или 1/20 + 1/7?
27. Нахождение приближенного значения корня методом
последовательных приближений
Пусть требуется вычислить J 2 с точностью до 0,0001. Ясно, что 1<J^2 <2.
Примем за первое приближение число 1,
Тогда
/2=1+ о,, (1)
где fli — погрешность первого приб тижени | причс я
0 < ел < 1.
Возведем обе части равенства (1) в квадрат, получим:
2=1 + 2cj + i*|.
Так как oi меньше елиниоы. то число О| меньше ai. Отбрасывая это число, мы
получим приближенное равенство:
2 ~ 1 + 2с
Из этого равенства найдем прпближе: ное значение <ц, получим, что aj ~ 0,6.
То: да
J/2 = 1 + 0,5 = 1,5.
За второе приближение примем найденное значение корня, т. е.
/2 = 1,5 4- а2,
Где д2 — погрешность второго приближения.
Чтобы найти более точное значение корня, понте риы описанный процесс
По. 1учим:
2 = 2,26 + За2 Ь а?,
ПЛ'1
2 = 2,2b + За2,
157
откуда
аа ~ — 0.083.
Следовательно,
У 2 ~ 1,6 — 0,083 = 1,417.
Приняв найденное приближенное значение корня за третье приближение, снова
ПОЛУЧИМ!
У 2 = 1,417 + а3,
где ав — погрешность третьего приближения.
Повторив весь процесс еще раз, найдем:
оэ s —0,00278
ж
У2 = 1,417 — 0,00278 = 1,41422.
Аналогичным путем найдем погрешность четвертого приближения. Получим»
ах ~ —0,000006 ...
Так как |а<| < 0,00001, то найденное приближение к У2 дает значение корня о
требуемой точностью.
Если обозначить последовательные приближения к } 2 через yi, у2, уй
я I. д., то можно заметить, что прь нахождении каждого следующего приближе-
ния использовалось предыдущее. Действительно, если
У 2 = Ух + Oi,
где ух — первое приближение и сгт — его погрешность, то
2 = 6'1 + 2yiOi -f- а|,
или
2 ~ v\ + 2yiai.
Отсюда
2 —У?
2У1
И
2-И У? + 2
Ра = У1 + ~7-- =—-------•
2^1 2yj
Если
У 2 = у, + «„
ОД® Уч — второе приближение и а2 — его погрешность, то получим?
2 —У2
Ж
2 — &2 Vz + 2
Уз У 2 + ~— = -----------.
2Ра 2уа
Вообще, если yn_j — приближение, полученное на (п — 1)-шаге, то
Уп । + 2 1 / 2 \
Уп = ~2и — ’ и™ Уп = -\ Уп х + „ (п = 2, 3, 4, ...).
Уп— 1 2 \ Уп 1 /
168
Эта формула позволяет находить каждое следующее приближение к /2,
если известно непосредственно предшествующее приближение. При этом необ-
ходимая точность достигается при совпадении двух последовательных прибли-
жений в пределах заданной точности. Проиллюстрируем это на гримере.
Пусть требуется вычислить /Б с точностью до 0,001. Формула для нахожд»"
иля последовательных приближений к /б будет иметь вид:
1 / 5
где л = 2, 3, 4, ...
За у, примем число 2, тогда
1 б\
у. = — 2 4- —1=2,25,
2 \ 2 /
1 / 5
у3 = — 2,25 +---------
2 \ 2,25
—(2,25 + 2,2222) = 2,2361,
= -| ( 2,2361 +
5 \ 1
------- = — (2,2361 + 2,2360) = 2,23605.
2,2361/ 2 '
Мы видим, что третье н четвертое приближения совпадают с точностью до
0,001. Следовательно, уже на третьем шаге был получен ответ на вопрос вадачи.
Приведенные рассуждения можно распространить на случай получения
последовательных приближений к корням из любых положительных чисел.
Так, для Ух формула для получения последовательных приближений будет
иметь вид:
1 / X \
У а = Т (Уп-14------- • 3- 4- -
z \ Уп-1 /
Замечание. За первое приближение, вообще говоря, можно принять
любое положительное число. Но если мы хотим получить нужный нам результат
быстрее, то следует по возможности выбирать yi точнее (с меньшей погрешностью).
660. Найдите методом последовательных приближений значение корна о
точностью до 0,001:
a) /26; 6) /36^5 в) /525] г) /95,28.
38. Таблица квадратов
В «Четырехзначных математических таблицах* В. М. Бреди-
са помещена таблица квадратов чисел. В этой таблице даны
квадраты чисел от 1 до 10 с шагом 0,001. Такие числа записы-
ваются не более чем четырьмя цифрами.
В первом столбце таблицы помещены числа от 1 до 10 с ша-
гом 0,1, т. е. числа, записываемые не более чем двумя цифрами.
159
В соседнем столбце даны точные значения квадратов этих чи-
сел. Например,
2,22 =4,840; 3,42=11,56; 6,02 =36,00.
Кроме рассмотренных двух столбцов, таблица содержит еще
девять столбцов, помеченных сверху и снизу цифрами от 1 до 9.
Эти столбцы используются для нахождения квадратов чисел от
1 до 10 с шагом 0,01, т. е. чисел, записываемых не более чем
тремя цифрами.
Покажем на примере, как находятся квадраты таких чисел.
Пусть требуется найти 7,342. В первом столбце находим число 7,3
(первые две цифры числа 7,34). Квадрат числа 7,34 помещен в
той же строке, на пересечении этой строки и столбца под номером
4. Он равен 53,88.
Полученный результат является приближенным. Какова
точность этого приближения?
Найдем значение выражения 7,342 обычным умножением:
7,342 =7,34 • 7,34 =53,8756.
Мы видим, что приближенное значение числа 7,342, равное
53,88, получено округлением до сотых числа 53,8756. Модуль
погрешности в этом случае не превышает половины единицы
разряда, до которого проводилось округление, т. е. половины
от 0,01. Таким образом, мы получили приближенное значение
с точностью до 0,005.
Вообще, приближенные значения квадратов чисел от 1 до 10
с шагом 0,01 получены в результате округления соответствую-
щих точных значений и отличаются от них не более чем на поло-
вину единицы разряда, до которого проводилось округление.
Например, 7,632^58,22. Модуль погрешности полученного
приближенного значения не превышает половины от 0,01, т. е.
0,005. Значит, 58,22—0,005 <7,632 <58,22+0,005, т. е. 58,215<
<7,632<58,225.
Для нахождения квадратов чисел от 1 до 10 с шагом 0,001
в таблице справа помещены еще 9 столбцов. Это так называемые
столбцы поправок.
Найдем, например, значение выражения 2,3422. На пересе-
чении строки «2,3» и столбца «4» помещен квадрат числа 2,34:
2,345,476. В столбце поправок под номером 2 находим на
пересечении с этой же строкой число 9, которое прибавляем к
последней цифре числа 5,476. Получаем: 2,3422^5,485.
Приведем еще пример. Пусть требуется найти 8,43722. Так
как в таблице даны квадраты чисел от 1 до 10, записанных с
помощью не более четырех цифр, то основание степени придется
округлить до тысячных. Получим: 8,43722«8,4372^71,18.
Мы разобрали на примерах, как с помощью таблицы находят-
ся квадраты чисел от 1 до 10 с шагом 0,1, 0,01 или 0,001. Эта
же таблица может быть использована для нахождения квадра-
160
тов положительных чисел, меньших 1 или больших 10. Для это-
го достаточно представить данное число в стандартном виде,
т. е. в виде а-10”, где <10 и п — целое число.
Найдем, например, значение выражения 342. Число 34 в 10
раз больше числа 3,4. Квадрат числа 3,4 находим по таблице:
3,42 = 11,56. Тогда
342 = (3,4 • 10)2 =(3,4)2 • 102 = 11,56 100 = 1156.
Приведем еще примеры:
0,3572 =(3,57 • 10-1)2 =3,572 • 10~2^12,74 10'2 =0,1274;
432,72 =(4,327 • 102)2 =4,3272 • 10 ‘^18,72 104 =187 200.
661. Найдите с помощью таблицы квадраты чисел:
а) 1,3; 4,7; 2,8; 5,7; 8,3; 7,2; 9,6;
б) 2,34; 5,12; 8,37; 9,56; 3,04; 6,19;
в) 1,243; 4,325; 7,239; 8,127; 6,571; 9,044.
662. Найдите значение выражения 1,0122 по таблице и вычисле-
нием. Определите модуль погрешности приближенного
значения, найденного по таблице.
663. Округлите число до тысячных и найдите его квадрат, поль-
зуясь таблицей:
а) 3,1238; б) 1,0058; в) 4,1405; г) 6,3752.
664. Найдите по таблице квадраты чисел:
а) 5,243; 52,43; 5243; 0,5243;
б) 1,315; 0,01315; 131,5; 13150;
в) 345; 290; 1281;
г) 0,351; 0,00425; 0.012482.
39. Таблица квадратных корней
В «Четырехзначных математических таблицах» В. М. Бради-
са помещена таблица значений арифметических квадратных кор-
ней. Устройство ее сходно с устройством таблицы квадратов.
Приближенные значения корней даны для чисел в промежут-
ке от 1 до 100. Причем числа от 1 до 10 берутся с шагом 0,001,
а от 10 до 100 — с шагом 0,01.
Покажем на примерах, как с помощью таблицы находятся
приближенные значения арифметических квадратных корней.
1. Найти значение выражения |. 5,6.
В первом столбце находим число 5,6, а в соседнем столбце
на той же строке читаем приближенное значение | 5,6:
| 5,6^2,366.
G Алгебра, 7 кл.
161
2. Найти значение выражения } 23,5.
В первом столбце находим число 23 и в этой же строке на
пересечении ее со столбцом под номером 5 читаем результат:
| 23,5 « 4,848.
3. Найти с помощью таблицы значение выражения /45,34.
В первом столбце находим число 45, затем на пересечении
этой строки и столбца под номером 3 находим приближенное
значение j 45,3:
/45,3^ 6.731.
В столбце поправок под номером 4 в той же строке нахо-
дим число 3. Прибавляя поправку к последней цифре числа
6,731, получаем: /45,34^6,734.
Заметим, что приближенные значения корней, приведенные
в таблице (без учета столбцов поправок), имеют модуль по-
грешности, не превышающий половины единицы последнего
разряда в записи приближенного значения корня.
Например, число 2,796 является приближенным значением
/7,82 с точностью до половины от 0,001, т. е. с точностью до
0,0005:
/7^82=2,796+0,0005.
С помощью этой же таблицы находят квадратные корни из
положительных чисел, меньших 1 или больших 100. Рассмотрим
примеры.
4. Най ги значение выражения ] 245.
Число 245 в 100 раз больше числа 2,45, квадратный корень
из которого можно найти по таблице. Поэтому
/245 = /2,45 101.
Легко проверить, что
У 2.45Л02 = /245 10.
Действительно,
(/245-10)2 = (/24б)г 10 2,45 102,
т. е. | 2,45 10 — неотрицательное число, квадрат которого
равен 2,45 102. Значит, / 2,45 10 - арифметический квадрат-
ный кореньиз 2,45 102, и равенство ) 2,45 10г=] 2,45 -10 верно.
Значение выражения /2,45 находим по таблице:
У 2,45 л 1,565.
Тогда
/245 - | 2’45 10 л 1,565 10 = 15,65.
162
5. Найти приближенное значение выражения ] 0,235.
Число 0,235 в 100 раз меньше числа 23,5. (Квадратный ко-
рень из числа 23,5 можно найти по таблице.) Поэтому
/0,235 = /23,5- 10 2.
Легко убедиться, что
/23,5 • 10-* ] 2-М 10-1.
Значит,
/0,235 = /23,5 101 ' 4.848 • 10 ’ 0,4848.
Вообще, чтобы найти корень из положительного числа, мень-
шего 1 или большего 100, следует представить это число в виде
а 102':, где 1^а<100 и k —целое число, и воспользоваться
формулой /а 103* = /а • 10'.
665. Пользуясь таблицей, найдите арифметические квадратные
корни из следующих чисел.
а) 4,3; 6,2; 8,9. 10; 50; 75;
б) 1,25; 14,7; 20,8; 40,1; 83,2;
в) 1,143; 4,835; 60,37; 81,92;
г) 1,0058; 6,83251; 20,156.
6S6. С помощью таблицы найдите приближенные значения
выражений:
а) ] 'бД; б) /б! г) | 2,07; д) 1 з/5; ж) //153; з) | 28,04; к) | 37,21; л) /53Д9;
в) /48; е) | 5/8; и) | 66,38; м) ] 87.25.
667. Представьте в виде а -10 , где 1^а<100 и k СИ, число: а) 115; в) 1230; д) 0,007; б) 692; г) 0.03; е) 0,00059.
668. Пусть 1 3 где k £Z, а) /300; и 1 30 *= р. число: б) /3000; Представьте в виде 10*а или 10' Р, в) | U.3, г) | 0,03.
669. С помощью таблицы найдите приближенные значения кор- ней: а) /6,52; /652; ] 6520; 1 0,652;
б) /3,278; /3278; /0,03278; /327800.
6*
J63
670. Найдите приближенное значение выражения:
а) /345; в) /1281; д) |/25740; ж) /0,0724;
б) /290; г) 1- 3720; е) ] О 351, з) /0,00425.
671. Найдите с помощью таблицы значение выражения и дока-
жите, что найденное значение является точным:
а) | 3,61; в) 1 676; д) /1521;
б)} 0 0256; г)/961; е) | 2,04.
672. Для каждого из чисел ) 7 и 1 3 укажите с помощью таб-
лицы две последовательные десятичные дроби с одним зна-
ком после запятой, между которыми заключено это число.
Методом границ найдите приближенное значение выраже-
ния:
а) | 7 —1,5; б) 1 3 + 0,2; в) | 7 | 3; г) J 7 /3
673. Найдите приближенное значение выражения | 3,1 -| /15,7.
(В качестве границ чисел 1 3,1 и I 15,7 возьмите две по-
следовательные десятичные дроби с одним знаком после
запятой.)
40. График функции у = 1 х
Каждому неотрицательному значению х соответствует един-
ственное значение выражения I х, Формулой у | х задается
функция, областью определения которой служит числовой про-
межуток ГО- т<»[.
Если х- 0, то у-0, следовательно, начало координат при-
надлежит графику функции. При х) 0 значение выражения х
положительно. Поэтому график функции у | х расположен в
I координатном углу.
Для построения графика функции у | х воспользуемся таб-
лицей:
X 0 0,5 1 2 3 4 5 6 7 8 9
0 0,71 1 1,41 1,73 2 2 24 2,45 2,65 2,83 3
Большему значению аргумента в этой таблице соответствует
большее значение функции. Можно доказать, что, вообще, если
л, и х, неотрицательные числа и хЛ>х1, то Г xs>| Xf, т. е.
функция у I х возрастает на всей области определения.
164
Рис. 48
Для доказательства составим разность выражений ) х2 и | х, и выполним
такие преобразования, в результате которых можно б] дет определить знак этол
разности:
, (| ^7 |/Х1)(|<^ Г Х|) х2 — х,
I Х2 I X, - _ — -- -----•
I Х2 | Xt I Xj I I X|
Так как x« > xt > 0, то x2 — Xi > 0 и ) х» -|- ) xL > 0. (Каждое из выра-
жений | X! и | x2 имеет смысл, причем t xt 0 и ] х5 > 0 )
х2 х, —
Значит, значение дроби —-----=^, а вместе с ним и значение разности | х» —
I х, -j | xt
— рх, положительно. Из неравенства j-Gr» — |z xt > 0 следует неравенство
) х2 > I х.
Функцию, кет эрая во >растает на всей области определеяи я,
принято называть возрастающей. Итак, функция у~] х воз-
растающая.
Построив в координатной плоскости точки, коордлнаты ко-
торых занесены в таблицу, и соединив их главной линией, полу-
чим график функции у Lx (рис. 48).
674. С помощью графика функции г j/x найдите значение
выражения | х, если х 2,5; 3; 5,5: 6: 8,4.
675. С помощью графика функции у =1 х найдите значение
переменной х, если 1 х 1,2; 1,7; 2,5.
676 Принадлежит ли график^- функции у J х точка А (64; 8),
В (81. 9) С (100: —101?
165
677. С помощью графика функции у~Ух сравните числа:
а) 1 1,7 и | 2,3; в) |л 2?5 и 2;
б) ] 4,5 и |Л3,е; г) | 6Д и 3.
678. Что больше:
a) ]/ 68 и. >и | 72; б) 8 или ] 60?
679. Оцените значение выражения У~х, если 0<^^4,
На какое множес гвп функция у -)/* итображает проме-
жуток:
а) [0; 9]; б) [100; 400]; в) ]0,01; Г?
680. Найдите границы значения выражения:
а) Ух+3,
б) I х—1,
если 0,16 <х <0,25;
если 0,255^*4^2,56.
681. С помощью трафика функпии у~У х выясните, пси каких
значениях х обращается в истинное высказывание пред-
ложение:
а) Ух — 2;
б) р х > 2;
в) Ух < 2.
682. Решите уравнение и неравенства:
а) ] гх — 10,
б) Ух = У7,
] х > 10.
Ух» 7,
] х < 10;
Ух< к 7.
683. Решите неравенство:
а) Ух >• 3;
б) j/х < 3;
в) 1<]/х<3;
г) Ух У5;
А) У < Кб;
е) | ' 2 <]/х </5.
684. Решите графи* ески уравнение ]/ х- 6 - х.
685. В какой координатной четверти расположен график функ-
ции:
а) У= ~Ух; б) у =]<=*?•
JK6
§ 12. ПРЕОБРАЗОВАНИЕ ВЫРАЖЕНИЙ, СОДЕРЖАЩИХ
КВАДРАТНЫЕ КОРНИ
41. Тождество = | х |
Сравним соответственные значения выражений ] х2 и х.
Из определения аоифметического квадратного каряя следует,
что при х^?0 соответственные значения этих выражений равны.
Напригтер,
при х - 6 | 'х* = J 6’ = 6,
при х — 0 У~х2 — У О1 = О.
Таким образом, при х^О верно равенство
У х2—х.
Если х <0, то соответственные значения выражений ] х- и
х — противоположные числа.
Например,
при х = —5
при х —0,3
Ух^=У( 5)г = 5,
Ух1 = У (—0,3)2 = q,3.
Значит, при х <0 верно равенство
] X — -----X.
Можно заметить, что при любых значениях х значение выра-
жения Г х* совпадает со значением выражения |х|, т. е. в^е
соответственные значения выражений ] х! и |х| равны, значит,
равенство
] л = |*| (1)
является тождеством.
Рассмотрим примеры преобразований выражений с исполь-
зованием тождества (1).
1. Найти значение выражения 0,?] х- гри х = —24,5. Так
как х2 = 1x1, то
0,2|> х2: 0,2 |х|=0,2-1—24,51 0,2-24,5- 1,9.
167
2. Упростить выражение ) 0,09а2, если а>0.
Представим подкоренное выражение | 0,09а2 в виде квадрата
одночлена и воспользуемся тождеством (1):
| 0,09а2 = | (0,3а)2 = 10,3а | = 0,3 • | а |.
При а^0 |а]=а, следовательно, |/б,09а2 —0,3а.
3. Упростить выражение ~| | а8.
Представим подкоренное выражение а8 в виде квадрата одно-
члена: а8 =(а4)2. Тогда
1| = W= v-|“4l-
ЛЛ А4
Значение выражения а4 неотрицательно при любом значении
переменной а. Значит, при любом а |а4|=а4
и -- } а8 = — а4.
2 v 2
686. а) При каких значениях переменной х из множества
{3; —4; 0; 10; —5} верно равенство | х2=х?
б) При каких значениях переменной с из множества
{4; —2; 7; —7; 0; —9) неверно равенство | с2—с?
в) При каких значениях переменной а из множества
{2; 9; —6; 1; —8} верно равенство ]/а2 = —а?
г) Назовите несколько значений переменной у, при кото-
рых неверно равенство ] у2——у.
687. Вычислите:
а) | (0,1)-; г) I (f,7p; ж) ]<(-23р;
б) | (—0,4р; д) | (1,9)-'; з) I 52г;
в) И(-0,8р; е) } и) |/ (=61р.
688. Найдите значение выражения:
а) 1 х2 при х — 22; — 35; —1-|-; 0;
б) 2] а2 при а = —7; 12;
в) 0,1 ] у2 при у = —15; 37.
689. Замените выражение тождественно равным:
в) j 9Ь2; д) | 0,01а ;
г) КЗбх2; е) Кб,04с2.
168
690. Преобразуйте выражение:
a) ]/с2,
б) |Ла2,
в) j/x2,
если с 0;
если а > 0;
если х < 0;
г) ] 4а2,
Д) |<07256%
если а 0;
если b 0;
если х < 0.
691. Замените выражение тождественно равным:
а) У (а - 1)%
б) 2‘Р;
в) Г х2 4- 2х 4-1;
г) Г 4f/2 — 4i/4- 1.
692. Преобразуйте выражение:
а) | (х — 4)2, если х 4;
б) ]/(а — 2)2, если а < 2;
в) | (3—7П)2, если т 3;
г) I (7 4- У)\
д) | (ЮТО2,
е) | (тГГ4р,
если у < —7;
если с —10;
если п < —4.
693. При каких значениях переменной верно равенство:
а) ] х2 — 2х 4-1 — х — 1;
б) К4а2 + 4а -Г1 = 1 4- 2а;
в) ]гс2— 6с 4- 9 = 3 — с;
г) ] х1 4- 2х" 4- 1 — х2 4-1?
694. Представьте подкоренное выражение в виде квадрата од-
ночлена и найдите значение выражения:
a) J. 24; в)
б) /3"; г) У"(-2)4;
д) 3 У(-2)‘;
е) -2|/С=10)г;
ж) 0.1J (-3)8;
з) 100 | Тб,!)™.
695. Упростите выражение:
если т 0;
если у < 0;
если х < 0;
если а > 0.
696. При каких значениях переменной верно равенство:
а) У у1 = — у;
б) I у‘ = у2;
в) pGc6 = х3;
г) с10 — —с5;
д) I а14 = —а7;
е) УУ = Ь4;
ж) ) х4=—х1;
з) уУ7 = Ь“?
697. Упростите выражение:
а) 1 (| 2-1)-’;
б) ] (1 -1 З)2;
в) I (|/11-1 io)2;
г)/(|<5-Г8)<
169
698. Решите уравнение:
а) V*2 = 4; в)] (х 1)! = 1;
б)]/ха 1-0; г)К(^77-3.
699. Постройте график функции у | х . На каком множестве
эта функция возрастает ?
42. Теорема о корне из произведения
Сравним значения выражений ] 81-4 и] 81 ] 4. Перемножив
числа 81 и 4, получим, что ] 81-4—} 324. Так как 324 =182, то
1 324=18. Таким образом,
]/8Ь4 = 18
Найдем теперь значение выр гжения 1 8i ] 4:
У81 |/4 = ] 9: - у 2- - 9-2 — 18.
Значит, । 81 4 = , 81 - } 4.
Теорема 1 Если а^О и b Ч, то ] ab 1 а 1 Ь.
Для того чтобы доказать, что равенство Уab | а [ Ь, где
а^О и t>^0, верно, достаточно убедиться в том, что значение
выражения ] a-J b неотрицательно и квадрат его равен ab.
Значение выражения ]/ а ]/ b неотрицательно, так как при
а ^>0 и Ь ^0 каждое из выражений \ а и 1 b имеет смысл и
принимает неотрицательное значение.
Найдем квадрат произведения ] а ] Ъ. получим:
(^a.}/b)s = (l/T)2.(l^r=ab.
Итак, на основании определения арифметического квадрат-
ного корня равенство ] ab=] а] Ь, где а^О и Ь^О, верно.
Таким образом, корень из произведения неотрицательных
множителей равен произведению корней из этих множителей.
Теорема верна и в том случае, если число мн< жителей под
знаком корня больше двух.
Приведем примеры применения этой теоремы.
1. Найти значение выражения У 64 0,04.
Воспользуемся доказанной теоремой:
У64 • 0,04 = [61 • ) 0.П1 -=<8.0,2 = 1,6.
2. Найти значение корня | 32 98.
Преобразуем подкоренное выражение:
32-98 (16 2) (49 2) 16-49 4.
170
Для нахождения значения выражения /16 49 4 восполь-
зуемся теоремой о корне из произведения неотрицательных
множит елей:
[ 16 49 ^4 = /16 • /49 /4 = 4 7 2 = 56.
3. Представить в виде одночлена выражение | 49а5Ь6, где
а <0 и b >0.
По теореме о корне из произведения неотрицательных мно-
жителей
] 49а:Ь6 = У49 у а- /б«= 7 | а | • | Ь3 |.
При с<0 и 0 | а | — — о и 1&?1 — 6*. еларвательно,
/ 49а"Ь6 = 7 • (—а) Ь3 — — 7аЬ3.
4 Найти значение произведения | 20 - ) 5.
Запишем формулу J ab = а - У Ь, где а>0 и Ь>0, иначе
У а • ] Ъ ] аЬ.
Тогда
/20 /5 = /100 = 10.
700. Найдите значение выражения:
а) /100 • 49; г) /81 -400;
в) /121 • С4; Д) У * • 81;
"> ( 9 Тй: .) у fg.
701. Найдите значение корня:
а) | 81U 40; в) /7м • 48;
б) |/ 72 82; г) [ 4,9 • 360;
702. Вычислите:
ж) /0,36 • 169;
з) /121 0,49:
и) /1,44 0 16;
к) ] ' 2,25 • 0,04.
д) /2,5 • 14,4 ;
е) | 90 6-4.
а) / 13» —12'; в) ], 172 — 82,
б) /313- — 312»; г) /117-— 10EF.
703. Сравните значения выражений:
а) /5?4 12г и 5 1-12; б) /10' — 62 и 10 — 6.
171
704. а) Найдите катет прямоугольного треугольника, если ги-
потенуза равна 41 см, а другой катет — 40 см.
б) Найдите площа, (ь прямоугольника, если одна из его
сторон равна 56 см, а диагональ — 65 см.
705. Представьте выражение в виде произведения корней:
a) J 15; б)/21; в) /7а; г)/=3с.
706. Разложите выражение на множители, вынеся за скобки I 2:
а) /10 4-/2; б)/6->10; в) ] 18+-/22; г) 2-/14.
707. Сократите дробь:
а)1 10-/5;
I 5
б) /2! 4/14; в) /б-/18. г) /15-5
/7 | 6 | 6 — у 10
708. Вычислите:
а) /2° - 3'; б) /5~4- 2~4; в) /4~2 10‘; г) | 11* • 10~в.
709. Вычислите значение выражения, разлож ив вначале под-
коренное выражение на множители:
а) | 576; б) | 1225; в) /1936; г) ( "19600.
710. П релсгавьте выражение в виде одночлена:
а) I 9а', где а 0;
б) | 25с1, где с^ 0;
в) /О,ЗбЬ2, где Ъ < 0;
i) 1 81 ухп, где у СО;
д) 1 а-с2, где ас 0 и с > 0;
е) /0,3652с4, где b С. 0;
ж) у/а®54, где а < 0;
з) У а1 хххи, где а > 0 и х < 0.
711. Используя формулу J а | b I ab, гдеа^О и Ь'^0, най-
дите значение произведения:
а) I М 8; д) Г 21 -> 2Г; у
б) | 10 • | 40; е) | 13 | 52;
в) р 12 •) 3; — . г/2 1/^3
п)27 |3-; ")1 Нз-
172
712. Найдите область определения выражения и упростите его:
а) х Г х • VX' в) | а5 J аа,
б) - V У I 'у*-, г) 4-1 F
у ЬЬг
713. Найдите область определения каждого из выражений и
выясните, какая из них является подмножеством дру! ой:
а) ] х(х —2) и Vx V х — 2;
б) ) 'х2 — 1 И \^Х + 1 • — 1.
43. Теорема о корне из дроби
Сравним значения выражений
<25 1 25
1 й я , я
/25 ) '5* 5
|/Ы /9а 9
25 1 25
81 1л
Теорема. Если а О и Ьу 0, то т —— —° •
У ь } Ь
Доказательство. Если с>0 и Г >0, то выражение
Vt
имеет смысл и принимает неотрицательное значение, так как
___ _______ /“
J'a>0 и V 0 >0. Докажем, что квалрат выражения -
О
а
равен —:
' г7 у = 0 7>2 = .°
I- ь / (/Т)2 ь‘
гг V о • | Л f
Так как значение выражения — неотрицательно и —— i
р Ь \ J b I
— — , то на основании определения арифметического квадратного
ь
> Q I С л т_ ~ /ч
корня равенство л — —. где а/ О и о О, верно.
J b
Итак, корень из дроби, числитель которой неотрицателен, а
знаменатель положителен, равен корню из числителя, деленно-
му на корень из знаменателя.
173
Приведем примеры.
1 36 р 36 6
V 109 |/169 13
2. _.
к 5 у s’ ) о
В результате преобразования выражения jZ - мы поз,учили
дробь -2—, знаменатель которой | 5 не является рациональ-
J 5
ным числом. Такие выражения иногда бывает удобно представ-
лять в ьиде а] Ь, где а — рациональное число, а Ъ — натураль-
ное.
Для того чтобы выражение -“= привести к виду а] Ь, вое-
пользуемся основным свойством дроби и умножим числитель
2 —
и знаменатель дроби —- на ] 5:
А- = = - — = 0-4 ] 5.
V 5 J 5 -1 5 5
В полученном выражении вида а ] b а~ 0,4 и b - 5.
Итак, jZ 4 • 0,45.
Выполняя некоторые преобразования, удобно пользоваться
формулой ч Z— = Z/ , Где д>. о и Ь>0, записав ее иначе:
г 6 У'ь
iZ" 75
П^сть, например, требуется упростить выражение По-
Г 12
лу чим:
Г?5
У12
- = 2,5.
2
714. Найдите значение корня:
а> VB в> /49’
б) 1ZJ; r)]Z^; e)]Zg; з) } 2
174
715. Представьте в виде частного корней выражение:
«>/& ">/|= »/-!
716. Представьте в виде a\fЬ, где а — рациональное число и
b — нач уральное, выражение:
2 6 з
а) у 10’ В) } 3* 4 У о'
1 9 21
6) у 2’ Г) 2/3’ е) 2/14*
717. Представьте гыражение в виде а]/~Ь, где а — рациональное
число и b — натуральное:
718. Представьте в виде а] 6, где а — рациональное число
и b — натуральное, выражение:
а)9]/-|; в) -1 j/±; д) 2/0,7; ж) 4 /12,1;
6)20j/j; г)|/А. е) 12//3] з) |/09.
719. Упростите выражение:
. у 2 ») ; в) & , J /15 д) -; ж) -—; . /51 и'- — ;
/13 /111 /4Ь 1 30 | 34
б)-& г)® е)® з)^5: . У 26 К) .
/ 2300 /28 } 65 /250 У 65
720. Найдите области определения каждого из выражений и
выясните, какая и з них явд яетея подмножеством другой:
а)
и
Г 5.
/^+з’
б> /ц/"
/ 2х — 4
/Юх
175
44. Вынесение множителя из-под знака корня
Выражение | 16а имеет смысл, если а^О. Преобразуем это
выражение, используя теорему о корне из произведения неот-
рицательных множителей. Получим:
] 16а /16 • У а 4 /а.
Мы заменили корень из выражения 16а, где а^О, произведе-
нием чисел 4 и | а. В этом случае принято говорить, что мно-
житель 4 вынесен из-под знака корня.
Приведем примеры.
Пример 1. Сравнить числа j 50 и 4] 2.
Преобразуем выражение | 50:
| 50 = ] 25 -2 = | 25 • | 2 = 5 | 2.
Ясно, что
5 | 2 > 4 | 2.
Поэтому
/50 > 4 | 2.'
Пример 2. Упростить выражение 2| 8+3| 2—2] 18.
Вынося в слагаемых 2| 8 и —2| 18 множитель из-под знака
корня, получим:
2 | 8-Ь 3] 2— 2| 18 2] 4-2"+3| 2 —2J 9~2 =
= 2/4 ] 2+31 2—2] 9 • | 2 =
= 4 /2 + 3/2 — 6| 2 = (4 + 3 — 6) /2 = /2.
П ример 3. Вынести множитель из-под знака корня в
выражении ] 9а7.
Выражение I 9а7 определено при а^О. Представим подко-
ренное выражение 9а7 в виде такого произведения, в котором
один из множителей тождественно равен квадрату одночлена:
9а7 —9а6-ц=(За3)2а. Тогда по теореме о корне из произведения
неотрицательных множителей
| 9a ‘ = |/(Зафа = | (За3)3 • /а = | За31 • J а = За3] 'а.
721. Вынести множитель из-под знака корня:
а) I 12; г) I 32; ж) • 363; к) ОД ] 20000.
б) ) 18; д) ] 108; з) J 845;
в) | 50; е) ]/180; и) А1 275;
176
722. Сравните числа:
а) 3 | 3 и | 12;
б) 1 20 и 3 /5;
в) i | 54 и - /150;
3 5
г) 3 | "120 и 2 /270;
д) । 72 и 0,5 | 162:
е) ]/24 и | | 216.
723. Упростите выражение и
приближенное значение:
найдите с помощью таблицы его
а) /12 -1/27 + 4 /48;
- I 18 + - | 8 —- J 50.
3 2 5
724. Упростите выражение:
а) 3/2 + | 32 — /200;
б) 2 | 72 — | 50 —2 | 8;
в) 5 J 3 + i 1 27 — | 48;
3
г) 1 80 + i I 20 + 31 45;
2
д) I 75—0,1 | 300 — | 27;
е) | 98 — J 72 — — | 8.
2
725.
Вынесите множитель
из-под знака корня:
a) I 7aJ, где а > 0;
б) | 10//-, где у < 0;
в) | 16х‘, где х>0;
г) 1 0,01b5, где Ъ 0;
д) I 50а7, где а>0;
е) 27с0, где с<0.
726. Найдите область определения выражения и вынесите
множитель из-под знака корня:
а) | 9х; в) ] 12г’2; д) 1 18х3; ж) J За4; и) | 45а7;
б) V— 16а; г) | b3; е) J — 18лг3; з) |5а°; к) ]/-45аЛ
727. Упростите выражение:
а) I 25а’ + 4а J а3 — а | а;
б) V- /6 — 4 J 166s + | 6s.
728. Вынесите положительный множитель из-под знака корня:
а) I гу, если х >0, у >0 и если х <0, у >0;
б) | xz/3, если х >0, у >0 и если х <0, у <0.
177
729. Вынесите множитель из-под знака корня в выражении
а) | 9а?Ь, где а < О, b > 0;
б) J 25а2Ь ‘, где а > О, b > 0;
в) } 144а3д3, где а <0, Ъ < 0;
г) | 32а4Ь3, где а < О, b > 0;
д) ] 75а3&% где а>0, &<0;
е) | 8а5Ь7, где а < О, Ъ < 0.
730. Представьте выражение в виде a]/ bt где а — рациональ-
ное число и b — натуральное:
а) ) 6 - 1 3; в) 2 /5 • /10; д) 0,5/3 • /24;
б) J 15 • /30; г) 0,5/2 /12; е) 2/2-0,5/48.
4
731. Докажите, что равенство верно:
а) (3 /5’— 21 3 ) • |/ 5 + /60 = 15;
б) (/28-2/3 + /7) - /7 + /84 - 21.
732. Упростите выражение:
а) (/12 + 2] 18) • | 2 —/150;
б) (/15 — /20) • 2 } 5 + /75;
в) (3) 2”—] 6 4-1)-2/2;
г) (4 /3 — 2 /6 — 1) • 2 /3.
733. Преобразуйте выражение:
а) (I 2 + 1/
б) (/3-2)2;
в) (/3-/2)2;
г) (2 /5 4- /2 )2;
д) (/64-/а)2;
е) (2/15-/6)2;
ж) (/10-3/5)’;
з) (/M + 2/I4)2.
45. Внесение множителя под знак корня
Пусть требуется сравнить числа 3|/б и 2/7. Это легко будет
сделать, если мы сумеем каждое из этих чисел представить в ви-
де арифметического квадратного корня.
В выражении 3] 5 положительный множитель 3 можно пред-
ставить в виде арифметического квадратного корня из 9. Тогда
3J 5 = 1 9 /5 | /5 = /45.
178
Преобразуем аналогично выражение 2 | 7:
2 |/7’= | 4 • ] rl = |/4^7 = V 28.
Ясно, что
] 45 > ] 28.
Поэтому
3]z5’>2] 7.
Итак, для сравнения чисел 3] 5 и 2] 7 мы каждое из них
представили в виде арифметического квадратного корня. В та-
ких случаях говорят, что в каждом из выражений 3| 5 и2|/7
мы внесли множитель под знак корня.
Рассмотрим теперь выражение —4J' 3. Его значение отри-
цательно. Поэтому это выражение нельзя представить в виде
арифметического квадратного корня. Однако выражение —4j 3
можно преобразовать так:
— 4/3’ — У16- /3 = — ]zifF3 = — 1^48.
Внеся положительный множитель 4 под знак корня, мы
представили —4|/ 3 в виде выражения, противоположного
арифметическому квадратному корню.
Приведем еще пример. В выражении а] 2 множитель а пе-
ред корнем может принимать любые значения. Поэтому для
преобразования этого выражения нужно рассмотреть два слу-
чая: и а <0.
Если о 0, то fl = 1 а2 и
а У2 = ] ? • Г2 2а2.
Если а < 0, то а = — J а2 и
а] 2 = —] а2 • ] 2 = -] 2^’7
734. Внесите множитель под знак корня:
а) 71'10; в) 5 , 0 ; д) 6 1;
6)51'2; г)10, 5; е) 2
735. Внесите положительный множитель под знак корня в вы-
ражении:
а) 3в) 2 J 7; д) 5 ж)| ] 6 г;
б) -51 2; г)—6J 3; е)-12]/^; з) -771 Зу.
179
736. Сравните числа:
а) 2 j 3 и 3| 2; в) 1).'6 и 61/1;
б) 5J 4 и 4] 5; г) 11/ 72 и 71/1
о г <5
737. а) При каких значениях переменной х из множества
2; 3; —5; —10} верно равенство х| 3 — Г Зх2?
б) При каких значениях переменной с из множества {—3;
1; 4; 10; —10} верно равенство с| 5 —| 5с2?
в) Назовите несколько значений переменной а, при кото-
рых неверно равенство а] 2 | 2аа.
г) Назовите несколько значений переменной Ь, при кото-
рых верно равенство b I 7 — —1 7Ь2.
738- Внесите множитель под знак корня:
а) с J 3, где а > 0; д) х |/1;
б) а } 3, где а < 0; е) х | — 1;
в) —b ( 3, где b 0; ж) у | 3;
г) — b | 3, где Ь < 0; з) — с ] 7а.
ДОПОЛНИТЕЛЬНЫЕ УПРАЖНЕНИЯ
К ГЛАВЕ III
К пункту 32
739- Пусть К — множество четных чисел и L — множество
чисел, кратных четырем.
Постройте «круги Эйлера» для множеств К и L Покажите
на вашем рисунке штриховкой множество четных чисел,
не кратных четырем.
Является ли истинным высказывание:
а) для того чтобы число было четным, достаточно, чтобы
оно было кратно четырем;
б) для того чтобы число было четным, необходимо, чтобы
оно было кратно четырем;
iso
в) для того чтобы число было кратно четырем, достаточ-
но, чтобы оно было четным;
г) для того чтобы число было кратно четырем, необходимо,
чтобы оно было четным?
740. Постройте «круги Эйлера» для множества В чисел, крат -
ных 6, и множества С чисел, кратных 3.
Является ли истинным высказывание;
а) для того чтобы число было кратно 6, достаточно, чтобы
оно было кратно 3;
б) для того чтобы число было кратно 6, необходимо, чтобы
оно было кратно 3?
741. Постройте «круги Эйлера» для множества В чисел, крат-
ных 6, множества С чисел, кратных 3, и множества Z це-
лых чисел.
742. Постройте «круги Эйлера» для множества рациональных
чисел Q, множества целых чисел Z и множества натураль-
ных чисел N.
743 Пусть А — множество равносторонних треугольников. В —
множество равнобедренных треугольников. Какое из мно-
жеств является подмножеством другого? Постройте «кру-
ги Эйлера» для множеств А и В.
744. Постройте «круги Эйлера» для множества А равносторон-
них треугольников, множества В равнобедренных тре-
угольников и множества С всех треугольников.
745. На рисунке 49 построены «круги Эйлера» дл я множества Z
целых чисел и множества Р положительных чисел. Какая
часть схемы соответствует множеству:
а) натуральных (целых положительных) чисел;
б) положительных, но не целых чисел;
в) целых, но не положительных чисел?
Назовите несколько элементов множества для каждого
из случаев а), б) и в).
746. Постройте «круги Эйлера» для множества С прямоуголь-
ников и множества D ромбов. Заштрихуйте часть схемы,
которая соответствует множеству
квадратов.
747. Постройте «круги Эйлера» для мно- --
жеств А, В, С и F, где: f
А — множество выпуклых четы- / Z ( \ Р \
рехугольников; I II I
В—множество параллелограммов; \ \ J J
С—множество прямоугольников; х------------------
F — множество квадратов. Рис. 49
1st
74В. Постройте «круги Эйлера» для множеств А, В, С, В п
F, где:
А — множество выпуклых четырехугольников;
В — множество параллелограммов;
С — множество прямоугольников;
D — множество ромбов;
F — множество квадрат ов.
749. Постройте «круги Эйлера» для множеств рациональных
чисел Q, цепых чисел Z, положительных чисел Р и чет-
ных чисел К.
750. Что является дополнением множества:
а) квадратов до множества прямоугольников;
б) равносторонних треугольников до множества всех тре-
угольников;
в) квадратов до множества ромбов;
г) чисел вида ЗА, где k — целое число, до множества целых
чисел?
751. Найдите дополнение до числового промежутка [3; 9] чис-
лового промежутка:
а) [3; 6]; б) [5; 6]; в) ]3; 9[; г) [3; 9[.
752. Найдите значение выражения:
1 - .2- • - 30,6 1-| 0.1.
\ 7 15 3 '
753. Вычислите:
7 : (- 1,05 —0,308 : 0,11 .
s
К пункту 33
754. Найдите значение выражения:
а) 0,3 /289;
б) — 4 КО 81;
•> /s-1'
. 4 1
г) -,—----—;
р25в )'С4
д) 2 /6,0121 + ] 100;
2 /0,04
ж) ) 2500 — ) 625;
з)1 ----L_;
I Ы ( 9
и) — 0,03 I '10000 + ] Тб:
182
735. Докажите, что верно равенство:
а) 5 - V 4-] 0,25 ] = 2,5;
б) 11 : (0,15 1-1600-0,29 ] 400) = 55;
в) (|'225 + 3 | 121) : У0,09 + 0,78 | 100 j = 6;
г) (-6/|+ф.^);1/Т5 = 3.
К пункту 34
756. Решите уравнение:
а)
+ ^-±-4 = 3
б) — = — 18.
х + 5 5 — х
757. Зная длины а и Ь катетов прямоугольного треугольника,
найдите длину его гипотенузы:
а) а~3 см, Ь — 4 см-, б) а = 2 аи, Ь = 3 см.
758. На рисунке 50 показано псстроение прямоугольных тре-
угольников. Известно, что
|ОА| = АВ = ВС = |CZ)| = 17>Е| = 1.
Докажите, что:
а) |ОВ| = | 2;
б) |ОС| = | 3;
в) OD| = 1 4:
г) |OEi = Ко.
759. Используя теорему Пифагора, постройте отрезок, длина
которого:
а) Кб; б) | 11.
760. Найдите область определения выражения:
а) 1 |*|;
б)
B)]Tir=^l;
г) х~ -|- 9;
д) | х3 — 9;
е) | 4 — х:;
ж) |
183
761. При каких значениях переменной имеет смысл выражение:
•’ 7=7. ») 7=7 л 1
9 1 ________________
6)77~5: r)V7TJ: е) 1 9 + 3«-lZ4«-12?
762. При каких значениях переменных а и Ъ имеет смысл вы-
ражение:
а) ) аЪ-, в) р а252; д) ] (о | by;
б) ] а25; г) V—ab’-, е) 1/ --Ц- ?
» (а — 6)-
763. Решите уравнение:
а) } х +1 1; е) ] х~ -|- 9 5;
б) р х — 2 = 5; ж) ] х- — Зх - х;
в) V5х — 4 = 0; з) ]/2х2 — 10х + 25 = х;
г) 0,5 |Лх -|- 4 3; и) | х 4 — х — 2;
Д) |/ Зх~ 4 = —10; к) | 2х = ж 2 1.
К пункту 35
764. Сократите дробь:
. 22 _ 14 6 + 1 .15 — 1^5
а)—; б) —; в)------------г) —~п
1'1 1 у 1 > 3 2 1'5
765. Упростите выражение:
а) (]/3-1>.(1 + /3); в) рг2‘ -|'6 Ц|/б +|<2);
б) 3| 3— 2)(2 4-3|/5); г) <3] 2 + 2} 10) (21410—3^2).
766. Представьте выражение в виде разности квадратов и раз-
ложите его на множите пи:
а) 9п2—с, где с>0; б) а—ib, где а >0 и Ъ >0.
767. Сократите дробь:
а) <-»_; б) 2~3 ; в) —’-Э—; г)
о—|<5 /. + 13 (t X — Я)! 1 uE/.l-a
768. Решите уравнение:
184
К пункту 36
769. Докажите, что:
а) 2< | 8 < 3;
б) 5<| 30< 6;
770. Сравните числа:
а) р 7 и —2,4;
771. Что больше:
a) Jz 13 или ]<3 4- 10;
б) У10 или У 20—]/б;
в) } 15—2 или ] 3 4 2;
в) 3,8 < 1 15 3,0;
г) 7,2 < | 52 7,3.
б) — | 7 и —2,4.
г) 7 — | 2 или 5 ]/2:
д) 2 | 8 или ' 15;
е) 0 5 | 24 или । 14?
К пункту 40
772. Расположите числа в порядке возрастания:
а) 1 40, | ^52 и 7; б) I 12, | 79’ и 10.
773. Расположите числа в порядке убывания:
а) | 60, 8 и | 56; б) [ 47, ] '93 и 7.
774. Найдите границы значения выражения;
а) 10 1 х, если 1 < х<1,44;
б) — —, если 4 < х <С 6,25.
' 5
775. Решите неравенство:
а) 2 |/х >5; б) А | х < 2; в) 0,5 < 0,1 |/х < 0,8.
3
776. Постройте график функции:
а) у = — I х; б) у = ]Л^х.
777. Реши ге графически у ра внение и неравенство:
а) 1 'х =х, | х > х; б) I х= - х, Vх < ± х.
778. Решите уравнение:
а) ] х 2х; в) — | х = 0;
б) J х 4 5х 0; г) х 5 J х.
18b
779. Рег-аите графически уравнение:
а) /х = х — 2; б) I х х— 6.
780. Найдите область определения функции:
а) У —=—; б) у = -1 2— .
V х +1 - 5 1 + ; х +16
К пункту 41
731. Назовите выражение, противоположное:
а) 5; в) /3; д) с; ж) т—п;
б) —15; г) — ] 7; е) а; з) с k.
732. Вычислите значение выражения (если оно имеет смысл):
а) ] ( — 12/; в) ] “10-; д) ] ( -15/;
б) —/10“ г) - | ( -117; е) | ( -20/.
783. Найдите значение выражения:
а) ) ( х)2 при х — 9; —13; 1,6, —2 8;
б) /(/и — и)! при т 25 и а = 10; т 15 и п — 20;
т — —30 и п = 40.
784. Вычислите:
а) /ТО5*; в) /2^; д) J '(- Ю/;
б) Г (-2/; г)] ( 37, е) | ( 9/.
785. Найдите значение выражения, пр< дварительно представив
подкоренное выражение в виде квадрата:
а)/45; Р)11& ; д) ] 4 - Зг: ж) /ТТ- /
б) V9"; г) 125 ; е) |> 2<9; з) /Й“Тв.
786- Замените выражение тождественно равным:
а) ] гх2, если х 10; rl 1 16г-’, если с < 25;
б) /а2, если а< — 5; д) ] т-, если —7;
в) V4j/> если у 100; е) | п', если п<~8.
166
787. Преобразуйте выражение:
a) /(Р 4 0,5)2, если р > 0;
б) У (с — 2)2, если с < 0;
в) /(Ь Ч • 2)-, если Ь > 4;
г) 1 (3 — k)-, если k > 20;
д) У(х— 5)?, если х' 0;
е) У(У—"6)4 если 10.
788. Упростите выражение:
а) V(2- |/2Г + 1/(Г2-1)2; в) К(/7-2)2+]/ (/7-б)2;
б) V(/3-5)2+/(1-/3)2; г) /(/15-2)=-К(]у15-3)2.
789. Решите ypai нение:
а) 0,1 У У- = 2; в) /х2 = х; д) ] (х-2)! 2-х;
б) 5/х2 = 4; г) У(х—10)2 = х—10; е) 1 (5 4*)? = 5 4х.
790. Решите неравенство:
а)/х?>1; б)|г<2.
791. Постройте график функции:
а) у =- Гг-; г) у = — х Ух2, ж) у = 1
б) у ~ ; А) У ] х®4-*; з) у = 0,5 (х—. Ух1,.
в) у - хУ х ; е) у = 1 х — х;
К пункту 42
792. Вычислите:
а) Г 196 б^КЬ.Зб;
о Г1.° 4 4ои
в) /0487449То,82 49;
г) J 1,44 • 121—1,44 0 4;
д) р 146,5‘—109^ 27 ТГб;
е) У117 5 — 26,ог—1440.
793. а) Найдите катет прямоугольного треугольника, если
гипотенуза равна 234 см, а другой катет 90 см.
б) НяЙ7|Ите площадь прямоу гол ьника, если одна из сторон
равна 72 дм, а диагональ 97 дм.
794. Представьте выражение ] ab, где а<0 и b <0, в виде про-
изведения корней.
187
795. Упростите:
а) | 64а"'Ь«,
б) 36x’t/36,
в) К25а "х‘,
г) | вТЛ1"?
д) |л0,01а’''6'-,
е) - Кб.гбх1^14,
5
где а > О, Ь > О;
где х > 0, у > О;
где а < О, х > О;
где с>0, *<0;
где а> О, Ъ <0;
где х<0, Ь<0.
К пункту 43
796. Найдите значение корня:
. ~|/" 165а — 1242 . т/ ПЭ2 —762
'г 164 * В) V 4572 — 3842’
1/ 98 ~~ . 1 т/ 145,52 -96,б2
' V 1762 — 1122 ’ Г' V 193,52 — 31,52 *
797. Упростите выражение:
а) У где х <0;
в> °-2
где О 0, 6>0;
, где а
0, Ь<0;
798. Представьте выражение
г) 4 У где х<0, i/<0.
где а <0 и Ъ <0, в виде
частного корней.
К пункту 4-1
799. Вынесите множитель из-под знака корня:
а) 0,5) 60; в) 0,01) 300; д) 1/1^; ж) l/GT;
» АО г A«-j
б)2Г150; г) 0,2) 375; е) )/1 3) j/'lg.
800. Сравните числа:
a) A )z26b и 10 | 8; в) 0,5 ) 108 и 9 )<3;
б) 7 1/^ и 0,8 ) 50; г) 4 I 63 и 4,5 ) 28.
Г л' м
188
801. Упростите выражение:
а) 3 /48 — /75 + 1 /147;
б) А] 200+ 2J 50—4/8;
5
в) 8 У2 | - /44 - /275 + 14 ]/|1;
г) /1300 — 2 I 52 — 12 ]/1 А + 5 |/ З^.
802. При каких значениях а и b верно равенство:
а) ] а2Ь = а ] д;
б) J а2Ь = — а] Ь’
в) Уa4b = а21 Ь\
г) | a“b = а3 /Б?
803. Вынесите множитель из-под знака корня:
а) j а’Ь,
б) | 8а:‘К,
в) | 9Sb’c>,
г) j 108fl17d13,
где а >• 0, b 2> 0;
где а < О, Ь <С 0;
где b 2> 0, с > 0;
где а < О, b < 0.
804. Представьте выражение в виде а] д, где а — рациональ
ное число ид — натуральное:
а) /I; б)б]/§; в)1,5]/Ц; г) 120 /И.
805. Упростите выражение:
а) а] а — а2 -------р 4а3;
о ч/зб 1 -1/—
б) х у - — -ух6 Ч- х]х.
806. Решите уравнение:
a) |/x-2/x = t/-6;
б) 2/Зх —4р Зх=2 —31 Зх;
в) 3 /2х — 5 |/8х + 7 /18х = 28.
189
807. Найдите значение выражения:
а) х2—4x4-3 при х = 2 1 J 3;
б) х2—6х+5 при х=3—]/2;
в) 2х2—6х—2 при х = 1—] И;
г) Зх2 + 2х — 5 V13 —1 при X = L .
808. Докажите, что значение выражения есть число рациональ-
ное:
а) (2 /3 + 5)(5-2/з) + (4- ) 5)2 ± 81 5;
б) 60/3 - (5 1 2 - 1) (1 + 5 /2) + (3 ' 3 - 10J2;
К пункту 45
809. Внесите множитель под знак корня:
а) |/8; ejaol/ZZ
То
G) ~ 18; ж) ab j- где а>0 и Ь>0;
в) — х2 J 3; з) 2аЪ У где а < 0 и b < 0;
г) и) ab V 4 +4’ где а и Ъ > °-
Д) -За
810. Расположите числа в порядке возрастания:
а) 1 1 72, 1 30 и 7 J 2;
О
6)5 1/1, |17 и 1/62;
в) 8] 02, /41 и 1/250;
5
г) 12 V б,5, /да и 1,/160.
190
811. Внесите положительный множитель под знак корня:
а) (х — 1) ]/ где х > 1;
б) (х + 5) у где х> — 5;
в) (х | 2) У 7^75, где х < — 2;
г) (х - 4) ) где х > 4.
812. Внесите множитель под знак корня:
а) (6—1)1 3; в) (х + 1) ] х;
6) (а + 2) ] 5; г) (х — 2) | ^х-.
\ f \ 1 За
Д) (а —1) У
е) (2-^)
813. Решите уравнение:
а) (х — 10) | х — 4 = 0;
Глава IV
КВАДРАТНЫЕ УРАВНЕНИЯ
§13. РЕШЕНИЕ КВАДРАТНЫХ УРАВНЕНИЙ
W
46. Графический способ решения квадратных уравнений
Задача. Одна сторона прямоугольника на 2 л меньше
другой, а площадь прямоугольника равна 8 лг. Найти стороны
прямоугольника.
Решение. Пусть меньшая сторона прямоугольника рав-
на х м\ тогда другая сторона равна (х + 2) лт, а площадь
х (х 2) м2. По условию задачи площадь прямоугольника рав-
на 8 лг.
Следовательно,
х (хН-2) = 8. '
Раскрывая скобки, получим:
х2+2х=8.
Решим уравнение графически. Для этого представим его в
виде
х2= 8— 2х.
В одной и той же системе координат построим графики функ-
ций у=х2 и у =8—2х (рис. 51). Парабола и прямая пересекают-
ся в точках А (—4; 16) и В (2; 4). При х ——4 и при х — 2 со-
ответственные значения выражений х“ и 8—2х равны, поэто-
му числа —4 и 2 являются корнями уравнения х2 —8—2х,
а следовательно, и корнями равносильного ему уравнения
х (х4-2)=8.
По смыслу задачи значения х и х -|-2 должны быть выраже-
ны положительными числами, значит, условию задачи удовлет-
воряет только положительный корень уравнения. Задача имеет
единственное решение: длины сторон прямоугольника равны
2 м и 4 м.
При решении задачи мы встретились с уравнением, которое
после переноса всех его членов в левую часть имеет вид:
хЧ 2х—8—0.
Всякое уравнение вида ах+Ьх + с—0, где а, b и с—неко-
торые числа, причем а=#0, а х — переменная, называется квадрат-
ным уравнением.
192
Рис. 52
В уравнении х2-[-2х—8—0 а — 1; Ь=2\ с = — 8.
Коэффициент а условились называть первым коэффициентом
квадратного уравнения, коэффициент Ь — вторым, ас — сво-
бодным членом.
Чтобы решить графически квадратное уравнение нхг4-дх-|-
4 с- 0, целесообразно записать уравнение в виде
ах2 — — Ьх—с
и построить в одной и той же системе координат графики функ-
ции у=ах2 и у =—Ьх—с.
Абсциссы точек пересечения графиков являются корнями
уравнения ах2 -\ Ьх с =4).
Если графики не имеют общих точек, то уравнение не имеет
корней.
7 Алгебра, 7 кл.
193
Приступая к графическому решению квадратного уравне-
ния, часто бывав’’’ удобно предварительно разделить все его
члены на первый коэффициент. Например, для графического
решения уравнения
2х2 6х—5 D (1)
заменим его равносильным уравнением:
х2 Зх—2,5 О. (2)
Представив уравнение (2) в виде
х- =—Зх 2,5,
найдем абсциссы точек пересечения параболы у —х2 и прямой
у = - Зх-} 2,5 (рис. 52).
Приближенные значения корней: —3.7 и 0.7.
Кзадратн эе уравнение, первый коэффициент которого равен
единице, называется приведенным. Графическое решение при-
веденных квадратных уравнений имеет то преимущество, что,
используя одну и ту же параболу у=х2, можно решить большое
число уравнений.
814. Решите графически уравнение:
а) х2 ’ Зх—4 0. д) 12х‘!—6х (-1 0;
б) х2—2х—3 0; е) Зх2-‘ 12х-10 0;
в) х2-‘г-3х 1 п- ж)--4х24 3х 7 0;
г) х2 . 2х 5 0; з) 9х24 6х 1-0.
815. Решите графически уравнение и неравенства:
а) х2 х 4-2;
х2 >х I 2;
х2 <х 4-2;
б) х2+>=12;
х2 I х—12 >0;
х2 4-х—12 <0;
в) х2- -2 =0,4х;
х2 2 >0,4х;
х2—2 <0,4х.
47. Решение квадратных уравнений выделением квадрата
двучлена
В предыдущем пункте при решении задачи мы получили
уравнение
х2 4-2х 8. (1)
Это уравнение было решено графически. Нельзя ли решить
его, не прибегая к построению графиков?
Уравнение (1) равносильно уравнению
х24 2х—8-0. (2)
Трехчлен х® 2х—8 лишь свободным членом отличается от
трехчлена х24~2х 1 1, тождественно равного квадрату двучлена
х41. Прибавим к левой части уравнения (2) сумму противопо-
л< жных чисел 1 и —1.
194
Получим:
х212х8 =(х24 2х П-1-8 (х- I)2— 9.
Мы выделили в левой части уравнения (2) квадрат двучле-
на. Уравнение (2) равносильно уравнению
(х I)2—9 О. (3)
Разложим левую часть уравнения (3) на множители как
разность квадратов:
(х44)(*—2) О (4)
Числа —4 и 2 — корни уравнения (4). Так как уравнение
(4) равносильно уравнению (1), то корни уравнения (1); —4 и 2.
Решим еще несколько уравнений вида ах2 4 bx 4 с О, при-
меняя способ выделения квадрата дзучлена в левой части урав-
нения.
Пример 1.
х2413х к 40 О. (5)
Из трехчлена х2 ! 13x4 40 выделим квадрат двучлена. Если
рассматривать х2 как квадрат первого члена двучлена, а 13х
как удвоенное произведение первого члена на второй (13х =
=2х — j, то вторым членом двучлена долме но служить число
13 _
—. Прибавим к левой части уравнения (5) сумму противо-
/13,2 13 2 s
положкых чисел | — I и — I I и преобразуем левую часть
уравнения в произведение:
х2 | 13х I- 40 = х2 4- 2х •
' 13\2 169 13 2 9
— (х 4- —1 • ——h 40 — I х 4- —I — ~ - (х + 8)(х 4- «>)•
Уравнение (5) примет вид:
(х -I 8)(х45) 0.
Его корни: —8 и - 5.
Пример 2.
Зх2- 11г- 20 0. (6)
Выделив квадрат двучлена из выражения Зх2 - 11х — 20,
получим:
7*
195
Уравнение (6) равносильно уравнению
3 (х 5) х + -4 О.
4
Следовательно, уравнение (6) имеет корни-и 5.
3
Пример 3.
4х2—4х 1 0. (7)
Трехчлен в левой части уравнения тождественно равен квад-
рату двучлена 2х—1. Значит, уравнение (7) можно записать
в виде
(2х I)2 О.
Очевидно, что левая часть уравнения обращается в нуль
1
ТОЛЬКО при X = —.
Уравнение (7) имеет единственный корень, равный
Пример 4.
х2 НЮх 26=0. (8)
Так как х2+10х 26=(х3+2х-5+25)—25+26 (х 5)2- 1, то
уравнение (8) примет вид:
(х |-5)2 + 1 0.
Выражение (х 5)2 - 1 при любом значении переменной х
положительно, следовательно, уравнение (8) не имеет корней.
816. Решите уравнение, выделяя квадрат двучлена:
а) х2—2х—35 0; д) х2+х 2 0;
б) х2 8х—20 0; е) 4х2Н 12х 9 0;
в) х2+64 —16х; ж) 5х2 + Зх 8 0,
г) 8 7х -х2; з) 2х2—9х 10 0.
817. Докажите, что уравнение не имеет корней:
a) z2+14z 50 0; в) Зх2—7х 5 0;
б) у2—11 у+32 0; с) 10х2—х 1 0.
48. Формула корней квадратного уравнения
Мы научились решать уравнения вида ахг Ьх с 0 гра
фически и путем выделения квадрата двучлена в левой части
уравнения Первый из этих способов не обеспечивает высокой
точности значений корней, второй — требует в каждом случае
106
выполнения громоздких преобразований. Поэтому удобнее,
решив квадратное уравнение в общем виде, вывести формулу
его корней.
Для решения уравнения
ах- Ьх-\-с 0, где а=^0, (1)
воспользуемся уже знакомым нам приемом выделения квадрата
двучлена;
ах2 4- Ьх 4- с = a iZ х2 4- — х -j- —=
\ а а /
х2 4- 2х • - Ь
2 i
Ь2 — 4ас
Обозначим выражение Ъ2—4ас буквой D. Тогда
, И ь\г D\
ах- 4 Ьх 4- с = a 1х 4—-------.
\\ 2а/ 4а2/
Пусть значение D отрицательно. Тогда отрицательно и зна-
чение дроби — (знаменатель дроби положителен, так как а
4а'
отлично от О). Б этом случае выражение 1x4 —) — —
положительно при любом х, и уравнение (1) корней не имеет.
Пусть значение D равно 0. Тогда равно 0 и значение дроби
—. Уравнение (1) примет вид:
4аа
а. [ х 4- —V — 0.
\ 2а/
Так как а#-0, то
х 4- - 0.
‘ 2а
Отсюда
h
х =-----.
2а
Уравнение (1) имеет единственный корень, равный —
2о
Пусть значение D положительно. Представим дробь ~ в
4а‘
виде квадрата: — [ J . Тогда vpaBHenne (1) будет равно-
4а2 \ 2а /
сильно уравнению
197
Разлагая разность ki адратов на множители, получим:
, ь ,
а х 1----------1
\ 2а '
- 0.
Так как 0, то
х I- — 4- О или
2а 2а
От сюда
х — ~ ь или х - — ь + V Д ,
2а 2а
Принята следующая краткая запись:
х =
2а
(А)
Мы видим, что наличие корней у квадратного уравнения и
их число зависят от выражения D Ь2 —4ас. Это выражение на-
зывают дискриминантом квадро тного уравнения (- дискрими-
нант» по-латыни — различите ль).
В зависимости от знака дискриминанта различают три
случая:
если D <0, то уравнение не имеет корней; если D = 0, то
уравнение имев™ один корень ——; если D >0, то уравнение
2а
имеет два корня, которые могут быть найдены по формуле (А).
Заметим, что формулой (А) можно пользоваться и в тем слу-
чае, когда D 0. Действительно, при D - 0 формула (А) примет
вид:
х —k ) о , т. е> х — — —.
2а 2а
Таким образом, формула (А) применима к любому квадрат-
ному уравнению, имеющему корни.
Рассмотрим примеры решения квадратных уравнений с ис
пользованием выведенной формулы.
Пример 1. 12х2 7х+1—0.
В этом уравнении а 12, Ъ 7, с 1.
Найдем дискриминант:
D 7г—4-12 1 = 1.
Так как дискриминант положителен, то уравнение имеет
два корня, которые можно найти, воспользовавшись формулой
(А):
х — —7 - * 1 . Корни уравнения: —• i и — ~.
>98
Пример 2. х2- 12х 36 О. Так как а 1, 5 = —12,
с =36, тэ Л (—12)'—4-1-36-0 Уравнение имеет единственный
корень: х — 12 £ 0 — 6.
Пример 3. 7х2 — 25x4 23 =0.
Здесь а 7, Ь = — 25, с=23.
Дискриминант D =(—25)2—4 7-23 625—644. Так как ди-
скриминант отрицателен, то ура внение не имеет корней.
Если хотя бы один из коэффициентов b или с квадратнэго
уравнения ах2-\-Ьх-\ с=0 равен нулю, то такое квадратное ; рав-
нение называется неполным.
Приведем примеры неполных квадратных ура вне ний:
1) Зх2-) 17х О. Здесь а 3, 5 = 17, с О.
2) 4х2—121—0. Б этом jравнении а-4, 5—0, с —121.
Как мы знаем, неполные квадратные уравнения легко ре-
шаются разложением на множители левой части уравнения:
1) Зх2 ' 17х=0; х(Зх+17) —0, х — 0 или х =—;
2) 4х2- 121=0, (2x4 11)(2х—11) 0, х~— 5 1 или х 5-.
2 2
Можно решать неполные квадратные уравнения и по фор-
муле (А), но это менее удобно, чем решение путем разложения
левой части уравнения на множител и.
Решим, например, рассмотренное выше непол ное квадрат-
ное уравнение 4х2—121 =0 по формуле (А).
Дискриминант D уравнения равен 02-f-4 4-121 = 16 121.
Применяя формулу (А), имеем:
х - 0 * >'16 121 - ±4 П х - — 5 1 ипп X - 5 1
Л . .. ., —. , Л ~ lxJ.ll «с — о •
8 8 2 2
Мы видим, что решение уравнения 4х2—121-0 путем не-
посредственного разложения левой части на множители проще,
чем по формуле.
Уравнение 7х2=0, в котором а 7. 5 0, с = 0, также являет-
ся неполны! I квадратным уравнением. Очевидно, чт о это урав-
нение имеет только один корень — число нуль.
818. В уравнении вида ох2 4 5x4 с 0 назовите коэффициенты
а, 5 и с, вычислите дискриминант и укажите число корней
уравнения:
а) 2x4 Зх+1--0; в) 2х24-х 1 0;
б) Зх217x4-2 0; г) 5х2 2х—3-0;
199
д) x2j-5x—6 О; ж) 9х2—6х -1 О;
е) х2+2x4-2 О, з) 4х2- 7х 2 О.
819. Решите уравнение по формуле (А):
а) Зх ' 7х 4 9; ж) 4х2 х—3 - 0;
б) 5х2 8х 3 0; з) 2х2- Зх- 9 О:
в) 2х2 7х 3 О; и) х'2 Зх -40 О;
г) 2х2 1 Lx 1 9 0; к) х2 7х -60 О;
ц) 2х2—9x 4 9 0; л) 12х2 7х О;
е) Зх2—13х i 14 =0; м) 81х2—49 О.
820. Решите уравнение:
а) 5х2 9х 2; д) z—5-г2- 25;
б) - х2+3х 40 О; е) z'5 = z2+25:
в) 14 -х2 5х; ж) 0,7х2= 1,3х 1-2;
г) —Зх24 8 10х; з)7 0,4г/4 0,2г/2.
821. Приведите уравнение к виду ах2 bx J с -0 и найдите ею
корни:
a) (x i-4) 3x |-40; в) (Зх—If 4(х -1)-’;
б) (2х-3)2-11х19; г) 4 (х , 3)2-(х 5)2.
822. Найдите методом границ приближенные значения корней
уравнения;
а) 5х2— х- 1-0; б) 2х2 7х )-4 —0.
Указание. В качестве приближенных значений арифметического
квадратного корня с недостатком и с избытком возьмите две последовательные
десятичные дроби с двимя знаками после запятой.
49. Другой вид формулы корней квадратного уравнения
Корни квадратного уравнения ах2 | Ьх с-0 могут быть
найдены, как известно, по формуле
х ~ь У ° , где D — Ъ2 — 4ас. (А)
2а
Иногда при решении квадратных уравнений удобно поль
зоваться формулой корней, записанной в другом виде.
„ Л _
Разделим числитель и знаменатель дроби —— на 2 и
1 тт
внесем множитель — под знак корня. Получим:
2
Ь 1 — Ь /'п
----- — - Ь 1/ -
- ь ± /Б = 2 ~ 2 = 2 И 4
2а а а
00
m T-> , о л D b2 — 4ac b2
Так как Z) = о — 4ac, to — — ------------------------ —---------ас, t. e.
4 4 4
Формула корней квадратного
уравнения примет вид:
- L 1/5
2 V 4
х
D lb \2
где — — I — — ас.
4 2
(В)
Формулой, записанной в таком виде, мож но пользоваться
для решения любого квадратного уравнения, дискриминант
которого неотрицателен (очевидно, что если ZJ^’O, то и—^>0).
Обычно на практике ее применяют в том случае, когда Ь — чет-
Ь
ное число и, значит,-----целое число,
2
Пусть, например, требуется решить уравнение
9х2—14х ' 5= О.
Применим формулу (В). Здесь — = - 7, а 9, с- 5.
-5 = (_7)2 -9-5 = 4.
9
X — — или X = 1.
9
Корни уравнения: — и 1.
Заметим, что использование формулы (А) привело бы к бо-
лее сложным вычислениям.
Приведем еще пример. Решим уравнение
5х248х46==0.
В этом уравнении — — 4, а ~ 5, с = 6. 5 = 4 —5 6 =— 14.
2 4
D г» О
Мы нашли, что — — отрицательное число. Знак — совпадает
со знаком D. Так как дискриминант отрицателен, то уравнение
не имеет корней.
201
823. Решите уравнение:
а) Зх2 — 14x4-16 0; е) 4х2- 36x477 0;
6) 5х2—6x41 0; эк) 15у2— 22у 37 0;
в) х242х—80=0; з) Зх2432х 80 0;
г) х2—10х— 24- 0; и) 7z2—20z 14 0;
д) х2—22х—23=0; к) у2—52у . 576 0.
824. Решите уравнение:
а) х2—1,6х-0,36-0; г) 8х2-4х 0,5 0;
б) х2—2x4-0.91 — 0; д) 2х2—10x4 12,5 0;
в) х2 6x4-19,7-0; е) ix242x—9=0.
3
825. При каких значениях х верно равенство:
а) (3x41)“—3x4 1; г) 4(х З)2 (4x4 З)2;
б) (3x4-1)* 3 (х4 1); д) 4 (х4-3)2-(2х 6)2;
в) (3x4 4)2=4 (х4 3), е) 9 (х—4)2=4 (х—9)2?
826. Существует ли такое значение а, при котором верно ра-
венство:
а) За 4-0,6 =9а2 I 0,36; б) 0,4а г 1,2=0,16а2 4 1,44?
827. Решите уравнение:
, х! 4 1 о . х2 — 4 2х + 3
а) —i-х — 2; г)-----— = 1;
2 '85
„5; (S+V_V-p= ,
' е 3 12 4 2
. Зх | 4 х2 — 4х — 6 .3 u i — 2 (и — £)’
в) ——--------— —1; е) —- — •---ь —-
' 5 10 5 4 8
828. Найдите множество корней уравнения:
а) 2х2 х —2 7х 6 х —2’ е) 3x41 х 4- 2 _ ж~1 _ х —2 1;
б) х2-6х 5 ж) 4 4 v - о-
х — 5 х — 5 »у« —1 Зу41 1-з7
в) 2х- 1. х 4 7 3x4 4. х— 1 ’ з) 4 х4 3 5 3 — х х 1; — 3
г) 5.7 4-1 _ У 4 2. и) 2x4 1 3(2х—1) 8г о-
У 41 •1 У 2х — 1 7(2x4 1) 4х--1
д) |_ х —2 Б 8 к) 2ц — 5 _ У 4 2 У24’-Зу 4 5 о
х4 2 Х- — 4* У2-Зу У3- Р
202
829. а) Существуют ли такие значения переменной у, при кото-
рых равны соответственные значения суммы дробей
у- 1 10
•--- И ----- и их произведения?
j/—5 у + 5
б) Существуют ли такие значения переменной у, при ко-
торых равны соответственные значения разности дробей
6 у „
---- и —~2 и их произведения?
830. Найдите множество значений I, при которых уравнение
не имеет корней:
а) Зх2—2х t 0; в) 4х2 -Их 4-1 = 0;
б) 5хгЦ-18х i-Z=0; г) 48x24~i’x—5==0.
831. Найдите множество значений v, при которых уравнение
имеет два корня:
а) 10х2 40х + v = 0; в) vx2 — 6х 4- 1 = 0;
б) 2х® + vx 18 0; г) 7х2 + ix — 25 = 0.
832. При каких значениях к уравнение имеет один корень:
а) 16х? + кх + 9 = 0; в) кх2 — 100х к 0;
б) 15х2 — 90х |- А 0; г) 25х2 + Ах 4-2 = 0?
50. Задачи, приводящие к решению квадратных уравнений
Многие задачи геометрии, физики, техники приводят к
квадратным уравнениям.
Рассмотрим, например, следующую задачу.
Тело брошено вертикально вверх с начальной скоростью
40 м/сек. Через сколько секунд теле окажется на высоте 60 л?
Решение. В курсе физики доказывается, что если не
учитывать сопротивление воздуха, то высота, на которой ока-
жется тело, брошенное вертикально вверх, может быть найдена
по формуле
А — v.l — — I2,
2
где h — высота в метрах, t — время в секундах и v0 — началь-
ная скорость тела, выраженная в м сек, g — ускорение свобод-
ного падения в м сек2. Подставим в формулу заданные значе-
ния v0 и h и будем считать, что — ~ 5*:
♦ Ускорение свободного падения в условиям Зел ли g х 9,8 м/сек* здесь
округлено до 10 м/сек-.
203
60—40Z—5f2, отсюда
t’— 8f+12 0.
Решая квадратное урав-
нение, находим его корни:
2 и 6.
На рисунке 53 дан гра-
фик зависимости h от t, где
h = 40Z — 5t“. Рассматри-
вая график, мы замечаем,
что тело, брошенное верти-
кально вверх, в течение
первых 4 сек поднимается
на высоту 80 м, а затем на
чинает снижаться и падает
на землю. На высоте 60 м
от земли тело оказывается
дважды: через 2 сек и через
6 сек после бросания.
Таким образом, усло-
вию задачи удовлетворяет
любой из найденных
корней.
Рассмотрим другую за-
дачу.
Моторная лодка пришла 42 км по течению реки и 20 км про-
тив течения за 5 ч.
Найти собственную скорость лодки, если известно, что
скорость течения реки на всем участке пути равна 2 км, ч.
Решение. Пусть х км ч — скорость лодки в стоячей
воде, тогда скорость лодки по течению реки (х 1 2) км ч, а про-
тив течения (х—2) км ч.
Время, затраченное на прохождение 42 км по течению реки,
42
--- ч, а время, за которое лодка прошла 20 км против тече-
х + 2
20
ния реки, - ч.
Время, затраченное лодкой на весь путь, равно । — - -- ч.
+ 2 х — 2/
Следовательно,
42_ , 20
х -|- 2 х — 2
(1)
По смыслу задачи собственная скорость лодки должна быть
больше скорости течения, значит, искомое значение х должно
удовлетворять неравенству
х >2.
204
Решение уравнения (1) сводится к решению системы:
|5х!—62х-|-24 О.
|(х 2) (х—2)^0.
2
Числа — и 12 — решения системы, из ник только число
5
12 удовлетворяет условию х >2.
Следовательно, задача имеет единственное решение: собст-
венная скорость моторной лодки равна 12 км ч.
833. а) Произведение двух натуральных чисел, одно из кото-
рых на 6 больше другого, равно 187. Найдите эти числа,
б) Представьте число 120 в виде произведения двух чисел,
одно из которых на 2 меньше другого.
834. а) Найдите периметр прямоугольника, длина которого
на 4 см больше ширины, а площадь равна 60 см'.
б) Периметр прямоугольника равен 62 м. Найдите его
стороны, если площадь прямоугольника 210 лг2.
835. а) Произведение двух последовательных натуральных чи-
сел больше их суммы на 109. Найдите эти натуральные
числа.
б) Квадрат суммы двух последова тельных натурал ьных
чисел больше суммы их квадратов на 112. Найдите эти
натуральные числа.
836. а) Доска прямоугольной формы имеет площадь, равную
4500 см2. От нее отрезали часть прямоугольной формы
той же ширины и длиной 120 см.. Оставшаяся часть доски
представляет собой квадрат. Найдите сторону этого квад-
рата.
б) От листа оконного стекла квадратной формы отрезали
прямоугольную полосу шириной 40 см. Оставшаяся пря-
моугол ьная часть стекла имеет площадь 3200 см2. Найдите
размеры куска стекла, от которого отрезали полосу.
837. а) Числитель некоторой обыкновенной дроби на 1 больше
знаменателя. Если к числителю дроби прибавить 3, а к
знаменателю 18, то полученная дробь б>дет меньше исход-
ной на 1. Найдите исходную дробь.
б) Числитель некоторой обыкновенной дроби на 4 меньше
знаменателя. Если числитель уменьшить на 3, то получен-
ная дробь будет вдвое меньше исходной. Найдите эту
дробь.
205
838. а) Спортивная площадка прямоугольной формы имеет пло-
щадь, рь внук» 840 м . Если ширину площадки увеличить ня
4 м, а длину уменьшить на 5 м, то ее площадь не изме-
нится. Найдите размеры спортивной площадки.
б) Площадь земельного участка прямоугольной формы
была равна IzOO м~. После увеличения длины участка на
8 м, а ширины на 6 м его площадь увеличилась на 528 м2.
Найдите первоначальные размеры участка.
839. а) В зрительном зале сельского клуба было 160 мест. При
расширении >ала число мест в каждом ряду учел ичили на
2, а число рядов увеличили на 1. В результате в зале ста-
ло на 38 мест больше, чем было первоначально. Сколько
рядов в зрительном зале?
б) Для перевозки 150 туристов предполагалось выделить
несколько автобусов, но так как приехало на 18 туристов
больше, то дооавили еще один автобус и в каждый пос а-
дили на 2 человека меньше, чем предполагали первона-
чально. Сколько автобусов было выделено для перевозки
туристов?
840. а) Катеты прямоугольного треугольника относятся как
8 : 15, а гипотенуза равна 6,8 м. Найдите площадь тре-
yi ольника.
б) Отношение гипотенузы прямоугольного i реугольника
к его катету равно 13 : 12, а друюй катет равен 15 см.
Найдите периметр треугольника.
841. а! Повысив скорость поезда на 10 кд ч, удалось сокра-
ти" ь на 1 ч время, затрачиваемое поездом на прохожде-
ние пути в 720 км. Найдите первоначальную скорость
поезда.
б) Велосипедист проехал расстояние 67 км за 4 ч, при-
чем на после дних 27 км пути ei о скорость была на 2 км!ч
больше, чем на предыдущем участке пути. Сколько време-
ни затратил велосипедист на последние 27 км пути?
842 а) Два автобуса отправились одновременно из города в
пионерлагерь, расстояние до которого 72 км. Первый
автобус двигался со скоростью, превышающей скорость
ьторого автобуса на 4 км ч, и прибыл в пионерлагерь на
15 мин раньше, чем второй автобус. Найдите скорость
каждого автобуса.
б) Из пункта А в пункт В, расстояние до которого 33 км,
одновременно выехали два велосипедиста. Один из вело-
сипедистов, двигаясь со скоростью, превышающей ско-
рость второго вел пси п: «-диета на 4 км ч, прибыл в пункт В
на 4R мин раньше, чем второй. Сколько времени находился
в нуги каждый велосипедист9
206
»43. а) Теплоход прошел 9 км по озеру и 20 км по реке (по
течению) за 1 ч. Найди е скорост ь теплохода в стоячей воде,
если скорость течения реки равна 3 км ч.
б) Тури< г проплыл по реке на лодке 6 км против течения
и 15 км по озеру, затратив на путь по озеру на 1 ч больше,
чем на путь по реке. Зная, что скорость течения реки рав-
на 2 км ч, найдите скорост ь лодки в стоячей воде.
844. а) Моторная лодка прошла 45 км по течению реки и 22 км
против течени я, затрст ив на весь путь 5 ч. Найдите ско-
рость лодки в стоячей воде, зная, что скорост ь течения
равна 2 км ч.
б) Катер, развивающий в стоячей воде скорость 20 км ч,
прошел 36 км против течения и 22 км по течению реки за
3 ч. Найдите скорость течения реки.
845. На расстоянии 80 м переднее колесо повоз ки сделало на
8 оборотов больше заднего. Найдич е длину окружности
каждого колеса, если известно, что длина скруж ности
переднего колеса на 0,5 м меньш в длины окружност и зад-
него колеса.
846. al При уборке урожая с каждого из двух участков собра-
но по 180 г картофеля. Площадь второго участка была
на 2 га меньше, чем плош адь первого участка. Сколько
тонн картофеля собрано с одного гектара на каждем уча-
стке, если урожай карт офеля на втор эм участке был на
Зге гектара больше, чем на первом участке?
б> При уборке урожая с каждого из двух участков собра-
но по 210 ц пшеницы. Площадь первого участ ка была на
0,5 га меньше площади второго участка. Сколько центне-
ров пшеницы собра но с одного гекта ра на каждом участ-
ке, если урожай пшениг ы на первом участке был на 1 и
с 1 ект ара больше, чем на втором участке?
51. Квадратные уравнения с параметрами
Рассмотрим квадратное уравнение
Зх2 — 5ах — 2ал = 0.
Д| скриминант этого уравнения
В = 25а2 + 24а2 = 49а2
при всех значениях а неотрицателен, значит, уравнение имеет корня при лю(см
значении а.
Если а — 0, то JD — О; уравнение имеет елииствеиный корень. Этот корень
можно найти, подставив значение а в уравнение. Полу тш Зх2 = 0, х — 0,
Если а =# 0, то D > 0; уравнение имеет два корня.
2Ci
По формуле (Al находим:
_ 5а, ± |Л49^ r _ 5а А I 7а |
Х 6 ’ Х 6
При а > 0 |7а| — 7а и корни уравнения вычисляются по формуле
5а + 7а
х □= -----•
6
При а < 0 |7а| — —7а и корни уравнения вычисляются по формуле
5а Чт 7а
Таким образом, при любом а, отличном от нуля, уравнение имеет два кор*
ня, которые вычисляются по формуле
5а. ± 7 а 1
х =------- , т е. х--------а или х — 2а.
6 3
Ответ. При а =/= 0 уравнение имеет два корня: ——а и 2а; при а = О
3
уравнение имеет единственный корень, равный 0.
Рассмотрим уравнение относительно х:
х (2х + 5) — Ь (х + 3) = 3. к
Чтобы решить его, представим это уравнение в стандартном виде. Получим
квадратное уравнение:
2х2 4- (5 — 6) х — 3 (6 + 1) - 0.
Найдем дискриминант уравнения:
/Э=(5—6)-+24(6- 1) =25—106 ЬЬ3+24&4-24=&г+14б+49=(Ы-7)г.
При любом значении 6 дискриминант неотрицателен. Значит, при любом b урав-
нение имеет корни.
Если 6=—7, то D=0 и уравнение имеет единственный корень. Подставив
в уравнение значение 6, равное —7, найдем, что х==—3.
Если 6 #= —7, то В >0 и уравнение имеет два корня. По формуле (А)
г _ Ь — 5 ± Г'(6 + О2* v ь — 5 ± lb + 71
4 ’ 4
Так как |6|7] = ЬН-7 при 6>—7 и |6+7|=—(b-f-7) при 6<—7, то корни
уравнения можно найти по формуле
6 — 5 ± (6 + 7)
х ---------------->
4
ь 4-1
Корни уравнения: —— н —3,
Ответ. При 6“—7 уравнение имеет единственный корень —3, при 6#=—7
b --1 ..
уравнение имеет два корня: ----- и —3.
847. Решите относительно х уравнение:
а) хЧ 26х—156г==О; в) х2—2/гх |-4/г—4=0; д) 2х2—(а+5)х | а+3-0; W
б) 18х*—15ах 2аг 0: г) х2—6х | 9—а- О; е) Зх2—(t—5)х—2(— 2=0.
208
52. Теорема Виега
Уравнение
5х2 —4х—12=0
имеет корни —1 £ и 2. Сумма корней равна — , а произведение
5 5
_12
5
Нетрудно заметить, что сумма корней рассматриваемого
уравнения равна отношению второго коэффициента к первому,
взятому с противоположным знаком, а произведение корней
равно отношению свободного члена к первому коэффициенту.
У всякого ли квадратного уравнения, имеющего два корня,
сумма и произведение корней обладают геми же свойствами?
Известно, что квадратное уравнение ах2-\-Ьх с—0 имеет
два корня при D >0. Обозначим их через xt и х2.
х —Ь—yD х _ 6-HD
1 2а. ’ 2 2с
Найдем сумму и произведение корней:
х 4- х = ~ь ~ । — ЬЧ-У-б _ —_ 6.
12 2а ' 2а 2а а ’
х. - х, = - ь ] - -ь- 1 =
2а 2а 4а8
Ъ~ — D Ь- — (Л2 — 4ас) 4ас с
4аа 4а2 4а2 а
Итак,
Ъ с
Xj ч- хй —---; Xj х„ = —.
а ~ а
При D = 0 квадратное уравнение ах24*Ьх+с О имеет един-
ственный корень, который может быть найден по формуле
Ь 4- УЪ
X------------
2а
Если условиться считать, что при D = 0 квадратное уравне-
ние имеет не один корень, а два равных корня, то вывод распро-
страняется на любое квадратное уравнение, имеющее корни.
Итак, справедлива теорема;
Сумма корней квадратного уравнения ахг+Ьх+с~0 равна
— —, а произведение корней равно
а а
Эта теорема называется теоремой Виета, по имени знамени-
того французского математика Франсуа Виета (1540—1603).
209
Виет — юрист по образованию, заинтересовавшись астрономией и ма ге-
матикой, быстра добил зя известности благодаря найденным им общим методам
решения уравнений 2-й, 3-й и 4-й степени. Виет впервые стал использовать бук-
венную символику для обозначения не только неизвестных величин, как делали
до него, но и для обозначения коэффициентов. Он внес большой вклад в развитие
математики, но сам из всех своих открытий больше всею ценил установление
зависимости между коэффициентами уравнения и его корнями.
В случае приведенного квадратного уравнения соотноше-
ния между его корнями и коэффициент ами принимают более
простой вид. В самом деле, если в уравнении ах2 + &г+с = 0,
имеющем корни, коэффициент а равен 1, то сумма корней рав-
на —Ь, а произведение корней равно с, т. е. сумма корней при-
веденного квадратного уравнения ровна второму коэффициенту,
взятому с противоположным знаком, а произведение корней раи-
на свободному члену.
Рассмотрим, например, уравнение
х2 -7х 4 10 0.
Так как дискриминант положителен (D (— 7)?—4-10 9). то
уравнение имеет два корня. Пусть Xj и х2 — корни уравнения.
По теореме Виета х,+х2 7, х,х 10
В тех случаях, когда нужно составить квадратное уравнение
по его корням, применяют теорему, обратную теореме Вие га.
Если числа тип таковы, что их сумма ра на —р, а произве-
дение равно q, та эти числа яв-гяются корнями уравнения
x2+px+q=Q. (1)
Докажем это
По условию т + п = —р и тп — q. Заменив в уравнении (1) коэффициенты
р и q соответственно на т + п.и тп, пол; чнм:
х- — (т -|- и) х j тп = 0. (2)
Преобразуем левую часть урлвненп...
х2 — (т + п)х г тп — х2 — тх — пх | тп — х (х — т) — п (х — т) =
(х — т) (х — п).
Очевидно, что уравнение (х — т) (х — п) ~ 0, равносильное уравне"ию (2),
имеет корни т и п и никаких других.
Следовательно, числа т и п, и только они, являются корнями уравнения
х2 + рх + q - 0.
Пуеть, например, нужно составить квадратное уравнение
с корнями — 15 и 22-
Коэффициенты р и q приведенного уравнения х2 рх 5 = 0,
имеющего данные корни, можно найти из равенств:
р =—(—15 I 22); q = —15 22.
210
Получим: р - —7; q — —330.
Значит, приведенное уравнение, имеющее данные корни,
будет иметь вид:
х:--7х 330 0.
(3)
Очевидно, что можно составить сколько угодно квадратных
уравнений, имеющих данные корн и 15 и 22. Для этого доста-
точно умножить все члены ура внения (3) на любое, не равное
нулю число. Например, умножая уравнение (3) почленно на 2,
получим: 2х2—14х—660 0.
848. Не решая уравнения, найдите сумму и произведение его
корней (если они существуют):
а) 2ха 9х 1 0 = 0; д) 1 г- -) г -7 = 0;
б) 5х2+12х 4 7 =0; е) Зх2 -8хч- 10 0;
в) х2—37х 21- 0; ж) 4у2- 19 0;
г) у2 I 411/—3710; з) х*—210х=0.
849. а) В уравнении ха рх—35 0 один из корней равен 7.
На идите другой корень и коэффициент р.
б) В уравнении х2—13х q~ 0 один из корней равен 12,5.
Найдите другой корень и коэффициент q.
850. а) В уравнении 5xs + &х-г24 ==0 один из корней равен 8.
Найдите другой корень и коэффицие нт Ь.
б) В уравнении 10х.—ЗЗх с- 0 один из корней равен 5,3.
Найдите другой корень и ко ’ффициент с.
851. Почему уравнение не может иметь корни одинаковых
знаков:
а) Зх* НЗх—7 0: в) 4х24 Ьх—100 0;
б) 5х'2- 291х 16 0; г) х; +6х t/2 = 0?
852. Не решая квадратных уравнений, определите, какие из
них имеют один положительный и один отрицательный
корень, два отрицательных корня, два положительных
корня:
а) х2+7х—1=0; г) 19х“—23х 1-5—0;
б) х2—7х 1 = 0; д) 2х2 51 3 х 11 0;
в) 5х2 4-17x4 16- 0; е) 11х2—9х 7—5J 2 0-
853. Решите уравнение и проверьте правильность решения на
основании теоремы, обратной теореме Виета:
а) х*+19х 88 =0; в)Зх2-4х-4 0; д)х2- 2 :-9 0,
б) х2—Зх 88 0; г) 2х:’4-7х4'6-0; е) 2х2 Эх-Щ- 0.
211
854. Составьте квадратное уравнение, имеющее:
а) два положительных корня;
б) два отрицательных корня;
в) корни разных знаков;
г) один положительный корень, а другой равный нулю.
855. Составьте квадратное уравнение по данным корням и для
проверки решите его.
а) 3; Ю; Д) 2 ]/3; 2 + /3;
б) —7; 4; е) ] 5; ]/5;
в) 8’ 3; ж) 5 - 3 |/ 2; 5 -I- 3 | '2;
г) 1,5; 3,5; з) — 7— 4|/3"; -7+4)/3
§ 14. КВАДРАТНЫЙ ТРЕХЧЛЕН
53. Корень многочлена
Каждому значению х соответствует одно и только одно зна-
чение многочлена х3—2х2 + 5х—10.
Найдем значения этого многочлена при некоторых значе-
ниях х.
X — 3 2 0 1 2 к
х3 — 2х2 -|- 5х — 10 - 70 — 36 -10 — 6 0 90
Мы видим, что среди взятых значений переменной х есть
такое (число 2), подстановка которого в многочлен обращает
этот многочлен в нуль. Говорят, что число 2 есть корень много-
члена хя—2х2-|-5х—10
Вообще, корнем многочлена с одной переменной называется
значение переменной, при котором значение многочлена равно
нулю.
Мы нашли один корень многочлена х3—2х2 }-5х—10. Имеет
ли этот многочлен другие корни, кроме 2? Чтобы ответить на
этот вопрос, нужно решить уравнение
х3—2х2+5х—10 О.
Разложим многочлен на множители:
х3—2х2+5х—10=х2 (х—2)1-5 (х—2)=(х—2) (х2 + 5).
Так как множитель х2 -5 положителен при всех значениях
х, то уравнение (х—2)(х2 5) - 0, а следовательно, и многочлен
х3—2х2-р5х—10 имеют только один корень: число 2.
212
Найдем множество корней многочлена х3+2х2 — 9х—18. Для
этого решим уравнение х3 т 2хг—9х—18 0:
х2(х+2)—9(x-J-2) 0,
(х+2)(х2—9)=0,
(х Ь2)(х 3)(х—3)---0;
к-—2, или х = —3, или х 3.
{—2, —3. 3) —множество корней многочлена х34-2х2—9х—18
Многочлен х4 + 5х* + 1 не имеет корней, так как при любом х
его значение положительно и, следовательно, ни при каком х
значение многочлена не равно нулю.
Иногда бывает нужно решить обратную задачу: найти мно-
гочлен, корнями которого служат данные числа (и только они).
Пусть, например, нужно найти многочлен с корнями 2; 3
и —4.
Запишем произведение трех множителей: (х—2) (х—3) (х-г4),
где х — переменная.
Очевидно, что это произведение обращается в нуль при х,
равном 2, 3, —4, и только при этих значениях х.
Преобразуем произведение (х—2) (х—3) (х+4) в многочлен
стандартного вида:
(х—2) (х—3) (х 4-4) =х3—х2—14х | 24.
Корнями этого многочлена являются числа 2; 3 и —4.
Очевидно, что существует сколько угодно многочленов с тем ясе множеством
корней {2; 3, —4). Например, любой многочлен вида ах8 — ах? — 14ах -| 24а,
где а 0, коэффициенты которого соответственно пропорциональны коэффи-
циентам многочлена х* — х2 — 14х - 24, будет иметь своими корнями числа 2;
3 и —4. и только эти числа. Это следует из тождества
ах3 — ах2 — 14ах 24а = а (х3 — х2 — 14х -(- 24).
856. Докаж ите, что многочлен не имее г корней:
а) х241; в) —х°—2; д) 2х2—4х-|-5;
б) 2х4+3; г) х2+2х ,2; е) —х3+Зх—11.
857. Найдите корни многочлена:
а) х3—4х; г) 3</“ F бг/— 2; ж) 4а3— 8а~ а—2;
б) 2х—3; д) х2—4х |-4; з) 63+562—4Ь—20.
в) ji4—1; е) х3+10х2—х—10;
213
858. Не выти ляя корней т рехчлена, найдите их сумму и про-
изведение:
а) 2х2- 5х -8; б) Зх-—^-х—12.
859. Найдите многочлен по множеству его корней:
а) {2; -3); в) (0; 7}; д) {1; 2; 3};
б) {5; -5); г) {4}; е) 0.
860. Почему число 3 не является корнем многочлена
х'-| 5х3-г4хг 418л 11?
8С1. П очему число —5 не являемся корнем многочлена
х’ Зх3 —4х2 |-28х 4-11?
54. Разложение квадратного трехчлена на множители
В предыдущем пункте были рассмотрены примеры разложе-
ния многочленов на множители. Решение этой задачи для произ-
вольных многочленов третьей и четвертой степени достаточно
трудно.
Здесь мы ограничимся рассмотрением задачи разложения
на линейные множители квадратного трехчлена — многочлена
второй степени с одной переменной.
Пусть известно, что квадратный трехчлен ах24Ьх4-с, где
х — переменная, а, Ь и с — числа, причем а==0, имеет корни
xt и х,. Покажем, «то в этом случае он может быть представлен
ь виде произведения:
ахг + Ьх- с —а (х— х,)(х—х2). (1)
Для доказательства тождества (1) преобразуем его правую
часть:
а (х—xj(x—х2) =а (х2—х3х—х;х 4xjX2)
а (х2 —(х'! х2)х XjX.).
Корни х( и Хо трехчлена ах2 -ЬЬх 4-е являются корнями урав-
нения ах24~ Ьх-1 с =0. По теореме Виета
। Ь с
X. 4’ Хо —---И Х.Хо------.
а “а
Выполнив подстановку, получим:
л / л Ь С \ О
а (х- — (х, х.,) х 4 XjX,) = а । х- -|-х 4— ах- 4- Ьх 4 с.
\ а а I
Тождество доказано.
Рассмотрим пример. Трехчлен 2х2—5х—3 имеет корни,
так как дискриминант квадратного уравнения 2х2- 5х—3—0
положителен. Корни этого трехчлена — числа — ' и 3.
214
Пользуясь тождеством (1), представим трехчлен в виде
произведения:
2х2 5х — 3 = 2 х + - ।. х — 3|,
Если множитель 2 внести в скобки, то полученное тождество
запишется так;
2х2—5х—3 =(2л 1) (х—3).
Тождество (1) может быть распространено и на квадратный
трехчлен, имеющий единственный корень. В этом случае х1- хг
и тождество (1) примет вид:
ах- ,-Ьх Гс а (х—xt) (х—х,), т. е.
ах'2 Ьх 1-с=а(х—х)\
Например, трехчлен —25х! LOx— 1 имеет единства нный
корень, равный i (в этом легко убедиться, решив уравнение
5
—25x2-f 10г—1=0). Применяя тождество (1), получим:
— 25x4 Юх —1 = —25.x—
Если квадратный трехчлен не имеет корней, то он не может
быть представлен в виде произведения двух многочленов первой
степени.
Действительно, пусть при D < 0 ах2 -,-Ъх-\ с (kx т)(рх+ q).
m
Очевидно, что в этом случае----и
k
Но это противоречит условию.
Рассмотрим примеры применения тождества (1).
Пример 1. Сократить дробь
Решение. Попытаемся разложить на множители знаме-
на гель дроби — квадратный трехчлен Зх2—13х 10.
D =132 •+ 4 • 3 10 289; D >0. Следовательно, квагра-ный трех-
член имеет два корня.
Применяя формулу корней квадратного
дем их:
q
— — корни трехчлена.
Р
уравнения, най-
11 17
Х„ — -----!--
6
13 — 17
X, —
1 6
Пользуясь тождеством (1), имеем:
9 X
10 = 3(*
Зх- — 13х —
5).
х — 5
2
3
Мы разя ожили на множите ш знаменатель дроби, и теперь
ее можно сокра гить:
Зх» - 13х - Ю
3x4 2’
215
Пример 2. Решить неравенство
х2—х—20 <0.
Решение. Выяснив, что дискриминант трехчлена
х2—х—20 больше нуля, найдем его корни —4 и 5. Разложим
трехчлен на множители:
х2 — х— 20 =(х 4 4)(х—5).
Множеством решений неравенства (х-|-4)(х—5) <0 служит
объединение множеств решений систем неравенств:
х 4-4 >0,
х—5 <0,
J х 4-4 <0,
и (х—5 >0.
Оно представляет собой числовой промежуток |—4; 5[.
Пример 3. Разложить многочлен 4х2 4~ 9Ьх 4_ 5Ь2 на множители.
Решение. Данный многочлен можно рассматривать как квадратный
трехчлен относительно х.
Выразим с помощью формулы корней квадратного уравнения переменную х
через Ъ:
D _ (9Ь)2 — 4 • 4 • 5b2 = 81b2 — 80b2 = b2; Z> > 0 при любых Ь.
Отсюда
н к- II 1 оо у о- 11 1 I СП м • —9Ь4-Ь х2 — — —Ь. 2 8
(х 4- Ь) = (4.Г + cb) (X 4- Ь).
Пользуясь тождеством (1), имеем:
4л2 4- 9Ьх 4- 5Ь2 = 4
862. Найдите корни трехчлена и разложите его на множители:
а) 2а2—5а4-3; в) 2х2—5х—7; д) —у2 \-6у—5;
б) 5j/24-2z/~3; г) х2—11х+30; е) — z2— 524-6.
863. Разложите трехчлен на множители, если это возможно:
а) 4х2—9x4-5;
б) 4Ь2—9Ь+7;
в) -Зу24 8у4-И;
г) 16а2—24а4 9;
д) х2— х—3;
е) 2у2— 5у 4 8;
ж) З22—1224-12;
з) —48а2—8а 4-1.
864. Зная, что числа —3,8 и 4 — корни квадратного трехчлена
10у2—2у—152, разложите на множители выражение:
а) —10z/24 2//4-152; в) 100г/2— 20// —1520;
б) 5г/2Ж-76; г) -у2 | 0,2г/ | 15,2.
216
865. Докажите тождество:
а) 7х24-19х—6=(7х—2) (х 4 3):
б) (5а—4) (3—а)--5а2+19а—12.
866. При каком значении р выражение хг \-рх 36 тождествен-
но равно произведению двучленов:
a) x-j-4 и х4~9;
б) х—2 и х—18;
867. Сократите дробь:
в) я+6 и х4-6;
г) х—1 и х—36?
а)
7л~2 -1- .Y — 8 .
7х — 7 ’
В)
b2 — 85 4-15
Ь* — 25 ’
с2 — с— 110
22 + 9с — с2 ’
5а 4- 10
2а2 4- 13с 4- 18 *
у2 — 5у — 36
81 —t/2
5а2 —| - 8а 4- 3
144-Зсг - 11с2*
868. Решите неравенство:
а) (х+Ю) (х—6) >0;
6) 2 (у+З) (у-ЭХО;
в) 2у2—7у+6> 0;
г) За2—10а—8 <0;
д) х24~6х—55^0;
е) х2—5x^0.
869. Найдите область определения функции:
а) у = V 81 — х2;
б) у = ]/16х —х2;
в) у = ^Тх^ХОх^ЗЗ;
г) у = х2 4- 20х 4-100;
Д) У = 1 2х — х2 — 2;
। 45 — 4х — х2
870. Постройте график функции:
ч х2 — 5х + 6
а) У = -------— I 6) у =
х — 2
—2х2 4- 7х — 3
2х— 1
871. Докажите, что значение выражения не зависит от значе-
ния переменной, принадлежащей области его определения.
872. Упростите выражение и найдите множество значений пе-
ременной х, при которых значение выражения положи-
тельно:
Зх2 — 4х 4 1
4- 4х 4- 3;
б) 5х 4- 4 —
6л2 -I- 13х 4- 2
х + 2
217
Рис. 54
55. График функции
у = axz 4- Ьх 4- с
Найдем значения функции
промежутка [—6; 2]:
Мы уже неоднократно встре-
чались с графиком функции
у =ах2, являющейся частным
случаем функции у =ax2-j- Ьх+с.
На рисунке 54 изображены
параболы — графики функции
р— ах1.
Напомним некоторые свой-
ства графика функции у —ах2:
1. График проходит через
начало координат.
2. График имеет ось симмет-
рии: это ось ординат.
3. При а>0 кривая распо-
ложена в верхней полуплос-
кости, причем ветви параболы
уходят вверх; при а<0 пара-
бола расположена в нижней по-
луплоскости, а ее ветви уходят
вниз.
4. От коэффициента а зави-
сит форма параболы: чем больше
|п ’, тем «круче» ветви параболы.
Перейдем теперь к построе-
нию графика функции у=ах2^
+ Ьх-]-с с любыми коэффициен-
тами а, & и с (а#=0).
Пусть нужно построить гра-
фик функции
у- .г24 4х—5.
для некоторых значений х из
X — 0 —5,5 5 -4,5 — 4 —3 —2 — 1 0 0,5 1 ' 1,5 2
У 7 3,25 0 — 2,75 —5 —8 —9 —8 —5 — 2,75 о: 3,25 7
Точки, координаты которых указаны в таблице, изображе-
ны на рисунке 55, они намечают некоторую кривую. Если при-
ложить шаблон параболы у=х~ так, чтобы вершина параболы
совпала с точкой (—2; —9), ось симметрии была параллельна
218
Рис. 56
оси ординат и ветви направлены вверх, то окажется, что все
построенные точки принадлежат параболе (рис. 56).
В последующих классах будет доказано, что графики функ-
ций р=ах2-ЬЬх + с и т£=«х2, где а-#0, при одном и том же зна-
чении с конгруэнтны и существует параллельный перенос,
переводящий график функции у—ах2 в график функции
у=ах2 + Ьх-\-с.
Так как график функции у=ах2 — парабола, ось симметрии
которой перпендикулярна оси абсцисс, а ветви при п>0 на-
правлены вверх, а при а <0 — вниз, то графиком функции
у = ах2-\-Ъх-\-с также является парабола с осью симметрии,
перпендикулярной к оси абсцисс, и ветвями, направленными
вверх при а >0 и вниз при а <0.
219
Для построения графика функции у ах2-{-Ьх \-с при D J-0
удобно найти точки пересечения графика с коирдина-j ными
осями и определить положение вершины параболы. Эти точки
позволят начертить график функции у =ах2 + Ьх |-с.
Рассмотрим пример.
II встроить график функции
у- х-—2х — 8. (1)
Найдем точку пересечения графика с осью у.
При х 0 значение у равно -8, следовательно, кривая
пересекает ось у в точке А (0; —8).
Подставляя в уравнение (1) значение у, равное нулю, опре-
делим точки пересечения параболы с осью х. Решая уравнение
х2—2х—8 0,
найдем его корни —2 и 4. Значит, точки пересечения графика
с осью абсцисс: В ( 2; 0) и С (4; 0) (рис. 57).
Точки В и С принадлежат параболе и лежат на перпендику-
ляре к ее оси симметрии, значит, точки В и С симметричны от-
носительно оси симметрии параболы.
Отсюда следует, что ось симметрии параболы пересекает
ось абсцисс в точке D, ра вноотстоящей от точек В и С. Абсцисса
точки D равна полусумме абсцисс точек В и С:
-2+4 JL
2
Очевидно, что вершина параболы лежит на ее оси симмет-
рии. Поэтому абсцисса вершины параболы та же, что и у точки
D, т. е. равна 1.
Подставляя в формулу (1) значение х =1, найдем ординату
вершины параболы:
у =1—2 1-8 = — 9.
Итак, вершина параболы Н имеет координаты (1; -9).
Наметив точки А, В, С и Н, строим график функции у~
- х" -2х —8 (рис. 57).
Если квад ра "ный трехчлен ах2 { Ьх { с не имеет корней, то
график функции у ах2 {-Ьх с не пересекает оси х. Для пост-
роения графика функции у — ax2-j- Ьх4~с в этом случае целесооб-
разно найти точки пересечения графика с какой-нибудь прямой,
параллельной оси абсцисс. За такую прямую удобно принять
прямую у с Дальнейшее построение выполняете я аналот и«но
рассмотренному выше.
Пример. Построить график функции
у --2х24 6х { 7. (2)
Парабола пересекает ось у в точке А (0; 7). Проведем пря-
мую у —7 и найдем точки пересечения параболы у -2х24 6х , 7
, 220
Рис. 5Ъ
с этой прямой. Для этого подставим в уравнение (2) значение у,
равное 7:
7=2х*+6х+7.
Приведя уравнение к стандартному виду, получим:
х2 + 3х -0.
Корни этого уравнения —3 и 0, значит, парабола у = 2х2А
4 6х + 7 и прямая у =7 пересекаются в точках А (0; 7) и В (—3; 7)
(рис. 58).
Точки А и В симметричны относительно оси симметрии па-
раболы, поэтому абсцисса вершины параболы равна полусумме
абсцисс точек А и В, т. е. —1 —.
221
Подставляя в уравнение (2) значение х =—l~t найдем ор-
динату вершины параболы:
Вершина Н параболы имеет координаты: (—1 2-1
Точки А, В и Н определяют параболу (рис. 58).
873. Используя график функции f (х)=х—2х—8 (см. рис. 57),
найдите:
а) значение функции, соответствующее х =—1,5; —8; 4;
б) значение аргумента, которому соответствует значение
функции, равное 7; —8; —27;
в) множество значений аргумента, на котором f (х) = О,
/(х) <0, f(x) >0;
г) множество значений аргумента, на котором функция f
убывает, возрастает;
д) значение переменной х, при котором функция принима-
ет наименьшее значение.
874. Не выполняя построения графика, найдите координаты
точек пересечения графика функции с осью х и с осью у:
а) у=х~—5х—6; б) у = —х2+2x4-3; в) у=х2—6х; г) у — —2х2+7х; д) г/=3х“ +9х; е) i/= 8х—-i х2; ж) z/=(x—5) (х+3); з) z/=(2x+l) (х—2); и) у=х2—7х+13; к) у ——2х2—5х—7.
875. Постройте график функции у=х'-\-2х—15. Рассматривая
построенный график, найдите:
а) множество значений х, на котором значения функции:
1) отрицательны, 2) положительны;
б) множество значений х, на котором функция: 1) возрас-
тает, 2) убывает;
в) наибольшее или наименьшее значение функции;
г) множество значений функции.
876. Постройте график функции и проведите исследование функ-
ции по схеме, предложенной в предыдущем упражнении:
а) у~х2-[4х; в) {/=х2+2х—3; д) у = — х~ +бх—10;
б) у 4х—х2; г) у=—х2—4х+6; е) у ——2х2—5х—2.
2
225
877. а) Сколько общих точек с осью абсцисс имеет график
функции у — х24 6x4 9?
б) Докажите, что график этой функции расположен в
верхней координатной полуплоскости.
в) Постройте график функции у— х24~6х4"9 по точкам,
заполняя таблицу:
X - 6 — 5 — 4 — 3 — 2 — 1 0
У
Рассматривая построенный график, укажите множест-
во значений х, на котором функция: 1) убывает, 2) воз-
растает.
878. Постройте график функции у=х2—2x4-1.
Рассматривая построенный график, найдите наименьшее
значение функции и укажите множество значений х, на
котором функция: 1) убывает, 2) возрастает.
879. Постройте график функции у — —х:?+4х—4 и укажите:
а) наибольшее значение функции;
б) множество значений функции;
е) множество значений х, на котором функция: 1) возрас-
тает, 2) убывает.
880. Постройте график функции у =(х-]-2)(х—4) и, пользуясь
им, решите неравенство:
а) (х+2) (х—4) >0; б) (х+2) (х—4) <0.
881. Укажите координаты вершины параболы:
a) i/=(x-J-5)(x 4-3); б) j/=2 (х—1) (х—5).
882. Постройте график функции у=х2—6x4-10. Рассматривая
график, укажите множество значений х, на котором функ-
ция: а) убывает, б) возрастает.
883. Постройте график функции:
а) у—х2—2х ,8; б) у ——* х 4“2х—3.
2
884. Докажите с помощью графика, что неравенство выпол-
няется при всех значениях х:
а) х2— 3x4 8 >0; б) —х24-6х—10 <0.
885. Проходит ли график функции у=х2—7х—31 через точки
А (3; —43), В (—8; 89), С (—5; —29)?
223
88G. а) При каком значении с график функции у=2х2- 7x-t-c
проходит через точку А (—10; 150)?
б) При каком значении b график функции у—х2 + Ьх—19
проходит через точку D (—11; —30)?
887. Известно, что график функпии у ах2 + Ьх— 48 проходит
через точки М (1; 2) и N (2; 10).
Найдите значения коэффициентов а и Ь.
888. Известно, что график функции у 2х2 + &х , с проходит
через точки Р (3; 2) и Q (—2; 12). Найдите значения коэф-
фициентов Ь и с.
ДОПОЛНИТЕЛЬНЫЕ УПРАЖНЕНИЯ
К Г Л А В Е IV
К пункту 46
889. Решите графически систему уравнений:
а) (2х 4 у = 8, У - х ; в) 8 У = X У = х2; д) | (х — 1)у 0, (у = 2х‘2;
б) 5х 2у 0, У х-'; г) ’н .. | -1Й II II е) |(х — у) (х4 у) = 0, (г/ - — х*.
890. Решите графически уравнение:
а) х2 = 5х - 8; г) — 2 х 7 - х; ж) х2 4- 6х 16 0;
б) х2 = 1 х -| 5; Д) X — х 12; з) -1х24 х 4 2- 0.
в) 2х2- 3> -|-10; е) Зх24~Зх —8;
891. Решите графически неравенство:
а) х2> - х 4 12; в) — х2<2х; 2 д) х2 — х 4 4> 0;
б) х2 < 5х 4 6; г) - х- > Зх; 2 е) 2х2 4- 5х -1 3 <0.
К пункту 47
892. Решите уравнение, выявляя квадрат двучлена:
а) х2- 16х | 48 0,
б) х2 г12х 1-27 0;
в) х1- 10х 39 0;
г) х2- 6х 55 0;
д) х2 7х -18 0;
е) х2- 11x4-28 0;
ж) 2х"- 5х I 2 0;
з) Зх2—х 70 0.
224
К пунктам 48 и 49
893. Решите по формуле (А) уравнение:
а) 4х2- Чх 1 3=0; д) 8х+х—75=0;
б) х24-х— 90=0; е) Зх®—Их—14 =0;
в) х2—х—90=0; ж) Зх24 Их—34=0;
г) 5х2—18x-t-16=0; з) х2—х—1 =0.
894. При каких значениях х справедливо равенство:
а) (5х . 3)2=5 (х f 3); д) (5х+3)2 =5x4-3;
б) (Зх , 10)2= 3 (х | 10); е) (5х4-3)2=(Зх4-5)2;
в) (Зх—8)2=3х2—8х; ж) (4х 4-5)! =4 (х4-5)2;
г) (4х 4~5)2 = 5х2 4 4х; з) (2х i 10)2 -4 (х+5)г?
895. Решите уравнение, применяя формулу (В):
а) х2--18x4 80= 0;
б) х2- 14х—15 = 0;
в) Зх2—22х—25=0;
г) 5х2 4-26x4-24=0;
д) 9х'--78x4-25=0;
е) х2—208x4-10!=0.
896. Решите уравнение и выполните проверку:
а) х2—2х—5= 0;
б) х24-4х 4-1=0;
в) 3z/24z/2 = 0;
г) 5у2-Ту4-1 0;
д) 2у24 Пу 4 Ю=0;
е) 4z2— 9z—2 = 0
897. Найдите приближенные значения корней уравнения:
а) х2—2х—2=0; в) Зх2—7x4-3=0;
б) х24-5х 4-3=0; г) 5х24-31х 20 = 0.
898. Решите уравнение:
б) (х 4- 2)3 = х (х
а) (х — 1)” = х (х 4-
(2 u-f-1)’ 4j- 1
8 5
. (У - 3)а _ А-У
'20 2
2)2 — 9; и _2С_ X— 1
I)2 4- 62; е) - 21
4 х- 4-2
. 12 8
= 1; Ж) - —
х — 1 х4 1
16 30
1J з) — + X —* о 1 — X
= 4;
= 2:
= 1;
( Алгсб] а, 7 кл
225
899. При каких значениях переменной у*
а) значение суммы дробей ---------- и —— равно значению
//4-1 у — 2
их произведения;
б) значение суммы дробей —— и —С-- равно значению
у — 3 у 4- 3
их произведения;
ч - о V 4- 12 у
в) значение разности дробей —— и —— равно значению
У — 4 у 4- 4
их произведения;
г) значение разности дробей -----и ------ равно значению
2^ — 1 2у 4
их произведения?
900. Решите уравнение:
а) 1---------1----3— = о;
i/2~9 j/24-3i/ бу-1-2^
б) 2у~г ч- 8 = 2У4-1 .
' 14{/2 4-7у “Г 121/2-3 61/2-31/’
. 3 1 3
В)------ —---------------------------.
Х‘ — 9 9 — 6х 4- х2 2ха 4- 6х
901. При каком значении а один из корней уравнения
ах2—Зх—5=0 равен 1?
902. Докажите, что один из корней уравнения ах2—(а 4-с)х 4-с — 0
равен 1.
903. Найдите соотношение между коэффициентами уравнения
ох24-Ьх4-с=0 в том случае, когда один из корней его:
а) равен —1; б) равен —, где с^0.
а
904. Найдите множество значений параметра а, при которых
уравнение имеет единственный корень:
а) 4х24-28х4-а=0; в) ах24-28x4-4=0;
б) 25х2 4-ах4-16 = О; г) х24-ах4-114=0.
905. Докажите, что корни уравнения сх24-Ьх4-о=0 (ст^О) об-
ратны корням уравнения ах24-дх4_с=0 (ат^О).
К пункту 50
906. а) Найдите пять таких последовательных целых чисел,
чтобы сумма квадратов трех первых чисел равнялась сум-
ме квадратов двух последних.
б) Найдите три таких последовательных четных числа,
чтобы сумма квадратов первых двух равнялась квадрату
третьего числа.
226
907. Сад и огород имеют форму прямоугольника; площадь каж-
дого из них равна 1500 №. Ширина сада на 5 м больше
ширины огорода, зато длина сада на 10 м меньше длины
огорода. Найти размеры сада и огорода.
908. а) Один завод должен был изготовить 720 станков, а дру-
гой за тот же срок — 660 станков. Первый завод, изготов-
ляя в день на 10 станков больше, чем второй, выполнил
заказ за 2 дня до срока, а второй завод, изготовив 22 стан-
ка сверх плана, закончил работу за 1 день до срока. Сколь-
ко станков изготовлял ежедневно каждый завод?
б) Две соревнующиеся бригады рабочих должны были
изготовить к некоторому сроку по 240 деталей. Изготовляя
в день на 8 деталей больше, чем вторая бригада, пер-
вая выполнила задание за 3 дня до срска, опередив вто-
рую бригаду на 1 день. Каков был срок выполнения ра-
боты?
909. а) Одна тракторная бригада должна была вспахать 240 га,
а другая на 35% больше, чем первая. Вспахивая ежеднев-
но на 3 га меньше второй бригады, первая все же закончи-
ла работу на 2 дня раньше, чем вторая бригада. Сколько
гектаров вспахивала каждая бригада ежедневно?
б) С одного участка собрали 1440 ц пшеницы, а с другого,
площадь которого была на 12 га меньше, — 1080 ц. Найти
площадь каждого участка, если известно, что на первом
участке собирали пшеницы с каждого гектара на 2 ц боль-
ше, чем на втором.
910. а) При постройке здания требовалось вынуть 4500 №
грунта в определенный срок. Перевыполняя дневную нор-
му на 45 лс3, строители уже за 4 дня до срока выполнили
96% задания. Определите срок работы.
б) Два звена должны были прополоть овощные культуры
на участке в 7200 лс2. Пропалывая в час на 120 № больше
второго звена, первое звено закончило работу на 1 час
позже второго и при этом выполнило 60% всей работы.
Сколько часов работало каждое звено?
911. а) Бригада рабочих должна была к определенному сроку
изготовить 360 деталей. Перевыполняя дневную норму на
9 деталей, бригада уже за 1 день до срока перевыполнила
плановое задание на 5%. Сколько деталей изготовит
бригада к сроку, если будет продолжать работать с той
же производительностью труда?
б) По плану колхозная бригада должна была к определен-
ному сроку прополоть овощные культуры. Начав работать
на 2 дня позже, чем было намечено первоначально, брига-
да перевыполняла дневную норму на 2 га и уже за 1 день
8*
22 Г
до срока прополола 49 га, что составляло 98% задания.
Какой срок был установлен бригаде для выполнения
задания?
912. а) Бригаде рабочих было поручено изготовить в опреде-
ленный срок 270 деталей. Перевыполняя задание, она
ежедневно изготовляла на 6 деталей больше, чем требова-
лось по заданию, а потому за 4 дня до срока бригада уже
сдала 264 готовые детали. Сколько деталей должна была
изготовлять бригада в один день по заданию и какой срок
ей был дан для его выполнения?
б) По плану бригада колхоза должна была убрать уро-
жай зерновых с 540 га к определенному сроку. После того
как убрали 30% урожая, бригада, получив дополнитель-
но комбайн, стала ежедневно убирать на 9 га больше, чем
первоначально, и закон- ила уборку на 1 день раньше
срока. Сколько дней продолжалась уборка урожая?
913. а) Отправляясь в путешествие, турист рассчитывал истра-
тить в дороге 72 руб. В течение первых 5 дней его расходы
совпадали с расчетными, затем он стал расходовать в
день в среднем на 1 руб. больше, чем предполагал, и, за-
державшись в пути на 1 день, вернулся домой, истратив
на все путешествие на 23 руб. больше, чем намечал. Сколь-
ко дней продолжалось путешествие?
б) Бригада рабочих должна была в определенный срок
изготовить 272 детали. Через 10 дней после начала работы
бригада стала перевыполнять дневную норму на 4 детали
и уже за один день до срока изготовила 280 деталей. Сколь-
ко деталей изготовит бригада к сроку?
914. а) Две машинистки получили для перепечатки рукопись.
После 2 ч совместной работы одна из машинисток полу-
чила другое задание и вторая, оставшись одна, закон-
чила работу через 1 ч 20 мин. За сколько часов могла
бы перепечатать рукопись каждая машинистка, если вто-
рой на это понадооилось бы на 1 ч 10 мин больше, чем
первой?
б) Уборку урожая с участка начал один комбайн. Через
2 ч к нему присоединился второй комбайн, и после 8 ч
совместной работы они убрали 80% урожая. За сколько
часов мог бы убрать урожай с участка каждый комбайн,
если известно, что первому на это понадобилось бы на 5 ч
больше, чем второму?
915. а) Цех завода получил заказ изготовить к определенному
сроку партию деталей. Если выполнение заказа поручить
первой бригаде, то она закончит работу на 3 дня позже
срока. Вторая бригада, работая одна, могла бы выпол-
Е28
нить заказ на 8 дней позже срока. Над исполнением зака-
за работали совместно обе бригады и закончили работу
за день до срока. Сколько дней понадобилось бы каждой
бригаде, чтобы одной выполнить заказ?
б) Два трактора могут вспатать зябь на 18 ч быстрее, чем
один первый трактор, и на 32 ч быстрее, чем один второй
трактор. За сколько часов может вспсхать зябь каждый
трактор, работая один?
916. а) Поезд вышел со станции А по направлению к станции В.
Пройдя 460 км, что составляло 75% всего пути, он был
задержан на полчаса, и машинист, увеличив скорость на
15 к.чч, привел его на станцию В без опоздания. Найти
первоначальную скорость поезд а.
б) Мотоциклист предполагал проехать расстояние S0 км
за определенное время. Проехав 54 км, он должен был
остановит ься у закрытого шлагбаума на 5 мин. Продол-
жая движение, он увеличил скорость на 6 км'ч и прибыл
к месту назначения в намеченное время. Найти первона-
чальную скорость моте ииклиста.
917. а) Расстояние между городами А и В 260 клс. Через 2 ч
после выхода автобуса из А в В он был задержан на 30 мин,
поэтому, чтобы прийти в В по расписанию, должен был
увеличить скорость на 5 км, ч. Найти первоначальную
скорость автобусе.
б) Велосипедист проехал 40 км от города до турбазы.
Возвращаясь обратно, он 2 ч ехал с той же скоростью, а
затем сделал остановку на 20 мин. Начав движение сно-
ва, он увеличил скорость на 4 км, ч, а пот ому затратил на
обратный путь столько же времени, сколько на путь
из города до турбазы. Сколько времени затратил велоси-
педист на путь из города до турбазы?
918. а) Катер, скорость которого в с гоячей воде 15 км ч. отпра-
вился от резного при,гала вниз по течению реки и, пройдя
36 кн, догнил плот, отправленный от того же причала за
10 ч до отправления катера. Найти скорость течения реки-
б) Турист, проплыл по течению реки на плоту 12 км,
возвратился o6pai но на лодке, скорость кот орой в стоя-
чей воде 5 км/ч. Найти скорость течения реки, если из-
вестно, что на все путешествие турист затратил 10 ч.
919. а) Моторная ледка прешла 39 км по течению реки и 28 км
против течения за то же время, за которое она могла в
стоячей воде пройти 70 км. Какую скорость имеет моторная
лодка в стоячей воде, если скорость течения реки 3 клг/ч?
б) Турист проплыл на байдарке 25 км по озеру и 9 км
против течения реки за столько же времени, сколько ему
£29
потребовалось бы для того, чтобы проплыть по течению
реки 56 км. Зная, что скорость течения реки равна 2 км'ч,
найти скорость лодки в стоячей воде.
920. а) Рыболов отправился на лодке от пункта N вверх по
течению реки. Проплыв 6 км, он бросил весла, и через
4 ч 30 мин после отправления из N течение снова отнесло
его к пункту N. Зная, что скорость лодки в стоячей воде
90 м’мин, найти скорость течения реки.
б) От пристани А в направлении пристани В, отстоящей
от А на 40 км, отправили плот. Через 3 ч 20 мин после
отправления плота навстречу ему от пристани В против
течения реки вышла моторная лодка, которая встретила
плот в 16 км от А. Найти скорость течения реки, если
известно, что скорость моторной лодки в стоячей воде
равна 15 км/ч.
921. а) Поезд должен был по расписанию пройти перегон, рав-
ный 420 км, за определенное время. Пройдя у всего расстоя-
ния, он был задержан в пути на 15 мин. Затем машинист
увеличил скорость на 10 км'ч, и перегон был пройден без
опоздания. Сколько времени затратил поезд на прохожде-
ние перегона?
б) Мотоциклист проехал расстояние MN, равное 180 км,
с некоторой средней скоростью. Возвращаясь обратно,
2
он — расстояния от N до М ехал с той же скоростью,
3
а ьа,ем увеличил скорость на 5 км'ч и возвратился в М,
затратив на обратный путь на 8 мин меньше, чем на путь
из М и N. Сколько времени затратил мотоциклист на весь
путь в оба конца?
922. Автотурист проехал расстояние между пунктами А и В,
равное 400 км, с нс которой средней скоростью. Возвра-
щаясь обратно, он 2 ч ехал с той же скорост ью, а затем
увеличил скорость на 10 км'ч и возвратился в пункт А,
затратив на обратный путь на 40 мин меньше, чем на путь
из А и В. Сколько времени затратил автотурист на обрат-
ный путь?
923. а) Расстояние между пунктами А и В велосипедист про-
ехал за 3 ч. Возвращаясь обратно, он первые 24 км ехал
с той же скоростью, а затем увеличит скорость на 2 км'ч
и прибыл в пункт А, затратив на обратный путь на 10 мин
меньше, чем на путь из А в В. Найти расстояние между
пунктами А и В.
б) Автобус проходит расстояние между городами М и N
по расписанию за 5 ч. Однажды, выйдя из М в N, авто-
230
бус был задержан на 10 мин в 56 км от М и, чтобы при-
быть в город N по расписанию, должен был оставшуюся
бол! шую часть пути проходить со скоростью, пр< выша к>-
щей первоначальную на 2 км/ч. Найти скорость автобуса
по расписанию.
924. а) Расстояние от прист ани М до пристани N по течению
реки катер проходит за 6 ч. Однажды, не дойдя до приста-
ни N 40 км, катер повернул назад и возвратился к при-
стани М, затратив на весь путь 9 ч. Найти скорост ь ка-
тера в стоячей воде, если скорость течения реки равна
2 км/ч.
б) Велосипедист предполагал проехать расстояние от тур-
базы А до турбазы В за 4 ч. Однако, проехав 30 км, он
вынужден был снизить скорость на 3 км/ч, так как
дорога пошла в гору, и прибит на турбазу В на полча-
са позже, чем предполагал. Найти расстояние между тур-
базами,
925. Из пункта А в пункт В, расстояние до которого 20 км,
выехал велосипедист, а через 15 мин вслед за ним со ско-
ростью 15 кле7ч отправился другой велосипедист, который,
дшнав первого, повернул назад и возвратился в пункт А
за 45 мин до прибытия первого велосипедиста в В. Найти
скорост ь первого велосипедиста.
926. Из А в В со скоростью 4 км. ч вышел турист. Спустя час
вслед за ним из А вышел второй турист, преходивший
в час 5 км, а еще через час из А выехал велосипедист,
который, обогнав одного туриста, через’ 10 мин сбогнал
И другого. Найти скорость велосипедиста.
927. а) На огороженном уч аст ке прямоугольной формы дли-
ной 150 м и шириной 110 ле разбит прямоугольный газон,
одинаково отстоящий от ограды. Найти длину и ширину
4
газона, если известно, что площадь газона составляет —
площади участка.
б) Участок прямоугольной формы имел площадь 1200 ле8.
После увеличения длины участка иг 4 ле, а ширины ьа
6 ле его площадь увеличилась на 35%. Найти первона-
чальную длину и ширину участка.
928. а) Коробка (без крышки) имеет форму прямоугольного
параллелепипеда с квадратным основанием. Площадь дна
коробки на 176 еле5 больше площади поверхности боковых
ее стенок. Высота коробки — 10 см. Найти площадь дна
коробки.
б) Из прямоугольного куска жести с измерениями 30 еле
и 48 еле нужно сделать открытую коробку. Для это-
го по углам прямоугольника вырезают квадраты, а
231
оставшукся часть сгибают
(рис. 59). Определить, ка-
кую длину должна име. ь
сторона вырезаемого квад-
рата, чтобы площадь осно-
вания коробки равнялась
ее боковой поверхности.
929. а) Длины сторон прямо-
yi олышка 37 м и 6 м.
Прямая, параллельная его
стороне, делит прямоуголь-
ник на два подобных, но не
kohi руэнтных прямоуголь-
ника. Н ли. и площадь каж-
дой части.
б) Прямая, параллельная стороне прямоу! ольника и от-
стоящая от нее на 9 м, отсекает прямоугольник, подобный
данному. На какие части делит эта прямая площадь пря-
моугольника, если его периметр равен 176 м?
930. Через вершину прямоугольника вне его проведена пря-
мая, отсекающая на продолжениях проти воположных
сторон отрезки в 15 см и 40 см. Найти площадь прямо-
угольника и его стороны, если известно, что периметр
прямоугольника равен 98 см.
931. а) Сплав меди с цинком, содержащий 5 кг цинка, сплав-
лен с 15 кг цинка. В результате содержание меди в сплаве
понизилось по сравнению с первоначальным на 30%.
Какова была первоначальная масса сплава?
б) Сплав золота с серебрим, содержащий 80 г золота,
сплавлен со 100 г чистого золотя. В результате содержа-
ние золота в сш аве повысилось по сравн. нич> с первона-
чальным на 20 %. Сколько серебра в сплаве?
К пункту 51
932. Дано уравнение относительно х. Решите его:
а) х2—13axf42a2 =0, г) Зх2—(4А—6)х <fe2 — 2ft =0;
б; 2х’+7ах -9а? =0; д) х(Зх-1)-2п(х— 2) = 10,
в) 4х2--(5с+4)х+с2-Ьс—0; е) <хх(х-г5) -х(х-|-2)=3—6а.
933. Найдите множество значений t, при которых уравнение
имеет по крайней мере один корень:
а) 9х2—12х-Н — 0; в) fx2<6x—1=0;
6У 4x2 + ix+9 ^0; г) х2—(2i+l)x + fa—1 0.
232
К пункту 62
$34. Найдите значение b и решите уравнение:
а) 2xtJt~bx—10=0, если оно имеет корень, равный 5;
б) 8х2 +6х+24=0, если оно имеет корень, равный 3;
в) (6—1)х2-Ь(Ь4-1)х«=72, если оно имеет корень, равный 3|
г) (6—5)х2—(6-|-2)х4-6=0, если оно имеет корень, рав-
„ 1
ный — .
2
935. Почему уравнение 7х2-\-Ъх—23=0 при любых значениях
6 и теет один положительный и один отрицательный
корень?
936. Почему уравнение 12х24-70х-|-а!-г1=0 при любых зна-
чениях а не имеет положительных корней?
937. В уравнении 6x24-6x-f-l=0 один из корней больше дру-
гого на —. Чему равно значение 6?
938. а) Разность корней уравнения 25х2—30х-гс = 0 равна 0,8.
Найдите коэффициент с.
6) Отношение корней уравнения 24х2 4-6x4-25=0 равно
1,5. Найдите коэффициент 6.
939. Разность квадратов корней уравнения 2х2+7х 4 с=0 рав-
на 1,75. Найдите с.
940. Один из корней уравнения Зх24-6х-гС=0 равен — 1 —,
3
а другой — второму коэффициенту уравнения. Найдите
коэффициенты бис.
941. Один из корней уравнения ах2—5х^-с = 0, где а >0 и Ст^О,
равен а, другой корень равен с. Найдите коэффициенты
а и с.
942. Составьте квадратное уравнение с корнями yt и у2, если:
a) i/i = 10; Ул =12:
б) = —3; у2 =8;
в) У1 = —7; у2=0;
Г) У1 = •£: у2 = 8;
о
е) у, = — Кб; _у2 = Кб;
ж) ух = 2 — К3; Уч = 2 4- К3;
з) У] =
11 — 2/80, „
- . Л
Х>у,—4;»з = -0.1; «)й = =“=112; ,.-=11212
D О О
943. Составьте уравнение по его корням yt и уа и для проверки
решите составленное уравнение:
а) У!=<И 5, у2= 3; б) yl = 2a-\l, у2 = —1.
233
944. Составьте квадратное уравнение, корни которого были
бы на 1 больше соответствующих корней уравнения
2х!—8х 4-3=0.
945. Составьте квадратное уравнение, корни которого были
бы на 0,2 меньше соответствующих корней уравнения
5х2— х—2=0.
946. Составьте квадратное уравнение, корни которого равня-
лись бы квадратам соответствующих корней уравнения
8х*4-7х-»-1 = 0.
947. Составьте квадратное уравнение, корни которого были бы
обратны соответствующим корням уравнения
4х?—13xi -7=0.
948. Пусть корни уравнения ах2 4 Ьх~г с—0 равны х, и х2. Вы-
полнив необходимые вычисления, найдите значения коэф-
фициентов и корней уравнения, соответствующие пустым
клеткам таблицы:
№ а . ь. с Х2
1 5 43 —132
2 2 1 2 6
3 180 —10 6
4 —100 0,7 1,3
5 —5 12 3
6 6 1 1 СО | Ь5
7 9 —7 1
К пунктам 53 и 54
949. Найдите корни многочленов:
а) х”—9х24х—9, в) х3—Зх21 Зх—1;
б) х”4-9х"— 4х—36; г) х4 —100.
950. Докажите, что число 15 не является корнем многочлена
х4—13х3—207х24 1681x48.
951. Докажите, что число —13 не является корнем многочлена
х4—20х4 | 919хг- 840х 1 26.
234
952. Напишите многочлен с целыми коэффициентами, зная
множество его корней:
а) X = {5; 10;;
б) X = {- 3; 0; 3};
в) X = {1; 2; 3};
г) X = (Д; 3; -6];
д)Х-{—Д;0; Д;
е) X = —1; —3; 2; 3
12 2
953. Разложите, если возможно, на линейные множители:
а) х2—Зх—21;
б) 5х24 13x4-8;
в) —4х2+7х—3;
г) 10х2+9х—63;
д) а2+а—20;
е) 7Ь2—ЗЬ-|-1;
ж) а2—а Ъ—6Ь2;
з) х~-^-ах -30а2;
и) Зу2— 2Ъу— 5Ь2:
к) г2—2г— 1;
л) 2c'!J cdJ 4d'2,
м) х3—12х24-20х.
954. Разложите на множители:
a) 6t3 —31Za— 31*4-6; в) 4Ь5—4Ь4—81(Ь—l)s;
б) а2(а —5)3—36а {-180; г) 5х3—19х2-38хт40.
955. Сократите, если возможно, дробь:
— 5а»т 13а 4-е
а) -----Т-----
(а — 2р — 1
б 27-(р 4-1)3 .
' 1р- — 9р — 10 ’
. Зс» — 11с 4- 10
й — С)3 — 8сг
. вс» —5а —4
г) ------------—.
27о» — (а — I)»
956. Докажите, что на
всей области определения выражения
его знгчение не зависит от а:
/_____4____________а 4- 1 х
I 5а® 4- а — 4 9 (5а - 4V
2 ) а 4-4 . / 9 (а — 1)
2 — о о “ 1 3 j 4
[-----“------ +
\ За» т а — 2 9а» — 4 '
15а - 12 _ 2
а 4 7 а 4- Г
__ (2а-7)» \
За» 4 а —4,’*
За 4-4______1_#
* 9а» — 4 а 4-1’
21 а» —25
4а ] 6 а 4- 2
—----1----------
23 - а» 2а» — 7а — 15
. 3 , За ’-12
д)---------------—
а - 2 25 - а»
2а- 1
а2- 25
а — 5
2а» 4- 9а — 5,
4 (а - 2)_ а —3 ,
а» — а — 6 4 — а» *
а2 4 2
а — 1 а — й
235
957. Решите уравнение:
35ж_______ж 4- 2 Зж — 1
4 Юж — 6ж» Зж 4-1' ж — 2
25ж—21 2ж — 3 ж-| 4
2ж»4-5ж—12 ж 4-4 3 —2ж
13 1 — -
2j/»4-j/-21 '2у4-7~ у2-9’
958. Решите неравенство:
а) х2—5x4-6 <0; в) Зх24-4х-7>0;
б) — х2— 7x4 6 >0; г) — Зх2—10х<3.
959. Найдите область определения функции:
а) у = /х2 — 49; д) у = —1^* — 3 ;
’ а г у ж2 —2ж-80
б) у = 1/144 — 9х2; е) у = — х ?
ж2 — 2ж —80
в) у = /х^-2х — 63; ж) у = jf*3 ~ 42 ;
. . ---5— --;—тёг~ х ж2 - ж — 6
Г) У = X2 4 x4- 42; з) у =
К пункту 55
960. Не выполняя построения графика, укажите, в каких точ-
ках пересекает координатные оси график функции:
а) у=х24-2х—120; д) ^—(5 — 2х) (1+х);
б) у=—х24-х4 56; е) у =х3— 2х2— 99х;
в) у — 2х2+9х 4-11; ж) у = х34-10х2 — 4х—40;
г) у = (х—3) (2x4*1); з) у—х*— 2х2+3.
961. Постройте график функции:
а) у = 2х2—5х; д) у=х2--2х—15;
6) у=6х -2х2; е) у=^хг—3х 4;
в) у=4х2—9; ж) у = (2х—7) (х4-1);
г) у =4— ix2; з) у=(2—х) (х4 6).
236
962. Найдите множество значений х, при которых перемен-
ная у возрастает с возрастанием х, если:
а) у 9—х2; в) у=х2— Зх—18;
б)у=^-х2—8; г) у = — х2— 4x4-5.
963. Решите графически неравенство:
а) х2—х—2<0; в) 2х24 3х— 5 <0;
б) х24-2х—15>0; г) i Xs—5x4-12>0.
2
964. Не выполняя построения графика, выясните, в кв ких
координатных четвертях расположена парабола, если:
а) у— 2х2—х+3; в) у -х2+16x4-3;
б) у=х2— 2х—63; г) у=— Зх---2х—7.
965. Постройте график функции:
а) у=|х2—х—12|; в) у=х2 — х| - 12;
б) у — х2- 2х—8,; г) у—х2+2[х[—8.
966. Напишите ураснение, соответствующее каждой из пара-
бол, изображенных на рисунке 60.
Гис 60
ОТВЕТЫ
Глава I
1. д) 6р4; е) 6g3 — 4р2д 4- 3g2; ж) 5/п — 12п; з) а1 4~ Ь*. 2. б) у2 + У — 56;
е) —g24-18g—81. 3. б) 9—4а2; ж) у2—2у5Ц-52; з) 9p2+6pg4«2. 4. а) -3 у!
о
в) 12; г) —100; д) 7; з) любое чисго; и) —2 —. 5. б) 5(5—с); д) 5а (Зх — 4у);
3
з) у (X — у); и) Зху (у2 + 2у — 6); к) 5а2Ь (За — 45 4- 2). 6. а) (5 — х) (у — 3);
в) (54-8) (а4-9); д) (q — 4) (р — 3); ж) (х — у) (х — 5). 7. а) (а 4- 3) (а — 3);
в) (х 4- 2у) (х — 2у); д) х (х 4~ 2) (х — 2); ж) (а — 3) (а — 3). 8. а) {2; —5};
- £1
Р 5 )
г) {0; 12}; е) {-8; 8}; ж) 0;
з)
9. а)
(а — 2) (а2 4- 2а 4- 4);
г) (У — 45) (у2 4- 45у 4~ 1652); д) (т — 1) (т 4~ 1) — «»4* D (т2 + лН"1);
е) (р‘4 ?‘) (Р2 4 52) (Р + 5) (Р - 0. И’ а) {-2; 2}; б) {0}; в) 0.
12. А — да; В — да; С — нет; D — да; Е — нет. 13. Длина 17,25 см,
а 2 у
ширина 5,75 см. 14. 144 см2. 15. 15 км/ч. 16. 40. 17. — ,- , — .
6 х — у 1
2 (21
19. а) —0,9; б) - ; в) 200; г) 206. 21. 3; —3; —1— ; 0,4; -; —1,5; —1,72}.
3 I о
22. а) 1,5; б) 0. 24^ а) ]-оо; 2[ (J ]2;4~ <4; д) ]—
— tUl~7; +°°С»«)]—оо;4-тоС«
4 4
25. а) ]— оо; 4- оо[; в) ] — оо; 1 [(J] 1; 4 [ U] 4; 4- «>[; ж) х #= 0 и х =# 2;
з) у =/= 0 и у =£2; и) х=£—5 и х=£5; к) ] — оо; 4~оо[. 28. а) При а=5; б) при а=—5;
в) при а — 0 и 5 = 0; г) при |а| — |5|; д) при а или 5 = 0; е) при а = 0 или 5 = 2.
38. а) {8}; б)
в) (3}; г) -3- ;
I "
д) 0; е) {—8}; ж) {-4; 4}; з) 0.
40. в) {—3; 6};
г) (0; 9). 46. б) ; г)
За
—а а а 9с8
б) —; в) — ; г) —. 48. в) — —;
10х 10х 10х 85
а 4- 45 35—4с х
6) 3. 53. а) — ; 6) —; в) — ;
с х3 3 а
— ; е) — ; з)--. 47. а) — ;
4ху у2 2х4у 10х
Эх’ з 4
г) — —; Д) — е> —49- а) 1:
5у2 4а4 а*
т а — 6 5у 2
г) __— . д) —— ; е) --ж)— ;
/п4~3п За 8х—Зу 3
з) — ; и) —; к) — . 54. в) 5—а; г) у—2х; ж) ; з) ------ . 57. а) — — •
6 а ох др — 2 о
238
59. в) -Ц; 6) -ф-т ») ; г, 2±-\ 62. а) ; 6) ; в)
а — 1 х4-у а—Ъ 7 c—d х-\-у
а—х
Д) а 4- Ъ', е)
1
У — 2
ж) у1 — 1; з) 1 + х4— х2. СЗ. а) 100; б) выражение не име-
ст значения. 65. а)
{0}; б) (2); в) 0; г)
35axs
к)
7m3 а2ц
—; ;д) -г; «)гг. б)
р2 2х 7 10х
3(х4-3)
2
4
1
в)
2
70. а) 4; б) - ——— ; в)
b (a ~J~ 25)
Зх
б)
2у
г) {7; -7}. 73. а)
1 9
ж)-------; з) --- . 74.
2а253 Юру
—2х2 л
е) ; ж) -
аг
х3
77. а) — ; б)
8у3
/4—х\5
.79.
а) ab' б)
з)
г)
2х‘ J
х — 5
85. а) ------- ;
У — 1
35 — 4
з) -------. 86.
7 10 —5
6р
68. а)-/; б)-
5g 4
b(a + b) 2а—b
------з)
1
°5 i
Р(Р4~ У). _.ч 2(т— Зл)
тп * 2а(а—5)’ ab
7
4х
—; в)
ху
3g
5(а—2)
5
Р
3g
Ъ_
4
В)
6 ’
3
г) —
%
7
—и)
а — 5
(^4-У)3 ч
----; к)
(х-уу
71. а) 2,5;
72а2
Ь2
о
б) —
35
г)
Д)
. 75.
б) (-3; 2}
Ъ ч У
— ; е) —
а х
(2а — 1) л
76. а) 6,25; б) —56
----7L ; к)
а — 55 д
(а—I)4
— . 78. а)
а4
X
25а2
v:,,)
(2- о) (34- Ь)
। ------------; е)
а (3 — 5)
а 4* б 2п—т
-----; в)
с— 3
б)
р—2
2
3 ’
354-5а
ab
2а53\2
х6 )
б)
2а \«
; в)
Ь2с4
Д)
б)
а)
90. а) 2; б) -
2с—7d
г)~^г;д)
25—15
б) ~т~-
6а
"*’4а2 — За5 — 352
Д)
а2Ь2
п — т
1; в)
а
в) 0; г) {—6;
8?/—7х
; е, -----
ху
—; б)
а25
е)
96.
а)
б)
2х— 10у
в)
2
24х
и)
4—9х2
а2
а — b
г)
К)
________________ g2
5Я(5— а)(5 4- а)2 ’
5р 3
-----; Д) о—
Р — 5 2а —
1
..; о —г; д)
— 3 а — 1
г)
7а
а)
1
б)
ж)
а — 5/
•г — У
3
6
1-У
5
х — 17
Зх — 1 ’
Зх — 1
; е) ----- . 88. 2
(х-1)з
5х—4 g
; б) ; в)
0). 91. а) — ,
6 20
13 1 7х 67а
; ж) — ; 3/ — ; и) —; к) — . 92. а)
Са
m— у
ту
12х ’ 30 ’ 60
4р2 -Ь 2pq — 8g*
---------------- г)
Р7
2 , ,2
; Ж)
; з)
З/Н-2?
3»
10g
Ъс1
----; б)--—
|- Ъ) у(х — у)
ах — 5а у
в) -------; г)
а
2(д24-9)
—:—д)
У“~9
4ха
102. а) {3};
в)
:Г) 5(е-1)
53х3
__ х—5г/
. 97. а)-----
1
х2 — 25г/2
-------- • 109- а)
б)
1 —X2
4а2 — 1
-----; е)
у2— х2
2ад
Р2— Q2
ж)
7И2 — П2
3)
б) {-1;
В)
а2—53
, 3 )
{-6; 6); г) -2-; 0
19
103. а)
6(х — у)
5
; б)---------; в)
12 (а 4- b) 6(2у—1)
У
Ъ
io (ь + 3) ’д)
а — 6
1
х2 +У2 , 3 (а2 4- 1>‘)
---------------; з) —----------------------; и)
ХУ (х2 — у2) ab (а2 — Ь2)
1 2
——— • '
1— т2 ’ л 4- 3 *
1
104. а) — —; б) 0.
239
- « 1 * 6у+19 3 8 1 1 2m+1
106. a) —; 6) • - — ; в)----; г) ---; д) 0; о)-------; ж) —; з)--------;
х4~2 у2 — & а—6 3—2Ь 2х (х — 1) 6 6(2т—1)
2 х 5 — х 2х 2(а24-ЗЬ2)
и) — —; к) ------------. 107. а)--------; 6) --------------------------;
а х (х — Ьу) (х + I)2 (х — 1) (а — Ь)2 (а + Ь)
36 8ху2 1 р — q 2 За
В) (а2 —9)2 *’ ° (х2 —у2)2 : Д) а—1* в) р2 4- рс 4- 02 ? ** х —21 3) а 4-4*
2ab 1 1 Зт 4- 5с
108. м4 Т ч; 2) 5ТЧ- 109’ --------------7г на 1 руб* 114’ а) 11ри п=1’ п=2»
о2— 25 6 3 т(т — 5)
п = 3, п = 4, п=6 или п = 12; б) при и = 1, п = 3 или п=Э. 116. а) а=—6;
10 2 10
б) а = 5; в) а=6; г) а=7. 117. а) 5 ——— ; б) — 2 —------- ; в) — 2 4---;
х4-2 х —1 5—х
г) — 14- —-— . 118. а) При А, где А = {—8; — 5; — 4; —3; —1; 0; 1; 4};
х— 2
б) при п£В, где В={—24; —10; —3; 0; 2; 3; 5; 6; 8; 11; 18; 32}. 119. а) а=2
1 — х [а 4- Ь\2 12
5 = 3; б) а = 8, Ъ = 3. 120 а) --------------; б) 1 —у; в) —— ; Д) -; е) 1;
2х — 1 \ b I а
х —2 ab 1 10
з) ——- . 121. а) ——- ; б) —2х; в) q2—pq; г) — —; д) —; е) 2; ж) 2х2 4- 2ху;
х 4- 6 а2— Ь2 4х х
2ах— а2 а — Ъ 4- Зс
з) а—2. 122. а) —8; б) 9. 123. а) --—-; б)----------
2ax-f- л2 а 4“ 5 — с
2х— у—5 1
* 2x-f- у+5 ’ а—1 ’
а2 а 27 4- 4х
125. а) —; б) — . 126. а)-----; 4,3 руб., 4,12 руб.; б) 12 кг; в) 50 кг.
b2 b х 4- 6
127. а) б) ; д) i; е) . 133. а) 8-’; б) 1б->»; в) (-2,7)-’.
И1» а* иь
1 1 1 57 13 1 1
134. а) б) 1; в) г) 16; д) 1-; е) 1-; ж)--;з)-. 139.а)9;в)-:
25 25 о 04 оо 1D 4
3
д) 16; ж) 0,5. 140. е) 8; ж) 1; з) —125; и) —;
8
к) —8-. 141. а) ЗЬ-2; б) xyh
V
ж) (а4-2)(а—2)-2; з) (Ь—5)3(Ь4-5)-Ч
142. д) ;е)
а 4- Ь
2х
(х—Зу)2 ’
144. а) — 1;
б)
а24- Ь2 2у2 — х2
—4. 145. а) - - ; б) - ; в)
а2Ь2 ху2
а4х6
5С7 з&2 — 2Ъ^
1 _ а2Ь2 2х2у2 — Зху—2 1
д) -------; е)------------------------; ж) -
ab ху al
a-\-h
— азьа
. 149. а) 7 • 109;
б) 2,86 • 10®; в) 3,092 • 10*°; г) 1,001 • 10е;
д) 2 • 10-2; е) 1,3 • 10'3;
ж) 5,72 • 10 е; з) 1,006 • 10“=. 150. а) 10а < 365 < 103; в) 10-’ < 0,0057 <10Л
153. г) 3,3 -10-’. 155. a) 5-1G-’; б) 2 10-’; в) 1,764 -10 ’; г) 1,25 -10*. 156.3 - 10п; 3 - 10е;
1,08 • 101а. 158. 8,09 • ЮЗ3. 160. а) Убывает; б) возрастает. 161. а)] — 1; —— ;
240
1
в) — 1; ——
4
в) [- 4; - 1]; г) [- 4; - 1].
162. а) Да; б) нет; в) да; г) да;
2 2
д) да; е) нет. 168. а) 35; б) 11; в) —2—; г) 1,5; д) —0,2; е) —; ж) 0,2;
3 11
1 3
3) 1. 169. а) —3; б) 5; в) {0; 1); г) 15. 170. а) 5; б) 0; в) {0; 5}; г) —. 171.—.
3 5
172. —. 173. 10 км!ч. 174. 1 км!ч. 175. 30 и 20 дней. 176.18 дней. 177. 64 км!ч,
6
178. 6 км/ч. 179- 840 км!ч. 183. а) Уравнение имеет единственный
8
корень —, если а Ф 0, и не имеет корней, если а = 0; б) уравнение
а
а
имеет единственный корень —
при любом а; в) уравнение имеет
20
единственный корень ------ , если а =/= 2, и не имеет корней, если а = 2;
а — 2
г) уравнение имеет единственный корень 2а — 2 при любых значениях а.
5
184. в) Уравнение имеет единственный корень---, если с^1, и не имеет корней,
с — 1
если с=1; г) уравнение имеет единственный корень 0, если сф—7, и имеет бес-
конечное множество корней (любое число — корень уравнения), если с = —7.
2 а 4а4~ 3
185. а) х «=---- ; б) х = а — 8; в) х— --- ; г) х = --. 186. а) у= 2а—
а — 1 2а — 1 а — 2
2а—25 аЪ аЪ
— 5; б) у = ——; в) у=——-; г) у= --------- . 189. а) 5; б) —1>, в) 22;
а -J- b a -J- Ъ Ъ — а
г) —5. 195. а) —3 и —5; в) 2 и 4. 197. а) (х—1) (х4-1) (х34-*+1) (х2 — х — 1);
г) (р2 4- Р + 1) (Р2 - Р + 1) (р4 — Р2 + 1); е) (а8 4- а 4* 1) (а3 - а + 1);
ж) (5s 4- 52 4- 1) (58 — 52 + 1). 199. д) Уравнение имеет бесконечное множество
корней. Любое неотрицательное число — его корень; е) ур; мнение имеет
бесконечное множество корней. Любое неположительное число — его
корень. 201. 9. 202. 10 и 11. 203. а) 3; б) 7; в) 30; г) 2; д) 37; е) 79. 205. к)]—оо; 0[.
206. а) Если х = 0 и у — 0; б) если х = 0 или у = 0; в) если х = у\
г) если |а — 5| = 1; д) если х ——1 и у = Г, е) если |а4-5|=1. 212. ж) ]—оо; 0[;
з) ] 0; 4-оо[. 217. б) (-3; 3}; г) 0; д) {6}. 221. а)
___1
57 4-1
; б)
В)
г а (а — с)
. 230. а) 7
1
е)
. пр ~ 2р2 .
_ . _ _ _ । О) 1' А >
ху—г2 х(10х— а) 5/гп — п2
(5Ь4-З)(3а4-55 4-5) _ ч 1
(За — 55) (За — 5) х2—Зх 7
х — v
в) ------—
7 2х — у—1
1
2х2 — 2х
в)
а2 — 52 2х—3
г) * д) -----------Г»
6* 4-4 2
3 ’ г) " 2х 4- 5 5
6аа4~3 2х—2у
а3 — 1 ’ в) х2 4" ху 4- у2’
1
232. а) 0; б) —- .
аЪс
249. а) а 4- 5. 253. а) 9;
241
6) 0. 255. a) x17; 6) у50; в) а12; г) 6я. 256. а) х3ра; б) ааЬ3; в) ——;
Ь— а
г) Ь 4- 1. 268. 17,5 км/ч. 272. 50 км. 283. а) Уравнение имеет единствен-
26
ный корень , если Ь 2. Если Ь = 2, то уравнение не имеет корней;
. 5 4а
в) уравнение имеет единственный корень -------, еслиа-^О и а=#—б. Урав-
нение ие имеет корней, если а=0 или а= —б; г) уравнение имеет единственный
а — 1
корень 1,
если a =/= —1. При а = —I уравнение корней не имеет.
284. в) Уравнение имеет единственный корень ----, если а =£ 3. Если а = 3,
4
то уравнение корней не имеет. 290. г) ad — be и bd =£ 0.
Глава II
293. в) Да; г) да; е) да; ж) да; з) да. 325. а) Да: б) нет. в) нет; г) да:
д) нет; е) да. 326. а) х > 11; б) у < 2; в) х > 1 1 ; г) а < —3,6. 337. а) Нет; б) да;
3
р) да; г) нет. 343. в) ]—4; 0[|J]3; 4-оо[. 360. а) ]1-~ + оо[: б) ] — оо; 2,5];
В) J—36; +оо[; г) ]—оо; —l,28j; д) ]—оо; 4|_; е) ]1,2; +оо [; ж) [—8; + оо[;
]3,б; 4-оо[; п) ]—оо; —2,4[; к) ]—2,2; 4-оо[; л) [1,5; 4-оо[; м) ]—оо; —1,25].
351. а) —оо; ——I; б) ]9; +оо[; в) ]—оо; —3,1[; г) ]—оо; 0,8[; д) ]Я; 4-°°[;
з)
7
J 8J’ '
7 2
е) J0; + оо[; ж) ]—оо; 3— [; з) ]—оо; —10[. 352. а) ]—оо;------[; б) ]—оо; 2,4];
1*5 3
в) ]17; +оо[; г) ]—оо: — Г; д) ]—оо; 3.5[; е) '—0,25; -f-oo[. 353. а) ]—оо; 3[;
б) ]7; + оо[. 354. а) ]2; +оо[: б) ]—оо; —2,б[. 355 а) ]—оо; 8_; б) ]2; + оо [.
356. ]6; + °°Г. 357. ]—оо; б[. 358. ]2; +оо[. 359. а) 0; б) ]—по; + «>[;
в) J—оо; +оо[: г) 0. 360. ]—оо; -f-oo[ 361 33. 362. —19- 363- 1, 2, 3, 4.
364. 1, 2. 365. Неравенство верно при всех положительных значениях х.
366. Неравенство верно при всех отрицательных значениях х. 367. ]—1, 2[.
368. ]4: 6]. 369. в) [2; +ооГ; г) ]—оо; б]; д) Г—; 4-“[; е) ]—оо; —2,6].
I ® I
370. Меньше 2 см. 371. Меньше 12,16 0м. 372. 7, 8, 9 пли 10 рая. 373. Не более
2
26- км. 374. а) ]17; 4-оо[; б) ]—оо; 1[; в) ]0: 6[; г) 0; д) [—1; 3]; е) J8; 20].
О
375. а) ]6; 4*оо[; б) J—оо; —1 ; в) ]0; 3- Г; г) 0. 376. а) ]0,8; |- оо[; б) [2; 41;
3
В) ]-i ; 4[; Г) ]0,1; 0,2[. 377. а) ]3; -|-оо[; б) ]-оо; —3[; в) [—11; 3]; г) 0.
О о
242
378. a) 0, 1,2, 3; б) 4, б, 6, 7; в) 1; г) 1. 380. а) ]—оо; 2,8[; 6)0.
381. а) 0, 1, 2; б) —6. —б, —4. —3, —2, —1, О: в) —2; —1,0; г) —2, —1,0.
382. а) ]2; +«>[; б) ]3; 6Г. 383. а) ]—1; 2 [; 6) [—7; 17], 384. а) [3; 4.2];
6) ]2,б; 3[. 385. а) ]8, + оо[; б) ]—оо; —5[; в) ]10; 12[; г) 0. 386. а) ]—оо; 2[;
б) ]12; 4-оо [•; в) ]1; 3[; г) ]1; 2[. 387. а) 51, 62, 73; б) 21, 32 или 43.
388- Более 4 км'ч, но менее 5 км/ч. 389. ]2; б[. 390. ]—оо; 1,5 [[]] б; 4" °°[-
391. а) ]1; 3[; 6) ]—оо; О [J ] 1; 4-оо[. 392. а) ]—оо; 0 [ J] б; + оо[; б)]1; 2[;
в) ]—Оо; —1 J] 1; 4-00 [; г) ] —6; О [. 393. а) ]—оо;—б[[]]0; + оо |:
б) ]0; 7,5[; в) ]—оо; —8[J]8; Н оо[; г) ]—0,5; 0,5[. 394. а) ]8; -f-oo [;
б) ]4; 4-00 [; в) ]3; 4-00 [; г) ]2,7; б EIJ] 5; 4-оо [. 395. а) ]—4; 4-°°Е;
б) ]—оо; 15[. 396. а) ]7,2; 4-оо[; б) ]—оо; 5[; в) ]37; + оо[; г) ]—оо; 13[.
397. ]—оо; з [U18; +°°[- Я98- ]—°°; —2[Ц13; +°°с зээ. а> I7;
б) ]0; 2[; в) ]—5; ±оо[; г) ]0; 1[. 401. а) —3. —2. —1, 0, 1, 2, 3; б) 2, 3, 4, б;
в) 1, 2; г) 1. 402. а) ]—оо; 0[UJO,7; + оо[; б) ]—оо; О [(JJ2; 4- оо[; в) ]—4; 4[;
г)]—оо; —5EJ15; + оо[. 433. 6) ]0; 3[. 404. а) ]— оо; — 1 [(]] 0; + °о[;
11 1 4П
6) ]0; 4 : в) ]0; — [; г) ]0; 1 - Г; д) ]—°о; 2[; е)]— оо; 1[; ж) [— —; 0[; а) ]0; —].
8 4 Z о
427. а) 16 С х+р С 19; 6) —6<х — р g, —3; в) 3 < у — х<6; г) 60 С, ху 84;
х 10 у о
д) 0,5< — С 0,7; е) — =^2. 430. а) б<За4-7Ь<7; б)—1,2<— 4-0,6Ь<— 0,4;
У 7 х 2
в) 1 < b1 — ab < 21; г) 7 < — 4- — < 12,5. 433. Нельзя. 434. Можно.
а b
436- 18г^СДВ<20°. 439- а) 11; 9; в) 7.6: 7,4. 442. 0,17 — лучшее приближение.
443- Подойдет. 444. 14.1 < nd < 14,5. 445. 810 860.
450. Не является приближением с точностью до 0,001. 461. Являются.
452- Являются, 453. Р = 18,2 ±0.4 сж; S = 20 ± 1 сж®. 455. 48 ± 4 см3.
кг
45«- 445 ± 15. 457. 2700± 40 — . Алюминий. 459. 7. 494. а) При положительных
JH3
значениях: б) при отринет тьных значениях. 495. а) Нет; б) да. 499. а) Да;
б' нет; в' да; г) нет; д) нет. Ь01- а) Да; б) да. 502- а) Нет; б) да;
в) нет: г) да; д) да: е) нет 507. б) ]—3; + °о[. 609. а) ]— оо; 2[;
б) ]—оо; —1»5[; в) 4; +°о[; г) ]—оо; — — [. 511. а) ]—оо, О CUJ 2; + °о [;
б) ]—оо; 0[J]2; +°о[. 613. а) ]—оо; —60 [; б) [4,8; +оо[; в) ]0,56; +оо[;
г) J—оо, —]. 614. а) ]—' оо; —115?, б) ]0,2; +оо[; в) ]—оо; 15[;
16
г) ]—оо; 1,4[. 515. а) ]—оо; 0,32Ь[; б) ]—1; +оо[. Ь16- а) {1; 2; 3; 4};
б) {1; 2; 3; 4; б}. 520- а) Нет; б) нет; я) ла; г) ла; ж) нет: з) нет.
521 а) Таких знач-ний нет; 6) гри любом значении х. 522. а) I—оо; +оо[ ;
б) ] —оо; + оо[. 624. а) ]0; F оо[; б) ]2; +оо[; в) ] —3; |+оо[; г) ]—7; -f-oo[.
243
525. a) ]—оо; 0[; б) ]— оо; — 4[; в) ]_оо; —3[; г)]— оо; — — [.
б
526. а) [8; +«>[; б) ]—оо; 2[; в) ]—оо; —6]; г) ]—оо; 3,5[. 527. а) 18; б) —1.
529. 4. 531. Не более 5 наборов. 532. Более 6 км/ч. 533. Более 18 км/ч,
2 1
534. Более 4— км/ч. 535. Более 16 км/ч, 536. в) ]6,5; 4~ои[; г) ]_____оо; 5—
3 4
537. б) ]—2,8; —1,7[; г) ]—2,01; —2,1[. 539. а) ]9; 4-оо[; б) ]—оо; 0[;
в) 0; г) 0. 541. а) 4-оо[; б) ]0, 1; 5[; в) 0; г) ]0,8‘, 4-оо[; д) ]—оо; — 0,2[;
О
5
е) ]1— ; 4-оо[. 542. б) —10; в) 1; г) 2, 3, 4, 5. 543. а) ]—3; 6[; б) 31,5; 2,5;
в) [0,8; 1]; г) [—2; 1]. 544. а) ]1,5; 4,5[; б) [5; 15]. 545. а) ]0; -[;
6
б) ]0; 0,8[. 546. а) ]—1; 0[; б) ]—5; 0[. 547. Дороже 1 руб. 16 коп., но дешев-
ле 2 руб. 04 коп. 548. Более 10 км и менее 16— км. 550. а)
4
6) [0; 22];
в) ]—оо; -“[U14; +°°[; г) — 2,5 [|J]—1; 4-<»[; д) ]—оо; I.SC;
о Z
е) ]7,5; 4-оо[. 551. а) ]— оо;— 4 [[]]!; 4-оо[; б) ]-оо; 2[|J]2; +оо[.
552. а) ]—оо; —5 [[)]—5; 6[; б) ]3,5; 5[|J]5;+oo[; в) ]-оо; 3 [JJ3; 15[;
г) ]5; 4-оо[. 553. а) ]2; 5[J] 7; +оо[; б) ]—оо; 0 [|J] 3; 4[.
554. а) ]—оо; 0[J]2; +оо[; б) ]0;2[; в) 0; г) ]-оо; -|-оо[.
556. а) ]—оо; 0 [[}]“•; + оо[; б) ]-оо; -1 [J] ~; 4-оо[; в) ]-1; 1];
Z 4
Г) ]-оо; -1[J [17,3; 4-оо[; д) ]—оо; —5 [(JJ—5; 8[; е) ]-оо; 7[.
557. а) 3; 4; б) 4; 5; 6; в) 1; 2; г) 1; 2. 558. а) ]—2; 0[;
б) ]—оо; 0[Ц]1; 4-оо[; в) ]0; 1,2[; г) ]-1; 4-оо[; д) ]—оо; 0[; е) ]—1; 4~оо[.
559. ]0; 2[. 566. а) Можно; б) нельзя; в) неизвестно. 571. г) 4^10—х 5;
11 1111
ж) 2—<-4-2 <2-; з) - < ----<-• 572. а) -0,4< с <0,1; в) - 0,3 <
ОХ О о X Z <
< с < 0,1. 584. а) [1 ; 4-°°[; б) ]—оо; —24]; в) [6; 4~ °°[» г) 0; — 1.
4 j
585. в) 12,3<5д4-7д<16; г) — 6< — — 5а<—5,25. 586. в) 12,1 < — 4- л<15,2;
4 тп
111 а
г) — < -< —. 590. а) Может; б) может. 591. б) 7,41 < — 4~ Ь < 7,44;
22 т+ л 20 с
а
в) 2,98 <--------< 3,05. 593. а) 35,8; б) 36. 594. а) 12,3; б) —7,6. 595. а) 5,9;
о — с
б) —9,2. 597. 3,142. 605. 1,46; 1,47; 1,463; 1,468. 607. 0,5 ± 0,1а. 608. Доста-
точно. 611. Неизвестно.
244
Глава III
625. а) 0,5; б) 1080. 631. б) —0,7; в) 2; г) 0,2; к) 0,5. 633. ж) з) 6,25.
638. а) /12; —/12; в) 0; г) 0,2; —0,2; з) /30; —/30. 639. а) [—/2; ]^2];
б) ]—сю; —I 2 [[)]) 2; +°°[- 641. в) При х 0; г) при х 0; д) при любых х.
642. д) ]2; 4-оо[; е) [—2,5; 4-оо[; ж) [0; 2[; з) ]— оо; —1[[)[9; 4-оо[.
644. ж) 2; з) 60; и) 0,13; л) 0,5. 668. а) 10а; б) 10(3; в) 0,1₽; г) 0,1а.
672. в) /7 4-) 3= 4,4±0,1;г)/7—/3=0,9±0,1. 673. /ЗД+] 15J=5,7±0,l.
680. а) 3,4</х+3<3,5; б) — 0,5</х—1<0,6. 683. а) ]9; + «>[; в) ]1; 9[;
д) [0; 5]; е) [2; 5]. 694. б) 27; г) 16; е) —200; ж) 8,1; з) 0,001. 697. а) /2 — 1;
в) /Й - /10. 698. в) 2; 0; г) —10; —4. 700. з) 7,7; и) 0,48; к) 0,3.
701. а) 180; б) 48; в) 6С; г) 42; д) 6; е) 24. 702. б) 25; г) 45. 704. а) 9 см;
б) 1848 см-. 708. а) 72; б) 0,01; в) 25; г) 0,121. 710. д) ас; е) —0,6Ьс2;
а3Ь2 I — г- г—
ж) —-----; з) —а7*5. 711. з) — ; и) 2. 716. г) 1,5/3; д) —0,15/5; е)—0,75) 14.
3 2
717. г) 718. б) 4 )Т; г) ± ] Й; е) 1,2|/130; з) 0, 51^16. 719. а)
15 11 3
в) /3; д) ЕД; ж) Ц.; и) Е1. 722. д) /72 > 0,5 /162; е) /24 = 4 / 216.
о о 2 о
724. б) 3) 2| г) 14 /5; е) 0. 725. а) а /7; б) —у /10; в) 4х }гх;
г) 0,1 Ь2 /Ь; д) 5а3 /2а; е) —Зе3 /7 727. а) 8а2/а- б) 0. 729. а) —За ) Ъ;
б) 5аЪ /Ь; в) 12ab Vab; г) 4а2д /2Ь; д) —5аЬ3 /За; е) —2а2Ь3 /2аЬ?
730. г) /6; д) 3/2; е) 0,5/б. 732. а) 12 — 3/б; б) 15J 3 — 20;
в) 12 — 4 /3 + 2) 2; г) 24 — 12/2—2/7. 733. б) 7 — 4/3; г) 22 + 4/10;
е) 66 — 12/10; з) 77 + 28 /б. 736. в) — /б<6 1/ — ; г) /72<7 1/ А.
2 f 2 3 F 3
751. а) ]6; 9]; б) [3; 5[|J]6; 9]; в) {3; 9}; г) {9}. 752. —3,32. 753. —3-^-.
О
4 1
754. а) 5,1; б) —3,6; в) — —; г) —; д) 10,2 ; е) 1. 756. а) ) 3, —) 3;
7 8
б) /20,—/20. 760. а) ]—ос; +°°[; 6) ]—оо; -|-оо[; в) ]—оо; —1 ]IJ[1; + °°[;
г) ]—оо; 4-оо[; д) ]—оо; — 3]J[3; е) [—2; 2]; ж) 0; з) ]0; + °°[;
и) ]—оо£—4[ J]4; +°°[« 761. а) При х>2; б) при х^0 и х=^4; в) при х>—2;
г) при х^0; д) при —2^х^15; е) при х^З. 762. а) а>0, Ь>0 или а<0, 5<0
или а = 0, Ь — любое или а — любое, Ь = 0; б) а — любое, не равное 0, Ъ 0
или а = 0, b — любое; в) а — любое, Ъ — любое; г) а^0, Ъ — любое, отличное
от 0, или а — любое, b = 0; д) а — любое, Ъ — любое; е) а — любое, Ъ —любое,
245
причем афЬ. 763. г) 32; д) 0; е) 4, —4; ж) 0; э) б; и) 5; к) 0.
764. а) 2 /11; б) 2/7; в) 2/зЦ- 1; С) 1 . 765. б) 41; г) 22.
768 а) 100; б) 0. 775. a) J6.25; +«>[; б) [0; 36[; в) ]25; 64Г,
780 а) [0; 24 [(J]24; +«>[; б) [—10; 0]. 784 6) 8; г) 81; “ е) 81.
785. а) 8; б) 243; в) 1024; г) 125; д) 18; е) 24; яс) 15; з) 12. 788. а) 1,
б) 6; в) 3; г) 1 789. г) [10; +«>[; д) ]—оо; 2]; е) [—5; +<ю[. 792. а) 7,56;
б)-; в) 9,1; г) 1,08; д) 128; е) 108. 796. а) 8,5; б)-7; в)—; г)—
24 _ 96 29 135 ’
801. а) 8 /3; 6) 4 /2; в) —/П; г) 4,5 /13. 803. 6) —2а /2аЬ; г) 6а8Ьв / ЗаЬ.
805. а) —2а ) а; б) 6х Ух 806 а) 36; б) 1— ; в) 2. 807 б) —2; г) —2,6.
3
809 в) —/Зх4; г) /а8; д) — /За5; е) —/—За* ж) /аЬ* з) /2а35-
и) — у аЬ(а-ЬЬ). 812. в) /х(х+1)2; г) — /—х(х—2)* д) — I П ~ (').
Г 1 +а ’
е> 1/50813-а)10; 4:6) -4; °;»>0; г> б= А) 61 е> 0-
Г о г -*
Глава IV
4
819. а) — —; —1; б) 0,6: 1; в) 0,5; 3; г) —4,5; —1; д) 1,5; 3;
0
13 7
в) 2; 2—; ж) —1; —; з) —1,5; 3; и)—5; 8; к)—12; 5; л) —-; 0;
34 12
7 7 2
м) — —; —. 820. а) —0,2; 2; б) —5, 8. в) —7; 2; г) —4; — ; д) —4, 5;
у у 3
е) 0; ж) —1; 2— ; з) —7; 5. 821. а) —8; 3; б) 1— ; 4; в) — — ; 3; г) —11; — —
7 4 5 3’
822
824-
825.
а)
а)
6)
0,558+0,0005 или —0,358+0,0005: б) —2,781+0,005; —0,719 + 0,005.
1,8; —0,2;
2 1
3 ’ 3 ’ Р'
б) 0,7; 1,3;
2
-2; 9 ; г)
в) 0; г) 0,25; д) 2,5; е) —9: 3.
—1,5; 1,5; д) любое число является корчем
уравнения; е) —6; 6. 826. а) — — ; —; б) 1; 1,5. 827- а) —1; 3; б) —5;
15 5
7; в) —2; 12; г) —2,8; 6; д) —4; 5; е) —2; 2,4. 828. а) 1,5;
2 1
в) —27; —1; д) —9; ж) 1; 2~; и) 0. 829. а) —11; б) 6. 830. а) ] —; -f-oo[;
б) 116,2; +оо[; в) ]—4; 4[; г) 0. 831. а) ]—оо; 40[; б).]—оо; —12 [1)]12; +<»[;
в) ]—оо; 0 [|J]0; 9[; г) ]—оо; + оо[. 832. а) А=+24; б) Л=135; в) Л=±50;
г) Л=±Ю/2. 835 а) 11 и 12; 6) 7 и 8 837. а) -; б) - .
3 10
839. а) 8 рядов или 10 рядов; б) 6 автобусов. 840. а) 9,6 л»2; 6) 90 см.
246
841. a) 80 км'ч; б) 1— ч. 844. а) 13 км.'ч’, б) 2 км/ч. 845. 2 м и 2,5 м.
846. а) 15 г и 18 г;
1 2
б) 21 ц и 20 ц. 847. а) —56; 36; б) —а; — а; в) 2k — 2; 2;
6 3
а 4- 3 «41
г) 3 —а; 3 + а; д) 1-—т-; е) — 2;——850. а) 0,6; 6^—43; б) — 2;
Z о
С = —106. 853- д) 1 ± /10. 855. э) х2 4- 14z Ь 1 = 0. 867
г) —--------;
f/4-9
/О-Ц^е) тг- 868- а) ]~°°: -lo'Ul6i +°о[; b)]-oo;1,5[U12;4-oo[;
с 4* ” И— На
2
г) ]— — ; 4[; д) [-11; 5]; е) ]—оо; 0] J[5; 4 ~[. 869. а) [—9; 9]; б) [0; 16];
3
в)
-ч]и
[3; 4-°°[; г) ]—+°°[; Д) функция не определена ни при
каких значениях х; е) ]—9; 5[. 871. а) Так как при всех допустимых значе-
ниях я данное выражение имеет только одно значение, равное 1, то оно не зависит
от х. б) Выражение имеет только одно значение, равное 1,5, следовательно,
оно не зависит от а. в) Значение выражения при любом (допустимом) у равно
— , значит, оно не зависит от у. г) Значение выражения при любых (допустимых)
4
• значениях 6 равно 1, следовательно, оно не зависит от 6. 881. а) (—4; —1);
б) (3; —8). 885. Через А и В проходит, через С не проходит. 886. а) с — 20:
б) 6 = 12. 887. а = —21; 6=71. 888. 6=—4; с=—4. 889. а) (—4; 16) и (2; 4);
б) (0; 0) и (2,5; 6,3); в) (2; 4); г) (—0,5; 0,3); д) (1; 2) и (0; 0); е) (0, 0);
(_1; —1), (1; —1). 890. а) Корией нет; б) —2; 2,5; в) —1,6; 3,1;
г) —4,9 и 2,9; д) корней нет; е) корней нет; ж) —8; 2; з) —1,4; 4.4.
891, а) ]—оо; —4[[J]3: 4-оо[; б) ]—1; 6 [; в) ]0; 4 ; г) ]—оо; —*5IIJ30; -f-oo[;
Д) ]_оо; 4-оо[; е) ]—1,5; —1[. 892. а) 4; 12; б) —9; —3; в) —13; 3;
2 „ 3
г) 11; —5; д) —9,2; е) 4; 7; ж) 0,5; 2; з) —4 — ; 5- 893- а) —1; *-
о 4
б) —10; 9; в) —9; 10; г) 2; 1,6; д) — 3 '; 3; е) —4 ; 1; ж) —5-^-; 2;
8 3 о
2 2 2 3
з) Т±'-- * 894. а) — 1.2; 0,2; б) — 4 д ; -1-; в) 2 — ; 4; г) —2—; — 1;
3 2
д) — — ; — — ; е) —1; 1; ж) —2,5; 2.5; з) любое число — корень уравие-
5 5
* 111
ния. 895. а) 8: 10; б) -15; 1; в) -1, 8- ; г) -4; - 1.2; д) - ; 8
3 о о
е) 200; 8. 896- а) 1 ± /б. е) 2*УГ- . 898 а) — ly; 1; б) - з|. 2;
1
в) —0,9, 1,5; г) —7; 3; д) 11; 13; е) —14; 5; ж) —3; 7; з) —5; 4- .
3
899. а) —4; 3; б) —6; в) 12; г) 5. 900. а) —1 . или 1; б) корней нет; в) 9.
247
9<*8. а) 72 станка и 62 станка; б) 8 дней. 909. а) 15 га и
18 га или 24 га и 27 га; б) 72 га и 60 га или 120 га и 108 га.
911. а) 432 детали; б) 10 дней. 912. а) 18 деталей; 15 дней; б) 9 дней.
913. а) 25 дней; б) 300 дета л< й. 914. а) 5 ч 50 мин\ 4 ч 40 мищ б) 25 ч и
20 ч. 915. а) 10 дней; 15 дней; б) за 42 ч и 56 ч. 918. а) 3 кж/ч; б) 2 кж/ч
пли 3 км ’ч, 919. а) 10 кж'ч; б) 5 км/ч. 920- а) 2,4 км/ч или 3 кж/ч; б) 3 км, ч.
921. а) 5 ч 15 жин; б) 7 ч 52 мин. 922. 6 ч. 923. а) 48 км или 54 жж;
б) 42 км/ч. 924. а) 18 кж/ч; б) 48 км или 60 км. 925. 10 км/ч. 926. 20 км/ч,
или 7 км/ч, или ==6,5 км/ч. 927. а) 100 ж и 60 ж; б) 50 ж и 24 ж или
16 ж и 75 ж. 928- а) 1936 сж2; б) 6 см. 929. а) 6 ж2 и 216 ж2; б) 1320 еж2 я 216 сж2.
930. 600 сж2; 24 сж; 25 сж. 931. а) 10 кг или 25 кг; б) 120 г. 932. б)—4.5а; а;
1 1 2л — 5
в) — с; с 4 1, г) — ft; fe — 2; д| 2; — — ; е) если а 1, то х - 3 или
4 3 3
2а —1
х=— - —; если а——1, то х =—3. 937- Ь=—5 или 5=5. 939. с=6. 940. 5=1;
а 4 1
с=— 4. 941. а= 1; с= 4. 942. е) у2—5=0; ж) у2—4у4-1 =0; з) 25у2—110j/4-
4-1 = 0; и) 9у* -*~60у+2 = 0. 944. 2у2 — 12у 4- 13 = 0. 945. 59Л4 у—2 = 0.
946. 9у2 43у4 5-10. 947. 7у2 — 13у 4- 4 = 0. 949. а) 9; б) —9; —2, 2;
в) 1; г) —/16; /16. 952. в) х3—6х24-11х—6=0; д) Ох3 4- Зх2 — 2х = 0;
е) 4х4 — 37х2 4- 9 = 0. 953. ж) (а — 35) (а 4- 2о); з) (х 1- 6а) (х — 5а).
и) (у F Ь) (Зу — 55); к) (г — 1 4" /2) (г — 1 — 1 2); л) не разлетается на линей-
ные множители; м) х (х — 2) (х — 10). 954. a) (I 4" 1) (< — 6) (6t — 1);
б) (а 4- 1) (а — 2) (а — 3) (а — 5) (а — 6); в) (5 — П (25—3) (5—3)(25’4-95—9);
„„„ 5а 4-2 р2 4- Ър 13 с—2
г) (х4-2)(ох—4)(х—5). 955. а) — -------; б)-------------; в) — - — ;
а2—За 1 3 ' 7р 4- 5 ’ Зс2 Ь 25 ’
За— 4
г) -----------. 956- а) При всех значениях переменной а из области опре-
13а2 —5а 4-1
1
деления значение данного выражснля равно----------------. следовательно.
3
3
оно не зависит от а: б) значение выражения равно — при любых
5
(допустимых) значениях а; в) значение выражения равно 1 при любых (до-
пустимых) значениях а; г) значение выражения равно — при любых (допуе-
3 1
тимых) значениях а. 957. а) —; б) 2 —. 959. а) ]—оо; —7 ] U [7; 4- о ;
16 3
б) [-4; 4]; в) J-oo; -71 IJ [9; 4-оо[; г) [-6; 7]; д) [0; 10[ J ]Ю; 4- <х> [;
е) —8 [ IJ ]—8; 5]; ж) ]—оо; —2] J ]2; 4-оо[; з) ]—3, 3[. 960. а) (—12; 0),
(10; 0), (0; - 120); б) (—7; 0), (8: 0), (0; 56); е) (0; 0), (—9; 0), (11; О);
ж) (—10; 0), (—2;0), (2; 0) (0; -40); з) (х*-2х21-1)4-2 (г2—I)2 F 2, следо-
вательно, график пересекает только ось ординат в точке (0; 3). 964. а) В 1 и II;
б) в I; II; Ши IV; в) в I; II и III; г) в III и IV-
ПРИЛОЖЕНИЕ
НЕКОТОРЫЕ МАТЕМАТИЧЕСКИЕ ЗНАКИ,
ВСТРЕЧАЮЩИЕСЯ В УЧЕБНИКЕ
— знак принадлежности множеству.
£— знак непринадлежности множеству.
0 — знак пустого множества.
cz — знак включения одного множества в другое,
f] — знак пересечения множеств.
(J — знак объединения множеств.
.—> — знак логическ ого следования,
знак равносильности.
)/ — знак арифметического квадрат но/о корня,
[а; Ь — множество решений неравенства а^х^Ь.
]а; Ь[ — множество решений неравенства а <х <&.
""а; + оо[ — множество решений неравенства х ~>а.
fa; 4-со[ —множество решений неравенства х>а.
]—ос; а[ — множество решений неравенства х<а.
]—оо; а1 — множество решений неравенства х^а.
ТАБЛИЦА КВАДРАТОВ НАТУРАЛЬНЫХ ЧИСЕЛ ОТ 10 ДО 99
2Б0
ТАБЛИЦА КУБОВ НАТУРАЛЬНЫХ ЧИСЕЛ ОТ 1 ДО 10
И СТЕПЕНЕЙ ЧИСЕЛ 2 И 3
п 1 2 8 4 5 6 7 8 9 10
п3 1 8 27 64 125 216 343 512 729 1000
2" 2 4 8 16 32 64 128 256 512 1024
3" 3 9 27 81 243 729 2187 6561 19683 Ь9049
СТЕПЕНЬ С ЦЕЛЫМ ПОКАЗАТЕЛЕМ
Определение 1. art= ааа ... а, где п£N и п =£ 1.
л раз
Определение 2. а* = а.
Определение 3. а° = 1, где а ¥=0.
Определение 4. а~п — - , где п N и а <^0.
ап
СВОЙСТВА СТЕПЕНИ С ЦЕЛЫМ ПОКАЗАТЕЛЕМ
Если тип — целые числа, а 0 и Ь 0, то:
1°. атап = с”!+п;
2°. а’п : а'1 = а"1-";
3°. (ат)п = ат"\
4°. (аЬ)" = а' Ьп;
ОЦЕНКА СУММЫ, РАЗНОСТИ, ПРОИЗВЕДЕНИЯ И ЧАСТНОГО
ас ху bd
(а>0)
(с>0)
(а>0)
(с>0)
ТОЖДЕСТВА СОКРАЩЕННОГО УМНОЖЕНИЯ
1. (а—Ь) (а-f Ь)=а2—Ь2;
2. (а + Ь)2 =а2+2а&-1 Ь2;
3. (a + &)s=as+3af&+3ab2 + bs;
4. (alfr) (a2— ab -bi)=a3 + bs;
5. (a-b) (a2+a& + bz)=as—bs.
ОГЛАВЛЕНИЕ
Глава I. ДРОБИ
§ 1. Понятие дроби .......................................... ... 8
1. Целые выражения ........................... . . —
2 Дробь. Область определения дроги . . . . ........... 6
§ 2. Свойства дробей .................... ....... 10
8. Условие равенства дроби нулю........................ . —
4. Основное свойство дроби. Сокращение дробей................ 13
§ 8. Тождественное преобразование в дробь произведения и частного
двух дробей ........................................ 19
5. Произведение дробей ......... .... ........... —
6 Частное двух дробей ... . . ... 22
7. Степень дроби ........................................... 21
§ 4. Тождественное преобра ювание в дробь суммы и разнос ги двух дробей 25
8. Сумма и разность дробей, имеющих равны* знаменатели ... —
9- Сумма и разность дробей, имеющих различные знаменатели . . 29
10. Представление дроби в виде суммы нескольких слагаемых ... 31
11. Тожде* гве.шые преобразования дробных выражений . . Зв
§ 5. Степень с целым пока„а гелем................................ 38
12. Onpej егегие степени с отрица гельным целым показателем ... —
13. Свойства степени с целым показателем.................... 41
14. Стандартный вид числа ...................................44
15. Степенная функция с целым показателем ...........46
§ 6. Уравнения, сод* ржащи< переменную в знаменателе ...... 50
16. Решение уравнений с переменной в знаменателе ... ... —
17. Уравнение с параметоом.................................. 51
Дополнительные упражнения к глаеь I................................57
Глава II. НЕРАВЕНСТВА И ИХ ПРИМЕНЕНИЕ
К ПРИБЛИЖЕННЫМ ВЫЧИСЛЕНИЯМ
§ 7. Неравенства и их свойства................................... 76
18 Понятия «меньше» и «больше............................... —
19. Свойства неравенств .................................... 80
253
20. Понятие логического следования ..................... 83
21. Равносильные предложения ........................... 86
$ 8. Неравенства с одной переменной.......................... 83
22. Графическое решение неравенств с одной переменно!.... —
23. Решение линейных неравенств с одной переменной...... 91
§ 9. Системы неравенств с одной переменной................... 96
24. Решение систем линейных неравенств с одной переменной ... —
25. Примеры решения нелинейных неравенств...............102
§ 10. Применение неравенств ж оценке точности приближенных вычисле-
ний ..........................................................106
26. Точные и приближенные значения величин............... —
27. Границы значения величины .....................108
28. Теоремы о почленном сложении и умножении верных числовых
неравенств .............................................111
29. Применение метода границ для оценки значения суммы, разно-
сти, произведения и частного........................... 114
30. Погрешность приближения .......................... 117
31. Точность приближения ...............................118
Дополнительные упражнения к главе II ........................123
Глава III. КВАДРАТНЫЕ КОРНИ
§ 11. Понятие квадратного корня .............................112
32. Рациональные числа .................................. —
33. Арифметический квадратный корень .................. 145
34. Уравнение х2 = а ...................................148
35. Тождество (У а)2 = а .................. 153
36. Приближенные значения квадратных корней из 'Положитель-
ных чисел ..............................................155
37. Нахождение приближенного значения корня методом последова-
тельных приближений .....................157
38. Таблица квадратов .....................159
39. Таблица квадратных корней ..........................151
40. График функции у = Ух ................ 164
§ 12. Преобразование выражений, содержащих квадратные корня . . . 167
41. Тождество У х2 = |х| ............................... —
42. Теорема о корне из произведения.....................170
43. Теорема о корне из дроби............................173
44. Вынесение множителя из-под знака корня..............176
45. Внесение множителя под знак корня...................178
Дополнительные упражнения к главе III........................180
254
к сожалению последующие страницы оказались вырваны из учебника.
I
график функции y=ax2+bx+c
26 к.