Текст
П Я. • М | п П
КО HI ЧНЫЕ
ЦЕПИ
МАРКОВА
ДЖОН ДЖ. КЕМЕНИ
ДЖ. ЛОРИ СНЕЛЛ
КОНЕЧНЫЕ
ЦЕПИ
МАРКОВА
Перевод с английского
С. А. МОЛЧАНОВА, Н. Б. ЛЕВИНОЙ
и Я. А. КОГАНА
Под редакцией
А. А. ЮШКЕВИЧА
ИЗДАТЕЛЬСТВО «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСК ВА 1970
517.8
К 35
УДК 519.2
FINITE MARKOV CHAINS
by
JOHN G. KEMENY
Professor of Mathematics
Dartmouth College
J. LAURIE SNELL
Associate Professor of Mathematics
Dartmouth College
THE UNIVERSITY SERIES IN
UNDERGRADUATE MATHEMATICS
Конечные цепи Маркова. Ke мен и Дж. и Снелл Дж. Глав
пая редакция физико-математической литературы изд-ва «Наука»,
1970.
В книге рассматриваются только цепи с конечным числом состоя-
ний и излагаются основные результаты теории таких цепей, имею-
щие значение в приложениях. Характерной чертой книги является
сочетание педантично строгого обоснования начальных понятий с
чрезвычайно элементарными аналитическими средствами, доступными
широкому кругу читателей. Благодаря последовательному использо-
ванию понятия резольвенты книга выгодно отличается от многих
руководств по теории вероятностей своим идейно-методическим един-
ством.
Рис. 12.
2*2*3
132-70
ОГЛАВЛЕНИЕ
Предисловие................................................6
Г л а в а I
Предварительные сведения ..................................9
1.1. Множества .....................................9
1.2. Высказывания..................................11
1.3. Отношения порядка.............................12
1.4. Отношения связи ............................ 15
1.5. Вероятностные меры............................18
1.6. Условная вероятность..........................20
1.7. Функции на пространстве возможностей..........22
1.8. Среднее значение и дисперсия функции..........24
1.9. Стохастические процессы.......................26
1.10. Суммируемость последовательностей и рядов ... 32
1.11. Матрицы.......................................33
Глава II
Основные понятия теории цепей Маркова.................. 39
2.1. Определение марковского процесса и цепи Маркова . 39
2.2. Примеры .......................................42
2.3. Связь с теорией матриц.........................48
2.4. Классификация состояний и цепей.............51
2.5. Чем мы будем заниматься........................56
Упражнения к главе II............................58
Глава III
Поглощающие цепи Маркова..................................62
3.1. Введение ......................................62
3.2. Фундаментальная матрица........................66
3.3. Приложения фундаментальной матрицы.............69
1*
4
ОГЛАВЛЕНИЕ
3.4. Примеры .......................................77
3.5. Распространение результатов....................81
Упражнения к главе III..........................89
Глава IV
Регулярные цепи Маркова..................................93
4.1. Основные теоремы...............................93
4.2. Закон больших чисел для регулярных цепей Маркова 98
4.3. Фундаментальная матрица регулярной цепи .... 100
4.4. Времена первого достижения....................104
4.5. Дисперсия времени первого достижения...........НО
4.6. Предельная ковариация.........................112
4.7. Сравнение двух примеров.......................119
4.8. Общая цепь с двумя состояниями................124
Упражнения к главе IV..........................126
Глава V
Эргодические цепи Маркова...............................129
5.1. Фундаментальная матрица.......................129
5.2. Примеры циклических цепей.....................134
5.3. Обращенные цепи Маркова.......................136
Упражнения к главе V...........................143
Г л а в а VI
Дальнейшие результаты...................................145
6.1. Приложение теории поглощающих цепей к эргодиче-
ским цепям........................................145
6.2. Приложение теории эргодических цепей к поглощаю-
щим цепям Маркова.................................151
6.3. Укрупнение состояний..........................159
6.4. Слабое укрупнение состояний...................169
6.5. Расширение цепи Маркова.......................181
Упражнения к главе VI..........................187
Глава VII
Приложения цепей Маркова ........191
7.1. Случайные блуждания ..........................191
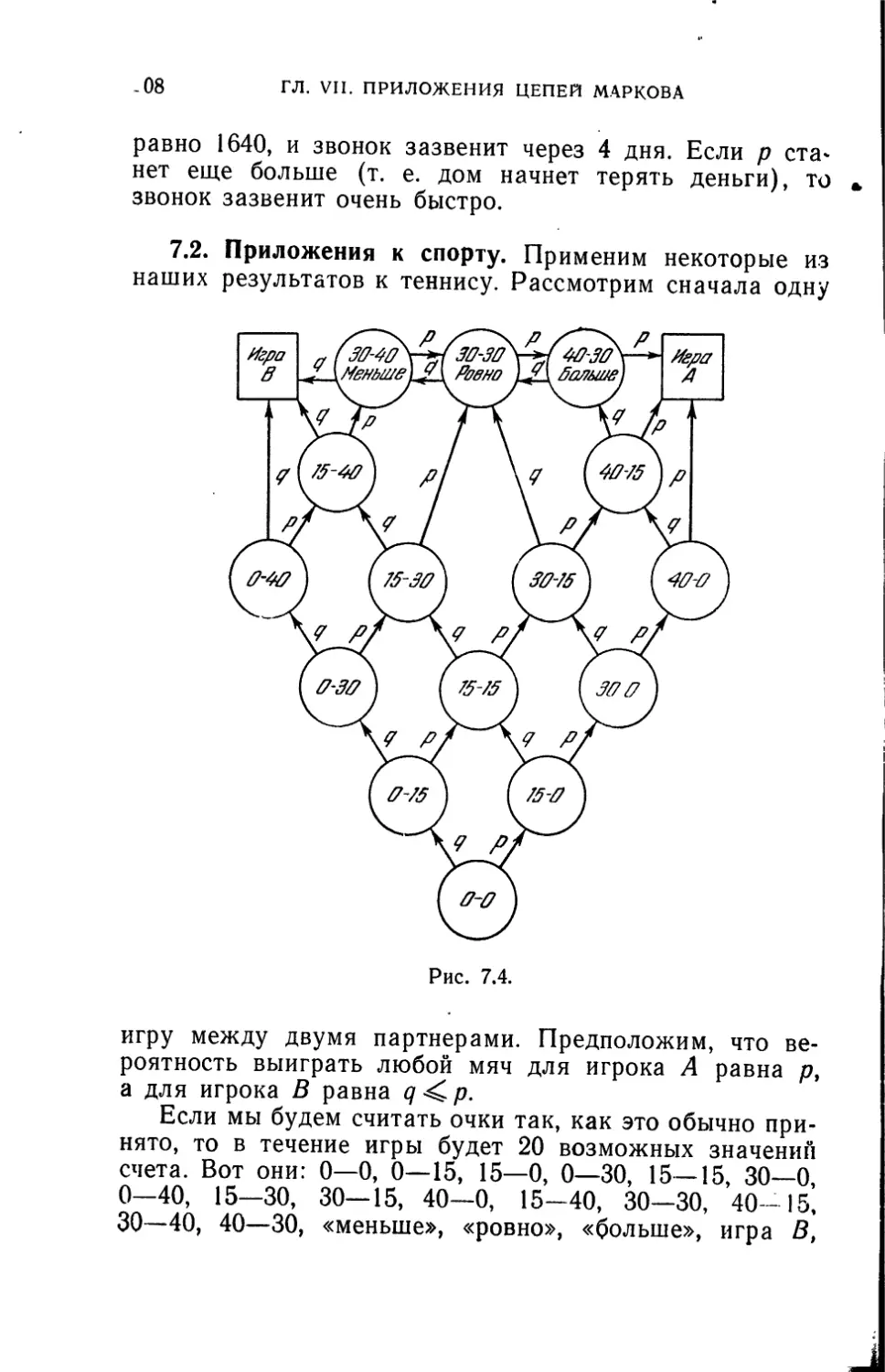
7.2. Приложения к спорту...........................208
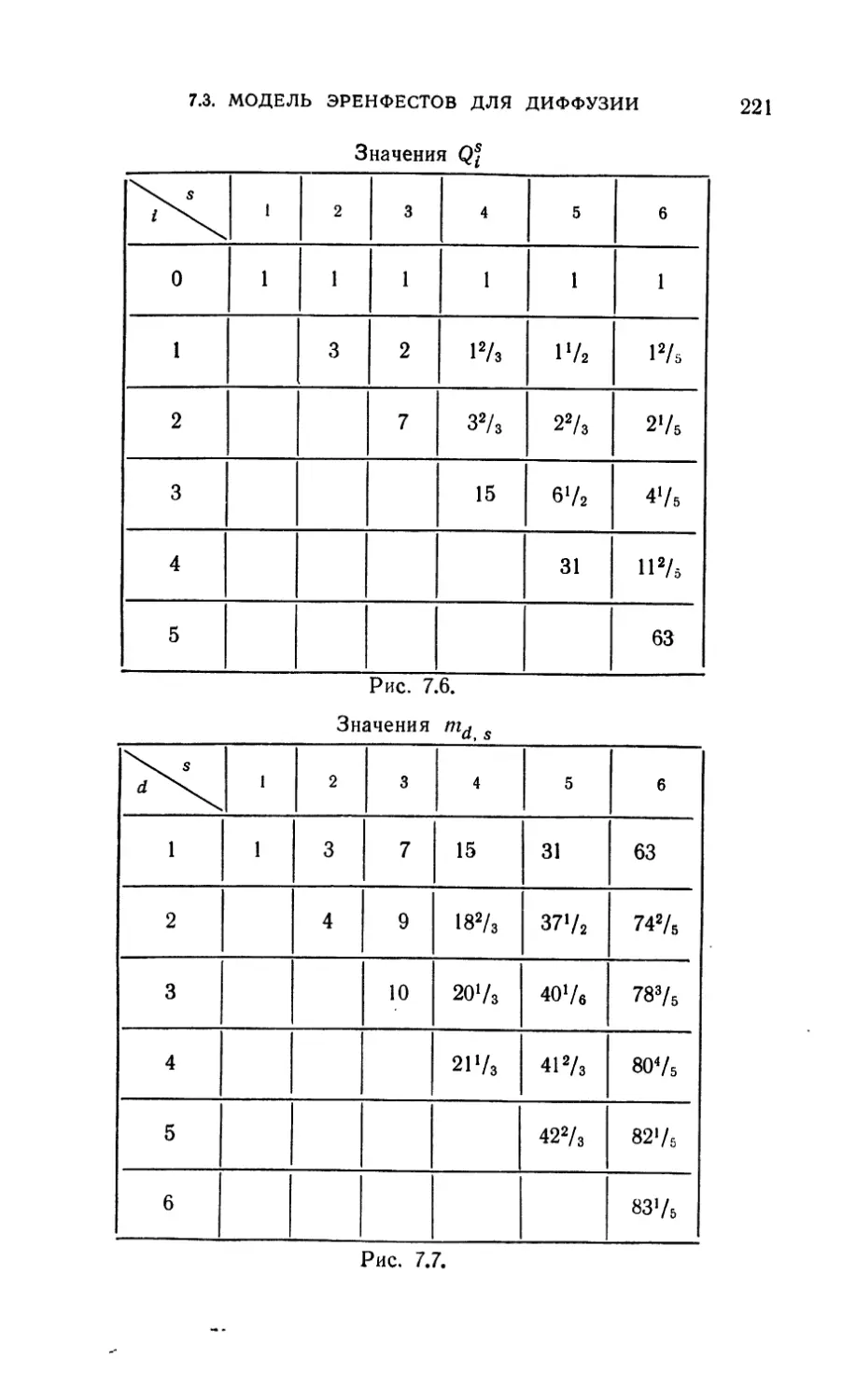
7.3. Модель Эренфестов для диффузии 215
ОГЛАВЛЕНИЕ 5
7.4. Применения к генетике......................... 227
7.5. Теория обучения................................ 235
7.6. Применения к теории мобильности................ 246
7.7. Открытая модель Леонтьева...................... 258
Добавление................................................267
I. Сводка основных обозначений......................267
II. Основные определения...........................267
III. Основные характеристики поглощающих цепей. . . . 268
IV. Основные формулы теории поглощающих цепей . 269
V. Основные характеристики эргодических цепей .... 270
VI. Основные формулы теории эргодических цепей . . .271
ПРЕДИСЛОВИЕ
Основные понятия теории марковских цепей ввел
А. А. Марков в 1907 г. С тех пор эту теорию развивали
многие ведущие математики. В самое последнее время
обнаружилась важная роль цепей Маркова в биологи-
ческих и социологических науках. Нам представляется,
что эти новые приложения настоятельно требуют изло-
жения на английском языке основных идей теории ко-
нечных цепей Маркова.
Ограничив наше внимание случаем конечных цепей,
мы смогли дать законченное изложение предмета, тре-
бующее минимальной математической подготовки. Книга
написана с таким расчетом, чтобы ее можно было ис-
пользовать как в начальном университетском курсе тео-
рии вероятностей, так и в качестве справочника для спе-
циалцстов-нематематиков.
Благодаря тому, что в книге рассматриваются толь-
ко конечные цепи, для многих характеристик вместо
обычно употребляемых бесконечных рядов удалось дать
простые матричные выражения. Показано, что для реше-
ния всех типов задач достаточно рассмотреть только два
типа марковских цепей, а именно поглощающие и эрго-
дические цепи. Для каждого из этих двух типов цепей
вводится «фундаментальная матрица», через которую
прочие интересующие нас величины выражаются с по-
мощью элементарных матричных операций.
Одно из практических преимуществ этого нового под-
хода состоит в том, что упомянутые матричные операции
легко реализуются на быстродействующих вычислитель-
ных машинах. Авторы построили две программы для
машины ИБМ-704, по одной для каждого из двух основ-
ных типов цепей. Эти программы позволяют непосред-
ственно по переходной матрице вычислять целый ряд
числовых характеристик цепи. Эти программы оказали
ПРЕДИСЛОВИЕ
7
неоценимую помощь при расчете примеров и численной
проверке теорем.
Существенное отличие нового подхода состоит еще и
в том, что отпадает нужда в использовании теории соб-
ственных значений и собственных векторов. Авторы счи-
тают, что в каждом рассматриваемом случае получен-
ные в книге матричные выражения проще, чем обычно
применяемые формулы, которые пишутся в терминах
собственных значений. Это связано, по-видимому, с тем
фактом, что фундаментальная матрица, в отличие от
собственных значений, допускает прямую вероятностную
интерпретацию.
Книга распадается на три части. Глава I представ-
ляет собой очень краткую сводку необходимых предва-
рительных сведений. В главах II—VI развивается тео-
рия цепей Маркова. Глава VII содержит приложения
этой теории к разнообразным задачам из других обла-
стей. Сводку использованных символов и основных опре-
делений и формул можно найти в добавлении. В книге
нет указателя, но нам кажется, что подробные оглав-
ление и добавление окажутся более полезными.
Вовсе не обязательно начинать чтение книги с де-
тального изучения главы I. Можно сразу же приступать
к главе II и обращаться к этому краткому введению
лишь по мере изучения последующих глав, при встрече
с незнакомыми понятиями1).
Книга написана с таким расчетом, чтобы ее можно
было использовать как материал для начального
*) Более подробное изложение большинства из этих вопросов
можно найти в любой из следующих книг: (1) М4 = Modern Mathe-
matical Methods and Models, тт. I и II, 1958 (книга составлена Дарт-
мутской группой авторов и издана Американской математической ас-
социацией) , (2) FM = К е m е п у, Snell, Thompson, Introduc-
tion to Finite Mathematics, Prentice-Hall, 1957 [русский перевод:
Дж. К e м e н и, Дж. Снелл, Дж. Томпсон, Введение в конечную
математику, «Мир», 1965. — Прим, перев}, (3) FMS = Kemeny,
Mirkil, Snell, Thompson, Finite Mathematical Structures,
Prentice-Hall, 1959. Предварительные сведения по теории вероятно-
стей, так же как изложение теории цепей Маркова с другой точки
зрения, читатель найдет в книге: W. Feller, Introduction to Proba-
bility Theory and Its Applications, Wiley, 1957 [русский перевод:
В. Феллер, Введение в теорию вероятностей и ее приложения, т. I,
«Мир», 1967. — Прим, перев.].
8
ПРЕДИСЛОВИЕ
университетского математического курса. Поэтому все
доказательства проведены на возможно более элементар-
ном уровне. Книга может служить основой полугодового
курса по теории цепей Маркова и приложениям. Выбо-
рочно ее можно использовать и в основном курсе теории
вероятностей (по нашему мнению, это относится к гла-
вам II, III, IV и частично VII). С этой же целью в конце
глав II—VI приводятся упражнения.
В книге принята следующая система обозначений:
числа обозначаются строчными латинскими буквами,
матрицы — прописными латинскими, векторы — грече-
скими. Функции, множества и прочие абстрактные объ-
екты обозначаются жирными буквами.
Авторы благодарят Национальный научный фонд за
поддержку Дартмутского математического проекта. Мно-
гие оригинальные результаты, приведенные в книге,
были получены авторами в период работы над этим
проектом. Авторы благодарны также MIT и Дартмут-
скому вычислительному центру за предоставление ма-
шинного времени, что дало возможность составить и ис-
пользовать упомянутые выше программы.
Авторы хотят поблагодарить своих научных сотруд-
ников П. Перкинса и Б. Барнса как за многие ценные
советы, так и за внимательное чтение рукописи.
Благодарим также миссис М. Эндрюс и миссис
X. Хэншетт за перепечатку рукописи.
Авторы
Гановер, Нью-Хэмпшир
сентябрь, 1959
г Л А В A I
ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ
1.1. Множества. Под множеством математик пони-
мает произвольную, но вполне определенную совокуп-
ность объектов. Объекты этой совокупности называются
элементами. Множества будут обозначаться жирными
прописными буквами.
Если дано множество А, и множество В состоит из
некоторых (не обязательно всех) элементов А, то мы
говорим, что В является подмножеством А, и обозначаем
это В А. Если два множества содержат одни и те же
элементы, то мы говорим, что эти множества равны,
А = В. Таким образом, А = В тогда и только тогда, ко-
гда А с В и В А. Если В является подмножеством
А и В не равно А, то мы говорим, что В — собственное
подмножество А, и пишем В с А. Если А и В не имеют
общих элементов, то мы называем их непер ссекающи-
мися множествами.
Очень часто мы будем иметь дело с некоторым за-
данным множеством объектов и будем рассматривать
различные его подмножества. В таком случае все это
множество мы будем называть универсальным множе-
ством U. Особый интерес среди подмножеств представ-
ляет множество, не содержащее никаких элементов, —
пустое множество Е.
Имея множество, можно разными способами из од-
них его подмножеств получать другие. Если А и В —
подмножества (/, то мы определим над ними следующие
операции.
(I) Дополнение А, А, имеет своими элементами все
элементы универсального множества, не содержащиеся
в А.
(2) Объединение А и В, A U В, имеет своими эле-
ментами все элементы А и все элементы В.
(3) Пересечение А и В, А А В, имеет своими элемен-
тами все элементы, которые принадлежат и А, и В.
10
ГЛ. I. ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ
(4) Разность А и В, А — В, имеет своими элемен-
тами все элементы А, которые не принадлежат В.
Чтобы проиллюстрировать эти операции, приведем
несколько легко доказываемых соотношений между мно-
жествами:
U = E,
1 = а,
А — В== AQB,
АЦВ = АПВ,
a7Tb = aub,
AUB = BUA,
АПВ = ВПА,
AUB = A,
Af|B = E.
Если Ai, А2, Ar— подмножества U и каждый
элемент U содержится в одном и только одном из мно-
жеств Aj, то мы говорим, что А = {Аь ..., Аг} является
разбиением множества U.
Если мы хотим задать множество, перечисляя его
элементы, то записываем эти элементы внутри фигур-
ных скобок. Например, множество пяти первых положи-
тельных целых чисел записывается как {1, 2, 3, 4, 5}.
Множество {1,3,5} является его собственным подмноже-
ством. Множество {2}, также являющееся подмноже-
ством нашего множества из пяти элементов, называется
единичным множеством, так как содержит только один
элемент.
В этой книге мы будем иметь дело как с конечными,
так и с бесконечными множествами, т. е. с множествами,
содержащими либо конечное, либо бесконечное число
элементов. Единственные бесконечные множества, кото-
рые нам будут встречаться, и притом довольно часто,—
это множество целых чисел {1, 2, 3, ...} и некоторые
его простые подмножества.
Для более детального знакомства с теорией множеств
мы отсылаем читателя к главе II FM или главе II
FMS1).
9 FM = Kemeny, Snell, Thompson, Introduction to Fi-
nite Mathematics, N. J., Prentice-Hall, Inc., 1957 [русский перевод:
Кемени, Снелл, Томпсон, Введение в конечную математику,
ИЛ, М., 1963. — Прим. ред.].
FMS = Kemen у, Mirkil, Snell, Thomson. Finite Mathe-
matical Structures, Englewood Cliffs, N. J., Prentice-Hall, Inc., 1959.
1.2. ВЫСКАЗЫВАНИЯ
И
1.2. Высказывания. Мы будем иметь дело с явле-
нием, которое чаще всего представляет собой научный
эксперимент или игру случая. У такого явления имеется
ряд различных возможных исходов. Мы будем рассмат-
ривать те или иные высказывания об этих исходах.
Образуем множество U всех логически возможных
исходов. Их нужно выбрать так, чтобы быть уверенны-
ми, что будет иметь место ровно один из этих исходов.
Множество U называется пространством возможностей.
Если р—какое-либо высказывание об исходах, то оно
будет, вообще говоря, истинно при одних возможностях
и ложно при других. Множество Р всех возможностей,
при которых р истинно, называется множеством истин-
ности высказывания р. Таким образом, каждому выска-
зыванию об исходах ставится в соответствие некоторое
подмножество множества U, а именно его множество
истинности. Выбор U для данного эксперимента не яв-
ляется единственным. Например, для двух бросаний мо-
неты можно анализировать возможности, используя
и - {НН, НТ, TH, ТТ} или U = {ОЯ, 1Я, 2Я) 1). В первом
случае указывается исход каждого бросания, во втором
только число выпавших гербов. (Более подробно эти
вопросы обсуждены в главе II FM и главе II FMS.)
Имея два высказывания р и q, относящиеся к одно-
му и тому же явлению (т. е. одному и тому же U), мы
можем различными способами формировать из них но-
вые высказывания (допустим, что эти высказывания
имеют соответственно множества истинности Р и Q):
(1) Высказывание ~р (читается «не р») истинно
тогда и только тогда, когда р ложно. Следовательно, вы-
сказывание ~р имеет множество истинности Р.
(2) Высказывание р V q (читается «р или q») ис-
тинно, если истинно либо р, либо q или истинны и р,
и q. Следовательно, высказывание р V q имеет множе-
ство истинности Р U Q.
(3) Высказывание р Aq (читается «р и <?») истинно,
если и р, и q истинны. Следовательно, высказывание
р Л q имеет множество истинности Р A Q.
9 Я ₽ head— герб, Т = tail — решетка [Прим, перев.].
12
ГЛ. I. ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ
Два частных типа высказываний принадлежат к чис-
лу основных понятий логики. Высказывание, истинное
для каждого логически возможного исхода, т. е. выска-
зывание, имеющее множество истинности 17, называется
логически истинным (такое высказывание называют ино-
гда тавтологией). Высказывание, ложное для каждого
логически возможного исхода, т. е. высказывание, имею-
щее множество истинности £, называется логически
ложным или внутренне противоречивым.
Два высказывания называются эквивалентными, ес-
ли они имеют одно и то же множество истинности. Это
означает, что одно высказывание истинно тогда и только
тогда, когда истинно другое.
Высказывания pi, р2, ..., pk являются несовместны-
ми, если пересечение их множеств истинности пусто, т. е.
если Р\ П Р2 А ... A Pk = Е. В остальных случаях эти
высказывания называются совместимыми. Если выска-
зывания несовместны, то они не могут быть все истинны.
Если высказывания совместимы, то они могут быть все
истинны.
Говорят, что высказывания образуют полное множе-
ство альтернатив, если для каждого элемента U истинно
ровно одно из этих высказываний. Это означает, что
пересечение любых двух множеств истинности пусто, а
объединение всех множеств истинности совпадает с U.
Таким образом, множества истинности полного множе-
ства альтернатив образуют разбиение U. Полное мно-
жество альтернатив представляет новый (вообще говоря,
менее подробный) способ анализа возможных исходов.
1.3. Отношения порядка. Нам понадобятся некото-
рые простые сведения из теории отношений порядка.
Полное изложение этих вопросов можно найти в М4,
т. II, часть 21), откуда мы заимствуем лишь отдельные
понятия.
Пусть R — какое-то отношение между двумя объекта-
ми (выбранными из данного множества U). Запись aRb
означает, что а находится в отношении R к Ь. Нас будут
интересовать следующие свойства таких отношений:
!) м4 = Modern Mathematical Methods and Models, Mathemati-
cal Association of America, 1958 (Дартмутская группа авюров).
1.3. ОТНОШЕНИЯ ПОРЯДКА
13
1.3.1. Определение. Отношение R называется рефлек-
сивным, если xRx выполняется для всех х из U.
1.3.2. Определение. Отношение R называется симмет-
ричным, если для любых х, у из U из выполнения xRy
вытекает yRx.
1.3.3. Определение. Отоношение £ называется тран-
зитивным, если для любых х, у, г из U из xRy A yRz
вытекает xRz.
1.3.4. Определение. Всякое рефлексивное, симметрич-
ное и транзитивное отношение называется отношением
эквивалентности.
Основное свойство отношения эквивалентности состо-
ит в том, что оно задает разбиение множества U. Имен-
но, пусть R — отношение эквивалентности, определенное
на U. Разобьем элементы U на классы, относя два эле-
мента а и Ь к одному классу, если aRb. Можно показать,
что получатся вполне определенные взаимно исключаю-
щие классы, образующие разбиение множества U. Они
называются классами эквивалентности отношения R.
Например, пусть xRy означает, что х имеет тот же
рост, что и у, где U — некоторое множество людей. Тогда
определенное выше разбиение делит этих людей по при-
знаку роста. Два человека окажутся в одном и том же
классе эквивалентности тогда и только тогда, когда они
одного роста.
1.3.5. Определение. Отношение Т называется совме-
стимым с отношением эквивалентности R, если при xRy
из xTz следует yTz и из zTx следует zTy.
1.3.6. Определение. Рефлексивное транзитивное отно-
шение называется отношением слабого упорядочения.
Отношение слабого упорядочения можно использо-
вать для упорядочения элементов множества U. При
слабом упорядочении Т для любых двух элементов а
и b из U существуют четыре возможности:
(1) аТЬ А ЬТа, тогда эти два элемента «подобны»
в смысле Т;
(2) аТЬ А ~ ЬТа, тогда а «предшествует» &;
(3) ~ аТЬ А ЬТа, тогда Ь «предшествует» а;
(4) ~аТЬ А ~ ЬТа, тогда эти два элемента несрав-
нимы.
14
ГЛ. I. ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ
Например, если хТу означает, что «я люблю х по
крайней мере так же, как и у», то такими четырьмя слу-
чаями будут: «Я люблю их одинаково», «Я предпочи-
таю х», «Я предпочитаю у» и «Я не могу сделать выбор
между ними».
Это отношение «подобия» действует как отношение
эквивалентности. В самом деле, можно показать, что
если Т — слабое упорядочение, то отношение xRy, выра-
жающее, что хТу Л уТх, является отношением эквива-
лентности, совместимым с Т, Таким образом, Т служит
и для классификации, и для упорядочения. Совмести-
мость гарантирует нам, что эквивалентные элементы I)
будут занимать одинаковые места при таком упорядо-
чении.
Например, если задать слабое упорядочение усло-
вием «не ниже», то это условие определит отношение
эквивалентности «одного и того же роста», совместимое
с первоначальным отношением.
1.3.7. Определение. Если Т — слабое упорядочение,
то порожденным им отношением эквивалентности назы-
вается отношение хТу А уТх.
1.3.8. Определение. Если Т — слабое упорядочение и
порожденное им отношение эквивалентности является
отношением тождества (х ~ У) , то Т называется частич-
ным упорядочением.
Сущность частичного упорядочения в том, что ника-
кие два различных элемента не являются при нем по-
добными. Один из способов частичного упорядочения
состоит в следующем. Пусть Т — слабое упорядочение,
определенное на U, Определим новое отношение Т*
на множестве классов эквивалентности, полагая uT*v,
если каждый элемент из и находится в отношении Т
к каждому элементу из v. Это частичное упорядочение
классов эквивалентности мы будем называть частичным
упорядочением, индуцированным Т.
1.3.9. Определение. Элемент а множества U назы-
вается минимальным, если из аТх следует хТа для лю-
бого х <=U. Если минимальный элемент является един-
ственным, то его называют минимумом.
Можно аналогичным образом определить «макси-
мальный элемент» и «максимум». Если U — конечное
1.4. ОТНОШЕНИЯ СВЯЗИ
15
множество, то легко показать, что для любого слабого
упорядочения существует по меньшей мере один мини-
мальный элемент. Однако этот минимальный элемент не
обязательно единственный. Аналогично, для слабого упо-
рядочения должен существовать максимальный элемент,
но не обязательно максимум.
1.4. Отношения связи. Отношения порядка находят
важное применение при изучении коммуникационных
сетей. Предположим, что г лиц связаны посредством
сложной сети. Каждое лицо может послать сообщение
некоторому подмножеству лиц. Это мы называем пря-
мой связью. Сообщения могут передаваться и в несколь-
ко этапов ретрансляцией. Это уже будет непрямая связь.
Заметим, что мы не предполагаем, что любое лицо имеет
прямую связь с самим собой. Пусть аТЬ означает, что а
имеет (прямую или непрямую) связь с b или что а = Ь.
Легко установить, что Т задает слабое упорядочение
рассматриваемого множества лиц. Это упорядочение по-
рождает отношение эквивалентности хТу А уТх, которое
читается как «х и у могут сообщаться друг с другом или
X = у».
Это отношение эквивалентности можно использовать
для классификации рассматриваемых лиц. Два лица
окажутся тогда в одном и том же классе эквивалентно-
сти, если они сообщаются друг с другом, т. е. если каж-
дый из них имеет связь с другим. Частичное упорядоче-
ние Т*, индуцированное Т, в данном случае имеет очень
простой смысл. Отношение uT*v выполняется, если все
представители класса и имеют связь со всеми представи-
телями класса V, но не наоборот (за исключением слу-
чая и — v). Таким образом, частичное упорядочение ука-
зывает на возможное направление передачи информации.
В частности, класс и является максимальным эле-
ментом частичного упорядочения, если представители
любого другого класса не имеют связи с представите-
лями и,н и является минимальным элементом, если его
представители не имеют связи с представителями дру-
гих классов. Таким образом, максимальные множества
являются источниками сообщений, а минимальные — их
конечными приемниками (см. М4, т. II, часть 2).
16
ГЛ. I. ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ
Рассмотрим подробнее некоторый класс эквивалент-
ности. Любые два элемента такого класса имеют связь
друг с другом. Поэтому любой элемент может передать
сообщение любому другому элементу. Возникает вопрос,
сколько времени требуется для такой передачи. За еди-
ницу времени примем время, необходимое для передачи
сообщения от любого элемента к любому другому эле-
менту при прямой связи. Эту единицу назовем шагом.
Предположим, что сообщение посылает элемент i, и за-
дадимся вопросом, где может оказаться это сообщение
через п шагов.
Пусть Nij — множество таких п, что сообщение, исхо-
дящее от /, может оказаться у / на n-м шаге. Вначале
рассмотрим Na, т. е. множество тех моментов времени,
за которые сообщение может вернуться к своему источ-
нику. Ясно, что если а е Na и & е Na, то а + b е Na,
так как сообщение может возвратиться через а шагов,
может быть снова послано и снова принято обратно еще
через b шагов. Таким образом, множество Na инва-
риантно относительно сложения. Нам понадобится сле-
дующий результат из теории чисел, доказательство ко-
торого приводится в конце этого пункта.
1.4.1. Теорема. Множество положительных целых чи-
сел, инвариантное относительно сложения, содержит все
целые кратные наибольшего общего делителя этих чисел,
за исключением быть может конечного числа таких
кратных.
Если наибольший общий делитель элементов Na ра-
вен di, то ясно, что все элементы Na делятся на di. Тео-
рема 1.4.1, сверх того, утверждает, что все достаточно
большие числа, кратные di, являются элементами этого
множества.
Так как каждый элемент имеет связь с каждым эле-
ментОхМ в своем классе эквивалентности, то множества
не пусты. Докажем теперь, что для in j, принадле-
жащих одному и тому же классу эквивалентности,
dt = dj = d и что числа данного множества N^ срав-
нимы друг с другом по модулю d (их разность де-
лится на d). Предположим, что а е Nij, b е Nij и
с Nji.
1.4. ОТНОШЕНИЯ СВЯЗИ
17
Прежде всего элемент i имеет связь с самим собой,
так как он может послать сообщение элементу / и за-
тем получить его обратно. Поэтому а + с е Na. С другой
стороны, сообщение может быть послано элементу /,
вернуться к нему снова, а затем передано элементу i.
Такая передача может быть осуществлена за a + kdj + c
шагов при любом достаточно большом k. Отсюда сле-
дует, что dj должно делиться на di. Но точно тем же
способом можно доказать, что di делится на dj, и по-
этому dj== di d.
Далее, сообщение может быть передано от i к / за
b шагов, а затем возвращено к I. Поэтому b + с е Na.
Значит, а + с и b + с оба делятся на d, и, таким обра-
зом, a^&(modd). Итак, все числа из множества
сравнимы друг с другом по модулю d. Поэтому можно
ввести такие числа Uj, 0 t^ < d, что любой элемент из
Nij сравним с по модулю d. Легко также убедиться,
что множество содержит все числа вида tij + kd за
конечным числом исключений.
В частности, видно, что в любом случае tn = 0, и по-
тому tij + tji = 0 (mod d). Кроме того, t^ + tjm =
= tim(modd). Отсюда легко усмотреть, что tij = 0 пред-
ставляет собой отношение эквивалентности. Назовем
соответствующий класс эквивалентности циклическим
классом.
Так как tij + tjm=tim(modd), то t^ = tim тогда и
только тогда, когда tjm = 0, а потому необходимым и
достаточным условием равенства tij = tim является
принадлежность элементов / и т к одному цикличе-
скому классу. Пусть п — любое целое число. Если
rc = ^(mod d), то сообщение, исходящее от i, через п
шагов может находиться только в соответствующем цик-
лическом классе. Отсюда сразу следует, что имеется
ровно d циклических классов и что сообщение передает-
ся циклически из класса в класс с периодом d. Легко
также показать, что по прошествии достаточно боль-
шого промежутка времени сообщение может оказаться
у любого представителя циклического класса, соответ-
ствующего данному п.
Приведенное описание класса эквивалентности ком-
муникационной сети справедливо во всех случаях, только
% Дж. Кемени, Дж. Снелл
18
ГЛ. I. ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ
при d == 1 цикл вырождается. В этом случае имеется
единственный «циклический класс», и по прошествии
достаточно большого отрезка времени сообщение может
оказаться в любой момент у любого элемента.
В частности, следует отметить, что если какой-нибудь
один элемент класса эквивалентности имеет прямую
связь с самим собой, то d = 1. Это сразу следует из того
факта, что d является делителем любого отрезка вре-
мени, за которое элемент может установить связь с са-
мим собой, и поэтому 1 должна делиться на d.
Приведенный под номером 1.4.1 результат из теория
чисел настолько важен, что мы дадим здесь его доказа-
тельство.
Прежде всего заметим, что если наибольший общий
делитель d элементов множества не равен 1, то все их
можно поделить на d и свести дело к случаю d = 1, ко-
торый мы и рассмотрим. Если имеется множество чисел
с наибольшим общим делителем, равным 1, то этим
Свойством обладает и некоторое конечное его подмноже-
ство. Поэтому, на основании хорошо известного резуль-
тата, существует линейная комбинация ахп\ + а2п2 + ...
... A-ahnh элементов множества (с положительными или
отрицательными целыми коэффициентами аг), которая
равна 1. Если мы сгруппируем все положительные и
все отрицательные члены отдельно и вспомним, что
наше множество инвариантно относительно сложения, то
получим, что этому множеству принадлежат такие чис-
ла т и п, что т — п = 1 (т является суммой положи-
тельных, а п — суммой отрицательных членов). Пусть
q — любое достаточно большое число, или, точнее,
q^n(n—1). Тогда можно написать, что q = ап 4- &,
где —1 и —1. Но в таком случае
q = (а — Ь)п + Ьт, и потому q принадлежит нашему мно-
жеству.
1.5. Вероятностные меры. При вероятностном ана-
лизе эксперимента имеется два основных этапа. Вначале
выбирается множество логических возможностей. Этот
вопрос обсуждался в 1.2. Затем вводится вероятностная
мера. Способы ее введения рассматриваются в этом
пункте. Обратимся сперва к случаю конечного простран-
1.5. ВЕРОЯТНОСТНЫЕ МЕРЫ
19
ства возможностей. (Для более подробного ознакомле-
ния с этими вопросами отсылаем читателя к FM, гла-
ве IV, или к FMS, главе III.)
1.5.1. Определение. Пусть U = {аь аг} — некото-
рое множество логических возможностей. Вероятностная
мера на U вводится путем приписывания каждому эле-
менту aj положительного числа называемого ве-
сом, так, чтобы эти веса давали в сумме 1. Мера под-
множества А множества U, обозначаемая через т(А),
полагается равной сумме весов, приписанных элементам
подмножества А.
1.5.2. Теорема. Вероятностная мера т, введенная на
множестве логических возможностей U, обладает сле-
дующими свойствами'.
(1) Для любого подмножества Р из U O^m(P)^ 1.
(2) Если Р и Q — непер ссекающие с я подмножества
U, то m(P U Q) = m(P) + m(Q).
(3) Для любых подмножеств Р и Q множества U
m(P U Q) = т(Р) + m(Q) —т(Р Г) Q).
(4) Для любого множества Р из U т(Р) = 1 —т(Р).
1.5.3. Определение. Пусть р — высказывание относи-
тельно множества U с множеством истинности Р. Тогда
вероятность р при данной вероятностной мере m пола-
гается равной т(Р) {и обозначается Р[р]).
В любом случае, когда вероятностная мера фиксиро-
вана, мы будем просто говорить о вероятности р, не упо-
миная каждый раз эту меру. Из теоремы 1.5.2 и связи
между операциями над высказываниями и операциями
над множествами вытекает следующий результат:
1.5.4. Теорема. Пусть U — множество возможностей,
на котором определена вероятностная мера. Тогда ве-
роятности высказываний, задаваемые этой мерой, обла-
дают следующими свойствами:
(1) Для любого высказывания р 0^Р[р]<С1.
(2) Если р и q несовместны, то Р [р V q] = Р [р] +
+ РМ,
(3) Для любых двух высказываний pug
Р Ь V - Р [р] + Р fa] - Р [р А д].
(4) Для любого высказывания р Р[~р] = 1 — Р[р].
2‘
20
ГЛ. I. ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ
1.5.5. Пример. На любом конечном множестве из s
элементов можно определить вероятностную меру, при-
писав каждому элементу вес 1/5. Такая мера называется
равновероятной. Для любого множества А, состоя-
щего из г элементов, m(A) = r/s. Например, такую меру
обычно используют, рассматривая бросание игральной
кости. В этом случае U = {1, 2, 3, 4, 5, 6} и каждому ис-
ходу приписывают вес 11в.
1.5.6. Пример. В качестве другого примера, когда на-
значаются различные веса, рассмотрим игру на скачках.
Игрок, делающий ставку, сравнивает лошадей а, b и с
и приходит к заключению, что лошади а п b имеют оди-
наковый шанс выиграть, тогда как шансы на выигрыш
у лошади с в два раза больше, нежели у а. Множество
логических возможностей в этом случае имеет вид
U = {а, &, с}, а его элементам назначаются веса w(a) =
= ’/4, W (&) = J/4 И W(c) = V2.
Часто требуется обобщение приведенных выше поня-
тий на случай, когда эксперимент имеет бесконечную по-
следовательность возможных исходов. Например, рас-
смотрим опыт, состоящий в бросании монеты до тех пор,
пока она впервые не упадет гербом вверх. Множеством
возможных исходов в этом случае будет С/ = {1, 2, 3,...}.
Приведенные выше определения и теоремы будут в рав-
ной степени применимы и к этому множеству возможных
исходов. Мы будем иметь теперь бесконечное число ве-
сов, но по-прежнему их сумма должна быть равна 1.
В данном случае следует назначить веса 7г, 74, 7в, ...»
которые, образуя геометрическую прогрессию, дают в
сумме 1.
1.6. Условная вероятность. Часто бывает, что вероят-
ностная мера уже введена на некотором множестве 17,
а затем выясняется, что относительно U справедливо не-
которое высказывание q. Располагая этой новой инфор-
мацией, мы переходим от прежнего множества возмож-
ностей к новому множеству возможностей, совпадающе-
му с множеством истинности Q высказывания q. На ос-
нове первоначальной меры т мы хотим определить ве-
роятностную меру на этом новом множестве. Мы делаем
это, требуя, чтобы элементы Q имели те же самые отно-
1.6. УСЛОВНАЯ ВЕРОЯТНОСТЬ
21
сительные веса, что и первоначально. Это означает, что
наши новые веса должны быть равны старым, умно-
женным на некоторую константу так, чтобы в сумме
снова получилась I. Константа будет равна обратной
величине суммы весов всех элементов в Q, т. е. I/m(Q).
(См. главу IV FM или главу III FMS.)
1.6.1. Определение. Пусть U = {аь ..., аг} — множе-
ство возможностей, на котором введена мера с помощью
весов w(aj). Пусть q — высказывание относительно мно-
жества U, не являющееся внутренне противоречивым.
Тогда условной вероятностной мерой при условии q на-
зывается вероятностная мера на множестве истинности
Q высказывания q, задаваемая весами
1.6.2. Определение. Пусть р и q — два высказывания
относительно множества U (и q не внутренне противоре
чиво). Условной вероятностью р при условии q, обозна-
чаемой Р [р | q], называется вероятность высказывания р,
вычисленная по условной вероятностной мере при усло-
вии q.
1.6.3. Теорема. Пусть р и q — два высказывания от-
носительно U (и q не внутренне противоречиво). Пред-
положим, что на множестве U определена вероятностная
мера m Тогда
Р[р|?1-Т^,
где Р[р A q] и Р[<?] определяются с помощью меры ш.
1.6.4. Пример. Допустим, что игрок на скачках из
примера 1.5.6 узнает, что лошадь b не будет выступать.
Это вынуждает его рассмотреть новое пространство воз-
можностей Q = {а, с}. Новые веса, определяющие услов-
ную меру, равны w (а) = = 7з и w (с) = =
= 2/3. По-прежнему вероятность выигрыша лошади с в
два раза больше вероятности выигрыша лошади а,
1.6.5. Определение. Два высказывания р и q (из ко-
торых ни одно не является внутренне противоречивым),
называются независимыми, если Р[рА<?]= Р[р]РМ.
22
ГЛ. I. ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ
Из теоремы 1.6.3 следует, что р и q независимы то-
гда и только тогда, когда P[pld=P[p] иРк1р]=Р[?].
Таким образом, независимость высказываний р и q озна-
чает, что известие об истинности одного высказывания
не влияет на вероятность, приписываемую другому.
1.6.6. Пример. Рассмотрим испытание, состоящее в
двукратном бросании монеты. Исходы испытаний состав-
ляют множество и = {НН, НТ, TH, ТТ}. Введем равно-
вероятную меру. Пусть р означает, что герб выпадает
при первом, a q — при втором бросании монеты. Тогда
Р[РА<7] = 74. Р[Р1 = РЫ = 72. Таким образом, р и q не-
зависимы.
1.7. Функции на пространстве возможностей. Пусть
U = {аь ..., а,} — пространство возможностей и f — не-
которая функция с областью определения U и областью
значений R = {ri,r2, ..., г}- Это значит, что f сопостав-
ляет каждому элементу U единственный элемент из R.
Если f сопоставляет элементу dj элемент rki то мы пи-
шем f(dj)~ Гк- Высказывание «значение функции равно
Г/.» записывается в виде f = Это высказывание яв-
ляется высказыванием относительно множества 17, так
как значение функции известно, когда известен исход
dj. Значит, это высказывание имеет множество истинно-
сти, являющееся подмножеством U. (См. главы II и III
FMS или М4, т. II, разд. I.)
1.7.1. Определение. Пусть f — функция с областью
определения U и областью значений R. Предположим,
что на множестве U задана мера. Для каждого rk из R
положим w(rk)= = Веса w(rk) определяют ве-
роятностную меру на множестве R, которая называется
мерой, индуцированной функцией f. Веса w(rk) назы-
ваются индуцированными весами.
Индуцированную меру мы будем обычно задавать,
указывая одновременно область значений и веса в виде
следующей таблицы:
е. f г2, .rs 1
' ' I Ни), w(r2), • w(rs)/’
Таким образом, индуцированный вес rh в R является
мерой множества истинности высказывания f г> в U.
1.7. ФУНКЦИИ НА ПРОСТРАНСТВЕ ВОЗМОЖНОСТЕЙ
23
1.7.2. Пример. Пусть в примере 1.6.6 функция f озна-
чает число выпавших гербов. Областью • значений f
является/? = {О, 1, 2}. Очевидно, P{f = 0} = '/4. Ptf = U=
= 72 и Р0 = 2} = 'Л. Значит, область значений и инду-
цированные веса задаются таблицей
О
4
1
72
2
74
1.7.3. Определение. Пусть U — пространство возмож-
ностей .и f и g— две функции с областью определения
U и областями значений, являющимися числовыми мно-
жествами. Тогда f+g обозначает функцию с областью
определения U, сопоставляющую элементу число
+ a f'g — функцию с областью определения
U, сопоставляющую элементу число f (а^) • g (aj). Для
любого числа с постоянной функцией с является функ-
ция, сопоставляющая число с любому элементу из U.
Пусть U — пространство возможностей, на котором
задана мера. Если f и g — две числовые функции с обла-
стью определения U, то f + g и f • g также будут функ-
циями с областью определения U, и как таковые они
индуцируют некоторые меры. Вообще говоря, не суще-
ствует простой связи между мерами, индуцированными
этими функциями, и мерами, индуцированными f и g.
1.7.4. Пример. Вернемся к примеру 1.6.6. Пусть
функция g принимает значение 1, если при первом бро-
сании выпал герб, и 0 — в противном случае. Функция h
принимает значение I, если герб выпал при втором бро-
сании, а 0 — если выпала решетка. Тогда области зна-
чений и индуцированные меры для g, h, g + h и g • h
можно представить в виде
Г ° В . ( О 11
fT/2 72Г i72 7J’
£ + А:{ °
I /4
V /4
1 2
7г 74
1 I
74Г
24
ГЛ. I. ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ
1.7.5. Определение. Пусть f — функция, определенная
на U, и пусть р — высказывание относительно U с мно-
жеством истинности Р. Предположим, что на U задана
мера т. Пусть f' — функция f, рассматриваемая только
на множестве Р. Тогда мера, индуцированная f и вы-
численная по условной мере при условии р, называется
условной мерой, индуцированной f при условии р.
1.7.6. Определение. Пусть f и g—две функции, опре-
деленные на пространстве U, на котором задана вероят-
ностная мера. Тогда fug называются независимыми,
если для любого rh из области значений f и любого sf
из области значений g высказывания f = rh и g = Sj не-
зависимы.
Эквивалентное определение независимости двух функ-
ций получится, если сказать, что мера, индуцированная
одной из функций, не меняется, когда становится из-
вестным значение другой функции.
1.8. Среднее значение и дисперсия функции. В этом
параграфе мы будем рассматривать функции, области
значений которых — числовые множества. Подробное об-
суждение понятий, вводимых в данном параграфе, см.
в FMS, глава III, или М4, т. II, разд. I.
1.8.1. Определение. Пусть f — функция, определенная
на пространстве возможностей U = {а\, а%, ..., ап}, на
котором с помощью весов w(aj) задана мера. Тогда
средним значением f (обозначается М [fl) называется ве-
личина
Вместо термина среднее значение часто используется
термин математическое ожидание.
1.8.2. Теорема. Пусть f—функция, определенная на
U. Предположим, что на U задана вероятностная мера
m и что функция f индуцирует меру
T'[w(ri), w(r2), ..w(rn) Г
Тогда
М1Л = 2 r/w(rz).
1.8. СРЕДНЕЕ ЗНАЧЕНИЕ И ДИСПЕРСИЯ ФУНКЦИИ
25
1.8.3. Пример. Пусть в условиях примера 1.6.6 функ-
ция f —это число выпавших гербов. По определению
среднего значения
М[Л = f (НН) • 74 + f (НТ) • >/4 + f (тн) • */4 + f (ТТ) • 74 =
= 2-74+1 • 74+1 • 74 + о-74= +
Среднее значение f можно также вычислить, воспользо-
вавшись теоремой 1.8.2. Область значений и мера, инду-
цированные f, задаются в виде
1 О 1 21
Г 1 74 72 74)’
По теореме 1.8.2
М[Л = о-74 +1 • 72 + 2 - 74= 1.
1.8.4. Определение. Пусть f — функция, определенная
на пространстве возможностей U, на котором задана
мера, и пусть M[fl = m— среднее значение этой функ-
ции. Тогда дисперсией f (обозначается D[fl) называется
среднее значение функции (f — m) 2. Стандартным откло-
нением (обозначается o[f]) называется квадратный ко-
рень из дисперсии,
1.8.5. Теорема. Пусть f — функция со средним зна-
чением т. Тогда D [Л = М [f2] — пг2.
1.8.6. Пример. Пусть / — функция из примера 1.8.3.
Мы нашли, что М[/]=1. Таким образом,
D [Л = (2 -1)2 • 74 + (1 -1)2 • 74 + (О — 1)2 • 74 = 72.
Другой метод подсчета дисперсии состоит в использо-
вании теоремы 1.8.5. Находим
М[Л] = 4.74+ 1-74+о-74 = 72.
Так как М [Л = 1, то D [Л = 72 ~ 1 = 72-
1.8.7. Теорема. Пусть f и g — любые две функции,
для которых определены средние значения и дисперсии.
Тогда
(1)М[с] = с. (4) DWWDtf].
(2) М[/ + £] = М[Л + М[£]. (5) D[<? + fl»D[fl.
(3) М [сЛ = сМ [Л- (6) D [с] = 0.
26
ГЛ. 1. ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ
Если функции fug независимы, то
(7) М[^ЬМ[ЛМИ.
(8) D [f + g] = D [f] + D[g].
1.8.8. Определение. Пусть р — некоторое высказыва-
ние относительно множества возможностей U, на кото-
ром задана мера, и пусть f — функция с областью опре-
деления U. Условным средним значением и условной
дисперсией f при условии р называются среднее значе-
ние и дисперсия f, вычисленные по условной мере при
условии р. Мы обозначаем их М[/|р] и D [/ |р].
1.8.9. Теорема. Пусть рь р2, рг — полное множе-
ство альтернатив для множества U и f — функция с об-
ластью определения U. Тогда
м[л = 5м[/|р/]Р[р/.
1.8.10. Теорема. Пусть /ь /г, • • • — последовательность
функций такая, что для некоторой постоянной с
при п-^ со. Тогда
М [/„]-> с
и для любого 8>0
Р[
При П~> ОО
1.8.11. Определение. Пусть fx и f2 — dee функции,
причем M[fi] = ai и = Тогда ковариация fx и
определяется формулой
К [А, М = М [(А
а коэффициент корреляции f{ и f2 — формулой
1.9. Стохастические процессы. В этом пункте мы
вкратце опишем понятие стохастического процесса. Бо-
лее полное изложение можно найти в главе IV FM или
в главе III FMS.
1.9. СТОХАСТИЧЕСКИЕ ПРОЦЕССЫ
27
Мы хотим задать вероятностную меру, которая опи-
сывала бы эксперимент, происходящий в несколько эта-
пов. Исход и-го этапа может зависеть от исходов
предыдущих этапов. Предполагается однако, что вероят-
ность каждого возможного исхода на определеннохм
этапе известна, если заданы исходы всех предыдущих
этапов. Зная эти вероятности, мы можем построить про-
странство возможностей и меру для всего эксперимента.
Мы проиллюстрируем построение пространства воз-
можностей и меры на частном примере, из которого бу-
дет ясна общая процедура.
1.9.1. Пример. Случайно выбирается одна из двух
монет А или В. Монета А — настоящая, а на монете В
с обеих сторон изображен герб. Выбранная монета под-
брасывается. Если выпала решетка, то бросают кость.
Если выпал герб, монету подбрасывают снова. Первый
этап эксперимента — выбор монеты. На втором этапе
бросают монету. На третьем этапе бросают кость или
монету, в зависимости от исходов первых двух этапов.
Возможные исходы эксперимента мы изображаем в
виде дерева, как это показано на рис. 1.1.
28
ГЛ. I. ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ
Возможны следующие исходы: t\ = (A, Н, Я), 12 =
-(А, Я, Т), /3 = (А, Т, 1), /4 = (А, Т, 2) и т. д. Каждый
исход отождествляется с некоторым путем на дереве.
Всякий путь состоит из прямолинейных отрезков, назы-
ваемых ветвями. На только что определенном дереве
имеется девять путей, каждый из которых состоит из
трех ветвей.
Мы знаем вероятности каждого исхода на данном
этапе, если известны исходы предыдущих этапов. На-
пример, если на первом этапе появилось А, а на втором
Т, то вероятность появления 1 на третьем этапе равна
Ve. Мы припишем эти известные вероятности ветвям и
назовем их вероятностями ветвей.
Определим теперь вес каждого пути как произведе-
ние вероятностей, приписанных образующим этот путь
ветвям. Например, путь /7 соответствует исходу А на
первом этапе, Т — на втором и 5 на третьем. Вес, при-
писанный этому пути, равен V2 • V2 • 1/б = 1/г4. Описанная
процедура задает вес каждого пути на дереве, причем
сумма всех весов равна 1. Множество U всех путей го-
дится в качестве пространства возможностей при рас-
смотрении любого высказывания, истинность которого
зависит от исходов всего эксперимента. Мера, заданная
весами путей, является при этом соответствующей ве-
роятностной мерой.
Описанное построение можно проделать для любого
эксперимента, происходящего по этапам. Требуется
только, чтобы на каждом этапе было конечное число
возможных исходов и чтобы нам была известна вероят-
ность'каждого отдельного исхода на j-м этапе при за-
данных исходах первых (/—1) этапов. Так для любого
/ получается дерево Uj. Множество путей этого дерева
служит пространством возможностей для любого выска-
зывания, связанного с первыми / этапами. Зададим меру
на множестве всех путей дерева Uj, во-первых, опреде-
лив вероятности ветвей, а затем положив вес, приписы-
ваемый какому-то пути, равным произведению вероятно*
стей всех его ветвей. Меры, заданные на каждом дереве,
согласованы между собой в следующем смысле. Выска-
зывание, истинность которого зависит лишь от первых
j этапов, можно, конечно, рассматривать как высказы-
1.9. СТОХАСТИЧЕСКИЕ ПРОЦЕССЫ
29
вание относительно любого дерева С7г- при i j. На каж-
дом из этих деревьев задана его собственная мера, и
вероятность высказывания можно найти по любой из
этих мер. Но в любом случае получится одна и та же
вероятность.
Предположим, что задано дерево некоторого экспе-
римента, состоящего из п этапов. Пусть ft —функция,
область определения которой — множество путей Un, а
значение — исход /-го этапа. Функции fi, ..., fn назы-
ваются функциями исходов. Множество функций ...
.fn называется стохастическим процессом. (В тео-
рии цепей Маркова удобно обозначить первый исход не
f„ а М
В нашем примере имеется три функции исходов. Мы
представили на рис. 1.1 значения каждой функции на
каждом из путей.
Между вероятностями ветвей и функциями исходов
имеется простая связь. Вероятности ветвей на первом
этапе — это вероятности
Р[А = пЬ
на втором этапе — это
P[f2 = r/|f1 = rz],
на третьем этапе —
P[f3 = rft = =гг]
И Т. д.
В нашем примере
р [А = 4] = №(#])+ ... +w(#8) = ’/2>
р [А = т If, = А] = =
_ «>«з)+ +«>(*8) I/.
w(h)+ ... +w(z8) >/2 /2>
Р [f, = 1 I f _ у д f _ я 1 _ Р Уз = 1ЛЬ = ГЛЬ = А]
1/з ИГ2 /ЛП-AJ- Ptf2 = rAfi=A] -
________w(/3)______= У24 _
®(*з)+ ••• +w(#8) Уз '6‘
1.9.2. Пример. Нам часто придется иметь дело с экс-
периментами, в которых допускается произвольное число
30
ГЛ. I. ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ
этапов. Например, рассматривая бросания монеты, мы
можем наблюдать любое число бросаний. Для случая
трех бросаний на рис. 1.2 представлены дерево и вероят-
ности путей.
Дерево можно сконструировать для любого количе-
ства бросаний. Достраивая дерево неограниченно дале-
ко, можно даже получить дерево с бесконечными пу-
тями. Наш метод построения меры в этом случае не
wftj
%
’/в
'/в
%
’/в
’/в
%
'/8
пригоден, так как он относит каждому пути меру 0. Нам
не придется, однако, задавать меру на бесконечном де-
реве. Дело в том, что интересующие нас высказывания
о процессе будут зависеть только от конечной части де-
рева, а для любого конечного числа этапов метод по-
строения меры уже имеется. Тем не менее мы будем
иногда рассматривать функции, в определении которых
участвует бесконечное дерево.
Пусть, скажем, в примере 1.9.2 функция f— это но-
мер бросания, при котором впервые появляется герб. То-
гда / определена для всех путей, на которых хотя бы
раз встречается герб. Эти пути образуют подмножество
бесконечного дерева. Мы будем говорить о среднем зна-
чении подобной функции, если выполнены следующие
условия:
1.9. СТОХАСТИЧЕСКИЕ ПРОЦЕССЫ
31
а) Найдется такая последовательность чисел
Гь Гг, • • • ’ чт0 истинность высказывания f == г, зависит
только от исходов конечного числа этапов и 2P[f = r/] = l.
Ь) 5 |Г/|Р[/ = Г/]<оо.
В случае выполнения условий а) и Ь) мы говорим, что
f имеет среднее значение, и определяем его формулой
м [Л =2 Г/Р [Г = Г/].
/
Если f имеет среднее значение а и определено сред-
нее значение для (f — а)2, то мы говорим, что функция f
имеет дисперсию D [fl, равную M[(f — а)2].
Все свойства средних и дисперсий, сформулирован-
ные в § 8, выполняются и в этом более общем случае.
Кроме того, нам потребуется следующая теорема.
1.9.3. Теорема1). Если fl,f2, ... — такие функции, что
область значений каждой fj есть подмножество одного и
того же конечного множества чисел, и если функция
s = fi + fz + ... имеет среднее значение, то
МЫ=2М[/;].
Назовем конечным стохастическим процессом такой
стохастический процесс, все функции исходов которого
принимают значения из данного конечного множества.
!) В такой форме, как показывают несложные примеры, тео-
рема не верна. Однако для последующих нужд вполне достаточно
более слабого утверждения:
Теорема. 1.9.3'. Если fi, fz, ... — такие функции, что их области
значений принадлежат одному и тому же конечному множеству не-
отрицательных чисел, и если s = + ... -ь fn + ..., причем М [$] су-
ществует, то
/
Это утверждение является очень частным случаем известной
теоремы Лебега о монотонном предельном переходе. Впрочем, его
можно доказать и элементарно, пользуясь тем, что абсолютно схо-
дящийся ряд допускает перестановку и группировку членов. (Прим,
перев.)
32
ГЛ. I. ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ
Тогда теорема 1.9.3 устанавливает, что в конечном сто-
хастическом процессе среднее суммы функций (если оно
существует) равно сумме средних значений этих функ-
ций.
1.10 Суммируемость последовательностей и рядов.
Бывает, что по расходящейся последовательности
So, si, ..., sn, ... можно построить такую последова-
тельность средних из что эта новая последователь-
ность сходится. В таком случае мы говорим, что исход-
ная последовательность суммируема с помощью данного
процесса осреднения. Мы будем иметь дело только с
двумя методами осреднения,
ft-l п
Пусть /„ = '/„]£ s‘ и w»= S
1=0 1=0
при некотором k из промежутка 0<6<1. Каждое из
этих выражений есть среднее членов последовательно-
сти Si с неотрицательными коэффициентами, сумма ко-
торых равна 1. Если последовательность /2, ... схо-
дится к пределу t, то мы говорим, что исходная после-
довательность суммируема по Чезаро к t. Если после-
довательность Ui, «2, ... сходится к пределу и, то мы
говорим, что исходная последовательность суммируема
по Эйлеру к и.
Рассмотрим, например, последовательность 1, 0, 1,
0, ... Легко видеть, что tn = V2, если п четно, и
tn = V2 + 7п, если п > 1 нечетно. Эта последователь-
ность сходится к V2 и, значит, исходная последователь-
ность суммируема по Чезаро к V2. Нетрудно проверить,
что limwrt = 1/2, и> следовательно, исходная последова-
->оо
тельность суммируема к У2 и по Эйлеру. Начальная же
последовательность расходится.
Нам потребуются два следующих простых факта от-
носительно суммируемости: (1) Если последователь-
ность сходится, то она суммируема каждым из указан-
ных методов к своему пределу. (2) Если последователь-
ность суммируема обоими методами, то обе суммы
должны совпадать.
1.11. МАТРИЦЫ
33
Понятие суммируемости применимо и к рядам,
оо
Утверждение, что ряд 2 ak суммируем данным мето-
/г=0
дом, означает, что последовательность частных сумм
i
s = 2 суммируема этим методом. Например, при-
/г=0
меняя к частным суммам метод Чезаро, мы приходим
п-1
Sn — k
—~ ak'
k—0
1,11. Матрицы. Матрица — это прямоугольная таб-
лица чисел. Матрица размерности (порядка) г X s
имеет г строк, s столбцов и r-s элементов (или компо-
нент). В этой книге особую роль будут играть три спе-
циальных типа матриц. Матрица, у которой число строк
равно числу столбцов, называется квадратной. Другими
словами, это матрица размерности г X г. Если г=1,
т. е. если матрица состоит из одной строки, то мы на-
зываем ее вектор-строкой. Если 5=1, т. е. матрица со-
стоит из одного столбца, то мы называем ее вектор-
столбцом. Матрицы будут обозначаться прописными ла-
тинскими, а векторы — строчными греческими буквами.
Пусть матрица А размерности г X s имеет элемен-
ты а матрица В размерности г'X s' — элементы Ьц.
Определим следующие операции и соотношения.
(1) Матрица kA имеет элементы т. е. умноже-
ние матрицы на число означает умножение на это число
каждого элемента. Матрица —А — это (—1)Д.
(2) Если г = г' и s = s', то сумма А + В имеет эле-
менты a-ij + btj. Другими словами, сложение осуще-
ствляется покомпонентно.
(3) Если s = г', то мы определим произведение АВ
s
как матрицу С с элементами Сц = 2 atkbkp Заметим,
fe= I
что произведение матриц размерностей г X s и «X/ —
это матрица размерности г X t. Наше определение при-
менимо также к произведению вектор-строки на мат-
рицу, аЛ, и к произведению матрицы на вектор-стол-
бец Лр, В первом из этих случаев произведение матриц
3 Дж. Кемени, Дж. Снелл
34
ГЛ. 1. ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ
размерностей 1 X г и г X s представляет собой матрицу
размерности 1 X s, т. е. вектор-строку. Если матрица А
квадратная, то получающаяся вектор-строка имеет го
же число компонент, что и а. Поэтому квадратная мат-
рица задает преобразование вектор-строк. Аналогично,
она определяет преобразование и вектор-столбцов. Глав-
ным образом ради таких преобразований мы и будем
использовать умножение векторов на матрицы.
(4) Скажем, что 4>В (или что А = В), если
> bij (или ац = Ьц) для всех i и /. Другими сло-
вами, эти соотношения между матрицами должны вы-
полняться покомпонентно — для всех соответствующих
элементов.
(5) Важную роль играют некоторые специальные
матрицы. Матрица размерности г X s, все элементы ко-
торой равны 0, обозначается OrXs. Индекс внизу будет
опускаться, если это не может привести к недоразуме-
нию. Матрица размерности г X г, у которой равны I
элементы ац («элементы главной диагонали») и равны О
все прочие элементы, обозначается 1Г. И здесь индекс
часто опускается. Роль этих матриц видна из следую-
щего. Пусть 4, / и О —матрицы размерности г X г,
а-г-мерная вектор-строка и р— r-мерный вектор-стол-
бец. Тогда
Л+0=0+ 4 = 4,
4 + (—4) = (—4) + 4 = О,
д/ = М = 4,
а/ = а,
/Р = Р,
40 = 04 = 0,
ор = о,
аО = О.
Таким образом, матрицы О и / играют примерно ту же
роль, что и числа 0 и 1.
(6) По аналогии с обратными числами определим
обратную матрицу. Говорят, что матрица 4 размерно-
сти г X г имеет обратную матрицу В размерности г X G
если АВ — /. Если такая матрица В существует, то она
1.11. МАТРИЦЫ
35
обозначается А~1. Обратную матрицу можно найти, ре-
шив систему из г2 линейных уравнений. Конечно, эти
уравнения могут оказаться несовместными. Но если они
имеют решение, то оно единственно, и можно показать,
что АА~1 — А~1А = /.
Различные арифметические действия над матрицами,
если только они определены, удовлетворяют обычным
законам арифметики. Существенным исключением из
этого правила является лишь то, что матричное умно-
жение не коммутативно, т. е. АВ не обязательно рав-
но ВА. В одном важном случае коммутативность все же
имеет место. Это случай степеней данной матрицы.
Пусть Ап — это Л, умноженная на самое себя п раз.
Тогда АпАт = АтАп для любых т и п. По определению
мы полагаем 4° = I.
Удобно ввести вектор-строку т}г и вектор-столбец gr,
все компоненты которых равны 1. Когда это возможно,
мы будем опускать индекс и в этих обозначениях. Век-
торы г| и g удобно использовать при суммировании ком-
понент векторов или строк или столбцов матриц. Произ-
ведение — это число (или, точнее, матрица из одного
элемента), которое равно сумме компонент а. То же
самое можно сказать об г)Р. Произведение — это век-
тор-столбец, t-я компонента которого равна сумме эле-
ментов f-й строки матрицы А. Аналогично, тр4 дает
суммы компонент А по столбцам. Обозначим через Е
квадратную матрицу, все элементы которой равны 1.
Заметим, что Е =
Приведем некоторые примеры этих операций и соот-
ношений:
3f2 1\ /6 3\
АО -1/ а -з/’
/2 П /-1 °VP
А -1/А о —2/ а -з/;
(1,2, 3) + (2, 1,0) = (3, 3, 3);
/2 1 \
(1, 2, 3)1 0 -1 | = (5, -1);
\1 о/
3*
36
ГЛ. 1. ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ
2 3\
о
1\ / 72\ •
о >( о ;
-1/ \—2/
/2 iy 1 -п/ 1 -1V2 ИД1 °V/
\1 1Д-1 2/ 1 2Д1 1/ \О 1/ ’
так что
/ 1 -1\_/2 IV*
(-1 2/(1 1/ '
Для квадратной матрицы А определим транспониро-
ванную матрицу Ат Элемент матрицы Ат с индексами ij
есть /7-й элемент А. Введем также матрицу Adg, главная
диагональ которой совпадает с главной диагональю А,
а прочие элементы равны 0. Матрица ASq получается
из А возведением в квадрат каждого элемента. Она, ко-
нечно, как правило, не совпадает с А2. (Но D2 = Dsq
для диагональных матриц, т. е. матриц, у которых все
отличные от нуля элементы стоят на главной диаго-
нали.) Аналогично определяется aSq для вектора а.
Часто бывает удобно задавать матрицы и векторы
их компонентами Так, мы обозначаем через {а^} мат-
рицу, ij-и элемент которой равен ац. Аналогично, че-
рез {aj} обозначается вектор-строка, а через {aj—век-
тор-столбец Эти обозначения можно проиллюстрировать
следующими соотношениями:
{вц} + {Ьц} = {ац + Ьц}\
О = {0};
= £ =
= {ац}>
{ац}т = {«/J;
3{aJ = {3aJ;
Последний пример показывает, что произведение век-
тор столбца на вектор-строку (каждый из векторов
1.11. МАТРИЦЫ
37
имеет г компонент) есть матрица размерности г X г.
Сопоставьте это с тем, что то же произведение, взятое
в обратном порядке, представляет собой матрицу с
единственным элементом. Например, если а —вектор-
строка, то а| дает сумму компонент а. Однако ga — это
матрица размерности г X г, каждая строка которой
равна а.
Пусть задана последовательность матриц Ah с эле-
ментами a!ff. Будем говорить, что ряд Ао + At 4- Д2 + .. •
сходится, если каждый из рядов, образованных компо-
нентами, сходится, т. е. если ряд а<® + а(и + а® + ...
сходится при любых i и /. Если сумма последнего ряда
равна ац для каждой пары i, j и А — матрица с эле-
ментами dij, то мы скажем, что А есть сумма нашего
бесконечного ряда матриц. Короче говоря, бесконечная
сумма матриц определяется покомпонентно.
1.11.1. Теорема. Если матрица Ап стремится к О (ну-
левой матрице) при п-*оо, то матрица I — А имеет
обратную, причем
(/_Д)-1 = / + д + а2+ ... = £а\
ьо
Доказательство. Рассмотрим тождество
(/-А)(7 + А + А2 + ... +Ап-1) = /-Ап,
которое легко проверить, раскрывая скобки в левой ча-
сти. По предположению, правая часть стремится к /
при п—>оо. Матрица 1 имеет определитель 1. Значит,
при достаточно больших п определитель 7— Ап отличен
от 0. Так как определитель произведения двух матриц
равен произведению определителей, то определитель
7 — А также не равен’ 0. Но если определитель матрицы
отличен от 0, то она имеет обратную, так что / — А об-
ратима. Теперь можно умножить обе части тождества
на матрицу, обратную к I — А. Тогда получим
7 + А + А2 + ... + = (/ —А)~1(/ — Ап).
Ясно, что правая часть полученного равенства стремится
к (7— А)-1, чем и заканчивается доказательство тео-
ремы.
38 ГЛ. I. ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ
/Чожно определить суммируемость последовательно-
стей и рядов матриц точно так же, как это было сде-
лано в 1.10, применяя метод усреднения к каждой ком-
поненте. Тогда предыдущая теорема допускает следую-
щее обобщение. Если последовательность Ап суммируе-
ма к О каким-либо методом, то матрица / — Л имеет
обратную, причем ряд / + А 4- А2 4- ... суммируем к
(/ — Д)”1 тем же методом.
1.11.2. Определение. Квадратная матрица А назы-
вается неотрицательно определенной, если для любого
вектор-столбца у утАу 0.
1.11.3. Теорема. Для любой неотрицательно опреде-
ленной матрицы А найдется матрица В такая, что
А = ВТВ,
г Л А В A II
ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ЦЕПЕЙ МАРКОВА
2.1. Определение марковского процесса и цепи Мар-
кова. Вспомним, что для конечного стохастического про-
цесса мы уже определили дерево и меру на множестве
всех его путей, а также последовательность функций
исходов fn, п = О, I, 2, ... Область определения fn —
это дерево Тп, а область значений — множество Un воз-
можных исходов п-го эксперимента. Функция fn прини-
мает значение sj, если Sj— исход п-го эксперимента
(см. 1.9). Всякий раз, когда в последующих определе-
ниях появляется условная вероятность Р [q | р], предпо-
лагается, что высказывание р непротиворечиво. Чита-
тель, возможно, сочтет удобным время от времени обра-
щаться к списку основных понятий и обозначений, при-
веденному в конце книги.
Конечный стохастический процесс называется про-
цессом с независимыми значениями, если
(I) Для любого высказывания р, истинность которого
зависит лишь от исходов экспериментов до п-го,
P{fn = Sl\P} = P{fn^Sl}.
Для таких процессов знание исходов уже наблюдав-
шихся экспериментов не влияет на наш прогноз отно-
сительно последующего эксперимента. Для марковских
процессов мы ослабим это требование, допустив, что зна-
чение непосредственно предшествующего исхода влияет
на этот прогноз.
2.1.1. Определение. Конечным марковским процессом
называется конечный стохастический процесс такой, что
(II) Для любого высказывания р, истинность кото-
рого зависит лишь от исходов экспериментов до п-го,
р [fn = Sj | (f„-i = s() A p] = P = Sj I = s,]
(предполагается, что fn_i = Si u p совместимы).
40 ГЛ. II. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ЦЕПЕЙ МАРКОВА
Мы будем называть условие (II) марковским свой-
ством1), Для марковских процессов знание исхода по-
следнего эксперимента позволяет пренебречь при пред-
сказании будущего любой другой информацией. Важно
понимать, что это верно лишь в том случае, когда исход
последнего эксперимента известен точно. Например, если
мы знаем только, что последний эксперимент привел
к исходу Si или sj, то знание того, истинно ли высказы-
вание р, связанное с предшествующими экспериментами,
может повлиять на наш прогноз будущего.
2.1.2. Определение. Переходные вероятности на
n-м шаге, которые будем обозначать р^, это
ЛIf.-,»»,]-
2.1.3. Определение. Конечной цепью Маркова назы-
вается конечный марковский процесс, для которого пе-
реходные вероятности pij(n) не зависят от п. В этом
случае они будут обозначаться рц. Элементы U назы-
ваются состояниями2).
2.1.4. Определение. Переходной матрицей цепи Мар-
кова называется матрица Р с элементами Pij- Вектором
начальных вероятностей {или начальным распределе-
нием) называется вектор л0 = {р9} = {Р [f0 = sjj.
Марковскую цепь можно представлять себе как про-
цесс, который движется из состояния в состояние. Он
начинается с вероятностью р(у0) в sr Если в какой-то
момент он находится в состоянии $г, то на следующем
«шаге» он попадает в з$ с вероятностью рц. Начальные
вероятности можно понимать как вероятности того или
иного возможного «старта». Вектор начальных вероят-
ностей вместе с переходной матрицей полностью опре-
!) В русской литературе термин «марковский процесс» приме-
няется обычно для обозначения стохастических процессов с непре-
рывным временем, удовлетворяющих марковскому свойству, а объ-
ект, определенный в 2.1.1, называется цепью Маркова с конечным
числом состояний. (Прим, ред.)
2) Стохастический процесс с таким определением в русской ли-
тературе принято называть однородной цепью Маркова с конечным
числом состояний. Неоднородные цепи, в которых переходные ве-
роятности зависят от п, в настоящей книге не рассматриваются.
(Прим, ред.)
2.1. ОПРЕДЕЛЕНИЕ МАРКОВСКОГО ПРОЦЕССА
41
деляют цепь Маркова как стохастический процесс, так
как их достаточно для построения полной меры на де-
реве. Поэтому если заданы некоторый вероятностный
вектор До и некоторая вероятностная матрица ’) Р, то
найдется единственная (с точностью до переобозначения
состояний) цепь Маркова, для которой ло— начальное
распределение, а Р —переходная матрица.
В большинстве случаев мы будем рассматривать фик-
сированную переходную матрицу Р, но менять при этом
начальный вектор л. Мера, заданная на дереве, будет,
конечно, зависеть от выбора начального распределения л.
Значит, если р — некоторое высказывание относительно
дерева или f — некоторая функция, областью определе-
ния которой служит дерево, то Р (р), М [fl и D [fl все
зависят от л. Мы будем указывать это, пользуясь обо-
значениями р«(р), мдя и оя[Л. В частном случае,
когда f-я компонента л равна 1 (процесс начинается
в состоянии Si), мы будем писать РДр), Mz[fl, Dz[fl.
В следующем пункте мы приведем несколько приме-
ров цепей Маркова. Настоящий параграф завершим не-
которыми замечаниями, относящимися к марковскому
свойству.
Легко доказать, что марковское свойство эквивалент-
но следующему свойству, формулировка которого более
симметрична.
(1Г) Пусть р— какое-нибудь высказывание, истин-
ность которого зависит от исходов экспериментов после
п-го, a q — какое-нибудь высказывание, истинность ко-
торого зависит от исходов экспериментов до п-го. Тогда
Р [р A q I fn = «/] = Р [р I fn = sj Р [q I fn = «/J.
Смысл этого условия в том, что при известном на-
стоящем прошлое и будущее процесса взаимно незави-
симы. Кроме того, это более, симметричное соотно-
шение наводит на мысль, что марковский процесс
должен остаться марковским, если наблюдения ведутся
9 Под вероятностным вектором понимается вектор с неотрица-
тельными элементами, дающими в сумме 1. Вероятностная матри-
ца— это квадратная матрица, все строки которой являются вероят-
ностными векторами. В русской литературе более распространен тер-
мин стохастическая матрица. (Прим, рев.)
42
ГЛ. II. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ЦЕПЕЙ МАРКОВА
в обратном порядке. Справедливость этого факта выте-
кает из следующей теоремы (доказательство которой
мы не приводим). '
2.1.5. Теорема. Пусть для данного марковского про-
цесса р — какое-нибудь высказывание, истинность кото-
рого зависит от экспериментов после п-го. Тогда
Р [L = Sj I (f„+1 = Si Л p)l = P [f„ = Si I fn+i = Si].
Так как марковский процесс, наблюдаемый в обрат-
ном порядке, остается марковским, то естественно пред-
положить, что то же верно и для цепей Маркова. Так
будет в том случае, если «обращенные переходные ве-
роятности» p*tJ (n) = Р [fn = Sj | = $.] не зависят от п.
Эти вероятности можно найти следующим образом:
. (пХ pP« = g/A/n+i = ad _
p[Ui = M
Р [tt-H = *< I = »/] Р [Ь = */] РцР [ti ~ */]
PIU1-M р[/п+1=^'
Полученные переходные вероятности не зависят от п
только тогда, когда вероятность находиться в отдельном
состоянии в момент п от п не зависит. Это, конечно,
вообще говоря, не верно. Скажем, если система стар-
тует из состояния с вероятностью 1, то на следующем
шаге она окажется в S| с вероятностью рп. Поэтому,
вообще говоря, Р [f0 = s/] =/= Р [fi = sj. Итак, цепь Мар-
кова, рассматриваемая в обращенном времени, будет
марковским процессом, но переходные вероятности этого
процесса в общем случае зависят от времени и, значит,
он не является цепью Маркова. Мы вернемся к этому
вопросу в пункте 5.3.
2.2. Примеры. В этом пункте мы приведем несколько
простых примеров марковских цепей. Эти примеры бу-
дут в дальнейшем использоваться с иллюстративными
целями. Первые пять примеров связаны с так называе-
мым «случайным блужданием». Представим частицу, ко-
торая движется по прямой единичными шагами. Каж-
дый шаг направлен вправо с вероятностью р и влево
С вероятностью q. Частица движется, пока не достигнет
2.2. ПРИМЕРЫ
43
одной из двух крайних точек, которые называются «гра-
ничными точками». Возможные типы поведения частицы
в этих точках приводят к различным цепям Маркова. Со-
стояния цепи — возможные положения частиц. Рассмот-
рим случай 5 состояний, когда состояния и «5 будут
«граничными», а состояния $2, $з, $4 — «внутренними».
$ 1_____s2_____S3_____$5
Пример 1. Допустим, что процесс, достигнув состоя-
ний $1 или «5, остается там навсегда. В этом случае пе-
реходная матрица имеет вид
$2 $3 54 55
0 0 0 0
0 р о о
q 0 р 0
0 q 0 р
0 0 0 1
(1)
Пример 2. Допустим теперь, что частица, достигнув
граничной точки, «отражается» и возвращается в состоя-
ние, из которого она пришла. Другими словами, если
она когда-либо попала в Si, то на следующем шаге она
идет назад в «2- Если она попала в s5, то на следующем
шаге она возвращается в «4- Матрица переходных ве-
роятностей имеет в этом случае вид:
S1 «2 53 $4 S5
10 0 0
0 р 0 0
q 0 р 0
0 q 0 р
0 0 10
(2)
Пример 3. В качестве третьей возможности рассмот-
рим случай, когда частица, достигнув одного из гранич-
ных состояний, непосредственно направляется в цент-
ральное состояние «з- Можно представить себе, что в
44 ГЛ. II. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ЦЕПЕЙ МАРКОВА
этом случае происходит процесс примера 1, начинаю-
щийся в s3 и возобновляющийся всякий раз после до-
стижения границы. Переходная матрица имеет вид
S| s2 S3 s4 s5
S| [ 0 0 1 0 0
CO N3 0 •X3 0 0
P = s3 0 q 0 p 0 (3)
s4 0 0 q 0 p
s5 0 0 1 0 0
Пример 4. Предположим теперь, что, достигнув од-
ного из граничных состояний, частица с вероятностью
7г в нем остается и с вероятностью 7г переходит в дру-
гое граничное состояние. В этом случае переходная мат-
рица имеет вид sl S2 S3 «4 «5
’/2 0 0 0 v2
S2 q 0 Р 0 0
P = s3 0 q 0 р 0 (4)
«4 0 0 q 0 р
S5 */2 0 0 0 '/J
Пример 5. В качестве последнего 1 типа граничного
поведения рассмотрим случай, когда частица, достигнув
однрй из границ, непосредственно переходит на другую.
Переходная матрица имеет вид
*2
P = s3
S4
S5
Sj S2
fo 0
я О
0 q
О О
Г О
S3 S4 S5
0 0 1
р о о
0 р о
р О р
ООО,
(5)
Пример 6. Рассмотрим теперь другой вариант слу-
чайного блуждания. Если частица находится в одном
из трех внутренних состояний, то она с равными вероят-
2.2. ПРИМЕРЫ
45
костями движется вправо, влево или остается на месте
Если частица находится на границе, то она не может
остаться на месте, и с равными вероятностями перехо-
дит в одно из четырех остальных состояний. Переходная
матрица имеет вид
Sj S2 S3 S4 S5
0 -/4 'Л 74 74
S2 73 7з 7з о о
Р ~ $3 о 7з 7з 7з о (6)
*4 о о 7з 7з 7з
55 74 74 74 74 о
Пример 7. Рассматривается последовательность
цифр, появляющихся случайно. Мы говорим, что про-
цесс находится в состоянии если появился 0, s2, если
появились 1 или 2, $з, если появились 3, 4, 5 или 6, «4,
если появились 7 или 8, и, наконец, $5, если появилась
цифра 9. Это процесс независимых испытаний, однако в
дальнейшем мы убедимся, что теория цепей Маркова по-
зволяет получить некоторую новую информацию даже
в этом частном случае. Переходная матрица здесь имеет
вид
*1
S2
Р = s3
«4
S5
S1
0,1
0,1
0,1
0,1
0,1
$3 ®4
0,2 0*4 0,2 0,1
0,2 0,4 0,2 0,1
0,2 0,4 0,2 0,1
0,2 0,4 0,2 0,1
0,2 0,4 0,2 0,1
<7)
Пример 8. Согласно «Введению в конечную матема-
тику» (глава V, § 8) в стране Оз никогда не бывает
подряд двух ясных дней. Если сегодня ясно, то завтра
будет плохая погода (снег или дождь с равной вероят-
ностью). Если сегодня снег (или дождь), то погода
на следующий день не изменится с вероятностью {/2.
Если все-таки она изменится, то лишь в половине слу-
чаев будет ясно. Образуем цепь Маркова с тремя со-
стояниями: R (дождь), N (ясно) и S (снег). Матрица
46 ГЛ. II. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ЦЕПЕЙ МАРКОВА
переходных вероятностей имеет вид
R N S
*/72 74 7Л
р = лг 72 о % . (8)
SV/4 74 72/
В предыдущих примерах марковское свойство вы-
полнялось очевидным образом. В последнем случае его
можно рассматривать лишь как некоторое приближение,
так как, например, знание погоды за два последних дня
может привести к другому прогнозу на завтра, чем зна-
ние погоды только за один день. Один из методов уточ-
нить нашу модель состоит в том, чтобы принять за со-
стояния цепи погоду за два последовательных дня. Эти
состояния можно обозначить NN, NR, NS, RN, RS, RR,
SN, SR, SS. Новые переходные вероятности еще нужно
оценить. Каждый переход в цепи происходит по-преж-
нему за один день, так что, например, из NR можно
попасть лишь в состояния RN, RR, RS. В примерах та-
кого сорта часто возможно бывает построить более точ-
ную модель, оставаясь в рамках цепей Маркова, но це-
ной увеличения числа состояний.
Пример 9. В урне содержится два неокрашенных
шара. В последовательные моменты времени случайно
извлекается шар, окрашивается в красный или черный
цвет и возвращается назад. Если шар не был окрашен,
выбор цвета случаен, если он был окрашен, то цвет
меняется. Образуем цепь Маркова, приняв за состоя-
ния тройки чисел (х, у, z), где х— число неокрашенных
шаров, у — число красных шаров и z — число черных
шаров. Тогда переходная матрица имеет вид
(0, 1, 1) (0, 2, 0) (0,0,2) (2,0, 0) (1, 1, 0) (1,0,1)
(0, 1, 1) 0 7г 72 0 0 0
(0, 2, 0) 1 0 0 0 0 0
(0, 0, 2) 1 0 0 0 0 0
(2, 0, 0) 0 0 0 0 >/2 */2 • (9)
(1, 1,0) 74 74 0 0 0 72
(1,0, 1) 74 0 74 0 */2 0
2.2. ПРИМЕРЫ
47
Пример 10. Предположим, что студент некоторого
колледжа каждый год с вероятностью р выбывает из
колледжа, с вероятностью q остается на том же курсе
на следующий год и с вероятностью г переходит на сле-
дующий курс. Образуем цепь Маркова, введя состояния:
— выбыл, «2 — окончил колледж, «з — четверокурсник,
s4 — третьекурсник, s5 — второкурсник, s6 — первокурс-
ник. Матрица переходных вероятностей имеет вид
Sj S2 S3 S4 S5 S6
II Со Со Со Со О) Со О СП rfa. ы ьэ — 1 0 0 0 0 0 0 10 0 0 0 р г q 0 0 0 р 0 г q 0 0 р 0 0 г q 0 р 0 0 0 г q (Ю)
Пример II. Некто опускает монету в один из двух
автоматов для азартной игры. Первый автомат произво-
дит выплату с вероятностью с, второй — с вероятно-
стью d. После проигрыша игрок продолжает игру с тем
же автоматом, в случае выигрыша переходит к другому.
Пусть Sj означает «в игре участвует i-й автомат». Тогда
матрица переходных вероятностей имеет вид
Sj s2
s2\
1 —с
d
(И)
Если с и d принимают все возможные значения
(О-^г^.1, 0 d 1), то мы получаем все цепи Мар-
кова с двумя состояниями.
Пример 12. Рассмотрим специальную цепь с двумя
состояниями (пример 11) и переходной матрицей
si
_ 51 / %
S2 \ V4
$2
(На)
(Это можно назвать примером На).
48 ГЛ. II. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ЦЕПЕЙ МАРКОВА |
I
По этой цепи Маркова построим новую цепь следую- I
щим образом. Примем за состояния новой цепи Мар-
кова пары состояний исходной. Таким образом, ее со-
стояния—это $i$i, $i$2, s2^2. Новая цепь на п-м
шагу находится в состоянии S{Sj, если старая цепь была
в состоянии Si на n-м шагу и перешла в s, на (и + 1)-м
шагу. Новые переходные вероятности (это и есть при-
мер 12) имеют вид
5 %S j SqSq
S[SX / v2 V2 о 0 >
М2 0 0 </4 %
Mil V2 V2 0 0
М2 ' 0 0 74 3/4Z
Мы увидим в дальнейшем (6.5), что изучение этой
новой цепи дает более подробную информацию об исход-
ном процессе, чем та, которую можно получить, рас-
сматривая непосредственно цепь с двумя состояниями.
(12)
2.3. Связь с теорией матриц. В этом параграфе мы
выясним связь между теорией цепей Маркова и теорией
матриц. Мы начнем с общих конечных марковских про-
цессов, а затем конкретизируем результаты для случая
конечных цепей Маркова.
2.3.1. Теорема. Пусть fn — функция исходов в мо-
мент п для конечногц марковского процесса с переход-
ными вероятностями рц(п). Тогда
Р [fn ~ S Р Ifn- 1 = Puv 70’
и
Доказательство. Высказывание fn = sv— это некото-
рое высказывание относительно дерева Тп. Чтобы найти
его вероятность, нужно сложить веса всех путей, вхо-
дящих в множество истинности высказывания. В это
множество входят те и только те пути, которые за-
канчиваются исходом sv. Поэтому если /, k, ..., и —
2.3. СВЯЗЬ С ТЕОРИЕЙ МАТРИЦ
49
возможная последовательность состояний, то
Plfn = sJ= S P[fo = S/A ••• Afrt-i=suAfre = s0] =
/, k.............и
= I иР[/о=«/Л ... Afra-i=su]X
x P[fn = s»lfo = S/A ... Afn-i=sJ.
Но по марковскому свойству это выражение равно
2 Р Но = в/ Л • • • Л fn-i = su] рио (п).
J, k.и
Фиксируя в последней сумме и и суммируя затем по
оставшимся индексам, получим
р = 2 Р И„-1 = S„] puv (n),
и
что и заканчивает доказательство.
Результат этой теоремы можно записать в матричной
форме. Пусть п„— вектор-строка, задающая меру, ин-
дуцированную функцией исходрв fn- Другими словами,
Jln = {/’(in)’ р(2}’ •••’ pH’
где р<”} = Р [fn = — вероятность того, что процесс по-
падает после п шагов в состояние Sj, В частности, л0—
это вектор начальных вероятностей. Пусть Р(п)—мат-
рица с элементами ргДи). Тогда результат теоре-
мы 2.3.1 можно записать в виде
лп = лп_1Р(и)
при п>1. Последовательным применением этой фор-
мулы находим
к = л0-Р(1)-Р(2). ... -Р(и).
В случае цепи Маркова все матрицы Р(п) равны между
собой и мы приходим к следующей фундаментальной
теореме.
2.3.2. Теорема. Пусть лп — мера, индуцированная
функцией исходов fn для конечной цепи Маркова с на-
чальным распределением л;0 w переходной матрицей Р.
4 Дж. Кемени, Дж. Снелл
50 ГЛ. II. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ЦЕПЕЙ МАРКОВА
Тогда
— ЭТд ’ Р .
Эта теорема показывает, что ключом к изучению мер,
индуцированных функциями исходов конечной цепи Мар-
кова, служит рассмотрение степеней переходной мат-
рицы. Элементы этих степеней сами по себе допускают
интересную вероятностную интерпретацию. Чтобы убе-
диться в этом, рассмотрим в качестве начального век-
тора по вектор, у которого Z-я компонента равна 1, а все
остальные —0. Тогда по теореме 2.3.2 лп = ло*-Рп. Но
лоРп — это ья строка матрицы Рп. Поэтому /-я строка
п-и степени матрицы перехода дает вероятности нахо-
ждения в каждом из возможных состояний при усло-
вии, что процесс начинается в состоянии
Допустим, что процесс примера 1 начинается в
Тогда л0 = {0, 0, 1, 0, 0}. Мы можем найти меры (см
пункт 1.7), индуцированные первыми тремя функциями
исходов, непосредственно конструируя дерево и меру на
дереве для первых трех экспериментов. Это дерево изо-
бражено на рис. 2.1.
2.4. КЛАССИФИКАЦИЯ СОСТОЯНИЙ И ЦЕПЕЙ
51
Исходя. из этого рисунка, можно легко подсчитать
меры, индуцированные функциями fbf2, h- Именно
Л!=(0, >/2, 0, */2, 0),
я2 = (*/4, 0, >/2, 0, >/4),
Лз = (74, ’Л. 0. 'А, ’А).
По теореме 2.3.2 эти же меры можно найти как третьи
строки матриц Р, Р2 и Р3, так как s3 — начальное со-
стояние процесса. Эти матрицы имеют вид
0 0 0 0
0 '/г 0 0
’/2 о '/2 о
о */2 0 >/2
0 0 0 1
0 0 0 0
74 О 'Л о
о ’/2 0 7л
'А 0 '/4 72
0 0 0 1
0 0 0 0
О 74 0 7з
'А о *А ’А
о 74 о 5/8
0 0 0 1
Мы видим, что эти матрицы дают нам сразу не-
сколько мер на деревьях Ть Т2 и Т3 (в зависимости от
начального состояния).
2.4. Классификация состояний и цепей. Мы хотим
классифицировать состояния цепи Маркова в зависи-
мости от того, может ли процесс попасть из данного
состояния в другое данное состояние. Эта проблема
вполне аналогична той, которой мы занимались в 1.4.
4*
52 ГЛ. II. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ЦЕПЕЙ МАРКОВА
Если мы интерпретируем отношение iTj как возмож-
ность для процесса попасть из состояния Sj в состоя-
ние (не обязательно за один шаг), то можем приме-
нить все результаты этого параграфа.
В частности, все состояния распадаются на классы
эквивалентных состояний. Два состояния принадлежат
одному классу эквивалентности, если они «сообщаются»,
т. е. если из одного состояния можно попасть в другое,
и наоборот. Возникающее при этом частичное упорядо-
чение показывает возможные направления, в которых
может развиваться процесс.
Минимальные элементы этого частичного упорядоче-
ния представляют особый интерес.
2.4.1. Определение. Минимальные элементы частич-
ного упорядочения классов эквивалентности называются
эргодическими множествами. Остальные элементы назы-
ваются невозвратными множествами. Состояния, входя-
щие в невозвратное множество, называются невозврат-
ными состояниями. Состояния эргодического множества
называются эргодическими (или возвратными) состоя-
ниями.
Так как при любом частичном упорядочении конеч-
ного множества должен быть по крайней мере один ми-
нимальный элемент, то в любой цепи Маркова найдется
хотя бы одно эргодическое множество. Однако наличие
невозвратных множеств не обязательно. Так бывает,
если вся цепь состоит из одного эргодического множе-
ства или же имеется несколько эргодических множеств,
не сообщающихся друг с другом.
Используя результаты 1.4, мы заключаем, что если
процесс выходит из невозвратного множества, то он ни-
когда уже не может вернуться в это множество. В то
же время, если он когда-нибудь попадет в эргодическое
множество, то он никогда не сможет его покинуть.
В частности, если эргодическое множество состоит лишь
из одного состояния, то это состояние таково, что, попав
в него, уже нельзя из него выйти. Такое состояние на-
зывается поглощающим. Поскольку из такого состояния
нельзя перейти ни в какое другое состояние, следующая
теорема полностью характеризует поглощающие со-
стояния.
2.4. КЛАССИФИКАЦИЯ СОСТОЯНИЙ И ЦЕПЕЙ
53
2.4.2. Теорема. Состояние Si— поглощающее тогда и
только тогда, когда рц = 1.
Нашу классификацию удобно использовать для по-
лучения канонической формы записи переходной мат-
рицы. Перенумеруем состояния следующим образом.
Элементы каждого класса эквивалентности обозначим
последовательными натуральными числами. Пусть сна-
чала идут минимальные множества, затем множества
«первого уровня» по отношению к минимальным, затем
множества «второго уровня» и т. д. Такая нумерация
гарантирует, что мы можем перейти из данного состоя-
ния в другие состояния того же класса, или в состояния
предшествующих классов, но не в состояния последую-
щих классов. Если классы эквивалентности, расположен-
ные как указано, обозначить ti\, #2, ...» то наша
матрица примет следующий вид (здесь для простоты
мы положили k = 5):
Здесь Pi представляет переходную матрицу внутри
данного класса эквивалентности. Область О состоит це-
ликом из нулей. Область содержит только нули, если
Рг — эргодическое множество, и имеет ненулевые эле-
менты в противном случае.
При такой форме записи легко понять, что будет про-
исходить при возведении в степень матрицы Р. Каждая
степень будет матрицей того же вида: верхний правый
угол Рп будет по-прежнему состоять из нулей, а в диа-
гональных областях будут стоять матрицы Р?. Это по-
казывает, что данный класс эквивалентности можно изу-
чать отдельно от других, обращаясь к подматрице Рг.
В дальнейшем этот вопрос будет детально исследован:
54 ГЛ. II. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ЦЕПЕЙ МАРКОВА
Мы можем воспользоваться также дальнейшим раз-
биением класса эквивалентности, рассмотренным в пре-
дыдущей главе. Там мы видели, что каждый такой
класс можно разделить на циклические подклассы. Если
имеется только один циклический подкласс, то мы назы-
ваем класс эквивалентности регулярным, в противном
случае мы говорим, что этот класс цикличен.
Если класс эквивалентности регулярен, то по про-
шествии достаточного времени процесс может оказаться
в любом из состояний класса, вне зависимости от того,
из какого состояния класса он начинался (см. 1.4). Это
значит, что все достаточно высокие степени соответст-
вующей матрицы Pi должны быть положительны (т. е.
состоять лишь из положительных элементов). Если
класс эквивалентности цикличен, то никакая степень Л
не может быть положительной.
Перейдем от классификации состояний к классифи-
кации цепей Маркова. Мы уже отмечали, что для каж-
дой цепи найдется хотя бы одно эргодическое множе-
ство, а невозвратных множеств может и не быть. Это
дает нам первоначальное разбиение множества всех це-
пей на два типа. Дальнейшую классификацию можно
проводить в зависимости от числа и характера эргоди-
ческих множеств.
I. Цепи без невозвратных множеств.
Если такая цепь состоит более чем из одного эргодиче-
ского множества, то между этими множествами нет аб-
солютно никакого взаимодействия. Значит, мы имеем
две или более изолированные цепи Маркова, объеди-
ненные вместе. Эти цепи можно изучать по отдельности,
и поэтому, не теряя общности, мы можем предположить,
что вся цепь представляет единственное эргодическое
множество. Цепи, состоящие из единственного эргоди-
ческого множества, называются эргодическими цепями,
I-А. Эргодическое множество регулярно. В этом слу-
чае цепь называется регулярной цепью Маркова, Как
мы только что видели, в этом случае все достаточно
высокие степени матрицы Р должны быть положитель-
ными. Следовательно, из какого бы состояния процесс
ни исходил, после достаточно большого количества ша-
гов он может находиться в любом состоянии.
2.4. КЛАССИФИКАЦИЯ СОСТОЯНИЙ И ЦЕПЕЙ
55
I-В. Эргодическое множество циклично. В этом слу-
чае цепь называется циклической цепью Маркова. Та-
кая цепь имеет некоторый период d (d> 1), и ее со-
стояния подразделяются на d циклических множеств.
При данном начальном положении цепь движется по
циклическим множествам в определенном порядке, воз-
вращаясь в множество, содержащее начальное состоя-
ние, через d шагов. Мы также знаем, что по проше-
ствии достаточного времени процесс может находиться
в любом состоянии циклического множества, соответст-
вующего выбранному моменту.
II. Цепи с невозвратными множествами.
В таких цепях процесс движется в направлении к эрго-
дическим множествам. Как мы увидим в следующей
главе, вероятность того, что процесс находится в одном
из эргодических множеств, стремится к единице. Кроме
того, попав в эргодическое множество, процесс не мо-
жет его покинуть. Поэтому естественно классифициро-
вать такие цепи по типу их эргодических множеств.
П-А. Каждое эргодическое множество состоит из
единственного состояния. Такие цепи называются погло-
щающими цепями. В этом случае процесс рано или
поздно останавливается в каком-то одном (поглощаю-
щем) состоянии. Этот тип процессов можно также оха-
рактеризовать тем, что все эргодические состояния яв-
ляются поглощающими.
П-В. Все эргодические множества регулярны, но не
все они состоят из одного элемента.
П-С. Все эргодические множества цикличны.
II-D. Имеются как циклические, так и регулярные
эргодические множества.
Естественно, в каждом из этих классов можно про-
изводить дальнейшую классификацию, учитывая коли-
чество имеющихся эргодических множеств. Особый ин-
терес представляет вопрос о том, имеется ли одно или
несколько эргодических множеств.
Все эти типы цепей, за исключением II-D, можно про-
иллюстрировать на примере случайных блужданий.
В примере 1 состояния $i и s5 — поглощающие. Со-
стояния s2, s3, «4 невозвратные. Между любыми двумя
из этих состояний возможны переходы. Значит, они
56
ГЛ. II. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ЦЕПЕЙ МАРКОВА
образуют единственное невозвратное множество. В итоге
мы имеем поглощающую цепь Маркова, т. е. случай
П-А.
В примере 2 можно из любого состояния попасть
в любое другое. Поэтому невозвратных множеств нет, а
имеется только одно эргодическое множество. Значит,
наша цепь эргодична. В любое состояние можно вер-
нуться лишь за четное число шагов. Поэтому период
каждого состояния равен 2. Имеется два циклических
множества {$ь$з, $б} и {$2, ty}. Это цепь типа I-B.
В примере 3 мы опять-таки из любого состояния мо-
жем попасть в любое другое. Значит, мы снова имеем
дело с эргодической цепью. Возвращение в $3 (исходя из
$з) возможно как за 2, так и за 3 шага. Наибольший об-
щий делитель этих чисел d = 1, и, стало быть, период
цепи равен 1. Это цепь типа I-A.
В примере 4 состояния {«i, $5} образуют эргодическое
множество, которое, очевидно, регулярно. Множество
{$2, $з, — единственное невозвратное множество. Это
цепь типа П-В.
В примере 5 мы имеем единственное эргодическое
множество {$1, $5} с периодом 2. Множество {«2, $з, $4
снова невозвратно. Это цепь типа П-С.
2.5. Чем мы будем заниматься. Рассмотрим различ-
ные типы цепей и наметим типы задач, которыми мы
собираемся заниматься в последующих главах.
Во-первых, хотелось бы заняться изучением регуляр-
ных цепей Маркова. В таких цепях процесс движется по
всем возможным состояниям, независимо от того, где он
начался. Вот некоторые из интересующих нас воп-
росов:
(1) Если цепь выходит из $2, то какова вероятность
через п шагов попасть в Sj?
(2) Можем ли мы предсказать среднее количество
времени, которое процесс проводит в $2? Если да, то как
оно зависит от начального положения процесса?
(3) Мы желаем, кроме того, рассмотреть поведение
процесса до его попадания в s?-, исходя из Како-
вы среднее значение и дисперсия необходимого для
2.5. ЧЕМ МЫ БУДЕМ ЗАНИМАТЬСЯ
57
этого числа шагов? Каковы среднее значение и диспер-
сия числа состояний, через которые пройдет при этом
процесс? Какова вероятность, что процесс пройдет че-
рез Sfe?
(4) Наконец, мы можем выделить некоторое подмно-
жество состояний и наблюдать процесс лишь в моменты
пребывания в этом подмножестве. Как отразится это
на предыдущих результатах? Все эти вопросы рассмат-
риваются в главе IV.
Затем хотелось бы изучить циклические цепи. Здесь
интерес представляют те же самые вопросы, что и в слу-
чае регулярных цепей. Естественно, изучать регулярные
цепи проще, но мы увидим, что если у нас есть ответы
для случая регулярных цепей, то мы легко сможем
найти соответствующие ответы для всех эргодических
цепей. Это распространение теории регулярных цепей на
все эргодические цепи осуществляется в главе V.
Далее хотелось бы рассмотреть цепи Маркова с не-
возвратными состояниями. Здесь есть два типа вопросов,
на которые нужно ответить. Одни касаются поведения
цепи до попадания в эргодическое множество, а другие
возникают уже после попадания цепи в эргодическое
множество. Последние вопросы не отличаются от рас-
смотренных выше. После того как цепь попадает в эр-
годическое множество, она уже не может из него выйти,
и поэтому состояния, находящиеся вне этого множества,
несущественны. Значит, на вопросы второго типа можно
ответить, рассматривая цепь, состоящую из одного эрго-
дического множества, т. е. эргодическую цепь.
Новые по существу вопросы возникают при изучении
поведения цепи до момента попадания в эргодическое
множество. В этих вопросах, однако, природа эргодиче-
ских состояний несущественна, и мы можем, если хо-
тим, заменить их все поглощающими состояниями. Во-
обще если мы хотим изучать процесс, пока он пребы-
вает в некотором множестве невозвратных состояний,
мы можем сделать все остальные состояния погло-
щающими. Этот преобразованный процесс дает всю
необходимую информацию. Итак, остаются новые за-
дачи, связанные только с поведением поглощающих
цепей.
58
ГЛ. II. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ЦЕПЕЙ МАРКОВА
Вот некоторые из вопросов, представляющих интерес
для данного невозвратного состояния
(1) Какова вероятность достигнуть данного эргоди-
ческого множества, исходя из $г?
(2) Каковы среднее значение и дисперсия времени,
проводимого в Sf до попадания в эргодическое множе-
ство, и как они зависят от начального положения?
(3) Каковы среднее значение и дисперсия числа ша-
гов, необходимых для достижения эргодического множе-
ства, ИСХОДЯ ИЗ Si?
(4) Каково среднее число состояний, в которых по-
бывает цепь, исходя из sit до момента попадания в эрго-
дическое множество?
В главе III мы будем иметь дело с поглощающими
цепями Маркова и ответим на все эти вопросы. Итак,
мы дадим ответы на наиболее интересные вопросы о ко-
нечных цепях Маркова в главах III, IV и V.
УПРАЖНЕНИЯ К ГЛАВЕ II
К 2.1
1. На окружности отмечено пять точек. Процесс попадает из лю-
бой данной точки в одну из соседних с ней с вероятностью !/2. Най-
ти переходную матрицу получающейся цепи Маркова.
2. Идет сражение между тремя танками. Танк А поражает свою
цель с вероятностью 2/з, танк В — с вероятностью */2, танк С — с ве-
роятностью 7з. Выстрелы производятся одновременно; если танк по-
ражен, он выбывает из сражения. Состоянием мы считаем множе-
ство танков, которые еще действуют. Проверить, что если каждый
раз танк стреляет в своего самого сильного противника, то процесс
описывается следующей переходной матрицей:
Е А в с АС ВС АВС
Е 1 0 0 0 0 0 0
А 0 1 0 0 0 0 0
В 0 0 1 0 0 0 0
С 0 0 0 1 0 0 0
АС 2/э 4/9 0 79 79 0 0
ВС 76 0 7з 7б 0 7з 0
АВС 0 0 0 4/9 2/9 2/9 79
3. Модифицировать переходную матрицу предыдущего упражне-
ния, предполагая, что когда все танки действуют, то А стреляет в
В в С и С в А.
УПРАЖНЕНИЯ К ГЛАВЕ II
59
4. Производится такая последовательность испытаний. В пер-
вом опыте бросается правильная монета. Если в п—1-м опыте вы-
пал герб, то в n-м опыте бросается правильная монета; если в п—1-м
опыте выпала решетка, то в я-м опыте бросается такая монета, для
которой вероятность выпадения герба равна \/п. Каковы переход-
ные вероятности? С каким процессом мы имеем дело?
К 2.2
5. Измените пример 1: предположите, что когда процесс дости-
гает состояния $i, то на следующем шаге он попадает в s2. Выпи-
шите переходную матрицу.
6. Измените пример 2: предположите, что когда процесс дости-
гает состояния Si, он остается там на двух последующих шагах, а на
третьем попадает в s2. Покажите, что полученный процесс не есть
цепь Маркова (с заданными пятью состояниями).
7. Покажите, что процесс упражнения 6 можно считать цепью
Маркова, если допустить большее число состояний. Напишите пе-
реходную матрицу.
8. Модифицируйте переходную матрицу примера 7, предполагая,
что цифра 0 появляется вдвое чаще, чем любая другая цифра.
9. Модифицируйте пример 7, предполагая, что одна и та же циф-
ра никогда не появляется два раза подряд, но в остальном все циф-
ры равноправны.
10. В примере 8 разрешены только 2 состояния: хорошая погода
и плохая погода. Покажите, что процесс по-прежнему остается цепью
Маркова, и найдите его переходную матрицу.
К 2.3
11. В примере Па вычислите Р2, Р4, Р8 и Р16 и запишите их эле-
менты десятичными дробями. Отметьте общую тенденцию и интер-
претируйте результат.
12. Покажите, что откуда бы ни начинался процесс примера 7,
вероятность находиться в каждом из состояний после первого шага
совпадает с соответствующей строкой переходной матрицы. Каковы
эти вероятности через п шагов?
13. Предположим, что процесс примера 8 имеет вектор началь-
ного распределения л0= (2/s, Vs, 2/s). Найдите jtj, Чему равно лп?
14. Сегодня в стране Оз хорошая погода. Какая погода наибо-
лее вероятна послезавтра?
15. В примере 11 положим с = V2 и d = V4. Человек случайно
выбирает автомат для первой игры. Какова вероятность того, что
он играет с лучшим автоматом (а) во * второй, (Ь) в третьей игре
и (с) в четвертой игре?
16. В примере 2 предположим, что процесс начинается из со-
стояния s3. Постройте дерево и меру на нем для первых трех испы-
таний. Используйте их для нахождения меры, индуцированной тремя
первыми функциями исходов. Проверьте, что ваши результаты совпа-
дают с вероятностями, найденными из Р, Р2 и Р3.
%
i
60 ГЛ. II. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ЦЕПЕЙ МАРКОВА
К 2.4
17. Дайте полную классификацию состояний для следующей це-
пи Маркова и приведите переходную матрицу к коническому виду: I
«1 $2 «3 «4 «5 «6 s7
0 0 0 1 0 0 0
$2 0 0 0 0 0 0 1
«3 0 0 1 0 0 0 0
Р = ^4 V2 0 0 V2 0 0 0
«5 0 0 0 0 1 0 0
$6 0 0 0 0 0 0 1
«7 . 0 ‘Л 0 0 0 ъ 0.
18. Цепь Маркова задана следующей матрицей переходных ве-
роятностей, в которой ненулевые элементы обозначены через х. Дай-
те полную классификацию состояний и приведите переходную ма-
трицу к каноническому виду
s2 «3 «4 s5 «6 s7 «8
X X 0 0 0 0 0 0 0
S2 X X X 0 0 0 X 0 0
S3 0 0 0 0 0 0 X 0 0
s4 0 0 0 X 0 0 0 0 X
P = s5 0 0 0 0 X 0 0 0 0
Se 0 0 X 0 0 X 0 0 0
S7 0 0 X 0 0 0 0 0 0
S8 0 X 0 0 0 X 0 X 0 .9
Sq 0 0 0 X 0 0 0 0 X
19. Какие из следующих цепей являются
кие — поглощающими? Какие из эргодических
эргодическими, а ка*
цепей регулярны?
УПРАЖНЕНИЯ К ГЛАВЕ II
61
20. Классифицируйте состояния в примере 9. Приведите матрицу
переходных вероятностей к каноническому виду. Каков тип этой
цепи?
21. В эргодической цепи сделаем i-e состояние поглощающим, за-
менив i-ю строку переходной матрицы строкой, в которой на i-м ме-
сте стоит 1. Докажите, что получившаяся цепь — поглощающая.
22. В примере 11 наложите такие условия на с и d, чтобы цепь
получилась: (а) эргодической, (Ь) регулярной, (с) циклической, (d)
поглощающей.
Ко всей главе
23. В некотором штате избиратель имеет право участвовать в
первичных выборах другой партии только после того, как он в пер-
вичных выборах предыдущего года воздержался !). Пусть озна-
чает, что в этом году он голосует за демократов, s2 — за республи-
канцев и s3 — воздерживается при голосовании. Опыт показывает, что
демократы воздерживаются при голосовании на первичных выборах
с вероятностью Vs, республиканцы — с вероятностью V4, в то время
как избиратель, который перед этим воздержался, с равной вероят-
ностью голосует на следующих выборах за любую из двух партий.
[Мы будем ссылаться на этот пример как на пример 13.]
(1) Найдите матрицу переходных вероятностей.
(2) Найдите вероятность того, что избиратель, который сейчас
голосует за демократов, через три года воздержится при голосова-
нии.
(3) Классифицируйте состояния.
(4) В данном году V4 избирателей голосовала за демократов,
V2 —за республиканцев, а остальные воздержались. Какую пропор-
цию следует ожидать на выборах следующего года?
24. Производится серия опытов, в каждом из которых подбра-
сывают две правильные монеты. Обозначим через si выпадение
двух гербов, через $2 — выпадение герба и решетки и через s3 — вы-
падение двух решеток. (В дальнейшем мы будем ссылаться на этот
пример, как на пример 14.)
(а) Найдите матрицу переходных вероятностей.
(Ь) Если при данном бросании получились два герба, то какова
вероятность, что два герба выпадут через три бросания?
(с) Классифицируйте состояния.
!) По установившейся в США традиции перед всеобщими выбо-
рами в отдельных штатах проводятся первичные выборы, на кото-
рых выясняется популярность предполагаемых кандидатов данной
партии среди сторонников этой партии. (Прим, ред.)
Г Л A В A III
ПОГЛОЩАЮЩИЕ ЦЕПИ МАРКОВА
3.1. Введение. Напомним основные определения, от-
носящиеся к поглощающим цепям. При классификации
состояний классы эквивалентности были разделены на
невозвратные и эргодические множества. Частица, по-
кинув класс первого типа, никогда в него не возвра-
щается, и, наоборот, достигнув класса второго типа, она
никогда уже его не покидает. Если эргодическое множе-
ство состоит из одного состояния, то это состояние назы-
вается поглощающим. Для такого состояния элемент
переходной матрицы ри должен быть равен 1 и, значит,
все остальные элементы соответствующей строки рав-
няются,^. Цепь, все эргодические состояния которой яв-
ляются поглощающими, называется поглощающей цепью.
Такими цепями мы будем заниматься в настоящей главе.
3.1.1. Теорема. В любой конечной цепи Маркова, не-
зависимо от того, где начался процесс, вероятность пос-
ле п шагов оказаться в эргодическом состоянии стре-
мится к 1 при п->оо.
Доказательство. Если процесс в какой-то момент
достиг некоторого эргодического состояния, то он навсе-
гда останется в соответствующем классе эквивалентно-
сти, и, следовательно, при дальнейшем своем движении
будет каждый раз снова попадать в эргодическое со-
стояние. Предположим, что процесс отправляется из не-
возвратного состояния. Его класс эквивалентности не
минимален, так что имеется минимальный класс, ему
подчиненный. Это значит, что из начального состояния
можно достигнуть некоторого эргодического множества.
Предположим, что из любого невозвратного состояния
можно не более чем за п шагов достигнуть какого-то
эргодического состояния (так как число всех состояний
конечно, то в качестве п можно взять просто максималь-
ное из чисел, достаточных для каждого из состояний). ?
3.1. ВВЕДЕНИЕ
63
Тогда найдется положительное число р такое, что для
любого невозвратного состояния вероятность за п шагов
попасть в какое-то эргодическое состояние не меньше р.
Отсюда следует, что вероятность не достигнуть какого-
нибудь эргодического состояния за п шагов не превос-
ходит 1 — р, что меньше 1. Вероятность не достигнуть
какого-то эргодического состояния за kn шагов не пре-
восходит (1 — p)h, а эта вероятность стремится к О
с ростом k. Теорема доказана.
3.1.2. Следствие. Найдутся числа b > 0, 0 < с < 1,
такие, что для любых невозвратных состояний Si и Sj
Это непосредственно вытекает из приведенного выше
доказательства. Следствие позволяет судить о скорости
убывания вероятностей pff при п—>оо.
Здесь удобно придать матрице Р несколько иной ка-
нонический вид, объединив все эргодические состояния
в одну группу и все невозвратные состояния — в другую
группу. (Пусть, скажем, имеется s невозвратных иг — s
эргодических состояний.) Тогда каноническая форма
будет
г — s s
( S О \} г — s
Р = ----------- *
\ Р Q
Здесь снова область О составлена целиком из нулей
Подматрица Q (размерности s X s) описывает поведение
процесса до выхода из множества невозвратных состоя-
ний, подматрица Р размерности s X (г — 5) отвечает пе-
реходам из невозвратных в эргодические состояния, а
матрица S размерности (г — s) X (г — s) относится к про-
цессу после достижения им эргодического множества.
Теорема 3.1.1 показывает, что степени Q стремятся к О.
Значит, при возведении матрицы Р во все более высо-
кие степени, все элементы последних s столбцов стре-
мятся к 0. Это матричный вариант теоремы 3.1.1.
Рассмотрим теперь поглощающую цепь. Из опреде-
ления следует, что S =/(r-s)x(r-s), т. е. S представляет
64
ГЛ. III. ПОГЛОЩАЮЩИЕ ЦЕПИ МАРКОВА
собой единичную матрицу размерности (г — s)X(r —s).
Поэтому каноническая форма матрицы Р имеет вид
г ~ s
s
О \ г — s
Q ) s
I
R
Из определения произведения матриц следует, что при
возведении матрицы Р в степень подматрица / не ме-
няется. Это соответствует тому факту, что после дости-
жения поглощающего состояния частица остается в нем
навсегда. Из теоремы 3.1.1 следует, что в поглощающей
цепи вероятность достигнуть одного из таких состояний
стремится к 1. Значит, мы можем сказать, что с вероят-
ностью 1 цепь рано или поздно достигнет некоторого по-
глощающего состояния и останется в нем, т. е. «погло-
тится».
Перепишем теперь некоторые из примеров пункта 2.2
главы II в новой канонической форме. В примере 1 со-
стояния «1 и s5 поглощающие, так что их нужно напи-
сать вначале. Тогда
«1
S2
S3
S5
Sj S2 $3 $4 $5
10 0 0 0
0 10 0 0
q 0 0 p 0
0 0 q 0 p
0 p 0 q 0
(разбиение матрицы на блоки /, О, R и Q обозначено
тонкими линиями).
Матрица примера 10 из 2.2 уже имеет каноническую
форму. Первые два состояния поглощающие. Поэтому
в этом примере блоки R и Q имеют размерности соот-
ветственно 4X2 и 4X4.
Цепь примера 9 — не поглощающая. Она имеет один
эргодический класс, в который входят первые три состоя-
ния. Матрица переходных вероятностей записана в ка-
нонической форме в 2.2. Если мы желаем изучить, пове-
3.1. ВВЕДЕНИЕ
65
дение этого процесса до попадания в эргодическое мно-
жество, то можем объявить эргодические состояния по-
глощающими. Переходная матрица примет тогда вид
1 0 0 ООО
0 1 0 ООО
* ГЛ 0 0 1 ООО
р =
ООО 0 ‘/2 >/2
о 0 0 </2
К 7< 0 о О
Если нас к тому же не интересует, какое именно из
эргодических состояний будет достигнуто, мы можем
объединить три эргодических состояния в одно. При
этом получится более простая матрица
10 0 0
В первой матрице сохраняются без изменения Q и R
и изменяется S, а во второй сохраняется только Q. Это
хорошо согласуется с той интерпретацией блоков Q, R
и S, которая была приведена выше.
Теперь должно быть ясно, что поглощающие цепи
являются тем средством, с помощью которого можно
ответить на все вопросы второго типа (относящиеся
к невозвратным состояниям), поставленные в 2.5. Но по-
глощающие цепи также важны и при изучении эргоди-
ческих множеств. Предположим, что нас интересует во-
прос о поведении процесса на пути из в Sj. Для этого
нам желательно «остановить» процесс после достижения
им Sj, а этого можно достигнуть, объявив Sj поглощаю-
щим состоянием. Так как в Sj можно попасть из всех со-
стояний его класса эквивалентности, то полученная цепь
Маркова окажется поглощающей. Этот прием будет раз-
вит в 6.1.
5 Дж. Кемени, Дж. Снелл
66
ГЛ. Ш. ПОГЛОЩАЮЩИЕ ЦЕПИ МАРКОВА
3.2. Фундаментальная матрица. Следующая основ-
ная теорема окажется прямым следствием теоремы о
матрицах, доказанной в 1.11, если мы вспомним, что Qn
стремится к О.
3.2.1. Теорема. Для любой поглощающей марковской
цепи матрица I — Q обратима, причем
оо
(Z-Q)~' = / + Q + Q2+ ... =SQ\
/г=0
3.2.2. Определение. Для поглощающей цепи Маркова
фундаментальной матрицей называется матрица N =
3.2.3. Определение. Обозначим через nj функцию,
равную общему числу моментов времени, проводимых
процессом в Sj (эта величина определена только для не-
возвратных состояний). Пусть также есть функция,
равная 1, если процесс после k шагов находится в Sj,
и равная 0 в противном случае. (По поводу обозначе-
ний, принятых в этом пункте, см. 1.7 и 1.8).
Теперь мы дадим вероятностную интерпретацию мат-
рицы N. Пусть Т — множество невозвратных состояний.
3.2.4. Теорема. {МЛ»/]} = jV, где sb Sj<=;T.
Доказательство. Легко видеть, что
Поэтому
оо
ОО оо
= S [р$] = S Qk (так как si и si невозвратны) =
= N (согласно 3.2.1, 3.2.2).
Это и завершает доказательство теоремы.
Эта теорема устанавливает, что среднее время, кото-
рое проводит процесс в данном невозвратном состоянии,
всегда конечно, и что эти средние времена попросту
даются матрицей N.
3.2. ФУНДАМЕНТАЛЬНАЯ МАТРИЦА
67
Имеется другое интересное доказательство этого ре-
зультата. Чтобы вычислить нужно прибавить к
вкладу, который дает начальное положение, вклады каж-
дого шага. Вклад начального положения равен 1 тогда
и только тогда, когда i = /. Условимся обозначить через
Ьц постоянную, равную 1, если i = /, и 0 в противном
случае. Тогда можно сказать, что вклад начального по-
ложения равен Через один шаг мы попадаем в со-
стояние sk с вероятностью Если это новое состояние
поглощающее, оно ничего не добавляет к интересующе-
му нас среднему, но если оно невозвратно, то его вклад
равен Значит,
М/[п/] = 6//+ 2 P/feMJn,],
{Mz[n/D = / + Q{Mz[n,l}.
Поэтому
Применим эти результаты к примерам предыдущего
пункта. Для случайного блуждания в примере 1 из 2.2
/ 1 -р 0\
I-Q =1 ~q 1 -Р I,
\ 0 — q 1/
так что
•$2 *3 $4
( р + д2 р р1
2 р2 + q2 р2 + q2 р2 + q2
N = (I~Q) ' = S3 р2 ’ p2 + q2 '
„ q2 q q + p2
4 p2 + q2 p2 +q2 p2 + q2
[Так как p + q = 1, а значит и (p + ?)2 = l, то I -~2pq =
= p2 4- q2} Мы видим, что если процесс начинается, ска-
жем, в «з (среднее состояние), то математическое ожида-
ние времени, проведенного им в среднем состоянии, рав-
но 1/(р2 Ч- <72). Эта величина всегда заключена между
1 и 2. Минимум, равный 1, достигается, когда р = 0 или
1, а максимум при р=х!2* В первом случае процесс
5*
68
ГЛ. III. ПОГЛОЩАЮЩИЕ ЦЕПИ МАРКОВА
выходит из s3 и детерминированно движется к одной из
границ, так что в $3 он находится только в начале. Но
даже в случае р = V2 мы можем ожидать в среднем
только одного возвращения в начальное состояние.
3.2.5. Пример 1а. В качестве иллюстрации приведем
фундаментальную матрицу для случая р = 2/3, т. е. для
ситуации, когда движение вправо в два раза более ве-
роятно, нежели влево:
$2 §3 $4
S2 / 7/б % 4/б\
N = s3 3/5 % % •
S4 % 7s'
В примере с колледжем (пример 10 из 2.2), вспоми-
ная, что р + q + г = I, получаем
/p + r 0 0 ° \
- ~r p + r 0 0 1
7-Q
1 0 — r p + r 0 1
\ 0 0 — r p + t '
= (Z-Q)"' =
S3 «4 S5 «6
1 s3 —— d p + r 0 0 0 четверокурсник
_ 54 (p + r)1 1 p + r 0 0 третьекурсник
r2 r 1
$5 (P + r)s (p + r)2 p + r 0 второкурсник
ra r2 r 1
s& (p + r)* (p + r)3 (P + r)2 P + r первокурсник
Нули матрицы W показывают, что в колледже невоз-
можно движение вспять. Так, например, третьекурсник
никогда в будущем не может стать уже второкурсником
или первокурсником. Для иллюстрации подсчитаем (при-
ближенно) матрицу N в случае (который мы будем на-
зывать примером 10а), когда вероятности «вылететь»,
3.3. ПРИЛОЖЕНИЯ ФУНДАМЕНТАЛЬНОЙ МАТРИЦЫ
69
остаться на том же курсе и перейти на следующий курс
равны соответственно р = 0,2, </= 0,1 и г =0,7
(1,11 0 0
0,86 1,11 0
0,67 0,86 1,11
0,52 0,67 0,86
четверокурсник
третьекурсник
второкурсник
первокурсник
В урновой схеме (пример 9 из 2.2) получаем
/1 ->/2 -*/Л
(7-Q) = Р 1 —Vs),
\0 ->/2 1 /
s4/l 1 1\ (2,0,0)
jV = (/-Q)-, = sJ 0 4/з 2/з 1(1,1,0).
«До 2/з 4/з/ (1,0, 1)
Если процесс достигает состояния (1,1,0) или (1,0,1),
то, считая с этого момента, он проводит в этом состоя-
нии в среднем 4/з единиц времени, и в другом состоя-
нии— 2/з единиц времени (4/з включает вклад началь-
ного положения). Состояние (2,0,0) вообще не может
быть достигнуто ни из одного из этих двух состояний,
так как окрашенный шар всегда остается окрашенным.
Если процесс вначале находится, как естественно пред-
положить, в состоянии (2,0,0), то он проводит в этом
состоянии только единицу времени. Математическое ожи-
дание времени пребывания в каждом из двух осталь-
ных состояний также равно 1, что является средним
между 4/3 и 2/з-
Фундаментальные матрицы этих примеров будут ис-
пользоваться для иллюстраций на протяжении всей на-
стоящей главы. ... • .
3.3. Приложения фундаментальной матрицы. Мы по-
кажем, что многие интересные величины могут-быть вы-
ражены в терминах фундаментальной матрицы. Здесь
эти результаты будут проиллюстрированы на примере
случайногр. блуждания (пример Да. из 3.2.5) ,. а . прочие
70
ГЛ. III. ПОГЛОЩАЮЩИЕ ЦЕПИ МАРКОВА
примеры поглощающих цепей будут рассмотрены в сле-
дующем пункте.
3.3Л. Определение. Введем следующие новые ма-
трицы и векторы'.
N2 = N (2A/dg — /) “ Afsq (s X в)-матрица,
В = NR, sX(r — в)-матрица,
т = N%, s-компонентный
вектор-столбец,
т2 = (2N — /) т ~ Tsq, s-компонентный
вектор-столбец.
3.3.2. Теорема. QN = NQ = N — I.
Доказательство. Из 3.2.1 и 3.2.2 следует, что
W = / + Q + Q2 + ...
Значит,
QAT=^Q = Q + Q2 + Q3 +
что совпадает с первоначальным рядом для N без сла-
гаемого I.
3.3.3. Теорема. {D, [л,]} = Л^2 при Sh Sf Т.
Доказательство. Напомним, что Dz [nJ = Mz [nJ2 —
— М?[пу]. Из теоремы 3.2.4 вытекает, что
поэтому остается только показать, что
Допустим, что среднее в левой части конечно (доказа-
тельство этого факта будет приведено в конце пункта).
Чтобы посчитать это среднее, снова рассмотрим, куда
может попасть процесс за один шаг при начальном по-
ложении Sf. С вероятностью p/k он переходит в состоя-
ние sh. Если это состояние поглощающее, то процесс уже
не может попасть в Sj, и вклад, равный 6ц, дает только
начальное состояние. Если же новое состояние невоз-
вратное, то начальное состояние дает вклад а после-
3.3. ПРИЛОЖЕНИЯ ФУНДАМЕНТАЛЬНОЙ МАТРИЦЫ
71
дующие шаги добавляют время tij. Поэтому с учетом
того, что Ьгэ постоянная и 6^ = 6^, получаем
[МДЛ/]} { + 2 Pif№k[(nj + ^i/)2] ~
(M4»;]+2M,|»j6,,)+q-
Рл s 7 J
= Q{MZ [«*])+2 (Qtf)d(f + Z.
Значит,
= Ы(2(Н-1)"+1)-Н(2Н<,-П.
Появление матрицы (QN)^g в приведенной выкладке объ-
ясняется тем, что множитель обращает в нуль все
элементы вне главной диагонали.
В примере 1а мы ранее посчитали N, теперь вычис-
лим также Л^2‘
(7/ 6/ 4/ \ /49/ 36/ 16/ \
/5 /5 /5 \ / /25 /25 /25 \
75 % % > tfSq= 725 8725 ^25 .
% 7/ь' ' V25 9/25 49/2Г»/
/7/5 о о\ /% о о\
Afdg= 0 % 0 1, 2tfdg-z= о 13/5 0 >
\ о о 7/5/ \0 о %/
(63/ 78/ 36/ \
/25 /25 /25 \
27/25 П725 54/25 ,
9/ 39/ 63/ /
/25 /25 /257
с / 14/ 42/ 20/ \
62 / /25 /25 /25 \
Л^2 = 5з1 18/25 36/25 18/25 )•
54 ' 8/25 3°/25 И/25'
ГЛ. III. ПОГЛОЩАЮЩИЕ ЦЕПИ МАРКОВА
В частности, видно, что наибольшая дисперсия при лю-
бом начальном состоянии получается для числа попада-
ний в среднее состояние. Отметим также, что матрица
Л;2 одного порядка по сравнению с Nsq, так что средние
для этой марковской цепи дают очень ненадежные
оценки. Это случается довольно часто.
3.3.4. Определение. Пусть функция t равна полному
времени (включая начальное положение), которое про-
цесс проводит в невозвратных состояниях.
Если процесс начинается в эргодическом состоянии,
то t = 0. Если процесс начинается в невозвратном со-
стоянии, то величина t показывает, сколько шагов нуж-
но сделать до попадания в эргодическое множество.
В поглощающей цепи — это время до поглощения.
3.3.5. Теорема. {Mz[Z]) = t, {Df[f]) = T2 при s^T.
Доказательство. Очевидно, t = 2 nj- Поэтому
{М [*]} = ( з
I s} е T I
так как это выражение дает суммы элементов строк
матрицы /V.
При вычислении дисперсии воспользуемся соображе-
ниями, аналогичными тем, которые применялись в 3.3.3.
Здесь начальное состояние всегда дает вклад. Имеем
{MjfD-l 2 p«-i + S pAWI-
(vfte=7- I
= ( 2 + =Q{MJ#2]} + 2QT + g.
Отсюда
{Mt.[f]} = (7-Q)-’(2QT + B) =
= 2NQx + Nl = 2(N-I)r + x = (2N-I)r. j
Итак,
{Df [/]} = {M, R2]} - {M, [/J2} - (2АГ - /) т - tsq.
3.3. ПРИЛОЖЕНИЯ ФУНДАМЕНТАЛЬНОЙ МАТРИЦЫ
73
В нашем примере
в2/17/5\
r = A^ = J 1% ,
sAn/J
12/s
2N — I = % 13/5 12/5 ,
V/5 % %/
/45725\ /28725\ /16725\
(2М-/)т = , xsq = I 324/25 , т3= ж/25 .
\ 241 / / \ 121 / / \ 120/ /
х /257 4 /25 7 х /25 7
Мы видим, что самого быстрого достижения границы
можно ожидать при начальном состоянии $4. Это и по-
нятно, так как на край проще попасть из «пригранич-
ных» состояний, чем из середины, и, кроме того, движе-
ние вправо более вероятно, чем влево. Но нужно снова
отметить, что дисперсия довольно значительна.
Мы вычислили средние для мер, связанных с про-
цессом, стартующим из фиксированного состояния $г-.
Отсюда нетрудно получить математические ожидания и
дисперсии при произвольном начальном распределении.
3.3.6. Следствие. Если л — начальное распределе-
ние для поглощающей цепи и я' состоит из последних s
компонент вектора л, т. е. п' дает начальные вероятно-
сти среди невозвратных состояний, то
{Мя [/»,]} = nW,
Юя [и,]} = n'N (2Nis -I)- (n'W)sq,
{МяИ) = л'т,
{D„ H} = «'(2iV-Z)T-(«'T)sq-
Доказательство. Это немедленно получается из того,
что для произвольной функции f
Мя[Л = лМг[Л,
что в свою очередь вытекает из строения меры, опреде-
ленной на дереве путей. Мы пишем в правой части л',
74
ГЛ. III. ПОГЛОЩАЮЩИЕ ЦЕПИ МАРКОВА
а не л, так как все интересующие нас средние равны О,
если начальное состояние поглощающее.
Остающиеся приложения фундаментальной матри-
цы связаны с вопросом о том, какое из поглощающих
состояний захватит блуждающую частицу.
3.3.7. Теорема. Если Ьц — вероятность того, что про-
цесс, выходящий из невозвратного состояния sif остано-
вится в поглощающем состоянии Sj, то
{Ьц} = В — NR, е Г, Sj е= Т.
Доказательство. Выйдя из состояния sif процесс мо-
жет поглотиться в Sj через один или более шагов. Ве-
роятность захвата на пёрвом шагу равна Pij. Если этого
не произошло, то процесс может попасть либо в другое
поглощающее состояние (и тогда достигнуть Sj невоз-
можно), либо в какое-то невозвратное состояние sk.
В последнем случае блуждающая частица может быть
захвачена нужным состоянием с вероятностью bkj. Сле-
довательно,
ьа = Ра+ 2 Pikbkh
что можно переписать и в матричной форме:
B = R + QB.
Отсюда
В = {I— Qj~l R = NR.
Другое доказательство основано на следующем на-
блюдении: каждый раз, когда процесс находится в не-
возвратном состоянии Sh, он с вероятностью попадает
в Sj. Поэтому можно установить, что
= 2 [«*] Pkj-
,k^T
Отсюда непосредственно вытекает
В = NR.
В нашем примере
f */з 0\ s2/7/i5 8/is\
Я = 1 0 0, B = NR = sA >/5 % .
'0 2/з' s4 '715 И/15'
3.3. ПРИЛОЖЕНИЯ ФУНДАМЕНТАЛЬНОЙ МАТРИЦЫ
75
Отметим, что для любого начального положения
сумма вероятностей поглощения равна 1. Из теоре-
мы 3.1.1 следует, что всегда NRlr-s = £s. Это также лег-
ко проверить и непосредственно.
Чем ближе к правому концу начальная точка, тем
больше, конечно, вероятность поглотиться справа. Инте-
ресно, однако, отметить, что даже для левой пригранич-
ной точки вероятность захвата на правом конце не-
сколько больше, чем на левом конце.
3.3.8. Следствие. Если ра— а-й столбец матрицы R,
т. е. ра = {рга} для Si из Т и фиксированного а, то век-
юр Npa дает вероятности поглощения в данном погло-
щающем состоянии sa для всех невозвратных начальных
состояний.
Это следствие полезно, когда нас интересует какое-
то одно поглощающее состояние.
3.3.9. Теорема. Если В* — матрица размерности г X г,
элементы Ьц которой представляют вероятности погло-
титься в Sj, выходя из sb то
РВ* = В*.
Доказательство. Если Sj^T, то Ь^ = 0. Значит, по-
следние s столбцов матрицы В* равны 0. Пусть состоя-
ние Sj —поглощающее. Если s< е Т, то согласно 3.3.7
Ь*ц = Ьц. Если же Si — также поглощающее состояние,
то bij — &ij. Значит,
0
0
/ /
РВ* = —
\ R
0 \ / I 0 \ / / о
Q Д В 0 / \ R + QB 0
Но R + QB = R + QNR = Я + (N — I)R = NR = В. Зна-
чит, РВ* = В*.
Итак, мы доказали, что r-мерный вектор-столбец,
дающий вероятности поглощения в данном поглощающем
состоянии Sj, является неподвижным вектором для Р.
76
ГЛ. III. ПОГЛОЩАЮЩИЕ ЦЕПИ МАРКОВА
Первые г — s компонент вектора равны 0, исключая /-ю,
равную 1. Этим вектор полностью определяется. Такой
метод нахождения вероятностей поглощения полезен,
если нас не интересует матрица А/.
В нашем примере легко проверить, что векторы
теоремы 3.3.3.
3.3.10. Теорема. В поглощающей
конечна при любых sp s^T.
Доказательство.
утверждение из
цепи величина
'/ сю \2'
(2 «/)
Lu-о '/
[нЭД] — это вероятность того, что процесс, начинаясь
из sif попадает в как на &-м, так и на /-м шагу. Если
мы положим m = min(6, /), d = \k — то эту вероят-
ность можно представить как вероятность попасть в Sj
за т шагов, а затем вернуться в это же состояние за
d шагов. Значит,
М, [nJ] = 22 p<7>p<f < 2 2 (b • ст) (b. cd) =
oo oo
= b2 5 2 C>1 (где « = гпах(й, /)) =
k=0 / = 0
oo
= &22 (2n+l)c", а эта величина конечна,
n-o
3.4. ПРИМЕРЫ
77
3.4. Примеры. Пример 3.4.1 (продолжение примера 1
из 2.2). Для случайного блуждания получим
/ p + q2 р р2 \
.. 1 I 1 I
Л^ = -у-—г q 1 р I
р2 + q2 i 4 r Р
\ q2 q q + p2/
/ p + q2 1 + 2p p + p2\
дг______pg I i о i I
Л2~ (p2 + <72)2 I 12 II,
\ q + q2 1 + 2q q + p2 '
/ 1 4- 2p2 \ / 1 + 2p \
- =____L_ о To =_______________________ 2 I
p2 + q2 \ ’ 2 (p2 + q2)2 I •
\ 1 + 2q2 / \ 1 + 2q /
/pq+q3 p3 \
В — J 2 I q2 p2 I.
p2 + q2 I 4 I
\ qz pq + p3/
В частности, если р — х!г (пример 1b), то
/3/2 1 */2\ /3Л 2 з/ч
Л' = 1 12 11, ЛГ2 = 1 12 1,
\'/2 1 3/2/ V/4 2 з/4/
а если р — 1 (пример 1с), то
/1 1 1\ /3\ /0 1\
JV=I 0 1 11, т = 1 2 I, В = 1 0 1 ],
\0 0 1/ \1/ \0 1/
и все дисперсии равны 0.
Последний результат легко понять, если вспомнить,
что рассматриваемый процесс представляет собой детер-
минированное движение вправо.
78
ГЛ. Ш. ПОГЛОЩАЮЩИЕ ЦЕПИ МАРКОВА
Пример 3.4.2 (продолжение примера 10 из 2.2). В за-
даче о студентах колледжа мы получаем, полагая
/ = г/(р + г):
(I 0 0 0\
t I 0 О I
t2 t 1 or
t3 е- t 1/
(q 0 0 0\
qt +1 — t2 q 0 0 |
qt2 + t2-t4 qt + t — t2 q О Г
qt3 + t3-te qt2 + t2-t4 qt + t — t2 q/
(1-/ \
\-t2 \
I — /3 r
1 -Г/
/ 9(1-0 \
1 [ q(i-t2) + t-2t2 + t3 ]
T2~ p(P + r) I <7(1 -fi) + t + t2-4t3 + t4 + t5 Г
\ q (1 — t4) + t + t2 +13 — 6t4 + t5 +16 + t7 /
Вероятность успешно закончить обучение в коллед-
же для студента любого курса зависит только от отно-
шения / = г/(р 4- г). Это отношение представляет собой
вероятность того, что студент будет переведен на сле-
дующий курс (а не будет исключен) при условии, что
он больше не будет учиться на нынешнем курсе. После-
довательные степени этого отношения допускают про-
стую интерпретацию: это произведения вероятностей то-
го, что всякий раз, когда студент оставляет очередной
курс, он переводится на следующий (а не прекращает
3.4. ПРИМЕРЫ
79
учебу), причем не накладывается никаких ограничений
на срок обучения на каждом из курсов. Формулы сильно
упрощаются, если мы исключим возможность остаться
на второй год на том же курсе, т. е. предположим, что
q = 0. Тогда t = г/ (р + г) = г и
(1 0 0 0ч
г 1 0 0 |
г2 г 10г
г3 г2 г 1 /
(0 0 0 0\
г-г2 0 0 0 |
г2 — г4 г — г2 0 0 г
г3 — г® г2 — г4 г — г2 0 /
(1 \ / 0\
1+r I _ | 1 |
1 + Г + Г2 1» Т2 — I 1 + Зг -р г2 I •
1 + г + г2 + г3 / х 1 + Зг + 6г2 + Зг3 + г4 /
Матрица В сохраняется без изменений.
При числовых данных примера 10а (см. 3.2.5) полу-
чается
/1,11 О О О X
/ 0,86 1,11 0 0 |
# = 1 0,67 0,86 1,11 О I’
\ 0,52 0,67 0,86 1,11 /
(0,12 О О О X
0,31 0,12 0 0 |
0,37 0,31 0,12 О I’
0,37 0,37 0,31 0,12/
(1,11\ /°’12\
1,98 ] / 0,43 I
2,65 Г Т2 = 1 1,13 Г
3,17/ \2,22/
80
ГЛ. III. ПОГЛОЩАЮЩИЕ ЦЕПИ МАРКОВА
Прекратить учебу Закончить учебу
0,22 0,78 > четверокурсник
0,40 0,60 I третьекурсник
0,53 0,47 J второкурсник
0,63 0,37/ первокурсник
Итак, студент должен стать третьекурсником, чтобы
иметь более половины шансов на окончание колледжа.
Пример 3.4.3 (пример 9 из 2.2). В этой урновой схе-
ме интересующие нас векторы и матрицы имеют вид
/I 1 1 \ /о 7з 2/з\
АГ = 1 0 % 2/з > ^2 = 1 0 % 2/з ,
\о 2/з ^0 2/з
$4 $5 S6
$4 /7г ^4 74\
В = s51 7г 7з 7б )•
$6'/2 7б 7з^
Так как процесс немедленно покидает состояние $4
и не может в него возвратиться, дисперсии времен, про-
веденных в этом состоянии, равны 0. Среди остальных
дисперсий наименьшими являются диагональные эле-
менты — это связано с эффектом стабилизации, который
вызывает вклад начального состояния.
Матрица В в рассматриваемом случае требует спе-
циального разъяснения. Так как состояния sb s2 и s3 для
исходного процесса не являются поглощающими, то «ве-
роятности поглощения» нужно трактовать как вероятно-
сти вхождения в эргодическое множество через данное
состояние. Например, если в начале оба шара не были
окрашены (состояние $4), то с вероятностью !/2 в пер-
вый раз, когда оба шара будут окрашены, они будут
иметь разные цвета, с вероятностью !/4 они будут оба
красные и с вероятностью у4 они будут оба черные.
Следует отметить, что в точности такие же вероятности
3.5. РАСПРОСТРАНЕНИЕ РЕЗУЛЬТАТОВ
81
получатся, если предположить, что оба шара окраши-
ваются независимо в случайно выбранный цвет (крас-
ный или черный).
3.5; Распространение результатов. Мы убедимся сей-
час, что результаты 3.3 можно прилагать к более широ-
кому кругу проблем,
3.5.1. Определение. Множество состояний S назы-
вается открытым, если из любого состояния, принадле-
жащего S, можно попасть в какое-то состояние из S.
Нетрудно привести примеры открытых множеств:
множество, составленное из единственного состояния,
открыто (если только это состояние не поглощающее),
открыты также множество невозвратных состояний, точ-
ное подмножество эргодического множества и т. п. Сле-
дующая теорема дает исчерпывающую характеристику
таких множеств.
3.5.2. Теорема. Множество состояний S открыто то-
гда и только тогда, когда никакое эргодическое множе-
ство не является подмножеством S.
Доказательство. Если какое-то эргодическое множе-
ство содержится в S, то, войдя в это множество, процесс
уже не может из него выйти, так что S не открыто.
С другой стороны, мы знаем, что из любого состоя-
ния можно достичь некоторого эргодического состояния.
Попав в эргодическое состояние, процесс может достиг-
нуть любого состояния в том же эргодическом классе.
Поэтому если S не содержит ни одного эргодического
множества, то для любого элемента, принадлежащего S,
найдется эргодическое состояние в S, достижимое из
этого элемента. Значит, S открыто.
3.5.3. Теорема. Если S — открытое множество и все
состояния из S превращены в поглощающие, то получен-
ная цепь Маркова будет поглощающей и множество всех
новозвратных состояний этой цепи будет совпадать с S.
Доказательство. Так как S открыто, то из каждого
состояния, принадлежащего S, можно достичь состояния,
принадлежащего S, которое, по условию, является погло-
щающим. Значит, цепь поглощающая. А так как из лю-
бого элемента S процесс может достичь поглощающего
О Дж. Кемени, Дж. Снелл
82
ГЛ. III. ПОГЛОЩАЮЩИЕ ЦЕПИ МАРКОВА
состояния, то все состояния S должны быть невозврат-
ными в новом процессе.
3.5.4. Теорема. Пусть S — открытое множество s со-
стояний и Q — подматрица размерности sXs матрицы
Р, отвечающая этим состояниям. Пусть также ра — век-
тор-столбец с s компонентами pia, где Sj — элементы S,
a sa е S. Допустим, что процесс начинается в состоянии
Si. Тогда'.
(1) ij-й элемент матрицы N = (/ — Q)-1 представляет
среднее значение времени, проведенного процессом в s}
до выхода из S.
(2) ij-й элемент матрицы N2 = N (2Ndg — I) — NSq
представляет дисперсию той же случайной величины.
(3) i-я компонента вектора т = представляет сред-
нее значение времени, проведенного в S.
(4) i-я компонента вектора Т2 = (2N — /)т — xsq пред-
ставляет дисперсию той же величины.
(5) i-я компонента вектора Мра представляет вероят-
ность того, что в момент выхода из S процесс попа-
дает в sa.
Доказательство. В силу теоремы 3.5.3 различные ча-
сти этой теоремы являются непосредственными след-
ствиями соответствующих результатов 3.3.
В качестве приложения предыдущей теоремы рас-
смотрим следующую задачу. Пусть Sj и sk — два каких-то
состояния регулярной марковской цепи. Предположим,
что процесс начинается в каком-то третьем состоянии.
Какова вероятность достичь sk раньше, чем Sj? Эту ве-
роятность можно отыскать, воспользовавшись предложе-
нием 3.5.4 (5) и взяв в качестве S множество всех эле-
ментов эргодического множества, кроме Sj и s^.
3.5.5. Пример. Рассмотрим случайное блуждание
примера 6 главы II. Соответствующая переходная мат-
рица имеет вид
$2
Р = S3
«4
О
7з
о
о
74
74 74 74 74
7з 7з о о
7з 7з 7з о
о 7з 7з 7з
74 74 74 о
3.5. РАСПРОСТРАНЕНИЕ РЕЗУЛЬТАТОВ
83
и так как из любого состояния в любое другое можно
попасть за два шага, то цепь регулярна. Значит, любое
собственное подмножество множества всех состояний от-
крыто. Предположим, что S состоит из последних трех
состояний. Тогда
s3 / 7з 7з ОД
Q = S4 7з 7з 7з ,
S5 V/.4 >/4 0 /
(21/ 12/ 4/ \
/9 /9 /9 \
,5/9 2% % ,
% % "/J
(252 / 324 / 44/ \
/81 /81 /81 \
27%1 360/81 56/81 ,
216/ 270/ 36/ /
/81 /81 /81 7
1220/ t \
11,4/81),
1062/si }
Матрица М дает нам средние значения времени пре-
бывания в каждом из последних трех состояний до до-
стижения процессом одного из первых двух состояний.
Мы видим, что соответствующие значения малы, когда
процесс начинается в последнем состоянии. Это интуи-
тивно вполне понятно, так как тогда процесс «захваты-
вается» с вероятностью V2 уже на первом шагу. По той
же причине среднее время пребывания в последнем со-
стоянии мало, откуда бы процесс ни начинался. Однако
матрица Мг показывает, что дисперсии, отвечающие вре-
менам пребывания в состояниях $з и $4, больше, чем
дисперсии, связанные с последним состоянием.
Из вида вектора т следует, что среднее время до по-
глощения больше всего при начальном положении $4,
которое не соприкасается непосредственно с S. Разница
в средних значениях времен до захвата объясняется раз-
личием в числе прямых связей, которые последние три
состояния имеют с первыми двумя. Отметим, что, тогда
6*
84
ГЛ. III. ПОГЛОЩАЮЩИЕ ЦЕПИ МАРКОВА
как средние заметно отличаются друг от друга, диспер-
сии почти одинаковы.
Наконец, вектор Wpi дает «вероятности выхода» в со-
стояние «1, т. е. вероятности (зависящие от начальной
точки) попасть в когда процесс выходит из S, или,
ГОВОРЯ ПО Другому, ВерОЯТНОСТИ ДОСТИЧЬ СОСТОЯНИЯ Sj
раньше, чем s2. Эти вероятности очень просто зависят от
числа шагов, необходимых для достижения Si из началь-
ной точки (при движении по S).
3.5.6. Теорема. Пусть функция гг равна времени, в те-
чение которого процесс остается в не поглощающем со-
стоянии Si, после того, как это состояние достигнуто
(включая момент достижения). Тогда
[г J = 1/(1 - ри), (а)
(Ь)
Условная вероятность того, что процесс перейдет в sj
при условии, что он покинул равна
(с)
Доказательство. Множество, состоящее из одного эле-
мента 8{, открыто. Применим теорему 3.5.4 к этому мно-
жеству. В этом случае N— матрица размерности 1X1,
и поэтому совпадает с т; величина единственного элемен-
та N равна 1/(1—рн). Значит, (а) вытекает из утвер-
ждений (1) или (3) теоремы 3.5.4. Аналогично, Nz = тз
и (Ь) следует из пунктов (2) или (4) той же теоремы.
Из (5) теоремы 3.5.4 следует утверждение (с), если вы-
брать в качестве р$ вектор с единственной компонентой
pij. Так как состояние а,- не поглощающее, то ри < 1, и
все наши величины имеют смысл.
Мы не интересовались еще до сих пор одним типом
задач, которые можно проиллюстрировать следующим
вопросом: попадет ли когда-нибудь процесс в данное
невозвратное состояние. Этот и похожие вопросы рас-
сматриваются в теоремах 3.5.7, 3.5.8 и 3.5.9. Введем
нужные обозначения. Пусть п, — время, которое прово-
дит процесс в невозвратном состоянии Sj, m — число раз-
личных невозвратных состояний, в которые когда-либо
попадает процесс, и Иц — вероятность того, что процесс
3.5. РАСПРОСТРАНЕНИЕ РЕЗУЛЬТАТОВ
85
когда-нибудь достигнет невозвратного состояния Sj, от-
правляясь из невозвратного состояния
3.5.7. Теорема.
Я = {М = (АГ-Wg*.
Доказательство.
или
{Пц} = / 4- {hijtiij},
т. е.
N = I+HNdg.
Значит,
H = (N — I)Nig.
3.5.8. Теорема. {Рг [п; — 6it = /г]} =
| Е — Н, если k = Q,
~\Н • Hk6g'[I- Hdg] = (N—1) Nig (I - Ndg), если k > 0.
Эта теорема определяет вероятность побывать в дан-
ном невозвратном состоянии ровно k раз. Теорема сразу
же получается из следующего замечания: чтобы побы-
вать в данном невозвратном состоянии k раз, нужно его
достигнуть по крайней мере один раз, затем вернуться
в него k — 1 раз, а затем навсегда покинуть.
3.5.9. Теорема.
Р = {Мг [т]} = [Я + (/ — Hdg)] I = NNi&
Доказательство. Среднее число невозвратных состоя-
ний, в которых побывает процесс, равно сумме вероятно-
стей побывать когда-нибудь в различных состояниях.
Если процесс начинается в то вероятность достичь
состояния Sj равна Л,у при i4= j и 1 при i = j.
Если мы применим теорему 3.5.7 к примеру 1, то по-
лучим
рд
\-pq
д
l-pq
<72
,1-РЧ
Р
4pq
q
р2
\-pq
Р
\-pq
РЧ
l-pq
Я =
86
ГЛ. II!.. ПОГЛОЩАЮЩИЕ ЦЕПИ МАРКОВА
Отсюда, например, видно, что при q = 0 все элементы
на главной диагонали и под ней равны 0. Это значит,
что если процесс движется вправо с вероятностью еди-
ница, то он не может возвратиться к начальному поло-
жению, а также не может попасть в состояния, располо-
женные левее начального. Далее,
/ 1 + р2 + р3 \
1 I о I
Н = 2-W .
\ 1 + q2 + q3 /
/3\
При 9 = 0 получается, что ц = 1 2 I. Результат очеви-
\1 /
ден, так как при этом условии процесс движется детер-
минированно вправо и проводит в каждом из промежу-
точных состояний единицу времени.
3.5.10. Теорема. Математическое ожидание и диспер-
сия числа перемен состояния в поглощающей цепи
можно подсчитать, положив для всех невозвратных со-
стояний ри — 0 п нормировав каждую строку так, чтобы
сумма ее элементов стала равна 1. Тогда i-я компонента
нового вектора т даст среднее значение числа перемен
состояний для исходного процесса. Дисперсия той же
величины будет равна i-й компоненте нового вектора Т2-
Доказательство. Предположим, что марковская цепь
стартует в непоглощающем состоянии. Построим новый
процесс, положение fn которого в момент п задается
следующим образом: если частица поглощена состоя-
нием Sh, причем число перемен состояний было меньше л,
то fn = sk. В противном случае fn — это состояние, в ко-
тором процесс находился после п-й смены состояния.
Очевидно, новый процесс является цепью Маркова. Ве-
роятности перехода из поглощающего состояния $г- у не-
го те же самые, что в матрице Р. Если же Si — невоз-
вратное состояние, то
Ра = Р< [?i = Л = 0,
оо
Ра = Pi [fl = /1 = s PhPii=т=77-
3.5. РАСПРОСТРАНЕНИЕ РЕЗУЛЬТАТОВ
87
По этой новой переходной матрице можно определить
математическое ожидание и дисперсию времени до по-
глощения для процесса /2, ... Это время представ-
ляет число перемен состояний в исходной цепи, выходя-
щей ИЗ S{.
Можно также найти среднее значение числа шагов,
во время которых процесс, находясь в множестве невоз-
вратных состояний, не меняет своего положения. Для
этого достаточно из среднего времени до достижения по-
глощающих состояний вычесть среднее число перемен
состояний.
Чтобы проиллюстрировать теорему 3.5.10 на примере
с колледжем (пример 10 из 2.2), положим ри = 0, i =
= 3, 4, 5, 6, и произведем нормировку. Тогда
1 0 0 1 0 0 0 0 0 0 0 0
р= 0,22 0,78 0 0 0 0
0,22 0 0,78 0 0 0
0,22 0 0 0,78 0 0
0,22 0 0 0 0,78 0
(1 0 0 Ох
0,78 1 0 0 |
0,61 0,78 1 0 I’
0,47 0,61 0,78 1 /
(1,00\ /0 \
1,78 | _( 0,17 1
2,38 Г Т2 = 1 0,68 Г
2,85/ \ 1,51 /
Сравнивая эти результаты с примером 3.4.2, отме-
тим, что среднее время до поглощения больше, чем сред-
нее число перемен состояний (но ненамного, так как
повторения состояния редки), и что дисперсия первой
величины заметно больше, чем второй.
Другое интересное применение условных вероятно-
стей к поглощающим цепям состоит в следующем.
88
ГЛ. III. ПОГЛОЩАЮЩИЕ ЦЕПИ МАРКОВА
Предположим, что поглощающая цепь стартует в непо-
глощающем состоянии, и вычислим все вероятности при
условии, что процесс заканчивается, скажем, в данном
поглощающем состоянии Sj. Тогда мы получим новую
поглощающую цепь с единственным поглощающим со-
стоянием «ь Невозвратные состояния останутся преж-
ними, но вероятности перехода из них изменятся. Вычис-
лим их. Пусть р — утверждение «исходный процесс по-
глощается в состоянии «1». Тогда для невозвратного
состояния Si переходные вероятности нового процесса
имеют вид
р Г. e |nl_ Ар) _
“Ifi-S/lpJ- р.[р] - р/[р]
А - ЬПРИ
bit •
Эта формула применима и при / = 1, если считать
fen = 1. Фундаментальная матрица для Р получается
следующим образом. Матрица R есть вектор-столбец
= Пусть Dо — диагональная матрица с диаго-
нальными элементами Ьц (при невозвратных $j). Тогда
Q = Dq 'QDq.
Отсюда
Qn = D^’IQrtD0
2V = Do"'[/ + Q + Q2+ ...\Dj = Dv'ND0.
В и т можно получить, исходя из N.
Пример. Рассмотрим пример 1а из 3.2.5. Изучим ус
ловный процесс при условищ что цепь поглощается в со
стоянии Новая матрица Q имеет вид
$2
z«/7 0 0 \ / О 2/з
$ = 0 15/з о 7з О
\о о ’5/t/\0 7з
«4
о\/715 о о\
7з 0 3/15 0 =
О/\ о О '/15/
/ о 2/7 0 \
= 79 0 2/9 ,
\ 0 1 о J
УПРАЖНЕНИЯ К ГЛАВЕ III
89
так что
$2 $3 $4
Sj / 1 О О О \
-U5/? О 2/7 О |
«з! О 7/9 О 2/9 I’
s4 \ О О 1 О /
/15/7 о о \/7з % 4/5\/715 О О\
лг = о 15/з О 3/5 % % О 715 О =
\ о о i5/J\l/5 75 75/\0 о 715/
/7б *8/з5 4/з5\
= 75 7S 75 ,
V/i 75 75/
УПРАЖНЕНИЯ К ГЛАВЕ III
К 3.1
1. Запишите следующие матрицы в канонической форме:
Sj $2 S3
s, / */з Vs Vs
P = s2 О 1 О
«з V Vs Vs Vs
Sj $2 S3 S4
P=S2
S3
S4
1
1
74
о
о
74
о
о о
о о
74 74
о 1
2. Примените теорему 3.1.1 к поглощающей цепи с единствен-
ным поглощающим состоянием.
3. Примените результат предыдущего упражнения к эргоди-
ческой цепи, в' которой одно из состояний заменено поглощающим
(см. упражнение 21 к главе 11).
90
ГЛ. Ш. ПОГЛОЩАЮЩИЕ ЦЕПИ МАРКОВА
4. В примере 8 из 2.2 замените состояние R поглощающим. Что
позволяет сказать о погоде в стране Оз теорема 3.1.1, примененная
к получившейся поглощающей цепи? (Другими словами, какую ин-
формацию мы получаем об исходном процессе?)
К 3.2
5. Найдите фундаментальную матрицу для поглощающей цепи
с переходной матрицей
$1 S2 S3
Si / 1 0 0 \
Р = 32 0 V2 v2 .
53 \ V2 0 V2'
6. Найдите фундаментальную матрицу для примера 11 из гла-
вы II при с = 0 и d =/= 0.
7. Получите в примере 9 из 2.2 поглощающую цепь, заменив все
эргодические состояния поглощающими. Найдите фундаментальную
матрицу и дайте истолкование элементам первой строки этой ма-
трицы.
8. Покажите, что если для поглощающей цепи задана фундамен-
тальная матрица N, то АН существует и Q — I — А/-*.
9. Докажите, что NQ = N — /.
10. Проверьте результаты упражнения 9 (см. выше) на примере
9 из 2.2.
К 3.3
И. Что можно сказать о матрице В, если в поглощающей цепи
только одно поглощающее состояние? Замените в примере 8 из 2.2
состояние Я поглощающим состоянием, вычислите N и В и про-
верьте ваше утверждение.
12. Получите в примере 7 из 2.2 поглощающую цепь, предполо-
жив, что процесс останавливается после достижения 0 или 9. Напи-
шите новую переходную матрицу в канонической форме.
13. Вычислите в примере из упражнения 12 (см. выше) N, N2, В,
т, т2.
14. В примере 8 из 2.2 замените состояние N поглощающим со-
стоянием. Вычислите фундаментальную матрицу полученной марков-
ской цепи. Найти N2, В, т, т2. Интерпретируйте результаты с точки
зрения исходной цепи.
15. Посчитайте матрицу N для танковой дуэли (упражнение 2
к главе II). Исходя из нее, найдите среднюю продолжительность
сражения и вероятность каждого возможного исхода.
16. Выполните выкладки упражнения 15 (см. выше) для моди-
фицированного танкового сражения (упражнение 3 из главы II).
В каком сражении у танка А больше шансов?
17. Для цепи примера 1а (см. 3.2.5) найдите вероятности успеш-
но закончить обучение методом, который дает теорема 3.3.9, т. е.
УПРАЖНЕНИЯ К ГЛАВЕ III
91
найдите соответствующий неподвижный вектор-столбец для переход-
ной матрицы.
18. В цепи примера 1а (см. 3.2.5) начальное состояние выби-
рается случайным образом с равными вероятностями из пяти воз-
можных состояний. Найдите математическое ожидание и дисперсию
для времен пребывания в различных невозвратных состояниях и чис-
ла шагов до поглощения.
К 3.5
19. Предположим, что в примере 9 из 2.2 оба шара первона-
чально не окрашены. Найдите среднее число извлечений до момента,
когда впервые оба шара будут окрашены. Какова вероятность, что
в этот момент оба шара будут красные?
20. Сегодня в стране Оз идет снег. Найдите среднее число раз-
личных типов погоды до ближайшего дождливого дня. Найдите ве-
роятность того, что перед дождливым будет хотя бы один яс-
ный день.
21. Предположим, что в примере 1 из 2.2 с р — V2 известно, что
процесс поглощается в состоянии Найдите переходную матрицу
нового условного процесса. Найдите среднее время до поглощения.
22. Вычислите следующие величины в задаче о танковой дуэли
(см. пример 2 из главы II):
(а) Математическое ожидание и дисперсию числа раундов, в ко-
торых все три танка еще действуют.
(Ь) Вероятность того, что на какой-то стадии танки А и С еще
действуют, а танк В уже подбит.
(с) Вероятность того, что на какой-то стадии танки А и В еще
действуют, а танк С уже подбит.
(d) Вероятность того, что танки А и В будут подбиты в одном
и том же раунде.
(е) Р, N, т, предполагая, что сражение выиграл С.
(f) Р, т, предполагая, что ни один танк не уцелел.
23. Пусть в танковом сражении (пример 2 из главы II) танк А
имеет вероятность попадания танк В — вероятность 3/5 и танк С—
неопределенную вероятность р (но р < 3/б)-
(а) Установите матрицу переходных вероятностей.
(Ь) Найдите вероятность того, что танк С уцелеет.
(с) В ответе на предыдущий вопрос устремите р к 0. Объясните
получившийся результат.
Ко всей главе
24. Семеро мальчиков играют в мяч.
Первый мальчик всегда бросает мяч второму.
Второй мальчик с равными вероятностями бросает мяч третьему
или седьмому.
Третий мальчик оставляет мяч у себя, когда он к нему по-
падает.
Четвертый мальчик всегда бросает шестому.
У2 ГЛ. III. ПОГЛОЩАЮЩИЕ ЦЕПИ МАРКОВА
Пятый мальчик с равными вероятностями бросает четвертому,
шестому или седьмому мальчику.
Шестой мальчик всегда бросает мяч четвертому.
Седьмой мальчик бросает мяч первому или четвертому с рав-
ными вероятностями.
(а) Напишите переходную матрицу Р.
(Ь) Классифицируйте состояния.
(с) Представьте Р в канонической форме.
(d) Объясните, что в данном случае означает попадание цепи
в конце концов в одно из эргодических множеств.
е) Пусть мяч у пятого мальчика. Найдите математическое ожи-
дание и дисперсию числа раз, когда мяч достается седьмому маль-
чику. Найдите также математическое ожидание и дисперсию времени
до достижения эргодического множества.
25. Дана поглощающая цепь Маркова. Проводится следую-
щая игра.
Мы отправляемся из фиксированного состояния и наблюдаем за
цепью до ее попадания в поглощающее состояние. Если достигнуто
состояние sa, то мы получаем плату са, Образуем вектор-столбец у,
t-я компонента которого равна среднему выигрышу при начальном
положении Si.
(а) Докажите, что Ру — у.
(Ь) Докажите, что если sa — поглощающее состояние, то а-я
компонента вектора у равна са.
(с) Докажите, что эти два условия однозначно определяют у.
[Указание: рассмотрите предел Рпу].
(d) Пусть уа — вектор, который дает вероятности поглощения в
sa (при различных начальных положениях). Как можно выразить у
через уа?
ГЛАВА IV
РЕГУЛЯРНЫЕ ЦЕПИ МАРКОВА
4.1. Основные теоремы. В этой главе мы будем изу-
чать поведение регулярной марковской цепи. Напомним,
что регулярной цепью Маркова называется цепь без не-
возвратных состояний, имеющая единственное эргоди-
ческое множество с одним циклическим классом.
4.1.1. Определение. Переходная матрица регулярной
марковской цепи называется регулярной переходной мат-
рицей.
4.1.2. Теорема. Переходная матрица регулярна тогда
и только тогда, когда при некотором N все элементы
матрицы PN отличны от нуля.
В главе II было показано, что цепь регулярна тогда
и только тогда, когда за некоторое число шагов N мож-
но попасть из любого состояния в любое другое. Это
возможно в том и только том случае, когда все эле-
менты матрицы PN не равны нулю.
4.1.3. Теорема. Пусть Р — переходная матрица раз-
мерности гХг, не содержащая нулевых элементов, иг—
наименьший элемент Р. Пусть х — произвольный г-мер-
ный вектор-столбец, имеющий максимальную компоненту
Mq и минимальную компоненту mQ, и пусть Mj и mi со-
ответственно максимальная и минимальная компоненты
вектора Рх. Тогда М\ -<Л10, mi > т0 и
Мх — mi ^(1 — 2в) (А40 — т0).
Доказательство. Пусть х' — вектор, полученный из х
заменой всех компонент, кроме т0, на Мо. Тогда х^х'.
Каждая компонента вектора Рх' имеет вид
ат0 + (1 — a) Мо = А10 — a (MQ — т0), ;
причем а > е. Поэтому каждая такая компонента не пре-
восходит Мо — 8 (Л1о — то). Отсюда и из неравенства
х^.х' получается, что
Mi^MQ-e(MQ-mQ). (1)
94
ГЛ. IV. РЕГУЛЯРНЫЕ ЦЕПИ МАРКОВА
Если мы применим те же рассуждения к вектору — х, то
получим
— тх < — mQ — е (— т0 + Л40).
(2)
Складывая соотношения (1) и (2), будем иметь
Мх — тх —— 2e(M0 — ш0) == (1 — 2е)(М0 —т0).
Из этого результата вытекает простое доказательство
следующей основной теоремы относительно регулярных
марковских цепей.
4.1.4. Теорема. Если Р— регулярная переходная мат-
рица, 70
(i) Степени Рп стремятся (при п—>оо) я вероятно-
стной матрице А.
(ii) Каждая строка матрицы А представляет один и
тот же вероятностный вектор а = {аь a2i ..., ап}, т. е.
А =
(iii) Все компоненты сс положительны.
Доказательство. Предположим сначала, что все эле-
менты матрицы Р отличны от нуля. Пусть pj— вектор-
столбец, все компоненты которого равны 0, кроме /-й,
равной 1. Пусть Мп и тп соответственно максимальная
и минимальная компоненты вектора Pnpj. Так как
рпр. = р. Рп~[р^ то из теоремы 4.1.3 следует, что
Мх М2 М3.. • и пгх пг2 пг3... и
Мп - mn < (1 - 2е) (М„-1 - m„-i)
при и>1. Положим dn = Mn — mn, тогда из предыду-
щего получается, что
4<(l-2erd0 = (l-2e)n.
Так как при п, стремящемся к бесконечности, последова-
тельность dn сходится к нулю, тоА1п и тп приближаются
к общему пределу. Значит, Pnpj сходится к вектору, все
компоненты которого равны между собой. Пусть aj—
их общее значение. Ясно, что тп-^,а^Мп при всех п.
В частности, так как 0 < тх и Afj < 1, то 0 < а,- < 1. За-
метим, что Pnpj — это /-й столбец матрицы Рп. Итак, /-й
столбец матрицы Рп стремится при п, стремящемся к
бесконечности, к вектору, все компоненты которого рав-
ны aj. Отсюда следует, что последовательность матриц
4.1. ОСНОВНЫЕ ТЕОРЕМЫ
95
Рп сходится к матрице Д, у которой по строкам стоит
один и тот же вектор а = (а\, а2, ..., аг). Так как сумма
элементов в каждой строке матрицы Рп равна 1, то
то же самое справедливо и для предельной матрицы.
Тем самым для матрицы, все элементы которой положи-
тельны, доказательство закончено.
Рассмотрим теперь произвольную регулярную матри-
цу Р. Пусть W таково, что все элементы PN отличны от
нуля и 8х — наименьший элемент PN. Применяя первую
часть доказательства к матрице PN, мы получаем, что
dftJV<(l-2e')ft. (3)
Поэтому последовательность dn, которая по доказанному
ранее не возрастает, имеет подпоследовательность, схо-
дящуюся к нулю. Значит, и dn стремится к 0, после чего
доказательство заканчивается так же, как и в случае
матрицы со всеми положительными элементами.
4.1.5. Следствие. Пусть Р — регулярная переходная
матрица и а, = lim Тогда найдутся постоянные bur
(причем 0<r< 1) такие, что
p^ = as + e^
и | е^ | b • гп.
Доказательство. Мы знаем, что Пусть N
таково, что матрица PN не содержит нулей, и 8 —
наименьший элемент PN. Положим г = (1—2e)1/2V,
b = 1/(1 — 2е) == r~N. Если п = kN, то по формуле (3)
dn^.rn. Если же n = kN + nb где то (так
как dn не возрастают) dn^.rn~ni ^гп • r~N = brn. Полу-
ченное здесь неравенство для eW полезно при доказа-
тельстве различных теорем, но слишком грубо как оценка
реальной скорости сходимости р(“} к пределу.
4.1.6. Теорема. Если Р — регулярная переходная мат-
рица, а А и а — те же, что и в теореме 4.1.4, то
(а) Для любого вероятностного вектора л последо-
вательность векторов пРп сходится к вектору а при
п-~* оо.
(Ь) Вектор а — единственный вероятностный вектор,
для которого аР = а.
(с) РА = АР = А.
96
ГЛ. IV. РЕГУЛЯРНЫЕ ЦЕПИ МАРКОВА
Доказательство. Если л — вероятностный вектор, то
ng=l, значит n;A=nga = a. Но векторы лРп сходятся
к лА, т. е. к а. Этим завершается доказательство пунк-
та (а).
Так как степени матрицы Р приближаются к матрице
А, то Рп+У = Рп • Р также приближается к А. Но после-
довательность матриц Рп • Р сходится к АР\ поэтому
АР — А. Аналогично устанавливается, что РА = А и
пункт (с) доказан. Покажем теперь, что вектор а един-
ственный. Пусть р — такой вероятностный вектор, что
рР = р. Согласно (а) последовательность рРп сходится
к а. Но рР = р, откуда рРп = р. Значит, а = р. Итак, мы
доказали (Ь).
Матрица А и вектор а будут в дальнейшем назы-
ваться предельной матрицей и предельным распределе-
нием (или предельным вектором) для марковской цепи,
определяемой регулярной матрицей Р1)-
Теорема 4.1.6 показывает, что для регулярной пере-
ходной матрицы существует вектор-строка а, остаю-
щаяся «неподвижной» при умножении на Р. Любой
другой вектор а' такой, что а'Р = а', пропорционален
вероятностному вектору а. Следующая теорема показы-
вает, что любой неподвижный вектор-столбец для Р
пропорционален g.
4.1.7. Теорема. Если Р — регулярная переходная мат-
рица и р = {rj — вектор-столбец такой, что Рр = р, то
р = eg, где с — постоянная.
Доказательство. Так как Рр = р, то Р2р = Рр = р и
вообще Рпр = р. Поэтому Ар = р. Значит, = ар. Но
это означает, что все компоненты вектора р равны меж-
ду собой. Поэтому при некотором с мы имеем р = eg.
В главе II было показано, что если процесс стартует
с начальным распределением л, то вероятности нахо-
диться в каждом из состояний через п шагов задаются
вектором лРп. По теореме 4.1.6 при больших п вектор
лРп близок к а. Так как предельный вектор а зависит
только от Р, но не от начального распределения л, то
можно сказать, что долгосрочное предсказание о поведе-
!) В русской литературе а называют также финальным распре-
делением цепи Маркова. (Прим, ред.)
4.1. ОСНОВНЫЕ ТЕОРЕМЫ
97
нии регулярной цепи не зависит от начальных вероятно-
стей. Проиллюстрируем это на примере 8 из главы II.
Переходная матрица в этом примере имеет вид
R N S
R/'h 74 74\
N 72 0 72 •
Ш 74 72/
Для нахождения вектора а = (tfj, а2, а3) мы должны оты-
скать вероятностное решение уравнения аР = а. Други-
ми словами, нужно найти решение следующей системы
уравнений:
1 — а,\ + а2 + #з,
Я1 = 72«1 + 74а2 + 74аз>
= 74«1 + 74а3,
а3= 74aj + '/ia2 + 1l2a3.
Единственное решение этой системы есть
а = (75, 7s> 7б)-
Тогда сразу же находится и предельная матрица
/0,4 0,2 0,4 \
Л==| 0,4 0,2 0,4 ].
\0,4 0,2 0,4/
Следствие 4Л .5 устанавливает, что скорость сходимости
к этому пределу экспоненциально быстрая. Поэтому мож-
но ожидать, что даже при сравнительно небольших зна-
чениях п матрицы Рп и А близки друг к другу. Матрица
Р5 равна
К N S
/? /0,4004 0,2002 0,3994
Р5 = ЛН 0,4004 0,1992 0,4004
S\ 0,3994 0,2002 0,4004
Каждая строка матрицы Р5 содержит вероятности того
или иного типа погоды через пять дней после данного
дня. Например, первая строка дает вероятности каждого
7 Дж. Кемени, Дж. Снелл
gg ГЛ. IV. РЕГУЛЯРНЫЕ ЦЕПИ Маркова
типа погоды через пять дней после дождливого дня.
Тот факт, что строки матрицы почти одинаковы, озна-
чает, что сегодняшняя погода в стране Оз оказывает
очень небольшое влияние на прогноз погоды через пять
дней.
4.2. Закон больших чисел для регулярных цепей
Маркова. Как мы убедились в 4.1, для регулярной цепи
Маркова существуют предельные вероятности aj нахо-
диться в состоянии Sj независимо от начального поло-
жения. В этом параграфе мы докажем, что если общее
число шагов велико, то aj представляет также ожидае-
мую долю числа шагов, после которых процесс будет
находиться в Sj. Этот результат также не зависит от на-
чального состояния.
Чтобы точно сформулировать приведенный резуль-
тат, мы должны ввести некоторые новые функции. Пусть
функция, заданная на дереве Un и равная I, если
п-й шаг приводит в Sj и 0 — в противном случае. Поло-
га
жим = 2 «?’. Тогда функция У\п} опять-таки опреде-
} £=1 J
лена на дереве Un и равна числу шагов до момента п
(без учета начального положения), после которых про-
цесс находится в состоянии Sj. Величина = у^/п дает
долю времени (за первые п шагов), которое процесс про-
водит В Sj.
4.2.1. Теорема (закон больших чисел). Рассмотрим
регулярную марковскую цепь с предельным вектором
а = (оь а2, .аг). Для любого начального распреде-
ления л
Мл [V/ra>] “* ai
и для любого е>0
PIt[|vW-a/|>e]->0 (b)
при п, стремящемся к бесконечности.
Доказательство. Согласно теореме 1.8.10, для дока-
зательства сформулированного утверждения достаточно
проверить, что Мл — aj2] -> 0 при п, стремящемся
к бесконечности. Это в свою очередь получится, если
4.2. ЗАКОН БОЛЬШИХ ЧИСЕЛ
99
мы установим, что [(v<n> — а.)2] —> 0 при любом /. Но
Пусть mkt = М. — а.)— а.)]. Тогда мы должны
доказать, что
п п
(1)
1=1 k=l
при п—>оо. Произведем умножение в выражении для
mkj. Имеем
mk i = — а;Мг — а;.М. [«<'>] + а|.
Пусть т = min (k,l) и d = | k — 11. Тогда
тк, i = Р{н]Рп ~ a/Pn ~ aiPn + аг
Используя следствие 4.1.5, получаем
mk, i = ai + ен ~ еп ~ ец) + eWi'
где | | Ьгп и 0<r< 1. Значит, при нужным обра-
зом выбранной постоянной с
I mkt к с | rm + rd + г* + г11. (2)
Каждая из величин m, d, k и I фигурирует в сумме (1)
не более 2п раз. Поэтому, используя соотношение (2),
мы получаем окончательно, что
п п
1 V1 I I 4с 2п __ 8с
п2 1 т>а 1 ‘ ТГТ _ я(1 - г)
/=1 k=l
Правая часть этого неравенства при п~*оо стремится
к нулю, значит, это верно и для левой части, что и тре-
бовалось доказать.
Применим эту теорему к примеру страны Оз. В кон-
це 4.1 мы нашли, что a = (2/5, Vs, 2/s). Следовательно, мы
7*
100
ГЛ. IV. РЕГУЛЯРНЫЕ ЦЕПИ МАРКОВА
можем ожидать, что на протяжении длительного интер-
вала времени примерно 2А дней будут дождливыми, око-
ло 1/б — ясными и примерно 2/5— снежными.
Рассмотрим один частный случай — процесс незави-
симых испытаний. Такой процесс является цепью Мар-
кова, переходная матрица которой имеет в каждой стро-
ке один и тот же вектор а и начальное распределение
которой задается тем же вектором а. Закон больших чи-
сел для независимых испытаний является, таким обра-
зом, частным случаем только что доказанной теоремы.
Но в этом случае можно дать значительно более про-
стое доказательство. Действительно, теперь Ма
для любого п; значит также и Ма = а,. Кроме того,
mki = 0 при 6 =/= / и mktk = o2 при всех k. Поэтому
Последнее выражение стремится к 0 при п—>оо.
Интерес представляет и другой частный случай: об-
щая марковская цепь с начальным распределением л = а.
Тогда, как и раньше, Ма = Ма == при всех п.
Значит,
В этом случае, однако, нельзя дать простое выражение
для дисперсии как функции от и, что нам удалось в слу-
чае независимых испытаний. Мы исследуем эту диспер-
сию в 4.6, где дадим для нее асимптотическое выражение.
4.3. Фундаментальная матрица регулярной цепи.
В главе II мы видели, что в теории поглощающих цепей
основную роль играет матрица (/ — Q)-1. (Матрица
Q —подматрица переходной матрицы, отвечающая не-
поглощающим состояниям.) Мы увидим, что соответст-
вующая фундаментальная матрица существует и для
регулярных цепей.
4.3.1. Теорема. Пусть Р — переходная матрица регу-
лярной цепи Маркова, а А — ее предельная матрица.
4.3. ФУНДАМЕНТАЛЬНАЯ МАТРИЦА РЕГУЛЯРНОЙ ЦЕПИ Ю|
Тогда матрица Z = (/ — (Р — Л))-1 существует и
Z = I + ^ (Рп — А).
п=1
Доказательство. Докажем, что (Р — А)п = Рп — А.
Так как Рп — Л—>0, то наша теорема будет тогда сле-
довать из теоремы о матрицах, установленной в 1.11.1.
Имеем А2 = = Л, значит Ah = Л, и
п
(Р-А)п = ^^У~ \)п~1 Р1Ап~1 =
1=0
ft—1
- Р'г + ^(")(-1)'г-/Д = Р"-Д.
i=0
4.3.2. Определение. Пусть Р — регулярная переходная
матрица. Матрица Z — (/ — (Р — Л))*1 называется фун-
даментальной матрицей марковской цепи, определяе-
мой Р.
Мы увидим, что матрица Z является тем основным
средством, с помощью которого вычисляется большин-
ство интересных характеристик, описывающих поведение
регулярной цепи Маркова. Установим предварительно
некоторые важные свойства этой матрицы, которые бу-
дут полезны в дальнейшем.
4.3.3. Теорема. Пусть Z — фундаментальная матрица
регулярной цепи Маркова с переходной матрицей Р, пре-
дельным вектором а и предельной матрицей А. Тогда
(a) PZ = ZP,
(b) = g,
(с) aZ = а,
(d) I — Z == Л — PZ.
Доказательство. Утверждение (а) вытекает из пред-
ставления Z в виде бесконечного ряда и того факта, что
матрица Р перестановочна с каждым членом этого ряда.
Утверждение (Ь) означает, что суммы элементов мат-
рицы Z по строкам равны 1. Это опять следует из
представления Z в виде ряда, так как суммы элемен-
тов по строкам первой матрицы / равны 1, а аналогич-
ные суммы для каждой из матриц Рп— А равны 0.
102
ГЛ. IV. РЕГУЛЯРНЫЕ ЦЕПИ МАРКОВА
Утверждение (с) вытекает из представления Z в виде
ряда и соотношений al = а и а(Рп— А) = 0. Для дока-
оо
зательства (d) умножим ряд Z = I + У (Рп — Л) на мат-
п — 1
рицу I — Р. Получится
(/ — P)Z = (I — P) + (P — Л) = I — А.
Стандартным примером для демонстрации приложе-
ний матрицы Z будет служить страна Оз. В этом при-
мере матрицы Р и А равны
R N S R N S
ИГ/2 'U 7Л 75 75\
P = N 72 0 72 . a=n 2/5 75 75 •
sv/4 74 */2/ s\2/5 >/5
Для нахождения матрицы Z мы должны обратить мат-
рицу
/ 0,9 -0,05 0,15 \
7-Р + Л = 1 -0,1 1,2 -0,1
\ 0,15 -0,05 0,9 '
Проделав это, получим
R N S
/ 86 3 -14\R
Z = yU 6 63 6 U.
\ —14 3 86/S
Хотя некоторые свойства фундаментальной матрицы Z
и совпадают со свойствами переходной матрицы, ее эле-
менты, как показывает этот пример, не обязаны быть не-
отрицательными.
Примером, в котором матрица Z имеет особенно про-
стой вид, является случай независимых испытаний. То-
гда Р — Л, так что Z = (/ — (Р— А))~х=1. Итак, для
процесса независимых испытаний фундаментальная мат-
рица— это единичная матрица.
4.3. ФУНДАМЕНТАЛЬНАЯ МАТРИЦА РЕГУЛЯРНОЙ ЦЕПИ ЮЗ
Пусть yW— число моментов времени, в которые про-
цесс находился в состоянии Sj за первые п шагов (на-
чальное положение плюс п— 1 шаг).
4.3.4. Теорема. Для любой регулярной цепи Маркова
и любого начального распределения л
(Мл [у^]} — яа] -> л (Z — Л) = %Z — а.
Доказательство. Для любого i
__ п-1 п-1
Значит,
_ п-1
{М, [ур] - па,} = 2 (Рк - Л) -> Z - А.
Поэтому
л [yf}\ — па^ —> л (Z — Л) — nZ — а.
Непосредственно из теоремы вытекает следующий ре-
зультат.
4.3.5. Следствие. Для любых двух начальных распре-
делений пил'
Мл [»/"’] - Мл' -* (rt - л') 2.
Если мы фиксируем некоторое начальное состояние,
скажем то теорема 4.3.4 показывает, что
М; [»(«>]
Итак, мы видим, что при больших п среднее время, про-
веденное в состоянии Sj, исходя из s^ отличается от
naj приблизительно на 2ц— aj. Напомним, что согласно
теореме 4.2.1 средняя доля времени, проведенного в Sj,
близка к aj независимо от начального положения. Таким
образом, элементы матрицы (Z — Л) дают нам интерес-
ную численную характеристику регулярной цепи, зави-
сящую от начального состояния. Мы можем сравнивать
различные начальные положения, так как по следствию
4.3.5
ГЛ. IV. РЕГУЛЯРНЫЕ ЦЕПИ МАРКОВА
(04-
Другое интересное применение теоремы 4.3.4 состоит в
следующем*
4.3.6. Следствие. Пусть c = Тогда
2(|М,[?«]-мл[^])^с-1
при п —► оо независимо от л.
Доказательство. В силу результата 4.3.5
М/ \уМ] - Мл [у(п>] -> zn - (лг)г
Суммируя по /, убеждаемся, что сумма стремится к
2zH-nZ^ = c- 1.
Этот результат допускает следующую интерпретацию.
При любом л имеем Мл[^п)]. Поэтому
М;. является наибольшим из возможных значений
среднего времени пребывания в состоянии Sj (до момен-
та и). Следствие устанавливает, что сумма отклонений
от максимума по всем состояниям стремится к пределу,
не зависящему от выбора л.
4.4. Времена первого достижения. В этом пункте мы
будем изучать продолжительность времени, за которое
процесс из Si впервые попадает в sj. Будет установлено,
что математические ожидания этих времен легко нахо-
дятся по фундаментальной матрице.
4.4.1. Определение. Для регулярной цепи Маркова
время первого достижения fk — это функция, равная чис-
лу шагов, за которое цепь впервые попадает в sk из на-
чального состояния.
4.4.2. Теорема. При любом i математическое ожида-
ние М i[fk] конечно.
Доказательство. Предположим сначала, что i Ф k.
Образуем новую цепь Маркова, сделав состояние sh по-
глощающим. Полученная марковская цепь — поглощаю-
щая с единственным поглощающим состоянием sh. Сред-
нее время перехода из $г- в Sj для исходной цепи — это
то же самое, что среднее время поглощения для новой
цепи. Но среднее время поглощения конечно по теореме
3.2.4.
4.4. ВРЕМЕНА ПЕРВОГО ДОСТИЖЕНИЯ
105
Если же i = k, то
Mt[fj = Pii +
k=^= i
и правая часть конечна, как следует из первой части до-
казательства.
4.4.3. Определение. Матрицей средних времен дости-
жения (обозначается М) называется матрица с элемен-
тами = МЯ/j].
Из 1.8.9 следует, что при начальном распределении л
средние времена достижения отдельных состояний равны
компонентам вектора пМ.
4.4.4. Теорема. Матрица М удовлетворяет уравне-
нию
M = P(M-Mdg) + E. (1)
Доказательство. Вычислим MJfJ, осреднив условные
математические ожидания при известных результатах
первого шага. Это дает
мдм= 2 р«(м, [/,] + \) + Pii =
ky=j
= 2 + i =
k^i
= 2№МИМ-/7(./мдм + 1,
k
или, другими словами,
mu = р1ктк1-- Рцтп+ 1.
k
Теорема доказана.
4.4.5. Теорема. Пусть а = {аь ..., аг} — вектор пре-
дельного распределения для Р. Тогда Шц = 1/а$.
Доказательство. Умножим приведенное выше урав-
нение (1) слева на а. Получится
аМ = аР(М — Mdg) + аЕ = а (М — Mdg) + аЕ.
Поэтому
aMdg = аЕ = г).
Это означает, что агпгц = I при любом i или тц =т
= 1/а«.
106
ГЛ. IV. РЕГУЛЯРНЫЕ ЦЕПИ МАРКОВА
4.4.6. Теорема. Уравнение (1) из теоремы 4.4.4 име-
ет единственное решение.
Доказательство. Пусть М и М' — два решения урав-
нения (1). Из доказательства теоремы 4.4.5 вытекает, что
aMdg = aMdg = т|. Поэтому Afdg = Afdg- Отсюда следует,
что
М-М' = Р(М-М').
Но это значит, что каждый столбец матрицы М — М'
является неподвижным вектором для Р. Воспользуемся
теперь теоремой 4.1.7. Она показывает, что все компо-
ненты такого столбца равны между собой. Так как диа-
гональные элементы матрицы М— М' равны 0, то все
эти столбцы состоят из нулей. Значит, М = М'.
$А.1. Теорема. Матрица М средних времен достиже-
ния дается формулой
M = (I-Z + EZdg)D, (2)
где D — диагональная матрица с диагональными эле-
ментами da = I/af.
Доказательство. С учетом теорем 4.4.4 и 4.4.6 оста-
ется лишь доказать, что матрица М, определенная фор-
мулой (2), удовлетворяет приведенному выше уравне-
нию (1).
Пусть
М = (I-Z + EZdg)D.
Тогда
A4-D = (-Z + £Zdg)D
и
Р (М - D) = (- PZ 4- £Zdg) D.
По теореме 4.3.3, пункт (d), последнее выражение равно
р (М - D) = М - AD = М - Е.
Согласно 4.4.5 D = и уравнение (1) выполняется.
4.4.8. Теорема. Пусть Р — переходная матрица про-
цесса независимых испытаний. Тогда М = {I/р^}.
Доказательство. Из теоремы 4.4.7 и того факта, что
для процесса независимых испытаний Z = /, получается,
что М = ED. Но для рассматриваемой цепи предельная
4.4. ВРЕМЕНА ПЕРВОГО ДОСТИЖЕНИЯ
107
матрица А совпадает с Р. Значит, рц = и 1/а^ = 1/рц.
Итак, М = ED = {\/рц}.
Проиллюстрируем вычисление матрицы средних вре-
мен достижения на примере страны Оз. Мы нашли в
свое время, что а = (2/s, Vs,2/s). Поэтому матрица D
имеет вид
/72 о о \
D = l 0 5 0 I.
\0 0
Матрица Z была найдена в 4.3. Стало быть, используя
теорему 4.4.7, мы можем определить матрицу М по
формуле М = (/ — Z + EZag)D. Произведя выкладки,
получаем
R N S
*/5/2 4 '0/3\
М = ЛИ 8/з 5 8/з |
«\'7з 4 б/2/
Так, например, если сегодня в стране Оз идет дождь,
то среднее число дней до ближайшего ясного дня рав-
но 4. Среднее число дней до следующего дождливого
дня равно 5/2, а до снегопада —10/3.
Теперь мы докажем теорему, которая связывает диа-
гональные элементы матрицы Z и средние времена до-
стижения отдельных состояний при начальном распре-
делении л. = а. Мы уже видели, что в этом случае сред-
ние времена пребывания в имеют особенно простой
вид. Такой выбор начального распределения представ-
ляет особый интерес по следующей причине. Допустим,
что мы начали наблюдать марковскую цепь по истече-
нии длительного промежутка времени после начала про-
цесса. Теорема 4.1.6 наводит на мысль, что тогда в ка-
честве нового начального распределения л естественно
выбрать а. При этом распределение в любой последую-
щий момент времени также будет задаваться векто-
ром а. Мы говорим в этом случае, что процесс имеет
стационарное распределение.
1.08
ГЛ. IV. РЕГУЛЯРНЫЕ ЦЕПИ МАРКОВА
4.4.9. Теорема. Для регулярной марковской цепи
аМ = {Мо [fj ]} = T]ZdgD = {zn/aj}.
Доказательство. Умножая соотношение (2) на а, по-
лучаем
аМ = а(/ — Z + EZdg) D = (а — а + T|Zdg) D,
аМ = ijZdgD.
4.4.10. Теорема. Пусть с = Тогда Мат = с^
i
Доказательство.
Мат = (/ - Z + fZdg) Dar = (/ — Z + EZdg) \ -% (nZdg£) == c%.
В 4.3. мы сравнили математические ожидания вре-
мен пребывания у^п} в состоянии Sj для двух различ-
ных начальных состояний. Аналогичное сравнение мож-
но сделать и для функции fj.
4.4.11. Теорема. Для любых двух начальных рас-
пределений п и п'
{Мя [/,]} - {Мл, [/,]} = (л - л') (/ — Z) D.
Доказательство.
{Мя[//]-М„ЧМ} = яЛ1-Я'Л4 =
= (n-n')(/-Z + EZdg)D = (n-n')(/-Z)D.
В примере со страной О3 мы имеем
МЛ/5]-Мл[^ = 8/з-10/з=-2/з.
Таким образом, после ясного дня придется ждать снега
в среднем меньше, чем после дождливого дня.
Заключим настоящий параграф доказательством
того, что марковская цепь полностью определяется чис-
лами тц при i 4= j. Мы используем эти числа как не-
нулевые элементы матрицы М = М — D. Итак, знания
п(п — I) ненулевых элементов матрицы М достаточно
для описания цепи. Если цепь определяется в терминах
переходной матрицы Р, то мы задаем п2 элементов, но
между ними имеется п соотношений (сумма элементов
по каждой из п строк равна I). Не существует есте-
ственного способа выделить среди них п(п—\) неза-
4.4, ВРЕМЕНА ПЕРВОГО ДОСТИЖЕНИЯ
109
висимых элементов. В то же время матрица М позво-
ляет естественным образом выделить минимальное чис-
ло определяющих параметров1).
4.4.12. Теорема. Для любой регулярной цепи Мар-
кова
(а) Матрица М имеет обратную.
(Ь) а = (с-1)СЙЛ2Г.
(с) P = I+ (D — E)M~l.
Доказательство. Из уравнения (1) в 4.4.4 следует,
что _ _
М + D = РМ + Е\
поэтому
(Р — I)M = D — E. (3)
Если матрица М не имела обратной, то существовал
бы ненулевой вектор у такой, что Му = 0. Но тогда из
формулы (3) следовало бы, что
(D-E)y = (P-/) Му = 0,
Dy = Еу,
Y = D~'Ey = = (тру) аГ>
где (tjy) = I — число. Так как у =# О, то I =# 0 и поэтому
_ ar = (l/0Y>
Л1аг = (1//) AfY = O.
Но, очевидно, Мат_> 0, и мы пришли к противоречию.
Значит, матрица М имеет обратную. Формула (с) те-
перь немедленно вытекает из соотношения (3). Для
доказательства (Ь) воспользуемся результатом 4.4.9 и
тем фактом, что £>ат = £. Имеем
_(M + D)aT = ct„
Маг = (с — 1)£,
аг = (с —
______________ а = (с - 1)
9 Рассуждения авторов о естественности того или иного спо-
соба задания цепи с помощью минимального числа параметров весь-
ма условны. Например, цепь можно задать с помощью n (п — 1) па-
раметров рц с i #= /. (Прим, ред.)
по
ГЛ. IV. РЕГУЛЯРНЫЕ ЦЕПИ МАРКОВА
Теперь мы можем найти вектор а, опираясь на фор-
мулу (Ь), и соотношение а£=1. Тем самым опреде-
ляется матрица D, а тогда в силу формулы (с) и пе-
реходная матрица Р. Итак, мы доказали, что цепь дей-
ствительно полностью задается матрицей средних М.
4.5. Дисперсия времени первого достижения. В пре-
дыдущем пункте мы установили, что матрица Z даег
возможность найти среднее значение времени первого
достижения состояния Sj, исходя из Si. Теперь мы пока-
жем, что матрица Z позволяет найти и дисперсию мо-
воспользоваться равенством Dz [f;] = М£. —
Обозначим через W матрицу с элементами
ментов первого достижения.
Напомним, что функция fj определялась как число
шагов, после которого впервые после начального со-
стояния достигается Sj. Мы уже нашли Поэтому
для определения Di[fj] необходимо найти лишь
и затем
4.5.1.
НИЮ
Теорема. Матрица W удовлетворяет уравне-
W = P(W- rdg) - 2Р [Z - EZdg] D + E.
(1)
Доказательство. Беря условные математические ожи-
дания, получаем
м,и- +
Или
F = P[r-№dg] + 2P[M-Mdg] + £. (2)
По теореме 4.4.7 М — Afdg = (—Z + EZdg)D. Подставляя
это выражение в (2), приходим к соотношению (1).
4.5.2. Теорема. Значения Mz даются формулой
Wdg = D(2ZdgD-I). (3)
Доказательство. Умножая уравнение (1) на а и поль-
зуясь тем, что аР = а, имеем
ar = a[r-Fdg]-2a[Z-£Zdg]£> + ri. (4)
4.5. ДИСПЕРСИЯ ВРЕМЕНИ ПЕРВОГО ДОСТИЖЕНИЯ
111
или, так как aZ = а и aD = аЕ = ц, aW'dg = — П + 2r]Zdg^.
Отсюда 2г., — — 1 Ч - ,
т. е. 1 , 2ги ®и= + 2 • ai ai
Представив это в матричной форме, придем к (3).
4.5.3. Теорема. Единственное решение уравнения (I)
равно
W = M (2ZdgD -1) + 2 (ZM—E (ZM)dg).
Доказательство. Доказательство единственности про-
водится так же, как для матрицы М в теореме 4.4.6.
Остается лишь проверить, что данное выражение для
W удовлетворяет уравнению (1). Эту выкладку мы опу-
скаем.
От матрицы W легко перейти к матрице дисперсий
{Df[f/]}. Обозначим эту матрицу через М2. Тогда М2 —
= W — M8q.
Определим дисперсии в примере со страной Оз. Мы
уже вычислили раньше матрицы М, D и Z для этой
цепи, так что для нахождения W нам потребуется толь-
ко одна новая матрица ZM. Она равна
/ 176 73 303 259 2/з
Z-M = 775(203 363 203
\2597з 303 176 7з
Теперь по формуле
W = М (2ZdgD — I) + 2(ZM — E (ZM)dg)
получаем
/776 26
Г = 4% 37
\54/з 28
7з\
7з •
7,/J
112
ГЛ. IV. РЕГУЛЯРНЫЕ ЦЕПИ МАРКОВА
Вычитая из этой матрицы матрицу MS(I, находим М2:
/6712 12 % \
м2= 12 .
\62А 12 67/12/
Отметим, что в этом примере дисперсии Diffj] очень
слабо зависят от выбора начального состояния. Мо-
менты первого достижения для регулярной цепи Мар-
кова по целому ряду свойств вполне аналогичны вре-
менам поглощения для поглощающих цепей. В частно-
сти, и в том и в другом случае дисперсии, как правило,
велики по сравнению со средними.
Формулы для W и М2 заметно упрощаются, если мы
имеем дело с процессом независимых испытаний.
4.5.4. Теорема. Для процесса независимых испыта-
ний
W = ED{2D-I) = {{\/Pii){2/Pii-l)}
И М2 = £(О2-/)) = {(1/А./)2-1/рг/).
Доказательство. Вспомним, что в рассматриваемом
случае Z — единичная матрица и М = ED. Поэтому в
силу теоремы 4.5.3
W = ED {2D - /) + 2 {ED - ED) = ED {2D - /).
Отсюда получается
М2 = W - Msq = 2ED2 -ED- {ED)sq = E{D2- D).
Другие представления для W и M2f приведенные в фор-
мулировке теоремы, следуют из того, что Pij = р^ при
любом L
4.6. Предельная ковариация. Пусть f и g— две функ-
ции, определенные на множестве состояний регулярной
цепи. Обозначим для краткости f{Si) = fi и g{Si) = gt.
Пусть и g(n} — значения этих функций на n-м шагу.
Мы хотим найти
lim - Кя
п 31
п. оо
~ П П
~/г=1 fe=l
Можно показать, что этот предел существует и не зави-
сит от л.
4.6. ПРЕДЕЛЬНАЯ КОВАРИАЦИЯ
113
4.6.1. Теорема.
где
lim
ft->oo
— Кя
п л
п п
2>>,
~/г=1 fe = l
= S ficagb
i. /=1
Сц = + cijZji - - ataj.
Доказательство. Мы примем без доказательства не-
зависимость предела от начального распределения и до-
кажем теорему только для случая л = а. Имеем
Ма
_fe=l
= П 2 a{fi
i = l
и
Стало быть,
п 1 г
2 g{k) = п^ atgj.
л=1 / = 1
n n
^g(k)
n
= -ма
п а
' \fe=i
n
n r
^g^-n^ajg!
= 7 Ма ^g(l} - « S fW S ~
Ц=1 z=i
/г=1
^=1
п п
nr r
-n^g^^aifi + n2 aiaifigi =
Z = 1 Z=1 i, / = 1
n r
"IS S (W-1A«y>-l]/,g,~
k, l=\ i, / = !
- P« [«'?* = П ffijg, - P [UT = !] g^ifi + ага/^/) =
n r
-IS S <>)
k, 1 = 1 i, j=l
Ho a(^~k\ k<l,
Pa[«<« = 1 Д uf = 1] = ajPfr>\ k>l, (2)
8 Дж. Кемени. Дж. Снелл
114
ГЛ. IV. РЕГУЛЯРНЫЕ ЦЕПИ МАРКОВА
Поэтому из (1) и (2) мы получаем
I На |s f{k\ S £(Z)] =4 S S +
Ц-i /=i J ц-i k<i
r r
+7 S aif^i 2 (PTrl)~ai)+ S (аА/“аЛ)^г
I, / = 1 k>l i, / = 1
Собирая члены с одним и тем же d = \l — fe |, получаем
г п~ 1
г,/ = 1 d=\
И__/ М) __
п
г п — 1 г
+ S S (аА/-«м
Z,/ — 1 d—1 i, / —1
Так как ряд Z = У (Р — A)d сходится, то он суммируем
d=0
по Чезаро (см. 1.10), так что
Значит,
п-1
Z = lim У ^-{Ра-А\
п^°° d=0 П
м-1
Z-l= lim У-^-^-Л),
d=i
n-l
Zij - 6Z/ = lim У -^4 (A? - a '
n -> 00 “ H
d— I
Поэтому из (3) вытекает
n n
z=i
lim7Ka 2^* =
= У [aifigr/(2z/-6i/)+a/Ag/(z/z-di/) + (aA/-ala/)fI^ =
/,/=1 r
Доказательство завершено.
4.6. ПРЕДЕЛЬНАЯ КОВАРИАЦИЯ
115
Если f и g— одна и та же функция, то приведенная
выше теорема позволяет установить
4.6.2. Следствие.
П->оо
= S Mi-
Нам понадобится некоторое усиление этого послед-
него результата. Предположим, что f не просто функ-
ция от состояния, но что в состоянии Si с вероятно-
стью fi эта функция равна I и с вероятностью I—fi
она равна 0. Можно представлять себе функцию f сле-
дующим образом: мы наблюдаем за цепью Маркова и,
когда в данный момент времени процесс попадает в si9
мы подбрасываем несимметричную монету (вероятность
герба — fi), чтобы определить равно ли f 0 или I. Пусть
снова — значение функции на п-м шагу. Тогда все
рассуждения относительно предельной ковариации, при-
веденные выше, проходят без изменений, за исключе-
нием небольшого исправления в формуле (I) при k — I.
Здесь член надо заменить просто на fi, и мы полу-
чаем дополнительный член
1=1
Итак, доказана
4.6.3. Теорема. Если f — функция, принимающая в
состоянии Si значения 1 и 0 с вероятностями fi и 1 — fi,
то
Результаты распространяются и на две функции та-
кого рода. Если их значения в каждом состоянии вы-
бираются независимо друг от друга, то доказательство
теоремы 4.6.1 проходит без изменений. Итак, установ-
лена
4.6.4. Теорема. Если f и g—две функции, прини-
мающие в Si с вероятностями fi и gi независимо
8*
116
ГЛ. IV. РЕГУЛЯРНЫЕ ЦЕПИ МАРКОВА
друг от друга значение 1, а в противном случае прини-
мающие значение 0, то
Одно из приложений ковариации состоит в том, что
через нее выражается коэффициент корреляции. Пусть
f и g— те же функции, что в предыдущей теореме.
4.6.5. Определение.
Рл
• D
п
7 = 1
Поделив числитель и знаменатель на п и исполь-
зуя 4.6.1 и 4.6.2, получаем, переходя к пределу, следую-
щий результат. .
4.6.6. Теорема.
^(/) =
Другое важное применение теоремы 4.6.1 состоит в
следующем. Пусть А и В— два множества состояний.
Пусть и времена пребывания в множест-
вах А и В за первые п шагов. Относительно этих функ-
ций справедлива следующая теорема.
4.6.7. Теорема.
д™ №]= 2 сч-
S ; €= А
Sj^A
Доказательство. Пусть f — функция, равна 1 на мно-
жестве А и 0 — вне него и, аналогично, g — функция,
4.6. ПРЕДЕЛЬНАЯ КОВАРИАЦИЯ
117
равная 1 на состояниях из В и 0 —вне В. Тогда
л fe=l /=1
и остается применить теорему 4.6.1.
Из предыдущего результата вытекает
4.6.8. Следствие.
Нш Р„[^> !#>]= 7--...
Если в качестве А и В взять множества, состоящие
из одного элемента, ’то получится, что представляет
предельную ковариацию для чисел попаданий в состоя-
ния Si и Sj за первые п шагов. Величина сц — это пре-
дельная дисперсия для числа попаданий в состояние s{.
Часто представляют интерес только эти дисперсии. Обо-
значим составленный из них вектор через £. Предельная
корреляция для чисел попаданий в и sj равна
си
- , При i = j эта корреляция обращается в 1.
V спсц
Для процесса независимых испытаний а} = —
— atOj, и все формулы, приведенные выше, упрощаются.
Например, если i =# /, то предельная корреляция равна
~'а1а! а1а1
('-“/) ' 0 “ “/) 0 “ ai) ’
Диагональные элементы матрицы С, т. е. предельные
дисперсии, имеют следующее важное применение. Пусть
р = {6J = Вектор р —это вектор предельных дис-
персий для чисел попаданий в каждое состояние. Ком-
поненты этого вектора используются в следующей глу-
бокой теореме (так называемая центральная предель-
ная теорема для цепей Маркова).
4.6.9. Теорема. Пусть задана эргодическая цепь, и
yW — число попаданий в состояние Sj за первые п шагов,
a ai = {а3} и р = {^} — соответственно неподвижный
118
ГЛ. IV. РЕГУЛЯРНЫЕ ЦЕПИ МАРКОВА
вероятностный вектор *) и вектор предельных дисперсий.
Тогда, если bj =# 0, то для любых двух чисел г < s
1
•> г___
/2л
х2
е 2 dx
при п-*оо, каково бы ни было начальное состояние k.
Доказательство этой теоремы выходит за рамки на-
стоящей книги и приводится только в более специаль-
ных монографиях по теории вероятностей. Впрочем, для
случая независимых испытаний эта теорема обсуж-
дается в FMS (гл. III). Интеграл, стоящий в правой
части, не выражается через элементарные функции.
С иллюстративными целями приводим его приближен-
ные значения при отдельных г и s. Если г = —1, s = I,
он равен 0,681, при г = —2, s = 2 его значение рав-
но 0,934 и при г = —3, s = 3 он равен 0,997.
Пример. Рассмотрим снова пример со страной Оз.
Б этом случае, как мы нашли ранее,
а = (2/5, ’/б,2Д)
R N S
/ 86 3
Z='/75 б 63
\ -14 3
Этой информации достаточно для вычисления матрицы
С = {tij}- Произведя выкладки, получаем
R N S
/ 134 -18 -116\R
С = 1/з75( 18 36 - 18 I1V.
\ —116 -18 134/S
Диагональные элементы матрицы С дают нам пре-
дельные дисперсии р = {134/з75. 36/з75. |34/з75) Для времен
!) Существование и единственность вектора а в данной главе
были yci ановлены только для регулярных цепей. Для произвольной
эргодической цепи это доказывается в теореме 5.1.2. (Прим, ред.)
4.7. СРАВНЕНИЕ ДВУХ ПРИМЕРОВ
119
пребывания в каждом состоянии. Поэтому применима
центральная предельная теорема и она утверждает, что,
скажем, случайная величина
- п/5
V (36/^)П
при больших п имеет приближенно нормальное распре-
деление. Исходя из этого, мы можем, например, оценить,
что число ясных дней среди 375 дней отличается от
75 больше, чем на 12, с очень маленькой вероятностью
(«0,046).
Предположим, что нас интересует только хорошая
или только плохая погода. Тогда мы могли бы рассмот-
реть времена пребывания процесса в множествах
41 = {/?, S} и А2 = {W}. Пусть ^- — предельная ковариа-
ция для чисел попаданий в эти множества. Теоре-
ма 4.6.7 показывает, что матрицу С = {^} можно полу-
чить, просто складывая соответствующие элементы мат-
рицы С. Например,
с12 = + <?sn = ~ 18/375— 18/375 = —36/375 = - 12/125,
41 42
Я __ / 12/125
"" J I _ 12/ 12/ •
Л2\ /125 /125 /
Нетрудно проверить, что суммы по строкам матри-
цы С должны равняться 0. Так как С симметрична, го
это же верно и для столбцов. Для матрицы размерно-
сти 2X2 отсюда следует, что все ее элементы равны
по абсолютной величине. Итак, можно было заранее
предвидеть, что матрица С имеет тот специальный вид,
который у нас получился.
4.7. Сравнение двух примеров. В этом пункте мы
сравним основные численные характеристики двух ре-
гулярных цепей Маркова с одним и тем же предельным
распределением. Одна из них — процесс независимых
испытаний, а другая — цепь общего вида, с зависимыми
испытаниями. Оба эти примера взяты из главы II. Один
из них — случайное блуждание примера 3 с р = V2 (мы
120
ГЛ. IV. РЕГУЛЯРНЫЕ ЦЕПИ МАРКОВА
условились называть это примером За), другой — при-
мер 7. Переходная матрица в примере За равна
«1 S2 «3 S4 «5
0 0 1 0 0
S2 v2 0 >/2 0 0
<п GO II Ом 0 */2 0 '/2 0
«4 0 0 */2 0 >/2
S5 0 0 1 0 0
Переходная матрица примера 7 имеет вид
S2 «3 S4 «5
0,1 0,2 0,4 0,2 0,1
S2 0,1 0,2 0,4 0,2 0,1
P = s3 0,1 0,2 0,4 0,2 0,1
«4 0,1 0,2 0,4 0,2 0,1
S5 0,1 0,2 0,4 0,2 0,1
Предельное распределение для каждого из этих двух
цепей одно и то же: а = {0,1; 0,2; 0,4; 0,2; 0,1}. По-
этому по закону больших чисел можно ожидать, что в
обоих случаях примерно одна десятая часть времени бу-
дет проводиться в «1, две десятых —в s2, и т. д.
Для регулярной цепи Маркова фундаментальная
матрица определяется формулой Z = (/ — Р + А )~1.
Проводя вычисления для примера За, получаем
«1 0,88 S2 -0,04
S2 0,33 0,86
Z = S3 -0,02 0,16
*4 -0,17 -0,14
S5 -0,12 -0,04
«3 «4 S5
0,32 -0,04 -0,12
0,12 -0,14 -0,17
0,72 0,16 -0,02
0,12 0,86 0,33
0,32 -0,04 0,68
Для процесса независимых испытаний фундамен-
тальная матрица Z—единичная матрица. Значит, в
примере 7 Z = /.
4.?. СРАВНЁНЙЕ ДВУХ ПРЙМЕЁОЙ
121
Первые сведения, которые мы получаем из матри-
цы Z, относятся к временам пребывания в каждом из
состояний за начальные п шагов. Пусть yW — время,
проведенное в состоянии Sj на протяжении первых п
шагов (с учетом начального положения). Тогда соглас-
но теореме 4.3.4
В случае независимых испытаний вместо стрелки нужно
поставить знак равенства. Для зависимого случая эле-
менты позволяют сравнить по величине средние
М.[у<га)] при фиксированном Sj и разных начальных со-
стояниях Так, скажем, в примере За £ц > ^21 > Z31 >
> Z51 > Z41, и поэтому при больших п
м, ЙЧ > мдй’] > М3 до>] > м5 до>] > м4 До”].
Тот факт, что, начиная из S5, процесс побывает в Si
в среднем чаще, чем начиная из s4, можно было бы
усмотреть и из того, что для достижения Sj как из s4,
так и из S5 нужно обязательно пройти через s3. Но из
состояния s5 первый шаг сразу же ведет в s3, а в со-
стоянии s4 есть две возможности — либо s3, либо s5.
Матрица_Z позволяет найти и предельные дисперсии
для y^fVn. Они определяются формулой
₽ ={0/(22// - 1 - Я/)}.
В примере За мы имеем
Р = (0,066, 0,104, 0,016, 0,104, 0,066).
Для независимых испытаний р = {аД1 —а^)}, так что
в примере 7
Р = (0,09, 0,16, 0,24, 0,16, 0,09).
В случае независимых испытаний дисперсия каждой
компоненты больше, чем соответствующая дисперсия в
зависимом случае, а дисперсия для состояния $3 суще-
ственно больше. Это значит, что относительно величины
у{£} в примере За можно сделать более точный прог-
ноз, чем в примере 7. Например, центральная предель-
ная теорема говорит нам, что за 1000 шагов в примере
122
ГЛ. IV. РЕГУЛЯРНЫЙ ЦЁПЙ МАРКОВА
За число попаданий в $3 с вероятностью 0,95 будет
отличаться от 400 не более чем на 2 ^/1000 • 0,016 =8.
В примере же 7 с той же самой вероятностью можно
лишь сказать, что время пребывания в $3 за 1000 шагов
отличается от 400 не более чем на 2 У1000 • 0,24 22.
Вычислим теперь матрицу ковариаций и некоторые
корреляции. В примере За имеем
0,066 0,042 -0,016 -0,058 -0,034
0,042 0,104 0,008 -0,096 -0,058
с = -0,016 0,008 0,016 0,08 -0,016
-0,058 -0,096 0,008 0,104 0,042
— 0,034 -0,058 -0,016 0,042 0,066
Предельные корреляции между и каждым из пяти
состояний равны (приближенно): (1,00,4-0,51,—0,49,
—0,70, —0,52).
В примере 7 матрица ковариаций равна
0,09 -0,02 -0,04 -0,02 -0,01
-0,02 0,16 -0,08 -0,04 -0,02
-0,04 -0,08 0,24 -0,08 -0,04
-0,02 -0,04 -0,08 0,16 -0,02
-0,01 -0,02 -0,04 -0,02 0,09
Предельные корреляции между и другими состоя-
ниями равны (1,00,—0,17,—0,28,—0,17,—0,11).
Следует ожидать, что предельные корреляции между
временами пребывания в двух различных состояниях
чаще всего будут отрицательны, так как, вообще го-
воря, чем больше времени процесс находится в одном
состоянии, тем меньше времени он проводит в другом.
Для процесса независимых испытаний все корреляции
для пар различных состояний отрицательны, хотя и не-
велики. Однако в примере За корреляции заметно
больше и корреляция между состояниями Si и поло-
жительна.
Изучим теперь функции дающие число шагов, за
которые впервые достигается состояние sj. Средние
4.7. СРАВНЕНИЕ ДВУХ ПРИМЕРОВ
123
м i[fj] даются матрицей М = (I— Z + EZdg). В при-
мере За S] S2 S3 «4 S5
«1 10 4,5 1 4,5 10
«2 5,5 5 1,5 5 10,5
Al = s3 9 3,5 2,5 3,5 9
«4 10,5 5 1,5 5 5,5
®5 10 4,5 1 4,5 10
Для процесса независимых испытаний формула, опре-
деляющая М, проще: М — ED. В примере 7
Si s2 S3 s4 S5
«I 10 5 2,5 5 10
S2 10 5 2,5 5 10
M = s3 10 5 2,5 5 10
«4 10 5 2,5 5 10
S5 10 5 2,5 5 10
В случае независимых испытаний среднее время до-
стижения состояния Sj не зависит от начального состоя-
ния. В зависимом случае это неверно. Действительно,
математическое ожидание времени достижения состоя-
ния $i, исходя из $2, почти в два раза меньше, чем
исходя из любого другого состояния. Заметим, что сред-
ние времена возвращения МЯМ одинаковы в обоих при
мерах. Это связано с тем, что такие средние опреде
ляются только вектором а.
Дисперсии ОЯЛ] задаются матрицей
М2 = М (2ZdgD -1) + 2 (ZM-E (ZM)dg) - Msc.
В примере За Sl s2 S3 s4 s5
si 66 123/4 0 123/4 66
S2 53 >/4 13 74 13 66 74
= 66 123/4 74 123/4 66
«4 66>/4 13 74 13 53‘/4
S5 .66 123/4 0 123/4 66
124
ГЛ. IV. РЕГУЛЯРНЫЕ ЦЕПИ МАРКОВА
В случае независимых испытаний формула для М? при-
водится к виду M2 = E(D2 — D). В примере 7
S] s2
®i
«2
Л1г =
«4
$5
90
90
90
90
90
20
20
20
20
20
$3 $4 S5
15/4 20 90
15/4 20 90
15/4 20 90
15/4 20 90
15/4 20 90
Точно так же, как и средние, дисперсии в случае не-
зависимых испытаний не зависят от начального поло-
жения. Однако, в отличие от средних, и в зависимом
случае примера За дисперсии почти не зависят от на-
чального состояния. Отметим, наконец, что для момен-
тов первого достижения fj, так же как для случайных
величин у^, дисперсии в независимом случае больше,
чем в зависимом.
4.8. Общая цепь с двумя состояниями. В этом пункте
мы найдем основные величины для цепи из примера 11
главы II, нужные для дальнейших ссылок. Напомним,
что это — общая марковская цепь с двумя состояниями.
Ее переходная матрица имела вид
/ 1 — с с \
Р = \ d l-dj’
Мы считаем, что 0 < с 1 и 0<d41, но с и d не
равны 1 одновременно. Это дает нам самую общую ре-
гулярную цепь с двумя состояниями.
Предельный вектор а равен
/ . с \
\с + d 9 с + d)
Фундаментальная матрица Z = (/ — Р + Л)-1 равна
1 j с + d
c + d I , d
\d~7+d
C c + d
4.8. ОБЩАЯ ЦЕПЬ С ДВУМЯ СОСТОЯНИЯМИ
125
Матрица средних времен первого достижения
с + d
1
d.
_1_
С
с + d
с
а матрица дисперсий времен первого достижения
(с (2 — с — d) 1 — с \
1 — d d(2-c-d) Г
d2 с2 /
Предельные дисперсии для времен пребывания в состоя-
ниях задаются вектором
□ _ / cd (2 — с — d) cd (2 ~ с — d) \
Р”\ (c + d)3 1 (c + d)3 Г
Сравним эти дисперсии с теми, которые получаются
для процесса независимых испытаний, имеющего то же
предельное распределение. Такой процесс имеет пере-
ходную матрицу
d
с -J- d
d
c + d
с
c + d
с
c + d
и предельные дисперсии для времен пребывания в со-
стояниях Sj у него равны
__ / cd cd \
P~[(c + d)2 ’ (c + d)2/
Отсюда видно, что предельная дисперсия для вре-
мени пребывания в Sj в зависимом случае будет больше
тогда и только тогда, когда
2 — с — d> с + d,
т. е. когда сумма диагональных элементов переходной
матрицы больше суммы двух других элементов. Иными
словами, когда сумма вероятностей остаться в старом
состоянии больше суммы вероятностей изменить поло-
жение.
126
ГЛ. IV. РЕГУЛЯРНЫЕ ЦЕПИ МАРКОВА
Матрица ковариаций имеет вид
r=cd(2-c-d){ 1
(c + dy l-l
-П
1/
Значит, Cij > 0 при i = j и Сц < 0 при i =# /. Предельные
корреляции в этих двух случаях равны соответствен-
но + 1 и — 1.
УПРАЖНЕНИЯ К ГЛАВЕ IV
К 4.1
1. Найдите предельную матрицу А в примере 13 (см. упражне-
ние 23 главы II).
2. Найдите предельную матрицу А в примере 14 (см. упражне-
ние 24 главы II).
3. Покажите, что цепь с четырьмя состояниями из примера 12
регулярна. Найдите неподвижный вектор а. Как связан этот вектор
с неподвижным вектором цепи с лвумя состояниями, из которой
была получена наша цепь?
4. Покажите, что если а — неподвижный вероятностный вектор
для цепи с переходной матрицей Р, то он также неподвижен и для
цепи с переходной матрицей Рп.
5. Докажите, что если у переходной матрицы суммы элементов
по столбцам равны 1, то все компоненты неподвижного вектора рав-
ны между собой.
6. Пусть дан вероятностный вектор а с положительными компо-
нентами. Постройте регулярную переходную матрицу, для которой
этот вектор был бы неподвижным.
К 4.2
7. Найдите математическое ожидание и дисперсию времени пре-
бывания в состоянии $i за первые п шагов в примере 14.
8. Рассмотрим цепь Маркова с переходной матрицей
$1 Sj
»?>/<• ч
S2V/2 '/J'
Пусть процесс начинается в состоянии s2. Посчитайте среднее значе-
ние v\n) при п = 1, 2, 3, 4, 5, 6. Результат сравните с Яь
К 4.3
9. Найдите фундаментальную матрицу для примера 11 при
с = V2 и d = ’/4-
10. Найдите предел разности между математическими ожида-
ниями числа ясных дней в стране Оз на протяжении первых п дней
УПРАЖНЕНИЯ К ГЛАВЕ IV
127
при двух различных условиях: в первый день игл дождь и в пер-
вый день было ясно.
11. Найдите фундаментальную матрицу для цепи из упражнения
8 (см. выше). Каков смысл разности гц — z2i?
12. Найдите фундаментальную матрицу в примере 14 (восполь-
зуйтесь результатом упражнения 2, см. выше).
13. Найдите фундаментальную матрицу в примере 13 (восполь-
зуйтесь результатом упражнения 1, см. выше).
К 4.4
14. Найдите матрицу средних времен достижения для примера 14
(воспользуйтесь результатом упражнения 12, см. выше).
15. Найдите матрицу средних времен достижения для примера
13 (воспользуйтесь результатом упражнения 13, см. выше).
16. Проверьте на примере 13 теоремы 4.4.9 и 4.4.10.
17. Докажите, что для процесса независимых испытаний все
строки матрицы М совпадают.
18. Известно, что матрица математических ожиданий времен пер-
вого достижения некоторой цепи имеет вид
/ х 2 6 \
М = ( 4 х 4 J.
\6 2 х/
Найти переходную матрицу цепи.
19. Укажите две различные переходные матрицы, имеющие одну
и ту же фундаментальную матрицу, и покажите тем самым, что фун-
даментальная матрица не определяет переходную матрицу одно-
значно.
20. Докажите, что суммы элементов по столбцам матрицы Р по-
стоянны тогда и только тогда, когда постоянны суммы по строкам
матрицы М.
К 4.5
21. Найдите М2 в примере 14.
22. Воспользовавшись результатом упражнения 15 (см. выше),
найдите М2 в примере 13.
23. Найдите М2 в примере 11 при с = 1/2 и d = 1/4.
24. Несколько раз подбрасывается игральная кость. Найдите ма-
тематическое ожидание и дисперсию числа бросаний между двумя
появлениями шестерки.
25. Найдите математические ожидания и дисперсии времен пер-
вого достижения для цепи из упражнения 8 (см. выше).
К 4.6
26. Найдите матрицу предельных ковариаций для примера 11
при с = V2 и d = V4.
27. Найдите матрицу предельных ковариаций для примера 13.
Истолкуйте диагональные элементы.
128
ГЛ. IV. РЕГУЛЯРНЫЕ ЦЕПИ МАРКОВА
28. Житель страны Оз берет с собой зонтик в ясный день с ве-
роятностью 1/2, в дождь — с вероятностью 1 и в снег — с вероят-
ностью 3/4. Найдите предельную дисперсию для числа дней, когда
он берет зонтик.
29. Дана поглощающая цепь. Пусть rij — время пребывания в со-
стоянии Sj до поглощения. Используя метод доказательства теоремы
4.6.1, покажите, что
мй [«г»/]=Vii+nkinu+&anki’
где N = {«i j} — фундаментальная матрица. Найдите КД/if, яj] и
Ол[пТ
К 4.8
30. Найдите предельную дисперсию для времени пребывания в
данном состоянии при с = d. Как меняется результат при измене-
нии с? В частности, что получится при с—>0?
31. Найдите предельное распределение и матрицу средних вре-
мен достижения для случая, когда с =2d. Как меняется результат
с изменением с? Интерпретируйте его при с~->0.
Ко всей главе
32. Рассмотрим следующую переходную матрицу цепи Маркова:
/72 7з 7б\
Р= 3/4 0 74 .
\ о 1 о /
(а) Регулярна ли цепь?
(Ь) Найдите а, А и Z.
(с) Найдите М и М2.
(d) Найдите матрицу ковариаций.
(е) Пользуясь методами поглощающих цепей, найдите матема-
тическое ожидание времени первого достижения состояния sb ис-
ходя из s3.
Проверьте результат, сравнив его с (с).
33. Пусть Р\ и Р2— две различные переходные матрицы для це-
пей с тремя состояниями. Случайно выбирается одна из этих матриц
и наблюдается получившаяся цепь (скажем, матрица Л выбирается
с вероятностью р).
(а) Является ли этот процесс марковской цепью?
(Ь) Покажите, что вероятности находиться в данном состоя-
нии стремятся к некоторым пределам. Как связаны предельные ве-
роятности с неподвижными векторами матриц Pi и Р2?
34. Предположим, что в упражнении 33 после каждого шага
применяется случайный выбор, который решает, какая матрица ис-
пользуется на следующем шагу.
(а) Является ли этот процесс марковской цепью?
(Ь) Покажите, что предельные вероятности пребывания в раз-
личных состояниях, вообще говоря, не совпадают с теми, которые
получились в упражнении 33 (Ь).
ГЛАВАХ/
ЭРГОДИЧЕСКИЕ ЦЕПИ МАРКОВА
5.1. Фундаментальная матрица. Мы обобщим теперь
результаты, полученные в предыдущей главе для регу-
лярных цепей, на произвольную цепь, состоящую из
одного эргодического множества, т. е. на произвольную
эргодическую цепь. Нам известно, что такая цепь дол-
жна быть либо регулярной, либо циклической. Цикли-
ческая цепь состоит из d циклических классов, и ре-
гулярную цепь можно мыслить как ее частный случай,
получающийся при d = 1. Излагаемые далее результаты
будут обобщением прежних в том смысле, что при d = 1
они будут сводиться к результатам предыдущей главы.
На самом деле в большинстве этих результатов d явно
не участвует, и поэтому они просто переносятся с регу-
лярных цепей на все эргодические.
Эргодическая цепь характеризуется тем, что она со-
стоит из одного эргодического класса, т. е. что можно
перейти из каждого состояния в любое другое. Но если
d>l, то такие переходы возможны только при неко-
торых специальных значениях числа шагов п. Таким
образом, никакая степень матрицы Р не является по-
ложительной матрицей, и различные степени содержат
нули на разных местах. С увеличением степени распо-
ложение этих нулей циклически повторяется. Следова-
тельно, последовательность Рп не может сходиться.
В этом и состоит основное различие между цикличе-
скими и регулярными цепями.
Но хотя последовательность степеней Рп не сходится,
имеет место следующий более слабый результат.
5.1.1. Теорема. Для любой эргодической цепи после-
довательность степеней Рп суммируема по Эйлеру к
предельной матрице А, и эта предельная матрица имеет
вид А = |а, где а — положительный вероятностный
вектор,
9 Дж. Кемени, Дж. Снелл
13^
ГЛ. V. ЭРГОДИЧЕСКИЕ ЦЕПИ МАРКОВА
Доказательство. Рассмотрим матрицу (&/+(!—k)P)
при некотором k, 0<&<1. Эта матрица снова яв-
ляется переходной матрицей. Она также задает эргоди-
ческую цепь, так как имеет положительные элементы на
всех тех же местах, что и Р. А поскольку, кроме того,
и диагональные элементы этой матрицы положительны,
то в каждое состояние можно возвратиться за один шаг
и, следовательно, d= 1. Таким образом, новая цепь яв-
ляется регулярной.
Из 4.1.4 следует, что (&/ + (!—k)P)n стремится
к матрице А == ga, где а — некоторый вероятностный
вектор. Таким образом,
А = lim (kI + (l-k)P)n,
П->оо
А = lim
гг->оо
Р‘.
1=0
(1)
Но последнее равенство в точности означает, что после-
довательность Рп суммируема по Эйлеру к А (см. 1.10),
причем суммируема при каждом значении k.
5.1.2. Теорема. Если Р — эргодическая переходная
матрица, а А и а такие же, как в теореме 5.1.1, то
(а) Для любого вероятностного вектора л последо-
вательность пРп суммируема по Эйлеру к а.
(Ь) Вектор а является единственным неподвижным
вероятностным вектором матрицы Р.
(с) РА = АР = А.
Доказательство. Умножая (1) на л, убеждаемся, что
предел последовательности лРп в смысле Эйлера равен
лА = л£а, что и доказывает (а).
Поскольку вектор а был получен из предельной мат-
рицы для (&/4-(1—k)P), являющейся регулярной пе-
реходной матрицей, то он будет ее единственным не-
подвижным вероятностным вектором. Но матрица
(kl + (1 — k)P) должна иметь те же неподвижные век-
торы, что и Р, так как из соотношения
л(й/ + (1— k)P)= л
следует, что
л(1—£)/> = л(1—ft),
5.1. ФУНДАМЕНТАЛЬНАЯ МАТРИЦА
131
и поскольку k ¥= 1, то пР = л. Тем самым доказано (Ь>.
Утверждение (с) следует из того, что Pg = g для любой
переходной матрицы и что аР = а.
Таким образом, мы видим, что в случае эргодиче-
ских цепей Лиа обладают почти теми же самыми свой-
ствами, что и в случае регулярных цепей, только в (а)
вместо обычной сходимости утверждается более слабое
свойство — суммируемость по Эйлеру. Покажем теперь,
что эргодические цепи имеют фундаментальную матрицу,
которая ведет себя совершенно так же, как и фундамен-
тальная матрица регулярных цепей.
5.1.3. Теорема. Если Р — эргодическая переходная
матрица, то обратная матрица Z = (I + (P— Л))-1 су-
ществует и
(a) PZ = ZP.
(b) Zg = g.
(с) aZ = a.
(d) (/ —P)Z = 7 —A.
Доказательство. Так как на основании 5.1.1 после-
довательность Рп суммируема по Эйлеру к Л, и в си-
лу 5.1.2 (с) (Р — Л)П = РП — А, то последовательность
(Р — А)п суммируема по Эйлеру к 0. Следовательно,
обратная матрица Z существует (см. 1.11) и ряд
оо
У+ЗСР'-Д) (2)
суммируем по Эйлеру к Z. Теперь для доказательства
(Ь) и (с) достаточно заметить, что /| = £, а/ = а и что
при умножении Pj— А на 2 справа или на а слева по-
лучается 0. Для доказательства (d) нужно умножить (2)
на I — Р.
До сих пор нам было достаточно суммируемости Рп
по Эйлеру, в дальнейшем же понадобятся следующие
более сильные результаты.
5.1.4. Теорема. Если Р — эргодическая переходная
матрица, то
(а) Последовательность Pri суммируема по Чезаро
к А.
оо
(Ь) Ряд /+ ^(Р‘ — А) суммируем по Чезаро к Z
9*
132
ГЛ. V. ЭРГОДИЧЕСКИЕ ЦЕПИ МАРКОВА
Доказательство. Если п = kd, то, начиная из со-
стояния Si, через п шагов мы должны оказаться в со-
стоянии того же циклического класса, которому принад-
лежит Si. И если k достаточно велико, то можно ока-
заться в любом состоянии этого класса. Поэтому Pd
можно рассматривать как переходную матрицу марков-
ской цепи с d отдельными эргодическими множествами,
ни одно из которых не циклично. Следовательно, Pkd
стремится к предельной матрице 40, элемент которой
с индексом ij равен 0, если $г- и Sj не принадлежат
одному и тому же циклическому классу, и получается
перенормировкой из компонент вектора а, принадлежа-
щих соответствующему циклическому классу, в против-
ном случае.
Если 0 / < d, то Phd+i стремится к PlAQ при k, стре-
мящемся к бесконечности. Поэтому последовательность
Р" состоит из d сходящихся подпоследовательностей и,
следовательно (см. 1.10), Рп суммируема по Чезаро к
среднему от их пределов. Но два различных метода
суммирования последовательностей не могут давать
различные ответы. Поэтому А и должно быть этим сред-
ним, т. е.
rf-i
z=o
и Рп суммируема по Чезаро к А. Отсюда сразу следует,
что Р1’— А суммируема по Чезаро к 0, и потому вы-
полняется (Ь).
Переформулируем (Ь) в виде обычного предела.
5.1.5. Следствие.
/ + lim 4) = Z.
П->оо П
Сумев обобщить многие важные свойства матрицы Z
на случай эргодических цепей и замечая, что при этом
нигде явно не входит d, мы можем теперь утверждать,
что многие результаты главы IV верны для всех эрго-
дических цепей. Это касается, в частности, всех свойств
матрицы средних времен первого достижения М и мат-
рицы дисперсий средних времен первого достиже-
5.1. ФУНДАМЕНТАЛЬНАЯ МАТРИЦА
133
ния М2, т. е. всех результатов из 4.4 и 4.5. Сохраняют
также свою силу результаты о предельных дисперсиях и
ковариациях из 4.6, так как при их доказательстве в
4.6.1 использовалась суммируемость соответствующего
ряда к Z только в смысле Чезаро (5.1.5). Поэтому все
основные формулы из 4.4, 4.5 и 4.6 можно применять к
любой эргодической цепи.
Стоит более подробно останови1ъся на результатах
4.4.12. Нам известно, что матрица М посредством фор-
мулы Р = (/ + (D — Е)М~') определяет переходную мат-
рицу любой эргодической цепи. В частности, по М мож-
но определить, является ли данная цепь циклической
или нет. Это совершенно неожиданный результат, и
было бы в высшей степени желательно найти необхо-
димые и достаточные условия того, что (I) М является
матрицей средних времен первого достижения некото-
рой эргодической цепи и (II) что М соответствует ре-
гулярной, а не циклической цепи. Хотелось бы,_чтобы
эти условия были проще, чем вычисление по М мат-
рицы Р и последующая ее проверка.
Какие свойства регулярных цепей мы пока не об-
общили? Главные из них — это геометрическая оценка
из 4.1.5, закон больших чисел из 4.2.1 и результа-
ты 4.3.4—4.3.6, касающиеся у\п}. Для их изучения не-
обходимо найти соответствующую верхнюю оценку для
Pi! иГ
Ясно, что в случае циклической цепи геометрическая
оценка 4.1.5 к этой разности неприменима, так как
часто будет обращаться в 0 и, следовательно, рассмат-
риваемая разность будет бесконечное число раз при-
нимать значение, равное по абсолютной величине aj.
Однако, используя идеи доказательства, приведенного
в 5.4.1, можно показать, что если прибавлять сразу по d
последовательных членов, т. е. рассматривать суммы
d—1
2 W/+Z)-a/)-
то для них будет иметь место геометрическая оценка.
Этого достаточно для доказательства закона больших
134
ГЛ. V. ЭРГОДИЧЕСКИЕ ЦЕПИ МАРКОВА
чисел, если в 4.2.1 в соответствующих местах поместить
сумму d последовательных членов. Рассмотренный ме-
тод позволяет также доказать аналоги результатов
4.3.4—4.3.6, но мы не станем этого делать.
5.2. Примеры циклических цепей. Самая простая ци-
клическая цепь получается из цепи с двумя состояниями
примера II при c = d=\. Назовем эту цепь приме-
ром На. Ее переходная матрица
Из доказательства теоремы 5.1.1 вытекает, что мат-
рицу А можно получить как предельную из матрицы
У2/ + Но последняя матрица сама является
для себя предельной. Отсюда
А = a = (V2, 72), ^ = 2,
( 3/2 -72\"’_/3/4 7Л
\-'/2 3/2/ "V/4 3/J’
Очень легко найти матрицу М непосредственно и
убедиться в том, что все элементы матрицы М2 равны 0.
Легко убедиться также в том, что равны нулю предель-
ные дисперсии.
В качестве менее тривиального примера рассмотрим
случайное блуждание 1?з примера 2 с р = ’/2 (назовем
это примером 2а). Здесь переходная матрица
®i
S2
P = s3
0 1 о
72 0 */2
О '/2 О
О о '/2
ООО
о о
о о
72 о
О 72
1 о
«4
®5
5.2. ПРИМЕРЫ ЦИКЛИЧЕСКИХ ЦЕПЕЙ
135
Начинаясь в состоянии с четным номером, этот про-
цесс может попадать в состояния с четными номерами
только через четное число шагов, а в состояния с не-
четными номерами — только через нечетное число ша-
гов. Поэтому состояния с четными и нечетными номе-
рами образуют два циклических класса. Вычисляя дру-
гие характеристики процесса, находим
а = (‘/в, ‘/4, ‘А, 74, */8),
23 18 -2 -14
9 22 2 -10
z = 'li6 -1 2 14 2
-7 - 10 2 22
-9 - 14 -2 18
-91
-7
-1
9
23
®i
®2
М = S3
®4
«5
Sl ®2 ®3 $4
8 1 4 9 16
7 4 3 8 15
12 5 4 5 12
15 8 3 4 7
16 9 4 1 8
si
S2
Л12 = ®з
®4
S5
112 0 8 48 160
112 24 8 48 160
152 40 8 40 152
160 48 8 24 112
160 48 8 0 112
Обратим внимание на некоторые элементы матриц М
и М2. Из каждого крайнего состояния можно попасть
в любое другое состояние только через состояние, со-
седнее с крайним. Поэтому элементы первой строки М,
за одним исключением, на 1 больше элементов второй
строки. То же самое справедливо для элементов пятой
и четвертой строк. Единственное исключение наблю-
дается для среднего времени первого достижения самого
состояния «4- Элементы третьей строки, за исключением
136
ГЛ. V. ЭРГОДИЧЕСКИЕ ЦЕПИ МАРКОВА
тех, которые соответствуют переходу в соседние состоя-
ния, равны среднему арифметическому элементов второй
и четвертой строк плюс 1.
В М2 стоит обратить внимание на равные элементы.
Некоторые из равенств вызваны симметрией процесса.
Но этим нельзя объяснить постоянство элементов
третьего столбца. Второй и четвертый элементы этого
столбца одинаковы вследствие симметрии. Остальные
три элемента равны 8, потому что, начиная из любого
состояния первого циклического множества, процесс
должен сначала попасть во второе циклическое множе-
ство, после чего дисперсия оказывается равной 8. На-
личие в матрице двух нулевых элементов объясняется
тем, что из крайнего состояния мы всегда за один шаг
переходим в соседнее состояние.
Интересная интерпретация средних столбцов мат-
риц М и М2 получится, если сделать состояние s3 по-
глощающим. Тогда процесс будет в основных чертах
подобен процессу, рассмотренному в 3.4.1 с р = '/2. По-
этому числа 3, 4 и 8 в этих столбцах совпадают с соот-
ветствующими элементами векторов т и тг, вычислен-
ными в 3.4.1.
Наконец, вычислим ковариационную матрицу
7 8 — 2 -8 -5
8 12 0 -12 -8
с — 7з2 -2 0 4 0 -2 •
-8 -12 0 12 8
1 -5 -8 — 2 8 7
Отсюда получаем предельные дисперсии
₽ = (7/з2, 3/s, 7s, 3/s, 7/зг)‘
Равенство нулю элементов с2з и с43 означает, что пре-
дельные корреляции между s2 и $3, и $4 и $3 равны 0.
С другой стороны, корреляция между и s2 равна
8/^84 «0,87. Этот результат легко объясняется видом
переходной матрицы.
5.3. Обращенные цепи Маркова. В 2.1 было пока-
зано, что марковский процесс, наблюдаемый в обратном
5.3. ОБРАЩЕННЫЕ ЦЕПИ МАРКОВА
137
порядке, тоже будет марковским с переходными вероят-
ностями
/ < Рл [fn-1 = 5/1 Рл [fn — fn-i — 5/1
РЙ’ ------------------------------
где fn — функция n-го исхода. Было также замечено, что
если прямой процесс является цепью Маркова, то обра-
щенный процесс будет цепью Маркова, только если ве-
роятность Pn\fn = sj] не зависит от п. Так будет в слу-
чае, когда обращенный процесс начинается со стационар-
ного распределения. В этом случае Pa[fn = sj = при
всех п и рц (п) принимает вид
5.3.1. Определение. Пусть Р — переходная матрица
некоторой эргодической цепи Маркова и а — ее непо-
движный вероятностный вектор. Тогда обращенной
цепью Маркова для Р называется цепь Маркова с пере-
ходной матрицей
P = {pll} = {~L] = DPTD~i.
Чтобы оправдать данное определение, нужно пока-
зать, что Р является переходной матрицей. В силу тео-
ремы 5.1.2 все а,- положительны, так что рц определены
и неотрицательны. Далее
Ь = DP^D~\ = DPrar = D (aP)T = DaT = |.
Следовательно, P — переходная матрица.
5.3.2. Определение. Цепь Маркова называется обра-
тимой, если Р = Р.
5.3.3. Теорема. Цепь Маркова обратима тогда и толь-
ко тогда, когда матрица D~XP симметрична.
Доказательство. Р = DPTD~'. Поэтому Р = Р тогда
и только тогда, когда
D-'P = PrD-1 = (D_1P)r,
т. е. тогда и только тогда, когда матрица D~'P симмет-
рична.
Обратимая марковская цепь со стационарным распре-
делением одна и та же как в прямом, так и в обратном
138
ГЛ. V. ЭРГОДИЧЕСКИЕ ЦЕПИ МАРКОВА
времени. Другой способ описания обратимости состоит
в следующем. Назовем процесс обратимым, если при
стационарном распределении для любых и Sj вероят-
ность следования Sj за совпадает с вероятностью сле-
дования Si за Sj, т. е. если для каждых п, s^ Sj
Ра [fn = si Л fn+l = $/] =# Ра [fn ~ Л fn+1 ~
Последнее равенство будет выполняться, если cttPij =
« cijPji или если pij = djPjilcii, т. е. если рц — рц для
всех i, j.
Очевидно, любая периодическая цепь с периодом,
большим 2, не может быть обратимой. В самом деле,
для такой цепи из состояния, в которое можно попасть
следующим шагом, нельзя за один шаг вернуться в пре-
дыдущее состояние. Таким образом, только цепи с пе-
риодом 1 и 2 могут быть обратимыми. Ясно, что если
цепь обратима, то ее период при обращении не ме-
няется.
В качестве примера обратимой цепи периода 1 рас-
смотрим пример со страной Оз. В этом случае матрица
R N S
/76 0 о\/*/2 *Л 7Л Н['/5 ‘/ю 7ю\
р-'р= о */5 0 ‘/2 о 72 710 0 710
\о о 2/5/\74 74 72/ s\7io 7ю 75/
является симметричной. Значит, по теореме 5.3.3 дан-
ная цепь обратима. Обратимую цепь с периодом 2 мы
имеем в примере 2а. В этом случае матрица
D"*P =
о 78 о о о
7в 0 7s 0 о
о 7в о 78 0
о 0 78 0 >/8
о о о 78 о
также является симметричной.
Займемся теперь вопросом, какие соотношения
имеются между данной эргодической цепью и связан-
ной с ней обращенной цепью. Мы найдем связь между
5.3. ОБРАЩЁННЫЕ ЦЕПИ МАРКОВА
139
их неподвижными векторами и фундаментальными мат-
рицами, а значит, между любыми зависящими от них
характеристиками. Для обращенной цепи матрицы А,
Z, М, ... будем обозначать A, Z, М, ...
5.3.4. Теорема. Неподвижные вероятностные векто-
ры матриц Р и Р совпадают.
Доказательство. Пусть <хР = а. Тогда aP=aDPTD~{ =
= т\РтD~{ = (РЮГ D~' = x\D~l = а.
5.3.5. Теорема. Z = DZTD~'.
Доказательство. Z = (/ — Р+ Л)”1.
Из вида матрицы А ясно, что А = DATD~l. Далее, из
теоремы 5.3.4 следует,’ что А = А. Таким образом,
Z = (/ - DPTD~' + ОАТО~1)~' =
= D (/ - Рт + Лг)~‘ Т>-1 = DZTD~'.
5.3.6. Теорема. Любая характеристика цепи, значе-
ние которой зависит только от Z&g и А, одинакова как
для прямого, так и для обращенного процесса.
Доказательство. По теореме 5.3.5 Zdg = ^dg, а в силу
5.3.4 А = А.
Доказанную теорему можно применять, например,
при вычислении для обращенной цепи среднего и дис-
персии времени первого достижения состояния sif если
процесс начинается из состояния в/ или если начальное
распределение задается вектором а. Предельная диспер-
сия относительного числа попаданий в любое состояние
также зависит только от Zdg и А. Следовательно, все эти
характеристики будут одинаковыми для прямого и об-
ращенного процессов. Новые примеры даются следую-
щей теоремой.
5.3.7. Теорема. С = С.
Доказательство, дц = + а^ — а$ц — ataj =
== ai (fljZjilai) + af (aiZijlai) - аД7 - a^ == afzfi + а^И - аД7 -
= C}].
Таким образом, все результаты для прямого процес-
са, зависящие только от матрицы ковариаций, сохра-
няются без изменений и для обращенного процесса.
140
ГЛ. V. ЭРГОДИЧЕСКИЕ ЦЕПИ МАРКОВА
5.3.8. Теорема. М - М = (ZD) - (ZD)T.
Доказательство. М — М = (/ — Z + EZds) D —
- (/ - Z + £Zdg) D = (Z - Z) Do.
Результат теоремы теперь следует из 5.3.5.
5.3.9. Теорема. W - W = (ZD -(ZD)T)(2ZdeD -3/) +
+ 2(Z2D-(Z2D)r).
Доказательство.
W - W = (М - М) (2ZdsD -/) +
+ 2 (ZtW — ZAf) — 2£(ZM — ZAf)dg, (1)
М - М = ZD - (ZD)T. (2)
Так как ZM = (Z-Z2+£Zdg)D и ZM = (Z-Z2+£Zdg)D,
то
ZM — ZM = (Z — Z) D + (Z2 — Z2) D =
= (ZD)r - (ZD) + (Z2D) - (Z2D)T. (3)
Поскольку полученное выражение представляет собой
разность между данной и транспонированной матрица-
ми, то матрица, стоящая в левой части равенства (3),
имеет нулевые диагональные элементы:
(ZJW-ZM)dg = 0. (4)
Объединяя (1), (2), (3) и (4), получаем утверждение
нашей теоремы.
Проиллюстрируем теперь применение доказанных вы-
ше теорем к необратимому процессу. Таким процессом
является случайное блуждание примера За. Здесь
»i
s2
Р = «з
«4
®5
о
*/2
о
0
0
§2 «3
0 1
о */2
'/2 0
0 72
0 1
S4 S5
о о
о о
72 о
о */2
0 0 J
5.3. ОБРАЩЕННЫЕ ЦЕПИ МАРКОВА
141
и а = (0,1; 0,2; 0,4; 0,2; 0,1). Отсюда находим
«1 0 1 0 0 0
®2 0 0 1 0 0
II <0. */4 7< 0 74 74
«4 0 0 1 0 0
ю со 0 0 0 1 0
Большинство значений элементов этой матрицы до-
пускает очевидную интерпретацию Например, когда рас-
сматриваемый прямой процесс попадает в состояние
он всегда приходит туда из $2,^ следовательно, р i2 = 1.
Неподвижным вектором для Р будет тот же вектор
а = (0,1; 0,2; 0,4; 0,2; 0,1).
В главе IV была найдена матрица Z для этого при-
мера:
®1 s2 S3 «4 «5
«1 0,88 -0,04 0,32 -0,04 -0,12
«2 0,33 0,86 0,12 -0,14 -0,17
Z — S3 -0,02 0,16 0,72 0,16 -0,02
«4 -0,17 -0,14 0,12 0,86 0,33
S5 -0,12 -0,04 0,32 -0,04 0,88
Отсюда находим Z = DZ D :
«1 s2 S3 «4 «5
«1 0,88 0,66 -0,08 -0,34 -0,12
s2 -0,02 0,86 0,32 -0,14 -0,02
Z = s3 0,08 0,06 0,72 0,06 0,08
«4 -0,02 -0,14 0,32 0,86 -0,02
S5 -0,12 -0,34 -0,08 0,66 0,88
142
ГЛ. V. ЭРГОДИЧЕСКИЕ ЦЕПИ МАРКОВА
Ранее мы нашли
«1
м = з3
«4
®5
S| S2 S3 S4 S5
10. 4,5 1 4,5 10
5,5 5 1,5 5 10,5
9 3,5 2,5 3,5 9
10,5 5 1,5 5 5,5
10 4,5 1 4,5 10
Отсюда получаем М = М + (ZD—(ZD)T);
S] s2 s3 s4 s5
St 10 1 2 6
s2 9 5 1 5
M = s3 8 4 2,5 4
s4 9 5 1 5
s5 10 6 2 1
10
9
8
9
10
Далее, мы имели
«1 S2 S3 «4 S5
«1 166 33 1 33 166
«2 83,5 38 2,5 38 176,5
IF = S3 147 25 6,5 25 147
«4 176,5 28 2,5 28 83,5
S5 166 33 1 33 166
Отсюда получаем W = W + (ZD — (ZD)T) (2Zdg D — 3/) +
+ 2 (Z2D - (Z2D)r):
166 1 4 49 166
147 38 1 38 147
W = 130 29 6,5 29 130
147 38 1 38 147
166 49 4 1 166
УПРАЖНЕНИЯ К ГЛАВЕ V
143
Следовательно,
66 0 0 13 66
66 13 0 13 66
м2= 66 13 74 13 66
66 13 0 13 66
66 13 0 0 66.
Наличие нулевых и равных
взглянув на матрицу А
дисперсий легко объяснить,
УПРАЖНЕНИЯ К ГЛАВЕ V
К 5,1
1. Вычислите предельную матрицу А и фундаментальную матри-
цу для эргодической цепи с переходной матрицей
О
1 О
О р
1 О
2. Для цепи из упражнения 1 вычислите М и М2.
3. Для цепи из упражнения 1 найдите ковариационную матри-
цу С.
4. В примере 2 положим р = 2/з. Найдите в этом случае непо-
движный вероятностный вектор и фундаментальную матрицу.
5. Для примера упражнения 4 найдите матрицу средних времен
первого достижения. Проверьте результаты, вычислив Р по М.
6. Дано, что эргодическая цепь имеет матрицу
3 3
4 4
4 4
2
М = I
Покажите, что эта цепь — циклическая.
7. Докажите, что матрица
3
7з
10/з
4 10/з
3 8/з
4 3
не является матрицей средних времен первого достижения ни для ка-
кой эргодической цепи.
8. Пусть Р — переходная матрица эргодической цепи и Р — ма-
трица, полученная из Р заменой диагональных элементов нулями И
144
ГЛ. V. ЭРГОДИЧЕСКИЕ ЦЕПИ МАРКОВА
последующей нормировкой ее строк с тем, чтобы сумма элементов в
каждой строке равнялась единице. Покажите, что полученная цепь
является опять эргодической, и если а = {а^} — неподвижный вектор
для первоначальной цепи, то вектор d = {яД1 — р^)} пропорциона-
лен неподвижному вектору для новой цепи. Как интерпретировать
компоненты нового неподвижного вектора в терминах первоначаль-
ной цепи?
9. Выполните процедуру, указанную в предыдущем упражнении,
для цепи из примера со страной Оз.
К 5.3
10. Найдите обращенную переходную матрицу для цепи из упра-
жнения 1. Вычислите фундаментальную матрицу для этой обращен-
ной цепи по фундаментальной матрице первоначальной цепи.
11. Для каких значений р цепь из упражнения 1 обратима?
12. Найдите обращенную переходную матрицу для цепи из при-
мера 2 при р = 2/з. Вычислите фундаментальную матрицу для этой
обращенной цепи и сравните результат с результатом, полученным
при решении упражнения 4.
13. Для примера из предыдущего упражнения вычислите М не-
посредственно из найденной там фундаментальной матрицы. Вычис-
лите М по М (см. упражнение 5), используя теорему 5.3.8, и срав-
ните ответы.
14. Докажите, что произвольный процесс независимых испытаний
обратим.
15. Докажите, что произвольная эргодическая цепь с двумя со-
стояниями обратима.
16. Докажите, что если эргодическая цепь имеет симметричную
переходную матрицу (т. е. ptj == pji), то эта цепь обратима.
17. Покажите, что для эргодической цепи
(а) Если эта цепь обратима, то = РjiPkjPik'
(b) Если все элементы ее переходной матрицы положительны,
то приведенное в (а) равенство обеспечивает обратимость [Указа-
ние: покажите, что для фиксированного i вектор-строка Л = {Pij/Рц}
является неподвижным вектором Р. Следовательно, этот вектор дол-
жен быть пропорционален а.]
Ко всей главе
18. Общее (конечное) случайное блуждание определяется сле-
дующим образом. Состояния перенумеровываются s0, sb ..., sn. Если
процесс находится в sit то он переходит в Si-i с вероятностью qi,
остается в Si с вероятностью г г и переходит в Sf+i с вероятностью
Pi. (Здесь Pi + qi + = 1, qQ = 0, pn = 0.)
(а) При каких условиях случайное блуждание эргодично?
(Ь) Из уравнения аР = а выведите методом математической ин-
дукции, что ai+iqi+i = aipi.
(с) Докажите, что эргодическое случайное блуждание обратимо.
(d) Найдите формулу для неподвижного вектора а.
г Л А В A VI
ДАЛЬНЕЙШИЕ РЕЗУЛЬТАТЫ
6.1 Приложение теории поглощающих цепей к эрго-
дическим цепям. Мы уже видели, что матрица Z позво-
ляет нам найти среднее значение и дисперсию времени
первого достижения любого состояния sj. Предположим
теперь, что нас интересуют более тонкие детали поведе-
ния процесса до попадания в Sj. Например, мы можем
спросить, какое время в среднем проводит процесс до
первого достижения Sj в каждом из остальных состоя-
ний. Теория поглощающих цепей Маркова позволяет по-
лучить ответ на этот и другие подобные вопросы. Чтобы
это сделать, изменим наш процесс, заменив Sj поглощаю-
щим состоянием. Получившийся процесс будет погло-
щающей цепью с единственным поглощающим состоя-
нием. Поведение этого процесса до поглощения в точ-
ности совпадает с поведением исходного процесса до
первого попадания в Sj. В силу этого всю информацию
о поглощающих цепях, которой мы располагаем, можно
превратить в информацию об исходной цепи. Это, в част-
ности, позволяет нам найти среднее время и дисперсию
времени первого достижения состояния исходя из sif
как среднее время и дисперсию времени до поглощения.
Так как любое собственное подмножество эргодического
множества открыто, то мы можем применить результа-
ты 3.5 для изучения поведения нашего процесса до мо-
мента первого попадания в некоторое подмножество со-
стояний.
Проиллюстрируем эти идеи на примере страны Оз.
Предположим, что мы интересуемся ходом процесса до
первого дождливого дня. Превратив состояние R в по-
глощающее, мы получаем поглощающую цепь Маркова
с переходной матрицей
R N S
R / 1 0 0 \
P = N '/2 0 '/2 .
S\‘/4 '/♦ */2/
10 Дж. Кемени, Дж. Снелл
146
ГЛ. VI. ДАЛЬНЕЙШИЕ РЕЗУЛЬТАТЫ
Основные результаты об этой поглощающей цепи по-
лучаются с помощью фундаментальной матрицы N =
= (/ — Q)-1, где Q — матрица, отвечающая непоглощаю-
щим состояниям. Пусть, например, /ij — время, проведен-
ное процессом в состоянии Sj до поглощения. Тогда
значения М/[п] даются матрицей N, которая в нашем
случае равна
N S
л._У/4/з 4М
SV/з 8/з/
Если, скажем, сегодня ясный день, то среднее число яс-
ных дней до первого дождя будет равно 4/з. Дисперсии
Dt [»j] можно найти из матрицы
N S
N/*/8 4 \
У2 = У (22Vdg - 7) - Nsq = s 40/J.
Пусть функция t равна полному числу шагов до по-
глощения. Тогда по теореме 3.3.5 вектор-столбец т =
= {МгИ1 задается формулой т = Wg. В рассматриваемом
нами примере
__ /4/з WO/V)
Т=Ч2/з 8/зД1/ к'7з/'
Для исходного процесса функция t представляет время
первого достижения состояния R. Итак, среднее время
до попадания в R равно 8/з, если процесс начинается
в 2V, и 10/з, если он начинается в S. Эти значения согла-
суются с теми, которые были определены из матрицы Л4,
вычисленной в 4.4 с помощью матрицы Z. Аналогично,
по теореме 3.3.5 получаем, что дисперсии D/H даются
вектор-столбцом тг — (2N—1)% — rSq. Произведя выклад-
ку, находим
Вектор тг дает нам дисперсию времени до поглоще-
ния. В терминах исходного процесса — это дисперсия
времени первого достижения состояния R. Найденные
6.1. ПРИЛОЖЕНИЕ ТЕОРИИ ПОГЛОЩАЮЩИХ ЦЕПЕЙ
147
только что значения опять совпадают с теми, которые
были определены в 4.5 с помощью матрицы М2.
Превращая последовательно одно за другим состоя-
ния цепи в поглощающие, мы можем найти для эргоди-
ческой цепи все недиагональные элементы матриц М и
М2. Однако более естественно и удобно использовать для
этой цели матрицу Z. Как правило, мы будем применять
метод поглощения лишь для получения более подробной
информации, которую не дает матрица Z.
В качестве примера циклической цепи рассмотрим
пример 2а. Превратим состояния Si и s2 в поглощающие.
Тогда
$3 $4 S5 S3 S4 S5
S3 / о 72 0 \ $3 / 2 2 I \
Q = s4| 72 0 72 , W = s4 2 4 2 I,
s5 \ 0 10/ s5 \2 4 3/
*3 $4 $5
s3/2 10 4\ s3/5\ s3 /40
Af2 = s4l 2 12 61, t = s4I 8 j, t2 = s4I 48
s5\2 12 6/ s5 \9/ s5 \48
Элементы матриц N и N2 дают среднее значение и дис-
персию времени, которое проводит процесс в каждом
состоянии до достижения s2 (состояния Si можно достиг-
нуть, только проходя через s2). Векторы т и т2 дают
среднее значение и дисперсию числа шагов до достиже-
ния s2, т. е. времени первого достижения. Можно прове-
рить, что компоненты векторов т и т2 совпадают с со-
ответствующими элементами вторых столбцов матриц
М и М2 из 5.2.
В качестве* второго приложения теории поглощаю-
щих цепей к эргодическим цепям рассмотрим следую-
щую задачу. Предположим, что задана цепь Маркова
с г состояниями и что процесс наблюдается только в те
моменты, когда он находится в множестве S, состоящем
из s элементов. Получается новая марковская цепь: од-
ному шагу нового процесса соответствует в старом про-
цессе переход (не обязательно за один шаг) из какого-то
Ю*
148
ГЛ. VI. ДАЛЬНЕЙШИЕ РЕЗУЛЬТАТЫ
состояния подмножества S в другое состояние этого же
подмножества. Пусть и — Два состояния из S. Мы
найдем новую вероятность перехода из Sj в Sj, если оп-
ределим вероятность того, что исходный процесс, начи-
наясь из sit впервые снова попадает в подмножество S,
находясь в состоянии Sj. Эта вероятность складывается
из вероятности попасть в s, за один шаг и вероятности,
попав в состояние из S, затем впервые войти в S через s$.
Используя результаты главы III, мы легко можем найти
эти вероятности. Чтобы сделать это, переобозначим со-
стояния так, чтобы состояния из S стояли впереди. То-
гда переходная матрица запишется в ви?^
S S
S /т и\
P = s\R Q/
Новый процесс будет цепью Маркова с s состояния-
ми. Найдем его переходную матрицу, которую мы обо-
значим Р, Предположим, что начальное состояние при-
надлежит S. Тогда вероятности попасть в любое из со-
стояний множества S за один шаг даются матрицей Т.
При переходе более чем за один шаг цепь должна сна-
чала попасть в какое-то из состояний множества S, ве-
роятности чего задаются матрицей U. Затем из данного
состояния множества S цепь достигает S впервые в со-
стоянии Sj с вероятностями, которые даются матрицей
(/ —Q)-1/? (см. теорему 3.3.7). Собирая все это вместе,
получаем, что
Р = Г 4- (/(/ —
Легко видеть, что матрица Р снова задает эргодическую
цепь.
6.1.1. Теорема. Пусть а = (аь а2, ..., а8, as+i, ..., аг)—
неподвижный вероятностный вектор для матрицы Р. То-
гда вектор а\ = (ai, а2, . • •, aQ, нормированный так, что-
бы сумма его компонент стала равна I, является непо-
движным вероятностным вектором матрицы Р.
Доказательство. Так как у всякой эргодической цепи
существует только один неподвижный вероятностный
6.1. ПРИЛОЖЕНИЕ ТЕОРИИ ПОГЛОЩАЮЩИХ ЦЕПЕЙ
149
вектор, то достаточно доказать, что ai — неподвижный
вектор для Р, Пусть a2 = (as+i, ..., аг). Тогда можно
записать a=(ai,a2). Так как а — неподвижный вектор
для Р, то
cq = щТ + а2Р
и
а2 = ci\U + a2Q.
Из последнего уравнения следует, что аг(/ — Q) = ctilZ,
или
a2 = a1C/(/ — Q)'"1.
Подставляя этот результат в первое уравнение, полу-
чаем
<Xj = щТ + (I — Q)-1 /?,
а это означает, что ai — неподвижный вектор для Р.
Для иллюстрации проделанных выше построений рас-
смотрим пример 6. Переходная матрица в этом случай-
ном блуждании имеет вид
$1 S2 $3 $4 $5
«1 [0 ‘/4 74 74 74
«2 7з Уз 7з 0 0
Р — $3 0 7з 7з 7з о
*4 0 0 7з 7з 7з
55 74 '/4 74 74 0.
Неподвижный вектор для этой цепи Маркова равен
a = (4/з8, 9/з8, 12/з8, 9/з8, 4/зв) • Предположим теперь, что про-
цесс наблюдается только в моменты пребывания в Sj
и s2- Тогда находим новые переходные вероятности сле-
дующим образом. При разборе этого примера в 3.5.5
мы получили
/21/э 12/э %
('-<?)"'= 15/9 24/9 %
% ‘%
150
ГЛ. VI. ДАЛЬНЕЙШИЕ РЕЗУЛЬТАТЫ
Поэтому новая переходная матрица равна
0 7Л. ГД 74 '1Л[
7з 7з/Л7з о оД
P = T+U(I-QrlR =
279 %\/0 '/з\
24/9 % 0 0 =
% % 'lj
% А
% Г
/
%
Неподвижный вектор для Р равен а= (4/1з, 9/1з)- Компо-
ненты этого вектора — попросту две первые компоненты
вектора а, нормированные так, чтобы их сумма равня-
лась 1.
В качестве примера циклической цепи рассмотрим
случайное блуждание примера 2а. Будем наблюдать за
процессом в множестве S = {si,s2, $з}- Имеем
р = 0 10 72 о 72 о 7г 0 0 0 0 0 72 0 , а = (7з, 74, 74. 7ч, 7в),
0 0 >/2 ООО 0 */2 1 о
-1/2\-'/0 0 '/2\
1 ) \0 0 0 /’
1 0 \ /0 0\
0 */2 ) + ( о о V 1
72 о/ V/2 оЛ-1
/ 0 1 0 \
р= '/2 0 >/2 , а = (75, 2/5) 7з)
\ 0 ‘/2 */2 /
Матрица Р здесь лишь немногим отличается от верхней
левой клетки матрицы Р. Процесс может выйти из S
только через состояние s3 и через него же должен вер-
нуться. Следовательно, изменяется только элемент р33.
Заметим, что в соответствии с 6.1.1 первые три компо-
ненты вектора а, нормированные нужным образом, со-
ставляют вектор а.
6.2. ПРИЛОЖЕНИЕ ТЕОРИИ ЭРГОДИЧЕСКИХ ЦЕПЕЙ
151
6.2. Приложение теории эргодических цепей к погло-
щающим цепям Маркова. В предыдущем пункте мы убе-
дились, что, используя теорию поглощающих цепей Мар-
кова, можно получить новые сведения об эргодических
цепях. Теперь мы покажем, что, наоборот, ряд резуль-
татов о поглощающих цепях можно вывести, используя
теорию эргодических цепей.
Нам потребуется следующее обобщение результата
5.1.2 (Ь).
6.2.1. Теорема. Для каждой цепи Маркова с одним
эргодическим множеством существует единственный не-
подвижный вероятностный вектор. Этот вектор имеет
положительные компоненты, отвечающие эргодическим
состояниям, и нулевые компоненты, отвечающие невоз-
вратным состояниям.
Доказательство. Запишем переходную матрицу в
канонической форме
/ SIO\
Р = [ -т— •
\r\qI
Матрица S — это матрица переходных вероятностей на
эргодическом множестве; значит, для нее существует
предельный вектор ai > 0. Пусть a = (ai, аг), где все
компоненты вектора аг равны 0. Тогда видно, что
a — неподвижный вероятностный вектор для Р. Обратно,
предположим, что 0 = (0ь 0)—неподвижный вероятност-
ный вектор матрицы Р. Тогда 02Q = 02- Отсюда 02Qn = 02
и, значит, 0г= lim 02Qn = O. Поэтому 01 — неподвижный
П->оо
вероятностный вектор для S и в силу результатов 5.1.2(b)
мы получаем, что 0i = ai и 0 = a.
Предположим теперь, что задана поглощающая мар-
ковская цепь с г состояниями, из которых г — s — по-
глощающие, а s — непоглощающие. Как обычно, зану-
меруем поглощающие состояния так, чтобы они стояли
впереди. Тогда переходная матрица принимает вид
/ 710 \
Р = -г- •
К 7? IQ /
Превратим теперь наш процесс в новый процесс сле-
дующим образом. Пусть л = (pi, ..., рг} — начальное
152
ГЛ. VI. ДАЛЬНЕЙШИЕ РЕЗУЛЬТАТЫ
распределение вероятностей в исходном процессе, и
пусть каждый раз, когда этот процесс достигает погло-
щающего состояния, он начинается опять с тем же на*
чальным распределением л. Тогда получается снова цепь
Маркова с переходной матрицей
Pr-s+1 • • • Рг
Pr-s+\ -- Рг
Q
Матрица Р' получается заменой всех строк, отвечающих
поглощающим состояниям, одним и тем же вектором я.
Пусть Л1 = (Р1, ..., Pr-s) И Л2 = (Pr-S+1, Рг). Тогда
Р' можно переписать в виде
= \ I Q /
6.2.2. Теорема. Матрица Р' представляет цепь Мар-
кова с единственным эргодическим множеством.
Доказательство. Пусть I — множество состояний, ко-
торым отвечают положительные компоненты вектора л,
a J — множество всех состояний, в которые процесс мо-
жет попасть, отправляясь из I. Ясно, что из состояний
sa, а = 1, 2, ..., г — s, можно попасть только в состоя-
ния множества /. С другой стороны, из любого состоя-
ния можно попасть в некоторое sa, так как исходная
цепь была поглощающей. Значит, все состояния J не-
возвратны.
Так как из любого состояния мы можем прийти в
одно из состояний sa, а из него в любое состояние из
множества I, а, значит, и J, то J — эргодическое множе-
ство. Значит, новый процесс имеет одно эргодическое
множество J и sa е J хотя бы для одного из а ~ 1,2, ...
..., г — s.
Пусть а — неподвижный вероятностный вектор для
Р'. Представим а в виде a = (ai,a2), где oci —
6.2. ПРИЛОЖЕНИЕ ТЕОРИИ ЭРГОДИЧЕСКИХ ЦЕПЕЙ
153
= («1, ar_s) и аг = (аг-з+1, Яг)- Тогда, так как
аР' = а, мы получаем два уравнения:
ai£r_/ii 4-а2Я = ab (1)
+ щО. == «2- (2)
Из 6.2.1 известно, что ои > 0; значит, и ai£r-s>0-
Пусть а = -^~—а. Новый вектор а= {аь а2} остается
неподвижным. Вспоминая, что digr-s=l. перепишем
наши уравнения в виде
л1 + а2/? = а1, (Г|
л2 + = a2. (2')
Из уравнения (2х) следует, что
d2 = л2(/ — Q)”1.
Обратная матрица существует, так как исходная цепь
была поглощающей. Из теоремы 3.3.5 мы видим, что век-
тор «2 дает нам средние значения времен, проводимых
цепью в каждом из состояний до поглощения при дан-
ном начальном распределении л.
Применяя только что полученный результат к урав-
нению (Г), имеем
dj = nj +л2 (/ — Q)”1
Вектор Л1 дает вероятности поглощения в каждом из
поглощающих состояний в начальный момент, а вектор
Я2(/ — Q)”1/? дает вероятности поглощения в тех же
состояниях при условии, что начальное состояние не по-
глощающее. Значит, di дает вероятности поглощения
в каждом из данных состояний при начальном распре-
делении л.
Итак, мы видим, что один и тот же вектор d дает нам
как вероятности поглощения, так и среднее время, про-
веденное в невозвратном состоянии до поглощения. Этот
метод более экономичен, чем метод главы III, если мы
интересуемся поведением процесса только при каком-то
одном начальном распределении. Зато в главе III приво-
дится решение сразу для всех начальных распределений.
154
ГЛ. VI. ДАЛЬНЕЙШИЕ РЕЗУЛЬТАТЫ
Применим изложенную процедуру к случайному блу-
жданию примера 1. Переходная матрица здесь имеет
вид
— см со чг щ СО СО СО СО СО II о. S2 S3 ®4 $5 1 0 0 0 0 0 10 0 0 q 0 0 р 0 0 0 q 0 р 0 р 0 q 0
Пусть л = (0,0,0, 1,0). Тогда новая цепь Маркова,
получаемая описанным выше образом, имеет переход-
ную матрицу
— СМ СО ЧГ Ю СО СО СО СО «о II а. S] ®3 ®4 0 0 0 1 0' 0 0 0 1 0 q 0 0 р 0 0 0 q 0 р 0 р 0 q 0
Это та же матрица, что в примере 3 из 2.2, с точ-
ностью до перестановки состояний. Неподвижный вектор
равен
«= 2+7Т?(?2> р2' ь р)-
Значит,
«=р2' q>
Отсюда видно, что вероятность поглощения исходного
процесса в состоянии $1 равна q2l(р2 + q2), а в состоя-
нии s2<—р2/(р2 + q2) и что средние времена пребывания
в каждом из состояний $з, $4, $5 равны соответственно
р/(р2 4- ?2), 1/(р2 + q2) и р!(р2 + ^2). Это совпадает с ре-
зультатами, полученными в 3.4.1.
Если мы положим л =(0,0, 0,0, 1), то полученная
цепь будет циклической с d = 2. То же самое справед-
6.2. ПРИЛОЖЕНИЕ ТЕОРИИ ЭРГОДИЧЕСКИХ ЦЕПЕЙ
155
либо, если л = (0, 0, с, 0, d),
пример. Здесь
Разберем этот
si
S2
Р —
$4
S5
О о
о о
<7 о
о о
О р
с О d
с О d
О р О
q о р
О q О
Вычислять вектор d проще всего непосредственно, не
отыскивая предварительно а. При решении уравнения
dP'=d следует воспользоваться соотношением di+a2=l.
Получаем
« = + p2qc ~ pq2d’ р2 + p(fd~ P2qc>
q + p2c — pqd, \ —qc— pd, p + q2d — pqc).
Если положить p = q = V2, to
a = (V2 + 74(c-d), 72 -74(c-d),
I + V2(c-d), 1, 1 — V2 (c —rf)).
Первые две компоненты дают вероятности поглощения
в Si и S5 при начальном распределении л. Как и можно
было ожидать, чем больше с, тем вероятнее поглощение
в Последующие три компоненты дают средние вре-
мена пребывания в состояних цепи до поглощения. Инте-
ресно отметить, что для $з соответствующая величина
равна 1, вне зависимости от с.
Последний результат допускает интересные прило-
жения к теории эргодических цепей. Пусть Р — переход-
ная матрица эргодической цепи с неподвижным вероят-
ностным вектором а. Превратим одно из состояний, ска-
жем «1, в поглощающее. Затем всякий раз, когда про-
цесс достигает будем возобновлять его с распределе-
нием л — {pij}. Тогда в силу изложенного выше резуль-
тата неподвижный вектор для этого нового процесса
даст среднее время пребывания в каждом из состояний
до поглощения. Но новый процесс совпадает с исходным
156
ГЛ. VI. ДАЛЬНЕЙШИЕ РЕЗУЛЬТАТЫ
и время до поглощения в означает время между по-
следовательными посещениями Значит, нормируя а
так, чтобы первая компонента равнялась 1, мы получим
для начальной эргодической цепи среднее время пребы-
вания в каждом состоянии между последовательными
попаданиями в Так как $1 произвольно, мы приходим
к следующей теореме.
6.2.3. Теорема. Пусть а — неподвижный вероятност-
ный вектор эргодической цепи. Тогда среднее время пре-
бывания в состоянии Sj между двумя последовательными
попаданиями в равно а^/а^.
Заметим, что если в переходной матрице цепи сумма
элементов каждого столбца равна I, то все компоненты
неподвижного вектора равны между собой. По нашей
теореме это означает, что средние времена пребывания
во всех прочих состояниях между двумя посещениями
данного состояния одинаковы.
6.2.4. Следствие. Пусть вектор а получается из а
вычеркиванием l-й компоненты, вектор р представляет
собой l-ю строку матрицы Р с вычеркнутой l-й компо-
нентой, а матрица Q получается из Р вычеркиванием
l-й строки и l-го столбца. Пусть также N = (/—Q)"*1,
т = Afg. Тогда
= (а)
4~=1+Р*- (Ь)
Доказательство. В левой части соотношения (а) фи-
гурируют средние времена пребывания в каждом из со-
стояний, кроме Si, между двумя последовательными по-
сещениями Si. В правой части стоят те же величины,
вычисленные с помощью теории поглощающих цепей.
В соотношении (Ь) мы имеем величину тц, вычислен-
ную с применением один раз — теории регулярных, дру-
гой раз — теории поглощающих цепей.
6.2.5. Теорема. Пусть Z — фундаментальная матрица
эргодической цепи, А — отвечающая ей предельная мат-
рица и N— фундаментальная матрица поглощающей це-
пи, полученной превращением состояния Si в поглощаю-
6.2. ПРИЛОЖЕНИЕ ТЕОРИИ ЭРГОДИЧЕСКИХ ЦЕПЕЙ
157
щее. Построим по N матрицу N*, добавив l-ю строку и
l-й столбец из нулей. Тогда
Z = A + (I — A) N* (I — А). (3)
Доказательство. Не ограничивая общности, можно
считать, что 1=1. Используя обозначения 6.2.4, запишем
Р и А в виде
Рп
Значит,
< I — Рп | -Р \ } Л Л ~ fl| I - а
и
Тогда
(Z-Р)ДГ (7-Л) = [
\ — «и
— pN + рта
I — |а
Используя результаты 6.2.4, получаем
(Z —Р)АГ(/ —4) = / —Д,
[1-Р+А]\А + (1-А)1Г(1-А)]=-
= Д + (/ - Р) У* (/ - Д) = Д + / - Д = /.
Поэтому
А + (/ - A)N’ (I - Д) = (7 - Р + Л)'1 = Z.
Интересно отметить, что в формуле (3) можно использо-
вать любую матрицу Л'*, полученную превращением ка-
кого-то одного состояния в поглощающее.
158
ГЛ. VI. ДАЛЬНЕЙШИЕ РЕЗУЛЬТАТЫ
6.2.6. Следствие. Если в 6.2.5 мы положим N =
N% = {№} и п{ц = пц = t{[} = 0 при i = Z, то
2ц = aj + п{ц - У aknk] - ajtf + a/ S aktk\ (a)
k^=i k^i
+ + (W
ai
Эти величины получаются непосредственно из 6.2.5,
с использованием при выводе (Ь) результатов 4.4.7. При-
веденные формулы можно использовать для получения
многих новых интересных соотношений. Некоторые из
них приводятся ниже. Величина п^. представляет собой
среднее время пребывания в sh исходя из st и до пер-
вого достижения Si.
6.2.7. Следствие.
„(/)
(a) mt/ + гпц = та + -^-(1 - М/) при i, j I.
al
„т № a
(b) m/z + mz/ = ^_ (c)^ = i.
at
Доказательство. Из 6.2.6 (b) при i, / =# l получается
mz/ + m/z = mz/ + - n® + й„) + mu,
_ л „(0 _ „(0 . д
1 _ ы> - 1 - i! - П </ + °г/
‘I nv) ~ n(l}
nil nil
Отсюда следует (а). Далее,
т11 + тц = ^ + ^-пи-^
Отсюда следует (b). Наконец,
t + ... nnlai
mn + mil nulal ’
что и доказывает (с).
6.3. УКРУПНЕНИЕ СОСТОЯНИЙ
159
В примере со страной Оз, сделав состояние К погло-
щающим, получаем (см. 6.1)
A+(I-.A)N'(I-A) =
/75 % 75\ / 3/з ~75 -75\
= 2Л 75 % + -75 4/5 -7s X
V/5 75 75/ \-75 -75 3/5/
/оо о \ / % -V8 -78\
х о 4/з 7з -75 4/5 -78 1 =
\о 7з 7з/\-75 -1/5 з/5/
/ 86 3 —14\
= 775( 6 63 6 I = z,
\—14 3 86/
как и в 4.3. Используя результаты 4.4 и 6.1, можно про-
иллюстрировать следствия 6.2.6 и 6.2.7:
mNS — ()/as) (nSS — nN$) + tN~ts —
= (72)(7з-7з) + 7з-’7з = 7з,
, nss 10 . 10 8/з
mSK + mRS = —, -у + Т=%--
6.3. Укрупнение состояний. Допустим, что задана
цепь Маркова с г состояниями, матрицей переходных
вероятностей Р и начальным распределением л. Пусть
А = {АЬ А2, ..., AJ- некоторое разбиение множества
всех состояний. Образуем новый процесс следующим об-
разом. Будем считать, что исходом /-го этапа в новом
процессе является множество Ahi если на /-м шагу ис-
ходная цепь попадает в Ak. Определим теперь вероятно-
сти ветвей. На нулевом уровне зададим их как
P«[f0^M (1)
на первом уровне — как
РЯ [fl ё= 4; |f0 <= А4
160
ГЛ. VI. ДАЛЬНЕЙШИЕ РЕЗУЛЬТАТЫ
и вообще на n-м уровне — как
ря [fn Л 1/«-1 е 4$ А ... А А е А/ л fo е Аг]. (2)
Описанную процедуру можно использовать для све-
дения процесса с очень большим числом состояний к про-
цессу с меньшим числом состояний. Назовем этот но-
вый процесс укрупненным процессом. В приложениях
часто случается, что интересующие нас вопросы сводят-
ся к этому более грубому анализу возможностей. По-
этому важно научиться определять, когда новый процесс
можно изучать методами цепей Маркова. I
6.3.1. Определение. Будем говорить, что состояния \
цепи Маркова можно укрупнить посредством разбиения
А = {А},А2,...,АГ}, если для любого начального рас- |
пределения л укрупненный процесс, определяемый фор-
мулами (I) и (2), является цепью Маркова, переходные
вероятности которой не зависят от л.
В следующем пункте мы увидим, что, по крайней
мере для регулярных цепей, условие независимости пере-
ходных вероятностей от л следует из требования, что
каждое начальное распределение приводит к цепи Мар-
кова.
Пусть PiA>= S Ptk* Тогда для первоначаль-
' k е Aj I
ной цепи Маркова piA. представляет вероятность по- j
пасть из состояния в множество Aj за один шаг. '
6.3.2. Теорема. Для того чтобы состояния цепи Мар-
кова можно было укрупнить посредством разбиения
А = {А:,А2,...,АГ}, необходимо и достаточно, чтобы
для любых двух множеств At и Aj вероятности pkAj |
имели одно и то же значение для всех k из А^ Эти об- :
щие значения {pi3} и образуют переходную матрицу
укрупненной цепи.
Доказательство. Для того чтобы цепь можно было
укрупнить, очевидно, необходимо, чтобы вероятности
РЯ Ц1 €=Д, Ио6= Aj]
имели бы одно и то же значение для всех л, для кото-
рых они определены. Обозначим это общее значение ;
через ptj. В частности, мы должны получить это зна-
чение, если &-я компонента л равна 1 и состояние
6.3. УКРУПНЕНИЕ СОСТОЯНИЙ
161
находится в множестве Аг. Значит, рАЛ/ = P*(/i eAJ =
= рц для всех sft из А{. Тем самым доказана необходи-
мость условия теоремы. Для доказательства достаточно-
сти надо проверить, что при выполнении условий теоре-
мы вероятность (2) зависит только от As и At. Вероят-
ность (2) можно представить в виде
Рл' [Л е Ad,
где л'— вектор, компоненты которого отличны от нуля
только для состояний из А«. Этот вектор зависит от л
и от исходов первых п испытаний. Однако если
PA[fi е А,] — pst для всех состояний sk из А8, то, очевид-
но, Pndfi s AJ = Pst- Следовательно, вероятность (2) за-
висит лишь от As и At.
6.3.3. Пример. Рассмотрим пример со страной Оз.
Напомним, что матрица Р имеет вид
R N S
*/V2 ’А VA
P = N Р/2 0 ’/2 .
sv/4 74 v2/
Предположим, что теперь нас интересует только «хо-
рошая» и «плохая» погода. Это приводит к объединению
состояний R и S. Заметим, что вероятности перехода
из этих двух состояний в N одинаковы. Значит, для раз-
биения А = ({2V}, {/?, S}) = {G, В}') условия, при которых
состояния цепи можно укрупнить, выполнены. Новая пе-
реходная матрица имеет вид
G В
_G( 0 1 \
Р = в[1/< yj-
Заметим, что для разбиения А = ({В}, {N, S}) условия
теоремы об укрупнении не выполняются, так как рил. =
= Pw = ‘/2. a psAi = Psr = ’А-
Допустим теперь, что нам задана цепь Маркова, со-
стояния которой можно укрупнить посредством разбиения
9 G — good — «хороший», В — bad — «плохой». (Прим, перев.)
11 Дж. Кемени, Дж. Снелл
162
ГЛ. VI. ДАЛЬНЕЙШИЕ РЕЗУЛЬТАТЫ
A = {Ai,A2, ...» AJ. Предположим, что первоначаль-
ная цепь имела г состояний, а новая цепь имеет s
состояний. Пусть U — матрица порядка s X г, i-я строка
которой представляет вероятностный вектор, имеющий
равные компоненты для состояний из Аг- и нули на про-
чих местах. Далее, пусть V — матрица порядка г X s,
/-й столбец которой представляет вектор, компоненты
которого, отвечающие состояниям из Aj, равны 1, а ос-
тальные компоненты — 0. Тогда укрупненная переходная
матрица Р дается формулой Р = UPV.
В примере со страной Оз имеем
U Р V
. /72
0 1 0 (7
*/2 0 >/2/1.
\ /4
1/4V0 Ц
1/2 1 0 =
72/\о 1/
и PV
О 1 0 Q ° 1 \
72 о */2Д3// V/4 3/4/
Х /4 /47
Отметим, что строки матрицы PV, отвечающие эле-
ментам одного и того же множества разбиения, одина-
ковы. Это верно для всех вообще цепей, удовлетворяю-
щих условиям укрупнения. Таким образом, матрица V
просто устраняет повторение одинаковых строк. Выбор
U отнюдь не однозначен. В действительности нужно
только, чтобы i-я строка представляла вероятностный
вектор, компоненты которого были бы отличны от нуля
лишь для состояний из А{. Для удобства мы выбрали
вектор, компоненты которого для этих состояний равны
между собой. В последующих рассуждениях удобно
предполагать, что состояния занумерованы так, что те
из них, которые входят в Д], идут первыми, затем идут
состояния из А2 и т. д. Мы будем считать во всех дока-
зательствах, что это условие выполнено.
Следующий результат полезен при выводе различ-
ных формул для укрупненных цепей.
6.3. УКРУПНЕНИЕ СОСТОЯНИЙ
163
6.3.4. Теорема. Если Р — переходная матрица цепи,
состояния которой можно укрупнить посредством раз-
биения А, и если матрицы U и V определены, как выше,
для этого разбиения, то
VUPV = PV. (3)
Доказательство. Матрица VU имеет вид
VI/-
где IVi, 1^2, ..., Ws— вероятностные матрицы. Соотно-
шение (3) означает, что столбцы матрицы PV — непод-
вижные векторы для VU. Но так как цепь можно укруп-
нить, то вероятности попасть из состояний Aj в множе-
ство A:i одинаковы для всех состояний из 4,; значит,
элементы столбцов матрицы PV, отвечающие множеству
Aj, равны между собой. Поэтому они образуют непод-
вижный вектор для Wj. Это доказывает (3).
6.3.5. Теорема. Если Р, A, U и V имеют тот же
смысл, что и в теореме 6.3.4, то условие (3) эквивалент-
но возможности укрупнения состояний.
Доказательство. Мы уже видели, что формула (3)
вытекает из того, что цепь можно укрупнить. Обратно,
предположим, что соотношение (3) имеет место. Каж-
дая из матриц Wj представляет собой переходную мат-
рицу эргодической цепи, так что единственный непод-
вижный вектор-столбец для нее равен Значит, все
компоненты столбцов матрицы PV, отвечающие одному
и тому же множеству Aj, должны быть равны между со-
бой. Следовательно, согласно 6.3.2 состояния цепи мож-
но укрупнить.
Заметим, что из формулы (3) следует равенство
P2=UPVUPV=UP2V
и вообще
Pn=UPnV.
Последний факт можно проверить и непосредственно.
11*
164
ГЛ. VI. ДАЛЬНЕЙШИЕ РЕЗУЛЬТАТЫ
Предположим теперь, что Р — переходная матрица
поглощающей цепи. Ограничимся случаем, когда мы
объединяем только состояния одинаковых типов. Дру-
гими словами, любое множество, входящее в наше раз-
биение, состоит либо из одних поглощающих, либо из
одних непоглощающих состояний. Напомним стандарт-
ную форму записи переходной матрицы, поглощающей
цепи:
/ I О
Р =------
Q
Запишем матрицу U в виде
где элементы матрицы U\ относятся к поглощающим со-
стояниям, а элементы (72—к непоглощающим состоя-
ниям. Аналогично, запишем матрицу V в виде
Vl
о
о
V2
Тогда равенство VUPV = PV, являющееся условием
для возможности укрупнения, обращается в систему ус-
ловий
^[/,1/, = ^. (4а)
V2U2PVX = RVU (4b)
V2tW2 = QV2. (4c)
Так как U\ Vi — 1, то первое условие выполняется авто-
матически. Стандартная запись переходной матрицы Р
получается из равенства
P = UPV
или
~ / Ui | О \ / / | О \ / Vt
\ о \uj\ r \q )\ о
о
6.3. УКРУПНЕНИЕ СОСТОЯНИЙ
165
Осуществив умножение, находим
~ { 1 I О \
Р= -------------- .
\ U2RV{ I C72QV2 J
Значит,
R = iWb
Q = [/2QV2.
Из условия (4c) находим
Q,= U2QV2U2QV2~U2Q2V2
и вообще
Qn=U2QnV2.
Используя представление фундаментальной матрицы N
в виде бесконечного ряда, получаем
yy = / + Q + Q2 + ... =U2IV2+U2QV2+ ... =
= t/2(/ + Q + Q2 + ...)И2,
fi=U2NV2.
Отсюда
x=U2NV&,
t=U2Nt,
t= U2x
и
в—nr = u2nv2u2rv2,
В = U2NRVlt
B = U2BVi.
Значит, все три основные характеристики N, т и В ук-
рупненной цепи легко получаются из соответствующих
характеристик исходной цепи.
Важное следствие нашего результата t = U2x состоит
в следующем. Пусть А, — какое-то непоглощающее мно-
жество” и 5* — состояние из А,. Можно так выбрать г-ую
166
ГЛ. VI. ДАЛЬНЕЙШИЕ РЕЗУЛЬТАТЫ
строку матрицы U2, чтобы она представляла вероятно-
стный вектор с компонентой 1 на месте sh. Но это озна-
чает, что t{ = tk для всех состояний sk из множества Ait
Значит, если цепь допускает укрупнение, то среднее вре-
мя поглощения одинаково для всех начальных состоя-
ний sk из одного и того же множества А^
Чтобы проиллюстрировать сказанное, рассмотрим
наш пример случайного блуждания с переходной матри-
цей
$1 S5 $2 S3 S4
«1 ®5 Р 1 0 0 1 ООО ООО
г —
«2 72 о 0 72 0
®3 0 0 72 о 72
«4 о 72 о 72 о
Возьмем разбиение A = ({si,s5}, {$2, $4}, {$3}). Условие
укрупнения для этого разбиения выполнено. Отметим,
что если вероятности движения вправо и влево не рав-
ны друг другу, то условие укрупнения уже нарушается.
Для исходной цепи мы ранее нашли
&2 «3 $4
s2 /3/г 1 7г \
= 12 11,
s4V/2 1 72/
/3
т —I 4
\3
55
S2
В ~ s3
^4
74 \
7г
6.3. УКРУПНЕНИЕ СОСТОЯНИЙ
167
Соответствующие величины для укрупненного процесса
равны
/7г
Р = 1 О
\ О
>/2 0 о
о 72 О
О 0 1
1 о
О 1
72 О
о о
о */2
о о
о о
О 72
*/2 О
о 72
о
о
о
о
о
10 0 Л| А-2 А3
1 0 0 41/1 0 О'
X 0 1 0 = А1 72 0 7г
0 0 1 А3 \ 0 1 0 ,
0 1 0
, /3/2 1 72\/1 О\ А* Аз
дМ/2 ° /2Н 12 10 1 =Л(2 П
ко 1 0/\1/2 1 з/2/\! 0/ Аз\2 2/
л2/з\
АД4/’
/ з \
А / V2 0 % \1 д ]
т = Л Л И 4
(з/ Ч \
* /4\/1\ А2/1\
h Л IГл, 1
/. V
Предположим теперь, что задана эргодическая цепь,
удовлетворяющая условию укрупнения с помощью раз-
биения А. Новая цепь будет также эргодической. Пусть
Я — предельная матрица укрупненной цепи. Тогда, как
мы знаем,
A- ||га Р + ... _
п->оо П
г UPV + UP2V + ... + UPnV
А = lim ----:-------------------,
И->=о «
A = UAV.
168
ГЛ. VI. ДАЛЬНЕЙШИЕ РЕЗУЛЬТАТЫ
Это означает, в частности, что компоненты вектора а по-
лучаются просто сложением компонент вектора а, отве-
чающих одному и тому же множеству разбиения. Анало-
гично, из представления фундаментальной матрицы Z
в виде бесконечного ряда находим, что
Z = UZV.
Вообще говоря, не существует простой связи между
матрицами М и М. Однако среднее время достижения
множества Aj из любого состояния множества А, одно и
то же (для исходного процесса). Чтобы убедиться в
этом, достаточно превратить состояния множества А;
в поглощающие. Мы уже знаем, что среднее время до
поглощения одинаково для всех начальных состояний из
одного и того же множества разбиения. Если, кроме
того, окажется, что Aj состоит из одного состояния, то
tiiij можно найти из М.
Мы можем вычислить ковариационную матрицу ук-
рупненного процесса. По существу, мы уже знаем (см.
4.6.7), что новые ковариации легко получить из матри-
цы С, даже если исходный процесс неукрупняем посред-
ством данного разбиения, т. е. если укрупненный про-
цесс не является цепью Маркова. В любом случае
С = i Qz.
k A j
Проведем эти выкладки в примере со страной Оз
Имеем
1/5 2/5 \/° Ц /•/ </
75 2/5 1 о = , 5 4 5
>/5 2/5Ао 1/ 5
3/75 - 14/75 \/0 1\
63/75 %5 1 0 =
3/75 8%5Ао 1/
63/
/75
3/
/75
|2м
72кГ
6.4. СЛАБОЕ УКРУПНЕНИЕ СОСТОЯНИИ
169
*2/125
12/125
-12/125\
12/125/
R
M — N
S
4 10/з\
5 8/з .
4 5/J
Я N S
Из фундаментальной матрицы Z получается, что
N В
N/5
В\4
1
5/4
Отметим, что среднее время достижения состояния N
как из /?, так и из S равно 4. В нашем случае множество
N составляет отдельное множество разбиения. Это общее
значение 4 и будет средним временем достижения со-
стояния N из В в укрупненном процессе. Точно так же
из матрицы М получается и элемент 5 матрицы М, За-
метим, что среднее время достижения состояния В, ис-
ходя из N, заметно меньше, чем средние времена дости-
жения первоначальным процессом, исходя из N, каждого
из состояний множества В в отдельности.
6.4. Слабое укрупнение состояний. Вообще говоря,
если мы хотим применять методы теории цепей Маркова
к процессу, состояния которого получены укрупнением
с помощью разбиения А = {Дь Д2, •4П}, то естест-
венно требовать, чтобы укрупненный процесс представ-
лял собой цепь Маркова вне зависимости от выбора на-
чального распределения. Однако ряд интересных резуль-
татов получается и в том случае, когда мы требуем,
чтобы, по крайней мере при одном начальном распре-
делении, возникала цепь Маркова. В этом случае мы
будем говорить, что процесс допускает слабое укрупне-
ние состояний посредством разбиения А. В настоящем
пункте мы рассмотрим некоторые следствия из этого
ослабленного предположения, причем ограничимся
170
. ГЛ. VI. ДАЛЬНЕЙШИЕ РЕЗУЛЬТАТЫ
классом регулярных цепей. Результаты пункта основаны
частично на работе Барка и Розенблатта1).
Чтобы определить, является ли результирующий про-
цесс цепью Маркова при данном начальном распреде-
лении л, мы должны изучить вероятности вида
ря [fn+1 €= At\fn «= Д ... A ft <= А/ A f0 €= 4J. (1)
Ответ будет положительным, если эти вероятности не за-
висят от исходов, предшествующих и-му.
Мы должны найти условия, при которых сведения об
исходах, предшествующих последнему, не отражаются
на величине вероятности (1). Посмотрим, какую роль
могли бы сыграть эти сведения. При информации, со-
держащейся в (1), мы знаем, что через п шагов исход-
ная цепь попадает в As, но, вообще говоря, нам неиз-
вестно, в каком из состояний этого множества она
находится. Однако можно посчитать вероятности нахо-
диться в том или ином состоянии из As. Именно для про-
извольного вероятностного вектора р обозначим через (V
вероятностный вектор, который получается из (3 так:
компоненты, отвечающие состояниям вне множества Aj,
заменяются нулями, а оставшиеся компоненты сохра-
няются пропорциональными своим прежним значениям.
Будем говорить, что — это сужение вектора р на мно-
жестве Aj. (Если все компоненты р, отвечающие состоя-
ниям из Aj, равны 0, то вектор JP’ не определен.) По-
смотрим, как в этих терминах выражается информация,
содержащаяся в (1). Тот факт, что можно выра-
зить, заменив начальное распределение л на л\ Допол-
нительная информация «fi Aj» означает превращение
вектора лФ в вектор (лг’Рр‘. Продолжая этот процесс до
тех пор, пока не будет исчерпана вся информация, со-
держащаяся в (1), в итоге мы получим некоторое рас-
пределение вероятностей на состояниях множества As.
С помощью этого распределения легко посчитать вероят-
ность перейти на следующем шаге в множество At. Важно
отметить, что эта вероятность может быть различной при
') С. К. Burke, М. Rosenblatt, A Markovian function of
a Markov chain, Annals of Mathematical Statistics 29, 1958,
1112-1122. -
6.4. СЛАБОЕ УКРУПНЕНИЕ СОСТОЯНИЙ
171
различной предшествующей информации. Например,
наша информация может привести к выводу, что цепь с
большой вероятностью на n-м шагу попадает в некое со-
стояние из ASi из которого обязательно происходит пере-
ход в At, Другая предыстория процесса может, напротив,
приписать этому состоянию маленькую вероятность. Эти
рассуждения дают ключ к пониманию того, когда, по-ви-
димому, прошлым можно пренебречь. Мыслимы два раз-
ных случая. Первым будет случай, когда информацию,
полученную из предыстории, вообще никак нельзя ис-
пользовать. Предположим, например, что вероятности
перейти в множество At одинаковы для всех состояний
из As. Тогда, очевидно, знание вероятностей нахождения
в состояниях множества никак не влияет на наш про-
гноз относительно следующего положения укрупненного
процесса. Именно в этом состоит условие из 6.3.2, при
котором возможно укрупнение (в полном смысле этого
слова). Второй случай заключается в том, что, какова
бы ни была информация о прошлом, мы всегда оказы-
ваемся в каждом из состояний множества с одними
и теми же вероятностями. Тогда, очевидно, предыстория
снова никак не влияет на наш прогноз. Мы увидим, что
такой случай также возможен.
Мы уже отмечали, что информация, содержащаяся
в (1), выражается посредством некоторого сужения на-
чального вероятностного вектора на As. Этот результи-
рующий вектор получается из начального распределения
л последовательными преобразованиями, каждое из ко-
торых учитывает информацию, полученную на очередном
шагу. Итак, образуем последовательность
Л] = л\
л2 = (л1Р)у,
л3 = (л2Р/,
(2)
1^) •
Обозначим через Ys совокупность всех векторов, кото-
рые получаются при рассмотрении всевозможных конеч-
ных последовательностей Aif Aj, ..., As, оканчиваю-
щихся на А$.
172
ГЛ. VI. ДАЛЬНЕЙШИЕ РЕЗУЛЬТАТЫ
6.4.1. Теорема. Укрупненный процесс является мар-
ковской цепью при начальном распределении л тогда
и только тогда, когда для любых s и t вероятность
Pftfl e4J сохраняет одно и то же значение при любом
распределении 0, принадлежащем У5. Это общее значе-
ние и дает вероятность перехода из множества 4S в мно-
жество At в укрупненном процессе.
Доказательство. Вероятность (1) можно представить
в виде PpIZi е 4/] при некотором нужным образом по-
добранном р. Это можно сделать, используя наши зна-
ния о первых п исходах и конструкцию (2). По предпо-
ложению, эта вероятность зависит только от s и /, что
и требовалось. Итак, в этом случае укрупненный про-
цесс— цепь Маркова. Предположим обратное, что про-
цесс, полученный после укрупнения, является марков-
ской цепью при начальном распределении л. Пусть р—
некоторый вектор из множества Ys. Это значит, что р
можно получить из некоторой последовательности
Aj, ..., As, скажем, длины п. Предположим, что
именно эти исходы использованы при подсчете вероят-
ности типа (1). Эта вероятность равняется тогда
Рр[/1 е 4J, и по марковскому свойству она не должна
зависеть от течения процесса до попадания в 4S. Зна-
чит, она принимает одно и то же значение при любом р
из Ys. Теорема доказана.
6.4.2. Пример. Рассмотрим цепь Маркова с переход-
ной матрицей
41 4г
А1 [7ч '/2
р = 0 76 %
Д2 7 /8 78 о.
Пусть 4 = ({$i}, {«2, $з}). Рассмотрим произвольный
вектор вида (1—За, а, 2а). Любой такой вектор сохра-
няет свою форму при умножении на матрицу Р. Кроме
того, сужение любого такого вектора на множествах 4j
и А2 — снова вектор того же вида. Значит, при любом
таком начальном распределении множество У1 содержит
только один элемент (1,0,0), a Y2— единственный эле-
6.4. СЛАБОЕ УКРУПНЕНИЕ СОСТОЯНИЙ
173
мент (О/АЛ/з). Поэтому условия теоремы 6.4.1 выпол-
няются тривиальным образом, каково бы ни было на-
чальное распределение такого вида. С другой стороны,
предположим, что выбрано начальное распределение
л = (0, 0, 1). Пусть
л2 = (яР)2 = (0, 1, 0) и л2 = (л1Р)2 = (0, 7б, 5/6)-
Векторы Л1 и л2 входят в класс У2, однако
Значит, при таком начальном распределении марковской
цепи не получается.
Итак, мы видим, что возможна ситуация, при кото-
рой некоторые начальные векторы приводят к цепи Мар-
кова, а другие — нет. Теперь докажем, что если какое-
нибудь начальное распределение приводит к цепи
Маркова, то это же верно и для стационарного распре-
деления а.
6.4.3. Теорема. Предположим, что регулярная цепь
Маркова допускает слабое укрупнение посредством раз-
биения А == {А], Д2, •••, As}. Тогда при начальном рас-
пределении а укрупненный процесс также является
цепью Маркова. Переходные вероятности этой цепи име-
ют вид
Рц — Ра* [f 1 е ^/]-
Любое другое начальное распределение, которое приво-
дит к цепи Маркова, приводит к тем же вероятностям
перехода.
Доказательство. Так как цепь допускает слабое ук-
рупнение состояний, то должен найтись начальный век-
тор л, приводящий к цепи Маркова. Пусть {Д;}—-ее пе-
реходная матрица. Тогда
РЛ [fn Aj | fn— 1 Ai /\ fп—2 = Рц
для всех множеств, для которых эта вероятность опре-
делена. Но это выражение можно переписать в виде
РЯр«-2 к е Л I f! е А А /о Ak\-
Устремляя п к бесконечности, получаем
Ра [f2 е А/1/, е Л,- Д «= = pi,.
174
ГЛ. VI. ДАЛЬНЕЙШИЕ РЕЗУЛЬТАТЫ
Тем самым мы доказали, что вероятности вида (1) с
п = 1 при начальном распределении а не зависят от про-
шлого (при условии, что учтен последний исход). Общий
случай совершенно аналогичен. Итак, если в качестве на-
чального распределения выбрать л = а, то укрупненный
процесс будет марковской цепью. В процессе доказатель-
ства мы попутно получили, что вероятности рц одни и
те же для начальных распределений л и а, а значит, и
для всех начальных распределений, приводящих к мар-
ковским цепям.
Согласно предыдущей теореме при проверке возмож-
ности слабого укрупнения состояний мы можем ограни-
читься начальным распределением а. В этом случае пе-
реходную матрицу Р можно записать в виде
Р = UPV,
где матрица V та же, что и выше (см. 6.3), а матрица U
определяется условием, что ее f-я строка равна а\ Когда
мы имели дело с укрупнением (в полном смысле), то
была большая свобода в выборе матрицы (7, и мы могли
придать ей максимально удобный вид. Иначе обстоит
дело при слабом укрупнении.
Изучим теперь условия, при которых можно рассчи-
тывать на возможность слабого укрупнения состояний.
Если при укрупнении снова получается цепь Маркова,
то матрицу Р2 можно посчитать двумя различными спо-
собами. Непосредственно^ из рассмотрения исходной
цепи следует, что Р2 = UP2V. С другой стороны, возведя
в квадрат матрицу Р, получаем UPVUPV. Значит, дол-
жно выполняться равенство
UPVUPV = UPPV.
Для этого достаточно, например, чтобы
VUPV^PV. (3)
Это условие укрупнения; выраженное в терминах нашей
новой матрицы U. Оно необходимо и достаточно для
укрупнения и, значит, достаточно для слабого укрупне-
ния состояний. Второе достаточное условие для написан-
ного выше равенства состоит в том, что
UPVU = UP. (4)
6.4. СЛАБОЕ УКРУПНЕНИЕ СОСТОЯНИЙ
175
Это условие означает, что строки матрицы UP являются
неподвижными векторами для матрицы VU. Но матрица
VU имеет вид
О I о
где Wj — переходная матрица, все строки которой рав-
ны aj. Утверждение, что ья строка матрицы UP есть не-
подвижный вектор для VU, означает, что этот вектор, су-
женный на множестве Aj, неподвижен для матрицы Wy
Но это в свою очередь значит, что компоненты этого век-
тора пропорциональны компонентам а< Итак, мы полу-
чили, что (5)
Это значит, что если мы начинаем с распределения а, то
класс Yu который определяется конструкцией (2), при
каждом i содержит только один элемент, а именно
Наоборот, если каждый такой класс состоит из един-
ственного элемента, то выполняется соотношение (5),
а, значит, и (4). Сказать: «Уг- при любом i состоит толь-
ко из одного элемента», все равно, что сказать: «Зна-
ние предыдущих исходов не оказывает влияния на зна-
чение вероятности оказаться в том или ином состоянии
множества 4г- на последнем шагу». Итак, доказано, что
условие (4) необходимо и достаточно, чтобы прошлое,
предшествующее последнему шагу, не добавляло ника-
кой новой информации. Значит, это условие достаточно
для слабого укрупнения состояний.
Пример 6.4.2 — это случай, в котором условие (4) вы-
полнено. Напомним, что в этом примере каждый из
классов Yi состоял из одного элемента.
Суммируем теперь результаты. В начале пункта от-
мечалось, что имеется две очевидные возможности сде-
лать ненужной информацию, содержащуюся в знании
исходов, предшествующих последнему. Во-первых, мож-
но потребовать, что если даже мы знаем точное положе-
ние исходного процесса на последнем шагу, все равно
176
ГЛ. VI. ДАЛЬНЕЙШИЕ РЕЗУЛЬТАТЫ
это не сказывается на нашем прогнозе следующего шага.
Это условие (3). Во-вторых, можно потребовать, чтобы
сведения об исходах, предшествующих последнему, не
несли в себе информации сверх даваемой последним ша-
гом. Это условие (4). Каждое из указанных условий де-
лает возможным слабое укрупнение. Итак, доказана
6.4.4. Теорема. Как условие (3), так и условие (4)
достаточны для слабого укрупнения состояний.
Имеется интересная связь между условиями (3) и
(4), выражаемая в терминах данного и связанного с ним
обращенного процесса (см. 5.3).
6.4.5. Теорема. Регулярная цепь удовлетворяет усло-
вию (3) тогда и только тогда, когда обращенная цепь
удовлетворяет условию (4).
Доказательство. Допустим, что процесс удовлетво-
ряет условию (3). Тогда
VUPV = PV.
Пусть Pq — переходная матрица обращенного процесса,
тогда Р = DP$D~'. Значит,
vudptqd~'v = dptod~'v
или, транспонируя,
VTD~'P0DU V = VTD~'P0D,
т. е.
VTD~'P0DUTVTD~l = VTD~'P0.
Заметим, что VTD~l = D~lU. Кроме того, матрица VUD
симметрична (это вытекает из определения матриц V,
U и D), так что VUD = DUTVT или DUTVTD~' = VU.
Используя эти два факта, преобразуем последнее равен-
ство к виду
D~'UP0VU = D~'UP0.
Умножая обе части слева на D, приходим к условию (4)
для Pq. Доказательство в обратную сторону проводится
аналогично.
6.4.6. Теорема. Если данный процесс допускает сла-
бое укрупнение состояний посредством разбиения А, то
это же верно и для обращенного процесса.
6.4. СЛАБОЕ УКРУПНЕНИЕ СОСТОЯНИЙ
177
Доказательство. Нужно проверить, что все вероят-
ности вида
Ра 1А е Л |f2 е= Aj л /з е= Ал л ... л fn е= Af]
зависят только от А,- и Aj. Эту вероятность можно пред-
ставить в следующей форме:
Ра Ifi Ai Л ^2 е Aj Л f3 е А^ Л Л fn^ Л/]
Ра [f2 €= А/ Л f3eAh/\ .’.. Л fn е AJ =
Ра [fn^At л ... Л f3€= Ah I f2& Aj A fl e Az] Pa [f2 (=Ajh f^Ai]
~ Pa [fn Л/ Д ... Д f3 e АЛ I f2 Aj] Pa [f2 €= Aj]
По предположению, прямой процесс является цепью
Маркова, так что первый множитель в числителе от Аг-
не зависит. Но тогда все выражение попросту равно
Pa [fi е Ai /\ f2 е Aj]
и зависит только от Аг- и Aj.
6.4.7. Теорема. Если регулярная обратимая цепь до-
пускает укрупнение состояний, то укрупненная цепь так-
же обратима. <
ДоказлтЕльство. По предположению об обратимости
P = DPrD-1.
Кроме того,
Р = UPV.
Поэтому
P=UDPTD~'V.
Мы уже знаем, что VTD~l = D~'U. Значит, UD = DVr,
а также D~lV = UTD~l. С учетом этого получаем, что
P = DVTPTUTD~'
ИЛИ
P = DPrD~\
Но это и означает, что укрупненный процесс обратим.
6.4.8. Теорема. Для обратимой регулярной цепи Мар-
кова из возможности слабого укрупнения состояний вы-
текает возможность их укрупнения (в полном смысле).
1g Дж. Кемени, Дж. Снедд
178
ГЛ. VI. дальнейшие результаты
Доказательство. Пусть Р — переходная матрица ре-
гулярной обратимой цепи. Тогда если цепь допускает
слабое укрупнение, то
UPPV = UPVUPV
или
UP(I -VU)PV = 0.
Так как U — DVTD~', то
DVTD~lP(I-VU) PV = Q.
Умножим это уравнение на D~l и воспользуемся тем
фактом, что для обратимой цепи D~]P = PTD~\ Полу-
чится, что
VTPTD~'(1— VU) PV = 0.
Пусть W = D-' — D-'VU. Тогда W = D~l — UW~'U.
Покажем, что матрица W неотрицательно определенная,
т. е. что для любого вектора р число pTW7p неотрица-
тельно. Для этого достаточно проверить, что
2 akbl^di (2 akbk\2,
Aj \k£= Aj ]
где di — г-ый диагональный элемент матрицы Ь. Напи-
санное неравенство эквивалентно следующему:
2 akdib‘k'^l 2 akdib^.
kAj \k s Aj J
Но так как коэффициенты ahdi неотрицательны и в сум-
ме дают 1, последнее соотношение сводится к стандарт-
ному вероятностному неравенству. В самом деле, рас-
смотрим случайную величину /, принимающую значения
Ьк с вероятностями ahdi. Из неотрицательности диспер-
сии вытекает, что М[/2]>(М[/])2 (см. 1.8.5), а это рав-
носильно доказываемому неравенству.
Так как матрица W неотрицательно определенная,
то найдется такая матрица X, что W = ХТХ. Но тогда
VTPTXTXPV = О
ИЛИ
(XPV)T (XPV) = 0,
6.4. СЛАБОЕ УКРУПНЕНИЕ СОСТОЯНИЙ
179
Это может быть верно лишь в том случае, когда
XPV = 0.
Поэтому
XTXPV = 0
или
D-'U-VUyPV = 0,
ИЛИ
(/- VU)PV = Q.
Окончательно
PV = VUPV.
Отметим, что в то время, как нам удалось дать необ-
ходимые и достаточные условия для возможности укруп-
нения состояний посредством разбиения А, аналогичные
условия для слабого укрупнения даны не были. Мы при-
вели два различных достаточных условия (3) и (4).
Можно было бы надеяться, что если слабое укрупнение
возможно, то одно из этих двух условий выполняется.
Нетрудно, однако, привести пример, когда не выполняет-
ся ни одно из них. Идея примера в следующем: возьмем
цепь Маркова, которая при каком-то укрупнении состоя-
ний превращается снова в цепь Маркова, и посмотрим,
не допускает ли укрупнения новая цепь. Если это так,
то результат этих двух операций можно рассматривать
как укрупнение состояний исходной марковской цепи.
Чтобы получить нужный контрпример, построим цепь,
допускающую слабое укрупнение в силу условия (3),
а затем последующее слабое укрупнение в силу усло-
вия (4). Результирующий процесс, который можно счи-
тать полученным укрупнением состояний исходной цепи,
очевидно, будет марковской цепью, но не будет удовле-
творять ни условию (3), ни условию (4). Рассмотрим,
например, цепь с переходной матрицей
Л, Vie 3/i6 _7г'
Р.Л 0 0 712 712 712 712 % %
Аз 78 7з2 3/з2 0
12*
180
Гл. VI. ДАЛЬНЕЙШИЕ РЕЗУЛЬТАТЫ
Для разбиения А = ({sj, {s2, «з}> {sj) выполняется более
сильное условие (3). После укрупнения состояний полу-
чается марковская цепь с переходной матрицей
Aj А2 A3
а, />/4
Р = А2 О
А3 V 7/s
74
7б
78
72\
% •
о /
Но это матрица примера 6.4.2, которая, как мы знаем,
удовлетворяет условию (4). Поэтому возможно слабое
укрупнение с помощью разбиения ({AJ, {А2, А3}). Ре-
зультатом будет слабое укрупнение исходной цепи по-
средством разбиения А = ({$]}, {$2, s3, s4J). Легко убе-
диться прямым подсчетом, что при таком разбиении
для исходной цепи не выполнены ни условие (3), ни
условие (4).
Закончим рядом замечаний об укрупненных процес-
сах, когда не выполняется даже условие слабого укруп-
нения. Предположим, что матрица Р регулярна. Если
исходная цепь начинается со стационарного распреде-
ления, то вероятность
Pt/ [f п+1 I fп ^«1
одна и та же для всех п. Поэтому матрицу Р = {ри)
по-прежнему можно считать матрицей вероятности пе-
реходов за один шаг. Кроме того, вероятность
~ Pct [fn AJ
также не зависит от п. Вектор а = {аг} является един-
ственным неподвижным вектором для Р. Его компо-
ненты можно получить простым сложением компонент
вектора а, отвечающих каждому множеству разбиения.
Аналогично предыдущему можно определить переход-
ные вероятности за два шага:
Р. Л
Матрица переходных вероятностей за два шага равна
по определению Р(2) = {р^}. Однако соотношение
Р' =г. р(2) уже не выполняется.
6.5. РАСШИРЕНИЕ ЦЕПИ МАРКОВА
181
Для укрупненного процесса (который не будет цепью
Маркова!) можно определить и матрицу математиче-
ских ожиданий времен первого достижения М. К со-
жалению, мы не можем воспользоваться стандартными
формулами теории марковских цепей. Чтобы получить
Л1, нужно сначала найти /и/, Лу — среднее время дости-
жения множества Aj, исходя из для исходного про-
цесса. Это можно сделать, объявив все элементы мно-
жества Aj поглощающими и вычислив затем среднее
время поглощения. (Если i входит в А;, рассуждения
нужно слегка видоизменить.) Из этих данных среднее
время перехода из Аг- в Aj получается по формуле
R. S А > J
где ak-k-n компонента вектора а*.
6.5. Расширение цепи Маркова. В двух предыдущих
пунктах мы показали, что при определенных условиях
цепь Маркова надлежащим укрупнением состояний мо-
жет быть сведена к цепи с меньшим числом состояний.
Эта новая цепь по-прежнему дает некоторые интерес-
ные сведения об исходном процессе. Таким путем, жерт-
вуя более детальной информацией, мы переходим к
объекту, требующему меньших вычислительных усилий.
В настоящем пункте мы покажем, что можно пойти и
в другом направлении. Именно из данной цепи Маркова
можно сконструировать некоторую большую цепь, ко-
торая дает более тонкую информацию о рассматривае-
мом первоначально процессе. Изложение основано на
результатах, полученных С. Худсоном в его дипломной
работе, выполненной в Дартмутском колледже.
Рассмотрим цепь Маркова с состояниями Sj, s2> ...
..., sr. Образуем новую марковскую цепь, которую на-
зовем расширенной цепью, следующим образом. Ее со-
стояния— это всевозможные пары ($г, $j), для которых
в исходном процессе рц > 0. Введем для этих состояний
обозначение s^). Предположим, что начальная цепь за
два последовательных шага переходит из в Sj и из Sj
в Sk. Условимся интерпретировать это как один шаг
расширенного процесса, ведущий из состояния в s^).
182
ГЛ. VI. ДАЛЬНЕЙШИЕ РЕЗУЛЬТАТЫ
При таком соглашении новый процесс может перейти
из состояния S(fj) в состояние за один шаг лишь
при / = k. Переходные вероятности определяются фор-
мулами
Р(И>Ш)~ Рц'
Pw(kn = °> i^k>
ИЛИ
Рщ) (kl) Pjfijk-
*6.5.1. Пример. Рассмотрим снова страну Оз. Состоя-
ниями расширенного процесса служат RR, RN, RS, NR,
NS, SR, SN, SS. Заметим, что состояние NN можно
исключить, так как для исходной цепи Pnn — 0. Пере-
ходная матрица расширенного процесса имеет вид
RR RN RS NR NS SR SN SS
RR Чг 74 74 0 0 0 0 0
RN 0 0 0 ‘/2 72 0 0 0
0 0 0 0 0 74 74 7г
nr 72 74 74 0 о о о о
NS 0 0 0 0 0 74 74 72
sr 72 74 74 о о о о о
SAT 0 0 0 72 72 о 0 0
ss( 0 0 0 0 0 ’/4 74 7г.
Рассмотрим сначала вопрос о классификации со-
стояний расширенного процесса в зависимости от струк-
туры исходной цепи. Заметим, что = Р(Д~°Р#>0
тогда и только тогда, когда р^“1)>0. Значит, если
исходная цепь эргодична, то это же верно и для рас-
ширенного процесса, точно так же, если исходная цепь
имеет период d, то и расширенная цепь имеет период d.
Состояние S(ij) расширенного процесса является погло-
щающим только тогда, когда i = j и Si — поглощающее
состояние исходной цепи.
Предположим теперь, что исходная цепь поглощаю-
щая. Пусть — непоглощающее состояние расширен-
6.5. РАСШИРЕНИЕ ЦЕПИ МАРКОВА
183:
ного процесса. Так как начальная цепь была поглощаю-
щей, то должно существовать поглощающее состояние
Sa- такое, что из Sj можно попасть в sk. Поэтому в рас-
ширенном процессе возможен переход из в S(kky
Значит, новый процесс также является поглощающим.
Интересно отметить, что от расширенного процесса
можно вернуться к исходному группировкой состояний.
С этой целью рассмотрим разбиение А = {Аь Д2, •. •, А,}
множества состояний расширенной цепи, где А^— это
совокупность всех состояний вида Условие, при ко-
тором возможно укрупнение состояний, как мы помним,
состоит в том, что вероятности P(ki)Af не зависят от k.
Но это очевидно в силу марковского свойства исходной
цепи. Укрупненный процесс совпадает с первоначальным.
В рассмотренном выше примере разбиение, о котором
только что шла речь, имеет вид
А = {(/?/?, SJ?, О), (SAT, RN), (RS, NS, SS)}.
Сравним теперь основные численные характеристики
расширенного процесса с соответствующими характерна
стиками исходной цепи, ограничиваясь регулярным слу-
чаем (другие случаи рассматриваются аналогично).
6.5.2. Теорема. Пусть а = {aj — неподвижный век-
тор регулярной цепи с переходной матрицей Р и
а = {ай;)} —неподвижный вектор расширенной цепи.
Тогда
^(ij) = ^iPij-
Доказательство. Очевидно, а^ц > 0. Кроме того,
#(//) = 2 aiPii = 2 Я/ = 1.
7 7
Остается лишь доказать, что d = {вгрц} — неподвижный
вектор для переходной матрицы расширенного процесса,
т. е. что
2a(//)P(i/) (ki) =
(tj)
Но
S o-anPan (w) 2 atPnPjfijk = 2 ^iPjfiik — akpki = a(ki)-
(i/) i, i j
184
ГЛ. VI. ДАЛЬНЕЙШИЕ РЕЗУЛЬТАТЫ
В нашем примере это дает следующее стационарное
распределение:
а = (0,2; 0,1; 0,1; 0,1; 0,1; 0,1; 0,1; 0,2).
Заметим, что доказанный нами результат интуитивно
очевиден, так как представляет вероятность того,
что после большого числа шагов процесс попадет в со-
стояние sif а затем перейдет в состояние s^ Ясно, что
вероятность этого события равняется Hip^.
6.5.3. Теорема. Фундаментальная матрица расширен-
ной цепи имеет вид
% = (ki)} = {ban (ki) + ~ ak) Pki}-
Доказательство.
co
zu/) (*/)= (ki) + (Pu/) (W)— aW))=
oo oo
(ki) + Si (Р(Д X]Pki akPki) = (ki, + Pki SQ (Р($““ ak)=
= b(ij) (kl) + Pkl (Zjk аь)»
В частности, в нашем примере
rr RN RS NR NS SR SN SS
rr ’ 1,373 0,187 0,187 —0,080 —0,080 -0,147 -0,147 -0,293
RN —0,160 0,920 —0,080 0,320 0,320 —0,080 —0,080 —0,160
RS -0,293 —0,147 0,853 —0,080 —0,080 0,187 0,187 0,373
NR 0,373 0,187 0,187 0,920 —0,080 —0,147 —0,147 —0,293
NS —0,293 —0,147 —0,147 —0,080 0,920 0,187 0,187 0,373
SR 0,373 0,187 0,187 —0,080 —0,080 0,853 -0,147 —0,293
SN -0,160 —0,080 -0,080 0,320 0,320 —0,080 0,920 —0,160
SS l —0,293 —0,147 —0,147 -0,080 —0,080 0,187 0,187 1,373
Рассмотрим теперь математические ожидания вре-
мен первого достижения в расширенном процессе.
6.5.4. Теорема.
1
(zjk~zlk)
Д'
&
6.5. РАСШИРЕНИЕ ЦЕПИ МАРКОВА
185
Доказательство. Воспользовавшись представлением
матрицы М через фундаментальную матрицу, получаем
ГП(Ц) (W) = <б(Ц) (kl) ~ Z(U) (feZ) + z(kl) <*z>) =
<M)
” [&(//) (kl) ~ Pkl(zlk — ak) — Ь(Ц) (kl) + Pkl(zlk — ak) + 1 ] 77- =
“k^kl
Hi_Pftz(2 2za)]_L_=_2—
I Pki\ Ik 1ЛН akPk{ akPki Uk
Как и раньше, элементы пцц) (ы) от i не зависят. Этого,
конечно, можно было ожидать заранее.
В рассматриваемом примере получается
RR RN RS NR NS SR SN SS
rr 1 5 77з 62/з 10 10 10 Ю2/з 87з
RN 72/з 10 97з 6 6 97з 10 72/з
RS 8’/3 102/3 10 10 10 62/3 77з 5
. NR 5 77з 62/3 10 10 10 Ю2/з 87з
М~ NS 8'/з Ю2/з 10 10 10 62/з 77з 5
SR 5 77з 62/з 10 10 10 Ю2/з 8'/3
SN 72/з 10 97з 6 6 97з 10 72/3
SS 8>/з кг/з 10 10 10 62/з 77з 5
Для сравнения напомним матрицу средних значе-
ний времен достижения для исходной цепи
R N S
R /2,5 4 3,3 \
М = АН 2,7 5 2,7 ].
S\3,3 4 2,5 /
Изучим теперь переходную матрицу цепи, полученной
186
ГЛ. VI. ДАЛЬНЕЙШИЕ РЕЗУЛЬТАТЫ
обращением расширенного процесса. Новые переходные
вероятности равны
й a{ki)P(ki)an
P(iDW=
Значит,
P(ij) (kl) — 0»
И
_ __ akPkiPil _ akPki = А
аап aiPn ai Pik'
Итак, цепь, полученная обращением расширенного про-
цесса, попросту совпадает с процессом, который полу-
чается расширением цепи, обратной к исходной.
Одно из приложений изложенного выше метода рас-
ширения цепи состоит в следующем. Часто бывает так,
что переходная матрица Р некоторой цепи не известна,
и мы хотим оценить ее по данным наблюдений. Если
известно большое число п исходов процесса, то очевид-
на следующая оценка:
У(1?
где у^ — число переходов из состояния S{ в состояние
sf, а у[п) — число попаданий в состояние Для ис-
следования свойств этой оценки нужно изучить случай-
ные величины yff и у^\ связанные с марковской
цепью. В частности, большую роль играют предельные
ковариации этих величин. Мы знаем, что предельную
ковариацию между у\п} и у^ можно выразить через
фундаментальную матрицу исходной цепи. Но как найти
предельную ковариацию между величинами у{^ и у(“>?
Проще всего заметить, что она совпадает с предельной
ковариацией для времен пребывания в состояниях (ij)
и (kl) расширенной цепи. Поэтому интересующую нас
характеристику удается выразить в терминах Z и а.
Используя затем теоремы 6.5.2 и 6.5.3, можно написать
выражение для предельной ковариации через величины,
связанные с исходной цепью. Выкладки приводят к сле-
дующему результату.
УПРАЖНЕНИЯ К ГЛАВЕ VI
187
6.5.5. Теорема. Предельные ковариации для расти
ренной цепи равны
С(И) (ki) = aiPuPki^jk + akpkipijZu + akpkfi(ij) (ki) “ ^iPuCikPki.
В нашем примере эти ковариации составляют матрицу
0,309 0,001 -0,012 0,001 - -0,065 - -0,012 - -0,065 - -0,157
0,001 0,074 -0,033 -0,041 0,007 0,001 - -0,026 - -0,065
—0,012 —0,033 0,061 0,001 - -0,033 0,027 0,001 - -0,012
0,001 0,041 0,001 0,074 -0,026 -0,033 0,007- -0,065
—0,065 0,007 - -0,033 - -0,026 0X174 0,001 0,041 0,001
—0,012 0,001 0,027 -0,033 0,001 0,061 - -0,033 - -0,002
—0,065 —0,026 0,001 0,007 -0,041 - -0,033 0,074 0,001
—0,157 —0,065 • -0,012 - -0,065 0,001 -0,012 0,001 0,309
УПРАЖНЕНИЯ К ГЛАВЕ VI
К 6.1
1. Рассмотрим пример 2 при р = ’/2. Предположим, что процесс
наблюдается только тогда, когда он находится в множестве
{$2, «з, sj- Найдите переходную матрицу и матрицу М для нового
процесса. Что означают элементы М в терминах первоначальной
цепи?
2. В следующей таблице даны вероятности того, что спортив-
ная команда займет в будущем году то или иное место, если из-
вестно, какое место она занимает в этом году. Для каждой коман-
ды второй группы вычислите, какое среднее число лет ей нужно,
чтобы попасть в первую группу.
1 2 3 4 5 6 7 8
1-е 0,3 0,3 0,3 0,1 0 0 0 0
2-е о,1 0,2 0,2 0,2 0,2 0,1 0 0
I группа 3-е 0,1 0,1 0,2 0,2 0,1 0,1 0,1 0,1
4-е 0 0,1 0,1 0,2 0,2 0,2 0,1 0,1
5-е 0 0,05 0,05 0,2 0,3 0,2 0,1 0,1
6-е 0 0 0,1 0,1 0,2 0,3 0,2 0,1
II группа 7-е 0 0 0 0 0,1 0,3 0,3 0,3
. 8-е 0 0 0 0 0,1 0,2 0,4 0,3
188
ГЛ. VI. ДАЛЬНЕЙШИЕ РЕЗУЛЬТАТЫ
3. Рассмотрим цепь с одним эргодическим множеством, имею-
щую невозвратные состояния. Пусть $г — невозвратное состояние и
si—эргодическое состояние. Пусть fj — время, необходимое, чтобы
достичь Sjt g— первое достигнутое эргодическое состояние, t — вре-
мя, необходимое для достижения эргодического множества. Тогда
МДМ- 2 р [г-+ !*“’*])•
— эргодические
Используя это, найдите в примере 4 при р — 2/3 среднее время
до первого попадания в $j, исходя из $3.
4. В стране Оз идет дождь. Сколько в среднем должно пройти
дней, пока не случится хотя бы раз другая погода?
5. Докажите, что если цепь наблюдается лишь в моменты пре-
бывания в некотором подмножестве эргодического множества, то
новый процесс также эргодичен.
К 6.2
6. Найдите среднее число дождливых дней между ясными дня-
ми в стране Оз.
7. В упражнении 2 к главе II предположим, что когда сраже-
ние кончается, то начинается новое сражение. Найдите неподвиж-
ный вектор полученной цепи. Используйте это для нахождения ве-
роятностей поглощения и среднего времени пребывания в каждом
состоянии для первоначальной цепи.
8. Рассмотрим цепь с переходной матрицей
$2 §3
Si / 0 1 0 \
о «/< .
$з \ 0 1 0 /
Найдите фундаментальную матрицу Z, приняв $1 за поглощаю-
щее состояние, вычислив N и используя теорему 6.2.5. Найдите
mu + т21 с помощью следствия 6.2.7.
9. Получите из 6.2.5 тождество
У* (I-A).
К 6.3
10. В примере 2 при р = У2 какое из следующих разбиений дает
при укрупнении состояний цепь Маркова?
(а) А = ({sj, s3, s5}, {s2, s4}).
(Ь) В = ({sb s5}, {s2, s4}> {s3}).
Какое из них дает цепь Маркова при р 4= Чъ?
11. Покажите, что процесс примера 3 допускает укрупнение
состояний посредством разбиения
A=({S1,S5}> {S2,S4}, W).
Найдите фундаментальную матрицу укрупненной цепи из фун-
даментальной матрицы первоначальной цепи (см. 4.7).
УПРАЖНЕНИЯ К ГЛАВЕ VI
189
12. Найдите такое разбиение на три группы, при котором про-
цесс примера 6 допускает укрупнение.
13. Пусть Р— переходная матрица цепи независимых испыта-
ний и а — любое число между 0 и 1. Покажите, что Р'= аР+
Ч-(1 — а)! допускает укрупнение по отношению к любому раз-
биению.
14. Покажите, что процесс примера 12 допускает укрупнение
посредством разбиения
А = ({s,si, S2«i}> {sis2, S2S2}).
Как новая матрица переходных вероятностей связана с цепью
из двух состояний, исходя из которой была построена цепь с че-
тырьмя состояниями?
15. Докажите, что если эргодическая цепь допускает укрупне-
ние, то d = aV.
16. Приведите пример цепи Маркова, которая не является цепью
независимых испытаний, но становится такой после укрупнения.
Проверьте ваш ответ, вычислив Z и UZV,
К 6.4
17, Покажите, что цепь Маркова с переходной матрицей
*1 /72 74 74\
32 72 72 О
*3 \ 0 74 3/4 '
допускает слабое укрупнение (но не укрупнение) посредством раз-
биения
A ® ({sj, {s2, S3}).
Найдите переходную матрицу укрупненного процесса.
Покажите, что обращенный процесс допускает укрупнение.
18. Покажите, что цепь Маркова с переходной матрицей
S1 0 74 7« 0 0
S2 ’/< 0 74 0 0
P=»s3 0 4о 7з 7» V»
S4 410 ’/и 7» 74 72
S5 7. 0 7» »/. 7»
допускает слабое укрупнение посредством разбиения
А = ({si,s2,s3}, {s4, s5}).
19. В примере со страной Оз положим At = {/?, /V}, А2 « {S}.
Вычислите Ро [A Ai I А е AJ и Ра [f2 €= Aj I A e Aj A fo sAJ. Ис-
пользуя результат, покажите, что цепь не допускает слабого укруп-
нения по отношению к А == (Аь А2).
20. Докажите, что если Р допускает укрупнение посредством
данного разбиения и суммы элементов Р по столбцам равны 1, то
Рт допускает слабое укрупнение посредством этого же разбиения.
190
ГЛ. VI. ДАЛЬНЕЙШИЕ РЕЗУЛЬТАТЫ
К 6.5
21. Раз за разом подбрасывается монета. Представьте это как
цепь Маркова с двумя состояниями. Образуйте расширенный про-
цесс. Найдите М и М2 для расширенной цепи. Интерпретируйте диа-
гональные элементы в терминах первоначальной цепи.
22. Пусть Р — переходная матрица цепи независимых испыта-
ний. Найдите формулы для Z и М, относящихся к расширенной
цепи. Проверьте их на примере упражнения 21.
23. Пусть Р— переходная матрица цепи независимых испыта-
ний. Найдите формулу для предельных ковариаций расширенной
цепи.
[Указание: запишите формулу в виде ..).] Используйте
эту формулу для нахождения предельных ковариаций в упражне-
нии 21.
г Л А В A VII
ПРИЛОЖЕНИЯ ЦЕПЕЙ МАРКОВА
7.1. Случайные блуждания. Мы будем рассматривать
четыре простых связанных друг с другом типа случай-
ных блужданий. Первые три — блуждания по прямой
с состояниями 0, 1, п. Во всех этих трех случаях
/ Р
Ч----1--1-------Н—Ч------------1---н
0 7 2 г-7 г г+7 л-7 л
Рис. 7.1.
мы движемся вправо (от i к i+ I) с вероятностью р
и влево (от i к i—I) — с вероятностью q. Они разли-
чаются между собой лишь своим поведением на «гра-
ницах» — в точках 0 и п. Введем для них следующее обо-
значения.
Рис. 7.2.
AARW: Оба состояния 0 и п являются поглощаю-
щими. ,
APRW: 0 является поглощающим состоянием, а в п
происходит «частичное отражение». Это значит, что из п
возвращаемся в п— 1с вероятностью q и остаемся в п с
вероятностью р.
192
ГЛ. VII. ПРИЛОЖЕНИЯ ЦЕПЕЙ МАРКОВА
PPRW: На обоих концах имеется частичное отраже-
ние, т. е. в п имеем то же, что в случае APRW, а в О
остаемся с вероятностью q и возвращаемся в 1 с вероят-
ностью р.
Четвертый тип — блуждание по окружности с со-
стояниями 1,2, ..., п, расположенными как на рис. 7.2.
CRW: Процесс движется по окружности; шаг по ча-
совой стрелке происходит с вероятностью р, против ча-
совой стрелки — с вероятностью q.
Будем иллюстрировать каждое из этих четырех
блужданий, считая п = 5. Так как при р = !/2 процесс
часто ведет себя совершенно иначе, чем при любом дру-
гом значении р, выкладки будем делать как для р = ’/г,
так и для р = 1 2 * 4/з. Для удобства обозначим отношение p/q
через г.
Рассмотрим сначала AARW. Это поглощающая цепь
с двумя поглощающими состояниями 0 и я.
AARW для п = 5, р = ’/2:
0 5 12
0 10 0 0
5 0 10 0
Р=1 Уг 0
2 0 0
3 0 0
4(0 >/2
0 >/2
'/2 0
0 ‘/2
о о
3 4
0 0
0 0
0 0
'/2 о
о >/2
*/2 0
1 /1,6 1,2 0,8 0,4 \
2 I 1,2 2,4 1,6 0,8 |
31 0,8 1,6 2,4 1,2 Г
4 \0,4 0,8 1,2 1,6/
4
6
т =
tl. СЛУЧАЙНЫЕ БЛУЖДАНИЯ
193
И
О 5
1 /0,8 0,2 \
2 / 0,6 0,4 |
й = з1 0,4 0,6 Г
4 \0,2 0,8/
AARW для п = 5, р = 2/3:
0 5 1 2 3 4
0 1 0 о о о о
5 0 1 о о о о
1 7з .о о 2/з о 0
2 0 0 7з 0 2/3 о
3 0 0 0 Чз 0 2/з
4 о 2/з 0 0 '/з 0
(45 42 36 24
21 63 54 36
9 27 63 42
3 9 21 45
О 5
(15 16\ 1
7 24 1 2
3 28 1 3
1 30/4
13 Дж. Кемени, Дж. Снелл
194
гл. vii. приложения цепей Маркова
Матрица I — Q при п = 5 имеет вид
I -р 0 0\
- q 1 - Р 0 1
0 ~q 1 -р I
О 0 — q 1/
В общем случае ее элементы Z, / = 1,2, ..., п—1,
равны 0, кроме = 1, sj—i, j = —p, = ~q. Ha
приведенных численных примерах замечаем, что эле-
меты матрицы N уменьшаются при удалении от главной
диагонали. При любом п матрица N будет иметь вид
1 f (г/— — 1),
i! (p-q)(rn-\) | (ft_ j>it U)
кроме случая p = V2; здесь выражение упрощается:
пц =
j^i,
j^i.
(2)
2
п
Проверим ответ при р = '1ъ, сосчитав N(I— Q). На
1-, j-м месте этой матрицы стоит
fin-i)(r---i)5»,+
L&=i
k=i+\
Напомним, что только для & = /—!, /, /+1.
Предположим, что / < I. Тогда во второй сумме все
члены равны 0, а первая сумма сводится к
1 .
- H-t+i -<ч)+(Р- 1+<)]-0.
7.1. СЛУЧАЙНЫЕ БЛУЖДАНИЯ
195
При / > i также получается 0. Таким образом, все
элементы, кроме диагональных, равны 0. Сосчитаем три
ненулевых члена t, i-ro элемента:
+ (г < - 1) (г-‘ - 1) (1) + (г‘ - 1) (г“-‘ - г) (- <7)1 =
=к (-?+1 (р -1+«)+
+ r.(f_1+r,) + (_p+1_r,)l = zM^ = l.
Таким образом, N = (/—Q)”1, как и должно быть.
Ответ для случая р = V2 можно проверить анало-
гичным образом. Можно также получить его из общего
случая с помощью предельного перехода: запишем
р — q — q(r — 1) и положим q —► V2, г —► 1.
Подсчитаем теперь т:
л-1 г i
/=i L/=i
+ 2 - ri~i) =
/=/ + 1
= (Р-q) (гП~‘ ~(S г1 ~+
(rt-1 X -
(n-/-l)r«-‘- 2 г/-Ч =
/ - i +1 /
__ (n-i) rn - пгп~1 + i
Упрощая, имеем
1 / \
и = (р-q) —ргт]----7» есЛИ р =# ’А • (3)
13*
196
ГЛ. VII. ПРИЛОЖЕНИЯ ЦЕПЕЙ МАРКОВА
Аналогично,
ti = — i), если р = 1/г- (4)
Интересно рассмотреть вопрос о нахождении наи-
большего значения Мы видим, что при р = V2 ti рас-
тет, пока не дойдет до середины, а потом симметрично
убывает. Если п четное, то в средней точке i = п/2 по-
лучается максимальное значение ti = (п/2)2. В общем
случае можно написать отношение двух соседних чле-
нов и найти значение i, при котором это отношение
равно I. Вообще говоря, мы не получим целое число,
но ближайшее к нему целое i дает искомый максимум.
Это приводит к приближенному решению
Алах = 10gr ( (Г - 1) tl).
Если р > q, т. е. г > 1, то получающееся /Юах близко
к П~^х .Таким образом, мы видим, что при рФЧъ
время поглощения при больших п имеет порядок более
низкий, чем при р = ’/г- Например, если р = 2/3, то г=2,
i’max = logs п, и /тах для больших п приблизительно
равно 3(п — log2 и). В нашем, примере для очень
малого п — 5 «шах = 2,3 и i — 2 — точка максимума, но
получаемое значение Апах слишком велико для такого
малого п.
Наконец, посчитаем В. Достаточно найти bin, так
как bto = 1 — bin. Заметим, что rin = 0, кроме rn-i,n=P-
Имеем
п—1
. V р(г1 -1)(гга-/
^{п P-i, п-1 ‘ Р (гп _ ])
fe=l
Поэтому
гп __ rn-i
= , если /?=/=’/г- (5)
Аналогично,
Ь1п = 11п, если р = */2. (6)
При р = У2 ответ очень нагляден: вероятность погло-
титься на правом конце пропорциональна начальному
7.1. СЛУЧАЙНЫЕ БЛУЖДАНИЯ
197
расстоянию от левого конца. Иначе обстоит дело при
р =£ i/2> когда из решения вытекают некоторые удиви-
тельные обстоятельства. Рассмотрим случай р > V2, т. е.
г>1. Тогда при заданном начальном положении i ве-
роятность окончания в п не будет пренебрежимо мала
ни при одном п. В самом деле, если фиксировать /, а п
устремить к бесконечности, то bin будет стремиться
к 1 — г~\ Если I достаточно велико, эта вероятность бу-
дет близка к 1, как бы велико не было п\ Даже для
i=l вероятность окончания в п не меньше (г— 1)/г.
Время поглощения в этом случае приблизительно рав-
но п/р, т. е. неожиданно мало. Для р = 2/з эта предель-
ная вероятность равна 7г. Это значит, что если р = 2/з,
то мы можем отодвинуть правую границу и так
далеко, как мы пожелаем, начать процесс в i = 1, и
все же будем иметь больше шансов поглотиться в п,
чем в 0.
Этот частный случай блуждания часто называют
«разорением игрока». Представим себе, что двое играют
в некоторую игру, и вероятность выигрыша игрока А
равна р. Пусть его начальный капитал равен i долла-
рам, капитал партнера равен п — i долларам, и пусть
каждый раз выигрывается 1 доллар. Тогда капитал Д
представляет случайное блуждание AARW с данным р.
Поглощение в п означает, что А выиграл все деньги,
а поглощение в 0 — что он разорился. Мы видим, что
при честной игре (р = V2) вероятность разорения равна
отношению начальных капиталов. Но ситуация резко
меняется, если игрок А имеет преимущество. В этом
случае он имеет хорошие шансы выиграть, даже если
у его противника гораздо больше денег. Например, если
у него р = 2/з, т. е. г = 2 (преимущество 2: 1 в его поль-
зу), то он имеет больше половины шансов разорить
противника, начиная игру всего лишь с одним дол-
ларом!
Упомянем кратко о двух приложениях этого резуль-
тата. Во-первых, игорные дома обязаны ему своим су-
ществованием. Они обеспечивают за собой такое пре-
имущество, чтобы г было больше единицы. Тогда,
запасшись достаточно большим (по отношению к разме-
рам одной ставки) начальным капиталом /, они будут
198
ГЛ. VII. ПРИЛОЖЕНИЯ ЦЕПЕЙ МАРКОВА
иметь вероятность 1—очень близкую к 1, сохра-
нить свое предприятие, независимо от того, кто и сколь-
ко выигрывает за их игорными столами. Мы также
видим, что время поглощения здесь колоссально ве-
лико; этим объясняется, почему игорные дома еще не
завладели всеми деньгами мира. Если г близко к 1,
то (3) приблизительно равно (4). Предположим (весь-
ма скромно), что игорный дом обладает капиталом
в 10 000 ставок, а игроки могут сделать 1000 000 ставок.
Тогда i(n— i) примерно равно 1010, так что время погло-
щения измеряется тысячелетиями. Это представляет
обильные возможности для появления новых игроков.
Второе приложение представляет собой простейшую
модель естественного отбора в теории эволюции. Пусть
на изолированном острове численность некоторого вида
не может превзойти п из-за ограниченности запасов
пищи. Предположим, что рождается мутант с несколь-
ко лучшими данными для выживания, чем обычный
представитель вида. Простейшую модель борьбы за су-
ществование получим, предположив, что в каждом по-
колении мутанты завоевывают одно место с вероятно-
стью р > V2 и теряют одно место с вероятностью q.
Тогда согласно найденному выше мутанты овладеют
островом с вероятностью большей, чем (г—1)/г. Если
р = 0,51, то эта вероятность равна 0,04; если р = 0,6,
она равна '/з- Мы видим, что относительно небольшие
преимущества могут привести к выживанию мутантов.
Эта простая модель служит иллюстрацией того, как
мутанты могут вытеснить многочисленный вид, но она
дает нереальное время поглощения. Даже для р = 0,6
и п такого малого, как 100, мы получаем, что потре-
буется п/р, т. е. около 167 поколений, прежде чем му-
танты окончательно возьмут верх. Причина этого ясна:
наше предположение о том, что в каждом поколении
заменяется лишь одно место, слишком неправдоподоб-
но. Для того чтобы получить действительное время по-
глощения, нужна более хитроумная модель.
Покажем теперь, что результаты для остальных
трех случайных блужданий можно получить из AARW
с помощью различных трюков. Проиллюстрируем сперва
APRWt считая п = 5.
7.1. СЛУЧАЙНЫЕ БЛУЖДАНИЯ
199
APRW при п = 5, р = 72:
0 1 2 3 4 5
1 0 0 0 0 0
0
1
Р = 2
3
4
5
’/2 О О О
О */2 О О
'/2 0 >/2 О
о </2 о >/2
о о >/2 '/2
1 2 2 2 2 2 10
2 2 4 4 4 4 18
W = 3 2 4 6 6 6 , т — 24
4 2 4 6 8 8 28
5 2 4 6 8 10 30
APRW при п = 5, р = 21з-
0 1 2 3 4 5
0 1 0 0 0 0 0
1 7з 0 73 0 0 0
II to 0 */з 0 2/з 0 0 .
3 0 0 */з 0 2/3 0
4 0 0 0 >/з 0 2/3
1 3 6 12 24 48
2 3 9 18 36 72
3 3 9 21 42 84
4 3 9 21 45 90
5 3 9 21 45 93
200
ГЛ. V11. ПРИЛОЖЕНИЯ ЦЕПЕЙ МАРКОВА
93
138
159
168
171
Матрицу N для APRW можно получить из соответ-
ствующей матрицы для AARW следующим образом.
Пусть i > /. Если процесс начинается в i, он в конце
-о-
/
-о
77
Рис. 7.3.
концов достигнет j. Поэтому Иц = (п^п^) = 1 и
= Пц (это бросается в глаза в выше приведенной
матрице N). Если k < /, то hkj можно получить как ве-
роятность окончиться в / для процесса AARW с п = /.
Поэтому nkj = = bkjtijj, где bkj взято из AARW.
Таким образом, остается найти Посчитаем их сна-
чала для р = V2. Заметим, что матрица Q (кроме по-
следней строки и последнего столбца) является подмат-
рицей матрицы Q для больших значений п, причем в
этих больших Q эти строки и столбцы заполнены нуля-
ми. Поэтому riij не зависит от и. Но если положить
и->оо, то разница между AARW и APRW исчезнет. По-
этому rijj для APRW есть предел для AAPW при
п->оо. Таким образом,
пи = 21, если />/, 1
•n-у о- (ДЛЯ р=’/2. (7)
Пц = t2jlj = 2i, если i /, j v '
Те же рассуждения применимы при г<1. Таким об-
разом,
= если
г1-г1~1 r'-\ ri-r!-1 (8)
ntj = —-----------------------, если i <1 /
г'-1 p-q p-q
для р Ч2.
7.1. СЛУЧАЙНЫЕ БЛУЖДАНИЯ
201
Мы можем также получить пц при i ¥= / из матрицы N
для AARW, положив п—*оо.
При г > 1 эти рассуждения не проходят, потому что,
как бы велико ни было п в AARW, вероятность погло-
титься в п не становится так мала, чтобы ею можно
было пренебречь. Но здесь мы воспользуемся тем, что
если в AARW переименовать I в п — I, то получится про-
цесс, в котором р и q поменяются местами. Отсюда вид-
но, что найденные формулы справедливы также и при
г > 1.
Для т получаем
tt = (2/г — i + 1) i, если р = '/г. (9)
1 Г гп+1 —• Z 4-1 1
= j-------']• если 0°)
Так как здесь имеется только одно поглощающее со-
стояние, то все вероятности поглощения равны 1.
И в AARW, и в APRW существует простое соотноше-
ние между riij и Hjf. В самом деле, из наших формул для
этих величин следует, что
Покажем, что существует простое вероятностное до-
казательство этого факта.
Пусть / < L Положим d = i — /. Тогда любой путь,
приводящий из i в / за п шагов, должен содержать на
d шагов больше влево, чем вправо. Поэтому вероятность
того, что процесс, начавшись в i, пойдет по такому пути,
равна
phqh+d,
где 2k + d = п. С другой стороны, любой такой путь,
пройденный в обратном направлении, можно рассматри-
вать как путь из / в I. Для того чтобы процесс пошел по
этому пути, надо сделать вправо на d шагов больше, чем
влево. Поэтому вероятность того, что процесс, начавшись
в /, пойдет по этому пути, равна
Число путей из i в /, состоящих из п шагов, такое же,
202
ГЛ. VII. ПРИЛОЖЕНИЯ ЦЕПЕЙ МАРКОВА
как и из / в I, а отношение вероятностей для каждого
пути равно
pk4k+d rj_t
pk+dqk~ pd~r
Следовательно, = Но тогда
Отсюда также
iiij = n,ji.
Обратимся
PPPW.
PPPW при
видно, что при р = V2, когда г = 1, имеем
теперь к регулярным
цепям, начиная с
п = 5, р = 72:
0
1
4
5
0
>/2
7г
0
о
о
о
1 2 3 4 5
7г О О О О
О >/2 О О О
72 о i/2 о о
о 7г о 1/2 О ’
0 о 1/2 о >/2
о о о v2 1/2.
« = (%, 76, 76, 76, 76, 76),
0 1
0 6 2
1 10 6
2 18 8
3 24 14
4 28 18
5 30 20
2 3 4 5
6 12 20 30
4 10 18 28
6 6 14 24
6 6 8 18
10 4 6 10
12 6 2 6
7.1. СЛУЧАЙНЫЕ БЛУЖДАНИЯ
203
PPRW при п = 5, р = 2/3:
0
О
1
4
5
7з
7з
о
о
о
о
1 2 3
2/з О О
О 2/3 О
7з 0 7з
О 7з о
о о 7з
ООО
4 5
о о
о о
о о
7з О
о 2/з
7з 2/з
а = (7бЗ. 2/бз> 4/бз> 8/бЗ> 16/ 32/ \ /63> /бЗ/>
0 1 2 3 4 5
0 63 3/2 578 l47i6 387/ /32
1 93 63/2 74 378 ,23/1б 339/ /32
2 138 45 63/4 27в 87i6 267/ /32
м = 3 159 66 21 63/8 45/i6 183/ /32 •
4 168 75 30 9 63/ /16 93/ /32
5 171 78 33 12 3 63/ /32
Можно получить APRW из PPRW, если сделать 0 по-
глотающим состоянием. Поэтому, если мы знаем а для
PPRW, мы можем получить матрицу М из матрицы N
для APRW, используя следствие 6.2.6. Имеем
та = -г(пн-пи) + ^~Ь ПРИ *=*/•
Если р = ’/г, то сумма элементов каждого столбца
равна 1, и поэтому а = Таким образом, получаем
та =
п+1, i=i,
(2п — i+ 1)/ — (2п — /+ 1)/, 1>/,
/(/+l)-i(i+1), /</,
при р = */2-
(И)
204
ГЛ. VII. ПРИЛОЖЕНИЯ ЦЕПЕЙ МАРКОВА
При р =# V2 пример, разобранный выше, подсказы-
вает, что Пг+1 = га*- И в самом деле, это дает нам не-
подвижный вектор, что можно усмотреть, записав наши
уравнения в виде
qa0 + qa{ = а0, или а{ = га0,
। р
pat-x+qai+i = ah или ai+i +qrat^l = at,
pan-i+qan = an, или a„_!=ya„.
Отсюда r 1
Тогда
rn+1-l 1
r - 1 Г1 ’
1 Г — /"Ы ___________ гП~/+1 1
^/= 7^[-----------—x---------(*-/)].
1 /. _ . _ — r1 \
P~4 IV 1 (г-1)г/+/ЛГ
p¥=V2. (12)
Сравним mOn с mno- Если p — */2, to mOn = mn0 —
= (n+l)n, т. e. является величиной порядка и2 при
больших п. Но когда р =# ’/г» мы наблюдаем совершенно
другое поведение. Положим г > 1, тогда
_ 1 Г гп-1 1
топ-р_д[п (r-i)rreJ’
что приблизительно равно * п для больших п. Сле-
довательно, на прохождение «всего пути» в благоприят-
ном направлении уходит удивительно мало времени.
Далее,
1 Ггге+1- г 1
'««о = тту [——~4
что приблизительно равно 7^.:^ • гп при боль-
ших п. Так как г > 1, то тп0 экспоненциально растет
с ростом п. При очень больших п прохождение «всего
7.1. СЛУЧАЙНЫЕ БЛУЖДАНИЯ
205
пути» в неблагоприятном направлении занимает неожи-
данно много времени. Такого рода поведение типично
для случайных блужданий. Мы увидим это еще раз в
модели Эренфестов.
Наконец, рассмотрим CRW.
CRW при п = 5, р = 1/г:
1 2 3 4 5
1
2
Р = 3
4
5
0
>/2
0
о
72
*/2 0 о </2
о */2 о о
7г 0 >/2 0
0 7г 0 7г
О 0 7г О
2
А1 = 3
4
5
4 6
5 4
4 5
6 4
6 6
6 4
6 6
4 6
5 4
4 5
1 '5
CRW при я = 5, р = 21з-
1 2 3 4 5
1 О
2 7з
Р = 3 О
4 О
5 Р/з
2/з 0 0 '/з
О 2/з О О
7з о 7з 0 »•
о 7з 0 2/з
о о 7з О
1 5 78/31 ,47з1 ,74/73 14731
2 ,47з1 5 7731 ,47з< ,74/31
А1 = 3 ,74/з1 147/з1 5 78/з. ,4731
4 147з1 174/з1 147/з1 5 78/31
5 78/31 147з1 174/31 147/31 5
206
ГЛ. VII. ПРИЛОЖЕНИЯ ЦЕПЕЙ МАРКОВА
В этом процессе всегда а = ~ т|» так как У матрицы
Р сумма элементов каждого столбца равна 1. Это видно
еще и из того, что на окружности все положения равно'
правны. По той же причине можно ожидать, что
будет зависеть лишь от расстояния между i и / (и от
направления, если р =# !/2). В приведенных выше приме-
рах дело обстоит именно так.
Если в CRW сделать п поглощающим состоянием, то
получим AARW, но с отождествленными концами 0 и п.
Значит, М для CRW можно получить из W для AARW.
Но есть еще более простой метод. Если мы хотим найти
т^, то перенумеровываем состояния так, чтобы / превра-
тилось в и, и тогда rtiij будет равно времени поглоще-
ния в AARW. Именно если расстояние от / до i (в на-
правлении часовой стрелки) равно d, то тц = td. Таким
образом,
та = п,
1 ( гп - rn~d 1
d • «¥=/, (13)
г Ч V ' 1-/
тц = d(n — d), р = i¥=j,
где d — расстояние от / до i по часовой стрелке.
Здесь применимы замечания, высказанные относи-
тельно т для AARW. Так, например, расстояние (по ча-
совой стрелке), для прохождения которого требуется
наибольшее время, приблизительно равно logr((r— 1)п).
Заметим также, что т^, вообще говоря, при любом
р =£ V2 имеют меньший порядок роста, чем при р = V2.
Найдем теперь переходные матрицы тех процессов,
которые получаются обращением во времени PPRW и
CR W.
Для PPRW, вспоминая, что aw = rat, имеем
а.., .
'+1 Л' + Ь ; = /7? = /7 = Pi, i + b
а. 1
&+!, * = 7 Р ~ У ~ Р* + ь **
Значит, процесс обратим, хотя интуиция и подсказывает
7.1. СЛУЧАЙНЫЕ БЛУЖДАНИЯ
207
противное. Но для CRW ai+\ = aif следовательно,
Pi, /+1 “ “Т”' Pi + 1, i —
I
л
Pi+1, 1 = a.+1 f+1 = P*
Значит, обращенный процесс — это CRW, но с заменой р
на 9, как и можно было ожидать, он обратим лишь
тогда, когда р = q = У2.
В завершение укажем одно практическое примене-
ние для PPRW. Рассмотрим игорный дом, который
хочет иметь простой способ постоянно следить за исправ-
ностью колеса рулетки. Предположим, что колесо в до-
полнение к номерам от 1 до 36, половина которых крас-
ная, а половина — черная, имеет номера 0 и 00, которые
не окрашены. Мы предлагаем следующий простой авто-
матический способ проверки, получает ли игорный дом
свою долю от ставок на красное. Установим электриче-
ский счетчик, который начинает с 0, добавляет 1 каж-
дый раз, когда выпадает красный цвет, и вычитает 1
каждый раз, когда красное не выпадает. Причем счет-
чик не опускается ниже 0. Если счетчик достигает отме-
ченного числа п, то раздается звонок, и тогда игорный
дом заменяет колесо.
Если колесо правильно сбалансировано, то получает-
ся PPRW с р = 18/з8 = 9/i9‘ Значит, надо очень много
времени, чтобы добраться до и. Игорный дом подбирает
п так, чтобы тОп соответствовало обычному сроку служ-
бы колеса. Однако если колесо неправильно функциони-
рует— например, если р увеличивается до У2 (при этом
дом уже не получает прибыли), — звонок зазвенит гораз-
до раньше. Подобная же проверка на черном дает воз-
можность убедиться, что дом получает свою прибыль при
любых ставках.
Рассмотрим конкретный пример: пусть выбрано
п = 40. Тогда тОп для правильно функционирующего
колеса равно примерно 18 000. Если колесо крутится
400 раз в день, то звонок будет звонить в среднем раз
в 45 дней, что соответствует нормальному сроку службы
колеса. Но если р возрастет до У2, то mOn станет
_08
ГЛ. VII. ПРИЛОЖЕНИЯ ЦЕПЕЙ МАРКОВА
равно 1640, и звонок зазвенит через 4 дня. Если р ста*
нет еще больше (т. е. дом начнет терять деньги), то
звонок зазвенит очень быстро.
7.2. Приложения к спорту. Применим некоторые из
наших результатов к теннису. Рассмотрим сначала одну
игру между двумя партнерами. Предположим, что ве-
роятность выиграть любой мяч для игрока А равна р,
а для игрока В равна q^p.
Если мы будем считать очки так, как это обычно при-
нято, то в течение игры будет 20 возможных значений
счета. Вот они: 0—0, 0—15, 15—0, 0—30, 15—15, 30—0,
0—40, 15—30, 30—15, 40—0, 15-40, 30—30, 40-15,
30—40, 40—30, «меньше», «ровно», «больше», игра В,
7.2. ПРИЛОЖЕНИЯ К СПОРТУ
209
игра А. Однако легко видеть, что состояния можно ук-
рупнить, объединив {30—30, «ровно»}, {30—40, «мень-
ше»} и {40—30, «больше»}. Полученное случайное блуж-
дание представлено на рис. 7.4.
Нам удобно разбить игру в теннис на две стадии.
Вначале процесс проходит через некоторые из нижних
двенадцати состояний, и за четыре или пять шагов он
доходит до одного из пяти состояний верхнего ряда. Мы
будем называть это предварительным процессом. Пред-
варительный процесс устроен исключительно просто. За
ним следует случайное блуждание типа AARW с п = 4.
Состояние «игра В» — это поглощающее состояние 0, а
состояние «игра А» — поглощающее состояние п.
Мы представим весь процесс как случайное блужда-
ние AARW с теми начальными вероятностями, которые
задаются предварительным процессом. Эти начальные
вероятности л •= (с0, сь с2, £з, с4) находятся элементарным
подсчетом. Находим, что
с0 = q4 (1 + 4р), Cj = 4p2q3t с2 = 6p2q2,
с3 = 4рV, с4 = р4 (1 + 4q).
ЕСЛИ P-V2, ТО С0 = 3/1б, Ct = 78, с2 = 3/8, Сз=78, f4 = 3/16.
Используя основные числовые характеристики процесса
AARW при п = 4:
N =-------!-----X
/(г— 1)(г3— 1) (г—1)(г3 —г) (г — 1)(г3 —г2)\
X (г — 1)(г2— 1) (г-1)2 (г2- 1)(г2 — г) ],
\ (г-1)2 (г - 1)(Г2_ 1) (г __ 1)(гз__ У
/72 1 72\ /3\ /74\
2V=( 1 2 1 )' . 1= 4 , {6/4} = 72 , р = 72,
\7г 1 3/2/ \3 / ' e/J
14 Дж. Кемени, Дж. Снелл
210
ГЛ. VII. ПРИЛОЖЕНИЯ ЦЕПЕЙ МАРКОВА
мы можем найти все интересующие нас величины. Самое
интересное, конечно, — найти вероятность победы игро-
ка А. При p = V2 получаем
3/1б • 0 + • */4 + 3/в • V2 + 7s • 3/4 + 3/1б • 1 = Уг-
Этого следовало ожидать из соображений симметрии.
Если р>Уг, имеем
нтгг к4 (1 + 4Р) ’ 0 + 4Р V У*4 “ г3) + 6Р V (f4 “ г2) +
+ W (г4 - г) + р4 (1 + 4р) (г4 - 1)]
и после упрощения
_ (1 _ 16<у4)
Pa- р4_д4 •
Например, если р = 0,51, то р& = 0,525, а если р = 0,6,
то Ра = 0,736. Время поглощения и время пребывания
в фиксированном состоянии мы посчитаем лишь для
случая р=У2. Интерес представляют те случаи, когда р
близко к V2, а время поглощения не слишком резко ме-
няется при изменении р.
При р = V2 находим, что среднее время пребывания
в трех невозвратных состояниях таково: I для «ровно»,
5/8 для «больше» и «меньше». Время поглощения равно
9/4. Чтобы найти полную продолжительность игры, надо
также учесть подготовительную стадию. Сделав это,
найдем, что средняя продолжительность игры между
одинаковыми по силе противниками равна 27/4 = 63/4.
Так как наименьшая продолжительность игры равна 4,
то отсюда видно, что для игроков одинаковой силы сред-
няя продолжительность ненамного превосходит мини-
мальную.
Если бы оказалось, что в действительности игры про-
должаются гораздо дольше, чем получилось у нас, и что
среднее время в состоянии ничьей значительно больше 1
(как, по-видимому, и бывает на самом деле), то это
означало бы, что наша модель игры в теннис слишком
проста. Надо думать, что игрок играет «с большой отда-
чей», когда он проигрывает. Это приводит к случайному
блужданию, несколько более сложному, чем наше.
Вернемся к вероятности того, что лучший игрок А
выиграет. Она всегда для всей игры больше, чем для
7.2. ПРИЛОЖЕНИЯ К СПОРТУ
211
каждого мяча. Таким образом, игра способствует уве-
личению разницы между игроками. Эта разница увели-
чивается и в дальнейшем, поскольку несколько игр объ-
единяются в сет, а несколько сетов — в матч. В сете иг-
рок должен выиграть не менее шести игр, причем с пере-
весом по меньшей мере в две игры. Вероятность того или
иного исхода сета можно подсчитать так же, как вероят-
ности исходов игры. Это приводит нас опять к блужда-
нию AARW, но с более длинной предварительной ста-
дией. Матч выигрывает тот, кто первым побеждает в
трех сетах. Здесь надо уже провести прямой подсчет.
Следующая таблица показывает, как увеличивается раз-
ница между игроками:
р = 0,51 р — 0,6
Вероятность выиграть мяч............ 0,510 0,600
Вероятность выиграть игру........... 0,525 0,736
Вероятность выиграть сет............ 0,573 0,966
Вероятность выиграть матч........... 0,625 0,9996
Таким образом, всегда велик шанс, что матч выиг-
рает лучший игрок. А если между игроками есть замет-
ная разница, то лучший игрок практически наверняка
выиграет.
Сравним эти результаты для тенниса с финалами
ежегодных чемпионатов США по бейсболу. Здесь объ-
является победителем команда, которая первая выиграет
четыре игры. Если предположим, что команда А вы-
игрывает игру с вероятностью р, то найдем, что
рл = р4(1+4?+ 10^2 + 20?3),
где различные члены соответствуют сериям из 4, 5, 6 и 7
игр соответственно. Если р = 0,51, то рА = 0,522, в то
время как если р = 0,6, то рА = 0,710. Серия игр в бей-
сболе также увеличивает разницу между игроками, но
не так сильно, как теннисный матч, или даже одна-един-
ственная игра в теннис.
Если мы посчитаем среднее число игр в финале бей-
сбольного чемпионата, то найдем, что
t = 4 (р 4 + q4) + 20 (p4q + pq4) + 60 (p4q2 + p2q4) +
+ 140(pV + p'V)
14*
212
ГЛ. VII. ПРИЛОЖЕНИЯ ЦЕПЕЙ МАРКОВА
Оно принимает наибольшее значение 5,81, когда р = 1/2>
и монотонно убывает до 4, когда р возрастает до 1. По-
этому мы имеем возможность оценить р по наблюдениям
за средней длиной финалов чемпионата США по бейс-
болу. Из 50 финалов бейсбольных первенств, сыгран-
ных по установленным правилам с 1905 по 1957 г., 10
окончились за четыре игры, 13 — за пять, 12 — за шесть
и 15 — за семь игр. Отсюда средняя длина 5,64 игры, и
значение р = ъ1ь прекрасно сюда подходит. Это застав-
ляет предположить, что команды, участвовавшие в фи-
нальных играх чемпионата, в среднем представляли со-
бой не равноценные пары.
Рассмотрим теперь влияние различных правил на уве-
личение разницы между игроками или командами. Мы
нашли, что теннис (одна игра) увеличивает ее немногим
больше, чем бейсбольный финал, но для этого требуется
в среднем большее число шагов. Чтобы сравнивать два
правила, их нужно рассмотреть так, чтобы средние дли-
ны серий были.одинаковы.
Теннис и бейсбол можно сравнить следующим обра-
зом. В бейсбольном финале надо выиграть 4 встречи,
а в теннисе — выиграть 4 мяча и быть впереди на два
мяча. Это явный гибрид двух типов правил. В чистом
виде правило выглядело бы так: побеждает тот, кто
опережает противника на четыре мяча. Легко видеть,
что это правило увеличивает разницу гораздо силь-
нее, чем другое, но также требует для этого значи-
тельно больше времени. Итак, рассмотрим правила двух
типов.
Правило Wn: Первый, кто выиграет п туров, объяв-
ляется победителем.
Правило Ап: Первый, кто опередит противника на
п туров, объявляется победителем.
Сравним эти два правила, выбирая п в каждом слу-
чае таким, чтобы средняя длина игры равнялась напе-
ред заданному большому числу (обозначим его №), н
посмотрим, насколько эти правила изменяют разницу
между играющими. Поскольку нас особенно интересуют
большие значения п, мы ограничимся асимптотическими
приближениями, и поскольку в нашем случае начальная
разница между игроками очень мала, то будем считать,
7.2. ПРИЛОЖЕНИЯ К СПОРТУ
213
1+8 1—8 о
что она равна е, т. е. положим р =—q = —Вы-
числим при этом первый член окончательной разницы
по отношению к е.
Мы воспользуемся такими тождествами1):
п
Ш‘Н2"П
/г=0
п
2ГГ)‘="ГНМ|'
fe=0
k=0
п
\ rv / \ £* / £i \ Г1> /
fe=0
Если действует правило Wn> то лучший игрок выиграет
с вероятностью
гг—1
fc=0
9 Эти тождества легко доказать по индукции, если воспользо-
ваться следующими почти очевидными соотношениями:
п‘Н“+:+,н^).
(Прим, перев.)
214
ГЛ. VII. ПРИЛОЖЕНИЯ ЦЕПЕЙ МАРКОВА
Используя формулу Стирлинга1) и упрощая, получаем
Рд«4 + ]/^ е.
Ожидаемая продолжительность игры (при этом мож-
но считать р = у) равна
П-1
Z = 2‘bJ 2j( k + =
6=0
= (1V’1 [«2"-' + n2re-' - /2" - 2 )1 «
\2/ L 2"-1 \ л-1 /]
~ 2n----У n .
Будем считать просто t « 2n. Таким образом, если мы
хотим, чтобы / Af2, то надо выбрать п = -у-. Отсюда
1 I „-./Г
Ра ~ —Г"'7— е> Ра ~~ Рв ~ N 1/ — е, и, следовательно,
2 У 2л т л
разница увеличивается в W j/", т. е. примерно в
0,8N раз.
Если применять Ап, то получается процесс AARW
с состояниями 0, 1, 2п, начинающийся в п. Поэтому
Г2П _ ГП
Ра = г2п _ । ’ •
Здесь оказывается, что члены порядка г сокращают-
ся и надо учитывать члены порядка е2. Мы находим
rn 1 + 2ие + 2 (п + п2) е2,
r2n ~ 1 + 4пе + 4 (п + 2/г2) е2,
2ne + 2(n + 3n2)e2_ T+2'(1+3/l)e 1 . п
рА~ 4пе + 4 (« +2п2) е2 1+(1+2п)е 2 2 е’
Находим среднюю длину (полагая Р 4): “
« п (2п — п) = п2. Поэтому выбираем n = ./V и получаем
!) См. В. Феллер, Введение в теорию вероятностей и ее при-
ложения, т. 1, гл. 2, «Мир», 1967.
7.3. МОДЕЛЬ ЭРЕНФЕСТОВ ДЛЯ ДИФФУЗИИ
215
рА « у + 8, рл — рв~ №, т. е. разница увеличивается
в W раз.
Мы находим, таким образом, что и AN сравнимы
2
в том смысле, что каждое из этих правил дает среднее
время примерно №. Первое увеличивает разницу при-
близительно в 0,8М раз, а второе — в N раз. Так что пра-
вило Ап более эффективно. Любая смесь этих двух пра-
вил, как, например, в теннисе, дает меньший эффект,
чем Ап.
7.3. Модель Эренфестов для диффузии. П. и Т. Эрен-
фест предложили простую модель одной системы
статистической механики. В этой модели рассматри-
вается газ, заключенный в сосуде, разделенном на две
части А и В проницаемой мембраной. Предположим,
что сосуд содержит $ молекул этого газа. В каждый мо-
мент времени случайно выбирается одна из этих моле-
кул и передвигается из той части, где она находится, в
другую. Нас интересует, как меняется со временем со-
держимое обеих частей. Например: пусть в начале все
молекулы находились в одной части; сколько в среднем
пройдет времени, пока в обеих частях будет поровну
молекул? На такие вопросы можно ответить, используя
методы цепей Маркова.
Построим цепь Маркова следующим образом. Буде^м
считать, что все молекулы одинаковы. В качестве состоя-
ний рассмотрим векторы у = (хь х2, ..., xs), где Xj— 1,
если /-я молекула находится в области 4, и 0 в против-
ном случае. Зная состояние, мы тем самым точно знаем
содержимое 4, а отсюда — и содержимое В. Всего име-
ется 2s состояний. Если процесс находится в состоя-
нии у, то после выбора одной молекулы и перемещения
ее в другую часть мы переходим из состояния у в состоя-
ние б, которое отличается от у одной координатой. Ясно,
что из у можно попасть в s состояний, и в каждое из
них — с вероятностью 1/s. Из любого состояния у можно
перейти в любое состояние б за какое-то число шагов,
но из у в у можно попасть только за четное число ша-
гов, например за два. Таким образом, мы здесь имеем
216
ГЛ. VII. ПРИЛОЖЕНИЯ ЦЕПЕЙ МАРКОВА
эргодическую цепь с периодом 2. Ясно также, что мож-
но попасть из у в б за один шаг тогда и только тогда,
когда из б в у можно попасть за один шаг. Если это воз-
можно, то вероятность каждого из этих событий равна
1/s. Поэтому матрица переходных вероятностей симмет-
рична. Это говорит о двух фактах: во-первых, процесс
обратим, а во-вторых, неподвижный вектор — это вектор,
все компоненты которого равны 1/28. Матрица переход-
ных вероятностей для случая s == 3 имеет вид
000 001 010 100 011 101 по 111
ООО 0 7з 7з 7з 0 0 0 0
001 */з 0 0 0 7з 7з 0 0
010 7з 0 0 0 7з 0 7з 0
100 7з 0 0 0 0 7з 7з 0
011 0 7з 7з 0 0 0 0 7з
101 0 7з 0 7з 0 0 0 */з
по 0 0 7з 7з 0 0 0 7з
111 0 0 0 0 7з 7з 7з 0
Неподвижный вектор а = (7s, 7e, 7в» 7e, Ve, Ve, Ve> Ve).
Из этого, например, видно, что среднее число шагов, ко-
торое требуется для возвращения в любое состояние,
равно 8. Кроме того, по теореме 6.2.3, среднее время,
проведенное в каждом состоянии в промежутке между
двумя пребываниями в каком-то одном состоянии, рав-
но 1. Вообще, для цепи с s молекулами среднее время
возвращения в данное состояние равно 2s, и среднее
время, проведенное в состоянии 6 между пребываниями
в состоянии у, равно 1.
Рассматриваемый процесс можно просто интерпре-
тировать с помощью следующего случайного блужда-
ния. Будем считать векторы у вершинами n-мерного ку-
ба. Тогда состояния, в которые можно попасть из у за
один шаг, — это вершины, соединенные с у ребром. Та-
ких вершин s, и вероятность продвинуться в любую из
них равна 1/s. Для s = 3 этот куб изображен на рис. 7.5.
МОДЁЛЬ ЭРЁНФЁС1ОЁ ДЛЯ ДИФФУЗЙИ
217
Определим расстояние d(y, 6) между двумя состоя-
ниями у и 6 как наименьшее число шагов, которое тре-
буется, чтобы из у прийти в 6. Его можно выразить че-
рез компоненты векторов у и б:
(am mj
d (у, 6) = S I xt - yt |.
1=1
Из нашей геометрической ин-
терпретации ясно, что средняя
продолжительность пути из у в б
зависит только от расстояния ме-
жду у и 6. Пусть mSd —это сред-
нее время для пары точек, находя-
щихся на расстоянии d. Зафик-
сировав s, посчитаем msd = md
Рис. 7.5.
следующим образом. Пусть у и S — две точки, удален-
ные друг от друга на расстояние d. Это значит, что
у них ровно d различных координат. На первом шаге
есть d возможностей приблизиться к б на единицу и
s— d возможностей отдалиться от 6 на единицу. Поэтому,
учитывая возможные способы сделать первый шаг, имеем
< । d . s d
tnd=\ + -md-x+——
О V
md+b Q<d^s,
где мы полагаем m0 — = 0. Эти уравнения имеют
единственное!) решение, которое можно записать
!) Единственность решения доказывается с помощью так на-
зываемого «принципа максимума». Приведем соответствующее рас-
суждение. Пусть md и md, d = 0, 1, ..., s, $ + 1, —два решения
нашей системы. Числа Md = md — md являются решением одно-
родной системы
Md-*-Md-x + ±^-Md+x.
о о
Очевидно, Мо = Мe+1 = 0. ПустьМ = max Md. Если = М, то
0Cd<s+l а°
= М = | Md>_x + Md>+X < 4 м + м = <
причем равенство возможно лишь тогда, когда =^о+1 = М.
Продолжая в том же духе, получим, что Mdo = } 2 = ...
... =M0 =0. Аналогично, можно показать, что т= min М^ = 0.
Значит, Конечно, эти рассуждения проходят в гораздо более
общей ситуации. (Прим, перев.)
218
ГЛ. VII. ПРИЛОЖЕНИЯ ЦЕПЕЙ МАРКОВА
в следующем виде. Положим
тогда1)
d
Qs-t,
i = l
0<d^s.
Значения Qs{ для s от 1 до 6 приведены на рис. 7.6. На
рис. 7.7 приведены значения msd для s от 1 до 6.
!) Приведем доказательство этого факта. Так как
то осталось проверить, что
что и было нужно. (Прим, перев.)
7.3. МОДЕЛЬ ЭРЕНФЕСТОВ ДЛЯ ДИФФУЗИИ
219:
Мы видим, что msd при фиксированном s возрастает
с увеличением расстояния. Этого и следовало ожидать.
Впрочем, они растут очень медленно.
Будем называть вышеописанную цепь микроскопиче-
ской цепью. В физических приложениях представляет
интерес не столько эта цепь, сколько та, которая полу-
чается из нее укрупнением состояний. Макроскопическая
цепь получается из микроскопической отождествлением
всех состояний, при которых в части А находится одно
и то же количество молекул. Проверим, что такое укруп-
нение возможно. Пусть Vi — множество состояний ми-
кроскопического процесса, при которых в А находится
i молекул. Множество Vi имеет ) элементов. Из лю-
бого элемента множества Vi процесс переходит в один
из ) элементов множества или в один из
(/~1) элементов множества Vj-i. Вероятность попасть
в равна -—а в V. Эти вероятности оди-
наковы для всех элементов V^ Значит, условие возмож-
ности укрупнения состояний выполнено, и мы получаем
новую цепь Маркова с состояниями Vo, Vi, V2, ..., Vs.
Вероятности перехода здесь равны
Pi, i+\ = 1 — у >
Pi,
рИ = 0 в остальных случаях.
Этот новый процесс будем в дальнейшем называть ма-
кроскопическим.
Из результатов 6.3 мы знаем, что укрупненный про-
цесс будет снова эргодическим, обратимым и иметь пе-
риод 2. Неподвижный вектор а этого процесса легко по-
лучить из а. Компоненты — это суммы компонент а
для состояний из множества V^ Так как Vi содержит
( s \ о
I t I состоянии, то мы имеем
. С)
«/--у-.
220
ГЛ. VII. ПРИЛОЖЕНИЯ ЦЕПЕЙ МАРКОВА
Поэтому
Из теоремы 6.2.3 следует, что среднее время, прове-
денное в любом состоянии Vi между последовательными
попаданиями в V,-, равно
В частности, среднее время, проведенное в i-м состоя-
нии между двумя попаданиями в Vo. равно^).
В нашем примере, т. е. при s = 3, состояния укруп-
няются так: {ООО}, {100,010,001}, {110,101,011}, {111}.
Матрица переходных вероятностей имеет вид
Vo V, V2 V3
V0/0 1 0 0\
v. / »/3 0 2/з 0 ]
V2I 0 2/3 0 Уз/
V3\0 0 1 о/
В случае макроскопической цепи нас также в первую
очередь интересует среднее время первого достижения.
Мы знаем, что в общем случае нелегко найти среднее
время первого достижения для укрупненной цепи по
аналогичной величине для первоначальной цепи. Но в
рассматриваемом случае нам помогут две особенности
нашего процесса. Во-первых, для новой цепи мы можем
найти все тц, зная только т,о- В самом деле, так как
перейти из Vt+i в Уо можно только через V,, то мы
имеем
и по симметрии
fni.i+i = = ms-i,Q - /ns-i-i,o. 0 <s.
7.3. МОДЕЛЬ ЭРЕНФЕСТОВ ДЛЯ ДИФФУЗИИ
221
Значения Q?
S 1 2 3 4 5 6
0 1 1 1 1 1 1
1 3 2 12/з 1‘/2 12/з
2 7 32/з 22/з 2‘/з
3 15 6«/г 4‘/з
4 31 П2/о
5 63
Рис. 7.6.
Значения tnd s
s d \ 1 2 3 4 5 6
1 1 3 7 15 31 63
2 4 9 182/3 371/2 742/в
3 10 20>/з 40»/в 78’/5
4 21'/з 412/з 804/з
5 422/з 82»/5
6 83’/&
Рис. 7.7.
222
ГЛ. VII. ПРИЛОЖЕНИЯ ЦЕПЕЙ МАРКОВА
Таким образом, нам нужно найти только среднее время
перехода из любого состояния в Vo- При укрупнении
состояние Vo было получено из множества, которое со-
стояло только из одного элемента, именно из вектора
у = (0, 0, ..., 0). Поэтому среднее время попадания из
Vi в Vo в укрупненной цепи совпадает со средним вре-
менем попадания из любого элемента множества Vi
в у = (0, 0, ..., 0). Но любой такой элемент расположен
на расстоянии i от вектора у. Значит, среднее время
равно mSi. Используя результаты для микроскопического
процесса, получаем значения тц для макроскопического
процесса, которые лучше всего записать в следующем
виде:
s—i s—i — \
i + X ~ ^s-i, 0 ms-i-X, 0 ~ 2 Qs-k 2 Qs-k = Qi,
fc=l Ы
0 i < s — 1.
Чтобы попасть из Vi в Vj, мы должны пройти через
все промежуточные точки. Поэтому
/-1
та = 2 Qn при i < ]
k — 1
и
s-i-\
т{! = ms-t,s-i= 3 QI при i>j.
k—s — i
Учитывая вид вектора а, имеем
Из этих значений получаем
Пусть «</+» — среднее время, проведенное в V, до до-
стижения Vi+i, если процесс начинается из состояния
7.3. МОДЕЛЬ ЭРЕНФЁСТОВ ДЛЯ ДИФФУЗИИ
223
Согласно 6.2.7 (Ь) мы имеем
Ш
яа+о = jZLLi+i±£!X±b_L = 25 . V1 ' = s
пи mu 2s s — i'
Пусть теперь s— четное число. Из (1) получаем
s/2-l
Кроме того, поскольку ms/2, о = rns/2, s, имеем
s/2—1
mo, s = mo, s/2 + m5/2, S = 25 (2)
‘s° I i )
С точки зрения физических приложений наиболее ин-
тересен случай большого числа молекул. Для этого слу-
чая нам хотелось бы оценить величины mo, $/2 и ms/2, о-
Первая из них представляет собой среднее время, тре-
буемое, чтобы молекулы, находившиеся сперва все в ча-
сти В, поровну распределялись между А и В, а вто-
рая— среднее время обратного перехода. Если наша
модель имеет хотя бы некоторое сходство с реальным
физическим явлением, то следует ожидать, что время,
необходимое, чтобы уравнять число молекул, гораздо
меньше, чем то, которое нужно, чтобы от равного числа
молекул в обеих частях перейти к случаю крайнего нару-
шения равновесия.
Рассмотрим сначала т0,5/2. Оценим время, нужное
для перехода из Vi в Мы знаем, что среднее число
попаданий в Vi до попадания в ViJr\ равно =
«= 1 4>—Каждое попадание в Vi (кроме последнего)
отнимает не менее двух шагов: попадание в V и воз-
вращение в V^ Поэтому среднее время перехода из V,
224 ГЛ. VII. ПРИЛОЖЕНИЯ ЦЕПЕЙ МАРКОВА
е Vi+i не меньше, чем
1+2_^ = £±4.
S—l S—I
Следовательно, то, 5/2 оценивается снизу суммой
s/2—1
Ss + i
s — i'
i=0
Эта сумма больше, чем
s/2
-2+ [ £i£dx = s(21og2-1/2)-2.
J ь л
О
Значит, s (2 log 2—*/г)—2 — нижняя граница для
то, s/г- Более точную оценку снизу можно получить сле-
дующим образом. Мы предполагали выше, что каждый
раз, когда процесс переходит из Vj_i в V,, это делается
за один шаг. Если вместо этого мы используем нашу
нижнюю оценку для времени перехода из Vt-i в Vi, то
получим новую нижнюю оценку для времени перехода
из Vi в Vt+i, а именно
1 + _(1 + £±1=±\ = 1 +_________*1______
1 + s-i \ s-z + 1 ) 1 r (s — Z) (.«— Z +1) •
Сумма этих выражений от Vo до Vs/2-i больше, чем
s/2
-4+ f (1+7-------,^sx ,.Adx =
J \ (s-x) (s-x + 1) )
о
= -4 + s[y — 2 log 2 + s (s + Olog-jiy].
Используя два первых члена тейлоровского разло-
1 s -Ь 2
жения для log—т-г, получаем улучшенную нижнюю
S г" 1
оценку
-5 + s(|-21og2).
7.3. МОДЕЛЬ ЭРЕНФЕСТОВ ДЛЯ ДИФФУЗИИ
225
Найдем верхнюю оценку для mo, s/2. Имеем
s/2—1
s — l _ s
з-2/ ~ A s-2l
1=0
s — l
2
<]* 7^27 dx + ,/4s = s(1/4 + l/2 1°gs).
О
Этот результат можно улучшить, если воспользовать-
ся более точной оценкой членов суммы при больших /.
Мы, таким образом, нашли, что
- 5 + s (% - 2 log 2) < т0, s/2 < s [74 + '4 log «]•
В действительности величина то, 5/г асимптотически
имеет больший порядок роста, чем константа на $, но
меньший, чем константа на s log s. Из этих оценок мы
видим, что на переход от 0 к s/2 уходит очень мало вре-
мени. Для s = 100 наименьшее возможное время равно
50, а истинное среднее время около 140.
Рассмотрим теперь mQ)S. Из (2) мы знаем, что
15 Дж- Кемени, Дж. Снелл
226
ГЛ. VII. ПРИЛОЖЕНИЯ ЦЕПЕЙ МАРКОВА
Поэтому
2’(1 + ^-).
Таким образом,
mo, s~2^1 +-7), где 1<Л<2.
Наши оценки для то, »/г показывают, что эта вели-
чина имеет меньший порядок роста, чем m0,«. Поэтому
приведенные здесь оценки годятся и для m$/2, s = ms/2, о
и мы имеем
ms/2,o~2’(l+-^-), где 1<Л<2.
Таким образом, как мы и предвидели, среднее время
перехода от равного числа молекул к 0 в одной часта
несравненно больше, чем среднее время перехода от О
к равному числу молекул. Для s = 100 первое из них
приблизительно равно 2100, т. е. примерно 1030, а вто-
рое— всего 140.
Интересны также значения т0, о и ms/2,s/2. Для них
имеем
то, о = 2\
2s
f^s/2, s/2— /
Для s = 100 число ^5о,5о приблизительно равно 12,5.
В заключение приведем несколько замечаний отно-
сительно макроскопической цепи и обратимости. Иногда
утверждают, что процесс рассматриваемого нами типа
имеет «направление», поскольку имеется очень сильная
тенденция к уравниванию. Действительно, если процесс
начинался не из состояния равновесия, а например,
из 0, то, конечно, он будет двигаться к центру. Однако
если от начала процесса до момента наблюдения прошло
достаточное время, то можно считать, что процесс на-
чался из состояния равновесия, и в этом случае процесс
и в прямом, и в обратном направлениях будет выглядеть
7.4. ПРИМЕНЕНИЯ К ГЕНЕТИКЕ
227
одинаково. Например, если процесс наблюдается в со-
стоянии Vx, то вероятность того, что он попадает в со-
стояние Vx-i, такая же, как вероятность того, что он
пришел из состояния Ух-ь Иначе это можно выразить
так. Если записать результаты последовательных наблю-
дений для большого числа шагов и показать их физику,
он не будет в состоянии сказать, записаны ли они в пря-
мом, или в обратном порядке.
7.4. Применения к генетике. В генетике часто обсуж-
дается следующая ситуация. Скрещивается пара жи-
вотных. Из их потомства каким-то образом выбирается
новая пара, опять скрещивается, и так далее. Такого
рода ситуацию можно трактовать как цепь Маркова.
В качестве состояний мы рассмотрим возможные комби-
нации родителей, а вероятности перехода возьмем из
законов генетики и предположения о способе выбора ро-
дителей.
Простейший из таких случаев получается, когда мы
классифицируем родителей только по одной паре генов,
занимающих одно и то же положение в хромосоме. Обсу-
дим этот случай. Мы можем еще больше упростить за-
дачу, предположив, что ген имеет две формы (аллели):
либо а, либо Ь, и, значит, любое животное имеет генотип
либо аа, либо ab, либо bb. Например, если а доминирует
над 6, то аа— чистый доминант, ab — гибрид, и bb — чи-
стый рецессив. Тогда пара родителей может быть одного
из следующих шести типов: (аа,аа), (aa,ab), (bb,bb),
(bb,ab), (aa,bb), (ab,ab). Эта задача для самого про-
стого случая — когда пары родителей случайно выби-
раются из потомства, — рассмотрена у Феллера и в FM.
Мы рассмотрим более широкий класс задач, част-
ным случаем которых является приведенная выше. Пред-
положим, что один из супругов случайно выбирается из
данного поколения, а затем сам подбирает себе пару.
При этом он (или она) с вероятностью, в k раз большей,
выбирает данное непохожее на себя животное, чем дан-
ное похожее. Таким образом, k служит мерой того, на-
сколько сильно «притягиваются противоположности».
При этом мы учитываем, что при простом доминирова-
нии животные генотипов аа и ab внешне одинаковы.
15*
228
ГЛ. VII. ПРИЛОЖЕНИЯ ЦЕПЕЙ МАРКОВА
В результате матрица переходных вероятностей выгля-
дит так 1)*
(аа, аа) I 0 0 0 0 0
(bb, bb) 0 1 0 0 0 0
(aa, ab) 1 4 0 1 2 0 0 2 4
P « (bb, ab) 0 1 0 6 0 1
2(6+1) 6+ 1 2(6+ 1)
(aa, bb) 0 0 0 0 0 1
(ab, ab) 1 1 1 26 (6+ 1) 6(6+1) 1
4(6 + 3) 4 (36 + 1) 6 + 3 (6+3) (36+ 1) (6 + 3) (36+ 1) 6 + 3
Первые два состояния — поглощающие. Они соответ-
ствуют образованию чистой породы — чисто доминант-
ной в первом состоянии и чисто рецессивной во втором.
Вычислим фундаментальную матрицу N, вектор т и мат-
рицу В:
N (2k+V)(k + 3) X
(4 (62+ 56+ 2)
2(36+1)
4(36 + 1)
4(36+1)
ktk+i)
(462+96+3)
2k (6+1)
2k (6+1)’
(46’+96+3)(6+l)
«(/г+1)2
46(6+1)’
/ 2fe3+ 12fe2 + 33fe+ 11
I 4&3 + 17&2 + 29& + 8
(2* + 1) (Л4-3) 4&з + 18£2 + 456 + 13
(3fc+l)(ft+3) \ (aa.ab)
(3A+1) (ft+3) 1 (bb, ab)
2 (36+1) (ft+3) l(aa, bb)>
2 (36+1) (6+3) / (ab, ab)
(aa, ab)
(bb, ab)
(aa, bb)'
4Л3 + 1 Gk2 + 386 + 10 / (ab, ab)
1
p _____________!_________
D 4 (2k + l)(fc + 3)
462 + 236 + 9
96 + 3
186 + 6
186 + 6
462 + 56 + 3 \ (aa, ab)
862+ 196 + 9 |(&6, ab)
862+ 106 + 6 l(aa, bb)'
862+ 106 + 6/ (ab, ab)
9 Напомним, что потомок заимствует от каждого из родителей
по одному гену, причем любой из двух генов родителя передается
ему с вероятностью Va- {Прим, перев,)
7.4. ПРИМЕНЕНИЯ К ГЕНЕТИКЕ
229
Так как мы знаем, что в конце концов мы получим
чистую породу, то два наиболее интересных вопроса —
это число поколений, необходимое для получения чистой
породы, и вероятность получения чистого доминанта или
чистого рецессива. В частности, нас интересует, как на
эти величины влияет k.
Большое k означает увеличение числа смешанных
пар. Поэтому следует ожидать, что увеличение k замед-
ляет процесс. Действительно, каждый элемент вектора г
монотонно растет с ростом k. Приведем некоторые ха-
рактерные значения этого вектора:
32/3\ /45/6\ /5,64\ /10,11
22/з ] 1 45/б 1 I 6,64 | | 16,11
47з 1 1 б2/з / 1 8,28 1 1 1'7,21
з’/3/ \52/3/ \ 7,28 / X 16,21
6 = 0 6=1 6 = 2 6 = 7
Мы видим, что увеличение k существенно замедляет
процесс, особенно если начинать в одном из трех послед-
них состояний. Заметим, что время поглощения при вы-
ходе из состояния (аа, ЬЬ) всегда на единицу больше,
чем при выходе из (ab, ab), так как из (аа,ЬЬ) первый
шаг обязательно ведет в (ab, ab) (пара, в которой один
родитель чисто доминантный, а другой — чисто рецес-
сивный, дает только-гибридное потомство).
Влияние k на вероятность поглощения не так оче-
видно. На первый взгляд кажется, что большое k бла-
гоприятствует рецессивной породе, так как и доминанты,
и гибриды стремятся выбрать рецессивную пару.; И дей-
ствительно, при k > 1 вероятность поглощения в (ЬЬ, ЬЬ)
растет с ростом k. Но при k < 1 положение удивитель-
ным образом меняется. Когда k уменьшается от значе-
ния 1, вероятность поглощения в (аа, аа) увеличивается,
пока не достигает максимума при k = !/з, а затем опять
уменьшается до того же значения, что при k = 1. Та-
ким образом, k = 0 и k = 1 дают одни и те же вероят-
ности поглощения. Это значит, что если при спарива-
нии подобные всегда выбирают подобных, то вероятности
поглощения такие же, как при случайном спаривании
230
ГЛ. VII. ПРИЛОЖЕНИЯ ЦЕПЕЙ МАРКОВА
(хотя, конечно, для случайного спаривания время
поглощения гораздо больше). Приведем несколько ха-
рактерных значений вероятностей поглощения в {аа, аа):
'0,75\ /0,77\ /0,75\ /0,71 \ /0,61'
0,25 | | о,27 | 1 0,25 | 1 0,21 1 | 0,11
0,50 1 1 0,54 1 1 0,50 1 1 0,42 1 1 0,22
,0,50/ \0,54/ \0,50/ \0,42/ \0,22-
k = 0 Л = 7з k= 1 k = 2 k = 7
Последние два элемента в каждом столбце всегда равны
между собой; это происходит оттого, что из состояния
(аа, bb) процесс обязательно сразу переходит в состоя-
ние {ab,ab). При начальном состоянии {bb, ab) вероят-
ность поглощения составляет половину этой величины,
так как при выходе из {bb, ab) одинаково вероятно по-
пасть в {ab, ab) или поглотиться в {bb,bb), Аналогично,
для {аа, ab) получаем половину значения для {ab, ab)
плюс V2- Интересно отметить, что при случайном спа-
ривании вероятность поглощения в {аа, аа) пропорцио-
нальна начальному количеству генов а.
Выпишем все величины для частного случая случай-
ного спаривания, когда k = 1:
1 0 0 0 0 0 (аа, аа)
0 1 0 0 0 0 (bb, bb)
74 0 72 0 о 74 (аа, ab)
о 74 о 72 о 74 (bb, ab)
0 0 0 0 0 0 (aa, bb)
716 Vie 74 74 7в 74. (ab, ab)
/7з 7з */б 4/з\ /4%\ 7л
( 7з 7з 76 4/з | _/ 4% | 74 *Л ]
I 4/з 4/з 4/з 7з Г Т I 62/з Г I 72 72 /
\4/з 4/з */з V \52/3/ v/2 72/
7А. ПРИМЕНЕНИЯ К ГЕНЕТИКЕ
231
Вычислим также
/5/в 74 7s 72 \ /769\
( 74 % 7s 72 ] ( 769 ]
I 72 72 74 1 Г Т2 /361 816 I
v/2 72 74 V \81б/
Среднеквадратическое отклонение для т — около 4,7 для
каждого элемента. Оно того же порядка, что элементы
самого т, поэтому следует ожидать очень больших коле-
баний.
Из матрицы Р следует, что процесс удовлетворяет
условию укрупнения состояний, при котором объеди-
няются два первых и два последующих состояния. Такое
разбиение допускает простую интерпретацию. Состояние
(ЬЬ, ЬЬ) получается из (аа, аа) заменой а на Ь и Ь на а,
и точно так же (bb, ab) получается из (аа, ab). В то же
время (аа, ЬЬ) и (ab, ab) при этом не меняются. Таким
образом, это разбиение соответствует процессу, в кото-
ром мы не различаем, какой из генов доминантный. Пер-
вое состояние нового процесса, которое мы обозначим
(аа,аа), представляет любую пару однотипных чистых
родителей. Второе состояние — обозначим его (аа, ab) —
представляет одного чистого и одного гибридного роди-
теля. Остальные 2 состояния представляют соответствен-
но пару неоднотипных чистых родителей и пару гибрид-
ных родителей. Матрица переходных вероятностей
укрупненного процесса равна
( 1 0 0 0 \ (аа, аа)
74 7г 0 74 |(аа, ab)
0001 1(аа, ЬЬ)
7в 7г 7s 74/ (ab, ab)
Чтобы получить матрицу N укрупненного процесса,
складываем первые два столбца прежней матрицы У,
которые соответствуют отождествленным невозвратным
232
ГЛ. VII. ПРИЛОЖЕНИЯ ЦЕПЕЙ МАРКОВА
состояниям:
/*7з 76 7з\
[ ’% 76 4/з I
I 8/з 4/з 7з I
' 7з 7з 8/з'
Мы теперь видим, что первые две строки совпадают,
как и должно быть в том случае, если укрупнение воз-
можно. Отсюда имеем
/*% 7e 4/з\И, ab)
# = ( 8/з 4/з 7з (а«. bb)
\8/з 7з 8/з/(а6. ab)
и
/45/6\
T = jVg = | 62/3 -
52/з/
Вектор t можно получить и непосредственно из т.
Те компоненты т, которые соответствуют отождествлен-
ным состояниям, совпадают, как и должно быть; вычерк-
нув одну из них, получим t. Информация, которую дает
новый процесс, вполне достаточна для многих целей.
(Конечно, мы не узнаем ничего интересного о вероятно-
стях поглощения, так как здесь после укрупнения остает-
ся только одно поглощающее состояние.) Например, т
полностью определяется вектором т. Далее, имеем
/7ю 7в 7г \ /2113/зб\
Я = 8/10 74 1 , ^2= 227з -
\710 74 5/в/ \227з J
Последние два столбца матрицы Н, соответствующие
неукрупненным состояниям, берутся непосредственно из
Н. Но первый столбец уже другой. т2 непосредственно
получается из тг.
Перейдем к обобщению такого укрупненного процес-
са, рассмотренному у Кемпторна1). Мы по-прежнему
•) О. К е m р t h о г n е, An Introduction to Genetic Statistics,'
New .York, John Wiley.& Son, Inc., 1950.
7А. ПРИМЕНЕНИЯ К ГЕНЕТИКЕ
233
ограничиваемся одной-единственной позицией в хромо-
соме (одним локусом), но не предполагаем больше, что
имеются только два типа генов: их может быть любое
число. Для простоты предположим, что таких типов
(аллелей) четыре: a, b, cf d. Рассмотрим укрупненный
процесс, т. е. будем интересоваться числом различных
генов и их комбинаций, не различая состояния, которые
получаются одно из другого, если поменять ролями два
или несколько генов. Тогда всего имеем семь состояний:
Sp (аа, аа),
s2-’ (аа, а&),
s3: (аа, bb),
s4: (ab, ab),
s5: (aa, be),
s6: (ab, ac),
s7: (ab, cd).
Матрица переходных вероятностей такова:
1 0 0 0 0 0 0 ®i
74 У2 0 74 0 0 0 S2
0 0 0 1 0 0 0 S3
р= у8 72 78 74 0 0 0 «4
0 0 0 'h 0 72 0 «5
Vie 74 0 Ч» У8 3/8 0 «6
0 0 0 0 72 У4.
В матрице переходных вероятностей мы указали
классы эквивалентности. Они определяются количеством
различных генов, имеющихся у родителей. Очевидно,
это число или остается тем же, или уменьшается, по-
этому < из класса эквивалентности с заданным, числом
генов процесс может попасть только в класс с меньшим
234
ГЛ. VII. ПРИЛОЖЕНИЯ ЦЕПЕЙ МАРКОВА
числом генов, т. е. в класс, расположенный выше в мат-
рице Р. Единственное состояние, в котором присутствует
только один тип генов, — поглощающее. Укрупненный
процесс с четырьмя состояниями, рассмотренный выше,
соответствует двум верхним классам эквивалентности в
настоящей цепи. Так как величины, относящиеся к этим
классам, не зависят от классов эквивалентности, лежа-
щих ниже, то верхние левые углы матриц, которые мы
сейчас вычислим, будут совпадать с ранее найденными
матрицами. Имеем
7ю */8 */2 о о о
8/ю 74 1 о о о
7ю 74 78 о о о
7ю 7г4 7в 71о 7г о
710 7б 7з 75 716 о
7ю 7зб 7э 715 7з 74
Мы видим, что Sj, s4 и $6 — «вероятные состояния»
в том смысле, что если процесс начинается достаточно
7.5. ТЕОРИЯ ОБУЧЕНИЯ
235
обозначим через
АвД-и V \
АД ш 1—w)
Рис. 7.8.
низко, чтобы иметь возможность достигнуть такого со-
стояния, то для этого имеются весьма хорошие шансы.
Остальные состояния совсем маловероятны, независимо
от того, где начинается процесс. Замечательно, что, от-
правляясь из s7i т. е. начиная с четырьмя различными
генами, мы ожидаем получить чистую породу уже через
72/з поколения. Но надо помнить, что среднеквадратиче-
ское отклонение этой величины равно 4,97, и поэтому
вполне вероятен гораздо более долгий процесс достиже-
ния поглощающего состояния.
7.5. Теория обучения. Этот пункт посвящен матема-
тической модели некоторых видов обучения, предложен-
ной Истизом (W. К. Estes). Мы рассмотрим лишь от-
дельные относительно простые частные случаи, но наша
техника применима и в более общей ситуации.
Типичный эксперимент состоит в том, что испытуе-
мого помещают перед парой ламп и предлагают ему
угадать, какая из них, левая или правая, будет сейчас
включена. Из двух возможных ответов
Ло ответ «левая», через А}— «правая».
Затем экспериментатор включает одну
из ламп. Пусть Ео означает включе-
ние левой лампы, а Е\— включение
правой лампы. Эта процедура повто-
ряется большое число раз, и ведется
запись последовательных результатов,
состоящих из Ai и Ei. Цель теории —
предсказать, как при заданном поведении эксперимен-
татора изменяются ответы испытуемого за долгий про-
межуток времени. Модель хорошо согласуется с мно-
гочисленными экспериментами.
В обширной группе интересных опытов эксперимента-
тор действует с постоянными вероятностями, завися-
щими только от действий испытуемого. Эти вероятности
удобно задать с помощью матрицы, приведенной на
рис. 7.8. Таким образом, ответ «левая» (Ло) подкреп-
ляется включением левой лампы (£0) с вероятностью
1 — и; догадка «правая» подкрепляется с вероятностью
1—ш. Здесь v и w— числа между 0 и 1, которые
остаются неизменными на протяжении эксперимента.
236
ГЛ. VII. ПРИЛОЖЕНИЯ ЦЕПЕЙ МАРКОВА
Обычно v и w положительны; однако случаи, когда
это не так, тоже представляют интерес. Например, если
v = 0, a w > 0, то До всегда подкрепляется, a At под-
крепляется лишь иногда. Случай v > 0, w = 0 аналоги-
чен. Если v = w = 0, то любой ответ испытуемого под-
крепляется.
Другой класс интересных частных случаев получается
при v + w = 1. Здесь 1 — v = w и v = 1 — w, т. е. ве-
роятности событий Ео и Е| не зависят от действий испы-
туемого.
В модели предполагается, что испытуемый имеет не-
которое неизвестное число $ стимулов, или раздражите-
лей. Каждый раздражитель на каждом этапе экспери-
мента связан с одним из двух возможных ответов At
(т. е. побуждает дать ответ А{), причем первоначальные
связи неизвестны. Затем предполагается, что на каждом
этапе эксперимента происходит следующее.
(1) В множестве раздражителей испытуемый выби-
рает подмножество; это делается с помощью процесса
независимых испытаний, в котором каждый раздражи-
тель выбирается с вероятностью t и не выбирается с ве-
роятностью 1 — t.
(2) Если в выбранном подмножестве k раздражите-
лей связано с Ао и / раздражителей с Ai, то испытуемый
дает ответ Ai с вероятностью // (k + /). Здесь нужно
дополнительное условие на тот случай, когда ни один
раздражитель не будет выбран; мы предположим, что
вероятность Ai в этом случае такая же, как если бы
были выбраны все раздражители.
(3) Если экспериментатор совершает действие Ео, то
те раздражители, связанные с А], которые перед этим
были Ьыбраны, испытуемый «перепривязывает» к Ао.
Аналогично, после действия Е\ все выбранные раздра-
жители связываются с Aj.
Эту модель можно представить как цепь Маркова с
(s + 1) состояниями, где состояние означает, что
имеется в точности i раздражителей, связанные с Aj,
i=0, 1, ..., s. Все интересные величины зависят только
от того, сколько раздражителей имеет ту или иную
связь, и являются функциями-этой цепи. Например, ве-
7.5. ТЕОРИЯ ОБУЧЕНИЯ
237
роятность ответа Ai при состоянии $г- получается так:-
s—I i
р, [л j - s ц (\') (;) <"(1 - о--”4-+(1 - о'4.
6=0 Z=0
где k и I — количество выбранных раздражителей, свя-
занных соответственно с Ао и с Ah т = k + /, и послед-
ний член отвечает случаю, когда не выбран ни один раз-
дражитель. Перепишем это выражение как сумму по
индексу т, а затем используем одно из биномиальных
тождеств *):
s
k+l^m
т=1
s
ЧИСН-о-М-
т=»0
Удобно записать эти вероятности в виде вектор-
столбца Y =
Построим теперь переходную матрицу Р. Для этого
нужно принять в расчет все четыре возможности, ука-
занные на рис. 7.8. При комбинации At и Ео вероятности
J) Действительно,
k+l=*m
k+l^m
Здесь мы воспользовались легко проверяемым (хотя бы из сравне-
ния коэффициентов при хп в левой и правой части соотношения
(1 4- х)а (1 4- х)ь = (1 4- х)а+ь) тождеством
(Прим, перев.)
238
ГЛ. VII. ПРИЛОЖЕНИЯ ЦЕПЕЙ МАРКОВА
перехода из s{ в Sj с понижением i задаются элементами
матрицы wX, где
хч —
при /</,
при j^i.
О
Для вероятностей перехода от st к Sj
при комбинации Ао и Ео имеем матрицу
где
с понижением i
(1 —гл) (У —X),
Уц =
(. 1
при
7<g
о
при j > Z.
Если мы положим х*. == хс . в . и у* = у, . то
иХ* и (1 — и>)(У‘ — X*) дадут вероятности переходов
с повышением числа I. Таким образом,
Р = а»Х + оГ + (1-»)(У-Х) + (1-ш)(Г-Г) +
+ (v-w + 1)(1 -t)4,
или
Р = о(Х + Г-У) + да(АЧ-Г-У’) + (У + П-(Л’ + Г) +
+ (v + w + 1)(1 - t)sI. (1)
Здесь последний член относится к тем не включенным
в предыдущие два члена случаям, когда не выбран ни
один раздражитель.
Мы хотим вычислить Ру. Сначала найдем Уу. Имеем
&=>0 k~0
fe=l k~l
= T S (‘ 7')- z)Z+'=-h1 - *)•
Таким образом,
Уу = (1-0у.
(2)
7.5. ТЕОРИЯ ОБУЧЕНИЯ
239
Совершенно аналогично
yY = ^+(i-/)Y. (3)
После несколько более долгих выкладок находим
(X + X‘)Y-^ + (l-2f-(l-04)Y. (4)
Если записать Ру с помощью (1) и затем воспользо-
ваться (2), (3) и (4), то получим
Ру = + (1 -2t -(1 - 0е)Y“(1 ~ t) Y] +
+ ^ + 2(l-/)Y-^-(l-2/-(l-/DY +
+ (i» + te> — 1)(1 — ffy.
После упрощения имеем
PY = o/| + [l — (о + u>)dY- (5)
Введем вектор S = Y — ( v^w j|, определенный для
случаев, когда v и w не равны одновременно 0. Впослед-
ствии будет показано, что эта величина играет важную
роль в модели. Имеем
= Ру - -L-g = [1 - (v 4- w) f] у - (7^) [I -(»+
ИЛИ
PS==[l-fa + ^)/]6 (6)
и
Р"б = [1 4-^)0. (7)
Величины v и w определяют природу цепи Маркова.
Если 0 < и 0 < w 1, то Р > О, и цепь, таким об-
разом, регулярна. Если v = 0, то i = 0 — поглощающее
состояние, а если w = 0, то i — s — поглощающее состоя-
ние. Таким образом, если v или w равны 0, то мы имеем
поглощающую цепь. Если v = w = 0, то имеется два
поглощающих состояния.
Найдем вероятность ответа после п шагов. Она
задается вектором Рпу (в зависимости от начального со-
стояния). Если v = w = 0, то из (5) видим, что Ру = у,
240
ГЛ. VII. ПРИЛОЖЕНИЯ ЦЕПЕЙ МАРКОВА
так что Рпу = у, и вероятность ответа Ai остается неиз-
менной. В остальных случаях получаем ответ из (7):
Первый член (как мы увидим ниже)—это предельная
вероятность для ответа Аь а второй представляет со-
бой отклонение, обусловленное начальным положением.
Рассмотрим сначала регулярный случай. Здесь у>0
и w > 0. Так как 0 < t < 1, то 11 — (v + w) 11 < 1. Из
(7) имеем
Аб = 0,
аб = а I у
v + w
и поэтому
ау = . (8)
1 V + W х '
Это показывает, что предельная вероятность ответа Ai
равна . Используя затем таблицу рис. 7.8, нахо-
дим, что предельная вероятность действия экспери-
ментатора равна
W I У /1 \ V
-------- у -|----(1 — до) =----- '
V + W V + w v 7 v + w
Следовательно, в состоянии равновесия (при стационар-
ном распределении) вероятности для экспериментатора
и испытуемого совпадают.
Интересно отметить, что испытуемый не максимизи-
рует число правильных догадок. Вместо этого он осу-
ществляет такое положение равновесия, в котором он
высказывает догадку «правая» с той же частотой, с ка-
кой «правая» появляется.
Так как ~ среднее число ответов А] на одно
испытание в положении равновесия, a i/s— среднее чис-
ло таких ответов в состоянии sif то вектор б = +У }
представляет разницу между средним числом ответов Ai
в данном состоянии и в положении равновесия.
7.5. ТЕОРИЯ ОБУЧЕНИЯ
241
Из (6) и (7) находим
(/ — Р + А) 6 = (v + и>) td, .
Z6 = -. -1 ..d,
(u + w) t
(Z-Л) 6 = 7-77-77 6,
v 7 (u + w) t *
(Z-4)y= < 1 r, d.
v ' r (y + w) t
Таким образом, суммарное отклонение от положе-
ния равновесия (для числа ответов Ai) пропорционально
вектору отклонения б. Поэтому суммарное отклонение
может быть велико, если i/s для исходного состояния
сильно отличается от v/(v + w), или если t мало.
Чтобы получить предельную дисперсию для числа
ответов Аь надо использовать 4.6, поскольку мы имеем
функцию от цепи, которая принимает значение 1 в S;
с вероятностью fi = i/s. Хотя у нас нет общей формулы
для этой предельной дисперсии, но в любом конкретном
примере ее легко посчитать, пользуясь 4.6.
Рассмотрим теперь случай поглощающей цепи с од-
ним поглощающим состоянием i = 0, т. е. случай, когда
v = 0, w > 0. (Случай v > 0, w = 0 аналогичен этому.)
В этом случае б = у. Пусть у получается из у отбрасы-
ванием первой компоненты (которая равна 0). Из (6)
имеем
Ру = Рб = (1 — wt)6 = (1 — wt) у,
Qy === (1 — wt) у,
(/ — Q)y = (wt) у, (Ю)
Это такой случай, в котором испытуемого побуждают
давать ответы До. Если он дает ответ Ао, то этот ответ
всегда подкрепляется. Ответ Ai тоже иногда подкреп-
ляется с вероятностью 1 — w. Л^удает среднее значение
общего числа ответов Ai (т. е. «неправильных» ответов).
Для начального состояния $г- оно равно (\/wt)(i/s).
16 Дж. Кемени, Дж. Снелл
242
ГЛ. VII. ПРИЛОЖЕНИЯ ЦЕПЕЙ МАРКОВА
Следовательно, большое число ошибок может быть по
одной из следующих трех причин: дробь //$, т. е. доля
раздражителей, которые надо ориентировать, вначале
была велика; или параметр обучения t мал; или w мало,
т. е. ответ Ai часто подкрепляется.
Иногда разумно бывает предположить, что перво-
начально раздражители были связаны с одним из двух
ответов случайно. Это приводит к начальному вектору
вероятностей Л = Тогда среднее суммарное
число «неправильных» ответов равно
1 1 1
Л . —- у = —- л у = .
wt ' wt r 2wt
Мы можем ожидать, что это число получится в качестве
среднего значения количества ответов А\ у большой од-
нородной популяции. Это один из простых путей для
оценки параметра t.
Наконец, рассмотрим случай v = w = 0, при котором
любое действие испытуемого подкрепляется. Тогда t=0
и i = s — поглощающие состояния, а самое интересное —
какие ответы будет в конце концов давать испытуемый,
Ао или Ai?
Из (5) мы видим, что в этом случае Ру = у. Но в у
состоянию «о соответствует компонента 0, а состоянию
ss — компонента 1, следовательно (см. теорему 3.3.9),
у дает вероятности поглощения в ss. Поэтому вероятность
того, что испытуемый в конце концов будет давать толь-
ко ответы Aj, равна доле раздражителей, первоначаль-
но связанных с Аь
Чтобы получить более подробную информацию о мо-
дели, нам придется сделать упрощающее предположение.
Пользуясь тем, что в большинстве приложений параметр
обучения t очень мал, мы предположим, что членами
высших порядков относительно t можно пренебречь. Это
предположение можно следующим образом истолковать
с точки зрения психологии. Если мы опускаем члены, со-
держащие i в степени выше первой, то мы тем самым
допускаем, что выбор одновременно более чем одного
раздражителя-стимула совершенно невероятен. При этом
7.5. ТЕОРИЯ ОБУЧЕНИЯ
243
предположении матрица Р существенно упрощается:
Pi.i+} = (s-i)tv,
piti-x — itw,
Ра = 1 —t(iw + (s — i) и),
pi! = 0 в остальных случаях.
Рассмотрим сначала регулярный случай при этом уп-
рощающем предположении. Наиболее важная величина,
не исследованная нами до сих пор, — это вектор а пре-
дельного распределения вероятностей. Покажем, что при
нашем нынешнем предположении
__ / $ \
О'1 — \ i / (v + w)s
Вычислим аР:
s
У akpkl = + ajPjj + ay+1p/+bJ =
= [(--i) v>~'ws~l+' (s — / + 1) tv +
+ [s.j v!ws~! [ 1 — t (jw 4- (s — /) u)] +
+ (/ +! ) (/+ 1)^] •. (-o+-m,)- =
, tv1ws~i Г/ s \ / • . 1 \
-( + (s - /)») + [^ )0’ + 1)»].
Теперь легко убедиться, что два члена, содержащие и,
взаимно уничтожаются, *и члены, содержащие w, тоже
уничтожаются, так что выражение в квадратных скобках
равно 0. Поэтому правая часть сводится к слагаемому
aj, и, значит, а = {яг} является неподвижным вектором
матрицы Р. Таким образом, если t мало, то предельные
вероятности очень близки к этому а. В действительно-
сти а — это предел предельного распределения при >0.
Интересно отметить, что при v == w — \jst полученный
процесс совпадает с макроскопическим процессом в мо-
дели Эренфестов.
16*
244
ГЛ. VII. ПРИЛОЖЕНИЯ ЦЕПЕЙ МАРКОВА
Рассмотрим теперь поглощающий случай; пусть для
определенности w > 0 и v = 0, т. е. испытуемого побуж-
дают давать ответ Ао. Тогда
Pii_x = itWi
Рн = 1 — itw,
а все остальные элементы равны нулю. Матрица I — Q =
= {Cij} имеет элементы Сц = itw, ;-1 = —itw и нули на
остальных местах. Покажем, что
1 .
-Г— При 1^1,
nij=zl ]tw
О в противном случае.
Вычислим М(/— Q):
2 n‘kCkj = Пц (jtw) + nt, i+i [- (/ + 1) tw] =
k=l
0 + 0 = 0, если i < /,
= -^-/7ш + 0=1, если i =/,
-^itw + (-(/ + 1)/w) = 1 - 1 = 0, если i>j.
Таким образом, данное N действительно является обрат-
ной матрицей для I — Q. Интересно отметить, что эле-
менты N зависят от it j, t, но не зависят от s. Далее
имеем
/“1
Таким образом, время поглощения обратно пропорцио-
нально t и w и зависит от количества раздражителей, ко-
торые нужно «перепривязать» от А[ к Ао. Это время бу-
дет большим, если t мало.- Оно будет также велико,
если w мало, т. е. если Ai часто подкрепляется. Но так
как ряд с общим членом 1// расходится, то время может
также быть велико за счет того, что первоначально с Ai
было связано много раздражителей.
7.5. ТЕОРИЯ ОБУЧЕНИЯ
245
Наконец, рассмотрим случай двух поглощающих со-
стояний: v = w = 0. Здесь члены первого порядка отно-
сительно t пропадают, и поэтому мы должны будем про-
извести подсчет членов, содержащих t2. Имеем
Pi,i~i = Pi,i+i = l/2i(s-i)t2,
Ри= l-i(s-i)t2.
С помощью вычислений, вполне аналогичных преды-
дущим, устанавливаем, что
^7 -
2 i
t2S j
2 (s - 0
t2S (s - j)
при i /,
при i j,
и, следовательно,
Здесь сумма снова может быть велика из-за мало-
сти t или из-за большого количества членов ($ велико).
Но в этом случае ti обратно пропорционально /2, и по-
этому надо ожидать, что время поглощения будет го-
раздо больше.
Есть один специальный случай, в котором можно по-
лучить более точную информацию, не делая вышеука-
занного упрощающего предположения. Это тот случай,
когда v + w = 1, т. е. w = 1 — v. Здесь действия экспе-
риментатора не зависят от поступков испытуемого.
В этом случае мы нашли точный способ вычисления а
с помощью простых рекуррентных уравнений1).
Установлено, что предельные вероятности могут быть
также получены с помощью следующего вспомогатель-
ного процесса: в начале имеется s раздражителей, не
связанных ни с одним из ответов. Мы образуем из них
подмножество, выбирая каждый элемент с вероятностью
t а затем относим это подмножество к с вероятно-
стью w и к А] с вероятностью 1 — w. Эта процедура
9 См. J. G. -Kem e ny and J. L. Snell, Markov. Processes in
Learning Theory, Psychometrika 22 (No. 3), 1957, 221—230.
246
ГЛ. VII. ПРИЛОЖЕНИЯ ЦЕПЕЙ МАРКОВА
повторяется с оставшимися раздражителями до тех пор,
пока все они не будут исчерпаны. Тогда предельная ве-
роятность в первоначальном процессе — это просто
вероятность того, что в нашем вспомогательном процессе
к At будет отнесено i раздражителей. Эти вероятности
легко найти для любого $, имеющего разумный порядок.
7.6. Применения к теории мобильности. В этом пункте
мы рассмотрим применение цепей Маркова к одной со-
циологической проблеме, — а именно проблеме мобиль-
ности профессий при смене поколений. Материалы этого
пункта подготовлены совместно с Бергером (J. Berger).
Задачу можно сформулировать следующим образом.
В множестве всех профессий или родов занятий произ-
водится разбиение А = {Аь А2, .AJ. Полученные
подмножества называются профессиональными класса-
ми. Они обычно упорядочиваются с помощью некоторого
подходящего социального критерия, например, престижа
профессии. Затем ставится вопрос, в какой мере про-
фессиональный класс отца, деда и т. д. влияет на про-
фессиональный класс сына. При изучении таких вопро-
сов всегда строится матрица, которая показывает, какая
в среднем доля сыновей в каждом классе изберет тот
или иной род занятий.
В качестве основного примера рассмотрим матрицу,
построенную по данным, собранным Глассом и Холлом
по Англии и Уэльсу в 1949 г.1)* Следуя Прейсу2), раз-
делим профессии на высшие, средние и низшие. Полу-
чается такая матрица:
высший средний низший
высший / 0,448 0,484 0,068
Р = средний| 0,054 0,699 0,247
низший \ 0,011 0,503 0,486
9 D. V. Glass, J. R. Hall, Social Mobility in Great Britain:
a Study of Intergeneration Changes in Status, in D. V. Glass (Ed.),
Social Mobility in Great Britain, London, Routledge & Kegan Paul,
1954.
2) S. J. P r a i s, Measuring Social Mobility, Journal of the Royal
Statistical Society 118, 1955, 56—66,
7.6. ПРИМЕНЕНИЯ К ТЕОРИИ МОБИЛЬНОСТИ
247
Мы видим, что например, из высшего класса 44,8%
сыновей остаются в высшем классе, 48,4% переходят в
средний и 6,8% —в низший классы.
Матрицу Р можно использовать двумя способами.
Один — это рассмотреть в каждом государстве все на-
селение и предсказать, какая его доля будет в каждом
из классов. Мы будем называть это «коллективным про-
цессом».
Другой путь состоит в изучении истории отдельной
семьи. С этой точки зрения история семьи рассматри-
вается нами как цепь Маркова с переходной матрицей Р.
Будем называть это «индивидуальным процессом». Мы
предполагаем, что в каждой семье есть ровно один сын.
Рассмотрим теперь, как связаны основные понятия
цепей Маркова с этими двумя процессами.
Начнем с предположений, которые нужно сделать,
чтобы получить цепь Маркова. Основным является пред-
положение, согласно которому знание того, что было до
последнего результата, не влияет на наши предсказания.
Например, в индивидуальном процессе знание профессии
деда не влияет на предсказание профессии сына (при
известной профессии отца).
Мы также предполагаем, что для всех поколений
справедлива одна и та же матрица. Ясно, что это пред-
положение не вполне реально. Однако весьма интересно,
что случилось бы, если бы нынешняя матрица оставалась
пригодной и в дальнейшем.
Кроме того, предполагается, что изменения в распре-
делении профессий от одного поколения к другому вы-
числяются только по процессу, описываемому матрицей
Р. Это значит, что мы пренебрегаем такими фактами,
как различие в рождаемости и объем миграций, хотя
они и влияют на распределение по классам.
Классификация состояний получает в теории мобиль-
ности очевидную интерпретацию. Эргодическое множе-
ство— это такое множество профессий, из которого
нельзя выбраться. Следует ожидать, что в наиболее ин-
дустриальных обществах будет только одно эргодическое
множество. Однако если в качестве состояния взять
пару: профессия и раса, то дискриминация какой-то расы
может привести к цепи с более чем одним эргодическим
248
ГЛ. VII. ПРИЛОЖЕНИЯ ЦЕПЕЙ МАРКОВА
множеством. Так как сын может избрать профессию от-
ца, то циклическая цепь, по-видимому, не возникнет.
Поглощающее состояние означает, что в данном про-
фессиональном классе сын обязан идти по стопам отца.
В индустриальных обществах профессии обычно не обла-
дают таким свойством. Поэтому мы предположим, что
наша основная цепь регулярна.
Истолкуем теперь степени матрицы Р. В индивиду-
альном процессе //-й элемент матрицы Рп есть вероят-
ность того, что семья, отправляясь из z-го профессиональ-
ного класса, через п поколений окажется в /-м. Для кол-
лективного процесса р{ц представляет собой ту долю
потомков в /i-м поколении /-го профессионального клас-
са, которая попадет в /-й класс. Пусть pi, р2, Рз — доли
населения, занимающие положение соответственно в
высшем, среднем и низшем классах, и л = (рь р2, рз).
Тогда через п поколений эти доли будут задаваться ком-
понентами вектора лРп. Предположим, что в нашем при-
мере в настоящее время 20% населения принадлежит
высшему, 70%—среднему и 10% — низшему классам.
Тогда в следующем поколении будет соответственно
12,9%, 63,6% и 23,5%. Мы получили это так:
/0,448 0,484 0,068
(0,200; 0,700; 0,100)1 0,054 0,699 0,247
\ 0,011 0,503 0,486
= (0,129; 0,636; 0,235).
Неподвижный вектор а имеет следующий смысл.
В индивидуальном процессе он представляет собой дол-
госрочный прогноз рода занятий одного индивидуума.
Наша основная теорема о регулярных цепях гласит, что
этот прогноз не зависит от нынешнего профессиональ-
ного класса. В коллективном процессе неподвижный век-
тор— это распределение по профессиям в положении
равновесия. Если такое распределение достигнуто, то
оно остается таким же и в следующем поколении. Ка-
ково бы ни было первоначальное распределение, после
многих поколений оно станет близким к распределению,
задаваемому неподвижным вектором.
7.6. ПРИМЕНЕНИЯ К ТЕОРИИ МОБИЛЬНОСТИ
245
В нашем примере неподвижный вектор а равен
(0,067; 0,624; 0,309). Фактическое же распределение по
классам (на основании тех же данных, по которым со-
ставлена матрица Р) задается вектором а — (0,076; 0,634;
0,290). Таким образом, мы видим, что система близка
к равновесию.
Средние времена первого достижения в индивидуаль-
ном процессе интерпретируются обычным образом, но
в коллективном процессе как будто не имеют естествен-
ного смысла. В нашем примере матрица, составленная
из средних времен первого достижения, равна
в С Н
в /14,9 2,1 5,6
м = с | 25,1 1,6 4,3
н \26,5 1,9 3,2
Среднеквадратические отклонения для времен пер-
вого достижения равны
вен
В /22,5 1,5 4,1 \
С[ 25,0 1,2 3,9 ).
Я\25,1 1,4 3,5/
Так как среднеквадратические отклонения времен
первого достижения того же порядка, что и средние
значения, то эти средние нельзя считать типичными зна-
чениями моментов первого достижения. Однако отноше-
ния их представляют интерес. Например, среднее время
перехода из низшего в высший класс почти в пять раз
больше, чем время перехода из высшего в низший.
Предположим теперь, что индивидуальный процесс
находится в положении равновесия. Тогда матрица, об-
ратная к матрице переходных вероятностей, задает ве-
роятности той или иной профессии отца при условии,
что известна профессия сына. Если матрица Р обратима,
то при условии принадлежности данного человека клас-
су z, вероятность того, что его сын попадет в заданный
класс /, равна вероятности того, что его отец находился
250
ГЛ. VII. ПРИЛОЖЕНИЯ ЦЕПЕЙ МАРКОВА
в этом классе /. Условие обратимости получает интерес-
ное истолкование в коллективном процессе. Напомним,
что условие обратимости сводится к тому, чтобы мат-
рица D~'P была симметрична, или другими словами,
чтобы aiPij = ajPji. В коллективном процессе в положе-
нии равновесия aiPtj означает долю тех людей среди
всего населения, которые из i-го профессионального
класса за одно поколение переходят в j-й класс. Анало-
гично, а^р^г означает ту долю населения, которая пере-
ходит из /-го класса в i-й. Таким образом, условие обра-
тимости означает равный обмен между классами. Ясно,
что при таком обмене число людей в каждом классе
неизменно, т. е. процесс находится в равновесии. Однако
условие равного обмена гораздо сильнее. Из приведен-
ных рассуждений можно заключить, что матрица D~'P
в коллективном процессе представляет большой интерес.
Мы назовем ее матрицей обмена. В нашем основном
примере она равна
вне
В / 0,030 0,032 0,005 \
D~'P = hI 0,034 0,436 0,154 ].
С \ 0,003 0,155 0,150/
Заметим, что здесь обмен между классами происхо-
дит примерно поровну1).
Наконец, рассмотрим вопрос об укрупнении в про-
цессах мобильности. Он особенно важен по следующей
причине. Раз мы решаем, что предположение марково-
сти разумно при определенном методе классификации,
то мы уже не можем произвольно обращаться с более
грубой классификацией как с цепью Маркова. Это про-
исходит потому, что более грубая классификация полу-
чается из более тонкой укрупнением состояний, а мы
знаем, что только при весьма специальных условиях
укрупнение снова приводит к цепи Маркова. Конечно,
тот или иной метод классификации представляет собой
9 Более детальное обсуждение вопросов обмена см. в работе:
J. Berger and J. L. Snell, On the Concept of Equal Exchange,
Behavioral Science 2 (No. 2), 1957, 111—118,
7.6. ПРИМЕНЕНИЯ К ТЕОРИИ МОБИЛЬНОСТИ
251
ценность и независимо от того, насколько при этом ме-
тоде оправдано предположение о марковости. Поэтому
при более грубой классификации мы можем оперировать
методами теории цепей Маркова даже тогда, когда усло-
вие укрупнения не выполнено; однако тогда мы должны
допустить, что при более тонкой классификации не по-
лучается цепь Маркова. Обе классификации дают цепь
Маркова лишь тогда, когда выполняется условие укруп-
нения.
Проиллюстрируем сказанное с помощью данных кон-
кретных исследований по мобильности. Числа рассмот-
ренного нами основного примера были на самом деле
получены из более подробных сведений, собранных Глас-
сом и Холлом по Англии и Уэльсу для 1949 г. Эти ав-
торы использовали следующие семь классов:
1. Специалисты и высшая администрация.
2. Директора и управляющие.
3. Заведующие, инспекторы и другие служащие (выс-
шего ранга).
4. Те же (низшего ранга).
5. Квалифицированные работники физического труда
и рядовые служащие.
6. Полуквалифицированные работники физического
труда.
7. Неквалифицированные работники физического
труда.
Из их данных получается такая матрица переходных
вероятностей:
1 2 3 4 5 6 7
0,388 0,147 0,202 0,062 0,140 0,047 0,016
0,107 0,267 0,227 0,120 0,207 0,053 0,020
0,035 0,101 0,188 0,191 0,357 0,067 0,061
0,021 0,039 0,112 0,212 0,431 0,124 0,062
0,009 0,024 0,075 0,123 0,4'73 0,171 0,125
0,000 0,013 0,041 0,088 0,391 0,312 0,155
0,000 0,008 0,036 0,083 0,364 0,235 0,274
252
ГЛ. VII. ПРИЛОЖЕНИЯ ЦЕПЕЙ МАРКОВА
Наш предыдущий пример получился из этого объедине-
нием {1,2} в высший, {3,4,5}—в средний, {6,7} — в низ-
ший классы.
Неподвижный вектор равен
а = (0,023; 0,041; 0,088; 0,127; 0,410; 0,182; 0,129).
Приведенная переходная матрица была получена из
выборки в 3497 человек. Распределение профессий в этой
выборке таково:
а = (0,030; 0,046; 0,094; 0,131; 0,409; 0,170; 0,121).
Мы видим, что этот вектор достаточно
подвижному. Далее,
близок к не-
1 2 3 4 5 6 7
1 43,9 26,2 9,9 9,2 4,0 8,4 11,5
2 63,1 24,2 10,1 8,5 3,5 8,1 П,1
3 70,3 30,5 11,4 8,0 2,9 7,6 10,3
Л4 = 4 72,3 33,0 12,7 7,9 2,6 7,0 10,0
5 73,7 33,9 13,5 8,7 2,4 6,5 9,3
6 74,9 34,6 14,1 9,1 2,6 5,5 8,8
7 75,0 34,8 14,3 9,2 2,7 5,9 7,7
Диагональные элементы матрицы М — это числа, об-
ратные компонентам неподвижного вектора. Эти компо-
ненты близки к истинным долям людей, занятых в соот-
ветствующем классе; поэтому если эта доля мала, то
среднее время возвращения соответственно велико. Ин-
тересно сравнить это время со средним времени для
достижения данного класса, исходя из любого другого
класса. Мы замечаем, что вообще среднее время пере-
хода из любого состояния i в данное состояние j умень-
шается, когда i становится ближе к /. Здесь имеется
в виду «ближе» в смысле общественного престижа, так
как профессиональные классы упорядочены именно по
этому признаку.
7.6. ПРИМЕНЕНИЯ К ТЕОРИИ МОБИЛЬНОСТИ
253
Мы пока занимались лишь понятиями, связанными
с регулярными цепями. Но мы знаем, что хорошие ре-
зультаты дает также применение поглощающих цепей
к регулярным. Например, мы можем изучить поведение
средних классов — 3, 4 и 5, — объявив высшие классы
1 и 2 и низшие — 6 и 7 — поглощающими состояниями.
После этого мы получим поглощающую цепь с матри-
цами Q и R, равными
3 4 5
3 /0,188 0,191 0,357
Q =4 । 0,112 0,212 0,431
5 \ 0,075 0,123 0,473
1 2 6 7
3 <0,035 0,101 0,067 0,061
Я=4( 0,021 0,039 0,124 0,062
5 ' \ 0,009 0,024 0,171 0,125
Основные характеристики этой цепи таковы:
3 4 6
3/1,44 0,58 1,45 \ 3 /3,47\
М = 4| 0,36 1,60 1,55 ], т = 4[ 3,51 ],
5 \ 0,29 0,45 2,47/ 5 \ 3,21/
12 6 7
3 / 0,08 0,20 0,42 0,30 \
В = 4| 0,06 0,14 0,49 0,32 ].
5 \ 0,04 0,11 0,49 0,36/
Вектор т дает нам среднее время до первого выхода
из множества {3,4,5} при любом начальном состоянии
в этом множестве. Мы видим, что оно при всех началь-
ных состояниях заключено между значениями 3 и 4.
Матрица В дает вероятности попадания в каждое из
состояний 1, 2, 6, 7 при выходе из множества {3, 4, 5}.
Объединяя 1 с 2 и 6 с 7, мы можем найти вероятности
254
ГЛ. VII. ПРИЛОЖЕНИЯ ЦЕПЕЙ МАРКОВА
попасть в высший или низший классы при выходе из
каждого из средних классов. Эти вероятности таковы:
В Н
3 /0,28 0,72 \
41 0,20 0,81 ].
5 \0,15 0,85/
В каждом случае вероятность перейти в низший класс
значительно больше, чем в высший.
Интересно отметить, что вероятность перейти в выс-
ший класс из среднего уменьшается с понижением уров-
ня профессионального класса.
Напомним, что основной пример этого параграфа
был получен с помощью укрупнения состояний данной
цепи с 7 состояниями. Было использовано разбиение
А—({1,2}, {3,4,5}, {6,7}) и первое множество названо
высшим классом, второе — средним, третье — низшим.
Интересно проверить условие возможности укрупнения
для этого разбиения. Для этого надо найти матрицу PV
(см. 6.3). Имеем
Ai А% А3
1 2 0,534 0,404 0,062' 0,374 0,553 0,073
3 PV = 4 5 0,136 0,736 0,128 0,060 0,754 0,128 0,033 0,671 0,296
6 7 0,013 0,520 0,467 0,008 0,483 0,509
Чтобы укрупнение было возможно, необходимо, что-
бы элементы каждого столбца оставались постоянными
в пределах каждого из множеств Аь А2, А3. Здесь это
условие, очевидно, нарушено. Например, вероятности по-
пасть в Ai из различных состояний, принадлежащих А2,
сильно разнятся между собой: 0,033 для состояния 5,
0,060 для состояния 4 и 0,136 для состояния 3. Следова-
7.6. ПРИМЕНЕНИЯ К ТЕОРИИ МОБИЛЬНОСТИ
255
тельно, мы не имеем права оба процесса считать цепями
Маркова.
Если мы предпочитаем поверить в марковость цепи
с 7 состояниями, то цепь с 3 состояниями уже не будет
марковской, однако в положении равновесия (при ста-
ционарном распределении) матрица Р, вектор а и мат-
рица М будут вполне определены. Вычисляя их мето-
дом, изложенным в § 4, получаем
вен
В / 0,43 0,50 0,07 \
Р = с1 0,05 0,70 0,25 ],
Н \ 0,01 0,50 0,48/
а = (0,06 0,63 0,31),
вен
В/15,7 2,0 5,9 \
А4 = С1 26,3 1,6 6,3
Н \ 28,0 2,0 3,0/
Мы видим, что эти величины весьма близки к тем,
которые получились раньше при обращении с цепью
с 3 состояниями как цепью Маркова.
Следующий пример, который мы рассмотрим, опи-
рается на данные, собранные Н. Роговым ’) на осно-
вании заявлений о вступлении в брак, поданных в окру-
ге Мэрион, штат Индиана. Этот пример интересен тем,
что данные собраны за два разных периода: с 1905
по 1912 г. и с 1938 по первую половину 1941 г. Поэтому
можно сравнить переходные матрицы, составленные для
каждого из этих периодов. В первой выборке было
10253, во второй — 9892 лица. В работе Рогова принята
очень детальная классификация профессий, мы же в
иллюстративных целях ограничимся более грубым де-
лением на работников умственного, физического и сель-
скохозяйственного труда. Рассмотрим сначала данные
') N. R о g о f f, Recent Trends in Occupational Mobility, Glencoe,
III., The Free Press, 1953.
256
ГЛ. VII. ПРИЛОЖЕНИЯ ЦЕПЕЙ МАРКОВА
вблизи 1910 г. В эти годы получается матрица переход-
ных вероятностей
умств. физич. с.-х.
у м с т в. / 0,594 0,396 0,009 \
Р = физич.1 0,211 0,782 0,007 ).
с.-х. \ 0,252 0,641 0,108 J
Неподвижный вектор равен
а1910 = (0,343; 0,648; 0,009).
Истинное же распределение по профессиям следующее:
а19ю = (0,10; 0,658; 0,034).
Отметим, что неподвижный вектор предсказывает за-
метно меньшее число фермеров, чем их есть на самом
деле. Поэтому можно предположить, что в данных
1940 г. доля фермеров уменьшится.
По данным в районе 1940 г. находим
умств. физич. с.-х.
умств. /0,622 0,375 0,003
Р = ф и з и ч.1 0,274 0,721 0,005
с.-х. \ 0,265 0,694 0,042
Неподвижный вектор равен
а1940 = (0,420; 0,576; 0,004).
Истинное распределение в 1940 г. задается вектором
d 1940 = (0,373; 0,616; 0,011).
Как и было предсказано, доля фермеров заметно умень-
шилась. Интересно отметить, что неподвижные векторы
как для 1910, так и для 1940 г. предсказывают боль-
шую долю принадлежащих высшему классу, чем это
есть в действйтельности. В то же время в Англии не-
подвижный вектор предсказывает меньшее количество
принадлежащих высшему классу.
В заключение рассмотрим пример, иллюстрирующий
равный обмен. Данные этого примера взяты из иссле-
7.6. ПРИМЕНЕНИЯ К ТЕОРИИ МОБИЛЬНОСТИ
257
дования по мобильности рабочих, проведенного Блюме-
ном, Коганом и Маккарти1)- Это очень обширное ис-
следование, основанное на данных социального страхо-
вания. Велась 1-процентная выборка из общего числа
всех рабочих, занимающих или занимавших места в
отраслях, охваченных системой социального страхования
со времени ее введения в 1937 г. Исследование осно-
вано на 10-процентной выборке из этих данных. Оно
приводит к следующей переходной матрице для группы
мужчин в возрасте от 20 до 24 лет (мы опускаем вопрос
о принципах классификации):
1 2 3 4 5
1 0,832 0,033 0,013 0,028 0,095
2 0,046 0,788 0,016 0,038 0,112
3 0,038 0,034 0,785 0,036 0,107
4 0,054 0,045 0,017 0,728 0,156
5 0,082 0,065 0,023 0,071 0,759
Неподвижный вектор равен
а = (0,270; 0,184; 0,076; 0,148; 0,322),
а истинное распределение по классам дается вектором
а= (0,282; 0,170; 0,068; 0,137; 0,343).
Наибольший интерес представляет здесь матрица
обмена. Вот она:
1 0,225 0,009 0,004 0,008 0,026
2 0,008 0,145 0,003 0,007 0,021
D~*P = 3 0,003 0,002 0,060 0,003 0,008
4 0,008 0,007 0,002 0,100 0,0023
5 0,026 0,021 0,007 0,023 0,244
9 J. В lumen, М. Kogan, Р. J. McCarthy, The Industrial
Mobility of Labor as a Probability Process, Cornell Studies in In-
dustrial and Labor Relations, Vol. VII, 1955.
Дж. Кеменц, Дж. Снелл
258
ГЛ. VII. ПРИЛОЖЕНИЯ ЦЕПЕЙ МАРКОВА
Почти полная симметрия этой матрицы указывает на
то, что в положении равновесия систему можно считать
находящейся в условиях равного обмена, или что про-
цесс обратим.
7.7. Открытая модель Леонтьева. В леонтьевской
модели затрат-выпуска (input-output model) рассматри-
вается экономическая система, состоящая из г отраслей.
Мы предполагаем для простоты, что каждая отрасль
производит только один вид товаров. Природные фак-
торы— такие, как земельные, лесные, минеральные и пр.
ресурсы — мы считаем свободными для безвозмездного
использования и не включаем их в стоимость конечной
продукции. Вообще говоря, отрасли связаны между со-
бой в том смысле, что каждая должна закупать опреде-
ленное (положительное или равное нулю) количество
продукции другой отрасли, чтобы продолжать свое про-
изводство. Определим технологические коэффициенты
таким образом: q^— это количество продукции j-й от-
расли, которую t-я отрасль должна приобрести для того,
чтобы самой произвести товаров на один доллар. Пусть
Q — квадратная матрица порядка г с элементами q^. По
определению технологические коэффициенты неотрица-
тельны.
Легко видеть, что сумма всех q^ при фиксирован-
ном i есть величина тех затрат, которые должна сделать
i-я отрасль, чтобы произвести товаров на 1 доллар.
Чтобы i-я отрасль приносила прибыль или хотя бы не
терпела убытков, эта сумма не должна превышать ве-
личины выпуска, т. е. должно быть
qa + qi2 + •. • qir 1-
Естественно назвать z-ю отрасль прибыльной, если вы-
полняется строгое неравенство, и бесприбыльной, если
имеет место равенство. Мы допускаем, что любая от-
расль либо прибыльна, либо бесприбыльна, т. е. исклю-
чаем возможность убыточных отраслей.
Сформулированные условия можно записать как
Q>0, (1)
(2)
7.7. ОТКРЫТАЯ МОДЕЛЬ ЛЕОНТЬЕВА
259
Рассмотрев затраты отраслей, перейдем теперь к вы-
пускаемой ими продукции. Пусть Xi — денежная стои-
мость продукции i-и отрасли, и пусть я= (хь х2,..., хг)—
вектор-строка из этих стоимостей. Так как f-я отрасль
нуждается в продукции /-й отрасли в количестве
то вектор необходимых затрат просто равен nQ. Иными
словами, /-я компонента вектора otQ дает стоимость той
части продукции /*-й отрасли, которую она должна про-
извести, чтобы удовлетворить потребности всех отрас-
лей в своей продукции.
Пусть из продукции f-й отрасли сумма сг- идет на .
конечное потребление.
Введем вектор потребления у = (сь с2, •••, сг)\ мы
требуем, чтобы
у>0. (3)
Теперь легко записать в векторной форме требова-
ние, чтобы экономика была сбалансирована так, что и
межотраслевые нужды, и нужды конечного потребления
удовлетворены:
л — nQ + у. (4)
Переписав (4) в виде
л(/ —Q) = y, (5)
мы видим, что это — система г уравнений с г неизвест-
ными.
Мы должны найти неотрицательные решения систе-
мы (5) (только они и имеют экономический смысл).
Так как вектор спроса у может быть произвольным,
то система уравнений (5), вообще говоря, неоднородна
и имеет решение тогда и только тогда, когда матрица
I — Q имеет обратную. Более того, решения системы (5)
будут неотрицательны при любом у тогда и только
тогда, когда все элементы матрицы (/—Q)-1 неотрица-
тельны. Поэтому нам надо найти необходимые и до-
статочные условия того, чтобы матрица, обратная к
/ — Q, была неотрицательна.
17*
260
ГЛ. VII. ПРИЛОЖЕНИЯ ЦЕПЕЙ МАРКОВА
Мы решим эту задачу с помощью погружения на-
шей модели в цепь Маркова. [Решение получено авто-
рами совместно с Томпсоном (G. L. Thompson).]
Под цепью Маркова, присоединенной к модели за-
трат-выпуска, мы будем понимать цепь Маркова со сле-
дующими свойствами:
(I) Состояниями служат г отраслей модели плюс
еще одно добавочное поглощающее состояние s0, назы-
ваемое банком.
(II) Матрица Р переходных вероятностей опреде-
ляется так:
Роо = 1>
Ро/ = О, />0,
Рц=Яц, />°>
Г
Pzo = 1 ““ 3 />0.
Вот интуитивная интерпретация этой цепи. Когда
в Z-ю отрасль поступает 1 доллар, то она использует
его, расходуя на покупку продукции /-й отрасли. Оста-
ток этого доллара, если он есть — т. е. величина рго,—
это прибыль; мы можем считать, что она поступает в
банк. Банк является поглощающим состоянием, т. е.
получает деньги, но не тратит их.
Теперь сразу видно, что если матрица Q удовлетво-
ряет условиям (I) и (2), то неотрицательное решение
системы (5) существует при любом г>0 тогда и только
тогда, когда присоединенная цепь Маркова поглощаю-
щая, причем банк з0 является единственным поглощаю-
щим состоянием. Действительно, если з0 — единственное
поглощающее состояние в поглощающей цепи, то мат-
рица N = (/—Q)”1 существует и неотрицательна; зна-
чит, л = yN является искомым решением. В противном
случае матрица (/—Q)-1, которая дает среднее время
пребывания в различных состояниях до достижения $0,
будет иметь бесконечные элементы, т. е. не существует.
Этот результат просто истолковывается с экономи-
ческой точки зрения. Как мы убедились, цепь должна
быть устроена так, чтобы из каждого состояния можно
было «добраться» до банка. Непосредственно в банк
7.7. ОТКРЫТАЯ МОДЕЛЬ ЛЕОНТЬЕВА
261
«попадает» только прибыльная отрасль; бесприбыльная
должна попасть в банк через прибыльную. Значит, наше
условие означает, что каждая отрасль либо прибыльна,
либо зависит от прибыльной отрасли. Например, если
предположить, что каждая отрасль зависит от труда,
и труд является прибыльной отраслью (по-видимому,
это значит, что плата за труд выше, чем зарплата, по-
крывающая стоимость средств существования), то наше
условие выполняется, и, значит, система может удов-
летворить любой спрос.
Если приведенное условие нарушается, то экономи-
ческая система уже не обладает этим свойством. По-
смотрим, какой спрос она все же может удовлетворить.
Прежде всего рассмотрим случай, когда нет прибыль-
ных отраслей. Это значит, что каждая отрасль расхо-
дует все, что производит, на закупку сырья, и, следует
думать, не может удовлетворить никакой спрос со сто-
роны. Легко доказать, что так оно и есть.
Если нет прибыльных отраслей, то сумма элементов
каждой строки матрицы Q равна 1, т. е. = £. Если
мы умножим уравнение (4) на % справа, то получим
+ у|,
откуда = 0. Это означает, что суммарный спрос со
стороны равен 0. Значит, никакой (положительный)
спрос не может быть удовлетворен.
Рассмотрим теперь общий случай нарушения на-
шего условия. В этом случае присоединенная цепь Мар-
кова не является поглощающей цепью с единственным
поглощающим состоянием. Значит, должно существо-
вать эргодическое множество, отличное от {$0}, т. е.
должна существовать замкнутая группа отраслей, каж-
дая из которых бесприбыльна и не зависит ни от одной
отрасли вне этой группы. Рассмотрим множество всех
таких отраслей, т. е. объединение всех эргодических
множеств, отличных от {s0}. Подматрица Q для этих от-
раслей обладает доказанным выше свойством Q% = | и,
значит, не может удовлетворить никакой спрос со сто-
роны. Поэтому и вся экономическая система не может
удовлетворить спрос на товары, производимые этими
отраслями. Невозможно и снабжение теми товарами,
262
ГЛ. VII. ПРИЛОЖЕНИЯ ЦЕПЕЙ МАРКОВА
производство которых требует в качестве сырья продук-
цию этих отраслей, поскольку по отношению к замкну-
той группе отраслей это было бы спросом со стороны.
Однако если мы удалим эту замкнутую группу бес-
прибыльных отраслей вместе с теми, которые от них
зависят, то для оставшихся отраслей (если они найдутся)
наше требование будет выполнено, и они смогут удов-
летворить любой спрос. Подведем итог: если есть такие
отрасли, которые не зависят ни от одной прибыльной
отрасли, то ни они, ни какая-либо отрасль, от них
зависящая, не могут удовлетворить спрос со стороны.
Остальные отрасли могут удовлетворить любой спрос.
В терминах цепей Маркова это значит, что любое эрго-
дическое состояние (отличное от s0), или любое невоз-
вратное состояние, из которого такое состояние дости-
жимо, не может удовлетворить никакого спроса.
Чтобы выяснить, какие отрасли могут поддержать
спрос, мы используем следующий простой алгоритм для
классификации состояний:
(а) Сделаем отметку против каждой строки мат-
рицы Q, сумма элементов которой меньше 1, другими
словами, отметим все строки, отвечающие прибыльным
отраслям.
(Ь) Отметим столбцы с теми же номерами, что от-
меченные строки; затем в этих столбцах отметим стро-
ки, все элементы которых положительны.
(с) Будем повторять операцию (Ь) до тех пор, пока
не перестанем получать новые строки. Тогда возможны
два окончательных исхода:
(1) Все строки будут отмечены.
(2) Не все строки будут отмечены.
Если имеет место случай (cl), то присоединенная
цепь Маркова является поглощающей с единственным
поглощающим состоянием s0. Поэтому любой неотри-
цательный спрос может быть удовлетворен. Если полу-
чится (с2), то неотмеченные строки и дадут максималь-
ную замкнутую группу из бесприбыльных отраслей. Мы
можем найти все состояния, зависящие от них, пометив
эти строки (предварительно удалив прежние отметки)
и повторно применяя операцию (Ь). Любое состояние,
7.7. ОТКРЫТАЯ МОДЕЛЬ ЛЕОНТЬЕВА
263
помеченное таким образом, не может удовлетворять
спрос со стороны.
Таким образом, мы видим, что весь вопрос о том,
какой спрос может удовлетворять экономическая си-
стема, решается с помощью очень простого алгоритма.
«Вычислить» нужно только суммы элементов строк, а
затем произвести простую итерацию, при которой про-
веряется только положительность элементов. Этот алго-
ритм удобен даже для очень больших матриц.
Отрасли, которые не могут удовлетворить никакого
спроса со стороны, образуют совершенно бесполезную
часть экономической системы. Начиная с этого момента,
мы предположим, что они исключены из рассмотрения;
тогда (/—Q)-1 существует.
Теперь поставим следующий вопрос: если потреби-
тель сделал заказ t-й отрасли на 1 доллар, то какая
часть этого доллара достанется в конечном счете той
или иной отрасли?
Прежде всего нужно определить, каков будет общий
спрос на продукцию различных отраслей. В данном
случае у — это вектор, у которого t-я компонента рав-
на 1, а остальные — нули. Значит, л = yN— это про-
сто t-я строка матрицы N. Таким образом, элементы
матрицы N получают простое истолкование: — это
количество продукции, которую должна произвести /-я
отрасль, чтобы отрасль i выполнила заказ на 1 доллар.
Так как /-я отрасль получает прибыли с продукции
стоимостью в 1 доллар, то ответ на наш вопрос таков:
если отрасль t получает доллар, то отрасль / получает
Прибыль riijpjQ.
Сумма всех прибылей равна 5 n{jpjo = biQ = 1 (так
как So — единственное поглощающее состояние). Отсюда
видно, что доллар, уплаченный заказчиком, оседает как
прибыль в прибыльно работающих отраслях.
С этим связан и такой вопрос: если t-я отрасль по-
лучает заказ на 1 доллар, то к какой деловой активно-
сти это приведет? От отрасли / требуется единиц
продукции. Сумма их равна — t-й компоненте век-
тора т. Она, как правило, гораздо больше единицы. Для
вектора спроса у общая продукция равна yN% ==
2о4
ГЛ. VII. ПРИЛОЖЕНИЯ ЦЕПЕЙ МАРКОВА
Рассмотрим пример. Пусть технологические коэффи-
циенты для шести отраслей задаются матрицей
72 0 74 0 0 0
74 74 74 0 0 0
72 0 7г 0 0 0
Q = 0 0 0 74 74 0 •
0 0 0 1 0 0
0 74 0 74 0 74.
Тогда 1 0 0 0 0 0 0 so
7ч 72 0 74 0 0 0 *1
74 74 74 74 0 0 0 S2
0 72 0 72 0 0 0 S3
0 0 0 0 74 74 0
0 0 0 0 1 0 0 S5
74 0 74 0 74 0 74 S6
Из первого столбца видно, что $i, s2 и s6 — прибыль-
ные отрасли. Классификация состояний показана на
рис. 7.9.
Здесь {$4, $5} — эргодическое множество бесприбыль-
ных отраслей, не зависящих от прибыльных отраслей.
Отрасль прибыльна, но зависит от {^4, s5}. Следова-
тельно, s4, $5, «6 бесполезны и могут быть исключены.
Отрасль $з бесприбыльна, но не бесполезна. Сокращен-
7.7. ОТКРЫТАЯ МОДЕЛЬ ЛЕОНТЬЕВА
265
ная матрица переходных вероятностей равна
Значит,
( 1 0 0 0 \ s0
'А '/2 о ’A I ®i
74 74 74 74 к’
О 7г 0 7г' ®з
/4 ° 2\ /6\
% 4/з 2 ], т= 6 ).
\ 0 0 4/ \8/
Так, например, заказ на 1 доллар отрасли «2 стиму-
лирует производство продукции всего на 6 долларов,
из них на 8/з, в S], на 4/з в «2 и на 2 в S3. Из этого
доллара s, получает прибыль 8/з • ’А = 2/з, «2 при-
быль 4/з • */4 = Уз и «з — прибыль 2-0 = 0 («з бес-
прибыльна).
Если мы зададим спрос у= (1,3,2), то наши от-
расли произведут yAf = (20, 4, 16) единиц продукции.
Стоимость всей продукции будет уг = 40 долларов.
Заметим, что Р допускает укрупнение состояний
[{•So}, {Si, «2}, {®з}]- Для укрупненного процесса
/ ! 0 0 \
р= 74 72 74 У
\о 72 72/
- /4 2>|
w= . л
\4 4/
/6\
Т = W’
Если у = (4,2), то yN = (24, 16), ут =40. Объеди-
ненные отрасли «1 и s2 рассматриваются здесь как одна
«отраслевая группа». При использовании этого процесса
получается спрос со всей отраслевой группы, без под-,
разделения его на спросы отдельным отраслям.
В реальных задачах вычисления могут оказаться
практически невыполнимы. Поэтому мы бываем рады,
266 ГЛ. VII. ПРИЛОЖЕНИЯ ЦЕПЕЙ МАРКОВА
когда удается решить «укрупненный» вариант экономи-
ческой системы. Условие возможности укрупнения при-
нимает здесь следующий вид: все отрасли одной отрас-
левой группы требуют одинаковое количество продук-
ции от членов (этой или) другой отраслевой группы при
заказе на единицу продукции. (Тогда все отрасли одной
группы получают одну и ту же прибыль на единицу про-
дукции.) Хотя трудно ожидать, чтобы такие условия вы-
полнялись в точности, тем не менее этот способ может
дать хорошие приближения. Укрупнение позволяет рас-
сматривать отраслевые группы как основные объекты и
приводит к меньшей и более податливой модели.
Таким образом, мы видим, что теория цепей Мар-
кова может дать довольно много информации даже при
изучении не вероятностной модели.
ДОБАВЛЕНИЕ
I. Сводка основных обозначений
МИЛ, Djn РДр] означают соответственно матема-
тическое ожидание (или среднее значение) функ-
ции f, дисперсию f и вероятность утверждения р
при условии, что цепь начинается в состоянии
R = — матрица с элементами
р = {/*;} — вектор-строка с компонентами rj.
У = {^} — вектор-столбец с компонентами cit
| — вектор-столбец, все элементы которого равны 1.
ц — вектор-строка, все элементы которой равны 1.
Е — матрица, все элементы которой равны 1.
I — единичная матрица.
О — матрица, все элементы которой равны 0.
( 1 при i = /,
1 I о при г#=/.
Ат — матрица, полученная из А транспонированием.
Xsq—матрица, полученная из А возведением в
квадрат каждого элемента.
Xdg — матрица, полученная из А заменой всех эле-
ментов, не лежащих на главной диагонали, нулями.
II. Основные определения
Конечная цепь Маркова — случайный процесс, про-
исходящий на конечном множестве состояний, для
которого вероятность попасть в некоторое состояние
зависит только от занимаемого перед этим состоя-
ния.
268
ДОБАВЛЕНИЕ
Эргодическое множество состояний — такое множе-
ство, в котором можно из любого состояния по-
пасть в любое и из которого, попав в него, нельзя
уйти.
Невозвратное множество состояний — такое множе-
ство, в котором можно из любого состояния попасть
в любое и из которого можно уйти.
Эргодическое состояние — элемент эргодического
множества состояний
Невозвратное состояние — элемент невозвратного
множества состояний.
Поглощающее состояние — состояние, попав в ко-
торое,.нельзя из него выйти.
Поглощающая цепь — цепь, все эргодические со^
стояния которой поглощающие, или, что эквива-
лентно,— цепь, имеющая по крайней мере одно
поглощающее состояние, причем из любого состоя-
ния можно попасть в поглощающее состояние.
Эргодическая цепь — цепь, состояния которой обра-
зуют одно эргодическое множество, или, что экви-
валентно,— цепь, в которой из любого состояния
можно попасть в любое другое.
Циклическая цепь — эргодическая цепь, в которой
в каждое состояние можно попадать только через
определенные периодические промежутки времени.
Регулярная цепь — эргодическая цепь, не являю-
щаяся циклической.
III. Основные характеристики поглощающих цепей
Каноническая форма переходной матрицы
О
Q
Р
jij — время, проведенное в состоянии $, .до погло-
щения
ДОБАВЛЕНИЕ
269
—функция, равная 1, если после #-го шага цепь
находится в состоянии Sj, и 0 — в противном случае.
t — полное число шагов до поглощения.
bij — вероятность ПОГЛОТИТЬСЯ В СОСТОЯНИИ Sj9 исхо-
дя из Si.
Гг — время пребывания в невозвратном состоянии
до выхода из этого состояния.
hij — вероятность того, что процесс когда-нибудь
побывает в Sj9 выходя из s^.
т — полное число невозвратных состояний, в ко-
торых процесс побывал до поглощения.
Аг = {Мг[п/]}.
^2 = {Ог[П;]}.
T = {hW
t2 = {D, [#]}.
В = (М-
ц = {М, [m]}.
Р — переходная матрица процесса изменения со-
стояний.
IV. Основные формулы теории поглощающих цепей
N = (/ — Q)-1 (фундаментальная матрица).
Л^2 = (2Af dg “ ^) — A^sq •
B = NR.
* = . •• . . . . - -
Т2 = (2Af — I) T — TSq .
M, [rd =1/(1-рн).
Dz [r,] = pa/(l - pa)2.
P = (AWd"gk
270
ДОБАВЛЕНИЕ
V. Основные характеристики эргодических цепей
а = {аг} — неподвижный вероятностный вектор для
матрицы Р (равновесное или стационарное распре-
деление) .
сц = Iim 7К4^п)’
П-+00 ™ L
Р = {bj} — вектор предельных дисперсий времен пре-
бывания в каждом из состояний.
А — матрица, каждая строка которой равна а.
D — диагональная матрица, /-й диагональный эле-
мент которой равен 1/aj.
Р— переходная матрица обращенного (сопряжен-
ного) процесса.
Z = (I — Р + Л)-1 (фундаментальная матрица)
i
М = {рпц} — матрица, элемент тг?- которой есть ма-
тематическое ожидание времени первого достиже-
ния СОСТОЯНИЯ Sj, исходя ИЗ 8/.
F = {a>ij) — матрица, элемент Юц которой есть дис-
персия времени первого достижения состояния
исходя ИЗ Si.
-- время пребывания в состоянии Si за первые и
шагов.
VI. Основные формулы теории эргодических цепей
P = DPTD~\
M = {mdl} = (I-Z + EZdg)D.
М = М- Mds.
ДОБАВЛЕНИЕ 271
И7 = {Wlj} = М (2ZdeD-I) + 2(ZM-E(ZM)dg).
С = {сц} = {aizlt + а}2ц - а$ц - а^}.
m{i = l/az.
^zu 1
®»== —-------•
«/ «»
aM = t\ZdgD.
MaT = cl.
а = (с-1)[(М)-Ч]Г-
P = I + (D-E){M)~'.
Джон Дж. Кемени, Дж. Лори Снелл
Конечные цепи Маркова
М., 1970 г., 272 стр. с илл.
Редактор В. В. Абгарян
Техн, редактор К. Ф. Брудно
Корректоры 3. В. Автонеева, Е. Я. Гороховская
Сдано в набор 4/VIII 1970 г. Подписано к печати 1/ХП 1970 г.
Бумага 84х108‘/з2- Физ. печ. л. 8,5. Условн. печ. л.14,28. Уч.-
изд. л. 13,59. Тираж 12000 экз. Цена книги 1 р. 18 к.
Заказ 726.
Издательство «Наука»
Главная редакция
физико-математической литературы.
Москва, В-71, Ленинский проспект, 15
Ордена Трудового Красного Знамени
Ленинградская типография № 2 •
имени Евгении Соколовой Главполиграфпрома
Комитета по печати при Совете Министров СССР.
Измайловский проспект, 29.