Аэродинамика вентиляции - Талиев В.Н.

Автор: Талиев В.Н.

Теги: отопление, вентиляция и кондиционирование воздуха в зданиях строительство кинематика методы аэродинамики вентиляции

Год: 1979

Похожие

Отопление и вентиляция. Часть 2

Основы промышленной вентиляции

Вентиляция и кондиционирование воздуха

Проектирование промышленной вентиляции

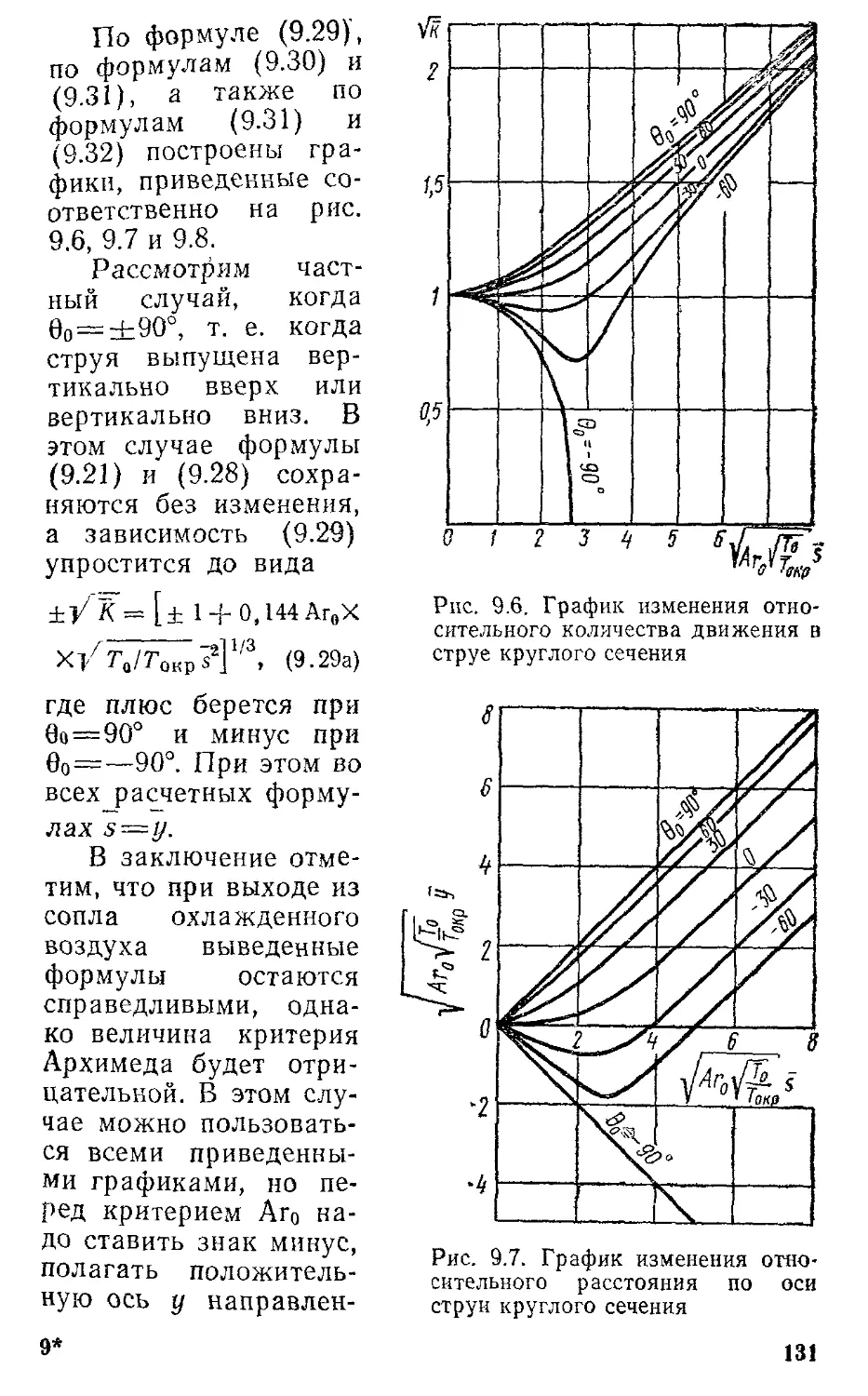
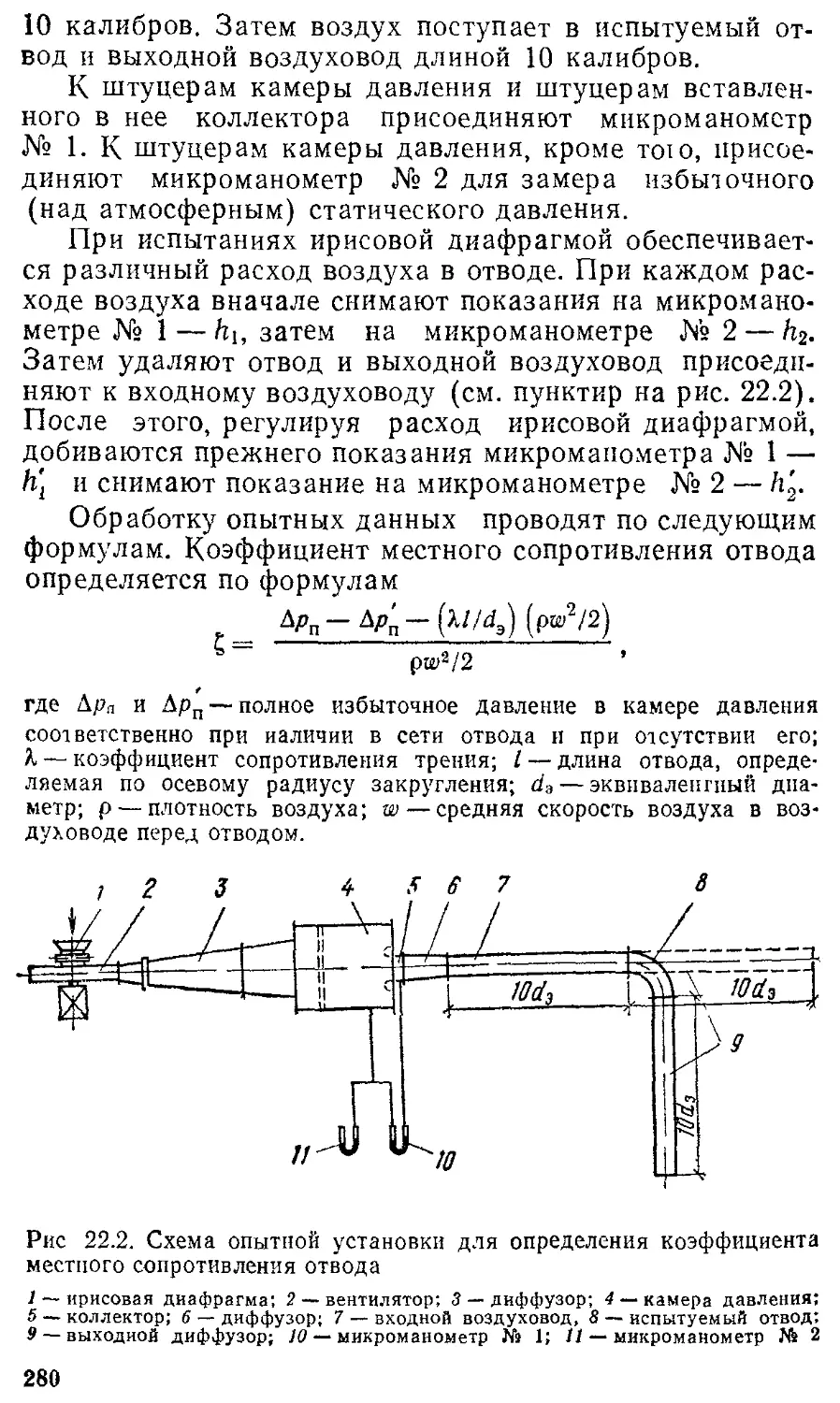
Текст

в. Н. ТАЛИЕВ, д-р техн, наук проф.
АЭРОДИНАМИКА
ВЕНТИЛЯЦИИ
Допущено
Министерством высшего и среднего специального образования СССР
в качестве учебного пособия для студентов вузов,
обучающихся по специальности «Теплогазоснабжение и вентиляция»
МОСКВА
СТРОЙИЗДАТ
1979
ББК 38 762.2
Т 16
УДК 697.92 : 533.6(075.8)
Рецензенты: кафедра «Отопление и вентиляция» Москов-
ского инжеиерно-строительиого института им. В В. Куйбышева (зав.
кафедрой д-р техн, наук проф. В. Н. Богословский), д-р техн, наук
проф. В. А. Бахарев.
Талиев В. Н.
Аэродинамика вентиляции: Учеб, пособие для
Т 16 вузов. — М.: Стройиздат, 1979. — 295 с., ил.
Описано применение методов аэродинамики для решения задач
вентиляции Рассмотрены уравнения аэродинамики, основы кинематики,
методы интегрирования уравнений аэродинамики и конформных ото-
бражений течений. Освещены вопросы обтекания тел потоком, приве-
дены зависимости для определения потерь давления в воздуховодах и
местных сопротивлениях. Проведено аэродинамическое исследование
приточных и конвективных струй, всасывающих факелов, бортовых от-
сосов и воздуховодов равномерной раздачи и всасывания. Даиы основы
моделирования вентиляции, описаны опытные установки, приборы и
методы лабораторного экспериментирования.
Пособие предназначено для студентов строительных вузов, обуча*
ющихся по специальности «Теплогазоснабжение и вентиляция».
30210__219
Т ----------- 216—79. 3206000000
047(01)—79
ББК 38.762.2
6С9.4
© Стройиздат, 1979
УСЛОВНЫЕ ОБОЗНАЧЕНИЯ ОСНОВНЫХ ВЕЛИЧИН
М — масса;
р — плотность жидкости или газа;
F — площадь поперечного сечеиия;
v — скорость потока;
vCp — средняя (по площади сечеиия) скорость?
k — коэффициент поля скоростей;
с»ос— осевая скорость, т. е. скорость на оси потока;
Q — количество тепла;
W — объем;
р — давление, статическое давление;
g — ускорение свободного падения;
О — массовый расход;
а — коэффициент Кориолиса;
К — количество движения;
₽ — коэффициент Буссинеска; *
V — кинематический коэффициент вязкости;
I — скорость линейной деформации частицы;
е — скорость угловой деформации частицы;
о —угловая скорость вращения частицы;
L — объемный расход;
Ф — потенциал скорости;
ф — функция тока;
w — ф+гф — комплексный потенциал;
z = x+iy— комплексная координата;
Re — число Рейнольдса;
kj — аэродинамический коэффициент;
Т — касательное напряжение;
Х< — коэффициент сопротивления трения;
Р — периметр поперечного сечения воздуховода;?
d$ — эквивалентный диаметр;
С — коэффициент местного сопротивления;
— коэффициент смягчения удара;
1)в—коэффициент смягчения входа;
— скорость в начале струи;
Е —кинетическая энергия;
to — температура в начале струи;
^окр — температура воздуха, окружающего струю;
Д6 “ to—^окр— избыточная температура в начале струи;
“Ср — средняя (по расходу) избыточная температура;
Кд/ — коэффициент поля избыточных температур;
^ОС — осевая избыточная температура, т. е. избыточная температуря вя ОСЯ
струи;
д,ср1 — средняя (по площади) избыточная температура;
Рд/ «— температурный аналог коэффициента Буссинеска;
Т — абсолютная температура;
АГо —число Архимеда;
М — коэффициент расхода;
б — ширина продольной щели в воздуховоде;
б — площадь бокового отверстия в воздуховоде;
^—скорость воздуха в воздуховоде в сечейии XJ
— скорость воздуха в воздуховоде в сечении I;
ил — параметр щели или отверстий;
X/ — параметр воздуховода;
г—относительное отклонение фактической скорости от средней;
Ьц — коэффициент полного сопротивления;
С — масштаб моделирования.
1*
ПРЕДИСЛОВИЕ
В материалах XXV съезда КПСС предусмотрено обеспечение
дальнейшего развития фундаментальных и прикладных научных ис-
следований в области общественных, естественных и технических
наук. В новой Конституции СССР отмечено, что государство обеспе-
чивает планомерное развитие науки и подготовку научных кадров,
организует внедрение результатов научных исследований в народ-
ное хозяйство
Все эти вопросы нашли конкретное отражение в беседе Гене-
рального секретаря ЦК КПСС, Председателя Президиума Верхов-
ного Совета СССР товарища Л. И Брежнева с партийно-хозяйст-
венным активом Новосибирской области, в ходе которой было под-
черкнуто, что активная роль ученых должна помогать решать во-
просы соединения науки с практикой н тем самым способствовать
росту производительных сил страны.
Вентиляция как наука за годы Советской власти также неуклон-
но развивалась. Теоретической базой для ее развития являлись такие
дисциплины, как «Аэродинамика», «Теплопередача» и «Тепломассо-
обмен»
К числу аналитически решаемых вопросов следует в первую
очередь отнести вопросы о закономерностях развития свободных
приточных изотермических и неизотермических струй, конвективных
струй, о взаимодействии их между собой и с набегающим на них
потоком воздуха, о стеснении струй твердыми стенками и вопрос о
затихании скоростей во всасывающих факелах
На основе этих аналитических решений были разработаны ме-
тодики расчета воздушных душей, подачи кондиционного охлажден-
ного воздуха в рабочую зону помещения с учетом заданных сани-
тарными нормами скорости и температуры, вентиляционных выбро-
сов как от приземных источников, так и от высоких труб
В дальнейшем были даны решения более сложных задач, а
именно о всевозможного рода воздушно-струйных укрытиях техно-
логического оборудования, выделяющего газовые вредные вещества,
бортовых отсосах и воздушных завесах и, кроме того, исследован
такой важный вопрос по организации воздухообмена, как вопрос о
создании температуры воздуха в рабочей зоне вентилируемого по-
мещения при наличии теплоисточников
На базе основных уравнений аэродинамики была решена также
задача о приточных и вытяжных воздуховодах с продольной щелью
или рядом боковых отверстий Настоящее учебное пособие посвяще-
но аналитическому решению некоторых нз перечисленных вопросов
методами аэродинамики
Автор выражает признательность коллективу кафедры «Отопле-
ние и вентиляция» Московского инженерно-строительного института
имени В В Куйбышева, возглавляемой д-ром техн наук проф.
В Н Богословским, и д-ру техн, наук проф. В А. Бахареву за цен-
ные замечания и советы, сделанные при рецензнрованин рукописи.
РАЗДЕЛ ПЕРВЫЙ
СВЕДЕНИЯ ПО ТЕОРЕТИЧЕСКОЙ АЭРОДИНАМИКЕ
ГЛАВА 1
УРАВНЕНИЯ АЭРОДИНАМИКИ
§ 1. Общие сведения
Гидроаэромеханика, как это следует из самого назва-
ния, явчяется механикой жидкой и газообразной среды,
она гораздо сложнее механики твердого тела. Если ме-
ханика твердого тела изучает систему жестко связанных
между собой молекул, то гидроаэромеханика исследует
среду с очень слабыми связями между молекулами. Эти
слабые связи позволяют молекулам жидкостей и осо-
бенно газов перемещаться в любом направлении, что
вызывает беспорядочное молекулярное движение. По-
следнее необычайно осложняет изучение различных
вопросов гидроаэромеханики.
Во избежание этих трудностей Д’Аламбер и Эйлер
предложили в гидроаэромеханике отказаться от рас-
смотрения молекулярного строения вещества, а изучать
жидкости и газы, не принимая во внимание отдельные
молекулы и имеющиеся между ними пустоты и считая
эти среды сплошными, непрерывно заполняющими
пространство. Это допущение носит название постула-
та о сплошности жидкой и газообразной среды.
Благодаря этому допущению все механические ха-
рактеристики жидкостей и газов (давление, скорость и
др.) можно рассматривать как непрерывные функции
координат точки и времени и при решении различных
задач гидроаэромеханики широко использовать ма-
тематический анализ. Однако для объяснения отдельных
явлений в гидроаэромеханике прибегают к рассмотре-
нию молекулярного строения среды и кинетической
теории газов.
Принятие постулата о сплошности практически озна-
чает, что при гидроаэромеханических исследованиях до-
статочно изучить поведение частиц (молей) жидкости
или газа, размер которых во много раз превосходит
размер молекул.
Движение жидкости и газа может быть неустановив-
шимся и установившимся. При неустановившемся дви-
5
жснии плотность, давление, скорость и прочие механи-
ческие характеристики в каждой точке потока с тече-
нием времени изменяются. В случае установившегося
движения все эти характеристики в каждой точке по-
тока остаются неизменными во времени.
Примером неустановившегося и установившегося
движения является истечение жидкости из сосуда со-
ответственно при переменном и постоянном уровне жид-
кости в нем. В дальнейшем, как правило, будет рас-
сматриваться только установившееся движение.
Гидроаэромеханика при изучении движения разли-
чает два режима течений: ламинарное и турбулентное.
Ламинарное течение характеризуется тем, что отдель-
ные струйки не смешиваются между собой. Турбулент-
ное течение характеризуется пульсациями, вследствие
которых происходит перемешивание отдельных струек.
При турбулентном движении частицы ведут себя
примерно так же, как молекулы, т. е. находятся в со-
стоянии беспорядочного движения, а скорости и давле-
ния в каждой точке жидкости или газа пульсируют,
т. е. изменяются с течением времени. Эти пульсации
чрезвычайно осложняют изучение движения. Поэтому
в целях облегчения исследования мгновенные истинные
скорости и давления подменяют их осредненными по
времени значениями.
В жидкостях и газах могут действовать разнооб-
разные силы. В зависимости от того, как они приложе-
ны к выделенному объему жидкости или газа, их раз-
деляют на объемные (массовые) и поверхностные.
Объемные силы приложены к любой частице дан-
ного объема. К ним относятся силы тяжести и инерции.
Поверхностные силы приложены только к частицам,
лежащим на поверхности данного объема. К ним отно-
сятся силы давления и трения. При этом сила давления
всегда направлена нормально к поверхности, а сила
трения — по касательной к ней.
Вследствие большой подвижности частиц силы яв-
ляются рассредоточенными (распределенными). Для
количественной характеристики сил используют понятие
«напряжение силы».
Напряжением объемной силы называется сила, при-
ходящаяся на единицу объема. В частном случае, ког-
да рассматривается сила тяжести, напряжением явля-
ется объемный вес.
6
Напряжением поверхностной силы называется сила,
приходящаяся на единицу поверхности. Напряжением
силы давления является давление, напряжением силы
трения — касательное напряжение. Необходимо отме-
тить, что касательное напряжение проявляется только
при движении жидкостей и газов. Величина его по
сравнению с величиной давления весьма мала.
В гидроаэромеханике для упрощения решения раз-
личных задач часто пренебрегают силами вязкости.
Жидкость и газ, не имеющие вязкости, принято назы-
вать идеальной жидкостью и идеальным газом.
Для описания движения вводятся понятия траекто-
рии частицы и струйки. Траекторией частицы называ-
ется линия, по которой происходит перемещение части-
цы последовательно во времени.
Понятие струйки определяется следующим образом.
Мысленно выделим в потоке некоторый достаточно
малый замкнутый контур abcde (рис. 1.1). Через все
точки этого контура, очевидно, проходят траектории
частиц, которые в своей совокупности образуют поверх-
ность. Часть жидкости или газа, ограниченная этой по-
верхностью, называется струйкой. Сама же поверхность
иосит название боковой поверхности струйки. Необхо-
димо отметить, что боковая поверхность струйки при-
нимается для жидкости и газа не-
проницаемой.
Поверхность, перпендикулярная
всем траекториям частиц в струйке,
называется поперечным или живым
сечением струйки.
Различают струйки элементар-
ные и конечного поперечного сече-
ния. Под элементарной струйкой
понимают бесконечно тонкую струй-
ку, по поперечному сечению которой
объемный вес, плотность и скорость
крайне мало изменяются и могут
быть приняты постоянными. В
струйке конечного поперечного се-
чения, как правило, эти величины
переменны по поперечному сечению
струйки.
Количество жидкости или газа,
протекающее через поперечное сече-
Рис. 1.1. Замкнутый
контур и проходящая
через него струйка
7
ние струйки в единицу времени, называется расходом.
Различают расход весовой, массовый и объемный в за-
висимости от того, в чем измеряют расход жидкости или
газа: в единицах веса, массы или объема.
В системе СИ весовой расход измеряется в Н/с,
массовый — в кг/с, а объемный — в м3/с или соответ-
ственно в Н/ч, кг/ч и м3/ч,
§ 2. Уравнение расхода
Выделим в движущейся жидкости или газе струйку
(рис. 1.2). Проведя два поперечных сечения 1—1 и
2—2, рассмотрим объем жидкости или газа в струйке,
заключенной между этими сечениями.
За время Д/ объем на участке 1, 2 переместится в
новое положение 1', 2'. Согласно закону сохранения ве-
щества, масса рассматриваемого объема струйки на
этих участках должна быть одинаковой:
Л412 — Л11'(2'
или
ДЛ4| j, Alj, 2 ~~ Alj. 2 т ДА1? о*.
При установившемся движении масса Мг, 2 до пере-
мещения будет равна массе 2 после перемещения.
Отсюда
AAfj j/ == ДЛ^2 2' •
Масса объема на участке /, 1'
ДЛ11(1, = р1 Fx
где pi — плотность воздуха; Ft — площадь поперечного сечения;
Д/1 —длина участка струи 1,1’.
Пусть скорости жидкости или газа в каждом сече-
нии одинаковы, тогда расстояние между сечениями
/—/ и 1'—Г равно произве-
, 2 2' 1 t —г?7г?' Рис 1 2 Элементарная струйка дению скорости на время: Д/1 = к1 &tv В таком случае ДЛ4; р = Р1 Аналогично получаем, что масса объема на участке 2,2':
8
&М22, = p2F2v2M.
Приравнивая полученные значения масс между со-
бой и сокращения на St, получим уравнение массового
расхода
Pi^i'i = (ПО
Такое название этому уравнению дано потому, что
произведение pFv является массовым расходом жид-
кости или газа (если представить себе, что сечение не-
подвижно, а жидкость или газ движется через него). Та-
ким образом, массовый расход вдоль струйки сохраня-
ется постоянным.
Если же плотности и скорости жидкости или газа
в каждом поперечном сечении не постоянны, то разде-
лим струйку на ряд элементарных струек. Массовый
расход вдоль каждой элементарной струйки [см. фор-
мулу (1.1)] будет постоянен:
PiM/i = Р2М/2.
где df — площадь поперечного сечения элементарной струйки
Массовый расход всех элементарных струек также
будет неизменным:
f == [ р2М/2.
FL Fi
Применяя известную в математике теорему о сред-
нем, получим иное уравнение массового расхода
(Pi^ilcp Pt — (Pa^alcp р2>
где рр — средняя по площади поперечного сечения массовая скорость.
Если в поперечном сечении струйки плотность жид-
кости или газа не изменяется, то уравнение массового
расхода несколько упрощается:
Pi^i^icp = • (1-2)
В частном случае, когда плотность вдоль струйки
является постоянной величиной, то р! = р2 и уравнения
массового расхода (1.1) и (1.2) упрощаются и принима-
ют вид уравнений объемного расхода:
F1vl = F2v2- (1.3)
^Лср ~ Pzv2C-p- (1-4)
Отсюда следует, что объемный расход вдоль струйки
остается постоянным.
Иногда удобно пользоваться уравнением объемного
расхода, содержащим осевую скорость. Такое уравне-
9
ние может быть получено, если среднюю по площади
скорость заменить на осевую по равенству
vcp —
где k — коэффициент поля скоростей
Тогда получим
= k2F2vz0C. (1.5)
При этом коэффициент
1
Vrr) 1 Р р — — л
k = =------ \vdf = vdf, (1.6)
"^ос ^ос F J J
F о
где v = v/voc и df=dflF.
Следует отметить, что этот коэффициент может быть
как меньше, так и больше единицы. В тех случаях, ког-
да осевая скорость является наибольшей, коэффициент
будет меньше единицы, когда же осевая скорость явля-
ется наименьшей, коэффициент будет больше единицы.
В иных случаях вопрос о том, меньше или больше еди-
ницы этот коэффициент, может быть решен только, ес-
ли известно поле скоростей.
Пример 1 1 Определить среднюю скорость воздуха иа выходе из
диффузора, имеющего диаметр на входе di=150 мм, а на выхо-
де da=300 мм. Средняя скорость воздуха на входе у1ср = 8 м/с.
Решение Проведем в начале и в конце диффузора попевеч-
ные сечения 1—-1 и 2—2. Напишем уравнение расхода (1.4):
ndf nd}
vicp = ~ Ггср-
Отсюда искомая скорость
/ dj \« /150,
и2Ср — ( , I У1СР — ( ° — 2 М'С>
\ Un ] \ OXjnj)
§ 3. Уравнение Бернулли
Выделим в потоке струйку и проведем в ней сечения
1—1 и 2—2 на бесконечно малом расстоянии друг от
друга (рис. 1.3). Рассмотрим участок струйки, заклю-
ченный между этими сечениями. Применим к выделен-
ному объему на участке 1, 2 закон сохранения энергии,
сформулированный следующим образом: количество
тепла, сообщенное выделенному объему за некоторый
промежуток времени, сложенное с работой, которую
10
произвели за то же время приложенные к объему си-
лы, равно изменению энергии выделенного объема за
это время.
Количество тепла, сообщенное объему, определяем
исходя из следующих соображений. Пусть объем на
участке 1, 2 за время Д/ переместится в новое положе-
ние 2'. Тогда количество тепла, которое сообщено
рассматриваемому объему за это время, составит
dQ — @1,2 = @1',2 “Ь ^@2,2' ^@1,1' — С1',2-
При установившемся движении количество тепла
QV2 до перемещения равно количеству тепла
Qj, 2 после перемещения.
Отсюда
dQ ~ Д@2 2' —
Обозначим тепло, приходящееся на единицу массы
жидкости или газа в объеме на участке 1,1', через q, а
в объеме на участке 2,2' — через q+dq.
Тогда количество тепла
dQ — AM, v (q -f- dq) — &М1 г, q.
Принимая во внимание, что
AAfj 1# = ДЛ12 2, = AM = const,
можем написать
dQ — AMdq.
Рис. 1.3. Струйка, в которой
объем на участке 1, 2 пере-
местился в положение объ-
ема на участке 1', 2'
Работа сил сложится из работы поверхностных и
объемных сил.
Работа нормальных поверхностных сил, приложен-
ных к объему на участке 1, 2, будет складываться из
работы сил давления, приложенных к обоим торцам
данного объема, так как рабо-
та нормальных сил, приложен-
ных к боковой поверхности
струйки, равна нулю (нормаль-
ные силы, приложенные к бо-
ковой поверхности струйки,
перпендикулярны направле-
нию перемещения частиц).
Обозначим давление в се-
чении 1—1 через р, а в сечении
2—2 — через p+dp. При этом
И
давление p-\-dp будет направлено в сторону, противо-
положную направлению потока. Обозначим также объ-
ем на участке 1,1' через AW, а объем на участке 2,2'
через &W-\-d&W.
Работа нормальных поверхностных сил без учета
бесконечно малых величин второго порядка будет равна:
рДГ — (р + dp) (ДГ + dAW) = — dpAW - pd/sW = — d (рДГ).
Работа касательных поверхностных сил, т. е. работа
сил трения, определяется таким же образом, каки ра-
нее найденное количество тепла. Не приводя этих рас-
суждений, по аналогии напишем, что работа касатель-
ных поверхностных сил равна —g&Mdh, где dh — по-
тери энергии на трение, приходящиеся на единицу веса
жидкости или газа.
Знак минус взят потому, что сила трения направле-
на в сторону, противоположную направлению потока.
Работа объемных сил сложится из работы по пере-
мещению центра тяжести объема на участке 1, Г в
центр тяжести объема на участке 2,2'.
Обозначим проекции ускорения, вызванные объем-
ными силами на оси координат, через X, Y и Z; рас-
стояние между центрами тяжести объемов на участках
1, Г и 2,2' — через ds, а проекции ds на оси координат —
через dx, dy и dz.
В таком случае работа объемных сил составит
DsM(Xdx+Ydy+Zdz').
Изменение энергии сложится, очевидно, из измене-
ния в рассматриваемом объеме внутренней и кинети-
ческой энергии. Изменение внутренней энергии будет
равно разности внутренних энергий жидкости или газа
в объемах на участках 1, 1' и 2, 2'.
Обозначив внутреннюю энергию объема на участке
1, 1', приходящуюся на единицу массы жидкости или
газа, через U, а объема на участке 2,2' — через U-\-dU,
получим, что искомое изменение внутренней энергии
равно AMdU.
Изменение кинетической энергии будет равно раз-
ности кинетических энергий жидкости или газа в объе-
мах на участках 1, 1' и 2, 2'.
Обозначив скорость в сечении 1—1 через и, а в се-
чении 2—2 через v-\-dv, получим, что изменение кине-
тической энергии без учета бесконечно малых величин
второго порядка составит
12
AM (v + dv)2 AMv2 , t v2 \
----------—------= AMd —— .
2 2 \ 2 J
Применяя закон сохранения энергии, получим
AMdq — d (pAW) — gAMdh + AM (Xdx + Ydy -f- Zdz) =
= AMdU + AMd (t>2/2).
Сокращая на ДМ = рЛЙ7, будем иметь уравнение
dq + Xdx + Ydy +Zdz=dU + d (р/р) + d (t>2/2) + gdh. (1.7)
Из термодинамики известно, что тепло, сообщенное
единице массы жидкости или газа, расходуется на по-
вышение их внутренней энергии и работу по расшире-
нию их объема:
dq = dU +pd (1/р).
Вычитая последнее уравнение из уравнения энер-
гии (1.7), получим обобщенное уравнение Бернулли:
Xdx + Ydy + Zdz = — +d(~} + gdh. (1.6)
р X /
Если из объемных сил действует только сила тя-
жести, то последнее уравнение упрощается.
Выберем прямоугольную систему координат, у ко-
торой оси х и у расположены горизонтально, а поло-
жительная ось z направлена навстречу силе тяжести.
Тогда проекции ускорений Л"=0; У=0; Z——g и
уравнение (1.8) примет вид
dp / v2 \
dz+—-)-dl— +d/i = 0. (1.9)
Pg \2g J
Интегрируя это уравнение, получаем уравнение
Бернулли:
Р dp v2
z “И । “Ь * “Ь h = const. (1*10)
J Pg 2g
Входящий в последнее уравнение интеграл можно
взять, если известно, как изменяются давление и плот-
ность вдоль рассматриваемой струйки.
В частном случае, когда p=const, интеграл легко
берется и уравнение Бернулли для жидкости или не-
сжимаемого газа примет вид
z + plpg + v2/2g -\-h = const. (1.11)
Если скорости в каждом поперечном сечении струи
неодинаковы, то, разделив струйку на элементарные
13
струйки, применим к одной из них уравнение (1 11).
Затем, умножив все члены этого уравнения на весовой
расход в элементарной струйке gdG, получим уравне-
ние энергий для элементарной струйки. Если затем
сложить энергии всех элементарных струек, то полу-
чим энергию струйки:
П \ f IT f*
г -J------gdG + 1 — dG + I hgdG = const.
< / J * J
(1.12)
При плавно изменяющемся движении, т. е. движе-
нии, очень мало отличающемся от параллельно-струй-
ного, все частицы, расположенные в одном и том же
перпендикулярном сечении струйки, имеют одинаковую
потенциальную энергию, т. е.
г + p/pg = const.
Учитывая это обстоятельство, уравнение (1.12) мож-
но записать в виде
р \ р V2 С
2 + —j gG + J — dG + J hgdG = const.
Сокращая на весовой расход gG и заменяя dG —
~=pvdf, получим
р 1 Г ov3 1 Г
г -1-----F — I —— df + — 1 hdG = const.
pg gG J 2 GJ
F
Применяя теорему о среднем и подставляя
G—pFvcp, можно написать
Р
Pg
(о8)ср
2gfCp
Ейср = const.
Заменим здесь среднюю величину куба скорости на
куб средней (по площади) скорости:
RcP=<>
где а — коэффициент Кориолиса.
Тогда окончательно получим следующее уравнение
Бернулли для жидкости или несжимаемого газа:
а+ — + а —— + йСп = const. (1.13)
Pg 2g
14
Применительно к двум сечениям струйки уравнение
(1.13) можно написать в виде
. Pi , Нср р2 , и^ср
*14---г«1—-— = г2Н-----Fa2—------J-Aft, (1.14)
Pg 2g Pg 2g
где ДЛ=Л2ср—hicp.
Очень часто уравнение Бернулли используют в дру-
гой форме. Чтобы ее получить, умножим все члены по-
следнего уравнения на pg:
9 2
Р^1 Р^2
PgZl+Pl+«l “у2-= PSZ2 + Р2 + «2 —+ АР> В-15)
где Ар=pg Д/г.
В этом уравнении: pgz— весовое давление; р— ста-
тическое давление; а - ср. —динамическое (скорост-
2
ное) давление (сумма этих трех давлений — полное
давление) и Др — потерянное давление.
В вентиляции принята иная форма уравнения Бер-
нулли. Приведем ниже ее вывод.
Для окружающей струйку неподвижной среды
о —0 и Др=0, а потому из уравнения (1.15) следует
Pog?i + Poi — Pogz2 + р02,
где индекс «о» означает, что эти величины относятся к
окружающей среде. Вычитая из уравнения (1.15) по-
следнее уравнение, получаем
(Р — Ро) gZl + (Pl — Pol) + «1 —= (Р — Ро) £22 +
Рр2со
+ (Р2 —РО2) +“2—^-4- ДР- (I-16)
Обычно струйка распространяется в среде одинако-
вых с ней физических характеристик и потому р=р0-
Введя понятие избыточные давления pi—Ро1=Р1изб
и рг — рО2=Р2изб, окончательно можем написать
, P^lcp Рр2ср
Ргизб + “1 2 —Ргизб 4" а2 g 4" Др- (I.’»)
Следует отметить, что под избыточным давлением
здесь понимается избыток над тем давлением окружа-
ющей среды, которое наблюдается вокруг струйки в
рассматриваемом сечеиии.
13
Необходимо оговорить, что под Др следует понимать
не только потери давления на трение, но вообще удель-
ные (приходящиеся на единицу объемного расхода)
потери механической энергии, затрачиваемые на лю-
бую работу (например, на вращение колеса турбины,
установленной между сечениями 1—1 и 2—2). Если же
между сечениями установлены насос, вентилятор или
Другая аналогичная машина, то под Др следует пони-
мать поступление удельной механической энергии от
насоса, вентилятора и др. При этом перед Др
* знак минус.
следует
изменить знак плюс на
Коэффициент
а _ (^3)ср _
v3 k3 F
vp UC
1
о
где v-v/Voc ndf=d[IF.
Коэффициент
сс> 1.
t
v3df,
(1.18)
(1.19)
Коэффициент a=l при равномерном поле скоро-
стей в поперечном сечении.
Пример 1.2. Определить давление, развиваемое вентилятором,
если потерн давления во всасывающей сети Дрвс, а в нагнетатель-
ной — Дрпг. Скорость на выходе из вентиляционной сети равна V.
Решение. Сечение 1—1 проведем вблизи входа в сеть, а
сечение 2—2 — на выходе из нее.
Вблизи входа в сеть скорость очень мала, так как всасывающие
факелы быстро затухают, и потому в сечении I—1 р1Изб=0 и щор =
= 0.
Из нагнетательной сети вытекает струя. По данным опыта дав-
ление в ией равно давлению окружающего воздуха, а потому
р2изб = 0. В таком случае, согласно уравнению (1.17), можем напи-
сать
pt'2
0 = a — J- ДрВс + Дрнг — ^Рв •
Отсюда
pt'2
Дрв = Дрв0 + Дрнг+a -у .
§ 4. Уравнение количества движения
Выделим в потоке жидкости или газа струйку. Про-
ведем в ней два сечения 1—1 и 2—2 и рассмотрим
объем струйки, находящейся между этими сечениями
(рис. 1.4).
16
Пусть этот объем за время А/ переместится в новое
положение, ограниченное сечениями Г—Г, 2'—2'. При-
меним к выделенному объему уравнение импульса сил
в таком же виде, как оно формулируется в механике
твердого тела: импульс результирующей силы равен
геометрической разности количеств движения.
Обозначив результирующую всех сил, приложенных
к рассматриваемому объему, через R , а количество
движения через К, можем написать векторное урав-
нение
~ Kv ^2' — ^12’
где Кл,2 и Ki>,2' — соответственно количество движения в объемах
на участках 1, 2 и 1', 2’.
При установившемся движении количество движе-
ния в объеме на участке Г2 во времени постоянно, и
потому справедливо
7?Д/ = K-2t2' — Kjjr.
Количество движения в объеме на участке 2, 2'
^2,2' “ ^^2,2' и2-
Количество движения в объеме на участке /, Г
Подставляя эти количества движения в уравнение
импульса сил, получим следующее уравнение количест-
ва движения:
RM = ИМ2 2 v2 — AAfjj, oj.
В этом уравнении в левой
части содержится геометриче-
ская сумма сил, а в правой —
геометрическая разность ко-
личеств движения, что затруд-
няет пользование им. Во избе-
жание этого проектируем все
силы и все скорости, входящие
в последнее уравнение, на
прямую п—п.
Обозначив проекцию ре-
зультирующей силы через Rn,
а проекцию скорости движения
Рис. 1.4. Струйка с векто-
рами скорости в сеченяях
и углами наклона их к ли-
нии п—п
2-741
17
воздуха через v cos 0 (0 — угол между линией п—п и
направлением скорости), будем иметь
Rn At — АМ2 2, v cos 02 — AAlj r t>1 cos 01.
Подставляя в это выражение AM2,2' = pfи
АМщ^р^щД/ и сокращая на А/, получим уравнение
количества движения
₽n = f>2 F2 t>2 cos 02 — Pi Fi »i cos 0P (1.20)
Если скорости в каждом поперечном сечении струй-
ки не одинаковы, то, разделив ее на элементарные
струйки, можно применить к каждой из них уравнение
количества движения (1.20):
dRn = р2 «гcos df? — Pi cos •
Проинтегрировав это уравнение (полагая, что в
каждом сечении р и 0 неизменны), получим
Rn ~ Р2 cos 62 Г dh — Pi cos 01 f tli d/i.
F F
Применяя теорему о среднем, будем иметь
Rn = P2F2(V2) ср COS 02 —Pl Fi (t>f)cpCOS0j.
Заменим здесь среднюю величину квадрата скоро-
сти на квадрат средней (по площади) скорости:
Иср=₽*2ср.
где Р — коэффициент Буссинеска.
Тогда окончательно получим уравнение количества
движения:
Rn = ₽2 р2 F2 v2ep cos 02 ~ ₽1 Pl Л "icp COS 01- 0 -21)
Коэффициент
(о2)ср 1
4 “
1
(1.22)

о
где о = ц/уос и df~df!F,
Коэффициент
(1.23)
здесь р—1 при равномерном поле скоростей.
18
Коэффициенты аир связаны следующим равенст-
вом
а = 3(3 —2. (1.24)
Пример 1.3. Определить тягу винта осевого вентилятора, уста-
новленною в воздуховоде круглого сечения диаметром d=2 м.
Избыточное статическое давление перед вентилятором Др1 =
= —100 Па, а за вентилятором Ap2 = +300 Па
Решение. Проведя сечения 1—1 и 2—2 и выделив между
ними объем, составим уравнение количества движения (1.21) в про-
екциях на продольную ось воздуховода.
При составлении этого уравнения будем полагать, что (31 =
= ₽2', Pi = Рг и П1ср = ^2ср, а сила трения о стеики воздуховода мала
и ею можно пренебречь. В таком случае уравнение количества дви-
жения будет следующим:
nd2 , nd2
&Pi — — Др2 + R = 0,
где R — результирующая сила давления винта на воздух, равная
численно тяге виита (тяга винта направлена в противоположную
сторону).
Отсюда
nd2 3 14<22
2? = (Др2 — Дрх) — - (300 + 100) -----= 1256 Па.
4 4
§ 5. Уравнение неразрывности
Рассмотрим в жидкости или газе некоторый объем
АН7, имеющий массу ДМ. Согласно основному закону
физики — закону сохранения вещества — масса этого
объема не будет изменяться с течением времени t, т. е.
d(AM)
di
В частном случае, когда плотность постоянна,
^(А1Г) _
di
(1.25)
(1.26)
Из равенства (1.26) следует, что объем жидкости
при всевозможных деформациях, сопровождающих ее
движение, остается неизменным, т. е. остается запол-
ненным сплошь, без образования пустот и разрывов
между отдельными ее частицами. Отсюда и происходит
название — уравнение неразрывности.
Выделим в движущейся среде некоторую точку А с
координатами х, у из. Пусть в этой точке проекции
скорости равны vx, vy и vz. Затем около точки А постро-
им весьма малый объем AW7. С этой целью дадим коор-
2*
19
динатам точки А элементарные приращения Ах, Ау и Аг.
Проводя затем через крайние точки этих отрезков коор-
динатные плоскости, выделим элементарный объем в ви-
де прямоугольного параллелепипеда (рис. 1.5).
Учитывая, что в разных точках параллелепипеда име-
ются различные скорости, примем, что скорость в конце
ребра длиной Ах будет равна иЛ+Аих, в конце ребра
длиной Ау— VyA-Avy и в конце ребра длиной
Аг—v?A~ Avz.
Вследствие различных скоростей в начале и конце
каждого упомянутого ребра последние за промежуток
времени dt получат приращения, а именно: ребро дли-
ной Ах превратится в ребро длиной Ax-\-Avxdt, ребро
длиной Ау — в ребро длиной AyA-Avvdt и ребро длиной
Аг — в ребро длиной Az-\-Avzdt.
Ввиду весьма малого объема параллелепипеда мож-
но принять, что во всех точках каждой грани нормаль-
ная к ней проекция скорости одинакова. Поэтому при-
ращение объема параллелепипеда за тот же промежу-
ток времени dt составит
d (All7) = (Дх + twx dt) (\у + Дау dt) (Дг + Дгк dt) — \х \у Дг.
Рис. 1 5. Элементарный параллелепипед с различными скоростями
на гранях
20
Произведя преобразования и пренебрегая бесконеч-
но малыми величинами высших порядков, получим
d (AF) — Дух Ay &zdt 4- \vy Av txzdt + Дуг Дх Дг/ d/.
Разделив обе части этого равенства на AxAyAzdt, а за-
тем стягивая выделенный объем к точке А, в пределе
получим уравнение неразрывности в следующем виде:
. дУу , дУг
дх ду дг
Пример 1.4. Проверить, может ли существовать движение при
р = const, заданное следующими проекциями скорости:
ц* = 6 (х 4-г/)2; vy = 2y-j-z- о2 = х+у + 4г.
Решение. Составляем уравнение неразрывности (1.27)!
^Л+^.,+1+4.,„0.
дх ду дг
(1.27)
Как видим, оно не равно нулю. Таким образом, условие нераз-
рывности не соблюдается. Следовательно, в каждой точке такого
потока имеется разрыв течения, поэтому такого движения быть не
может.
Необходимо отметить, что если бы в выражении проекции ско-
рости на ось абсцисс перед скобкой стоял знак минус, а остальные
выражения проекции скорости были прежними, то такое течение
было бы возможно.
§ 6. Уравнения движения
Предположим, что на какое-либо тело с массой ДМ
оказывает воздействие сила R, вызывающая ускорение
тела а. В таком случае, как известно из механики, бу-
дет справедливо равенство
R — АМа.
Если заменить силу и ускорение их проекциями на
оси координат, то последнее равенство можно предста-
вить в виде следующих трех равенств:
7?х = ДЛ4ах; Ry = &Мау-, Rz — ^Maz.
Эти равенства в аэродинамике могут быть представ-
лены в более явной форме.
С этой целью в пространстве с движущимся возду-
хом отметим точку А, в которой давление равно р, а
проекции скорости vx, vy и vz. После этого выделим
около точки А весьма малый параллелепипед с ребрами
21
Ax, Ay и Аг (рис. 1.6). На его противоположных гра-
нях будут следующие давления: р и n-f- — Дх;
<3х
Р и р+ ~~ Ау, р и р+ ~~Az.
оу дг
Примем, что проекции ускорения массовых сил па-
раллелепипеда равны X, Y и Z.
Рассмотрим теперь одно из трех исходных уравне-
ний, составленное из проекций величин на ось абсцисс.
Проекция силы Rx равна сумме поверхностных сил
Rx пов и объемных РЖоб
Рх ~ Рх пов Рх об •
Проекция поверхностных сил слагается из нормаль-
ных и касательных сил. В целях облегчения вывода
уравнения движения касательные силы пока не будем
учитывать. Тогда проекция поверхностных сил будет
равна разности сил, действующих на противоположные
грани параллелепипеда, перпендикулярные оси х. Сле-
довательно, можно написать
Rx пов = Р^уХг — (p-f~ ~~~ Дх 'l Ди Да = — — Дх Дг/ Дг.
\ дх / дх
Проекция объемных сил будет равна:
Rx об = &МХ.
Проекцию же ускорения можно представить в виде
Рис. 1 6. Элементарный параллелепипед с различными давлениями
иа гранях
22
Поэтому уравнение, составленное из проекций вели-
чин на ось абсцисс, запишется следующим образом:
др dvx
— AxAy\z + ДЛ« — ДМ — .
дх dt
Разделим все члены последнего равенства на массу
параллелепипеда ДЛ1 = рДхДy\z. В пределе, когда Дх,
Ду и Дг одновременно стремятся к нулю, т. е. паралле-
лепипед стягивается в точку А, получим уравнение дви-
жения, относящееся только к упомянутой точке:
Y _ 1 др ~ dvx
р дх dt '
По аналогии напишем два других уравнения движе-
ния, содержащие проекции величин на другие оси ко-
ординат:
„ 1 др dvy 1 др dvz
р ду dt р dz dt
Входящие в уравнения проекции скорости при уста-
новившемся движении являются только функциями ко-
ординат пространства, а потому справедливо равенство:
dv dv dx dv dy dv dz dv dv dv
'17—T~~7rJr—-7~+~~ = vx—~+vy— + vz-—.
dt dx dt dy dt дг dt dx dy dz
В таком случае уравнения движения (без учета в
них сил вязкости) окончательно запишутся в следующем
виде:
Z-----
1 dp dvx dvx dvx
x---------Г" = v* "Z—• vy —г ;
p dx dx y dy dz
1 dp dvy dvy dvy
Y---------= vx —- + vu —— + v, —— ;
p dy dx ydy dz
1 dp dvz dvz dvz
p dz dx y dy dz
(1.28)
Эти три уравнения носят название уравнений движе-
ния Эйлера. В уравнениях отражена связь, которая су-
ществует между проекциями ускорения объемных сил,
плотностью, давлением и проекциями скорости в какой-
либо точке потока.
При учете сил вязкости уравнения движения прини-
мают более сложную форму:
23
v 1 dp _i_д2{>х _i_ д^х
p dx \ dx2 dy2 dz2 )
dvx dvx dvx
= vx —---F vy ~ + vz ;
дх u dy dz
Y 1 Др _i_ v (d'vv -L д2иУ . dh'y
p dy \dx2 dy2 dz2 /
dvu dVu , dvu
*=vx—-+vy—- + v2—^-;
dx dy dz
7 1 dp _i_ (d2vz ,d2vz d2vz\
p dz \ dx2 dy2 dz2 J
dvz , dvz , dvz
= vx ——F vy ——F vz —— ,
dx dy dz
(1.29)
dvz
~ду
где v — кинематический коэффициент вязкости.
Эти три уравнения носят название уравнений движе-
ния Навье—Стокса.
Пример 1.5. Определить, как изменяется давление воздуха по
высоте комнаты, если воздух находится в состоянии покоя.
Решение. Для этого случая в уравнениях Эйлера (1.28) на-
до положить, что проекции скорости воздуха
= Vy = vz = 0.
Тогда упомянутая система уравнений принимает следующий
вид:
= у_А5р=0. z_A> = 0.
р дх р dy р дг
Эти три уравнения носят название уравнений равновесия, так
как ими определяются условия покоя.
Ориентировав оси координат в пространстве так, чтобы поло-
жительная ось г была направлена навстречу силе тяжести, будем
иметь:
X = 0; У = 0 и Z = —g.
В результате ранее написанные уравнения равновесия примут внд:
Умножив первое уравнение на dx, второе — на dy, и третье —
па dz, а после этого порознь сложив их левые н правые части, по-
лучим
dp = — pgdz.
Интегрируя это уравнение и принимая во внимание, что плот-
ность воздуха является неизменной, будем иметь
Р + Рё2 ~ с ~ const.
24
Произвольная постоянная интегрирования определяется из
граничного условия, например состоящего в том, что на уровне пола
комнаты (г = 0) давление р—ра. В этом случае с=ро, н потому
справедлива следующая формула:
Р = —P£Z.
Отсюда следует, что давление воздуха в комнате уменьшается
по мере удаления от пола вверх.
ГЛАВА 2
ОСНОВЫ КИНЕМАТИКИ
§ 7. Траектории частиц, линии тока
и линии отмеченных частиц
Для геометрического изображения потока можно
воспользоваться понятием траектории частицы. Как из-
вестно, траектория — это путь движущейся частицы. Из
определения следует, что траектория фиксирует измене-
ние положения частицы с течением времени.
Выведем уравнение траектории частицы. Если части-
ца за бесконечно малый промежуток времени dt прошла
путь ds, то скорость ее движения составит
Проекции этой скорости на прямоугольные оси ко-
ординат
dx dy dz
vx = ~ ; vu = — ; v, — — ,
dt ’ y dt dt
где dx, dy n dz — проекции пути ds на оси координат.
Из этих трех равенств следует:
dx a, dy dz
--= dt; — = di; ---------- dt.
Vx Vy vz
Поскольку левые части последних равенств равны одной
и той же величине, их можно приравнять между собой.
Осуществив это, получим дифференциальное уравнение
траектории частиц
25
В ряде случаев оказывается удобнее пользоваться
понятием линии тока. Представим себе поле скоростей
в потоке, соответствующее какому-либо времени to.
Выделим произвольную точку Дь в которой скорость
равна щ (рис. 2.1). Вблизи от точки А[ на направлении
вектора vt выделим точку Л2 со скоростью v2, затем точ-
ки А3, Д4 и т. д. и, соединив их последовательно отрез-
ками прямых, получим ломаную линию.
Если все прямые этой ломаной линии одновременно
уменьшить до нуля, то в пределе получим линию, в
каждой точке которой вектор скорости будет располо-
жен по касательной. Эта линия явится огибающей
всех векторов скорости и будет называться лини-
ей тока.
Итак, линия тока представляет собой огибающую
векторов скорости в различных точках потока, взятых
в единый для всех точек момент времени.
Очевидно, через каждую точку потока можно прове-
сти линию тока. Ряд линий тока даст картину движения
жидкости в данный момент времени — фотографический
снимок направлений скоростей в потоке.
Основное отличие траектории частицы от линии тока
состоит в следующем.
Если траектория фиксирует положение во времени
одной только частицы, то линия тока в один и тот же
момент времени указывает направление скоростей мно-
гих частиц. Необходимо отметить, что при установив-
шемся движении траектории частиц и линии тока сов-
падают.
Наряду с траекторией частицы и линией тока в аэ-
родинамике пользуются понятием линии отмеченных
частиц. Это линия, на которой находятся все частицы,
прошедшие через одну какую-либо точку в пространстве.
Линию отмеченных ча-
стиц можно получить, ес-
ли в поток жидкости или
газа поместить трубку и
вводить через нее краску.
Каждая частица, проходя
около отверстия трубки,
будет окрашиваться. В
результате получится ли-
ния окрашенных или от-
меченных частиц.
В случае установившегося движения линия отмечен-
ных частиц будет совпадать с траекторией частиц, а
также и с линией тока.
§ 8. Скорости деформации
и угловые скорости
вращения частиц
Отнесем движущуюся среду к системе прямоуголь-
ных координат и выделим в потоке частицу в виде пря-
моугольного параллелепипеда с длиной ребер Дх, ДуиДх.
Ребра длиной Дх параллельны оси х, ребра длиной
Ду— оси у, а ребра длиной Дг — оси г.
По истечении некоторого времени этот прямоуголь-
ный параллелепипед переместится в новое положение,
При этом вследствие различных скоростей точек парал-
лелепипед может деформироваться и вращаться.
Рассмотрим сначала деформацию параллелепипеда.
Различают деформацию линейную и угловую.
Для выявления линейной деформации исследуем по-
ведение ребра параллелепипеда длиной Дх. Пусть ско-
рость в начале этого ребра будет равна vx, а в его кон-
це— уж+Ауж. Поскольку скорость движения в конце
ребра другая, чем в его начале, ребро будет вытягивать-
ся или сжиматься.
В качестве скорости линейной деформации ребра,
казалось бы, можно было принять величину Диж. Одна-
ко эта величина не может характеризовать скорость
линейной деформации ребра, так как зависит от длины
ребра Дх.
Поэтому для возможности сравнения линейной де-
формации у разных ребер следует ввести понятие ско-
рости линейной деформации, равной отношению вели-
чины Дух к длине ребра Дх, т. е. ДуДДх. Последняя ве-
личина будет характеризовать среднюю скорость
линейной деформации на участке длиной Дх.
Если требуется установить скорость линейной дефор-
мации в точке, то параллелепипед, очевидно, следует
сжать к этой точке. В этом случае
&>х dvx
дж->о Дх дх
Частная производная написана здесь потому, что про-
екция скорости на ось абсцисс есть функция всех трех
координат и времени.
27
Рассматривая линейную деформацию ребер длиной
Дг/ и Дг, получим аналогичные выражения для скорости
линейной деформации:
дни cvz
—— и-----.
ду дг
Обозначая каждую из полученных частных произ-
водных через i с соответствующим индексом х, у или г,
можем написать
^Vy
х дх ’ ty ду ’ 1г дг
(2.2)
Каждая из этих величин является скоростью линей-
ной деформации вдоль соответствующей оси координат.
Исследуем теперь деформацию углов грани паралле-
лепипеда, образованной ребрами длиной Дг/ и Дг. Пусть
в начале ребра длиной Дг/ проекция скорости на ось г
равна иг, а в конце его — иг4-ДУг- В начале ребра дли-
ной Дг проекция скорости на ось у равна vy, а в конце —
Цу+Дщ, (рис. 2.2). Очевидно, угловая скорость враще-
ния ребра Дг/ составит \vzf\y, а ребра Лг—
Средняя скорость угловой деформации рассматрива-
емой грани могла бы быть охарактеризована суммой
'названных угловых скоростей. Однако в аэродинамике
среднюю скорость угловой деформации принято характе-
ризовать полусуммой угловых скоростей. В таком слу-
чае средняя скорость угловой деформации рассматри-
ваемой грани будет равна
1 / Дег Avy \
—------------- .
2 \ Д(/ Дг /
Рис. 2.2. Деформация грани парал-
лелепипеда с ребрами Дг/ и Дг
Если мы хотим уста-
новить скорость угловой
деформации в точке, то,
очевидно, параллелепипед
следует стянуть к одной
точке.
Тогда
1 Г,- , .. Ао,/
—- lim ------f- lim —
2 ay дг->о az .
____1 / dvz \
2 \ ду дг / ‘
28
Рассматривая скорости угловых деформаций других
граней, образованных ребрами Дх и Дг, а также ребра*
ми Дх и Дг/, получим аналогичные выражения.
Обозначая каждую полусумму частных производных
через е с соответствующими индексами х, у и г, получим
____1_ / дуг । дуу \ ___1_ tdv* . dvz\ .
“ 2 \ ду дг ] ’ 2 \ дг + дх J ’
1 (дУу Лд\
ег = — —— + — |.
1 \дх ду]
(2.3)
Каждая из этих величин является скоростью угловой
деформации в плоскости, перпендикулярной той или
иной оси координат. Индексы при букве е не следует
понимать как проекции. На самом деле они указывают
направление перпендикуляра к площадке, которая де*
формируется.
Рассмотрим теперь вращение частиц. С этой целью
снова рассмотрим грань параллелепипеда, образован-
ную ребрами Дг/ и Дг (см. рис. 2.2).
Как было установлено ранее, угловая скорость вра-
щения ребра Дг/ равна kvz]b.y, а ребра г — &vy]\z.
Если условиться, что угловые скорости вращения по-
ложительны при вращении от оси х к оси г/, от оси у к
оси г и от оси г к оси х, то средняя угловая скорость
вращения грани может характеризоваться средним
арифметическим из соответствующих угловых скоростей
1 /ДУ, ДУц \ г,
вращения ребер — —--------- . Для средних угловых
2 \Ду Дг )
скоростей вращения других граней параллелепипеда
получим аналогичные выражения.
Переходя к точке и обозначая среднюю арифмети-
ческую величину угловых скоростей вращения через <о с
соответствующими индексами х, у и г, будем иметь про-
екции угловых скоростей вращения:
1 / диг dvy \ 1 fdvx дуг \ _
2 \ ду дг ] ’ у 2 (дг дх ] ’
1 [ dVy dvx\
~~ ~~ "л ' I ~ I •
2 \ дх ду]
(2.4)
Коэффициент V2 принят для того, чтобы данные фор-
мулы аэродинамики не противоречили соответствующим
формулам механики твердого тела. В самом деле, если
29
бы рассматриваемая грань не деформировалась, то
8х=0 и, следовательно,
дУу диг
dz ду
Подставляя это выражение в первую формулу (2.4),
имеем обычную формулу для угловой скорости враще-
ния твердого тела
dvz
а, —-----.
ду
Пример 2.1. Выяснить, сопровождается ли турбулентное тече-
ние внутри прямой трубы деформацией и вращением частиц, если
изменение скорости в поперечном сечении трубы подчиняется за-
кону
где v — скорость воздуха в точке, удаленной на расстояние г от оси
трубы; R — внутренний радиус трубы.
Решение. Ориентируем прямоугольные оси координат в
пространстве таким образом, чтобы ось абсцисс совпадала с осью
трубы. Тогда расстояние от оси трубы до рассматриваемой точки
можно определить по равенству
г = V У* + z2 ,
а проекции скорости будут равны:
(, Vp2+z2 YA
VX — VOC I 1 D /5
\ A /
n^ = 0; Vz — 0.
В таком случае частные производные от проекций скорости на
осн равны нулю, за исключением
dvx _____1 Пос У Л___L't’7’.
ду 7 R г \ R }
dvx =_____!_ 2L А _
dz ~ 7 R г \ R }
Следовательно, угловые скорости деформации и вращения ча-
стиц будут иметь вид:
1 ^ос У I. г
ez —----------------1---------;
г 14 R г k R!
36
1
<вл = 0; <»«/ = - —
Voc ?
R r
___£oc _У_ Л _ r
14 R r \ Я /
Таким образом, турбулентное движение воздуха в трубе проис-
ходит с деформацией и вращением частиц.
§ 9. Простейшие течения
Однородный поступательный поток. Имеется без-
граничный поток, все частицы которого движутся пря-
молинейно и параллельно друг другу (рис. 2.3). Опре-
делим скорость как функцию координат точки.
Ориентировав оси координат таким образом, чтобы
направление положительной оси абсцисс совпало с на-
правлением движения, получим проекции скорости:
vx = const; Vy — 0; v2 = 0.
Проекция скорости на ось абсцисс постоянна, так
как если бы она была переменна, то, согласно уравне-
нию расхода, траектории частиц не были бы параллель-
ны. Поэтому
v — const. (2.5)
Следовательно, скорость не зависит от координат
точки. Заметим, что в таком потоке не будет деформа-
ции и вращения частиц. В самом деле, любая производ-
ная от постоянной скорости равна нулю, поэтому ско-
рости деформации и вращения частиц также будут
равны нулю.
Пространственный источник — точка. Жидкость или
газ нагнетается по очень тонкой трубке в пустотелый
шарик. На поверхности шарика равномерно расположе-
но много мелких отверстий. Через эти отверстия жид-
кость или газ вытекает из шарика и распространяется
во все стороны равномерно и прямолинейно. Объемный
расход равен L.
Если допустить, что трубка шарика становится бес-
конечно тонкой, радиус шарика бесконечно малым, а
число отверстий бесконечно большим, то в пределе по-
лучим пространственное истечение воздуха из точки.
Такое нереальное течение называется пространствен-
ным течением из источника — точки (рис. 2.4).
31
У
Рис. 2 4 Пространствен-
ный источник — точка
Рис. 2.3. Одонородный
поступательный поток
Рис 2 5. Плоский источ
ник — точка
В аэродинамике при реше-
нии практических задач реаль-
ные течения весьма часто за-
меняют течением из совокуп-
ности таких источников — то-
чек.
Выясним, как изменяется
скорость с удалением от ис-
точника — точки. Приняв за начало прямоугольных ко-
ординат источник — точку, опишем сферу радиусом г.
По условию задачи все частицы, расположенные на
сфере, обладают одинаковыми скоростями, направлен-
ными перпендикулярно поверхности сферы. Применяя
уравнение расхода (1.3) к источнику — точке и сфере,
можно написать
L = 4лг2 V.
Отсюда скорость в любой точке, удаленной от нача-
ла координат на расстояние г, равна:
о = Д/4лг3. (2.6)
Таким образом, скорость обратно пропорциональна
квадрату расстояния любой точки от пространственного
источника — точки.
Определим проекции скорости на осп координат.
С этой целью воспользуемся равенствами
= v cos бх; vy == v cos 0у; vz = vcos0z,
где fir, 0а и Qz— углы между скоростью v и осями координат. ,
В этих равенствах:
Проекции скорости на оси координат будут равны;
L х L у
4л (^+i/« + ?)3/2 : = 4л (/+^+^3 1
L г
Vt~ 4л •
Нетрудно убедиться, что в этом потоке деформация
имеется, а вращения частиц не происходит.
Плоский источник — точка. Жидкость пли газ на-
гнетается в бесконечно длинную тонкую трубку. По всей
боковой поверхности равномерно расположено много
мелких отверстий. Через эти отверстия жидкость или
газ вытекает из трубки и распространяется равномерно
и прямолинейно во все стороны.
Если предположить, что трубка стала бесконечно
тонкой, а число отверстий в трубке стало бесконечно
большим, то в пределе получим пространственное исте-
чение воздуха из прямой, причем течение в любой плос-
кости, перпендикулярной этой прямой, будет одинако-
вым, Такие течения в аэродинамике получили название
плоских течений.
Будем рассматривать течение в одной какой-либо
плоскости. Это новое нереальное течение называется
плоским течением из источника — точки (рис. 2.5). При
решении задач аэродинамики реальные течения также
часто подменяют течением из группы таких источни-
ков — точек.
Выясним, как изменяется скорость с удалением
частицы воздуха от плоского источника — точки. Прове-
дем вокруг него окружность радиусом г. По условию
задачи все частицы, расположенные на окружности,
обладают одинаковыми скоростями, направленными
перпендикулярно окружности. Применяя уравнение рас-
хода (1.3) к источнику — точке и к окружности, можем
написать
L = 2лго,
где L — расход воздуха в плоском источнике — точке.
Отсюда скорость в какой-либо точке, находящейся
на расстоянии г от плоского источника — точки, равна:
п = Т/2лг. (2.7)
Таким образом, скорость обратно пропорциональна
расстоянию любой точки от плоского источника — точки.
3-741
33
Найдем проекции скорости. Для этого ориентируем
оси координат так, чтобы ось z совпала с осью плоского
источника — точки, тогда будут справедливы следующие
равенства:
vx = v cos 0;{; vy = v cos Qy,
где cos 0x = x/r; cos Qy = ylr и r= У хг + у2.
В таком случае проекции скорости окажутся рав-
ними
L х L у
v*= ~2л х2Н-г/2 ’ Vy ~2л х2 Дг/2’
Нетрудно убедиться, что это течение также происхо-
дит с деформацией, но без вращения частиц.
ГЛАВА 3
ИНТЕГРИРОВАНИЕ УРАВНЕНИИ АЭРОДИНАМИКИ
§10 . Потенциал скорости
Для определения поля скоростей применяют следу-
ющие функции течения, потенциал скорости, функцию
тока и комплексный потенциал.
Выясним, что представляет собой потенциал скоро-
сти. При пространственном движении без вращения ча-
стиц проекции угловых скоростей вращения равны
нулю:
ых = == и2 = 0,
В таком случае, как это следует из формул угловых
скоростей вращения частиц (2.4), будут справедливы
равенства
dvz со у дих _ дуг дУу дох
ду дг ’ дг дх ’ дх ду
Как известно из математики, наличие таких равенств
является условием того, что выражение vxdx-\-vydy-\-
-\-vzdz есть полный дифференциал некоторой функции.
Если мы обозначим эту функцию через q>=<p(x, у, z),
то
4ф = vxdx-(- vvdy + vzdz. (3.1)
Вместе с тем полный дифференциал можно выразить
через частные производные следующим образом:
34
дф , , dtp , д<р
dp — —— dx + — dy + dz.
дх ду dz
Сопоставляя в последних двух равенствах правые их
части, обнаруживаем зависимости:
др дф
у ду дг
что полная производная функ-
линии тока даст скорость воздуч
д<р
vx~ ——;
ox
(3.2)
Нетрудно показать,
ция <р по направлению
ха. В самом деле,
dtp <Эф dx , Sep dy dtp dz
~ 7-4- — ~ + ““Г- = охc°sО* + Ogc°s0у +
ds дх ds ду ds дг ds
-}-VZCOS0Z.
Сумма членов правой части последнего равенства
равна скорости воздуха и потому
d<p
ds ~~v‘
(3.3)
Из механики твердого тела известно, что производ-
ная потенциала сил по направлению равна ускорению.
Поэтому по аналогии с потенциалом сил функцию ф на-
звали потенциалом скорости, а движение без вращения
частиц, как имеющее потенциал скорости,— потенциаль-
ным.
Необходимо отметить, что поскольку потенциал ско-
рости является функцией только координат, то в каждой
точке потока он будет иметь вполне определенное значе-
ние. Поверхности, проведенные в среде таким образом,
что все их точки имеют одинаковое значение потенциала
скорости, называются эквипотенциальными поверхно-
стями.
Эквипотенциальные поверхности всегда перпендику-
лярны векторам скорости. Векторы же скорости каса-
тельны к линиям тока, и поэтому эквипотенциальные
поверхности и линии тока будут взаимно перпендику-
лярны.
§11 . Функция тока
Рассмотрим плоское движение, т. е. течение, при ко-
тором среда движется параллельно некоторой плоско-
сти, причем в параллельных ей плоскостях все явления,
3*
35
характеризующие поток, совершенно одинаковы. Оче-
видно, такой поток будет двухмерен, скорость в данной
точке будет функцией только двух ее координат.
Выбрав оси координат таким образом, чтобы ось г
была перпендикулярна параллельным плоскостям, мож-
но уравнение неразрывности записать в виде
dvx dvu
---— +---J- = 0.
дх ду
Отсюда
дУх ди у
дх ду
и потому выражение vxdy—vydx является полным диф-
ференциалом некоторой функции.
Если обозначить эту функцию через ф=ф(х, у), то
будет справедливо равенство
dty = vxdy— Vydx. (3.4)
Вместе с тем полный дифференциал выражается
через частные производные следующим образом:
дф chb
d$ =---di' -U--dy.
дх ду
Сравнивая между собой правые части последних
двух равенств, установим зависимости:
Необходимо отметить, что поскольку ф является
функцией только координат, то в каждой точке потока
она имеет вполне определенное значение. Можно в по-
токе выделить линии, все точки которых имеют одинако-
вые значения этой функции. Уравнением этих линий
явится xp = const, причем для отдельных линий это урав-
нение будет отличаться только значением постоянной.
Исследуем, что представляют собой линии равного
значения функции ф. Для этого воспользуемся уравне-
нием линии тока
dx dy
Vx Vy
Преобразуя его, получим vxdy—vydx=0. Последнее
уравнение является дифференциалом функции ф. Сле-
довательно, для линии тока </ф = 0 или ф = const. Та-
зе
ким образом, линия равного
значения функции ф явля-
ется линией тока. Исходя из
этого функцию ф назвали
функцией тока.
Заметим, что, поскольку
эквипотенциальные линии
перпендикулярны линиям
тока, линии равных значе-
ний функции тока и эквипо-
Рис. 3.1. Элементарная пло-
щадка эквипотенциальной
поверхности с вектором
скорости
тенциальные линии взаимно
перпендикулярны.
Установим физический
смысл функции тока. С этой
целью рассмотрим движе-
ние среды через элементарную площадку ds, происхо-
дящее со скоростью v (рис. 3.1). Очевидно, элементар-
ный расход будет равен: dL—vds.
При этом скорость, выраженная через ее проек-
ции, с учетом отрицательной проекции скорости на ось
ординат составит
V = vx sin © — Vy cos О,
где & — угол наклона площадки ds к оси абсцисс.
Вследствие этого элементарный расход может быть
определен по формуле
dL — vx ds sin О — Vy ds cos
Зная, что справедливы равенства
ds sin О = dy; ds cos © = dx,
получим для элементарного расхода иное уравнение:
dL = vxdy — vu dx —--dy 4----dx = dib,
dy dx
Интегрируя это уравнение, будем иметь ф=£-[-с.
Чтобы в интеграле освободиться от произвольной посто-
янной интегрирования, функцию тока всегда определя-
ют так, чтобы ф = 0 при расходе L=0. В таком случае
с=0, и мы окончательно будем иметь
ф = £. (3.6)
Таким образом, функция тока численно равна расхо-
ду жидкости или газа,
37
§ 12. Комплексный потенциал
Рассмотрим плоское движение без вращения частиц.
Проведем в потоке эквипотенциальные линии (ф=
=const) и линии тока (ip = const). Оба семейства кри-
вых образуют ортогональную сетку. Отнесем поток к
прямоугольным координатам и постараемся уменьшить
число переменных. Объединим для этого потенциал ско-
рости и функцию тока, а также координаты точки со-
ответственно в следующие комплексные величины:
= z — x-^iy, (3.7)
где i= / —1.
Затем будем рассматривать первую величину как
функцию второй величины w = w(z). Функция w назы-
вается комплексным потенциалом, а аргумент z— ком-
плексной координатой точки.
Введение такой зависимости позволяет не только
сократить число функций течения, но и число координат,
т. е. позволяет уменьшить число переменных.
Приведем необходимые сведения о комплексных
числах. Для этого рассмотрим на плоскости г некоторую
точку А с прямоугольными координатами х и у и с по-
лярными координатами гиб. Как известно, полярные и
прямоугольные координаты связаны равенствами х—
—rcosO и у—rsin0.
Используя эти равенства, можно комплексное число
представить в тригонометрической форме:
г= r (cos 0 -f- i sin в). (3.8)
Разложим cos 8 и sin 0 в степенные ряды
03 0* 0в
cos 0=1 —---4-----—-----4-...,
2! 4! 6! 1
0 03 . 05 0’
s>n0 р - 3! 5! ' 7! +--
и составим сумму
<0
cos 0 +1 sin 0 = 1 -j-
02 103 0* <05
1! 2! ~ .3' + 4! + 5!
i0 (t0)2 (t0)3 (i0)4 (if))5
1! + 2! + 3! 4! + 5!
Ряд в правой части равенства представляет собой
разложение основания натуральных логарифмов е, взя-
38
того в степени (б. Таким образом, справедливо равен-
ство
cos 0 + г sin 0 = е • (3-9)
Это известная формула Эйлера, связывающая триго-
нометрические функции с показательной функцией. Ес-
ли воспользоваться этой формулой, то комплексное число
можно представить в показательной форме
г = гЛ (3.10)
где г= уГ х2+г/2 и 0=arctg —. (311)
Определим теперь, чему равна производная от ком-
плексного потенциала по комплексной координате. Если
комплексный потенциал w рассматривать как функцию
от двух переменных х и у, то его дифференциал может
быть найден в виде
, dw , dw / дф , , дф \ / дф , . дф \ ,
tto = —— dx —— dy = (—- 4- i —— рл 4-1 — + * — dy.
dx dy \ dx dx / \ dy dy }
Ранее установленные свойства потенциала скорости
и функции тока, состоящие в том, что частные произ-
водные от этих функций течения по координатам дают
проекции скорости, позволяют написать следующих два
равенства:
(3.12)
д<р дф дф дф
дх ду ' ду дх
Эти равенства в математике носят название условий
Коши — Римана. Они выражают собой необходимое и
достаточное условие существования производной от
комплексной функции по комплексному аргументу.
В этом легко убедиться и в нашем случае. Исполь-
зуя последние два равенства, можем написать
. / 0ф , дф \ / дф , дф \ / дф
dw — I---4- i----j dx 4- —----р I----) dy — I--4-
\ дх дх ] \ дх дх ) \дх
, дф \ / дф дф \
+ i — (rfx 4- idy) = I —- 4- i - dz
dx J \ dx dx I
ИЛИ
dw дф . дф
dz dx dx '
Таково будет выражение для производной от ком-
плексной функции по комплексному аргументу, если
39
соблюдаются условия Коши — Римана. Отметим, чго
функция, удовлетворяющая условиям Коши — Римана,
называется аналитической функцией.
Для комплексного потенциала соблюдаются не
только условия Коши — Римана, но и следующие:
Сф <?ф
дх ~Vx’ дх
Вследствие этого производная от этой функции те-
чения может быть представлена в виде
dw
—^-=vx — ivy. <3.13)
Таким образом, производная от комплексного по-
тенциала по комплексному аргументу равна комплекс-
ной скорости.
В дальнейшем будет показано, как при помощи рас-
смотренных функций течения можно облегчить решение
задач и расширить круг известных течений. Особенно
следует отметить значение комплексного потенциала,
вводя который, при разыскании течений можно пользо-
ваться также методом конформных отображений.
Пример 3.1. Определить функции течения однородного посту-
пательного потока воздуха, параллельного оси абсцисс и направлен-
ного в ту же сторону, что н ее положительная полуось. Скорость
равна Vx.
Решение. Проекция скорости vv=0. Поэтому имеем два
уравнения
Интегрируя эти уравнения, находим для потенциала скорости и
функции тока соответственно следующие выражения:
ф == VxX + Cj и ф = vx у + с2,
где Ci и сз — произвольные постоянные интегрирования.
Выбираем такую систему значений этих функций, при которой
потенциал скорости на оси ординат (х=0) был бы равен нулю
(ф=0) н функция тока на оси абсцисс (г/ = 0) была бы также равна
нулю (ф = 0).
В таком случае обе произвольные постоянные интегрирования
равны нулю, а потому окончательно получим
Ф = xvx и ф = yvx.
Комплексный потенциал будет равен:
w = <р + :ф = vx (х + iy) = гож.
41»
Пример 3.2. Определить функции течения
для потока, рассмотренного в предыдущем
примере, но параллельного оси ординат и на-
правленного в ту же сторону, что и ее поло-
жительная полуось.
Решение. Проекция скорости цх = 0.
Следовательно, будут справедливы уравнения
rf<p drj)
dy u' dx y
Интегрируя эти уравнения и принимая
соответствующую систему значений функций
течения, получим
<р = yvy и ф = — xvy.
Комплексный потенциал будет равен:
Рис. 3.2. Поток
в верхней полупо-
лоске
w = vy (у — tx) = — i (х + iy) vy = — izvy.
Если поток воздуха будет не безграничен, а заключен в верх-
ней полуполоске шириной Ь (рис. 3.2) и его расход будет равен L,
то, очевидно,
L L L
Ч=~ГУ, ф = —— х; ш = — I— г.
ООО
При направлении же скорости и сторону отрицательной оси ор-
динат
L L L
<Р ---—У, Ф = — х; w = t — z,
0 0 о
Пример 3.3. Определить функции течения, уравнение эквипотен-
циальных линий и уравнение линий тока для плоского течения из
источника — точки, расположенного в начале координат.
Решение. Линии тока в этом потоке представляют собой лу-
чи, расходящиеся радиально из начала координат. Известно, что
эквипотенциальные линии перпендикулярны линиям тока. Следова-
тельно, эквипотенциальные линии должны быть окружностями с
Центром в начале координат. Вследствие этого потенциал скорости
следует рассматривать как функцию только одной переменной t,
т. е. расстояния частиц воздуха от полюса (центра) источника, а
функцию тока — как функцию только одной переменной 0 — угла,
заключенного между линией тока н осью абсцисс.
Перейдем теперь к определению потенциала скорости. Исходя
3<р
нз основных свойств этой функции, можно написать — = V,
В этом равенстве частную производную можно заменить полной
dtp
производной — —V. Подставляя сюда [см. формулу (2.7)] t>==)
==L/2nr, будем иметь
L dr
"’’"STT
41
Интегрируя это уравнение, получаем
L
ф = _ lnr_|_Cli
2Л
Произвольную постоянную интегрирования найдем из условия,
что на окружности с радиусом, равным единице (г=1), потенциал
скорости будет равен нулю. Тогда постоянная интегрирования бу-
дет также равна нулю, а потому окончательно получим
Определим теперь функцию тока. Ее частная производная по
координате равна:
Эф Эф/Эу
56 = dQldy '
Но, как известно, справедливы равенства
5ф L
— = vz> vx = vcos9; v = -—;
ду 2лг
х у
cos 0— — и 9 = arctg — ,
Г X
а потому верны и следующие два равенства:
t х да 1 /х х
ду ~2л г2 “ ду 1 +(у/х)2== г2 ’
Пользуясь найденными выражениями для частных производных,
приводим исходное равенство к виду:
г/Ф = да.
Y 2л
Интегрируя его, получаем
L
Ф =— 0-гС3.
2Л
Произвольную постоянную интегрирования найдем из условия,
что на положительной осн абсцисс (9=0) функция тока равна
нулю. Тогда постоянная также будет равна нулю, вследствие чего
функция тока примет следующий вид:
L п L и
ф = — 9 = ~— arctg — .
2л 2л х
Из найденных решений для потенциала скорости и функции то-
ка следует, что эквипотенциальные линии и линии тока опреде-
ляются уравнениями
431 "Г / ф \
х2 + у2 — е L и у = х tg 12л —— к
\ А/ /
где <риф следует рассматривать как параметры.
42
Комплексный потенциал можно найтн на основании следую-
щего равенства:
w = <р + (1р = —- (In г 4- 16) = — In (re10) = — In г.
J L JI J L
Заметим, что если источник — точка будет находиться не в на-
чале координат, а в некоторой точке zo=Xo-H#o> то комплексный
потенциал этого течения будет равен
L
w = — In (a —afl),
ZJX
Необходимо сказать, что для плоского течения нз стока — точ-
ки, т. е. течения, при котором все частицы среды на плоскости дви-
жутся из бесконечности по прямым в одну точку, комплексный потен-
циал имеет такое же аналитическое выражение, как и для плоского
течения из источника — точки. Однако перед величиной расхода L
должен стоять знак минус, так как сток — точка есть источник —
точка с отрицательным расходом.
§ 13. Приемы интегрирования уравнений
неразрывности и движения
Интегрирование системы уравнений неразрывности
и движения в общем виде представляет настолько боль-
шую трудность, что до сих пор эта задача никем не осу-
ществлена.
В настоящее время предложены методы интегриро-
вания системы этих уравнений лишь для отдельных ви-
дов движения и даны решения для отдельных конкрет-
ных течений. Рассмотрим методы интегрирования урав-
нений аэродинамики, соответствующие трем движениям:
пространственному без вращения частиц, плоскому
с вращением частиц и плоскому без вращения частиц.
Вначале рассмотрим пространственное движение без
вращения частиц. Как известно, такое движение имеет
потенциал скорости. Поскольку все проекции скорости
могут быть выражены через потенциал скорости, нет
необходимости интегрировать все четыре уравнения,
а достаточно проинтегрировать только уравнение нераз-
рывности.
В самом деле, уравнение неразрывности при введе-
нии в него потенциала скорости принимает следующий
вид:
<32<р t д2<р
дх2 ду2
д2<р
~ =0.
ог2
(3.14)
43
Это уравнение носит название уравнения Лапласа.
При этом про потенциал скорости говорят, что он удов-
летворяет уравнению Лапласа. Проинтегрировав это
уравнение, мы найдем потенциал скорости q>=q>(x, у, z).
Рассмотрим теперь плоское движение с вращением
частиц. Такое движение имеет, как известно, функцию
тока. Введение функции тока в уравнение неразрывнос-
ти приводит к тождеству:
О2ф б2!))
дх ду ду дх '
так как частные производные не зависят от порядка
дифференцирования.
Вследствие этого при решении задач на плоское дви-
жение с вращением частиц приходится прибегать
к уравнениям движения. Подставив в первые два урав-
нения Навье— Стокса (1.29) величины:
дф дих д2ф дих д2ф
у _----- . ----—---------- ----—--------
ду дх дх ду ду ду2
д2 vx д^ф д2 vx д3ф
дх2 д2х ду ’ ду2 ду3 ’
дф дуу д2ф ди у д2ф
дх ’ дх дх2 ' ду ду дх
д2Уу___д^ф д2уу__________д3ф
дх2 дх3 ’ ду2 дх ду ’
получим
1 др / , д3ф \ _ дф д2ф _
р дх \ д2х ду "И ду3 / ду дх ду
дф д,2ф
~ дх ду2 1
1 др / д2ф д3ф \ дф д2ф
р ду у дх3 дх ду2 / ду дх2
(3.15)
дф д2ф
дх дх ду
Проинтегрировав эти уравнения, находим функцию
тока ф=ф(х, у).
Рассмотрим теперь плоское движение без вращения
частиц. Во-первых, в этом случае интегрирование основ-
ных уравнений аэродинамики может быть проведено
44
й помощи потенциала скорости и теми же приемами,
как при пространственном движении без вращения
частиц. ,
Во-вторых, при решении можно использовать функ-
цию тока. Однако прием решения будет несколько иным,
чем описанный ранее при решении задач на плоское те-
чение с вращением частиц. В данном случае введение
функции тока также обращает уравнение неразрывнос-
ти в тождество, но вместе с тем справедливы равен-
ства:
э2Ф д / эф \ _ д _ д { d<f \ __ э2ф _
дх2 ~ дх \ дх ) дх Vtl дх \ ду ) дхду
Э2ф д I Эф \ д д I Эф \ Э2<р
—— —-------I---- =------(у,.) =--I-----I =------,
ф/2 ду \ ду j ду ду \ дх / дудх
потому
Э2Ф д2ф
дх2 ду2
(3.16)
Таким образом, при отсутствии вращения частиц
функция тока удовлетворяет уравнению Лапласа. Сле-
довательно, для решения задачи достаточно только про-
интегрировать это уравнение, т. е. найти функцию
тока ф.
В-третьих, при решении можно использовать комп-
лексный потенциал. В самом деле, комплексный потен-
циал удовлетворяет уравнению Лапласа, так как спра-
ведлив следующий ряд равенств:
d2w д2ш 32ф . Э2ф д2ф . Э2ф
дх2 + ду2 ~ дх2 +1 дх2 ' ду2 ‘ ду2'
Э2Ф Э2Ф \ . / д2ф Э2ф \ _
дх2 + ду2 /+ Ч дх2 + ду2 J ~
(3.17)
§ 14. Наложение потоков
Для определения скорости в какой-либо точке потока
как функции координат этой точки достаточно проинте-
грировать уравнение неразрывности. К сожалению,
осуществить интегрирование нелегко, причем по мере
45
усложнения течения трудности все более и более увели-
чиваются.
Вследствие сказанного в аэродинамике вместо пря-
мого интегрирования уравнения неразрывности часто
прибегают к иным приемам нахождения интегралов это-
го уравнения. Одним из таких приемов является метод
наложения потоков, сущность которого состоит в следу-
ющем.
Для разыскания неизвестного нам сложного потока
необходимо определить, из каких более простых извест-
ных потоков, одновременно действующих в рассматри-
ваемом пространстве, может быть образован искомый
сложный поток.
При одновременном же действии нескольких потоков
скорости в одной и той же точке, как известно, склады-
ваются по правилу векторов. Следовательно, вектор
скорости в каждой точке неизвестного сложного потока
будет равен векторной сумме скоростей в той же точке
простых потоков. Поэтому можно написать следующее
векторное равенство:
t> = t'1+t'J + t'8+...+»«» (3.18)
где v — вектор скорости искомого сложного потока; щ, из, »з, ....
vn — векторы скорости известных простых потоков.
Сложение векторов скорости по данной формуле про-
водится последовательно по правилу параллелограмма.
Ранее написанное векторное равенство представим
в виде трех равенств, связывающих проекции скорости
на оси координат, а именно:
vx — Vxi + vx2 + Vxb +•. .-f- vxn,
Vy = Vtn + Ощ+Чуз+... + Чуп,
VZ — VZ1 + VZ2 + VZ3 +• • •+ vzn-
(3.19)
Поскольку проекции вектора скорости на одну ка-
кую-либо ось координат имеют одинаковое направление,
то достаточно только выполнять их алгебраическое сло-
жение. Однако такое сложение надо выполнять 3 раза,
соответственно числу осей координат. Это имеет также
известные неудобства.
Нетрудно убедиться, что найденные таким образом
проекции скорости сложного потока действительно явля-
ются интегралами уравнения неразрывности,
46
Предложенный выше общий метод наложения пото-
ков может быть несколько упрощен для движений, обла-
дающих функциями течения. Оказывается, в этих случаях
вместо составления трех сумм проекций скоростей доста-
точно составить сумму функций течения отдельных со-
ставляющих потоков.
При пространственном движении без вращения частиц
оказывается, что потенциал скорости искомого потока
равен алгебраической сумме потенциалов скоростей
составляющих потоков
<р = <pt + %+<Рз+ •.+%.
(3.20)
При плоском движении независимо от наличия или
отсутствия в нем вращения частиц функция тока неиз-
вестного потока равна сумме функций токов составляю-
щих потоков
Ф = & +'рз + + +
(3.21)
При плоском движении без вращения частиц комп-
лексный потенциал неизвестного потока равен сумме
комплексных потенциалов составляющих потоков
W = Wj 4- Шг w3 +. . . + wn
(3.22)
Однако для построения неизвестного потока этих
проекций скорости недостаточно, а необходимо еще знать,
как проходят линии тока. Построение их может быть
проведено по уравнению семейств линии тока, получен-
ному в результате интегрирования дифференциального
уравнения:
dx dy dz
vx vy vz
Однако для частного случая движения, а именно
плоского течения, можно предложить другой, более прос-
той графический способ построения линии тока. Предпо-
ложим, что имеются два потока с построенными семей-
ствами линий тока. Наложим один поток на другой,
точнее наложим семейство линий тока одного потока на
семейство линий тока другого потока (рис. 3.3).
47
Рис. 3 4. Клетка, выделенная из
сетки линий тока
се-
Рис. 3 3. Сетка, образован-
ная наложением двух
мейств линии тока
масштабе векторы
В результате получим сет-
ку, образованную линиями
тока. Пусть стороны клеток
в сетке линии тока будут
изображать в определенном
скорости накладываемых пото-
ков.
Тогда, очевидно, диагональ любой клетки будет
в том же масштабе изображать вектор скорости резуль-
тирующего потока. Таким образом, линии тока сложно-
го течения выявятся в результате последовательного со-
единения точек пересечения линий тока накладываемых
потоков.
Установим, какому условию должна удовлетворять
густота линий тока обоих накладываемых потоков. С этой
целью рассмотрим какую-либо клетку. Обозначим сторо-
ны клетки через A$i и Дз2. Условие, что скорость пропор-
циональна длине стороны клетки, запишем в виде
Р1 = сА$1 и v2—aAs2 (где а — коэффициент пропорцио-
нальности) .
В таком случае справедливо отношение
v1/v2 = Asx/Asa.
При большой густоте линий тока каждая клетка бу-
дет представлять собой почти параллелограмм (рис. 3.4).
Проведя из одной его вершины высоты A/ii и Д/г2, обна-
руживаем, что треугольники (заштрихованные) подобны,
и поэтому можно написать
Д51/Д52 — Д/ц/Д^з-
Сопоставляя последнюю пропорцию с ранее написан-
ной, получим Vi/Xh2=v2^hl или окончательно
Д£1 = Д£а. (3.23)
48
Рис. 3.5. Цепочка плоских источников — точек
Таким образом, при графическом определении линии
тока неизвестного потока необходимо так чертить линии
тока накладываемых друг на друга двух потоков, чтобы
расходы между парой смежных линий тока первого
и второго потоков были одинаковыми.
Пример 3.4. Определить функции течения однородного посту-
пательного потока, направленного под углом к оси абсцисс.
Решение. Такой поток может быть образован в результате
наложения плоского однородного поступательного потока, парал-
лельного оси абсцисс на плоский однородный поступательный по-
ток, параллельный оси ординат. Функции течения обоих этих пото-
ков были найдены в примерах 3.1 и 3 2. Используя эти функции,
можем написать
Ф = <Р1 + Фа = хих + W Ф = '1’1 + Ф2=№— xvy-,
W = U/t W2~— ZVX — iZVy = z(vx — iVy) .
Пример 3.5. Определить комплексный потенциал. Плоские источ-
ники— точки одинакового расхода расположены равномерно на оси
абсцисс. Расстояние между двумя соседними центрами источников
равно Ь (рис. 3 5).
Решение. Комплексный потенциал всех источников — точек
будет равен:
L
w п —— [In а + In (z—b) + In (z+&) + In (z—2b) + In (z~-2&) -f-.. ,j=
= ~ [In Z (2a — o2) (za — 22&2) . . .] =
r f R—cc 1
= —1п г П =
2л I
T f Г k=<X> /
= -^ In ?П 1
2л I L *=1 \
где П — произведение.
za \
kW )
+ In П kW
Л=1
4—741
Отбрасывая несущественную для исследования течения постоян-
ную часть и вводя новую переменною t, связанную с г равенством
z—ibt/n, получим

L
w =-----
2л
In
L
=-------1п
2л
L ( b \
=----- In — sin it .
2л \ л /
Возвращаясь к прежней переменной z и снова отбрасывая по-
стоянное слагаемое, будем иметь
L лг
w —-------In sin----.
2л Ь
ГЛАВА 4
КОНФОРМНЫЕ ОТОБРАЖЕНИЯ ТЕЧЕНИЙ
§ 15. Общие сведения
о конформном отображении
В случае плоского потенциального потока интегралы
уравнения неразрывности можно находить методом
конформных отображений. Но прежде чем перейти к опи-
санию этого метода, ознакомимся вообще с конформным
отображением.
Пусть имеется аналитическая функция M=f(z), где
комплексные переменные a z~x-[-iy. Будем
вычислять и, задаваясь различными значениями г.
Каждую пару значений этих величин фиксируем в виде
точек на плоскостях комплексных переменных г и и. Та-
ким образом, точке на плоскости z будет соответствовать
вполне определенная точка н% плоскости и или, как
говорят, она отобразится с плоскости z на плоскость и.
Проделывая такую операцию по отображению точек,
допустим, что нам удалось все точки некоторой области
на плоскости z перенести в точки другой области на
плоскости и.
Исследуем, что происходит при отображении одной
области в другую. С этой целью выделим в области на
плоскости z некоторую точку А (рис. 4.1,а), которая
в соответствии с функцией f(z) переходит в точку В
области на плоскости и (рис. 4.1,6).
Пусть комплексные координаты точек А и В соответ-
ственно равны: z—x-^-iy и м=£+гг)> что в показательной
форме даст
50
z — Гх е‘91‘, и — г.2 егвг,
г, = У” л'2 4- у2; 9j = arctg —;
где 1 г 1 х
.-------- И
Га = У £2 + Ч2! Оа = arcts ~ •
Рассмотрим производную от функции комплексного
переменного:
du Аи
—— = Нт —— .
dz дг->-о Az
В правой части равенства конечные приращения мо-
гут быть найдены геометрически. Дав координате z при-
ращение Дг, тем самым переместим точку А с координатой
z в точку Ai с координатой гф-Дг. Соответственно (со-
гласно отображению) точка с координатой и перейдет
в точку Bi с координатой «+Ди. При этом точка А1 бу-
дет удалена от точки А на расстояние ДГ1 и прямая AAi
составит с осью абсцисс угол точка Bi будет
удалена от точки В на расстояние Дг2 и прямая ВВ< со-
ставит с осью абсцисс угол бг+ДЭг.
В таком случае конечные приращения можно пред-
ставить в виде комплексных чисел:
Дг = Дг1^<9*+д0>>;
Дц = Дг2
и потому производная будет равна:
= ит ЛИ. е/1Эг-М-Д&-дед e Jd ег(б2-0,)е
dz Дгг dt\
Следовательно, при отображении с одной плоскости
на другую окрестность каждой точки независимо от на-
Рис. 4.1. Конформное отображение отрезка AAi в отрезок BBi
4*
61
правления, во-первых, изменяется в dr^dr^ раз и, во-
вторых, поворачивается на один и тот же угол 02 — 01.
Разумеется, что это сжатие пли растяжение окрестнос-
ти, а также поворот будут различными для разных то-
чек области течения._______________________________
Гаким образом,“ОТОоражение при помощи аналити-
тгеский функции сохраняет подооие форм в бесконечно
1^ТШ^е^Нта~5!.7ГГреобразованиё~такбти рида иблдсТби
с кШТстантными формами в бесконечно малых элемен-
тах называется конформным отображением.
Перейдем теперь к рассмотрению методов конформ-
ных отображений, применяемых в аэродинамике.
§ 16. Конформное отображение безотрывного течения
Предположим, что нам необходимо разыскать ком-
плексный потенциал w=F(z) некоторой области тече-
ния на плоскости комплексного переменного z—x-^-iy.
Для решения этой задачи рассмотрим какую-либо
новую область течения на плоскости другого комплексно-
го переменного и=£4-1т] с известным нам комплексным
потенциалом w=F(u). Затем найдем отображающую
функцию, т. е. аналитическую функцию, которая отобра-
зит все точки области течения на плоскости z в точки
области течения на плоскости и. Эту функцию обычно
находят, пользуясь известными в математике формула-
ми конформных отображений или устанавливая новые
формулы. При этом для определения вида формулы ис-
пользуют граничные условия течения. Допустим, что та-
кая функция найдена в виде
« = /(2). >
Тогда, поставив ее в выражение известного комп-
лексного потенциала, получим
= (г)].
Найденная таким образом функция и явится разыс-
киваемым комплексным потенциалом. Метод, которым
эта функция была найдена, называется методом кон-
формных отображений.
В зависимости от выбранной области течения с из-
вестным комплексным потенциалом, точнее в зависимос-
ти от ее формы, различают конформное отображение
разыскиваемого течения на полуполоску, верхнюю полу-
плоскость и т. д.
52
Если известен комплексный потенциал разыскиваемо'
го течения, то не представляет труда определить проек-
ции скорости. Как известно, они находятся по формуле
йш
' Кроме описанного метода конформного отображения,
в аэродинамике приняты и другие методы, в частности
метод, при котором связь между областями течения на
плоскостях «иг устанавливается в виде функции г==
==f(w). В таком случае полученное решение для комп-
лексного потенциала будет задано в параметрическом
виде от и, т. е. двумя функциями:
w — F (и) и г ~ f (и).
Известен метод годографа, при котором связь уста-
навливается между скоростью на плоскости z и комп-
лексным потенциалом течения на плоскости и. Эта связь
во многих случаях очень проста, однако для ее установ-
ления необходимо располагать сведениями о характере
скоростного поля на плоскости г.
§ 17. Конформное отображение течения
с отрывом струй
При конформных отображениях течений с отрывом
струй обычно принимается упрощенная схема течения,
предложенная Гельмгольцем и Кирхгофом. Эта более
простая схема соответствует течению воздуха (без учета
вязкости) и кратко состоит в следующем.
Допустим, что некоторое тело обтекается потоком.
В потоке всегда можно выделить такую линию тока МА,
которая, 'приходя из бес-
конечности, встречает те-
ло нормально в точке А.
Затем эта линия тока раз-
деляется на две ветви, ко-
торые прилегают к телу
до некоторых точек В\ и
В?. После этого обе ветви
отделяются от тела и ухо-
дят в бесконечность (рис.
4.2). При такой схеме
область течения, располо-
Рис. 4.2. Упрощенная схема
обтекания тела
53
женная слева от линии СВ\АВ2С, резко отделяется от
области покоя, расположенной внутри этой линии.
В области течения поле скоростей принимается не-
прерывным и потенциальным, а скорость в точке А — рав-
ной нулю. В области покоя предполагается, что отсутст-
вуют массовые силы, а поскольку скорость воздуха
здесь равна нулю, то давление воздуха здесь должно
быть постоянным. Это обстоятельство позволяет линии
тока В1С и В2С рассматривать как свободные границы
течения воздуха, а скорость на этих линиях постоянной
и равной скорости течения в бесконечности.
Необходимо отметить, что при реальных течениях
воздуха струи будут отрываться от тела, но не уходить
в бесконечность, а постепенно размываться вследствие
затухания вихрей в области покоя. Поэтому к методам
конформного отображения течения с отрывом струй не-
обходимо относиться с известной осторожностью и ре-
зультаты решения каждой задачи проверять экспери-
ментами. Существует несколько методов конформного
отображения течения с отрывом струй. Ниже мы подроб-
но ознакомимся только с методом Н. Е. Жуковского [6],
представляющим для инженера большую ценность, по-
скольку автором этого метода были даны подробные
правила по составлению как комплексного потенциала,
так и отображающей функции.
§ 18. Метод Н. Е. Жуковского
Для определения неизвестного двухмерного движе-
ния воздуха на плоскости z—xA-iy Н. Е. Жуковский
предлагает рассмотреть новое двухмерное движение воз-
духа па верхней полуплоскости:
U = £ + 1Г|.
Новое движение воздуха выбирается таким образом,
чтобы в самом общем случае течение было вызвано раз-
личным числом точечных источников и стоков, по-разно-
му расположенных вдоль действительной оси. Число
этих источников и стоков, а также их взаимное распо-
ложение устанавливаются по числу потоков или струй,
и их взаимному расположению в разыскиваемом тече-
нии.
Комплексный потенциал нового течения выражается
в общепринятом виде, т. е. в виде аналитической функ-
ции:
w—F (и).
(4Д)
54
Разыскивание комплексного потенциала нового тече-
ния не представляет большого труда, поскольку он ра-
вен сумме известных комплексных потенциалов элемен-
тарных движений, вызванных источниками и стоками.
Связь между разыскиваемым и новым движениями
воздуха Н. Е. Жуковский устанавливает при помощи
конформного отображения. В качестве отображающей
функции им принимается функция
& + ie = f(u), (4.2)
причем
О = 1п^, (4.3)
и
где Vo и v — скорости течения на плоскости z соответственно на кон-
туре струи н в любой точке потока; 0 — угол между вектором ско-
рости в рассматриваемой точке потока и действительной осью плос-
кости г.
При составлении аналитических зависимостей для
комплексного потенциала и отображающей функции
Н. Е. Жуковский рекомендует руководствоваться следу-
ющими правилами.
Комплексный потенциал определять по формуле
£, и — Vi £» и — у,
ф + гф = Ф1 (и) Ч—- In—-—i4—- In —---(4.4)
Л Pi Л pg
где Ф1(п) —алгебраическая рациональная целая функция с действи-
тельными коэффициентами; прн потоке с конечным расходом проте-
кающей жидкости равна нулю, а прн бесконечном расходе не должна
быть выше второй степени; в отдельных случаях может содержать
также мнимое постоянное; £, р, у — действительные величины, при-
чем £— расход воздуха источника или стока; р — величина, позво-
ляющая в определенном месте иметь потенциал скорости, равный ну-
лю, а также обусловить определенную систему отсчета линии тока;
у — абсцисса центра источника или стока.
Отображающая функция в случае прямолинейных
границ течения разыскивается по формуле
„ г f (и) du
-&+tO=m I —..... —---- (4.5)
J K(u—®i) (« —®2)«».
При этом т=\ или т=1 в зависимости от того, че-
му соответствует ось g на плоскости z — твердой стенке
млн контуру струи. Неизвестная функция, стоящая под
интегралом в числителе;
А А
f (и) — Фг (и)-5-+-----?-+.», - (4.6)
и — ei и — е2
55
где Ф;(и)—целая рациональная функция, А и е — действительные
величины, нз которых А — некоторый коэффициент; е — абсцисса на
плоскости и, соответствующая точке излома границ потока, т. е.
соответствующая вершине угла стенок на плоскости г.
Величины сон 0)2 •••— абсциссы на плоскости и, соот-
ветствующие краям твердой стенки, с которой сбегают
струи.
Входящие в последнее равенство неизвестные коэф-
фициенты определяются по формуле
Л = — — ]/(е, — coj (е( — w2) (4.7)
тл,
где А0 — угол излома стенки на плоскости г.
Если комплексный потенциал и отображающая функ-
ция найдены, то можно решать различные задачи.
Предположим, что необходимо найти уравнение ли-
нии тока. Решая известное равенство
— — V
ds
совместно с равенством (4.3) и исключая скорость V, по-
лучим
1 л
ds — — ev d<p.
«о
Умножим левую н правую части последнего уравне-
ния сначала на cos0, а затем на sin0 и заменим
ds cos Q — dx, a ds sin Q—dy. Тогда уравнение линии тока
можно записать в параметрическом виде:
1 л
dx = — е co# 0d<p;
1 Л
dy =— е sin 0d<p.
»o
В частном случае, а именно на контуре струи, ско-
рость v—vq и, следовательно, v=1п_!!_== in 1 =0. Поэто-
V
му последние уравнения для контура струи примут бо-
лее простой вид:
х — — f cos 0d<p; (4.8)
Со J
у = — Г bin 0d<Pi (4.9)
Vo J
5G
РАЗДЕЛ ВТОРОЙ
ПРИМЕНЕНИЕ МЕТОДОВ АЭРОДИНАМИКИ
ПРИ РЕШЕНИИ ВОПРОСОВ ВЕНТИЛЯЦИИ
ГЛАВА 5
ОБТЕКАНИЕ ТЕЛ ПОТОКОМ
§ 19. Распределение давлений на поверхности
обтекаемых тел
При обтекании потоком неугловатого тела, например
шара, возникает пограничный слой, который вначале
прилегает к поверхности шара, а затем отрывается от
нее. Объясняется это тем, что в первый момент поток
обтекает шар без срыва. Тогда вблизи поверхности ша-
ра по наибольшему поперечному сечению возникают по-
вышенные скорости, что, согласно уравнению Бернулли,
приводит к пониженному давлению в этих местах. Начи-
нается перетекание воздуха с передней и задней частей
шара и последующее его стекание с этой части поверх-
ности шара.
При небольшом значении числа Рейнольдса погра-
ничный слой ламинарен и точки его отрыва находятся
почти на наибольшем поперечном сечении шара.
Под числом Рейнольдса понимается величина
Re=t>od/v, (5.1)
где d — диаметр шара; Vo — скорость набегающего потока вдали
от гола.
При турбулентном пограничном слое точка отрыва
смещается к задней части шара. Объясняется это тем,
что турбулентный невозмущенный поток вследствие по-
перечного переноса частиц убыстряет движение воздуха,
движущегося впереди, к точке отрыва и замедляет дви-
жение воздуха, движущегося сзади, к этой точке. В ре-
зультате точка отрыва смещается к задней части шара.
Необходимо отметить, что схема обтекания шара
в большой степени зависит от начальной турбулентнос-
ти потока.
Опытами установлено, что давление воздуха вблизи
поверхности шара неодинаково (рис. 5.1). Здесь на ра-
диусах отложено значение аэродинамического коэффи-
циента, т. е. избыточного статического давления, выра-
57
Рис. 5.1. Эпюра аэродинамических
коэффициентов на поверхности
шара
женного в долях скоростно-
го давления набегающего
потока:
Рис. 5.2. Эпюра аэродина-
мических коэффициентов на
поверхности параллелепипе-
да
__Pl Ра
Р^/2
(5.2)
где рг — статическое давление в
точке, взятой на поверхности ша-
ра; р0 — статическое давление в
набегающем потоке.
Как видим, на передней части шара в пределах
0<С ±45° давление положительно, а на остальной час-
ти — отрицательно.
При обтекании потоком угловатых тел, например
прямоугольного параллелепипеда, между горизонталь-
ной плоскостью н передней стенкой параллелепипеда об-
разуется вихрь. После срыва потока с переднего угла
параллелепипеда на верхней грани его образуются
вихри. Позади параллелепипеда также наблюдается зо-
на завихрения.
Необходимо отметить, что геометрические размеры
параллелепипеда не сказываются на схеме обтекания,
но существенно влияют на значение аэродинамических
коэффициентов.
Распределение аэродинамических коэффициентов по
поверхности такого параллелепипеда при разных на-
правлениях потока представлено эпюрами (рис. 5.2). На
основании этих эпюр видно, что положительные давле-
ния наблюдаются только на той грани параллелепипеда,
на которую набегает поток. Остальные грани, омывае-
мые воздухом, находятся под разрежением,
58.
При направлении потока под углом 6=0° аэродина-
ические коэффициенты составляют около 0,2. На на-
поенной грани при направлении потока под углом
I—X450 они равны в среднем 0,35, а под углом 6=90° —
около 0,7о.
В этих же условиях другая грань параллелепипеда
прИ 0=45 и 90° находится постоянно под разрежением
и значения средних аэродинамических коэффициентов
для нее колеблются от 0,2 до 0,7.
Во всех случаях не заметно влияния относительной
ширины параллелепипеда В/Н на изменение значения
аэродинамических коэффициентов. Исключение из это-
го правила составляют аэродинамические коэффициенты
на заветренной грани при направлении потока под углом
0=90°.
§ 20. Аэродинамические сила и момент
При обтекании тела потоком на каждую элементар-
ную площадку его поверхности воздействуют силы дав-
ления и трения. Сложение этих сил (по правилу парал-
лелограмма) в самом общем случае, как известно из те-
оретической механики, приведет к, главному вектору R
и главному моменту М (рис. 5.3).
В аэродинамике главный вектор называют аэродина-
мической силой, а главный момент — аэродинамическим
моментом.
Пользуясь приемом неопределенных коэффициентов,
выведем формулу для определения аэродинамической
силы R по способу анализа размерностей.
Очевидно, сила R зависит от площади наибольшего
поперечного сечения тела F, кинематического коэффици-
ента вязкости воздуха v,
плотности воздуха р и
скорости набегающего по-
тока v0:
R = f(F, v, р, с0).
Эту неизвестную функ-
цию будем искать в сле-
дующем виде:
R = AFX vlJ рг vnQ, (5.3)
где А — безразмерный коэф-
фициент; x,y,z и п — пока не-
известные показатели степени.
Рис. 5.3. Обтекание потоком тела
с векторами аэродинамических
силы и момента
5»
Чтобы найти эти показатели, в зависимость (5.3)
вместо величин подставим единицы их измерения в си-
стеме СИ:
у ( м2 \р / кг \г ! м
1 щ) Ы (т)
или
КГ-М , « г / М2 V / КГ \2 { м
----=(м2) — — —1
с2 1 \ с / к м3 м с /
что дает
кг-м _ КГг..м2х+2у~3г+п
С2 су+п
Показатели степени у единиц измерения величин
слева должны быть такими же, как и показатели степе-
ни у единиц измерения соответствующих величин спра-
ва. С учетом этого обстоятельства будет справедлива
следующая система уравнений:
г=1; 2л' + 2// — Зг ~г/г = 1; z/ + n = 2.
Итак, получили три уравнения с четырьмя неизвест-
ными. Будем считать, что один показатель степени, на-
пример п, нам известен. Тогда, решая систему уравне-
ний, получаем
х = я/2; у = 2 — п; г—1.
Подставляя эти значения х, у и г в зависимость
(5.3), будем иметь
R = AFn/2 v2~n pv^. (5.4)
В большинстве практических расчетов наблюдается
развитая турбулентность и тогда, согласно опытам, п=.
=2, что дает
= AFpvl.
Умножив и разделив правую часть на 2 и обозначив
2A = Cr, окончательно получим
2
Р^о
* = CrF—, (5.5)
где Сп — коэффициент аэродинамической силы; F — площадь наи-
большего поперечного сечения обтекаемого тела (площадь миделе-
восо сечения).
60
Аналогично рассуждая, можно вывести формулу для
аэродинамического момента
Р^о
M = CnFl~, (5.6)
где с,„ —коэффициент аэродинамического момента; I — характер-
пая длина.
Вследствие того что сила R и момент М являются
векторами, при практических расчетах удобно пользо-
ваться их проекциями на прямоугольные оси координат.
В качестве таковых выбираются так называемые по-
точные оси координат. Начало координат принимается
в центре тяжести обтекаемого тела, ось х направляется
вдоль по течению, ось z — вбок, в горизонтальной плос-
кости, а ось у — перпендикулярно плоскости xoz. Тогда
вместо равенства (5.5) получаем следующие три равен-
ства:
2 2 2
ру0 ру0 pv0
Rr=CxF — ; Ry^CvF —; RZ^CZF~ , (5.7)
где /?х — сила лобового сопротивления; Rv — подъемная сила; —
боковая сила; Сх, Су и С2— соответственно коэффициенты сил ло-
бового сопротивления, подъемной и боковой.
Аналогично вместо равенства (5.6) будем иметь:
2 2 2
ру0 ру0 ру0
Л4д; — Стх FI 2 ! Му — Сту FI 2 ; Мг — Cmz Fl i (5.8)
где Л4Х, и Mz — проекции аэродинамического момента на оси ко-
ординат; Стх, Сту и Стг — соответственно коэффициенты этих про-
екций.
В случае равномерного поля скоростей в набегаю-
щем потоке и симметричных тел, каковыми являются,
например, пластинка, поставленная перпендикулярно
потоку, шар и т. п., силовое взаимодействие потока с те-
лом сводится к одной аэродинамической силе. При этом
эта сила совпадает с направлением течения, т. е. явля-
ется одновременно и силой лобового сопротивления.
При неравномерном поле скоростей в набегающем
потоке и симметричных телах возникают еще подъемная
сила и аэродинамический момент.
Если, например, поток горизонтален и скорость уве-
личивается по оси у, а тело является шаром, то в верх-
ней части шара скорость воздуха больше, чем в нижней.
61
Поэтому, согласно уравнению Бернулли, над шаром
давление будет меньше, чем под шаром, и появится
подъемная сила. Разность скоростей в верхней и ниж-
ней частях шара обусловит появление аэродинамическо-
го момента.
При теоретическом определении проекций аэродина-
мических силы и момента силы давления и трения
порознь геометрически суммируют. В результате, напри-
мер, для силы лобового сопротивления получают
Р«о
Rx — Rxn 4" Rxt = (Х-хп F + Cxi Ft) g •
где /?хД и — составляющие силы лобового сопротивления, обус-
ловленные силами давления и трения; С1Д и Сет — коэффициенты
составляющей силы лобового сопротивления, обусловленные соот-
ветственно силами давления и силами трения; FT — поверхность
трения.
Соотношение между составляющими /?жд и RX1 мо-
жет быть совершенно различным. При обтекании, на-
пример, плоской тонкой пластины, поставленной пер-
пендикулярно потоку воздуха, будет значительна сила
/?жд и очень мала сила /?Жт- Если же пластинку поста-
вить по направлению потока воздуха, то Яхя—0, a RXT
значительна.
§ 21. Коэффициент силы лобового сопротивления
симметричных тел
Коэффициенты проекций аэродинамических силы
и момента определяются экспериментально в потоке
с равномерным полем скоростей. Значение их зависит от
числа Рейнольдса.
Изменение коэффициента силы лобового сопротивле-
ния шара в зависимости от числа Рейнольдса представ-
лено на графике (рис. 5.4).
При малых значениях числа Рейнольдса (/?<С1)
кривая приближенно описывается формулой Стокса:
C* = 24/Re. (5.9)
В несколько большем диапазоне значений числа Рей-
нольдса точнее формула Озина:
(5.10)
Re 1о /
62
Как видим, с увеличе-
нием числа Рейнольдса
коэффициент лобового со-
противления уменьшает-
ся и при Re = 1034-105 до-
стигает значения 0,4—
0,48. Затем при дальней-
шем увеличении Re (при-
мерно от 105 до 4-Ю5)
значение коэффициента
Сх резко уменьшается
до 0,2. Эта зона падения
сопротивления носит на-
звание критической.
Оказывается, что кри-
тическая зона связана с
Рис. 5.4. График изменения коэф-
фициента силы лобового сопроти-
вления шара
1, 2 и 3 — кривые соответственно по
Стоксу, Озину и опытная
переходом пограничного
слоя шара нз ламинарного состояния в турбулентное.
Таким образом, при переходе пограничного слоя из ла-
минарного режима в турбулентный коэффициент лобо-
вого сопротивления резко уменьшается.
§ 22. Скорости витания и трогания
Как известно, при пневматическом транспортирова-
нии твердых примесей скорость воздуха в воздуховодах
должна быть больше скорости витания и трогания с тем,
чтобы примеси можно было перемещать в вертикальных
воздуховодах вверх и в случае их оседания на дне гори-
зонтальных воздуховодов стронуть с места.
Рассмотрим, как с помощью законов аэродинамики
устанавливаются зависимости для этих двух скоростей.
Вначале установим зависимость для скорости вита-
ния. Пусть на тело весом Mg (М — масса тела) набега-
ет поток воздуха, двигающийся снизу вверх с такой ско-
ростью vB, что тело не поднимается и не опускается,
а находится на одном и том же уровне, как бы повисает
в воздухе (рис. 5.5). При этом оно может перемещаться
в горизонтальной плоскости под действием подъемной
и боковой сил. Итак, тело будет висеть в воздухе. Ско-
рость, при которой это происходит, называется скоростью
витания.
Очевидно, эта скорость определяется при условии,
что сила лобового сопротивления равна весу тела
63
Rx~Mg
или
₽ав
CxF—^Mg
Учитывая, что Cs=fs (Re), получаем
Рав
F~ = Mg
(5.11)
Из этого уравнения, если известна функция fx, мож*
но определить скорость витания. В частном случае для
шара диаметром d при Re<l имеем Сх—24/Re, и тогда
Их
' Мд
О'
Рис. 5.5. Тело в восходя-
щем потоке с приложен-
ными к нему силами
24v nd2 Ррв nd3
3 ~7~ п ~ Рм с g<
vad 42 6
где Рм — плотность материала шара.
Из последнего уравнения еле
дует, что скорость витания
_ Рм£42
Vb 18pv ’
Если скорость воздуха V>ua,
то тело начнет двигаться вверх
со скоростью vT, определяемой
уравнением
Rx — Mg=M-~
dl
(5.12)
или
о dvr
CXF у .
Рис. 5 6. Тело, лежащее на горизонтальной плоскости с приложен-
ными к нему силами
а— при Mg, б — при Ry < Mg
64
Следует отметить, что скорость воздуха v>vT, так
как часть энергии потока воздуха будет расходоваться
на подъем тела. Вместе с тем следует отметить, что Сх=
(v — vT) d
=fx(Re), но уже Re= ; •
Установим теперь зависимость для скорости трога-
ния. Ввиду сложности вопроса аэродинамический мо-
мент будем полагать равным нулю. Пусть на тело весом
Mg, лежащее на горизонтальной плоскости, набегает
горизонтальный поток воздуха с такой скоростью, что
тело поднимается в воздух или скользит по плоскости по
направлению течения (рис. 5.6).
В первом случае Mg—Rv и, очевидно, скорость тро-
гания будет определяться из условия, что подъемная си-
ла равна силе тяжести (рис. 5.6, а)
Ru = Mg
или
о
Учитывая, что можем написать
' (fiprf \ гРС'тр
/d—(5.13)
Из этого уравнения, если известна функция fv, можно
определить скорость трогания.
Если скорость воздуха п>пТр> то тело начнет дви-
гаться со скоростью ит, определяемой уравнением
R„-Mg-M-^
ИЛИ
_ „РФ — От)2 .. .. dVf
CVF---~----- Mg = М — .
Во втором случае Mg>Rv (см. рис 5 6, б) и ско-
рость трогания определяется из условия, что сила лобо-
вого сопротивления равна силе трения Rx — T или
Rx = f(Mg-gy),
где f — коэффициент трения
5—741 65
Отсюда
О ! 0
Рутр ( Р«Тр
Сх F= f [ Mg — CyF
или
2 Г 2 "
<5|4)
Из этого уравнения, если известны функции fx и fy,
можно найти скорость трогания.
Если скорость воздуха v>oTp, то тело начнет сколь-
зить по плоскости со скоростью vT, определяемой урав-
нением
uV'p
Rx-f(Mg-Rg) = M-^
или
CXF ~ (о - от)2 - f |мй - CyF~ (v - t)T)2] = М.
Необходимо отметить, что если скорость витания оп-
ределяется по одной зависимости, то скорость трогания
определяется по двум зависимостям. Очевидно, для ско-
рости трогания первый случай характерен для легких
тел, а второй — для тяжелых тел.
Пример 5.1. Определить силу лобового сопротивления для шара,
если диаметр d, a Re<; 1.
Решение. Подставляя в первую формулу (5.7) Сх из выра-
жения (5.9) и F=itd2/4, получаем Rx=3npvu0d-
Эта зависимость носит название закона Стокса.
ГЛАВА6
ПОТЕРИ ДАВЛЕНИЯ В ВОЗДУХОВОДАХ
§ 23. Распределение скоростей
в поперечном сечении воздуховода
Движение воздуха в воздуховодах может быть ла-
минарным и турбулентным.
Ламинарное течение существует в воздуховодах при
Re = yd/v<2320, где v — средняя скорость воздуха в
воздуховоде и d — диаметр воздуховода. Турбулентное
66
Рис. 6.1. Профиль скоростей
в поперечном сечении возду- Рис. 6.2. Соосный с воздуховодом
ховода цилиндр радиусом г
течение наблюдается при Re>2320. Если при наличии
предварительно успокоенного воздуха осторожно увели-
чивать скорость, то можно переход ламинарного течения
в турбулентное осуществить даже при Re—50 000.
Установим, как изменяется скорость в поперечном се-
чении воздуховода круглого поперечного сечения. Воздух
вследствие наличия вязкости будет прилипать к стенкам
воздуховода и тормозить движение смежных слоев. По-
этому скорость v увеличивается по мере удаления от
поверхности воздуховода (где она была равна нулю) и
достигает наибольшей величины иос на оси воздуховода
(рис. 6.1).
Выявим зависимость между скоростями v и иос. Вна-
чале рассмотрим ламинарное течение. Согласно закону
Ньютона, касательное напряжение
do ,
т = —рт—, (6.1)
dr
где v — скорость воздуха на расстоянии г от оси воздуховода
Наличие знака минус объясняется тем, что с увели-
чением радиуса г скорость v уменьшается и, следова-
тельно, градиент dvfdr отрицателен, а величина т всегда
положительна. Полная производная взята вместо част-
ной производной потому, что скорость в круглом возду-
ховоде постоянного сечения обычно изменяется лишь по
радиусу трубы.
Из равенства (6.1) следует
dv = ——idr. (6.2)
pv
5*
67
Для определения t проведем в воздуховоде два по*'
перечных сечения 1—1 и 2—2 на расстоянии I одно от
другого. Пусть статическое давление в сечении 1—1 рав-
но Р[, а в сечении 2—2 — р2. Выделим в объеме между
сечениями 1—1 и 2—2 соосный с воздуховодом цилиндр
радиусом г (рис. 6.2).
Напишем для объема этого цилиндра уравнение ко-
личества движения в проекциях на его ось, полагая, что
количества движения, проходящие через сечеиия, оди-
наковы:
(Pi — Р2) nr'1 — x2nrl = 0.
Из этого равенства следует
Подставляя это значение х в равенство (6.2), по-
лучим
Интегрирование этого уравнения дает
Pt — Рг
2pv/ 2
Постоянная интегрирования определяется из усло-
вия, что на стенке трубы (r—R) скорость равна нулю
(у=0). Следовательно,
с= Pt — Pi R*
2pvl 2 ’
поэтому
Зная, что на оси трубы (г = 0) скорость v = uoc> на-
ходим
(6.4)
Совместное решение двух последних уравнений окон-
чательно дает
(6.5)
Как видим, скорость по радиусу трубы при ламинар-
ном течении изменяется согласно параболическому за-
кону.
Рассмотрим теперь турбулентное течение. Согласно
Прандтлю, касательное напряжение
2 / dv
где /я —длина пути перемешивания.
Отсюда
da = l/ -~dr.
У Pin
Подставляя сюда т из выражения (6.3), получим
dv^]/'^^-dr,
V 2lPln
Интегрирование этого уравнения затрудняется из-за
того, что длина пути перемешивания /п является неиз-
вестной функцией.
В настоящее время имеется несколько решений дан-
ной задачи, когда относительно /п принимаются различ-
ные гипотезы, например гипотеза об увеличении /п пря-
мо пропорционально удалению от стенки трубы, т. е.
—г), где х — коэффициент пропорциональности.
Однако до сих пор для турбулентного течения не
удалось теоретически точно решить задачу об измене-
нии скорости по радиусу трубы. Вследствие этого исполь-
зуем экспериментальные данные.
При турбулентном течении опытами было установ-
лено, что
о = оос (1 - r!R)x/n. (6.6)
Показатель степени 1/л по данным опытов уменьша-
ется с увеличением турбулизации воздуха. Анализ
зависимости (6.6) обнаруживает, что с увеличением тур-
булентности воздуха, т. е. числа Re, распределение ско-
ростей по сечению воздуховода делается более равно-
мерным и при 1/п->0 имеем о = оОс- Обычно в расчетах
принимают п~1, тогда зависимость (6.6) именуют за-
коном 1/7 степени.
Пример 6.1. Определить коэффициент поля ламинарного тече-
ния в круглой трубе.
69
Решение. Для определения коэффициента поля используем
формулу (1 6). В нашем случае
г2
R2
2nrdr
nR2
= 2rdr.
v
и -------
Voc
Поэтому
i
k = 2 f (1 — ?) ~rdr = 2 (--------------- ) = 0,5.
J \ 2 4 /
о
§ 24. Потери давления в воздуховоде
постоянного сечения
Определим потери давления на трение в воздухово-
де постоянного сечения (рис. 6.3). Проведя в нем два
поперечных сечения 1—1 и 2—2, напишем уравнение
Бернулли, полагая, что в обоих сечениях скоростные
давления одинаковы. Тогда
Pi = Р2 + &Р-
Отсюда найдем потери давления на трение:
Ap = pi — р2. (6.7)
Рассмотрим вначале воздуховод круглого сечения.
Выделив объем воздуха, заключенный между сечениями
1—1 и 2—2, напишем уравнение количества движения
в проекциях на ось воздуховода:
nd2
(Pi — Ра) “ — т0 ndl—0,
где d— диаметр воздуховода; I — расстояние между сечениями 1—1
и 2—2; то — касательное напряжение на стенке воздуховода.
Из последнего уравнения следует
Pi — Рг — 4то ~ .
а
Подставив в равенство
(6.7) эту разность статиче-
ских давлений, получим
Др = 4т0-у-. (6.8)
а
Рис. 6 3. Воздуховод постоянного
сечения На основании опытов
70
было замечено, чго касательное напряжение на стенке
трубопровода пропорционально скоростному давлению,
вычисленному по средней скорости:
Рисп
То=ф — , (6-9)
где Ф — коэффициент пропорциональности.
Заменив в формуле (6.8) величину То выражением
(6.9), будем иметь
d 2
Обозначая здесь 4ф = Х, окончательно получим
Л 1 1
(6.10)
где к — коэффициент сопротивления трения.
Рассмотрим теперь воздуховод произвольного попе-
речного сечения. Для объема воздуха, заключенного
между рассматриваемыми сечениями, напишем уравне-
ние количества движения в проекциях на ось воздухо-
вода:
(Pi — Ра) F — т0 Р1 = 0,
где F и Р— соответственно площадь и периметр поперечного сече-
ния воздуховода.
Отсюда
Р1 к Р1 Р"ср
Л-р2-т0 р ~ 4 р 2 .
Подставляя эту разность статических давлений в ра-
венство (6.7), получим
Последняя формула может быть преобразована к ви-
ду формулы для воздуховода круглого сечения, если вве-
сти обозначение
4f/P=d3. (6.12)
Тогда потери давления на трение в воздуховоде про-
извольного сечения составят
I Руср
----(6.13)
da 2
где Дэ — эквивалентный диаметр.
71
Если, например, воздуховод прямоугольного сечения,
то F=ab и Р=2(а4-Ь), где а и b — длины сторон пря-
моугольного сечения. В этом случае эквивалентный диа-
метр
d^ = 2abl(a-Fb). (6.14)
§ 25. Коэффициент сопротивления грения
В случае ламинарного течения коэффициент сопро-
тивления трения достаточно просто можно установить
теоретически.
Действительно, потери давления на трение опреде-
ляются формулой (6.7).
Разность статических давлений может быть найдена
из зависимости для осевой скорости в трубе (6.4):
4pvZuOc
Pl - Р2 = .
Заменяя радиус воздуховода диаметром (# = tf/2),
получим
16pvZ
Pi — Pi = ~voc
а3
Поскольку в примере 6.1 было установлено, что ко-
эффициент поля скоростей k при ламинарном течении
равен 0,5, то
Гос = р.
С учетом последних двух равенств потери давления
на трение составят
32 pvZ
Ар^= ——t'cp. (6.15)
d2
Таким образом, потери давления па трение при ла-
минарном течении прямо пропорциональны скорости
движения Држиср.
Приравнивая потери на трение по формулам (6.10)
и (6.15) и производя сокращение общих множителей в
левой и правой частях равенства, будем иметь
t>cp 32v
Отсюда
Z=64/Re. (6.16)
72
Следовательно, этот коэффициент обратно пропор-
ционален числу Рейнольдса. Формула хорошо подтвер-
ждается опытными данными.
В случае турбулентного течения вывести аналогич-
ную формулу для коэффициента сопротивления трения
не удается, так как не известна зависимость для опре-
деления осевой скорости. Вследствие этого воспользу-
емся имеющимися экспериментальными данными.
Согласно опытам, коэффициент сопротивления тре-
ния при турбулентном течении зависит от числа Рей-
нольдса и шероховатости стенок воздуховода. По
А. Д. Альтшулю, он равен
А. = 0,11^ 68/Re + й/d , (6.17)
где k — эквивалентная шероховатость, т е такая шероховатость
стенок воздуховода, которая при данных Re и d дает фактическое А.
На основании опытов установлено, что значение k
для воздуховодов из стали, винипласта, асбестоцемен-
та и фанеры равно 0,1 мм, шлакоалебастра — 1 мм, кир-
пича — 4 мм и штукатурки по сетке — 10 мм.
§ 26. Потери давления в пневмотранспортном
воздуховоде постоянного сечения
Рассмотрим вопрос о потерях давления на трение при
движении воздуха с твердыми примесями в прямом го-
ризонтальном воздуховоде постоянного сечения (рис.
6.4). Напишем уравнение Бернулли для сечений 1—1
и 2—2-
Pi ~ Pi Лрпн>
где Лрпа—потери давления на трепне между сечениями 1—1 и 2—2.
Отсюда потеря давления
== Pl ~ Р1 (6.18)
Напишем теперь уравнение количества движения в
проекциях на ось воздуховода:
P1F — PiF — -^Pl— 2Rx = 0, (6.19)
где то — напряжение трения на степке трубопровода; 2RX — реак-
тивная сила всех частиц примесей, численно равная силе лобового
сопротивления всех частиц примесей, но направленная в противопо-
ложную сторону.
Из уравнения (6.19) следует
Р1
Р1 Р1 — т0
\
73
Рис. 6.4. Пневмотранспортный воз-
духовод постоянного сечения
Подставляя эту раз-
ницу статических дав-
лений в уравнение
(6,18) и учитывая, что
Р1
то —равно потере
F
ления Др того же уча-
стка воздуховода
движении в нем возду-
ха без примесей, полу-
чим
дав-
при
X ptF
Т Т
Подставляя
RX = CXF-P- ф-ст)2
и т0 =
(здесь v — скорость воздуха, a vT — скорость твердых примесей),
будем иметь
Арпа = АрГ1+.4'2Схр('1--—У]. (6.21)
L хр/ \ v j j
Анализируя это выражение, можно заметить, что
увеличение потери давления за счет примесей зависит
от Сх, т. е, от вида примесей и числа Рейнольдса, от
суммарной площади миделевых сечений всех примесей
и от vT/v — отношения горизонтальной скорости мате-
риала к скорости воздуха, т. е. от плотностей материа-
ла и воздуха (известно, что чем тяжелее материал, тем
меньше его скорость по сравнению со скоростью возду-
ха). При расчетах пневмотранспортных воздуховодов
число Re меняется незначительно, поэтому можно сде-
лать допущение, что второе слагаемое в прямоугольных
скобках равенства (6.21) пропорционально массовой
концентрации примесей рПр’.
4 / vT \2
— j =АИпр,
где k — коэффициент пропорциональности; pDp = GT/G— массовая
концентрация примесей (GT—массовый расход примесей, G — мас-
совый расход воздуха).
Учитывая последнее равенство, формулу (6.21) мож-
но записать в виде
Арпн — Ар (1 4” ^Рпр)
(6,22)
74
Экспериментальные исследования по определению
потерь давления в воздуховодах при движении в них
воздуха с твердыми примесями подтвердили эту зави-
симость.
ГЛАВА 7
ПОТЕРИ ДАВЛЕНИЯ
В МЕСТНЫХ СОПРОТИВЛЕНИЯХ
§ 27. Общие сведения
о местных сопротивлениях
Местным сопротивлением называется аэродинамиче-
ское сопротивление, сосредоточенное в одном месте на
коротком участке воздуховода. Типичным примером
местного сопротивления является колено, тройник, ре-
шетка, дроссель-клапан и т. д.
В местных сопротивлениях всегда происходит пере-
стройка поля скоростей и образование на границах по-
токов вихрей. Перестройка поля скоростей и поддержа-
ние вращения вихрей требуют затраты энергии. Таким
образом, течение воздуха через местные сопротивления
всегда сопровождается потерями давления.
Теоретическим определением величины потерь дав-
ления в местных сопротивлениях занимаются давно. Од-
нако число аналитически решенных случаев в настоящее
время невелико. Объясняется это тем, что до сих пор
не разработан общий аналитический метод расчета
местных сопротивлений. Привлекаемые же для решения
этой задачи основные уравнения аэродинамики, как
правило, нуждаются в тех или иных допущениях. В ре-
зультате решение получается приближенным.
Вследствие этого определение потерь давления в
местных сопротивлениях главным образом пошло по
экспериментальному пути. Как показывают опыты, по-
тери давления в местных сопротивлениях обычно про-
порциональны квадрату скорости. Поэтому для опреде-
ления потерь давления в местных сопротивлениях при-
нята формула
pv2
(7.1)
где 5 — коэффициент местного сопротивления.
75
—в-----*--- - - «—
АВ С
Рис 7 1 Движение воздуха окочо
стенки
Необходимо отметить,
что коэффициент £ при
турбулентном движении
зависит почти исключи-
тельно от геометрии мест-
ного сопротивления.
Определение потерь
давления в местных со-
противлениях производит-
ся всегда при условии равномерного поля скоростей на
входе в него. Практически такой случай бывает довольно
редко. Наоборот, почти всегда поле скоростей неравно-
мерно, и фактические значения коэффициентов местных
сопротивлений несколько отличаются от расчетных. Од-
нако при расчетах воздуховодов этой ошибкой прене-
брегают.
Ниже рассматриваются только такие местные сопро-
тивления, для которых имеются аналитические решения,
полученные при совместном использовании уравнения
Бернулли и уравнения количества движения. При этом
предполагается, что поля скоростей до и после местного
сопротивления равномерны. Вместе с тем стенки воздухо-
водов предполагаются гладкими, что позволяет прене-
бречь потерями на трение. Поскольку местные сопро-
тивления заполнены таким же воздухом, как и снару-
жи, то можно также пренебречь силами тяжести.
Таким образом, в уравнении количества движения учиты-
ваются только поверхностные силы и притом лишь нор-
мальные.
Эти силы представляют собой силы давления в рас-
сматриваемых сечениях и силы реакции со стороны сте-
нок воздуховода. Величина последних устанавливается
следующим образом.
Представим себе движение воздуха около стенки
(рис. 7.1). Воздух в начале течения (точка Л) имеет
статическое давление р0 и скорость п0 Статическое дав-
ление в какой-либо точке на поверхности стенки, напри-
мер в точке В, согласно выражению (5.2), составит
(Mj
Pi^P0 + kt-^’
где kt — аэродинамический коэффициент.
При рассмотрении не отдельной точки, а целой по-
76
верхности среднее статическое давление будет опреде-
ляться равенством
if 1 \( , Р1,о V
Пер = TJ pidf = ~Ф J И» + Т df'
ф ф
1де df — элементарная поверхность, выделенная около точки В;
ф — площадь поверхности стенки на протяжении линии АС.
Применяя теорему о среднем и сокращая на Ф, по-
лучим
^ср = ^о +Пере-
учитывая, что среднее статическое давление возду-
ха на стенку равно реактивному давлению стенки на
воздух (Р1ср=Лср), опуская индекс «ср», окончательно
будем иметь
о
рУо
G=Po+*t — (7.2)
Сила же реакции стенки на воздух будет равна:
( Р°о\
— г, Ф[ — I 2 I <Р‘"
§ 28. Потери давления при входе
в воздуховод постоянного сечения
Вход воздуха в торец воздуховода. Воздух засасыва-
ется в открытый торец воздуховода. При входе поток
сначала сжимается, а затем расширяется и заполняет
все поперечное сечение воздуховода (рис. 7.2).
Выбрав в потоке сечение 1—1 вдали от входа, на
таком расстоянии, где скоростью можно пренебречь, и
сечение 2—2 в том месте, где сжатый поток расширяет-
ся и поле скоростей становится равномерным, напишем
уравнение Бернулли:
9
ТО
Pl = Pl + — + др
Отсюда потери давления при входе в воздуховод соста-
вят
9
ДР==Р1 —Ра_—
77
Разность статических давлений pi и р2 может быть
установлена с помощью уравнения количества движе-
ния. С этой целью проведем вне воздуховода сечение
3—3 и рассмотрим объем, ограниченный контуром /, 3,
3, 2, 2, 3, 3, 1. Напишем применительно к этому объему
Рис. 7.2. Вход воздуха в торец воздуховода
Рис. 7.3. Вход воздуха в наветренный торец воздуховода
78
уравнение количества движения в проекциях на ось
воздуховода
PtF — P2 F = PFvz
При составлении этого уравнения полагаем, сгто ста-
тические давления в сечениях 1—1 и 3—3 весьма близ-
ки между собой, а скорости на границе контура вне
воздуховода пренебрежимо малы.
Сокращая последнее уравнение на F, получим
Pt Р1~ Ру2 •
Подставляя эту разность статических давлений в ра-
нее установленную зависимость для потерь давления,
будем иметь
Дд=--рУ]/2. (7.3)
Итак, при входе воздуха в воздуховод потеря давле-
ния равна одному скоростному давлению. Коэффициент
местного сопротивления входа
Вход воздуха в наветренный торец воздуховода. Воз-
духовод обращен открытым концом навстречу потоку.
При этом в зависимости от отношения скоростей Vtlvt
(г») — скорость потока, vz— скорость внутри воздухово-
да) возможны различные схемы течения (рис. 7.3).
Случай, при котором ц1/ц2==0, был рассмотрен раньше,
и схема течения для него изображена на рис. 7.2.
Выбрав в потоке сечение 1—1 и внутри воздуховода
сечение 2—2 на таком расстоянии от входа, чтобы в
этих сечениях поля скоростей были равномерны, напи-
шем уравнение Бернулли для потока, направляющего-
ся в воздуховод:
2 2
РИ pv^
Pt + ~ = Ръ + — +
Отсюда потери давления составят
Др = Р1-Ра + -^-(а1-аг)-
Разность статических давлений pt—Pz определяем,
используя уравнение количества движения. Для этого
вне воздуховода проводим сечение 3—3 на таком рас-
79
стоянии от входа, чтобы по всему сечению скорости бы-
ли одинаковы. Далее рассмотрим объем, ограниченный
всеми тремя сечениями и стенками воздуховода, и на-
пишем применительно к нему уравнение количества дви-
жения в проекциях на ось воздуховода:
PiF ~ Р2F = PFvi ~ PFvl
При составлении этого уравнения полагаем, что как
статические давления, так и скорости в сечениях 1—1 и
3—3 весьма близки между собой
Сокращая последнее уравнение на F, получим
РХ-Р2 = Р (^~ vi)'
Подставляя эту разность статических давлений в ра-
нее установленную зависимость для потерь давления,
будем иметь
' (7-5)
Коэффициент местного сопротивления входа
c=-^-=i-№.
pv]/2 \ »2 /
(7-6)
Анализируя эту зависимость, обнаруживаем, что
>0 при vjv2<. 1, а £<0 при Ui/v2> 1. Отрицательные
значения объясняются тем, что набегающий поток на-
гнетает воздух в воздуховод и на его всасывание энер-
гия не затрачивается. В частном случае, когда Vi = 0,
имеем С=1, что было установлено ранее.
Вход воздуха в заветренный торец воздуховода.
В этом случае схема течения
Рис. 7 4. Вход воздуха в завет-
ренный торец воздуховода
представлена на рис. 7.4.
Выбрав сечения 1—1 и
2—2 на достаточном уда-
лении от входа, составля-
ем уравнение Бернулли:
. PV1 , РУ2 , ,
Pi + ~ = Рг + — + Др-
Отсюда потери давления
составят
др = р1-р2 + '7’(°?-
Проводя сечение 3—3,
рассмотрим объем, огра-
80
ничепный всеми тремя сечениями и стенками воздухово-
да. Применительно к этому объему напишем уравнение
количества движения в проекциях на ось воздуховода:
ряР~ p2F = pFv‘22 + pFvl.
Сокращая это уравнение на F и учитывая, что р\ —
=рз и Vi = t>3, получим
Pi - = Р Н + "1) •
Подставляя эту разность статических давлений в ра-
нее установленную зависимость для потерь давления,
будем иметь
Др = Р (а? + tty + -у (у? — = -у (Зр? + . (7.7)
Коэффициент местного сопротивления входа
Др I щ V
C = -f-=l+3p- . (7.8)
р»]/2 \ «2 /
Анализ последней формулы обнаруживает, что £
всегда больше единицы. В частном случае, когда v1 = 0,
имеем £=1, т. е. получаем ранее известный результат.
§ 29. Потери давления при изменении
поперечного сечения воздуховода
Расширение воздуховода. Представим воздуховод, у
которого по направлению течения потока происходит
внезапное расширение поперечного сечения (рис. 7.5).
Проведем в широкой
части воздуховода се- чение /—1, а на доста- точном удалении от него сечение 2—2, где поток расширяется и заполняет все сечение воздуховода. Для выбранных та- ким образом сечений напишем уравнение Бернулли: ptf pv^ Pi+~ — Ра + 2 +Др. 1 1 2 Рис. 7.5. Внезапное расширение поперечного сечения воздуховода
6—741
81
Отсюда потери давления составят
Др = рг — р2 + (р/2) (v{ — vty.
Выделим объем, заключенный между обоими сече-
ниями и стенками воздуховода, и применительно к не-
му составим уравнение количества движения в проек-
циях на ось воздуховода:
Р1 F1 + Г1 (F2 - Fl) ~P2F2 = PF2 U2 - pf2 a2 al
где rt — среднее реактивное давление торцовой стенки широкой ча-
сти воздуховода.
В соответствии с равенством (7.2) можем написать
pt»i
Г1 = Р1 + .
Подставляя rj в уравнение количества движения,
получим
Pl Fl + Pl (f2 — fl) —P>F> = Pf2 —
— pf2 a2 al — kl {F1 — fl) Pal/2‘
Упрощая это выражение и сокращая его на F2, бу-
дем иметь
Рх — Р2 = (Р/2) [2с] — 2v2v1 — k1(l — Fl/F2'j с(].
Согласно уравнению расхода,
Fl/F2 = а2/а1»
поэтому
Pi — Р2 = (р/2) [2v| — 2v2 v1 — (tij — t>2)].
Подставим эту разность статических давлений в ра-
нее найденную зависимость для потерь давления. Тогда
Др = (р/2) [(V1 — с2)2 — (vt — оа)]. (7.9)
Опытами доказано, что ri = pi. В таком случае fei =
=0, и потому
ДР=(Р/2)(С!-С2)2. (7.10)
Как видим, потери давления при внезапном расши-
рении воздуховода равны скоростному давлению поте-
рянной скорости.
Следует отметить, что явление, происходящее при
внезапном расширении воздуховода, аналогично явле-
нию удара в механике твердого тела. Поэтому потери
«2
давления при внезапном расширении воздуховода очень
часто называют потерями на удар.
Коэффициент местного сопротивления, отнесенный к
скорости в узкой части воздуховода, составит
С = -^-
pt^/2
(7.11)
В частном случае, когда воздух выходит из воздухо-
вода в бесконечно большой объем, площадь F2—o°, а
скорость и2=0- Следовательно, будем иметь Др = рг^/2
и ?=1.
При постепенном расширении воздуховода значение
аэродинамического коэффициента неизвестно, но, по-ви-
димому, близко к нулю. Вследствие этого, если в равен-
стве (7.9) принять ^! = 0, то его правую часть необхо-
димо умножить на поправочный коэффициент 1, что
даст
ДР = П у" fa ~г>2)8 (7.12)
и соответственно
? = n(i-fi/f2)2.
(7.13)
где коэффициент ц носит название коэффициента смяг-
чения удара.
Сужение воздуховода. Вначале рассмотрим воздухо-
вод, у которого по направлению течения потока про-
исходит внезапное сужение поперечного сечения, при-
чем в этом месте имеется достаточно длинный патрубок
с тонкими стенками (рис.
Выбрав два сечения 1
ленные от входа в узкую
часть воздуховода, про-
ведем такие же выкладки,
как и в случае расшире-
ния воздуховода [7]. В ре-
зультате получим, что по-
тери давления при суже-
нии определяются по
формуле
&р = (р/2) [(у2 — гц)2 +
+*А (t»2 — t»i)]. (7.14)
На основании опытов
установлено, что Г1=Р1+,
бл
7.6).
—1 и 2—2, значительно уда-
Рис. 7 6. Внезапное сужение попе-
речного сечения воздуховода при
наличии патрубка
83
(7.15)
4-pU;/2 и, следовательно, &i=l. Подставляя это значе-
ние ki в формулу (7.14), будем иметь
р
—«2^2 —У1).
Коэффициент местного сопротивления, отнесенный к
скорости в узкой части воздуховода, равен:
; _ &Р _ J = J
рР;/2 F1
(7.16)
В частном случае, когда воздух поступает в воздухо-
вод из бесконечно большого объема, площадь Ft — ос, а
скорость Vi—0. Следовательно, получим Др=ри^/2 и
5=1.
При коротком патрубке значение аэродинамического
коэффициента будет несколько меньше единицы. Поэто-
му если в формуле (7.14) принять Л1 = 1, то правую ее
часть следует умножить на поправочный коэффициент
т]в< 1, что даст
р
Ар = Цв ~ v2 (t'2 — t'l)
(7.17)
и соответственно
? = Чв(1-ВД). (7.18)
где коэффициент г]в носит название коэффициента смяг-
чения входа.
Опытами установлено, что для внезапного сужения
воздуховода без патрубка г]в=0,5. В этом случае
р
Ар = 0,5 —(У2 — И1)
(7.19)
C = 0,5(l —F2/Fx).
(7.20)
§ 30. Потери давления в колене
Рассмотрим прямоугольное колено с изменением пло-
щади поперечного сечения (рис. 7.7). Проведем сечение
1—1 до поворота и сечение 2—2 после поворота, где по-
ток расширяется и заполняет все сечение воздуховода.
Составляем уравнение Бернулли:
р, -|- pt/j/2 = р2 + Р^/2 + Ар.
«4
Отсюда потери давления
Др = Pi — Р2 + (Р/2) •
Рассмотрим объем, заключенный между обоими се-
чениями и стенками колена, и применительно к нему на-
пишем уравнение количества движения в проекциях на
ось колена после поворота:
PlFi COS 0 + S1П 0 — p2f2 = pf2C2 (t»2 — Vi cos 0),
где fl — среднее реактивное давление на площади Ф, расположен-
ной от сечения 7—1 до вершины внешнего угла.
Заменяя здесь
pt>!
ri — Pi+ h -у и Ф1 sin 0 = Г2 — Ficos 0,
получаем
PiFi cos 0 + Pi (f2 — Fi cos 0) — p2F2 =
= pf2 o2 (o2 — cos 0) — kr (Рг — Fr cos 0) pvj/2.
Упрощая это выражение и сокращая его на F%, бу-
дем иметь
Р / F1 \
Pi~Pi = ~ [2v2( v2 — vr cos 0) - Ц1 - у cos 0 ) tij
Согласно уравнению расхода,
Fj/F2 — v2/vi,
и потому
Pi — Ра = (P/2)[2v2 (v2 — Vi cos 0) — kiVi (Vi — v2 cos 0)].
Подставляя эту разность статических давлений в
формулу для потерь дав-
ления, получим
Лр = (р/2) jvj — 2v{ v2 cos 0 +
+°2—V2COS0)]. (7.21)
Если воздуховод пос-
ле поворота расширя-
ется (vi>V2), то, подоб-
но ранее рассмотренному
случаю постепенного рас-
ширения воздуховода, в
формуле (7.21) примем
Рис. 7.7. Колено прямоугольного
сечения
85
и для всего выражения введем коэффициент смяг-
чения удара т]. Тогда получим
Др = г] —- — 2v,t v2 cos 0 + t'jj; (7.22)
?=-V-=nfl-2fbcos0+^-Y (7.23)
po|/2 у Рг F% }
Если же после поворота наблюдается сужение пото-
ка (wi<02), то в формуле (7.21) принимаем &i = l, а
для всего выражения вводим коэффициент смягчения
входа т]в, что дает
Др = Пв ~ fa (ия — «1 cos 0); (7.24)
Z = ~~ = Пв(1~72-coso') , (7.25)
pu?/2 \ Pi 1
В случае, если колено имеет постоянное сечение, в
формуле (7.21) следует принять vi = v2 = v, и тогда
р 9 pt>a
Др = — [2v2 (1 — cos 0) — Лтг2 (1 — cos 0)J = (2 — Aj) 2 sin2 -g-— .
При Aj —0 получаем
0 pt>a
Др = 4т] sin2— — ; (7.26)
? = -^Г = 4г] sin2-|-. (7.27)
pt'2/2 2
Следует сказать, что значения коэффициентов смяг-
чения удара и входа почти не исследованы. Однако для
колена постоянного сечения установлено, что т] — 0,55.
Выведенные здесь формулы для прямоугольного коле-
на, по-видимому, могут быть распространены и на ко-
лена круглого сечения.
§ 31. Потери давления в тройнике
Деление потока в тройнике. Прямоугольный тройник
состоит из общего воздуховода площадью поперечного
сечения F, ответвления площадью f0 и прохода пло-
щадью fn. В зависимости от положения линии тока МО
в тройнике все течения потока могут быть сведены к
трем вариантам (рис. 7.8).
88
Определим потери давле-
ния в тройнике. Вначале вы-
явим их в потоке, направляю-
щемся в ответвление. Исходя
из уравнения Бернулли, со-
ставленного для двух попереч-
ных сечений 1—1 и 2—2, про-
веденных через общий возду-
ховод и ответвление (см. рис.
7.8, а), эти потери будут равны:
М) = Р —Р0 + (р/2) (и2 — »о).
Выделим теперь объем, ог-
раниченный обоими попереч-
ными сечениями, стенками
тройника и линией тока МО, и
применительно к нему напи-
шем уравнение количества
движения в проекциях на ось
ответвления
pf cos 0 -f- г\Ф} si n 0 — г2Ф2 si n 0 —
—г3Фг sin 0 — pafa = pfovo (v0— w COS9),
где fl, r2 и r3 — среднее реактивное
давление соответственно на площа-
дях Фь Ф2 и Ф3.
Рис. 7. 8. Деление потока в
тройнике
а — при г>п<а", б — при пп=®;
в — при Va>W
Заменяя здесь
рю2 ргш2
rl ~ Р + 2 ’ Г2 = р + ^2 2 ’
рю2
гз — Р + Рз 2 ’
получим
р (f cos 0 + Ф1 sin 9 — Фг sin 9 — Ф3 sin 9) — pafo —
раа2
= Pfo Vo (vo — w cos 9) — Uh Фх — fe2 Ф2 — k3 Ф3) -у- sin 9.
Учитывая, что
f cos 9 -|- sin 9 — Ф2 sin 9 — Фо sin 9 = f0,
можем написать
1 paa2
P — Po = P^'o (vo — w cos 9) — — (&x Фх — fe2 Ф2 — k3 Ф8) —— sin 0.
to *
87
Подставляя эту разность статических давлений в ра-
нее найденное выражение для определения потерь дав-
ления в ответвлении, будем иметь
Др0 = (р/5) [со - 2v0 оа cos 9 + w2 - (1 //Q) Фг — k,2 Ф2 - k3 Ф3) X
X w" sin 9).
Отбрасывая в этой формуле последний член, содер-
жащий неизвестные аэродинамические коэффициенты, и
вводя поправочный коэффициент Цо, окончательно по-
лучим
&Ро = Чо(уо — 2% c°s 9 + ^2) • (7.28)
Для установления зависимости местных потерь дав-
ления от скорости воздуха в ответвлении возьмем пер-
вую производную от потерь давления по этой скорости:
<9Лр„ р
—— = По о (2ио — cos 9) •
Приравняв правую часть этого равенства к нулю и
решив затем полученное уравнение относительно скоро-
сти воздуха в ответвлении, будем иметь
иОпт = cos 9 • (7.29)
Следовательно, оптимальная скорость воздуха в от-
ветвлении равна скорости воздуха в общем канале,
умноженной на косинус угла поворота.
Чтобы решить, наибольшие или наименьшие потери
давления в ответвлении наблюдаются при оптимальной
скорости в нем, берем вторую производную
Д Др/5^ = г)0 Р > 0.
Таким образом, оптимальная скорость воздуха ооу-
словлпваег наименьшие местные потери давления в от-
ветвлении.
Для определения наименьших местных потерь дав-
ления следует в формулу (7.28) вместо скорости возду-
ха ио подставить оптимальную скорость. Осуществив
это, получим
рои2
Арпаим — По sin2 9. (7.30)
В результате проведенного анализа можно утверж-
дать, что потери давления в ответвлении тройника при
увеличении скорости сначала уменьшаются и достигают
88
наименьшего значения, определяемого выражением
(7.30), а затем увеличиваются.
Для определения местных потерь давления в прохо-
де тройника можно воспользоваться формулой (7.28),
сменив у входящих в нее величин индекс «о» на индекс
«п» и приняв угол 0=0, что даст
р
ЛРп-= Пп — (Ч>~1-п)2.
(7.31)
Значения поправочных коэффициентов ц0 и цп поч-
ти не исследованы.
Сравнение результатов расчета по формулам (7.28)
и (7.31) с данными опыта показывает, что для трой-
ников с углом ответвления 0 < 30° т0=1 и почти для
всех тройников тп=0,3—0,35.
Необходимо отметить, что выведенные здесь форму-
лы для прямоугольного тройника справедливы и для
тройника круглого сечения.
Слияние потоков в тройнике. Прямоугольный трой-
ник состоит из ответвления, прохода и общего воздухо-
вода (рис. 7.9).
Проведем три поперечных сечения (два 1—1 и 2—2
ДО слияния и одно 3—3 после). Линия тока СШ являет-
ся линией раздела двух потоков.
Составим уравнение Бернулли для потока, вытекаю-
щего из ответвления, и решим его относительно потерь
89
давления. Тогда получим
&р0 = Ро ~ Р + <Р/2) Н — м2) •
Выделим теперь объем воздуха внутри тройника, за-
ключенный между избранными сечениями, и примени-
тельно к нему напишем уравнение количества движе-
ния в направлении оси общего воздуховода:
Ро f0 cos 0 + ра /п — pF — гх Фх sin 0 + г2 Ф2 sin 0 =
= pFw2 — pf0 «о cos 0 — Р/п vn
Заменяя здесь средние реактивные давления
7 9
pt'o Ру0
Г1 — Ро “Т ki 2 > Г2 — Ро ^2 2 ’
получаем
Ро fo cos 0 + ра fa — pF — р0 (Ф± — Ф2) sin 0 =
= pFw2 — pf0 v20 cos 0 — pfa v2 4- (fej Фг — fe2 Фг) — sin 0.
Учитывая, что (Ф1—Ф^) sin Q—f0 cos 0+/n—F, имеем
Po fo cos 0 Pa fa — pF — Po (fo cos 0 -f- fa — F) —
2 9 9 РУ0
= pFw — p/0 Pqcos 0 — p/n V2n + (kt Фг — k2 Ф2} — sin 0.
Принимая во внимание, что по данным опытов р0
Ра, будем иметь
( „ VoCOS0+fnVn
Ро — Р = Р -----
/гхФх — к2Ф2 Рсо .
+-------Z--------Z- 51П0.
F 2
Воспользуемся известным в теоретической механике
понятием неупругого удара тел и введем проекцию
средней скорости слившихся потоков на ось общего воз-
духовода:
v cos© = (/0 V2 cos 0 + fn v^)/F,
где v — скорость слившихся потоков; © — угол, заключенный между
этой скоростью и осью общего воздуховода.
В таком случае
/о о. , ^1Ф1 — к2Ф2 Руо . Л
pQ — р = р (и?2 — wv cos и) Н--т--------- sin 9.
г 2
90
Подставляя найденную разность статических давле-
ний в ранее определенное равенство для подсчета по-
терь давления в ответвлении, будем иметь
Р I 9 2
Др0 = —— nJ — 2ш v cos 0+ w
£ \
, fei Ф1 ^2 Фг
’Г F
Vq sin 0
Отбрасывая неизвестные последние слагаемые и вво-
дя поправочный коэффициент г|0, окончательно получим
Л Р ( 2
Ар = Йо — (5о
— 2wv cos
(7.32)
й ~f- ar2).
Установим, как зависят потери давления в ответвле-
нии от скорости в общем воздуховоде. С этой целью
возьмем первую производную от потерь давления. При-
равняв ее нулю, будем иметь
шОпт —гсозй. (7.33)
Вследствие того что вторая производная больше ну-
ля, оптимальная скорость обусловливает наименьшие
потери в ответвлении.
Заменяя скорость w в формуле (7.32) оптимальной
скоростью, получим наименьшие потери давления в от-
ветвлении:
Ар = п — (о? — и2 cos2 й).
гпаим ’о 2 и )
(7.34)
Из проведенного анализа видно, что местные потери
давления в ответвлении с увеличением скорости воздуха
в общем воздуховоде вначале уменьшаются и достига-
ют наименьшего значения, определяемого формулой
(7.34), а затем увеличиваются.
Для определения местных потерь давления в про-
ходе можно воспользоваться формулой (7.32), сменив у
входящих в нее величин индекс «о» на «п». В результа-
те получим
ДРП = йп Дп — 2шг cos 0 + w2y
(7.35)
Сравнение результатов расчета по формулам (7.32)
и (7.35) с данными опыта показывает, что во всех слу-
чаях значения т]0 и т]п близки к единице.
Следует отметить, что названные формулы могут
быть распространены и на тройники круглого сечения.
91
ГЛАВА 8
СВОБОДНЫЕ ИЗОТЕРМИЧЕСКИЕ СТРУИ
§ 32. Схема изотермической струи
Струей называется поток жидкости или газа с ко-
нечными поперечными размерами. Различают струи сво-
бодные и несвободные, изотермические и неизотермиче-
ские, ламинарные и турбулентные.
Свободная струя не стеснена никакими границами,
а несвободная в той или иной мере ими ограничена.
Изотермическая струя имеет по всему объему одну
температуру. Это может быть в том случае, если струя
не участвует в теплообмене с окружающей средой, т. е.
температура в начале струи равна температуре окру-
жающей среды. В противном случае струя нагревается
или охлаждается по течению и становится неизотерми-
ческой.
Ламинарная или турбулентная струя характеризует-
ся соответственно ламинарным или турбулентным ре-
жимом течения.
В вентиляции имеют дело с турбулентными воздуш-
ными струями, поэтому в дальнейшем будут рассматри-
ваться только такие струп.
В настоящее время имеется много работ, посвящен-
ных исследованию струй. Наиболее глубокое и полное
исследование этого вопроса принадлежит Г. Н. Абрамо-
вичу [1]. Ниже в несколько упрощенном виде излагает-
ся эта теория свободных изотермических струй.
Турбулентная струя, как и всякое турбулентное тече-
ние, характеризуется интенсивным поперечным переме-
щением частиц. Вследствие этого периферийные слои
струи подтормаживаются, а слои окружающего непо-
движного воздуха, находящиеся вблизи струп, приходят
в движение. В результате создается пограничный слой
струи, который по направлению течения непрерывно
утолщается. Таким образом, размеры струи по течению
увеличиваются, масса ее растет, а скорость убывает.
В результате наблюдений над подкрашенными изо-
термическими струями с начальным равномерным по-
лем скоростей и замеров скоростей в таких струях при-
нята схема струи, показанная на рис. 8.1.
Воздух, вытекая из сопла, образует струю с криво-
линейными границами АВС и DEF, которые прибли-
92
Рис. 8.1. Схема струи с равномерным начальным полем скоростей
женно могут быть заменены прямыми АВ, ВС и DE,
EF. В струе различают два участка: начальный ABED
и основной CBEF. Сечение BE называют переходным
сечением.
На начальном участке струи равномерное поле ско-
ростей переходит в поле скоростей основного участка.
Участок разделяется на ядро постоянных скоростей
AGD и пограничные слои ABG и DGE.
На основном участке струи поле скоростей нерав-
номерно. Участок сплошь состоит из пограничного слоя.
Границы основного участка ВС и EF при их продолже-
нии пересекаются в точке О, находящейся в центре вы-
ходного отверстия. Точка О называется полюсом основ-
ного участка струи. Боковой угол расширения основного
участка струи 0=12°25'.
На начальном участке скорость на оси струи посто-
янна и равна начальной, а на основном участке ско-
рость по мере удаления от отверстия непрерывно умень-
шается. В пограничном слое по мере удаления от оси
струи скорость уменьшается и на границе струи стано-
вится равной нулю.
Относительная скорость в поперечном сечении основ-
ного участка струи изменяется в соответствии с анали-
тической зависимостью Шлихтинга:
^ = (1-?'5)2, (8.1)
где v — v/voc; у=у1уг-р (у— скорость в точке, удаленной от осн струи
на расстояние у, угр— полуширина струи).
93
Относительная скорость в пограничной слое началь-
ного участка также изменяется в соответствии с зависи-
мостью (8.1). Однако в этом случае
У = У/(.Угр — УяУ, v = v/v0,
где уя — полуширина ядра; v0 — скорость в начале струи.
Замеры давления в струе показывают, что статичес-
кое давление в ней одинаково и равно статическому дав-
лению окружающего воздуха. Это приводит к выводу,
что количество движения в струе должно быть неизмен-
ным.
В самом деле, проведя контур HK.LM (см. рис. 8.1)
и пренебрегая малыми скоростями эжектируемого в
струю окружающего воздуха, можно написать уравне-
ние количества движения в проекциях на ось струи:
К-Хо-0,
где К— количество движения, проходящее через поперечное сече-
ние струи, на расстоянии s от отверстия; Ко — количество движе-
ния в струе на выходе из отверстия.
Отсюда
К = К0. (8.2)
Используя описанную схему изотермической струи,
установим безразмерные зависимости между геометри-
ческими и физическими величинами различных струй
При этом вначале выявим зависимости для начального
и основного участков, переходного сечения, а затем ус-
тановим константы струи и дадим расчетные формулы.
§ 33. Плоская изотермическая струя
Из бесконечно длинной щели постоянной ширины
вытекает воздух, образуя плоскую струю (рис. 8.2). По-
ле скоростей в щели равномерно.
Начальный участок. Начало координат поместим в
центре щели, а ось абсцисс s направим по оси струи.
Относительная полуширина струи
B = B/B0 = (B0+stgOH)/B()= 1 +stg0„, (8.3)
где Во — полуширина щели; s=s/B0 — относительная абсцисса;
Он — боковой угол расширения струн в начальном участке.
Относительный объемный расход
В = L/L^ — (Вя -р Вц)/В(> = -|- £П)
где Во, Вя и — объемные расходы соответственно в начале струи,
в ядре постоянных скоростей и в обоих пограничных слоях.
W
Относительный объемный расход в ядре постоянных
скоростей
бя — Вя/Во 2ВЯ Vq/QBq Vq = Вя!Bq — Вя,
где Вя — полуширина ядра постоянных скоростей; v0 — скорость в
щели
Относительный объемный расход в пограничном слое
- La 2 (в — вя) vn t— — ч -
in — . — ~ =(В — Вя) vn,
Во 2В0 Vq
где Vn — средняя скорость в поперечном сечении пограничного слоя.
Относительная полуширина ядра постоянных скоро-
стей может быть определена, если воспользоваться ра-
нее отмеченным свойством струи, заключающимся в по-
стоянстве количества движения во всех ее поперечных
сечениях. Применительно к двум сечениям начального
участка струи, выбранным одно на расстоянии s от от-
верстия, а другое в начале струи, согласно выражению
(8.2), можно написать
2Рвя г02 + 2рР (В - вя) v2 = 2рВ0 $
Разделив левую и правую части последнего равен-
ства на 2рВ0о2, получим
вя+₽(в-вя)^=1.
Решая это равенство относительно полуширины ядра
постоянных скоростей, будем иметь
вя = (1 - рв^)/(1 - ₽v*).
Рис. 8.2. Схема изотермической плоской струи
95
Кориолиса воспользуемся формулами (1.6), (1.22) и
Относительная скорость на основном участке опре-
деляется по зависимости (8.1), где у—b и утр—В. От-
носительная площадь плоской струи равна:
df = df/F = 2db/2B = db/B = db.
В таком случае
k = J (1 — ft1’5)2 = 0,45;
о
1 i
₽=— f (1 —bt’5)idb = 0,316/0,452 = 1.56;
ьЛ J
* 0
a = 3₽ —2 = 3-1,56 — 2 = 2,68.
Таблица 8.1. Расчетные формулы для плоской струи
Относительная величина Значения относительной величины
ьа начальном участке в пере- ходном сечении на основном участие
Расстояние от отвер- стия S <14,4 14,4 >14,4
Полуширина струи В 1+0,151 Г 3,16 0,22 7
Средняя скорость Оср 1+0,0295 7 1+0,151 7 0,45 1,71
Скорость на оси струи ^ОС 1 1 3,8 1/7
Объемный расход L 1+0,02957 1,425 0,375]/Т
Кинетическая энер- гия Е 1—0,01587 0,775 2,93
Тангенс бокового угла расширения струи tg0H = 0,151 tgO = 0,22
«8
Поскольку tg 0 = tg 12°25'=0,22, то получаем
. ,, Впер — Bo Впер — 1
tg U;I = -----— —-------—
sne₽ Snep
1M2P — 1
= i/fe2Ptge = (1~O) tg0 =(l - °-316) °’22 = °’151 •
Расчетные формулы. Подставляя полученные значе-
ния коэффициентов k, £ и а, а также tg0H и tg 0 в зави-
симости (8.3) — (8.14), получим для плоской струи рас-
четные формулы, сведенные в табл. 8.1.
Необходимо отметить, что расчетные формулы спра-
ведливы и для щели конечной длины, если отношение
длины щели к ее ширине не менее 20. В противном слу-
чае струя трансформируется в струю круглого сечения.
§ 34. Изотермическая струя
круглого сечения
Из круглого отверстия вытекает воздух, образуя
струю круглого сечения (рис. 8.3). Поле скоростей в
круглом отверстии равномерно.
Начальный участок. Начало координат поместим в
центре круглого отверстия, а ось абсцисс s направим по
оси струи. Относительный радиус струи
- R ^o + stg0n -
В==—=----------------=l+stg0H, (8.15)
Ко Ко
где Ro— радиус круглого отверстия; s—s/Ra— относительная абс-
цисса; 0п — боковой угол расширения струи в начальном участке.
Рис. 8.3. Схема изотермической струи круглого сечения
7*
99
Относительный объемный расход
L = LiL0 = (i-я La)!L0 — La Ln,
где Lo, L„ н L„—объемные расходы соответственно в начале струи,
в ядре постоянных скоростей и в пограничном слое.
Относительный объемный расход в ядре постоянных
скоростей
= £я' Lo = nRn
где Ля — радиус ядра постоянных скоростей; t’a — скорость в круг-
лом отверстии.
Относительный объемный расход в пограничном
слое
L° nRo vo
где i>B — средняя скорость в поперечном сечении пограничного слоя.
Для определения радиуса ядра постоянных скоро-
стей воспользуемся ранее установленным свойством
струп, состоящим в том, что она имеет во всех своих
поперечных сечениях одинаковые количества движения.
Поэтому для двух сечений начального участка струи,
выбранных одно на расстоянии s от отверстия, а дру-
гое в начале струи, согласно выражению (8.2), можно
написать
Vq н Ррл (/?2 — /?я) t>2 = рл/?о с2.
Разделив все члены последнего равенства на
будем иметь
Решая это равенство относительно радиуса ядра по-
стоянных скоростей, получим
Относительная средняя скорость в поперечном сече-
нии пограничного слоя
уп = ап/Ч) = й.
Подставляя величины R, R4 и vn в формулы для от*
носительных объемных расходов в ядре постоянных ско-
ростей и в пограничном слое, получим:
г i-fe2P (1+stge,,)2 _ fe2P
La~ (2 + ИбОн)ИбОн,
100
Zo= O+stg%)2-l
b2R _ T
P -------Zaft (2 + s tg On) s tg Оц \k =
1 — R3p J
= z—(2+*tg 0ц) *tg 0,1
i — A-p
Подставляя величины Ья и Ln в формулу относитель-
ного объемного расхода, будем иметь
1_, + ^=Ж^6ви + ^й-;!,8.9.. (8.1Й
I — /гр I — /гр
Относительная средняя скорость в поперечном сече-
нии струн
nRp L _
До = R2
s2tg20Hi
-------- Р--------------. (8.17)
t»cp L
Сер = -- = —™ •
v0 п/с
2fe(l-feP) ,
1+"—Z^--stg0H +
(l+stg Он)3
Относительная скорость на оси струи
Сое ~ еос/со ~ уо/^о “ 1 (0.18)
Относительная кинетическая энергия так же, как и
для начального участка плоской струи, равна:
£ = Дя+<хДпо2.
Подставляя в это выражение относительные расхо-
ды в струе круглого сечения, будем иметь
_ В — ak - В — ak -
Г=1~2Н------fe2s2tg20H. (8.19)
1 — Zrp 1 —
Основной участок. Относительный радиус струи
R=R/R0^^gOIR0 = stgQ. (8 20)
Относительная средняя скорость в поперечном сече-
нии струи находится из условия постоянства количества
движения. Согласно выражению (8.2), можно написать
рл/?б 4 = РрлЯ2 е2р.
Разделив обе части этого равенства на pnJ?o v%, бу-
дем иметь
₽^ср = 1-
Отсюда относительная средняя скорость
% = %/%= !/«/₽“= 1//Fstg0. (8.21)
101
Относительная скорость на оси струи
Ь'ос = — = — йср =---------. (8.22)
1’° й &ZPstg0
Относительный объемный расход
— L лЯгаСп — 1 -
L==T~= ^-=^ср=—=5tg0, (8.23)
Ьл УР
Относительная кинетическая энергия [см. формулу
(8.12)]
Ё = £7£о = аГ^р = а/р/Гз!§е. (8.24)
Переходное сечение. Относительное расстояние до
переходного сечения находим из формулы для относи-
тельной скорости на оси основного участка, положив
в ней о00 = 1. Тогда получим
Snep = 1М Т^"Р tg 0. (8.25)
Подставив Ядер в формулы (8.20) — (8.24), будем
иметь:
t?ncp — 1 Ik Р ; иср пер = k\ уос пер = 1: 1
Z-nep = £пер =а^/Р- J
Константы струи. Для определения коэффициента
поля скоростей, а также коэффициентов Буссинеска и
Кориолиса следует воспользоваться формулами (1.6),
(1.22) и (1.24).
Относительная скорость на основном участке струи
определяется по зависимости (8.1), где у=г, yrv=R.
Относительная площадь струи круглого сечения равна:
df = df IF — d (nr2) /л/?2 = 2nrdrlnR? — 2rdr.
Тогда
i
k = 2 f (1 — P’5)W = 0,258;
0
2 1
P = —r j'(l — rl’!J7dr = 0,134/0)2582 = 2,02;
k“ ti
a = 3P — 2 = 3.2,02 — 2 = 4,06.
102
(1-й/₽ )tgO =
Поскольку tg9=tg 12°25,=9,22, то имеем
, п Rnep — Ro Rnep — 1
tg он=------------------ = —~ ~
snep Snep
= щ/{Г-1
1/k //tge
= (1 — 0,258//02) 0,22 = 0,14.
Расчетные формулы. Подставляя полученные значе-
ния коэффициентов k, р и а, а также tg9a и tg 0 в фор-
мулы (8.15) — (8.26), получим для струи круглого сече-
ния расчетные формулы, сведенные в табл. 8.2.
Таблица 8.2. Расчетные формулы для струи круглого сечения
Относительная величина Значения относительной величины
на начальном участке в пере- ходгкиг сечении иа основном участке
Расстояние от отверстия s <12,4 12,4 >12,4
Радиус отвер- стия R 1+0,14 s 2,73 0,22 "s
Средняя ско- рость уср l+0,0396s+0,00278? (1+0,14 s)2 0,258 3,2 S
Скорость на оси СТруИ Уос 1 1 12,4 S
Объемный рас- ход L 1+0,0390's +0,00278? 1,92 0,155 s
Кинетическая энергия Е 1—0,0206 s—0,00141 ? 0,518 6,42 S
Тангенс боково- го угла расшире- ния струн tg0H = O,14 — tg9 = 0,22
Необходимо отметить, что расчетные формулы для
основного участка справедливы и для струи, вытекаю-
щей из прямоугольного отверстия с отношением сторон
103
менее 20 и из любого отверстия с отношением сторон,
близким к единице, если под относительной абсциссой
понимать
s = s/7?3>
где /?.,— эквивалентный по площади радиус.
Эквивалентный радиус находится из условия, что
площадь выходного отверстия Fo равна равновеликой
площади круга:
Fo = п/?|.
Отсюда
/?э
Fa = 0,565 "КК-
§ 35. Изотермическая струя
кольцевого сечения
Из кольцевой щели постоянной ширины вытекает
воздух под некоторым углом к оси симметрии, образуя
струю кольцевого сечения (рис. 8.4). Поле скоростей в
кольцевой щели равномерно.
Ряс. 8.4. Схема изотермической струи кольцевого сечения
N4
1 +-#-) Вя,
«ц/
Начальный участок. Начало координат поместим в
центре щели, а ось абсцисс s направим по оси струи.
Относительная полуширина струи
В = В/Во = (Во + s tg 0н)/Во - 1 + ?tg 0п, <8.27)
гце Во — полуширина кольцевой щели; s=i/Bt>— относительная абс-
цисса; 0н — боковой угол расширения струи иа начальном участке.
Относительный объемный расход
L — L/Lo ~ (Вя -}- Ln)/B0 = Ln 4- Ln,
где io, in, io — объемные расходы соответственно в начале струи,
в ядре постоянных скоростей и в пограничном слое
Относительный объемный расход в ядре постоянных
скоростей
£ — (S ~Ь Slfl ^Bfl V9
я i0 2л5,( sin й2В0о0
где Хц — расстояние между центром щели и точкой пересечения оси
струн с осью симметрии; О — угол, заключенный между осью струи
к осью симметрии, Вп — полуширина ядра постоянных скоростей;
ио — скорость в кольцевой щели; su=sn/Bo.
Относительный объемный расход в пограничном
слое
— in 2л (чц -j- s) sirs 02 (В — Вя)
Lq 2л5ц sin v2BqVq
«='[•+ ~ ] (В — Вя) Уп>
\ su /
где Vn — средняя скорость по площади поперечного сечения погра-
ничного слоя.
С целью определения полуширины ядра постоянных
скоростей воспользуемся условием постоянства количе-
ства движения в струе. Это условие применительно к
двум сечениям начального участка (одно на расстоянии
s от отверстия, а другое в начале струи), согласно вы-
ражению (8.2), можно записать в следующем виде;
р2л«ц sin $2Bqv0 cos & — р2л (чц 4- s) sin &2ВЯ v% cos 0 +
4- Ррл (Sg 4- s) sin й2 (В — Вя) cos ft.
Здесь количества движения взяты в проекциях на
ось симметрии. Разделив обе части этого равенства на
левую часть, получим
1 4-4-| Вл 4-₽ (1 4-77-) (в — 5Я) 1.
Бц / \ /
105
Отсюда
Л , S 1 - ₽ t1 + s/sa) В%
| 1 — ня ----------------—------.
\ «ц / 1 — р U„
Относительная средняя скорость в поперечном сече-
нии пограничного слоя
св — va!v0 — k.
Подставляя величины В, (1+$/«ц)Вя и пп в формулы
для относительных объемных расходов воздуха в ядре
постоянных скоростей и в пограничном слое, получим:
Вя = 1 — ~: ттг* ~ (1 -h Зц tg 0Н -р s tg 0н)’
Ец ~ 1 ~~~ (1 sig Он)’
Подставляя величины Ья и Ln в формулы для отно-
сительного объемного расхода в струе, будем иметь
L 1 + - ° ~ k^ k - 4- (1 + зц tg 0„ + s tg 0н) . (8.28)
1 ~ к ₽ sn
Относительная средняя скорость в поперечном сече-
нии струи
vCp Е2л,5ц 2Д0 sin 0 _____L_____________
Vcp~ v0 ’ 2л (s4 + s) 2В sin ОЕо ~ ~
1 3'Д~~Г' + «ц tg 0H-F s tg 0H)
=------------1—. (8.29)
(1 + s/sn) (1 +itgOJ
Относительная скорость на оси
Сое = Сое /с0 =• с0 /с„ 1. (8.30)
Относительная кинетическая энер1Ия, так же как и
для начальною участка плоской струи, равна:
Е _
Е — — La кЕц с„ ~
Еа
(В — ka) k2 s ,
= 1~ i “ О + 5ц tg 0H + stg 0ц). (8.31)
1 К 0 s4
106
Основной участок. Относительная полуширина струи
S = S/fi,=stgO/Se =JtgO. (8.32)
Относительная средняя скорость в поперечном сече-
нии струи находится из условия постоянства количества
движения, например в направлении оси симметрии. Со-
гласно выражению (8.2), можем написать
р2лзц sin 025^ cos О = рр2л (зц + s) sin 02Во|р cos О.
Разделив обе части этого равенства на левую часть,
получим
Р (1 +s/su) В^ = 1.
Отсюда относительная средняя скорость
5ср-»сРЧ=--1/КрО +з/зц)в =l/yrp(l+'s/sIl)stge. (8.33)
Относительная скорость на оси струи
Ьос = = 4- ёср = 1 Ik Кр(1+Vsn)Hg0 . (8.34)
Vo k v
Относительный объемный расход
- L 2л (зд 4- s) sin 025рср
Ло 2л3ц sin &2Bava
l_f1+A.Vtg0 . (8.35)
Р \ sn /
Относительная кинетическая энергия [см. формулу
(8.12)]
— Е —1 а,
Ez= =aLv2 ---------- ... . (8.36)
РИЗ(1 +s/sn)stg0
Переходное сечение. Относительное расстояние до пе-
реходного сечения найдем из формулы для относитель-
ной скорости на оси основного участка, положив voc=l.
Тогда получим _______________________
k Р (1 + Snep/Sil) snep tg 0 =1
пли
®nep + »ц «пер — tg 0 == 0.
Отсюда
«пер = ~ V2+Z??4 +• (8.37)
107
Подставляя snep tg 6= 1//г2р (1 -Нтер/«ц)
(8.32) — (8.36), будем иметь
£иер W(l+snep/s4); 1
1'ср.пер ~ Срс.пер ~ 1;
^пер —В11ер —016/3-
в формулы
(8.38)
Константы струи. Значение коэффициента поля ско-
ростей, а также коэффициентов Буссинеска и Кориоли-
са вычисляют по формулам (1.6), (1.22) и (1.24). При
этом относительная скорость на основном участке струи
определяется по зависимости (8.1), где у=Ь и г/гр=В.
Величина
- df d |2л (чц -F s) sin O2t>] db -
df —---- --------------------—-----= db.
F 2л (>n s) sin 02В В
Как видим, для струи кольцевого сечения получено
то же значение величины df, что и для плоской струи.
В таком случае для струи кольцевого сечения будут
справедливы полученные ранее для плоской струи зна-
чения 6=0,45; Р —1,56 п а=2,68. Поскольку tg0 =
=tg 12°25'=0,22, то
tg 0н = (^иер — Во)/5пер = (^пер — 1)/Snep1
Расчетные формулы. Подставляя значения коэффи-
циентов k, р и а, а также tg 0Н и tg 0 в формулы (8.27) —
(8.38), получим для струи кольцевого сечения расчет-
ные формулы, сведенные в табл. 8.3.
Необходимо заметить, что при больших удалениях
от кольцевой щели расчетные формулы для основного
участка могут быть заменены приближенными, более
простыми.
В самом деле, в формулах для иСр, ^ос, L и Е при
значительном s можно пренебречь единицей, и тогда эти
формулы примут следующий вид:
рср -
Сое — 3,8 у s4/s;
(8.39)
Sn/s.
Расчетные формулы, приведенные в табл. 8.3, спра-
ведливы при 0>30°. При О<30° ось струи начинает
искривляться в сторону оси симметрии и струя транс-
формируется в струю круглого сечения.
108
Таблица 8.3. Расчетные формулы для струи кольцевого сечения
Относительная величина Значения относительной величины
на начальном участке в переходном сечении iа основном участке
Расстояпие_ от отверстия s < Snep /F- - 14,4«ц — — _£s_ 2 > $пер
Полуширина струи В 1 + s tg 0tl 3,16 । । 5пер 5ц 0,22s
Средняя ско- рость УСр 1 1-0,198-4- 11 + sn 0,45 1,71
/, s \ 1+ — )x \ SH / + 5д+ s)tgoj x(l +stgOji) 1Z (i + ~\ r \ sn ]
Скорость на оси струн Voc 1 1 3,8 r \ ^ц/
Объемный расход L 1 + 0,198-4“ fl 4- ’ц + Ь'Ц + S) tg 0HI 1,425 0,375x xjZ (1+ +-J-V s4 /
109
Продолжение табл. 8.3
Относительная величина Значения относительной величины
на начальном участке в переходном сечении на основном участке
Кинетиче- ская энергия Е 1—0,105^-11 + + (s4 + s) tg eHl 0,775 2,93 г \ «Ц /
Тангенс бо- кового угла расширения струи tg9H = 2^PzJ Snep tg 0 = 0,22
Следует также отметить, что эти расчетные форму-
лы справедливы и для веерной струи, когда 0=90°.
Нетрудно убедиться, что формулы для струи коль-
цевого сечения, приведенные в табл. 8.3, при зц=оо пе-
реходят в формулы для плоской струи.
§ 36. Струи с неравномерным начальным
полем скоростей
Струя с неравномерным начальным полем скоро-
стей характеризуется схемой, показанной на рис. 8.5.
Рис 8.5. Схема струи с неравномерным начальным полем скоростей
НО
Схема такой струи отличается от схемы струи с рав-
номерным начальным полем скоростей следующими
особенностями. На начальном участке нет ядра посто-
янных скоростей и сам участок короче. На оси струи
начального участка скорость переменна и может по те-
чению воздуха или убывать (при выпуклом начальном
поле скоростей), или вначале увеличиваться, а затем
уменьшаться (при вогнутом начальном поле скоростей).
Границы основного участка при их продолжении пере-
секаются в полюсе М, находящемся внутри патрубка.
Поле скоростей струи с неравномерным начальным
полем на основном участке описывается зависимостью
Шлихтинга, и потому для таких струй удается устано-
вить зависимости только для этого участка.
Рассмотрим эти зависимости, поместив начало коор-
динат в центре отверстия и направив ось абсцисс s по
оси струи. Вначале рассмотрим плоскую струю.
Относительная полуширина струи
— В s — Зл ,
В Т = R--------- fg 0 = <S — So) fg 0-
Bq
rflfi Sg—So/Ba — относительная абсцисса полюса основного участка
струи (So<O).
Относительная средняя скорость в поперечном сече-
нии струи находится из уравнения количества движения.
Согласно выражению (8.2), можем написать
2Р^р=2Р0В^02,
где Ро — коэффициент Бусси песка для начального сечения струи;
v0 — средняя скорость воздуха в отверстии.
Разделив обе части равенства на 25оУд, получим
Отсюда
Ё'ср = УСр/1'0 = Кри/|//'рв =У’Ро/]/Лр(а —So)tge .
Относительная скорость на осн струи
. 1 - V7T
уос —' t'oc/^o — , — г - •
k feyp(s_;o)tg0
Относительный объемный расход
L = L/Lo = ВБср= J/^-у- G - s0) tg в
1И
Относительная кинетическая энергия
Ё = Л = А f ? = У Ро
£о а° СР аа8 Кр G - ^о) tg 9
Подставив в эти формулы 6=0,45; 0 = 1,56 и а=2,68,
будем иметь для плоской струи:
5 = 0,22 (s — s0); сср=1,71
Pqc = 3,81/^~/Vs— Sq ; <8 40)
1 = 0,3751^00 G — So);
Е = 2,93 0О К₽Г/а» /«-«о.
Проведя такие же, как для плоской струи, выклад-
ки, получим:
для струи круглого сечения
_ 3,2К₽Г
R = 0,22 (s — so); оср == —z—z-
s —s0
«ос =12,4 l/0o f(s—so); (8.41)
L = O,155K₽TG-;o);
6,42 .
«0 (s — So)
для струи кольцевого сечения
В = 0,22 (s — s0);
- i,7i/рГ
«ср — ..... ;
V (1 + s/sjO (s — s0)
s.sVpT
«ос = —; (8.42)
V (1 4-s/Sij) (s —So)
L = 0,375 /00 (1 -bs/s^G-So) ’,
- 2,930o /07
£ ==----— - —' .
«0 17(1 +«/5ц) G — So)
Необходимо отметить, что формулы (8.40) — (8.42)
справедливы при s>snep. Входящие в эти расчетные
112
формулы коэффициенты Буссинеска и Кориолиса могут
быть вычислены по формулам (1.22) и (1.24), если из-
вестно начальное поле скоростей в струе. Относительная
абсцисса полюса основного участка струи s0 и относи-
тельное расстояние до переходного сечения snep до на-
стоящею времени изучены недостаточно.
Единственное аналитическое решение для этих вели-
чин было дано Г. Н. Абрамовичем для случая началь-
ного поля скоростей, состоящего из центральной части
равномерной скорости и скоростей у стенок сопла, умень-
шающихся по закону У7степени.
Относительная абсцисса полюса основного участка
струи «о может быть вычислена по формуле для относи-
тельной осевой скорости:
для плоской струи
;o = s-14,4po/^c;
для струи круглого сечения
J0=S'-12,4/M4;
для струи кольцевого сечения
s0 = s'-14,4P0/(1 +?5Ц)^С.
Здесь значения s, р0 и о0с принимаются по данным
опыта. Следует указать, что, согласно опытам, скорости
в струях с неравномерным начальным полем скоростей
затухают быстрее, чем в струях с равномерным началь-
ным полем скоростей.
Сравнивая формулы (8.40) — (8.42) с формулами,
приведенными в табл. 8.1—8.3, замечаем, что они отли-
чаются от них наличием у формул для оср, ооо и L ко-
эффициента |/ZPo, у формулы _для Е — коэффициента
₽о VРо/ао, а также разности s—s0 (где s0<0) вместо s.
Учитывая, что в формулы для струи с неравномерным
полем скоростей входят три неизвестные величины,
а именно р0, а0 и s0, было предложено пренебречь вели-
чиной s0. Однако просто отбросить эту величину нельзя,
так как тогда в струях с неравномерным начальным по-
лем скоростей скорости будут медленнее затухать, чем
в струях с равномерным полем скоростей, поскольку
Ро>1, что противоречит опытам. Поэтому, отбрасывая
в формулах величину sOl следует ввести поправочный
коэффициент 1.
8-741 113
В таком случае формулы для струй с неравномерным
полем скоростей будут отличаться от формул для струй
с равномерным полем скоростей наличием для относи-
тельной полуширины или радиуса коэффициента g, от-
носительных скоростей — коэффициента g 7 р0, отно-
сительного расхода — коэффициента / f}0/g и относи-
тельной энергии — коэффициента gp0 V Po/cto- Величина
совершенно не изучена.
Наибольший интерес для вентиляции представляет
зависимость для скорости на оси, которая с введением
указанных коэффициентов запишется для плоской струи
и для струй круглого и кольцевого сечений соответствен-
но следующим образом:
3,8g/К _ 12,4g 77”
т'ое — ; е»с — _ >
7 s
- 3,8g 77 3,8g 1'77
V Q С ~~~~ " ~ 1
7(1 + s/sI() s S
ИЛИ
»ос = Atvjyr; t>oc = Л1’-,/'5,'
Гос = A^/s,
где Л1== 3,8g Л2 = 12,4g/Оо!
= 3,8 7ро5ц В„.
Коэффициенты At, А2 и А3 обычно устанавливаются
экспериментально для каждого насадка, из которого
вытекает струя.
§ 37. Некоторые случаи особых струй
Струя иногда по выходе из отверстия претерпевает
сжатие, а затем за счет турбулентности — расширение
(рис. 8.6). В таком случае все ранее выведенные расчет-
ные формулы справедливы для участка струи, располо-
женного справа ог сжатого сечения.
При расчете же бывают заданы ширина или ра-
диус отверстия и средняя скорость воздуха в отвер-
стии. Поэтому при пользовании расчетными формулами
для таких струй вначале необходимо определить шири-
ну или радиус сжатого сечения и скорость в нем.
114
Как известно, пло-
щадь сжатого сечения
= е/; отв,
где е — коэффициент сжатия
струи; foTs— площадь отвер-
стия.
Из этой зависимости
вытекает, что полушири-
на струи и радиус сжато-
го сечения определяются
по формулам:
Вд — е50тв; ^о = РЛё”^отв-
(8.43)
Рис. 8.6. Схема струи с начальным
поджатием
Скорость в сжатом сечении
^ОТВ Чотв (
р — Г’отв,
Fg е
(8.44)
где цОтв — средняя скорость в отверстии.
В формулы для струй вместо расстояния s надо вве-
сти величину s—As, где As — расстояние от отверстия до
сжатого сечения. Однако величина As незначительна и
ею можно пренебречь.
Таким образом, при расчете таких особых струй вна-
чале по формулам (8.43) и (8.44) определяются полу-
ширина струи или радиус сжатого сечения, а затем ис-
пользуются формулы, приведенные в табл. 8.1—8.3.
Рассмотрим струи, отличающиеся от окружающей их
среды концентрацией примесей. Исследуем, как изме-
няется средняя концентрация примесей по течению струи.
Обозначим средние концентрации в струе и в среде со-
ответственно через сср и сокр. В таком случае относи-
тельная избыточная средняя концентрация примесей мо-
жет быть представлена в виде
J (с — Сокр) dL
Сер — сокр _L
Со Сокр (с0 с0Кр) 5
где со — средняя концентрация примесей в начале струи; с — кон-
центрация в любой точке поперечного сечения струи.
Заметим, что избыточное содержание примесей в раз-
личных поперечных сечениях струи одинаково. Поэтому
8*
115
справедливо следующее равенство:
I” сокр) dL = (с0 сОкр) Т-о-
L
Заменяя в ранее написанной формуле интеграл пра-
вой частью последнего равенства и производя сокраще-
ние, получаем
с0 сОкр L
Как видим, изменение средней избыточной концент-
рации примесей по течению струи обратно пропорцио-
нально относительному расходу.
Пример 8.1. Определить параметры воздушной струи на рас-
стоянии 4,5 м от выходного отверстия диаметром 0,3 м. Поле скоро-
стей на выходе равномерно и характеризуется скоростью 8 м/с.
Температура подаваемого воздуха равна температуре окружающего
воздуха.
Решение. Поскольку начальное поле скоростей равномерно,
коэффициент Ро—1, относительная абсцисса основного участка
струн So=O.
Находим относительное расстояние
s = s/R0 = 4,5/0,15 = 30 > 12,4.
Определяем начальный объемный расход воздуха
Z.o = 3,14-0,152-8 = 0,365 м3/с
И начальную кинетическую энергию
1,2-82
£о = 0,365 —---- =0,365-38,4 = 14 Вт,
0 2 ’
где 1,2 — плотность воздуха, кг/м3.
Вычисляем по формулам, приведенным в табл. 8.2, для основного
участка струи:
£= 0,22-30 = 6,6; цср = 3,2/30 = 0,107;
уос = 12,4/30 = 0,413; L = 0,155-30 = 4,65;
Отсюда
R = 6,6-0,15 = 0,99 м; оср = 0,107-8 = 0,856 м/с;
ц00 = 0,413-8 = 3,4 м/с; L = 4,65-0,365 — 1,7 м3/с;
£ = 0,214-14 = 3 Вт.
116
Пример 8.2. Определить для условий предыдущего примера ра-
диус круга на расстоянии 4,5 м от выходного отверстия, в пределах
которого скорости превышают 0,5 м/с.
Решение. Используем аналитическую зависимость Шлихтии-
га (8.1), из которой следует:
r — R
2/3
= 0,7 м.
ГЛАВА 9
СВОБОДНЫЕ НЕИЗОТЕРМИЧЕСКИЕ СТРУИ
§ 38. Схема неизотермической струи
Неизотермическая струя образуется в том случае,
когда температура воздуха в струе на выходе из отвер-
стия t0 отличается от температуры окружающего возду-
ха /окр. Поскольку такая струя легче или тяжелее объ-
ема вытесненного ею воздуха, то по закону Архимеда
она будет всплывать или тонуть в окружающем возду-
хе. При этом траектория струи искривляется.
За основу излагаемой ниже теории свободных неизо-
термпческих струи принята
бодных изотермических
струй.
Схема неизотермиче-
ской струи нагретого воз-
духа, вытекающего из от-
верстия под углом 6о к
горизонту, приведена на
рис. 9.1. Границы струи
криволинейны. В струе
имеются начальный и ос-
новной участки с разде-
ляющим их переходным
сечением. На начальном
участке происходит пере-
стройка полей скоростей
и температур в поля ос-
новного участка.
Начальный участок
неизотермической струи
в настоящее время плохо
упрощенная теория сво
Рис. 9.1. Схема нагретой
струи, выпущенной под уг-
лом к горизонту
117
изучен. Поэтому в дальнейшем будем рассматривать
только основной ее участок, полагая, что вначале струя
имеет равномерные поля скоростей и температур. Рас-
ширение основного участка неизотермической струи при-
нимается таким же, как и расширение основного участ-
ка изотермической струи.
На оси струи основного участка скорость непрерыв-
но уменьшается. С удалением от оси к периферии ско-
рость также непрерывно уменьшается и на границе
струи становится равной нулю. Изменение относитель-
ной скорости v в поперечном сечении основного участка
струи принимается по Шлихтингу [см. формулу (8.1)].
Изменение относительной избыточной температуры
в поперечном сечении основного участка струи прини-
мается по Тейлору:
— Д//Д/Ос— 0 ^окр)/(^ос — ^окр) —> (9.1)
где t — температура в любой точке поперечного сечения струи; toc —
температура на оси струн того же сечения; /Окр — температура окру-
жающею воздуха.
Статическое давление изменяется по длине струи и
не равно статическому давлению окружающего воздуха.
Для отмеряемого по искривленной оси струи на рас-
стоянии s от отверстия элементарного слоя толщиной
ds можно написать следующие уравнения количества
движения:
в проекциях на ось абсцисс
(К + dK) cos (0 + d0) — /< cos 0 = 0;
в проекциях на ось ординат
(К + dK) sin (0 + d0) — К sin 0 = Ra - (Ra + dRa),
где К — количество движения, проходящее через сечение, удаленное
на расстояние s от отверстия; /?.,— архимедова сила; 0 — угол меж-
ду осью струи в сечении s и осью абсцисс.
Преобразовывая оба эти уравнения количества дви-
жения, а именно заменяя косинус и синус суммы двух
углов, перемножая выражения в скобках, учитывая, что
cos<10 = l; sindO=d0; sin BdB =—dcosB; cosd0 — sin 0,
и отбрасывая бесконечно малые величины второго по-
рядка, соответственно получим
d (К cos 0) = 0; (9.2)
d (К sin 9) = ~ dRa. (9.3)
118
Количество избыточного тепла по длине струи оста-
ется неизменным:
Q = Qo> (9.4)
где Q — избыточное количество тепла, проходящее в сечении s;
Qo — то же, в начале струи.
При изучении неизотермических струй дополнитель-
но вводятся следующие коэффициенты:
коэффициент поля избыточных температур
(9’5)
Д/ос ДгОс г J J
F О
температурный аналог коэффициента Буссинеска
1
„ д/Сп 1 С if_____________________________
Рд/ = ~~~ = Р ^df = -тт—- Д/ vdf, (9.6)
A^cpl ^cpi^cp J J
F 0
где Д/Ср(иД/Ср — средняя избыточная температура в поперечном се-
чении струп соответственно по площади и по расходу; F— площадь
поперечного сечения струи.
На основе описанной схемы неизотермической струи
и ее особенностей установим зависимости для основно-
го участка, а также выявим уравнение для определе-
ния искривления оси различных струй.
§ 39. Плоская
неизотермическая струя
Из бесконечно длинной
щели постоянной ширины
под углом Оо к горизонту
вытекает нагретый воздух,
образуя искривленную
струю (рис. 9.2). Поля ско-
ростей и температур на вы-
ходе из щели равномерны.
Начало координат поме-
стим посередине ширины
щели, ось абсцисс х напра-
вим горизонтально, а ось
ординат у—вертикально
(навстречу силе тяжести),
Рис. 9 2. Схема нагретой
плоской струи
119
Относительная полуширина струи
B = BIBn = 0,22s,Bo = 0,22s, (9.7)
где s = s/Bo— относительное расстояние от сопла до рассматриваемо-
го сечения, отмеряемое по искривленной оси струи; Во — полушири-
на ше in
Относительную среднюю скорость установим, введя
понятие относительного количества движения:
к- х _ PpWcp К« Ро25о ао Отсюда
ьср = ^Н/ ЯО V Т7Т- м
Относительная скорость на оси
Vqc —
Ср С___। -__________। 1 / I Ро К
v9 k *ср k V ₽ р в
(9.9)
Относительную среднюю избыточную температуру
найдем из уравнения (9.4):
ср2ВиСр Л/Ср =
где с — удельная теплоемкость воздуха.
Отсюда _______
А? _ _ Ро * 1 / о Ро 1 Q . m
Д/о - р Всср ~ |/ Р р КВ • (9J0)
Относительная избыточная температура на оси струи
__ Д^ос Д^сР! Д^р____1___ ,т
ос~ д/0 - Д/ср, Д/ср’ Д/о ~ Waz Лср
или
(9">
Относительный объемный расход
1 = Г==^==®^р=1/'т'7^5' <9л2)
^0 ^^0^0 * Р Р
Относительная кинетическая энергия
£ а /(р0/р)3 К3
Е== aL^ . (9.13)
ьо Rl/fiB
’20
Входящие в зависимости (9 8) — (9.13) коэффициен-
ты имеют следующие значения: £=0,45; [3= 1,56 н а —
=2,68 (см. § 33).
Значения коэффициентов и вычисляем, ис-
пользуя формулы (9 5) и (9.6), где v принимаем по за-
висимости (8.1), а Л/ — по зависимости (9.1), и пола-
гая, что У = Ъ\ угр = В и df—db. В таком случае:
1
— j (1 — ?’5M& = 0,6;
и
= 51,5)3
о
0,368
0,45-0,6
= 1,36.
Отношение плотности
состояния газа, равно:
воздуха, согласно уравнению
Ра __ Ро 71__Т______Т Токр Т'окр
Р Р То То ТоКр То То
где ро и р — давление в начале струн н на расстоянии $ от щели;
То, Т, Тоир — абсолютные температуры воздуха в начале струи, на
расстоянии s от щели и в окружающем воздухе (здесь принято, что
р<.«р и Т/То„р«1).
Подставляя в полученные для струи зависимости
значения констант, заменяя отношение плотностей и под-
ставляя В, получим следующие расчетные формулы:
(9.14)
121
В эти формулы входят неизвестные величины К и $.
Определяем вначале К. С этой целью в струе на рас-
стоянии s от сопла выделим элементарный слой толщи-
ной ds (см. рис. 9.2) и применительно к нему напишем
уравнения количества движения в проекциях на оси ко-
ординат:
d (К cos 0) = 0;
d (К sin 0) = (рокр — Pcpi) g^Bds,
где 0—текущий угол наклона оси струи к оси абсцисс; pCpi — сред-
няя по площади сечения струи плотность воздуха.
Из первого уравнения количества движения полу-
чаем
К cos 0 — Ко cos 0О
или
К = cos 0o/cos 0.
Учитывая, что
Рокр Pcpi — р 1 (Рокр ~
F
FR J ТокрГ
F
Рокр
F
= д^
Т'окр
1 р Р f 1 1
F R J \Токр “ Т
F
F
,________1 Рокр Л.
CP1 — 3л/ T СР’
Г окр
Рокр Ы
В J ^окр
второе уравнение можем представить в виде
d (К si п 0) —
2gB Рокр
Рд^ Т’окр
Л Ар ds.
Разделив это уравнение на А'0=р02В0^, получим
_ gBBa
d(KsinO)=£—*-
Рд/
Рокр А^сР ДА
7’окр Токр Uq
ds.
Вводя число Архимеда
Аг0 = gBQ Д^0/7’окрOq,
можем написать
d (К sin 0) = ~ В^р ds.
РД/ Ро

Согласно выражению (9.10), имеем
/Рро/р _ 1 Z Р Ро ~
ср УКВ ’ к В Рокр
поэтому получим
./т> ,,, . Л. ' РАг0 1 / Рокр т;,-
у Л 4(6 sin 6) =-— j/ —-—Bds =
у/0,226
Рд/ АГ°
или
/Td(Ksin6) = О,432Аго 1/ -^-s ds. (9.15)
Г ' окр
Подставляя в выражение (9.15) K=cos 0o/cos 0, бу-
дем иметь
/cos 0а / cos 0П \ i / Тл
---d ------7 sin О = О,432Аго / —2- sds
cos 0 (cosO / 0 V Токр
или
3/2 Лв
cos3/2 е„
—g7I-=O,432Aro l/y^sds.
COS V F 1 окр
Интегрирование этого дифференциального уравнения
дает
,,, I 2 sin 0
cos 00 (т cos3/2 е
de
cos1/2 0
= О,288Аго ]/ -A-s^+c.
J окр
В этом равенстве интеграл при cos0=z приводится
к интегралу от биномиального дифференциала. Соглас-
но теореме Чебышева, он не выражается в элементар-
ных функциях. Приближенно он может быть принят рав-
f rf0
ным 0. При этом ошибка в вычислении —— не пре-
J COS /20
взойдет 2%. Следовательно, справедливо
,/9 / 2 sirl'O 1
C0S ' 00 Usings ‘ 3
-ZA--s3/2+c.
vKp
123
Постоянную интегрирования следовало бы искать из
условий, существующих в переходном сечении, т. е. при
s«— Snep и 0=0Пер. Однако ни относительное расстояние
до переходного сечения, ни угол наклона оси струи к
горизонту в этом сечении неизвестны. Поэтому опреде-
лим постоянную интегрирования приближенным путем.
С этой целью распространим последнюю зависимость и
на начальный участок струи. В этом случае, положив
s = 0, имеем 0=0О, и тогда
с = -|“ sin 0 -р 0e cos3/2 0О.
О и
В результате будет справедливо равенство
COS 0П \3/2 -1/9 „
----— sin 0 — sin 0О + 0,5 (0 — 0О) cos3'2 0О =
COS0 /
Т0
Т'окр
(9.1^
Заменяя здесь
„ cos 0.д „ ч / cos2 0л
cosO--^-; sin0=±j/ 1--=г-
А г №
I г—---------- / cos (
= ± у № — cos2 0О ; 0 — £ arccos (—=-
К ( л
можем написать
± К (А2 — cos2 0о) — siп 0о + 0,5 | ± arccos
cos 0о
= 0,432Ar0 1/ -^-s3'2,
v Т’окр
0O j cos3'2 0ft —
(9.17)
где плюс берется при 0>О и минус — при 0<О.
По этой формуле построен график зависимости р
3 /------_
от 1/ Аг2—s при разных значениях 0О (рис. 9.3).
V Т'окр _
Выявим теперь зависимость для s. Как известно,
у = J sin Ods,
где у=у/В0.
124
Рис. 9.3. График изменения относительного количества движения в
плоской струе
Из уравнения (9.16) имеем
3 /*' ' '
1/ Arg s = 1,75С°$в° 'j sinO —sin0o +
V ° Токр [Д cos 0 )
12/3
(9.18)
Определяя из_ этой формулы ds и подставляя ее в
зависимость для у, получим
Arg -р- у = 0,583 cos3/2 0О X
Лэкр
125
е
х (
(2 + sin2 0 4- cos"1” O’) sin 0d0
(9.19)
cos 0„ \3/2
----— sin 0 — sin 0О + 0,5 (0 — 0О) cos3/2 0О cos5,20.
0.
По формуле
(9.18) были вычислены значения
Гр -
Гокр
а по формуле
разных 9 и 0а.
Используя полученные
МОСТЕ
(9.19) —значения
значения,
1/ Аг2-Д~(/ при
Г ' окр
построили зависи-
3/.---- ----------------
1/ Аг? ОТ 1/ Лг’ЛЧ
» JОКр F i QKp
при разных 0о (рис. 9.4).
Уравнение искривления оси струи
х — J cos Ods,
где х=х1Вв.
Подставляя сюда ранее найденное ds, получим
Аг^ —х = 0,583 cos3/2 0ОХ
г 'окр
0
X С, (2+ ОМ (9 20)
J (cos O0/cos 0)3/2 sin 0—sin 0о+О,5 (9—Оо) cos 3/2 0О cos3/20
о&
Уравнения (9.19) и (9.20) определяют траекторию
оси струи. По этим уравнениям была построена зависи-
мость
3 у--------—
V Г0/7^р у от]/
г 1 окр
при разных 0о (рис. 9.5).
Рассмотрим частный случай, когда 0О — ±90°, т. е.
когда струя выпущена вертикально вверх или вертикаль-
но вниз. В этом случае формулы (9.7) и (9.14) сохра-
нятся без изменения, а зависимость (9.17) упростится
до вида
± Vк = [± 1 + 0,432Аг0 /Т0/Токр ]1/3, (9.17а)
126
где плюс берется при 0о=9О° и минус^—при 0о =—90°,
При этом во всех расчетных формулах s=y.
В заключение отметим, что при выходе из сопла
охлажденного воздуха выведенные формулы остаются
справедливыми, однако величина критерия Архимеда
будет отрицательной. В этом случае можно пользовать-
ся всеми приведенными графиками, но перед критери-
ем Аг,, надо ставить знак минус на всех трех графиках
(см. рис. 9.3—9.5), положительные углы 0О и положи-
тельную ось у считать
отрицательными, а отри-
цательные углы 9о и от-
рицательную ось у — по-
ложительными (см. рис.
9.4 и 9.5).
Необходимо отметить,
что все расчетные форму-
лы справедливы и для
щели конечной длины,
если отношение длины
щели к ее ширине не ме-
нее 20. В противном слу-
чае струя трансформиру-
ется в струю круглого се-
чения.
Рис. 9.4. График изменения отно-
сительного расстояния по осн пло-
ской струн
Рис. 9.5. График зависимости координат оси плоской струи
127
Следует также заметить, что при пользовании фор-
мулами относительное расстояние s должно быть боль-
ше относительного расстояния до переходного сечения
8перЛ которое, однако, неизвестно. Поэтому рекомендует-
ся 5Пер принимать в первом приближении как для плос-
кой изотермической струи, т. е. snep=14,4.
§ 40. Неизотермическая струя круглого сечения
Из круглого отверстия под углом 0О к горизонту вы-
текает нагретый воздух и образует искривленную струю
(см. рис. 9.2, заменяя Во и В на /?о и R). Поля скоро-
стей и температур на выходе из отверстия равномерны.
Начало координат поместим в центре выходного се-
чения сопла, ось абсцисс х направим горизонтально,
а ось ординат у — вертикально (навстречу силе тяже-
сти). Относительный радиус струи
А? == O,22s//?o = 0,22s, (9.21)
где s=s//?o — относительное расстояние от сопла до рассматриваемо-
го сечения, отмеряемое по искривленной оси струи; Ro — радиус от-
верстия.
Относительную среднюю скорость установим из
уравнения относительного количества движения:
Ко р0 Vq Р»
Отсюда
(9.22)
Относительная скорость на оси струи
= Еяс._ j_i/j_Po_A
V,y k С'СР = ~ V Р Р £2
(9.23)
Относительную среднюю избыточную температуру
найдем из уравнения постоянства избыточного тепла в
струе. Согласно выражению (9.4),
еря/?2 есрД/ср = ср0 nR20 v0 Д?о,
где с — удельная теплоемкость воздуха.
128
Отсюда
Д7ср=-^- = -£й--=^—= 1/ ₽ — (9.24)
Относительная избыточная температура на оси струи
7 Д^ос Д^ос Дс^р1 Д^со I
Д'ос = “ ----------И-
Д‘О
а^ср ________!____ду
Д/cpi Mo kbt ₽д; ср
или
1
Ро 1
^ос~ Wa< к ₽р W‘
Относительный объемный расход
L - — = —2'С'С-Р - 02 V
L — J п2 ~~ К СР
Относительная кинетическая энергия
р Е тг> _л К(р0/р)3Х3
£ - т~ =а£ % ;f~
(9.25)
(9.26)
(9 27)
^K~R\
Входящие в зависимости (9.22) — (9.27) коэффици-
енты имеют следующие значения: fe=0,258; |3 = 2,02 и
(1=4,06 (см. § 34).
Значения коэффициентов ks/ и рд( вычислим, ис-
пользуя формулы (9.5) и (9.6), где А? принимаем по за-
висимости (9.1), a v — по зависимости (8.1), и пола!ая,
что у—г, yrP=R и df — 2rdr. Тогда
1
£д/ = 2 J (1 — r1,s) rdr 0,428;
о
1
2 2-0,09
В.. = -Гт— 1 (1 — ri,5)3rdf =---------= 1,63.
^Д/ J 0,258-0,428
о
Отношение плотностей (см. § 33) заменяем отноше-
нием абсолютных температур
Ро/р Т’окр/Т’о-
Подставляя в полученные для струи зависимости
значения констант, заменяя отношение плотностей и под-
ставляя R, будем иметь следующие расчетные формулы.
9—741
129
В эти формулы входят неизвестные величины К и s.
Определяя их таким же образом, как и для плоской не-
изотермической струи, получим:
± К (.К2 — cos2 0О — sin 0О + 0,5 ( ± arecos
COS09
К ~
О0 I cos3,2 Оо —
= 0,144 Аг0 1/ -Д-?; (9.29)
У ' окр
У Аг01/ -Д-«=2,64Х
’ У 'окр
X 1/ (-^Дг-ГДпО — sin0О +0,5(0 — 0О) cos3'20o; (9.30)
у \ cos 0 /
=0,66 cos3'2 Оо X
е
х
(2 + sin2 0 + cos5/2 0) sin 0 dQ
— .. .... . J
| 1 sin 0 — sin 0O + 0,5 (0 — 0O) cos3'2 0O cos5'2 0
(9.31)
е
X
' ------5— x =0,66 cos3'2 0o X
Т’окр
(2 + sin2 0 + COS5/2 Q) (ft
- sin 0О + 0,5 (0 — 0о) cos3'2 0e cos3'2 0
(9.32)
е,
где
130
^Г0 ^о^окр
По формуле (9.29)',
по формулам (9.30) и
(9.31), а также по
формулам (9.31) и
(9.32) построены гра-
фики, приведенные со-
ответственно на рис.
9.6, 9.7 и 9.8.
Рассмотрим част-
ный случай, когда
0о=±90°, т. е. когда
струя выпущена вер-
тикально вверх или
вертикально вниз. В
этом случае формулы
(9.21) и (9.28) сохра-
няются без изменения,
а зависимость (9.29)
упростится до вида
±/К=[± 1 + 0,144 АгвХ
Х1/Га/Гокр?]1/3. (9.29а)
где плюс берется при
0о==9О° и минус при
0о=—90°. При этом во
всех расчетных форму-
лах s=y.
В заключение отме-
тим, что при выходе из
сопла охлажденного
воздуха выведенные
формулы остаются
справедливыми, одна-
ко величина критерия
Архимеда будет отри-
цательной. В этом слу-
чае можно пользовать-
ся всеми приведенны-
ми графиками, но пе-
ред критерием Аг0 на-
до ставить знак минус,
полагать положитель-
ную ось у направлен-
Рис. 9.6. График изменения отно-
сительного количества движения в
струе круглого сечения
Рис. 9.7. График изменения отно-
сительного расстояния по оси
струи круглого сечения
9*
131
Рис. 9.8. График зависимости координат оси струи круглого сечения
ной вниз, а отрицательную — вверх (см. рис. 9.7 и 9.8),
а также на всех трех графиках (см. рис. 9.6—9.8) поло-
жительные углы 0о считать отрицательными.
Следует сказать, что расчетные формулы применимы
и для струи, вытекающей из прямоугольного отверстия
с отношением сторон менее 20 и вообще из любого от-
верстия с отношением сторон, близким к единице, если
вместо А*о ввести вычисляемое по формуле
== |/ -^-Го = 0,565/ЁЁ
где Fo — площадь отверстия.
При пользовании расчетными формулами необходи-
мо, чтобы s>Snep, где Sne£—расстояние до переходного
сечения. Ввиду того что snep неизвестно, рекомендуется
его принимать таким же, как и для изотермической
струи круглого сечения, т. е. snep —12,4.
§ 41. Неизотермическая струя
кольцевого сечения
Из кольцевой щели под углом 0о к горизонту выте-
кает нагретый воздух и образует искривленную струю
(рис. 9.9). Поля скоростей и температур на выходе из
кольцевой щели равномерны. Начало координат поме-
стим в точке пересечения осей струн, ось х направим
132
горизонтально, а ось у
вертикально (навстречу
силе тяжести). Относи-
тельная полуширина струи
В = В/Во = O,22s/Bo = 0,22s,
(9.33)
где s=s/B0 — относительное
расстояние, отмеряемое от на-
чала координат по искривлен-
ной оси струи; Во — полуши-
рина кольцевой щели.
Относительную сред-
нюю скорость установим
из уравнения относитель-
ного количества движения
Рис. 9.9. Схема нагретой струи
кольцевого сечения
_ Рр2ях2Л-4р _ р
Ка Р02яХц 2S0 "о Ро СР
где х = х/В0 и хц = хц/Во— относительные абсциссы; х и хц ~ абс-
циссы точек, лежащих на осп s в произвольном н начальном сечениях
струи.
Отсюда ______________
иср = -^- = ]/' j--Рв- . (9.34)
V ₽ Р х В
Относительная скорость на оси струи
500 = — = 4^ = 4 iZ— — — — • (9-35)
v» k k V b P x в
Относительную среднюю избыточную температуру
найдем из уравнения постоянства избыточного тепла в
струе. Согласно выражению (9.4),
ср 2лх 2£цср Д/ср = ср0 2лхц 2Ва о, Д/о,
где с — удельная теплоемкость воздуха.
Отсюда
= = = 1/ р_Ри_А_1_. (9.36)
&‘о Р х Bvcp г Р х В К
Относительная избыточная температура на оси струи
•7 __ Д^ос _ ДДзс A/Cpi Д^ср _ 1 .7
°С Д/о Д/ор1 Д/Ор Д/о Рдт °р
133
или
Относительный объемный расход
Z = — = _g?l2ZfoeP . = JL= д/ J__Po__£_
Ло 2лхц 2В0 и0 хц V р р х
(9.37)
ВК .
(9 38)
Относительная кинетическая энергия
Е а]/-^-(рв/р)3К3
Е = = a L ;2ср = ---Х— --------- . (9.39)
£° Ру рв
Входящие в зависимости (9.34) — (9.39) коэффици-
енты имеют следующие значения: £=0,45; р=1,56 и
а = 2,68 (см. § 35).
Значения коэффициентов kA, и рд/ не требуется вы-
числять, так как при рассмотрении изотермической струи
кольцевого сечения было обнаружено, что k, (3 и а име-
ют те же значения, что и у плоской изотермической струи,
т. е. kAi —0,6 и рд — 1,36.
Отношение плотностей (см. § 39)
Ро/р ~ Т'окр/Т’о-
Подставляя в полученные для струи зависимости
значениЯ-Констант, заменяя отношение плотностей и под-
ставляя В, будем иметь следующие формулы:
(9.40)
134
В эти формулы входят неизвестные величины К и s.
Определяя их таким же образом, как и для плоской не-
изотермической струи, получим:
±1^К (№ — cos2 0О) — sin 0О + 0,5 ( + arc cos
cos 0О
К
— 0ujcos3/2Oo =
(2 -f- sin2 0 -f- cos5/2 0) sin 0 d0
| sin 0 — sin 0O 4- 0,5 (0 — 0O) cos3,2 0O cos5/~0
(9.43)
e .__________________(2 4- sin2 0 4- C0S5/2 0) de________________
X I -j f 7cos0o \3/2
J |/ \T0S~g~I sin0 — sin 0O-f-0,5 (9 — 09) cos3/2 0e cos3/2 0
(9.44)
ГДС АГ0 = ^‘$0Д/д/ТокрУд<
135
По формуле (9.41), по формулам (9.42) и (9.43),
а также по формулам (9.43) и (9.44) построены графи-
ки, приведенные соответственно на рис. 9.10, 9.11 и 9.12.
Рис. 9.10 График изменения
относительного количества
движения в струе кольцево-
го сечения
Рис. 9 11. График измене-
ния относительного расстоя-
ния по оси струи кольцевого
сечения
Рис 9 12. График зависимости коордииш оси струи кольцевого
есчспгя
136
Рассмотрим частный случай, когда 0о—±90°, т. е.
когда струя выпущена вертикально вверх или вниз.
В этом случае формулы (9.33) и (9.40) сохраняются без
изменения, а зависимость (9.41) упростится до вида
+ ) Х =
1 0,324
Аг0
(9.41а)
где плюс берется при 0о=9О° и минус — при 0О = —90°.
При этом во всех расчетных формулах s=y.
Заметим, что при выходе из кольцевой щели холод-
ного воздуха выведенные формулы остаются справед-
ливыми, однако величина критерия Архимеда будет от-
рицательной. В этом случае можно пользоваться всеми
приведенными графиками, но на графиках (см. рис. 9.10—
9.12) положительные углы 0О и положительную ось ор-
динат надо считать отрицательными, а отрицательные
углы 0о и отрицательную ось ординат (см. рис. 9.11 и
9.12) — положительными.
Необходимо отметить, что при пользовании расчет-
ными формулами относительное расстояние s должно
быть больше относительного расстояния до переходного
сечения Зпер- Поскольку Snep для неизотермической струи
неизвестно, то рекомендуется его принимать таким же,
как и для изотермической струи кольцевого сечения.
§ 42. Упрощенные зависимости
для неизотермических струй
В случае неизотермических струй справедливы рас-
четные формулы (9.14), (9.28) и (9.40), а зависимости
для определения относительного количества движения,
относительного расстояния, а также уравнения искрив-
ления оси струи могут быть упрощены. Выведем эти
упрощенные зависимости для трех ранее рассмотренных
струй.
Плоская струя. Используя зависимость (9.15) и за-
меняя в ней
sin 0 — )/ 1 — cos2 0 = / 1 — cos3 0n/\ = -Jr- /к2 — cos20o,
X
получим
V К d [ К'1 — cos2 0O =- 0,432Aro )/Z Tq/Toup yAs ds.
137
Если струя слабо нагрета или охлаждена, то значе-
ние К будет близко к единице. Приняв К~ 1 и про-
интегрировав последнее уравнение, имеем
К2-cos2 0О =а I 0,288Аг0 1/ —Г° s3'2 + с .
Постоянную интегрирования находим из условия, что
К— 1 при s=0, а потому с — У 1—cos20o = sin 9о. В та-
ком случае
УК = [cos20o-j- (о,288 Аг0/Т0/Токр;3/2+ sm09)2]1/4. (9 45)
_ Опять используя зависимость (9.15) и заменяя в ней
7< = cos 9o/cos 9 и sin Q—dyjds, получим
=°.432A^o i/ZZZ
V COS0 COS0 £ ] ° У T0KpySdS-
Если струя слабо нагрета или охлаждена, то вели-
чина 9 будет близка к 9о- Положив 0 = 0О, будем иметь
d (dy/ds) — 0,432Аго }/ Тй/Т0Кр Уs ds.
Дважды интегрируя это уравнение, можем написать
У — 0,115Аг0 1 / — s5 ‘ -j- s с2.
г ' окр
Постоянную интегрирования находим из условий:
1) г/=0 при 5=0, что дает с2=0; 2) y=ssin90
при Аго = О, что дает c1 = sin9o. Поэтому справедливо
~у = s sin 0О + 0,115Аг0 У Т0/Токр s512. (9 46)
Уравнение искривления оси струи можно получить
в следующем виде, если в уравнении (9.46) положить
S"=T/cos 9q:
у~у~ / х У2
у = х tg 0„+0,115Аг0 1/ —-7- • (9.47)
V T0KV \ cos0o /
Струя круглого сечения. Проводя такие же выклад-
ки, как и для плоской неизотермической струи, получим:
Ук= [cos2 0О + (о, О96Аго У Т0/Токр ? + sin 0О)2]1/4; (9.48)
у — s sin 0О О(О32Аго Т$1Токр s3» (9.49)
— х tg еоo,O32Ar0\f <9-50)
г Т^окр \ Cos % /
138
Струя кольцевогосечения. Проводя такие же выклад-
ки, как и для плоской неизотермической струи, получим:
§ 43. Воздушные фонтаны
Воздушным фонтаном можно назвать неизотермиче-
скую охлажденную струю, выпущенную под положитель-
ным углом к горизонту. Название такой струе дано по
аналогии с водяным фонтаном. В обоих случаях наблю-
дается сначала подъем струи, а затем ее опускание.
Воздушные фонтаны характеризуются в основном
тремя величинами, а именно: расстоянием до максиму-
ма их подъема, высотой подъема и расстоянием до точ-
ки пересечения оси струи с уровнем, на котором струя
была выпущена, так называемой дальнобойностью фон-
тана. Эти величины, вычисленные по зависимостям для
неизотермических струй, приведены в табл. 9.1—9.3.
Таблица 9.1. Характеристики плоского фонтана
Угол 0О, град Значения характеристик
3 /~ п 'г 1 / Аг2 1/ ° т в У 1 окр 1/4'"Г^5- У 1 окр 3 / Т 1/ У 1 окр
30 1,61 0,43 2,38
60 1,245 1,215 2,3
90 0 1,75 0
139
Таблица 9.2. Характеристики фонтана круглого сечения
Угол в , град Значения характеристик
V V I7 Дкр
30 1,87 0,78 3,42
60 1,64 1,8 3,04
90 0 2,64 0
Таблица 9.3. Характеристики фонтана кольцевого сечения
Угол град ^на ч евия характеристик
/ ^1/ Л =• г ц у окр |/ ^1/ г ьц у 1 окр
30 1,25 0,52 2,28
60 1,1 1,2 2,03
90 0 1,76 0
Для этих трех величин можно вывести упрощенные
формулы.
Плоский фонтан. Уравнение искривления оси плос-
кого фонтана
г/ х tg е0 — 0,115Аг0
(9.54)
Относительную абсциссу вершины фонтана находим,
беря первую производную от у по х и приравнивая ее
нулю. Это дает
хв=2,29
3/~sin2 0О cos3 е0 70ИП
У Ард Та
140
Относительную высоту фонтана находим, беря вто-
рую производную от у по х и подставляя в нее х=хв.
Получаем
V Аг0i, 2 То
Относительную дальнобойность фонтана находим,
полагая в уравнении (9.54) у—О и решая его относи-
тельно абсциссы. В результате получим
'Хл = 4 24-I3/-in26(|CO--a
Из анализа этих зависимостей видно, что высота
фонтана ув наибольшая при 0о=9О°, а дальнобойность
максимальная при 0о=39°1О'.
Фонтан круглого сечения. Уравнение искривления
оси фонтана круглого сечения
у = ~х tg 0О - 0,032Аго ) . (9 55)
У Токр \ cos е0 /
Проведя такие же выкладки, как и для плоского фон-
тана, получим следующие зависимости для фонтана
круглого сечения:
относительная абсцисса вершины
хв = 3,221/*in 0°c°?a5 1/^7 .
' Ar0 г Та
относительная высота
n ..-I/ sin3 0О । /~ Токр
9-ет2’,5(/ ~^у ~
относительная дальнобойность
i, - 5,591Z]/г» .
д ’ г Аг0 V Тп
При этом высота фонтана ув наибольшая при 60 =
=90°, а дальнобойность хд максимальная при 0О=34°55/.
Фонтан кольцевого сечения. Уравнение искривления
оси фонтана кольцевого сечения
141
p = xfgO3 — 0,072 -АГд ]/ f—-- j . (0 SO)
/Тц V T0KV \cos0j
Проведя такие же выкладки, как и для плоского
фонтана, будем иметь следующие зависимости для фон-
тана кольцевого сечения:
относительная абсцисса вершины
хв = 2,15 ]/ sin6°cos26° 1/1,^ ;
Аг0 г То
относительная высота
1 лъ\/ sin 0О 1 / - Т’окр .
относительная дальнобойность
sin0ocos20o -] Токр
Хд = 3<73|/ --------- |/ •
При этом высота фонтана ув наибольшая при 0о=
= 90°, а дальнобойность хд максимальная при 0О =
=34°55'.
Необходимо отметить, что название «воздушный
фонтан» распространяют также и на неизотермическую
нагретую струю, выпущенную под отрицательным уг-
лом к горизонту. Для таких струй справедливы все три
характеристики фонтана, приведенные в табл. 9.1—9.3,
или упрощенные зависимости для неизотермических
струй. Однако во всех случаях перед высотой фонтана
нужно ставить знак минус. Эта величина будет назы-
ваться глубиной фонтана.
Пример 9 1. Определить на расстоянии 1,05 м (по горизонтали)
от сопла высоту подъема струи, скорость и температуру на оси струи,
вытекающей из круглого сопла горизонтально. Диаметр сопла
0,15 м, начальная скорость 2 м/с, начальная температура 133° С,
температура окружающего воздуха 18° С.
Решение. Проводим расчет по формулам (9.28) и графикам
(см. рис. 9.6—9 8).
9,81-0,075(133— 18)
(273+ 18) 22
= 0,0727;
Го - 1 /~273 + 133 , /~ 406 1Я,
Токр V 273 +18 |/ 291
142
у’ _
—°— = К0,0727-1,18 = 0,293;
‘ окр
1,05
х =-------= 14;
0,075
То -
р2—х = 0,293-14 = 4,1,
' окр
По графику (см. рис. 9.8) при 0о=О им_еемУ Агор 7’0/7’окрУ=
= 2,8. Следовательно, </ = 2,8/0,293=9,55 и </=9,55 0,075=0,716 м.
По графику (см. _рис. 9.7) при 00 = 0 имеемР^Аг0 У'т’о/Т’окр S =
=5,5. Следовательно, «=5,5/0,293=18,8.
По графику (см. рис. 9.6) при 0о = О имеем = 1,58.
По формуле для voc и Afoc [см. формулы (9.28)] получаем;
12,4.1,58
«ос = 1Й й , ,о = 0,885; гос = 0,885-2 = 1,77 м/с;
10,0-1,10
9,24
18,8 1,58-1,18
Д/оо = 0,264-115 = 30,3°С;
/00 = 18 4-30,3 = 48,3°С.
1
= 0,264;
‘ Л^оо —
ГЛАВА 10
СВОБОДНЫЕ КОНВЕКТИВНЫЕ СТРУИ
§ 44. Схема свободной конвективной струи
Конвективная, или тепловая, струя возникает над ис-
точником тепла. Тепло от источника передается приле-
гающим слоям воздуха, которые, расширяясь, становят-
ся менее плотными по сравнению с окружающим возду-
хом и поднимаются вверх. Их место занимает воздух из
окружающего пространства, который, нагреваясь, так-
же поднимается вверх. Таким образом, создается кон-
вективная струя. Если мощность источника тепла до-
статочно велика, то вызванная им конвективная струя
будет турбулентна.
Теория конвективных турбулентных струй излагает-
ся в основном по Г. Н. Абрамовичу [1].
143
Наблюдения над подкрашенными конвективными
струями и замеры скоростей в них позволяют принять
упрощенную схему струи, показанную на рис. 10.1. При-
близившись к нагретой поверхности, воздух затем под-
нимается вертикально вверх и образует струю с искрив-
ленными границами ABCD и EFGH.
В конвективной струе различают три участка: раз-
гонный ABFE, переходный BCGF и основной DCGH. Се-
чение BF называют сжатым сечением, а сечение CG —
переходным.
На разгонном участке в основном проявляются ар-
химедовы силы, под действием которых скорость дви-
жения непрерывно нарастает. На переходном участке
происходит перестройка полей скоростей и температур
в поля этих же величин основного участка.
На переходном и основном участках наряду с подъ-
емными силами проявляются силы турбулентной вязко-
сти. Под действием последних струя непрерывно расши-
ряется по течению.
Границы переходного и основного участков BCD и
FGH при их продолжении пересекаются в некоторой
точкеМ, называемой полюсом конвективной струи. Угол
бокового расширения 0 переходного и основного участ-
ков струи так же, как и для изотермических струй, ра-
вен 12°25'.
Разгонный и переходный участки конвективных струй
Рис. 10.1. Схема свободной
конвективной струи
до сих пор плохо изучены.
Вследствие этого в дальней-
шем будет рассматриваться
лишь основной участок струи.
На основном участке струи
наблюдается уменьшение по
течению скорости и темпера-
туры воздуха. Поля скоростей
в поперечных сечениях основ-
ного участка струи удовлетво-
рительно описываются анали-
тической зависимостью Шлих-
тинга (8.1), а поля избыточ-
ных температур — зависимо-
стью Тейлора (9.1).
Если выделить в струе на
расстоянии s от источника
тепла элементарный слой тол-
144
щиной ds, то применительно к этому объему можно на-
писать уравнение количества движения в проекциях на
оси струи:
dK = — dRa, (10.1)
где К — количество движения, проходящего через сечение, удаленное
на расстояние s от источника тепла; Ra — архимедова сила.
Количество избыточного тепла по длине струи сохра-
няется постоянным
Q = Q0, (Ю.2)
где Q — избыточное количество тепла, проходящего через сечение,
удаленное на расстояние s от источника тепла, в единицу времени;
Qo — количество конвективного тепла, выделяемого источником теп-
ла в единицу времени
Для конвективных струй коэффициенты поля скоро-
стей, Буссинеска и Кориолиса, коэффициент поля избы-
точных температур и температурный аналог коэффици-
ента Буссинеска принимаются такими же, как и для не-
изотермических струй.
На основе описанной схемы и уравнений (10.1) и
(10.2) установим зависимости для основного участка
плоской конвективной струи и струи круглого сечения.
§ 45. Плоская конвективная струя
Над бесконечно длинным источником тепла постоян-
ной ширины 2В0 поднимается плоская конвективная
струя (см. рис. 10.1).
Начало координат поместим посередине верхней гра-
ни источника тепла, а ось абсцисс s направим вверх по
оси струи. Полуширину струи определим по формуле
В = (s— sB) tg 0 = 0,22 (s — s0), (Ю.З)
где So — абсцисса полюса струи; на основании опытов установлено,
что so=—2В0.
Среднюю скорость в поперечном сечении струи на-
ходим, используя уравнение количества движения, при-
ходящегося на единицу длины источника тепла;
K = ₽p2Bv2cp.
Отсюда
«ср = 1/К/Рр2В.
Полагая, что р~рокр, где рокр— плотность окружаю-
10—741 145
щего струю воздуха, и заменяя В согласно выражению
(10.3), получим
vcp-]/' o,44BpOItp(s-So) ' (10'4)
Входящее в эту зависимость количество движения
определим из уравнения (10.1), которое применительно
к плоской струе примет вид
dK — (Рокр • Pcpi)
где pcpi — средняя по площади поперечною сечения струи плот-
ность воздуха.
Разность плотностей (см. § 39) представим в виде
1 Рокр ,.
Рокр Pcpi— g ~ “'ср-
НД/ J окр
Подставляя эту разность плотностей в уравнение ко-
личества движения и заменяя В согласно выражению
(10.3), получим
°,44g Рокр . . .
ад — — Д^ср (s — s0) ds.
Среднюю избыточную температуру определим из
уравнения (10.2), которое применительно к плоской
струе примет вид
ср2ВоСр Д^ср = Qo,
где с — удельная теплоемкость воздуха; Qo — количество конвектив-
ного тепла, выделенного единицей длины источника тепла в се-
кунду
При р«рокр имеем
д/ =__________Qo________=_________/pQo_________
ср 0,44срокрГср(« — So) с-/ 0,44рОКр К (s — s0)
В таком случае
°’ 44₽РокР
V КаК =-------7л~т------- г s — sQds.
сРд/ ‘ ОКР
Интегрируя это уравнение, будем иметь
хз/2 тЧ^ррокргОо (s _ So)3;2 + с (105)
срд;Токр
Постоянную интегрирования следует искать исходя
из того, что в переходном сечении s=snep и Л=ЛПер, по-
этому
146
3'2 1^0ftp.il: p gQo , 3/2
ncp~ С₽Д<7ОКР (SneP-S»’ •
Как видим, постоянная интегрирования зависит от
количества движения в переходном сечении. Для его
определения необходимо знать уравнение контура раз-
гонного участка и зависимости для поля скоростей и
температур в горизонтальных сечениях разгонного и пе-
реходного участков струи. Все эти зависимости неизвест-
ны. Вследствие этого Кпер определим приближенно сле-
дующим образом.
Заменяя разгонный и переходный участки струи
объемом постоянного сечения с шириной 2Впср и высо-
той 8цер—s0 и полагая, что по высоте объема средняя
избыточная температура равна /Пер, получим
Кпер = (Рокр — Pnepi) g2Bnep (snep — s0),
где paep i — средняя по площади сжатого сечения струи плотность
воздуха.
Заменяя здесь разность плотностей ранее найденным
выражением, можем написать
Кпер— а Р Л^пер 2ВПер («пер— so)-
2 окр
Избыточную температуру в сжатом сечении найдем
из уравнения (10.2):
А,____________Q»______
Л‘пер —
сРокр •‘Опер ^пер
Подставляя А/пер в предыдущую зависимость, полу-
чим
,z SQ (sneP so)
Лпер- u—y ~ .
ГД' окр пер
Подставляя сюда иПеР согласно выражению (10.4),
имеем
д-3/2 _ У" 0.44 рРокр gQo 3/2
А пер- т (?пер so)
С₽Д/ Токр
Подставляя это значение в зависимость для оп-
ределения с, получаем, что с=0. Следовательно,
2/3
(s —s0).
0,44ррОкр gQp
К =
10*
147
Подставляя полученное значение К в зависимость
(10.4), будем иметь
_ 1 /Л gQo
^Р-|/ 0,44^д/Ронр7окр-
Поскольку £=9,81 м/с2; с = 1 кДж/(кг-°С); (3 = 1,56;
рд/ = 1,36; рокр=1,2 кг/м3 и ТОкр=273, то окончательно
получим
ccp = 0,31Q’/3. (10.6)
Скорость на оси струи
t, =_L„ =— 0,31 Q;/3 = 0,69Q,1/3. (Ю.7)
ос k ср 0,45 ° и
Средняя избыточная температура
д/ -------2о----=-------------О»----------=
Фокр-2Врер 1-1,2-0,44(5 —s0) 0,31 Qq/3
С
= 6,1 . (10.8)
s — «о
Избыточная температура на оси струи
1 6,1 <
-----------------------= 7,5--------. (10.9)
kM^\t 0,6-1,36 (s — s0) s —s0
Объемный расход, приходящийся на единицу длины
источника тепла в секунду:
L = 2Виср = 0,44 (s — s0) 0,31 Qj/3 = 0,136 Q'y 3 (s - s0). (10.10)
Кинетическая энергия, приходящаяся на единицу
длины источника тепла:
E=aL = 2,68-0,136Qj/3 (s — s0) 0,312 Q2/3 =
= 0,021 <?0(s — s0). (10.11)
Формулы (10.6) — (10.11) справедливы при s>sne₽,
где saep=10B0. Однако для приближенных расчетов они
верны и при s=sc»=2Bo.
Конвективное тепло, кВт, выделяемое единицей дли-
ны источника, подсчитывается по формуле
Q0 = a2B0 (/п-^вр)/1000,
148
где а _ коэффициент теплоотдачи, Вт/(м2-°С); /п температура
поверхности источника тепла, °C.
Необходимо отметить, что выведенные расчетные
формулы для плоской струи и для струи над источни-
ком тепла конечной длины справедливы, если отноше-
ние его длины к ширине не менее 20,
§ 46. Конвективная струя круглого сечения
Над круглым в плане источником тепла радиусом /?о
поднимается конвективная струя круглого сечения
(см. рис. 10.1).
Начало координат поместим в центре верхней грани
источника тепла, а ось абсцисс направим вверх по оси
струи.
Радиус струи на переходном и основном участках
R=(s — s0)tg 0 = 0,22(7 — s0), (10.12)
где so — абсцисса полюса струп; на основании опытов установлено,
что so = — 2Ro
Среднюю скорость в поперечном сечении этих двух
участков струи определим, используя уравнение коли-
чества движения:
К -= Ррш?2 t’2p
Отсюда
гср = Ук/fcml? .
Принимая р=рокр, где рОкР — плотность окружающе-
го воздуха, и заменяя R согласно выражению (10 12),
получим
1 I / к 1
Уравнение количества движения (10.1) для основно-
го участка струи круглого сечения примет вид
dK = (рокр — Pcpi) ds,
где pep i—средняя по площади поперечного сечения струп плот-
ность воздуха.
Разность плотностей (см.§ 39)
I Рокр ..
Poi.p — Рсрг— Й ~ ДЦ'Р-
ИД/ 1 окр
149
Подставляя эту разность плотностей в уравнение ко-
личества движения и заменяя /? согласи» выражению
(10.12), получим
0,22^л рокр
ЛК = —s--------- Л'ср (s — s0)2 ds.
гД/ 10Кр
Среднюю избыточную температуру находим из урав-
нения (10.2), которое в нашем случае запишется в виде
срл/?2 Vpp Л/Ср = Qo,
где с — удельная теплоемкость воздуха, Qo — количество конвектив-
ного тепла, выделяемое источником тепла в секунду
Отсюда при р»рОкр получим
Л/с =_________%___________= VI Qa 1 .
срокрэт-0,222(з — s0)2 уср 0,22 с У^ярокрК s — s®
В таком случае
cht токр
Интегрируя это уравнение, имеем
К3/2 = 0,165 <9p_(s _ Sfl)2 -р с (10.14)
С$М Tw<p
Постоянную интегрирования следует искать исходя
из того, что в переходном сечении s—snep и К=Кпер,
поэтому
с = к«-0.1Ю ^StaM2L(Sw_s<),.
1 окр
Проводя такие же выкладки, как и для плоской кон-
вективной струи, получим
0,0551//~лррокр sQo
С₽Д/ Гокр
Опер so)2.
Следовательно,
хз/2 = 0> 165KngPoKpgQo. (s_So)a +
СР\t ^ОКр
+ 0,055 ~Pp°*Pgg°-(SneI,-So)2.
* онр
159
Второе слагаемое здесь мало по сравнению с первым,
и им можно пренебречь. Тогда окончательно получим
2/3
(s-s0)4/3.
0 165 УлРРокр gQo
Ум Гокр
Подставляя это значение К в зависимость (10.13),
будем иметь
к =
_ , У_________1,55<30
^р-|/ ™₽₽A/PokpTokp(s-s0) •
Поскольку £ = 9,81 м/с2; с—1 кДж/(кг-°С); р=2,02;
=1,63; рокр = 1,2 кг/м3 и ТОкр=293, то окончательно
получаем
/ Qo W3
vcp = 0,346 —— .
\s — $о /
Скорость на оси струи
1 0,346 / Q. V/з / Qo у/3
Сос= — 'Vp = y^ НМ = 1,34 1—
k F 0,258 \s — sa / \s — s0 /
Средняя избыточная температура
________Qo ~_______Qo_______
ср срл£2 сср ~ срокр л£2 сср
Qo(s-so)V3
(10.15)
(10.16)
1.1,2л.0,22^ (s-s0)2 0,346 Q?/3 15,8 zs_s V/3 1
(10.17)
Избыточная температура на оси струи
1 t 15,8Q9y
*д*₽д/ А/С₽ 0,428-1,63 (s — «оУ3
_JL_
(s-s0y3 '
Объемный расход в секунду
Д^ОС —
= 22,5
(10.18)
/ О„ \1/з
L = л£2 рср = л • 0,222 (5 — s0)2 0,346 —=
\s — Зд /
= 0,052 Qo/3(s-s0)5/3.
(10.19)
151
Кинетическая энергия
2
Е = aL = 4,06.0,052 Q^s - S())5/3 X
/ Qn W3
Х 0.3462 — ° = 0,0152 Q0(s — s0). (10 20)
\s — s0 /
Формулы (10.15) — (10.20) справедливы при s>snep,
где Snep —10 Ro. Однако для приближенных расчетов они
верны и при s>sCHS=2R0.
Количество конвективного тепла, кВт, определяется
по формуле
<20--=аЯ/?20(/п-/№р)/1ООО,
где а — коэффициент теплоотдачи, Вт/(м2-°С); (л — температура
поверхности источника тепла, °C.
Следует указать, что выведенные расчетные форму-
лы применимы для конвективной струи, возникающей
над прямоугольным в плане источником тепла, если от-
ношение его сторон менее 20, и вообще над любым ис-
точником тепла с отношением сторон, близким к единице.
Однако в этих случаях при подсчете количества кон-
вективного тепла вместо Ro надо ввести Ra, вычисляе-
мое по формуле
Ro = ]/ -^-Го = 0,565 1/7Г,
где Го — теплоотдающая поверхность источника тепла.
Пример 10.1. Определить скорость и температуру на оси кон-
вективной струи на высоте 3 м от круглого в плайе источника тепла
радиусом 1 м. Температура его поверхности 70° С, а окружающего
воздуха 20° С.
Решение. Находим расстояние до сжатого сечеиия sCh< =
= 27?о = 2 м. Следовательно, s>Sc,K, и можно пользоваться формула-
ми основного участка струи. Коэффициент конвективной теплоотдачи
а -- 1,3-1,575 (ta — /0Kp)I/J = 2,05 (70 — 20)1/3 =
= 2,05-3,68 = 7,55 Вт/(м.сС).
Здесь введен коэффициент 1,3, так как теплоотдача происходит
от горизонтальной поверхности.
Количество конвективного тепла
Qo = алГ2 (/и —фкр) = 7,55-3,14-12-50 = 1185 Вт =1,185 кВт.
Абсцисса полюса струп s0 = — 2 Ra = —2 м. Скорость на осн
[см. формулу (10.16)]
!'ос
= 1,34
1,185 у/з
Зф 2/
з-------
= 1,34/ 0,237 =1,34-0,62 = 0,83
м/с.
152
Избыточная температура на оси [см. формулу (10.18)]
Д^ос
1,1852/3
(3 + 2)5/3
22,5-1,12
14,6
= 1,7 °C;
foc = 20+ 1,7 = 21,7 rC.
ГЛАВА 11
ВСАСЫВАЮЩИЕ ФАКЕЛЫ
§ 47. Общие сведения
о всасывающих факелах
Всасывающим факелом называется течение, возни-
кающее около вытяжного отверстия или патрубка. Вса-
сывающий факел всегда в большей или меньшей степе-
ни стеснен твердыми стенками. Зависимости для всасы-
вающих факелов коренным образом отличаются от за-
висимостей для приточных и конвективных струй.
Течение во всасывающих факелах можно считать
потенциальным. Влияние вязкости проявляется только
в очень узком пограничном слое вблизи стенок, где про-
исходит быстрое падение скорости до нуля. Вследствие
этого к исследованию всасывающих факелов примени-
мы все методы аэродинамики, разработанные для по-
тенциальных течений.
В настоящее время для установления зависимостей
для скоростей во всасывающих факелах применяются
следующие методы: интегрирование уравнения Лапла-
са, наложение потоков, конформное отображение и маг-
нитная аналогия.
Воздух к вытяжному отверстию движется обычно со
всех сторон, в результате чего резко сокращается район
активного действия всасывающего факела. При этом
скорости во всасывающих факелах на удалении в один-
два калибра1 и более начинают подчиняться зависимо-
стям для точечных стоков на плоскости или в простран-
стве.
Ниже рассматриваются наиболее простые, подтверж-
денные опытными данными зависимости для скорости
воздуха на оси различных факелов.
1 Калибром называется отношение удаления от всасывающего
отверстия к ширине щели или диаметру этого отверстия.
153
§ 48. Скорость на оси факела
у отверстий в плоской стенке
Прямоугольное отверстие имеет длину 2 а и шири-
ну 2 b (рис. 11.1). Начало координат поместим в цент-
ре отверстия, оси к и у направим по стенке, а ось z —
по оси факела [14].
Выделим на расстоянии х и у от центра отверстия
элементарное отверстие площадью dxdy. Объемный рас-
ход воздуха через это отверстие
dL = dx dy,
где «о — скорость воздуха в элементарном отверстии.
Рассматривая элементарное отверстие как точечный
сток в полупространстве, можем определить скорость,
которую сток вызывает в точке А, лежащей на оси z:
dv — dL/Zns* = v0 dx dyllns2,
где s — расстояние от элементарною отверстия до точки А.
Проекция этой скорости на ось факела
dv? = dv cos 0.
Таким образом,
154
Псдстазляя сюда
s — Ух2 + У2 + г2 и cos 0 — г/s = z/Ух2 + у2 4- г® ,
получим
_________уог dx dy
Vz~ 2п (х2+у2 + z2)3/2 '
В таком случае скорость на оси факела
Ь а
, f Г____Pg z dx dy
Vz J J 2л (x2 + У2 + z2)3'2 ’
0 0
Полагая Уо==Уср=А/4«& и дважды интегрируя, бу
дем иметь
_ 2 -Г Ьа
йг = —arcctg г! 1/ 14- —(1 + ?), (11.1)
где Vz — Vz/vn, z=z/b.
В частном случае для квадратного отверстия а—Ь
и зависимость (11.1) упрощается до вида
vz = — arcctg z У 2 4- za .
Л
В случае бесконечно длинной щели а —сю и полу-
чаем
2
vz = — arcctg г.
л
Круглое отверстие имеет радиус R (рис. 11.2). На-
чало координат поместим в центре отверстия, ось р на-
правим по стенке, а ось z — по оси факела [14].
Выделим на расстоянии р от центра отверстия эле-
ментарное отверстие площадью pdcpr/p. Объемный рас-
ход воздуха через это отверстие
dL = v0 pdqdp.
Скорость в точке А, вызываемая элементарным вса-
сывающим отверстием:
dv = dL/2ns2 = ve pd pd(p/2ns2,
где s — расстояние or элементарного отверстия до точки А.
Проекция этой скорости на ось факела
v0 pdpdtp
dvz = —-—-— cos 0.
t55
Подставляя сюда
s — Уp2+z2 и cos 0 = ?/s = г/Т'""p2 + z2,
получим
du2 =-v0 zpdpd(p/2n (p2 + z2)3/2
В таком случае скорость на оси факела
2л А"
У С f vo 2PrfPd?
J J 2л(р2 + г2)5'2 ‘
oo u '
Полагая v0 — vcp==L/tiR2 и дважды интегрируя,
имеем
У=1 — г/К'1 -Ь г2- (И. 2)
где гь = гч/о<>; г=г!И
Кольцевое отверстие имеет наружный радиус Rn и
внутренний RB. Начало координат поместим в центре
кольцевого отверстия, а ось z направим перпендикуляр-
но [14].
Рассматривая площадь кольцевого отверстия как
разность площадей круглого отверстия радиусами Ra
и RB, можем найти
с’г = £’о I 0 ~ 2 'V+ г2) — (1 — г/]/ Яв+ г2)]
Рис 1 i 2 Круглое отверстие в плоской стенке
156
или
b2=v/i+*l-*H/l/i+^ (”з>
ГДе Vz = V2/Vq', z^—-ziRv, Zr.=z[R^
Эллиптическое отверстие имеет большую ось 2 а и
малую ось 2 b (рис. 11.3). Начало координат поместим
в центре эллипса, ось р направим по стенке, а ось z—
по оси факела [3].
Выделим на расстоянии р от центра эллипса элемен-
тарное отверстие площадью pdpdcp. Проводя такие же,
как и для круглого отверстия, выкладки, получим
Л/2 г
. Г С t.’ozp</<>d<p
. 4 । —i • •
J J 2л (p2 +z2)3/2
где r — расстояние от начала координат до любой точки, лежащей
на эллипсе.
Для определения величины г воспользуемся уравне-
нием эллипса:
х2/а2 + «/2Д2 = 1,
где х и г/ — координаты точки, лежащей на эллипсе; при этом ось
х направлена по большой оси эллипса, а ось у — по малой.
Используя формулы перехода от цилиндрических
координат к прямоугольным x=rcoscp и y=rsin<p,
уравнение эллипса представим в виде
г2 cos2 ф/а2 + г2 sin2 <р/&2 — 1.
1S7
Отсюда
а2 b2
a2 sin2 <р + &2 cos2 ф '
Полагая скорость и0 — иср=L/nab и интегрируя пор,
получим
л/2
2 \
-............... \ 4ф.
а2 Ь2
a2 sin3 <р + 63cos2 ф ,
Интегрируя теперь по ср, будем иметь
я/2--------------------------------------------
2 Г -j / о2 sin2 ф + b2 cos2 (р
л J |/ a2 sin2 ф+Ь2 cos2 ф + а2 Ь'Чг2
о
Преобразуем дробь под радикалом:
a2 sin2 ф 4~ b2 cos2 ф &2 + (а2 — b2) sin2 ф
a2 sin2 ф+&2 cos2 ф + а2 Ь21х2 Ь2~Ч(а2 — b2) sin2 ф + a2 b2/z2
1 + (a2/&2 — 1) sin2 ф 1 + (а2 — 1) sin2 ф
1+(а2/&2 — 1) sin2 ф + а2/х2 1 -j-(а2 — 1) sin3 ф + 1/г2 '
где а-а/Ь, г—г/а.
В таком случае для скорости на оси факела получим
следующую зависимость:
Д 1'2 г~-------—---------------
2 f / 1 4-(а2 — 1) sin2 ф
vz = 1—— I 1/----------т=--------;-------—<4ф (П-4)
л J у 1 4" (а2—1) sin2 ф4-1/г2
о
Интеграл в этой зависимости взять или свести к таб-
личному не удалось, вследствие чего он был вычислен
приближенно. По полученным результатам расчета был
построен график, приведенный на рис. 11.4.
§ 49. Скорость на оси факела
у отверстий в криволинейной стенке
Щель конечной ширины расположена вдоль круглой
трубы. Ширина щели определяется центральным углом
2а0, радиус трубы R (рис. 11.5, а).
Начало координат поместим в центре поперечного
сечения трубы, ось х направим так, чтобы она прошла
через середину ширины щели, а ось у — перпендикуляр-
но ей [10].
158
Выделим на расстоянии х0 и у0 от центра круга под
углом ±а две элементарные щели шириной Rda (точ-
ки и Л2). Объемный расход воздуха через обе щели
на единицу их длины составит
dL = 2г' г; Rda,
тде Vo — скорость воздуха в элементарной щели.
Воспользуемся отображающей функцией
и = г-f- R'“/z,
которая переводит круг ра-
диусом R на плоскости z в
отрезок прямой длиной 47?
на плоскости и (см. рис.
11.5,6). При этом точки Л1
и А3 перейдут в точку В на
плоскости и с координатой
Но ^о.
Комплексный потенциал
течения на плоскости и за-
пишется в виде
- dL
dw = -—ln (« — &,).
Используя отображаю-
щую функцию для опреде-
ления величины go, можем
написать
Рис. 11.4. График изменения
скорости на оси всасываю-
щего факела у эллиптичес-
кого отверстия
Рис. 11.5. Продольная всасывающая щель в круглой трубе и ее
отображение
° труба со щелью; б — отрезок прямой со стоком — точкой
о
159
g + й] = x + iy + -А- = x + iy+ R2 .
X + iy x2+y2
Выделяя действительную часть, получаем
+ TTY-
хг+у2
Для точки В справедливо g=g0> а для точек At и Аг
имеем x=Xq и у—+у0, Поэтому
?о = ха + R2 л = 2х0 — 2R cos а.
Xq+ijq
Подставляя в комплексный потенциал величины и
и §о, будем иметь
dL ( R2 \
dw — — In z 4- — — 27? cos а I .
2л \ 2 /
Беря производную, получим
d (dw) , ., dL 1 — 7?a/z2
dz y 2л z-J-/?2/z —27?cosa
При y=Q имеем z=x и vy=Q. Поэтому
dL x2 — R2
dvr — — — --------------- .
2nx x2 -j- R2 — 2Rx cos a
В таком случае при замене dL ранее найденной ве-
личиной можем написать
о
7? С v0 (х2 — 7?2) da
Vr = — — i -----------------,
л х J х2 + R2—2Rx cos a
о
Принимая vo=vcp=L/2Rao, отбрасывая знак минус
и интегрируя, окончательно получаем
2 . (х+ 1 , «0 \
^ = — arctg Н-----tg— , (11.о)
tix \x— 1 * /
где l)x — vxlv0-, x—xjR, причем x>l.
§ 50. Скорость на оси факела у патрубков
Плоский патрубок. Щель, образованная двумя па-
раллельными стенками, имеет бесконечную длину и ко-
нечную ширину 2Ь (рис. 11.6,а). Поток воздуха, вли-
ваясь в щель, сжимается. Скорость воздуха на границе
потока после щели и в сжатом сечении равна t»o-
160
Начало координат поместим посередине щели, ось х
направим по оси факела, а ось у — перпендикулярно ей.
Выявим, как изменяется скорость на оси факела. По-
скольку течение плоское, воспользуемся методом кон-
формного отображения Н. Е. Жуковского. Отобразим
область искомого течения на плоскости z на верхнюю
полуплоскость и с течением, обусловленным источни-
ком— точкой (рис. 11.6,6).
Как известно, нроекции скорости искомого течения
на оси координат
yx = i/cos0; i>j, = fsin0,
где v — скорость во всасывающем факеле; 0—угол между векто-
ром скорости и осью абсцисс.
Н. Е. Жуковский предложил связывать скорость и
со скоростью г)0 следующей зависимостью:
_#
V = v0 е v,
где ft — переменная величина.
В таком случае проекции скорости
их — vo е~&cos0; vv = voe—tf sin 0.
Комплексную координату будет искать в виде
dz
dz = — dw,
dw
где z=x+iy, w — комплексный потенциал.
Величина
= 1 , 1 __________J________ 1
dvu dwldz vx — ivg v0 e~& (cos 0—i sin 0) v0
X
Рис. 11.6. Плоский всасывающий патрубок и его отображение
а патрубок; б — источник — точка
11—741
(«1
Комплексный потенциал источника — точки на полу-
плоскости и
L
w = — In и,
л
где L —объемный расход воздуха; w=g-j-tr|.
Тогда
, L du
dw =-----.
л и
Отображающая функция, по Н. Е. Жуковскому,
© 4- i0 = 2i arcsin — ,
и
где оз — абсцисса на плоскости и, соответствующая краю щели.
Отсюда
иг ch (fl+i0) d Г— ('0' г'0)
(01 2 I 2
------------ -------------------------------—:
sh — (в1 + г'0) sh2 — (fl+г 0)
В таком случае
dw ~ — — cth[-^-(©4-i0)d-^-(©4-i0) .
Подставляя в зависимость для комплексной коорди-
наты dz величины dzjdw, dw и L=2ebv0, где е— коэф-
фициент сжатия потока в щели, получим
dz
2eb
л
e^i(’ cth |у (fl + id)d -у (fl + г'0)
— (1 + e’?+w + cth 14- (fl + I0)d 4- (fl+ * 0)
л I, |_ Z Z
dy(fl+i0).
Интегрируя, получаем
г = x + iy = — [4" + l0) + 4" +ln sh V
л I z z z
4-c.
Постоянную интегрирования находим из условия, что
в точках F и К] величины х=0; г/=Ч:&; fl—0 и 0=±л.
Подставляя эти величины в последнюю зависимость и
учитывая, что =—1, получим
е/> / „ л .
с = — — 1 ± 2nt Т — г
л \ е
1С2
Постоянная интегрирования не может иметь два раз-
_____________________________________л
ных значения. Поэтому с=—eb/n и ±2nt-t-“t=0. По-
следнее равенство дает е = ’/2-
Подставляя в зависимость для комплексной коорди-
наты dz величины е и с, будем иметь
х + = + О + «О +
2л L
+ 2 In sh ~ (& + i0)
Выделяя действительную часть, получаем
ь

2л
1 + Ф + cos 0 + 2 In
О
+ 21nsh —
Для оси факела 0=0, и поэтому

bl л
х = — —— I 1 + б +
2л \
Заменяя здесь v0 = vcp/e,—2vcp, где t’cp — средняя
скорость в щели, и вводя относительные величины ох=
= VxlVcp и х—х/b, получим
vx = 2е~
1 / ,,, О \
х = — — 1 + О + е+* + 2 In sh — .
л \ 2 j
Решая последние две зависимости совместно и от-
брасывая знак минус, будем иметь формулу для скоро-
сти в виде обратной функции:
х=(1/л)[0,5 + 1/ёх+1п(1/ёж —0,5)]. (11.6)
По данной формуле построен график, показанный
на рис. 11.7.
Патрубок круглого сечения полубесконечной длины
имеет радиус R (рис. 11.8). Начало цилиндрических ко-
ординат поместим на входе в центре трубы, ось р рас-
положим в плоскости всасывающего отверстия, а ось г
направим по оси факела.
Выявим, как изменяется скорость на оси факела.
При решении задачи воспользуемся методом магнитной
аналогии [8]. Как известно, существует аналогия меж-
ду магнитнымУПблями постоянных электрических токов'
• и потенциальными течениями воздуха. Те и другие опи-~
"сываются зависимостями, которые переходят друг в дру-
*Га При замене'магнитной индукции на скорость потока^
'ТГ наоборот. ————л——— .
44*----- 163
Рис 117 График изменения
скорости по оси всасываю-
щего факела у плоского па
трубка
Рис. 11.8. Цилиндрический
всасывающий патрубок
Рис 119. К закону Бпо —
Савара — Лапласа
В основу метода положен
закон Био — Савара — Лапла-
са, который устанавливает ве-
личину и направление вектора
магнитной индукции в произ-
вольной точке магнитного по-
ля (рис. 11.9):
ui
dB —----— sin adl,
4nr2
где и — магнитная проницаемость
среды; I — сила тока; dl — элемент
проводника, вектор которого совпа-
дает с направлением силы тока; г —
радиус-вектор, проведенный нз эле-
мента проводника в рассматриваемую точку С; а — угол между
векторами dl и г.
Вектор В перпендикулярен плоскости, в которой ле-
жат векторы dl и г, и направлен таким образом, чтобы
из его конца кратчайшее вращение вектора dl до совме-
щения с вектором г происходило бы против часовой
стрелки.
Если применить этот закон к круговому витку ра-
диусом R (рис. 11.10) и рассматривать магнитную ин-
дукцию в точке, лежащей на оси витка, то, очевидно,
а=90° и dl—Rdtp, а поэтому
164
Рис. 11.10. Круговой виток
с током и вызываемая им
магнитная индукция
Рис 11.11. Соленоид и вы-
зываемая им на его оси маг-
нитная индукция
Проекция же магнитной индукции на ось кругового
витка
dBz = dB sin р = -у- dB.
Следовательно,
dB.
-----Ар.
4nrJ
г = Уф + .

Заменяя здесь
получим
dBz
4л (7Г+ ЛТ'а
Интегрируя от 0 до 2л, будем иметь
В j»7?2
2 2(7?2 + й2)3/2
185
Рассмотрим теперь полубесконечный соленоид
(рис. 11.11) радиусом /?. Выделим в соленоиде элемент
высотой dz. Пусть число витков, приходящееся на еди-
ницу высоты соленоида, равно п; тогда число витков в
элементе высотой dz составит ndz.
Используя последнюю зависимость, можем написать
для полубесконечного соленоида
рш С R-dz pnt ' h
При h=—оо получаем
оо = pni.
Известно, что в глубине соленоида магнитное поле
равномерно по всему поперечному сечению. Следова-
тельно, S-oo есть не только индукция на оси соленоида,
но и средняя индукция, т. е.
В—х = ^ср.
Средняя индукция внутри соленоида в любом сече-
нии постоянна, следовательно, она является и средней
индукцией на входе в соленоид. Подставляя р,ш —Вср
в зависимость для Вл, будем иметь
JL* /, h А
2 1— Л------- •
z 1 У/?24-й2 /
1—
Bk
Заменяя здесь Bh на vz, Bcp на ocp и ft на z, оконча
тельно получим
1 /
’--Г 1
z
(11.7)
где v2=v2/vCj>', z=z/R.
Пример 11.1. Определить осевую скорость во всасывающем фа-
келе на расстоянии 1 м от плоскости всасывания. Всасывание про-
исходит через круглое отверстие в плоской стейке диаметром 250 мм
при скорости 15 м/с.
Решение. Относительное расстояние
z = z/Т? == 1/0,125 = 8.
Тогда, согласно выражению (11.2), имеемз
v2 = 1 — 8/V 1 4- 64 = 1 — 8/8,05 = 1 —0,99 = 0,01;
ог = 0,01.15 = 0,15 м/с.
166
Пример 11.2. Определить скорость на расстоянии 0,5 м от оси
круглой трубы диаметром 200 мм, на поверхности которой устроена
продольная щель с центральным углом 2а0 —60°. Скорость в щели
равна 20 м/с.
Решение. Относительное расстояние
£ = х/Я = 0,5/0,1 =5.
Находим
tga0/2 = tg30°/2 = tg 15° = 0,2679.
Тогда, согласно выражению (11.5), получим:
2 /54-1 \
vx = —— arctg [ --— -0,2679 I =
\ 5 — 1 j
= 0,1275 arctg (0,4) =0,1275-0,38 = 0,0485;
vx = 0,0485-20 = 0,97 м/с.
ГЛАВА 12
ОБЫЧНЫЕ БОРТОВЫЕ ОТСОСЫ
ОТ ПРОМЫШЛЕННЫХ ПРЯМОУГОЛЬНЫХ ВАНН
§51. Постановка задачи о бортовом отсосе
и метод ее решения
При аналитическом решении задачи о бортовом от-
сосе сложный процесс, происходящий над ванной с от-
сосом, расчленяют на два более простых: восхождение
потока над ванной без работы отсосов и образование
вытяжного факела под действием только бортового от-
соса без работы ванны.
Горячая жидкая поверхность ванны вызывает нагре-
вание воздуха над ней. Это создает подъемную силу,
под действием которой возникает свободная конвектив-
ная струя.
Промышленные ванны могут быть различным обра-
зом установлены в помещении, а именно: ванна с одно-
бортовым отсосом — свободно в помещении или у сте-
ны, ванна с двухбортовым отсосом — свободно в поме-
щении, у стены или между двух стен.
Для каждого варианта установки ванны характерно
определенное течение воздуха. Разнообразие течений
при различных вариантах установки ванны, казалось
бы, обусловливает необходимость решения задачи о бор-
товом отсосе для каждого варианта в отдельности. Од-
нако такой путь решения поставленной задачи трудо-
167
емок и весьма сложен. Поэтому рассмотрим решение
задачи о бортовом отсосе только для случаев, когда
ванна с однобортовым отсосом находится у степы, а ван-
на с двухбортовым отсосом — между двумя стенами.
Экспериментальная проверка этих решений показала,
что они справедливы и для других вариантов установки
ванн.
С целью более простого решения рассматриваемой
задачи принимаются следующие допущения:
1) течение воздуха над ванной не изменяется по ее
длине, т. е. рассматривается плоское течение;
2) поток воздуха, поднимающийся от жидкой по-
верхности ванны без работы отсоса, имеет одинаковую
скорость в любой точке над ванной;
3) всасывающий факел бортового отсоса обусловлен
весьма узкой щелью, несколько заглубленной и распо-
ложенной выше уровня жидкости в ванне. При этом те-
чение в факеле ограничено уровнем жидкости в ванне
и стенкой пли стенками.
Задача об однобортовом и двухбортовоМ отсосе ре-
шается с учетом расстояния от уровня жидкости в ван-
не до оси щели.
§ 52. Однобортовой отсос
Промышленная ванна с однобортовым отсосом рас-
положена у стены. Пусть ширина ванны Ъ, а расстояние
между осью щели и уровнем жидкости в ванне Н
(рис. 12.1).
Наиболее удаленная от бортового отсоса частиття.
поднимающаяся со~свободной поверхности жидкости
ванны, описывает траекторию, превышающую расстоя-
1Ше~от уровня жидкости'ДО ОСИ щели на величину Д/Л
наз"ываемую высотой спектра всасывания.
----Примем"Качало КООрдиНй'т’Т'вёрШИНёпрямого угла,
образованного стенкой и зеркалом ванны. Ось абсцисс
х направим по зеркалу ванны, а ось ординат у — по
стенке, перпендикулярно свободной поверхности жид-
кости.
Движение, обусловленное совместной работой ванны
и бортового отсоса, может быть получено в результате
наложения течения в верхней полуполоске шириной Ъ
(см. рис. 3.2) на течение, возникающее при наличии
двух плоских стоков — точек с одинаковым расходом,
168
Рис 12.1. Схема ванны с
однобортовым отсосом
Рис. 12.2 Линии токов двух
плоских стоков — точек
расположенных на оси ординат и на расстояниях Н от
оси абсцисс (рис. 12.2).
Для изучения движения над ванной воспользуемся
областью течения в правом квадранте верхней полу-
плоскости. Схема течения будет зависеть от соотноше-
ния расхода половины одного стока — точки Lo и рас-
хода в верхней полуполоске Ln, т. е. от отношения L0/Ln.
Из различных случаев течения представляют инте-
рес те, при которых L0IL^ \, так как при этом не на-
блюдается прорыва восходящего потока.
Для аналитического определения отношения расхо-
дов воспользуемся комплексными потенциалами ранее
рассмотренных течений.
Комплексный потенциал параллельного течения в
верхней полуполоске при направлении потока в сторону
положительной оси ординат (см. пример 3.2) будет
равен:
Комплексные потенциалы стоков — точек (см. при-
мер 3.3) в верхней и нижней полуплоскостях соответст-
венно равны:
Lo
w2 — — — In (г— iH);
л
w3 — — — In (г + iH).
Я
В таком случае комплексный потенциал течения над
однобортовой ванной выразится в виде
w — + ш2 + wa = — i г — — [In (г — iH) + ln(z + iH)].
о л
169
Возьмем первую производную:
dw . £п Lo / 1 1
dz 1 b л \z — iH z + iH
Тогда комплексная скорость [см. формулу (3.13)]
будет равна:
. Ln Lo f 1 1
п, — iv == — -------------------+----------
b я [x + i(y—H) x+i(y+H)
и проекция скорости на ось ординат составит
La Lo Г у — Н у + Н
у Ь л х2+(1/—Н)2 хЧ-(Н-Я)2 J
В точке максимума граничной линии тока, имеющей
абсциссу х0 и ординату уа=Н-}-1\.Н (см. рис. 12.1), про-
екция скорости на ось ординат иу=0. Поэтому справед-
ливо следующее уравнение:
Ln _ L„ Г АН 2Н + ЛН j 0
ь л х^+ЛН2 х%+(2Н+ЛН)2
Из этого уравнения можно получить следующую
формулу для определения интересующего нас отноше-
ния расходов:
-- =----------------*— ----------f (12.1)
L° 277 + ЛЯ
+ ^ + (2^ + ДЯ)2
где xo=xo/b.
Входящая в эту формулу неизвестная относительная
абсцисса максимума xq может быть найдена таким об-
разом. Из выражения для комплексного потенциала
[см. формулу (3.11)] имеем
Д П
<р — i —— (х 4. iy)------------------
Ь л
In У*2 + (у-Н)2+
+ In /х2 + (у +//)2 + i arctg -—— -f- i arctg ,
X X j
Тогда функция тока будет равна:
. La Lo Г у — Н уА-Н'
г|? = —----х —--- arctg-------+ arctg----- .
ь -< L x x
Из этого равенства следует, что значение функций
тока для линии тока, проходящей через точку х — Ь и
у=0, равно:
ф-------La.
170
В таком случае уравнение граничной линии тока
будет
Ln Lq Г У—Н
х — arctg-f- arctg
b---------------------л L x
//+Я] ,
= Ln.
Отсюда
y—H , y+H
arctg--------f- arctg —
Ln I, x
~ n~i—~T
Lo \ b
Беря тангенс от левой и правой частей этого равен-
ства, получим
2ху
Х2+ _^ = tg
Ln
я~
‘-О
Преобразуя последнее равенство, имеем
у2 + 2ху ctg
L / х \“|
я-Н- 1-— — (х2 + /72)=0.
Lo \ b
Решая его, получим
у — — xctgfn~"/1—-~У| ± %/ *2tga [л у3-/1 — +*2+//2.
L L0 \ Ь /J у L L0 \ и /J
В правой части последней формулы перед радика-
лом должен стоять плюс, так как ордината (при рас-
смотрении течений к верхней полуплоскости) всегда по-
ложительна.
Для точки максимума (х0, уй=Н-\-^Н) последнее
уравнение примет вид
[/ / у \ Д
л ——11--2- +
Lo \ о /J
+ |/ ^ctg2L -М1- vIM+tf2-
г L Lo \ 0 /А
Разделив левую и правую части этого уравнения на
величину b и переходя к безразмерным величинам, по-
лучим
__ ___ _ Г г ~ д') 2 Г L — "1 _
н + Д/z + хй ctg л ~~ (1 — ха) I > = х0 CSC2 л -2- (1—ха) -f- Н%.
L Lo J/ L Lo J
Подставив в это равенство ранее найденное отноше-
ние расходов, относительную абсциссу максимума х$
найдем из следующего уравнения:
171
Н + ЛЯ + х0 ctg
ЛЯ
*о + д^2
2Я+ ЛЯ
(2Я+ЛЯ)2
л2
(1—Хо)} =
= Xq csca
ЛЯ 2Я + ЛЯ
х2 + ЛЯ2 "л-2 + (2Я4-ДЯ)2
(1-^+Яа. (12.2)
Для частного случая, когда расстояние от уровня
жидкости до оси щели незначительно, т. е. //«О, фор-
мула (12.1) и уравнение (12.2) упрощаются:
Рис. 12 3. График для расчета од-
нобортового отсоса
Z-o л хо + .
ТГ “ Т ан
кН = х0 tg
ЛЯ(1-хо)
*5 + ЛЯ2
По формулам (12.1)
и (12.2) были вычис-
лены отношения рас-
ходов, приведенные в
табл. 12.1.
По данным этой
таблицы построен гра-
фик, показанный на
рис. 12.3. Из графика
видно, что расход воз-
духа, удаляемого од-
нобортовым отсосом,
уменьшается с увели-
чением относительного
Таблица 12.1. Отношения расходов Л0/Лп при однобортовом отсосе
Г/ Значения отношения LQ/Ln при Д/Д равных
0 0,05 0,1 0,15 0,2 0.25 0,3
0 оо 7,5 4,2 2,8 2,15 1,7 1,5
0,05 7,5 4,3 2,8 2,1 1,65 1,5 1,35
0,1 4,1 2,9 2,2 1,7 1,45 1,35 1,2
0,15 3 2,3 1,8 1,55 1,4 1,25 1,15
0,2 2,5 1,9 1,65 1,45 1,3 1,2 1,1
0,25 2,1 1,8 1,5 1,4 1,25 1,15 1
172
расстояния от уровня жидкости до оси щели. Это умень-
шение происходит интенсивнее при незначительной от*
носительной высоте спектра всасывания.
§ 53. Двухбортовой отсос
Промышленная ванна с двухбортовым отсосом рас-
положена между двумя стенками. Пусть ширина ванны
Ь, а расстояние между осью щелей и уровнем жидкости
в ванне Н (рис. 12.4).
Частица, поднимающаяся из середины поверхности
ванны, описывает траекторию, превышающую расстоя-
ние от уровня жидкости до оси щелей на величину Д/7,
называемую высотой спектра всасывания.
Примем начало координат в вершине угла, образо-
ванного левой ётенкой и зеркалом ванны. Ось абсцисс х
направим по зеркалу ванны, а ось ординат у—по стен-
ке нормально к свободной поверхности жидкости.
Движение, обусловленное совместной работой ванны
и обоих бортовых отсо-
сов, может быть получено
в результате наложения
течения в верхней полу-
полоске шириной b (см.
рис. 3.2) на течение, обус-
ловленное двумя беско-
нечными цепочками плос-
Рис. 12.4. Схема ванны с двухбор-
товым отсосом
ких стоков — точек оди-
накового расхода, распо-
ложенных с интервалами
b параллельно оси абс-
цисс и на расстояниях от
нее Н (рис. 12.5). Для
изучения течения над
ванной достаточно рас-
смотреть область течения
в верхней полуполоске,
ограниченной осью орди-
нат и прямой х—Ь.
Схема течения в полу-
полоске будет зависеть
от соотношения суммарно-
го расхода половинок
двух стоков — точек Z.o и
Рис. 12.5. Линии тока двух плос-
ких цепочек стоков — точек
173
расхода в верхней полуполоске £п, т. е. от отношения
LolLn. Из различных случаев течения интересны те, при
которых Л0/£п> 1, так как при этом не наблюдается про-
рыва восходящего потока.
Для аналитического определения отношения расхо-
дов воспользуемся комплексными потенциалами ранее
рассмотренных течений.
Комплексный потенциал параллельного течения в
верхней полуполоске при направлении потока в сторону
положительной оси ординат (см. пример 3.2) будет
равен:
Комплексные потенциалы двух цепочек стоков — то-
чек (см. пример 3.5) равны:
Lq Л
= — —— In sin (г — iff);
2л b
(2 — iH)-)-
О
te)3 = —Insin-^- (z + iH).
2л b
Следовательно, комплексный потенциал течения над
двухбортовой ванной будет равен:
. . . Ьц Lq
w = оу, + в — I---г—-----in sin
133 Ь 2п
+ In sin (г + 1Н).
2л b
Берем первую производную:
dw ,La Lo [ л
— =— i ~ — — ctg — (г — iff) + cfg
dz b 2b i b
Тогда комплексная скорость будет равна:
2л
sin--г
Ь
-7-(г-МЯ)|.
& J
. La Lo
Vx — IVU= — I------— -----
* » ь 2b
sin — (г — iff) sin — (г + iff)
b b
2л 2л 2л 2л
sin— xch —— у4- icos —— xsh — у
Ljj Lq b b b b
1 b 2b 2л 2л 2л 2л , 2л ’
ch--ff—cos----x ch —— у + i sin-x sh — у
b b b b b
Отсюда проекция скорости на ось ординат составит
174
Ln , l-o
v^— + ~rx
2л 2л , 2л „ 2л , 2л 2л
cos-— xsh—— у ch — Я — cos2 —— х sh —— z/ch —— z/
Ь_________b_____b____________b_______b________b______
X ( v. 2л u 2n v, 2л V I
(ch —— H — cos-----x ch----у +
\ b b b J
л 2л 2л 2л
4- sin3---у sh----у ch----у
, b У b у b У
/ 2л 2л \2
4- sin----х sh-----у
\ b /
В точке максимума линии тока, имеющей абсциссу
х0=й/2 и ординату уа — Н-\-Ь.Н, проекция скорости на
ось ординат будет равна нулю (оа=0). Поэтому
ведливо следующее уравнение:
2л
sh—— (Н-1-ЛН)
ь
2л, 2л,
ch----Н + ch — (Я -j- ДЯ)
b ь
Решая это уравнение относительно расходов
реходя к безразмерным величинам, окончательно
чим следующую формулу:
Ln ch 2л Я Ц- ch 2л (Я + ДЯ)
La
спра-
и не-
полу-
(12.3)
sh 2л (fi + ДЯ)
где Н=Н[Ь\ &Н=&Н/Ь.
Таблица 12.2. Отношения расходов L0/La при двухбортовом отсосе
н Значения отношения bQ/Ln при АН, равных
0 0,05 0,1 0,15 0,2 0,25 0,3
0 00 6,42 3,29 2,27 1,8 1,56 1,29
0,05 6,59 3,79 2,33 1,83 1,54 1,31 1,23
0,1 3,6 2,47 1,93 1,62 1,35 1,26 1.2
0,15 2,72 2,1 1,73 1,43 1,32 1,25 1,18
0,2 2,36 1,92 1,56 1,41 1,31 1,24 1,17
0,25 2,18 1,75 1,55 1,4 1,3 1,22 1,16
175
Рис. 12.6. График для расчета
двухбортового отсоса
Если расстояние от
уровня жидкости до
оси щелей незначи-
тельно, то в формуле
_£12.3) можно принять
/7=0, вследствие чего
формула приобретает
более простой вид:
L0/Ln = cth лДЯ.
По формуле (12.3)
вычислены значения
отношений расходов,
приведенные в табл.
12.2.
На основании этой
таблицы построен гра-
фик, показанный на
рис. 12.6. На графике
видно, что расход воз-
духа, удаляемого бор-
товым отсосом, зависит от относительного расстояния
от уровня жидкости до оси щели: при увеличении это-
го расстояния и высоты спектра всасывания он умень-
шается.
§ 54. Расчет бортовых отсосов
Для проведения расчета бортового отсоса должны
быть известны: длина ванны а, ширина Ь, расстояние
от уровня жидкости до оси щели Н и высота спектра
всасывания Д/7. Расчет бортового отсоса ведется в та-
кой последовательности. Вычисляют относительное рас-
стояние от уровня жидкости до оси щели:
Н = Н!Ь.
Определяют относительную высоту спектра всасы-
вания:
ДЯ = Д/7/6.
По графикам (см. рис. 12.3 и 12.6) находят отноше-
ние расходов LojLn.
176
Вычисляют коэффициент теплоотдачи, Вт/(м2-°С):
а = 2,05(Лк-/в)Ч
где 6к и t3—температура жидкости ванны и воздуха помещения.
Вычисляют количество конвективного тепла, кВт,
выделяющегося от зеркала ванны длиной 1 м:
Qo — a.b —/8)/1000.
Подсчитывают скорость подъема паровоздушной
смеси, полагая ее у зеркала ваниы равной нулю, а пос-
ле сжатого сечения струи определяемой по формуле
(10.6). Тогда средняя скорость, м/с:
и = 0,155(3^.
Находят расход восходящего над ванной потока,
м3/ч:
£п = 3600 abu.
Подсчитывают расход отсасываемого воздуха, м3/ч:
Lq — (L0/La) Ьц*
Пример 12.1. Определить расход воздуха, отсасываемого двух-
бортовым отсосом от ванны хромирования длиной а=1,2 м, шири-
ной Я = 0,75 м. Расстояние от уровня жидкости до оси щели Я=
= 105 мм. Температура жидкости £« = 60° С, а температура воздуха
помещения /В=16°С Высота спектра всасывания ДЯ принята
равной 90 мм.
Решение. Вычисляем
Н = 105/750 = 0,14; ДЯ = 90/750 = 0,12.
По графику (см. рис. 12.6) находим
L0!La — 1,6.
Определяем:
а = 2,05 (60 — 16)7’ = 2,05-3,52 = 7,25 Вт/(м2-°С);
Qo = 7,25-0,75(60— 16)/1000 = 0,239 кВт;
и = 0,155-0,2397, = 0,155-0,62 = 0,96 м/с;
£п = 3600-1,2-0,75-0,96 = 3120 м3/ч.
Тогда
Lo = 1,6-3120 = 5000 м3/ч.
12-741
177
ГЛАВА 13
РАВНОМЕРНАЯ РАЗДАЧА И ВСАСЫВАНИЕ ВОЗДУХА
ВОЗДУХОВОДАМИ С ПРОДОЛЬНОЙ ЩЕЛЬЮ
ИЛИ С БОКОВЫМИ ОТВЕРСТИЯМИ
§ 55. Схема явлений при раздаче
и всасывании воздуха воздуховодами
В воздуховодах с продольной щелью или с боковы-
ми отверстиями для выхода воздуха, т. е. в воздухорас-
пределителях, движение воздуха значительно сложнее,
чем в обычных воздуховодах.
Экспериментальные наблюдения над воздухораспре-
делителями постоянного сечения показывают, что по их
поперечному сечению происходят: изменение направле-
ния скорости, деформация поля скоростей и изменение
статического давления воздуха.
Направление скорости меняется у частиц воздуха,
находящихся вблизи щели или отверстия, причем части-
цы тем больше отклоняются от оси воздухораспредели-
теля, чем ближе подходят к щели или отверстию.
Деформация поля скоростей состоит в том, что поле
скоростей воздуха имеет перекошенный профиль: от оси
воздухораспределителя в сторону щели или отверстия
наблюдаются повышенные скорости, а в обратную сто-
рону (стенка без щели или отверстия)—пониженные.
Статическое давление воздуха изменяется по попе-
речному сечению в обратном порядке: являясь наимень-
шим в щели или отверстии, оно непрерывно возрастает
по направлению к противоположной щели или отверстию
стенки. При переходе от одного поперечного сечения
к другому средняя скорость воздуха, среднее динамиче-
ское и среднее статическое давления, как правило, из-
меняются.
По направлению от начала к концу воздухораспре-
делителя (по потоку воздуха) средняя скорость возду-
ха все время уменьшается, так как часть воздуха выте-
кает через щель или боковые отверстия. Таким образом,
динамическое давление будет уменьшаться по направ-
лению потока воздуха на некоторую величину, которая
по закону сохранения энергии будет переходить в ста-
тическое давление. Эта величина динамиче-жого давле-
ния получила название освободившегося динамического
давления.
178
Рис 13 1. Векторы скоростей струй, вытекающих из отверстий воз-
духораспределителя
Благодаря освободившемуся динамическому давле-
нию статическое давление воздуха внутри воздухорас-
пределителя должно увеличиваться по направлению по-
тока. Однако оно в том же направлении одновременно
будет расходоваться на преодоление трения и местных
сопротивлений. Очевидно, что если освободившееся ди-
намическое давление будет больше потерь давления на
трение и местные сопротивления, то статическое давле-
ние в итоге возрастет, а если оно будет меньше этих по-
терь давления, то статическое давление уменьшится.
Если же освободившееся динамическое давление будет
равно потере давления, то статическое давление возду-
ха внутри воздухораспределителя будет неизменным.
Таким образом, характер изменения статического
давления воздуха внутри воздухораспределителя цели-
ком зависит от соотношения освободившегося динами-
ческого давления и потерь давления.
В более общем случае, когда имеется воздухораспре-
делитель переменного поперечного сечения, к описанным
явлениям добавляются еще добавочные явления, свя-
занные с изменением скорости, вызванным различной
площадью поперечного сечения, и процесс течения воз-
духа еще более усложняется.
Величина и направление скорости истечения воздуха
из отверстий различны в отверстиях одного и того же
воздухораспределителя (рис. 13.1). В начале воздухо-
распределителя скорость воздуха, вытекающего из от-
верстия 23, почти параллельна оси воздухораспредели-
теля. Затем, если двигаться по потоку воздуха внутри
воздухораспределителя, она все сильнее отклоняется от
оси и в конце его скорость истечения из отверстия 1 поч-
ти перпендикулярна оси.
При уменьшении площади отверстий эта картина
сглаживается, и все скорости становятся почти перпен-
12* 179
дикулярпы оси. При применении насадок или лопаток
в отверстиях все скорости истечения воздуха могут иметь
одно направление.
В воздуховодах постоянного сечения со щелью или
с боковыми отверстиями для входа воздуха, т. е. в вы-
тяжных воздуховодах, по поперечному сечению также
наблюдается изменение направления скорости, дефор-
мация поля скоростей и изменение статического давле-
ния. При этом по потоку средняя скорость и среднее
динамическое давление будут увеличиваться. Следова-
тельно, статическое давление будет уменьшаться, а раз-
режение расти. Разрежение также будет расходоваться
на преодоление трения и местных сопротивлений.
В случае воздуховодов переменного сечения добав-
ляется такое новое явление, как изменение средней ско-
рости вследствие изменения поперечного сечения возду-
ховода. Скорости всасывания в щель или в отверстие
подчиняются зависимости точечного стока. При этом
ось всасывающего факела у всех отверстий перпенди-
кулярна оси воздуховода, а сам факел симметричен от-
носительно своей оси.
§ 56. Зависимости и уравнения,
используемые при исследовании воздуховодов
Расчет воздухораспределителей и вытяжных возду-
ховодов, как и обычных воздуховодов, следовало бы
проводить по полным давлениям, учитывая удельную
потерю давления на трение и коэффициенты местного
сопротивления; при раздаче — на проход мимо отвер-
стия и на истечение из отверстия, при всасывании — на
вход в отверстие и дальнейшее слияние с основным по-
током в воздуховоде.
Однако такой путь расчета воздухораспределителей
и вытяжных воздуховодов весьма сложен, поскольку
коэффициенты местных сопротивлений прохода и отвер-
стий переменны и зависят от соотношения площадей от-
верстия и поперечного сечения воздуховода, а также от
отношения расходов воздуха в них. Поэтому К. К. Бау-
лин предложил вести расчет воздуховодов по статиче-
ским давлениям. Этот путь оказался значительно про-
ще и получил всеобщее признание.
180
В воздухораспределителях нормальную к оси возду-
ховода среднюю скорость в отверстии определяют по
формуле
и = li уЛ2 (р — ра) Ф = ц 2Дд/р, (13.1)
где ц _ коэффициент расхода; р и ра — статическое давление cooi-
ветственно внутри и вне воздухораспределителя; Др=р—Ра — избы-
точное статическое давление.
В случае вытяжного воздуховода формула (13.1)
принимает несколько иной вид:
V = |Л / 2 (ра — р)/р = р р' — 2 Лр/р. (13 2)
Входящую в зависимости (13.1) и (13.2) величину
Др можно установить, если воспользоваться уравнени-
ем Бернулли или уравнением количества движения. При
этом оказывается целесообразнее при расчете воздухо-
распределителей использовать уравнение Бернулли,
а при расчете вытяжных воздуховодов — уравнение ко-
личества движения.
Это объясняется следующим образом. При определе-
нии величины Др в воздухораспределителях достаточно
воспользоваться уравнением Бернулли для потока воз-
духа. находящегося внутри воздухораспределителя. При
этом потери давления на трение и местное сопротивле-
ние на проход известны. Если же применить уравнение
количества движения, то проекция количества движе-
ния в воздухе, истекающем из отверстия, не извест-
на, так как не известен угол истечения. При наличии
насадок и лопаток необходимо также учесть силы реак-
ции, которые также не известны.
При определении величины Др в вытяжных воздухо-
водах надо в уравнении Бернулли учесть потери давле-
ния на трение и местные сопротивления на проход. Яв-
ления, происходящие в местных сопротивлениях, слож-
ны и до сих пор точные аналитические зависимости для
них не установлены. В случае же использования урав-
нения количества движения потери давления на проход
не надо учитывать, а проекция количества движения
всасываемого воздуха на ось воздуховода равна нулю.
При аналитическом исследовании воздуховодов рав-
номерной раздачи или всасывания воздуха принимают-
ся следующие допущения:
а) коэффициент расхода по всей длине щели или для
всех отверстий воздуховода принят постоянным;
181
б) поля скоростей в поперечных сечениях воздухово-
да приняты равномерными (коэффициенты Кориолиса
и Буссинеска равны единице);
в) коэффициент сопротивления трения по всей дли-
не воздуховода принят постоянным.
§ 57. Способы обеспечения
равномерной раздачи
или всасывания воздуха
На основании формул (13.1) и (13.2) напишем за-
висимости для расхода воздуха в щелях шириной 6 еди-
ничной длины и в отверстиях площадью о:
=цбуЛ2(± Др)/р;
Lo = ца (± Др)/р.
Исходя из этих формул видно, чго равномерную раз-
дачу или всасывание воздуха можно осуществить сле-
дующими способами:
1) изменением ширины щели или площади отвер-
стий по длине воздуховода (см. гл. 14, 15, 18, § 75 и 76);
2) сохранением разности статических давлений по-
стоянной по длине воздуховода (см. гл. 16, § 66);
3) незначительным изменением разности статических
давлений по длине воздуховода (см. гл. 16, § 67, 68, 69,
гл. 17 и гл. 18, § 77 и 78);
4) изменением коэффициента расхода.
Первый способ, обеспечивая одинаковые расходы
воздуха по длине щели или в огверсгиях, не обеспечи-
вает в них одинаковых скоростей воздуха. Этот способ
рекомендуется при регулировании воздуховодов.
Второй способ эффективен для коротких воздухово-
дов, например при устройстве воздушно-струйных укры-
тий, воздушных завес и т. п.
Третий способ надо применять при осуществлении
общеобменной рассредоточенной подачи и отсасывания
воздуха, например в системах кондиционирования воз-
духа в прядильных и ткацких цехах.
Четвертый способ почти не получил развития из-за
сложности и неизученности.
В отдельных случаях раздача воздуха воздухорас-
пределителями может осуществляться через перфориро-
ванные отверстия в боковой поверхности, т. е. через пер-
форированную поверхность воздухораспределителя.
!82
Перфорированные воздухораспределители можно
рассчитывать, как обычные. При этом если перфора-
цию поверхности воздухораспределителя намечено про-
извести по всей длине, то такой воздухораспределитель
рассчитывается как воздухораспределитель с продоль-
ной щелью. В этом случае, сделав расчет ширины ус-
ловной щели и необходимого полного давления при зна-
чении коэффициента расхода, соответствующем значе-
нию коэффициента расхода перфорированного отверстия,
устанавливают степень частоты перфорированных от-
верстий на каждом метре. Очевидно, что число перфо-
рированных отверстий пгх на 1 м составит
тх = 6х/о,
где 6х — ширина условной щели, о — площадь одного перфориро-
ванного отверстия.
Индекс х показывает, что число перфорированных
отверстий будет изменяться по длине воздухораспреде-
лителя.
Если же перфорацию поверхности воздухораспреде-
лителя намечено произвести участками, расположенны-
ми на некотором расстоянии друг от Друга, то расчет
такого перфорированного воздухораспределителя ведет-
ся так же, как расчет воздухораспределителя с отвер-
стиями.
Произведя обычный расчет площадей условных от-
верстий и необходимого полного давления при значе-
нии коэффициента расхода, соответствующем значению
коэффициента расхода перфорированного отверстия,
устанавливают число перфорированных отверстий в
каждом условном отвергни. Очевидно, что число пер-
форированных отверстий тг в условном отверстии со-
ставит
mt = ojo,
где о, — площадь условного отверстия
Индекс i показывает, что число перфорированных
отверстий на каждом участке будет различно.
Наконец, если перфорацию воздухораспределителя
намечено произвести равномерно по одной какой-либо
грани, по двум граням или по всей боковой поверхно-
сти воздухораспределителя, то для обеспечения прибли-
женной равномерной раздачи воздуха необходимо при-
нять такое значение параметров условной щели или от-
183
верстий, которое обеспечивало бы заданную неравно-
мерность.
Вытяжные конусные и клиновидные воздуховоды с
продольной щелью постоянной ширины или с рядом бо-
ковых отверстий одинаковой площади обусловливают
большие относительные отклонения неравномерного вса-
сывания от равномерного, чем вытяжные воздуховоды
постоянного сечения. Вследствие этого ниже приводит-
ся расчет только вытяжных воздуховодов постоянного
сечения. Необходимо отметить, что во всех случаях рас-
сматриваются воздуховоды с заглушенным концом.
ГЛАВА 14
ВОЗДУХОРАСПРЕДЕЛИТЕЛИ С ПРОДОЛЬНОЙ ЩЕЛЬЮ
ПЕРЕМЕННОЙ ШИРИНЫ
Рис. 14.1. Схема воздухораспре-
делителя постоянного сечения с
продольной щелью
§ 58. Воздухораспределитель
постоянного сечения
с продольной щелью
переменной ширины
Воздухораспределитель постоянного сечения длиной
I имеет периметр Р и площадь поперечного сечения F
(рис. 14.1). Вдоль возду-
хораспределителя в боко-
вой его поверхности уст-
роена щель переменной
ширины бж. Расход возду-
ха в начале воздухорас-
пределителя равен LH.
Требуется установить,
как должна изменяться
ширина щели по длине
воздухораспределителя,
чтобы обеспечить равно-
мерную раздачу воздуха
по всей длине щели, и оп-
ределить сопротивление
воздухораспределителя.
Примем начало коор-
динат у заглушенного
конца воздухораспреде-
лителя и направим ось
Рис. 14.2. Кривая изменения шири-
ны щелп по ее длине
184
абсцисс навстречу потоку воздуха. Проведем в воздухо-
распределителе поперечное сечение х. Ширина щели в
сечении х при равномерной раздаче воздуха равна:
§x = Lallvx — Fwallvx. (14.1)
Нормальная скорость воздуха в щели
определена по формуле
может быть
(14.2)
Составим применительно к сечениям х и х=0 (сече-
ние у заглушенного конца воздухораспределителя) урав-
нение Бернулли:
, Pwx . , f X Pwx
Ьрх -ь —— = + 1 -----—dx,
о
где d3 — 4FIP.
При равномерной раздаче воздуха
шх = waxll.
Подставляя в уравнение Бернулли wx и интегрируя,
получаем
&рх = Ар0-(х2//2)(1 -ЛхШэ)р^/2. (14 3)
Подставляя в зависимость (14.1) величины vx и &рх
согласно выражениям (14.2) и (14.3), будем иметь
j, f 1 ц2 х2 / Ах \
бх=1 I/-------— —----- 1— —— , (14.4)
I V Я k 3da /
где 6о — ширина щели у заглушенного конца воздухораспределителя.
Анализ па экстремум зависимости (14.4) обнару-
живает, что при Xi = 0 ширина минимальна, а при х2—
= ‘2ds/K— максимальна. Отсюда следует, что щель в кон-
це воздухораспределителя узкая, затем с удалением от
заглушенного конца ее ширина увеличивается и дости-
гает максимума, после чего уменьшается. Представляет
интерес определить значение х>х2, при котором шири-
на щели будет равна ширине щели в конце воздухорас-
пределителя. С этой целью, положив в зависимости
(14.4) ширину 6х=6о и решив уравнение относительно
х, получим x8=3d3/X. Сказанное иллюстрируется графи-
ком, приведенным на рис. 14.2.
185
На основании проведенного анализа можно устано-
вить ширину продольной щели в конце воздухораспре-
делителя таким образом, чтобы по всей длине воздухо-
распределителя скорости истечения воздуха из про-
дольной щели не превышали максимально допустимого
значения, В самом деле, если 1^х3, то б0^бн и, следо-
вательно, б0=бмин; если 1>Хз, то д0>6н и, следователь-
но, 6п=6мин- Поэтому ширину продольной щели в конце
воздухораспределителя определяют по формулам:
при /'х3
= ^-н/^макс; (И. 5)
при 1>Хз—«о формуле, полученной из зависимости
(14.4), при х—I
где
бы = 7-н/^макс> (14.7)
В расчетах после нахождения ширины продольной
щели 6о рекомендуется сразу же определять начальную
(при /^х2) или максимальную (при />хз) ширину про-
дольной щели, так как они могут быть настолько вели-
ки, что их нельзя осуществить конструктивно. В таких
случаях решение невозможно, и следует увеличить по-
перечные размеры воздухораспределителя или умень-
шить конечную ширину продольной щели, в результате
чего повысятся скорости истечения воздуха.
Сопротивление воздухораспределителя равно полно-
му избыточному давлению в его начале:
ЛР = Лря + р^/2,
где Лря — избыточное статическое давление в начале воздухораспре-
делителя.
Согласно формуле (14.2),
Тогда
ро2я pw2 I v2H
Ртн
2
t86
или
где
(14.8)
(14.9)
§ 59. Конусный воздухораспределитель
с продольной щелью переменной ширины
Конусный воздухораспределитель длиной I имеет ди-
аметр в начале dH, а в конце do (рис. 14.3). Вдоль воз-
духораспределителя устроена щель переменной ширины.
Расход воздуха в начале воздухораспределителя £н.
Требуется установить, как должна изменяться шири-
на щели по длине воздухораспределителя, чтобы обеспе-
чить равномерную раздачу воздуха по всей длине щели,
и определить сопротивление воздухораспределителя.
Примем начало координат у заглушенного конца
воздухораспределителя и направим ось абсцисс навстре-
чу потоку воздуха. Проведем в воздухораспределителе
поперечное сечение х. Ширина щели в сечении х при
равномерной раздаче воздуха равна:
„ La cos 0 л^ШдСозО
Or =x ------- — ---------
lvx 4fox
(14.10)
где 0 — боковой угол раскрытия конуса.
Нормальная скорость воздуха в щели в сечении х
определяется по формуле (14.2).
Составим применительно к сечениям х и х=0 (сече-
ние у заглушенного конца воздухораспределителя) урав-
нение Бернулли:
Рис. 14.3. Схема конусного возду-
хораспределителя с продольной
щелью
При равномерной раз-
даче
187
Ln x F„wttx dKwnx
wx = ~----- = ———=---------------- ,
F* 1 d' I
где Fx и FH — площадь поперечного сечения соответственно в сече*
иии х а в начале воздухораспределителя.
Подставляя в уравнение Бернулли w* и dx=tfo4-
,4~2xtg9, получим
X
4 Р^н X- , Adj pw- f x2dx
Px~ Pa d4x 2 Г- I2 2 J (d04-2x tg 0)° •
о
Интегрируя и принимая во внимание, что tg9— (dH—-
—do) 121, можем написать
4 pw2B х* Adj (3dta+dx)x3
— ТГ+—---------------~
Подставляя в зависимость (14.10) величины vx и
Дрх согласно выражениям (14.2) и (14.11), будем иметь
о2 X' Г A(3d04-dx)x
Fx cos3 0 12d5
(14.12)
Анализ зависимости (14.12) на экстремум показыва-
ет, что щель минимальную ширину имеет в конце воз-
духораспределителя (xi=0), затем с увеличением х ши-
рина ее увеличивается и при х2 достигает максимума,
после чего убывает.
Величина х2 определяется по формуле
xa = 2d0/(A+4tge).
Поскольку боковой угол раскрытия конуса 9 всегда
положителен, то справедливо
2d0/(A 4- 4 tg 9) < 2d0/A < 2dH/A.
Отсюда следует, что продольная щель в конусном
воздухораспределителе имеет наибольшую ширину бли-
же к ее концу по сравнению с воздухораспределителем
постоянного сечения.
Ширину щели, равную ширине щели в конце возду-
хораспределителя, определяют по формуле (14.12). По-
ложив в ней бж—б0 и решив ее относительно х, получим
188
Ширина продольной щели в конце воздухораспреде-
лителя может быть установлена по формулам:
при I СХз
&о = cos ЭУ/Омакс! (14,13)
при 1>Х3
(14.14)
Л (Sdp 4~ da) 1
где
= 2<нcos 0//умакв. (14.15)
Сопротивление воздухораспределителя определяется
по формуле (14.8), где
гп = ^со530/р2 l42tt+ I. (14.16)
§ 60. Клиновидный воздухораспределитель
с продольной щелью переменной ширины
Клиновидный воздухораспределитель длиной I с по-
стоянной высотой Ъ имеет ширину в начале ап и в кон-
це а0 (рис. 14.4). Вдоль воздухораспределителя устрое-
на щель переменной ширины. Расход воздуха в начале
воздухораспределителя LH-
Требуется установить, как должна изменяться шири-
на щели по длине воздухораспределителя, чтобы обеспе-
чить равномерную раздачу воздуха по всей длине щели,
и определить сопротивление воздухораспределителя.
Примем начало координат у заглушенного конца воз-
духораспределителя и направим ось абсцисс навстречу
потоку воздуха. Проведем в воздухораспределителе по-
перечное сечение х. Ширина щели в сечении х при рав-
номерной раздаче возду-
ха определяется по фор-
муле
6х = Z-u COS C/lVx =
= ав bwB cos Q/lvx, (14.17)
где 0 — боковой угол раскры-
тия клина.
Рис. 14.4. Схема клиновидного
воздухораспределителя с продоль-
ной щелью
Нормальная скорость
воздуха в щели определя-
ется по формуле (14.2).
189
Составим применительно к сечениям х и х—0 (се-
чение у заглушенного торца воздухораспределителя)
уравнение Бернулли:
X
Дрх+—_=Apo+j___—
и
4Э1 — эквивалентный диаметр в сечении х.
Подставим в это уравнение
Z-n х ан ©н х
wx = — — =------------—;
Fx I axl
2ах b
d3X =---—; ax = ao4-2xtg0,
ax +b
где Fx — площадь поперечного сечения воздухораспределителя в се-
чении х; ах—ширина воздухораспределителя в сечеиии х.
Тогда получим
«н
Дрх — ДРо „
al
Р^н х2
2 I2
2Ы3
Ршн
~lh + bl2],
где
I р х2 dx__________
2 J (ao + 2xtg0)3 ’
о
имеем
ао
р x2dx
Z1 = J (а0 + 2х tg 0)2 1
о
Проинтегрировав Ц и 12,
1 Г 2(ao4-xtg0) a04-2xtg9
Z, =------ ~~— 2х tg 0 — 2a„ In-------------
1 8tgs0L a» + 2xtg9 S 0
1 Г a04-2xtg9 ao + 3xtg0 .
I, =---- In-------------------------2x tg 91.
8tg39[ a0 (a0 4-2x tg 0)a J
Для упрощения этих зависимостей целесообразно
освободиться от логарифмов. С этой целью воспользуем-
ся формулой разложения логарифмической функции в
ряд:
Гх—1 1 !х—1\3 1 /х — 1\5 1
In х — 2 ---Д — |---- 4- — (-----
Lx4-1 3 \x4-l/ 5 \x4-l/ J
Прн этом ограничимся первым членом ряда, что даст
а0 4- 2х tg 0 2х tg 0
1П-------------------- га--------- .
a0 a04-xtg9
Такая замена для самого невыгодного случая, когда
х—1 и сужение клина значительно, например в 2 раза
190
(Оо: ан=о,5), дает ошибку в 3,8%.
Тогда
х3 ______х3_____
(«о + Щ) ак ’ 2 2 {а0 + aj а2
и, следовательно,
Л + &/2 =
(ах+ 0,5b) х3
(а0 "I- ах) ах
Лрх = &Ра
В таком случае
°Н РШН X2 Ршн (Ид- + 0.5b) X3
a2 2 I2 + 2bl2 2 (ап+а)а2х '
х \ о ‘ х/ х
(14.18)
Подставляя в зависимость (14.17) величины vx и Арх
согласно зависимостям (14.2) и (14.18), будем иметь
6х=1
|Л2 X2
T^cosO
Хх 1
1 —----с,— (ах + 0,5b) .
2(fe + fx) * J
(14.19)
Анализ зависимости (14.19) на экстремум показыва-
ет, что щель минимальную ширину имеет в конце возду-
хораспределителя (%i = 0), затем с увеличением х ее ши-
рина увеличивается и при х2 достигает максимума, пос-
ле чего убывает.
Величина х2, вычисленная при точном значении ин-
тегралов /1 и I2, равна:
1 / (а + Ь)2 2а0Ь ~~а0+Ь
*2 V 16 tg2 0 +Xtg0 4 tg 0
Ширина щели, равная ширине щели в конце возду-
хораспределителя, находится на расстоянии х3. Однако
это расстояние определить не удалось. Поэтому в пер-
вом приближении по аналогии с воздухораспределите-
лем постоянного сечения можно принять х3=1,5х2.
Ширину продольной щели в конце воздухораспреде-
лителя д0 при I <х3 следует определять по формуле
(14.13), а при 1>х3 — по следующей формуле:
б» = Jl/i + —f-— Г1 + о-5*)] •
|F 6* F^cosQ I 2 (Fo + Дн) J
где би находится по формуле (14.15).
191
Сопротивление воздухораспределителя подсчитыва-
ется по формуле (14.8), где определяется по формуле
(14.16).
§ 61. Расчет воздухораспределителей
с продольной щелью
переменной ширины
Заданными величинами являются: d или а, b или da,
dQ или ав, «о, Ь и I, ц, vM!lKc. Кроме того, надо знать k —.
абсолютную шероховатость стенок воздухораспредели-
теля. Расчет ведется в такой последовательности:
1) вычисляют:
da — 2аЪЦа + Ь) или da — 2ав Ь/(ая + Ь);
F = лФ/4, F = ab; Fu = л42/4; Fa = ан b;
wB = LBfF или wB = LB!FB,
2) подсчитывают число Рейнольдса:
Re = d9 wH/v;
3) определяют коэффициент сопротивления трения
по формуле (6.17);
4) вычисляют х3 и устанавливают 1<х3 или />х3;
5) подсчитывают ширину щели у заглушенного кон-
ца воздухораспределителя 6о!
6) вычисляют ширину щели бж;
7) устанавливают сопротивление воздухораспредели-
теля Др.
Необходимо отметить, что ширину продольной щели
на любом расстоянии от конца воздухораспределителя
проще определять по формуле
6ж = Мо, (14.21)
где бх — относительная ширина продольной щели, равная отноше-
нию ширины щели в сечении х к конечной ширине щели.
Относительную ширину продольной щели на основа-
нии формул (14.4), (14.12) и (14.19) можно определить
по следующему равенству:
6Х = - • -- (14.22)
/ 1 — Аг(1 —Вх)хг
При этом имеем для воздухораспределителя:
постоянного сечения
192
КОНУСНОГО
«О D MSdp + dJ
Л -- г д > “ -- о »
Fxcos 9 12^5
КЛИНОВИДНОГО
. X (я*+ 0,56)
иРАсоз0’ 2(Fe + Fx)
где соответственно:
F = —— d2 или F = аб;
4
Fx = 7^ dx = do + 2xtg0;
tg 0 = ~П~° 1 Fх = ах 6;
aA = ao + 2xtg0; tg0= .
Пример 14.1. Определить ширину щели и сопротивление возду-
хораспределителя прямоугольного сечения, если а=2,5 м, 6=1 м;
1=20 м; й=0,1 мм; ц = 0,65; £а=15 м3/с; v=l,5.10—5 м2/с;
^макс — б М/с.
Решение. Вычисляем исходные величины;
2-2,5-1
da =---7-— = 1,43 м; F = 2,5m2;
•3, □
15
— "ГТ" — 6 м/с;
1,43-6
Re = —7-7 Ю& = 5,7 • 10»;
1,5
, У 68 0,1
.-О.п|/ —— = 0.013;
3-1,43
х3 = ’ - - = 330 м; I = 20 < х3 = 330;
v. U10
15
Вычисляем;
О 125 0,013
А = 0,65 —----- 0,03; В = —:-------= 0,003.
’ 2,5 3.1,43
Подформуле (14.22) подсчитываем относительную ширину про-
дольной щели, азатем по формуле (14.21) и ширину продольной ще-
13—741
193
ли. Вычисления ведем для сечений, расположенных через каждые
2 м, по форме, указанной в табл. 14.1.
Таблица 14.1. Относительная и абсолютная ширина щели
X, м 0 2 4 6 8 10 12 14 16 18 20
1 X ‘•Q 1 1,002 1,008 1,015 1,03 1,05 1.07 1.1 1.13 1.18 1,23
6Х’ « 0,125 0,1255 0,126 0,127 0,127 0,131 0,134 0,138 0,141 0,148 0,153
Коэффициент полного сопротивления, скоростное давление и пол-
ное сопротивление равны:
( 2 5 \2
?п = I л «с «л п “ 2,58;
\ 0,65-20-0,153 /
= 21,6 Па; Др = 2,58-21,6 — 56 Па.
ГЛАВА 15
ВОЗДУХОРАСПРЕДЕЛИТЕЛИ С ОТВЕРСТИЯМИ
РАЗЛИЧНОЙ ПЛОЩАДИ
§ 62. Воздухораспределитель
постоянного сечения
с отверстиями различной площади
Воздухораспределитель постоянного сечения длиной
I имеет периметр Р и площадь поперечного сечения F
(рис. 15.1). Вдоль воздухораспределителя в его боковой
Рис. 15.1. Схема воздухораспределителя постояннэго сечения с от-
верстиями
194
поверхности равномерно расположено п отверстий. Пло-
щади всех отверстий различны. Расход воздуха в на-
чале воздухораспределителя равен LH.
Требуется установить, как должны изменяться пло-
щади отверстий по длине воздухораспределителя, что-
бы обеспечить равномерную раздачу воздуха по отвер-
стиям, и определить сопротивление воздухораспредели-
теля.
Пронумеруем все отверстия против движения потока
воздуха и проведем поперечные сечения 1—1, 2—2,...,
к—к, ..., i—i, п—п перед каждым отверстием. Пло-
щадь l-го отверстия при равномерной раздаче возду-
ха равна:
= Ln/nvi — Fw^/nvi. (15.1)
Нормальная скорость воздуха в i-м отверстии
vt= Н
(15.2)
Напишем применительно к i- и i — 1-му сечениям
уравнение Бернулли:
2 2
дл+^-=др1_1+£^ +
где Zo — расстояние между i- и i—1-м сечениями; Т|=0,4 — коэффи-
циент смягчения удара (потери на проход воздуха мимо отверстия
приняты как смягченные потери давления при внезапном расшире-
нии воздуховода).
При равномерной раздаче воздуха
1 — 1
= .
н п
W. — wa------
* n
Подставляя в уравнение Бернулли скорости и
Wi-i, получим
Др. = Дрг_] — р — (1 — I)2 —
Подставляя в зависимость (15.1) величины Vi и
13*
195
&рг согласно выражениям (15.2) и (15.3) и заменяя
1п=1]п, будем иметь
L Г 1 и2 г л/ 1
““‘IV (15-4’
где аг_1 —площадь i—1-го отверстия.
По формуле (15.4) можно последовательно подсчи-
тать все площади отверстий, задаваясь 1=2, 3,..., п.
При этом так же, как и для воздухораспределителя по-
стоянного сечения с продольной щелью переменной ши-
рины, при /<х3 площадь первого отверстия
Щ — £н/дамакс> (15.5)
где у,икс — максимально допустимая скорость истечения воздуха из
отверстия.
В случае же 1>хй зависимость (15.4) надо решать
относительно o,_j и задаваться 1=п, п—1, ..., 2, причем
площадь «-го отверстия определять по формуле
ап — Т-н/^^маьс- (15.6)
Величину х3 установить не удалось, поэтому ее следу-
ет подсчитывать по формуле для воздухораспределителя
постоянного сечения с продольной щелью переменной
ширины.
Сопротивление воздухораспределителя равно полно-
му избыточному давлению в начале воздухораспредели-
теля
ЛР = Лрп + ргг/ц/2,
где Дрп — избыточное статическое давление внутри воздухораспре-
делителя в /г-м сечении.
Величина Дрп, согласно формуле (15.2), равна:
&Рп = Ру^2И2-
Тогда
ЛО < ра)» / ЛрШ«
- 2^ + 2 (у + J 2
или
Ршп
ДР = ?п—, (15.7)
где
196
§ 63. Конусный воздухораспределитель
с отверстиями различной площади
Конусный воздухораспределитель длиной I имеет диа-
метр в начале da, а в конце dQ. Вдоль воздухораспреде-
лителя равномерно расположено п отверстий. Площадь
отверстий различна. Расход воздуха в начале воздухо-
распределителя LH-
Требуется установить, как должны изменяться пло-
щади отверстий по длине воздухораспределителя, чтобы
обеспечить равномерную раздачу воздуха по отверсти-
ям, и определить сопротивление воздухораспределителя.
Пронумеруем все отверстия против движения потока
воздуха и проведем поперечные сечения перед каждым
отверстием. Площадь i-ro отверстия при равномерной
раздаче воздуха определяется по формуле
<y. = L„lm = nd?wJ4nv.. (15.9)
L П I u ti i '
Нормальная скорость воздуха в i-м отверстии опре-
деляется по формуле (15.2).
Применительно к i- и i — I-му сечениям напишем
уравнение Бернулли:
i.
, Г х РИ’Ь-м о
+ J —2—dX + П 2 (“>*— “’‘-1) ’ (15J0)
и
где /0 — расстояние между i- и I— 1-м сечениями; — диаметр
воздухораспределителя на расстоянии х от i—1-го сечения; я—
скорость внутри воздухораспределителя в сечении с диаметром
di-i, »; г; = 0,4 — коэффициент смягчения удара
Подставим в уравнение (15.10):
i i-1
w, —-----------: w , —-----------------
d2 n d2_, n
d2 i _ i
wt-i,x = —------------и d(_x x = + 2x tg 0,
ll—l,X
где d, и d,_i—диаметры воздухораспределителя в i- и t—1-м сече-
ниях, 0 — боковой угол раскрытия конуса.
197
Тогда после интегрирования получим
. . \i2 (i-1)2 Ч^-<С-1)<‘~1)2
Др. = ap; « — <------- — —------------- —
1 U M<!tge
i2 _ (« — !)* Т1 4 Р^н
4 J J “а 2 ’
(15.11)
Подставляя в зависимость (15.9) величины vt и Др<
согласно выражениям (15.2) и (15.11), будем иметь
Г ? (f_1)8 X(F?-F?_Q(1-1)2
1Л Fl-i F^F^tge
-п(тг—ТрМ2]» (15-12)
\F( г<-1 I
где о.-i — площадь i—1-ro отверстия.
В этой формуле
nd? i
Л = —d^do + 21— tgG.
4 n
По формуле (15.12) можно последовательно подсчи-
тать все площади отверстий, задаваясь i=2, 3, .... п. При
этом так же, как и для конусного воздухораспределителя
с продольной щелью переменной ширины, при /</з пло-
щадь первого отверстия щ определяется по формуле
(15.5).
В случае же 1>хз зависимость (15.12) надо решать
относительно Oi-i и задаваться i=n, п—1 2, причем
площадь n-го отверстия ога определять по формуле
(15.6).
Величину х3 установить не удалось, поэтому ее следу-
ет определять по формуле для конусного воздухораспре-
делителя с продольной щелью переменной ширины.
Сопротивление воздухораспределителя определяется
по формуле (15.7), где £п подсчитывается по формуле
(15.8),
198
§ 64. Клиновидный воздухораспределитель
с отверстиями различной площади
Клиновидный воздухораспределитель длиной I с по-
стоянной высотой b имеет ширину в начале ан, а в кон-
це а0. Вдоль воздухораспределителя равномерно распо-
ложено п отверстий. Площадь отверстий различна. Рас-
ход воздуха в начале воздухораспределителя LB.
Требуется установить, как должны изменяться пло-
щади отверстий по длине воздухораспределителя, чтобы
обеспечить равномерную раздачу воздуха по отверстиям,
и определить сопротивление воздухораспределителя.
Пронумеруем все отверстия против движения потока
воздуха и проведем поперечные сечения перед каждым
отверстием. Площадь i-ro отверстия при равномерной
раздаче воздуха определяется по формуле
а, — LBlnvi = ан bwBlnvi. (15.13)
Нормальная скорость воздуха в i-м отверстии опреде-
ляется по формуле (15.2).
Применительно к i- и i — 1-му сечениям справедливо
уравнение Бернулли (15.10) при условии, что под вели-
чиной di-lrX надо понимать эквивалентный диаметр.
Подставим в уравнение (15.10):
ан i а„ i — 1
а<-1л = а,-1 +2я tg 0,
где а, и a,--i —ширина воздухораспределителя в i- и I—1-м сечени-
ях; di-i, х — ширина воздухораспределителя на расстоянии х от
i—1-го сечения; «—скорость воздуха внутри воздухораспре-
делителя в сечении с шириной а<-1, х; 0 — боковой угол раскрытия
клина.
д/\ = Др,_1 —
Тогда после интегрирования получим
2а. а, , + 6 (а. + а, ,)
'х 2 2
L ai ai—i
\ 9 9
_ (1 _ ‘ -1 у I а«
** \ а/ ai—1 / J п8 2
(15.14)
199
Подставляя в зависимость (15.13) величины Vi и Др/
согласно выражениям (15.2) и (15.14), будем иметь
где а,-! — площадь i—1-го отверстия.
В формуле (15.15)
ас = аа + 21— tg0.
п
По формуле (15.15) последовательно можно подсчи-
тать площади всех отверстий, задаваясь t=2, 3, ..., п.
Причем при /<Сх3 величина Oi определяется по формуле
(15.5), а при 1>х3 зависимость (15.15) надо решать от-
носительно Oi-i н задаваться i—n, п—1, ..., 2, а оп опре-
делять по формуле (15.6).
Величину х3 установить не удалось, поэтому ее сле-
дует определять по формуле для клиновидного воздухо-
распределителя с продольной щелью переменной ши-
рины.
Сопротивление воздухораспределителя определяется
по формуле (15.7), где £п подсчитывается по форму»
ле (15.8).
§ 65. Расчет воздухораспределителей
с отверстиями различной площади
Расчет этих воздухораспределителей проводится та-
ким же образом, как и расчет воздухораспределителей
с продольной щелью переменной ширины. При этом Хз
подсчитывается по ранее приведенным формулам для
воздухораспределителей с продольной щелью перемен-
ной ширины.
Площади отверстий рекомендуется рассчитывать по
формуле
°z = °(CTz-i> (15.16)
где а, — относительная площадь отверстия, равная отношению пло-
щади г-го отверстия к площади i—1-го отверстия.
200
Относительную же площадь (-го отверстия на основа-
нии зависимостей (15.4), (15.12) и (15.15) можно опре-
делять по следующей формуле:
0i = 1//1—Л2 [I3 — B(i — 1)'2J. (15.17)
При этом для воздухораспределителей:
постоянного сечения
А = р ~г~ ; В = 1 Н—- |- - —-,
F nda (i— I)2
конусного
клиновидного
а?
В =—-
a'L
А = и
<4
ai—i
2
где
F = —— d3 или F — ab;
4
= -Г d. = d+2l—tgB = d +(da-d.) — ;
* * C U Л U\n (J/ д
F( = at b; at = a0 + 21 — tg 9 = a0 + (aH — a0) — .
n n
Пример 15.1. Определить площади отверстий и сопротивление
воздухораспределителя прямоугольного сечения, если а=2,5 м;
Ь=1 м; /=30 м; 6 = 0,1 мм; n=10; pi = 0,65; Ln—15 м/с; v =
= 1,5.10-5 М2/с и Смаке = 6 м/с.
Решение. Используя решение, приведенное в примере (14.1),
имеем: <£>=1,43 м; шн=6 м/с; А=0,013; х3=ЗЗО м; /=ЗО<х3=ЗЗО.
Следовательно, в нашем случае:
15
а1==“БТ = 0’25м;
Д=.0,65-^- = 0,2€аь
2,5
201
В = 1 +
0,013-30
10-1,43
0,4
О'-I)3
= 1,027 +
0,4
О-I)3’
Расчет ведем в такой последовательности: вначале вычисляем
А к В, затем по формуле (15 17)—относительную площадь отвер-
стия, после этого по формуле (15.16)—площадь отверстия. Ре-
зультаты расчета записываем в виде табл. 15.1
Таблица 15.1. Коэффициенты А, В, относительная и абсолютная
площади отверстий
i 1 2 3 4 5 6 7 8 9 10
А 0,065 0,065 0,0652 0.066 0,067 0,685 0,0705 0,0727 0,076 0,079
В 00 1,427 1,127 1,071 1,052 1,043 1,038 1,035 1,033 17032
1 1,005 1,01 1,015 1,02 1,025 1,032 1,04 1,05 1,06
0(t м2 0,25 0,251 0,254 0,258 0,264 0,271 0,28 0,292 0,307 0,325
давление и
Коэффициент полного сопротивления, скоростное
полное сопротивление воздуховода равны:
/ 2,5 \2
= --------------- + 1 = 2,18;
\ 0,65-10-0,325 )
Р“<н 1-2-63 „
----=----------= 21,6 Па;
2 2 ’
ДР =2,18-21,6 = 47 Па.
ГЛАВА 16
ВОЗДУХОРАСПРЕДЕЛИТЕЛИ С ПРОДОЛЬНОЙ ЩЕЛЬЮ
ПОСТОЯННОЙ ШИРИНЫ
§ 66. Воздухораспределитель переменного
прямоугольного поперечного сечения
Воздухораспределитель переменного прямоугольного
поперечного сечения длиной I имеет ширину в начале аа
и постоянную высоту b (рис. 16.1). Одна боковая стенка
у воздухораспределителя плоская и в ней устроена про-
дольная щель постоянной ширины б. Другая боковая
стенка криволинейная. Расход воздуха в начале возду-
хораспределителя LH,
2W
Рис. 16.1. Схема воздухораспреде-
лителя постоянного статического
давления
Требуется установить,
как должна изменяться
ширина воздухораспреде-
лителя, чтобы обеспечить
равномерное статическое
давление воздуха по всей
его длине, а также опре-
делить сопротивление
воздухораспределителя.
Поместим начало ко-
ординат в конце воздухо-
распределителя и напра-
вим ось абсцисс навстречу
потоку воздуха {4]. Проведем
в воздухораспределителе два поперечных сечения: пер-
вое— на расстоянии х от заглушенного конца, а вто-
рое — рядом с ним на расстоянии dx.
•Очевидно, уменьшение расхода воздуха внутри возду-
хораспределителя от сечения x+dx к сечению х равно
расходу воздуха, вытекающего через щель между этими
сечениями.
Обозначив расход воздуха в сечении х через Lx, а в
сечении x+dx через Lx + dLx и нормальную скорость ис-
течения воздуха из щели в сечении х через v, можем на-
писать
dLx = v8dx.
Нормальная скорость воздуха в щели
(16.1)
(16.2)
Из зависимости (16.2) следует, что если Ap = const, то
У —const. В таком случае, интегрируя уравнение (16.1),
получаем Lx—v8x.
Составим применительно к обоим сечениям уравнение
Бернулли:
Р^х
2
Л
К Р®х
-----dx.
d3 2
,. Вычитая из левой и правой частей уравнения одина-
ковые члены, дифференцируя, сокращая на wx и подстав-
ляя d9, получаем
Л (ах + Ь)
^ахЪ

Подставляя сюда
Lx vbx
wx = —- — —- и w
axb axb
vb ax Xax
~b a2
X
получаем уравнение
ax~xa’x~ fix/4Ь) (ax -Г b).
Приводя его к нормальному виду, имеем следующее
линейное дифференциальное уравнение:
а'х + (ЩЬ — 1/х)аа. + Х/4 = 0. (16.3)
Интегрируя его, можем написать
Произвольную постоянную с находим из граничных
условий. Приняв в последнем равенстве х=/, получаем
(i \
С ^/4^1 ^/46,
4 J х /
о /
Отсюда
i
с — — С g^/4b — .
I 4 J х
О
В таком случае ширина воздухораспределителя
i
ах = + А. j е^ь хе~^ь. (16.4)
X
На основании равенства (16.4) можно предложить
для определения ширины следующую расчетную фор-
мулу:
ах = ЛаГ1 + ВЬ, (16.5)
где
и - I и - ,
— (1—х) Л , —Л-Х Г, —X Jr
А=хе4Ь ; В— — хе ® I е46 —, (16.6)
46 J х
х
здесь x—xll.
204
По формулам (16.5) и (16.6) построена номограмма,
приведенная на рис. 16.2.
Сопротивление воздухораспределителя переменного
поперечного сечения равно полному избыточному давле-
нию в его начале:
д? = Др + _2!-,
где Др — избыточное статическое давление в воздухораспределите-
ле; wB — скорость воздуха в начале воздухораспределителя.
Согласно формуле (16.2),
Др = ро2/2р2.
Тогда
ДР =
Р^Н
2
Рис. 16.2. Номограмма для расчета ширины воздухораспределителя
постоянного статического давления
205
или
Д^ = Сп
Р^н
2 ’
(16.7)
где
Сп = v2/g2 а«н +• 1 • (16.8)
§ 67. Воздухораспределитель
постоянного сечения
с продольной щелью постоянной ширины
Воздухораспределитель постоянного сечения длиной
I имеет периметр Р и площадь поперечного сечения F
(см. рис. 14.1). Вдоль воздухораспределителя устроена
щель постоянной ширины 6. Расход воздуха в начале
воздухораспределителя Лн.
Требуется установить, насколько отклоняется нерав-
номерная раздача воздуха таким воздухораспределите-
лем от равномерной, и определить сопротивление возду-
хораспределителя.
Примем начало координат у заглушенного конца
воздухораспределителя и направим ось абсцисс навстре-
чу потоку воздуха. Проведем в воздухораспределителе
два поперечных сечения на расстояниях х и x+dx от за-
глушенного конца.
Очевидно, уменьшение расхода воздуха внутри воз-
духораспределителя от сечения x + dx к сечению х равно
расходу воздуха, вытекающему через щель между этими
сечениями.
Обозначив скорость воздуха в сечении х через wx,
а в сечении x+dx через wx + dwx и нормальную скорость
истечения из щели в сечении х через vx, можем написать
Fdwx = vx 6dx.
Переходя к производной»щолучаем
^ = -уРж. (16.9)
Нормальная скорость воздуха в щели
= &Рх‘ (16.10)
* г
206
Составим применительно к сечениям х и x+dx урав-
нение Бернулли:
, Р®1 , а ,РШх , х P-'z ,
+ ----— +d — у = &рх + 2 +— 2 dx.
Уничтожая в левой и правой частях уравнения одина-
ковые члены и переходя к производным, получаем
, , X Р®х
Дрх + ршхшх——— =0. (16.11)
Выразим Др* через скорость wx. Из уравнения (16.10)
следует
= Р^/2|Л
.Согласно выражению (16.9) vx — — wx , и потому
pf2 -2
Лр* — 2р2 б2 Wx •
Беря производную, получаем
. Pf2 ' ”
apr — wr
х р2б2 Х Х
Подставляя в уравнение (16.11) величину Др’ и ум-
ножая на pt262/pF2, будем иметь
„ , , р2 б2 . и2 б2 % , Л
+7Гшхг£’х-0>5 —— шх = 0.
Введем обозначения:
шх = шх/аин; х—хЦ,
где wB—скорость воздуха в начале воздухораспределителя.
Тогда
wx = Шн wx\ х — Гх;
„ dwx wH dwx Wj,
<rtl =-- —-------=------- •
x dx I2 dx I2 x'
Подставляя найденные значения wXl wx и wx в по-
следнее уравнение и сокращая на w2H/l3, получим сле-
207
дующее дифференциальное уравнение:
w' + Р + <7 = О,
А А • А А ’ А '
(16.12)
где
p=g2 (2; q = — 0,5 g2 f2 17;
f = f/F = 6//F; 7=//d3.
Величину nf называют параметром щели, а 17 — па-
раметром воздуховода.
Дифференциальное уравнение можно проинтегриро-
вать численными методами на ЭЦВМ.
При расчетах было принято:
g/ = 0,4 ч- 2,4 при шаге Дц/ = 0,2;
17 = Оч-4 при шаге Д17 = О,5;
х = 0 ч- 1 при шаге Д х = 0,05.
Относительная скорость истечения воздуха из щели
составит
vx Fw* Fwa
, = — = --------= ------w = w
x ^cp O^cp о/^ср
(16.13)
где yCp — средняя скорость воздуха в щели.
Заметим, что при равномерной раздаче относитель-
ная скорость воздуха в продольной щелн равна единице.
Вследствие этого отклонение неравномерной раздачи
воздуха от равномерной составит
гх=йх-1. (16.14)
В результате расчета были получены таблицы с изме-
нением гх в зависимости от х. Анализ этих таблиц позво-
ляет отметить, что относительное отклонение в общем
случае изменяется следующим образом: в конце возду-
хораспределителя гх имеет какое-то значение, затем по
мере увеличения х величина гх уменьшается и достигает
минимума, после чего при дальнейшем увеличении х ве-
личина гх растет и достигает некоторого значения в на-
чале воздухораспределителя. Вследствие такой законо-
мерности изменения гх был построен график (рис. 16.3).
На графиках отклонения г0, гмин и гн даны соответст-
венно в конце, в сечении с минимальной скоростью исте-
чения и в начале воздуховода,
208
Как видим, абсолютные значения го, гКт и гн увели-
чиваются с увеличением параметра щели ц/. Отклонение
га при М=0 отрицательно и с увеличением параметра
канала kl сначала убывает, достигая минимума при
Х7=2,5, после чего увеличивается. Отклонение гыиц всег-
да отрицательно и с увеличением параметра канала kl
только убывает. Отклонение же го всегда положительно
Рис. 16.3. График изменения относительных отклонений для воз-
духораспределителя постоянного сечения с продольной щелью
14—741 209
и с увеличением параметра канала К1 тоже только убы-
вает.
Полное сопротивление воздухораспределителя равно
избыточному полному давлению в начале воздухорас-
пределителя:
ДР = Арн + ра»и/2.
Согласно выражению (16.10), Дрн=рц2/2ц2, поэтому
ДР=(^/р2 га2 + Г) (кгг/2
или
рщ)2
(16.15)
где
= -^- + 1 = lUfo-l2 4-1. (16.16)
ц2 /а /2
§ 68. Конусный воздухораспределитель
с продольной щелью
постоянной ширины
Конусный воздухораспределитель длиной I имеет
диаметр в начале da, а в конце d0 (см. рис. 14.3). Вдоль
воздухораспределителя устроена щель постоянной шири-
ны 6. Расход воздуха в начале воздухораспределите-
ля Тн.
Требуется установить, насколько отклоняется нерав-
номерная раздача воздуха таким воздухораспределите-
лем от равномерной, и определить сопротивление возду-
хораспределителя.
Примем начало координат у заглушенного конца
воздухораспределителя и направим ось абсцисс навстре-
чу потоку воздуха [9]. Проведем в воздухораспредели-
теле два поперечных сечения на расстояниях х и x-$-dx
от заглушенного конца.
Обозначив расход воздуха в сечении х через Lx, а в
сечении x-\-dx через Lx-\-dLx и нормальную скорость ис-
течения из щели в сечении х через vx, можем написать
dx
dLx = vxb---------------------— ,
cos О
где 0 — боковой угол раскрытия конуса.
210
Переходя к производной, получим
Lx — vx б/cos 0. (16 17)
Нормальная скорость истечения воздуха из щели оп-
ределяется по формуле (16 10).
Составим применительно к сечениям х и x-\-dx урав-
нение Бернулли:
р^ / рОУх \ рш* % pwx
&Рх + dfxpx + —~ + d I —~ I = Лрх + — +~ — dx
Проводя преобразования и переходя к производным,
получим
, , ' х п
Д/>х+ pwxwx — — — =°.
Выразим Др'; wx и w’x через объемный расход Lx. Из
зависимостей (16.10) и (16 17) следует
/р / Lx cos2 0\ р cos2 0 , „
Рх=\2^1 = 2|Г2 к б2 / р2б2 xL*'
Величины же
(16 18)
Lx Fx Lx Fx
Lx
w = — И W.
х р
г х
р1
1 X
где Fx — площадь поперечного сечения воздухораспределителя в се-
чении г
Подставляя в уравнение (16.18) величины \р’х, wx
и wx и деля на р cos2 0/р2б2, будем иметь
„ , ц2 б2 , ц2 б2 (FX L \ ,
Lx Lx + ; •„ Lx Lx- 2 — + — =°. (16.19)
Fxcos 0 P2cos20 \Гх L.ax/
Введем обозначения
Lx — LxlLa, FX = FX/Fn; dx = dx/dn, x — x/l,
где FB — площадь поперечного сечения в начале воздухораспреде-
лителя.
Тогда
Lx = La Lx', Fx — Fa Fx, dx — dB dx; x = I x;
,' dL* LH d Lx LB
Lx^~= = ~T Lx,
dx Id x 1
14»
211
Г = —= ^-Г-
х dx р *'
dFx Fn ,
Fr =---= — F„.
dx Iх
Подставляя найденные величины Lx, L'x, L’x, Fx и F’
в уравнение (16.19), обозначая f=/7FH=6Z/FHcos 0, 1=
—llda и умножая на lsIL?a, получим
ьх ьх ' р2 ьх
, 4МП = 0, (16.20)
Fx 2dxJ
где nf — параметр щели; XZ — параметр воздуховода.
В формуле (16.20):
dx 1 1 /
г/Л = /=7’(г/о+2х1§0) = -7’ Ро+2ж
х dn dB ' и > d3 \ u
4н — 40
2/ .
(16.21)
(16.22)
(16.23)
из щели
(16.24)
скорости
где do=do/dH.
Относительная скорость истечения воздуха
vx Fx cos 0 £н cos 0
и = — = —---------------= —-----Lr — Lr,
X Vcp 6t>cp 6/Vcp
где vCp — средняя скорость воздуха в щели.
Относительное отклонение относительной
истечения от относительной скорости при равномерной
раздаче определяется по формул^ (16.14).
Интегрирование дифференциального уравнения
(16.20) проводилось по методу Рунге — Кутта. ГраниЧ'
ными условиями являлись: х=0, Lx==0 и х=1, Lx=l.
Значение первой производной Lx при х=0 содержалось
в интервале значений l<Lx<oo.
Ввиду трудоемкости вычислений Lx, vx и гх расчеты
проводились на ЭЦВМ. При расчетах было принято:
р / = 0,2 -т- 2 при шаге Др f = 0,2;
Л.7 = 0-т-4 при шаге ДХ7=О,5;
3e = 0,2-s-l при шаге д5о = 0,2;
х = 0 н- 1 при шаге Д х — 0,1.
212
По результатам расчета
при разных значениях d0 бы-
ли построены графики отно-
сительного отклонения в кон-
це, в сечении с наименьшей
скоростью истечения и в на-
чале воздухораспределите-
ля: Го, Г мин, 1" н.
Наименьшие отклонения
при обычно допускаемых
относительных отклонениях
гх<0,5 оказались у_ возду-
хораспределителя с do=O,8.
Вследствие этого графики
отклонений приводятся толь-
ко для воздухораспредели-
теля с таким сужением (рис.
16.4). Из графиков видно,
что относительное отклоне-
ние увеличивается с увели-
чением параметра щели.
Сопротивление конусно-
го воздухораспределителя с
продольной щелью постоян-
ной ширины определяется
по формуле (16.15), где £п
находится по формуле
(16.16).
Рис. 16 4. График изменения
относительною отклонения
для конусного воздухорас-
пределителя с продольной
щелью при do = 0,8
§ 69. Клиновидный воздухораспределитель
с продольной щелью постоянной ширины
Клиновидный воздухораспределитель длиной I с по-
стоянной высотой b имеет ширину в начале ан и в конце
«о (см. рис. 14.4). Вдоль воздухораспределителя устрое-
на щель постоянной ширины б. Расход воздуха в начале
воздухораспределителя равен La.
Требуется установить, насколько отклоняется неравно-
мерная раздача воздуха таким воздухораспределителем
от равномерной, и определить сопротивление воздухо-
распределителя.
Примем начало координат у заглушенного конца
воздухораспределителя и направим ось абсцисс навстре-
чу потоку воздуха [12]. Проведем в воздухораспредели-
213
теле два поперечных сечения на расстояниях х и x-j-dx
от заглушенного конца.
Проводя такие же выкладки, как и для конусного
воздухораспределителя с продольной щелью постоянной
ширины, получим равенства, аналогичные равенствам
(16.17) — (16.19). Переходя к безразмерным величинам,
получаем следующее, соответствующее равенству (16.20),
уравнение:
LxLx^ -р LxLx р
'х М
F х 24эх
7.2 = 0, (16.25)
где
f = f/Fw = 6l/FncosQ- FX^FX/FU- l =
dax — d$x/aui LX = LXILB.
Для клиновидного воздухораспределителя справед-
ливо
ах 1 „ 1 / ан — ап\
ах =— =— (fle + 2х tg 0) =— at+2x—-—i =
°н ап аи \ 21 j
= а0 Н-(1 — а0) i, (16.26)
где
а0 — а0/аа; ~х = х/1.
В таком случае:
Fx — ахЬ/аиЬ — ах = -р (1—ав) х; (16.27)
?' = 1 —о0; (16.28)
1 2axb 2axb 2la0-p(l—а0)х!б
Ъх =-------fl = ° у7-5 —, (16.29)
°н ах + b ax-j-b а,/п~ (1 — а0)х -р b
где
Ь — Ь/ая.
Относительная скорость истечения воздуха из щели
будет определяться по формуле (16.24), а относительное
отклонение относительной скорости истечения от относи-
тельной скорости истечения при равномерной раздаче —
по формуле (16.14.)
Интегрирование дифференциального уравнения
(16.25) проводилось численными методами с помощью
ЭЦВМ. При расчетах было принято:
р7 = О,5; 1; 1,5; 2; М = 0; 1; 2; 3; 4; ло = О,4; 0,6; 0,8; 6 = 0,5;
х = 0; 0,2; 0,4; 0,6; 0,8; 1.
214
По результатам расчета
при разных аа и b были по-
строены графики относитель-
ных отклонений г0, гмин и
гв. На рис. 16.5 приведен гра-
фик относительного отклоне-
ния для случая ао=0,8 и Ь =
= 0,5. Сопротивление клино-
видного воздухораспредели-
теля со щелью постоянной
ширины определяется по
формуле (16.15), где £п на-
ходится по формуле (16.16).
§ 70. Расчет
воздухор аспредел ител ей
с продольной щелью
постоянной ширины
При расчете воздухорас-
пределителя переменного
прямоугольного поперечного
сечения обычно заданы ан,
b, I, Lb, ц. Кроме того, на-
до знать k — абсолютную
шероховатость стенок возду-
хораспределителя и Пмакс —
максимально допустимую
скорость истечения воздуха
из щели. Расчет ведется в
такой последовательности:
Рис. 16.5. График изменения
относительного отклонения
для клиновидного воздухо-
распределителя с продоль-
ной щелью
1) вычисляют da—2aKb/(an-^-b); FH=aH&; Wb—Lh/Fh,
2) находят число Рейнольдса: Re=d3u»H/v;
3) вычисляют коэффициент сопротивления трения по
формуле (6.17);
4) определяют по номограмме (см. рис. 16.2) А и В,
а затем пх;
5) находят ширину продольной щели:
Ь — IUmbhc',
(16.30)
6) вычисляют £п И А.Р.
При расчете воздухораспределителя постоянного сече-
ния обычно заданы d или а и b, I, Ln, р, г и k — абсолют-
215
теле два поперечных сечения на расстояниях х и x-^-dx
от заглушенного конца.
Проводя такие же выкладки, как и для конусного
воздухораспределителя с продольной щелью постоянной
ширины, получим равенства, аналогичные равенствам
(16.17) — (16.19). Переходя к безразмерным величинам,
получаем следующее, соответствующее равенству (16.20),
уравнение:
—Л» — f
^х ^х
Ц2 /2---
LXL
Ьх
[X
F2 F
X L X
(16.25)
где
f = //fH = 6//FHcos6; FX = FX/FH; 1^Цая,
^вх — ^эх/^н', Lx = Lx/Lh-
Для клиновидного воздухораспределителя справед-
ливо
— бу J 1 / tZfl ~~ аД
ах —— = — (а0 + 2х tg 6) =—lfle4-2x—-— =
\ 2/ /
= aft-р (1 — a0) x, (16.26)
где
a0 = a0/aH; x = x/l.
В таком случае:
Fx = ax b/au b = ax = a0 4- (1—ae)x; (16.27)
= (16.28)
1 2aJ) 2axb 2 [a0 -f- (1 — a0) xl b
d3X =------77 = z—— = _------- --—=——, (16.29)
cn 11 x + b ax-j-b a0'4~ (1 — a0)x + b
где
b=b/aH.
Относительная скорость истечения воздуха из щели
будет определяться по формуле (16.24), а относительное
отклонение относительной скорости истечения от относи-
тельной скорости истечения при равномерной раздаче —
по формуле (16.14.)
Интегрирование дифференциального уравнения
(16.25) проводилось численными методами с помощью
ЭЦВМ. При расчетах было принято:
р/ = 0,5; 1; 1,5; 2; W = 0; 1; 2; 3; 4; йо = О,4; 0,6; 0,8; Ь = 0,5;
х = 0; 0,2; 0,4; 0,6; 0,8; 1.
214
По результатам расчета
при разных cio и b были по-
строены графики относитель-
ных отклонений г0, гмин и
гв. На рис. 16.5 приведен гра-
фик относительного отклоне-
ния для случая по = О,8 и Ь =
= 0,5. Сопротивление клино-
видного воздухораспредели-
теля со щелью постоянной
ширины определяется по
формуле (16.15), где £п на-
ходится по формуле (16.16).
§ 70. Расчет
воздухор аспределител ей
с продольной щелью
постоянной ширины
При расчете воздухорас-
пределителя переменного
прямоугольного поперечного
сечения обычно заданы ан,
b, I, La, ц. Кроме того, на-
до знать k — абсолютную
шероховатость стенок возду-
хораспределителя И Умакс —
максиматьно допустимую
скорость истечения воздуха
из щели. Расчет ведется в
такой последовательности:
Рис. 16.5. График изменения
относительного отклонения
для клиновидного воздухо-
распределителя с продоль-
ной щелью
1) вычисляют <Уэ=2пнЬ/(«н+Ь); Кн=ан&; te»H==i-H/FH;
2) находят число Рейнольдса: Re=d3te»H/v;
3) вычисляют коэффициент сопротивления трения по
формуле (6.17);
4) определяют по номограмме (см. рис. 16.2) А и В,
а затем ах;
5) находят ширину продольной щели:
в — Гн/ 1Имакс‘>
(16.30)
6) ВЫЧИСЛЯЮТ £п и АР.
При расчете воздухораспределителя постоянного сече-
ния обычно заданы d или а и b, I, La, ц, г и k — абсолют-
215
ная шероховатость стенок воздухораспределителя. Рас*
чет ведется в такой последовательности:
1) вычисляют б?э, F, wB;
2) находят Re, % и XI;
3) по значениям г и XI на графике (см. рис. 16.3)
находят значения р/ и выбирают наименьшее из них;
4) подсчитывают ширину щели
8==1eZLL. (16.31)
5) вычисляют £ и ДР.
При расчете конусного и клиновидного воздухорас-
пределителей обычно заданы da или ап, b, I, Ln, ц, г и
k — абсолютная шероховатость стенок воздухораспреде-
лителя. Расчет ведется в такой последовательности:
1) вычисляют б?э, Рн, wa;
2) находят Re, X и XI, используя da;
3) по значениям г п XI на графиках (см. рис. 16.4,
и 16.5) находят значения р/ и выбирают наименьшие
из них;
4) вычисляют б?о = О,8 dn или ао = 0,8 аи;
5) подсчитывают ширину щели:
_ (р./) FHcosO ~ (ц/)Ря
р/ ~ р/ ’ ( • )
6) вычисляют £п и Др.
Пример 16 1. Определить ширину продольной щели и сопроти-
вление воздухораспределителя постоянжио сечения, если а=1,2 м;
i> = 0,8 м; /=35 м; fe=0,l мм; v = l,5.10~5 м2/с; р=0,62; wn =
= 6,5 м/с; г=±0,2.
Решение. Вычисляем исходные величины;
2-1,2-0,8 6,5-0,96
= 1 9 . п я = °>96 м; Re = Г<~1051=14’151
1,1 -f- U, о 1,0
л 1 У 68 оТ
Х= 0,111/ —— 10-?+ ~ = 0,014;
’ V 4,16 960 ’
35
Л/=0,014----— = 0,51.
’ 0,96
По графику (см. рис, 16 3) для гп=—0,2 находим р/=0,86; для го=
= +0,2 находим pf=l,2.
216
Принимаем р/ = 0,86, тогда: „ 0,86-1,2-0,8 6 = ’ ’ ’ = 0,038 м; 0,62-35 (1 — 0,2)2 gn = -J У— + 1 = 1,86; ьп 0,862 9 2^=Ч^. = 25>з Па; 2 2 ’ ДР= 1,86-25,3 = 47 Па.
ГЛАВА 17
ВОЗДУХОРАСПРЕДЕЛИТЕЛИ С ОТВЕРСТИЯМИ
ОДИНАКОВОЙ ПЛОЩАДИ
§71. Воздухораспределитель
постоянного сечения
с отверстиями одинаковой площади
Воздухораспределитель постоянного сечения длиной
I имеет периметр Р и площадь поперечного сечения F
(см. рис. 15.1). Вдоль боковой поверхности воздухорас-
пределителя равномерно расположено п отверстий. Пло-
щадь всех отверстий одинакова и равна о. Расход воз-
духа в начале воздухораспределителя равен Lu.
Требуется установить, насколько отклоняется нерав-
номерная раздача воздуха таким воздухораспределите-
лем от равномерной, и определить сопротивление
воздухораспределителя.
Пронумеруем все отверстия против движения потока
воздуха и проведем поперечные сечения перед каждым
отверстием.
Очевидно, уменьшение расхода воздуха внутри воз-
духораспределителя от сечения i к сечению i — 1 равно
расходу воздуха, вытекающему через i-e отверстие меж-
ду этими сечениями. Обозначив скорость воздуха в се-
чении I через wh а в сечении i— 1 через wt-\ и нормаль-
ную скорость истечения воздуха через i-e отверстие че-
рез и,, можем написать
F(wt — = (17.1)
Нормальная скорость воздуха в i-м отверстии
217
Напишем применительно к i- и i—1-му сечениям
уравнение Бернулли.
Apt + ~ “"г = + 1 у- -у
, „ р
(17 3)
где 1о— расстояние между двумя смежными сечениями, т]=0,4 —
коэффициент смягчения удара (потери на проход воздуха мимо от-
верстия приняты как смягченные потери при внезапном расширении
канала)
В уравнении (17 3) неизвестные избыточные стати-
ческие давления можно исключить, если воспользовать-
ся формулой (17 2) В результате имеем.
Ар, = Р^/2р2 ; \р^ = ро2_; /2р.2.
Согласно зависимости (17.1):
vl = (F/o)(wi—
t\_l = (F/о) (a/f_i-t0t_2).
В таком случае;
pF’
pF3
Подставляя Др, и Др,-1 в уравнение (17.3) и осу-
ществляя преобразования, будем иметь следующее
квадратное уравнение-
[1+-^
L п J к
U2 7а / 17 \ —9 — — —9
— ( 1 +~ + Ч I rf-i + 2 t0,_! Wt_2 — w2_2 = о, (17.4)
где f=fIF=nv/F, и, = и1;Д|я; = а»,_2 = а»<_2/:0в: l~
~lid3 = nlripdbl wa — скорость воздуха в начале воздухораспреде-
лителя
Отсюда относительная скорость воздуха внутри воз-
духораспределителя в i-м сечении
7 И’/’ \_ , / V-2
li--^-nk-i+ (1- — пI +
^1= --------
р2/2 -
— пт

п3
2Г8
и2/2
1+4- (1-n)
я2
р272 /,,х7 \-2 ,-2
—I 1+— Г) I ш(_!—2wl_1wl_2+wl_2
Р2/2
я2
(1—п)
(17 5)
Перед радикалом взят знак плюс, так как всегда
>7^,-1 Необходимо отметить, что в формуле (17.5)
1= 2, 3, 4,.. , п.
Для расчета должны быть известны рД л/ и число
отверстий. Подставляя в формулу (17^5) значения рД
и п, полагая 1=2 и учитывая, что w0—0, получаем
w2=A2Wi, где А2 — конкретное число^ Полагая затем
/=3 и подставляя w2—A2wlt находят W3==A3Wi_ Далее,
полагая i=4, 5,..., i,.... п и_подставляя w2—A2Wi, w3=
=AsW{ и т. д., получают ге»!=Л,ге»1 и, наконец, wn=
=AnW\. Поскольку wn=l> то Wi — i/An, а потому
wt=AJAn, (17.6)
где i=l, 2, 3, . , я
Теперь установим, как будет изменяться скорость
истечения воздуха из отверстий. Из уравнения (17.1)
следует
х>г = (Flo) (wi — о\_г) = (Fla) (wt — te>n. (17.7)
Составим уравнение расхода:
Fwa = яогср,
где Сер — средняя скорость истечения из отверстий, равная скорости
истечения при равномерной раздаче
Подставляя в зависимость (17.7) найденную величи-
ну Fwa, получим относительную скорость истечения.
«4 = ^1-1) Л> О7-8)
где ; = 1, 2,.., я
Относительное отклонение скорости истечения от
средней скорости истечения
где i=l, 2,..., п.
2W-
Рис. 17.1. График изменения
относительных отклонений
для воздухораспределителя
постоянного сечения с от-
верстиями
а — при |xf=0,5; б — при pf = 1
Вычисления гг- были выполнены на ЭЦВМ. При рас-
чете было принято:
р/= 0,5 4- 2 при шаге Ар/ = 0,5;
й = 0 ч- 4 при шаге A/J = 1;
п = 2 - :20 при шаге An — 1.
В результате вычислений получены таблицы, анализ
которых выявил, что ri изменяется следующим образом.
В общем случае п всегда положительно, затем с увели-
чением i достигает минимума гмин, после чего начинает
увеличиваться и достигает тп.
На рис. 17.1 приводятся зависимости этих относи-
тельных отклонений от параметров отверстий и воздухо-
вода, а также от числа отверстий.
Как видим, абсолютные значения и, гмин и гп увели-
чиваются с увеличением параметра отверстий pf и их
числа.
Параметр воздуховода при своем увеличении снача-
ла обусловливает снижение отклонений, а затем их уве-
личение.
Сопротивление воздухораспределителя
др==Арп + рЕг)2/2.
Согласно выражению (17.2), разность статических
давлений
&рп = py>iA
220
а потому
9 9/9 \ О
2P 2 |y J 2
или
pw„
&P^=tu~-. (17.10)
Здесь
9 9 —9
, _ _ v- I !_ V" I 1
гЧ, p.2n2(0/F)2v2cp
Подставляя сюда, согласно выражению (17.9), вели-
чину vn, окончательно получаем
gn = ~ta)2 +1-
М2/2
§ 72. Конусный воздухораспределитель
с отверстиями одинаковой площади
Конусный воздухораспределитель длиной I имеет диа-
метр в начале dH, а в конце d0. Вдоль воздухораспреде-
лителя равномерно расположено п отверстий. Площадь'
каждого отверстия равна о. Расход воздуха в начале
воздухораспределителя Ан.
Требуется установить, насколько отклоняется нерав-
номерная раздача воздуха таким воздухораспределите-
лем от равномерной, и определить сопротивление возду-
хораспределителя.
Пронумеруем все отверстия против движения потока
воздуха и проведем поперечные сечения перед каждым
отверстием [11]. Обозначив расход воздуха в сечении i
через Li, а в сечении i— 1 через Lt-i и нормальную ско-
рость истечения воздуха из г-го отверстия через Vi, мо-
жем написать уравнение расхода:
7г —= (17.12)
Нормальная скорость истечения воздуха из отверстия
определяется по формуле (17.2),
221
Напишем применительно к i-му и i—1-му сечениям
уравнение Бернулли:
Др. + y = д^-1 + a'Li +
/о
С к Pwi—1,х , , р ,
’ J ~^~гх —2— +11Т'
о
где 1о — расстояние между смежными сечениями; di-i, х — диаметр
воздухораспределителя в сечении, удаленном на расстояние х от
i—1-го сечения; w,-i,x — скорость внутри воздухораспределителя в
сечении с диаметром d>~i,x; r)=0,4— коэффициент смягчения
удара.
Выразим давления и скорости, входящие в уравнение
Бернулли, через расход воздуха внутри воздухораспре-
делителя.
Воспользовавшись для определения избыточных ста-
тических давлений формулой (17.2), получим:
Др, = ро-/2р.2; Др(._] = p^_i/2p2,
где Vi и tj-i — скорости истечения из t-ro и t—1-го отверстий.
Воспользовавшись для определения скорости истече-
ния уравнением расхода (17.12), получим следующие за-
висимости:
о. = 1 /а(L. - L{_xy, vt_x = 1 /а (L{_x - LM),
где Lt, Li-i, Li-i — расходы воздуха внутри воздухораспределите-
ля, соответственно в i-, i—1- и i—2-м сечениях.
Скорости внутри воздухораспределителя:
wt = Li/Fi' wi-i ==
где Fi, F,-i и fi-i,x — площади поперечных сечений воздухорас-
пределителя.
Подставляя в уравнение Бернулли величины Др(-,
Д/Ъ-1, Vi, Vi-X, Wt, Wi-x, Юг-1,х, ПОЛуЧИМ
L2 L1-
(L. - L^f + рго9- = (£<_, - Lc_2)*+ |W +
i.
+ И2а2и?_Л---------+ . (17.13)
222
Для вычисления имеющегося в этом уравнении инте»
грала находим.
диаметр воздухораспределителя
1,х = + 2х tg 0,
где д — боковой угол раскрытия конуса;
площадь сечения
Jt п Л .л
Ъ-1.Х = Т 4-1.Х = V (*<-! + 2* tg Э)2.
В результате вычислений получаем
I. I,
р_______dx_____ 16 р dx
J “ * J <4'-‘+2' *8 е)‘=
о о
2 Г 1 %
“ л2 tg 0 [(^_1 + 2х tg fl)4j0 *
Принимая во внимание,что di-i-j-2l0tgd—di и tgO=]
= (dB — d0)/2l, будем иметь
i.
р dx I Г 1 1 ~
J ^.xFti.x ~ И, :
Подставляя в уравнение (17.13) вычисленный нн«
теграл и осуществляя преобразования, получим
Р2/2 ~ U Г 1 L
«2 4(1 -50) 1Л-1 ??
n2
где
~Li=LiIL^ ^-2 = Li-ilLj
f = f/FB = nalFB-, Ft=Fi/Fn;
F^F^/F», ~l = l/da; d0^d0/dB.
Раскрывая скобки в уравнении
мальному виду, можем написать
и приводя его к нор-
1 +
р2/2 I-, / р2/2 \-----
п2р2 (1 -fl) J Ч -2 П j
223
н2?
2 7?2
п Fl~l
й /
------- 1
4(1 —d0) (
+ *1 +
+ 7-(—2 ^1—2 — 0
(17.14)
Отсюда относительный расход воздуха внутри возду-
хораспределителя в f-м сечении
(17.15)
где i=2, 3,.... п.
В формуле (17.15):
Л = ^=^Г==^^+2'7о‘е0)2 =
dH
Гд .л £ Т
= No + (1 — ^о) — ;
п J
IzziLl2
I ’
'^‘ + 2U‘ 2Ц,
~ da + (1 — do)
F.
(17.16)
(17.17)
По формуле (17.15) можно подсчитать относитель-,
ные расходы воздуха в каждом сечении воздухораспре-
делителя. Для этого необходимо знать [if, М, число от-
верстий п и_сужение конуса d0. Подставляя в формулу
(17.15) pf, id, п и do, полагая i=2, вычисляя Fj, Fi-i,
подставляя_ их в формулу (17.15) и учитывая, что Ао=О,
получаем L2=^2Fi, где А2 — конкретное число.
Полагая 1=3, вычисляя F, и Д-_ь подставляя их
в формулу (17.15) и учитывая, что Ь2=А21.1, находим
Lo=AoL\.
224
Далее, полагая i=4, 5,п, вычисляя Fi, Fj—i, под-
ставлявших в формулу (17.15)_и учитывая, что L^—A^Ly
Ls=AsLl и т. д., получаем Li=AiLi и, наконец, Ln =
=AnLi. Поскольку Лп=1, то Ь{ = \/Ап, а потому
Ц = АМП, (17.18)
где i= 1, 2, п.
Относительная скорость истечения из отверстия
Vt = --- =------------ =-------------- =
vcp ovcp otcp
= (17.19)
где fcp — средняя скорость истечения из всех отверстий.
Относительное отклонение
Г/ = 2'(-Др. =7,._1, (17.20)
°ср
где 1=1,2,.... п.
Вычисления rt были выполнены на ЭЦВМ. При рабо-
те было принято:
р/ = 0,5 н- 2 при шаге Др/ = 0,5;
М = 0 -+• 4 при шаге ДХГ=0,5;
d0 — 0,2 ч- 1 при шаге Дф> = 0,2;
п = 2 20 при шаге &.п - 2.
По результатам расчета построены зависимости от-
носительного отклонения в первом отверстии гь в отвер-
Рис. 17.2. График изменения
относительных отклонений
для конусного воздухорас-
пределителя с отверстиями
при do ==0,8
а — при pf-0,5; б — при pF-1
15-741
225
стии с минимальным отклонением Гмин и в n-м отверс-
тии гп.
Наименьшие отклонения при прочих равных услови-
ях оказались у воздухораспределителя с do=O,8. Поэто-
му на рис. 17.2 приводятся графики только для такого
воздухораспределителя.
Сопротивление воздухораспределителя определяется
по формулам (17.10) и (17.11).
§ 73. Клиновидный воздухораспределитель
с отверстиями одинаковой площади
Клиновидный воздухораспределитель длиной I с по-
стоянной высотой b имеет ширину в начале аЕ и в конце
а0 Вдоль воздухораспределителя равномерно располо-
жено п отверстий. Площадь каждого отверстия равна о.
Расход воздуха в начале воздухораспределителя ра-
вен
Требуется установить, насколько отклоняется скорость
истечения из отверстий при неравномерной раздаче воз-
духа от скорости истечения при равномерной раздаче
воздуха, а также определить сопротивление воздухорас-
пределителя
Пронумеруем все отверстия против движения потока
воздуха и проведем поперечные сечения перед каждым
отверстием [13]
Проводя такие же выкладки, как и для конусного
воздухораспределителя с отверстиями одинаковой пло-
щади, получим равенства, аналогичные равенствам
(17.12) и (17.13).
Для вычисления имеющегося в равенстве (17 13) ин-
теграла находим
эквивалентный диаметр
2at_! ХЬ
_j х — J
а.-1,х + &
площадь сечения
Д—1,Х = ai—1 X Ь’
ширину воздухораспределителя
at_i.x = a,_i+2x tg0,
-де х — расстояние от сечения I—1 до сечения х, 0 — боковой угол
раскрытия клина.
226
в таком случае
2&3
1
2&3 tg е
т 2х tg е
Ь ' 1а
2(а,_!+ 2xtge)2 0‘
Принимая во внимание, что a,-i+2/otg9 = а( и tg0 =
== (ан — а0)/21, б) дем иметь
Р dx____________I Г 1 / 1 J_\
J <_1 х х 2 (ая — аа) L &2 I F:-i Ft ] +
* о
Г
F-t
Подставляя в уравнение (17 13) найденный интеграл
и осуществляя преобразования, получим
1
К
цУ М М
2«2 1 — а0 ~b
Р2/2 / Lt
«2 \Ft
1 ( 1
где
Lt — LJL^, Lt_x — — Lt_^IL^
f = F/Fa=™/Fa-, Ft = Ft/Fa-, Ft^F^lFn,
1=1! Он! Oq = л01аа.
Раскрывая в уравнении скобки и приводя его к нор,
мальному виду, можем написать
И2/2 1-9 /
1 +5W(1 - П) t?-2 1
П Г f \
И2/2 \ - -
2 ъ “п Л I L
п Ft F(-i J
15*
227
(17.21)
где b = b'aa.
Решая это уравнение относительно расхода в i-м се-
чении, будем иметь
Ц2 /2
« Fi
Ин2/2 , xi
iW-iP 2(1-Б0)
1 I 1 £
2 I 7?2 F2
VZ-l
LI2 72
« Fi
~Hl{ Fi—1 Fi—1 ~Ь
(17.22)
где t—2, 3, .... n.
В этой формуле:
1 / 1 / Сн—ал\
( ao + 2i70 tg 0) = I c0 + 2il0 - j =
\ ян \ 2c/0 /
= c0 + (l~-a0) —; (17.23)
n
Р^ = ^+{\-а0)* 1^ - 07.24)
По формуле (17.22) можно подсчитать относитель-
ные расходы воздуха в каждом сечении воздухораспре-
делителя. Для этого необходимо знать рД XI, п, а0 и Ь.
Последовательные вычисления проводятся таким же об-
разом, как и для конусного воздухораспределителя
с отверстиями одинаковой площади.
228
Рис. 17.3. График изменения
относительного отклонения
для клиновидного воздухо-
распределителя с отверстия-
ми при ао = 0,8; 6 = 0,5
, а — при ц7=О,5; б — при ц|=1
В итоге относительный расход воздуха определяется
по формуле (17.18), относительная скорость истечения —
по формуле (17.19), а относительное отклонение — по
формуле (17.20).
Вычисления г, были выполнены на ЭЦВМ. При рас-
чете было принято:
IV = 0,5; 1; й = 0; 1; 2; 3; 4; а0 = 0,4; 0,6;'.0,8; 6 = 0,5;
п = 2; 4; 6; 8; 10; 12; 14; 16; 18; 20.
По результатам расчета были построены зависимос-
ти для г\, и гп- На рис. 17.3 приводятся графики
для йо=О,8 и 6=0,5 при ц/=0,5 и ц/=1.
Сопротивление клиновидного воздухораспределителя
определяется по формулам (17.10) и (17.11).
§ 74. Расчет воздухораспределителей
с отверстиями одинаковой площади
Расчет воздухораспределителей с отверстиями прово-
дится таким же образом, как и расчет воздухораспреде-
лителей с продольной щелью (см. гл. 16). Однако вмес-
то ширины продольной щели определяют площадь от-
верстия по формуле
a = (tf)F/y.n. (17.25)
15а—741
229
Пример 17.1. Определить площадь отверстия и сопротивление
воздухораспределителя прямоугольного сечения с отверстиями оди-
наковой площади, если а=1 м; 6=0,5 м; /=60 м; £=10 мм; га=20,
v= 1,5.10“5 м2/с; |1=0,65; о>н = 5 м/с; г=0,05.
Решение. Вычисляем исходные величины:
2-1,0-0,5 5-0,667
<^Э - = — = 0,667 м; Re = / 106 = 2,22-Ю6; 1,5 1,5 „ У 68 10 Л = 0,111/ 10-5-1- =0,0384; |/ 2,22 667 60 U = 0,0384 = 3,46. ’ 0,667
По графикам для г= ±0,05; W = 3,46 и га=20 находим и| = 0,5.
Тогда 0,5-0,5 а = — — = 0,02 м2; 0,65-20 (1 —- 0,05)2 Sn- 0>53 1 1-4,6; Р^н 1.2-52 = — = 15 Па; 2 2 ДР =4,6-15 = 69 Па.
ГЛАВА 18
ВЫТЯЖНЫЕ ВОЗДУХОВОДЫ ПОСТОЯННОГО СЕЧЕНИЯ
§ 75. Вытяжной воздуховод
с продольной щелью
переменной ширины
Рис. 18.1. Схема вытяжного
воздуховода постоянного
сечения с продольной щелью
Воздуховод постоянного сечения длиной I имеет пе-
риметр Р и площадь поперечного сечения F (рис. 18.1).
Вдоль воздуховода с боко-
вой его поверхности устрое-
на щель переменной шири-
ны. Расход воздуха в конце
воздуховода равен LK.
Требуется установить,
как должна изменяться ши-
рина щели по длине возду-
ховода, чтобы обеспечить
равномерное всасывание
230
воздуха по всей длине щели, и определить сопротивление
воздуховода.
Примем начало координат у заглушенного конца
воздуховода и направим ось абсцисс по направлению
движения воздуха.
Ширина щели в сечении х при равномерном всасы-
вании воздуха равна:
Ьх = LK/lvx = FwK!lvx. (18.1)
Скорость всасывания воздуха в щель в сечении х:
1»х = рУ(2/р)(ра — рх). (18.2)
Применительно к объему, ограниченному сечениями
х и х=0 (сечение у заглушенного конца воздуховода)
и стенками воздуховода, напишем уравнение количества
движения в проекциях на ось воздуховода:
Ро F ~ Рх F ~ Г тх pdx = PFwx-
' о
Напряжение трения
X (™х
Подставляя в уравнение количества движения вели-
чину тх и деля все члены уравнения на F, получим
с х 2
РО~РХ- \Т 2 dx=Pwx
о
При равномерном всасывании воздуха wx=wKxfl.
Подставляя в последнее уравнение wx и интегрируя, бу-
дем иметь
х* (и.
Рх Ро 2
(18.3)
В зависимость (18.1) подставим величины vx и рх со-
гласно выражениям (18.2) и (18.3), в результате по-
лучим
где 6о — ширина щели у заглушенного конца воздуховода.
15а*
231
Из зависимости (18.4) следует, что наибольшая ши-
рина щели будет при х=0, затем с увеличением х ши-
рина щели уменьшается и при х = 1 достигает наимень-
шего значения. На основании этого ширину щели
у заглушенного конца можно установить таким образом,
чтобы скорость всасывания в щель по всей ее длине бы-
ла бы не меньше минимально допустимого значения.
Для этого ширину щели у заглушенного конца следует
определять по формуле
бо = £к//°мин- (18.5)
Сопротивление воздуховода установим на основании
уравнения Бернулли для сечения вне воздуховода у за-
глушенного конца при входе в щель и в сечении х=1:
ра = рк+р1Ик/2+ДР>
где рк — статическое давление воздуха внутри воздуховода на вы-
ходе из него; АР — сопротивление воздуховода
Отсюда
др = Ра- Рк- Р^/2.
Согласно уравнению (18.2):
Ра-Рк^Р'^2!'2’
где Гк — скорость всасывания в конце щели.
В таком случае
или
Р^к
ДР = ^п—. (18.6)
где
= (18.7)
§ 76. Вытяжной воздуховод с отверстиями
различной площади
Воздуховод постоянного сечения длиной I (рис. 18.2)
имеет периметр Р и площадь поперечного сечения F.
Вдоль воздуховода в боковой его поверхности равномер-
но расположено п отверстий. Площадь всех отверстий
232
различна. Расход воздуха в конце воздуховода ра-
вен LK.
Требуется установить, как должны изменяться пло-
щади отверстий по длине воздуховода, чтобы обеспечить
равномерное всасывание воздуха в отверстия, и опреде-
лить сопротивление воздуховода.
Пронумеруем все отверстия по ходу движения потока
воздуха и проведем поперечные сечения 1—1, i—1 —
i — 1, i — I,n — n после каждого отверстия.
Площадь t-го отверстия при равномерном всасывании
воздуха
а/ = LK]mt <= FwK/nvi. (18.8)
Скорость всасывания воздуха в i-e отверстие
О, = ц]/(2/р)(ра-Л). (18.9)
Напишем применительно к объему, ограниченному
i-м 'и i—1-м сечениями и стенками воздуховода, уравне-
ние количества движения в проекциях на ось воздухо-
вода:
Pt-i Т — р.Г — Р1й = pFrf — рГю?_Р
где /о — расстояние между осями двух смежных отверстий.
Подставляя в это уравнение =я —---------—
и деля все члены уравнения на F, получаем
Рис. 18 2. Схема вытяжного воздуховода постоянного сечения с от-
верстиями
233
При равномерной раздаче воздуха
i i— 1
wi = — и иь_, — w„--- .
п К п.
Подставляя в последнее уравнение и w^, будем
иметь
Г Х/о 1 2 Ршк
Р^Л-i- . (18 10)
I 2аэ J
Подставив в зависимость (18.8) величины Vi и pt со-
гласно выражениям (18.9) и (18.10) и заменив 10=1/п,
получаем
*=1/1/ -Т- + -^- k-(i-’)2+-^-(i-I)2l, (18-И)
/ ' 1 г3 L 2паэ J
где cTi-i — площадь i—1-го отверстия.
По формуле (18.11) можно последовательно подсчи-
тать площади всех отверстий, задаваясь 1=2, 3,..., п.
Из зависимости (18.11) видно, что наибольшая пло-
щадь будет у первого отверстия, затем с увеличением i
площадь отверстий уменьшается и достигает наименьше-
го значения у n-го отверстия. Отсюда следует, что если
скорость в любом отверстии не должна быть меньше
Умин, то площадь первого отверстия можно определить по
формуле
Щ =-^к/лУмин- (18.12)
Сопротивление воздуховода (см. § 75) равно.
ДР = Ра-Рп-ра£/2.
Согласно выражению (18.9):
Pa-Pn = Pvn/2V^
поэтому
ДР =
Р^ __
2р.2
Ртк
2
или
где
Р^К
ДР = ?п^-
(18.13)
(18.14)
234
§ 77. Вытяжной воздуховод
с продольной щелью
постоянной ширины
Воздуховод постоянного сечения длиной I имеет пери-
метр Р и площадь поперечного сечения F (см. рис. 18.1).
Вдоль воздуховода устроена щель постоянной ширины 6.
Расход воздуха в конце воздуховода равен LK.
Требуется установить, насколько отклонится нерав-
номерное всасывание таким воздухом от равномерного,
и определить сопротивление воздуховода.
Примем начало координат у заглушенного конца и
направим ось абсцисс по направлению движения возду-
ха. Проведем в воздуховоде два поперечных сечения на
расстояниях х и x-}-dx от заглушенного конца. Очевидно,
увеличение расхода воздуха внутри воздуховода между
этими двумя сечениями будет равно расходу воздуха
через участок щели длиной dx. Следовательно, можно
написать равенство
Fdwx = vx 8dx,
где wx — скорость воздуха внутри воздуховода; V* — скорость вса-
сывания воздуха в щель.
Переходя к производной, получаем
6
wx = -fvx- (18-15)
Скорость всасывания воздуха в щель определяется по
формуле (18.2).
Применительно к объему, ограниченному сечениями х
и x-j-dx и стенками воздуховода, напишем уравнение ко-
личества движения в проекциях на ось воздуховода:
Рх F - (Рх + dPj F~\ Pdx == PFw* + d (pM) - pM-
Проводя преобразования, получаем
р^ + 2риГш^ + тл.7’/Г = °. (18.16)
Заменим в этом уравнении р'х и тж. Из зависимости (18.2)
следует
РХ = Р&-Р^2^-
Согласно выражению (18,15), имеем vx = — ш',
235
поэтому
pF2 „
P* ~ P& ~ 2p2 62 W* ‘
Беря производную, получаем
. pF3 . .
PX—^VX.
Напряжение трения
X
Tx~ 4 2 '
Подставляя в уравнение (18.16) величины р' и тх и
умножая все члены этого уравнения на ц263/р/?2, будем
иметь
» ' „ p62 , u.2p2 X 2
wxwx-2—^~wxV>x-°'5—^-------^"^ = 0-
Введем обозначения
шх=чих/а|к и x^=xll,
где шк— скорость воздуха внутри воздуховода в его открытом конце.
Тогда
wx
KI.
а>х==шка>х; x=lx\
dwx а>к -r
= ~7~wx'
dx I *
d®x kik
—— =s —
dx I2 x
Подставляя w х, w'x и w’x в последнее уравнение и ум-
ножая все члены уравнения на /3/ю2, получим следующее
дифференциальное уравнение:
wx wx + pwx wx + = 0,
(18.17)
где
р = —2ц2/2; q = — 0,5р2/2Л1;
/ = f/F = MIF-, 1 = lld,.
Дифференциальное уравнение (18.17) отличается от
ранее полученного для воздухораспределителя постоян-
236
ного сечения с продольной
щелью постоянной ширины
уравнения (16.12) только
коэффициентом р.
Проведем интегрирова-
ние дифференциального
уравнения (18.17) числен-
ным методом на ЭЦВМ. При
расчете было принято:
К) = 0.4? 2,4 при шаге Др/= 0,2;
17 = 0—4 при шаге Д17=О,5;
х = 0-ь 1 при шаге’Дх =0,1.
Относительная скорость
всасывания воздуха в щель
вычислялась по формуле
vx Fw'x Fte)K
=-----=-------=s------X
t'cp
X w'x = wx, (18.18)
Рис. 18.3. График изменения
относительных отклонений
для вытяжного воздуховода
постоянного сечения с про^
дольной щелью (на оси ор^
цинаг отложены значения
гк/2)
где Vcp — средняя скорость воздуха в щелн.
Относительное отклонение
Гж=- Рср=йя-1. (18.19)
Чср
В результате расчета были получены таблицы зави-
симости гх от х. Анализ этих данных показал, что гх с
увеличением х непрерывно увеличивается. Вследствие
этого приводятся зависимости только для г0 и гк
(рис. 18.3).
Сопротивление воздуховода определяется по форму-
ле (18.6), где
t = А______, , Р+'к)» .
1^72цР и2/2 и8/8
(18.20)
§ 78. Вытяжной воздуховод с отверстиями
одинаковой площади
Воздуховод постоянного сечения длиной I имеет пе-
риметр Р и площадь поперечного сечения F. Вдоль воз-
духовода равномерно расположено п отверстий. Пло-
237
щадь всех отверстий одинакова и равна а. Расход возду-
ха в конце воздуховода Lv (см. рис. 18.2).
Требуется установить, насколько отклонится неравно-
мерное всасывание таким воздуховодом от равномерного,
и определить сопротивление воздуховода.
Пронумеруем все отверстия по ходу движения пото-
ка воздуха и проведем поперечные сечения после каж-
дого отверстия. Очевидно, увеличение расхода воздуха
от сечения i—1 к сечению i равно расходу воздуха, вте-
кающего в i-e отверстие. Следовательно, можно напи-
сать:
Р (wt — wi—d=avt. (18.21)
Скорость всасывания Vi определяется по формуле (18.9).
Применительно к объему, ограниченному сечениями
i—1 и i, а также стенками воздуховода, напишем урав-
нение количества движения в проекциях на ось воздухо-
вода:
pi-1 F — pF — т£_! Р/о = pFw] — pFwj-i-
Разделив все члены этого уравнения на F, получим
Р;-1 — р. = р + т£-1 -у Zo. (18.22)
Исключим из этого уравнения величины рг-\—Pi и
Ti-ь Разность статических давлений на основе зависимо-
сти (18.9) можно представить в виде
Р;_1 — Рг = ру?/2ра — pv?_i/2|?.
Согласно выражению (18.21), имеем
vc = (F /а) (Wt — o»£-i); Vi-J = (F /0) (wt—L — wt-2).
В таком случае
Pi-i — Pi =№4^? 02)[(ш£ — Ш(-1)2 — (wt-i. — wt-2)2].
Напряжение трения
X P®Li
T'-i ~ 4 2 ’
Подставляя в уравнение (18.22) величины pc—i—рг и
тг-1 и осуществляя преобразования, будем иметь следу-
ющее уравнение:
(1 — 2|? JL j wj — 2 wt w^ -j- (2 — j + 2шг-1 Wi-‘T~
_ й?_2 = 0, (18.23)
238
где
"f = f/Р = rujlF; Wi=wJwK; tWi-i = Wi-i/wK;
Wi—2 = —з/^К> = l/^Э ~ tllflldg .
Отсюда относительная скорость воздуха внутри воз-
духовода в i-м сечении
(2 — ИГ) + 2ш‘“1 Wi~2 ~ W^2
(18.24)
n2
Под'радикалом взят знак плюс, так как всегда wt >
>Wf_i. Необходимо отметить, что в формуле (18.24)
(—2, 3...п. _ _
Для расчета должны быть известны значения р/,
а также число отверстий. Подставим в формулу (18.24)
значения pf, U и п.
Полагая i=2 и учитывая, что №о=О, получаем
w2=A2wb где А2— конкретное число. Полагая затем
1=3 и подставляя w2=A2wi, находят w3—A3Wi. Далее,
полагая i=4, 5,..., п и подставляя w2=^2®i, w3=A3Wi
и т. д., получают Wi=AiWi и, наконец, wn=AnWi.
Поскольку дап=1, то W\=\/An, а следовательно,
wi = AilAn,
(18.25)
где i=l, 2, .... п.
Теперь установим, как будет изменяться скорость
всасывания в отверстиях. Из уравнения (18.21) следуе’т
vi=(F/o){wi — Wi-i) =(Д/а)(шг — Wi-Awn. (18.26)
Составим уравнение расхода:
Дшк = паиср,
где ^ср—средняя скорость всасывания в отверстиях.
239
Подставляя FwK в зависимость (18.26), получим от-
носительную скорость всасывания:
vi = vi!vcp =(®« — w(—i) n, (18.27)
где i= 1, 2, ..., n.
Относительное отклонение скорости всасывания от
средней скорости всасывания составит
= — »cp)/»cp = «i — И (18.28)
где 1=1, 2, ..., п.
Вычисления выполнены на ЭЦВМ. При расчетах
было принято
ц/ = 0,5Н ,5 при шагеДрЦ = 0,5;
XZ = 0ч-4 при шаге ДХ? = 1»
п = 2 20 при шаге An = 1.
В результате вычислений получены таблицы. Анализ
данных таблиц выявил, что г.
а)
с увеличением i всегда уве-
личивается. Поэтому на
рис. 18.4 приводятся толь-
ко зависимости Г[ и гп от
ц/ и X/.
Сопротивление возду-
ховода будет определять-
ся по формулам (18.13)
и (18.20).
Рис. 18.4 График изменения
относительных отклонений
для вытяжного воздухово-
да постоянного сечения с
отверстиями
а —при nf-0,5; б —при |if=l
§ 79. Расчет вытяжных
воздуховодов
При расчете вытяж-
ных воздуховодов задан-
ными величинами явля-
ются: d или а и b, I, k, ц,
LK и г, где k — абсолют-
ная шероховатость стенок
воздуховода. Расчет ве-
дется в такой последова-
тельности:
1) ВЫЧИСЛЯЮТ d3 —
=2ab/(a+b)-, F=nd2/4
или F—ab\ wk=Lk]F\
2) находят число Рей-
нольдса: Re=6?8twK/v 5
240
3) определяют коэффициент сопротивления трения
по формуле (6.17);
4) для воздуховодов со щелью переменной ширины
или с отверстиями различной площади подсчитывают
ширину щели до или площадь о;, а затем ширину щели
дх или площади о,. Для воздуховодов со щелью постоян-
ной ширины или_с отверстиями одинаковой площади по
значениям г и А/ или г, XI и п находят на графиках зна-
чение ц/, а затем подсчитывают d==(p7)F/p,l или о=
= (иЛ
5) устанавливают сопротивление воздуховода.
Пример 18.1. Определить ширину щели и сопротивление цилин-
дрического вытяжного воздуховода, если d = 0,3 м; 1=3 м; k —
= 0,1 мм; ц=0,735; шк = 5 м/с; /'=0,3; v=l,5-10~5 м2/с.
Решение. Вычисляем исходные величины:
0,3.6
Re =-i— 105= 1,2.105;
1,5
4 '
’•-“•“I/
(1+0,3)3
6п 0,682
— 1 =2,65;
3
М =0,019--------=0,19.
* 0,3
По графику (см. рис. 18.3), полагая Гк/2=0,3/2=0,15, находим
р/=0,68. Далее вычисляем:
п 0,68.0,0675
F = — 0,32 = 0,0675 м2; 6 = —--------;---= 0,0208 м;
4 ’ * ’ 0,735.3
Ршк 1.2.62
-----=----------= 21,6 Па.
2 2 •
ДР = 2,65.21,6 = 47,5 Па.
Пример 18.2. Определить площадь отверстия и сопротивление
вытяжного воздуховода прямоугольного сечения, если а=1 м; Ь =
= 0,5; 1 = 60 м; /?=20; 6=10 мм; ц = 0,735; шк=5 м/с; /'=0,12;
V— 1,5.10~5 м2/с.
Решение. Используя решение примера 17.1, имеем А/= 3,46.
Тогда по графику (см. рис. 18.4) находим [Д=0,5.
Далее вычисляем
0,5.0,5
- ' - = 0,092 м2;
0,735.20
(1+0.12)2
0,52
о =
Си —
Ртк
2
1 2-52
—------= 15 Па; ДР = 4-15 = 60 Па.
2
241
РАЗДЕЛ ТРЕТИЙ
СВЕДЕНИЯ ПО ЭКСПЕРИМЕНТАЛЬНОЙ
АЭРОДИНАМИКЕ
ГЛАВА 19
ОСНОВЫ МОДЕЛИРОВАНИЯ ВЕНТИЛЯЦИИ
§ 80. Постановка задачи
Разработку новых эффективных систем вентиляции,
а также проверку существующих систем в условиях, от-
личающихся от условий эксплуатации, весьма удобно
проводить на моделях. Для правильной организации экс-
перимента на моделях необходимо владеть методом мо-
делирования.
Для изучения метода моделирования рассмотрим
отдельно стоящее здание (рис. 19.1). В его ограждении
имеются открытые проемы, а внутри расположены источ-
ники тепла и влаги, а также смонтированы системы ме-
ханической вентиляции. Снаружи здание обдувается вет-
ром. В результате совместного действия тепла, ветра и
механической вентиляции в здании происходит опреде-
ленный воздухообмен и создается некоторый температур-
ный режим.
Процесс воздухообмена и температурный режим ре-
комендуется изучать на модели здания при рабочей сре-
де в модели воздух. Очевидно, что для такого изучения
необходимо располагать зависимостями, по которым мо-
жет быть рассчитана мо-
дель, знать габариты мо-
дели, а также скорость
ветра и мощность источ-
ников тепла и влаги в
модели. Кроме того, над-
лежит знать и те форму-
лы, по которым будет
производиться пересчет
замеренных в модели ско-
ростей, температур и
влажностей на соответ-
Рис. 19.1. Схема здания в попереч-
ном разрезе
ствующие им в натуре
величины.
242
С целью выяснения поставленных вопросов допустим,
что модель выполнена в определенном геометрическом
масштабе и явление, происходящее внутри модели зда-
ния, подобно явлению, происходящему внутри здания.
В таком случае в соответствии с теорией подобия должна
соблюдаться определенная пропорциональность, или,
иначе, масштабность между соответствующими физиче-
скими величинами, характеризующими явления, проис-
ходящие в здании и его модели. При этом у каждой фи-
зической величины будет свой масштаб. Пользуясь этим
положением теории подобия, выявим необходимые для
моделирования масштабы.
§ 81. Моделирование воздухообмена
Масштаб скорости определяем как отношение скоро-
сти воздуха соответственно в проемах модели и здания
Cv = v"/v' = р" j/ у ~^Р'= С^УС^ , (19.1)
где v — средняя скорость в проеме; р.— коэффициент расхода;
Ар—разность давлений до и после проема; р — плотность воздуха
(р'—р"); при этом величины с одним штрихом относятся к зда-
нию, а с двумя штрихами — к его модели.
Масштаб разности давлений установим исходя из по-
нятия избыточного (над атмосферным) давления возду-
ха соответственно на внешней поверхности ограждения
модели и здания:
где k, — аэродинамический коэффициент; w — скорость ветра.
Поскольку здание и его модель являются плохо обте-
каемыми телами, а турбулизация потоков воздуха обыч-
но почти одинакова, то их аэродинамические коэффици-
енты равны (&' — .
Подставляя в уравнение (19.1) масштаб разности
давлений и принимая во внимание, что CKi = 1, полу-
чаем
Сц = 1.
(19.2)
243
Известно, что коэффициент расхода зависит от числа
Рейнольдса: Rq—Iv/v, где I — характерный размер; v~
кинематическая вязкость. При этом, когда число Ре
увеличивается, то вначале возрастает и коэффициент
расхода, а затем, начиная с некоторого значения Re =
=2400, коэффициент расхода ц остается неизменным.
Для проемов здания число Рейнольдса всегда больше
указанной величины (Re'>2400), поэтому для соблюде-
ния требования, указанного в формуле (19.2), необходи-
мо и для проемов модели здания исходить из условия,
что Re" >2400.
Масштаб разности давлений может быть установлен
и из понятия гравитационного давления:
где h — высота рассматриваемого столба воздуха; Др — разность
плотностей воздуха в столбе и вне его; g — ускорение свободного
падения; Ci--h"lh'— геометрический масштаб модели.
Подставляя найденный масштаб разности давлений
в уравнение (19.1) и учитывая, что С^ = 1, получаем
следующую общую формулу для определения масштаба
скорости:
CO = V~C^- <19-3)
Эта формула может быть представлена иначе. С этой
целью воспользуемся известной зависимостью для плот-
ности воздуха:
Р = Рн/(1 + ₽Д0,
где рн — плотность наружного воздуха при температуре /н; Р—ко-
эффициент объемного расширения; Д>£в—tB <t„— средняя темпе-
ратура воздуха соответственно в здании или его модели).
Тогда для воздуха:
в здании
др’= Рн — р’= Рр’д/”;
в модели здания
лр'=р;-р"=рР"дг.
Следовательно:
Сдр = Др"/Др' = С&!.
244
Подставляя найденный масштаб разности плотностей
в уравнение (19.3), получаем, что масштаб скорости
Cv = VC^t. (19.4)
Масштаб массового расхода
Gg=G’/G' = p"F"u''/p'f'u’ = c2C0, (19.5)
где G — массовый расход; F — площадь открытого проема.
§ 82. Моделирование тепловыделений
Масштаб количества тепла
Q Q'
(19.6)
— Cq^AI’
где с — удельная теплоемкость; /Ух — температура воздуха, уходя-
щего из здания или его модели.
Согласно теории подобия, такой же масштаб должен
быть и у количества конвективного тепла:
aW-fl
С<3 = ~ J = с“ ct ’ (19-7)
где а — коэффициент теплоотдачи; Ф — площадь поверхности ис-
точника тепла или его модели; tn — температура на поверхности ис-
точника тепла или его модели.
Уточним масштаб коэффициента теплоотдачи. Этот
коэффициент в соответствии с теорией теплопередачи
определяется по формуле
X
а = от — (Gr Рг)",
где X— коэффициент теплопроводности; Gr и Рг — критерии Грас-
гофа и Прандтля.
Коэффициент т и показатель степени п зависят от
произведения критериев Gr Рг, которые определяют по
формулам:
ст/8 V
Gr = £-PA/; Рг = — ,
v= 1 а
где А/ = /п—tB; а — коэффициент температуропроводности.
При этом X, v и а находят по средней температуре
^ср=0,5(г'н+(в). При Gr Рг = 5-1024-2-107 имеем т=
=0,54 и п==1/4, а при GrPr>2-107— m=0,135 и п=
= >/з.
16—741
245
Для источников тепла в здании Gr'Pr'>2-107. Сле-
довательно, чтобы масштаб коэффициента теплоотдачи
был безразмерен, для источников тепла в модели дол-
жно соблюдаться неравенство Gr"Pr">2-107. В этом
случае
Са=Ск/Г
Подставляя величину Са в формулу (19.7), будем
иметь
(19.8)
Совместное решение равенств (19.4) — (19.6) и (19.8)
позволяет установить геометрический масштаб модели:
Cz = l/C7?. (19.9)
Масштаб лучистого тепла
4,9бе1е2ф Ф 9 ^п-/огр)
4,96eje^q>’ ф’ О' (<-^гр)
= Ср с] се сд(,
(19.10)
где 4,96 — коэффициент лучеиспускания абсолютно черного тела;
81 и 82 — степени черноты поверхностей, участвующих в теплообме-
не; ф •—угловой коэффициент облучения; 9 — температурный фак-
тор; Сгр— температура на внутренней поверхности ограждения зда-
ния или его модели.
При этом температурный фактор
(ТП/100)*-(ТОГР/100)«
С Сгр
где Ти — 273-р/п; 71огр^273-|-/огр
Заметим, что масштаб С =1 вследствие геометриче-
ского подобия, а масштаб С0 =1, поскольку абсолютные
температуры при вентиляционных процессах незначи-
тельно отличаются друг от друга. Поэтому равенство
(19.10) примет следующий вид:
CQ=clc2lC&i. (19.11)
Совместное решение равенств (19.5), (19.6) и (19.11)
позволяет установить, что масштаб степени черноты по-
верхностей
Cs
(19.12)
246
Масштаб теплопотерь через ограждения
k S (t"~ Q
= 7) = C^Ct Сд<’ (19J3)
k S Иогр-гн)
где k — неполный коэффициент теплопередачи; 5 — площадь по-
верхности ограждения здания или его модели.
Входящий в равенство (19.13) неполный коэффици-
ент теплопередачи
где 6 — толщина слоя ограждения, X — коэффициент теплопровод-
ности этого слоя; ао—‘Коэффициент теплопередачи ог ограждения к
наружному воздуху или рабочей среде; при этом в целях упроще-
ния моделирования будем считать, что а0 =а0 .
Решая совместно равенство (19.5), (19.6) и (19.13),
получаем, что масштаб неполного коэффициента тепло-
передачи ограждений
СК = СВ. (19.15)
Из равенства (19.9) следует
Сд,= 1/С?.
Отсюда видно, что если модель по сравнению с натурой
будет уменьшена в 10 раз, то разность температур в мо-
дели должна быть примерно в 1000 раз больше разности
температур в натуре, что практически невыполнимо.
При необходимости изучения вентиляционных про-
цессов на модели приходится геометрический масштаб
считать произвольным. Экспериментальная проверка та-
кого рода приближенного моделирования устанавливает,
что получаемая при этом ошибка не превышает 5и/о, что
вполне допустимо.
§ 83. Моделирование влаговыделений
Масштаб количества влаги
Cd~D'
'ух
(19.16)
~ — CG CAd,
где D расход влаги, dH и dyx — влагосодержание наружного воз-
духа и воздуха, уходящего из здания или его модели.
16*
247
Входящий в это равенство масштаб разности влаго-
содержания может быть установлен, если воспользо-
ваться понятием углового масштаба, применяемого при
графическом построении вентиляционных процессов на
i—d-диаграмме.
При подобии процессов тепло- и влагообмена в зда-
нии и его модели угловые масштабы должны быть оди-
наковыми
Ai'/Ad'= Ai"/Ad" (19,17)
или
A/'/Ad' =A/"/Ad".
Отсюда следует
СД(/ = СД/, (19.18)
значит,
CD = CQ. (19.19)
§ 84. Практические приемы моделирования
Метод расчета модели и обработки опытных данных
состоит в следующем.
1. Задаются геометрическим масштабом модели Ci и
масштабом разности температур Сд(.
2. Вычисляют масштабы: Cv— У^С[СЛ(; Ce — Cj С»;
CQ = CGC^; Се = У~Св- СК=С„.
3. Вычисляют для модели скорость ветра и скорости
воздуха на выходе из приточных вентиляционных систем
и на входе в вытяжные устройства, мощности источников
тепла, степень черноты и неполный коэффициент тепло-
передачи по формулам:
w" = Cvai'; v" = Cv — v';
Q"=CqQ'; e" = cee'; k=CRk'.
4. Определяют термическое сопротивление огражде-
ния модели:
2б'А" = 1/й"- 1/4
5. Затем, выбрав определенный материал ограждения
модели, т. е. зная %", находят б".
6. После запуска модели проверяют соблюдение усло-
вий Re">2400 и GrPr>2-107,
248
7. Проводят замеры скоростей и температур.
8. Замеренные в модели скорости и температуры пе-
ресчитывают на натурные данные по следующим фор-
мулам:
с =и/С0; t = lH+i + <В/СД/.
При наличии влаговыделений дополнительно опре-
деляют мощности источников влаговыделений в модели,
используя равенство (19.19).
Влагосодержание, замеренное в модели, на натурное
значение пересчитывается по формуле
где С= С др
Пример 19.1. Необходимо исследовать аэрацию проектируемого
машинного зала электрической станции.
Ограждения здания этого зала характеризуются следующими
неполными коэффициентами теплопередачи, Вт/(м2.°С): для стен
1,52; остекления 17,4; кровли 1,65 и пола 0,35.
В зале имеются две турбины, четыре крупных трубопровода,
четыре подогревателя и две группы насосов. Количество тепла, кВт,
выделяемое оборудованием модели, составит: турбиной 1045, трубо-
проводом 174, подогревателем 116 и одной группой насосов 116.
Всего выделяется тепла 3482 кВт. Количество пара, выделяемого
турбиной, равно 460 кг/ч. Всего выделяется пара 920 кг/ч.
Приточная механическая вентиляция подает 80000 кг/ч воздуха
на рабочие площадки турбин при скорости воздуха 0,25 м/с и темпе-
ратуре 35° С. Температура наружного воздуха 26° С, а влагосодержа-
ние 9 г/кг.
Проведем это исследование на модели, выполненной в масштабе
Cj=l:50. Пусть рабочей средой будет воздух при температуре 25° С
и влагосодержании 7 г/кг. Примем масштаб избыточных температур
Сд(=2. Тогда масштабы составят:
Се =/2/50 = 1/5; CG = 1/502-5 — 1/12 500;
CQ= 1/6250; Cs = 1/2,24; Ск=1/5.
Отсюда следует, что ограждения модели зала должны характе-
ризоваться следующими неполными коэффициентами теплопередачи,
Вт/(м2-°С): для стен 0,302, остекления 3,5, кровли 0,33 и пола 0,07.
Такие коэффициенты возможны, если ограждения модели вы-
полнять из двух слоев фанеры (V = 0,15) толщиной 4 мм с проклад-
кой между ними теплоизоляции различной толщины, например мипо-
ры (Х"=0,03). В этом случае неполный коэффициент теплопередачи
[см. формулы (19 14)] при а —20 равен:
2-0,004/0,15 + 6'70,03 + 0,05 *
Отсюда
249
По последней формуле получают толщину мипоры, мм. для
стен 111, остекления 7, кровли 104 и пола 500.
Количество тепла, Вт, выделяемое оборудованием модели, соста-
вит: турбиной 167, трубопроводом 28, подогревателем 18,5 и одной
группой насосов 18,5. Всего выделяется тепла 557 Вт. Количество
пара, выделяемое моделью турбины, равно 74 г/ч. Всего выделяется
пара 148 г/ч.
В модели степень черноты поверхностей оборудования н ограж-
дения, если принять, что они в натуре равны 0,91, очевидно, соста-
вит 0,4.
Для достижения такой степени черноты воспользуемся следу-
ющим приемом. Какую-то часть поверхности (например, п) оклеиваем
алюминиевой фольгой со степенью черноты 0,195, известно, что сте-
пень черноты фанеры равна 0,78. Тогда величина п определится из
уравнения 0,4 = 0,195«+0,78(1—я) и составит 0,65. Чтобы реализо-
вать это значение в модели, оклеиваем поверхность лентами алюми-
ниевой фольги шириной 13 мм с промежутками в 7 мм [«=13/(13+
+7) =0,65].
Количество приточного воздуха в модели составит 6,4 кг/ч при
скорости 0,05 м/с и температуре 25+2(35—26) =43° С.
Для пересчета на натурные данные скоростей, температур и
влагосодержания, замеренных в модели, следует пользоваться фор-
мулами:
v' = 5и"; Г = 26 + 0,5 (/" — 25) = 0,5?" + 13,5;
d' =9 + 0,5(d" —7) =0,5d" + 5,5.
ГЛАВА 20
ОПЫТНЫЕ УСТАНОВКИ
§ 85. Аэродинамическая труба
Аэродинамическая труба позволяет изучить работу
аэрационных фонарей, шахт, дефлекторов, взаимодейст-
вие струи с набегающим на них потоком воздуха, а так-
же аэрацию зданий и промышленных площадок.
Наиболее целесообразна при исследовании процес-
сов вентиляции аэродинамическая труба с открытой ра-
бочей частью (рис. 20.1).
При запуске воздушного винта воздух засасывается
через входное отверстие коллектора. В коллекторе по-
перечные сечения по ходу воздуха уменьшаются, поэто-
му скорость воздуха вдоль него увеличивается, в резуль-
тате чего воздух с большой скоростью входит в сопло.
Отсюда он при равномерном поле скоростей поступает
в рабочую часть. В рабочей части свободная струя,
эжектируя воздух камеры, обтекает испытываемую мо-
250
дель и достигает входной кромки диффузора, которая
отсекает вышедший из сопла поток и пропускает его
внутрь диффузора, а подсасываемые массы воздуха от-
брасывает наружу.
При входе в диффузор для разрушения вихревых
колец, охватывающих свободную струю, в рабочей части
предусматривается установка кольцевого раструба,
уменьшающего пульсацию трубы.
Воздух внутри диффузора проходит через сетку и
выбрасывается винтом в помещение. Сетка, имеющая
ячейки размером 2\2 см, предохраняет винт от попа-
дания предметов, которые могут быть унесены из поме-
щения или из рабочей части трубы и вызвать поврежде-
ние или разрушение винта.
Для возможности изменения скорости воздуха в тру-
бе рекомендуется винт приводить в движение электро-
двигателем постоянного тока с числом оборотов,
регулируемых реостатом, включенным в сеть обмотки
статора. Для получения постоянного тока необходим
умформер.
Скорость в рабочей части трубы на выходе из сопла
определяется скоростной трубой, соединенной резиновы-
ми шлангами с микроманометром.
Приведем расчет контура и аэродинамического сопротивления
трубы. Примем габарит здания равным 80X40X10 (h) м, а масштаб
модели 1:100. Тогда модель будет иметь размер 0,8X0,4X0,1 (к) м.
Рис. 20.1. Контур аэродинамической трубы
/ — коллектор; 2 — патрубок; 3 — сопло; 4—камера; 5—рабочая часть; 6 —
кольцевой раструб; 7 — диффузор; 8— сетка; 9 —воздушный винт; 10 — элект-
родвигатель; 11 — осветительный плафон
251
При установке модели в трубе площадь ее миделевого сечения, т. е.
наибольшая площадь поперечного сечения, составит
/ = 0,8-0,1 = 0,08 м2.
Площадь миделевого сечения модели не должна превышать
10% площади поперечного сечения рабочей части трубы, так как
иначе испытание модели в трубе не будет соответствовать задаче
обтекания тела безграничным потоком. Поэтому в среднем площадь
поперечного сечения рабочей части трубы не должна быть менее
0,08/0,1 =0,8 м2.
Если принять поперечное сечение рабочей части трубы в виде
прямоугольника с высотой йо = О,9 м, то его ширина не должна
быть менее 0,8/0,9=0,9 м.
Остановимся на ширине ао=1,2 м. В таком случае площадь
поперечного сечения на выходе из коллектора будет равна:
Ео = = 1.2-0,9 = 1,08 м2.
За образующую коллектора возьмем лемнискату. Уравнение по-
следней в полярных координатах следующее:
р = a ]/cos 20 ,
где р — радиус-вектор; 0 — угол, изменяемый от 0 до 45°, а — пара-
метр кривой, принимаемый равным 0,8 ширины на выходе коллек-
тора. В нашем случае а=0,8 ао = О,8.1,2 = 0,96 м.
Длина коллектора составит
1К = Роs>n45° — 0,96.0,708 = 0,68 м.
Длину патрубка коллектора (прямой участок у коллектора) в
целях удобства монтажа примем равной /п = 0,15 м.
Внутренние поперечные размеры сопла будут такими же, как
и на выходе из коллектора. Длина сопла (исходя из того, что по
обеим его сторонам можно поставить столы) принимается
/0 = О,8ао = 0,8.1,2 = 0,96 м.
Длина открытой рабочей части трубы из соображений удобства
работы равна:
/рл = 1,25а0 = 1,25.1,2= 1,5 м.
Размеры входного поперечного сечения диффузора для пропуска
массы воздуха, вышедшей из сопла, принимаются по Г. Н. Абрамо-
вичу [1] следующими:
Hi = а0+ 0,038/рл = 1,2-1-0,038.1,5 = 1,26 м
и
йх = ft0 + 0,038/рЛ = 0,9+0,038.1,5 = 0,96 м.
Заметим, что площадь поперечного сечения на входе в диффузор
/4=1,26-0,96=1,21 м2.
Диаметр выходного сечения диффузора примем равным 0 =
= 1,62 м (площадь £=2,06 м2). Тогда длина диффузора при боко-
вом угле ею раскрытия 0 = 4° должна составить
£>—1,62— 1,26 0,36
Д~ 2 tg 0 ~ 2-0,07 = 0,14 ~2' 7М
252
или
_ р —ft! 1,62 — 0,96 _ 0,66
я~ 2 tg в “ 2.0,07 “ 0,14
Принимаем среднее значение
/я = 0,5 (2,57 + 4,7) = 3,63 м.
Из-за отсутствия данных по расчету относительные размеры
кольцевого раструба диффузора и боковых отверстий принимаются
такими же, как и в существующих однотипных аэродинамических тру-
бах. Для рассматриваемой трубы абсолютные размеры этих частей
даны на рис. 20.2. В числителе даны размеры по вертикали, в зна-
менателе— по горизонтали).
Исходя из удобства экспериментирования в рабочей части ось
трубы располагаем на расстоянии 1,4 м от пола. В таком случае для
симметрии высота камеры рабочей части должна быть равна 2,8 м.
Остальные размеры камеры назначаем исходя из возможности раз-
мещения в ней рабочих столов (по обе стороны сопла) и удобства
работы в рабочей части трубы, а именно: ширину камеры принима-
ем равной 3 м, а ее длину — 3,6 м.
Длина аэродинамической трубы будет равна:
/ = /к+/п + *с+ /рл + /д = 0,68 + 0,15 + 0,96+1,5 +
+ 3,63 = 6,92 м.
Ширина трубы составит 3 м, а высота — 2,8 м.
Аэродинамическое сопротивление трубы слагается из сопроти-
влений:
коллектора
2 2
ра’о Р®0
ДРк = Ек-у- = 0,01— ,
где £к — коэффициент местного
сопротивления коллектора; Wo —
скорость воздуха в сопле;
патрубка коллектора и сопла
. . . , /п-Но Р^О
Арп + Арс — Л , 0 —
Ug Z
0,15 + 0,96 Р^о
= 0,01
1,03 2
Р^о
0,01------,
2
где Л=0,01—обычно принимае-
мое значение коэффициента сопро-
тивления трения аэродинамиче-
ской трубы;
Рис. 20 2. Вход в диффузор
с кольцевым раструбом
253
J 2аЛ 2-1,2-0,9
4 ==-------- =-------—------= 1,03 м.
ао + «о 2,1
рабочей части трубы, согласно Г. Н. Абрамовичу [1]:
Р^о
ЛРр.ч = 5 ~
р.ч
/о ч / /„ „ \й1 №%
0,1 -^2_ — 0,008 -^2-1 2- =
\ d$ } J 2
г 1,5 /1,5 \2] Р®о Р“>о
= РЛ-Лт— 0,008 —-5- —г- = о,1з—
L 1,03 \ 1,03 J J 2 ’ 2
диффузора (пренебрегая незначительным расширением его сече-
ния)
2 2 9 9
, , 1д , 3,63 P^i л _ Р^Г р^о
Дрд==Л-+ —— = 0,01 —2——— = 0,033—— =0,03--------------
<7э 2 ’ 1,09 2 2 2
где
2-1,26-0,96
---ТГТН— = 1,09 м;
2,2
, 1,08
4 —
о>0 — 0,90ауо;
Fo
1 Ft 0 1,21
скоростною давления на выходе из диффузора
рш2 / Fo \2 Р^о / 108 2 ра'о Р^о
Дрных —-----= I------I ----=----------------= 0 28----- ,
Рвых 2 [ F ] 2 \ 2,06 J 2 ’ 2 ’
Общее сопротивление трубы составит
Др = Дрк 4- Дрп 4- Др0 4- дРрл 4- Дрг 4- Дрвых =
Р+) Р®0
= (0,01 + 0,01 + 0,13 + 0,03 + 0,28) —— = 0,46 .
Принимая, что плотность воздуха р=1,2 кг/м3, скорость воздуха
в сопле ш0=25 м/с, получим
1 2•252
Др = 0,46—-------= 172 Па.
н 2
Расход воздуха
L = 36OOFot>o = 3600 • 1,08 • 25 = 97 000 мз/ч.
Зная сопротивление трубы и расход воздуха в ней, подбираем
по каталогу осевой вентилятор У-12 № 16 с производительностью
L—100 000 м3/ч, полным давлением Др=250 Па, углом установки
лопаток 23°, числом оборотов п=725 об/мин и коэффициентом по-
лезного действия т] = 0,62. Тогда расход электроэнергии составит
ДДр 100 000-250 „ „ „
Л/ =------------- =----------------= 11,2 кВт.
3600-10001] 3600-1000-0,62
Исходя из этой мощности подбираем электродвигатель.
254
§ 86. Аэродинамический стенд
Аэродинамический стенд предназначается для изу-
чения потерь давления на трение и местные сопротивле-
ния в воздуховодах, а также исследования свободных
и стесненных струй равномерной раздачи и всасывания
воздуха воздуховодами с продольной щелью или отвер-
стиями.
Аэродинамический стенд (рис. 20.3) состоит из ради-
ального вентилятора, переходной части, камеры давле-
ния и сети воздуховодов, включающей и испытываемый
элемент. Составные части стенда собирают по схеме
«нагнетание» (см. рис. 20.3, а) или «всасывание» (см.
рис. 20.3, б). Сеть воздуховодов стенда в зависимости от
объекта испытания и принятой методики эксперименти-
рования может быть различной. В отдельных случаях,
например при тарировании коллектора по эталонному
коллектору, исследований местных сопротивлений трой-
ников и крестовин, в состав стенда вводятся вторая ка-
мера давления и второй вентилятор.
Рассмотрим отдельные элементы аэродинамического
стенда. Радиальный вентилятор предпочтительно иметь
высокого, в крайнем случае, среднего давления с ча-
стотой вращения 3000 об/мин.
Диафрагма может быть ирисовая и простая. Простая
диафрагма (рис. 20.4) представляет собой кассету с
набором бленд различного живого сечения.
Камера давления состоит из сваренных между собой
тележки и корпуса (рис. 20.5); размеры на рисунке
даны в миллиметрах. Тележка сваривается из угловой
стали и имеет четыре ролика для облегчения передви-
жения камеры по полу. Корпус камеры представляет со-
бой цилиндрическую трубу, внутри которой устанавли-
вается на болтах обруч с натянутыми на него двумя сет-
ками. Снаружи цилиндрическая труба снабжена четырь-
мя штуцерами, расположенными равномерно по периметру
ее поперечного сечения. По краям трубы имеются флан-
цы. К одному фланцу приболчивается крышка с прива-
ренным к ней диффузором. Другой фланец снаружи
снабжен восемью откидными болтами с гайками, а с
торца — резиновым кольцом.
Открытый торец корпуса камеры давления может
герметично закрываться диском, имеющим по периметоч
восемь радиальных вырезов. Для этого диск подводят
255
Рис. 20 3 Схема аэродинамического стенда
/ — вентилятор; 2 —диафрагма; 3 —диффузор; 4— камера давтения; 5 —
сетка; 6 — коллектор; 7 — сеть воздуховодов; 8 — микроманометр
Рис 20 5. Камера давления
/ — сетка, 2 — стопорный болт
256
к камере давления, откидные болты вводят в вырезы
диска и завинчивают гайки откидных болтов. В центре
диска имеется круглое отверстие для ввода коллектора.
Поперечные размеры камеры давления устанавлива-
ются на основании следующих соображений. Диаметр
корпуса должен быть таким, чтобы измерение полного
давления Арп можно было заменить измерением стати-
ческого давления АрСт- Это освобождает эксперимента-
тора от замеров скорости воздуха и выявления коэффи-
циента поля и коэффициента Кориолиса. В этом случае
ошибка не должна превышать 0,2% полного давления,
т. е. должно соблюдаться условие
(Дрп— Дрст)МРп < 0,002;
< 0,002 Дрп,
где Дрп и окам — давление и скорость воздуха в камере.
Проведем расчет для неблагоприятного случая, ког-
да полное давление будет минимальным, т. е. когда к
камере давления не будет подключена сеть. В этом слу-
чае давление в камере (согласно уравнению Бернулли
при условии пренебрежения весьма малым сопротивле-
нием коллектора) будет равно:
ДРп = Р0кол/2>
где Укол — скорость в патрубке коллектора.
Подставляя в последнее неравенство Арп, получим
Окол/°кам > V500 = 22,4.
Принимая во внимание, что
^кол/°кам — Plf,
где F и f — соответственно площади поперечных сечений камеры,
и патрубка коллектора
будем иметь
F > 22,4(
или окончательно
D > 4,74d,
где D и d — соответственно диаметры камеры давления и патрубка
коллектора.
Наибольший диаметр коллектора d обычно равен
150 мм, поэтому диаметр камеры давления 7)>4,74Х
Х150=710 мм. Принимаем диаметр камеры давления
£)=800 мм.
257
Рис. 20.6, Коллектор
1 — головка; 2 — манжет; <3 —штуцер; 4 — патрубок; 5 — фланец
Коллекторов (рис. 20.6) должно быть несколько со
следующими внутренними диаметрами патрубков: 25,
50, 75, 100, 125 и 150 мм. Образующей коллектора при-
нята лемниската с параметром а=0,8 d.
Длина патрубка коллектора берется в один калибр,
а штуцера устанавливаются на расстоянии 0,5 калибра
от входа в патрубок. Манжет коллектора приболчивает-
ся к диску камеры давления.
В числе элементов сети необходимо иметь диффузо-
ры к коллекторам. Кроме того, должны быть переходы
с круглого сечения на прямоугольное, прямые воздухо-
воды, отводы, тройники круглого и различного прямо-
угольного сечения.
Аэродинамический стенд должен иметь набор раз-
личных пневмометрических трубок, микроманометры и
координатник.
§ 87. Гидравлический лоток
Гидравлический лоток служит для изучения плоских
течений. С его помощью можно установить схему тече-
ния внутри каналов и около обтекаемых тел.
Наиболее удачной конструкцией гидравлического
лотка является циркуляционный лоток с двумя обратны-
ми каналами и эжекторным побуждением движения во-
ды (рис. 20.7). Такой лоток обычно представляет собой
резервуар длиной 2450 мм, шириной с одного конца
1330 мм, с другого 1000 мм при глубине от 300 до 95 мм,
с рабочей частью шириной 750 и глубиной 95 мм.
Входная камера имеет плавный переход к рабочей
части. В переходе наблюдается значительное поджатие
258
поперечного сечения в горизонтальной и вертикальной
плоскостях. Коэффициент поджатия
k =
1330-300
750-95
В горизонтальной плоскости вход в рабочую часть
лотка выполнен в виде коллектора.
Два обратных канала расположены по обеим сторо-
нам рабочей части и имеют каждый ширину 120 и глу-
бину 95 мм. Затем по течению глубина постепенно уве-
личивается и достигает 300 мм.
В начале каждого обратного канала установлено по
три эжекторных насадка. Они смонтированы на движ-
ке, перемещаемом по направляющим пластинам. Насад-
ки могут поворачиваться и перемещаться вниз, вверх
и поперек обратного канала. Насадки каждого обратно-
го канала присоединены резиновыми шлангами к на-
порной трубе. Для регулирования подачи воды на ней
имеется вентиль. Обе напорные трубы подключены к во-
допроводной сети.
Лоток оборудован переливным устройством, позво-
ляющим во время работы удалять в канализацию воду.
Рис. 20.7. Схема гидравлического лотка с эжекторами
259
Переливное устройство состоит из трубы диаметром 2",
возвышающейся над днищем рабочей части и навинчи-
вающейся на нее муфты, а также ограждающей
пластинки. Пластинка не доходит до днища на 10 мм и
возвышается над уровнем воды. Вода, проникая через
зазор между ограждающей пластинкой и днищем, по-
ступает в отверстие муфты и затем сливается. Установ-
ка муфты на той или иной высоте обеспечивает различ-
ный уровень жидкости в лотке. Ограждающая пластин-
ка не позволяет порошку, плавающему на поверхности
воды, уходить из гидравлического лотка.
Для полного опорожнения гидравлического лотка в
наиболее глубокой его части в днище входной камеры
вварена сливная труба диаметром Р/г", имеющая вен-
тиль. Скорость воды в рабочей части обеспечивается сов-
местной регулировкой вентилей на напорных линиях и
переливном устройстве. Рекомендуемая скорость движе-
ния воды в лотке 10—12 см/с. Необходимо иметь в ви-
ду, что при больших скоростях на поверхности воды по-
являются волны.
Скорость воды определяется по скорости движения
какого-либо легкого предмета (кусочка пробки, спички
и т. д.), плывущего на поверхности воды в рабочей
части.
Для удобства проведения опытов в гидравлическом
лотке желательно иметь набор металлических пластин
и тел различного профиля, чтобы составлять каналы и
тела различного очертания и иметь возможность изме-
нять его в процессе испытания.
Модель, устанавливаемая в рабочей части лотка,
должна возвышаться над уровнем воды на 5—10 мм.
Чтобы она лучше выделялась на фоне воды, ее следует
окрашивать в белый цвет.
Для получения схемы течения поверхность воды по-
сыпают порошком алюминия, ликоподия и др. Схему те-
чения с целью большей объективности наблюдения ре-
комендуется фотографировать. Для лучшей освещенно-
сти софиты по бортам лотка следует устанавливать так,
чтобы они не давали отблесков от зеркала воды и лотка.
Последний должен быть окрашен нитрокраской темно-
го цвета. Софиты должны иметь лампы мощностью
около 1000 Вт и располагаться на расстоянии 1—1,5 м
от фотографируемой поверхности. Экспозиция при нор-
мальной скорости движения воды составляет Vs—V20 с.
260
§ 88. Вентиляционный стенд
С помощью вентиляционного стенда на моделях зда-
ний проводятся исследования процесса вентиляции.
Основными частями стенда являются: стол для
установки на нем модели здания, вентиляторы, воздухо-
воды, щит управления и тарировочная труба. При вен-
тиляционном стенде необходимо иметь электроизмери-
тельную аппаратуру, набор термопар, электроанемо-
метр и один-два микроманометра.
Стол для установки модели здания представляет со-
бой обычный лабораторный стол без крышки. Размеры
его в плане 1X1,5 м, а высота 0,8 м. Отсутствие крыш-
ки позволяет удобно подводить вентиляционные систе-
мы и провода к электронагревателям снизу модели зда-
ния.
Применяются радиальные вентиляторы низкого дав-
ления. Набор воздуховодов имеет прямые участки, от-
воды, тройники, мерные диафрагмы с круглым попереч-
ным сечением диаметром 50—100 мм. Воздуховоды же-
лательно изготовлять из белой жести.
Щит управления состоит из трех школьных электро-
распределительных щитов ШЭС-59, монтируемых в ви-
де блока на стене. К щиту управления подводится ток
Рнс. 20.8. Тарировочная труба
/ — коллектор большой; 2 —коллектор малый; 3 — диффузор; 4 — кольцерой
шибер; 5 — спрямляющая решетка; 6 — вентилятор; 7 — электродвигатель; 3—
стойки
261
для питания электронагревателей и радиальных венти-
ляторов в модели здания.
Тарировочная труба предназначена для тарировки
насадков электроанемометров. Труба имеет радиаль-
ный вентилятор низкого давления, соединенный осью с
электродвигателем переменного тока. В собранном ви-
де труба показана на рис. 20.8. К ней придан комплект
бленд, устанавливаемых на выхлопе вентилятора, и од-
ноосевой координатник, в который укрепляется тарируе-
мый прибор.
Скорость потока в рабочем звене трубы определяет-
ся по перепаду статических давлений. Диапазоны из-
меряемых скоростей могут изменяться от 0,05 до 8 м/с.
Скорость воздуха регулируется кольцевым шибером и
блендами.
Тарировочную трубу несложно изготовить из уста-
новки для поверки ручных анемометров УПАР-01.
К установке добавляется приставка в виде трубы диа-
метром 400 и длиной 500 мм, имеющая плавный вход.
В этой приставке и производится тарирование насадка
электроанемометра.
ГЛАВА 21
ПРИБОРЫ И ИХ ТАРИРОВАНИЕ
§ 89. Микроманометр
В последнее время получил распространение микро-
манометр чашечный многопредельный ММН (рис. 21.1),
рабочей жидкостью в котором является спирт с плот-
ностью р0=0,8095 г/см3. Заполнение бачка 1 спиртом
производится через отверстие 2. Вращая регулятор 3,
можно уровень спирта в стеклянной трубке 4 вывести
на нулевое деление.
На крышке бачка имеется трехходовой кран 5 с тре-
мя штуцерами, а также с отверстием для сообщения с
атмосферой. Первый штуцер используется для постоян-
ного соединения крана со стеклянной трубкой.
При измерении избыточного (над атмосферным)
давления используется второй штуцер, а при измерении
разрежения — третий штуцер. В случае перепада дав-
ления для измерения повышенного давления использует-
ся второй штуцер, а пониженного — третий.
262
Рис. 21.1. Микроманометр ММН
При повороте крана по часовой стрелке до упора
производят замеры, а при повороте против часовой
стрелки до упора — контроль нуля.
На стеклянной трубке через 1 мм нанесены деления
от нуля до 250 мм. Стеклянная трубка может находить-
ся в пяти наклонных положениях, ошеченных на стой-
ке цифрами 0,8; 0,6; 0,4; 0,3 и 0,2. Эти цифры означают
величину произведения Л=р0'', где i — синус угла на-
клона стеклянной трубки.
Перепад давлений определяется по формуле
Лрм = kA —gh, (21.1)
K 1 0,8095 s v ’
где k — коэффициент микроманометра; р— плотность спирта во
время замера, h — уровень спирта при замере
Плотность спирта замеряется ареометром при ка-
кой-либо температуре /0, а опыт ведется при иной тем-
пературе t, поэтому плотность спирта
Ро
Р = <212J
где ро — плотность спирта при температуре /о
§ 90. Пневмометрические трубки
Пневмометрические трубки вводятся в поток возду-
ха и воспринимают то или иное его давление, которое
затем с помощью резиновых шлангов передается на
микроманометр.
263
a)
Рис. 21.4. Аэ-
родинамический
крючок
Пневмометрические трубки разделяются на трубки
полного, статического и динамического давления.
Пневмометрическая трубка полного давления про-
стейшей конструкции представлена на рис. 21.2, я. Оба
конца ее открыты. При этом короткий участок трубки
носит название носика, а длинный — державки или
стебля.
При замере давления трубка вводится в поток та-
ким образом, чтобы носик открытым торцом был обра-
щен навстречу потоку воздуха. При необходимости
замера полного давления в узких щелях или вблизи
264
стенки носик трубки изготовляется из более тонкой тру-
бочки, например из иглы шприца. Такие тонкие трубки
получили название микротрубок (рис. 21.2,6).
Трубка статического давления не имеет отверстия
в носике, а на расстоянии 3d (d— диаметр носика) от
торца носика равномерно по поперечному сечению про-
сверлены два или четыре отверстия диаметром 0,5—
0,6 мм. При замерах носик трубки также устанавлива-
ется навстречу потоку воздуха.
Трубка динамического давления, иначе называемая
скоростной трубкой (рис. 21.3), является соединением в
одной конструкции двух ранее описанных трубок полно-
го и статического давления. Радиус закругления конца
носика принимается r=0,5 d.
Рекомендуется при изготовлении носика трубки
тщательно соблюдать размеры, приведенные на рис.
21.3, чтобы в дальнейшем не требовалось тарирование
трубки.
Отклонение оси трубки от направления движения
воздуха до ±17° практически не сказывается на точно-
сти замера. Такое свойство трубки является весьма цен-
ным, поскольку во многих случаях установить ось носи-
ка по потоку воздуха можно лишь ориентировочно.
На конце державки выведены два штуцера для при-
соединения резиновых трубок, идущих к микроманомет-
ру. Плюсом обозначен штуцер, передающий полное дав-
ление, а минусом — статическое давление.
При замере давления и скорости воздуха во всасы-
вающих отверстиях применяются аэродинамические
крючки (рис. 21.4). Они представляют собой ранее опи-
санные трубки, но носик у них имеет два поворота. Эти
повороты могут быть выполнены даже в разных пло-
скостях.
Аэродинамические крючки так же, как и трубки, мо-
гут быть полного, статического и динамического давле-
ния. На рис. 21.4 изображен крючок полного давления.
Если необходимо в потоке замерить не только дина-
мическое давление, но и направление скорости воздуха,
то применяют цилиндрический насадок (рис. 21.5), ко-
торый вводится в поток так, чтобы его ось была перпен-
дикулярна направлению скорости.
Насадок имеет три отверстия. Каждое отверстие
тонкой трубочкой соединено со штуцером. Боковые шту-
цера с помощью резиновых шлангов соединены с
17—741
265
Рис. 21.5. Цилиндрический насадок
V-образной трубкой, а центральный и какой-либо боко-
вой штуцер —с микроманометром. Насадок имеет по-
перечно установленный уровень.
При замерах насадок устанавливают вначале по
уровню, а затем вращают до тех пор, пока в V-образ-
ной трубке уровень в обоих коленах не будет одинако-
вым, после чего снимают отсчет с микроманометра.
При работе с цилиндрическим насадком координат-
ник должен иметь вращательное приспособление с угло-
мерным кругом.
Давление с помощью трубок полного или статичес-
кого давления определяют по формуле
= (21.3)
где — коэффициент скоростной трубки при замере полного и ста-
тического давлений (обычно с«1).
Скорость воздуха с помощью скоростной трубки или
цилиндрического насадка находят по формуле
V = |/Г~" -2 ’ (21 -4)
где р — плотность воздуха; — коэффициент скоростной трубки
или насадка.
Плотность воздуха в период опытов подсчитывают
по уравнению состояния газов
266
1 /? (273 + t) 287 (273 + t) ’
где p — давление; R— газовая постоянная; t — температура возду-
ха, °C.
Коэффициенты пневмометрических трубок устанав-
ливаются экспериментально при их тарировании.
§ 91. Электроанемометры
Электроанемометры применяются для замера ско-
ростей воздуха от 0,1 до 5—6 м/с. В основу их работы
положен принцип охлаждения воздушным потоком на-
гретого электрическим током проводника или полупро-
водника.
Наиболее распространенным электроанемометром
является термоанемометр марки ТА-ЛИОТ (рис. 21.6).
Насадок этого термоанемометра представляет собой од-
но плечо моста сопротивления. Для питания служит пе-
ременный ток напряжением 127 или 220 В, включаемый
через феррорезонансный стабилизатор — трансформа-
тор и выпрямители (германиевые диоды).
Перед началом работы проверяется нулевая точка
Рис. 21.6. Общий вид электроанемометра ТА-ЛИОТ
17* 267
гальванометра. С этой целью переключатель ставят в
правое положение и с помощью реостата стрелку галь-
ванометра выводят на нуль. Затем при среднем поло-
жении этого переключателя фиксируют температуру на
гальванометре — микроамперметре марки М-24 на
50 мА, отградуированном на шкалы температур и ско-
ростей потока. С помощью другого переключателя вво-
дится компенсационное сопротивление, исключающее
влияние температуры потока на показание скорости.
После этого первый переключатель переводят в ле-
вое положение и фиксируют на гальванометре скорость
потока. Прибор может замерять скорости потока от 0,1
до 5 м/с.
Необходимо отметить, что в случае неисправности
насадки не могут быть заменены, поскольку полупро-
водники нестандартны, а для новых полупроводников
необходимо заново подбирать многие элементы схемы.
В последние годы Уральским Промстройниипроек-
том стал выпускаться полупроводниковый термоанемо-
метр марки.ЭА-2М, который может измерять темпера-
туру, скорость воздуха и направление воздушных пото-
ков. Диапазон его измерения: скорости от 0 до 5 м/с,
температуры от 10 до 60° С и направления потока от 0
до 360°. Датчик прибора состоит из двух терморезисто-
ров, подогревной обмотки, цилиндрической обечайки и
крепится на трубке держателя, внутри которой проходят
выводы от терморезисторов. На ручке держателя датчи-
ка расположен угломерный лимб, а стрелка указателя
угла поворота датчика крепится к трубке, скользящей
по держателю. При хранении и настройке датчик теле-
скопическим держателем вдвигается в защитный фут-
ляр.
Термоанемометр работает на четырех элементах ти-
па 373 «Марс» или от аккумуляторной батареи 7 В, а
также с помощью стабилизированного источника пита-
ния СИП-1 на 220 В.
При определении направления потока совмещают
стрелку указателя поворота с нулевым делением лим-
ба. Плавно поворачивая ручку датчика, находят мини-
мальное значение тока и производят отсчет на лимбе.
Затем ручку датчика поворачивают на 180° и фиксиру-
ют силу тока. Угол, при котором получилось минималь-
ное значение силы тока, дает направление потока воз-
духа.
268
§ 92. Координатники
Координатники служат для закрепления пневмомет-
рической трубки или насадка электроанемометра в оп-
ределенном положении и перемещения их в заданное
положение. Различают координатники одноосевые,
двухосевые и трехосевые в зависимости от возможности
передвижения пневмометрической трубки или насадка
в одном, двух или в трех направлениях. В отдельных
случаях координатник может снабжаться поворотным
устройством с угломерным кругом, позволяющим отсчи-
тывать углы поворота трубки, что необходимо, напри-
мер, при работе с цилиндрическим насадком.
Наиболее простой конструкцией одноосевого коорди-
натника является координатник со струбцинкой (рис.
21.7), состоящий из платформы /, червяка 2 с головкой
3, каретки 4 и струбцины 5. Платформа имеет шкалу
6 для фиксации положения каретки. Вращение головки
червяка вызывает перемещение каретки.
Каретка снабжена откидной крышкой 7 и прижим-
ным болтом 8. В теле каретки имеются три отверстия
для вкладки в них пневмометрических трубок различно-
го диаметра. Струбцинка позволяет укрепить коорди-
натник в нужном месте, используя ближайшую высту-
пающую часть опытной установки.
Более сложной конструкцией является двухосевой
координатник (рис. 21.8), состоящий из двух частей:
собственно координатника (см. рис. 21.8, а) и стойки
(см. рис. 21.8,6).
Координатник включает в себя неподвижную верти-
кальную ось I и подвижную горизонтальную ось 2. На
обеих осях имеются шкалы с точностью до 1 мм. Муфта
3 горизонтальной оси имеет нониус. По горизонтальной
оси может перемещаться каретка 4 с поворотным меха-
низмом 5. Каретка снабжена нониусом, а поворотный
механизм снабжен сектором с градусной шкалой 6.
Стойка состоит из вертикальной трубы 7 и круглой
платформы 8 с уровнями и установочными винтами.
При сборке координатника неподвижная вертикаль-
ная ось вкладывается в верхний открытый торец трубы
стойки и зажимается стопорными винтами. При работе
пневмометрическая трубка вводится в отверстие пово-
ротного механизма и зажимается конусом. Перемеще-
ние трубки по горизонтальной и вертикальной осям, а
269
Рис. 21.7. Одноосевой координатник
S)
Рис. 21.8. Двухосевой координатник
270
670
также ее вращение осуществляются соответствующими
винтами.
Трехосевой координатник состоит из тележки, верти-
кальной стойки и каретки. Под координатник прокла-
дывается специальный двухрельсовый путь. Управление
передвижением каретки сосредоточено на крышке стола
тележки. Каретка по вертикали перемещается с по-
мощью тросов, а по горизонтали — посредством кониче-
ской передачи.
§ 93. Тарирование приборов
Тарирование производится для определения значе-
ния коэффициента прибора и осуществляется обычно
путем сравнения показаний тарируемого прибора с по-
казаниями другого точно выверенного прибора, назы-
ваемого эталонным.
При тарировании микроманометра берут эталонный
и тарируемый микроманометры и проверяют их герме-
тичность. Затем резиновыми шлангами соединяют их
штуцера повышенного и пониженного давления (рис.
21.9).
Осуществив такую сборку, оба микроманометра ус-
танавливают строго по уровням и фиксируют началь-
ные показания. Затем закрывают кран и накачивают
воздух. Подняв уровень спирта до верхних делений
шкалы тарируемого микроманометра, записывают пока-
зания обоих микроманометров. Затем с помощью кра-
на выпускают постепенно воздух и каждый раз запи-
сывают показания микроманометров. В результате по-
лучают ряд значений высоты столба спирта ha и hT. При
этом учитывают, что давление в эталонном и тарируе-
мом микроманометрах
каждый раз должно быть
одинаковым:
Адэ = Арт
ИЛИ
kg Ад Рэ ёЪ — Ат Рт ё^т
Отсюда коэффициент
тарируемого микромано-
метра
«т — , (21.6)
**т Рт^т
Рис. 21.9. Схема установки для
тарирования микроманометра
271
В целях повышения точности тарирования микрома-
нометры устанавливают с одинаковым наклоном стек-
лянных трубок (Аэ=Дт) и заливают спирт одинаковой
плотности (рэ=рт). Тогда
, , ft?
«т — «э .
пт
Имея несколько значений коэффициента тарируемо-
го микроманометра, вычисляют их среднеарифметичес-
кое значение:
*ср=1/«2*т, (21.7)
1
где п — число проведенных опытов.
Наличие в схеме установки для тарирования резер-
вуара облегчает взятие отсчетов на шкалах микромано-
метров, изолируя их от атмосферы, и тем самым позво-
ляет более точно определить коэффициент микромано-
метра.
Тарирование скоростной трубки производится сле-
дующим образом. В поток воздуха с равномерным по-
лем скоростей вводят две скоростные трубки. Коэффи-
циент эталонной трубки известен, коэффициент тариру-
емой трубки должен быть определен.
К каждой трубке с помощью резинового шланга
присоединен микроманометр. При тарировании создают
различные скорости воздуха и записывают при каждой
скорости воздуха в обоих микроманометрах высоты
столба спирта h0 и 1гг.
Скорости, замеряемые обеими скоростными трубка-
ми, должны быть одинаковы:
t'a = Vt
ИЛИ
== j/” ?т АРт •
Освобождаясь от радикала, сокращая на 2/р и рас-
крывая Ар, получим
Ад Рэ 8^3 ~ -т Рг
Отсюда
g = g3 fo AJlP^ , (21,8)
йт Ат Рт/гт
272
В целях повышения точности тарирования стеклян-
ные трубки устанавливают с одинаковыми наклонами
(ЛО=АТ), а микроманометры заливают спиртом одина-
ковой плотности (рэ=рт). При этих условиях
6 _6 С
St — ёэ , , •
Если же поток не пульсирует (показания на микро-
манометрах не колеблются), то можно обе трубки при-
соединить с помощью крана-переключателя к одному
микроманометру. При тарировании к микроманометру
присоединяют краном сначала одну, а потом другую
скоростную трубку и последовательно записывают по-
казания микроманометра.
При таком способе тарирования в последней форму-
ле будут равны и коэффициенты обоих микроманомет-
ров (ka-kv). Следовательно, в этом случае будет спра-
ведлива еще более простая формула;
hy
Подсчитав значение коэффициентов скоростной
трубки при каждой скорости воздуха, находят их сред-
нее арифметическое значение:
п
Bep —
(21 9)
где n — число проведенных испытаний.
Аналогичным образом тарируются трубки полною
и статического давления, а также цилиндрический на-
садок.
Коллекторы могут быть протарированы двумя спосо-
бами: по эталонной пневмометрической трубке и по эта-
лонному коллектору.
При первом способе тарируемый (обычно круглый)
коллектор вставляется в камеру давления аэродинами-
ческого стенда, собранного по схеме «нагнетание» (рис.
21.10). К штуцерам камеры давления и штуцерам кот-
лектора присоединяется один микроманометр.
На выходе из коллектора устанавливается микро-
трубка полного давления, вставленная в координатник
и соединенная с другим микроманометром. При опреде-
ленной скорости воздуха в коллекторе замеряют микро-
273
трубкой давление воздуха по двум взаимно перпендику-
лярным диаметрам патрубка коллектора. Замер полей
давления всегда начинают от внутренней поверхности
патрубка коллектора, первый раз устанавливая ось но-
сика трубки (иглы шприца) вдоль внутренней образую-
щей патрубка. Затем трубку устанавливают через 1 мм,
а при удалении носика на 10—15 мм — через 5—10 мм.
При каждой установке трубки записывают отсчет на
координатнике, показания микроманометра коллектора
hK и показания микроманометра трубки йт.
После этого вычисляют коэффициент коллектора по
формуле тарирования. Эту формулу можно получить,
для тарирования коллектора
с помощью пневмометриче-
ской трубки
Рис. 21.11. График, получаемый
при тарировании коллектора
Рис. 21.12. Схема установки для тарирования коллектора по эталон-
ному коллектору
/ — ирисовая диафрагма; 2 — вентилятор, 3 —первая камера давления, 4 —
эталонный коллектор; 5 —вторая камера давления, 6 — тарируемый коллектор;
7 — микроманометр №1;в - микроманометр Ns 2
274
учитывая, что средние скорости воздуха, замеряемые
коллектором и пневмометрической трубкой, должны
быть одинаковы:
Ск.ср = f-r.cp •
Средняя скорость воздуха, определяемая с помощью
пневмометрической трубки, может быть представлена в
следующем виде:
Ст.ср=(1 IP) С vdf I
F
где F — площадь поперечного сечения патрубка коллектора; v —
скорость воздуха в данной точке того же сечения; df — элементар-
ная площадка.
Для круглого коллектора при осесимметричном про-
филе скоростей воздуха справедливо
F = nR2- df = 2nrdr,
где R— внутренний радиус патрубка коллектора; г — удаление дан-
ной точки от центра поперечного сечения патрубка коллектора
В таком случае будем иметь следующее равенство:
I
Гн.ср = 2j vrdr,
и
где r = r/R — относительный радиус данной точки.
В последнем равенстве, заменяя скорости воздуха
динамическими давлениями согласно формуле (21.4),
а затем давления высотами столба cnnpia, по формуле
(21.1) получим
Г 2 Г •. /~~2 _ _
I/ Вк Лк рк ghK = 2 1 I/ - г k? Лт Рт ght г d г.
о
Решая это равенство относительно неизвестного ко-
эффициента коллектора, окончательно будем иметь сле-
дующую расчетную формулу:
^=^-“4 • (21.Ю)
'пДк Рк Jr
Интеграл расчетной формулы обычно вычисляется
графически. С этой целью для каждого из четырех ра-
диусов, вдоль которых проводился замер давлений,
строится график функций
сУ\/Лк = /(д-
27&
В качестве образца приводится один такой график
для коллектора с диаметром патрубка d— 150 мм (рис.
21.11). Искомый интеграл равен площади, заключенной
между кривой и осью абсцисс. Эту площадь проще все-
го определять планиметром.
При втором способе тарирования кроме аэродинами-
ческого стенда необходимо иметь вторую камеру дав-
ления. Эталонный коллектор вставляют в камеру дав-
ления аэродинамического стенда, собранного, например,
по схеме «нагнетание». Вторую камеру давления при-
соединяют к эталонному коллектору и в нее вставляют
тарируемый коллектор (рис. 21.12).
К штуцерам каждой камеры давления и к штуцерам
вставленных в них коллекторов присоединяют по одно-
му микроманометру. Создавая внутри установки раз-
личные расходы воздуха, записывают показания обоих
микроманометров, получают два ряда значений h3 и /гт.
Имея эти значения, можно вычислить неизвестный ко-
эффициент тарируемого коллектора.
Действительно, расходы воздуха в эталонном и та-
рируемом коллекторах должны быть одинаковыми. По-
этому можно написать равенство L3=LT. Заменяя рас-
ходы воздуха произведением площади на скорость воз-
духа, получим
/э v3 — fl Vlf
где и fT — площади поперечных сечений эталонного и тарируемо-
го коллекторов; v3 и иг— средние скорости воздуха в тех же сече-
ниях.
Последнее равенство можно представить в виде
/э Рг
Отсюда следует, что коэффициент тарируемого кол-
лектора
= (2М1)
/?т Рт \ / т /
Заметим, что, как и в ранее рассмотренных случаях,
эта формула существенно упростится, если работать на
двух микроманометрах при одинаковых наклонах стек-
лянных трубок и наполнении бачков спиртом одной
плотности или в процессе тарирования использовать
один микроманометр.
Определив значения коэффициента коллектора при
разных расходах воздуха, вычисляют его среднеарифме-
тическое значение.
276
Первый способ тарирования не рекомендуется про*
водить с прямоугольными коллекторами, так как даже
при увеличении числа замеров давлений этот способ не
обеспечит необходимой точности. Второй способ тариро-
вания допустим как для круглых, так и для прямо-
угольных коллекторов. Для обеспечения достаточной
точности тарирования желательно площади поперечных
сечений патрубков обоих коллекторов принимать по
возможности равными ((э~/ст). Необходимо отметить,
что по второму способу тарирования коллектора могут
быть протарированы также труба Вентури и диа-
фрагма.
Тарирование электроанемометров производится в та-
рировочной трубе. Насадок устанавливается в широкой
ее части. Замеряя перепад давлений с помощью микро-
манометра, определяют скорость потока, а на электро-
анемометре фиксируют деления гальванометра, отмеча-
емые стрелкой. Затем строится график, где по оси абс-
цисс откладывают число делений гальванометра, а по
оси ординат — скорость потока.
ГЛАВА 22
ЛАБОРАТОРНОЕ ЭКСПЕРИМЕНТИРОВАНИЕ
§ 94. Определение коэффициента
сопротивления треиия
Испытание прямого воздуховода проводится на аэро-
динамическом стенде, собранном по схеме «нагнета-
ния» (рис. 22.1). При работе этого стенда воздух, прой-
Рис. 22.1. Схема опытной установки для определения коэффициента
сопротивления трения
J —диафрагма; 2 — вентилятор; 3 —диффузор; 4 — камера давления; 5 — кол-
лектор; 6 — входной воздуховод; 7 — испытуемый воздуховод; 8 — микрома-
нометр № 1; 9 — микроманометр № 2
277
дя диафрагму и вентилятор, нагнетается последним в
диффузор и камеру давления. Из камеры давления воз-
дух выдавливается в коллектор, входной воздуховод
длиной 10 калибров и испытуемый воздуховод длиной
30—40 калибров. Диафрагма установлена для того, что-
бы изменять расход воздуха в сети.
Кроме штуцеров, имеющихся на поверхности камеры
давления и патрубка коллектора, установлены штуцера
на расстоянии двух калибров от начала испытуемого
воздуховода.
К штуцерам камеры давления и штуцерам патруб-
ка коллектора присоединен микроманометр № 1, а к
штуцерам испытуемого воздуховода — микроманометр
№ 2.
При испытаниях в кассету диафрагмы вводят блен-
ды различного живого сечения и снимают показания на
микроманометре № 1—hi и на микроманометре № 2 —
/12-
Обработку опытных данных проводят по следующим
формулам. Коэффициент сопротивления трения опреде-
ляется по формуле
_ Ара+ ИаР^/2~ авР^2
pw2/2
где Лра — избыточное статическое давление воздуха в воздуховоде
в точке а; аа — коэффициент Кориолиса для поля скоростей в точ-
ке а; р— плотность воздуха; va — средняя по площади поперечного
сечения воздуховода скорость воздуха в точке а; ав — коэффициент
Кориолиса для поля скоростей на выходе из воздуховода; пв— сред-
няя по площади поперечного сечения воздуховода скорость воздуха
на выходе из него; w — средняя скорость воздуха, замеренная по
коллектору.
Обычно разность динамических давлений, стоящая в
числителе правой части этой формулы, невелика, и ею
можно пренебречь. В этом можно убедиться, если заме-
рить поле скоростей в точке а и на выходе из воздухо-
вода и подсчитать динамические давления в них. Про-
водится это измерение с помощью микротрубки (см. гл.
21, § 5). В таком случае
рю2/2
Заменим в этой зависимости
Лра = й2 Я2 Рг §Л2>
278
где kz — коэффициент микроманометра; Аг— произведение плотно-
cm спирта на синус угла наклона; ра — плотность спирта; g— уско-
рение свободного падения,
И
pw2/2 = рд! = g ki At pi ghlt
где рД1—динамическое давление; g — коэффициент коллектора.
Тогда получим
Л = (22 Л)
где
А = (1/g) (*а pa/*i Ai рО.
Число Рейнольдса находится по формуле
Re = wd/v = 2/рЛрщ ,
где v — кинематическая вязкость воздуха.
Отсюда
Re = В/ft?, (22.2)
где
B=(d/v)V 2ikiAiPig/p .
Эквивалентная абсолютная шероховатость определя-
ется по формуле, получаемой из зависимости А. Д. Альт-
шуля:
Подсчитав k при каждой установленной бленде, на-
ходят их среднее арифметическое значение:
/гср=1/п2Х (22.4)
где п — число проведенных испытаний,
§ 95. Определение коэффициента
местного сопротивления отвода
Испытание отвода проводится на аэродинамическом
стенде, собранном по схеме «нагнетание» (рис. 22.2).
При работе этой установки воздух, пройдя ирисовую
диафрагму и вентилятор, нагнетается последним в диф-
фузор и камеру давления. Из нее воздух выдавливается
в коллектор, диффузор и входной воздуховод длиной
279
10 калибров. Затем воздух поступает в испытуемый от-
вод и выходной воздуховод длиной 10 калибров.
К штуцерам камеры давления и штуцерам вставлен-
ного в нее коллектора присоединяют микроманометр
№ 1. К штуцерам камеры давления, кроме тою, присое-
диняют микроманометр № 2 для замера избыточного
(над атмосферным) статического давления.
При испытаниях ирисовой диафрагмой обеспечивает-
ся различный расход воздуха в отводе. При каждом рас-
ходе воздуха вначале снимают показания на микромано-
метре № 1 — hi, затем на микроманометре № 2 — /г2.
Затем удаляют отвод и выходной воздуховод присоеди-
няют к входному воздуховоду (см. пунктир на рис. 22.2).
После этого, регулируя расход ирисовой диафрагмой,
добиваются прежнего показания микроманометра № 1 —
h\ и снимают показание на микроманометре № 2 — h'2.
Обработку опытных данных проводят по следующим
формулам. Коэффициент местного сопротивления отвода
определяется по формулам
ДРп-ДРп-(Х/^э) (ць.г/2)
6 “ рш2/2
где Лря и Дрп — полное избыточное давление в камере давления
соответственно при наличии в сети отвода и при отсутствии его;
Л — коэффициент сопротивления трения; I — длина отвода, опреде-
ляемая по осевому радиусу закругления; da — эквивалентный диа-
метр; р— плотность воздуха; w — средняя скорость воздуха в воз-
духоводе перед отводом.
Рис 22.2. Схема опытной установки для определения коэффициента
местного сопротивления отвода
/ — ирисовая диафрагма; 2 — вентилятор; 3 —диффузор; 4 — камера давления;
5 — коллектор; 6 — диффузор; 7 — входной воздуховод, 8— испытуемый отвод;
9 — выходной диффузор; J0 — микроманометр № 1; // — микроманометр № 2
280
Принимая во внимание, что скорости в камере давле-
ния весьма малы, можно заменить разность полных
избыточных давлений в камере давления разностью ста-
тических избыточных давлений. Тогда
рш2/2 d3
Заменяем в этой зависимости
Дрст = k2 А2 р2 gh.2, Apct = k2A2p2gh^
P®*/2 = (f IF)* pt>2/2 = (f IF)* Арю = (f IF)2 Л! Pt ghit
где f и F — площадь поперечного сечения соответственно патрубка
коллектора н воздуховода; v—скорость воздуха в патрубке кол-
лектора.
В таком случае
h2 — h2 I
t = A ----- - -X ~r , (22.5)
hi d3
где
A _ 1 MaPa / f V
6 feiAPi \ f j '
Коэффициент сопротивления трения находится по
формуле А. Д. Альтшуля, если известна эквивалентная
шероховатость стенок отвода. При этом значение числа
Рейнольдса находится по формуле
wd3 d3 fv d3 f 2
где v — кинематическая вязкость воздуха.
Отсюда
Re = В Vhx , (22.6)
где
„ аз f 1 /~~2
TfV
Если эквивалентная шероховатость стенок воздухо-
вода неизвестна, то ее следует установить по методике,
изложенной в предыдущем параграфе. Подсчитав С и Re
при каждом расходе воздуха в отводе, получают зависи-
мость £ от Re,
18—741
281
§ 96. Определение коэффициентов
местных сопротивлений тройника
при делении потока
Испытание тройника при делении потока проводится
на аэродинамическом стенде, собранном по схеме «на-
гнетание», с присоединением к его вентиляционной сети
вторых камеры давления, коллектора, диафрагмы и вен-
тилятора (рис. 22.3).
При работе этой установки воздух засасывается ос-
новным вентилятором, проходит диафрагму, диффузор и
поступает в камеру давления. Из нее воздух выдавлива-
ется в коллектор и течет по прямому воздуховоду длиной
10 калибров. Затем воздух поступает в испытываемый
тройник, а часть его направляется в ответвление. Остав-
шаяся часть воздуха далее течет по прямому воздухово-
ду длиной 10 калибров и поступает во вторую камеру
давления. Из этой камеры воздух выдавливается во вто-
рой коллектор. Затем воздух проходит вторую диафраг-
му и вспомогательным вентилятором выбрасывается
наружу.
Обе диафрагмы установлены для того, чтобы можно
было изменять общий расход воздуха и создавать раз-
личные расходы воздуха в ответвлении и проходе трой-
ника. Вспомогательный вентилятор поставлен с тем, что-
бы «взять на себя» сопротивление проходной части вен-
тиляционной сети и тем самым обеспечить и такой режим
работы установки, при котором воздух не поступает в от-
ветвление.
Рис. 22.3. Схема опытной установки для определения коэффициен-
тов местного сопротивления тройника при делении потока
1 — основной вентилятор; 2 — первая диафрагма; 3 —диффузор; 4 —первая
камера давления; 5 — первый коллектор; 6 — входной участок; 7 — испытуемый
тройннк; 8 — выходные участки; 9— вторая камера давления; 10 — второй
коллектор; 11 — вторая диафрагма; 12 — вспомогательный вентилятор; 13, 14,
15, 16 — микроманометры соответственно 2-, 3* и 4 й
282
Кроме штуцеров, имеющихся на поверхностях каме-
ры давления, и патрубков коллекторов установлены
штуцера на поверхности прямых участков, а именно: шту-
цер а на расстоянии двух калибров и штуцер b на рас-
стоянии восьми калибров от тройника.
К штуцерам каждой камеры давления и штуцерам
вставленного в нее коллектора присоединяют по одному
микроманометру, к штуцеру а — третий микроманометр,
к штуцерам а и b—четвертый микроманометр.
Испытание начинают при открытой первой диафраг-
ме и закрытой второй диафрагме. Затем в кассету вто-
рой диафрагмы последовательно вводят бленды все
большего и большего живого сечения. Наконец, вторая
диафрагма становится полностью открытой. После этого
в первую диафрагму начинают последовательно вводить
бленды все меньшего и меньшего живого сечения. Это
осуществляется до тех пор, пока из ответвления не пере-
станет выходить воздух. Для определения направления
движения воздуха у открытого конца ответвления подве-
шивают вблизи торца несколько шелковых нитей. При
отсутствии расхода воздуха в ответвлении эти нити бу-
дут висеть отвесно, никуда не отклоняясь. При каждой
установке бленды снимают показания на микроманомет-
рах № 13—16: /гь h2, h3 и Л4.
Обработку опытных данных проводят по следующим
формулам. Коэффициенты местных сопротивлений ответ-
вления и прохода тройника, как известно, зависят от от-
носительного расхода воздуха в ответвлении:
to = ф До); ?п = Ч До);
Lo = L0!Llt
где La — расход воздуха в ответвлении; Li — расход воздуха в воз-
духоводе, установленном до тройника.
Коэффициент местного сопротивления ответвления
тройника установим с помощью уравнения Бернулли, на-
писанного для сечений А—А и Б—Б:
2 2 2 2 2
рш ро0 I рш рш I рр
Ра 2 и 2 d 2 2 do 2 ’
где ра и р — статическое давление воздуха соответственно в возду-
ховоде у штуцера а н в помещении (ра—Р замеряется микромано-
метром № 3); w — скорость воздуха в воздуховоде, установленном
до тройника; Va — скорость воздуха в воздуховоде, присоединенном
к ответвлению тройника; I — расстояние от штуцера а до места де-
18*
283
ления потока; lo — расстояние or места деления потока до конца
воздуховода, присоединенного к ответвлению тройника; d и do — эк-
вивалентные диаметры соответственно воздуховода, установленного
до тройника, и воздуховода, присоединенного к ответвлению трой-
ника; Л и Ло — коэффициенты сопротивления трения.
Решая последнее равенство относительно неизвестно-
го коэффициента местного сопротивления ответвления и
обозначая ра—р=^Ар0, получаем
Заменяем в этой формуле величины;
Дро = А3 Psgh3;
рш2 / f V po2 if у / Л У
-у- = J ~у = ( у j Дрдг = j
Volw = LBFI foLt = Loifo,
где /i — площадь поперечного сечения патрубка первого коллекто-
ра; Vi — скорость воздуха в патрубке первого коллектора; F и fo —
площадь поперечного сечения соответственно воздуховода, установ-
ленного до тройника, и воздуховода, присоединенного к ответвлению.
Тогда после простейших преобразований будем иметь
to = Ао~ + (1 - X у ) - (1 - Ло у) (v) • (22.7)
Коэффициент Ао вычисляется по формуле
А 1 *3Л3р3 IF у
£i ki Аа Pi \ /1 /
Коэффициент местного сопротивления прохода трой-
ника установим с помощью уравнения Бернулли, напи-
санного для сечений А—А и В—В:
2 о о ? 2
ОШ OV„ 1 ОШ" р[£Г 1 pVn
г *__ . _*______П I >___ г <п * П
Ра+ 2 -рЬ+ 2 +Л d 2 +?п 2 +*п 2 ,
где рь-—статическое давление воздуха в сечении воздуховода, про-
ходящем через штуцер b (ра—рь замеряется микроманометром №4);
vn—скорость воздуха в воздуховоде, присоединенном к проходу
тройника; Zn — расстояние от места деления потока до штуцера 6;
— эквивалентный диаметр воздуховода, присоединенного к про-
ходу тройника.
Если ввести обозначение ра—ръ = А.ра, то из послед-
него уравнения следует:
г _
fen pto2/2
। j.,
1 тГп , I
da J\ w j
284
Заменяем в нем величины:
Дрп = ki Ai р4 gh4;
рш2/2 = (Л/F)2 Хх pi g/ij;
va!w = (L- Lo) F!faL, = (1 - L0)lfa,
где Л — площадь поперечного сечения воздуховода, присоединенно-
го к проходу тройника.
В таком случае получим
h / I \ / I \ ( ^ — \
?п = А,-~-+ 1-Х— - l+Xn-f- —=----- , (22.8)
«1 \ « 1 \ dn / \ /п /
где
л _ 1 МаРа / F У
51 ^1X1 Pi \ Л /
Коэффициенты сопротивления трения могут быть вы-
числены аналитически по формуле А. Д. Альтшуля, если
известна эквивалентная шероховатость стенок воздухо-
водов.
Значение числа Рейнольдса вычисляется по следую-
щим формулам:
для воздуховода, установленного до тройника:
wd d flvi d fi л /~ 2
Re=vv~“VT V T
или
Re = B]/fti, (22.9)
если
R d 1/ 2 e А Л
~ ~F V V 5lW1W ’
где v — кинематическая вязкость воздуха;
для воздуховода, присоединенного к проходу трой-
ника:
Ren = Bu/'ft2, (22.10)
если
п 1 2 е а л
Вп=~— I/ — ЬМгР^;
* /п < р
285
для воздуховода, присоединенного к ответвлению
тройника:
vodo d0 Lo d0 d0
Re0 =----=-----— = —— (bi — i2) = — (ftvi — M =
v v f0 vfo vf0
= iikiAiPiShi — ~~ ]/r~
vf0 V p vf0 V p
ИЛИ
Re0 = ^Re--y--^-Ren. (22.11)
Ufo «И /О
Если эквивалентная шероховатость стенок воздухово-
да неизвестна, то следует вначале ее установить по ме-
тодике, изложенной в § 94.
Относительный расход воздуха в ответвлении
Li ц
где Li и Дг — расходы воздуха соответственно в первом и втором
коллекторах (микроманометры № 1 и 2).
Заменяя в первой части последнего равенства расхо-
ды воздуха произведением площади поперечных сечений
патрубков коллекторов и f2 на соответствующие сред-
ние скорости воздуха в этих сечениях Vi и v2, получим
L0 = l—cVhJh1, (22.12)
После вычисления £0, £п и Lo строят зависимости ко-
эффициента местного сопротивления ответвления от от-
носительного расхода в ответвлении Lo и коэффициента
местного сопротивления прохода от относительного рас-
хода в проходе, равного Ln=En/Li=(LI—Lo)/Ll = l—L0.
§ 97. Выявление оптимальной схемы
всасывающего патрубка
Всасывающий патрубок имеет плавный вход, выпол-
ненный с радиусом закругления г, и горло шириной b
(рис. 22.4). Необходимо выявить, при каком сочетании
г и b в условиях постоянного расхода воздуха в патруб-
ке скорость всасывания v на определенном расстоянии
286
от входа в патрубок будет наибольшей. При этом радиус
закругления г не должен превышать 40 мм, а ширина
горла Ъ—100 мм [5].
Для решения этой задачи следовало бы изготовить
серию патрубков, например, со следующими значениями:
г=0; 5; 10; 20; 30 и 40 мм — 6 вариантов и & = 5; 10;
15; 20; 25; 30; 40; 60; 80 и 100 мм — 10 вариантов.
Таким образом, пришлось бы изготовить 60 патруб-
ков. Затем их надо было бы подвергнуть испытанию иа
аэродинамическом стенде, собранном по схеме «всасы-
вание», и выявить скорость всасывания у каждого
патрубка. Для этого на оси абсцисс следовало бы от-
кладывать значения Ь, а на оси ординат — значения г и
затем проводить из этих то-
чек прямые, параллельные
осям координат. В результате
получили бы сетку, каждый
узел которой соответствует
опыту с определенным значе-
нием г и b (рис. 22.5).
Затем рядом с каждым уз-
лом необходимо написать зна-
чения скорости всасывания и
затем установить наибольшее
из них. Изготовление 60 пат-
Рис. 22 4. Схема всасываю-
щего патрубка
Рис. 22 5. Сетка с нанесением на ней номеров проведенных опытов
и значений скорости всасывания
287
рубков и их испытание потребовало бы больших средств
и времени.
Современная теория математического планирования
экстремального эксперимента [2] позволяет значитель-
но сократить число опытов. В основу этой теории поло-
жена кибернетическая система, состоящая из черного
ящика (в нашем случае патрубка), ряда входных пара-
метров X), х2, ... — (в нашем случае г и 5) и ряде выход-
ных параметров — параметров оптимизации ylt у2,-.- (в
нашем случае п).
Ниже в весьма упрощенном виде изложим метод
математического планирования эксперимента при поиске
оптимального всасывающего патрубка. Вначале выбираем
четыре патрубка со смежными значениями г и Ь, напри-
мер с радиусом г=30 и 40 мм и шириной &=60 и 80мм
(см. рис. 22.5) и составляем табл. 22.1.
Таблица 22.1. Обозначения параметров и уровни их варьирования
Параметр Уровня варьирования. мм, при кодированные значениях
—1 0 4-1
г 30 35 40
ь 60 70 80
Здесь в среднем столбце записаны средние значения
уровней варьирования параметров:
гср — (гпаим 4" Гнаиб)/2;
= (^наим 4* ^наиб)/2.
Цифрами —1; 0 и 4-1 обозначены кодированные зна-
чения уровней варьирования параметров (наименьшее
значение параметра принимается за —1, наибольшее за
4-1, среднее за 0). Для кодированных уровней парамет-
ров составляем табл. 22.2.
Таблица 22.2. Матрица планирования эксперимента
№ опыта Xj X, с', М/С
1 __l_ 2,64
2 I- + 2,22
3 1 2,48
4 — — 2,78
288
В табл. 22.2 при знаках плюс и минус опущены для
простоты записи единицы. Последовательность опытов
принята произвольная (случайная).
Проведя испытания четырех намеченных патрубков,
устанавливаем скорость и. Полученное значение v зано-
сим в табл. 22.2. Вместе с тем у соответствующих узлов
сетки (см. рис. 22.5) наносим номер опыта и в кружке
полученное значение скорости и. Принимаем зависимость
v в виде полинома
V = а0 + alxt +а2х2.
Коэффициенты Со, + и а2 находим по методу наимень-
ших квадратов, причем этот метод для кодированных
параметров весьма упрощается, а именно:
а0 =2с = (1/4)(2,б4 + 2,22 + 2,48 + 2,78) = 2,5;
Щ = -2-2x^=0/4)(2,64+ 2,22 —2,48 —2,78) = —0,1;
1
а2 = — 2x.,v = (1 /4)(—2,64 + 2,22 + 2,48 — 2,78) = — 0,175
В результате получаем так называемое уравнение
регрессии:
у = 2,5 — 0,1АЦ — 0, 175х2. (22.13)
После вывода уравнения регрессии значения коэффи-
циентов проверяют по критерию Стъюдента, а истинность
уравнения (адекватность)—по критерию Фишера. В
целях упрощения изложения эти проверки опущены.
Уравнение регрессии справедливо при + +J + 1
и при значениях 30+1г<^40 и 60+++180. При
этом в центре клетки, ограниченной г=30; 40 и 0 = 60;
80 величины *1=0 и х2=0, а потому ц=2,5 м/с.
В дальнейшем для поиска значений г и Ь, дающих
наибольшую скорость v (оптимальные г и Ь), применим
метод градиента. Он состоит в следующем. Если из то-
чек, соответствующих опытам 7, 2, 3 и 4, а также из
точки в центре клетки с вершинами 1, 2, 3 и 4 восстано-
вить перпендикуляры и отложить на них соответствую-
щие значения v и провести через концы векторов v по-
верхность, то получим так называемую поверхность
отклика. Очевидно, поверхность отклика есть геометри-
ческое представление функциональной связи v=f (Xi, х2).
Для быстрейшего нахождения оптимальных г и b надо
289
ставить следующий опыт в направлении градиента v на
поверхности отклика.
Из уравнения регрессии (22.13) следует, что наиболь-
шее значение скорости будет получено при значении ко-
дированных координат Xi=—1 и х2——1 или при значе-
нии неполированных координат г=30 и Ь = 60. Отсюда
следует, что направление градиента определяется пря-
мой, проведенной из центра клетки 1, 2, 3, 4 (г=35; Ь =
= 70) через точку с координатами г=30 и Ь=60 (см.
рис. 22.5).
В этом направлении намечаем опыты 5, 6 и 7, дав-
шие соответственно п = 3,16; 3,26 и 2,83 м/с (см.
рис. 22.5). Опыт 6 дал наибольшее значение скорости.
Следовательно, в окрестности этой точки необходимо
провести еще опыты. Проведя опыты 8, 9, 10 и И, обна-
руживаем, что они дали скорости 3,05; 3,12; 2,9 и 3,2 м/с
(см. рис. 22.5), т. е. меньшие скорости, чем в опыте 6.
Таким образом, патрубок, дающий максимальную ско-
рость 3,26 м/с на оси всасывающего факела, должен
иметь радиус закругления 10 мм и ширину горла 25 мм.
Как видим, вместо 60 опытов понадобилось провести
всего 11.
СПИСОК ЛИТЕРАТУРЫ
1. Абрамович Г. Н. Теория турбулентных струй. М., Физматгиз,
1960.
V 2. Адлер Ю. П., Маркова Е. В, Грановский Ю. В. Планирование
эксперимента прн поиске оптимальных условий. М., Наука, 1971.
3 Алтынова А. Л. Изменение осевой скорости во всасывающем
факеле у эллиптического отверстия в плоской стенке — Водоснаб-
жение и санитарная техника, 1974, № 5.
4. Баулин К. К. О равномерной раздаче воздуха из трубопро-
водов. — Отопление и вентиляция, 1937, № 5—6.
5 Ваганов Р. Ф., Конышев И. И. Оптимизация методов исследо-
ваний аспирационных устройств. — Научные работы институтов
охраны труда ВЦСПС, вып. 102, 1976.
6. Жуковский Н. Е. Видоизменение метода Кирхгофа для опре-
деления движения жидкости в двух измерениях при постоянной ско-
рости, данной па неизвестной линии тока. Избр. соч., т. 1. М„ Гос-
техиздат, 1948.
7. Идельчик И. Е. Справочник по гидравлическим сопротивле-
ниям. М., Госэнергоиздат, 1960.
8. Конышев И. И , Чесиоков А. Г., Щадрова С. Н. Расчет неко-
торых пространственных всасывающих факелов. — Известия вузов.
Технология текстильной промышленности, 1976, № 4.
9. Лебедев Г. О. Раздача воздуха конусным воздуховодом с
продольной щелью неизменной ширины. — Водоснабжение и сани-
тарная техника, 1977, № 8.
10 Маховер В. Л., Халезов Л. С., Чесиоков А. Г. Всасывающий
факел у щелевидных отверстий. — Известия вузов. Технология тек-
стильной промышленности, 1969, № 1.
11. Талиев В. Н, Лебедев Г. О. Раздача воздуха конусным воз-
духоводом с боковыми отверстиями одинаковых размеров. — Извес-
тия вузов. Технология текстильной промышленности, 1977, № 4.
12. Талиев В. Н., Цирекидзе Т. В. Раздача воздуха клиновид-
ным воздуховодом с продольной щелью постоянной ширины. — Во-
доснабжение и санитарная техника, 1979, № 3.
13. Цирекидзе Т. В. Раздача воздуха клиновидным воздухово-
дом с боковыми отверстиями одинаковых размеров. — Известия ву-
зов Технология текстильной промышленности, 1979, № 1.
14. Шепелев И А Воздушные потоки вблизи всасывающих от-
верстий.— Труды НИИ санитарной техники, сб. 24, 1967.
ОГЛАВЛЕНИЕ
Стр.
Условные обозначения основных величин ........ 3
Предисловие........................................ • 4
РАЗДЕЛ ПЕРВЫЙ
СВЕДЕНИЯ ПО ТЕОРЕТИЧЕСКОЙ АЭРОДИНАМИКЕ
Глава 1. Уравнения аэродинамики
§ 1. Общие сведения................................... 5
§ 2. Уравнение расхода ............................... 8
§ 3. Уравнение Бернулли............................... Ю
§ 4. Уравнение количества движения ....... 16
§ 5. Уравнение неразрывности......................... 19
§ 6. Уравнения движения.............................. 21
Глава 2. Основы кинематики
§ 7. Траектории частиц, линии тока и линии отмеченных
частиц ............................................ 25
§ 8. Скорости деформации и угловые скорости вращения
частиц............................................. 27
§ 9. Простейшие течения...................... . 31
Глава 3. Интегрирование уравнений аэродинамики
§ 10. Потенциал скорости.................... 34
§ И. Функция тока.......................... 35
§ 12. Комплексный потенциал................. 38
§ 13. Приемы интегрирования уравнений неразрывности
и движения............................ 43
§ 14. Наложение потоков...............................45
Глава 4. Конформные отображения течений
§ 15. Общие сведения о конформном отображении . 50
§ 16. Конформное отображение безотрывного течения. 52
§ 17. Конформное отображение течения с отрывом струй. 53
§ 18. Метод Н. Е. Жуковского................ 54
РАЗДЕЛ ВТОРОЙ
ПРИМЕНЕНИЕ МЕТОДОВ АЭРОДИНАМИКИ ПРИ РЕ-
' ШЕНИИ ВОПРОСОВ ВЕНТИЛЯЦИИ
Глава 5. Обтекание тел потоком
§ 19. Распределение давлений на поверхности обтекае-
мых тел . .................................... . . 57
§ 20. Аэродинамические сила и момент................ 59
§ 21. Коэффициент силы лобового сопротивления сим-
метричных тел................................ . 62
§ 22. Скорости витания и трогания ....... 63
Глава 6. Потери давления в воздуховодах
§ 23. Распределение скоростей в поперечном сечении
воздуховода...................................... 66
292
Стр.
§ 24. Потери давления в воздуховоде постоянного се-
чения .......................................... ... 70
§ 25. Коэффициент сопротивления трения................ 72
§ 26. Потери давления в пневмотранспортом воздухо-
воде постоянного сечения ...................... .... 73
Глава 7. Потери давления в местных сопротивлениях
§ 27 Общие сведения о местных сопротивлениях ... 7®
§ 28. Потери давления при входе в воздуховод постоян-
ного сечения ................................. 77
§ 29. Потери давления при изменении поперечного сече-
ния воздуховода................................. 81
§ 30. Потери давления в колене 84
§ 31. Потери давления в тройнике............... 86
Глава 8. Свободные изотермические струи
§ 32. Схема изотермической струи ......... 92
§ 33. Плоская изотермическая струя.................... 94
§ 34. Изотермическая струя круглого сечения ... 99
§ 35. Изотермическая струя кольцевого сечения ... 104
§ 36. Струи с неравномерным начальным полем скоро-
стей ............................................ : 110
§ 37. Некоторые случаи особых струй................. 114
Глава 9. Свободные неизотермические струи
§ 38. Схема неизотермической струи................. 117
§ 39. Плоская неизотермическая струя................. 119
§ 40. Неизотермическая струя круглого сечения ... 128
§ 41. Неизотермическая струя кольцевого сечения . . 132
§ 42. Упрощенные зависимости для неизотермических
струй..............................................: 137
§ 43. Воздушные фонтаны.............................. 139
Глава 10. Свободные конвективные струи
§ 44. Схема свободной конвективной струи ..... 143
§ 45. Плоская конвективная струя................. . 145
§ 46. Конвективная струя круглого сечения ........... 149
Глава 11. Всасывающие факелы
§ 47. Общие сведения о всасывающих факелах . . . 153
§ 48. Скорость на оси факела у отверстий в плоской
стенке...........................................; 154
§ 49. Скорость на оси факела у отверстий в криволи-
нейной стенке . .......................... 158
§ 50. Скорость на оси факела у патрубков............ 160
Глава 12. Обычные бортовые отсосы от промышленных
прямоугольных ванн
§ 51. Постановка задачи о бортовом отсосе и метод ее
решения...................................... 167
§ 52. Однобортовой отсос...........................168
§ 53. Двухбортовой отсос .......................... 173
§ 54. Расчет бортовых отсосов . ................... 176
293
Стр.
Глава 13. Равномерная раздача и всасывание воздуха воздухо-
водами с продольной щелью или с боковыми отвер-
стиями
§ 55. Схема явлений при раздаче и всасывании воздуха
воздуховодами........................................ 178
§ 56. Зависимости и уравнения, используемые при ис-
следовании воздуховодов .... ......... 180
§ 57. Способы обеспечения равномерной раздачи или
всасывания воздуха ................................... 182
Глава 14. Воздухораспределители с продольной щелью пере-
менной ширины
§ 58. Воздухораспределитель постоянного сечения с
продольной щелью переменной ширины .... 184
§ 59. Конусный воздухораспределитель с продольной
щелью переменной ширины . . .......... 187
§ 60. Клиновидный воздухораспределитель с продоль-
ной щелью переменной ширины........................... 189
§ 61. Расчет воздухораспределителей с продольной ще-
лью переменной ширины................................. 192
Глава 15. Воздухораспределители с отверстиями различной
площади
§ 62. Воздухораспределитель постоянного сечения с от-
верстиями различной площади........................... 194
§ 63. Конусный воздухораспределитель с отверстиями
различной площади............................ . . 197
§ 64. Клиновидный воздухораспределитель с отверстия-
ми различной площади.............................. . 199
§ 65. Расчет воздухораспределителей с отверстиями
различной площади................................. . 200
Глава 16. Воздухораспределители с продольной щелью посто-
янной ширины
§ 66. Воздухораспределитель переменного прямоуголь-
ного поперечного сечения .......................... . 202
§ 67. Воздухораспределитель постоянного сечения с про-
дольной щелью постоянной ширины.......................206
§ 68. Конусный воздухораспределитель с продольной
щелью постоянной ширины ... . . 210
§ 69. Клиновидный воздухораспределитель с продольной
щелью постоянной ширины...............................213
§ 70 Расчет воздухораспределителей с продольной ще-
лью постоянной ширины.................................215
Глава 17. Воздухораспределители с отверстиями одинаковой
площади
§ 71. Воздухораспределитель постоянного сечения с от-
верстиями одинаковой площади..........................217
§ 72. Конусный воздухораспределитель с отверстиями
одинаковой площади....................................221
§ 73. Клиновидный воздухораспределитель с отверстия-
ми одинаковой площади............................... 226
294
Стр.
§ 74. Расчет воздухораспределителей с отверстиями оди-
наковой площади....................................229
Глава 18. Вытяжные воздуховоды постоянного сечения
§ 75. Вытяжной воздуховод с продольной щелью пере-
менной ширины..................................... 230
§ 76. Вытяжной воздуховод с отверстиями различной
площади.......................................... 232
§ 77. Вытяжной воздуховод с продольной щелью по-
стоянной ширины................................... 235
§ 78. Вытяжной воздуховод с отверстиями одинаковой
площади .........................................» 237
§ 79. Расчет вытяжных воздуховодов............ . 240
РАЗДЕЛ ТРЕТИЙ
СВЕДЕНИЯ ПО ЭКСПЕРИМЕНТАЛЬНОЙ
АЭРОДИНАМИКЕ
Глава 19. Основы моделирования вентиляции
§ 80. Постановка задачи . .......... 242
§ 81. Моделирование воздухообмена .................243
§ 82. Моделирование тепловыделений............... 245
§ 83. Моделирование влаговыделений.................247
§ 84. Практические приемы моделирования ..... 248
Глава 20. Опытные установки
§ 85. Аэродинамическая труба.......................250
§ 86. Аэродинамический стенд ......................255
§ 87. Гидравлический лоток . . ....................258
§ 88 Вентиляционный стенд.........................261
Глава 21. Приборы и их тарирование
§ 89. Микроманометр................................262
§ 90. Пневмометрические трубки ....................263
§ 91. Электроанемометры.......................... 267
§ 92. Координатники................................269
§ 93. Тарирование приборов ....................... 271
Глава 22. Лабораторное экспериментирование
§ 94. Определение коэффициента сопротивления трения. 277
§ 95. Определение коэффициента местного сопротивления
отвода ... . *........................ 279
§ 96. Определение коэффициентов местных сопротивле-
ний тройника при делении потока ................. 282
§ 97. Выявление оптимальной схемы всасывающего пат-
рубка ....................................... ( . 286
Список литературы . . ....................... , . , , 291
295