ДЛЯ ВУЗОВ
ГС.Самошович
ГВДРО-
ГАЗОДИНАМИКА
2-е издание, переработанное и дополненное
Допущено
Государственным комитеюм СССР
по народному образованию
в качестве учебника
для студентов вузов,
обучающихся по специальности
"Турбостроение"
Москва
Машиностроение -
1990

ББК 30.123я73
С17
УДК 621.438 : [532+533] @75.8)
Рецензенты: кафедра аэродинамики летательных
аппаратов Московского авиационного института, Г. Ю. Степанов
Самойлович Г. С.
С17 Гидрогазодинамика: Учебник для студентов вузов,
обучающихся по специальности «Турбостроение». — 2-е изд..
перераб. и доп. — М.: Машиностроение, 1990. — 384 с: ил.
ISBN 5-217-01092-4
Изложены теоретические основы газодинамики, до-, транс- и
сверхзвуковых потоков, пограничного слоя, турбулентных течений и т. п.
Основные уравнения приведены в тензорной (индексной) форме записи.
Учебник ориентирован на использование ЭВМ. Второе издание A-е изд.
1980 г.) существенно переработано и дополнено. В него включены
разделы, освещающие осесимметричные и неустановившиеся течения, теорию
подобия, численное моделирование, построение оптимальных решеток.
ISBN 5-217-01092-4
Издательство «Машиностроение», 1980
С. С. Самойлович, 1990 с изменениями

ПРЕДИСЛОВИЕ
Второе полностью переработанное и расширенное издание
учебника содержит систематическое изложение теоретических основ механики
жидкости и газа в объеме курса для соответствующей специальности. В
связи с требованием совершенствования образования обобщен ряд выводов.
Вместе с тем показано применение общих законов к решению конкретных
технических проблем, с которыми сталкивается инженер-механик при
создании новой техники.
Автор обращает особое внимание на физическую сущность задач и их
расчетную сторону, что особенно важно для инженеров. Ввиду этого всо
изложенные методы доведены для практического приложения.
Основные уравнения выведены в интегральной и дифференциальной
формах с применением индексной записи. Это позволяет сделать все
преобразования компактными.и наглядными, особенно при рассмотрении общих
случаев. Такой подход, что не ^енее важно, естественно согласован с
применением ЭВМ в учебном процессе и последующей работе. В связи с этим
следует также подчеркнуть, что учебник содержит изложение основ современного
численного и физического моделирования в механике жидкости и газа.
Инженеры-механики широко применяют подобные методы при расчетном и
экспериментальном исследовании и оптимизации оборудования.
Учебник знакомит с методами расчета до-, транс-и сверхзвуковых
потоков, с расчетом двухфазных течений, расчетом течений при разного рода
воздействиях, расчетом пограничного слоя, аэродинамических решеток,
лабиринтовых уплотнений и рядом других вопросов, которые служат основой
теории турбомашин.
При изложении материала особое внимание обращено на расширение
самостоятельной работы студентов в процессе обучения. Все главы
снабжены вопросами для самопроверки» а с учебником согласован задачник.
Учебник и задачник построены так, что студенты могут использовать их в
самостоятельной работе, в частности, при выполнении курсовых работ, проектов и
лабораторных работ, которые они делают при изучении курса.
Автор выражает признательность акад. Ю. А. Рыжову и проф.
Е. Н. Бондареву, сделавшим ценные замечания по рукописи учебника,
и проф. Г. КХ Степанову за конструктивные советы.

ОСНОВНЫЕ УСЛОВНЫЕ ОБОЗНАЧЕНИЯ
а — скорость звука, м/с;
с — абсолютная скорость, м/с;
ср — удельная теплоемкость при постоянном давлении, Дж/(кг«К);
Су — удельная теплоемкость при постоянном объеме, Дж/(кг'К);
е — внутренняя удельная энергия потока, Дж/кг; -
F — сила, Н;
g — ускорение свободного падения» м/с2;
h — удельная энтальпия потока, Дж/кг;
i — мнимая единица (i = "]/ — 1);
/ — длина, мм, м;
М — число Маха;
т — массовый расход, кг/с;
р— давление, Па;
q — газодинамическая функция расхода;
Н —газовая постоянная, Дж/(кг-К);
г — радиус, м;
5 — площадь, м2;
s—удельная энтропия потока, Дж/(кг«К);
Т — термодинамическая температура потока, К;
t — время, с;
и, v, w — проекции скорости на оси х> у, г, м/с;
х, yt z — декартовы координаты;
z = х + iy — комплексная координата;
а — угол Маха;
Г — циркуляция скорости, ма/с;
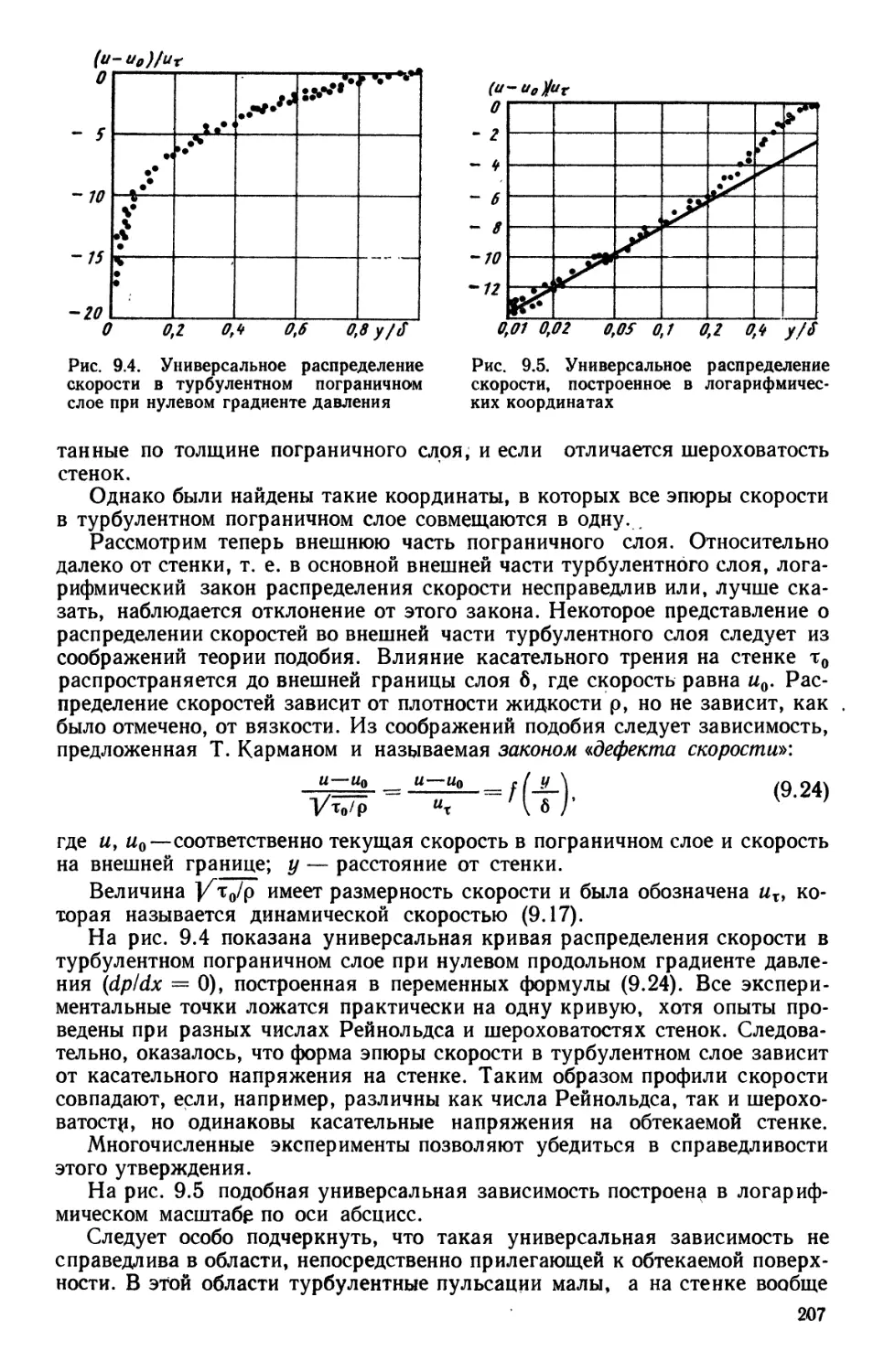
б — толщина пограничного слоя;
х—показатель изоэнтропы;
X — приведенная скорость (безразмерная);
fi — динамическая вязкость, Па-с;
v — кинематическая вязкость, м2/с;
р — плотность, кг/м3;
а — напряжение, Па;
Ф — потенциал скорости, ма/с;
г|) — функция тока, м2/с;
со — угловая скорость (вихрь скорости), рад/с.

ГЛАВА 1
ЖИДКОСТИ, ГАЗЫ И ПАРЫ КАК СПЛОШНЫЕ
ДЕФОРМИРУЕМЫЕ СРЕДЫ
1.1. ФИЗИЧЕСКИЕ СВОЙСТВА ЖИДКОСТЕЙ, ГАЗОВ И ПАРОВ
Жидкости отличаются относительным постоянством объема и
легкостью, с которой можно деформировать их форму. Весьма малые силы,
действуя достаточно долгое время, могут произвольно изменить
первоначальную форму жидкости. Однако жидкости все же сопротивляются
деформации, причем величина сопротивления зависит от скорости деформации.
Если скорость деформации стремится к нулю, то и сопротивление этой
деформации стремится к нулю. Свойство жидкости сопротивляться
деформации называется вязкостью. Такие технически важные жидкости, как вода
или масло, обладают относительно малой вязкостью и являются типичными
жидкостями.
Некоторые вещества, обладающие большой вязкостью, при медленной
деформации ведут себя как жидкости, а при быстрой — как твердые тела. Так,
например, вар при очень медленной деформации вытекает как жидкость, а
при ударе разрушается как хрупкое твердое тело.
Газы, как и жидкости, под влиянием внешних сил легко изменяют
форму, причем сопротивление изменению формы также характеризуется
вязкостью, т. е. зависит от скорости деформации. Однако в отличие от жидкости
объем газа (и, следовательно, его плотность) может существенно изменяться
при изменении давления и температуры.
Газы, в отличие от жидкости, занимают весь предоставленный им объем.
Жидкости способны образовывать свободную поверхность и капли.
Пар отличается от газа тем, что его состояние рассматривают
достаточно близко от кривой насыщения. Поэтому он может при определенных
условиях частично конденсироваться и образовывать двухфазную среду. При
быстром расширении процесс конденсации запаздывает, а затем при
достижении определенного переохлаждения происходит лавинообразно. В этом
случае законы течения пара могут существенно отличаться от законов
течения жидкостей и газов. Очевидно, что плотность пара зависит от давления
и температуры, но по иным, более сложным законам, чем для газа.
Если в процессе течения плотность газа или пара меняется мало, то
законы их движения будут мало отличаться от-законов движения
несжимаемой жидкости. С другой стороны, капельные жидкости, которые в обычных
условиях можно считать несжимаемыми, как известно, также могут
сжиматься при достаточно большом повышении давления (например, при
взрыве). Поэтому в гидрогазодинамике как газ, так и капельную жидкость, а
при определенных условиях и пар именуют жидкостью. В тех случаях,
когда эффектом сжимаемости можно пренебречь, вводят понятие несжимаемой
жидкости, т. е. жидкости, которая по определению имеет постоянную
плотность.
Если же плотность жидкости в процессе течения меняется, то говорят о
сжимаемой жидкости.

Ёсе реальные жидкости обладают вязкостью и поэтому их называют
вязкими жидкостями.*Под термином вязкая жидкость не следует понимать, что
жидкость обладает большой вязкостью, речь идет только о том, что она
имеет вязкость. В некоторых задачах влиянием вязкости можно пренебречь
и ввести понятие «идеальная жидкость», понимая под этим жидкость,
вязкость которой равна нулю. Для всех реальных жидкостей и газов такие
физические характеристики, как вязкость, теплоемкость, теплопроводность
и т. п., зависят от их параметров, например, от температуры. Во многих
задачах с достаточной степенью точности можно полагать эти величины
постоянными, как это и сделано в дальнейшем, без особых оговорок.
Очевидно, имеются задачи, в которых такое предположение было бы не
оправданным, как, например, при горении движущейся смеси.
1.2. СКАЛЯРНЫЕ, ВЕКТОРНЫЕ И ТЕНЗОРНЫЕ ПОЛЯ
В ГИДРОГАЗОДИНАМИКЕ
При изучении движения жидкости рассматривают ее как
сплошную среду. Таким образом рассматривают не движение конечного числа
отдельных частиц, а поля различных физических величин: скорости,
плотности, давления и т.д. Такие поля можно назвать материальными полями.
Математически эти поля описывают системой функций от координат и
времени. Такой подход типичен не только для механики сплошных сред
(аэродинамики, теории упругости, реологии и т.д.), но и для ряда других облас-
стей физики.
В общем случае поле является пространственным (трехмерным), однако
иногда можно упростить задачу и изучать одномерные или плоские
(двумерные) поля. В этом случае предполагают, что физические величины зависят
соответственно только от одной или двух пространственных координат.
Если физические величины не зависят от времени, то поле называется
стационарным, в противоположном случае — нестационарным.
При математическом описаний полей предполагают, что существуют
пределы значений физических величин в точке. Так, например, плотность
жидкости в точке определяется как предел отношения массы жидкости,
заключенной в некотором объеме, к этому объему, когда он стремится к нулю.
Такой подход приводит к упрощению физической реальности, так как не
учитывает дискретности строения материи. Очевидно, что такая абстракция
вполне оправдана и нужно только разумно ограничить область применения
полученных результатов.
Так, основываясь на предыдущем примере, следует принять, что
элементарный объем, в котором вычисляют среднюю плотность жидкости,
значительно больше атомных размеров, но в то же время значительно меньше
некоторой характерной длины, на которой происходит заметное изменение
плотности. Так как в практических задачах размеры обтекаемых тел,
длины звуковых волн и т.п. на много порядков больше молекулярных размеров,
то в этих задачах жидкость можно рассматривать как сплошную среду.
Опишем кратко характеристики полей, которые встречаются в
гидроаэромеханике.
Скалярным называют поле, которое характеризуют в каждой точке
пространства одним числом. Такое поле описывают одной функцией, зависящей
от трех координат. Скалярным будет, например, поле плотности или
температуры.
Вместо обычного обозначения декартовых координат х, у% z удобно
принять обозначения хъ х2у х3. Это позволит ввести индексные обозначения, что
в дальнейшем сократит и упростит зсе преобразования,
6

Основное свойство скалярной функции a (xl9 x2f x3) состоит в том, что
ее численное значение не изменяется при преобразовании координат. Если
перейти от старой хг, х2, х3 к новой х\у х'ъ, х3 системе координат, то значения
плотности или температуры в фиксированной точке пространства,
естественно, не изменяются:
а (х'и х2, х'3) = а (х1у х29 х3). A.1)
Векторным называют поле, которое характеризуют в каждой точке
пространства величиной и направлением. Векторным будет, например, поле
скоростей жидкости. Вектор а (в пространстве трех измерений), как
известно, может быть задан тремя компонентами:
ах {хъ лг2, х3), а2 (х1у хъ х3)у а3 (хъ х2, х3), A.2)
т. е. тремя функциями от трех переменных.
Это можно записать также в виде таблицы из трех величин (матрицы-
столбца):
01
а3
или, более кратко, одной величиной с индексом, который принимает
значение 1, 2, 3:
а &аь i = 1, 2, 3. A.4)
При такой записи предполагается, что at — это i-я компонента вектора а.
В дальнейшем применяется эта индексная запись.
Введем новую декартову систему координат х[, Хг, *з с тем же началом,
но другим направлением осей. Обозначим через lif направляющий косинус
оси х) относительно оси х% (i== 1,2,3; / = 1, 2, 3). Вычислим проекции
того же вектора на новые оси координат:
а\ = 1паг ¦+• 121а2 + 1зга3\
а'2 = 112аг + 122аг + l32a3; \ A.5)
Следовательно, вектор подчиняется определенному закону
преобразования его компонент A.5) и отличается от скалярной величины, численное
значение которой не меняется при преобразовании координат. Очевидно, что
сам вектор не меняется в новых координатах, а меняются только его
компоненты.
Целесообразно принять индексную форму записи, основанную на
общепринятых соглашениях.
Выражения A.5) можно представить в виде суммы
В дальнейшем, как это принято, будем применять еще более короткую запись:
а} = luat. A.6)
При такой записи пользуются двумя правилами.
1. Соглашение о суммировании. По индексу, встречающемуся дважды
(немой индекс), производят суммирование от 1 до 3.
2. Соглашение о ранге. Индекс, встречающийся один раз (свободный
индекс), пробегает значения от 1 до 3.
7

Таким образом, уравнение с одним свободным индексом означает запись
трех уравнений. Очевидно, что для двумерного движения суммирование по
немому индексу производят от 1 до 2, а свободный индекс принимает
значения 1 и 2. В одномерном движении необходимости в подобных индексах
вообще нет.
Соглашения о суммировании и ранге относятся не только к векторам, а вообще
к любой записи и любым операциям (если нет специальной оговорки о противном.
Так, например, краткая запись
д at
д xk
означает (здесь индекс k — немой, индекс / — свободный):
д ах
д аг да
+ а2
дхг
д а2
~дх^
о х2 о х3
¦+«2
д а2
д х2
да3
д х2
да2
дх3
д а3
дхя
=**;
¦=v.
Отметим, что немой индекс при суммировании заменяют цифрами, поэтому немой
индекс пропадает и его можно заменить любой буквой. Можно, например, заменить
индекс к на я, но не на it так как i в данном случае принят в качестве свободного
индекса.
Приведем другой пример (индекс i — немой, свободного индекса нет):
Отметим также, что все члены уравнения должны иметь один и тот же свободный
индекс (или вообще не иметь свободного индекса). Это означает, что все члены
уравнения представляют проекцию на одну и ту же ось координат.
Приведем в качестве примера, на который будем ссылаться в дальнейшем,
индексную запись скалярного произведения векторов.
Пусть имеются два вектора а и Ь, которые можно задать их проекциями at и bt.
Как известно, скалярное произведение двух векторов можно выразить через сумму
произведений проекций:
A.7)
Следовательно, в индексной записи скалярное произведение выглядит так:
031?
032
*3
011'"
><>13
"п
/
1
/
022
РИС. 1
гранях
8
1. Система напряжений на
элементарного объема
Помимо скалярных и векторных
полей в механике сплошной среды
рассматривают еще тензорные поля. Введение
тензорных полей, так же как
скалярных и векторных, вызвано
необходимостью наиболее удобного описания
основных свойств материальных полей.
Вырежем в жидкости элементарный
параллелепипед с ребрами dxly dx2 и dx3
(рис. 1.1). На грани этого
параллелепипеда со стороны остальной жидкости
действуют поверхностные напряжения.
В общем случае на каждую грань
действуют как нормальные, так и
касательные напряжения. В принятой
записи (см. рис. 11) каждое из напряжений
аи имеет два индекса. Первый индекс

означает ориентацию площадки, на которую действует напряжение,
второй — ось проектирования. Так, например, а21 — это напряжение,
которое действует нц площадку, перпендикулярную оси х2 и параллельно оси xt.
Компоненты напряжений можно записать в виде таблицы (матрицы
тензора напряжений) или коротко одной буквой с двумя индексами:
013
аг1
при t = 1,2,3; /=1,2,3.
A.8)
Здесь первый индекс означает номер строки, второй — номер столбца.
Нормальные напряжения имеют два одинаковых индекса (диагональ
матрицы), касательные напряжения имеют разные индексы. Такой тензор
называют тензором второго ранга (по числу индексов у компонент).
Тензор—более общее понятие, чем вектор или скаляр. Компоненты
вектора имеют один индекс A.4) и он может быть записан матрицей (таблицей)
из одного столбца A.3). Вектор называют тензором первого ранга.
Скаляр, представляемый буквой без индекса A.1), называют тензором
нулевого ранга.
Тензор второго ранга в общем случае описывается девятью функциями
трех переменных. Однако тензор напряжений A.8) обладает одной важной
особенностью. Из условия равенства нулю моментов, действующих на
элементарный объем (см. рис. 1.1), следует, что касательные напряжения с
одинаковыми, но расположенными в обратном порядке индексами равны:
аи — ан- Такой тензор называют симметричным и вместо A.8) можно
написать:
оп а12 а13
О\2 @22 ^23
<*13 <*32 <*33
Следовательно, тензор напряжений выражается через шесть функций
трех переменных.
Конечно, не каждые шесть функций трех переменных образуют тензор
напряжений. Тензор должен удовлетворять определенному закону пересчета
компонент при изменении координат. Это свойство должно быть
согласовано с особенностью изменения напряжений, действующих на площадку, при
изменении ориентации площадки.
Компоненты напряжений представляют как нормальные (сгп, а22, а33),
так и касательные (<т12, а13, а23) напряжения. Касательные напряжения
возникают вследствие вязкости, которой обладают все реальные жидкости.
Однако вязкость и, следовательно, касательные напряжения проявляются
только при движении жидкости. В покоящейся вязкой жидкости
касательные напряжения отсутствуют (так как скорости деформации равны нулю),
а нормальные напряжения вызваны только давлением и не зависят от
ориентации площадки (закон Паскаля).
Напомним, что в гидрогазодинамике введено понятие идеальной
жидкости как жидкости, полностью лишенной вязкости. Следовательно, в
идеальной жидкости касательные напряжения отсутствуют и при движении, а
матрица тензора напряжений принимает вид
О О
—Р
О — р О
О О — р
A.10)

Перед р по условию поставлен знак минус,
так как давление обычно сжимает жидкость, т. е.
действует против положительного направления
.нормали к площадке.
Матрицу 1.10 можно сокращенно записать
в виде
ои = — pbih A.11)
где введен символ, определяемый условиями
(символ Кронекера):
6^=1 при 1 = /, 6^=0 при %Ф /. A.12)
1 О РяВНОВбСИв 3JI6MGH-
тарного тетраэдра ^Ри рассмотрении движения вязкой жидкости
также целесообразно выделить ту часть
нормального напряжения, которая не зависит от вязкости, и записать
тензор напряжений A.9) в таком виде:
°'и- A.13)
Здесь напряжения а'ц зависят только от вязкости.
Если i Ф /до второй член справа представляет касательные
напряжения. Если i ==/, то этот член выражает добавочные нормальные напряжения,
вызванные вязкостью жидкости.
Величины оц представляют компоненты напряжений по трем взаимно
перпендикулярным граням, нормальным осям координат. Однако при
выводе основных законов движения жидкости необходимо также знать
напряжения, которые действуют на произвольно ориентированную
площадку./Покажем, что эти напряжения можно выразить через ац.
Для того чтобы найти напряжения, действующие на произвольно
ориентированную площадку, рассмотрим малый тетраэдр, вырезанный из
жидкости (рис. 1.2), и положим, что на него действуют только поверхностные
силы.
Пусть три грани тетраэдра АОС, ВОС, АОВ перпендикулярны
соответствующим осям координат, а ориентация четвертой грани ABC определяется
единичной внешней нормалью п (пъ /i2, п3).
Поскольку вектор единичной нормали имеет длину, равную единице, то
его компоненты по осям координат равны направляющим косинусам:
л?= cos (n, *,), i = 1, 2, 3.
Обозначим площадь грани ABC через dS, тогда площади остальных
граней будут равны ее проекциям: n^S, n2dS, nsdS.
Из условий равновесия бесконечно малого тетраэдра найдем
Gt}dS=:oljn1dS+G2jn2dS+a3jnsdS
или, применив индексную запись, получим
оУ-Л|а„. A.14)
Эта формула Коши выражает о1} — проекцию на ось Xj напряжения на
площадке (ориентация которой задана нормалью nt) через тензор
напряжений Gij.
Повернув оси координат, можно показать, что компоненты о^ пересчиты-
ваются по формуле, которая обобщает формулу A.6) для преобразования
компонент вектора:
0/m»/<j/fcm0fft' A.15)
10

Напомним, что так как здесь дважды повторяются индексы i и k, то по
ним необходимо суммировать. Следовательно, краткая запись по существу
представляет собой двойную сумму.
Если набор из девяти величин (а^) подчиняется преобразованию A.15),
то это может служить определением тензора (второгоранга). Если набор
из трех величин (at) подчиняется преобразованию A.6), то это служит
определением вектора (в трехмерном пространстве). Если же численное
значение а не меняется с преобразованием координат, то это скаляр. Ранее
упоминалась зависимость компонент от трех координат. В том случае, если
рассматривается неустановившееся течение, они должны зависеть также от
времени.
Необходимо сделать еще одно замечание относительно давления в вязкой
жидкости. В идеальной жидкости касательные силы отсутствуют и давление
не зависит от ориентации площадки. В вязкой жидкости нормальные напря-
жения в общем случае не равны, однако можно показать, что суммы трех
нормальных напряжений не зависят от ориентации площадки. Для
идеальной жидкости эта сумма согласно формуле A.11) равна — Зр. Поэтому для
вязкой жидкости принимают в качестве понятия давления среднее значение
нормальных напряжений со знаком минус:
Следовательно, давление, определяемое таким образом, не зависит от
ориентации площадки и его используют как давление, входящее в формулы
термодинамики. Справедливость этого подтверждена опытом.
1.3. ДЕФОРМАЦИЯ И ВРАЩЕНИЕ ЖИДКОЙ ЧАСТИЦЫ
Пусть Xj — координата, отмечающая положение точки о в
декартовой системе координат. Поместим в эту точку вершину элементарного
куба с ребрами 6xjt которые в начальный момент времени параллельны осям
координат. Проследим движение этого жидкого элемента, состоящего из
одних и тех же частиц жидкости.
Через малое время 8t вершина куба переместится в соседнюю точку оъ
а жидкий элемент повернется и деформируется. Это объясняется тем, что
скорости точек жидкого элемента отличаются от скорости в точке о.
Пусть в точке о компоненты скорости равны щ. Тогда в малой окрестности
точки о компоненты скорости можно представить выражением
в^. A.16)
Поскольку индекс / включен дважды, то он является немым и по нему
производится суммирование согласно общему правилу. Так как в этом
выражении есть свободный индекс, то это — сокращенная запись
приращения скорости в направлении всех трех осей координат.
Жидкий элемент переносится как целое со скоростью иь.
Последний член этого выражения представляет приращение скорости
щ вдоль координаты Xj, т. е. (в индексной записи) полное приращение
функции трех переменных через соответствующие частные производные. Поворот
и деформация жидкого элемента определяются только приращением
скоростей, поэтому рассмотрим член (дщ/dxf) бх/ при различных значениях
индексов. Для наглядности графического изображения исследуем сначала
поворот и деформацию однрй из граней куба, например, нижней грани,
параллельной плоскости х%х% (рис. 1.3).
11

Рис. 1.3. Определение
деформации и вращения граней
элементарного объема
Величина (диг1дх^) Ьхх показывает, насколько
компонента иг в точке а больше, чем в точке о.
Следовательно, величину (ди^дх^) Ьхг можно
трактовать как скорость удлинения ребра оа.
Значит, dujdxx представляет скорость
относительного удлинения ребра, т. е. скорость
удлинения, отнесенную к первоначальной длине
ребра.
Величина (du2fdxt) Ьхг выражает скорость
вращения ребра оа относительно точки о.
Следовательно, ди2!дх1 представляет угловую
скорость вращения ребра в указанной
плоскости.
Аналогично дих1дх2 равно угловой скорости
ребра ос в плоскости хгх2, а ди21дх2 равно
скорости относительного удлинения этого ребра. Перед первым из этих
выражений поставлен знак минус, так как принято считать положительным
вращение против часовой стрелки.
Удлинение ребер вызывает, очевидно, деформацию элемента. Вращение
ребер в общем случае приводит как к деформации элемента, так и к чистому
вращению элемента как твердого тела. Для последующего нужно выделить
чистую деформацию и чистое вращение.
Чистое вращение — оба ребра вращаются в одну сторону с одинаковой
угловой скоростью (угол между ребрами не изменяется). Чистая угловая
деформация — ребра вращаются с одинаковой угловой скоростью в
противоположные стороны (биссектриса угла не вращается).
Угловая скорость чистого вращения равна угловой скорости биссектрисы,
которую представляет полусумма угловых скоростей ребер (причина
появления знака минус объяснена раньше):
0I2 = 2 [ дхг
дх2
Скорость угловой деформации сдвига характеризуют полуразностью
угловых скоростей ребер (перед вторым слагаемым был знак минус):
ди2 , диг
-i(-
¦+•
д Хо
Рассуждения относительно деформации и вращения других граней куба
совершенно аналогичны. Поэтому, возвращаясь к общему случаю,
целесообразно представить приращение скоростей в таком виде:
Введем обозначения:
dtij , дщ
д Xi д Xj
1 f duj дщ
dxt dxj
1 / Э^ ^Ц; \
^ 2 \ dxt dXj I
и перепишем предыдущую формулу:
A.18)
A.19)
Из проведенных рассуждений следует, что величина ги характеризует
скорость деформации жидкой частицы. Эта характеристика является
тензором и поэтому ее называют тензором скоростей деформации.
Ш

В частности eu характеризует скорость удлинения нижней грани куба
(рис. 1.4) вдоль оси хг:
д иг
__!_ / v **i . |
2 V дх1 дхг
Аналогично е22 дает скорость удлинения этой грани вдоль оси х2\
ди2 ди2
¦)-
дх2 дх2 ) дх2
Наконец, е12 = е21 есть скорость деформации сдвига:
ди2 дщ
д хл
-)¦
Возвращаясь снова к общему случаю, отметим, что ги- = eJf и матрицу
тензора скоростей деформации жидкой частицы можно представить в виде:
дхг
ди2 ,
дхг
у i ди3 .
ди2
д щ
-И
д иг
д х2
дЩ \ J_
dxs J 2
ди2
д х2
ди3
дх*
ди2
дхя
ди3
дхг
д и3
д х2
ди3
+
д х3
д и2
д х3
дх3
Вычисление тензора скоростей деформации необходимо при выводе
уравнений течения вязкой жидкости, так как силы трения зависят от скоростей
деформации.
Рассмотрим теперь другую важную характеристику движения
жидкости — выражение для угловой скорости частицы, т. е. ее частоты вращения
A.18). Эту характеристику
принято называть завихрен- ____.. I 1 ^ — "*""~7
ностью. ] 1 I
Завихренность также пред- */' ?„ ' г?2 ' ?}2 /
ставляется тензором. Однако
это тензор особого рода, так
как три его составляющие,
для которых индексы
одинаковы (i = /), равны нулю, а
для остальных шести
составляющих справедливо
соотношение (ofJ- = — (Oij (i Ф j). Таким образом, независимыми являются
только три составляющие. Подобный тензор называют псев до вектором.
Угловая скорость частицы жидкости представляется вектором и тогда ее можно
обозначить буквой с одним индексом. Составляющие этого вектора следует
записать одним столбцом, в котором представлены проекции на оси
координат:
1
1
1
1
.....
*„•
_ , - •—¦
/<¦<
Рис. 1.4. Деформации элементарного объема
1 / ди3
2 V дх2
2 I дх3
дх3
ди2
д x-i
ди2
дх3
дхг
дх2
A.21)
13

Следует подчеркнуть, что со$ характеризует угловую скорость в точке,
т. е. предполагается, что ось вращения проходит через частицу, которая
стягивается в точку.
Окончательный вывод формулируется теоремой Гельмгольца: общее
движение жидкого элемента состоит из: 1) поступательного
движения вместе с центром; 2) вращения с некоторой угловой скоростью
вокруг оси, проходящей через центр; 3) деформационного движения.
Завихренность является важной характеристикой. Те течения, в
которых (ог = 0,-составляют класс безвихревых течений.
Очевидно, для того чтобы трехмерное течение было безвихревым,
необходимо, чтобы все проекции вектора угловой скорости A.21) были равны
нулю. Для плоских течений остается одна составляющая вектора угловой
скорости. Поэтому, например, чтобы течение в плоскости хгх2 было
безвихревым, достаточно выполнить условие:
^q A.22)
д хг д xz
Важно отметить, что все течение в некоторых подобластях может быть
вихревым, а в других подобластях — безвихревым, т. е. завихренность
характеризует вращение частиц в точках.
1.4. ЗАПИСЬ ВЕКТОРНЫХ ОПЕРАЦИЙ В ИНДЕКСНОЙ ФОРМЕ
В работах по аэродинамике и теории турбомашин часто применяют
векторную запись основных уравнений, В ряде случаев удобно- записать все векторные
операции через компоненты вектора, т. е. в индексной форме, так как эта форма записи
идеально приспособлена к вычислениям на ЭВМ и использована в дальнейшем
изложении.
Прежде всего введем два символа.
1. Единичный тензор (символ Кронекера) по определению обладает следующими
свойствами:
6^=1 при ifs{f 6^ = 0 при 1Ф\.
2. Тензор перестановок (тензор Леви — Чивиты) по определению обладает
следующими свойствами:
ецк ~ 1 при циклическом порядке индексов: 1, 2, 3, 1, 2 ...
eijk ~ — 1 ПРИ антициклическом порядке индексов: 3, 2, 1, 3, 2, ...
eijk — 0> если любые два индекса равны.
Пусть даны два вектора а и Ь, которые в индексной записи можно задать их
компонентами cii и Ь$.
Известно, что скалярное произведение двух векторов является скаляром и его
выражают через сумму произведений проекций
а. b = axbx+аф%+a9b3.
Следовательно, в индексной записи скалярное произведение выглядит так:
a-b^a^j. A.23)
Векторное произведение является вектором, i-ю проекцию которого можно
записать через тензор перестановок:
A.24)
Операция по вычислению дивергенции вектора изображается следующим
выражением:
A.25)
Ротор вектора является вектором и его проекции определены формулой
(roX&)i^eiJk$ah/dxj. A.26)
И

Градиент скалярной функции является вектором и в индексной форме выглядит
так:
A.27)
При выводе уравнений сохранения и других выкладках часто используют общую
формулу преобразования интеграла по объему в интеграл по поверхности (и наоборот).
Пусть / будет скалярной, векторной или тензорной функцией.
Тогда при известных ограничениях о дйфференцируемостн функций и гладкости
поверхности можно записать:
A.28)
Здесь v — фиксированный объем, ограниченный поверхностью S; щ — внешняя нор*
маль к поверхности.
Из общей формулы A.28) и выражения A.25) следует формула Гаусса —
Остроградского о дивергенции в индексной записи:
\$. > A.29)
Аналогично из формул A,28) й (L26) следует теорема Стокса также в индексной
записи:
J4j* (д bk/d xj) dv^ f eijk bknf dS. A.30)
V '$
Наконец, для компонент тензора второго ранга из A.28) получим
J (dbij/dxj)do.^: \bijnjdS. A.31)
V $
Формулы преобразования интегралов известны из курса высшей математики, где
их, однако, обычно приводят в векторной записи. Ниже они использованы при выводе
основных законов механики жидкости, где и будет подчеркнут их физический смысл.
Вопросы дли самопроверки
1. Опишите основные свойства жидкостей, газов и паров.
2. Поля каких физических величин описывают скаляры, векторы и тензоры?
3. Запишите условия безвихревого движения жидкости.
4. В чем состоит теорема Гельмгольца о движении жидкого элемента?

ГЛАВА 2
УРАВНЕНИЯ СОХРАНЕНИЯ
2.1. УРАВНЕНИЕ НЕРАЗРЫВНОСТИ
Основные уравнения гидрогазодинамики основаны на законах
сохранения массы, количества движения и энергии, которые вместе обычно
кратко именуют законами сохранения. Особенность заключается в том, что
в механике жидкости эти законы необходимо записать в форме, пригодной для
изучения движения сплошной деформируемой среды. Закон сохранения
массы обычно называют уравнением неразрывности, хотя это название нельзя
считать удачным.
Рассмотрим в потоке жидкости некоторую фиксированную замкнутую
поверхность s, ограничивающую объем v. Выделим на поверхности элемент
площади ds и построим единичный вектор п, направленный наружу по
нормали к поверхности (рис. 2.1). Поток жидкости пронизывает замкнутую
поверхность, причем через выделенный элемент поверхности за единицу
времени протекает масса жидкости, равная punds, где ип — нормальная к
поверхности составляющая скорости жидкости; р — плотность жидкости.
Проекцию скорости на нормаль можно заменить через скалярное произведение
вектора скорости и на единичную нормаль n: pn-uds. В индексной записи по
формуле A.23) это выражение примет вид pntUids.
Интегрируя по поверхности, получим массу, вытекающую за единицу
времени из фиксированного объема:
Jp n«iij?far B.1)
s
Пусть в общем случае в жидкости распределены источники массы,
которые подают на единицу объема в единицу времени массу ти кг/(м3«с). Тогда
внутрь фиксированного объема за единицу времени поступает масса
B.2)
Здесь поставлен знак минус, так как в выражении B.1) было принято,
что вытекающая масса берется со знаком плюс.
Масса жидкости, заключенная внутри выделенного объема, за единицу
времени, как следует из выражений B.1) и B.2), изменится на
f p tiiUt ds — f ти dv. B.3)
Масса в фиксированном объеме может изменяться только в том случае,
если изменяется во,времени плотность жидкости.
Скорость изменения массы, заключенной в объеме, можно представить
следующим образом:
д С , С до j /о л\
1 р dv = \ —— dv. B.4)
dt -} J dt
16

Здесь переход к дифференцированию
под знаком интеграла возможен, так
как объем постоянен.
Из выражений B.3) и B.4) можно на
основании закона сохранения массы
записать уравнение неразрывности в
интегральной форме:
\(— mK)dv +\ pUitiids^O.
v \ °1 J s
Для того чтобы получить это урав- ™,
нение в дифференциальной форме, вое- Р)ИС 2л Поток ЖИДКости через про-
пользуемся формулой Гаусса — Ост- извольную поверхность
роградского, которая позволяет
преобразовать интеграл по поверхности в интеграл по объему, ограниченному
этой поверхностью.
Положив в формуле A.29) Ьг равным рии заменив в выражении B.5)
интеграл по поверхности интегралом по объему, получим
Полученное уравнение справедливо для произвольно выбранного объема.
Интеграл может быть равен нулю только тогда, если равно нулю
подынтегральное выражение. Отсюда следует уравнение неразрывности в
дифференциальной форме:
д р 1 д (он) —т (9.Ы
dt dxt и \ '
Запишем это уравнение для частных случаев, на которые будем
ссылаться в последующем изложении. Если источник массы отсутствует, то
^+_i_(pUl)=0. B.7)
Если рассматриваем стационарное движение сжимаемой жидкости; то
dp/dt = 0 и, следовательно,
-А_(р „.)=(). B.8)
d Xi
Если жидкость несжимаема, то уравнение неразрывности принимает
наиболее простую форму:
-^- = 0. B.9)
d Xi
2.2. УРАВНЕНИЕ ДВИЖЕНИЯ
Уравнения движения можно вывести с помощью теоремы о
количестве движения, примененной к сплошной движущейся среде.
Пусть произвольная фиксированная замкнутая поверхность s
ограничивает постоянный объем v. Применим к жидкости, протекающей через этот
объем, закон количества движения: скорость изменения количества
движения жидкости внутри объема равна действующей на объем силе.
Найдем сначала скорость изменения количества движения жидкости в
выделенном объеме.
17

Обозначим п вектор внешней единичной нормали к поверхности s (см.
рис, 2.1). Тогда масса жидкости, вытекающая в единицу времени через
элемент поверхности, как и ранее, равна pw^ds. Вытекающая масса выносит из
объема некоторое количество движения, которое является векторной
величиной и может быть найдено умножением массы на вектор скорости:
ptiiUjtiids. Это выражение представляет собой количество движения,
вынесенное из объема через элемент поверхности в единицу времени (в
проекции на ось Xj). Следовательно, через всю поверхность текущей жидкостью
выносится количество движения:
s. B.10)
Количество движения жидкости, заключенной в объеме, может
изменяться также вследствие изменения скорости и плотности жидкости внутри
объема во времени. Это изменение представляется интегралом по объему:
ypujdv.
B.П)
Сумма выражений B.10) и B.11) дает полную скорость изменения
количества движения выделенного объема жидкости и должна быть равна
действующей на объем силе:
J-~ (Рuj)dv+$pujл< л * <fa »Fj. B.12)
Под Fj следует понимать результирующую всех сил, приложенных к
жидкости в выделенном объеме. Все члены этого уравнения имеют один и тот
же свободный индекс /, так как изменение количества движения и сила
должны проектироваться на одну и ту же ось координат.
Силы, действующие на выделенный объем жидкости, можно
подразделить на массовые и поверхностные. Силы, действующие на единицу массы
жидкости, обозначим // — это могут быть сила тяжести или сила
электромагнитного происхождения, возникающая в токопроводящей жидкости.
Тогда проекция на ось / полной массовой силы, действующей на
выделенный объем жидкости:
jp/,«fo. • B.13)
V
Поверхностными называются силы, действующие только на поверхность.
жидкости выделенного объема со стороны окружающей жидкости или
стенки. Эти силы в общем случае действуют как по нормалям, так и по
касательным к поверхности. Поверхностные силы, как показано в разд. 1.2,
представляются напряжениями а^. В данном случае необходимо найти
напряжения на площадке, которой соответствует нормаль п.
Согласно формуле AЛ4) напряжения на такой площадке равны п(ои
(напомним, что второй индекс у а означает ось проектирования).
Следовательно, проекция на ось / полной силы, действующей на
поверхность выделенного объема жидкости:
^niOtjds. B,14)
s
18

Заменив Fj в уравнении B.12) через сумму выражений B.13) и B.14),
получим уравнение движения в интегральной форме:
f _J? (р uj) do + f p Uj ut nt ds =
V * S
* S
J J B.15)
Для того чтобы получить уравнение движения в дифференциальной
форме, необходимо, как и при выводе уравнения неразрывности, заменить
интегралы по поверхности интегралами по объему с помощью формулы Гаусса-
Остроградского (см. разд. 1.4):
Полученное выражение справедливо для произвольного объема v,
поэтому подынтегральное выражение должно быть равно нулю. Отсюда
получаем уравнение движения в дифференциальной форме:
д t д xi д Xi
Первый член уравнения характеризует изменение количества движения
частицы жидкости (на единицу ее объема) и не равен нулю только при
нестационарном течении. Второй член уравнения учитывает изменение
количества движения жидкости той же частицы из-за конвекции. Наконец,
члены, записанные справа, учитывают соответственно массовую и
поверхностную силы, действующие на эту частицу.
Такая форма записи уравнения движения носит название дивергентной
и имеет преимущества при разработке численных методов расчета движения
сплошной среды (см. гл. 12).
При аналитическом решении задач уравнение движения B.16) обычно
удобнее записать в другом виде. Продифференцируем произведения,
стоящие в скобках:
ди* , да , д
и заметим, что сумма второго и третьего членов равна нулю в силу
уравнения неразрывности B.7). Тогда получим
B.17)
В этом уравнении целесообразно явно выделить член, зависящий от
давления, воспользовавшись представлением напряжений по формуле A.13).
Покажем, что последний член уравнения B.17) можно преобразовать
следующим образом:
datj __ d(pdjj) , dat/ _ dp . dot/
д xt "* dxt ' д xt '" dxj ~*~ д Xi
В уравнении B.17) индекс / — свободный, т. е. должен последовательно
принимать значений 1,2, 3. Но 6^- = 0 при i ф\ и только при i — /
получим Ьц ~ I,
19

Окончательно уравнение движения вязкой жидкости примет вид
— ^-+— 42L. B.18)
p dxj р dxt v '
Последний член этого уравнения учитывает влияние сил вязкости.
Для .жидкости, лишенной вязкости (идеальная жидкость), последний
член уравнения равен нулю и оно переходит в уравнение
называемое уравнением Эйлера, в честь Л. Эйлера, получившего это
уравнение A755 г.).
2.3. УРАВНЕНИЕ ЭНЕРГИИ
Третье основное уравнение гидрогазодинамики представляет
запись уравнения энергии. При движении жидкости поверхностные и массовые
силы совершают работу. К жидкости может подводиться теплоГа.
Вследствие этого может изменяться как кинетическая, так и внутренняя энергия
жидкости.
Для движущейся жидкости удобнее рассматривать скорость изменения
энергии. В этом случае очевидно надо подсчитывать работу поверхностных
и объемных сил в единицу времени, т. е. их мощность, а также скорость
подвода теплоты.
Рассмотрим замкнутую поверхность s (см. рис. 2.1), окружающую
фиксированный объем Vy и составим баланс энергий для текущей жидкости.
Энергию, отнесенную к единице объема жидкости, можно записать как сумму ки-
нетическсж и внутренней энергии (энергия — скалярная величина и поэтому
полученное выражение не имеет индексов):
где и2 = UiUi = м| + и! + мз — квадрат модуля вектора скорости; е —
внутренняя энергия единицы массы жидкости.
Тогда скорость изменения энергии жидкости, заключенной в
фиксированном объеме:
( ) !( )*"«-<Ь- B.20)
Первый интеграл выражает скорость изменения энергии внутри объема в
результате изменения параметров потока (скорости, плотности и т.д.) во
времени при неустановившемся движении. Второй интеграл представляет
скорость выноса энергии из объема текущей жидкостью. Следовательно, сумма
интегралов равна скорости «появления» энергии внутри объема. Источником
этой энергии служит работа, производимая в единицу времени массовыми и
поверхностными силами, а также подводимая к объему жидкости теплота.
Работа в единицу времени равна мощности. Мощность можно представить
как скалярное произведение векторов силы и скорости или в индексной
записи произведением Т7^.
Массовые силы развивают внутри объема мощность
v. B.21)
V
20

Поверхностная сила, действующая на элемент поверхности, как следует
из формулы A.14), равна (проекция на /-ю ось) a^riids. Следовательно,
чтобы получить мощность, развиваемую этими силами, надо помножить это
выражение на и, — проекцию скорости на /-ю ось. Тогда полную мощность
поверхностных сил представляет интеграл по поверхности
\ujOijntds. B.22)
s
Рассмотрим теперь подвод теплоты к выделенному объему жидкости.
Теплота может подводиться к выделенному объему жидкости благодаря
внутренним источникам. Обозначим q скорость подвода теплоты к единице
массы жидкости благодаря источникам. Тогда скорость подвода теплоты к
выделенному объему жидкости
$pqdv, B.23)
V
Теплота может подводиться к жидкости данного объема также извне,
т. е. от окружающей жидкости. Обозначим Q вектор потока теплоты через
единицу площади в единицу времени. Тогда скорость передачи теплоты
через элемент поверхности из объема наружу равна Qftitds (п — внешняя
единичная нормаль к поверхности). Передача теплоты через поверхность
происходит вследствие теплопроводности жидкости, и тогда проекции вектора
Qt можно выразить через градиент температурного поля и коэффициент
теплопроводности k формулой Фурье:
Qt = — kdT/dxh
Следовательно, скорость подвода теплоты к жидкости в объеме (знак минус)
можно представить интегралом по поверхности:
-iQtriids. B.24)
S
Сумма выражений B.21) — B.24) представляет скорость подвода энергии к
жидкости в фиксированном объеме. На основании закона сохранения
энергии эта сумма равна скорости изменения энергии жидкости в объеме,
определяемой выражением B.20). Следовательно, уравнение энергии в
интегральной форме имеет вид
V S V S
Заменив интегралы по поверхности интегралами по объему с помощью
формулы Гаусса-Остроградского (см. подразд. 1.4) точно так же, как это было
сделано в разд. 2.1, 2.2, получим уравнение энергии в дифференциальной
форме:
@,5р и2 + р ё) -\ 1@,5р и2 + р ё) щ\ — р ut ft +
д t dxt
B.26)
21

В газовой динамике обычно изучают движение сжимаемой жидкости
с большой скоростью и в относительно малом пространстве. Тогда влияние
сил тяжести ничтожно мало. В этом случае вместо уравнения B.26) следует
записать
(,5ри + р) + | [(,p+p)*l j (juQd + pq. B.27)
о t a xt a xt
Воспользуемся представлением напряжений формулой A.13) и выделим
отдельно члены уравнения, которые учитывают работу сил давления и
работу сил вязкости. Тогда правую часть уравнения B.27) можно представить
таким образом:
(ttaQ)(PU) +
Подставим выражение B.28) в уравнение B.27), а также прибавим к
обеим частям этого уравнения dpldt. Тогда, после группировки членов,
получим
д
at
-^<LL+ _JL_ (и о• _ Qt) + p g. B.29)
at a xt
Для совершенного газа, как известно из термодинамики, можно ввести
энтальпию по формуле
h = е + р/р. ' B.30)
Тогда уравнение энергии B.29) примет вид:
-3- [@,5^ + Л) Р1 + ^— [@,5и*+ h) p щ] -
at а х,
B.31)
Это так называемая дивергентная форма записи уравнения энергии, из
которой видно, что единица массы жидкости переносит энергию h + и?72.
Напомним, что в дивергентной форме были уже записаны уравнения
неразрывности B.7) и количества движения B.16). Такая форма записи имеет
определенные преимущества в некоторых практических расчетах и, в
частности, при численном моделировании течения жидкости.
Уравнение B.31) можно записать и в ином виде, если
продифференцировать выражения в квадратных скобках по частям:
= д р/д t + d/dXi(iij о}/ — Qt)
и заметить, что второй сомножитель в первом члене равен нулю на
основании уравнения неразрывности B.7).
Тогда получим
-?- @,5u*+h) + щ ^— @$5u2+h) =
Qt a xt
= jt+j lh-^-Qo + Я. B.32)
22

В случае установившегося течения в уравнении B.32) следует отбросить
члены с частными производными по времени:
B.33)
а Х\
2.4. УРАВНЕНИЕ ПЕРЕНОСА
Движущаяся жидкость может переносить не только массу,
количество движения, энергию, что рассматривалось при выводе основных
уравнений сохранения, но также иные вещества и свойства. Так, в общем случае
жидкость может переносить примеси: мелкие твердые частицы, капли
другой жидкости и т. п. или какие-нибудь свойства и качества: завихренность,
энтропию и т.д.
Положим, что жидкость переносит какую-нибудь материальную среду
или свойство, подчиняющееся закону сохранения. Обозначим F содержание
переносимого вещества или свойства в единице объема жидкости. Тогда по
полной аналогии с изложенным в подразд. 2.1 можем записать уравнение
переноса в интегральной форме:
ЦЛ /W + Jfii|nids«O. B.34)
Здесь / можно назвать источником величины F внутри выделенного объема.
Следовательно, / показывает, какое количество F возникает на единицу
объема жидкости в единицу времени.
Уравнение B.34) может быть записано в дифференциальной форме
(также по аналогии с предыдущими выводами):
dF + ^<F «)«/. B.35)
dt dxi
В данном случае рассматривается перенос какой-либо среды или
свойства благодаря движению жидкости. Если скорость жидкости равна нулю, а
источники переносимого вещества отсутствуют, то, как следует из
уравнения B.35), dFldt = 0. Следовательно, концентрация вещества не меняется в
данной точке со временем. Значит в данном случае не рассматривается
перенос путем диффузии, который происходит и в покоящейся жидкости, если
концентрация вещества распределена неоднородно по объему. Для примера
достаточно вспомнить рассеивание дыма, т. е. диффузию мельчайших
твердых частиц.
Учесть рассеивание переносимого вещества вследствие диффузии можно
так же, как это было сделано в разд. 2.3 при подсчете теплоты, переданной
объему благодаря теплопроводности (диффузии молекул). Тогда вместо
B.35) получим уравнение
д F д д* F
1 (Fщ)~ f + k , B.36)
dt д хь dxtdxi
где k-коэффициент диффузии.
2.5. ПРИМЕНЕНИЕ УРАВНЕНИЙ СОХРАНЕНИЯ В ИНТЕГРАЛЬНОЙ
ФОРМЕ
Некоторые задачи могут быть просто решены применением
уравнений сохранения, записанных в интегральной форме. Наиболее просто
решаются задачи для установившегося течения, так как в этом случае
необходимы данные о потоке только на поверхностях, ограничивающих область
23

течения, и нет необходимости рассматривать особенности течения внутри
области. Таким образом могут быть получены только суммарные
характеристики потока. Важно также отметить, что уравнения в интегральной форме
пригодны для расчета потоков с разрывами, т. е. скачкообразными
изменениями параметров.
Приведем несколько примеров применения уравнений сохранения в
интегральной форме, на которых можно глубже разобраться в существе
самих уравнений и методике их использования. Полученные результаты
представляют также самостоятельный интерес, так как используются в
технических расчетах.
1. Установившееся одномерное течение идеальной несжимаемой жидкости в поле
тяжести. Пусть площадь трубы изменяется столь плавно, что в каждом поперечном
сечении скорость постоянна по сечению и перпендикулярна ему (одномерность течения).
Найдем запись уравнения энергии для данного случая.
Рассмотрим сначала уравнение неразрывности в интегральной форме B.5).
Первый интеграл равен нулю, так как плотность не изменяется, а источников массы внутри
трубы нет. Второй интеграл следует взять по площади, ограничивающей выделенный
объем жидкости. Объем жидкости ограничен стенками трубы и двумя произвольно
выбранными поперечными сечениями St и S2. Интеграл, вычисленный по поверхности
стенок, равен нулю, так как равна нулю нормальная к ним проекция скорости (стенки
непроницаемы). Скорость нормальна к поперечным сечениям и поэтому имеем
O. B.37)
Перед первым членом поставлен знак минус, так как жидкость втекает в объем.
Уравнение выражает тот факт, что расход массы через каждое поперечное сечение
постоянен. В данном случае плотность жидкости постоянна и поэтому постоянен объемный
расход.
Используем уравнение энергии в интегральной форме B.25). Первый интеграл
равен нулю, так как течение установившееся. Пятый и шестой интегралы равны нулю,
так как подвода теплоты и теплообмена нет. Во втором интеграле можно опустить член,
учитывающий внутреннюю энергию, так как температура жидкости не меняется. При
вычислении второго интеграла интегрирование проводится только по площади
поперечных сечений, так как проекция скорости на нормаль к стене трубы равна нулю.
Следовательно, получим
Третий интеграл вычисляется по объему жидкости, заключенному между выбранными
поперечными сечениями. Запишем следующие выражения:
dv = Sdl, щ fi=ug cos a,
где dl — элемент длины вдоль оси трубы; а — угол между касательной к оси трубы в
данной точке и направлением действия силы тяжести. Сила /,-, действующая на
единицу массы жидкости, в данном случае равна ускорению свободного падения.
Третий интеграл вычисляется также просто:
J g р и S cos a dl = g р и S J dz = g р и S (гл_ — г2). B.38)
Произведение puS вынесено за знак интеграла, так как оно постоянно для любого
сечения в силу уравнения неразрывности B.37). Координата г измеряется в
направлении действия силы тяжести.
В четвертый интеграл уравнения B.25) входят напряжения, действующие на
поверхности выделенного объема. Поскольку в идеальной жидкости силы трения равны
нулю, то напряжения равны силам давления, действующим по нормали к поверхности.
На стенках трубы нормальная проекция скорости равна нулю, поэтому интеграл
вычисляется только по выбранным поперечным сечениям, т. е. равен
Силы давления на контрольных поверхностях направлены внутрь выделенного
объема. Перед вторым членом поставлен знак минус, так как направление силы
противоположно направлению скорости.
После преобразований получим так называемое уравнение Бернулли A738 г.):
B.39)
24 (

которое является одним из основных уравнений механики несжимаемой жидкости.
Каждый член уравнения Бернулли выражает энергию единицы массы жидкости.
Первый член соответствует кинетической энергии, второй представляет работу сил
давления,, а третий — потенциальную энергию силы тяжести. Как будет показано далее,
уравнение Бернулли является интегралом уравнения движения и совпадает с
уравнением энергии только в частйых случаях.
2. Уравнение Бернулли для потока в системе, вращающейся с постоянной
угловой скоростью. Пусть ось трубы переменного сечения лежит в плоскости, проходящей
через ось вращения. Труба, по которой течет несжимаемая идеальная жидкость,
вращается с постоянной угловой скоростью о).
Рассматриваем течение в относительном движении, т. е. в системе координат,
связанной с вращающейся трубой. Уравнения механики справедливы и во вращающихся
системах, если к действующим в абсолютной системе силам добавить две массовые
силы (силы инерции), соответствующие центростремительному ускорению и ускорению
Кориолиса, взятым с обратным знаком. Ускорение Кориолиса направлено по нормали
к относительной скорости жидкости и поэтому при вычислении третьего интеграла в
уравнении B.25) даст результат, равный нулю. Тогда вывод уравнения не отличается
от предыдущего вывода и только.при вычислении третьего интеграла в уравнении B.25)
надо подставить центростремительное ускорение, взятое с обратным знаком.
Интеграл по объему вычисляется по аналогии с проделанным ранее вычислением
B.38):
— j* оJ г р и S cos a dl = — со2 р и S J r d г = 0,5р и S (г2 — г\),
где г — текущий радиус, а — угол между касательной к оси трубы в данной точке и
радиусом. Тогда окончательное уравнение представим в таком виде (член,
учитывающий силу тяжести, в данном случае не записываем):
Cbj+^-Q.
— 0,5оJ/-2
B.40)
Это уравнение применяется, например, при расчете центробежных насосов.
3. Потери при внезапном расширении трубы. Пусть поток несжимаемой жидкости
течет по трубе с площадью поперечного сечения Slt а затем внезапно переходит в
трубу с площадью S2 > St (рис. 2.2). При выходе из трубы с меньшей площадью поток
не может сразу заполнить все сечение и образуется струя. Поверхность раздела струи
и окружающей ее жидкости неустойчива, происходит обмен количеством движения, а
часть механической энергии переходит в тепловую (внутреннюю энергию), которая
считается «потерянной энергией». На некотором отдалении струя занимает всю площадь
поперечного сечения.
Применим уравнение движения B.15) к объему жидкости, ограниченному стенками
трубы и контрольными сечениями J—/ и 2—2. Ввиду одномерности течения есть только
одна ось проектирования, направленная вдоль
трубы.
Первый и третий интегралы равны нулю,
а второй и четвертый необходимо вычислить Р1 \^^fig
только по площади контрольных сечений.
Рис. 2.2. Труба с внезапным
расширением
Рис. 2.3. Поворот потока в густой
решетке бесконечно тонких
пластин
25

В результате получим (предполагаем давление постоянным по сечению)
= S2(p1-p2). B.41)
При вычислении четвертого интеграла пренебрегаем силами трения, так как на
коротком участке потери трения много меньше потерь от внезапного расширения. В таком
случае напряжения о равны давлению, которое действует по нормали к поверхности.
Преобразовав уравнение B.41) с помощью уравнения неразрывности B.37), имеем
P2-Pi = P («j—«2). B-42)
Если бы труба расширялась плавно и потери отсутствовали, то разность давлений
при тех же скоростях определялась из уравнения Бернулли B.39):
Р2-/>1 = 0,5р(и12-н|). B.43)
Следовательно, внезапное расширение вызывает потерю давления, равную
[вычитаем почленно из уравнения B.43) уравнение B.42)]
P2-P2 = 0,5p(Wl-W2J. B.44)
Относительная величина потерянной кинетической энергии определяется
безразмерным коэффициентом потерь «внезапного расширения»
4. Потери при внезапном повороте потока в аэродинамической решетке.
Рассмотрим решетку, составленную из пластин, расстояние t (шаг) между которыми много
меньше их длины (рис. 2.3). На решетку набегает поток несжимаемой жидкости,
направленный под углом, отличающимся от угла направления пластин. На острых
кромках пластин происходит отрыв потока, а затем под влиянием вязкости поток
выравнивается и течет между пластинами по всему сечению. Определим потерю, которая возникает
при повороте, и отрыве потока на кромках пластин. Трением по поверхности пластин
пренебрежем.
Уравнение неразрывности можно записать таким образом:
, B.45)
где их и и2 — скорость соответственно перед решеткой и внутри канала, где поток вы-
равнялся; рг — угол направления скорости перед решеткой; $2 — Угол наклона
пластин.
Уравнение движения в проекции на направление пластин
Pi t sin fa+pul t sin ?! cos 6 = p21 sin ftj-Ьрu\ t sin p2. B.46)
Левая часть уравнения относится к сечению на входе в решетку, а правая — к
сечению канала между пластинами, где поток стал однородным, б = Р2 — pj. Уравнения
составлены для потока, приходящегося на один шаг решетки, так как картина течения
периодична.
Выразим из уравнения B.46) разность давлений
Pi
ft cos6—ра|.
P2Pi=pM? . ft
sin p2
Преобразуем первый член в правой части, воспользовавшись уравнением
неразрывности B.45):
P2—Pi = pti1 щ cos 6—р и\.
При отсутствии потерь на входе в решетку разность давлений можно найти с помощью
уравнения Бернулли:
Pi —Р2 = 0.5ри! — 0,5ри|.
Тогда потеря давления равна разности последних выражений:
Д2-Р2=-0,5р {и\-2игщcos 6+и|). B.47)
На основании теоремы косинусов очевидно, что выражение в скобках представляет
отрезок АВ. Отрезок А В изображает разность векторов скоростей ulf и2.
Следовательно, потеря давления эквивалентна кинетической энергии «потерянной,» скорости.
Обратим внимание, что потери при внезапном расширении трубы также рыражздись через
кинетическую энергию «потерянной» скорости B.44),
26

Для более удобной записи окончательной формулы потерь выразим отрезок А В из
треугольника А ОВ по теореме синусов и запишем выражение B.47) в виде
безразмерного коэффициента потерь:
? = 2(p2-p2)/P«f=-sin26/sin2p1. B.48)
Следует заметить, что потери сильно зависят от угла Р2 установки пластин. Эта
формула с некоторыми изменениями используется для определения потерь в
аэродинамических решетках турбомашин при отклонении угла входа потока от расчетного значения.
5.Потери при смешении потоков. В ряде технических задач приходится
иметь дело с расчетом смешения или выравнивания потоков. К подобным
задачам относятся расчеты эжектора, струй, вихревых следов и др.
Характерным является то, что в подобных течениях либо смешиваются потоки с
разными скоростями, либо поток имеет неоднородное поле скорости, которое
затем выравнивается. Во всех случаях выравнивание происходит благодаря
работе сил вязкости, что приводит к потере некоторой доли механической
энергии и переходе ее в тепловую (внутреннюю энергию).
Рассмотрим расчет потери, которая возникает при смешении двух потоков для
случая, когда статическое давление остается постоянным. Трением по границам
пренебрежем.
Пусть смешиваются и затем выравниваются два потока с массовыми расходами ml9
т2 и соответственно скоростями шъ w2. Обозначим общую скорость потока после
выравнивания w3. При постоянном давлении эту скорость можно найти из условия
постоянства количества движения:
Кинетическая энергия потоков до смешения
Кинетическая энергия потока после смешения меньше этой величины:
? = 0,5(m1-hm2) ц>1=0,Ъ(т1 w1+m2 w
так как разность всегда положительна:
3 1 j^^) A2
Запишем выражение для относительной потери механической энергии:
А Е __ mlm2(w1—w2J
Е (j (m1wl + т2ш|)
Вопросы для самопроверки
1. Какие физические законы описывают уравнения сохранения?
2. В каком случае применимо уравнение движения Эйлера?
3. В чем состоит особенность дивергентной формы записи уравнений сохранения?
4. Выведите уравнения сохранения, исходя из уравнения переноса.
5. Какие преимущества дает применение уравнений сохранения в интегральной
форме?
6. Выведите уравнение Бернулли для тяжелой жидкости, если система координат
вращается с постоянной угловой скоростью.

ГЛАВА 3
МЕТОДЫ РАЗМЕРНОСТИ И ПОДОБИЯ
В ГИДРОГАЗОДИНАМИКЕ
3.1. АНАЛИЗ РАЗМЕРНОСТЕЙ. ФОРМУЛА РАЗМЕРНОСТИ
Для измерения физических величин необходимо введение
определенных масштабов. Как известно, выбор таких масштабов произволен
(здесь отвлекаемся от выбора удобных физических эталонов для хранения
масштабов, так как в данном случае это не относится к сути дела). Так,
длину можно измерять, например, в метрах, аршинах, футах или других
единицах.
Выбор нескольких единиц физических величин, которые называют
основными, образует систему единиц физических величин. Выбор единиц
физических величин, принятых в качестве основных, также произволен. Так, в
в СИ в качестве основных механических единиц физических величин
приняты: единица длины—метр, единица массы — килограмм, единица
времени—секунда. До этого в технике широко применялась так называемая
техническая система единиц физических величин: единица длины — метр,
единица силы — килограмм, единица времени — секунда. Конечно,
целесообразно выбрать основные единицы физических величин для тех понятий,
которые имеют фундаментальное значение, как это и сделано в СИ (или в
технической системе).
Однако важно отметить (и это будет использовано в теории подобия и
размерности), что в качестве основных единиц физических величин можно
выбрать, например, скорость, плотность, ускорение.
Величины, численные значения которых зависят от принятых единиц
физических величин, называют размерными. Время, энергия, сила — это
примеры размерных величин.
Величины, численные значения которых не зависят от принятых единиц
физических величин, называют безразмерными. Угол, число я (отношение
длины окружности к ее диаметру), отношение газовой постоянной к
теплоемкости R/Cp (т. е. отношение двух размерных величин, имеющих одинаковую
размерность) — примеры безразмерных величин.
Кроме основных единиц физических величин, очевидно необходимо иметь
единицы других физических величин, которые рассматривают при изучении
той или иной проблемы. Эти величины связаны с величинами, принятыми в
качестве основных, определенными физическими формулами. Поэтому
размерность остальных физических величин можно выразить через размерности
основных единиц физических величин.
Единицы физических величин, выраженные через основные, называют
производными. Так, например, в СИ единицы скорости (м/с) и
плотности (кг/м3) являются производными единицами основных физических
величин.
Для дальнейшего изложения удобно принять четыре основные единицы
физических величин и обозначения для их размерностей: единицы длины
/ — метр, размерность [Л = L; единицы массы т — килограмм,
размерность [т] = М; единицы времени / — секунда, размерность [t] = Т; едини-
28

цы температуры Т — градус Кельвина, размерность [71 = К. Здесь, как
обычно принято, квадратные скобки означают размерность
соответствующих величин.
Тогда, например, размерность скорости и плотности, которые являются
производными, должны быть записаны таким образом:
[o>]=LT-\ [p] = L-3M.
Единицу силы в СИ называют ньютоном, однако это производная
размерность, так как по закону Ньютона сила равна массе, умноженной на
ускорение, и, следовательно, размерность силы такова:
Единицей давления является паскаль. Так как 1 Па по определению
равен 1 Н/м2, то единица давления имеет производную размерность [р] =
В общем случае для принятых основных единиц производные
размерности могут быть записаны с помощью формулы размерности Фурье:
L«M*T'Krf, C.1)
который положил начало систематическому применению соображений
теории размерности и подобия к физическим задачам. Показатели степени в
формуле размерности C.1), естественно, являются безразмерными
величинами.
Если размерность данной физической величины может быть выражена
через размерности некоторых других указанных физических величин, то
ее называют зависимой (от размерности указанных величин). В противном
случае размерность называют независимой.
Размерность скорости [w] = LT независима от размерностей
ускорения [g] =^ LT-2 и плотности [р] = LM.
Размерность скорости [w] = LT зависима от размерностей ускорения
[g] = LT и длины [/] = L.
Рассмотрим применение метода анализа размерностей к решению
физических задач сначала на одном наглядном частном примере, а затем перейдем
к обобщению.
Решения Задач методом анализа размерностей надо начинать с
рассмотрения физического существа задачи. Прежде всего надо выбрать основные
факторы, которые определяют изучаемое явление, и выяснить, какими
эффектами можно пренебречь.
Эта часть работы является творческой и по существу единственно
трудной, так как требует понимания существа проблемы и физической интуиции.
В сложном случае можно анализировать последовательно несколько
правдоподобных предположений, а затем с помощью теоретических выкЛа-
док, расчетов или опытов выбрать правильное. Во всяком случае
предварительное применение метода анализа размерностей сократит и облегчит
работу.
Пусть в сосуд налита тяжелая жидкость и уровень ее поддерживается
постоянным (тяжелой называют жидкость в том случае, если необходим учет
веса жидкости). Жидкость вытекает через насадок в дне сосуда (рис. 3.1).
Надо определить расход, т. е. количество массы жидкости, вытекающее в
единицу времени.
В поставленной задаче можно пренебречь влиянием трения, так как если
размеры бака велики по сравнению с размером отверстия, то скорость
жидкости в баке очень мала. Влиянием трения в насадке также можно пренебречь,
так как полагаем, что он короткий.
29

В поставленной задаче логично
предположить, что массовый расход жидкости т зависит
от высоты уровня / жидкости над выходным
отверстием насадка, площади отверстия насадка
S, плотности жидкости р и ускорения
свободного падения g.
Логично также предположить, что расход
жидкости пропорционален площади отверстия.
Тогда запишем зависимость в таком виде:
= SF(/, p, g):
C.2)
Рис. 3.1. Вытекание тяжелой
жидкости из сосуда
Задача состоит в том, чтобы найти вид этой
функциональной зависимости.
Сначала следует выразить размерности всех величин:
Из записи C.3) следует, что три аргумента в скобках функциональной
зависимости C.2) имеют независимую размерность, т. е. размерность любого
из них нельзя выразить через размерности двух других.
Выберем в качестве новых единиц физических величин длину /, плотность
р и ускорение g. Тогда очевидно, что искомая функция в уравнении C.2)
превратится в постоянную величину, так как
F(l, I, 1) = С. C.4)
Единица длины изменена в / раз. Для того чтобы р была единицей
плотности, необходимо единицу массы изменить в р/3 раз. А для того чтобы# была
единицей ускорения, необходимо единицу времени изменить в \fllg раз.
Расход т имеет размерность масса/время. Тогда в новых единицах
величина mIS должна быть записана в таком виде:
(m VTJg)/plS в tk/pS Vgl.
Из формул C.2), C.4), C.5) следует окончательный результат:
C.5)
C.6)
Постоянная С может быть найдена из опыта.
Приведенные выкладки можно проделать и несколько иным путем, kojo-
рый имеет преимущество, так как проводится по стандартной схеме.
Размерность tn/S можно представить через размерности новых единиц
физических величин в виде степенного одночлена по типу формулы C.1):
Перейдя к символической записи размерностей входящих величин,
получим соотношение
Отсюда получим три уравнения для определения показателей степени
1 = 6, — 1 = —2 с, —2 = а — ЗЬ + с, из которых следует: а = 1/2, b =1,
с - 1/2.
30

Искомый расход жидкости, отнесенный к площади отверстия, в новых
единицах равен
mis m
что, естественно, совпадает с условием C.6).
Приведенная задача имеет известное теоретическое решение. Скорость
вытекания жидкости из отверстия по формуле Торичелли равна
w ^
Расход находим по уравнению неразрывности:
что совпадает с формулой C.6) при значении постоянной С = У 2.
3.2. П-ТЕОРЕМА. ВЫБОР ОПРЕДЕЛЯЮЩИХ ПАРАМЕТРОВ
В предыдущем разделе на частном примере показано, что
формальный переход к новой системе единиц физических величин позволяет
достаточно просто установить структурную форму физической зависимости.
Рассмотрим функцию, которая описывает физическую закономерность:
Q-F(Q,, Q2,..., Qk ..., Qn). C.7)
и не зависит от выбора системы единиц физических величин.
Пусть первые k < п аргументов Qx, Q2, ..., Qh имеют независимые
размерности. Тогда размерности функции и остальных п — k аргументов Q,
Qk+ъ Qfe+2> • ••» Qn можно выразить через размерности первых k
аргументов, которые и выбираем в качестве новых единиц физических величин.
Формулы размерности физических величин должны иметь вид степенных
одночленов, т. е. должны быть записаны через размерности новых
единиц в таком виде:
C.8)
После введения новых едикиц физических величин изменяются
численные значения всех величин. Величины Q1% Q2, ..., Qh сами приняты за новые
единицы физических величин и, следовательно, в новой системе равны
единицам.
Численные значения Q, Qfc+I> Qft+2 «-•> Qn в новой системе единиц будут
соответственно равны:
п =
Q?#...Q°*
3!

Тогда зависимость C.7) примет вид
n = F(l,l, ..., l/nlf П2, ..., nn_fe).
При k<iri первые k единиц можно не писать:
n=F(nlt П2, ..., Пп.к). C.10)
Если k = я, то функция F просто равна постоянной, как это и было
продемонстрировано в предыдущем разделе на частном примере.
Из сравнения выражения C.8), C.9) видно, что параметры П, Пь П2, ...
... Пп_ь являются безразмерными.
Изложенное можно сформулировать в виде так называемой П-теоремы:
связь между п + 1 размерными величинами, независимую от выбора единиц
физических величин, можно преобразовать в функциональную зависимость
между п — k + 1 безразмерными величинами, где k — число аргументов с
независимой размерностью.
Таким образом, каждое физическое соотношение, записанное для
размерных величин C.7), может быть преобразовано в соотношение между
безразмерными величинами C.10).
Такое преобразование полезно по крайней мере по двум причинам: 1)
количество аргументов, от которых зависит функция, уменьшается от п до
я — k\ 2) соотношение C.9) показывает, что размерные физические
величины оказывают влияние на результат расчета или опыта по существу не в
отдельности, а только в определенной комбинации с другими размерными
величинами. Эти выводы значительно облегчают экспериментальные,
расчетные и теоретические исследования.
Для использования отмеченных выгод надо прежде всего правильно
составить зависимость C.10). Тут могут представиться два случая. Если
известны дифференциальные уравнения и краевые условия, которые
математически описывают поставленную физическую задачу, то отыскание
безразмерных критериев C.9) производится довольно просто. Если же изучаемое
явление настолько сложно, что не имеет вообще или не имеет достаточно
надежного математического описания, то в помощь необходимо привлечь
физические соображения.
Преобразование дифференциальных уравнений и определение
безразмерных критериев рассмотрим при изложении теории физического подобия
(разд. 3.3).
Определить безразмерные критерии можно из соображений теории
размерности и не имея уравнений движения. Однако тогда связь между этими
безразмерными критериями можно установить только опытом.
Анализ надо начинать со схематизации физического явления,
отбрасывания второстепенных факторов и установления основных размерных
параметров, определяющих явление. В число таких параметров должны быть
включены как переменные, так и постоянные размерные величины, от
которых зависит изучаемый процесс. Так, при рассмотрении движения тяжелой
жидкости (разд. 3.1) необходимо было включить в качестве основного
параметра ускорение свободного падения.
Рекомендации по анализу задач и применению П-теоремы могут быть
очень многословны и расплывчаты. Поэтому лучше всего изучить этот
метод прямо в действии.
В цилиндрический сосуд, вращающийся с постоянной угловой скоростью
вокруг оси 2 (рис. 3.2), налита несжимаемая тяжелая жидкость. Требуется
определить уравнение поверхности жидкости.
Если в неподвижный сосуд налита жидкость, а затем сосуд приводится
во вращение, то жидкость также начнет вращаться под действием сил тре-
32

J
—
2
2r
Рис. З.2. Вращение тяжелой
жидкости в сосуде
ния. После того как движение установится,
влияние сил вязкости можно не учитывать.
Тогда можно предположить, что
исследуемое явление зависит от следующих
параметров: р, gy m, угловой скорости Й, радиуса
сосуда г. Рассмотрим, все ли эти параметры
необходимо учитывать? Из рис. 3.2 можно
заключить, что если в сосуд налить больше
жидкости, то это не изменит формы
свободной поверхности, а только сместит. эту
поверхность вверх. В этом случае параметр т
не следует включать в число определяющих.
Удобно поместить начало координат в точке
О и обозначить искомую функцию h — h (г)
(см. рис. 3.2).
Выпишем размерности всех выбранных величин:
[ft]=L, [Q]=T-\ [/•]== L, [p]=L-3M, [g] = LT-2.
Прежде всего следует отметить, что размерность массы входит только в
один параметр. Следовательно, плотность не может входить в число
определяющих параметров, так как иначе из них нельзя составить безразмерную
комбинацию, что требует П-теорема.
Можно сделать общий вывод: система выбранных параметров должна
обладать такими размерностями, чтобы из них можно было составить
безразмерные комбинации. Если это не так, то либо некоторые параметры не
являются определяющими, либо, наоборот, — среди выбранных не хватает каких-
то определяющих параметров.
Теперь общее число переменных стало п + 1 = 4, а число независимых
единиц измерения k = 2. Так как п + 1 — k = 2, то из всех параметров
можно составить две безразмерные комбинации. Безразмерную функцию
удобно взять в таком виде: П = hi r = F (Пг). Для определения
безразмерного аргумента запишем выражение
Пх = [Q]a [r]b [g]c = Т ~а Lb V Т~2с,
из которого следуют уравнения для определения показателей степени:
— а — 2с = О, Ь + с = 0.
Число неизвестных превышает число уравнений на единицу, поэтому один
из показателей степени можно выбрать произвольно (но не 0и не об). Это
не влияет на полученное соотношение, так как искомая функция неизвестна
и аргумент, который в нее входит, может быть взят в произвольной степени.
Этот вывод не относится только к рассматриваемому примеру, а является
общим.
Вернемся к примеру и выберем а = 1, тогда: с== —1/2, Ь =1/2.
Следовательно, безразмерный аргумент равен fl^ = Qj/V/g и искомая зависимость
приобретает вид
/i/r=F(Q)/
Если принять а = 2, то следует написать
2 Зак. 2638
33

что математически равноценно, но физически более наглядно, так как
аргумент можно представить как отношение центробежной силы к массе:
pQ2r/(pg). Эта запись также поясняет, почему плотность жидкости не
вошла в число определяющих параметров.
Можно продолжить рассуждения и полупить более конкретный
результат. Разложим функцию F (&2r/g) в ряд по степеням аргумента:
hi г = сг (Q2r/g) + c2 (Q2 rlgf +...
Величины коэффициентов из приведенного анализа определены быть не
могут. Однако, если использовать граничные условия на свободной
поверхности, то из уравнения Бернулли получим (р0 = const)
Ро/Р—0,5Q2r2 + gz = const.
Если принять г = h и 2 = 0 при г = 0, то получим уравнение свободной
поверхности жидкости
3.3. ФИЗИЧЕСКОЕ ПОДОБИЕ. МОДЕЛИРОВАНИЕ.
КОЭФФИЦИЕНТЫ ПОДОБИЯ
В приложениях гидрогазодинамики к инженерным проблемам
часто приходится сталкиваться с очень сложными задачами, которые, если
и поддаются решению, то после предварительных существенных упрощений.
Для большинства сложных задач решение может быть получено только с
помощью численных методов на ЭВМ, что также вносит схемные погрешности.
Все это приводит к необходимости как чисто экспериментальных
исследований, так и экспериментальной проверке теоретических расчетов.
Во многих областях техники при создании новых объектов необходимо
предварительное проведение широких экспериментальных исследований.
В этом случае создаваемый объект, который далее будем называть натурным,
отсутствует. Следовательно, такие испытания могут быть проведены только
на каких-то моделях. При этом естественно встает вопрос: возможно ли
такое моделирование физических явлений и какие условия должны быть
соблюдены при моделировании.
Уже созданные машины и установки или отдельные их элементы также
обычно подвергают экспериментальным исследованиям. Такой эксперимент
может быть проведен на натурном объекте. При планировании эксперимента
желательно сократить до минимума время и стоимость проведения
испытаний, но вместе с тем обработать полученную информацию в таком виде, чтобы
она имела наиболее общий характер. В таких задачах возникает вопрос о
правильном выборе представления общей функциональной зависимости от
минимального количества аргументов.
Соображения о физическом подобии позволяют, например, провести
ограниченное количество частных экспериментов, а научно-обоснованный
результат выдать и для тех случаев, для которых прямой эксперимент не
производился.
Наконец, в теоретических исследованиях и расчетах сложных процессов
соображения о физическом подобии также играют очень большую роль. На
первом этапе изучения задачи эти соображения помогают лучше
разобраться в существе явлений и выбрать основные безразмерные аргументы, от
которых зависит изучаемое явление. Далее наиболее простым образом
обосновывается вид искомой функциональной зависимости. Наконец, становится
более очевидным, каким образом следует проверить экспериментом
допущения, принятые в теории.
34

Если добавить к изложенному, что соображения теории размерности и
подобия достаточно просты, то станет очевидным, что они всегда должны
предшествовать как теоретическим, так и экспериментальным
исследованиям.
Соображения теории подобия следует применять и после окончания
теоретической или экспериментальной работы, т. е. на этапе представления
итоговых зависимостей. В таком случае эти зависимости будут наиболее общи,
логичны и удобны.
В аэродинамике теорию подобия применяют широко и сравнительно
давно. Также широко она применяется для построения обобщенных
характеристик паровых и газовых турбин, осевых компрессоров, насосов и других
машин, работающих на газе и жидкости.
Представление о физическом подобии сложилось, вероятно, как
обобщение понятия геометрического подобия. Поэтому вначале приведем простой
пример, основанный на понятиях только геометрического подобия.
Два треугольника подобны, если отношения сторон одного к
соответствующим сторонам другого равны одному и тому же числу: коэффициенту
подобия. Можно рассуждать и по-другому. Введем для подобных
треугольников разные единицы физических величин для длин, причем такие, что
численные значения сходственных сторон треугольников станут одинаковы.
Тот же коэффициент подобия можно представить как отношение единиц
физических величин для длин. Аналогичные рассуждения справедливы и в
более общем случае, когда изменяют единицы физических величин не только
длин, но и других физических величин. /
Физические явления подобны, если по характеристикам одного можно
определить характеристики другого простым пересчетом масштабовло
коэффициентам подобия.
Рассмотрим условия, которые необходимо выдержать для того, чтобы
явления были подобны.
Пусть Q зависит от п определяющих параметров Ql4 ..., Qn:
Q = F(QIf'Qlf ..., Qk9 ..., Qn), C.11)
среди которых первые k < п имеют независимую размерность.
На основании П-теоремы эту зависимость можно представить уравнением
C.10) с меньшим числом безразмерных аргументов:
U^F(Ulf П2, ..., П^), C.12)
где П, Пг, ..., nn_ft определены условиями C.9).
Важно отметить, что безразмерные параметры П1э П2, ..., Iln_ft
полностью определяют явление, а под П следует понимать различные безразмерные
величины, которые изучают в данном явлении. Все они зависят от одних и
тех же безразмерных аргументов П1ч П2, П3, ..., П„__ь, которые в
совокупности называют базой.
Рассмотрим некоторое физическое явление, аналогичное описываемому
уравнением C.11):
Q'=F(Q,', <й, ..., QL ..., Q'n). C.13)
Допустим, например, что в обоих случаях изучают течение в трубах, но
жидкости различны, скорости их не равны, трубы имеют различные
диаметры и т.д.
Уравнение C.13) на основании П-теоремы также можно привести к
безразмерному виду:
II'=F(II,\ Щ Щ_4). C.14)
2* 35

Потребуем, чтобы в уравнениях C.14) и C.13) выполнялось условие
Щ^п19 Щ = П2, ..., Щ_*=ПП^. C.15)
Поскольку рассматриваются явления одного класса, то
П'=П. C.16)
Необходимым и достаточным условием подобия явлений служит
равенство численных значений безразмерных комбинаций, образующих базу C.15).
Безразмерные комбинации C.15) называют в таком случае критериями
подобия.
Введем обозначения для коэффициентов подобия:
/C = Q7Q, /d-Qi/Qi, tf.-QJ/Qi. ..., Kn-k^Qk-k/Qn^- C.17)
Из равенств C.15), C.16), определяющих подобие, а также выражений
для критериев подобия C.9) и обозначений C.17) получим
C.18)
Если известны коэффициенты подобия для определяющих параметров, то
по формулам C.18) можно вычислить коэффициенты подобия для всех
остальных параметров.
Из теории подобия следует, что возможно моделирование физических
явлений.
Моделированием называют замену исследования явления на натурном
объекте экспериментальным изучением этого явления на модели.
Рассмотрим простой пример, на- котором продемонстрируем применение
всей методики расчета. Пусть требуется оценить на модели сопротивление,
которое возникает при подаче смазочного масла по длинному
горизонтальному трубопроводу круглого поперечного сечения.
Для этого необходимо определить падение давления на единицу длины
трубопровода Др//. Определяющими размерными параметрами являются:
d — диаметр трубопровода; w — средняя по расходу скорость жидкости и
величины, характеризующие физические свойства жидкости р и |х.
Для размерных параметров искомая зависимость имеет вид
p, (I, w). C.19)
Выпишем размерности выбранных величин:
Из п + 1 = 5 размерных величин имеют независимую размерность k=?3.
Согласно П-теореме зависимость C.19) можно записать как зависимость
между двумя безразмерными величинами: П = F (П^).
Пользуясь правилами, изложенными в разд. 3.2, можно составить два
безразмерных критерия П — /ipdllpw* и Пх = d/
3,6

Записав такие критерии для модели й натуры и воспользовавшись
условиями подобия C.15) и C.16), получим
Apd __ Ар' d1 pwd __ pf w' df
Ipw* ~ Up'' w'9' ц ~~ ц'
Выразим эти условия через коэффициенты подобия:
If If 2 lf~\ ¦., If If If If /О ОЛ\
= /\p t\w i\(i И Ajm === *\p /\ w *Vd• \У• ^v//
Коэффициент К показывает отношение величины сопротивления в
модели к аналогичной величине в натуре. В остальных коэффициентах подобия
индекс указывает, какой физической величине соответствует коэффициент
пересчета.
Допустим, что для проведения эксперимента на модели удобно выбрать
вместо масла воду. С помощью таблиц определяем, что отношение вязкости
воды (при 20 °С) к вязкости масла (при рабочей температуре 60° С) Кц=
— 0,079, а соответствующее отношение плотностей Кр = 1,15. Тогда по
второй формуле C.20) подсчитываем KwKd =0,0687. Выберем для
испытаний на модели диаметр трубки в 5 раз меньше, чем в натуре: Ка = 0>2.
Тогда для соблюдения подобия скорость воды в модели должна быть
примерно в 3 раза меньше, чем скорость масла в натурных условиях: Kw = 0,0687/
/0,2 = 0,344. Определив экспериментально падение давления в модели на
мерном участке Г, найдем падение давления в натурном трубопроводе на
участке /:
Ар// = (Kd/KP К1) (tiP9 IV) = 1,47ЛР'//'.
Этот пример, хотя и носит учебный характер, ясно показывает, каких
преимуществ можно достичь испытанием моделей. Стенд имеет малые
размеры и требует для подачи воды насос малой мощности, так как расход на
модели во много раз меньше расхода масла в натурной установке:
т
Однако следует особо подчеркнуть трудности, которые могут возникнуть
особенно при моделировании сложных явлений, когда требуется соблюдать
подобие по многим безразмерным критериям (а не по одному, как это было
в приведенном примере).
Моделирование, при котором соблюдено подобие по всем критериям
подобия, как этого требует П-теорема, называют полным моделированием.
На практике соблюдение полного подобия часто оказывается технически
невозможным. Так, даже в приведенном ранее примере, для того чтобы
выдержать полное геометрическое подобие, надо было бы выдержать
подобие по шероховатости стенок трубы (хотя это далеко не всегда существенно,
как показано в гл. 9). -При испытании на стендах моделей турбомашин,
уменьшенных по сравнению с натурой, практически невозможно выдержать
в масштабе зазоры между ротором и статором и т. д.
При испытании малых моделей, в которых используется та же
жидкость, что и в натурной установке, необходимо соблюдение условия /С^/Сш =
= const, что может привести к недопустимо высоким скоростям течения.
Здесь приведены только простые частные примеры. Несколько подробнее
этот вопрос будет рассмотрен при использовании моделирования в теории
турбомашин (см. подразд. 3.4).
Важно заметить, что на практике часто приходится отказаться от полного
моделирования и применить частичное, т. е. соблюсти подобие только по
наиболее существенным критериям. В этом случае при переносе полученных ре-
37

Зультатов на натурный объект необходимо введение расчетных или опытных
поправок.
Рассмотрим применение теории подобия к преобразованию уравнений
сохранения и выводу основных определяющих критериев подобия. Для
определенности рассмотрим задачу обтекания тела неограниченным потоком
вязкой жидкости без теплообмена. Пусть в бесконечности известны и^,
Poo» 7"oo» a также р^. Вязкость жидкости количественно характеризуется
величиной fx. Характерный размер тела L. Для большой общности положим,
что обтекаемое тело совершает периодические колебания с частотой Q.
Приведенные величины можно применять в качестве характерных
масштабов и перейти к безразмерным параметрам.
Введем следующие безразмерные величины, которые обозначим чертой
сверху:
t = t/ulf х% = Lxi р = Роо р,
h = cp Too Л, o'i/ = (\iUcolL) о}/.
Заменив в уравнениях неразрывности B.7), движения B.18), где
пренебрежем силой тяжести, и энергии B.32) размерные величины
безразмерными, получим
" ш
dUj = Г Poo "I I dp [
dXi [ Poo ulo \ p dXj
dt [ \ p j
Z.Q 1 1 др
Выражения в квадратных скобках являются безразмерными постоянными.
Из курса физики известно, что скорость распространения звука в газе
можно определить по формулам (в гл. 4 дан вывод этих формул): а^ =
= V*pJpoo = VkRT^ х = cplcv.
Безразмерные критерии принято называть по именам ученых, много
сделавших в соответствующих областях науки. В данном случае получено три
таких критерия:
Sh = QZ./ttoo — число Струхала;
M==Uoo/aoo—число Маха; C.22)
Re = poo Woo ll\x—число Рейнольдса,
38

Запишем уравнения сохранения C.21) в безразмерной форме через
критерии подобия C.22):
Sh Л +-±- (р~т) =0;
dt dxt
+ 5,+
dt dxt *m p faj Re dx.
cu д I 1 -2 , 1 1 -\ , ^ / 1 -2 . 1 1 t\
Sh [—u2-\ h)-\ f—u2-{ h =
Численные значения коэффициентов этих уравнений зависят только от
безразмерных величин Sh, M, Re, и показателя изоэнтропы х, который
также является критерием подобия.
3.4. ПОДОБИЕ И МОДЕЛИРОВАНИЕ ТУРБОМАШИН.
БЕЗРАЗМЕРНЫЕ ХАРАКТЕРИСТИКИ ТУРБОМАШИН
Здесь будут рассмотрены условия подобия процессов в турбома-
шинах и построение их безразмерных характеристик.
Зададим некоторый режим работы неохлаждаемой турбомашины
(турбины или компрессора) и выберем размерные определяющие параметры,
которые характеризуют этот режим. Если рассматривать группу подобных
турбомашин, то они должны быть геометрически подобны и, следовательно,
конкретную турбомашину можно характеризовать одним линейным
размером. В качестве характерного размера удобно принять диаметр какой-либо
(например, первой) ступени d.
Режим работы будет определен, если задать параметры газа на входе в
турбомашину, давление на выходе из нее и частоту вращения ротора. Таким
образом, чтобы выделить конкретную турбомашину из группы ей подобных
и задать определенный режим ее работы, следует считать известными (п —
частота вращения):
d, p, Г„ р2, п. C.24)
Индексом 1 отмечены параметры перед турбомашиной, а индексом 2 — за
ней. Следует подчеркнуть, что это не единственный и не во всех случаях
самый удобный способ фиксировать режим работы турбомашины.
Так, например, можно задать режим работы турбомашины, выбрав
следующие размерные параметры:
dyply Тът,п. C.25).
Здесь вместо давления на выходе задан расход газа через турбомашину.
Это во многих случаях удобный способ задания режима работы, однако он
применим не всегда. Так, если расход газа равен критическому, то в
варианте задания C.25) давление за турбомашиной не может быть однозначно
определено.
Ввиду этого представляет интерес и другой вариант задания режима
работы, например, для ступени турбины, в которой возникают сверхзвуковые
скорости. Режим работы в этом случае можно однозначно определить, задав
параметры:
d% m, р%ь Г2, п. C.26)
39

Поэтому выбор размерных параметров, характеризующих режим работы
турбомашины в целом или ступени турбомашины, должен зависеть от
существа задачи и удобства анализа.
Помимо фиксации режима работы турбомашины, для анализа условий
подобия необходимо также указать характеристики, определяющие свойства
рабочего тела. Для упрощения задачи будем рассматривать только
совершенный газ и пренебрегать теплообменом. В таком случае рабочее тело
может быть характеризовано параметрами:
Таким образом, в любом из вариантов в качестве определяющих должно
быть выбрано восемь размерных параметров. Если для определенности
выбрать вариант задания C.25), то определяющими параметрами будут
следующие:
d, ръ Тъ т, я, #, ср, и. C.27)
Размерности этих восьми параметров можно выразить в системе СИ
через размерности четырех единиц измерения: L, Т, М, К. Напомним, что
такие размерности, как джоуль и паскаль, можно рассматривать как
производные и выразить через размерности основных единиц физических величин.
Тогда согласно П-теореме из восьми размерных определяющих
параметров можно образовать четыре безразмерных. В данном случае в качестве
таких безразмерных критериев удобно выбрать приведенные ниже.
1. Показатель изоэнтропы
х = cp/cv=cpl(cp—R). C.28)
2. Безразмерный расход газа (по существу величину,
пропорциональную отношению расхода к критическому расходу)
~G^mVRT\ld2px. C.29)
3. Отношение окружной скорости на среднем радиусе к скорости звука
Ми = и/а1 = ndnlV*RT~i • C.30)
4. Число Рейнольдса
Re =udp1/ii = up1d/\iRTv C.31)
Тогда на основании П-теоремы можно получить такую
функциональную зависимость: П = F (и, G, MM, Re).
Здесь под критерием П понимается любая искомая функция,
представленная в безразмерном виде согласно правилам физического подобия
(которая зависит только от выбранных аргументов).
Полное соблюдение условий подобия при испытании моделей турбома-
шин затруднительно. Так, практически невозможно соблюсти полное
геометрическое подобие натуры и модели по зазорам между ротором и статором
и относительной шероховатости поверхности лопаток. Обычно невозможно
выдержать равенство чисел Рейнольдса, так как размеры модели обычно в
два-три раза меньше натуры, а соответствующее повышение плотности [см.
формулу C.31)] недостижимо.
Ввиду этого приходится применять частичное моделирование, а затем
вводить поправки к опытным результатам. Поправки на изменение утечки
через зазоры или влияние толщин выходных кромок лопаток могут быть
определены расчетным путем. Также расчетом или вспомогательными
исследованиями могут быть оценены поправки на совместное влияние числа Re и
шероховатости поверхности.
40

Важное значение имеет вопрос о влиянии свойств рабочего тела на
процессы в компрессорах и турбинах. Практическое значение этой проблемы
состоит в том, что приходится проектировать турбомашины, которые должны
работать на газах с физическими свойствами, резко отличающимися от
свойств воздуха.
Так, например, газовая постоянная гелия в 7,2 раза, коэффициент
теплопроводности в 6 раз и показатель изоэнтропы в 1,19 раза больше, чем у
воздуха.
С другой стороны, в практике моделирования турбомашин применяют в
качестве рабочего тела фреон, газовая постоянная которого в 4,75 раза, а
показатель изоэнтропы в 1,27 раза меньше, чем у воздуха, Поскольку скорость
звука в фреоне существенно меньше, чем в воздухе, то это позволяет
значительно снизить мощность и частоту вращения экспериментальных
установок при соблюдении подобия по числу Маха. Однако при этом возникает
вопрос о необходимых поправках, так как показатель изоэнтропы является
одним из критериев подобия. Подобная задача встает также при
моделировании ступеней паровых турбин на воздухе и ступеней газовых турбин на
относительно холодном воздухе. Правда, в последних случаях отклонение
показателя изоэнтропы не будет столь значительным.
Положим, что модельная и натурная турбомашина работает на одном
и том же газе, а по числу Re могут быть, если это необходимо, введены
поправки.
Тогда процессы в турбомашинах будут подобны, если они геометрически
подобны, а сходственные критерии одинаковы. Из формул C.29) и C.30)
получим
/3 33)
Здесь индексами мин отмечены параметры, относящиеся
соответственно к модели и натуре.
Из соотношений C.32) и C.33) можно найти связь между
коэффициентами подобия, необходимыми для пересчета характеристик. Обозначим
H, Kd=dJdH, Kp=pJph, Кт = Ты/Тн, Кп=пы/пл. C.34)
Тогда из C.32), C.33) и C.34) следует
KmVWr^KlKP9 Kd Кп = VTt- C.35)
Для установления связи между искомыми характеристиками следует
подставить их сначала в безразмерном виде. Пусть, например, надо найти
внутреннюю мощность натурной ступени турбины по измеренной на стенде
мощности модельной ступени. Соотношение между указанными мощностями
^м/^„ = (тмЯмЛ )/(тнЯнЧ). C.36)
Здесь внутренние КПД даны без индексов, так как они у подобных
ступеней одинаковы: г\ы = цн = ц.
Для совершенного газа теплоперепад
н=-^зт RTl [1 - (р*/р^ ]
4!

20 25 т,кг/с
Рис. 3.3. Характеристика осевого
компрессора, построенная в
размерах переменных. Кружком отмечена
расчетная точка
0,5 0,8 1,0 1,2 т
Рис. 3.4. Характеристика осевого
компрессора, построенная в
безразмерных переменных (универсальная
характеристика)
Поскольку отношения давлений, взятых в сходственных сечениях, для
модели и натуры одинаковы, то отношение теплоперепадов равно отношению
абсолютных температур. Тогда из формул C.37), C.34) и C.36) получим
ш? р Iр Г?2 TS2 \flf~ C 38)
Аналогичным образом можно найти коэффициенты пересчета для
других величин, например крутящего момента.
Выше были рассмотрены соотношения между параметрами подобных
турбомашин. Другим приложением теории подобия к турбомашинам
является установление подобных режимов работы одной и той же турбомашины.
Так, два режима работы компрессора могут быть подобны, хотя абсолютные
значения параметров в этих режимах различны. Установление подобных
режимов позволяет строить характеристики в безразмерном виде и, самое
главное, с меньшим числом переменных. Вместе с тем характеристики являются
более общими, т. е. позволяют получать на основании условий физического
подобия сведения о тех режимах работы, на которых фактически испытания
не производились.
Следует отметить, что в данном приложении вопрос о соблюдении
подобия по числам х и Re, если не совсем отпадает, то все же стоит не так остро,
так как в разных режимах эти величины хотя и будут отличаться, но не
столь значительно.
Из C.32) и C.33) следует, что в подобных режимах должны соблюдаться
условия
Pi
eidem, !L_ eidem.
C.39)
Полученные критерии удобны в инженерных приложениях, так как в
них входят величины, которые характеризуют режим эксплуатации.
Неудобство состоит в том, что эти критерии не безразмерны (так как
отброшены размерные постоянные), и кроме того, величина их ничего не говорит о
характере работы турбомашины, например, близости к расчетному режиму.
42

Эти недостатки будут устранены, если критерии C.39) отнести к их
значению в расчетном режиме работы турбомашины. Тогда получим
безразмерные параметры, которые называют приведенным расходом и приведенной
частотой вращения:
AS ?/Г /Ж C.40)
т0 Pi V Тю п0
Здесь индексом нуль отмечены параметры при расчетном режиме
работы.
Безразмерную характеристику турбомашины можно представить в виде
n-F(m, n). C.41)
Под критерием П можно понимать, например, КПД, степень повышения
давления в компрессоре, приведенную мощность.
На рис. 3.3 дана экспериментально полученная характеристика осевого
компрессора. Испытания проведены при давлении на входе рх =
= 1,0-Ю5 Па и температуре 7\ = 295 К. Расчетный расход m = 25 кг/с,
расчетная частота вращения п = 100 1/с. Характеристика приведена в
размерных величинах (получена во время испытаний).Такой характеристикой
можно пользоваться только при указанных параметрах воздуха на входе.
Пересчитав ее к приведенным параметрам (рис. 3.4) по формулам C.40) и
C.41), т. е. по существу изменив только масштабы по осям координат и на
линиях постоянной частоты вращения, получим универсальную
характеристику. Такую характеристику можно использовать при различных
параметрах воздуха на входе в компрессор без дополнительных испытаний.
Вопросы для самопроверки
1. Каковы условия подобия физических явлений?
2. Что такое коэффициенты подобия и как их вычислить?
3. Что называют полным и частичным подобием?
4. Какие преимущества дает применение теории подобия?
5. Запишите выражение для безразмерного крутящего момента на валу турбины.

^ЛАВА 4
ОДНОМЕРНЫЕ ТЕЧЕНИЯ
4.1. УРАВНЕНИЯ СОХРАНЕНИЯ ДЛЯ ОДНОМЕРНЫХ ТЕЧЕНИИ
Одномерные установившиеся течения являются самым
простым видом течений. При рассмотрении одномерных течений делают
основное предположение о том, что параметры потока не меняются по
поперечному сечению канала (или что эти параметры осреднены по сечению). В связи
с этим предполагают, что хотя площадь поперечного сечения канала и
может меняться произвольным образом, однако достаточно плавно. Поэтому
правильнее было бы рассматривать не одномерную, а квазиодномерную
задачу. Значение одномерных задач для технических расчетов трудно
переоценить, так как в них удается учесть все виды воздействий на поток:
подвод теплоты, трение, подвод другого газа или жидкости, конденсацию,
испарение, горение и т.д. Конечно, все полученные результаты будут
приближенными, но их получают очень просто и они обычно в целом достаточно
хорошо согласуются с экспериментальными. Отсюда не следует делать
вывод о том, что вообще все задачи могут быть удовлетворительно решены в
одномерной постановке.
Следует отметить, что полнее понять происходящие процессы и
оптимизировать конструкцию можно после рассмотрения более сложных плоских
или пространственных задач.
Уравнения сохранения массы, количества движения и энергии для
установившегося одномерного течения могут быть получены из общих уравнений
сохранения, выведенных в подразд. 2.1, 2.2, 2.3. Однако проще получить
эти уравнения непосредственно для одномерного течения, тем более что при
исследований поставленной задачи целесообразно ввести некоторые
изменения.
Рассмотрим установившееся течение сжимаемой жидкости вдоль трубы с
переменной площадью поперечного сечения S = S (х), где координата х
измеряется вдоль оси канала (рис. 4.1). Уравнение неразрывности, т. е. закон
сохранения массы, йримет вид
т = puS. D.1)
Эта запись выражает тот факт, что через любое поперечное сечение трубы
в единицу времени проходит постоянная масса жидкости.
Запишем уравнение сохранения количества движения для идеальной
жидкости, предположив, что силы трения отсутствуют:
d (mu) = —d (pS) + pdS. D.2)
В этом предположении изменение количества движения жидкости вдоль
трубы может быть вызвано только действием сил давления.
Первый член уравнения D.2) представляет приращение количества
движения текущей жидкости, второй член равен сумме сил давления,
действующих на поперечные сечения выделенного элемента жидкости. Знак минус
44

объясняется тем, что при d(pS) >0 эта
сила действует против движения.
Третий член учитывает силы давления,
действующие на жидкий элемент со
стороны стенок трубы в проекции на
направление движения. Расход массы на
основании уравнения неразрывности
постоянен вдоль трубы. Вынесем т в
уравнении D.2) за знак дифференциала и
объединим второй и третий члены этого
уравнения. Тогда получим уравнение
движения для идеальной жидкости в
виде
udu + dp/p = 0. D.3)
В данном случае будем считать, что труба, по которой течет жидкость,
теплоизолирована, т. е. нет подвода теплоты извне. Тогда поток энергии
через каждое поперечное сечение трубы постоянен:
Рис. 4.1. Одномерное течение в трубе
Из условия постоянства потока массы следует запись уравнения энергии
в дифференциальной форме
dh^O, D.4)
а также в конечном виде
и2/2 + Л = const.
D.5)
Получены три основных уравнения сохранения: массы D.1), количества
движения D.3) и энергии D.5). Уравнение движения в форме D.3)
справедливо только для идеальной жидкости, т. е. при отсутствии сил трения.
Уравнение энергии в формах D.4), D.5) справедливо и при наличии сил трения, но
при отсутствии теплообмена. Следовательно, система уравнений в
приведенной форме применима только для изучения движения невязкой,
нетеплопроводной жидкости.
Из уравнений D.3) и D.4) следует dh — dp/p = 0.
Из термодинамики известно, что Tds = dh — dp/p.
Сравнив два последних уравнения, приходим к выводу что при
введенных ограничениях энтропия текущей сжимаемой жидкости должна быть
постоянной ds = (dh — dp/p)/T = 0, s = const. Следовательно, течение
невязкого нетеплопроводного газа является изоэнтропийным. Тогда между
термодинамическими параметрами существуют соотношения, справедливые для
изоэнтропийного процесса:
Поскольку условие постоянства энтропии было получено из
сопоставления уравнений движения и энергии, то одно из этих уравнений можно
заменить уравнением D.6), Очевидно, что это допустимо только при сделанных
ограничениях об отсутствии трения и теплообмена.
4.2. СКОРОСТЬ РАСПРОСТРАНЕНИЯ ЗВУКА
Введем важное в теории течения сжимаемой жидкости понятие о
скорости распространения звука. Скоростью звука называют скорость
распространения слабых возмущений в упругой среде.
45

Пусть сжимаемая жидкость с
заданными параметрами р, р, Т находится в
длинной трубе, ограниченной слева поршнем
(рис. 4.2). В некоторый момент времени
поршень начинает двигаться слева
направо с постоянной скоростью du, сжимая
газ. В газе начинает распространяться
слабая волна сжатия, фронт которой /—/
отделяет сжатую массу газа с
параметрами р + dp, р + dp, Т + dT от области,
куда возмущения еще не проникли.
Скорость движения фронта слабой волны
(относительно газа) а называют скоростью
звука.
Через время dt фронт волны передвинется из сечения 1—/ в сечение
2—2 и при этом будет сжата новая порция газа. Из уравнения
неразрывности следует (S — площадь сечения трубы) (р + ф) Sdudt = Sadpdt. Слева
в этом уравнении — масса газа, прошедшая за время dt со скоростью du
через сечение /—У, а справа — вызванное этим приращение массы в
элементарном объеме. Тогда с точностью до малых первого порядка получим
du
Рис. 4.2
волны
1 1
p + dp
p + dp
T+dT
7
. Распростр
1
1 '
1 '
I T
анен
Z
adT
ле слабой
adp = pdu.
D.7)
Из уравнения движения следует Sdpdt = Sadt (p + dp)du. Слева стоит
импульс сил, действующих на элемент, а справа приращение
количества движения элемента. Отсюда получим второе соотношение
dp. D.8)
Исключим из уравнений D.7) и D.8) du, получим формулу для
определения скорости звука
а=У dp/dp. D.9)
При распространении слабых возмущений можно пренебречь
теплообменом, что хорошо подтверждается опытом, и считать, что
плотность и давление связаны уравнением изоэнтропы.
Выразим производную давления по плотности с помощью
формулы D.6):
к — 1— р о* — 1 — к р
р р
Тогда из D.9) найдем скорость распространения звука
Воспользуемся уравнением состояния совершенного газа
D.10)
DЛ1)
Выразим скорость распространения звука через температуру
D.12)
В движущемся газе температура является переменной величиной и
поэтому можно говорить только о местной скорости звука, определенной в
данной точке.
46

4.3. ОДНОМЕРНОЕ ИЗОЭНТРОПИЙНОЕ ТЕЧЕНИЕ
Прежде чем переходить к общему анализу одномерного
движения жидкости при различного рода воздействиях на поток, исследуем
подробнее один важный частный случай.
Рассмотрим одномерное установившееся течение идеальной сжимаемой
жидкости по теплоизолированной трубе переменного поперечного сечения.
При этих предположениях, как показано в разд. 4.1, течение можно описать:
уравнением неразрывности D.1), уравнением движения D.3) и уравнением
энергии D.5). Там же было показано, что в этом частном случае течения
энтропия сжимаемой жидкости остается постоянной (s = s0 — const), а
значит термодинамические параметры связаны уравнением изоэнтропы D.6).
Проинтегрируем уравнение движения D.3), записанное в
дифференциальной форме. Выразив плотность через давление из уравнения
изоэнтропы D.6) и подставив в уравнение D.3), после интегрирования получим
— + — ^(-M~=const. D.13)
2 х — 1 ро \ Ро I
Справа стоит постоянная интегрирования, которую удобно определить
через так называемые параметры изоэнтропийного торможения.
Параметрами торможения называют параметры жидкости в той
точке, где скорость равна нулю. В том случае, если торможение потока до
скорости, равной нулю, произведено при постоянной энтропии, то такие
параметры жидкости называют параметрами изоэнтропийного торможения.
Следует подчеркнуть, что при определении параметров торможения не
обязательно имеется в виду реальное торможение потока. Параметры
торможения можно формально вычислить в любой точке потока по
соответствующим формулам. Так, например, параметры изоэнтропийного торможения
можно вычислить в данной точке потока, хотя само течение может и не быть
изоэнтропийным. Вместе с тем важно отметить, что параметры
изоэнтропийного торможения являются физическими понятиями, т. е.
соответствующие параметры могут быть измерены, хотя, конечно, с определенной
погрешностью, так как при измерении нельзя полностью исключить
теплообмен. Измерение параметров изоэнтропийного торможения имеет большое
значение при проведении аэродинамических экспериментов.
В уравнении D.13) обозначим индексом нуль параметры изоэнтропийного
торможения. Тогда, очевидно, нужно принять р = р0 при и = 0, и,
следовательно, правая часть уравнения будет записана через параметры
изоэнтропийного торможения:
2 х-1 Ро \ Ро )
D.14)
Это уравнение имеет большое значение в теории течения и носит
название уравнения Бернулли для сжимаемой жидкости. Подчеркнем еще раз,
что оно пригодно только для расчета изоэнтропийных потоков. Напомним,
что ранее было выведено уравнение Бернулли B.39) для несжимаемой
жидкости.
Получим теперь различные виды записи уравнения энергии. В уравнении
D.5) выразим правую часть через энтальпию торможения:
1г2/2 + Л=Л0. D.15)
Это уравнение отражает тот факт, что сумма кинетической и тепловой
энергии текущей сжимаемой жидкости постоянна.
47

При постоянной теплоемкости энтальпию
можно выразить через абсолютную
температуру и записать уравнение энергии D.15) в таком
виде:
иУ2 + срТ==срТ0. D.16)
Исключим из уравнения D.16) температуру с
помощью уравнения состояния D.11) и
воспользуемся известными формулами для
термодинамически совершенного газа:
R=cp—cv; x=cp/cv. D.17)
После элементарных преобразований
получим еще один вид уравнения энергии:
р
р
Рис. 4.3. Определение
параметров торможения в
тепловой диаграмме
_25_>?<L D.18)
2 х-Ч р х— 1 ро
Напомним, что уравнение энергии в форме
D.15), а также в формах D.16), D.18)
эквивалентны и пригодны для расчета течений без
теплообмена. Уравнения энергии применимы и для
расчета неизоэнтропийных потоков, например
одномерного течения с трением в
теплоизолированной трубе.
Сравним уравнения D.14) и D.18). Уравнение Бернулли D.14)
связывает два параметра (скорость и давление) и справедливо только для
изоэнтропийного течения. Уравнение энергии D.18) связывает три параметра
(скорость, давление и плотность), но оно справедливо и для неизоэнтропийного
течения. Если в уравнении D.18) исключить плотность, выразив ее через
давление с помощью уравнения изоэнтропы D.6), то оно совпадает с
уравнением D.14).
Поясним понятие параметров торможения с помощью тепловой
диаграммы. Пусть точка / (рис. 4.3) соответствует статическим параметрам и в ней
известны скорость потока и, давление р и температура Т. Если затормозить
поток при постоянной энтропии до скорости, равной нулю, то параметрам
изоэнтропийного торможения соответствует точка 0. Эту точку можно
найти прямо по тепловой диаграмме, отложив от точки / вверх отрезок, равный
u2l2. Температуру торможения можно найти и расчетом по уравнению
энергии D.16), а затем определить давление изоэнтропийного торможения с
помощью уравнения изоэнтропы D.6).
На рис. 4.3 показано также торможение потока до скорости, равной
нулю, по линии 1 — 0'. Из уравнения энергии D.15) следует, что скорость
будет равна нулю для той же изоэнтальпы Ло, что и ранее. Следовательно,
энтальпия торможения не зависит от того, как тормозят поток, так как вся
кинетическая энергия все равно переходит в тепловую (теплообмена нет).
Температура торможения также не зависит от того, как тормозят поток, если
газ термодинамически совершенен. Однако давление торможения рб < Ро>
т. е. зависит от процесса торможения.
Уравнения D.14), D.16) устанавливают связь между скоростью потока,
давлением и температурой. Найдем теперь зависимость между заданным
законом изменения площади трубы и скоростью.
Прологарифмировав уравнение неразрывности D.1) и найдя приращение,
получим
dp/p+du/u+dS/S =
D.19)
48

Запишем уравнение Бернулли D.3) в таком виде!
udu + (dp /dp) (dp/p) = 0.
Воспользуемся формулой для скорости звука D.9) и преобразуем
предыдущее уравнение к виду
udu+a2dp/p = 0. D.20)
Следует отметить, что в данном случае такая замена возможна, так как
и уравнение . Бернулли, и формула для скорости звука записаны
для изоэнтропийного течения, т. е. изменения плотности однозначно
связаны с изменением давления.
Отношение скорости потока к местной скорости звука называется числом
Маха и является важной характеристикой в теории течения сжимаемой
жидкости:
М = и/а. D.21)
На основании выражений D.20), D.21) следует такая запись уравнения
Бернулли:
_^Р__М2^ D.22)
р и
Следовательно, число М может служить мерой сжимаемости
движущейся среды. Чем больше число М, тем больше относительное изменение
плотности, вызванное изменением скорости потока. Если М< 1, то поток
называют дозвуковым, если М > 1, то — сверхзвуковым.
Исключив с помощью уравнения D.22) плотность из уравнения D.19),
получим искомую формулу, связывающую изменение площади трубы (вдоль
оси х) с изменением скорости:
Проведем сначала качественный анализ полученной зависимости.
1. Скорость потока меньше местной скорости звука (М < 1). Если труба
суживается в направлении течения (dS < 0), то скорость потока возрастает,
так как du >0. Если труба расширяется (dS >0), то скорость вдоль трубы
уменьшается (du < 0).
2. Скорость потока больше местной скорости звука (М >1).
Сверхзвуковой поток ведет себя противоположно дозвуковому. В суживающейся
трубе (dS < 0) скорость уменьшается (du < 0), а в расширяющейся —
возрастает (du >0).
Следовательно, для того чтобы разогнать дозвуковой поток до
сверхзвуковой скорости, необходимо сначала суживать трубу, а затем
расширять. Переход через скорость звука (М = 1) может произойти только в
минимальном сечении трубы, так как при М = 1 только при dS = 0 левая
часть уравнения D.23) не становится бесконечно большой. Такие трубы (или
каналы) называются соплами Лаваля, который впервые применил их в
паровых турбинах для получения сверхзвуковых скоростей.
4.4. ГАЗОДИНАМИЧЕСКИЕ ФУНКЦИИ
В разд. 4.3 получены основные уравнения для расчета
одномерного изоэнтропийного потока. Анализ уравнений и расчеты могут быть
значительно упрощены, если ввести безразмерные параметры. Это
позволяет также затабулировать основные функции.
49

Так, в качестве безразмерной скорости можно принять число
РЛ=и/а. D.24)
Температуру, давление и плотность удобно измерять в долях от их значения
в заторможенном потоке:
т = Г/Го, е= р/р0, б = р/р0. D.25)
Установим зависимости между безразмерными параметрами. Запишем
уравнение энергии D.18), заменив отношение давления к плотности с
помощью формулы D.10) для скорости звука:
^ ^^ D.26)
х—1 х—1
Здесь справа стоит скорость звука, подсчитанная по температуре
торможения, которая для заданного потока постоянна (как следует из уравнения
энергии и формулы для скорости звука):
а0 - j/x/WPo - КкК70. D.27)
Скорость звука, записанная в левой части уравнения D.26), переменная
величина, так как зависит от местной скорости потока. Поделив все члены
уравнения энергии D.26) на а2 и воспользовавшись обозначением D.24) и
очевидным условием аЬ/а2 = TJT, получим зависимость для безразмерной
температуры
— = -I*- - 1 + —— М2. D.28)
т Т 2 v
Из полученного уравнения и уравнения изоэнтропы D.6)
следуют формулы для безразмерных давления и плотности:
1\ D.29)
". D.зо)
В точке, где М = 1, скорость потока равна местной скорости звука.
Такую скорость называют критической и отмечают специальным индексом
и* = а*. Понятие критической скорости является весьма важным, так как
поток со скоростью ниже критической будет дозвуковым, а со скоростью выше
критической —сверхзвуковым. Свойства дозвуковых и сверхзвуковых
потоков различны, как можно было понять из предварительного анализа
формулы D.23).
Выразим постоянную (для данного потока) правую часть уравнения
энергии D.26) через критическую скорость:
 . а2 = <** | в? ^ *+1 а\ - /4 3П
2 х—1 2 х—1 х—1 2 ' К
Сравнив правые части уравнений D.26) и D.31), получим, что критическую
скорость можно выразить через температуру торможения
50

В точке, где скорость равна критической, все параметры также
называются критическими. Соотношения между критическими параметрами и
параметрами торможения устанавливаются из формул D.28) — D.30) при
М = 1:
__ Г* __ 2 __ р* __
То х+1 ро
Р* /2 У /С* *) ,» QQ\
= = 1 . D.оо)
Ро \ х+1 /
В частности, для воздуха (х = 1,4): т* = 0,833, е* = 0,528, 6* = 0,634;
для перегретого водяного пара (х = 1,3): т^ = 0,870, е^ = 0,546, 6^ =
= 0,628.
Во многих задачах вместо безразмерной скорости М удобно
использовать другую безразмерную скорость
D.34)
которая пропорциональна скорости потока, так как критическая скорость
а* постоянна в энергетически изолированных потоках. Между введенными
безразмерными скоростями существует однозначная зависимость. Поделив
члены уравнения D.31) на и2 и выразив из полученного уравнения М2 или
X2, найдем
М*= ^ , Л»= (Х+1)М2 D 35)
(Х+1) — (х— 1) № 2+(х— 1)М2 ' v
При и = 0 получим: М = 0, X = 0; при и = а* получим: М = 1, X = 1.
При истечении в абсолютный вакуум (Т —>- 0, а ->¦ 0)
D.36)
С помощью первой формулы D.35) выражения для безразмерных
параметров D.28) — D.30) могут быть записаны через безразмерную скорость X:
x=-J-=l_^U"; D.37)
D.38)
в—Е /i_JLnl х«У/<к""П. D.39)
РО \ Х+1 j ^
Легко видеть, что безразмерные параметры т, е, 6 изменяются в пределах
от 0 до 1, что представляет известное удобство. Для расчета потока
необходимо установить формулу, связывающую безразмерные параметры с
безразмерной площадью трубы.
Сечение трубы, в котором устанавливается критическая скорость,
называется критическим, и площадь его обозначается S*. Из рассуждений,
проведенных в подразд. 4.3, следует, что критическим может быть только то
сечение, где площадь трубы S (х) достигает минимума. Однако обратное
утверждение не справедливо, так как минимальное сечение может и не быть
критическим, если там не достигается критическая скорость.
Безразмерную площадь трубы можно определить отношением S/S*,
однако удобнее рассматривать отношение q = SJS, так как оно изменя-
е1ся р стандартных пределах от 0 до 1. С помощью уравнения неразрывно-
51

сти D.1) функцию расхода q можно представить также через отношение
плотностей и скоростей в двух сравниваемых сечениях:
*. D.40)
Представив правую часть этого выражения в таком виде:
q
Р* Ро а*
легко выразить q через безразмерную скорость А, с помощью формул D.33),
D.34), D.39) или М по формуле D.35):
D.41)
2A-К)
м.
Следует отметить, что обратная зависимость X (<?) (и М (q)) является
двухзначной, так как заданному q соответствуют по одному значению Х<С 1 и
X > 1. Смысл этого ясен из определения q через отношения площадей, так как
S = S* при X = 1 и S > S* при Я > 1 и X < 1.
Выше было отмечено, что параметры изоэнтропийного торможения
можно определить в любой точке потока, хотя фактически в этой точке скорость
неравна нулю. Точно также можно формально найти критические
параметры, критическую площадь и функцию расхода q> хотя фактически в потоке
критическая скорость может не достигаться. Найденная формально
критическая площадь всегда меньше любой действительной площади поперечного
сечения трубы, и только если она равна самой минимальной площади, то там
действительно возникла критическая скорость.
Зависимости D.28) — D.30), D.37) — D.39), D.41) называются
газодинамическими функциями и для них составлены таблицы, которые сильно
упрощают расчеты.
Рассмотрим решение двух задач с применением газодинамических
функций. Эти задачи представляют самостоятельный технический интерес.
Сначала, исследуем задачу о переходе через скорость звука в соплах Лаваля,
которая в разд. 4.3 была рассмотрена только качественно. Функция расхода
q D.41) по существу является интегралом уравнения D.23).
Отложим по оси ординат (рис. 4.4) отношение произвольной площади S к
минимальной площади заданного сопла Smln. Если в минимальном сечении
возникает критическая скорость, то Smln = S* и для этого режима
течения S/Smin = SIS* = l/q. Значению q = 1 соответствует X = 1. Любому
другому значению q соответствует два значения X, которые можно найти по
формуле D.41) или газодинамическим таблицам. Так, например, в сечении
Si/Smln определяем точки / и Г, а в сечении S2/Smin —точки 2 и 2'. Тогда
режим 102 соответствует разгону дозвукового потока до сверхзвуковой
скорости, а режим Г02' — торможению сверхзвукового потока до дозвуковой
скорости. Возможны также режимы течения 102' и Г02, Возможны также
другие режимы течения, при которых скорость в минимальном сечении не
равна критической. Зададим в сечении Si/Smin скорость, выбрав точку 3.
По соответствующему значению X можно найти q = S^/St. Отсюда S* =
= 4\SX Ф Smln. Значение q в любом другом сечении сопла находится по
формуле q = SJS = qiSx/S. Соответствующий режим изображается кривой 345,
причем скорости всюду дозвуковые. Аналогичный режим для
сверхзвуковых скоростей соответствует линии 678.
52

Рис. 4.4. Режимы
течений в соплах Лаваля
Рис. 4.5. Течение через
суживающееся сопло
Ро
Го
Ро
Однако в заданном сечении скорость не может быть выбрана совершенно
произвольно. Так, если выбрать скорости в области ЮГ (или 202'), то такое
течение не может быть реализовано, что ясно из протекания построенных там
кривых. Это объясняется тем, то расходы газа, соответствующие этим
скоростям, не могут пройти через фиксированное минимальное сечение.
Поставим задачу определения расхода через суживающееся сопло
(рис. 4.5) при заданных площади выходного (минимального) сечения S,
параметрах торможения р0, То и давления р в пространстве за соплом.
Запишем уравнение неразрывности для выходного сечения, полагая, что
в нем устанавливается давление р и соответствующие ему скорость и
плотность:
m=puS. D.42)
Определим скорость потока в выходном сечении сопла из уравнения
D.13):
к—1
U =
х—1 Ро L \ Ро /
Плотность газа в выходном сечении выразим через известную плотность
изоэнтропийного торможения с помощью уравнения изоэнтропы D.6):
Теперь можно определит^ расход через суживающееся сопло по формуле
D.42) через отношение давлений е = р/р0:
D.43)
х-1
При е=1, как и следовало ожидать, расход равен нулю. Однако он
равен нулю и при е = 0, что очевидно противоречит логике. Для объяснения
этого парадокса фиксируем параметры торможения и будем изменять е,
изменяя только давление в пространстве за соплом.
53

Найдем то е, при котором расход т достигает максимального значения.
Для этого достаточно найти то е, при котором выражение в скобках формулы
D.43) равно максимуму. Продифференцировав выражение в скобках,
приравняв результат нулю и выразив е, получим
2 \х/<х-1) лл.
что соответствует по формуле D.33) критическому отношению давлений. Это
объясняет парадокс, так как применение формулы D.43) при е < е* для
определения расхода недопустимо; давление в минимальном сечении сопла не
может быть меньше критического. Это было показано при качественном
анализе формулы D.23). Дозвуковой поток внутри суживающегося сопла
ускоряется, но скорость в минимальном сечении не может превосходить
критическую скорость, а следовательно, давление там не может быть ниже
критического давления.
Предположение, что давление в выходном сечении суживающегося сопла
равно давлению в окружающем пространстве, справедливо только, если
давление за соплом больше или равно критическому. Если же давление в
пространстве за соплом меньше критического, то в выходном сечении сопла
устанавливается критическое давление.
В том случае, если в минимальном сечении параметры равны
критическим, то расход называют критическим:
т* •= р* w* S* = р* я* S*. D.45)
Критический расход можно определить так же, как максимальный
расход при фиксированных параметрах торможения.
Подставим в формулу D.43) е = е* из формулы D.44) и заменим
плотность изоэнтропийного торможения через соответствующие давление и
температуру с помощью уравнения состояния. Тогда получим формулу для
определения критического расхода в таком виде:
х-Н
* & D.46)
Критический расход будет выражен в килограммах на секунду, если принять
для воздуха С = 0,0405 с«К1/2/м, а для перегретого водяного пара С =
-0,0311 с-К^/м.
Покажем, что расход газа через сопло можно определять с помощью
газодинамических функций. Фиксируем параметры торможения ро> То и
будем менять давление в пространстве за суживающимся соплом в таких
пределах, что е = plp0 > е*. В этом случае давление в выходном сечении
сопла равно давлению в окружающем пространстве за соплом. При е >е^
для расхода справедлива формула D.42), а при е = е* для критического
расхода можно записать формулу D.45).
Найдем отношение произвольного расхода через суживающееся сопло к
критическому расходу при тех же параметрах торможения:
т puS ри /А л*
-—. = —г =—^ =q. D.47)
При выводе этой формулы учтено, что в данном случае S численно равно
S*, так как это одна и та же площадь выходного сечения сопла. Таким
образом, газодинамическую функцию расхода q можно трактовать как
отношение произвольного расхода через суживающееся сопло к критическому
расходу при тех же параметрах торможения,
54 -

Воспользовавшись формулами D.43), D.46) и D.47), получим выражение
для функции расхода через отношение давлений:
-4—]/-
х+1
D.48)
Эта формула используется для расчета расхода через суживающиеся
сопла, так как в практических задачах известны давление перед соплом и за
ним. Расход можно найти по формуле D.47), в которую входит критический
расход, представленный формулой D.46), и функция q. которую следует
найти по таблицам газодинамических функций или формуле D.48). На рис. 4.6
показаны зависимости
функции расхода через
суживающееся сопло от отношения
давлений при постоянных
параметрах изоэнтропийного
торможения.
ч
0,8
0,6
0,*
0,1
\
\
}
0,2 0,Ь е, 0,6 0,8 €
Рис 4.6. Зависимость функции
расхода от относительного
давления за суживающимся
соплом (/эо=const, Го=const,
14)
0,2 0Л 0.6 0.8 1.0
Рис. 4.7. Зависимость функции расхода от
относительных давлений перед и за
суживающимся соплом (х=1,4)
При расчете паровых и газовых турбин необходимо определять расход
через сопла при изменении как давления за ними, так и параметров
торможения. Из зависимости D.43) следует, что расход обратно пропорционален
корню квадратному из абсолютной температуры торможения, так как
плотность обратно пропорциональна температуре. Зависимость расхода от
давления изоэнтропийного торможения сложнее, так как при изменений
давления р0 меняется также отношение р/р0.
Для наглядного представления зависимости расхода от давления перед и
за соплом удобно ввести в качестве масштаба некоторое максимальное
давление изоэнтропийного торможения, которое обозначим рот. Всегда можно
выбрать такое максимальное давление, что в конкретной группе задач нет
давления, которое превосходит рот.
Отнесем давление перед соплом и давление в пространстве за соплом рг к
максимальному давлению и введем обозначения:
— Ро/Рот* h—
D.49)
55

Величины 80 и бг изменяются в стандартных пределах!: О < е0 < 1,
О < ег < е0. Критический расход по формуле D.45) пропорционален
давлению торможения и поэтому при постоянной температуре торможения
максимальный критический расход т^т соответствует давлению рот,
причем mJm^m = E0. Обозначим q0 отношение произвольного расхода через
сопло к максимальному критическому расходу q0 = т/т#т, 0 < q0 < 1.
После введения указанных переменных с учетом формулы D.47) получим
q9 ^=m/th*m = qmJm*m=sQ q. D.50)
Функция q в выражении D.50) может быть определена через отношение
давлений е из уравнения D.48), однако е следует прежде выразить через
введенные переменные D.49): е = е1/е0. В итоге выразим функцию расхода
<7о от относительного давления торможения е0 и относительного давления за
СОПЛАМ 8x1
?
На рис. 4.7 эта зависимость представлена графически поверхностью в
координатах е0, гъ q0. На криволинейном участке поверхности ОВС расход
через сопло меньше критического расхода. На участке поверхности,
представленном плоскостью ОАВу расход равен критическому. На поверхности
нанесена сетка линий. На линиях одного семейства постоянно относительное
давление торможения, на линиях другого — относительное давление за
соплом.
4.5. ОДНОМЕРНЫЕ ТЕЧЕНИЯ ПРИ РАЗЛИЧНЫХ ВОЗДЕЙСТВИЯХ
НА ПОТОК
В подразд. 4.3 и 4.4 рассмотрен частный случай одномерного
течения, когда воздействие на поток было осуществлено только изменением
площади поперечного сечения канала. В технических устройствах на поток
могут действовать также силы трения, подвод теплоты, массы, количества
движения и т. п. Для анализа этих задач надо записать уравнения
сохранения в более общем виде, чем это было сделано в подразд. 4.1.
Закон сохранения массы:
m-=m(A;)=pSw. D.52)
Наличие аргумента х указывает на то, что в общем случае расход массы
может изменяться вдоль канала вследствие подвода или отвода жидкости.
Уравнение сохранения количества движения представим в форме
d(mu) = — Sdp+dF. D.53)
Здесь и далее в общем случае следует рассматривать расход массы как
переменную величину. Первый член представляет изменение количества
движения текущей жидкости, второй член равен сумме сил давления,
действующих на выделенный элемент жидкости. Третий член учитывает действие
дополнительных сил, приложенных к выделенному элементу (например, сил
трения о стенки трубы).
Уравнение сохранения энергии
d[(u2/2+h)rh} =dQ + dP. D.54)
56

Слева — выражение для приращения потока энергии текущей
жидкости; первый член справа — скорость подвода теплоты, а второй — работа
внешних сил в единицу времени. Здесь всюду записаны полные
дифференциалы, так как течение полагаем установившимся, а следовательно, все
величины зависят только от одного аргумента — координаты вдоль оси канала.
Приведенные уравнения следует дополнить уравнением состояния
D.55)
где #0 = 8,314 Дж/(моль- К). В данном случае |х следует считать
переменной величиной, так как к потоку при движении могут подмешиваться газы с
различной молекулярной массой.
Будем считать искомыми функциями параметры и, р, р, Т и рассмотрим,
как они меняются при различного рода воздействиях на поток.
Прологарифмировав уравнения неразрывности D.52) и состояния D.55)
и взяв приращения, запишем их, в дифференциальной форме:
dp/p + da/и = dm/m —dS/S; D.56)
dp/p —dp/p —dT/T = — d\i/\i. D.57)
Продифференцировав в уравнении D.53) выражение в скобках по частям,
поделив все члены на mu и перенеся искомые функции в левую часть,
получим
*L + J!!E-=-J!L + J!La D.58)
и mu m mu
Преобразуем уравнение энергии D.54), продифференцировав левую часть:
(udu ¦+ dh) m + (h + и2/2) dm^dQ + dP. D.59)
-Приращение энтальпии, стоящее в первой скобке, представим следующим
образом:
Примем, что теплоемкость смеси ср изменилась только в результате
подмешивания к основному потоку газа с теплоемкостью с'р газообразного
вещества с другой теплоемкостью ср. Тогда, записав уравнение теплового
баланса, можно найти приращение теплоемкости (пг + dm) cp = mc'p + cp dm,
dcp = (c"p — c'p)dmlm и приращение энтальпии в таком виде: dh =
= cpdT + Т (спр — с'р) dm/m.
Подмешивание к основному потоку вещества с другими физическими
характеристиками вызывает также изменение средней молекулярной массы.
Следовательно, в общем случае правая часть уравнения D.57) не равна
нулю. Выкладки можно провести до конца с учетом всех этих эффектов, но они
будут несколько громоздки.
Для большой наглядности выводов рассмотрим частный случай, когда
расход массы постоянен, а воздействия на поток осуществляются изменением
площади, воздействием силы, подводом теплоты и механической энергии.
Тогда уравнение D.54) примет вид (udu + cpdT) m = dQ + dP.
Поделим все члены этого уравнения на сртТ и оставим в левой части
только искомые функции:
udu ,JT__ dQ-\-dP
1 rr>
cpT T tncpT '
57

Преобразуем первый член уравнения, использовав выражения для
скорости звука D.11) и числа М D.21);
udu
срТ
xRu* du
cpkRT и сра2 и
Окончательное уравнение энергии в безразмерном виде
и. 1члд2 * , dT __ dQ + dP
D.60)
" Г mcpT
Всего получены четыре уравнения D.56), D.57), D.58) и D.60), в левых
частях которых стоят относительные приращения искомых функций, а в
правых — относительные элементарные воздействия. Уравнения линейны
относительно искомых величин. Из этих уравнений простыми
алгебраическими преобразованиями можно найти приращение каждой искомой функции
в отдельности. Для того чтобы найти, например, относительное приращение
скорости, необходимо исключить из основных уравнений приращения
температуры, давления и плотности. Исключим в уравнении D.60) температуру
с помощью уравнения D.57), затем исключим давление и плотность с
помощью уравнений D.56) и D.57). Поступив аналогичным образом для других
искомых функций, получим, опустив преобразования, окончательные
выражения.
В качестве примера приведем уравнение для скорости
du I dS »,« dF , dQ-\-dP \ 1 /л />1Ч
—- — I . *л ДД «S I ^- ' I ____________ | ?L f\ I I
и \ S mu mcpT J 1—,Ma
Аналогичные уравнения могут быть получены для давления, температуры
и плотности. Однако окончательный результат удобно представить в
несколько ином виде. Из D.61) следует, что относительное изменение скорости
зависит от суммы элементарных воздействий и поэтому решение можно
представить в виде табл. 4.1.
Таблица 4.1
Прираще -
ние
функции
du
и
dp
Р
dT
Т
dp
Р
dm
М2
Элементарное воздействие
dS
S
1
1—М2
хМ2
1—М2
(х—1)М2
1—М2
М2
1— М2
2-f (x--l)M2
1 — М2 '
dF
m и
хМ2
1—М2
хМ2[1 + (х— 1)М2]
1—М2
х(х— 1)М4
1—М2
хМ2
1 — М2
[2+(х— 1)М2]хМ2
1-М2
dP+dQ
mcvT
1
1—М2
хМ2
1-М2
1—хМ2
1-М2
1
1—М2
1+хМ2
1-М2
58

Таблица составлена так, что в каждой клетке стоит коэффициент
пропорциональности между элементарным воздействием и относительным
приращением искомой функции. Так, например, если необходимо узнать, как
изменяется скорость от изменения площади поперечного сечения канала, то из
первой строки и первого столбца получим dulu = — dSI\S A — М2)]. Это,
естественно, совпадает с ранее выведенной зависимостью D.23). В этом
случае, если на поток воздействует не только изменение площади, но и другие
факторы, коэффициент пропорциональности следует записать как сумму
соответствующих коэффициентов.
В последней строке табл. 4.1 дополнена коэффициентами, необходимыми
для расчета изменения числа М. Из формулы Лг = и2!а2 = u2IkRT следует,
что логарифмический дифференциал
du dT
М2 и Т
Так как правая часть этого уравнения может быть по данным
табл. 4.1 представлена как функция числа М, то это дает возможность просто
найти коэффициенты в последней строке.
Рассмотрим одномерное течение сжимаемой жидкости с трением в
теплоизолированной трубе с постоянной площадью поперечного сечения. В
данном случае единственным воздействием является трение, т. е. воздействие
силы. Дифференциальное уравнение задачи можно получить с помощью
табл. 4.1. Коэффициент пропорциональности для приращения скорости
находим в первой строке и втором столбце.
Следовательно, основное уравнение имеет вид
du хМ2 dF ,462)
62)
и 1-М« пги '
Силу трения, действующую на кольцевой элемент поверхности круглой
трубы диаметром D, можно выразить через касательное напряжение т на
стенке трубы:
dF=--—TnDdx. D.63)
Знак минус указывает, что сила трения направлена против движения.
Разность давлений на участке трубы длиной / уравновешивается
касательными напряжениями на стенке:
= (Рх—р2) nD2/4. D.64)
Введем безразмерный коэффициент сопротивления \ в выражение
Pi-Pi =_LH*L D 65)
Очевидно, что эта запись отвечает условиям теории размерности (см.
подразд. 3.3).
Из зависимостей D.64) и D.65) следует выражение касательного
напряжения через коэффициент сопротивления
т = 1ри2/8. D.66)
Использовав формулы D.63), D.66), а также уравнение неразрывности
m = nD2pu/Ay представим дифференциальное уравнение D.62) в виде
J*- D.67)
1-М* D ' к '
59

0,8 х
Рис. 4.8. Изменение безразмерной
скорости при течении в трубе
постоянного сечения с трением от пара-
*
Рис. 4.9. Процесс течения в трубе
постоянного сечения с трением в
тепловой диаграмме
Прежде чем интегрировать это уравнение, учтем следующее. При работе
сил трения от потока отводится мощность dP = — udF, но так как труба
теплоизолирована, то вся эта энергия передается в виде теплоты текущей
жидкости, причем dQ + dP = 0. В таком случае из уравнения энергии
следует, что температура торможения потока остается постоянной.
Следовательно, постоянной является также критическая скорость, которая
зависит от температуры торможения по формуле D.32).
Перейдем в уравнении D.67) к безразмерной скорости К = и/а*у так как
в этом случае просто преобразовать дифференциальное выражение в левой
части. Число М в правой части уравнения заменим через к с помощью сорт-
ношения D.35).
Тогда
Проинтегрируем это уравнение при g = const, выбрав постоянную
интегрирования так, чтобы в сечении х = 0 скорость потока была Хо:
1 / 1
D.68)
График полученного решения дан на рис. 4.8. Из полученного решения
следует, что если к0 < 1, то поток ускоряется. На некотором расстоянии,
которое называется критической длиндй трубы, поток достигает
критической скорости (Х= 1). Если критическая скорость достигнута, то
критическое сечение обязательно должно совйадать с выходным сечением трубы,
так как поток не может стать сверхзвуковым без изменения знака
воздействия (а сила трения всегда направлена против течения). Конечно, возможны
промежуточные случаи, когда поток выходит из трубы с дозвуковой
скоростью Ко < Ж 1.
Процесс при течении в трубе постоянного сечения с трением показан в
тепловой диаграмме (рис. 4.9). При дозвуковом течении давление и
температура газа вдоль трубы уменьшаются. Падение давления вызвано
сопротивлением трубы. Скорость вдоль.трубы растет, так как растет объемный
расход вдоль трубы из-за уменьшения плотности газа. Характер изменения
всех параметров потока устанавливается вторым столбцом табл. 4.1,
причем следует помнить, что сила трения направлена против потока, т. е. отри-
60

цательна. Распределение температуры находится по известной скорости с
помощью уравнения энергии D.16). Применение уравнения энергии в
таком виде допустимо, так как подвода теплоты извне нет, а выделение
теплоты внутри трубы, благодаря работе сил трения приводит к условию dQ+
+dP = 0.
Из табл. 4.1 следует запись дифференциального уравнения для давления
dp = хМ2 [! + (*— 1) М2] dF
р 1 — М2 ти
Поделив это уравнение почленно на уравнение D.62), получим
_^ = _-^__(х_1)М2^-.
р и и
Введем безразмерную скорость kj тогда
dp ____rf^ 2(х —1) kdk
р ~~ к (х-Ы) —(х—1) X2
Проинтегрировав, найдем, что
~1)Яр 1 = const. . D.69)
—(X—1) Х2 V
С помощью этого уравнения и уравнения D.68) для скорости легко найти
давление в любом сечении трубы, если оно известно для какого-нибудь
исходного сечения.
Точка А на тепловой диаграмме соответствует критическим параметрам
и, следовательно, критическому расходу через трубу.
Подчеркнем, что критическое давление р% при течении с трением не
равно критическому давлению при изоэнтропийном движении p%ty хотя
критические скорости в обоих случаях одинаковы. Критическим параметрам при
изоэнтропийном течении соответствует точка В (см. рис. 4.9).
Режимы, соответствующие сверхзвуковой скорости на входе в трубу,
изображены на рис. 4.9 штриховой линией. Опыт показывает, что эти режимы
оказываются неустойчивыми и процесс идет более сложным образом с
образованием скачков уплотнения.
Рассмотрим переход потока через критическую скорость в трубе
переменной площади при течении с трением. В данном случае рассматриваем два
воздействия: изменение площади и работу сил трения. Дифференциальное
уравнение, описывающее изменение скорости, можно получить с помощью
табл. 4.1, взяв сумму коэффициентов в первой строке для первого и второго
столбцов. Чтобы не повторять преобразования, возьмем уравнение D.67)
и добавим из табл. 4.1 коэффициент, учитывающий влияние изменения
площади трубы:
du = -dS/S+xl№dx/BD) 4 70)
и 1 —М2 : * ' '
Полученное уравнение отличается от уравнения D.23), выведенного для
изоэнтропийного течения, наличием второго слагаемого в числителе,
которое учитывает трение.
В месте перехода потока через критическую скорость (М = 1) в трубе
переменного сечения с трением должно выполняться условие
— dS/S + xgM2 dx/BD) = 0. D.71)
Из этого условия следует, что при наличии трения одномерный поток
переходит через критическую скорость в сечении, где dS/dx >0, т. е. в
расширяющейся части сопла Лаваля, а не в минимальном сечении (см. подразд.
61

4.3). Однако трение обычно столь мало, что этой поправкой можно
пренебречь, как и поступают на практике.
Рассмотрим задачу о подводе теплоты к газу, текущему в трубе
постоянного сечения. Из первой и третьей строк третьего столбца (см. табл. 4.1)
получим дифференциальные уравнения для скорости и температуры:
du _ \ dQ dT ^ 1-хМ2 dQ
и 1—М2 тсрТ ' Т 1--М2 тсрТ V • /
Из уравнения D.72) следует, что при подводе теплоты к дозвуковому
потоку он ускоряется, так как при dQ >0, М < 1: du >0. Однако в трубе
постоянного сечения скорость не может превзойти скорость звука.
Следовательно, если при подводе теплоты достигается скорость звука, то это может
произойти только в выходном сечении трубы. Из уравнения D.72) следует,
что при хМ2 < 1 температура газа растет, а при хМ2 > 1, несмотря на
подвод теплоты, температура падает.
4.6. НЕОДНОРОДНЫЕ ПОТОКИ И РАЗЛИЧНЫЕ СПОСОБЫ
ОСРЕДНЕНИЯ
В технических устройствах параметры потока (скорость,
давление, температура, плотность) зависят от координат, т. е. поток является
неоднородным.
Для того чтобы воспользоваться теорией одномерного течения в
практических задачах, необходимо прибегать к осреднению потоков по сечению.
При экспериментальном исследовании течений в машинах и других
технических устройствах необходимо по результатам измерений вычислять
некоторые суммарные характеристики: потоки массы, количества движения,
энергии и др. Для этого необходимо правильно производить осреднение.
Осреднение потоков приходится также применять в теоретических методах
расчета, например, при использовании способов численного моделирования
течения.
Это краткое перечисление показывает, что задача правильного
осреднения потоков является важной и достаточно общей.
Осреднение представляет замену неоднородного потока некоторым од-
нородным при условии сохранения наиболее существенных для
рассматриваемой проблемы свойств течения. Следует, конечно, помнить, что при любом
осреднении не могут быть сохранены все свойства потока, так как при
осреднении часть информации о потоке неизбежно теряется.
Будем рассматривать установившееся течение и запишем потоки
основных физических величин, характеризующих это течение, через контрольную
поверхность.
Поток массы
m^^pUiHidS. D.73)
Поток импульса в проекции на /-ю ось
ij = f (pnj + рщ щ uj) dS. D.74)
s
Поток энергии (или энтальпии полного торможения)
Е - Яо = J (h + u*/2) put л, dS, D.75)
5

Поток энтропии
jMS. D.76)
Именно эти характеристики выбраны по следующим причинам.
Во-первых, они являются основными при расчете течений во всяком техническом
устройстве и поэтому желательно, когда это возможно, чтобы осредненный
поток имел те же суммарные характеристики, что и осредняемый.
Во-вторых, разность значений этих характеристик между двумя
контрольными поверхностями позволяет вычислить внешние воздействия на
поток, которые происходят между этими поверхностями. Разность потоков
массы позволяет найти подведенную или отведенную массу. Разность
потоков импульсов дает возможность определить внешнюю силу, действующую
на выделенный объем жидкости. Разность потоков полной энергии равна
подведенной (например, в компрессоре) или отведенной (например, в
турбине) энергии. Наконец, разность потоков энтропии позволяет определить
потери, т. е. ту долю энергии, которая перешла-в тепловую, например, из-за
трения. Кроме того, выбранные характеристики обладают свойством
суммируемости, т. е. суммарное значение характеристики для всего потока
равно сумме значений этих характеристик для отдельных его частей.
Дальнейшие операции зависят от того, с какой целью производят
осреднение потока. Рассмотрим некоторые основные случаи, причем нельзя
указать наилучшего метода осреднения для всех задач, так как выбор метода
зависит от существа задачи.
Дело заключается в том, что нельзя одновременно выдержать как для
реального, так и для осредненного течения одинаковыми потоки массы,
импульса, энергии и энтропии. Например, всегда можно потребовать, чтобы
для двух течений были одинаковы потоки массы, импульса и энергии.
Однако в этом случае при осреднении возрастет суммарная энтропия, т. е.
течению искусственно будут приписаны потери, которые в действительности не
возникли, а возможно и не возникнут, так как в реальном течении
выравнивание полей за счет сил вязкости может происходить в конфузоре,
диффузоре или в иных условиях, от которых зависит фактическая величина потерь.
Если потребовать, чтобы для реального и осредненного течений были
одинаковы потоки массы, энергии и энтропии, то течению не будут
искусственно приписаны дополнительные потери. Однако в этом случае искусственно
будет изменен поток импульса, что может быть также нежелательным, так
как внесет некоторую ошибку в определение сил.
При различном подходе к осреднению течения будут отличаться также
другие параметры: давление, скорость, температура и плотность.
Допустимое искажение тех или иных из этих параметров зависит от конкретной
технической задачи. Кроме того, при практическом осреднении следует иметь
в виду информацию, которую мо^кно получить о потоке измерениями.
Информация о величине некоторых параметров может или вообще отсутствовать,
так как ее трудно получить, или быть недостаточно надежной по сравнению
с информацией о других параметрах.
Наконец, для слабо неоднородных потоков, которые достаточно часто
встречаются в технических задачах, может оказаться, что способ
осреднения практически не влияет на результат осреднения, т. е., точнее,
внесенная погрешность меньше допустимой. В этом случае надо принимать во
внимание простоту выбранного метода.
Для лучшего изучения эффектов, сопутствующих осреднению
неоднородного потока, рассмотрим сначала случай, когда все скорости нормальны
плоскости сечения, в котором производят осреднение.
03

Массовый расход, определяемый формулой D.73), может быть записан
через критический расход D.46) и функцию расхода q с помощью формулы
D.47):
D.77)
где q (e) определено формулой D.48), а постоянная С зависит только от
физических свойств газа.
Аналогичным образом через функцию расхода можно выразить и поток
импульса D.74):
/ = j pdS + CVxR J риq (e) X(e) dS. D.78)
s s
Здесь помимо функции расхода входит безразмерная скорость (.4.34).
Поток энтальпии торможения D.75) выразим через функцию расхода и
параметры торможения:
#о = ср С J Ро УП q (е) dS. D.79)
Чтобы преобразовать формулу для потока энтропии D.76), запишем
уравнение второго начала термодинамики Tds = dh — dp/p, которое для
совершенного газа при помощи уравнения состояния р = pRT и зависимости
h = срТ приведем к виду
ds = cpdT/T— Rdp/p.
Выразим энтропию через параметры заторможенного потока
(несущественная постоянная интегрирования отброшена), тогда
-1). D.80)
Теперь формула для потока энтропии D.76) примет вид
() In p0T*/<x-i>dS. D.81)
При осреднении во всех случаях желательно сохранить величину потока
массы. Тогда с помощью приведенных формул обычно рассматривают два
способа осреднения.
1. Осреднение при сохранении потоков массы, энергии и энтропии.
Сначала определим среднюю температуру торможения и среднюю
энтропию
D.82)
и по
D.83)
Далее можно определить среднее значение функции расхода
q=mJp*a*S. D.84)
По среднему значению функции расхода и параметрам торможения,
пользуясь газодинамическими функциями или таблицами, можно найти
средние значения статических параметров. В формулу D.84) входят сред-
64
Тогда среднее давление изоэнтропийного торможения можно найти по
формуле D.80), записав ее для средних величин:

ние критические плотность и скорость, которые йзйестны, так как их можно
выразить через найденные параметры торможения:
х+1
2. Осреднение при сохранении потоков массы, импульса и энергии.
Среднюю температуру торможения, по-прежнему, находим по формуле
D.82). Выразим известный поток импульса чрез осредненные параметры
/= mu + 'pS=m{u+~p/{pu)).
Используя уравнение состояния для осредненных параметров и введя осред-
ненное число М, преобразуем предыдущую формулу к виду
Применив первую формулу D.35), получим окончательно
— *— =к+ -i-. D.86)
"+1 та* к
Численное значение левой части этого уравнения известно, так как
критическая скорость может быть подсчитана по формуле D.85). Решив это
квадратное уравнение, следует выбрать корень, согласуясь с тем, является ли
поток до- или сверхзвуковым.
По к можно найти среднюю скорость и = а* к и статическую температуру
Т = хТ0. Определив по найденному к функцию расхода q = q (к), можно,
применив формулу D.46) для осредненных параметров, найти осредненное
давление торможения
Ро —m у I0/Lo%q. D.o7)
Среднее статическое давление р = г (к) р0.
Л. И.Седов и Г. Г. Черный, которые проводили анализ способов
осреднения, отметили, что осреднение с сохранением потоков массы, импульса
и энергии не всегда возможно, так как уравнение D.86) не имеет
действительных корней, если его левая часть менее двух.
Прежде чем делать практические выводы, рассмотрим другой способ
осреднения, который наиболее часто применяют именно в практических
исследованиях.
Определим среднее статическое давление как среднее по площади:
р=— \pdS. D.88)
S
Такое определение логично, так как правильно определяет величину
полной статической силы и, как будет показано далее, приводит к хорошим
результатам.
В таком случае поток полного импульса, определенный_формулой D.78),
удобно представить двумя слагаемыми / = 1г + /2 = Sp + mu, которые
имеют тот же физический смысл, что и в строго одномерном течении. Как
следует из формулы D.78),
/2 = С YxR j p{} q (e) к (е) dS. D.89)
3 Зэк. 2638 65

Этим определена средняя по количеству движения скорость
и= /2/т. D.90)
Среднюю плотность определяем из уравнения неразрывности р = mISu.
Тогда из уравнения состояния, записанного для осредненных параметров,
определим осредненную температуру
. D.91)
Поток полной энергии D.75) также представим двумя слагаемыми
Е = Ег + ?2 = j cp TpudS + J — ри2 udS,
S S
первое из которых определяет поток тепловой энергии, а второе —
кинетической.
Этим определены правила осреднения температуры торможения и
статической температуры
7>- -V f TopudS, T -4- f TpudS, D.92)
m J m J
а также скорости
J? 4f D.93)
m
здесь средние величины обозначены сверху знаком «тильда», так как они
в общем случае не равны средним величинам, найденным с помощью
уравнения количества движения и обозначенных чертой.
Среднее давление, которое не входит в уравнение энергии, по-прежнему,
определено формулой D.88).
Уравнение энергии может быть записано для средних величин в обычном
виде
срТ+й*/2= cjro-
Как уже отмечалось, каждый способ осреднения приводит к потере
части информации о потоке и, как следствие, к погрешности. В только что
рассмотренном способе осреднения погрешность можно оценить, сравнивая
значения параметров, осредненных по уравнениям движения и энергии.
Соответствующие коэффициенты можно назвать коэффициентами
неоднородности: __
а = Т/Т, $=={и/пJ. D.94)
Если аир близки к единице, то возможно использование уравнений
одномерного потока в обычном виде. Ошибка, которая при этом возникает,
имеет порядок отклонения этих коэффициентов от единицы. Можно показать,
что всегда р > 1, а в подавляющем большинстве практических задач
а < 1, причем знаки равенства относятся только к равномерному потоку.
Подробно вопросы осреднения проанализированы Л. Крокко.
Вопросы для самопроверки
1. Покажите, что для изоэнтропийного течения уравнение сохранения энергии и
уравнение Бернулли для сжимаемой жидкости совпадают.
2. Как подсчитать параметры изоэйтропийного торможения?
3. Как подсчитать критические параметры?
4. Запишите уравнение, которое выражает зависимость числа М от площади
поперечного сечения трубы при одномерном изоэнтропийном течении.
66

ГЛАВА 5
ПЛОСКОЕ ДОЗВУКОВОЕ ДВИЖЕНИЕ
ИДЕАЛЬНОЙ ЖИДКОСТИ
5.1. ВИХРЕВОЕ И БЕЗВИХРЕВОЕ ДВИЖЕНИЕ. ТЕОРЕМА СТОКСА.
УРАВНЕНИЯ ЭЙЛЕРА И ГРОМЕКИ-ЛЭМБА
В этой главе будут изучены основные свойства течений
идеальной жидкости, т.е. жидкости, вязкость которой по определению равна нулю.
Все реальные жидкости обладают вязкостью. Поэтому важно понять, какое
значение имеет теория течения невязкой жидкости и где она может быть
приложена к практическим задачам.
Полностью и обосновано можно ответить на этот вопрос после изучения
основных свойств течения жидкости, обладающей вязкостью (см. гл. 8, 9).
Сейчас отметим, что теория течения идеальной жидкости находит широкое
практическое применение. Важно только знать рамки, в которых эту теорию
можно применять.
В разд. 1.3 было показано, что в общем случае элементарная частица
жидкости перемещается с поступательной скоростью, деформируется и
вращается вокруг оси, проходящей через частицу. Рассмотрим сейчас только
вращение. Матрица A.21) представляет компоненты вектора угловой
скорости. В плоском движении частицы могут вращаться только вокруг оси,
перпендикулярной плоскости течения. В этом случае останется только
проекция оK и поэтому индекс 3 можно отбросить. Далее удобно принять также
обозначения хх ss х, х2 г= у, иг ша и, и2 « v. В новых обозначениях
проекция (о3 примет вид
G)~-
2 \ дх ду
Так как величина со характеризует вращение в точке, то она называется
местной завихренностью. Безвихревым называется такое движение
жидкости, при котором (о = 0 в рассматриваемой области. Плоское течение будет
безвихревым, если выполняется условие
-т"Чгв0- E-2)
дх ду
Если это условие не соблюдается, то течение называют вихревым.
Для дальнейшего исследования особенностей вихревого и безвихревого
течений введем понятие циркуляции скорости. Циркуляцию скорости Г по
замкнутому контуру / определяют интегралом (рис. 5.1, а):
hdl, E.3)
где Wi — проекция скорости на касательную к контуру; dl — элемент дуги
контура.
Положительным считается обход против часовой стрелки.
Криволинейный интеграл E.3) можно представить в декартовых
координатах и применить формулу Стокса для выражения криволинейного интегра-
3* 67

\Л/
ла через интеграл по
площади S, охватываемой
кривой /:
= (ft udx—
dv ди \
-^—^jdxdy.
E4)
Рис. 5.1. Обход односвязной и двусвязной областей:
а — односвязная область; б — двусвязная область
Заменив в этой
формуле выражение в скобках
через завихренность E.1), получим теорему Стокса (dS — элемент
площади):
r = 2$oodS. E.5)
s
Следовательно, если течение безвихревое, то циркуляция скорости по
любому замкнутому контуру равна нулю. Обратное утверждение неверно, т. е.
нельзя считать течение безвихревым, если циркуляция скорости по данному
контуру равна нулю. В этом случае можно утверждать, что нулю равна
суммарная завихренность внутри контура.
Выше предполагалось, что контур области может быть стянут в точку,
не пересекая никакой другой контур. Рассмотрим теперь обтекание профиля
1Х безвихревым потоком и подсчитаем циркуляцию скорости по контуру /2,
охватывающему профиль (см. рис. 5.1, б). Для того чтобы сделать область
односвязной, сделаем разрез. Область с контуром 123456 будет односвязной,
и из теоремы Стокса Г12345в = Г123 + Г34 + Г45в + Гв1 = 0. Здесь
цифрами обозначены участки, по которым подсчитывается циркуляция скорости.
Поскольку Г34 = — Гв1, имеем Г123 = — Г45в = Г654. Следовательно, в
безвихревом потоке циркуляция скорости по произвольному контуру,
охватывающему профиль, равна циркуляции скорости по самому профилю.
Рассмотрим плоское установившееся движение идеальной сжимаемой
жидкости при отсутствии массовых сил. Положим в уравнении BA9)duj/dt=
=?= 0, fj = 0, i = 1,2, / = 1,2 и обозначим, как было принято, хх =лг,
х2 = у, их яш и, и2 = v. Тогда получим уравнение Эйлера в таком
виде:
ди . ди 1 dp
дх ду р дх
E.6)
дх
ду
Эти уравнения пригодны для изучения общего случая движения
идеальной жидкости, когда имеется завихренность.
Безвихревое движение является важным частным случаем движения
жидкости. Рассмотрим, какие упрощения основных уравнений возможны при
изучении безвихревых движений.
Для этого сначала запишем уравнения E.6) в другом виде, выделив явно
члены, в которые входит завихренность. Добавим к левой части первого
уравнения и вычтем из нее выражение vdv/dx. Аналогичное преобразование
68

проведем со вторым уравнением, добавив и вычтя выражение иди/ду.
Сгруппировав члены, перепишем уравнения E.6);
2 дх [дх ду ) р дх
2 ду { ^ '^ \дх ду) р ду-
Введем обозначение для модуля скорости
О,2=а2 + О2. E.8)
Уравнения E.7) с учетом обозначений E.1), E.8) можно записать в
окончательном виде, указанном Громекой и Лэмбом:
2ш
E.9)
+2«<o .
2 ду 9 ду
Эти уравнения эквивалентны уравнениям E.6), так как при выводе их
не сделано никаких дополнительных предположений. Преимущество
уравнений E.9) заключается в том, что они в явном виде включают величину со
и позволяют просто рассмотреть наиболее важный частный случай <о = 0.
Для безвихревого движения уравнения E.9) принимают простой вид и их
можно проинтегрировать:
_^
2 дх р дх ' 2 дц р ду
Умножив левую и правую части первого уравнения на dx, а второго —
на dy и сложив, получим
• if. dx +^.7у) = --Uf. dx+ 1l dy\
2 \ дх ду } p \ дх ду }
Тогда в полных дифференциалах
wdw+dp/p=0. E.10)
Проинтегрировав это уравнение при р = const, получим уравнение Бер-
нулли для несжимаемой жидкости:
_Ei.+_?_ = _??_==COnst. E.11)
2 Р Р
Для изоэнтропийного течения сжимаемой жидкости можно выразить
плотность через давление и также проинтегрировать уравнение E.10):
^!.+^_ J^/^\^e.JL-JL.eConst E.12)
2 х-1 ро \ Ро / х-1 Ро
Уравнение E.11) совпадает с ранее выведенным уравнением Бернулли
B.39), если в последнем пренебречь силой тяжести. Уравнение E.12)
совпадает с уравнением D.13).
Различие заключается в том, что для безвихревого движения, как сейчас
показано, постоянная будет общей для всей области течения. Ранее
утверждалось, что левая часть уравнения постоянна только для одномерного
течения, т. е. для струйки.

5.2. ПЛОСКОЕ БЕЗВИХРЕВОЕ ДВИЖЕНИЕ ИДЕАЛЬНОЙ
НЕСЖИМАЕМОЙ ЖИДКОСТИ
Рассмотрим плоское установившееся безвихревое движение
идеальной несжимаемой жидкости. Уравнение неразрывности B.9) в принятых
обозначениях примет вид
|L+^.-0. E.13)
дх ду
Для безвихревого движения справедливо уравнение E.2) и уравнение Бер-
нулли E.11):
JiL+JL^Je*-, а?=и1+Л E.14)
2 р р
Это же уравнение справедливо для пространственного безвихревого течения,
причем вывод его совершенно аналогичен.
Полученная система является полной, так как содержит три уравнения
и три неизвестных: и, vi р [модуль скорости можно просто исключить из
первого уравнения E.14)].
Прежде чем перейти к исследованию системы уравнений для несжимаемой
жидкости, посмотрим, насколько существенным может быть влияние
сжимаемости, и установим, когда им можно пренебречь.
Для сжимаемой жидкости уравнение неразрывности в форме E.13) надо
Заменить на уравнение B.8):
*±№L+1SS2L=q9 E.I5)
дх ду
которое, введя плотность изоэнтропийноготорможения, постоянную для
конкретного течения, запишем в виде
-?¦ (Ри/Ро) + ^ (ро/Ро) = 0. E.16)
Уравнение отсутствия вихрей E.2) не зависит от сжимаемости и поэтому
вид его не изменится. Уравнение E.14) надо заменить на уравнение E.12),
справедливое для сжимаемой жидкости.
Покажем, что если число М = w/a мало, то в первом приближении
эффектом сжимаемости жидкости можно пренебречь.
С помощью формул D.29), D.30) или таблиц газодинамических функций
легко определить, что при М< 0,3 отношения р/р0 >0,96 и р/р0 >0,94,
т. е. плотность и давление мало отличаются от их значений в
заторможенном потоке.
Если в уравнении E.16) пренебречь малым изменением плотности, то
оно перейдет в уравнение E.13). Покажем, что уравнение для сжимаемой
жидкости E.12) также перейдет в уравнение для несжимаемой жидкости
E.14).
' Отношение давлений представим в виде р/р0 =1 — (р0 — РУро-
Подставим это выражение в скобки формулы E.12), разложим в ряд по степеням
параметра (рц — р)/ро и удержим только первую степень ввиду малости
этого параметра. Тогда
и>2 | * Л х—1 ро-р j \ Ро ^ и
2 х—1 \ к ро '"/ ро х—1
Очевидно, что после приведения подобных членов это уравнение
перейдет в уравнение Бернулли для несжимаемой жидкости <5.14).
70

По определению несжимаемой жидкостью называется жидкость,
плотность которой строго постоянна. Однако, если число М мало, то для расчета
течений газов и паров можно приближенно применять все формулы,
выведенные для несжимаемой жидкости. Так, например, при нормальных
условиях скорость звука в воздухе 330 м/с. Следовательно, можно пренебречь
сжимаемостью воздуха для скоростей менее 100 м/с. Скорость звука в
перегретом водяном паре при давлении 20 МПа и температуре 550 °С равна
656 м/с, Следовательно, в этом случае можно пренебречь сжимаемостью пара
да:ш>рьст^почти 200 м/с.
Вернемся к решению основной задачи и отметим, что основная сложность
состоит в определении поля скоростей, т. е. совместном решении
дифференциальных уравнений E.13) и E.2). Поле давлений определяется простыми
алгебраическими операциями по формулам E.14).
Систему двух линейных дифференциальных уравнений первого порядка
можно привести к одному линейному дифференциальному уравнению второго
порядка.
Для безвихревого движения можно ввести функцию ср (#, у), которая
называется потенциалом скорости:
cp=q>(*, у). E.17)
При этом уравнение отсутствия завихренности E.2) удовлетворяется
(смешанные производные равны вне зависимости от порядка
дифференцирования), не накладывая никаких условий на выбор функции ср. Так как
потенциал скорости можно ввести только для безвихревого движения, то такие
течения называют также потенциальными. Подставив выражения E.17) в
уравнение неразрывности E.13), найдем, что потенциал скорости для
несжимаемой жидкости должен удовлетворять уравнению Лапласа:
ЛФ+^Ф=0. E.18)
Решение уравнения Лапласа (при соответствующих граничных условиях,
которые будут сформулированы позже) дает решение задачи о движении
жидкости, так как скорости находятся по формулам E.17). Однако удобно
ввести еще одну функцию г|? (х, у), называемую функцией тока:
E.19)
Тогда уравнение неразрывности E.13) удовлетворяется автоматически.
Подставив выражения E.19) в уравнение E.2), найдем, что функция ty
также должна удовлетворять уравнению Лапласа:
i!±+ -*!. = о, E.20)
однако, естественно, при других граничных условиях, чем для ф.
Если функция г|) найдена, то задачу также можно считать решенной.
Для последующей формулировки граничных условий следует рассмотреть
некоторые свойства функций ф и if». Введем сначала понятие линии тока.
Линия, в каждой точке которой скорость направлена по касательной,
называется линией тока. При установившемся движении линия тока
совпадает с траекторией движения фиксированной частицы жидкости. Из этого
свойства может быть найдено уравнение линий тока.
Рассмотрим линию тока АВ (рис. 5.2). В точке А построим вектор
скорости и его проекции на оси координат. Поместим точку Л' на линии тока
вблизи точки Л так, что координаты точки Л' получают приращение на Ах и
dy по сравнению с координатами точки Л,
71

У\
Рис. 5.2. Линия тока t|)=const
Рис. 5.3. Ортогональная сетка линий
тока и эквипотенциалей
Из условия подобия треугольников при А' -+ А следует
дифференциальное уравнение линий тока dxlu = dy/v.
Заменив в этом уравнении скорости через производные функции тока с
помощью выражений E.19), получим уравнение линии тока в таком виде:
i
—vdx + udy = -^ dx+ -^ dy^d^^O.
дх ду
Следовательно, на линии тока функция тока принимает постоянное
значение я|> = const. Если постоянной придать конкретное значение, то это
будет уравнение одной линии тока. Если же подразумевать, что постоянная
может принимать произвольные значения, то уравнение ^ = const
описывает семейство линий тока данного потока.
Рассмотрим свойства потенциала скорости. Производные <р в направлении
осей координат дают проекции скорости на эти оси E.17).
Получим выражение для производной потенциала скорости по
произвольному направлению /:
дф дф dx , дф dy
dl ~~ дх dl ду dt '
Его можно представить в виде
дц>/д1 = и cos (xl) + v cos (yl).
Здесь использованы зависимости E.17) и введены углы между направлением
/ и осями координат. Полученное выражение равно сумме проекций unv
на направление /, т. е. равно проекции скорости w на направление /:
w^ E.21)
Следовательно, производная потенциала скорости по произвольному
направлению равна проекции скорости на это направление.
В частности, обозначив sun — направления вдоль линии тока и по
нормали к ней, получим
= wn = 0. E.22)
Эти равенства очевидны из определения линии тока.
Рассмотрим сетку, образованную семейством линий тока (ф = const)
и линий равного потенциала (<р = const), которая дает наглядное
представление о потоке (рис. 5.3). Скорости касательны к линиям тока и на основании
формул E.22) нормальны к линиям равного потенциала (эквипотенциалям).
Следовательно, сетка ортогональна. Поскольку жидкость не может
пересекать линий тока, то между двумя линиями тока расход жидкости в любом
72

сечении одинаков. Отсюда следует, что чем ближе сходятся выбранные
линии тока, тем больше скорость жидкости, и наоборот.
Покажем, что объемный расход (в слое постоянной толщины),
протекающий между двумя линиями тока, равен разности значений функций тока на
этих линиях. Проведем между точками а и ft произвольную кривую/ и
вычислим расход жидкости через нее (wn — проекция скорости на нормаль к
кривой (см. рис. 5.3):
Q= j wndl = j [иcos(xn) + v (yn)\dl = Judy—vdx =*
где г|)х hi|>2—значения функции тока на концах кривой, т. е. на
соответствующих линиях тока.
Рассмотрим теперь граничные условия на твердой поверхности,
обтекаемой невязкой жидкостью. Так как жидкость не может пронизывать твердую
поверхность или вытекать из нее, то проекция скорости на нормаль к
поверхности должна быть равна нулю, т. е. скорость должна быть направлена
по касательной к поверхности. Следовательно, на обтекаемой поверхности
потенциал скорости и функция тока должны удовлетворять следующим
граничным условиям (п — нормаль к поверхности):
дц>/дп=0, г|? = const. E.23)
Очевидно, что это те же условия, которые определяют линию тока.
Значит, для удовлетворения граничных условий достаточно потребовать, чтобы
обтекаемая поверхность была линией тока (или частью линии тока) или,
наоборот, любую линию тока можно считать твердой поверхностью.
Остановимся еще на одном важном свойстве введенных функций, на
котором основаны по существу все методы расчета плоских потенциальных
потоков.
Из основных формул, определяющих потенциал скорости E.17) и
функцию тока E.19), следует, что они связаны соотношениями Коши—Рима-
на:
дх ду ' ду дх * К
Из теории функций комплексного переменного известно, что
действительная и мнимая части произвольной аналитической функции комплексного
переменного также удовлетворяют соотношению Коши — Римана. На этом
основано приложение теории функций комплексного переменного к расчету
потенциальных потоков идеальной несжимаемой жидкости.
Таким образом, действительную часть произвольной функции
комплексного переменного можно рассматривать как потенциал скорости, а
мнимую—как функцию тока, т. е. положить
z=x + iy. E.25)
Функция F (г) называется комплексным потенциалом потока.
Следовательно, любой функции комплексного переменного можно
сопоставить плоский потенциальный поток несжимаемой жидкости.
Очевидно, что этим избегаем интегрирования исходных уравнений.
Следует иметь в виду, что произвольная функция F (г) приведет к
построению произвольного потенциального потока. Для того чтобы построить
потенциальный поток по заданным граничным условиям, надо отыскать функ-
7?

цию F (z), удовлетворяющую этим условиям. В этом теперь и состоит основ
ная трудность задачи.
При использовании комплексного потенциала F (г) удобно вычислять
скорости потока не через <р или г|), а прямо через F (г).
Представим выражение E.25) в виде
dF =dy + idy = (^dx+ ^ dy)+i№ dx +^
\ дх ду ) \ дх ду
Выражения в скобках представляют полные дифференциалы потенциала
скорости и функции тока.
Заменим производные в правой части через скорости по формулам E.17)
и E.19) и сгруппируем члены:
dF = (udx + vdy) + i (— vdx + udy) = (u — iv) (dx + idy) = (u—iv) dz.
Тогда получим формулу для скорости через производную комплексного
потенциала
E.26)
где и — iv — выражение скорости потока в комплексном виде. Так как перед
мнимой частью стоит знак минус, то по существу это сопряженная
комплексная скорость. Обычно она называется просто комплексной скоростью.
Рассмотрим простейшие потенциальные потоки идеальной несжимаемой
жидкости, причем следует обращать внимание на физическую
интерпретацию течений, представляемых различными функциями комплексного
переменного. Выбор приведенных простейших течений не является случайным,
так как дальше они использованы для решения конкретных практических
задач.
1. Источник. Выберем комплексный потенциал в виде
^(г)-Ф + п|>==-|-1пг, E.27)
где Q — действительная постоянная.
Покажем, что эта функция описывает течение, вызванное источником.
Ввиду симметрии задачи удобно применить для комплексного переменного
полярные координаты:
0 -arctg(f//;c),
где г — модуль; 8 — аргумент комплексного переменного.
Тогда, отделив в E.27) действительную и мнимую части, получим
потенциал скорости и функцию тока:
Линии тока г|> = const будут лучами, выходящими из начала координат,
а линии равного потенциала ср == const — концентрическими
окружностями с центрами в начале координат (рис. 5.4).
При построении сетки линий тока и эквипотенциалей функциям ф и i|>
придают постоянные приращения, так как это дает более наглядную
картину. Поэтому в данном случае радиусы окружностей, представляющих
линии равного потенциала, возрастают по экспоненте.
Найдем радиальную и окружную проекции скорости с помощью
формулы E.21):
74

Рис. 5.4. Линии тока и эквипотенциа-
ли точечного источника
Рис. 5.5. Линии тока и эквипотенциа-
ли потока, вызванного точечным
вихрем
Следует обратить внимание на то, что дифференцирование проведено по
радиусу и дуге окружности.
Для плоского течения можно представить, что жидкость вытекает из
точечного источника, расположенного в начале координат. Через любую
окружность с центром в Начале координат протекает расход
2nrwr = 2nr (Q/2nr) эв Q.
Эту величину называют производительностью источника (или стока, если
Q < 0 и скорости направлены к центру).
В начале координат (г = 0) функция E.27) теряет аналитичность и эта
точка является особой. Физически это проявляется в том, что в этой точке
скорость имеет произвольное направление: именно здесь и расположен
точечный источник.
Такое течение можно представить и как пространственное, вызванное
источниками, непрерывно распределенными вдоль линии, перпендикулярной
плоскостям течения.
2. Вихрь. Возьмем комплексный потенциал в виде (Г—действительная
постоянная)
F{Z):
2л1
lnz.
Проведя преобразования, аналогичные приведенным ранее, найдем
г г ,
Ф = 8, ф = lnr.
E.28)
E.28а)
Здесь линии тока будут окружностями, а линии равного потенциала —
лучами (рис. 5.5). В данном случае потенциал скорости многозначная
функция, так как при обходе начала координат он меняется на ± Г (знак
зависит от направления обхода).
Радиальная и окружная скорости соответственно
=г —5L ?55
И 1#й 5=
Г
2я
E.29)
75

-const
-const
Вычислим интеграл E.3) по
замкнутому контуру, охватывающему
начало координат. Выберем в качестве
такого контура любую окружность с
центром в начале координат и,
проинтегрировав в направлении против
часовой стрелки, получим
ше rdQ = 2яг (Г/2яг) = Г.
Здесь окружная скорость взята из
формулы E.29).
Такой же интеграл, вычисленный
по любому контуру, не
охватывающему начало координат, равен нулю.
Таким образом, в начале координат
согласно формуле E.5) расположен
вихрь-точка. Величина Г —
циркуляция скорости — характеризует
интенсивность вихря, а ее знак —
направление вращения жидкости
(положительно против часовой стрелки).
Следует отметить, что течение во всей плоскости является потен щаль-
ным, т. е. безвихревым. Это можно представить наглядно следующим
образом. Маленький крестик, помещенный в жидкость, будет двигаться по
окружности (по линии тока), не вращаясь вокруг собственной оси. Крестик,
помещенный в начало координат, будет вращаться: точка, где расположен
вихрь, является особой.
3. Диполь. Запишем комплексный потенциал в виде
Рис. 5.6. Линии тока и эквипотенциали
диполя
F(z)=q/z,
E.30)
где q — действительная постоянная.
Отделив действительную и мнимую части в декартовой системе координат,
найдем (для упрощения положим q = 1)
и * = —
хЧ-У2
Приняв ч|> = const, получим уравнение семейства окружностей,
проходящих через начало координат с центрами на оси ординат (рис. 5.6):
Аналогично, линии равного потенциала изображаются семейством
окружностей, центры которых смещены по оси абсцисс и которые также
проходят через начало координат:
Величину q называют моментом диполя. При q >0 жидкость вытекает
из начала координат в отрицательном направлении оси абсцисс и снова
возвращается в начало координат со" стороны положительного направления.
Диполь можно получить в результате слияния источника и стока:
О О
2лг 2л;
76
In г.

Первый член — это комплексный потенциал источника, помещённого в
точке z =—Л, а второй —.потенциал стока, расположенного в точке z =0,
В пределе при Л -^ 0 и условии Qh = q это выражение представляет
производную логарифма и переходит в формулу E.30).
Очевидно, что сумма функций комплексного переменного, являясь
также функцией комплексного переменного, представляет некоторый
потенциальный поток или, иначе, потенциальное потоки несжимаемой жидкости
можно складывать. При этом потенциалы скорости и функции тока
складывают алгебраически, как это следует из формулы для комплексного
потенциала E.25). Поля скоростей складывают геометрически, так как
алгебраически складывают проекции скоростей. -
Возможность сложения потенциалов скорости и функций тока
несжимаемой жидкости объясняется тем, что они удовлетворяют линейным
дифференциальным уравнениям E.18), E.20). Подобное сложение полей течения для
сжимаемой жидкости недопустимо, так как потенциал скорости и функция
тока для них удовлетворяют нелинейным дифференциальным уравнениям.
Рассмотрим теперь потенциальные течения несжимаемой жидкости,
полученные сложением элементарных потоков.
4.Обтекание окружности (или бесконечно длинного кругового цилинд-
ра).
Комплексный потенциал
J ^) ^(^A E.31)
где */«,, г0 и Г — действительные постоянные.
Покажем, что потенциал E.31) соответствует обтеканию окружности.
Комплексный потенциал (если раскрыть скобки) состоит из трех слагаемых.
Первое слагаемое, как легко убедиться, представляет комплексный
потенциал плоскопараллельного потока, параллельного оси абсцисс и имеющего
скорость и^.Второе слагаемое — комплексный потенциал диполя с моментом
ujr\, а третье — комплексный потенциал течения, вызванного вихрем с
циркуляцией Г.
Применив полярную систему координат z = re'e, как и ранее, отделим
действительную и мнимую части в E.31) и получим
-?-6; E.32)
y = Ueo Ir—r-L\ sin в — -I- ln(j-Y E.33)
В преобразованиях использована формула Эйлера e'e = cos 6 + i sin0.
Рассмотрим сначала частный случай течения при Г = 0. Ясно, что на
окружности радиуса г0 с центром в начале координат функция тока
принимает постоянные значения (ф = 0). Следовательно, окружность является
линией тока, а точнее частью линии тока, так как ^ = 0 также на оси абсцисс
F = 0, 6 = л). Следовательно, скорости жидкости направлены по
касательным к окружности, и она может рассматриваться как непроницаемое
твердое тело. Можно считать также, что рассматривается обтекание
безграничного круглого цилиндра, перпендикулярного к плоскостям течения.
Вычислим радиальную и окружную проекции скорости потока через потенциал
скорости E.21):
wr =^ = ы /l_-l.)cose; E.34)
дг \ г2 /
4 ^)ne + ir- <5-35>.
77

Продифференцировав согласно формуле E.26) комплексный потенциал
E.31) по г, можно найти комплексную скорость
dF
dz
E.36)
Из последней формулы следует, что далеко от цилиндра (z->oo)
скорость потока постоянна и параллельна оси абсцисс, т.е. на цилиндр
набегает плоскопараллельный поток со скоростью и^. Линии тока при обтекании
цилиндра (для Г = 0) показаны на рис. 5.7, а.
В полярной системе координат скорость положительна, если она
направлена в сторону отсчета угля.
Скорость на цилиндре можно найти, положив в формулах E.34) и E.35)
г = га (рассматриваем случай Г = 0): wr = 0, w = щ = — 2«O0sin8.
В точках 8 = 0, 8 = я скорость равна нулю. В этих точках поток
разветвляется, и они называются точками ветвления. Максимальная скорость,
равная 2uQoy достигается в точках 8 == я/2, 8 = Зя/2. Распределение давления
на цилиндре находится по уравнению Бернулли для несжимаемой
жидкости E.14).
В общем случае при Г Ф 0 окружность г = г0 также является линией
тока, как это следует из выражения E.33). Вдали от окружности
набегающий поток по-прежнему плоскопараллелен, а скорость его равна иж.
Линии тока для этого случая показаны на рис. 5.7, б, причем Г < 0. Для
Г > 0 картина зеркально отобразится относительно оси абсцисс.
Положение точек ветвления, в которых скорость равна нулю, можно определить,
положив г = г0 и приравняв выражение E.35) нулю. В результате найдем
sin 8 = Г/Dяг0 Woo). E.37)
Если правая часть по модулю меньше единицы, то это уравнение имеет два
решения для угловой координаты, причем обе точки располагаются
симметрично относительно оси ординат. Если правая часть по модулю равна
единице, то обе критические точки совпадают (8 = я/2 для Г > 0, 8 = Зя/2 для
Г < 0). Наконец, когда правая часть по модулю больше единицы, то точка
в явления одна и находится в потоке на оси ординат. Ее положение легко
найти из условия wr = w$ = 0.
Рассмотрим некоторые случаи обтекания окружности, когда в потоке
расположены особые точки. Полученные решения будут использованы в методе
годографа скорости (см. подразд. 5.7) и при построении численной модели
обтекания тел с отрывом потока (гл. 12).
Рис. 5.7. Линии тока при обтекании цилиндра;
а — Г«=0; ^ — Г<0, | Г/4 |
78

M-s
Рис. 5.8. Обтекание окружности
потоком, вызванным точечным
вихрем (ММ\~г{\ ММ2~г2)
Рис. 5.9. Обтекание окружности
потоком, вызванным точечным
источником
Пусть в плоскости комплексного переменного z = х + iy расположена
окружность радиуса г0 с центром в начале координат (рис. 5.8). Найдем
комплексный потенциал потока, обтекающего окружность, если поток вызван
вихрем с циркуляцией Г, расположенным в точке Мх вне окружности. Поместим
вихрь с циркуляцией —Г в точку М2> которая является зеркальным
отображением точки Мх относительно окружности (т. е. ОМХ-ОМ2 = г§).
Покажем, что в этом случае окружность будет лянией тока.
Пусть точка М — произвольная точка на окружности. Функция тока
в точке М только от вихря, расположенного в точке Мъ по формуле E.28а)
будет г|)г (М) = —(Г/2л) In гх (рис. 5.8). Аналогично функция тока в'точке М от
вихря в точке М2 будет \|э2 (Af) = (Г/2я) In г2 (знак плюс, так как циркуляция
этого вихря отрицательна). Пользуясь принципом сложения потенциальных
потоков несжимаемой жидкости, получим функцию тока в точке М от двух
вихрей г|) (М) - ^ (М) + г|>2 (Л!) = (Г/2я) In (r2/rx). Треугольники ОММХ и
и ОММ2 подобны, так как угол МОМЛ у них общий, а две пары сторон
пропорциональны по условию OMJOM = ОМЮМ2. Из подобия
треугольников следует г21гг = rJOMx,
Поскольку радиус окружности и положение вихря, а следовательно,
отрезок 0Мх заданы, то отношение г2/гх =? const для всех точек М,
лежащих на окружности. Тогда окружность является линией тока, так как на
ней значение функции тока постоянно.
Запишем на этом основании комплексный потенциал потока,
вызванного вихрем в точке Мх и обтекающего окружность. Если принять, что
комплексная координата точки Мх равна гъ то координата точки М2,
зеркально отображенной относительно окружности, будет г2 = rllzx, где Тх=
=хх — хуу. Это следует из того, что аргументы гх и г2 одинаковы (они лежат
на одном луче), а произведение модулей равно г§.
Комплексный потенциал потока может быть записан с помощью формулы
E.28).
2ш
In
— гх
E.37а)
Рассмотрим обтекание окружности радиуса г0 потоком, вызванным
источником производительностью Q, расположенным в точке Мх (рис. 5.9).
Поместим источник той же производительности в точку М2, являющуюся
зеркальным отображением точки Мх относительно окружности (ОМХ*ОМ2==
=гЬ)9 з также сток производительностью — Q э центр окружности.
79

Функция тока в потоке, вызванном
источником (или стоком), принимает
постоянное значение на лучах,
проведенных из точки расположения
источника (стока). Функция тока на луче,
составляющем угол 0 с осью абсцисс,
от источника производительностью Q
будет if = QQ/2n. Тогда в
произвольной точке М на окружности функция
тока от двух источников и стока
Рис. 5.10. Обтекание окружности пото- Тпл„пл пилил пилил
ком, вызванным диполем Треугольники ОММХ и 0ММ2
подобны, и L 0ММ2 = |_ ММгО =
= я — 92. Треугольник 0ММ2 имеет углы, равные 9, я — 92, я — 91#
Так как сумма углов треугольника равна я, то отсюда следует, что 9Х +
+ 92 — 9 = я. В таком случае значение функции тока в любой точке на
окружности равно ф (М) = Q/2, т. е. постоянно. Окружность является
линией тока, что и требовалось доказать. Следовательно, комплексный
потенциал рассматриваемого потока следует записать в таком виде:
= _g-ln (z-*t>(*-'
2я
E.38)
Эта запись следует из формулы E.27) и условия, что поток представлен
суммой потоков, вызванных двумя источниками и стоком. Положено, что
точке Мг соответствует комплексная координата zx. Тогда, как показано в
предыдущем примере, координата зеркально отображенной точки М2
равна г2 = r\lzx.
В заключение рассмотрим обтекание окружности радиуса г0 потоком,
вызванным дцполем, расположенным в точке Мг (рис. 5.10).
Диполь, как было показано в п. 3 этого раздела, можно получить
предельным переходом при слиянии источника и стока. Осью диполя
называется прямая, вдоль которой диполь выбрасывает и подсасывает жидкость.
Так, на рис. 5.6 осью диполя является ось абсцисс и соответственно
постоянная q — действительная величина. Если q будет чисто мнимой величиной,
то ось диполя будет направлена вдоль оси ординат. В общем случае
постоянная q может быть комплексной, что и определяет направление оси диполя.
Если источник и сток при слиянии и образовании диполя расположены на
оси абсцисс, то ось диполя совпадает с осью абсцисс. Если источник и сток
были расположены на произвольно направленной прямой, то она и будет
являться осью диполя.
Поскольку диполи могут быть образованы источниками и стоками, то
задача построения комплексного потенциала потока от диполя, обтекающего
окружность, может быть сведена к предыдущей.
Пусть в точке Мх (рис. 5.10) ос^ диполя направлена по линии АВ,
наклоненной под углом 8 к оси абсцисс. Чтобы окружность была линией тока,
необходимо поместить диполь в зеркально отображенную точку (ОМг X
80

X ОМ 2 — /•§), причем ось этого диполя А В должна составлять угол л —в
с осью абсцисс.
Обозначим: q — момент диполя, в — угол наклона оси диполя к оси
абсцисс, г, — комплексная координата, определяющая место расположения
диполя. Тогда комплексный потенциал потока, вызванного диполем и
обтекающего окружность с центром в начале координат:
qt1
qt
—1*0
E.39)
5.3. ТЕОРЕМА ЖУКОВСКОГО. ПОСТУЛАТ ЖУКОВСКОГО —
ЧАПЛЫГИНА 1
Н.Е. Жуковский доказал теорему о подъемной силе для
произвольного крыла в плоском потоке в 1904 г. и о подъемной силе лопатки в
решетке в 1912 г. С тех пор эта важная теорема была доказана и другими
способами. Рассмотрим доказательство теоремы Жуковского для решетки
и получим теорему для одиночного профиля предельным переходом.
Решеткой называют систему из бесконечного числа одинаково
ориентированных профилей, размещенных вдоль прямой на одинаковом
расстоянии (шаг решетки).
Рассмотрим обтекание аэродинамической решетки установившимся
плоским потенциальным потоком идеальной несжимаемой жидкости (рис. 5.11).
Поставим задачу определения силы, с которой поток действует на лопатку.
Выберем контур 1234, который состоит из двух отрезков, параллельных
фронту решетки, и двух произвольных линий, расположенных на
расстоянии шага t.
Параллельные сечения выберем столь далеко от решетки, что параметры
потока в них можно считать постоянными. Поток набегает на решетку слева
со скоростью тг (давление рх), поворачивает в решетке и уходит в
бесконечность справа со скоростью w2 (давление р2). Ориентируем ось ординат
параллельно фронту решетки.
Из уравнения неразрывности, записанного для контрольных сечений,
следует, что для несжимаемой жидкости нормальные к фронту проекции
скорости до и после решетки
m = p«1/=pw2<, иг = и2 =и. E.40)
Здесь т — расход, приходящийся
на один шаг.
Применим к жидкости,
заключенной внутри контура, теорему о
количестве движения и запишем ее
в проекциях на фронт решетки и
нормаль к нему:
—Fx = т (и2—иг) +1 (p2—Pi) =
= /(/>2-Pi); E.41)
-Fy^m(vt-vx)9 E.42)
где Fx и Fy — проекции на оси
координат СИЛЫ, С которой ПОТОК Рис 5.11. Обтекание аэродинамической ре-
действует на лопатку. шетки
81

В уравнениях перед ними поставлены знаки минус, так как там
необходимо записать силу, с которой лопатка действует на поток. В уравнения не
вошли силы давления, действующие на выделенные линии тока, так как из-
за периодичности потока сумма их равна нулю (периодом является шаг
решетки).
Найдем циркуляцию скорости по выбранному замкнутому контуру с
помощью формулы E.3). Интегралы вдоль линий /—2 и 3—4 можно исключить,
так как распределение скоростей вдоль них одинаково, а обход их
совершается в противоположных направлениях. Тогда при обходе контура против
часовой стрелки
Г = /@2— Vl). E.43)
По теореме Стокса (см. подразд. 5.1) эта циркуляция не зависит от
формы контрольного контура и равна циркуляции скорости по лопатке.
Дальнейшие преобразования заключаются в выражении силы через
циркуляцию скорости. Из уравнений E.42), E.40) и E.43) следует
Fy= — pitf (Г/Г)== —риТ. E.44)
В уравнении E.41) заменим разность давлений с помощью уравнения
E.14):
Fx = t (Рх -Р2) = 0,5р* К - «»?)• E.45)
Затем, воспользовавшись условием w\ = мг + v\, wl = и2 + v\ и
уравнением E.43), запишем уравнение E.45) в таком виде:
Fx = 0,5p/ (vl -vl)~0,5pt ta-t^to + oi) =0,5рГ (о, + о,). E.46)
Следовательно, полная сила, действующая на лопатку в решетке:
F =У7ГЩ =ра>оГ. E.47)
Здесь введено обозначение для модуля вектора полусуммы скоростей до
решетки и после нее (см. рис. 5.11):
E-48)
Отношение проекций сил на оси у и х пропорционально отношению
проекций скорости w0 на оси хну:
Тогда полная сила перпендикулярна векторной полусумме скоростей до и
после решетки. Вектор силы F повернут относительно вектора скорости w0
на прямой угол в сторону, противоположную знаку циркуляции скорости.
Сила действует на единицу длины бесконечно длинной лопатки.
Если безгранично увеличивать шаг решетки, сохраняя циркуляцию
постоянной, то в пределе получим задачу обтекания одиночного профиля.
Одиночный профиль (в отличие от решетки) не может повернуть безграничный
поток на конечный угол. Следовательно, скорости в бесконечности
одинаковы и можно обозначить .
Тогда из формулы E.47) следует формула Жуковского о подъемной силе
для одиночного крыла:
F~pw*r. E.49)
82

Рис. 5.12. Положение точки ветвления
постулата Жуковского—Чаплыгина)
потока на обтекаемом контуре (объяснение
Формулы E.47) и E.49) составляют содержание теоремы Жуковского о
подъемной силе. В общем случае на одиночное тело, обтекаемое вязкой
жидкостью, действуют как сила сопротивления (направленная вдоль
скорости потока), так и подъемная сила (перпендикулярная скорости потока).
В идеальной несжимаемой жидкости, как следует из теоремы Жуковского,
сила сопротивления равна нулю, а подъемная сила возникает только при
наличии циркуляции скорости по профилю (рассмотрено течение без отрыва).
Сила сопротивления равна нулю также в дозвуковом потоке идеальной
сжимаемой жидкости.
Для определения подъемной силы необходимо найти циркуляцию
скорости по профилю. Однако величина циркуляции не входит ни в основные
уравнения, ни в граничные условия и в идеальной жидкости, чисто
теоретически может быть выбрана произвольно. Примером этому служит задача об
обтекании окружности, рассмотренная в разд. 5.2. Неопределенность в
выборе циркуляции снимает постулат Жуковского — Чаплыгина.
Рассмотрим обтекание крыла с абсолютно острой задней кромкой
(рис. 5.12). Величина циркуляции, как выяснено в разд. 5.2, влияет на
положение задней точки ветвления, в которой поток сходит с обтекаемого тела.
На рис. 5.12, а, б точки схода лежат соответственно на верхней и нижней
сторонах профиля, поток огибает острую кромку и внезапно поворачивает на
180°. На острой кромке возникают бесконечно большие скорости и
бесконечно большое отрицательное давление, что нереально. На рис. 5.12, в поток
сбегает с задней кромки по касательной. В этом единственном варианте
обтекания скорость и давление конечны на задней кромке и можно
предполагать, что он будет согласовываться с результатами эксперимента. Постулат
Жуковского — Чаплыгина предписывает такой выбор циркуляции скорости,
чтобы сбег потока происходил с острой задней кромки.
В заключение отметим, что для хорошо обтекаемых тел (крылья, лопатки
турбомашин и т. п.) теория идеальной жидкости в целом согласуется с
экспериментом по распределению давления и величине подъемной силы
Однако естественно, что эта теория не пригодна для определения силы
сопротивления.
Для плохо обтекаемых тел (цилиндр и т.п.) теория расходится с
экспериментом, так как в реальной жидкости возникает отрыв потока.
5.4. РАСЧЕТ ОБТЕКАНИЯ ТЕЛ ПОТЕНЦИАЛЬНЫМ ПОТОКОМ
НЕСЖИМАЕМОЙ ЖИДКОСТИ МЕТОДОМ КОНФОРМНОГО
ПРЕОБРАЗОВАНИЯ
Рассмотрим путь, которым может быть решена задача обтекания
плоским потенциальным потоком идеальной несжимаемой жидкости профиля
заданной формы. Выше такая задача была решена для случая, когда
профиль имел простую форму; окружность.

Рис. 5.13. Конформное
соответствие плоскостей:
а — плоскость крыла; б —
плоскость окружности
Обозначим комплексный потенциал потока, обтекающего окружность
расположенную в плоскости г = х + iy:
F(z)=q>(x, у) + Ц(х, у). E.50)
Положим, что комплексная переменная г = х + /у в свою очередь
является аналитической функцией комплексной переменной ?= | + 1ц:
*=/F + Л1) = /@. E.51)
Очевидно, что сложная функция
Л)> E.52)
как и всякая аналитическая функция комплексного переменного,
описывает некоторый плоский потенциальный поток идеальной несжимаемой
жидкости. Этот новый поток существует в плоскости комплексного переменного
С = I + it), а ф (?, т)), -ф (?, т)) являются соответственно потенциалом
скорости и функцией тока этого потока.
Если функция E.51) и обратная ей функция однозначны, то точке
плоскости комплексного переменного z = х + iy соответствует определенная
точка плоскости комплексного переменного ? = | + и], и наоборот.
Следовательно, если точка z будет пробегать по окружности, то точка
? будет описывать некоторый замкнутый контур. Подчеркнем, что все
приведенные функции рассматривают только в области поля течения, т. е. вне
окружности и вне профиля, в который преобразуется окружность.
Таким образом, можно считать, что функция E.51) преобразует поток
вокруг профиля в поток вокруг окружности. Задача обтекания окружности
была решена, и соответствующий комплексный потенциал в общем случае
(при г0 = 1) имеет вид E.31):
E.53)
где w^ — комплексная скорость потока в бесконечности.
Тогда комплексный потенциал потока вокруг профиля сконструируем с
помощью выражений E.51) и E.53):
Следовательно, задача обтекания произвольного профиля в принципе
может быть всегда сведена к решенной задаче обтекания окружности. Вся
сложность заключается в нахождении такой функции E.51), которая
преобразует поток вокруг профиля заданной формы в поток вокруг окружности.
Пусть в плоскости комплексного переменного ? = 6 + «л задан профиль
(рис. 5.13, а).
84

, В соответствии с изложенными выше соображениями расположим в
плоскости комплексного переменного z = х + iу окружность (рис. 5.13, б).
Радиус окружности для сокращения последующих записей удобно принять
равным единице, что не принципиально, так как определяет только выбор
масштаба.
Практически удобнее искать не функцию E.51), преобразующую поток
вокруг профиля в поток вокруг окружности, а обратную ей функцию,
которая преобразует поток вокруг окружности в поток вокруг профиля:
E.55)
Это объясняется тем, что в этом случае искомую функцию легко строить
в виде ряда Лорана.
Если рассматривать вопрос преобразования геометрически, то следует
говорить, что однозначная аналитическая функция E.55) преобразует
область вне окружности в область вне профиля, а саму окружность — на
профиль.
Любая линия в плоскости z преобразуется в соответствующую ей линию
в плоскости ?.
Такое преобразование, осуществляемое аналитической функцией
комплексного переменного, называется конформным и основное его свойство
состоит в том, что при отображении сохраняются углы. Если две линии
пересекаются в плоскости z под некоторым углом, то соответствующие им
линии в плоскости С будут пересекаться под тем же углом. Это следует из того,
что производная аналитической функции не зависит от направления, в
котором она вычисляется. Ортогональная сеть эквипотенциалей ср (дс, у) =
= const и линий тока \|) (х, у) = const, расположенных в плоскости z,
переходит в ортогональную сеть ср (?, ц) = const, \|э (?, ц) = const в плоскости
Пусть профиль, расположенный в плоскости ? (см. рис. 5.13, а),
обтекается потенциальным потоком идеальной несжимаемой жидкости с заданной
скоростью в бесконечности.
Обозначим комплексный потенциал потока в плоскости профиля
F&)=4>(t, f|) + *HE. Л)- E.56)
Тогда комплексная скорость по формуле E.26) может быть найдена
через его производную и (?, ч\) — ш (?, ч\) = dF (?)/d?. Поскольку
переменная ? является функцией переменной z, то по правилам дифференцирования
сложной функции получим формулу для пересчета скоростей в плоскостях
5@ -«ю-ио-^-^-!---^-^-. E-57)
d? dz dt, dz dt/dz
Здесь у всех функций отмечены аргументы, что позволяет легко, понять, в
какой плоскости рассматривается функция. Так слева стоит искомая
комплексная скорость в плоскости профиля, а справа — комплексный
потенциал обтекания окружности F (г) [см. выражение E.53)] и производная
функции, совершающей конформное преобразование E.55).
Для того чтобы плоскопараллельный поток перед профилем переходил
в плоскопараллельный поток перед окружностью, точке ? = оо должна
соответствовать точка z = оо, а производная dt,!dz должна быть конечна.
Тогда по общей формуле для пересчета скоростей E.57) найдем соответствие
между скоростями в бесконечности перед профилем и перед окружностью:
5 e.. E.58)
86

При заданной согласно постановке задачи скорости в бесконечности
перед профилем w (? = оо) можно найти соответствующую ей скорость в
бесконечности перед окружностью w (z = оо), если известно значение
производной отображающей функции при z = оо.
Таким образом основная сложность в решении поставленной задачи
состоит в нахождении такой функции E.55), которая конформно преобразует
внешность окружности на внешность заданного профиля.
Рассмотрим теперь практическую и вычислительную стороны задачи:
построение преобразующей функции.
Ищем функцию E.55) в виде ряда Лорана по переменной z не выше чем
в первой степени, что обеспечивает условие ? = оо при z = оо и dt>ldz Ф оо;
^ — + ... E.59)
0 +
г г2
Здесь искомые коэффициенты являются в общем случае комплексными
постоянными:
A^a + ib, An = an + ibnf /t = 0, 1, 2, ... E.60)
Найдем уравнение профиля, в который переходит окружность при
использовании преобразования E.59). Так как для точек на окружности
единичного радиуса z = е1'9, где 8 — полярный угол (см. рис. 5.13, б), то,
подставив это выражение в ряд E.59), получим параметрическое
представление профиля в комплексном виде:
Z = Aei*'+A0 + A1e-i*+A2e-v* + ... E.61)
Используем формулу Эйлера е'е = cos в + i sin 0 и заменим
коэффициенты в уравнении E.61) с помощью обозначения E.60). После отделения в
уравнении E.61) действительной и мнимой частей получим параметрическое
представление профиля в таком виде:
N N
N
2 bncosnQ— E.62)
1=2
— 2 ans\nnQ.
2
n—2
Подобное параметрическое представление замкнутой кривой называют
нормальным. Главное заключается в том, что такое параметрическое
представление отличается от бесчисленного множества других возможных
параметрических представлений того же контура тем, что коэффициенты при
cosn9 и sin л9 в двух рядах I (9), г\ (9) взаимозависимы определенным
образом. Для п > 2 коэффициент при cos nQ в ряду для I равен по абсолютной
величине и обратен по знаку коэффициенту при sin л9 в ряду для ч\. А
коэффициент при sin л9 в ряду для | равен коэффициенту при cos n9 в ряду
ДЛЯТ).
Через W обозначено число гармоник, при котором достигнута нужная
точность описания профиля (детали будут пояснены ниже, чтобы не
перебивать существа изложения).
Очевидно, что если найдено нормальное параметрическое уравнение
контура E.62), то задачу построения функции, совершающей конформное
преобразование, можно считать решенной. В самом деле, по найденным
действительным коэффициентам а, Ь, апу Ьп с помощью E.60) определяем комп-
86

лексные коэффициенты Л, Ап и, следовательно, ряд Лорана E.59), которым
представлена искомая функция комплексного переменного.
Прежде чем перейти к общему случаю построения обтекания профиля
произвольной формы, рассмотрим некоторые частные виды профилей. Это
позволит хорошо понять существо дела и не потребует громоздких
преобразований и вычислений.
Вместо общего ряда E.59) запишем только три члена:
? = z + -- +-т—. E.63)
г 2г2
Следовательно, примем А = 1, так как этот коэффициент по существу
влияет только на масштаб изображения. Примем Ло = 0, что также
несущественно и определяет выбор начала координат. Запись коэффициентов в
принятой форме Ах = а2 — ft2, Л2 = аЬ2/2 просто удобна для анализа, как
это будет видно из дальнейшего изложения.
Положим сначала b = О и рассмотрим конформное преобразование,
представляемое функцией
г, E.64)
которое называют преобразованием Жуковского, применившим его для
получения серии профилей крыльев самолета.
Здесь рассмотрим только два простейших профиля Жуковского: эллипс
и бесконечно тонкую пластину.
При действительном а < 1 функция E.64) отображает внешность
окружности единичного радиуса на внешность эллипса. Подставив в E.64) г = е'е,
получим, после отделения действительной и мнимой частей,
параметрическое уравнение профиля в таком виде:
g=(l+a2)cose, т| = A — a2)sin6.
Это уравнение эллипса в параметрической форме, причем A + а2) — его
большая, а A — а2) — малая полуоси.
Пусть требуется вычислить скорости на эллипсе, обтекаемом безцирку-
ляционным (Г = 0) потенциальным потоком идеальной несжимаемой
жидкости со скоростью в бесконечности и^ параллельной оси абсцисс.
Найдем производную преобразующей функции E.64):
^l— а*/г\ E.65)
Значение этой производной в бесконечности равно единице. Следовательно,
в данном случае соответствующая скорость в бесконечности перед
окружностью, как следует из формулы E.58), равна скорости в бесконечности перед
эллипсом w^ = и^.
Теперь можно вычислить скорость в любой точке плоскости эллипса по
формуле E.57), в которую следует подставить производную комплексного
потенциала потока вокруг окружности E.53) при Г = 0:
w (г) =dF(z)/dz = uoo A — 1/z2) E.66)
и найденную производную отображающей функции E.65). Для
иллюстрации вычислим скорости в точках ? = ± A + а2), ? = ± A — a2) i,
лежащих на концах осей эллипса. Первой паре точек на эллипсе соответствуют
точки z = ± 1 на окружности, как это следует из зависимости E.64). В этих
тбчках скорость на окружности по формуле E.66) равна нулю.
Следовательно, по формуле E.57) скорость в соответствующих им точках эллипса также
равна нулю (точки ветвления). Второй паре точек на эллипсе соответствуют
точки ± i на окружности, в которых скорость равна 2и00. Тогда по формуле
87

E.57) находим искомые скорости на эллипсе, подсчитав предварительно
значение производной E.65) при z = ±i (dtldz = 1 + a2)tHv = 2иоо 1(\+а2).
Рассмотрим теперь обтекание крыла в виде бесконечно тонкой пластины.
При а -»- 1 эллипс «сплющивается» и превращается в пластину, так как
большая его ось стремится к 4, а малая — к 0. Значение производной E.65)
в точках z = ±1, соответствующих на окружности концам пластины, равно
нулю. В этих точках нарушается конформность преобразования, т. е.
сохраняемость углов, так как гладкой окружности соответствует пластина с
бесконечно острыми кромками.
Положим теперь в зависимости E.63) по-прежнему 6 = 0, но примем
a =tia и покажем, что в этом случае внешность окружности отображается
на внешность пластины, ориентированной под углом а. Одновременно
введем масштабный множитель, чтобы сделать длину пластины равной В.
Тогда из E.63) имеем
С = Е + *Ч = (г+е»'«/г)В/4. E.67)
При z = е|в запишем параметрическое уравнение
Б = [cos0 + cos( —0 + 2а)]В/4, ц = [sin8 + sin(—0 + 2а)]В/4.
Применив формулы сложения тригонометрических функций, получим
I = {В 12) cos а-cos (в—а), ц = (В/2) sin а-cos (в —а). E.68)
Отсюда следует, что это уравнение пластины длиной В, наклоненной к
оси абсцисс под углом а, так как х\ = | tg а. Подчеркнем, что когда угол
0 пробегает значения от 0 до 2я, то пластина обходится дважды: по одной и
другой стороне, т. е. ее следует рассматривать как замкнутую кривую, а не
как отрезок прямой.
Пусть пластина обтекается потенциальным потоком идеальной
несжимаемой жидкости со скоростью в бесконечности иЖУ параллельной оси абсцисс.
Найдем подъемную силу, действующую на пластину, наклоненную под
углом а к оси абсцисс.
Производная отображающей функции E.67)
да*= A — е«*/Л В/4. E.69)
Значение производной при г->оо равно В/4. Следовательно,
соответствующая скорость в бесконечности перед окружностью будет
действительной величиной, равной по формуле E.58) uJBl\. Тогда эквивалентный
комплексный потенциал потока вокруг окружности E.53) примет вид
Для того чтобы определить подъемную силу, действующую на пластину,
надо найти значение циркуляции скорости Г. Согласно постулату
Жуковского — Чаплыгина сбег потока должен происходить с острой задней
кромки пластины. Острым кромкам пластины соответствуют на окружности
точки z — ±е'а, в которых производная отображающей функции E.69) равна
нулю. Циркуляцию скорости надо определить таким образом, чтобы сбег
потока с окружности происходил в точке z = e'°, соответствующей задней
кромке пластины.
По формуле E.37), приняв 0 = а, г0 = 1 и подставив вместо и^
значение м^В/4, определим величину циркуляции Г = пВи^ sin а. Величину
подъемной силы, действующей на пластину, определим по формуле
Жуковского E.49): F = пВри? sin а. Эта сила, как отмечалось, перпендикулярна
88

Рис. 5.14. Профили, полученные конформным преобразованием:
а — Ь*=О,Ь; б — *>2=-0,5
направлению скорости в бесконечности. Обычно рассматривают
безразмерный коэффициент подъемной силы
Су = 2F/pul В = 2л sin a.
Вычисленное значение Су несколько больше (примерно на 10 %)
экспериментального, полученного для тонких хорошо обтекаемых крыльев,
поставленных под малым углом атаки (сс< 10°). При значительных углах
атаки на передней кромке крыла возникает отрыв потока и в этом случае
рассматриваемая теория не применима. В этих режимах обтекания
необходимо учитывать дополнительные эффекты, вызванные отрывом (см. гл. 12).
Вернемся к преобразованию с помощью функции E.63), найдем
производную и приравняем ее нулю, чтобы определить положение точек, в
которых нарушается конформность:
dt I a»—ft»! ab2 Л
dz z* г3
Один из корней этого уравнения г = а и, следовательно, уравнение можно
представить в таком виде (Ь Ф 0):
Выбрав а = е'а, т. е. поместив один из корней на окружность, получим
профиль с острой задней кромкой. Можно положить а = 1, так как это
вызовет только поворот профиля. Если же принять а< 1, то задняя кромка
будет скругленной. Выбор постоянной b определит два других корня
уравнения, от положения которых будет зависеть форма профиля. Профили
при а = 1 и различных b показаны на рис. 5.14.
В некоторых практических задачах форму профиля следует считать
заданной, а в других ее необходимо произвольно варьировать, чтобы добиться
определенных эффектов. Во всяком случае желательно иметь метод, который
позволяет решать задачу для профиля произвольной формы.
Изложим метод последовательных приближений, удобный для
реализации на ЭВМ, который позволяет решить задачу конформного
преобразования для профиля заданной формы.
Произвольное параметрическое уравнение заданного профиля получить,
конечно, очень просто. Будем исходить из того, что параметрическое
представление профиля задано в виде
N N
I = (Б/2) cos 0, ц == с9 + 2 Сп cos пб + 2 dn sin nQ. E.70)
Здесь В обозначена хорда профиля в выбранном масштабе.

Задача состоит в том, чтобы по заданному параметрическому
представлению E.70) найти нормальное параметрическое представление того же
профиля E.62).
Как нормальное представление E.62), так и заданное E.70) являются
частными случаями параметрического уравнения профиля в более общем
виде:
N N
S ]? bn sin nG;
E.71)
n n
cncosnQ+
я
Для того чтобы ряды E.71) приняли нормальную форму, нужно выполнить
условия:
an = —dn, Ьп--=сп при я>2. E.72)
На коэффициенты а0, с0, аи сг требования нормальной формы рядов не
налагают каких-либо условий, и эти коэффициенты должны быть определены
так, чтобы ряды описывали заданный профиль. Ряды E.70), коэффициенты
которых по условию известны, дают точное представление профиля в
параметрической форме (или с точностью, которая считается достаточной), но
не имеют нормальной формы.
Рассмотрим метод последовательных приближений, который позволяет
построить параметрическое представление профиля в нормальной форме по
заданному представлению E.70). Пусть нижний индекс у коэффициентов
рядов Фурье по-прежнему обозначает номер гармоники, а верхний —
номер приближений. Примем следующий метод определения приближений:
™>+A — а) с^\ E.73)
= 0, 1, 2, ...,
где а — коэффициент релаксации, который определяет долю взаимного
влияния коэффициентов двух рядов при подсчете следующего
приближения по предыдущему. В качестве нулевого приближения (т = 0), очевидно,
следует принять коэффициенты рядов E.70) при п > 2.
Если последовательные приближения сходятся, то согласно условию
E.72) для п ^ 2 получим ап ->• — dny bn-+- cn и из соотношения E.73)
следует, что коэффициенты стремятся к некоторым значениям, которые
являются искомыми.
Таким образом, в каждом приближении по условию E.73) определены
коэффициенты ап и Ьп только для п > 2. Покажем, как должны быть
определены в каждом приближении коэффициенты ao> <*i и Ьг.
Очевидно, что если параметр 0 изменяется от 0 до 2 я, то точка I должна
дважды пробегать отрезок, соответствующий хорде профиля.
Следовательно, функция | (9) должна достигать максимума в точке % (9Х) = В/2 и
минимума в точке | (92) = — В/2. Этим определены четыре условия: значения
0i и 92, при которых функция достигает соответственно максимума и
минимума, и значения максимума и минимума. Таким образом, с помощью ряда
E.71) можно составить четыре уравнения:
при 9 = 9Х
i-B/2, d|/dO = O; E.74)
при 9 = 92 *
90

Значения 8Х (или 62) можно выбрать произвольно. Примем 6Х = 0. Тогда
из условий E.74) и ряда E.71) получим
ао+аг+ 2 ап^В12\ E.75)
н=2
Ь1==_ 2 nbn; E.76)
л =2
JV N
а0 +аг cos 02+S a» cos "вз + 2 b» sin n92 = ~#/2; E.77)
/1 = 2 п=1
— a1sin68— 2 nansinnQ2+ 2 я^п cos n68 = 0. E.78)
/i — 2 /г = 1
При решении системы E.75) — E.78) возможны два случая. Из
сравнения E.76) и E.78) следует, что вариант 62 = я возможен только, если &п=0,
где п = 1,2, 3, ... Тогда из E.75) и E.77)
ао = а2==а4 = ... =0, ах—(В/2)—as—a5—... E.79)
Если 82 ф я, то решение будет иным. Уравнения E.75) — E.79)
записаны таким образом, что под знаками сумм стоят только известные
коэффициенты, так как коэффициент Ьх определен выражением E.76). Исключим
а0 в уравнении E.77) с помощью уравнения E.75). Затем из полученного
выражения исключим аъ выразив его из уравнения E.78). В результате
получим уравнение с одним неизвестным 62:
N N N \
rt=2 /t = 2 /1 = 1 / *
— I S л6цСО8лв,— V пап sin n%) (I— cos82)=0. E.80)
\я=1 /г=2 /
Решение трансцендентного уравнения на ЭВМ не представляет
сложности (напомним только, что 82 Ф я). Определив 82, находим ах из уравнения
E.78), а затем а0 из уравнения E.75). Эти вычисления элементарны, так как
все входящие в уравнения величины известны.
Теперь все коэффициенты первого ряда E.71) вычислены, а сам ряд
представляет более точное параметрическое представление координаты |, чем
исходный.
Следующий шаг — это определение нового параметрического
представления координаты т) согласно второму ряду E.71). Для этого задаем
значения 8 (например, через 10°) и подсчитываем соответствующие значения \
с помощью первого ряда E.71). Затем по этим значениям | определяем
соответствующие новые значения 8 с помощью исходного выражения E.70);
6= ±arccosB?/B). E.81)
Здесь знак плюс следует выбирать при 8 < 82 и знак минус в обратном
случае. По этим новым значениям 8 находим новые значения т), используя
исходное параметрическое представление E.70). В результате этого расчета
находим зависимость т) (8). Разложив ее обычным путем в ряд Фурье,
получим коэффициенты второго ряда E.71).
Далее цикл расчетов повторяется, начиная с формул E.73). Расчет
проводится до тех пор, пока условия E.72) будут удовлетворены с принятой
точностью. Важно подчеркнуть, что так как во время каждого цикла исполь-
91

©.
2/ о
Рис. 5.15. Профиль лопатки турбины
зуется заданное параметрическое представление E.70), то в процессе
приближений форма профиля остается неизменной. Расчеты удобны для
программирования, так как все циклы совершенно идентичны и состоят из трех
основных стандартных операций: 1) разложение в ряд Фурье, т. е.
гармонический анализ; 2) решение уравнения E.80); 3) вычисление координат по
заданному ряду Фурье, т. е. гармонический синтез.
В качестве примера приведем результаты расчета конформного преобразования
внешности окружности единичного радиуса на внешность толстого сильно изогнутого
профиля (рис. 5.15).
Для В = 118, 0 [см. зависимость E.70)] коэффициенты сп и dn
приведены ниже.
п о
сп 44,Ш
dn 0,0
Результаты расчета коэффициентов ап и Ьп первого приближения и всех
коэффициентов рядов E.71) девятнадцатого приближения приведены в
табл. 5.1 (для сокращения записи результаты 2—18 приближений
пропущены).
Коэффициенты даны только для двух приближений при N = 7. В
качестве исходного (нулевого) приближения принято [см. E.70)]: аг = В/2 =
= 59,000; все остальные коэффициенты anibn, cn, dn имеют нулевое значение,
что соответствует бесконечно тонкой плоской пластине, весьма далекой по
форме от толстого и сильно изогнутого профиля (рис. 5.15), для которого
ищем функцию, совершающую конформное преобразование.
Таблица 5.1
—6
16
1
,171
,798
2
-16
-8
,568
,683
3
1,438
1,662
4
0,448
—0,418
0
0
5
,004
,384
п
0
1
2
3
4
5
6
7
Приближение m
первое
а
0,730
54,552
4,342
-0,831
0,209
—0,002
0,0
0,0
Ъ
13,515
-8,284
0,719
0,224
0,0
0,0
0,0
девяти адцатое
а
—5,381
55,259
11,053
0,790
—2,046
— 1,363
0,111
0,577
Ь
19,706
—5,214
—4,921
— 1,492
0,784
0,798
0,392
с
24,789
— 13,427
-5,257
—4,893
— 1,510
0,796
0,793
0,392
d
20,710
— 11,045
—0,798
2,045
1,368
—0,117
—0,575
92

На рис. 5.15 номера точек на профиле (умноженные на 10)
соответствуют значениям угла 9 для нулевого приближения.
Очевидно, что полученные результаты достаточно хорошо согласуются
с условием E.72).
5.5. ПЛОСКОЕ ДОЗВУКОВОЕ ТЕЧЕНИЕ ИДЕАЛЬНОЙ ЖИДКОСТИ.
УРАВНЕНИЕ ГОДОГРАФА СКОРОСТИ
Рассмотрим плоское, установившееся, безвихревое течение
идеальной сжимаемой жидкости с дозвуковыми скоростями. Такое движение
можно описать уравнениями неразрывности E.15):
= 0, E.82)
ox ay
отсутствия вихрей E.2)
E.83)
дх ду
Бернулли для сжимаемой жидкости E.12)
и— 1
х ро
E.84)
2 х—1 ро \ Ро / к—1 ро
изоэнтропы, связывающим давление и плотность:
р/р*= PilPi» E.85)
При безвихревом движении сжимаемой жидкости можно ввести
потенциал скорости так же, как это было сделано для несжимаемой жидкости:
и = dq>/dxf v = дц)/ду. E.86)
Введем функцию тока, чтобы удовлетворить уравнение неразрывности E.82)
ри = dty/ду, pv = — дЦ/дх, р' = р/р0. E.87)
Связь между потенциалом скорости и функцией тока можно установить на
основании формул E.86) и E.87):
дх р ду ' ду р дх
Полученные уравнения нелинейны, так как плотность жидкости зависит
от скорости, и не совпадают с соотношениями Коши — Римана E.24), как
это было в случае несжимаемой жидкости. Нелинейность уравнений
делает весьма трудным использование их для решения задач.
Однако существует способ преобразования этих точных нелинейных
уравнений в точные линейные уравнения. Такие преобразования были применены
в газовой динамике С. А. Чаплыгиным A902 г.). Большинство современных
исследований дозвуковых (и трансзвуковых) течений основаны на
применении уравнений Чаплыгина. Эти точные преобразования не следует
смешивать с методом линеаризации, под которым понимают упрощение нелинейных
уравнений путем отбрасывания нелинейных членов.
Общая идея преобразований заключается в следующем. В приведенных
уравнениях независимыми переменными являются координаты дс, у, а
функциями — скорости потока и (х, у), v (х, у), функция тока ty = \|? (#, у) и
потенциал скорости ф= ф (jc, у). Из этих зависимостей в принципе можно
исключить х, у и считать, что функция тока и потенциал скорости являются
93

ил,
Рис. 5.16. Соответствие между физической
плоскостью и плоскостью годографа
скорости:
а — физическая плоскость; б — плоскость
годографа скорости
функциями скоростей ф = Ф (и, v),
г[) = г|) (и> v). Следовательно, ф иг|э
будут и дальше оставлены в
качестве независимых переменных, но
вместо декартовых координат х> у
введены декартовы координаты и, v.
Плоскость, в которой
происходит течение, называется физической
плоскостью или плоскостью
течения, а плоскость с координатами
и, v — плоскостью годографа
скорости.
Рассмотрим соответствие между
этими плоскостями. Пусть в
физической плоскости известна линия
тока, на которой отметим точку А (рис. 5.16). Пусть в этой точке
скорость равна до, а угол ее наклона к оси абсцисс 6. Тогда точке А
соответствует в плоскости годографа точка А' с декартовыми координатами и, v
или, что то же самое, с полярными координатами до, 6. Повторяя эти
построения для точек, находящихся на линии в физической плоскости,
можно найти соответствующую ей линию тока в плоскости годографа.
Получим основные уравнения в плоскости годографа, используя путь,
аналогичный тому, который был принят при выводе формулы E.26) для
несжимаемой жидкости.
С помощью формул E.86) и E.87) найдем следующее соотношение (при
разложении метода годографа будем для сокращения записи обозначать через
р относительную плотность р/ро):
E.89)
Вместо декартовых координат и, v удобнее использовать полярные до, 8,
представив комплексное число в тригонометрической форме:
Р \ дх ду ) р \ дх ду
(udx + vdy) + i(—vdx + udy) = (и — iv) dz,
и — iv~
E.90)
Тогда из формул E.89) и E.90) получим важное для дальнейшего
выражение
w
Если рассматривать доив как независимые переменные, то
dz
dw
w
(J2.+jLJ±.)
\ dw p dw /'
w
E.91)
(+-LJ±) E.92)
Для того чтобы найти уравнения годографа, из этих выражений следует
исключить г. Продифференцировав первое выражение E.92) по 0, второе по
w и исключив смешанную производную, найдем.
pw
i dw 1 dw , . d / 1 \ dty
• —— sss « ~p ^ I j: ' I ' ' ' ,
w dw w2 ^^ ^w \ pw / d$
94

Отделив действительные и мнимые части, получим дба уравнения:
J <*ф ^A-(-L-\J!$L J^^JL.iSL E 93)
w dw dw \ pw j d6 ' dw w dd
Преобразуем полную производную в первом уравнении E.93):
d ( 1 \ 1 /- , dp \
dw \ pw / p2w2 \ dw I
Производную в правой части можно найти с помощью уравнения E.10) и
формулы для скорости звука с учетом того, что процесс течения также изо-
энтропийный и плотность является функцией только давления
dp dp dp pw
dw dp dw a2
Окончательно имеем
l—M2
dw \ pw j pi
pw2
Заменив в первом уравнении E.93) полную производную полученным
выражением, приходим к уравнениям годографа Чаплыгина:
dg> = 1—М2 дф ^L^i^L E.94)
dw pw dQ ' dw w dQ '
Так как р — известная функция w, a M = w/a, то эти уравнения годографа
линейны, что и является основным их преимуществом в отличие от
нелинейных уравнений E.88) в физической плоскости. Ввиду линейности
уравнений к ним мргут быть применены известные общие методы построения
решений. Однако не будем здесь рассматривать некоторые точные решения,
а остановимся только на приближенном методе, также предложенном
С. А. Чаплыгиным. _
Прежде всего отметим, что для несжимаемой жидкости (М = 0, р = 1)
уравнения годографа E.94) переходят в соотношения Коши — Римана,
записанные в полярной системе координат:
дф = L^L J^L^J-^L E 95)
dw w дб ' dw w дВ '
Соотношения E.95) приводят к использованию методов теории функций
комплексной переменной, как это показано в подразд. 5.2. Точные
уравнения годографа не сводятся к соотношениям Коши — Римана, но их можно
привести к этим соотношениям для некоторого гипотетического газа и на
этой основе создать приближённый метод расчета.
Вместо скорости w введем новую независимую переменную s (w). Тогда
согласно правилу дифференцирования уравнения годографа E.94) примут
вид
дф ds 1— М2 dty Jhj> jis j> o^
ds dw pw dQ ds dw w dB
Выберем новую переменную s (w) так, чтобы уравнения годографа E.96)
превратились в соотношения Коши — Римана, т. е.совпали с
соотношениями E.95) при замене w на s:
LJ?$_ _?$_:__!-j?3L E 97)
ds s dd ' d$ $ ^9 '

Для этого необходимо принять
_?_=_bMLs, JL=i.s. E.98
aw pW aw w
Уравнения E.98) совместны только при условии
A — М2)/рш == р/ад,
из которого следует, что плотность газа и число М связаны формулой
4-= -^ = VI— М2 или КЬ^М^/Р = 1. E.99
Р Р
Полученная зависимость плотности от числа М не совпадает с точной за
висимостью для изоэнтропийного течения D.30)
) E.100
Однако для дозвукового течения зависимость E.99) является хорошей ап
проксимацией точной формулы. В этом можно убедиться, разложив левук
часть второй формулы E.99) с использованием точной зависимости для плот
кости E.100) в ряд по М2 (напомним, что через р обозначается фактически
р/ро):
у 1-0,ЗМ4+... при х = 1,4.
Р 8
Таким образом, левая часть этого выражения отличается от единиць
только на члены порядка М4 и выше.
Можно трактовать зависимость E.99) как точную, но для
гипотетического газа, называемого газом Чаплыгина. Если принять в точной формуле
E.100) х = — 1, то она полностью совпадает с формулой E.99).
Аналогичным образом при х = — 1 могут быть установлены остальные
зависимости для газа Чаплыгина. Из уравнения Бернулли E.84) следует
связь между скоростью потока и скоростью звука:
a2— w2=al E.101)
Для газа Чаплыгина скорость звука растет с ростом скорости, а не
уменьшается, как в обычном газе. Можно потребовать, чтобы уравнение E.101)
удовлетворялось для некоторого значения скорости wl9 приняв
al^al-wl E.102)
Из уравнения E.101) следует выражение для числа М в газе Чаплыгина:
MJ^». E.103)
С помощью формул E.99) и E.100) найдем зависимость безразмерной
плотности от скорости
-?- = —а° E.104)
Зависимость давления от скорости установим из уравнения Бернулли
E.10), исключив в нем плотность с помощью формулы E.104):
aowdw . dp ~
96

После интегрирования и определе- р/р2
ния постоянной из условия р = р0 при 1>°
w = 0 имеем а^п\ -\- w% + р/р0 —
0,6
Исключив скорости с помощью
формулы E.104), получим зависимость
между давлением и плотностью
E.105)
0,2 0,4 0,6 0,8 X
Рис. 5.17. Зависимость безразмерной
плоскости от безразмерной скорости:
/ _ точная зависимость при х=1,4; 2 —
приближенная зависимость
которая для газа Чаплыгина заменяет
уравнение изоэнтропы.
Выбор постоянной а0 в формулах
E.104) или E.105) можно, используя
зависимость E.102), произвести так, чтобы достичь лучшего
согласования с точными формулами. Формулу E.104) можно записать в таком виде:
1/1/" Г+Ж
Р/Ро=
E.106)
Сравнение результатов расчета по формуле E.106) и точной формуле
D.39) дано на рис. 5.17.
Заменив во втором уравнении E.98) плотность с помощью формулы
E.104), получим зависимость между новой независимой переменной и
скоростью
ds ^
s У'с
Проинтегрировав это выражение, имеем
aw
dw
w
s ==•
Определим постоянную интегрирования а из условия, что при w <^ а0
следует принять s = до, так как при малых скоростях законы движения
сжимаемой и несжимаемой жидкости совпадают. Тогда
2anw
«в-г
или
W =•
Плотность из формулы E.104) также можно выразить через s:
р 4а§—s2
Ро 4uj+s* '
E.107)
E.108)
E.109)
Подытожим полученные результаты. Если ввести газ Чаплыгина, то
точные уравнения годографа E.88) превращаются в соотношения Коши —
Римана E.97), что дает возможность использовать хорошо разработанные
методы теории несжимаемой жидкости. Хотя газ Чаплыгина обладает
необычными свойствами, но при х = — 1 зависимость между плотностью
и давлением или плотностью и скоростью значительно ближе к изоэнтро-
пийной. При помощи метода С. А. Чаплыгина можно рассматривать только
4 За к. 2638 97

дозвуковые течения, так как даже при до-> оо из формулы EЛ03) следует
М—>• 1.
Поскольку приближенные уравнения годографа — это соотношения
Коши — Римана, то можно считать, что им соответствует в плоскости
годографа s, Э некоторое течение идеальной несжимаемой жидкости. Течение в
плоскости годографа иногда называют фиктивным течением в отличие от
действительного течения в физической плоскости.
Расчет течений с помощью метода годографа состоит из следующих
этапов.
1. Согласно заданным условиям задачи строят годограф скорости.
2. В плоскости годографа находят точки, соответствующие бесконечно
удаленным точкам в физической плоскости . В этих точках годографа могут
быть особенности типа источник (сток), диполь, вихрь и др., смотря по
условиям течения в физической плоскости.
3. Строят фиктивное течение в плоскости годографа.
4. Решение, полученное в плоскости годографа, переносят в физическую
плоскость.
Подчеркнем особенность применения метода годографа. В
гидродинамике различают прямые и обратные задачи. В прямых задачах считают
заданным форму обтекаемого тела, а ищут закон распределения скорости.
Некоторые методы решения прямых задач изложены в подразд. 5.5. и гл. 13. В
обратных задачах задано распределение скорости по обтекаемому телу или
скорость на границе струи, решение состоит в определении формы тела или
струи. Примеры применения метода годографа даны в подразд. 5.6. и гл.13.
Таким образом, области применения прямой и обратной задач различны и в
технике следует использовать оба подхода.
Преимущество метода годографа, в силу его особенности, состоит в
возможности непосредственного построения профилей с целесообразным
распределением скорости.
5.6. ПОСТРОЕНИЕ ТЕЧЕНИЙ МЕТОДОМ ГОДОГРАФА СКОРОСТИ
Первые задачи в теории струй идеальной несжимаемой
жидкости были решены Г. Гельмгольцем A868 г.) и Г. Кирхгофом A869 г.),
крупный вклад в теорию сделан Н. Е. Жуковским A890 г.). Первое точное
решение в теории струй сжимаемой жидкости получил С. А. Чаплыгин A902 г.)
В качестве первого примера, в
котором выясняются особенности
метода годографа, рассмотрим
задачу о струйном течении. Это
решение находит практическое
применение, в частности, в теории
лабиринтных уплотнений турбомашин.
Плоская струя идеальной
несжимаемой жидкости вытекает из
отверстия в стенке с острыми
кромками (рис. 5.18, а). Давление на
границе струи равно заданному
давлению в окружающем
пространстве, т. е. постоянно. Следовательно,
на основании уравнения Бернулли
на границе струи величина
скорости также постоянна, хотя
направление скорости меняется. На стен-
6)
Рис. 5.18. Истечение струи из отверстия:
а — физическая плоскость; б — плоскость
годографа скорости
98

ках, наоборот, постоянно направление скорости, однако ее величина
изменяется. Эти соображения дают возможность нарисовать годограф
скорости (рис. 5.18, б). В точках Л^, D^, бесконечно удаленных от отверстия
(в левой полуплоскости), скорость жидкости равна нулю и поэтому им
соответствует начало координат в плоскости годографа (и = 0, v = 0). В
точке В скорость направлена по касательной к стенке, а значение ее равно
значению известной скорости на границе струи wx. В плоскости годографа
соответствующие точки обозначаются теми же буквами. На границе струи ВС^
скорость постоянна по величине и поэтому на годографе границе струи
соответствует дуга окружности, Течение симметрично и поэтому нет
необходимости пояснять положение остальных точек. В физической плоскости все
линии тока выходят из бесконечности слева и идут в бесконечность справа.
Следовательно, в плоскости годографа они должны выходить из начала
координат и идти в точку С^. ртсюда следует, что течению в физической
плоскости соответствует фиктивное течение в плоскости годографа, вызванное
источником в начале координат и стоком в точке С^, Это фиктивное
течение происходит в полукруге.
Скорости в физической плоскости не могут быть больше, чем на границе
струи, а углы наклона скоростей лежат в первом и четвертом квадрантах.
При построении годографа принято, что соответствующие скорости в
физической плоскости и плоскости течения совпадают по направлению. Это
делает построение более наглядным. Однако надо помнить, что согласно
условию E.90) в плоскости годографа следует изображать сопряженные
скорости. В этом случае годограф зеркально отобразится относительно оси
абсцисс, что не принципиально.
Следующий этап состоит в построении фиктивного течения в полукруге
плоскости годографа. Запишем комплексный потенциал в таком виде
(пользуясь возможностью сложения комплексных потенциалов):
2д wx 2я о*!
—g-ln ¦"-*+-' , E.110)
2я w, V '
Координатами в плоскости годографа служат скорости, причем ше~'е — это
переменная сопряженная скорость. Первые два члена в правой части
представляют комплексные потенциалы соответственно источника в начале
координат и стока в точке С^, координата которой равна величине постоянной
скорости wx на границе струи. Последний член справа — это комплексный
потенциал стока, помещенного в точке с координатой — wx. Следовательно,
этот сток находится вне области годографа и добавлен, как ниже будет
показано, для удовлетворения граничных условий на контуре годографа.
Упростим выражение E.110), воспользовавшись основным свойством
логарифма:
Q . ib
Ф t пЬ In
I е
2л \ wj )
in (L-e-w —В-еЧ E.111)
и покажем, что фиктивное течение происходит в полукруге, так как его
контур состоит из линий тока.
4* 99

На отрезке А^В (см. рис. 5.18) 9 = я/2 и, следовательно, из E.111)
получим
\i w
На полуокружности w = wx и, значит, комплексный потенциал
<р + й|>= — JLinBsin6)(— I). E.112)
В частности, на четверти окружности ВС^: 0 < 9 < я/2, sin 9 > 0 и
тогда
<р + /ф == 2- In B sin 9) iQ.
Следовательно, отрезок А^ В и четверть окружности ВС^ составляют
одну линию тока, на которой функция тока постоянна г|э =—C/4) Q.
Аналогично можно показать, что отрезок 9 = — я/2 и нижняя четверть
окружности совпадают с линией тока л|) = — A/4) Q. Расход жидкости,
протекающей между двумя линиями тока, равен разности значений функции тока на
этих линиях: Дф = — A/4) Q + C/4) Q = A/2) Q. Полученная величина
равна расходу жидкости в струе. Это дает возможность выразить
полученную величину Q/2 из уравнения неразрывности, записанного для струи на
бесконечном расстоянии от отверстия, где поток полностью выравнялся:
Q/2=2b1wli E.113)
где 2&х обозначена ширина струи в бесконечности.
Последний этап заключается в построении контура струи в физической
плоскости. Связь между физической плоскостью и плоскостью годографа
устанавливает формула E.91). Поскольку струя является линией тока, на
ней dt|) = 0 и, кроме того, w = до,, то координаты контура струи находятся
по формуле (р = 1)
z = х + iy = I e'e dy + const. E.114)
щ J
Из формулы E.112) следует
d(p== 2-d[lnBsin6)]J= ^-ctg9d9 = — i^bctg9d9. E.115)
2я 2л я
Здесь величина Q исключена с помощью уравнения неразрывности E.113).
Подставив выражение E.115) в формулу E.114) и отделив действительную и
мнимую части, получим уравнение контура струи (верхней границы EF^)
в параметрической форме:
е
??i- f cos9ctg9d9= —^~ fcos в + In I tg — I);
я J я \ 12/
-*/* /[ E.116)
f
J
J
Нижний предел выбран равным — я/2, так как соответствует началу струи
в точке Е с координатами х = 0, у = Ь9 где Ь—половина ширины отверстия.
100

Для определения bx следует вычислить у при 6 = 0: Ьг = Ь — 2bjn.
Найдем коэффициент сжатия струи, который показывает, что расход через
щель меньше расхода через сопло той же площади:
|i = &!/& = я/(я + 2) = 0,611. E.117)
Формулы E.116) используют также для построения контура входных
устройств, например, в аэродинамических трубах. Преимуществом является то,
что на стенках скорость только возрастает.
Следует отметить, что в данном случае решение было получено довольно
просто, так как простой была форма годографа. Простота годографа
объясняется тем, что течение ограничено прямолинейными стенками (на которых
9 = const) и границей струи (на которой wl = const).
Рассмотрим эту же задачу для сжимаемой жидкости на основе
приближенного метода С. А. Чаплыгина. В данном случае расчет проводится по
уравнениям годографа E.97), которые полностью совпадают с уравнениями
годографа несжимаемой жидкости E.95). Следовательно, все расчеты,
которые относятся к годографу, в данном случае проводятся точно так же, как
ранее, но с заменой скорости w на фиктивную скорость s. Следует особо
отметить, что такая замена возможна только в плоскости годографа, так как
в физической плоскости по-прежнему рассматриваем скорость w. Ввиду
этого вместо уравнения неразрывности E.113), которое записано в
физической плоскости, следует записать с учетом сжимаемости
Ро
где Pi и р0 — плотность газа соответственно на границе струи и в точке
торможения.
В этом случае вместо формулы E.115) получим
p g
я Ро
Дальнейшие преобразования аналогичны предыдущим. Для
коэффициента сжатия струи вместо формулы E.117) получим приближенное решение
для сжимаемой жидкости
5. E.118)
Отношение плотностей надо вычислять по формуле E.106).
Задача об истечении струи сжимаемого газа в точной постановке решена
С. А. Чаплыгиным для М < 1. Ниже приведены точные расчетные значения
коэффициента расхода (х = 1,4), а также приближенные значения,
полученные по формуле E.118).
Я 0,00 0,25 0,50 0,75 1,00 1,90
е 1,00 0,964 0,862 0,709 0,528 0,0388
точное значение 0,611 0,617 0,637 0,676 0,745 0,850
приближенное значение . . 0,611 0,617 0,636 0,668 0,712 —
Задача об истечении струи при сверхкритическом отношении давлений
была решена Ф. Й. Франклем. Им было обнаружено, что при понижении
давления за отверстием ниже критического давления расход не остается
постоянным (как для сопла), а продолжает возрастать. Расход возрастает
вплоть до достижения так называемого второго критического давления
(?** = 0,0388 при х = 1,4). При дальнейшем понижении давления расход
101

Рис. 5.19. Построение аэродинамической решетки по заданному годографу скорости:
о — физическая плоскость; б — плоскость годографа скорости
не изменяется. Расчетные результаты, полученныеФ. И. Франклем,
записаны в последнем столбце.
Напомним, что все расчеты проведены для невязкого газа. При
истечении вязкого газа струя вовлекает в движение окружающие массы газа,
размывается и замедляется. Однако, как следует из теории, почти расчетное
сужение струи происходит близко от отверстия, и поэтому расход,
подсчитанный теоретически, хорошо согласуется с экспериментом. Ввиду этого
коэффициент \i будем далее называть коэффициентом расхода.
Аналогичным путем определены коэффициенты расхода при истечении из
отверстия, образованного наклонными стенками, и отверстия в камере
конечной ширины. Теория находит применение, например, при расчетах
лабиринтных уплотнений турбомашин.
Рассмотрим построение аэродинамических решеток методом годографа.
Метод годографа скорости впервые применен к теории решеток Н. Е.
Жуковским A890 г.) и С. А. Чаплыгиным, рассмотревшим обтекание решетки
пластин и со срывом струй у кромок.
Изложим метод, предложенный Г. Ю. Степановым. Как было показано,
сначала следует построить годограф скорости, а потом найти течение в
физической плоскости. Однако вначале для выяснения основных особенностей
поступим противоположным образом. Положим, что задана плоская
аэродинамическая решетка (рис. 5.19, а), обтекаемая потоком идеальной
несжимаемой жидкости. Считаем, что задача обтекания решена, т.е. для заданной
скорости набегающего потока известно распределение скоростей на профиле
и скорость в бесконечности за решеткой. На профиле имеются две точки ог и
о2 (точки ветвления потока), в которых скорость равна нулю. Этим точкам
соответствует начало координат плоскости годографа (рис. 5.19,6). В
каждой точке профиля лопатки известны величина и направление скорости.
Отложим соответствующие векторы от начала координат годографа и получим
годограф распределения скорости на контуре лопатки (рис. 5.19, б).
Течению в одном периоде решетки в физической плоскости соответствует
внутренняя часть годографа, т. е. область, ограниченная построенной замкнутой
кривой.
Отложим в плоскости годографа векторы скорости в бесконечности перед
решеткой и в бесконечности за решеткой. Им будут соответствовать точки
А и В (рис. 5.19, б). Покажем, что в этих точках плоскости годографа сле-
J02

дует поместить источник и вихрь, сток и вихрь. Проведем в физической
плоскости две эквидистантные линии ab и а'Ь', ограничивающие один период
течения. Линиям аа' и ЬЬ' в плоскости годографа соответствуют замкнутые
кривые, окружающие точки А и В. Это следует из условия периодичности
течения в физической плоскости: скорости в точках а и а' равны и им в
плоскости годографа соответствует одна и та же точка (аналогично для Ъ и Ь').
В физической плоскости через линию аа' проходит расход Q = to1sinpl.
а через ЬЬ' — расход Q = tw2 sin р2. Следовательно, в плоскости
годографа в точке А надо поместить источник производительности Q, а в точке
В — сток производительности — Q. Из условия неразрывности очевидно
twx sin Pi = tw2 sin p2.
Циркуляции скорости по линиям аа и ЬЬГ соответственно:
Тг = —twt cos pi, Г2 = — tw2 cos p2. E.119)
Знаки минус выбраны потому, что положительным считается обход против
часовой стрелки.
Следовательно, в точках А и В годографа скорости следует расположить
вихри указанной интенсивности.
Циркуляция скорости по замкнутому контуру аа'Ъ'Ъа равна сумме
указанных циркуляции: Г = 1\ + Г2 = — twx cospx — tw2 cosp2. Это
следует из того, что суммарная циркуляция по линиям Ьа и а'Ь' равна нулю,
так как они обходятся в противоположных направлениях, а скорости в
соответственных точках указанных линий равны. Найденная циркуляция Г
равна (в силу периодичности течения) циркуляции скорости вокруг одного
профиля решетки.
Таким образом, фиктивное течение в плоскости годографа вызвано
вихреисточником и вихрестоком. Поскольку точка 0 соответствует точкам
разветвления потока в физической плоскости, то она является точкой
разветвления и в плоскости годографа. На рис. 5.19, б показаны линии тока,
которые идут в точку О и разветвляются на контуре годографа.
Следовательно, точка 0 должна быть точкой нулевой скорости также и для
фиктивного потока в плоскости годографа.
Метод годографа в приложении к теории аэродинамических решеток
обладает двумя преимуществами: 1) построенная решетка имеет некоторое
заданное оптимальное распределение скорости; 2) учет сжимаемости не
усложняет решения задачи и достаточно точен. К недостаткам следует
отнести сложность построения фиктивного течения в плоскости годографа
сложной формы.
Рассмотрим общий метод построения аэродинамической решетки с
углом входа р,, углом выхода Р2 при безразмерной скорости входа ^ —wx/a*.
Шаг решетки примем t = 1, так как это единственный геометрический
размер и поэтому он по существу определяет масштаб чертежа решетки.
При расчетах отсутствует необходимость построения истинного
годографа скорости we™ (или Хе'в) течения сжимаемой жидкости, а достаточно
рассмотреть только годограф фиктивного течения sel'e. Поэтому далее, когда
говорится о плоскости годографа, подразумевается плоскость sel*e.
По формулеч E.107) находим фиктивную скорость, соответствующую
скорости входа потока в решетку:
Уравнение неразрывности для решетки
(Pi/Po) Щ sin рг = (р2/р0) w% sin p2.
103

С помощью формулы E.104)
уравнение неразрывности
представляем в виде
fi щ sin p2
Рис. 5.20. Годограф скорости
аэродинамической решетки
Отсюда определяем скорость w2
потока за решеткой и по формуле
E.107) соответствующую ей
фиктивную скорость s2.
Интенсивность источника (и
стока) найдем по уравнению
неразрывности
Q = (Рг/Ро) twx sin px.
Циркуляцию вихрей подсчитываем по формулам E.119).
Важным этапом является выбор годографа скорости для проектируемой
решетки. При выборе формы годографа следует иметь в виду, что в
действительности решетка будет обтекаться жидкостью, обладающей вязкостью.
Хорошие результаты показывают решетки, в которых скорость постоянна
на большей части выпуклой и вогнутой сторонах лопаток. Это позволяет
избежать лишних диффузорных участков, где возможен отрыв потока. Кроме
того, в дозвуковых решетках не следует допускать возникновения
сверхзвуковых скоростей на выпуклой стороне лопатки, что также снижает
потери.
На рис. 5.20 показан годограф скорости фиктивного течения для
заданных: Хх = 0,65, рг — 30°, р2 = 25°. Максимальная скорость на выпуклой
стороне лопатки принята равной Хт = 0,95, Соответствующая часть
годографа очерчена дугой окружности аЬ с центром в начале координат.
Участок ей, соответствующий вогнутой стороне лопатки, очерчен дугой
окружности с тем же центром. Это обеспечивает постоянство скоростей на
указанных участках лопатки. Наибольшее влияние на форму лопатки оказывает
—
о А
0,2 \
X
1,0
0,8
0,6 /ч
/ /
b 0 е
Рис. 5.21. Распределение скорости по
профилю решетки (см. рис. 5.22)
Рис. 5.22. Аэродинамическая
решетка, построенная по годографу
скорости (см. рис. 5.20)
104

выбор именно этих участков годографа. Дуга окружности bof касается дуги
ab и проходит через начало координат. Клиновидный участок годографа
определяет угол схождения выходной кромки лопатки и принимается
равным 8° ... 15°. Остальные участки годографа не имеют столь
принципиального значения и их очерчивают плавными кривыми. Длину разрезов fe и
dc следует выбирать так, чтобы выполнить условие совпадения точек
ветвления с точкой 0.
Далее нужно построить фиктивное течение несжимаемой жидкости
внутри построенного годографа, вызванное вихреисточником и вихрестоком.
Аналитическое решение при столь сложной форме годографа получить
невозможно, поэтому прибегают к расчетным методам. Опустим описание
этих специфических вопросов и приведем конечный результат:
распределение скорости (рис. 5.21) по развертке профиля решетки, изображенной на
рис. 5.22.
Изложенный выше способ наглядно показывает общую идею метода.
Однако практические расчеты и построение оптимальных
аэродинамических решеток лучше вести несколько иным путем, который изложен в гл.13.
5.7. РАСЧЕТ ПОТЕНЦИАЛЬНЫХ ТЕЧЕНИИ МЕТОДОМ
ДИСКРЕТНЫХ ВИХРЕЙ
Существуют различные способы расчета обтекания профилей
потенциальным потоком несжимаемой жидкости: метод конформного
преобразования (см. подразд. 5.4), метод годографа (см. подразд. 5.6), метод
интегральных уравнений, метод дискретных вихрей и др. Все они имеют
определенные преимущества и недостатки. В этом разделе рассмотрим метод
дискретных вихрей, который обладает простотой, хорошо приспособлен для
машинного счета и может быть применен при решении трехмерных задач.
Недостатком является то, что полученные решения необходимо сглаживать.
Поясним суть метода следующим образом. Заменим действие обтекаемого
тела на окружающую жидкость нормальными напряжениями,
распределенными по контуру тела.
Скорость жидкости направлена по касательной к поверхности тела, а
силы давления — нормальны к этой поверхности. По теореме Жуковского
сила, действующая на вихрь, нормальна к скорости основного потока в
точке расположения вихря. Если заменить поверхность тела непрерывной
вихревой пеленой и подобрать распределение ее интенсивности так, что
скорости будут направлены по касательной к ней, то силы, вызванные
вихревой пеленой, будут действовать только по нормали. Следовательно, можно
заменить обтекаемое тело вихревой пеленой, которая вызовет тот же
силовой эффект.
Если переложить эти рассуждения на язык математики, то получим
интегральное уравнение для определения интенсивности вихревой пелены,
как функции точки на контуре тела.
При такой трактовке можно упростить задачу и заменить ее более
грубой схемой. Непрерывный вихревой слой, о котором говорилось, заменим
сосредоточенными вихрями, расположенными по контуру тела. Это
равносильно замене распределенной нагрузки сосредоточенными силами,
действующими в месте расположения вихрей. Вихревая пелена или заменяющие
ее вихри как бы связаны с обтекаемым телом и их называют
присоединенными вихрями Жуковского.
Замена вихревой пелены дискретными вихрями — это самая грубая
схема, хотя практика расчетов показывает, что она работает весьма надежно.
В принципе можно заменить вихревую пелену отрезками с постоянной или
105

линейно изменяющейся завихренностью (сплайны первого порядка). Это
усложнит расчеты, но и приведет к более точным результатам. Описание
вихревой пелены сплайнами более высокого порядка даст большую точность.
Чтобы разобрать практически существо расчета, рассмотрим сначала
простой пример. Пусть плоскопараллельный поток, имеющий в
бесконечности скорость до^, обтекает плоскую пластину шириной Ь. Задан угол а
между направлением скорости в бесконечности и пластиной. Требуется
найти подъемную силу и момент аэродинамических сил, действующих на
пластину.
Разобьем пластину на N отрезков и в середине каждого поместим вихрь,
заменяющий вихревую пелену, расположенную на этом участке.
Циркуляции вихрей Г,, Г2, ... неизвестны и должны быть найдены из граничных
условий. Пластина непроницаема и нормальные проекции скорости на ней
должны быть равны нулю. Так как число уравнений для определения
циркуляции должно быть равно числу вихрей, то граничному условию можно
удовлетворить не на всей пластине, а только в N точках. Поместим эти
контрольные точки между вихрями на равных расстояниях. На задней острой
кромке следует поместить контрольную точку, а не вихрь, так как согласно
постулату Жуковского — Чаплыгина перепад давления на этой кромке
равен нулю и, следовательно, на задней кромке отсутствует подъемная сила,
а значит и завихренность.
Для первоначального пояснения заменим вихревую пелену всего тремя
вихрями, положение которых на рис. 5.23 показано черными кружками.
Места, где удовлетворяются граничные условия, отмечены крестиками.
Нумерацию как кружков, так и крестиков проведем слева направо.
В такой постановке условие Жуковского — Чаплыгина на острой задней
кромке будет удовлетворено, так как скорость на ней направлена но
касательной.
В качестве примера составим уравнение для удовлетворения граничного
условия в первой точке, отмеченной крестиком:
. тх 1 г2 1 г, 1 Л
до по sina-i : — 0.
2л Ь/6 2л Ь/6 2л Ь/2
Первое слагаемое равно проекции скорости набегающего потока на
нормаль к пластине. Остальные члены уравнения равны нормальным скоростям,
вызванным вихрями. Определение этих скоростей производим по формуле
E.29), причем в данном случае вместо г следует подставлять расстояние от
вихря до данной точки. Знак плюс принят для скорости, направленной
вверх.
Составив все уравнения, получим систему, решив которую найдем
циркуляции вихрей. Полная циркуляция равна сумме циркуляции вихрей.
Подъемная сила должна быть подсчитана по формуле E.49). Силу,
действующую на каждый вихрь в отдельности, можно определить по той же
формуле, не учитывая те скорости, которые вихри индуцируют один на другой,
так как эти составляющие вызывают только внутренние силы. Иначе /л-й
вихрь вызывает на я-м вихре силу, равную
и противоположную силе, которую
вызывает я-й вихрь на m-м. Подсчитав силу,
действующую на каждый вихрь, легко оп-
ределить момент аэродинамических сил,
действующих на пластину.
Сделаем еще некоторые общие замеча-
Рис. 5.23. Присоединенные вихри ния к методу дискретных вихрей. Рассмот-
на обтекаемой пластине рим обтекание произвольного контура.

У
1
У
I
Г "***
\ )
J
)г
Рис. 5.24. Присоединенные вихри на профилях решетки
Рис. 5.25. Цепочка вихрей, расположенных на оеи ординат
Расположим дискретные вихри в середине каждого из участков, на кото-
рьь разбит контур. Это равносильно предположению, что распределенная
по участку сила давления заменена дискретной силой, приложенной по
середине каждого участка, что имеет известное обоснование.
Если расположить контрольные точки, в которых удовлетворены
граничные условия, на контуре обтекаемого тела между вихрями, то в общем
случае в местах расположения вихрей нормальные скорости не будут строго
равны нулю. Можно совместить точки расположения вихрей с точками, в
которых удовлетворяют граничные условия. Тогда дискретные силы в местах
расположения вихрей будут направлены по нормалям к контуру, как это
должно быть для сил давления. При этом, естественно, следует учесть, что в
месте расположения каждого вихря самоиндуцированная скорость равна
нулю. Однако при таком подходе возникнет сложность, если крыло имеет
абсолютно острую заднюю кромку, так как на ней не будет строго
удовлетворено условие Жуковского — Чаплыгина.
Если же обтекаемый контур не имеет острой задней кромки, то задача,
как известно, имеет бесчисленное множество решений в зависимости от
выбранной величины циркуляции скорости. В таком случае при N вихрях на
контуре граничному условию можно удовлетворить только в N — 1 точке.
Тогда в качестве дополнительного уравнения следует выбрать условие
2) Г| = Г, при котором суммарная циркуляция скорости может быть выбра-
i = 1
на произвольно.
Рассмотрим подробно более общую задачу: расчет обтекания
аэродинамической решетки методом дискретных вихрей.
Пусть дана решетка произвольных профилей с острой задней кромкой
(рис. 5.24). В бесконечности перед решеткой заданы комплексная скорость
потока их — ш1 и давление рх. Требуется определить скорость за решеткой
и2 — iv2, давление р2 и подъемную силу, действующую на профиль.
Расположим решетку в плоскости комплексного переменного z = х + iy,
направив ось ординат вдоль фронта решетки.
Все профили решетки находятся в одинаковых условиях и поэтому
течение имеет периодом шаг решетки. Если на одном из профилей поместить
вихрь с циркуляцией Г, то точно такие же вихри должны быть помещены в
!07

сходственных точках всех профилей. Комплексный потенциал одиночного
вихря дается формулой E.28). Продифференцировав это выражение по z,
найдем комплексную скорость для одиночного вихря, расположенного в
начале координат:
„__to = ——. E.120)
2 л i z
Разместим теперь в сходственных точках, т. е. в точках с координатами
int (п = ± 1, ±2, ±3,...), вихри с такой же циркуляцией. Тогда
комплексная скорость, вызванная всеми вихрями, будет представлена рядом:
2ni z *A \ z — int z + int /J 2ni *
Эта сумма равна гиперболическому котангенсу. В результате получим
комплексную скорость, которую индуцирует бесконечная цепочка точечных
вихрей, размещенных на оси ординат (рис. 5.25):
и-fo=--L-cth—, 0<|z\<*. E.121)
При возрастании шага до бесконечности формула E.121), как можно
показать, разложив гиперболический котангенс в ряд, переходит в формулу
E.120):
2*7 t J^oo 2// I nz 3 /
Формула E.121) заменяет для решетки формулу E.120), которая
использована в предыдущих примерах для подсчета скорости, вызванной одним
точечным вихрем.
Если исходный вихрь поместить не в начало координат, а в точку zky
то остальные вихри следует поместить в сходственных точках zk + int
(п = ±1, ±2, ±3, ...). Следовательно, для такой цепочки вихрей
комплексная скорость согласно формуле E.121)
^cth[-=-(z-**)]. E.122)
Разместим по профилю в решетке N вихрей с циркуляцией Гк в точках
zk (k = 1, 2, 3, ..., N). Разумеется, такие же вихри размещаем в
сходственных точках остальных профилей. Тогда комплексную скорость,
индуцированную такой системой вихрей, можно с помощью записи E.122) выразить
суммой
> . w
E.123)
Пусть эта система вихрей, которые заменяют аэродинамическую решетку,
обтекается плоскопараллельным потоком с комплексной скоростью и0 —
Тогда комплексная скорость суммарного потока, образованного
системой вихрей, расположенных на профилях, и плоскопараллельным потоком:
N - 1
-(*-**)]. E.124)
108

Комплексная постоянная uo—ivo пока неизвестна. Определим ее по
заданной скорости в бесконечности перед решеткой. Для того чтобы
определить по формуле E.124) скорость в бесконечности перед решеткой, надо
положить х -> — оо. Покажем, что в этом случае cth f^ (г — zh)] -*• — 1.
Поскольку zk — конечная величина, ее в,этой оценке можно не учитывать.
Тогда имеем
cth nz —fenz/t _[_е~"яг//)/(еЯг// е""Я2//)» еЯг// = еп*л+*пУГ*.
При х -* оо первые члены в скобках стремятся к нулю, а отношение '
вторых — к минус единице. Следовательно, далеко nepei решеткой из
формулы E.124) имеем
Ul-iVl=uQ-ivQ—^ V rfc. E.125)
Аналогично за решеткой х-> + оо, cth["(z — zk)] ->- + 1 и из формулы
E.124) следует
1 ^
u2 — iv2=u0—ivo+-^~ 2^ Tfe. E.126)
Исключив в выражении E.124) и0 — ivOy с помощью соотношения E.125)
получим
\^ l E.127)
2lt k^
Эта формула позволяет определить скорость и — iv в произвольной
точке z по известной скорости перед решеткой и неизвестным пока циркуляциям
вихрей, расположенных на профиле.
Неизвестные Th определяем с помощью граничных условий. Выберем
координаты точек zm, в которых удовлетворяются граничные условия. Число
этих точек, как уже объяснялось, должно соответствовать числу вихрей.
Запишем E.127) для произвольной точки zm (т = 1, 2, 3, ..., /V):
j^ ] E.128)
Обозначим для краткости действительную и мнимую части
гиперболического котангенса буквами с двумя индексами
cth у- (гт —zh)= Amk + iBmk.
Отделим в уравнении E.128) действительные и мнимые части, чтобы найти
проекции скорости потока в точке:
1 N
u(tn)^ut+— 2 I\Bwfe;
N k~l E.129)
»09

Потребуем удовлетворения граничного условия в точке с номером т.
Направление нормали к профилю в этой точке определяем углом 9W (см.
рис. 5.24). Проекция скорости потока в точке т на нормаль должна б}ять
равна нулю, т. е.
w(m)cosew + t;(m)sinem=:0. E.130)
Тогда из выражений для скоростей E.129) и условия E.130) получаем
систему из N уравнений, из которой определяем искомые Циркуляции (т = 1,
2, 3, ..., Л0 вихрей 1\:
1 N
«1cosew + y1sinem+—- У Tk[BmkcosQM + (Amk + l)sinQm]^0. E.131)
м ~\
Напомним, что zk — это координаты вихрей на профиле, a zm —
координаты точек, где удовлетворены граничные условия. Граничные условия
достаточно удовлетворить только на одном профиле, так как на остальных
они будут удовлетворены автоматически в силу периодичности течения.
Если задняя кромка не абсолютно острая, то следует записать
дополнительное уравнение
Г надо выбирать так, чтобы скорость на кромке была равна нулю.
Из формул E.125) и E.126) следует
"i — iVi^Uo—&о+~г, Иг —й>2—Ио—*Ц>—-¦—. E.133)
At At
После отделения действительных и мнимых частей получим
EЛ34)
Выражение (Vi + v2) следует вычислять как алгебраическую сумму.
Сравнив это выражение с формулами E.47) и E.48), можно убедиться,
что w0—это та же скорость, которая входит в уравнение Жуковского для
подъемной силы профиля в решетке.
Из уравнений E.133) можно найти проекцию скорости за решеткой на
ось ординат
E.135)
Давление за решеткой находим с помощью уравнения Бернулли:
После вычисления суммарной циркуляции скорости E.132) можно
найти подъемную силу по формуле Жуковского для профиля в решетке E.47).
По известному распределению сил можно определить также
аэродинамический момент, действующий на профиль.
Обычно требуется подсчитать аэродинамические характеристики
(аэродинамическую силу, момент и угол выхода) для различных режимов
обтекания данной решетки. Вычисления можно сильно сократить, если учесть,
что потенциальные потоки можно складывать.
Так, если решить основную систему уравнений E.131) для двух случаев:
1) и\ — 1, v\ я= 0 (поперечное обтекание решетки); 2) и\ « 0, vl = 1 (про-
ПО

дольное обтекание решетки), то любой другой режим обтекания и
соответствующие ему характеристики можно найти элементарным пересчетом.
Пусть, например, требуется найти обтекание решетки при заданных ии
vr (или wlt Pj). Циркуляцию скорости в этом режиме обтекания находим из
принципа сложения двух рассмотренных потоков:
Г --, Лк- Г' + -^- Г" = их Г' +vx Г",
где Г' и Г" — циркуляции, подсчитанные для единичных скоростей нате-
кания.
Далее на основании общих формул можно найти
Запишем очевидную цепь равенств
и2 иг tut t t
Так как для данной решетки величины Г' и Г" вполне определенные и
постоянные, из предыдущей записи следует линейная зависимость между
тангенсами угла входа и выхода потока:
tgP*—(l+r/Otgpx^r'/f. E.136)
Если /~-коо, то вместо решетки получим одиночное крыло, которое не
поворачивает поток: р2 = |32. Для густых решеток угол выхода
практически не зависит от угла входа.
Если дискретные вихри на профиле заменить сплошным вихревым слоем,
то сумму в уравнении E.128) следует заменить интегралом и в результате
получим интегральное уравнение. В этом случае искомой функцией будет
интенсивность вихревого слоя на црофиле у (s), причем dT = y(s)ds
(s — координата, изменяемая по контуру лопатки).
5.8. УРАВНЕНИЯ ДВИЖЕНИЯ В ЕСТЕСТВЕННЫХ КООРДИНАТАХ.
РАСЧЕТ ПОТОКА В КАНАЛЕ
При решении граничных задач всегда желательно выбрать
систему координат, согласуясь с формой обтекаемой поверхности, так как в этом
случае легче удовлетворять граничным условиям. В этом смысле
представляет интерес вид основных уравнений в так называемой естественной
системе координат. Такие уравнения позволяют просто и наглядно проводить
некоторые доказательства, а также дают возможность построить простые
приближенные методы расчета.
Естественными называют ортогональные криволинейные координаты,
в которых в качестве координатных линий выбираются линии тока и их
ортогональные траектории (т. е. семейство линий, ортогональных к линиям
тока). Если движение безвихревое, т. е. существует потенциал скорости, то
ортогональные траектории совпадают с эквипотенциальными линиями.
Рассмотрим плоское установившееся течение идеальной сжимаемой
жидкости. Обозначим s и п длины дуг, измеряемых соответственно
вдоль линии тока и ее ортогональной траектории от некоторой точки А
(рис. 5.26). Поместим в точку А систему координат и отождествим
направление осей с направлениями § и п.
Ш

Запишем уравнения Эйлера
E.6):
ds '
dwn
1 ds
dn
, dwn
rwn dn
p ds
E.137)
1 dp
p dn
E.138)
Рис. 5.26. Естественная система координат
где шв) wn — проекции скорости
^ Поскольку направление 5
совпадаете касательной к линии
тока, то очевидно, что в точке Л: w8 = w, wn=0. Однако производные от
wn в общем случае не равны нулю. Обозначим
и wn =
E.139)
где 6 — угол наклона скорости, измеряемый от фиксированного
направления, за которое принято направление 5 в точке А.
Отметим, что s и п — это криволинейные координаты, т. е.
дифференцирование производится по дугам, вдоль которых угол наклона
скорости .меняется определенным образом. Вычислим производные
проекции скорости:
— (wn) =— (ay sin в) = sinO—— + до cos 6 —;
ds ds ds ds
(w) = (w sin в) = sin 8 —^- + до cos 6 .
dn dn dn dn
Поскольку в точке А угол 6 = 0, то
dwn
ds
= w-
dQ
ds
E.140)
Аналогичным образом могут быть вычислены производные второй
проекции скорости в точке А:
dws dw dws dw /r 1
ds
ds
dn
dn
В формулы E.140) входят производные угла по дуге, которые, как-
известно, равны кривизне дуги:
— = —=к дв ^ д
ds гя
dn
rn
E.142)
где rs и rn — радиус кривизны соответственно линий тока и их
ортогональных траекторий; К8 и Кп — соответствующие кривизны.
Тогда формулы E.140) принимают вид
^ * E.143)
ds
dn
Преобразуем уравнения Эйлера E.137) и E.138) с помощью
полученных зависимостей E.141) и E.143). При этом учитываем, что нормальная к
линии тока проекция скорости равна нулю, а производные давления оста-
112

ются без изменения, так как величина давления не зависит от ориентации
площадки. В результате
, &К = 1__Ё?_. E.144)
ds р ds р dn
Преобразуем к естественным координатам уравнение неразрывности
dn
Продифференцировав произведения в скобках, получим
^) + w+wnf0.
дп ] ds дп
Заменив производные скоростей по формулам E.141) и E.143) и положив
нормальную к линии тока проекцию скорости равной нулю, найдем
4 = а E.145)
Преобразуем уравнение для завихренности E.1):
dwn dWg f\
ds dn
Заменив производные скоростей по формулам E.141), E.143), имеем
— —wKR= —2(o. E.146)
dn
Поскольку положение точки А выбрано произвольно, то уравнения
справедливы для всего потока. Для безвихревого, т. е. потенциального, потока
уравнение E.146) примет вид
-*L—wK4=0. E.147)
dn
Для изоэнтропийного течения уравнение неразрывности можно
преобразовать к более удобному виду. Поскольку произведение pw зависит
только от wf то уравнение E.145) можно записать в форме
4- (pw) -i" + pwKn = 0. E.148)
dw ds
Преобразуем полную производную, пользуясь тем, что рассматривается
изоэнтропийное течение
{pw)p+wp + wj?-Jp-. E.148 а)
dw dw dp dw
Воспользовавшись выражением для скорости звука D.9) и уравнением
Бернулли в дифференциальной форме D.3) dp/dp =a2, dp/dw — — pw,
предыдущее выражение можно записать так:
4,(раОРр^
dw a2
Тогда уравнение неразрывности E.148) примет окончательный вид:
^¦+-^—/С„=0. E.149)
ПЗ

Рис. 5.27. Система
координат и обозначения при
приближенном расчете
потенциального течения
в канале
При использовании полученных уравнений следует помнить, что
кривизна кривой может иметь знак плюс или минус. Положительным направлением
для линии тока считается направление скорости потока. Положительное
направление нормали к линии тока получается поворотом вектора скорости на
+ 90°. Кривизна линии тока положительна, если центр кривизны лежит на
положительной нормали. Другими словами, линия тока имеет
положительную кривизну, если она обращена вогнутостью в сторону положительного
направления нормали (как на рис. 5.26). Для линий, ортогональных линиям
тока, положительная нормаль определяется направлением вектора скорости,
а знак кривизны находится по тому же правилу.
С помощью уравнении, записанных в естественной системе координат,
можно строить различные приближенные методы расчета дозвуковых
течений в каналах. Расчеты, которые необходимо провести, элементарны, а
результаты всегда более точны, чем в одномерной теории.
Для пояснения основной идеи рассмотрим сначала потенциальное
течение несжимаемой жидкости в заданном плоском канале. При расчете
считаются заданными очертание стенок канала и расход жидкости. Требуется
найти распределение скоростей в канале.
Стенки канала являются линиями тока и, следовательно, две граничные
линии тока известны. На стенке скорость должна быть направлена по
касательной. Ортогональными траекториями линий тока в потенциальном
потоке являются линии равного потенциала или эквипотенциали. Форма экви-
потенциалей неизвестна и они могут быть построены только методом
последовательных приближений, который не будем применять. Экви потенциал и
должны быть нормальны к линиям тока и, следовательно, к стенкам канала.
Построим экви потенциал ь приближенно в виде дуги окружности 12
(рис. 5.27), нормальной по концам к стенкам канала. Для этого впишем r
канал окружность, построим касательные к стенкам канала в точках / и 2 и
найдем центр О упомянутой дуги. Скорости должны быть нормальны к эк-
випотенциали. Однако отклонение построенной дуги окружности от
истинной эквипотенциали не приведет к существенным ошибкам. Так, если
направление скорости найдено с ошибкой 10°, то ошибка в величине скорости
составляет 1,5 %.
Начало координат поместим в точке /. Найдем распределение скорости
поперек канала вдоль дуги 12. В данном случае можно выставить три
условия, которым должно удовлетворять распределение скорости. На каждой
стенке должны быть удовлетворены граничные условия для производной
скорости по нормали к стенке. Для безвихревого потока это условие дает
формула E.147): dwldn ^wK или dlnw/dn =/(. Здесь отброшен индекс «s» у
кривизны, так как используем только кривизну линий тока,
114

Выпишем граничные условия на стенках:
n==0: *L=wKi; E.150)
дп
n^h: -?*.=ц,къ E.151)
где индексами 1 и 2 отмечены величины, относящиеся к первой и второй
стенкам канала; h — ширина канала, измеряемая вдоль дуги 12 и
приближенно равная диаметру вписанной окружности.
Распределение скорости должно удовлетворять уравнению
неразрывности, которое запишем в интегральной форме (размер, перпендикулярный
чертежу, берем равным единице):
h
т = р f wdn. E.152)
Очевидно, что в выборе закона распределения скорости поперек канала
имеется известный произвол. Однако это не должно привести в расчете к
существенной ошибке, так как интенсивность изменения скорости по
нормали к стенкам определена точно, а различия в выборе эпюры скоростей внутри
канала сглаживает применение уравнения неразрывности в интегральной
форме.
Поскольку распределение скорости имеет гиперболический характер,
имеет смысл задать его в виде
, E.153)
Три неизвестные постоянные определим так, чтобы удовлетворить трем
введенным условиям. Удовлетворив двум граничным условиям E.150),
E.151), найдем
=—Кх и с = К* +Ki*th-b E 154)
Покажем, что полученное распределение скорости совпадает с точным
решением в двух важных частных случаях. При потенциальном течении
жидкости в кольцевом канале, образованном двумя концентрическими
окружностями, точное распределение скорости выражено формулой E.29):
w = Wifjr.
Если канал образован окружностями с радиусами г2 > гъ то его ширина
h = г2 — гг. Кривизны обеих стенок в данном случае отрицательны: Кг =
= — 1/г*!, К2 ¦='- — 1//V Подставив эти значения в формулы E.154), найдем
значения постоянных: Ь == \1гх ис=0. Тогда из формулы E.153) следует
точное распределение скорости. Если канал образован двумя лучами, то
скорости на каждой эквипотенциали постоянны. Поскольку кривизны
стенок канала равны нулю, то это же следует из рассматриваемого решения.
Распределение скорости вдоль канала и форма эквипотенциалей для этих
двух частных случаев также согласуются с точным решением.
Вернемся к рассмотрению общей задачи и определим неизвестную
скорость wx с помощью уравнения неразрывности E.152):
in = pay, f — ~ pwCX) ft.
J 1 + bn + en2 '
115

1,2 1,6 h/гу
Здесь введена средняя по сечению
скорость потока, которая известна, так как
расход тю условию задан. Введем
также некоторый коэффициент ц, определив
который, можно найти скорость на
первой стенке через среднюю скорость
E-g^—!-f...¦* .-¦ E-155)
wt
h
I
\-\-bn + en2
Введем безразмерные величины
Рис. 5.28. График вспомогательной
функции для расчета течения в
канале
где /*! и г2 — радиусы кривизны стенок, которые нужно выбирать с
соответствующими знаками.
Тогда интеграл E.155) запишется следующим образом:
i
E.156)
Здесь вместо коэффициентов Ь, с E.154) введены безразмерные величины
-А. E.157)
1» — Т
При вычислении интеграла возможны два случая в зависимости от знака
дискриминанта Д = 4с — Ь2:
ц=—=-arctg
Уд
2
А +6
А<0.
Величина [х зависит от двух параметров: безразмерного радиуса кривизны
и безразмерной ширины канала. На рис. 5.28 приведен график этой
величины.
Таким образом, расчет основан на том, что распределение скорости
поперек канала зависит главным образом от местных условий: радиусов
кривизны стенок и ширины канала. Приближенные расчеты согласуются с
точными, если ширина канала существенно не превосходит радиуса кривизны,
а очертание стенок меняется достаточно плавно.
Если сравнить распределение скоростей в криволинейном канале для
потоков сжимаемой и несжимаемой жидкости, то они, естественно, будут
отличаться. Такое отличие наблюдается в распределении скоростей как
поперек, так и вдоль канала и происходит вследствие зависимости плотности
жидкости от скорости. Однако характер распределения скорости поперек
канала для дозвукового потока должен слабо зависеть от сжимаемости. Это
объясняется тем, что, как было показано, характер распределения скоростей
поперек канала определен в основном производной скорости по нормали к
стенке. Это условие следует из уравнения отсутствия вихрей, которое
одинаково для сжимаемой и несжимаемой жидкости. Для двух частных случаев:
течения в кольцевом канале постоянной ширины и течения в клиновидном
канале — поперечное распределение скоростей вообще не зависит от
сжимаемости.
116

Таким образом, в рассматриваемой приближенной постановке закон
распределения скоростей поперек канала вместо E.153) можно принять в
форме
Я= _Xl _ . E.158)
НЦ+2
Это предположение подтверждается, например, при расчете дозвукового
потока в каналах между лопатками решеток турбомашин. Следовательно,
все выкладки, проведенные для несжимаемого потока, включая
определение величины (х, остаются справедливыми и для дозвукового потока.
Различие состоит только в применении уравнения неразрывности в
интегральной форме, в котором необходимо учесть изменение плотности газа поперек
канала:
1
т =ha* f рЫц.
о
Выразив плотность через скорость, можно, как и ранее, найти скорость
на первой стенке канала Хг. Однако этот прямой путь приведет к большим
вычислениям, так как зависимость плотности жидкости от скорости
довольно сложна. Достаточно точный результат дает следующий простой прием.
Используя теорему о среднем, в уравнении неразрывности E.152) можно
вынести за знак интеграла некоторое среднее по сечению значение плотности
жидкости
1
т = a* Pep h j Ыц.
о
Интеграл в этом случае равен |д,Х,, где \i имеет тот же смысл и определяется
теми же формулами, что для несжимаемой жидкости. Очевидно также, что
(иЯ-! равно средней по расходу скорости при постоянной плотности. Тогда
уравнение неразрывности может быть записано в таком виде: т — а*рср^ср/1.
Средняя плотность и средняя скорость, входящие в это уравнение, не
связаны зависимостью, обычной для одномерного изоэнтропийного потока,
так как они зависят от неравномерности поля скоростей поперек канала.
Другими словами, эти величины выражают плотность и скорость в
некоторых, вообще говоря различных, точках фиксированного поперечного
сечения.
Ввиду того, что изменение плотности жидкости поперек канала даже при
больших дозвуковых скоростях не очень значительно, можно считать, что
эти точки совпадают. Если это так, то рс р и кс р связаны известной
зависимостью и их произведение можно заменить через функцию расхода qc9 =
= рсДср/р*. Тогда уравнение неразрывности примет вид т - a^qcph.
Чтобы иметь представление о погрешностях, связанных с этим
предположением, рассмотрим пример, который может считаться весьма
неблагоприятным по сравнению со многими практическими задачами. Пусть поток газа
движется в канале, образованном концентрическими окружностями.
Относительная ширина канала равна h/'rl = 1. Скорость на выпуклой стенке равна
критической. Точное значение функции расхода при этом рабно qcp —
= 0,865, а найденная по этой величине с помощью газодинамических таблиц
средняя скорость Яср = 0,664. Точное же значение среднерасходной
скорости (при постоянной плотности) равно Кср —0,700. Таким образом, ошибка в
очень неблагоприятном случае составляет менее 5 %.
117

Общий порядок расчета течения в канале следующий.
1. В канал вписывают окружности и строят дуги^ заменяющие эквипотенциали.
2. Определяют радиусы кривизны стенок канала в расчетных сечениях.
3. Для расчетных сечений определяют величину \i.
4. По заданному расходу газа через канал находим qc$ и по таблицам
соответствующее ему значение Яср.
5. Определяют Хх = Яср/[х и по формуле E.158) вычисляют скорость на второй
стенке или во всем сечении.
Соображения, изложенные выше, позволяют также произвести расчет скоростей
по контуру канала, если известно распределение скоростей при течении несжимаемой
жидкости и течении при другом числе М. Формула пересчета следует из подобия эпюр
скоростей
Аналогичный приближенный метод с небольшими изменениями может быть применен
к расчету течений в осесимметричных каналах.
Вопросы для самопроверки
1. Какое течение называют потенциальным?
2. Почему допустимо сложение потенциальных потоков несжимаемой жидкости?
3. Постройте линии тока для плоского течения несжимаемой жидкости,
вызванного точечными источником и вихрем, расположенными в начале координат.
4.. Что называют прямой и обратной задачей в аэродинамике и каковы области их
практического приложения?
5. Нарисуйте годограф скорости, соответствующий вытеканию струи из отверстия,
образованного стенками, расположенными под заданным углом.
6. Почему метод Чаплыгина не применим для построения течений, в которых
происходит переход через критическую скорость?
7. Определите подъемную силу, которая действует на бесконечно тонкую
пластину, обтекаемую потоком идеальной несжимаемой жидкости под заданным углом атаки.
Задачу решите методом конформного преобразования.
8. Решите предыдущую задачу методом дискретных вихрей.
9. Какие преимущества и недостатки имеет метод дискретных вихрей по
сравнению с методом конформного преобразования при решении задач обтекания тел?
10. Какие координаты называют естественными?

ГЛАВА 6
ПЛОСКОЕ СВЕРХЗВУКОВОЕ ТЕЧЕНИЕ
ИДЕАЛЬНОЙ ЖИДКОСТИ.
ТЕЧЕНИЯ С ПЕРЕХОДОМ ЧЕРЕЗ СКОРОСТЬ ЗВУКА
6.1. РАСПРОСТРАНЕНИЕ ВОЗМУЩЕНИЙ В ПОТОКЕ.
ХАРАКТЕРИСТИКИ
Движение газа со скоростями, превышающими скорость звука,
существенно отличается от дозвукового движения. Для того чтобы отметить
эти особенности, рассмотрим некоторые примеры. Пусть в
плоскопараллельном дозвуковом потоке (М<С 1) находится источник слабых возмущений
(рис. 6.1, а). Возмущения, вызываемые неподвижным источником О,
распространяются относительно газа со скоростью звука а и одновременно
сносятся потоком со скоростью w. Сигнал, посланный из начала координат,
через время / достигнет окружности радиуса г = at, центр которой находится
в точке х =- wt. Очевидно, что со временем возмущения достигнут любой
точки пространства. В сверхзвуковом потоке (М > 1) возмущения будут
распространяться только внутри острого угла, образованного лучами,
исходящими из источника возмущений (рис. 6.1, б). Линии ОА, ОВ называют
линиями Маха или характеристиками, угол, который они составляют с
вектором скорости, называют углом Маха. Из геометрических соображений
очевидно
s\na^=a/w = 1/M. F.1)
В общем случае (рассматриваем установившееся движение) величина и
направление скорости различны для различных точек потока, а линии тока
криволинейны. Скорость звука зависит от скорости потока и, следовательно,
тоже меняется от точки к точке. В таком потоке характеристики будут
криволинейны.
Через каждую точку можно провести две характеристики АА\ ВВ'
(рис. 6.2), которые наклонены к вектору скорости под углом а;
определяемым местным числом М. Если провести через точку О линию тока, то
характеристики будут составлять с ней также углы а, так как вектор скорости
направлен по касательной к линии тока.
Если в точке О вызвать слабое возмущение потока, то оно может влиять
на течение в области АОВ. В свою очередь, на течение в точке О могут
влиять возмущения, произведенные только в области А'О'В'.
В большинстве случаев исследования сверхзвуковых течений
основывают на применении характеристик. Каждая точка в плоскости потока
может быть определена пересечением двух характеристик, которые можно
рассматривать как криволинейные координаты. Если нанести такую
координатную сетку, то по ней можно построить линии тока.
Характеристики обладают некоторым универсальным свойством,
которое позволяет построить их раз и навсегда, но не в плоскости течения, а
во вспомогательной плоскости годографа скорости.
Покажем, что вдоль характеристик изменение величины скорости
потока определенным образом связано с изменением угла направления
скорости.
119

Будем рассматривать плоский,
установившийся и безвихревой
сверхзвуковой поток идеальной
жидкости. Выпишем уравнения
неразрывности и отсутствия вихрей
в естественной системе координат
E.147), E.149) в таком виде:
dw w dO d(d dQ
ds M2— 1 dn ' dn ds
F.2)
Рис. 6.1. Распространение слабых
возмущений:
а — в дозвуковом потоке; б — в сверхзвуковом
где sun — координаты,
измеряемые соответственно вдоль линии
тока и по нормали к ней; 6 — угол
наклона скорости к оси абсцисс.
Пусть через произвольную точку о проведены две характеристики тх и
т2 (рис. 6.3). Они составляют в точке о углы а с вектором скорости, который
направлен по касательной к линии тока. Следовательно, координата s на
малом участке отсчитывается,вдоль направления os. Координата п отсчиты-
вается по нормали on.
Полное приращение скорости как функции двух переменных
dw j , dw л
ds-] dn.
ds dn
F.3)
Рассмотрим приращение величины скорости при перемещении вдоль
характеристики от точки о в бесконечно близкую точку о,. Поскольку
характеристика составляет угол а с направлением скорости, то между
приращением координат dn и ds имеется зависимость (см. рис. 6.3).
dn = ds tg a = ds
sin a
cos a
1/M
ds
T/i —1/M2
F.4)
В этом преобразовании использована формула F.1).
Заменим в выражении F.3) производные скорости через производные
угла с помощью формул F.2):
w
dQ
dQ , , д9 ,
ds+w dn.
M2—1 dn ds
Пиния
В тона
Рис. 6.2. Характеристики в
сверхзвуковом потоке
Рис. 6.3. Характеристики в плоскости
течения
120

Заменим Лна dn, a dn на ds,
воспользовавшись для этого зависимостью
F.4), и вынесем общий множитель за
скобку:
dtv-\—— ds .
2—1 V дп ds J
90-л
90°-*
Рис. 6.4. Характерстики в плоскости
годографа скорости
Выражение в скобках представляет
полный дифференциал, поэтому
d0= ±yW^l —. F.5)
w
Знаки «+» и «—» oтнoqятcя
соответственно к первой и второй характеристикам,
проходящим через точку о, в чем можно
убедиться, повторив те же рассуждения.
Затем эти знаки для сокращения записи
опустим, имен в виду, что их следует
выбирать, согласуясь с условиями
конкретной задачи.
Следовательно, вдоль характеристик изменение величины скорости
однозначно связано с изменением ее направления. Графически будем откладывать
векторы скорости от общего начала в координатах и, и, т. е. в плоскости
годографа скорости (рис. 6.4). Точкам о, ох в плоскости потока (см. рис.6.3)
соответствуют точки О', О\ в плоскости годографа (см. рис. 6.4), причем d9,
dw связаны уравнением F.5). Линии т'и m^ которые вычерчивают конец
вектора скорости, также называют характеристиками, но в плоскости
годографа скорости. Следовательно, характеристикам т1у т2 в плоскости потока
соответствуют характеристики ml, m'2 в/плоскости годографа.
Выделим одну особенность характеристик в плоскости годографа,
которая важна для практических расчетов. Рассмотрим прямоугольный
треугольник А00\ с катетами АО' ~~wdQ> АО\ -- dw (см. рис. 6.4) и покажем,
что угол ЛО'О'ь равен углу Маха:
i'MO' =
Это преобразование проделано с помощью формул F.1), F.5). В таком
случае характеристики mj, m'2 в точке О' составляют с вектором скорости углы
90° — а. Тогда нормаль к характеристике т2 (в плоскости годографа)
параллельна характеристике тх (в плоскости потока), а нормаль к т[
параллельна т2. Разумеется, следует помнить, что характеристики
криволинейны, и это соответствие соблюдается в точке.
Вернемся к уравнению F.5) характеристик в плоскости годографа и
проинтегрируем его. Перейдем в правой части уравнения F.5) к
безразмерной скорости X, заменив М через X по формуле D.35) и исключив размерные
скорости (а* — постоянна для всего потока и поэтому ее можно внести под
знак дифференциала):
dX
F.6)
121
После элементарных преобразований окончательно имеем

Проинтегрировав эту
зависимость от А = 1 до
текущего значения А, получим
уравнение эпициклоиды
в(Я)
Рис. 6.5. Диаграмма характеристик
+ const. F.7)
Таким образом, вдоль
характеристик изменение угла
наклона скорости
определенным образом связано с
изменением скорости.
Подчеркнем, что эта связь не зависит
от условий конкретной
задачи, т. е. одними таблицами и
диаграммами можно прльзо-
ваться в различных случаях.
Постоянная интегрирования в
формуле F.7) может быть принята равной нулю, так как начало отсчета
углов можно выбрать произвольно. Фактически необходимо знать, на
какой угол повернет поток при изменении скорости от Ах до А,2. Этот угол
поворота, очевидно,
6 = 6(А2)—в(Х1)=ва—в,. F.8)
Наибольший возможный угол поворота соответствует Хг = I, А2 = Атах:
F.9)
По формуле F.7) вычислены таблицы. Поскольку рассматриваем изоэнт-
ропийный процесс, то таблицы устанавливают связь между изменениями
всех параметров потока при движении по характеристике. В таблицах
также дано значение угла а, подсчитанное по формуле F.1).
Для проведения расчетов характеристики в плоскости годографа
изображают графически в виде так называемой диаграммы характеристик (рис.6.5).
В принципе для расчетов достаточно одной характеристики, однако для
удобства их строят для разного значения начального угла (разной постоянной
интегрирования) и знаков плюс и минус (что соответствует двум семействам
характеристик в плоскости течения). Все характеристики располагаются
в кольце 1 < А < Атах, однако для расчетов достаточно изображение
сектора.
Характеристики в плоскости течения не обладают такой
универсальностью и построение их с помощью диаграммы характеристик нужно
рассматривать для конкретных задач.
6.2. ВОЛНЫ РАЗРЕЖЕНИЯ И СЖАТИЯ В СВЕРХЗВУКОВОМ ПОТОКЕ
Рассмотрим элементарные решения, на основе которых можно
построить решения более общих задач.
Пусть сверхзвуковой поток движется вдоль стенки, которая в точке
В изменяет направление на малый угол Дб (рис. 6.6, а). Для соблюдения
122

граничных условий поток также должен повернуть до направления,
параллельного стенке ВС. Отложим в плоскости годографа вектор X (отрезок 01).
Через точку / проходят две характеристики. Согласуясь с направлением
поворота и условием, что скорость потока увеличивается, выбираем правую
нижнюю ветвь характеристик. Построив в диаграмме характеристик заданный
угол поворота, находим величину и направление скорости потока после
поворота (отрезок 02). Нормаль к элементу характеристики 12 в плоскости
годографа дает направление характеристики тх в плоскости потока. Эту
характеристику называют элементарной волной разрежения (волной Маха),
так как после ее прохождения давление в потоке уменьшается, а скорость
растет. Характеристика т1 делит поток на две области: область /, где
перелом стенки не повлиял на течение, и область 2, где вследствие перелома
стенки поток повернул. В этой задаче отсутствует необходимость в построении
характеристик второго семейства, так как построение линий тока очевидно.
Отметим, что элементарная волна разрежения составляет со скоростью
невозмущенного потока угол а = arcsin A/M).
Рассмотрим движение сверхзвукового потока в канале, форма которого
изображена на рис. 6.7. Элементарную волну разрежения АВ и
характеристику 12 в плоскости годографа строят точно так же, как в предыдущем
примере. После прохождения элементарной волны разрежения скорость
потока в области 2 определена вектором 02. Этот вектор не параллелен нижней
стенке и поэтому возникает отраженная волна ВС, которой соответствует в
плоскости годографа характеристика второго семейства 23. Элементарная
волна ВС также является волной разрежения, так как скорость 03 больше
скорости 02. Направление отраженной волны определено нормалью к дуге
23. В результате расчета поток разбит на три области, скорости в которых
определены точками с той же нумерацией. Элементарная волна ВС на рис. 6.7.
оборвана в точке С условно, так как в действительности она дойдет до
верхней стенки, отразится от нее, вновь достигнет нижней стенки и т.д.
Если в точке А верхняя стенка будет повернута в противоположную
сторону (на бесконечно малый угол!), то вместо волн разрежения возникнут
элементарные волны сжатия. Следовательно, волны отражаются от твердой
стенки, не меняя знака, волны разрежения отражаются волнами
разрежения, а волны сжатия — волнами сжатия.
Пусть сверхзвуковой поток движется между параллельными стенками,
причем верхняя в точке А имеет излом (рис. 6.8). Нижняя стенка
заканчивается в точке В. Давление в окружающем пространстве равно давлению в
Рис. 6.6. Элементарная волна
разрежении
Рис. 67. Отражение элементарной волны
разрежения от стенки
123

канале ра = р. Отрезок АС изображает элементарную волну сжатия,
которой в плоскости годографа соответствует характеристика 12, выбранная из
условия, что поворот потока происходит по часовой стрелке, а скорость его
должна уменьшаться (площадь, через которую идет сверхзвуковой поток,
уменьшается). Отрезок ВС изображает границу струи, которая называется
свободной границей. Давления по обе стороны свободной границы, т. е. в
потоке и окружающем пространстве, должны быть равны, что в данном
случае соблюдается по условию задачи. После прохождения элементарной
волны сжатия АС поток в области 2 имеет более высокое давление, чем в
окружающем пространстве (скорость 02 меньше скорости 01). Следовательно,
прежде чем поток образует дальнейший участок свободной границы,
давление в нем должно понизиться до давления в окружающем пространстве.
Давление понижается при прохождении потоком отраженной от
свободной границы элементарной волны разрежения CD. Построение этой волны
производится следующим образом. Для того чтобы давление в области 2 было
таким же, как в области /, поток должен иметь в них одинаковые по
величине скорости (это следует из уравнения Бернулли). В таком случае точка 3
должна лежать на дуге окружности, проведенной из центра диаграммы
характеристик радиусом 01. Таким образом, в диаграме строят
характеристику 23 и в плоскости течения элементарную отраженную волну разрежения
CD. Скорость в области 3 определена вектором 03.
Следовательно, свободная граница СЕ параллельна вектору 03.
Подчеркнем, что волна отражается от свободной границы с изменением знака.
В данном случае волна сжатия отразилась волной разрежения.
Обратимся теперь к построению волн разрежения и сжатия конечной
интенсивности.
Рассмотрим сначала один простой, но важный частный случай
сверхзвукового течения (течение Прандтля — Майера). Пусть плоскопараллельный
сверхзвуковой поток движется вдоль прямой стенки АВ (рис. 6j9). В точке В
стенка меняет направление на угол 6. От точки 5, которая является очагом
возмущений, идет первая линия Маха (характеристика) ВС.
Так как набегающий поток плоскопараллелен, то линия ВС прямая и
составляет с ним угол ах = arcsin A/Мх). Левее этой линии потЬк невозмущен,
правее — начинает
поворачивать по часовой стрелке.
Поворот на угол 6 можно разбить
на элементарные повороты db.
После поворота в элементарной
волне Маха поток остается
однородным и следующая
элементарная волна также
прямолинейна. Просуммировав
бесконечное количество бесконечно
слабых волн, получим волну
разрежения конечной интенсивности.
Это соответствует
интегрированию дифференциального
уравнения F.6) и переходу к
уравнению F.7). Последняя
элементарная волна Маха BD
составляет угол а2 со скоростью М2
(см. рис. 6, 9, а).
Рис. 6.8. Отражение элементарной волны ежа- Волну разрежения конечной
тия от границы струи интенсивности, расположенную
124 ,
'/////////////////А,

Рис. 6.9. Волна разрежения, образующаяся
при обтекании сверхзвуковым потоком
выпуклого угла (течение Прандтля—Майера)
внутри клина CBD, называюг
центрированной, так как все
характеристики в плоскости
течения сходятся в одной точке.
Соответствующая волне
характеристика в плоскости годографа
изображена на диаграмме
дугой 12.
Углы ах и а2 могут быть
найдены по формуле F.1), таблицам
газодинамических функций или
с помощью диаграммы
характеристик. По Мх находим 8Ь далее
по формуле F.8) определяем
Э2 ~ Bi + 6. Для этого
значения 02 по таблицам находим М2
и а2. Для определения углов ах
и сс2 по диаграмме
характеристик необходимо построить
нормали к дуге характеристики в
точках 1 и 2 (рис. 6.9, б).
При повороте скорость сверхзвукового потока увеличивается и
поэтому М2 > Mt, а2 < ах, Т2 < Тъ р2 < р1у р2 < рх. Течение в волнах
разрежения (и сжатия) подчиняется изоэнтропийному закону и поэтому
параметры изоэнтропийного торможения постоянны для всего потока.
Параметры потока за волной разрежения могут быть найдены с помощью таблиц
газодинамических функций. Объясним порядок расчета, например, при
определении давления за волной. По Мх находим г1 = рг/р0 и по заданному
рх определяем давление изоэнтропийного торможения р0. По М2 находим
е2 ~ pJPo и определяем ра, так как давление торможения постоянно.
В данном расчете нет необходимости строить характеристики второго
семейства, так как линии тока находятся на основании простых соображений.
Выберем произвольную точку Е на характеристике ВС и найдем другие
точки, лежащие на этой же линии тока. Запишем уравнение неразрывности,
воспользовавшись тем» что скорость составляет с характеристикой угол аг:
rl^lwlsinal=^rf р' w' sina\ F.10)
где г — расстояние вдоль характеристики от точки В до заданной линии
тока.
Величины, отмеченные индексом 1, относятся к первой характеристике,
а величины со штрихом — к произвольной. Поделив левую и правую
части уравнения F.10) на а*р* и воспользовавшись формулой F.1), получим
r'lr^q'Mlq^. ч F.11)
Задаваясь произвольными М' (Мг < М' < М2), находим г', так как
величины, относящиеся к первой характеристике, известны. Остается
определить положение характеристики, к которой относится найденный радиус.
Каждому М' соответствуют определенные текущие значения угла поворота
потока б' и угла а'. Очевидно, что характеристика наклонена к
направлению АВ под углом q/ = а — б'. Из пропорции F.11) следует, что все
линии тока подобны.
Простая, но не центрированная волна разрежения образуется при
обтекании сверхзвуковым потоком выпуклой стенки (рис. 6.10). Пусть до
точки А стенка прямолинейна, а далее криволинейна и выпукла. Первая
125

Рис. 6.10. Волна разрежения, образующаяся
при обтекании сверхзвуковым потоком
выпуклой стенки
Рис. 6.11. Расширение и
отклонение потока в волне разрежения:
AD — граница струи
характеристика, а также все последующие будут прямолинейны на
основании приведенных ранее рассуждений. Метод расчета остается тем же.
В любой точке на стенке поток направлен по касательной.
Следовательно, в любой точке можно найти угол поворота потока от первоначального
направления и по нему с помощью газодинамических таблиц определить все
параметры потока. Следует отметить, что скорость потока растет вдоль
стенки и поэтому волны Маха составляют с ней все меньшие углы.
По мере увеличения скорости сверхзвукового потока линии тока
расходятся. Любые две линии тока можно считать твердыми стенками (в
идеальной жидкости) и тогда получим сверхзвуковое течение в криволинейном
расширяющемся канале.
В рассмотренных примерах граничные условия были заданы
требованием поворота потока на заданный угол до нового направления стенки.
Могут быть выставлены и другие условия. Сверхзвуковой поток течет вдоль
стенки, которая в точке А кончается (рис. 6.11). В окружающем
пространстве задано давление р2 < рг. Очевидно, что в точке А образуется
центрированная волна такой интенсивности, чтобы давление за ней было равно
внешнему давлению р2. По Mi с помощью таблиц находим гг = pjp^.
Определяем относительное давление за волной разрежения е2 = р2/Ро — Z\P^P\-
По гг находим аг и 8Ь а по е», — М2, а2 и 62. Угол поворота потока по
формуле F.8) б = в2 — в,.
Рассмотрим более общую задачу, в которой необходимо построение
характеристик в поле потока. Сверхзвуковой поток движется в канале, одна из
стенок которого в точке А терпит излом (рис. 6.12). Поток ограничен твер-
Рис. 6.12. Отражение волны разрежения от стенки:
а — плоскость течения; 6 — плоскость годографа скорости
126

дыми стенками и граничные условия заключаются в том, что на стенках
задано направление скорости. В точке А возникнет центрированная волна
разрежения, в которой поток повернет на заданный угол б до направления
АВ. Для расчета методом характеристик разобьем весь поворот на п
элементарных поворотов с углами 6М. Для наглядности построения выберем
п = 3. Центрированная волна разрежений конечной интенсивности
изображена на диаграмме характеристик линией 1234, а в плоскости течения заменена
тремя элементарными волнами. Эти элементарные волны, идущие из точки Л,
построены как нормали к участкам характеристики 12, 23 и 34. Вектор
скорости после первой элементарной волны изображен в диаграмме
характеристик отрезком 02 и, следовательно, не параллелен нижней стенке.
Поэтому первая элементарная волна в точке С отражается от твердой стенки.
Отраженная волна изображена в диаграмме характеристик кривой 25 и
вектор 05 параллелен нижней стенке. Отраженная волна от точки С до встречи
со второй элементарной волной будет отрезком прямой, нормальным к
эпициклоиде 25.
В плоскости потока области обозначены теми же номерами, что и
соответствующие-им точки в плоскости годографа. Так, например, в области
3 скорость потока определена вектором 03 и т.д.
Поток из областей 3 и 5 в плоскости течения должен попасть в область
6У где он должен иметь определенную общую скорость. Этому в плоскости
годографа соответствует переход из точек 3 и 5 в точку б, лежащую на
пересечении эпициклоид. Эпициклоиды, выходящие из точек 3 и 5, выбраны так,
что они, во-первых, соответствуют волнам разрежения, а во-вторых,
пересекаются. Это позволяет по общему правилу построить следующие
элементарные участки волн. Дальнейшие построения идут тем же путем, в чем
легко разобраться с помощью нумерации в плоскости годографа и плоскости
течения.
Волна ACD называется падающей, а волна CDEF — отраженной
волной. Отраженная волна изображена эпициклоидой 48910 и, следовательно,
также является волной разрежения. В области CDG обе волны
взаимодействуют.
Во всех областях течения, которые граничат с твердыми стенками,
векторы скорости параллельны стенкам.
Распределение давления, плотности и температуры можно найти,
например, с помощью таблиц по известным скоростям А,.
В области интерференции CDG волны изображены ломаными прямыми
и, следовательно, в действительности они будут там криволинейны.
Рассмотрим задачу об отражении волны разрежения от границы струи.
Сверхзвуковой поток движется в канале с параллельными стенками
(рис. 6.13, а). В точке В нижняя стенка кончается, но в окружающем
пространстве поддерживается то же статическое давление, что и в канале,
поэтому граница струи имеет (в невязкой жидкости) направление,
параллельное нижней стенке. В точке А возникает центрированная волна разрежения,
которая падает на границу струи.
Граничное условие заключается в том, что давление на границе струи
должно быть равно давлению в окружающем пространстве. Поскольку
течение в струе изоэнтропично, то это равносильно условию постоянства
скорости. Точка 1 в плоскости годографа (рис. 6.13, б) изображает всю область
течения до первой элементарной волны АС. Центрированная волна
изображена эпициклоидой 1234.
Скорость в области 2 выше, а следовательно, давление ниже, чем на
границе струи. Поэтому первая элементарная волна разрежения отражается
от свободной границы элементарной волны сжатия, которая изображена от-
127

Рис. 6.13. Отражение волны разрежения от границы струи:
а — плоскость течения; б — плоскость годографа скорости
резком эпициклоиды 25. Точка 5 лежит на окружности радиуса 01 и,
следовательно, в соответствующей ей области 5, которая граничит с
окружающим пространством, давление такое же, как в области /. Дальнейшее
построение очевидно из принятой нумерации. Построение проводим таким
образом, что давление в областях /, 5, 7, 10, лежащих на границе,
постоянно. Это обеспечено тем, что точки /, 5,7, 10 в плоскости годографа
лежат на дуге окружности с центром в точке 0, т. е. соответствующие скорости
одинаковы по величине. Участки границы струи для областей 5, 7, 10
построены параллельно векторам 05, 07, 010. Падающая волна разрежения
ACD (штрихи) отражается от границы струи волной сжатия CDEF
(сплошные линии). В области интерференции CDG характеристики в
действительности криволинейны, также в действительности криволинейна и граница
струи на участке CD.
Таким путем может быть решен ряд практических задач, когда в
плоских сверхзвуковых потоках образуются волны разрежения и сжатия, г
поток ограничивается твердыми стенками или свободными границами. Hi
рис. 6.14 показано течение в плоской сверхзвуковой струе, выходящей из
устья сопла Лаваля, в пространство с более низким давлением рокр, чем t
канале. В точках Л и В возникают центрированные волны разрежения, в ко
торых поток расширяется до окружающего давления. Эти волны отражаютс*
от границы струи на участках А А" и В'В" и образуют волны сжатия. В точ
ках А'" и В'" волны сжатия вновь от
ражаются и образуют волны разреже
ния. Далее (в невязкой жидкости) кар
тина повторяется. Для наглядности все
волны изображены прямыми линиями
хотя, как было показано, в области ин
терференции они искривлены.
В тех областях струи, которые гра
ничат с окружающим пространством
давление равно давлению в этом про
странстве. Внутри струи имеется об
ласть, где давление падает ниже, чем i
Рис. 6.14. Схема сверхзвуковой струи окружающем пространстве, так ка*
при истечении в область с понижен- rj г г
ным давлением (волны условно по- поток последовательно проходит ДВ<
казаны прямыми) волны разрежения. Затем поток прохо
128
А1 А

дит две волны сжатия и во внутренней области давление его становится
равным давлению в устье сопла, т. е. больше, чем в окружающем
пространстве.
6.3. СКАЧКИ УПЛОТНЕНИЯ В СВЕРХЗВУКОВОМ ПОТОКЕ
Помимо волн разрежения и сжатия, в которых параметры потока
меняются плавно, в сверхзвуковом потоке могут существовать поверхности,
при переходе через которые параметры меняются скачком. В разд. 6.2
рассмотрена задача обтекания выпуклого угла сверхзвуковым потоком с
образованием волны разрежения.
Если сверхзвуковой поток набегает на вогнутый угол (рис. 6.15), то
очевидно, должно происходить сжатие газа. Однако волна сжатия в этом
случае существовать не может. При торможении потока М2 < Мг и,
следовательно, по формуле F.1) а2 >ocj. В таком случае первая характеристика тъ
на которой должно начаться сжатие, окажется ниже по потоку, чем
последняя характеристика т2, на которой сжатие заканчивается, что, естественно,
не реально. В действительности при таком течении газа возникает фронт
разрыва АВ, при переходе через который все параметры потока изменяются
скачком.
Рассмотрим скачок уплотнения, который составляет с направлением
потока угол Р < я/2 (рис. 6.16). Индексом 1 отмечаем все величины до скачка,
а индексом 2 — после скачка. Для того чтобы найти соотношения между
параметрами потока до и после скачка, применим уравнения сохранения.
Из условия непрерывности потока массы следует (при использовании
уравнений сохранения можно опустить величины площадок, через которые
переносится масса, количество движения и энергия, так как параметры
потока не меняются вдоль фронта скачка)
Pi^«i = P2^ia. F.12)
Индексом п отмечены проекции скорости на ^нормаль к фронту скачка.
Из уравнения сохранения количества движения в проекции на фронт
скачка следует
Pi wn i Щ1 = Р2 wn2 wt2. F.13)
Здесь индексом t отмечены проекции скорости на направление фронта.
Из уравнения сохранения количества движения в проекции на нормаль
к фронту получим
Pi wl i 4 рг == р2 wfa -f p2. F.14)
В
т2
Рис. 6.15. Скачок уплотнения при
обтекании вогнутого угла
5 За к. 2638
Рис. 6.16. Расчетная схема для
косого скачка уплотнений
J39

Наконец, из условия сохранения энергии
и>\ | * Рг __. »| ., * ра _ X-П aS ,g ш
2 х-~! Pl 2 х-I р2 x-l 2 * l '
Отметим, что заранее нельзя оценить термодинамический процесс,
протекающий в газе, т. е. о связи между параметрами газа до скачка и после
него. Уравнение термодинамического процесса должно быть установлено с
помощью уравнений сохранения.
Найдем сначала соотношения между скоростями потока до скачка и
после него.
Из уравнений F.12) и F.13) следует, что тангенциальные проекции
скорости до скачка и после него равны
Wn — Wtt—до*. FЛ6)
Из этого условия имеем
F.17)
Для того чтобы найти соотношение между нормальными проекциями,
исключим из основных уравнений давление и плотность. Поделим левую и
правую части уравнения F.14) соответственно на левую и правую части
уравнения F.12):
JlйF.18)
Умножим это уравнение на произведение нормальных скоростей wnlwn2
и получим
w?i\ wn2+ -&- шп2 = шп1 wfo + — wni. F.19)
Pi P2
Отношение давления к плотности можно выразить из уравнения энергии
FЛ 5) через скорости
Рг ^ *+» at *-[ w^ JUL. = JldJL a» _ -2LZJL да|в
Исключим отношения давления к плотности из уравнения F.19) с
помощью найденных зависимостей и запишем
™р~ <*l (Wn2—wnx)—~d- (mi wn2—wl wnl)—wnlwnb(wn2—wnl).
Заменив в этом уравнении w\ и w\ через нормальные и тангенциальные
проекции скоростей по формуле FЛ7), после простых преобразований найдем
-~Г а! + ~^ »?) -0.
Одно решение wnx == wn2 соответствует течению без скачка, второе —
приводит к искомому соотношению между нормальными проекциями
скоростей (напомним, что тангенциальные проекции равны)
wnl wn* « а\ - ^L- wl F.20)
Поделив все члены на al, запишем это условие, а также условие F.16) в
безразмерном виде:
^«i ^пч ^ 1 Т7" ^** ^«1 ^ ^«а ^" ^ F.21)
Ураэнение F.21) устанавливает зависимость между скоростями потока
130

до скачка и после него. Для
практических расчетов удобно
представить эту зависимость графически.
Если фиксировать скорость Хг до
скачка, то конец вектора J опишет
кривую, называемую декартовым
листом (рис. 6.17). Ветви АА' этой
кривой соответствуют увеличению
скорости после скачка, т. е. скачку
разрежения, который, как будет
доказано ниже, невозможен из условий
термодинамики. Поэтому будем
рассматривать только оставшуюся
замкнутую часть кривой, которую назыЦ Рис. 6.17. Характерные точки ударной
вают ударной полярой. Угол 8 (см. поляры
рис. 6.16, 6.17) называют углом
поворота потока в скачке. Векторы О А и ОВ имеют общую составляющую ОС,
которая по доказанному равна тангенциальной составляющей скорости Kt.
Следовательно, отрезок ОС параллелен фронту скачка в плоскости
течения, который составляет угол |$ с набегающим потоком. Нормальные
составляющие скоростей до и после скачка представлены отрезками
соответственно АС и ВС.
Если р <С я/2, то скачок называют косым. В частном случае при Р =
= я/2 скачок называют прямым. В прямом скачке поток не отклоняется
(Kt = 0, Xnl = Xl9 Кп2 = Х2) и скорость за ним изображена отрезком OD.
Для прямого скачка из формулы F.21) следует соотношение Прандтля:
Pt^-1. F.22)
Поток не отклоняется также в другом предельном случае, когда на
диаграмме поляр точка В стремится к точке Л, т. е. Я2 -> %х.
Скачок вырождается в элементарную волну Маха сжатия и угол его
наклона стремится к углу Маха. Отсюда следует, что в малой окрестности
точки А элементарные отрезки ударной поляры совпадают с элементарными
отрезками эпициклоид на диаграмме характеристик. Следовательно,
достаточно слабый скачок можно заменить элементарной волной Маха сжатия.
Проведем к ударной поляре касательную ОЕ. Угол ЕОА равен
максимальному углу отклонения потока в косом скачке (при фиксированном Xj).
Для угла отклонения меньше, чем максимальный, луч пересекает поляру
в двух точках, т. е. для заданного угла отклонения потока возможно два
скачка уплотнений: сильный и слабый. Слабым называется скачок, за
которым скорость потока получается большей. Имеются предположения, что
слабый скачок неустойчив и поэтому реализуется сильный. Однако это
утверждение не имеет убедительных доказательств.
На рис. 6.17 из центра О проведена окружность радиусом к = 1
(штриховая линия). Скорость за косым скачком может быть как сверхзвуковой
(на участке AF)y так и дозвуковой (на участке EF). Скорость за прямым
скачком всегда дозвуковая (точка D).
Диаграмма ударных поляр (рис. 6.18) представляег собой семейство
ударных поляр, построенных для разных значений начальной скорости.
Ударная поляра, соответствующая максимально возможной безразмерной
начальной скорости, является, как можно показать из общих уравнений,
окружностью.
Из уравнений сохранения можно получить формулу для
относительного повышения давления в скачке,
5* 131

о
о
Уравнение F.14)
представим в виде р2 —
— Pi ^ РМ\ ~ Р2Я>«2.
Преобразуем последний
член с помощью
уравнения F.12) и перейдем к
безразмерному виду,
поделив все члены на рл:
^-^-(wh—wHlwn2).
Pi
Заменим
произведение нормальных
скоростей по формуле F.20) и
введем скорость звука
Рис. 6.18. Диаграмма ударных поляр
х+1
Исключим критическую скорость с помощью уравнения F.15) и положим
согласно рис. 6.16 wnl = щ sin р, wt = wx cos р. После приведения
подобных членов получим
a—Pi 2
р,
х+1
(M?sin2p —1).
F.23)
Эта формула дает возможность по известным параметрам до скачка вы
числить статическое давление за скачком. Так как в скачке уплотнений
(р2—р1)/рг>0, из формулы F.23) следует Щ sin2 р —1>0, sin p >1/М! =
= sin а1# Угол наклона фронта скачка больше угла Маха, Р >а,.
Из формулы F.23) также следует, что нормальная к фронту проекция
скорости до скачка должна быть сверхзвуковой. Следовательно, по формуле
F.21) нормальная проекция скорости после скачка — дозвуковая, хотя,
как уже было отмечено, полная скорость за косым скачком может быть как
сверхзвуковой, так и дозвуковой.
Найдем отношение плотности газа до скачка к плотности за скачком
(в этом случае формула более компактна). Из уравнений F.12) и F.20)
следует
Pi
Р2
WU\
w\
**nl
¦+
к-1-1
w
Выразив проекции скоростей через полную скорость до скачка (см.
рис. 6.16), получим
Pi __ 1 х—1 2ft
р2 Я? sin2 p х+1
Заменив безразмерную скорость через число М по формуле D.35), после
простых преобразований найдем
р2 " х i-1 (х-i-l) Mf sin» |
F.24)
132

Определив р2 по формуле F.23) и р2 по формуле F.24), получим
отношение абсолютных температур газа с помощью уравнения состояния:
Wi=PtPi/(PiP«). • F.25)
Для аналитического расчета необходимо получить соотношение между
углом поворота потока в скачке и наклоном фронта скачка. Из рис. 6.17
A*— A* cos p, Хп]^:Ji1sinp,
Xn2==X2sin(p—б),
Подставив эти соотношения в формулу F.21), установим искомую
зависимость
A,? sinPcosptg(P — б)- 1—?li- X\ cos2p.
Для дальнейшего анализа эту формулу удобнее выразить через число М.
Используя зависимость D.35), после простых преобразований имеем
e)= 24 (к-Ц-Mfsintp
; (к+1) М? sin p cos p *
Раскрыв тангенс разности углов и приведя подобные члены, найдем
формулу для угла поворота потока
Угол наклона фронта скачка должен находиться в пределах а < р <
< я/2. Левый предел соответствует вырождению скачка в элементарную
волну сжатия (бесконечно слабый скачок), а правый — прямому скачку
(самый сильный скачок при заданном Mi). На границах этого интервала
выражение F.26) равно нулю, а внутри интервала — положительно.
Следовательно, угол поворота потока при заданном Мг имеет внутри указанного
интервала максимум. Этот максимум бгпах равен углу наклона касательной,
проведенной из точки О к поляре (см. рис. 6.17).
Если угол поворота сверхзвукового потока,при данном ^ больше бтах,
то косой скачок невозможен.
Получим уравнение, которое будет связывать термодинамические
величины по обе стороны скачка. Запишем F.18) в виде
Умножим обе части уравнения на (wn2 + wnl), тогда
Р\ И^П2 Pi I P2
I '
Pi ttJni Pi P2
Помножим и поделим первый член уравнения на р2, а четвертый член
уравнения — на рх, исключим скорости в левой части этого уравнения с
помощью уравнения неразрывности F.12), а правую, воспользовавшись
условием F.17), выразим через полные скорости до скачка и после него:
Р2 Pi P2 PJ
Исключив скорости в правой части с помощью уравнения F.15), получим
Pi Р\_^ , Jh Рг_. _ _ 2х Pi 2х р2
р2 р{ р2 р, х—1 р! х—1 р2

Р2
Pi
х+1
н—I
x+I
X—l
Pi
92
Pi
Поделим все члены на Pi/pi и выразим отношение давлений через отношение
плотностей [адиабата Рэнкина A870 г.) — Гюгонио A889 г.)]
F.27)
Это соотношение называют уравнением ударной адиабаты. Очевидно,
что процесс сжатия в скачке не является изоэнтропийным. При
прохождении газа через скачок изменение энтропии происходит скачком (так же, как
и других термодинамических величин). Изменение энтропии можно
определить по формуле, известной из термодинамики:
Н <6-28)
Согласно условию возрастания энтропии возможно лишь такое течение
газа, при котором s2 — st > 0 (второй закон термодинамики).
На рис. 6.19 представлены кривые, соответствующие ударной адиабате
и изоэнтропе. При изоэнтропийном сжатии приращение энтропии равно
нулю. Тогда, как следует из формулы F.28),
При той же степени повышения давления pJPi в ударной адиабате
согласно рис. 6.19 отношение плотностей рг/р2 больше, чем при
изоэнтропийном сжатии. Следовательно, при течении через скачок уплотнения
энтропия возрастает, так как
Аналогичные рассуждения приводят к тому, что скачок разрежения
физически невозможен, так как это связано с уменьшением энтропии.
Реальный скачок не бесконечно тонок, а имеет толщину порядка длины
свободного пробега молекул, и диссипация энергии происходит в этом
тонком слое. Выведенные формулы не применимы в слое, а дают связь между
начальным и конечным состоянием газа.
При течении в скачке возникают потери. Часть механической энергий
переходит в тепловую энергию (внутреннюю энергию), что вызывает
большее повышение температуры газа, чем при изоэнтропийном сжатии. Это и
приводит при той же степени повышения давления к меньшему
возрастанию плотности.
На рис. 6.20 приведена /is-диаграмма, на которой точка / соответствует
состоянию до скачка, а точка 2 — после скачка. «Процесс» в скачке
условно показан штриховой линией. Точка 0 соответствует параметрам изо-
энтропийного торможения перед скачком, а точка 0' — после скачка.
Температура торможения остается постоянной на основании уравнения
энергии, а давление изоэнтропийного торможения после скачка ниже, чем перед
скачком. Отрезок АА изображает часть кинетической энергии, которая
s перешла в теплоту из-за наличия потерь. Можно показать, что для слабых
скачков приращение энтропии является величиной третьего порядка
малости по сравнению с приращением давления
134

w
15 P2IP1
Рис. 6.19. Сравнение ударной адиабаты
и изоэнтропы
Рис. 6.20. Определение параметров
торможения после скачка
Ро
н
Ру
Тогда для слабых скачков с помощью формулы F.23) найдем
*-* = о '*¦>, '(Ml Sin^P—1K.
F.29)
В предельном случае бесконечно слабого скачка он вырождается в
элементарную волну Маха сжатия. Угол наклона фронта скачка стремится к
углу Маха (Р -их) и так как Mt sin ot^ — 1, то процесс сжатия переходит в
изоэнтропийный.
Очевидно, что в этом случае уравнение ударной адиабаты Рэнкина —
Гюгонио F.27) должно перейти в уравнение изоэнтропы. Обозначим Pi=p,
Pi = Р> Р2 =¦¦ Р Л dp и р2 -= р + dp. Заменив в формуле F.27)
обозначения и оставив только члены первого порядка малости, получим
уравнение изоэнтропы в дифференциальной форме dplp = xdp/p.
В предельном случае, когда скачок вырождается в элементарную волну
сжатия, угол поворота потока стремится к нулю. Если угол поворота
достаточно мал, то скачки будут слабыми и вместо точных формул можно
получить простые приближенные формулы первого порядка точности. Чтобы
снизить интенсивность скачков и потери в сверхзвуковом потоке, применяют
тонкие крылья и лопатки турбомашин. В этом случае такие формулы имеют
практическое применение.
Точную формулу F.26), после замены косинуса двойного угла cos 2(J~
= 1—2 sin2p, запишем в таком виде:
2(Mfsin2P—l-)=tgetgP|(x+l)Mf + 2(Mfsin1P-»l)J. F.30)
Для малого угла отклонения потока б
tg6=6, P=
1 положим
где а — угол Maxa; sin a =
Подставив эти выражения в правую часть формулы F.30) и удержав
только члены первого порядка малости, получим приближенную формулу
для угла наклона фронта скачка
х+1
М|
F.31)
135

Рис. 6.21. Расчет косого
скачка уплотнений:
а — косой скачок; б —
схема расчета по диаграмме
б)
С учетом этой зависимости из точной формулы F.23) найдем
приближенную формулу для относительного повышения давления при сжатии газа
в слабом скачке
__ У.Щ
F.32)
Следовательно* интенсивность слабого скачка пропорциональна углу
отклонения потока.
Прирост энтропии при сжатии газа в слабом скачке, как следует из
формул F.29) и F.31), пропорционален третьей степени угла отклонения
потока
х(х+1)
12
м?
(M'f-1K/2
Получим соотношение между скоростями до и после слабого косого скачка.
Тангенциальные проекции скоростей до и после скачка равны. Тогда из
рис. 6.17 вытекает, что
Xt = Xt cos р = Х2 cos (Р — б).
Если угол отклонения мал, то приближенно cos(P — б) = cos р +
+ б sin p и, следовательно,
С учетом зависимости F.31) получим окончательную формулу,
справедливую с точностью до членов первого порядка малости:
F.33)
Рассмотрим порядок расчета косого скачка уплотнения произвольной
интенсивности. Сверхзвуковой поток течет параллельно стенке АВ
(рис. 6.21, а). В точке В стенка изменяет направление и образует
относительно потока вогнутый угол. Если угол поворота стенки меньше
максимального б <; бтах при заданном числе Хг набегающего потока, то возникнет
косой скачок уплотнения BD. Определение скорости после скачка А,2 и угла
наклона фронта скачка к набегающему потоку Р произведено с помощью
ударной поляры (рис. 6.21, б).
Как было показано, процесс сжатия газа в скачке является неизоэнтро-
пийным, поэтому для расчета параметров потока за скачком нельзя
воспользоваться обычными таблицами газодинамических функций. Статическое
Давление следует определять по формуле F.23). Давление изоэнтропийного
торможения за скачком р02 вычисляют но найденным Х.г и /?2,
136

6.4. ОТРАЖЕНИЕ И ВЗАИМОДЕЙСТВИЕ СКАЧКОВ И ВОЛН.
ОБТЕКАНИЕ ТЕЛ ПЛОСКИМ СВЕРХЗВУКОВЫМ ПОТОКОМ
Разберем основные задачи, связанные с отражением и
пересечением скачков уплотнения, а также со взаимодействием скачков и волн.
Рассмотрим движение сверхзвукового потока в канале, изображенном
на рис. 6.22. Если угол отклонения стенки 6 < бтах при заданном ix (что
устанавливаем с помощью диаграммы ударных поляр), то в месте перелома
стенки возникнет косой скачок уплотнения. Угол наклона скачка рх и
скорость после него Я2 находим по соответствующей ударной поляре. В точке В
возникнет отраженный скачок J3C, в котором поток повернет на тот же угол
8 в обратную сторону так, что скорость после отраженного скачка К3 будет
параллельна нижней стенке. На рис. 6.22 изображен вариант, для которого
угол поворота потока меньше угла 6max, найденного по скорости А,2. В этом
случае определение р2 и к3 проводится точйо так же, как для первого
скачка. Такое отражение называется правильным отражением. Статические
давление, температуру и плотность газа после скачков находим по формулам
F.23), F.24), F.25). Давление изоэнтропийного торможения в каждой
области находится с помощью газодинамических таблиц по местному
статическому давлению и местной безразмерной скорости. На рис. 6.22
изображена также одна из линий тока.
В том случае, если угол поворота во втором скачке становится больше
максимального, правильное отражение невозможно. Падающий скачок
разветвляется на некотором расстоянии от стенки и возникает так называемое
маховское отражение (рис. 6.23). В точке В встречаются три скачка: два
косых и прямой. Поток, прошедший косые скачки АВ и BDy по
пунктирной линии BE соприкасается с потоком, прошедшим прямой скачок ВС.
Давления в обоих потоках вдоль линии соприкосновения BE должны быть
одинаковы. Следовательно, степень повышения давления в двух косых скачках
равна степени повышения давления в прямом скачке. При фиксированной
степени повышения давления сжатие газа в двух скачках сопровождается
меньшими потерями, чем сжатие в одном, так как чем больше скачков, тем
ближе они к волне сжатия, в которой происходит изоэнтропийный процесс.
При одинаковом статическом давлении скорость потока над линией BE
будет выше, чем под ней. Линия BE является линией тангенциального разрыва
поля скоростей, т. е. является вихревой линией.
Построение скачков при пересечении основано на тех же соображениях,
что и при отражении. В частности, если рассматривать течение в
симметричных каналах, то центральную линию тока можно заменить стенкой и решать
'////////А/,.
Рис./ 6.22. Правильное отражение косого скачка
от стенки
Рис. 6.23. Маховское
отражение косого скачка от стенки
J37

задачу отражения. Другими словами, зеркальное отражение течений на
рис. 6.22, 6.23 относительно нижних стенок даст картину течения в
симметричных каналах. Следовательно, при течении в каналах возможно как
правильное пересечение, так и маховская конфигурация скачков. Для примера
на рис. 6.23 зеркальное отображение выполнено штрих пунктирной линией.
В предыдущих примерах граничные условия определялись твердыми
стенками. Рассмотрим теперь задачу об отражении скачка уплотнений от
границы струи (рис. 6.24). Косой скачок уплотнения АС падает на границу
струи в точке С. Так как принято р2 = рг, то участок границы струи ВС
является продолжением нижней стенки. Поскольку давление за скачком
больше давления на границе струи, то скачок отражается волной
разрежения CDE такой интенсивности, что давление за ней становится равным
давлению в окружающем пространстве.
Расчет скачка и волны разрежения может быть произведен описанным
методом. Отметим только, что так как в скачке возникают потери, то
равенство статических давлений в каких-либо областях не означает, что там
равны и величины скоростей. Так р4 = р1ч но вследствие потерь в скачке ХА <
<КТ€>ТХ.
В описанных задачах исследовалось взаимодействие скачков,
отклоняющих поток в противоположных направлениях. Возможен случай, когда
пересекаются два скачка, которые отклоняют поток в одном и том же
направлении (рис. 6.25). Скачки А В и ВС\ вызванные изломами стенки,
встречаются в точке В. Рассмотрим линию тока, проходящую через точку В,
По этой линии не должен происходить разрыв давления и нормальных
составляющих скоростейт хотя тангенциальные составляющие, как уже
отмечалось, могут терпеть разрыв. Эти граничные условия по линии АЕ нельзя
удовлетворить одним скачком BDt так как повышение давления в нем
связано однозначно с поворотом потока, поэтому возникает отраженная волна
BF, интенсивность которой обычно очень мала по сравнению с
пересекающимися скачками.
Интенсивность скачка BD и слабой отраженной волны BF, которая
принадлежит другому семейству, находят из упомянутых граничных условий
на линии BE. Отраженная волна BF может быть как волной сжатия, так и
волной разрежения, что зависит от расположения пересекающихся скачков.
Аналогичная картина возникает при обтекании сверхзвуковым потоком
вогнутой стенки (рис. 6.26). При обтекании выпуклой стенки (см. рис. 6.10
волны разрежения расходились. При обтекании вогнутой стенки образуют
Рис. 6.24. Отражение скачка от
границы струи волной
разрежения
138
Рис. 6.25: Взаимодействие скачков,
отклоняющих поток в одном и том
же направлении

'A///VA 777/У В
Рис. 6.26. Схема обтекания
сверхзвуковым потоком вогнутой
стенки
Рис. 6.27. Взаимодействие скачка с волной
разрежения
ся элементарные волны сжатия, которые пересекаются, так как скорость
потока вдоль стенки падает, а следовательно, углы Маха, под которыми
наклонены волны, растут, В результате интерференции волн сжатия
образуется криволинейный скачок. Скачок CD начинается не на поверхности тела,
а внутри потока, интенсивность, его в начальной точке равна нулю и
переменна вдоль фронта.
Рассмотрим взаимодействие скачка уплотнения и волны разрежения
(рис. 6.27). Такое взаимодействие всегда наблюдается при обтекании тела
сверхзвуковым потоком. Пусть за косым скачком уплотнения, идущим от
точки Л, поток сверхзвуковой. Тогда в точке В возникнет центрированная
волна разрежения, которая, как можно показать, определив углы р и а,
обязательно будет пересекать скачок, так как ах + 6 >р.
Рассмотрим характеристику (линию Маха) BE, которая пересекает
скачок в точке Е. При фиксированных параметрах М1ч рг перед скачком угол
поворота потока в скачке, давление за скачком и наклон его фронта связаны
между собой. Так как BE — элементарная волна разрежения, то давление
за ней меньше, чем перед ней. Следовательно, повышение давления в скачке
на участке СЕ должно быть больше, чем на участке ED. Угол поворота
потока в скачке на участке СЕ должен быть также больше, чем на участке ED.
Следовательно, скачок на участке ED должен быть более слабым, чем на
участке СЕ. Более слабому скачку соответствует меньший угол наклона,
следовательно, скачок должен искривляться, а от него будут отходить
слабые отраженные волны. Угол наклона скачка не может быть меньше угла
Маха, подсчитанного по скорости набегающего потока. Вдали от
обтекаемого тела скачок вырождается в звуковую волну. Эти соображения
являются наводящими, так как в действительности течение за искривленным
скачком станет вихревым вследствие того, что потери вдоль фронта
криволинейного скачка изменяются.
Рассмотрим обтекание сверхзвуковым потоком плоского тела, имеющего
ромбовидную форму (рис. 6.28, а). Если угол раствора клина меньше
удвоенного максимального угла отклонения, то на передней кромке возникнут
косые скачки уплотнения АВ, АВ\ Если скорость за скачками также
сверхзвуковая, то дальнейший поворот потока совершается в центрированных
волнах разрежения CDE, CD E'. На задней кромке возникают скачки
уплотнения KG, KG\ в которых потрки, обтекающие тело сверху и снизу,
поворачивают и сливаются вдоль общей границы. Поскольку давление на
гранях АС, АС больше, чем давление на гранях СК, С К. то на тело со стороны
жидкости действует сила. Таким образом» в сверхзвуковом потоке невязкой
139

Af,>
\v
Рис. 6.28. Схемы обтекания плоских тел
сверхзвуковым потоком:
а — острые передняя и задняя кромки; б — острая
передняя и тупая задняя кромки; в — тупая
передняя кромка; г — пластина под углом атаки
жидкости возникает сопротивление, не связанное с трением. Это
сопротивление называют волновым, так как оно вызвано возникновением ударных
волн (скачков), в которых процесс сжатия не является изоэнтропийным. На
рис. 6.28 система волн изображена вблизи обтекаемого тела. На некотором
отдалении волны разрежения будут взаимодЬйствовать со скачками
уплотнения. Скачки будут искривляться, интенсивность их, как уже было
объяснено, уменьшится и они превратятся в звуковые волны, наклоненные под
углом Маха к набегающему потоку.
На рис. 6.28, б показано обтекание тела с тупой выходной кромкой.
Обтекание головной части тела происходит точно так же, как пояснено выше.
В точках А у В возникают центрированные волны разрежения. Верхний и
нижний потоки встречаются в точке С. Поскольку потоки не могут
пересекаться, то появляются скачки уплотнения CD, СЕ и наблюдается течение
внутри вогнутого угла. Интенсивность волн разрежения, возникающих в
точках Л, В, и, следовательно, положение точки С определяются так
называемым донным давлением в области ABC. Теоретический расчет донного
давления является сложной задачей и может быть выполнен только при
учете вязкости .жидкости. Сила сопротивления для тела с тупой задней
кромкой больше, чем для тела с острой задней кромкой (при прочих равных
условиях) из-за низкого донного давления.
В том случае, если угол раствора клина, образующего переднюю кромку,
больше 2бтах или если входная кромка тупая (рис. 6.28, в), то косой
скачок не может обеспечить соответствующего поворота потока. Другими
словами, сверхзвуковой поток не может повернуть на угол, необходимый для
обтекания кромки. Это приводит к образованию криволинейного скачка,
отсоединенного от тела. Элемент скачка на оси симметрии следует
рассматривать как прямой скачок. В некоторой окрестности углы наклона элементов
скачка столь велики, что поток за ними также дозвуковой. Входная кромка
обтекается дозвуковым потоком, в котором угол поворота не связан жестко
с изменением величины скорости.
Форма криволинейного скачка и расстояние его от обтекаемого тела
зависят от формы тела и числа Мх. В таком скачке могут реализоваться все
участки ударной поляры, в том числе и те, которые относятся к сильным косым
скачкам.
Чем интенсивнее скачок, тем больше потери. Наиболее интенсивным
является прямой скачок. Следовательно, в сверхзвуковом потоке тело с тупой
передней кромкой имеет большее волновое сопротивление, чем с острой.
но

В дозвуковом потоке хорошо обтекаемые тела должны иметь скругленную
входную кромку.
Расчет криволинеййого отошедшего от.тела скачка является трудной
задачей, так как образование дозвуковой зоны приводит к тому, что сам
скачок зависит от условий вниз по течению. Однако один частный расчет,
имеющий практический интерес, проводится просто. При измерении полного
давления в сверхзвуковом потоке с помощью зонда перед измерительной
трубкой расположен скачок, элемент которого можно считать прямым. Так
как в скачке имеются потери, то полное давление, измеренное зондом, ниже
истинного давления изоэнтроиийного торможения. Задача состоит в
определении истинного давления изоэнтропийного торможения pin по
измеренным: давлению торможения за скачком р02 и статическому давлению в
набегающем потоке рх. В потоке до скачка справедлива формула D.29):
JHL ,(И JLzl_Mff<4-". F.34)
Р\ \ 2 /
Аналогичная формула справедлива после скачка
I^^h + J^Lmf{^\ F.35)
Отношение статических давлений после и до прямого скачка определим
по формуле F.23), которую представим в виде
Jl. ,- 1 -|- _*1_ (Mf - 1). F.36)
Р. * ! 1
Исключим из формул F.35) и F,36) неизвестное давление за скачком и
получим
A-L h f_2x_ Mf_ X)UX^^zLmYf^X\ F.37)
Pi I * ! ! П 2 /
Соотношение между безразмерными скоростями до скачка и после него
определяет формула F.22). Запишем ее с помощью формулы D.35) через числа
М:
2
xM'f — (х— 1)/2 "
Исключим в уравнении F.37) скорость М2 и получим выражение с
одним неизвестным Мъ которое называют формулой Рэлея:
x1) F.38)
Вычислив Мь можно определить истинное давление торможения в потоке по
формуле F.34).
Рассмотрим обтекание сверхзвуковым потоком тонкой пластины,
поставленной под малым углом атаки (рис. 6.28, г), как пример обтекания крыла.
Сверху при обтекании передней кромки образуется центрированная волна
разрежения, так как можно считать, что поток обтекает выпуклый угол.
Снизу от передней кромки идет косой скачок уплотнения, так как поток
обтекает вогнутый угол. Давление над пластиной (область 2) меньше, чем под
ней (область 3). Потоки, идущие над пластиной и под ней, должны после
прохождения задней кромки иметь общую границу (штриховая линия).
Следовательно, по обе стороны этой границы (области 4 и 5) скорости должны быть
параллельны, а статические давления равны. Из этих двух условий
рассчитывают интенсивность волны разрежения и скачка уплотнения, идущих
141

от задней кромки пластины. Скорости в областях 4 и 5, строго говоря, не
равны, так как потери в потоках, текущих над и под пластиной,
неодинаковы. Потери в хвостовом скачке уплотнения, который расположен после
волны разрежения, больше, чем в головном, так так М2 >М3. Следовательно,
скорость потока в области 4 меньше, чем в области 5. Пунктирная линия
изображает вихревую линию разрыва поля скоростей.
Ввиду перепада давлений на пластину действует нормальная к ней сила.
Проектируя эту силу на направление потока и нормаль к этому
направлению, можно определить подъемную силу и силу волнового сопротивления.
Результирующая сила /\ которая приложена к середине пластины и
перпендикулярна к ней, а также ее проекции: подъемная сила Fu и сила
сопротивления F х показаны на рис. 6.28, г.
6.5. СВЕРХЗВУКОВЫЕ ТЕЧЕНИЯ В СОПЛАХ И РЕШЕТКАХ
При вытекании из сопла сверхзвуковой струи в пространство,
где давление выше, чем на срезе сопла, образуются скачки уплотнения
(рис. 6,29, а). Интенсивность скачков определяется так, чтобы давление
после них было равно давлению в окружающем пространстве. Граница струи
на участках AD и BE параллельна скоростям потока после скачков.
Скачки посл§ пересечения падают на свободную границу в точках D и Е.
Давление в потоке после прохождения двух скачков становится больше,
чем давление в окружающем пространстве, поэтому скачки отражаются от
границы струи волнами разрежения. Дальнейшая картина строится так же,
как на рис. 6.14, так как волны разрежения отражаются волнами сжатия.
Построенная система волн не является единственно возможной,
При повышении давления в окружающем пространстве скачки станут
более интенсивными, угол наклона их увеличится и правильное пересечение
станет возможным. Возникнет другая конфигурация скачков (рис. 6,29, б),
показанная ранее на рис. 6,22. Такие картины течения наблюдаются в
струях, выходящих из сопла Лаваля, если давление за соплом выше расчетного.
Следует, конечно, иметь в виду, что при течении вязкого газа результаты
расчета совпадают с опытом только на некотором начальном участке, так
как дальше струя подтормаживается, становится дозвуковой и размывается.
При дальнейшем повышении давления за соплом описанная система
скачков превратится в один прямой скачок, который войдет внутрь
расширяющейся части сопла, Рассмотрим различные режимы работы сопла Лаваля
для тех случаев, когда скачок находится внутри сопла. Будем считать
течение одномерным, а жидкость идеальной.
На рис. 6.30 кривая пЬс изображает распределение безразмерном)
давления вдоль сопла при расчетном режиме работы. Давление в минимальном
сечении равно критическому (точка Ь)\ расчетное давление за соплом «г
изображается точкой с, Если давление в пространстве за соплом
(противодавление) выше расчетного, то давление в потоке где-то должно
повыситься. Положим, что повышение давления происходит в прямом скачке у плот*
нения, который располагается точно в выходном сечении сопла. Давление
за скачком р2 определяется по формуле F,23) при известном расчетном дав*
лении рл и расчетном числе Мг (Р = я/2):
А» ____: *--* / Зн щ _ Л
Следовательно, если относительное противодавление равно е8 - рар
то изменение давления внутри сопла изображается кривой abed. Если
относительное противодавление лежит в пределах ц <, в < et, то повышение
142

'//////Л
Рис. 6.29. Схема сверхзвуковой струи при истечении в пространство с повышенным
давлением:
а - пересечение косых скачков; б — образование мостообразного скачка
Рис. 6.30. Распределение давления вдоль сопла Лаваля при различных давлениях на
выходе
давления менее интенсивно и происходит в скачках, расположенных вне
сопла, как это описано выше»
Во всех рассмотренных случаях расход через сопло равен критическому,
так как в минимальном сечении сопла поддерживаются критические
параметры. Рассмотрим наибольшее относительное противодавление, при
котором параметры в минимальном сечении остаются критическими. Это
относительное противодавление называется предельным «пр^Рпр/Ро и
соответствует точке е. При этом противодавлении процесс идет по линии abe. В
суживающейся части давление падает, в горле достигает критического значения, а в
расширяющейся части давление повышается, как в дозвуковом диффузоре.
Если известны площади минимального и выходного сечений сопла, то
расчетное давление за соплом (точка с) и предельное противодавление
(точка е) можно определить таким образом. В двух рассматриваемых режимах в
минимальном сечении сопла скорость равна критической и, следовательно,
Smin " $*- Тогда можно определить значение газодинамической функции
q -- SJSX> где S, — площадь выходного сечения. Определив no q, например
с помощью таблиц, значение ер в сверхзвуковой области, получим
расчетное противодавление рр~Ерр0. Найдя по тому же значению q величину
епр в дозвуковой области, найдем предельное противодавление р11р е11Рр0.
Если относительное противодавление лежит в пределах е2 < е < епру
то скачок уплотнения находится между выходным и минимальным сечением
сопла. В частности, если противодавление соответствует точке /, то
изменение давления внутри сопла описывается кривой aghf. На участке ag
расширение идет, как при расчетном режиме, отрезок gh изображает повышение
давления в скачке, кривая ft/ соответствует сжатию дозвукового потока в
ИЗ

б)
Pric. 6.31. Расширение потока в косом срезе аэродинамической решетки:
а — схема потока; б — годограф скорости
диффузоре. Штриховая линия bhd показывает возможное положение точки
h для различных положений точки / в пределах отрезка ed.
Если противодавление за соплом больше предельного (например,
соответствует точке к), то течение внутри сопла становится всюду дозвуковым.
Распределение давления изображается кривой dik, давление в минимальном
сечении (точка i) становится больше критического, а расход будет меньше
критического расхода.
Подчеркнем, что нерасчетные режимы работы сопла Лаваля
рассмотрены здесь в одномерной постановке и на модели идеальной жидкости. В
вязкой жидкости при возникновении скачков уплотнения возможно появление
более сложных отрывных течений.
Выше рассматривался сверхзвуковой поток в расширяющихся соплах.
При определенных условиях сверхзвуковой поток может возникнуть и в
решетке с суживающимися каналами.
Пусть имеется плоская аэродинамическая решетка, спроектированная
для дозвуковой скорости на выходе, т. е. с суживающимися каналами. Для
упрощения предположим, что решетка имеет бесконечно тонкие
прямолинейные выходные кромки (рис. 6.31, а), расположенные под углом {$1в В
случае, если относительное давление за решеткой выше критического е =
=- pjpo >е* (Ро — давление торможения; рх — давление за решеткой),
то поток за решеткой дозвуковой и направлен под углом pt. Если установить
давление за решеткой ниже критического, то поток на выходе станет
сверхзвуковым, причем возникнет отклонение потока в косом срезе.
Косым срезом называется область, ограниченная треугольниками aba,
причем размер ab соответствует минимальной площади сечения канала
между лопатками. При давлении за решеткой ниже критического в точках а
возникнут центрированные волны разрежения abd. При протекании через
эти волны давление в потоке понижается от/?* (на линии иЬ) до давления за
решеткой Рх< Р*. Волны разрежения представлены в диаграмме
характеристик эпициклоидой 12 (рис. 6.31, б), причем при прохождении волн
струйки / повернуты на угол б, а скорость потока станет равной Xi.
Струйки //, расположенные по другую сторону кромки, пройдут не только
прямую, но и отраженную волну разрежения bdef (рис. 6.31, а), которая
изображается в диаграмме характеристик эпициклоидой 23 (рис. 6.31, б).
После точек а струйки / и // имеют общую границу (отмечены точками на
рис. 6.31, а), по обе стороны которой давление должно быть одинаковым, а
144

скорости параллельны. Поэтому образуются косые скачки уплотнений
ag. Если, как обычно, угол отклонения невелик, то скачок уплотнений
имеет малую интенсивность и может быть заменен элементарной волной сжатия.
Эта волна сжатия представлена в диаграмме характеристик эпициклоидой
32. Следовательно, скачки параллельны нормали к этой эпициклоиде.
Таким образом, в суживающихся соплах с косым срезом поток может
стать сверхзвуковым, причем одновременно произойдет увеличение угла
выхода потока. Это свойство решеток с косым срезом имеет большое значение
в теории турбомашин.
Получим приближенную формулу для определения угла отклонения
потока в косом срезе решеток с суживающимися каналами. При давлении за
решеткой ниже критического в минимальном сечении ab устанавливаются
критические параметры. Запишем уравнение неразрывности для сечений аЬ и
ЛЛ, предполагая течение одномерным и изоэнтропийным: /р*а* sin рг =
-= tpxwx sin фх + 6), где wx и рх — соответственно скорость и плотность за
решеткой; б — угол отклонения потока в косом срезе.
Окончательное выражение можно получить Мерез газодинамическую
функцию q
J— sinpt. F.39)
Покажем, что косой срез обладает некоторой предельной
расширительной способностью.
При понижении давления за решеткой волна разрежения занимает все
большее пространство в косом срезе. Если волна разрежения займет весь
косой срез, то дальнейшее понижение давления за решеткой не может
изменить распределения давления на лопатках. В этом случае сила,
действующая на лопатку, достигает максимального значения (при фиксированных
параметрах торможения). Максимальной проекции силы на фронт решетки
соответствует максимальная проекция скорости на это же направление
(расход постоянен).
Рассмотрим проекцию скорости на фронт решетки wx cos фх + 6).
С помощью формулы F.39) это выражение можно записать в виде [w\ —
— vo\ (VtaJpiWj1 s'm'%]1^.
Продифференцировав это выражение по до,, найдем, что оно достигает
максимума при условии
1
я*
Pi
Заменив производную с помощью формулы E.148, а), получим
соотношение, при котором достигается максимум:
(sin р,)/^=1 /Ml F.40)
Отсюда при максимально возможном расширении в косом срезе
проекция скорости за решеткой на нормаль к фронту решетки равна скорости зву-
дса, как видно из формулы F.30):
^{wx sinHj)/^^ wl/M1 = av
По формуле F.40) находится число М, соответствующее предельной
расширительной способности косого среза.
Дальнейшее расширение и отклонение возможней только в неплоском
потоке за пределами косого среза. При этом проекция скорости на фронт
решетки остается постоянной, а проекция скорости на нормаль к решетке
возрастает.
145

Рис. 6.32. Различные режимы обтекания
решетки пластин сверхзвуковым потоком
Рис. 6.33. Обтекание решетки
телесных профилей безотрывным
сверхзвуковым потоком
Рассмотрим некоторые задачи обтекания аэродинамических решеток
сверхзвуковым потоком. Сначала обратим внимание на некоторые
особенности течения. Пусть аэродинамическая решетка из тонких пластин
обтекается сверхзвуковым потоком с нулевым углом атаки. Возможны три
характерных режима обтекания.
г В первом режиме волны Маха (характеристики) выходят в пространство
перед решеткой (рис. 6.32, а), во втором режиме возмущения
распространяются только за передним фронтом решетки (рис. 6.32, б), но имеется
взаимное влияние профилей, наконец, в третьем режиме каждый из прбфилей
обтекается как одиночное крыло (рис. 6.32, в). Границей между первым и
вторым режимом является случай, когда волны Маха идут точно вдоль
переднего фронта решетки. Очевидно, что в этом случае проекция скорости
набегающего потока на нормаль к фронту равна скорости звука sin а = 1/М =
= а/до, до„ — w sin а == а.
Следовательно, в первом режиме нормальная составляющая скорости
меньше скорости звука.
Рассмотрим более подробно обтекание решетки тонких телесных профилей
сверхзвуковым потоком, когда нормальная составляющая скорости меньше
скорости звука (рис. 6.33). На тонких передних кромках возникают косые
скачки уплотнений, а на выпуклой поверхности лопаток — волны
разрежения. Скачки и волны разрежения расположены перед фронтом и,
следовательно, возмущают поток перед решеткой. Скачки уплотнения
интерферируют с волнами разрежения и возмущения затухают при отдалении от
решетки, так как иначе поток не мог бы быть периодическим. Характеристики
каждой волны разрежения интерферируют с соседними скачками уплотнения и
скачки вырождаются в волны сжатия. Следовательно, в каждой волне
разрежения имеется одна характеристика, которая уходит в бесконечность
перед решеткой, не пересекаясь со скачками (допустим характеристика АВ
на рис. 6.33). При достаточно слабых скачках течение можно считать изо-
энтропийным, и тогда характеристика АВ будет прямой. Поскольку вдоль
прямой характеристики все параметры потока постоянны, то очевидно, что
значение скорости и угла натекания потока в бесконечности соответствует
их значению на характеристике АВ. Этим объясняется так называемое
«направляющее» свойство решетки в сверхзвуковом потоке: заданной скорости
потока в бесконечности Хх соответствует только один угол натекания (З^ при
котором течение всюду сверхзвуковое и безотрывное.
Действительно, для заданного &г возможно только такое V при котором
для характеристики/ уходящей из точки Л в бесконечность, справедливо
146

Заметим, что при образовании дозвуковых зон около входных кромок
или возникновении отрыва столь жесткой связи между величиной и
направлением скорости в бесконечности перед решеткой нет.
6.6. ТЕЧЕНИЯ С ПЕРЕХОДОМ ЧЕРЕЗ СКОРОСТЬ ЗВУКА
Трансзвуковыми или смешанными течениями называют течения,
в которых имеются области как с дозвуковыми, так и сверхзвуковыми
скоростями. Границу между областями называют звуковой поверхностью или,
если течение двумерное, — звуковой линией. В подразд. 4.4 рассмотрена
простейшая одномерная задача о переходе потока через скорость звука в
соплах Л аваля. В этом случае звуковая линия была прямой и располагалась
точно в горле сопла. Сейчас рассмотрим значительно более сложную задачу
о переходе через скорость звука в двумерном потоке.
Итйк положим, что течение плоское и безвихревое, а следовательно,
описывается уравнениями неразрывности и отсутствия вихрей:
ди ft R *
и, — и. ^о. ft i;
ду дх ду
Расположим ось абсцисс вдоль оси симметрии сопла. Тогда вблизи
минимального сечения, в котором может возникнуть трансзвуковой поток,
проекции скорости накось ординат много меньше проекции скорости на ось
абсцисс v <t uy w% *— и2 + v2 ж и2, vlw я& viu — tg Q я& в <^ 1, где w —
скорость потока; в — угол наклона скорости к оси абсцисс.
При этом условии основные уравнения принимают вид
4~ttw)+4-{iwQ) в0* 4-(ше> -4-w^a <М2)
дх ду дх ду
В дальнейшем удобно оперировать известными газодинамическими
функциями. Поделив члены первого уравнения на р*а*, а второго — на
введем безразмерную скорость К — w/a+ и функцию расхода q = /
dg [ d(Qq) Q>
дх ду * ' дх ду
Перепишем первое из этих уравнений в таком виде:
jL JL JLo. F.44)
+ b + go.
дх ду ду
Для безвихревого изоэнтропийного потока q зависит только от скорости
А, и тогда можно записать
dq dq dh dq ^ dq dK
дх dX дх * ду dX ду
Следовательно, уравнению неразрывности F.44) можно придать такой
вид:
ЛЦ^+еЛ)+дЛ=*о. F.45)
dk \ дх ду ) ду Х ¦
Покажем, что второй член в скобках много меньше первого и им можно
пренебречь.
Заменив dkldy на д(Щ1дх согласно второму уравнению F.43),
преобразуем выражение в скобках:
дх ду / дх
14?

Предполагаем, что можно пренебречь членами, в которые входят
произведения малых величин. После упрощения основные уравнения примут вид
d\ng дк* дв _0 д(Ък) дк _0 46
dk дх ду ' дх ду
Поскольку предполагаем исследовать трансзвуковой поток вблизи
звуковой линии, на которой К = 1, естественно принять, что вблизи этой линии
X не сильно отклоняется от 1. Обозначим
X = l-K s« 1, F.47)
где s — некоторый малый добавок к безразмерной критической скорости
(для сокращения будем называть s скоростью).
Функция In (/, которая входит в уравнение F.46), зависит только от X,
а следовательно, может быть выражена через s. Подставив в формулу D.41)
X — 1 4- s и отбросив члены высшего порядка малости, получим
х11 9 d\nq dlnq . , 1ч /п АОХ
S2 ^L_^= (X+I)s F.48)
2 dk ds
Заменив в уравнении F.48) искомые функции через s, получим основные
уравнения трансзвукового потока
* х+1" ds* dQ ds dQ
дх ду ' ду дх
F.49)
Продифференцируем первое уравнение по х, второе по у и почленным
вычитанием, исключив 9, найдем уравнение для неизвестной скорости
JLhL^!iL_^!^^o. F.50)
2 дл-2 ду* V ;
Можно поступить иначе, чтобы получить уравнение для одной
неизвестной функции. Введем потенциал
0ф o dw /г» г 1 \
s гг-.—, ti——- . E.51)
В этом случае второе уравнение F.49) будет удовлетворено
автоматически, а из первого найдем уравнение для определения потенциала
/ i i\ 0ф 02Ф 02Ф л /с со\
(X-J-1; U. (D.DZ)
0.V дх2 ду2
В свою очередь, первое уравнение F.49) можно удовлетворить, если
ввести функцию
00 ' х-} 1 0а:
Тогда из второго уравнения F.49) получим уравнение для этой функции,
которое менее удобно:
F.54)
4 у ду дх2 ду*
Как следует из формул F.51) и F.53), между ср и \|) существует
зависимость
К-\- 1 / 0ф \2 0t|) 0ф 0t|? ,« --.
I . I —: , -"-• . (и. ОГ))
2 \ дх I ду ду . дх
148

в)
Рис. 6.34. Трансзвуковой поток внутри сопла Лаваля:
а — расчетный режим течения; б — местная сверхзвуковая зона занимает всю ширину сопла;
в — сверхзвуковые области на стенках
Полученные уравнения F.50), F.52) и F.54) эквивалентны и выбор их
должен определяться только простотой решения. Прежде чем приступить к
решению уравнений, сделаем некоторые общие замечания об их свойствах.
Все полученные уравнения нелинейны, так как в них искомые функции
входят не в первой степени, что, как известно, чрезвычайно затрудняет решение.
Кроме того, напомним, что согласно определению F.47) s — 0 соответствует
звуковому потоку, s < 0 — дозвуковому, a s >0 — сверхзвуковому.
Тогда легко отметить, что все основные уравнения [например F.52I в
дозвуковой области — эллиптического типа, а в сверхзвуковой —
гиперболического. Это также осложняет решение, так как методы его получения
различны для эллиптических и гиперболических уравнений. Следует отметить,
что задача о трансзвуковом потоке даже после упрощений остается одной из
самых сложных в газовой динамике. Эти замечания касаются сложности
решения краевых задач. Некоторые частные решения, имеющие практическую
ценность, строятся достаточно просто. Рассмотрим два таких решения,
которые позволяют выяснить особенность перехода через скорость звука в
соплах Лаваля.
Расположим начало координат в центре сопла (рис. 6.34) и направим ось
абсцисс вдоль потока. Легко проверить, что функция
Ф = —
и-И
а2 ху1
24
• a3*Д
F.56)
где а — произвольная постоянная, будет точным решением основного
уравнения F.52).
В таком случае дополнительная скорость и угол наклона могут быть
вычислены по формулам F.51):
—г—а2 у2; F.57)
-а6 у3
F.58)
Это решение, как будет показано ниже, описывает течение через плоское
симметричное сопло Лаваля с переходом через скорость звука. За стенки
сопла можно принять произвольные линии тока. Так как принято s < 1, 6<^1,
то решение имеет физический смысл только вблизи звуковой линии, т. е.
вблизи начала координат. В этом случае конкретное сопло можно
характеризовать размером минимального сечения и кривизной его стенки в этом
сечении. Положив 9 --- 0, найдем уравнение линии от (на рис. 6.34, а,
штриховая), на которой вектор скорости горизонтален:
х Ь (х 4 1) ау*/Ь --: 0. F.59)
149

Обозначив у0 половину ширины минимального сечения сопла, найдем
по формуле F.59) х0 —расстояние этого сечения от начала координат (см.
рис. 6.34). Радиус кривизны стенки сопла Ro в минимальном сечении
находится ло известной формуле для кривизны кривой (при условии dy/dx = 0):
r) (*+!) а2 (Л, F.60)
Ах )х=х0
Ширина сопла и радиус кривизны стенок в минимальном сечении
известны, если дано конкретное сопло.
Отсюда при известных у0 и Ro находим постоянную а, которая, как
следует из формулы F.57), характеризует интенсивность изменения скорости
вдоль оси сопла.
Поскольку X = 1 + s, то звуковой линии (X = 1) соответствует s = 0
в формуле F.57). Следовательно, в данном случае уравнение звуковой линии
представляет параболу О А (см. рис. 6.34, а):
Эта парабола, как видно из сравнения с уравнением F.59), лежит выше
по потоку, чем минимальное сечение, обозначенное штриховой линией.
Слева от звуковой линии (s < 0) поток дозвуковой, справа —
сверхзвуковой (s >0). Переход через скорость звука происходит раньше всего на
выпуклой стенке, где давления меньше, а скорость больше, чем на оси сопла,
что объясняется центробежным эффектом, возникающим при искривлении
линий тока.
Найдем расход газа через сопло. Выразим х через у из уравнения F.59) и
а через у0 и /?0 из формулы F.60) и подставим в уравнение F.57):
s=y*/C.yQRol F.61)
Эта формула дает распределение дополнительных скоростей вдоль
линии, на которой скорости горизонтальны.
Распределение приведенного расхода вдоль линии, где скорость
горизонтальна, находим с помощью формул F.48) и F.61):
С учетом того, что скорости горизонтальны, расход через половину сопла
Ул
J
Случай t/o'/?0 ~ 0 соответствует одномерной теории. Следовательно,
второй член в скобках дает относительную поправку при двумерном течении,
которая даже при yJRQ = 0,3 составляет всего 0,24 %.
Рассмотренный пример показывает особенности перехода потока через
скорость звука в двумерной задаче.
В одномерной теории сопла Лаваля (см. подразд. 4.4) был рассмотрен
также случай, когда поток, пройдя минимальное сечение, остается
дозвуковым. Рассмотрим соответствующую задачу в двумерной постановке.
Ищем решение уравнений F.49) в виде
s = Ff (x+l)aV; F-62)
8-(>c+l)a(/F
150

Здесь введена неизвестная пока функция F (z):
F (г), г = х + -^±±- ау\ F.63)
где а — постоянная.
Предполагаемое решение похоже на рассмотренное ранее F.57), F.58),
однако является более общим. Из формул F.62) следует, что при у = 0
функция F задает распределение скорости по оси сопла.
Если подставить предполагаемое решение F.62) во второе уравнение
F.49), то можно убедиться, что оно удовлетворено автоматически.
Подставив предполагаемое решение в первое уравнение F.49), находим
дифференциальное уравнение, которому должна удовлетворять искомая функция:
FF' — aF—2a*(x+ -?±L ay2) = 0. . F.64)
В предыдущих операциях вычисление частных производных функции
произведено по известным правилам, как для функции двух переменных dF/dx—
= F\ dF/ду = (х + 1) ayF'. Уравнение F.64) согласно принятому
обозначению F.63) можно переписать следующим образом:
FF' — aF1 — 2dl z = 0. F.65)
Рассматривая /\ как функцию одной неременной z, имеем dFldz — F'.
Решением дифференциального уравнения являются корни кубического
уравнения
(F + az) (F~2azf=b, F.66)
где b — произвольная постоянная.
В этом можно убедиться, если продифференцировать решение F.66)
по г и, представив результат в виде 3 (F — 2 az) (FF' — aFr — 2a2z) = 0,
сравнить его с дифференциальным уравнением F.65).
Проанализируем полученное решение. Если сначала положить b ^= 0,
то корнями уравнения F.66) будут Ft = — az, F2 = 2oz, т.е.
ay*).
F.67)
Для первого корня из формул F.62) имеем решение
3== „OX+iLhbfll^; F.68)
в =Ы + 1) а1 ху — (х + 1 f а3 у»/6.
Это решение совпадает с полученными ранее уравнениями F.57) и F.58),
если принять а = — а. Возьмем второй корень, тогда
& = 2ах -г 2 (х +1) а2 у\ F.69)
Такое решение совпадает с полученным ранее, если принять а - 2а.
Таким образом, при 6 = 0 имеются два решения. Первое решение F.68)
описывает переход сверхзвукового потока в дозвуковой (при а < 0 и
и х < 0 поток сверхзвуковой, так как s >0), а второе F.69) — переход
дозвукового потока в сверхзвуковой. Такой вывод следует, если рассматривать
151

Рис. 6.35. График вспомогательной
функции F(z) = F (*+X+1 ауЛ
отдельно только первое решение или
только второе. Полученным результатам
можно дать другую трактовку. Из
сравнения выражений F.67) следует, что Fx = F2
на линии г --= 0, т. е. на линии
х + 0,5(х-М)ш/2=0. F.70)
Д это значит, что на этой линии
совпадают значения s и 9, взятые как для
первого F.68), так и для второго F.69)
решений. Следовательно, при z >0 можно
рассматривать первое решение, при z<0—
второе, а на линии z = 0 решения совпа-
21 дают. Таким образом, сращивая
полученные решения по указанной линии, получим
новое единое решение. Кривизны линий
тока в месте сращивания будут разными.
Рассмотрим особенности полученного
течения. Для первого решения F.68)
звуковая линия s = 0 (ОА рис. 6.34, б) построена по уравнению
—х + (х + 1) ау2/2 = 0. Для второго решения F.69) звуковая линия ОВ
построена по уравнению х + (х + 1) ау% = 0.
Линия ОС, по которой произведено сращивание, определена уравнением
F.70) и лежит между указанными звуковыми линиями. Следовательно,
дозвуковой поток, пересекая звуковую линию ОВ, становится сверхзвуковым,
а затем, пересекая звуковую линию ОА — дозвуковым. На оси сопла
скорость дозвуковая и только в точке О равна скорости звука.
Для анализа общего случая с помощью кубического уравнения F.66)
можно построить график F как функции z или az. На рис. 6.35 прямые
линии ЮГ и 202' построены по уравнениям F.67) и соответствуют решениям
F = — az и F = 2az при b = 0.
Если в этих решениях принять у = 0, то график описывает изменение
дополнительной скорости вдоль оси сопла. Например, рассмотренной только
что задаче соответствует распределение 102'. В области / находятся кривые,
соответствующие решению b >0. Здесь F < 0, а следовательно, на оси
сопла скорости дозвуковые. В области // F >0 и скорости на оси сопла
сверхзвуковые. Области II и III нереальны, так как не соответствуют
физическому смыслу задач (аналогично нереальным областям в одномерной
задаче, см. подразд. 4.4). Для примера в области / построена кривая b = const.
Соответствующая картина течения показана на рис. 6.34, в. Несмотря на то,
что всюду F < 0, около стенок сопла могут быть области, где поток
сверхзвуковой, т. е. s >0, так как второй член в решении {6.62)
положителен.
Выбрав в качестве стенок канала произвольные линии тока, можно
распространить это решение на построение околозвуковых течений в
криволинейных каналах.
Таким рбразом, при обтекании тела дозвуковым потоком на выпуклой
поверхности могут возникать местные сверхзвуковые зоны. В
рассмотренных решениях не учитывалась возможность возникновения скачков
уплотнения, которые возникают при торможении -сверхзвукового потока и
замыкают сверхзвуковую зону.
Современные численные методы позволяют установить положение такого
скачка.
152

Вопросы для самопроверки
1. Какими свойствами обладают характеристики?
2. Покажите, что нормальные к фронту косого скачка составляющие скорости до
скачка больше скорости звука, а после него — меньше.
3. Как вычислить давление изоэнтропийного торможения после прямого скачка,
если перед ним известно М^ и рх?
4. Определите погрешность, которую дает приближенная формула F.32) по
сравнению с точным расчетом при Mj = 1,25 и б = 5°.
5. Рассчитайте и постройте положение косых скачков уплотнения и волн
разрежения около ромба, обтекаемого сверхзвуковым потоком.
6. Как определить предельное противодавление для сопла Лаваля в одномерной
постановке?
7. Как влияет кривизна стенок сопла Лаваля в минимальном сечении на
распределение скорости?

ГЛАВА 7
ОДНОМЕРНЫЕ НЕУСТАНОВИВШИЕСЯ ТЕЧЕНИЯ
l
7.1. РАСПРОСТРАНЕНИЕ СЛАБЫХ ВОЗМУЩЕНИЙ В ПОТОКЕ.
АКУСТИЧЕСКИЕ УРАВНЕНИЯ
Теория неустановившегося течения сжимаемой жидкости имеет
большое прикладное значение в ряде областей техники. Эту теорию
используют при расчете переходных процессов в турбомашинах, газовых сетях,
определении устойчивости работы систем, содержащих компрессоры, и т.п.
Особенности неустановившегося течения необходимо учитывать при
расчете систем измерения давления в пульсирующих потоках, при
конструировании как инерционных, так и малоинерционных зондов. Наконец, теория
неустановившегося течения используется в численных методах также и при
расчете установившегося течения, рассматриваемого как предельный
случай.
Одним из широко применяемых в инженерных расчетах методов является
метод, использующий решение о так называемом распаде разрыва. Поэтому
прежде чем излагать сам метод расчета, необходимо рассмотреть решение о
распаде разрыва, которое кстати и само по себе имеет важное теоретическое
и практическое значение.
Прежде чем перейти к обобщению, получим основные закономерности
распространения относительно слабых волн сжатия и разрежения.
Целесообразно начать с этих задач, так как они наиболее просты. Вместе с тем
подобные решения также используются, например, при анализе шума турбо-
машин, возбуждаемого движущимися аэродинамическими решетками.
Пусть труба заполнена идеальной сжимаемой жидкостью, которая
неподвижна и имеет параметры р и р, поршень скачком преобретает малую
постоянную скорость du вправо (рис. 7.1, а). Слабая волна сжатия
распространяется вправо со скоростью звука а = х р/р. После прохождения волны
сжатия жидкость имеет параметры р + dp, p + dp и скорость du.
Если за время dt волна сжатия переместится от сечения / — /до
сечения 2—2, то в этом элементарном объеме жидкость будет сжата до
параметров р +• dp и р + dp. Необходимое для этого количество жидкости втечет
со скоростью du через сечение /—/.
Для выделенного элементарного объема уравнение неразрывности
G.1)
и уравнение количества движения
G.2)
где S обозначена площадь поперечного сечения трубы.
Из уравнения G.1) найдем скорость жидкости после прохождения
слабой волны сжатия
G.3)
Скорость жидкости направлена в сторону движения волны сжатия.
154

Рис. 7.1.
Распространение слабых волн:
а — сжатия; б —
разрежения
1 \г
I t
Р + dp
4*
a at
du
pi-dp
I. I P
adt
Поделив почленно уравнение G.1) на уравнение G.2), получим
уравнение процесса, протекающего при сжатии жидкости:
dp = a2 dp. G.4)
Исключив скорость звука а2 = хр/р, можно представить соотношение
G.4) в виде (уравнение изоэнтропийного процесса)
dplp = xdpjp. G.5)
Если придать поршню малую скорость du влево (рис. 7.1, б), то по
жидкости побежит слабая волна разрежения. Аналогичным образом вновь
придем к формулам G.3), G.4) и G.5). Однако теперь dp < 0, ф < 0, а
следовательно, после прохождения волны разрежения скорость жидкости
направлена в сторону, противоположную распространению волны. Поэтому
формулу G.3) для волн сжатия и разрежения можно записать единым образом:
du = ± dp/pa.
G.6)
С помощью полученных формул решим задачу о распаде слабого разрыва.
Пусть труба разделена перегородкой (рис. 7.2, а), по обе стороны от которой
находится газ при разном давлении, причем Ар >0, Ар >0 (Ар/р < 1,
Ар/р <^ 1.) При удалении перегородки произойдет распад разрыва:
направо побежит слабая волна разрежения, а налево — слабая волна сжатия.
В рассматриваемом акустическом приближении скорости обеих волн будут
одинаковы и равны скорости распространения звука. Через время t после
удаления перегородки волны пройдут расстояние at (рис. 7.2, б). После
прохождения волн образуется область АВ, на которой разрывы должны
отсутствовать, т. е. как давление, так и скорость потока во всей этой области
должны быть постоянны. Если давление после волны разрежения упадет на
Ар/2, а после волны сжатия возрастет на Др/2, то в этом случае скорости
газа как после волны разрежения, так и после волны сжатия будут одина-
§
ч
\А
Р+&Р
Р+Др/2
¦ at
at
Рис. 7.2. Распад слабого разрыва
155

ковыми по величине и направлению и по формуле G.6) равными Ли =
— —Ар/2ра. Знак минус указывает на то, что скорость направлена справа
налево, т. е. газ естественно движется из области высокого давления в
область низкого.
В общем случае в потоке могут распространяться как волны разрежения,
так и вЬлны сжатия конечной интенсивности.
Процесс расширения и сжатия газа в волнах конечной амплитуды
является изоэнтропийным. Поэтому решение может быть получено
интегрированием уравнения G.6), которое устанавливает зависимость между
изменением скорости и давления в бесконечно слабой волне. Рассмотрение
ударных волн требует другого подхода, так как процесс сжатия в них не
является изоэнтропийным.
Получим сначала уравнения для волн разрежения и сжатия. Исключив
давление из уравнений G.4) и G.6), найдем
du= ±adp/p. G.7)
Для изоэнтропийного процесса отношение скоростей звука можно
выразить через отношение плотностей
G.8)
Прологарифмировав это выражение и вычислив дифференциал от
обеих частей равенства, получим da/a = ((х—1)/2) (dp/p). Исключив из
уравнения G.7) плотность и проинтегрировав полученное дифференциальное
уравнение, найдем формулу для определения скорости газа в бегущей волне
w = ±—i—(a—дв) G.9)
к— 1
и формулу для местной скорости звука
а=Оо±-?=^-и. G.10)
Здесь через а0 обозначена скорость звука в неподвижном газе.
Отметим, что скорость звука всегда считают положительной величиной,
в то время как скорость газа может быть как положительной, так и
отрицательной, что определено направлением отсчета координаты х. Будем считать,
что скорость газа положительна, если он движется слева направо.
Поэтому в уравнении G.9) следует брать знак плюс, если волна
распространяется направо, и минус, если — налево.
Местная скорость распространения волны относительно газа равна
местной скорости звука. Тогда местная скорость распространения волны
относительно неподвижного наблюдателя
с=а±и. G.11)
Скорость волны с, как и скороеь звука а, всегда считают
положительными, т. е. рассматривают их модули. Поэтому, если волна
распространяется направо, то в формуле G.11) следует брать знак плюс, а если налево—
знак минус.
Из соотношений G.9), G.11) находим формулу для определения местной
скорости распространения волны
G.12)
Из полученных формул следуют важные выводы, которые для физической
наглядности проиллюстрируем примерами.
156

Пусть труба справа от поршня
заполнена неподвижным газом,
скорость звука в котором равна а0.
В некоторый момент времени
поршень внезапно начинает двигаться
налево с постоянной скоростью
ип < 0. По газу пойдет волна
разрежения. Газ в пространстве,
через которое прошла волна
разрежения, будет иметь скорость
поршня (ниже будет показано, что это
справедливо, если скорость
поршня не выше определенного
предела).
Передний фронт волны
разрежения будет проходить по
неподвижной жидкости (и -- 0), а следовательно, скорость его перемещения
согласно формуле G.12) будет равна скорости а0 звука в неподвижной
жидкости.
В движущейся за передним фронтом волне разрежения плотность
жидкости уменьшается и, следовательно, уменьшается местная скорость звука,
т. е. а <С а0. В таком случае из формулы G.9) ясно, что абсолютная величина
скорости жидкости возрастает, но и < 0, так как жидкость движетсй в
сторону движения поршня. Волна разрежения движется вправо и в формуле
G.12) надо выбрать знак плюс:
G.13)
Рис. 7.3. Образование волны разрежения
конечной интенсивности
Так как #<0, скорость элементов волны разрежения, бегущих за передним
фронтом, тем меньше, чем они дальше от переднего фронта. Следовательно,
волна разрежения размывается, т. е. становится с течением времени более
пологой.
После прохождения волны разрежения скорость жидкости равна
скорости поршня и м7,<0, и скорость заднего фронта волны разрежения
является наименьшей:
с -= а0 +
X+I
G.14)
Представим, все графически (рис. 7.3) в координатах х (расстояние) и
t (время). В исходный момент времени поршень находится в начале
координат, а дальнейший его путь представлен прямой во втором квадранте x^=unt.
В первом квадранте прямые показывают траекторию волны разрежения
(линия ОВ — х — (а0 +
х+1
ип) t, линия ОС — х = а() t). В частности,
в момент времени tx поршень находится в положении А А; положение
переднего и заднего фронтов волны разрежения обозначено соответственно ВВ и
СС.
Передний фронт волны разрежения всегда движется в сторону,
противоположную перемещению поршня. На рис. 7.3 показано, что и задний фронт
движется направо. Однако он может быть неподвижен или двигаться влево
при достаточно большой отрицательной скорости поршня. На рис. 7.3
показаны характеристики ОВС.
157

Сделаем еще важное замечание относительно предельной скорости
течения. Максимальная скорость течения достигается по уравнению G.9) при
а- 0:
| -1). G.15)
Такая скорость возникнет, если начнется истечение из трубы,
наполненной газом, в абсолютный вакуум. Если скорость поршня превышает это
значение, то можно считать, что происходит истечение в абсолютный вакуум, а
величина скорости поршня уже не оказывает влияния на течение.
Если поршень не выдвигать, а вдвигать (ип ;> 0) в трубу, наполненную
газом, то возникнет волна сжатия, для которой справедливы соотношения
G.9), G.10) и G.11). В этомслучае скорость газа за волной сжатия будет
направлена в сторону движения волны. Скорость звука за волной сжатия будет
выше, чем перед ней. Тогда скорость заднего фронта волны сжатия будет
выше, чем переднего. Фронт волны сжатия (в противоположность волне
разрежения) будет становиться все круче и она в конце концов превратится в
ударную волну, бегущую по неподвижному газу. Формулы для расчета
ударной волны будут выведены далее, а здесь продолжим изучение слабых
возмущений.
Запишем уравнение движения для одномерного неустановившегося
течения идеальной сжимаемой жидкости
J!L+U*L= L-E?_ G.16)
dt ' дх р дх
и уравнение неразрывности
^ + ^<Р«>=0. ,7.17)
Будем считать, что газ неподвижен, имеет постоянную плотность р0 и
давление р0. Пусть в газе распространяются слабые возмущения, т. е.
возможны слабые пульсации плотности, давленияи скорости (р' <? р0, р'<
)
и = и*. G.18)
Подставим эти выражения в основные уравнения G.16) и G.17) и
отбросим члены, в которых встречаются произведения величин со штрихами, т. е.
члены второго порядка малости. Преобразование первых двух членов
уравнения G.16) очевидно, а третий член принимает вид
1 др ^ 1 др' __ 1 Л р' \ dp' = I dp'
р дх Ро + Р' дх ро I ро " / дх ро дх
Тогда получим линейные уравнения, которые называют акустическими
так как они пригодны для изучения только слабых ^колебаний газа:
JaL+J-JEL^o, G.19)
dt p0 дх
2eLJ*!l0. G.20)
dt дх
Подобные уравнения могут быть применимы для потока газа,
движущегося с постоянной скоростью.
При слабых колебаниях происходит изоэнтропийное сжатие или
расширение газа, поэтому давление и плотность связаны уравнением
Ро + Р' _ / Ро+Р'
Ро V Ро
158

Разложив правую часть в ряд и сохранив только члены первого порядка
малости 1 + р'/ро ~ 1 + >ф'/р0, получим формулу, связывающую
пульсации плотности и давления:
p' = (KA/p,)p' = aSp', G.21)
где а0 - - скорость звука в неподвижном газе согласно формуле D.10).
Приближенное уравнение изоэнтропы G.21) дает достаточно точный '
результат, даже при относительно большем уровне пульсаций давления.
Так при pf/p0 = 0,1 и х = 1,4 точное значение р'/р0 = 0,0704, а
приближенное — р7р0 = 0,0714.
Исключив р' из уравнения G.20) с помощью уравнения G.21), получим
a% dt дх N
Таким образом, получены два уравнения G.19) и G.22), содержащие
две искомые функции. После нахождения давления и скорости как функции
координаты и времени, пульсация плотности может быть найдена из
уравнения G.21).
Два основных уравнения первого порядка G.19) и G.22) с двумя
неизвестными функциями можно свести к одному уравнению второго порядка,
исключив скорость или давление.
Продифференцировав уравнение G.19) по *, а уравнение G.22) по / и
вычтя одно из другого, исключим скорость и получим
?-=0. G.23)
дх* a*
и
Это линейное уравнение второго порядка называют волновым, так как
оно описывает распространение волн (в данном случае волн давления).
Точно такие же уравнения, как легко показать, могут быть получены для
р' и и'.
Общее решение уравнения G.23) можно записать в виде
р' =/^<*-Oi>/)+F2(x + a0/), G.24)
где Fx и F2 — произвольные функции, что можно проверить, подставив
решение в уравнение (решение Даламбера).
Физический смысл решения ясен из следующего. Положим сначала F2=
0. Пусть в газе создано какое-нибудь возмущение. Тогда давление зависит
от координаты и времени. Пусть, например, в момент времени tx в точке хх
возмущенное давление равно pi. Так как общее решение имеет вид р' =
, „ рх (х ___ Qi)t)y такое же давление будет там, где аргументы написанных
функций равны, т. е. х — aot = хх — я0/,.
Следовательно, в точке х такое же давление будет через промежуток
времени / — tx -~ (х — xt) laQ> x >хг. Значит решение Fx описывает
простую волну возмущения, бегущую со скоростью звука в положительном
направлении. Точно так же решение F2 описывает простую волну, бегущую в
отрицательном направлении. Подчеркнем, что из решения G.24) следует
отмеченный ранее факт, что слабые возмущения распространяются в газе со
скоростью звука.
Решение системы уравнений G.19), G.22) удобно выразить через одну
функцию Ф (х, t), положив
* «•-?-. «7.25,
159

р
Рг ¦
S Pi
При подстановке этих выражений в
уравнение G.22) убеждаемся, что оно
автоматически удовлетворено, а при подстановке в
уравнение G.19) получим уравнение, которому
должна удовлетворять введенная функция:
Г--0. G.26)
дх* а% dt*
Рис. 7А. Схема зонда для из- ^
мерения давления Это волновое уравнение того же типа, что
и уравнение G.23).
Следовательно, общее решение опять имеет вид
F2{x + aJ). G.27)
Рассмотрим задачу, которая находит применение при расчете пневмомет-
рических систем.
Система состоит из трубки длиной / и площадью поперечного сечения S
(рис. 7.4). Открытый конец трубки выведен в пространство, где измеряется
давление, а другой соединен с камерой объема V, где расположен датчик,
регистрирующий давление. Пусть переменная часть измеряемого давления
меняется по закону:
pjcosco/, G.28)
где р[ — амплитуда; со — круговая частота колебаний.
Требуется определить закон изменения давления в объеме, где
поставлен датчик. В трубке возникают гармонические колебания воздуха с частотой
о, поэтому аргументы функции G.27) следует записать так:
Решение следует искать как сумму четырех членов с неизвестными
постоянными коэффициентами, которые определяются из граничных условий:
Ф- A sin (— +Ы) + В sin (-22- — ю/W Ccos (— f «>/) +
\ а0 ! \ а0 I \ а0 ]
+Dcos(— — (оЛ. G.29)
\ <*о /
Волны возбуждаются на правом конце трубки и распространяются в
отрицательном направлении (первый и третий члены), отражаются от
левого конод и движутся в положительном направлении (второй и четвертый
члены).
Интенсивность прямых и отраженных волн одинакова и при их
сложении образуется стоячая волна. Можно сократить дальнейшие
преобразования, если сразу положить В = А и D = С.
В этом случае выражение G.29), использовав формулы сумм
тригонометрических функций, можно записать так:
Ф - 2Л sin (— ) cos со/ f 2C cos (—) cos со/. G.30)
\ «о / V «о /
Постоянные А и С определяют из граничных условий. На правом конце
трубки закон изменения давления задан G.28). Тогда, выразив давление
через функцию Ф по формуле G.25), получим граничное условие, которому
должна удовлетворять искомая функция на правом конце трубки:
~~роа* дФ/дх=-р[ cos со/, x^t. G.31)
160

На левом конце трубки (х = 0) граничное условие можно получить из
закона сохранения массы. Количество жидкости, вытекающей из объема за
время dt, dm = —p0u'Sdt. Тогда изменение плотности жидкости внутри
объема dp' = dmIV = — pou'SdtIV.
Заменив р' через р' по формуле G.21), имеем
+ «' = 0
dt V
Считаем, что д авление в камере одинаково во всех точках, так как скорость
там пренебрежимо мала.
Воспользовавшись условиями G.25), запишем граничное условие для
функции Ф при х = 0 в таком виде:
Поскольку функция Ф зависит от времени, а производная по времени от
выражения, стоящего в скобках, равна нулю, то очевидно, что выражение
в скобках равно постоянной. Эту постоянную можно принять равной нулю,
так как давление и скорость находятся согласно формулам G.25)
дифференцированием. Следовательно, на левом конце трубки граничное условие
имеет вид — дФ/дх + SO IV = 0.
Вычислив постоянные с помощью граничных условий G.31), G.32),
получим
Ц2С - -2L.2Л. G.33)
aS x '
2Л = Ц 2С - -2L
(G>V7a0 S) sin Sh—cosSh a0S
Здесь введено обозначение для безразмерной величины, называемой числом
Струхала: Sh = о//а0, которое характеризует относительную частоту
колебаний.
Решение G.30) при известных постоянных G.33) позволяет по формуле
G.25) найти пульсацию давления в любом сечении трубки. Положив *=0,
получим пульсацию давления в камере
pj cos ш
2
cosSh—
Проанализируем решение G.34). Прежде всего очевидно, что амплитуда
пульсаций давлений в камере, где установлен Aat4HK, в общем случае не
равна амплитуде измеряемых пульсаций. Решение зависит от двух
безразмерных критериев (при условии, что влияние трения не учитываем): Sh=
= (dl/aOi T = G)V7a0S.
Если число Струхала равно нулю, то амплитуда пульсаций в камере
равна амплитуде измеряемых пульсаций. Следовательно, чтобы обеспечить
точное измерение пульсирующего давления, в измерительной системе должно
быть обеспечено достаточно малое число Струхала. Если частота пульсаций
и скорость звука заданы, то этого можно добиться только уменьшением
длины приемной трубки. Для того чтобы подавить влияние второго члена в
знаменателе, необходимо выдержать достаточно малую безразмерную величину
Г. Следовательно, надо уменьшать объем камеры и увеличивать площадь
поперечного сечения трубки. Но площадь поперечного сечения трубки, с
другой стороны, нельзя сделать большой, так как обычно желательно обеспе-
шть измерение пульсаций в небольшой окрестности заданной точки потока.
Высказанные требования учитывают при расчете малоинерционного
измерительного прибора, предназначенного для возможно точного измерения
временной составляющей давления.
> Зак. 2638 161

В ряде случаев необходима регистрация только среднего давления. Для
этого применяется инерционная измерительная система, причем пульсация
давления в камере только затрудняет измерения и должна быть подавлена.
Очевидно, что в этом случае, наоборот, нужно выбрать параметр Т столь
большим, чтобы пульсации в камере были пренебрежимо малыми.
Вернемся к рассмотрению общего случая. При стремлении знаменателя
формулы G.34) к нулю погрешность измерения пульсирующей величины
безгранично возрастает. Строго говоря, теория не применима к этому случаю,
так как пульсации, которые при вводе предполагались малыми,, становятся
бесконечно большими (при учете трения пульсации будут большими, но
ограниченными). Безграничное возрастание амплитуды колебаний связано
с явлением резонанса в измерительной системе.
Следовательно, собственные частоты колебаний воздуха в системе
трубка — камера определяются по формуле
G.35)
Если камера отсутствует (V = 0), то из формулы G.35) следует
J^-=B*-l)^, * = 1, 2, 3, ... G.36)
«о 2
Эта формула служит для определения собственных частот колебаний
воздуха в трубке. Число собственных частот безгранично, так как столб
воздуха имеет бесконечное число степеней свободы.
7.2. ОСНОВНЫЕ УРАВНЕНИЯ НЕУСТАНОВИВШЕГОСЯ ТЕЧЕНИЯ.
ИНВАРИАНТЫ РИМА НА
В подразд. 7.1 рассмотрены линейные акустические уравнения,
которые описывают распространение слабых возмущений. Во многих
технических системах, например в газовых турбомашинах, возмущения потока
могут быть сильными. В частности, в потоке могут распространяться
ударные волны. Кроме того, поток может быть подвержен различного рода
воздействиям: подводу теплоты, трению, подводу массы и т. д. Получим в этом
разделе основные уравнения, пригодные для анализа этих явлений, и
проанализируем особенности распространения сильных возмущений в потоке.
Запишем уравнения сохранения для квазиодномерного неустановившегося
течения идеальной сжимаемой жидкости с учетом различного вида
воздействий на поток.
Уравнение неразрывности
4 ^ G.37)
at дх at
где 5 — площадь поперечного сечения; х—координата, измеряемая вдоль
тракта; dmldt — скорость подвода массы на единицу массы текущего газа.
Уравнение движения
¦S"+«-r-+JL-r—^ <7-38>
dt дх р дх
где F — сила, действующая на единицу массы газа.
Уравнение энергии
(h + *l2) + u(h + u/2)^ 7T+»F> G-39)
at дх р at at
где dQIdt — скорость подвода теплоты к единице массы газа.
162

В уравнениях площадь поперечного сечения зависит от координаты, а
остальные переменные в общем случае являются функциями как координаты,
так и времени. Члены, которые стоят в правых частях уравнений,
позволяют учитывать различного рода воздействия на поток, движущийся в
технических устройствах. Так, например, член dmldt может учитывать отвод
воздуха в противопомпажное устройство осевого компрессора. Сила F может
представлять действие лопаток турбомашины на поток, центробежные силы,
действующие на газ в центробежном компрессоре или центростремительной
турбине, или силы трения. Член dQ/dt учитывает внутренний подвод
теплоты к текущему газу из-за наличия сопротивления или подвод теплоты извне.
В частном случае установившегося течения уравнениями G.37), G.38),
G.39) можно, например, описывать статические характеристики турбин,
компрессоров и иного оборудования, в котором поток испытывает
различного рода воздействия. При неустановившемся течении можно рассчитывать
динамические зависимости, а уравнения будут описывать законы
генерации, распространения и затухания волн давления, плотности, скорости и
энтропии.
Для анализа и практических расчетов уравнения G.37), G.38), G.39)
целесообразно преобразовать к так называемым характеристическим
переменным.
Будем считать газ совершенным и дополним систему уравнений
сохранения термодинамическими соотношениями.
Приращение энтропии газа определяют зависимостью
ds~cvd\np—cpd\np. G.40)
Использовав уравнение-состояния
P=pRT9 R^cp~cv% G.41)
из выражения G.40) получим
, ds=cpd\nT—Rd\np = cvdlnp—cpd\np. G.42)
С помощью формул для скорости распространения звука
a2=xp/p, h^cp/cv G.43)
найдем остальные зависимости, необходимые для дальнейших
преобразований:
ds= 2cvd\n a—Rd lnp = 2cpd In a— Rd \np. G.44)
Выразим энтальпию совершенного газа через давление и плотность
А«хр/(х-1)р G.45)
и запишем уравнение G.39) в виде
d/ I x—1 p 2 Г дх V x—1 p 2 У
p dt dt
Продифференцировав выражение в скобках и исключив производную du/dt
с помощью уравнения G.38), получим после приведения подобных
членов
L(^? JL\^/EE Jp)^ G.46)
dt дх ) р» \ dt дх) v 'it
. 163

Поделив и помножив первую скобку на р и применив формулу G.43) для
скорости звука, запишем это уравнение в виде
= (x-"тгGA7)
Выражения в круглых скобках с помощью зависимости G.42) можно
заменить через энтропию и записать уравнение энергии в виде
(•*¦¦?• '
Из этого уравнения следует, что энтропия переносится со скоростью
потока, а источником ее изменения является подвод теплоты. Если подвода
теплоты нет, то процесс является изоэнтропийным (здесь рассматриваем
течение без ударных волн).
Преобразуем теперь уравнения сохранения массы G.37) и количества
движения G.38), введя вместо давления р и плотности р новые переменные:
энтропию s и скорость звука а.
Продифференцировав в уравнении G.37) выражение в скобках и поделив
все члены на pS, запишем его в таком виде:
dlnp ди ^ dm d\nS . .g
дх дх dt dx ' К ' '
Из формул G.44) следует
dlnp==—^— din a— — dins. G.50)
Исключив плотность из уравнения G.49) с помощью соотношения G.50).,
имеем
Вторую скобку в уравнении G.51) выразим из уравнения энергии G.48) и
запишем уравнение неразрывности в окончательном виде:
Аналогичным путем преобразуем уравнение G.38). Помножив и поделив
третий член уравнения G.38) на р и введя скорость звука, получим
F. G.53)
dt дх х дх
Из соотношения G.44) следует
После исключения давления уравнение G.53) примет вид
ди , ди , 2а2 д In a a2 dins
dt U~d7 х—1 djc kR ~дх
164

Для использования метода характеристик полученные уравнения следует
записать в несколько ином симметричном виде. Умножим уравнение G.52)
на а и сложим с уравнением G.54):
Ve+)H+L(V«+
х— 1 / дх \ х—1 /
+ a^L-au^^+F *_-*.. G.55)
dt dx kR дх , '
Умножим уравнение G.52) на а и вычтем из него уравнение G.54), тогда
д / 2 \ . , ч д I 2 \ х dQ , dm
— [ а—и ) + (и—а)— ( а—и) = — + а
dt \ х— 1 / v дх \ х—1 / a dt dt
-au-*^-F + ——. G.56)
dx xR дх
Рассмотрим подробнее важный частный случай: одномерное изоэнтро-
пийное неустановившееся течение при отсутствии внешних воздействий.
Тогда уравнения G.55), G.56) примут вид
Kdh H; G.57)
Введем так называемые инварианты Римана, который дал основу метода
характеристик:
У-—— a + a, Z=—?—а—и, G.59)
X—1 X—1
и запишем основные уравнения G.57), G.58) в виде
a) dY/dx = 0; G.60)
-a)dZ/dx=0. . G.61)
Эти нелинейные уравнения описывают распространение волн в газе.
Инварианты являются функциями двух переменных: координаты и времени,
поэтому можно записать
^^-df, G.62)
ОХ О1
dx+
dx+ dt. G.63)
дх dt v ;
Из выражения G.62) и уравнений G.60) вытекает, что если dx/dt = и+а
то dYldt = 0, т. е. если наблюдатель движется со скоростью и + а, то для
него величина Y остается неизменной. Если же наблюдатель движется со
скоростью dx/dt = и — а, то из G.63) и G.61) следует, что для него
величина Z остается неизменной. Необходимо подчеркнуть, что скорость потока
и скорость звука в общем случае изменяются. Неизменными остаются только
их комбинации, выражаемые инвариантами G.59).
Скорость и + а можно физически трактовать как местную скорость
распространения слабых возмущений по потоку, а скорость и' — а — против
потока. Это следует из того, что слабые возмущения распространяются
относительно неподвижного газа с местной скоростью звука, а в
движущемся газе дополнительно к этому их еще переносит поток. Следовательно, ес-
165

ли наблюдатель движется со скоростью, равной местной скорости
распространения слабых возмущений, то для него один из инвариантов Римана
остается неизменным.
Инварианты Y и Z описывают распрцстранение волн, бегущих
соответственно по потоку и против потока, поэтому их можно назвать Y и Z
волнами.
Под термином «волна» следует понимать то, что возмущение,
характеризуемое параметрами а и иу распространяется со скоростью и + а (или
и — а), в то время как частицы газа движутся" со скоростью и.
Из основных уравнений G.60), G.61) видно, что существуют решения,
для которых один из инвариантов постоянен для любых х и t, т. е. во всем
пространстве и на протяжении всего времени. Это соответствует
распространению волны только в одном направлении. Такие волны называют
простыми. Так, если
Z- —— a-u=ZOy G.64)
к—1
то распространяется простая волна Y. Ее можно назвать волной, бегущей
вперед (по потоку). Таким образом, для волны, бегущей вперед, инвариант Z
вообще постоянная величина, а инвариант Y постоянен только вдоль линий
и + а = const (характеристик), на которых
Y =—— а + и -const. G.65)
х—1
Из условий G.64), G.65) следует, что в простой волне вдоль характеристик
постоянно не только значение инварианта, но и скорости звука.
Аналогично, если Y = Уо и постоянно во всем потоке, то против потока
распространяется простая волна Z, причем этот инвариант постоянен вдоль
характеристик и — а =.const. Вдоль этих же характеристик постоянны
скорость потока и скорость звука.
Если оба инварианта постоянны во всем потоке и в любой момент
времени, то в потоке нет возмущений и он однороден.
Вернемся к задаче о распространении волны разрежения в трубе,
заполненной газом, из которой выдвигается поршень (см. рис. 7.3), и поясним ее
решение с помощью инвариантов Римана.
Передний фронт волны разрежения бежит по неподвижному газу со
скоростью звука в нем а0, т. е. его путь изображен прямой ОС, для которой х=
= aot.
Инвариант Z в данном случае постоянен во всей области / и его значение
можно определить по параметрам неподвижного газа (и = 0, а = а0). Тогда
по формуле G.59) получим
Z — Zo= а — и = а0.
X—1 X—1
Отсюда определяем скорость звука в области 2 (и = — иа)
а = а{)—^— ип. G.66)
Поскольку процесс расширения газа в волне изоэнтропийный, то связь
между давлением до волны (область 1) и за ней (область 2)
-Й--/ 1— *-',, jifg_L)" G 67)
166

Аналогичная формула для отношения плотностей имеет вид
n 8
Pi V 2 а,
Волна разрежения ВОС состоит из веера характеристик, вдоль которых
параметры потока постоянны. Так как в данном случае распространяется
простая волна У, то уравнение характеристик следует записать в форме х —
== (а + и) t. Выразив текущую скорость звука через скорость потока из
формулы G.66), получим уравнение характеристик х — (а0 -\—~- и) t,
— ип < и < 0. На этих характеристиках инвариант У принимает
постоянные значения.
Ранее было показано, что после возникновения волна разрежения
размывается и становится более пологой. Рассмотрим, каким образом будет
искажаться со временем форма произвольной простой волны.
Пусть в начальный момент времени задана форма волны. Так как это по
условию простая волна, то значение второго инварианта постоянно Z =
= Zo. Изменение волны в последующие моменты времени можно описать,
пользуясь тем, что значение У (л\ /) не изменяется вдоль характеристик
и + а = cons.
Из определения инвариантов G.59) получим
—C—x)Z/4; G.69)
G.70)
Если в начальный момент времени задана форма простой волны Y (x, t0)
на рис. 7.5, то можно найти ее форму в последующие моменты времени.
Определим по заданным У (*, /0) и Z = Z.o наклон характеристик с помощью
формулы G. 69). Вдоль этих характеристик (штриховые линии) У (х, t) =
= У (х, t0). Точки, для которых значения инварианта одинаковы, остаются
при распространении волны на том же расстоянии одна от другой.
Форма сильной простой волны изменяется. Участок волны, на котором
происходит сжатие газа, становится все более крутым, а участок, где
наблюдается разрежение, — наоборот, все более пологим. Это объясняется тем,
что чем больше У, тем больше скорость распространения возмущений, как
это следует из формулы G.69).
Таким образом, в области сжатия последующие возмущения догоняют
предыдущие и сливаются с ними. Это в конце концов приводит к появлению
разрыва, т. е. скачкообразному изменению параметров потока. В потоке
появляется бегущая ударная волна.
Если рассмотреть распространение простой Z-волны, то все эти
рассуждения останутся справедливыми, т. е. участки сжатия будут становиться
все более крутыми (вплоть до появления разрыва), а участки разрежения—
более пологими. Отмеченная особенность является характерной для сильных
волн, так какчслабые акустические волны распространяются, не изменяя в
первом приближении своей формы.
В общем случае волны не являются простыми, т. е. в потоке
одновременно имеются возмущения обоих типов: У и Z.
Рассмотрим плоскость xt (рис. 7.6) и положим, что в некоторый момент
времени t0 известно распределение а и и как функций х. По этим данным и
формулам G.59) можно найти распределение инвариантов для того же
момента времени. Пусть требуется найти распределение скорости потока и
скорости звука в следующий момент времени: t = t0 + At.
Если Да: и А/ достаточно малы, то их отношение приближенно
представляет скорость. Пусть из точки А проведена прямая Axx/kt = и + а, а из
167

Рис. 7.5. Распространение простой волны
Рис. 7.6. Схема расчета методом
характеристик
точки В — прямая Д*2/Д/ = и — а, которые пересекаются в точке С.
Вдоль первой прямой постоянен инвариант У, а вдоль второй — инвариант
Z. Так как по условию в точках Аи В значения соответствующих
инвариантов известны, то, следовательно, известны их значения и в точке С. Тогда
можно найти значения искомых параметров потока в точке С с помощью
формул G.59):
a=(x-l)(V + Z)/4, u = (Y-Z)/4. G.71)
Пользуясь этим правилом, по начальным условиям можно найти
значения параметров потока в каждый момент времени в серии точек,
которые приняты контрольными. Таким путем мо^но решать задачи об
отражении и интерференции волн. Однако на этой основе может быть построен
и несколько видоизмененный метод расчета, который более удобен для
программирования .и применения ЭВМ. Такой способ будет изложен в гл. 12,
посвященной численным методам. Однако, прежде чем применять данный
метод, необходимо более подробно рассмотреть особенности
распространения ударных волн и задачу о распаде разрыва,'что и сделано в последних
двух разделах этой главы.
7.3. УДАРНЫЕ ВОЛНЫ
В разд. 7.2 показано, что крутизна фронта волн сжатия
увеличивается и в потоке возникают ударные волны.
Ударная волна возникнет также, если поршень внезапно начнет двигаться
с постоянной скоростью unt сжимая газ в трубе. На рис. 7.7 прямая О А
изображает путь поршня х — unt, а прямая
ОВ — путь ударной волны х = ct. Газ
за ударной волной движется в ту же
сторону, что и волна. В данном примере газ
перед ударной волной неподвижен, что
следует рассматривать как частный
случай. Газ за ударной волной сжат:
давление, плотность и температура его выше,
чем перед волной.
Будем, как обычно, обозначать и —
скорость потока относительно
неподвижного наблюдателя. Обозначим с —
скорость ударной волны относительно того
же наблюдателя. Индексом 1 обозначим
параметры газа перед, а индексом 2 —
Рис. 7.7. Образование ударной волны за ударной волной.
168

Запишем уравнения сохранения, используя скорости газа, измеренные
относительно бегущего фронта ударной волны, т. е. те скорости, с которой
поток пересекает фронт.
Уравнение неразрывности
Pi(«i—с) =Р2(«2—с), G.72)
уравнение сохранения количества движения
^J, % G.73)
уравнение сохранения энергии
• (th—W2+aV(* — l) = (u*—W2+al/(x — l). G.74)
Эти уравнения совпадут с уравнениями для прямого скачка уплотнений,
если рассматривать (иг — с) как скорость перед, а (и2 — с) — за скачком,
т. е. принять теперь, что наблюдатель движется со скоростью ударной волны.
Скачок можно рассма*ривать как стационарную ударную волну. В
таком случае очевидно, что те формулы для скачка уплотнения, в которые не
входят скорости, останутся справедливыми и для ударной волны. Те же
формулы, в которые входят скорости, должны быть записаны с учетом движения
ударной волны относительно движущегося потока.
При исследовании ударных волн в качестве аргумента удобно выбрать
степень повышения давления p2lpi или относительный прирост давления
(р2 — Pi)/pi> Эти характерные параметры позволяют наглядно оценивать
интенсивность волн и в некоторых практически важных случаях получать
приближенные зависимости.
Уравнение сжатия газа в ударной волне описано ударной адиабатой
F.27), которую запишем в таком виде;
Р2 =
Аналогично может быть записана формула для степени повышения
температуры
Т Р (*+!) +(и l)P/P ПШ
Тх Pi <х-
Скорость распространения ударной волны относительно неподвижного
газа равна скорости потока перед прямым скачком уплотнения с той же
степенью повышения давления. В таком случае эту скорость можно найти
по формуле F.23) при Р = л/2, причем под Мх следует понимать
отношение скорости ударной волны к скорости звука в газе перед волной.
Разрешим формулу F.23) относительно Мх и получим
Тогда скорость ударной волны относительно газа
При p2lpi = 1 скорость бесконечно слабой волны равна скорости
распространения звука. Скорость ударной волны конечной интенсивности тем
больше, чем больше ее интенсивности, и всегда больше скорости звука.
Для рарчета ударных волн удобно вычислить разность скоростей потока
до и после волны, так как разность скоростей не зависит от относительного
движения принятой системы координат.
169

Применив формулу F.21) для прямого скачка, имеем uL — и2 == мх —
— аЦиг = Ui (I — 1/М). Заменим безразмерную скорость А,х через число Мг
по формуле D.35) и запишем предыдущее выражение в виде
Здесь по-прежнему число Mi определяет скорость движения ударной волны,
представленную формулой G.77).
Поэтому разность скоростей потока до и после ударной волны можно
выразить через отношение давлений
)[+1>-^]-1" G.79)
В предельном случае очень слабой ударной волны она вырождается в
элементарную волну сжатия. Для этого частного случая, обозначив рх =р,
Рг — Р + ^Р» щ — и2 = du, из формулы G.79) получим соотношение
G.3), справедливое для акустических волн.
Процесс сжатия газа в ударных волнах происходит с ростом энтропии.
В ряде технических задач ударные волны имеют умеренную интенсивность
и поэтому практический интерес представляет оценка отклонения
процесса сжатия от изоэнтропийного.
Интенсивность скачка или ударной волны целесообразно
характеризовать безразмерной величиной
G.80)
С учетом этого обозначения выпишем уравнение ударной адиабаты
G.75) в виде
р2 _ 2х+(х+1)г ,78j,
Pl 2х+(х-1)г '
Для волн умеренной интенсивности (г < 1) можно воспользоваться
разложением по степеням г:
Рх х 2х2 4х3
Для изрэнтропийного сжатия соответствующее отношение плотностей
равно
Pi I Pi / 'x 2x* ^
G.83)
Из сравнения рядов G.82), G.83) следует, что отношения плотностей
при сжатии газа в ударной волне отличаются от изоэнтропийного сжатия,
начиная только с третьей степени малого параметра.
Изменение энтропии при сжатии газа в ударной волне умеренной
интенсивности по формуле F.28) также равно величине третьего порядка малости:
<7-84>
Эти оценки позволяют предположить, что инварианты Римана G.59),
которые строго постоянны для изоэнтропийных волн конечной
интенсивности, црактически будут мало изменяться также при сжатии газа в ударных
волнах умеренной интенсивности.
170

Относительное изменение
инвариантов G.59) при сжатии газа в ударной
волне можно записать таким образом:
А
AZ _ 2 / а2 Л
ах х— I \ ах )
ах
G.86) ¦
Рис. 7.8. Изменение инвариантов
Рима на в скачке уплотнения
Искомые величины AY/aXt AZIax при
сжатии газа в ударной волне зависят
только от p2/Pi, так как а2/ах — VT2lfx>
и, следовательно, определено формулой
G.76), а (и2 — Ui)lax определено
формулой G.79). Поэтому AY/ax можно
рассматривать как функцию только АЦау
или, наоборот, &Zlax только как
функцию AYIav Уравнения G.85), G.86) ,
можно рассматривать как заданные в параметрической форме, причем в
качестве параметра выступает отношение давлений p^Pv Соответствующая
зависимость изображена на рис. 7.8. Смысл состоит в том, что при
значительном изменении величины AY/at величина AZ/ax практически не
изменяется, и, наоборот, при значительном изменении AZIax величина AYIcii
почти постоянна.
Отсюда следует практический вывод, что скачки умеренной
интенсивности можно рассчитывать по формулам для волн сжатия. Можно
рассматривать К-скачки и Z-скачки, причем при сжатии газа в них один или другой
инвариант G.59) остается практически постоянным.
7.4. РАСПАД РАЗРЫВА. ЗАДАЧА Н. ?. КОЧИНА
Пусть в начальный момент времени по некоторой плоскости
соприкасаются две массы газа с произвольно заданными параметрами:
давлением, температурой и скоростью. Поверхность соприкосновения является
поверхностью разрыва, т. е. при переходе через нее параметры изменяются
скачком. Начальные значения величин разрывов параметров могут быть
произвольны, т. е. между ними не существует каких-либо соотношений.
Однако такое состояние может существовать только в первое
мгновение, так как дальнейшее движение всей системы описывается уравнениями
сохранения. Начальный разрыв распадается на устойчивые образования,
которые могут существовать в газе: ударные волны, волны разрежения и так
называемые слабые разрывы.
Общее исследование этой задачи было дано Н. Е. Кочиным A926 г.). В
настоящее время эта задача широко применяется в численной аэродинамике,
в том числе при решении широкого круга инженерных проблем.
Рассмотрим сначала общее физическое описание возможных случаев
распада произвольного разрыва, а затем подробнее остановимся на расчете
тех задач, которые имеют практическое применение в инженерных расчетах
и будут использованы в гл. 12.
Пусть в начальный момент времени плоскость разрыва
перпендикулярна оси х и проходит через начало координат. В следующие моменты времени
течение является одномерным и неустановившимся, т. е, зависит от одной
координаты и времени»
17!

и,
б) г)
Рис. 7.9. Различные варианты распада разрыва •
Состояние газа можно определить тремя переменными:
давлением р, температурой Т и скоростью и. Пусть в начальный
момент времени слева от плоскости разрыва (х < 0) эти переменные
обозначены индексом 1, а справа (х >0) — индексом 2.
При распаде заданного произвольного разрыва влево и вправо от него
начнут распространяться возмущения: ударные волны или волны
разрежения, причем в каждую сторону может двигаться только одна из волн. Позади
каждой из этих волн, т. е. вблизи начала координат, статическое давление
в газе должно выравниться и он должен иметь общую скорость. Этим и
должны быть определены знаки и интенсивность тех волн, которые побегут
влево и вправо от первоначального произвольного разрыва.
Массы газа, прошедшие разбегающиеся влево и вправо волны, в месте
соприкосновения, как уже отмечено, должны иметь одинаковые статические
давления и скорости. Однако температуры этих масс газа, а следовательно,
их плотности и энтропии могут быть различны. Такой разрыв плотностей
(температур и энтропии) называют слабым. Наличие такого слабого
разрыва естественно не нарушает физических требований к граничным условиям,
в месте соприкосновения двух масс газа.
Возможность появления такого слабого разрыва объяснима и из
математических соображений. Ударная волна и волна разрежения, которые
распространяются по газу с заданными параметрами, зависят только от одной
* переменной (например, отношения давлений.) Следовательно, для двух
разбегающихся волн имеются две свободные переменные, которыми можно
распорядиться. Однако состояние газа за этими волнами определено тремя
переменными: давлением, скоростью и плотностью. Потребовав для
двух масс газа выравнивания давлений и скоростей, нельзя уравнять
плотности.
Рассмотрим теперь возможные случаи распада произвольного разрыва.
В том случае, если сталкиваются две массы тела, движущиеся с
противоположными скоростями, то возникают две разбегающиеся ударные волны.
На рис. 7.9, а сплошными линиями показано распределение давления, а
штриховой линией — положение слабого разрыва. Стрелками с буквами и
обозначены скорости газа, а стрелками с буквами с — скорости волн.
Области 3 и 3' образовались после распада первоначального разрыва.
На рис. 7.9, б изображен случай, когда первоначально соприкасались
две неподвижные (или движущиеся в одну сторону с одинаковыми
скоростями) массы газа, сжатые до разных давлений. В таком примере в одну
сторону побежит ударная волна (на рис. 7.9, б налево), а в другую — ролна
172

у ^ J У1
разрежения. Границы волны разрежения отмечены пунктирными линиями,
а штриховая линия по-прежнему обозначает слабый разрыв.
На рис. 7.9, в изображен случай, когда в обе стороны распространяются
волны разрежения. Такой вариант возникнет, если в начальный момент
времени соприкасающиеся массы газа имели скорости, направленные в
противоположные стороны, и разлетались.
Если же скорость разлета выше определенного предела (см. подразд.7.1),
то в зоне 3 будет достигнут абсолютный вакуум (рис. 7.9, г), а в обе стороны
побегут волны разрежения.
Все эти случаи могут быть рассчитаны с помощью формул, полученных
для волн разрежения и ударных волн в подразд. 7.3 и 7.4.
Скачки уплотнения можно рассчитывать по точным формулам G.75),
G.76), G.79) или, как показано для скачков умеренной интенсивности, с
помощью инвариантов G.59).
Наконец, можно воспользоваться разложениями по параметру г
G.87)
G#88)
G-89)
и производить расчеты с точностью до второй или первой степени малого
параметра. Формула G.90) дает приближенную зависимость скорости
распространения скачка относительно неподвижного газа.
Задачу о распаде произвольного разрыва можно обобщить на случай,
который представляет практический интерес.
Рассмотрим разрыв в начальных данных, расположенный в месте скачка
площади трубы. Можно, как и прежде, предполагать, что в начальный
момент времени произвольно заданы параметры газа и скорости по обе
стороны от'разрыва. Так как ударные волны или волны разрежения будут
распространяться в обе стороны от первоначального разрыва, то они будут
двигаться по трубам постоянной площади поперечного сечения, т. е. течение
по-прежнему будет одномерным. Различие от прежней задачи заключается
в согласовании параметров в месте скачка площади.
Если считать, что сказки площади введены искусственно, т. е.
приближенно заменяют плавное изменение площади трубы, то следует принять,
что течение через скачок площади является изоэнтропийным. Тогда
течения по обе стороны от скачка площади должны быть согласованы с
помощью уравнений неразрывности и Бернулли.
Вопросы для самопроверки
1. Какими свойствами обладают инварианты Римана?
2. Запишите инварианты Римана для акустического уравнения.
3. Выведите акустическое уравнение для потока, движущегося с постоянной
скоростью.
4. Какие характеристики должны иметь тракты пневмометрических систем для
измерения: а) пульсирующего давления; б) среднего давления в пульсирующем
потоке?
5. В каком случае при распаде разрыва возникает контактный разрыв?
173

ГЛАВА 8
ЛАМИНАРНОЕ ТЕЧЕНИЕ ВЯЗКОЙ ЖИДКОСТИ
8.1. УРАВНЕНИЕ НАВЬЕ-СТОКСА. ЛАМИНАРНОЕ ТЕЧЕНИЕ
В предыдущих главах рассмотрено движение идеальных
жидкостей, т. е. жидкостей невязких. Все реальные жидкости обладают
определенной вязкостью, которая приводит к появлению внутреннего трения при
деформации частиц жидкости.
В твердых телах деформация (если она относительно мала) обычно
прямо пропорциональна приложенному напряжению, что выражено законом
Гука. При деформации жидкостей дело обстоит несколько иначе. В этом
случае при ламинарном (слоистом) течении касательные напряжения
пропорциональны скорости деформации частицы.
Если жидкость движется параллельными слоями вдоль оси х, т. е.
наблюдается деформация чистого сдвига, то касательные напряжения между
слоями могут быть описаны законом трения Ньютона:
(8.1)
где т — касательное напряжение, т. е. сила трения, отнесенная к единице
площади; duldy — градиент скорости в поперечном направлении.
Коэффициент динамической вязкости \i является физической характеристикой
жидкости, зависит от температуры и в меньшей степени от давления.
Закон трения Ньютона записан для движения простейшего вида и,
следовательно, простейшего вида деформации частиц жидкости. В общем
случае, при рассмотрении произвольного движения жидкости, необходимо
обобщение закона трения. Если продолжать аналогию с теорией упругости, то
такое обобщение соответствует переходу от закона Гука для простого
растяжения к обобщенному закону Гука при сложном напряженном
состоянии.
Обобщение закона трения Ньютона было выполнено Стоксом A845 г.),
причем в предположении, что напряжения пропорциональны
соответствующим скоростям деформации. Скорости деформации и напряжения можно
выразить, как показано в гл. 1, соответствующими тензорами.
Напомним, что тензор напряжений можно записать следующим
образом A.13): Ofj = — pbu + o'jj.
Первый член справа не зависит от вязкости и представляет нормальные
напряжения от давления. Второй член справа представляет дополнительные
напряжения, вызванные вязкостью жидкости.
Тензор скоростей деформаций можно записать следующим образом
A.18):
1 / duf . ди
Согласно закону трения Ньютона в его простейшей записи (8.1)
напряжения, вызванные вязкостью жидкости, пропорциональны скорости
деформации сдвига, При рассмотрении произвольного пространственного дви-
174

жения вязкой жидкости также полагают, что напряжения, вызванные
вязкостью, пропорциональны соответствующим скоростям деформации
^тензор вязких напряжений пропорционален тензору скоростей
деформаций):
(??) (8.2,
Множитель 2 в этой формуле позволяет сохранить коэффициент
пропорциональности и в частном случае формулы Ньютона (8.1).
Физические соображения, которые положены в основу формулировки
закона трения, заключаются в том, что внутреннее трение должно проявляться
в жидкости только при взаимном перемещении ее частиц. Следовательно,
напряжения должны зависеть от скоростей деформации. Если скорости
деформации не очень велики, то можно предположить (и это косвенно
подтверждено опытом), что напряжения пропорциональны первым степеням
скоростей деформации. Если жидкость движется поступательно или вращается
как твердое тело, то скорость деформации равна нулю и трение также
должно быть равно нулю. Этому условию удовлетворяет сумма производных в
формуле (8.2).
Если жидкость сжимается, то возможно объемное расширение, причем
скорость объемной деформации в точке, как это следует из разд. 2.1, равна
dujdxi. Поэтому для сжимаемой жидкости следует предположить такую
зависимость напряжений от деформации:
дщ
где \i' — скалярный коэффициент пропорциональности; 6^ — символ,
введенный в разд. 1.4 F^- = 1 при i = /, 6О- = 0 при i = /).
Эту зависимость принято записывать в несколько ином виде (закон
трения Стокса):
duJ i dui 2 А ди* \ I .." X duh /о о\
3 dxh I
dxk
где |ii"—скалярная величина, которую называют вторым коэффициентом
вязкости. Смысл записи в такой форме состоит в том, что при
t=/выражение в скобках равно нулю как для сжимаемой, так и для несжимаемой
жидкости, в чем легко убедиться, пользуясь правилами суммирования по
индексам, которые изложены в разд. 1.2. В таком случае при i = j из
зависимости (8.3) имеем
Для несжимаемой жидкости выражение в скобках равно нулю на основании
уравнения неразрывности B.9). Следовательно, последний член в
выражении (8.3) не равен нулю только в сжимаемой жидкости, если не равна нулю
скорость объемного расширения. Поэтому \к" называют коэффициентом
объемной вязкости или вторым коэффициентом вязкости. Далее будем
полагать \i" = 0, так как учет второй вязкости существенен при большой
скорости объемного расширения (например, в сильных ударных волнах).
Закон трения Стокса (8.3) представляет обобщение закона трения
Ньютона. Вязкие жидкости, трение в которых может быть описано этим законом,
называют ньютоновскими жидкостями. К ньютоновским жидкостям
принадлежат такие технически важные жидкости, как вода, масло, воздух и т. д.
Однако встречаются жидкости, например, в биологии, химическом
производстве, которые не подчиняются этому закону,
175

Подставив выражение для вязких напряжений (8.3) в уравнение
движения B.18), получим уравнение движения сжимаемой вязкой жидкости в
форме Навье — Стокса:
+ Bl/;+ +
dt dxi р dXj р dxt I \ dxi dx
Для несжимаемой жидкости последний член в круглых скобках равен
нулю и уравнение Навье — Стокса принимает вид
dt dxt u p dxj p \ dxidxt dxtdxj
Здесь коэффициент динамической вязкости вынесен за знак
дифференцирования, что допустимо при малом изменении температуры жидкости в
процессе движения.
В уравнении (8.5) второй член в скобках равен нулю на основании
уравнения неразрывности для несжимаемой жидкости B.9):
д2 щ _ д / дщ \ q
дхг dxj dxj \ dxi )
Тогда окончательно уравнение Навье — Стокса для несжимаемой жидкости
можно записать в виде
dt ^ l dxt n p dxj dxidxt V ;
Здесь введено обозначение для так называемого кинематического
коэффициента вязкости v = (л/р.
В основе вывода уравнения Навье — Стокса лежит предположение о
законе трения, которое может быть проведено только экспериментально.
Имеющиеся немногие частные решения уравнения Навье — Стокса (например,
ламинарное или слоистое течение в трубе) подтверждены экспериментами.
Запишем уравнение (8;6) для установившегося течения и при отсутствии
массовой силы
1ц+v
dxi p dxj dxi дхг
Рассмотрим обтекание какого-нибудь тела потоком вязкой жидкости,
имеющим в бесконечности скорость и^. Пусть некоторый характерный
размер тела (например, его длина) равен L. Введем безразмерные скорость,
длину и давление:
щ = щ/и„9 Xt^XilL, P=2p/pul.
Тогда предыдущее уравнение можно записать через безразмерные величины
(см. гл. 3):
щ +(8.7)
dxj 2 dxj L"oo dxtdxi
Следовательно, в уравнение Навье-Стокса для несжимаемой
жидкости входит только один безразмерный коэффициент, который зависит от
условий конкретной задачи (все члены уравнения также безразмерны), —
число Рейнольдса Re = u^L/v.
Если рассмотреть обтекание двух геометрически подобных тел
потоками, которые имеют различные скорости в бесконечности и разные вязкости,
176

Рис. 8.1.
течение
канале
Ламинарное
в плоском
но такие, что числа Re для них одинаковы, то и
решения уравнения (8.7) будут одинаковы.
Такие течения называют подобными. По
характеристикам одного течения (найденным теоретически
или экспериментально) можно получить
характеристики другого течения простым пересчетом
масштабов.
Если рассмотреть обтекание фиксированного
тела безграничным потоком вязкой несжимаемой
жидкости, то безразмерные характеристики, например
безразмерная сила сопротивления, должны зависеть
только от величины Re.
Из уравнения (8.7) следует, что Re можно
трактовать как величину, характеризующую отношение сил инерции (первый член
этого уравнения) к силам вязкости (последний член уравнения).
Следовательно^ для течений, в крторых преобладают силы вязкости,
число Re должно быть малым. Если же число Re велико, то велико и
влияние сил инерции.
Отметим, что формально уравнение Навье — Стокса (8.7) пригодно для
расчета течений вязкой жидкости при любых значениях числа Re. Однако,
как будет объяснено в гл. 9, фактически ламинарное течение при
достаточно больших числах Re становится неустойчивым и переходит в турбулентное.
Запишем уравнения (8.6) для плоского установившегося движения при
отсутствии массовых сил. В этом случае удобно положить:
дх
ду
р дх
дх*
—
ду*
V
дх*
(8.8)
(8.9)
дх ду р ду
Для решения задач уравнения (8.8), (8.9) следует дополнить уравне
нием неразрывности
дх ду
Решим сначала простые задачи.
(8.10)
1. Течение в плоском канале. Рассмотрим течение несжимаемой вязкой
жидкости в канале с двумя безграничными параллельными плоскими стенками (рис. 8.1).
Из условий задачи следует заключить, что ди/дх = 0, v = 0. Тогда из уравнения
(8.9) получим др/ду = 0. Уравнение (8.8) упрощается и в нем можно записать полные
производные
dx
d2u
dy2
(8.11)
Опыт показывает, что вязкая жидкость как бы прилипает к твердым стенкам, т. е.
скорость жидкости на стенках равна нулю. Следовательно, уравнение (8.11) необходимо
решить при граничных условиях:
и = 0 при у— ± А.
Тогда получим
U=z
2ц dx
(S.12)
177

Распределение скоростей в любом поперечном сечении канала описано
квадратичной параболой. Поскольку давление не зависит от у, то dpldx постоянно вдоль канала.
В формуле (8.12) справа стоит знак минус, так как из-за силы сопротивления трения на
стенках давление вдоль канала уменьшается.
2. Ламинарное течение в круглой трубе. Для решения удобно выписать
уравнения Навье — Стокса в цилиндрической системе координат. Проще, однако, получить
решение непосредственно с помощью закона трения Ньютона (8.1), воспользовавшись
тем, что течение в трубе слоистое. Выделим в жидкости цилиндр длиной / и радиусом у
с осью, совпадающей с осью трубы. Из условия равновесия следует
Щ2 (Р1—Р2) + 2nyl\idu/dy = 0. (8.13)
Первый член в уравнении (8.13) равен силе давления, действующей на торцовые
поверхности выделенного цилиндра. Второй член равен силе трения по боковым
поверхностям цилиндра. Величина (рг — /?2) равна падению давления на длине /.
Проинтегрировав уравнение (8.13) с условием, что скорость на стенках трубы (у = г) равна
нулю, имеем
/
u
4ц /
Следовательно, распределение скоростей в поперечном сечении трубы также
параболическое.
Вычислим среднюю по сечению трубы скорость
- i j^jif ^j^ (814)
4ц / яг2 J 8м- /
о
В расчетах принято вводить безразмерный коэффициент сопротивления ?,
характеризующий падение давления на единицу длины трубы в долях от кинетической
энергии, подсчитанной по средней скорости (такая структура формулы следует из
соображений теории подобия):
Из выражений (8.14), (8.15) следует Запись для коэффициента сопротивления
I = 64 \ifpud.
В результате получим, как это и должно следовать из теории подобия, что
коэффициент сопротивления зависит только от числа Рейнольдса:
g==64/Re,.Re = «d/v. (8.16)
Эта формула, называемая законом Хагена — Пуазейля, хорошо подтверждена
экспериментальными данными до Re < 2300. При больших числах Re ламинарное течение
теряет устойчивость и переходит в турбулентное, и закон трения становится иным.
8.2. ГИДРОДИНАМИЧЕСКАЯ ТЕОРИЯ СМАЗКИ
Уравнения Навье — Стокса (8.8), (8.9) содержат члены,
учитывающие как силы инерции (первые два члена уравнений), так и силы
вязкости (последние члены). При очень медленном движении или при течении
очень вязких жидкостей силы вязкости могут быть много больше, чем силы
инерции. Поскольку отношение силы инерции к силам вязкости
характеризуется числом Re, то течения с преобладающей ролью вязкости
соответствуют очень малым числам Re. Если можно пренебречь инерционными
силами, то уравнения (8.8), (8.9) примут вид
—?_ =и, / . (о. 17)
дх* ду* ) ду г\ дх* ду2 )
Эти уравнения могут описывать движение тонкой вязкой пленки в
подшипниках скольжения, движения мелких частиц в суспензии, осаждение
капелек тумана и т.п,
178
др ( д2и
дх 1 \ дх*

Рис. 8.2. Схема течения «_
в упорном подшипнике ^
скольжения
Первые работы по гидродинамической теории смазки были опубликованы
Н. П. Петровым A883 г.) и О. Рейнольдсом A886 г.).
Рассмотрим течение вязкой пленки в упорном подшипнике скольжения.
Тонкий слой масла находится между неподвижной колодкой,
установленной под малым углом а, и движущейся со скоростью и0 опорной
поверхностью (рис. 8.2).
Порядок отношения сил инерции Ft к силам трения Ff в данной задаче
можно оценить, заменив соответствующие производные отношением
конечных величин:
Fi риди/дх apul/h __ apuoh
Ff [id2u/dy2 цщ/h2 ц
В реальных условиях масляная пленка очень тонка h <? /, а угол
наклона колодки к опорной поверхности мал а < 1. Если apujx/\i < 1, то
силами инерции можно пренебречь. В этом случае возможно дальнейшее
упрощение уравнений. Поскольку v<^uOt то второе уравнение (8.17) можно
отбросить, приняв др/ду=0, т. е. считать, что давление меняется только вдоль
оси абсцисс. Граничные условия следуют из того, что вязкая жидкость
прилипает к поверхности, т. е. скорость жидкости равна нулю на колодке и
равна и0 на опорной поверхности. Отсюда при условии h <^ l можно заключить,
что д2и/дх2 < д2и/ду2, т. е. скорость значительно интенсивнее изменяется
поперек слоя, нежели вдоль течения. После этих упрощений получим
уравнение движения (8.17) в виде
dx
ду*
К этому уравнению (8.18) нужно добавить уравнение неразрывности,
которое следует из условия, что количество жидкости, протекающее через любое
поперечное сечение пленки, постоянно:
h(x) .
Q =: J Udy^ const. (8.19)
о
Уравнения (8.18), (8.19) должны быть решены при заданных граничных
условиях для скорости:
при у = 0 и = а0, при у = h и = 0 (8.20)
и давления:
при х = 0 /? = /?а, при х = I р = ра> (8.21)
где /г = Л (х) — толщина масляного слоя; ра — давление в окружающем
пространстве.
179

Проинтегрировав уравнение (8.18) по у, получим
Определив постоянные с помощью граничных условий (8.20) для
скорости, найдем
u = -±-W-hy)-?- + -!?-(h-y). (8.22)
2ft dx h
Подставим полученное выражение в уравнение неразрывности (8.19) и
проинтегрируем поперек масляного слоя:
q_ uoh hz dp
2 12ц dx '
Для того чтобы найти распределение давления вдоль оси абсцисс, выразим
dp ^ 12ц / uoh
dx Л3 I 2
и проинтегрируем полученное выражение по х:
) <8-23)
где с3 — постоянная интегрирования.
Для вычисления интегралов нужно выразить h = h (x) или, что удобнее,
х = х (h). Ввиду малости угла а можно записать (hx — толщина слоя при
* = 0)
А= Л1—ах, dx = — dh/a. (8.24)
Заменим в интегралах (8.23) переменную интегрирования х на Л,
воспользовавшись выражениями (8.24):
После вычисления интегралов имеем
В это уравнение входят две постоянные Q и с3, которые находим с помощью
граничных условий для давления (8.21), причем х = 0 соответствует
h = hl9 а х = / соответствует h = /ц.
После подстановки граничных условий (8.21) в формулу (8.25)
Определив постоянные и подставив их снова в формулу (8.25), получим
окончательную формулу для распределения давления в слое смазочного
материала
180
V,yir^ (8-26)
а № (Л+Л)

При h2 < ft< hx второй член формулы (8.26)
положителен и, следовательно, давление под колодкой
больше, чем давление ра по ее краям. Распределения
давления и скорости в слое смазочного материала
показаны на рис. 8.2. Максимальное давление
находится из условия dpldh = 0:
i 3 * h\—h<*
Рт=Ра+—\Шо1 ,' *
2 h1
вание масляного
В этом выражении угол наклона колодки заменен с по- клина в опорном
мощью формулы, которая ясна из геометрических сооб- п°дшипнике
ражений (см. рис. 8.2): а = (hx — h2)/L
Максимальное (и, следовательно, среднее) давление при достаточно
тонком смазочном слое может быть очень большим. В то же время трение
определено жидкостным трением и поэтому очень мало.
С помощью приведенных формул можно определить полную нормальную
силу, действующую на опорную поверхность:
К h1+hi Г
о
и полную касательную силу, приложенную к опорной поверхности:
)
Отношение касательной силы к нормальной по аналогии с трением
твердых поверхностей можно условно назвать «коэффициентом трения». Легко
видеть, что этот коэффициент не зависит от вязкости жидкости и
теоретически может быть сделан сколь угодно малым, что объясняется эффектом
клина. v '
Из рис. 8.2 следует, что колодка может поворачиваться вокруг шарнира
А. Угол при вершине клина а саморегулируется и зависит от величины
упорной силы. Поэтому величину а следует найти из условий равновесия
колодки.
В опорных подшипниках (рис. 8.3) наблюдается примерно такая же
картина течения в масляной пленке,/как в упорных. Эксцентрично
расположенный вал вращается в подшипнике и увлекает масло в образующийся
клиновидный зазор, в котором возникает высокое давление. Вал не может
располагаться в подшипнике концентрично, так как в этрм случае ввиду
симметрии течения в пленке не возникнет поддерживающей силы,
уравновешивающей вес ротора.
Первое точное решение задачи гидродинамической теорий смазки для
опорного подшипника было дано Н. Е. Жуковским и С. А. Чаплыгиным
A904 г.).
При расчете реальных подшипников конечной длины учитывают
вытекание масла из зазора по торцам, а также изменение вязкости масла при его
нагревании в слое.
181

8.3. ОСНОВНЫЕ СВОЙСТВА ПОГРАНИЧНОГО СЛОЯ.
ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ПОГРАНИЧНОГО СЛОЯ
ПРАНДТЛЯ
В большинстве технических задач приходится иметь дело с мало-
вязкимй жидкостями, движущимися с относительно большими скоростями.
Рассмотрим особенности такого течения на примере обтекания тела вязкой
жидкостью при большом числе Re.
Опыт показывает, что жидкость, обладающая вязкостью, прилипает к
поверхности тела, т. е. скорость жидкости на поверхности неподвижного тела
равна нулю. \
Если бы жидкость не обладала вязкостью (идеальная жидкость), то
поток скользил бы по поверхности тела. Отсюда следует, что сколь бы ни мала
была вязкость жидкости, она будет оказывать существенное влияние^на
течение непосредственно возле поверхности. Если число Re велико, то на
некотором отдалении от поверхности силы инерции во много раз превосходят
силы вязкости и жидкость течет практически как идеальная, т. е.
лишенная вязкости. v
Следовательно, можно ожидать, что при достаточно большом числе Re
влияние трения будет ощущаться только в тонком слое возле поверхности
тела. Этот слой получил название пограничного слоя II (рис. 8.4). В
поперечных сечениях пограничного слоя (см. А на рис. 8.4) скорость возрастает
от нуля (на поверхности) до скорости внешнего потока. Ввиду малой
толщины слоя поперечный градиент скорости очень велик. Подторможенные в
пограничном слое частицы жидкости сбегают с обтекаемого тела и образуют
вихревой след III, который сносится потоком вниз по течению. Поперечный
градиент скорости в вихревом следе вначале также велик и, следовательно,
там существенно влияние трения. В области,/ вне пограничного слоя и
вихревого следа влиянием вязкости можно пренебречь и рассматривать
потенциальное течение.
Таким образом, задачу обтекания тела вязкой жидкостью при большом
числе Re можно разделить на три значительно более простые задачи:
1) задачу обтекания заданного тела потенциальным потоком (пользуясь
тем, что пограничный слой очень тонок); 2) задачу о движении вязкой
жидкости в тонком пограничном слое; 3) задачу о движении в вихревом следе (в
почти параллельном потоке за телом).
Следует подчеркнуть, что гипотеза о пограничном слое не только дает
возможность упростить решение уравнений Навье — Стокса, но и
позволяет подойти к решению задачи о течении вязкой жидкости в слое другими
методами.
Рассмотрим упрощение уравнений Навье-Стокса и некоторые оценки,
относящиеся к пограничному слою. То, что влияние вязкости сказывается
А
Рис. 8.4. Схема
обтекания крылового профиля
потоком вязкой
жидкости при большом числе
Re
182

лишь вблизи обтекаемой поверхности, было отмечено еще Д. И. Менделеевым
A880 г.). Математический анализ задачи и вывод уравнения пограничного
слоя принадлежит Л. Прандтлю A904 г.).
Обозначим / длину обтекаемого тела, а б <^ / — толщину пограничного
слоя. Считаем также, что толщина пограничного слоя много меньше радиуса
кривизны поверхности обтекаемого тела, б <? R. Координату х отсчитываем
вдоль поверхности тела, а у — по нормали к ней.
Поперек пограничного слоя скорость изменяется от нулевого значения
на поверхности до скорости внешнего потока и0 на малом расстоянии 6.
Изменение скоростей вдоль потока, т. е. по координате лг, происходит
значительно медленнее. Тогда можно считать, что в пограничном слое
справедливы оценки:
дх I /
Производные оцениваем по порядку изменения соответствующих величин
на заданной характерной длине. Поэтому в уравнении (8.8) можно
отбросить первый член в скобках, что приведет к уравнению Л. Прандтля для
ламинарного пограничного слоя:
(8.27)
ди
ду
. «о
б '
д*и
дх*
. «0 //
/2 ХХ
д*и
ду*
дх ду р дх ду*
По определению, внешней границей слоя считаем ту границу, на которой
можно пренебречь силами трения. На внутренней границе слоя, т. е. на
поверхности тела, наоборот, равны нулю силы инерции (так как и = 0, v —0).
Следовательно, внутри пограничного слоя силы трения должны быть одного
порядка с силами инерции.
Учитывая, что продольная скорость в пограничном слое имеет порядок
скорости внешнего потока и ~ и0, получим оценки порядков первого и
последнего членов уравнения (8.27):
дх I I ду* ду \ду ] 6* v '
Здесь производные оцениваются по порядку изменения скорости на
заданной длине. Поскольку порядки оцененных членов должны быть одинаковы,
то отсюда следует оценка относительной толщины ламинарного
пограничного слоя:
L J /1Е! Re==Jfo_L. (829)
ио1
Следовательно, как и предполагалось, относительная толщина
пограничного слоя может быть очень мала при достаточно большом числе Re.
Поскольку уравнение (8.27) на внешней границе должно переходить в
уравнение, описывающее движение идеальной жидкости, т. е. уравнение
Эйлера E.6), то все эти члены должны быть оставлены и в уравнении
пограничного слоя (8.27). Отсюда следует, что второй член в уравнении (8.27)
должен иметь тот же порядок, что и первый. Тогда с помощью условия
(8.28) получим
u9 T.e. *. (8.30)
ду дх I I
183

Следовательно, скорость v в пограничном слое должна быть величиной
первого порядка малости по сравнению со скоростью на внешней границе
пограничного слоя и0. Эта оценка согласуется с оценкой по уравнению
неразрывности. В уравнении (8.10) оба члена должны иметь один порядок:
dv ди
ду дх I I
Оценивая порядки первых двух членов уравнения (8.9) с помощью
условия (8.30), находим
dv Uq б Uq б
dv Uq б Uq б Uq б
V~dy~~l /б"~" /2 '
Убеждаемся, что они в пограничном слое имеют первый порядок малости.
В уравнении (8.9) можно пренебречь первым членом в скобках по
сравнению со вторым членом в скобках. Тогда остается оценить порядок члена
v&v/dy2. Оценка порядка вязкости жидкости следует из условия (8.29):
v ~ ао62//. Тогда порядок последнего члена в уравнении (8.9)
d2 V Uq б2 Ы0 б Ы2, б
ду2 I /б2 /2 '
Так как третий член уравнения (8.9) не может иметь порядок больше,
чем все остальные члены, то
1 др и%6
р ду /2
Проинтегрировав это выражение по у от 0 до 6, найдем, что можно
пренебречь изменением давления поперек пограничного слоя, так как эта
величина второго порядка малости:
Др/р^б2//2. (8.31)
Подытожив все оценки, приходим к выводам: 1) при большом числе Re
на поверхности тела образуется относительно тонкий пограничный слой
(8.29); 2) давление поперек слоя не меняется (8.31), и, следовательно, равно
давлению в соответствующей точке внешней границы; 3) течение в
пограничном слое описывается одним упрощенным уравнением (8.27), которое
должно быть решено совместно с уравнением неразрывности (8.10).
8.4. ПОДОБНЫЕ РЕШЕНИЯ ДЛЯ ЛАМИНАРНОГО
ПОГРАНИЧНОГО СЛОЯ
В общем случае аналитическое решение уравнения Прандтля
получить невозможно, поэтому приходится прибегать к приближенным
методам расчета пограничного слоя.
Прежде чем переходить к изложению приближенных метбдов,
рассмотрим одно частное, но важное решение. Анализ этого решения представляет
интерес по крайней мере по трем причинам.
1. Решение позволяет выяснить основные свойства пограничного слоя:
зависимость распределения скорости от распределения давления,
возможность отрыва слоя, изменение толщины слоя.
2. Решение может служить контрольным при сравнении тестовых задач,
решаемых на основе приближенных методов.
184

3. Метод, основанный на подобии решений, является очень важным в
механике жидкости, так как позволяет свести уравнения в частных
производных к обыкновенному дифференциальному уравнению, что
принципиально упрощает задачу.
Под подобными (или автомодельными) решениями понимаем такие
решения, в которых профили скорости в поперечных сечениях пограничного
слоя отличаются только масштабами. Другими словами, все профили
скорости будут совпадать, если их изобразить в безразмерных координатах.
Рассмотрим задачу обтекания плоской полубесконечной пластины
потоком вязкой несжимаемой жидкости со скоростью и0 = и0 (х). Для
внешнего потока несжимаемой жидкости можно пренебречь влиянием трения и
применить уравнение Бернулли, из которого следует
1 dp __ du0
щ -—•— .
р dx dx
Тогда уравнение Прандтля (8.27) примет вид
MT!yTM»f
дх ду dx
Это уравнение необходимо решить совместно с уравнением неразрывности
JJL+-?-=<>. (8.33)
дх ду v '
Введем функцию тока
ду дх
которая удовлетворит уравнение неразрывности и, следовательно, приведет
систему уравнения (8.32), (8.33) к одному уравнению
Juo_ ?± 834)
dx ду9 v '
ду дхду дх ду2 dx ду9
Это нелинейное дифференциальное уравнение в частных производных
третьего порядка. Его необходимо решить при следующих граничных условиях:
л|>= 0 при # = О, — оо < х < оо.
= 0 при у = 0, 0 < х < оо; (8.35)
при #-*оо, —оо^дс<оо.
Первое из этих условий отвечает требованию, что набегающий поток
параллелен пластине, которая расположена вдоль положительной оси
абсцисс. Второе условие обеспечивает прилипание вязкой жидкости на
поверхности пластины. Третье условие подчиняет решение требованию, что
бесконечно далеко от пластины поток является плоскопараллельным и
потенциальным. По поводу последнего граничного условия уместно сделать
следующее замечание. При выводе уравнения (8.27) показано, что при
большом числе Рейнольдса влияние вязкости существенно только в тонком
пограничном слое, прилегающем непосредственно к поверхности обтекаемого тела.
Справедливость этого утверждения будет дальше подтверждена при
приближенном решении этой задачи. Однако в действительности возмущения,
вызванные пластиной, ощущаются вплоть до бесконечности, где скорость
асимптотически стремится к скорости внешнего потока. Таким образом,
в данном случае рассматриваем точное решение задачи о ламинарном
пограничном слое.
185

Будем далее считать, что скорость внешнего потока задана степенной
зависимостью
ио(х)*=Кхт, (8.36)
где Ку т — некоторые постоянные.
Тогда из общего уравнения (8.34) получим уравнение для выбранного
частного случая:
ду дхду дх ду* ду\ V '
Для того чтобы просто найти вид решения, проведем так называемый
инспекционный анализ.
Перейдем в уравнении (8.37) к новым переменным согласно условию
= Ьхъ у=суи (8.38)
где а, Ьу с — некоторые безразмерные постоянные, которые можно
рассматривать как масштабные множители.
Тогда уравнение (8.37) примет вид
be* дУ1 дхгдУ1 Ъс* дхг х с3 ду\ ' V '
Первое и второе граничные условия (8.35) при введении новых масштабов
не изменяются. Третье граничное условие (8.35) при новых масштабах с
учетом формулы (8.36) примет вид
bKxf. (8.40)
с дух
Потребуем, чтобы полученное уравнение (8.39) совпало с исходным
(8.37) и граничное условие (8.40) не изменилось.
Поделив все члены уравнения (8.39) на б2-1, а левую и правую части
условия (8.40) на Ьт, получим, что указанное требование будет выполнено,
если
fJffl 1 ?*> ffffl Q
Отсюда следует, что при преобразовании (8.38) ни уравнение, ни
граничные условия не изменяются, если принять
2 \—т
г .Ш -4- 1 ~1 ~\~Я1 /О АЛ\
о = а , с~ а . (8*41)
В таком случае говорят, что задача инвариантна относительно принятого
преобразования.
Так как при переходе к новым масштабам и соблюдении условия (8.41)
ни уравнение, ни граничные условия не изменились, то не должно измениться
и решение. Следовательно, искомая функциональная зависимость ty =
^ Мх> У) должна иметь такой вид, чтобы при новых масштабах решение не
менялось. Этому требованию удовлетворяет функциональная
зависимость вида
гр/х 2 =F[yx 2 ) (8.42)
или вида (что не имеет принципиального значения)
l+m / 2
186

Таким образом, простыми рассуждениями установлен вид (8.42),
которое должно иметь решение уравнения (8.37). Самое главное состоит в том,
что вместо двух независимых переменных ху (/теперь можно рассматривать
т — 1
только одну переменную ух ^ * Это позволит свести уравнение в частных
производных к обыкновенному дифференциальному уравнению. Для
удобства приведем сначала предполагаемое решение к безразмерному виду.
Входящие в зависимость (8.42) и условие (8.36) величины имеют следующие
размерности:
h|>]^L2T-\ [x]=[y]=U [«0]=LT-\
[v]=L2T-\ [K] = V-mT~\ (8.43)
Тогда с помощью зависимости (8.42) устанавливаем безразмерный вид
искомого решения
ф = VKvxm+l F {у VKxm~4v). (8.44;
Этот вид решения получен из свойств уравнения (8.37), т. е. из
соображений математики, а не физики, хотя, конечно, особенности уравнения
зависят от физической задачи, которую оно описывает.
Обозначим для краткости безразмерный аргумент
Чу>. (8.45)
Для того чтобы преобразовать уравнение (8.37), вычислим входящие
в него производные. С учетом зависимости (8.44) и обозначения (8.45)
получим
V
Зт — 1
ду9
т—\
(8.46)
Здесь и далее штрихами обозначены производные по переменной т|.
Заменив в уравнении (8.37) производные с помощью соотношений (8.46),
приведем его к обыкновенному дифференциальному уравнению
F'''=m(F'2 — 1) — JH±L FF". . (8.47)
#
Это уравнение (полученное В. М. Фокнером и С. Скэн) необходимо
решить при граничных условиях:
*(Л) = О, F'(T,) = 0npnr,=0; ) •
F' (ц)-+ 1 при т)-*оо. J
Решение уравнения (8.47) может быть получено только численными
методами. В результате такого численного решения составлены подробные
таблицы функций F'(r\) и Fn(t\) при различных значениях параметра т.
На рис. 8.5 и 8.6 эти функции представлены графически. Из условия
187

(8.36) и первой формулы (8.46) следует, что производная F'(i\) дает
распределение безразмерной скорости в любом поперечном сечении по нормали
к обтекаемой поверхности
u/uo=:F' (ц). (8.49)
Из рис. 8.5 видно, что скорость и довольно быстро стремится к
асимптотическому значению uOi которое достигает только в бесконечности. Если
обозначить через тH ту безразмерную координату, при которой, например,
и/и0 = 0,99 или 0,95, то по формуле (8.45) ей будет соответствовать
некоторое значение у0, 'которое по определению можно назвать толщиной
пограничного слоя, т. е. принять б = у0.
Следовательно, для толщины ламинарного пограничного слоя в
рассматриваемом классе задач получим формулу
\—т
b^r\0VvJKx 2 , (8.50)
в которой значение tj0 можно брать из рис. 8.5. Смысл такого определения
заключается в том, что при у\ >т|0» т. е. у >8, поперечный градиент
скорости ди/ду столь мал, что можно пренебречь трением.
Отметим тот важный факт, что величина т]0, а следовательно, толщина
пограничного слоя зависит от продольного градиента скорости во внешнем
потоке dujdx (в данном случае от /л, так как и0 = Кхт).
При т = 0 скорость внешнего потока постоянна, при т >0 поток
ускоряется (конфузорное течение), а при т < 0 — замедляется (диффу-
зорное течение). При конфузорном течении эпюра скоростей в пограничном
слое более полная, а толщина пограничного слоя меньше, чем при диффузор-
ном.
При т = —0,0904 эпюра скоростей у стенки имеет вертикальную
касательную (ди/ду = 0 при у = 0), что соответствует предотрывному состоянию
пограничного слоя и далее будет более подробно пояснено.
Исключив в формуле (8.50) коэффициент К с помощью зависимости (8.36),
после простых преобразований найдем относительную толщину
пограничного слоя
б/лг-noRe--1/2, Re^
(8.51)
и/и0
По)
12
1,0
0,6
1
1
/
г
0,2-
f
у*
-0,2 0 0,2 0,4 0,6 0,8 т
Рис. 8.5. Распределение скорости в погранич- Рис. 8.6. Значение функции, опреде-
ном слое ляющей трение на стенке
188

Поскольку при заданном течении г\0 является постоянной, то эта формула
согласуется с оценкой толщины пограничного слоя, полученной при выводе
уравнения Прандтля.
Значение второй производной F"@) при г\ = 0, приведенное на рис. 8.6,
необходимо для определения касательного напряжения на обтекаемой
поверхности. Из второй формулы (8.46) следует
ду ду2
Тогда касательное напряжение на поверхности по формуле Ньютона (8.1)
-1 F" @), (8.52)
ду
где F"@) — значение второй производной при ц = 0.
Из этой формулы видно, что касательное напряжение может как
возрастать, так и уменьшаться вдоль обтекаемой поверхности. При т = 1/3
касательное напряжение на поверхности постоянно.
Воспользовавшись зависимостями (8.36) и (8.52), найдем безразмерное
касательное напряжение на поверхности
где F"@) = f(m) = const для заданного течения.
Следовательно, полученная формула также согласуется с анализом
Прандтля.
По рассмотренному решению можно сделать такие выводы.
1. Эпюра скорости в поперечном сечении пограничного слоя зависит от
продольного градиента давления. При отрицательном градиенте давлени^,
т. е. при возрастании скорости внешнего потока вдоль обтекаемого тела,
эпюра более полная (см. рис. 8.5).
2. При положительном градиенте давления возможен отрыв пограничного
слоя, т. е. возникновение обратного течения возле обтекаемой поверхности.
В данном решении предельному предотрывному течению соответствует
значение т = —0,0904, при котором (ди/ду)у==0=0 (см. рис. 8.5).
3. Законы изменения толщины пограничного слоя [см. формулу (8.50I
и касательного напряжения на обтекаемой поверхности 1см. формулу (8.52)]
зависят от величины продольного градиента давления. При значительном
отрицательном градиенте давления пограничный слой может даже
утоняться.
Следует отметить, что здесь рассмотрен только один класс частных
решений, однако качественно эти выводы являются общими для любого
пограничного слоя.
Используем полученное точное решение для оценки возможностей
приближенных методов расчета ламинарного пограничного слоя.
Прежде всего отметим, что второе граничное условие (8.48) для
дифференциального уравнения (8.47) поставлено на бесконечности. В
практических задачах эти граничные условия приходится переносить на внешнюю
границу тонкого пограничного слоя.
В приближенных методах эпюру скорости в поперечных сечениях
пограничного слоя описывают полиномом относительно невысокой степени.
Получим приближенное решение для пограничного слоя со степенной
зависимостью скорости внешнего потока (8.36).
Следует подчеркнуть, что строгое решение уравнения (8.47) представляет
трудную задачу, которая требует сращивания внутреннего и внешнего
разложений и доказательства единственности. Смысл приближенного решения
189

состоит в использовании отмеченных и обычно применяемых упрощений с
последующим сравнением с точными расчетами, полученными численными
методами.
Используем основное свойство пограничного слоя — то, что при
достаточно больших числах Рейнольдса он является относительно тонким.
Следовательно, можно считать, что продольная скорость в пограничном слое
достигает предельного значения не в бесконечности, а на некотором
конечном расстоянии от обтекаемой поверхности. Обозначим это безразмерное
расстояние через т]0. Оно имеет тот же смысл, что и ранее: представляет собой
численный коэффициент в формуле для толщины пограничного слоя, как
в формуле (8.50).
Решим уравнение (8.47) методом последовательных приближений,
оставив первое граничное условие (8.48) без изменений и заменив второе условие
на
F'(r\) = l при г)-г|о. (8.54)
Примем в качестве исходного приближения F = ц2/2ц0у так как эта
функция удовлетворяет всем граничным условиям. Подсчитав правую часть
уравнения (8.48), получим в следующем приближении:
?„,^Ът±_ 2_т
Последовательно проинтегрировав это уравнение, имеем
(8.55)
F =
с 171 о , С п
240г|§ ' 6 ' 2 '
где с — постоянная интегрирования.
В последних двух выражениях постоянные интегрирования приняты
равными нулю согласно первому граничному условию (8.48).
Постоянную интегрирования определим из граничного условия (8.54):
,0+-L.. (8.56)
48
На внешней границе пограничного слоя можно пренебречь трением, а
следовательно, как это следует из формулы (8.1), положить ди/ду = 0. Это
соответствует условию F" = 0 при г] = ti0. Тогда из первого выражения
(8.55) и значения постоянной {8.56) получим
(8.57)
Следовательно, постоянная интегрирования (8.56)
с = A + 9т)/3 ]Л+5т. (8.58)
Подставив значение (8.58) во второе выражение (8.55), получим закон
изменения безразмерной скорости в поперечных сечениях пограничного слоя:
«о 3yi + 5m 2 ' 768
Ограничимся этим перрым приближением
190

Безразмерное касательное напряжение
на обтекаемой поверхности по формуле
(8.53) пропорционально значению F" при
ц = 0. Из первого выражения (8.55) и
формулы (8.57) находим это значение
второй производной:
+5m. (8.60)
0,8
0,6
о,*
f
7
Сравнение приближенного [формула 0,2
(8.60I — штриховая линия — и точного
значения F"(Q) — сплошная линия (а еле- 0
довательно, безразмерного касательного
напряжения) на обтекаемой поверхности
при разных значениях т дано на рис. 8.6.
Наилучшее согласие наблюдается при
т = 0, что по формуле (8.36)
соответствует безградиентному течению, т. е.
обтеканию плоской пластины, поставленной под нулевым углом атаки. Для
этого случая известно решение Блазиуса:
02 = 0,332/j/Re^ Rex = щx/v.
1
Рис. 8.7. Сравнение расчетного
распределения скорости в
пограничном слое с экспериментом:
Н х=30 мм, О — *=100 мм, ф — х=
= 150 мм
(8.61)
Приближенное значение числового коэффициента по формуле (8.60)
при т = 0 равно 1/3 = 0,333.
Полная сила трения, действующая на одну сторону пластины длиной /
и шириной Ь:
i
FTp = Ь J т0 dx -0,664ft Vwlu\ ¦ (8.62)
о
Эти расчеты применимы только при ламинарном пограничном слое, что
соответствует примерно следующему ограничению для чисел Re* = uol/v <
<5 • 1О5...1О6, причем теория подтверждена экспериментальными
результатами с большой степенью точности.
Для более удобного представления результата (8.62) вводят суммарный
коэффициент трения
CTP = 2FTp/puJS, S=/fc. . (8.63)
С помощью (8.62) и (8.63) получим расчетное значение коэффициента
трения
Стр-1,328/KR^". (8.64)
Это значение согласуется с опытами с погрешностью менее 1%.
Хорошо согласуются также расчетные и опытные данные по
распределению скорости в поперечных сечениях пограничного слоя (рис. 8.7).
Сплошная кривая соответствует точному решению, а экспериментальные точки
получены измерениями скорости в поперечных сечениях, расположенных
на разных расстояниях от передней кромки пластины. Этот график
подтверждает также подобие эпюр скоростей, построенных в безразмерных
координатах и/иОг ц — у\^ио/\х.
Толщину пограничного слоя можно найти только приближенно, так как
согласно точной теории скорость потока стремится к скорости в
бесконечности асимптотически. При т — 0 из (8.36) следует К = Uq. Тогда из формулы
191

(8.45) получим выражение для безразмерной толщины ламинарного слоя
(у = б при т] = т|р) т]0 = бУи^хх. Так как при т = 0 из формулы (8,57)
следует ti0 = 4, то получим такое выражение для безразмерной толщины
ламинарного слоя на пластине
6/* = 4/KRe~. (8.65)
По точному расчету при безразмерной толщине т]0 = 4 (и т — 0)
скорость в пограничном слое достигает 0,956 своего асимптотического значения
на бесконечности. Понятие физической толщины пограничного слоя
является условным. Более обоснованное сравнение будет приведено в разд. 8.6.
Из формулы (8.65), после подстановки текущего значения числа Рей-
нольдса, следует
б = 4 Vvx/tio. (8.66)
Местное касательное напряжение на пластине изменяется по ее длине и
согласно формуле (8.61) становится бесконечно большим на носике пластины
(х = 0). Дело в том, что вблизи носика пластины происходит резкое местное
изменение скорости потока и оценки, принятые в теории пограничного слоя,
здесь не применимы. Однако это практически не сказывается на величине
полной силы трения, действующей на пластину.
8.5. ПРИБЛИЖЕННЫЙ МЕТОД РАСЧЕТА ЛАМИНАРНОГО
ПОГРАНИЧНОГО СЛОЯ
Точное решение уравнения Прандтля для пограничного слоя
возможно лишь в отдельных частных случаях. Под точным понимаем такое
решение обыкновенного дифференциального уравнения (возможно
численное), к которому сведены уравнения Прандтля и уравнение неразрывности.
Конечно, возможно и прямое численное решение этой системы из двух
уравнений в частных производных с помощью ЭВМ. Однако большое значение
имеют и приближенные методы расчета, особенно те, которые опираются на
ясную физическую основу.
Со времени создания теории пограничного слоя начали создавать и
усовершенствовать приближенные методы его расчета. В основе приближенных
способов лежит выбор некоторого семейства профилей скорости в
пограничном слое. Обычно такое семейство зависит от одного параметра, величина
которого пропорциональна градиенту скорости внешнего потока: dujdx.
Поскольку распределение скорости в пограничном слое зависит от
распределения скорости во внешнем потоке, то очевидно, что число таких
параметров в произвольном случае теоретически должно быть неограниченным, а
практически зависеть от нескольких высших производных: d2u0/dx2y
d3u0/dxB... Однако много- и даже двухпараметрические методы приводят к
очень сложным вычислениям и поэтому развития не получили.
Представим однопараметрическое семейство профилей скорости в
поперечных сечениях пограничного слоя зависимостью
и (х, у) = и0 (х) [F (у/Ь) + AG (у/Ь)], (8.67)
.где и(х> у), ио(х) — скорости соответственно внутри пограничного слоя и
на внешней его грайице; * > 0, 0 < # < 8 — соответственно продольная и
поперечная координаты; Ь(х) — толщина пограничного слоя; Л —
параметр, вид которого будет определен ниже.
Скорость и(х, у) должна удовлетворять граничным условиям,
сформулированным на внутренней и внешней границах слоя. В приближенных мето-
192

дах число граничных условий может быть выбрано, вообще говоря, разным,
а если расчет идет последовательными приближениями, то зависеть и от
номера приближения. Во всех приближенных методах обычно обязательно
удовлетворяют следующим граничным условиям:
и=0, vd2u/dy2=—ui)du0/dx при */ = 0; (8.68)
и=иОу ди/ду'^0, д2и/ду2=-0 при у= 6. (8.69)
Первое условие (8.68) объясняется прилипанием вязкой жидкости к
твердой стенке, а второе следует из уравнения пограничного слоя (8.27).
Условия (8.69) следуют из того, что на внешней границе слоя трением можно
пренебречь (ди/ду = 0), а эпюра скорости в пограничном слое плавно
сопрягается со скоростью во внешнем потоке (д2и/ду2 = 0).
Функции F((//5), G(y/&) в первом по времени методе Польгаузена были
выбраны полиномами четвертой степени, коэффициенты которых
определены из сформулированных выше граничных условий для скорости. Однако
такой прием оказался не очень удачным, так как выбор указанных функций
не был согласован с особенностями уравнения (8.27).
Рассмотрим приближенный метод решения уравнения для ламинарного
пограничного слоя, пригодный для произвольно заданного закона изменения
скорости на внешней границе и0 = ио(х).
При выводе уравнения (8.27) отмечено, что при достаточно больших
числах Рейнольдса пограничный слой относительно тонок, и тогда граничные
условия можно выставлять не на бесконечности, а на расстоянии 6 от
обтекаемой поверхности, равном толщине пограничного слоя.
Запишем уравнение (8.27) в виде (
^ *JJ < (8.70)
v u+vUo.
д(/2 дх ду dx
Уравнение неразрывности (8.33) проинтегрируем поперек слоя
Будем решать систему этих уравнений методом последовательных
приближений и для того, чтобы не усложнять выкладок, ограничимся только одним
приближением.
В качестве исходного приближения возьмем эпюру скоростей в виде
и = иоу/Ь, которая удовлетворяет только двум первым граничным условиям
(8.68), (8.69). Однако в следующем приближении будут удовлетворены три
граничных условия.
Вычислим сначала величины, входящие в основные уравнения, причем
напомним, что и0 и б являются функциями только х. Штрихами будем
обозначать производные по х:
JOL^u' Л У6' ди = и°
дх ° б ° 62 ' ду 6 f
дх и ° 26 ' " 262
о
Подставив эти выражения в уравнение (8.70), после приведения подобных
членов получим
7 зак. :

Проинтегрируем это выражение по у:
v-|L = _«;j?il + ,leB;j?—иои'оу+С1. (8.72)
ду 662 6о2
Постоянную интегрирования находим из условия duldy = 0 при у — б;
??! = iiJ676 + 5ад6/6.
Подставим это значение постоянной интегрирования в
дифференциальное уравнение (8.72) и, еще раз проинтегрировав по у, найдем
?+т*и'.**- <8-73)
Постоянная интегрирования принята равной нулю согласно условию
и = 0 при у = 0. Подставим в это решение у = б; тогда согласно
граничному условию должно быть и = и9.
После проведения этой операции и приведения подобных членов получим
обыкновенное линейное дифференциальное уравнение первого порядка для
определения толщины пограничного слоя
Fy + 6-?i-6*« —. (8.74)
«о «о
Это уравнение легко интегрируемо по общему правилу и при условии
6 = 0 при х = 0 имеем
ЦГ .*<**• (8-75)
Аналогичные формулы для расчета ламинарного пограничного слоя при
несколько иных значениях числового множителя и показателях степени
получены другим более сложным путем различными авторами. Подобный путь
вывода предложен М. Е. Швецом.
Преимуществом формулы (8.75) является то, что в нее не входят
производные скорости, т. е. не требуется операции численного
дифференцирования, которая всегда не очень точна.
Далее следует получить формулы для распределения скоростей в
поперечном сечении пограничного слоя и касательное напряжение на обтекаемой
поверхности. Покажем, что эти формулы легко могут быть получены и в них
не требуется численного дифференцирования.
Запишем сначала уравнение (8.73) в безразмерном виде
Из дифференциального уравнения (8.74) следует
«O68' = 8v—За; б2.
Исключив с помощью этого выражения ао66' из уравнения (8.76), после
простых преобразований получим выражение для эпюры скоростей в
ламинарном пограничном слое
J!--±JL-.±(jrf + ±A\2Jt—.3(JL)t + lJLL (8.77)
Здесь введено обозначение безразмерного параметра, который
характеризует влияние градиента скорости внешнего потока на пограничный слой:
«!_-*?_. (8.78)
fju/o dx
194

Этот параметр выражен также через
градиент давления, что сделано с
помощью уравнения Бернулли (8.31),
записанного для внешней границы слоя.
Местное касательное напряжение на
обтекаемой поверхности находим с
помощью формулы (8.1) и уравнения (8.77):
u/u0
0,8
причем толщину пограничного слоя
следует определять из соотношения (8.75)
по заданному распределению скорости
во внешнем потоке.
С помощью формулы (8.79)
выясняется физический смысл безразмерного
параметра Л. Запишем выражение
(8.78) следующим образом:
6 (dp/dx) dx
(—\шо/Ь) dx '
г-
ш
/
у/.
у/
'/
Y/,
f
Л =¦
0,2
0,2 0,t 0,6 0,8 y/S
Рис. 8.8. Распределение скорости
в ламинарном пограничном слое при
различных градиентах давления
Числитель этой дроби представляет собой силу давления, действующую
на элемент пограничного слоя длиной dx, а знаменатель — величину,
пропорциональную силе трения, действующую на этот же элемент со стороны
обтекаемой поверхности. Отметим только, что знаменатель пропорционален
силе трения при безградиентном течении. Это, конечно, не меняет сути дела,
однако в некоторых случаях удобнее сравнивать свойства пограничных
слоев, введя отношение силы давления к истинной силе трения при данном
градиенте давления. Тогда в качестве характерного параметра следует
рассматривать выражение
(8.80)
dp _
dx
ЗЛ
4 + Л
В заключение сделаем вывод, что распределение скорости в сечении
пограничного слоя (8.77) и местная сила трения (8.79) зависят от параметра
Л.
Распределение скоростей в пограничном слое показано на рис. 8.8.
Параметр Л может изменяться только в интервале — 4 < Л. При нижнем
пределе сила трения по формуле (8.79) равна нулю и это соответствует, как будет
объяснено ниже, предотрывному состоянию пограничного слоя. При
меньших значениях Л возникнет возвратное течение жидкости вблизи
поверхности, а при этом несправедливо приближенное соотношение для
пограничного слоя (хотя такое течение в действительности наблюдается при больших
положительных градиентах давления). Следует отметить, что при конфузор-
ных течениях (Л >0) эпюра скоростей более полная, чем при диффузорных
(Л < 0).
Сравним течение в ламинарном пограничном слое с ламинарным течением
между параллельными стенками. Расположим одну стенку вдоль оси
абсцисс, а другую — на расстоянии 2й. Ввиду симметрии картины можно
считать, что толщина «пограничного слоя» равна половине ширины канала:
6 = ft.
Полной аналогии между течением в канале и течением в пограничном
слое нет. На внешней границе слоя можно пренебречь трением и применять
уравнение Бернулли, т. е. изменение давления вдоль пограничного слоя
7* 195

жестко связано с изменением скорости внешнего потока. При течении между
стенками скорость на внешней границе «пограничного слоя» (в центре
канала) постоянна, хотя давление уменьшается вдоль потока из-за
сопротивления.
Однако для приведенного выше метода расчета подобное сравнение все
же возможно, так как уравнение распределения скорости в слое (8.77)
получено интегрированием (хотя и приближенным) общих уравнений движения
жидкости.
При течении в канале безразмерный параметр Л находим по формуле
(8.78), что в данном случае следует сделать только через градиент давления
Л==ь !*L-lL
М^о dx
где и0— скорость в центре канала.
Запишем условие равновесия между силами давления и трения для
элемента жидкости, расположенного в канале:
2h
dx
где т0 — касательное напряжение на стенках канала.
Из двух последних уравнений следует: т0 = pAuJh. Исключив т0 из
формулы (8.79), получим для данного случая Л = 2. Подставив это значение
в уравнение (8.77), найдем закон распределения скорости в поперечном
сечении канала:
Это решение совпадает с известным точным параболическим распределением
скорости. Следует только иметь в виду, что в данном случае ордината у
измеряется от стенки канала, а не от его середины.
8.6. УСЛОВНЫЕ ТОЛЩИНЫ ПОГРАНИЧНОГО СЛОЯ
Толщиной пограничного слоя можно назвать расстояние,
измеренное по нормали к обтекаемому телу, в пределах которого существенно
влияние трения. На внешней границе пограничного слоя поперечный
градиент скорости столь мал, что можно пренебречь трением. В
действительности эту границу трудно установить, так как на некотором отдалении от
поверхности тела скорость меняется мало и граница становится нечеткой.
Поэтому вводят некоторые условные толщины пограничного слоя, которые
уменьшают указанный произвол и имеют определенный физический смысл.
Рассмотрим выражение, в котором интегрирование проводим поперек
слоя:
б
Р"(А=Р \(uo—u)dy.
о
Интеграл справа показывает, на сколько меньше стал расход жидкости
вблизи стенки в слое толщиной б из-за появления пограничного слоя.
Соответствующая площадь на рис. 8.9 заштрихована. Если увеличивать
верхний предел интеграла даже до бесконечности, то величина интеграла мало
изменится. Величину бг называют толщиной вытеснения, так как она
показывает, на какое расстояние будут оттеснены линии тока от обтекаемого тела

из-за того, что через пограничный слой
проходит меньший расход:
(8.81)
При наличии пограничного слоя вблизи
поверхности обтекаемого тела будет меньше не
только поток массы, но и потоки количества
движения и энергии. Поэтому кроме толщины
вытеснения вводят еще две другие условные
толщины пограничного слоя.
Вследствие трения поток импульса в пограничном слое станет меньше,
чем поток импульса в потенциальном течении, на величину
б
P^62=pju(ao—u)dy.
Отсюда получим формулу для определения толщины потери импульса
У- (8.82)
Поток энергии в пограничном слое меньше, чем поток энергии в
потенциальном течении, на величину
6
Отсюда следует формула для определения толщины потери энергии
"* ^ , (8.83)
Для иллюстрации определим условные толщины, выбрав, ради
упрощения, распределение скорости поперек пограничного слоя линейным: и =
= иоу/6. По формулам (8.81), (8.82), (8.83) найдем соответственно: 8г=
= 6/2, 62 - 6/6, 63 = 6/4.
Если изменение плотности жидкости в поперечном сечении пограничного
слоя существенно, то легко получить такие же формулы и для этого случая.
Определим толщину вытеснения для ламинарного пограничного слоя с
продольным градиентом давления, характеризуемым параметром Л (8.78).
Вычислим интеграл (8.81) для приближенного изменения скорости поперек
слоя (8.77).
Опустив простые вычисления, получим выражение толщины вытеснения
через физическую толщину пограничного слоя
6i =6 F/15—Л/30).
(8.84)
Здесь толщину 6 пограничного слоя следует определять по формуле
(8.75).
197

В частности, при нулевом градиенте давления (Л = 0), что
соответствует постоянной скорости внешнего потока, из формул (8.84), (8.75) имеем
. (8.85)
Напомним, что для данного случая (ламинарный пограничный слой с
нулевым градиентом давления) известно точное решение. Для этого точного
решения численный коэффициент в формуле (8.85) равен 1,72.
Вопросы для самопроверки
1. Какие жидкости называют ньютоновскими?
2. Получите общий вид функциональной зависимости для падения давления на
единицу длины трубы (рх — Pi)ll при течении несжимаемой вязкой жидкости, исходя из
соображений теории подобия.
3. Как влияет величина продольного градиента давления на форму эпюры
распределения скорости в поперечном сечении ламинарного пограничного слоя?
4. Что называют автомодельным решением в применении к ламинарному
пограничному слою?
5. Получите общий вид зависимости для среднего коэффициента трения на плоской
пластине, обтекаемой без угла атаки, исходя из соображений теории подобия.
6. Что называют физической толщиной пограничного слоя?
7. Какой физический смысл имеют условные толщины пограничного слоя?
8. Для каких практических целей могут быть использованы вычисления условных
толщин пограничного слоя?

ГЛАВА 9
ТУРБУЛЕНТНОЕ ТЕЧЕНИЕ ВЯЗКОЙ ЖИДКОСТИ
9.1. ОСОБЕННОСТИ ТУРБУЛЕНТНОГО ТЕЧЕНИЯ.
УРАВНЕНИЯ РЕЙНОЛЬДСА
Теоретические решения задач о движении вязкой жидкости с
помощью уравнений Навье—Стокса, как уже отмечалось, хорошо
совпадают с экспериментом. Однако это совпадение наблюдается только при
достаточно малых числах Re, Опыт показывает, что если числа Re превосходят
некоторый предел, то ламинарное течение становится невозможным и
возникает другой тип течения, которое называют турбулентным.
Систематические исследования в этом направлении начались с известного опыта Рейнольд-
са A883 г.).
Если в трубу с прозрачными стенками, по которой движется жидкость,
пустить струйку краски, то окрашенная струйка при ламинарном течении
будет двигаться вдоль трубы, почти не размываясь. Скорость поперек трубы
при этом, как предсказывает теория, меняется по параболическому закону
(рис. 9.1, а).
При увеличении расхода жидкости через трубу увеличивается скорость
и, следовательно, число Re. При некотором числе Re характер движения
жидкости в трубе изменяется. Струйка краски начнет испытывать поперечные
пульсации, размоется и окрасит весь поток. При этом распределение
средней по времени скорости в поперечном сечении трубы станет более полным
(рис. 9.1, б). Изменение эпюры скорости указывает на то, что изменился и
закон трения, так как ламинарному закону трения соответствует параболичес
кое распределение скорости.
Аналогичная картина может наблюдаться и в пограничном слое,
например, на плоской пластине. Сначала окрашенная струйка движется в
пограничном слое вдоль пластины, не размываясь. На некотором расстоянии
в струйке возникнут усиливающиеся поперечные пульсации и краска
размоется. При возникновении пульсаций эпюра скоростей в поперечном сечении
пограничного слоя также изменяется, становится более полной, т. е. не
соответствует закону трения при ламинарном течении.
Таким образом, опыт показывает, что в вязкой жидкости возможны две
формы течения: ламинарная, когда жидкость движется слоями, и
турбулентная, когда в потоке возникают малые хаотические пульсации скорости и
давления вокруг средних значений этих величин.
Формально решения уравнения Навье—Стокса могут быть получены и
для очень больших чисел Re. Однако в действительности ламинарные
течения наблюдаются только при достаточно малых числах Re. Это
объясняется тем, что при больших числах Re ламинарные течения теряют
устойчивость и переходят в турбулентные. Так, опыт показывает, что ламинарное
течение в круглой трубе существует, если Re = ud/v < 2300. Однако эта
граница довольно условна, так как устойчивость ламинарного течения
зависит также от возмущений потока на входе в трубу. Весьма тщательным
устранением источников возмущений удалось, например, добиться ламинарного
течения в трубе для Re « 40 000. С другой стороны, следует отметить, что,
!99

Рис. 9.1. Распределение скорости в
трубе:
а — при ламинарном течении; б — при
турбулентном течении
сколь бы сильными не были
возмущения на входе, они гаснут, и поток
в трубе остается ламинарным, если
Re < 2000.
Большое практическое значение
имеет вопрос об устойчивости
ламинарного пограничного слоя. Все
причины, которые могут вызвать
пульсации в ламинарном пограничном слое,
понижают его устойчивость, т. е.
вызывают его переход в турбулентный
при меньших числах Re.
Устойчивость ламинарного пограничного слоя понижается при увеличении
пульсаций во внешнем потоке, увеличении положительного градиента давления,
увеличении шероховатости ртенки.
Основной особенностью турбулентного течения является хаотическая
пульсация скорости и давления в любой фиксированной точке пространства.
Пульсации вызываются быстрым и хаотическим перемещением и
перемешиванием элементарных^ частиц жидкости. Эти малые пульсации накладываются
на основное установившееся течение жидкости. Хотя пульсации весьма малы
по сравнению со скоростью основного потока, они, как показал Рейнольде,
приводят к появлению турбулентного трения, которое существенно больше
трения при ламинарном движении. „
Поскольку теоретическое изучение турбулентных течений с хаотическими
пульсациями встречает непреодолимые трудности, прибегают к осреднению
по времени и составляют уравнения для осредненных параметров.
, Рассмотрим турбулентное течение несжимаемой жидкости.
Представим составляющую скорости в турбулентном потоке суммой
среднего значения и «пульсационного добавка»:
ut^Hi+ui. (9.1)
Под средним значением понимаем результат осреднения скорости по
времени в фиксированной точке пространства
(9.2)
Полагаем, что осреднение проводится за такой достаточно большой
промежуток времени Т, что результат осреднения не зависит от данного
промежутка времени. Очевидно, что при этом также предполагается, что среднее
течение является установившимся.
Из закона осреднения (9.2) следует, что средние значения пульсационных
составляющих равны нулю:
и/=0, (9.3)
так как за большой промежуток времени равновероятны положительные и
отрицательные пульсации одинаковой величины.
Если осреднить квадрат пульсационной скорости, то результат не будет
равен нулю. Полученную среднюю величину можно взять за меру
пульсаций скорости. В качестве одной из главных характеристик турбулентности
принимают безразмерную величину
~~/«t (9.4)
200

называемую степенью турбулентности. Эту величину принято выражать
в процентах. Для примера укажем, что в аэродинамических трубах, если
предпринимаются специальные меры для успокоения потока, степень
турбулентности может составлять десятые доли процента. В турбомашинах, где
пульсации возбуждаются движущимися лопатками, степень турбулентности
достигает десятка и более процентов.
Давление в фиксированной точке пространства также можно представить
средним значением и пульсационной составляющей
р' = 0. (9.5)
Совокупность средних значений скоростей и давлений определяет
некоторое установившееся течение. Поэтому соответствующее турбулентное
течение можно назвать в среднем установившимся.
Далее с помощью формулы типа (9.2) будем осреднять более сложные
выражения, поэтому приведем общие правила. Пусть осреднению подлежат
две функции Fx и F2, тогда следует
dFjdx^dFJdx. (9.6)
Для того чтобы получить уравнение движения турбулентного потока,
выпишем уравнение Навье—Стокса (8.6) для несжимаемой жидкости в
таком виде: *
dt j
Второй член в этом уравнении в данном случае удобнее записать иначе:
д , ч dp , д2 uj
т— (" Ъ) = г- + JA J
+ Р т ("г Ъ) г + JA . (9.8)
dt dxi dxj dxi dxi
Справедливость такой замены очевидна из выражения
Легко видеть, что здесь второй член справа равен нулю на основании
уравнения неразрывности для несжимаемой жидкости.
Подставим в уравнение (9.8) скорости и давление, выраженные через
средние по времени значения и пульсационные составляющие из формул
(9.1), (9.5), а затем осредним все члены уравнения по времени. Осреднение
членов уравнения производим по формулам (9.6).
Осреднение первого члена уравнения (9.8):
S.A+S^o. (9.9)
dt dt ' dt y '
Этот результат следует из того, что среднее движение установившееся
т. е. средняя скорость не зависит от времени, а средняя по времени от пуль
сационной составляющей равна по условию (9.3) нулю.
Осреднение следующего члена уравнения (9.8):
I Uj) ==—— [ut Uj + Щ U) +U'i Uj+ Щ Uj) =
0X( ¦
= — {uiUj) + — {uTui)< (9.10)
dxi dxi '
201

Очевидно, что операция осреднения
членов квадратичных относительно средних
значений скоростей, оставляет их без
изменений. Операция осреднения членов
уравнений, содержащих первые степени пульса-
i ционных скоростей, дает результат, равный
нулю, а от членов, квадратичных
относительно пульсационных скоростей, — не
равный нулю. После осреднения третьего
-^ и четвертого членов уравнения (9.8) по-
U1 лучим уравнения Рейнольдса для турбу-
Рис. 9.2. Схема турбулентного мнтного течения'.
обмена при пульсациях скорости
и,(х2 +
дх / Г dxtdxi dxt
Так как уравнение неразрывности B.9) содержит только первые степени
скорости, то получим, что как средние, так и пульсационные скорости
должны удовлетворять уравнению неразрывности:
=о,4^=о.
Таким образом, для средних скоростей уравнение неразрывности не
изменилось, а уравнение Рейнольдса (9.И) отличается от уравнения Навье—
Стокса (8.8) наличием последнего члена:
OXi
который зависит от осредненного произведения пульсационных скоростей.
Следовательно, закон распределения средних скоростей зависит отосред-
ненных пульсационных скоростей. Это - главный вывод из проделанных
Р%Уы^нНимИна простом примере, какой физический смысл имеет выраже-
"^Рассмотримдля простоты двумерное плоскопараллельное течение
средняя скорость которого «! зависит только от координаты х2 (рис. 9.2).
Проведем контрольную поверхность аа. Благодаря поперечным
пульсациям скорости «г частицы жидкости пересекают эту K°«7frbHMyPI" им„ в
ность Частицы, для которых и'2 > 0, попадают из области с меньшими в
Хасть с большими средними скоростями. Эти частицы, имея меньшую
продольную скорость, тормозят слои жидкости, расположенные выше конт-
рЬльной поверхности, т. е. вызывают отрицательные проД^ьные^пульс*
ции «i < 0. Для частиц, которые пересекают контрольную поверхность в
обратном направлении, «2 < 0, и\ > 0. Таким образом, возникает^
касательное напряжение между слоями, появление которых можно объяснить
переносом количества движения при пульсациях. „атт1л ипнг
Величина рмо пропорциональна массе жидкости, пересекающей
контрольную поверхность. Величина р«2 «1 пропорциональна перенесенному
. через контрольную поверхность количеству движения в проекции на ось
абсцисс.
Тогда, после осреднения по времени, получим
т,,-1—ри,«1-
202

Правая часть представляет количество движения (в проекции на ось
jCi), перенесенное через единицу площади в единицу времени, а левая —
равна касательной силе, приходящейся на единицу площади.
Следовательно, эта формула выражает закон трения в турбулентном течении.
Возвращаясь к общему случаю произвольного трехмерного течения,
можно утверждать, что выражение (9.12)
Oij^—puiu/ (9.13)
представляет собой тензор напряжений, вызванных пульсациями при
турбулентном течении.
Это же заключение можно было бы сделать без пояснений, формально
сравнивая уравнение Рейнольдса (9.11) с уравнением движения B,17),
записанным через напряжения для произвольного закона трения.
Ранее было пояснено, что когда индексы i и / не одинаковы, то формула
(9.13) дает касательные напряжения. Таким же образом легко показать,
что при одинаковых индексах получаются нормальные напряжения.
В заключение запишем уравнения Рейнольдса_для плоского движения
(i = 1, 2j_/=l, 2), положив хг = х, х2=У, иг^и, u2 = vy u[=u\
U2 зз v\ p = р. Тогда из уравнения (9Л1) получим
дх
[ dv , dv \
lu \-V =
\ дх ду
Анализ этих уравнений и сравнительная оценка величины членов,
учитывающих трение, рассмотрены в подразд. 9.2.
9.2. УНИВЕРСАЛЬНЫЕ ЗАКОНЫ РАСПРЕДЕЛЕНИЯ СКОРОСТИ.
УНИВЕРСАЛЬНЫЕ ЗАКОНЫ СОПРОТИВЛЕНИЯ
Ламинарные течения жидкости описаны уравнениями Навье—
Стокса (8.4), в которых использован закон трения Ньютона (8.1).
Турбулентные течения должны быть описаны уравнениями Рейнольдса (9.11) и из них
следует, что турбулентное трение возникает при турбулентных пульсациях.
Однако уравнения Рейнольдса не содержат закона турбулентного трения,
т.е. связи между распределением скорости и величиной трения. Поэтому
система уравнений не замкнута и для решения ее необходимо дополнить
законом трения.
Рассмотрим плоский турбулентный слой в нержимаемой жидкости и
воспользуемся уравнениями Рейнольдса (9.14).
Теория пограничного слоя, т. е. предложение о том, что влияние трения
наиболее существенно в тонком слое, непосредственно прилегающем к
твердой обтекаемой поверхности, справедлива как для ламинарного, так и
для турбулентного течения. В обоих случаях при большом числе Re
справедливы общие положения теории: 1) пограничный слой тонок по сравнению
с продольным размером обтекаемого тела; 2) поперечный градиент скорости
в пограничнЬм слое много больше продольного градиента скорости; 3)
давление поперек слоя практически не меняется.
При этих условиях уравнения Навье—Стокса упрощаются и переходят
в уравнение ламинарного пограничного слоя (8.27). Точно такие же упро-
203

щения справедливы для уравнений Рей-
нольдса (9.14). В правой части первого
уравнения можно ввиду малости
отбросить производные скоростей по х, тогда
имеем
(9.15)
Фо Это уравнение отличается от уравнения
(8.27) только наличием последнего чле-
Рис. 9.3. Схема турбулентного по- на, который учитывает касательные на-
граничного слоя пряжения, вызванные турбулентными
пульсациями.
Таким образом, суммарные касательные напряжения формально состоят
из ламинарных xt и турбулентных rt:
*и д
р .
ду
Ламинарные напряжения зависят от осредненной скорости, а турбулентные
определены пульсационными составляющими. Естественно предположить,
что турбулентные пульсации непосредственно вблизи твердой стенки
весьма малы, что и подтверждено прямыми измерениями. Следовательно, очень
близко от стенки трение определено ламинарным законом, в котором
коэффициент трения зависит от молекулярного перемешивания.
На некотором отдалении от стенки турбулентное трение, вызванное xad-
тическим перемешиванием элементарных масс жидкости, станет много
больше ламинарного. Течение в турбулентном пограничном слое можно
разбить на три характерные области (рис. 9.3).
В слое толщиной @,001...0,01N, который называют вязким подслоем
(область /), трение определено ламинарным законом. В основной части
слоя толщиной @,8...0,9) б (область///) турбулентное трение много больше
ламинарного. В переходной области // оба вида трения соизмеримы. Эта
оценка является чисто описательной и требует уточнений, которые
приведены дальше.
В вязком подслое закон распределения скорости по оси ординат может
быть определен с помощью уравнений Навье—Стокса. В остальной части
слоя закон трения не известен, и поэтому распределение осредненной
скорости должно быть найдено из дополнительных соображений.
Прежде всего отметим, что эпюра скоростей, приведенная на рис. 9.3,
в действительности зависит от величины числа Re, шероховатости стенки
и градиента давлений вдоль слоя. Очевидно, что желательно найти закон
распределения скорости в турбулентной части слоя в зависимости от таких
параметров, которые делали бы его наиболее универсальным. Некоторые
соображения позволяют установить общий характер распределения скорости.
Положим, что известно касательное напряжение на стенке т0.
Градиент скорости в турбулентном потоке на некотором расстоянии от стенки
зависит от т0, расстояния от стенки у и плотности жидкости р. Величина
вязкости жидкости в турбулентном потоке при больших числах Re, как уже
было сказано, не должна оказывать влияния на результат. Градиент ско-
204

рости ди/ду имеет размерность Т. Из указанных величин можно составить
только одну комбинацию, которая имеет ту же размерность:
Тогда на основании теории подобия градиент скорости должен быть
пропорционален этой величине:
ду У у 9
где А — безразмерная постоянная, которая может быть найдена
экспериментально.
Зависимость (9.16) была получена Л. Прандтлем.
Для дальнейшего удобно ввести обозначение величины, имеющей
размерность скорости: ,
Ux=VrJp. (9Л7)
Эту характерную скорость называют динамической скоростью.
Проинтегрировав выражение (9.16), получим
и 2= Aux In (у/уо), (9.18)
где у0 — постоянная интегрирования, имеющая размерность длины. Этот
закон распределения скорости не применим в подслое, так как там велико
влияние вязкого трения, которое не учитывалось. Он не применим и
далеко от стенки, так как по смыслу вывода ясно, что т0 полагалось
постоянным, а стенка — бесконечно длинной. В действительности стенка имеет
конечную длину, а касательное напряжение на стенке переменно. Однако
вблизи от стенки распределение скоростей зависит в основном от местного
значения касательного напряжения. И поэтому вблизи от стенки (в
турбулентной части слоя) формула (9.18) должна давать правильный результат.
Особенно точной эта формула должна быть, например, при турбулентном
течении в очень длинной трубе, так как стенку можно считать бесконечно
длинной, а касательные напряжения действительно не меняются вдоль
трубы.
Выразим в формуле (9.18) неизвестную постоянную интегрирования,
имеющую размерность длины, через динамическую скорость (9.17).
Из соображений подобия можно полагать, что размер у0 определен
числом Re, составленным из у0, иХу v:
где С — некоторая постоянная.
Выразив отсюда у0 и йодставив в формулу (9.18), получим
логарифмический закон распределения скорости в турбулентной части слоя вблизи
стенки вне тонкого подслоя:
Л-=А1п^-—В. (9.19)
" v
Здесь для сокращения записи введена новая постоянная В = AlnC.
Внутри очень тонкого вязкого подслоя касательное напряжение
изменяется мало, и поэтому согласно формуле трения Ньютона (8.1)
распределение скорости в нем будет линейным:
205

Выразив касательное напряжение на стенке через динамическую
скорость по формуле (9Л7), получим
u=u\ylv. (9.20)
Таким образом, решение (9.20) дает распределение скорости в вязком
подслое у самой стенки, а решение (9.19) в турбулентной части слоя вблизи
стенки. Эти два решения нужно стыковать на каком-то небольшом
расстоянии от стенки. Теоретически можно оценить только порядок этого
расстояния. Опыт показывает, что вязкий подслой имеет такую толщину fiz, что
число Re, подсчитанное по скорости щ на его внешней границе, имеет
порядок а2 = lOO-f-150:
a*6j/v = a2. (9.21)
Можно и не производить такой стыковки, а определить постоянные А и В
в формуле (9.19) из эксперимента.
Главное заключается в следующем. Распределение скорости в
турбулентной части пограничного слоя вблизи стенки подчиняется
логарифмическому закону, поэтому этот закон называется универсальным.
Распределение скоростей по формулам (9.19), (9.20) зависит только от касательного
напряжения на стенке. Следовательно, распределение скорости вблизи
стенки практически не зависит от внешних воздействий: продольного
давления и степени турбулентности внешнего потока. Поэтому постоянные в
формуле (9.19) также оказываются универсальными. Однако здесь необходимо
сделать одно существенное замечание.
Поскольку вязкий подслой очень тонок, то касательное напряжение на
стенке сильно зависит от ее шероховатости. Если бугорки шероховатости
не выступают за вязкий подслой, то касательное напряжение не зависит от
шероховатости и стенка называется гладкой. Для гладких стенок
постоянные в формуле (9.19) будут универсальны. Исследования в трубах показали,
что стенку можно считать гладкой, если размер шероховатостей h таков,
что удовлетворяет условию
/mT/v<4. (9.22)
Если же бугорки выступают за вязкий подслой, то касательное
напряжение на стенке зависит от шероховатости. В этом случае шероховатость
влияет на тонкий вязкий подслой и, следовательно, на распределение скорости
вблизи этого подслоя. Однако это влияет только на сдвиг профиля скорости
вне подслоя в полулогарифмических координатах, т. е. на величину
постоянной В (причина этого выясняется дальше). Величина В становится
функцией h высоты выступов шероховатости:
B = B(hux/v). (9.23)
Остановимся сначала на простейшей задаче о пограничном слое на плоской
пластине, обтекаемой потоком при нулевом градиенте давления.
Для ламинарного пограничного слоя решение этой задачи было приведено
в гл. 8, а на рис. 8.5 дана эпюра распределения скорости в пограничном слое
для этого частного случая. Здесь важно отметить то, что в координатах
и/и0 = F(y/b) она является универсальной и не зависит от числа Рейнольд-
са.
Для турбулентного пограничного слоя дело обстоит иначе., Эпюры
скоростей в турбулентном пограничном слое, построенные в координатах и/и0 =
= /(«//б), в общем случае не совпадают, причем было замечено, что
совпадения не наблюдается, если различны числа Рейиольдса Re = «06/v, подсчи-
206

(и- uo)fut
•<
••
•
•
1.»
- 5
-10
-15
„
0,2 0,<t 0,6 0,8 у/d
Рис. 9.4. Универсальное распределение
скорости в турбулентном пограничном
слое при нулевом градиенте давления
(и-и o)ftir
0
- 2
- 6
- 8
-12
f
>**
0,01 0,02 0,0S 0,1 0,2 0t<t y/S
Рис. 9.5. Универсальное распределение
скорости, построенное в
логарифмических координатах
тайные по толщине пограничного слоя, и если отличается шероховатость
стенок.
Однако были найдены такие координаты, в которых все эпюры скорости
в турбулентном пограничном слое совмещаются в одну. .
Рассмотрим теперь внешнюю часть пограничного слоя. Относительно
далеко от стенки, т. е. в основной внешней части турбулентного слоя,
логарифмический закон распределения скорости несправедлив или, лучше
сказать, наблюдается отклонение от этого закона. Некоторое представление о
распределении скоростей во внешней части турбулентного слоя следует из
соображений теории подобия. Влияние касательного трения на стенке т0
распространяется до внешней границы слоя 6, где скорость равна и0.
Распределение скоростей зависит от плотности жидкости р, но не зависит, как
было отмечено, от вязкости. Из соображений подобия следует зависимость,
предложенная Т. Карманом и называемая законом «дефекта скорости»:
и—и0
и—и0
(9.24)
где и, Uq—соответственно текущая скорость в пограничном слое и скорость
на внешней границе; у — расстояние от стенки.
Величина ]/то/р имеет размерность скорости и была обозначена их,
которая называется динамической скоростью (9.17).
На рис. 9.4 показана универсальная кривая распределения скорости в
турбулентном пограничном слое при нулевом продольном градиенте
давления (dpldx = 0), построенная в переменных формулы (9.24). Все
экспериментальные точки ложатся практически на одну кривую, хотя опыты
проведены при разных числах Рейнольдса и шероховатостях стенок.
Следовательно, оказалось, что форма эпюры скорости в турбулентном слое зависит
от касательного напряжения на стенке. Таким образом профили скорости
совпадают, если, например, различны как числа Рейнольдса, так и
шероховатости, но одинаковы касательные напряжения на обтекаемой стенке.
Многочисленные эксперименты позволяют убедиться в справедливости
этого утверждения.
На рис. 9.5 подобная универсальная зависимость построена в
логарифмическом масштабе по оси абсцисс.
Следует особо подчеркнуть, что такая универсальная зависимость не
справедлива в области, непосредственно прилегающей к обтекаемой
поверхности. В этой области турбулентные пульсации малы, а на стенке вообще
207

равны нулю, и, следовательно, трение зависит от осредненной скорости
иным образом, чем вдали от стенки.
Закон трения у стенки основан на предположении о том, что касательные
напряжения должны зависеть от и, расстояния от стенки у и параметров
ЖИДКОСТИ р И |Л.
В таком случае должна быть справедлива зависимость, записанная в
безразмерном виде:
/v), (9.25)
где их — введенная выше динамическая скорость.
Зависимость (9.25), предложенная Л. Прэндтлем, также является
универсальной. Все экспериментальные точки распределения скорости возле
гладких стенок лежат на одной кривой.
Такая зависимость распределения скорости на некотором отдалении от
стенки будет сохраняться и при наличии продольного градиента давления,
так как силы трения вблизи стенки существенно больше сил давления. Это
заключение также подтверждено многочисленными опытами.
Таким образом, во внешней части турбулентного пограничного слоя
распределение скорости описано зависимостью (9.24) в переменных: (и — ио)/их,
у/6> а во внутренней части зависимостью (9.25) в переменных: и/их, yuxlv.
Если на некотором участке пограничного слоя зависимости (9.24) и
(9.25) перекрываются, то это позволяет сделать важные выводы.
Перепишем зависимость (9.24) в виде
(9.26)
а зависимость (9.25) представим таким образом:
. (9.27)
Если левые части выражений (9.26), (9.27) одинаковы, то и правые части
в зоне перекрытия также должны совпадать. Для того чтобы функцию от
произведения аргументов можно было представить как сумму функций от
каждого аргумента, она должна быть логарифмической. Следовательно,
зависимость (9.27) для согласования с зависимостью (9.26) в зоне перекрытия
должна иметь вид
x = Alg(y/b)+AlgFux/v)+Bt (9.28)
где Л и Б — некоторые постоянные.
Тогда очевидно, что и зависимость (9.26) в зоне перекрытия должна быть
логарифмической функцией
(9.29)
На рис. 9.6 построена экспериментальная зависимость скорости в
турбулентном пограничном слое, обработанная в форме (9.29), причем по оси
абсцисс выбран логарифмический масштаб. Из рис. 9.6 следует, что йа
некотором участке зависимость является линейной:
u/ux=:Alg(yuxM+C. (9.30)
Это означает, что зависимость скорости для внешней части пограничного
слоя, представленная формулой (9.24), на этом участке может быть
представлена формулой (9.25), справедливой только для внутренней части
пограничного слоя. Отметим, что перекрытие этих зависимостей осуществляется
не обязательно на всем прямолинейном участке, а возможно только на
какой-то его части.
208

2'10
Рис. 9.6. Экспериментальная зависимость
распределения скорости в турбулентном
пограничном слое
Постоянные в формуле (9.30) и1а*
получены из обработки
экспериментальных результатов:
по данным Клаузера:
А =5,65; С = 4,90;
по данным Коулса:
А =5,75, С=5,Ю.
(9.31)
Расхождение можно
объяснить тем, что зависимость (9.30)
отклоняется от прямолинейной
очень плавно и участок
перекрытия выделяется недостаточно
четко.
Рассмотрим теперь более подробно закон распределения скорости в
турбулентном пограничном слое. Для того чтобы показать детально
распределение, скорости вблизи от стенки, по оси абсцисс выбран логарифмический
масштаб.
Из рис. 9.6 очевидно, что действительно можно выделить три указанные
выше характерные зоны.
На очень близком расстоянии от стенки (участок ab) течение является
ламинарным и эта область называется вязким подслоем. Толщина вязкого
подслоя ух такова, что число Рейнольдса на его внешней границе u^Jv «
« 150. При большей толщине ламинарное течение вблизи стенки
неустойчиво из-за пульсаций во внешней основной части турбулентного слоя.
Число Рейнольдса, подсчитанное по всей толщине турбулентного пограничного
слоя, может быть порядка Re = uoblv = 1500... 150 000. Следовательно,
относительная толщина вязкого подслоя лежит в пределах yjb ^ 0,0J...
0,001.
В тонком вязком подслое можно практически принять, что касательное
напряжение постоянно и равно напряжению на стенке и тогда из формулы
(8.1) следует, что скорость в нем меняется линейно. Воспользовавшись
обозначением (9.17), эту линейную зависимость можно представить в форме
(9.25):
Эксперимент на рис. 9.6 подтверждает эту зависимость для участка ab
(напомним, что для оси абсцисс применен логарифмический масштаб).
Участок be на рис. 9.6 соответствует логарифмическому закону
распределения скорости (9.30). Протяженность этого участка @,1...0,2N.
На этом участке должен быть справедлив закон трения Прандтля,
пригодный вблизи стенки, но вне ламинарного подслоя. Этот закон трения
соответствует логарифмическому распределению скорости, что и подтверждено
экспериментом.
На участках cd (см. рис. 9.6) протяженностью @,8...0,9)8 распределение
скорости во внешней части пограничного слоя отклоняется от
логарифмического закона. Участки cd в переменных и/их, yux/vt как уже отмечалось,
изображаются не единой униэерсальной кривой, а серией кривых,
зависимых от т0 (а в общем случае и от продольного градиента давления).
Из рассмотрения физической картины течения в турбулентном слое
можно сделать важные практические выводы.
209

Из факта перекрытия на некотором участке зависимостей (9.24) и (9.25),
который отнюдь не был очевидным, следуют формулы (9.28) и (9.29), из
которых можно получить формулу для местного касательного напряжения
на стенке. Вычтем из зависимости (9.28) зависимость (9.29) и получим
u/Ux = AlgFthM+B. . (9.32)
Исключим их через Tq с помощью обозначения (9.17) и введем безразмерное
касательное напряжение и число Рейнольдса по формулам:
re=xe/piijf Reft = H08/v. (9.33)
Тогда из формулы (9.32) следует зависимость для местного касательного
напряжения на стенке плоской пластины
^A\gRe6+B, (9.34)
где А — 5,65, В ~ 4,90 для гладкой пластины.
Далее можно заключить, что распределение скорости вблизи стенки
обладает универсальностью даже при наличии градиента давления, так как
там силы трения много больше сил давления. В противоположность этому
величина градиента давления сильно влияет на форму эпюры скорости
внешней части пограничного слоя.
Разберем теперь вопрос о влиянии шероховатости стенки на профиль
скорости в пограничном слое и на касательное напряжение.
Очевидно, что при любой чистоте обработки поверхность стенки не может
быть сделана абсолютно гладкой. В данном случае гладкой (или, точнее,
гидравлически гладкой) называют поверхность, если бугорки шероховатости
столь малы, что не влияют на форму эпюры скорости и касательное
напряжение.
Турбулентный пограничный слой особенно чувствителен к величине
шероховатости, так как вязкий подслой весьма тонок.
Следует ожидать, что вблизи стенки распределение скорости подчинено
зависимости, включающей два безразмерных аргумента:
x^g(yux/vt uxh/v), (9.35)
где uxh/v — число Рейнольдса, подсчитанное по величине бугорков
шероховатости h. Если uxh/v меньше определенной величины, то бугорки не
выступают за вязкий подслой и не влияют на течение в слое и поверхность
следует считать гидравлически гладкой. В этом случае зависимость (9.35)
переходит в зависимость (9.25).
При увеличении uxh/v на течение вблизи стенки в зависимости (9.35)
влияют оба аргумента.
Наконец, если uxh/v превосходит определенную величину, вязкий
подслой разрушается и бугорки сами индуцируют турбулентные пульсации.
Такой режим называют течением с полным проявлением шероховатости и для
него вместо (9.35) должна быть справедлива зависимость, в которую явно
не входит вязкость жидкости:
u/ux=g[(yux/v) (v/hux)\ =g(y/h) (9.36)
и которая в дальнейших выкладках заменит формулу (9.25). Закон дефекта
скорости (9.24) сохраняет свой вид, так как для внешней части
турбулентного слоя существенна только величина касательного напряжения на стенке.
210

Повторив приведенные выше рассуждения об области перекрытия
законов стенки и дефекта скорости, приходим к выводу, что функциональная
зависимость (9.36) также должна быть логарифмической:
ufux - A lg (у/6) + A lg (y/h) + Вг. (9.37)
Эта зависимость справедлива, как и ранее, только в области, примыкающей
к стенке, причем постоянная А имеет то же числовое значение, что и для
^гладкой стенки. ;
Вычтем из уравнения (9.37) уравнение (9.29) и воспользуемся
обозначениями (9.17) и (9.33). В результате получим закон для местного касательного
напряжения на плоской пластине для режима течения с полностью
выраженной шероховатостью:
l/YT0=AlgF/h)+Bv (9.38)
Если шероховатость поверхности однородна, то, как показывают
опыты, такая поверхность может считаться гидравлически гладкой при
huxlv <C 4. Режим течения с полным проявлением влияния шероховатости
возникает примерно при hu%h >50. Толщина вязкого подслоя, в котором
справедлив закон ламинарного течения, примерно равна ЬЛА1Лих1\ « 12.
Тогда очевидно, что при Шлам < 1/3, т. е. когда бугорки шероховатости
в три раза меньше толщины подслоя, стенку можно считать гидравлически
гладкой. Если размер бугорков шероховатости существенно больше
толщины подслоя /1/6лам >4, то подслой разрушается и прямого влияния
вязкости на сопротивление трения не обнаруживается.
Хорошее подтверждение универсальности зависимости (9.24) получено
при обработке экспериментов с течением в трубах. Известно, что при
турбулентном течении в трубах с разной шероховатостью стенок эпюры
скоростей различны и соответственно различны касательные напряжения на
стенках. Если перестроить опытные зависимости в координатах, диктуемых
формулой (9.24), то они все совместятся в одну универсальную кривую
распределения скоростей (за исключением области вязкого подслоя). Эта
зависимость в данном случае оказывается весьма близкой к логарифмической.
При аналогичной обработке измерений, проведенных с турбулентными
слоями на пластинах (без градиента давления), также получается
универсальная зависимость, однако во внешней части слоя уклоняющаяся от
логарифмической.
Универсальность закона стенки (9.19) также подтверждена различными
экспериментами.
Опыты подтверждают, что при изменении шероховатости стенки эпюра
скоростей сдвигается только вследствие изменения коэффициента Вг.
Закон стенки в целом хорошо согласуется с эпюрой скоростей в трубе,
но в применении к трубам следует положить «толщину пограничного слоя»
равной радиусу трубы.
Для гладких труб при больших числах Re = ad/v справедлив
универсальный закон распределения скоростей:
u/ih = 5,75 lg (yux/v) + 5,5, (9.39)
где у — текущее значение радиуса.
Запишем формулу (9.39) для центра трубы:
uju -5,75 ig(atd/2v) + 5,5, (9.40)
где и0 — скорость в центре трубы; d — диаметр трубы,
211

Из формул (9.39), (9.19) получим закон распределения скорости в виде
uo—u^uxlg(d/2y). (9.41)
При расчете сопротивления труб удобно иметь дело со среднерасходной
скоростью, так как ее легко подсчитать по расходу жидкости:
_ d/2
й = -4г Г 2nyudy. (9.42)
о
Из формул (9.41), (9.42), опустив простые вычисления, получим выражение
для средней скорости
п=ио—3,75их. (9.43)
Исключив скорость в центре трубы с помощью формулы (9.40), найдем из
(9.43) окончательное выражение для средней скорости
и = их [5,75 lg (lit dp) + 1,75]. (9.44)
Из этой формулы можно получить зависимость, выражающую
универсальный, закон сопротивления при турбулентном течении в гладких
трубах.
Разность давлений на участке трубы длиной I уравновешена
касательными напряжениями на стенке трубы
jTd/T0 = (Pl— p2) nd2/4. (9.45)
Введем безразмерный коэффициент сопротивления |, определенный через
среднюю скорость жидкости (9.42):
JL РбУ . (9.46)
Из формул (9.45), (9.46) следует зависимость между касательным
напряжением и коэффициентом сопротивления
то = |р(«J/8. (9.47)
Заменим в выражении (9.44) динамическую скорость через касательное
напряжение по формуле (9.17):
Исключив из этого выражения т0 с помощью формулы (9.47) и
подсчитав численные коэффициенты, получим
Общий вид этой зависимости очень хорошо подтвержден многочисленными
экспериментами, причем наилучшее согласие наблюдается, если несколько
изменить числовые коэффициенты:
l//!=21g(ReVT)-0,8, Re= Jid/v. (9.48)
Эта формула выражает универсальный закон сопротивления для гладких
труб (закон Прандтля). Некоторые значения коэффициента сопротивления
для гладких труб, подсчитанные по формуле (9.48), приведены ниже:
Re
|
212
.... 5-Ю3
.... 0,0374
10*
0,0309
105
0,0180
10е
0,0116
107
0,0081

X 1
V
\
W
10*
Re
Рис. 9.7. Зависимость сопротивления гладких труб от
числа Рейнольдса при различном течении:
/ — ламинарном, формула (8.16); 2 — турбулентном,
формула (9.48); 3 — турбулентном, формула (9.79)
Эксперименты
подтверждают, что формула (9.48)
применима также для
расчета сопротивления в
трубах и при течении
сжимаемой жидкости с большими
дозвуковыми скоростями.
Это объясняется тем, что
сопротивление зависит
только от числа Re [см.
формулу (9.48)], значения
которого на основании
уравнения неразрывности
не изменяются вдоль
трубы и при течении
сжимаемой жидкости
(произведение плотности и скорости
остается постоянным).
На рис. 9.7 даны
опытные значения
коэффициента сопротивления гладких
труб в зависимости от
числа Re, подсчитанного по средней скорости. Прямая I соответствует
ламинарному течению и построена по теоретической формуле (8.16). Кривая 2
соответствует турбулентному течению в трубе и построена по формуле
(9.48). Теоретические кривые хорошо подтверждаются экспериментальными
исследованиями, проведенными многими авторами. Эксперимент также
показывает, что .между режимами ламинарного течения и развитого
турбулентного течения в трубах существует некоторая переходная область,
соответствующая числам Re = ud/v примерно 2,3 • 103...8 • 103.
Приведенные коэффициенты сопротивления относятся к достаточно
длинным трубам, так как на начальном участке при входе в трубу эпюра
скоростей изменяется.
Выше было показано, что логарифмический закон распределения
скорости в трубах позволяет получить универсальный закон сопротивления,
пригодный для произвольно больших чисел Re. Очевидно, желательно
получить такой же закон для сил турбулентного трения на пластине.
• Необходимо напомнить, что между распределением скорости в трубе и
в пограничном слое на пластине нет полной аналогии. На внешней части
пограничного слоя распределение скорости отклоняется от распределения
скорости в трубе.
Исходя из логарифмического закона распределения скорости в
пограничном слое, Т. Карман получил формулу для местного коэффициента трения:
l/j/CTP-4,151g(RexCTP)+l,7, Стр =
(9.49)
в которой Re^ = u()x/v — текущее значение числа Re.
Для подсчета полной силы трения удобнее рассматривать средний
коэффициент трения Стр = 2FTP/pWQ /?/, где FTl) — полная сила трения на
длине пластины /; Ъ — ширина пластины. Для определения этого
коэффициента трения обычно используют формулу Кармана—Шёнхера:
1/|/Стр -4,1
(9.50)
213

или интерполяционную формулу Шлихтинга, которая удобнее тем, что в
ней средний коэффициент трения явно выражен через число Re,
подсчитанное по длине пластины:
CTP^0,455/(lgRe,J.*8. (9.51)
9.3. ТРЕНИЕ ПРИ ТУРБУЛЕНТНОМ ТЕЧЕНИИ
В разд. 9.2 получены закон распределения скорости и закон
трения для частного случая, когда скорость не изменяется вдоль потока.
Однако в большинстве технических задач скорость и давление меняются
вдоль обтекаемого тела и это может существенно изменять характеристики
турбулентного пограничного слоя, возникающего на поверхности. Общей
теории турбулентных течений не существует и поэтому прибегают к
полуэмпирическим теориям.
Для расчета турбулентного пограничного слоя необходимо иметь закон
трения, применяемый в данных условиях.
Согласно теории Рейнольдса касательное напряжение при турбулентном
течении
' x==_pu'v\ (9 52)
Величины пульсаций скорости, входящие в это выражение, неизвестны
и могут быть получены только путем специальных измерений. Поэтому для
практических расчетов необходимо выразить касательное напряжение через
осредненную скорость основного потока.
Вернемся к рис. 9,2, на котором изображена эпюра скоростей в
пограничном слое. Пусть благодаря турбулентным пульсациям малая жидкая
частица из слоя (у — /) попадает в слой у, не смешиваясь по пути. Тогда
скорость этой частицы будет меньше скорости слоя на величину
Аи=и(у—/)—и(у)~1ди/ду.
Считаем, что эта разность скоростей и представляет собой осредненную
по времени абсолютную величину пульсации
\и\=1 — . (9.53)
Величину /, имеющую размерность длины, называют путем
перемешивания.
Порядок величины поперечной пульсации скорости v' должен быть
таким же, как и продольной и\ как это следует из уравнения
неразрывности, записанного для пульсационных скоростей. Тогда на основании
выражения (9.53) можно записать аналогичную зависимость для поперечной
пульсации скорости
\l'\=$lJ!L9 (9.54)
где р — некоторое число порядка единицы.
Частица попадает из слоя (у — /) в слой у благодаря положительной
пульсации у' >0, но вносит туда отрицательную пульсацию и1 < 0. И
наоборот, частица попадает из слоя {у \- I) в слой у из-за возникновения
отрицательной пульсации vr < 0, но вносит в новый слой положительную
пульсацию и' >0.
Следовательно, осредненное по времени произведение продольных и
поперечных пульсаций не равно нулю и отрицательно. Тогда из выражений
214

(9.52), (9.53), (9.54) следует формула Л. Прандтля для турбулентного
трения
Т =1
Здесь множитель р включен в /, которое пока также неизвестно. Формулу
(9.55) правильнее было бы написать в виде
(9.56)
du
dy
du
dy
так как касательное напряжение имеет тот же знак, что и градиент скорости.
Наводящие соображения о структуре формул турбулентного трения
могут быть получены также с помощью теории подобия. Для пояснения
рассмотрим сначала задачу о законе трения при ламинарном течении, для
которой ответ известен. Пусть вязкая жидкость движется параллельными
слоями вдоль твердой стенки. Можно ожидать, что безразмерное касательное
напряжение т/рм2 между слоями жидкости зависит от кинематической
вязкости v, скорости течения и и градиента скорости поперек течения du/dy,
т. е. скорости деформации. Из размерных аргументов можно составить один
безразмерный критерий и искать зависимость в виде
/) /9 57)
ри2 ' { Ф dy )' , V • /
Логично считать, что само касательное напряжение не зависит от скорости
течения, а зависит только от скорости деформации сдвига. Тогда из (9.57),
если принять функцию т пропорциональной аргументу, следует известный
закон трения Ньютона:
который, как известно, хорошо подтвержден опытом.
Безразмерный аргумент, входящий в формулу (9.57), можно назвать
локальным числом Рейнольдса (или, точнее, величиной, обратной
локальному числу Рейнольдса, что не существенно), так как он представляет собой
комбинацию типа ul/v.
Переходя к поиску формулы для закона трения в турбулентном
пограничном слое, можно ожидать, что безразмерное касательное напряжение
также зависит от этого и аналогичных ему локальных чисел Рейнольдса,
в которые входят производные высших порядков:
j_Ju_ J^__rfi« (958)
и2 dy и3 dy2
Однако при турбулентном течении, как уже было отмечено, напряжения
определяются макроскопическими пульсациями скорости 1см. формулу
(9.52I и поэтому в качестве аргумента следует ввести также некоторую
характерную длину /. Таким характерным размером может быть, например,
расстояние от стенки, так как очевидно, что величина макроскопических
пульсаций скорости зависит от этого расстояния. В таком случае следует
добавить еще один безразмерный аргумент: число Рейнольдса,
подсчитанное по характерному размеру lu/v.
Поэтому следует ожидать, что безразмерное напряжение при
турбулентном трении должно быть выражено зависимостью
=/р-, -V-?-. 4 ТТ. •••)•
\ v и2 dy и3 dy2 ]
215

Эта функциональная зависимость согласуется с соображениями теории
размерности, но, конечно, оставляет большой произвол при выборе
окончательной формулы. Для получения той или иной формулы необходимы
дополнительные физические соображения о природе турбулентного трения.
Прежде всего отметим, что трение зависит не от скорости движения
жидкости, а от скорости деформации, т. е. от производной скорости по
координате.
Далее отметим, что хотя турбулентное течение возникает, конечно, при
наличии вязкости, однако касательные турбулентные напряжения вызваны
макропульсациями. В этом случае в развитом турбулентном течении можно
пренебречь влиянием вязкости, т.е. переносом количества движения при
хаотическом движении молекул.
Рассматривая в зависимости (9.59) в качестве нового безразмерного
аргумента произведение первых двух аргументов, исключим вязкость и
получим
т __ с/ / du
ри2 \ и dy
Касательное напряжение не будет зависеть от скорости, если положить,
что функция пропорциональна квадрату аргумента:
(9.60)
где х — коэффициент пропорциональности, т. е. некоторая постоянная,
которую можно найти из опыта.
Физическое обоснование этой формулы было дано выше.
Другую формулу для турбулентного трения, в которую не входит
вязкость, можно получить, если скомбинировать второй и третий аргументы в
исходной зависимости (9.59):
«Г 1 (du/dy)* 1
, [ и (d*u/dy*) ]
ри*
Чтобы исключить скорость, запишем формулу в виде
т = хр ldu/dy)* {961
Эта формула имеет и более тонкое физическое обоснование, связанное с
предположением о подобии поля скоростей, выдвинутым Т. Карманом.
Формула (9.60) более проста, чем (9.61), и поэтому используется
значительно чаще при расчете турбулентных течений в трубах, пограничных
слоях, струях, следах.
Очевидно, что из общей функциональной зависимости (9.59) можно
получить и другие формулы для турбулентного трения. Основная сложность,
конечно, заключается в том, что при этом должна быть предложена
правдоподобная и достаточно общая гипотеза, хорошо подтверждаемая опытом.
Наибольшее распространение получила формула (9.55), так как она
проста, и расчеты, построенные на ее основе, обычно достаточно хорошо
согласуются с экспериментом.
Путь перемешивания /, введенный Л. Прандтлем, имеет ясный
физический смысл — он характеризует осредненный размер пути, на котором
пульсирующие частицы сохраняют свою^ скорость. Кроме того, и это особенно
важно, оказалось, что это довольно устойчивая функция, поведение
которой можно предсказать, сообразуясь с конкретной задачей.
216

Зависимость пути перемешивания от расстояния до стенки определялась
обработкой опытных результатов. Прежде всего следует отметить, что возле
стенки @ < у/Ь < 0,2) путь перемешивания линейно зависит от расстояния
до стенки. У самой стенки / = 0, так как там отсутствуют,пульсащш
скорости. На этом участке принимают
/ = ху, х;=0,4. (9.62)
Если подставить эти значения в формулу (9.55), то получим, что в
турбулентной части пограничного слоя вблизи стенки Справедлива зависимость
dy ку
Если положить, что касательное напряжение вблизи стенки меняется
мало, то эта формула совпадает с выведенной ранее из соображений
подобия зависимостью (9.16), причем А = 1/х.
Во внешней части пограничного слоя наблюдается приблизительное
постоянство пути перемешивания, хотя экспериментальные точки сильно
разбросаны.
Отметим, что этот разброс не сильно сказывается на результатах
расчетов, так как возле внешней границы пограничного слоя мал градиент
средней скорости, квадрат которого входит в основную формулу (9.55).
Другие опыты показывают, что путь перемешивания слабо зависит от
числа Re и продольного градиента давления.
Для пути перемешивания известен ряд зависимостей, аппроксимирующих
опытные результаты. Так для не очень точных расчетов можно применять
формулу (9.62) поперек всего пограничного слоя, учитывая высказанное
ранее замечание. В более точных расчетах для внешней части слоя берут
//6 = 0,08~0,Ш или применяют формулу
//6 = 0,4^/6-0,5 (у/8)* + 0,2 (у/6K.
(9.63)
чо
¦ J
9.4. ИНТЕГРАЛЬНОЕ СООТНОШЕНИЕ ДЛЯ ПОГРАНИЧНОГО СЛОЯ
В практических расчетах обычно проводят осреднение скоростей
поперек пограничного слоя и по существу сводят задачу к одномерной. Для
этого используют так называемое интегральное соотношение для
пограничного слоя, основанное на применении законов сохранения в интегральной
форме. Для получения уравнения обычно
используют законы сохранения массы и коли- у
чества движения.
При выводе интегрального соотношения
опираются на основные свойства
пограничного слоя.
Пусть твердая поверхность обтекается
вязкой жидкостью при достаточно большом
числе Re, так что можно выделить
относительно тонкий пограничный слой. Течение
считаем плоским, установившимся, а жид-
кость несжимаемой. Направим ось абсцисс 'У/?/у/у/1
вдоль обтекаемой поверхности (рис. 9.8),
которая в общем случае может быть
криволинейной, но при условии, что радиус кривизны
много больше толщины пограничного слоя.
Пусть линия АВ изображает внешнюю гра-
У///////////
'3/////
рис 9 8 -Течение через элемен-
тарный объем в пограничном
слое
217

ницу пограничного слоя, т. е. границу, на которой можно пренебречь
силами трения.
Примерная эпюра скоростей и(х, у) в пограничном слое начерчена для
сечения 12. Скорость на обтекаемой стенке равна нулю, так как жидкость
прилипает к стенке. На внешней границе скорость равна скорости внешнего
потенциального потока ио(х). Скорости можно считать параллельными
твердой стенке, так как в разд. 8.3 было доказано, что проекции скорости по оси
ординат очень малы.
Выделим элементарный объем 1234 (рис. 9.8), ограниченный двумя
поперечными сечениями, участком твердой стенки и внешней границей. Ввиду
того, что рассматривается плоское сечение, размер, перпендикулярный
чертежу, можно считать равным единице.
Через сечение 12 внутри объема втекает в единицу времени масса
жидкости
J pad*/,
где Цх) — текущая толщина пограничного слоя.
Этот интеграл является функцией верхнего предела, т. е. зависит
только от х.
Расход жидкости через бесконечно близкое сечение 34 отличается от
расхода через сечение 12 на величину
б
— [pudydx, (9.64)
dx J
о
которая найдена как приращение записанного интеграла. Таким образом,
через правое сечение вытекает больше, чем втекает через левое, если, как
это принято, вытекающей массе присвоен знак плюс. Так как жидкость
несжимаема, то масса жидкости в выделенном объеме неизменна.
Недостающая масса жидкости должна втекать внутрь объема через верхнюю границу
пограничного слоя 24. Следовательно, через грань 24 втекает в единицу
времени масса, равная выражению (9.64), но взятому со знаком минус.
Применим теперь теорему о количестве движения. Количество движения
в проекции на ось абсцисс, которое вносит поток в единицу времени через
грань 12:
б
о
Тогда разность количеств движения, выносимого через грань 34 и вносимого
через грань 12:
— [pu2dydx. (9.65)
dx J
о
Количество движения будет внесено внутрь объема также и через верхнюю
грань вместе с втекающей жидкостью. Это количество движения равно
втекающей в единицу времени через верхнюю грань массе (9.64), умноженной
на скорость жидкости и0 (знак минус отмечает, что это количество движения
внесено в объем):
ь
—«0— [pudydx. (9.66)
dx J
о
218

Таким образом, полное изменение количества движения в единицу
времени и в проекции на ось абсцисс равно сумме выражений (9.65) и (9.66):
б б
— f pu2dydx ~-uQ—[pudydx. (9.67)
dx J dx J
о о
Подсчитаем силы, действующие на выделенный элемент жидкости.
Разность сил давления, действующих на левую и правую грани выделенного
элемента, равна (величинами второго порядка малости пренебрегаем)
= —Ыр—pdb. (9.68)
При подсчете сил давления использовано доказанное условие, что
давление поперек пограничного слоя не меняется.
Сила давления, которая действует на верхнюю грань элемента, также
дает проекцию на ось абсцисс, так как эта грань наклонена:
pdb. (9.69)
На нижнюю грань элемента действует сила трения, направленная
против движения (знак минус):
—x{)dx, (9.70)
где to(x) — касательное напряжение между потоком и стенкой, что
отмечено индексом нуль (у = 0).
Сила трения на верхней грани элемента согласно определению
пограничного слоя отсутствует. Таким образом, полная сила, действующая на
выделенный элемент жидкости, равна сумме выражений (9.68), (9.69), (9.70):
— bdp—T0dx. (9.71)
Приравняв изменение количества движения в единицу времени (9.67)
силе (9.71), получим интегральное соотношение Кармана для
пограничного слоя:
р ±- f и« dy-pa,, -!L-\udy= _ т„ - 8-^. (9.72)
dx J dx J dx
о о
Прежде всего подчеркнем, что при выводе интегрального соотношения
(9.72) не было сделано никаких предположений о законе трения и о форме
эпюры скоростей. Поэтому полученное уравнение пригодно как для расчета
ламинарного, так и турбулентного пограничных слоев.
Остановимся на особенностях решения интегрального соотношения (9.72).
При расчете считаем известным закон распределения скорости по внешней
границе пограничного слоя и0 = и(х). Это распределение можно найти,
решив задачу обтекания тела потенциальным потоком идеальной жидкости.
Ввиду того, что пограничный слой очень тонок, найденное распределение
скорости можно отнести к внешней границе слоя.
В принципе, после расчета пограничного слоя можно ввести поправку
на фиктивное искажение формы обтекаемого тела из-за наличия
пограничного слоя. Для этого необходимо подсчитать толщину вытеснения (см.
разд. 8.6) и соответственно этому изменить контур обтекаемого тела. Во
многих случаях этой поправкой пренебрегают.
По распределению скорости на внешней границе пограничного слоя
можно найти распределение давления р(х). Давление следует определять с
помощью уравнения Бернулли, которое можно записать для внешней границы
219

0.8
0,6
О,*
0,2
у
2.
У
/
-г
/
—
0,2
0,*t 0,6 0,8 y/J
Рис. 9.9. Сравнение профилей
скорости в пограничных слоях:
/ — ламинарном; 2 — турбулентном
и/ио пограничного слоя, так как по
определению на этой границе можно
пренебречь трением. Напомним, что давление
поперек слоя не изменяется.
Искомыми функциями являются
толщина пограничного слоя Ъ(х) и
касательное напряжение на стенке то(лс).
Однако в уравнение (9.72) входит,
кроме этого, неизвестное распределение
скоростей в поперечных сечениях
пограничного слоя и(х, у). Для того чтобы
воспользоваться уравнением (9.72),
необходимо задать это распределение из
дополнительных соображений,
согласуясь с характером задачи и
граничными условиями для скорости на
внутренней и внешней границах
пограничного слоя.
При задании эпюры скоростей в
пограничном слое должно быть учтено,
является ли он ламинарным или турбулентным. Типичные профили
скорости для ламинарного — /и турбулентного — 2 слоев приведены на
рис. 9.9 для постоянной скорости внешнего потока.
Скорость в турбулентном пограничном слое возле стенки возрастает
значительно более интенсивно, чем в ламинарном. Это связано с тем, что
турбулентное трение возле стенки меньше, чем на некотором отдалении от нее.
Соответственно этому градиент скорости по нормали к стенке при отдалении
от нее уменьшается [см. формулу для турбулентного трения (9.55) и
выражение для длины пути перемешивания (9.62)].
На форму эпюры скоростей влияет также продольный градиент
давления. Для ламинарного слоя этот вопрос подробно рассмотрен в гл. 8. Там
же обсуждены граничные условия на внешней и внутренней границах
слоя.
Для решения задачи необходимо также принять из дополнительных
соображений закон трения, т. е. связь между касательным напряжением и
поперечным градиентом скорости в пограничном слое.
Для ламинарного слоя это, очевидно, закон трения Ньютона (8.1). Для
турбулентного трения применяют, как будет показано далее,
полуэмпирические формулы.
Подытоживая сказанное., можно отметить, что функции, входящие в
интегральное соотношение, можно разбить на три группы.
1. Заданные: ио(х), р(х).
2. Искомые: to(jc), 6(*).
3. Выбираемые из дополнительных соображений: и(х, у)у т(ху у).
Закон трения, входящий в третью группу, может быть задан различным
образом. Для ламинарного течения — это общий закон трения,
выраженный через скорость деформации сдвига. Для турбулентного трения может
быть задано касательное напряжение на обтекаемой поверхности,
выраженное через толщину пограничного слоя.
Преобразуем уравнение (9.72) к виду, более удобному для расчета, имея
в виду привести его к обыкновенному дифференциальному уравнению
относительно искомой функции. В качестве такой функции удобно выбрать
толщину потери импульса, введенную в подразд. 8.6,
220 v

Воспользовавшись уравнением Бернулли на внешней границе
пограничного слоя, напишем
-*—р*-*-. (9.73)
Поскольку скорость на внешней границе слоя не зависит от у, ее можно
в формуле (8.81) вынести за знак интеграла:
б
Wo81=ao6 — §udy. (9.74)
Из уравнений (9.73), (9.74) следует
6-
Исключим
в таком виде:
6
d {и2
dx У
0
dp du0 с
dx dx v
в интегральном
6
! A it и I tiA
dx J
° dx
соотношении
6
ti ° ( ttdt
i/i uuy
0
(9.
72)
dx
dpldx
9
6
- Г udy.
о
и представим его
и б dUo
Второй и третий члены можно записать как производную от произведения
и тогда, объединив их с первым интегралом, получим
dx I J
J p dx
Воспользовавшись формулой (8.82), можно записать
Введем обозначение
Я = б!/62. (9.76)
Эта характеристика зависит от формы эпюры скоростей в пограничном слое
и ее называют формпараметром.
Продифференцировав произведение в скобках в уравнении (9.75) и
исключив во втором члене 6j с помощью формпараметра, получим
окончательное уравнение для толщины потери импульса
dx V u0 dx pul V '
Точно таким же способом подобное уравнение может быть выведено для
пограничного слоя в сжимаемой жидкости
d6 A* (9.78)
dx u0 dx pul
где Mft = uola — число Маха на внешней границе пограничного слоя.
9.5. РАСЧЕТ ПЛОСКИХ ТУРБУЛЕНТНЫХ ПОГРАНИЧНЫХ СЛОЕВ
Расчет турбулентных пограничных слоев является трудной
задачей, которую нельзя считать полностью решенной. Сложность Заключается
в том, что нет теоретически полностью обоснованного метода расчета трения

при турбулентном течении. Даже если бы такой метод существовал, то все
равно точный расчет в общем случае был бы весьма труден, так как
турбулентный пограничный слой является составным, т. е. имеет ламинарный
подслой и переходную область (см. подразд. 9.1).
Вместе с тем это практически очень важная задача, без решения которой
невозможно надежное проектирование ряда технических объектов.
Поэтому в настоящее время для расчета привлекают эмпирические и
полуэмпирические зависимости, которые дают возможность достаточно надежно
подсчитать силы сопротивления в ограниченном диапазоне изменения чисел
Рейнольдса.
Ограничимся здесь применением наиболее простого способа из-за его
наглядности и так как он позволяет получить в общем правильные оценки
суммарных характеристик в основных задачах теории турбомашин.
При экспериментальном исследовании турбулентного течения в трубах
и пограничных слоях было замечено, что профили скорости и законы
сопротивления могут быть с достаточной степенью точности представлены
степенными зависимостями. Было также обнаружено, что между течением в
трубе и в плоском пограничном слое существует некоторая аналогия.
Эквивалентными размерами являются радиус трубы и толщина пограничного
слоя, а эквивалентными скоростями — скорость в центре трубы и на
внешней границе пограничного слоя. Следует подчеркнуть, что эта аналогия
является приблизительной.
Измерение потока в трубе значительно проще, чем в пограничном слое.
Так для измерения сопротивления достаточно измерить разность
статических давлений между двумя сечениями трубы, что может быть выполнено
просто и с большой точностью.
Степенной закон сопротивления для труб предложил Г. Блазиус A911 г.),
обработав экспериментальный материал на основе теории подобия:
I -0,3164 Re-1/4, Re=ud/v. (9.79)
Расчеты по формуле (9.79) хорошо совпадают с экспериментом (см.
рис. 9.7) в диапазоне 3 • 103 < Re < 105, причем число Рейнольдса
подсчитано по средней скорости.
Из формул (9.47), (9.79), исключив ?, можно найти касательное
напряжение на стенке трубы
т0 - 0,03955р« • Re-» /4. (9.80)
Имея в виду использовать аналогию между течением в трубе и noi ранич-
ном слое, выразим в формуле (9.80) диаметр через радиус, а касательное
напряжение заменим по формуле (9.17). Тогда получим
Средняя скорость отличается от скорости в центре трубы только
числовым множителем и поэтому аналогичную формулу можно записать для
(9.81)
Этот закон справедлив и для распределения скорости по радиусу трубы
(9.82)
что подтверждено независимыми экспериментами. Расхождение
наблюдается только в очень тонком вязком подслое и вблизи оси трубы, что
объяснимо и существенного значения не имеет.
222

Из формул (9.81), (9.82) следует такая запись зависимости распределения
скорости в поперечном сечении трубы:
Полученные формулы просты и в то же время хорошо аппроксимируют
основные зависимости. Однако они не совпадают с универсальными (см.
разд. 9.2) и поэтому все числовые коэффициенты хотя и являются довольно
стабильными, но все же зависят от Re.
Вместо (9.82) вводят также более общую зависимость для распределения
скорости
@/О|/я- (9.83)
Ниже приведены значения я, полученные в опытах И. Никурадзе для
различных чисел Re = ud/v:
Re 4-Ш3 2,3-10* 1,1-10* 1,1-10е 2,0-106 3,2* 10е
п . 6,0 6,6 7,0 8,8 10,0 10,0
п/и0 0,791 0,807 0,817 0,850 0,865 0,865
Для расчетов необходимо отношение средней скорости к максимальной,
которое можно найти с помощью формулы (9.83):
Расчетные значения, полученные по этой формуле, приведены в последней
строке. Для сравнения заметим, что при ламинарном течении в трубе и/и0 =
= 0,5, т. е. турбулентному течению соответствует значительно более полная
эпюра скорости.
Для использования аналогии между течением в трубе и пограничном слое
выразим правую часть формулы для касательного напряжения (9.80) через
скорость в центре трубы и ее радиус. С помощью приведенных значений для
п получим новый численный коэффициент в формуле касательного
напряжения, записав вместо радиуса толщину пограничного слоя:
(9.84)
Распределение скорости поперек турбулентного пограничного слоя
следует взять по аналогии с формулой (9.83):
иК~(у!Ьуп. (9.85)
Рассмотрим на основе этих данных расчет турбулентного пограничного
слоя на плоской пластине, обтекаемой несжимаемой жидкостью. Поскольку
в данном случае uQ = const, то интегральное соотношение (9.77) примет вид
d62/dx =то/(ри1). (9.86)
Выразим толщину потери импульса через физическую толщину
пограничного слря с помощью формул (8.82), (9.85). Опустив простые вычисления,
получим б2 =. 78/72. Запишем формулу (9.84) через толщину потери
импульса, пересчитав численный коэффициент:
то-0,0130ра>/(МоI1/4. (9.87)
Заменив правую часть уравнения (9.86) с помощью формулы (9.87) и отделив
переменные, получим
?4^ 0,0130 (v/woI/4.
223

После интегрирования и простых преобразований найдем
б2 = 0,0370* [ v/(iio x)]1 'ъ. (9.88)
Здесь принято, что турбулентный пограничный слой возникает на передней
кромке пластины и поэтому постоянная интегрирования принята равной
нулю.
Для физической толщины пограничного слоя из формулы (9.88) получим
б = 0,380* [v/(w0 x)Y /5. (9.89)
Толщина турбулентного пограничного слоя растет пропорциональн9
степени 4/5, т. е. значительно быстрее, чем ламинарного слоя, для которого
показатель степени равен 1!/2 (см. гл. 8). Это вызвано тем, что при
турбулентном слое трение больше, чем при ламинарном.
Исключив в формуле (9.84) толщину слоя с помощью формулы (9.89),
найдем выражение для местного касательного напряжения
т0 :=0,0297pii; [v/(iio х)]1/*. (9.90)
Полная сила трения, действующая на одну сторону пластины длиной /
и шириной Ь:
i
FTV^b ^T0dx^0fi370pulbl(v/u0iyt5. (9.91)
о
Тогда для среднего.коэффициента трения получим формулу
Стр =2FTP/pwJ &/ = 0,0742 Re,-1/5, Re,=«0//v. (9.92)
Расчеты по этой формуле хорошо совпадают с экспериментом для
гладких пластин в диапазоне 5 • 106 < Re/'< 107 при условии, что на пластине
образуется только турбулентный слой. Нижний из указанных пределов
объясняется тем, что на пластине образуется ламинарный слой, а верх->
ний — приближенностью исходной зависимости. Если в исходной
зависимости для скорости (9.85) взять показатель 1/8, 1/9 или 1/10, то полученные
формулы будут хорошо согласовываться с опытом для еще больших чисел
Re, однако будут менее точны при малых.
В большинстве случаев скорость и давление во внешнем потоке
меняются вдоль обтекаемой поверхности. Поэтому наибольший интерес
представляет расчет пограничного слоя для этих условий. Если абсолютная величина
градиента давления (особенно положительного) не очень велика, то
описанный метод может быть распространен и на этот случай.
Для большей общности выберем вместо исходной формулы для трения
(9.84) формулу
v/buory (9.93)
где Лит — постоянные, которые будут выбраны далее.
Заменим касательное напряжение через динамическую скорость по
формуле (9.17) и получим
и/их = А (их 6/v)«/<2-m>. (9.94)
Распределение скорости поперек пограничного слоя будет выражено
аналогичной формулой
и/их = А(иху/\)тН2-т1 (9.95)
Из формул (9.94), (9.95) следует
и/и0=(у/Ь)т'<0~-'пК - (9.96)
ПА

Подчеркнем, что показатели степени в формулах для распределения
скорости (9.96) и местного касательного напряжения (9.93) взаимозависимы.
Было отмечено выше, что показатель степени в формуле (9.96) зависит от
числа Re. Следовательно, от числа Re зависит и показатель степени в формуле
(9.93). - .
По выбранному закону распределения скорости (9.96) вычислим по
формуле (8.81) толщину вытеснения
6г/6=т/2, (9.97)
а по формуле (8.82) — толщину потери импульса
А-= "И2-"*) (9.98)
б 2(т+2) * К '
Формпараметр по формулам (9.76), (9.97), (9.98) зависит от выбранного в
формуле (9.93) показателя степени
(9.99)
хотя эта зависимость слабая, так как т существенно меньше 2.
Поскольку толщина потери импульса при выбранном т
пропорциональна физической толщине пограничного слоя (9.98), то исходную формулу
(9.93) можно записать так:
(9Л00)
где Ах — постоянная величина.
Подставив найденные зависимости (9.99), (9.100) в уравнение (9.77),
имеем
462 /о 2+т\ \ du0 fi __ - / у \"*
djc V 2 — т ] щ dx ' \ 62 «о /
После элементарных преобразований это уравнение примет такой вид:
dx 2—m dx
щ )
Это — линейное дифференциальное уравнение первого порядка и его
можно проинтегрировать в замкнутой форме:
^bdx\. (9.102)
' Xt /
Здесь введено обозначение безразмерных постоянных
а-{\+т)Аъ 6 =F—m)(l+m)/B—m). ч (9.103)
Постоянную интегрирования с следует определить по условиям, заданным
в точке х = хА.
Величина т в формуле (9.93) должна быть в пределах 1/4... 1/6, что
соответствует изменению показателя степени в формуле (9.96) в пределах
1/7...1/11.
Постоянная Ах и, следовательно, а зависят также только от т и должны
быть выбраны так, чтобы результат расчета по формуле (9.102) совпадал
с известным результатом для плоской пластины.
Для постоянного а0» положив с = 0, из формулы (9.102) получим
bz(uo62/v)m=ax
8 Зак. 2638 w 225

или после простых преобразований
К (9.103,а)
При т = 1/4 выражение (9Л03,а) можно сопоставить с формулой (9.88), в
результате имеем а = 0,03701+ш = 0,0162.
Для этого случая по формуле (9.103) получим Ь = 4,11. Округлив,
обычно принимают v
я= 0,016, 6-4.
(9.104)
Следует иметь в виду, что расчетная формула (9.102) является
приближенной, так как в ней не учтено изменение формы эпюры скорости от
градиента давления.
9.6. СОПРОТИВЛЕНИЕ. ОТРЫВ ПОГРАНИЧНОГО СЛОЯ.
КРИЗИС СОПРОТИВЛЕНИЯ ПЛОХООБТЕКАЕМЫХ ТЕЛ
При обтекании тела со скругленными кромками идеальной
жидкостью на теле имеются две точки (точки ветвления), в которых скорость
равна нулю, а давление максимально. Следовательно, при движении
жидкости вдоль поверхности тела давление сначала падает, а затем вновь
возрастает, т. е. при обтекании тела обязательно возникают диффузорные
участки (dp/dx > 0). При обтекании тела реальной, т.е. вязкой жидкостью,
в диффузорной области в некоторой точке может возникнуть отрыв
пограничного слоя от твердой стенки. Отрыв обычно приводит к нежелательным
последствиям; возрастанию сопротивления и появлению нестационарных
аэродинамических сил, вызывающих вибрацию конструкции. В связи с этим
большое практическое значение имеет оценка возможности безотрывного
обтекания и установление режимов, при которых появляется отрыв.
Отрыв потока возникает на поверхности тела и определен законом
движения пограничного слоя и, следовательно, прежде всего зависит от такого
свойства жидкости, как вязкость. Рассмотрим схему (рис. 9.10), которая
поясняет причину отрыва пограничного слоя. Пусть вязкая жидкость
движется вдоль стенки в сторону возрастающего давления. Скорость
основного потока вдоль внешней границы пограничного слоя уменьшается, так
как кинетическая энергия переходит в потенциальную. Скорость частиц
жидкости в пограничном слое уменьшается еще в большей степени, так как
там, кроме того, затрачивается дополнительная энергия на преодоление
трения. В окрестности некоторой точки А частицы жидкости вблизи стенки
будут'остановлены. Математически это означает, что в точке А при у = 0
не только и = 0, но и ди/ду = 0.
Правее точки А жидкость под
воздействием положительного
градиента давления течет в
направлении, обратном основному потоку.
Область отрыва ограничена
стенкой и линией А В,
Таким образом, отрыв
пограничного потока вязкой жидкости
может произойти там, где имеется
положительный градиент давления
(dp/dx > 0). Однако, когда
положительный градиент давления до-
-Рис. 9 10. Схема отрыва пограничного слоя статочно мал, то может и не про-
226 ч,

исходить отрыва пограничного слоя, если запаса кинетической энергий
в нем будет достаточно для преодоления диффузорной области. Следует
заметить, что отрыв зависит не только от общего запаса кинетической
энергии в слое, но и от закона трения, так как частицы вблизи стенки имеют
очень малую кинетическую энергию и могут преодолеть положительный
градиент давления благодаря силам трения между ними и внешней частью
пограничного слоя.
Турбулентный пограничный слой из-за интенсивного поперечного
перемешивания имеет более полную эпюру скорости, чем ламинарный, т. е.
обладает большим запасом кинетической энергии непосредственно вблизи
стенки. Отсюда следует тот важный вывод, что турбулентный пограничный слой
более устойчив в отношении отрыва. Другими словами, если ламинарный
пограничный слой отрывается в некоторой точке, то турбулентный
пограничный слой при сравнимых условиях оторвется в точке, лежащей ниже по
потоку, или вообще не оторвется»
Рассмотрим возможность количественной оценки условий отсутствия
отрыва пограничного слоя.
Следует иметь в виду, что расчеты вблизи точки отрыва, если он
действительно происходит, нельзя производить с помощью теории пограничного
слоя, так как там нарушается основное предположение о малости
поперечной скорости.
Ламинарный пограничный слой. Точка отрыва, как было указано,
определена условием
~) -0, (9.105)
ду /у=.= о
Отсюда следует, что касательное напряжение на стенке в точке отрыва
равно нулю. Воспользовавшись условием (9,105) и представлением эпюры
скоростей в ламинарном слое полиномом по формуле (8,77), получим значение
параметра Л в точке отрыва:
-4. (9,106)
д 4.
v dx [iu0 dx
Следует иметь в виду, что это грубая оценка. Другие расчетные методы
дают большие по абсолютной величине значения параметра при отрыве.
Вообще все оценки условия отрыва по приведенному параметру не могут
быть достаточно точными. Из решения Фокнера и Скэн (см. подразд, 8,4)
можно сделать вывод, что ламинарный пограничный слой отрывается при
очень малом положительном градиенте „давления. При степенной
зависимости и0 = Д>~0'0904 уже наступает отрыв.
В точке отрыва пограничного слоя принимают
р«| dx u0 dx
Re3 =к uQ Sj/v.
Для ламинарного слоя по различным данным/(Re2) = @,06...0,)$
Турбулентный пограничный слой. Определение точки отрыва
турбулентного пограничного слоя является более важной, но и более трудной
проблемой. В большинстве технических устройств (например, турбома-
шинах) пограничный слой турбулентен. Это позволяет применять сильно
изогнутые профили и относительно большие углы атаки при безотрывном
обтекании. Однако при отклонении режима работы турбомашины от
расчетного возникают такие положительные градиенты давления, которые при-
%* , 227

водят к отрыву турбулентного слоя. В этих режимах снижается
эффективность и надежность работы машины.
Условием отрыва» как было указано, является равенство нулю
касательного напряжения на стенке. Отсюда следует, что для предсказания
отрыва должна быть установлена достаточно точная связь между формой
эпюры скоростей, продольным градиентом давления и касательным
напряжением на стенке. Известно много критериев, служащих для определения
точки отрыва турбулентного пограничного слоя. Оценку иногда производят
по величине формпараметра Н (9.76), если при определении его значения
учтено влияние градиента давления.
Для турбулентного пограничного слоя применяют критерий отрыва,
предложенный Л. Г. Лойцянским:
/(R*) =@,013^- 0,20)Re2-'/e#
Рассмотрим теперь вопрос о сопротивлении тел, обтекаемых вязкой
жидкостью. Силой сопротивления называют силу, действующую на тело в
направлении потока. Введем безразмерный коэффициент сопротивления,
который согласно теории подобия зависит от формы тела, чисел Re и М:
(9Л07)
где F — сила сопротивления; иж — скорость плоскопараллельного потока
в бесконечности; S — наибольшая площадь поперечного сечения тела.
В дозвуковом потоке сила сопротивления складывается из двух
составляющих; силы трения по поверхности и результирующей сил давления.
Суммарная сила давления не равна нулю, как в идеальной жидкости, так
как пограничный слой искажает основной поток и изменяет распределение
давления. Следует подчеркнуть, что в конечном счете эти силы
сопротивления вызваны влиянием вязкости жидкости. Хорошо обтекаемым называют
тело, для которого сопротивление трения много больше сопротивления
давления (пластина, параллельная потоку, крыло с малым углом атаки). Для
плохо обтекаемого тела (шар, цилиндр) основным является сопротивление
давления (или, как иногда называют, сопротивление формы). На рис. 9.11
для наглядности показаны профиль крыла и цилиндр (точка на рисунке),
имеющие одинаковый коэффициент сопротивления. Этот рисунок
показывает, насколько велико может быть сопротивление давления для плохооб-
текаемого тела по сравнению с сопротивлением трения хорошообтекаемого
тела.
При отрыве пограничного слоя от поверхности тела течение обычно
становится неустановившимся. С поверхности тела периодически сбегают
вихри, попеременно образующиеся то на одной, то на другой стороне тела.
Ввиду этого точки отрыва могут периодически перемещаться по
поверхности, а давление на кормовой части тела пульсировать.
В сверхзвуковом потоке или при наличии местных сверхзвуковых зон,
заканчивающихся скачками уплотнения, возникает волновое сопротивление,
которое не связано с вязкостью жидкости (см. подразд. 6.3). Однако скачки,
взаимодействуя с пограничным слоем, могут изменять и сопротивление
трения и сопротивление давления (например, вызывать отрыв пограничного
слоя).
Рассмотрим особенность сопротивления плохо обтекаемых тел. На
рис. 9.12 дана зависимость коэффициента сопротивления Сх = 2/Vpw«
от числа Re для цилиндра. Из графика следует, что при Re = dujv =
— C...5I05 коэффициент сопротивления резко уменьшается. Это явление
получило название кризиса сопротив4ения плохо обтекаемого тела и объяс-
228

10°
яг»
Рис. 9.11. Профиль крыла и
цилиндр, имеющие одинаковое
сопротивление
\
и
"Ч 1
Ж
t-ч
а)
10°
7Or
1Ог 103
10'
10s
Re
Рис. 9.12. Зависимость коэффициента сопротивления цилиндра от числа Рейнольдса:
а — положение точек отрыва на цилиндре для ламинарного - / и турбулентного — t слоев; б —
зависимость коэффициента сопротивления от числа Re
няется следующим образом. Распределение давления по цилиндру при
отрывном обтекании, конечно, отличается Ът расчетного распределения при
потенциальном обтекании. При докритическом числе Re минимум давления
наблюдается в точке тх при 9 « 70°.
На передней части цилиндра существует ламинарный пограничный слой,
который отрывается в точке / F « 80°). На задней части цилиндра при
отрыве давление ниже, чем на передней, что и вызывает сопротивление формы.
При достижении критического числа Re ламинарный слой становится
турбулентным до точки отрыва. Поскольку турбулентный слой способен
преодолеть большой градиент давления, то отрыв смещается в точку / при Э «
« 110° (а минимум давления в точку /л2 при 6 « 90°). Эти значения зависят
от числа Re. Так как в этом случае область пониженного давления на задней
стороне цилиндра уменьшается, то резко уменьшается и коэффициент
сопротивления. S^roro же эффекта можно добиться при меньшем числе Re,
турбулизовав ламинарный слой введением, например, шероховатости
поверхности или повышением турбулентности внешнего потока. Эти
воздействия приводят к переходу ламинарного пограничного слоя в
турбулентный при меньших числах Re и соответственно к перемещению точки
отрыва и снижению сопротивления.
При обтекании шара и очень малых числах Re для коэффициента
сопротивления справедлива теоретическая формула Стокса: Сх = 24/Re, Re =
=¦¦ ^ d/v < 1.
Эта формула находит применение, например, при расчете осаждения
капелек тумана или расчете движения очень малых капелек жидкости при
течении влажного пара. С увеличением числа Re изменение коэффициента
сопротивления шара качественно совпадает с законом, приведенным для
цилиндра. В частности, кризис сопротивления возникает при Re « 5 X
X 105. На этом принципе основана работа простого прибора для измерения
степени турбулентности внешнего потока. По уменьшению сопротивления
маленького шарика регистрируют критическое число Re. Зависимость
критического числа Re от степени турбулентности известна по измерениям
турбулентности с помощью малоинерционного прибора, которым можно
измерять малые пульсации скорости.
БыЛи рассмотрены особенности изменения силы сопротивления
округлых плохообтекаемых тел, для которых точка отрыва заранее не фиксирова-
,на, а определена режимом обтекания. Плохообтекаемое тело может иметь
острые выступающие углы (например, пластина, поставленная поперек
потока), тогда положение точек отрыра определено и не зависит от числа
229

Рис. 9.13. Схема взаимодействия
скачка с пограничным слоем
Re (в данном случае это кромки
пластины). Для таких тел сопротивление
слабо зависит или вообще не зависит от
числа Re и кризиса сопротивления,
естественно, не наблюдается. В частности,
для пластины, поставленной поперек
потока, коэффициент сопротивления в
диапазоне чисел Re от 4 • 103 до 1 • 10е
не изменяется и равен 1,1.
Рассмотрим еще одну причину,
которая может привести к отрыву
пограничного слоя. В сверхзвуковом потоке
большой положительный градиент
давления может быть вызван не только
формой обвода обтекаемого тела, но и
скачком уплотнения. Скачок уплотнения,
падая на поверхность, покрытую пограничным слоем, не достигает стенки,
так как во внутренней части слоя вблизи стенки скорости потока
дозвуковые. Поэтому давление вблизи стенки меняется не скачкообразно, а более
плавно, но положительный градиент давления все же может быть очень
большим.
В области взаимодействия скачка с пограничным слоем не справедливы
как основные допущения теории пограничного слоя (велик продольный
градиент скорости и давление меняется поперек слоя), так и теория
скачка (протяженность скачка становится порядка десятков толщин
пограничного слоя). Возможно много вариантов взаимодействия в зависимости от
того, является ли слой ламинарным или турбулентным, происходит ли
отрыв, а также происходит ли последующее присоединение слоя к
поверхности.
Рассмотрим подробнее только вариант отражения скачка от
поверхности, покрытой турбулентным слоем, при отсутствии отрыва (рис. 9.13).
Пограничный слой утолщается перед скачком, так как там возникает
положительный градиент давления, вызванный передачей возмущений через
дозвуковую часть слоя вверх по потоку. На этой части пограничного слоя,
как при обтекании вогнутой стенки, появляются сходящиеся волны сжатия,
образующие при слиянии отраженный скачок уплотнений. В том месте,
где утолщение слоя заканчивается, возможно появление волн разрежения,
как при обтекании сверхзвуковым потоком выпуклой поверхности.
Возможность отрыва пограничного слоя зависит от интенсивности
скачка и характеристик пограничного слоя.
В области отрыва распределение давления по поверхности тела
существенно связано с изменением толщины слоя, иначе говоря, наблюдается
сильное взаимодействие пограничного слоя с внешним потоком.
Пусть в области падения скачка на некоторой малой длине / (см. рис. 9.13)
происходит повышение давления Ар = р2 — рл <^ роа§ с большим
градиентом давления dpldx ~ Ар/1 > риЬ/1 (/ ~ х — характерная длина).
Разделим пограничный слой на две части: наружную часть и пристеночный слой
малой толщины у19 в котором и происходит формирование отрыва. Течение
в пристеночной части пограничного слоя можно считать течением вязкой
несжимаемой жидкости, с линейным распределением скорости
я = (tw/Vvv) У = (?Ро ullVw) # = &о ? Re (Po/Pw) (ytfh
где ? = тш/(р0«§), Re = po#o'/lV> Р^ и Vw — плотность газа и
коэффициент вязкости в пристеночном слое; р0, щ — то же, во внешнем потоке.
230

Ввиду малости длины / области взаимодействия толщина у2 = 6 — уг
и профиль скорости и = и(#) в ней изменяются мало, и эту часть можно
рассматривать как вихревой слой невязкого газа, отклоняющийся на
длине / на малый угол Д0.
На участке длиной / пристеночный слой тормозится, а форма эпюры
скорости становится менее наполненной. Если принять для оценки, что эпюра
из прямоугольной станет треугольной, то увеличение толщины
пристеночного слоя равно A#j ~ уг. Это утолщение и определяет угол отклонения
наружной части слоя Д6 ~ yJL
Из формулы F.5) и F.10) следует формула Прандтля—Майера для
малого угла отклонения. Тогда, с учетом приведенной оценки, получим
безразмерное повышение давления
Ум*—1 Ум*— 1
При установившемся течении силы давления, действующие на
пристеночный слой, должны быть уравновешены силами трения (поток импульса
pwu\ < А/?, поэтому им можно пренебречь)
Исключив из написанных соотношений r/t//, найдем
Для практического использования полученных оценок их надо
превратить в расчетные формулы.
В случае сверхзвукового обтекания теплоизолированной пластинки с
ламинарным пограничным слоем можно приближенно принять
Тогда
Др, =CiRe-4*(l +0,126 М2)-°°5(М2 —I)-1/4.
Если применить основную оценку в случае турбулентного слоя в
предположении (не имеющем строгого обоснования), что пристеночный слой
ламинарный, и воспользоваться приближенной формулой
то
Apt=CtRe-l'l4(l +0,1М2)-°'35(М2 — I)-*/4.
На рис. 9.14 приведены экспериментальные значения предельных А/?,
соответствующих отрыву пограничного слоя при взаимодействии со
скачком уплотнения. Расчетные значения, представленные в логарифмических
координатах прямыми, согласуются с экспериментом, если Сл == 1,6 для
ламинарного и Ct = 1,2 для турбулентного слоев.
После рассмотрения условий отрыва пограничного слоя и сопротивления
тЪ\ можно сделать некоторые общие выводы. Обычно в технике требуется
отыскание такой формы тела, при которой сопротивление будет
минимальным (точнее, коэффициент сопротивления при определенных условиях и
ограничениях на форму тела). Основным условием получения хорошо
обтекаемого тела обычно является предотвращение отрыва пограничного слоя.
23)

Рис. 9.14. Предельное приращение давления за скачком уплотнения, вызывающее
отрыв пограничного слоя:
4-_м=3; # — М = 2; в~М=1,8; Э-М=1,7; D - М= 1,4; О - М= 1,2
Ввиду этого главное внимание при дозвуковом потоке надо обратить на вы-
бор*очертания кормовой части тела, где происходит повышение давления.
Выполняя кормовую часть вытянутой, можно снизить величину
положительного градиента давления и не допустить отрыва пограничного слоя
вплоть до выходной кромки. Головную часть тела лучше выполнять
скругленной, так как это предотвращает образование областей пониженного
давления и последующих диффузорных участков при изменении угла натека-
ния потока. В тех случаях, когда это возможно, лучше иметь на
поверхности ламинарный пограничный слой, чем турбулентный, так как Ьри этом
сопротивление трения будет меньшим.
Для затягивания точки перехода ламинарного слоя в турбулентный
вниз по потоку необходимо иметь гладкую поверхность, уменьшить
пульсацию внешнего потока, а также избегать больших положительных
градиентов давления. Последнего можно добиться, уменьшая максимальную
толщину тела. Вместе с тем поддержание ламинарного пограничного слоя часто
невозможно из-за пульсаций внешнего потока (например, в турбомашинах),
да и нежелательно, так как ламинарный слой легче отрывается. Наличие
турбулентного слоя на лопатках турбомашин, хотя и приводит к некоторому
увеличению сопротивления трения, но позволяет выполнять лопатки
сильно изогнутыми и поворачивать поток на большой угол без отрыва.
Поверхность тела при турбулентном слое должна выполняться столь гладкой, чтобы
бугорки шероховатости не вызывали нарушения вязкого подслоя и не
привели к увеличению сопротивления трения. При отсутствии отрыва
распределение давления по поверхности обтекаемого тела может быть найдено
расчетом потенциального потока. Это позволяет применять модель
идеальной жидкости для построения хорошо обтекаемых тел.
При обтекании тела потоком с большой дозвуковой скоростью
желательно, если это возможно, не допускать образования сверхзвуковых зон на
поверхности. Сверхзвуковые зоны обычно заканчиваются скачком
уплотнения, что, как уже подчеркивалось, приводит к дополнительным потерям.
Этого можцо добиться, уменьшая толщины и кривизну обтекаемого тела,
23?

9.7. СВОБОДНАЯ ТУРБУЛЕНТНОСТЬ. ТУРБУЛЕНТНЫЕ СЛЕДЫ
И СТРУИ
Под свободной турбулентностью понимают турбулентность в
потоках, которые не ограничены стенками. К таким течениям можно отнести
турбулентные струи, вытекающие из сопл, и вихревые следы,
распространяющиеся за обтекаемым телом.
Подобные задачи представляют интерес для многих областей техники,
в том числе для энергетики и теории турбомашин. Практически, конечно,
все течения в той или иной степени ограничены твердыми поверхностями.
В ряде случаев, однако, можно считать, что эти твердые поверхности не
оказывают существенного воздействия на поток вр всем ограниченном
пространстве или по крайней мере в какой-то его части. К таким течениям с
достаточной степенью точности можно отнести течение в открытой
аэродинамической трубе, в камере эжектора и т. п. Для всех подобных течений
характерно постоянство давления в исследуемом пространстве.
Во многих задачах ограничивающие стенки существенно влияют на
характер течения и там это предположение было бы ошибочным. К таким
задачам можно отнести, например, задачи об отклонении струи стенкой,
распространения струи или вихревого следа в канале с переменной площадью
поперечного сечения.
При расчете свободных турбулентных течений используют
полуэмпирические теории турбулентности так же, как и в^теории пограничного слоя.
Однако при этом возникают некоторые специфические особенности,
характерные для всего класса рассматриваемых задач.
Далее при решении задач свободной турбулентности будем
использовать только формулу для турбулентного трения (9.55), соответствующую
гипотезе Прандтля об обмене количеством'движения, ввиду ее
универсальности. Отметим, только, что задачи о следах и струях исследованы с
применением различных полуэмпирических теорий турбулентности и
соответственно были получены различные конечйые формулы. Эти исследования
важны, так как позволяют глубже понять особенности турбулентного
обмена. Однако с практической точки зрения различия в окончательных
формулах не принципиальны, так как количественные расхождения малы, а
теории хорошо согласуются с экспериментом.
Будем рассматривать плоское установившееся свободное турбулентное
течение и запишем уравнение движения в таком виде, учитывая
постоянство давления:
u*L + v^-^±-^-. (9.108)
дх ду р ду
где т — касательное напряжение, вызванное турбулентным трением.
Выбрав формулу для турбулентного трения (9.55), запишем уравнение
(9.108):
uJlL+vJ!L=jL.\t*(*LYl (9.109)
дх ду ду [ [ду ) J
Это уравнение необходимо решить совместно с уравнением
неразрывности для несжимаемой жидкости
JlL+JL^o. (9.110)
-дх ду '
Задачи о свободном турбулентном течении р такой постановке могут быть
решены как точными, так и приближенными методами, рассмотрение
которых представляет интерес, как пример простого подхода к практическим
233

8
Рис. 9.15. Турбулентное перемешивание
потока
инженерным задачам, который
может быть распространен и на более
сложные случаи, не поддающиеся
точному решению.
Рассмотрим сначала задачу о
турбулентном перемешивании
плоскопараллельного потока с
неподвижной окружающей
жидкостью (рис. 9.15), Эта задача
соответствует картине течения на
краю турбулентной струи,
вытекающей из плоского сопла.
Поток со скоростью ие течет вдоль стенки АО. Турбулентное смешение
происходит в области ВОС. То, что эта область ограничена лучами ОВ и
ОС, следует из соображений подобия. В данной задаче нет никаких
параметров с размерностью длины. Поэтому в качестве аргумента должны
выступать не х и у в отдельности, а комбинация т) = у/х. Ординаты границ
области смешения должны быть прямо пропорциональны х:
y/x—r\i = tgBu yjx — tg&2~i\2. (9.111)
Длина пути перемешивания также должна быть пропорциональна х, где
с —безразмерная опытная постоянная:
My) ст /О 1 10}
Рассмотрим решение Толлмина A926 г.). Введем функцию тока, которая
удовлетворит уравнение неразрывности (9.110):
(9.113)
и =
Тогда уравнение (9Л09) примет вид
ду дхду дх дуг
Размерность функции тока [ip] = LT"
й б
ду2 дуъ
(9.114)
р фу p следовательно, на основании
соображений теории подобия решение уравнения (9.114) следует искать в
автомодельной форме
(9.115)
Вычислим частные производные, входящие в уравнение (9.114):
дх
дхду
ущ
х2
ду*
Щ р„
ду*
(9.116)
Здесь штрихами отмечены производные по ц = у/х соответствующего
порядка.
Подставив выражения производных в уравнение (9Л14), получим
обыкновенное (так как задача автомодельна) дифференциальное уравнение для
искомой функции
Уравнение (9.117) распадается на два уравнения:
(9Л18)
234

Решение первого из них соответствует плоскопараллельному потоку вне
области турбулентного смешения:
г|> •= хи0F(т)) =хи0(ац +b)=auoy + bu0х.
Для принятого расположения осей координат (см, рис. 9.15) следует
положить а = 1,6 = 0 для потока вне области смешения и а — 0 для области,
занятой неподвижной жидкостью также вне области смешения.
Решение второго дифференциального уравнения (9.118),
описывающего течение в области турбулентного смешения, имеет вид
+A3sin -^- агЛ. (9.119)
Постоянная а = Bс)/3, постоянные А19 Л2, А3 и положения лучей
ОВ и ОС, ограничивающих зону смешения (см. рис. 9.15), должны быть
определены из граничных условий.
На верхней границе области смешения скорость должна быть равна
скорости основного потока, а трение по определению равно нулю — при
ц — %: и — uOj v — 0, ди/ду = 0. На йижней границе области смешения
горизонтальная проекция скорости равна нулю и трение отсутствует — при
ц = у\2: и = 0, ди/ду = 0.
На основании выражений (9.113), (9.116) перепишем эти граничные
условия для функции F(r\):
при т)=Л1-^/(л)=1» ^(ч) = Ль Fff(t\)=0; (9 120)
при Ч = Л1^'(Л)=О, F'(r])^0.
В. Толлмин, который решил изложенную задачу, нашел по этим данным
^ = -0,0062, Л2 =
Аз-0,577, сети-0,981, аг]2 = —2,040.
Ширина зоны смешения по условию (9.111) равна
Ь = х (к\г — гJ) = х (ат|1'—ат|а)/а = 3,021д:/а.
Измерениями было установлено, что
6=0,255*. (9.122)
По этим данным и условиям (9.121) можно найти значение
экспериментальной постоянной с = 0,0174 в формуле (9.112).
Логично выразить путь перемешивания через ширину зоны смешения.
Из зависимостей (9.112), (9.122) и найденного значения экспериментальной
постоянной получим
1/Ь = 0,0682. (9.123)
Жидкость втекает в зону перемешивания из окружающей среды через
границу т] = тJ. Скорость втекания по условиям (9.116), (9.120)
(производная Г(гJ) = 0)
0 {Чд •¦= — д^1дх = —^о F Ш + % "о F' Ш = —u0F (т]2).
Можно подсчитать, что эта скорость составляет 0,032и0, т. е. около 3%
от скорости основного потока.
Жидкость втекает в зону смешения также через границу т] = %, но так
как скорость i>(r)i) = 0, то расход определяется только наклоном этой
границы. Наклон границы находим из условия (9.121):
1 -0,981 {2с*уг\
235

Для найденного значения с = 0,0174 получим угол наклона границы
9Х = 4,7°. Поэтому нормальная к границе проекция скорости равна 0,083и0.
Угол наклона границы ц = г\2 также находим из условия (9.121), и он
составляет 62 = 9,8°. '
Можно также вычислить, что избыточное давление в зоне смешения
равно примерно 0,5% от кинетической энергии ри§/2. Следовательно,
предположение о постоянстве статического давления выполняется с достаточной
степенью точности.
Таким образом решение с точностью до эмпирической постоянной дает
исчерпывающую информацию о характеристиках, которые представляют
практический интерес.
Подчеркнем только, что при смешении потоков влияние трения
распространяется до бесконечности. Выделение зоны смещения конечной ширины
является условностью, совершенно аналогичной предположению о конечной
толщине пограничного слоя. Такое предположение, как известно, оправдано.
Скорость стремится к значению в бесконечности асимптотически и вне
условно выделенной зоны смешения можно пренебречь влиянием трения.
Эту задачу можно решить (с хорошей степенью точности) гораздо проще.
Примем линейный профиль скорости в зоне смешения и учтем, что
и = иоу/уг, ух=Ьх
р == const.
По теореме импульсов
Ух
(Уг — Уо)и1 = {u2dy =-j-yi> Уо = -|-У1.
о
Отсюда получим
Чг=-Уо1х~= — 26/3 = —tg9f.
Если (из экспериментов) Ь = 0,255, то % = 0,085 (вх ±= 4,9°), ц2 = —0,170
@2 = 9,8°), что хорошо согласуется с предыдущим решением. Представляет
интерес еще нулевая (разделяющая) линия тока. Для ее определения
используют уравнение расхода
у
Ух
Уг
Чо = —(Уо -УъЦх - 0,023 (в0 = 1,3°).
Поперечная скорость vx = иог\о "= Q,023w0. Присоединенный объемный
расход
ух
т Г . __ yl 1
Р J 2^i 6
о
v2 - -2L = Л и0 = 0,042а0.
рл: 6
Ясно, чтр t; <g и0, поэтому их можно не учитывать при формулировке
начальных условий.
236

Рис. 9.16.
струи
Схема плоской турбулентной
На основании
проанализированного -ранее решения можно
нарисовать схему плоской
затопленной турбулентной струи.
Затопленной называют струю, которая
распространяется в покоящейся
среде.
Пусть из сопла с прямым срезом
выходит поток с постоянной по
сечению скоростью и0. На начальном
участке струи образуются
турбулентные зоны смешения CAB и
СХАХВ (рис. 9.16), аналогичные
описанным ранее. Внутри
треугольника АВАЪ включая его границы, поток имеет скорость и0. На
линиях АС и АХСХ скорость и = 0 (расположение системы координат показано
на рисунке). На линиях АВ и АХВ скорость v = 0 и основной поток
проникает в зоны смешения только из-за наклона границ. На линиях АС и АгСг
скорость v мала, но не равна нулю, и струя подсасывает окружающую
жидкость. Струя ускоряет подсасывающую жидкость, но сама замедляется, так
как при постоянном давлении суммарное количество движения постоянно.
Участок, в котором скорость по оси струи равна и0, называют начальным.
Ниже по течению за начальным участком скорость начнет уменьшаться
также и по оси струи. До сечения ССХ этот участок называют переходным.
Далее течение в струе будет таким, как будто оно вызвано источником в точке
О (рис. 9.16). За сечением ССХ расположен участок струи, который называют
основным. На всем протяжении струя вовлекает в движение окружающую
неподвижную жидкость, расширяется и подтормаживается.
Такая схема струи с гладкими границами является идеализированной
(подобная идеализация полезна при создании расчетных методов).
Осредненное по времени течение в зонах смешения начального участка
и развитой струе должно удовлетворять уравнению движения (9.108) и
неразрывности (9.110).
Эти уравнения и соображения подобия позволяют установить основные
закономерности для струи: закон увеличения ширины струи 2Ь(х) и
уменьшения скорости на оси струи ит(х).
В полностью раавитом свободном турбулентном течении вязкость не
влияет на осредненное движение, и поля скоростей в каждом сечении струи
подобны, т. е. отличаются только масштабами.
При подобии поли скоростей справедливо условие
и/ит ~/(*//Ь). (9.124)
Достаточно далеко от устья сопла на основном участке закон изменения
ширины струи не зависит от ширины сопла, так как такая же струя может
быть создана точечным источником. Тогда можно считать, что ширина струи
на большом расстоянии пропорциональна х (при надлежащем выборе
начала координат). -
Количество движения жидкости для любого сечения струи должно
быть постоянным:
р ^ и2 dy =
= const.
-1
(9.125)
237

А
т
А
V.
У
Рис. 9.17. Универсальное распределение
скорости в турбулентной струе (схема)
Рис. 9.18. Сравнение расчетного и
опытного распределения скорости в
турбулентных струях и следах:
/ — след; 2 — струя
Здесь обозначено ц = у/b. Преобразование интеграла выполнено с
помощью формулы (9.124). Поскольку интеграл в формуле (9.125) равен
постоянной, то ulmb = const и при Ъ ~ ху ит ~ MYH.
Следовательно, скорость на оси сопла пропорциональна 1/}/лГи служит
масштабным множителем для эпюр скоростей. Масштабным множителем
для координаты у может служить Ь — половина ширины струи, как в
формуле (9.125). Однако величину Ь трудно измерить при проведении
эксперимента, так как скорость стремится к нулю на границе струи асимптотически,
а, кроме того, там наблюдаются хаотические пульсации. Поэтому в качестве
масштабного множителя выбирают другую величину Ь1/2, которая
пропорциональна Ь, но которую легко измерить.
Величиной frj/2 называют расстояние от оси струи до той точки, где
скорость в струе равна половине скорости на оси струи (см. рис. 9.17). Тогда
зависимость (9.124) можно записать в таком виде:
u/um=f(ylb\/2).
(9.126)
Многочисленный эксперимент очень хорошо подтверждает подобие эпюр
скоростей в струях, а как дальше будет доказано, также и в турбулентных
вихревых следах, распространяющихся за обтекаемым телом.
Экспериментальные точки сгруппированы вокруг единой кривой (рис. 9.18), построенной
в координатах формулы (9.126).
Универсальные зависимости (9.126) могут быть получены аналитически
различными методами теории свободной турбулентности. Для получения
этой зависимости можно проинтегрировать уравнение (9.118) при граничном
условии на оси — при у = 0 F(v\) = 0; условие следует из того, что ось струи
является линией тока.
Граничные условия на границе струи при у = Ъ F'(ri) = 0, F"(r\) =
= 0 следуют из того, что там скорость равна нулю, а трение отсутствует.
Однако проще (и с вполне достаточной точностью) определить зависимость
(9.126) только из условий для скорости.
Будем искать распределение скорости в струе в виде полинома, причем
выберем только четные степени, так как струя симметрична:
и/ит = а+
f т] = у/Ь.
238

Потребуем выполнения следующих условий на оси струи и ее границе —
при л = 0 ulum = 1; при т| = 1 ulum = 0, йи!йц = 0, d?u/dv\2 = 0.
Последнее условие обеспечивает плавный переход к нулевой скорости
на границе струи. Определив коэффициенты полинома из этих условий,
найдем а = 1, b = —3, с = 3, d = — 1.
В таком случае для распределения скорости на основном участке струи
получим удобную формулу
и/«и = A—Ч1)*. (9.127)
Для сравнения с экспериментом, как уже было отмечено, введем такое
расстояние от оси следа btj2, при котором и/ит = 0,5. Из формулы (9.127)
следует
= 0,454. (9.128)
В новых координатах, удобных для сравнения с экспериментом [для
расчета скорости в струе следует по-прежнему использовать ту же формулу
(9Л27)], из формулы (9.127) получим*
2,
(9.129)
На рис. 9.18 видно, что кривая, построенная по формуле (9.129),
удовлетворительно совпадает с экспериментальными значениями, хотя, конечно,
можно подобрать и лучшую зависимость. Однако в этом нет необходимости
из-за приближенности всех методов расчета.
Рассмотрим другую задачу из теории свободной турбулентности,
которая находит практическое приложение во многих областях и в том числе
в турбомашинах при расчете кромочных следов.
Турбулентный (при большом Re) след возникает за неподвижным телом,
обтекаемым потоком вязкой жидкости. Скорость в следе за телом меньше,
чем скорость в набегающем потоке, так как количество движения в потоке
стало меньше из-за силы сопротивления.
Условная граница отделяет след от внешнего потока, в котором можно
пренебречь трением (рис. 9.19) и считать, что там скорость и = uQ.
Вблизи обтекаемого тела поля скоростей и давлений могут быть сильно
неоднородны, а течение неустановившимся из-за срыва вихрей. На
некотором удалении от тела течение становится более однородным, поле
давлений выравнивается раньше, чем поле скоростей, и в потоке наблюдаются
только мелкомасштабные турбулентные пульсации.
На достаточном отдалении течение в следе не зависит от конкретной
формы тела, породившего след. Картина, аналогичная течению в следе,
наблюдается и в турбулентной струе (вдали от источника),
распространяющейся в окружающем потоке. На границе следа или струи скорость равна
скорости основного потока. Различие
состоит в том, что внутри следа скорости
меньше скорости внешнего потока, а
внутри струи — наоборот, больше.
На большом расстоянии от обтекаемого
тела расчет течения можно вести по
теории свободной турбулентности. Такие
течения обладают свойствами,
характерными для пограничного слоя: давление
постоянно, градиент скорости в поперечном
направлении велик по сравнению с
градиентом в продольном направлении. В то
Рис 919 Схема
следа за телом
турбулентного
239

же время расчет следов более прост, чем
расчет пограничного слоя, так как
следует учитывать только турбулентное
трение, и нет областей, где скорость
потока падала бы до нуля.
Будем рассматривать течение столь
далеко за обтекаемым телом, что
можно линеаризовать уравнение движения.
Введем новые обозначения для
скорости потока, что позволит подчеркнуть
аналогию между течением в следе и
струе.
Обозначим w скорость потока и
пренебрежем вторым членом в уравнении
(9.108) ввиду малости скорости v. Тогда
Рис. 9.20. Эпюра распределения
дополнительной скорости в следе
Обозначим
дх
р дх
ду
ду
(9.130)
С<1, (9.131)
где w0 — постоянная скорость набегающего потока; w — скорость в следе;
и — так называемая дополнительная скорость в следе.
Эпюра скоростей в следе с введенными обозначениями показана на
рис. 9.20.
Из уравнения (9.130) при обозначениях (9.131) получим уравнение
задачи
дх
ду
(9.132)
Здесь длина пути перемешивания вынесена за знак дифференцирова- .
ния, так как в задачах свободной турбулентности оправдывает себя
предположение, что она зависит только от ширины зоны перемешивания.
В задачах о распространении струи / было принято
пропорциональным ширине струи. Теперь логично принять пропорциональную
зависимость между длиной пути перемешивания и шириной следа
(9.133)
где Ь(х) — половины ширины симметричного следа; р — безразмерная
универсальная постоянная, которая будет определена из опыта.
Эпюры дополнительных скоростей в следе, как показывает опыт,
подобны, т. е. отличаются только масштабами скорости и длины. В таком
случае справедлива зависимость
(9.134)
где ит = ит(х) — дополнительная скорость на оси следа, т. е.
максимальная дополнительная скорость в данном сечении следа (см. рис. 9.20).
Следует подчеркнуть, что след автомоделей только на достаточно
большом расстоянии от тела.
Оценим, как изменяется максимальная дополнительная скорость в
зависимости от расстояния до источника возмущений, т. е. тела, вызвавшего
след. На большом расстоянии от обтекаемого тела статическое давление
постоянно и равно статическому давлению в невозмущенном потоке. Поэтому
240

на основании теоремы о сохранении количества движения, записанной в
интегральной форме, получим для плоского течения
+ ь
F=p f w(wo—w)dy> (9,135)
где F — сила сопротивления, действующая на единицу длины тела.
Интегрирование ведем поперек симметричного следа конечной
ширины. Исключим из формулы (9.135) скорость w с помощью зависимости
(9.131) и пренебрежем квадратом малой величины, получим
+ь +ь
. F = p f u(wQ — u)dy = pw0 f udy.
Л Л
Преобразуем этот интеграл, воспользовавшись уравнением (9.134) и
тем, что скорость ит зависит только от х:
+ i
(9.136)
Силу сопротивления, действующую на единицу длины тела, можно, на
основании теории подобия, представить в виде
F=Cxdpw*/29 (9.137)
где Сх — безразмерный коэффициент сопротивления; d — характерный
размер тела (например, диаметр цилиндра).
Исключив из формул (9.136), (9.137) силу сопротивления, имеем
Cxdw0=>2umb f /ft)*,. (9.138)
Отсюда следует, что вдоль следа сохраняется постоянным произведение
Ьит, хотя сомножители зависят от х.
Если принять
b = btxn, (9.139)
где bly n — некоторые постоянные, то можно найти такой показатель
степени, при котором дифференциальное уравнение (9.132) дает автомодельное
решение, что согласуется с условием (9.134).
Из формул (9.138), (9.139) получим степенную зависимость для ит:
ит = (Сх w0 d/2bt J) x~n. (9.140)
Здесь введено обозначение для постоянной, которой равен интеграл в
формуле (9.138):
+ (9-141)
Из зависимостей (9.134), (9.139), (9.140) следует, что решение надо
искать в виде
и = (С, w0 d/2bt J)x~nf (y/bt x"). (9.142)
Из формул (9.133) и (9.139) следует зависимость для пути перемешивания
/=РМ«, (9-143)
24!

Подставив выражения (9.142) и (9.143) в уравнение (9.132), проведем
дифференцирование и после упрощений получим
nf+ п _!_ /'« c*Pd *- 2«+1 р р\
На основании формул (9.134) и (9.139) запишем это уравнение в виде
nf (ц) + пцГ <Ч) - (С, р2dlb\ J) х- "¦+'/' <ч) Г (Л)-
Следует принять п = 1/2, так как искомая функция зависит только от
переменной rj = y/b, но не х. Окончательно получим следующее
дифференциальное уравнение:
Здесь введено обозначение для безразмерной постоянной
A^2Cx^dlb\J. (9.145)
Уравнение (9.144) необходимо решить с граничными условиями:
при т] = 1 /(Ч)=0, Г(Ч)=О- - t (9Л46)
Эти условия соответствуют тому, что на границе следа дополнительная
скорость (9.134) равна нулю, а трение отсутствует.
Интегрируя уравнение (9.144) один раз, имеем
Постоянная интегрирования принята равной нулю на основании
граничного условия (9.146). Проинтегрировав уравнение второй раз, найдем
Согласно зависимости (9.134) на оси следа дополнительная скорость
максимальна. Тогда следует принять (f(r\) = 1 при ц = 0)
А = 2/9 (9.147)
и решение уравнения (9.144) записать в виде
/М = A-т]3/2)г = м/«т- (9.148)
Вычислив интеграл (9.141) по найденной функции, получим
+ i
У = Г A _43/*)*A|=-JL. (9.149)
Далее следует найти коэффициент пропорциональности Ьх в зависимости
,9.139), выразив его через единственную экспериментальную постоянную р.
Из формулы (9.145), подставив вместо Л и У их численные значения (9.147)
и (9.149), получим
b^frVTOCTd. (9.150)
Тогда из зависимостей (9.139) и (9.150) при п = 1/2 найдем формулу
для определения ширины следа
dx. (9.151)
242

Аналогичным образом из формул (9.140) и (9.150) получим выражение
для дополнительной скорости на оси следа
18
(9152)
Тогда по формулам (9.134), (9.148) и (9.152) можно найти скорость в
любой точке дальнего следа
^ /^иЩ*'*]\ (9.153)
Вовсе итоговые формулы (9.151), (9.152), (9.153), полученные Г. Шлих-
тингом, входит одна универсальная постоянная, которую можно
определить только из опыта. Эту постоянную можно найти из формулы (9.151),
измерив ширину следа на выбранном расстоянии от обтекаемого тела, или
по формуле (9.у32), измерив скорость на оси следа. В принципе достаточно
одного измерения, однако проводят серию измерений на разных
расстояниях, что повышает точность и позволяет проверить справедливость общей
зависимости.
Непосредственное измерение ширины следа b приводит, как было
объяснено ранее, к большим погрешностям. Поэтому следует измерять величину
bj/2, которая по определению равна расстоянию от оси следа до точки, где
дополнительная скорость равна половине дополнительной скорости на оси
следа.
Согласно этому определению из формулы (9.148) получим
ll-(fci/2/ftK/2l2 = l/2, fri/2/fr = 0t441. (9.154)
Измерения, проведенные в следах на больших расстояниях за круглыми
цилиндрами, дают такую зависимость:
(9.155)
Тогда из формул (9.151), (9.154), (9.155) можно найти
Р-0,18. (9.156)
Формулы (9.151), (9.152), (9.153) следует применять, используя это
значение р.
Зависимость (9.155) хорошо согласуется с измерениями для
безразмерных расстояний xlCxd >50. При этих же условиях хорошо совпадает с
экспериментом расчетная зависимость безразмерных дополнительных
скоростей в следе (9.148). Подчеркнем, что зависимости для скоростей в
турбулентном следе и турбулентной струе, выраженные в принятых координатах,
совпадают, как это показано на рис. 9.18.
Заметим, что во всех задачах теории следов можно использовать единый
профиль дополнительной скорости (9.127) или (9.148), или иной, который
можно получить, применив другой закон турбулентного трения.
Таким образом, ширина плоского следа растет пропорционально, а
максимальная скорость падает обратно пропорционально корню
квадратному из расстояния до тела. Следовательно, границы следа описываются
квадратичной параболой. Полученные зависимости справедливы только на
достаточном удалении от обтекаемого тела, где давление практически
постоянно, а дополнительные скорости малы. Для плохообтекаемых тел
(цилиндр) теория применима только с расстояний в несколько десятков диа-
243

метров цилиндров (хотя достаточно хорошее согласование наблюдается с
расстояния в пятнадцать диаметров). Для хорошо обтекаемых тел с острой
задней кромкой расчет хорошо согласуется с экспериментом на значительно
меньших расстояниях.
Вопросы для самопроверки
1. Как можно объяснить причину появления касательных напряжений при
турбулентном течении?
2. Почему логарифмический закон распределения скорости в турбулентном
пограничном слое называют универсальным?
3. Что называют гидравлически гладкой поверхностью?
4. Как влияет продольный градиент давления на закон изменения толщины
пограничного слоя вдоль поверхности?
5. Какова причина возникновения кризиса сопротивления гглохообтекаемых тел?
6. Дайте классификацию составляющих силы сопротивления.
7. Как следует поставить эксперимент и провести обработку результатов
наблюдения, чтобы подтвердить подобие эпюр дополнительных скоростей в турбулентном
следе?
8. Получите основные формулы для турбулентного следа, выбрав для простоты
линейный закон изменения дополнительной скорости на половине ширины следа.

ГЛАВА 10
ОСЕСИММЕТРИЧНЫЕ ТЕЧЕНИЯ ИДЕАЛЬНОЙ ЖИДКОСТИ
10.1. УРАВНЕНИЯ ДВИЖЕНИЯ, НЕРАЗРЫВНОСТИ
И ЗАВИХРЕННОСТИ ДЛЯ ОСЕСИММЕТРИЧНЫХ ТЕЧЕНИЙ
Расчет осесимметричных течений имеет большое значение в
технике и, в частности в теории турбомашин, так как корпуса турбомашин,
внутри которых движется жидкость, являются телами вращения. В
некоторых случаях, как например в патрубках кольцевой формы турбин,
компрессоров и насосов, течение практически является осесимметричным.
Течение же через ступени турбомашин, т. е. через системы неподвижных
и вращающихся кольцевых аэродинамических решеток, можно также
приближенно рассматривать как осесимметричные после определенным образом
произведенных осреднений потока в окружном направлении.
При рассмотрении осесимметричных течений следует различать
осевые течения, в которых окружная составляющая скорости равна нулю.
Другой тип осесимметричных течений — это так называемые
закрученные потоки, которые имеют окружную составляющую скорости.
Рассмотрение закрученных потоков представляет особую важность в теории
турбомашин, так как принцип работы турбомашин основан именно на
изменении момента количества движения жидкости, текущей через
кольцевые аэродинамические решетки. Вместе с тем следует заметить, что
осесимметричные течения более сложны для анализа, чем плоские.
В этой главе будут рассмотрены установившиеся течения идеальной
жидкости, что позволит наглядно установить основные закономерности для
осевых и закрученных потоков.
Аэродинамические решетки, расположенные на роторе турбомашины,
вращаются относительно неподвижных решеток, связанных со статором.
Ввиду этого параметры потока периодически меняются во времени. Поток
в турбомашинах турбулентен, причем степень турбулентности велика, так
как хаотические пульсации возбуждаются аэродинамическими решетками,
движущимися в неоднородном потоке.
Общая задача столь сложна, что для ее решения необходимо ввести
разумные упрощения. Эти упрощения основываются на том, что для
практических целей нет необходимости в расчете всех деталей картины течения.
Прежде всего, пользуясь тем, что пульсационные составляющие
параметров потока малы по сравнению с их средними значениями, можно
произвести осреднение по времени аналогично тому, как это делается при
изучении турбулентного потока.
Далее предполагают, что поверхности тока представляют собой
поверхности вращения. Это предположение не вносит существенной ошибки.
Обоснование этого предположения можно пояснить следующим. Кольцевые
аэродинамические решетки, состоящие из конечного числа лопаток,
имеющих определенную толщину, условно заменяют решетками из бесконечно
тонких лопаток. Такая система лопаток оказывает силовое воздействие на
поток, эквивалентное реальной решетке, но не нарушает осесимметричности
течения. Таким образом, на этом этапе расчета течение рассматривают уста-
245

новившимся и осесимметрйчным, т. е.
зависящим только от двух координат. Это
существенным образом упрощает задачу.
Цель расчета состоит в построении осесим-
метричных поверхностей тока и определении
закона изменения параметров потока по радиусу.
В кольцевых решетках с относительно
длинными лопатками изменения давления, скорости,
углов и других параметров потока весьма
существенны.
Рис. 10.1. Цилиндричес- После того как построены осесимметрич-
кая система координат ные поверхности тока, можно вернуться к
исследованию обтекания реальной
аэродинамической решетки. При течении невязкой жидкости поверхности тока можно
рассматривать как непроницаемые стенки. Можно считать, что они
образуют кольцевые каналы и вырезают в потоке слои переменной
толщины. На этом этапе задача состоит в расчете обтекания
аэродинамической решетки, ограниченной двумя осесимметричными поверхностями.
Выбрав близкие поверхности тока, приходим к задаче обтекания
аэродинамической решетки, расположенной на поверхности вращения в слое
переменной толщины. Толщину каждого слоя всегда можно выбрать малой
и пренебречь изменением параметров потока поперек слоя. В таком случае
эту задачу также можно рассматривать как двумерную. Следует обратить
внимание, что лопатки пересекаются поверхностями вращения наискось,
а слой имеет переменную толщину. Следовательно, распределение
давления на лопатках решетки и ее характеристики не будут совпадать с теми,
которые получены при обтекании прямой решетки.
Таким образом, трехмерная задача расчета течения в турбомашине
разбита на две значительно более простые двумерные задачи: 1) построения осе-
симметричных поверхностей тока, 2) расчета обтекания аэродинамической
решетки, расположенной на поверхности вращения в слое переменной
толщины.
Решения, полученные на основе такой постановки, удовлетворяют
требованиям практики, так как позволяют найти изменение параметров
потока по радиусу, а также установить условия обтекания каждого сечения
решетки.
Решение задачи в такой постановке может быть получено численными
методами с помощью вычислительных машин. Следует, однако, отметить,
что решение трудоемко и поэтому наряду с таким более общим и правильным
подходом используются различные приближенные способы.
Для рассмотрения осесимметричных течений (рис/10.1) удобно ввести
цилиндрическую систему координат» (х, г, 6) с соответствующими
проекциями скорости (и, v, w).
Уравнения Эйлера для осесимметричного течения должны быть
записаны в таком виде:
дг дх г р дг
A0.2)
дг дх р дх
246
дг дх
^L±1L Fx, A0.3)

где /у, Fq, Fx — проекции силы соответственно на радиальное, окружное и
осевое направления.
В теории турбомашин эти силы можно трактовать как силы, действующие
на жидкость со стороны лопаток.
Следует подчеркнуть, что в написанных уравнениях, так же как и в
других уравнениях этой главы, все производные в окружном направлении
равны нулю, так как здесь рассматриваем только осесимметричные
течения.
Уравнение A0.1) называют уравнением радиального равновесия.
Уравнение A0.2) утверждает тот факт, что момент количества движения жидкой
частицы может быть изменен только под действием окружной составляющей
силы. Наконец, уравнение A0.3) представляет проекцию уравнения
количества движения на осевое направление.
Уравнение сохранения массы или, иначе, уравнение неразрывности для
осесимметричного течения жидкости имеет вид
i ~j7{pru)^°' (la4>
Проекции локальной угловой скорости вращения частицы жидкости для
осесимметричного течения определены формулами:
1 «?0
2 дг
2г
1
2
' dv
дг '
dw
дх '
дг
A0.7)
Уравнения движения в форме Эйлера A0.1), A0,2), A0.3) можно
преобразовать к эквивалентным им уравнениям в форме Громеки—Лэмба,
введя выражения для угловых скоростей вращения A0.5), A0.6), A0,7).
Опустив преобразования, которые просты (и совершенно аналогичны
проделанным в гл. 5 в декартовой системе координат), запишем уравнения в
окончательном виде:
(L&L?)A0.8)
A0.9)
^+ . (ШЛО)
р дх 2 дх ]
Здесь для краткости введено обозначение для величины полной
скорости
A0.11)
Уравнение неразрывности A0.4) будет автоматически удовлетворено,
если ввести функцию тока ty = ty(x, г) в таком виде:
p,/==JLit, pp«_JLJL. (Ю.12)
г дг г дх
Уравнение i|)(x, r) = const, где постоянная принимает конкретное
значение, описывает поверхность вращения. При различных значениях
постоянной уравнение ty(x< r) ~ const представляет семейство поверхностей
вращения.
247

Каждая частица жидкости движется по поверхностям тока. Для чисто
осевого течения в силу симметрии задачи достаточно изучить движение
жидкости в произвольно выбранной меридиональной плоскости, т.
е.плоскости, проходящей через ось симметрии. Если поток является
закрученным, то частицы жидкости движутся по линиям тока, также лежащим на
поверхностях вращения. Различие состоит в том, что частицы жидкости
имеют составляющую скорости, нормальную к меридиональной плоскости.
Из уравнения A0.9); эквивалентного уравнению A0.2), следует, что
момент количества движения wr для частицы жидкости, движущейся по
поверхности тока при Fq = 0, остается постоянным. Можно также сказать,
что в этом случае остается постоянной циркуляция скорости по
окружностям, образованным сечением поверхностей тока плоскостями, нормальными
к оси симметрии.
Следовательно, на поверхности тока
A0.13)
и справедливо уравнение Бернулли:
dp/p+cdc = 0. A0.14)
Следует отметить, что в общем случае как циркуляция скорости в
уравнении A0.13), так и постоянная, полученная после интегрирования
уравнения A0.14), постоянны только на каждой поверхности тока, но не для
всего потока.
Выразим окружную составляющую локальной угловой скорости
вращения через функцию тока. Из формул A0.7) и A0.12) для несжимаемой
жидкости следует
о)е = —
2г V д*2 дг*
г дг )
Если течение безвихревое, т. е. сол = (ог = сое = 0, то для такого
течения функция тока должна удовлетворять уравнению
±± + »±-.±Я.=о.' A0.16)
дх* дг* г дг v
Как следует из условия A0.7), для безвихревого течения можно ввести
потенциал скорости
„=-*?., v=J2.m A0.17)
дх дг
Для безвихревого осесимметричного течения несжимаемой жидкости
потенциал скорости и функция тока на основании их определения
формулами A0.12) и A0.17) должны удовлетворять соотношениям
S-. A0.18)
дх г дг ' дг г дх '
Исключив из соотношений A0.18) функцию тока перекрестным
дифференцированием, получим для потенциала скорости уравнение Лапласа в
цилиндрических координатах:
4? . A0.19)
дх* г дг дг*
Для идеальной жидкости поверхность обтекаемого тела должна
совпадать с поверхностью тока, и поэтому граничным условием для уравнения
A0.16) является г|э = const на твердой поверхности.
248

На неподвижном обтекаемом теле нормальная составляющая скорости
должна быть равна нулю. Поэтому граничным условием для уравнения
A0.19) будет dyldn = 0 на поверхности тела.
Из уравнения A0.8), A0.10) следует, что для потенциального течения
постоянная в уравнении Бернулли одинакова для всего потока, а из
уравнения A0.5) получим также, что во всем потоке постоянна и
циркуляция скорости wr = const.
10.2. ТОЧНЫЕ РЕШЕНИЯ ДЛЯ ОСЕСИММЕТРИЧНЫХ
ЗАКРУЧЕННЫХ ПОТОКОВ
Рассмотрим осесимметричные течения, изучение которых
представляет практический интерес в теории турбомашин.
В первой задаче поставим условие, что поверхности тока
цилиндрические, а лопатки отсутствуют. Исследуем течение идеальной сжимаемой
жидкости.
Поскольку поверхности тока цилиндрические, то радиальная проекция
скорости равна нулю, а все параметры потока зависят только от радиуса.
В таком случае можно записать
±lL+cJL^Jb<Lf A0.20)
р dr dr dr
где h0 = /io(r) — распределение энтальпии торможения по радиусу,
которое следует считать Заданным.
В цилиндрическом течении уравнения A0.2), A0.3), A0.4)
удовлетворены автоматически, а из уравнения A0.1) получим
-2L-J-.*- A0.21)
г р dr '
Введя в рассмотрение полную скорость с2 = и2 + w2 и обозначив w =
= с cosa, где a = a(r), как это принято в теории турбомашин, угол наклона
скорости к плоскости, нормальной оси симметрии, из A0.20), A0.21)
получим
1 dc2 , с* cos2 a dh0
• —; Г" • ¦ —
2 dr r dr
Это дифференциальное уравнение первого порядка относительно
функции с2(г) может быть проинтегрировано в общем виде. Обозначив
/W(r) = f 2со^ш<г, A0.22)
можно записать решение в виде
^ expy(r)drlexp(-A A0.23)
lexp(-
где cv— пфстоянная, соответствует заданной скорости на некотором радиусе
Значение угла наклона скорости и распределение энтальпии торможения
по радиусу могут быть заданы произвольно. Решение A0.23) представляет
интерес при расчете закрученного потока за кольцевой аэродинамической
решеткой осевой турбомашины. Следует, однако, помнить, что подобное
решение непригодно для изучения течения внутри самой кольцевой решетки,

закручивающей поток, так как там поверхности тока не являются
цилиндрическими. Следовательно, решение A0.23) представляет закрученный поток
только на некотором (теоретически бесконечном) расстоянии от
аэродинамической решетки.
Анализ движения потока в кольцевой решетке и асимптотическое
приближение такого решения за решеткой к решению A0.23) является
существенно более сложной задачей. Некоторые приближенные методы ее решения
будут рассмотрены далее.
Если энтальпия торможения в потоке постоянна по радиусу, то решение
A0.23) значительно упрощается:
(ji2?u*LY A0.24)
Самое простое решение, которое также имеет практический интерес,
соответствует случаю, когда угол постоянен. Тогда интеграл в A0.24)
может быть вычислен явно и решение имеет вид
JL_/Mco*'a ' A0.25)
с, \ г }
Из A0.24), A0.25) очевидно, что скорость потока уменьшается по
радиусу, что легко объяснимо, так как в закрученном потоке из-за центробежного
эффекта давление по радиусу растет.
Отметим, что решения A0.23), A0.24), A0.25) в общем случае
соответствуют завихренному потоку и это можно проверить с помощью формул A0.5),
A0.7).
Однако из общего решения можно выделить одно решение, которое
соответствует потенциальному закрученному потоку с цилиндрическими
поверхностями тока. Из A0.6) видно, что <ог = 0 во всех цилиндрических
потоках. Если йоложить юх = 0 (см. 10.5), то необходимо принять
rw = const или в соответствии с принятыми выше обозначениями
г с cos а = rx cx cos av A0.26)
Для того чтобы сов = 0 [см. A0.7I, следует принять постоянной
осевую скорость и = их = const, a следовательно, положить
с sin a = сг sin аг. A0.27)
Во всех случаях по-прежнему индекс I соответствует значению
параметров на произвольно выбранном радиусе г1.
Из формул A0.26), A0.27) следует, что для того чтобы поток был
безвихревым, угол закрутки должен изменяться вдоль радиуса по закону:
tga = (r/r1)tgo1. A0.28)
Выразив в формуле A0.26) cos a через tg a из формулы A0.28), после
простых преобразований найдем закон изменения полной скорости по радиусу
для цилиндрического потенциального закрученного потока:
A0.29)
Во всех рассмотренных выше закрученных потоках линии тока
представляли винтовые линии, расположенные на цилиндрических поверхностях.
Величина радиального градиента давления в этом случае зависит от
величины окружной проекции скорости и радиуса кривизны цилиндрической
поверхности тока [левый член уравнения A0.21I.
250

Однако в общем случае радиальный градиент давления зависит от трёх
членов в левой части уравнения A0.1), так как вообще поверхности то^а не
являются цилиндрическими.
Радиальный градиент давления и связанные с ним законы распределения
по радиусу величины скорости потока и угла ее направления весьма
существенно влияют на конструкцию ступени турбомашины и ее
характеристики. Здесь кратко коснемся этого вопроса только в той мере, которая
относится к общей аэродинамике осесиммет*ричных течений.
В осесимметричных течениях линии тока лежат на поверхностях
вращения, которые обладают кривизной. Однако линии (в данном случае линии
тока), принадлежащие криволинейной поверхности, не обязательно
являются кривыми. Так, поверхность называется линейчатой, если она
получена как след движущейся прямой линии. Линейчатыми поверхностями
вращения являются: цилиндр, конус и однополостный гиперболоид.
В первых двух случаях прямые линии, образующие поверхности
вращения, если их рассматривать как линии тока, соответствуют незакручен-
ным потокам. Если же поверхностью тока является однополостный
гиперболоид вращения, то прямые линии, образующие эту поверхность,
соответствуют закрученному потоку. Это наводит на мысль, что, возможно,
существуют закрученные потоки, для которых градиенты давления отсутствуют,
т. е. давление постоянно во всем потоке. Очевидно, что это утверждение
требует доказательства.
Если давление во всем потоке постоянно, а внешние силы отсутствуют,
то уравнения движения A0.1), A0.2), A0.3) примут вид:
ojL+tt_*L__"L = 0; A0.30)
дг дх г
_а(?Е)_=0; (]031
дг д х
JOLbL. A0.32)
дг дх
Для изоэнтропийного течения должна быть постоянная полная скорость
потока
u2 + v2 + w2 = cl A0.33)
Уравнение A0.32) будет удовлетворено, если во всем потоке постоянна
осевая скорость и = и0. Покажем, что это не противоречит остальным
уравнениям.
Из уравнения неразрывности A0.4) следует, что при постоянной
осевой скорости радиальная скорость должна быть представлена в таком виде:
v=F(x)/r9 A0.34)
где F(x) — искомая функция только координаты х9 так как при изоэнтро-
пийном течении и постоянном давлении плотность также постоянна.
Из уравнений A0.33), A0.34) следует зависимость для окружной
составляющей скорости
w* = d- ub -F* (х)/г\ A0.35)
Подставив выражения для радиальной A0.34) и окружной A0.35)
скоростей в левую часть уравнения A0.30), получим
— F2 (х)/г* —ц0 F (х)/г — <сЬ —иЬ)/г —F2 (х)/г* = 0.
251

Отсюда следует, что уравнение A0.30) будет удовлетворено, если принять
F (х) = (d/Uo—Uo) х. A0.36)
Остается показать, что будет удовлетворено также уравнение A0.31),
выражающее условие постоянства момента количества движения для частиц
жидкости, находящихся на поверхности тока.
Уравнение поверхности тока следует найти из условия
d t|> = (д t Id х) dx + (д ф/d г) d r.
Заменив частные производные из определения функции тока A0.12),
получим
dt|)= —pvrdx + prudr. A0.37)
Воспользовавшись уравнениями A0.34), A0.36) и условиями постоянства
осевой скорости и плотности, получим после интегрирования A0.37)
уравнение поверхности тока
const. A0.38)
Это уравнение семейства однополостных гиперболоидов вращения,
имеющих общую ось. Один из таких гиперболоидов показан на рис. 10.2.
, Помножив обе части уравнения A0.35) на г2 и воспользовавшись
условием A0.36), получим
r*w2=(cl — ul)lr2 — (c2jul — l)x2}. A0.39)
Из сравнения уравнений A0.38), A0.39) следует, что на произвольной
поверхности токаг|) = \|H момент количества движения постоянен, что и
требуется для доказательства удовлетворения уравнения A0.31).
Таким образом, возможно закрученное осесимметричное течение
идеальной сжимаемой жидкости, в котором давление и скорость постоянны.
Очевидно, что в общем случае радиальный градиент давления зависит от
формы меридиональных обводов осесимметричной поверхности, т. е. формы
кривых, образованных сечением этой поверхности меридиональной
плоскостью. Это заслуживает более подробного изучения. Выбирая форму
меридиональных обводов в турбомашинах, можно в известных пределах
изменять распределение параметров потока по радиусу.
В цилиндрических течениях радиальный градиент давления вызван
окружной проекцией скорости. В течениях, где поверхности тока имеют
кривизну в меридиональной плоскости, радиальный градиент давления
вызван также осевой и радиальной проекциями скорости. Рассмотрим третье
течение, которое выбрано так, что кривизны поверхностей тока в
меридиональной плоскости равны нулю, но
течение не цилиндрическое.
Рассмотрим потенциальное течение
несжимаемой жидкости и выберем
потенциалом скорбсти функцию
х2+г2 , A0.40)
которая, как легко проверить, удовлет-
Рис. 10.2. Поверхность тока в виде В0Ряет Уравнению Лапласа A0.19) в ци-
однрполостного гиперболоида враще- линдрическои системе коордийат (А —
ния произвольная постоянная),
252

Осевую и радиальную проекции
скорости определим по формулам
A0.17):
и- —Лл;(л:2+/-2)--3/2,
+ y2)-^2. A0.41)
Окружную составляющую
скорости зададим в таком виде:
= B/rf
A0.42)
Рис. 10.3. Течение в конической трубе
где В — произвольная постоянная.
Три проекции скорости A0.41), A0.42) определяют осесимметричное
потенциальное закрученное течение, так как легко видеть, что все проекции
локальной угловой скорости вращения A0.5), A0.6), A0.7) равны нулю.
Записав полный дифференциал функции тока A0.37) и подставив в него
проекции скорости A0.41), после интегрирования получим (для
несжимаемой жидкости, не уменьшая общности, можно принять р = 1)
A0.43)
Поверхности тока являются семейством конических поверхностей с
общей вершиной в начале координат.
Если рассматривать область х > 0 и принять А <С 0, то в начале
координат располджен источник, а формулы A0.40), A0.41), A0.43) описывают
незакрученное течение внутри кольцевой трубы, образованной коническими
стенками. Добавление окружной составляющей скорости A0.42) делает
суммарный поток закрученным (в данном случае потоки можно складывать,
так как жидкость несжимаема, а течения потенциальны).
Квадрат полной скорости закрученного потока, определенный с помощью
формул A0.41), A0.42):
с2 = А2/(х2 + г2J+В2/г2. A0.44)
При изучении течения в турбомашинах практический интерес
представляет оценка влияния конусности на радиальный градиент давления (или
скорости). Для этого анализа в соответствии с физическим смыслом задачи
в формулах A0.41), A0.42) следует принять
А^-игг1 В^шггъ A0.45)
где ии ы>1 — соответственно осевая и окружная проекции скорости на
фиксированном радиусе гг.
Продифференцировав функцию A0.44) по г при фиксированном х и
использовав условие A0.45), найдем градиент квадрата полной скорости в
фиксированной точке
/ д с2 \ __ 2и\ г\ 2w\
\ дг jreri -~ (xj + rf)» ~'
A0.46)
Введем по аналогии с цилиндрическим течением угол направления
скорости а, а также угол конусности е (см. рис. 10.3):
iga—u/w, tge = u/«- A0.47)
Поскольку х — rctge (см. рис. 10.3), то из формул A0.46), A0.47) следует
ltg2«1)/rl. A0.48)
253

Здесь и далее индексом 1 всюду отмечено значение переменных на
фиксированном радиусе.
Определим значение полной скорости в расчетной точке
cl^u\ + v\-\w\ -^(l+tg'^axcos2^). A0.49)
Исключив w\ из формулы A0.48) с помощью формулы A0.49), запишем
окончательное выражение градиента для конического закрученного
течения
/ дс* \ _ 2gfcosai l + sinfleltg««1 A0 50)
\ дг )г—гх гл cos2a!+cos2ei sin2aj
Для сравнения вычислим с помощью формулы A0.25) значение градиента
квадрата скорости для цилиндрического течения:
дс2
При гг = 0 формулы A0.50) и A0.51) естественно совпадают. Следова-
тельно, второй сомножитель в формуле A0.50) дает поправку на влияния
конусности:
4i'M»A0.52)
К.
cos2 aj + cos2 8i sin2 at
В сильно закрученных потоках даже при большом угле конусности эта
поправка мала, так как радиальный градиент вызван в основном закруткой,
а не продольным градиентом скорости. Так, при гг = 20°, а, -= 15° по
формуле A0.52) получим К = 1,06.
Для более ясного понимания зависимости радиального градиента давле*
ния от различных факторов следует преобразовать уравнение радиального
равновесия (ЮЛ).
Пусть дана осесимметричная поверхность тока. Направим одну ось
координат вдоль оси симметрии (рис. 10,4). Сечение поверхности
плоскостями, проходящими через ось симметрии (меридиональные сечения),
образует на поверхности вращения семейство линий, называемых меридианами.
Сечение поверхности плоскостями, перпендикулярными оси симметрии,
дает на поверхности семейство окружностей (параллели). В меридиональном
сечении (см. рис. 10.4) меридиан изображается кривой АВ без искажения,
а проекция одной из параллелей — отрезком CD. В цилиндрической
системе координат были рассмотрены проекции полной скорости: осевая и,
радиальная v, окружная w (перпендикулярная чертежу).
Течение на осееимметричных поверхностях является двумерным и
поэтому удобнее ввести две проекции скорости: меридиональную wM и
окружную wq. В таком случае осевую wx и радиальную wr проекции полной
скорости w также логично обозначить буквой w с соответствующими
индексами.
Меридиональная проекция (см. рис. 10.4)
wm = Vwl + w*- - (Ю.53)
Отметим следующее соответствие между проекциями скоростей
(рис. 10.5):
Щ = wm sin е, w.x = wm cos е, A0.54)
где е — угол между осевой и меридиональной проекциями скорости.
254

Рис. 10.4. Меридиональное сечение осе-
симметричной поверхности тока
Рис. 10.5. Полная скорость и ее
проекции на оси координат
W
В дальнейшем понадобится также преобразование производных от одной
системы координат к другой. Соответствие между производными следует из
рис. 10.4:
д ' д ' д A0.55)
ds
д , д
¦ = sin е \- cos в
дг дх
где s — длина дуги, измерена на поверхности тока вдоль меридиана.
Заменив проекции скоростей в цилиндрической системе координат в
уравнении A0.1) через меридиональную скорость по формуле A0.54),
получим
wm [sin e ~f~ (wm sin г) -{- cos в — (wm sin в) I ^L ^=f —— —
L or ^x J г г р дг
Выражение в квадратных скобках по формуле A0.55) можно заменить
через производную по s:
2,
ds r r p дг
Продифференцировав выражение в скобках, получим
т v* ь о - -у- шт ЫН о ¦ == Г г —— . AU.OO)
as ds r p дг
Производная угла по дуговой координате выражается через радиус
кривизны кривой
rfe/ds- l/Rmf ' A0.57)
где Rm — радиус кривизны меридиана (см. рис. 10.4).
Тогда уравнение A0.56) запишем в такой форме:
Wm
cose —
we
+ wm sin e
dwn
и т
dp
dr
A0.58)
Rm ww ^ Т~"л Wm O111 ° ~~d7
Это уравнение описывает условие равновесия потока в радиальном
направлении.
Поясним физический смысл членов, входящих в уравнение равновесия
A0.58). Они представляют проекцию на радиус сил, действующих на
единицу массы жидкости, т. е. имеют размерность ускорения. Первый член
выражает проекцию (на радиус) центростремительного ускорения,
возникающего при движении жидкости вдоль криволинейной поверхности тока.
Второй член равен центростремительному ускорению, возникающему при вра-
255

Щении частицы жидкости вокруг оси симметрии. Третий член выражает
проекцию касательного ускорения частицы жидкости в ее движении вдоль
поверхности тока. Четвертый член представляет проекцию силы, действующей
на единицу массы жидкости со стороны лопаток решетки.
Градиент давления по-прежнему выражен в цилиндрической системе
координат, так как при расчете турбомашин главным образом надо знать
изменение параметров потока по радиусу.
Преобразовав описанным способом уравнение A0.3), получим
выражение для градиента давления в осевом направлении
-*-*.+*. —Ъ--'--7~%" A0-59>
Физический смысл членов этого уравнения ясен из предыдущих
объяснений.
Заменим в уравнении A0.2) проекции скорости в цилиндрической
системе координат на меридиональную скорость по формулам A0.54):
wm sin e — (гwe) + a>m cos e -— (лад) -= rFid.
dr dx
Продифференцировав выражения в скобках, после простых
преобразований получим это уравнение в таком виде:
Заменив sine = drlds, как это следует из рис. 10.4, придем к
уравнению
Отсюда получим окончательное выражение
w
(<>) re A0.60)
ds
Следовательно, момент количества движения на данной поверхности
тока может изменяться только в том случае, если на поток действует сила
в окружном направлении. Если же сцла равна нулю, т. е. поток
движется вне аэродинамической решетки, то на поверхности тока
г we = const ' A0.61)
и момент количества движения жидкой частицы остается постоянным.
Постоянная может иметь различные значения для различных
поверхностей тока. В вязкой жидкости момент количества движения изменяется
благодаря силам трения. Однако на некотором расстоянии от твердых стенок
силы трения малы, и изменение момента количества движения происходит
достаточно медленно.
В результате преобразований получены три уравнения движения,
записанные через меридиональную проекцию скорости: A0.58), A0.59), A0.60).
В сильно закрученных потоках турбомашин наибольшее значение имеет
второй член уравнения A0.58), так как окружная составляющая скорости
существенно больше меридиональной. Легко заметить, что закрутка
потока всегда приводит к росту давления по радиусу.
Знак первого члена может быть как положительным, так и
отрицательным — это зависит от знака кривизны меридиана. Если поверхность тока
вогнутая (см. рис. 10.4), то первый член положителен и, следовательно, сум-
256

марный градиент давления уменьшается. Таким образом, изменяя контуры
корпуса турбомашины, можно в некоторых пределах изменять величину
радиального градиента давления.
Уравнения движения в форме A0.58), A0.59), A0.60) позволяют яснее
понять влияние кривизн поверхностей тока на градиент давления. На это
следует обратить внимание также потому, что существуют приближенные
методы расчета течений в турбомашинах, основанные на расчете кривизн.
10.3. ОСЕСИММЕТРИЧНЫЕ ТЕЧЕНИЯ ЧЕРЕЗ КОЛЬЦЕВЫЕ
АЭРОДИНАМИЧЕСКИЕ РЕШЕТКИ
В разд. 10.2 приведены некоторые точные решения для
закрученных потоков. Подобные решения используют при расчете течений в
осевых турбомашинах, хотя теоретически они справедливы только на
бесконечном расстоянии от кольцевых аэродинамических реше+ок.
В этом разделе рассмотрим особенности течения через саму кольцевую
аэродинамическую решетку, закручивающую поток, и процесс
выравнивания этого потока за решеткой.
Положим, что жидкость идеальна и несжимаема. Течение происходит
между двумя цилиндрическими концентрическими поверхностями, а
кольцевая аэродинамическая решетка, закручивающая поток, состоит из
бесконечного количества бесконечно тонких лопаток.
В такой постановке задачи течение осесимметрично.
Однако теперь, и это особенно важно подчеркнуть, поверхности тока
не будут цилиндрическими ни внутри аэродинамической решетки, ни за
ней, хотя ограничивающие стенки являются цилиндрическими.
Как было сказано, лопатки приняты бесконечно тонкими, однако их
суммарная толщина на любой окружности может быть взята точно такой
же, как суммарная толщина лопаток реальной кольцевой решетки. Это
весьма существенно, так как суммарная толщина лопаток в осевых
турбинах может занимать до 50—60% проходной площади.
В связи со сказанным, уравнение неразрывности для несжимаемой
жидкости в цилиндрической системе координат следует записать в таком виде:
— (т rv) + — (т г и) - 0, A0.62)
дг дх
где т = т(х, г) < 1 — функция, определяемая геометрическими
характеристиками кольцевой аэродинамической решетки, учитывает стеснение
проходной площади лопатками. В потоке вне решетки т = 1.
^ля удовлетворения уравнения неразрывности A0.62) введем функцию
тока, приняв в отличие от A0.12):
тги = д$/дг, тд>-:— dty/dx, A0.63)
Даже если течение до кольцевой аэродинамической решетки было
безвихревым, то при закрутке потока в решетке оно станет вихревым.
Выразим проекции локальной угловой скорости вращения частиц жидкости
через введенную функцию тока A0.63).
Сама функция тока связана только с осевой и радиальной проекциями
скорости, а проекции завихренности по формулам A0.5), A0.6) зависят
также от окружной проекций скорости.
При течении внутри аэродинамической решетки окружную проекцию
скорости можно выразить через осевую, исходя из граничных условий на
лопатках. Действительно, в принятой постановке угол между осевой и
9 Зак. 2638 257

окружной составляющими скорости следует считать известным из заданных
геометрических характеристик решетки:
w^uctga, A0.64)
где а == а(лг, г) — известная функция координат (внутри аэродинамической
решетки).
С помощью формул A0.5), A0.6), A0.7), A0.63), A0.64) получим
искомые зависимости:
iJ f( ft) A0.65)
ж (r«ctga) f(
г дг г дг \ т
> —-f-<«ctga) —-L -f
дх г дх
<io.67)
Из уравнений A0.65), A0.66) следует, что при повороте потока в решетке
изменяется его завихренность.
Далее рассмотрим силы, с которыми действуют на поток лопатки
решетки. В данной постановке эти силы следует считать распределенными
или как бы «размазанными» внутри всего пространства, занятого решеткой.
При заданных геометрических характеристиках решетки эти силы
нельзя задать произвольно. При течении идеальной жидкости силы должны
быть нормальны к поверхности лопаток. Другими словами, в каждой
точке вектор силы должен быть нормален к вектору скорости.
Это условие можно записать через проекции силы и скорости на оси
координат:
0. A0.68)
В кольцевых решетках осевых турбомашин практически во всех
случаях можно пренебречь по малости радиальной проекцией силы
(исключение составляют специальные конструкции, в которых лопатки установлены
не радиально).
Тогда учитывая к тому же, что и радиальная проекция скорости мала,
вместо зависимости A0.68) запишем
uFx + wFb = 0. A0.69)
Сопоставив уравнения A0.64), A0.69), запишем соотношение между
осевой и окружной проекциями силы:
^-Fectga. A0.70)
Форма поверхностей тока заранее неизвестна. Положим, что
уравнение семейства этих поверхностей может быть описано функцией
(обоснование этого будет дано далее сравнением с известными точными решениями)
^^~u^l2+u,F{x){r-ri)(r~r2). A0.71)
Здесь rlt г2 — радиусы соответственно внутренней и* внешней
ограничивающей поверхностей; г — текущий радиус; и0 — постоянная. При таком
выборе уравнение неразрывности и граничные условия на цилиндрических
ограничивающих стенках удовлетворены автоматически при любом
значении функции F = F(x), так как функция тока принимает постоянные
значения на цилиндрических поверхностях.
258

Радиальную и осевую скорости определяем через функцию тока A0.71)
по формулам A0.63):
if_ri)(r_rj); A0.72)
v (rri)(rrj);
f T (XX
и ^Л» ' 2^L(r_r0). A0.73)
т г т
Здесь принято обозначение для среднего радиуса г0 - (гх + г2)/2. Из
формулы A0.71) следует, что и0 — осевая скорость потока на среднем
радиусе вне аэродинамической решетки. Эту скорость следует считать известной,
так как по ней и размерам кольцевого канала можно выразить объемный
расход через кольцевую аэродинамическую решетку, который считаем
известным:
г*
Q = 2л J т rudr = п (г\ — г'\) и0 --- л Ши0. A0.74)
ri
Здесь введены обозначения среднего диаметра и длины лопаток
аэродинамической решетки, обычно используемые при расчете турбин:
d~rH r2 = 2r0, г^гъ — гь A0.75)
Запишем уравнение радиального равновесия A0.1), в котором, как
было^отмечено, можно пренебречь по малости радиальной силой, так как
поверхности лопаток мало отклоняются от радиального направления:
v [_w = ?_ A0.76)
д г д х г р д г
Выразим радиальный градиент давления через радиальный градиент
полной скорости с помощью уравнения Бернулли для несжимаемой
жидкости:
(U + Xj + W)—L Jl^t A0.77)
p д г 2 д г р д г
Здесь в общем случае полное давление не является постоянным для
всего потока и его следует рассматривать как известную функцию радиуса
Ро = Ро(г)> Хотя в данном случае поверхности тока и не будут
цилиндрическими, но мало уклоняются от них и такое предположение допустимо.
Исключив в уравнении A0.76) статическое давление с помощью
уравнения A0.77), получим
dv w* I ди* . 1 dw* I др0 ПП7Я\
дх г 2 дг 2 дг р дг v ;
Геометрические характеристики кольцевой аэродинамической решетки
полагаем известными. В таком случае окружную проекцию скорости
можно выразить через ее осевую проекцию A0.64). Объединив третий и
четвертый члены уравнения A0.78) и воспользовавшись условием A0.64),
получим
«f-^^ =-f (l + cttf «)-?*- +
дх г 2 дг
+ ±^J^t^^±Il^, A0.79)
^ 2 дг р дг х '

Для приближенного решения этого дифференциального уравнения в
частных производных примем, что распределение скоростей соответствует
уравнениям A0.72), A0.73), которые точно удовлетворяют уравнению
неразрывности и граничному условию на цилиндрических стенках.
Для определения неизвестной функции F = F(x) потребуем точного
удовлетворения уравнения A0.93) на расчетном радиусе г0.
Определим последовательно значение всех членов уравнения A0.79) на
расчетном радиусе, используя для этого уравнения A0.72), A0.73) и
обозначения A0.75). Для упрощения записи, не будем вводить
дополнительной индексации, но следует помнить, что функции и их производные,
зависящие от радиуса, следует подсчитывать на расчетном радиусе.
Ниже выписаны значения членов уравнения A0.79) при г = г0:
(и dv \= "о/2 / d2F | I дт dF \
[ дх ) 2r*d [ dx* т dx dx у
и2 ctg2 q \ _ 2u% ctg2 q
~ J d "
[ 2 dr ) 2t2
I \ д Pq \ 1
\ p dr ) p
2t2 dr
д Pq
dr
Посла подстановки этих значений в уравнение A0.79) получим для
искомой функции F = F(x) обыкновенное дифференциальное уравнение
второго порядка:
дх дх
L. ""*-<* 4. '-«* _J1_/ ^о \ A0.80)
/2 dr /2 dr \ pa2 }' v
Введем безразмерные координаты, отнеся их к среднему радиусу, а также
безразмерный параметр 6, который характеризует веерность кольцевой
решетки (веерностью называют отношение lid):
x--2x/d, r=2r/d, Q-^d/l. A0.81;
С помощью соотношений A0.81) запишем уравнение в безразмерном виде
Ц^= ^2e(l + ctga)F
dx* т дх dx
—т2 92 ctg2 a +— A + ctg2 a) -21- —
x д г
-e2 ^ctg!a + т2е2 -4г (-3&-) <io.82)
2д г д r \ pw0 /'
В этом уравнении единственная неизвестная функция — это F(x)> В
общем случае уравнение A0.82) может быть решено численным методом, что
достаточно просто, так как оно является обыкновенные дифференциальным
260

уравнением второго порядка. Прежде чем переходить к общему случаю И
обсуждать граничные условия, рассмотрим некоторые частные решения,
которые можно сравнить с точными.
Бесконечно далеко за кольцевой решеткой течение будет
цилиндрическим, а эта задача имеет точное решение при любых заданных законах
изменения по радиусу угла а и давления торможения р0 (см. разд. 10.2).
В частности, при р0 = const, a = const из формулы A0.25) следует
известный закон изменения осевой скорости в принятых здесь обозначениях:
u=u0(rjr)cos*a. A0.83)
При цилиндрическом течении вне решетки должно быть F = const,
т = 1. Для принятых выше условий в уравнении A0.82) не равны нулю
только третий и четвертый члены. Тогда найдем искомую функцию
cos,
2(l+ctg2a) 2
а из формулы A0.73) — такую приближенную зависимость для
распределения осевой скорости
.= 1+ r°~~r
+
Для сравнения разложим точное решение A0.83) в ряд:
cos2 a. A0.84)
•¦ <10-85>
Разложение ведем по степеням параметра (г — го)/г, который по
абсолютной величине всегда существенно меньше 1/2, так как наибольшее его
значение равно отношению длины лопатки к диаметру 2гх кольцевой
решетки: (г0 — гг)/г} = ll(d — /).
Приближенное решение A0.84) совпадает с первыми двумя членами
точного решения A0.85). Максимальное значение третьего члена в разложении
A0.85) равно 0,125(//d—/Jsin22a, так что даже при 6 = d// = 5 и a = 15°
ошибка будет составлять 1%.
В подразд. 10.2 рассмотрено также точное решение задачи о
закрученном потенциальном потоке, для которого угол зависит от радиуса по
формуле A0.28).
В принятых здесь обозначениях эта формула примет вид
(l^)i A0.86)
гдеа0 — значение угла на расчетном радиусе. В уравнении A0.82) не равны
нулю члены третий, четвертый и шестой, причем в последнем из них
производную следует вычислить с помощью формулы A0.86) при Г=--- 1. В
результате получим F — 0, а тогда из формулы A0.73) следует постоянство
осевой скорости, что соответствует точному решению.
Вернемся к общей задаче и перейдем к рассмотрению граничных
условий.
Положим, что в безграничном в осевом направлении канале,
образованном концентричными цилиндрическими поверхностями, расположена одна
кольцевая аэродинамическая решетка. Геометрические характеристики
решетки известны,
261

Граничные условия на цилиндрических поверхностях соблюдены при
любом F(x) выбором функции тока A0.71).
Граничные условия на лопатках в аэродинамической решетке
удовлетворены в осесимметричной постановке заданием функции a(je, г),
определяемой только геометрической характеристикой лопаток.
Остается рассмотреть граничные условия на бесконечности до и после
аэродинамической решетки. В принятой постановке задачи течения в
бесконечных кольцевых трубах до и после решетки можно приближенно
рассматривать отдельно.
В бесконечности перед одиночной аэродинамической решеткой течение
должно быть цилиндрическим. В разд. 10.2 было показано, что для
цилиндрического течения распределения по радиусу угла направления скорости и
давления полного торможения можно задать произвольно. Поскольку в
данной постановке задачи аэродинамическая решетка не возмущает течение пе-
ре# собой, то течение будет цилиндрическим вплоть до ее переднего фронта.
Тогда граничные условия можно приближенно перенести из бесконечности
перед решеткой на плоскость ее переднего фронта. Распределение угла
направления потока по радиусу будем считать известным, так как
направление потока согласовано а углом входной кромки в общем случае закрученной
лопатки (рассматриваем расчетный режим обтекания).
Таким образом, в плоскости переднего фронта решетки следует считать
известными как значение функции F(x), так и ее первой производной
dF(x)/dx=0. Второе из этих условий следует из цилиндричности течения
на входе и формулы A0.72). Граничное условие для функции F(x) следует
из аппроксимации формулой A0.73) заданной осевой скорости
и (*i> г) = с (r)sin a» a ="•a (*i> 0>
причем для цилиндрического течения на входе полная скорость определена
формулой A0.23); хх — координата, соответствующая плоскости переднего
фронта решетки.
Таким образом для обыкновенного дифференциального уравнения
второго порядка A0.82) известны два граничных условия и оно может быть
решено (в общем случае численным методом). В результате решения станут
известны значения F(x) и (dFldx) при х = хъ что соответствует плоскости
заднего фронта аэродинамической решетки. Эти данные будут граничными
условиями для решения задачи о течении в полубесконечной кольцевой трубе
за аэродинамической решеткой. Течение должно быть описано тем же общим
дифференциальным уравнением A0.82), но при т = 1. Однако угол
направления потока a(jc, г), который был известен внутри аэродинамической
решетки, теперь также будет искомой функцией и должен быть выражен через
F(x).
Вне аэродинамической решетки окружная проекция силы равна нулю,
и на основании уравнения A0.2) момент количества движения должен быть
постоянен на поверхностях тока.
Как принято в этом разделе, будем применять это уравнение на
расчетном радиусе. На этом радиусе, как следует из формулы A0.73),, осевая
скорость вне решетки постоянна. На основании принятых приближений примем
на расчетном радиусе постоянными безразмерные радиальные градиенты
момента количества движения и полного давления:
uodr
262
-l JB*-\ = b при г = 1, A0.87)
г V Р «о /

где А, В — безразмерные постоянные, которые известны из расчета течений
в аэродинамической решетке, так как равны значениям соответствующих
градиентов в выходном сечении на среднем радиусе.
Записав уравнение A0.2) при г = г/г0 = 1 с учетом зависимостей A0.72),
A0.73) и обозначений A0.81) после простых преобразований, получим
л^4-е2 дс1еа° -о
л^4е - о-
dx д х
После интегрирования по х найдем
62ctga0—AF=C, A0.88)
где С — безразмерная постоянная интегрирования, которую следует
считать известной, так как известно а(х2, г0) и F(x2), где х2 -— координата,
определяющая положение плоскости заднего фронта решетки.
Заменим в первом выражении A0.87) окружную проекцию скорости через
осевую с помощью формулы A0.47) и затем продифференцируем полученное
выражение по частям:
7JLi?*|?L7^=A A0.89)
or
ctga+7|
и0 и0 д г
Записав это выражение для расчетного радиуса, имеем
ctgao + ( дс^а ) + 2ctgaQF=A. A0.90)
При дифференцировании осевой проекции скорости в уравнении A0.89)
была использована зависимость A0.73).
Соотношения A0.88) и A0.90) позволяют выразить ctga0 и (dctga/dr)ro
через искомую функцию F(x) и исключить их из основного
дифференциального уравнения A0.82).
Опустив простые алгебраические преобразования, запишем уравнение
A0.82) в форме, пригодной для расчета закрученного потока вне
аэродинамической решетки:
. -^4-+92B+ЛС + Ла)/'=в2В. A0.91)
Все постоянные в этом уравнении известны. В бесконечности за
решеткой функция F(x) должна стремиться к некоторой постоянной, так как
только в этом случае радиальная скорость стремится к нулю и поток становится
цилиндрическим. Для расчета течения за решеткой удобно поместить
начало координат так, чтобы плоскость заднего фронта решетки
соответствовала х = 0. Тогда решение уравнения A0.91) следует записать в таком
виде (х > 0):
F(x)=Dexp[—QxV 2 + АС + А* +В/B+А С + А2)). A0.92)
Постоянную D находим по известному значению функции jF(O):
-\ A2). A0.93)
Из решения A0.92) определяем значение искомой функции в
бесконечности за решеткой;
F (оо) = В 1B + АС +Л2)# A0.94)
263

а затем по формуле A0.73) — соответствующее ей распределение осевой
скорости. Угол направления скорости на расчетном радиусе в
бесконечности подсчитываем с помощью формулы A0.88):
A0.95)
По формуле A0.90) можно найти dctga/dr в бесконечности за решеткой.
Вопросы для самопроверки
1. Какие причины вызывают радиальный градиент давления в осесимметричном
закрученном потоке?
2. Как влияет кривизна поверхности тока в меридиональной плоскости на
радиальный градиент давления?
3. Найдите проекции угловых скоростей вращения жидкости дл# закрученного
цилиндрического потока при a = const.
4. Запишите уравнения движения жидкости в цилиндрической системе координат,
вращающейся с постоянной угловой скоростью. v

ГЛАВА И
ДВУХФАЗНЫЕ И ДВУХКОМПОНЁНТНЫЕ ТЕЧЕНИЯ
П.1. ОСОБЕННОСТИ ДВУХКОМПОНЕНТНЫХ И ДВУХФАЗНЫХ
ТЕЧЕНИИ
В предыдущих разделах книги было рассмотрено движение
однородных газов или жидкостей. В технике возникает много задач, в которых
необходимо рассматривать движение смесей (при изучении горения,
конденсации, испарения, кавитации и т. д.). Такими смесями могут быть: газ
и твердые частицы (например, дым), пар или газ с жидкими частицами
(например, влажный пар или влажный воздух), жидкость с пузырьками
пара или газа, жидкость с твердыми частицами или капельками другой
жидкости.
Компоненты системы — различные вещества, наименьшее число
которых достаточно для образования всех фаз термодинамической системы. Они
могут находиться в твердом, жидком или газообразном состоянии. Эти
состояния вещества называют соответственно твердой, жидкой или
газообразной фазами. Компоненты состоят из одного и того же химического вещества
(например, водяной пар и капельки воды).
Когда одно и то же вещество одновременно находится в двух фазах, то
возможен переход его из одной фазы в другую, т. е. массообмен. Следует
подчеркнуть, что этот массообмен сопровождается также поглощением или
выделением скрытой теплоты.
Компоненты могут находиться в одной фазе, например воздух с
примесью водяного пара. Свойства такой смеси будут мало отличаться от свойств
обычного газа до тех пор, пока при определенных условиях водяной пар не
начнет конденсироваться. Между капельками воды и водяным паром
возможен тепло- и массообмен, что скажется на свойствах всего потока. Однако,
если содержание пара в воздухе невелико, то течение такой смеси будет,
естественно, отличаться от течения чистого пара с капельками той же
жидкости.
Теплообмен происходит также, например, между воздухом и
переносимыми им мелкими твердыми частицами, однако количество теплоты, которое
при этом передается, обычно не столь велико, как при фазовом переходе.
Между фазами веществ различной химической природы возможен и
массообмен, например, растворение или выделение пузырьков в воде. Поэтому
подчеркнем, что в двухфазных потоках одного вещества тепло- и массообмен
существенно влияют на характер течения.
Течение однофазных многокомпонентных потоков также имеет свои
особенности. Воздух представляет собой смесь азота, кислорода и других
газов. Концентрация этих газов постоянна и между ними не происходит
реакций. Поэтому, если каждый компонент подчиняется уравнениям
совершенного газа, то и вся смесь подчиняется этим уравнениям, причем
соответствующие постоянные (теплоемкости, показатель изоэнтропы,
газовая постоянная) могут быть вычислены по правилам смешения.
Если же газ, например кислород, диссоциирует при высокой
температуре, то образуется реагирующая смесь из молекулярного и атомарного кисло-
265

рода, свойства которой определяются степенью диссоциации, т. е.
концентрацией компонентов. Поскольку концентрация зависит от температуры и
давления, то смесь не подчиняется уравнениям совершенного газа, хотя ее
компоненты можно рассматривать как совершенные газы. При течении
диссоциирующего газа степень диссоциации будет изменяться, т. е. будет
наблюдаться массообмен, который сопровождается поглощением или
выделением теплоты диссоциации.
В потоке смесей могут происходить химические реакции, например
горение, при которых состав смесей также изменяется и выделяется теплота.
Если одно и то же химическое вещество находится в двух фазах, то
между ними соблюдается фазовое равновесие. Температура и давление
насыщения связаны между собой. Однако при быстром изменении состояния
системы фазовое равновесие устанавливается не мгновенно. При быстром
расширении пара в соплах пар переохлаждается, так как для конденсации
требуется определенное время для образования первичных ядер
конденсации и теплообмена. Если фазы состоят из веществ различной химической
природы, tq связи между давлением и температурой нет, однако и там
теплообмен происходит не мгновенно, т. е. для установления теплового
равновесия среды требуется определенное время.
Так как физические и химические процессы происходят с конечной
скоростью, то при быстром изменении параметров смеси будут наблюдаться
неравновесные течения.
Установление с течением времени нарушенного равновесия среды
называется релаксацией. Явление релаксации существенно при изучении
быстрого движения двухфазных сред.
Процесс установления равновесия идет асимптотически. Однако можно
ввести некоторое характерное время установления, называемое временем
релаксации. Если время релаксации мало по сравнению с характерным
временем изменения состояния смеси, то течение можно рассматривать как
равновесное. Если, наоборот, относительное время релаксации очень
велико, то можно пренебречь теплообменом и массообменом и рассматривать
течение смеси неизменного состава.
Виды течений двухфазных сред могут быть весьма многообразны. Обе
фазы могут быть сплошными: пленка жидкости может двигаться по
поверхности твердого тела, увлекаемая потоком газа. Одна фаза может быть
сплошной* а другая — распыленной в виде мельчайших частиц. Сплошной фазой
может быть газ или пар, а распыленной (дисперсной) — твердые частицы
(дым) или капельки жидкости (влажный пар).
Если сплошной фазой является жидкость, то она может содержать
пузырьки газа или пара (кипящая жидкость), твердые частицы (суспензия)
или капельки другой несмешивающейся жидкости (эмульсия масла и воды).
Смесь характеризуется размерами распыленных частиц (дисперсностью)
и концентрацией» т. е. массой частиц, содержащихся в единице массы
смеси. Последняя характеристика называется массовой концентрацией. Можно
ввести также объемную концентрацию как отношение объема частиц к
объему смеси, в котором они содержатся. Кроме того, смесь характеризуется
относительным расстоянием между частицами.
Свойства текущей смеси зависят от дисперсности и концентрации. Так,
например, при малой концентрации газа в жидкости мелкие ну*
эырькн рассеяны в потоке, а при объемной концентрации газа,
близкой к единице, поток движется в виде пены, где газовые включения
разделены пленкой жидкости. Мелкие жидкие или твердые включения
переносятся потоком, причем скорость частиц ке совпадает с местной
скоростью потокаА Это рассогласование скоростей или скольжение зависит от

дисперсности. Так как масса частицы пропорциональна кубу характерного
размера частицы, а сила сопротивления для очень мелких частиц —
первой степени размера, то включения с высокой степенью дисперсности будут;
двигаться с малым рассогласованием скоростей. А так как траектория
движения частиц зависит от рассогласования скоростей, то траектории
движения более мелких и более крупных частиц будут различны.
Практически смеси не состоят из частиц одного размера, поэтому
вводится также характеристика распределения частиц по размерам. Размеры
частиц могут быть заданы (например, при пневмотранспорте сыпучей среды),
а в общем случае они зависят от тех процессов, которые протекают в смеси,
как при конденсации текущего пара.
Общая задача о движении двухфазных систем весьма сложна и не
может быть решена только методами термодинамики и газодинамики, а
требует расчета скорости фазовых переходов. Однако предельные случаи очень
большого и очень малого времени релаксации рассматриваются
достаточно просто. Решение таких задач позволяет выяснить основные
закономерности и оценить пределы, в которых могут влиять те или иные воздействия
(теплообмен и т. п.). Далее в этой главе рассмотрены такие предельные
случаи.
11.2. СОВЕРШЕННЫЙ ПАР
В гидрогазодинамике широко используют понятие
совершенного газа, который по определению удовлетворяет уравнению состояния
p==pRT,.R = const. A1.1)
Известно, что реальные газы удовлетворяют этому уравнению лишь
приближенно. Отличия особенно существенны при очень высоких давлениях и
очень низких температурах, т. е. в области, где газ следует рассматривать
как пар.
В общем случае вместо уравнения состояния A1.1) необходимо
применять уравнение типа
Р=Р(Р,Т). A1.2)
Для расчета течений совершенного газа широко используют
газодинамические функции (см. гл. 4). Очевидно, что очень полезным было бы
распространение этого метода на пар. Для этого необходимо иметь простое
уравнение состояния пара и найти связь между параметрами пара при изоэнтро-
пийном процессе.
В общем случае можно записать уравнение состояния в таком виде:
p^zpRT, A1.3)
где z — безразмерная величина, называемая коэффициентом сжимаемости,
отклонение которой от единицы показывает, насколько свойства реального
газа или пара отличаются от совершенного газа.
Отклонение коэффициента сжимаемости от единицу! вызвано в основном
влиянием двух причин; При высоких температурах и низких давлениях в
газе происходит диссоциация. При низких температурах и высоких
давлениях влияют межмолекулярные силы и газ близок к сжижению. В последнем
случае можно говорить о паре, причем для такого технически важного
вещества, как водяной пар, конденсация происходит в диапазоне изменения
параметров, при которых работают паровые турбины.
267

В общем случае коэффициент сжимаемости является функцией двух
независимых параметров:
9). A1.4)
В. Траупель постулирует свойства совершенного пара следующим
образом.
Совершенный пар удовлетворяет термическому уравнению состояния в
форме A1.3) (коэффициент сжимаемости будет определен позднее), а для
энтальпии справедлива зависимость
h = -* —
r „, A1.5)
где hH — произвольная постоянная, соответствующая выбору начальной
точки отсчета для энтальпии. При этом предложено, что х и hH изменяются
столь слабо, что в относительно небольшой области их можно считать
постоянными.
Уравнение A1.5) называют калорическим уравнением состояния.
Термическое уравнение состояния A1.3) и калорическое уравнение
состояния A1.5) не могут быть введены независимо одно от другого.
Запишем уравнение второго закона термодинамики
Tds=dh—dplp> '• A1.6)
Поделим все члены уравнения на pip и получим
9Т , pdh dp
——— i^^ —— ——^——"—— —~¦—¦¦¦ t
р Р Р
Первый член этого уравнения преобразуем с помощью формулы A1.3),
а второй — формулы A1.5):
х— 1 ds dh L х—1 dp /11 7\
———— —^— ————— I ————— ——-— ^ I 1 1 . I I
x zR h—/iH x p
Для того чтобы не были нарушены законы термодинамики, результат
интегрирования этого уравнения не должен зависеть от пути, по которому
выполнено интегрирование. Все слагаемые в уравнении A1.7) должны быть
полными дифференциалами некоторых функций. В правой части уравнения
это условие выполнено. Так как ds — уже полный дифференциал, то для
того чтобы левую часть записать как полный дифференциал, необходимо,
чтобы коэффициент сжимаемости был функцией только энтропии:
z=-z(s). A1.8)
Этот вид зависимости является более частным случаем, чем общая
зависимость A1.4). Ввиду этого пар какого-либо вещества не обязательно должен
удовлетворять условию A1.8), а следовательно, для него, вообще говоря,
нельзя ввести уравнение состояния в форме A1.5).
Однако водяной пар, который здесь представляет основной интерес,
удовлетворяет условию A1.8) с приемлемой для приближенных расчетов
точностью.
На рис. 11.1 показана зависимость коэффициента сжимаемости от
энтропии в широком диапазоне изменения параметров для перегретого и
насыщенного водяного пара. Газовая постоянная R по расчетам, выполненным с
помощью таблиц водяного пара, равна 461,5 Дж/(кг • К).
Из расчетов следует, что при s > 7,5 Дж/(кг • К) водяной пар можно
рассматривать как совершенный газ, так как z>0,99. Вместе с тем в
области рабош паровых турбин коэффициент сжимаемости лежит в пределах z =
268

I
0.950
0,900
0,850
0,800
6,0
6,5
1,0
15
Рис. 11.1. Зависимость коэффициента сжимаемости от энтропии для водяного пара:
О — насыщенный пар; 4- — / = 200 °С; О — /=300 °С; D — / = 600 °С
=- 0,8-М ,0, т. е. перегретый водяной пар можно приближенно рассматривать
как совершенный пар, но нельзя считать совершенным газом. При этом
следует отметить, что в принятом диапазоне изменения параметров разброс
точек не превосходит 0,02, а следовательно, отклонение от некоторой
средней зависимости z = z(s) не превысит 1 %.
Для изоэнтропийного процесса после интегрирования уравнения A1.7)
получим
к~1
(Л-Ан)/(А1-Лн)==(Р/Р1) * . A1.9)
Исключив из уравнения изоэнтропы A1.9) давление с помощью
уравнения, определяющего показатель х, найдем
(h~h^Hhx-K)^{9l9l)^\ A1.10)
Заменим в формуле A1.9) давление через плотность и температуру из
уравнения состояния A1.2) и затем исключим плотность по формуле A1.10),
тогда
(h-hJ/(bi-hJ = TlTv A1.11)
В предыдущих формулах уравнения изоэнтропы записаны через
энтальпию. Исключив из них энтальпию, можно записать для совершенного
пара, как для совершенного газа:
/V/\ (P/Pi)x, TITx^{pIpx) * , T/T^ip/pJ*-1. A1.12)
Чтобы использовать формулы для совершенного пара, необходимо
сначала определить показатель изоэнтропы. Напомним, что под этим надо
понимать некоторую среднюю величину, которую следует найти из уравнения
A1.5) с помощью таблиц водяного пара.
Приведем численный пример, который позволяет судить о точности
формул, хотя следует иметь в виду, что погрешность зависит от области, в
которой производят расчеты. Ниже приведены'точные и приближенные значения
плотности перегретого пара на изоэнтропе s = 6,2626 кДж/(кг • К) в
зависимости от давления:
р, МПа
р, кг/м5*:
точное значение
приближенное значение
36
. 36
10
,846
,846
30
30
8
,941
,942
24
24
6
,691
,705
17
17
4
,982
,989
14
14
3
,358
,362
2
12
12
,44
,226
,225
269

Постоянные в формуле A1.5) определены ее применением при давлениях
\р = 10 МПа и р = 3 МПа как решение системы из двух линейных
уравнений; х = 1,278, hn = 2783,3 кДж/кг.
Расчеты приведены по первой формуле A1.12), причем за основу бралась
плотность пара при давлении р = 10 Mlia. Расхождение в значениях
плотностей при давлении р — 3 МПа объясняется округлением значения
показателя изоэнтропы. Последний столбец соответствует насыщенному пару,
т. е. наинизшему давлению, при котором справедливы формулы.
Влажный пар нельзя рассматривать как совершенный, однако и в этом
случае приведенные формулы могут существенно упростить расчеты. Так,
например, при s >7,5 кДж/(кг • К) можно считать, что насыщенный пар,
который используется в расчете свойства влажного пара, подчинен
обычному уравнению состояния A1.1). В других случаях наосноверис. 1J.1
можно получить простую аппроксимацию коэффициента сжимаемости.
11.3. гомогенное течение газа с постоянной
концентрацией примесей
Гомогенным называют такое течение двухфазной среды, когда
смесзь рассматривают как однофазную среду, обладающую некоторыми осред-
ненными характеристиками. Такой подход сильно упрощает исследование и
позволяет использовать все уравнения гидрогазодинамики в обычном виде.
Осреднение свойств двухфазной среды производят в предположении о
равновесном состоянии смеси в процессе движения, В действительности при
движении двухфазной смеси процесс может быть неравновесным. Например,
при течении пара с каплями через сопло теплообмен происходит не
мгновенно и, следовательно, параметры каждой из фаз и всей смеси зависят от
скорости протекания процесса. Скорость процесса расширения зависит от
ускорения потока, т. е, при установившемся движении от градиента скорости
потока вдоль оси сопла.
Массообмен, т. е. конденсация на каплях или испарение капель связаны
с теплообменом. Следовательно, конденсация жидкой фазы в паре меняется
и также зависит от градиента скорости потока. Несмотря на эти замечания,
изучение гомогенных течений двухфазной среды представляет определенный
интерес. Во-первых, имеются технически важные задачи, в которых
процесс изменения параметров смеси идет достаточно медленно. Во-вторых, с
помощью теории гомогенных течений можно просто рассмотреть предельные
частные случаи и установить границы, в которых может сказываться
влияние неравновесности процессов.
При изучении двухфазных потоков будем применять термины: газ, пар
и жидкость в их обычном значении, так как общий термин «жидкость»
может привести к неясностям. В тех случаях, когда различие между газом и
паром из-за введенных упрощений не существенно, будет применяться
термин «газ». Вторая фаза, которая может быть жидкостью или твердыми
частицами, если это из-за упрощений задачи не существенно, будет называться
жидкостью.
В тех случаях, когда жидкость содержится в газе или паре в виде мелких
капелек, или твердые включения распылены в виде мелких частиц, можно
определить некоторые средние свойства смеси. Будем сейчас рассматривать
задачи, в которых можно пренебречь массообменом между фазами. Таким
образом, будем полагать, что жидкость, находясь в паре или газе, не
испаряется, а пар не конденсируется. Следовательно, полагаем, что состав смеси
как бы заморожен, т. е. концентрация массы одного вещества в другом
неизменна. Будем считать также, что скорости фаз одинаковы. Это, конечно,
270

приводит к упрощениям явления, но позволяет произвести некоторые
количественные оценки влияния второй фазы.
Величины, относящиеся к жидкости, будем обозначать штрихом, к
газу — двумя штрихами и к смеси — без штрихов. Величины, которые
одинаковы как для всей смеси, так и для каждой фазы, пишем без штрихов.
Обозначим ф массовую концентрацию жидкости в смеси, т, е. отношение
массы жидкости в некотором объеме смеси к массе смеси в атом объеме:
Ф = m'l{mf -f m") = trilm, m — m' + m". Запишем выражения для плот*
ностей фаз и средней плотности среды: р' — m'/V\ p" — m"/V'\ p = m/V,
V = V + V'\ где V\ V" — объемы, занимаемые фазами в выделенном
объеме среды 1Л Тогда среднюю плотность среды можно выразить через
концентрацию и плотности фаз;
Далее рассмотрим два частных случая равновесного процесса: фазы
находятся в тепловом равновесии (скорость тешюобмева между фазами бес*
кбнечно велика); тешюобмен между фазами отсутствует, В
действительности теплообмен происходит с какой-то конечной скоростью и указанные слу*
чаи будут предельными, т. е. по ним можно оценить влияние теплообмена
между фазами на характеристики течения.
Фазы находятся в тепловом равновесии. В этом случае температуры
обеих фаз равны и теплоемкость двухфазной среды определяется с помощью
теплового баланса. Следовательно; теплоемкости двухфазной среды при по*
стоянном давлении и постоянном объеме находятся по формулам: Чч
ср^A — <$)с"р + ч>с\ cv^{\— <р}ср + ус'. A1.14)
Газ полагаем совершенным, жидкость несжимаемой, а теплоемкости т
постоянными.
Определим газовую постоянную двухфазной среды через найденные
теплоемкости:
Тогда с помощью формулы A1,15) можно записать уравнение состояния длят
смеси (давление и температура одинаковы для каждого компонента и всей
смеси):
Показатель изоэнтропы для смесей находим как отношение
соответствующих теплоешостеЙ шеен:
Энтальпию массы смеси определим по формуле
Внутренняя энергия единицы массы смеси
Г, A1,19)
Следовательно, в данной постановке смесь можно рассматривать как
совершенный газ, но с постоянными, отличающимися от «чистого» газа.
Тогда все расчеты потока могут быть проведены по общим формулам,
используемым для совершенного газа,
271

Подчеркнем, что этими формулами можно пользоваться только тогда,
если одна фаза представляет собой сплошную среду, а другая — мелко-
дисперсна. Очевидно, что если жидкость течет в виде пленки, над которой
движется газ, или газ переносит жидкость в виде пены, то свойства такой
среды будут совершенно отличаться от найденных.
Теплообмена между фазами нет. В этом случае температура капель
остается постоянной. Следовательно, удельные теплоемкости смеси следует
определять по формулам, которые учитывают только то, что в единице массы
смеси из-за наличия второй фазы находится меньше газа:
сР = A —Ф)*р, cv^(l-(f)cy. A1.20)
Эти же формулы следуют из формул A1.14), если в них положить
теплоемкость жидкой фазы равной нулю, так как теперь при подсчете свойств
смеси жидкая фаза не участвует в теплообмене.
Для газовой постоянной смеси получим ту же формулу, что и ранее
A1.15). Следовательно, уравнение состояния A1.16) также не изменится,
так как его вид не зависит от теплоемкости жидкой фазы. Показатель изо-
энтропы смеси в рассматриваемом частном случае не отличается от
показателя изоэнтропы газа, переносящего капли:
х^ср/су==с;/су = к". A1.21)
Энтальпия и внутренняя энергия единицы массы смеси определяются по
формулам:
h = cpT^ A — ф) стр Т + ц>С Г; A1.22)
+ чс' Т. A1.23)
Как в первом, так и во втором случае можно считать, что смесь является
псевдогазом, и применять обычные уравнения одномерного течения. В
частности, для псевдогаза можно рассматривать и изоэнтропийное течение (при
отсутствии трения о стенки и подвода теплоты извне).
Рассмотрим теперь в той же постановке задачи вопрос о скорости
распространения звука в двухфазной среде, состоящей из газа и мелких
капелек. По определению скорость звука — это скорость распространения
слабых возмущений. Скорость звука зависит от упругости среды, ее плотности
и термодинамического процесса, происходящего при сжатии и разрежении.
Газ с очень мелкими капельками воды можно представить как смесь двух
газов: обычного газа и «газа» с тяжелыми молекулами (капельками),
который имеет массу, но не имее^ упругости. Если капельки столь малы, что
при прохождении звуковой волны колеблются вместе с газом, то скорость
звука можно определять по обычной формуле а = У х/?7\ Следовательно,
скорость звука будет различна для двух рассмотренных случаев.
Относительно большие капельки остаются при колебании газа
неподвижными, и тогда скорость звука будет равна скорости звука в «чистом» газе.
Присутствие относительно больших капелек влияет только на рассеивание
звука.
Общий случай, когда капельки частично вовлекают звуковой волной в
колебательный процесс или возможен частичный теплообмен, гораздо
сложнее и скорость звука зависит от частоты колебаний.
Критические параметры зависят от показателя изоэнтропы псевдогаза и
поэтому будут различными для двух рассмотренных частных случаев.
Для того чтобы представить степень влияния теплообмена между
фазами на параметры потока, рассмотрим пример.
272

Пример. Рассчитать параметры потока воздуха с капельками воды на выходе из
сопла, если концентрация капелек воды смеси равна ф — 0,10. Параметры торможения
перед сошюм: р0 — Ю5 Па, То = 300 К. Давление за соплом рх — 0,8-105 Па.
Теплоемкости воздуха: с"р = 1010 Дж/(кг- К), Су — 718 Дж/(кг«К). Теплоемкость воды
с' = 4190 Дж/(кг-К).
Фазы находятся в тепловом равновесии. Теплоемкости и газовая постоянная
смеси равны: ср == 1328 Дж/(кг-К), cv -•= 1065 Дж/(кг-К), R = 263 Дж/(кг-К).
Температура и плотность смеси за соплом: 7\ = 285К, pi = 1,07 кг/м3. Скорость потока и=
= 200 м/с, скорость звука аг = 311,5 м/с, число М равно 0,642, плотность потока
массы 213 кг/(м2-с). Критическое отношение давлений 0,547. , ,
Теплообмена между фазами нет. Теплоемкости и газовая постоянная смеси
равны: ср = 909 Дж/(кгК), cv = 643 Дж/(кг-К), Л = 263 Дж/(кг-К). Температура и
плотность смеси за соплом: Тг ~ 281,5К, рх = 1,08 кг/м3. Скорость потока и =
— 183,5 м/с, скорость звука а = 321,9 м/с, число М равно 0,570, плотность потока массы
198,3 кг/(м2-с). Критическое отношение давлений 0,528.
При наличии теплообмена между фазами капельки передают теплоту
расширяющемуся воздуху, и поэтому температура смеси за соплом и ее
скорость в первом случае больше. При истечении сухого воздуха
температура потока за соплом равна, естественно, соответствующей температуре
для второго случая. Скорость истечения, равная 195,5 м/с, больше, чем во
втором случае, в котором поток потратил энергию на разгон капель, но
несколько меньше, чем при наличии теплообмена.
11.4. ГОМОГЕННОЕ ТЕЧЕНИЕ ЖИДКОСТИ С ПУЗЫРЬКАМИ ГАЗА
Задача о движении жидкости с пузырьками газа находит
технически важное приложение при изучении течения жидкого топлива, в
насосах. Эта задача имеет особенности по сравнению с задачей о движении
газа с капельками жидкости.
Рассмотрим смесь, сплошной фазой которой является жидкость, а
дисперсной — мелкие пузырьки газа, равномерно рассеянные по объему.
Будем считать, что газ не растворяется в жидкости, а парциальное давление
паров жидкости мало и, следовательно, можно пренебречь массообменом
между фазами. Положим также, что жидкость и пузырьки газа находятся в
тепловом равновесии.
В данном случае удобнее характеризовать смесь концентрацией газа в
смеси ф. Тогда формулу для средней плотности смеси запишем в таком виде
(один штрих отмечает параметры жидкости, а два штриха — газа):
1/Р = A-ф)/р' + ф/р'. A1.24)
В технически важных случаях массовая концентрация газа в смеси очень
мала, так как количество его обычно не велика, а плотность много меньше
плотности жидкости.
Основной особенностью течения жидкости, в которой рассеяны мелкие
пузырьки газа, является то, что смесь имеет большую плотность, порядка
плотности жидкости, так как масса газа ничтожно мала из-за его малой
плотности и малого количества. Вместе с тем, смесь обладает сжимаемостью
вследствие сжимаемости пузырьков газа, в то время как жидкость
практически несжимаема. Сочетание этих свойств резко отличает свойства
смеси от свойств жидкости и газа.
Газ подчиняется уравнению для совершенного газа (давление и
температура выписаны без индексов, так как они общие для всей смеси)
р=9*ц*Т. A1.25)
273

Выразив в уравнении A1.24) плотность газа через давление и
температуру, получим уравнение состояния для смеси
1/р«ф/Г7> + A—<р)/р\ A1.26)
которое fenepb не совпадает с уравнением состояния для совершенного
газа, так как содержит справа дополнительный член. Теплоемкости смеси при
постоянном давлении и постоянном объеме определяем формулами:
A1.27)
и ввиду малости концентрации газа практически равны теплоемкости
жидкости. В таком случае показатель изоэнтропы для смеси весьма близок к
единице:
^ »»Юф)«' > A1#28)
Добавив и вычтя справа единицу, придадим этой формуле вид
Таким образом, при изоэнтропийном движении смеси изменение
температуры должно быть весьма малым. Это объясняется предположением об
идеальном теплообмене между пузырьками газа и жидкостью, которая
имеет относительно большую массу. Даже существенное повышение
температуры газа в пузырьках при быстром сжатии приводят? после теплообмена к
ничтожно малому повышению ?емпературы смеси. Предположение о
тепловом равновесий в данном случае близко к истине, так как жидкости
движутся в технических устройствах с относительно малыми градиентами
скорости.
Определим внутреннюю энергию единицы массы смеси
e*=cvT**tocy + (l— ч>)с'\Т A1.30)
и энтальпию единицы массы смеси h — е + р/р.
Заменив в этом выражений внутреннюю энергию по формуле A1.30),
плотность смеси по формуле A1.26) н выразив газовую постоянную через
теплоемкости газа, получим
h^[<pc; + (l~$)c']T + (l~-y)ptp'^c'>T+(l-~<p)pfp'. A1.31)
В данном случае энтальпия зависит не только от температуры, как для
совершенного газа, но и от давления, что выражается последним членом
уравнения* Это объясняется тем, что смесь подчиняется уравнению состоя*
ння A1.26), которое, как подчеркивалось, также отличается от уравнения
ддя совершенного газа.
Уравнение энергии должно быть записано в обычном виде
В соответствующих частных случаях (ф ~ 1, q> — 0) оно переходит в
уравнение энергий для совершенного газа или уравнение Бериулли для
несжимаемой жидкости, В случае, если рассматривается движение смеси, можно
также пренебречь членом, зависящим от температуры, так как было
показано, что она не меняется.
Вычислим скорость распространения звука в жидкости с пузырьками
газа. Ввиду того, что плотность смеси велика, а упругость определена
упругостью воздушных пузырьков, скорость распространения звука в смеси
должна быть низкой. Тогда, если и яри распространении звуковой волну
274

в смеси происходит идеальный теплообмен, то можно считать температуру
практически постоянной, В этом случае давление и плотность смеси
связаны уравнением A1.26). Если же при распространении звуковой волны
теплообмен между пузырьками газа и жидкостью не успевает произойти,
то для газа в пузырьках справедливо уравнение изоэнтропы. Вычислим
скорость звука в предположении постоянства температуры. Из уравнения
A1.26) получим
р = 1EJLL . A1.32)
1—A—ф) р/р'
Согласно уравнению D.9) скорость звука выражается через производную
давления по плотности среды:
а2^ dp _^ 4>R"T
dp П~A-ф)р/р']2 '
Заменив в этом выражении знаменатель с помощью формулы A1.32),
найдем выражение для скорости звука в смеси
а^= ,\ - -?-. ' A1.33)
Исключив из этой формулы плотность среды с помощью формулы A1,26),
выразим скорость звука через давление и температуру:
При ф = 1 получим скорость звука в газе при изотермическом процессе.
При ф-^0 скорость звука стремится к бесконечности, так как жидкость
предполагается несжимаемой. Массовая концентрация воздуха в смеси очень
мала (ф < 10~а), поэтому далее можно пренебречь этой величиной по
сравнению с единицей в формулах A1.26), A1.34). Продифференцировав A1.34)
по ф и приравняв производную нулю, найдем, что минимальная скорость
звука достигается при концентрации
'T. A1.35)
При этой концентрации, как следует из формулы A1.26), плотность среды
в два раза меньше плотности жидкости, т. е. объемное содержание газа в
жидкости равно 1/2. При условии A1.35) из формулы A1.34) получим
формулу для минимальной скорости звука в смеси
rjF A1.36)
При большом объемном содержании воздуха пузырьки газа начнут
сливаться и течение нельзя рассматривать как гомогенное.
Так как плотность жидкости велика, то минимальная скорость звука
мала. В воздушно-водяной смеси эта скорость при атмосферном давлении
порядка 20 м/с, причем расчеты удовлетворительно согласуются с
измерениями.
В тех случаях, когда размеры пузырьков очень малы, во всех формулах
необходимо учесть дополнительное давление, создаваемое поверхностным
натяжением.
Таким образом, критическая скорость в двухфазном потоке пузырьковой
структуры может быть малой.
Так как в сужениях скорость потока не может превосходить
критического значения, то это ограничивает расход газированной жидкости
критическим расходом. Следовательно, для газированной жидкости возможны за-
Щ

пирания, которые могут существенно ограничивать пропускную способность
трубопроводов.
Наконец, в газированной жидкости при прохождении сначала
суживающейся, а затем расширяющейся трубы могут возникнуть сверхзвуковые
скорости (сами по себе небольшой величины, так как критическая скорость
мала). Далее очевидно, что при сверхзвуковых скоростях в газированной
жидкости могут возникать скачки уплотнения аналогично тому, как они
возникают при сверхзвуковом течении газа.
Рассмотрим особенности скачка уплотнений в двухфазной среде
пузырьковой структуры. Запишем уравнения неразрывности и количества
движения в сечениях до и после скачка:
р1^ = р2«2; A1.37)
Рг—Pi = pi w, (Uj — u2). A1.38)
Исключив из уравнения A1.37) плотности с помощью формулы для
скорости звука A1.32), имеем
Рз/Рг-^М^Мз, М1 = и1/о1, М2 = и2/а2. A1.39)
Здесь учтено, что течение изотермическое и введены числа М.
Запишем уравнение A1.38) в виде
г—Pi — 9iui[ 1.
\ Pi р2 /
Воспользовавшись уравнением A1.35), вынесем общий множитель за
скобки:
(J Ц. A1.40)
Pi P2 /
Записав уравнение A1.26) для сечений до и после скачка и составив
их разность, получим
Pi P2 \ Pi P2
После замены в уравнении A1.40) выражения в скобках с помощью
уравнения A1.41) и введения скорости звука по формуле A1.33) найдем
^=ф#''Т-Я1^?--М2. A1.42)
Pi P?
Объединив формулы A1.39), A1.42), получим соотношение между числами
М до и после прямого скачка:
МгМ2-:1. A1.43)
Процесс в скачке происходит столь быстро, что газ в пузырьках
сжимается изоэнтропийно. Затем происходит теплообмен между газом и
жидкостью, т. е. наблюдается термическая релаксация. После теплообмена
температура смеси практически не изменяется из-за большой массы жидкости.
Зона теплообмена, т. е. по существу толщина скачка, может иметь
протяженность десять—двадцать* миллиметров и ее величина зависит от
дисперсности газовой фазы.
Наличие пузырьков газа в капельной жидкости имеет большое
значение при возникновении гидравлического удара. Пусть капельная жидкость
движется по трубопроводу и в некоторый момент времени внезапно
закрывается задвижка. Скорость жидкости перед задвижкой становится равной
276

нулю. Давление перед задвижкой поднимается столь значительно, что
становится существенной сжимаемость капельной жидкости. В потоке
возникает ударная волна, которая начинает распространяться против течения.
Скорость потока до прохождения ударной волны равна первоначальной
скорости и, а после прохождения волны скорость становится равной нулю.
Скорость распространения волны относительно среды зависит от объемной
упругости жидкости ? и ее плотности:
A1.44)
Упругость и плотность капельной жидкости почти не меняются с
изменением давления, и поэтому скорость распространения ударной волны не
зависит от ее интенсивности, т. е. равна скорости звука в жидкости.
Напомним, что в газе скорость ударной волны зависит от степени сжатия и
ударная волна движется со сверхзвуковой скоростью.
Свяжем систему координат с ударной волной, тогда можно
рассматривать ее как неподвижный скачок уплотнений. В данной задаче для решения
достаточно одного уравнения A1.38), так как температура жидкости также
практически не меняется. В относительном движении скорости потока до и
после скачка соответственно равны (скорость жидкости много меньше
скорости ударной волны): иг =• а, и2 = а — и. Тогда из уравнения A1.38)
получим формулу Жуковского для прироста давления при гидравлическом
ударе:
A1.45)
Рассмотрим теперь гидравлический удар в жидкости с пузырьками
газа. Обозначим w — скорость перемещения фронта ударной волны
относительно среды перед фронтом. Тогда относительная скорость среды перед
фронтом (т. е. перед скачком) равна w, а за фронтом w — и. Уравнения
A1.37), A1.40) примут вид
A1.46)
) (П.47)
Pi 92 I
Исключив w в уравнении A1.46) с помощью уравнения A1.47), получим
Pi Р2
Исключив плотности с помощью уравнения A1.41), найдем искомую
зависимость для определения степени повышения давления в ударной
волне, распространяющейся в смеси:
fh \ Pi
A1.48)
Найдем повышение давления при гидравлическом ударе в трубе при скорости по»
тока и -~ 10 м/с для: 1) воды, 2) воды с пузырьками воздуха при массовой
концентрации ф — Ю-4. Объемный модуль упругости чистой воды при 20° С равен Е==22,5х
ХЮ8 Па, давление смеси до гидравлического удара pL — 105 Па.
1. Скорость звука в воде 1500 м/с находим по формуле A1.44). Повышение
давления при гидравлическом ударе по формуле A1.45) равно 15-Ю6 Па. При столь
значительном повышении давления необходимо учитывать упругость трубы, что
существенно снизит заброс давления.
2. Степень сжатия при гидравлическом ударе в смеси по формуле A1.48) равна
13,5, т. е. повышение давления 12,5-105 Па, При большом начальном давлении смеси
277

повышение давления также будет значительным и необходимо учитывать сжимаемость
жидкой фазы и упругость трубы. Расчет правильнее вести, предполагая изоэнтропий-
ное сжатие воздуха в пузырьках.
При концентрации воздуха <р ~ Ю-3 повышение давления при гидравлическом
ударе будет всего 1,8-105 Па.
11.5. ТЕЧЕНИЕ ДВУХФАЗНОЙ СРЕДЫ ПРИ ФАЗОВОМ
РАВНОВЕСИИ ИЛИ ПОЛНОМ ПЕРЕОХЛАЖДЕНИИ
При расширении пара в соплах давление и температура его
падают и при пересечении верхней пограничной кривой должна начаться
конденсация. Если бы расширение пара происходило очень медленно, то
конденсация и началась бы на пограничной кривой, так как переохлажденный
пар находится в неустойчивом состоянии и система стремится перейти к
устойчивому двухфазному состоянию: насыщенному пару и капелькам
жидкости. Однако конденсация не может произойти мгновенно, так как
необходимо время на образование ядер конденсации и теплообмен. Так как
процесс расширения идет очень быстро, то конденсация запаздывает, и пар
при расширении переохлаждается. Переохлаждение может достигать
определенного предела, после чего начинается бурная конденсация. Скорость
потока и параметры переохлажденного пара не равны скорости и
параметрам влажного пара, найденным с помощью таблиц, так как таблицы
вычислены только для равновесных состояний.
Для анализа этой задачи рассмотрим два предельных случая: 1) пар
при расширении полностью переохлаждается; 2) пар при расширении
находится в тепловом равновесии с непрерывно образующимися при
конденсации капельками жидкости.
1. Пар при расширении полностью переохлаждается. Будем полагать,
что переохлажденный пар подчиняется уравнениям совершенного газа,
со всеми постоянными, взятыми на верхней пограничной кривой, т. е. для
сухого пара при тех же давлениях. Каждый конкретный расчет ведется в
относительно узком диапазоне изменения параметров и поэтому можно
предполагать, что теплоемкости, показатель изоэнтропы и т. п. постоянны (см.
разд. UЛ).
Таким образом, в данном предположении расчет течения
переохлажденного пара ведется как обычной однофазной среды и могут быть
использованы все формулы, полученные для газов.
Это предположение может приводить к более существенным неточностям
вблизи точки, где переохлаждение достигает предельного значения и
начинается бурная конденсация, так как в переохлажденном паре начинают
стремительно образовываться ядра конденсации.
2. Течение пара, находящегося в тепловом равновесии с капельками
жидкости* Рассмотрим одномерное изоэнтропийное течение пара,
находящегося в тепловом равновесии с мелко распыленными капельками жидкости,
образующимися при конденсации. Считаем, что капельки жидкости имеют
ту же скорость, что и пар.
Обозначим ф концентрацию жидкой фазы в двухфазной среде:
A1.49)
где т — общий расход среды, который постоянен вдоль сопла; т! и т" —
расход фаз соответственно жидкой и паровой, которые меняются вдоль сопла
вследствие конденсации паровой фазы. Следовательно, концентрация
является также переменной величиной.
Так как фазы находятся в тепловом равновесии, то пар и жидкость имеют
одинаковые температуры и давления, которые называются температурой и
278

давлением насыщения. При равновесном существовании жидкой и паровой
фазы давление и температура насыщения связаны формулой Клапейрона—
Клаузиуса:
-42- = ——. A1.50)
dT T (v"-v') v '
где г — теплота фазового перехода, т. е. теплота, которая выделяется при
конденсации пара или поглощается при испарении жидкости; v" и v' —
удельный объем соответственно паровой и Жидкой фаз.
Ввиду того, что v <^ v", можно упростить формулу A1.50) и, обозначив
v" = 1/р (р — плотность пара), представить ее в виде
dp[dT=:pr/T. A1.51)
Таким образом, в рассматриваемой системе пар—жидкость температура
и давление не являются независимыми параметрами.
Выпишем уравнения сохранения для потока влажного пара, текущего в
трубе переменного сечения.
Уравнение неразрывности запишем только для паровой фазы, так как
объем, занимаемый жидкой фазой, пренебрежимо мал:
puS=(l— cp)m. A1.52)
Уравнение количества движения запишем для среды в целом с учетом
того, что обе фазы имеют одинаковую скорость:
d(um) = —Sdp. AL53)
Здесь правая часть равна внешней силе давления, действующей на
выделенный элемент текущей среды.
При отсутствии подвода теплоты и работы уравнение энергии имеет
вид
d {l(l-q>)(h"+u2/2)+<p(h' + u42)\m\ =0, A1.54)
где h"y ti—энтальпии фаз соответственно паровой и жидкой. В выражении
A1.54) полная энергия потока представлена как сумма энергий,
переносимых паровой и жидкой фазами.
Пар находится в тепловом равновесии с жидкостью, т. е. является
насыщенным. В этом случае можно считать, что пар подчиняется уравнению
состояния для совершенного газа, если энтропия достаточно велика (см. под-
разд. ИЛ):
р = рЯГ. A1.55)
Преобразуем полученные уравнения, имея в виду исследование
изменения параметров потока и концентрации жидкости в потоке вдоль сопла при
заданном законе изменения площади. Исключим в уравнении A1.51)
плотность с помощью уравнения A1.55) и придадим ему вид
dp r dT
Р RT
= 0. AL56)
Прологарифмировав уравнение A1.52) и взяв приращение, приведем его
к виду
4EL * 4 i? A1.57)
р и \— <р ф S
Уравнение A1.53) можно записать в такой форме:
279

Заменив расход по уравнению неразрывности A1.52), а затем исключив
плотность пара, с помощью уравнения состояния A1.55), получим
+
и и2 р
Уравнение энергии A1.54) можно записать в такой форме:
' — (h'f—h')dq>4-udu=0.
Заменим приращение энтальпий пара и жидкости через приращение
температур и теплоемкости и введем теплоту фазового перехода:
' dhT^cvdT, dti = cdT, /t"~ Л' = г.
Тогда уравнение энергии примет вид
[(I —y)cp + <pc]dT—rd<f + udu=*O. A1.59)
Здесь первый член представляет теплоту, полученную паром и жидкостью
при изменении температуры, второй член выражает теплоту, выделившуюся
при конденсации некоторой доли пара, а последний равен приращению
кинетической энергии двухфазной среды. Введем обозначение для средней
теплоемкости двухфазной среды
xc^(l-i)cp + Vc9 A1.60)
и, поделив все члены уравнения A1.59) на и2, придадим ему окончательный
вид
12L*JLULAV J!L A1.61)
м2 Т м2 ф и
Запишем уравнение A1.55) в дифференциальной форме
-*Р—А?. Л- = о. A1.62)
Р 9 Т
Окончательно получена система из пяти уравнений A1.56), A1.57),
A1.58), A1.61), A1.62), которая содержит пять неизвестных (относительных
приращений искомых величин). В качестве единственного аргумента
выступает заданное относительное изменение площади сопла.
При решении системы уравнений необходимо выразить относительные
приращения искомых функций через относительное приращение площади
сопла. В частности, для приращения скорости получим
1 2 *¦ 1 '« (".ад
~ [~1ё A—ф) RT ^ A-Ф) Г ' A—ф2Jг2 J^—"^Г
В минимальном сечении сопла правая часть уравнения равна нулю. Если
в минимальном сечении происходит переход через критическую скорость, то
du Ф0 и, следовательно, должно быть равно нулю выражение в квадратных
скобках. Так как скорость потока при этом равна местной скорости звука,
то отсюда получаем формулу для скорости распространения звука в
двухфазной среде:
? Ь °1 , M-w/a. A1.64)
A—ф) г A-фJГ*'
280

Тогда решение системы уравнений A1.56) ... A1.58), A1.61) и A1.62)
представляется следующими формулами:
du dS/S dT = 1 kRT №dS/S A165)
и "* 1 —M2 ' Г ~~ 1 —ф г 1—М2 ' '
dp __ М2 dS/S dp x [л RT \M*dS/$ /n ftft.
——— ~~ _____ ______ ______. ~— ————— I j ~__ —____— I i ^ 111. 00 /
p 1—<p 1 —M2 p 1—ф \ r ) 1—M2
. A1.67)
Проанализируем полученное решение. Прежде всего отметим, что
скорость звука в двухфазной среде вблизи пограничной кривой не равна
скорости звука в сухом паре непосредственно над пограничной кривой. Это
объясняется тем, что при распространении звуковой волны во влажном
паре, т. е. при сжатии и разрежении среды, происходит переход вещества из
одной фазы в другую. Скорость звука в двухфазной среде меньше, чем в
газе с теми же газовой постоянной и показателем изоэнтропы, что следует
из формулы A1.64).
Отметим, что скорость звука, которую определяет формула A1.64),
можно назвать скоростью звука при нулевой частоте, так как насыщенный
пар и капельки жидкости все время находятся в термодинамическом
равновесии. Именно эту скорость и необходимо вычислить для нахождения
критической скорости при равновесном расширении пара. Для примера
определим скорость звука во влажном паре вблизи пограничной кривой (ф « 0),
что исключит влияние инертной массы капелек и позволит оценить
влияние фазовых переходов.
Определим скорость звука в насыщенном водяном паре при давлении р 10& Па.
Взяв необходимые постоянные в таблицах водяного пара, по формуле A1.64) найдем
а — 441,4 м/с.
Скорость звука, подсчитанная по обычной формуле для сухого пара, при том же
давлении вблизи пограничной кривой а - 469,4 м/с. Для оценки влияния инертной
массы капелек приведем значение скорости звука во влажном паре (<р = 0,1) при том
же давлении а — 417,4 м/с.
Для анализа формул A1.65)—A1.67) сравним их с формулами,
выведенными для газа (см. табл. 4.1, первый столбец), которые в данном случае
применяются для расчета переохлажденного пара. Формулы для
приращения скорости в обоих случаях совпадают, однако при одинаковых
скоростях потока число М во влажном паре будет больше из-за меньшей
скорости звука. Следовательно, при равновесном течении скорость
дозвукового потока будет возрастать несколько быстрее. Это является результатом
действия нескольких факторов: отвод массы пара при конденсации и
затрата энергии на разгон капель уменьшают скорость потока, однако выделение
теплоты конденсации увеличивает скорость дозвукового потока. Как
видно, последний фактор, связанный с выделением теплоты конденсации,
воздействует более сильно.
Температура при равновесном расширении будет уменьшаться
медленнее, чем при расширении переохлажденного пара. Это объясняется
подводом теплоты при конденсации. Коэффициент пропорциональности
в формуле A1.65) меньше, чем соответствующий коэффициент в
табл. 4.1.
Плотность пара при равновесном расширении будет уменьшаться
существеннее, чем при расширении с переохлаждением. Это следует из ко-
281

эффициентов соответствующих формул и объясняется тем, что температура
пара при равновесном расширении падает медленнее. Множитель в
квадратных скобках формулы A1.67) всегда положителен, так как конденсация
происходит как в звуковом, так и в сверхзвуковом потоке.
Для оценки численных результатов произведем расчет потока водяного пара для
двух рассматриваемых предельных случаев. Расширение начинается от пограничной
кривой при давлении р ~ 1 • 105 Па. Давление за соплом рх — 0,6-105 Па. Степень
сухости в конце изоэнтропийного равновесного расширения х — 0,974 находим по
формуле (энтропию, энтальпию и удельный объем берем по таблицам)
so -xsI-Ml—x)si -х-7,5332 + A— х) 1,1459 = 7,3608 кДж/(кг.К).
Удельный объем смеси в конце расширения
vx - хщ 4- A — х) v\ - 0,974.2,733 + A — 0,974) 0,001 - 2,662 м3/кг.
Энтальпия в конце расширения
Aix = jc/^i -Ь<1 —Jc)/ii =0,974-2653,6 + A—0,974K59,9 = 2593 кДж/кг.
Скорость потока на выходе из сопла
их - V 2 (Ло—ft,) - V2 B675—2593) 103 = 403 м/с.
Плотность потока массы
m/S = р, их =^/0! =403/2,662 = 151,5 кг/(м2-с).
Расчет течения переохлажденного пара дает следующие значения:
vx = 2,489 кг/м3, иг = 401,4 м/с,
m/S=: 161,3 кг/(м2-с).
Наиболее существенным результатом является то, что плотность
потока массы для переохлажденного пара на 6% больше, чем для равновесного
течения. Так как обычно наблюдается переохлаждение пара при
расширении, то расчет по равновесному состоянию требует соответствующей
коррекции. Следует также напомнить, что числа М и критическое отношение
давлений в этих двух условиях будут различны.
Рассмотрим теперь задачу определения скорости звука в жидкости с
пузырьками пара. Положим, что пар и жидкость находятся в фазовом
равновесии. Запишем уравнение теплового баланса
0. A1.68)
Первый член представляет изменение количества теплоты, содержащейся в
жидкости, а второй — количество выделившейся скрытой теплоты при
изменении массовой концентрации пара ср. Изменением количества теплоты,
содержащейся в пузырьках пара, можно пренебречь ввиду того, что
массовая концентрация пара очень мала. Полагая, что сухой пар подчиняется
уравнению состояния для совершенного газа, запишем уравнение для
плотности смеси:
1/р=фЯ7>—1/р'. A1.69)
о с еди-
A1.70)
Здесь также учтено, что можно пренебречь величиной ср по сравнению с
единицей. Уравнение фазового равновесия запишем в виде
d T RT*
dp rp
В полученной системе уравнений все переменные величины можно считать
функциями давления насыщения.
282

Продифференцируем уравнение A1.69) по давлению
1 dp __ RT dq> , q>R dT фRT
p2 dp p dp p dp p2
Производную плотности по давлению заменим по формуле D.9) через
скорость звука. Производную концентрации по давлению заменим с помощью
уравнения A1.68) через dT/dp: ,
1 ^ R /cT \dT {
а2 р \ г } dp
р2
Исключив производную с помощью уравнения A1.70) и выразив плотность
среды по уравнению A1.69), получим формулу для определения скорости
распространения звука в жидкости с пузырьками пара:
R2T2 q>RT
rp\
A1.71)
Следует подчеркнуть, что давление и температура в этой формуле не
независимы, а связаны условием фазового равновесия, т. е. должны браться на
кривой насыщения. Можно пренебречь членами, содержащими множитель
Ф, и тогда получим
а =-
утг
A1.72)
Скорость звука в кипящей жидкости с пузырьками пара очень мала.
Пузырьки пара могут возникать в жидкости, когда при движении ее с
местной большой скоростью давление в ней падает ниже давления насыщения.
Это явление называется паровой кавитацией и играет большую роль при
работе гидравлических турбин, насосов, гребных винтов и т. п.
11.6. ТЕПЛОВОЙ СКАЧОК
В разд. 6.3 были рассмотрены адиабатические скачки, которые
могут возникать в сверхзвуковых потоках. В некоторых технических
устройствах в потоках наблюдается скачкообразное изменение параметров при
внезапном подводе теплоты. Такие процессы возможны при горении смеси
или конденсации переохлажденного пара, текущего в соплах. Если длина
участка, на котором происходит подвод теплоты, очень мала по сравнению с
размером области, где наблюдается явление, то можно рассматривать фронт
пламени или зону конденсации, как поверхности разрыва. В таком случае
можно считать, что бесконечно тонкий фронт пламени отделяет горючую
смесь от продуктов сгорания или фронт скачка конденсации разделяет
области, где движется переохлажденный и влажный пар. Некоторые
особенности скачка конденсации связаны с тем, что после скачка образуется
двухфазная система насыщенный пар —
жидкость (см. разд. 11.7).
Рассмотрим тепловой скачок.
Пусть газ течет в трубе, и в некотором
сечении к нему подводится теплота Q на
единицу массы газа (рис. 11.2). Составим
уравнения сохранения, выбрав
контрольные сечения непосредственно до и после
разрыва. Поскольку скачок полагается
бесконечно тонким, то площади сечений
трубы до и после скачка одинаковы и урав-
PtrPf \P2fPz
Т1,и1 \Т2,иг
Рис. 11.2. Тепловой скачок при
подводе теплоты к потоку
283

кения можно составить для единицы площади фронта. Индексами 1 и 2
отмечаем параметры потока соответственно до и после скачка.
Уравнение сохранения массы
PiWi = p2. A1.73)
Уравнение количества движения
Pi + Pi и! = Р2 + р2  (U. 74)
Уравнение сохранения энергии
Q + cplTx + u\/2^cp2Tt+ul/2. A1.75)
Полагаем, что теплоемкости газа до и после скачка постоянны, но в
общем случае не одинаковы как вследствие химической реакции в скачке, так
и из-за значительного повышения температуры.
Уравнение энергии можно записать через температуры торможения
до Т01 и после Т02 скачка:
Q + cplT01=cptTn. (П.76)
Полагая, что газы до и после скачка можно считать совершенными,
напишем соответствующие уравнения состояния:
V (П.77)
Найдем соотношение скоростей потока до и после теплового скачка
аналогично тому, как это было сделано для адиабатического скачка. Поделив
левую и правую части уравнения A1.74) соответственно на левую и правую
части уравнения A1.73), получим
Pi , ,, Р2 _!_„
(- их = h Иг-
Pi «1 Р2 «2
Исключим отношения давления к плотности с помощью уравнений
состояния A1.77) и умножим полученное уравнение на скорость за скачком:
0. A1.78)
Температуру газа за скачком можно выразить из уравнений A1.65), A1.76)
CpiT2=cpl Tol T Q-ull2. A1.79)
Исключив из уравнения A1.78) температуру за скачком с помощью
уравнения A1.79) и сгруппировав члены, получим
cP2
_/_*iIi + Ul)uM\ +-«-.) *a?ffil2i=0. A1.80)
\ ux / \ cpiTx I cP2
Преобразуем это уравнение к безразмерному видуч. Введем безразмерные
скорости и безразмерную теплоту:
и тогда из уравнения A1.80) получим
) RCT =0. A1.81)
CP2
Критические скорости до а%х и после а%2 скачка не равны и их можно найти
по формуле D.32) через температуры торможения:
all - -^V RiT01, aU - ^7 RtTn. A1-82)
284

Температура торможения за скачком может быть выражена через заданные
величины с помощью уравнения энергии A1.76). Тогда
aU=-*b--??i-RtTol{H-Q). A1.83)
х1 1 с
Воспользовавшись этими соотношениями, а также известными
зависимостями:
p р pylt /?2=?p2 — Су2>
после подстановки и преобразований запишем уравнение A1.71) в
следующем виде:
2^/JEI№ )^ ' 1 -f 1=0.
Отношение температур во втором члене заменим по формуле
То1
Тогда получаем окончательное уравнение теплового скачка
X! — К—1+Ц _ К + 1 = 0. A1.84)
X.V l-t-Q
Здесь для сокращения записи введено обозначение
/C=-^-l/*IEI. A1.85)
Проанализируем полученное решение. Выразим из уравнения A1.84)
скорость за тепловым скачком
+ с?) J • '
Если теплового скачка нет (Q ¦=¦- 0), то, полагая Xj --= х2, т. е. К = 1,
получим следующие решения:
2 2 Я,! 2Л, "
Первое решение (знак плюс): ХХХ2 -^ 1 соответствует адиабатическому
скачку уплотнений (см. разд. 6.3); второе решение, Хг — Х2 — течению без
скачка.
Далее отметим, что, как следует из общего решения A1.86), количество
подводимой к газу теплоты ограничено условием (выражение под радикалом
не может быть отрицательным)
>4M(l+Q), A1,87)
которое можно для К = 1 записать в таком виде:
4Q<(X,—1AJ8. A1.88)
Смысл этого ограничения состоит в том, что при подводе теплоты
дозвуковой поток ускоряется, а сверхзвуковой — замедляется, но ни в одном,
ни в другом случае поток не может перейти через критическую скорость
(см. разд. 4.5). Так, например, к потоку, движущемуся с критической
скоростью, теплота не может быть подведена и, следовательно, при
критической скорости не может существовать тепловой скачок.
285

Рис. 11.3. Зависимость между
безразмерными скоростями до и
после теплового скачка
Таким образом, максимальное
количество теплоты, которое может быть
подведено к потоку при данной скорости
согласно уравнению A1.87), равно
Qm ,,, JL К* (X л. 1 /ХЛ2— 1. A1.89)
4
Подставив в решение A1.86) Q == Qw,
получим единственное решение Х2, = 1,
что понятно из только что приведенных
рассуждений.
Проанализируем более подробно
уравнение скачка для случая хг — х2.
Уравнение^ 1.86) связывает три величины Х1%
Х2 и Q.
Будем откладывать по оси абсцисс
(рис. 11.3) скорость до теплового скачка
Х1у а по оси ординат — скорость после скачка Х2. Прямая О А
соответствует течению без скачка (Хг = Х2) и, следовательно, без подвода теплоты.
Кривая ВС соответствует прямому адиабатическому скачку (Q — 0) и
построена по уравнению ХгХ2 = 1.
Кривая DEF построена по уравнению A1.86) при Q = const >0.
В общем случае при постоянном Q каждому значению Хг соответствует
два значения Х2. Ветвь DE (Х2 > 1) соответствует чисто тепловому скачку,
так как за тепловым скачком при Xt > 1 всегда Х2 < 1. Ветвь EF (Х2 <
< 1) соответствует совмещению теплового скачка с адиабатическим прямым
скачком. Точка Е (Х2 =•= 1) отвечает максимально возможному подводу
теплоты при фиксированной скорости Х1.
В области OBG тепловой скачок существует при дозвуковой скорости
^ < 1 и Х2 < 1. При подводе теплоты Q = const >0 скорость за скачком
больше скорости до скачка Х2 >Хг. Точка Н соответствует максимально
возможному подводу теплоты при данном) х (Х2 = 1).
В области, ограниченной прямыми АВ, BJ, и области, ограниченной
осью абсцисс, прямой 05 и кривой ВС, могут существовать скачки с отводом
теплоты.
Область, ограниченная осью ординат, прямой GB и прямой BJ,
соответствует скачкам разрежения и физически не реальна, так как там процессы
приводят к уменьшению энтропии замкнутой системы.
Таким образом, тепловой скачок может существовать при сверхзвуковой
скорости потока, причем скорость за скачком также сверхзвуковая. Если
же тепловой скачок совмещается с прямым адиабатическим скачком, то
скорость за ним дозвуковая. В обоих случаях давление за скачком
повышается, причем во втором случае, естественно, более значительно.
При дозвуковом тепловом скачке возможен только один вариант, когда
скорость за скачком дозвуковая и больше, чем скорость до скачка. Эти
выводы согласуются с качественным анализом влияния подвода теплоты к
дозвуковому и сверхзвуковому потокам (см. разд. 4.5).
Пусть дозвуковая скорость потока на входе задана точкой а, (см.
рис. 11.3). Скорость на выходе может быть определена точкой а2 (подвод
теплоты отсутствует) или точкой а9 — при простом горении смеси. Если
скорость на входе сверхзвуковая (точка bt), то возможны четыре варианта на
выходе. При отсутствии подвода теплоты получим точки Ь2 и й5 (прямой
скачок). При подводе теплоты точка Ьх соответствует быстрому горению сме-
286

си или сильной детонации. Точка ft3 соответствует так называемой слабой
детонации.
Точке ft а может соответствовать также процесс в скачке конденсации,
так как пар с капельками за скачком может рассматриваться как псевдогаз
с некоторыми осредненными характеристиками.
Следует особо подчеркнуть, что сейчас анализируются свойства только
теплового скачка, а не процессов горения или конденсации в целом. Для
анализа задачи в целом необходимы дополнительные сведения о процессе.
При горении смеси скорость химической реакции зависит от состава
смеси, коэффициента температуропроводности и т. д. Стационарное
горение, которому соответствует стационарный разрывной прямой фронт,
возможно, если скорость пламени равна скорости набегающего потока газа.
Следовательно, скорость движения горючей смеси должна быть увязана
со скоростью реакции горения и количеством подвезенной при этом теплоты
уравнением теплового скачка.
При скачке конденсации давление и температура за скачком такжр не
могут быть произвольными, так как они связаны, кроме уравнения
скачка, также условием равновесия фаз.
При рассмотрении потока в целом должны быть удовлетворены
граничные условия по концам трубы и местные условия существования потока.
Так, даже в трубе постоянного сечения скорость за тепловым скачком не
может быть равна критической, поскольку при наличии трения на стенках
трубы за скачком критическая скорость может установиться только в
выходном сечении. При возникновении скачка в расширяющейся части сопла
Лаваля скорость за скачком также не может быть равна критической, так
как поток с критической скоростью не может существовать в
расширяющейся трубе.
11.7. СКАЧОК КОНДЕНСАЦИИ
Уже упоминалось, что при быстром расширении в соплах пар
переохлаждается. При достижении определенного переохлаждения
начинается бурная конденсация, сопровождающаяся выделением теплоты,
связанной с фазовым переходом. В пределе этот процесс может
рассматриваться как скачкообразный. Напомним, что противоположный предельный
случай, соответствующий расширению и конденсации пара при тепловом
равновесии с жидкостью, рассматривался в разд. 11.5.
Рассмотрим скачок конденсации в предположении: 1) пар перед скачком
переохлажден и не содержит капелек жидкости; 2) насыщенный пар и
мелкие капельки жидкости за скачком находятся в тепловом равновесии; 3)
скорости капелек жидкости за скачком равны скорости пара.
Общее между тепловым скачком и скачком конденсации состоит в том,
что в обоих случаях к потоку подводится теплота. Однако в тепловом
скачке эта теплота подводится извне, и поэтому энтальпия торможения после
скачка возрастает. В скачке конденсации теплота выделяется при
конденсации части текущего пара, и поэтому полная энергия потока до и после
скачка остается постоянной. Кроме того, различие состоит в том, что после
скачка конденсации давление и температура связаны условием фазового
равновесия. Поэтому количество выделившейся при конденсации теплоты
не может быть установлено произвольно, а связано с интенсивностью
скачка.
Обозначим ф концентрацию жидкой фазы в двухфазной среде после
скачка:
<p==m'An, l~-<p^m7m, m-m' 4-га", A1.90)

где m', m" и т — расход через единицу площади соответственно жидкой
фазы, паровой фазы и среды.
Поскольку объем, занимаемый жидкой фазой, очень мал, то уравнение
неразрывности запишем только для первой фазы:
.PiKi^fWU—Ф). A1.91)
где pj и р2 — плотность переохлажденного пара соответственно до скачка и
насыщенного пара после' скачка.
Уравнение движения запишем на основе предположения, чтр нар и
капельки после скачка имеют одинаковую скорость
где и1у и2 — скорости потока соответственно до и после скачка.
Запишем уравнение энергии через энтальпии
=A—Ф)ЛМ фЛ?-Ьи|/2, A1.93)
где Hq и h'{ — энтальпии соответственно торможения и переохлажденного
пара до скачка; /i<> и hf2 — энтальпии соответственно насыщенного пара и
жидкости после скачка.
Уравнение*энергии A1.93) удобно записать в следующем виде:
«f/2 —(A5 —ЛТ) + Ф(Л2 —Лг)—*«|/2-=0. A1.94)
Повышение температуры в скачках конденсации составляет несколько
десятков градусов. Считая теплоемкость пара в этом диапазоне изменения
температур постоянной, можно написать
Й2—Л1 ==с,,(Г4—Tj). A1.95)
Напомним, что по условию за скачком конденсации пар находится в
фазовом равновесии с жидкостью, и поэтому в уравнении A1.94) выражение
во второй скобке равно теплоте, выделяющейся при конденсации единицы
массы пара:
Ii2 — h'2^r. , A1.96)
Для скачка конденсации эта величина может считаться известной
постоянной, так как она может быть найдена по таблицам насыщенного пара
для заданной области существования скачка.
После сделанных замен уравнение энергии A1.94) принимает следующий
вид:
и?/2-и|/2=ср(Г,—Г,)-фг. A1.97)
Это уравнение энергии по форме совпадает с аналогичным уравнением,
записанным для теплового скачка, так как последний член выражает количество
теплоты, выделившееся при конденсации. Однако теперь количество
теплоты нельзя рассматривать как свободный параметр.
Считаем, что переохлажденный и насыщенный пар подчиняются
уравнению состояния совершенного газа, т. е.
pr-.pRT. A1.98)
При этом следует, конечно, помнить, что для насыщенного пара
температура и давление дополнительно связаны условием фазового равновесия, т. е.
не могут быть выбраны произвольным образом.
Предположение о том, что переохлажденный пар имеет в достаточно
узком диапазоне изменения параметров постоянную теплоемкость и
подчиняется уравнению состояния совершенного газа, в данной задаче не явля-
288

ется обязательным. Расчеты могут быть проведены по соответствующим
таблицам.
Полученная система уравнений A1.91), A1.92), A1.97), A1.98)
незамкнута, и ее необходимо дополнить уравнением фазового равновесия, которое
связывает давление и температуру насыщения за скачком. Таким
уравнением является уравнение Клапейрона—Клаузиуса A1.56).
Проинтегрировав это уравнение, получим
In^^JL/^L L\ A1.99)
Pi * V г; т2 /
где Р2, Т'2 -- постоянные интегрирования (некоторые давление и
температура насыщения), которые могут быть взяты из таблиц насыщенного пара в
области существования скачка. Теплота фазового перехода, как уже было
сказано, может считаться постоянной, так как уравнение используется в
узких пределах изменения параметров. В частности, уравнение A1.99)
можно записать в виде
1п-^-= — (-! U A1.100)
Pi R \ Ts> 72 Г
где Т81 - температура насыщения при давлении перед скачком рх. Вместо
уравнения A1.100) в расчетах можно использовать таблицу насыщенного
пара.
Теперь полученная система уравнений замкнута и содержит пять
неизвестных. При решении системы удобно исключить скорости и плотности и
найти зависимость между давлением и температурой насыщенного пара за
скачком.
Из уравнений A1.91), A1.98) получим
ф=П—PlHl._i_^_Zi_ J&l A1.101)
Pi «i Pi T2 ux
Тогда уравнение энергии A1.97) можно записать в таком виде:
"И1 -(¦*-
Из уравнения движения A1.92) следует
f й) A1.103)
Pi Pi/Pi
Здесь введено число Мх перед скачком:
М1=и1/о1=а1
Для сокращения записи введем дал^е обозначения для степени повышения
давления и температуры в скачке (не следует путать с газодинамическими
функциями, обозначенными теми же буквами):
e=P«/Pi, т = Т,/Г1в A1.104)
Тогда из уравнения A1.102) получим
JfL.^. i^lZlL A1.105)
и, хЩ l 7
Исключив отношение скоростей из уравнения A1.102) с помощью
полученной зависимости, после простых преобразований найдем уравнение
скачка конденсации
JLz±„JLzi '_[х _JL). (Ц.106)
Ю Зак. 2638

u
Умножив и поделив правую часть
уравнения A1Л00) на х7\ и использовав
обозначения A1.104), получим
[l L\ (Ц.107)
si Т /
Полученные уравнения A1.106),
A1.107) должны быть решены совместно.
Однако вместо уравнения A1.107)
проще использовать таблицы
насыщенного пара. Расчет достаточно прост.
Укажем порядок расчета, который не
ff требует последовательных приближений.
—* Задаем параметры переохлажденного
г пара перед скачком plf Tx. Выбираем
Рис. П.4. Степень повышения дав- степень повышения давления в скачке
ления в скачке конденсации (водя- е — p2/plf т. е. давление за скачком
ной пар, р1 = 106 Па) конденсации р2. Поскольку за скачком
пар находится в фазовом равновесии с
жидкостью, то по давлению рг с помощью таблиц насыщенного пара
находим температуру насыщения Т2 и затем т = Т21Тг. Тогда из уравнения
(8.106) легко определяется единственная неизвестная — число Mt перед
скачком. Расчет удобно вести при фиксированных параметрах перед
скачком, т. е. при постоянной величине переохлаждения пара:
ДГ = ГЙ —7V A1.108)
Температура насыщения Tsl находится по давлению перед скачком с
помощью таблиц насыщенного пара.
Пусть давление перед скачком конденсации равно ръ = 10е Па, а величина
переохлаждения водяного пара составляет AT = 30 К. Определив по таблицам
насыщенного пара температуру насыщения при давлении перед скачком TS1 = 45S К, найдем
температуру пара перед скачком 7^ = 423 К. Задаем степень повышения давления в
скачке 6= 1,2 и находим: давление за скачком р2 — f»2- Ш* Па, температуру насыщения» при
этом давлении Тг = 462 К, степень повышения температуры т. == 1,032, скрытую
теплоту конденсации г— 2000 кДж/кг. Подставив полученные значения в уравнение A1,
106), определим число Мг перед скачком конденсации: Мг = 1,198.
Задавая различные степени сжатия, можно построить зависимость их
от числа Мх перед скачком при постоянной величине переохлаждения
(рис, 11.4). Ветвь аЬ соответствует «чистому» скачку конденсации, причем
поток после скачка остается сверхзвуковым. Ветвь ас соответствует
совмещению скачка конденсации с адиабатическим скачком. В данном случае
скорость за скачком дозвуковая. Точка а отвечает минимально возможному
числу Мг перед скачком при данном переохлаждении. При меньшем числе
Мг поток не может воспринять то количество теплоты, которое выделяется
при полной конденсации, соответствующей данному переохлаждению перед
скачком.
Концентрацию жидкости в смеси после скачка находим с помощью
уравнений A1Л01), A1.105):
A1.109)
Поскольку по предположению в скачке происходит полная конденсация,
т. е. за- скачком система пар—жидкость находится в термодинамическом
равновесии, то давление и концентрация жидкости позволяю! определить
состояние смеси после скачка.
290

Скачок конденсации (при заданных параметрах пара перед соплом) не
может существовать в произвольно выбранном сечении сопла. Число М
перед скачком согласно формуле A1.106) зависит от величины
переохлаждения пара. Для того чтобы существовал устойчивый скачок, скорость
конденсации должна быть такова, чтобы в скачке конденсировалось
определенное количество жидкости A1.109). Скорость конденсации также зависит
от величины переохлаждения. Согласование между скоростью
конденсации и числом М перед скачком позволяет установить сечение, где происходит
скачок и интенсивность скачка.
В действительности наблюдается релаксация и скачок имеет
определенную протяженность.
Подчеркнем, что при расчете скачков конденсации в расширяющейся
части сопла Лаваля нужно выдерживать граничные условия на выходе из
сопла. Поэтому, например, если давление за соплом выше расчетного
давления, за скачком конденсации может располагаться адиабатический скачок
уплотнения.
В предыдущих разделах этой главы было принято, что капли,
переносимые потоком пара или газа, движутся со скоростью потока. В
действительности в общем случае наблюдается рассогласование скоростей жидкой и
газообразных фаз. Пусть, например, пар с капельками воды поступает в
сопло. Пар расширяется и ускоряется, Капельки увлекаются потоком, но
имеют, естественно, меньшую скорость. В практических задачах, таких,
например, как оценка скорости эрозии рабочих лопаток турбины, вызванной
ударами капелек, необходимо знать величину рассогласования скоростей
пара и жидкости за соплом.
Рассмотрим задачу о разгоне капель потоком газа в одномерной поста-'
новке и будем пренебрегать тепло- и массообменом, которые мало влияют на
закон распределения скоростей. На каплю действуют: сила сопротивления
в однородном потоке, сила, вызванная градиентом давления, сила инерции,
а также сила тяжести и архимедова сила. Ввиду того, что плотность
жидкости много больше плотности газа и капли движутся со скоростями,
значительно превышающими скорость свободного падения, будем
пренебрегать всеми силами, кроме силы сопротивления. Сила сопротивления
зависит от формы капли и числа Re, подсчитанного но скорости капли
относительно газа. В общем случае эта зависимость определяется только
экспериментально.
Общий случай движения очень сложен. Капля стремится сохранить
сферическую форму под действием сил поверхностного натяжения. Однако
силы давления и трения, действующие на каплю, искажают эту форму, а при
определенных соотношениях сил большая капля теряет устойчивость и
разбивается на более мелкие. Ради упрощения будем считать, что капельки
малы, имеют сферическую форму и тогда силу сопротивления можно
определить по закону Стокса, справедливому при малых числах Re:
F-6jxjji(«—w), Ue^(u—шJгр7|*<Ю). A1.110)
Здесь jul — коэффициент динамической вязкости газа; г — радиус капли;
и — скорость потока; w — скорость капли; р" — плотность газа.
Полагая течение одномерным, запишем уравнение движения капли под
действием аэродинамической силы
зтрг—. A1.111)
3 dt
Слева написана сила сопротивления, а справа — масса капли, умноженная
на ее ускорение, р — плотность жидкости.
10* т

Для сокращения записи введем постоянную, имеющую размерность
времени (время релаксации):
Тогда уравнение движения капли A1.111)
т-^=ы—ш. A1.113)
at
Рассмотрим сначала разгон капель потоком постоянной скорости. Пусть
в начальный момент времени (t = 0) скорость капли равна wx. Тогда
решение уравнения A1.113) запишем в виде
а; = и —(м—аОе-'/*. . A1.114)
Практически необходимо знать, на каком отрезке пути произошел разгон
капли до определенной скорости. Проинтегрировав выражение A1.114),
найдем зависимость пути, пройденного каплей, от времени
^ut —т(и—ша)A— е~'/*). 1 A1.115)
Введем обозначение для безразмерной разности скоростей газа и капли и
безразмерного пути, пройденного каплей:
, ...... -. A1.116)
Тогда выражение для относительной безразмерной скорости капли A1.114)
можно записать в виде
и> = ще~!'*9 A1.117)
а для пути, пройденного каплей, в виде
*=- щA — е~'/т). A1.118)
Следует заметить, что безразмерное время зависит от квадрата радиуса
капли и входит в показательную функцию. Следовательно, разгон капли
сильно зависит от ее размера.
Рассмотрим теперь разгон капли с постоянным градиентом скорости:
и~иг + $х, j5 = (w2—илIЬ, и2>и1, jc^O, A1.119)
где Ь — длина участка, на котором скорость газа возрастает от их до м2.
Представив скорость капли производной пути по времени аь = dxldty
напишем уравнение движения капли A1.113) следующим образом:
т -?JL = W 1+Ъх~~ —. ' A1.120)
Ш2 dt
Ищем решение этого уравнения в таком виде:
A1.121)
где б0, си с\2, otlt a2 — постоянные.
Подставив предполагаемое решение A1.121) в уравнение A1.120) , найдем
постоянные:
1-A -V"
292

Постоянные си с2 находим из начальных условий, которые можно
записать для капли в начале участка разгона:
при / = О х — 0; при / = 0 w. — w1.
Тогда из выражения A1.121) следует
Отсюда искомые постоянные:
аг —а2 ах — а2
Таким образом, все постоянные в решении A1.121) найдены. Зависимость
скорости капли от времени находится дифференцированием решения
A1.121) по времени:
e0»'. A1.124)
Зависимость скорости капли от координаты представлена уравнениями
A1.121), A1.124), в которых время выступает в качестве параметра.
Формулы получены при использовании закона сопротивления Стокса,
т. е. пригодны только при малых числах Re, подсчитанных по размеру
капли и ее относительной скорости. Предполагалось также, что распределение
скорости газа вдоль сопла задано и не зависит от закона разгона капель.
Такое предположение справедливо, если концентрация жидкой фазы мала.
В общем случае, после нахождения скорости капель, с помощью уравнений
сохранения можно уточнить распределение скорости газообразной фазы.
Были рассмотрены задачи о разгоне капель в потоке газа, имеющем
постоянную скорость или постоянный градиент скорости. При заданном
произвольном законе распределения скорости газообразной фазы вдоль сопла
можно вести расчет по участкам, используя полученные формулы.
Вопросы для самопроверки
1. Что называют совершенным паром?
2. Почему скорость звука в жидкости с пузырьками газа очень низка?
3. Почему скорость звука в двухфазной среде может зависеть от частоты
колебаний?
4. Какие особенности имеет скачок конденсации по сравнению с тепловым скачком?
5. Почему при расширении влажного пара в соплах поток массы фактически
больше, чем следует из расчетов, проведенных по таблицам водяного пара?

ГЛАВА 12
ВЫЧИСЛИТЕЛЬНАЯ ГИДРОГАЗОДИНАМИКА
12.1. ВЫЧИСЛИТЕЛЬНАЯ ГИДРОГАЗОДИНАМИКА И ЕЕ ЗАДАЧИ.
ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ И ЧИСЛЕННЫЙ ЭКСПЕРИМЕНТ
Исторически механика жидкости и газа как физическая наука
делилась на теоретическую и экспериментальную. Относительно недавно,
после развития ЭВМ, в этой дисциплине появилась новая ветвь, которую
назырают вычислительной гидрогазодинамикой.
В вычислительной гидрогазодинамике изучают и применяют методы
математического моделирования законов движения деформируемой сплошной
среды. При этом моделируют законы сохранения, т. е. те физические
законы, на основе которых построена теоретическая механика жидкости и газа.
Затем с помощью ЭВМ проводят численный эксперимент. Проведение такого
эксперимента на ЭВМ в сущности похоже на проведение физического
опыта в экспериментальной гидрогазодинамике. Таким образом
вычислительный процесс носит как бы физический характер.
Вычислительная аэродинамика имеет нечто общее как с теоретической,
так и экспериментальной аэродинамикой. Однако численный эксперимент
не может заменить ни теоретическое решение, ни физический эксперимент.
Численные методы могут, с одной стороны, претендовать на общность и
точность теоретического анализа, ас другой,— учесть некоторые реальные
тонкие эффекты, которые можно измерить при физическом эксперименте.
Однако и численный эксперимент в свою очередь не может быть
заменен ни теоретическим анализом, ни физическим экспериментом.
Большое количество новых задач, которые ставит современная техника,
не могут быть решены теоретически ввиду их сложности. Более того, для
многих задач не существует еще строгой математической постановки. Часто
и физический эксперимент не может решить проблемы либо из-за
невозможности удовлетворительного физического моделирования, либо из-за
колоссальной стоимости эксперимента и очень большого времени,
необходимого на его подготовку. Кроме того, в численном эксперименте можно
изучать модельные задачи, вообще недоступные для физического эксперимента.
Т ак, можно изучить чисто плоское течение, в любых пределах независимо
изменять различные физические свойства газа, варьировать любыми
упрощениями и т. д.
Для того чтобы представить особенности численного моделирования и
трудности, которые при этом возникают, рассмотрим более конкретно один
из возможных подходов.
Физическую наглядность и другие важные преимущества имеют методы
расчета, основанные на применении уравнений сохранения в интегральной
форме. При подобном подходе особенно ясно, каким образом моделируются
законы сохранения массы, количества движения и энергии в текущей
жидкости.
Разобьем всю область течения на некоторые достаточно малые
контрольные объемы. В принципе форма таких объемов, как ясно из вывода
уравнений сохранения (см. гл. 1), может быть произвольной. Однако, когда речь
294

Рис. 12Л. Контрольный объем
идет о практическом расчете на ЭВМ,
форма их должна быть достаточно
простой: например, параллелепипеды,
треугольные призмы, тетраэдры и т. д.
Рассмотрим течение жидкости через
такой фиксированный контрольный
объем с центром в точке х, у, z
(рис. 12.1). Запишем уравнение
переноса некоторой физической величины,
которая подчиняется законам сохранения.
Пусть в момент времени / в
фиксированном контрольном объеме
содержится количество М переносимой величины. Определим среднюю плотность
распределения величины М в контрольном объеме:
li=M/V, V =:&xAyAz. A2.1)
Будем относить эту плотность распределения к некоторой
характерной узловой точке контрольного объема. Жидкость течет через
выделенный контрольный объем и в общем случае меняет в нем плотность
распределения благодаря конвекции переносимой величины.
За время А/ из контрольного объема через правую грань вытекает
некоторое количество рассматриваемой физической величины
(положительным считаем направление скорости по внешней нормали к элементу):
За это же в^емя через левую грань элемента втекает количество
Следовательно, изменение количества М внутри контрольного объема
за счет течения через эти две грани
("ИМ
Z A t.
A2.2)
Здесь (u\i)x 2 — плотности потока величины М соответственно на
правой и левой гранях контрольного объема в момент времени t.
Аналогично могут быть учтены потоки через остальные грани элемента.
Однако такое суммирование не внесет принципиально нового в общие
рассуждения, поэтому ниже будем рассматривать только течение через
выбранные выше грани, т. е. одномерное течение.
При неустановившемся течении содержание М внутри контрольного
объема за время Д/ изменится на величину
(ц4+ ш — \лх) Д х А у А г. A2.3)
Здесь нижний индекс отмечает то, что плотность соответствует
контрольному объему, узловая точка которого имеет координату дс, а верхний
индекс отмечает момент времени, в который определена плотность.
Согласно закону сохранения при отсутствии источников полное
изменение величины М внутри контрольного объема должно быть равно
разности втекшего и вытекшего количества.
Тогда из A2.2) и A2.3) получим уравнение в конечных разностях:
Ах
A2.4)
295

Поскольку все пространство разбито на конечные элементы, то их
можно пронумеровать и вместо координаты х фиксировать каждый элемент
номером его узловой точки /. В таком случае граням элемента удобно присвоить
дробные индексы. Например, правой и левой граням элемента на рис. 12.1
удобно присвоить соответственно индексы / + 1/2, i — 1/2. Эти индексы
принято писать снизу.
При расчете на ЭВМ неустановившихся процессов время также
необходимо менять дискретно через выбранные промежутки Д/. Тогда время можно
фиксировать некоторым индексом n(t = пД/), который принято писать
сверху.
Таким образом, для примера, запись {и\л). /* обозначает плотность
потока на правой грани t-го элемента в момент времени п. При введенных
обозначениях конечно-разностное уравнение A2.4) имеет вид
Л/ Ал-
Теперь обратим внимание на то, чтобы проверить, насколько правильно
полученное уравнение может описывать основные свойства течения
жидкости. Суть заключается в том, что вместо непрерывного поля
рассматривается дискретный аналог. При такой замене какие-то свойства реального
течения могут быть не учтены и, наоборот, появятся какие-то новые
свойства, не характерные для описываемого течения.
Напомним, что в дискретном аналоге все физические величины
определены только в узловых точках. Следовательно, значения этих величин в
промежутках между точками на гранях контрольных объемов (что соответствует
дробным индексам) определяются произвольно. Вообще говоря,
аналогично произвольно выбираются характерные моменты времени в левой части
уравнения A2.5). Очевидно, что это следует учитывать таким образом,
чтобы уравнение A2.5) некоторым наилучшим образом описывало характерные
для течения физические закономерности. Вместе с тем принятая схема
должна быть по возможности простой. Конструирование такой расчетной
схемы является сложной проблемой и решение ее не однозначно.
Рассмотрим основные физические требования, которые могут быть
предъявлены к расчетной схеме. . , <
Определим скорости потока на гранях контрольного объема в уравнении
A2.5) как средние арифметические их значений в соседних узловых точках:
Это соответствует простой линейной интерполяции и представляется
естественным.
Теперь следует определить, каким образом надо находить значения (ы
слева и справа от фиксированного контрольного объема. Этот выбор разумно
сделать таким образом, чтобы удовлетворить двум физическим соображениям:
свойству транспортивности и свойству консервативности.
Расчетная схема обладает свойством транспортивности, если перенос
количества \л происходит в направлении скорости потока.
Расчетная схема обладает свойством консервативности, если накопление
переносимой величины в любой области разно количеству, внесенному через
границы области,
296

t
n+2
n+1
t
n+1
. I
t
n+2
n+1
а) б) * в) * ¦
Рис. 12.2. Рост ошибки в конечно-разностной схеме
Обозначим значение переносимой величины слева от контрольного
объема |i_ ц справа \i+ и примем следующие условия:
(H-i-i при и_>0; _/^г ПРИ и+>0;
\[ii при м_<0; l(xi+1 прим+<0.
A2.7)
Легко видеть, что эти условия выбраны из того соображения, что если
поток вытекает из рассматриваемого t-ro контрольного объема, то он с собой
переносит вещество или свойство с плотностью [i^ Если же поток втекает в
/-й фиксированный контрольный объем, то он вносит в него вещество или
свойство с плотностью в той ячейке, откуда он попадает в t-й объем.
Скорость считаем положительной, если она направлена в сторону
возрастания номеров ячеек.
После введения обозначений A2.6), A2.7) основное разностное уравнение
примет вид
+1
минус — к
А/ Ад:
где индекс плюс относится к правой грани элемента, а индекс
левой.
Обратим внимание на очень важное свойство уравнения переноса,
записанное в разностной форме. Для упрощения рассуждений положим, что
скорость потока постоянна и положительна: и+ = и_ = и > 0. В этом
случае из условия A2.7) следует, что ц_ = |ij_lf |ui+ = (хь и уравнение
A2.8) примет вид
l- + 1-- _u ^-^-i , A2.9)
¦tf
А/
Ах
Выразим из этого уравнения значение переносимой потоком величины в
момент времени (п + 1) через ее значение в предыдущий момент времени п:
li7+'«tf--c(|i7-|i7_i). A2.10)
Здесь С обозначено так называемое число Куранта, которое
существенно при изучении дискретных полей и разностных схем:
Д. A2.11)
Если число Куранта С = 1, то из уравнения A2.10) следует (х^+1 —
^ f1^!- ^то очевиДно соответствует правильному решению, так как
благодаря конвекции осуществляется перенос плотности \i по потоку в соседнюю
ячейку без изменения ее величины. Графически такое решение можно
изобразить иа плоскости xl (рис. 12.2, а). Пусть в момент времени п имеем
297

i
I
h
|xj — 1, а во всех остальных узловых
точках jut« = 0 (i Ф\). Тогда в следующий
момент времени п + 1 из A2.10) следует
ц«-Н = lt ji«+i = 0 при / Ф2 и т. д.
Рассмотрим теперь случай С< 1,
например С -=-- 0,8. Тогда при тех же
начальных условиях в момент времени п + 1 из
уравнения A2.10) получим
-0,2^ + 0,8^-0,2,
Рис.
схемы
4-1
12.3.
Ячейки разностной
jO Aф19 1ф2).
В следующий момент времени ji
4 +2 032 ?+2
?4 r"
= 0,04; *^+2 --- 0,32;
^«+2 = о (i: ^= 1, / ^= 2, t ^= 3)v Графически эта картина распространения
изображена на рис. 12.2, б.
В каждый момент времени или, как говорят, на каждом временном слое
суммарное значение всех \i остается равным единице, т. е. соблюдается
закон сохранения. Однако к эффекту переноса добавляется рассеивание
величины fi, которое можно считать влиянием некоторой диффузии или
вязкости. Это явление не свойственно дифференциальному аналогу уравнения
A2 9)' ;
д1дг д&д A2.12)
а является следствием применения уравнения в конечно-разностной форме,
поэтому такую вязкость называют схемной вязкостью.
Если число Куранта С > 1, например С ¦= 1,2, то при тех же
начальных условиях получим (см. рис. 12.2, в) jiy+I — —0,2, f^+! = 1,2,
ц?+2 =.0,04, fx?+2 = -0,48, fi?+2 - 1,44...
В этом случае получаем физически нереальную картину переноса.
Схема расчета становится неустойчивой, так как любое возмущение, например
случайно внесенная ошибка, не затухает, а неограниченно растет.
В этом параграфе рассмотрена одна из возможных простейших моделей
переноса и схем расчета. Однако на этом примере выявлены основные
особенности, которые необходимо иметь в виду при применении разностных
моделей течения жидкости.
Следует ожидать, что лучше основываться не на применении
формальных методов решения дифференциальных уравнений, описывающих
свойства непрерывных полей, а на удовлетворении физических законов для малых
конечных элементов и макроскопических объемов.
Необходимо иметь в виду, что применение расчетных схем к объемам
конечного размера привносит в законы переноса свойства, которые
отсутствуют в точных дифференциальных уравнениях: схемную вязкость.
При определенных условиях численные решения, получаемые, казалось
бы, на правдоподобной схеме, могут не соответствовать реальной
физической картине течения. Так, расчетная схема окажется неустойчивой, если,
например, число Куранта С > 1. Поскольку скорость потока не одинакова
во всей области течения, то ограничение числа Куранта A2.11) по
наибольшей скорости потока приведет к проявлению схемной вязкости в остальных
областях.
В заключение отметим, что для расчетов следует применять только
хорошо отработанные методы, прошедшие серьезную теоретическую и особенно
298

расчетную проверку на разнообразных тестовых задачах. Ниже
изложены несколько таких методов, широко применяемых в инженерных
расчетах.
12.2. МЕТОД РАСПАДА РАЗРЫВА
Уже было подчеркнуто, что современные методы расчета течений
жидкости должны иметь ясные основы. Поэтому прежде чем излагать
расчетную сторону метода распада разрыва, ознакомимся с его физической
сущностью. Такое ознакомление удобно провести на примере одномерного
течения, как более простого.
Рассмотрим одномерное неустановившееся течение идеальной сжимаемой
жидкости в теплоизолированной бесконечной трубе. Пусть в некоторый
момент времени известно распределение вдоль трубы всех параметров потока.
Все численные методы основаны на дискретном счете, т. е. в
предположении, что пространство разбито на ячейки, а состояние потока
рассчитывают через малые конечные промежутки времени.
Разделим трубу на малые ячейки и будем считать все параметры потока
внутри каждой ячейки в данный момент времени постоянными.
Если параметры потока были распределены вдоль трубы непрерывно, то
теперь это распределение приближенно представлено некоторой
ступенчатой функцией. Для примера, на рис. 12.3 плотности переносимой величины
будут постоянны в квадратах.
Можно считать, что параметры потока осреднены внутри ячеек. Такое
осреднение проведено для всех параметров: давления, температуры,
плотности и скорости.
Теперь подчеркнем, что мгновенное ступенчатое распределение
параметра вдоль трубы физически возможно. Это соответствует разрывам в
начальных условиях, когда параметры в соприкасающихся объемах сжимаемой
жидкости различны (см. гл. 7). В следующее мгновение разрывы будут
распадаться, от мест разрыва будут распространяться ударные волны и волны
разрежения, а жидкость начнет перетекать из ячейки в ячейку. Через
некоторый промежуток времени можно вновь осреднить параметры потока
внутри ячеек. Получим новое ступенчатое распределение параметров, так
как за прошедший промежуток времени между ячейками произошел обмен
массой, количеством движения и энергией. Этим цикл расчета закончен.
Дальнейший расчет состоит ил повторения однотипных циклов, что удобно
для применения ЭВМ.
Таким образом цикл состоит из двух этапов. На первом этапе
рассчитывают распады разрывов и находят количество жидкости, которое перетекает
из ячейки в ячейку. На втором этапе производят осреднение параметров в
ячейках и вновь получают ступенчатое распределение.
Общее решение задачи о распаде одиночного разрыва известно (см. гл. 7).
Пока волны, образующиеся при распаде разрыва на границах любых двух
ячеек, не доходят до соседних ячеек, то распад каждого разрыва можно
считать по формулам одиночного.
Промежуток времени, за который волны пробегают от ойной границы
ячейки до другой ее границы, является характерным временем. Шаг по
времени не должен превосходить минимальное характерное время.
При вычислениях на втором этапе необходимо найти три средних
параметра: давление, температуру и скорость. Поэтому для осреднения потока
внутри ячеек применяют три уравнения сохранения: сохранение массы,
импульса и энергии.
299

Рассмотрим теперь вычислительную сторону метода, по-прежнему иола-
гая течение одномерным, а для наглядности изложения возмущения столь
слабыми, что можно применить акустические уравнения.
Расчетная область разбита на ячейки, границы которых (узлы
разностной сетки) обозначим xi% где i — целочисленный индекс (рис. 12.3).
Расстояние между узлами сетки h = xi+1 — xt называют шагом сетки. В данном
случае будем считать его постоянным.
В акустическом приближении скорость звука во всем газе постоянна и
равна а0 (см. разд. 7.1). Давление обозначим р0 + /?, где р <^ р0 — малое
отклонение давления от постоянной величины, которое вызвано
прохождением слабых волн сжатия и разрежения (акустических волн).
Плотность жидкости обозначим р0 + р, где р 4's Po также малая
величина. Из уравнения изоэнтропы с точностью до малых первого порядка
следует зависимость между приращением давления и приращением плотности:
р^аЬр. A2.13)
Скорость жидкости, вызванная прохождением акустических волн,
также мала, и <^ а0.
В расчетные моменты времени параметры потока в ячейках постоянны.
Обозначим параметры среды в ячейке, расположенной между сечениями х%
и Xt+V буквами с полуцелыми индексами: wl+1/2, Pi+i/2-
Рассмотрим распад разрыва, первоначально расположенного в сечении
xt. При распаде слабого разрыва в сторону большого давления побежит
элементарная волна разрежения, а в сторону меньшего давления —
элементарная волна сжатия. Скорости обеих волн равны скорости звука, а их
интенсивности следует определить так, чтобы давление и скорость были
постоянны во всем пространстве между разбегающимися волнами. Задача о
распаде слабого разрыва в неподвижном газе была рассмотрена в под-
разд. 7.1. Здесь отличие состоит в том, что среда имеет скорость и до распада
разрыва.
Выберем положительное направление оси абсцисс в сторону возрастания
номеров сечений. Это также соответствует положительному направлению
скорости. Обозначим pit ut соответственно давление и скорость,которые
возникают между разбегающимися волнами при распаде разрыва в сечении xt.
Если Pi+i/2> Pi-иъ то в положительном направлении побежит
волна разрежения, а в отрицательном — волна сжатия. Скорость среды после
волны разрежения
A2.14)
Равная ей скорость среды после волны сжатия
Ui = Ui-\i2 — {Pi~Pi~\ /2)/Ро «о. A2.15)
Первый член в формуле A2.14) равен первоначальной скорости среды в
правой ячейке, а второй — дополнительной скорости, вызванной
прохождением волны разрежения. Перед вторым членом поставлен знак минус,
так как за волной разрежения среда приобретает скорость в сторону,
противоположную движению волны. Перед вторым членом в формуле A2.15)
также стоит знак минус, так как волна сжатия бежит в отрицательном
направлении и вызывает движение среды в ту же сторону.
Решив совместно уравнения A2.14) и A2.15), выразим параметры потока
между разбегающимися волнами через известные величины:
щ = (щ _ 1/2 +и* +1 /г)/2—(Рс + i/2 —Pi -1 /2)/2роЯо; A2.16)
Pi^(Pi-i/2 + Pi + \f 2)/2 — (^+ 1/2 — Щ -1 / 2) Ро во/2. A2.17)
300

Эти формулы не изменятся, если Pi+i/2 < Pi-i/г» чт0 легко
показать рассуждениями, аналогичными приведенным выше. Формулы A2.16)
и A2.17) просто получить также из свойств инвариантов Римана (см.
разд. 7.2). На этом закончен первый этап расчета. На втором этапе следует
определить новые значения средних скоростей и давлений в каждой из
ячеек. Прежде всего заметим, что скорости и давления на торцовых
поверхностях каждой из ячеек, т. е. в узлах сетки, постоянны до тех пор, пока
волны, возникшие при распаде разрывов, не прошли всю ячейку.
Рассмотрим ячейку между сечениями Xt и #1+1 и запишем для нее
уравнение неразрывности (все выкладки проводим, откидывая члены высшего
. порядка малости)
р^ + ,/2). A2.18)
Слева стоит масса жидкости, которая втекла через торцовые
поверхности ячейки за время т, а справа — увеличение массы жидкости внутри
ячейки благодаря приращению плотности. Верхним индексом принято
обозначать то же самое, что и нижним, но в нбвый момент времени.
Исключив плотности в формуле A2.18) по формуле A2.13), найдем
новое давление в ячейке
р'н-1 /2 = p, + f /2 + (М| —И|+1) а» Рох/Л. A2.19)
Запишем для выбранной ячейки уравнение движения
f po h (U*'' + 1 /2 — Ut + 1 /2) = (Pi —Pi+i) Т. "
. Слева записано приращение количества движения жидкости в ячейке, а
справа — импульс сил давления.
Отсюда найдем новую среднюю скорость в ячейке
|—Р«+1)т/р0Л. A2.20)
В формулы A2.19) и A2.20) входят вычисленные ранее по формулам
A2.16) и A2.17) скорости и давления в узлах сетки.
На этом закончен второй этап расчета и, следовательно, один цикл.
Далее расчет следует проводить вновь по формулам A2.16) и A2.17), причем
верхние индексы станут нижними.
Как было отмечено, полученные формулы справедливы при ограничении
шага по времени т < h/a0. Вместо этого неравенства можно рассматривать
число Курант^ (см. подразд. 12,1):
1. A2.21)
При С> 1 схема расчета неустойчива и ее применять нельзя.
Физическая причина этого ясна из вывода формул. При С <С 1 возникнет
схемная вязкость, которая приводит к «размазыванию» волн (см. разд. 12.1).
В этом разделе было схематически рассмотрено построение решения
акустических уравнений в безграничной трубе. Во всех практических задачах
область, занятая потоком, ограничена и поэтому необходимо удовлетворять
заданным граничным условиям.
Для пояснения способа удовлетворения граничных условий рассмотрим
трубу конечной длины, которая разбита на ячейки я сечениями (рис. 12.4).
Для определенности положим, что левый конец трубы закрыт, а правый
открыт и сообщается с безграничным пространством, в котором
поддерживается давление ра.
Граничные условия таковы: в сечении / скорость равна нулю, а в сечении
п давление разно ра,
301

Рз/г
Pn-T/2
1 Пусть в некоторый момент вре-
I мени заданы значения скоростей и
I давлений во всех ячейках. При-
т ¦* строим к трубе слева и справа
п~ п фиктивные ячейки, показанные
штриховой линией, и обозначим в
Рис. 12.4. Фиктивные граничные ячейки них парамеТры потока согласно
принятой индексации (рис. 12.4).
Так как в сечениях параметры потока изменяются скачкообразно, то
возникнут распады разрывов, в том числе и в граничных сечениях.
Для того чтобы при распаде разрыва в сечении 1 скорость была равна
нулю, в формуле A2.16) надо положить: ul/2 = —и3/2, plfi = /?а/2. Тогда
из формул A2.16), (}2,17) получим
и1 = 0, рг •== р\ /2 — ро ®о иt /2- A2.22)
Для удовлетворения граничного условия на правом конце в фиктивной
ячейке следует принять: е/„+1/2 ^= и„_1/2, 2ра -= />п_,/2 + рп+г/2- Тогда
из формул A2.16), A2.17) получим
При расчете распада разрывов во всех внутренних сечениях следует
использовать формулы A2,16) и A2.17), а в граничных сечениях —
формулы A2.22) и A2.23).
Аналогичные формулы легко получить и для более сложных граничных
условий, например, в том случае, когда скорость зависит от давления (см.
разд. 7.1). Формулы для граничных условий следуют также
непосредственно из ^свойств инвариантов Римана (см. разд. 7.2).
Вышефассмотрен простейший вариант метода распада разрыва, на
котором продемонстрирована общая идея. Авторы метода (С, К. Годунов и др.)
разработали его для решения сложных многомерных задач газовой
динамики при наличии сильных разрывов. В общем случае при распаде разрывов
будут возникать ударные волны, течение будет неизоэнтропийным и
осреднение потока в ячейках надо проводить по уравнениям сохранения массы,
количества движения и энергии.
В настоящее время известно большое количество задач, решенных этим
методом, и в том числе расчетов трансзвуковых течений в плоских
аэродинамических решетках и трехмерных течений в ступенях турбомашин.
В очень многих практических задачах скачки уплотнения либо вообще
отсутствуют, либо интенсивность их мала. В таких случаях можно
существенно упростить расчет, обращаясь к инвариантам Римана для расчета не
только волн разрежения и сжатия, но и ударных волн (см. подразд. 7.3).
В подразд. 7.3 приведены приближенные формулы, которые можно
использовать для расчета распада разрыва.
12.3. МЕТОД КРУПНЫХ ЧАСТИЦ В ЯЧЕЙКАХ
Рассмотрим нестационарное двумерное течение идеальной
сжимаемой жидкости. Запишем уравнения сохранения в единой дивергентной
форме уравнений переноса по типу формулы B.35):
±L + ±±L + llL ,= ._/. A2.24)
д t дх - дц
302

Здесь F представляет переносимую величину,а / — источник этой
величины:
F =
р
pv
lp?J
• /=
о
dpjdx
dp Id у
d(pu)!dx + d(pv)ldy
A2.25)
Если выбрать первые строки в записи A2.25), то уравнение A2.24)
станет уравнением неразрывности, т. е. записью закона сохранения массы.
Вторые строки дадут запись переноса количества движения в проекции на
ось абсцисс, третьи — на ось ординат. Наконец, четвертые строки
соответствуют записи уравнения переноса энергии, причем
Е = е + (м2 + 0*)/2, A2.26)
где первый член представляет внутреннюю, а второй—кинетическую энер -
гию единицы массы жидкости.
Как следует из форм записи A2.24) и A2.25), в данном случае источники
массы отсутствуют. В качестве источника изменения количества движения
жидкой частицы выступают силы давления (т рения нет, так как вязкость
равна нулю). Источником изменения энергии является работа сил давления
в единицу времени.
К этим уравнениям надо добавить ур авнение состояния, которое можно
записать в форме:
р=(х—1)ре. A2.27)
Уравнения сохранения, записанные в дифференциальной форме
уравнений переноса A2.24), можно представить также в интегральной форме:
JL f fds + f FwndC ^ ~ \ GdC. A2.28)
Ol s с с
Здесь S — площадь элемента, по которому проведено интегрирование;
С — дуга, охватывающая эту площадь.
Запись в интегральной форме A2.28) однотипна для всех трех уравнений
сохранения, если ввести обозначения: '
О
0 =
Pi
рпг
A2.29)
где /, т — направляющие косинусы скорости; wn — проекции скорости на
внешнюю нормаль к ко'нтуру;
wn—ul-\-vtn. A2.30)
Если выбрать первую строку в записи A2.29), то уравнение A2.28)
представит уравнение неразрывности в интегральной форме. Вторая и третья
строки в записи A2.29) соответствуют интегральным формам уравнения
сохранения количества движения в проекции на оси абсцисс и ординат
соответственно. Четвертая строка дает уравнение сохранения энергии.
Три члена в уравнении A2.28) имеют ясный физический смысл, на
который следует обратить внимание, так как это использованочв построении
метода расчета.
303

Первый член в уравнении A2.28) выражает скорость изменения
некоторой физической величины, содержащейся внутри площади, ограниченной
выбранным контуром. Если обратиться к записи A2.25), то ясно, что такой
физической величиной может быть масса жидкости, количество движения
или энергия, присущие этой массе.
Второй член уравнения A2.28) представляет скорость изменения
указанной физической величины внутри контура благодаря потоку ее через
контур. Очевидно, что расход через контур зависит от нормальной к
контуру проекции скорости, как это и записано в уравнении. ;
Наконец, третий член в уравнении A2.28) выражает скорость изменения
выбранной величины внутри площади благодаря физическим воздействиям
по ее границе. Источник массы отсутствует.
Как следует из выражений A2.28) и A2.29), приложенные по контуру
силы определяют скорость изменения количества движения внутри
контура. Работа этих сил в единицу времени, т. е. мощность,определяет скорость
изменения энергии. Сумма всех трех членов в уравнении A2.28) равна нулю,
что и выражает соответствующие законы сохранения.
Выше говорилось о площади и контуре, так как рассматривается
плоская задача. Очевидно, что когда речь идет о физических величинах, то
лучше говорить, что они заключены в объеме, ограниченном поверхностью, и
о потоках через поверхность. Для плоской задачи размер,
перпендикулярный плоскости течения, можно выбрать равным единице длины и
рассматривать соответствующие объемы и поверхности, не изменяя сути
изложения и формул.
Рассмотрим теперь, как на основе законов сохранения может быть
развито численное моделирование течения сплошной среды.
Существует много методов моделирования и все они в конечном счете
опираются на законы сохранения, однако между ними имеются
существенные различия. Рассмотрим так называемый метод крупных частиц.
Разобьем всю область, занятую жидкостью, неподвижной сеткой из
прямоугольных ячеек. Прямые, образующие сетку, параллельны осям координат.
Присвоим столбцам целочисленный индекс «', а строкам /. Тогда, для
примера, ии будет означать скорость жидкости в ячейке /, /.
Решение стационарных задач ищут методом установления, т. е. исходя
из некоторого произвольно заданного начального состояния, и после ряда
шагов по времени приходят к искомому установившемуся потоку.
Обозначив / = мт, где т — шаг по времени, будем обозначать верхним индексом
момент времени, в который определена данная переменная. Так р*.
означает давление жидкости в ячейке t, у в момент времени /г.
Расчет каждого шага по времени в методе крупных частиц состоит из
трех этапов.
1. На первом этапе пренебрегают конвективными членами в уравнениях
сохранения (вторым и третьим членом в уравнении A2.24) и вторым членом
в уравнении A2.28)). Таким образом рассматривают изменение количества
движения и энергии жидкого элемента в целом под влиянием градиента
давления. Масса элемента жидкости остается постоянной.
2. На втором этапе учитывают перетекание жидкости, т. е. вычисляют
потоки массы через границы неподвижной сетки.
3. На третьем этапе с помощью уравнений сохранения находят
окончательные значения массы, количества движения и энергии жидкости в
ячейке.
Таким образом в этом методе расчета (как и в некоторых других)
произведено, как принято называть, расщепление уравнений по физическим
процессам.
304

Следовательно, для первого этапа уравнение A2.24) должно быть
записано в таком виде:
—f, A2.31)
а уравнение A2.28) так:
-±-§FdS= -§GdC. A2.32)
о С
Как цз уравнения A2.31) с учетом обозначений A2.25), так, естественно,
и из уравнения A2.32) с учетом обозначений A2.29) следует, что на первом
этапе плотность элемента жидкости остается постоянной.
Применив на этом этапе уравнение A2.31) для записи изменения
количества движения, получим
pjL=_.3?.f pJL = __2?.. A2.33)
v dt dx dt ду V
Здесь плотность вынесена за знак дифференцирования, так как было
показано, что на этом этапе она постоянна.
Производную скорости заменим через конечные разности первого
порядка точности
(Йг./-и7./)/т. A2.34)
Здесь новое значение скорости и?. можно назвать промежуточным, так
как на этом этапе не было учтено влияние конвективных членов.
Производную давления запишем
(р? + 1/2-р7-1/2)/Д*,. A2.35)
где Ах — сторона ячейки, параллельная оси абсцисс; величины с дробными
индексами соответствуют границам ячеек и их можно вычислить по
формулам:
p?h-i/2./ = (p?./ + p?+i./)/2, p7-i/2=(p7-i./ + p7./)/2. A2.36)
Таким образом производная по давлению определена по формуле
второго порядка точности.
Из уравнения A2.33) с учетом обозначений A2.34) и A2.35) получим
промежуточные значения проекции скорости:
. A2.37)
Аналогично для второй проекции скорости
{^ A2.38)
Такие же зависимости можно получить с помощью уравнения A2.32),
так как давления, входящие в обозначение A2.29)* — это давления на
гранях выделенного элемента.
Далее для сокращения записи будем выписывать формулы только для
одномерного течения. Обобщение на многомерный случай очевидно.
Промежуточное значение энергии
A2.39)
На втором этапе определяем протекание массы жидкости между
ячейками, используя промежуточные значения скоростей,
305

Если учесть направление перетекания и применить формулы первого
порядка точности, то получим значение массы, пересекающей одну грань
ячейки, в таком виде:
«?+i)p? А У т/2, если и? + п?+1>0;1
0.)
Здесь по понятным причинам взяты разные значения плотности в
зависимости от того, течет ли жидкость из i-й ячейки в (/ + 1)-ю или наоборот.
Полное изменение массы жидкости, заключенной в данной ячейке, равно
алгебраической сумме перетеканий массы через все грани (в одномерном
случае через две):
А У т/2, если и? + п?+1>0;1
, если unt )
На третьем этапе вычисляют окончательные значения массы, скорости и
энергии таким образом, чтобы соблюдались уравнения сохранения.
Новое значение плотности жидкости в ячейке
Р? + 2ЛМ2/Д*Л*/. A2.42)
Значение количества движения жидкости в ячейке в новый момент
времени следует представить суммой
Ду. A2.43)
Эта запись соответствует расщеплению по физическим процессам, о
котором было сказано ранее. Первый член справа соответствует изменению
количества движения, определенному на первом этапе расчета, когда
плотность не изменилась, а скорость изменилась для ячейки в целом. Второй
член справа учитывает изменение количества движения, которое поток
вносит в ячейку через грани. Суммирование идет по граням (в данном случае
двум). Из формулы A2.43) найдем значение скорости потока в новый момент
времени
A2.44)
Точно таким же образом определим новое значение энергии
??+t =??+lp?/P?+l + 2Кл«/р?+1 Д х Д у. A2.45)
Из уравнения A2.26) находим внутреннюю энергию
е?+1 = ??+1-(м?+1J/2. A2.46)
Давление определяем из уравнения состояния A2.27)
A2.47)
Следует подчеркнуть, что в данном методе строго выполняются уравнения
сохранения массы, импульса и энергии. Это важное условие, которое
необходимо выдержать при численном моделировании в механике сплошных сред.
Изложенный метод расчета развит О. М. Белоцерковским и Ю. М.
Давыдовым и опробован на решении ряда сложных задач газовой динамики для
до,- транс- и сверхзвуковых течений. Метод позволяет производить
сквозной счет, не выделяя заранее места расположения скачков уплотнения.
Приведенные выше формулы приспособлены для расчета течений в
прямоугольных ячейках. Такой способ удобен, когда ячейки лежат во
внутренней области, но ими неудобно описывать криволинейную границу
обтекаемого тела, так как приходится вводить дробные или фиктивные ячейки.
306

В принципе, если применять запись уравнений сохранения в
интегральном виде A2.28), форма ячеек может быть произвольна. Наиболее удобной
является треугольная форма, так как она позволяет гораздо лучше
описывать криволинейные границы тела и не сильно усложняет расчеты. При
разбиении области на треугольные ячейки легко, не изменяя расчетных формул,
измельчать их в зоне резкого изменения параметров потока. Это позволяет
более точно проводить расчет, например, вблизи входных кромок лопаток
аэродинамической решетки.
Выше кратко изложены два метода расчета, причем особое внимание
было обращено на их физическую сущность. Для анализа устойчивости
и сходимости следует обратиться к оригинальным работам.
12.4. МЕТОД ДИСКРЕТНЫХ ВИХРЕЙ И РАСЧЕТ СРЫВНОГО
ОБТЕКАНИЯ
Задачи, связанные с отрывом потока от поверхности тела,
представляют большой интерес во многих областях техники: энергетике,
авиации, судостроении, ракетной технике. Отрыв потока приводит к
увеличению сил сопротивления и появлению нестационарных аэродинамических
сил, вызывающих опасные вибрации конструкции.
Характерной особенностью отрывного обтекания является образование
вихревой пелены из оторвавшегося пограничного слоя. Эта вихревая
пелена неустойчива и свертывается в вихревые жгуты, образующие
относительно правильную дорожку с шахматным расположением крупных вихр'ей.
Для численного моделирования нестационарного срывного обтекания
особенно подходит метод дискретных вихрей, которыми заменяют
сплошную вихревую пелену, сбегающую с тела, а затем прослеживают ее
эволюцию в потоке.
Метод дискретных вихрей пригоден для расчета срывного обтекания тел
произвольной формы. В данном случае для определенности будем
рассматривать обтекание цилиндра, так как на этом простом примере можно
выяснить основные свойства метода. Кроме того, для цилиндра накоплен
наиболее богатый экспериментальный материал, что позволит сравнить
результаты численного и физического эксперимента.
Заметим также, что расчет обтекания цилиндра представляет
практический интерес при оценке вибрации трубок теплообменников, проводов
электропередач, дымовых труб, колонн химического производства и т. д.
Рассмотрим схему обтекания цилиндра вязкой жидкостью при больших
числах Re (рис. 12.5).
Опыт показывает, что в некоторых
точках А пограничный слой
отрывается от поверхности цилиндра и
образует турбулентные вихревые слои,
которые будучи неустойчивыми,
сворачиваются в крупные вихри дорожки
Кармана. В модели идеальной
жидкости вихревую пелену заменим
дискретными вихрями малой
интенсивности. Важным вопросом является
подсчет интенсивности сбегающей
вихревой пелены.
Положим, что основная вихревая
пелена сбегает в точке А и состоит из
частиц жидкости, попавших из погра-
Рис. 12.5. Схема обтекания цилиндра
вязкой жидкостью
307

Яичного слоя лобовой части цилиндра. На кормовой части цилиндра
существует встречное движение и поэтому к основной вихревой пелене
(предположительно в треугольнике ABC) подмешивается завихренность
обратного знака.
Завихренность, сходящая из пограничного слоя в точке А за элемент
времени А/, равна циркуляции скорости ДГ вокруг элемента пелены:
ДГ= —I и -^-dyM = —u20M/2t A2.48)
J ду
о
где и0 — скорость на внешней границе пограничного слоя толщиной 6.
Количество завихренности обратного знака, подмешиваемой в
треугольнике А ВС, можно оценить расчетом, но не очень надежно. Однако ясно,
что это количество существенно меньше подсчитанного по формуле A2.48),
так как скорость на кормовой части цилиндра (входящая к тому же в
квадрате) много меньше, чем в точке А.
Поэтому циркуляцию дискретных вихрей, сбегающих с цилиндра,
можно представить так:
ДГ = — уи\М/2у A2.49)
где Y <. 1 — величина, близкая к единице (опыт дает значение у ~ 0,85).
Все свободные вихри в выбранной схеме движутся со скоростью потока
в данном месте, а вихревая пелена в точке А имеет скорость ио/2.
Комплексный потенциал потока несжимаемой жидкости вокруг цилиндра для
рассматриваемой задачи имеет вид (г0 = 1 — радиус цилиндра)
F(z)^uoo(z + —)+ -V V ДГЛ[In(г-гп)-In(*-*„,)], A2.50)
п = I
где и^ — скорость потока в бесконечности; zn = х„ + iyny zni = xni +
+ iy'ni — координаты вихрей в потоке и фиктивных вихрей внутри
цилиндра, добавленных для удовлетворения граничных условий на цилиндре (см.
разд. 5.2); ДГ^ — циркуляция n-го вихря в потоке.
Циркуляции сбегающих с цилиндра вихрей следует подсчитывать по
формуле A2.49). Эти вихри попадают в поток и их называют свободными.
Движение свободных вихрей определяем по полной скорости, которая
для каждого вихря складывается из скоростей: 1) основного
потенциального потока, обтекающего цилиндр; 2) наводимой свободными вихрями; 3)
наводимой фиктивными вихрями. Таким образом за один шаг по времени
следует выполнить следующие операции.
1. Найти по формуле A2.49) циркуляции двух новых вихрей, которые
появятся в потоке,
2. Подсчитать скорости на всех вихрях в потоке, вычислив комплексную
скорости, с помощью комплексного потенциала A2.50).
3. Переместить все свободные вихри в новые положения, определив
приращение координат по скоростям, подсчитанным в п. 2, и заданному шагу по
времени.
4. Подсчитать по новым координатам свободных вихрей новые
координаты фиктивных вихрей внутри цилиндра по формулам разд. 5.2.
5: Определить две проекции силы, действующие на цилиндр. Силы
можно найти, либо проинтегрировав распределение давления по поверхности
цилиндра, либо подсчитав количество движения, вносимое в поток
системой свободных и фиктивных вихрей,
308

••
•
•
*
•
•
<
• ...
••
¦i
У
jjji~
1Оз
ю5
Рис. 12.6. Зависимость угла отрыва от
числа Рейнольдса
Положение точек отрыва
пограничного слоя на цилиндре зависит
от числа Re. Опыт показывает, что
при фиксированном числе Re эти
точки совершают небольшие
периодические колебания вокруг среднего
положения.
Положение точек отрыва можно в
принципе получить расчетом по
теории пограничного слоя, хотя лишь
весьма приближенно. В данном
разделе более важным является проверка
возможностей численного
моделирования отрывных явлений. Поэтому
следует исключить все погрешности,
не связанные с самим механизмом отрыва, возникновением и сворачиванием
вихревой пелены и распространением вихревой дорожки, состоящей из
крупных вихрей. Ввиду этого приведем результаты расчетов при
различном заданном положении точек отрыва, основываясь на опытной
зависимости а — a(Re), показанной на рис. 12.6.
Опыты показывают, что для Re < 60—70 течение в следе за цилиндром
ламинарное. При больших числах Re происходит постепенный переход к
вихревой дорожке. При умеренных числах Re хорошее согласие с
экспериментом дает численное моделирование, основанное на уравнении Навье—
Стокса. ,
Диапазон, в котором вихревая дорожка хорошо стабилизирована,
лежит примерно при 103< Re< 105. При Re = 3 • 105~5 • 10б в следе за
цилиндром происходит быстрое турбулентное перемешивание вихрей и
картина обтекания изменяется.
Таким образом, выбором положения точек отрыва по рис. 12.6 на
модели идеальной жидкости можно косвенно учитывать влияние числа Рей-
нбльдса A03< Re< 5 • 105).
Расчеты показывают, что при таком подходе метод дискретных вихрей
дает значения силы сопротивления, подъемной силы, числа Струхала и
других характеристик, согласующиеся с аналогичными характеристиками,
полученными экспериментально.
Прежде всего следует подчеркнуть, что расчетная схема приводит к
возникновению гидродинамического автоколебательного процесса,
наблюдаемого на опыте. Вихревая пелена, моделируемая дискретными вихрями малой
интенсивности, сворачивается в вихревые клубки, которые попеременно то
с одной, то с другой стороны отходят от цилиндра. Эти вихревые клубки
образуют шахматную дорожку, подобную той, которую наблюдают на
опыте.
На рис. 12.7 показаны расчетные значения безразмерных коэффициентов
сопротивления и подъемной силы:
1 Cx=2Fx/pulld9 Cv=2Fy/pulld9 , A2.51)
где Fx и Flf — проекции аэродинамической силы на оси координат (см.
рис. 12.5); d — диаметр цилиндра; / — условная толщина,
перпендикулярная чертежу.
По оси абсцисс рис. 12.7 отложено безразмерное время
где г0 — радиус цилиндра.
A2.52)
309

Рис 12.7. Расчетные значения
коэффициентов сопротивления и подъемной
силы
10s 10s Re
Рис. 12.8. Сравнение расчетных и экспериментальных значений коэффициента
сопротивления:
0— результаты эксперимента; О — результаты расчета
Начальный участок /< 6 соответствует установлению автоколебаний,
так как начало работы схемы осуществляется внесением свободного вихря
для создания начальной асимметрии.
Из рис. 12.7 следует, что наблюдаются значительные колебания
подъемной силы вокруг среднего нулевого значения. Именно переменная сила
приводит к колебаниям или даже разрушению цилиндрических конструкций в
потоке с постоянной скоростью.
Коэффициент сопротивления практически постоянен, Сх = 1 , что
хорошо согласуется с экспериментом, как показано на рис. 12.8.
Расчеты показали, что при угле срыва а в диапазоне 80° < а <С 100р за
цилиндром наблюдается четкая дорожка Кармана и практически
синусоидальное изменение подъемной силы во времени. В том же диапазоне
стабилен и коэффициент сопротивления.
При Re = 5 • 105 возникает кризис сопротивления цилиндра (см. под-
разд. 9.6). Расчетное значение коэффициента сопротивления также резко
уменьшается, что находится в согласии с экспериментом (см. рис. 12.8).
При а > 100° картина обтекания на модели идеальной жидкости
становится непериодической. Это примерно соответствует Re = 5 • Ю5, т. е.
режиму, когда в вязкой жидкости наступает разрушение дорожки Кармана.
На рис. 12.9 расчетные значения числа Sh = fdlu^ где/ — частота
отрыва крупных вихрей, сравниваются с экспериментом. В этом случае также
наблюдается
удовлетворительное согласие расчетов с
опытами. В диапазоне Re =
= Ю3-т-3 • Ю5 числа Струха-
ла приблизительно
постоянны: Sh - 0,2G4-0,22.
При подходе к
критическому числу Re расчет, как и
эксперимент, указывают на
резкое падение
сопротивления и рост числа Sh.
Точки, отмеченные
стрелками на рис. 12.8 и 12.9,
относятся к диапазону Re =
= 2 • 103—6 • Ю\ в котором
положение точки отрыва по
Sh
0,38
0,2*
0,08
J
••
4
ф
СФ
w
•
103
to5
Re
и
эксперименРис. 12.9. Сравнение расчетных
тальных значений числа Струхала:
ф — реэультаты эксперимента; О — результаты расчета
310

экспериментальным данным практически не изменяется. Зависимость
некоторых характеристик вихревой дорожки Кармана от угла отрыва (т. е.
для вязкой жидкости от чисел Re) также согласуется с
экспериментальными значениями. Так, по данным расчета для а = 80° отношение lid = 4,5,
где / — расстояние между соседними вихрями одной цепочки; d — диаметр
цилиндра. При этом расчетная относительная интенсивность одного вихря
Кармана Т = Tlru^ = 9.
Построение обтекания тел с отрывом, имеющих угловые точки, например
пластины или прямоугольника, проще тем, что там места отрыва
фиксированы и не зависят от числа Re. Более сложным является расчет обтекания
крыльев и особенно решеток турбомашин. В последнем случае срывы с
лопаток могут происходить со сдвигом по фазе или возникать
перемещающийся отрыв.
В приведенных расчетах сила сопротивления и подъемная сила
подсчитаны по количеству движения, вносимому в поток парами вихрей
противоположного вращения (свободными и фиктивными). Вектор количества
движения равен I = np/Г, где п — нормаль к линии длиной /, соединяющей
вихри, направлен по скорости, сообщаемой ими жидкости. Тогда вектор силы,
действующей от этой пары вихрей, равен F = —dl/dt. Этот расчет не
требует определения нестационарного давления на цилиндре по формуле Лаг-
ранжа.
В заключение по всей главе отметим, что в ней изложены в большей
степени только основные физические соображения по численному
моделированию.
Подчеркнем, что метод установления позволяет решить стационарные
задачи, в том числе трансзвуковые. Подчеркнем, что схемная вязкость
автоматически обеспечивает выполнение условий на задней кромке крыла (в
идеальной жидкости), позволяет установить положение точек отрыва и
скачков.
Вопросы для самопроверки
1. Какими особенностями обладает численный эксперимент?
2. Почему при численном моделировании стремятся обеспечить консервативность
и транспортивность схемы?
3. Что такое число Куранта и как оно влияет на результаты расчета при
численном моделировании?
4. В чем состоит основная идея применения метода распада разрыва?
5. Почему стационарные задачи в некоторых случаях решают методом
установления?

ГЛАВА 1$
АЭРОДИНАМИКА ЭЛЕМЕНТОВ ТУРБОМАШИН
13.1. РАСЧЕТ ОБТЕКАНИЯ РЕШЕТОК ПЛОСКИМ
ПОТЕНЦИАЛЬНЫМ ПОТОКОМ
Высокий коэффициент полезного действия турбомашин может
быть достигнут только при правильных, основанных на знании
законов аэродинамики, расчете и проектировании аэродинамических
решеток.
В теории аэродинамических решеток различают прямую и обратную
задачи. Прямая задача заключается в построении потока, обтекающего
решетку, состоящую из профилей заданной формы.Требуется найти
распределение скоростей и давлений по профилю. Обратная задача состоит в
построении решетки, обладающей определенными, предписанными заранее
свойствами. При решении обратной задачи заданным считают распределение
скорости по профилю в решетке, а ищут форму профиля.
Необходимость решения этих задач вытекает из практики: обе
являются одинаково важными. Обратную задачу следует применять для
построения вновь проектируемой решетки. Такая решетка, найденная в результате
решения обратной задачи, будет иметь заданное гидродинамически
целесообразное распределение скорости. Однако в практических задачах помимо
выполнения требований аэродинамики необходимо выполнить
конструкторские и другие требования.
Прямая задача применяется в том случае, если при проектировании
необходимо, не меняя профиля лопатки, изменить шаг лопаток или угол их
установки в решетке. Постановка подобной/проблемы продиктована
технико-экономическими соображениями, так как дает возможность
использовать лопатки с отлаженной технологией производства в более широком
классе турбомашин. Решение прямой задачи позволяет также проверить
эффективность измененной решетки по сравнению с исходной.
Оценка эффективности работы решеток возможна на основе теории
пограничного слоя, для расчета которого необходимо знать распределение
скоростей или давлений на профиле.
В этом разделе изложим решение прямой задачи расчета обтекания
решетки методом конформного преобразования.
Рассмотрим плоскую аэродинамическую решетку, составленную из
профилей произвольной формы, обтекаемую потенциальным потоком
идеальной несжимаемой жидкости (рис. 13.1). Подобная задача для одиночного
профиля произвольной формы была решена в подразд.5.4, причем там
предложен алгоритм решения, который реализован на ЭВМ.
Задача обтекания аэродинамической решетки имеет свои особенности
и несколько сложнее, поэтому сначала выведем общие зависимости, на
основе которых можно построить расчет. Подчеркнем, что на основе этих же
зависимостей может быть решена прямая задача, а так как она опирается на
метод годографа скорости (см. подразд. 5.6), то решение можно получить
312

Рис. 13.1. Плоская аэродинамическая решетка
для дозвукового потенциального потока
сжимаемой жидкости в приближении
Чаплыгина.
Течение вокруг решетки периодично.
Если лопатки расположить вдоль мнимой
оси комплексной плоскости, то периодом
будет itu где tx — абсолютная величина
шага решетки, которую далее будем
называть просто шагом.
Метод конформного преобразования
основан на преобразовании сложной области,
занятой потоком, на некоторую более
простую область, для которой легко получить
решение. Для решения задачи обтекания
одиночного профиля в качестве такой
простой области была выбрана область вне
круга единичного радиуса. В принципе на эту
же область можно преобразовать область,/
соответствующую течению в одном периоде
решетки. Однако практически это приведет
к значительным погрешностям при
вычислениях. Дело в том, что для толстых силь- ,
но изогнутых лопаток, расположенных
с относительно малым шагом, контур
лопаток будет преобразован на окружность с очень большой деформацией. Если
на контуре лопаток точки расположить равномерно, то соответствующие
им точки на окружности в некоторых местах будут очень сильно сближены,
а в других — разрежены. Этот недостаток будет
не столь сильным, если в качестве простой
стандартной области выбрать внешность решетки
кругов единичного радиуса (рис. 13.2).
Практически удобнее преобразовывать не
внешность решетки профилей на внешность решетки
кругов, а, наоборот, внешность решетки кругов
на внешность решетки профилей.
Решение состоит из трех основных
этапов.
1. Преобразования решетки кругов на
решетку профилей.
2. Решения задачи обтекания для решетки
кругов.
3. Пересчета результатов решения для кругов
на решетку профилей.
Рассмотрим сначала часть задачи, связанную с
первым этапом, который составляет основную
сложность.
Расположим решетку кругов в плоскости
комплексного переменного z = х + iy (см. рис. 13.2),
а решетку профилей в плоскости ? == | + ix\ (см.
рис. 13.1).
313
Рис. 13.2.
кругов
Решетка

Функцию, совершающую указанное конформное преобразование,
можно записать в таком виде
?=« + />(*). A3.I)
Функция Р (z) должна обладать следующими свойствами.
1. Быть периодической с периодом it, т. е.
P{z±ikt)=P(z), *=1, 2, 3, ..., A3.2)
где t — шаг решетки кругов.
2. Быть ограниченной при а:-^±оо.
3. В окрестности начала координат (а вследствие периодичности и в
окрестности любой окружности) должно быть справедливо разложение
33
Первое свойство следует из того, что при изменении комплексной
переменной г на ikt переменная ? должна получить приращение iktx. Тогда
функция Р (ц) не должна измениться, а постоянная должна быть равна
а = t^lt, где р — угол наклона оси решетки. Второе свойство
определено тем, что в бесконечной дали перед и за обеими решетками потоки должны
быть однородными. Тогда между переменными z и ? должна быть линейная
зависимость, так как производная одной переменной ро другой должна быть
равна постоянной (см. гл. 5).
В качестве функции Р (г) можно было бы принять такое выражение:
Я(*) = У. hnc№(m/t), A3.4)
/1 = 1
т, е. сумму степеней гиперболического котангенса, так как такая функция
удовлетворяет поставленным требованиям.
Однако такое задание функции неудобно, как будет видно дальше, для
ее фактического построения, т. е. нахождения коэффициентов Ьп при
заданной решетке профилей.
Рассмотрим такое выражение для: искомой функции
P{z) = V пп — eth— , A3.5)
т. е. представим эту функцию как сумму производных гиперболического
котангенса.
В принципе ряд A3.5) можно привести к виду A3.4), так как любая
производная гиперболического котангенса может быть выражена через
сумму егоч степеней, в чем легко убедиться после элементарных
преобразований. Покажем, что выбор искомой функции в форме ряда A3.5)
особенно удобен для решения поставленной задачи.
Для выяснения в дальнейшем аналогии между конформным
преобразованием решеток профилей и одиночных профилей целесообразно записать
ряд типа A3.5) в несколько ином виде:
Яг)-— V .1—J_a __cth —. A3.6)
/ —¦* ll\ dzn t
n =r 0
Каждый член ряда A3.6) отличается от соответствующего'ему члена
ряда A3.5) только тем, что он умножен на некоторую постоянную, что не
меняет существа дела, но сделает более прозрачными последующие
преобразования.
314

Итак, с помощью выражений A3.1) и A3.6) запишем функцию,
совершающую конформное преобразование внешности решетки кругов на внешность
решетки профилей, в таком виде:
f l^^L-^. A3.7)
t ~*n n\ dzn
n- с
Запишем ряд, в который разлагается cth (nzlt) в окрестности начала
координат:
JLcth-=LB=J-+ V Jl^
k —-1
где Bk — числа Бернулли, первые из которых выписаны ниже:
Вв = 691/2730, ... ' A3.9)
Прежде всего заметим, что если шаг решетки неограниченно возрастает
(/->оо), то, как следует из выражения A3.8),
— cth-^--+—. A3.10)
/ -fc z
Тогда очевидно, что
п\ dzn t zn
Следовательно, при этом условии вместо ряда A3.7) можно записать
ряд
2
л-0
Этот ряд представляет функцию, которая преобразует внешность
одиночной окружности на внешность одиночного профиля. В разд. 5.4
изложен алгоритм, позволяющий найти коэффициенты ряда A3.11) для
получения заданного произвольного профиля.
Обращаем внимание на аналогию, на которой далее будет основан
метод расчета. Ряд A3.7) при расчете аэродинамических решеток имеет то же
значение, что и ряд Лорана A3.11) при расчете одиночного профиля. Когда
шаг решетки t—>¦ оо, то ряд A3.7) переходит в ряд A3.11), Это свойство ряда
A3J) позволяет связать закон обтекания одиночного профиля с законом
обтекания аэродинамической решетки, составленной из тех же профилей.
Для построения решения необходимо преобразовать ряд A3.7) по
производным гиперболическо}-о котангенса в ряд по степеням переменной z.
Это можно сделать с помощью разложения в ряд A3.8) гиперболического
котангенса.
Вычислим я-ю производную левой и правой частей выражения A3.8)^
подставим результат в ряд A3.7) и, опустив преобразования, получим
(ряды сходятся абсолютно и равномерно),
? = «+ 2 «пгч 2 bnZn> <13Л2)
н — 1 // - 0
где обозначено
315

Суммирование по к следует проводить от k ¦== (п + 1)/2 при нечетном
п и от k = (п + 2)/2 при четном п.
Поясним полученный результат, так как ряд A3.12) с обозначением
A3.13) является основным при построении метода расчета обтекания
аэродинамических решеток.
Ряд A3.12) дает разложение функции, представленной функциональным
рядом A3.7), в окрестности начала координат. Ряд A3.12) сходится при
условии 0 < \z\ < /, причем внешний радиус области сходимости определен
расстоянием до ближайших особых точек, лежащих в центре окружностей
(см. рис. 13.2).
Шаг решетки входит только в выражение для коэффициентов Ьп.
Если шаг решетки безгранично возрастает, то эти коэффициенты
стремятся к нулю:
*-*оо, Ьп-+0. . A3.14)
В этом случае вместо ряда A3.12) следует записать ряд
?=ог+ 2 ап/г'\ A3.15)
/? .-= 1
который дает преобразование одиночной окружности в одиночный профиль.
Ряд для преобразования решетки окружностей в решетку профилей
A3.12) отличается от ряда A3.15), преобразующего одиночную окружность
в одиночный профиль, наличием положительных степеней z, причем
коэффициенты Ьп зависят от всех коэффициентов ап.
Рассмотрим решетку, составленную из профилей произвольной формы
(см. рис. 13.1), и решетку окружностей единичного радиуса (см. рис. 13.2).
Пусть ряд A3.7) дает конформное преобразование решетки окружностей
на решетку профилей.
Если точка z пробегает по окружности, то соответствующая ей точка
? очерчивает один из профилей решетки. В силу периодичности функции,
представленной рядом A3.7), каждой окружности соответствует свой
профиль. Для основной окружности, расположенной в начале координат,
функциональный ряд A3.7) можно представить рядом A3.12). Если точка z
находится на основной окружности, то z — е'е, где 6 — полярный угол
(см. рис. 13.2). Тогда из выражения ,A3.12) следует то параметрическое
представление профиля в решетке, которое соответствует конформному
преобразованию решеток:
?=ое'» + 2 flne-'«e + 2 ^е"*. * A3.16)
Следовательно, достаточно представить профиль в решетке уравнением
A3.16), чтобы решить задачу искомого конформного преобразования.
Напомним, что коэффициенты Ьп, входящие в ряды A3.12), A3.16), зависят
от коэффициентов ап по условию A3.13). Преобразуем эту зависимость к
более удобному для численных операций виду.
Для решетки окружностей единичного радиуса (см. рис. 13.2) шаг / >2,
так как при / = 2 окружности касаются. Введем безразмерный параметр
s< 1, характеризующий густоту решетки окружностей (г = 1 —радиус
окружностей):
5-2г//-2//. A3.17)
316

Таблица 13.1
к
1
2
3
4
5
6
7
8
9
10
' 1
0,8225
—0,4059
0,1590
-0,0549
0,0176
-0,0054
0,0016
—0,0005
—
—
2
0,4059
—0,3179
0,1647
—0,0704
0,0269
—0,0095
0,0032
—0,0010
—.
3
—0,1353
0,3179
-^0,2746
0,1642
—0,0806
0,0349
—0,0139
0,0052
—
п
4
—0,1590
0,2746
—0,2463
0,1612
—0,0873
0,0417
—0,0182
0,0074
5
0,0318
—0,1647
0,2463
—0,2256
0,1571
—0,0916
0,0472
—0,0222
6
—
—
0,0549
—0,1642
0,2256
—0,2095
0,1527
—0,0944
0,0518
7
—0,0078
0,0704
—0,1612
0,2095
-0,1964
0,1484
—0,0961
8
-0,0176
0,0806
—0,1571
0,1964
—0,1855
0,1442
Тогда зависимость A3.13) можно записать в эквивалентном виде, где
верхний предел суммы неуказан, так как его следует выбирать, исходя из
допустимой погрешности расчета:
k^ /i = lf 2, 3, ...
Здесь числа
М(п9 k)^
2kBk—n—\)\n\
A3.18)
A3.19)
A3.20)
для п < 8, к < 10, что достаточно для практических целей, приведены в
табл. 13.1.
Суммирование в формуле A3.18) следует проводить от: к = (п + 1)/2
при п нечетном, к = (п + 2)/2 при, п четном.
Выпишем с помощью зависимости A3.18) и табл. 13.1 значения
коэффициентов Ьп с точностью до членов, в которые входят степени s не выше
шестой:
Ьх = 0,8225s2 аг — 0,4059s4 as + 0,1590s6 a5 —...;
b2 = 0,4059s4 a2 — 0,3179s6 a4 +...;
&8= — 0,1353s4 a14-0,3179s6a3—...;
fe4-—0,1590s6 a2 + ....
fe5-0,0318s6 ax —....
Если параметр s --= 0, то все коэффициенты Ьп равны нулю и
параметрическое представление профиля в решетке A3.16) переходит в нормальное
параметрическое представление для одиночного профиля:
C^ce'v-t- 2 с»е""/йф» A3.21)
где ф — полярный угол в плоскости одиночного круга.
Процедура получения параметрического представления для профиля
произвольной формы изложена в подразд. 5.4 и, таким образом, если
задана форма профиля, то коэффициенты ряда A3.21) можно считать
известными.
Теперь требуется найти параметрическое представление того же
профиля в форме ряда A3.16). Будем считать, что задана форма профиля и
известно параметрическое представление A3.21). Покажем, как для того
же профиля построить параметрическое представление A3.16).
317

Очевидно, что зависимость между полярным углом в плоскости
одиночного круга и полярным углом в плоскости решетки окружностей можно
записать в виде ряда по степеням параметра s:
q):=e+s4e4+se66+... A3.22)
Здесь 04, 6в, ...—действительные периодические функции угла 0,
имеющие период 2я.
Если в зависимости A3.21) исключить <р с помощью зависимости A3.22),
то форма профиля не изменится, а параметром станет угол в плоскости
решетки кругов.
Выберем функции 04, 8в, ... таким образом, чтобы ряд A3.21)
превратился в ряд A3.16) с заданной точностью.
В зависимости A3.22) разложение идет только по четным степеням s,
так как коэффициенты Ьп по формуле A3.18) зависят только от четных
степеней. Первой четной степенью следует взять четвертую, так как при
п>2в коэффициенты входят степени не ниже четвертой.
Подставив зависимость A3.22) в ряд A3.21) и разложив полученное
выражение в ряд по степеням s, получим
e-"*!^-!-... A3.23)
Функции 04, 06, ... следует выбрать таким образом, чтобы.ряд A3.23)
был построен по типу ряда A3.16), т, е. коэффициенты при положительных
степенях tinQ зависели от коэффициентов при отрицательных степенях
е-шв по условию A3Л8).
Поскольку искомые функции должны быть действительными, то положим:
Вп*=оя+~оЯ9 A3.24)
где черта сверху обозначает сопряженную величину.
Ограничим вычисления членами, содержащими степени s не выше
шестой, что дает достаточную точность в практических задачах расчета
аэродинамических решеток турбомашин.
Опустив вычисления, приведем окончательный результат:
а4 = i [о, 1353-^- е*'в —0,4059 -й- е'е ];
1 с с \
а6 = / Г—0,0318 -^ е«* + 0,1590 ?- е3* — f0,0318 ?- + A3.25)
[ с с \ с2
+ 0,3180 ^e2i*0 + (o,3180^+0,0954
Функцию A3.22) можно назвать функцией смещения. Она устанавливает
соответствие между точками окружности в решетке и точками профиля в
решетке ори конформном преобразовании, если известно такое же
соответствие между точками одиночной окружности и одиночного профиля.
Каждому значению 0 по зависимостям A3.25), A3.24), A3.22) можно
найти значение ф. Каждому значению ср соответствует точка на профиле,
так как ряд A3.21) по условию известен. Можно сказать по-другому:
одной и той же точке на одиночном профиле и том же профиле в решетке
соответствуют разные точки на одиночной окружности и окружности в
решетке.
318

В процессе вычисления функций A3.25) были последовательно
определены коэффициенты ряда A3.16), из которых для практических расчетов
необходим только первый:
а -- с—0,8225s2 ct + /о,4О59с3 Ь 0,1353 -?Ц s* + / _ о, 1590 Л- +
\ с ] \ с
+ 0,9856-?-—0,7471 -^ — 0,0318-^-W. A3.26)
с с с2 /
Прежде чем переходить к изложению порядка расчета обтекания
решетки, обратим внимание на одну особенность.
При конформном преобразовании одиночного профиля в общем не
важна его ориентация относительно принятой системы координат, так как
существенно только выдержать направление скорости в бесконечности
относительного профиля.
При конформном преобразовании решетки необходимо строго выдержать
ориентацию профиля относительно ее оси. Для этого необходимо уметь
поворачивать профиль на заданный угол относительно принятой системы
координат.
Функция A3.21) дает преобразование одиночной окружности на
одиночный профиль. Рассмотрим функцию
?^ei«e4a>4- 2 б'Ле~'««>+«>, A3.27)
п — 1
где а — действительная постоянная.
Очевидно, что функция A3.27) преобразует окружность в тот же самый
профиль и не изменяет его ориентации.
Умножим лравую часть выражения A3.27) на е~'а:
V сп е-'<"+ ' >« е"*«>. A3.28)
п 1
При таком преобразовании форма профиля останется прежней, но он
будет повернут на угол —а относительно прежнего расположения.
Следовательно, если в функции A3.21) заменить коэффициенты сп на
спе~'(л+1)а, а коэффициент с оставить без изменения, то это приводит
к повороту профиля на угол —а. Так как функция, преобразующая
решетку окружностей на решетку профилей, выражена через те же самые
коэффициенты, то и в решетке профиль будет повернут на тот же угол.
В этом состоит одно из преимуществ изложенного метода по сравнению
с другими, так как по известному нормальному представлению одиночного
профиля получена функция, конформно отображающая внешность
эквивалентных решеток окружностей на решетки профилей, в которых этот
заданный профиль расположен с любым шагом и углом установки.
Полученные формулы могут быть применимы также для построения
теоретических решеток с профилями практически произвольной формы.
Формула A3.7) дает возможность находить поле скоростей вне
решетки, что имеет практическое значение при расчете возмущений, вызванных
решеткой.
Отметим также, что все расчеты приспособлены для выполнения на
ЭВМ. Алгоритм построения функции A3.21) для произвольного профиля
дан в разд. 5.4, где также приведен пример расчета. Для расчета
преобразования решетки с тем же профилем необходимо провести вычисления по
формулам A3.25), приведенным здесь в общем виде,
319

Так как решетка профилей преобразована на решетку окружностей, то
для полного решения задачи необходимо рассмотреть обтекание последней.
Для решения используем общие формулы. Не уменьшая общности задачи,
расположим центры окружностей на оси у, а центр основной окружности
в начале координат (см. рис. 13.2). Комплексный потенциал потока,
обтекающего решетку окружностей, обладает теми же свойствами, что и функция
A3.7). Однако это будет комплексный потенциал бесциркуляционного
потока. Член, определяющий циркуляционное обтекание, может быть найден
как интеграл от cth z точно так же, как для одиночной окружности In г,
это — интеграл от Иг.
Запишем комплексный потенциал в виде
п = 0 П'
cth
dztl t
A3.29)
где w^ ~ u^ — iv^ — комплексная скорость бесциркуляционного
обтекания в бесконечности; Г — циркуляция скорости; Л„ — в общем случае
комплексные постоянные.
В случае, если. шаг решетки окружностей неограниченно возрастает,
следует положить
Al^wOOi Л„ = 0 при я>1,
и тогда A3.29) перейдет, в известный комплексный потенциал потока,
обтекающего одиночную окружность:
Ряд A3.29) представляет комплексный потенциал во всей области вне
решетки окружностей. Для определения входящих туда коэффициентов
разложим комплексный потенциал в ряд в окрестности начала координат.
Для разложения второго члена в выражении A3.29) проинтегрируем
ряд A3.8), введем обозначение A3.17) и получим
ln-Lsh —-lnz+ У Ы(п)з*«г*п. A3.30)
Здесь введено обозначение
У **"*"<"l)"+1 . A3.31)
п = 1
Первые пять чисел N (п) даны ниже:
п 1 2 3 4 5
Л/(л) 0,4113 —0,0338 0,0053 —0,0010 0,0002
Разложение комплексного потенциала обтекания решетки окружностей
A3.29) в окрестности начала координат с учетом формул A3.16), A3.18),
A3.30), A3.31) можно представить рядом
lV N(n)s2nz2n +
\nz{
2ni 2ni .
n— 1
+ V Anz~"+ V V #*М(пъ k)A^nz«. A3.32)
/t l=\ k
320

Для решения задачи обтекания решетки окружностей целесообразно
рассмотреть отдельно случаи поперечного, продольного и чисто
циркуляционного потоков. Произвольный поток вокруг решетки будет суммой этих
трех потоков.
При поперечном обтекании w^ - иж, Г - 0. Вследствие симметрии
задачи коэффициенты A2k — 0, а коэффициенты А2к„г (Л = 1, 2, 3, ...) —
действительные числа.
Так как основная окружность (а в силу периодичности картины
обтекания и все остальные) является линией тока, то мнимую часть
комплексного потенциала на ней можно положить равной нулю.
Подставив в ряд A3.32) z = е':е и приравняв мнимую часть нулю, получим
бесконечную систему линейных уравнений:
A3.33)
(л, fe)s2M2ft_n, л-3, 5, 7, ...
Суммирование следует начинать с k = (п f 1)/2. Числа М (n9k) были йри-
ведены в табл. 13.1.
Система A3.33) может быть легко решена методом скользящих
последовательных приближений, которое сходятся очень быстро.
Скорость на окружности в решетке можно представить рядом
w=2 2 nAnsinnQ, n -1, 3, 5, ... • A3.34)
При продольном обтекании w^ — ш^, Г = 0. Коэффициенты Ап с
четным индексом равны нулю, а с нечетным должны быть чисто мнимыми:
Ах ¦=¦- гСъ А3 = /С3, ... Приравняв нулю мнимую часть комплексного
потенциала на окружности в решетке, получим систему уравнений:
A3.35)
Остальные замечания те же, что и к системе A3.33).
Скорость на окружности в решетке определена тригонометрическим рядом
w
= 2^ nCncosnQ, п«1, 3, 5, ... A3.36)
При чисто циркуляционном обтекании w^ - = 0. Все коэффициенты Л„ с
нечетным индексом равны нулю, а с четным — чисто мнимые: А2 — t*D2,
Л4 = Ю4, ...
Приравняв нулю мнимую часть комплексного потенциала на
окружности в решетке A3.32), получим систему уравнений:
Г a;(a*)s2" Dn j \з*М(пч k)IXlh „. A3.37)
2л
Суммирование следует начинать с к — (п 4 2)/2.
П Зак. 2638 32!

Скорость на окружности
, "=2> 4> 6, ...
A3.38)
Приведем результаты расчета обтекания рабочей решетки турбины.
Вычисления (здесь опущенные) дают коэффициенты ряда Лорана, в который
разложена функция, отображающая внешность единичного круга на
внешность профиля:
?4 = —2,206-1,29Н;
с5=—1,364+0.859*;
св -0,096 + 0,80Ш;
с0-—5,329+ 24,706г,
?==38,183 — 16,366/;
cv = 17,337 + 3,020/;
с2 = 11,028—5,085/;
с3= 0,7430—4,955/;
?7---= 0,515 + 0,358/.
На рис. 13.3 показана решетка из этих профилей с шагом tx = 164 в
масштабе чертежа и углом между фронтом решетки и осью абсцисс Р = 108°.
Запишем зависимость между шагом решетки кругов и шагом решетки
профилей
iat = tx e# или 2iaftx = se'p. A3.39)
Зависимость A3.39) при замене коэффициента а его значением по
формуле A3.26) станет уравнением, из которого надо найти значение
параметра, характеризующего густоту решетки кругов. Параметр s должен быть
действительным числом. Это всегда может быть достигнуто поворотом
изолированной окружности, как это следует из зависимости A3.27). По
существу надо просто определить из уравнения A3.39) корень se~*\ где а и будет
искомый угол.
Решение уравнения A3.39) легко получить методом последовательных
приближений, чтобы найти единственный корень, модуль которого меньше
единицы.
В результате расчета получим
s= 0,7945, а-—33°. A3.40)
Зададим скорость перед решеткой
профилей
|о>+в0| = 1, arg
=78°
Рис. 13.3. Рабочая решетка турбины
322
Значение производной функции,
отображающей внешность решетки
кругов на внешность решетки
профилей, на бесконечности слева
согласно ряду A3.7) равно а.
Значение этой производной в общем
виде представлено формулой A3.26),
в которую входят известные
величины. Отметим только, что в
связи с поворотом круга на угол
а = —33° коэффициенты съ спч
вычисленные выше, следует умно-
жить на е~'« и tinn. Опустив вы-

M/lW.ool
^——
r
Irn/t
Рис. 13.4. Распределение скорости по профилю решетки (см. рис. 13.3)
числения, приведем значение производной отображающей функции на
бесконечности:
\а\ -32,574, arg a -18°.
Далее вычисляем скорость в бесконечности перед решеткой кругов
l/ + «="Htt!4.-.=F 16,288 +28,2 Ш.
Так как профиль не имеет абсолютно острой задней кромки, то полагаем,
что сбег происходит в точке, для которой модуль производной,
отображающей функции, имеет минимум. В данном случае это приводит к равенству
скоростей с двух сторон выходной кромки, что согласуется с реальной
картиной обтекания лопатки вязкой жидкостью.
В решетке этой точке соответствует 90 = —35°.
Для определения а0, v0 и Г составим уравнения.
1. Условие равенства нулю скоростей в точке Эо = —35°.
2,0691/0 + 0,951 v0 -(- 0,475717/ - 0.
2. Условие для скорости в бесконечности перед решеткой окружностей
"о f too — iT/2* - 16,288+ 28,211 i.
Решив эти уравнения, получим
и0- 16,288, 1>0=0§630, Г/2л = —22,10.
Значение модуля скорости на профиле в решетке определяем по формуле
где \V\ — модуль скорости на окружности в решетке.
Распределение скорости по профилю в решетке показано на рис. 13.4.
По оси абсцисс отложена развертка контура лопатки /. Начало координат
помещено в переднюю точку ветвления.
13.2. ПОСТРОЕНИЕ РЕШЕТОК С ГИДРОДИНАМИЧЕСКИ
ЦЕЛЕСООБРАЗНЫМ РАСПРЕДЕЛЕНИЕМ СКОРОСТИ
Рассмотрим решение обратной задачи, т. е. построение решетки
с заданным распределением скорости по профилю. Изложим кратко метод,
предложенный Г, Ю. Степановым,
И* . 323

На рис. 13.5 показана плоская решетка, обтекаемая потоком идеальной
несжимаемой жидкости, и даны основные применяемые здесь обозначения.
В данном случае будем рассматривать так называемое струйное обтекание,
которое удобно реализовать в методе годографа и которое лучше
соответствует действительному течению с отрывом потока на задних кромках
профилей.
В принятой схеме такое течение имитировано струями, на границе
которых и до бесконечности за решеткой скорость, а следовательно, и
давление постоянны. Эта классическая схема Кирхгофа в случае тонких кромок
вполне оправдана.
Напомним, что в методе годографа легко учесть сжимаемость,
используя приближенный метод Чаплыгина (см. родразд. 5.5), однако ради более
компактного изложения будем рассматривать течение несжимаемой
жидкости. ,
На рис. 13.6 показано желательное распределение скорости V V (s)
на контуре профиля в решетке. Началу координат соответствует точка о
разветвления потока на носике профиля (см. рис. 13.5), а по оси абсцисс
отложена развертка дуг по выпуклой С и вогнутой В сторонам профиля и
кромочной струи. Положительным считаем то направление по дуге, которое
совпадает с направлением скорости на профиле.
Кривая oabc соответствует распределению скорости по выпуклом
стороне профиля, а кривая aefgc — по вогнутой.
Отрезок cd изображает начальный участок границ струи, rta которых
скорость постоянна и равна скорости V2 потока в бесконечности за
решеткой. На рис. 13.6 показана также
скорость V1 потока в бесконечности
перед решеткой, которая меньше
максимальной скорости Vc на
выпуклой стороне профиля (спинке),
но больше, чем скорость Vb на
вогнутой.
Скорость Vc > V2 на спинке
профиля ограничена постоянной
величиной 1/0, выбор которой
может быть подчинен условию, чтобы
в сжимаемой жидкости скорость не
превосходила, например, числа
М - 0,8.
Рис. 13.5. Струйная схема
аэродинамической решетки
324
обтекания
0 5а
Рис. 13.6. Заданное распределение
скорости по профилю

В данном случае рассмотрено обтекание решетки осевого компрессора
и поэтому особое значение имеет диффузорный участок be падения скорости
на спинке профиля. На этом участке отрицательный градиент скорости
должен быть таким, чтобы не происходил отрыв пограничного слоя. В
общем случае еще один диффузорный участок может быть на вогнутой
стороне профиля.
Запишем уравнение неразрывности
tfV\ cos о^ = A— a)/K2cosa2, A3.41)
где безразмерная величина а учитывает, что из-за струйного обтекания за
решеткой проходная площадь меньше, чем до решетки.
В потенциальном потоке циркуляция скорости по любому замкнутому
контуру равна нулю. Вычисляя равную нулю циркуляцию скорости по
бесконечному замкнутому контуру А1С1А2В (см. рис. 13.5), охватывающему
течение в межлопаточном канале и в одном периоде решетки, найдем
<рс—<р, = Г= f V(s)ds—[ V{s)ds = tV1sinoL1— A— a)tV2sina2t A3.42)
о о
где <р — потенциал скорости на контуре профиля.
Положительным считаем обход контура против часовой стрелки. Справа
стоят результаты, полученные интегрированием вдоль шага в бесконечности
перед решеткой и за ней. .
Для практических целей желательно строить компрессорные решетки с
наибольшей диффузорностью, при которой, однако, не происходило бы
отрыва пограничного слоя.
На диффузорных участках s >sb (см. рис. 13.6) для компрессорной
решетки выставим условие равновероятностного отрыва:
? __^ Rer/™, Re2 —1/6,/v, A3.43)
V ds
где для турбулентного пограничного слоя при предотрывном состоянии
можно принять
m-6, A = 0,013-f-0,020. A3.44)
Определим толщину потери импульса турбулентного пограничного слоя
в конце участка постоянной скорости, т. е. непосредственно перед участком
be (см. рис. 13.6). В турбомашинах поток сильно турбулизован, поэтому
можно считать, что турбулентный пограничный слой начинается на
входной кромке профиля. Длина дуги s , на которой происходит разгон потока
(см. рис. 13.6), обычно мала и можно для упрощения считать, что на всей
длине дуги s0 поток на спинке лопатки имеет постоянную скорость V = Vc.
(Легко получить общую формулу и не вводя этого упрощения),
По формуле (9.102) при постоянной скорости V = Vo получим
б«о -0,016 [v/(l/o62o)]0'25 % A3.45)
Эту формулу удобно записать в виде
На диффузорном участке при градиенте скорости, близком к
предельному по отрыву, касательное напряжение на стенке мало. Тогда интегральное
соотношение (9.77) можно записать так:
a°2 Iff] I 2) 2 = (
dx V dx
325

Проинтегрируем это уравнение и найдем
+ (#+2IпК=1пС.
Постоянную интегрирования следует принять такой, чтобы при V = Vo
получить б2 = б20, что соответствует толщине потери импульса
пограничного слоя в точке Ь (см. рис. 13.6). Тогда
Распределение скорости поперек предотрывного пограничного слоя
примерно такое же, как в свободной турбулентной струе, и формпараметр
Н ж 3. Удовлетворительное согласие с экспериментом дает зависимость
62-(V»/VO4-8Ao. A3.47)
которую и примем для дальнейших расчетов.
Формулы A3.43), A3.46), A3.47) дают возможность задать такое
распределение скорости на диффузорном участке be (см. рис. 13.6), при котором
положительный градиент давления будет возможно большим, но отрыва
пограничного слоя не произойдет.
Из формул A3.46) и A3.47) получим зависимость толщины потери
импульса на диффузорном участке от скорости V:
82 = 0,0366Re-0"s0(V0/Vy<*, Re0 -Vosjv. A3.48)
Исключив 62 из условия A3.43) с помощью выражения A3.48) и взяв,
как более надежное, меньшее значение постоянной Л, после преобразований
получим
— (—) -0,6164 Reg
Проинтегрировав это уравнение, найдем
634 =2,856
Постоянную интегрирования С следует определить из условия, чтобы при
s = s0 было V = Vo.
Окончательно получим желаемое распределение скорости на
диффузорном участке:
— -[1 +2,856Reg»0667 (s—So)/So)-°'151. A3.49)
Такой закон изменения скорости удовлетворяет условию
безотрывного обтекания A3.43), а решетка будет иметь максимально допустимую на
этом участке диффузорность.
Следует отметить, что точное получение такого распределения
необходимо только для компрессорных решеток. Хорошие турбинные решетки
обычно имеют незначительные диффузорные участки и на них достаточно
лишь проверять условие безотрывного обтекания.
Потенциальному течению вокруг решетки в физической плоскости
можно сопоставить потенциальное течение в плоскости годографа скорости
(см. подразд. 5.6). Область внутри годографа скорости можно, далее,
конформно отобразить на другую удобную для вычислений область (см.
подразд. 5.4) и в ней также рассматривать соответствующее потенциальное
течение несжимаемой жидкости. В качестве такой удобной стандартной (как
говорят, канонической) области удобно взять окружность единичного
радиуса.
326

Рис. 13.7. Эквивалентное
течение в круге
Фактически можно миновать преобразование
течения из области годографа, а прямо
рассматривать соответствие между течением вокруг
решетки и течением внутри окружности, иначе
говоря, конформное отображение внешности
решетки (в полосе одного периода) на
внутренность единичной окружности.
Расположим круг в плоскости комплексного
переменного ? (рис. 13.7). Пусть бесконечности
А1 перед решеткой соответствует центр круга
С — 0, а бесконечности Л2 за решеткой —
точка ? = I-
Соображения, аналогичные приведенным в
подразд. 5.2, позволяют заключить, что для
соответствия рассматриваемых течений в центр круга следует поместить
вихрь и источник, а в точку ? ¦== 1 — сток.
Интенсивность вихря
T1-/l/lsina1. A3.50)
Производительность источника равна расходу жидкости в одном
периоде решетки:
Q=/l/1cosal. A3.51)
Производительность стока по уравнению неразрывности равна
производительности источника.
Комплексный потенциал течения, вызванного этими особенностями,
должен быть записан таким образом, чтобы окружность единичного
радиуса была линией тока. Построение комплексного потенциала обтекания
окружности потоком, вызванным источниками и вихрями, было
рассмотрено в подразд. 5.2. В данном случае выражение комплексного потенциала
принимает вид
-1). A3.52)
Для построения профиля в решетке необходимо найти распределение
потенциала скорости по окружности.
На окружности единичного радиуса ? = et6, где 8 — полярный угол
(см. рис. 13.7). Тогда комплексный потенциал на окружности
F (е*в) = (-I*- -г —) *6 5- In (cos 6 — 1 + i sin 6).
\ 2ш 2л / л
Разделяя в написанном выражении действительную и мнимую части,
находим, что последняя, равная функции тока \|>, конечно, постоянна (равна
нулю), а действительная часть — потенциал скорости — имеет выражение
Г О ft
ср @) = —L 0 — In sin h const.
2л л 2
Вычислим производную потенциала A3.53):
иф Г» Q . Э
d$ ~~ 2л 2л 2
A3.53)
A3.54)
Используя формулы A3.50) и A3.51), после тригонометрических
преобразований из выражения A3.54) получим
2л
I * 1 6 2 /
2л sin @/2)
1
327

В плоскости круга поток течет из источника в начале координат в сток,
расположенный в точке ? =*= 1. В точке с угловой координатой 90 (см.
рис. 13.7) поток разветвляется. В этой точке скорость потока, а значит, и
производная потенциала равна нулю. Из выражения A3.55) находим, что
этой точке соответствуют
60=я—2alf ax^{n — 90)/2. A3.56)
Исключив ах в формуле A3.55) с помощью зависимости A3.56), получим
= — —-. A3.57)
dQ 2л sin F/2)
Найдем соответствие между точками окружности и точками профиля в
решетке.
Зависимость потенциала скорости на профиле от дуги следует из его
определения
A3.58)
где отсчет дуги s >0 определен на рис. 13.6 в сторону возрастания V > 0.
Так как поток вокруг решетки соответствует потоку внутри круга, то
в сходственных точках профиля и окружности потенциалы должны быть
равны
= Г
J
о
A3.59)
Здесь учтено, что точке разветвления потока на передней кромке профиля
s = 0 соответствует точка разветвления на окружности 0 — 60. Если,
например, задать распределение скорости по профилю V (s), то при прочих
известных параметрах по формуле A3.59) можно найти соответствие между
точками профиля и окружности.
Практически удобнее задавать скорость не как функцию дуги s, а как
функцию полярного угла 9, что очевидно возможно, так как s = s (9) есть
однозначная функция.
Распределение скорости V (9) должно быть задано конечно так, чтобы
распределение скорости V (s) удовлетворяло указанным выше условиям,
а также соответствовало заданным параметрам потока через решетку.
По заданному V (9) можно найти
s(9) =
С 1 </<р
J 1/@) ИГ1
A3.60)
где производная dcp/d9 задана формулой A3.55).
Рассмотрим постановку задачи, естественную по техническим
требованиям: построить гидродинамически совершенную решетку с заданными
величиной Vx и направлением аг скорости в бесконечности перед решеткой и
направлением а2 потока за ней.
Выбор шага / по существу определяет только масштаб чертежа профиля,
т. е. его площадь, моменты инерции и сопротивления, необходимые для
расчета прочности и вибрационных характеристик. Следует еще задать
величину а, безразмерную толщину струйной зоны, очевидно, связанную с
толщиной выходной кромки.
328 л •*.

Величина V2 скорости в бесконечности за решеткой будет найдена при
этом из уравнения неразрывности A3.41).
Перейдем к математической формулировке задачи. Уравнения в
плоскости годографа скорости E.95) записаны в полярной системе координат V,
а. Они перейдут к декартовой системе координат, если рассматривать
переменные In V и —а, т.е. логарифм скорости и угол ее наклона к оси абсцисс
с обратным знаком, действительная и мнимая части функции
комплексного переменного V ---= Veria.
Из теории функций комплексного переменного известно, что если задать
на окружности действительную часть функции, то всю эту функцию в круге
можно восстановить с точностью до мнимой постоянной. Эту задачу решает
интеграл Шварца. Следовательно, если задать на окружности In V (в) и
значение а — аг в центре круга (он соответствует бесконечности перед
решеткой), то функция In V (?) в круге будет однозначно определена. В
частности, угол на окружности, как мнимая часть этой функции, может быть
определен несобственным интегралом .
2Л
а (8):=— f In V(e)ctg-^=^-de+-<*,. A3.61)
2я
В точке е = 0 подынтегральная функция обращается в бесконечность как
(е —- 6)-\ и интеграл надо понимать в смысле главного значения.
В принятой постановке задачи необходимо удовлетворить еще двум
условиям.
В бесконечности за решеткой задан угол а2 направления скорости.
Следовательно, в точке I = 1 значение'угла известно. Оно же по формуле
A3.61) при 9-0
2Я
=4- f
ZTL J
0
Задана также величина Vx скорости в бесконечности перед решеткой и,
следовательно, в соответствующей ей точке — центре окружности ? — 0.
В то же время из интеграла Шварца следует, что в этой точке
2Л
^-i- f lnV(eUe. A3.63)
о
(Заметим, что это соответствует известной теореме о том, что значение
гармонической функции в центре круга есть среднее арифметическое ее
значение на окружности.)
По заданному распределению скорости V (8) интеграл A3.61) полностью
определяет угол а (8) ее наклона. Однако распределение скорости
произвольно задавать нельзя,, оно должно обеспечивать определенную циркуляцию
скорости A3.42) и удовлетворять указанным условиям A3.62) и A3.63).
Для их выполнения при заданных величинах Vb и Ус и общем виде
распределения скорости V (s) (см. рис. 13.6) остаются три свободных параметра:
угол наклона прямой оеа„ длина участка аЬ постоянной скорости Vc, а
также участка ef постоянной скорости Vb (или, более общем, все
распределение скорости на вогнутой поверхности, начиная от точки е).
Применим для удобства расчета линейные распределения V — k (б —
— 80), (в0 < 8 < ва) и V - k (в0 — в), (8^ < в < в0) с угловым
коэффициентом k. (При этом соответствующие распределения V (s) будут незна-
329

чительно отличаться от линейных, что никакого значения не имеет.) Кроме
того, для решеток реальной густоты с очень малой погрешностью можно
считать, что V (9 >6а) =-- Vc и V (9 < 9е) .-= VB. Тогда, интеграл в
формуле A3.63) можно вычислить в явном виде и найти
(я-2а,) In
(.3.64)
Чтобы удовлетворить условию A3.62), приходится делать несколько
пробных численных расчетов интеграла в формуле A3.62), изменяя угол Qh и
соответственно распределение скорости на дйффузррном участке be, а также
угол 6^ (и, возможно, еще 9^) так, ^тобы выдержать заданную величину
циркуляции Г A3.42). В выражении A3.42) потенциалы <рг -- ф {Qc) и
Ф# — Ф (Qg) определены теперь формулой A3.53).
После того как по формуле A3.61) определен угол а ¦=-¦ а (9), можно
строить контур профиля в решетке; для этого используем формулу A3.60)
и выражение для производной потенциала A3.57):
+e/2) dQ 65
1 dQ
t/\ 2я J V(B) [stna(e) J sin F/2)
Oi
Для удобства проведения численного интегрирования A3.61) надо
исключить особенности подынтегральной функции в точках г = 90 и е ~ 9.
Прежде всего целесообразно превратить интеграл в обычный,, учитывая,
что при любых 9 главное значение несобственного интеграла
2Л
Вычитая его из интеграла A3.61), получим обыкновенный интеграл, не
имеющий особенности при е — 0:
2 я
ос(в)= 4— f 1п1гЙгс^^<*е + а'- <13'66>
in J v (о) 1
0
Аналогичную замену In V (г) на In (V (e)/V2) полезно произвести и в
интеграле A3.62).
Осталась еще особенность при е = 90. В небольшой 6-окрестности
этой точки (90 — 8 < е < 0О + б) при |9 — 90| >6 можно записать:
Формула A3.67) справедлива при условии V (90 + б) = V (90 — 6), т. е.
если вся б-окрестность точки 90 не выходит за пределы участка еоа (см.
рис. 13.6).
Численное интегрирование по г затрудняется еще тем, что вблизи
Э ^ о и 9 = 2я функция V (9) изменяется на очень малых углах.
Целесообразно «растянуть» их путем подходящей замены переменной. Для этого
оказалась удобной функция
Т = — 1пBя/в- 1), т -л — In (Зл/г -1). A3.68)
330

v=v2
h
a
*\
\
V
p V=VC
f ?
пй
Ort
b
#\
d '
-30 -20 40
10
20 T
t t
' 2Я-Ю'* Л
Рис. 13.8. Заданное распределение скорости
После такой замены формула A3.66) принимает вид
-f-oo
V(T)
Аналогично преобразуется и условие A3.62):
A3.69)
A3.70)
Ввиду уменьшения подынтегральной функции с ростом |т| как е~'х
пределы интегрирования по т можно заменить на конечные (практически
1ттаХ I ^ 20 ... 25). Интегрирование можно проводить по формуле трапеций
с равномерным делением промежутка интегрирования. Ввиду того, что
функция а (Т) в точке разветвления Г--То(9 ~ 00) испытывает разрыв на
ят точку Т Г,* надо располагать в середине одного из отрезков AT.
Значения а (То ± 0) следует находить экстраполяцией а (Т) слева и справа в
точку Т Т{).
Рассмотрим пример построения решетки турбины. Зададим шаг решетки / = 1
и величину скорости на входе V| ~ !f чем определим линейный масштаб и масштаб
скоростей. Примем углы входа и выхода потока <%j — 60°, сс2 — — 65°. Выберем о = 0,1,
что определит реальную безразмерную толщину выходных кромок лопаток ^ 0,05.
По уравнению неразрывности A3.41) определим величину скорости за решеткой V2~
— lt3l46. Зададим скорости на спинке и вогнутой стороне лопатки (см. рис. 13.6):
Vc U К2 -1,4461, Ve-0,6 Vi= 0,6000.
(Отметим, что для получения реальных сужающихся выходных кромок в любых
решетках следует принимать Vc > K2.) Далее по формуле A3.42) подсчитаем циркуляцию
Г - 1,9383 и по формуле A3.56) — угловую координату 0О ~ 60° точки о
разветвления потока.
Теперь по формуле A3.53) можно найти распределение потенциала скорости по
окружности ? - е10 (см. рис. 13.7), вычислив постоянное слагаемое так, чтобы было
<Г @„) 0:
Ф@) 0,2546 12,406-10~эВ~041592 in sin (B/'2b A3.71)
где- угол 0 измерен в градусах.
331

После этого прн любом задаваемом
распределении скорости, используя
формулы A3.60), A3.68) и A3.70), можно
найти однозначное соответствие дуги s
контура профиля (с каждой его
стороны), угловой координаты 0 и
параметра Г.
Гидродинамически целесообразное
распределение скорости по контуру
профиля проектируемой решетки
обсуждалось по рис. 13.6 в функции дуги $.
Однако, как уже было сказано, удобнее
задавать скорость как функцию
параметра Т (рис. 13.8). Для этого находим
по формуле A3.64) угловой
коэффициент к — 1,4652 линейного
распределения скорости V F) в окрестности
точки разветвления 0=0О и определяем
Qa=,% + Vc/k-= 116,5°,
По формуле A3.68) переходим к
параметру Т: Го= — 1,609; Та - —0,7366,
Те — — 2,181. Затем строим
распределение скорости V (Т) (рис. 13.8),
задавая точки Ь, с, f и g сначала
ориентировочно, но так, чтобы на диффузор ном
участке be выполнялось условие A3.49)
безотрывного обтекания, а разность
фс —" Ф# была равна Г. Далее
проверяем условие A3.70) и изменяем
положения точек с, / и g до его
удовлетворения. Заметим, что 0С и 0^ обычно очень
близки соответственно к 2я и 0,
благодаря чему все формулы и построения
весьма упрощаются.
На рис. 13.8 показано окончательно принятое распределение V (Г). Определение
а (Т) производилось численно по формуле A3.69) в пределах интегрирования от т -
= Те до т = Tdt удовлетворяющих условию A3.42) (при этом Td — Tc^Tg~ Th).
Распределение скорости V (s) по контуру профиля качественно не отличается от
распределения V (Т) и в расчетах не использовалось.
Профили в решетке, координаты х, у которых вычислены по формуле A3.65) с
указанием всех характерных точек, построены на рис. 13.9.
Точность расчетов и построения подтверждается тем, что отрезок dh параллелен
фронту решетки, а его длина равна заданной величине а/. Кроме того, при постоянных
Рис. 13.9. Решетка,
графу скорости
построенная по годо-
скоростях Vв и Vc на стенках
значительной части
межлопаточного канала он содержит участок
практически постоянной ширины,
ограниченный дугами
окружностей, радиусы которых
удовлетворяют условию потенциальности
течения, гв Vв ~-~ rcVc.
Реальный профиль надо
закончить вблизи точек с и g
начала струй, на границах которых
скорость V — V2 — const. Эти
точки * в отличие от точек d и Л, не
лежат на одной вертикали. На
рис. 13.9 штриховыми линиями
показано окончание выходной
кромки, выполненное по дуге
окружности. Строго говоря,
полученный профиль следовало бы еще
утонить по всему контуру на
332
Рис. 13.10. Распределение скорости по профилю

толщину 6, вытеснения пограничного слоя, в чем, однако, ввиду малости 6Х
необходимости нет.
По существу построения известно соответствие s — s F) точек контура
профиля и окружности в плоскости ? (см. рис. 13.7), поэтому распределение
скорости V (s) при любых других «нерасчетных» условиях на входе в решет,
ку, otj и Vu вычисляется элементарно:
ds
dO dy> ds
dy/dQ
где производная dcp/d9 определена формулами A3.57)^и A3.56) на расчетном
режиме, a dcp/d8 — теми же формулами, но при Г\ = tV1 sin alf Q =
= tVi cos al% т. e. при ax = a1? Vx = V\ и00 = 0О.
Итак, при заданных величинах t, а1э Кь а2 и а построена решетка с
гидродинамически целесообразным распределением скорости, которое
характеризуется тем, что на входной кромке профиля (ае) скорость только
увеличивается, на большей части межлопаточного канала имеет заданные
постоянные величины Vb и Vc и уменьшается только на одном коротком диф-
фузорном участке (be) с выполненным условием безотрывного обтекания
(рис. 13.10).
Изложенный метод достаточно прост и может быть реализован на мини-
ЭВМ. В случае необходимости его можно распространить на дозвуковые
течения газа в приближении Чаплыгина, рассмотренном в подразд. 5.5.
13.3. ХАРАКТЕРИСТИКИ РЕШЕТОК ОСЕВОЙ ТУРБИНЫ
Рассмотрим плоскую аэродинамическую решетку (рис. 13.11),
обтекаемую без отрыва дозвуковым потоком вязкой жидкости. При
достаточно большом числе Re пограничный слой на лопатках будет тонким, и в
этом случае весь поток можно разбить на четыре характерные области.
Область / — безвихревой, т. е. потенциальный поток, где трением можно
пренебречь, область // — относительно тонкий пограничный слой на
лопатках, в котором существенно влияние трения и наблюдается большой
поперечный градиент скорости, область /// — кромочные следы, образующиеся
за лопатками, где также существенно влияние трения, область IV —
кромочные следы после слияния, где под влиянием трения продолжается
выравнивание потока.
рис. 13.11, Схема течения в решетке при больших числах Re
333

Очевидно, что поток за аэродинамической решеткой неоднороден, т. е.
величина и направление скорости, давление, плотность газа различны в
различных точках. Расчет турбомашин проводится обычно на основе одномерг
ной теории. Для применения такой теории необходимо осреднить
неоднородный поток.
Для полного описания неоднородного потока необходимо задать
значение его параметров во всех точках. Задача осреднения состоит в описании
неоднородного потока меньшим числом параметров, но при условии
сохранения основных его свойств, существенных для данного исследования.
Очевидно, что при осреднении некоторые свойства утрачиваются и
поэтому осредненный поток не может быть полностью эквивалентен
неоднородному. Вместе с тем после осреднения задача существенно упрощается,
что позволяет провести исследование и получить количественные
результаты.
Возможны различные методы осреднения, причем выбор метода, как
было сказано, должен быть согласован с задачей исследования. В турбома-
шинах целесообразно проводить осреднение по расходу, количеству
движения и энергии, так как эти уравнения положены в основу одномерного
расчета.
Проведем контрольное сечение 2—2 за решеткой (см. рис. 13.11) и
будем проводить осреднение потока в этом сечении на протяжении шага
решетки /, равного периоду неоднородности потока.
Найдем поток массы, пересекающий контрольную поверхность:
t
m= f Pepsinpg dy,
b
Здесь p3, w%> p2 — соответственно плотность, скоррсть и угол направления
потока в контрольном сечении.
Аналогично определим количество движения, переносимое потоком через
контрольную поверхность. Поскольку эта величина —вектор, рассмотрим
проекции его на оси координат, положение которых показано на рис. 13.11:
' . t
lx » J* ра wl sin p2 cos p2 dy, \u = f pa w\ sin2 P2"dj/.
о 6
Угол направления суммарного вектора количества движения будем
считать средним углом направления потока за решеткой:
Определение среднего угла через количество движения принято дото-
му, что по этому углу в теории турбомашин строят треугольники скоростей
и определяют силу, действующую на лопатки в решетке.
Определим среднее статическое давление в контрольном сечении как
среднее по шагу t
j
о
Введем теперь одномерный изоэнтропийный поток, который имеет те же
параметры торможения, что и реальный поток перед решеткой. Пусть в
сечении 2—2 идеальный поток направлен под углом, равным среднему углу ?а,
и его статическое давление равно среднему давлению в реальном потоке ра.
334

Тогда поток массы для идеального течения
Здесь индексом t отмечены теоретические значения параметров, которые
могут быть определены обычным путем из расчета одномерного изоэнтропий-
ного течения.
Коэффициентом расхода, по определению, называют отношение
действительного расхода к теоретическому, который проходит через ту же
площадь и при том же статическом давлении:
!('pM>sinpd0 A3.72)
Коэффициентом скорости называют отношение количества движения,
переносимого единицей массы реального потока, к аналогичной величине
для теоретического потока:
( {\ A3.73)
Здесь использовано условие, что для теоретического потока можно записать
\tlmt = mtw2tlmt = w2t.
Коэффициентом полезного действия решетки ц называют отношение
кинетической энергии, переносимой единицей массы действительного
потока, к аналогичной величине для теоретического потока:
A A3.74)
Вместо коэффициента полезного действия решетки обычно используют
величину, называемую коэффициентом потерь:
С =1-4. A3.75)
Таким образом, после введения трех безразмерных коэффициентов
по формулам A3.72), A3.73), A3.75) неоднородный поток заменяется
однородным, который^ имеет тот же расход и переносит те же количества
движения и энергии:
; A3.76)
Ё = (I/2)Mtot wits\npt=(l/2)r\whm,
или, точнее, тремя однородными потоками со скоростями, осредненными по
расходу \iw2t> количеству движения tyw2t и энергии Уц w2t-
Введенные коэффициенты и средний угол выхода потока называют
аэродинамическими характеристиками решетки. Если эти характеристики
известны, то расчет решетки производят по одномерной теории для изоэн-
тропийного течения, а действительные значения расхода, количества
движения и энергии находят по формулам A3.76).
Аэродинамические характеристики зависят от геометрических
характеристик решетки и режима обтекания, т. е. угла входа потока в решетку, чисел
М, Re и степени турбулентности потока.
335

Экспериментальный метод определения аэродинамических
характеристик состоит в измерении параметров потока в контрольном сечении и
обработке результатов опытов по формулам A3.72), A3.73), A3.74).
Контрольное сечение, в котором производят измерения, обычно выбирают на таком
расстоянии от данной решетки, которое примерно соответствует положению
фронта соседней решетки в турбомашине. В таком случае возможно
упрощение основных формул и соответственно программы эксперимента.
Возмущения, вносимые решеткой, могут быть вызваны: 1) неоднородностью
потенциального потока; 2) вязкостью жидкости. Возмущения первого рода
связаны с тем, что решетка, помещенная в поток (даже невязкой жидкости),
делает его неоднородным, т. е. поле скоростей и давлений зависит от
координат. Возмущения второго рода связаны с вязкостью жидкости и
выражены главным образом неоднородностью поля скоростей в кромочных следах
(неоднородность в пограничном слое сейчас не рассматриваем). Эта
классификация возмущений несколько условна для областей вблизи выходных
кромок, где сбегают пограничные слои.
Возмущения в потенциальном потоке быстро гаснут при отдалении от
решетки (по экспоненциальному закону, см. подразд. 13.1).
Следовательно, поля углов и давлений (а значит и плотностей) выравниваются
довольно быстро. Наиболее неоднородным остается поле скоростей в кромочных
следах. Будем считать, что поле углов и давлений в контрольном сечении
практически однородно. Тогда можно считать, что действительная плотность
равна теоретической, так как давления в обоих потоках по условию
одинаковы, а небольшим различием в температурах можно пренебречь.
Из формулы A3.72) получаем упрощенное выражение для
коэффициента расхода:
tw2t
{w2dy. A3.77)
Производя соответствующие упрощения в формулах для вектора
количества движения с учетом A3.73), получим выражение для коэффициента
скорости:
§ A3.78)
Из формул A3.74), A3.75) имеем
т]- 1 —?=( f Kdy \l\w\t \wtdy\ A3.79)
Типичное распределение давления торможения за решеткой показано
на рис. 13.12, а, соответствующие параметры отмечены также в /is-диаграм-
ме (рис. 13.12, б). В зоне кромочных следов наблюдается уменьшение
полного давления, так как при том же статическом давлении там скорости
меньшие, чем в основном потоке. На рис. 13.12 р0 — давление торможения
перед решеткой, рщ — давление торможения за решеткой, 01 — изоэнтро-
пийный процесс расширения; 02 — действительный процесс расширения
для какой-либо струйки.
Можно показать, что между найденными характеристиками имеется
следующее соотношение:
1КЦ<Уг)<*- A3.80)
336

5 б)
Рис. 13.12. Давление торможения за решеткой:
а - распределение относительного давления торможения по шагу; б — процесс в тепловой
диаграмме
Во многих практически важных случаях возможно дальнейшее
упрощение формул A3.77)—A3.79). Если поле скоростей в контрольном сечении
слабо неоднородно, то
W2/W2t = l — (l~W2/W2t)9 A —W2/W2t) С 1.
Подставив это отношение скоростей в формулы A3.77) — A3.79) и
воспользовавшись формулой бинома с точностью до величин первого порядка
малости, легко получить приближенные зависимости:
jjt^=4t>=- 1—?/2, tj=i|>2, ? = 1— ф2. A3.81)
В практике помимо введенного коэффициента расхода целесообразно
использовать также коэффициент расхода, определенный для выходного
сечения решетки КК (см. рис. 13.11). Запишем уравнение неразрывности
для этого сечения при изоэнтропийном процессе:
trii ™р$ t sin рк ^2<» (lu.oz)
где Рк — угол наклона выходных кромок.
В действительном течении расход будет меньше из-за наличия
пограничных слоев, что можно учесть, уменьшив размер сечения на толщину
вытеснения пограничного слоя (см. разд. 8.6):
m==p,(*siripK —
A3.83)
где бх — суммарная толщина вытеснения пограничных слоев по обе
стороны кротки.
Тогда коэффициент расхода
jjik^ m/mt= I —61//sinpK- A3.84)
Толщину вытеснения можно определить расчетом пограничного слоя.
При экспериментальном определении непосредственно измеряют
действительный расход и сравнивают его с теоретическим. Введение коэффициента
расхода для выходного сечения имеет то преимущество, что таким образом
при расчете турбомашины более точно определяют выходную площадь
решетки, в то время как средний угол выхода потока не всегда известен с
достаточной точностью. Следует учесть, что [лк >№•
Таким образом, можно отметить, что коэффициент расхода меньше
единицы из-за наличия пограничного слоя. Это замечание справедливо при
течении газа или перегретого пара, В случае течения пара с переохлажде-
337

нием коэффициент расхода может
принимать значения и больше единицы,
если, как обычно, расчет проведен в
предположении о фазовом равновесии.
Это объясняется тем, что
наблюдающееся в действительности
переохлаждение пара приводит к увеличению
расхода в большей степени, чем
снижение расхода из-за присутствия
пограничного слоя.,
Коэффициент потерь, который
определен ранее для плоской
решетки, называют коэффициентом
профильных потерь. Эти потери можно представить суммой двух потерь:
Рис. 13.13. Схема
ками лопаток
течения за
кромгДе Спр ~~ профильные потери; ?тр — потери трения; ?кр — кромочные
потери.
Потери трения вызваны наличием пограничного слоя на поверхности
лопаток и, следовательно, могут быть выражены через толщину потери
энергии слоя. Из формул A3.72), A3.74), A3.75) следует
Стр = 1-?/|х?|. . A3.86)
Количество энергии, которое несут теоретический и действительный
потоки через выходное сечение решетки, может быть записано так:
(lO.Ol)
где 63 — суммарная толщина потери энергии в пограничных слоях по обе
стороны кромки в выходном сечении. Из формул A3.86), A3.87) следует
<|А « 1)
CTP=e.//sinpK. A3.88)
Потери трения могут быть вычислены после расчета пограничного слоя
или определены экспериментально по измерениям толщины потерь энергии
на выходной кромке.
Кромочные потери включают потери, возникающие при обтекании с
отрывом кромки конечной толщины, и потери, которые происходят при
выравнивании вязкого потока за решеткой.
Рассмотрим решетку с прямолинейными выходными кромками (рис. 13.13)
и произведем теоретическую оценку влияния толщины кромок на
кромочные потери и угол выхода потока. Положим, что в контрольных сечениях,
выходном КК и за решеткой 22, поток однороден. Запишем для этих
сечений уравнение неразрывности, полагая жидкость несжимаемой:
t' sinjJK =
A3.89)
Составим уравнение количества движения в проекции на фронт решетки:
рШк/sinPK cospK ^tpw\ sinp2cosp2 A3.90)
и нормаль к фронту:
Рк*' +р' Ц—П + рпУ* sin*fLK=ptt +(w\s\n*h9 A3.91)
338

где р' — давление за кромками, которое ниже, чем давление в каналах
решетки из-за эжектирующего действия вязкого потока, срывающегося с
кромок.
Возведя левую и правую части уравнения A3.89) в квадрат и поделив
его почленно на уравнение A3.90), получим формулу для определения угла
выхода потока:
a = (*'//) tgPK. A3.92)
Угол выхода потока меньше, чем угол наклона кромок, так как площадь,
занимаемая потоком за решеткой, больше, чем площадь каналов. Следует
также обратить внимание на то, что угол выхода не зависит от величины
разрежения за кромками.
Относительные кромочные потери определяем как отношение
абсолютной потери к кинетической энергии потока:
?кр=2ДА/ри;4к. A3.93)
В числителе записана разность полных энергий потока в контрольных
сечениях:
ДА = (рк—рО/Р + Нс—о#/2. A3.94)
Преобразуем выражения в скобках. Разность давлений выразим из
уравнения A3.91):
pK_pa===±z?l(pK_p') + pa,jsinfp2 ypa;2Ksin2pK. A3.95)
Из уравнения A3.89) следует
w\ sin2 02 = 1-jA2 wk sin2 pK. A3.96)
Исключив из соотношения A3.96) sin P2 с помощью уравнения A3.92),
получим
A3.97)
Заменив разность давлений в выражении A3.94) с помощью уравнения
A3.95) и исключив w2 и sin p2 c помощью зависимостей A3.97), A3.89),
получим
Тогда из формулы A3.93) следует формула для относительных кромочных
потерь:
Здесь введено обозначение для относительного разрежения за кромками:
A3.99)
Относительное разрежение за кромками зависит от их формы и числа
Re, а для сжимаемой жидкости также и от числа М. Прямые опыты по
измерению разрежения, а также опыты по измерению кромочных потерь в
общем согласуются, причем в качестве среднего значения можно принять
этот коэффициент равным 0,2.. Для относительно тонких кромок второй член
339

в формуле A3.98) можно отбросить и в этом случае кромочные потери
пропорциональны толщине кромки:
трк. A3.100)
При относительно толстых кромках и больших углах выхода потока второй
член в формуле A3.98) дает ощутимую поправку.
Течение через плоскую решетку не отличается от течения через решетку
с бесконечно длинными лопатками, образующие которых нормальны к
плоскостям течения. Рассмотрим теперь течение через прямую решетку,
образованную лопатками конечной длины и ограниченную по торцам
плоскостями П (рис. 13.14). При течении вязкой жидкости через такую решетку
возникают некоторые явления, изучение которых важно для практических
приложений.
При достаточной длине лопаток течение в средней части каналов, т. е.
на некотором удалении от торцовых поверхностей, не отличается от
течения в решетке бесконечно длинных лопаток. Поток проходит через
криволинейные каналы и поворачивает. Это течение называют основным или
первичным. По концам Лопаток при повороте потока возникают так
называемые вторичные течения в пограничном слое на торцовых поверхностях.
Частицы жидкости в пограничном слое на торцовых поверхностях движутся
не только вдоль канала, но и поперек его, перемещаясь от вогнутой
поверхности лопаток к выпуклой.
В результате сложения этих движений частицы перемещаются в
направлениях, указанных на рис. 13.14 стрелками. Причину возникновения
вторичных течений можно объяснить следующим образом. На частицы
жидкости, движущиеся в средней по высоте части канала, при повороте
действуют центробежные силы, которые вызывают градиент давления поперек
канала. Давление на 'вогнутой поверхности лопаток больше, чем на
выпуклой. Частица движется вдоль канала по криволинейной траектории,
а центробежная сила уравновешивает разность давлений.
Частицы жидкости, текущие в пограничном слое на торцовых
поверхностях, имеют меньшие скорости, чем скорости частиц в средней по высоте
части канала. Меньшие центробежные силы не могут уравновесить разности
давлений поперек канала, которые вызваны основным потоком. Поэтому
в пограничном слое на торцовых поверхностях наблюдается перетекание от
вогнутой поверхности лопаток
к выпуклой. Суммарное
движение вблизи торцовых
поверхностей определяется сложением
продольных и поперечных
скоростей.
По высоте канала возникают
перетекания жидкости в
обратном направлении в силу
уравнения неразрывности — от
выпуклой поверхности лопаток к
вогнутой. Поскольку эти
компенсирующие перетекания
наблюдаются по всей высоте
канала, то соответствующие
поперечные скорости малы.
В результате вторичного те-
Рис. 13.14. Вторичные течения в решетке с ло- чения подторможенные частицы
патками конечной длины жидкости из пограничного слоя
340

г ft
075
0,25
f
1
z/t
0,75
0,50
0,25
У
)
a)
0,2
Ю
6)
Рис. 13.15. Распределение
относительных потерь и углов по высоте
лопаток:
а — распределение относительных потерь;
б — распределение углов выхода потока
на торцовой поверхности попадают на
спинку лопатки и свертываются в
вихревые жгуты. Это приводит к резкому
утолщению пограничного слоя на
спинке, как это видно из рис. 13.14, на
котором изображено распределение тол- Ц50
щин пограничного слоя в выходном
сечении. Местные утолщения
пограничного слоя в выходном сечении
несколько смещены от торцовых
поверхностей, так как из-за вторичного
течения на спинке лопатки имеются
составляющие скорости вдоль оси г,
направленные от торцов. Ближе к торцовым
поверхностям наблюдается небольшой
участок, где толщина пограничного
слоя мала. Этот слой состоит из частиц,
которые попали с торцовой
поверхности, т. е. из зоны с большими давлениями и меньшими скоростями. Сле-?
довательно, эти частицы по дороге ускорялись и не успели затормозиться
на выпуклой поверхности лопатки.
Выберем контрольную плоскость за решеткой, расположенную на
некотором расстоянии х = х2 и параллельную плоскости yz (рис. 13.14). Для
каждого сечения 2 -= const можно произвести измерение параметров
потока по шагу решетки и вычислить средние аэродинамические
характеристики по тем же формулам, как для плоской решетки. На рис. 13.15, а
показано распределение средних по шагу потерь по высоте решетки. В средней
части решетки потери постоянны и равны потерям, которые возникли бы
в решетке с бесконечно длинными лопатками. Осредненный угол выхода
потока на этом участке также постоянен (см. рис. 13.15, б). Ближе к
торцовым поверхностям наблюдается значительное увеличение потерь,
объясняемое утолщением пограничного слоя на спинке лопатки из-за вторичного
течения. В этих же сечениях средний угол выхода потока больше, чем в
центральной части решетки. Угол выхода растет из-за оттеснения линий
тока от спинки лопатки в месте набухания пограничного слоя. При
приближении к торцовым поверхностям толщина пограничного слоя на
небольшом участке вновь уменьшается, что приводит к уменьшению потерь
и угла выхода потока. Непосредственно вблизи ограничивающих стенок
потери резко возрастают, так как эти сечения соответствуют области
пограничного слоя на торцовых поверхностях.
Средние потери в решетке вычисляются по обычным формулам, но
интегрирование теперь следует выполнять по всей контрольной плоскости,
выбранной за решеткой. Это соответствует вычислению средних по высоте
лопаток потерь с помощью графика (рис. 13.15, а). Относительные потери
в решетке с ¦, лопатками конечной длины можно представить суммой
гДе Спр — профильные потери, которые соответствуют потерям в решетке
с бесконечно длинными лопатками и в действительности наблюдаются в
средних сечениях решетки; ?к — концевые потери, вызванные вторичными
течениями и возникающие у торцовых стенок.
Предположим, что высота лопаток исследуемой решетки увеличена,
например, вдвое при сохранении всех прочих геометрических размеров ре-
щетки. Тогда очевидно, что при том же режиме обтекания распределение
341

потерь по высоте решетки изменится только вследствие увеличения
протяженности зоны профильных потерь. Длина участков концевых потерь и
закон распределения потерь на этих участках останутся прежними.
Следовательно, доля относительных концевых потерь в общем балансе уменьшится
вдвое. Отсюда следует, что относительные концевые потери обратно
пропорциональны длине лопаток, что согласно требованиям теории подобия можно
записать в виде
?к=КЬ/1. A3.102)
Величина lib характеризует относительную длину лопатки. При
уменьшении длины лопатки пропорциональное изменение концевых потерь будет
наблюдаться до тех пор, пока зоны концевых потерь не начнут смыкаться.
Зависимость A3.102) хорошо согласуется с опытами, в которых меняется
высота лопатки. При изменении хорды лопатки (и прочих равных условиях)
изменяется также число Re, что влияет на вторичные течения и нарушает
строгую пропорциональность. На рис. 13.16 полные потери в решетке
(прямая А В) представлены как сумма профильных и концевых потерь.
Поскольку профильные потери не зависят от длины лопаток, то, определив их и
полные потери для решетки с какой-либо длиной лопаток, можно вычислить
полные потери при другой длине лопаток.
Концевые потери зависят от трения на торцовых поверхностях и
расхода энергии на поддержание вторичного течения. Коэффициент
пропорциональности в формуле A3.102) зависит от геометрических характеристик
решетки и режима обтекания: угла входа потока, чисел Re, M и степени
турбулентности. В настоящее время нет вполне удовлетворительного
теоретического решения этой сложной задачи и поэтому приходится обращаться
к эксперименту. Так, Е. А. Гукасовой в результате обработки
экспериментов предложена формула для коэффициента К в формуле A3.102):
К -0,0085 + 0,0185 (sin fc/sin
A3.103)
пригодная как для сопловых, так и для рабочих решеток.
Для заданных условий: углов входа и выхода, хорды профиля, высоты
лопатки и известных чисел М и Re в принципе можно найти наилучшую
решетку, в которой потери будут минимальны. Однако при проектировании
бесконечная вариация формы профилей практически неудобна по
технологическим соображениям. Поэтому на практике используется набор
стандартных профилей, из которых можно составить ряд решеток с
характеристиками, весьма близкими к оптимальным.
Рис. 13.16. Зависимость
относительных потерь от относительной длины
лопатки
342
Рис. 13.17. Аэродинамическая решетка
из профилей Р-4629 А

Oflb
0,02
=-—=
^=
Pr50°
fif+f
- f
-
=====
«5/7
Рис. 13.18. Профильные потери в_ решетке
(см. рис. 13.17) при М2 = 0,7; /^=//& = оо;
Р 80°
Рассмотрим
аэродинамическую решетку, в которой
профиль лопатки фиксирован, а
хорда лопатки 6, шаг /, угол
установки Ру и высота лопатки /
могут варьироваться (рис. 13.17).
Исследования показывают, что
варьирование относительного
шага t = tlb, угла установки,
чисел М и угла входа в
определенном диапазоне приводит к
малому изменению потерь.
Число Re, подсчитанное по хорде лопатки, в крупных турбинах обычно столь
велико, что находится в области автомодельности, т. е. не влияет на
потери. Это позволяет использовать решетку, оптимальную для
определенного сочетания параметров, в некоторой области, где эти параметры
варьируются.
Весьма небольшое увеличение потерь компенсируется
технологическими преимуществами. Каждую из таких оптимальных решеток можно
применять в определенном диапазоне вариации параметров, за пределами
которого потери начинают существенно возрастать. Поэтому применяют
серии оптимальных решеток, которые перекрывает практически необходимый
диапазон вариаций параметров. Для каждой из таких решеток проведены
экспериментальные исследования и указан возможный диапазон изменений
числа М, углов входа рх и выхода Р2 потока, относительного шага и угла
установки. Это дает возможность подобрать решетку на заданные условия
работы.
На рис. 13.18, 13.19, 13.20 приведены для примера характеристики
решетки, применяемой для углов выхода потока 25—32°, углов входа
потока 45—60°, при относительных шагах 0,45—0,58 с углом установки 75—80°
в диапазоне чисел М 0,55—0,85.
При подборе решетки считаются заданными: число М на выходе М2 =
— w2/a2i углы входа рх и выхода Р2, высота лопаток. По рис. 13.18 находим
оптимальный относительный шаг и'профильные потери, по рис. 13.19
по углу выхода и оптимальному шагу — угол установки профиля в
решетке, а с помощью рис. 13.20 и заданных высоты лопаток и угла входа —
суммарные потери в решетке (в этом случае необходимо знать хорду профиля,
которую выбирают из условий прочности и вибрационных характеристик
лопаток).
28
26
—-
Ь5 050 0.55 t
Рис. 13.19. Углы выхода потока из решетки
(см. рис.,13.17)
0,25 0,50 0,75 1ft bli
Рис. 13,20. Суммарные потери в
решетке (см. рис. 13.17) при 7=0,59;
343

13.4. ХАРАКТЕРИСТИКИ РЕШЕТОК ОСЕВОГО КОМПРЕССОРА
Аэродинамические решетки осевых компрессоров, в отличие от
турбинных решеток, имеют диффузорные каналы, т. е. скорость потока при
прохождении через решетку уменьшается, а давление возрастает. При диф-
фузорных течениях пограничный слой склонен к отрыву (см. гл. 9),
поэтому степень повышения давления в компрессорных решетках весьма
ограничена.
Рассмотрим геометрические характеристики компрессорных решеток,
которые определяют поведение их аэродинамических характеристик.
Для заданных углов входа и выхода потока, чисел М и Re в принципе
можно найти наилучшую форму профиля и геометрические параметры
решетки, при которых потери будут минимальны. Так, например, используя
метод годографа, можно построить компрессорную решетку для
дозвукового потока с заданным распределением скорости по профилю. Однако так же,
как и при проектировании турбинных решеток, многочисленные и иногда
незначительные вариации формы профилей практически неудобны.
Поэтому часто применяют некотррые стандартные профили и стандартные
решетки, которые в определенных диапазонах изменения характерных
размеров дают вполне удовлетворительные результаты, близкие к
оптимальным.
Кроме того, и это весьма важно, работа аэродинамической решетки в
условиях реальной ступени отличается от идеальных условий обтекания
плоской решетки. В ступени кольцевые решетки обтекаются потоком с
повышенной степенью турбулентности, при наличии пограничных слоев на
корпусе и роторе и т. п.
Влияние этих факторов на режим работы решетки в ступени
компрессора существеннее, чем в турбине. Поэтому оптимизировать компрессорную
решетку в условиях работы ее в ступени более необходимо, чем турбинную.
Однако теоретическое и экспериментальное изучение характеристик
одиночных прямых и плоских компрессорных решеток также необходимо, так
как позволяет выяснить основные закономерности.
Лопатки осевого компрессора и вентилятора по форме напоминают
профиль крыла, и это позволило использовать богатый опыт, накопленный при
отработке формы крыльев самолета. В частности, для построения диффузор-
ных решеток иногда используют симметричный профиль крыла (рис. 13.21).
Изогнутую лопатку в решетке строят на основе симметричного профиля
следующим образом. Среднюю
линию профиля задают
обычно уравнением параболы
у b—x
A3.104)
где Ь - хорда
компрессорной лопатки; %i и, %i — углы
направления касательных по
концам средней линии
(рис. 13.21, б);
Рис. 13.21. Профиль лопатки
компрессорной решетки:
а — исходный симметричный; б —
изогнутый
A3.105)
344

с --- XiJ-X* — кривизна
профиля; xj xflb — положение
максимальной вогнутости
средней линии.
Хорду исходного
симметричного профиля берут
равной длине средней линии
проектируемой лопатки, а
ординату исходного профиля
откладывают по нормали к
средней линии. Исходный
профиль имеет относительную
толщину 10 %. Если
относительная толщина изогнутого
профиля 7-=clb принята
другой, то все ординаты
исходного профиля изменяют
пропорционально
Рис. 13.22. Решетка осевого
новными обозначениями
компрессора с ос-
НижеаЛприведены относительные размеры (в процентах от хорды)
симметричного'профиля А-40. Для этого профиля радиус округления
передней кромки равен 0,055b, а радиус скругленной задней - 0,05Ь. Профиль
применяют для относительно больших дозвуковых чисел М.
0
0
30
4,927
1,0
1,14
35
4,986
1,5
1,43
40
5,00
2 5 5 7,5 !0 15 20 25
К85 2,55 3,09 3,525 4,16 4,55 4 788
50 60 70 80 90 95 100
4 858 4,442 3,783 2,850 1,722 1,003 0
Компрессорную решетку характеризуют следующие параметры
(рис 13 22): /-шаг решетки; Ру - угол установки профиля р„ ра,-
углы между касательными к средней линии и фронтом решетки; h - мини-
МаЛ5сновСнаяНзадача состоит в отыскании зависимости аэродинамических
характеристик реШетки от ее геометрических характеристик и режима обте-
^Ткомпрессорных решетках течение диффузорное, шаг относительно
велик а входные кромки-тонкие, поэтому они более чувствительны к
режиму обтекаГя? чеРм турбинные. Другими словами, изменение угла входа
Тела М числа Re и турбулентности внешнего потока может сильно
сказываться на изменении аэродинамических характеристик решетки. При
изменении указашьГх режимных параметров сильно изменяются
характеристики пограничного слоя: он может оторваться и образовать спутную струю
или после отрыва вновь присоединиться к поверхности лопатки ^
Опыты показывают, что автомодельность наступает при Re ~ «*'v ~
« 3- 10е. Далее будем считать, что число Re находится в автомодельной оО
ласти
Обозначим р, угол входа, а р,- угол выхода потока (рис. 13.22). В
компрессорных решетках вводят понятие угла атаки
/ = в;-в, A3.Ю6)
и угла отставания
A3.107)
345

В подразд. 5.8 было показано, что угол выхода потока из решетки в
общем случае зависит от угла входа. Для турбинных решеток, которые имеют
относительно малый шаг, этой зависимостью можно пренебречь (если нет
отрыва), т. е. считать угол выхода постоянным. В компрессорных решетках
шаг относительно велик и поэтому нельзя пренебрегать зависимостью угла
выхода от угла входа потока. Следовательно, угол отставания зависит от
угла атаки. Вместо угла отставания в качестве искомой аэродинамической'
характеристики обычно вводят угол поворота потока в решетке
ЛР-Р2— Pi. A3.I08)
С помощью формул A3.106), A3.107), A3.108) угол поворота можно
выразить через угол отставания и угол атаки
Др =р2 — Pi—б + ?=е — 6Н-?. A3.109)
Для конкретной решетки кривизна профиля е известна, а угол атаки
рассматривают как аргумент, определяющий режим обтеканий.
В качестве второй искомой аэродинамической характеристики решетки
вводят коэффициент потерь
A3.110)
Рассмотрим сначала влияние угла атаки на распределение скорости по
профилю. Обтекание компрессорной решетки потоком идеальной
несжимаемой жидкости при разных углах атаки было рассчитано методом,
изложенным в подразд. 13.1. Относительный шаг решетки tlb = 1, угол установки
профиля Ру =; 45°. В качестве лопатки выбран крыловой профиль, для
которого известно конформное преобразование на внешность единичной
окружности:
+ c2z-\ A3.111)
где с = 109,25, с3 - 90,32 + 2,65 /, с2 = 4,34 — 7,75/.
Для компрессорной решетки, имеющей тонкий профиль и большой шаг,
значение функции смещения мало:
ф = 9—40,8° + 0,241 cos 6 + 0,138 sin 0 — 0,895 cos 29 —
—0,190 sin 29+ 0,057 cos 49.
Распределение скорости по развертке профиля при различных углах
атаки показано на рис. 13.23.
При нулевом угле атаки распределение скоростей по профилю
является благоприятным. Скорость резко возрастает от нулевого значения в
передней точке ветвления Ог до максимального значения на спинке профиля и
несколько меньшего на вогнутой стороне, а затем плавно уменьшается к
выходной кромке, что объясняется диффузорностью решетки. В этом режиме
в вязкой жидкости течение будет безотрывным, так как градиент давления
на спинке лопатки хотя и положителен, но мал.
По мере увеличения положительного угла атаки картина обтекания
изменяется. Передняя точка ветвления несколько смещается в сторону
вогнутой поверхности (точка О2). Возле этой точки со стороны выпуклой
поверхности лопатки образуется все более острый пик скорости,
возникающий благодаря ускорению потока при обтекании носика профиля, имеющего
малый радиус кривизны. После подъема скорости происходит ее резкий спад.
В месте появления этого значительного положительного градиента давле-
346

10
Рис. 13.23. Распределение скорости по
профилю лопатки решетки осевого
компрессора при разных углах атаки
-Ю
Рис. 13.24. Характеристики
компрессорной решетки:
а — относительные потери: б —
угол поворота потока
ния в вязкой жидкости произойдет отрыв пограничного слоя (для решеток
подобного типа при угле атаки больше 8—10°) и картина обтекания резко
изменится.
До появления отрыва распределение скорости, полученное
теоретически, хорошо согласуется с экспериментами, если, разумеется, относить эту
скорость к внешней границе пограничного слоя.
Следует также отметить, что при положительном угле атаки
аэродинамическая диффузорность решетки, т. е. степень повышения давления,
возрастает.
При больших дозвуковых скоростях на входе в решетку влияние угла
атаки на распределение скорости по профилю будет еще существеннее, так
как эффект сжимаемости увеличивает пики скоростей.
Второй вывод, который можно сделать, заключается в том, что по
результатам расчета обтекания решетки потенциальным потоком можно
приблизительно предсказать момент появления отрыва.
На рис. 13.24, а приведен экспериментальный график изменения потерь
в компрессорной решетке при малых дозвуковых скоростях (М < 0,4). При
малых скоростях влияния сжимаемости нет, и зависимость потерь от угла
атаки изображена одной кривой. Изменение угла атаки в пределах
(—10 ~ +7)° практически не приводит к возрастанию потерь; очевидно, что
данная решетка в этом диапазоне изменения углов атаки обтекается без
отрыва (или срыв локализуется на носике лопатки). Если угол атаки
превосходит 7°, то потери начинают сильно возрастать.
Зависимость угла поворота потока в решетке от угла атаки приведена
на рис. 13.24, б. Если угол атаки лежит в указанных ранее пределах, то
приращение угла поворота примерно равно приращению угла атаки. Из
этого можно заключить, что в данной решетке (густота tlb — 0,75) угол
отставания мало зависит от угла атаки. При больших положительных углах
атаки и появлении отрыва наблюдается замедление роста угла поворота.
Рассмотрим характеристики компрессорных решеток при больших
дозвуковых скоростях, когда влияние сжимаемости жидкости становится
ощутимым. На рис. 13.25 (кривая /) дана зависимость профильных потерь от
числа Ь\у на входе в диффузорную решетку, составленную из крыловых про-
347

филей, типичных для малых дозвуковых скоростей (подобные профили имеют
относительно большую толщину и кривизну).
При малых числах Мг < 0,65, когда влияние сжимаемости невелико,
коэффициент потерь остается постоянным. При Щ > 0,65 происходит
резкое увеличение коэффициента потерь. Это увеличение потерь вызвано
появлением в потоке местных зон со сверхзвуковой скоростью,
заканчивающихся скачками уплотнений.
В описываемом случае местная сверхзвуковая зона возникает на
выпуклой поверхности профиля при числе М, на входе в решетку примерно 0,65.
Как можно установить с помощью оптической установки, сверхзвуковая
область заканчивается слабым скачком уплотнения, который вызывает
отрыв ламинарного пограничного слоя на спинке лопатки.
При дальнейшем росте числа !Лг на входе внутри каналов между
лопатками образуется система значительно более сложных скачков. При этом
возрастают как волновые потери, так и потери, вызванные отрывом.
Можно сделать вывод, что диффузорные аэродинамические решетки,
составленные из крыловых профилей, типичных для малых скоростей,
имеют малые потери вплоть до чисел Mj = 0,6—0,65. В этом диапазоне
скоростей потери составляют 0,02—0,03 при расчетном угле атаки.
Резкое возрастание потерь в решетке происходит при появлении слабых
скачков уплотнения, вызывающих отрыв пограничного слоя. Так как
скачки могут возникать только в сверхзвуковом потоке, то возрастания потерь
можно ожидать с того момента, когда на лопатках в решетке скорость
потока станет критической. ' '
Чтобы отметить верхний предел безразмерной скорости входа, начиная с
которой наблюдается резкий рост потерь, вводят понятие критического числа
Маха М#.
Критическим числом М# называют такую безразмерную скорость на
входе в решетку, при которой где-либо на профиле возникает критическая
скорость, т. е. М = 1.
На профиле всегда имеется область, где скорость больше, чем скорость
на входе (см., например, рис. 13.23).
Величина критической скорости зависит от формы профиля (прежде
всего его толщины и кривизны), угла его установки в решетке, безразмерного
шага и угла атаки. Чем больше толщина и кривизна профиля, тем
значительнее местная скорость на нем превосходит скорость на входе.
Чем больше угол атаки (положительный или отрицательный), тем
значительнее пик скоростей на входной кромке, соответственно со стороны
спинки или вогнутой стороны
профиля.
Критическое число М* с достаточной
степенью точности может быть опреде-
qi\ | | | /1/1 лено расчетным путем. Для этого
необходимо рассмотреть обтекание решетки
потенциальным потоком сжимаемой
жидкости.
Рассмотрим теперь явление, которое
называют запиранией решетки. Число
М на входе в решетку и угол атаки не
могут быть заданы совершенно
произвольно, так как решетка не может
пропустить расход больше критического
расхода. Следовательно, второй
характерной безразмерной скоростью входа
7
0,2 0,Ь 0,6 0,8 М
Рис. 13.25. Зависимость профильных
потерь в компрессорных решетках от
числа Mi
348

является максимально допустимое число
Маха на входе.
Максимальным числом Маха Мтах
называют такое число М на входе в решетку, при
котором расход через решетку становится
максимальным, т. е. критическим.
Положим, что режим обтекания решетки
соответствует критическому по расходу. Если
в первом приближении считать течение
одномерным и изоэнтропийным, то критическая
скорость возникает в сечении канала, где
площадь минимальна, а звуковую линию
можно принять прямой.
Запишем уравнение неразрывности для
сечения перед решеткой и минимального сечения канала между лопатками
(см. рис. 13.22):
у/
— '
Мтах
\
0,8
0,6
Рис. 13.26. Зависимость
критического и максимального чисел
М. от угла атаки
wx t sin ф{ — i) =г
ft.
Выразим это уравнение через газодинамическую функцию —¦
приведенный расход
^ = (Л//) sin (PI — i). A3.112)
Подсчитанному значению q соответствуют два значения числа Мг в
дозвуковой и сверхзвуковой областях: М[ < 1, Mf > 1. При заданном угле
атаки работа внутри найденного диапазона чисел Мх исключена, так как
расход не может быть больше критического. Если рассматривать только
дозвуковые скорости на входе в решетку, то, очевидно, Мтах = М|, и
возможны только такие режимы обтекания, при которых Мх < Мтах.
Типичные графики зависимости критического и максимального чисел
Маха от угла атаки приведены на рис. 13.26.
Наибольшего значения М* достигает при угле атаки, близком к нулю, так
как при этом распределение скорости на профиле наиболее благоприятное,
без пиков. При положительном или отрицательном угле атаки значение
М* заметно меньше, потому что на входной кромке профиля появляется
.область больших скоростей.
Возрастание Мшах с увеличением угла атаки легко объяснимо при
рассмотрении струйки газа, проходящей через один межлопаточный канал.
Чем больше положительный угол атаки, тем меньше ширина струйки перед
решеткой и, следовательно, тем больше Мтах, так как ширина струйки в
критическом сечении постоянна.
При проектировании диффузорных решеток, предназначенных для
работы при больших околозвуковых скоростях входа, надо стремиться к
увеличению М#, чтобы иметь допустимый уровень потерь.
Проблема повышения числа М# для решетки напоминает такую же
задачу в аэродинамике одиночного профиля при проектировании крыльев для
самолетов, летящих с околозвуковой скоростью.
Для того чтобы увеличить М#, неЬбходимо уменьшить относительную
толщину профиля, расположить сечение максимальной толщины дальше от
входной кромки, уменьшить кривизну профиля. Входную кромку профиля,
приспособленного для больших скоростей, нужно делать более острой. В
случае решетки на характеристики должны влиять также два дополнительных
параметра, которыми можно варьировать: относительный шаг и угол
установки.
349

0,10
0,05
¦0
\
SS
1,0
1,5 Re-HT
Рис. 13.27. Зависимость профильных
потерь в компрессорной решетке от
числа Re и степени турбулентности
Для иллюстрации сказанного на
рис. 13.25 кривая 2 показывает
зависимость профильных потерь от числа М2 на
входе для решетки лопаток, очерченных
двумя дугами окружностей. Лопатки
имеют острую кромку, а максимальная
толщина профиля расположена
посредине хорды. Отношение площади струйки
на входе, приходящейся на один шаг, к
минимальной площади канала при
нулевом угле атаки равно приблизительно
единице. Максимальная толщина
профиля примерно 0,08 6. Сравнив кривую 2 с
кривой /, которая соответствует
решетке для малых дозвуковых скоростей,
можно убедиться, что обе решетки имеют
примерно одинаковые потери при Mj < 0,65. При дальнейшем повышении
скорости входа потери в первой решетке возрастают гораздо интенсивнее,
чем во втЬрой, что подтверждает преимущество второй решетки при
больших околозвуковых скоростях.
При отклонении угла атаки от расчетного значения потери во второй
решетке резко возрастают, так как происходит отрыв потока на острых
передних кромках.
Потери в решетках зависят от числа Re. В зависимости от величины
числа Re пограничный слой может быть ламинарным или турбулентным (что
изменит потери трения), пограничный слой может оторваться или не
отрываться. Поскольку отрыв ведет к полной перестройке всего потока, то
изменение характеристик решетки будет не только количественным, но и
качественным. Влияние числа Re особенно существенно на течение в
компрессорных решетках, так как отрыв пограничного слоя возникает в диффузорных
потоках.
Помимо числа Re на течение в пограничном слое существенно влияет
турбулентность внешнего потока, поэтому влияние этих двух факторов
необходимо изучать совместно.
На рис. 13.27 показана зависимость профильных потерь в
компрессорной решетке от числа Re и степени турбулентности. Кривая / соответствует
степени турбулентности 1%, а кривая 2 — степени турбулентности 3,5%.
Автомодельность по числу Re достигнута примерно при Re -¦= 2 • 105,
причем при более низкой турбулентности несколько позже, чем при
большой.
Начиная с Re > 1,2 • 105, потери в решетке при малой степени
турбулентности ниже, чем при большой, что объясняется меньшими потерями
трения. При Re< 1,2 • 105 потери меньше при большой степени
турбулентности внешнего потока. Это можно объяснить таким образом. При низких
числах Re увеличение потерь вызвано отрывом ламинарного пограничного
слоя, который не может преодолеть заданный положительный градиент
давления. Если оторвавшийся ламинарный слой турбулизируется и снова
присоединяется к поверхности лопатки, то отрыв локализуется и потери
возрастают незначительно. Если такое повторное присоединение
пограничного слоя не происходит, то потери сильно возрастают. Чем выше степень
турбулентности, тем при меньшем числе Re происходит полный отрыв.
Следует иметь в виду,что большинство исследований решеток проведено
в аэродинамических трубах, где степень турбулентности набегающего потока
350

около 0,25%, в то время как степень турбулентности в компрессоре порядка
десятков процентов.
Для подбора компрессорных решеток и установления количественных
зависимостей используют обобщенные характеристики, которые строят на
основании многочисленных экспериментальных исследований и
теоретических соображений. Такие обобщенные характеристики не могут быть
полностью универсальными, т. е. пригодными для любого типа профилей и
решеток. Однако они дают возможность подобрать аэродинамическую
решетку в классе оптимальных с приемлемой для инженерной практики
точностью.
Были рассмотрены характеристики плоских компрессорных решеток.
В реальных компрессорных решетках возникают дрполнительные потери
по концам лопаток. В случае, если лопатки ограничены по торцам
твердыми стенками, то появляются вторичные течения того же типа, что и
описанные для турбинных решеток. Если между лопатками и корпусом
компрессора имеется зазор, то воздух перетекает через этот зазор с вогнутой
стороны лопатки к выпуклой, т, е. в направлении^ обратном вторичным течениям
без зазора. Такие вторичные течения также приводят к дополнительным
концевым потерям и изменяют угол выхода потока из решетки. Поскольку эти
перетекания происходят по концам лопаток и не зависят от их абсолютной
длины, то относительные концевые потери также обратно пропорциональны
длине лопаток.
13.5. РАСЧЕТ ПОТЕРЬ ТРЕНИЯ В АЭРОДИНАМИЧЕСКИХ
РЕШЕТКАХ
Потери трения в аэродинамических решетках могут быть
определены расчетным путем с помощью теории пограничного слоя. Для
проведения таких расчетов сначала должны быть найдены распределения скоростей
и давлений по профилю в решетке. Эти распределения также могут быть
получены расчетом при построении потенциального потока вокруг решетки
различными методами, например, изложенными в подразд. 13.1, 13.2.
Для получения обобщенных характеристик потерь в рабочих решетках
воспользуемся приближенным способом.
В аэродинамически совершенной рабочей решетке скорость на спинке
профиля должна быть практически постоянной. Скорость постоянна также
на большей части вогнутой стороны лопатки. Примем, что эта скорость
также постоянна, что не внесет сколь-либо существенной ошибки, так как
потери трения в пограничном слое на спинке лопатки значительно больше,
чем на ее вогнутой стороне,
Найдем указанные средние скорости на спинке и вогнутой стороне
лопатки, исходя из аэродинамических соображений и общих геометрических
характеристик решетки, которые известны до ее детального проектирования.
Рассмотрим потенциальный поток жидкости внутри канала между
рабочими лопатками (рис. 13.28). Запишем уравнение отсутствия вихрей в
естественной системе координат E.147):
, dw.'dn- Kw. A3.113)
Проведем внутри канала среднюю линию (риг. 13.28) и обозначим
среднюю кривизну этой линии Кт и скорость на ней wm. В таком приближении
следует считать, что скорость по нормали к средней линии поперек канала
изменяется по линейному закону. Из формулы A3.113) получим
w^wni(l К-Ктп). A3.114)
т

За среднюю кривизну канала
естественно принять
Кда-(*-р,~Р,)/я. 03.115)
где л Pj — р2 — угол поворота потока
в решетке, рад; ^— длина средней линии
внутри канала.
Из формул A3.114) и A3.115) следуют
выражения для средних скоростей по
спинке и вогнутой стороне лопатки:
e--= wm + (я-Р,-
««а>т -(я —р,
A3.116)
A3.117)
где h -- ширина канала между
лопатками, измеренная но эквипотенциали.
Так как скорость нормальна
эквипотенциали и согласно формуле A3.114)
изменяется вдоль нее по линейному
закону, то произведение hwmB формулах
A3.116) и A3.117) равно расходу
жидкости. Тогда по уравнению неразрывности, для несжимаемой жидкости
можно записать
Рис. 13.28. Аэродинамическая
решетка с основными обозначениями к
выводу формул A3.127), A3.128)
hwm - iwx sin p? — to2 sin p2.
В таком случае формулы A3.116) и A3.117) примут вид:
2s
to2 sin p
2;
2s
¦ to2sinpa.
A3.118)
A3.119)
A3.120)
Подобная* замена справедлива для любого поперечного сечения канала.
Таким образом, остается свобода в выборе места положения характерного
поперечного сечения канала. Этот выбор равносилен выбору характерной
величины средней скорости. Выберем среднюю скорость так, чтобы
удовлетворить интегральному условию, от которого зависит аэродинамическая
сила, действующая на лопатку. (
Выразим силу, действующую на лопатку в проекции на ось ординат
(см. рис. 13.28), с помощью уравнения количества движения:
Fи~р(до, cospL ~bt02cosp2) to2sinp2. A3.121)
Эту же проекцию силы можно записать через разность средних давлений на
спинке и вогнутой поверхности лопатки:
Fu:-2(t>B—Pc)Bf A3.122)
где В — ширина решетки (см. рис. 13.28).
Заменим разность давлений через средние скорости по уравнению Бер-
нулли для несжимаемой жидкости и перепишем формулу A3.122) в таком
виде:
у — {){Wc~— w&) ВB. (\o.\2o)
352

Приравняв правые части формул A3.121) и A3.123), так как они выражают
одну и ту же силу, получим еще одно соотношение, которому должны
удовлетворять средние скорости на спинке и вогнутой стороне лопатки:
(wb — wl) B^2t (щ cosp, +w cos P2)w2 sin p2. A3.124)
Подставим в формулу A3.124) выражения для скоростей на спинке и
вогнутой поверхности лопаток из формул A3.119) и A3.120). После
сокращений получим
Bwm(n—pl-p2)-(a;1cosp1+^2cosp2)s. A3.125)
Исключив в формуле A3.125) скорость перед решеткой с помощью
уравнения неразрывности A3.118), найдем характерное значение средней
скорости
»ж = Ь sMh+bLj,. A3.126)
Подставив значение средней скорости A3.126) в формулы A3.119) и
A3.120), получим формулы для скоростей на спинке и вогнутой поверхности
лопатки:
с |(jl_P_p)sinP в
я-р1-р2)зшр2 П
2 s J V '
Г sin(p1 + p2) ^_(^-Р|-р2>зтр2^_1
в [(n-pl-p2)sinpl В 2 s J '- v
В предельно частном случае решетки пластин имеем: рх = р2 = я/2 и
s =- В. Тогда из формул A3.127) и A3.128), как и следовало ожидать,
получим We = wq = w2. Для получения этого результата следует раскрыть
неопределенность в первом члене указанных формул.
Результаты используем для оценки потерь трения в рабочих решетках
турбин. Будем считать, что турбулентный пограничный.слой возникает в
точке ветвления на передней кромке лопатки, так как в ступени турбины
внешний поток сильно турбулизирован.
Для определения толщины потери импульса используем формулу (9.102),
причем выпишем ее сначала в прежних обозначениях, а потом сделаем
некоторые существенные замечания, которые надо учесть при расчете
пограничного слоя по выбранной схеме:
s
,0,016м,;4 CmJ^s. A3.129)
U
Под интегралом в формуле A3.129) стоит скорость во внешнем потоке,
которую следует проинтегрировать по всей длине участка рассчитываемого
пограничного слоя. Следовательно, под интеграл должны быть поставлены
скорости wc и W&. Скорости, которые записаны вне интеграла,— это
скорости потока в конечной точке участка. Значит, вместо них следует
записать скорость выхода потока из решетки w2.
Это следует понимать так, что скорости на спинке лопатки и ее вогнутой
стороне считаем постоянными вплоть до выходной кромки, где они скачком
принимают значение до2. Это необходимо для соблюдения условия
Жуковского—Чаплыгина о равенстве скоростей по обе стороны выходной кромки.
С учетом этих замечаний из формулы A3.129) получим толщину потери
импульса на выходной кромке со стороны спинки лопатки
«2С--0,0366Re*~••* (^ V'2 б0-2 s?*. A3.130)
\ w2 j
12 Зак 2638 . 353

Itp
0,0в
0,06
Qfib
0,02
\
N
К
Аналогично для вогнутой стороны
получим
62в -0,0366
ZQ 40
60
80
Рис. 13.29. Расчетные значения потерь
трения при турбулентном пограничном
слое в рабочих решетках турбин
(Re = 5*105)
3.2
A3.131)
Здесь, как это принято в
практике расчета решеток, число Рейнольд-
са подсчитано по хорде лопатки и
скорости за решеткой:
Re,, -wtbN. A3.132)
Потери трения в решетке следует
определять через условную толщину
потери энергии. С помощью формул
(8.82) и (8.83) найдем для показателя
степени 1/7» который принят в
расчете
62/6 -772, ЛЯ'6-7/40, fia/V^lA
A3.133)
Тогда согласно определению понятия толщины потери энергии можно
найти потери трения в решетке по формуле
ьтр = <*зс + 6зв)/* sin ft, ^ 1,8 (вас + 62B)/f sin р2, A3.134)
где в2С и в2В следует определять по формулам A3.130) и A3.131).
Полученные формулы позволяют сделать следующие выводы: 1) потери
трения на спинке лопатки во много раз больше, чем на вогнутой стороне,
так как там больше скорость и длина дуги; 2) потери трения
пропорциональны Re~?'\
Полученные формулы справедливы для аэродинамически гладкой
поверхности, при которой бугорки шероховатости не разрушают вязкий
подслой (см. гл. 9).
Допустимой величиной шероховатости называют ту наибольшую
относительную шероховатость, которая не приводит к увеличению
сопротивления по сравнению с гидродинамически гладкой поверхностью. Это понятие
имеет большое практическое значение, так как определяет необходимую
чистоту обработки поверхности лопаток турбомашин.
Допустимую шероховатость можно оценить по формуле
hjxon/l =• 100/Reb Re/- wl/vf A3.135)
где йдоп — допустимая высота выступов на обтекаемой поверхности; / -
характерный размер обтекаемой поверхности.
Из формулы A3.135) следует, что при больших числах Re, характерных
для аэродинамических решеток паровых турбин, допустимая шероховатость
очень мала. Так, при Re, - 107 получим Адоп// 10~\ что, например, при
/ = 50 мм соответствует допустимой величине выступов йД01| 0,0005 мм.
Для сравнения укажем, что полированная лопатка имеет высоту выступов
h « 0,001 мм.
В случае коррозии, эрозии и появления отложений шероховатость
поверхности лопаток может увеличиться в сотню раз.
На рис. 13.29 приведены потери трения для серии рабочих решеток,
рассчитанные по изложенной методике. Напомним, что как на спинке, так и на
вогнутой поверхности лопаток существует только турбулентный погранич-
354

ный слой (Re = 5 • 105). Таким образом, эти значения потерь больше
соответствуют рабочим решеткам, находящимся в ступени турбины. При
статических продувках решеток в аэродинамических трубах получены меньшие
значения потерь.
Из рис. 13.29 следует, что расчетные значения потерь трения,
показанные точками, закономерно уменьшаются с увеличением суммы углов входа
потока в решетку и выхода из нее. Это объясняется тем, что величина A80° —
— р! — р2) равна углу поворота в решетке и чем она больше, тем больше
кривизна канала между лопатками, больше (wc/w2) и sc. А чем больше эти
величины, тем больше толщина потери энергии на спинке лопатки, от
которой в основном и зависят потери трения 1см. формулы A3.127), A3.130)
и A3.134)].
Представляет интерес сравнение полученных потерь трения в решетках
реальной формы с минимально возможными потерями трения, которые
соответствуют решетке пластин, т. е. нулевому углу поворота pt ! р2 -~
-- 180°.
Для такой решетки шв - wc = w2y «с - sB ^ ^ и тогДа из формул
A3.130) и A3.131) следует
62с + 62В - 2.0,0366 Re* "•* Ь.
По формуле A3.134) находим потери трения
В рассчитанной серии реальных рабочих решеток турбин (все размеры
взяты по чертежам) относительные шаги лежат в пределах tlb = 0,5—0,7.
При расчете принято Re - 5 • 10\
G учетом указанных условий для решетки пластин ?тр = 0,016.
Эта величина может служить оценкой нижнего предела потерь трения для
рабочих решеток с гидродинамически гладкой поверхностью (штриховая
линия на рис. 13.29).
!3.6. РАСЧЕТ КРОМОЧНЫХ СЛЕДОВ
На некотором отдалении за решеткой неоднородность поля
потока определяется в основном турбулентными кромочными следами. В тур-
бомашине неподвижные решетки чередуются с вращающимися, поэтому
вращающаяся решетка движется в неоднородном поле, т. е. обтекается в
относительном движении периодически пульсирующим потоком. Определение
неоднородности потока необходимо для оценки: 1) аэродинамических сил,
возбуждающих колебания лопаток; 2) дополнительных потерь энергии в
решетке; 3) уровня шума, возникающего при работе турбомашины.
Для оценки неоднородности потока в кромочных следах решетки можно
применить теоретические методы расчета1 следа за одиночным профилем
(см. гл. 9). Направим ось абсцисс вдоль следа, а ось ординат поперек
(рис. 13.30). Вблизи выходных кромок наблюдается значительная
неоднородность поля скоростей, статических давлений и углов. Эта
неоднородность вызвана как конечной толщиной кромок лопаток, так и
пограничными слоями, уносимыми потоком в кромочный след. В этой области обычная
теория турбулентных следов неприменима, так как в ней предполагается
постоянство давления, неизменность угла направления потока и малая
неоднородность поля скоростей. Несколько дальше от кромок ширина тур-

булентных следов увеличивается, поля статических давлений и углов потока
существенно выравниваются, выравнивается также и поле скоростей, хотя
его неоднородность и остается наиболее существенной. Далее кромочные
следы смыкаются и дальше их ширина не изменяется, так как картина
течения периодична.
Поля статических давлений и углов практически становятся
однородными еще до смыкания следов, хотя, строго говоря, процесс выравнивания
происходит асимптотически. Поле скоростей сохраняет заметную
неоднородность и после смыкания следов.
Законы распространения вихревых следов за лопатками турбомашины на
участке до смыкания аналбгичны законам распространения следа за
плоским одиночным телом, обтекаемым вязкой жидкостью при большом числе
Re. Соответствующие решения базируются на полуэмпирических теориях
свободной турбулентности. Во всех случаях рассматривается слабая
неоднородность, т. е. решения имеют асимптотический характер и пригодны
только на значительном отдалении от обтекаемого тела. При расчете следов
за решетками будет наблюдаться несколько худшее (чем для одиночных тел)
совпадение теории и эксперимента в деталях, так как приходится делать
дополнительные предположения и рассматривать следы на более близких
расстояниях за лопатками, чем это допускается классической теорией.
На больших расстояниях результаты расчета также отличаются от
классических, так как в этом случае следы смыкаются, чего не возникает при
одиночном следе. Отметим, что некоторое несовпадение теории и эксперимента
в деталях не имеет существенного значения, так как в перечисленных
приложениях теории необходима интегральная оценка неоднородности,
которая вычислена более надежно.
Рассмотрим расчет поля скоростей и ширины следа (см. рис. 13.30) на
участке до смыкания и применим теорию турбулентных струй (см. гл. 9),
изменив только обозначения на те, которые приняты в теории решеток.
Теория следов как за сопловыми, так и за рабочими решетками одинакова,
поэтому для сокращения записи примем единое обозначение для скоростей вне
зависимости от типа решетки.
Обозначим w2t — постоянную скорость потока вне следа. Эта скорость
соответствует изоэнтропийному процессу, так как потерями вне
пограничного слоя и следа можно пренебречь. Дополнительную скорость в следе
обозначим v(x, у), а ее максимальное значение на оси следа vm(x).
Рис. 13.30. Кромочные следы за лопатками аэродинамической решетки
356

Распределение дополнительных Фт
скоростей в следе до смыкания, как
показано в гл. 9, может быть описа- 08
но универсальной зависимостью
A3.136)
где 2s — ширина следа.
Непосредственное измерение
ширины следа приведет к большой
погрешности, так как скорость в следе
переходит в скорость внешнего потока
асимптотически.
Поэтому, как обычно в теории
следов, следует ввести sx/2 (х)—
расстояние от оси следа до точки в данном
сечении, где дополнительная скорость
равна половине максимальной
дополнительной скорости. Тогда, положив у — s1/2,
ношение
1\
\
<
ч
1
к
•
0.2
Ofi 0,6 1,2 1,6 2fly/st/2
Рис. 13.31. Сравнение расчетных
значений дополнительной скорости в следах
за решетками с опытами Г. Ю. Степанова
1/2, найдем соот-
s = 2,27si/2. A3.137)
v В экспериментах определяют измерениями s1/t, и затем вычисляют
полуширину следа по формуле A3.137).
Сравнение теоретической зависимости
с измерениями скоростей в следах решеток турбин показано на рис. 13.31.
Общая зависимость удовлетворительно подтверждается, однако разброс
экспериментальных точек довольно значителен. Это можно объяснить тем,
что измерения в следах проведены на относительно малом расстоянии от
решетки, где неоднородность потока велика.
Исследование кромочных следов представляет практический интерес
именно на близком расстоянии, соизмеримом с зазором между сопловой и
рабочей решетками и ступени турбины.
Как уже отмечалось, подобный разброс не снижает ценность
теоретических расчетов, так как в данном случае важен только интегральный
эффект неоднородности поля скоростей, оценку которого расчеты дают
достаточно точно.
Скорость потока в следе
w2=w2t—v. A3.138)
Ввиду периодичности потока за решеткой все расчеты можно вести в
пределах одного шага.
Количество движения, которое переносит поток в одном периоде
решетки:
1
i=2p
w\dy.
A3.139)
Здесь интегрирование ведется поперек следа, причем ввиду его симметрии
относительно оси абсцисс в верхнем пределе поставлен множитель 1/2,
а перед интегралом — множитель 2; р2 — угол наклона скорости к фронту
решетки; t — шаг решетки (см* рис. 13.30).
357

В формуле A3.139) плотность вынесена за знак интеграла, что возможно
даже при больших дозвуковых скоростях, так давление в потоке
практически постоянно.
Подставим под интеграл A3.139) значение скорости из формулы A3.138)
и, полагая, что неоднородность поля скоростей невелика, откинем член
второго порядка малости:
I=2p I wltdy—2p I 2vw2tdy. A3.140)
Во втором интеграле верхний предел взят равным полуширине следа, что
можно сделать,, так как дополнительная скорость вне следа равна нулю.
Окончательно из выражения A3.140) получим
{vdy.
y A3.141)
о
Количество движения вдоль следа должно быть постоянно, так как на
след не действуют внешние силы. Обратим внимание на то, что при
постоянстве количества движения одновременно удовлетворено уравнение
неразрывности (при выбранной точности расчета, когда отброшена величина
второго порядка малости).
Количество движения, переносимое потоком, можно выразить также
через коэффициент скорости, т. е. известную аэродинамическую
характеристику решетки (см. подразд. 13.3):
I=i|>*pa>l/sinp2. A3.I42)
Приравняв выражения A3.141) и A3.142), получим
s
f A3.143)
Здесь коэффициент скорости выражен через коэффициент профильных
потерь, что можно сделать для слабо неоднородного потока согласно
формуле A3.81).
Подставив в интеграл A3.143) значение дополнительной скорости в следе
из формулы A3.136) и произведя вычисления, имеем
Лш-.^ A-Lj; sinp2. A3.144)
w2t 9 s
Второе уравнение, которое связывает ширину следа и максимальную
дополнительную скорость, получим из уравнения движения.
Для движения жидкости внутри следа справедливо упрощенное
уравнение
dw \ дх /%п л лс\
w == , A3.145)
дх р ду
которое следует из того, что поперечные проекции скорости в следе очень
малы.
Уравнение A3.145) с учетом обозначения A3.138) и условия слабой
неоднородности потока (v <? w2t) примет вид
_o,2|-*L=:-LJ?L. A3.146)
дк р ду
358

Запишем уравнение A3.146), выбрав для касательного напряжения при
турбулентном течении формулу (9.55):
-ш2(-|^=2/2-^-^-. A3.147)
дх ду ду2
Длину пути перемешивания, как было отмечено при расчете
турбулентных следов, можно принять постоянной поперек следа и пропорциональной
его ширине
/ ^ / (х) - cs (х). A3.148)
Уравнение 1C.147) должно быть справедливо и на оси следа, поэтому
можно записать
— Щг—- ^c2s2\ . A3.149)
dx I ду ду2 Ji/ = o
Здесь были использованы формулы ПЗ. 136) и A3.148). Слева записана
обычная производная, так как максимальная дополнительная скорость
зависит только от х.
Производные, стоящие в скобках в уравнении A3.149), вычислим с
помощью зависимости A3.136) и получим
L*LJ!fL] =AJ*, A3.150)
что позволяет представить уравнение A3.149) в виде
— о>а|-^==—с1—. A3.151)
dx 2 s
Исключив в уравнении A3.151) s с помощью уравнения A3.144),
получим дифференциальное уравнение, описывающее закон изменения
дополнительной скорости на оси следа:
=-?JLc»i&. A3.152)
Проинтегрировав уравнение A3.152), найдем
A3.153)
Здесь все постоянные включены в новую постоянную съ которую можно
определить только опытом, так как в нее входит постоянная, определяющая
турбулентное перемешивание в кромочных следах.
По результатам многочисленных опытов, проведенных с разными
решетками при малых и больших дозвуковых скоростях (см. рис. 13.32), можно
принять постоянную в формуле A3.153): сх = 0,66.
Тогда из зависимостей A3.144) и A3.153) следует формула для
определения ширины кромочного следа
2з = 1,68 Ух'Ср sin P,. A3.154)
Формулы A3.136), A3.153) и A3.154) решают задачу о расчете
кромочного следа на участке до смыкания. По формуле A3.153) можно определить
максимальную дополнительную скорость, а по формуле A3.154) — ширину
следа, что дает масштабы для построения эпюры скоростей по формуле
A3.136).
Рассмотрим особенности распространения следов после смыкания.
Прежде всего следует отметить, что ширина следа после смыкания в силу периодич-
359

V2t
/
1
•
Ofi
Рис. 13.32. Опытные значения
максимальной дополнительной
скорости в следе за решеткой
о,об 0,16xhp
Рис. 13.33. Опытные и расчетные
значения максимальной
дополнительной скорости в зоне смыкания
следов
ности течения остается постоянной и равной t sin p2. Это приведет к тому, что
изменится величина турбулентного трения. Так как путь перемешивания
пропорционален ширине следа, то в данном случае он будет постоянным.
Для определения характера изменения дополнительной скорости вдоль
оси абсцисс рассмотрим основное уравнение A3.147). Положим v ~ хп и
найдем показатель степени. Из условий пропорциональности
dv/дх ~х"-\ (dv/dy) (д2 v/dy2) ~ х2п
и уравнения A3.147) следует, что п = — 1. Таким образом^после смыкания
дополнительные скорости изменяются пропорционально дг1, а не х~ /2, как
до смыкания.
Еще одна особенность течения после смыкания следов заключается э
том, что поток не имеет потенциального ядра и, следовательно, на границах
следа скорость также будет уменьшаться.
Строго говоря, по описанной выше методике расчет кромочного следа
можно вести только до сечения аа (см. рис. 13.30), где два соседних следа
соприкасаются. Однако приближенно можно считать, что расчет можно вести
до сечения ЬЬ, где ширина следа 2s = /sin P2. Вообще говоря, место слияния
следов трудно четко выделить, так кщ по их границам происходят
турбулентные пульсации.
Из формулы A3.54) можно найти, что смыкание следов происходит на
расстоянии
х= @,354* sin p2)/?np. A3.155)
Тогда в зоне смыкания максимальная относительная дополнительная
скорость, как Следует из формул A3.153) и A3.155),
0m/ttto = UCnp- A3.156)
Таким образом, относительная неоднородность поля скоростей в
сечении, где смыкаются следы, не зависит явно ни от геометрических
характеристик рещетки, ни от режимных параметров,
360

На рис. 13.33 дано экспериментальное подтверждение формулы A3.156).
Сравнение произведено для решеток с различными углами выхода потока,
при различных числах Маха и Рейнольдса. Влияние всех этих факторов
сказывается только через безразмерный коэффициент профильных потерь.
Оценка расстояния, на котором выравнивается поток, представляет практический
интерес. Произведем такую оценку для сопловой решетки при характерных условиях:
/ = 50 мм, Р2 --= 15°, Спр = 0,025.
Расстояние по оси следа до смыкания, подсчитанное по формуле (Id.155), х =
— 183 мм, что соответствует расстоянию от фронта решетки 47,5 мм. Относительная
неоднородность потока в этом сечении по формуле A3.156) vm/w2t — 0,0275.
При осевом расстоянии 10 мм, чему соответствует х = 38,6 мм, относительная
степень неоднородности, определяемая по формуле A3.153), также мала: vmlw2t = 0,060.
13.7. РАСЧЕТ ЛАБИРИНТНЫХ УПЛОТНЕНИИ
Для уменьшения утечки газа между вращающимися и
неподвижными деталями турбомашин применяют лабиринтные уплотнения.
Уплотнения состоят из ряда расположенных один за другим гребней с острыми
кромками. Между гребнями образуются камеры (рис. 13.34). Скорость газа
при прохождении через щель под гребнем увеличивается, а затем
кинетическая энергия струи гасится в камере и переходит в тепловую энергию. Так
как размер камеры велик по сравнению с размером щели, то в каждой из
них давление практически постоянно и можно считать, что торможение
струи происходит изобарически. Подобный процесс повторяется от гребня
к гребню, и давление вдоль лабиринта падает. Сопротивление лабиринта
больше, чём гладкой щели, и поэтому при тех же параметрах газа расход через
него меньше, чем через щель.
Если все гребни уплотнения расположены на одном диаметре, т. е. газ,
текущий через уплотнение, движется вдоль оси турбомашины, то
уплотнение называют* осевым. Если гребни расположены на разных диаметрах,
так что газ течет в радиальном направлении, то и уплотнение называют
радиальным.
В осевом уплотнении площади щелей под гребнями одинаковы (или
практически одинаковы), а в радиальном — пропорциональны радиусам, на
которых расположены гребни.
Если можно считать, что кинетическая энергия струй, вытекающих из-
под гребней, полностью гасится в камерах, то уплотнение называют
ступенчатым. В противном случае уплотнение называют прямоточным.
Процесс течения газа через осевое ступенчатое уплотнение
изображен в тепловой диаграмме на рис. 13.34. Отрезок 01 соответствует
разгону потока под первым гребнем, отрезок 12 — изобарическому торможению
в камере, отрезок 23 — разгону потока под вторым гребнем и т. д. Посколь-
V////
Рис. 13.34. Ступенчатое лабиринтное уплотнение:
а — схема уплотнения: и — процесс течения в тепловой дна!раммс
361

0J35
0,5
т
1—.
г
i,
i
s
N
\
Кг
\
\
V
\
-—
\
\
и
\\
\1
о
Рис. 13.35. Зависимость относительного
расхода от относительного давления:
/ _ через сопло; 2 — щель (ро = const,
Го^ const)
т/т* , ку полная энергия потока остается
во время течения постоянной, то все
точки, характеризующие состояние
газа в камерах, лежат на общей изо-
энтальпе, соответствующей
заторможенному потоку. Таким образом,
если не вдаваться в детали, то
процесс в целом можно характеризовать
как процесс дросселирования газа.
Точки, характеризующие
состояние газа в суженных сечениях, лежат
на линии Фанно, так как можно
считать, что эти участки составляют
трубу постоянного сечения, через
которую движется вязкий сжимаемый газ.
Скорость под каждым последующим
гребнем больше, чем иод
предыдущим, так как расход массы через
каждую щель одинаков, а плотность
газа по ходу потока уменьшается
из-за падения давления. Ввиду того
что температура газа в камерах практически одинакова, то величина
критической скорости всюду одинакова. Следовательно, критическая
скорость, если она при данном режиме достигается, возникает под последним
гребнем, так как там скорость потока наибольшая. Этим течение в
лабиринтном уплотнении также напоминает дозвуковое течение вязкого газа в
трубе постоянного сечения, где критическая скорость может быть
достигнута только в выходном сечении трубы.
Следует, однако, иметь в виду, что лабиринтные уплотнения обычно
рассчитывают на низкие дозвуковые скорости, т. е. при данных давлениях
до и после уплотнения число гребней выбирают столь большим, чтобы
относительный перепад давлений на каждом гребне был мал. Именно это
позволяет уменьшить утечку газа, так как при малом перепаде мала скорость.
Уже упоминалось, что гребни выполняют с острыми кромками: это
позволяет использовать эффект сужения струи и также уменьшить утечку.
Задача об истечении через щель рассмотрена в подразд. 5.7 и там
показано, что расход через щель меньше, чем расход через сопло, имеющее ту же
площадь поперечного сечения на выходе (при тех же параметрах торможения
на входе и том же давлении на выходе). Обозначим jli отношение расхода
через щель к расходу через сопло в сопоставимых условиях, о которых
говорилось ранее. На рис. 13.35 представлена теоретическая зависимость
приведенного расхода через сопло в функции отношения давлений г р/р0
(кривая /). Кривая 2 на той же фигуре изображает отношение расхода через
щель к критическому расходу через сопло с той же площадью выхода.
Следовательно, отношение ординат двух кривых есть коэффициент расхода,
взятый по данным теории С. А. Чаплыгина (и Ф. И. Франкля при *-**).
При теоретическом рассмотрении задачи кромки предполагаются
абсолютно острыми (стенка сосуда, из которого происходит истечение,
бесконечно тонкая). Понятно, что практически стенка не может быть бесконечно
тонкой, и кромка более или менее скруглена. Поэтому при сравнении
теории с экспериментом надо быть осторожным, так как расхождение может
объясняться неправильной постановкой опыта. В том случае, когда стенка
может рассматриваться как бесконечно тонкая, результаты опыта хорошо
подтверждают теорию,
.162

При истечении газа через отверстие в стенке с острыми краями
коэффициент расхода должен быть несколько ниже, чем для случая плоской
бесконечной щели. Это объясняется тем, что сужение круглой струи
происходит во всех азимутальных направлениях. Однако различие должно быть
незначительным, что и подтверждается опытами при числе Re > 105, когда
наступает автомодельность по числу Re. Таким образом, можно сделать
вывод, что теория подтверждена экспериментом.
Формула для расчета сопла сложна, а для коэффициента расхода вообще
нельзя написать формулу в явном виде. Очевидно, что упрощенную
формулу для определения расхода через щель следует искать, не выделяя
коэффициента расхода, так как он также зависит от отношения давлений.
Зависимость относительного расхода газа через щель может быть хорошо
аппроксимирована уравнением эллипса
Vie A3.I57)
Здесь под q следует понимать отношение расхода через щель к критическому
расходу через щель, а не через сопло, как на рис. 13.35. Это соответствует
изменению масштаба по оси ординат в отношении 1 : 0,85, где 0,85 —
коэффициент расхода через щель при давлении ниже, чем второе критическое
давление е <*¦•**. Второе критическое давление зависит не только от
показателя изоэнтропы, но и от формы кромок, приближаясь при скруглении
кромок к обычному критическому отношению давлений для сопла, которое
можно рассматривать как отверстие с идеально скругленными стенками.
Окончательно расход через щель можно определять но формуле
tn~ \bm*%qm*s A3.158)
где |ы1Пах — максимальный коэффициент расхода через щель, равный 0,85
для абсолютно острой прямой кромки; q относительный расход,
определяемый из уравнения A3.157); т* критический расход через сопло с той
же площадью выхода, что и щель.
Действительная картина течения газа через щель в уплотнении несколько
отличается от того, что было описано в подразд. 5.6. Рассмотрим один
гребень уплотнения и обозначим его толщину Д, а зазор между гребнем и
стенкой 6, При течении вязкого газа на стенке образуется пограничный слой.
Если при постоянной величине зазора сильно увеличить толщину гребня,
то картина течения изменится, и коэффициент расхода будет определяться
не срывом потока на кромке, а пограничным слоем, возникающим на
стенке. Такое течение будет представлять собой течение в узкой длинной щели.
Такого же эффекта можно добиться, уменьшая величину зазора при той же
величине гребня. Очевидно, что во внимание нужно принимать
относительную толщину гребня Д/6.
Когда гребень относительно тонок, коэффициенты расхода имеют
приблизительно то значение, которое следует из теории для бесконечно тонкого
гребня. При увеличении относительной толщины гребня коэффициент
расхода вначале растет; это объясняется тем, что отрыв локализуется на
входном участке и течение напоминает течение в короткой трубе. При
дальнейшем увеличении толщины гребня коэффициент расхода снижается, так как
возникают достаточно толстые пограничные слои, и течение больше
начинает напоминать течение в длинной трубе.
Влияние формы гребня на коэффициент расхода можно представить,
рассматривая экспериментальные результаты, полученные при исследовании
увеличенных моделей уплотнений (рис. 13.36). Эти результаты не требуют

a)
0,7
0,6
Ot5
*=135 °
L
90
a=45° -
6)
Ofiufh
Рис. 13.36. Опытные значения
коэффициентов расхода для гребней
различной формы (по опытам Б. М.
Трояновского)
Рис. 13.37. Влияние угла наклона
гребня на коэффициент расхода:
а — схема расположения гребня; б —
коэффициент расхода
особых пояснений. Следует только подчеркнуть, что особенно нежелательно
скруглить кромку гребня на входе и что подобное скругление при
эксплуатации сильно увеличивает утечку через уплотнение.
Кроме относительной толщины кромки и ее формы* большое влияние на
коэффициент расхода оказывает наклон гребня. Рассмотрим поток,
движущийся в камере бесконечной длины и конечной ширины; поперек камеры
установлен гребень, наклоненный под углом а навстречу потоку
(рис. 13.37, а). Если жидкость идеальная, а гребень бесконечно тонок, то
коэффициент расхода можно определить, решив задачу методом годографа
(см. рис. 13.37, б). Для практически применяемых зазоров (8 — 0,3...
0,5 мм) и размеров камеры (Л --= 4... 10 мм) коэффициент расхода не зависит
от отношения б/А. Как и следовало ожидать, уменьшение угла гребня
уменьшает коэффициент расхода. Однако в действительности наивыгоднейший
угол наклона лежит в пределах а ~ 35...45°. Это объясняется тем, что
толщина гребня не может быть взята меньше А = 0,3—0,5 мм, а тогда
уменьшение угла А вызовет увеличение A' A/sina и вместе с тем необходимость
скругления входной кромки, и то и другое увеличивает коэффициент
расхода.
Выведем формулу для расчета утечки через прямоточное лабиринтное
уплотнение. Рассмотрим сразу более общий случай, когда площадь щели
под каждым гребнем может быть различной (такой случай встречается, когда
уплотнение расположено радиально).
Обозначим давление в камере за //-м гребнем р„. Пользуясь тем, что
относительный перепад давления на каждом гребне уплотнения мал (pn^L -
— РпУрп <^ 1» можно определить скорость жидкости под гребнем по
уравнению Бернулли для несжимаемой жидкости
A3.159)
364

Здесь использовано условие, что давление торможения в камерах
ступенчатого уплотнения равно статическому давлению, так как скорость жидкости в
камерах пренебрежимо мала.
Расход газа через щель найдем по уравнению неразрывности (расход
одинаков вдоль всего уплотнения)
pn-i-Pn), A3.160)
где fx — коэффициент расхода; Sn — площадь щели гГод п-ы гребнем.
Плотность жидкости в формулах A3.159), A3.160) также отмечена
индексом /г, так как хотя в окрестности одного гребня ее изменением можно
пренебречь, но для всего уплотнения она может измениться очень значительно
(например, в десять раз). Определим плотность жидкости под п-м гребнем,
выбрав среднее давление для этого гребня:
Pn-(Pn-i+Pn)/2RT». A3.161)
Исключив в формуле A3.160) плотность с помощью формулы A3.161),
найдем выражение для расхода
Перепишем эту формулу в виде
ПТ / ' / \8/l/C V2 «2 nt /1Q 1 М\
l\In\fTll\i) f 1 /*->/?/ == /^/г 1 —Рп> (lu.lOZ/
Просуммировав левую и правую части формулы A3.162) от п = 1 до
п - г, где z — число гребней в уплотнении, исключим этим все
неизвестные давления и получим формулу для расчета утечки
Pl-Pl
A3.163)
В осевом ступенчатом уплотнении площади всех щелей одинаковы и из
формулы A3.163) получим известную формулу А. Стодолы:
A3.164)
=fiS у
zRTQ
Отметим только, что при выводе было положено, что температура газа,
газовая постоянная и коэффициент расхода не изменяются вдоль уплотнения.
Если их изменения существенны, то они войдут под знак суммы.
В турбомашинах применяют также прямоточное лабиринтное
уплотнение (рис. 13.38, а). Процесс расширения газа в таком уплотнении (см.
рис. 13.33, б) характерен тем, что не вся кинетическая энергия струи
гасится в камере, а некоторая доля ее используется под следующим гребнем.
П 2
'////////////////////А
\РОП
Pz
'///////////////////////////А
а)
Рис. 13.38. Осевое прямоточное лабиринтное уплотнение:
а — схема уплотнения; 0 — процесс течения в тепловой диаграмме
365

V
0,2
Рис. 13.39. Коэффициент К для
расчета прямоточного
лабиринтного уплотнения
Процесс расширения изображен в тепловой
диаграмме на рис. 13.38, б. Отрезок 01
соответствует расширению под первым гребнем,
отрезок 12 — изобарному торможению в
камере между гребнями. Точка 2' соответствует
параметрам изоэнтропийного торможения
перед вторым гребнем и т. д. Поскольку
давление изоэнтропийного торможения перед
гребнем в прямоточном уплотнении выше,
чем в ступенчатом (см. рис. 13.38, б), то
утечка газа через него при сравнимых условиях
больше.
Получим формулу для расчета осевого
прямоточного лабиринтного уплотнения.
Вместо формулы A3.162) в данном случае
следует записать
К 1 о \/П/|ХО/ = Ро(п--1)— Рпч (lo. lOO)
где Po(n-i) — давлени/е торможения в камере
перед п-м гребнем.
Запишем формулу, которая связывает
давление полного торможения со статическим
давлением в той же камере в виде
^pbn-pl A3.166)
где / — коэффициент восстановления давления.
Если / == 0, то из формулы A3.166) следует, что давление полного
торможения равно статическому давлению в камере, т. е. кинетическая энергия
струи, вытекающей из-под гребня, полностью гасится и переходит в тепловую.
Если / -- I, то из сравнения формул A3.165) и A3.166) следует, что
давление торможения в последующей камере равно давлению торможения
в предыдущей. Это соответствует случаю, когда кинетическая энергия струи
полностью без потерь переходит в потенциальную.
Таким образом коэффициент 0 < / < 1 показывает, какая доля
кинетической энергии струи, вытекающей из-под предыдущего гребня, может быть
использована под следующим.
Просуммируем левую и правую части формулы A3.165) от п = 1 до
п = г:
A3.167)
Формулу A3.166) просуммируем от п = 1 до п = z — 1, так как
восстановление давления возможно только в камерах между гребнями:
/(z-l)#ro(m/fiSJ =*2 (Pon-Pnl A3.168)
Если вычесть из формулы A3.167) формулу A3.168), то все
промежуточные давления будут взаимно уничтожены и останутся только известные
давления перед лабиринтным, уплотнением р0 = р00 и ?а ним. После
элементарных преобразований получим формулу для определения утечки через
прямоточное лабиринтное уплотнение:
A3.169)
1
366

В частном случае, когда происходит полное гашение скорости в камерах
(/ — 0), эта формула совпадает с формулой для ступенчатого уплотнения.
При отсутствии потерь (/ — 1) утечка, как это понятно, не зависит от
числа гребней в уплотнении, так как давление торможения перед каждым
гребнем равно давлению торможения перед лабиринтным уплотнением.
Для того чтобы определить, во сколько раз утечка через прямоточное
лабиринтное уплотнение больше, чем через ступенчатое, введем коэффициент
/С, равный отношению соответствующих расходов.
Из формул A3.164) и A3.169) следует
К Л/ - . A3.170)
Л/
Параметр / зависит от конструктивных форм и прежде всего от
отношения величины зазора под гребнем к длине камеры. Для определения
параметра / можно воспользоваться опытными результатами, причем сравнение
проще всего провести при большом числе гребней, так как в этом случае
формула A3.170) принимает простой вид
/С-/1/A-/). г-voo. A3.171)
Если высота камеры прямоточного уплотнения много больше размера
зазора, то опыты дают линейную зависимость /С от bit:
К=~ 1+об/Л а -8,9, A3.172)
где а — безразмерный опытный коэффициент; 6 — радиальный зазор; t -^
шаг гребней прямоточного уплотнения.
Сопоставив формулы A3.171) и A3.172), получим выражение для
коэффициента использования кинетической энергии
/= 1—A—а6//)-а. A3.173)
График функции /С(г, б//), построенный по формулам A3.170) и A3.173),
причем с экспериментальными значениями совмещена только прямая при
z - оо, дан на рис. 13.39.
Увеличение числа гребней в прямоточном уплотнении уменьшает
приведенный расход, но вместе с тем (при фиксированной длине уплотнения /)
уменьшает расстояние между гребнями и, следовательно, увеличивает
использование кинетической энергии. Следовательно, упри заданной длине
уплотнения имеется оптимальное число гребней, при котором утечка
минимальна. Используя формулы A3.170), A3.173), находим оптимальное число
гребней и оптимальный шаг между гребнями
го= 1+/М6, /о-//(го—1)=а6. A3.174)
Результаты расчета хорошо согласуются с экспериментами.
Вопросы для самопроверки
1. Что называют прямой и обратными задачами теории решеток и каковы области
их применения?
2. Вычислите распределение скорости на решетке окружностей, если s = 2г//=
-=- 0,6.
3. Из каких условий следует выбрать гидродинамически целесообразное
распределение скорости на лопатке в решетке?
4. Какие измерения необходимо произвести при экспериментальном определении
коэффициента потерь?
5. Классифицируйте потери в решетке и объясните, от каких факторов они
зависят.
6. Почему в Компрессорных решетках угол выхода потока зависит от угла входа,
'л в турбинных решетках практически не зависит?
367

СПИСОК ЛИТЕРАТУРЫ
1. Абрамович Г. Н. Прикладная газовая динамика. М.: Наука, 1976. 888 с.
2. Белоцерковский О. М. Численное моделирование в механике сплошных сред. М:
Наука, 1984. 520 с.
3. Белоцерковский С. М., Ништ М. И. Отрывное и безотрывное обтекание тонких тел
идеальной жидкостью. М.: Наука, 1978. 352 с.
4. Гогиш Л. В., Степанов Г. Ю. Турбулентные течения. М.: Наука, 1979. 367 с.
5. Гостелоу Дж. Аэродинамика решеток турбомашин. М.: Мир, 1987. 391 с.
6. Дейч М. Е„ Зарянкин А. Е. Гидрогазодинамика. М1.: Энергоатомиздат, 1984. 384 с.
7. Дейч М. Е., Филиппов Г. А. Двухфазные течения в элементах теплоэнергетического
оборудования. М.: Энергоатомиздат, 1987. 328 с.
8. Емцев Б. Т. Техническая гидромеханика. М.: Машиностроение, 1987. 440 с.
9. Лаврентьев М. А., Шабат Б. В. Методы теории функций комплексного
переменного. М.: Наука, 1978. 736 с.
10. Ландау Л. Д., Лифшиц Е. М. Теоретическая физика. Т. 6. Гидродинамика. М.:
Наука, 1986. 736 с.
11. Лойцянский Л. Г. Механика жидкостей и газов. М.: Наука, 1987. 840 с.
12. Нигматулин Р. И. Динамика многофазных сред. М.: Т. 1. 464 с, т. 2. 369 с. Наука,
1987.
13. Самойлович Г. С., Нитусов В. В. Сборник задач по гидроаэромеханике. М.:
Машиностроение, 1986. 152 с.
14. Седов Л. И. Методы подобия и размерности в механике. М.: Наука, 1987. 430 с.
15. Степанов Г. Ю. Гидродинамика решеток турбомашин. М.: Физматгиз, 1962. 512 с.
16. Холщевников К.. В., Емин О. Н., Митрохин В. Т. Теория и расчет авиационных
лопаточных машин. М.: Машиностроение, 1986. 432 с.
17. Шлихтинг Г. Теория пограничного слоя. М.: Наука, 1969. 742 с.
18. Численные решения многомерных задач газовой динамики / С. К. Годунов,
А. В. Забродин, М. Я. Иванов и др. М.: Наука, 1976. 400 с.

ПРИЛОЖЕНИЯ
1. Таблица газодинамических функций (к=|,4)
0,000
0,005
0,010
0,015
0,020
0,025
0,030
0,035
0,040
0,045
0,050
0,055
0,060
0,065
0,070
0,075
0,080
0,085
0,090
0,095
0,100
0,105
0,110
0,115
0,120
0,125
0,130
0,135
0,140
0,145
0,150
0,155
0,160
0,165
0,170
0,175
0,180
0,185
0,190
0,195
0,200
0,205
0,210
0,215
0,220
0,225
0,230
0,235
0,240
0,245
0,250
0,255
0.260
0,265
0,270
0,275
0,280
0,285
0,290
0,295
1,0000
1,0000
1,0000
1,0000
0,9999
0,9999
0,9999
0,9998
0,9997
0,9997
0,9996
0,9995
0,9994
0,9993
0,9992
0,9990
0,9989
0,9988
0,9987
0,9985
0,9983
0,9982
0,9980
0,9978
0,9976
0,9974
0,9972
0,9969
0,9967
0,9965
0,9963
0,9960
0,9957
0,9955
0,9952
0,9950
0,9946
0,9943
0,9940
0,9936
0,9933
0,9930
0,9927
0,9923
0,9919
0,9915
0,9912
0,9908
0,9904
0,9900
0,9896
0,9892
0,9887
0,9883
0,9879
0,9874
0,9869
0,9864
0,9860
0,9855
е=р/ро
1,0000
1,0000
0,9999
0,9999
0,9998
0,9997
0,9995
0,9993
0,9990
0,9988
0,9986
0,9982
0,9979
0,9975
0,9971
0,9967
0,9963
0,9958
0,9953
0,9948
0,9942
0,9935
0,9929
0,9922
0,9916
0,9909
0,9901
0,9894
0,9886
0,9878
0,9870
0,9861
0,9851
0,9842
0,9832
0,9822
0,9812
0,9802
0,9791
0,9779
0,9768
0,9757
0,9745
0,9733
0,9720
0,9707
0,9695
0,9681
0,9668
0,9653
0,9640
0,9626
0,9611
0,9596
0,9581
... 0,9565
О,'955О
0,9534
0,9518
0,9501
6 = Р/Ро
1,0000
1,0000
0,9999
0,9999
0,9998
0,9998
0,9997
0,9995
0,9993
0,9992
0,9990
0,9987
0,9985
0,9982
0,9979
0,9977
0,9974
0,9971
0,9967
0,9963
0,9959
0,9954
0.9949
0,9945
0,9940
0,9935
0,9929
0,9924
0,9918
0,9913
0,9907
0,9900
0,9893
0,9887
0.9880
0,9872.
0,9866
0,9858
0,9850
0,9842
0.9834
0.9827
0,9817
. 0,9808
0,9799
0,9790
0.9781
0,9772
0,9762
0.9752
0,9742
0,9731
0,9721
0.9710
0,9699
0,9688
0,9677
0,9665
0,9653
0,9641
0
0,0078
0,0158
0,0236
0,0315
0,0395
0,0473
0,0552
0,0631
0,0710
0,0788
0,0866
0,0945
0,1026
0,1102
0,1181
0,1259
0,1336
0,1415
0,1493
0,1571
0,1649
0,1726
0,1804
0,1832
0,1960
0,2036
0,2113
0,2190
0,2267
0,2344
0,2421
0,2497
0,2572
0,2649
0,2725
0,2801
0,2877
0,2952
0,3028
0,3102
0,3178
0,3253
0,3327
0,3401
0,3476
0,3549
0,3622
0,3696
0,3769
0,3842
0,3914
0,3987
0,4059
0,4131
0,4202
0,4274
0,4345
0,4416
0,4486
М=и/а
0
0,0045 *
0,0091
0,0136
0,0183
0,0228
0,0274
0,0322
0,0365
0,0411
0,0457
0,0503
0,0548
0,0593
0,0639
0,0685
0,0731
0,0777
0,0822
0,0868
0,0914
0,0959
0,1005
0,1051
0,1097
0,1143
0,1190
0,1235
0,1280
0,1326
0,1372
0,1416
0,1460
0,1510
0,1560
, 0,1605
0,1650
0,1694
0,1740
0,1785
0,1830
0,1874
0,1920
0,1970
0,2020
0,2064
0,2109
0,2155
0,2202
0,2246
0,2290
0,2339
0,2387
0,2433
0,2480
0,2526
0,2573
0,2622
0,2670
0,2715

Продолжение
0,300
0,305
0,310
0,315
0,320
0,325
0,330
0,335
0,340
0,345
0,350
0,355
0,360
0,365
0,370
0,375
0,380
0,385
0,390
0,395
0,400
0,405
0,410
0,415
0,420
0,425
0,430
0,435
0,440
0,445
0,450
0,455
0,460
0,465
0,470
0,475
0,480
0,485
0,490
0,495
0,500
0,505
0,510
0,515
0,520
0,525
0,530
0,535
0,540
0,545
0,550
0,555
0,560
0,565
0,570
0,575
0,580
0,585
0,590
0,595
0,600
0,9850
0,9845
0,9840
0,9835
0,9829
0,9824
0,9819
0,9813
0,9807
0,9802
0,9796
0,9790
0,9784
0,9778
0,9772
0,9765
0,9759
0,9753
0,9747
0,9740
0,9733
0,9726
0,9720
0,9713
0,9707
0,9701
0,9692
0,9685
0,9677
0,9670
0,9663
0,9655
0,9647
0,9640
0,9632
0,9624
0,9616
0,9608
0,9600
0,9592
0,9583
0,9575
0,9567
0,9558
0,9549
0,9540
0,9532
0,9523
0,9514
0,9505
0,9496
0,9487
0,9477
0,9468
0,9459
0,9449
0,943Q
0,9430
0,9420
0,9410
0,9400
0,9485
0,9468
0,9451
0,9434
0,9415
0,9397
0,9379
0,9360
0,9342
0,9323
0,9303
0,9284
0,9265
0,9244
0,9224
0,9203
0,9183
0,9162
0,9141
0,9119
0,9097
0,9075
0,9053
0,9031
0,9008
0,8985
0,8962
0,8938
0,8915
0,8891
0,8868
0,8844
0,8819
0,8795
0,8770
0,8744
0,8719
0,8693
0,8668
0,8640
0,8616
0,8590
0,8563
0,8537
0,8509
0,8482
0,8455
0,8429
0,8400
0,8369
0,8344
0,8316
0,8287
0,8258
0,8230
0,8201
0,8172
0,8142
0,8112
0,8083
0,8053
6-р/р«
0,9630
0,9618
0,9605
0,9592
0,9579
0,9569
0,9552
0,9538
0,9525
0,9511
. 0,9497
0,9483
0,9469
0,9454
0,9439
0,9424
0.9409
0,9393
0,9378
0,9362
0,9346
0,9330
0,9314
0,9298
0,9281
0,9264
0,9247
0,9230
0,9212
0,9195
0,9178
0,9160
0,9142
0,9123
0,9105
0,9086
0,9067
0,9048
0,9029
0,9010
0,8991
0,8971
0,8951
0,8931
0,8911
0,8891
0,8871
0,8850
0,8829
0,8808
0,8787
4 0„8766
0,8744
Q,8723
0,8701
0,8679
0,8657
0,8635
0,8612
0,8590
0,8567
0,4557
0,4627
0,4697
0,4766
0,4835
0,4904
0,4972
0,5041
0,5109
0,5176
0,5243
0,5311
0,5377
0,5443
0,5509
0,5575
0,5640
0,5704
0,5769
0,5833
0,5897
0,5961
0,6024
0,6086
0,6149
0,6210
0,6272
0,6333
0,6394
0,6455
0,6515
0,6574
А6633
0,6691
0,6750
0,6808
0,6865
0,6922
0,6979
0,703о
0,7091
0,7146
0,7201
0,7255
0,7309
0,7362
0,7416
0,7468
0,7520
0,7572
0,7623
0,7674
0,7724
0,7773
0,7823
0,7871
0,7920
0,7967
0,8015
0,8062
0,8109
0,2760
0,2805
0,2850
0,2898
0,2947
0,2993
0,3040
0,3087
0,3134
0,3181
0,3228
0,3275
0,3322
0,3369
0,3417
0,3464
0,3511
0,3558
0,3606
«0,3653
0,3701
0,3748
0,3796
0,3844
0,3892
0,3939
0,3987
0,4034
0,4083
0,4131
0,4179
0,4226
0,4275
0,4324
0,4372
0,4420
0,4468
0,4516
0,4565
0,4614
0,4663
0,4711
0,4760
0,4809
0,4858
0,4907
0,4956
0,5005 ,
0,5054
0,5103
0,5152
0,5201
0,5251
0,5300
0,5350
0,5400
0,5450
0,5499
0,5549
0,5599
0,5649
370

Продолжение
0,605
0,610
0,615
0,620
0,625
0,630
0,635
0,640
0,645
0,650
0,655
0,660
0,665
0,670
0,675
0,680
0,685
0,690
0,695
0,700
0,705
0,710
0,715
0,720
0,725
0,730
0,735
0,740
0,745
0,750
0,755
0,760
0,765
0,770
0,775
0,780
0,785
0,790
0,795
0,800
0,805
0,810
0,815
0,820
0,825
0,830
0,835
0,840
0,845
0,850
0,855
0,860
0,865
0,870
0,875
0,880
0,885
0,890
0,895
0,900
0,905
0,9390
-0,9380
0,9370
0,9359
- 0,9349
0,9339
0,9328
0,9317
0,9306
0,9296
0,9285
0,9274
0,9263
0,9252
0,9240
0,9229
0,9218
0,9207
0,9195
0,9183
0,9172
0,9160
0,9148
0,9136
0,9124
0,9112
0,9100
0,9087
0,9075
0,9063
0,9050
0,9037
0,9024
0,9012
0,8999
0,8986
0,8972
0,8960
0,8946
0,8933
0,8920
0,8907
0,8893
0,8879
0,8865
0,8852
0,8838
0,8824
0,8810
0,8796
0,8781
0,8767
0,8753
0,8739
0,8724
0,8709
0,8695
0,8680
0,8665
0,8650
0,8635
е = р//>о
0,8022
0,7992
0,7962
0,7932
0,7901
0,7870
0,7839
0,7808
0,7777
0,7745
0,7713
0,7681
0,7651
0,7617
0,7585
0,7553
0,7520
0,7488
0,7455
0,7422
0,7389
0,7356
0,7322
0,7289
0,7255
0,7221
0,7187
0,7154
0,9120
0,7086
0,7051
0,7017
0,6982
0,6948
0,6913
0,6878
0,6843
0,6809
0,6774
0,6738
0,6703
0,6668
0,6633
0,6597
0,6562
0,6526
0,6490
0,6454
0,6418
0,6382
0,6346
0,6310
0,6274
0,6238
0,6201
0,6165
0,6128
0,6092
0,6055
0.6019
0,5983
0,8544
0,8521
0,8497
0,8475
0,8451
0,8428
0,8404
0,8380
0,8356
0,8332
0,8308
0,8283
0,8258
0,8233
0,8208
0,8183
0,8158
0,8133
О.,81О7
0,8082
0,8056
0,8030
0,8004
0,7978
0,7952
0,7925
0,7899
0,7872
0,7845
0,7819
0,7792
0,7764
0,7737
0,7710
0,7682
0,7655
0,7627
0,7599
0,7570
0,7543
0,7514
0,7486
0,7457
0,7429
0,7400
0,7372
0,7343
0,7314
0,7285
0,7256
0,7227 *
0,7197
0,7167
0,7138
0,7109
0,7079
0,7049
0,7019
0,6989
0,6959
0,6928
q ~S*/S
0,8153
0,8198
0,8243
0,8288
0,8332
0,8375
0,8417
0,8459
0,8501
0,8543
0,8583
0,8623
0,8662
0,8701
0,8740
0,8778
0,8815
0,8852
0,8888
0,8924
0,8958
0,8993
0,9027
0,9061
0,9094
0,9126
0,9158
0,9189
0,9219
0,9250
0,9279
0,9308
0,9336
0,9364
0,9391
0,9418
0,9443
0,9469
0^9494
0,9518
0.9541
0,9565
0,9588
0,9610
0,9631
0,9652
0,9672
0,9691
0,9710
9^9729
0,9746
0,9764
0^9780
0,9796
0,9811
0,9826
0,9840
о'9854
0,9866
0,9879
0^9890
M~ula
0,5700
0,5750
0,5800
0,5850
0,5901
0,5951
0,6002
0,6053
0,6104
0,6154
0,6205
0,6256
0,6307
0,6359
0,6410
0,6461
0,6513
0,6565
0,6616
0,6668
0,6720
0,6772
0,6824
0,6876
0,6929
0,6981
0,7033
0,7086
0,7138
0,7192
0,7244
0,7298
0J35I
0,7404
0,7457
0,7511
0,7565
0,7619
0,7673
0,7727
0,7782
0,7835
0,7890
0,7944
0,7998
0,8053
0,8108
0,8163
0,8218
0,8274
0,8329
0,8384
0,8440
0,8496
0,7552
0.8608
0,8664
0,8721
0,8777
0,8833
0.8890
371

Продолжение
0,910
0,915
0,920
0,925
0,930
0,935
0,940
0,945
0,950
0,955
0,960
0,965
0,970
Q,975
0,980
0,985
0,990
0,995
1,000
1,005
1,010
1.015
1,020
1,025
1,030
1,035
1,040
1,045
1,050
1,055
1,060
1,065
1,070
1,075
1,080
1,085
1,090
1,095
1,100
1,105
1,110
},115
1,120
1,125
1,130
1,135
1,140
1,145
1,150
1,155
1,160
1,165
1,170
1,175
1,180
1,185
1,190
1,195
1,200
1,205
1,210
0.8620
0,8604
0,8589
0,8574
0,8559
0,8543
0,8527
0,8512
0,8496
0,8480
0,8464
0,8448
0,8432
0,8416
0,8399
0,8383
0,8367
0,8350
0,8333
0,8317
0,8300
0,8283
0,8266
0,8249
0,8232
0,8215
0,8197
0,8180
0,8163
0,8145
0,8127
0,8110
0,8092
0,8074
0,8056
0,8039
0,8020
0,8001
0.7983
0,7965
0,7947
0,7928
0,7909
0,7890
0,7872
0,7853
0,7834
0,7815
0,7796
0,7777
0,7757
0,7738
0,7719
0,7699
0J679
0,7660
0,7640
0,7620
0,7600
0,7580
0,7560
0,5946
0,5910
0,5873
0,5836
0,5800
0,5763
0,5726
0,5690
0,5653
0,5616
0,5579
0,5542
0,5505
0,5468
0,5431
0,5394
0,5357
0,5320
0,5283
0,5246
0,5209
0,5172
0,5135
0,5098
0,5061
0,5024
0,4987
0,4950
0,4913
0,4877
0,4840
0,4803
0,4766
0,4730
0,4693
1 0,4656
0,4619
0,4583
0,4546
0,4510
0,4473
0,4437
0,4400
0,4364
0,4328
0,4292
0,4255
0,4220
0,4184
0,4148
0,4111
0,4076
0,4040
0,4005
0,3969
0,3933
0,3898
0,3862
0,3827
0,3792
0,3757
0,6898
0,6868
0,6838
0,6807
0,6776
0,6745
0,6715
0,6684
0,6653
0,6622
0,6591
0,6560
0,6528
0,6497
0,6466
0,6434
0,6403
0,6372
0,6340
0,6307
0,6276
0,6244
0,6212
0,6180
0,6148
0,6116
0,6084
0,6052
0,6019
0,5987
0,5955
0,5923
0,5890
0,5858
0,5826
0,5793
0,5760
0.5727 .
0,5694 i
0,5662
0,5629
0,5596
0.5564
0.5533
0,5498
0,5465
0,5432
0,5399
0,5366
0,5333
0.5309
0,5267
0,5234
0,5200
0,5168
0,5135
0,5102
0,5069
0,5035
0,5002
0,4969
q^SJS
0,9902
0,9912
0,9923
0,9932
0,9941
0,9948
0,9957
0,9964
0,9970
0,9975
0,9981
0,9985
0,9989
0,9992
0,9995
0,9997
0,9999
0,9999
1,0000
0,9999
0,9999
0,9997
0,9995
0,9992
0,9989
0,9984
0,9980
0,9975
0,9969
0,9963
0,9957
0,9948
0,9941
0,9932
0,9924
0,9914
0,9903
0,9891
0,9880
0,9868
0,9856
0,9843
0,9829
0,9815
0,9800
0,9784
0,9768
0,9752
0,9735
0,9717
0,9698 .
0,9678
0,9659
0,9640
0,9620
0,9599
0,9577
0,9555
0,9531
0,9507
0,9484
0,8947
0,9004
0,9062
0,9120
0,9177
0,9235
0.9292
0,9348
0.9409
0,9467
0,9526
0,9584
0,9644
0,9702
0,9761
0,9820
0,9880
0,9940
1,0000
1,0060
1,0120
1,0180
1,0241
1,0302
1,0363
1 0424
1,0486
1,0548
1,0609
1,0671
1,0733
1,0795
1,0858
1,0921
1,0985
1,1048
1,1111
1,1174
1,1239
1,1303
1,1367
1,1431
1,1496
1 1562
1,1627
1,1693
1,1758
1,1824
1,1890
1,1956
1,2023
1,2090
1,2157
1,2224
1.2292
1,2360
1,2428
1,2497
1,2566
1,2637
1.2708
372

Продолжение
1,215
1,220
1,225
1,230
1,235
1,240
1,245
1,250
1,255'
1,260
1,265
1,270
1,275
1,280
1,285
1,290
1,295
1,300
1,305
1,310
1,315
1,320
1,325
1,330
1,335
1,340
1,345
1,350
1,355
1,360
1,365
1,370
1,375
1,380
1,385
1,390
1,395
1,400
1,405
1,410
1,415
1,420
1,425
1,430
1,435
1,440
1,445
1,450
1,455
1,460
1,465
1,470
1,475
1,480
1,485
1,490
1,495
1,500
1,505
1,510
1,515
0,7539
0,7519
0,7498
0,7478
0,7457
0,7437
0J416
0,7396
0J375
0,7354
0,7334
0,7312
0,7290
0,7269
0,7248
0,7227
0,7205
0,7183
0,7162
0,7140
0,7119
0,7096
0,7074
0,7052
0,7030
0,7007
0,6985
0,6962
0.6940
0,6917
0,6895
0,6872
0,6849
0,6826
0,6803
0,6780
0,6756
0,6733
0,6710
0,6687
0,6664
0,6639
0,6616
0,6592
0,6568
0,6544
0,6520
0,6496
0,6472
0,6447
0,6423
0,6398
0,6374
0,6349
0,6325
0,6300
0,6275
0,6250
0,6225
0,6200
0,6175
е^р/р0
0,3722
0,3687
0,3652
0,3617
0,3582
0,3548
0,3514
0,3479
0,3445
0,3411
0,3377
0,3343
0,3309
0,3275
0,3241
0,3208
0,3175
0,3142
0,3108
0,3075
0,3042
0,3010
0,2977
0,2945
0,2912
0,2880
0,2848
0,2816
0,2785
0,2753
0,2723
0,2690
0,2659
0,2628
0,2597
0,2566
0,2536
0,2505
0,2475
0,2445
0,2415
Q.2385
0,2355
0,2326
0,2297
0,2267
0,2238
0,2209
0,2.180
0,2152
0,2123
0,2095
0,2067
0,2040
0,2012
0,1985
0,1956
0,1930
0,1903
0,1876
0,1850
6 = р/ро
0,4936
0,4903
0,4870
0,4837
0,4804
0,4770
0,4737
0,4704
0,4671
0,4638
0,4605
0,4572
0,4538
0,4505
0,4472
0,4439
0,4406
0,4374
0,4349
0,4307
0,4275
0,4241
0,4208
0,4176
0,4143
0,4110
0,4078
0,4045
0,4012
0,3980
0,3948
0,3914
0,3882
0,3850
0,3818
0,3785
0,3752
0,3720
0,3687
0,3656
0,3624
0,3592
0,3560
0,3528
0,3496
0,3464
0,3433
0,3401
0,3370
0,3338
0,3307
0,3275
0,3243
0,3212
0,3181
0,3150 .
0,3121
0,3088
0,3057
0,3027
0.2996
0,9460
0,9435
0,9410
0,9384
0,9358
0,9331
0,9304
0,9275
0,9246
0,9217
0,9187
0,9159
0,9128
0,9096
0,9065
0,9033
0,9001
0,8969
0,8935
0,8901
0,8866
0,8831
0,8796
0,8761
0,8725
0,8688
0,8651
0,8614
0,8577
0,8538
0,8499
0,8459
0,8420
0,8380
0,8340
0,8299
0,8258
0,8216
0,8175
0,8131
0,8088
0,8046
0,8002
0,7958
0,7914
0,7869 '
0,7823
0,7778
0,7732
0,7687
0,7640
0,7593
0,7546
0,7499
0,7452
0,7404
0,7356
0,7301
0,7258
0,7209
0,7160
1,2776
1,2843
1,2909
1,2974
1,3050
1,3126
1,3195
1,3268
1,3340
1,3413
1,3485
1,3558
1,3632
1,3705
1,3779
1,3853
1,3927
1,4002
1,4078
1,4153
1,4229
1,4305
1,4382
1,4458
1,4534
1,4613
1,4691
1,4769
1,4848
1,4927
1,5007
1,5087
1,5168
1,5248
1,5329
1,5410
1,5492
1,5575
,5657
l,574t
1,5824
1,5909
1,5995
1,6078
1,6163
,6250
1,6336
1,6423
1,6510
1,6598
1,6687
1,6776
1,6865
1,6955
1,7045
1,7137
1,7229
1,7321
1,7414
1,7506
1,7600
373

Продолжение
1,520
1,525
1,530
1,535
1,540
1,545
1,550
1,555
1,560
1,565
1,570
1,575
1,5вО '
1,585
1,590
1,595
1,600
1,605
1,610
1,615
1,620
1,625
1,630
1,635
1,640
1,645
1,650
1,655
1,660
1,665
1,670
1,675
1,680 ч
1,685
, 1,690
1,695
1,700
1,705
1,710
1,715
1,720
1,725
1,730
1,735
1,740
1,745
1,750
1,755
1,760
1.765
1,770
1,775
1,780
1,785
1,790
1,795
1,800
1,805
1,810
1,815
1,820
т=Г/Г«
0,6149
0,6124
0,6090
0,6073
0,6048
0,6022
0,5996
0,5970
0,5944
0,5918
0,5892
0,5866
0,5839
0,5813
0,5786
0,5759
0,5733
0,5707
0,5680
0,5653
0,5625
0,5599
0,5572
0,5543
0,5517
0,5490
0,5463
0,5435
0,5407
0,5380
0,5352
0,5324
0,5296
0,5268
0,5240
0,5211
0,5183
0,5154
0,5126
0,5097
0,5069
0,5040
0,5012
0,4983
0,4954
0,4925
0,4896
0,4867
0,4837
0,4808
0,4779
0,4749
0,4719
0,4690
0,4660
0,4630
0,4600
0,4570
0,4540
0,4510
0,4479
0,1824
0,1798
0,1771
0,1746 "
0,1720
0,1694
0,1669
0,1644
0,1619
0,1594
0,1570
0,1546
0,1522
0,1498
0,1474
0,1450
0,1427
0,1403
0,1381
0,1359
0,1336
0,1313
0,1291
0,1270
0,1248 -
0,1227
0,1205
0,1184
0,1163
0,1142
0,1121
0,1101
0,1081
0,1061
0,1041
0,1022
0,1003
0,0984
0,0965
0,0946
0,0928
0,0909
0,0891
0,0873v
0,0856
0,0839
0,0821
0,0803
0,0787-
0,0771
0,0754
0,0738
0,0722
0,0706
0,0691
0,0675
0,0660
0,0645
• 0,0630
0,0616
0,0602
0,2965
0,2934
0,2904
0,2(874
0,2844
0,2814
0,2784
0,2754
0,2724
0,2695
0,2665
0,2636
0,2606
0,2576
0,2547
0,2518
0.2489
0,2460
0,2431
0,2401
0,2374
0,2347
0,2317
0,2289
0,2261
0,2233
0,2205
0,2177
0,2150
0,2123
0,2095
0,2068
0,2041
0,2015
0,1988
0,1961
0,1934
0,1908
0,1881
0,1855
0,1830
0,1804
0J778
,0,1751
0,1727
0,1702
0.1677
0,1653
0,1628
0,1603
0,1578
0,1554
0,1530
0,1506
0,1482
0,1458
0,1435
0,1412
0,1389
0,1366
0,1343
0,7110
0,7060
0,7009
0,6959
0,6909
0,6858
0,6807
0,6756
0,6703
0,6651
0,6599
0,6546
0,6494
0,6441
0,6389
0,6335
0,6282
0,6228
0,6175
0,6121
0,6067
0,6012
0,5958
0,5904
0,5850
0,5795
0,5740
0,5685
0,5630
0,5575
0,5520
0,5464
0,5409
0,5353
0,5298
0,5243
0,5187
0,5131
0,5075
0,5020
0,4965
0,4909
0,4852
0,4796
0,4741
0,4685
0,4630
0,4575
0,4520
0,4464
0,4407
0,4352
0,4296
0,4241
0,4185
0,4! 30
0,4075
0,4020
0,3965
0,3910
0,3855
1,7694
1,7789
1,7885
1,7981
1,8078
1,8176
1,8273
1,8372
1,8471
1,8572
1,8672
1,8773
1,8875
1,8978
1,9081
1,9185
1,9290 -
1,9396
1,9501
1,9509
1,9716
1,9824
1,9934
2,0045
2,0155
2,0267
2,0380
2,0493
2,0607
2,0723
2,0839
2,0956
2,1073
2,1193
2,1313
2,1434
2,1555
2,1678
2,1802
2,1928
2,2053
2,2180
2,2308
2,2437
2,2567
2,2699
2,2831
2,2965
2,3100
2,3235
2,3374
2,3513
2,3653
2,3795
2,3937
2,4082
2,4227
2,4375
2,4523
2,4674
2,4824
374

Продолжение
% — ula^
1,825
1,830
1,835
1,840
1,845
1,850 .
1,855
1,860
1,865
1,870
1,875
1,880
1,885
1,890
1,895
1,900
1,905
1,910 "
1,915
1.920
1,925
1,930
1,935
1,940
1,945
1,950
1,955
1,960
1,965
1,970
1,975
1,980
1,985
1,990
1,995
2,00
Х = Т/То
0,4449
0,4418
0,4388
0,4357
0,4327
0,4296
0,4265
0,4234
0,4203
0,4171
0,4140
0,4109
0,4078
0,4047
0,4015
0,3983
0,3952
0,3920
0,3888
0,3856
0,3824
0,3792
0,3760
• 0,3727
0,3694
0,3662
0,3630
0,3597
0,3565
0,3532
0,3499
0,3460
0,3433
0,3400
9,3366
0,3333
е = р/р„
0,0588
0,0573
0,0559
0,0546
0,0533
0,0520 ,
0,05Q7
0,0494
0,0481
0,0469
0,0457
0,0445
0,0434
0,0422
0,0411
0,0399
0,0388
0,0377
0,0367
0,0356
0,0346
0,0336
0,0326
0,0316
0,0307
0,0297
0,0288
0,0279
0,0270
0,0262
0,0253
0,0245
0,0237
0,0229
0,0221
0,0214
6 = р/ро
0,1320
0,1298
0,1275
0,1253
0,1232
0,1210
0,1189
0,1167
0,1146
0,1124
0,1103
0,1083
0,1063
0,1042
0.1022
0,1002
0,0982
0,0962
0,0942
0,0923
0.0904
0,0885
0,0866
0,0848
0,0830
0,0812
0,0794
0,0776
0,0758
0,0741
0,0724
0,0707
0,0691
0,0674
0,0658
0,0642
0,3800
0,3746
0,3692
0,3638
0,3584
0,3530
0,3476
0,3423
0,3370
0,3316
0,3263
0,3211
0,3158
0,3105
0,3054
0,3002*
0,2950
0,2898
0,2848
0,2797
0,2746
0,2695
0,2646
0,2596
0,2547
0,2497
0,2448
0,2400
0,2352
0,2304
0,2256
0,2209
0,2163
0,2116
0,2070
0,2024
2,4978
2,5132
2,5290
2,5449
2,5608
2,5766
2,5930
2,6094
2,6261
2,6429
2,6600
2,6772
2,6948
2,7123
2,7302
2,7481
2,7666
2,7840
2,8037
2,8225
2,8419
2,8612
2,8810
2,9007
2,9211
2,9414
2,9623
2,9831
3,0066
3,0301
3,0501
3,0701
3,0929
3,1155
3,1389
3,1622

в, °
0
1,00
1.5
2,00
2,5
3.00 -
3,5
4,00
4,5
5,00
6,00
7,00
8,00
9,00
10,00
11,00
12,00
13,00
14,00
15,00
16,00
17,00
18,00
19,00
20,00
21,00
22,00
23,00
24,00
25,00
26.00
27,00
28,00
29,00
30,00
Таблица для
ф
0
23,53
27,00
30,00
32,55
34,90
37,00
38,87
40,65
42,30
45,40
48,30
51.00
53,47
55,83
58,10
60.33
62,40
64,42
66,40
68,40
70,30-
72,10
73,95
75,70
77,45
79,20
80,87
82,50
84.17
85,80
87,40
/ 89.00
90,50
92,00
расчета волнь
м
1,000
1,083
1,109
1,133
1,155
1,178
1,199
1,219
1,238
1,257
1,294
1,331
1,367
1,401
1,435
1,469
1,504
1,536
1,569
1,603
1,639
1,673
1,705
1,741
1,775
1,809
1,846
Г,880
1,914
1,951
1,988
2,028
2,063
2,096
2,130
i разрежения (х=1,4)
к
1,000
1,067
1,088
,107
1,125
1,142
1,157
1,172
1,186
1,200
1,227
1,253
,277
1,300
,323
1,345
1,367
1,388
1,408
1,428
1,448
1,467
1,486
1,505
1,523
1,542
1,559
1,576
,594
,610
1,628
1,644
1,660
,675
1,691
е
0,528
0,479
0,463
0,450
0,464
0,424
0,413
0,402
0,392
0,383
0,364
0,346
0,330
0,314
0,299
Л, 285
0,271
0,258
0,246
0,234
0,222
0,211
0,201
0,190
0,181
0,171
0,162
0,154
0,146
0,138
0,130
0,123
0,116
0,110
0,104
6
0,634
0,591
0,577
0,565
0,553
0,542
0,532
0,522
0,513
0,504
0,497
0,468
0,452
0,437
0,422
0,408
0,393
0,380
0,367
0,354
0,341
0,329
0,318
0,306
0,295
0,284
0,273
0,263
0,253
0,243
0,233
0,224
0,215
0,207
0,198
т
0,833
0,810
0,803
0,796
0,789
0,783
0,777
0,771
0,766
0,760
0,749
0,738
0,728
0,718
0,708
0,698
0,688
0,679
0,670
0,660
0,650
0,641
0,632
0,622
0,613
0,604
0,595
0,586
0,576
0,568
0,558
0,550
0,541
0,532
0,523
о, °
90,00
67,47
64,40
62,00
59,95
58,10
56,50
55,13
53,85
52,70
50,60
48,70
47,00
45,53
44,17
42,90
41,67
40,60
39,58
38,60
37,60
36,70
35,90
35,05
34,30
33,55
32,80
32,13
31,50
30,83
30,20
29,55
29,00
28,50
28,00

3, Таблица газодинамических функций (х-1,3)
0,02
0,04
0,06
0,08
0,10
0,12
0,14
0,16
0,18
0,20
0,22
0,24
0,26
0,28
0,30
0,32
0,34
0,36
0,38
0,40
0,42
0,44
0,46
0,48-
0,50
0,52
0,54
0,56
0,58
0,60
0,62
0,64
0,66
0,68
0,70 ,
0,72
0,74
0,76
0,78
0,80
0,82
0,84
0,86
0,88
0,90
0,92
0,94
0,96
0,98
,00
,02
,04
,06
,08
,10
,12
,14
,16
,18
,20
/>//>0
0,99977
0,99910
0,99797
0,99639
0,99436
0,99189
0,98897
0,98561
0,98182
0,97759
0,97293
0,96785
0,96235
0,95644
0,95012
0,94340
0,93628
0,92878
0,92091
0,91266
0,90405
0,89509
0,88578
0,87615
0,86618
0,85591
0,84532
0.83445
0,82330
0,81187
0,80019
0,78826
0,77610
0.76371
0,75111
0,73831
0,72533
0,71218
0,6^887
0,68541
0,67182
0,65811
0,64430
0,63039
0,61640
0,60234
0,58824
0,57409
0,55991
0,54573
0,53154
0,51737
0,50822
0,48911
0,47505
0,46106
0,44714
0,43331
0,41958
0,40596
т/и
0,99995
0,99979
0,99953
0,99917
0,99870
0,99812
0,99744
0,99666
0,99577
0,99478
0,99369
0,99249
0,99118
0,98977
0,98826
0,98664
0,98492
0,98310
0,98117
0,97913
0,97699
0,97475
0,97240
0,96995
0,96740
0,96474
0,96197
0,95910
0,95612
0,95304
0,94986 '
0,94657
0,94318
0,93969
0,93609
0,93238
0,92857
0,92466
0,92064
0,91652
0,91230
0,90797
0,90353
0,89899
0,89435
0,88960
0,88475
0,87979
0,87473
0,86957
0,86430
0,85892
0,85344
0.84786
0,84217
0,83638
0,83049
0,82449
0,81838
0,81217
, РФ»
0,99983
0,99930
0,99844
0,99722
0,99566
0,99375
0,99150
0,98891
0,98598
0,98271
0,97911
0,97518
0,97091
0,96632
0,96140
0,95617
0,95062
0,94476
0,98859
0,93211
0,92534
0,91828
0,91093
0,90329
0,89538
0,88720
0,87875
0,87004
0,86108
0,85187
0,84243
0,83275
0,82285
0,81273
0,80239
0,79186
0,78113
0,77021
0,75911
0,74784
0,73641
0,72482
0,71309
0,70122
0,68935
0,67709
0.66486
0,65253 -
0,64010
0,62759
0,61500
0,60235
0.58963
0,57688
0.56408
0,55125
0,53841
, 0,52555
0,51269
0,49984
я
0,03186
0,06369
0,09545
0,12712
0,15865
0,19001
0,22118
0,25212
0,28279
0,31317
0,34223
0,37292
0,40223
0,43113
0,45957
0,48754
0,51500
0,54194 .
0,56831
0,59409
0,61927
0,64380
0,66768
0,69087
0,71335
0,73511
0,75611
0,77634
0,79579
0,81443
0,83224
0,84922
0,86535
0,88060
0,89498
0,90846
0,92104
0,93271
0,94346
0,95329
0,96219
0,97014
0,97716
0,98324
0,98922
0,99257
0,99583
0,99815
0,99954
1,00000
0,99954
0,99817
0,99590
0,99273
0,98869
0,98377
0,97800
0,97140
0,96397
0,95574
6
—
—
—
—
—
—.
—
—
—
—
—
—
—
—
—
—
—
—
—
—
—
—
—
—
—
—
—
—
—
• —
—
,—
0°
0°10'
0°30'
0°55'
1°25'
1°55'
2°25'
3°28'
3°28'
4° 19'
4°52'
м
0,01865
0,03730
0,05596
0,07463
0,09331
0,11201
0,13072
0,14945
0,16821
0,18699
0,20580
0,22465
0,24353
0,26245
0,28141
0,30041
0,31947
0,33858
0,35774
0,37696
0,39624
0,41558
0,43500
0,45448
0,47404
0,49367
0,51341
0,53322
0,55312
0,57312
0,59322
0,61341
0,63372
0,65414
0,67467
0,69532
0,71610
0,73701
0,75805
0,77924
0,80057
0,82205
0,84368
0,86548
0,88744
0,90958
0,93190
0,95440
0,97710
,00000
,02310
,04642
,069%
,09374
,11775
,14200
,16651
,19129
,21634
,24164
377

Продолжение табл. 3
х ¦
,22
,24
,26
,28
,30
,32
,34
,36
,38
,40
,42
,44
,46
,48
1,50
1,52
1,54
;•
с
,56
,58
,60
,62
,64
,66
,68
,70
,72
,74
,76
1,78
,80
,82
,84
,86
1,88
1,90
,92
1,94
,96
,98
>,00
Р/Ра
0,39246
0,37909
0,36587
0,35281
0,33991
0,32718
0,31464
0,30229
0,29014
0,27820
0,26648
0,25499 '
0,24373
0,23270
0,22193
0,21140
0,20113
0,19112
0,18138
0,17191
0,16271
0,15379
0,14514
0,13678
0,12870
0,12090
0,11339
0,10616
0,09921
0,09255
0,08617
0,08006
0,07424
0.06888
0,06340
0,05839
0,05364
0,04914
0,04490
0,0409
Т/То
< 0,80586
0,79944
0,79292
0,78630
0,77957
0,77273
0,76579
0,75875
0,75160
0,74435
0,73699
0,72953 '
0,72197 '
0,71430
0,70652
0,69864
0,69065
0,68257
0,67438
0,66609
0,65769
0,64918
0,64057
0,63186
0,62304
0,61412
0,60510
0,59597
0,58673
0,57739
0,56795
0,55840
0,54875
0,53899
0,52913
0,51916
0,50909
0,49802
0,48864
0,4783
Р/Ро
0,48701
0,47420
0,46142
0,44870
0,43602
0,42341
0,41087
0,39841
0,38603
0,37375
0,36158
0,34952
0,33759
0,32578
0,31411
0,30259
0,29122
0,28000
0,26896
0,25809
0,24740
0,23690
0,22658
0,21647
0,20657
0,19687
0,18739
0,17813
0,16909
0,16029
0,15171
0,14338
0,13528
0,12743
0,11982
0,11246
0,10536
0,09850
0,09190.
0,0856
я
0,94672
0,93693
0,92640
0,91514
0,90319
0,89056
0,87727
0,86336
0,84884
0,83376
0,81813
0,80109
0,78636
0,76827
0,75076
0,73286
0,71460
0,69601
0,67713
0,65798
0,63861
0,61905
0,59933
- 0,57948
0,55955
Д53956
0,51954
0,49955
0,47960
0,45973
0,43997
0,42073
0,40094
0,38173
0,36276
0,34407
0,32568
0,30762
0,28993
0,2796
6
5°37'
6°20'
7°08'
7°52'
8°44'
9°32'
10°16'
1Г18'
12°01'
13°17'
14°04'
14°52'
15°59'
J6°59'
18°00'
18°54'
20°05'
21°06'
22°ов'
23° 15'
24°2Г
25°29'
26°38'
27°4Г
28°55'
30°07'
31°13'
32°2Г
33°43'
35°04'
36°24'
37°33'
38°53'
40°22'
41°33'
43°06'
44° 14'
45°36'
47°04'
48°26'
м
1,26730
1,29324
1,31949
1,34607
1,37299
1,40027
1,42791
1,45593
1,48435
1,51318
1,54244
1,57214
1,60231
1,63295
1,66410
1,69577
1,72798
1,76076
1,79413
1,82812
1,86276
1,89807
1,93408
1,97083
2,00836
2,04669
2,08588
2,12595
2,16696
2,20896
2,2520
2,2962
2,3414
2,3879
2,4357
2,4849
2,5355
2,5876
2,6414
2,697

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Автомодельность 185
Адиабата ударная 134
Безразмерные величины 28, 32
Вектор 6, 7, 9, 14
Вихрь 13
— присоединенный 106, 107
Волна звуковая 110
-~ Маха ПО
— разрежения, 122, 123, 125, 126, 155, 157
— сжатия 46, 122, 123, 128
— ударная 167, 168, 170
Вязкость динамическая 174
кинематическая 176
Газодинамические функции 49
Газ Чаплыгина 96, 97
Годограф скорости 93, 94, 98
Гомогенное течение 278
Давление торможения 47, 48, 141
Движение безвихревое 67, 68, 69, 70, 71
— вихревое 67, 68
— потенциальное 71
Двухкомпонентные течения 265
Двухфазные течения 265
Диаграмма ударных поляр 132
Диаграмма характеристик 122
Диполь 76
Длина пути перемешивания 214
Единицы измерений 28
Жидкость вязкая 6
— идеальная 6
— несжимаемая 5
сжимаемая 5
Инварианты Римана 162, 165
Индексная форма записи 7
Источник точечный 74, 75
Количество движения 17, 18
Консервативность 296
Конформность 83, 85, 89
Координаты естественные 111
Косой срез решетки 144
Коэффициент подобия 41
— подъемной силы 89
— потерь 27, 335
расхода 335, 363
- сжимаемости 267
— сопротивления 178, 213, 299
Кризис сопротивлений 226, 228
Критерий Маха 38
— подобия 36
379

•-- Рейнольде а 38
— Струхала 38
Критические параметры 51
Лабиринтовое уплотнение 361
Ламинарный подслой 204
I— слой 184, 188
Линия равного потенциала 72, 75, 76
— тока 72, 75, 76, 77, 78, 94
Моделирование физическое 34, 39
— численное 294
Напряжения касательные 8, 9
— нормальные 8, 9
Нестационарное течение 154
Обтекание окружности 78, 79
— пластины 88, 106
— решетки 107, 312, 313, 324
— тел сверхзвуковым потоком 137, 140
Осесимметричные течения 245
Осреднение потока 62, 65, 66
Отрыв пограничного слоя 226, 227, 228, 232
Пар совершенный 267, 268
Переохлаждение 266
Плоскость годографа 98, 102
— физического течения 98, 102
Пограничный слой 182
ламинарный 184, 185, 192, 195, 220, 227
турбулентный 204, 205, 207, 220, 227
Подобие турбомашин 39, 41, 42
— физическое 34, 36
Подшипник упорный 179
Постулат Жуковского—Чаплыгина 83
Потенциал комплексный 73, 77
— скорости 71
Потенциальный поток 71
-= и метод сложения 77
Потери концевые 340
— кромочные 338, 340
— профильные 338
— трения 338
Пульсации турбулентные 214, 199, 200, 202
Путь смешения 214, 215
Распад разрыва 155, 209
Решетка аэродинамическая 102, 103, 107, 323
— компрессорная 345, 344, 347
турбинная 107, 322
Сила массовая 18
— поверхностная 18
— подъемная 81, 82
— сопротивления 140, 228, 229
Скачок конденсации 287
— тепловой 283
— уплотнения 129, 130, 131, 132
Скорость звука 45, 46, 280
— деформации 12, 13
— динамическая 205
— истечения 53
— комплексная 74
— критическая 50
Смазки теория 178
Сопло Л аваля 53, 149, 143
— расширяющееся 53
380

— суживающееся 53
Сопротивление волновое 140
— давления 228
— трения 228
Струя идеальной жидкости 98
— турбулентная 237, 233
Тензор напряжения 9
— скоростей деформации 13
Течение гомогенное 273
— дозвуковое 49, 50, 52
— несжимаемой жидкости 71
— потенциальное 71
— сверхзвуковое 49, 50, 52, 142
— смесей 270, 271, 272, 265
— трансзвуковое 147, 149
Толщина вытеснения 197
— потери импульса 197
— потери энергии 197
Транспортивность 296
Ударная адиабата 134, 135
Универсальный закон сопротивления 203
— профиль скорости 205, 207
Уравнение акустики 158
— Бернулли 24, 69
— Громеки—Лэмба 67, 69
— Кош и—Римана 73, 95
— Навье—Стокса 176, 177
— неограниченного слоя 182, 183
— неразрывности 16
— Рейнольде а
— сохранения 16, 17, 20
— Эйлера 20
— энергии 20, 21, 22
Фазовое равновесие 271
Физические свойства среды 5, 6.
Формпараметр 221
Формула Гаусса—Остроградского 15
Жуковского 82
—ч трения Ньютона 174, 215
— Прандтля 215, 216
— —- Стокса 175
— размерности Фурье 29
— Хагена—Пуазейля 178
Характеристики 121, 122, 123
— решеток 333, 344
Циркуляция скорости 67
Численное моделирование 294
Число Маха 38, 49
критическое 348, 349
максимальное 349
__ Рейнольдса 38
— Струхала 38
Шаг решетки 81
Шероховатость 210
Эжекция 27
Эквипотенциаль 72, 75
Эксперимент численный 294
Энергия внутренняя 20
—- кинетическая 20
— полная 20
381

ОГЛАВЛЕНИЕ
Предисловие ' 3
Основные условные обозначения * 4
Глава 1. Жидкости, газы и пары как сплошные деформируемые среды ... 5
1.1. Физические свойства жидкостей, газов и паров 5
1.2. Скалярные, векторные и тензорные поля в гидрогазодинамике 6
1.3. Деформация и вращение жидкой частицы 1 {
1.4. Запись векторных операций в индексной форме 14
Глава 2. Уравнения сохранения 16
2.1. Уравнение неразрывности . . . . 1б
2.2. Уравнение движения 17
2.3. Уравнение энергии 20
2.4. Уравнение переноса 23
2.5. Применение уравнений сохранения в интегральной форме . . 23
Глава 3. Методы размерности и подобия в гидрогазодинамике 28
3.1. Анализ размерностей. Формула размерности 28
3.2. П-теорема. Выбор определяющих параметров 31
3.3. Физическое подобие. Моделирование. Коэффициенты подобия 34
3.4. Подобие и моделирование турбомашин. Безразмерные
характеристики турбомашин 39
Глава 4. Одномерные течения 44
4.1. Уравнения сохранения для одномерных течений 44
4.2. Скорость распространения звука 45
4.3. Одномерное изоэнтропийное течение 47
4.4. Газодинамические функции 49
4.5. Одномерные течения при различных воздействиях на поток . . 56
4.6. Неоднородные потоки и различные способы осреднения ... 62
Глава 5. Плоское дозвуковое движение идеальной жидкости ....... 67
5.1. Вихревое и безвихревое движение. Теорема Стокса. Уравнения
Эйлера и Громеки — Лэмба 67
5.2. Плоское безвихревое движение идеальной несжимаемой
жидкости 70
5.3. Теорема Жуковского. Постулат Жуковского—Чаплыгина ... 81
5.4. Расчет обтекания тел потенциальным потоком несжимаемой
жидкости методом конформного преобразования 83
5.5. Плоское дозвуковое течение идеальной жидкости. Уравнение
годографа скорости 93
5.6. Построение течений методом годографа скорости 98
5.7. Расчет потенциальных течений методом дискретных вихрей 105
5.8. Уравнения движения в естественных координатах. Расчет
потока в канале 111
Глава 6. Плоское сверхзвуковое движение идеальной жидкости. Течения
с переходом через скорость звука 119
6.1. Распространение возмущений в потоке. Характеристики . 119
6.2. Волны разрежения и сжатия в сверхзвуковом потоке .... 122
6.3. Скачки уплотнения в сверхзвуковом потоке 129
6.4. Отражение и взаимодействие скачков и волн. Обтекание тел
плоским сверхзвуковым потоком. 137
6.5. Сверхзвуковые течения в соплах и решетках 142
6.6. Течения с переходом через скорость звука 147
382

Глава 7. Одномерные неустановившиеся течения 154
7.1. Распространение слабых возмущений в потоке. Акустические
уравнения # 154
7.2. Основные уравнения неустановившегося течения.
Инварианты Рима на 162
7.3. Ударные волны 168
7.4 Распад разрыва. Задача Н.Е. Кочина 171
Глава 8. Ламинарное течение вязкой жидкости . ¦ 174
8.1. Уравнение Навье — Стокса. Ламинарное течение 174
8.2. Гидродинамическая теория смазки 178
8.3. Основные свойства пограничного слоя. Дифференциальное
уравнение пограничного слоя Прандтля 182
8.4. Подобные решения для ламинарного пограничного слоя . . , 184
8.5. Приближенный метод расчета ламинарного пограничного слоя 192
8.6. Условные толщины пограничного слоя . . . 196
Глава 9. Турбулентное течение вязкой жидкости 199
9.1. Особенности турбулентного течения. Уравнения Рейнольдса 199
9.2. Универсальные законы распределения скорости.
Универсальные законы сопротивления 203
9.3. Трение при турбулентном течении 214
9.4. Интегральное соотношение для пограничного слоя 217
9.5. Расчет плоских турбулентных пограничных слоев 221
9.6. Сопротивление. Отрыв пограничного слоя. Кризис
сопротивления илохообтекаемых тел 226
9.7. Свободная турбулентность. Турбулентные следы и струи . . 233
Глава 10. Осесимметричные течения идеальной жидкости 245
10.1. Уравнения движения, неразрывности и завихренности для
осесимметричных течений 245
10.2. Точные решения для осесимметричных закрученных потоков 249
10.3. Осесимметричные течения через кольцевые аэродинамические
решетки 257
Глава 11. Двухфазные и двухкомпонентные течения , . 265
11.1. Особенности двухкомпонентных и двухфазных течений. . . 265
11.2. Совершенный пар 267
11.3. Гомогенное течение газа с постоянной концентрацией
примесей 270
11.4. Гомогенное течение жидкости с пузырьками газа 273
11.5. Течение двухфазной среды при фазовом равновесии или
полном переохлаждении 278
11.6. Тепловой скачок 283
11.7. Скачок конденсации 287
Глава 12. Вычислительная гидрогазодинамика 294
12.1. Вычислительная гидрогазодинамика и ее задачи. Численное
моделирование и численный эксперимент 294
12.2. Метод распада разрыва 299
12.3. Метод крупных частиц в ячейках 302
12.4. Метод дискретных вихрей и расчет срывного обтекания . . 307
Глава 13. Аэродинамика элементов турбомашин 312
13.1. Расчет обтекания решеток плоским потенциальным
потоком , 312
13.2. Построение решеток с гидродинамически целесообразным
распределением скорости 323
13.3. Характеристики решеток осевой турбины 333
13.4. Характеристики решеток осевого компрессора 344
13.5. Расчет потерь трения в аэродинамических решетках .... 351
13.6. Расчет кромочных следов 355
13.7. Расчет лабиринтных уплотнений 361
Список литературы 368
Приложения 369
Предметный указатель . , 379

УЧВБНОК ИЗДАНИЕ
Самойлович Георгий Семенович
ГИДРОГАЗОДИНАМИКА
Редактор В. В. Нитусов
Художественный редактор В. В. Лебедев
Технический редактор Л. А. Макарова
Корректоры О. Е. Мишина, О. Ю. Сады ков а
И Б № 4433
Сдано в набор 20.12.89. Подписано в печать 23.07.90. Т-07210. Формат 70x1007*.
Бумага офсетная № 2. Гарнитура литературная. Печать офсетная. Усл. печ. л. 31,2.
Усл. кр.-отт. 62,4. Уч.-изд. л. 29,67. Тираж 5500 экз. Заказ 2638. Цена I р. 40 к.
Ордена Трудового Красного Знамени издательство «Машиностроение»,
107076, Москва, Стромынский пер., 4.
Московская типография № 4 Государственного комитета СССР по печати,
129041, Москва, Б. Переяславская ул., 46.