Синхронизация динамических систем - Блехман И.И.

Автор: Блехман И.И.
Теги: динамика кинетика физика механика
Год: 1971
Похожие
Основы автоматического регулирования. Теория
Математическая энциклопедия. Предметный указатель
Стохастические и хаотические колебания
Автоволновые процессы
Текст
                    СИНХРОНИЗАЦИЯ
ДИНАМИЧЕСКИХ
СИСТЕМ
И.И.БЛЕХМАН
И. И. БЛЕХМАН
СИНХРОНИЗАЦИЯ
ДИНАМИЧЕСКИХ
СИСТЕМ
ИЗДАТЕЛЬСТВО «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОИ ЛИТЕРАТУРЫ
МОСКВА 1971
531
Б 68
УДК 531.3
2-4-2
112—71
ОГЛАВЛЕНИЕ
Предисловие..........................................................11
Введение............................................................15
§ 1.	Проблема	синхронизации	динамических	систем...............15
§ 2.	Об	исследованиях	в	области	синхронизации.................19
§ 3. Обзор основных фактов и результатов, изложенных в книге . 22
ЧАСТЬ 1
ПОСТАНОВКА И ОСНОВНЫЕ ОСОБЕННОСТИ ЗАДАЧ
О СИНХРОНИЗАЦИИ ДИНАМИЧЕСКИХ СИСТЕМ
Глава I. Задачи о синхронизации динамических объектов...............63
§ 1.	Синхронизация возбудителей механических колебаний .... 63
§ 2.	Динамика автоматического балансира для уравновешивания
вращающихся роторов...........................................66
§ 3.	Изгибно-крутильные колебания вращающегося вала с неурав-
новешенными дисками...........................................69
§ 4.	Взаимная синхронизация маятниковых часов, висящих на под-
вижном основании (задача Гюйгенса)..........................  72
§ 5.	Синхронизация при параллельной работе	электрических машин 76
§ 6.	Синхронизация ламповых генераторов.......................79
§ 7.	Синхронизация квантовых генераторов......................86
§ 8.	Явления синхронизации в биологии и медицине..............88
§ 9.	Синхронизация и некоторые нерешенные проблемы биологии,
физики и астрономии...........................................92
Глава П. Общая задача о синхронизации динамических систем ... 98
§ 1.	Постановка общей задачи о синхронизации..................98
§ 2.	Основные особенности задач о синхронизации..............102
1*
4
ОГЛАВЛЕНИЕ
ЧАСТЬ П
МЕТОДЫ И МАТЕМАТИЧЕСКИЙ АППАРАТ ТЕОРИИ
СИНХРОНИЗАЦИИ ДИНАМИЧЕСКИХ СИСТЕМ
Глава III. Методы Пуанкаре и Ляпунова.................................107
§ 1.	Предварительные замечания...................................107
§ 2.	Основные идеи метода Пуанкаре...............................108
§ 3.	Об устойчивости периодических решений ......................115
§ 4.	Краткий обзор исследований по развитию методов Пуанкаре
и Ляпунова, существенных для теории синхронизации . . . 136
Глава IV. Методы Пуанкаре и Ляпунова как средства получения прав-
доподобных результатов в прикладной теории нелинейных
колебаний........................................................139
§ 1.	О пестрогостях, допускаемых при практическом применении ме-
тодов Пуанкаре н Ляпунова. Правдоподобные рассуждения и
их ценность при решении прикладных задач этими методами 139
§ 2.	О применимости методов малого параметра к системам, не
содержащим физического малого параметра ........ 141
§ 3.	О сходимости рядов, найденных методом Пуанкаре. Правдопо-
добность результатов, полученных при отсутствии доказатель-
ства сходимости. О внутренней и внешней правдоподобности 144
§ 4.	О правдоподобности качественных результатов локального
исследования при их «нелокальном» применении ...... 146
Глава V. О существовании, устойчивости и практическом вычислении
периодических и синхронных решений некоторых систем не-
линейных дифференциальных уравнений..............................154
§	1.	Предварительные замечания.........................154
§	2.	Квазилинейные неавтономные системы................154
§	3.	Квазилинейные автономные системы..................169
§	4.	Неавтономные системы, близкие к произвольным	нелинейным	186
§	5.	Автономные системы, близкие к произвольным	нелинейным	.	202
§ 6.	Системы почти периодические, с разрывными правыми ча-
стями и с запаздыванием.....................................209
§ 7.	Применимость теорем о существовании и устойчивости перио-
дических движений в случае синхронных движений .... 217
§ 8.	Интегральный критерий устойчивости периодических и син-
хронных движений............................................219
§ 9.	Практическое вычисление периодических решений систем
уравнений с малым параметром................................224
§ 10.	О случаях, когда уравнения для определения порождающих
параметров имеют непростые решения или удовлетворяются
тождественно................................................230
§ И.	Случай нелинейных (непростых) элементарных делителей
корней характеристического уравнения......................  232
ОГЛАВЛЕНИЕ
5
"лава VI. Некоторые другие методы решения задач о синхронизации
§ 1.	Асимптотические методы.................................233
§ 2.	Метод математического моделирования (применение аналого-
вых устройств и цифровых вычислительных машин) .... 234
§ 3.	Физическое моделирование.............................  236
Ч .4 С Т Ь 111
СИНХРОНИЗАЦИЯ НЕКОТОРЫХ КЛАССОВ ДИНАМИЧЕСКИХ
СИСТЕМ СО СЛАБЫМИ ВЗАИМНЫМИ СВЯЗЯМИ
Глава VII. Общий случай слабо связанных объектов . ..............238
§ 1.	Уравнения движения системы.............................238
§ 2.	Задача о внешней синхронизации.......................  238
§ 3.	Задача о внутренней синхронизации..................... 243
Глава VIII. Объекты с одной степенью свободы, близкие к линейным 248
§ 1.	Предварительные замечания..............................248
§ 2.	Уравнения движения системы и основные предположения;
главные частные случаи...................................  248
§ 3.	Объекты с немалым демпфированием и немалыми частотами
свободных колебании ...................................... 251
§ 4.	Объекты с малым демпфированием или малыми частотами
свободных колебаний	................................. 252
§ 5.	Объекты с малым демпфированием и с малыми частотами
свободных колебаний	................................. 267
Глава IX. Объекты с почти равномерными вращательными движениями 283
§ 1.	Постановка задачи и	уравнения движения.................283
§ 2.	Уравнения для определения*порождающих фаз. Условия су-
ществования н устойчивости синхронных движений.............285
§ 3.	Развернутая форма и физическое истолкование уравнений для
определения порождающих фаз................................287
§ 4.	Об одном важном соотношении для систем, линейных в исход-
ном приближении относительно колебательных координат . . 290
§ 5.	Интегральный критерий устойчивости синхронных движений
в системах с почти равномерными вращениями.................294
§ 6.	О зависимости результатов исследования от характера идеа-
лизации объектов...........................................296
Глава X. Объекты, близкие к нелинейным консервативным............299
§ 1.	Почти консервативные объекты с одной степенью свободы . . 299
§ 2.	Обобщение на случай объектов и связей со многими степе-
нями свободы...............................................308
§ 3.	О зависимости условий устойчивости синхронных движений от
характера анизохронизма объектов в связей между ними . . 3|9
6
ОГЛАВЛЕНИЕ
Глава XI Объекты, близкие к системам Ляпунова....................324
§ 1.	О системах Ляпунова....................................324
§ 2.	Уравнения движения.................................... 326
§ 3.	Уравнения для определения параметров порождающего реше-
ния. Условие существования синхронных движений..............326
§ 4.	Необходимые условия устойчивости синхронных движений . . 329
ЧАСТЬ IV
ТЕОРИЯ СИНХРОНИЗАЦИИ МЕХАНИЧЕСКИХ ВИБРАТОРОВ
Глава XII. Задача о синхронизации механических вибраторов .... 336
§ 1.	О механических вибраторах..............................336
§ 2.	Основные задачи о синхронизации вибраторов.............360
§ 3.	Краткий обзор исследований в области синхронизации меха-
нических вибраторов........................................ 367
Глава XIII. Синхронизация механических вибраторов в машинах и
установках с плоским движением ..................................372
§	1.	Предварительные замечания...........................372
§	2.	Уравнения движения системы..........................373
§ 3.	Математическая постановка задачи. Введение малого пара-
метра ....................................................  394
§ 4.	Условия существования и основные условия устойчивости
синхронных движений вдали от резонанса. Уравнения для
определения фаз вращения вибраторов в синхронных движе-
ниях ...................................................... 399
§ 5.	Дополнительные условия устойчивости синхронных движений
вдали от резонанса . .с..................................   404
§ 6.	Развернутая форма основных уравнений теории синхрониза-
ции вибраторов и их интерпретация. Вибрационные моменты 415
§ 7.	Различные формы записи и способы вычисления вибрацион-
ных моментов и моментов системы принудительной синхрони-
зации .  ...................................................422
§ 8.	Выражения для вибрационных моментов в некоторых част-
ных случаях ............................................... 425
§ 9.	Потенциальная функция и интегральный критерий устойчиво-
сти синхронных движении вибраторов..........................428
§ 10.	Основные соотношения и общий анализ задачи о самосин-
хронизации вибраторов...................................... 4"2
§ 11.	Основные соотношения и общий анализ задачи о принуди-
тельной синхронизации вибраторов .......................... 440
§ 12.	О комбинировании различных способов синхронизации вибра-
торов ......................................................445
§ 13.	Синхронизация вибраторов, установленных на вибрирующем
органе с одной степенью свободы, в случае резонанса . . . 446
ОГЛ,ХВЛЕ1ШЕ
7
§ 14.	О законе движения системы при установившемся синхронном
вращении вибраторов..........................................464
§ 15.	Условия, при которых ролики или кольца планетарных виб-
раторов движутся без	отрыва	и	скольжения...............467
§	16.	Случай двух вибраторов...............................470
§	17.	Замечания о способе	решения	рассмотренной задачи . . . 492
7 а в а XIV. Обобщения задачи о синхронизации механических вибра-
торов .............................................................493
§ 1.	Предварительные замечания................................493
§ 2.	Общая задача о простой (некратной) синхронизации вибра-
торов ................................................... .  494
§ 3.	Синхронизация вибраторов, связанных с квазилинейной коле-
бательной системой...........................................505
§ 4.	Интегральный критерий устойчивости синхронных движений
механических вибраторов .................................... 514
§ 5.	Решение задачи о синхронизации при квазикоисервативной
идеализации вибраторов. Сравнение с «неквазиконсерватив-
ным» решением................................................517
§ 6.	О кратной синхронизации вибраторов.......................523
§ 7.	О синхронизации вибраторов в системах с соударениями . -.525
§ 8.	Некоторые важные частные случаи, примеры.................527
Глава XV. О синтезе вибрационных машин с механическими вибрато-
рами ..............................................................568
§ 1.	Проблема синтеза вибрационного поля......................568
§ 2.	Синтез вибрационных машин с механическими вибраторами . 571
§ 3.	Обеспечение устойчивости требуемого режима синхронного
вращения вибраторов путем изменения колебательной части
системы......................................................579
§ 4.	Обеспечение устойчивости требуемого режима синхронного
вращения вибраторов путем изменения числа вибраторов . . 589
§ 5.	Оптимальная система связен между роторами вибраторов,
обеспечивающая устойчивость заданного режима вращения . 590
Глава XVI. О стабильности режима колебаний рабочих органов вибра-
ционных машин с механическими вибраторами..........................599
§ 1.	Понятие стабильности режима колебаний вибрационной ма-
шины ......................................................  599
§ 2.	О стабильности режима колебаний вибрационных машин с
несколькими механическими вибраторами........................603
Глава XVII. Взаимодействие механического вибратора с колебательной
системой (случай одного вибратора) ................................ 605
§ 1.	О неприменимости концепции теории вынужденных колебаний
для объяснения некоторых явлений в колебательных системах
с механическими возбудителями. Краткий обзор исследований 605
8
ОГЛАВЛЕНИИ
§ 2.	Основные уравнения в случае одного вибратора..........607
§ 3.	Взаимодействие синхронного вибратора с простейшей колеба-
тельной системой...........................................609
§ 4.	Случай асинхронного вибратора. Эффект Зоммерфельда . . . 614
§ 5.	О динамике регулятора Буасса— Сарда.................. 619
Глава XVIII. Вращение неуравновешенного ротора под действием ко-
лебаний его осн.................................................625
§ 1.	Предварительные замечания. Краткий обзор исследований . . 625
§ 2.	Уравнение движения и постановка задачи................628
§ 3.	Основной режим стационарного вращения рогора..........630
§ 4.	Субротацнонные режимы вращения ротора.................641
§ 5.	Связь между задачей о движении вибратора с колеблющейся
осью и задачей о синхронизации вибраторов...............  .	650
§ 6.	Об условиях возбуждения стационарных режимов вращения 654
Глава XIX. Экспериментальные исследования синхронизации вибра-
торов ...........................................................659
§ 1.	Предварительные замечания. Цели экспериментального иссле-
дования ................................................   659
§ 2.	Описание экспериментальных установок и техники экспери-
ментов ....................................................660
§ 3.	Проверка некоторых выводов теории самосинхронизации виб-
раторов ...................................................665
§ 4.	Исследование режимов установления синхронного вращения
вибраторов ................................................672
§ 5.	Краткий обзор других экспериментальных исследовании. За-
ключение ...............................................   683
ЧАСТЬ V
ПРИЛОЖЕНИЯ ТЕОРИИ СИНХРОНИЗАЦИИ
МЕХАНИЧЕСКИХ ВИБРАТОРОВ
Глава XX. Вибрационные грохоты, конвейеры, питатели и дозаторы;
вибрационные площадки и некоторые другие машины . . , 686
§ 1.	О возможностях использования эффекта самосинхронизации
для получения прямолинейных, круговых, эллиптических, вин-
товых и поворотных колебаний рабочего органа вибрационной
машины.....................................................686
§ 2.	О стабильности колебаний рабочих органов некоторых вибра-
ционных машин с самосинхронизирующимися вибраторами . . 695
§ 3.	О необходимых условиях нормальной работы некоторых виб-
рационных машин со многими вибраторами, приводимыми от
синхронных электродвигателей...............................712
§ 4.	Вибрационные грохоты с самосинхронизирующимися вибрато-
рами ......................................................720
ОГЛАВЛЕНИЕ
9
§ 5.	Вибрационные конвейеры с самоспнхроппзирующимися и с
принудительно синхронизированными вибраторами................729
§ 6.	Вибрационные питатели с самоспнхроппзирующимися вибра-
торами . . ..................................................737
§ 7.	Вибрационные площадки с самосипхроиизирующимнся и при-
нудительно синхронизированными вибраторами...................739
§ 8.	Универсальный вибрационный стенд с самосиихропизнрующи-
мися вибраторами.............................................740
Глава XXI. Вибрационные дробильно-измельчительные машины . . . 742
§ I.	Инерционная дробилка и вибрационные измельчители институ-
та «Мехапобр». Связь их теории с теорией самосинхрониза-
ции вибраторов............................................  .	742
§ 2.	Критическая щель инерционной дробилки и некоторых других
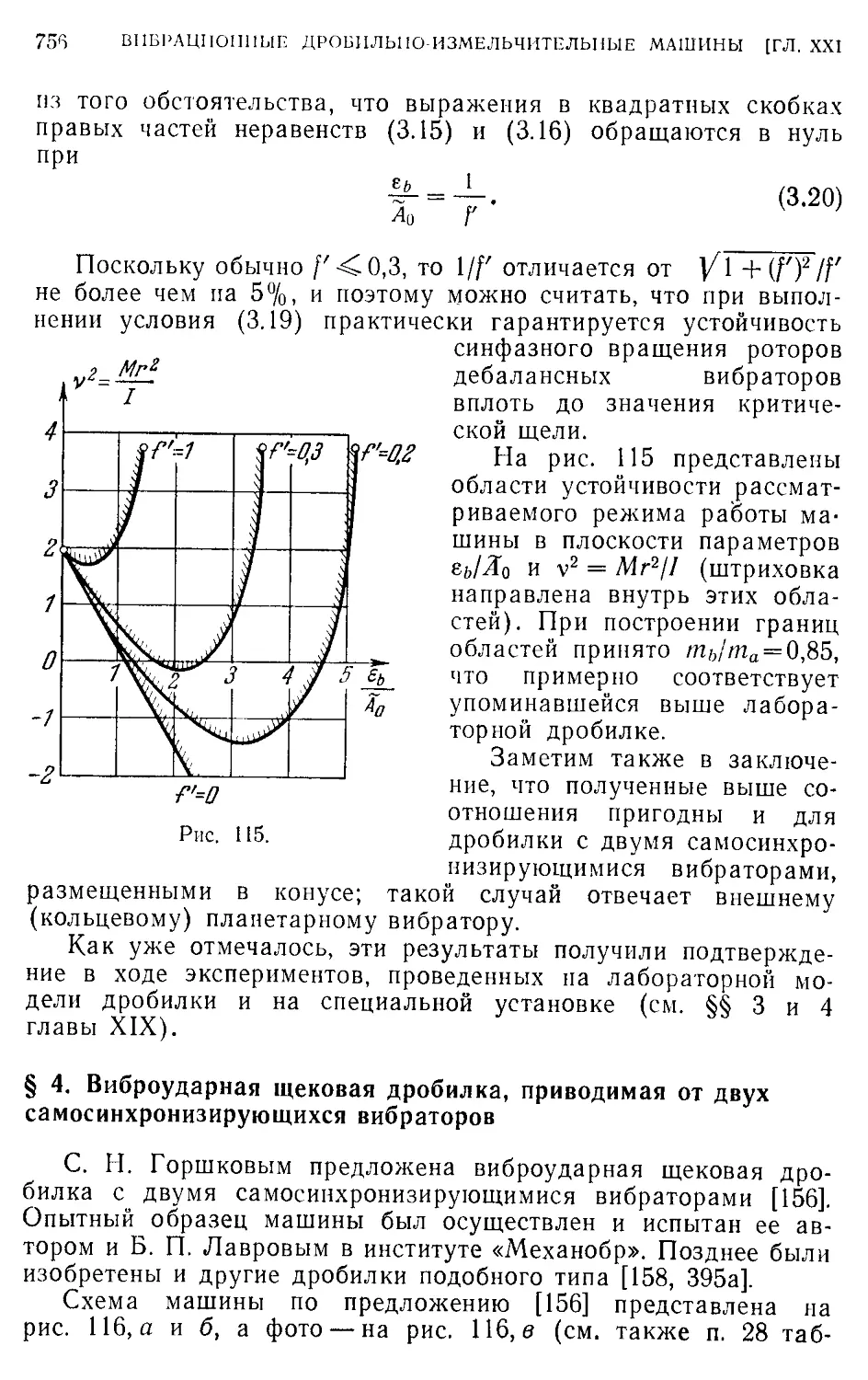
машин........................................................748
§ 3.	Инерционные дробилки, приводимые от двух самоспнхрони-
зпрующихся вибраторов........................................750
§ 4.	Впброударпая щековая дробилка, приводимая от двух само-
сиихронизпрующихся вибраторов  ..............................756
§ 5.	Вибрационные шаровые мельницы с самосннхроиизнрующп-
мися или принудительно синхронизированными вибраторами . 763
Глава XXII. Вибрационные погружатели свай, шпунта и оболочек . . 766
§ 1.	Об особенностях использования самосннхронизнрующихся или
принудительно синхронизированных вибраторов в изучаемом
классе машин...............................................  766
§ 2.	О невозможности использования двух самосиихронизирующих-
ся вибраторов в простейшем вибропогружателе с продольными
колебаниями..................................................766
§ 3.	Вибропогружатель с самосинхронизирующимися вибраторами,
установленными па мягко амортизированной платформе . . . 768
§ 4.	О некоторых возможностях использования самосннхронизи-
рующихся вибраторов при погружении оболочек..................770
Глава XXIII. Групповые фундаменты под неуравновешенные машины 774
§ 1.	Проблема групповых фундаментов с точки зрения теории син-
хронизации вибраторов. Общий план теоретического исследо-
вания .......................................................774
§ 2.	Одно следствие из интегрального критерия устойчивости син-
хронных движений вибраторов . ...............................777
§ 3.	Пример: фундамент под две машины, развивающие неуравно-
вешенные силы постоянного направления ...................... 778
§ 4.	О случае, когда машины приводятся от синхронных двига-
телей .....................................................  788
10
ОГЛАВЛЕНИЕ
ЧАСТЬ VI
НЕКОТОРЫЕ ДРУГИЕ ПРИЛОЖЕНИЯ ТЕОРИИ
СИНХРОНИЗАЦИИ ДИНАМИЧЕСКИХ СИСТЕМ
Глава XXIV. Системы с вращающимися роторами..........................791
§ 1.	Автоматический балансир для уравновешивания вращающихся
роторов ................................................ 791
§ 2.	Вращающийся ротор с маятниковыми подвесками................797
§ 3.	Вращающийся гибкий вал с неуравновешенными дисками . . 803
Глава XXV. Системы со слабо связанными квазилинейными осцилля-
торами .......................................................808
§ 1.	Взаимная синхронизация слабо связанных осцилляторов Ван-
дер-Поля..............................................   808
§ 2.	Взаимная синхронизация маятниковых часов (задача Гюй-
генса) ...............................................   815
§ 3.	Синхронные колебания в..системе	со	многими	электромагнит-
ными возбудителями	 	820
Добавление 1. Методика исследования синхронизации механических
вибраторов..................................................826
§ 1.	Основной случай.....................................826
§ 2.	Более сложные случаи................................833
§ 3.	Об исследовании стабильности	рабочего	режима колебаний	.	.	835
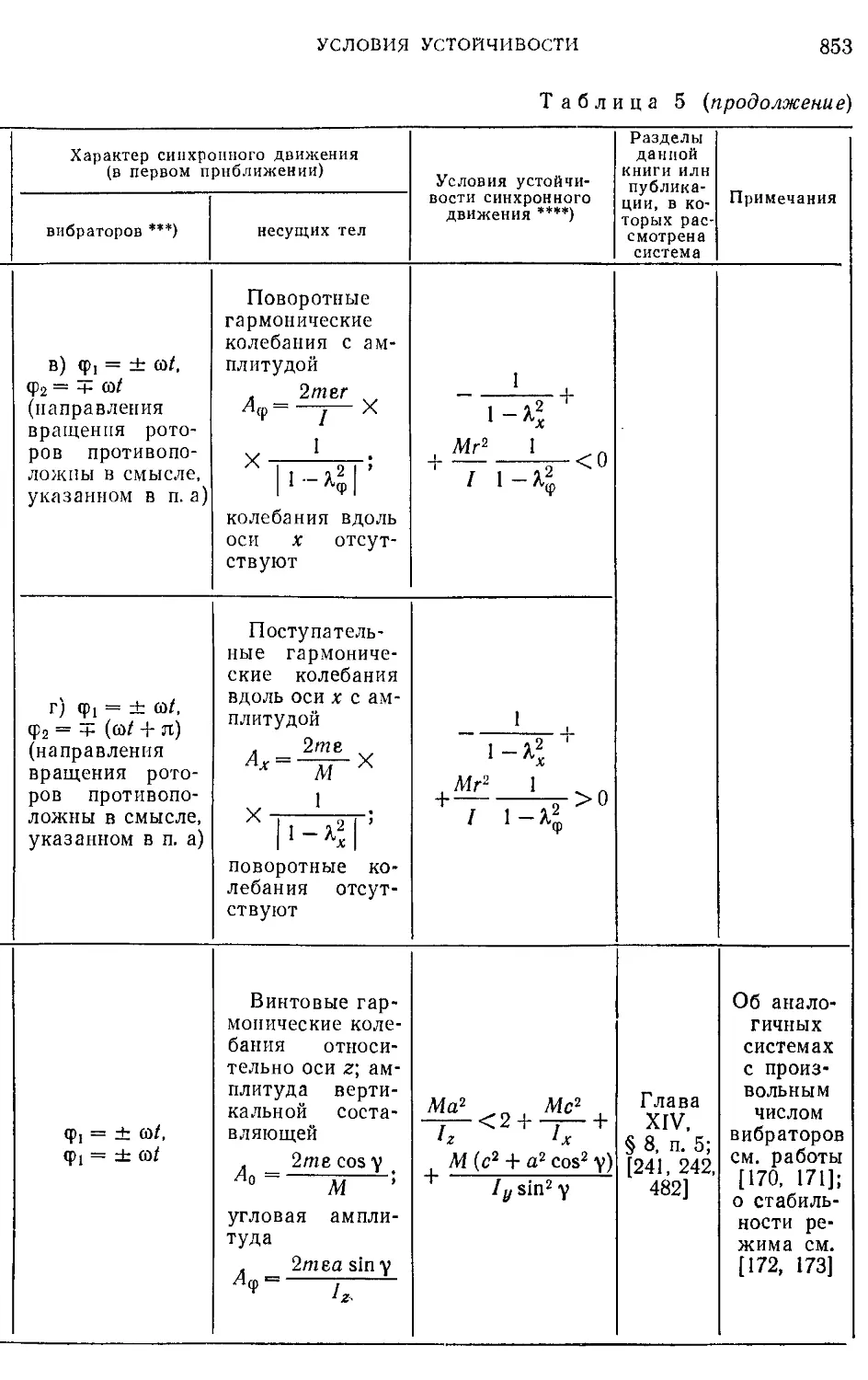
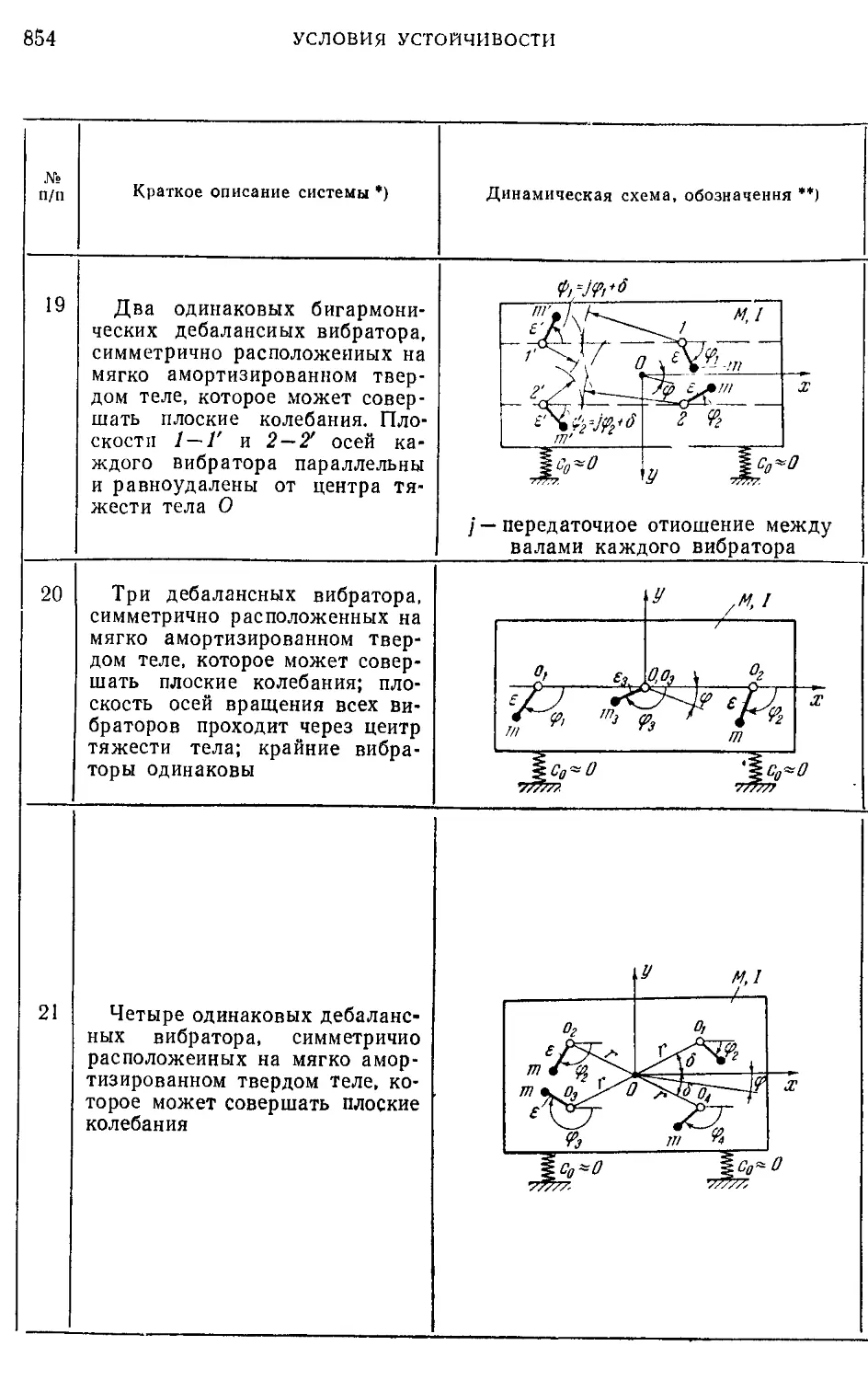
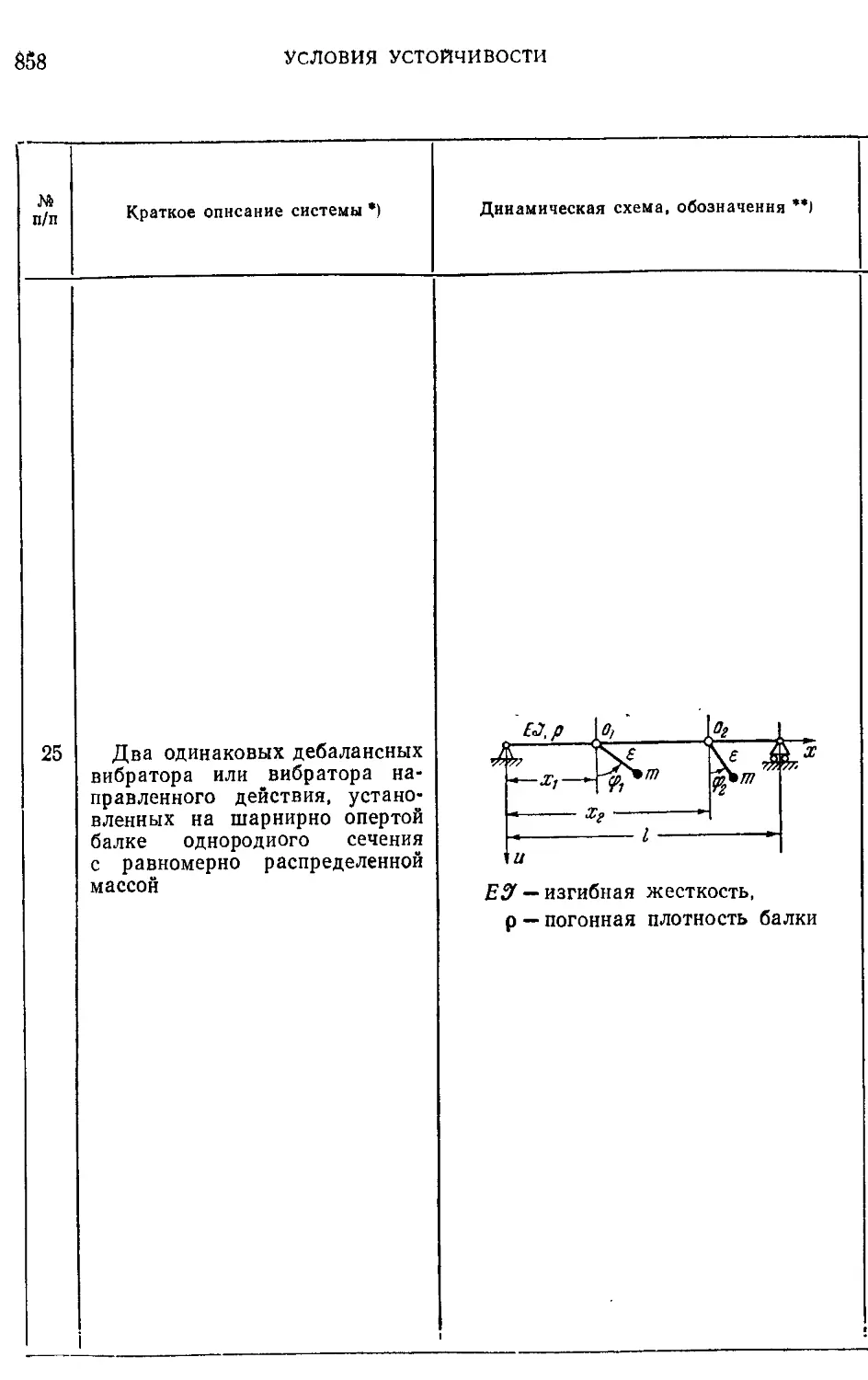
Добавление 2. Условия устойчивости важнейших синхронных дви-
жений вибраторов в некоторых колебательных си-
стемах .......................................................836
Литература...........................................................864
Именной указатель................................................... 888
Предметный указатель.................................................892
Доброй памяти моих родителей.
Автор
ПРЕДИСЛОВИЕ
В настоящей книге делается попытка систематического из-
ложения фактов и результатов, относящихся к быстро развиваю-
щейся области науки и техники — синхронизации динамических
систем.
Грубо говоря, синхронизацию можно определить как свой-
ство материальных объектов самой различной природы выраба-
тывать единый ритм совместного существования, несмотря на
различие индивидуальных ритмов и на подчас крайне слабые
взаимные связи. Это удивительное свойство, заслуживающее,
как нам представляется, обсуждения с философских позиций,
находит свое отражение в свойстве нелинейных дифференциаль-
ных уравнений некоторого определенного вида допускать устой-
чивые периодические решения. Синхронизация, по-видимому,
представляет собой одну из форм самоорганизации материи, и
поэтому с определенной точки зрения изучаемую проблему мож-
но рассматривать как относящуюся к кибернетике.
Нет ничего странного в том, что два вала, связанные парой
одинаковых зубчатых колес, вращаются с одинаковыми угло-
выми скоростями, — это синхронизация посредством «сильных»,
жестких связей. Однако когда, например, двое маятниковых
часов, ходивших по-разному, начинают ходить совершенно оди-
наково (синхронно), если их подвесить к общей подвижной бал-
ке вместо стены, то это воспринимается как парадокс. Здесь
синхронизация осуществляется посредством «слабой» связи —
едва заметных колебаний балки. (Говорят, что этот эффект,
описанный X. Гюйгенсом еще в начале второй половины сем-
надцатого столетия, недобросовестные часовщики не раз исполь-
зовали для обмана доверчивых клиентов.)
Тенденция к синхронизации при наличии слабых связей свой-
ственна ,очень многим техническим объектам, например близко
расположенным органным трубам, неуравновешенным машинам,
размещенным на общем фундаменте, электрическим генерато-
рам, работающим на общую нагрузку; она характерна и для
жизнедеятельности живых организмов.
С момента опубликования Гюйгенсом его знаменитых мемуа-
ров прошло более трехсот лет. В настоящее время явление син-
хронизации широко используется в технике, например в электро-
п радиотехнических устройствах и в вибрационных машинах;
12
ПРЕДИСЛОВИЕ
оно объясняет также своеобразие поведения ряда биологических
систем. В различных изданиях, особенно за последние годы,
опубликовано много статей, посвященных отдельным частным
задачам теории синхронизации. Однако данная книга представ-
ляет собой, по-видимому, первую попытку изложения различных
аспектов проблемы синхронизации с единой точки зрения.
Автор стремился прежде всего подчеркнуть общность явле-
ний синхронизации объектов самой различной природы. Пони-
мание этой общности, возможно, будет способствовать тому, что-
бы достижения в одной из областей стали достоянием других
областей.
Особенности предмета предопределили структуру книги, со-
стоящей из шести частей.
Во введении и в первой части сообщается об основных прояв-
лениях эффекта синхронизации в природе и в технике и дается
постановка ряда прикладных задач теории синхронизации. Пос-
ле этого формулируется общая задача о синхронизации и рас-
сматриваются ее характерные особенности. Вторая часть посвя-
щена изложению и развитию математического аппарата теории;
таким аппаратом в данной книге является теория периодических
решений нелинейных дифференциальных уравнений, содержа-
щих малый параметр. В третьей части указанный аппарат ис-
пользуется для исследования синхронизации некоторых основ-
ных общих классов слабо связанных динамических объектов.
Первые три части книги адресованы главным образом иссле-
дователям, работающим в различных областях прикладной ма-
тематики и механики, в особенности специалистам по теории не-
линейных колебаний. Возможно, они окажутся полезными и для
математиков, занимающихся теорией дифференциальных урав-
нений и ищущих области приложения своих знаний и усилий.
Последующие три части посвящены применению изложенных
ранее общих результатов к решению прикладных задач теории
синхронизации.
Наибольшее внимание здесь уделено теории синхронизации
механических вибраторов (четвертая часть), получившей в пос-
ледние годы значительное развитие и послужившей источником
многих изобретений. Приложения теории к созданию новых п
усовершенствованию существующих вибрационных машин, а
также к проектированию групповых фундаментов под неурав-
новешенные машины являются предметом пятой части книги.
Четвертая и пятая части предназначены главным образом для
исследователей-механиков и конструкторов вибрационных
устройств. Эти специалисты могут без ущерба для понимания
начать изучение книги непосредственно с ее четвертой части.
К тому же, чтобы облегчить использование результатов иссле-
дования инженерами, заинтересованными только приложения-
ПРЕДИСЛОВИЕ
13
ми, эти результаты сведены в обширную таблицу (таблица 5
Добавления 2), содержащую около тридцати схем устройств
с самосинхронизирующимися или принудительно синхронизируе-
мыми вибраторами. Приведена также методика получения усло-
вий синхронизации вибраторов, не предполагающая знания тео-
рии в полном объеме (Добавление 1).
В заключительной, шестой части книги рассмотрен ряд дру-
гих прикладных задач теории синхронизации, в частности за-
дача об автоматических балансировочных устройствах, об изгиб-
но-крутильных колебаниях вала с неуравновешенными дисками
и упоминавшаяся выше задача о маятниковых часах.
Большая часть книги основана на результатах, полученных
автором и его коллегами Б. П. Лавровым, Р. Ф. Нагаевым и
К. III. Ходжаевым в 1953—1969 гг.В ней, однако, нашли свое
отражение и работы других исследователей.
Как указывалось, в прикладных разделах книги наибольшее
внимание уделено проблеме синхронизации механических вибра-
торов. Это, однако, вовсе не означает, что другие, лишь конспек-
тивно рассмотренные задачи имеют меньшее прикладное значе-
ние. К тому же автор убежден, что изложенные в книге методы
и многие результаты могут быть с успехом применены для не
менее подробного развития теории синхронизации электрических
устройств, а также для рассмотрения вопросов функционирова-
ния биологических объектов.
В книге почти не затронут весьма интересный и важный во-
прос о синхронизации объектов при наличии случайных воздей-
ствий; этот пробел в определенной мере восполняется недавно
появившейся монографией А. Н. ^Малахова [265].
Автору приятно, что излагаемое в книге учение о синхрони-
зации оптимистично: оно подчеркивает наличие в окружающем
нас мире ярко выраженных тенденций к градации и порядку, а
не только противоположных тенденций, существование которых
отражается вторым началом термодинамики.
Автор огорчен, что книга — возможно, из-за многоплановости
темы — получилась толстой: как и большинство людей, он лю-
бит тонкие книги на научные темы. Хотелось бы надеяться, что
этот недостаток все же не помешает читателям испытать то же
чувство восторженного удивления перед любопытнейшими зако-
номерностями явлений синхронизации, которое было испытано
им самим в процессе работы над проблемой. Для того чтобы
описания этих закономерностей не затерялись в глубине текста,
наиболее интересные факты изложены во введении с использо-
ванием минимума математических средств и без претензии на
строгость.
Несколько слов о терминологии. Под синхронизацией (а так-
же взаимной или внутренней синхронизацией) мы понимаем
14
ПРЕДИСЛОВИЕ
здесь наиболее общий случай, когда определенные частотные
соотношения устанавливаются в результате взаимодействия объ-
ектов, рассматриваемых как равноправные. В идеализированном
же случае, когда один из объектов считается настолько мощ-
ным, что он навязывает свой ритм движения (предполагаемый
заранее заданным и неизменным) другим автоколебательным
объектам, будем говорить о явлении захватывания или о внеш-
ней синхронизации, причем первый термин будем употреблять
в случае одного синхронизируемого объекта. Отметим, что в ли-
тературе, говоря о синхронизации, часто имеют в виду только
захватывание.
В книге применена сквозная нумерация глав и нумерация
параграфов по главам. При этом нумерация формул указывает
лишь на номер параграфа (первая цифра) и на номер формулы
(вторая цифра). Если ссылка дается на формулу внутри главы,
то ее номер не указывается; это делается лишь при ссылках на
формулы других глав.
Интерес автора к работ'е над проблемами синхронизации ви-
браторов пробудил изобретатель, исследователь и конструктор
вибрационных машин Д. А. Плисс. Г. А. Финкельштейн под-
держал эти исследования на том этапе, когда их прикладное
значение было далеко не очевидным. Б. П. Лавров воплотил в
реальные конструкции ряд туманных мыслей автора в области
синхронизации вибраторов, а затем выдвинул и осуществил
много собственных плодотворных идей.
Большое значение для автора имела возможность постоянно-
го общения со своими учителями А. И. Лурье и Г. 10. Джане-
лидзе, а также частые беседы с Я- Г. Пановко.
Существенное влияние на характер и содержание ряда раз-
делов книги оказал непрерывный творческий контакт с веду-
щими конструкторами и исследователями вибрационных машин:
Э. А. Аграновской, И. И. Быховским, Г. А. Денисовым, Б. Н. Ду-
бровиным, В. В. Дубровиным, А. И. Макаровым, Р. Ф. Нагае-
вым, Г. И. Николенко, В. А. Олевским, А. Д. Рудиным, К. А. Рунд-
квистом, А. К- Рундквистом, О. А. Савиновым, К. Ш. Ходжаевым.
Руководители института «Механобр» неизменно интересова-
лись исследованиями по синхронизации вибраторов и по мере
возможности поддерживали соответствующие разработки.
Значительную помощь в подготовке публикаций, лежащих
в основе книги, оказал Н. А. Талицких.
Много ценных замечаний сделал редактор книги М. 3. Ко-
ловский.
Всем этим лицам автор выражает свою глубокую благодар-
ность.
4 ноября 1969 г.	И. И. Блехман
Ленинград.
ВВЕДЕНИЕ
§ 1. Проблема синхронизации динамических систем
1. О явлениях синхронизации. Явление синхронизации состо-
ит в том, что несколько искусственно созданных или природных
объектов, совершающих при отсутствии взаимодействия коле-
бательные или вращательные движения с различными часто-
тами (угловыми скоростями), при наложении подчас весьма
слабых связей начинают двигаться с одинаковыми, кратными
или находящимися в рациональных отношениях частотами (уг-
ловыми скоростями), йричем устанавливаются определенные
фазовые соотношения между колебаниями и вращениями.
Частные случаи синхронизации давно известны. Еще в на-
чале второй половины семнадцатого столетия Христиан Гюй-
генс установил, что пара часов, ходивших по-разному, самосин-
хронизировалась, когда их прикрепляли к легкой балке вместо
стены. В одном из своих мемуаров [164] Гюйгенс описывает
сделанное им во время одного из плаваний наблюдение следую-
щим образом:
«Маятник этих часов имел длину 9 дюймов и груз полфунта.
Механизм приводился в движение гирями, заключенными в
ящик вместе с механизмом. Длина ящика была 4 фута. Внизу
он был отягчен по крайней мере 100 фунтами свинца, чтобы
весь механизм возможно лучше сохранял в судне вертикаль-
ное положение... С этими часами было сделано следующее чрез-
вычайно интересное наблюдение.
Двое таких часов висели на одной и той же балке, покоящей-
ся на двух опорах. Оба маятника двигались всегда в противо-
положные стороны, и колебания так точно совпадали, что ни-
когда пи насколько не расходились. Тиканье обоих часов было
слышно в одно и то же мгновение. Если искусственно нарушить
это совпадение, то оно само восстанавливалось в короткое вре-
мя. Сначала я был поражен этим странным явлением, но на-
конец, после внимательного исследования, нашел, что причина
лежит в незаметном движении самой балки. Колебания маят-
ника сообщают некоторое движение и самим часам, как бы тя-
желы они пи были. А это движение передается балке, и если
маятники сами не двигались в противоположных направлениях,
16
ВВЕДЕНИЕ
то теперь это произойдет с необходимостью, и только тогда дви-
жение балки прекратится. Но эта причина не была бы доста-
точно эффективна, если бы ход обоих часов не был бы с самого
начала очень однороден и согласован».
Приходится поражаться точности и глубине этого описания,
сделанного в эпоху, когда еще не были точно сформулированы
основные законы механики. Естественно, однако, что количест-
венного исследования открытого явления Гюйгенс выполнить
не мог.
Фото устройства с маятниками, воспроизведенного в инсти-
туте «Механобр» (Ленинград), приводится на рис. 11,6 и в. Как
видно из фотографии, устойчивыми, при определенных условиях,
являются не только противофазные колебания маятников, на-
блюдавшиеся Гюйгенсом, но также и синфазные колебания;
к такому заключению приводит и теоретическое исследование
(см. § 2 главы XXV).
Синхронизацию в акустических и электроакустических си-
стемах обнаружил Рэлей в конце XIX века. Наблюдая две
органные трубы с расположенными рядом отверстиями, он
установил, что при достаточно малой расстройке они звучат в
унисон, то есть происходит взаимная синхронизация обеих авто-
колебательных систем. Иногда при этом трубы могут заставить
почти полностью «замолчать» одна другую.
Аналогичное явление было обнаружено Рэлеем и для двух
камертонов с электромагнитным возбуждением, связанных меж-
ду собой либо электрически, либо механически — при помощи
упругой нити, — либо, наконец, посредством резонаторного ящи-
ка [386].
Позднее, примерно в начале текущего столетия, явления син-
хронизации были открыты в электрических цепях и в некоторых
электромеханических системах. С этими объектами до недав-
него времени были связаны главные технические приложения
явлений синхронизации (синхронизация электрических генера-
торов, синхронизация ламповых генераторов в радио- и телеви-
зионных устройствах).
Наконец, в 1947—1948 гг. в СССР было обнаружено явление
самосинхронизации механических дебалансных вибраторов, ус-
тановленных на одном вибрирующем органе [44, 77, 78, 339]; че,-
рез несколько лет — в 1950—1956 гг. — появились первые публи-
кации (в виде патентных описаний) и за рубежом [451, 474, 478,
479, 483, 485]. Оказалось, что вибраторы, представляющие со-
бой в простейшем случае неуравновешенные роторы, приводи-
мые от каких-либо двигателей асинхронного типа, при опреде-
ленных условиях работают синхронно, несмотря на возможное
различие параметров вибраторов и на отсутствие каких-либо
кинематических или электрических связей между их роторами.
I
ПРОБЛЕМА СИНХРОНИЗАЦИИ ДИНАМИЧЕСКИХ СИСТЕМ
17
В настоящее время самосинхронизация, а также родственное
ей явление вибрационного поддержания вращения неуравнове-
шенных роторов находит все более широкое применение в но-
вых конструкциях вибрационных машин, выпускаемых как
в СССР, так и за его пределами.
В Советском Союзе предложен и ряд способов принудитель-
ной электрической синхронизации и фазировки вращения ви-
браторов [326, 52, 58, 242]. Эффект вибрационного возбуждения
и поддержания вращения, по существу, используется также
в ядерной технике при создании циклических ускорителей заря-
женных частиц — синхротронов, фазотронов, синхрофазотронов
и других [100, 122—124, 60].
Эффекты взаимной синхронизации были обнаружены и в по-
ведении биологических объектов [497, 141, 460]. Н. Винер пола-
гал, что явление синхронизации лежит в основе возникновения
альфа-ритмов головного мозга, а также высказал далеко иду-
щие предположения о роли этого явления в процессах само-
организации и самовоспроизведения некоторых биологических
объектов, в частности в процессах развития злокачественных
опухолей [127—129].
Н. Винеру принадлежит и мысль о том, что определенные
закономерности распределения периодов обращения астероидов
объясняются «возможным притяжением частот», то есть, по су-
ществу, также тенденцией к синхронизации.
В своеобразной форме явления синхронизации наблюдаются
и в поведении коллективов людей. В качестве простейших при-
меров можно указать на скандированные аплодисменты ауди-
тории и на хождение строем «в ногу».
Сказанное подтверждает, что тенденция к синхронизации
является своеобразной закономерностью поведения материаль-
ных объектов самой различной природы. Несомненно, что такая
закономерность представляет собой одно из проявлений тенден-
ции материальных форм к самоорганизации. Эта последняя
более общая закономерность не раз отмечалась представите-
лями различных наук. Процитируем в качестве примера выска-
зывания известного американского астронома X. Шепли [425а, б]:
«Живое п неживое обладает тенденцией к организации...
Основной тенденцией природы является все более и более вы-
сокая степень организации. Можно проследить непрерывную
последовательность организации от атома до Метагалактики...»
«Классифицируя звездные скопления, мы прежде всего ясно
отметим, что тысячи случаев неравномерного распределения
звезд, которые можно обнаружить в густо усеянных звездами
областях Млечного Пути, должны рассматриваться как отдель-
ные группы п классифицироваться поэтому наряду с явными,
«открытыми» звездными скоплениями.
18
ВВЕДЕНИЕ
Легко показать на основании законов теории вероятности,
что случайное распределение звезд в пространстве дало бы нам
некоторую неравномерность в распределении на любой малой
области неба. Но те случаи неравномерного распределения, ко-
торые мы на деле наблюдаем во многих областях, далеко пре-
восходят все то, что дозволяется законами теории вероятности.
Иногда это можно объяснить присутствием темных туманно-
стей, закрывающих звезды, но большая часть звездных полей
неравномерной плотности должна быть приписана едва выра-
женной тенденции к группировкам, которая представляет собой
слабый намек на организацию, намек на следы когда-то суще-
ствовавших систем и на зачатки новых, более определенных
скоплений».
Наиболее обобщенное отражение тенденция материальных
форм к самоорганизации нашла в концепциях кибернетики—
«науки о связи, управлении и организации в природе, технике
и обществе» [126]. К одной из специальных проблем этой науки
можно отнести и проблему синхронизации.
2. Задачи о синхронизации в технике и науке. Самосинхро-
низация и принудительная синхронизация. Сделанный краткий
обзор истории открытия и технического использования синхро-
низации динамических систем убедительно показывает, что про-
блема синхронизации рано или поздно возникает всюду, где име-
ются колебательные процессы; от эффективности решения этой
проблемы зачастую существенно зависит прогресс в определен-
ной области техники. Сказанным и определяется ее большое
практическое и теоретическое значение.
Технические задачи синхронизации представляют собой ча-
стный случай более общей проблемы — обеспечения согласован-
ного функционирования нескольких однотипных объектов.
Синхронизация динамических объектов осуществляется по-
средством имеющихся между ними связей (в широком смысле
этого слова). При этом в некоторых случаях синхронизация и
фазировка имеют место в силу уже присутствующих в системе
естественных связей. Так, например, в задаче о синхронизации
генераторов электрических или механических колебаний синхро-
низация зачастую осуществляется за счет свойств самой систе-
мы генератор — нагрузка. Такой тип синхронизации обычно
называют самосинхронизацией. В других случаях эффект син-
хронизации и фазпровки достигается путем введения дополни-
тельных синхронизирующих элементов {принудительная синхро-
низация) .
Как уже отмечалось, наибольший интерес представляют слу-
чаи слабых связей между объектами.
Важнейшими примерами современных прикладных задач
о синхронизации являются:
иг, ИССЛЕДОВАНИЯХ В ОБЛАСТИ СИНХРОНИЗАЦИИ
19
1.	Получение условий синхронизации и надлежащей фазп-
ровкп механических вибраторов — одна из узловых проблем,
возникающих при разработке новых типов современных вибра-
ционных машин (грохотов, конвейеров, дробилок, мельниц и
Других).
2.	Исследование условий устойчивой параллельной работы
нескольких синхронных электрических генераторов на общую
нагрузку; эта задача приобретает особое значение в связи
с объединением сложных энергетических систем.
3.	Получение условий синхронизации и определенной фази-
ровки автоколебаний, возбуждающихся в нескольких ламповых
пли молекулярных генераторах.
К этому же классу задач приводятся исследование работы
некоторых типов ускорителей заряженных частиц, изучение сов-
местных изгибно-крутилытых колебаний вращающихся валов
с неуравновешенными дисками, анализ динамики специальных
автоматических балансиров для компенсации неуравновешенно-
стей быстро вращающихся роторов, изучение поведения несколь-
ких неуравновешенных машин, установленных на общем фунда-
менте или на связанных между собою опорных сооружениях,
исследование принципов работы ряда акустических приборов,
в частности особенностей звучания некоторых музыкальных ин-
струментов, исследование совместного функционирования не-
скольких взаимно связанных однотипных биологических систем.
§ 2.	Об исследованиях в области синхронизации
Из конкретных проблем синхронизации до недавнего време-
ни наибольшее число исследований было посвящено задаче о
совместной параллельной работе нескольких синхронных элек-
трических машин*). В числе первых публикаций по этому во-
просу необходимо упомянуть труды Ф. Оллендорфа и В. Петерса
[471] (1925—1926 гг.), Н. М. Крылова и Н. И. Боголюбова [231]
(1932 г.), П. С. Жданова и С. А. Лебедева [188, 189] (1940—
1948 гг.), А. А. Горева [151, 152] (1950 г.); позднее были опубли-
кованы исследования В. А. Андреюка [14], Г. В. Ароновича [21],
Д. Н. Быстрицкого [112], В. Витека [130], В. М. Горнштейна [154],
Л. А. Жукова и А А. Хачатурова [190], Б. С. Иноземцева [197],
И. А. Картвелишвили [205—207], Э. Кимбарка [211], М. П. Кос-
тенко [228], В. М. Матюхина [288, 289], Г. В. Михневича и
Г. Ф. Козловского [298, 299], В. Т. Морозовского [305], В. И. Пи-
щикова и И. И. Соколова [337], М. И. Розанова [359], Р. Рюден-
берга [371], И. А. Сыромятникова [389], Л. В. Цукерника [419,
*) Необходимо отметить, что в электротехнике термин «синхронизация»
обычно употребляется в несколько ином смысле.
20
ВВЕДЕНИЕ
420], А. А. Япко-Триницкого [441] и других авторов. Обстоятель-
ную библиографию и характеристику состояния вопроса можно
найти в работах [205, 211, 371] (см. также § 5 главы I).
В перечисленных исследованиях был получен ряд весьма су-
щественных результатов, однако многие важные стороны про-
блемы, ввиду их крайней сложности, до сих пор остаются не-
изученными. В частности, почти не рассмотрены несимметрич-
ные режимы работы машин и вообще случаи, когда переходные
процессы описываются уравнениями с периодическими коэффи-
циентами.
Большой цикл работ посвящен задаче о синхронизации лам-
повых генераторов, применяемых в различных радиотехнических
устройствах, в частности и проблеме синхронизации систем ти-
па нелинейных осцилляторов вообще.
Первоначально эти задачи рассматривались в весьма упро-
щенной постановке—в виде задач о захватывании. Явление за-
хватывания заключается в том, что при определенных условиях
автоколебательная система, на которую действует внешняя воз-
мущающая (сила периода То, совершает устойчивые колебания
с периодом Т = plqt0, где р и q— целые положительные числа.
Работы по теории захватывания, принадлежащие Эпплтону [443]
(1922 г.), Ван-дер-Полю [119] (1927—1934 гг.), А. А. Андронову
и А. А. Вигту [15, 19] (1930 г.), сыграли важную роль в разви-
тии общей теории нелинейных колебаний.
Из дальнейших многочисленных исследований в этом направ-
лении можно упомянуть статьи К. К. Теодорчика и С. Э. Хай-
кина [390], И. Берштейна и Е. Иконникова [41], А. Г. Майера
[262], Н. М. Крылова, Н. Н. Боголюбова и Ю. А. Митропольско-
го [232, 94—97], И. Г. Малкина [268, 274], Н. В. Бутенина [109,
111], Н. Н. Баутина [31], Л. И. Холоденко [412], А. Н. Малахова
[265], Р. Шалеа [424], Н. Минорского [292], Ж. Хаага [461—463],
В. С. Лауда [249]; см. также монографию Л. Чезари [419]. В цити-
рованных работах (и особенно в [19, 96, 265]) можно найти более
полные библиографические данные, Р. Фора [456].
В работах по теории захватывания, если их рассматривать
€ позиций общей теории синхронизации, изучен вырожденный ча-
стный случай — задача о внешней синхронизации лишь одного
автоколебательного объекта (см. § 3 введения). Естественно, что
сведение задачи о синхронизации к задаче о захватывании воз-
можно далеко не всегда. Поэтому в последнее время появляется
все больше работ, где вопрос рассматривается в более полной
постановке. Одними из первых исследований этого направления
являются статьи В. И. Гапонова [139], А. С. Бремзена и
И. С. Файнберга [102], Н. И. Есафова [187]; краткий обзор упо-
мянутых и других работ приведен в § 6 первой главы настоящей
книги.
$ 2J	ОБ ИССЛЕДОВАНИЯХ В ОБЛАСТИ СИНХРОНИЗАЦИИ	21
В связи с созданием приборов и устройств, основанных на
использовании квантовых генераторов радио- и оптического диа-
пазонов (так называемых лазеров и мазеров), начали появлять-
ся исследования, посвященные синхронизации подобных генера-
торов. Одной из первых работ в этой области была статья
П. К- Манешина и Р. В. Хохлова [280] (1958 г.).
Своеобразный класс задач о синхронизации в радиоэлектро-
нике представляют задачи теории фазовой автоподстройки ча-
стоты. Обзор состояния этого вопроса и библиографические
данные приводятся в монографии В. В. Шахгильдяна и А. А. Ля-
ховкина [425].
В 1953 г. появилась статья автора [44], посвященная изуче-
нию явления самосинхронизации механических вибраторов. С тех
пор было опубликовано много исследований по теории синхро-
низации вибраторов и сделан ряд изобретений, нашедших про-
мышленное применение. Краткий обзор соответствующих работ
приведен в § 3 главы XII настоящей книги.
Наконец, для последних лет характерно повышение интереса
к проблемам синхронизации в биологии и медицине. Начало
этим исследованиям было положено трудами Ван-дер-Поля и
Вап-дер-Марка [495] (1928 г.), В. Вольтерра [497] (1931 г.),
Г. Ф. Гаузе и А. А. Витта [141] (1934 г.). Обзор работ этого
направления и краткое обсуждение ряда высказанных до-
статочно смелых гипотез о синхронизационном механизме не-
которых биологических явлений приведены в §§ 8 и 9 главы
первой.
Для последнего времени характерно также совершенствова-
ние и развитие основного математического аппарата теории син-
хронизации динамических систем — теории периодических реше-
ний нелинейных дифференциальных уравнений, содержащих ма-
лый параметр. Обзор соответствующих работ, в основе которых
лежат классические сочинения А. Пуанкаре и А. М. Ляпунова,
приведен в § 4 главы III книги. К упомянутым математическим
исследованиям примыкают работы, посвященные изучению син-
хронизации отдельных общих классов динамических объектов
[62, 68, 93, 309—312, 316, 411].
Анализу различных частных задач и постановке общей за-
дачи о синхронизации динамических систем посвящена работа
автора [74].
Из приведенного весьма краткого обзора видно, что все воз-
растающий поток публикаций в области синхронизации динами-
ческих систем рассредоточен по многим периодическим и эпи-
зодическим изданиям. Исследования синхронизации различных
технических объектов часто выполняются изолированно, без уче-
та достижений в смежных областях, и с использованием не
наиболее подходящего математического аппарата. Поэтому
22
ВВЕДЕНИЕ
настоящая книга и посвящена (с оговорками, сделанными в
предисловии) попытке систематического изложения проблем
синхронизации динамических систем с единой точки зрения.
§ 3.	Обзор основных фактов и результатов,
изложенных в книге
1.	Общая постановка и главные особенности задачи о син-
хронизации динамических систем. В весьма распространенном,
хотя и не в самом общем случае задача о синхронизации ста-
вится следующим образом. Пусть имеется некоторое число k
автоколебательных объектов, которые при отсутствии взаимных
связей могут совершать движения с некоторыми «индивидуаль-
ными» частотами (угловыми или линейными скоростями) ид
величины (os естественно назвать парциальными частотами (ско-
ростями) объектов. Задача заключается в нахождении усло-
ви^, при которых после установления связей между объектами
последние будут совершать движения с одинаковой частотой
(скоростью) и или же с частотами (скоростями) вида nsw, где
ti„— взаимно простые положительные целые числа. Соответст-
вующие движения назовем синхронными, причем в случае, когда
все ns= 1, будем говорить о простой, а в случае, когда встре-
чаются ns =# 1, — о кратной синхронизации.
Для приложений весьма существенна и противоположная за-
дача (задача синтеза), состоящая в таком выборе связей меж-
ду объектами, при котором последние будут совершать синхрон-
ные движения заданного вида.
Несколько обобщая поставленную задачу*), можно придать
ей следующую математическую формулировку.
Рис. 1.
Рассмотрим систему из k взаимно связанных динамических
объектов, схематически представленную на рис. 1. Пусть x(s) =
= [x(1s), ..., x)s)J есть г3-мерный вектор, компоненты которого х^
*) Отказавшись от предположения об автоколебательном характере объ-
ектов.
§ 3]	ОБЗОР ОСНОВНЫХ ФАКТОВ И РЕЗУЛЬТАТОВ	23
определяют состояние s-ro объекта в фазовом пространстве си-
стемы (s = 1, .... k). Объекты могут быть связаны один с дру-
гим как непосредственно, так и через систему связи, состояние
которой характеризуется v-мерным вектором и.
Пусть, далее, движение системы описывается дифференци-
альными уравнениями
x(s} = X<s} (x<s}) + F(s} (x(I>.x<k\ u) (s = 1, .. ., k),
ii = U(xw, ..., x(k}, u),	(3,1)
где X's}, F(s) nV — соответственно rs и v-мерные вектор-функ-
ции, удовлетворяющие некоторым весьма общим требованиям,
при которых система (3.1) является динамической.
Первые k уравнений (3.1)—уравнения движения объектов
под действием связей, а последнее — уравнение движения си-
стемы связи. Функции F.s и V, характеризующие связи между
объектами, назовем функциями связей. При F, ^0 мы имеем,
очевидно, k взаимно независимых динамических объектов.
Под основной задачей теории синхронизации, согласно изло-
женному выше, в данной книге будем понимать установление
условий существования и устойчивости решений уравнений (3.1),
имеющих вид
x(s> _ CT(s)	+ у(р	(/=1, ..., rs; s= 1,	k),
up = % [qPnp(ot + (mpat)] (p = 1, ..., v),
где и — положительная постоянная	и op(mpwf) — пе-
риодические функции с периодами 2n/mjs) и 2л/тр по at
(то есть также и с общим периодом 2л по at), q^ и qp —
числа, каждое из которых может быть равно нулю или единице,
тр, n<s> и пр — взаимно простые целые положительные
числа, а и ар — числа, равные либо +1, либо —1. Фазовые
координаты, для которых число q^ или qp равно нулю, условно
назовем колебательными, а координаты, для которых указан-
ное число равно единице, — вращательными.
Иными словами, будем интересоваться колебательными или
равномерными в среднем движениями по каждой из координат
с одинаковыми для всех координат или кратными частотами
(угловыми или линейными скоростями); такие движения и на-
зовем синхронными.
Помимо сформулированной основной задачи о синхрониза-
ции, для приложений зачастую представляет интерес также ре-
альное вычисление синхронной угловой скорости (частоты) а
И устойчивых синхронных решений (3.2), а также решение
24
ВВЕДЕНИЕ
упоминавшейся выше задачи синтеза. Особый интерес представ-
ляет иногда и решение весьма трудной задачи о нахождении
«области захвата» определенного синхронного движения в фазо-
вом пространстве системы, то есть такой области начальных
значений координат, для которой с течением времени соответ-
ствующее движение неограниченно приближается к данному
синхронному движению.
В зависимости от характера постановки задачи о синхрони-
зации систем, содержащих автоколебательные объекты, следует
различать задачи о внутренней (взаимной, автономной) и
о внешней (неавтономной) синхронизации.
Первый случай является наиболее общим: здесь все объек-
ты рассматриваются как равноправные элементы единой авто-
номной динамической системы; частота синхронного движения
w при этом устанавливается в результате взаимодействия всех
объектов. Значение синхронной частоты и заранее неизвестно и
подлежит определению в процессе решения задачи.
Во втором случае считают, что один из объектов является
значительно более мощным по сравнению со всеми остальными,
и поэтому его движение считается не зависящим от характера
движения прочих элементов системы. Воздействие указанного
объекта на остальные элементы системы и тем самым частота
(скорость) синхронного движения <о предполагаются наперед
заданными и неизменными. Система уравнений движения при
этом подходе к задаче оказывается неавтономной и имеет более
низкий порядок, нежели исходная автономная система.
Заметим, что может оказаться целесообразным расширение
приведенного выше понятия синхронизации как на случай объ-
ектов более общей природы, так и на случай непериодических и
неравномерных в среднем движений. Можно предполагать так-
же, что функции у^ и ир в выражениях (3.2) являются почти
периодическими. Однако для подавляющего большинства при-
ложений вполне достаточно ограничиться изложенным выше ме-
нее общим толкованием синхронизации.
Отметим также, что понятие о синхронизации предполагает
возможность (и целесообразность) выделения в единой системе
нескольких объектов, состояние которых характеризуется «соб-
ственными» фазовыми координатами. Между тем такое расчле-
нение системы на «объекты» и «связи» в принципиальном отно-
шении достаточно условно; это вытекает, например, из того
обстоятельства, что если не сделано никаких оговорок о харак-
тере функций связей и U, то все переменные входят в си-
стему уравнений (3.1) вполне равноправно.
Однако при рассмотрении конкретных задач о синхронизации
обычно не возникает вопроса о выделении отдельных объектов.
Дело здесь не только (и не столько) в том, что эти объекты
S3)
ОВЗОР ОСНОВНЫХ ФАКТОВ И РЕЗУЛЬТАТОВ
25
представляют собой обособленные физические или биологиче-
ские системы (маятники, электрические генераторы, насекомые
и т. н.), а в том, что связи между отдельными объектами
в практически интересных случаях значительно слабее, чем
между отдельными элементами самих объектов.
При наличии сильных связей между объектами их выделе-
ние (по крайней мере, при математическом решении задачи)
часто нецелесообразно, и явление взаимной синхронизации ни-
чем не выделяется из класса автоколебательных явлений, к ко-
торым оно, несомненно, во всех случаях относится.
Именно слабость связей между объектами и определяет
главную специфику задач о синхронизации. Математически эта
специфика отражается в том, что функции связей F3 малы по
сравнению с X(s>, и поэтому уравнения (3.1) могут быть пред-
ставлены в форме
x(s) = X(s)(x(s)) + Hf(S)(x(l).xk\ и, ц) (S=l, .... k),
и = U' (х(1), . . ., x(ft), и, ц),	(
где ц— малый параметр, который ниже удобно считать поло-
жительным.
2.	Математический аппарат теории синхронизации. Инте-
гральный критерий устойчивости синхронных движений. Если
в уравнения движения (3.3) подставить вместо x<s> и и выраже-
ния (3.2), то мы придем к системе дифференциальных уравне-
ний относительно новых неизвестных функций y<s) и v. Основная
задача теории синхронизации сводится тем самым к исследова-
нию периодических решений системы нелинейных дифферен-
циальных уравнений с периодическими правыми частями*),
содержащими малый параметр. Для решения этой последней
задачи могут быть использованы методы малого параметра
Пуанкаре и Ляпунова, а также асимптотические методы, пред-
ставляющие собой различные варианты метода осреднения. Обе
группы методов получили в последние десятилетия существен-
ное развитие преимущественно в трудах отечественных уче-
ных**). В настоящей книге предпочтение отдано методам Пу-
анкаре и Ляпунова.
Применение методов Пуанкаре и Ляпунова для решения
задач о синхронизации имеет ряд существенных особенностей и
*) То обстоятельство, что в результате подстановки (3.2) правые части
дифференциальных уравнений (3.3) оказываются периодическими функциями
времен.!!, представляет характерную особенность задач о синхронизации ди-
намических объектов.
**) Краткие обзоры соответствующих исследований приведены в § 4
главы III, а также в § 1 главы VI.
26
ВВЕДЕНИЕ
наталкивается на определенные специфические трудности. Рас-
смотрим эти особенности в общих чертах.
Как известно, основная идея метода Пуанкаре состоит в рас-
смотрении вместо исходной системы уравнений так называемой
порождающей системы, получающейся из исходной при ц = 0;
естественно, что решение порождающей системы может ока-
заться более простым, нежели решение исходной системы. Наи-
более существенным этапом дальнейшего исследования является
установление условий, при выполнении которых периодическому
решению порождающей системы действительно отвечает одно-
единственное периодическое же решение исходной системы,
обращающееся в него при ц = 0. Только при выполнении этих
условий периодическое решение порождающей системы можно
рассматривать как приближенное решение исходной, основной
системы, а дальнейшие приближения, если это необходимо, вы-
числять в виде рядов по степеням малого параметра. Затем
надлежит исследовать устойчивость найденных решений, для
чего обычно используют теорию устойчивости А. М. Ляпунова.
Естественно, что характер всего исследования существенно за-
висит от характера порождающей системы и ее решения.
В задачах о синхронизации слабо связанных объектов по-
рождающая система, согласно (3.3), имеет вид*)
xf,5’ = X(s)Ws)) (s=l,
(3.4)
и0=1Г(х<‘), ...,	u0, 0),
то есть распадается на k независимых уравнений, определяю-
щих движение изолированных объектов, и на уравнение, опи-
сывающее поведение системы связи при известных движениях
объектов. Если мы теперь допустим, что каждое из первых k
уравнений (3.4) имеет некоторое решение
х/о (0 =	(3.5)
то есть решение типа (3.2), то выражение
(7 + as) = [q^n^cot + q^n^aa,. + y$ [m<s)co (t + as)]]	(3.6)
(/ = 1....rs> «= 1. • • •, ^)>
где as — произвольная постоянная, также будет решением типа
*) Здесь и в дальнейшем вместо того, чтобы говорить о периодических
решениях y(s) и у системы, получающейся из (3.3) в результате подстановки
(3.2), мы говорим о синхронных решениях (3.2) исходной системы (3.3) и
соответствующей ей порождающей системы. Существо дела от этого, есте-
ственно, не меняется.
§ 3]	ОБЗОР ОСНОВНЫХ ФАКТОВ И РЕЗУЛЬТАТОВ	27
(3.2). Отсюда следует, что если порождающая система для
рассматриваемого наиболее важного класса задач о синхрони-
зации допускает некоторое синхронное решение
Х& = x(.s> (t)	(/=1,..., г; s
/о 10 ' ' V	s	У)
WpO = Mpo(O ' (р= 1...v),
то эта система, вследствие автономности объектов, допускает
также и семейство синхронных решений
4o=x/o(/ + as)	(/=l,...,rs; s=l.......k),
«po = »p(z- a,, . . afe) (p= 1, . . ., v),
зависящее по крайней мере от k произвольных постоянных as.
Указанные постоянные играют роль фазовых сдвигов объектов
в синхронных движениях системы.
Случай, когда порождающая система допускает решение,
зависящее от некоторого числа произвольных постоянных, яв-
ляется в теории периодических решений, во-первых, особенным,
требующим специального исследования и, во-вторых, наиболее
интересным с принципиальной точки зрения. Как устанавли-
вается путем соответствующего исследования*), в этом случае,
вообще говоря, нет полного качественного соответствия между
рассматриваемыми решениями исходной и порождающей си-
стем уравнений. А именно оказывается, что синхронные реше-
ния исходной системы (3.3), обращающиеся при ц = 0 в син-
хронные решения (3.8) порождающей системы (3.4), могут
соответствовать далеко не всем значениям постоянных as,
а лишь значениям, удовлетворяющим некоторой системе ко-
нечных уравнений
РДа„ ..., а,) = 0	(s=l,...,fc),	(3.9)
составляемых по определенному правилу (см. ниже).
Однако, вообще говоря, не всем решениям уравнений
(3.9) будут отвечать устойчивые синхронные движения. Ис-
следование устойчивости показывает, что для достаточно широ-
кого класса систем основную роль в отборе устойчивых реше-
ний играет требование, чтобы для определенного решения
уравнений (3.9) все корни (за исключением, быть может, одного
*) Обзор работ, развивающих идеи методов Пуанкаре и Ляпунова в
интересующем здесь нас направлении, приведен в § 4 главы III настоящей
книги.
28
ВВЕДЕНИЕ
нулевого корня) алгебраического уравнения /г-й степени
дРг	дРх	dPt		
	да.	dak		
дР2	дР,	дР2		
да{	да, % 	да. К.	= 0	(3.10)
dPk	дРь	дРк X		
да j	да2	<9ct. К		
имели отрицательные вещественные части. Для многих систем
сформулированное требование является не только необходимым,
нс> и достаточным условием устойчивости (в малом и при до-
статочно малых значениях параметра ц); кроме того, при вы-
полнении данного требования для соответствующего решения
уравнений (3.9) этому решению действительно отвечает един-
ственное решение исходной системы дифференциальных урав-
нений (3.3), обращающееся при ц = 0в порождающее реше-
ние (3.8).
Таким образом, если постоянные as найдены из уравнений
(3.9) и для них к тому же все корни х уравнения (3.10) —
кроме, быть может, одного — удовлетворяют условиям
Rex/<0 (/=1,..., k),	(3.11)
то выражения (3.8) могут рассматриваться как полноценные
первые приближения к решению задачи.
Условия наличия у уравнений (3.9) вещественных решений
относительно постоянных аь ..., могут рассматриваться
как необходимые условия возможности синхронизации объ-
ектов *).
Решения исходной системы (3.3) при необходимости можно
разыскивать в виде рядов по степеням малого параметра.
К счастью, однако, в большинстве задач о синхронизации
вполне достаточно ограничиться нахождением первых членов
рядов, определяемых приближением (3.8), при условии, конечно,
что постоянные найдены из уравнений (3.9); эти постоянные
определяют фазировку движения объектов в синхронных ре-
жимах системы.
Таким образом, уравнения (3.9) играют весьма важную
роль при решении задач о синхронизации: они служат для вы-
числения фаз движения объектов в исходном приближении, для
установления условий существования синхронных движений
в системе; через левые части этих уравнений Л(аь ..., ал)
*) Мы имеем в виду случай, когда постоянные а. по своему физиче-
скому смыслу должны быть вещественными.
§ 3]	ОБЗОР ОСНОВНЫХ ФАКТОВ И РЕЗУЛЬТАТОВ	29
выражаются и условия устойчивости синхронных движений.
Назовем указанные уравнения основными уравнениями задачи
о синхронизации слабо связанных объектов. О роли основных
уравнений (3.9) и величин as более подробно будет сказано
в п. 12 настоящего параграфа. Здесь же мы отметим, что эти
уравнения не могут быть составлены только на основе инфор-
мации, содержащейся в порождающей системе (3.4); для этого
необходимо как-то учесть также те члены в исходных уравне-
ниях (3.3), которые содержат малый параметр, в частности
члены, отвечающие функциям связей ^^(хЮ, ..., х<А>, и, р).
Впрочем, для составления функций Ps(ai, •••, а/{) (их можно
назвать порождающими функциями) обычно оказываются до-
статочными линейные относительно р члены разложений функ-
ций то есть выражения
....4".0).
Следует отметить, что выше мы умышленно несколько упро-
стили ситуацию, чтобы не загромождать изложение второсте-
пенными деталями и оговорками. Из опущенных подробностей
отметим лишь, что число произвольных постоянных в порождаю-
щем решении (3.8) может быть большим, нежели число k, по-
скольку появление этих постоянных вовсе не обязательно свя-
зано с произвольностью выбора начала отсчета в синхронном
движении каждого из изолированных автономных объектов.
В пятой главе настоящей книги на основе развития в опре-
деленном направлении методов Пуанкаре и Ляпунова изложен-
ные выше результаты получены для различных типов диффе-
ренциальных уравнений, содержащих малый параметр; при этом
найдены также общие выражения для порождающих функций
Ps(ai, a,t). Применению указанных результатов к исследо-
ванию синхронизации некоторых основных классов слабо свя-
занных объектов посвящена отдельная, третья часть книги.
В сущности, здесь конкретизируется вид порождающих функ-
ций Ps и уравнений (3.10) для объектов и связей определенного
типа и делается ряд общих заключений о характере возмож-
ных синхронных режимов.
Весьма существенно, что трудности получения выражений
для порождающих функций Ps в явной форме для задач о син-
хронизации слабо связанных объектов определяются не сте-
пенью сложности всей системы в целом, а лишь степенью слож-
ности отдельных изолированных объектов и системы связи. Это
обстоятельство значительно облегчает решение задач о синхро-
низации объектов со слабыми связями.
Рассмотренным результатам исследования синхронизации
слабо связанных объектов часто можно придать форму, зна-
чительно более удобную во многих отношениях. Предположим,
30
ВВЕДЕНИЕ
например, что существует такая функция D = D(at, .... ад),
что выполняются соотношения
....«д)	(5=1,..., k),	(3.12)
где Ря— по-прежнему порождающие функции задачи. Функ-
цию D (последняя, как и Ps, предполагается вещественной)
можно назвать потенциальной функцией.
Рассматривая совместно соотношения (3.9) — (3.12), нетруд-
но прийти к выводу, что устойчивые синхронные движения си-
стемы могут соответствовать тем стационарным точкам
а*, . а* потенциальной функции D(a\, ..., ад), в которых
эта функция имеет минимум; стационарным же точкам, в ко-
торых минимум потенциальной функции D отсутствует, отве-
чают неустойчивые синхронные движения *).
Таким образом, функция D в рассматриваемых задачах
о синхронизации играет ту же роль, что и потенциальная энер-
гия системы в задаче об отыскании и исследовании устойчиво-
сти положений равновесия консервативных систем.
Сформулированный критерий устойчивости синхронных дви-
жений! был назван интегральным, поскольку функция D, так же
как и порождающие функции Ps, зависит от осредненных за
период характеристик движения системы, вычисленных для по-
рождающего решения. Значение этого критерия определяется
тем, что потенциальная функция D во многих конкретных за-
дачах о синхронизации имеет отчетливый физический смысл,
что облегчает решение задачи синтеза систем с синхронизирую-
щимися объектами. Так, например, в задаче о синхронизации
вибраторов (см. и. 4 настоящего параграфа) потенциальная
функция оказывается равной среднему за период значению
функции Лагранжа системы, взятой со знаком минус. Другое
достоинство интегрального критерия состоит в том, что он
открывает возможности для использования хорошо разрабо-
танных алгоритмов поиска экстремумов функций многих пере-
менных, допускающих применение современных вычислитель-
ных машин. При наличии этого критерия условия устойчивости
движения могут быть к тому же выражены в явной форме с по-
мощью известной теоремы Сильвестра.
Несмотря на то, что существование функции D, казалось
бы, накладывает на рассматриваемую систему достаточно жест-
кие требования, эта функция существует во многих важных
задачах о синхронизации, а также и в других задачах теории
нелинейных колебаний, для которых порождающая система до-
*) Доказательство, а также более точная формулировка этого утвержде-
ния приводятся в § 8 пятой главы книги,
§ 3]	ОБЗОР ОСНОВНЫХ ФАКТОВ И РЕЗУЛЬТАТОВ	31
пускает семейство периодических решений, зависящее от не-
которого числа произвольных параметров. Расширению класса
систем, для которых справедлив интегральный критерий, спо-
собствует также и то обстоятельство, что, как можно показать,
для его наличия достаточно существования функции D, удов-
летворяющей не условиям (3.12), а гораздо менее жестким со-
отношениям
bsi ~да^ + ~да7 +	~	  > ak)> (3.13)
(s = 1....k)
где bSj = bjs — любые постоянные, подчиненные требованию,
чтобы квадратичная форма
k k
B(z, г)= 2 2	(3.14)
s-l /-I
была положительной*).
В заключение настоящего пункта коснемся существенного и,
к сожалению, часто неправильно освещаемого вопроса о «стро-
гости» методов Пуанкаре и Ляпунова при их применении к ре-
шению прикладных задач.
Дело в том, что основной «работающий» аппарат этих мето-
дов позволяет установить факты существования и устойчивости
решения, а также сходимости соответствующих рядов при до-
статочно малых значениях параметра ц и при достаточно малых
начальных отклонениях. Значительно труднее определить гра-
ницы областей изменения малого параметра и начальных от-
клонений, в которых эти факты имеют место: несмотря на на-
личие ряда интересных результатов, эффективных универсаль-
ных методов здесь до сих пор не существует. Поэтому
в подавляющем большинстве прикладных исследований (и дан-
ная книга не составляет исключения) авторы ограничиваются
установлением результатов «в малом», не определяя радиусов
сходимости рядов и областей притяжения найденных режимов
в фазовом пространстве системы. Между тем при практическом
использовании указанных результатов приходится иметь дело
с конечными значениями параметра ц и начальных отклонений.
Иными словами, результаты локального исследования исполь-
зуются вовсе не локально.
Естественно, что такое применение рассматриваемых мето-
дов не является строгим и в принципе может приводить к ошиб-
кам. Иначе говоря, в приложении к практическим задачам
*) На возможность подобного обобщения внимание автора обратили
Р. Ф. Нагаев и К. Ш. Ходжаев.
32
ВВЕДЕНИЕ
локальные результаты, найденные методами Пуанкаре и Ляпу-
нова, являются не достоверными, а лишь правдоподобными. Та-
кие взгляды на рассматриваемые методы высказывались еще
А. А. Андроновым и представителями его научной школы
[32, 151]. Однако опыт использования методов Пуанкаре и Ля-
пунова показывает, что «степень правдоподобности» при ука-
занном нестрогом, но осмотрительном применении локальных
результатов па деле оказывается весьма высокой: как правило,
эти результаты хорошо согласуются с экспериментом. Причина
такого положения, по мнению автора книги, состоит, грубо
говоря, в хорошей «корреляции» между математическим и ин-
туитивным понятиями «достаточной малости»; по этой, а также
и по некоторым другим причинам реальное попадание в об-
ласть, где локальные результаты несправедливы, «менее ве-
роятно», чем в ту область, где они верны.
Подробному рассмотрению изложенных соображений по-
священа четвертая глава настоящей книги, а также статья
А. Д. Мышкиса, Я. Г. Пановко и автора [82].
В указанной главе обсуждается также вопрос о возможно-
сти использования метода малого параметра для изучения си-
стем, не содержащих физического малого параметра. Здесь
высказывается соображение, что основой для успеха примене-
ния этого метода может служить правильная гипотеза о виде
разыскиваемых решений; в основу такой гипотезы могут лечь
физические соображения или результаты экспериментов. Если
указанная гипотеза принята, то несложный формальный прием
позволяет ввести малый параметр в систему, в которой он фор-
мально отсутствует. Соответствующие рассуждения, как пред-
ставляется, позволяют пролить некоторый свет на так назы-
ваемое «чудо большого ц», состоящее в справедливости для
ряда случаев результатов, найденных в предположении о до-
статочной малости [х, также и при «немалых» значениях этого
параметра.
3.	Основные закономерности синхронизации динамических
объектов. Перечислим некоторые общие закономерности, ха-
рактерные для синхронизации динамических объектов вне за-
висимости от их природы.
а)	Основным фактом, обнаруживаемым при исследований
синхронизации динамических систем, является отсутствие по-
рога синхронизации. Речь идет о том, что синхронизация может
иметь место при как угодно слабой связи между объектами,
если только достаточно мало отличие соответствующих одно-
именных параметров объектов.
Иными словами, как бы слабо ни были связаны объекты
один с другим, всегда существуют определенные условия, при
которых их взаимное влияние приведет к качественному эф-
§ 3]	ОБЗОР ОСНОВНЫХ ФАКТОВ И РЕЗУЛЬТАТОВ	33
фекту, который может быть зафиксирован, — к установлению
синхронизации.
Отмеченная закономерность обнаруживается и в вырожден-
ном случае синхронизации — захватывании [15, 18]; эта законо-
мерность проявляется в своеобразной форме и при наличии
флуктуаций параметров объектов и системы связи [265].
б)	Наиболее существенно возможность или невозможность
синхронизации автоколебательных объектов зависит от зна-
чений их парциальных частот (угловых скоростей) cos. Если,
например, все парциальные частоты достаточно близки или
одинаковы, то простая взаимная синхронизация объектов, во-
обще говоря, всегда возможна вне зависимости от значений
прочих параметров объектов и системы связи.
Вместе с тем даже при «слабых» взаимных связях между
объектами их тенденция к синхронизации может быть столь
сильна, что синхронизируются объекты с существенно различ-
ными частотами. Более того, в ряде случаев могут синхронизи-
роваться объекты, часть из которых имеет нулевые парциаль-
ные частоты, то есть при отсутствии взаимодействия вообще не
генерирует колебаний.
в)	Синхронная частота (угловая скорость) со при простой
взаимной синхронизации автоколебательных объектов обычно не
больше, чем наибольшая, и не меньше, чем наименьшая из
парциальных частот (угловых скоростей) cos отдельных
объектов:
Inf [со,, ..., coj ^со Sup [со,.со*].	(3.15)
Во многих случаях, особенно при близких значениях cos, син-
хронная частота со близка к средневзвешенному значению пар-
циальных частот со8:
со	... + bka>k (6,+ ... +bft=l), (3.16)
где b\, ..., bk— некоторые функции параметров системы. От-
сюда, в соответствии с известным положением теории вероятно-
сти, следует, что среднеквадратическое отклонение со при слу-
чайных отклонениях величин cos может быть значительно
меньше, чем среднеквадратические отклонения cos. Указанное
обстоятельство лежит в основе применения взаимной синхро-
низации для получения весьма точных генераторов частоты или
регистраторов промежутков времени: ошибка, получаемая
в связанной системе таких генераторов, значительно меньше
ошибки, характерной для одного генератора.
г)	В связанной системе объектов во многих случаях воз-
можно не одно, а несколько устойчивых (в малом) синхрон-
ных движений, отличающихся, например, фазами движения
объектов as (см. п. 2 настоящего параграфа); существуют, как
2 И. И. Блехман
34
ВВЕДЕНИЕ
правило, и другие (не синхронные) устойчивые в малом движе-
ния. В таких случаях характер реально устанавливающегося
движения в системе определяется начальными условиями. В не-
которых системах, однако, имеется лишь единственный устой-
чивый в большом синхронный режим движения, устанавливаю-
щийся при любых начальных условиях. В первом, наиболее
общем случае мы будем говорить о жестком возбуждении син-
хронного режима, или о несамоустанавливающемся синхронном
режиме, а во втором — о мягко возбуждаемом, или самоустанав-
ливающемся, режиме.
д) Характер и число устойчивых синхронных движений си-
стемы существенно зависят от числа степеней свободы и харак-
тера системы связи, а также от характера и числа объектов
в системе. Так, например, неустойчивое синфазное синхронное
движение автоколебательных объектов (aj = аг = ... = «/<) во
многих случаях можно сделать устойчивым, изменив на еди-
ницу число степеней свободы системы связи или число взаимо-
действующих объектов. Это обстоятельство указывает на кон-
кретные пути решения задачи синтеза систем с синхронно ра-
ботающими объектами (см. пп. 1 и 5 настоящего параграфа).
Для иллюстрации зависимости характера синхронного дви-
жения от свойств объектов приведем следующий результат, при-
надлежащий Р. Ф. Нагаеву (см. § 3 главы X). Пусть имеется
система слабо связанных объектов, близких к консервативным.
Назовем объект изохронным, если в консервативном прибли-
жении частота его движения не зависит от энергетического
уровня движения системы. В случае, если частота возрастает
с ростом энергетического уровня движения, будем говорить
о жестком, а в противном случае — о мягком анизохронизме
(см. рис. 20). Тогда при некоторых предположениях оказы-
вается, что мягко-апизохронные объекты синхронизируются та-
ким образом, что некоторая функция Ло(аь ..., ал) (среднее
значение функции Лагранжа системы связей) в устойчивых
синхронных движениях имеет минимум. Устойчивым же син-
хронным движениям жестко-анизохронных объектов отвечают
максимумы функции Ao(ai, ..., ал).
4. Задача о синхронизации механических вибраторов. Меха-
нические вибраторы, основными элементами которых являются
вращающиеся неуравновешенные роторы, используются в ка-
честве приводных устройств в большинстве вибрационных ма-
шин и установок: в вибрационных конвейерах, грохотах, пита-
телях, дробилках, мельницах, вибрационных площадках для
уплотнения бетона, вибропогружателях свай, шпунта и оболо-
чек и других устройствах.
В значительном числе вибрационных машин по различным
причинам применяются несколько механических вибраторов.
§ 3]	ОБЗОР ОСНОВНЫХ ФАКТОВ И РЕЗУЛЬТАТОВ	35
При этом для обеспечения нормальной работы машин, как пра-
вило, приходится добиваться одинаковости или кратности сред-
них угловых скоростей, а иногда и наличия определенных соот-
ношений между фазами вращения вибраторов, то есть возни-
кает необходимость решения задачи о синхронизации.
Представление о машинах и устройствах, для которых суще-
ственна проблема синхронизации, а также об условиях, накла-
дываемых на вращение их роторов, дает таблица 2 (см.
стр. 340—358.
Известны три основных способа синхронизации механиче-
ских вибраторов: принудительная кинематическая синхрониза-
ция (с помощью специальных валов, шестеренных или цепных
передач), принудительная электрическая синхронизация (путем
использования системы электрического вала или синхронных
двигателей) и, наконец, самосинхронизация.
Естественно, что самым предпочтительным способом синхро-
низации является самосинхронизация, ибо она не требует вспо-
могательных устройств, усложняющих конструкцию и вообще
не всегда применимых. При самосинхронизации же синхрон-
ность и требуемая фазировка достигаются благодаря вибра-
циям системы тел, па которых установлены вибраторы. Исполь-
зование эффекта самосинхронизации позволило не только усо-
вершенствовать привод существующих вибрационных устройств,
но и создать принципиально новые машины и установки.
Существует, однако, особый случай, когда самосинхрониза-
ция систем типа механических вибраторов является не полез-
ной, а весьма опасной. При установке нескольких динамически
неуравновешенных машин на едином (групповом) фундаменте
или другом опорном сооружении синхронная и синфазная ра-
бота машин иногда приводит к недопустимо большим колеба-
ниям, вызывающим разрушения. С другой стороны, при пра-
вильно спроектированном групповом фундаменте можно до-
биться взаимного уравновешивания самосинхронизирующихся
машин, обеспечив значительное снижение уровня колебаний
фундамента (см. п. 7 настоящего параграфа).
Таким образом, задача о синхронизации механических ви-
браторов представляет существенное прикладное значение; ее
общей постановке и решению посвящена четвертая часть на-
стоящей книги.
Основные особенности задачи могут быть выяснены на про-
стейшем примере, относящемся к самосинхронизации дебаланс-
ных вибраторов, установленных на абсолютно жесткой плат-
форме, имеющей одну степень свободы.
Динамическая схема рассматриваемой системы представлена
на рис. 2. Вибрирующий орган машины 1 (жесткая плат-
форма) связан с неподвижным основанием 2 системой плоских
2’
36
ВВЕДЕНИЕ
пружинных опор 3 (рессор) или шарнирных стоек. Оси рессор
или стоек предполагаются нерастяжимыми, и поэтому платформа
может поступательно смещаться только в направлении, перпен-
дикулярном этим осям.
На платформе установлено некоторое число k дебалансных
вибраторов 4, представляющих собой неуравновешенные ро-
торы, оси которых перпендикулярны плоскости колебаний плат-
формы и которые приводятся во вращение вокруг этих осей
Рис. 2.
какими-либо двигателями асинхронного типа. Положение рас-
сматриваемой системы определяется отклонением платформы х
от положения статического равновесия и углами поворота ро-
торов вибраторов ф«, отсчитываемыми по ходу часовой стрелки.
Дифференциальные уравнения движения системы имеют вид
ДФз = mszs [х sin + g cos (q>s - %)] + Ls (ф5) - Rs (<ps)
(s = 1, ..., k),
k
Mx + kxx + cxx = 2 tns&s (ips sin <ps + ф2 cos <p5).
S=«l
(3.17)
Первые k уравнений (3.17) представляют уравнения движе-
ния роторов вибраторов, а последнее является уравнением
малых колебаний платформы. При этом приняты следующие обо-
значения: Is — момент инерции ротора s-ro вибратора относи-
тельно его оси вращения; ms и es — соответственно масса и экс-
центриситет ротора; Ls(<ps) — вращающий момент асинхронного
двигателя; /?5(ф5) = ф3 [) sign ф5 — момент сил сопротивле-
§ 3]	ОБЗОР ОСНОВНЫХ ФАКТОВ И РЕЗУЛЬТАТОВ	37
ния вращению; Л4 — масса системы; kx— коэффициент вязкого
сопротивления колебаниям платформы; сх— жесткость упругой
системы; g— ускорение силы тяжести; % — угол между направ-
лением оси Ох и горизонталью.
Очевидно, что по своей структуре уравнения (3.17) вполне
соответствуют общим уравнениям задачи о синхронизации ди-
намических объектов; в них нетрудно выделить фазовые коор-
динаты объектов (cps и ф8) и системы связи (х и х), а также и
функции связей. Отметим, что особую роль в этих последних
функциях играют члены msesxsincps в уравнениях движения
роторов. Указанные члены отражают обратное влияние коле-
баний платформы на движение роторов. Именно эти члены,
которыми зачастую пренебрегают, и предопределяют синхро-
низацию вибраторов и другие важные эффекты в рассматривае-
мых системах.
Основная задача о самосинхронизации вибраторов сводится
к выяснению условий, при выполнении которых все вибраторы
будут вращаться с одинаковыми по абсолютной величине сред-
ними угловыми скоростями, несмотря на отсутствие каких-либо
непосредственных связей между их роторами (кроме косвенной
связи — общей колеблющейся платформы, на которой установ-
лены вибраторы) и несмотря на различие параметров, характе-
ризующих вибраторы и действующие на них силы.
Иными словами, речь идет о выяснении условий
вания и устойчивости решений системы (3.17) вида
Фз = <js [©/ + фЛ©01	(s=l,	k),
х = x(<j>t).
Здесь со — абсолютная величина средней скорости
роторов вибраторов, ф«(со/) и x(a>t)— периодические функции
времени t с периодом Т = 2л/со, а каждая из величин щ, равна
либо 1, либо —1; первому случаю отвечает вращение ротора s-ro
вибратора в положительном, второму — в отрицательном на-
правлении.
Движения типа (3.18), в соответствии с принятой выше тер-
минологией, назовем простыми синхронными; иногда интерес
представляют и кратно-синхронные движения, когда |ф8|ср =
= ns(n, где п„— целые положительные числа. Отметим, что
модуль угловой скорости синхронного вращения со заранее не-
известен и подлежит определению в процессе решения задачи.
Как показывает опыт, в изучаемых синхронных движениях
системы вращение роторов вибраторов мало отличается от рав-
номерного. Учитывая это обстоятельство и принимая во вни-
мание относительный порядок величин, входящих в первые k
уравнений (3.17) (см. § 3 главы XIII), можно представить эти
существо-
(3.18)
вращения
38
ВВЕДЕНИЕ
уравнения в форме
+ ks (<ps - osa>) = р,Ф5 (jps, x) (s = 1, .. ., k) (3.19)
где
рФ5 (<PS> *) = mses [x sin <ps + g cos (<ps - x)] + Ls (as©) - Rs (osa>),
а ц есть малый параметр, который, не нарушая общности,
можно считать положительным; положительными обычно яв-
ляются также и постоянные ks и ks.
Уравнения (3.19), очевидно, вполне соответствуют первым k
общим уравнениям (3.3). При ц = 0 эти уравнения становятся
взаимно независимыми и допускают синхронное решение
<₽s =	+ аЛ	(3-21)
где а,— произвольные постоянные, играющие роль начальных
фаз вращения вибраторов.
Отметим, что к виду (3.19) приводятся уравнения движения
вибраторов также и в гораздо более общем случае, чем рас-
смотренный. Так, колебательная система, на которой установ-
лены вибраторы, может представлять собой не одно, а не-
сколько твердых или даже упругих тел (назовем их несущими
телами или несущей системой)-, эти тела могут иметь более
одной степени свободы; система может быть и нелинейной.
Вибраторы могут быть не простейшими дебалансными, а плане-
тарными вибраторами или вибраторами направленного дей-
ствия того или иного типа (см. § 1 главы XII); они могут при-
водиться во вращение как асинхронными, так и синхронными
двигателями. Наконец, роторы вибраторов могут быть связаны
непосредственно той или иной системой «несомых связей»
(системой принудительной синхронизации).
При решении подавляющего большинства задач о синхро-
низации вибраторов вполне достаточно ограничиться исходным
приближением, которому отвечает равномерное вращение ро-
торов вибраторов по закону (3.21) и установившиеся вынужден-
ные колебания несущих тел под действием возмущающих сил,
развиваемых вибраторами при равномерном вращении. Дело
сводится, таким образом, к определению начальных фаз вра-
щения роторов cci, ..., в возможных устойчивых синхронных
движениях, что невозможно в рамках обычной теории выну-
жденных колебаний и что позволяет сделать теория синхрони-
зации вибраторов.
Не приводя здесь результата исследования в наиболее об-
щей форме, остановимся на случае дебалансных вибраторов,
§ 3]
О133ОР ОСНОВНЫХ ФАКТОВ И РЕЗУЛЬТАТОВ
39
роторы которых могут быть связаны безынерционными упру-
гими элементами или элементами типа электрического вала.
Колебательную систему будем считать мало отличающейся от
линейной консервативной системы с произвольным числом сте-
пеней свободы, собственные частоты которой не связаны с син-
хронной угловой скоростью со так называемыми резонансными
соотношениями (см. главы XIII и XIV книги). Тогда использо-
вание аппарата, кратко изложенного во втором пункте настоя-
щего параграфа, приводит к следующему заключению.
Синхронные движения вибраторов с одинаковой по абсолют-
ной величине средней угловой скоростью со могут соответство-
вать лишь тем значениям фаз as, входящих в решения (3.21),
которые удовлетворяют уравнениям *)
Ps(ai....ак, ©) = L(sm} (as, oscd) - Rs (co) — (on, ak) -
— Ws (ab ..., aA, co) = 0 (s = 1, ..., k). (3.22)
Каждому решению = a*.........ak = a* системы (3.22) дей-
ствительно отвечает единственное и асимптотически устойчивое
синхронное движение вибраторов, если для этого решения все
корни х алгебраического уравнения (3.10) отрицательны. Если
хотя бы один из корней указанного уравнения положителен, то
соответствующее движение неустойчиво; случай нулевых корней
требует дополнительного исследования.
Сказанное относилось к задаче о внешней синхронизации;
последняя отвечает, например, случаю, когда хотя бы один из
вибраторов приводится от синхронного двигателя и угловая
скорость синхронного движения со заранее задана. Задача
о внутренней синхронизации (в частности, о самосинхрониза-
ции) отличается тем, что фазы а, находятся из системы (3.22)
лишь с точностью до произвольной постоянной, но зато из этих
уравнений определяется и неизвестное заранее приближенное
значение синхронной угловой скорости со. Что же касается урав-
нения (3.10), то оно непременно имеет в этом случае один
нулевой корень, никак не влияющий на решение вопроса об
устойчивости.
Таким образом, для возможности синхронных движений
уравнения (3.22) должны допускать решения, вещественные от-
носительно ccj и (в случае внутренней синхронизации) положи-
тельные относительно со. Указанные условия и приводят обычно
к условиям возможности синхронизации вибраторов.
Рассмотрим уравнения (3.22) несколько подробнее и по-
ясним принятые в них обозначения. Прежде всего заметим, что
*) Обозначения, принятые в уравнениях (3.22) —как и ранее, будем на^
зывать их основными уравнениями, — поясняются ниже.
40
введение
эти уравнения имеют достаточно простой физический смысл:
они представляют собой уравнения равновесия средних (за
один оборот) моментов сил, действующих на роторы каждого
вибратора при условии, что последние равномерно вращаются
по закону (3.21), а несущие тела совершают установившиеся
вынужденные колебания под действием возмущающих сил, раз-
виваемых роторами при их равномерном вращении по указан-
ному закону. Рассматриваемые уравнения могут быть получены
путем простого осреднения уравнений движения роторов ви-
браторов при указанном движении системы.
В соответствии с изложенным, через (as, crsG>) в равен-
ствах (3.22) обозначен средний момент, передаваемый на вал
вибратора от электродвигателя, а через 7?° (со) — средний мо-
мент сил сопротивления. При обычных предположениях
2л/<а
Llm)(as> asco) = -^ f
о s s
<ysL''sa’ (crsco) для асинхронного двигателя,
[as(as — ₽s)] Для синхронного двигателя, (3-23)
где ps — установочный угол, определяемый расположением об-
моток статора синхронного двигателя, а /?°(со) представляет
собой монотонно возрастающую неотрицательную функцию со.
Моменты Ws(a\, .... ah, со) играют основную роль в рас-
сматриваемых явлениях. Они отражают обратное влияние коле-
баний несущих тел на движение роторов вибраторов, и поэтому
их можно назвать вибрационными моментами.
Вибрационные моменты получаются путем осреднения
в уравнениях движения роторов членов того же типа, что и
члены mses^sinq)s в первых k уравнениях (3.17). Эти моменты
представляют собой как бы дополнительные средние внешние
нагрузки (в случае > 0) или вращающие моменты (если
Ws < 0). С другой стороны, каждый вибрационный момент мо-
жет быть представлен в виде суммы
k
wst	(3.24)
/-I
«частных вибрационных моментов» wSj, характеризующих влия-
ние /-го вибратора на s-й вибратор. Этим влиянием и объяс-
няется самосинхронизация вибраторов и ряд нелинейных эф-
фектов, наблюдаемых при принудительной синхронизации.
Проследим роль вибрационных моментов в случае задачи
о самосинхронизации вибраторов, когда Ss ss 0 и =
5 3]
ОБЗОР ОСНОВНЫХ ФАКТОВ И РЕЗУЛЬТАТОВ
41
= asL(sa} (orsco). Уравнения (3.22) при этом приобретают вид
Ps(ai, ak, (t>)^asLsa) — Rs(a>)~ lF.s(a......... ak, <o) = 0 (3.25)
(s = 1, ..., k).
Введем в рассмотрение парциальные угловые скорости вра-
щения роторов вибраторов <в.„ которые положим равными угло-
вым скоростям установившегося вращения роторов при усло-
вии, что вибраторы установлены не на колеблющихся телах,
а на неподвижном основании. За положительное направление
угловой скорости примем при этом направление, в котором ро-
тор s-ro вибратора вращается в изучаемом синхронном движе-
нии. Тогда, как можно показать (см. § 10 главы XIII), при
o)s > 0 двигатель s-ro вибратора в этом движении работает
в обычном, а при ws < 0 — в генераторном режиме.
В случае, когда парциальные скорости положительны, они
определяются из уравнений
asT(a) (ors<os) = Rs (<os),	(3.26)
получающихся из (3.25) при = 0. Если моменты L(^, разви-
ваемые двигателями, и моменты сопротивления R°s различны
для различных вибраторов, то различными, вообще говоря, бу-
дут также и скорости вращения роторов cog этих вибраторов
при установке их на неподвижном основании. Если, однако,
такие вибраторы установить на систему тел, которые могут со-
вершать колебания, то за счет появления вибрационных момен-
тов может произойти выравнивание угловых скоростей враще-
ния роторов вибраторов — их самосинхронизация.
Можно показать, что наличие или отсутствие самосинхрони-
зации существенно зависит от того, насколько разнятся между
собой парциальные угловые скорости Если все cos одинаковы
и положительны, то самосинхронизация, вообще говоря, имеет
место независимо от значений других параметров системы.
Однако одинаковость и положительность со., совсем не обяза-
тельны для самосинхронизации; в частности, один или несколько
вибраторов могут быть выключены из сети (<bs = 0) или даже
работать в генераторном режиме («, < 0) и, несмотря на это,
вращаться синхронно с другими вибраторами, двигатели кото-
рых включены в сеть и работают в обычном режиме (<bs>0).
Энергия, необходимая для преодоления сопротивления в вы-
ключенных (или в генерирующих) вибраторах, передается от
нормально включенных в сеть вибраторов благодаря вибрациям
тел, на которых они установлены. В последнем случае имеет
место так называемый эффект вибрационного поддержания
вращения, о котором более подробно говорится в п. 9 настоя-
щего параграфа.
42
ВВЕДЕНИЕ
Исследование показывает, что возможность или невозмож-
ность самосинхронизации существенно зависит от числа сте-
пеней свободы несущих тел, от соотношений между частотами
их собственных колебаний и угловой скоростью синхронного
движения о, от расположения осей вибраторов на несущих те-
лах и от направлений вращения роторов в изучаемом синхрон-
ном движении.
Наличие вибрационных моментов может существенно отра-
зиться также и на работе системы принудительной синхрониза-
ции вибраторов. В этом случае могут существенно изменяться
начальные фазы вращения вибраторов в устойчивом синхрон-
ном движении (по сравнению с их значениями при установке
вибраторов на неподвижном основании). Кроме того, устано-
вившееся движение вибраторов, устойчивое в случае их уста-
новки на неподвижном основании, может оказаться неустойчи-
вым при размещении вибраторов на колеблющихся телах, и
наоборот. Вместе с тем путем надлежащего подбора парамет-
ров системы принудительной синхронизации всегда оказывается
возможным обеспечить существование и устойчивость синхрон-
ного движения с наперед заданной комбинацией начальных фаз.
Особое прикладное значение имеет случай самосинхрониза-
ции вибраторов с одинаковыми и положительными парциаль-
ными скоростями. Для систем рассматриваемого типа в этом
случае имеют место равенства (3.26), и поэтому уравнения
(3.25) приобретают вид
Ps(ab ..ак, <о) = - U7s(ai> . .., ак, со) = 0	(3.27)
(s=l....k),
а уравнение (3.10) записывается в форме
К да}	dW, da2	dWt dak	
dW2 det]	dW2 , -5	F- x . da2	dW2 da. Я	= 0.
dWk да,	dWk da2	da, R	
(3.28)
Иными словами, значения фаз вращения а,, .... aft, а тем
самым и характер колебаний несущих тел в устойчивых син-
хронных движениях, в данном случае определяются исключи-
тельно выражениями для вибрационных моментов.
На практике парциальные скорости отдельных номинально
одинаковых вибраторов всегда несколько отличаются одна от
другой вследствие неточностей изготовления и других случай-
§ 3]	ОБЗОР ОСНОВНЫХ ФАКТОВ Л РЕЗУЛЬТАТОВ	43
них причин. При этом устойчивые комбинации фаз «,=«*, ...
..., ak = а*, найденные из уравнений (3.27), будут как бы
«центрами рассеяния» значений тех же фаз в реальных систе-
мах. Существенно, чтобы указанное рассеяние было не слиш-
ком велико, то есть чтобы фазы а*, ..., а* были «достаточно
стабильными». Этот важный вопрос кратко обсуждается в п. 6
настоящего параграфа.
Из сказанного ясно, что вычисление вибрационных момен-
тов является одним из главных элементов решения задачи
о синхронизации: составление выражений для прочих слагае-
мых в левых частях основных уравнений (3.22) обычно не
представляет труда.
Существует несколько способов нахождения вибрационных
моментов. Наиболее универсальный из них состоит в непосред-
ственном осреднении соответствующих членов в уравнениях
движения роторов вибраторов.
Другой способ, часто значительно более удобный, основан
на соотношении (см. § 7 главы XIII и §§ 2 и 3 главы XIV) *)
rs(a„ .... ak, <о) =	(3.29)
где
2л/о	2л/<а
А = А(а.......	= (L)odi = ^j (Т-П)0Л	(3.30)
о	о
есть среднее за период значение функции Лагранжа системы
L = T—П (Г —кинетическая, а П — потенциальная энергия),
вычисленное в исходном приближении. Это приближение обычно
является известным: оно отвечает равномерному вращению ро-
торов вибраторов по закону (3.21) и соответствующим устано-
вившимся вынужденным колебаниям несущих тел.
Если колебательная система, на которой установлены вибра-
торы, близка к линейной, то вибрационные моменты могут быть
найдены по еще более простой формуле:
..., ak, <о) = -^-,	(3.31)
где А^^А^Да.........ал, w)—среднее значение лагранжиана
только колебательной части системы (то есть несущей системы).
Наконец, в последнем случае вибрационные моменты мо-
гут быть выражены через так называемые гармонические
*) Здесь мы рассматриваем для упрощения рассуждения случай, когда
несомые связи (синхронизирующие элементы) между роторами вибраторов
отсутствуют.
44
ВВЕДЕНИЕ
коэффициенты влияния, легко вычисляемые, если известны уста-
новившиеся вынужденные колебания осей роторов вибраторов
под действием единичных гармонических возмущающих сил, так-
же приложенных к осям роторов (см. п. 2 § 3 главы XIV). Одно
из достоинств этого последнего способа, предложенного
К. Ш. Ходжаевым, состоит в том, что гармонические коэффи-
циенты могут быть найдены экспериментальным путем и, таким
образом, выражения для вибрационных моментов можно со-
ставить не решая (и даже не выписывая) дифференциальных
уравнений движения несущих тел.
Сопоставление формул (3.29) и (3.31) с формулами (3.27)
и (3.12) приводит к заключению, что в рассматриваемых слу-
чаях задачи о синхронизации вибраторов справедлив интеграль-
ный критерий устойчивости (см. п. 2 настоящего параграфа),
причем в первом случае роль потенциальной функции D играет
осредненный лагранжиан системы Л, взятый со знаком минус,
а во втором — осредненный лагранжиан несущей системы А<т>.
Определение значений фаз аь ..., а.к, которым соответствуют
устойчивые синхронные движения роторов вибраторов, сводится
при этом к отысканию точек минимума соответственно функ-
ций Л и А<1>.
На практике часто встречается случай, когда вибраторы
с одинаковыми парциальными угловыми скоростями установ-
лены на мягко амортизированном твердом теле*). При этом
потенциальной энергией несущей системы можно пренебречь,
и устойчивые синхронные движения будут соответствовать ми-
нимуму осредненной кинетической энергии тела. Отсюда сле-
дует вывод (см. § 2 главы XXIII), что роторы вибраторов в рас-
сматриваемом случае стремятся вращаться таким образом,
чтобы развиваемые ими возмущающие силы как можно полнее
взаимно компенсировались и тело совершало «минимальные»
(в смысле величины средней кинетической энергии) колебания.
Этот вывод особенно важен для теории групповых фундаментов
под неуравновешенные машины (см. п. 7 настоящего параграфа
и главу XXIII книги), а также при решении задач синтеза
машин с самосинхронизирующимися вибраторами.
Простейшим примером, иллюстрирующим изложенное, мо-
жет служить поведение двух одинаковых дебалансных вибра-
торов, установленных на платформе с одной степенью свободы
(рис. 3, а). Пусть жесткость опорных пружин с относительно
мала, так что |/с/Л4<(й, где М — масса системы, то есть ча-
стота свободных колебаний платформы меньше угловой скоро-
*) Под мягко амортизированным твердым телом понимается тело, свя-
занное с неподвижным основанием столь мягкими упругими элементами, что
частоты собственных колебаний тела весьма малы по сравнению с угловой
скоростью вращения роторов вибраторов.
§ 3]	ОБЗОР ОСНОВНЫХ ФАКТОВ И РЕЗУЛЬТАТОВ	45
сти вращения роторов. Тогда в устойчивом синхронном движе-
нии роторы вращаются в противофазах, как показано на
рис. 3, а сплошными линиями. При этом те составляющие воз-
мущающих сил, развиваемых вибраторами, которые направ-
лены вдоль направления возможного движения, взаимно урав-
новешиваются, и платформа остается неподвижной (в рассмат-
риваемом приближении). Подобная ситуация представляется
парадоксальной, ибо на первый взгляд кажется непонятным,
Рис. 3.
каким образом может обеспечиваться определенная фазировка
роторов при «неработающей обратной связи», то есть при не-
подвижной платформе. Дело, однако, в том, что при возмущении
противофазного вращения роторов обратная связь начинает
работать — платформа перестает быть неподвижной. При этом
возникающие колебания платформы как раз таковы, что спо-
собствуют восстановлению противофазного вращения. Картина
здесь во многом аналогична той, которая наблюдалась
X. Гюйгенсом в опыте с часами (см. цитату в п. 1 § 1 настоя-
щего введения).
В заключение пункта отметим, что соотношения типа (3.29)
и (3.31), а, значит, также и интегральный критерий устойчиво-
сти имеют место и для значительно более общих случаев за-
дачи о синхронизации вибраторов, нежели рассматриваемые
выше. Кроме того, интегральному критерию могут быть при-
даны различные формы и интерпретации (см. § 9 главы XIII
46
ВВЕДЕНИЕ
и § 4 главы XIV), удобные при решении практических задач,
в том числе задачи синтеза, о которой подробно говорится ниже.
Полученные или изложенные в настоящей книге результаты
исследования синхронизации вибраторов в различных конкрет-
ных системах сведены в таблицу 5 (см. Добавление 2).
5. Проблема синтеза вибрационного поля и задачи синтеза
устройств с механическими вибраторами. Полезное применение
механических колебаний — создание вибрационных машин и
устройств — делает все более актуальной следующую своеобраз-
ную задачу: требуется обеспечить с заданной точностью
периодические колебания определенных частей упругой системы
по некоторым заданным законам, допускаемым связями. 'Гак,
например, при создании вибрационных транспортирующих ма-
шин необходимо сообщить колебания упругой балке или обо-
лочке, мало отличающиеся от их прямолинейных поступатель-
ных колебаний как твердых тел.
Данную задачу можно назвать задачей синтеза вибрацион-
ного поля. Ее особенности и трудности решения определяются
в основном следующими обстоятельствами. Во-первых, приме-
няемые в настоящее время возбудители колебаний развивают
возмущающие усилия, распределенные по некоторой небольшой
части поверхности упругих тел, входящих в колебательную
систему; эти усилия уместно считать сосредоточенными. Во-
вторых, число возбудителей практически всегда ограни-
ченно; более того, по экономическим и эксплуатационным со-
ображениям желательно, чтобы число возбудителей было по
возможности минимальным. Наконец, в-третьих, действие реаль-
ных вибраторов на колебательную систему далеко не всегда
можно сводить к действию заданных возмущающих сил, как
это обычно делается в теории вынужденных колебаний. Дело
в том, что указанные возмущающие силы существенно зависят
от колебаний тех участков упругой системы, с которыми свя-
заны вибраторы. Иными словами, вибраторы образуют с упру-
гой системой единую колебательную систему с большим, не-
жели у исходной системы, числом степеней свободы за счет
добавочных «собственных» степеней свободы вибраторов. Урав-
нения движения совокупной системы оказываются при этом,
как правило, нелинейными.
Изложенное хорошо иллюстрируется системой уравнений
(3.17) настоящего параграфа: указанная система была бы ли-
нейной, если отбросить уравнения движения роторов вибра-
торов и считать это движение заданным и равномерным. Не-
сомненно, однако, что подобное упрощение сделало бы невоз-
можным решение задачи о синхронизации вибраторов и не
позволило бы учесть многие важные эффекты (см. п. 8 настоя-
щего параграфа),
§ 3]	ОБЗОР ОСНОВНЫХ ФАКТОВ И РЕЗУЛЬТАТОВ	47
Решение рассматриваемой задачи все же удается существен-
но упростить благодаря тому, что обратное влияние колебаний
упругой системы на вибраторы, как правило, допустимо считать
малым, подобно тому как это было сделано при решении задачи
о синхронизации вибраторов (см. п. 4 настоящего параграфа).
В указанном предположении задача может быть разбита на
две последовательно решаемые задачи — задачу о синтезе за-
данного поля вынужденных колебаний упругой системы по-
средством некоторого (по возможности меньшего) числа за-
данных сосредоточенных периодических возмущающих сил и
задачу о синтезе системы возбуждения. В результате решения
первой задачи определяются, в частности, значения начальных
фаз вращения валов вибраторов а*, a*k, обеспечивающие
требуемое поле колебаний упругой системы. Вторая же задача
по существу представляет собой упоминавшуюся выше задачу
о синтезе систем с синхронно работающими вибраторами. Она
состоит в таком выборе свободных параметров системы, при
котором определенные решением первой задачи начальные
фазы а*, а* удовлетворяют основным уравнениям (3.22) и
условию устойчивости (3.10).
Как отмечалось, указанные условия всегда могут быть удов-
летворены путем надлежащего выбора системы принудительной
синхронизации. Однако к такому способу следует прибегать
лишь в том случае, если нельзя достигнуть цели посредством
использования эффекта самосинхронизации.
В отдельных случаях может оказаться, что условия суще-
ствования и устойчивости требуемого движения самосинхрони-
зирующихся вибраторов либо удовлетворяются автоматически,
либо могут быть удовлетворены путем простого варьирования
параметров заданной системы. Относительно широкий набор
таких «удачных» вариантов приведен в таблице 5 (Добавле-
ние 2). Чаще же оказывается, что требуемый режим в задан-
ной системе при самосинхронизации не обеспечивается. .Тогда
следует попытаться добиться цели либо путем изменения
числа степеней свободы несущей упругой системы, либо путем
изменения числа вибраторов. Выше уже указывалось, что
в результате таких изменений характер устойчивых синхрон-
ных движений роторов вибраторов может существенно из-
мениться. В ряде случаев для определения необходимых изме-
нений системы можно опять-таки использовать данные таб-
лицы 5.
Чтобы пояснить указанные способы синтеза систем с само-
синхронизирующимися вибраторами, приведем два простых
примера.
48
ВВЕДЕНИЕ
Пусть сначала необходимо обеспечить прямолинейные по-
ступательные колебания мягко амортизированного твердого
тела по закону, близкому к гармоническому (рис. 3). Для этой
цели могут быть использованы два одинаковых дебалансных
вибратора, приводимых от асинхронных двигателей с роторами,
вращающимися в противоположных направлениях. Для гаран-
тии колебаний тела в нужном направлении на первый взгляд
представляется полезным поместить тело в направляющие, ко-
торые допускают перемещения тела только в этом направлении
(рис. 3,а). Однако, как отмечалось в конце предыдущего
пункта, исследование показывает, что в этом случае вибраторы
будут устойчиво самосинхронизироваться с таким соотношением
фаз, которое показано на рисунке сплошными линиями. Иными
словами, в устойчивом синхронном движении возмущающие
силы, развиваемые вибраторами, будут взаимно уравновеши-
ваться, а тело останется практически неподвижным. Требуемая
же для обеспечения колебаний тела фазировка вращения ви-
браторов в данном случае является неустойчивой (на рис. 3, а
эта фазировка показана пунктиром).
Исследование показывает, что существуют по крайней мере
два способа обеспечения устойчивости требуемого синхронного
вращения роторов: либо присоединить к основной массе ДТ;
посредством пружины с2 некоторую добавочную массу *) М2
(рис. 3,6), либо, как это ни кажется парадоксальным, просто
убрать направляющие (рис. 3, в). Отметим, что в обоих случаях
желаемый результат достигается, по существу, одним и тем же
способом — изменением числа степеней свободы колебательной
части системы.
В качестве другого примера рассмотрим случай, когда не-
обходимо обеспечить круговые поступательные колебания мягко
амортизированного твердого тела. Этой цели можно достигнуть,
применив два одинаковых дебалансных вибратора, приводимых
от асинхронных двигателей, роторы которых вращаются в оди-
наковых направлениях. Оси вращения роторов лежат в одной
плоскости с центром тяжести тела О| и удалены от него на
одинаковые расстояния г. Исследование показывает, что в этом
случае (см. § 4 главы XV) при выполнении условия
л^>2
(3.32)
(через М и I обозначены соответственно масса и момент инер-
ции тела) устойчиво синхронное и синфазное вращение роторов,
которое как раз и обеспечивает круговые поступательные коле-
*) Величины М2 и с2 должны удовлетворять при этом некоторому нера-
венству, в которое входят также масса Л11 и синхронная угловая скорость 0)
(см. условие (3.6) главы XV).
§ 3]
ОБЗОР ОСНОВНЫХ ФАКТОВ И РЕЗУЛЬТАТОВ
49
бания тела (рис. 4, а). При невыполнении условия (3.32) ро-
торы вибраторов в устойчивом синхронном движении вра-
щаются в противофазе (рис. 4,6), и поэтому тело совершает
поворотные колебания относительно центра тяжести Оь
Часто удовлетворить условию (3.32) оказывается практиче-
ски затруднительным. Поэтому желательно добиться устойчи-
вости синфазного вращения обоих роторов при Мг2!1 < 2. Как
в)
Рис. 4.
показывает исследование, для этого достаточно снабдить си-
стему дополнительным центрально расположенным дебалансным
вибратором, обладающим той же парциальной скоростью и
вращающимся в том же направлении. При выполнении соотно-
шения
Mr2 2 _ '”383
I	те
(те и тзвз — статические моменты роторов соответственно
каждого из основных и дополнительного вибраторов) роторы
основных вибраторов будут в устойчивом синхронном режиме
вращаться синфазно, а ротор дополнительного вибратора —
в противофазе по отношению к роторам основных (рис. 4,в).
Колебания тела при этом окажутся круговыми поступатель-
ными, несмотря на несоблюдение условия (3.32), хотя ампли-
туда колебаний несколько уменьшится.
50
ВВЕДЕНИЕ
Рассмотренные способы обеспечения устойчивости требуе-
мого режима синхронного вращения вибраторов значительно
расширяют возможности использования явления самосинхрони-
зации. Однако могут представиться случаи, когда соответствую-
щие принципиальные и конструктивные решения оказываются
нецелесообразными или даже невозможными. В таких случаях
можно прибегнуть к тому или иному способу принудительной
синхронизации.
Практически почти всегда желательно, чтобы система при-
нудительной синхронизации удовлетворяла некоторым условиям
оптимальности. Можно потребовать, например, чтобы число свя-
зей между валами вибраторов было минимально возможным,
а «жесткости» связей — минимально допустимыми.
В ряде относительно простых случаев указанный оптималь-
ный выбор системы принудительной синхронизации может быть
выполнен без особого труда (см. пп. 5 и 6 § 16 главы XIII,
а также § 3 главы XX). Допускает решение в общей форме и
задача об обеспечении устойчивости требуемой фазировки вра-
щения роторов вибраторов путем наложения минимального
числа абсолютно жестких (кинематических) связей между ро-
торами (см. § 5 главы XV).
6. О стабильности синхронного режима движения системы.
Стабильность колебаний, возбуждаемых самосинхронизирую-
щимися вибраторами. Для возможности практического исполь-
зования системы с синхронно работающими объектами еще не-
достаточно, чтобы требуемый синхронный режим существовал
и был устойчив. Необходимо также, чтобы этот режим был до-
статочно «стабилен», то есть чтобы отклонения показателей
работы устройства (назовем эти показатели контрольными па-
раметрами), обусловленные либо неточностями изготовления
элементов системы, либо изменениями их параметров в про-
цессе работы, не превосходили определенных пределов.
Проблема стабильности синхронного режима работы устрой-
ства, естественно, представляет собой часть проблемы надеж-
ности этого устройства, а именно ту ее часть, которая связана
с динамикой совместно функционирующих объектов. Наиболее
последовательной является вероятностная форма определения
стабильности, когда выдвигается условие, чтобы не превышала
определенного предела вероятность появления недопустимо
больших отклонений контрольных параметров от их номиналь-
ных значений.
Следуя традиции, в настоящей книге мы различаем понятия
устойчивости и стабильности движения. Заметим, однако, что
этого можно было бы не делать, ибо в обоих случаях инже-
нера-прикладника, в сущности, интересует характер зависимо-
сти некоторых функционалов от решений уравнений движения
§ 3]	ОБЗОР ОСНОВНЫХ ФАКТОВ И РЕЗУЛЬТАТОВ	51
системы (контрольных параметров), от параметров, определяю-
щих ее движение. Практически используемая система должна
быть достаточно «грубой», малочувствительной по отношению
к отклонениям этих последних параметров. То обстоятельство,
что, например, в задаче об устойчивости за контрольные пара-
метры, как правило, принимаются значения фазовых координат
системы при Z-*oo, а из числа параметров, определяющих дви-
жение, выделяются начальные условия, принципиального зна-
чения не имеет.
В важном классе задач о синхронизации слабо связанных
объектов характер устойчивого синхронного режима опреде-
ляется соответствующей системой значений фазовых сдвигов
ой, ..., as и синхронной частоты <л. Поэтому «стабильность»
(или, наоборот, «чувствительность») указанных величин по от-
ношению к изменениям параметров системы, по существу, и
определяет стабильность режима. Что же касается параметров
системы, влияющих на ее движение, то наиболее важными из
них в задаче о синхронизации автоколебательных объектов яв-
ляются парциальные скорости (частоты) этих объектов.
Применительно к вибрационным машинам с несколькими
механическими вибраторами проблема стабильности ставится и
рассматривается соответственно в главе XVI и в § 2 главы XX
настоящей книги. За контрольные в этом случае можно при-
нять параметры, характеризующие закон колебаний некоторых
точек рабочего органа машины. Тогда задача сведется к задаче
о стабильности вибрационного поля упругой системы (или не-
которой ее части), возбуждаемого вибраторами.
Особенно важной проблема стабильности является для ви-
брационных машин с самосинхронизирующимися вибраторами.
Как правило, в таких машинах используются номинально оди-
наковые вибраторы (см. таблицы 2 и 4). Пусть при этом суще-
ствует устойчивый режим синхронного вращения роторов ви-
браторов, характеризующийся значениями начальных фаз
вращения а1 = а*, ..., aft = а*, при которых осуществляется
требуемый закон колебаний рабочих органов машины.
В действительности, однако, одноименные параметры вибра-
торов (в том числе, конечно, и парциальные угловые скорости)
никогда не могут быть выдержаны при изготовлении в точности
одинаковыми. Вследствие этого изменяются по сравнению
с расчетными и значения углов <zj, ..., ah в устойчивом син-
хронном движении вибраторов, а значит, и поле колебаний
рабочего органа машины. При разбросе парциальных угловых
скоростей, превышающем определенные пределы, вибраторы
могут даже выпасть из синхронизма. Для возможности прак-
тического использования устройства необходимо, чтобы этого
не происходило и чтобы указанное искажение поля колебаний
52
ВВЕДЕНИЕ
было не слишком значительно. Последнее условие и является
условием стабильности колебаний.
В случае машин, приводимых от двух самосинхронизирую-
щихся вибраторов, условие стабильности, как правило, может
быть записано в форме
•	о
— > х*	(3.33)
Здесь р°а — максимально допустимое значение относительного
отклонения парциальных угловых скоростей вибраторов, кото-
рое еще не приводит к выпадению из синхронизма, a qti,— мак-
симально возможное значение этого отклонения, обусловленное
неточностями изготовления и сборки вибраторов и их двигате-
лей. Величина хш, таким образом, представляет собой коэффи-
циент запаса по самосинхронизации-, согласно условию (3.33)
для обеспечения стабильности колебаний рабочего органа ма-
шины этот коэффициент должен быть не ниже некоторого ми-
нимально допустимого значения х^. Рекомендуемые значения
х^ в зависимости от типа и назначения машины, а также фор-
мулы для определения величин и q® приводятся в п. 6 § 2
главы XX настоящей книги. Здесь мы отметим лишь, что %*
варьирует в пределах от 3,5 до 20
отклонение парциальных угловых
формулам вида
о 1 I (dj СО2
и что предельно допустимое
скоростей определяется по
^0 (©о)
где СГо(соо)—максимальное значение вибрационного момента
(как функции углов ai и аг), вычисленное для случая совер-
шенно одинаковых вибраторов и номинальных значений пара-
метров системы, coo — номинальное значение угловой скорости
вращения роторов вибраторов, zL и zR— номинальные значе-
ния жесткостей характеристик соответственно вращающих мо-
ментов асинхронных двигателей и моментов сопротивления вра-
щению роторов.
Соотношения (3.34) и (3.33) еще раз подчеркивают роль
вибрационного момента W как синхронизирующего фактора:
чем больше величина ТГо(о)о), тем большие различия в пар-
циальных угловых скоростях вибраторов являются допусти-
мыми, тем как бы сильнее «притяжение» фаз вращения роторов
а, и аг к их значениям а* и а*, отвечающим одинаковым ви-
браторам. Иными словами, чем больше ТГо(соо), тем при про-
чих равных условиях стабильнее режим колебаний рабочего
органа машины.
§ 3]	ОБЗОР ОСНОВНЫХ ФАКТОВ И РЕЗУЛЬТАТОВ	53
7. Приложения теории синхронизации механических вибра-
торов. Простейшие примеры, рассмотренные в п. 5 настоящего
параграфа (см. рис. 3 и 4), а также многочисленные более
сложные примеры, изучаемые в четвертой и пятой частях книги
(см. таблицу 5 Добавления 2), свидетельствуют о том, что мно-
гие практически важные закономерности синхронизации вибра-
торов вряд ли могли бы быть предсказаны на основе интуитив-
ных соображений до приведения теоретического или эксперимен-
тального исследования. Сказанным и определяется прикладное
значение теории синхронизации вибраторов, явившейся в по-
следние годы базой для создания многих новых вибрационных
машин и устройств (см., в частности, рис. 86—120 и обзор в §3
главы XII).
Обстоятельства, по которым использование явления само-
синхронизации и некоторых средств принудительной синхрони-
зации позволяет усовершенствовать существующие и создать
новые вибрационные машины, были уже указаны выше (см. п. 4
настоящего параграфа). Поэтому остановимся лишь на одном
специальном приложении теории самосинхронизации, относя-
щемся к расчету и проектированию групповых фундаментов
под однотипные неуравновешенные машины. Поскольку указан-
ные машины, как правило, могут рассматриваться как вибра-
торы, установленные на некоторой колебательной системе и
приводимые от независимых двигателей асинхронного типа, то
здесь приходится иметь дело с двумя случаями:
а)	Тенденция машин к самосинхронизации, определяемая,
как указывалось выше, максимальными значениями вибрацион-
ных моментов, слаба по сравнению с десинхронизирующим
влиянием разброса парциальных угловых скоростей отдельных
машин. При этом вероятность наступления самосинхронизации
достаточно мала и взаимодействие машин можно не учитывать.
Колебания фундамента в данном случае носят характер биений.
б)	Тенденция к самосинхронизации относительно сильна,
так что синхронное движение неуравновешенных масс машин
весьма вероятно. В этом последнем случае взаимодействие ма-
шин существенно, причем оно оказывается весьма опасным,
если устойчивым будет такое синхронное движение, при котором
неуравновешенности отдельных машин складываются. С другой
стороны, если устойчивым является синхронный режим, при
котором неуравновешенные усилия и моменты, развиваемые
отдельными машинами, взаимно компенсируются, то установка
машин на групповом фундаменте может привести к значитель-
ному снижению уровня колебаний.
В рассматриваемом случае задача состоит в таком выборе
параметров фундамента и его основания, при котором, во-пер-
вых, существует и устойчив указанный «компенсирующий»
54
ВВЕДЕНИЕ
режим синхронной работы машин и, во-вторых, при котором этот
режим достаточно стабилен по отношению к разбросам пара-
метров отдельных машин.
Рассмотрению поставленной задачи посвящена глава ХХШ
книги; при ее решении оказывается полезным следствие из ин-
тегрального критерия устойчивости синхронных движений ви-
браторов, упомянутое в конце п. 4 настоящего параграфа. Со-
гласно этому следствию тенденция к «компенсирующему» син-
хронному режиму непременно имеется в случае установки
машин на фундаменте, частоты собственных колебаний которого
в достаточной мере ниже угловых скоростей вращения валов
машин.
8.	Взаимодействие механического вибратора с колебатель-
ной системой. Задача о синхронизации вибраторов, по суще-
ству, представляет собой задачу о взаимодействии возбудите-
лей через колебательную систему. Поэтому она включает в себя
как составную часть задачу о взаимодействии одного вибратора
с колебательной системой, с которой он связан. Последняя про-
блема представляет также и самостоятельный интерес и по-
этому явилась в последние годы предметом ряда специальных
исследований (их обзор приводится в § 1 главы XVII).
Существенная особенность рассматриваемых задач состоит
в том, что при их решении недопустимо оставаться в рамках
обычной концепции теории вынужденных колебаний, когда воз-
мущающая сила предполагается заданной и не зависящей от
движения колебательной части системы. Такая идеализация
в случае системы, описанной в п. 4 настоящего параграфа, от-
вечала бы отбрасыванию первых k дифференциальных уравне-
ний (3.17) и предположению, что <ps = os(at + а°), где а°—
заранее заданные числа. Здесь же приходится рассматривать
совместное движение возбудителей и колебательной системы,
в результате чего порядок уравнений движения существен-
но повышается и к тому же система в целом становится нели-
нейной.
Задача о взаимодействии вибратора с колебательной систе-
мой может рассматриваться как простейший частный случай
задачи о синхронизации, когда имеется всего лишь один вибра-
тор. Вместе с тем рассмотрение этой задачи позволяет выявить
ряд особенностей поведения систем с любым числом возбуди-
телей.
Наиболее интересные закономерности обнаруживаются при
взаимодействии возбудителя с колебательной системой вблизи
области резонанса, когда угловая скорость синхронного враще-
ния близка к одной из частот собственных колебаний системы.
Одно из наиболее ярких явлений, характерных для рассматри-
ваемых систем в случае, когда вибратор приводится от двига-
ОБЗОР ОСНОВНЫХ ФАКТОВ И РЕЗУЛЬТАТОВ
65
§ 3]
теля асинхронного типа, состоит в стабилизации частоты коле-
баний вблизи собственных частот колебательной части системы
и последующем резком срыве колебаний с переходом на после-
резонансный режим. Речь идет об эффекте, по-видимому, впер-
вые описанном А. Зоммерфельдом еще в 1902 г. и часто свя-
зываемом с его именем.
Другой примечательной особенностью, обнаруживаемой при
анализе взаимодействия вибратора с колебательной системой,
является то, что ниспадающие ветви пиков резонансных кривых
линейной колебательной системы оказываются практически не-
реализуемыми вследствие неустойчивости послерезонансных ре-
жимов (см. рис. 5, й, где нереализуемые участки кривых нане-
сены пунктиром). В случае синхронного двигателя при плав-
ном изменении синхронной угловой скорости со или частоты
собственных колебаний системы р нереализуемыми оказываются
все верхние части резонансных пиков (рис. 5,6).
Анализ описанных явлений может быть выполнен на основе
уравнения
L(m) (а, ай) = R (и) + W (и),	(3.35)
где Г (со)—по-прежнему вибрационный момент, представляю-
щий как бы дополнительную внешнюю нагрузку на двигатель
вибратора. Функция W(со) имеет ярко выраженные экстре-
мумы вблизи собственных частот колебательной части си-
стемы. Подчеркнем, что по своему виду уравнение (3.35) впол-
не соответствует виду основных уравнений (3.22) задачи о син-
хронизации вибраторов; это уравнение также может быть по-
лучено путем соответствующего осреднения уравнения движения
вибратора, то есть уравнения типа первых k уравнений (3.17).
Подробное рассмотрение указанных задач, а также связан-
ной с ними задачи о динамике регулятора Буасса — Сарда, по-
священа XVII глава настоящей книги.
9.	Вращение неуравновешенного ротора под действием ко-
лебаний его оси. Выше уже указывалось (см. п. 4 настоящего
56
ВВЕДЕНИЕ
параграфа), что тенденция нескольких вибраторов к синхрон-
ному вращению может оказаться столь сильной, что при выклю-
чении из сети электродвигателей одного или нескольких рабо-
тающих вибраторов роторы выключенных вибраторов не вы-
падают из синхронизма, продолжая вращаться неограниченно
долго. Вращение роторов происходит за счет энергии, переда-
ваемой от включенных вибраторов колебаниями несущих тел,
на которых вибраторы размещены. Подобное весьма эффектное
явление, которое можно назвать вибрационным поддержанием
вращения неуравновешенного ротора, находит многочисленные
технические применения; оно лежит также в основе известной
игры-упражнения «хула-хуп».
Задача о вибрационном поддержании вращения неуравнове-
шенного ротора, а также и более общая задача о движении
ротора вибратора с колеблющейся осью, может быть, вообще
говоря, рассмотрена в рамках задачи о синхронизации вибра-
торов как соответствующий частный случай. Однако зачастую
оказывается вполне достаточным рассмотреть значительно бо-
лее простую задачу о стационарном вращении ротора вибра-
тора, ось которого совершает заданные колебания, например
гармонические колебания с определенными частотой со и ам-
плитудой А. Иными словами, вместо внутренней синхронизации
можно рассматривать внешнюю синхронизацию (захватыва-
ние). То обстоятельство, что в данном случае речь идет о за-
хватывании вращательного, а не колебательного (как обычно)
движения, особой роли не играет. Рассмотрению сформулиро-
ванной задачи посвящена глава XVIII настоящей книги.
Теоретическое и экспериментальное исследования показы-
вают, что возможны режимы стационарного вращения ротора
не только со средней угловой скоростью |фср], совпадающей
с частотой колебаний оси вибратора со, но и со скоростями
|фср| = усо, где р и q — целые положительные числа. Однако
обычно режиму, для которого |фср| — со, отвечает наиболее ши-
рокая область существования и устойчивости в пространстве
параметров и наибольшая «область притяжения» в фазовом
пространстве; назовем этот режим основным.
Применение теорем, о которых говорилось в п. 2 настоящего
параграфа, приводит для определения фазы вращения вала
вибратора а к уравнению типа (3.35), с той лишь разницей, что
в данном случае вибрационный момент W = W (а, со) зависит
от угла а. Требование наличия у этого уравнения веществен-
ных решений относительно а и приводит к условию существова-
ния рассматриваемого движения.
Исследование показывает, что если частота колебаний оси и
достаточно близка к парциальной угловой скорости ротора
§ 3]	ОБЗОР ОСНОВНЫХ ФАКТОВ и результатов	5;
вибратора, приводимого от асинхронного двигателя, то враще-
ние ротора всегда захватывается частотой ы, как бы мала ни
была амплитуда колебаний оси ротора. Здесь мы, как обычно,
имеем отсутствие так называемого порога захватывания. Более
примечательно, однако, то, что стационарные режимы враще-
ния ротора существуют и устойчивы в достаточно широкой об-
ласти значений параметров даже при отсутствии двигателя,
приводящего ротор во вращение, то есть в случае, когда вибра-
тор представляет собой обычный физический маятник (речь
идет о вибрационном поддержании вращения). Роль «актив-
ного», вращающего момента в данном случае играет вибра-
ционный момент 1Е(<в, а), который при этом отрицателен (в про-
тивном случае уравнение (3.35) при Z/m>(a, ооз) = 0 не имело
бы решений).
В качестве примера приведем условие существования устой-
чивого основного режима вращения маятника, ось которого со-
вершает гармонические колебания в двух взаимно перпенди-
кулярных направлениях (рис. 65, а). Это условие имеет следую-
щий простой вид:
2A/d>f.	(3.36)
Здесь d — диаметр внутреннего кольца подшипников, в которых
вращается ротор, f — коэффициент трения в подшипниках, а
Л = у(й+а7>)	(3.37)
— так называемая эффективная амплитуда колебаний оси ро-
тора, причем а и b — соответственно большая и малая полуоси
эллиптической траектории колебаний оси, а число о* равно 1,
если рассматривается вращение ротора в направлении, совпа-
дающем с направлением движения оси по эллиптической траек-
тории; в случае, когда указанные направления противополож-
ны, о* = —1.
Из формулы (3.37) видно, что при а* = —1 условие (3.36)
является более «жестким», чем при о* = 1: вращение ротора
в направлении движения оси по траектории поддерживать, во-
обще говоря, проще, нежели вращение в противоположном на-
правлении. Различие, естественно, отсутствует лишь в случае
прямолинейных колебаний оси, когда 6 = 0иЛ = -^а. В слу-
чае же круговых колебаний, когда а = b = г0, при а* = —1
имеем А — 0, а при о* = 1 получаем А — г0, то есть вращение
в направлении, противоположном направлению движения оси,
вообще невозможно.
Если заметить, что коэффициент ( лежит в пределах от 0,001
до 0,01, то можно заключить, что условию (3.36) удовлетворить
практически достаточно легко.
58
ВВЕДЕНИЕ
Отметим в заключение, что вибрационное поддержание вра-
щения маятника может рассматриваться как своеобразный слу-
чай вибрационного перемещения — «направленного в среднем»
движения, происходящего под действием «ненаправленных в
среднем» (колебательных) воздействий [73].
10.	Синхронизация некоторых систем с вращающимися ро-
торами. Задачи динамики ряда устройств с вращающимися
роторами могут быть рассмотрены как задачи о синхронизации
объектов с почти равномерными вращательными движениями.
К таким устройствам относится автоматический балансир, пред-
ложенный Е. Сирлем. Этот балансир в простейшем случае со-
стоит из двух шариков, вложенных в цилиндрическую полость
неуравновешенного диска, который сидит на вращающемся
гибком валу (рис. 7). При определенных условиях шарики рас-
полагаются в полости таким образом, что неуравновешенность
диска ими компенсируется; задача состоит в нахождении ука-
занных условий.
Другой системой подобного рода является сидящий на гиб-
ком валу вращающийся ротор, снабженный двумя маятнико-
выми подвесками (рис. 125). Здесь также требуется найти ус-
ловия самоуравновешивания.
В §§ 1 и 2 главы XXIV книги показано, что основные резуль-
тативные уравнения для определения параметров устойчивого
установившегося режима движения описанных систем имеют ту
же форму, что и соответствующие уравнения задачи о синхро-
низации вибраторов, причем и здесь имеет место интегральный
критерий устойчивости. Исследование в обоих случаях приво-
дит к следующему главному условию самоуравновешивания
систем:
(£>> р,	(3.38)
где <в — угловая скорость вращения валов, а р — частота соб-
ственных колебаний диска с жестко закрепленными на нем ша-
риками или маятниками. Иными словами, условие самобалан-
сировки совпадает с классическим условием самоуравновеши-
вания диска без шариков и маятников. В последнем случае,
однако, при уравновешивании вал, на котором сидит диск, не-
сколько деформируется.
Иным примером систем рассматриваемого типа является
вращающийся вал с несколькими неуравновешенными дисками,
совершающий изгибно-крутильные колебания (см. рис. 9, а так-
же § 3 главы XXIV книги). Основные уравнения и в данном
случае имеют вид уравнений (3.22), так что ситуацию по-преж-
нему можно трактовать таким образом, будто ко всем обычно
учитываемым моментам, действующим на диски, добавляются
некоторые дополнительные вибрационные крутящие моменты,
§ 3]	ОБЗОР ОСНОВНЫХ ФАКТОВ И РЕЗУЛЬТАТОВ	69
которые возникают вследствие изгибных колебаний вала и от-
ражают наличие связи между изгибными и крутильными коле-
баниями. В результате при определенных условиях участки
вала могут оказаться закрученными на значительные дополни-
тельные углы, так что крутильные колебания будут происходить
относительно иных средних положений. При этом в сечениях
вала могут возникнуть значительные напряжения, а характер
воздействия вала па опоры существенно измениться.
Подобные эффекты должны проявляться тем сильнее, чем
больше максимальные значения вибрационных моментов
по сравнению с наибольшими упругими крутящими момента-
ми Ss, то есть чем меньше жесткости участков вала, чем боль-
ше неуравновешенность дисков и чем выше угловая скорость
вала оз.
Для рассматриваемой задачи, так же как и для большин-
ства предыдущих, может быть сформулирован интегральный
критерий устойчивости.
11.	Синхронизация систем типа слабо связанных квазили-
нейных осцилляторов. Задача о синхронизации объектов типа
слабо связанных осцилляторов представляет интерес в связи
со многими приложениями из области механики, электро- и ра-
диотехники. К ней, в частности, приводится упоминавшаяся
классическая задача о синхронизации маятниковых часов, вися-
щих на подвижной балке (рис. 11). В § 2 главы XXV эта за-
дача рассмотрена при некоторых упрощающих предположениях,
причем получено объяснение наблюдений Гюйгенса, описание
которых было приведено в начале § 1 введения. Показано, что
двое часов с достаточно близкими «парциальными» частотами
колебаний маятников и некоторыми другими одноименными
параметрами синхронизируются таким образом, что их колеба-
ния близки к противофазным.
Исследованию синхронизации слабо связанных осцилляторов
Ван-дер-Поля посвящен § 1 главы XXV; библиографические све-
дения приведены в § 6 главы I.
К своеобразной задаче о внешней синхронизации слабо свя-
занных квазилинейных объектов приводит исследование дина-
мики устройств с несколькими электромагнитными возбудите-
лями. Рассмотрению этой задачи была посвящена работа
К. Ш. Ходжаева [406], кратко излагаемая в § 3 главы XXV. Ис-
следование показывает, что в случае одинаковых возбудителей
справедлив (с некоторыми оговорками) интегральный критерий
устойчивости синхронных движений, причем потенциальная
функция D выражается теперь через физические величины, ха-
рактерные для устройств с электромагнитами, — энергию маг-
нитного поля в системе, магнитные потоки и магнитодвижущие
силы подмагничивания.
60
ВВЕДЕНИЕ
12.	Об иерархичности рассматриваемых систем. Дополни-
тельные замечания о вибрационных моментах. Бросим в заклю-
чение общий взгляд на некоторые из полученных результатов.
Заметим, что в итоге решения всех задач о синхронизации
механических систем получалась некоторая система урав-
нений относительно постоянных ai, ..., сц и ю. Эти уравнения,
названные основными, можно рассматривать как уравнения
установившихся режимов движения объектов (например, ви-
браторов) в условиях, когда на них действуют некоторые до-
полнительные моменты, названные вибрационными.
Такой результат является следствием иерархичности изучен-
ных систем: в них можно выделить относительно небольшую
группу переменных (это как раз и есть переменные <zi, . . . , аь
и со), которые в изучаемых движениях остаются неизменными
и которые как раз и определяют эти движения в главных чер-
тах; прочие же переменные, претерпевающие «быстрые» изме-
нения, описывают второстепенные детали рассматриваемых
процессов.
Естественно, что основные уравнения, из которых опреде-
ляются величины «I, . . . , а/, и со, представляют собой осреднен-
ные уравнения движения системы, в которые входят осреднен-
ные характеристики «быстрых» процессов — вибрационные
моменты.
В сущности, установление подобной иерархии представляет
собой одну из главных идей теоретической физики вообще и не-
бесной механики в частности. Эта идея состоит в разбиении
процесса на «медленные» и «быстрые» составляющие и в полу-
чении уравнений для «медленных» составляющих, которые
обычно оказываются гораздо более простыми, нежели уравне-
ния, описывающие процесс в целом.
Значение методов малого параметра (методов Пуанкаре—•
Ляпунова и асимптотических методов) в значительной степени
как раз и состоит в том, что они представляют некоторые регу-
лярные процедуры для реализации указанной идеи в теории
нелинейных колебаний. В теоретической физике, отчасти ввиду
сложности изучаемых систем, эти методы не всегда используют-
ся, и тогда для получения уравнений «медленных» процессов
прибегают к интуитивным соображениям. Вместе с тем при та-
ком полуинтуитивном подходе члены в уравнениях «медлен-
ных» процессов, отражающие осредненное воздействие «бы-
стрых» факторов, автоматически получают отчетливую физиче-
скую трактовку.
При решении же задач нелинейной механики на физической
интерпретации слагаемых в уравнениях «медленных» процессов,
как правило, не останавливаются. Между тем, как нам пред-
ставляется, такая интерпретация полезна во многих отноше-
§ 3]	ОБЗОР ОСНОВНЫХ ФАКТОВ И РЕЗУЛЬТАТОВ	61
ниях. В частности, при исследовании поведения механических
систем, в которых, наряду с «медленными» силами или момен-
тами, действуют «быстрые» (обусловленные колебаниями) силы
или моменты, весьма удобной оказывается интерпретация осред-
ненных воздействий как вибрационных сил или моментов. От-
метим, что такие понятия удобны и при рассмотрении многих
задач теории вибрационного перемещения [73].
Обсуждению затронутых аспектов теории нелинейных коле-
баний посвящен доклад автора [88], в котором рассмотрен так-
же и вопрос о границах применимости понятий о вибрационных
силах и моментах. Применительно к проблемам колебаний
в биологических системах вопрос о иерархичности колебатель-
ных систем обсуждается в статье А. М. Молчанова [303].
ЧАСТЬ I
ПОСТАНОВКА И ОСНОВНЫЕ ОСОБЕННОСТИ
ЗАДАЧ О СИНХРОНИЗАЦИИ
ДИНАМИЧЕСКИХ СИСТЕМ
В первой главе настоящей первой части книги рассматри-
вается ряд прикладных задач, естественно приводящих к проб-
леме синхронизации динамических объектов. Затем во второй
главе делается попытка сформулировать эту проблему в об-
щей форме и установить ее основные особенности.
Подавляющее большинство обсуждаемых частных задач от-
носится к задачам о синхронизации слабо связанных объектов,
поэтому таким объектам уделяется наибольшее внимание как
в данной, так и в последующих частях книги.
Наиболее просто формулируются задачи о синхронизации
технических объектов — возбудителей механических колебаний,
маятниковых часов, ламповых генераторов и других устройств,
удовлетворительные математические модели которых достаточно
хорошо известны. Значительно сложнее дело обстоит, например,
с биологическими объектами, модели которых лишь начинают
создаваться: несмотря на отчетливую «синхронизационную»
внешнюю картину явлений, их математическое описание и изу-
чение в настоящее время можно выполнить лишь в некоторых
простейших случаях. Обсуждению других, еще более сложных
и далеко еще не разрешенных вопросов биологии, медицины,
физики и астрономии, по-видимому, связанных с явлением син-
хронизации, посвящен специальный, девятый параграф первой
главы.
Во второй главе предлагается математическая формулировка
задачи о синхронизации динамических систем, охватывающая
как частные случаи постановки известных в настоящее время
конкретных задач. Следует, однако, заметить, что приведенное
определение синхронизации допускает естественное обобщение
как применительно к объектам более сложной природы, так и в
отношении расширения самого понятия синхронизации. Так, на-
пример, под синхронизацией можно понимать совпадение у свя-
занных объектов некоторых «временных» функционалов от их
движений, которые для изолированных объектов не совпадали.
В приводимом определении за такие функционалы приняты пе-
риоды колебаний или вращений, хотя в принципе это вовсе не
обязательно.
ГЛАВА 1
ЗАДАЧИ О СИНХРОНИЗАЦИИ ДИНАМИЧЕСКИХ
ОБЪЕКТОВ
§ 1. Синхронизация возбудителей механических колебаний
Как отмечалось во введении (см. и. 5 § 3), изучение способов
возбуждения заданных колебаний некоторой упругой системы
представляет одну из главных проблем теории вибрационных
машин и устройств. При этом, естественно, возникает задача
о синхронной работе нескольких возбудителей, связанных с еди-
ной колебательной системой.
Постановка простейшей задачи о самосинхронизации меха-
нических вибраторов была приведена в п. 4 § 3 введения, по-
этому здесь мы остановимся на задаче о синхронных колеба-
ниях системы с несколькими двухзазорными электромагнитными
возбудителями. Каждый такой возбудитель (рис. 6, а) в одном
в)
Рис. 6.
из простейших случаев состоит из электромагнита С («сердеч-
ника»), связанного с определенной частью механической коле-
бательной системы и взаимодействующего через воздушный
промежуток (зазор) с «якорем» Я, связанным с другой частью
колебательной системы*). Находят применение и так называе-
мые двухзазорные возбудители [253], в которых «якорь»
*) Иногда «якорь» или «сердечник» располагаются на неподвижном
основании.
64
ЗАДАЧИ О СИНХРОНИЗАЦИИ ДИНАМИЧЕСКИХ ОБЪЕКТОВ
[ГЛ. I
(рис. 6, б) или «сердечник» состоит из двух жестко связанных
одна с другой одинаковых и симметрично расположенных частей.
Рис. 6, а и б отвечают возбудителям с электрически независи-
мыми цепями обмоток подмагничивания, питаемых от источни-
ков постоянного тока. Встречаются также однозазорные и двух-
зазорные возбудители с электрическими схемами, отличными
от изображенных на рис. 6, а и б.
Во всех возбудителях рассматриваемого типа электромаг-
нитная сила взаимодействия якоря с сердечником играет роль
возмущающей силы, величина которой может регулироваться
путем изменения напряжения постоянного тока, приложенного
к обмоткам подмагничивания. Эта сила имеет частоту, которая
для двухзазорного возбудителя равна, а для однозазорного воз-
будителя в два раза больше, чем частота напряжения питаю-
щей сети и, подаваемого к обмоткам переменного тока.
Частота со может обычно считаться заранее заданной и не
зависящей от режима работы системы с возбудителями, ибо
мощность источника питания значительно больше, нежели сум-
марная мощность возбудителей. Что же касается возмущающей
силы, развиваемой возбудителем, то она не может считаться
наперед заданной, ибо существенно зависит от величины за-
зора между якорем и сердечником, который в свою очередь
существенно изменяется в процессе колебаний и зависит от той
же возмущающей силы. Таким образом, мы имеем здесь ти-
пичный случай механической колебательной системы, взаимо-
действующей с источником возбуждения (см. пп. 4 и 8 § 3 вве-
дения). Естественно, что при наличии нескольких электромаг-
нитных возбудителей последние будут взаимодействовать один
с другим через механическую колебательную систему. Поэтому
и в данном случае при последовательном рассмотрении системы
возникает своеобразная задача о совместном движении не-
скольких однотипных объектов — электромагнитных возбуди-
телей.
Схема машины — электровибрационного конвейера, приво-
димого от нескольких электромагнитных возбудителей, — изо-
бражена на рис. 6, в.
При определенных предположениях уравнения, описывающие
изменение магнитных потоков в зазорах двухзазорных вибра-
торов, могут быть представлены в форме
dm, dm .
---—= sin т + иЕ, (<р„ Фс L;
, *	я	o-1)
dm,	dm,
-dr-^W = s,nT + ^(^’ -es)
(s = 1, ..k),
§ 1|	СИНХРОНИЗАЦИЯ ВОЗБУДИТЕЛЕН ВИБРАЦИИ	65
где
(<ps, ф;. и о=
- - «. 3F К1 + У f. - (' “ W фЗ “ р. (! + М *.+<1 • 2)
причем q>s и ф* — безразмерные магнитные потоки в зазорах
s-ro вибратора, — безразмерное перемещение якоря s-ro ви-
братора относительно сердечника из положения статического
равновесия, отсчитываемое в направлении увеличения того из
зазоров, который пронизывает поток ф8, т — at — безразмерное
время, р. > 0 — малый параметр, %s, 6S, ps и es — безразмерные
постоянные, выражения для которых через размерные пара-
метры вибраторов можно найти в работе [405], k — общее число
возбудителей. В соответствии с обозначениями (1.2) предпола-
гается, что величины 6.ч, рч и es — малые одного п того же по-
рядка.
Электромагнитные силы, развиваемые возбудителями, с до-
статочной точностью определяются выражениями
(1-3)
где Fqs — некоторая постоянная.
К уравнениям (1.1) необходимо присоединить дифферен-
циальные уравнения колебаний механической части системы
под действием возмущающих сил (1.3). Запишем совокупность
этих уравнений в следующей форме:
й= 17(фр ...» фй; ф;....Фй, «, Н).	(1-4)
Здесь и — вектор, определяющий координаты механической ча-
сти системы, в том числе и величины gs, входящие в уравнения
(1.1):
5S = M«).	(1-5)
Задача состоит в определении условий существования и
устойчивости решений уравнений (1.1), (1.4), имеющих общий
период 2л по безмерному времени т = at, то есть период
Т = 2л/а по времени t.
Как и уравнения движения механических вибраторов (см.
уравнения (3.1) введения), уравнения (1.1) при ц = О, то есть
в исходном приближении, превращаются в k независимых урав-
нений. Иными словами, и здесь мы имеем дело с задачей о син-
хронизации слабо связанных объектов. Отличие уравнений (1.1)
от уравнений (3.17) введения состоит, однако, в том, что в пра-
вые части первых уравнений время х = at входит в явной форме,
3 И. И. Блехман
66
ЗАДАЧИ О СИНХРОНИЗАЦИИ ДИНАМИЧЕСКИХ ОБЪЕКТОВ
[ГЛ. I
то есть рассматриваемая здесь система является неавтоном-
ной. Это является прямым следствием предположения о значи-
тельно большей мощности генераторов питающей сети по срав-
нению с мощностью возбудителей.
Решение задачи о совместной работе двухзазорных электро-
магнитных возбудителей, связанных с линейной колебательной
системой, было выполнено К. Ш. Ходжаевым [406]; оно при-
водится в § 3 главы XXIV настоящей книги.
§ 2. Динамика автоматического балансира
Для уравновешивания вращающихся роторов
Много общего с задачей о самосинхронизации механических
вибраторов имеет задача об исследовании специального балан-
сира для автоматической компен-
сации небаланса вращающихся
дисков.
Одна из возможных конструк-
тивных форм такого балансира
схематически представлена на
рис. 7 и 8. На гибком вращающемся валу 1 закреплен диск 2,
центр тяжести которого С не лежит на оси вала АОВ. Диск
имеет залитую маслом цилиндрическую или тороидальную по-
лость, ось которой совпадает с касательной к оси вала в точке
крепления диска Oj. В полость помещены два шарика 3,
которые при определенных условиях располагаются во вращаю-
щемся диске таким образом, что компенсируют небаланс диска
и тем самым устраняют колебания вала и передачу динамиче-
ских нагрузок на его опоры.
В иных конструктивных вариантах автобалансира вместо
полости в диске и шариков имеются либо кольца, надетые на
вал с большим зазором, либо рычажки, один из концов которых
§ 2]	ДИНАМИКА АВТОМАТИЧЕСКОГО БАЛАНСИРА	67
связан со свободно поворачивающейся на валу втулкой, а дру-
гой несет неуравновешенный груз.
Описанные автобалансиры были изобретены Е. Сирлем
[488, 489] и находят применение в машинах типа центрифуг; они
особенно эффективны в случаях, когда небаланс ротора может
несколько изменяться в процессе работы машины.
Элементы теории автобалансира приведены в книгах Ден-
Гартога [165] и Я- Г. Пановко [332], а подробное исследование
его динамики выполнено Ф. М. Детинко [174]; в несколько иной
постановке задача рассмотрена А. И. Муйжниеком [306].
Уравнения движения системы с шариковым автобалансиром
и одним неуравновешенным диском, сидящим посредине неве-
сомого вала, имеют вид [174]*)
фз + ₽о (ф5 - ®) = ~ (х sin <ps + у cos ф9)	(s = 1, ..., k)\	(2.1)
k
Mx + 0x + ex = Afrco2 cos at + mR 3 (<PS sin фх + ф2 cos фД
(2.2)
Mi) + ?>y + су = — Mra2 sin at + mR 3 (<PS cos ф5 — ф2 sin фА
Здесь (см. рис. 8) x и у — координаты центра диска О, в непод-
вижной системе осей хОу, начало которой находится в точке
пересечения плоскости диска с осью подшипников; <ps — отсчи-
тываемый по ходу часовой стрелки угол между прямой, соеди-
няющей центр диска Oi с центром s-ro шарика, и направлением
оси Ох\ Л— масса диска, т — масса шарика, М = Л + km —
масса всей системы; г — эксцентриситет диска; R — расстояние
от центра шарика до оси вала; со— угловая скорость враще-
ния вала; 0О и 0 — коэффициенты вязкого сопротивления; с —
жесткость вала на изгиб по отношению к силе, приложенной
в точке О[.
Исследование динамики автобалансира сводится к выясне-
нию условий существования и устойчивости решений системы
дифференциальных уравнений (2.1), (2.2) вида
Ф5 = at + фл,(at) (s = 1, ..., k),
х = х (at), у = у (®0>
где х и у — периодические функции времени t с периодом
2л/м. Особый интерес представляют при этом те решения типа
*) Нами используются обозначения, несколько отличные от обозначений
цитируемой работы; кроме того, мы считаем для общности число шариков k
произвольным.
68
ЗАДАЧИ О СИНХРОНИЗАЦИИ ДИНАМИЧЕСКИХ ОБЪЕКТОВ
[ГЛ. I
(2.3), в которых x(at) == y(wt) 0 (или по крайней мере ос-
таются достаточно малыми), то есть решения, отвечающие
самоуравновешиванию системы, когда колебания вала отсут-
ствуют.
Сформулированная выше задача динамики автобалансира
и была, по существу, рассмотрена в статье Ф. М. Детинко [174]
с помощью методов, отличных от используемых в данной книге.
Ф. М. Детинко изучил также и значительно более сложный
случай, когда вал имеет распределенный по длине неба-
ланс и несет произвольное число п неуравновешенных дисков
с двумя шариками каждый; при этом имеется п групп урав-
нений типа (2.1), а уравнения (2.2) заменяются уравнениями
в частных производных.
Обратим внимание на наличие большого сходства в поста-
новках данной задачи и задачи о самосинхронизации вибрато-
ров (см. и. 4 § 3 введения к книге). Различие состоит лишь
в том, что исходные уравнения задачи о самосинхронизации
(уравнения (3.17) введения) автономны, в то время как си-
стема (2.1), (2.2) является неавтономной; в первом случае
частота и была заранее неизвестной, а во втором считается
заданной.
Однако, как уже отмечалось во введении, в случае задачи
о внешней синхронизации вибраторов также получились бы не-
автономные уравнения. Кроме того, и в задаче об автобалан-
сире можно получить автономную систему, если, не считая угол
поворота вала ср = (at заранее заданным, присоединить к си-
стеме (2.1), (2.2) уравнение движения двигателя, приводящего
вал во вращение.
Если ввести обозначение
цФ (<ps, х, у) = у (х sin <р4. + у cos cps),	(2.4)
то первые k уравнений (2.1) примут вид
Ф« + ₽о(Ф^~®) = Н(1,(ф5, У) (s=l,	k),	(2.5)
вполне аналогичный виду уравнений задачи о самосинхрониза-
ции вибраторов (см. уравнения (3.19) введения к книге). Ве-
личину ц > 0 при этом, как и в задаче о вибраторах, можно
принять за малый параметр, что отвечает предположению о ма-
лости отклонений центра диска х и у по сравнению с радиу-
сом R. Таким образом, и в данном случае при ц = 0 все урав-
нения (2.5) оказываются независимыми, то есть мы опять имеем
случай слабо связанных объектов.
Задаче о динамическом балансире во многом аналогична
задача о движении вращающегося на гибком валу диска, несу-
§ 3] ИЗГИБНО-КРУТИЛЬНЫЕ КОЛЕБАНИЯ ВРАЩАЮЩЕГОСЯ ВАЛА 69
щего несколько маятниковых подвесов. Эта последняя задача,
имеющая ряд практических приложений, рассмотрена Л. И. Ма-
чабели [290]; ее постановка и решение будут приведены в § 2
главы XXIV настоящей книги.
§ 3. Изгибно-крутильные колебания вращающегося вала
с неуравновешенными дисками
В настоящем параграфе будет изложена постановка задачи
о совместных изгибно-крутильных колебаниях вращающегося
вала с неуравновешенными дисками. Эта задача, так же как
и предыдущая, во многом аналогична задаче о синхронизации
вибраторов.
В наиболее общем случае рассматриваемая система (рис. 9)
представляет собой многоопорный вал с некоторым числом k
Рис. 9.
статически и динамически неуравновешенных дисков, приводи-
мых от каких-либо двигателей; при этом считается, что вал
в процессе движения может совершать не только изгибные, но
и крутильные колебания, то есть жесткости на кручение отдель-
ных участков вала предполагаются конечными. Опоры вала
могут быть как жесткими, так и упругими, с неодинаковыми
жесткостями в различных направлениях.
Будем считать, что некоторые из дисков представляют со-
бой роторы двигателей, приводящих вал во вращение.
Пусть Oxyz — неподвижная система прямоугольных коорди-
нат, ось Oz которой направлена вдоль осей подшипников вала,
a O'sx'sy'sz's — системы осей, параллельных соответствующим
осям системы Oxyz и имеющих начала в точках пересечения
O's плоскостей дисков с изогнутой осью вала оо (рис. 10).
Пусть, далее, O'susvsws — системы осей координат, жестко связан-
ных с дисками и совпадающих с их главными осями инерции.
Положение каждого диска определяется пятью обобщенны-
ми координатами—декартовыми координатами л;ч и точки
О' в неподвижной системе Oxyz и тремя эйлеровыми углами
70
ЗАДАЧИ О СИНХРОНИЗАЦИИ ДИНАМИЧЕСКИХ ОБЪЕКТОВ
[ГЛ. 1
as, ps и q>s, выбранными в соответствии с рис. 10: as есть угол
между осью O'sws и плоскостью x'sO'sz's, р, — угол между осью
O'sz's и проекцией оси O'sws на плоскость x'sO'z's, и, наконец, cps
есть угол между линией п пересечения плоскости x'0'z' с пло-
Рис. 10.
скостью usO'svs и осью Osus
(указанную линию обычно
называют линией узлов, а
угол <ps — углом собственно-
го вращения).
Ограничиваясь рассмот-
рением случая статической
неуравновешенности дисков,
будем предполагать, что их
центры тяжести Cs лежат
на осях O'sus.
Если пренебречь гиро-
скопическими членами, а
также членами, имеющими
относительно координат х.„
уа, as, Ps и соответствующих
скоростей порядок выше
второго, и не учитывать
влияния силы тяжести, то выражения для потенциальной и ки-
нетической энергии системы будут
k k
П = IS S (csXjxsxj + 4/Ча/ + 2сТхза! +	+
№ 1 I «=1
£-1
+ 2^’#sPy) + S Cs, S+1 (^+1 ~	~	+ Xs)2>	(3-1)
1
k
T = 1X И + y2^ - 2mA (Дcos + ys sin <₽s) % +
+ А(^ + ^) + Ш (3.2)
Выражение (3.2) наиболее просто может быть получено из
формулы для кинетической энергии твердого тела, отвечающей
общему случаю, когда за полюс принимается произвольная точ-
ка этого тела, а не обязательно его центр тяжести [259].
В равенствах (3.1) и (3.2) обозначено: ms, es, Д и Is — со-
ответственно масса, эксцентриситет, экваториальный и поляр-
ный момент инерции 5-го диска; с.,. s+i — жесткость на круче-
ние участка вала между s-м и ,s + 1-м дисками, причем с0] =
*=ск„ k+1= °! csX]’ csp с<з1’ cs/a'> ^’—соответствующие жест-
§ 3] ИЗП1БНО КРУТИЛЫ1ЫЕ КОЛЕБАНИЯ ВРАЩАЮЩЕГОСЯ ВАЛА 71
кости вала на изгиб, вычисленные с учетом податливости опор;
х«— значения углов <ps, при которых упругие крутящие моменты
в пролетах вала равны нулю; эти углы, определенные с точ-
ностью до постоянного поворота хо, характеризуют направления
векторов-эксцентриситетов ss — O'sCs дисков при нескручен-
пом вале.
Дифференциальные уравнения движения системы, составлен-
ные в соответствии с равенствами (3.1) и (3.2) в форме урав-
нений Лагранжа второго рода, имеют вид*)
= mses (xs cos <ps + ys sin <ps) ~ s (qps - <ps-i -	+
^s, $4 1 (ф$ + 1 Ф$ +1 “Ь xs) + Ls
k
msxs + 2 (c^xj + c^'a,) = mses (ys cos <ps - ф* sin <ps) + Qf,
(3.3)
msijs + 2 (c^yj +	= mses (ips sin <ps + <p* cos <ps) + QW,
1 1	k
Asas + 2 (c<a/)a/ + c^x,) = Q<“>,
k
As^ + ^c^ + c^y^Q^
(s = 1....k)
Здесь Q(x), Q(x\ Q® и Q® — силы и моменты внутреннего и
внешнего сопротивления колебаниям вала, которые могут за-
висеть от всех обобщенных координат и скоростей системы, при-
чем координаты <р8 и скорости ф8 входят в выражения для Q
только в виде разностей <ps — <р/ и ф5 — ф;; Ls и Rs — соответ-
ственно вращающие моменты двигателей и моменты сил со-
противления вращению; обычно достаточно предполагать, что
эти моменты суть функции <ps — <ру, ф, —ф/ и ф’5> а также, быть
может, периодические функции <ps с периодом 2л.
Как и в рассмотренных выше задачах, основной целью ис-
следования является установление условий существования и
устойчивости, а также вычисление с той или иной степенью
точности синхронных движений системы, то есть движений вида
<ps = со/ + ф8 (at),
xs = xs (at), ys = ys (at),	(3.4)
ct8 ct8 (at), P8 Ps (at),
*) Уравнения (3.3) во многом аналогичны уравнениям задачи о синхро-
низации вибраторов, подробный вывод которых приводится в главе XIII.
Различные частные случаи этих уравнений можно найти, например, в моно-
графиях Ф. М. Диментберга [176] и В. А. Гробова [161].
72
ЗАДАЧИ О СИНХРОНИЗАЦИИ ДИНАМИЧЕСКИХ ОБЪЕКТОВ
[ГЛ I
где ips, xs, ys, as и |35 — периодические функции времени с перио-
дом 2л/со. При этом значение синхронной частоты со, вообще го-
воря, заранее неизвестно и должно быть определено в ходе
решения задачи.
Рассмотрению поставленной задачи при некоторых упро-
щающих предположениях посвящен § 3 главы XXIV настоящей
книги.
Заметим, что частный случай описанной выше системы, от-
вечающий одному диску, с различных точек зрения и с различ-
ными целями изучался в работах А. Тондла [394], В. О. Коно-
ненко [219] и Л. А. Растригина [356]. Об этих работах, не
относящихся, однако, непосредственно к задаче о синхрониза-
ции, подробнее будет сказано ниже (см. § 1 главы XVII).
§ 4. Взаимная синхронизация маятниковых часов,
висящих на подвижном основании (задача Гюйгенса)
Как уже отмечалось во введении к книге, явление синхро-
низации динамических систем, по-видимому, впервые было
экспериментально обнаружено X. Гюйгенсом именно на примере
самосинхронизации и фазировки хода двух маятниковых часов,
висевших на общей легкой балке [164].
Рассмотрение соответствующей задачи, которую с полным
основанием можно назвать задачей Гюйгенса, представляется
небезынтересным не только в связи с попыткой теоретического
объяснения описанных X. Гюйгенсом явлений, но также и в
связи с аналогиями и параллелями, которые здесь обнаружи-
ваются с иными самосинхронизирующимися объектами, напри-
мер с механическими вибраторами и ламповыми генераторами.
Приведем постановку задачи Гюйгенса для одной из наи-
более простых, однако зачастую вполне приемлемых моделей
часовых ходов с одной степенью свободы*). При этом будем
предполагать, что часы висят на упруго опертой жесткой плат-
форме, также имеющей одну степень свободы (рис. 11).
Дифференциальные уравнения движения рассматриваемой
системы в точности совпадают с уравнениями движения (3.17)
введения для соответствующей задачи о самосинхронизации ви-
браторов, роторы которых, по существу, также являются фи-
зическими маятниками (ср. рис. 2 и 11).
Изменяются в задаче о часах в основном лишь смысл и вы-
ражения движущих моментов Ls, которые при оговоренных
выше предположениях следует считать зависящими от углов
*) Наиболее полное описание и исследование динамических моделей ме-
ханизмов часов (часовых ходов) дано в работах 3. М. Аксельрода [8, 9] и
Н. Н. Баутина [33, 34]. Ударные и безударные модели ходов с одной сте-
пенью свободы рассмотрены также в монографии [19].
§ 4]
ВЗАИМНАЯ СИНХРОНИЗАЦИЯ МАЯТНИКОВЫХ ЧАСОВ
73
поворота маятников <ps и угловых скоростей ф5. При этом воз-
действие момента Ls(q>s, <ps) на маятник с целью упрощения
теоретического анализа задачи иногда считают имеющим ха-
рактер мгновенного импульса; в последнем случае Д(ф5, cps)
ZZ2
Рис. И.
представляет неаналитическую функцию своих аргументов. Не-
сколько иной характер в рассматриваемой здесь задаче могут
носить и выражения для моментов сил сопротивления будем
считать их, так же как и Ls, зависящими не только от угловой
скорости ф8, но и от угла <ps, то есть положим Rs = /?«(ф8, <ps).
Дифференциальные уравнения движения системы часы —
платформа запишутся в виде (в отличие от задачи о самосин-
74
ЗАДАЧИ О СИНХРОНИЗАЦИИ ДИНАМИЧЕСКИХ ОБЪЕКТОВ
[ГЛ. I
хронизации вибраторов, углы поворота маятников <ps отсчиты-
ваются не от направления колебаний платформы, а от вер-
тикали)
ls<Ps + т xg&s sin <ps = т4ед cos (<ps + x) +
+ l-s (<H> fl’s) - Rs (<Ps, <Ps) (s= 1, ..., k),	(4.1)
k
Mx + kxX + CxX = 2 tnses [fl’s C0S (fl’s + %) “ fl’s sin (fl’s + X)]-
Здесь приняты те же обозначения, что и в п. 4 § 3 введения.
При рассмотрении задачи о самосинхронизации часов углы
отклонения маятников от вертикали <ps допустимо считать до-
статочно малыми по сравнению с единицей, и поэтому в урав-
нениях (4.1) можно произвести линеаризацию аналитических
относительно q>s членов*). Тогда уравнения (4.1) примут вид
фх + “sTs =	* cos % + [Ls (q)s, <ps) - /?s (ф5, <ps)]	(4.2)
(s= 1, .... k),
k
Mx + kxX + CxX = 2 ^sesTsC0SX>
s = I
где
— частоты малых свободных колебаний маятников при условии,
что точки подвеса их неподвижны; эти величины будем назы-
вать парциальными частотами колебаний маятников.
Задача о самосинхронизации часов заключается в основном
в выяснении условий существования и устойчивости периодиче-
ских колебаний маятников с общей частотой со, имеющих место,
несмотря на возможное различие парциальных частот колеба-
ний ю, отдельных маятников, моментов инерции Is и моментов
Ls и Rs-
Иными словами, речь идет об исследовании условий суще-
ствования и устойчивости периодических решений уравнений
(4.3) с заранее неизвестным периодом Т = 2л/со, подлежащим
определению в процессе решения задачи. Представляет инте-
рес также вычисление (хотя бы приближенное) самих перио-
дических решений.
*) Подобная частичная линеаризация недопустима лить при % = — л, то
есть в случае вертикальных колебаний платформы, па которой висят часы:
в этом случае линеаризированные уравнения движения часов и платформы
оказываются независимыми друг от друга.
§41	ВЗАИМНАЯ СИНХРОНИЗАЦИЯ МАЯТНИКОВЫХ ЧАСОВ	/5
Исходя из наблюдений X. Гюйгенса (см. цитату, приведен-
ную во введении на стр. 15 и 16), можно ожидать, что синхрони-
зация часов возможна лишь при условии, что парциальные ча-
стоты &s мало отличаются друг от друга. Учитывая это обстоя-
тельство, а также соображения о возможных порядках малости
отдельных величин, естественно ввести в систему (4.2) малый
параметр ц, представив ее в следующей форме:
+ w2(ps =	(ф5, qps, х) (s=l, ..., k),
k	(4.4)
Afx + CxX = 2j m&tPs COS X — P-k'xX,
S=1
где
нФ; (<Ps. <Ps> *) = ®2%X + X cos X +
+7r[M^- О-ЯДчф <pj|’	= s2 = a2(i -Xs), (4.5)
причем за величину й можно принять либо одно из й8, либо
какое-нибудь среднее от чисел й>; можно также определить й
в процессе решения задачи из условия близости первого при-
ближения к исходному подобно тому, как это сделано в работах
[44, 46, 54] при решении задачи о самосинхронизации вибрато-
ров (см. также п. 5 § 3 и § 5 главы V).
Как и в рассмотренных ранее задачах, при ц = 0 первые k
уравнений (4.4) становятся независимыми, то есть мы снова
пришли к задаче о синхронизации слабо связанных объектов.
Заметим в заключение, что может быть поставлена задача
и о внутренней синхронизации часов посредством электромаг-
нитных связей между их механизмами, а также задача о внеш-
ней синхронизации заданным возмущением.
Случай, отвечающий синхронизации (захватыванию) одного
маятника, когда координата х считается заданной гармониче-
ской функцией времени I, рассмотрен в работе Н. В. Бутенина
[111]. В этом исследовании «подталкивающая сила» L аппрок-
симируется выражением Е' sign ф, где Е'— положительная по-
стоянная; при этом учитывается также запаздывание значений
функции L на некоторый постоянный отрезок времени \t по
отношению к соответствующему нулевому значению аргу-
мента ф.
В другой работе Н. В. Бутенина рассматривается задача
Кельвина о влиянии способа подвешивания часов на их движе-
ние [108]. Задачи о взаимной синхронизации двух часов ка-
сается также Н. Минорский в работе [292]; об этой работе
более подробно будет сказано в главе XXV настоящей книги,
один из параграфов которой специально посвящен рассмотре-
нию поставленной выше задачи Гюйгенса.
76
ЗАДАЧИ О СИНХРОНИЗАЦИИ ДИНАМИЧЕСКИХ ОВЪЕКТОВ
[ГЛ. I
§ 5. Синхронизация при параллельной работе
электрических машин
Задача об устойчивости стационарных режимов параллель-
ной работы нескольких синхронных электрических машин, несом-
ненно, является одной из наиболее важных конкретных проблем
теории синхронизации динамических систем*). Этой проблеме
посвящено значительное число интересных исследований, упо-
минавшихся во введении. Тем не менее задача в общей поста-
новке столь сложна, что многие ее существенные стороны до
сих пор остаются неизученными. В частности, почти не рассмот-
рены случаи, когда вопрос об устойчивости приводится к ис-
следованию системы дифференциальных уравнений с периоди-
ческими коэффициентами. Обстоятельный обзор современного
состояния этого вопроса можно найти в работах [205, 211, 371].
Рассмотрим вначале постановку задачи о параллельной ра-
боте некоторого числа k генераторов Gt, . . . , Gfi на общую
нагрузку. Состояние s-ro генератора характеризуется одной
«вращательной» координатой — углом поворота ротора по от-
ношению к статору q>s, а также совокупностью «колебательных»
фазовых координат х*4’ , .. . , х*®\ которыми могут являться как
электрические, так и механические величины.
Пусть сначала каждый генератор работает на независимые
нагрузки /?ь . . ., Rk, состояние которых характеризуется фазо-
выми координатами u\s\	(рис. 12, о). Тогда мы имеем k
независимых автономных систем, в которых при определенных
условиях устанавливаются движения вида
Фе “	"I” Фз
Xifs) = x<s) (cosf),	‘ '
(/ = 1, ..., rs; p = 1, .. ., vs; s = 1, . .., k),
где ф5, x(ys) и u<f — периодические функции времени t с перио-
дом 2л/со, а каждое из — постоянная, которую можно на-
звать парциальной частотой генератора, отвечающей данной
нагрузке Rs. Вследствие неодинаковости нагрузок Rs, неточно-
стей изготовления, а также неидеальности регуляторов часто-
ты (os для различных генераторов, вообще говоря, будут раз-
личными.
Предположим теперь, что все генераторы включены парал-
лельно для работы на общую нагрузку R, состояние которой
характеризуется фазовыми координатами «v (рис. 12,6).
*) Как уже подчеркивалось, термин «синхронизация» в электротехнике
употребляется в несколько ином смысле, нежели в настоящей книге.
§ 5]
СИНХРОНИЗАЦИЯ ПРИ РАГЮТН ЭЛ1-КТРПЧГСКИХ МАШИН
77
Тогда основная задача о параллельной работе генераторов за-
ключается в установлении условий, при которых, несмотря на
возможное различие парциальных частот as, в объединенной
Генератор С, Генератор Гг Генератор
й2
Нагрузка R
Генерит up	Генератор 0г Генератор Б/,
б)
Рис. 12.
системе устанавливается режим с общей синхронной часто-
той со. Иными словами, и в данном случае речь идет о выясне-
нии условий существования и устойчивости движений совокуп-
ной системы вида
<ps = at + фДсо/), x^ = x^(at), Up~up(at) (5.2)
(/ = 1, . .., rs; р= 1, ..., v; s = 1, ..., k)
где i|)s, x^ и up — периодические функции времени t с общим
периодом 2л/со, а со — постоянная, которая точно заранее не-
известна. Иными словами, и здесь речь идет о задаче, назван-
ной выше основной задачей о синхронизации.
Вполне аналогичным образом ставится задача о параллель-
ной работе энергетических систем, каждая из которых содер-
жит несколько синхронных машин: по-прежнему речь идет об
исследовании условий существования и устойчивости движений
вида (5.2) в случае, когда парциальные частоты <о« отдельных
систем, вообще говоря, различны.
Мы не приводим здесь дифференциальных уравнений дви-
жения рассматриваемых систем; в общем случае они столь
сложны, что само составление их представляет нетривиаль-
ную задачу, которая до сих пор не получила окончательного
78
ЗАДАЧИ О СИНХРОНИЗАЦИИ ДИНАМИЧЕСКИХ ОБЪЕКТОВ
[ГЛ, 1
решения. Для различных практически интересных случаев эти
уравнения, написанные как правило, для функций	и ир,
приводятся в цитированных выше работах (см. стр. 19 и 20).
В определенных случаях целесообразен переход от модели с ко-
нечным числом дискретных генераторов к континуальной мо-
дели [207].
Особый класс задач о синхронизации связан с электротех-
ническими способами обеспечения одинаковости углов поворота
нескольких валов, каждый или отдельные из которых приво-
дятся во вращение от тех или иных двигателей (не обязательно
электрических). Речь идет о системах типа электрического вала,
достаточно подробно описанных в литературе (см., например,
[326, 376а, 377а, 445, 466, 492]).
Для правильного и экономичного выбора параметров си-
стемы электрического вала, вообще говоря, необходимо реше-
ние задачи о синхронизации нескольких связанных объектов,
подобной тем задачам, о которых говорилось выше: динамиче-
ские (а не только статические) особенности объектов, связан-
ных с каждым из валов, естественно, могут существенно влиять
на значения параметров системы, обеспечивающих наличие син-
хронного и синфазного вращения валов. Механические вибра-
торы (см. п. 4 § 3 введения) являются одними из объектов,
для которых представляет интерес решение задачи о синхрони-
зации и фазировке посредством электрического вала. Эта задача
будет подробно рассмотрена в главе XIII.
Как правило, хотя и не всегда, уравнения движения систем
с электрическими машинами могут быть записаны в виде урав-
нений Лагранжа — Максвелла, представляющих обобщение
уравнений Лагранжа второго рода на электромеханические си-
стемы [140].
В переменных x<s>, ир и т = at задача о параллельной
работе электрических синхронных машин, как и все рассмот-
ренные выше задачи о синхронизации, приводится к исследо-
ванию условий существования и устойчивости периодических
(с периодом 2л) решений некоторой системы дифференциаль-
ных уравнений, правые части которых также суть периодические
функции т = at с периодом 2л. Впрочем, подавляющее большин-
ство изученных до сих пор систем таково, что указанные урав-
нения могут быть в результате ряда допущений преобразованы
к переменным, для которых правые части уравнений не содер-
жат время в явном виде, а установившимся режимам отвечают
постоянные значения новых переменных*). Естественно, что при
*) Это объясняется тем, что рассматриваются такие режимы работы ма-
шин, которые с достаточной степенью точности могут быть сведены к так
называемым симметричным.
§ 6]	СИНХРОНИЗАЦИЯ ЛАМПОВЫХ ГЕНЕРАТОРОВ	79
этом, как отмечалось выше, анализ устойчивости сводится к
рассмотрению системы дифференциальных уравнений с постоян-
ными коэффициентами.
Как и в разобранных выше задачах о синхронизации дина-
мических систем, дифференциальные уравнения параллельно
работающих электрических машин и энергетических систем до-
пускают эффективное введение малых параметров, причем это
обусловлено не только характером связей между синхронизи-
руемыми объектами, но и существенным различием в порядках
постоянных времени, характеризующих переходные процессы в
различных частях системы [22, 205].
Помимо сформулированной выше основной задачи, в теории
параллельной работы синхронных электрических машин суще-
ственный интерес представляет также вопрос об изучении усло-
вий захвата в синхронный режим подключаемой к работающей
сети синхронной машины, а также исследование возникающего
при этом переходного процесса. Эти достаточно трудные в об-
щей постановке задачи, по существу, связанные с рассмотре-
нием поведения системы «в целом», также изучались в ряде ци-
тированных выше работ (в частности, в работах [14, 21, 22, 152,
154, 359, 441]).
Заметим далее, что задача о синхронизации электрических
машин часто ставится и решается как задача о внешней син-
хронизации, то есть предполагается, что один или несколько
генераторов системы значительно более мощные, чем все про-
чие, и поэтому их движение заранее задано и не зависит от по-
ведения остальных объектов. При этом, естественно, синхронная
частота со совпадает с частотой колебаний, генерируемых «мощ-
ными» генераторами.
§ 6.	Синхронизация ламповых генераторов
Проблема синхронизации ламповых генераторов имеет боль-
шое значение в радиотехнике и телевидении. Так, например, при
отсутствии строгой синхронизации и фазировки движения элек-
тронного луча передающей трубки, находящейся в передающей
камере телевизионного центра, и электронных лучей во всех
телевизорах телепередача оказывается невозможной. Поэтому
генераторы телевизионной развертки всегда содержат специаль-
ные синхронизирующие устройства [377].
Существует значительное число работ, начало которым было
положено известными исследованиями Ван-дер-Поля [119, 493,
494], Эпплтона [443], А. А. Андронова и А. А. Витта [15, 19], где
задача о синхронизации генераторов решалась в простейшей
постановке — как задача о внешней синхронизации (захватыва-
нии) одного генератора заданным периодическим воздействием
80
ЗАДАЧИ О СИНХРОНИЗАЦИИ ДИНАМИЧЕСКИХ ОБЪЕКТОВ
[ГЛ, I
(см. § 2 введения). Обширную библиографию можно найти, на-
пример, в трудах Международного симпозиума по нелинейным
колебаниям (издание АН УССР, Киев, 1963 г.), а также в моно-
графии А. Н. Малахова [265].
Естественно, что сведение задачи о взаимной синхронизации
ламповых генераторов к вырожденной задаче о захватывании
возможно далеко не всегда, особенно в случае, когда взаимо-
действующие генераторы обладают сравнимой мощностью. По-
этому все возрастающее внимание уделялось исследованию
взаимной синхронизации нескольких генераторов. Одна из пер-
вых работ данного направления принадлежит А. Г. Майеру
(1935 г.) [469]. В ней, как и в появившейся несколько позднее
работе В. И. Гапонова [139] (1936 г.), рассмотрены два связан-
ных генератора с мягким самовозбуждением колебаний.
Самосинхронизация двух связанных релаксационных лампо-
вых генераторов (мультивибраторов) рассматривалась
А. С. Бремзеном и И. С. Файнбергом [102] (1941 г.), причем
были обнаружены режимы кратной синхронизации и показана
возможность генерирования колебаний связанной системой в
случае, когда каждый из генераторов в отдельности не возбу-
ждается. Пренебрежение так называемыми паразитными сте-
пенями свободы привело авторов к необходимости рассматри-
вать колебания системы как разрывные, причем наряду с из-
вестной гипотезой скачка пришлось сделать дополнительные
предположения о характере поведения системы. Эти предполо-
жения (вне связи с задачей о синхронизации) обоснованы
Л. В. Родыгиным в работе [358] (1955 г.) путем рассмотрения
системы с «паразитными емкостями».
Теория взаимной синхронизации двух автогенераторов том-
соновского типа была рассмотрена К. Ф. Теодорчиком [391]
(1946 г); ряд выводов этой работы был проверен Н. И. Еса-
фовым [187] (1947 г.). В работе И. В. Акаловского [7] (1950 г.)
взаимная синхронизация двух генераторов изучена путем рас-
смотрения частотно-фазовых диаграмм.
Задачи о взаимной синхронизации двух квазилинейных и су-
щественно нелинейных осцилляторов изучались также Г. Колом-
бо (1950 г. и позднее) и Г. Джиованнини (1954—1955 гг.).
Краткий обзор этих исследований и библиографические ссылки
приводятся в докладе [223].
Взаимная синхронизация трех слабо связанных ламповых
генераторов, по-видимому, впервые была подробно рассмотрена
В. Н. Парыгиным [334, 335] (1956—1957 гг.), использовавшим
асимптотический метод и прием приближенного решения, пред-
ложенный Р. В. Хохловым [413] (1954г.). В. Н. Парыгиным изу-
чен как случай далеких по мощности генераторов, так и случай
генераторов близкой мощности. Применение ряда приближен-
§ 6]	СИНХРОНИЗАЦИЯ ЛАМПОВЫХ ГЕНЕРАТОРОВ	81
них приемов позволило автору построить области существова-
ния и устойчивости синхронных режимов генераторов в зависи-
мости от их взаимных расстроек и других параметров системы;
результаты были подтверждены экспериментальным исследо-
ванием.
Взаимная синхронизация двух индуктивно связанных отра-
жательных клистронов рассмотрена Р. В. Хохловым в работе
[414] (1956 г.). Кратная синхронизация в двухконтурном гене-
раторе изучена Г. М. Уткиным [397] (1958 г.).
Н. Минорский изучил задачу о взаимной синхронизации двух
осцилляторов Ван-дер-Поля с помощью метода, названного им
стробоскопическим [292] (1961 г.). Ранее близкая задача изуча-
лась С. В. Беллюстиным [39] (1939 г.), использовавшим метод
Пуанкаре.
Ряд задач о взаимной синхронизации генераторов рассмот-
рен В. П. Рубаником и Ю. И. Марченко [284—287, 362—364]
(1962 г. и позднее). Особенно подробно в указанных исследова-
ниях, выполненных с помощью асимптотического метода, изу-
чено влияние на процесс синхронизации наличия запаздывания
в элементах связи между контурами генераторов. Это направле-
ние, начало которому было положено, по-видимому, в работах
Б. Н. Горожанкина [154а] и Г. Н. Рапопорта [355], возникло, в
частности, потому, что в виде запаздывания часто идеализирует-
ся (с целью упрощения исследования) действие волновых свя-
зей между генераторами. Важный вопрос о допустимости подоб-
ной идеализации рассмотрен па примере простых механических
систем В. П. Рубаником и Ю. И. Марченко [285, 286] (1966 г. и
позднее). Работы данного направления суммированы в моногра-
фии [364а].
Взаимная синхронизация двух генераторов рассматривалась
также Суезаки Теруо и Мори Шиузаки [487] (1964 г.). Захваты-
вание и взаимная синхронизация генераторов при наличии
флуктуационных явлений систематически рассмотрены в уже
упоминавшейся монографии А. Н. Малахова [265] (1968-г.).
Вопросу о синхронизации ламповых генераторов родственна
задача об автоколебаниях в двух взаимно связанных контурах,
один из которых самовозбуждается, а другой не возбужден. Эта
задача, поставленная еще Ван-дер-Полем, впервые в достаточно
строгой постановке для случая «сильной» связи между конту-
рами рассматривалась А. А. Андроновым и А. А. Виттом [17]
(1934 г.)„ А. П. Скибарко и С. П. Стрелковым [380] (1934 г.).
Для случая слабой связи соответствующее исследование вы-
полнено С. В. Беллюстиным [39] (1939 г.). Следует сослаться
также на работы Л. П. Холоденко [412] (1940 г.), М. Н. Гущи-
на [163] (1960 г.), Б. А. Альтшуля и В. П. Рубаника [11] (1963 г.).
Механический аналог одной нз указанных выше систем, но с
82
ЗАДАЧИ О СИНХРОНИЗАЦИИ ДИНАМИЧЕСКИХ ОБЪЕКТОВ
[ГЛ. I
ударным возбуждением изучен в исследовании Н. В. Бутенина
(1940 г.) [108], посвященном решению задачи Кельвина из тео-
рии часов.
Приведенный краткий обзор работ в области синхронизации
генераторов не претендует на полноту. Заметим также, что бо-
лее подробно о некоторых из работ будет сказано ниже в дан-
ном параграфе, а также в § 1 главы XXV.
Выясним теперь особенности постановки задачи о синхрони-
зации ламповых генераторов на некоторых примерах, заимство-
ванных в основном из цитированных исследований.
Рассмотрим сначала схему, состоящую из двух связанных
между собой релаксационных генераторов (рис. 13, а). Исследо-
ванию этой системы (вне прямой связи с задачей о синхрони-
зации) посвящена работа Л. В. Родыгина [358].
Рис. 13
Схема не предполагается симметричной, то есть генераторы
не считаются одинаковыми: емкости С] и Сг, а также «паразит-
ные» емкости Cgi и Cg2, вообще говоря, могут быть различными.
Сопротивление aRg играет роль связи между генераторами:
при а = 0 последние становятся независимыми.
При условии пренебрежения сеточными токами и анодной
реакцией для рассматриваемой системы получаются следующие
дифференциальные уравнения [358] (принятые обозначения рас-
шифрованы непосредственно на рис. 13, а):
/a(ut) + C,», =
la (иа) +	=
п . П	»1~ ац2
_а2) >
с2й2-с^2=^^-.
§ 6]
СИНХРОНИЗАЦИЯ ЛАМПОВЫХ ГЕНЕРАТОРОВ
83
Здесь /о(и)=/0[1 — <р(у/уо)] — характеристика ламповых ча-
стей схемы, причем /0 и и0—постоянные, а <р(и/р0) —нелиней-
ная функция, примерный вид которой показан на рис. 13, б
сплошной линией. Часто принимают кусочно-линейную аппро-
ксимацию характеристики, полагая
Ф (х) =
-1,
Л',
1,
X «С — 1,
(см. пунктирную линию на рис. 13, б).
После перехода к безразмерным переменным хь х2, У\, Уг и
т согласно равенствам
/ cg'	\
t»i = Еа + и0 х, + Кху{у,
/ cs-2	\
«2 Еа + Cq (	х2 4" К2у21 >	(6 2)
Vi = Uo-r,, V2 = цо^2. T = tlRaC\,
С gs	Ra
= 1 + (s=1>2)
уравнения (6.1) запишутся в форме*)
ZjXj = — х{ + k\ [<р (xt) — 1] + ах!х2 — t/b
А.2х2 = — х2 + k2 [<р (х2) — 1 ] + ах2Х1 — у2,
У\ =«1 Сч -ах2),
z/2 = vx2 (х2 — axj).
Здесь обозначено:
« _ css .
~ CSKS ’
, RaJo	Ra
ks = VG ’ Zs =	1 cET\
M‘-«2) П + -Л- l + Ra
X	l
(s=l,2),
v = С[/С2.
В случае a = 0 уравнения (6.3) распадаются на две незави-
симые группы, соответствующие не связанным между собой ге-
нераторам:
^"S^S =	3" ^-s [ф (•*-$)	1] Уз>
ys = vsKsxs (V1 = l>V2 = v) (s=l,2).
*) В соответствующие уравнениям (6.1), (6.3) и равенствам (6.2) соот-
ношения работы [358] вкрался ряд мелких погрешностей, которые здесь
устранены.
81
ЗАДАЧИ О СИНХРОНИЗАЦИИ ДИНАМИЧЕСКИХ О1> ЬГКТОВ
ИД. 1
Каждая группа уравнений при этом может иметь периодиче-
ское решение с некоторым периодом Ts = 2л/юв или вообще не
иметь периодических решений; иными словами, генераторы мо-
гут иметь автоколебательные режимы, вообще говоря, с различ-
ными частотами или даже вообще не иметь таких режимов.
Тем не менее, если генераторы связать указанным выше об-
разом, то связанная система при прочих неизменных параметрах
может обладать автоколебательным режимом с периодом
Т = 2л/а. Иначе говоря, система (6.3) может иметь периоди-
ческое решение периода Т, несмотря на то что уравнения (6.4)
имеют периодические решения с различными периодами Та или
даже вовсе не имеют периодических решений *).
Выяснение условий существования и устойчивости, а также
вычисление периодических решений системы (6.3) и составляют
основное содержание рассматриваемой задачи о синхронизации
генераторов.
Иногда интерес представляет также изучение случая крат-
ной синхронизации, когда отношение частот колебаний генерато-
ров равно p/q, где р и q— целые положительные числа.
Решение задачи о синхронизации генераторов существенно
упрощается, если параметр ос, а также величины (Cgi — C^/Cgz
и (Ci — С2)/Сг малы по сравнению с единицей. Тогда система
(6.3) может быть представлена в форме
kxs = xs + k [ф (xs) - 1] - ys + рФ4. (xi, x2, уh y2),
ys = %xs + jPFs (x1; x2) (s = 1, 2),
где p— малый параметр, величины X, k и x— каким-либо обра-
зом определенные средние значения от Xs, ks и xs, а Ф8 и W., —
функции, конкретные выражения для которых могут быть легко
получены путем сопоставления уравнений (6.5) и (6.3).
При ц = 0 уравнения (6.5) распадаются па две одинаковые
независимые группы, то есть мы приходим в рассматриваемом
случае к задаче о синхронизации двух почти одинаковых слабо
связанных объектов.
Заметим, что в цитированной выше работе А. С. Бремзена и
И. С. Файнберга [102] задача о синхронизации релаксационных
генераторов рассмотрена в предположении, соответствующем
пренебрежению членами с параметрами Z, и к2 в уравнениях
(6.3). При этом система (6.3) вырождается в систему второго
порядка; ее колебания носят разрывный характер, и для их
♦) Как уже указывалось, возможность генерирования колебаний связан-
ной системой релаксационных генераторов в случае, когда каждый из гене-
раторов в отдельности не возбуждается, была впервые установлена
А. С. Бремзеном и И. С. Файнбергом в работе [102]. Ниже мы неоднократно
будем сталкиваться с подобными явлениями и в других динамических си-
стемах.
СИНХРОНИЗАЦИЯ ЛАМПОВЫХ 1 I.lIlXP.Vi Ol’Oli
85
изучения приходится делать ряд дополнительных предположе-
ний (в том числе принимать известную «гипотезу скачка» [19]).
Строгое обоснование этих предположений удается получить пу-
тем рассмотрения описанной выше невырожденной системы; по-
следнее и было выполнено Л. В. Родыгиным в работе [358].
В качестве второго примера рассмотрим синхронизацию не-
которого числа 1г ламповых генераторов, поведение каждого из
которых описывается дифференциальным уравнением
х + й2х = \ш (1 — х2) х,	(6.6)
широко известным под названием уравнения Ван-дер-Поля. Это
уравнение при ряде упрощающих предположений отвечает не
только симметричному мультивибратору с самоиндукцией, пер-
воначально изучавшемуся Ван-дер-Полем [493, 494], но также
и ряду других электрических, механических и иных автоколеба-
тельных систем с одной степенью свободы. Поэтому системы,
описываемые уравнением (6.6), иногда называют осциллятора-
ми Ван-дер-Поля.
В предположении, что генераторы связаны между собой ин-
дуктивно, будем иметь следующие дифференциальные уравне-
ния системы:
[k
М1 “	+ 2
(S= 1, . .., k).
(6.7)
Здесь &s > 0, ц > 0, as > 0 — постоянные. При bsj = 0 уравне-
ния (6.7) обращаются в k независимых нелинейных уравнений
типа (6.6).
Известно, что уравнение (6.6) допускает периодическое ре-
шение периода Т =2л[1 + 6 (ц)]/&s, где 6(0) = 0; поэтому в слу-
чае отсутствия .связи между генераторами (bSj = 0) каждый из
них в установившемся режиме генерирует колебания, частоты
которых <o.s(p) = й8/[1 + 6S(р.)], вообще говоря, различны. Эти
частоты можно назвать парциальными частотами колебаний ге-
нераторов.
Основным в рассматриваемой задаче о синхронизации по-
прежнему является установление условий, при которых все свя-
занные генераторы работают с общей (заранее неизвестной)
частотой (о, несмотря на возможное различие парциальных ча-
стот <os(|i). Иными словами, речь идет опять об отыскании ус-
ловий существования и устойчивости периодических решений
системы (6.7).
Если частоты й,. = ws(0) мало отличаются одна от другой,
так что можно положить й2 = й2 (1 — pxs), то уравнения (6.7)
приводятся к виду
xs + &2xs = (xs, хц х,.....хк) (s = 1.......k) (6.8)
86
ЗАДАЧИ О СИНХРОНИЗАЦИИ ДИНАМИЧЕСКИХ ОБЪЕКТОВ
[ГЛ. I
где
иФс(х , X • X,,
s\ s’ s’ 1’
= И
k
as (1 “ *s)*s + %S54 + S bs/*/
(6.9)
Уравнения (6.8) представляют квазилинейную автономную
систему, аналогичную системе (4.5) задачи Гюйгенса. По-преж-
нему при ц = 0 эта система распадается на k независимых си-
стем, то есть осцилляторы являются слабо связанными.
Как отмечалось выше, частный случай данной задачи, отве-
чающий двум осцилляторам (k = 2), рассмотрен в работе
Н. Мипорского [292] с помощью так называемого стробоскопи-
ческого метода. Ранее близкая задача изучалась также
С. В. Беллюстиным [39], использовавшим для этой цели метод
Пуанкаре.
Общему исследованию синхронизации k почти одинаковых
осцилляторов Ван-дер-Поля при наличии слабых взаимных свя-
зей посвящен § 1 главы XXV настоящей книги.
§ 7.	Синхронизация квантовых генераторов
Создание квантовых генераторов радиодиапазона (мазеров)
и оптического диапазона (лазеров) является одним из наиболее
существенных достижений современной технической физики [329].
За короткий промежуток времени приборы и устройства, осно-
ванные на использовании квантовых генераторов, нашли многие
важные применения как в научных исследованиях, так и при ре-
шении технических задач, в том числе при создании приборов
для весьма точного измерения отрезков времени и частот коле-
баний; в сверхчувствительных приемниках, примененных, в част-
ности, для локации Венеры и Марса, а также для улавливания
слабых сигналов, приходящих из дальних областей Вселенной;
для создания тонких пучков мощного излучения в узком частот-
ном диапазоне. Имеются основания ожидать завоевания кванто-
вой электроникой и других важных областей: с ее помощью
представляется возможным внести ряд коренных усовершенство-
ваний в технику передачи энергии и информации, в химическую
технологию, в изучение и использование биологических явлений.
В основе квантовой электроники лежит явление индуциро-
ванного — синхронного и синфазного — выделения энергии воз-
бужденными атомами вещества под действием внешнего источ-
ника импульсов, в результате чего возникает интенсивное
высококогерентное излучение. Это явление было предсказано
А. Эйнштейном ещев 1917г. Однако начало интенсивного разви-
тия квантовой электроники относится к 1954—1955 гг., когда
американский физик Ч. Таунс и советские ученые Н. Г. Басов и
$ 7]	СИНХРОНИЗАЦИЯ КВАНТОВЫХ ГЕНЕРАТОРОВ	87
А. М. Прохоров независимо и почти одновременно опублико-
вали статьи, в которых излагались основы теории мазеров и
сообщалось о создании радиоспектроскопов высокой разрешаю-
щей силы с использованием молекулярных пучков. Позднее,
в 1960 г., был создан первый лазер — квантовый генератор оп-
тического диапазона.
Для теории ряда устройств, в которых используются кван-
товые генераторы, представляет интерес задача о взаимной син-
хронизации нескольких связанных тем или иным образом гене-
раторов. Приведем постановку этой задачи для частного случая
двух взаимодействующих молекулярных генераторов [280]. Если
обозначить через Xi и х2 напряженности электрического поля
соответственно в резонаторах первого и второго генераторов, то
при ряде упрощающих предположений процессы в генераторах
могут быть описаны системой дифференциальных уравнений
+ к>2х1 + 4nP, (%]) + а|2х2 = 0,
J	-	(7-1)
х2 + Х2 + Ч>2х? + 4пР2 (х2) + a2|xt = 0.
Здесь <01 и (02, Qi и Qz— соответственно частоты и добротности
первого и второго резонаторов, <%|2 и a2i— коэффициенты связи
между генераторами (предполагаемые малыми), ДДлт) и
Р2(х2)—усредненные по длине резонаторов поляризации соот-
ветственно первого и второго резонаторов, являющиеся доста-
точно сложными функциями своих аргументов.
Основная задача по-прежпему состоит в выяснении условий,
при которых, несмотря на различие параметров генераторов, в
последних будут возбуждаться колебания с общим периодом
2л/(о, то есть в нахождении условий существования и устойчи-
вости периодических решений уравнений (7.1) с периодом
Т = 2л/(о. Как и в рассмотренных выше задачах о взаимной
(внутренней) синхронизации, этот период заранее неизвестен и
подлежит определению в процессе решения. Таким образом, за-
дача о синхронизации молекулярных генераторов во многом
аналогична соответствующей задаче о ламповых генераторах
(см. § 6 настоящей главы). Различие состоит лишь в особен-
ностях структуры нелинейных функций, входящих в уравнения
движения, а также в характере членов, описывающих связи
между генераторами. Из указанной специфики вытекают свое-
образные особенности поведения связанных молекулярных гене-
раторов, изучение которых в различных случаях приводится в
цитированной выше статье [280], а также в работах [37, 284,
329]. Уравнения колебаний в генераторах обсуждаются в статьях
[260, 398].
88
ЗАДАЧИ О СИНХРОНИЗАЦИИ ДИНАМИЧЕСКИХ ОБЪЕКТОВ
[ГЛ. I
§ 8.	Явления синхронизации в биологии и медицине
Как уже отмечалось во введении, явления синхронизации
широко распространены не только в технике, но и в природе,
где колебательные процессы играют весьма важную роль. «Го-
ворят, что природа не терпит пустоты, по очень любит ритм и
цикличность», — пишет Р. Гольдэкр, посвятивший вопросу о ре-
гуляции ритма и состоянии гомеостазиса в биологии и меди-
цине специальную статью [460]. Сошлемся также на интересную
работу А. М. Молчанова [303].
Один из примеров взаимной синхронизации в поведении лю-
дей хорошо известен. Он состоит в том, что большая аудитория
(иногда в несколько тысяч человек), стремящаяся аплодировать
по возможности более громко, довольно быстро переходит от
беспорядочных хлопков к скандированным (синхронным и син-
фазным) аплодисментам.
Другим примером является хождение большой группы людей
«в ногу» под звуки оркестра или по счету командира. Здесь си-
туация близка к тому, что во введении к книге было названо
принудительной синхронизацией. Вполне аналогичные явления
иногда наблюдаются при полете стаи птиц и движении косяка
рыб: взмахи крыльев (плавников, хвоста) носят синхронный
характер.
Н. Винером высказано предположение, что ритмическое мер-
цание света, излучаемого несколькими жуками-светляками, на-
ходящимися в пределах «взаимной видимости», не является
простой оптической иллюзией, а представляет один из приме-
ров взаимной синхронизации и фазировки биологических объ-
ектов.
Интересные данные о синхронных колебаниях макромолекул,
а также о синхронном изменении размеров клеточных ядер при-
водятся соответственно в статьях С. Э. Шполя [435] и В. М. Ми-
тюшкина, Л. Л. Литинской, Л. Б. Каминира [297].
Большое значение в жизни человека и животных имеет су-
точный ритм, навязанный вращением Земли вокруг своей оси,
а также годовой период, обусловленный движением Земли по
орбите вокруг Солнца. Эти ритмы характерны для многих физи-
ологических процессов и, кроме того, для механических явлений
п химических реакций, происходящих па Земле.
Четко прослеживаются ритмы, связанные с циклическим из-
менением солнечной активности и имеющие своими периодами
одиннадцать и двадцать два года. Оказалось, что с солнечными
пятнами связаны такие процессы, как колебания температуры
воды мирового океана и интенсивности морских течений, раз-
множение и передвижение рыбы, саранчи и некоторых других
видов живых организмов, эпидемии и пандемии гриппа, чумы,
§81	ЯВЛЕНИЯ СИНХРОНИЗАЦИИ В БИОЛОГИИ И МЕДИЦИНЕ	89
вспышки туляремии, ящура и некоторых других заболеваний
[421, 422].
Последние явления можно рассматривать как принудитель-
ную синхронизацию — захватывание ряда объектов в заданный
ритм одного весьма мощного объекта, обратное влияние на ко-
торый со стороны синхронизируемых объектов не имеет суще-
ственного значения.
Принцип захватывания лежит также в основе работы элек-
трических стимуляторов сердечной деятельности — приборов, ко-
торые посылают в определенные области сердца электрические
импульсы заданной частоты, навязывая мышцам необходимую
частоту сокращений (обычно порядка 60—70 в минуту). Такие
приборы являются незаменимыми при ряде операций, а также
при спасении больных с поперечной блокадой сердца, возникаю-
щей в результате инфаркта миокарда, кардиосклероза или дру-
гих заболеваний [26].
Несомненно, что все перечисленные выше явления синхрони-
зации могут быть феноменологически описаны моделями, ото-
бражающими поведение живых организмов или их отдельных
органов при определенных условиях. Напомним, в частности, что
модель системы кровообращения и сердца как автоколебатель-
ной системы была предложена Б. Ван-дер-Полем и М. Ван-дер-
Марком еще в 1928 г. [495].
Модели, описывающие поведение человека, используются при
решении ряда задач об управлении движением транспорта. От-
метим, что для построения таких моделей часто достаточно
использовать обычные элементы и понятия теории автоматиче-
ского регулирования, такие, например, как инерционность, за-
паздывание, обратная связь и т. п.
Примером проблемы о взаимной синхронизации (самосин-
хронизации) природных объектов, для которой разработана
удовлетворительная математическая модель, могут служить ко-
лебания численности популяции двух видов живых организмов,
один из которых питается продуктами внешней среды (предпо-
лагается, что последние всегда имеются в изобилии), а другой,
хищный, — организмами первого вида.
Соответствующая задача была подробно изучена В. Воль-
терра [497], а затем Г. Ф. Гаузе и А. А. Виттом [141]; в основ-
ных чертах ее решение воспроизведено в монографии [19]. Как
полагает Р. Гольдэкр в уже цитированной работе [460], меха-
низм, рассмотренный В. Вольтерра, в действительности лежит
в основе также очень многих других физиологических процес-
сов, внешне не имеющих ничего общего с колебаниями числен-
ности популяции. Та же модель пригодна для описания кине-
тики некоторых химических реакций [399].
90
ЗАДАЧИ О СИНХРОНИЗАЦИИ ДИНАМИЧЕСКИХ ОБЪЕКТОВ
[ГЛ. I
Приведем постановку указанной задачи. Обозначим число
особей первого вида через Nit а второго — через N2- Если бы
первый вид жил один, то естественно было бы предположить,
что скорость увеличения числа его особей пропорциональна чис-
лу имеющихся налицо особей:
TF-W.	(8.1)
Здесь положительный «коэффициент увеличения» е° зависит от
смертности и рождаемости.
Если бы второй вид жил один, то он бы постепенно выми-
рал, так как ему нечем было бы питаться, причем опять-таки
можно предположить, что
= - 82Х,	'	(8.2)
где Ej > 0.
Допустим теперь, что оба вида живут совместно. Тогда ко-
эффициент увеличения числа особей первого вида будет тем
меньше, чем больше число так как особей первого вида пое-
дают особи второго вида. Сделаем простейшее предположение,
что коэффициент увеличения е° уменьшается пропорционально
N2', аналогичным образом будем считать, что коэффициент умень-
шения для второго вида е° при наличии особей первого вида
(то есть пищи) изменяется пропорционально Ni. Тогда изме-
нение численности обоих видов при их совместном существова-
нии будет описываться следующей системой дифференциальных
уравнений:
-^-= - А^-уМ,
где Ei, е2, Yi и у2— положительные постоянные.
Нетрудно видеть, что система уравнений (8.3) допускает
однозначный аналитический интеграл. Действительно, умножив
первое уравнение на уг, а второе на yi и сложив их, получим
У2-^- + У1-^- = е|У2^1- е2у^2.	(8.4)
Умножив же первое уравнение на Ег/М, а второе на ei/N2 и
сложив, найдем
е2 дГ+ е‘= “ e2Yi^2 + eiy2^i.	(8.5)
2V | til	IV 2 I»»
§ 81
ЯВЛЕНИЯ СИНХРОНИЗАЦИИ В БИОЛОГИИ И МЕДИЦИНЕ
91
Сопоставляя (8.4) и (8.5), получаем
Y2
dNf
dt
dN2
din IV!
dt
d In Л^2
dt
~ ei
Непосредственное интегрирование последнего равенства и
приводит к упомянутому интегралу:
y2A^i + Yi^2 — е2 In Л^! — ё! In Af2 = const.	(8.6)
Несложный анализ равенства (8.6) показывает, что в пло-
скости AAAf2 ему отвечают замкнутые кривые; эти кривые обе-
гаются изображающей точкой, вообще говоря, за некоторое ко-
нечное время Т, представляющее собой общий период колеба-
ний численности видов. Как установлено В. Вольтерра,
(8.7)
где Ti — время, необходимое для удвоения числа особей первого
(поедаемого) вида при отсутствии особей второго (поедающе-
го) вида, а Т2 — время, необходимое для уменьшения вдвое чис-
ла особей поедающего вида в отсутствии поедаемого вида. Не-
трудно видеть, что величины Ti и Т2 (а значит и Т) зависят не
только от параметров системы, но и от начального количества
особей соответствующих ви-
дов. Примерный вид графи-
ков изменения величин Ati и
.V2 представлен на рис. 14;
как видно, максимумы кри-
вых и несколь-
ко сдвинуты по фазе.
Таким образом, и в рас-
смотренном своеобразном
случае вследствие «взаимо-
действия» видов наступает
взаимная синхронизация колебаний их численности*). Любо-
пытно при этом, что изменение численности каждого вида в от-
сутствии особей другого вида представляет собой монотонно
протекающий, а вовсе не колебательный процесс. Аналогичная
ситуация была обнаружена А. С. Брсмзеном и И. С. Файнбер-
гом в задаче о синхронизации двух связанных ламповых гене-
раторов, каждый из которых в отдельности не самовозбуждает-
ся [102].
*) Заметим, что здесь мы имеем дело со случаем сильных связей между’
объектами, когда взаимная синхронизация формально ничем не выделяется
из класса автоколебательных явлений (см. п. 1 § 3 введения к книге).
92
ЗАДАЧИ О СИНХРОНИЗАЦИИ ДИНАМИЧЕСКИХ ОБЪЕКТОВ
[ГЛ. I
Число примеров, свидетельствующих о широком распростра-
нении явлений синхронизации в биологических и биохимических
системах, могло бы быть значительно увеличено.
О ряде биологических закономерностей, механизм которых
предположительно также связан с синхронизацией, будет ска-
зано в следующем параграфе.
§ 9. Синхронизация и некоторые нерешенные проблемы
биологии, физики и астрономии
б)
Рис. 15.
анализу, то получается картина,
Ведущая роль явлений синхронизации в рассмотренных вы-
ше случаях представляется несомненной. Вместе с тем в послед-
ние годы был высказан ряд гипотез о синхронизационной при-
роде механизма некоторых неразгаданных до сих пор явлений
из различных областей нау-
ки. Остановимся па некото-
рых из таких гипотез.
Известно, что если поме-
стить пару электродов на
кожу головы, то можно об-
наружить меняющееся во
времени электрическое на-
пряжение. Усилив и записав
соответствующие биотоки,
получают так называемую
электроэнцефалограмму —
характеристику состояния
головного мозга, используе-
мую как в медицинской
практике, так и в научных
исследованиях.
Если подвергнуть запись
мощности колебаний биото-
ков мозга спектральному
схематически представленная
па рис. 15, а, где по оси абсцисс отложена частота в герцах,
а по оси ординат — спектральная плотность мощности S. Ока-
зывается, что наиболее заметная активность биотоков имеет
место вблизи частоты 10 гц\ эта особенность электроэнцефало-
граммы получила название альфа-ритма. Более тщательное изу-
чение спектра мощности биотоков вблизи 10 гц, выполненное
посредством анализа автокорреляционной функции, записанной
по специально разработанной методике [127], привело к кри-
вой, изображенной па рис. 15, б. Из рисунка видно, что имеет
место как бы «притяжение частот», близких к десяти герцам:
по обе стороны от пика, отвечающего 10 гц, в спектральной кри-
§ 9] СИНХРОНИЗАЦИЯ И НЕКОТОРЫЕ ШЧ’ЕШЕИПЫЕ ПРОБЛЕМЫ 93
вой имеются впадины. Для объяснения подобного явления
Н. Випер [127, 129] предположил, что в мозге имеются своего
рода нелинейные автоколебательные осцилляторы*), генерирую-
щие частоты, близкие к 10 гц. В результате взаимодействия
этих осцилляторов и происходит взаимное «притяжение ча-
стот»— самосинхронизация с частотой около 10 гц**).
Как указывает Н. Винер, такая гипотеза, по крайней мере
косвенно, подтверждается рядом опытов. В одном из таких опы-
тов человек помещался в комнату, к потолку которой был под-
вешен лист жести. К листу подводилось переменное напряже-
ние с амплитудой порядка 400 в. Вследствие этого в любом
предмете, расположенном в комнате, возникала электростати-
ческая индукция. Оказалось, что при частоте колебаний напря-
жения около 10 гц у человека, находящегося в комнате, возни-
кали «определенно неприятные ощущения».
Подтверждением наличия в мозге объектов типа нелинейных
осцилляторов с частотой около 10 гц является также то обстоя-
тельство, что в результате посылки в мозг внезапного электри-
ческого импульса следует четко фиксируемая разрядка с часто-
той, равной примерно десяти колебаниям в секунду. Кроме
того, наблюдалось захватывание частоты альфа-ритма внеш-
ним источником возмущения (вспышками света) с частотой око-
ло 10 гц.
Отметим, что описанный Н. Винером опыт с листом жести
весьма интересен еще и тем, что он является одним из свиде-
тельств возможности посылки сигналов в мозг человека не через
известные нам органы чувств.
Быть может, именно этот опыт навел Н. Винера па мысль о
возможности найти научное объяснение эффектам обмена сиг-
налами между людьми, находящимися на таком расстоянии или
в таких условиях, когда исключено обычное непосредственное
чувственное восприятие. Подобные эффекты, сама реальность
которых в настоящее время многими не без оснований подвер-
гается сомнению вследствие отсутствия достаточно убедитель-
ных экспериментальных данных, называют телепатическими [120,
128]. Изучением этих предполагаемых эффектов занимались
многие видные биологи, психологи и физики как в СССР, так и
за рубежом. Краткая характеристика современного состояния
вопроса, а также описание ряда интересных экспериментов и
наблюдений приведены в книге Л. Л. Васильева [120].
В конце прошлого — начале текущего столетия довольно
широкое распространение получила гипотеза об электромагнит-
ной природе связи между нервными системами людей. Однако
*) До II. Винера гниотеза об осцилляцпоннон природе структурных эле-
ментов нервной ткани была выдвинута Г>. Б, Кажиискпм [200, 201].
*♦) И. Випер, как правило, нс пользуется термином «синхронизация».
94
ЗАДАЧИ О СИНХРОНИЗАЦИИ ДИНАМИЧЕСКИХ ОБЪЕКТОВ
[ГЛ. I
эта мысль, казалось бы, была опровергнута расчетами, свиде-
тельствующими о том, что мощность электромагнитных полей,
создаваемых биотоками мозга, значительно меньше той пороговой
величины, которая, по мнению физиологов, еще может быть
воспринята нервной системой. Такая точка зрения высказана,
например, в статье В. Аркадьева [20], где говорится, в част-
ности, что мощность электромагнитных полей, возникающих при
работе окружающих нас электрических устройств, значительно
больше мощности электромагнитных полей биологического про-
исхождения. Отсюда автор пришел к заключению о несостоя-
тельности гипотезы об электромагнитной природе взаимосвязи
между нервными системами людей.
Из работ последнего времени отметим статью А. Н. Мала-
хова, А. С. Максимова и Ю. Я. Нефедова [264]. На основе из-
мерений спектра биопотенциалов некоторых биологических объ-
ектов в диапазоне частот от 1 до 500 гц и непосредственного об-
наружения электромагнитного излучения на частотах 3 и 150 кгц
авторы также приходят к выводу, что электромагнитное излу-
чение в силу своей малости не может служить носителем ин-
формации в биологической связи, по крайней мере в диапазоне
частот до 150 кгц. Однако авторы не исключают, что электро-
магнитное излучение может служить основой биологической свя-
зи на более высоких частотах. Таким высокочастотным излуче-
нием, по их мнению, может быть резонансное излучение какого-
либо белкового комплекса; оно должно играть роль несущей,
а информация может передаваться от биотоков в виде модуля-
ции несущей.
Из теории синхронизации вытекает, что как при электромаг-
нитном, так и при ином «колебательном» механизме взаимодей-
ствия вопрос о пороге чувствительности может быть рассмотрен
с иных позиций.
Действительно, одной из главных закономерностей синхрони-
зации (см. п. 3 § 3 введения к книге) является отсутствие по-
рога синхронизации: как бы слаба пн была связь между авто-
колебательными объектами, их самосинхронизация непременно
наступит, если только достаточно мало различие между парци-
альными частотами объектов*). При этом вхождение в синхро-
низм сопровождается установлением вполне определенных
фазовых соотношений между колебаниями, тогда как при отсут-
ствии самосинхронизации фазы были случайны.
Таким образом, при достаточной близости парциальных ча-
стот даже сколь угодно слабая связь между генерирующими
объектами может привести к заметному качественному измене-
*) Мы не касаемся здесь существенного вопроса о времени, необходимом
для установления синхронного режима,
§ II] СИНХРОНИЗАЦИЯ Н НЕКОТОРЫЕ НЕРЕШЕННЫЕ ПРОБЛЕМЫ 95
нию характера движения, а значит, соответствующий слабый
сигнал может быть воспринят. Если это так, то никакого уни-
версального физиологического порога чувствительности не суще-
ствует: указанный порог различен для различных пар людей.
Мощность посылаемого сигнала, конечно, играет при этом опре-
деленную роль, однако даже при весьма малой мощности сиг-
нал может быть воспринят, если он обладает определенным ча-
стотным спектром, который играет, таким образом, роль своеоб-
разного ключа.
Как известно, необходимым условием успеха телепатических
опытов считают соответствие участников: они должны образо-
вывать так называемую телепатическую пару. Если признавать
реальность телепатических явлений, то можно предполагать, что
люди, образующие такую пару, как раз и отличаются близкими
парциальными частотами генерируемых воли.
Конечно, вывод об отсутствии «порога синхронизации» отно-
сится к детерминированным системам. При наличии шумовых
эффектов картина получается более сложной. Однако сообра-
жения вероятностного характера, которые должны в таких усло-
виях лечь в основу определения эффективного порога возбуж-
дения, будут совершенно иными, и можно ожидать, что этот по-
рог окажется значительно более низким, чем упоминавшийся
выше «физиологический порог».
Одна из наиболее смелых и далеко идущих гипотез, касаю-
щихся синхронизации в биологии, выдвинута Н. Винером при
рассмотрении возможных механизмов самоорганизации и само-
воспроизведения биологических объектов [129].
Н. Винер отмечает, что одной из основных проблем биологии
является изучение способа, посредством которого главные веще-
ства, составляющие гены или вирусы, или возможные специфи-
ческие вещества, вызывающие рак, самовоспроизводятся из
материалов, лишенных этой специфики, например из смеси
аминокислот и нуклеиновых кислот. Часто говорят, что одна
макромолекула рассматриваемых веществ действует как шаб-
лон, по которому меньшие молекулы составляющего вещества
формируются в аналогичную макромолекулу. Вместе с тем о ме-
ханизме такого воспроизведения почти ничего не известно.
Сущность гипотезы Н. Винера состоит в том, что активный
носитель специфики макромолекулы лежит в частотном строении
ее молекулярного излучения, значительная часть которого пред-
положительно находится в области инфракрасных электро-
магнитных частот или даже ниже. «Может оказаться, — пишет
Н. Винер, — что специфические вещества вируса при некоторых
обстоятельствах излучают инфракрасные колебания, которые
обладают способностью содействовать формированию других мо-
лекул вируса из неопределенной магмы аминокислот и нуклеи-
96
ЗАДАЧИ О СИНХРОНИЗАЦИИ ДИНАМИЧЕСКИХ ОБЪЕКТОВ
[ГЛ. I
новых кислот. Вполне возможно, что такое явление позволитель-
но рассматривать как своего рода взаимное притягательное
взаимодействие частот».
Разумеется, описанный механизм воспроизведения макромо-
лекул далеко не единственно возможный, и поэтому изложен-
ная гипотеза нуждается в тщательной проверке. Один из путей
такой проверки, по мнению Н. Випера, состоит в том, чтобы изу-
чить спектры поглощения и излучения вирусного вещества, а
затем проследить действие света этих частот на' образование
дальнейших вирусов от существующего вируса в надлежащей
питательной среде.
Третья гипотеза, на которой следует остановиться, также
принадлежит Н. Винеру [127], но относится к астрономии. От-
мечая, что планеты являются объектами типа нелинейных ос-
цилляторов, он обращает внимание на тот факт, что периоды
обращения малых планет — астероидов — распределены весьма
неравномерно. Некоторые полосы значений периодов обраще-
ния отсутствуют, причем оказывается, что эти полосы лежат
вблизи периодов, находящихся в простом отношении к периоду
обращения Юпитера. Н. Винер высказывает предположение, что
здесь также имеет место «притяжение частот», то есть синхро-
низация.
Другой весьма примечательный факт, относящийся к астро-
номии и также еще не получивший достаточного объяснения,
состоит в следующем. Периоды обращения Земли и Венеры во-
круг Солнца связаны с периодом вращения Венеры вокруг сво-
ей оси некоторым соотношением с целочисленными коэффици-
ентами таким образом, что в моменты, когда центры Солнца,
Земли и Венеры лежат на одной прямой линии *), Венера всегда
обращена к Земле одним и тем же участком своей поверхности.
Высказываются предположения, что такая согласованность пе-
риодов— синхронизация — объясняется неравномерным распре-
делением массы планеты.
По-видимому, приведенное в п. 1 § 1 введения высказыва-
ние X. Шепли о роли явлений самоорганизации материи в раз-
витии Вселенной в полной мере относится и к явлениям синхро-
низации.
В заключение коснемся одной принципиальной физической
проблемы. Пусть имеется статистическая совокупность слабо
взаимодействующих почти одинаковых объектов типа нелиней-
ных осцилляторов, например автоколебательных объектов. В
этом случае вследствие возможности синхронизационных явле-
ний нельзя ожидать равномерного распределения кинетической
*) Такие моменты противостояния повторяются через каждые полтора
года.
§ 9] СИНХРОНИЗАЦИЯ И НЕКОТОРЫЕ НЕРЕШЕННЫЕ ПРОБЛЕМЫ 97
энергии по степеням свободы, как это предполагается в класси-
ческой статистике. О том, что такие ситуации могут иметь место
и служить причиной ряда «аномальных» явлений, косвенно сви-
детельствуют математические эксперименты, проведенные
Э. Ферми, Д. Паста и С. Уламом в известной Лос-Аламосской
лаборатории на цифровых электронных вычислительных маши-
нах (см. § 8 главы VII монографии [396а]). В этих эксперимен-
тах, по существу, рассматривалось слабо нелинейное взаимо-
действие осцилляторов, находящихся под действием начального
импульса или начального смещения. Поведение системы оказа-
лось не соответствующим равномерному распределению энергии
по степеням свободы: как говорится в цитированной моногра-
фии, в подобных системах «не очень-то много перемешивания».
Добавим, что при этом, как явствует из описания хода экспе-
риментов, движение осцилляторов сопровождается явлениями
синхронизации.
ГЛАВА //
ОБЩАЯ ЗАДАЧА О СИНХРОНИЗАЦИИ
ДИНАМИЧЕСКИХ СИСТЕМ
§ 1.	Постановка общей задачи о синхронизации
Для эффективной разработки общих методов решения зада-
чи о синхронизации представляется важным дать ее общую ма-
тематическую формулировку, охватывающую, как частные слу-
чаи, постановки рассмотренных выше основных частных задач.
Рассмотрим некоторое число k динамических объектов, свя-
занных друг с другом в единую систему (рис. 1). Пусть состоя-
ние s-ro объекта определяется гв-мерным вектором x(s) =
= [x(]s),	x'«](s = 1, ..., й), компоненты которогох^являются
координатами объекта в фазовом пространстве системы.
Движение системы в целом определяется как совокупностью
введенных выше векторов так и v-мерным вектором
и = [«1, ..., uv], характеризующим состояние связей между
объектами. Таким образом, фазовое пространство системы имеет
/ = Г] + ... + rh + v измерений.
Пусть движение рассматриваемой системы описывается диф-
ференциальными уравнениями
*<s) = Xм (x(s)) + F(s) (х(1).xw, «) (s = 1, ..., k),
(1.1)
и = V (x(1), .... x(k), «),
где
X(s} = |x(is>, . . ., X^], Fis} = [ F . .., F'ss|,
U = [Ult Uv]
— соответственно rs и v-мерные вектор-функции, удовлетворяю-
щие весьма общим требованиям, при которых система (1.1)
является динамической (см., например, [323]), и некоторому спе-
циальному требованию, которое будет указано ниже. Вектор-
функции Fs и U, характеризующие связи между отдельными
объектами, назовем функциями связей.
§ 1]	ПОСТАНОВКА ОБЩЕЙ ЗАДАЧИ О СИНХРОНИЗАЦИИ	Q9
Из структурной схемы системы, представленной на рис. 1,
а также из рассмотрения уравнений (1.1) видно, что каждый
из объектов может быть связан со всеми прочими как непо-
средственно, так и через специальную систему связи, состояние
которой характеризуется фазовыми координатами ир. Вместе
с тем из уравнений видно, что координаты х<л\ определяющие
состояние объектов, и координаты «р системы связи, по суще-
ству, входят в уравнения (1.1) вполне «равноправно». Характер-
ная для многих задач о синхронизации специфика каждой груп-
пы переменных выяснится ниже.
Под основной задачей теории синхронизации понимается уста-
новление условий существования и устойчивости решений урав-
нений (1.1), имеющих вид
x(s) = СТЦ) ^qt^n^at + у^ (m^'co/)] (/=1, , rs', s=l.k),
Up = tfp [qpnpat + vp (mpat)] (p = 1, ..., v),
где и —положительная постоянная, (/n<sW) и п()(/пр®/) — пе-
риодические функции соответственно с периодами 2nlm^ и 2л/тр
по at (то есть также с общим периодом 2л по at), q1^ и qp —
числа, каждое из которых может быть равно нулю или едини-
це: в первом случае соответствующую координату х^ или ир
будем условно называть колебательной, во втором случае —
вращательной *). Через ст'.’1 и <тр обозначены числа, любое из ко-
торых может быть равно +1 или —1, а через тр, п'р и
яр —целые положительные числа, которые, не нарушая общ-
ности, можно считать взаимно простыми. Решениям вида (1.2)
отвечают колебательные или «равномерные в среднем» движе-
ния по каждой из фазовых координат с одинаковыми для всех
координат или кратными частотами (угловыми или линейными
скоростями); такие движения назовем синхронными. При этом,
если все числа и равны единице, то будем говорить
о простых синхронных движениях, а если имеется хотя бы одно
число m<f или n<s\ отличное от единицы, — о кратно-синхронных
*) Движения, отвечающие вращательным координатам (</=£0), иногда
называют также ротационными, а отвечающие колебательным координатам —
либрационными [106, 145]. Если для первых движении х^ (со/ + 2л) —	+
+x^(at), где C(f- — постоянные, то для вторых x'f* (св/ + 2л) = x^f1 (at).
Для скоростей изменения обобщенных координат в обоих случаях имеет
место периодичность (св/ + 2л) = Гу5 (со/). Подчеркнем, что принятый нами
термин «вращательная координата» условен: в реальной системе такой коор-
динате может отвечать также и прямолинейное движение некоторой точки
или тела с постоянной средней скоростью.
100
ОБЩАЯ ЗАДАЧА О СИНХРОНИЗАЦИИ
[ГЛ. II
движениях. Соответственно будем различать задачи о простой
и о кратной синхронизации динамических объектов. Величину
и > 0 назовем синхронной скоростью (частотой).
Конкретизируем теперь вид правых частей уравнений (1.1).
Будем предполагать, что функции F^ и (jp зависят от
своих аргументов таким образом, что после подстановки вме-
сто х(р и ир их значений согласно формулам (1.2) эти функции
становятся периодическими функциями «безразмерного време-
ни» т = at с периодом 2л.
Последнее условие не является обязательным для существо-
вания у системы (II) синхронных движений, однако оно выпол-
няется во всех рассмотренных в главе I основных конкретных
задачах о синхронизации и существенно упрощает их решение;
поэтому далее это условие предполагается удовлетворенным.
Заметим, что для его справедливости достаточно, чтобы xf и
Up были периодическими функциями вращательных координат
с периодом 2л, а также, быть может, функциями разностей
or(,s)x(,s)	° iul арир a()S)X^ CpUp
!	!	a a	1 1__P P >	'	_ P P ГПР t-(S) y(P) f! и
„(s)	“ n(₽>	’ n	n	’ Ks)	n	’ A 1 ’ “ ’ 1
nl	na	nl	np	nj	nP
Up — вращательные координаты.
Переходя в уравнениях (1.1) по формулам (1-2) от перемен-
ных х, и и t к переменным у, v и т = at, получаем систему вида
--= У<s> (у^, т) + ф<*’ (у^, ..., y<k\ V, т) ($ = 1, ..., k),
,	(1.3)
-g- = V(^\ ..., y<k\ v, т),
где, в соответствии с предположениями о характере вектор-функ-
ций X<s) и U, функции и V являются периодическими отно-
сительно безразмерного времени т с периодом 2л.
Таким образом, основная задача о синхронизации сводится
к установлению условий существования и устойчивости периоди-
ческих решений системы уравнений (1.3), имеющих период 2л.
Помимо сформулированной выше основной задачи о синхро-
низации зачастую представляет также интерес решение следую-
щих задач.
1. Реальное вычисление синхронной скорости (частоты) со,
а также решений (1.2), отвечающих устойчивым синхронным
движениям. При этом во многих случаях можно ограничиться
определением средних за период 2л значений функции y(s>(x)
и и(т), то есть величин
2л	2л
= 2^ J y{S}(i:)dT, a = -2^J v(x)dx, (1.4)
о	о
§ 1]	ПОСТАНОВКА ОБЩЕЙ ЗАДАЧИ О СИНХРОНИЗАЦИИ	|01
а также максимальных отклонений | у’?} (т) — a<s) |max и|г?р(т) —
— “plmax 0Т ЭТИХ СРВДИИХ ЗНЗЧеНИЙ.
2. Выбор системы связи, при котором обеспечивается суще-
ствование и устойчивость синхронного движения (1.2) задан-
ного вида. Эта задача, которую можно назвать задачей синтеза,
является в известной мере обратной по отношению к основной.
В ряде случаев представляет интерес также решение весьма
трудной задачи об определении в фазовом пространстве систе-
мы таких областей начальных значений ее координат («обла
стей захвата»), для которых с течением времени движение не-
ограниченно приближается к определенному синхронному дви-
жению.
Один из наиболее важных классов задач о синхронизации
образуют задачи о синхронизации автоколебательных объек-
тов, то есть объектов (как правило, однотипных), каждый из
которых, будучи изолирован от остальных (функции связей fW
и ф(8> соответственно в уравнениях (1.1) и (1.3) отсутствуют),
при определенных условиях может совершать движения типа
(1.2), характеризующиеся некоторой частотой (угловой ско-
ростью) од. Величину со« естественно назвать парциальной ча-
стотой (скоростью) объекта. Задача о синхронизации при этом
заключается в установлении условий, при которых после объеди-
нения всех объектов в единую систему последние смогут совер-
шать движения того же типа, но с одинаковой частотой (ско-
ростью) и или же с частотами (скоростями) вида п.чсо.
В зависимости от характера постановки задачи о синхрони-
зации автоколебательных объектов или систем, содержащих та-
ковые, следует различать задачу о внутренней (взаимной, авто-
номной) синхронизации и задачу о внешней (неавтономной)
синхронизации.
В первом, наиболее общем случае, к которому и относилась
приведенная выше постановка задачи о синхронизации, все син-
хронизируемые объекты рассматриваются как равноправные
элементы единой автономной динамической системы; частота
синхронного движения со при этом устанавливается в результате
взаимодействия всех элементов системы. Правые части уравне-
ний (1.1) в таком случае не содержат в явной форме времени
t, а значение синхронной частоты со заранее неизвестно и под-
лежит определению в процессе решения задачи.
Во втором случае предполагается, что один из синхронизи-
руемых автоколебательных объектов является значительно бо-
лее мощным по сравнению со всеми остальными, и поэтому его
движение считается не зависящим от характера движения про-
чих элементов системы. Воздействие указанного объекта на
остальные элементы системы и тем самым частота (или угловая
102
ОБЩАЯ ЗАДАЧА О СИНХРОНИЗАЦИИ
[ГЛ. II
скорость) синхронного движения предполагаются наперед за-
данными и неизменными. Исходная система (1.1) при этом под-
ходе к задаче обращается в неавтономную, и ее порядок пони-
жается.
Нетрудно видеть, что все рассмотренные в главе I конкрет-
ные задачи о синхронизации представляют частные случаи сфор-
мулированной общей задачи.
Заметим в заключение параграфа, что выражения (1.2),
определяющие синхронные движения, можно записать в более
простой форме:
x(s) =	у(р	(/ = 1, • • • > rs’’ s = 1 > • • • > &)>
ZZ„ =/7pO)f +	(/Ир0)/)	(Р=1......V),	(1'5)
где nf и «р — целые числа, и тр — целые положительные
числа, a и vp — периодические функции —> соответственно с
периодами 2n/m)s) и 2л/тр по <о/. Однако мы, как правило, бу-
дем придерживаться в дальнейшем более развернутой записи
(1.2), ибо она удобней для ряда приложений.
Отметим, далее, что для некоторых приложений может ока-
заться целесообразным расширить приведенное выше понятие
синхронизации, распространив его па объекты более общей при-
роды и охватив некоторые типы непериодических и неравномер-
ных в среднем движений. Можно предполагать также, что функ-
ции ур и vp являются почти периодическими. Вместе с тем во
всех задачах, изучаемых в данной книге, достаточно ограни-
читься изложенным выше менее общим толкованием синхрони-
зации, и поэтому мы, как правило, придерживаемся его в даль-
нейшем.
Укажем также, что для ряда приложений (см., например,
§§ 2 и 3 главы XIV) представляет интерес задача о синхрониза-
ции в системах с распределенными параметрами. В этом случае
в числе уравнений (1.1) содержатся уравнения в частных про-
изводных. Естественно, что все сказанное может быть распро-
странено и па такую систему уравнений.
§ 2. Основные особенности задач о синхронизации
Остановимся па основных общих особенностях задач о син-
хронизации, которые были выяснены в главе I на частных при-
мерах.
Прежде всего заметим, что уравнения подобных задач, как
правило, являются существенно нелинейными. К счастью, одна-
ко, в них зачастую удается ввести малый параметр, что дает
возможность воспользоваться для решения методами теории
§ 2J	ОСНОВНЫЕ ОСОБЕННОСТИ ЗАДАЧ О СИНХРОНИЗАЦИИ	ЮЗ
периодических решений нелинейных дифференциальных уравне-
ний, основы которых развиты в классических сочинениях
А. Пуанкаре и А. М. Ляпунова.
Можно указать две важные группы задач о синхронизации,
допускающих эффективное использование метода малого пара-
метра.
К первой группе относятся задачи о синхронизации объектов
со «слабыми» взаимными связями. Именно такие задачи пред-
ставляют основной прикладной интерес, ибо, с одной стороны,
синхронизацию технически наиболее просто и экономично осу-
ществлять именно посредством «слабых» связей и, с другой сто-
роны, если все же приходится применять «сильные» связи ме-
жду какими-либо объектами, то последние, как правило, после
наложения таких связей можно рассматривать как единую си-
стему, для которой задачи о синхронизации не возникает. Так,
например, два механических дебалансных вибратора, валы ко-
торых связаны шестеренной передачей с жесткими промежуточ-
ными элементами, расположенными между дебалансами и ше-
стернями, практически образуют один двухвальный вибратор.
К категории задач о синхронизации объектов со слабыми
взаимными связями, как явствует из изложенного в главе I, мо-
жет быть отнесено большинство конкретных задач о синхрони-
зации вибраторов, задача об автоматическом балансире для
уравновешивания вращающихся роторов, ряд задач об изгибно-
крутильных колебаниях вращающихся валов с неуравновешен-
ными дисками, задача Гюйгенса о синхронизации часов, задачи
о синхронизации ламповых генераторов и многие другие.
В задачах о синхронизации объектов со слабыми взаимными
связями основные уравнения (1.1) могут быть представлены в
виде
?s’ = X's>(x(i)) + pFw(x(1),	*<*>, и, ц) (s=l.....k),
« = 1Г(*»’,	«, р)	(2Л)
или, в переменных z/(S), v и т = <£>/,— в форме
^ = У^(^,т) + цФ^(У<1’,	у^, V, т, ц) (s=l, .... Я
~	v, т, ц).
Здесь F(i), U*, Ф(1) и V* — вектор-функции того же класса,
что и функции F(S) и U, Ф(5) и V в уравнениях (1.1) и (1.3),
причем F(i), U*, $'s’ и V* являются также функциями малого
параметра р>0, которые достаточно считать аналитическими
по р при р < р0, где pQ>0.
104
ОБЩАЯ ЗАДАЧА О СИНХРОНИЗАЦИИ
[ГЛ. II
Весьма распространенным классом задач являются задачи
о синхронизации одинаковых или почти одинаковых объектов,
слабо взаимодействующих один с другим. В этом случае функ-
ции Х^ в уравнениях (2.1) и функции в уравнениях (2.2) не
зависят от индекса s.
Уравнения (2.2), к исследованию периодических решений ко-
торых приводится решение основной задачи о синхронизации в
случае слабых связей между объектами, обладают той особен-
ностью, что в отвечающей им порождающей системе (то есть
системе, получающейся при ц = 0) каждое из первых k уравне-
ний является независимым; после определения из них векторов
у№ вектор Vo может быть найден из последнего уравнения. Это
обстоятельство с одной стороны, существенно облегчает реше-
ние порождающей системы, но, с другой стороны, оно приводит
к ряду осложнений при исследовании полной системы.
Дело в том, что порождающая система, отвечающая уравне-
ниям (2.2), допускает не одно периодическое решение, а семей-
ство таких решений:
y{fo=y{io(x’ ai> • • •> %) (/=1, rs; s=l, (2.3)
зависящее от некоторого числа р произвольных параметров aq,
где число р равно или больше числа объектов k. Причину ска-
занного нетрудно понять: поскольку в порождающем приближе-
нии уравнения движения объектов (2.2) независимы, то, допу-
ская периодическое решение !/$(т), в силу автономности
каждого из исходных уравнений (2.1), они, согласно (1.2), до-
пускают также и периодические решения вида (т +	+
+ p<.s)/ijs)asw, где a5 — произвольные постоянные, общее число ко-
торых равно числу объектов k (см. также п. 2 § 3 введения
к книге).
Из теории метода Пуанкаре известно (см. § 2 главы III на-
стоящей книги), что наличию у порождающей системы перио-
дических решений типа (2.3), зависящих от некоторого числа р
произвольных постоянных, отвечает особый случай, когда так
называемый определитель Пуанкаре обращается в нуль вместе
со своими минорами до I — р+ 1-го порядка включительно.
В данном случае осложняется изучение не только условий су-
ществования, но и условий устойчивости периодических реше-
ний, ибо характеристическое уравнение для системы, отвечаю-
щей порождающей системе и порождающему решению, непре-
менно имеет р-кратный корень, равный единице. В результате
исходное приближение к корням характеристического уравнения
еще не дает ответа на вопрос об устойчивости, и поэтому необ-
ходимо рассматривать следующее приближение.
§ 2]	ОСНОВНЫЕ ОСОБЕННОСТИ ЗАДАЧ О СИНХРОНИЗАЦИИ	105
Наличие кратных (или близких) корней у характеристиче-
ского уравнения в задачах о синхронизации может быть связано
не только с автономностью объектов и слабостью связей, но и
с наличием в системе нескольких одинаковых (или почти одина-
ковых) объектов.
Другая категория задач о синхронизации, при решении ко-
торых может быть эффективно использован метод малого пара-
метра, характеризуется тем, что можно ограничиться исследо-
ванием синхронизации при условии, что объекты совершают
движения, близкие к какому-либо известному движению. Так,
например, ряд задач о синхронизации вибраторов, об автоба-
лансире, об изгибно-крутильных колебаниях валов, о синхрони-
зации генераторов зачастую достаточно решить в предположе-
нии, что в синхронных движениях изменение во времени всех
вращательных координат (углов поворота роторов) происходит
по закону, близкому к равномерному вращению с синхронной
угловой скоростью.
Более подробно математические особенности задач о син-
хронизации будут рассмотрены в третьей и седьмой главах на-
стоящей книги.
ЧАСТЬ II
МЕТОДЫ И МАТЕМАТИЧЕСКИЙ АППАРАТ
ТЕОРИИ СИНХРОНИЗАЦИИ ДИНАМИЧЕСКИХ СИСТЕМ
Вторая часть книги посвящена изложению методов решения
задач теории синхронизации динамических систем. Основное
внимание уделяется методу малого параметра Пуанкаре, кото-
рый по причинам, изложенным во втором параграфе предыду-
щей главы, особенно удобен при изучении проблем синхрони-
зации.
После изложения основных идей методов Пуанкаре и Ля-
пунова рассматриваются особенности исследования с помощью
этих методов задач о синхронизации динамических объектов.
Далее доказывается ряд теорем о существовании и устойчиво-
сти периодических и синхронных решений систем нелинейных
дифференциальных уравнений, типичных для задач о синхро-
низации. По существу, эти теоремы развивают математический
аппарат методов Пуанкаре и Ляпунова применительно к таким
задачам. Показывается, что результат исследования при опре-
деленных условиях может быть представлен в удобной форме —
в виде так называемого интегрального критерия устойчивости
синхронных и периодических движений.
Обычно при решении прикладных задач методами Ляпунова
и Пуанкаре ограничиваются установлением фактов существо-
вания и устойчивости решений при достаточно малых значениях
параметра и начальных отклонений от решения, отвечающего
невозмущенному движению. Области сходимости получаемых
рядов по малому параметру и области устойчивости решений в
пространстве начальных отклонений, как правило, не опреде-
ляются. Между тем полученные данные используются для су-
ждения о поведении системы при конечных значениях параметра
и при конечных отклонениях. Подобное «нелокальное» исполь-
зование результатов «локального» исследования не является
строгим. Однако практика оправдывает такой нестрогий об-
раз действий, ибо, как правило, он не приводит к ошибкам.
Затронутые существенные вопросы, часто неправильно трак-
туемые в литературе, обсуждаются в четвертой главе. Там же
рассматриваются вопросы об использовании метода малого па-
раметра для исследования систем, формально не содержащих
такого параметра. Шестая глава посвящена краткому рассмот-
рению некоторых других возможных методов решения задачи
о синхронизации, в том числе методов математического и физи-
ческого моделирования.
глава ///
МЕТОДЫ ПУАНКАРЕ И ЛЯПУНОВА
§ 1. Предварительные замечания
Метод малого параметра, представляющий собой, по суще-
ству, вариант метода возмущений, является в настоящее время
одним из наиболее эффективных и универсальных способов ре-
шения задач теории нелинейных колебаний.
Особенности задач о синхронизации, отмеченные в первой
части книги, требуют развития математического аппарата мето-
да малого параметра во вполне определенных направлениях.
Этому вопросу посвящено основное содержание пятой главы.
В данной же главе мы остановимся на краткой характеристике
метода, уделив особое внимание обзору результатов, имеющих
непосредственное отношение к теории синхронизации.
Математические основы метода малого параметра примени-
тельно к теории периодических решений дифференциальных
уравнений были заложены в классических сочинениях А. Пуан-
каре [472] в конце XIX столетия.
Первостепенную роль при использовании метода Пуанкаре
играет теория устойчивости движения и теория периодических
решений дифференциальных уравнений, развитая примерно в
тот же период А. М. Ляпуновым в его основополагающем труде
«Общая задача об устойчивости движения» [261].
Широкое использование методов Пуанкаре — Ляпунова в
теории нелинейных колебаний началось, однако, только в три-
дцатых годах текущего столетия. Основная заслуга в деле раз-
вития и применения этих методов к решению задач механики,
радиотехники и теории автоматического регулирования, несо-
мненно, принадлежит отечественным ученым — Л. И. Ман-
дельштаму, Н. Д. Папалекси, А. А. Андронову, А. А. Витту,
а также их последователям — Б. В. Булгакову и И. Г. Малки-
ну [276—279, 15—19, 105, 106, 266—275].
Методы А. Пуанкаре и А. М. Ляпунова за последние два де-
сятилетия получили интенсивное развитие в трудах многих ис-
следователей; эти методы были с успехом использованы при
решении ряда важных прикладных задач. Подробному изло-
жению методов А. Пуанкаре и А. М. Ляпунова посвящена пре-
восходная монография И. Г. Малкина [275], оригинальное изло-
жение метода и обобщения содержатся в работах [142, 181];
краткий обзор исследований и обширная библиография содер-
жатся в книге Л. Чезари [419]. К наиболее значительным зару-
бежным работам, посвященным развитию и изложению метода,
следует отнести исследования С. Дилиберто и Г. Хуффорда
[453], Э. Коддингтона и Н. Левинсона [450, 215], В. Мак-Милла-
на [467, 263], Дж. Стокера [486, 384], Р. Фора [455, 456],
108
МЕТОДЫ ПУАНКАРЕ И ЛЯПУНОВА
(ГЛ ш
К. Фридрихса [457], Дж. Хаага [461—463], Дж. Хейла [464, 403] и
М. Розо [360а]. Обзоры исследований отечественных ученых и не-
которые точки зрения на методы Пуанкаре и Ляпунова изло-
жены в статьях А. П. Проскурякова [350] и автора [90].
О результатах работ, имеющих прямое отношение к вопро-
сам, затрагиваемым в настоящей книге, будет сказано ниже
(см., в частности, § 4 главы III).
§ 2. Основные идеи метода Пуанкаре
I. Случай неавтономной системы. Напомним в общих чертах
основные идеи метода Пуанкаре, причем специально остано-
вимся на вопросах, касающихся задач о синхронизации. Рас-
смотрим вначале систему дифференциальных уравнений
xs = АДхн . . ., хп, t) + pFs(xi, хп, t, jx) (2.1)
($ = 1.................п),
где Xs и Fs для простоты рассуждений будем считать аналити-
ческими функциями переменных Х\, . . ., хп в замкнутой обла-
сти G, которой принадлежат все рассматриваемые ниже реше-
ния уравнений, и непрерывными периодическими функциями
переменной t с периодом 2л*) в любой точке области G. По-
ложим также, что функции Fs являются аналитическими функ-
циями малого параметра р 0 при р р0, где р0 > 0.
Система (2.1) неавтономна: предполагается, что правые
части уравнений содержат время t в явной форме. Более слож-
ный случай автономной системы будет рассмотрен ниже.
Отыскание периодических решений системы
(S=l......п),	(2.2)
получающейся из (2.1) при р = 0 и называемой порождающей
системой, может оказаться более простым, нежели нахождение
периодических решений системы (2.1).
Возникает, однако, вопрос, можно ли «доверять» периодиче-
ским решениям порождающей системы в том смысле, что этим
решениям действительно соответствуют «близкие» периодиче-
ские решения исходной системы уравнений (2.1), то есть реше-
ния исходной системы, обращающиеся при р = 0 в решения по-
рождающей системы.
А. Пуанкаре показал, что указанное соответствие имеет мес-
то далеко не всегда. А именно в зависимости от характера пра-
*) Если период иной, то можно всегда сделать его равным 2л путем
простой замены независимой переменной t.
ОСНОВНЫЕ ИДЕИ МЕТОДА ПУАНКАРЕ
109
§ 2]
вых частей уравнений (2.1) может оказаться, что периодиче-
скому решению порождающей системы (2.2) не соответствует
периодическое решение основной системы (2.1). С другой сто-
роны, возможны и случаи, когда решению порождающей си-
стемы отвечает несколько и даже бесчисленное множество пе-
риодических решений основной системы.
Для выяснения сформулированного выше вопроса о соответ-
ствии между периодическими решениями основной и порож-
дающей систем рассуждают, следуя А. Пуанкаре, таким об-
разом.
Пусть
< = <(/)	($ = 1,	(2.3)
есть какое-нибудь периодическое решение порождающей систе-
мы (2.2). Рассмотрим решение
Xs = xs(t, pi,	р) ($=!,...,«)	(2.4)
основной системы (2.1), удовлетворяющее начальным условиям
хДО, рр ..., р„, p) = x;(0) + Ps.	(2.5)
Попытаемся подобрать параметры ps как функции р, обра-
щающиеся в нуль при р = 0, таким образом, чтобы решение
(2.4) было периодическим с периодом 2л. Если это удастся сде-
лать, то основная система, по крайней мере при достаточно ма-
лом р, будет иметь периодическое решение, обращающееся при
р = 0 в «порождающее решение» (2.3).
Условия периодичности решения (2.4) имеют вид
= xs (2л, рь ..., р„, р) - xs (0, р1( ..., р„, р) = 0	(2.6)
($ = 1, .. ., п).
В силу сделанных выше предположений о характере правых
частей уравнений (2.1) функции фа будут аналитическими отно-
сительно Pi, ..., рп и р при достаточно малых значениях этих
величин. Кроме того, при Pj = . . . = рп = р = 0 функции фя об-
ращаются в нуль, так как в этом случае решение (2.4) в силу
(2.5) обращается в порождающее решение (2.3), которое пе-
риодично по условию.
Поэтому если якобиан
I — I (Ф*...Ч’п) I	/9 71
I <?(₽!..₽„) Ц
отличен от нуля, то в силу теоремы о существовании неявных
функций из системы уравнений (2.6) могут быть однозначно
110
МЕТОДЫ ПУАНКАРЕ И ЛЯПУНОВА
[ГЛ. 111
определены функции 0s = ps(p), обращающиеся в нуль при
р = 0 и аналитические при достаточно малых значениях ц. Под-
ставив эти функции в (2.4), получим аналитическое относитель-
но р решение основной системы (2.1), обращающееся при р = 0
в порождающее решение (2.3).
Таким образом, в случае отличного от нуля определителя
(2.7), который в дальнейшем будем называть определителем
Пуанкаре, существует единственное периодическое решение си-
стемы (2.1), обращающееся при р = 0 в решение порождаю-
щей системы. Иначе говоря, вопрос о соответствии периодиче-
ских решений систем (2.1) и (2.2) в этом случае решается по-
ложительно*). Последнее утверждение и представляет собой
известную теорему А. Пуанкаре [472, 275].
Значительно более сложным становится изучение рассматри-
ваемого вопроса, если определитель Пуанкаре (2.7) равен нулю.
Здесь уже недостаточно теоремы о существовании неявных
функций в ее простейшей формулировке. Между тем такие, ка-
залось бы, весьма специальные с математической точки зрения
случаи представляют наибольший интерес для теории нелиней-
ных колебаний. Действительно, именно в этих случаях, согласно
сказанному выше, нет однозначного соответствия между перио-
дическими решениями исходной и порождающей систем урав-
нений. Поэтому при обращении определителя (2.7) в нуль, с пе-
реходом от р, = 0 к р Ф 0, как раз и получаются качественные
Изменения.
Можно, следовательно, сказать, что основное содержание
теории метода Пуанкаре представляет исследование различных
случаев обращения в нуль определителя (2.7).
Необходимо подчеркнуть также (отметим, что это не всегда
делается при изложении метода) особую роль, которую играет
в методе Пуанкаре теорема о существовании неявных функций.
По существу, основная идея метода и состоит в сведении во-
проса о существовании периодических решений системы диффе-
ренциальных уравнений к вопросу о существовании неявных
функций. Специфика заключается лишь в том, что особый инте-
рес представляют специальные случаи, как правило, не рас-
сматриваемые в общих курсах и руководствах.
Важный класс таких специальных случаев, когда определи-
тель (2.7) обращается в нуль, характеризуется тем, что порож-
дающая система (2.2) имеет семейство периодических решений
= ai> • • •> ak) (s	(2.8)
*) Отметим, что метод Пуанкаре позволяет получить лишь те периоди-
ческие решения основной системы (2.1), которые обращаются при ц = 0
в порождающее решение (2.3). В принципе основная система может иметь
и иные периодические решения.
§ 2]
ОСНОВНЫЕ ИДЕИ МЕТОДА ПУАНКАРЕ
111
зависящее от k п произвольных параметров ось а*. Имен-
но этот случай, как отмечалось в главе II, представляет особый
интерес для теории синхронизации.
Если постоянные ои, . . ., а& входят в выражения (2.8) неза-
висимо, то есть хотя бы один из определителей k-vo порядка
матрицы
дх°	дх°
dai ‘ ' да!
дх°	дх°п
dak ' ' ' dak
(2.9)
не обращается в нуль в интересующей нас области, то, как не- -
трудно показать [275], определитель Пуанкаре (2.7) обращается
в нуль вместе со своими минорами до п — k + 1-го порядка
включительно. Если при этом не обращается в нуль по крайней
мере один из миноров п — k-vo порядка определителя (2.7), то,
как показывает исследование [275], 2л-периодические решения
исходной системы, обращающиеся при р = 0 в порождающее
решение, могут отвечать, вообще говоря, лишь избранным си-
стемам значений параметров, а именно значениям, удовлетво-
ряющим некоторой системе уравнений
Ps(a1; ..aft) = 0 (s = 1.....k).	(2.10)
Определенному решению а^а]...........ak = ak уравнений
(2.10) действительно отвечает единственное периодическое ре-
шение исходной системы дифференциальных уравнений, анали-
тическое относительно р и обращающееся при р = 0 в порож-
дающее, если определитель матрицы
dPt
dat
dPk
да!
дРх
dak
dPk
dak
(2.U)
отличен от нуля.
Естественно, что вопрос о нахождении функций Ps по из-
вестным правым частям исходных уравнений (2.1) и порождаю-
щему решению (2.3) имеет первостепенное значение. Как отме-
чалось во введении к книге (см. п. 2 § 3) знание этих функций,
названных порождающими функциями, как правило, позволяет
решить соответствующую задачу о синхронизации с достаточ-
ной полнотой. Поэтому получению развернутых выражений
112
МЕТОДЫ ПУАНКАРЕ II ЛЯПУНОВА
[ГЛ. III
функций Рь для ряда систем уравнений, существенных в теории
синхронизации, посвящена значительная часть V и VII—XI глав
книги.
2. Случай автономной системы. Выше предполагалось, что
исходная система уравнений (2.1) неавтономна, то есть что пра-
вые части этих уравнений содержат время t в явной форме.
Рассмотрим теперь автономную систему
xs = Xs (х,, .. ., хп) + p,Fs (Xj.x„, ц)	n), (2.12)
в которой правые части уравнений явно не зависят от времени.
Пусть относительно Х„ и Fs как функций переменных Xi, . .. , хп
и ц справедливы те же простейшие предположения, что и вп. 1
настоящего параграфа.
Как отмечалось в § 2 главы II, автономные системы пред-
ставляют особый интерес для теории синхронизации, ибо к их
рассмотрению приводится изучение наиболее общей задачи —
задачи о внутренней синхронизации. Неавтономные системы
уравнений отвечают случаям, когда допустимо ограничиться
рассмотрением задачи о внешней синхронизации, то есть счи-
тать, что движение одного (или нескольких) наиболее «мощ-
ного» объекта заранее задано; тем самым считается заданным
и период (частота) синхронного движения.
Случай автономной системы уравнений существенно отли-
чается от случая неавтономной системы. Прежде всего, если
для системы неавтономной искомые периодические решения
имели заданный период, равный (или кратный) периоду правых
частей уравнений, то автономная система уравнений (2.12) мо-
жет иметь периодические решения любого и притом неизвест-
ного заранее периода Т, который, вообще говоря, будет зави-
сеть от параметра ц.
Далее следует отметить, что автономная система не может
иметь изолированных периодических решений: любое периоди-
ческое решение остается таковым, если заменить в нем t на
t + h, где h — произвольная постоянная.
Пусть соответствующая уравнениям (2.12) порождающая
система
.... о (*=1,.... п) (2.13)
допускает периодическое решение
=	(s- 1, .... и)	(2.14)
некоторого периода Т.
Разыскивая периодическое решение исходной системы (2.12),
мы должны предполагать, что его период отличен от Т; обозна-
чим этот период через Т + у.
§2]	ОСНОВНЫЕ ИДЕИ МЕТОДА ПУАНКАРЕ	1 ]3
Подобно случаю неавтономной системы, рассмотрим решение
xs = xs(t, р,...........р„, р) (s= 1.......п) (2.15)
исходной системы (2.12), удовлетворяющее «смещенным» на-
чальным условиям
хДО.р,, ..., р„, p) = <(O) + ps (s=l, .... п). (2.16)
Поставим вопрос о том, можно ли подобрать параметры ps
и параметр у как функции р, обращающиеся в нуль при р = О,
таким образом, чтобы решение (2.15) было периодическим с пе-
риодом Т + у. Если это удастся сделать, то основная система
(2.12), по крайней мере при достаточно малом р, будет иметь
периодическое решение, обращающееся при р = 0 в порождаю-
щее решение (2.14).
Условия периодичности решения (2.15) имеют вид
.....₽«> V, н) = ^(?’ + у, Pi, •••> Рп, ц)-
- xs (0,	р) = 0 (s=l, ...,«).	(2.17)
При этом, в силу сделанных выше предположений об аналитич-
ности правых частей уравнений (2.12) и известных теорем тео-
рии дифференциальных уравнений, функции ф., будут аналити-
ческими относительно рь . . . , рп и у при достаточно малых зна-
чениях этих величин; кроме того, при 0j = . . . =	= у = р = О
функции фя обращаются в нуль, так как при этом рассматри-
ваемое решение (2.15) обращается в порождающее решение
(2.14), которое периодично по условию.
Число уравнений (2.17) на единицу меньше числа неизвест-
ных	и у. Поэтому одно из неизвестных можно назна-
чить произвольно. Пусть, например,
Рп = 0.	(2.18)
Тогда, если якобиан
\	.... Рп-^У) |р1=...=Р„_1-Г=Ц=О	(2,19)
отличен от нуля, то, в силу теоремы о существовании неявных
функций, из системы уравнений (2.17) могут быть однозначно
определены функции pt = f3i(p), ..., 0n-t = Pn-t(p) и у = у(р),
обращающиеся в нуль при р = 0 и аналитические при доста-
точно малых значениях р. Подставив эти функции в (2.15), по-
лучим аналитическое относительно р решение основной систе-
мы (2.12), обращающееся при р = 0в порождающее решение
(2.14); определится также и период Т + у(р) этого решения.
Если функциональный определитель (2.19) обращается в
нуль, то вместо рп можно положить равной нулю какую-нибудь
114
МЕТОДЫ ПУАНКАРЕ И ЛЯПУНОВА
[ГЛ. ПГ
другую неизвестную функцию. Таким образом, в итоге полу-
чается, что основная система (2.12) допускает одно и только
одно периодическое решение, обращающееся при ц = 0 в по-
рождающее, если по крайней мере один из определителей /1-го
порядка, заключающихся в матрице
dipi	dip] dipi
dPi ‘ ' dp„ dy
dipn dipn dipn |
d₽i ' ’ ' dp„ dy II
не обращается в нуль при Pi = . . . =	= у = ц = 0.
Отметим, что один из таких определителей, а именно
г = I d (ip......... ip„) I
"+’ I d(p,.......p„) |ф1=...=ф„=у=1х=о’
(2.20)
(2.21)
непременно обращается в нуль и поэтому нельзя вместо р„ = О
положить у = 0. Обращение в нуль определителя (2.21) яв-
ляется следствием автономности исходной системы (2.12): по-
рождающее решение (2.14) остается периодическим в резуль-
тате замены t на t + а, и, следовательно, уравнения (2.17) при
у = ц = 0 должны допускать бесчисленное множество решений,
отличных от тривиального, отвечающего Pi = ... =	= 0. Та-
ким образом, отличным от нуля при 01 = . .. = 0П = у = 0 мо-
жет быть лишь какой-либо иной определитель матрицы (2.20).
Как следует из изложенного выше, если такой определитель
действительно имеется, то вопрос о соответствии периодических
решений основной и порождающей систем решается положи-
тельно.
Более сложными являются случаи, когда все определители
п-го порядка матрицы (2.20) обращаются в нуль при Pi = . . . =
= рп = у = р, = 0. Как и для неавтономной системы, именно эти
случаи представляют особый интерес для теории нелинейных
колебаний, ибо здесь нет однозначного соответствия между пе-
риодическими решениями исходной и порождающей систем: при
переходе от ц = 0 к ц #= 0 возникают качественные изменения.
Эти случаи, как и ранее, имеют место, например, тогда, ко-
гда порождающая система (2.13) имеет семейство периодиче-
ских решений
*; = <(/, ар ..., аА) (s=l, ..., п),	(2.22)
зависящее, кроме указанной выше постоянной а, которую все-
гда можно добавить к t, также и от некоторого числа k п
других постоянных «1, . . . , ак-
Предположим, что эти постоянные входят в (2.22) незави-
симо, то есть хотя бы один из определителей k-ro порядка мат-
§ 3J	OB УСТОЙЧИВОСТИ ПЕРИОДИЧЕСКИХ РЕШЕНИЙ	Ц5
рицы (2.9) в интересующей нас области отличен от нуля. То-
гда, как нетрудно показать [275], все определители до порядка
п — k + 1 включительно, содержащиеся в матрице (2.20), обра-
щаются в нуль при Pi= ... =Рп= у= ц = 0. Если, далее, хотя бы
один из определителей п — k-ro порядка, содержащийся в мат-
рице (2.20), отличен от нуля (этот определитель непременно
должен включать столбец с производными по у), то, как пока-
зывает исследование [275], периодические решения периода
Т + у, обращающиеся при ц = 0 в Т-периодические решения
(2.14) порождающей системы (2.13), могут отвечать, вообще го-
воря, лишь избранным системам значений параметров он, .. .
..., «/<, а именно значениям, удовлетворяющим некоторой си-
стеме уравнений
РДа,, ..аА) = 0	(2.23)
Как и в случае неавтономной системы, определенному решению
а,=(Хр ..., ак = а"к уравнений (2.23) действительно отвечает
единственное периодическое решение исходной системы диффе-
ренциальных уравнений, аналитическое относительно ц и обра-
щающееся при ц = 0 в порождающее, если рассматриваемое
решение уравнений (2.23) является изолированным, то есть если
отличен от нуля определитель (2.11).
§ 3.	Об устойчивости периодических решений
1.	Определение устойчивости по А. М. Ляпунову. Для того
чтобы определенному решению дифференциальных уравнений,
описывающих поведение рассматриваемой системы, отвечало
физически реализуемое движение, это решение должно быть
устойчивым. При исследовании устойчивости решений в настоя-
щее время наиболее широко используются методы, развитые
в классическом сочинении А. М. Ляпунова «Общая задача об
устойчивости движения» [261].
В настоящем параграфе будут кратко изложены некоторые
основные положения теории устойчивости по А. М. Ляпунову.
Затем мы остановимся на особенностях исследования устойчи-
вости периодических решений вообще и на особенностях изуче-
ния устойчивости решений в задачах о синхронизации в част-
ности*). Как правило, при этом доказательства формулируе-
мых положений воспроизводиться не будут.
*) Подробному изложению и развитию теории устойчивости движения
посвящен ряд монографий [420, 271, 194, 229, 35, 38, 247]. Обстоятельный
обзор исследований в этой области содержится в статьях В. В. Румянцева
[366а] и И. П. Еругипа [186]. В пп. 1—5 настоящего параграфа мы придер-
живались в основном стиля изложения ряда главных фактов теории, приня-
того в монографии И. Г. Малкина [271] и отчасти — Н. Г. Четаева [420].
116
МЕТОДЫ ПУАНКАРЕ И ЛЯПУНОВА
[ГЛ 111
Пусть движение рассматриваемой системы описывается диф-
ференциальными уравнениями
xs = Xs(Xi, • • •> xb t) (s ~ 1, ..., /),	(3.1)
где правые части не обязательно периодичны относительно t
и вообще не обязательно зависят от t. Предполагается, если не
делаются иные допущения, что эти правые части определены
при всех значениях . . ., Xi, лежащих в некоторой области G,
и при всех значениях t, лежащих в интервале О/ < оо. Счи-
тается также, что функции Xs в указанной области изменения
переменных допускают непрерывные и ограниченные производ-
ные первого порядка по переменным х\, . . . , Xi.
Рассмотрим определенное частное решение системы (3.1)
xs = x;(0	(s=l, ...,/).	(3.2)
Для суждения об устойчивости решения (3.2) рассмотрим
какое-нибудь другое решение системы, удовлетворяющее «воз-
мущенным» начальным условиям
Xs (Q = Xs (Q + Уз (Q = Х’о + У SO’	(3 -3)
и изучим поведение во времени «возмущений», т. о. разностей
^(0 = *Л)-Ш	(3.4)
Движение x*s(f) будет называть невозмущенным, а всевозмож-
ные движения xs(t) —возмущенными.
Следуя А. М. Ляпунову, будем говорить, что исследуемое
движение устойчиво, если возмущения ys(t) остаются малыми
при всех t > to, если только они были достаточно малыми в на-
чальный момент времени to > 0.
Иными словами, невозмущенное движение называется устой-
чивым по Ляпунову, если для всякого положительного числа е,
как бы мало оно пи было, можно найти другое положительное
число б, такое, что для всех возмущенных движений, для кото-
рых в начальный момент времени to выполняются неравенства
’ 1>’	(З-5)
будут при всех t > to выполняться неравенства
К(0-<(0|<е (S = 1, ...,/).	(3.6)
Решения, не удовлетворяющие сформулированному условию
устойчивости, называются неустойчивыми.
ОБ УСТОЙЧИВОСТИ ПЕРИОДИЧЕСКИХ РЕШЕНИЙ
117
§ SJ
Устойчивые невозмущенные движения, для которых при до-
статочно малом 6 выполняются не только условия (3.6), но и
более сильные соотношения
1нпхД/) = х;(0,	(3.7)
оо
называются асимптотически устойчивыми.
Устойчивость по А. М. Ляпунову в указанном выше смысле
часто называют устойчивостью в малом, подчеркивая от обстоя-
тельство, что такое понятие об устойчивости связано лишь
с поведением движений системы, близких к рассматриваемому
невозмущенному. Зная, что движение устойчиво (или неустой-
чиво) по А. М. Ляпунову, вообще говоря, еще ничего нельзя
сказать о движениях, удаленных от рассматриваемого на «ко-
нечное» расстояние. Более подробно этот вопрос обсуждается
в § 4 главы IV.
Как правило, при исследовании устойчивости в уравнениях
движения (3.1) переходят от переменных xs к переменным ys.
В результате получаются так называемые уравнения возмущен-
ного движения
Уя Xs(xi + yi.....xi + У о О	•••> Х1Л ty
(«=1.....О,
которые можно представить также в форме
ys = Mi + ••• + PsiXi + Ys(yi, •••> l/i,	(3.8)
(з=1......О,
где
дХ.(х",..............................х,*,	/)
P4/=Ps/(0 =-------—5------- >	(3.9)
dxj
а функции У8 удовлетворяют условиям
lim	j’yj = ° ПРИ 1^1 1+ +lyzH>6.
Уравнения (3.8) имеют тривиальное решение гд = . . . = yi =
= 0, соответствующее невозмущенному движению. В перемен-
ных уъ . . . , yi условие устойчивости выражается в виде требо-
вания, чтобы для всякого положительного е можно было вы-
брать такое положительное число б, что неравенства |ys(/) |<
< е будут выполняться при всех t > to для любого решения,
удовлетворяющего условиям | ys (t0) | -С б. При выполнении бо-
лее сильных соотношений lim ys(/) = 0 невозмущенное движе-
I -> ОО
ние асимптотически устойчиво.
118
МЕТОДЫ ПУАНКАРЕ И ЛЯПУНОВА
[ГЛ. ш
2.	Уравнения в вариациях, их значения и свойства. Если в
уравнениях возмущенного движения (3.8) отбросить члены выс-
ших порядков, то получится система линейных однородных
уравнений с переменными коэффициентами
= pslZi + ... + pstzt (s=l, ...,/),	(3.10)
которые, следуя Пуанкаре, называют уравнениями в вариациях
для системы (3.1) и решения (3.2). Уравнения в вариациях иг-
рают важную роль при исследовании устойчивости. Дело в
том, что в большинстве случаев, кроме особых, так называемых
«критических» случаев, для суждения об устойчивости или не-
устойчивости достаточно вместо полной системы уравнений воз-
мущенного движения (3.8) рассматривать лишь ее первое при-
ближение, т. е. уравнения в вариациях (3.10).
Одно из важнейших свойств уравнений в вариациях, уста-
новленное А. Пуанкаре, состоит в том, что если исходная си-
стема (3.1) допускает семейство решений
xs = xs(t, а,, .. ., а*),	(3.11)
зависящее от k произвольных параметров он, ..., ай, и невоз-
мущенное движение х* = х*(/) соответствует некоторым фикси-
рованным значениям этих параметров а^а*, ..., ak = а*, то
уравнения в вариациях (3.10) допускают k решений
= <s=1> •••>/=1’ •••’ <ЗЛ2>
где производные вычисляются для невозмущепного движения.
Справедливость этого утверждения выясняется путем подста-
новки (3.11) в уравнения (3.1), дифференцирования получен-
ных тождеств по aj и перехода к невозмущенному движению,
то есть путем замены а, на а*.
Отметим и другое важное свойство уравнений в вариациях:
если исходная система (3.1) допускает первый интеграл
F(X], ..., Xi, t) = const,
то система в вариациях (3.10) допускает первый интеграл вида
Н = (z{+ ... + (zt = const,
(dr, /	\dxt j ‘	’
где скобки указывают, что производные вычислены для невоз-
мущенного движения.
Справедливость этого утверждения легко обнаруживается
п^тем составления полных производных функций F и Н по t
при учете уравнений (3.1) и (3.10).
§ 3]
ОБ УСТОЙЧИВОСТИ ПЕРИОДИЧЕСКИХ РЕШЕНИЙ
119
3.	Случай периодических движений. Характеристическое
уравнение и аналитический вид решений линейных однородных
дифференциальных уравнений с периодическими коэффициен-
тами. Если правые части уравнений движения (2.1) периодичны
по t с некоторым периодом Т и если исследуется устойчивость
Т-периодического решения этих уравнений, то есть функции
х* (/) являются также периодическими, то правые части урав-
нений возмущенного движения, а также и уравнений в вариа-
циях, окажутся периодическими относительно t с тем же перио-
дом. Поэтому задача об устойчивости периодических решений
приводится прежде всего к изучению системы линейных урав-
нений с периодическими коэффициентами. При исследовании
поведения решений такой системы особую роль играет так на-
зываемое характеристическое уравнение. К этому уравнению
можно прийти следующим образом.
Пусть zsj(t)—фундаментальная система решений уравнений
(3.10), удовлетворяющая начальным условиям
zst (0) = 6s/,
(3.13)
где 6SJ- — символ Кронекера*). Тогда характеристическим урав-
нением системы будет следующее алгебраическое уравнение /-й
степени:
ZnCO-p z]2(T)	...zu(T)
Z21 (Г)	z22 (Г) — р ... z2t (Т)
= 0.
(3.14)
2ц (Г) zt2 (Т)	... zlL (Т) - р
Одно из основных свойств характеристического уравнения
состоит в независимости его корней р от выбранной фундамен-
тальной системы решений. Кроме того, характеристическое урав-
нение не изменяется, если систему (3.10) подвергнуть неособен-
ному линейному преобразованию с Т-периодическими коэффи-
циентами.
Система уравнений (3.10) с периодическими коэффициентами
не интегрируется в замкнутой форме. Можно, однако, указать
общий аналитический вид ее решений, вполне аналогичный виду
решений линейных уравнений с постоянными коэффициентами.
Введем в рассмотрение так называемые характеристические
показатели системы Кч, связанные с корнями характеристиче-
ского уравнения pf; следующими соотношениями:
^ = ^1пР?’	=	(3-15)
*) Здесь и ниже в аналогичных случаях первый индекс указывает на
номер функции в решении, а второй — на номер решения.
Под фундаментальной системой понимают любую систему I линейно не-
зависимых решений.
120
МЕТОДЫ ПУАНКАРЕ И ЛЯПУНОВА
[ГЛ. Ill
Тогда оказывается, что для каждого корня рч характеристиче-
ского уравнения можно подобрать частное решение уравнений
(3.10) вида
=	(3-16)
где qps(/) — некоторые периодические функции периода Т; в силу
(3.15) для этого решения справедливо равенство
гЛ/-1Т) = р9гЛ0 = ЛггД0-	(3.17)
При этом если корень рд является простым, то для него суще-
ствует только одно (с точностью до постоянного множителя)
решение вида (3.16). Если все корни характеристического урав-
нения простые, то для системы (3.10) будет существовать I раз-
личных частных решений вида (3.16). Эти решения, как не-
трудно видеть, независимы и образуют, следовательно, фунда-
ментальную систему.
Пусть теперь корень р,; является кратным и кратность его
равна rq. Будем различать два случая в зависимости от ранга
характеристического определителя (3.14) при р = pQ. Предполо-
жим сначала, что этот ранг равен I—1, так что корень р? не
обращает в нуль по крайней мере один из миноров I—l-ro
порядка характеристического определителя. В этом случае для
корня рд можно построить частное решение вида
zs = zsl = A>s(0>	(3.18)
где Ps(t) —полиномы относительно t с периодическими коэффи-
циентами периода Т. Степени полиномов Ps(t) не превосходят
rq—1, и степень хотя бы одного из них равна rq—1.
Кроме решения (3.18), для корня р7 существует еще rq—1
независимых частных решений уравнении (3.10), которые вместе
с решением (3.18) могут быть записаны в виде
zsi =	(S=l, ..., k~, i=l, .... rq). (3.19)
Здесь через DjDt обозначен оператор такого условного диффе-
ренцирования по t полинома Р(/) с периодическими коэффи-
циентами, при котором эти коэффициенты считаются постоян-
ными. Так, если
Р(0 = /тф1(0 + ^-,ф-(0+ ••• -I- /фт(0 + фт+1> (0
где <рДО —периодические функции t, то
(0 + (m - 1) /т-2ф2 (0 + ... + 2/фт_! (0 +	(/).
Будем говорить, что решения (3.19) образуют одну группу
и что в рассматриваемом случае корню р9 отвечает одна группа
решений.
§ 3J	ОБ УСТОЙЧИВОСТИ ПЕРИОДИЧЕСКИХ РЕШЕНИЙ	121
Допустим теперь, что кратный кореньр9 обращает в нуль все
миноры характеристического определителя до порядка I — р + 1
включительно, не обращая в нуль хотя бы один из миноров
I — р-го порядка, так что ранг характеристического определи-
теля (3.14) при р = р? равен I — р. В этом случае рассматривае-
мому корню будет, как и ранее, отвечать rq решений уравнений
(3.10), но эти решения разбиваются па р самостоятельных
групп. Если мы обозначим через число решений в /-й груп-
пе (заметим, что п(^ + ... +и^ = г q}, то решения этой группы
имеют вид
п(«-1)р(Р
+w = Л' =1.......................+)	<3-20)
Здесь Ps' — полиномы относительно I с Г-периодическими ко-
эффициентами, степени которых не превосходят — 1, причем
степень хотя бы одного из них равна nj^—l. Можно поэтому
написать:
л<<7)-2
+	  • + «. о,2')
где ф$ — периодические функции t периода Т, причем для вся-
кого / хотя бы одна из функций ф</> не обращается тождествен-
но в нуль.
Число р, естественно, не превосходит кратности rq рассмат-
риваемого корня, но может этого предела достигать. В послед-
нем случае каждая группа будет состоять из одного решения,
которое при этом имеет вид (3.16), то есть, как и в случае про-
стых корней, не содержит полиномиального множителя.
Отметим, что справедливо также утверждение, обратное при-
веденному выше [271]: если для системы уравнений (3.10) с пе-
риодическими коэффициентами удалось найти rq частных ре-
шений, разбивающихся на р групп вида (3.20), то величина р,;
является корнем характеристического уравнения (3.14), крат-
ность которого не менее rq, причем этот корень обращает в нуль
все миноры характеристического определителя до порядка по
крайней мере I — р + 1.
Итак, ранг характеристического определителя (3.14) при
р = р9 в общих чертах определяет вид решений системы урав-
нений (3.10) с периодическими коэффициентами. При заданном
ранге I — р неопределенными остаются лишь числа решений
в каждой группе (то есть числа n^j.
Полная характеристика структуры решений системы (3.10),
в том числе и величины п^', определяется так называемыми
122
МЕТОДЫ ПУАНКАРЕ И ЛЯПУНОВА
[ГЛ. III
элементарными делителями характеристической матрицы (то
есть матрицы, образованной из элементов характеристического
определителя).
Известно (см., например, [400, 420]), что путем элементарных
преобразований характеристической матрицы *) последняя все-
гда может быть приведена к форме
Е{ 0... 0
0	^2 • • • ° (	(3 22)
0	0 ... Et
где
„(1)	n,v>
£/(р) = (р-р.) ' ...(р-р/',	(3.23)
причем pi, ..., pv — попарно различные корни характеристиче-
ского уравнения (3.14), а — целые положительные числа
или нули, удовлетворяющие условию
(/ = 2, ...,/)•	(3.24)
Таким образом, каждый полином Е, является делителем лю-
бого полинома Е3-, для которого / > I. Иными словами, поли-
номы Е3 имеют вид
£] (р) = 61;
£2 (р) = 6j62,	(3.25)
Ez(p) = 6IS2 ... 6Z,
где каждое из б., есть либо единица, либо полином от р с коэф-
фициентом при старшем члене, равным единице. Очевидно, что
сумма
п\и +	+ ... Н-п*1’= г<”
есть не что иное, как кратность корня р = pi уравнения (3.14),
и вообще
+ ... 4- пр =	(3.26)
есть кратность корня р7.
*) Под элементарными преобразованиями матрицы понимаются переста-
новки двух строк или столбцов, умножение всех элементов строки или столб-
ца на отличный от нуля постоянный множитель, сложение элементов неко-
торой строки (столбца), умноженных на один и тот же полином от р, с со-
ответствующими элементами другой строки (столбца). Если все определители
i-ro порядка матрицы имеют множителем полином ср(р), то этим множителем
обладают также все определители t-го порядка элементарно преобразованных
матриц.
§ 3]	ОБ УСТОЙЧИВОСТИ ПЕРИОДИЧЕСКИХ РЕШЕНИЙ	123
Входящие в функции ЕДр) множители
„(<?)
(р-р//	(3.27)
с отличными от нуля показателями и называются элементар-
ными делителями характеристической матрицы, отвечающими
корню pq.
Один из основных фактов теории состоит в том [420], что
число показателей элементарных делителей (3.27) как раз
равно числу р групп решений (3.20), отвечающих корню р = pq,
а сами эти показатели равны числу решений в /-й группе.
Нетрудно усмотреть соответствие между этим утверждением
и сказанным выше относительно зависимости характера решений
уравнений (3.10) от ранга определителя (3.14) при р = р9. Дей-
ствительно, если, например, ранг матрицы (3.22) при р = р,?
равен /—1, то есть корень р(; не обращает в нуль по крайней
мере один из миноров I—1-го порядка этой матрицы, то в силу
(3.23) —(3.25)
= nf - ... = п/ = 0,	= rq,
и мы имеем всего одну группу решений (3.20) с числом реше-
ний в ней, равным кратности г,, корня pq. Далее, если ранг мат-
рицы (3.22) при р = р, равен l — rq, то есть корень р, обращает
в нуль все миноры этой матрицы до порядка I — rq + 1 вклю-
чительно, не обращая в нуль по крайней мере один из миноров
порядка I — rq, то, в соответствии с (3.23) — (3.25), должно быть
= nW1 =• ... =	= О,
. .	. .	’	.	(3.28)
n)\+I = «^+2=---=«|” = l.
Таким образом, в данном случае, как и говорилось выше,
число групп решений равно кратности rq корня р = р?, и все эти
решения не содержат полиномиального множителя. Элементар-
ные делители (3.27), отвечающие этому важному для теории
синхронизации частному случаю, согласно равенствам (3.28)
являются линейными, или, как иногда говорят, простыми.
Из равенств (3.16) и (3.17) следует, что если характери-
стическое уравнение имеет корень pq, равный единице, то си-
стема в вариациях (3.10) непременно допускает периодическое
решение периода Т. Справедливо, очевидно, и обратное утвер-
ждение: при наличии Г-периодического решения уравнений в
вариациях характеристическое уравнение непременно имеет ко-
рень рд = 1.
Как было установлено А. М. Ляпуновым, всякую систему
линейных уравнений с периодическими коэффициентами в прин-
ципе можно преобразовать посредством неособенной линейной
124
МЕТОДЫ ПУАНКАРЕ И ЛЯПУНОВА
[ГЛ. HI
подстановки с периодическими же коэффициентами в систему
с постоянными коэффициентами*). Этой последней системе все-
гда можно придать так называемую каноническую или нор-
мальную форму, вид которой определяется показателями эле-
ментарных делителей характеристической матрицы. Для того
чтобы записать указанные канонические уравнения по возмож-
ности просто, изменим несколько обозначения корней характе-
ристического уравнения р7 и чисел п'л\ перенумеровав их
согласно следующей таблице:
Pl > Р2, • • • > Pm
X], %2> • • • > ^m
«I. П2, tlm
Здесь каждый корень р характеристического уравнения и отве-
чающий ему показатель Л выписаны столько раз, сколько групп
решений им соответствует. Среди чисел р;- (и Л,), таким обра-
зом, могут встречаться и равные, но каждому числу отвечает
только одна группа решений; число решений в этой группе обо-
значается через tij.
Сумма всех чисел /г,, очевидно, равна порядку системы:
+ п2 + ... + /l„i = I.
В указанных обозначениях каждой /-й группе с числом ре-
шений tij соответствует следующая группа дифференциальных
уравнений с постоянными коэффициентами в канонической
записи:
= ksy^, )
у(Ф = ЪлЛр — y'f, I ,. ,	,
В частном случае, когда все элементарные делители линей-
ны, число групп решений равно кратностям корней, все числа
tij равны единице и т = I. При этом- каноническая запись си-
стемы существенно упрощается:
= (/=1,...,/).
4.	Сопряженные системы уравнений и свойства их решений.
В теории линейных дифференциальных уравнений с переменными
*) Естественно, однако, что трудности, связанные с фактическим нахо-
ждением такого преобразования, вполне эквивалентны тем трудностям, кото-
рые возникают при решении системы уравнений с периодическими коэффи-
циентами.
§ 3]	ОБ УСТОЙЧИВОСТИ ПЕРИОДИЧЕСКИХ РЕШЕНИЙ	125
коэффициентами заметную роль играет система
К + Р^* + ••• +Р/Л = °	(«=!>•••-	(3-29)
называемая системой, сопряженной с (3.10).
А. М. Ляпуновым показано, что если pQ есть корень харак-
теристического уравнения некоторой системы линейных уравне-
ний с периодическими коэффициентами, то величина 1/р, яв-
ляется корнем характеристического уравнения сопряженной
системы. При этом кратности обоих корней, число групп реше-
ний, им соответствующих, числа решений в соответствующих
группах и их аналитический вид совпадают.
Остановимся на соотношениях, существующих между реше-
ниями сопряженных систем. Пусть us(t) — какое-либо частное
решение системы
«s = Psi«i+ ••• + psiUi + fs(t) (s=l, ..., /), (3.30)
отличающейся от системы (3.10) лишь наличием в правых ча-
стях функций fs(t). Тогда, если z’s(t) есть решение сопряженной
системы (3.29), то в силу уравнений (3.29) и (3.30) будем иметь
i	i
S-l	S-1
ИЛИ
I	I
(з.з1)
3 = 1	S“1
При fs(/) = 0 предыдущее равенство приводит к следующему
соотношению между решениями сопряженных систем:
i
^zs(f)z*(/) = const.	(3.32)
3=1
Здесь через za(t) обозначено частное решение системы (3.10),
совпадающей при fs(t) = 0 с системой (3.30).
Пусть zsi(/), ..., zSh(t)—некоторая система, состоящая из
k периодических решений уравнений (3.10) с периодическими
коэффициентами, a z’si (/), ..., z*sk(t)— система из k периодиче-
ских решений сопряженной системы. Тогда, как нетрудно убе-
диться (см. [275], стр. 206—207), в случае линейных элементар-
ных делителей, отвечающих кратным корням характеристиче-
ского уравнения, постоянные в равенствах типа (3.32) всегда.
126
МЕТОДЫ ПУАНКАРЕ И ЛЯПУНОВА
[ГЛ. HI
можно выбрать так, чтобы выполнялись соотношения
(0(3.33)
5-1	1 *’ а~Р
(а, р = 1, . .., k).
Через полную совокупность независимых периодических ре-
шений (J = 1, •••, k) сопряженной системы (3.29) удобно
выражаются необходимые и достаточные условия существова-
ния Т-периодических решений неоднородной системы уравнений
вида (3.30) с Т-периодическими коэффициентами. Эти условия,
которые неоднократно понадобятся в дальнейшем, имеют вид
[275]
т I
= Q (/=1, ..., k).
0 5-1
Сказанное выше о случае, когда уравнения в вариациях
представляют собой систему уравнений с периодическими коэф-
фициентами, относится, разумеется, и к частному случаю урав-
нений с постоянными коэффициентами. Периодические функции
<ps(Z) и коэффициенты <р^(/) полиномов Р^р в выражениях
(3.16), (3.18) — (3.21) заменяются при этом постоянными. Харак-
теристические же показатели 7.q = у- 1п р? оказываются совпа-
дающими с корнями обычного характеристического уравнения
системы линейных уравнений с постоянными коэффициентами*).
5.	Теорема А. М. Ляпунова об устойчивости по первому
приближению. Как уже отмечалось в п. 2 настоящего пара-
графа, значение уравнений в вариациях (3.10) определяется
тем, что суждение об устойчивости или неустойчивости периоди-
ческих движений в малом, как правило, может быть получено
на основе рассмотрения этих уравнений, независимо от вида
нелинейных членов в уравнениях возмущенного движения (3.8).
А именно имеет место следующая теорема, принадлежащая
А. М. Ляпунову.
Теорема. Если все характеристические показатели системы
уравнений в вариациях, отвечающей рассматриваемому невоз-
мущенному периодическому движению, имеют отрицательные
вещественные части, то это движение асимптотически устойчиво.
*) Заметим, что выше под характеристическим уравнением мы понимали
уравнение (3.14), из которого определялись не характеристические показа-
,	ЩТ _
тели А.,, а величины рз=е * .1акая часто допускаемая непоследовательность
в терминологии не может вызвать серьезных недоразумений, ибо всякий раз
из текста ясно, о каком уравнении и о каких величинах (р, или А,„) идет
речь.
§ 3J	ОБ УСТОЙЧИВОСТИ ПЕРИОДИЧЕСКИХ РЕШЕНИЙ	127
Если хотя бы один из указанных характеристических показате-
лей имеет положительную вещественную часть, то невозмущен-
ное движение неустойчиво. Если некоторые характеристические
показатели имеют вещественные части, равные нулю, но ни один
из них не имеет положительной вещественной части, то для
решения задачи устойчивости необходимо рассмотреть нелиней-
ные члены в уравнениях возмущенного движения.
Поскольку корни pi, . . . , pi характеристического уравнения
системы связаны с характеристическими показателями А,ь . . .
соотношениями (3.15), то предыдущую теорему можно сфор-
мулировать также следующим образом.
Если все корни характеристического уравнения системы в
вариациях исследуемого периодического движения имеют мо-
дули, меньшие единицы, то это движение асимптотически устой-
чиво. Если хотя бы один из этих корней имеет модуль, больший
единицы, то исследуемое периодическое движение неустойчиво.
Если некоторые из указанных корней имеют модули, равные
единице, а остальные — модули, меньшие единицы, то вопрос
об устойчивости исследуемого периодического движения ре-
шается нелинейными членами в уравнениях возмущенного дви-
жения.
Таким образом, изучение только уравнений в вариациях при
исследовании устойчивости периодического движения оказы-
вается недостаточным лишь в случаях, когда при отсутствии
характеристических показателей с положительными веществен-
ными частями имеются нулевые или чисто мнимые показатели.
Эти случаи называют критическими; их изучению в настоящее
время посвящена обширная литература (см., например,
[194, 419]).
Отметим, что поскольку положения равновесия системы (3.1)
Xi = х10,	. .., Xi = Хю
(хю, Хю — постоянные) могут рассматриваться как перио-
дические движения произвольного периода, то приведенная тео-
рема А. М.. Ляпунова справедлива и для этого более простого
случая.
6.	Теорема А. А. Андронова и А. А. Витта об устойчивости
автономных систем и ее обобщения. При изучении периодиче-
ских решений автономных систем как раз приходится сталки-
ваться со случаем, когда один из корней характеристического
уравнения системы в вариациях всегда равен единице и, тем
самым, один из характеристических показателей всегда имеет
вещественную часть, равную пулю. Это связано с тем обстоя-
тельством, что если автономная система
xs = As(x!, . xt) (s = 1......./)	(3.34)
128
МЕТОДЫ ПУАНКАРЕ И ЛЯПУНОВА
[ГЛ. HI
допускает некоторое периодическое решение xs = x*(Z), то она
допускает также и семейство периодических решений
х = х’(/+ а), зависящее от произвольной постоянной а. Отсюда
в силу свойства уравнений в вариациях, отмеченного в п. 2 на-
стоящего параграфа, следует, что система уравнений в вариа-
циях для рассматриваемого решения также допускает периоди-
ческое решение
дх',. (I + а)
с,, = -------•
s да
Поэтому, согласно сказанному в конце п. 3, соответствующее
характеристическое уравнение непременно должно иметь ко-
рень, равный единице; таким образом, налицо критический
случай.
Тем не менее А. А. Андроновым и А. А. Виттом была
доказана теорема [16], согласно которой для изучения воп-
роса об устойчивости периодических решений автономных си-
стем нет надобности в специальном рассмотрении нелинейных
членов в уравнениях возмущенного движения, если только ука-
занный корень р = 1 характеристического уравнения является
простым, а все прочие корни имеют модули, меньшие единицы.
Периодическое движение при этом является устойчивым, хотя
и не асимптотически*).
Существенное обобщение упомянутой теоремы А. А. Андро-
нова и А. А. Витта было дано Н. Ф. Строковым [330] и
И. Г. Малкиным [266], показавшими, что если система (не обя-
зательно автономная)
xs = XS(X], . .., xh t) (s = 1, . . ., I),	(3.35)
где Xs— периодическая функция t с периодом T, допускает се-
мейство периодических решений того же периода
xs = <ps(Z, а,, .. ., am) ($ = 1.../),	(3.36)
зависящее от некоторого числа т^.1 произвольных постоянных
aj, то при наличии у характеристического уравнения системы
в вариациях для каких-либо из решений семейства (3.36) I — т
корней, по модулю меньших единицы, рассматриваемое перио-
дическое решение устойчиво.
В цитированных исследованиях предполагалось, что если
функции Xs не зависят явно от t, то период решения не зависит
от постоянных ар Т. Н. Трибелевой, однако, было показано
[395], что последнее ограничение не является существенным. Со-
*) Здесь имеет место, однако, так называемая орбитальная асимптоти-
ческая устойчивость [247, 255].
§ 3]	ОБ УСТОЙЧИВОСТИ ПЕРИОДИЧЕСКИХ РЕШЕНИЙ	[29
ответствующее наиболее общее утверждение мы и условимся
называть расширенной теоремой А. А. Андронова и А. А. Витта.
7.	Об исследовании устойчивости периодических решений,
найденных методом малого параметра. Поскольку уравнения
типа (3.10) с периодическими коэффициентами не интегрируют-
ся в замкнутой форме, то реальное построение характеристиче-
ского уравнения (3.14) в общем случае наталкивается на су-
щественные технические трудности. В задачах о синхронизации
дело, однако, часто упрощается в связи с тем, что исходные
дифференциальные уравнения имеют вид уравнений (2.1):
xs = Xs(xb .... xt, t) + ^Fs{xb .... xh t, p) (3.37)
(s=l, .... 0,
то есть содержат малый параметр р^>0. Тот же параметр, есте-
ственно, содержат и исследуемые периодические решения.
Вследствие этого коэффициенты pSj уравнений в вариациях
(3.10) будут также зависеть от параметра р. Если исходные
уравнения движения и рассматриваемое периодическое реше-
ние являются аналитическими функциями р, то и коэффициенты
pSj будут аналитическими функциями р.
Сделаем более общее предположение, что коэффициенты
зависят от m параметров pi, . . ., pm, относительно которых они
аналитичны в области, определяемой неравенствами
|рг|<Л4г (/=1, ..., ш),	(3.38)
где Mi — некоторые положительные числа. Предполагается при
этом, что период Т от указанных параметров не зависит.
Тогда, в силу известных теорем теории дифференциальных
уравнений, любое решение ys = ys(t, рь ..., pm) уравнений
(3.10), начальные значения для которого не зависят от пара-
метров, будет также аналитическим относительно р,, ..., рт
в той же области (3.38). В частности, аналитическими относи-
тельно р, будут решения zSj, фигурирующие в форме (3.14) ха-
рактеристического уравнения. Это приводит к следующей тео-
реме, принадлежащей А. М. Ляпунову.
Теорема. Если коэффициенты psj системы (3.10) являются
аналитическими функциями параметров рь ..., рт в области
(3.38), то коэффициенты характеристического уравнения (3.14)
будут аналитическими функциями pi, ..., рт в той же области.
Существенно, что область аналитичности коэффициентов ха-
рактеристического уравнения совпадает с областью аналитич-
ности коэффициентов исследуемых дифференциальных уравне-
ний. В частности, если коэффициенты изучаемых уравнений
являются целыми функциями параметров, то и коэффициенты
характеристического уравнения будут также целыми функциями
параметров.
5 И И. Блехман
130
МЕТОДЫ ПУАНКАРЕ И ЛЯПУНОВА
(ГЛ. III
Сформулированную теорему можно использовать для при-
ближенного вычисления коэффициентов характеристического
уравнения. Допустим с этой целью, что коэффициенты системы
(3.10) зависят только от одного параметра ц, так что можно
написать:
Ps/ (t) = Р<$ (0 +	(/) + «> (0 + ...,	(3.39)
где	непрерывные периодические функции периода Т и
ряды сходятся при | р, | М.
Рассмотрим фундаментальную систему решений zsj(t, ц)
уравнений (3.10), определяемую начальными условиями
f 1, «= /,
*3/(0. H) = 6S/=4O( S74>	(3.40)
В соответствии с теоремой А. М. Ляпунова можно написать:
zsl (/, и) = 4°/ (0 + р4У (/)+•••>	(3.41)
где ряды при всех значениях t сходятся в области | ц | М. Под-
ставив ряды (3.41) в уравнения (3.10) и начальные условия
(3.40) и приравняв коэффициенты при одинаковых степенях ц
в обеих частях получившихся равенств, приходим к следующим
системам дифференциальных уравнений и начальных условий
для определения функций 4°/(0> 4/(^’ • • ••
^ = р№] + •••	4?(Q) = V
4? р(0)2(П + .. . +	+ 2 р^.,	(3.42)
41? (о) = о,
I q — 1
47 = 4? 4? + ... + р^ + 2 р2 р%~^,
4‘7/)(0) = °	(<7 = 2,3,...).
У всех этих систем неоднородных линейных уравнений оди-
наковая однородная часть
4 = р'0?21 + ••• +4°/4	(3.43)
которая представляет собой не что иное, как уравнения в ва-
риациях для порождающей системы уравнений и порождающего
решения (см. § 2 настоящей главы), ибо согласно (3.9), (3.37)
и (3-39)
§ 3J	ОБ УСТОЙЧИВОСТИ ПЕРИОДИЧЕСКИХ РЕШЕНИЙ	131
В систему (3.43) переходят уравнения в вариациях (3.10) при
М =0.
Предположим, что мы можем проинтегрировать систему
(3.43) в замкнутой форме. Такая ситуация имеет место, напри-
мер, в случае, когда коэффициенты постоянны (что бывает,
в частности, если исходная система (3.37) квазилинейна), а так-
же в случае, когда порождающая система полностью интегри-
руется, и поэтому, согласно теореме А. Пуанкаре (см. п. 2 на-
стоящего параграфа), можно сразу найти фундаментальную
систему решений системы (3.43), дифференцируя общий инте-
грал по входящим в него произвольным постоянным.
Указанная ситуация весьма благоприятна, ибо если изве-
стно общее решение системы (3.43), то не представляет прин-
ципиальных затруднений последовательно найти из системы
(3.42) все функции (/), начиная с q = 0.
Следовательно решения (3.41) могут быть вычислены с ка-
кой угодно степенью точности. Полагая в этих решениях t = Т,
получим элементы характеристического определителя (3.14).
Заметим, однако, что для выяснения характера корней характе-
ристического уравнения при достаточно малых значениях пара-
метра р, как правило, необходимо выполнить вычисление лишь
небольшого числа приближений. Действительно, исходное при-
ближение р<°> к корням р характеристического уравнения (3.14)
отвечает ц = 0, то есть уравнениям в вариациях (3.43), состав-
ленным для порождающей системы и порождающего решения.
Поэтому можно предполагать, что указанное приближение к
корням нам известно.
Предположим сначала, что модули всех корней р(°> меньше
единицы (все характеристические показатели имеют отри-
цательные вещественные части). Тогда, в силу непрерывности, эти
корни будут оставаться меньшими единицы также и при доста-
точно малых значениях параметра ц. Поэтому согласно теореме
А. М. Ляпунова, приведенной в п. 5 настоящего параграфа, рас-
сматриваемое движение будет устойчивым; надобности в вычис-
лении следующих приближений к корням характеристического
уравнения при данном подходе к задаче не возникает.
Не нужно вычислять дальнейшие приближения и в случае,
если модуль одного или нескольких корней р<°> больше единицы:
при этом изучаемое движение неустойчиво, по крайней мере при
достаточно малых значениях р.
Необходимость в нахождении последующих приближений
возникает лишь в случаях, когда среди корней р*0) имеются рав-
ные по модулю единице, а все прочие корни имеют модули,
меньшие единицы. Здесь характер корней р,-, даже при до-
статочно малых р, определяется следующим приближением
5*
132
МЕТОДЫ ПУАНКАРЕ И ЛЯПУНОВА
[ГЛ. Ш
к указанным корням. Естественно, что вычисление приближений
следует вести лишь до тех пор, пока характер корней р, при до-
статочно малых р не окажется выясненным. Обычно для этого
бывает достаточно вычислить одно или в крайнем случае два
приближения.
Отметим, что случаи, когда среди корней р)0’ имеются кор-
ни с модулями, равными единице, а модули всех прочих корней
меньше единицы, представляют, как выяснится ниже (см. п. 8
настоящего параграфа), основной интерес для задач о синхро-
низации. Соответствующие корни условимся называть крити-
ческими.
Следует заметить, что при аналитических относительно ц
(вблизи ц = 0) коэффициентах алгебраического уравнения
корни последнего далеко не всегда будут аналитическими функ-
циями ц. Единственность и аналитичность имеют место лишь
при условии, что при ц = 0 соответствующий корень уравне-
ния р<°) является простым. Если же корень р<°> алгебраического
уравнения при ц = 0 является m-кратным (т-^/), то это урав-
нение при достаточно малых ц будет иметь пг корней, обращаю-
щихся при ц = 0 в р<°>, и эти корни разлагаются в ряды по целым
положительным степеням величины ц1/г, где	Дока-
зательство сформулированного предложения, представляющего
собой не что иное, как обобщение теоремы о неявных функ-
циях, можно найти, например, в курсе [162], а также в работе
[418], в которой дается удобный способ построения решений
с помощью так называемого многоугольника Ньютона.
Заметим далее, что условия устойчивости |рД < 1, требую-
щие расположения всех корней уравнения (3.14) внутри единич-
ного круга в плоскости комплексной переменной р, могут быть
выражены в явной форме через коэффициенты этого уравнения
[475]. Соответствующие условия вполне аналогичны известным
условиям Гурвица. Можно воспользоваться также и непосред-
ственно условиями Гурвица, если предварительно перейти в
уравнении (3.14) к новой переменной г, связанной с р соотно-
шением
1 + Z	е
р — 1 _ 2 •	(3.45)
Такая подстановка преобразует круг единичного радиуса с цент-
ром в начале координат плоскости комплексной переменной р
в левую полуплоскость комплексной переменной z. Поэтому тре-
бование | pj [ < 1 эквивалентно неравенствам Re Zj < 0, выра-
жающимся условиями Гурвица.
Приведем еще одну форму записи характеристического
уравнения (3.14), иногда более удобную при исследовании
§ 3]
ОБ устойчивости периодических решений
133
устойчивости решений, найденных			методом Пуанкаре [268, 275]:	
	-эр,	-1-0 -^i- Р <эр2 ^+1-0	зр; Зфг	
	фЗ, <эр.	<эр2 1 р 34 г Зр2	зр4 ... -^Z- + 1 - 0 -ЭР/	р	= 0.	(3.46)
Здесь через Pj = Р>(ц) обозначены функции, определяемые из
уравнений (2.6) или (2.17) настоящей главы, а через
фь = ф8(Р1, ..., Р/, ц) или ф8 = ф8(Р/, -	0;, 6, ц) — правые ча-
сти указанных уравнений, выражающих условия периодичности
рассматриваемого решения.
Остановимся вкратце также на способе вычисления харак-
теристических показателей систем с малым параметром, пред-
ложенном Н. А. Артемьевым [23] и развитом С. Н. Шимановым
и И. Г. Малкиным [275].
Предположим, как и выше, что исходное приближение (ц = 0)
к характеристическим показателям — у- In р(® найдено. То-
гда, согласно сказанному выше, характеристические показатели
при р 0 можно искать в виде
Ч = Ч0) + а»-	(3.47)
где ад(ц)—непрерывные функции, обращающиеся в нуль при
ц = 0. Эти функции можно найти следующим образом.
Как было отмечено в п. 3 настоящего параграфа, если Zg
есть характеристический показатель системы уравнений в вари-
ациях (3.10), то эта система должна иметь по крайней мере
одно решение вида
Zs(f) =
где <ps(Z) — периодическая функция периода Т. Но тогда если
в указанных уравнениях произвести замену переменных
г5 = М>+а"(^Ч(0,	(3.48)
преобразованная система
+РзЛ-(Н0) + а<М («=!, •••,/), (3.49)
должна допускать Т-периодическое решение. Это условие и по-
зволяет определить величины aq = ад(ц); для систем, допускаю-
щих при ц = 0 интегрирование в замкнутой форме, доведение
134
МЕТОДЫ ПУАНКАРЕ И ЛЯПУНОВА
[ГЛ. Ш
вычислений до конца не представляет принципиальных затруд-
нений. Если, как обычно, решается вопрос об устойчивости дви-
жения при достаточно малых значениях параметра р, то, как
уже отмечалось, достаточно найти поправки а9(ц) только к
«критическим» характеристическим показателям Хд, то есть
к показателям, для которых ReA.(90> = 0.
Изложенные выше положения и методы используются в гла-
ве V настоящей книги для изучения устойчивости решений
системы уравнений, характерных для задач о синхронизации.
8. Особенности исследования устойчивости решений в зада-
чах о синхронизации динамических систем. Исследование устой-
чивости периодических решений в задачах о синхронизации
имеет ряд особенностей, которые и будут рассмотрены ниже.
Порождающая система, соответствующая уравнениям основ-
ного класса таких задач — задач о синхронизации объектов со
слабыми взаимными связями, имеет вид (см. уравнения (2.1)
и (2.2) главы II)
x’е. * * * * * * * * * * * * * s) =	(х^) (s = 1.k),
(3.50)
«0 = СГ(х''), ..., х<*>, «0, 0)
или, в переменных у^ и V, связанных с х<«) и и соотношениями
(1.2) главы II,
е. 0) (Т = со0.
Напомним, что здесь х^ и у'^ — rs-мерные векторы, а и0 и
v0 — векторы размерности у.
Таким образом, как уже отмечалось, каждое из первых k
уравнений (3.50) и (3.51) является независимым. Если уравне-
ния (3.50) допускают синхронные движения, то есть решения
вида
х^ (/) =	+ у*$ (m^W)]
(/= 1, . . ., rs- s= 1, . . ., k),	(3.52)
«ро (0 = Op [qpnp^t + vpo (mp®t)] (P = 1,  • •, v),
то, в силу автономности каждого объекта, они допускают также
решения
х/о (* + as)= O/s) {qfnfat + 7/s)/2/Mas + y(jSo (t + as)]}
(/=1.....rs; S = l, ..., k),	(3.53)
иро = «р(Ж «I. • • , aj (p = 1, . . ., v).
§ 3]	ОБ УСТОЙЧИВОСТИ ПЕРИОДИЧЕСКИХ РЕШЕНИЙ	135
получающиеся из (3.52) путем замены t на t 4- в выраже-
ниях для Хд>(0> где as — произвольные постоянные.
Отсюда следует, что уравнения (3.51) допускают семейство
периодических решений
(Т- О = У(10 1тТ (Т + ЮО] +	. ,,
{0.04/
бро(т, а,, . . ., ak),
зависящее от k произвольных параметров as. Поэтому, соглас-
но теореме А. Пуанкаре (см. п. 2 настоящего параграфа), урав-
нения в вариациях для порождающей системы (3.51) и решения
(3.54) допускают k периодических решений, получающихся пу-
тем дифференцирования (3.54) по каждому из параметров as.
Соответствующее характеристическое уравнение, то есть харак-
теристическое уравнение системы в вариациях для системы
в целом при ц = 0, имеет корень р(°) = 1, кратность которого не
менее k. Эта кратность была бы в точности равна k, если бы
все элементарные делители, отвечающие корню р(°> = 1, были
линейны и если бы к тому же уравнения в вариациях не имели
иных периодических решений периода Т, кроме указанных выше.
Таким образом, в задачах о синхронизации как раз имеет место
случай наличия критических корней у характеристического урав-
нения порождающей системы, взятого для порождающего реше-
ния. В этом случае для решения вопроса об устойчивости необ-
ходимо вычисление следующих приближений к корням харак-
теристического уравнения полной системы.
Нетрудно видеть, что вследствие независимости первых k
уравнений (3.51) характеристическое уравнение системы в ва-
риациях для этих уравнений распадается на k + 1 отдельных
уравнений, соответствующих каждому из k объектов и системе
связи. Но, очевидно, элементарные делители системы в целом
представляют собой совокупность элементарных делителей всех
подсистем. Поэтому элементарные делители всей системы, отве-
чающие корню р(°> — 1, будут линейными, если только линейны
элементарные делители, соответствующие отдельным объектам
и системе связи. Так будет, в частности, если корень р(°)= 1 для
характеристических уравнений каждого из объектов является
простым, а у характеристического уравнения системы связи либо
вовсе отсутствует, либо является простым, либо имеет линейные
элементарные делители.
Иными словами, нелинейность элементарных делителей ука-
занйых кратных корней в задачах о синхронизации порождается
не наличием многих объектов, а свойствами объектов и системы
связи. Случаи кратных корней с линейными элементарными
делителями у рассматриваемого характеристического уравне-
ния довольно часто встречаются в задачах о синхронизации
136
МЕТОДЫ ПУАНКАРЕ И ЛЯПУНОВА
(ГЛ. III
динамических объектов. Поэтому таким случаям в дальнейшем
уделяется значительное внимание.
Отметим, что наличие кратных корней у соответствующего
характеристического уравнения в задачах о синхронизации мо-
жет быть связано не только с автономностью объектов и сла-
бостью связей между ними, но и с наличием в системе несколь-
ких одинаковых или почти одинаковых объектов. По поводу
элементарных делителей кратных корней, порождаемых указан-
ными обстоятельствами, можно было бы, однако, повторить все
сказанное относительно делителей, отвечающих корню р<°) = 1:
и здесь нелинейность элементарных делителей порождается не
множественностью объектов, а свойствами этих объектов и
системы связи.
Общему исследованию вопроса о существовании и устойчи-
вости синхронных движений слабо связанных объектов посвя-
щена седьмая глава книги.
§ 4. Краткий обзор исследований
по развитию методов Пуанкаре и Ляпунова,
существенных для теории синхронизации
Отмеченные выше специфические особенности задач о синхро-
низации потребовали развития в определенных направлениях
математического аппарата методов Пуанкаре и Ляпунова. Со-
ответствующие исследования, результаты которых в значитель-
ной мере отражены в настоящей части книги, были выполнены
преимущественно в последние годы как безотносительно к тео-
рии синхронизации, так и под непосредственным влиянием за-
дач этой теории. Здесь мы приведем краткий обзор работ в дан-
ном направлении.
Монография И. Г. Малкина [268] была работой, в которой
начато систематическое рассмотрение отмеченного в § 2 общего
случая зависимости порождающего решения х“ от произ-
вольного числа k независимых параметров а,. До этого
изучались лишь случаи зависимости х° от одного или двух
параметров *).
Позднее вопрос о существовании периодических и почти пе-
риодических решений при наличии зависимости порождающего
решения от произвольного числа параметров aj подвергся даль-
нейшему рассмотрению. В частности, в работах И. Г. Малкина
[267, 269, 270, 272, 273], Ж. Хаага [462, 463], С. Н. Шиманова [429,
430, 433, 434], Г. А. Мермана [291], Э. Коддингтона и Н. Левин-
сона [450], Н. Г. Булгакова [107], И. М Волка [132—134], Р. Фора
*) Случай зависимости порождающего решения от одного параметра
рассмотрен в классическом сочинении А. Пуанкаре [472].
$ 4] ОБЗОР ИССЛЕДОВАНИЙ МЕТОДОВ ПУАНКАРЕ И ЛЯПУНОВА 137
[456], Ю. И. Неймарка [319], В. М. Волосова [136], Ю. И. Ней-
марка и Л. П. Шильникова [320], М. 3. Коловского [216, 217],
М. Розо [360а], М. Я. Кушуля [236], А. М. Родионова [357] полу-
чены развернутые выражения или указан конкретный способ
построения уравнений Ps(ai, ak) =0 для определения пара-
метров ось • • •, аь применительно к различным системам диф-
ференциальных уравнений. При этом Г. А. Мерманом изучен
особый случай, когда уравнения Ps(ai, ..., а/£) = 0 удовле-
творяются тождественно [291]. Особые случаи, когда оп-
ределитель матрицы (2.11) обращается в нуль, то есть когда
решение at =а‘, ..., аА = а* уравнений (2.10) или (2.23) яв-
ляется непростым для различных систем с одной и несколь-
кими степенями свободы, рассмотрены в цикле работ А. П. Про-
скурякова и его последователей — Г. В. Плотниковой и
Ю. М. Копнина. Результаты этих работ суммированы в статьях
[348—350, 224].
Изученная нами в работе [44] (1953 г.) задача о самосин-
хронизации вибраторов представила пример конкретной техни-
ческой задачи, для решения которой как раз оказалось необхо-
димым рассмотрение общего случая зависимости порождаю-
щего решения от k произвольных параметров и выполнение
исследования устойчивости при условии, что характеристическое
уравнение для порождающей системы и порождающего реше-
ния имеет /?-кратный корень, равный единице (с линейными
элементарными делителями). В цитированной работе для упо-
минавшейся частной задачи было показано, что исследование
устойчивости периодических решений системы уравнений при
достаточно малых р может быть сведено к вопросу о знаке ве-
щественных частей корней алгебраического уравнения k-n сте-
пени, получающегося приравниванием нулю характеристиче-
ского определителя матрицы (2.11), то есть к задаче Гурвица
для алгебраического уравнения, которое может быть легко со-
ставлено, если известны выражения для функций Ps.
В статье [47] (1955 г.) соответствующая теорема об устойчи-
вости была доказана нами для квазилинейных неавтономных
систем. Доказательство ряда аналогичных теорем для периоди-
ческих и почти периодических решений неавтономных нелиней-
ных систем более общего вида было дано в монографии
И. Г. Малкина [275], вышедшей в 1956 г.
В заметке [49] (1957 г.) соответствующий результат получен
нами для периодических решений квазилинейных автономных
систем.
Наконец, в работе [434] (1960 г.) аналогичная теорема дока-
зана С. Н. Шимановым для почти периодических колебаний
квазилинейных систем с запаздыванием.
138
МЕТОДЫ ПУАНКАРЕ И ЛЯПУНОВА
[ГЛ. III
Необходимо отметить также, что вопрос о вычислении ха-
рактеристических показателей системы линейных дифферен-
циальных уравнений с периодическими коэффициентами, близ-
кими к постоянным, при наличии критических корней рассмат-
ривался в работах С. Н. Шиманова [428] (1952 г.) и [431]
(1956 г.). В первой работе намечен путь вычисления характери-
стических показателей с помощью метода вспомогательных си-
стем. Во второй рассмотрен весьма общий случай критических
корней с нелинейными элементарными делителями*). При этом
использован метод, примененный ранее Н. А. Артемьевым [23]
при изучении менее общего случая, когда кратные показатели
отсутствуют. Та же задача, что и в работе [431], позднее рас-
сматривалась М. Я. Кушулем [235] (1958 г.).
Во всех четырех цитированных работах, однако, вопрос о
связи коэффициентов результативных алгебраических уравне-
ний для вычисления характеристических показателей с упомя-
нутыми выше функциями Ps не рассматривался.
В работе Дж. А. Ноэля [470] (1960 г.) некоторые результаты
наших статей [47, 49] получены путем несколько иных рассуж-
дений и дополнены рядом новых теорем.
Помимо упомянутых выше исследований, имеющих непо-
средственное отношение к рассматриваемым в настоящей книге
задачам, вопрос о выяснении знаков вещественных частей ха-
рактеристических показателей систем линейных дифференциаль-
ных уравнений, содержащих малый параметр, безотносительно
к методу Пуанкаре рассматривался в работах Н. Н. Боголюбова
(младшего) и Б. И. Садовникова [98], К- Г. Валеева [116],
Л. Л. Вознюка [131], Р. Гамбила [458, 459], Г. Бейли и Р. Гам-
била [444], Н. П. Еругина [184, 185], Сибуйя [477], Дж. Хейла
[403, 464], Л. Чезари [419], Н. Г. Четаева [420], И. 3. Штокало
[439], В. А. Якубовича [440] и других авторов. Краткий обзор
соответствующих результатов можно найти в монографиях
Л. Чезари [419] и Дж. Хейла [403].
*) В более подробном и дополненном виде результаты этой работы
опубликованы С. Н. Шимановым в статье [432] (1958 г.).
ГЛАВА IV
МЕТОДЫ ПУАНКАРЕ И ЛЯПУНОВА КАК СРЕДСТВА
ПОЛУЧЕНИЯ ПРАВДОПОДОБНЫХ РЕЗУЛЬТАТОВ
В ПРИКЛАДНОЙ ТЕОРИИ НЕЛИНЕЙНЫХ
КОЛЕБАНИЙ*)
§1.0 нестрогостях, допускаемых при практическом
применении методов Пуанкаре и Ляпунова.
Правдоподобные рассуждения и их ценность
при решении прикладных задач этими методами
В настоящей главе будут изложены некоторые точки зрения на приемы
использования методов Пуанкаре и Ляпунова при решении прикладных за-
дач. В дальнейшем мы будем систематически опираться на эти точки зрения
в процессе рассмотрения проблем синхронизации динамических систем.
Хорошо известно, что методы Пуанкаре и Ляпунова являются матема-
тически вполне строгими. Однако не всегда подчеркивается, что результаты,
получаемые с их помощью, используются, как правило, далеко не строго.
Так, например, обычно в прикладных исследованиях ограничиваются уста-
новлением факта существования решения при достаточно малых значениях
малого параметра, а факта устойчивости движения —еще и при достаточно
малых начальных отклонениях. Далее эти факты (как правило, без оговорок)
используются для суждения о существовании и устойчивости изучаемых
движений в реальных системах, в которых значения параметра и начальных
отклонений всегда конечны**).
Проще всего было бы забраковать такие приемы, не отвечающие требо-
ваниям формальной логики. Однако практика показывает, что они, позволяя
значительно упростить исследование, как правило, не приводят к ошибкам.
Между тем строго последовательное решение тех же задач сопряжено со
значительными трудностями, связанными с установлением областей сходимо-
сти рядов и с изучением поведения системы в большом. Не отрицая важности
таких исследований, мы попытаемся подчеркнуть полезность упомянутых
выше и некоторых других нестрогих приемов при решении прикладных задач,
показав, что эти приемы представляют собой типичные случаи так называе-
мых правдоподобных рассуждений.
*) Данная глава в основном воспроизводит содержание доклада автора,
прочитанного на совещании по проблемам нелинейных колебаний механиче-
ских систем (Ленинград, декабрь 1965 г.). В более широком плане — приме-
нительно к методам прикладной математики вообще — вопрос о правдопо-
добности и доказательности был затем обсужден в статье А. Д. Мышкиса,
Я. Г. Пановко и автора [82].
**) На эти обстоятельства обращали внимание А. А. Андропов и пред-
ставители его научной школы [32, 153].
140
МЕТОДЫ ПУАНКАРЕ И ЛЯПУНОВА
П л. iv
Под правдоподобным здесь можно понимать такое рассуждение (за-
ключение), которое имеет определенные шансы сказаться справедливым,
в отличие от доказательного рассуждения (заключения), которое непременно
справедливо. Правдоподобным рассуждениям в математике посвящена полу-
чившая широкую известность превосходная книга Д. Попа [340].
Говоря ниже о правдоподобном качественном результате (например, об
утверждении типа «величина а больше величины 6», «данное движение устой-
чиво» и т. п.), будем понимать правдоподобность соответствующего утвер-
ждения. Под правдоподобностью количественных результатов будет пони-
маться правдоподобность заключения о том, что эти результаты с требуемой
по условиям задачи точностью воспроизводят истинные результаты.
Относимые к реальной действительности результаты математического ре-
шения прикладной задачи почти всегда (за исключением простейших слу-
чаев) лишь правдоподобны, ибо только правдоподобным является отождест-
вление реального объекта или процесса с его математической моделью. По-
этому, даже если решение проведено вполне строго, полученный результат
все равно нуждается в экспериментальной проверке, повышающей степень
его правдоподобности*). При этом повышение общей правдоподобности ре-
зультата путем его экспериментальной проверки может оказаться более эко-
номичным по затрате времени и усилий, нежели повышение правдоподобно-
сти за счет большей строгости математического решения.
Отмеченное обстоятельство делает оправданным применение правдопо-
добных рассуждений не только при построении, но также и в процессе изу-
чения математической модели. Однако это обстоятельство является не един-
ственным доводом в пользу обсуждаемых нестрогих приемов. Другой важный
довод, как уже говорилось, состоит в относительно высокой степени правдо-
подобности результатов, полученных с помощью этих приемов. Мы попы-
таемся, в частности, показать (правда, также только путем правдоподобных,
а не доказательных рассуждений), что сведения о поведении системы при
достаточно малых значениях параметра и начальных отклонений несут зна-
чительную информацию о поведении системы при «не слишком больших»
конечных отклонениях. Иными словами, практически «более вероятно», что,
достаточно осторожно перенося результаты локального исследования на
реальные системы, мы не совершим ошибки, чем ее совершим. В сущности,
речь идет, по-видимому, о «хорошей корреляции» между математическим и
интуитивным пониманием малости.
В заключение подчеркнем, что применение обсуждаемых в данной главе
нестрогих приемов позволяет не только значительно упростить процесс иссле-
дования, но и существенно расширить класс прикладных задач, поддающихся
изучению с помощью методов Пуанкаре и Ляпунова.
Мы не выступаем, однако, и против определения областей сходимости
рядов и особенно против отыскания областей притяжения устойчивых реше-
ний в тех случаях, когда затраты труда на такие исследования оправданы
значением задачи и ценностью получаемых результатов.
Автор, с одной стороны, отдает себе отчет в спорности и пестрогости
некоторых выводов и оценок в пользу обсуждаемых приемов, а с другой
стороны, знает, что излагаемые соображения хорошо известны многим иссле-
дователям, активно работающим в области прикладной теории колебаний.
Вместе с тем представляется неправильным молчаливо обходить существую-
щие трудные вопросы, не акцентируя внимания читателя на ситуации, сло-
жившейся в практике применения методов Пуанкаре и Ляпунова при реше-
нии прикладных задач.
*) Эксперимент является решающим средством контроля правдоподоб-
ности результата, однако хорошо известно, что ссылка на подтверждающий
изолированный эксперимент тоже служит лишь правдоподобным соображе-
нием в пользу доброкачественности теории.
§2]	О ПРИМЕНИМОСТИ МЕТОДОВ МАЛОГО ПАРАМЕТРА	141
§ 2. О применимости методов малого параметра к системам,
не содержащим физического малого параметра*)
Один из приемов, расширяющих область применимости метода Пуанкаре
при решении задач теории нелинейных колебаний (в том числе и задач
о синхронизации), состоит в формальном введении малого параметра в си-
стему уравнений, непосредственно не содержащую малого параметра. Такие
системы в дальнейшем иногда будут называться системами без физического
малого параметра.
Упомянутый прием основан на том соображении, что для успеха приме-
нения метода Пуанкаре вовсе не обязательна малость определенных членов
уравнений: главным является наличие близких по характеру решений у по-
рождающей и у исходной систем.
Дело в том, что определенная группа членов в дифференциальных урав-
нениях обычно практически никогда не мала «в целом», на всех возможных
траекториях системы. Однако эта группа членов может оказаться малой на
определенном классе периодических движений и вблизи таких движений.
При этом отдельные члены могут и не быть малыми каждый по отдельно-
сти, но их сумма может все же оказаться малой. При рассмотрении разных
классов периодических решений одной и той же системы дифференциальных
уравнений, как правило, малыми могут считаться совершенно различные чле-
ны или совокупности членов уравнений. Указанное обстоятельство ниже будет
проиллюстрировано на конкретном примере.
Основное значение при использовании метода Пуанкаре, таким образом,
приобретает не столько правильность сделанного предположения о малости
того или иного параметра или определенных членов уравнений, сколько пра-
вильность гипотезы о виде разыскиваемых решений. Основой для такой гипо-
тезы могут служить физические соображения или результаты экспериментов.
После того как гипотеза о примерном виде разыскиваемых решений
сформулирована, не составит особого труда выделить в дифференциальных
уравнениях движения такую группу членов, предположение о малости кото-
рой соответствует гипотезе о близости разыскиваемых решений к функциям
определенного вида. Это можно сделать, например, с помощью такого фор-
мального приема. Пусть имеется дифференциальное уравнение (или система
уравнений, записанная в векторной форме)
х = Х(х, t),	(2.1)
относительно которого представляется правдоподобным предположить, что
оно допускает решения, близкие к некоторой функции **)
х0 = х0(/,	aj.	(2.2)
В последней записи подчеркнуто, что в общем случае эта функция мо-
жет быть не вполне определенной, а включать некоторые параметры
ai, .... ак, подлежащие определению в процессе решения задачи.
Обычно нетрудно построить дифференциальное уравнение, которому удо-
влетворяет функция Xq:
х0 = Хо (х0, О-	(2.3)
*)	С иных точек зрения некоторые аспекты данного вопроса рассматри-
вались в работах М. А. Айзермана и И. М. Смирновой [5, 6], А. П. Проску-
рякова [347], Е. П. Попова и И. П. Пальтова [344] и Е. Н. Розенвассера [360].
**	) Отметим, что предположения о характере рассматриваемых движений
фактически почти всегда приходится делать уже на этапе составления урав-
нений движения системы, то есть при построении математической модели
задачи. Иными словами, для того чтобы успешно разыскать нечто, всегда
следует хотя бы приблизительно знать, что именно разыскивается,
142
МЕТОДЫ ПУАНКАРЕ И ЛЯПУНОВА
Н'Л. IV
Если теперь прибавить к правой части исходного уравнения (2.1) и вы-
честь из нее выражение X0(x,t), а затем ввести обозначение
gXj (х, /) = X (х, t) - Хо (х, /),	(2.4)
где |х — малый параметр, то уравнение (2.1) представится в форме
х = Хо (х, I) + цХ, (х, /),	(2.5)
как раз и отвечающей предположению, что уравнение (2.1) может допускать
решения, близкие к (2.2). Действительно, при |х — 0 уравнение (2.5) превра-
щается в (2.3), которое, по предположению, имеет решение (2.2).
Изложенный выше способ введения малого параметра использован памп
(см. [61, 62], а также главу IX настоящей книги) при решении задачи о син-
хронизации слабо связанных автоколебательных объектов с почти равномер-
ными вращательными движениями. Исходной системе (2.1) в этой задаче
отвечали уравнения движения в форме уравнений Лагранжа второго рода.
Предполагалось, что в искомых движениях определенная часть обобщенных
координат изменяется по закону
<р° = os (со/ + as), as=±l,	(2.6)
близкому к равномерному вращению с угловой скоростью, равной по мо-
дулю со, и с некоторыми фазовыми сдвигами as; постоянные as и <о при
этом считались заранее неизвестными и подлежащими определению в про-
цессе решения задачи. В соответствии с видом решений (2.6) уравнения,
отвечающие системе (2.3), для координат q>s записывались в форме
+ ks (<₽Z - as“) = °-	(2-7)
где /s и ks — положительные постоянные.
Решения, полученные таким путем, для рассмотренных классов конкрет-
ных задач, в частности для задачи о синхронизации вибраторов, оказались
вполне согласующимися с экспериментальными данными; эти решения для
задач с соответствующим физическим малым параметром к тому же совпали
с решениями, полученными посредством обычной методики.
Если принять указанный выше способ введения малого параметра и
учесть, что обычно при решении задач редко вычисляют приближения выше
второго, то следует заключить, что успех применения метода Пуанкаре в
такой трактовке существенно зависит от справедливости гипотезы о харак-
тере решений, то есть от удачпости выбора исходного приближения (2.2). Это
обстоятельство существенно снижало бы «автоматизм» применения метода
в рассматриваемом виде, если бы не одно дополнительное обстоятельство,
которое необходимо учитывать.
Дело в том, что метод Пуанкаре дает как бы средство контроля пра-
вильности гипотезы о виде решений: уравнения, получающиеся для определе-
ния параметров ai, ..., п <о (это уравнения (2.10) предыдущей главы),
в случае удачной гипотезы допускают вещественные решения, удовлетворяю-
щие смыслу задачи, а в случае неудачной гипотезы не допускают таких
решений. В ряде случаев при одних значениях параметров системы веществен-
ные решения нужного типа существуют, а при других не существуют; усло-
вия наличия таких решений являются одновременно условиями существова-
ния у уравнения (2.1) решений изучаемого класса, то есть решений близких
к (2.2).
Отметим к тому же, что уравнения для определения параметров
он, .... и>, и со порождающего решения обычно имеют четкий физический
смысл: они, как правило, могут быть трактованы либо как усредненные за
период колебаний исходные уравнения движения, либо как уравнения балан-
са энергии (см., например, § 3 главы IX и § 3 главы XIII),
§2]	О ПРИМЕНИМОСТИ МЕТОДОВ МАЛОГО ПАРАМЕТРА	143
Естественно, что результаты, получаемые при описанном выше способе
решения задач, не могут претендовать на математическую строгость, на до-
казательность. Они должны рассматриваться лишь как правдоподобные, не-
пременно подлежащие экспериментальной проверке. Но следует иметь в виду,
что и при применении метода Пуанкаре к системам с физическим малым
параметром решения также обычно носят характер правдоподобных. При-
чины такого положения будут рассмотрены в § 3 настоящей главы. Здесь
же мы приведем конкретный пример, иллюстрирующий то обстоятельство,
что при разыскании различных классов решений одного и того же дифферен-
циального уравнения следует делать различные предположения относительно
малости тех или иных членов или их комбинаций.
Рассмотрим движение физического маятника, точка подвеса которого со-
вершает заданные гармонические колебания с некоторой частотой а
(рис. 65, а).
Пусть закон колебаний маятника по отношению к неподвижной системе
осей хОу выражается формулами
x = Z/sin<o/, у = G cos (oV 4- Ф),	(2.8)
где G и Н— амплитуды колебаний в горизонтальном и вертикальном напра-
влениях, О—'постоянный угол, характеризующий сдвиг фаз между составляю-
щими колебаний. Соотношениям (2.8) отвечает движение оси маятника по
эллиптической траектории с центром в начале О неподвижной системы коор-
динат.
Дифференциальное уравнение движения маятника имеет вид
/б + АО + mge sin 0 — шею2 [G cos (а/ + О) sin 0 — H sin a/ cos 9] = 0 (2,9)
или
/б + k& + mge | sin 0 +	sin ю/cos 0 — -y cos (a/ + 0) sin O^j |= 0 (2.10)
(S = Y H2 + G2').
Здесь 0 — угол поворота маятника, отсчитываемый от вертикального (устой-
чивого при отсутствии вибраций оси) положения равновесия по ходу часовой
стрелки, т — масса маятника, 1 — его момент инерции относительно оси вра-
щения, е — расстояние от центра тяжести маятника до оси вращения, k —
коэффициент вязкого трения, g — ускорение силы тяжести.
Как показывают теоретические исследования и эксперименты (см., на-
пример, [45, 59, 214, 352, 387], а также главы XVIII и XIX настоящей книги),
при одних и тех же параметрах системы, в зависимости от начальных усло-
вий, могут оказаться возможными по крайней мере два рода устойчивых уста-
новившихся движений маятника*) —колебания вблизи некоторого положения
с частотой возмущения со и вращение с постоянной средней скоростью, также
равной по модулю частоте ю.
При изучении движений первого рода в зависимости от характера за-
дачи считают малыми те или иные «физические» параметры, входящие в
уравнение (2.10), или некоторые их комбинации, например отношение Sa2lg
«амплитуды» ускорения колебаний к ускорению силы тяжести, коэффициент
трения k, разность между частотой собственных малых колебаний маятника
K=YmgelI и частотой возмущения ю и т. п.; как правило, уравнение (2.10)
при этом линеаризируют вблизи некоторого значения угла 0. Однако всегда
(за исключением задач, относящихся к вырожденному случаю) член mge sin О
не считают малым по сравнению с другими членами.
*) Возможны, вообще говоря, и иные, более сложные движения.
144
МЕТОДЫ ПУАНКАРЕ И ЛЯПУНОВА
[ГЛ. IV
sin 0 -t-
В случае же, когда интересуются движениями второго рода, целесооб'
разно считать малой следующую комбинацию членов*):
рФ (6, 0, 0 = <тйо> — mge.
+	£-2. sin cd? cos 0 — cos (cd? + •&) sin oj |	(o=±l), (2.11)
представив уравнение движения (2.10) в форме
/0 + й(0-аа) = рФ(0, 0, ?),
(2.12)
где ц— малый параметр, иение	Отвечающее уравнению (2.12) порождающее урав- /бо + й(0о-<т<о) = О	(2.13)
допускает решение	0О = <т (<of + а),	(2.14)
как раз и соответствующее вращению маятника с постоянной угловой ско
ростью. Условия наличия у уравнения (2.10) решений искомого вида
0 = о [со? + а + 0* (ю0],
а также периодическая функция 0*(со1) с периодом
найдены методом Пуанкаре.
(2.15)
2л по (fit могут быть
§ 3. О сходимости рядов, найденных методом Пуанкаре.
Правдоподобность результатов, полученных при отсутствии
доказательства сходимости. О внутренней
и внешней правдоподобности
Как отмечалось в § 2 предыдущей главы, теорема Пуанкаре гарантирует
существование периодического решения, обращающегося при ц = 0 в поро-
ждающее, лишь при достаточно малых значениях ц, не давая никаких ука-
заний относительно того, каковы эти значения.
Между тем при решении конкретной технической задачи (пусть речь
идет для простоты о задаче с физическим малым параметром) приходится
иметь дело с некоторыми определенными, конечными значениями малого па-
раметра. Со строго математической точки зрения для того чтобы быть уве-
ренным в правильности найденного методом Пуанкаре результата, необхо-
димо провести дополнительное исследование — оценить область сходимости
полученных рядов по малому параметру и убедиться, что интересующие иас
значения параметра принадлежат этой области. Более того, необходимо выяс-
нить, насколько найденные приближения (обычно их одно или Ава) отли-
чаются от точного решения: хорошо известно, что сумма любого конечного
числа членов сходящегося ряда в принципе может сколь угодно отличаться
от суммы ряда.
Получение указанных оценок представляет достаточно трудную задачу
(см., например, работы [373, 374]). Существующие более илц мунее общие
оценки крайне «пессимистичны», что вполне понятно, ибо они отвечает са-
мому неблагоприятному случаю.
) Подробно этот случай рассмотрен в § 3 главы XVIII.
§ Ч] О СХОДИМОСТИ РЯДОВ, НАЙДЕННЫХ МЕТОДОМ ПУАНКАРЕ 145
Все сказанное приводит к тому, что оценки областей сходимости рядов
по малому параметру и величин остаточных членов в прикладных исследо-
ваниях обычно не делаются. Спрашивается, как относиться к подобным ис-
следованиям, имеют ли полученные в них результаты какую-либо практиче-
скую ценность? По этому поводу высказываются две противоположные точки
зрения. Некоторые математики полагают, что такие результаты совершенно
лишены какой-либо ценности. С другой стороны, ряд исследователей-при-
кладников склонен считать результаты, получаемые методом Пуанкаре, без-
условно практически приложимыми, невзирая на отсутствие указанных выше
оценок.
С последним суждением, разумеется, нельзя согласиться. Однако нельзя
принять и первую точку зрения. Правильная позиция, по мнению автора,
состоит в том, что результаты, найденные для конкретных случаев без ана-
лиза областей сходимости рядов и оценки погрешности, должны рассматри-
ваться как правдоподобные, имеющие «хорошие шансы» оказаться спра-
ведливыми (но, разумеется, верные не всегда).
Для того чтобы убедиться в правильности или, точнее, повысить степень
правдоподобности этих результатов, можно осуществить их эксперименталь-
ную проверку. Такая проверка все равно нужна при математическом мо-
делировании прикладных задач: в процессе моделирования — при составлении
дифференциальных уравнений, начальных и граничных условий и т. п. — не-
избежно приходится прибегать к упрощающим предположениям и пренебре-
жению многими факторами. Иными словами, правдоподобность результатов
решения прикладной задачи связана не только с «внутренними» причинами —
приближенностью математического решения уже поставленной задачи, но и
с «внешними» причинами — приближенностью математической модели. По-
этому следует заботиться не только о внутренней правдоподобности, степень
которой определяется точностью решения, но и о внешней правдоподобности,
определяемой соответствием математической модели изучаемому явлению
или процессу.
С точки зрения прикладной математики было бы неправильным доби-
ваться крайне высокой степени внутренней правдоподобности при низкой сте-
пени внешней правдоподобности. По этому поводу можно было бы повторить
то же самое, что в настоящее время является общепризнанным в отношении
приближенных вычислений: степень точности таких вычислений должна соот-
ветствовать степени точности исходных уравнений, начальных и граничных
условий, степени точности при определении параметров, от которых зависит
решение, и т. п. *).
Возвращаясь к вопросу о внутренней правдоподобности результатов, по-
лучаемых методом малого параметра, естественно попытаться понять при-
чины, по которым результаты, справедливые лишь при «достаточно малом ц»,
имеют хорошие шансы оказаться справедливыми при заданном значении ц.
О том, что эти шансы действительно не так уж плохи, свидетельствуют ре-
зультаты использования решений многих прикладных задач для конечных
значений р и притом иногда даже для таких, которые не представляются
интуитивно малыми**).
Причины относительно высокой степени правдоподобности указанных ре-
зультатов вполне аналогичны тем причинам, которые предопределяют высо-
кую степень правдоподобности заключений об устойчивости движения системы
при конечных отклонениях (или конечных значениях некоторого параметра)
на основании изучения поведения системы при достаточно малых отклоне-
ниях (или при достаточно малых значениях параметра). Можно сказать, что во
*) Исключения из этого правила, а также различные точки зрения на
затронутый вопрос обсуждены в уже упоминавшейся статье [82].
**) В последних случаях иногда говорят о «чуде малого р» [32].
146	МЕТОДЫ ПУАНКАРЕ И ЛЯПУНОВА	[ГЛ. IV
всех указанных случаях речь идет, по существу, об оценке правдоподобности
качественных результатов, найденных посредством локального исследова-
ния, при их использовании для конечной области. Этот вопрос и рассматри-
вается в следующем параграфе.
§ 4. О правдоподобности качественных результатов
локального исследования при их «нелокальном» применении
1. Недостаточность локального исследования при решении прикладных
задач. Рассмотрим вначале ситуацию, возникающую при исследовании устой-
чивости движения. Как отмечалось в § 3 главы III, при изучении устойчи-
вости обычно ограничиваются рассмотрением устойчивости «в малом», то
есть при достаточно малых отклонениях от изучаемого невозмущенного дви-
жения. При этом в случае периодического певозмущенпого движения вопрос
об устойчивости сводится к нахождению характеристических показателей для
уравнения в вариациях, отвечающего рассматриваемому периодическому ре-
шению: для устойчивости (в малом) достаточно, чтобы вещественные части
всех характеристических показателей были отрицательны; при наличии хотя
бы одного показателя с положительной вещественной частью изучаемое дви-
жение неустойчиво, а случай, когда имеются нулевые или чисто мнимые по-
казатели, требует специальною исследования.
Далее, как указывалось в п. 7 § 3 главы III, при изучении вопроса об
устойчивости периодических решений, найденных методом Пуанкаре, как пра-
вило, ограничиваются выяснением знаков вещественных частей характеристи-
ческих показателей при достаточно малых значениях параметра ц. А именно,
рассуждают следующим образом. Пусть
Re	+ ...	(4.1)
— разложение вещественной части характеристического показателя Xs по сте-
пеням параметра р., причем as есть первый отличный от нуля коэффициент
разложения, a k, — целое положительное число, представляющее степень па-
раметра ц при члене с этим коэффициентом *). Все дальнейшие коэффициенты
разложений (4.1) обычно не вычисляют на том основании, что при достаточно
малых значениях ц знак Re будет определяться знаком коэффициента а„
(напомним, что параметр ц мы всегда считаем неотрицательным).
Таким образом, результат исследования устойчивости движения является
с математической точки зрения справедливым лишь при достаточно малых
отклонениях и при достаточно малых значениях параметра ц, причем вопрос
о том, каковы на самом деле соответствующие предельные значения откло-
нений и предельное значение ц, остается открытым. Между тем в реальной
прикладной задаче приходится иметь дело с конкретными конечными знача
ниями отклонений и с конечным значением параметра Ц.
Иными словами, мы приходим к выводу, что заключение об устойчиво-
сти движения при описанном выше использовании методов Пуанкаре и Ля-
пунова для решения прикладных задач также является не доказательным,
а лишь правдоподобным, подлежащим экспериментальной проверке. Вместе
с тем результаты исследования, получаемые указанным путем, довольно ча-
сто оказываются верными; хорошо известно, например, большое практическое
значение методов исследования устойчивости движения по первому прибли-
жению. Аналогичное положение имеет место при практическом использовании
рядов по некоторой переменной, сходимость которых доказана лишь для
достаточно малых значений этой переменной. Иначе говоря, степень правдо-
подобности «локальных» качественных результатов оказывается относительно
*) В случае, когда характеристические показатели разлагаются по дроб-
ным степеням |х, приводимые ниже рассуждения изменяются незначительно
§ 4J
О ПРАИДоИОДОЕНиСТИ КАЧЕСТВЕННЫХ РЕЗУЛЬТАТОВ	147
высокой, несмотря на их «нелокальное» использование: существует как бы
достаточно хорошая «корреляция» между математическим и интуитивным
пониманием малости.
2. О причинах высокой степени правдоподобности локальных качествен-
ных результатов при их «нелокальном» практическом применении. Обратимся
сначала к выяснению, насколько «вероятна» ситуация, что из факта отрица-
тельности коэффициента о» в выражении (4.1) будет следовать отрицатель-
ность величины Re Z,s.
Заранее очевидно, что рассматриваемая «вероятность» тем выше, чем
меньше значение и чем больше значение as. Однако прежде чем переходить
к более подробному обсуждению поставленного вопроса, отметим, что слово
«вероятность», равно как и некоторые другие термины теории вероятности,
заключенные нами в кавычки, употребляются в настоящем параграфе не в
обычном смысле, а для оценки степени правдоподобности (иногда называе-
мой «вероятность-один» в отличие от обычной «вероятности-два», основанной
на понятии частоты; Д. Пойа [340] говорит соответственно о «качественной»
и «количественной» вероятности). Правдоподобности же образуют лишь ча-
стично упорядоченное множество, и поэтому их, вообще говоря, нельзя оце-
нивать числами, множество которых линейно упорядочено. Однако для того
чтобы чисто качественно пояснить причины относительно высокой степени
правдоподобности при нелокальном использовании результатов, полученных
при изучении устойчивости «в малом и при достаточно малых р», мы в чисто
иллюстративных целях примем некоторые грубые гипотезы, в результате ко-
торых «вероятпостн-одип», то есть степени правдоподобности, окажется воз-
можным приписать некоторое число, то есть трактовать ее как обычную
вероятность — «вероятность-два». Отметим, что примеры такого сведения
вероятности одного рода к вероятности другого рода известны: можно со-
слаться, в частности, на весьма эффектный результат решения задачи о вы-
числении «в среднем» числа вещественных корней полинома некоторой
степени п с вещественными коэффициентами [210].
Представим выражение (4.1) в форме
k
Re Ks = Ц s [as + р/д (n)J.	(4.2)
где через Fs(p) обозначена соответствующая часть ряда для вещественной
части характеристического показателя
Сделаем теперь простейшее (но достаточно произвольное) допущение,
что в задачах, которые могут встретиться, функция Fs(p) может принимать
значения в интервале от As до —А„, причем каждое значение из этого ин-
тервала является «равновероятным». «Математическое ожидание» функции
Fa(p), таким образом, считается равным нулю, что вполне естественно.
Функция распределения «вероятности» для случайной величины pFs(p)
представлена па рис. 16, а в виде линии N'M'MN-, на том же рисунке нане-
сены абсциссы, соответствующие +а„ и —as. Теперь нетрудно найти «ве-
роятность» Р интересующего пас события, состоящего в совпадении знаков
вещественной части характеристического показателя As и первого ненулевого
коэффициента а„ в разложении Re Л, по степеням р. Эта «вероятность», в
соответствии с (4.2), при ц/1.., > as > 0 численно равна площади прямоуголь-
ника KLMN, а при — рА, < аа < 0— площади прямоугольника K'L'M'N',
который равен прямоугольнику KLMN. При | as | > рЛа рассматриваемая
«вероятность» численно равна площади прямоугольника N'M'MN, то есть
единице.
Таким образом,
148
МЕТОДЫ ПУАНКАРЕ И ЛЯПУНОВА
п л. iv
или, если ввести обозначение z=y,Aslas,
График функции Р = Чг(г) представлен на рис. 16,6, из которого видно,
что при заданных а8 и Д, и достаточно малом значении параметра р. «ве-
роятность» получения правильного результата, как п следовало ожидать,
б)	а>
Рис. 16.
равна единице — результат является «достоверным». Эта «вероятность» по
мере возрастания р вначале продолжает оставаться равной единице, а затем
достаточно медленно убывает, приближаясь в пределе при р->-оо к значе-
нию 0,5. При заданном значении р «вероятность» успеха тем выше, чем
больше значение коэффициента as по сравнению с предельным значением А,
функции Л (И)- В° всех случаях рассматриваемая «вероятность» (правдопо-
добность) остается больше 0,5.
Рассмотрим теперь в том же духе вопрос о причинах относительно вы-
сокой степени правдоподобности нелокального использования результатов,
получаемых при исследовании устойчивости движения системы «в малом».
Изучим в качестве примера вопрос об устойчивости в случае, когда возму-
щенное движение системы описывается дифференциальными уравнениями
x-altx + ai2y + fi (х, у),
y = a2ix + a22y + f2(x, у),
О ПРАВДОПОДОБНОСТИ КАЧЕСТВЕННЫХ РЕЗУЛЬТАТОВ
149
§ 4]
где ац — постоянные, а функции h и [2 содержат в своих разложениях по
целым положительным степеням х п у члены не ниже второго порядка.
Пусть оба корня Л] и характеристического уравнения
Иц — Л а12
6^21	^22 ~~
(4.5)
= 0
системы первого приближения для уравнений (4.4) имеют отрицательные
вещественные части. Тогда в силу известной теоремы А. М. Ляпунова (см.
п. 5 § 3 главы III) при достаточно малых значениях начальных отклонений
х0 = х(0) и Уо = У(0) рассматриваемое движение асимптотически устойчиво
независимо от вида функций f>(x, у) и f2(x,y).
Как уже говорилось, однако, наличие устойчивости «в малом» еще не
гарантирует убывания возмущений х и у с течением времени при заданных
конечных значениях х0 = *(0) и уо = у(О), то есть «фактической» устойчи-
вости движения.
Для рассматриваемой относительно простой системы (4.4) вопрос во
всей полноте может быть решен путем построения «фазового портрета», схе-
матически представленного для одного из возможных случаев на рис. 17, а.
В условиях этого рисунка «область притяжения» рассматриваемого движе-
ния (область «фактической устойчивости») ограничивается неустойчивым
предельным циклом С,: если точка, отвечающая начальным условиям, лежит
внутри этого цикла, то возмущенное движение с течением времени затухает
(изображающая точка приближается к началу координат); если же началь-
ная точка лежит за пределами цикла, то возмущенное движение никогда не
затухнет.
Вообще говоря, может иметь место картина более сложная, чем представ-
ленная на рис. 17, а (см., например, монографию [19]), однако для дальней-
шего нам важно одно: в изучаемом случае наличия асимптотической устой-
чивости «в малом» всегда существует такой круг радиуса г*, что если на-
чальная точка Л4о(хо, Уо) лежит внутри этого круга, то в дальнейшем
изображающая точка асимптотически приближается к началу координат (воз-
мущения затухают); с другой стороны, вне указанного круга, как угодно
близко к нему, имеются такие точки фазовой плоскости, через которые
проходят траектории, не пересекающие окружность г*, то есть не подходящие
к началу координат ближе чем на расстояние г*. Естественно, что нахожде-
ние радиуса г* должно основываться на анализе нелинейных членов уравне-
ний (4.4), то есть функций [> и f2. Этому вопросу посвящен ряд интересных
исследований, основанных, в частности, на использовании второго метода
А. М. Ляпунова; обзор указанных исследований и краткое изложение их
результатов можно найти, например, в монографиях [19, 35, 247, 301, 419].
Сделаем теперь достаточно грубые предположения о характере величин
r0 = V х'о + Уд и Гц. Будем предполагать, что распределение случайной
(в обычном смысле) величины — начального радиуса га — отвечает распреде-
лению Рэлея, то есть характеризуется плотностью
0	при — оо < г0 < О,
<₽1 (Го) =
2
г0
^2" 6	ПРИ 0<Г0<ОО.
(4.6)
Как известно, такое распределение имеет модуль вектора на плоскости, со-
ставляющие которого х и у по обеим осям координат имеют нормальное
распределение со средним значением, равным нулю, и со средним квадрати-
150
МЕТОДЫ ПУАНКАРЕ И ЛЯПУНОВА
(ГЛ. IV
веским отклонением о (подчеркнем, что а
отклонение для величины г0 — У + у^).
не есть среднее квадратическое
е)
Радиус предельной окружности г* будем считать «случайной» величиной
(изменяющейся при переходе от одной задачи к другой), распределенной на
некотором отрезке 0 г* Л с равномерной плотностью
1 0 при
<Р2('-.)=| при
г, <0 и г, >Л,
(4.7)
0 < г, < А.
Графики функций ср, и q>2 представлены на рис. 17,6 и в.
§4]	О ПРАВДОПОДОБНОСТИ КАЧЕСТВЕННЫХ РЕЗУЛЬТАТОВ	151
Как это часто делается (см., например, [125]), примем за максимально
возможное значение начального радиуса г0 величину
Г о max ж	“Ь Зоо,
где /По и По — соответственно математическое ожидание и среднее квадрати-
ческое отклонение величины го- Для закона распределения (4.6) имеем
00
_2	| „2„ / .. \ л- _,2 In	\ о
ао я J гоФ 1 (ro) dro — — ^2 — j п >
и поэтому
г о max = (]/у + 3]/2 --у) а = 3,21а.	(4.8)
Постоянную А в выражении (4.7) будем считать как бы радиусом естествен-
ной границы фазового пространства системы для определеииого класса задач,
так ЧТО Готах А.
Оценим теперь «вероятность» (правдоподобность) получения «фактиче-
ской» устойчивости при наличии асимптотической устойчивости «в малом».
Очевидно, что рассматриваемая вероятность Р ие меньше вероятности Ро
выполнения неравенства г0<г*, гарантирующего попадание начальной точки
Ма внутрь «области притяжения» начала координат:
Здесь
р > Ро (Го < г.) = J J ср (г0, г.) dra dr.
(Го < г»)
ф (г0. Г*) = <Р1 (г0) ср2 (г.)
(4.9)
(4.Ю)
— плотность распределения системы двух независимых величин го и г#, а
интегрирование распространяется на часть плоскости го, г#, для которой
Го < г*.
Производя интегрирование, в соответствии с (4.6) — (4.10) находим
00
О, г.) dra dr. =	<Р! (г0) dra <р2 (г,) dr,
о	о
152
МЕТОДЫ ПУАНКАРЕ И ЛЯПУНОВА
[ГЛ, IV
Таким образом,
Р>Ро(Го<г.) = 1-0,39-^^.	(4.11)
График функции
Po(ro<r.) = 'F. (-^)
представлен на рис. 17, г сплошной линией. Из рисунка видно, что при малых
отклонениях рассматриваемая вероятность (степень правдоподобности)
весьма близка к единице — результат практически достоверен. Однако и при
увеличении максимально возможного начального отклонения r0 max степень
правдоподобности убывает достаточно медленно: «вероятность» получения
верного результата остается относительно высокой.
Отметим, что последнее заключение будет справедливым, даже если счи-
тать величину начального отклонения г0 не случайной, а равной наиболь-
шему возможному значению го тах. В последнем случае, как нетрудно видеть,
Получаем
B>Po(romax<r»)=l-Z^.	(4.12)
Соответствующий график зависимости Ро (r0 тах < г.) =	( Г° 'п,?х | представ-
лен иа рис. 17, г пунктирной линией.
Подчеркнем еще раз, что приведенные выше рассуждения и выкладки
носят чисто иллюстративный характер и не претендуют иа строгость. Пред-
ставляется, однако, что иным путем было бы весьма трудно понять несо-
мненный, практически установленный факт: высокую степень правдоподобно-
сти результатов исследования устойчивости «в малом» и «при достаточно
малом у.» в случае суждения по этим результатам о поведении системы при
конечных отклонениях и при конечных значениях у..
Отметим также, что в обоих рассмотренных выше примерах мы скорее
занижали, нежели завышали, степень правдоподобности, ибо предполагали
«равномерное» распределение тех величин (максимального значения остаточ-
ного члена ряда, предельного радиуса области притяжения г*), которые на
самом деле «распределены» более благоприятно: значения этих величин, при-
водящие к явно неправильным результатам, встречаются более редко, ибо
обычно имеется ряд правдоподобных признаков неблагополучия. Таким
признаком может быть, например, оценка относительной величины учтенных
и неучтенных членов в разложениях правых частей равенств (4.1) и (4.4).
Иными словами, точки сгущаются вблизи области достоверности результатов
вследствие наличия дополнительных признаков правдоподобности, как пра-
вило, учитываемых при решении конкретных задач.
Заметим также, что если на недостаточность рассмотрения устойчивости
«в малом» для суждения о фактической устойчивости системы Неоднократно
обращалось внимание*), то причины в известной мере противоположного
факта — относительно высокой степени правдоподобности результатов иссле-
дования устойчивости «в малом» при их «нелокальном» использовании — до
сих пор, насколько нам известно, не обсуждались.
*) Это отмечается, например, во введении к монографии Н. Н. Баутина
[32]. ж. Ла-Салль и С. Лефшец [247, 248], указывая, что асимптотически
устойчивая система может быть «практически неустойчива», а неустойчивая
система — «практически устойчива» (из-за малости соответствующих обла-
стей устойчивости или неустойчивости), предлагают новое определение «прак-
тической устойчивости» и применяют второй метод А. М. Ляпунова для до-
казательства интересной теоремы о практической устойчивости.
§4]	О ПРАВДОПОДОБНОСТИ КАЧЕСТВЕННЫХ РЕЗУЛЬТАТОВ	153
Рассмотрение, аналогичное приведеииому выше, могло бы быть прове-
дено и в отношении сходимости рядов по малому параметру, которая, как
отмечалось, также гарантируется лишь при достаточно малом р.
То же самое можно сказать и относительно другого аспекта правдо-
подобности результатов исследования устойчивости — влияния на устойчи-
вость так называемых постоянно действующих возмущений. Как известно
(см., например, [271]), периодическое или установившееся движение, асимп-
тотически устойчивое по отношению к достаточно малым отклонениям на-
чальных условий, то есть в обычном ляпуиовском смысле, устойчиво (при
довольно широких предположениях) также и по отношению к достаточно
малым постоянно действующим возмущениям. Реальные же возмущения
всегда конечны. Таким образом, и в данном случае речь может идти о прав-
доподобности результатов, строго справедливых при достаточно малых по-
стоянно действующих возмущениях, то есть локально, при их применении
к случаям заданных, то есть конечных, возмущений.
ГЛАВА V
О СУЩЕСТВОВАНИИ, УСТОЙЧИВОСТИ
И ПРАКТИЧЕСКОМ ВЫЧИСЛЕНИИ ПЕРИОДИЧЕСКИХ
И СИНХРОННЫХ РЕШЕНИЙ НЕКОТОРЫХ СИСТЕМ
НЕЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
§ 1.	Предварительные замечания
Выше, в § 2 главы II и в п. 8 § 3 главы III, были выяснены
основные особенности систем дифференциальных уравнений,
к изучению которых приводится решение задач о синхрониза-
ции динамических систем.
В настоящей главе приводится ряд теорем о существовании
и устойчивости периодических и синхронных решений таких си-
стем уравнений. Эти теоремы, по существу, развивают в опре-
деленных специфических направлениях классический аппарат
теории Пуанкаре и Ляпунова периодических решений систем
с малым параметром. Главной особенностью изучаемых урав-
нений является существование у порождающей системы семей-
ства периодических (или синхронных) решений, зависящих от
некоторого числа k произвольных параметров.
В данной главе рассматривается также вопрос о практиче-
ском вычислении изучаемых решений.
Излагаемые результаты будут использованы в последующих
частях книги при решении различных задач о синхронизации
динамических систем.
§ 2.	Квазилинейные неавтономные системы [47]
1.	О рассматриваемой системе уравнений. Пусть движение
системы описывается дифференциальными уравнениями вида
i
xs = 2 as/(0*/ + <Ps(0 + li®s(xi, •••> хь ц, t) (s=l.I),
/-i
(2.1)
где Ф8 — вещественные аналитические функции переменных
хь ..., Xi в некоторой замкнутой области G, которой будем пред-
5 2]
КВАЗИЛИНЕЙНЫЕ НЕАВТОНОМНЫЕ СИСТЕМЫ
155
полагать принадлежащими все рассматриваемые ниже реше-
ния уравнений, и параметра р$>0 при достаточно малых его
значениях. По вещественной переменной t функции Ф5, aSj(t)
и <ps(/) являются периодическими с периодом Т = 2п/<в и непре-
рывными, причем функции Ф., удовлетворяют этим требованиям
в любой точке области*).
Система (2.1) относится к так называемым квазилинейным
системам: при ц = 0 она обращается в систему линейных урав-
нений с периодическими коэффициентами.
Пусть x*sj(f) есть фундаментальная система решений од-
нородных дифференциальных уравнений
i
х^^а^х* (з = 1, ...,/),	(2.2)
удовлетворяющая начальным условиям
^/(0) = 6s/	(з,/=1, ...,/)>	(2.3)
где 6SJ- — символ Кронекера.
Тогда характеристическое уравнение системы (2.2) можно
записать в форме (см. и. 3 § 3 главы III) **)
К/<Г)-М0,| = 0	(з, / = 1, • • •, /).	(2.4)
Будем предполагать, что уравнение (2.4) имеет произволь-
ное число корней любой кратности, модули которых равны еди-
нице; эти корни, в соответствии со сказанным в пи. 7 и 8 § 3
главы III, назовем критическими.
Пусть модули всех прочих корней меньше единицы, а эле-
ментарные делители матрицы, из элементов которой составлен
определитель в уравнении (2.4), для всех кратных корней яв-
ляются линейными. Как указывалось выше, именно такой слу-
чай представляет особый интерес для ряда задач о синхрони-
зации.
В изучаемом случае система уравнений (2.2) путем неосо-
бенного линейного преобразования с периодическими коэффи-
циентами
^ = 2^/0^ (s=l...........П	(2.5)
может быть приведена к следующей канонической форме:
У,~\Уз (з=1,...,/),
*) О возможности ослабления сделанных предположений см. п. 2 § 6
настоящей главы.
**) Здесь и ниже используется сокращенная запись определителя по-
рядка q с элементами а.,,- в виде I asj | (s, j = 1, ..., <?)'.
156
СУЩЕСТВОВАНИЕ II УСТОЙЧИВОСТЬ РЕШЕНИЙ
[ГЛ. V
где = -у In р(0) — характеристические показатели (см. п. 4 § 3
главы III; индекс (0) при Xs для упрощения записи здесь и да-
лее опускаем).
Характеристические показатели ks, отвечающие критическим
корням | р(0) |=1, являются чисто мнимыми числами или нуля-
ми; эти показатели также условимся называть критическими.
Для всех прочих корней | pW |<1 характеристические показа-
тели являются, вообще говоря, комплексными числами с отри-
цательными вещественными частями.
Разобьем все критические характеристические показатели на
группы, каждая из которых объединяет кратные показатели и
показатели, отличающиеся друг от друга на 1пы, где п— любое
целое положительное или отрицательное число или нуль.
Из этих групп выделим две особые группы, объединяющие
показатели вида Х = утсо, где п — целые положительные или
отрицательные числа или нули. К первой особой группе (назо-
вем ее ведущей особой группой) отнесем показатели вида X =
= ina, а ко второй особой группе — показатели вида Х =
= у i (2п + 1)со.
Мнимые части vs всех прочих критических показателей от-
1	г-
личны от чисел вида уто. I руппы, к которым они относятся,
назовем неособыми.
Обозначив через	характеристический показатель
из неособой группы г, в соответствии с вышесказанным будем
иметь
insG), s = 1, .. ., k,
у г (2щ+1) w, s = k + 1, ..., k + m,
iv(sr\ s = k + m + mx + ... +mr~i + l, ...
..., k + ni + nix+ ... + mr
(r= 1, . .., p),
— us+ivs, s = k + m + ml+ ... +mp + 1, .... I
(us > 0).
(2.6)
Здесь k — число корней в ведущей особой группе, m — число
корней во второй особой группе, mr — число корней в неособых
группах, р — общее число неособых групп и, наконец, согласно
принципу разбиения корней на группы,
) v(sr) — v^r) I =/гео,	|	| #= /ко, r =4= q. (2.7)
КВАЗИЛИНЕЙНЫЕ НЕАВТОНОМНЫЕ СИСТЕМЫ
157
§ 2]
Заметим, что среди чисел X,s может быть сколько угодно оди-
наковых: каждое число повторяется столько раз, какова крат-
ность соответствующего корня.
Поясним теперь смысл выделения в особые группы характе-
ристических показателей вида X = -^znco. Поскольку предпола-
гается, что коэффициенты aSj(t) в уравнениях (2.1) и (2.2) ве-
щественны, то все комплексные (в частности, чисто мнимые)
характеристические показатели встречаются только в виде
комплексно-сопряженных пар. Но тогда характеристические
показатели особых групп X = у та попадают, в соответствии
с (2.7), в ту же особую группу, что и комплексно-сопряженные
им показатели X =—% та. В то же время комплексно-сопря-
женные показатели вида X = iva попадают в разные неособые
группы. Иными словами, особые группы содержат пары комп-
лексно-сопряженных показателей, а неособые таковых не со-
держат.
При этом для каждой неособой группы можно найти другую
неособую группу, которая содержит характеристические пока-
затели, комплексно-сопряженные показателям первой группы.
Отсюда следует, что общее число неособых групп р всегда чет-
ное, то есть можно положить р = 2р', где р' — целое число.
Будем в дальнейшем для конкретности считать, что неосо-
бая группа с номером р' + г содержит показатели, комплексно-
сопряженные по отношению к показателям группы с номером г.
Иначе говоря, положим в дополнение к формулам (2.6)
<r) = - v(₽;+r>+ .. +mpt, mr = mp,+r	(2,8)
(r=l,	p'; s=^k + m + ml + ... +mr_! + 1, ...
..., k + m + m1 + ... + mr).
Путем того же преобразования (2.5) над переменными xs
исходную систему уравнений (2.1) можно привести к виду
ys = ^sys + fs(.i) + lifs(.yi, •••, Ун Ц, t)	(2.9)
(s=l......О,
где Xs по-прежнему определяются формулами (2.6) — (2.8), a fs
и Fs — линейные комбинации функций <ps и Ф8. При этом, по-
скольку мы предположили, что функции tps и Ф8 в уравнениях
(2.1) вещественные, можно, не нарушая общности, считать, что
в уравнениях (2.9) каждой паре комплексно-сопряженных зна-
чений Xs соответствуют комплексно-сопряженные функции
и F*-
158
СУЩЕСТВОВАНИЕ И УСТОЙЧИВОСТЬ РЕШЕНИЙ
[ГЛ. V
Напомним (см. п. 4 § 3 главы III), что фактическое отыска-
ние преобразования (2.5), приводящего систему уравнений с пе-
риодическими коэффициентами к системе уравнений с постоян-
ными коэффициентами канонического вида, в общем случае
представляет достаточно сложную задачу, ибо для ее решения
необходимо знать фундаментальную систему решений уравне-
ний, сопряженных с (2.2), то есть тоже дифференциальных
уравнений с периодическими коэффициентами.
Проще всего найти преобразование (2.5) в случае, когда
коэффициенты aSj(t) в уравнениях (2.2) постоянны. Однако и
в случае периодических коэффициентов преобразование (2.5)
иногда все же удается найти, поскольку оказывается возмож-
ным построить указанную выше фундаментальную систему (см.
п. 2 § 9 настоящей главы). Наконец, дело значительно облег-
чается тем, что для справедливости получаемых ниже результа-
тов достаточно осуществить приведение системы к канонической
форме лишь частично — только для критических переменных
уь yk+m+m^ +тр- При этом все прочие уравнения могут
даже и не быть квазилинейными. Важно лишь, чтобы при р = О
все некритические корни характеристического уравнения для
системы в вариациях были по модулю меньше единицы.
Иными словами, для получения результатов, о которых пой-
дет речь ниже, достаточно осуществить преобразование урав-
нений (2.1) к форме
Уз ~ ^sl/s 4” f s (0 4“ yFs (l/ь • • • > Уь О
(s = 1, . . ., k + т -\- mY + ... 4- mp),
yr = ^(y^  . О + н^’Чг/р •••> Уг н, 0 (2,10)
(r = k + m + m{-\- ... +тр + 1, ..., /),
ибо эти результаты не зависят от конкретного вида функций
Е® и Fr1 в «некритических» уравнениях.
Естественно, что преобразование системы уравнений к «не-
полному каноническому виду» (2.10) осуществляется значитель-
но проще, чем преобразование к канонической форме (2.9).
В частности, неполное каноническое преобразование легко про-
водится для дифференциальных уравнений теории синхрониза-
ции многих классов динамических объектов (см. часть III на-
стоящей книги).
Ниже нас будут интересовать только такие системы уравне-
ний (2.9), для которых порождающая система
+	(s=l, ...,/)	(2.11)
2зт
допускает периодические решения того же периода Т = —, что
и период правых частей уравнений (2.9). Последнее требование
§ 2]
Квазилинейные неавтономные системы
159
приводит, как нетрудно видеть, к следующим условиям, накла-
дываемым на функции соответствующие переменным ве-
дущей группы:
т
J fs(t)e~ln^‘dt = O	(2.12)
о
При выполнении условий (2.12) порождающая система
(2.11) допускает не одно решение, а семейство периодических
решений, зависящее от k произвольных постоянных а/.
1 aseinsU>t + us (/), s=l, k,
I us (/),	s = k + 1, .... I.
(2.13)
Здесь через us(Z) обозначены периодические функции вре-
мени t, определяемые формулами
Щ (0 = us(t + Г) =
J fs(x)einsa(t~x)dx, s=l..........k,
о
1
1
— е s
Jfs(T)A(/-T)dT
О
(2.14)
s — k 4" 1, Z.
2.	Условия существования периодических решений. Рассмот-
рим, следуя основной идее метода А. Пуанкаре (см. п. 1 § 2
главы III), вопрос о существовании периодических решений ис-
ходной системы уравнений (2.9), обращающихся при ц = 0 в
периодические решения (2.13) порождающей системы (2.11).
В силу сдела1нных выше предположений о характере правых
частей уравнений (2.1) и известных теорем о зависимости реше-
ний дифференциальных уравнений от параметров, решение
ys = ys(t, Pi, . . . , Рг, |i) системы уравнений (2.9), удовлетворяю-
щее начальным условиям
г/ДО, р,, .... pz, p) = z/°(O) + ps (s=l, ...,Z).	(2.15)
будет аналитической функцией параметров 0Ь ..., р( и ц, по
крайней мере при достаточно малых их значениях, и поэтому
160
СУЩЕСТВОВАНИЕ И УСТОЙЧИВОСТЬ РЕШЕНИЙ
(ГЛ. V
указанное решение можно искать в виде ряда
i
ys(t, ₽,..₽р hW;(0 + 2 Az(O₽z + hA(O +
I	I I
+ h2^(03z + ^(0h2 + 2 3^(0^,+ ... (2.16)
по целым положительным степеням 01.Рг и ц.
Подставим выражение (2.16) в уравнения (2.9) и началь-
ные условия (2.15). Учитывая, что
ps(yv г/р ц, 0 = 7Ш- •••> у°1> °- 0 +
! I
(круглые скобки, в которые заключены производные функций Fs
и г/8, означают, что эти производные вычислены при 0i = ... =0; =
= у. = 0, то есть для порождающего решения), приравняем вы-
ражения при одинаковых степенях 01, ..., 0/ и ц в левых и пра-
вых частях полученных соотношений. Тогда для определения
Л8»(/), В8(0 и CSj(t) получим следующие дифференциальные
уравнения и начальные условия:
Az— AAz.	Az (0) — ^>sV
Bs=^sBs + Fstf, y°,Q, t), Bs(0) = 0,
csi = ACsz + S(^-) Az. Csi(0) = 0
(s, i = 1, ..., /).
(2.17)
Функции Ds(t) в дальнейшем существенной роли не играют;
что же касается функций Е(ц (/), то они, как нетрудно убе-
диться, равны нулю.
Действительно, при ц = 0 решение z/s(Pi, . >., ₽z, 0, t) должно
зависеть от 08 линейно, поскольку эти параметры входят в на-
чальные условия (2.15) линейно, и при ц = 0 уравнения (2.9)
КВАЗИЛИНЕЙНЫЕ НЕАВТОНОМНЫЕ СИСТЕМЫ
161
§ 21
превращаются в линейные. Поэтому все нелинейные члены раз-
ложения (2.16) непременно должны содержать параметр ц в
качестве множителя, то есть, в частности, должно быть
Е^ (/)	0.
Интегрируя уравнения (2.17) при соответствующих началь-
ных условиях, находим
Bs(t) = e4 j F^y°, .... у°, 0, r)e~^xdr, (2.18)
о
Csf(/) = eVj№)^-^TdT.
о \ i /
Составим теперь уравнения, выражающие необходимые и
достаточные условия периодичности решения (2.16):
ФДРь • • •» Pz. = Ы33 2 [AdPz + p-[ss] +
Z = I
+ lxS[Csz]₽z + UW+ ... =0 (2.19)
i = l
(s=l, ..., Z).
Здесь обозначено:
[F] = F \t_T - F |^0.	(2.20)
При учете равенств (2.6) и (2.18) уравнения (2.19) записы-
ваются в форме
Ф| =	И [Fj] + Pz + Н2 + ••• =0,
z-i
Ф/г —	И [Ffe] + HStCfeilPz + Н2 + ••• =0>
z=i
i
фй+1 = (^+‘Г- 1)pft+i Ш+1] + lxS[Cft+i.zlPz + [^+i]lx2+ • • • =о,
1 = 1
^ = (eV-l)Pz + li[Bz] + 1фС/г1 рг + UW + ... =0.
(2.21)
Для того чтобы исходная система (2.9) допускала периоди-
ческое решение с периодом Т, обращающееся при ц = 0 в пе-
риодическое решение (2.13) порождающей системы (2.11), урав-
нения (2.21) должны допускать решение относительно функций
6 И. И. Влехман
162
СУЩЕСТВОВАНИЕ И УСТОЙЧИВОСТЬ РЕШЕНИЙ
[ГЛ. V
Pi = 0i(p), ••> 0/= Ml1), обращающееся в нуль при р = 0.
Получим условия, при которых последнее имеет место.
Первые k уравнений (2.21) можно сократить на р, поскольку,
как было сказано выше, разложения (2.16) функций ys =
= £/s(pi, Рг, р) не могут содержать нелинейных членов, не
имеющих р в виде множителя. Но тогда, для того чтобы эти
уравнения допускали решение относительно ps, обращающееся
в нуль при р = 0, необходимо выполнение равенства [Bs] = 0
(s = 1, ..., k), которые в соответствии с (2.18), (2.6) и (2.13)
могут быть записаны в форме
т
Ps(ait .... aft)=sj Fs(y°, у°, 0, ty~in^dt = O (2.22)
о
(s —= 1, . . ., k).
Последние соотношения представляют систему k уравнений отно-
сительно параметров ai, ..., сц порождающего решения (2.13).
Таким образом, периодические решения исходной системы
(2.9), обращающиеся при р = 0 в периодические решения (2.13)
порождающей системы (2.11), могут соответствовать лишь тем
решениям (2.13), для которых параметры ah ..., as удовлетво-
ряют уравнениям (2.22).
В соответствии с теоремой о существовании неявных функ-
ций каждой системе значений параметров (эти значения часто
называют порождающими) a(=a*, ..., а^ = а*, найденной из
(2.22), действительно отвечает единственное и притом аналити-
ческое относительно р решение Pi = 0i(p), ..., 0/ = рг(р) си-
стемы уравнений (2.21), если функциональный определитель
<Э(^......l4 1>н-1> ъ)
5 (Pi, .... Р/)
3]= ••• =Pz = 4 = 0
где ф' = ф5/р (s = 1, ..., k), отличен от нуля.
Согласно (2.18), (2.6), (2.13) и (2.22) имеем
[Cs/] = [ №\^rWdt = f
1 oJ U//	oJ д1Л daiT
<2-24>
(s, / = 1.k).
§ 2]	КВАЗИЛИНЕЙНЫЕ НЕАВТОНОМНЫЕ СИСТЕМЫ	16,3
Далее заметим, что в силу (2.6) ни одна из величин — 1
при s = k + 1, .. . , I не равна нулю. Поэтому условие неравен-
ства нулю определителя (2.23) может быть, в соответствии
с (2.24), представлено в форме
I^R0 (*> / = 1, .... k).	(2.25)
Таким образом, каждому простому решению а*, ..., а* урав-
нений (2.22) соответствует единственное периодическое (с пе-
2л \
риодом Т ~ решение исходной системы (2.9), обращаю-
щееся при ц — 0 в периодическое решение (2.13) порождающей
системы (2.11). Это решение будет аналитическим относительно
параметра р при достаточно малых его значениях.
Отметим, что сформулированный результат можно было бы
получить, используя общие теоремы, принадлежащие И. Г. Мал-
кину (см. [275], а также § 4 настоящей главы). Мы привели
здесь непосредственный вывод соотношений (2.22) и (2.25) для
изучаемого случая, во-первых, поскольку построенные выше
функции ф.ч(Pi, . .. , Р/, р) все равно понадобятся при исследова-
нии устойчивости периодических движений и, во-вторых, чтобы
показать, насколько этот вывод упрощается для канонической
системы уравнений.
3. Условия устойчивости периодических решений. Обращаясь
к изучению вопроса об устойчивости периодических решений,
рассмотрим характеристическое уравнение системы уравнений
в вариациях, взятое для какого-либо из упоминавшихся выше
периодических решений системы уравнений (2.9).
Запишем указанное характеристическое уравнение в форме
+	= ° U, /=1, .... О, (2.26)
указанной А. Пуанкаре (см. п. 7 § 3 главы III). Предполагается,
что элементы определителя (2.26) вычислены для значений
функций Pi = pi (р), •••> Мр)> удовлетворяющих условиям пе-
риодичности (2.21).
Если все корни р уравнения (2.26) имеют модули, меньшие
единицы, то рассматриваемое периодическое решение асимпто-
тически устойчиво; если имеется хотя бы один корень, по мо-
дулю больший единицы, то это решение неустойчиво; случаи,
когда наряду с корнями, по модулю меньшими единицы, имеются
корни с модулями, равными единице, требуют, вообще говоря,
дополнительного исследования.
Подставим в характеристическое уравнение (2.26) выраже-
ния для функций ф3 согласно формулам (2.19). Тогда при учете
164
СУЩЕСТВОВАНИЕ И УСТОЙЧИВОСТЬ РЕШЕНИЙ
[ГЛ. V
равенств (2.18) это уравнение примет вид
|(A7’-p)6s/ + |x[Cs/]+ .. .| = 0	(s, /=1,	I), (2.27)
где невыписа-нные слагаемые имеют относительно ц порядок
выше второго, а функции [Сч] предполагаются вычисленными
для соответствующего порождающего решения (2.13).
При ц = 0 все недиагональные элементы определителя в ле-
вой части уравнения (2.27) обращаются в нуль, и это уравнение
имеет корни
ps==p(o) = eV	(2.28)
Модули первых k + т + mi + ... + пгр этих корней (то есть
модули критических корней) согласно (2.6) равны единице, а
модули всех прочих I —(k + т + mi + . .. + тр) корней мень-
ше единицы. При достаточно малых значениях ц модули пос-
ледних корней в силу непрерывности останутся меньшими еди-
ницы, и вопрос об устойчивости сводится, таким образом, к из-
учению следующего приближения к первым k + т + mi + ...
.. . + trip корням.
Рассмотрим сначала k корней, для которыхр® = eKsT = e2ltifls =
= 1, то есть корни, образующие ведущую особую группу.
С этой целью раскроем определитель в левой части уравнения
(2.27) по минорам первых /? столбцов в соответствии с теоремой
Бине — Коши [106]. Тогда, если учесть также равенства (2.24),
уравнение (2.27) представится в форме
/? = /?(|х, р) =
<?р2
дР,
Р да2
- .	1	, дР2
да, Р + (Х <?а2	•
н —
дак
дР2
ц ~5—
<?а*
X
dPk
да.
dPk ,	„ , „ dPk
Ц, -z-- ...	1 — р + Ц —z----
1 <?а2	dak
х	1) + /?*(|л, Р) = о,
s-HI
(2.29)
где функция R* содержит в своем разложении по степеням ц
и 1—р лишь члены не ниже k + 1-го порядка относительно
этих величин, в то время как член с определителем имеет отно-
сительно тех же величин порядок k.
Так как при ц = 0 корень р(0, = 1 уравнения (2.29) имеет
кратность k, то функция /?(ц, р) при ц = 0, р = 1 обращается
в нуль вместе со своими производными до k—1-го порядка
§ 2]
КВАЗИЛИНЕЙНЫЕ НЕАВТОНОМНЫЕ СИСТЕМЫ
165
включительно. В данном случае теорема о существовании не-
явной функции р = р(ц) в ее элементарной формулировке не-
применима, и поэтому следует воспользоваться более глубо-
кими теоремами. Хорошее изложение этих теорем и их интер-
претация с помощью так называемого многоугольника Ньютона
даны, например, в работе Н. Г. Чеботарева [418].
Поскольку в разложении /?(ц, р) по степеням р— 1 наимень-
шая степень р в члене с (р—1р, где q = 0, 1, ..., k, равна
k — q, то из упомянутых теорем вытекает, что все корни уравне-
ния (2.29), обращающиеся в единицу при ц = 0, можно разы-
скивать в виде *)
р = 1 + цх + цЛ"0 (pi),	(2.30)
где /Со(О) = 0.
Подставив выражения (2.30) в уравнение (2.29), будем
иметь
R [|Ч 1 + цх + цКо (н)] =
	dPi -г-5	х дР2	dPi да2 дР2	dPi dak дР2	♦ I
= ц':	<Эа,	—х • да2	да. k	Д (Лг-1)+ ... =o,
				
	dPk	dPk	dPk J	
				
	да.	<Эа2	‘ dak %	(2.31)
где невыписанные слагаемые имеют относительно ц порядок не
ниже k + 1.
Из условия равенства нулю коэффициента при ц& в левой
части уравнения (2.31) получаем следующее алгебраическое
уравнение k-й степени для определения поправок х к первым
k критическим корням характеристического уравнения (2.27):
|1^-М| = °	(s, /=1, .... k).	(2.32)
Остается получить уравнения для определения поправок
к прочим т + mi + . .. + тр критическим корням характери-
стического уравнения (2.27).
Рассуждения и выкладки, совершенно аналогичные прове-
денным выше, приводят к выводу, что эти корни для каждой
из групп можно искать соответственно в виде
р = — [1 + цх 4- ц/С (ц)],	•	(2.33)
pr — es [ 1 + цх + ц Кг (ц)]	(г=1,...,р),	(2.34)
*) Многоугольник Ньютона в этом случае вырождается в прямую линию,
проходящую через точки (0, к) п (k, 0).
166
СУЩЕСТВОВАНИЕ И УСТОЙЧИВОСТЬ РЕШЕНИЙ
ЦЛ. V
где v^’— какое-либо из чисел а К. (0) = Кг (0) = 0. При этом
для определения поправок и к указанным корням получаются
следующие г + 1 алгебраических уравнений, степень каждого
из которых равна числу корней в соответствующей группе:
I — [Cs/] — 6s/x | = 0	(s, j = k + 1.k + tn), (2.35)
|[Cs/]^r)r-6s/x| = 0	(2.36)
(s, j = k + m + ml + ... +mr_, + l, ..., k + tn + m{ + ... + mr)
(r = l, .... p).
Величины [CSJ], фигурирующие в уравнениях (2.35) и (2.36),
выражаются непосредственно через левые части уравнений
(2.9). В соответствии с равенствами (2.18) имеем
[Cs/] = - f dFs^1’ lJl’ °-)- e‘<nrnJdi (2.37)
5 д‘Л
(s, j = k+ 1....k + m),
(2.38)
0 dVi
(s, j = k + m +	+ ... +	+ 1, ..., k + tn + пц + ... + mr)
(r= 1, p)
Подставив последние выражения в уравнения (2.35) и (2.36),
представим их в форме
г	°-f\ (nrns} t dt _ б
! ду>
(2.39)
(s, j = k + 1, ..., k + m),
(2.40)
(s, j = k -r- tn + m{ + ... +	_! + 1, ..., k + tn + tn{ + ... 4- mr)
(r=l......p).
Покажем теперь, что число уравнений (2.40), действительно
подлежащих рассмотрению, может быть уменьшено вдвое, то
есть на р' = j Р единиц,
§ 2]
КВАЗИЛИНЕЙНЫЕ НЕАВТОНОМНЫЕ СИСТЕМЫ
167
С этой целью напомним, что характеристические показатели
Z'r = i-ytp, а также и соответствующие им функции Fs из г-й
S ( , , 1 )
группы I г = 1... Р	~ Р) являются комплексно-сопряжен-
ными по отношению к соответствующим показателям и функ-
циям г + р'-й группы. Поэтому коэффициенты первых р' урав-
нений (2.40) будут комплексно-сопряженными по отношению
к коэффициентам других р' уравнений. Отсюда следует, что кор-
ни соответствующих уравнений также являются комплексно-со-
пряженными, и, таким образом, достаточно ограничиться рас-
смотрением только первых р' = у р уравнений (2.40).
Далее заметим, что, как следует из формул (2.30), (2.33) и
(2.34), при достаточно малом ц условия устойчивости |рг|<1
эквивалентны требованиям отрицательности вещественных ча-
стей поправок х, определяемых из уравнений (2.32), (2.39) и
(2.40). Условия |pi|> 1, очевидно, эквивалентны неравенству
Rexj > 0; при Re % = 0 для суждения об устойчивости необхо-
димо знать |р| с точностью до членов с р в степени выше
первой.
Иными словами, решение вопроса об устойчивости перио-
дических решений сводится к обычной задаче Гурвица для ал-
гебраических уравнений (2.32), (2.39) и (2.40). Существенно,
что неравенство нулю вещественных частей корней уравнения
(2.32) обеспечивает автоматическое выполнение условия
(2.25) *).
4. Теорема о существовании и устойчивости периодических
решений. Результаты, изложенные в настоящем параграфе,
можно сформулировать в виде следующей теоремы [47].
Теорема. Периодические решения неавтономной системы
уравнений (2.9), обращающиеся при ц = 0 в периодические ре-
шения (2.13) порождающей системы (2.11), могут соответство-
вать лишь тем значениям постоянных си, .... «а, которые удо-
влетворяют уравнениям
т
р,(«„....	=	....о,	(зли
о
(з = 1, ..., k).
Если для определенной системы постоянных ai =а’, ...
,удовлетворяющих уравнениям (2.41), вещественные
*) Отметим, что это обстоятельство не является случайным; оно имеет
место для всех рассматриваемых ниже систем и является отражением того
общего факта, что часть границы области устойчивости динамической системы
в пространстве параметров совпадает с границей области существования, то
есть с поверхностью, на которой определитель (2.25) обращается в нуль [321].
16S
СУЩЕСТВОВАНИЕ И УСТОЙЧИВОСТЬ РЕШЕНИЙ
(ГЛ. V
части всех корней к алгебраических уравнений *)
<3PS	8 п
-5-----бо/Х = О
да/ s'
(s, / = 1..........k),
(2.42)
(2.43)
(2.44)
(s, j = k + m + mI-]- ... +mr_1 + l, .... k + m + tni + ... + mr)
(r= 1, .... p'; p' = ^p)
(6Sj — символ Кронекера) отрицательны, то при достаточно ма-
лых ц этой системе постоянных действительно соответствует
единственное аналитическое относительно ц асимптотически
устойчивое периодическое решение уравнений (2.9), обращаю-
щееся при ц = 0 в порождающее решение (2.13).
Если вещественная часть хотя бы одного из корней уравне-
ний (2.42) — (2.44) положительна, то соответствующее решение
неустойчиво; при наличии чисто мнимых или нулевых корней,
вообще говоря, необходимо дополнительное исследование.
Таким образом, исследование устойчивости периодических
решений системы уравнений (2.9) сводится к задаче Гурвица
для алгебраических уравнений, коэффициенты которых выра-
жаются непосредственно через правые части первых k + ш +
+ пг1+ ... + тр' уравнений (2.9).
5. Дополнительные замечания. Можно показать, что сфор-
мулированная выше теорема непосредственно справедлива не
только для канонической системы уравнений (2.9), но также и
для системы (2.10), имеющей неполную каноническую форму;
неканонические уравнения последней системы при этом могут и
не быть квазилинейными. Существенно лишь, чтобы при ц = 0
все некритические корни характеристического уравнения систе-
мы в вариациях имели модули, меньшие единицы.
Более того, для получения уравнений (2.41) и (2.42), из
которых определяются параметры порождающего решения а3
и поправки к критическим корням ведущей группы, достаточно
*) Напомним, что здесь используется сокращенная запись определителя
порядка q с элементами aaj в виде | asj | (s, / = 1, ..., q).
§ 3J	КВАЗИЛИНЕЙНЫЕ АВТОНОМНЫЕ СИСТЕМЫ	139
привести исходную систему уравнений к канонической форме
только для переменных yit . . ., yh ведущей критической груп-
пы. Прочие l — k уравнений опять-таки могут при этом не быть
квазилинейными.
Последнее замечание существенно, поскольку уравнения
(2.41) и (2.42) зачастую играют основную роль, тогда как усло-
вия устойчивости, вытекающие из рассмотрения критических
корней неведущих групп, особого значения не имеют (см., на-
пример, § 5 главы XIII).
Все указанные дополнения к сформулированной теореме мо-
гут быть без особых затруднений доказаны путем некоторого
усложнения приведенных выше рассуждений. Однако на этих
рассуждениях можно не останавливаться, поскольку та же цель,
правда при некотором ограничении, более просто достигается
в результате использования теоремы И. Г. Малкина, изложению
которой посвящен четвертый параграф настоящей главы.
Отметим, наконец, что выше нигде не предполагалось, что
Т = 2п/(л есть наименьший период функций asj, <ps и Ф8 по
переменной t. Поэтому все изложенное вполне приложимо и
к случаю субгармонических колебаний системы, то есть колеба-
ний с периодом, в целое число раз превышающим наименьший
период возмущающих сил.
§ 3. Квазилинейные автономные системы [49]
1. О рассматриваемой системе уравнений. Случай, когда
правые части дифференциальных уравнений (2.1) не зависят
явно от времени t, то есть когда эти уравнения являются авто-
номными, имеет существенные особенности и поэтому должен
быть изучен отдельно.
Итак, рассмотрим квазилинейную автономную систему диф-
ференциальных уравнений
i
xs = S aslXj + цФ5(х,, ..хь ц) (s = l,..., Z),	(3.1)
/=i
где asj — вещественные постоянные, а Ф8 — вещественные ана-
литические функции переменных Xi.....xt в замкнутой обла-
сти G, которой предполагаются принадлежащими все рассмат-
риваемые ниже решения уравнений, и параметра ц 0 при до-
статочно малых его значениях *).
При р = 0 уравнения (3.1) обращаются в систему линей-
ных однородных дифференциальных уравнений с постоянными
*) О возможности смягчения этих предположении см. п. 2 § 6 настоя-
щей главы.
17'0	СУЩЕСТВОВАНИЕ И УСТОЙЧИВОСТЬ РЕШЕНИЙ	[ГЛ. V
коэффициентами. Будем предполагать, что характеристическое
уравнение этой системы
|<ф-М = 0	(s, /= 1, .... Z)	(3.2)
имеет кратный нулевой, а также произвольное число чисто мни-
мых корней любой кратности*). Вещественные части всех про-
чих корней предполагаются отрицательными, а элементарные
делители, соответствующие всем кратным корням, — линейными.
При сделанных предположениях систему уравнений (3.1)
с помощью неособенного линейного преобразования с постоян-
ными коэффициентами можно привести к канонической форме
Уз = U + РА(1/1, • • Уь Н) (s =!,...,/),	(3.3)
где Fs — линейные комбинации функций Фд при этом можно
считать, что каждой паре комплексно-сопряженных чисел Xs
соответствует пара комплексно-сопряженных функций Fs.
Отыскание преобразования, приводящего уравнения к кано-
нической форме, в данном случае не представляет существен-
ных трудностей, поскольку при ц = 0 система (3.1) обращается
в линейную систему с постоянными коэффициентами.
Как известно [107, 450], периодические решения системы (3.3)
с периодом Tq,0, близким к Т° д = 2nqlva (<7=?^0 — целое поло-
жительное число), могут соответствовать любой паре чисто мни-
мых корней ±zv0 характеристического уравнения. Рассматривая
вопрос о существовании и устойчивости решений с периодом Т,
близким к какому-либо из указанных периодов, разобьем ,нуле-
вые и все чисто мнимые корни Xs (то есть критические корни)
на группы в точности таким же образом, как и в § 2.
Иными словами, будем считать, что числа /,,ч в уравнениях
(3.3) определяются по-прежнему соотношениями (2.6) — (2.8)
с единственной оговоркой: по крайней мере одно из чисел X., =
= 2ninsIT = ia>ns ведущей группы (1 s < й) должно быть от-
лично от нуля, ибо в противном случае будет неопределенным
период рассматриваемого решения.
Соответствующая уравнениям (3.3) порождающая система
У>^зУз (s=1.........о	(3-4)
допускает периодическое решение с периодом Т = 2л/ю:
зависящее от k произвольных параметров 0ц, ... , a)t.
!) См. сноску на стр. 126.
§ 3J	КВАЗИЛИНЕЙНЫЕ АВТОНОМНЫЕ СИСТЕМЫ	|7|
В рассматриваемом случае автономной системы периодиче-
ские решения уравнений (3.3), обращающиеся при р = 0 в по-
рождающие решения (3.4), будут иметь период, вообще говоря,
отличный от Т и зависящий от р.
Обозначим этот период через 7* = 7*(р) = 7[1— 6(р)], где
6(р)—пока неизвестная функция р, обращающаяся в нуль при
р = 0, и произведем замену независимой переменной по фор-
муле ([261, 232])
t — т[1 — 5(р)].	(3.6)
Тогда система (3.3) примет вид
-^ = (l-6)[Ms + H^(i/i.......Уь н) (S=l, .... Z).	(3.7)
В результате замены (3.6) исследование периодических ре-
шений системы (3.3) с периодом 7*(р) сводится к исследова-
нию периодических решений системы (3.7) с периодом Т.
2. Условия существования периодических решений. Для из-
учения вопроса о существовании и устойчивости периодических
решений системы (3.7), обращающихся при р = 0 в решения
(3.5) порождающей системы (3.4), а также для вычисления
неизвестной функции 6(р), как и в § 2, рассмотрим решение
z/s(x, pi, ..., Рг, 6, р) системы (3.7), определенное начальными
условиями
ys(Q, р„ .... pz, 5, p) = r/;(O) + Ps (s=l...Z).	(3.8)
Будем разыскивать это решение (которое должно быть ана-
литической функцией своих аргументов по крайней мере при
достаточно малых их значениях) в виде ряда по целым поло-
жительным степеням pi, . . ., рг, 6 и р:
i
ys(x, рр .... pz, 6, р) = y°s (т) + 2 Asi (т) pz + Gs (т) 6 + рВ, (т) +
I	I.
+ н 2 Csl (т) pz + н5 (т) рб + 6 2 ls1 СО Pz +
i=i	/-1
+ Ds (т) P2 +	(т) d2 + 2 2	(T) Pip/ + ...	(3.9)
<=i/=i
(s=l....../)•
Подставив этот ряд в уравнения (3.7) и начальные условия
(3.8), приравняем выражения при одинаковых степенях рь ...
..., Pi, 6 и р в левой и правой частях полученных соотноше-
ний. Тогда придем к следующим уравнениям и начальным
172
СУЩЕСТВОВАНИЕ И УСТОЙЧИВОСТЬ РЕШЕНИЙ
[ГЛ. V
условиям для определения функций ^4Si(r), Gs(r), Bs(x), CSi(x)
Hs(r) и Lsi(x):
Ai(0) = d^;
=	gs(O) = o,
^-^sBs + Fs(y\, .... y], 0),	Bs(0) = 0,
z	(3.10)
= ^sCsi + jL (5^7) A>h ^si (°) = °’
= ksHs - lsBs + ^^)Gi-Fs (y°........y°,	0), Hs (0) = 0,
<-i
-~L = ksLsi —ksAsi, Lsi(0) = 0.
Выражения для функций £)s(x) и Afs(x) далее не понадо-
бятся; функции (х), а также и все прочие коэффициенты при
р; в степенях выше первой непременно равны нулю по тем же
причинам, что и соответствующие функции в § 2.
Интегрирование уравнений (3.10) при учете равенств (3.5)
дает
Asl (т) = дцЛт, Bs (х) = Лт / Fs (у°,	у°,0) е~К°и du,
о
. _ г „	.	( — asXsxeXs%, s — 1, k,
Gs(x)=-A%J y°(u)e~Ks du = \ 0) s = ft+1) <>t> z>
0 ’ ’ ’	(3 H)
Lsi (?) = - Xs6sixc?i'T.
Условиями периодичности решения (3.9) являются равен-
ства
i
фДР1, Pz, б, ц) = [z/s] = Д [Дн]Р( + [Gs] 5 + ц [Bs] +
1	1
+ |Х 2 [Csi] Pz + [И5] цб + 6 2 [Lsi] pz + ц2 + [MJ & + ... (3.12)
1= [	i=*l
(3=1,	I),
где по-прежнему использовано обозначение (2.20).
КВАЗИЛИНЕЙНЫЕ АВТОНОМНЫЕ СИСТЕМЫ
173
§ 3]
Принимая во внимание равенства (3.11) и (2.6), запишем
уравнения (3.12) в форме
i
Ф1 = - oqTAjd + р [В 1] + и 2 [Сн] Pi 4- [#1] +
/=1
+ 6 2 [Aii]Pi + [П,]и2 + [Лф]д2 + ... =0,
I
Фй-1 = ~	+ и [Bk - ] ] + Ц 2 [Сй - 1, ;] Р; + [//fe — 1] рб +
i = I
I
+ 6 2 l^-i, ilPi + [Да-i] р2 + [И/г—i] б2 + ... =0,
i=1	Z	(3.13)
ф* = — a/jT’M' + р [В&] + р 2 [CwlPi + [#*] рб +
/=»1
Z
+ б 2 Pi + [О*] р2 + [Afft] 62 + ... =0,
(-1
Фа+i = (eKk+lT — l)Pfe+i + р [Bft+1] + ... =0,
^ = (eV- 1)P, + 14BZ]+ ... =0.
Невыписанные здесь члены, имеющие по совокупности пере-
менных р, Pi.....Р/ и 6 порядок не ниже второго, существен-
ного значения для дальнейшего не имеют.
Рассмотрим теперь условия, при которых уравнения (3.13)
допускают решение относительно Рь ..., рг и 6, обращающееся
в нуль при р = 0, и тем самым система уравнений (3.3) допу-
скает периодическое решение с периодом 7* = 7\(р), обращаю-
щееся при р = 0 в периодическое (с периодом Т (0) = Т) реше-
ние (3.5) порождающей системы (3.4).
Сделаем предварительно несколько замечаний. Прежде все-
го напомним, что по условию по крайней мере одно из чисел
ctiA.i = i/iicooii, ... , осаАа = in/t(i)ah отлично от нуля. Пусть это
будет со<А/< = 1пьыак-
Далее заметим, что среди чисел А,, . . ., Аа непременно долж-
но содержаться число, комплексно-сопряженное по отношению
к Аа = tnhw; пусть это будет Aa-i = —1пьа>.
Наконец, необходимо отметить, что число уравнений (3.13)
на единицу меньше числа неизвестных . .., и 6. Это об-
стоятельство обусловлено автономностью системы уравне-
ний (3.3).
174
СУЩЕСТВОВАНИЕ И УСТОЙЧИВОСТЬ РЕШЕНИЙ
[ГЛ. V
Действительно, условия периодичности (в данном случае
уравнения (3.13)) принципиально могут определить периоди-
ческие решения автономной системы лишь с точностью до произ-
вольной постоянной, ибо если ys — (s = 1, . .., /) есть ка-
кое-либо периодическое решение системы (3.3), то ys — y*s (t + h),
где h — произвольная постоянная, также является периодиче-
ским решением этой системы.
Ввиду изложенного одно из неизвестных можно задать
произвольно (за исключением, конечно, величины 6, поскольку
от нее зависит период искомого решения). Положим, например,
Рл-i = Pft.
Итак, в дальнейшем будем считать справедливыми соотно-
шения
?-к = Xfc-] = inka, пк=£0, ак¥=0, Pfe-i = Pft. (3.14)
Составив k—1 линейных комбинаций функций фь ф&
вида Ys = ХассаФз — (s = 1, .... k), заменим уравнения
(3.13) следующими:
= МЛ - /.5щф/г = Ц {Ккак [Bs] - Zsas [В J} +
i
+ И 2 [CJ - Xsas [Cft J} P, + {lkak [tfj - /..A [H fe]} p6 +
/-I
/
+ 6 2 {^kak — 7-sas	+
i=> 1
+ {Xftaft[Ds]- Xsas[Dft]}n2 + {Mftl^s]-Ms[^J}62+ ... =0
(s = 1, .... k — 1),
(3.15)
Фй = —	+ ц [В J + Ц 2 [Си] Pz + [H*] H6 +
i=»l
+ 5 2 [MPi + UW + [MZi]62+ ... =o,
i=l
Фй+i =(ex*+ir - l)pi+i + p-[Bft+1] + ... =0,
ф, = (^г- i)p/ + |I[Bz]+ ... =0.
Из й-го уравнения (3.15) всегда можно, в соответствии
с (3.14), определить 6 как аналитическую функцию величин
Рь .... р/ и ц:
б = нб.+ ....	=	<3-16)
aftAfe-'
Здесь невыписанные члены имеют относительно рь ..., рг и ц
порядок выше первого.
Если подставить выражение (3.16) в первые k—1 уравне-
ний (3.15), то их можно будет сократить на р. Но тогда, для
§ 3]
квазилинейные автономные системы
175
того чтобы эти уравнения допускали относительно рь рг
решение, обращающееся в нуль при р. = 0, необходимо выпол-
нение следующих k— 1 равенств:
«(«......................................(3.17)
(s = 1, ..., k — 1).
При учете формул (3.5) и (3.11) уравнения (3.17) могут
быть представлены в виде
QXai> •••-	afc)-Wfc(ai> •••> а*) = 0 <ЗЛ8)
(s = 1,	6-1),
где
Ps(alt ak) = [Bs] =
т
= J	ake^\ 0.....6)e~^xdx (3.19)
(s = 1, ..6).
Число неизвестных a,, ..., a/f опять-таки на единицу боль-
ше числа уравнений (3.18). Это, конечно, объясняется той же
причиной, что и отмеченное выше превышение числа неизвест-
ных Рь ..., Ра и 6 над числом уравнений (3.13), определяющих
эти величины. Поэтому в уравнениях (3.18) можно положить
= а.	(3.20)
При выполнении условий (3.18) и (3.20) уравнения (3.15)
действительно допускают одно (и только одно) решение относи-
тельно
Pi = Pi (ц), •••» Pa-i ~ Ра—1 (и) =i Ра — Ра(ц)> Pa+i — Pa+i (М-)> ••> Pz =
= р;(ц), обращающееся в нуль при ц = 0 и аналитическое отно-
сительно ц при достаточно малых значениях этого параметра,
если отличен от нуля функциональный определитель
...К-1. ........ */)
(Pl’ Pa-I’ Pfe + l’ Р/) |3j= ... =3z=U = 0
/?П	Rl2	• Rl, A-l
Ри	R22	• Rq, a-i
Rk-i,	Rk-l,2 •	• Rk-i, A-l
хЦ^-О, (3.21)
176
СУЩЕСТВОВАНИЕ И УСТОЙЧИВОСТЬ РЕШЕНИЙ
[ГЛ. V
где через
(3.22)
обозначен результат подстановки в выражение для Ws/pt значе-
ния функции 6 = Sip + ... из формулы (3.16),
=	•••> aft) =
= ^kak{[£«/] + 6] [Z.s/]} — A.sas{[Cft/] + 6] [Z.fe/]}	(3.23)
(s,	k — 1),
а под aj понимаются значения величин aj, удовлетворяющие
уравнениям (3.18) и условию (3.20).
Поскольку в силу (2.6) ни один из сомножителей
где s = k + 1, ..., I, не может быть равен нулю, то требование
неравенства нулю функционального определителя (3.21) сво-
дится к условию *)
1Я5/1^0	(з, / = 1, ..., k- 1).	(3.24)
Покажем теперь, что, как и в случае неавтономной системы
уравнений, элементы определителя (3.24) представляют собой
частные производные от левых частей уравнений (3.18). С этой
целью заметим предварительно, что в силу равенств (2.6),
(3.11), (3.16) и (3.19) имеем
°	Рк	(3.25)
[Ls/]= -KsT6sl,
Поэтому выражения (3.23) могут быть представлены в форме
Psl (“'.........=	("day “ Рк) ~ (lay ~ "af)
(s ~ 1....k- 1; / = 1, ..., k).	(3.26)
Вычислим теперь производные от функций Q*(aI; ..., ал).
Согласно равенствам (3.18) имеем
dQ*(a,, ..., а Л	др	дРк
—- = Kkak ~д^+W (3-27)
(з = 1, ..., k-\‘, j=l, k).
*) См. сноску на стр. 168.
§ 3]
КВАЗИЛИНЕЙНЫЕ АВТОНОМНЫЕ СИСТЕМЫ
177
Сопоставляя формулы (3.26) и (3.27) при учете равенств
(3.18), находим
(* \
<?оД
^7	.	.	<3-28)
1 аГа1...“а”“а
(з — 1, .... k — Г, j = 1, .... k).
Таким образом,
в форме
условие (3.24) может быть представлено
#=0	(з, /=1, ..., £-1).	(3.29)
Отсюда при учете сказанного выше следует, что каждому
простому решению «( = а‘, ..., afe_2 = а‘_2, aft_1 = afe = a’ урав-
нений (3.18) соответствует единственное периодическое реше-
ние (с периодом Т*(ц)) исходной системы (3.3), обращающееся
при ц = 0 в периодическое (с периодом 7’*(0) = Т) решение
(3.5) порождающей системы (3.4). Это решение является ана-
литической функцией параметра ц при достаточно малых его
значениях.
К сформулированному выводу можно также прийти, исходя
из результатов, полученных Н. Г. Булгаковым [107] и отчасти
также Э. Коддингтоном и Н. Левинсоном [450]. Мы, однако,
предпочли получить этот результат несколько иным путем спе-
циально для рассматриваемой системы в основном потому, что
многие из приведенных выше выкладок все равно предстояло
бы выполнить при исследовании устойчивости решений.
3. Условия устойчивости периодических решений. Обра-
тимся к изучению вопроса об устойчивости рассмотренных выше
периодических решений [49]. Характеристическое уравнение
в форме А. Пуанкаре (см. п. 8 § 3 главы III) системы в ва-
риациях для уравнений (3.3), взятое для какого-либо из этих
решений, имеет вид

б-б (ji), (3, =(3. (JI), ....
(3.30)
(s, / =1............/).
Предполагается, что элементы определителя вычислены
здесь для значений б(,ц) и рДц), найденных из уравнений
(3.13) при учете условия р^..! = pft = р(ц).
178
СУЩЕСТВОВАНИЕ И УСТОЙЧИВОСТЬ РЕШЕНИЙ
[ГЛ. V
Подставим в уравнение (3.30) выражения функций со-
гласно равенствам (3.12). Тогда при учете соотношений (3.11),
(3.19) и (3.25) это уравнение запишется в форме
s = |(Ar-p)6s/ + ^s/+а _а- =о (3.31)
а1~“1............................... ak-2~ak-2-
ak-i=ak=a*
(S, /= 1, . .	I),
где обозначено
NSj = [Cs/] + [Ts/]6,
= e s
ЛЛК dr-
(3.32)
^S&sjPk
(«, /=1, /),
а невыписанные в элементах определителя члены имеют отно-
сительно ц порядок выше первого.
При [1 = 0 все недиагональные элементы определителя S
обращаются в нуль и уравнение (3.31) имеет корни ps = p^0> =
= e%sT (s = 1,	/). Согласно (2.6) модули первых k + m +
+ /И1 + ... 4- тр корней равны единице, а модули всех прочих
корней меньше единицы. При ц достаточно малом в силу не-
прерывности модули этих последних корней останутся меньше
единицы, и вопрос об устойчивости сводится, таким образом,
к изучению следующего приближения к первым k + т +
+ т\ + ... + тр корням (то есть к критическим корням).
Как и в § 2, поправки к критическим корням следует разы-
скивать отдельно для корней каждой из р + 2 групп. Рассу-
ждения и выкладки здесь вполне аналогичны проведенным
в § 2: они сводятся к применению теоремы Бине — Коши для
раскрытия определителя S по минорам столбцов, отвечающих
рассматриваемой группе корней, и к последующему использо-
ванию теоремы о существовании неявных функций для «нетри-
виального» случая.
В результате приходим к выводу, что критические корни
можно разыскивать в виде р = р(ц) = 1 + цх + цЛо(ц) (для
ведущей критической группы), р = р(ц) = —[1 + цх + цК(ц)]
(для второй особой критической группы), р(г> = р<г) (ц) — е s [1 +
+ цх + рКг(р.)], где г = 1, ..., р (для прочих р критических
групп). Здесь /Со (0) = К(0) = КДО) = 0, а через v<.r), как и в § 2,
обозначено какое-либо из чисел v<,r).
Для определения поправок х к критическим корням полу-
чаем следующие алгебраические уравнения, степень которых
§ 3J	КВАЗИЛИНЕЙНЫЕ автономные системы	17 )
равна числу корней в группе:
= 0	(S, /=1,	(3.33)
I - jVs/-6s/x| * = 0	(з, / = /г+1...k + tri), (3.34)
ао
U/e~^’?-6sXo_a. = 0	(3.35)
(s, / = k + m + m-. + ... + mr-i + 1, ..., k + m + mi + ... + mr)
(r= 1............................p).
Рассмотрим несколько подробнее уравнение (3.33) для по-
правок к критическим корням ведущей группы. Покажем, что
это уравнение всегда имеет один корень, равный нулю. С этой
целью заметим, что согласно (3.32) и (3.19)
dPs hs6si
=	^-/ = 1....k).	(3.36)
Рассмотрим далее выражение, получающееся из (3.19) путем
замены функции е 1 , ..., ек соответственно на е 1	, ...
... , e^k{x+h\ Тогда, вводя новую переменную интегрирования
и = т + h и имея в виду, что подынтегральная функция при
s=l, ..., k является периодической по т (а также и по
и = т + h) с периодом Т, находим
j Fs(ai?'(T+/1)...aftA(T+/1),	0...^e~'^xdx =
О
т
e^h / Fs (a/‘“, ..., a/‘“, 0, ..., О) e~^u du (3.37)
(s = 1....k).
Продифференцировав последнее тождество no h и полагая
затем h = 0, получаем при учете (3.19)
k
(3.38)
/=i	1
Умножим теперь последний столбец определителя, фигури-
рующего в левой части уравнения (3.33), на и прибавим
к нему все прочие столбцы, предварительно умноженные на
180
СУЩЕСТВОВАНИЕ II УСТОЙЧИВОСТЬ РЕШЕНИИ
П'Л. V
aj^j. Тогда, в соответствии с (3.36), получим столбец с элемен-
тами
k
= As (я,, .. ., <ik) 	fLjhjNsj	x dsKs —
/=i
k
V IdPs
( da,
/=i 4	1
as^s
sS*kh
bsPk']
xashs.
(3.39)
a^j — 6
Учитывая, что при a, = a*, aft_9 = a’_9, aA_j = a =a*
справедливы уравнения (3.18), в силу тождества (3.38) находим
’ ak-2’ a*> a*)= - xaX	(3-40)
Таким образом, уравнение (3.33) может быть представлено
в форме
х
	Nu -х A2i	Nl2 IV 22 X .		k-i • N2,k-i	Ct j Л4 «9 ^2
	Nk-i,i	Nk-l,2 •	• Afc-l,*-!	
	Nkl	N k2		ak^k
= 0. (3.41)
-a = aa

Отсюда и следует, что один корень уравнения (3.33) всегда
равен пулю. Это обстоятельство не является случайным: как
было отмечено в п. 6 § 3 главы III, характеристическое уравне-
ние (3.31) для любого периодического решения автономной си-
стемы уравнений непременно имеет один корень р = pi = 1.
Естественно, что этому корню отвечает поправка х = х, = 0.
Однако, как указывалось, в соответствии с теоремой А. А. Ан-
дронова и А. А. Витта наличие у характеристического уравне-
ния системы в вариациях для автономной системы одного корня
р = pi = 1 не приводит, вопреки общему правилу, к необходи-
мости специального изучения членов высших порядков в урав-
нениях возмущенного движения. Суждение об устойчивости
в данном случае целиком зависит от модулей прочих I—1
корней характеристического уравнения, то есть дело обстоит
так, как будто указанный корень р = pi = 1 вообще отсутствует
(с оговоркой, приведенной в сноске на стр. 128).
Сократив уравнение (3.41) на х, получим уравнение для
определения поправок х к прочим k—1 критическим корням
ведущей группы.
Преобразуем это уравнение к более удобному для исполь-
зования виду. С этой целью умножим первые k—1 строк опре-
КВАЗИЛИНЕЙНЫЕ АВТОНОМНЫЕ СИСТЕМЫ
181
§ 3]
делителя в левой части уравнения (3.41) на и вычтем из
них последнюю строку, предварительно умноженную на asXs
(s — номер строки).
Тогда уравнение (3.41) представится в следующей форме:
~aiKiNki ~akkkK... akKkN\,k~\~a\'k\Nk,k-\	Q
akKkNk-\, \~ak-\Kk-\Nk\.akkkNk-\, 4-1 -“4-14-1^, 4 -1 ~ a4?'4z a _ *
“a~ua
или, в более компактной записи, — в виде
I akKkNs/ - asksNkl - akKkt>slx la^a* = 0	(3.42)
(s, j = 1, ..., k — 1).
В соответствии с (3.18) и (3.36) при s, j = 1, ..., k—1 имеем
dP, дРк	<?Q*
a4^4^s/ V-j-s^ki = a4^4	а^5~да~^ ^s^sl^k ~	•	(3.43)
Поэтому уравнению (3.42) можно придать следующую оконча-
тельную форму:
dQs
akkkl>si'X
= 0	(s, / = 1, .... k- 1). (3.44)
%-“0
Рассмотрим
венствам (3.32)
теперь
и (2.6)
Г Т
уравнения (3.34) и (3.35). Согласно ра-
имеем
L0
ei (nrns) <ot j 1 (2»s + О
2 пЛ
&sjPk
Ns! = e s
(s, j = k + 1, ..., k + m),
Г T
(3.45)
V)rf4
bsjPk
L0
(s, j = k 4- m 4- mx 4- ... + mr-x 4-1,..., k 4- m 4- mx + ... 4- mr)
(r= 1....p).
Далее заметим, что, как и в § 2, здесь можно ограничиться
изучением только первых / = |р уравнений (3.35), ибо корни
прочих р' уравнений имеют коэффициенты (а значит, и корни),
комплексно-сопряженные по отношению к корням первых р'
уравнений. При учете этого обстоятельства, а также формул

182
СУЩЕСТВОВАНИЕ II УСТОЙЧИВОСТЬ РЕШЕНИИ
(ГЛ. V
(3.45), подлежащие рассмотрению уравнения (3.34) и
будут
(3.35)
(3.46)
/ (2ns +!)/*&
\ 2nkak
+ X
= 0
(s, j = k + 1, ..., k + m),
(3.47)
(lx 6 . . .
1 к

= 0
(s, j = k + m 4- mi + • • • + fnr-i + 1, • • •, k + m + m, + ... + mr)
(r= 1, ..., p' = -| p).
При достаточно малом p условия устойчивости периодиче-
ского решения | р51 < 1 эквивалентны неравенствам Rex,<0,
а условия |рл1 > 1 сводятся к неравенствам Re Xj > 0; при
Rexj = 0 для суждения об устойчивости необходимо знать |pj
с точностью до членов с р в степени выше первой. Таким обра-
зом, решение вопроса об устойчивости сводится к задаче Гур-
вица для уравнений (3.44), (3.46) и (3.47).
Заметим в заключение, что, как и в случае неавтономной си-
стемы (§ 2), условие отсутствия у уравнения (3.44) нулевого
корня х = 0 равноценно неравенству (3.29), обеспечивающему
при выполнении уравнений (3.18) существование и аналитич-
ность относительно р периодических решений рассматриваемого
типа *).
Приведем в заключение тождество, которое может оказаться
полезным при исследовании уравнения (3.44). Это тождество
имеет вид
fe >	*	\
(« = 1......*-!)•	(З-48)
/=1 V	' %“ая
Последнее соотношение легко получается из формул (3.18) при
учете (3.38).
4. Теорема о существовании и устойчивости периодических
решений. Основные результаты, приведенные в настоящем па-
раграфе, могут быть сформулированы в виде следующей тео-
ремы [49].
Теорема. Периодические (с периодом 7\(p)= Д1 — б(р)])
решения автономной системы уравнений (3.3), обращающиеся
) См. сноску на стр. 167.
§ 3]
КВАЗИЛИНЕЙНЫЕ АВТОНОМНЫЕ СИСТЕМЫ
183
при ц = 0 в периодические (с периодом Т) решения (3.5) поро-
ждающей системы (3.4), могут соответствовать лишь тем зна-
чениям постоянных схь . . . , ak-2, «/г-i = Ль = а, которые удов-
летворяют уравнениям*)
Qs (ai> ak) = aknkPs - asnsPk = 0	(3.49)
(s = 1, ..k — 1),
где
т
....ak)= / Fs(y°, •••, У°{, O)e~in^xdx =
0
T
= j Л(а1е^1'вт) akeink<i>x, 0,	0) e~in^x dx (3.50)
о
(s = 1, . . . , k).
Если для определенной системы постоянных а1 = а1, ...
..ak_2 = a*k_2, ак_} = ak = а, удовлетворяющих уравнениям (3.49),
вещественные части всех корней х алгебраических уравнений **)
^--алМ=0	(s, j = 1, .... k-1),	(3.51)
[	dx -	+ x =0 (3.52)
J \дУ] I	ц 2	V >
(s, j = k + 1, ..., k + m),
(s, i = k + m + tn, + ... + mr_, + 1, ..., k + m + гщ + ... + mr
(r=l, .... p' =|pj,
(3.53)
(6Sj — символ Кронекера) отрицательны, то при достаточно ма-
лых ц этой системе постоянных действительно соответствует
единственное, аналитическое относительно ц, устойчивое (ррби-
тально асимптотически устойчивое) периодическое решение си-
стемы (3.3) с периодом 7\(р,) = Д1 — 6(ц)], обращающееся при
ц = 0 в периодическое (с периодом Т) решение (3.5) порождаю-
щей системы (3.4).
*) Здесь обозначено Qs = Q*/ia>.
**) См. сноску па стр. 168.
184
СУЩЕСТВОВАНИЕ И УСТОЙЧИВОСТЬ РЕШЕНИЙ
[ГЛ. V
* *
аА 2> а , а )
(3.54)
Если вещественная часть хотя бы одного из корней уравне-
ний (3.51) — (3.53) положительна, то соответствующее решение
неустойчиво', при наличии чисто мнимых или нулевых корней,
вообще говоря, необходимо дополнительное исследование.
С точностью до членов порядка ц поправка к периоду при
этом определяется формулой
6	~ и	ia*nkT
Таким образом, и в случае автономной квазилинейной си-
стемы уравнений (3.3) исследование устойчивости периодиче-
ских решений сводится к задаче Гурвица для алгебраических
уравнений, коэффициенты которых выражаются непосредствен-
но через правые части первых k 4- m +	4- ... + пгр- уравне-
ний (3.3).
5. Дополнительные замечания. Заметим, что сформулирован-
ная теорема, как и теорема § 2, остается справедливой и для
системы уравнений, приведенной к канонической форме лишь
частично, то есть только относительно переменных, отвечающих
критическим корням характеристического уравнения. При этом
для получения уравнений (3.49) и (3.51), играющих, как пра-
вило, основную роль, достаточно привести систему к канониче-
ской форме лишь для переменных у\, . . ., yh, соответствующих
ведущей критической группе корней. Прочие уравнения могут
даже не быть квазилинейными; существенно лишь, чтобы все
некритические корни характеристического уравнения системы
в вариациях были по модулю меньше единицы.
Необходимо сделать также следующее существенное замеча-
ние. Во многих практически важных задачах, в частности в за-
дачах о внутренней синхронизации динамических систем (см.
главы VIII, IX, XIII и XIV), период порождающего решения Т
заранее неизвестен*). В таких случаях естественно попытаться
определить этот период, исходя из условия, чтобы он был по
возможности ближе к периоду 7\(ц) исходной системы (3.3),
а именно из условия, чтобы поправка к периоду 6(ц) с точ-
ностью до членов порядка ц обращалась в нуль**). Тогда вме-
сто уравнений (3.54) и (3.49) получаются равенства
Ps(cti, . . ., aJ = 0	(s=\,...,k).	(3.55)
Из этих уравнений, в силу автономности системы, принципиаль-
но могут быть определены лишь k — 1 постоянных аь ...,
*) Следует отличать случай неизвестности периода порождающего при-
ближения от факта неизвестности периода синхронного движения в задачах
о внутренней синхронизации (см. § 1 главы II).
**) Такой прием применялся при решении ряда задач теории нелиней-
ных колебаний (см., например, работы [106, 44]).
§ 31
квазилинейные автономные системы
185
при условии, что одна из постоянных задана произвольно или
что задано какое-либо одно соотношение между постоянными
(например, положено, как это было сделано выше, = а)г = а).
Вместе с тем уравнения (3.55), вообще говоря, позволяют
определить, наряду с постоянными as, период порождающего
решения Т.
Уравнения (3.51) — (3.53) в рассматриваемом случае упро-
щаются и могут быть, в силу равенств (3.43) и (3.55), представ-
лены в форме
dPs	dPk < n
aknk ------- — asns -3----OSM = 0
я я да.] s s дй] S1
т
(s, j = 1, .... k — 1),
(3.56)
dx-bsl% =0
(3.57)
0	‘
(s, j k + 1, ..., k + m),
-v«rt)r
dx — dsyz = О
J \UU I
0	‘
(3.58)
(s, j = k + m + гщ + ... + mr_x + 1
., k + m + m{ + ... + тг)
, P =
Примечательно, что результативные соотношения (3.55) —
(3.58) могут быть формально получены непосредственно из со-
ответствующих соотношений (2.41) —(2.44), найденных для не-
автономной системы.
Действительно, если применить соотношения (2.41) — (2.44)
для указанного выше автономного случая, то следует учесть,
что одна из постоянных в уравнениях (2.41) может быть на-
значена произвольно, и эти k уравнений, вообще говоря, могут
быть использованы для определения прочих k—1 постоянных
и неизвестного периода порождающего приближения Т. Далее
следует принять во внимание, что при переходе к автономному
случаю будет иметь место соотношение
k
S4?-a^=0	....<3-59)
/=i	1
вытекающее из равенства (3.38) при учете (3.55). Тогда, при-
бавляя первые k—1 столбцов определителя (2.42), предвари-
тельно умноженные на ccj-Xj (/ — номер столбца), к последнему
столбцу, умноженному на аДл, получим столбец с элементами
а «Дух.
186
СУЩЕСТВОВАНИЕ II УСТОЙЧИВОСТЬ РЕШЕНИЙ
(ГЛ. V
Таким образом, один из корней уравнения (2.42) в данном
случае непременно будет равен нулю. Отделив этот корень, ко-
торый, согласно теореме А. А. Андронова и А. А. Витта (см.
п. 6 § 3 главы III), следует считать несущественным вследствие
автономности системы, как раз и придем к уравнению (3.56),
специально полученному для рассматриваемого автономного
случая. Что же касается уравнений (2.43) и (2.44), то они
в точности совпадают с уравнениями (3.57) и (3.58).
С отмеченным фактом нам неоднократно придется сталки-
ваться в дальнейшем: благодаря ему окажется возможным фор-
мулировать результаты решения ряда задач о синхронизации
в виде, одновременно пригодном как для случая внешней син-
хронизации, так и для случая внутренней синхронизации. Более
того, при определенных условиях можно будет не останавли-
ваться специально на рассмотрении наиболее сложной задачи
о внутренней синхронизации, получая результаты чисто фор-
мальным путем из решения более простой задачи о внешней
синхронизации.
§ 4. Неавтономные системы, близкие к произвольным
нелинейным
1. Теоремы о существовании и устойчивости периодических
решений. Рассмотрим систему дифференциальных уравнений
Xs X s (-4 > • • •, % h 0 4" Ц^'з (^ 1 , • • • >	> н) (5 1» • • •, О, (4.1)
где Xs и Fs — аналитические функции Хь ..., Xi в замкнутой
области G, которой предполагаются принадлежащими все изу-
чаемые ниже периодические решения.
По времени t функции Xs и Fs предполагаются непрерыв-
ными периодическими функциями периода Г; Fs к тому же яв-
ляются аналитическими функциями параметра ц >0 при доста-
точно малых его значениях *).
Пусть соответствующая уравнениям (4.1) порождающая си-
стема
....4 0	(5 = 1,...,/)	(4.2)
допускает семейство периодических решений
а„ ..., аА) (S=l,	/),	(4.3)
зависящее от k-^l произвольных параметров а1( ..., ан и ана-
литическое относительно этих параметров вблизи изучаемых
ниже «порождающих» значений = а*........ak = а*. Предпола-
*) О возможности смягчения этих предположений см. п. 2 § 6 настоящей
главы.
§ 4]
НЕАВТОНОМНЫЕ СИСТЕМЫ, БЛИЗКИЕ К НЕЛИНЕЙНЫМ
187
гается, что параметры ссь ..., сс& входят в выражения (4.3)
независимо, то есть что по крайней мере один из определителей
k-vo порядка, содержащихся в матрице
дх°	дх°	
дщ		(4.4)
дх°	дх°	
да{	dak	
не обращается в нуль при упомянутых порождающих значениях
параметров.
Рассмотрим соответствующую уравнениям (4.2) и решению
(4.3) систему уравнений в вариациях
zs = PsiZi + • • • + PsiZi (s =!,..., /),	(4.5)
где
/ дХ \ дХ (х°., ..х°,, t)
Psi = Psi (t) = (j =	~°	(4-6)
U Л j j	UX j
— периодические функции t периода T, причем круглые скобки,
в которые заключены производные от функции Xs, здесь, как
и выше, указывают, что эти производные вычислены для какого-
либо из порождающих решений (4.3).
В силу известного свойства уравнений в вариациях (см. и. 2
§ 3 главы III) система (4.5) допускает по крайней мере k пе-
риодических решений вида
_ о
дх
=	(s=l, .... Z; / = 1, .... Й),	(4.7)
получающихся путем дифференцирования решений (4.3) по па-
раметрам. Согласно изложенному в п. 4 § 3 главы III также по
меньшей мере k периодических решений z*sj (/) имеет система
линейных уравнений
••• +М = °	(s=l,	(4.8)
сопряженная с (4.5). Будем предполагать, что число независи-
мых периодических решений систем (4.5) и (4.8) в точности
равно k, то есть что система (4.5) не имеет периодических ре-
шений, отличных от (4.7).
При сформулированных условиях справедлива следующая
теорема, принадлежащая И. Г. Малкину [275].
Теорема 1. Для того чтобы система (4.1) допускала пе-
риодическое решение периода Т, обращающееся при ц = 0 в поро-
ждающее, принадлежащее семейству (4.3), необходимо, чтобы
188
СУЩЕСТВОВАНИЕ И УСТОЙЧИВОСТЬ РЕШЕНИЙ
[ГЛ. V
параметры ссь ..., этого порождающего решения удовлет-
воряли системе уравнений
т I
«,) - J S F! (<’ • • • > Х°’ °) dt = ° <4-9)
О / = !
(в = 1, . . . , k).
Каждому простому решению этой системы уравнений, то есть
такому решению, для которого выполняется условие*)
|^| ¥= 0	(s, /=!, .... k),	(4.10)
действительно отвечает при достаточно малых значениях ц.
единственное, аналитическое относительно ц, Т-периодическое
решение уравнений (4.1), обращающееся при ц = 0 в порож-
дающее.
Сформулируем теперь результат, относящийся к устойчиво-
сти периодических решений. С этой целью необходимо принять
некоторые дополнительные допущения.
Поскольку система в вариациях (4.5), как указывалось,
имеет k независимых Т’-периодических решений, то не менее k
корней характеристического уравнения этой системы равны
единице (см. п. 3 § 3 главы III). Будем предполагать, что число
единичных корней характеристического уравнения в точности
равно k и что все прочие корни имеют модули, меньше единицы.
При таком предположении число групп решений системы
в вариациях (4.5), отвечающих корню р = 1, будет в точности
равно кратности корня, и поэтому данному корню будут соот-
ветствовать линейные элементарные делители (см. там же).
Пусть, далее, периодические решения z'sj (t) сопряженной
системы (4.8) выбраны так, что удовлетворяются соотношения
2 zsizsi = f>u = { 0> f	(4.11)
в соответствии со сказанным в п. 4 § 3 главы III в рассматри-
ваемом случае это всегда можно сделать.
В указанных условиях справедлива следующая теорема.
Теорема 2. Периодическое решение системы уравнений
(4.1), отвечающее определенному решению а, = а’, . . ., со = ak
уравнений (4.9), является асимптотически устойчивым при
достаточно малых значениях параметра р, если все корни
) См. сноску па стр. 168.
§ 4]
НЕАВТОНОМНЫЕ СИСТЕМЫ, БЛИЗКИЕ К НЕЛИНЕЙНЫМ
189
алгебраического уравнения k-й степени
dPs
да,]
bsfx, =0	(s, j = 1...........k),
(4.12)
имеют отрицательные вещественные части. При наличии хотя
бы одного корня с положительной вещественной частью соответ-
ствующее решение неустойчиво-, случай нулевых или чисто мни-
мых корней требует, вообще говоря, дополнительного иссле-
дования.
Сформулированная теорема, в основном, вытекает из резуль-
татов И. Г. Малкина [275]. Отличие состоит лишь в том, что
И. Г. Малкиным оговаривается требование отсутствия кратных
корней у уравнения (4.12). Как будет показано ниже, это огра-
ничение является необязательным; оно понадобилось лишь в
процессе исследования устойчивости избранным И. Г. Малки-
ным способом (с использованием подстановки Н. А. Артемьева
[23]; см. п. 7 § 3 главы III). Отметим, что оговорки относительно
отсутствия кратных корней соответствующих уравнений не по-
надобились также и при доказательстве аналогичных теорем
в §§ 2 и 3 настоящей главы. Указанное ослабление ограничений
существенно для ряда задач о синхронизации одинаковых или
почти одинаковых объектов, когда имеет место случай равных
корней уравнения (4.12).
Заметим, что если характеристическое уравнение системы
(4.5) имеет, помимо указанных выше k корней р = 1, еще и дру-
гие корни, модули которых равны единице (по которые, однако,
не равны единице!), а все прочие корни этого уравнения имеют
модули, меньшие единицы, то условия отрицательности веще-
ственных частей уравнения (4.12) будут необходимыми, но уже
не достаточными условиями устойчивости. В этом последнем
случае к уравнениям (4.12) должны быть добавлены некоторые
дополнительные алгебраические уравнения, аналогичные соот-
ветствующим уравнениям §§ 2 и 3 настоящей главы; от харак-
тера корней этих уравнений также зависит решение вопроса
об устойчивости периодического движения. В указанном смы-
сле приведенная в настоящем параграфе теорема является ме-
нее общей, нежели теорема § 2.
Вместе с тем в частном случае, когда первые k уравнений
(4.1) имеют вид
xs = i<nnsxs + pFs(x{, . . xh t, ц) (s = 1, ..k),
то есть представляют собой квазилинейные уравнения в канони-
ческой записи, функции z*sj (t), согласно (4.8) и (4.5), будут
(s = i,.... 1-, /=1,.... k),
190
СУЩЕСТВОВАНИЕ И УСТОЙЧИВОСТЬ РЕШЕНИЙ
(ГЛ. V
и поэтому выражения (2.41) получатся из выражений (4.9).
Отсюда непосредственно вытекает возможность обобщения тео-
ремы § 2, упомянутого в п. 5 указанного параграфа.
Практическое использование сформулированных выше тео-
рем связано с трудностями, обусловленными необходимостью
знать функции z*; (/), то есть периодические решения системы
линейных однородных уравнений (4.8) с периодическими ко-
эффициентами. О путях преодоления этих трудностей будет
сказано в § 9 настоящей главы.
Заметим в заключение, что условие отсутствия у уравне-
ния (4.12) корня х = 0 совпадает с условием (4.10), обеспечи-
вающим существование периодических решений. Закономер-
ность такого совпадения уже подчеркивалась выше (см. сноску
на стр. 167).
2. Доказательство теорем. Обратимся к доказательству сформулирован-
ных выше теорем. Проведем это доказательство несколько иначе, чем в мо-
нографии [275], что, как отмечалось, позволит обойти ограничение относи-
тельно отсутствия кратных корней у уравнения (4.12).
а) Доказательство теоремы 1. Как и в §§ 2 и 3 настоящей главы, попы-
таемся так подобрать начальные условия
М°> ₽1....₽/•	g) = x°(0) + ₽s (s=l......1}	(4.13)
для решения xs(Z, Pi...|Ф, pi) исходной системы уравнений (4.1), чтобы
оно было периодическим по t с периодом Т. В силу сделанных предположе-
ний о характере правых частей уравнений (4.1) рассматриваемое решение
будет аналитическим относительно (31, ..., р( и pi, по крайней мере при
достаточно малых значениях перечисленных параметров, и поэтому его мож-
но искать в виде ряда
I
*s = *s (t, Р,.Pz, pi) = х° (/) + 2	(0 ₽г +	(/) +
i-1
l	1	’
+ В 2 csi « Pz + DS H2 + 2 2 < (0 ₽iP/ + • • • (4.14)
z-1	z-j /==!
по целым положительным степеням Pi, ... , Р/, pi.
Подставив выражения (4.14) в дифференциальные уравнения (4.1) и
начальные условия (4.13), разлагая в ряды и приравнивая коэффициенты при
одинаковых степенях параметров в обеих частях равенств, придем, в частно-
сти, к следующим уравнениям и начальным условиям для определения функ-
ций z4sl(/) и ВД1) (прочие коэффициенты рядов (4.14) в дальнейшем не
понадобятся):
I
= S (-^1	Л/(0)=б^
/-1 '	1 7
,	(4.15)
+ ВИ0) = 0.
i=»l V 1 '
§ 4]
НЕАВТОНОМНЫЕ СИСТЕМЫ, БЛИЗКИЕ К НЕЛИНЕЙНЫМ
191
Напомним, что круглые скобки, в которые заключены функции F, и X, и их
производные, указывают на то, что эти величины вычислены для решения
(4.3) порождающей системы (4.2) и при р, = 0.
Уравнения (4.15) представляют собой линейные системы с периодически-
ми коэффициентами, однородная часть которых совпадает с уравнениями в
вариациях (4.5) для порождающей системы (4.2) и решения (4.3).
Необходимыми п достаточными условиями периодичности решения (4.14)
будут равенства
I	I
ФИ ₽ь  •₽z. И) ss [xs] У, [4si] ₽/ + р [В.,] + р У [CS1-] рг +
i=i	/=1
+ [*М Н2 + 2 2 [^/]	+ • • - = 0 (s=l........./), (4.16)
i=l /!
где, подобно предыдущему, использовано обозначение
[F] — F\l=T — F\t=Q.
Для того чтобы исходная система (4.1) допускала периодическое реше-
ние с периодом Т, обращающееся при р = 0 в периодическое решение (4.3)
порождающей системы (4.2), уравнения (4.16) должны допускать относи-
тельно функций pi(p)......Рг(ц) решение, обращающееся в нуль при р = 0.
Получим условия, при которых последнее имеет место. Решение вопроса было
бы тривиальным, если бы функциональный определитель
дСФр	Ф;)
^(₽1....₽/)	р
= I [Л,-] | = I Л, (Г) - Asi (0) I =
=pz=n=o
=	(s, /=1.....Z)
(4.17)
был отличен от нуля. Однако поскольку по условиям теоремы система (4.1)
при р = 0 допускает периодическое решение (4.3), зависящее от k произволь-
ных параметров a,i, .... ал, то и система (4.16) при р = 0 должна допу-
скать относительно ..., р( решение, зависящее от такого же числа пара-
метров; это решение, в соответствии с равенствами (4.13), имеет вид
₽s(0) = x°(0, <х1( .... ak)-x°(0, <х‘, .... ак) (s=l../),	(4.18)
где	а^—некоторые фиксированные значения величин а1...........ал.
Отсюда следует, что не только определитель (4.17), ио и все его миноры до
I — k + 1-го порядка включительно должны обращаться в нуль.
Сказанное вытекает также из следующего рассуждения. В силу равенств
(4.15) функции Asi(t) образуют фундаментальную систему решений уравне-
ний в вариациях (4.5). Поэтому характеристическое уравнение этой системы
может быть записано в форме (см. п. 3 § 3 главы III)
1А((П-М1 = 0	(S, /=1./)-	(4.19)
Но ввиду наличия у системы в вариациях k периодических решений (4.7)
это уравнение должно иметь корень р = 1 кратности k. Отсюда и следует,
что определитель (4.17) должен обращаться в нуль вместе со своими мино-
рами до I — k + 1-го порядка включительно.
Допустим теперь в согласии с условием теоремы, что по крайней мере
один из миноров / — k-ro порядка определителя (4.17) отличен от нуля, то
192
СУЩЕСТВОВАНИЕ II УСТОЙЧИВОСТЬ РЕШЕНИЙ
[ГЛ. V
есть что система в вариациях (4.5) имеет в точности k периодических реше-
ний; пусть для определенности
a(^+i....^z)
....₽/) р
-Pz-H-0
+1, Zs + i] • • • \Ak +1, z]
Mi. 4+d	• • • Mz/]
¥= 0.
(4.20)
Покажем, ибо в дальнейшем это понадобится, что из последнего условия
следует отличие от нуля определителя
Rk =
д(Х!.....4)
Э(а1.....ak) (_0
(4.21)
матрицы (4.4).
Рассмотрим систему линейных однородных алгебраических уравнений
I
2	= °	<s=1......О-	(4.22)
z=i
Так как согласно сказанному выше определитель этой системы, совпадающий
с определителем (4.17), обращается в нуль вместе со своими минорами до
I — k+ 1-го порядка включительно, то указанная система допускает k ли-
нейно независимых решений. Чтобы получить такую систему решений, рас-
смотрим последние l — k уравнений (4.22). В силу (4.20) можно разрешить
эти уравнения относительно + ь .... qt, выразив последние через q\, ..., q^.
Придавая q\, ..., qh какие-либо численные значения, мы получим решение
системы (4.22). Рассматривая k систем таких численных значений с отлич-
ным от нуля определителем, получим полную совокупность из k независимых
решений уравнений (4.22). Обозначим указанные системы решений через
?1Ь . • •, qn (j — 1, ..  , 6) и выберем величины qij, .... q^j следующим
образом:
fl, s = /,
“to.	(“3>
Можно, однако, указать и иную систему решений уравнений (4.22).
С этой целью папомним, что при ц = 0 уравнения (4.16) должны тожде-
ственно удовлетворяться при значениях ря, взятых согласно равенствам
(4.18). Дифференцируя эти тождества по cii...ось и полагая затем
Pi = ... =Р< = 0, будем иметь
Sdx°, (0, а,, .... аД
Msil---Л-----------~ = ° (s = 1....1’ ' = 1......(4-24)
z-i	1
Таким образом, уравнения (4.22) имеют систему решений
dxs(0, Ct,, .... ak)
rsJ	да.]
(s=l........I; i= 1, .... k),	(4.25)
которые, естественно, должны быть линейными комбинациями решений q,j:
k
rsj= 2 aaj4sa (s == 1...............................(4.26)
a=l
где oaj—некоторые постоянные. Из равенств (4.26) вытекает, что всевоз-
можные определители ft-го порядка, состоящие из величин rtj, равны произ-
НЕАВТОНОМНЫЕ СИСТЕМЫ, БЛИЗКИЕ К НЕЛИНЕЙНЫМ
193
ведению определи геля | ацi| (г, j = 1, k) на соответствующие определи-
тели из величин qai. Но так как по условию хотя бы один из определителей
матрицы
II ^(0, а,...а,)
I а(а!.....
(4.27)
отличен от нуля, то определитель | ащ| также отличен от нуля. Полагая
теперь в равенствах (4.26) s = 1, ..., k, будем иметь согласно (4.23) и
(4.25)
йх (0, а,.....а.)
-- = asj (s, / = 1..........k).	(4.28)
Следовательно, определитель (4.21) равен определителю | a3j | и, таким обра-
зом, будет отличен от пуля.
Вернемся теперь к изучению вопроса о существовании интересующих
нас решений уравнений (4.16) в рассматриваемом особом случае. С этой
целью несколько преобразуем указанные уравнения. Рассмотрим, наряду с
Л.,;(/), фундаментальную систему решений 71si(l, т) уравнений в вариациях
(4.5), определенную начальными условиями не при 7 = 0, как Ла,(/), а при
t = т:
Asi (т, т) = Ssi.	(4.29)
Очевидно, что
As{ (Л 0) = Asl (/).	(4.30)
Если z*! (/), .... z*ft(/) суть k периодических решений системы (4.8), со-
пряженной с системой в вариациях (4.5), то, в силу свойства решений со-
пряженных систем (см. п. 4 § 3 главы III), для каждой пары решений этих
систем будет иметь место соотношение
k
=	(; = 1..../;	7=1, .... k).	(4.31)
S = I
В соответствии с равенствами (4.15), (4.29) и (4.30) уравнения (4.15) могут
быть записаны в форме
= 2 ~Asi (Т, 0) ₽(. - ₽s + Ц [Bs] + и 2	₽1 +
l-I	i-1
I I
+ Ps]lx2+2 2[£17]₽Л+ ••• =°	(s»l...../)• (4.32)
i-1 /-I
Умножим каждое из этих уравнений на z*sq(T) и просуммируем по
индексу s. В силу соотношений (4.31) и периодичности функций zsq (/) имеем
2 2	°)4 (пih - 2 << (п2 (°)₽/ - 2 4k=°-
$.1 1=1	4=1	1=1	4=1
7 И И Кпрхмян
194
СУЩЕСТВОВАНИЕ И УСТОЙЧИВОСТЬ РЕШЕНИЙ
[ГЛ. V
Поэтому в результате указанного суммирования получатся следующие k ра-
венств, которыми заменим первые k уравнений (4.16):
!	I 1
*q=и 2 [bj(пъ 2 2 [<Ч]z'sq₽/ +
S=1	S=1 i=l
+ н2 2 Pdz'sq(n + 2 2 2 [£o] zsq(Ш+ ••• =o (4.33)
s-l	S-1 /=1 /=1
(9=1,..., k).
В качестве остальных уравнений возьмем последние I—k уравнении
(4.16). В силу условия (4.20) эти уравнения имеют решение относительно
неизвестных Р^ +....... которые будут аналитическими функциями
Pi, '.. ., [ц и (.1 вблизи точки 01. 0ft = (.1 = 0, обращающимися в нуль
в этой точке. Подставив указанные величины в уравнения (4.33), будем иметь
k уравнений для определения k неизвестных Pi.......Рй. Остается, таким
образом, изучить вопрос о решениях этих последних уравнений.
Как уже отмечалось, при ц = 0 уравнения (4.16) допускают для р... р;
решение (4.18), зависящее от k произвольных параметров. Вследствие не-
равенства нулю определителя (4.21) за такие параметры могут быть приняты
величины Pi(0),..., Pt(O). Но тогда при ц = 0 уравнения (4.33) после под-
становки в них Pft+i.Pi должны удовлетворяться тождественно при любых
значениях Pi,..., 0й. Поэтому указанные уравнения непременно должны со-
держать параметр ц в качестве множителя. Сократив на этот множитель,
получим для определения Pi..fb< систему вида
I
Ф,(₽......в)=2РМ4?(П + Ф; (Р1..............РЛ, н) = 0	(4.34)
s=l
(<7=1.... k),
где — аналитическая функция своих аргументов вблизи точки Р] = ,.. =
= Рй = р = 0, обращающаяся в нуль в указанной точке.
Необходимым условием существования решения уравнений (4.34), обра-
щающегося в нуль при р = 0, являются равенства
I
Pq(«i......«а) = 2 РЧ z'sq (П = 0	(<7= !>•••, k).	(4.35)
s==l
Рассмотрим полученные соотношения. Решение уравнений (4.15) для функ-
ций при соответствующих начальных условиях может быть записано
в форме
BS(O=J	....х°, г, 0)Ast(i, r)dr. (4.36)
о 1-1
Если учесть теперь обозначения [f] = F — F |/с=0 и равенства (4.31), то
условия (4.35) могут быть представлены в следующем окончательном виде:
т I
Pq(al’ > <4= f	....х°, /, 0)z’^(/)d/ = 0 (9=1...k).	(4.37)
0 i = l
Эти равенства, которые служат для определения параметров порождающего
решения оч....ан, совпадают с уравнениями (4.9), фигурирующими в фор-
мулировке доказываемой теоремы.
§ 4]
НЕАВТОНОМНЫЕ СИСТЕМЫ, БЛИЗКИЕ К НЕЛИНЕЙНЫМ
195
При выполнении соотношений (4.37) для существования рассматриваемых
решений уравнений (4.34) достаточно, чтобы был отличен от нуля функцио-
нальный определитель
Покажем, что последний
(4.39)
лишь не равным нулю множителем. Это можно было бы сделать подобно
§§ 2 и 3 настоящей главы — путем рассмотрения коэффициентов ряда (4.14)
при квадратичных членах. Однако в данном случае проще, следуя И. Г. Мал-
кину [275], воспользоваться иным путем, тем более что основные элементы
доказательства подготовлены предшествующими рассуждениями.
Заметим, что согласно (4.34) н (4.35)
Pq = Ф? (°....°-	°).
и заменим в функциях Ф, величины р,, ..., (м величинами ai.......а/, при
помощи подстановки (4.18). Обозначим результат этой подстановки через
ip,(ai....сс/,,р). Тогда будем иметь
pq-®q(*........«А-	0)	(4.40)
_______., Ф&) I
_______1₽1
<3(Ф„
(4.38)
определитель отличается
^-ц=0
от определителя
и определитель (4.38) представится в форме
, = д(ф,......ФА) ^(Р,........Pfe)
k <5(«r ak) ' д(^.............ak) ^=o
или, согласно (4.18), (4.40) и (4.21), в виде
d(Pj.....Pfe) .	.... 4) I 1 d(pi............Pk)
k <5(«1.......ak) ‘ <3(ai.....afe) “ Rk a(ai> ak) '
Так как по доказанному выше определитель Rk отличен от нуля, то условие
неравенства нулю определителя Л сводится к требованию
Таким образом, мы показали, что каждому простому решению уравнений
(4.9) соответствует единственное решение уравнений (4.16), обращающееся
в нуль при ц = 0; это решение будет аналитическим относительно р вблизи
точки р = 0. Тем самым показано, что каждому простому решению уравне-
ний (4.9) отвечает единственное периодическое решение исходной системы
дифференциальных уравнений (4.1), обращающееся при р = 0 в периодиче-
ское решение (4.3) порождающей системы (4.2) и аналитическое относитель-
но параметра р при достаточно малых его значениях. Иными словами, тео-
рема 1 доказана.
б) Доказательство теоремы 2. Рассмотрим теперь вопрос об устойчивости
периодических решений уравнений (4.1). Использование в данном случае ха-
рактеристического уравнения в форме А. Пуанкаре (см. п. 7 § 3 главы III)
196
СУЩЕСТВОВАНИЕ И УСТОЙЧИВОСТЬ РЕШЕНИЙ
[ГЛ, V
потребовало бы вычисления коэффициентов при квадратичных членах в раз-
ложениях (4.14). Избежать указанных чисто технических трудностей можно
путем применения подстановки Н. А. Артемьева, как это сделано в моногра-
фии [275], однако при этом возникнет ограничение, о котором говорилось
в п. 1 настоящего параграфа. Поэтому мы воспользуемся здесь записью
характеристического уравнения в обычной форме:
IZMD-WI = O («-/='.О-	(4.42)
Здесь ysj(fj—фундаментальная система решений уравнений в вариациях
для системы (4.1) и изучаемого периодического решения.
Указанные уравнения в вариациях имеют вид
ХС)„.
дх,	дх, дх / ч
‘	<7=1	‘	4
(«= 1.....О,
(4.43)
где круглые скобки означают, что заключенные в них производные вычислены
при р = 0 и для порождающего решения (4.3), а иевыписанные члены имеют
относительно р порядок выше первого.
Через x^(t) в уравнениях (4.43) обозначен коэффициент при первой сте-
пени р в разложении
xq (0 = x°q (0 + P*,’ U) + P242) (0 +	(4-44)
невозмущенного периодического решения уравнений (4.1); согласно доказан-
ному выше данное решение при условиях (4.37) н (4.41), выполнение кото-
рых предполагается, является аналитической функцией р при достаточно ма-
лых его значениях и поэтому представимо в виде ряда (4.44). Коэффициенты
этого ряда являются периодическими функциями t с периодом Т, причем xt (t)
удовлетворяет уравнениям (4.2) (порождающей системе), а х^ (Г)— уравне-
ниям
=S (4г') +(s=1......................°’ м
1-1 '	1
получающимся в результате подстановки ряда (4.44) в исходные уравнения
(4.1) и приравнивания коэффициентов при р в обеих частях равенства.
Будем искать фундаментальную систему решений уравнений в вариациях
(4.43), удовлетворяющую начальным условиям
>Jsj (0) — f>sj । Q
s = i,
S=Aj,
(4.46)
в виде ряда
У si	“ y°sl (0 + РУ«/ (0 + • • •
(s,	1, .... I)-	(4.47)
Подставив выражения (4.47) в уравнения (4.43) и начальные условия (4.46)
и приравнивая коэффициенты при одинаковых степенях р в обеих частях
§ 41
НЕАВТОНОМНЫЕ СИСТЕМЫ, БЛИЗКИЕ К НЕЛИНЕЙНЫМ
197
получившихся равенств, приходим к следующим дифференциальным урав-
нениям и начальным условиям для определения функций ySJ- (/) и у^) (/):
УЦ’
(8. /=1............/),
V ( д!Х°
ЛчЛ I дх. дх

(4.48)
(4.49)
(8, j = 1.........../).
Функции у°] (t), таким образом, образуют уже рассматривавшуюся
выше фундаментальную систему решений 4SJ(/) уравнений в вариациях (4.5)
для порождающей системы (4.2) и порождающего решения (4.3):
У°, = ASj (/)	(s, j = 1..../).	(4.50)
Что же касается решений уравнений (4.49), то они могут быть представлены
в форме
У*1 (0 = / xj S	+	}xv}yU Asq(t,x)dx (1.51)
0 q=1 i=l L4 ‘ ' v=i 4 1 v/	J/ = r
(8, /=1...../).
Здесь Asr(t, t)—введенная выше фундаментальная система решений урав-
нений в вариациях (4.5), определенная начальными условиями (4.29).
При учете (4.44) характеристическое уравнение (4.42) может быть пред-
ставлено в следующей матричной записи:
I У°(7-) + цУ(1>(Л + --Ер 1 = 0,	(4.52)
где У°(Г) и У(,)(7')—квадратные (Z X /(-матрицы, элементами которых яв-
ляются соответственно у°, (Г) и у^} (Т), а Е — единичная (/X/)-матрица.
Введем в рассмотрение матрицы
zH(0)	...	zu(0)	0	...	0
г/г:(0)	• • •	zkk (°)	о	...	о
гА + 1, 1 (°)   •	Zk+1, k (°) 1	• • •	0
ZZ1 (0)	...	zlk (0)	0	...	1
Z’(T) =
z'n(T)	...	zki(T)	z;+1>1(7-)	...	zn(T)
...	zkk(T)	zM'k(T)	...	4(Г)
0	...	0	1	...	0
0	...	0	0	...	1
(4.53)
198
СУЩЕСТВОВАНИЕ И УСТОЙЧИВОСТЬ РЕШЕНИЙ
[ГЛ. V
Обе эти матрицы невырожденные: первая — вследствие отличия от нуля
определителя (4.21) и соотношений (4.7), вторая — в силу указанных соот-
ношений, равенств (4.11) и периодичности функций z*sl (/). Поэтому урав-
нение
I Z* (Г)[У° (Г) + цУ(1) (Г) + ... -£p]-Z(0)| = 0
равносильно характеристическому уравнению (4.52). Введя обозначения
С° = Z* (Г) У° (Г) Z (0), С' = Z* (Г) Z (0) = Z* (0) Z (0),
С(1) = Z (T)YW (Т) Z (0),	(4'54)
представим полученное уравнение в следующей форме:
/?(ц, р) = | С°-рС' + рС(1)+ ...| = 0.	(4.55)
Вычислим элементы с°г, с'рг и матриц С°, С' и С(1). Предварительно
заметим, что имеют место соотношения
Z	-О
So	дхп
zjr (°) у Pi Ш = zpr W “ -^7 (р = 1.......Z; г = 1.....k).	(4.56)
/-1
Действительно, рассматриваемая сумма есть решение уравнений (4.48) (или,
что то же самое, уравнений (4.5)), удовлетворяющее начальным условиям
/	I
2 zfr (0) У°р1 (t) = 2 zir (0) бр/ = Zpr (О)-
/-1	/-1
Но в силу теоремы о единственности решений таким начальным условиям мо-
гут удовлетворять только функции, совпадающие с zpr(t); согласно равен-
ствам (4.7) эти функции равны производным дх°р/даг.
Используя равенства (4.50), (4.30), (4.31), (4.9) и (4.56), находим:
при р, г = 1....k
срг=2 2 z}p{T)y^T) zlr(0) =
/-1 S=1
I	I	I
= 2 zir W 2 ZSP (Л Asi 0) = 2 zir (°) zip (0) - bpr.
/=1	s=l	/=1
I
cpr ~ 2 Zip (0) zir (0) = &pr cpr"’
при p = k+ 1....../;	r = 1..k
i	i
^pr- 2 zir (°) Api °) = 2 zir (0)У°Р1 (Л = zpr (0),
/=1	/=1
z
cpr ~ 2 ^ipzjr (0) = Zpr (0) = cpr’
§ 4]
НЕАВТОНОМНЫЕ СИСТЕМЫ, БЛИЗКИЕ К НЕЛИНЕЙНЫМ
199
при р = 1, ..k; г = k + 1, ../
I	I
с°Рг = 2 4 CD y°sr СП = 2 <р СП Asr (Т, 0) = zrp (0),
с'рг = 2 г/р (°) б/г = 2ГР (°) = Срг’
/ = 1
при р, г = k + 1.Z
I I
4 = 2 2М/г4 (7’)=4(л)
/«1
I
4=2M/p = V	(4-57)
/=1
Далее при учете тех же соотношений, а также равенств (4.51) находим
последовательно (для р, г = 1.k)
I I
^рСП$(Пг1г(0)~
1=1 S=1
I	I
x S уОч zir (°) S CH t) z'sp (П dt =
/=1	S=1
Преобразуем последнее выражение, использовав равенство
d дХ^ _^1дХДд^	д 1дХД1 d(Fq)
dt даг \ dxv / даг v даг \ 3xv / + до-т
v-i	i-1
200
СУЩЕСТВОВАНИЕ И УСТОЙЧИВОСТЬ РЕШЕНИЙ
[ГЛ. V
которое получается дифференцированием соотношения (4.45) по параметру ar.
Тогда
л) = f у Сдхч)\ _ у (дХ«\ дхУ
Cpr J di \ даг / ^4 \ dxv ) диг
о <7=1 L	v=i
z«prf<
(р, г = 1.........k).
Интегрируя по частям и учитывая, что функции zqp удовлетворяют уравне-
ниям (4.8), находим
Т I	I Г	I
о) I V дхч)	*	С V	v (дх<Л	дх^'	*
CPr~\2j dar	Zpp	J 21	dar	Z4P+ 21\dxv)	dar	Z«p
0 <j=l	0 <7 = 1 L	V=1
dt =
0 <7 = 1	0 <7 = 1
T
Знак | F (/) обозначает здесь подстановку F(T)—^(0). Поскольку функ-
о
ции х^ являются периодическими только при определенных значениях пара-
метров аг (а именно лишь при значениях, удовлетворяющих уравнениям
(4.9)), то производные дх^/даг, вообще говоря, не будут периодическими,
а поэтому выражения отличны от нуля. Вместе с тем функции z*ip
являются периодическими при любых значениях параметров аг, и поэтому
dz*
выражения г(1) чр также периодические. Но тогда получаем
« даг
О <7 = 1	0 <7 = 1	0 <7 = 1
,d)£i
« да
0 <7=1
.(!)_
<7 ^<?р'
Используем теперь соотношение
^-S414p=S(?«) zpp’
<7 = 1	<7 = 1
/1\	•
которое легко получается, если учесть, что функции xq и zqp удовлетво-
ряют соответственно уравнениям (4.45) и (4.8). Тогда при учете обозначений
(4.9) приведем выражения для величин к следующей окончательной
форме:
I I
5 । V . дРр
ср’’=-^;] 1(^)гчРЛ=-^Г	(Р, г=1, .... fe). (4.58)
0 <7-1
§ 4]
НЕАВТОНОМНЫЕ системы, близкие к нелинейным
201
В соответствии с равенствами (4.54), (4.57) и (4.58) уравнение (4.55)
может быть представлено в виде
R(p- Р) =
ЗР, 1-р+ц-^	ар, и dak	4+i, i(0) (i~p)+ +pci4+i •	zj, (0) (I-p) + + pciz
dPk р За,	dPk 1"p + paS7	4+i, k (°> < -p>+ +p4'4+i •	4fe (0) (1 -p) + +p4z
2М1. 1(0) (1-р) +	с-р’ +	&k+i, k+i (Г)~р +	4+1,/<г> +
+Н+1,1 	+ w(I) + p 4+1,4	+ p4+ 1. 4+1 ’	•• +p4+i, z
гп (0) (1 -р) +	2lk (0) “ p) +	'//, ft+1 <V +	y°a (D-P +
+ ЦС(1)	+pc!4	+p44+i 	+ uc(D
= 0
(4.59)
Здесь все элементы определителя выписаны с точностью до членов, имеющих
относительно р порядок не выше первого.
При р = 0 уравнение (4.59) имеет корень р<°> = 1 кратности /г; все про-
чие корни, в соответствии с условиями теоремы, имеют модули, меньше еди-
ницы. При достаточно малых р модули этих последних корней, в силу не-
прерывности, останутся меньшими единицы, и решение вопроса об устойчи-
вости будет зависеть от характера следующего приближения к корням, обра-
щающимся в единицу при р = 0.
Обратимся к вычислению указанного приближения. Как и в §§ 2 и 3 на-
стоящей главы, раскроем определитель в левой части уравнения (4.59) по
минорам первых k столбцов в соответствии с теоремой Бине—Коши [106].
Тогда рассматриваемое уравнение представится в форме
Я(Р> Р) =
,	, dPf	dPt
1 — р + р -=-- . . . Ц -;-
da,	oak
dPk
да
, дРк
••• *-р + ^
4+1,а+1(Л-1 ... 4+1. z (Л
Л,/г+,(Л	••• Л; (Л ~ 1
+
+ R* (р, р) = О. (4.60)
где функция R*(p, р) содержит в своем разложении по степеням р и 1—р
лишь члены не ниже k + 1-го порядка относительно этих величин, в то время
как член, представленный в виде произведения определителей, имеет относи-
тельно совокупности тех же величин порядок k.
Дальнейшие рассуждения вполне аналогичны проведенным в §§ 2 и 3
настоящей главы: из теоремы о неявных функциях [162] следует, что инте-
ресующие нас корни уравнения (4.60) можно разыскивать в виде рядов
р = 1 + рх + рК (р),	(4.61)
202
СУЩЕСТВОВАНИЕ И УСТОЙЧИВОСТЬ РЕШЕНИЙ
[ГЛ. V
где К(0) =0. Подставив выражения (4.61) в уравнение (4.60), будем иметь
R [р, 1 + цх + рЛ (ц)] =
= И*
дР,	dPt
да, Х	"	да.
1	к
дРк	дРк
'tai	'''	дак
Ук + l, k+l ID 1 ‘ ' Uk+1, I Ю
	+ . . . = 0,
У I,	1 (Г)	... У°и (Г) — 1 I (4.62)
где невыписанные слагаемые имеют относительно [1 порядок не ниже k + 1.
Второй определитель в равенстве (4.62) отличен от нуля, ибо в силу соотно-
шений (4.50) и (4.48) он совпадает с определителем (4.20). Поэтому из усло-
вия равенства пулю коэффициента при рк в левой части уравнения (4.62)
получаем следующее уравнение /г-й степени для определения поправок х
к изучаемым корням уравнения (4.59):
д,/х =0	(s, /=1......k).
(4.63)
Но при достаточно малом р условия устойчивости |ps| < 1 эквивалентны
неравенствам Re xs < 0, а условия I ps I > 1—неравенствам Re xs > 0; при
Re Xs — 0 для суждения об устойчивости необходимо знать | р., | с точностью
до членов с ц в степени выше первой.
Но уравнение (4.63) совпадает с (4.12). Таким образом, теорема дока-
зана.
§ 5. Автономные системы, близкие к произвольным нелинейным
Рассмотрим теперь автономную систему
..., xz) + hFhxI( ..., xt, и) (s=l, ...,/) (5.1)
где Xs и Fs — аналитические функции переменных хь ... , х;
в замкнутой области G, которой принадлежат все изучаемые
ниже периодические решения; Д, к тому же являются аналити-
ческими функциями параметра ц 0 при достаточно малых, его
значениях *).
Пусть отвечающая уравнениям (5.1) порождающая система
х>ХДх°, ..., х°) (s = l, ..., /),	(5.2)
допускает семейство периодических решений
< = ai> aA-i)’	(5-3)
зависящее, кроме постоянной а, которая вследствие автономно-
сти системы всегда может быть добавлена к t. также от некото-
рого числа k—1<С/—1 произвольных параметров аь . .., а^-ь
Допустим, что решение (5.3) является аналитическим относи-
тельно этих параметров вблизи рассматриваемых ниже «порож-
*) О возможности смягчения этих требований см. п. 2 § 6 настоящей
главы.
§ 5]
АВТОНОМНЫЕ СИСТЕМЫ, БЛИЗКИЕ К НЕЛИНЕЙНЫМ
203
дающих» значений а^а*, aft_I=a^_I. Как и в § 4, пред-
полагаем, что параметры ai, . .., a^-i входят в выражения
(5.3) независимо, то есть что при упомянутых порождающих
значениях параметров а, = а*, ak_i = a*k_i отличен от нуля
по крайней мере один из определителей k— 1-го порядка, содер-
жащийся в матрице (4.4).
Рассмотрим систему уравнений в вариациях, отвечающую
порождающей системе (5.2) и порождающему решению:
Здесь
zs = psiZi + ... 4 pslzi (s = 1, ..., /).
Л/ =---------------- (s,/= 1, ..., /).
OXj
(5.4)
(5.5)
В силу свойства уравнений в вариациях (см. п. 2 § 3 гла-
вы III) система (5.4) допускает k решений вида
дх°
^/(0 = -^-	(s=l, ..., fe-l),	(5.6)
^(0 = ^,	(5.7)
получающихся путем дифференцирования решений (5.3) соот-
ветственно по ai, . .., ос/<—1 и по t (напомним, что к t всегда
можно добавить еще одну постоянную а).
В дальнейшем необходимо различать два случая: когда пе-
риод порождающего решения Т не зависит от параметров
ai, ..., aft_i и когда он зависит по крайней мере от одного из
этих параметров.
Рассмотрим сначала первый случай. В этом случае можно
утверждать, что производные (5.6) являются Г-периодическими
функциями t и уравнения (5.4) допускают, таким образом, Апе-
риодических решений того же периода. Согласно п. 4 § 3 гла-
вы III столько же Г-периодических решений будет допускать
и система
^s + PiZ+ + Pisz'i =0	(S=l, ...,/),	(5.8)
сопряженная с (5.4). Обозначим эти решения через z*y(/) (/ =
= 1, ..., А) и будем предполагать, что иных периодических ре-
шений система (5.8) не имеет*); не имеет тогда периодиче-
ских решений, помимо (5.6) и (5.7), и система в вариациях
(5.4).
*) Относительно функций z*y не предполагается, что они удовлетворяют
соотношениям типа (4.11), ибо последнее в рассматриваемом случае воз-
можно лишь при выполнении некоторых дополнительных условий (см. стр. 207).
204
СУЩЕСТВОВАНИЕ И УСТОЙЧИВОСТЬ РЕШЕНИЙ
[ГЛ. V
При сформулированных выше условиях имеет место следую-
щая теорема, вытекающая из результатов И. Г. Малкина [275],
которую приведем здесь без доказательства *).
Теорема 1. В случае, когда период порождающего реше-
ния Т не зависит от параметров аь . . ., ай-i, периодические
решения с периодом 7\(р) = Т[1—6(р)] исходной системы урав-
нений (5.1), обращающиеся при р = 0 в периодические (с пе-
риодом Т) решения семейства (5.3) порождающей системы
(5.2), могут соответствовать лишь тем значениям постоянных
ai, . . ., ал-i указанного семейства, которые удовлетворяют
уравнениям
<?>(«!- •••-vHA~U=o (s=i, .... £-1), (5.9)
где
т I
Qs = Qs(ai,	4
° /=1	(5.10)
А =	^х°г^т
(s = 1, ..., k).
Каждому простому решению этих уравнений, то есть реше-
нию, для которого
dQ"s
^-=#0 (s, / = 1,	1),	(5.11)
действительно отвечает при достаточно малых значениях р един-
ственное аналитическое относительно р периодическое решение
системы (5.1) с периодом 7\(р), обращающееся при р = 0 в по-
рождающее.
С точностью до членов порядка р поправка б(р) к периоду
решения при этом определяется по формуле**)
6(p)~-^-g-.	(5.12)
Рассмотрим теперь случай, когда период порождающего ре-
шения Т зависит по крайней мере от одного из параметров
*) Мы формулируем соответствующие результаты в несколько изменен-
ном виде; кроме того, исправлена небольшая описка, вкравшаяся в форму-
лу (9.13) на стр. 417 монографии [275] (в этой формуле перед интегралом
п \
должно СТОЯТЬ р У] | 
р-1/
**) Предполагается, что величина Вк отлична от нуля.
§ 5]	АВТОНОМНЫЕ СИСТЕМЫ, БЛИЗКИЕ К НЕЛИНЕЙНЫМ	205
«1, . . . , aft-ь В этом случае решение уравнений в вариациях
(5.7) по-прежнему является 7-периодическим; что же касается
решений (5.6), то они теперь не являются периодическими. Дей-
ствительно, дифференцируя по aj тождества
хЛН’7'(а1.....ai............aA-i] = ^(f> ан •••’ aA-i)>
находим
о -	„,	,	, дТ дх°	дх°
х 17 •+ Т (а . . ., а. .), а , .. ., а. .1 -ч-|--з—	= я—	(5.13)
«I \ 1’	’ k-lj’ I’ ’ A-IJ да, 1 да, ,	да, , '	’
I I t + T I t
или, при учете 7-периодичности производной х°,
_	ч дТ
~ x„(t, а., а, .)-:—.	(5.14)
да,	да,	s\ ’ I’ ’ да,	v ’
1 t+T I t	1
Отсюда нетрудно усмотреть, что решения (5.6) можно пред-
ставить в форме
t дТ .о .
г5/ = -7^Ш/>	(5.15)
где через ySj = ai, ..., Oto-i) обозначена 7-периодическая
функция
У si	У si (Л ®| > • • • ,	1)
=	.....а' ... а' 11	= 1-^° + ^-.
I da'j s[_7 (ар .... аА_,) р ' k ']/а'=а(.	7 За/ 5 das
(5.16)
Непосредственная подстановка при учете того, что и
dx°/da;. — решения уравнений в вариациях (5.4), показывает,
что функции ySj удовлетворяют неоднородной системе уравнений
1 лт
^/ = Psi//i/+ •••	+	<5-17)
(s = 1....I; j = 1, ..., k — 1).
Если теперь составить комбинации
дТ	дТ __ дТ	дТ ,
Zs^ ^ak-i Zs’ /‘~J daj ^ak-i Vs’k~x дау	' ’ '
(/=1, .... A-2),
то они будут, очевидно, представлять собой k — 2 периодических
решений уравнений в вариациях (5.4). Вместе с решением (5.7)
эти уравнения, таким образом, допускают в изучаемом случае
206
СУЩЕСТВОВАНИЕ И УСТОЙЧИВОСТЬ РЕШЕНИИ
|ГЛ. V
k—1 периодических решений. Как и выше, будем считать, что
иных периодических решений уравнения в вариациях (5.4) не
имеют.
Тогда в точности k—1 периодических решений zsj (t) (j—
= 1, ..., k—1) допускает также система, сопряженная с (5.4).
При этом будут иметь место соотношения *)
= 0	(/=1, ..., k-\).	(5.19)
s= 1
Действительно, поскольку система (5.17) имеет периодиче-
ское решение, то согласно изложенному в п. 4 § 3 главы III
т I
= 0 (/=1.	*-!)•
о s=l
Справедливость равенств (5.19) непосредственно очевидна те-
перь, если учесть, что х° и z*sj представляют решения сопря-
женных систем и поэтому для них имеют место соотношения
(3.32) главы III.
При сформулированных предположениях И. Г. Малкиным
установлено следующее утверждение, на доказательстве кото-
рого также не будем останавливаться.
Теорема 2. В случае, когда период порождающего реше-
ния Т зависит от параметров а\, . . ., ай_ь периодические ре-
шения с некоторым периодом 7\(ц) исходной системы уравне-
ний (5.1), обращающиеся при ц = 0 в периодические (с перио-
дом Т) решения семейства (5.3) порождающей системы (5.2),
могут соответствовать лишь тем значениям постоянных
ось . . . , as-i указанного семейства, которые удовлетворяют
уравнениям
ViHSW •••’ Х°’ 0)^(0^ = 0 (5.20)
о /=|
(s = 1, .... k — 1).
Каждому простому решению этих уравнений, то есть реше-
нию, для которого
(s> /=1.....^-1).	(5-21)
действительно отвечает при достаточно малых значениях ц
единственное аналитическое относительно ц периодическое ре-
♦) См. сноску на стр. 203.
§ 5]
АВТОНОМНЫЕ СИСТЕМЫ, БЛИЗКИЕ К НЕЛИНЕЙНЫМ
207
шение системы (5.1) с периодом 7\(ц), обращающееся при ц = 0
в порождающее.
Рассмотрим теперь снова более подробно случай, когда пе-
риод порождающего решения Т не зависит от параметров
ан . . • , a/i-ь Наличие k независимых периодических решений
(5.6) и (5.7) системы в вариациях (5.4) в этом случае означает
(см. п. 3 § 3 главы III), что соответствующее характеристиче-
ское уравнение имеет по крайней мере k корней, равных еди-
нице. Предположим, что единице равно именно k корней харак-
теристического уравнения и что все прочие корни имеют модули,
меньшие единицы. Тогда число групп решений системы в вариа-
циях (5.4), отвечающих корню р = 1, будет в точности равно
кратности корня, и этому корню будут отвечать линейные эле-
ментарные делители.
Напомним, далее (см. п. 4 § 3 главы III), что в указанном
предположении решения z*. (/) сопряженной системы (5.8) мо-
гут быть выбраны так, чтобы выполнялись соотношения
=	(*, /= 1, .••> £).	(5.22)
Но тогда, согласно (5.7), при i — k имеем
v .о *	(° ПРИ 1 = ’• • • •- k~ !>
i = ii	-и
_i s s/ 11 при ] = k
и формулы (5.10) для величин Bs дают
Й!= ... =5^ = 0, Bk=l.	(5.23)
При учете последних равенств уравнения (5.9) для определе-
ния величин см, . . . , аь-\ принимают вид
т I
<?. = («...........................У. о)г;,ю<и = о
О / = |
(5=1, ..., k).
В рассматриваемом случае существенно упрощается также
и исследование устойчивости периодических решений, что и было
выполнено Р. Ф. Нагаевым [309]. Приведем соответствующий
результат без доказательства, объединив утверждения, касаю-
щиеся существования и устойчивости решений.
Теорема 3. Периодические решения с периодом 7\(ц) =
= Л1 - б(р)] исходной системы уравнений (5.1), обращаю-
щиеся при ц = 0 в периодические (с периодом Т, не зависящим
208
СУЩЕСТВОВАНИЕ И УСТОЙЧИВОСТЬ РЕШЕНИЙ
[ГЛ. V
от параметров а,, ал-i) решения семейства (5.3) порож-
дающей системы (5.2), могут соответствовать лишь тем значе-
ниям параметров ои, . . ., указанного семейства, которые
удовлетворяют уравнениям
т I
Qs(ap .... «fe_,) =	....х°, 0) z]s(t) dt = 0 (5.24)
о / = |
(s= 1....k- 1).
Определенному решению этих уравнений действительно соот-
ветствует при достаточно малых значениях р единственное ана-
литическое относительно ц и устойчивое (асимптотически орби-
тально устойчивое) периодическое решение системы (5.1) с пе-
риодом Т*(р.), обращающееся при ц = 0 в порождающее, если
все корни алгебраического уравнения k— l-й степени
4^--М| = 0	(s, j=l, k-\)	(5.25)
имеют отрицательные вещественные части. При наличии у урав-
нения (5.25) хотя бы одного корня с положительной веществен-
ной частью рассматриваемое решение неустойчиво-, случай нуле-
вых или чисто мнимых корней требует, вообще говоря, допол-
нительного исследования.
С точностью до членов порядка р поправка 6(р) к периоду
решения при этом определяется формулой
т I
6 (Н) - Т J S Fs (х°, ..., х°, 0) z*sk (t) dt. (5.26)
0 s=l
Как и И. Г. Малкин при исследовании устойчивости соответ-
ствующей неавтономной системы [275], Р. Ф. Нагаев использо-
вал в процессе доказательства данной теоремы подстановку
Н. А. Артемьева (см. п. 7 § 3 главы III). При этом, как указы-
валось в § 4 настоящей главы, строго говоря, приходится пред-
полагать, что уравнение (5.25) имеет только простые корни.
Однако, как и в § 4, это ограничение можно обойти, если вос-
пользоваться иным способом исследования устойчивости. На
необходимых при этом достаточно громоздких рассуждениях
и выкладках, аналогичных приведенным в § 4, здесь останавли-
ваться не будем.
В п. 5 § 3 настоящей главы уже отмечалось, что в ряде за-
дач период порождающего решения Т заранее неизвестен и его
можно пытаться определить из условия равенства нулю (с точ-
ностью до членов порядка р) поправки к периоду б(р). Тогда
i 61
СИСТЕМЫ ПОЧТИ ПЕРИОДИЧЕСКИЕ
209
вместо равенств (5.24) и (5.26) получаются k уравнений
Qs(аь а*_1) = 0 (s — 1..........k),	(5.27)
которые служат одновременно для определения постоянных
аь . . ., аы и периода Т порождающего решения.
Подобно тому как это было установлено в п. 5 § 3 для ква-
зилинейных систем, уравнения (5.27) и (5.25) могут быть фор-
мально получены из соответствующих уравнений (4.9) и (4.12),
найденных для неавтономного случая. Для этого при переходе
от неавтономной системы к автономной следует учесть, что
одна из постоянных (пусть это будет оц) в автономном случае
может быть назначена произвольно, и что уравнение (4.12)
будет непременно иметь один нулевой корень. Отделив этот ко-
рень, несущественный в силу автономности системы (см. п. 6
§ 3 главы III), как раз и придем к уравнению (5.25), специально
полученному для автономного случая.
По поводу взаимоотношения теорем, приведенных в настоя-
щем параграфе, с теоремой § 3, доказанной для квазилинейной
системы, можно повторить сказанное в п. 1 § 4 по аналогич-
ному поводу*). То же касается замечания относительно совпа-
дения условия (5.11) с условием отсутствия нулевого корня
у уравнения (5.25) (см. п. 3 § 3 и п. 1 § 4 настоящей главы).
Следует лишь добавить, что в случае квазилинейных автоном-
ных систем период порождающего решения Т всегда не зависит
от параметров ац . . ., ап порождающего решения.
Вопрос об устойчивости периодических решений в случае,
когда период порождающего решения зависит хотя бы от од-
ного из параметров аь . .. , аь-ь является более сложным, ибо,
как следует из изложенного выше, в этом случае элементарные
делители, отвечающие корню р<°> = 1 характеристического урав-
нения системы в вариациях, не являются линейными. Исследо-
вание устойчивости движения для ряда конкретизированных
систем в указанном случае приводится в третьей части книги.
§ 6. Системы почти периодические, с разрывными
правыми частями и с запаздыванием
1. Почти периодические системы. Теоремы предыдущих па-
раграфов допускают обобщение на случаи почти периодиче-
ских систем, а также систем с запаздыванием и систем
*) При сопоставлении теоремы § 3 с теоремой 3 настоящего параграфа
следует иметь в виду, что функции zst- — (>sje~tniai в § 3, в отличие от функ-
ций zSj настоящего параграфа и в отличие от случая неавтономной системы,
рассмотренной в § 2, не удовлетворяют условиям (5.22). Сказанное следует
из соотношений (5.6) и (5.7), определяющих в случае автономной системы
независимые решения уравнения в вариациях (5.4).
210
СУЩЕСТВОВАНИЕ II УСТОЙЧИВОСТЬ РЕШЕНИЙ
[ГЛ. V
с разрывными правыми частями. Соответствующие результаты
приведем здесь без доказательства.
Рассмотрим вначале систему уравнений
xs = Xs(xlt .. ., xb t) + nFs(xb . .xb t, p) (s =-- 1, . .I), (6.1)
где независимая переменная t изменяется в интервале
(—оо, +оо), переменные хь ..., xt — в некоторой области G
пространства этих переменных и параметр ц^О— на отрезке
[0, ро]. При этом функции Xs обладают производными второго
порядка по Х\, ..., X/, а функции Fs — производными первого
порядка по Xi, . . . , Xi и р, и эти производные удовлетворяют
относительно указанных переменных условиям Коши — Лип-
шица с не зависящими от t коэффициентами. По отношению
к t функции Xs непрерывны и периодичны с периодом Т, а функ-
ции Fs почти периодичны*) и притом такие, что при всяком
фиксированном р функции Fs[xi(t), .... xt(t),t, р], где Xj(t) —
произвольные почти периодические функции t, лежащие в обла-
сти G, будут также почти периодическими. Более того, предпо-
лагается, что функции Fs могут быть представлены в виде ко-
нечных сумм
Fs(x}, xpt, p^SpW^, ..., xpt, p)cosv/ +
+ FS(*i> •••> xz, p)sinvpt], (6.2)
где vP — вещественные числа, а функции F^ относительно t не-
прерывны и периодичны с периодом Т.
Пусть, далее, отвечающая уравнениям (6.1) порождающая
система
х° = Х,(х°....х°, /)	(s=l,...,Z)	(6.3)
допускает семейство Т’-периодических решений
= x°(Z, «J (s=l, ...,/),	(6.4)
*) Напомним, что непрерывная функция /(/), определенная при
— оо < / < + оо, называется почти периодической по Г. Бору, если для
всякого сколь угодно малого положительного числа е можно найти такое
положительное число /(е), что внутри каждого интервала длины I можно
найти хотя бы одно число т(е), для которого при всех t выполняется нера-
венство
Конечные суммы вида
f (t) - aQ + 2 (ар cos + bp sin Vpt),
p
где vp — произвольные вещественные числа, вообще говоря, несоиз!иерпмые
между собой, являются почти периодическими функциями.
§ (i[	СИСТЕМЫ ПОЧТИ ПЕРИОДИЧЕСКИЕ	211
зависящее от k-^.1 произвольных параметров ои, осл; как
и выше, предполагается, что эти параметры входят в выраже-
ния (6.4) независимо. Тогда система уравнений в вариациях,
отвечающая порождающей системе (6.3) и порождающему ре-
шению (6.4), допускает k независимых Т-периодических част-
ных решений
дх°
Zsi^==~d^	(s= 1,	1.....k).	(6.5)
При этом характеристическое уравнение указанной системы
в вариациях будет иметь ^-кратный корень р<°) = 1, которому
отвечают линейные элементарные делители (число групп ре-
шений равно кратности корня). Будем предполагать, что
остальные I — k корней имеют модули, отличные от единицы.
При указанных условиях система, сопряженная с системой
в вариациях для уравнений (6.3) и решения (6.4), имеет k
(и только k) периодических решений г’Д/); как и выше, эти
решения всегда можно выбрать так, чтобы выполнялись условия
Введем обозначение
* i
Ps = Ps(at, aj = lim4 J ...............х°,	t, G)zjs(t)dt. (6.7)
о y-i
Тогда при сформулированных условиях будет справедлива
следующая теорема, принадлежащая И. Г. Малкину [275].
Теорема. Для каждого порождающего решения семей-
ства (6.4), лежащего в области G, для которого параметры сц
удовлетворяют уравнениям
Ps(ab ..., aft) = 0	(s=l,	(6.8)
и при этом алгебраическое уравнение k-й степени
лр	I
-^--6s/p| = o (s,/ = 1, ..., k)	(6.9)
не имеет корней с вещественными частями, равными нулю, су-
ществует при достаточно малом ц почти периодическое реше-
ние системы (6.1), обращающееся при ц = 0 в порождающее.
Это почти периодическое решение системы (6.1) будет
асимптотически устойчивым, если все корни уравнения (6.9) и
I — k характеристических показателей системы в вариациях для
212
СУЩЕСТВОВАНИЕ И УСТОЙЧИВОСТЬ РЕШЕНИЙ
[ГЛ. V
порождающей системы и порождающего решения имеют отри-
цательные вещественные части-, если хотя бы одна из веще-
ственных частей указанных величин положительна, то соответ-
ствующее решение неустойчиво. Случай нулевых вещественных
частей требует дополнительного исследования.
Если число параметров порождающего решения равно по-
рядку системы, то есть k — I, сформулированная выше теорема
остается справедливой также и в предположении, что функ-
ции Xs почти периодичны относительно t и при любом выборе
почти периодических функций хД0, лежащих в области G,
функции Xs[x\(t), ..., Xi(/),/] почти периодичны; также почти
периодическими предполагаются в рассматриваемом случае ре-
шения порождающей системы (6.4) и их производные по а;
[275].
Заметим также дополнительно, что если соотношения (6.4)
при k = I рассматривать как уравнения преобразования от пе-
ременных X], ..., х; к новым переменным аь ..., а/, то после
перехода к новым переменным при использовании равенств
(6.3), (6.5) и (6.6) исходная система уравнений (6.1) прини-
мает вид
(
as =	«j....az)....x°(t, a,, t, y]z’s(t)dt (6.10)
/-I
(s=-l, ..., /),
то есть приводится к так называемой стандартной форме. Для
систем такого рода Н. М. Крыловым и Н. И. Боголюбовым
развиты эффективные асимптотические методы исследования не
только стационарных режимов, но и процессов установления
[232, 95, 96].
Поскольку периодические функции представляют собой
частный случай почти периодических, то последний результат,
естественно, справедлив и в случае периодических функций Х3,
Fs и решений х°.
Если в указанном случае от уравнений (6.10) перейти
к осредненный за период Т уравнениям
т I
as = p•••’ х/°> ^z!S^dt .........................0,
о /-1
то непосредственно видно, что условия для нахождения по-
стоянных а,, отвечающих стационарным периодическим режи-
мам, совпадут с уравнениями (4.9) настоящей главы, а вопрос
об устойчивости этих режимов будет решаться знаками веще-
ственных частей корней алгебраического уравнения (4.12).
§ 6]	СИСТЕМЫ ПОЧТИ ПЕРИОДИЧЕСКИ	213
2. Системы с разрывными правыми частями. Как уже отме-
чалось, требования, предъявляемые к правым частям диффе-
ренциальных уравнений, достаточные для справедливости зна-
чительной части результатов, излагаемых в настоящей главе,
с математической точки зрения могут быть значительно ослаб-
лены. Можно сослаться на формулировки соответствующих тео-
рем в монографиях [275, 450], а также в других работах, где,
например, во многих случаях от функций Xs в уравнениях
(4.1), (5.1) и т. д. требуется не аналитичность по переменным
Л'ь ..., Xi, а лишь наличие непрерывных частных производных
второго порядка, а от функций Fs— непрерывных частных про-
изводных первого порядка.
Однако с прикладной точки зрения подобные обобщения
вряд ли имеют большое значение, ибо в обычно встречающихся
па практике задачах правые части дифференциальных урав-
нений движения либо аналитичны, либо разрывны («кусочно-
аналитичны»), Поэтому мы остановимся здесь лишь на этом
последнем случае неаналитичности, который представляет осо-
бый интерес, например, в связи с задачами о синхронизации
вибраторов в системах с сухим трением или с ударами (см. § 7
главы XIV).
Ю. И. Неймарк и Л. П. Шильников с помощью метода то-
чечных отображений показали [320], что для уравнений типа
(4.1), но с разрывными правыми частями, для которых по-
рождающая система допускает периодическое решение, зави-
сящее от k произвольных параметров ai, ..., as, могут суще-
ствовать периодические решения, близкие к решениям поро-
ждающей системы и непрерывно в них переходящие при р—>0.
Для наличия такого соответствия параметры ..., дол-
жны удовлетворять определенным k соотношениям, которые,
однако, в цитированных работах были представлены не в форме
уравнений типа (2.41), (3.49), (4.9), (5.9), а выражены через
определители с элементами, вычисляемыми по так называемой
функции последования. Знание этой функции, характеризую-
щей точечное преобразование, совершаемое решениями системы,
по существу эквивалентно знанию общего интеграла уравнений
движения и поэтому позволяет также подойти к решению во-
проса об устойчивости периодических движений.
Несколько позднее М. 3. Коловский показал [216], что упо-
мянутые условия для определения параметров си, .... ая могут
быть представлены для случая уравнений с разрывными пра-
выми частями в той же интегральной форме (4.9), (5.9) и т. п.,
что и для уравнений с «гладкими» правыми частями. Этот ре-
зультат, обобщенный затем М. 3. Коловским также на случай,
когда сами решения разрывны [217], может быть сформулиро-
ван следующим образом.
214
CJ ШЕСТВОВАНИЕ И УСТОЙЧИВОСТЬ РЕШЕНИЙ
[ГЛ. V
Пусть система
xs = Xs (лу, . .., xz, f) + [iFs (л-,, . . ., Xt, t, p) (s - 1, . .., /) (6.11)
удовлетворяет условиям:
1)	Функции A's и Fs однозначно определены при всех веще-
ственных t, при всех р, лежащих на отрезке О-<р4(ро, и при
всех хь .... Xi, лежащих в области G, которой предполагаются
принадлежащими все рассматриваемые ниже решения уравне-
ний (6.11).
2)	При всех х\,...xt из G и при 0 < р < р0 функции Х3
и Fs непрерывны и периодичны по t с периодом Т.
3)	Область G может быть разбита гладкими поверхностями
на области Gi, Gs, ..., в каждой из которых, вплоть до границ,
Xs обладает непрерывными частными производными второго
порядка по X], .... xh a Fs — непрерывными производными пер-
вого порядка по этим переменным и по р при О^р<^ро.
4)	На границах
<₽„(%!, ..., xz) = 0	(<7=1,2,...)	(6.12)
между областями Gq и Gg+i (называемых поверхностями раз-
рыва) могут иметь место разрывы первого рода либо самих
функций Xs и Fs, либо их производных, перечисленных в п. 3).
Кроме того, при переходе через границу <р? = 0 искомые ре-
шения претерпевают скачки, определяемые «условиями раз-
рыва»
xs (т„ - 0) =	[х, (т? + 0), .... xz(t? + 0), р],	(6.13)
где хд—момент пересечения фазовой траектории с поверхно-
стью разрыва <р? = 0. Функции <р7 и Ф? имеют непрерывные
частные производные второго порядка по Xi, ..., xz и р по
крайней мере на частях поверхностей разрыва, лежащих в об-
ласти G.
5)	Отвечающая уравнениям (6.11) порождающая система
допускает семейство Г-периодических решений
x° = x°(t, ai> ’ ak) (s=l,...,/),	(6.14)
зависящее от k независимых параметров, причем все интеграль-
ные кривые этого семейства проходят через одну и ту же со-
вокупность областей Gq, и для всех этих кривых в точках пере-
сечения их с поверхностями (6.12) выполняются условия
(тг)	<6-15’
/_1 /
Пусть интегральные кривые (6.14) проходят последовательно
через области Gi, ..., Gm. Вследствие замкнутости из области
§ 6]
СИСТЕМЫ ПОЧТИ ПЕРИОДИЧЕСКИЕ
215
0,„ эти кривые должны возвратиться в область Gt; уравнение
границы между G,„ и G, запишем в виде <p„>(xi,	х?) = 0.
Моменты времени п, тш, в которые интегральные кривые
пересекают поверхности <рь срт, вообще говоря, являются
функциями параметров aj, .... ah.
Как и в рассмотренных ранее случаях уравнений с «глад-
кими» правыми частями, уравнения, сопряженные по отноше-
нию к уравнениям в вариациях, составленным для порождаю-
щей системы и порождающего решения, допускают k периоди-
ческих (периода 7') решений z*s. (t) (s = 1, ...,/;/ = 1, ..., k);
теперь, однако, эти решения не будут непрерывными, а должны
удовлетворять следующим условиям:
(s = 1, . . ., /; / — 1, . . ., /г; q = 1, . . ., tri),
(6.16)
где обозначено
(т,) = (Xv)t=x^_0-	\ дхр (т? + 0) /	+о>	(6-17)
р=1
а круглые скобки указывают, что заключенные в них функции
вычислены для порождающего решения (ц = 0).
При сформулированных условиях М. 3. Коловским доказана
следующая теорема [216, 217].
Теорема. Периодические решения исходной системы (6.11),
обращающиеся при ц = 0 в решения порождающей системы,
могут отвечать лишь тем значениям постоянных at, ..., aft, ко-
торые удовлетворяют уравнениям
т 1
Р/(а„ ..., a,)-J £ W •••- x°r
0 $ = 1
-2 iHrL гЖ-0)=°	0=1........(6.18)
q 1 .s = 1	Я
Каждому простому решению уравнений (6.18), то есть ре-
шению, для которого
дР; I
¥=0	(i,j= 1, ..., k),	(6.19)
UU. j
216
СУЩЕСТВОВАНИЕ И УСТОЙЧИВОСТЬ РЕШЕНИЙ
[ГЛ. V
действительно отвечает единственное решение исходной системы
(6.11), переходящее при ц = 0 в решение порождающей си-
стемы.
Сформулированная теорема в работе [217] обобщена также
на случай автономной системы, для которой период порождаю-
щего решения может зависеть от параметров аь ..., а*, на
случай, когда функции д,, в уравнениях поверхностей разрыва
(6.12) являются не только функциями xh ..., xt, но и Г-перио-
дическими функциями t, а также на случай, когда разрыв
в решениях происходит за некоторое конечное время.
Там же показано, что функции 2^(0 обладают тем свой-
ством, что величины
1 л 0
Zsi да,
s = l	!
сохраняются при прохождении через поверхности разрыва.
Заметим, что при отсутствии разрывов, когда
xs (Т?	0) = xs (Т? 0)>	= xs (т<7 0),	= (-^s\=r +о>
имеем
<?Ф?., х fl, s = v, <?Ф,р.
<?XV (Т? + 0)	= ( 0, S=£v, ~фГ = 0,	Л^(Д) = 0,
и поэтому условия (6.16) превращаются в требования непре-
рывности и периодичности функций .?*,(/), а уравнения (6.18)
принимают форму, соответствующую дифференциальным урав-
нениям с «гладкими» правыми частями и решениями.
Вопрос об устойчивости рассмотренных периодических реше-
ний в той форме, как он был решен выше для «гладких» систем,
до сих пор остается неизученным. Однако на основе рассмотре-
ния частных задач (см. [308, 193], а также § 7 главы XIV) и по
аналогии можно ожидать, что результат, найденный для «глад-
ких» систем, сохранится и в данном случае. Иными словами, при
соответствующих оговорках условием устойчивости, по-види-
мому, будет требование отрицательности вещественных частей
корней алгебраического уравнения вида (4.12). Заметим, что
частный случай описанных выше разрывных систем рассмотрен
в работах [436—438].
3. Системы с запаздыванием. Без каких-либо общих допол-
нительных ограничений теоремы предыдущих параграфов рас-
пространяются также и на системы с запаздыванием. Для слу-
чая почти периодических решений квазилинейных систем это
сделано в работе С. Н. Шиманова [434].
§ 7]	СЛУЧАЙ СИНХРОННЫХ ДВИЖЕНИЙ	217
§ 7. Применимость теорем о существовании и устойчивости
периодических движений в случае синхронных движений
Согласно изложенному в § 1 главы II основная задача тео-
рии синхронизации динамических систем состоит в изучении так
называемых синхронных движений, то есть движений вида
Xj = О; [qjtij&t + yt (m/toZ)],	(7.1)
где ms и п, — взаимно простые целые положительные числа, ка-
ждое из чисел oj может быть равно +1 или —1, а каждое из чи-
сел qj — нулю или единице, со > 0, a y^rn^t)—периодические
функции времени t с периодами Г; = 2л/сот, (то есть с общим
периодом Т = 2л/со).
При этом движение системы, как правило, описывается си-
стемой дифференциальных уравнений *)
xs = Xs(x{, ..., xh t) + pFs (xi,..., xb t, p) (s=l.Z). (7.2)
Если, как это бывает в большинстве прикладных задач,
функции Xs и Fs таковы, что в результате подстановки (7.1)
они становятся (или остаются) Т'-периодическими функциями Z,
то после перехода от переменных Xj к переменным у, по фор-
мулам (7.1) задача сводится к исследованию Г-периодических
решений системы дифференциальных уравнений
Уз~ - qsns® + osXs [<Ji (qxnx&t + у,), . .., az (qLtii®t + yi), Z] +
+ ki (^i«i<oZ + z/1), .. ., crz (qini®t + yi), t, p] (7.3)
(s= 1, .... Z)
с Г-периодическими правыми частями.
Применяя теоремы настоящей главы, можно получить усло-
вия существования и устойчивости периодических решений урав-
нений (7.3) и тем самым — синхронных решений (7.1) исходных
уравнений (7.2). Однако в большинстве случаев теоремы
§§ 4—6 можно непосредственно применять не только для пе-
риодических, но и для синхронных решений.
Справедливость теорем §§ 4—6 для движений типа (7.1)
обеспечивается отмеченным выше свойством функций Xs и Fs,
а также следующими обстоятельствами.
1.	Система уравнений в вариациях, составленная для урав-
нений (7.2) и какого-либо синхронного решения, есть система
с Т-периодическими коэффициентами.
2.	Пусть порождающая система
х° = Xs(x°, ..., xj, Z) (s=l,...,Z),	(7.4)
*) Мы записываем здесь эти уравнения в несколько иной форме, игно-
рируя несущественное в данном случае различие между координатами объек-
тов и координатами системы связи.
218
СУЩЕСТВОВАНИЕ II УСТОЙЧИВОСТЬ РЕШЕНИЙ
|ГЛ. V
соответствующая уравнениям (7.2), допускает синхронное ре-
шение
^ = <^/70/ +z/°(w/, ар ..., afe)],	(7.5)
где у° — периодические функции t периода Т = 2л/со, завися-
щее от k произвольных - независимо входящих* **)) параметров
ai, Ok- Тогда система в вариациях
•••+(4^)^	....<7-6)
составленная для порождающей системы (7.4) и порождающего
решения (7.5), также является системой с Т-периодическими
коэффициентами. Пусть, далее, период 7' = 2 л/со порождающего
решения (7.5) не зависит от постоянных а1; ..., а***). Тогда
функции
<Эл:° ду°
=	($= 1, ...,/; г = 1.k) (7.7)
образуют k независимых периодических (а не синхронных!)
решений этой системы с тем же периодом (см. п. 2 § 3 гла-
вы III).
3.	Функции
zs=[w+у° (X ai.............О] (7-8)
являются Т'-периодическими по t и в случае автономности си-
стемы (7.4) образуют решение уравнений в вариациях (7.6).
Сказанное следует из того факта, что в указанном случае
в решение (7.5) всегда можно ввести еще одну постоянную,
добавив ее к времени t. Производная от такого решения по
указанной постоянной, то есть в конечном счете производная
по времени, и является решением системы в вариациях (7.6).
Что касается теорем §§ 2 и 3 настоящей главы, то последние
более специализированы для случая периодических движений.
Но и в этих случаях можно рассуждать следующим образом.
Пусть системы уравнений §§ 2 и 3 получены путем перехода
от функций Xj к функциям у} по формулам (7.1). Тогда, как и
в уравнениях (7.3), роль функций Fs, фигурировавших в исход-
ных уравнениях (см. уравнения (7.2)), будут играть функции
*) Имеется в виду, что по крайней мере один из определителей &-го
порядка, содержащихся в матрице (4.4), отличен от нуля.
**) Отметим, что последнее требование является единственным сущест-
венным ограничением для рассматриваемого обобщения теорем на случай
синхронных решений. Это требование, однако, не выполняется лишь в усло-
виях теоремы 2 § 5 настоящей главы.
§8]	ИНТЕ! РАЛЫ1ЫЙ КРИТЕРИИ УСТОЙЧИВОСТИ	219
crsFs. Поэтому при применении теорем §§ 2 и 3 настоящей
главы к решениям типа (7.1) следует лишь заменить функ-
ции Fs на функции asFs.
Отметим, далее, что теорема А. А. Андронова и А. А. Витта
о периодических решениях автономных систем, обобщенная
Н. Ф. Строковым и И. Г. Малкиным на неавтономные системы
(см. п. 6 § 3 главы III), распространяется также и на синхрон-
ные движения. На указанное обстоятельство было обращено
внимание в пашей работе [44]. Позднее соответствующая тео-
рема была доказана О. Вейводой [121, 496], который, по-види-
мому, не знал о работах [330, 266, 44]; в своем доказательстве
О. Вейвода не использует теорем Н. Ф. Отрокова и И. Г. Мал-
кина, и поэтому оно более сложно.
§ 8. Интегральный критерий устойчивости
периодических и синхронных движений
Основному содержанию теорем настоящей главы можно при
определенных условиях придать своеобразную форму, удобную
при решении ряда прикладных задач. С этой целью рассмотрим
сначала случай неавтономных систем и напомним, что согласно
указанным теоремам периодические (или синхронные) движе-
ния отвечают простым решениям aj=a*, ..., аА = а* некото-
рой системы уравнений
РДа„ ..., аА) = 0	($=1......k),	(8.1)
названных основными уравнениями.
Вопрос об устойчивости каждого конкретного движения за-
висит от знаков вещественных частей корней х алгебраиче-
ского уравнения Ай степени
I - ds/x I = 0
da. 57 I ,
1
(s, / = 1, . . ., k).	(8.2)
Функции Ps(ai, ..., ал) при этом выражаются через некоторые
интегралы, вычисленные за период движения Т и зависящие
от правых частей рассматриваемых дифференциальных уравне-
ний; эти функции выше были названы порождающими.
Пусть существует функция D = D(ai, ..., а&) параметров
порождающего решения, обладающая непрерывными частными
производными до второго порядка включительно, такая, что
^;= ~ Ps(ai, •••> ак) (s= 1, ..., /г).
(8.3)
220
СУЩЕСТВОВАНИЕ И УСТОЙЧИВОСТЬ РЕШЕНИЙ
[ГЛ. V
При этом предположим также, что функции Ps вещественны
вблизи порождающих значений параметров а*, ak, которые
тоже будем считать вещественными*).
Заметим, что последнее условие, например, в случае си-
стемы уравнений (2.9) наверняка выполняется, если все крити-
ческие характеристические показатели ведущей группы равны
нулю, то есть если Zi = ... = Х/{ = 0.
Назовем функцию D потенциальной функцией. Очевидно,
для ее существования необходимо и достаточно выполнение со-
отношений
dPs	dPi	/	• i	ю
"5--=	—	(S,	/=1, •••>	k).
da.j	das	v	1
Разлагая эту функцию по	формуле Тейлора вблизи поро-
ждающих значений параметров а, = а*	аА = а*, в соответ-
ствии с (8.1) и (8.3) получаем
£)(ai, ...,	•••,<) =
k k
=	.(a.-<)(a/-aD+ ••• =
s=l/-lV *
k k
"-П1Э	.(»,-«>,-%)+  (8-4)
j.! /.|	1 ai = ai
где не выписаны слагаемые выше второго порядка относитель-
но а. — а*.
Для того чтобы функция D в точке (а), . . ., cQ имела мини-
мум, достаточно, чтобы квадратичная форма в равенстве (8.4)
была знакоопределенной положительной. А для этого в свою
очередь необходимо и достаточно [138], чтобы все корни алгеб-
раического уравнения й-й степени
|^- + 5l/x|	(«,/-!......ч
1	5	/	'а «а
Q Q
(8.5)
были отрицательны. Заметим, что все корни этого уравнения
вещественны в силу известной теоремы о характеристических
числах вещественной симметрической матрицы [138].
Если хотя бы один корень уравнения (8.5) положителен, то
квадратичная форма не является знакоопределенной, и мини
мум отсутствует. Случай, когда имеются корни, равные нулю,
*) Напомним, что под порождающими значениями параметров пони-
маются значения, удовлетворяющие уравнениям (8.1).
§8]	ИНТЕГРАЛЬНЫЙ КРИТЕРИЙ УСТОЙЧИВОСТИ	221
является сомнительным и, вообще говоря, требует изучения
членов разложения (8.4), имеющих более высокий порядок.
Но уравнение (8.5) при наличии соотношений (8.3) эквива-
лентно уравнению (8.2). Поэтому условия строгого минимума
функции D в точке (а*....cQ, основанные на анализе членов
второго порядка в разложении (8.4), в рассматриваемом слу-
чае совпадают с условиями устойчивости периодических (или
синхронных) решений соответствующих систем уравнений.
Итак, в задаче о существовании и устойчивости периодиче-
ских или синхронных движений функция D играет такую же
роль, как и потенциальная энергия системы II в задаче об
отыскании и исследовании устойчивости положений равновесия
консервативной системы с голономными стационарными свя-
зями. Иначе говоря, для периодических (или синхронных) ре-
шений уравнений изучаемого типа справедливы теоремы, ана-
логичные известным теоремам Лагранжа (Лежен-Дирихле) и
А. М. Ляпунова [261, 271].
Сформулированный выше критерий устойчивости может быть
назван интегральным, поскольку функция D, согласно сказан-
ному выше о порождающих функциях Ps, зависит от осреднен-
ных за период характеристик движения системы, вычисленных
для порождающего решения.
Заметим, что если характеристическое уравнение для урав-
нений в вариациях порождающей системы, помимо k критиче-
ских корней «ведущей группы» (см. §§ 2 и 3), имеет еще и дру-
гие критические корни, то указанные условия минимума функ-
ции D будут не достаточными, а лишь необходимыми условиями
устойчивости*). Другие случаи, когда интегральный критерий
устойчивости дает лишь необходимые, но не достаточные усло-
вия устойчивости, указаны в части Ш.
Отметим, что интегральный критерий устойчивости с не-
большими дополнениями и видоизменениями может быть сфор-
мулирован и для автономных систем, изученных в §§ 3 и 5
настоящей главы.
Класс систем, для которых справедлив интегральный крите-
рий устойчивости, может быть значительно расширен, если за-
метить, что для его наличия достаточно существования функ-
ции D, удовлетворяющей не условиям (8.3), а менее жестким
соотношениям
, dD , , dD ,	, , dD n ,	, /О
да, + ^s2 da/’ ' " ^~^skda. ~	• • •> ak) (8-6)
1	2	k
(s = 1, .... k),
*) Однако, как правило, в практических задачах условия устойчивости,
выраженные интегральным критерием, играют основную роль (см., например,
§ 5 главы XIII).
222
СУЩЕСТВОВАНИЕ И УСТОЙЧИВОСТЬ РЕШЕНИЙ
[ГЛ. V
где bsj = bjS — любые вещественные постоянные, подчиненные
лишь требованию
k k
 B(z,	(8.7)
/-]
то есть условию, чтобы соответствующая им квадратичная
форма была положительной.
На возможность подобного обобщения внимание автора
было обращено Р. Ф. Нагаевым и К. Ш. Ходжаевым; его спра-
ведливость устанавливается следующим образом.
Прежде всего, поскольку определитель |£SJ| отличен от
нуля, то основные уравнения (8.1) по-прежнему эквивалентны
условиям стационарности функции D. Остается, таким образом,
показать, что соответствующие условия минимума функции D
совпадают с требованием отрицательности корней уравнения
(8.2). Подставив выражения (8.6) в указанное уравнение, за-
пишем его в форме
|ВА + Ех| = 0,	(8.8)
где А — симметрическая матрица с элементами <Э2О/<Эа,,<Эаа,
В — симметрическая матрица коэффициентов bSj, а Е — единич-
ная матрица. Так как по условию форма (8.7) положительна,
то матрица В-1 невырожденная и уравнение (8.8) можно пред-
ставить в форме
|А + В-1х| = 0,	(8.9)
где обратная матрица В1 также симметрическая и
В-1 (z, z)>0.	(8.10)
В силу известных положений теории матриц (см., напри-
мер, [138], § 9 главы I) корни уравнения (8.9) вещественны, и
к тому же, как нетрудно убедиться, знаки наименьшего (xmln)
и наибольшего (хтах) из них совпадают со знаками наимень-
шего (xmin) и наибольшего (йтах) корней
| А + Ей [ = 0.
уравнения
(8.П)
минимаксимальных
квадратичных
Действительно, из так называемых
свойств характеристических чисел пучка
вытекает (см. там же, § 10 главы I)
Д (г, г)	Д (г, г)
- xmin = mm	,	- хтах = max —m,
В (г, г)	В (г, г)
Д (г, г)	_	А (г, г)
Xmln mln । i2 , Xmax ГЛЯХ . ,2
Отсюда, в силу (8.10), и следует, что
sign xniIn = sign xmln, sign xmax = sign xmax>
форм
(8.12)
(8.13)
§ 81
ИНТЕГРАЛЬНЫЙ КРИТЕРИЙ УСТОЙЧИВОСТИ
223
и поэтому вместо уравнения (8.8) при исследовании устойчи-
вости можно рассматривать более простое уравнение (8.11). Но
последнее уравнение представляет собой лишь иную запись
уравнения (8.3), условие отрицательности корней которого, как
было показано в начале параграфа, эквивалентно соответствую-
щему условию минимума функции D в рассматриваемой ста-
ционарной точке. Таким образом, утверждение доказано.
Отметим, что из установленного факта вытекает также спра-
ведливость интегрального критерия устойчивости в случае су-
ществования функции D, удовлетворяющей равенствам
~(Plcsl+P2cs2+ ... +Pkcsk) (s=\,...,k),	(8.14)
где cSj = CjS — любые вещественные числа такие, что
k k
C(z, Z)^ 2 2 cs!zsZj>0.
S-1
(8.15)
В случае справедливости интегрального критерия исследо-
вание устойчивости существенно упрощается, ибо условия
устойчивости могут быть легко выписаны в явной форме. Дей-
ствительно, согласно известной теореме Сильвестра (см., на-
пример, [138]) необходимым и достаточным условием положи-
тельности квадратичной формы является положительность всех
главных миноров ее матрицы. Поэтому, согласно (8.5), необ-
ходимыми и достаточными условиями минимума функции D
в точке а, =- а*, . .., ak = ak будут неравенства
			д2Р	д2Р	
д2Р _ да?	>0,		да? д'2Р	dat да2 д2Р	>0,
			да} да2		
			д2Р	д2Р	
			да?	Set] dak	
			д2Р	d2P	>0.
		За, dak		dak	
(8.16;
Последние соотношения особенно удобны при решении за-
дачи о синтезе системы объектов, имеющих синхронное дви-
жение с заданным сочетанием порождающих параметров
а’, . . ., ak (см. §§ 3—5 главы XV).
В случае, когда аналитическое исследование представляется
затруднительным или нецелесообразным, при наличии инте-
грального критерия можно использовать известные хорошо
224	существование и УСТОЙЧИВОСТЬ РЕШЕНИЙ	[ГЛ, V
разработанные алгоритмы численного (в том числе машинного)
поиска экстремумов функции многих переменных [318, 254, 396].
Значение интегрального критерия устойчивости опреде-
ляется также тем обстоятельством, что в ряде случаев функ-
ция D имеет отчетливый физический смысл. Это также облег-
чает синтез систем синхронно работающих объектов. Так, на-
пример, в случае задачи о самосинхронизации дебалансных
вибраторов потенциальная функция D оказывается равной
среднему за период значению функции Лагранжа системы, взя-
той с противоположным знаком и вычисленной для порождаю-
щего решения (см. § 9 главы XIII и §§ 4 и 8 главы XIV настоя-
щей книги). Для этого частного случая интегральный критерий
и был первоначально сформулирован на основе интуитивных
соображений, проверенных на ряде примеров, Б. П. Лавровым
и автором [60], а затем обоснован и обобщен в работах ав-
тора [61, 62]. Дальнейшее развитие указанные исследования
получили в работах Р. Ф. Нагаева [311, 314, 316, 86, 93],
Б. П. Лаврова [242, 244], К- Ш. Ходжаева [406, 407, 411, 316],
автора [68, 93], К- Г. Валеева и Р. Ф. Ганиева [117]. Изложение
основных результатов цитированных работ будет приведено
ниже (см. § 5 главы IX, п. 3 § 1 и п. 3 § 2 главы X, § 9 гла-
вы XIII, § 4 главы XIV, § 2 главы XXIII и п. 4 § 3 главы XXV).
Заметим в заключение, что если рассматривать положения
равновесия системы как вырожденные периодические движения
произвольного периода, то функция D для ряда механических
систем переходит при определенных условиях в потенциальную
энергию системы. Таким образом, существует не только анало-
гия, но и прямая связь полученных результатов с теоремой
Лагранжа (Лежен-Дирихле).
§ 9.	Практическое вычисление периодических решений
систем уравнений с малым параметром*)
1.	О вычислении периодических решений в виде рядов по
степеням малого параметра. Если выполняются условия соот-
ветствующих теорем §§ 2—5 настоящей главы, то искомые пе-
риодические решения дифференциальных уравнений**)
xs = Xs(xb Xi, t) + nFs(xh .... xb t, p) (s — 1......../)
(9.1)
*)	Содержание настоящего параграфа во многом базируется на соот-
ветствующих результатах монографии [275].
**	) Рассматриваем случай неавтономной системы; для автономной си-
стемы рассуждения изменятся весьма незначительно, и поэтому не будем на
них останавливаться.
§ 9] ПРАКТИЧЕСКОЕ ВЫЧИСЛЕНИЕ ПЕРИОДИЧЕСКИХ РЕШЕНИЙ 225
являются аналитическими функциями параметра ц, и поэтому
их можно разыскивать в виде рядов
xs(t) = x°s(t, а;, .... а;) + ихО)(0 + ^)(/)+ ...	(5 = 1, ...,0
(9.2)
по целым положительным степеням этого параметра с периоди-
ческими коэффициентами периода Т.
Подставляя ряды (9.2) в дифференциальные уравнения
(9.1) и приравнивая коэффициенты при одинаковых степе-
нях ц в обеих частях получившихся равенств, придем для опре-
деления коэффициентов к линейным дифференциальным
уравнениям с периодическими коэффициентами следующего
вида:	J
*(sq) = PsixiQ> + ••• +Psix(iq'> + Fs) (S=I> •••« l> <7==I> 2> •••)>
(9.3)
a Ff — полиномы с периодическими коэффициентами от пре-
дыдущих приближений х°, хР\ .... х^-1). В частности,
.....4 »)•	(9-5)
Однородная часть уравнений (9.3), очевидно, совпадает
с уравнениями в вариациях (4.5) для порождающей системы
и порождающего решения.
Проследим в общих чертах за процессом последовательного
определения коэффициентов рядов (9.2).
Для того чтобы линейные уравнения (9.3) допускали Т-пе-
рйоДйческое решение х^\ необходимо и достаточно выполне-
ние равенств (см. [275], а также п. 4 § 3 главы III)
т I
JS^4/(O^ = O (/=1, .... k\ <7=1,2, ...). (9.6)
О s=l
Здесь z*^/), как и выше, — периодические решения уравнений
(4.8), сопряженных по отношению к уравнениям в вариациях
(4.5).
При q — 1, то есть для первого приближения, условия (9.6),
согласно (9.5), принимают вид
т t
Р^, ....	....х°>	= O (9.7)
о S=1
(/=1, ...» k)t
Я И И Блехман
226
СУЩЕСТВОВАНИЕ И УСТОЙЧИВОСТЬ РЕШЕНИЙ
[ГЛ. V
1о есть совпадают с уравнениями (4.9), и так же, как и послед-
ние, служат для определения параметров а*, . . ., а* порождаю-
щего решения.
При выполнении равенств (9.7) уравнения (9.3) для q = 1
допускают относительно лф* периодическое решение вида
я'*’= <*,>+ •••	+	(9-8)
где — какое-нибудь частное решение уравнений, zSj — пе-
риодические решения уравнений в вариациях (4.5), определяе-
мые равенствами (4.7), а Л4/1’ произвольные постоянные, кото-
рые находятся из условий периодичности для функций х<_2), то
есть из равенств (9.6) при q — 2.
И вообще, если все функции лф*, ..., x<v) уже вычислены и
оказались периодическими, то функции x<.v+1> будут иметь вид
<+,, = <+%+	+<+% + <+,)*.	(9-9)
где x<v+,)4 — какое-либо частное решение уравнений (9.3) для
a4v+i), a AfjV+1) — постоянные, которые определятся из условий
периодичности функций хр’+2>.
Если рассмотреть вытекающие из равенств (9.6) условия
для определения указанных постоянных, то окажется [275], что
они всегда представляют собой систему линейных алгебраиче-
ских уравнений с определителем
|^|	•	(s,'/=l, .... /г),	(9.10)
I aaJ la^=af
вычисленным для рассматриваемой системы порождающих па-
раметров. Но в силу условий упомянутых теорем определи-
тель (9.10) отличен от нуля, ибо в противном случае уравнения
типа (4.12) имели бы нулевой корень. Поэтому при выполнении
условий указанных теорем ряды (9.2) определятся единствен-
ным образом и, в силу аналитичности, также гарантируемой
теоремами, будут сходиться и Действительно представят иско-
мое периодическое решение.
Таким образом, периодические решения изучаемого вида
действительно могут быть найдены в виде рядов (9.2) для
каждого простого решения а], ..., а/г’ уравнений (9.7).
Если правые части уравнений (9.1) не аналитичны относи-
тельно Xi, ..., Xi и ц, то для вычисления периодического ре-
шения можно воспользоваться методом последовательных при-
ближений [275, 217]. Не останавливаясь на подробностях, отме-
§ 9] ПРАКТИЧЕСКОЕ ВЫЧИСЛЕНИЕ ПЕРИОДИЧЕСКИХ РЕШЕНИЙ 227
тим, что и в этом случае задача приводится к нахождению
периодических решений уравнений вида (9.3).
2. О технических трудностях, связанных с реальным вычис-
лением периодических решений. При решении методом малого
параметра значительного числа задач о синхронизации динами-
ческих систем оказывается вполне достаточным найти поро-
ждающее решение, а также условия существования и устойчи-
вости периодических решений, обращающихся при ц = 0 в по-
рождающие. Как явствует из теорем §§ 2—6 настоящей главы,
для этой цели необходимо найти по формулам (9.7) порождаю-
щие функции Pj(ai, ..., ал), входящие в уравнения для опре-
деления параметров aj и в соответствующие условия устойчи-
вости. В свою очередь для составления выражений Р, необ-
ходимо знать функции z*s! (t), образующие k независимых пе-
риодических решений системы (4.8), сопряженной по отношению
к системе в вариациях (4.5) для порождающей системы и по-
рождающего решения.
Нахождение функций z"s! (t) требует, вообще говоря, знания
общего решения системы в вариациях, то есть системы линей-
ных уравнений с периодическими коэффициентами. Но, как из-
вестно, общих методов решения таких систем не существует.
Поэтому для возможности доведения решения задачи до конца
весьма желательно вводить малый параметр таким образом,
чтобы было известно не только периодическое, но и общее ре-
шение порождающей системы*). Действительно, если таким
общим решением является
x° = x°(t, ai> •••> “/)	(« = !.•••> О,
где at, ai — произвольные постоянные, то производные
дх°
^(0 = 4- (/ = 1-•••>0,
вычисленные для значений постоянных, соответствующих по-
рождающему решению, определяют I независимых частных ре-
шений уравнений в вариациях (см. п. 2 § 3 главы III). Вообще
же для полного интегрирования уравнений в вариациях доста-
точно найти только I—1 их частных решений, для чего доста-
точно знать не общее решение порождающей системы, а реше-
ние, зависящее от I— 1 произвольных постоянных. В частности,
уравнения в вариациях могут быть полностью проинтегри-
рованы в том случае, когда число k параметров а, в порож-
дающем решении равно /—1. Отметим, что для указанных
*) Вопрос о введении малого параметра подробно обсуждался в § 2
главы IV.
8*
228
СУЩЕСТВОВАНИЕ И УСТОЙЧИВОСТЬ РЕШЕНИЙ
[ГЛ. V
систем — систем, близких к точно интегрируемым, просто полу-
чаются и уравнения, определяющие изменение параметров а,
в режимах установления (см. § 6 настоящей главы).
Естественно, что трудностей не возникает, если порождаю-
щая система представляет собой систему линейных уравнений
с постоянными коэффициентами или систему, которая приво-
дится к таковой (см. §§ 2 и 3 настоящей главы). Однако такое
жесткое ограничение иа порождающую систему вовсе не обя-
зательно. Как явствует из рассмотрения примеров, приведенных
в главе I, во многих задачах о синхронизации динамических
объектов малый параметр естественно вводится в уравнения
как раз таким образом, что общее решение порождающей си-
стемы является известным. Это характерно, например, для за-
дач о синхронизации слабо связанных объектов (см. § 2
главы II), когда при ц = 0 система распадается на k незави-
симых систем, отвечающих несвязанным объектам, и на систему,
отвечающую системе связи. В этом случае, как нетрудно ви-
деть, периодические решения	системы, сопряженной по
отношению к системе в вариациях, без труда находятся, если
такие решения известны для каждого из изолированных объек-
тов в отдельности. Последние же решения часто легко нахо-
дятся. Во всяком случае, их всегда можно найти, если известно
общее решение уравнений движения изолированных объектов.
Сказанное будет неоднократно иллюстрироваться ниже при
решении различных задач о синхронизации (см. главы VII—XI
настоящей книги).
Здесь же мы заметим, что в ряде случаев для нахождения
функций г’ДО и, следовательно, для составления уравнений
(9.7) нет необходимости искать общее решение уравнений в ва-
риациях: эти функции могут быть определены непосредственно
по порождающему решению [275]. Наиболее простым случаем
такого рода будет тот, когда система в вариациях является
самосопряженной, то есть когда выполняются соотношения
Psi ~ Pjs-
В этом случае можно положить z*sJ = zsj, причем* функции zSj
определяются равенствами (4.7) непосредственно по порождаю-
щему решению.
Другим, более общим и практически значительно более важ-
ным является случай системы, близкой к канонической, когда
уравнения (9.1) допускают запись в форме
Xs~ dxn+s^^s’ xn+s~ dXs +мЛг+з (s-1, ...» n = //2),
(9.11)
где функции H = H(x.......x2n) и Ft(xi.....x2n,t, ц) таковы,
§ 9]
ПРАКТИЧЕСКОЕ ВЫЧИСЛЕНИЕ ПЕРИОДИЧЕСКИХ РЕШЕНИИ
229
что выполняются общие условия, которым удовлетворяют пра-
вые части уравнений (9.1). Предположим, как и ранее, что
порождающая система допускает периодическое решение
x°s = x°s(*’	  ’ ak)	I, ..2n),	(9.12)
зависящее от k произвольных постоянных. Уравнения в вариа-
циях (4.5) для какого-нибудь решения этого семейства имеют
вид
2п	2п
..................................................
' n+s 1 '	/ = 1 ' s / '•
(9.13)
где производные вычислены для решения (9.12).
Уравнения (9.13) имеют k периодических решений
дх. (t, а,, ..аь
Z =	р——2L	(j = ! . k .
s/	f)a^	V ,	,	/
Системой, сопряженной с (9.13), будет
<’-м)
\ S п + 1 /	' s * '
(s = 1, .... 2п).
Но эти уравнения переходят в (9.13) при замене z* на zn+s и
zn+s на —Zs (s	п)- Отсюда следует, что уравнения
(9.14) имеют k периодических решений
_ dx°n+s(t, а,.aft)	_ _ а,..........ak) ,Q .
Zsi	да.]	’	»+«. /	da.j	' ’	'
(s = 1, ..., n; j = 1, ..., k).
Выражения для порождающих функций Pj(ai, ..., ак) при
этом принимают вид
..., afe) = J 2(xi.........х2п’ °)~гйГ
О 5“° 1
о \
дх I
.....°)^7\dt = 1.......................<9-16)
Еще один важный случай характеризуется тем, что для по-
рождающей системы известны первые интегралы
ФДхр ..., х°, /) = const (t=l, ..., k),	(9.17)
число которых равно числу k параметров, входящих в поро-
ждающее решение. Предполагается, что являются периоди-
ческими функциями t периода Т. В этом случае, согласно
230	СУЩЕСТВОВАНИЕ И УСТОЙЧИВОСТЬ РЕШЕНИИ	[ГЛ. V
изложенному в пп. 2 и 4 § 3 главы III, функции
являются первыми интегралами системы в вариациях (4.5) и,,
следовательно, функции дФг(х°, ..., x°L,	образуют k не-
зависимых периодических решений сопряженной системы (4.8)..
Линейные комбинации этих функций с коэффициентами, вы-
бранными из условий (4.11), и будут искомыми функциями
г^(/), необходимыми для составления выражений РДаь ..., а&)..
Если помимо порождающего решения интерес представляет
также и вычисление следующих приближений, то, как было.'
установлено в п. 1 настоящего параграфа, дело сводится к на-
хождению периодических решений системы неоднородных урав-
нений (9.3) с периодическими коэффициентами. Однородная
часть этих уравнений совпадает с уравнениями в вариациях
(4.5) для порождающей системы и порождающего решения.
Поскольку для нахождения периодических решений системы
линейных неоднородных уравнений вида (9.3) требуется, во-
обще говоря, знание общего решения соответствующих однород-
ных уравнений, то для вычисления приближений требуется зна-
ние общего решения указанных уравнений в вариациях. Од-
нако поскольку речь идет о вычислении не основных членов
искомого решения, которые определяются порождающим реше-
нием, а поправочных членов, то можно воспользоваться какими-
нибудь из известных приближенных методов нахождения перио-
дических решений, не требующих интегрирования однородной
части уравнений (9.3).
Если, как это часто бывает, коэффициенты pSj мало отли-
чаются от постоянных, то периодические решения уравнений
(9.3) можно найти, воспользовавшись разложениями в ряды
или методом последовательных приближений.
Подчеркнем, однако, что, как правило, при решении задач
о синхронизации надобности в вычислении высших приближе-
ний не возникает.
§10. О случаях, когда уравнения для определения
порождающих параметров имеют непростые решения
или удовлетворяются тождественно
Теоремы, приведенные в §§ 2—6 настоящей главы, обеспечи-
вают существование периодического решения исходной системы
уравнений, обращающегося при ц = 0 в решение порождающей
системы, для каждого простого решения уравнений
Р?(аь ..., <хА) = Q ($=1.......k),	(10.1)
I dPs
I да1
dPs ,
-Т-----Ое/Х
да, s/
§ 10]	О СЛУЧАЯХ НЕПРОСТЫХ РЕШЕНИЙ	231
то есть для каждого решения а^а*, аА = а*, для которого
. =#0	(з, / = 1, .... k).	(10.2)
%
Выполнение последнего условия гарантировалось при этом
выполнением условия устойчивости соответствующего периоди-
ческого решения, то есть условием отрицательности веществен-
ных частей корней алгебраического уравнения
. = 0	(s, /=1.....k),	(10.3)
‘<7
ибо условие (Ю.2) совпадает с требованием отсутствия нуле-
вого корня у уравнения (10.3). Закономерность такого совпадет-
ния, обусловливающего совпадение определенной части обла-
сти устойчивости решения в пространстве параметров системы
с границей области существования этого решения, отмечалась
выше (см. сноску на стр. 167).
Если предположить, что условие (10.2) не выполняется, то
есть что соответствующее решение уравнений (10.1) является
кратным, то изучение вопроса о существовании и об устойчиво-
сти периодических решений осложняется: искомые решения,
а также и корни характеристического уравнения оказываются,
вообще говоря, представимыми в виде рядов не по целым, а по
дробным степеням малого параметра ц. Ряд таких особых слу-
чаев подробно изучен А. П. Проскуряковым и его последовате-
лями Г. В. Плотниковой и Ю. М. Крпниным [350, 224]. Изуче-
ние этих случаев интересно с принципиальной точки зрения,
поскольку речь идет, по существу, об исследовании решений
вблизи точек бифуркации. Однако для приложений указанные
случаи представляют ограниченный интерес, ибо им соответ-
ствуют значения параметров, при которых имеют место трудно-
реализуемые, весьма чувствительные к различного рода возму-
щениям режимы.
Относительно больший интерес с точки зрения приложений
представляет случай, когда уравнения (10.1) удовлетворяются
тождественно. Его подробное исследование в связи с некото-
рыми классическими задачами небесной механики было выпол-
нено Г. А. Мерманом [291]. Результат Г. А. Мермана состоит
в следующем. Как отмечалось в § 9 настоящей главы, уравне-
ния (10.1), совпадающие с уравнениями (9.7), представляют
собой условия периодичности первого приближения при
отыскании периодического решения уравнений (9.1) в виде
рядов (9.2) по степеням параметра р. Если уравнения (10-1).
удовлетворяются тождественно, то необходимо последовательно
дР™
да.
232	СУЩЕСТВОВАНИЕ И УСТОЙЧИВОСТЬ РЕШЕНИЙ	[ГЛ. V
рассмотреть условия периодичности следующих приближений,
определяемых из уравнений (9.3) при q = 2, 3, ... Эти условия
выразятся в виде некоторых уравнений
•••> «а) = °	(<7 = 2, 3, ...; s=l...k). (10.4)
Если при q = 2, 3, ..., т— 1 уравнения (10.4) удовлетворяются
тождественно относительно cxi, ..., ад, а при q = т допускают
простое решение а^а*, ..., aft = a^, то есть решение, для ко-
торого
ar_a; = 0	(S, /=1, .... k),	(10.5)
то исходная система дифференциальных уравнений (9.1) допу-
скает единственное периодическое решение, обращающееся при
ц = 0 в порождающее и аналитическое относительно ц.
§ 11. Случай нелинейных (непростых) элементарных
делителей корней характеристического уравнения
Основные теоремы, Приведенные в данной главе, в своих
частях, касающихся устойчивости решений, относились к слу-
чаю, когда элементарные делители, отвечающие кратным кор-
ням характеристического уравнения системы в вариациях, со-
ставленной для порождающей системы и порождающего реше-
ния, являются линейными. Иными словами, речь всегда шла
о случаях, когда число групп решений указанной системы в ва-
риациях равно кратности соответствующего корня характери-
стического уравнения. Между тем, как отмечалось в п. 8 § 3
главы III, в теории синхронизации встречаются задачи, которым
отвечают нелинейные (непростые) элементарные делители крат-
ных корней.
В таких случаях для отыскания корней характеристического
уравнения пользуются одним из способов, рассмотренных в п. 7
§ 3 главы III. При этом указанные корни, вообще говоря, не
являются более аналитическими функциями параметра ц, если
Таким свойством обладают коэффициенты характеристического
уравнения. Эти корни, однако, как упоминалось, могут быть
найдены в виде рядов по степеням ц1/г, где г — целое число, не
превышающее кратности соответствующего корня. Аналитиче-
ский вид указанных разложений может быть определен с по-
мощью уже упоминавшегося многоугольника Ньютона [418].
Исследование случая нелинейных элементарных делителей
Кратных корней содержится в ряде работ [419]; в частности,
этому исследованию специально посвящены статьи С. Н. Ши-
манова [431, 432] и М. Я- Кушуля [235].
ГЛАВА VI
НЕКОТОРЫЕ ДРУГИЕ МЕТОДЫ РЕШЕНИЯ ЗАДАЧ
О СИНХРОНИЗАЦИИ
§ 1.	Асимптотические методы
Асимптотические методы в виде различных вариантов так
называемого принципа осреднения являются эффективным сред-
ством решения задач современной теории нелинейных колеба-
ний. Эти методы, одним из истоков которых явились известные
работы Ван-дер-Поля, получили существенное развитие преиму-
щественно в трудах отечественных ученых и в особенности в ра-
ботах Н. М. Крылова, Н. Н. Боголюбова и Ю. А. Митрополь-
ского [232, 293—295].
Асимптотические методы могут быть использованы и при
исследовании синхронизации динамических систем. При этом
наибольшее значение здесь имеет обобщение методов осредне-
ния на так называемые системы уравнений с «многомерной бы-
стро вращающейся фазой», развитое в работах В. М. Волосова
[135—137]. Речь идет о системах вида
х = цХ(х, у, t, ц),
y—Y(x, у, t, ц),
где х и X— п-мерные векторы, а у и Y— m-мерные векторы; пе-
ременные х описывают «медленные», а переменные у — «бы-
стрые» движения. К исследованию именно таких уравнений
в так называемом резонансном случае приводятся многие за-
дачи о синхронизации динамических систем (см. часть III на-
стоящей книги).
Различные модификации асимптотических методов были
применены для исследования синхронизации объектов типа
ламповых и квантовых генераторов (см. §§ 6 и 7 главы I),
а также для решения некоторых задач о синхронизации меха-
нических вибраторов [352—354, 426, 427].
Мы не будем излагать здесь асимптотические методы, во-
первых, в связи с тем, что им посвящены специальные
234
ДРУГИЕ МЕТОДЫ РЕШЕНИЯ ЗАДАЧ О СИНХРОНИЗАЦИИ
[ГЛ. VI
монографии и статьи [232, 293—295, 135—137, 302], и, во-вторых,
потому, что эти методы не используются в настоящей книге.
Отметим лишь, что применение асимптотических методов к ре-
шению основных задач теории синхронизации — задач, сводя-
щихся к исследованию стационарных движений, по меньшей
мере не дает каких-либо преимуществ по сравнению с исполь-
зованием метода Пуанкаре.
В принципе асимптотические методы приводят к уравнениям,
описывающим не только стационарные режимы, но и процессы
установления. Следует, однако, иметь в виду, что построение
асимптотической процедуры для уравнений (1.1) в «резонанс-
ном» случае, характерном для задач о синхронизации, вообще
говоря, наталкивается на трудности, связанные с известной про-
блемой малых знаменателей. Некоторые пути преодоления этих
трудностей при изучении стационарных движений рассматри-
ваются в статье В. М. Волосова и Б. И. Моргунова [137].
§ 2.	Метод математического моделирования (применение
аналоговых устройств и цифровых вычислительных машин)
Аналитическое решение многих вопросов теории синхрони-
зации- динамических объектов в настоящее время представляет-
ся крайне трудным или даже вообще практически невозможным.
К числу таких вопросов относятся, например, установление
областей захвата в определенный синхронный режим, а также
многие задачи о синхронизации в существенно нелинейных си-
стемах. Кроме того, как отмечалось выше, аналитические ре-
шения, если их и удается получить, часто носят характер
правдоподобных результатов, подлежащих проверке. В связи
со сказанным особое значение при решении задач о синхрони-
зации приобретает использование аналоговых и цифровых вы-
числительных машин. По сравнению с натурным экспериментом
и с физическим моделированием метод математического моде-
лирования выгодно отличается возможностью легко изменять
условия задачи и параметры системы, а также легко фиксиро-
вать получаемые результаты.
В аналоговых устройствах, как известно, вместо рассматри-
ваемого физического процесса изучается иной процесс, описы-
вающийся теми же дифференциальными уравнениями. Наи-
большее распространение в настоящее время получил метод
электронного моделирования, применительно к которому созда-
но значительное число машин и установок и которому посвя-
щено большое число специальных исследований и руководств.
Что касается проблем синхронизации, то к настоящему вре-
мени выполнен ряд работ по исследованию методом электрон-
ного моделирования совместной работы электрических генера-
§21
МЕТОД МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ
235
торов. Значительно меньшее число исследований посвящено ре-
шению этим методом задач теории синхронизации вибраторов.
Здесь можно упомянуть лишь работы по определению областей
захвата в простейшей «вырожденной» задаче о вибрационном
поддержании вращения неуравновешенного ротора (см. § 1
главы XVIII и [352]), а также работу [101], в которой изучена
синхронизация в виброударной системе с двумя дебалансными
возбудителями.
При решении многих задач теории синхронизации (в частно-
сти, задач о синхронизации механических вибраторов) методом
электронного моделирования оказывается необходимым вос-
произведение на значительном интервале нелинейных периоди-
ческих функций зависимой переменной, например функций
sin ф, cos ф и т. п. Как правило, серийно выпускаемые электрон-
ные модели не имеют соответствующих блоков, и поэтому для
указанной цели было предложено несколько специальных схем
(см., например, [2, 354, 378]).
Отметим также, что при решении на аналоговых машинах
задач теории синхронизации целесообразно иметь отдельные
специальные блоки, моделирующие синхронизируемые объекты,
а основное моделирующее устройство использовать.для имита-
ции связи между объектами. При этом окажется особенно удоб-
ным воспроизводить различные типы связей, изменять число
синхронизируемых объектов и т. п.
Для решения ряда задач теории синхронизации представ-
ляется целесообразным использование также и цифровых вычис-
лительных машин. Этим путем 3. С. Баталовой была изучена
задача об определении областей захвата неуравновешенного
ротора в режим стационарного вращения под действием колеба-
ний его оси [29]; краткое изложение соответствующих резуль-
татов приводится в § 6 главы XVIII настоящей книги.
При исследовании с помощью цифровых машин стационар-
ных режимов движения динамических систем возникает ряд спе-
цифических вопросов, связанных с ограниченными точностью
и временем вычислений, а также с тем, что при изучении пове-
дения траекторий в фазовом пространстве практически всегда
можно «перебрать» лишь конечное число начальных точек. Эти
обстоятельства приводят к тому, что результаты исследования
режимов движения динамических систем с помощью цифровых
вычислительных машин являются лишь правдоподобными (см.
§ 1 главы IV). Степень точности и достоверности результатов
определяется заданием некоторых постоянных, характеризую-
щих время интегрирования, расстояния между «пробными» точ-
ками в фазовом пространстве, предельную «сложность» изучае-
мых режимов и т. п. Рассмотрению указанных принципиальных
вопросов посвящена работа 3. С. Баталовой [30].
236
ДРУГИЕ МЕТОДЫ РЕШЕНИЯ ЗАДАЧ О СИНХРОНИЗАЦИИ [ГЛ. VI
§ 3.	Физическое моделирование
Как было отмечено в предыдущем параграфе, математиче-
ское моделирование с помощью аналоговых или цифровых вы-
числительных машин необходимо, с одной стороны, для реше-
ния вопросов, аналитическое рассмотрение которых затруднено,
и, с другой стороны, для проверки, как правило, нестрогих или
неточных аналитических решений, то есть для изучения внут-
ренней правдоподобности результатов (см. § 1 главы IV).
Физическое моделирование, то есть воспроизведение системы
в ином (как правило, меньшем) масштабе, наряду с решением
перечисленных задач, позволяет проверить внешнюю правдо-
подобность теоретического результата — соответствие математи-
ческой модели реальной системе. Естественно, что при разра-
ботке физических моделей явлений синхронизации необходимо
придерживаться известных общих принципов, в частности прин-
ципов теории подобия.
Метод физического моделирования широко использован нами
и другими исследователями при решении прикладных задач тео-
рии синхронизации механических вибраторов. Описание ряда
соответствующих установок и стендов приводится в главе XIX
настоящей книги.
ЧАСТЬ 111
СИНХРОНИЗАЦИЯ НЕКОТОРЫХ КЛАССОВ
ДИНАМИЧЕСКИХ СИСТЕМ СО СЛАБЫМИ
ВЗАИМНЫМИ связями
Как указывалось в первой части книги, задачи о синхрониза-
ции слабо связанных объектов представляют особый интерес
для приложений. Вместе с тем наличие слабых связей между
объектами предопределяет возможность введения малого пара-
метра в уравнения движения системы, что позволяет использо-
вать эффективные методы нелинейной механики.
В настоящей, третьей части книги будут изучены задачи
о синхронизации ряда важнейших классов слабо связанных объ-
ектов. Вначале, в главе седьмой, рассматривается относительно
общая система слабо взаимодействующих нелинейных объектов.
Основная цель этой главы — выявить несколько более подроб-
но, чем это было сделано выше, особенности задач о синхрони-
зации объектов со слабыми взаимными связями. Главная из
этих особенностей состоит в том, что трудности получения ре-
зультативных соотношений в явной форме определяются не
сложностью всей системы в целом, а лишь сложностями, по-
рождаемыми характером отдельных изолированных объектов
и характером связей. Это обстоятельство, конечно, значительно
облегчает решение соответствующих задач.
В главе восьмой рассматривается синхронизация слабо свя-
занных объектов простейшего типа — объектов с одной степенью
свободы, близких к линейным. При этом подробно изучаются
различные варианты вырождения объектов, представляющие
в данном случае наибольший прикладной и теоретический инте-
рес. В числе таких вырожденных объектов особое место зани-
мают объекты, допускающие установившиеся вращательные
движения и, в частности, объекты с почти равномерными вра-
щениями. Исследованию синхронизации подобных объектов по-
священа специальная, девятая глава.
В десятой и одиннадцатой главах рассматривается синхро-
низация существенно нелинейных систем с одной и со многими
степенями свободы — почти консервативных объектов и объек-
тов, близких к системам Ляпунова.
Во всех случаях особое внимание уделяется установлению
и формулировке интегрального критерия устойчивости синхрон-
ных движений.
ГЛАВА Vll
ОБЩИЙ СЛУЧАИ СЛАБО СВЯЗАННЫХ ОБЪЕКТОВ
§ 1.	Уравнения движения системы
Рассмотрим наиболее общий случай системы слабо взаимо-
действующих нелинейных объектов, движение которой описы-
вается уравнениями (2.1) главы II. В скалярной записи эти
уравнения имеют вид
+ pFp(х\'\	х^-, х\к\	«р •••, nv’, Л в)
(/•=1.....G; S-1........k),	(1.1)
ziz = ЦЦх*1'...х)0; ...; x\k\ x(®; ult uv; t, p.)
(z = 1,	v).
Здесь x<s> — фазовые координаты объектов*), «j —фазовые ко-
ординаты системы связи, k — число объектов, rs — число фазо-
вых координат, определяющих состояние s-ro объекта. Струк-
турная схема системы соответствует изображенной на рис. 1.
Рассматривая задачу о внешней синхронизации, будем пред-
полагать, что функции Т7’/’ и Ui явно зависят от времени t\
о характере этой зависимости говорится ниже. В случае задачи
о внутренней синхронизации правые части уравнений (1.1) от t
не зависят, то есть система автономна. Относительно гладкости
функций Х^, F\s} и Ui делаются предположения, обеспечи-
вающие справедливость используемых ниже теорем главы V.
О некоторых других предположениях будет сказано ниже.
Цель исследования состоит прежде всего в выяснении усло-
вий существования и устойчивости синхронных решений си-
стемы (1.1).
§ 2.	Задача о внешней синхронизации
Рассмотрим вначале задачу о внешней синхронизации. Со-
ответствующая уравнениям (1.1) порождающая система имеет
вид
xf° == Х^(х^°, .... х<5>°)	(/= 1, ..., rs; s= 1, ..., &)>
ц“=ЦЦх<1)0, ...,	...; x®°.....x®°; u\......<2Л)
(' = 1, • • •, v).
*) Как и в главе II, верхний индекс, если он имеется при обозначении
какой-либо величины, указывает на номер объекта, а нижний — на номер
координаты.
§2]
ЗАДАЧА О ВНЕШНЕЙ СИНХРОНИЗАЦИИ
239
Пусть уравнения (2.1), отвечающие каждому из объектов,
допускают порождающее синхронное решение периода 7’=2л/со:
X»’ = <р(«) (t + cQ.	(2.2)
Здесь as — произвольные постоянные, которые всегда можно
добавить ко времени t вследствие автономности объектов в ис-
ходном приближении, а функции ф^>(/) имеют вид
(/) =	(тf)],	(2.3)
причем, как и в § 1 главы II, и «^ — взаимно простые
целые положительные числа, числа q^ могут быть равны нулю
или единице, о& = ± 1, а ф<5) — периодические функции t с пе-
риодами Т/5) = 2n/m/s)co, то есть также и с общим периодом
Т = 2л/а>. Производные от функций <р(«> по времени, очевидно,
всегда являются Т-периодическими, то есть
Ф7)(М-Т) = ф(;)(0.	(2.4)
Пусть, далее, последние v уравнений (2.1) после подстанов-
ки в них выражений (2.2) также допускают одно или несколько
синхронных решений
.....«д	(2-5)
имеющих тот же период Т и зависящих от тех же постоянных
ai, .... as- При этом считается, что после подстановки (2.2),
(2.5) правые части уравнений (1.1) становятся (или остаются)
Т = 2л/«-периодичсскими функциями t.
Уравнения в вариациях, отвечающие системе (2.1) и реше-
нию (2.2), (2.5), имеют вид
z<s) = (t + as) zf> + ... + pW + as) zW
(/ = 1, . . ., Гs', s = 1.............k),
k
= qllZi + ... + qivzv + 3 Iq^zW + ... + ee>],
ffl ta ] L	in Ifl Л
(2.6)
где
dXf ...<Р^(01
P$(0=——----------1
(0
rs; s = 1, ..., k),
(2.7)
fdU,'
qui = -—
\duht
(/, p, d= 1, ..., rs; i, h = 1, ..., v; s= !,...,&),
240
ОБЩИЙ СЛУЧАЙ СЛАБО СВЯЗАННЫХ ОБЪЕКТОВ
[ГЛ. VII
а круглые скобки, в которые заключены производные от Ui,
означают, что эти производные вычислены для порождающего
решения.
В силу известного свойства уравнений в вариациях (см. п. 2
§ 3 главы III) система (2.6) допускает k независимых /-перио-
дических решений
4v) = <p<s’(/ + as)6vs, =	(j=l, ..., rs’, s, Y=l, ..., k),
(2.8)
которые получаются последовательным дифференцированием
порождающего решения (2.2), (2.5) по аь .... ал. Через 6YS
здесь, как и выше, обозначен символ Кронекера:
6SY =
1, s = y,
0, s^=y.
(2.9)
Первый нижний индекс при обозначениях функций z указывает
на номер координаты, а второй — на номер решения.
Пусть уравнения в вариациях (2.6) не имеют периодических
решений, отличных от (2.8). Тогда характеристические уравне-
ния для каждой из первых k подсистем (2.6) имеют по одному
корню, равному единице. Все прочие корни указанных характе-
ристических уравнений, а также корни характеристического
уравнения, отвечающего уравнениям в вариациях для системы
связей
zl = qlizl+ ... +qivzv (z=l.......v),	(2.10)
пусть имеют модули, меньшие единицы *).
При сделанных предположениях к системе (1.1) оказы-
ваются применимыми теоремы 1 и 2 § 4 главы V, а также ска-
занное в § 7 той же главы. Для использования этих теорем
остается лишь рассмотреть систему уравнений, сопряженную
по отношению к системе в вариациях (2.6) (см. п. 4 § 3 гла-
вы III).
*) Тем самым мы ограничиваемся здесь рассмотрением случая, когда
число критических корней характеристического уравнения системы в вариа-
циях в точности равно числу объектов k и когда 6-кратному критическому
корню р = 1 отвечают простые элементарные делители. Такое ограничение,
как будет ясно из дальнейшего, отвечает случаю неквазиконсервативных
объектов. Задачи о синхронизации квазпконсервативных объектов, при ре-
шении которых приходится сталкиваться с дополнительными критическими
корнями, а также с непростыми (нелинейными) элементарными делителями
кратных корней, изучаются в следующих главах данной части книги.
ЗАДАЧА О ВНЕШНЕЙ СИНХРОНИЗАЦИИ
241
§ 2]
Нетрудно заметить, что последние v уравнений указанной
сопряженной системы имеют вид
zl + qilZ]+ ... +<7vX = °	(2.11)
то есть содержат только переменные, отвечающие координатам
системы связи. Это обстоятельство не случайно; как уже отме-
чалось в п. 2 § 9 главы V, оно характерно для всех задач о син-
хронизации слабо связанных объектов.
В силу предположения о корнях характеристического урав-
нения системы (2.10), уравнения (2.11) допускают единствен-
ное тривиальное Т-периодическое решение zj = 0. Поэтому Т-пе-
риодические решения системы, сопряженной по отношению к си-
стеме в вариациях (2.6), следует искать из систем уравнений
^(s) + p's/)(/ + a5)<)+ ... +^(Has)2^' = 0	(2.12)
(/ = I...s = 1.........k),
отвечающих координатам объектов и независимых для каждого
объекта.
В силу сделанных выше предположений каждая из подси-
стем (2.12), так же как и каждая из соответствующих подси-
стем (2.6), допускает единственное Т-периодическое решение;
обозначим это решение через х\(р (t 4- as) (/=1, .... rs\
s = 1, ..., k). Тогда система (2.12) в целом допускает k линей-
но независимых Т-периодических решений, которые могут быть
представлены в форме
4s> = nJs’(' + aM₽ (₽=!,..., 6).	(2.13)
Как указывалось в п. 1 § 4 главы V, решения (2.13) в дан-
ном случае могут быть выбраны так, чтобы удовлетворялись
равенства *)
k S
S	(₽, Y=l, ...» Я (2.14)
При учете выражений (2.8) и (2.13) соотношения (2.14) сво-
дятся к условиям
S<p's’(O^)(O=l (s=l...........k),	(2.15)
которым и должен быть подчинен выбор периодических реше-
ний Т)^>.
*) Здесь мы учитываем, что функции (i = 1, ..., v) тождественно
равны нулю.
242
ОБЩИЙ СЛУЧАЙ СЛАБО СВЯЗАННЫХ ОБЪЕКТОВ
(ГЛ. VII
Уравнения (4.9) главы V для определения порождающих
фаз as при учете выражений (2.13) могут быть представлены
в форме *)
т k rs
(а,, ..., aft) / 2 £ (/f) (t + as) dt = 0 (2.16)
О s-l /-1
(₽= 1,	k).
Здесь, как и выше, круглые скобки, в которые заключены функ-
ции F(j\ указывают на то, что эти функции вычисляются для
порождающего решения и при ц = 0.
Учитывая наличие символа Кронекера под знаком суммиро-
вания и заменяя затем индекс |3 на индекс s, представим урав-
нения (2.16) в виде
т rs
Ps(alt ...,aA) = J	+	= 0 (s=1- •••>	<2-17)
о /=1
В соответствии с теоремами § 4 главы V синхронные движе-
ния системы (1.1), обращающиеся при р = 0 в решения (2.2),
(2.5) порождающей системы, могут отвечать только тем значе-
ниям фаз аь . • • , ал, которые удовлетворяют уравнениям (2.17).
Каждому решению уравнений (2.17), для которого все корни
алгебраического уравнения k-й степени
|4§--6^| = 0	($, / = 1, .... k) (2.18)
имеют отрицательные вещественные части, действительно отве-
чает (по крайней мере при достаточно малом ц) единственное
асимптотически устойчивое синхронное движение указанного
типа.
Подводя итог, еще раз отметим, что для составления усло-
вий существования, и устойчивости синхронных движений (то
есть для составления порождающих функций Ps) в рассматри-
ваемом случае необходимо, кроме решения порождающей си-
стемы, знать решения системы, сопряженной по отношению
к уравнениям в вариациях лишь для изолированных объектов.
Особо отметим также, что форма записи результативных
соотношений при сделанных предположениях о характере си-
*) Заметим, что суммированию по индексу s от 1 до / в обозначениях
главы V здесь отвечает суммирование по индексу / от 1 до ге, а затем по
индексу s от 1 до k и, наконец, суммирование по индексу I от 1 до v.
Иными словами, суммирование ведется по всем фазовым координатам си-
стемы. При этом следует также иметь в виду, что функции г*, отвечающие
координатам системы связи, равны нулю.
§ 3]	ЗАДАЧА О ВНУТРЕННЕЙ СИНХРОНИЗАЦИЙ	243
стемы связи оказалась не зависящей от конкретного вида урав-
нений связи. Это обстоятельство объясняется общими соображе-
ниями, изложенными вп. 5 § 2 и в п. 5 § 3 главы V;. более кон-
кретно о его значении будет сказано в п. 4 § 4 главы VIII.
§ 3. Задача о внутренней синхронизации
Рассмотрим теперь случай, отличающийся от изученного
в предыдущем параграфе только тем, что исходная система
(1.1) является автономной; такой случай отвечает задаче о вну-
тренней синхронизации объектов.
Рассмотрим вначале вариант задачи, когда период Т порож-
дающего решения (2.2), (2.5) известен; будем предполагать,
что этот период не зависит от фаз аь .. ., <zh. Ввиду автоном-
ности системы одну из этих фаз, например ал, можно, не нару-
шая общности, принять равной нулю. С другой стороны, одну
постоянную а всегда можно ввести, добавив ее ко времени /;
таким образом, порождающее решение по-прежнему будет со-
держать k независимо входящих постоянных.
В соответствии со сказанным уравнения в вариациях (2.6)
по-прежнему допускают k независимых Т-периодических реше-
ний, которые, однако, теперь имеют вид
^==T^(/ + a6.)dvs, =
(Y=l......*-1),	(3.1)
z$ = qf(/ + as), zik = ur
Первые k—1 решений получаются путем дифференцирования
порождающего решения (2.2), (2.5) последовательно по
ось ..., as-], а последнее, k-e решение — путем дифференциро-
вания порождающего решения по а (или, что то же самое,
по t).
Будем, как и в § 2 под r|)s)(Z + а,) (/= 1, .... rs; s= 1, .... k)
понимать решения подсистем (2.12), удовлетворяющие соотно-
шению (2.15). Но тогда, как нетрудно видеть, окажется, что
решения
+	(₽=1, ...,^)	(3.2)
системы, сопряженной по отношению к уравнениям в вариа-
циях, в отличие от решений (2.13), не удовлетворяют условиям
(2.14). Поэтому будем искать решения сопряженной си-
стемы в виде линейной комбинации решений (3.2), то есть
244
ОБЩИЙ СЛУЧАЙ СЛАБО СВЯЗАННЫХ ОБЪЕКТОВ
[ГЛ. VI1
в форме *)
k	k
- 2 с^' - 2 V',” (I+».)	(' + «.) (3.3)
<7=1	<7“ 1
(P=l.......k).
Для определения коэффициентов с9р подставим выражения
(3.1) и (3.3) в равенство (2.14). Тогда при учете соотношения
(2.15) получим:
а)	для у=1, ..., k — 1
k rs
3 3 Ф'х) + as) 6Y(' + as) °
= Sp 3 <P(/Y) tf + cQ n}Y> (t + aY) =	(3.4)
1
б)	для y = Z>
k rs	k	k-1
2 3 <P(/S) (* + as) cs^ (/ + as) = 3 csjJ = 3 6sjJ + = 6Aj},
s=l /»1	S=1	S=1
то есть
. V x _ f - 1 > ₽=!>•••> A-l,
2j°s₽ I j,
Таким образом, матрица коэффициентов cgp имеет вид
1	0	...	0	0 0	1	...	0	0 0	0	...	10 -1	-1	... -1	1	
(3.5)
и является невырожденной.
Решения (3.3) сопряженной системы теперь могут быть пред-
ставлены в форме (напомним, что ah считается равным нулю)
. (»)
/₽
М(7’(/+аЛ s=i, ₽=1>
-n(/ft)(0, s = k-, Р= 1, .... k- 1;
Т]® (f), S = Р = k
(/=1, ..., rs).
• > k;
(3.6)
Теперь можно воспользоваться теоремой 3 § 5 главы V. Со-
гласно этой теореме уравнениями для определения порождающих
*) Соответствующие вычисления аналогичны проведенным Р. Ф. Нагае-
вым [309] при рассмотрении частного случая данной задачи, о котором го-
ворится в конце настоящего параграфа.
§ 3]	ЗАДАЧА О ВНУТРЕННЕЙ СИНХРОНИЗАЦИИ	245
фаз аь .... «л-i будут*)
Т k rs
Qp (аь ..., afe_,) J 2 £ (Tf) zf{t) dt = 0	(3.7)
0 № 1 /Q1
0=1,	6-1)
или, после учета равенств (3.6), упрощений и замены индексар
на индекс s,
Qs(ai> ..., a^O^PJaj.......ak-i)~ Рк{щ.......aft_]) = 0	(3.8)
(s=l, .... 6-1).
Здесь, как и выше (см. равенства (2.17)),
т rs
Ps(ai> .... aft_!)= JS(f(/S>)^(/ + as)d/ (s=l,..., 6), (3.9)
о /-1
причем следует помнить, что а* = 0.
Формула (5.26) главы V для определения поправки 6(н)
к периоду 7\(jx)= Г[1—6(h)] решения исходной системы в дан-
ном случае примет вид
Г г«
О sel /=»1
г rk
=	=	....aft->).	(З.Ю)
О /°1
Для действительного существования и устойчивости {по
крайней мере при достаточно малых значениях ц) синхронного
решения рассматриваемого типа, отвечающего определенной си-
стеме фаз аь ..., ал-ь найденных из уравнений (3.8), доста-
точно, чтобы все корни % алгебраического уравнения 6 — 1-й
степени
I"Х~~М=0 («>/=1>•••, ^-i) (з.и)
имели отрицательные вещественные части. Присутствие хотя бы
одного корня с положительной вещественной частью свидетель-
ствует о неустойчивости, а при наличии чисто мнимых или нуле-
вых корней, вообще говоря, требуется дополнительное исследо-
вание.
*) См. сноску на стр. 242.
246
ОБЩИЙ СЛУЧАЙ СЛАБО СВЯЗАННЫХ ОБЪЕКТОВ
[ГЛ. VI!
Если период порождающего решения Т заранее неизвестен
и определяется из условия обращения в нуль (с точностью до
членов порядка р) поправки 6(ц), то вместо уравнений (3.8)
и (3.10) получается система k уравнений
т rs
Ps(ab ...,	+	= Q (3.12)
о /=1
($=!,...,&; ak = 0).
Из этих уравнений теперь должны быть определены не только
фазы аь ..., aft_i, но и период порождающего решения Т.
Отметим, что система (3.12) и уравнение (3.11) могут быть
формально получены и из уравнений (2.17) и (2.18), найденных
для задачи о внешней синхронизации (см. замечания в п. 5 § 3
и в конце § 5 главы V). Действительно, в случае автономной
исходной системы в уравнениях (2.17) можно, не нарушая общ-
ности, положить аА = 0 и рассматривать эти уравнения как
соотношения для определения k—1-й постоянной ai, ..., a^-i
и неизвестного периода порождающего решения Т. Далее заме-
тим, что в задаче о внутренней синхронизации фазы оц, ..., aft
принципиально определяются лишь с точностью до аддитивной
постоянной, ибо в любом решении (2.2) всегда можно заменить
t на t + а. Поэтому должны иметь место тождества *)
Ps(a, + а, ..., а* + а>Р5(аь ..., aj (s = 1....k).	(3.13)
Дифференцируя последние равенства по а и полагая затем
а = 0, получим
k
= 0	<s=1.................0.14)
/-1 7
Покажем теперь, что уравнение (2.18), в силу последних
соотношений, непременно имеет нулевой корень, и отделим
этот корень, несущественный в автономном случае.
Прибавив к последнему столбцу определителя (2.18) все
другие столбцы, получим, согласно (3.14), столбец с элемен-
тами
*) Заметим, что соотношения (3.13) вытекают также и непосредственно
из формул (2.17), если функции F^ не зависят явно от времени.
§ 3]
ЗАДАЧА О ВНУТРЕННЕЙ СИНХРОНИЗАЦИИ
247
В результате уравнение		(2-18)	представится в форме	
	дР, -д—!	X . . да1	дРх dak~	- 1	
х •	dPk-i det]	dPk- dak-	L-x -1	= 0,	(3.15)
	dPk ddj	dPk dak-	- 1	
то есть будет всегда иметь корень х = 0. Сократив на х и вычи-
тая последнюю строку определителя (3.15) из всех прочих
строк, как раз и придем к уравнению (3.11), специально по-
лученному для случая внутренней синхронизации.
Таким образом, результативные соотношения задачи о вну-
тренней синхронизации формально получаются в данном случае
из соответствующих уравнений задачи о внешней синхрониза-
ции, что, как отмечалось, удобно при решении конкретных клас-
сов задач *).
В частном случае задачи о внутренней синхронизации почти
одинаковых линейно связанных объектов, когда в уравнениях
(1.1) следует положить
г, = ... = rt = r,
Х<р = . .. = х<р = хг
v	(3 16)
F(S) = f(s) (x(s).X(.s)-J + 2 IZW (x<f, xf) Ut,
k
+ ... +aVJ«v+S tWP)- •••> 4P))>
полученные выше соотношения, как нетрудно убедиться, пере-
ходят в найденные Р. Ф. Нагаевым [309].
•) Неверно было бы видеть противоречие между установленным здесь
фактом и тем обстоятельством (см. § 1 главы II), что задача о внутренней
(автономной) синхронизации является более общей, нежели задача о внешней
(неавтономной) синхронизации. На - самом деле противоречие отсутствует:
в § 2 главы II говорится, что задача о внешней синхронизации k—1-го
объекта является предельным частным случаем задачи о внутренней синхро-
низации k автономных объектов. Здесь же речь идет о том, что результаты
решения задачи о внутренней синхронизации k автономных объектов полу-
чаются как особый случай задачи о синхронизации того же числа неавтоном-
ных объектов, то есть из решения более общей математической задачи.
ГЛАВА VIII
ОБЪЕКТЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ, БЛИЗКИЕ
К ЛИНЕЙНЫМ
§ 1. Предварительные замечания
Ниже в настоящей, третьей части книги изучаются задачи
о синхронизации ряда важнейших классов объектов со слабыми
взаимными связями. Простейший из таких классов образуют
квазилинейные объекты с одной степенью свободы, подробно
рассматриваемые в данной главе.
Задача о синхронизации квазилинейных объектов представ-
ляет интерес в связи со многими приложениями. В виде таких
объектов могут быть идеализированы определенные типы лам-
повых генераторов, а также механических и электромагнитных
вибраторов; к рассмотрению взаимной синхронизации квази-
линейных осцилляторов может быть сведено и решение задачи
Гюйгенса о маятниковых часах (см. § 4 главы I и § 2 гла-
вы XXV).
§ 2. Уравнения движения системы и основные предположения;
главные частные случаи
Уравнения движения системы k взаимосвязанных осцилля-
торов с одной степенью свободы, близких к линейным, в общем
случае могут быть записаны в форме
x<s> + a,J№ + (£>2x(s) =
=fe(©O + M^s(x(1)> • • •>	*(1)> • • •> иъ • • •> н)
(s=l,	k),	(2.1)
ii{=> UiixM, ....	x(1),	щ, ..., uv, at, ц)
(Z= 1, ..v).
Здесь через xM обозначены обобщенные координаты объектов,
а через ut — фазовые координаты системы связи; ц_>0, как и
выше, — малый параметр. Величины as и со^ представляют со-
бой неотрицательные постоянные, характеризующие соответ-
УРАВНЕНИЯ ДВИЖЕНИЯ СИСТЕМЫ
249
§ 2J
ственно линейное затухание и собственную частоту s-ro объекта
при р = 0. Относительно гладкости вещественных функций Д„
Fs и U{ по отношению к их аргументам делаются предположе-
ния, обеспечивающие справедливость используемых ниже тео-
рем главы V; fs предполагаются Т = 2л/(о-периодическими функ-
циями t; о характере зависимости Fs и Ui от t будет сказано
ниже.
Структурная схема рассматриваемой системы соответствует
общей схеме, представленной на рис. 1.
Процесс и результат решения задачи, естественно, в значи-
тельной степени зависят от характера порождающей системы
x<s)0 + asx&° + (o2sx^° = fs (<of) (s = 1.k),
й° = и^х^°.....x(k)0.	x(i)o...xwo, u°......и°, o) (2.2)
(i= 1....v),
а также от свойств системы уравнений в вариациях
z(s) 4- as?(s) +	=0 (s = 1, ..., k),	(2.3)
zt = pu(t)z™ + ... +	+qn(t)z^ + ... +
+ qlk(t)z^ + rli(t)zl+ ... +rlvzv (z= 1, ..., v),	(2.4)
составленной для порождающего периодического или синхрон-
ного решения уравнений (2.2) (везде ниже предполагается, что
по крайней мере одно такое решение существует).
В уравнениях (2.3) и (2.4) обозначено:
„ - [ dUt\ п ( dUi\ г I dUl	(9РЛ
а круглые скобки указывают на то, что заключенные в них
производные вычислены для порождающего решения и при зна-
чении ц = 0.
Поскольку первые k уравнений являются независимыми, то,
как нетрудно видеть, характеристическое уравнение системы
(2.4) распадется на k + 1 независимых характеристических
уравнений. Первые k этих уравнений соответствуют уравнениям
в вариациях (2.3) для отдельных объектов. Вместо указанных
характеристических уравнений удобнее ввиду линейности си-
стемы рассматривать уравнения для характеристических пока-
зателей Л5 = у1пр(.0), то есть уравнения
^ + «Л + ^ = 0	(s=l, .... k).	(2.6)
Последнее же из k + 1 упомянутых характеристических уравне-
ний отвечает системе связи и совпадает с характеристическим
2S0
ОБЪЕКТЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ
[ГЛ. Vllt
уравнением *)
K-CO-V’hO (/, /=1..............v) (2.7)
системы
Z/ = r,-i(0z;+ ... +r.v(/)z; (i=l....v) (2.8)
(функции z'y. (t) представляют фундаментальную систему ре-
шений уравнений (2.7), удовлетворяющую начальным условиям
z'if(0) = 6Z/). В дальнейшем будем предполагать, что система
(2.8) не имеет периодических решений и поэтому (см. п. 3 § 3
главы III) уравнение (2.7) не имеет корня р<°> = 1. Иными сло-
вами, допустим, что выполняется условие
(i, /=1, .... v).	(2.9)
Более того, будем считать, что все корни уравнения (2.7) имеют
модули, меньшие единицы.
При таких предположениях характер решения задачи о син-
хронизации будет зависеть в основном от корней характеристи-
ческих уравнений (2.6), отвечающих объектам, то есть опреде-
ляться коэффициентами as и Поэтому в дальнейшем рас-
смотрены отдельно следующие случаи, отвечающие различным
вариантам объектов и различным вариантам их идеализации:
1)	Все коэффициенты as и отличны от нуля и не малы;
назовем условно соответствующие объекты объектами с нема-
лым демпфированием и немалыми частотами свободных коле-
баний.
2)	Среди коэффициентов as и имеются малые или рав-
ные нулю, однако если какое-либо as мало или равно нулю,
то соответствующее отлично от нуля и не мало. Назовем
условно соответствующие объекты объектами с малым демпфи-
рованием или с малыми частотами свободных колебаний.
3)	Среди пар as и имеются такие, в которых одновре-
менно as и малы или равны нулю; соответствующие объек-
ты условно1 назовем объектами с малым демпфированием и с
малыми частотами свободных колебаний.
Возможен, конечно, и случай, объединяющий случаи 2) и 3),
однако его изучение не представит труда после раздельного
рассмотрения указанных случаев.
В силу уже обсуждавшихся особенностей отдельно должен
быть рассмотрен случай взаимной синхронизации, когда правые
*) Здесь, как и выше, 6ц — символ Кропекера, и использована сокращен-
ная запись характеристического определителя, поясненная в сноске па
стр. 168.
$ 3]	НЕМАЛОЕ ДЕМПФИРОВАНИЕ И НЕМАЛЫЕ ЧАСТОТЫ	251
части уравнений (2.1) не зависят явно от времени I, то есть
когда рассматриваемая система является автономной.
Ниже, как правило, будут рассматриваться не только чисто
периодические, но и синхронные движения объектов, то есть
движения вида (см. § 1 главы II)
x(s) = [qsnsat + у& (msat)],	(2.10)
где os=±l, со = 2л/Т > 0 — частота синхронного движения,
уЮ— периодическая функция t с периодом Ts = 2n/ams, а каж-
дое из чисел qs может быть равным нулю или единице (в пер-
вом случае соответствующая координата х(я) называется коле-
бательной, во втором — вращательной). Синхронные движения
заданной системы могут отвечать, вообще говоря, различным
комбинациям чисел qs и щ. Через ms и tij обозначены взаимно
простые целые положительные числа.
При изучении синхронных движений, как и в общем случае
(см. главу II), будет предполагаться, что функции F, и Uj
в уравнениях движения (2.1) таковы, что в результате подста-
новки (2.10) они обращаются (или остаются) в периодические
функции t с периодом Т = 2л/<о. Как уже отмечалось, всегда
будет предполагаться также, что порождающая система (2.2)
действительно допускает хотя бы одно решение типа (2.10).
§ 3.	Объекты с немалым демпфированием и немалыми
частотами свободных колебаний
Первый из перечисленных выше случаев, когда все коэф-
фициенты а,и о, в уравнениях объектов отличны от нуля и не
малы, является наиболее простым. Ввиду положительности ве-
личин as и o)s все корни уравнений (2.6) имеют отрицательные
вещественные части, то есть все корни р<°> характеристического
уравнения, составленного для порождающей системы и порож-
дающего решения, имеют модули, меньшие единицы.
Первые k порождающих уравнений (2.2) в изучаемом случае
допускают единственное /’-периодическое решение
x<s)° = <ps(f)	(s=l,	k).	(3.1)
В согласии с принятым выше допущением о характере корней
уравнения (2.7) будем считать, что существует Т’-периодическое
решение
Ы° = Ы’(0 = и°а + П	(1=1......V) (3.2)
также и последних v уравнений (2.2), в которые подставлены
функции (3.1).
Функциональный определитель Пуанкаре (см. формулу (2.7)'
главы III), в соответствии с равенством {4.17) главы V, может
252
ОБЪЕКТЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ
[ГЛ. VIII
быть представлен в форме
. = I д	tyl) I
I 5(₽j........Pi) |(
(s, 1=1...........I),
(3.3)
= I zsi (Т) - bsi |
где I = 2k + v — порядок рассматриваемой системы, а г8!(/) —
фундаментальная система решений уравнений в вариациях
(2.3), (2.4), удовлетворяющая начальным условиям zsi(0) = 6si.
Но последний определитель отличен от нуля, ибо в силу сде-
ланных выше предположений характеристическое уравнение си-
стемы в вариациях
1^(Л-W0) 1 = 0	(s, i=l, /)	(3.4)
не имеет корней, равных единице (система в вариациях не име-
ет периодических решений, отличных от тривиального).
Согласно теореме А. Пуанкаре (см. п. 1 § 2 главы III) от-
сюда следует, что порождающему решению (3.1), (3.2) при до-
статочно малых значениях ц отвечает единственное аналитиче-
ское относительно р, Т-периодическое решение исходной систе-
мы (2.1), обращающееся при ц = 0 в порождающее. Это решение
к тому же будет асимптотически устойчивым при достаточно
малых ц.
Таким образом, в данном случае синхронизация объектов
всегда имеет место. Следует отметить, что этот случай является
малоинтересным с точки зрения теории синхронизации, ибо за-
дача утрачивает здесь характерные' особенности задач о син-
хронизации и, по существу, представляет собой обычную задачу
о вынужденных колебаниях в слабо нелинейной системе.
На рассмотрении задачи о внутренней синхронизации, когда
система (2.1) является автономной, не будем останавливаться.
В изучаемом случае эта задача является вырожденной в том
смысле, что периодические решения первых k уравнений порож-
дающей системы (2.2) представляют собой постоянные, то есть
имеют произвольный период.
§ 4.	Объекты с малым демпфированием или малыми частотами
свободных колебаний *)
1.	Внешняя синхронизация. Пусть теперь среди k синхрони-
зируемых объектов имеется некоторое число k' таких, для ко-
торых коэффициенты имеют порядок ц (или равны нулю),
но коэффициенты as не малы, и k" таких, для которых as имеют
•) В настоящем параграфе обобщаются результаты работ автора [44,
62, 68, 74].
§ 4]
МАЛОЕ ДЕМПФИРОВАНИЕ ИЛИ МАЛЫЕ ЧАСТОТЫ
253
порядок ц, но коэффициенты и* не малы; при этом, естественно,
k' + k"^.k. Тогда, отнеся члены порядка ц в первых k'+ k"
дифференциальных уравнениях (2.1) к функциям pFs, можем
считать, что в указанных уравнениях
at =# 0, ..., ak, =# 0; со, = ... = соА, = 0;
ak'+i=	= ak'+k„= °; ®б'+1	°> •••>“/!'+к» °;	(4-о
ak'+k"+i • • •> ak^°’ ak'+k"+\	ak °*
При этом уравнения (2.6) будут иметь следующие корни:
41 = о,
41 =
42
ks2 ~ ~ г>(0;
(s = 1, ..., k');
(з = 4 + 1..........k' + k")-, (4.2)
4г —
(з = k' + k" + 1, • • . , k).
Иными словами, первые k' уравнений (2.6) имеют по одному
нулевому и одному отрицательному корню, следующие k" урав-
нений— два чисто мнимых корня и, наконец, последние
k—(k' + k") уравнений — два комплексных корня с отрица-
тельными вещественными частями или два отрицательных кор-
ня; при этом чисто мнимые и комплексные корни, естественно,
являются комплексно-сопряженными.
Рассмотрим вначале задачу о внешней синхронизации, то
есть будем предполагать, что явная зависимость правых частей
уравнений (2.1) от t действительно имеет место. Пусть среди
cos(s = 4+l, ..., k' + k") имеется k'" чисел, мало отличаю-
щихся от целых кратностей частоты со = 2л/Г, соответствую-
щей периоду Т. Тогда всегда можно, отнеся соответствующие
малые добавки к функциям в уравнениях движения
тов, считать, что
2л
cos = — ns = cons (s = k +1......k' + k"'),
объек-
(4.3)
где ns — целые положительные
При выполнении условий
т
J fs (со/) di = osqstisaas
числа, a O^-k'"^k".
(s = 1.....4),
т
J fs (со/) cos ns at dt = 0,
о
т
J fs (со/) sin nsat dt = 0
о
(4.4)
41 —
—

($ = 4 + 1, ..., 4 + k'")
254
ОБЪЕКТЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ
[ГЛ. VIII
порождающая система (2.1) допускает в рассматриваемом слу-
чае семейство синхронных решений
= <ys (qsnsat + as) + cps (co/) (s = 1, . . ., k'),
x<s)° = gs cos nsat — hs sin nsat + <ps («/) (s = k' + 1, .. ., k' + k"'),
x<*>° = <ps (&t) (s = k' + k"' +1, .... k),	(4.5) *
u° = u°(T + t) = u°(t)	(/=!,..., v),
зависящее от k'+2k'" произвольных параметров ai, ....a*';
gV+1......gk'+k'"’ hk'+i’ hk'+k"' (через cps(®/) обозначены
Г-периодические функции времени t, вычисление которых не
представляет каких-либо затруднений). Как видно из выраже-
ний (4.5), движения первых k' объектов могут быть не просто
периодическими (<?s = 0), но и синхронными (<7S= 1)- Напомним,
что через щ (см. § 2) обозначены числа, каждое из которых
может быть равно +1 или —1.
Преобразуем теперь первые k уравнений (2.1) к канониче-
ской форме. С этой целью введем вместо Хц .... xft;
xi, ..., новые фазовые координаты г)!,0;	по
формулам
x(s) = 2. ^(s) + x<s) = -L (A,sl-n<js) + M^') (s = 1, ..., k).	(4.6)
В результате, как нетрудно видеть, эти уравнения запишутся
в форме
П?’ = М” + zsl-zs2	+ ц XS1-ZS2 Fs’
F. (S-I.........<4-7)
ili = U i (i = 1....v).
Здесь предполагается, что в выражения для функций Fs и Ui
вместо х<5> и x<s> подставлены их значения согласно (4.6).
В новых переменных порождающее решение (4.5) предста-
вится в виде
< ° = 2<rs (qsns&t + as) +	osnsqsa + (<ps -I- ns<ps),
n(S)o = _ А	_ A <ps (s = i.......k'),
t)<js)° = asetan^ +	(<ps + irts®<ps)(
Ml
МАЛОЕ ДЕМПФИРОВАНИЕ ИЛИ МАЛЫЕ ЧАСТОТЫ
233
= ase-(<ps - ms<oq>s) (s = k' + 1, ..., kr + k'"), (4.8)
)0 = 7^7 (Ф*+ /(°Л)» <° = ~ 17? (<₽* “ Z(0(₽s)
(s = k' + k'" + 1.k),
u° = u°(i)	(/= 1, ..., v),
Еде вместо 2k'" вещественных постоянных gs и hs введены kr>'
комплексных постоянных
as = gs + ihs, as = gs~ihs (s = k' + 1, ..k' + k'"). (4.9)
Заметим теперь, что уравнения (4.7) как раз таковы, что
к рассматриваемой системе применима теорема § 2 главы V
с дополнением, указанным в п. 5 упомянутого параграфа. При-
менение этой теоремы при учете сказанного в § 7 главы V и ре-
шает вопрос о существовании и устойчивости синхронных дви-
жений.
Уравнения (2.41) главы V для данной задачи, в соответ-
ствии с равенствами (4.2), (4.3) и (4.7), будут иметь вид
(числу И = k' + 2k'" ведущей группы критических корней в § 2
главы V соответствует число k; в уравнениях (2.41) полагаем
ns = 0 при s = 1, ..., k' и nk,+s = nk,+s, nk,+k,„+s = - nk,+s при
s = 1, . . . , k'")
••> a^'! a*'+i> •••> ak'+k’”'’ “a'+i.
T
^^p-[(Fs)dt~O (s=l...........k'),
S о	(4.10)
T
Pv+S (...) = - у-Ц- f (?v+s) e-^’+^dt = 0,
T
=	[ (FA4s)e^+^ = 0 (s=l, ...» k'").
nk'-^s w *
Здесь круглые скобки указывают на то, что функции Fs вычис-
лены для порождающего решения, определяемого согласно фор-
мулам (4.5) или (4.8) и при ц = 0. Поскольку выражения
256
ОБЪЕКТЫ с одной степенью СЙОБОДЫ
(Гл. vtii
(Fk'-i-s) вещественны, то последняя группа из k'" уравнений
(4.10) является комплексно-сопряженной по отношению ко вто-
рой группе этих уравнений. Поэтому нетрудно перейти от
k'+ 2 k'" уравнений (4.10) к k' + 2k'" вещественным уравне-
ниям относительно такого же числа вещественных постоянных
°i<	•••> gk'+k'"‘>	hk'+k’"'‘
^ = /Uai> •••> a*'’ gfe'+i’ •••> Sk'+k’"^ ^k’+i> •••
т
.... hk,+k.^^Ps^\(Fs)dt (S = l, .... k'),
0
ftk'+s s Rk'+s (•••) = ~ 2	(Pk'+s “ Pk'+k"'+s) —
т	(4.11)
ss J cos dt == 0,
о
m^+s(d
R.k’+k'"+s — Rk'+k"'+s(- • •) ==-2 (Pk'+s + Pk'+k"'+s)
1
ss J (Fk’+s) sin iik'+s&t dt — 0 (s = 1, ..., k'").
о
Для существования синхронных движений исходной системы
уравнений, обращающихся при р, = 0 в порождающее, необхо-
димо, чтобы уравнения (4.11) допускали вещественные решения
относительно постоянных a, g и h; каждому изолированному
решению уравнений (4.11) действительно отвечает единствен-
ное аналитическое относительно ц при достаточно малых его
значениях синхронное движение исходной системы, обращаю-
щееся при ц = 0 в порождающее.
Вопрос об устойчивости синхронных движений решается в
зависимости от знаков вещественных частей корней алгебраиче-
ских уравнений (2.42) — (2.44) главы V. При этом число и сте-
пени уравнений (2.43) и (2.44) зависят от характера чисел cos
(s = k' + k'" +1, ..., k") в выражениях (4.2) для XS1 и Хв2. Эти
уравнения, как и уравнения (4.10), можно привести к уравне-
ниям с вещественными коэффициентами, на чем мы, однако,
останавливаться не будем.
2. Внутренняя синхронизация. Случай известного периода
исходного приближения. Рассмотрим теперь задачу о внутрен-
ней синхронизации, когда правые части уравнений (2.1) не за-
висят явно от времени t, и поэтому система является автоном-
ной. В этом случае любой паре чисто мнимых чисел Xoi = йо0
и Ла2 = —могут соответствовать периодические решения си-
§ 41	МАЛОЕ ДЕМПФИРОВАНИЕ ИЛИ МАЛЫЕ ЧАСТОТЫ	257
стемы (2.1) с периодом Г’о (ц), близким к Tqa=‘^- (<?=#0 —
целое положительное число). Будем интересоваться синхрон-
ными движениями с каким-либо из таких периодов 7\(ц) =
= Г[1-6(ц)], где 6(0) = 0. Числа Xsi и Xs2 пусть по-прежнему
определяются соотношениями (4.2) и (4.3), причем в данном
пункте будем предполагать, что число k" > 0, то есть что чисто
мнимые величины A,si и Z,s2 непременно имеются.
Функции fs(cot) в рассматриваемом случае заменяются по-
стоянными, причем для того, чтобы порождающая система по-
прежнему допускала синхронные движения, следует положить
fs = asqs&asns (s= 1, ..k');	(4.12)
что же касается постоянных Д для прочих k — k' объектов, то
эти постоянные могут иметь любые значения.
При выполнении условий (4.12) порождающая система допу-
скает семейство синхронных решений
х(«)° = <rs (qsns&t + as) (s = 1, ..., k'),
x(s)0 = ff cos nsat — hs sin nsat + 4 (s = k' + 1, ..., k' + k'"),
(4.13)
x(s)° = 4 (S = k' + k"'+l........k),
°>s
u° = tf^t + T) —	(t=l,	v),
зависящее по-прежнему от k' + 2k'" произвольных постоянных
ctp aft,; gk,+ l, •••, gk'+k'"’	•••>
В рассматриваемом автономном случае, однако, одну из по-
стоянных или какое-либо одно соотношение между постоянными
можно выбрать произвольно; с другой стороны, одну дополни-
тельную постоянную всегда можно добавить к аргументу t
в решении (4.13).
После перехода к переменным t]<s) и ^s) по формулам (4.6)
порождающее решение (4.13) примет вид
П|(о) = 2(Т (q П cot + a ) + 4 a л га со,
1	О \ ' О О	О/	О'ОО
= - 4 osqs<i>ns (s = 1, .... k'),
us
тГ° = ae1^ + 4, пГ = %e~	+ 4	(4.14)
1	(Oj	s	COj
(S = fe'+ 1, .... k' + k'"),
T]<s)o = T]<2S)O = 4 (s = k' + k'" +1, .... k),
U° = U°(t) (i=l........V).
a И И. Влехман
258
ОБЪЕКТЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ
[ГЛ. УШ
Вопрос о существовании и устойчивости синхронных дви-
жений в рассматриваемом случае решается посредством при-
менения теоремы § 3 главы V при учете дополнения, сделан-
ного в п. 5 того же параграфа. Следует учесть одновременно
сказанное в § 7 главы V о применимости теорем, относящихся
к периодическим движениям, также и к синхронным движе-
ниям.
Уравнения (3.49) главы V для данной задачи будут иметь
вид (как и в п. 1, в этих уравнениях следует положить
k = k' + 2k'", ns = 0 при s = 1....k' и nk,+s = nk,+s, пк,+к,„+~
= ->h'+s при s= 1, ..., k'")
Qs(alt aft,; ak,+l, ..., ak,+k„,-, ak,+l, .... aw,)^
— ~ ^k'+k"'^k'+k'''^s = 0	($=!,...,&),
Qfc'+SG • •) — ~ ak,+ k,„nk,+k,"Pk,+s — %.+A'+sPft'+2ft"' = 0	(4-15)
(s= 1, .... k'"),
Qk’ + k"' + S (• • •) s — ^k'+k'"^k'+k'"^k'+k'" + s 4*
4" ^k'+s^k'+s^k'+2k'" ~ 0
(s= 1........k'"-	1).
Здесь функции P, по-прежнему определяются равенствами
(4.10).
К уравнениям (4.15) следует присоединить дополнительное
соотношение
ak'+k'" = ®k'+k"'= Sk'+k'">	(4.16)
после чего число уравнений, связывающих постоянные а, совпа-
дет с числом этих постоянных.
Как и в п. 1 настоящего параграфа,
Pv+s— Pk'+k"'+s	(s=l, ..., k'").	(4.17)
Но тогда при учете равенства (4.16) из k' + k'"-vo уравнения
(4.15) вытекает соотношение
Pk'+k'" — ~ Pk'+2k'" = IP*,	(4.18)
где Р* также непременно вещественно.
Теперь нетрудно заключить, что
Qk'+k-'+s-Qk'+s	(s=l, .... k'"-V).	(4.19)
Поэтому можно перейти от уравнений (4.15) к k' + 2k'"—1
вещественным уравнениям относительно величин gs = Re as =
~Reas и /i8=lmas = —Im as (s = k' + 1, ..., k' + k'"), по-
добно тому как это было сделано, в п. 1 настоящего параграфа.
§ 4)	МАЛОЕ ДЕМПФИРОВАНИЕ ИЛИ МАЛЫЕ ЧАСТОТЫ	259
При учете соотношений (4.10) и (4.16) — (4.18) эти уравнения
могут быть представлены в форме
#s=#s(ai>	%'’> Sk'+l’ ’••> Sk’+k’"’ dk'+l> •••> ^A'+fe'"-l)S
т
s “ 2g = f dt = 0 (s = 1..........................*'),
^Sk'+k"'nk'+k"'	*
n , s   (Qfe' + S + Qk'+k'" + s)
Rk’+s^	2	ank'+k"'nk'+s —
T
= gk,+k,„n2k,+k,„ J* (Fft,+s) sin nk,+s®t dt +
0
T
+ hk'+s^k'+s I (Fk'+k">)cos nk’+k'"&t dt = O,
о	(4.20)
Rk’+k"'+s (• • •)	2	ank'+k'"nk'+s —
T
S ёк'+^+к"' f (f K+s) C0S "k'+s^ dt -
0
T
- hk' + sdl+S f ('W") cos dk,+k,^t dt = O
(s=l, ...,
T
nk,+k,„a Im P* J (Fft,+V„) sin nk,+k,„&t dt = O.
о
Наличие вещественных решений у уравнений (4.20) и будет
необходимым условием существования синхронных движений
в системе. Каждому простому решению действительно соответ-
ствует при достаточно малых р единственное синхронное реше-
ние с периодом = Г[1 — 6(р)], обращающееся при р, = 0
в порождающее решение с периодом Т.
Поправка к периоду искомого движения 6(р) в первом при-
ближении определяется формулой (см. равенство (3.54) главы V)
. , .	P/e+ik’"
О (р) ~ — р -------z-----тр- —
lak' + k”'nk' + k'"
Т
= - н 2дй2 1 g--------/ (Л'-Н'") cos пк'+^ dF (4.21)
2nnk'+li"'gk'+k'" д'
9*
260
ОБЪЕКТЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ
[ГЛ. VIII
Вопрос об устойчивости синхронных движений решается в за-
висимости от знаков вещественных частей корней уравнений
(3.51) — (3.53) той же главы-, как и в п. 1, число и степени этих
уравнений зависят от характера чисел cos (s = k' + k"' +1, ...
..., k") в выражениях (4.2) и (4.3) для Xsi и Х.,2- Указанные урав-
нения также можно привести к уравнениям с вещественными
коэффициентами.
3. Внутренняя синхронизация. Случай неизвестного периода
исходного приближения. Пусть теперь период порождающего
решения Т = 2л/а заранее неизвестен; как и выше (см. п. 5 § 3
и § 5 главы V, а также § 3 главы VII), попытаемся определить
этот период из условия, чтобы поправка 6(ц.) к периоду иско-
мого движения 7\(ц)=Г[1 — 6(ц)] обратилась в нуль с точ-
ностью до членов порядка ц.:
б(ц)~О.	(4.22)
Будем по-прежнему интересоваться движениями, синхрон-
ными по координатам хь х?, то есть движениями типа
(2.10). В данном случае нет надобности считать, что чисто мни-
мые корни Xs непременно имеются. Вместе с тем теперь примем,
что числа a., (s = k' + 1,. .. , k"), отвечающие таким корням, от-
личны от nsu>, где ns — целые положительные числа, а а =
= 2п/Т — неизвестная заранее частота порождающего решения,
ибо в противном случае решение изучаемой задачи получилось
бы при 6(ц) ~ 0 из решения задачи предыдущего пункта. Иными
словами, положим, что k'" = 0.
При таком допущении решение рассматриваемой задачи не
может быть непосредственно получено при 6(ц)~ 0 из решения
задачи п. 2, ибо там существенно предполагалось, что k'" =/= 0,
то есть что непременно имеется хотя бы одно число оц типа nsa.
Учитывая изложенное, исходную систему уравнений движе-
ния будем записывать в форме
x<s) + asx(s) = osqsnsaas + j.iFs (s = 1, ..., k'),
x<s> + <o2x(s) =	(s = k'+l, ..., k' + k"),
x<s) + asx(s) + (o^x^ = p,Fs (s = fe' + fe"+l, k), (4-23)
ut = Vt (1= 1, ..v).
Здесь постоянные fs — Gsqsnsaas в первых k' уравнениях, как и
выше, отвечают условию, чтобы эти уравнения в порождающем
приближении действительно допускали синхронное решение
x(s)o = crs (qsns&t + as) (s=l, ..., k'),	(4.24)
а постоянные fs в прочих уравнениях объектов могут быть лю-
быми.
§ 4]	МАЛОЕ ДЕМПФИРОВАНИЕ ИЛИ МАЛЫЕ ЧАСТОТЫ	261
Отвечающая уравнениям (4.23) порождающая система до-
пускает, таким образом, семейство синхронных решений, опре-
деляемое, наряду с (4.24), равенствами
x(s,° = j	(s = k' 4- I, ..., k),
= ap ..aft) (i =« 1...........v).	(4‘25)
Это семейство зависит от k' произвольных параметров
один из которых, в силу автономности, может быть выбран про-
извольно; положим, например,
а,у = 0.	(4.26)
С другой стороны, в решениё (4.24), (4.25) всегда можно ввести
еще одну постоянную, добавив ее ко времени t.
В переменных r|is). Л?'1 и м> система (4.23), согласно (4.2)
и (4.7), примет вид
ПУ - “ “Л" - 2»,4А» “ ТТ	<s = 1....
V " Ч*’ + 7^ Г. + И 7^ F,.	(4'27’
+ 1....*).
Ui^Ui	v),
а порождающее решение запишется в форме
С)с = 2<т, (qsn^t + cQ + osqsans,
n(2s)0= - ~^sqsnsa (s= 1,k'),	(4 28)
T|)s)o = n(s)o _ f	(s = k'+l,	k),
u°==u°(t)	(Z=l, .... V).
Для решения вопроса о существовании и устойчивости син-
хронных движений системы (4.27) можно использовать теорему 3
§ 5 главы V при учете изложенного в § 7 той же главы. Для
этой цели нербходимо лишь найти систему из k периодических
решений z‘s(Z) уравнений, сопряженных по отношению к урав-
нениям в вариациях, составленным для порождающей системы
и порождающего решения, причем функции должны удо-
влетворять условиям (5.22) главы V.
262
ОБЪЕКТЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ
[ГЛ. VIII
Упомянутые выше уравнения в вариациях имеют вид
= 0, z<s) = — asz^ (s = 1.....................k'),
z(s) = X..z(.s), z<s> = Xs2z<s) (s = k' + 1......k),	(4.29)
1	Oil	4	04 X	'	- r •	у
k	V
*/ = 2 [ Ait (/) z</> + BiS (t) £(/)] + 2 rlp (t) zp
i-l	P”!
(z = 1, ..v),
где
а круглые скобки, в которые заключены производные от функ-
ций Uit означают, что эти производные вычислены для порож-
дающего решения и при ц = 0.
Система (4.29), в соответствии со сказанным в п. 2 § 3
главы III, допускает k'—1 периодических решений, получаю-
щихся дифференцированием решения (4.28) последовательно по
параметрам ai, ..., а^-1, и одно периодическое решение, полу-
чающееся дифференцированием того же решения по t:
2(s) = _= 2a б	zls, = —= 0 (s=l	k]
Z4 да j zas°sj’	z2j da/		.......
du°
=	(*= 1, •••> v); (/=!,..., /г — 1),	(4.30)
Ask' = n(is) = 2ors(7s®ras>	= 0	(s=l,	k),
Zik, = u° (z=l,...,v),
где, как обычно, 6SJ- — символ Кронекера.
Система, сопряженная с уравнениями (4.29), имеет вид (см.
п. 4 § 3 главы III)
z;<s) + 2As(/)2; = o,
^> + v;'s> + 2Bjs(i)z;=o (s = i,.... П
^>-v;<*> + 2 As(Oz>o,	(4.31)
z;<s) - as2z;(’> + 2 в .s (0 z> о (s = k' +1.k),
i=l
^i+itr (t)z =Q (i^l,...,v).
§4]
МАЛОЕ ДЕМПФИРОВАНИЕ ИЛИ МАЛЫЕ ЧАСТОТЫ
263
Эта система имеет k' периодических решений *)
Z*lr} = ^sr’ ^2г} = О	(S = 1 > • • •» ^)>
z‘(.s) = z*<s) = 0	(s = k' + 1, ..., k),	(4.32)
z*r = 0 (i = 1........v);	(r = 1, ..., k').
Выписанные решения, однако, не удовлетворяют условиям (5.22)
главы V, которые, в силу равенств (4.30), в данном случае мо-
гут быть представлены в форме
k'
= б (/, r=l,..., k').	(4.33)
3 = 1
Будем, подобно тому как это было сделано в § 3 главы VII,
искать решения удовлетворяющие условиям (4.33), в виде
линейной комбинации решений (4.32):
k'	k.'
z;<s) = S = 2	= Csr.	(4.34)
P=1	pel
Тогда при учете выражений (4.30) получим следующие уравне-
ния для определения постоянных csr:
k'	te
2 z<s;z*w = 2 2<Ts6s/cSr = 2<T/C/r = 6/r
(/ = 1, .... k'- 1),	(4.35)
k'	k'
2	= 2 2asqsanscsr = 6^.
Из первых k'— 1 уравнений находим
г;(/)=с/г=4°гАг	(/=i.........k'~1’	r=1......п (4.зб)
после чего последнее уравнение дает
?ЛЙ + 2°^Л'(ЙСА7 = 6А'г.
или
г^ = с
1г к'г
(/• = 1........k').
(4.37)
Из равенства (4.37) видно, что для существования искомого
преобразования необходимо предполагать отличие от нуля
числа qk', иными словами, существенно, чтобы движение по
♦) Напомним, что второй нижний индекс указывает на номер решения,
а все прочие — на номер переменной.
264
ОБЪЕКТЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ
[ГЛ. viit
координате xv было «вращательным», а не колебательным. По-
скольку, однако, за k'-ю координату можно принять любую из
Первых k' координат, то, по существу, важно, чтобы по крайней
мере одно из движений (4.24) действительно было вращатель-
ным; последнее и будем предполагать, считая, что

(4.38)
Нетрудно убедиться, что преобразование (4.34), определяе-
мое равенствами (4.36) и (4.37), является неособенным.
Для составления уравнений (5.24) главы V теперь следует
учесть, что все функции г*, кроме найденных выше, равны
тождественно нулю и что функции F j в рассматриваемом случае
следует заменить на
а) 1
Тогда при учете равенств (4.36) —
(4.38) получаем
Г k'
Q,(«n > J	dtss
о i-i 1
..............................Н-ЭД
(s = 1, . .., k'-l),
где обозначено
т
Ps(a1,...)a^_1) = -^- ((Fs)dt,
Us J
0
(4.40)
причем, как и выШе, круглые скобки, в которые заключены
функции Fs, указывают, что эти функции вычисляются для по-
рождающего решения.
Приравнивая далее нулю, в соответствии с (4.22), выраже-
ние (5.26) главы V для первой поправки к периоду, приходим
к равенству
Pfc'(ai, .... afe'_i) = 0.	(4.41)
Уравнения (4.39) и (4.41), таким образом, могут быть запи-
саны в следующей окончательной форме:
т
......f (Fs)d/ = 0 (s = 1........................k').	(4.42)
US V
0
§ 4]
МАЛОЕ ДЕМПФИРОВАНИЕ ИЛИ МАЛЫЕ ЧАСТОТЫ
265
Эти k' уравнений и служат для определения k'— 1-й постоян-
ной «1, ctfe'_ 1 порождающего решения и неизвестного пе-
риода Т = 2л/о) этого решения. Вопрос об устойчивости синхрон-
ного движения, соответствующего каждой определенной системе
постоянных, найденных из уравнений (4.42), решается в зави-
симости от знаков вещественных частей корней уравнения
k' — 1-й степени *)
dlps-qs—
U 3 Ч') .
daj
= 0
(s, /=1, .... k'-l), (4.43)
а также корней уравнений, соответствующих уравнениям (3.56)
и (3.57) главы V.
4.	Дополнительные замечания
а)	Заметим, что в рассмотренных выше случаях наличие
в системе объектов, для которых оба коэффициента as и ы2 не
малы (число таких объектов равно k — (k'+ k")), никак не
отразилось на форме результативных соотношений, равно как
не отразилось и наличие системы связи. Это объясняется, с од-
ной стороны, предположением, что уравнения связей, а также и
указанные k — (k' + k") объектов с немалыми as и не вно-
сят дополнительных критических корней характеристического
уравнения системы в вариациях**). С другой стороны, имеет
значение тот факт, что критическим корням при ц = 0 отвечают
простые элементарные делители. Указанное обстоятельство уже
отмечалось в общей форме в п. 5 § 2, в п. 5 § 3 главы V и для
конкретизированной системы — в § 2 главы VII.
Надо, конечно, иметь в виду, что речь идет только о форме
результативных соотношений—уравнений для определения по-
рождающих параметров и уравнений для изучения вопроса об
устойчивости. Что же касается конкретных результатов решения
задачи о синхронизации, то они весьма существенно зависят от
общего числа степеней свободы системы, а также от характера
системы связи, даже если эти степени свободы и не порождают
критических корней характеристического уравнения (см., напри-
мер, §§ 3 и 4 главы XV). Этого и следует ожидать, поскольку
*) Заметим, что уравнение (4.43) несколько отличается от аналогичного
уравнения (3.11) главы VII вследствие того, что постоянные а, введены в
данном случае иным образом (ср. выражения (2.4) и (2.3) главы VII с вы-
ражениями (4.5) настоящей главы).
**) Напомним (см. § 2 главы V), что критическими называются такие
корни р, модули которых при р. = 0 обращаются в единицу. Ведущими крити-
ческими корнями при этом называются корни, обращающиеся при [1 = 0
в единицу.
266
ОБЪЕКТЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ
[ГЛ. VIII
порождающие приближения для координат всех объектов и ко-
ординат системы связи входят в уравнения (4.11) и (4.18) для
определения параметров порождающего решения ау, они входят
также и в коэффициенты уравнений, от характера корней кото-
рых зависит решение вопроса об устойчивости движения.
б)	Отметим, далее, что результаты п. 3, а также результаты
п. 2 в случае, если считать, как и в п. 3, период Т неизвестным
и положить равным нулю выражение (4.21) для поправки 6(ц),
могут быть формально получены из соответствующих результа-
тов, найденных для задачи о внешней синхронизации (п. 1). На
это обстоятельство уже обращалось внимание в п. 5 § 3, в § 5
главы V, а также в § 3 главы VII. Тем не менее представляется
полезным остановиться на получении результатов п. 3 из соот-
ношений п. 1, поскольку в указанных пунктах применялись тео-
ремы, относящиеся к различным классам уравнений.
С этой целью заметим, что в случае задачи о внешней син-
хронизации вместо уравнений (4.42) получились бы следующие
соотношения (см. равенства (4.10)):
т
Р,{рл....= f (Fs)di = 0	(s=l,..., k), (4.44)
0
а вместо уравнения (4.43) — алгебраическое уравнение
|-^--6s/x| = 0	(s,/=l,..., k').	(4.45)
Если теперь при переходе к задаче о внутренней синхрониза-
ции положить в уравнениях (4.44) постоянную а/г- равной нулю,
то получатся как раз уравнения (4.42), служащие для опреде-
ления ai, ..., afe'_i и неизвестного в этом случае периода Т.
Далее, если учесть, что в задаче о внутренней синхронизации
уравнения (4.44) не должны измениться при замене в порождаю-
щем решении at на at + h (h — постоянная), то будем иметь
при учете выражений (4.24)
ps(ai> • • • > М = ps(ai + 4^h, ..., afe, + qkfnk,h).
Дифференцируя последнее тождество no h и полагая затем
h = 0, находим
kr
(*=!,.-.,*')•	(4.46)
/=i	1
Прибавляя теперь к последнему столбцу определителя (4.45),
предварительно умноженному на qk,nk,, все другие столбцы,
SB]
МАЛОЕ ДЕМПФИРОВАНИЕ И МАЛЫЕ ЧАСТОТЫ
26?
умноженные на qjtij, получим в силу (4.46) столбец с элемен-
тами
к'
2 ( да
/=1 V 1 '
В результате уравнение (4.45) представится в форме (напом-
ним, что qk, = I)
	dPi да{ х	дРх	q^i		
		dak'-\			
X •		dPk’-x			= 0.
	5а,	dak'-i			
		dPk,			
	да}	дак'-1		"k'	
(4.47)
Отсюда следует, что при формальном применении уравнения
(4.45) к задаче о внутренней синхронизации один из корней
этого уравнения, в силу автономности задачи, непременно будет
равен нулю. Но, отделив этот корень, как раз и приходим
к уравнению (4.43), специально полученному для задачи о вну-
тренней синхронизации. Действительно, вычитая из первых
k' — 1 строк определителя в левой части уравнения (4.47) его
последнюю строку, предварительно умноженную на
tls
— qs, ПО-
nk'
лучаем определитель, лишь знаком отличающийся от определи-
теля (4.43).
О значении отмеченных фактов с точки зрения упрощения
формулировки и получения результатов решения задач о син-
хронизации уже говорилось в п. 5 § 3 главы V. Подчеркнем,
однако, что эти факты, вообще говоря, не имеют места, когда
критическим корням характеристического уравнения системы
отвечают непростые элементарные делители (см. § 5 настоя-
щей главы).
§ 5. Объекты с малым демпфированием и с малыми
частотами свободных колебаний
1. Уравнения движения системы. Особенности рассматривае-
мого случая. Обратимся теперь к изучению наиболее сложного
для исследования случая, когда среди объектов имеются такие,
для которых одновременно и коэффициенты as и коэффи-
циенты 0)2 имеют порядок малости р или равны нулю. Величины
as и для всех прочих объектов будем считать отличными от
нуля и немалыми.
268
ОБЪЕКТЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ
[ГЛ. VI11
Уравнения движения системы (2.1) в рассматриваемом слу-
чае будут иметь вид
x(s) = fs(®0 + мА(х(1), •••> х{к\ х'1\ ....	uv', &t, ц)
(s = 1, .... k'),
x(i) -} nsx(s) + cojx(s) = fs (co/) + Fs (x<’>.x<fe); x(1>, ...
.... x(fe); ....uv‘, co/, p)	(s = k' + 1, ..k),
iii=* U((х(,)...x<*>; x(,)....№>;	.....uv; со/, p)
(i= 1, ..., v).
Будем, как и выше, интересоваться синхронными движениями
системы, то есть движениями вида (2.10). Существенное отли-
чие рассматриваемого случая от изучавшихся в §§ 3 и 4 настоя-
щей главы состоит в том, что уравнения (2.6) теперь имеют по
два нулевых корня Zs = 0, в связи с чем характеристическое
уравнение системы в вариациях (2.3), (2.4) имеет 2/г'-кратный
корень р(0) = 1, причем этому корню отвечают элементарные де-
лители второй степени.
Действительно, в данном случае система (2.3), (2.4) допу-
скает k' групп решений, отвечающих указанному корню:
4S) = W + A)^
zil — zi. k + l = 0
(s = 1, .... /г; / = 1..v; j — 1, ..., k).
Здесь Ms и Ns — постоянные, a 6S3-, как и ранее, — символ Кро-
некера. Поскольку каждая группа решений (5.2) содержит два
решения (отвечающие значениям индекса j и k + j), то, со-
гласно сказанному в п. 3 § 3 главы III, отсюда как раз и выте-
кает наличие 2/г'-кратного корня р(,,) = I с элементарными дели-
телями второй степени.
Наличие нелинейных элементарных делителей делает непри-
менимыми к данному случаю теоремы §§ 2 и 3, а также тео-
рему 3 § 5 главы V в частях, касающихся устойчивости периоди-
ческих движений. Здесь необходимо специальное исследование,
которое можно выполнить, например, одним из методов, указан-
ных в п. 7 § 3 главы III. Как будет ясно из дальнейшего, нали-
чие последних k — k' + v уравнений (5.1) существенно отра-
жается по форме записи результата исследования, несмотря на
предположение об отсутствии критических корней, отличных от
2/г'-кратного корня р<°) = 1. Иными словами, для рассматривае-
мой задачи несправедливо первое замечание, сделанное в п. 4
§ 4 настоящей главы.
§ 5)	МАЛОЕ ДЕМПФИРОВАНИЕ И МАЛЫЕ ЧАСТОТЫ	269
Уравнения типа (5.1) часто называют системами с многомер-
ной быстро вращающейся фазой. Различные частные случаи та-
кой системы изучались многими авторами. В частности,
К. Л. Штельмахер [484] рассмотрел уравнение
х = pF(x, t, р),
указал метод нахождения периодического решения и исследовал
его устойчивость. Более просто и для случая произвольного
числа уравнений типа первых k' уравнений (5.1)—но при от-
сутствии прочих уравнений — задача построения периодических
решений рассмотрена И. Г. Малкиным [275]. В. М. Волосов при-
менил к изучению систем типа (5.1) специально разработанный
вариант метода усреднения [135—137]. Также с помощью асимп-
тотических методов почти периодические решения системы типа
(5.1) при некоторых упрощающих предположениях изучены
М. Я. Кушулем [237]. Вопрос об устойчивости периодических ре-
шений системы типа первых k' уравнений (5.1) рассмотрен
Р. Ф. Нагаевым [311], результаты которого позднее были обоб-
щены им и К. Ш. Ходжаевым [316] для системы, включающей
также и прочие уравнения системы (5.1), но при определенных
предположениях о характере их правых частей. В настоящем
параграфе и излагается с некоторыми видоизменениями и до-
полнениями один из разделов этой последней работы.
Будем предполагать, что уравнения системы связи квази-
линейны относительно фазовых координат связей щ, uv,
а также относительно х<*'+1).......х(/г> и х(*'+|), .... x(fe):
2 (k — fe,)4-’V
Ut = 2 bilVl + иГ (x(l>, ..., x^'\ x(1), .... x(V), (Of) +
/=i
+	x(fe); x(1>, ..., x(fe); щ, uv, at, p), (5.3)
где Ьц — постоянные, а через обозначены соответствую-
щим образом перенумерованные переменные х<*'+1>, ..., x(fe);
х<*'+|)....х^; щ, ..., uv. Тогда, положив
x(s) = x;s),	^(S)_x(s)	($= 1, ..., /г),	(5.4)
запишем систему (5.1) в форме
x)s) = fs (®0 + pFs (x^, ..., x<fe,); x)», .... x<V); v, at, p,),
£Gs) = x(s) (s = 1, . . ., k'),
v = Av + V(0)(x^.....х(ф'>;	xp, ..., x)*'!; cof) +
+ HV(,)(xf'>, .... xp, x™, ..	X(k'). v>	(5.5)
Здесь первые k' уравнений системы (5.1) записаны в виде 2k'
уравнений первого порядка, а все прочие уравнения — в виде
270
объекты с одной степенью свободы
[ГЛ. VIII
одного векторного уравнения, квазилинейного относительно пе-
ременных x(|V+l),	х<А); х<*'+1),	х<А); и{, uv. (В по-
следнем уравнении v, V<°) и суть 2 (k— k') + v-мерные
векторы, а А — постоянная [2(/г — k') + v] X 2[(/г— k') + v]-Ma-
трица.) Поскольку это понадобится в дальнейшем, будем вме-
сто системы (5.5) рассматривать несколько более общую си-
стему
x<s) = ф5 (®f) + цФ5,
xS>s) = x<s) + ips (со/) + gTs (s = 1, ..k'),	(5.6)
v = Av + V<°) +
где функции ф8(со/), фДсо/) и Ф8, Чт, в точности того же типа, что
и соответственно функции fs(at) и Fs в уравнениях (5.5). Си-
стема (5.6) переходит в (5.5) при ф«(со/) = fs(at), Фв = Fs,
фДсо/) = 0 и Ts = 0.
2. Внешняя синхронизация. Как и ранее, рассмотрим вначале
задачу о внешней синхронизации. Порождающая система
№)° = ф (со/), xls)o = X<s)o + ф (со#)	($ = 1....k'),
I s	z I s	(5 7)
v° = Av° + У<°)(х(,>0> ..., x«°; x^°, ..., x^°- co/, 0),	* ’
соответствующая уравнениям (5.6), при выполнении условий
т
J q>s(at)dt = 0 (s = 1.........k')	(5.8)
о
допускает синхронное решение
4)0 = °s [4sns® + as И)|> xf° = os [qsnsat + as + bs (at) ]
(s = l..........................k'),	(5.9)
v° = v° (at, eq, ..., aw),
зависящее от k' произвольных постоянных aj, ..., a^. Через
as(at) и bs(at) в равенствах (5.10) обозначены Т = 2л/со-перио-
дические функции, определяемые равенствами
t
asas (at) = J qps (сот,) dxx + csa,
\ T	t	(5.10)
asbs (at) = J с/т J фя (cotj) dxi + csat 4- J ф\ (сот) dx,
0	0	0
где
T X	т
cs = —jr J dx J ф5 (cotj dxx — jr J i|)s (cot) dx (5.11)
0	0	0
§ 5]
МАЛОЕ ДЕМПФИРОВАНИЕ И МАЛЫЕ ЧАСТОТЫ
271
— постоянная, определенная из условия периодичности функ-
ций х<?>°.
Предполагается, как и выше, что последнее уравнение (5.7)
таково, что оно допускает единственное синхронное решение
относительно v° при значениях х(^°, опредёляемых равенства-
ми (5.9).
Для получения условий существования Т-периодических ре-
шений исходной системы (5.6), обращающихся при ц = О
в порождающее, можно воспользоваться теоремой I § 4 главы V
с учетом сказанного в § 7 той же главы. С этой целью заметим,
что система уравнений
2*<s> = — z*(s),	z‘(s) = 0 (s = 1, ..., k'),	(5.12)
сопряженная по отношению к уравнениям в вариациях
z(s) = 0, z^ = z& (s= 1, ..., k'),	(5.13)
допускает k' периодических решений, которые можно выбрать
в форме
zi/s)==aA/> 4/s>==0	(s, 7 = 1, ..., /г')-	(5.14)
Поэтому уравнения (4.9) главы V для определения пара-
метров порождающего решения ai, ..., as в рассматриваемом
случае имеют вид
т
РДа|, ..., М = ^рФ5)<Д = 0	(s=l, .... k'), (5.15)
о
где круглые скобки, в которые заключены обозначения функ-
ций Ф„ означают, что эти функции вычислены при ц = 0 и для
порождающего решения; несущественный положительный мно-
житель 1/7 введен для удобства записи последующих соотно-
шений.
Каждому простому решению уравнений (5.15), то есть реше-
нию, для которого
-^-рО	(s,j=l, ..., k'),	(5.16)
при достаточно малых ц отвечает единственное аналитическое
по ц периодическое решение системы (5.6), обращающееся при
ц = 0 в порождающее. Синхронные решения уравнений (5.7),
о которых говорилось выше, можно искать в виде рядов
X(S) — x(s)o цХ(5)1 + . . ., Х^ = X<s)o + ЦХ*’’1 + . . .
(S= 1,  •., k'),	(5.17)
V = V° + |W(1) + . . .
т
ОБЪЕКТЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ
[ГЛ. VIII
с Т-периодическими коэффициентами (за исключением коэффи-
циента x(]S)0). Не останавливаясь на вычислении этих коэффи-
циентов (для частного случая оно весьма изящно выполнено
в цитированной выше монографии И. Г. Малкина [275]), перей-
дем к рассмотрению вопроса об устойчивости синхронных дви-
жений.
Уравнения в вариациях, отвечающие системе (5.6) и реше-
нию (5.17), имеют вид
(s — 1, ..., k'),
k'
Az
/«. 1 -
z(/’ +
дх\п
--------- 2«(/)	_1_
дх^ ) 2 +
Здесь через z<s), z^s) и г обозначены соответственно вариации
функций x(]S), х!/1 и V; круглые скобки, в которые заключёны
производные функции Ф8, и У<°>, указывают на то, что они
вычислены при ц = 0 и для порождающего решения; невыписан-
ные в правых частях уравнений слагаемые имеют относительно
р более высокий порядок, нежели выписанные.
При ц = 0, как указывалось выше, характеристическое урав-
нение системы (5.18) имеет 2£'-кратный корень р<°> = е''-т = 1
или, что то же самое, 2&'-кратный характеристический показа-
тель А = у-In р(0) = 0. Все прочие корни характеристического
уравнения системы при ц = 0, в силу сделанных выше предпо-
ложений (см. § 2 данной главы и п. I настоящего параграфа),
имеют модули, меньшие единицы. Поэтому решение вопроса об
устойчивости движения при достаточно малом ц будет зависеть
от последующих приближений к 2k' критическим характеристи-
ческим показателям. С целью нахождения указанных прибли-
жений поступим следующим образом.
Исключим прежде всего из системы (5.18) вариацию z век-
тора V. Для этого будем искать вектор z в виде
k'
г = 2 [?/ (t н) 4у) + (*, н)	(5.19)
где через и обозначены Т = 2л/о)-периодические вектор-
функции времени. Подставив выражение (5.19) в последнее
$ 5)
МАЛОЕ ДЕМПФИРОВАНИЕ И МАЛЫЕ ЧАСТОТЫ
273
уравнение системы (5.18) и использовав выражения для произ-
водных г*/* и согласно первым 2k' уравнениям, приходим
для определения функций и Цу к некоторой системе квазили-
нейных уравнений. Разыскивая Т-периодическое решение этих
уравнений в виде рядов
§/ = 5; + ^°+ •••> П/ = П/ + ^|)+ •••	(5.20)
по степеням параметра ц с периодическими коэффициентами,
для определения функций и t]J получим систему
Заменив в порождающем решении (5.9) в выражении для
произведение qsns<as на vs, получим эквивалентные выражения
[vs + as (®0]. 4S)' = 4s’ = CTs + as + bs M)],
vs = «/л® (s = 1, • • •, k').	(5.22)
Обозначим, далее, через
v°' = v°' (ffl/; a], ..., av; V], ..., v*')	(5.23)
единственное синхронное решение уравнения
v°' = Av°' + (V(0))'.	(5.24)
Здесь и далее штрих при круглых скобках означает, что стоя-
щая в скобках функция вычисляется для x\s> = х^>' и х^'.
Продифференцировав это равенство последовательно по aj
и Vj и полагая затем vs = <7snsa>, найдем при учете (5.22)
/ dv° V _ . / dv°\ , /дУ*°> \
\ да, }	\ да, ) удх-/1 J
, м х	(5-25)
/<Э®°'\"	я/ду°'\ , д^0}\
I---1 = А |----1 -И—ПГ <7/.
\ 5v/ /* \ ^v/ /» \ /
Здесь и ниже значок «*» при скобках, в которые заключены
производные, означает, что после дифференцирования пола-
гается vs = (aqsns.
Сравнивая последние соотношения с уравнениями (5.21) и
учитывая, что a'j = I, получим
:° _ дг>°
7 ~	’
О ldv°'\ , «.
\	/ /(0^=ж (0
(5.26)
274
ОБЪЕКТЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ
[ГЛ, VIII
где через & обозначены функции, удовлетворяющие уравнению
<5.27)
Заметим, что производная просто выражается через про-
изводную от функции v°. Действительно, если в последнем урав-
нении (5.7) перейти к безразмерному времени т = со/, а затем
продифференцировать частным образом по явно входящей ча-
стоте со, то получим
да А ( да J a V ’	(5.28)
Сравнивая это равенство с уравнением (5.27), находим
г д2у° (т)	оп.
^-а> dadaf •	(5,29Э
Исключим теперь с помощью соотношения (5.19) величину г
из первых двух уравнений (5.18). Тогда придем к следующей
системе из 2k' уравнений относительно функций 2^ и 2<s>;
k'
zf = р У а (g 1 г(/) + ±Ж2</) 1 + ...,
1	I I gv I у gv I j g„ 2 I	’
/=1	<1\	/ /»	'	7 J	/	)
k'	(5.30)
= Z& + Ц У О, (	+ Г 1 г(/) I Ж 2(/) 1 +
2	z) т и	I ду Т I дц L,/ Д । да	IT ...
(s= 1, ..., k').
Здесь использованы соотношения
д (Ф5) _ / <9Ф, \	/ дФ$ \ dv°
да, \дх^)	\ dv I да, ’
,	(5.31)
д (®sy _ / (9Ф.9 \ а/ дФз \ ду°
dVj узД/)/ ;	\ dv / dVj
и аналогичные равенства для функций ЧД полученные при уче-
те формул (5.9) и (5.22).
Характеристические показатели системы (5.31), число кото-
рых равно 2k', совпадают с критическими характеристическими
показателями системы (5.18). Учитывая, что элементарные де-
лители, отвечающие 2&'-кратному нулевому характеристиче-
скому показателю, при р = 0 являются квадратными, их можно
искать в виде рядов по степеням ц|/2 (см. п. 7 § 3 главы III):
Л(ц) = Л1^ + Л2ц + Лз11’/г+ ...	(5.32)
9 S]	МАЛОЕ ДЕМПФИРОВАНИЕ И МАЛЫЕ ЧАСТОТЫ	275
С целью определения коэффициентов последнего разложения
воспользуемся подстановкой Н. А. Артемьева (см. там же)
zf = е^>‘wf (s = 1, г= 1, 2),	(5.33)
разыскивая показатели (5.32) из условия периодичности функ-
ций w\s"'. Эти функции удовлетворяют уравнениям
k’
V (Г/<5(фЭ'\ । /<?ФНо1 ,п , <9(ФЭ „и
® I = Н Zj	fc/ + "я w’ —
1 г-I I	j ' \ dv 1 \ 1 да,	2 [
/-1 ЧА	/ /.	J	/	)
— (^1Ц,/2 +	+ ^зН3/г + • • •) ®(!S) + . . .,
»»_ +и i о, {[1^.+S/] +	(5-з4>
Н—да	J ~	+ ^зН’/2 + • • •) W2S) + • • •
(s = 1, . . . , k'),
которые получаются из системы (5.30) в результате замены
(5.33).
Функции wf будем также разыскивать в виде рядов
®w° + pil/2®)s)I + pi®)s)2 + ps/2®<s)3 + ...	(5.35)
с периодическими коэффициентами.
Для определения исходного приближения из системы (5.34)
получаем уравнения
wf° = 0,	= w^°,	(5.36)
которые допускают периодическое решение*)
tef>° = 0,	w^° = Ms,	(5.37)
зависящее от k' произвольных постоянных Ms.
Уравнения первого приближения, составленные при учете
(5.37), имеют вид
^>‘ = 0,	w<2s>1 = ®<s>1 - AjMs	(5.38)
и допускают периодическое решение
w <s>1 = wf1 = Ns,	(5.39)
где Ns — также произвольные постоянные.
*) Как уже отмечалось, постоянную следует рассматривать как функ-
цию любого периода.
Й76	ОБЪЕКТЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ	[ГЛ. VII»
Для определения второго приближения при учете (5.37) и
(5.39) получаем уравнения
/=1	k,	(5.40)
^(S)2 =	_ ^Ns _	+ 2 <rz
/=i	1
Для существования Г-периодического решения последней си-
стемы должны выполняться равенства
(5=1,...,^). (5.41)
Если учесть, что согласно (5.15)
т	т
[ dt =	[ (Ф.) dt = osT^,	(5.42)
J да, да, J v	s da, ’	'	’
o'	' о	'
то уравнения (5.41) запишутся в форме (б.,/ —символ Кронекера)
k’
Mj (o/as	= 0	(s= 1...k').	(5.43)
/=i	'	1	7
Поскольку
а/аА/ = (Т/^/ = бз/’	(5-44)
то уравнения (5.43) можно представить в виде
k'
S^(4^~x^) = 0 (х = ^) (s=1...............k'Y А45)
/=i V 1	7
Условие нетривиальности решений этих линейных однородных
относительно Mt уравнений
|	- xtsl | = 0	(s,/=l, .... й')	(5.46)
и послужит для определения первых приближений х = к ха-
рактеристическим показателям.
5 5]
МАЛОЕ ДЕМПФИРОВАНИЕ И МАЛЫЕ ЧАСТОТЫ
27/
При выполнении условий (5.45) дифференциальные уравне-
ния (5.40) допускают Г-периодическое решение вида
к
— mN s + ZjAfs + Ds — kiMst + (TyAf
/-i
k’	c
2 1	da. J
' о
(5.47)
где постоянные Cs произвольны, а постоянные
определены из условий периодичности функций и>^)2.
Выпишем уравнения для определения третьего приближе-
ния к функциям
k'
<)3 = 2 Г О/ - N/ -	(у - t) +
/»iL 1	J
k*	t	k'
- ч 2 4-1 (ф-) dt+2 °'	+ OsHs'] M>-
‘Q	/=1	'	(5.49)
Условия существования Г-периодического решения этих урав-
нений состоят в равенстве нулю средних за период значений их
правых частей. Эти условия при учете (5.42) могут быть пред-
ставлены в форме
(5.50)
278
ОБЪЕКТЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ
[ГЛ. VIII
или, если ввести обозначения
т
=-Rs (ai.....Ok') = Os Y J (WJ dt,
0
T
ps = p's{av •••> ak’> vi- •••>	=	(5.51)
0
T
0
— в виде
ад, (др'\
да, 1 \ дх, /	s‘
i \ i /•
(5.52)
(s = 1, ..., k').
Наличие периодического решения уравнений для определе-
ния функций w^3 обеспечивается, аналогично предыдущему, вы-
бором постоянных, появляющихся при интегрировании уравне-
ний (5.49). Мы не будем выписывать соответствующих уравне-
ний, поскольку в дальнейшем они не понадобятся.
Равенства (5.52) представляют собой систему линейных не-
однородных уравнений относительно постоянных N}. Согласно
(5.44) и (5.46) определитель этой системы равен нулю. Поэтому
для ее разрешимости должно выполняться условие
JdPs} , р
да, ' \ dv, /
AG = 0, (5.53)
k'	к
J} 2Z,2MS-
i-i	/=i
где постоянные Afs определяются из системы линейных одно-
родных уравнений
ft' др .
= 0	(s=h---.n	(5.54)
/=i
сопряженной по отношению к системе (5.45).
§ 5)
МАЛОЕ ДЕМПФИРОВАНИЕ И МАЛЫЕ ЧАСТОТЫ
279
Из равенства (5.53) легко находится второе приближение
к характеристическим показателям:
!	° J 6
7^2 —
dR. (дР'\
-----Ь “л-- ) + ^sf
. да1 \ dvi л 7
(5.55)
k'
5 = 1
Теперь можно сформулировать условия устойчивости реше-
ний. Прежде всего заметим, что если хотя бы одни из корней
х = Zi уравнения (5.46) является комплексным или положи-
тельным, то одно из значений Xi непременно будет иметь поло-
жительную вещественную часть, и поэтому, по крайней мере
при достаточно малых ц, рассматриваемое движение будет не-
устойчивым. Таким образом, для устойчивости движения необ-
ходимо, чтобы корни алгебраического уравнения k'-й степени
|^--6s/x| = 0	(s,/ = l, ..., k'),	(5.56)
были вещественны и отрицательны*).
При выполнении указанного условия числа Xj=]/x будут
чисто мнимыми, и для устойчивости движения, согласно (5.32),
достаточно выполнения неравенства ReX2<0. Впрочем, знак
«Re» в последнем неравенстве может быть опущен, ибо при
Xi = x^0 величины Х2 получаются вещественными. Таким об-
разом, достаточные условия устойчивости периодических реше-
ний (при достаточно малых значениях р) сводятся к неравен-
ствам
Х? = х<0,	Х2<0.	(5.57)
Если хотя бы один корень х является положительным или ком-
плексным, а также при Х2 > 0, соответствующее движение не-
устойчиво; случай, когда при выполнении первого условия (5.57)
имеет место равенство Х2 = 0, вообще говоря, требует дополни-
тельного исследования**).
*) Случай, когда имеется нулевой корень, исключаем из рассмотрения,
ибо при этом не выполняется условие (5.16).
**) Условия, связанные с возможностью нахождения величин Mj из урав-
нений (5.45), а также с возможностью однозначного построения рядов (5.35)
для каждого показателя 7.(ц), приводят к дополнительному требованию
о некратности корней уравнения (5.56) (см. стр. 195—201 книги [275]).
Однако, как отмечалось в п. 1 § 4 главы V, это требование можно обойти,
например, применяя иной способ определения характеристических показа-
телей.
280
ОБЪЕКТЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ
[ГЛ. VIII
Возвращаясь теперь к исходной задаче — о синхронных ^дви-
жениях системы (5.5), в полученных выше соотношениях" сле-
дует положить
<ps (Ы) = fs (at), Ф5 = Л>	^ = 0.
Тогда при запишутся	учете соотношений (5.4), (5.9) —(5.11) уравнения (5.15) в форме т
Ps(ai		ctfe') ss у j* (Fg) dt ss 0
т J*F 0 СГ] [f/j/ZjCO + с	s (<Л [wpt + ai + Z>i (©/)], ..., ck,[qk,nk,at+ak,+ bk,(at)]’, I] (©/)], .... ck,\qk,nk,a +ak,(ai)]-, at, p.](ft = 0	(5.58) (s = 1, ..., k'),
где	t asa3 (at) = J fs (©t,) dti + csa = asbs (at), °t t	(5.59) o3b3 (at) = J dx J f3 (ax:) dxt + c3at 0	0 /	T	z	x 1 C3 = - 2^- j" dx J f3 (©T1) dxi j.
Условиг сохраняют нимает вид]	устойчивости (5.57) и уравнение (5.56) полностью свою форму, а формула (5.55) в силу (5.51) при- S	+Es} 	р	—	,	(5.60) 2Г 2
где	,5-6|) 0
Таким образом, каждому вещественному решению уравнений
(5.58) относительно постоянных а1? .может соответ-
§ 5]	МАЛОЕ ДЕМПФИРОВАНИЕ И МАЛЫЕ ЧАСТОТЫ	281
ствовать синхронное движение вида (2.10), обращающееся при
[1 = 0 в порождающее. Такое движение действительно суще-
ствует и является асимптотически устойчивым при достаточно
малых значениях ц, если выполняются условия (5.57).
3. Внутренняя синхронизация. В случае задачи о внутренней
синхронизации, когда система автономна, в соответствии с усло-
вием (5.8) функции (ps в уравнениях (5.6) и функции fs в урав-
нениях (5.1) и (5.5) должны тождественно равняться нулю.
Как и в п. 3 § 4 настоящей главы, период порождающего ре-
шения Т в этом случае неизвестен, и его можно пытаться опре-
делить из условия обращения в нуль первого приближения для
поправки к периоду б(ц).
Порождающее решение в рассматриваемом случае будет
иметь вид *)
x(s)o = (ts (qsnsat + as) (s = 1.k'),	(5.62)
причем одну из постоянных а, можно назначить произвольно;
будем считать для конкретности, что &k' = 0. При этом уравне-
ния (5.58) запишутся в форме
т
Рз(щ.....afe'_i)^asy J (Fs)dt=ss
о
т
S crs J- j* Fs [а, (дщщй! + щ), ...
о
....	ok,qk,nk^t-
, ak,nk,qk,(A\ O\dt = 0 (s — 1, ..., k'), (5.63)
и из них, кроме ap ..., aA,_p определится период порождаю-
щего решения Т = 2л/и.
Условие существования у уравнений (5.63) решений, веще-
ственных относительно сц, ..., ak-i и положительных относи-
тельно Т = 2л/со, и будет необходимым условием существования
синхронных решений рассматриваемой системы, обращающихся
при [1 = 0 в порождающее.
Далее, совершенно аналогично тому, как это было сделано
в п. 4 § 4 настоящей главы, можно показать, что один из корней
x = Ai уравнения (5.56) непременно равен нулю. Отделив этот
*) Как и в п. 4 § 4, предполагается, что qki = 1.
282
ОБЪЕКТЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ
[ГЛ. VHI
д(р -q — PkA
\	4 nk' к I	.
да.
корень, придем к следующему уравнению k'—1-й степени для
определения прочих корней:
= 0	(s, /=1......fe'-l).	(5.64)
Необходимые условия устойчивости движения состоят в тре-
бовании отрицательности всех корней х уравнения (5.64).
Получение достаточных условий устойчивости в данном
случае более сложно. Это объясняется наличием двукратного
нулевого корня Zi—х = 0 у уравнения (5.56) относительно пер-
вого приближения Xi к характеристическим показателям. Один
из этих нулевых корней соответствует нулевому характеристи-
ческому показателю, всегда имеющемуся (и не влияющему на
суждение об устойчивости) в случае автономной системы. Вто-
рой же из показателей, для которого Xi = 0, является суще-
ственным. С целью вычисления второго приближения к этому
показателю можно воспользоваться известной теоремой, со-
гласно которой сумма характеристических показателей системы
линейных уравнений с периодическими коэффициентами равна
среднему за период значению следа матрицы коэффициентов
системы. Не останавливаясь на указанном вычислении, выпол-
ненном в работе [316], отметим, что в результате получается
формула, совпадающая с точностью до числового множителя
с формулой (5.55) или, в частном случае, с формулой (5.60).
Таким образом, достаточные условия устойчивости в задаче
о внутренней синхронизации сводятся к требованию выполнения
первого из неравенств (5.57) для k'—1-го корня уравнения
(5.56) — или, что то же самое, для всех корней уравнения
(5.64)—и к требованию выполнения второго неравенства (5.57)
для всех корней уравнения (5.56), включая нулевой. Иными
словами, и в данном случае результаты, относящиеся к задаче
о внутренней синхронизации, формально получаются из соответ-
ствующих результатов решения задачи о внешней синхрониза-
ции, хотя здесь это и не вытекает из общих соображений (см.
п. 4 § 4 настоящей главы).
ГЛАВА IX
ОБЪЕКТЫ С ПОЧТИ РАВНОМЕРНЫМИ
ВРАЩАТЕЛЬНЫМИ ДВИЖЕНИЯМИ
§ 1. Постановка задачи и уравнения движения
В настоящей главе будут получены в общей форме условия
существования и устойчивости синхронных движений достаточно
широкого класса систем с вращательными координатами, отли-
чающихся той особенностью, что вращательные координаты
изменяются по закону, близкому к равномерному вращению,
а также тем, что связи между отдельными вращательными
степенями свободы являются «слабыми». Такими системами
являются многие вибрационные машины и установки с механи-
ческими вибраторами; к ним относятся также специальные авто-
балансиры для динамической балансировки вращающихся ро-
торов, гибкие валы с неуравновешенными дисками, а также ряд
электромеханических систем с параллельно работающими син-
хронными машинами (см. главы 1 и XXIV). Настоящая глава
в основном воспроизводит результаты работ автора [61, 62, 68].
Итак, рассмотрим задачу о синхронизации для системы, по-
ложение которой характеризуется k обобщенными вращатель-
ными координатами <р(, . . ., <pft и v обобщенными колебатель-
ными координатами Хь . . . , xv.
Предположим, что интерес представляют лишь те синхрон-
ные движения, которым отвечают решения уравнений движения
системы вида
Ts == [n> + as + НФ* (®0] (s = l...k),
xr = xr(<nf) (r = 1, ..v),
где <rs по-прежнему есть 1 или —1, ns — взаимно простые целые
положительные числа, as — постоянные, со > 0 — угловая ско-
рость синхронного вращения, ф*(со/) и хг(и/)— периодические
функции времени t с периодом 2n/co, причем для определенности
284
ОБЪЕКТЫ С ПОЧТИ РАВНОМЕРНЫМИ ВРАЩЕНИЯМИ
[ГЛ. IX
задачи можно принять, что средние за период значения функ-
ций ф* (w/) равны нулю, то есть
2л/щ
-£/ *;мл=0;	(1.2)
о
величина ц >0, как и выше,— малый параметр.
Иными словами, будем изучать задачу о синхронизации в
предположении, что движение по вращательным координатам
мало отличается от равномерного.
Пусть движение системы описывается дифференциальными
уравнениями
d	<9Z, _ dL
dt	<5<ps	<5<ps
d	dL	dL
dt	dxr	dxr
(s — 1, .... k),
(1.3)
(/= 1.......v),
где L — T — II — функция Лагранжа системы (Г — кинетиче-
ская, П — потенциальная энергия), Qs и Qr — непотенциальные
обобщенные силы.
Считается, что функции L, Qs и Qr могут зависеть как от
обобщенных координат и скоростей системы, так и от вре-
мени t, относительно которого они являются периодическими
с периодом 2л/со. Что касается предположений о гладкости
этих функций, то они такие же, как и допущения о правых ча-
стях дифференциальных уравнений в §§ 2—5 главы V.
В соответствии с общей постановкой задачи о синхрони-
зации (см. главу II) считаем также характер зависимости
функций L, Qs и Qr от q>s и от t таким, что после подстановки
в них вместо tps выражений (1.1) эти функции становятся (или
остаются) периодическими функциями t с периодом 2л/со. По-
следнее условие наверняка выполняется, если Qs, Qr и L отно-
сительно фз являются периодическими функциями с периодом
2л, относительно t — периодическими функциями с периодом
(Т.ф,	<т,<р,
2n/w, а также, быть может, функциями разностей —— -----— и
nt nt
ni
Отметим, что, например, в задаче о синхронизации вибрато-
ров обобщенные силы Qs (s = 1, ..., k) в уравнениях (1.3)
для вращательных координат представляют сумму вращающих
моментов двигателей и моментов сил сопротивления, приведен-
ных к валу вибратора, а силы Qr (r= 1, ..., v) в уравнениях
для колебательных координат — суммы сил или моментов со-
противления, отвечающих этим координатам, и реактивных мо-
§ 2]
УРАВНЕНИЯ ДЛЯ ОПРЕДЕЛЕНИЯ ПОРОЖДАЮЩИХ ФАЗ
285
ментов сопротивления, передаваемых на вибрирующие органы
роторами вибраторов, а также основаниями двигателей, если
последние установлены непосредственно на вибрирующем ор-
гане (см. главу XIII). Аналогичный смысл имеют обобщенные
силы Qs и Qr в задачах об автобалансире и в задаче об изгиб-
но-крутильных колебаниях вала с неуравновешенными дисками
(глава XXIV). По своему характеру указанные силы и моменты
таковы, что они удовлетворяют сформулированным требова-
ниям.
Учитывая вид интересующих нас решений (1.1), а также
наличие слабых связей между отдельными вращательными
степенями свободы, естественно ввести малый параметр у, в си-
стему уравнений (1.3) таким образом, чтобы она представилась
в форме
IsVs + ks (ф5 - Osnsw) = |1ФХ (S = 1, . . ., k)		(1.4) (1.5)
	atd^r	(г 1.....V),	
где	ЦФз	Is4>S	ksGsfis® dt d(j)s 1 (9<Ps '	(1.6)
pQ'I) = Qr - Q<0),
Is и ks — существенно положительные постоянные, a Q(r0) — функ-
ции того же типа, что и Qr.
Общие соображения в оправдание такого образа действий
были приведены в § 2 главы IV.
Заметим, что именно такой способ введения малого пара-
метра использован в задаче о синхронизации вибраторов (см.
§ 1 главы I и § 3 главы XIII) и об автобалансире (см. § 2
главы I), причем к уравнениям вида (1.4), (1.5) в ряде случаев
нетрудно прийти также и посредством оценки порядков входя-
щих в основные уравнения величин.
Постоянные Is и ks в задаче о синхронизации вибраторов
представляют соответственно момент инерции и суммарный ко-
эффициент демпфирования.
§ 2. Уравнения для определения порождающих фаз.
Условия существования и устойчивости синхронных движений
Обратимся к получению условий существования и устойчи-
вости решений системы (1.4), (1.5), имеющих вид (1.1), то есть
синхронных движений.
286
ОБЪЕКТЫ С ПОЧТИ РАВНОМЕРНЫМИ ВРАЩЕНИЯМИ
[ГЛ. IX
Порождающая система для уравнений (1.4) и (1.5) имеет
вид*)
+ МФя~<W°) = 0	(s==1- •••> ^)>	(2Л)
(r=l, ...,v)	(2.2)
L dt dxr dxr	r Jo	'	'	'
и допускает для вращательных координат систему решений
ф° =(nsat + as) (s=l,	(2.3)
зависящую от k произвольных параметров.
Пусть
х° =	а,, ..., cQ (г = 1, ..., v) (2.4)
— соответствующее периодическое решение (с периодом по вре-
мени t, равным 2л/о>) для колебательных координат, найденное
из уравнений (2.2) после подстановки в них выражений (2.3).
Предполагаем, что существует некоторое конечное число (но не
менее одного) таких решений для каждой системы рассматри-
ваемых значений постоянных ai, . . . , щ. Будем сначала счи-
тать также, что характеристическое уравнение системы в вариа-
циях, отвечающее уравнениям (2.2), имеет только корни, мень-
шие единицы по модулю.
При сделанных предположениях рассматриваемая задача
о синхронизации сводится к частному случаю задачи, подробно
изученной в § 4 главы VIII, а именно к случаю, когда имеются
только объекты с малыми частотами свободных колебаний.
Уравнения (4.10) указанной главы для определения порождаю-
щих параметров ctj, .... сц в данном случае будут иметь вид
(в рассматриваемом случае k"' = 0, k' = k, as = kjls, РЯ = Ф,Д.:)
2я/(о
....	= J [ФМ/ = 0 (s=l...............k). (2.5)
6
Для существования синхронных движений типа (1.1) необхо-
димо, чтобы система (2.5) допускала вещественное решение от-
носительно постоянных ai, . . . , аь-
Каждому такому решению а’, . .., ak при достаточно малых
значениях параметра ц > 0 действительно отвечает единствен-
ное и притом асимптотически устойчивое синхронное движение
*) Квадратные скобки и значок «0» здесь и ниже в данной главе ука-
зывают, что в заключенное в скобки выражение вместо неизвестных под-
ставлены их значения, соответствующие порождающему решению.
УРАВНЕНИЯ ДЛЯ ОПРЕДЕЛЕНИЯ ПОРОЖДАЮЩИХ ФАЗ
28?
§ 3]
типа (1.1), обращающееся при р = 0 в соответствующее движе-
ние (2.3), (2.4), если все корни х алгебраического уравнения
k-й степени
-^-6s/x| = 0	(s, 7=1, k)	(2.6)
при a, = а*, ..., ak = а* имеют отрицательные вещественные
части. При наличии хотя бы одного корня х с положительной
вещественной частью соответствующее решение неустойчиво;
в случае нулевых или чисто мнимых корней требуется, вообще
говоря, дополнительное исследование *).
Сказанное выше относилось к задаче о внешней синхрони-
зации, когда частота и (угловая скорость) заранее задана.
В случае задачи о внутренней синхронизации, когда частота по-
рождающего решения со заранее неизвестна, согласно сказан-
ному в п. 3 § 4 главы VIII эта частота (в соответствующем при-
ближении) определится из уравнений (2.5). Вместе с тем фазы
a.j могут быть определены из уравнений (2.5) лишь с точностью
до произвольной постоянной: из этих уравнений найдутся толь-
ко разности фаз as — а*. Один из корней уравнения (2.6) при
этом непременно будет равен нулю, а прочие корни опреде-
лятся из уравнения
($, / = 1, k- 1),	(2.7)
которое получается из равенств (4.43) главы VIII, если учесть,
что в рассматриваемом случае q\ = ... = q^ = 1.
§ 3. Развернутая форма и физическое истолкование
уравнений для определения порождающих фаз
Рассмотрим подробнее уравнения (2.5) для определения по-
рождающих фаз ai, .. ., as, играющие основную роль при ре-
шении задачи о синхронизации.
*) Если, в отличие от принятого выше предположения, характеристиче-
ское уравнение системы в вариациях для уравнений (2.2) имеет корни р,
равные по модулю единице, то сформулированные выше условия устойчиво-
сти (назовем их основными) являются лишь необходимыми, но не достаточ-
ными. Для получения достаточных условий устойчивости к этим условиям
следует присоединить дополнительные соотношения, вытекающие из требова-
ний |р| < 1 при ц=#0 и достаточно малом. Отметим, однако, что эти до-
полнительные условия устойчивости часто фактически не играют существен-
ной роли (см., например, § 5 главы XIII).
288
ОБЪЕКТЫ С ПОЧТИ РАВНОМЕРНЫМИ ВРАЩЕНИЯМИ
[рл. ix
Заменив в указанных уравнениях функции [Ф8]о их выраже-
ниями согласно (1.6) и учтя равенства (2.1), получим*)
2л/ш
Ps(at, .... ак, ш)^-^--^- [ Г - 4 (#-] + 4^ + Qs] Л = 0 (3.1)
sv ”	’ я ’ 2л ks J L dt \dqs j 1 <5<ps ^sJo '	’
о
(s = l, .... k).
Отсюда следует, что уравнения (2.5) или, что то же самое,
уравнения (3.1), по существу, представляют результат осред-
нения за период дифференциальных уравнений движения (1.3),
причем в качестве функций tps и хг в процессе этого осреднения
взяты их значения в порождающем решении (2.3) и (2.4).
Введем функцию
2л/<о
А = А(аь ..., aft, о)==-^/ [L]adt,	(3.2)
о
представляющую среднее за период значение функции Лагран-
жа системы L = T — П, вычисленной для порождающего ре-
шения (2.3), (2.4).
В результате несложных преобразований, включающих инте-
грирование по частям при учете равенств (2.2) — (2.4), находим
dL
а]о
dt +
дх°г
да^
(3.3)
*J В функции Р, введен для удобства несущественный с принципиаль-
,	со и
иой точки зрения положительный множитель jx Кроме того, подчеркну-
та зависимость функций Р, от частоты о>.
§ 3] УРАВНЕНИЯ ДЛЯ ОПРЕДЕЛЕНИЯ ПОРОЖДАЮЩИХ ФАЗ	289
Используя последнее соотношение, можно уравнения (3.1)
представить в следующей форме:
дК
das
РДа,, ..ак, =
Kg
2л/ш	0
I т«й-<«+
О
2л/(0
о
= 0 (s = 1...............k).
(3.4)
Уравнения (3.4) по смыслу представляют уравнения равно-
весия средних за период моментов (обобщенных сил), соответ-
ствующих каждой из вращательных обобщенных координат cps;
их можно рассматривать также как уравнения баланса энергии
за период.
Величины
Ms = -	(3.5)
® das	4	'
представляют средние моменты, которые зачастую не связаны
непосредственно с потерями или с притоком энергии в системе,
а характеризуют лишь перераспределение энергии между от-
дельными вращательными степенями свободы, необходимое для
синхронизации. Это имеет место, например, если функция Ла-
гранжа системы L не зависит явно от времени t. Действительно,
тогда имеем (рассматриваем для упрощения простые синхрон-
ные движения, когда th = ... = пк = 1)
A(a[ + a0....aA + a0, co)==A(ai.....ak, со), (3.6)
где осо — произвольная постоянная. Дифференцируя последнее
тождество по осо и, полагая затем ао = 0, находим
k	k
UVAg
S-I	S=I
Таким образом, сумма всех моментов ЛД в рассматриваемом
случае равна нулю. Замечая, что знаки ЛД выбраны с учетом
«направлений вращений» по координатам tps (уравнения (3.1)
или, что то же самое, уравнения (3.4) получены путем осредне-
ния уравнений движения (1.3), предварительно умноженных на
ств), заключаем, что работа указанных средних моментов в син-
k
хронном движении определяется выражением 2л 2 ЛД, то есть
также оказывается равной нулю.
Ю И. И. Блехман
290
ОБЪЕКТЫ С ПОЧТИ РАВНОМЕРНЫМИ ВРАЩЕНИЯМИ
[ГЛ. IX
Моменты
V 2"/И	о
(3.8)
г-1 0
наряду с перераспределением энергии между вращательными
координатами, могут отражать убыль или приток энергии, свя-
занные с колебательными обобщенными координатами и учиты-
ваемые в исходном приближении.
Наконец, средние моменты
2Л/Ю
<3-9)
0
связаны с убылью или притоком энергии, соответствующими
вращательным координатам. Например, в задаче о синхрони-
зации вибраторов они представляют собой «избыточные момен-
ты»— разности между средними вращающими моментами дви-
гателей вибраторов Lsm) (если последние имеются) и средними
моментами сил сопротивления вращению роторов Мт) (см. § 6
главы XIII и § 2 главы XIV).
Величина
AS~ZS-GS,	(3.10)
таким образом, характеризует общий средний момент неконсер-
вативных сил, отвечающих s-му объекту.
.Отметим, что моменты Zs, Gs и As могут быть истолкованы
также как величины, пропорциональные средней за период ра-
боте соответствующих непотенциальных сил (см. §§ 1 и 2 гла-
вы X).
При учете равенств (3.5), (3.8) и (3.9) уравнения (3.4) мо-
гут быть записаны в следующей форме:
Ps(ai....aA, w)sJ-Hs-Afs) = 0	(3.11)
или также в виде
Л(а„ .... аА, со)^(а + ^) = 0 (s=l............k). (3.12)
Заметим, что моменты Z„ Ms и Gs, вообще говоря, зависят
как от ai, ..., ak, так и от со.
§ 4.	Об одном важном соотношении для систем, линейных
в исходном приближении относительно колебательных
координат
Рассмотрим системы, для которых функции Лагранжа
L = Т — П может быть представлена в форме
L = L+L^ + LW,	(4.1)
ОБ ОДНОМ ВАЖНОМ СООТНОШЕНИИ
291
§ 4]
где
k k	V	k
£’ = у	+ S fr (Ф1.....Фь Фь •••> Фа) xr + 2 F? ^s).
s»l / = 1	r = l	S=»I
V V	v v
~ у 2 2 arlxrXj “ у 2 brjxrXj,
r=l /-1	r-l /=i	'n.x)
Л(11) = 11Г(Ф1.Фа; <Pt, • •Фа).
Здесь arj, brj и drj — постоянные, fr, Fs и T — функции соответ-
ствующих аргументов, причем fr и Fs периодичны по фв с пе-
риодом 2л. Иначе говоря, предполагается, что функция Ла-
гранжа есть сумма однородных квадратичных форм с постоян-
ными коэффициентами от переменных хг, фз, хт, и линейной
однородной формы от хг с коэффициентами, 2л-периодическими
по фь ..., фа и зависящими от ф1, ..., Фа, а также некоторой
функции фь фа и фь .... Фа, не обязательно периодической
ПО Ф1, . . . , фА.
Указанное выше разбиение лагранжиана системы на ряд
слагаемых в рассматриваемых далее задачах имеет отчетливый
физический смысл. Так, например, в задаче о синхронизации
вибраторов слагаемое LW соответствует лагранжиану системы
тел, на которых установлены вибраторы («несущих» связей),
&
слагаемое L* = Lt\L* отвечает сумме «собственных» ла-
<-1
гранжианов вибраторов Lt и добавочного слагаемого АЛ*, отра-
жающего влияние подвижности «есущих связей на кинетиче-
скую энергию вибраторов. Наконец, слагаемое Л<п> отвечает
лагранжиану «несомых» связей между роторами вибраторов
(например, гибких валов, инерционных муфт и т. п.). Наличие
несомых связей, в отличие от связей несущих, не приводит
к появлению дополнительной подвижности вибраторов. Несу-
щие связи в дальнейшем иногда будут называться связями
первого рода, а несомые — связями второго рода.
Допустим, далее, что непотенциальные обобщенные силы,
отвечающие колебательным координатам, имеют порядок мало-
сти ц, то есть в уравнениях (1.5) и (2.2)
Q<o) = O (г=1........v).	(4.3)
К изучению описанных систем сводится большинство задач
о синхронизации механических вибраторов, многие задачи об
изгибно-крутильных колебаниях вращающихся валов с неурав-
новешенными дисками, задача об автобалансире и ряд других
ш»
292
ОБЪЕКТЫ С ПОЧТИ РАВНОМЕРНЫМИ ВРАЩЕНИЯМИ
[ГЛ. IX
(см. главу I). Как нетрудно видеть, порождающие уравнения
(2.1), (2.2) для подобных систем линейны относительно коле-
бательных координат Xi, ..., xv.
Покажем, что при сделанных выше предположениях спра-
ведливы соотношения
=	Л<2)=_^	(s=1.....k)>	(44)
где
2л/ш	2л/ш
Д(1) = ^ f [L(I)U,	=	[L'"U	(4.5)
о	0
причем Л® есть среднее за период значение функции Ла-
гранжа LW, соответствующей только колебательным координа-
там системы *) и подсчитанной для порождающего решения
(2.3), (2.4). Равенства (4.4) играют существенную роль при
решении ряда задач о синхронизации.
Для доказательства заметим предварительно, что в силу
(4.2) и (2.3) имеют место соотношения
V I  dZ.(I>
Г=1
2 л До
= У [Л‘]0Л + В0,
о
X,
dLw
дхг
) = 2Л(Ъ,
(4.6)
где Во — не зависящая от ои, ».., ak постоянная.
Дифференцируя по а, тождества (4.6), взятые для поро-
ждающего решения (2.3), (2.4), получаем после сокращений
следующие равенства:
'dLa> . .О а Г dL(I) 1
дхг Jo +Хг да! д*г Jo J
(4.7)
дх°
да^
dLi]s 1 дх° 1
д*г Jo “^7 Г
*) Функция Лагранжа в соответствии с (4.2), определяется так, как
будто степени свободы системы, отвечающие вращательным обобщенным ко-
ординатам <р>, отсутствуют.
§ 4]
ОБ ОДНОМ ВАЖНОМ СООТНОШЕНИИ
293
Используя эти соотношения,
(3.3), (4.2), (4.5) и (4.3),
имеем, в соответствии с (3.2),
dL
аф .
Ts JO
(Эфе 1
^а! J
v 2л/(о
со Г д dL* ,,	аЛ*11»
2п J Хг да, дх п да,
г-1 о	‘ J	‘
ЭЛ*1»
да^
дх°
да^
ал*1» дх°г ,
-Tv- \dt
дхг _0 да J
(4.8)
v 2п/со
со v< Г ( о д ал*1»	. .о а г ал 1 1
2"J I г^Гм
Складывая последние равенства, учитывая (4.2), (4.3) и (2.2)
и периодичность функций fr по ср,, ..., <pfe, находим
Отсюда непосредственно следует справедливость соотноше-
ний (4.4). Отметим, что при учете равенств (4.1) и (4.5) они
могут быть записаны в форме
a(A* + 2A(1>) __0
das
(s=l.........k). (4.9)
Значение полученных тождеств состоит в том, что они по-
зволяют существенно упростить рассуждения и выкладки, свя-
занные с исследованием устойчивости синхронных движений.
294
ОБЪЕКТЫ С ПОЧТИ РАВНОМЕРНЫМИ ВРАЩЕНИЯМИ
[ГЛ. IX
§ 5. Интегральный критерий устойчивости синхронных
движений в системах с почти равномерными
вращениями
Для определенного достаточно широкого класса систем с по-
чти равномерными вращательными движениями оказывается
справедливым интегральный критерий устойчивости периодиче-
ских или синхронных движений, рассмотренный в § 8 главы V.
Действительно, пусть существует функция В = В(аь ...
..., a,k, w), такая, что
v 2л/<0	о	2л/(0
^- = AS = ZS-Gs — f [QWl dt + f [QJod/
das s s s 2л Ай J Jo das 2л J L^SJJ
r=i о	о
(s = 1,	k). (5.1)
Тогда основные уравнения (3.4) запишутся в форме
Л(а„ ....	<о)^-£	=0	U=1.......k), (5.2)
и поскольку коэффициенты ks положительны, то функция
D = - (А + В)	(5.3)
может быть принята за потенциальную функцию системы. Урав-
нения (5.2) при этом эквивалентны равенствам
^- = «	(*->......ч,	(5.4)
то есть порождающие фазы он, ..., ал находятся из условий
стационарности функции D.
Определенной стационарной точке = a‘, ak = a*k дей-
ствительно отвечает единственное и притом асимптотически
устойчивое синхронное движение изучаемого типа, если этой
точке соответствует строгий минимум функции D, определяе-
мый на основании анализа членов не выше второго порядка
в разложении D, вблизи стационарной точки.
Отсутствию минимума в точке а, = а’, ..., ак — a*k, обнару-
живаемому тем же путем, отвечает неустойчивое синхронное
движение; неопределенный случай, вообще говоря, требует спе-
циального исследования*).
Если исходные дифференциальные уравнения движения си-
стемы (1.3) автономны (задача о внутренней синхронизации),
то согласно сказанному в § 2 настоящей главы из уравнений
*) См. сноску на стр. 287.
§5]	ИНТЕГРАЛЬНЫЙ КРИТЕРИИ УСТОЙЧИВОСТИ	295
(5.4) фактически определяются лишь разности фаз as — aj, но
зато находится одновременно угловая скорость (частота) син-
хронного вращения и. В этом случае одну из фаз а, в уравне-
ниях (5.4) можно назначить произвольно, в частности положить
равной нулю. Достаточным условием устойчивости при этом
будет наличие строгого минимума функции D по остальным
k— 1 переменным as.
При наличии потенциальной функции D, как указывалось
в § 8 главы V, условия устойчивости могут быть выражены
в явной форме путем использования теоремы Сильвестра.
Если функция В не зависит от фаз ai, ..., ak, то можно по-
ложить
D = - А,	(5.5)
то есть принять за функцию D среднее за период значение
функции Лагранжа системы, вычисленное для порождающего
решения (2.3), (2.4) и взятое с противоположным знаком.
Наконец, в случае рассмотренных в предыдущем параграфе
систем, для которых справедливы соотношения (4.4) и (4.9),
можно положить либо
П = А(” -Л<’” -В,	(5.6)
либо
£> = - (л(11) +^Л’ + В).	(5.7)
Любопытно, что осредненные лагранжианы ЛЛ и Л<П) вхо-
дят в выражение (5.6) с противоположными знаками, то есть
действие связей первого и второго рода в известном смысле
является взаимно противоположным (подробнее об этом гово-
рится в § 3 главы X). Примечательно также, что в силу (5.5)
и (5.6) при В = const и Л<п) = const устойчивые синхронные
движения соответствуют минимумам функции Л®, в то время
как для функции Л устойчивым движениям отвечают макси-
мумы.
Заметим в заключение, что если условие стационарности
функции Z) = — (Л + В) для синхронных движений рассматри-
ваемых систем можно, по существу, вывести из обобщенного
на неконсервативные системы принципа стационарного действия
Гамильтона — Остроградского*), то наличие минимума этой
функции для устойчивых синхронных движений отнюдь не вы-
текает из упомянутого принципа. Действительно, выражение
2л/со
о
*) Соответствующие выкладки см. в § 6 монографии М. 3. Коловского
[218].
296
ОБЪЕКТЫ С ПОЧТИ РАВНОМЕРНЫМИ ВРАЩЕНИЯМИ
(ГЛ. IX
представляет (с точностью до постоянного множителя) действие
по Гамильтону, вычисленное за период. При этом можно гово-
рить лишь о стационарности, а отнюдь не о минимальности
действия для истинных путей системы. Минимальность же
можно утверждать лишь для действия по Гамильтону за до-
статочно малые промежутки времени.
Подробное рассмотрение этого вопроса, связанного с тео-
рией кинетических фокусов для задач о колебаниях, дано в ра-
боте Г. Ю. Джанелидзе и А. И. Лурье [175], а также в моно-
графии А. И. Лурье [259].
Изложенное в настоящем параграфе перекликается с неко-
торыми результатами Томсона и Тэта [490], развитыми впослед-
ствии в известной докторской диссертации Н. Е. Жуковского
«О прочности движения» [191]. Рассмотрев вопрос об устойчи-
вости консервативной системы, Томсон и Тэт пришли к выводу,
что «действие будет наименьшим между всякими двумя поло-
жениями в непрочном движении и не будет обладать этим
свойством при прочном движении»*).
§ 6. О зависимости результатов исследования от характера
идеализации объектов
Выше при изучении синхронизации объектов с почти равно-
мерными вращательными движениями предполагалось, что
уравнения Лагранжа (1.4), отвечающие вращательным коорди-
натам, соответствуют квазилинейным объектам с малыми часто-
тами свободных колебаний, но с конечным демпфированием.
При этом для получения условий существования и устойчиво-
сти синхронных движений использовались результаты, изложен-
ные в § 4 главы VIII.
Для ряда приложений (см., например, § 5 главы XIV) пред-
ставляет интерес также получение соответствующих соотноше-
ний для случая, когда уравнения движения по вращательным
координатам отвечают почти консервативным квазилинейным
объектам, то есть объектам с малым демпфированием и с ма-
лыми частотами свободных колебаний; синхронизация таких
объектов в общей форме была рассмотрена в § 5 главы VIII.
Представляет интерес также сопоставление результатов, полу-
чающихся при двух указанных выше идеализациях.
Обращаясь к рассмотрению поставленных вопросов, поло-
жим в дифференциальных уравнениях (1.4)
=	(6.1)
*) Цитируется по переводу, приведенному в указанном выше труде
Н. Е. Жуковского [191]; по этому вопросу см. также упоминавшуюся моно-
графию [259].
§ 6]
ВЛИЯНИЕ ХАРАКТЕРА ИДЕАЛИЗАЦИИ ОБЪЕКТОВ
297
и запишем их в форме
(s= 1,	k),	(6.2)
где *)
Фз = ®s - &s (Фз - <М>)-	(6.3)
При этом будем считать, что функции цФ8 по-прежнему
определяются равенствами (1.6), а уравнения (1.5), описываю-
щие изменение колебательных координат, отвечают предполо-
жениям п. 1 § 5 главы VIII, то есть являются квазилинейными
относительно колебательных координат и скоростей. Тогда, при-
меняя для изучения движений вида (1.1) рассматриваемой си-
стемы результаты, изложенные в § 5 главы VIII, придем к сле-
дующему:
1) Уравнения для определения порождающих фаз ai, ..., ал
в изучаемом случае будут (см. уравнения (5.58) и (5.5) ука-
занной главы, а также уравнения (6.2) настоящего параграфа)
2л/и>
Ж«1...........aft, = f [Фз - ^(Фз - dt = О
1 $ Z.J L
о
($ = I, k),
или, при учете (2.3),
2л/ы
.... аь = f [Фз1о^ = 0	(3=1..............k).	(6.4)
1 §	V gj
О
2) Условия устойчивости синхронных движений, согласно со-
отношениям (5.56) и (5.57) главы VIII, будут заключаться, во-
первых, в требовании вещественности и отрицательности кор-
ней уравнения
=0	(S, /=1, .... k)	(6.5)
и, во-вторых, в выполнении для всех корней этого уравнения
условия
(6.6)
где величина fa определяется равенствами (5.60) и (5.51) гла-
вы VIII.
*) Здесь и ниже постоянные величины и функции со значком
(тильда) относятся только к случаю квазиконсервативной идеализации, а
так же обозначенные постоянные или функции, но без этого значка — к слу-
чаю неквазиконсервативной идеализации.
298
ОБЪЕКТЫ С ПОЧТИ РАВНОМЕРНЫМИ ВРАЩЕНИЯМИ
[ГЛ. IX
Сопоставим сформулированные результаты с полученными
ранее для случая неквазиконсервативной идеализации объектов.
С этой целью заметим, что согласно (2.5) и (6.4) порождающие
функции Ps отличаются от функций Ps лишь положительным
множителем:
Ps = -^-1lp	(6-7)
s 4л Is s	v ’
Поэтому основные уравнения (2.5) и (6.4) равносильны и
значения фаз ац .... ал, которым могут отвечать изучаемые
синхронные движения, в обоих сравниваемых случаях будут
одними и теми же.
Что касается условий, определяющих отбор устойчивых дви-
жений, то последние, вообще говоря, являются несколько раз-
личными. Однако, как нетрудно убедиться, и эти условия сов-
падают, по крайней мере для достаточно широкого класса си-
стем. Так, например, если для системы справедлив интеграль-
ный критерий устойчивости (см. § 5), то условия устойчивости,
связанные с уравнениями (6.5) и (2.6), совпадут, ибо в силу
(6.7) обоим случаям будет отвечать одна и та же потенциаль-
ная функция. В отношении же дополнительных условий устой-
чивости (6.6) можно сказать, что по крайней мере в ряде прак-
тически важных случаев они оказываются несущественными,
ибо выполняются автоматически (см., например, § 5 гла-
вы XIV).
ГЛАВА X
ОБЪЕКТЫ, БЛИЗКИЕ К НЕЛИНЕЙНЫМ
КОНСЕРВАТИВНЫМ
§ 1. Почти консервативные объекты с одной
степенью свободы
1. Уравнения движения. Рассмотрим задачу о синхрониза-
ции под действием слабых связей системы k объектов с одной
степенью свободы, близких к нелинейным консервативным; эта
задача была изучена Р. Ф. Нагаевым в работе [311].
Пусть состояние каждого объекта как при отсутствии свя-
зей, так и при их наличии определяется обобщенной координа-
той Допустим также, что связи между объектами не вносят
в систему новых степеней свободы и, вообще говоря (в случае
задачи о внешней синхронизации), передают на объекты внеш-
нее периодическое воздействие периода Т = 2л/со.
Структурная схема изучаемой системы представлена на
рис. 18; естественно, что она является менее общей, нежели
Рис. 18.
схема, изображенная на рис. 1. Обобщение на случай объектов
и связей со многими степенями свободы будет рассмотрено в
следующем параграфе настоящей главы.
Обобщенная функция Лагранжа системы может быть пред-
ставлена в форме
k
l = S L,(х^, х(/)) + pA0(x<l)> *(1); •••, х</г)>	®0 + ....	(i.i)
/=i
где Lj = Tj — Ilj — функции Лагранжа объектов (Tj— кинети-
ческая, Tlj—.потенциальная энергия), Lo — лагранжиан системы
связи, а невыписанные слагаемые имеют относительно ц поря-
док выше первого.
300
ОБЪЕКТЫ. БЛИЗКИЕ К НЕЛИНЕЙНЫМ КОНСЕРВАТИВНЫМ (ГЛ. X
Будем считать, что связи между объектами с точностью до
величин порядка р2 являются консервативными, все непотен-
циальные обобщенные силы Q’ имеют порядок малости ц и
с точностью до членов с ц2 носят «парциальный» характер,
то есть могут быть представлены в форме pQ;(x<j), x<J)).
Функции Q* и I. считаются аналитическими по всем своим
аргументам в областях, в которых лежат изучаемые ниже ре-
шения; рассматривая вначале задачу о внешней синхрониза-
ции, будем полагать, что эти функции имеют по времени t пе-
риод Т = 2л/со.
Обобщенные импульсы
дТ dL dLj dL0
р</) = = = + и (1,2)
вводимые посредством выражения для общей кинетической
энергии системы*), вообще говоря, зависят от характера свя-
зей. Эта зависимость отсутствует (с точностью до величин по-
рядка ц) лишь при условии, что dLo/дх^ zss 0.
Обобщенные скорости x(J>, выраженные через новые канони-
ческие переменные хб') и посредством равенств (1.2), пред-
ставятся в виде рядов
х(/) = ц(/>(%(/), p(/)) + jW(/)(x(’)) p(i);	pw. &t)+ ...	(1.3)
(/ = 1, .... k).
Подставив эти ряды в выражение для обобщенной функции
Гамильтона И рассматриваемой системы и учитывая, что со-
гласно (1.2) и (1.3)
р<п =	ц(/>) +
будем иметь
k
— L —
/“I
k
p^)-iiL0(xW, v^;	x®,	(o/)+	(1.4)
где
/7/(хФ, р^) = р^(х^, p^-LjfxW, о</>)	(/=1......k) (1.5)
— «парциальный» гамильтониан /-го объекта.
*) Ниже используются некоторые положения аналитической механики и
теории колебаний консервативных систем, которые подробно излагаются, на-
пример, в монографиях А. И. Лурье [259], Б. В. Булгакова [106] и Г. Голд-
стейна [145]
§ П
ОБЪЕКТЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ
301
В итоге уравнения движения взаимосвязанной системы объ-
ектов в канонической форме будут иметь вид
дН,	дЬй
X(/)----77Г = — Р  ТТГ + .
др^	др^
dfft ( dLa
(1-6)
(/ = 1.......k).
2. Синхронные решения порождающей системы. Переход
к переменным «фаза — частота». В порождающем приближе-
нии (ц = 0) система уравнений (1.6) принимает вид
х(°П = ’д^> Ро)==~	(/=1, •.,&),	(Ь7)
°Ро	ах0
то есть распадается на k независимых чисто консервативных
подсистем. Каждая из этих подсистем в некоторой области Gj
фазовой плоскости (хб>, р(Л) допускает общее решение вида
х</> = Xt (ф,, S,) = <т; [qfr +	(Ф/> S/)],
где
ф/ = ©;(5;)/ + а/,	(1.9)
а} и Sj — произвольные постоянные, а и р^ — периодиче-
ские функции фв с периодом 2л по этой переменной (то есть
с периодом Tj = 2nl&j по времени /). Как и выше, любое из
чисел <Tj может быть равно +1 или —1, а любое — нулю
или единице; в первом случае координата хд) является колеба-
тельной, во втором — вращательной*). При этом в случае
= 1 соответствующая функция Hj(xd\ рЧ>) должна быть
2л-периодичной по x(j).
Под постоянной Sj в общем решении (1.8) будем понимать
так называемый интеграл действия, определяемый соотноше-
нием
2n	<П
s," i J РПЪ-	О-1»)
о	'
Интеграл действия взаимно однозначно и непрерывно связан
в областях Gj с интегралом энергии
Н}(х^, p^hjlSj)	(1.11)
*) Как уже отмечалось в § 1 главы II, движения, отвечающие qj = 0,
часто называют либрационными, а отвечающие q.i = 1 — ротационными.
302
объекты, близкие к НЕЛИНЕЙНЫМ КОНСЕРВАТИВНЫМ (ГЛ. X
и поэтому по своему смыслу также является характеристикой
энергетического уровня движения системы, устанавливающе-
гося в зависимости от начальных условий. От энергетического
уровня зависит и частота колебаний, которая определяется со-
отношением
/ох dh)	/< IQX
®/(•$/) —' ~ф$~>	(Ь12)
то есть как производная от энергии по действию, и может из-
меняться на интегральных кривых в области Gj в некотором
конечном или бесконечном интервале (частотном диапазоне)
сой) < со, < со®.	(1.13)
Не рассматриваемый здесь вопрос о фактическом нахожде-
нии решений (1.8), равно как и вывод приведенных соотноше-
ний, подробно излагается, например, в цитированной выше
книге Б. В. Булгакова [106].
Дальнейшее исследование значительно упрощается, если
применить метод вариации произвольных постоянных Лагранжа
и перейти в системе (1.6) от переменных хд) и рО) к новым пе-
ременным <pj и Jj, использовав для этой цели выражения (1.8),
то есть положив
х('> = Х/(<Р/, Jj), p^Y^, Jf) (/=1.............k). (1.14)
Переменные <pj, Jj являются каноническими [259, 145], ибо, как
можно убедиться, используя равенства (1.7) — (1-12), преобра-
зование (1.8) удовлетворяет условию
<Э<р,	dJj
Переменные Jj, <pj носят название переменных действие —
угол, они были введены Делоне при решении задач теории воз-
мущений в небесной механике, а затем с успехом использова-
лись Зоммерфельдом в так называемом старом варианте кван-
товой механики [145].
После перехода к переменным действие — угол система урав-
нений (1.6) при учете соотношения (1.15) представится в форме
/<ЭХ, л дЬЛ
JI — ti (— Q j + — । + ...,
1 f\ dw, ‘ йф,/
V 1	(1.16)
[dXi dL0\	х ’
Ф/ = ®/ (Л)_ н ("ату Q/ +	+ • • •	(/ = 1. • • • - &)•
Более характерны для задач о синхронизации переменные
фаза — частота <pj, coj; система (1.16) в этих переменных будет
§ 1]
ОБЪЕКТЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ
303
иметь вид
	_ И ( дХ> П Л. 9L° \ .
ц / dXj dLa \
в] (Шу) у д(й] Q да)/ J +
(/ = 1, .... &). (1-17)
Здесь, в соответствии с равенством (1.12),
бу (&]) =
d/i (m/)
(Zffly
1 ^/[Л(ю/)]
(By da> i
(1.18)
Если величина e3(coj) имеет порядок единицы, что мы и бу-
дем предполагать, то последнее преобразование является не-
особенным. Это соответствует допущению об анизохронности
объектов (см. § 3 настоящей главы), то есть предположению
о том, что частоты «у существенно зависят от постоянных энер-
гии hj\ более простой случай изохронных объектов будет кратко
обсужден в конце следующего параграфа.
3. Условия существования и устойчивости синхронных дви-
жений. Интегральный критерий устойчивости. Система (1.17)
является квазилинейной; она представляет собой частный слу-
чай системы (5.6) главы VIII, и поэтому здесь можно непосред-
ственно воспользоваться полученными там результатами.
Отвечающая уравнениям (1.17) порождающая система име-
ет вид
йу = 0, ф° = и°.	(1.19)
Пусть частотные диапазоны объектов (1.13) пересекаются
и содержат к тому же частоту внешнего возмущения со, то есть
существуют такие числа со(’) и со<2>, что *)
k
(со(1), со(2)) =	(«/Д ей2»),	со(1) < со < со(2).	(1.20)
/=1
Тогда система (1.19) допускает синхронное решение**)
со° = со, <р° = со/ + сОу	(1.21)
*) Знаком П. как обычно, обозначено пересечение частотных диапазо-
нов (1.13).
**) Отметим, что здесь можно ограничиться рассмотрением синхронных
движений частного вида, которому отвечает ?[ = ... = qh = 61 = ... = вь = 1,
ибо соответствующая общность по отношению к исходным переменным за-
дачи уже предусмотрена соотношениями (1.8), использованными в качестве
формул преобразования к новым переменным. Ограничиваемся также изуче-
нием простой синхронизации; обобщение на случай кратной синхронизации,
как и ранее, не вызывает затруднений.
304
ОБЪЕКТЫ, БЛИЗКИЕ К НЕЛИНЕЙНЫМ КОНСЕРВАТИВНЫМ [ГЛ. X
с частотой возмущения со, зависящее от k произвольных по-
стоянных а,.
Применим теперь к системе (1.17) результаты § 5 гла-
вы VIII. В соответствии с формулами (5.15) указанной главы
заключаем, что синхронные движения связанных объектов, об-
ращающиеся при ц = 0 в движения (1.21), могут отвечать лишь
тем значениям фаз аь ..., ал, которые удовлетворяют урав-
нениям
2Л/(й
1 м f / дХ, dLn \
Р,(а1, ..., aj = —т—+ ]dt = O (1.22)
u	е{(&) 2л J dqp, дор, /	v 7
1 о4 1	1 '
(i=i.....k),
где круглые скобки, в которые заключено подынтегральное
выражение, указывают на то, что оно вычислено для поро-
ждающего решения.
При учете равенств (1.21) уравнения (1.22) могут быть
представлены в форме
....+	.....<1-23)
Здесь
2л/ш	2 л/о
a f I дХ,\ If
^-srj W‘" = sd	0.24)
o' '	0
— величина, пропорциональная средней за период работе не-
потенциальной силы, действующей на объект, а
2Л/(й
A0 = A0(a,......<»*)	= -£/ (^о)^	(1-25)
о
— среднее за период значение функции Лагранжа системы
связи, причем обе величины вычислены тля порождающего
приближения (1.21).
Обратимся к получению условий устойчивости синхронных
движений. Уравнение (5.46) главы VIII в рассматриваемом слу-
чае имеет вид
Ь,Ы	(S. /-1.......4),	(1.26)
так как величины А}, определяемые согласно (1.24), от по-
стоянных ai, ..., ал не зависят*).
---------------- )
*) Сказанное связано с тем обстоятельством, что обобщенные силы Qj,
по предположению, зависят только от координат /-го объекта, а подынте-
гральные функции в выражениях (1.24) являются 2л/ш-периодическими по /.
§ 1]
ОБЪЕКТЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ
305
Необходимые условия устойчивости движения, отвечающего
определенной системе значений постоянных аь ..., ал, найден-
ных из уравнений (1.23), состоят в вещественности и отрица-
тельности всех корней уравнения (1.26).
Пусть все величины еДы) имеют одинаковые знаки, то есть
sign ех (и) = ... = sign ek (и) = о,	(1.27)
где а равно +1 или —1. Тогда из равенств (1.23) и (1.26) при
учете независимости величин Aj от аь .... «л следует, что
в рассматриваемом случае справедлив интегральный критерий
устойчивости (см. § 8 главы V), причем за потенциальную
функцию можно принять выражение
/ k	ч
D (ai, ..., aft) = - I 2 Ла/ + Ло/<*•
(1.28)
В соответствии с указанным критерием синхронные движения
изучаемого типа могут соответствовать лишь стационарным зна-
чениям функции D, причем устойчивыми могут быть движения,
которым отвечает минимум функции D, обнаруживаемый на
основе анализа членов второго порядка в разложении D
вблизи стационарной точки.
В частном случае чисто консервативных объектов, когда
Aj = 0, за функцию D может быть принято среднее за период
значение функции Лагранжа системы связи Ло, взятое со зна-
ком, противоположным знаку коэффициентов еДи).
Рассмотрим теперь достаточное условие устойчивости, выра-
жающееся соотношениями (5.55) и (5.57) главы VIII. Для
этого, в соответствии с равенствами (5.54) и (5.45) указанной
главы, сначала рассмотрим систему линейных однородных урав-
нений
k
2>;к<5Гаг73Г-М] = 0	(«-1.....*).	(1-29)
/-1 L 1 ‘ s J
сопряженных по отношению к системе
k
,~H = 0 <s-‘............*>.	(1-30)
Используя тождество еДы)б^ == es(co)6Sj, уравнения (1.29)
можно представить в форме
М,	1 32ЛП
У—А-------------------=0 (s = 1, .... k). (1.31)
XJ e, (<л)	e(<o) da da, SI	'	’	’ '	'	'
/-1 1 u 4 4 1 J
306
ОБЪЕКТЫ, БЛИЗКИЕ К НЕЛИНЕЙНЫМ КОНСЕРВАТИВНЫМ [ГЛ. X
Сравнивая эти уравнения с (1.30), находим следующую про-
стую связь между решениями сопряженных систем (1.29) и
(1.30):
м; = (со) Мг	(1.32)
Сопоставляя далее уравнения (1.17) настоящей главы с
уравнениями (5.6) главы VIII, заключаем, что в рассматривае-
мом здесь случае
Чг = -
* 5
1 (dxs п аг0\
es (®s) \ da>s das / ’
=	(1.33)
Поэтому, согласно равенствам (5.51) главы VIII и формуле
(1.22) данной главы,
Esj = 0,
ад, др'\	1 д а Г дХ, dLn\
да, ^\dvt I	е (со) да, 2л J {дш dw /
» J о'6	5'
д Г 1	/ <ЭД£ \'|)
—— —т—г- 14 5 4 “з— j г •
да, е (а \ \ 6 dec /
j L s \ S/ \	s / J) *
(1-34)
Отметим, что поскольку в рассматриваемом случае q\ = ...
... = qh, то vi = coi, ..., v/t = (Ofe. Напомним, что здесь, как и
в главе VIII, штрих при обозначениях величин указывает, что
они вычисляются не для порождающего решения (1.21), а для
значений со8 и ф8, определяемых равенствами
Фя = ф'= со/+ as, cos = co'.	(1.35)
Скобки же со значком ««•» означают, что заключенное в них
выражение вычисляется при coi = ... = сол = со, то есть снова
для порождающего решения.
Вследствие предположения о том, что обобщенные силы
Qs зависят только от координат s-ro объекта, интеграл
СО Г / dXs п \
2л J \ dco8
о
dt
фактически не зависит от величин аь ..., ал, а величины 4$
(см. равенство' (1.24)) не зависят от со,-, где j 4= s. Поэтому
2л/а
д со Г / дХ \
х— -5-	-^<24^ = 0,
да, 2л J \ дю	I
' о	4 5	1
дСО/ [еДсоД
d
bs! 3----
s‘ do>s
-^^ + 4'6
es (со j dcos « si
d [	1	’
dcos L es (“s).
(1.36)
S п
ОБЪЕКТЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ
307
При учете последних соотношений выражение (1.34) может
быть представлено в виде
daij
дР' \	1
---I 4- Р 1 =--------
dvl /» S es
д2Лр
das д(й] да^ das
дА‘
д<л
Но последнее слагаемое этого выражения обращается в нуль
в силу уравнений (1.22). Таким образом, окончательно
дР, , (дР'Д	1 Г <ЭЛ' <ЭЛ' dA's '
да \ ду, j si ~~ е (со) да дю, да.дш дю
S \ J /*	S ' ' о J	J s	S
(1.37)
Теперь нетрудно упростить выражение для величины А,2,
определяемой по формуле (5.55) главы VIII. При учете ра-
венств (1.32) и (1.37) находим
dasда/
<Э2Лр дА'
_______о t о Д
d№j dws da>s s<
к
2 2 M2ses (со)
1
» /\ I
<L38)
3-1 V s/*	/	3-1
Напомним, что согласно результатам § 5 главы VIII достаточ-
ные условия устойчивости синхронных движений (при доста-
точно малом ц) состоят в выполнении неравенств
^ = к<0,	^2<0.	(1.39)
Если хотя бы один корень х уравнения (1.26) является поло-
жительным или комплексным, а также при > 0, соответствую-
щее движение неустойчиво; случай, когда при отрицательности
всех корней х величины равна нулю, вообще говоря, требует
дополнительного исследования. Как и следовало ожидать,
именно такой случай имеет место для чисто консервативной
системы, то есть при Qs = 0. Отметим, что уравнение (1.26)
в этом случае не изменяется, и требование отрицательности его
корней по-прежнему представляет необходимое условие устой-
чивости.
Заметим в заключение, что производная (dA's/d(as^ , фигури-
рующая в выражении (1.38), может быть представлена в более
308
ОБЪЕКТЫ, БЛИЗКИЕ к НЕЛИНЕЙНЫМ КОНСЕРВАТИВНЫМ [ГЛ. X
простой форме. Используя равенства (1.24), (1.14), (1.15), (1.8)
и (1.18), получаем
{2л/(о	ч	2л/(о
д <й Г ( дХЛ	а Г fdQ,\
-Х—УГ-	dt\ =^(со)лт- \dt- U-40)
д<о 2л J \^s dw I	s' ' 2я J \ др! '	’
з о	5	> *	о 4
Сказанное относилось к задаче о внешней синхронизации.
В случае внутренней синхронизации функция Lo не зависит
явно от времени и уравнения движения являются автономными.
При этом из уравнений (1.23) фазы aj определятся лишь с точ-
ностью до аддитивной постоянной, но из тех же уравнений,
вообще говоря, может быть найдено исходное приближение
к частоте искомого решения со = 2п/Т. Уравнение для опреде-
ления со получается из системы (1.23) следующим образом.
Заметим, что в изучаемом случае функция Ао не изменяется
при замене а, на а, + а, где а — произвольная постоянная.
Отсюда, как и в § 3 главы IX, получается соотношение
k
2-Э^-О.	(1.41)
/=1 '
Если теперь сложить уравнения (1.23), предварительно умно-
женные на еД<в), то при учете (1.41) получим
k
2Д. = 0.	(1.42)
/-1
Последнее соотношение и является искомым уравнением для
определения о и по своему смыслу представляет собой урав-
нение баланса энергии в системе. Уравнение (1.26) в случае
задачи о внутренней синхронизации непременно имеет нулевой
корень, который, однако, не влияет на решение вопроса об
устойчивости движения. Условия устойчивости отличаются при
этом от (1.39) лишь тем, что первое из фигурирующих там не-
равенств должно выполняться для k—1-го корня уравнения
(1.26). В вырожденном частном случае единственного объекта
приведенные выше условия существования и устойчивости дви-
жения непосредственно переходят в соответствующие соотноше-
ния, найденные А. М. Кацем [209, 180].
§ 2. Обобщение на случай объектов и связей со многими
степенями свободы
1.	Характеристика рассматриваемой системы. Несущие и не-
сомые связи. Результаты предыдущего параграфа допускают
обобщение на случай почти консервативных объектов со мно-
гими степенями свободы, находящихся под действием слабых
связей, которые вносят в систему дополнительные степени сво-
§ 2] объекты и связи со многими степенями свободы 309
боды. Такое обобщение было выполнено Р. Ф. Нагаевым и
К. Ш. Ходжаевым в работах [312, 316]; эти работы можно рас-
сматривать также как распространение на случай почти кон-
сервативных объектов результатов наших работ [62, 68] о син-
хронизации механических вибраторов и объектов с почти рав-
номерными вращательными движениями (см. главы IX и XIII
настоящей книги). В данном параграфе будут изложены ре-
зультаты упомянутой статьи Р. Ф. Нагаева [312].
Структурная схема рассматриваемой системы представлена
на рис. 19. Подобно предыдущему предполагаем, что состояние
Рис. 19.
каждого из k объектов как при отсутствии связей, так и при их
наличии определяется одними и теми же обобщенными коорди-
натами x(s) = (УД	(s — 1, ..., k). Подчеркнем, что,
в отличие от § 1 главы II, здесь под компонентами вектора-
столбца понимаются именно обобщенные, а не фазовые
координаты; то же относится и к компонентам векторов, опреде-
ляющих состояние связей.
«Собственные» кинетическая и потенциальная энергии объ-
екта могут быть представлены в виде
Тв = 1?(5)А(5>(*и))?Д Щ = ПДх(Д, (2.1)
где A(s) = A'(s)—симметрическая «инерционная» rs X ^-матри-
ца, а штрихом обозначается операция транспонирования.
Сформулируем теперь предположения о системе связей
между объектами. Имея в виду определенные приложения, бу-
дем рассматривать, подобно тому как это было сдедане в § 4
главы IX, связи двух родов.
Связи первого рода, состояние которых определяется векто-
ром-столбцом обобщенных координат u=(«i, ..., ит), можно
трактовать как обусловленные наличием некоторого «несущего
тела-» или системы «несущих тел» с т степенями свободы. Бу-
дучи связаны с указанными телами, объекты приобретают
310
ОБЪЕКТЫ, БЛИЗКИЕ К НЕЛИНЕЙНЫМ КОНСЕРВАТИВНЫМ [ГЛ. X
дополнительную подвижность, так что их общие кинетическая и
обобщенная потенциальная энергии представляются в виде
k	k
r=^Ts + ДГ,	П = 2 Щ + ДП\ (2.2)
S“1	S=1
где
k
Д 7” = J x'{s} Asm (х, и) й + j й'Ат (х, и) и,
ДП* = и'С (х, со/) + ...
— добавочные кинетическая и потенциальная энергии объектов,
причем выписаны лишь первые слагаемые разложений соответ-
ствующих величин в ряды по степеням и, под х понимается
совокупность всех векторов хМ, а через Asm и Ат обозначены
соответственно некоторые rs X т- и т X т матрицы.
Считается, что, вообще говоря, через систему связей может
передаваться Т = 2л/со-периодическое внешнее воздействие, ко-
торое может быть учтено в ДП*.
Собственные кинетическая и потенциальная энергии связей
первого рода (несущих связей) могут быть представлены
в форме
Tw=ju'Mm(u)u, II(n = |«'Cm« + ...	(2.4)
При этом можно считать, что координаты и являются нормаль-
ными, так что симметрические т X /n-матрицы Afm|u=o и Ст
имеют диагональную форму. Последнее предположение, однако,
не обязательно.
Связи второго рода условно назовем несомыми. Они не при-
водят к увеличению подвижности объектов, но их наличие
также может быть (хотя и не обязательно) связано с увеличе-
нием числа степеней свободы взаимосвязанной системы, так что
для определения состояния системы необходимо, кроме
хб), ..., x<ft>; и, задать также и вектор-столбец обобщенных
координат v(wi, ..., vn). Кинетическая и обобщенная потен-
циальная энергии связей второго рода соответственно будут
7(П) = 1 v'NT (х, и, v) v + 2 x'(S)NsXn 0) (х, и, v) v +
k k
+ 1 S S (*’	*(/) +	(x, U, v)v +
/—I
k
+ 2 x'{s}N[smU} (X, u, v) ii + ju'N{m (x, u, v) ii,
n("> = n(,I)(x, u, v, co/).	(2.5)
§2] ОБЪЕКТЫ И СВЯЗИ СО МНОГИМИ СТЕПЕНЯМИ СВОБОДЫ 31]
Здесь N<n\ N[xnv\ N^j, N(mn\ N(smU} И N%} — соответственно
n X n-, rs X n-, rs X rj-, rm X rn-, r,X in- и m X m-матрицы и,
как и для связей первого рода, предполагается, что обобщенная
потенциальная энергия может содержать внешнее 2л/со-перио-
дическое возмущение.
В задаче о синхронизации вибраторов, подробно рассматри-
ваемой в четвертой части книги, несущими связями являются
тела, па которых размещены вибраторы, а несомыми связями —
упругие или какие-либо иные непосредственные связи между
роторами вибраторов (см. рис. 25, 26 и 37).
В соответствии с предположением о почти консервативности
объектов и о слабости связей будем считать, что после нало-
жения связей кинетическая и потенциальная энергии системы
в целом изменяются незначительно, то есть что можно положить
k
т = т' + т’(!) + tw = 2 ts + о (ц),
(2-6)
п = п* + п(,) + п(И) = 2щ+о (ц),
5=1
где через О(ц) обозначены члены, имеющие порядок малого
параметра ц.
Соотношения (2.6) могут выполняться, например, при сле-
дующих условиях:
1)	Динамические и кинематические характеристики движе-
ния объектов имеют порядок единицы, то есть
x(s> = O(|i°), А = О(ц°),	С=О(р°).	(2.7)
2)	В предположении, что компоненты rs X /n-матриц Asm,
характеризующих инерционные свойства объектов, имеют поря-
док единицы, для справедливости оценки ДР = О(ц) изменение
координат несущей системы в процессе движения должно счи-
таться малым, то есть
и =
5 = о (р°).	(2,8)
3)	При выполнении последнего условия для малости вели-
чин Т® и П<Т) достаточно, чтобы было
 >°	—О
с
М,„ = ^ + О(р°), Ст = -^+О(ц0),	(2.9)
где М°т и ^т~ постоянные т X т-матрицы.
312
ОБЪЕКТЫ, БЛИЗКИЕ К НЕЛИНЕЙНЫМ КОНСЕРВАТИВНЫМ [ГЛ. X
4)	Инерционные и силовые характеристики элементов свя-
зей второго рода малы, так что
У (х, и, v) = р№ (х, и) + О (р2),
(ft	к к	\
-г v'N°nv + 2 x'(s)№smv + j- У У х’ (s)N°s!x + О (р2),
J (2.10)
П(,,) = рл("'(х, v, +
где под N понимается любая из соответствующих матриц, фи-
гурирующих в выражениях (2.5).
В указанных предположениях слабость связей первого рода
обусловлена малостью колебаний несущей системы, а слабость
связей второго рода — малостью соответствующих импульсов.
Следствием этих предположений является линейность уравне-
ний движения системы по координатам несущей системы с точ-
ностью до величин порядка р2.
Как и в предыдущем параграфе, будем предполагать, что
взаимодействие между объектами (с точностью до членов с р2)
имеет консервативную природу и что непотенциальные обоб-
щенные силы Q*(s)(Qi(,s>, ..., отвечающие координатам
объектов, малы и носят «парциальный» характер, то есть каж-
дое из Q*<s) зависит от обобщенных координат и скоростей
только s-ro объекта.
2. У равнения движения. Пусть
Pw = -^- = A*(s) + O(p) (5=1,...,й)	(2.11)
дх' ’
есть вектор-столбец обобщенных импульсов объектов. Разре-
шив систему (2.11) относительно обобщенных скоростей х<4\
получим
х(5)==ЛГ'р(5) + рх{'”(х, х, t v, v) + O(yf). (2.12)
Уравнения движения системы удобно записать в форме
Рауса (см., например, [259]). Для этого введем функцию Рауса
к	к
r=т - j p'wx,s)=- j 2 p'<s)^_1p(s)+
S—l	S“1
f	k
+ P I у	+ 2 p'^r’ALt + у v'Nnv +
k	k k	X
+2р'("л"^+42^	+°(p2) <2-13)
4-1	4-1 /-1	J
S 2]
ОЬЪЕКТЫ И СВЯЗИ СО МНОГИМИ СТЕПЕНЯМИ СВОБОДЫ
313
и кинетический потенциал Рауса
k
	I R = R — П= — 2 77,+ liL0 + О (ц2,. S=sl	(2.14)
Здесь		
	L0 = \L +L(1) + L( \	(2.15)
причем		
	^ = ур'(5)ДГ‘р(5) + Щ	(2.16)
есть «собственные» энергии (функции Гамильтона)		объектов,
вычисленные	с точностью до величин порядка щ, / k	\	
	ц AL* = ц 2 p'(s)Ar'Asmt - С'5)	(2.17)
—добавочный кинетический потенциал всех объектов, обуслов-
ленный малыми колебаниями несущей системы,
цЛ(,) = ц(4 «л	(2.18)
— кинетический потенциал несущей системы,
(k
у v'N°nv + 2 p'(s}A7lrfstlv +
S=1
k k	\
+ 4S ^p'{s)A7'№s!A7'p(s} - n(">	(2.19)
s=l/=l	/
— кинетический потенциал элементов несомой системы (связей
второго рода).
Уравнения движения системы в форме Рауса можно полу-
чить, например, при помощи вариационного способа с исполь-
зованием центрального уравнения Лагранжа [259]. Эти урав-
нения имеют вид
- ттг - -1* -П*	+L"") + ° W.
дрк ’	др{ '
р‘“+-»]<гм(»м. р“)++А111’)] + О w
(J X	(J X	|
(s = 1, ..., k),	(2.20)
<h^=-(|4-|)AL‘ + O(n) = O,
\ dt dl dt, /
(—4-------) l(,,) + о (ц) = о.
\dt dv dv j	v ’
314
ОБЪЕКТЫ, БЛИЗКИЕ К НЕЛИНЕЙНЫМ КОНСЕРВАТИВНЫМ [ГЛ. X
3, Порождающее решение. Условия существования и устой-
чивости синхронных движений. Порождающая система, отве-
чающая уравнениям (2.20), относительно координат объектов
распадается на k отдельных консервативных автономных под-
систем:
4'-^.	<s“‘............<221>
иР()	ихо
Каждая из этих подсистем в некоторой области Gs «пар-
циального» фазового пространства (x<s>, р<«>) допускает един-
ственный однозначный аналитический первый интеграл — ин-
теграл энергии — и имеет орбитально устойчивое частное реше-
ние вида
= xf (Ф5, Cs) = of + yf (ф5, Cs)],
(i = 1, .. •> rs; s = 1, ..k),
где
i|>s = a>s (cs) t + as,	(2.23)
причем as и cs — произвольные постоянные, a yf и pf — пе-
риодические функции ф8 с периодом 2л по этой переменной (то
есть с периодом Ts = 2n/as(cs) по t). Как и в предыдущем па-
раграфе, <r<s)=± 1, а qf = O или 1; если qf=\, то соответ-
ствующая функция H,!i> при этом должна быть 2л-периодической
по xf.
Постоянные as представляют собой фазовые сдвиги, произ-
вольные в силу автономности изолированных объектов, а по-
стоянные cs на траекториях, отвечающих решению (2.22), вза-
имно однозначно и непрерывно связаны с постоянной энергии:
Л5(^)=^(*Г.РГ)-	(2-24)
От постоянной cs, а значит и от постоянной энергии hs, за-
висит и частота (os(cs) решения (2.22); эта частота изменяется
для решений (2.22), лежащих в области Gs, в некотором диа-
пазоне
< cos < ®<2>.	(2.25)
Синхронные движения объектов с частотой внешнего воз-
мущения о), то есть движения, для которых *)
СО] = ... = соА = со,	(2.26)
*) Рассматривается задача о простой синхронизации, ибо обобщение на
случай кратной синхронизации, как и ранее, не встречает затруднений.
§2]
ОБЪЕКТЫ И СВЯЗИ СО МНОГИМИ СТЕПЕНЯМИ СВОБОДЫ
315
возможны лишь при условии, что частотные диапазоны всех
объектов (2.25) пересекаются и содержат частоту ш (см. соот-
ношения (1.20)).
Будем далее предполагать, что имеет место нерезонансный
случай, то есть что частоты Xj собственных малых колебаний
несущей системы, определяемые из уравнения
| С°т - Х2М°т I = О,	(2.27)
удовлетворяют условию
Xj =/= pa (j = 1, . • •, т),	(2.28
где р — любое целое положительное число. Тогда последние
два уравнения (2.20) в порождающем приближении будут до-
пускать единственное Т — 2л/й)-периодическое решение
§ = сь ck\ а!, .... ak),
v = v(^t; сх, .... ck; аь ak),
зависящее от тех же 2k постоянных с и а, что и решение (2.22)
уравнений (2.21). Будем считать решения (2.29) соответствую-
щих порождающих уравнений асимптотически устойчивыми.
Сформулируем теперь результаты исследования вопроса
о существовании и устойчивости синхронных решений уравне-
ний (2.20), обращающихся при ц = 0 в порождающее, не оста-
навливаясь на получении этих результатов.
Пусть объекты в порождающем приближении существенно
неизохронны, так что везде внутри областей Gs зависимость
cos = (Ds(cs) является существенной. Иными словами, положим,
что
_ „(о = о (цО),	= О (ц°),	(2.30)
то есть что частотные диапазоны объектов не малы. Тогда
параметры cj, ..., ch однозначно определяются из равенств
(2.26). Что же касается параметров порождающего решения
аь ..., «ft, то их значения, которым могут отвечать синхронные
решения системы (2.20), обращающиеся при ц = 0в порождаю-
щее, определяются из системы уравнений
РДа,( ..., a^^-U + ^) = 0	($=1, ..., k). (2.31)
Здесь
г9 2Л/(о	rs 2л/ю
(?")«<« “Ж Sf	(2.32)
/—10	1-1 о	г
316
ОБЪЕКТЫ, БЛИЗКИЕ К НЕЛИНЕЙНЫМ КОНСЕРВАТИВНЫМ [ГЛ. X
—	величина, пропорциональная средней за период Т = 2я/и ра-
боте непотенциальных обобщенных сил в порождающем при-
ближении*), а
2л/а
Ао(а,.....a*) = ^J (^о)^	(2.33)
о
—	среднее за период значение функции Лагранжа, вычислен-
ное для системы связей (см. равенство (2.15)) также в по-
рождающем приближении;
е (ш ) = JL :	(^)J t (2.34)
6 v s/ cos dcs dcs (ns d(&s	x 1
Можно показать [312], что имеет место соотношение
2л/а
(2Л(,) + ДЛ’)с// = О,	(2.35)
о
то есть средний за период добавочный кинетический потенциал
объектов равен удвоенному среднему значению кинетического
потенциала (функции Лагранжа) несущей системы, взятому
с противоположным знаком. Это соотношение аналогично ра-
венству (4.9) главы IX.
Отметим также, что поскольку средние за период значения
функций Hs и Ls изолированных объектов не зависят от фазо-
вых сдвигов а«, то
2л/а	2л/а
(L)^ = p^-J (L0)dt + C,	(2.38)
о	о
где L есть функция Лагранжа всей системы в целом, а С —
величина, не зависящая от ось •••, «ь
Используя равенство (2.35), при учете соотношения (2.15)
будем иметь
Д0 = ЛП1)-Л(1),	(2.37)
2я/а	2л/<0
Л(1) = ^Г (L^dt, = (L^dt.
о	о
Необходимым условием устойчивости синхронных движений
рассматриваемого типа при достаточно малом ц является ве-
*) Как и выше, круглые скобки в равенствах (2.32) и (2.33) указывают
на то, что заключенные в них выражения вычисляются для порождающего
решения.
§ 2]
ОБЪЕКТЫ И СВЯЗИ СО МНОГИМИ СТЕПЕНЯМИ СВОБОДЫ
317
щественность и отрицательность всех корней алгебраического
уравнения
. !-г-ъ-"--М| = 0	(s, / = 1..k).	(2.38)
es(w) dasdaf s> |	v ’ 1	’	’ '	'	'
Получение достаточных условий устойчивости является бо-
лее затруднительным, чем в случае объектов с одной степенью
свободы; на соответствующем исследовании здесь не будем
останавливаться. Отметим лишь, что для объектов с одной сте-
пенью свободы, находящихся под действием слабых линейных
связей определенного вида, указанное исследование выполнено
в работе Р. Ф. Нагаева и К. Ш. Ходжаева [316].
Примечательно, что слагаемые А<г) и Л(П) входят в выраже-
ние (2.37) с различными знаками. Это свидетельствует о том,
что связи первого и второго рода могут в известном смысле
полностью или частично «гасить» действие друг друга. Более
отчетливо смысл последнего утверждения будет ясен при рас-
смотрении конкретных систем.
Отметим, далее, что существует определенное соответствие
полученных здесь результатов с результатами, установленными
в главе IX для систем с почти равномерными вращательными
движениями. В частности, при учете равенства (2.36) уравне-
ния (2.31) для определения фаз ось •••, оказываются вполне
аналогичными уравнениям (3.12) главы IX.
Если величины es(<n) для всех объектов имеют одинаковый
знак, то, как и в случае объектов с одной стороны свободы, бу-
дет справедлив интегральный критерий устойчивости движений,
причем потенциальная функция D по-прежнему будет опреде-
ляться равенством (1.28). Устойчивые синхронные движения
могут отвечать точкам минимума функции D, обнаруживаемого
на основе рассмотрения членов второго порядка в разложе-
нии D вблизи стационарной точки.
В случае чисто консервативных объектов (Д, = 0) за функ-
цию D может быть принята функция До, взятая со знаком, про-
тивоположным знакам коэффициентов es(co).
Нетрудно проверить, что при соответствующих частных
предположениях приведенные результативные соотношения пе-
реходят в формулы, полученные в предыдущем параграфе для
объектов с одной степенью свободы.
По поводу задачи о внутренней синхронизации здесь можно
было бы повторить все сказанное в конце предыдущего пара-
графа.
4. Случай объектов, изохронных в порождающем приближе-
нии. Выше предполагалось, что объекты являются существенно
анизохронными уже в порождающем приближении. Приведем
318
ОБЪЕКТЫ, БЛИЗКИЕ К НЕЛИНЕЙНЫМ КОНСЕРВАТИВНЫМ
[ГЛ. X
в заключение параграфа результаты [312], относящиеся к осо-
бому случаю, когда порождающая система может быть вы-
брана так, что частота не зависит от энергии, частотные диапа-
зоны объектов (2.25) вырождаются в точку, соответствующую
(в случае задачи о внешней синхронизации) частоте возмуще-
ния со. Этот случай наиболее прост для исследования; ему соот-
ветствует ряд подробно рассмотренных конкретных задач о син-
хронизации.
Порождающее синхронное решение в данном случае зависит
не только от фаз аь ..., аь, но и от энергетических параметров
Сь ..., Ch, то есть содержит 2k произвольных постоянных. Зна-
чения этих постоянных, которым могут при достаточно малом
ц отвечать синхронные движения системы, определяются из
уравнений
а+4^=°. ^+4^=° <s==1...................*>• <2-39>
(7U.S	'Ji'S
Здесь величины As(cs) и Ao = Ao(ai, ..., а&; С\, ..., ch) по
смыслу совпадают с введенными выше и вычисляются по тем
же формулам, а
г, 2л/<0
=	(QT)-ardt.	(2.40)
/ = 1 о
Необходимые и достаточные условия асимптотической устой-
чивости рассматриваемого синхронного режима состоят в от-
рицательности вещественных частей всех корней алгебраиче-
ского уравнения 2&-й степени
дХ0
dasда^
д2Х0
-bsj%
да, дс.
1 *
д2Л0 . dAs .
dasdcs + dcs s!
а2л0  Mgs.
/s/
(s, / = 1, ..., k).
(2.41)
= о
В случае чисто консервативной системы (или в предположе-
нии, что непотенциальные силы имеют более высокий порядок
малости) по-прежнему справедлив интегральный критерий
устойчивости: устойчивому движению отвечает строгий макси-
мум функции Ло = —D по переменным ai, ..., a/,; Ci, ..., сь,
обнаруживаемый на основе анализа членов второго порядка
в разложении функции Ло вблизи стационарной точки.
Отметим, что иным путем аналогичный результат для не-
сколько отличного случая был получен позднее также К- Г. Ва-
леевым и Р. Ф. Ганиевым [117].
§ 3] ВЛИЯНИЕ АНИЗОХРОНИЗМА ОБЪЕКТОВ И СВЯЗЕЙ МЕЖДУ НИМИ 319
§ 3. О зависимости условий устойчивости синхронных
движений от характера анизохронизма объектов
и связей между ними
Как отмечалось в предыдущих параграфах, частота со дви-
жения изолированного чисто консервативного объекта устанав-
ливается в зависимости от энергетического уровня движения h,
определяемого начальными условиями. При этом от вида функ-
ции и (/г), которую можно назвать скелетной характеристикой
объекта, существенно зависит вид синхронного движения в си-
стеме взаимно связанных объектов. Рассмотрим, следуя работе
[314], различные возможные здесь случаи.
Прежде всего выделим вырожденный случай чисто изохрон-
ного объекта, когда частота колебаний не зависит от постоян-
ной энергии h. Примером такого объекта может служить ли-
нейный осциллятор, описываемый уравнением
X + СО2Х = 0.	(3.1)
Частота колебаний m определяется здесь только параметрами
объекта и не зависит (в пределах справедливости уравнения
Рис. 20.
(3.1)) от начальных условий. «Скелетной кривой» изохронного
объекта ® = и(/г) является прямая линия, параллельная оси
абсцисс*) (рис. 20, а).
Консервативные объекты, не обладающие указанным выше
свойством, называются анизохронными. При этом в случае,
когда частота колебаний возрастает с ростом постоянной энер-
гии h, будем говорить о жестком анизохронизме, а в случае,
когда частота убывает по мере увеличения h, — о мягком анизо-
хронизме. Скелетные кривые анизохронных объектов также
изображены на рис. 20, а.
*) Обычно под скелетной кривой понимают обратную зависимость
h = Л (со) или 4 = 4(со), где А— размах, или амплитуда, колебаний.
320
ОБЪЕКТЫ, БЛИЗКИЕ К НЕЛИНЕЙНЫМ КОНСЕРВАТИВНЫМ (ГЛ. X
Примером жестко-анизохронного консервативного объекта
может служить твердое тело, вращающееся без трения вокруг
некоторой оси. Уравнением движения такого тела будет
/ф = 0,	(3.2)
где / — момент инерции, а ф — угол поворота. Зависимость
угловой скорости и (частоты) вращения тела от его энергии h
в этом случае имеет вид
со = V2h/T.	(3.3)
Объект, описываемый уравнением Дуффипга
тх + сх + у Д' = 0,	(3.4)
где т> 0 и с>0, в случае у > 0 будет жестко-анизохронным,
а при у<0 — мягко-анизохронным.
Другим примером мягко-анизохронного консервативного
объекта может служить шарик, движущийся в поле силы тя-
жести над горизонтальной плоскостью и абсолютно упруго со-
ударяющийся с последней. Зависимость периода колебаний
шарика Т (то есть промежутка времени между двумя последо-
вательными соударениями) от его энергии h определяется от-
ношением h/mg = у g ly Л , где т —масса шарика, g — уско-
рение силы тяжести. Таким образом, частота колебаний
O =	=	(3,5)
монотонно убывает по мере увеличения постоянной энергии.
Встречаются объекты, которые в одних областях фазового
пространства являются мягко-анизохронными, а в других —
жестко-анизохронными. Так, например, обычный физический
маятник из мягко-анизохронного объекта становится жестко-
анизохронным при переходе из области колебательных в об-
ласть вращательных движений. Это видно из рассмотрения ске-
летной кривой маятника, представленной на рис. 20,6; точка на
этой кривой, где ш = 0, соответствует неограниченно увеличи-
вающемуся периоду колебаний при приближении амплитуды
колебаний к значению ф* = л.
В принципе могут встретиться и объекты, частота колеба-
ний которых изменяется в ограниченном диапазоне при любом
изменении энергетического уровня (рис. 20,в).
Для того чтобы проследить влияние характера анизохро-
йизма объектов и типа связей между ними на вид устойчивого
синхронного режима, рассмотрим случай внутренней синхрони-
зации нескольких одинаковых анизохронных объектов, когда
Л] = ... = Ак = А (и),	М®)3 • • • = еь (“) е (со)» (3.6)
§ 3] ВЛИЯНИЕ АНИЗОХРОНИЗМА ОБЪЕКТОВ И СВЯЗЕЙ МЕЖДУ НИМИ 321
Уравнение баланса энергии (1.42) в данном случае дает
А = 0, а уравнения (1.23) или (2.31) принимают вид
^Г = °-	М
Таким образом, синхронные режимы в данном случае отве-
чают стационарным значениям функции Ао = А<Т1> — А®, при-
чем характер экстремума *) этой функции, соответствующего
устойчивому движению, определяется знаком «коэффициента
жесткости» скелетной кривой объектов:
е(со) = —= —(3.8)
v ' co d«> co dh	х '
А именно в силу уравнения (2.38) и рассуждений, аналогичных
проведенным в § 8 главы V, в случае жесткого анизохронизма
[е(со)>0] устойчивому движению отвечает максимум, а в слу-
чае мягкого анизохронизма—минимум функции Ар.
Если, далее, заметить, что согласно (2.37) при наличии
только несущих связей Ао = —АВ), а при наличии только не-
сомых связей Ао = А<п>, то приходим к следующей таблице.
Таблица 1
Характер экстремумов функции А'1* или А(11\
отвечающих устойчивым синхронным движениям
	Жесткий анизохроннзм е (со) > 0	Мягкий анизохроннзм е (со) < 0
Несущие связи А(11> = 0, Ао= -А(1)	Минимум А*1'	Максимум Л*1’
Несомые связи А(1> = 0, л0 = л<Н)	Максимум А^б	Минимум Л<и>
В случае объектов с одной степенью свободы наличие соот-
ветствующего экстремума вместе с неравенством (1.39) пред-
ставляют необходимые и достаточные условия устойчивости син-
хронного движения. Во избежание недоразумений отметим
также, что, в отличие от функций Ao, A<T> и А(ГГ>, введенная
в § 8 главы V и в §§ 1 и 2 настоящей главы потенциальная
*) Вследствие автономности задачи один из корней уравнения (2.38),
как указывалось выше, всегда равен пулю, и поэтому здесь речь идет о не-
строгих экстремумах соответствующих функций по переменным аь ... , сц
или о строгих экстремумах по отношению к разностям ai — a*, ...
..., оц-i •— a*.
И И. И. Блехман
322
ОБЪЕКТЫ, БЛИЗКИЕ к нелинейным КОНСЕРВАТИВНЫМ [Гл. X
функция D выбрана так, что устойчивому движению всегда от-
вечает минимум этой функции.
Приведем в заключение параграфа простой иллюстративный
пример [314].
Пусть два одинаковых почти консервативных механических
вибратора установлены на некотором свободном несущем теле
массы М (рис. 21). Оси вращения роторов вибраторов прохо-
тела, а тело может двигаться в пло-
скости, перпендикулярной осям вра-
щения роторов. Указанное выше те-
ло представляет собой несущую
связь между вибраторами; несомая
связь осуществляется посредством
массы то, помещенной в вершине
шарнирно-стержневого ромба ОАСВ
(предполагается, что точки А и В
совпадают с центрами тяжести ро-
торов). Связи между вибраторами
действительно слабы, если доста-
точно малы отношения
дят через центр тяжести
т	т«	/О
Hi м >	1*2 т ,	(3.9)
где т — массы роторов вибраторов.
В порождающем приближении синхронное движение вибра-
торов
<р° = со/ + а,,	<р° = mt + а2
(3.10)
представляет собой равномерное вращение с некоторой угловой
скоростью ш и с произвольными фазами ai и а2-
Кинетические энергии соответственно элементов связей пер-
вого и второго рода, подсчитанные с точностью до членов по-
рядка ц2, не зависят от времени и равны
7’<1) = — М (Л<о)2 =	[1 + cos (а! — а2)],
7’(,1) = у m0(Rmf = ц2"*е2сй2 [1 + cos (а, — а,)].
Здесь е — эксцентриситет роторов вибраторов,
X = ^cos
(3.11)
2
— амплитуда колебаний тела М под действием центробежных
сил, развиваемых вибраторами при их движении по закону
(3.10), и
R = 2е cos
§ 3] ВЛИЯНИЕ АНИЗОХРОНИЗМА ОБЪЕКТОВ И СВЯЗЕЙ МЕЖДУ НИМИ 323
— расстояние от центра тяжести массы т0 до оси вращения
роторов О.
Поскольку потенциальные энергии связей равны нулю, то
согласно (2.37)
цА0 = Г*11' —	= те2ш2(ц2 — Pi) 0 + cos а) (а = а, — а2). (3.12)
Условия стационарности функции Ао приводят к выводу,
что возможными являются синфазное (а = а(|) = 0) и противо-
фазное (а = а<2* = л) синхронные движения вибраторов. По-
скольку, далее, как отмечалось выше, вибраторы являются
жестко-анизохронными объектами, то устойчивым будет дви-
жение, отвечающее максимуму функции Ао- Отсюда заключаем,
что при отсутствии связей второго рода (ц2 = 0) устойчиво про-
тивофазное движение вибраторов, то есть движение, для кото-
рого кинетическая энергия несущего тела Л1) минимальна
(в данном случае — равна нулю). При отсутствии же связей
первого рода (ц, = 0) устойчив синфазный режим вращения, ко-
торому отвечает максимум кинетической энергии массы то.
При наличии связей обоих родов характер устойчивого дви-
жения зависит от знака разности р2— Ць то есть от того, какая
из связей преобладает.
ГЛАВА XI
ОБЪЕКТЫ, БЛИЗКИЕ К СИСТЕМАМ ЛЯПУНОВА
§1.0 системах Ляпунова
Системами Ляпунова называют нелинейные автономные
системы дифференциальных уравнений вида
i
*s= 2	+	..., xz) ($=1, ...,/),	(1.1)
где aSj — постоянные, а Л'* —функции, аналитические в окрест-
ности начала координат xz = ... = xz = О, разложения которых
по степеням хь ..., Xi начинаются членами не ниже второго по-
рядка. Правые части уравнений (1.1) при этом должны обла-
дать следующими свойствами:
1. Характеристическое уравнение линейной части системы
| as/- д5/х | = О (s, / = 1..I)	(1.2)
имеет по крайней мере одну пару простых чисто мнимых корней
±Xi и не имеет иных корней вида ±nAi, где п — целое число или
нуль.
Нетрудно показать, что при таком предположении путем
неособенного линейного преобразования с постоянными коэф-
фициентами система (1.1) может быть приведена к виду
х = — 7. у + X (х, у, х1( ..., Xz_2),
z/ = Zx + F(x, у, Xj..xz_2),
(1.3)
xs — 2j bslXf + Xs(x, у, X], .... xz_2)
(s = 1, ..., 1 — 2),
где bSj — постоянные, a X, У и Xs—функции того же типа, что
и нелинейные члены в уравнениях (1.1).
2. Система допускает первый интеграл, который в перемен-
ных х, у, Xi, .... xZ-2 может быть представлен в виде
// = x2 + z/2+IF(xb .... xz_2) + S(x, у, xb xz_2), (1.4)
О СИСТЕМАХ ЛЯПУНОВА
325
§ U
где W—квадратичная форма переменных xh	Xz—2, aS —
аналитическая функция от х, у, xlt ..., xi-2.
Системами Ляпунова часто называют также физические
объекты, удовлетворительно описываемые соответствующими
дифференциальными уравнениями.
Системы вида (1.1) или (1.3) рассматривались А. М. Ляпу-
новым при изучении одного из особенных случаев задачи об
устойчивости движения, когда для решения вопроса об устой-
чивости необходим учет нелинейных членов в уравнениях воз-
мущенного движения. А. М. Ляпунов показал, что такие си-
стемы допускают семейство периодических решений
х = х \t + а, с) у = у (t + а, с),
xs = xs(Z + a, с) ($=1, Z — 2),
зависящее как от параметра а, который всегда может быть до-
бавлен ко времени t вследствие автономности системы, так и
от параметра с, представляющего собой начальное значение ко-
ординат х (предполагаемое достаточно малым). Начальные зна-
чения прочих координат, а также период Т = Т(с) периодиче-
ского решения являются при этом аналитическими функциями
параметра с. При с = 0 период решения обращается в 2л/Х,
а само решение переходит в тривиальное решение х = у = х\ =
= ... = Xi-2 = 0.	,
А. М. Ляпуновым был указан также эффективный метод вы-
числения решений (1.5).
Системы Ляпунова играют заметную роль в современной
теории нелинейных колебаний и в небесной механике, ибо ими,
в частности, описываются при достаточно общих предположе-
ниях «немалые» (нелинейные) свободные колебания консерва-
тивных систем около положения равновесия или вблизи стацио-
нарного движения. Системы Ляпунова и их обобщения явились
предметом ряда исследований (см., например, [275, 381]).
И. Г. Малкиным [268, 275] с помощью метода Пуанкаре по-
дробно изучены колебания систем, мало отличающихся от си-
стем Ляпунова, причем показано, что, несмотря на нелинейность
порождающей системы, основные вычисления удается довести
до конца.
В настоящей главе изучается задача о синхронизации не-
скольких слабо связанных объектов, которые могут рассматри-
ваться как близкие к системам Ляпунова. Эта задача была ре-
шена Р. Ф. Нагаевым [310] для почти одинаковых объектов,
однако проведенное им исследование, как явствует из дальней-
шего изложения, легко распространяется также и на случай
любых объектов рассматриваемого типа.
326
ОБЪЕКТЫ, БЛИЗКИЕ К СИСТЕМАМ ЛЯПУНОВА
[ГЛ. XI
§ 2.	Уравнения движения
Будем, как и в § 1 главы X, предполагать, что система связи
не вносит дополнительных степеней свободы, то есть уравне-
ния связи представляют собой конечные соотношения. Струк-
турная схема системы отвечает тогда представленной на рис. 18.
Движение системы описывается дифференциальными урав-
нениями
(2.1)
(/=1, ..., rs- s = 1, ..., k).
Здесь, как и в главе VII, k есть число объектов в системе, rs —
число фазовых координат, определяющих состояние s-ro объек-
та; верхний индекс при х, X и f указывает на номер объекта,
а нижний — на номер координаты. При ц = 0 система (2.1) об-
ращается в k независимых систем Ляпунова, описываемых
уравнениями
xT° = Xf(xT0, ..., 4*)0)	(/=1, ...,	s-1......fe). (2.2)
Функции в отличие от Х^\ могут, вообще говоря,
зависеть от координат всех объектов, а также от времени t,
относительно которого они имеют период Т — 2л/ю, и от ма-
лого параметра р.; к гладкости этих функций предъявляются
требования, необходимые и достаточные для справедливости
используемой ниже теоремы.
§ 3.	Уравнения для определения параметров порождающего
решения. Условие существования синхронных движений
В соответствии со сказанным в § 1, порождающая система
(2.2) допускает семейство решений
= <pW (/+ as, с^)	(/ = 1, ..., rs-, s = 1, ..., fe), (3.1)
соответствующих движению изолированных объектов с перио-
дами Ts ~ Ts(cs). Семейство решений (3.1) зависит от 2k про-
извольных постоянных аь ..., ал и щ, ..., ch. Порождающее
решение при этом определяется условиями*)
Ts(cs) = T (s=l, ...,£).	(3.2)
Как и в § 1 главы X, будем считать, что рассматриваемые
объекты анизохронны (то есть что зависимости Ts(cs) являются
*) См. сноску на стр. 314.
§ 3] УРАВНЕНИЯ Для ОПРЕДЕЛЕНИЯ ПОРОЖДАЮЩИХ ПАРАМЕТРОВ 327
существенными) и что пересечение частотных диапазонов объ-
ектов содержит частоту внешнего воздействия со = 2л/Т. Тем
самым будет считаться, что уравнения (3.2) непременно имеют
соответствующие решения cs = с«.
Уравнения в вариациях, отвечающие порождающей системе
(2.2) и порождающему решению (3.1), имеют вид
g(s) = p(s) + а*) z(s) + ... + рФ + as) гД>	(3.3)
(7=1,	/у, s= 1, .... k),
где
и допускают 2k независимых решений
Z$ = qf(' + “s.	(P=1.................(3.4)
,	(t + a., c.)
2i? =	,e,	4	»" С  - 4	<3'5>
где, как и ранее, 6sp — символ Кронекера. В соответствии со
свойствами уравнений в вариациях (см. п. 2 § 3 главы III)
решения (3.4) получаются путем дифференцирования решений
(3.1) по фазам ai, .... as, а решения (3.5) — по постоянным
С1, ..., ck.
Между решениями (3.4) и (3.5) имеется существенное раз-
личие: если первые являются Г, (cs)-периодическими функ-
циями t, то последние этим свойством не обладают. Действи-
тельно, поскольку <p*.s)(Z + as, cs) есть Т-периодические функ-
ции t, то и их производные по t также представляют собой
Т-периодические функции. С другой стороны, дифференцируя
по cs условие периодичности
Ф(;ф + 7\(сД cs] = <O> СД
находим
Ф'/Ф + тДсД с5]
dTs(cs)
dcs
d<V(!S}
dcs
dcs
l + TS (*s)
t
или, при учете Ts(cs)-периодичности производной ф^>,

dcs
t+Ts (cs) dcs
dT,
(3.6)
328
ОБЪЕКТЫ, БЛИЗКИЕ К СИСТЕМАМ ЛЯПУНОВА
[ГЛ. XI
Таким образом, решения (3.5) являются непериодическими;
эти решения, как нетрудно проверить, можно представить
в форме
4? - [ - 77Й- 4я (' + “= С) + 4я (' + О]4. <3-7>
(₽=1, .... k),
где через у(Р (t, cs} обозначена следующая функция:
( д
CJ = [~d^
Ts(c's)
= qf(7, Cs)
/ dTs
Ts(cs) dcs
(3.8)

' dcs
Учитывая равенство (3.6), можно заключить, что функция
cs) является Л(cs)-периодической по I, а путем непо-
средственной подстановки — проверить, что опа является реше-
нием неоднородной системы * *)
y^ = p^(t)y\s} + •••	+	cs) (3-9)
при начальных условиях
dq)(s> (0, с.)
'd(Cs • ’3-10>
Система, сопряженная с уравнениями в вариациях (3.2):
2*(Ц + р(«>(1-р а^) 2*(«) + ... 4- р1-^ (f 4- а^) z*(s} = 0	(3.11)
(/ = 1, ..., rs; s= 1, ..., /?),
допускает k периодических решений с периодами Ts(cs):
^ = ф</>(^ + а5, c5)dsp,	(3.12)
отвечающих решениям (3.4) системы (3.2). Пусть иных перио-
дических решений эти системы не имеют. Тогда решения (3.4)
и (3.12) связаны соотношениями
Cs) = °	(S=1......k),	(3.13)
/=|
справедливость которых выясняется исходя из наличия
Ts(cs)-периодического решения у системы (3.9) в точности так
же, как и справедливость равенств (5.19) главы V.
. дфЛТ/, cs)
*) Следует принять во внимание, что функции Ф/ (Л c,s) и ------
удовлетворяют соответствующим однородным уоавнениям.
НЕОБХОДИМЫЕ УСЛОВИЯ УСТОЙЧИВОСТИ
329
§ 4]
Пусть теперь с] являются простыми корнями уравнений
(3.2). Тогда, в соответствии с теоремой 1 § 4 главы V, необхо-
димыми условиями существования синхронного Т-периодиче-
ского режима во взаимосвязанной системе будут *)
О s=l /=1
. . .; <рр> (/ + ak, с°), . . ., <pW + ak, е°); t, 0] (t + as, с°) dt = 0
(7=1, •••, k),
или, после упрощения и замены индекса q на индекс s,
т rs
о /=1
. ..,<pW(/ + aA, с°), ..., <P<*>(7 + aft, с°); t, 0]	(7 + as, с°)^ = 0
(3.14)
(s = 1, ..., k).
Каждому решению последних уравнений при достаточно ма-
лых р действительно отвечает единственное синхронное движе-
ние рассматриваемого типа с периодом Т, если для этого ре-
шения выполняется условие
~р0	(s, /=1, ..., k).	(3.15)
Решение исходной системы уравнений (2.1), отвечающее
указанному синхронному движению, при этом можно искать
в виде рядов
х(?'’(0 =	cs) +	(3.16)
(/ = 1, • • •, g; s = 1, ..., k)
с Т-периодическими коэффициентами.
§ 4.	Необходимые условия устойчивости синхронных
движений
Вопрос об устойчивости синхронных движений в данном слу-
чае не может быть решен путем использования теоремы 2 § 4
главы V: элементарные делители, отвечающие 2й-кратному
корню р<0) = 1 характеристического уравнения для системы
*) Суммированию по индексу s от 1 до I в обозначениях § 4 главы V
отвечает суммирование по индексу j от 1 до г, и по индексу s от 1 до к.
330
ОБЪЕКТЫ, БЛИЗКИЕ К СИСТЕМАМ ЛЯПУНОВА
[ГЛ. XI
в вариациях (3.3), являются не линейными, а имеют степень,
равную двум, — числу решений в каждой из k групп (см.
формулы (3.4) и (3.7), а также п. 3 § 3 главы III). Поэтому
здесь необходимо специальное рассмотрение одним из спосо-
бов, упомянутых в п. 7 § 3 главы III.
Уравнения в вариациях, отвечающие Г-периодическому ре-
шению исходной системы уравнений (2.1), могут быть записаны
в форме
rs	k rs
= 2 pfi {t + as) z^ + p (2 2 qfflz® + ...	(4.1)
(/=1, ..., rs; s=l.....k),
где
rs
V=1
4-
|	......xty ...; x{®..............x%;	t, 0)
(4.2)
причем круглые скобки означают, что заключенные в них ве-
личины вычисляются для порождающего решения; невыписан-
ные в уравнениях (4.1) члены имеют относительно ц порядок
выше первого.
Будем искать характеристические показатели А.(р) системы
(4.1) с помощью подстановки Н. А. Артемьева (см. [23], а так-
же п. 7 § 3 главы III)
(Ц)
(4.3)
из условия существования Т-периодического решения у системы
г §	k S
= 2 P(ji (t + as) n)s) + P 2 S	(h) n(/s) + • • •, (4.4)
которая получается из (4.1) в результате замены (4.3).
Интерес представляют характеристические показатели си-
стемы (4.1), которые отвечают указанному выше 26-кратному
корню р<°> =	= 1 характеристического уравнения системы
в вариациях (3.3). Для этих показателей, очевидно, 7Д0) = 0.
В соответствии со сказанным в п. 7 § 3 главы III эти показа-
тели в данном случае (то есть случае наличия 26-кратного
корня, которому отвечают 6 групп решений (3.4) и (3.7))
можно искать в виде рядов по степеням ц1'2:
X (р) = AiP1'2 + Х2р + ^зр3/2 + •..	(4.5)
§ 4]	НЕОБХОДИМЫЕ УСЛОВИЯ УСТОЙЧИВОСТИ	331
Разыскивая Г-периодическое решение системы уравнений
(4.4) также в виде рядов
= r]js)0 4	1 + p/r^s) 2 + ...	(4.6)
(/=1, ..., rs; s= 1, ..., k),
Т-периодическое решение уравнений исходного (нулевого) при-
ближения получим в виде
^° = <ф^(/ + а5, <),	(4.7)
где Ms — произвольные постоянные.
Уравнения для определения первого приближения будут
иметь вид
^is)i = 2 p^)(/ + a^)Ti(/)I ~xiMM’(/ + aS’ <0-	<4-8)
Сопоставляя эту систему с системой (3.9), заключаем, что
она также допускает /'-периодическое решение
(< + а„ О+М'1 ('+“• О («)
(/= 1, ..., rs; s= 1, ..., k),
зависящее от 2k постоянных Ms и Ns.
Наконец, для определения второго приближения получаем
систему
rs	k Г|3
f] w 2 = £	(7 + cQ n(S> 2 +	V M^f+ ajj( +
1=1	3=1 z=i
+ dT (c°^ldc° "1”	~	as’ Cj) ~
+ <)• (4-10)
Составим необходимые и достаточные условия существова-
ния Г-периодического решения у последней системы (см. п. 4
§ 3 главы III):
О s=I 1-1 1-3-1 1=1
+	!l"i ('+ °- - VW’ О -
-. 01*,ООл-0 (V-1........ч- Н-И)
332
ОБЪЕКТЫ, БЛИЗКИЕ К СИСТЕМАМ ЛЯПУНОВА
|ГЛ, У!
Заметим, что, подобно тому как это было сделано при до-
казательстве теоремы 2 § 4 главы V, можно доказать тожде-
ства *)
г|3 4 Т
S S J +	<W(, + ay, = U (4.12)
/=1 /=1 о	11
(0, Y=1.......k),
в которых функции Ру определяются равенствами (3.14).
Далее, поскольку функции и являются решениями
взаимно сопряженных систем, то в силу равенств (3.7), (З.Ю),
(3.12), (3.13) и сказанного в п. 4 § 3 главы III величины
S	5 Л (S) /п
=	c^Ks (4.13)
/=|	/=| S
являются постоянными.
При учете соотношений (3.13), (4.12) и (4.13) условия пе-
риодичности (4.11) могут быть представлены в следующей
форме:
k
S (-Я7 - «М») " ° Ф. V - 1..................Ч, (4.14)
₽=1
где
ТК„	„ dm., (с,,)
Условие нетривиальности решения системы линейных урав-
нений (4.14) приводит к алгебраическому уравнению /г-й сте-
пени относительно
= °	(s./'-l.......k),	(4.16)
которое определит первые приближения A.i к 2k критическим
характеристическим показателям.
Очевидно, что если хотя бы один из корней уравнения
(4.16) является комплексным, то одна из величин Zi непре-
менно будет иметь положительную вещественную часть, и по-
этому по крайней мере при достаточно малых значениях ц
рассматриваемое решение будет неустойчивым. Для устойчиво-
*) См. стр. 199—200; левым частям равенства (4.12) отвечают величины
фигурирующие в формулах (4.58) главы V.
§4]	НЕОБХОДИМЫЕ УСЛОВИЯ УСТОЙЧИВОСТИ	333
сти решения необходимо, чтобы все корни уравнения (4.16)
были вещественными и отрицательными.
Для получения необходимых и достаточных условий устой-
чивости следует вычислить дальнейшие приближения к рас-
смотренным выше критическим характеристическим показате-
лям, а также к показателям, обращающимся при ц = 0 в чисто
мнимые числа (если такие показатели имеются). На соответ-
ствующем исследовании, однако, останавливаться не будем.
Очевидно, что если все коэффициенты ач имеют одинаковый
знак, то есть
sign а{ = ... =signaft = a,	(4.17)
и к тому же существует функция D* такая, что
8D*
-^-= - Ps(aI; ..., aj (s=l,	k),	(4.18)
то для рассматриваемой системы справедлив интегральный кри-
терий устойчивости (в смысле необходимых условий устойчи-
вости, зависящих от корней уравнения (4.16)), причем за по-
тенциальную функцию D можно принять выражение
D = aD’.	(4.19)
Нетрудно усмотреть вполне понятное соответствие между со-
отношениями, полученными в настоящем параграфе, и резуль-
татами исследования синхронизации почти консервативных объ-
ектов (см. главу I).
Выше речь шла о случае внешней синхронизации объектов.
Приведем в заключение главы результаты, относящиеся к за-
даче о внутренней синхронизации, когда исходная система урав-
нений (2.1) автономна, то есть функции /js) не зависят явно
от времени t.
В рассматриваемом случае из уравнений (3.14) могут быть
принципиально найдены не сами фазы cxi, ..., аь, а лишь k— 1
разностей этих фаз, например ai— аь, ..., ccs-i — ah', с другой
стороны, из тех же уравнений, вообще говоря, определится пе-
риод порождающего решения Т.
Необходимые условия устойчивости решений будут заклю-
чаться в отрицательности k— 1-го корпя уравнения (4.16). Один
же корень указанного уравнения непременно будет равен нулю;
обнаружить данное обстоятельство и отделить несущественный
нулевой корень можно совершенно аналогично тому, как это
неоднократно делалось выше (см., например, заключительную
часть § 3 главы VII).
ЧАСТЬ IV
ТЕОРИЯ СИНХРОНИЗАЦИИ МЕХАНИЧЕСКИХ
ВИБРАТОРОВ
Настоящая четвертая часть книги посвящена изложению
теории синхронизации конкретных технических объектов — ме-
ханических вибраторов; эта теория, развитая в последние годы,
явилась основной для ряда технических приложений.
Вначале даются общая постановка задачи и обзор состоя-
ния вопроса. Затем в главе XIII подробно рассматривается
существенный для приложений частный случай синхронизации
простейших вибраторов, установленных на твердом теле, совер-
шающем плоскопараллельное движение. При изучении этой
системы выясняются основные особенности данной задачи.
Иные, более сложные случаи синхронизации вибраторов рас-
сматриваются в четырнадцатой главе, где дается также общая
методика исследования и получен ряд соотношений общего ха-
рактера. Особое внимание уделено рассмотрению синхрониза-
ции вибраторов, связанных с квазилинейной колебательной
системой. Подробно обсуждается интегральный критерий устой-
чивости синхронных движений вибраторов, во многих случаях
упрощающий решение прикладных задач. В заключение гла-
вы XIII применение общих результатов иллюстрируется на раз-
нообразных примерах, имеющих и самостоятельное значение.
В главе XV дается постановка задачи о создании заданных
колебаний упругой системы или некоторой ее части; эта задача
является одной из основных в теории вибрационных устройств.
Основное содержание главы посвящено изучению способов ре-
шения этой задачи посредством использования механических
возбудителей и, в частности, самосинхронизирующихся и прину-
дительно синхронизированных механических вибраторов.
В главе шестнадцатой, по существу, ставится вопрос о на-
дежности работы вибрационного устройства, связанной с его
способностью обеспечивать требуемый по технологическим усло-
виям закон колебаний рабочего органа в условиях неточного
изготовления возбудителен и колебательной системы, а также
при наличии «дрейфа» параметров как самой системы, так и
технологической нагрузки.
Рассматриваемый вопрос имеет особенно важное значение
применительно к вибрационным машинам с самосинхронизирую-
щимися вибраторами, а также к вибрационным машинам резо-
ТЕОРИЯ СИНХРОНИЗАЦИИ ВИБРАТОРОВ
335
нансного типа. А именно, для возможности практического
использования явления самосинхронизации вибраторов в каж-
дом конкретном случае необходимо обеспечить не только суще-
ствование и устойчивость нужного режима синхронного вра-
щения номинально одинаковых вибраторов, приводимых от
номинально одинаковых двигателей, но и добиться «стабильно-
сти» этого режима, то есть относительно слабой чувствительно-
сти характера возбуждаемых колебаний по отношению к не-
идентичности вибраторов и их двигателей и к различного рода
несовершенствам. Неучет указанного обстоятельства приводит
к грубым ошибкам.
Общие положения, изложенные в шестнадцатой главе, ниже
используются при рассмотрении конкретных машин и устройств
с самосинхронизирующимися вибраторами (см. § 2 главы XX
и главу XXIII пятой части книги).
Семнадцатая и восемнадцатая главы посвящены изучению
двух вырожденных частных случаев задачи о синхронизации
вибраторов, представляющих, однако, принципиальный и прак-
тический интерес. В первом случае рассматривается взаимодей-
ствие одного механического вибратора, приводимого от асин-
хронного или от синхронного двигателя, с колебательной систе-
мой, а во втором — задача о вращении неуравновешенного
ротора, ось которого совершает заданные колебания в двух вза-
имно перпендикулярных направлениях.
Обе эти задачи в последние годы явились предметом доста-
точно многочисленных исследований; их краткий обзор приво-
дится в начале указанных глав. Однако почти всегда (исключе-
нием являются некоторые работы автора книги) рассмотрение
проводилось вне связи с задачей о самосинхронизации меха-
нических вибраторов. Поэтому установлению и использованию
такой связи здесь уделяется определенное внимание.
Наконец, в последней, девятнадцатой главе данной части
приводятся результаты экспериментальных исследований про-
цессов синхронизации механических вибраторов, выполнявше-
гося как на специально разработанных экспериментальных
стендах и установках, так и на моделях и промышленных об-
разцах вибрационных устройств. Особое внимание уделяется
исследованию процессов установления синхронных режимов дви-
жения вибраторов; как уже отмечалось, чисто аналитическое
рассмотрение этого вопроса представляет значительные труд-
ности.
Ряд приложений теории синхронизации вибраторов рассмат-
ривается в следующей, пятой части книги.
ГЛАВА XII
ЗАДАЧА О СИНХРОНИЗАЦИИ МЕХАНИЧЕСКИХ
ВИБРАТОРОВ
§1.0 механических вибраторах
Под механическим вибратором (рис. 22) в дальнейшем, как
правило, будем понимать некоторое тело, кинематически связан-
ное с другим телом (называемым несущим телом), которое
может совершать относительно последнего периодические дви-
жения (обычно колебательного или вращательного, харак-
тера). При таких движениях на не-
сущее тело со стороны вибратора,
вообще говоря, действуют некото-
рые силы инерционного происхожде-
ния. Движение вибратора по отно-
шению к несущему телу, как пра-
вило, обеспечивается внутренними
или внешними по отношению к си-
стеме вибратор — несущее тело си-
лами, развиваемыми двигателем
того или иного типа.
В технике под механическим вибратором часто понимают
устройство, включающее не только указанное выше твердое
тело, но также и «корпус», присоединяемый к несущему телу
и представляющий, таким образом, часть последнего; иногда
к вибратору относят также и приводной двигатель.
Мы будем пользоваться термином «механический вибратор»
в обоих указанных смыслах, особо оговаривая, о чем идет речь
лишь в случаях, когда такая неоднозначность терминологии
может привести к недоразумениям.
Понятию о механическом вибраторе можно было бы дать бо-
лее широкое толкование, однако для целей дальнейшего изло-
жения в этом нет особой необходимости.
Рассмотрим основные типы существующих механических ви-
браторов.
Простейшим является так называемый механический деба-
лансный вибратор (рис. 23, а), представляющий собой неурав-
новешенный вал, приводимый во вращение тем или иным спо-
собом. Дебалансные вибраторы, развивающие вращающуюся
возмущающую силу, широко применяются в качестве приводных
устройств вибрационных машин и установок.
Дебалансными вибраторами снабжены, в частности, вибра-
ционные грохоты, конвейеры и питатели различных типов, ви-
броразгрузчики вагонов и вагонеток, вибрационные дробилки
и мельницы, виброплощадки и другие устройства для уплотне-
ния материалов, а также вибропогружатели свай, шпунта и
Ободочек.
О МЕХАНИЧЕСКИХ ВИБРАТОРАХ
337
Рис. 23.
338
ЗАДАЧА О СИНХРОНИЗАЦИИ МЕХАНИЧЕСКИХ ВИБРАТОРОВ [ГЛ. XII
Внешний вид одного из типов дебалапсных вибраторов пред-
ставлен на рис. 24, а. Этот вибратор, часто называемый мотор-
вибратором, состоит из электродвигателя, к обоим концам вала
которого присоединены заключенные в тот же корпус неуравно-
вешенные роторы (дебалансы). Указанные роторы обычно вра-
щаются в подшипниках качения, которые значительно усилены
по сравнению с подшипниками двигателя, имеющего те же па-
раметры, что и двигатель вибратора.
Наряду с обычными дебалансными вибраторами находят
применение вибраторы планетарного типа, или, как их иногда
называют, катковые вибраторы [146, 147]. Основным элементом
планетарного вибратора (рис. 23, б) является тело вращения 1,
которое может катиться по поверхности полости корпуса ви-
братора 2 под действием тем или иным образом передаваемого
вращающего момента двигателя.
Своеобразный планетарный вибратор с пневматическим при-
водом выпускается американской фирмой «Вибролатор». Схема
этого вибратора представлена на рис. 23,в, а схематический
разрез — на рис. 24,6. В данном вибраторе роль дебаланса
играет шарик 1, катящийся по кольцевой канавке 5 внутри кор-
пуса вибратора 2. Движение шарика возбуждается и поддер-
живается струей сжатого воздуха, подводимой через сопло
для отвода воздуха служит отверстие 4 в средней части кор-
пуса.
Вибраторы, соответствующие рис. 23, б и 23, в, можно на-
звать внутренними планетарными вибраторами. Встречаются
также и внешние планетарные вибраторы (рис. 23, г), представ-
ляющие собой кольцо 1, которое может обкатываться своей
внутренней поверхностью по оси 2, связанной с корпусом (не-
сущим телом). Движение кольца может возбуждаться различ-
ным образом; существуют, в частности, пневматические коль-
цевые планетарные вибраторы.
При определенных условиях планетарные вибраторы имеют
преимущества перед дебалансными; они нашли применение
в вибрационных машинах для уплотнения бетона, в качестве ви-
бропобудителей для предотвращения зависания сыпучих мате-
риалов в бункерах, а также и в некоторых других устройствах.
Механизмы, вполне аналогичные вибраторам планетарного
типа, используются, однако, не только как возбудители коле-
баний. В машинах типа инерционной дробилки, вибрационной
роликовой мельницы и вибрационных измельчителей института
«Механобр», в вибрационных распределительных и питающих
устройствах институтов ВНИИЗ и ВНИИНСМ, а также в неко-
торых типах грохотов, выпускаемых зарубежными фирмами,
элементы «планетарных вибраторов» выполняют функции ра-
бочих органов машины.
§ 1]	О МЕХАНИЧЕСКИХ ВИБРАТОРАХ	339
Так, в вибрационных измельчателях и инерционных дробил-
ках «Мехаиобра» (см. пи. 15, 16 и 22 таблицы 2 и рис. 107—114)
рабочий орган представляет собой цилиндрическое или конусо-
образное тело, которое под действием вибраций катится по ци-
линдрической или конусообразной полости в другом теле (кор-
пусе машины) *); в процессе такого движения происходит раз-
рушение руды, поступающей в полость.
В вибрационном грохоте шведской фирмы «АгЬга» [454] (см.
п. 7 таблицы 2) просеивающую поверхность образуют стержни,
которые под воздействием вибраций короба грохота обкаты-
ваются (или вибрируют) в круговых цилиндрических отверстиях
в его бортах точно таким же образом, как ролики в стаканах
вибрационных мельниц.
По аналогичному принципу работают и вибрационные шне-
ковые питатели, предложенные во ВНИИНСМ. Основной де-
талью питателя является шнек, вложенный в цилиндрический
стакан большего диаметра. Под действием вибраций стакана
шнек обкатывается по его поверхности, обеспечивая подачу ма-
териала вдоль оси стакана.
В грохоте фирмы «Bixby zimmer engineering» (США), схема
которого представлена в п. 6 таблицы 2, рабочий орган (просеи-
вающая поверхность) осуществлен в виде приваренных к коль-
цам продольных стержней; кольца насажены на поперечные
стержни значительно меньшего диаметра, укрепленные в вибри-
рующем корпусе грохота. Под действием вибраций стержней
кольца обкатываются (со скольжением) по стержням, и вместе
с ними все сито совершает круговые поступательные колебания.
Наконец, по аналогичному принципу, то есть по принципу
внешнего планетарного вибратора, осуществлено распредели-
тельное устройство разработанное во ВНИИЗ и описанное в ра-
боте В. В. Гортинского [155].
Помимо описанных выше вибраторов, предназначенных для
создания вращающегося возмущающего усилия, широкое приме-
нение находят механические возбудители направленного дей-
ствия.
На рис. 23, д представлен так называемый поршневой вибра-
тор, в котором возмущающая сила развивается массой т,
возвратно-поступательно движущейся в полости корпуса. Коле-
бательное движение массе («поршню») сообщается либо по-
средством кривошипно-шатунного механизма от обособленного
двигателя, либо пневматическим приводом. Известны вибра-
торы, выполненные на базе обычного поршневого двигателя,
в которых роль инерционной массы играет утяжеленный пор-
шень.
*) Это своеобразное явление, названное вибрационным поддержанием
вращения, подробно рассматривается в главе XVI11 настоящей книги.
Примеры вибрационных машин и установок с несколькими вибраторами и требования,
предъявляемые к движению роторов вибраторов ')
Таблица 2
№	Краткая характеристика типа или назначения вибрационной машины (установки)	Динамическая схема	Необходимые для нормальной работы машины соотношения		Примечания
			а) между углами пово- рота роторов вибрато- ров	б) между сред- ними угловыми скоростя ми роторов вибра- . * торов	
А. МАШИНЫ И УСТАНОВКИ С ВИБРИРУЮЩИМ ОРГАНОМ, ИМЕЮЩИМ ОДНУ СУЩЕСТВЕННУЮ СТЕПЕНЬ СВОБОДЫ
1 Вибрационные резо-
нансные а послерезо-
нансные машины и ус-
тановки с прямолиней-
ными поступательными
колебаниями рабочего
органа. обеспечивае-
мыми специальными
направляющими эле-
ментами (некоторые
типы вибрационных
грохотов, конвейеров,
питателей, вибрацион-
ные столы).
ЗАДАЧА О СИНХРОНИЗАЦИИ МЕХАНИЧЕСКИХ ВИБРАТОРОВ [ГЛ, ХИ
I
2
Вибрационные резо-
нансные и послерезо-
нансные машины с вин-
товыми или поворот-
ными колебаниями ра-
бочего органа, обеспе-
чиваемыми специаль-
ными направляющими
элементами (некото-
рые типы вибрацион-
ных бункерных питате-
лей и вертикальных
конвейеров).
Число вибра-
торов может
быть более двух
Ф1
Ф1 Ф2
Б. МАШИНЫ И УСТАНОВКИ С ВИБРИРУЮЩИМ ОРГАНОМ, ИМЕЮЩИМ ДВЕ СУЩЕСТВЕННЫЕ СТЕПЕНИ СВОБОДЫ
Вибропогружатели
свай и шпунта с ви-
браторами, жестко свя-
занными с погружае-
мым элементом [361].
<Pj ~ —ср2 ±
±180°
Ф1 — ф2
Погружае-
мый элемент
может сме-
щаться вдоль
своей оси и по-
ворачиваться
вокруг некото-
рой прямой, пе-
ресекающей эту
ось и перпенди-
кулярной пло-
скости враще-
ния роторов
вибраторов
О МЕХАНИЧЕСКИХ ВИБРАТОРАХ
’) В схемах таблицы приняты следующие обозначения: Oxyz — неподвижная в пространстве система координат, O\uvw — система
координат, связанная с основными вибрирующими органами, osos — оси вращения роторов вибраторов, ms, 1 s~массы и моменты инерции
вибрирующих органов или их частей, рассматриваемых как отдельные твердые тела.
2) На всех схемах стр. 340—358 для упрощения изображены дебалаисные вибраторы, однако в большинстве случаев могут быть
применены и вибраторы других типов.
Таблица 2 (продолжение)
to
№	Краткая характеристика типа или иазиачеиия вибрационной машины (установки)	Динамическая схема				Необходимые для нормальной работы машины соотношения		Примечания
						а) между углами пово- рота роторов вибрато- ров Ф5	 б) между средними угловыми скоростями роторов вибра- . * торов <Р5	
					и			
				0	,,,			
								
4	Вибропогружатель свай и шпунта свибра-	/		О,	1Г'М, -т- м,			Ввиду достаточно малой жесткости рес-
	торами, установленны-	(		1 ‘				сор в направлении оси
	ми на подрессорной платформе с одной сте- пенью относительной подвижности [361].					Ф1 ~ ~(?2 — ±180°	ф] = — ф2	Оу и малости расстоя- ния О\О2 допустимо счи- тать, что погружаемый элемент может переме- щаться только в про- дольном направлении.
ЗАДАЧА О СИНХРОНИЗАЦИИ МЕХАНИЧЕСКИХ ВИБРАТОРОВ [ГЛ. XII
В. МАШИНЫ И УСТАНОВКИ С ВИБРИРУЮЩИМ ОРГАНОМ, ИМЕЮЩИМ ТРИ СУЩЕСТВЕННЫЕ СТЕПЕНИ СВОБОДЫ
5
Вибрационные гро-
хоты, конвейеры и пи-
татели с прямолиней-
ными колебаниями ра-
бочего органа, приво-
димые от двух деба-
лансных вибраторов,
вращающихся в проти-
воположных направ-
лениях [51, 56, 68, 241,
242, 245, 498—508].
+1	+1 «о е-о е-о 1“ |2 8 +1 » +1 & ё	Ф1 — Фг ф[ = — ф2	
41 ~ ~ Ср2± ±180°	Ф1 = ~Фг	В общем случае ма- шины по схеме в) дол- жны рассматриваться как системы с шестью степенями свободы ви- брирующего органа.
О МЕХАНИЧЕСКИХ ВИБРАТОРАХ	343
Таблица 2 (продолжение)
№	Краткая характеристика типа или назначения вибрационной машины (установки)	Динамическая схема		Необходимые для нормальной работы машины соотношения		Примечания
				а) между углами пово- рота роторов вибрато- ров <ps	б) между средними угловыми скоростями роторов вибра- торов ф	
6	Вибрационный гро- хот со специальной просеивающей поверх- ностью, совершающей круговые поступатель- ные колебания [509].	/ / Й тЖ / / ь&г / I Нк > //'/^Аг'7 С	йУэт —/-ЖТчрзк'	л / 1 1	)rl и л			Ф1 =Ч>2	Круговые поступатель- ные колебания сита 1 возбу- ждаются ко- лебаниями стержней 2, укрепленных в вибрирую- щем коробе грохота 3.
7	Вибрационный гро- хот с просеивающей поверхностью, образо- ванной вибрирующими стержнями [454].	few Ж \ 1	‘V т—	 су XfelLCV			Обкатка или колебания стержней 1 в цилиндических отверстиях 2, расположен- ных в коробе грохота 3. осущест- вляются вслед- ствие вибра- ции короба.
344 ЗАДАЧА О СИНХРОНИЗАЦИИ МЕХАНИЧЕСКИХ ВИБРАТОРОВ [ГЛ. XII
8
Вибрационные ма-
шины с бигармониче-
скими колебаниями ра-
бочего органа (вибра-
ционный конвейер с
бигармоническими про-
дольными колебаниями
[1, 73], концентрацион-
ный стол с бигармони-
ческим вибратором [73,
510], вибропогружа-
тель свай).
9
М.1
Вибрационные пс-
слерезонансные (инер-
ционные) машины и
установки с колеба-
ниями рабочего орга-
на, близкими к круго-
вым поступательным
(некоторые типы ви-
брационных грохотов,
грохотов-конвейеров,
вибрационных площа-
док).
		 X ffp *	-е -е 4*.	Ю » » 1 1 -е -в « *“	 Ф*= -Фг = = 2фз = 	2ф‘	
____MJ	<Pi~q>2==	ф’ = ф‘ =	Число виб- раторов может быть любым.
	=а q>3 =s q)4	= Фз = Ф<	
co-
иг
О МЕХАНИЧЕСКИХ ВИБРАТОРАХ
Таблица 2 (продолжение)
№	Краткая характеристика типа или назначения вибрационной машины (установки)	Динамическая схема	Необходимые работы маш* а) между углами пово- рота роторов вибрато- ров <ps	для нормальной ты соотношения б) между сред- ними угловыми скоростями роторов вибра- . * торов <Р5	Примечания
10	Вибрационные по- слерезонансные (инер- ционные) машины и установки с колеба- ниями рабочего орга- на, близкими к прямо- линейным поступатель- ным	(вибрационные конвейеры и грохоты- конвейеры, некоторые типы	вибрационных площадок и другие машины) [52, 246, 326].	\У/ U/	)	нЛ нЛ i+Л нЛ 00 1 00 1 00 1 00 1 О-в о-в о-в о-в Осо	о св	Ojfc	Oto 1+ 1+	1+	1+	„	II	II	.	« II * * & •©• # см	’©*	’©*	I •е-	।	1	1 1	II	II	.1 II » со ♦ ю •©• •э-	II	II	11	Число ви- браторов мо- жет быть лю- бым.
и	Самоходный вибра- ционный уплотнитель грунта [73].	fV .	/	M.I J 1	II	Ф1~—ф2± ±180°	Ф1	Фг	
1					
ЗАДАЧА О СИНХРОНИЗАЦИИ МЕХАНИЧЕСКИХ ВИБРАТОРОВ [ТЛ. ХП
12
Вибрационный кабе-
стан для завинчивания
свай и некоторые дру-
гие машины с поворот-
ными колебаниями ра-
бочего органа [375].
Ф2~Ф1 + 360° + k	Фт — Фг — • ••• =<Pfe	Число	ВИ-
фз«ф2 + 360°		браторов	мо-
+~г		жет быть бым.	ЛЮ’
~ cpfe —! +
, 360°
13
Вибрационные моло-
ты для погружения
свай и шпунта [415, 183].
О МЕХАНИЧЕСКИХ ВИБРАТОРАХ
Таблица 2 (продолжение)
№	Краткая характеристика типа или назначения вибрационной машины (установки)	Динамическая схема	Необходимые для нормальной работы машины соотношения		Примечания
			а) между углами пово- рота роторов вибрато- ров <ps	б) между средними угловыми скоростями роторов вибра- торов <ps	
14	Вибрационная шаро- вая мельница, приво- димая от нескольких дебалансных вибрато- ров [53].	If *\//О °\э° °/\ vzxa W n° o/o Л/Х \\ VZ°s>f \И II О	OS \J4 Ио ° °	Я о о о 0	\ о	\>^ \ ч P:	+1 £	Э-о «	1 2 £	II +1 "S’ о gi	ф* = ф* <h= -Ч>2	1. Число вибрато- ров может быть более двух. 2. Случай (а) соответствует круго- вым, случай (б) — прямолинейным посту- пательным колебаниям корпуса мельницы.
					
ЗАДАЧА О СИНХРОНИЗАЦИИ МЕХАНИЧЕСКИХ ВИБРАТОРОВ [ГЛ. XII
15 Вибрационная конус-
ная (безэксцентрико-
вая) дробилка с одним
дебалансным вибрато-
ром, размешенным в
конусе (плоская схе-
ма) [212, 367, 369].
Ф1 ~ Фг
Пространственная
динамическая схема
дробилки представлена
в п. 22 настоящей таб-
лицы.
О МЕХАНИЧЕСКИХ ВИБРАТОРАХ
со
о
Таблица 2 (продолжение)
	Краткая характе- ристика типа или назначения вибра- ционной машины (установки)			Необходимые для нормальной работы машины соотношения		
№		Динамическая схема		а) между углами пово- рота роторов вибрато- ров cps	б) между средними угловыми скоростями роторов вибра- торов <р5	Примечания
16	Вибрационные (инерционные) дробильно-из- мельчительные машины с не- сколькими деба- лансными вибра- торами и не- сколькими из- мельчающими те- лами (плоская схема) [45, 69]	1 \	Ж-Sr I	Ч>1 ~(р2~ф1	ф* = фг = ... ••• =Ф*+Я	Число вибраторов Z и число роликов п мо- гут быть любыми.
		\ Пи \	тп				
ЗАДАЧА О СИНХРОНИЗАЦИИ МЕХАНИЧЕСКИХ ВИБРАТОРОВ [ГЛ. XII
Г. МАШИНЫ И УСТАНОВКИ С ВИБРИРУЮЩИМИ ОРГАНАМИ, ИМЕЮЩИМИ БОЛЕЕ ТРЕХ СУЩЕСТВЕННЫХ СТЕПЕНЕЙ
СВОБОДЫ
17
Вибрационные
машины и уста-
новки с прямо-
линейными коле-
баниями рабо-
чего органа, при-
водимые от не-
скольких маят-
никовых вибра-
торов (схема а))
или от качаю-
щихся вибрато-
ров (схема б))
[70, 239] — неко-
торые типы ви-
брационных гро-
хотов и конвейе-
ров, вибрацион-
ные столы.
Ф1 ~Ф2	Ф1 — Фг
Ф1 « — q>2	ф* = -ф
Фз ~ — ф4	Фз = — ф
1. Число вибраторов
может быть любым.
2. Число степеней сво-
боды вибрирующих ор-
ганов равно к + 3, где
k — число вибраторов.
1.	Число вибраторов
может быть любым.
2.	Вибраторы могут
свободно поворачи-
ваться вокруг осей, па-
раллельных оси Ojtw.
3.	Число степеней
свободы вибрирующих
органов равно k + 6
ik—число вибрато-
ров), если корпусы ви-
браторов не связаны
между собой, и равно
к
-g- + о, если корпусы
каждой пары вибрато-
ров (1 и 2, 3 и 4 и т.
д.) соединены жестки-
ми элементами.
О МЕХАНИЧЕСКИХ ВИБРАТОРАХ
Таблица 2 (продолжение)
№	Краткая характе- ристика типа или назначения вибра- ционной машины (установки)
18	Вибрационные резонансные ма- шины с прямо- линейными (или близкими к пря- молинейным) ко- лебаниями рабо- чего органа, мяг- кой амортизацией и с приводом от нескольких деба- лансных вибра- торов — вибраци- онные грохоты, конвейеры, пита- тели, сепараторы и другие машины.
zz;

Динамическая схема
Необходимые для нормальной работы машины соотношения		
а) между углами пово- рота роторов вибрато- ров	б) между средними угловыми скоростями роторов вибра- торов <ps	Примечания
Ф1«<р2« ... «<рk	• * л» II -е- II II : * —	1. Число сте- пеней свободы вибрирующих органов равно четырем.
Ф1 — Ч>2± ±180“ Фз~ — q>4± ±180“	. * * = -q>2 = = ф’ = . * = -<р4= ...	2. Вибраторы могут быть раз- мещены также и на теле Л12.
« - <pfe±180°	И •е- 1 II II	
ЗАДАЧА О СИНХРОНИЗАЦИИ МЕХАНИЧЕСКИХ ВИБРАТОРОВ [ГЛ. XII
12 И. И. Блехман
19	Вибрационные машины с вин- товыми или по- воротными коле- баниями рабочего органа, мягкой амортизацией и с приводом от нескольких де- балансных вибра- торов — вибраци- онные вертикаль- ные конвейеры и сушилки, ви- брационный стенд [167, 66].			W	Ф1 ~фз	. * . * ф] = Ф2	1. Число вибра- торов может быть любым четным числом. 2. Число сте- пеней свободы вибрирующего органа	равно шести.
				j- &			
					с			
		°’ ~^в					
20	Вибрационные резонансные ма- шины с винто- выми или с пово- ротными колеба- ниями рабочего органа, с мягкой амортизацией — вертикальные ви- брационные кон- вейеры и пита- тели, некоторые типы вибрацион- ных мельниц.				Ф1~фг	. * . * Ф^Фг	1.	Вибраторы могут быть раз- мещены также и на теле М2. 2.	Число ви- браторов может быть любым. 3.	Число сте- пеней свободы вибрирующих ор- ганов равно семи
							
		Мг	О;				
О МЕХАНИЧЕСКИХ ВИБРАТОРАХ
Таблица 2 (продолжение)
№	Краткая характеристика типа или назначения вибрационной машины (установки)	Динамическая схема	Необходимые работы машии а) между углами пово- рота роторов вибрато- ров <ps	1ля нормальной ы соотношения б) между средними угловыми скоростями роторов вибра- . * торов	Примечания
21
Вибрационная уста-
новка для погружения
в грунт свай-оболочек
и тонкостенных цилин-
дров [375, 427].



	1		
ms^5_		^V,
	1	т4	
|<Р1 I - 1<Р21 =
|ф11 — 1фз 1 =
= а13
*
г
I <Р11 -1 Фе I=
=«16
ai}- = const
(/ = 1....6)
1. Вибрирую-
щий орган в об-
щем случае имеет
шесть существен-
ных степеней сво-
боды.
2. Значения
разностей
вращения
торов aj/
раются в
симости от тре-
буемого харак-
тера колебаний
погружаемого
элемента.
фаз
вибра-
выби-
зави-
ЗАДАЧА О СИНХРОНИЗАЦИИ МЕХАНИЧЕСКИХ ВИБРАТОРОВ [ГЛ. XtI
24
Инерционная конус-
ная дробилка с одним
дебалансным вибрато-
ром, размещенным в
конусе [212, 367, 369]
(пространственная схе-
ма).
Ф1 = Ф2
О МЕХАНИЧЕСКИХ ВИБРАТОРАХ
№	Краткая характеристика типа или назначения вибрационной машины (установки»	Динамическая схема
23
Вибрационная щеко-
вая дробилка с приво-
дом от двух дебаланс-
ных вибраторов [156].
Таблица 2 (продолжение)
	Необходимые для нормальной работы машины соотношения		
	а) между углами пово- рота роторов вибрато- ров	б) между средними угловыми скоростями роторов вибра- . * торов	Примечания
	Ф1 = ф2 — ±180°	Ф1 = -Фг	
ЗАДАЧА О СИНХРОНИЗАЦИИ МЕХАНИЧЕСКИХ ВИБРАТОРОВ [ГЛ. XII
24
Несколько неуравно-
вешенных машин (кон-
центрационных столов,
дробилок и др.) уста-
новлены на едином
групповом фундамен-
те [46, 83].
Отсутствие самосин-
хронизации
(|Фз| + |Ф*|. s = j)
или по возможности
полное взаимное урав-
новешивание инерцион-
ных сил и моментов,
возникающих при ра-
боте машин в случае
самосинхронизации.
Колеблющееся
тело имеет в об-
щем случае шесть
существенных
степеней свободы.
О МЕХАНИЧЕСКИХ ВИБРАТОРАХ
Таблица 2 (продолжение)
сл
				Необходимые для нормальной работы машины соотношения		
№	Краткая характеристика типа или назначения вибрационной машины (установки)		Динамическая схема	а) между углами пово- рота роторов вибрато- ров ф5	б) между средними угловыми скоростями роторов вибра- . * торов	Примечания
25	Вибрационные ма- шины и установки со многими дебалансными вибраторами, располо- женными на вибрирую- щем органе, ряд частот собственных колеба- ний которого меньше рабочей частоты коле- баний (многовибратор- ные конвейеры, грохо- ты-конвейеры и вибро- площадки с рабочим органом значительных размеров) [52, 246, 315, 326].		V ц/ X	ifXS- S)	а а ;	+	+	а	~ «	т,	ц	•	»и- »	t	ё-	е-	.	'Lt	g. £»	II	। & 8- »	II»	.	& 1	11 &	-2-	:	II	о.	?’. 11 11 X 11 11 * • -я 1 V 1 и '*'* -•1 11 	и :	II	Вибрирующий орган предста- вляет собой упру- гое тело (в част- ности, балку) с распределенной массой («беско- нечное число сте- пеней свободы»).
ЗАДАЧА О СИНХРОНИЗАЦИИ МЕХАНИЧЕСКИХ ВИБРАТОРОВ (ГЛ. XII
§ 11
О МЕХАНИЧЕСКИХ ВИБРАТОРАХ
359
Наиболее часто, однако, для создания возмущающей силы
постоянного направления используются два дебалансных ви-
братора, роторы которых связаны зубчатым зацеплением с пе-
редаточным отношением, равным единице*) (рис. 23, е). Такой
составной вибратор иногда
называют самобалансным.
Развиваемое им возмущаю-
щее усилие направлено
вдоль прямой, перпендику-
лярной плоскости, в которой
лежат оси вращения не-
уравновешенных валов.
Все рассмотренные выше
вибраторы можно назвать
одночастотными (иногда их
называют также моногар-
моническими). Встречаются,
однако, и многочастотные
(полигармонические) меха-
нические вибраторы, генери-
рующие возмущение не-
скольких (наиболее ча-
сто— двух) частот. Они
представляют собой, напри-
мер, дебалансные вибрато-
ры, валы которых связаны
зубчатыми зацеплениями
с передаточными отноше-
ниями, отличными от еди-
ницы. На рис. 23, ж изобра-
жена схема такого состав-
ного вибратора, развиваю-
щего вращающиеся возму-
щающие силы. Схема состав-
ного двухчастотного (бигар-
монического) вибратора на-
правленного действия пред-
ставлена на рис. 23,з, а об-
щий вид этого вибратора в
разрезе — на рис. 24, в.
Рис. 24.
В заключение отметим, что недавно были предложены так
называемые гироскопические вибраторы (рис. 23,и), основой
которых служит быстро вращающийся ротор. Ось ротора
*) Как будет ясно из дальнейшего, зачастую такая кинематическая связь
не обязательна, ибо желаемый эффект достигается «автоматически» благо-
даря явлению самосинхронизации вибраторов.
260
ЗАДАЧА О СИНХРОНИЗАЦИИ МЕХАНИЧЕСКИХ ВИБРАТОРОВ [ГЛ. XII
совершает относительно несущего тела заданное периодическое
движение (например, вращение вокруг некоторой оси, связанной
с этим телом) [10, 213, 196]. Если ротор уравновешен, то такой
вибратор развивает гироскопический момент, вектор которого
изменяется в зависимости от характера движения оси ротора.
В более сложном случае ротор и промежуточное тело, в кото-
ром закреплена его ось, не уравновешены, и тогда генерируют-
ся также и неуравновешенные силы. Можно ожидать, что такие
возбудители в будущем найдут техническое применение.
§ 2. Основные задачи о синхронизации вибраторов
1. Технические задачи, приводящие к проблеме синхрониза-
ции вибраторов. В значительном числе, если не в большинстве,
вибрационных машин и установок применяется не один, а не-
сколько вибраторов, установленных либо на одном общем несу-
щем теле (вибрирующем органе машины), либо на двух или
более тем или иным способом связанных телах.
Так, в упоминавшихся выше машинах с планетарными ви-
браторами, используемыми в качестве рабочих тел, имеется по
крайней мере еще один вибратор, играющий роль возбудителя
колебаний.
В других случаях применение нескольких относительно
маломощных вибраторов, вместо одного более мощного, обус-
ловлено необходимостью рассредоточить возмущающую силу по
вибрирующему ограну значительных размеров (см. п. 25 таб-
лицы 2, а также рис. 101 и 104). Таким путем при соблюдении
определенных условий удается обеспечить колебания рабочего
органа вибрационной машины, мало отличающиеся от коле-
баний его как абсолютно твердого тела, несмотря на то что ча-
стота возмущающей силы превышает ряд частот собственных
упругих колебаний рабочего органа, то есть несмотря на его
«нежесткость» (см. [50, 84, 85], а также главы XV и XX настоя-
щей книги).
В ряде случаев использование нескольких вибраторов, вме-
сто одного, вызвано стремлением уменьшить нагрузку на каж-
дый подшипник вибраторов, распределив ее на большее число
подшипников. Такая задача возникает в тяжелых промышлен-
ных машинах, максимальный размер которых (в случае исполь-
зования одного вибратора) предопределяется максимальной
работоспособностью освоенных промышленностью подшипников
качения.
Применение двух (или любого четного числа) вибраторов,
вращающихся с одинаковой угловой скоростью в противополож-
ных направлениях, позволяет получить возмущающую силу по-
стоянного направления. Эта возможность широко используется
§ 2]	ОСНОВНЫЕ ЗАДАЧИ О СИНХРОНИЗАЦИИ ВИБРАТОРОВ	36]
в вибрационных машинах с прямолинейными поступательными
рабочими колебаниями (см. пп. 3, 4, 5, 8, 10, 11, 13, 17, 18, 23
и 25 таблицы 2, а также рис. 86—90, 102, 104 и 105).
Два или несколько одинаковых вибраторов со скрещиваю-
щимися осями при определенном согласовании фаз и направ-
лений вращения обеспечивают винтовые колебания вибрирую-
щего органа (см. пп. 19—21 таблицы 2, а также рис. 93, 98
и 103).
Несколько дебалансных вибраторов, вращающихся с различ-
ными по абсолютной величине (как правило, с кратными) угло-
выми скоростями, используются в вибрационных машинах со
сложным полигармоническим законом колебаний рабочего
органа (см. рис. 23, ж, з, 24, в, а также п. 8 таблицы 2).
В подавляющем большинстве перечисленных выше вибра-
ционных машин и установок с несколькими вибраторами необ-
ходимым условием нормальной работы является синхронность
вращения, а иногда и наличие определенных соотношений ме-
жду фазами вращения роторов отдельных вибраторов, напри-
мер наличие синфазности или противофазности.
В ряде случаев, подобных указанному в п. 8 таблицы 2, воз-
никает задача обеспечения кратно-синхронного движения, то
есть вращения роторов вибраторов с угловыми скоростями,
кратными некоторой заданной скорости, и с определенными
разностями фаз.
Некоторое, хотя и неполное, представление о разнообразии
типов вибрационных машин и установок с несколькими вибра-
торами дает уже упоминавшаяся таблица 2. В этой же таблице
приведена сводка требований, которым должны удовлетворять
фазы и угловые скорости вращения роторов вибраторов, для
того чтобы машина или установка работала нормально. Схемы
машин расположены в таблице в порядке увеличения числа су-
щественных степеней свободы тел, несущих вибраторы; вначале
показаны машины, вибрирующий орган которых (несущее тело)
может рассматриваться как система всего лишь с одной сте-
пенью свободы, а в самом конце — с бесконечно большим чис-
лом степеней свободы.
Следует отметить, что обычно можно удовлетвориться не
точным, а лишь приближенным соблюдением определенных со-
отношений между фазами вращения вибраторов: малые коле-
бания, накладывающиеся на вращательное движение роторов,
не приводят к нарушению рабочего процесса. Аналогичным
образом почти всегда достаточно обеспечить равенство не мгно-
венных, а средних за один оборот значений угловых скоростей
вращения роторов вибраторов.
В настоящее время известны три основных способа согласо-
вания вращения роторов механических вибраторов.
362
ЗАДАЧА О СИНХРОНИЗАЦИИ МЕХАНИЧЕСКИХ ВИБРАТОРОВ [ГЛ. XII
Наиболее простым и исторически первым способом является
введение кинематических связей между роторами вибраторов.
Такими связями являются, например, зубчатые или цепные
передачи, синхронизирующие валы и т. и.
Кинематическая синхронизация вращения роторов вибрато-
ров обладает, однако, рядом существенных недостатков. Пре-
жде всего, она не может быть целесообразно применена во мно-
гих практически важных случаях, например в большинстве пла-
нетарных вибраторов, а также при значительных расстояниях
между вибраторами, достигающих в некоторых машинах де-
сяти и более метров. Другим недостатком является значитель-
ный шум, сопровождающий работу зубчатой или цепной пере-
дачи в вибрационных машинах, и повышенный износ шесте-
рен и цепей.
Следует отметить, что кинематическая синхронизация, не-
смотря на указанные выше недостатки, до недавнего времени
оставалась единственным применяемым способом синхрониза-
ции и фазировки вращения роторов вибраторов, что существен-
но ограничивало возможности совершенствования конструкций
вибрационных машин.
Лишь сравнительно недавно был предложен другой метод
согласования вращения роторов вибраторов, который состоит
в использовании электрических связей между двигателями, при-
водящими роторы во вращение. Известно при этом несколько
приемов электрической синхронизации и фазировки. Один из
них, разработанный для данного класса машин П. И. Новосель-
ским, А. В. Борщевским и В. Н. Сильвановичем (ВНИИстрой-
дормаш), состоит в применении специализированной системы
электрического вала [326].
Другой способ, который был предложен автором и разрабо-
тан для использования в конкретных вибрационных машинах
А. В. Ватсон, А. И. Кириченко и Б. П. Лавровым (институт
«Механобр»), заключается в применении для привода вибрато-
ров синхронных двухполюсных нереактивных электродвигателей
[52, 58, 68]. Известно, что при постоянной внешней нагрузке
роторы таких двигателей, включенных в одну достаточно мощ-
ную сеть, вращаются синхронно и с постоянным сдвигом по
фазе относительно вращающегося с синхронной угловой ско-
ростью поля статора. В многоиолюспых двигателях существует
не одно, а несколько устойчивых положений ротора по отно-
шению к указанному полю, поэтому непосредственное исполь-
зование таких двигателей в машинах, где существенна не толь-
ко синхронизация, по и определенная фазпровка вращения ви-
браторов, не представляется возможным.
Б. П. Лавровым, однако, было предложено несложное уст-
ройство, обеспечивающее автоматическую установку требуемой
§ 2j	ОСНОВНЫЕ ЗАДАЧИ О СИНХРОНИЗАЦИИ ВИБРАТОРОВ	363
устойчивой конфигурации фаз вращения вибраторов [240]. Это
устройство может позволить существенно расширить класс син-
хронных электродвигателей, пригодных для привода мпогови-
браторных машин, и, кроме того, делает возможной работу на
частотах, мепыиих частоты промышленного тока, без использо-
вания специальных преобразователей частоты.
Оба описанных выше способа согласования вращения рото-
ров вибраторов — кинематический и электрический — относятся
к принудительной синхронизации.
Существует, однако, и третий способ, при котором синхрон-
ность н требуемая фазировка вращения роторов нескольких
вибраторов, установленных на вибрационной машине и приводи-
мых от отдельных, не связанных между собой двигателей (на-
пример, от асинхронных электродвигателей или от электродви-
гателей постоянного тока), достигается автоматически, в силу
внутренних свойств самой колебательной системы. Речь идет
о своеобразном физическом явлении — самосинхронизации виб-
раторов.
Самосинхронизация и тем более требуемая по условиям ра-
боты машины фазировка вращения роторов вибраторов имеют
место, конечно, далеко не всегда. Тем не менее теоретические
и экспериментальные исследования, о которых будет сказано
в § 3 настоящей главы и которые излагаются в четвертой и пя-
той частях книги, показывают, что явление самосинхронизации
при умелом подходе можно успешно использовать в достаточно
широком классе вибрационных машин и устройств. Очевидно,
что в таких случаях нет никакой надобности прибегать к при-
нудительной — кинематической или электрической — синхрони-
зации и фазировке вращения роторов.
Встречаются случаи, когда в одной машине целесообразно
использовать сразу несколько способов синхронизации вибра-
торов. Так, например, в дробилках и мельницах с несколькими
возбудителями, схематически представленных в и. 16 таблицы 2
(см. также рис. 112—114), для синхронизации вибраторов-воз-
будителей иногда (если невозможно использовать явление само-
синхронизации) приходится применять принудительную элек-
трическую синхронизацию или синхронизацию посредством
механических связей. Для синхронизации же планетарных ви-
браторов-рабочих тел (роликов, конусов и т. п.), как правило,
применима лишь самосинхронизация. Можно привести также
и другие примеры целесообразного комбинирования различных
способов синхронизации вибраторов.
Вопрос о возможности использования того или иного спо-
соба синхронизации и фазировки вращения вибраторов имеет
очень важное значение для усовершенствования существующих
и для создания новых типов вибрационных машин; от его
364
ЗАДАЧА О СИНХРОНИЗАЦИИ МЕХАНИЧЕСКИХ ВИБРАТОРОВ [ГЛ, ХИ
Рис. 25.
решения часто зависят максимально возможный размер и со-
вершенство конструктивной схемы машины определенного типа.
Поэтому исследование различных способов синхронизации вра-
щения вибраторов, и особенно самосинхронизации и электри-
ческой синхронизации, представляет одну из узловых задач
динамики привода вибрационных машин.
Такие исследования необходимы не только для установле-
ния условий самосинхронизации вибраторов. При электрической
и кинематической синхронизации в вибрационных машинах так-
же имеет место ряд свое-
образных нелинейных эф-
фектов, которые следует
учитывать при расчете и
проектировании вибра-
ционных машин.
Укажем, далее, на
один особенный случай,
когда, в отличие от ра-
нее рассмотренных си-
стем, самосинхронизация
не только не является
полезной, но представля-
ет прямую опасность.
Речь идет об установке нескольких динамически неуравновешен-
ных машин (дробилок, грохотов, концентрационных столов, не-
которых ткацких машин и т. п.) на едином (групповом) фунда-
менте или перекрытии. Опыт показывает, что в ряде случаев
машины, являющиеся в указанном выше смысле механическими
вибраторами, начинают работать синхронно и синфазно, приводя
к недопустимо большим колебаниям, а иногда и к разрушению
сооружений. Для подобных систем представляет интерес полу-
чение условий, при которых либо окажется невозможной синх-
ронная и синфазная работа машин, либо при наличии само-
синхронизации будет иметь место взаимное динамическое урав-
новешивание (см. п. 24 таблицы 2).
Рассмотрению перечисленных вопросов в основном и посвя-
щены четвертая и пятая части книги.
2. Постановка основных задач о синхронизации вибраторов.
Обратимся теперь к рассмотрению общей постановки основных
задач о синхронизации вибраторов.
В достаточно общем случае вибрационная машина может
быть идеализирована в виде системы, состоящей из некоторого
числа п твердых или деформируемых тел В\, .... Вп (рис. 25),
связанных одно с другим и с неподвижным основанием 1 неко-
торыми «сосредоточенными» геометрическими связями 2, а так-
же «сосредоточенными» упругими 3 и демпфирующими 4 эле-
§ 2]
ОСНОВНЫЕ ЗАДАЧИ О СИНХРОНИЗАЦИИ ВИБРАТОРОВ
365
ментами. Состояние тел В\, .. . , Вп определяется вектором об-
общенных координат и(«ь и2, ...), который, в соответствии сс
сказанным выше, может быть как конечномерным, так и беско-
нечномерным.
Пусть па телах Blt .... Вп (назовем их несущими телами)
размещено некоторое число k механических вибраторов, оси
вращения которых osos могут быть расположены любым обра-
зом, а основные параметры — различными. Состояние вибрато-
ров определяется углами поворота фц . . . , фл их роторов (в слу-
чае поршневых вибраторов можно считать, что угол д., есть
угол поворота кривошипа кривошипно-шатунного механизма,
фактически или мысленно связанного с инерционной массой ви-
братора) .
Пусть, далее, на роторы вибраторов действуют некоторые
внутренние или внешние по отношению к рассматриваемой си-
стеме моменты, которыми могут быть моменты сил сопротивле-
ния вращению роторов, вращающие моменты, передавае-
мые от двигателей, и моменты сил, обусловленных наличием
электрических или механических (упругих, фрикционных, цен-
тробежно-инерционных*)) или каких-либо иных связей между
роторами вибраторов. Эти моменты могут быть различными для
различных вибраторов и зависеть как от углов поворота рото-
ров ф[, ..., фл и координат и2, ... , так и от их производ-
ных по времени t, а также и непосредственно от t. Указанные
моменты могут быть различными для каждого вибратора; их
конкретные выражения зависят от типа вибратора, характера
сил сопротивления в нем и от принятого способа синхронизации.
Эти выражения будут подробно рассмотрены в дальнейшем.
Оставив для дальнейшего также и рассмотрение дифферен-
циальных уравнений движения описанной выше системы, заме-
тим, что они относятся к тому же типу, что и общие уравнения
задач о синхронизации (см. § 1 главы I и главу II).
Главные задачи о синхронизации вибраторов вытекают из
практических проблем, представление о которых дает рассмот-
ренная выше таблица 2.
В случае одночастотных вибраторов основная задача о син-
хронизации состоит в выяснении условий, при выполнении кото-
рых все роторы, несмотря на возможное различие параметров
вибраторов и действующих на них сил, вращаются с одинако-
выми по модулю средними за оборот угловыми скоростями
|ф* | = и (s = 1, .. ., k), а несущие тела В\, . . ., Вп совершают
при этом колебания с периодом Т = 2л/ш. Такую задачу назо-
вем задачей о простой синхронизации вибраторов.
) О центробежно-инерционных связях (рис. 35) см. п. 1 § 2 главы XIV,
366
ЗАДАЧА О СИНХРОНИЗАЦИИ МЕХАНИЧЕСКИХ ВИБРАТОРОВ [ГЛ. ХП
Иными словами, речь идет об установлении необходимых
и достаточных условий существования и устойчивости синхрон-
ных движений системы вида
<ps == crs [со/+ as + ф^ (со/)]
иг = иг (со/)	(г = I, 2, . ..),
где cr.s — числа, каждое из которых может быть равно +1 или
— 1 в зависимости от направления вращения роторов вибрато-
ров в рассматриваемом движении, а*— постоянные и ф*(со/) и
и ur(co/)—периодические функции времени / с периодом, рав-
ным 2л/со, причем постоянные as удобно считать определенными
таким образом, что средние за период значения функций ф*
равны нулю.
В случае многочастотных вибраторов, а иногда и в случае
вибраторов одночастотных, представляет интерес также и не-
сколько более общая задача (будем ее называть задачей о крат-
ной синхронизации вибраторов), когда речь идет о выяснении
условий существования и устойчивости движений вида
% = \nsat + as + € И)]	(s=l, fe),
ur — ur (co/)	(r = 1, 2, ...),
где ns — произвольные целые взаимно простые положительные
числа.
В случае, если рассматриваемая система автономна, в част-
ности в задаче о самосинхронизации, угловая скорость со не яв-
ляется заданной заранее, а подлежит определению в процессе
решения задачи.
Помимо выяснения условий существования и устойчивости
движений типа (2.1) или (2.2), интерес представляет также вы-
числение средних за период значений фаз as в устойчивых син-
хронных движениях, а иногда также вычисление наибольших
размахов колебаний фаз (ФДпах вблизи этих средних значений
и обусловленных колебаниями ф’(со/) «искажений» движения
несущих тел Si, .... Вп но сравнению с движением, которое
имело бы место при ф* (со/) = 0, то есть при заданном равно-
мерном вращении вибраторов с начальными фазами as.
Особое значение для проектирования вибрационных машин
и установок имеет и обратная задача (ее можно назвать зада-
чей синтеза в отличие от сформулированной выше задачи ана-
лиза), заключающаяся в таком выборе параметров системы,
при котором обеспечивается устойчивое синхронное (или крат-
но-синхронное) движение вибраторов с наперед заданными
§ з]
КРАТКИЙ ОБЗОР ИССЛЕДОВАНИЙ
367
средними значениями фаз as, предопределяющими в основном
требуемый закон колебаний вибрирующего органа машины (не-
сущих тел Si, Вп). Более подробно задача синтеза обсуж-
дается в главе XV настоящей книги.
Во многих случаях представляет интерес также задача
о «стабильности» определенного устойчивого синхронного или
кратно-синхронного движения системы по отношению к возмож-
ным отклонениям параметров от их номинальных значений.
Для теории ряда вибрационных машин существенно изуче-
ние синхронизации вибраторов при условии, что некоторые из
тел В|, . . . , Вп в процессе движения могут соударяться.
Отметим, что о простейшем частном случае поставленной
выше общей задачи о синхронизации вибраторов уже говори-
лось в § 1 главы I. Заметим также, что разобранные в §§ 2 и 3
главы I задачи об автобалансире и об изгибно-крутильных ко-
лебаниях вращающихся валов с неуравновешенными дисками,
по существу, также могут рассматриваться как частные слу-
чаи общей задачи о синхронизации вибраторов.
§ 3. Краткий обзор исследований в области синхронизации
механических вибраторов
1.	Открытие явления самосинхронизации вибраторов. На-
сколько нам известно, в Советском Союзе явление самосинхро-
низации двух механических вибраторов впервые было обнару-
жено в институте «Механобр» при проведении работ по созданию
вибрационных машин, осуществлявшихся под руководством
Д. А. Плисса (1947—1948 гг.). В том же институте выполнено
большее число из опубликованных до настоящего времени ис-
следований в области теории синхронизации вибраторов, а так-
же конструкторских разработок (см. ниже). Ряд опытов по ис-
пользованию явления самосинхронизации в конце сороковых
годов был поставлен также во ВНИИстройдормаше.
Первая из известных нам зарубежных публикаций, касаю-
щихся самосинхронизации вибраторов, появилась позднее—в
1950 г. — в виде патентного описания [478]. Соответствующая
заявка, относящаяся к простейшему случаю симосинхрониза-
ции двух дебалапсных вибраторов, была, однако, сделана
в Швеции в 1946 г.
2.	Теоретические и экспериментальные исследования в обла-
сти синхронизации вибраторов*). В 1953 г. была опубликована
*) В настоящем параграфе мы не касаемся работ по теории вибрацион-
ного поддержания вращения неуравновешенного ротора, а также по теории
колебательных систем, возбуждаемых единственным вибратором, приводимым
от двигателя ограниченной мощности. Обзор соответствующих исследований,
относящихся с точки зрения теории синхронизации вибраторов к вырожден-
358
ЗАДАЧА О СИНХРОНИЗАЦИИ МЕХАНИЧЕСКИХ ВИБРАТОРОВ [ГЛ. XII
статья автора [44], в которой дано теоретическое объяснение
синхронизации механических вибраторов. В этой работе рас-
смотрена задача о самосинхронизации вибраторов в простей-
шем случае, когда вибрирующий орган машины (несущее тело)
имеет всего одну существенную степень свободы, получены не-
обходимые и достаточные условия существования и устойчиво-
сти синхронных движений роторов вибраторов.
Более сложная задача о самосинхронизации вибраторов в
машинах, вибрирующий орган которых может совершать произ-
вольное плоское движение, то есть имеет три степени свободы,
изучена автором в работах [54, 56, 57, 59], опубликованных
в 1958—1960 гг.
Основы теории принудительной электрической синхронизации,
а также синхронизации посредством введения упругих элемен-
тов между роторами вибраторов рассмотрены автором в ста-
тьях [58, 63] (1960 -1961 гг.).
В работе Б. П. Лаврова и автора [60] (1960 г.) был предло-
жен так называемый интегральный критерий устойчивости дви-
жения в задачах о самосинхронизации вибраторов. Обоснование
и обобщение этого критерия даны в публикациях автора [61, 62,
68] (1960—1963 гг.). Дальнейшие модификации и обобщения
предложены в работах Б. П. Лаврова [242, 244] (1966 г.),
Р. Ф. Нагаева и К- Ш. Ходжаева [311, 312, 314, 316, 406, 411]
(1964—1969 гг.).
В 1961 г. появилась работа О. Я. Шехтер [427], в которой за-
дача о самосинхронизации вибраторов в машине с двумя
степенями свободы вибрирующего органа рассмотрена при-
менительно к установке для вибрационного погружения обо-
лочек.
В статье Б. П. Лаврова [241] (1961 г.) изучена задача
о синхронизации вибраторов, установленных на свободном
твердом теле. При этом рассмотрен случай, когда среди вибра-
торов имеются так называемые качающиеся вибраторы, или
вибраторы маятникового типа.
В монографии К- М. Рагульскиса [352] (1963 г.) изучен ряд
систем с самосинхронизируюгцимися вибраторами, в том числе
рассмотрены для простейших случаев кратная самосинхрониза-
ция и самосинхронизация при наличии ударов.
Сложная система с ударами, колебания в которой возбуж-
даются двумя самосинхронизирующнмися вибраторами, иссле-
дована применительно к теории вибрационной щековой дро-
ным частным случаям, приводится в § 1 главы XVII и в § 1 главы XVIII.
Не рассматриваются также работы, посвященные изучению синхронизации
объектов, аналогичных механическим вибраторам (см., например, п. 3 § 2
главы XIV н главу XXIV). Не упоминаются нами и некоторые (к счастью,
весьма немногочисленные) ошибочные работы.
§ 3]	КРАТКИЙ ОБЗОР ИССЛЕДОВАНИЙ	369
билки Р. Ф. Нагаевым [308] (1963 г.); им же изучен ряд задач
о синхронизации вибраторов, установленных на твердых телах,
совершающих пространственные колебания, а также вибрато-
ров, связанных с системами, обладающими распределенными
параметрами [307] (1963 г.). Самосинхронизация нескольких пар
дебалансных вибраторов, размещенных вдоль упругой балки
с распределенной массой, рассмотрена Р. Ф. Нагаевым и
И. А. Поповой [315] (1967 г.). Самосинхронизация вибраторов
в виброударных системах изучена Л. Б. Зарецким [192, 193]
(1967—1968 гг.), воспользовавшимся для получения результата
иными методами, нежели К. М. Рагульскис и Р. Ф. Нагаев.
В работе К- Ш. Ходжаева [407] (1967 г.) рассмотрена задача
о синхронизации дебалансных вибраторов, связанных с произ-
вольной квазилинейной колебательной системой, и предложены
выражения для так называемых вибрационных моментов через
гармонические коэффициенты влияния. Аналогичные выраже-
ния, содержащие, однако, гармонические коэффициенты влия-
ния, определенные иным образом, были почти одновременно и
независимо получены Л. Шперлингом [482] (1967 г), рассмот-
ревшим также синхронизацию вибраторов в ряде практически
интересных конкретных систем. Л. Шперлингом изучена не-
сколько ранее и задача о самосинхронизации вибраторов, свя-
занных с линейной цепной колебательной системой [481] (1965 г.).
Самосинхронизация вибраторов, связанных со своеобразной
трехмассной линейной колебательной системой, рассмотрена
А. Д. Рудиным [365] (1966 г.).
Существенный для теории и расчета машин с самосинхрони-
зирующимися и принудительно синхронизированными механи-
ческими вибраторами вопрос о стабильности (надежности) за-
кона колебаний рабочего органа изучен в работах автора
[56, 68] (1960, 1962 гг.), Б. П. Лаврова [242] (1966 г.), Г. А. Де-
нисова [172, 173] (1969 г.).
В работе автора [68] (1962 г.) было предложено использо-
вать явление самосинхронизации при проектировании группо-
вых фундаментов под неуравновешенные машины. Дальнейшая
разработка этого вопроса дана в статьях автора [76, 83]
(1965—1967 гг.), А. Л. Кумпикаса и К. М. Рагульскиса [233]
(1966 г.).
Самосинхронизация двух вибраторов в системе с одной по-
воротной степенью свободы изучена в работе П. М. Алабужева,
А. К. Зуева и М. Ш. Кирнарского [9а] (1965 г.).
Основы теории синхронизации обобщенных вибраторов, ге-
нерирующих практически любые силовые и моментные возбуж-
дающие воздействия, разработаны Р. Ф. Нагаевым [317] (1968 г.).
Эта теория послужила основой для исследования синхрониза-
ции гироскопических вибраторов, которое выполнено в работах
370
ЗАДАЧА О СИНХРОНИЗАЦИИ МЕХАНИЧЕСКИХ ВИБРАТОРОВ [ГЛ, XII
П. М. Алабужева, А. К- Зуева, Е. Н. Иванова и М. Ш. Кирнар-
ского [10, 196, 213] (1969 г.).
В статье Ю. И. Марченко и автора [92] (1969 г.) рассмотрен
вопрос о влиянии реологических свойств рабочей среды на само-
синхронизацию возбудителей вибрационных устройств и полу-
чены некоторые результаты, касающиеся синтеза машин с само-
синхронизирующимися вибраторами.
О немногочисленных работах по применению для решения
задач теории синхронизации аналоговых и вычислительных ма-
шин говорилось в § 2 главы VI.
Ряд положений теории самосинхронизации вибраторов из-
ложен в работах В. Богуша и 3. Энгеля [447] (1965 г.), Иноуэ
Дзюнкити, Араки Иосиаки, Хаяси Сэцуко и Мияура Суга [198,
199] (1967 г.), Я. Г. Пановко и И. И. Губановой [331] (1967 г.).
Экспериментальные исследования синхронизации механиче-
ских вибраторов проводились С. А. Цаплиным [415] (1953 г.),
автором [44, 46, 59, 68] (1953—1962 гг.), К. А. Олехновичем [327]
(1956 г.), И. И. Долицким [178] (1958 г.), Б. П. Лавровым [242]
(1958 г. и позднее), Н. А. Карповым [204] (1962 г.), В. Богушем
и 3. Энгелем [447] (1965 г.), А. Д. Лесиным [250] (1966 г.),
Ю. Ю. Гецявичусом и К. М. Рагульскисом [142а] (1966 г.),
М. И. Забылиным [191а] (1966 г.) и другими исследователями.
Приведенный краткий обзор показывает, что приоритет в ис-
следовании явления самосинхронизации и электрической син-
хронизации вибраторов, а также подавляющее большинство ра-
бот в этой области, несомненно, принадлежат отечественным
ученым, в частности сотрудникам института «Механобр» (Ле-
нинград) .
Результаты большего числа исследований, цитированных
в настоящем пункте, будут изложены и частично обобщены
в соответствующих главах данной части книги.
3.	Работы по созданию машин с самосинхронизирующимися
и электрически синхронизированными вибраторами. Как было
отмечено, толчком для исследований в области теории самосин-
хронизации послужили экспериментальные наблюдения. С дру-
гой стороны, последующее развитие теории и постановка спе-
циальных опытов способствовали изобретательской и конструк-
торской деятельности в области создания новых вибрационных
машин, приводимых от нескольких самосинхронизирующихся
или электрически синхронизированных вибраторов.
Значение теории при создании таких машин определяется
тем, что многие существенные факты и расчетные соотношения
вряд ли могут быть предсказаны на основе интуиции и отдель-
ных экспериментов; это обстоятельство неоднократно будет ил-
люстрировано в дальнейшем. В частности, возможность исполь-
зорапия двух одинаковых самосинхронизирующихся вибраторов
§ 3]	КРАТКИЙ ОБЗОР ИССЛЕДОВАНИЙ	37 [
для получения круговых поступательных колебаний мягко амор-
тизированного твердого тела была вначале установлена чисто
теоретическим путем [54], что послужило основой ряда изобре-
тений (см., например, [53, 66, 69], §§ 1 и 8 главы XX, а также
§§ 3 и 5 главы XXI настоящей книги).
К настоящему времени в различных странах мира выдано
значительное число патентов и авторских свидетельств на ви-
брационные машины и устройства, приводимые от самосин-
хронизирующихся или электрически синхронизированных ви-
браторов (см., в частности, [51—53, 66, 67, 72, 104, 156—159,
166—169, 212, 238—240, 243, 246, 326, 339, 361, 367, 368, 375,
395а, 451, 474, 478, 479, 483, 485]). Несколько десятков различ-
ных типов таких машин выпускается в СССР и за рубежом
(см. [498—508], а также таблицу 2), причем достигнут весьма
значительный технико-экономический эффект. В нашей стране
наибольшее число конструкторских разработок до настоящего
времени выполнено в институте «Механобр» под руководством
Б. П. Лаврова, а также К. А. Рундквиста и автора книги.
Значительная часть цитированных выше публикаций о ма-
шинах и устройствах с самосинхронизирующимися и электриче-
ски синхронизированными механическими вибраторами будет
более подробно описана в соответствующих главах пятой части.
ГЛАВА XIII
СИНХРОНИЗАЦИЯ МЕХАНИЧЕСКИХ
ВИБРАТОРОВ В МАШИНАХ И УСТАНОВКАХ
С ПЛОСКИМ ДВИЖЕНИЕМ
§ 1. Предварительные замечания
В настоящей главе задача о синхронизации вибраторов
рассматривается в предположении, что вибрирующий орган
Рис, 26.
машины, на котором установлены вибраторы, представляет еди-
ное твердое тело В (несущее тело), которое может совершать
плоскопараллельное движение, то есть имеет, вообще говоря,
§ 2]	УРАВНЕНИЯ ДВИЖЕНИЯ СИСТЕМЫ	373
три степени свободы (рис. 26). Вибраторы предполагаются одно-
частотными, дебалансного или планетарного типа (см. главу XII);
при этом изучается простая (некратная) синхронизация.
Указанный частный случай имеет широкое поле приложений:
ему соответствует большая часть типов вибрационных машин
и установок, динамические схемы которых представлены в таб-
лице 2 (см. пп. 1, 2—14, 16, 17).
С другой стороны, на примере проводимого в данной главе
исследования будет проиллюстрирована методика решения ана-
логичных задач в более сложных случаях и выяснятся основные
качественные закономерности рассматриваемых явлений. В этом
отношении изучаемый случай является «предельными, дальней-
шие упрощения приводят к исчезновению некоторых важных
эффектов.
Исследованию будут подвергнуты три упомянутых в преды-
дущей главе способа синхронизации: самосинхронизация, при-
нудительная электрическая синхронизация и принудительная
синхронизация с помощью упругих элементов, введенных между
роторами вибраторов (кинематическая синхронизация).
Основное содержание главы воспроизводит в дополненном и
переработанном виде работы автора [44, 46, 54, 56—58, 60—
63, 68].
§ 2. Уравнения движения системы
1. Динамическая схема. Динамическая схема рассматривае-
мой в настоящей главе системы представлена на рис. 26. Несу-
щее тело В (вибрирующий орган машины) считается твердым
телом, которое может совершать плоскопараллельное движе-
ние и которое связано с неподвижным основанием системой уп-
ругих элементов 4.
В теле размещено k' дебалансных и k" планетарных (внут-
ренних или внешних) вибраторов. Общее число вибраторов, та-
ким образом, есть k = k' -j- k".
Дебалансные вибраторы 1, в соответствии со сказанным
в § 1 главы XII, представляют неуравновешенные роторы, при-
водимые во вращение от каких-либо двигателей. Под внутрен-
ними (катковыми) планетарными вибраторами понимаются
тела вращения 2 (как правило, цилиндрической формы), вло-
женные в стаканы 3, которые укреплены в вибрирующем органе.
Под внешними (кольцевыми) планетарными вибраторами по-
нимаются кольца 2', которые могут обкатываться своей внут-
ренней поверхностью по оси 3', связанной с вибрирующим орга-
ном. Оси вибраторов считаются перпендикулярными плоскости,
параллельно которой происходит движение тела; последнее ог-
раничение, впрочем, не является особенно существенным.
374
ПЛОСКАЯ ЗАДАЧА О СИНХРОНИЗАЦИИ ВИБРАТОРОВ
[ГЛ. л!1|
Предполагается, что в рассматриваемых ниже движениях
ролики планетарных вибраторов катятся в стаканах без отрыва
от стенок последних, а кольца не отрываются от осей, то есть
что не происходит нарушения неудерживающих связей. Усло-
вия, при выполнении которых такое допущение справедливо,
будут получены в § 15 настоящей главы.
Электрические или какие-либо иные двигатели вибраторов
могут быть размещены либо на самом вибрирующем органе,
либо на неподвижной раме; в последнем случае вращающий
момент передается через клипоременную передачу, специальный
вал или муфту.
Роторы вибраторов могут быть связаны друг с другом си-
стемой линейно-упругих синхронизирующих элементов (несомых
связей).
Пусть хОу— неподвижная система прямоугольных осей ко-
ординат, uO\V — система осей, жестко связанная с телом В и
совпадающая с хОу в положении статического равновесия си-
стемы.
Положение подвижных осей координат uO\V в теле В пока
считается произвольным; в дальнейшем, однако, оно будет вы-
брано однозначным образом из условий упрощения записи урав-
нений движения.
Примем за обобщенные координаты системы координаты х
и у точки 01 твердого тела В в системе неподвижных осей хОу,
угол поворота ф тела В, отсчитываемый по ходу часовой стрел-
ки, и углы поворота ф8 векторов-эксцентриситетов вибраторов
по отношению к неподвижной оси Ох, отсчитываемые в том же
направлении.
В дальнейшем координаты х, у и ф, определяющие положе-
ние несущего тела В (вибрирующего органа машины), в соот-
ветствии с введенной в главе II терминологией иногда будут
называться колебательными координатами, а координаты ф8,
определяющие положение роторов (неуравновешенных валов,
роликов или колец), — вращательными координатами.
2. Кинетическая и потенциальная энергии. Выражение для
кинетической энергии системы может быть записано в виде
т=4 ж ч- г?2,)+4 ^сф2+4 S и +*&)+^cS^s]+
S ==» 1
fe
+1 S [тх*«+сн-МУз-Ф)2]- с2-1)
1
Здесь Ж — масса твердого тела В, У— его момент инерции
относительно центральной оси, перпендикулярной плоскости
§ 2]	УРАВНЕНИЯ ДВИЖЕНИЯ СИСТЕМЫ	375
хОу, ms и S/'cs — соответственно масса и центральный момент
инерции ротора, неуравновешенного вала, ролика или кольца
s-ro вибратора; дебалансным вибраторам приписаны номера от
s = 1 до s = k', планетарным — от s = k' + 1 до s = k' + k" = k.
Через xc, yc, xcs и ycs обозначены соответственно координаты
центров тяжести твердого тела и роторов в неподвижных осях
хОу, через ys— угол поворота некоторого фиксированного ради-
уса s-ro ролика или кольца, отсчитываемый от оси Ощ против
хода часовой стрелки в случае роликового и по ходу часовой
стрелки в случае кольцевого планетарного вибратора (рис. 26).
Выразим кинетическую энергию системы через введенные
выше обобщенные координаты. С этой целью воспользуемся
геометрическими соотношениями
хс = х + a cos ф + b sin ф,
ус~- у + b cosф — a sinф,
xcs = х + uos cos ф + vos sin ф + es cos ф,,
ycs — у + vos cos ф — uos sin Ф — es sin ф5,
вытекающими из рассмотрения рис. 26. В последних формулах
через а и b обозначены координаты центра тяжести С тела В
в системе осей иО}и, связанной с телом, через uos и vos — коор-
динаты оси s-ro вибратора в той же системе и через е„ — экс-
центриситет (расстояние от оси вращения до центра тяжести)
s-ro вибратора.
В дальнейшем будут рассматриваться движения, в которых
тело В совершает малые колебания вблизи положения стати-
ческого равновесия. Поэтому угол поворота тела ф можно счи-
тать малым по сравнению с единицей и пренебрегать при вы-
числении координат хс, Ус, xcs и ycs степенями ф более высокими,
чем первая. Тогда приведенные выше формулы примут вид
хс = х + а + 6ф,	ус = у + b - яф,
xcs = х + uos+ vos<f + es cos ф5, ycs = у T vos - uos<p - es sin ф5.
Между угловыми скоростями ys, <ps и ф в случае планетар-
ных вибраторов имеет место соотношение
Y А = (<PS ~ ф)л A (s = k' + 1, ..., k),	(2.3)
где (см. рис. 26) в случае внутреннего вибратора bs = /?* — es
есть радиус ролика, а в случае внешнего вибратора &8 = /?5 + е5—
внутренний радиус кольца; Bs—радиус стакана в случае внут-
реннего и радиус оси в случае внешнего вибратора. Отметим,
что такие обозначения позволят записать основные формулы
в виде, одинаково пригодном как для случая внутренних, так
376
ПЛОСКАЯ ЗАДАЧА О СИНХРОНИЗАЦИИ ВИБРАТОРОВ
[ГЛ. XIII
и для случая внешних планетарных вибраторов. Число X* в ра-
венстве (2.3) равно единице при условии, что ролик или кольцо
катятся без скольжения. Если же ролик или кольцо скользят
по соответствующей поверхности, не поворачиваясь относитель-
но несущего тела, то = 0. Возможны, естественно, и иные
случаи, однако в настоящей главе мы ограничимся изучением
только этих двух, представляющих особый практический инте-
рес. Условия, при которых имеет место движение того или
иного вида, будут рассмотрены в § 15 настоящей главы.
Подставив выражения (2.2) и (2.3) в формулу (21), пред-
ставим кинетическую энергию системы Т в следующем виде:
т = у ai (%2 + т/2) + ~ /ф2Ч~4 S + 5и*ф ~	-
ь
~ У ms^s (х sin cps + i/ cos cps) -
k
- Ф <i>s mses (vos sin ф6. - uos cos ф5) 4- hsS(,
CS
b'i
(2.4)
Здесь введены обозначения
k
М = Л -I- У ms,
S — 1
fe
I = Зс + Л {о?
bs +	V
bs	/ .
7=7
1 s u cs
~ьГ
k
Sa = ЛЬ 4- У msvos,
4- ms&s,
k
Sv = Ла 4- У msuos.
(2.5)
- 1
Через hs в формулах (2.4) и (2.5) обозначен параметр, равный
нулю для дебалансных вибраторов и единице для планетарных
вибраторов:
10, s=l.........k',
As = ( 1, s = k'+\.......k' + k" = k. (2,6)
Составим выражение для потенциальной энергии системы П.
Последняя слагается из потенциальной энергии силы тяжести
Пг, потенциальной энергии Пе упругих опор, связывающих тело
с неподвижным основанием, и — в задаче о синхронизации по-
УРАВНЕНИЯ ДВИЖЕНИЯ СИСТЕМЫ
377
§ 2]
средством введения упругих элементов между роторами — также
из потенциальной энергии Пс этих элементов (несомых связей):
П = Пг + Щ + Пс.	(2.7)
Выражения для энергий Пя и Пе, отсчитываемых от поло-
жения статического равновесия, могут быть представлены в
форме
k
пг = 2 msesg [ 1 - sin (<ps - %)],
S=I	(2.8)
П* = 4 (Cxx2 + СуУ2 + СУ + 2СхуХУ + 4</(₽ + 2сучУУ)-
Здесь g— ускорение силы тяжести, % — угол между осью Ох
и горизонталью *), сх, су, с<Р, с?у, схч> и суч>— постоянные («квази-
упругие коэффициенты»), зависящие от жесткостей упругих
элементов и их расположения в положении равновесия тела.
Вычисление этих постоянных обычно не представляет затрудне-
ний; в более сложных случаях можно воспользоваться форму-
лами, приводимыми, например, в монографии П. Ф. Папковича
[333], работе Г. И. Николенко [325] (см. также монографию
А. И. Лурье [259], стр. 271—276), а также в книге Н. Г. Бели-
ковского [40].
Предполагая упругие элементы системы принудительной син-
хронизации линейными, запишем потенциальную энергию этих
элементов Пс в форме**)
k k
Пс = -4 Y ^cs/K4s-CT/<P/-xs + xy)2.	(2.9)
S=1 /=1
Здесь cSj = CjS и к., — постоянные, crs —числа, равные +1 для
вибраторов, которые в допускаемом системой синхронизации
стационарном движении вращаются в положительном направ-
лениик (по ходу часовой стрелки), и равные —1 для вибрато-
ров, вращающихся при стационарном движении в отрицатель-
ном направлении, щ<р8— углы поворота роторов, отсчитываемые
в направлении стационарного вращения. В выражение для
*) Для конкретности предполагается, что рассматриваемая система дви-
жется параллельно вертикальной плоскости; этот случай является наиболее
часто встречающимся на практике. Не представляет, конечно, затруднений и
составление выражения для Пй в иных случаях. Забегая вперед, заметим,
однако, что сила тяжести вообще не оказывает существенного влияния на
основные результаты исследования в случае простой синхронизации.
**) Заметим, что, говоря здесь и ниже об упругих синхронизирующих
элементах, мы имеем в виду не обязательно механические элементы, связы-
вающие роторы вибраторов, но также и соответствующие указанным пред-
положениям устройства типа электрического вала.
378
ПЛОСКАЯ ЗАДАЧА О СИНХРОНИЗАЦИИ ВИБРАТОРОВ
[ГЛ. ХП1
потенциальной энергии входят лишь разности указанных углов,
поскольку при повороте всех роторов на один и тот же угол
в направлениях стационарного вращения, допускаемых системой
синхронизации, потенциальная энергия этой системы не должна
измениться.
Для выяснения смысла постоянных xs заметим, что при зна-
чениях углов одр.ч = хя — хо, где хо—произвольная постоянная,
потенциальная энергия синхронизирующих элементов обращает-
ся в нуль.
Выбор углов xs определяется необходимой для работы ма-
шины фазировкой вращения роторов вибраторов; назовем эти
углы установочными углами системы синхронизации. Одно из
xs, как нетрудно видеть, может быть выбрано совершенно про-
извольно.
Выражение (2.9) относится к случаю, когда система синхро-
низации предназначена для обеспечения вращения вибраторов
с равными по абсолютной величине средними угловыми скоро-
стями, то есть если эта система не содержит редукторов. Если
же система синхронизации упругими элементами осуществлена
так, что стационарное вращение роторов происходит с различ-
ными угловыми скоростями osvstt), где vs — произвольные числа,
то для получения соответствующего выражения для Пс в фор-
муле (2.9) следует заменить os на o5/vs.
Составление выражения (2.9) для потенциальной энергии Пс
в конкретных случаях синхронизации посредством упругих эле-
ментов не представляет существенных трудностей. Как правило,
большая часть коэффициентов csj квадратичной формы Пс ока-
зывается равной нулю (отметим, что с!(- = 0, если г-н и /-й ви-
браторы не связаны синхронизирующими элементами).
Воспользуемся теперь произволом в выборе осей координат
хОу и uO\V с целью максимального упрощения выражений (2.4)
и (2.7) для кинетической и потенциальной энергии системы и
тем самым для соответствующего упрощения дифференциаль-
ных уравнений движения системы.
Прежде всего выберем начало координат О, подвижной си-
стемы uO\V таким образом, чтобы выполнялись соотношения
k	k
Sa = ЛЬ + 2 msvos=-Q, Sj, = Ла + 2 msuos = {). (2.10)
S=“l	S = 1
Иначе говоря, примем за начало координат точку твердого тела,
которая является центром тяжести этого тела, если присоеди-
нить к нему массы всех роторов ins, сосредоточив их на осях
вращения. Эту точку в дальнейшем для краткости будем назы-
вать центром тяжести вспомогательного тела или условным
центром тяжести
§ 2]
УРАВНЕНИЯ ДВИЖЕНИЯ СИСТЕМЫ
379
Далее выберем наклон осей координат хОу таким образом,
чтобы коэффициент сху в выражении (2.8) для потенциальной
энергии упругих опор Пе был равен нулю:
сху = 0.	(2.11)
Как нетрудно убедиться, такой выбор осей всегда возможен.
При учете равенств (2.8) —(2.11) выражения (2.4) и (2.7)
для кинетической и потенциальной энергии системы принимают
следующий окончательный вид:
k
Т = ±М(х2 + у2) + | 7ф2 + -1 £ /X +
8=1
k
+ J} mses<ps (i sin <ps + у cos <ps) -
S=|
k
mfis (vos sin <ps - uos cos <ps) + h:
b'z
(2.12)
k
11 = у (cxx2 + Cyy2 + 2сСфхф + 2Сучу(р) + msge,s [ 1 - sin (ф5 - x)] +
8 = 1
fe fe
+ —J ~СТ/Ф/~xs + x/)2- (2-13)
s=l / = 1
3. Обобщенные силы-, выражения для моментов, развивае-
мых двигателями вибраторов, и для сил и моментов сопро-
тивления. Остается составить выражения для обобщенных сил
системы, к которым следует отнести вращающие моменты, пере-
даваемые на роторы вибраторов электрическими или какими-
либо иными двигателями, силы сопротивления вращению рото-
ров и силы сопротивления при колебаниях твердого тела В.
Структура выражений для обобщенных сил, таким образом,
различна для вращательных и для колебательных координат,
причем для вращательных координат она существенно зависит
от типа вибратора (дебалансный или планетарный), от типа
двигателей вибраторов (синхронный или асинхронный). По-
этому приведем выражения для обобщенных сил, отвечающие
основным случаям задачи.
Рассмотрим сначала выражения для обобщенных сил Q<ps,
соответствующих вращательным обобщенным координатам. Эти
обобщенные силы могут быть представлены в форме
Q =LS-RS (s=l, ...,&),	(2.14)
Ts
380
ПЛОСКАЯ ЗАДАЧА О СИНХРОНИЗАЦИИ ВИБРАТОРОВ
[ГЛ. XIII’
где Ls — приведенные к координатам <ps вращающие моменты
двигателей вибраторов и /?., — приведенные моменты сил со-
противления.
Обратимся к составлению выражений для моментов Ls. Бу-
дем предполагать, что вращающий момент двигателя с до-
статочной степенью точности определяется так называемой
статической характеристикой. Основанием для подобного допу-
щения является то обстоятельство, что в изучаемых установив-
шихся синхронных движениях вибраторов угловые скорости
вращения роторов изменяются вблизи некоторого стационар-
ного значения и притом, как правило, достаточно медленно.
Косвенным подтверждением возможности использования стати-
ческих характеристик двигателей является хорошее согласие
получающихся теоретических результатов с данными экспери-
мента. Отметим также, что для случая электродвигателей по-
стоянного тока вопрос о возможности использования статиче-
ских характеристик рассмотрен в работах М. Л. Быховского,
В. А. Зиновьева и Т. Т. Павловой [114, 115].
В дальнейшем будем различать двигатели двух видов — дви-
гатели асинхронного типа и двигатели синхронного типа.
Вращающий момент двигателя асинхронного типа*), в со-
ответствии с предположением о возможности использования
статической характеристики, будем считать зависящим только
от угловой скорости вращения ротора двигателя по отношению
к статору:
=	(2-15)
Здесь, в соответствии с принятой системой отсчета углов <ps и <р
(см. рис. 26), число qs должно быть взято равным единице, если
двигатель s-ro вибратора установлен непосредственно на вибри-
рующем органе машины (то есть на теле В), и равным нулю
в случае установки двигателя на неподвижном основании **).
Примерный вид статической характеристики обычного асин-
хронного электродвигателя схематически показан на рис. 27, где
и —соответственно номинальная угловая скорость и
номинальный момент двигателя
Вращающий момент двигателя синхронного типа явно зави-
сит от времени t. Рассмотрим сначала наиболее простой случай
двухполюсного синхронного электродвигателя, причем будем
*) Такими двигателями являются, например, обычные асинхронные элек-
тродвигатели и электродвигатели постоянного тока.
**) Строго говоря, при установке двигателя па неподвижном основании
и при соединении валов вибратора и двигателя, например, посредством кли-
ноременной передачи некоторый относительный поворот валов возникает и
при поступательных перемещениях тела В. Однако это обстоятельство не
влияет па результат решения задачи и поэтому здесь не учитывается.
§ 2]
УРАВНЕНИЯ ДВИЖЕНИЯ СИСТЕМЫ
381
предполагать, что вращение от вала двигателя на вал вибра-
тора передается «напрямую», без промежуточного редуктора.
Пусть A^sst)SsSt> есть мгновенное положение оси главного
магнитного потока статора двигателя s-ro вибратора (рис. 28).
Эта ось равномерно вращается с синхронной угловой скоростью
щи относительно обмотки статора*). Обозначим через 1% =
=	+ Щф + Gs<i>t угол между положительным направлением
оси Ох и упомянутой осью Mst)slst), отсчитываемый по ходу ча-
совой стрелки. Угол asps, где ps — постоянная, при этом опре-
деляет ориентацию обмотки статора относительно основания, на
котором установлен двигатель:
в случае расположения двигате-
ля на вибрирующем органе ма-
шины (щ = 1) величина щр5
есть угол между направлением оси главного магнитного потока
статора N os в момент времени t = 0 и направлением под-
вижной оси О|«; в случае же установки двигателя на неподвиж-
ном основании (щ = 0) величина <т8р8 есть угол между напра-
влением yist'Slst) при t = 0 и направлением неподвижной
оси Ох. В дальнейшем углы р8 будем называть установочными
углами синхронных электродвигателей. Эти углы во многом ана-
логичны введенным выше установочным углам xs системы син-
хронизации посредством использования упругих элементов ме-
жду роторами.
Далее, не нарушая общности, можно считать, что положи-
тельное направление оси главного магнитного потока ротора
Ssrot)Mrot’ совпадает с направлением вектора-эксцентриситета
о8с8 неуравновешенного ротора вибратора. Тогда 08 = ф8—	=
*) Напомним, что под
вращения, а — ±1.
(о > 0 понимается модуль синхронной скорости
382
ПЛОСКАЯ ЗАДАЧА О СИНХРОНИЗАЦИИ ВИБРАТОРОВ
[ГЛ. XIII
= q>s — <7s<p — o.,(ps + со/) будет углом между направлениями
осей главных магнитных потоков ротора и статора.
Интересующий нас момент Ls, передаваемый ротору вибра-
тора от электродвигателя, теперь можно представить в форме *)
Ls = - ksSs + Ls(Qs),	(2.16)
где
6S = <Ps - qs<$ ~ 0Д - os(o/.	(2.17)
Первое слагаемое в выражении (2.16) представляет демпфи-
рующий момент электродвигателя, обращающийся в нуль при
вращении ротора с синхронной угловой скоростью, то есть при
Фх~ Ws = asM’ постоянную k's>Q иногда называют коэффи-
циентом демпфирующего момента.
Второе слагаемое представляет синхронизирующий момент
электродвигателя; этот момент обращается в нуль при 0S = 0.
Обычно при | 0s |<Ох, где 0S—так называемое критическое
значение угла 0S, имеют место соотношения
«
0sL;(0s)<0 (0s^0),	^<0.	(2.18)
UUs
Если, как предполагалось первоначально, синхронный дви-
гатель является двухполюсным и промежуточный редуктор от-
сутствует, то LS(0S) есть периодическая функция 0S с перио-
дом 2л; ее примерный график представлен на рис. 29. Функция
Ls (О») такова, что каждому значению постоянной внешней на-
грузки на двигатель, не превышающей критической нагрузки
*) Предполагается, что питание электродвигателей вибраторов осуществ-
ляется от одной сети бесконечной мощности, так что синхронная угловая
скорость о) есть заданная величина, не зависящая от нагрузок на двигатели.
Таким образом, задача о синхронизации вибраторов, но крайней мере один
из которых снабжен синхронным двигателем, ставится и решается здесь как
задача о внешней синхронизации (см. § 1 главы II).
§ 21
УРАВНЕНИЯ ДВИЖЕНИЯ СИСТЕМЫ
383
Л111ах, отвечает единственное (с точностью до 2лп, где п — це-
лое число) устойчивое установившееся значение угла 0S. Иными
словами, роторы вибраторов в рассматриваемом случае вра-
щаются с некоторым практически постоянным, вполне опреде-
ленным сдвигом по фазе относительно оси главного магнитного
потока статора, в свою очередь равномерно вращающейся с син-
хронной угловой скоростью (о. Это обстоятельство н делает воз-
можным применение синхронных двухполюсных двигателей
как для целей синхронизации, так и для обеспечения требуемой
фазировки вращения роторов вибраторов. Аналогичное положе-
ние, очевидно, будет иметь место при использовании редуктора,
повышающего угловую скорость вращения при переходе от вала
синхронного двухполюсного двигателя к валу вибратора в це-
лое число раз.
Иначе обстоит дело в случае привода вибраторов от синхрон-
ных двигателей с числом пар полюсов п, большим единицы, или
в случае привода от двухполюсных синхронных двигателей, но
при применении понижающего обороты редуктора с передаточ-
ным отношением от вала двигателя к валу вибратора, рав-
ным п, где п — целое число*). Стремление использовать такие
многополюсные двигатели или редукторы может быть связано
с желанием обеспечить работу вибраторов на рабочей частоте,
меньшей частоты сети о) (314 i/сек = 3000 кол/мин. в европей-
ских странах).
В этих случаях существует не одно направление Ssrot)jVxot),
а п связанных с ротором вибратора направлений, при совпаде-
нии которых с равномерно вращающимся направлением Alst>SsSt)
момент A.s(9s) равен нулю. Указанный момент при этом яв-
ляется периодической функцией угла 0S с периодом 2л/«, и
поэтому при постоянной внешней нагрузке на двигатель су-
ществует несколько существенно различных устойчивых уста-
новившихся значений угла 0S. Таким образом, определенная
фазировка вращения роторов вибраторов сама по себе здесь не
обеспечивается.
Для получения однозначной фазировки в этих случаях, од-
нако, можно применять устройства, аналогичные уже упоми-
навшемуся автоматическому устройству Б. П. Лаврова [240].
Выбор требуемого, а не какого-либо случайного устойчивого
положения каждого ротора по отношению к вращающемуся
полю статора здесь обеспечивается автоматическим переключе-
нием фаз при «застревании» ротора в одном из нежелательных
устойчивых положений.
*) Из последующего станет ясным, что применение редукторов с переда-
точными отношениями tp =£ 1/л или ip^n в рассматриваемых системах
смысла не имеет.
384
ПЛОСКАЯ ЗАДАЧА О СИНХРОНИЗАЦИИ ВИБРАТОРОВ
[ГЛ. XIII
Следует, конечно, иметь в виду, что в особых случаях и при
изучении ряда специальных задач может оказаться необходи-
мым учет динамических явлений в двигателе*). При этом по-
рядок дифференциальных уравнений, описывающих движение
вибраторов, увеличивается, и решение задачи о синхронизации,
естественно, осложняется, хотя оно и может быть, как правило,
выполнено рассматриваемыми в настоящей книге методами.
Для того чтобы дать представление о характере возможных
осложнений, рассмотрим достаточно полную систему уравнений,
определяющую вращающий момент на валу асинхронного ко-
роткозамкнутого электродвигателя Иа> с учетом влияния про-
текающих в нем переходных процессов.
Указанный выше момент в данном случае может быть пред-
ставлен в форме **) [388, 441]
L(a} = jLad(ipdiC4-ipqicd).	(2.19)
Здесь iCd, icq, ipd, ipq — мгновенные значения расчетных токов,
представляющие собой определенные комбинации мгновенных
токов фаз и определяемые из системы дифференциальных урав-
нений
d i cd	di pd	,
Lc H Lad I- r^cd Чщ sin at,
diCq , . dipq .
l^c dt	c^cq	Um COS (Hlt
t.	(2.20)
dlpd	died .	•*(! • T • X
dt ' ~dt Гplpd	Ф x^ad^cq < ^ptpq)t
~~^r + Lad ~dT + rpipy = ^adied + LpipdL
где Lc, Lp, Lad, тс и rp — параметры статора и ротора электро-
двигателя, ф1* — угловая скорость вращения ротора двигателя,
с» — синхронная угловая скорость (частота тока в сети).
*) Одним из таких особых случаев является, например, случай близости
частот колебаний внешней нагрузки на двигатель вибратора (в рассматри-
ваемом случае — частоты синхронного вращения и ее целых кратностей) к
так называемой частоте собственных колебаний скорости вращения асинхрон-
ного двигателя [300, 336].
К особым задачам, при решении которых может понадобиться учет ди-
намических явлений в двигателе, следует отнести задачи о синхронизации
вибраторов, когда для достижения полезного эффекта параметры вибраторов
и двигателей специально подбираются таким образом, чтобы имело место
динамическое взаимодействие механической и электрической частей системы
(не исключено, что указанное направление таит в себе новые интересные
возможности).
**) Индекс s, указывающий номер вибратора, для упрощения записи в
соотношениях (2.19) — (2.20) опущен.
§ 2]	УРАВНЕНИЯ ДВИЖЕНИЯ СИСТЕМЫ	385
Таким образом, в данном случае выражение для электромаг-
нитного вращающего момента двигателя (2.19) содержит ве-
личины, связанные системой дифференциальных уравнений чет-
вертого порядка. В результате порядок уравнений, описываю-
щих движение каждого из вибраторов данного типа (см. ниже
первые k уравнений (2.44)), увеличивается на четыре единицы.
К счастью, как уже отмечалось, обычно не возникает надоб-
ности в рассмотрении такой усложненной системы.
Обратимся к составлению выражений для слагающих обоб-
щенных сил Q9, обусловленных наличием сопротивления вра-
щению вибраторов.
Момент Rs сил сопротивления, действующих на ротор вибра-
тора, можно представить в виде суммы двух слагаемых:
Rs = RsA + RsB-	(2.21)
Здесь RsB — момент сил сопротивления, обусловленный в деба-
лансном вибраторе трением в подшипниках, а в планетарных
вибраторах — сопротивлением при качении ролика по стакану
или кольца по оси. Момент отражает наличие дополнитель-
ных сопротивлений, которые могут вызываться, например, при-
соединением к ротору вибратора крыльчатки вентилятора си-
стемы охлаждения, масляного насоса или других устройств.
Относительно момента Rsa в дальнейшем будем предпола-
гать, что он зависит только от угловой скорости ротора вибра-
тора ф5, причем его модуль = есть неубывающая
функция от | фз |:
dR°
^А = ^л(|Фх|)51ёпф5,	(1ФЛ=И=О).	(2.22)
Обратимся к составлению выражения для момента RsB. Рас-
смотрим сначала случай дебалансного вибратора, ротор кото-
рого вращается в подшипниках качения (рис. 30, а) или
жидкостного трения. Момент сил трения в таких подшипниках
обычно подсчитывают по формуле *) [36]
Rsb = у М si£n	(2.23)
где — модуль радиальной составляющей реакции в подшип-
нике, ds—диаметр внутреннего кольца подшипника качения
или диаметр вала подшипника жидкостного трения.
*) Строго говоря, в выражении (2.23) под знаком sign должна фигури-
ровать не абсолютная угловая скорость ротора вибратора ф$, а скорость
вращения ротора по отношению к корпусу машины фз —ф. Однако во всех
рассматриваемых ниже движениях системы | фз1 « (о > | ф |, и поэтому
sign (фз - Ф) = sign фз.
13 Ил И. Блехман
386
ПЛОСКАЯ ЗАДАЧА О СИНХРОНИЗАЦИИ ВИБРАТОРОВ
[ГЛ. ХН1
Безразмерный условный коэффициент трения в подшипнике f,
зависит от типа подшипника, вида смазки и ряда других фак-
торов; для подшипников, обычно применяемых в вибраторах,
fs варьирует в пределах 0,001—0,01 (см., например, [36]).
Рис. 30.
С целью получения формулы для модуля силы N, рассмо-
трим уравнения движения центра тяжести с3 неуравновешен-
ного вала в проекциях на неподвижные оси координат хОу
(рис. 30, а)
msxcs = ~NS cos ф5 + Fs sin ф5 sign <ps - msg sin x,
msycs = Ns sin $S + FS cos cps sign <j>s-msg cos x- 1	'
Здесь Fs — модуль силы трения в подшипнике, связанный с мо-
дулем силы Ns соотношением
Fs — fsNs,	> (2.25)
а через qjs обозначен угол между вектором-радиусом о3А3 точки
приложения реакции в подшипнике и осью о3х, отсчитываемый
по ходу часовой стрелки; этот угол, вообще говоря, не совпа-
дает с углом фз.
Из уравнений (2.24) при использовании равенства (2.25) и
формул (2.2) для хсз и усз нетрудно найти искомое выражение
для Ns:
2
[в2ф* + X2 + у2 + г2ф2 + g2 + е2ф2 +
*	/ s
+ 2г<.ф (х sin Ss — ij cos Ss) — 2estps (x sin ф4. + у cos ф5) —
- 2es<p2 (x cos фJ - у sin фл.) + 2g (x sin x + у cos x) +
+ 2e/s q>q>s cos (ф, + Ss) - 2е/5фф2 sin (ф4 + Ss) -
- -2grsif cos (d, + x) ~ 2£84ф4 cos (ф, - x) + 2ge^2 sin (ф4 - x)[ (2.26)
§ 2]	УРАВНЕНИЯ ДВИЖЕНИЯ СИСТЕМЫ	387
Здесь учтены следующие соотношения между декартовыми и
полярными координатами оси вращения ротора s-ro вибратора
(см. рис. 26):
uos = rs cos 6S,	vos = rs sin Ss.	(2.27)
Обратимся к анализу порядков слагаемых, входящих в вы-
ражение (2.26), в интересующих нас движениях системы. Йусть
А есть наибольшая амплитуда колебаний точек тела В в таких
движениях; тогда порядок величин х, у и г, ср не будет превы-
шать А. Далее естественно предположить, что порядок вели-
чин х, у и Лф есть Дсо, а порядок х, у, rsips соответствует Дм2.
В указанных предположениях выражение для реакции Ns,
согласно формуле (2.26), может быть представлено в виде
Ns=адф + о, (-£.	.
где через 0^-^-,	обозначены члены, имеющие отно-
сительно величин A/e.s, g’/esW2 и fs порядок не ниже первого.
В реальных системах изучаемого типа отношение A/es имеет
порядок 0,1; отношение g/e,s&2 редко превышает 0,05; величина
коэффициента трения fs, как отмечалось выше, лежит в преде-
лах 0,01—0,001. Поэтому для дебалансных вибраторов можно
с достаточной степенью точности принять, подобно тому как
это делается в случае неуравновешенных роторов, установлен-
ных на неподвижном основании,
I	I
RsB = 2 W* Si^n <PS = 2 dM siSn ‘Ps-
Следует, однако, отметить, что если по каким-либо причинам
желательно использовать более точное выражение для реак-
ции Ns, вытекающее из формулы (2.26), то это не приведет
к особым затруднениям в процессе решения задачи.
Составим теперь выражение для момента сопротивления RsB
движению ролика или кольца планетарного вибратора; рассмо-
трим вначале случай качения без скольжения*). В соответ-
ствии с обычной гипотезой примем **)
RsB = fsRsNssiSn^s,	(2.29)
*) Как уже отмечалось, условия, при выполнении которых в рассматри-
ваемых движениях отсутствует иарушеиие неудерживающей связи (отрыв
ролика от поверхности стакана) и не происходит проскальзывания в зоне
контакта ролика со стаканом, подробно рассматриваются в § 16 настоящей
главы.
**) См. сноску на стр. 385.
1 о»
388
ПЛОСКАЯ ЗАДАЧА О СИНХРОНИЗАЦИИ ВИБРАТОРОВ
[ГЛ. XIII
где /' — безразмерный коэффициент сопротивления перекатыва-
нию, a Ns — нормальная реакция, действующая на ролик
(кольцо) со стороны стакана (оси) в точке контакта.
Отметим, что момент Rsb, входящий в виде слагаемого в вы-
ражение для обобщенной силы по координате <р8, следует отли-
чать от момента сопротивления перекатыванию
/^ = WVignvs,	(2-30)
действующего непосредственно на ролик или кольцо (см.
рис, 30, б, в). Выражение (2.29) для момента /?.,в получается из
условия равенства работ RsB ((ps — ф) = при учете кинема-
тического соотношения (2.3), взятого для случая Л* = 1 (каче-
ние без скольжения),
Обратимся к вычислению реакции Ns. Из уравнения движе-
ния центра тяжести ролика (кольца) с3 в проекциях на нормаль
к его траектории, рассматриваемой в подвижных осях x'sosy',
параллельных неподвижным осям хОу, получаем
Ns =	sin (4>s - X) - cos 4>s + ,nsyos sin 4>s- (2.31)
Здесь через xos и yos обозначены координаты оси s-ro вибра-
тора; последние могут быть легко выражены через обобщенные
координаты системы х, у и ср (см. рис. 26; как и ранее, мы пре-
небрегаем степенями <р выше первой):
Xqs = ^os "В х + vos<p, yos vos у uosy. (2.32)
Подставляя последние выражения в равенство (2.31), а за-
тем (2.31)—в формулу (2.29), получаем при учете (2.27) сле-
дующие выражения для нормальной реакции Ns и момента со-
противления Rsb в случае планетарного вибратора:
Ns = ms Ms + У Sin <ps - X COS <ps - Г/р Sin (<ps + ds) + g Sin (<ps - %)],
RsB = f'sesNs sign <Ps = f'smsRs [es<P* + У sin <ps - X cos <PS -	(2.33)
- rsq> sin (<ps + Ss) + g sin (<ps - %)] sign <ps.
Отметим, что эти формулы благодаря принято?! системе
обозначений пригодны как для случая внутреннего (ролико-
вого), так и для случая внешнего (кольцевого) планетарного
вибратора.
Анализ порядков величин, подобный проведенному выше для
дебалансного вибратора, показывает, что группа членов в квад-
ратных скобках формул (2.33), содержащая х, у и rsip, имеет
§ 2]	УРАВНЕНИЯ ДВИЖЕНИЯ СИСТЕМЫ	389
по сравнению с членом es<p2 порядок Д/е8, а член с ускорением
силы тяжести — порядок gle^a1. Однако отношение Л/е«, в от-
личие от дебалансных вибраторов, для планетарных вибраторов
далеко не всегда мало: зачастую оно имеет порядок 0,5; отно-
шение же glzstf может достигать величины 0,3. Поэтому чле-
нами с х, у, г8ф и g в данном случае не всегда можно прене-
бречь по сравнению с членом es<p2.
Для ряда приложений, в частности при изучении машин типа
грохота, представленного в п. 6 таблицы 2 и описанного в § 2
главы XII, интересно рассмотрение случая, когда имеет место
скольжение роликов или колец по стакану, причем угловая ско-
рость вращения указанных тел относительно вибрирующего
органа ys равна нулю. Несложное рассмотрение показывает,
что полученные выше выражения (2.33) для нормальной реак-
ции и момента сопротивления сохраняют силу и в этом случае,
если заменить коэффициент сопротивления перекатыванию f's
на коэффициент трения скольжения fs.
Таким образом, окончательное выражение момента сопро-
тивления Rsb для планетарных вибраторов, как правило, оказы-
вается значительно более сложным, нежели для дебалансных:
момент RSB в данном случае может существенно зависеть не
только от угловой скорости вращения вектора-эксцентриситета
ролика фз, но также и от ускорения оси вибратора.
Подводя итог сказанному, заключаем, что обобщенные силы
Q(S,s, отвечающие координатам <ps, могут быть представлены
в следующей форме (см. формулы (2.14) — (2.22), (2.28) и
(2.33)):
Q<ps= Q<ps (Фз> ф®> У’ ф> Ф> ф> =
= Ls(ф,, <ps, ф, ф, asat) - Rs (фд., ф5, Л, i), ф) (2.34)
(s=l..............k).
Здесь обозначено:
£я = £Дфз, Фз, ф, Ф, <Jsai) =
L'f (ф^ — qsty для двигателя
асинхронного типа,
- АЖ + Zj(0s) Для синхронного
двигателя
(0S (ps QS<P O5ps
^sA	Фз> Уч Ф) в
WI фJ(%>	ф)] siKn
390
ПЛОСКАЯ ЗАДАЧА О СИНХРОНИЗАЦИИ ВИБРАТОРОВ
[ГЛ. XIII
где
*°В (I <М) = 'Wfi [| fA + hs [f>s ~ 4 fsd)] •
^') = fl(b (ф5> x, ij, ф) = hsf'smse.s [y sin <ps - x cos ф5 -
- г,ф sin (<ps + 6S) + g sin (<ps - %)].
При этом R°A (| фх |) есть модуль приведенного момента допол-
нительных сопротивлений, а В°в + В^в~ модуль приведенного
момента сил сопротивления в подшипниках дебалансного виб-
ратора или момента сил сопротивления движению ротора пла-
нетарного вибратора *).
Поскольку в дальнейшем будут рассматриваться только та-
кие движения системы, в которых скорости вращения роторов
вибраторов изменяются вблизи постоянных значений стцо,
а тело В совершает малые колебания вблизи положения равно-
весия, то выражение (2.34) для обобщенной силы QVs можно
линеаризировать по ф8 вблизи значений <ps = сгдо и по ф и ф
вблизи ф = 0 и ф = 0. Производя указанную линеаризацию, бу-
дем иметь **)
Ls = Ls (Фз> <PS> Ф> Ф> crs(o/) =
L\a' (аЛ) ~ ‘ (ф« ~	“ ст5®) Для Двигателя
асинхронного
типа,
-	• (ф5 - ^ф - сг^со) + L* (фя - аД - as®i) -
~  (ф5 ~	— а4®0  ^Ф для синхрон- (2.37)
ного двигателя,
Ч = RSA + #sB = (<PS’ Ф5- ф) = - k°S (Ч - М +
+ [Я° (®) + /?<’) (<PS> X, у, ф)] as,
♦) Напомним, что через hs обозначены числа, равные нулю для деба-
лансных и единице — для планетарных вибраторов; в случае движения
роторов планетарных вибраторов с проскальзыванием и при условии, что соб-
ственные угловые скорости роторов у3 равны нулю, коэффициенты сопротив-
ления перекатыванию fs должны быть заменены коэффициентами трения
скольжения fe.
**) Отметим, что задача может быть решена, хотя и несколько более
сложно, и без предположения о возможности такой линеаризации.
§ 2]
УРАВНЕНИЯ ДВИЖЕНИЯ СИСТЕМЫ
391
где обозначено:
b° = Ь° -4- b° b° = ( dR°A (| Н - dR°sA (О)
Rs RsA'RsB’ RsA \ d I фз I /|фД=о> rfw ’
ko (а£в(\Фз I) \	__
sB \ d I фз |	/| <t>s |-<o rfco
= 2mses [4 Ms + hs	~ I f/s)] »
причем величина ks для синхронных двигателей совпадает с фи-
гурирующей в равенствах (2.35), а для двигателей асинхрон-
ного типа определяется формулой
( dL(f (Q) \
\ dQ „
(2.39)
После линеаризации выражение (2.34) для обобщенной
силы Q<ps представится в следующей окончательной форме:
Q<PS = Qvs (Фз> Фз> X, у, ф, ф, Ф, crs®/) = - ks (фз - СГ3С0) +
+ Ls (crsG), Фз, Фз, ф, (ТзСО^) - Rs (crsG), Фз, х, у, ф),	(2.40)
где обозначено:
=	=	+	+	(2-41)
В соответствии с (2.22) и в силу положительности величин
fs и f's коэффициенты k°A и k°B существенно положительны.
Для синхронного двигателя, а также при работе двигателя асин-
хронного типа в нормальном режиме положителен также и ко-
эффициент k*s (см. рис. 27). Поэтому всюду в дальнейшем (если
только не оговаривается противное) мы будем считать «суммар-
ный коэффициент демпфирования» ks = k?aA + k°sB + k*s положи-
тельным.
Заметим, что функции Ls, Rs и Qq,s являются периодическими
по аргументам ф8 и at с периодом, равным 2л.
Остается составить выражения для обобщенных сил Qx, Qv
и Q((>, отвечающих колебательны,м координатам х, у и ф. Пред-
полагая сопротивления колебаниям тела В пропорциональ-
ными первой степени скорости условного центра тяжести тела,
392
ПЛОСКАЯ ЗАДАЧА О СИНХРОНИЗАЦИИ ВИБРАТОРОВ (ГЛ, Xtil
а момент сил сопротивления пропорциональным скорости ф, бу-
дем иметь
Qx = ~ kxx, Qy= — kyy,
Q<p=~ M + Q№i> •••> Ф^ Фр •••> Фа! Ф> Ф> Ф>
где
= <Эф(Ф1.....ФА;_Ф1......фа; *> у> Ф> Ф> <₽> ®0 =
k	k'
е ~ 2 Л (фз, Фз> Ф> Ф> <М>0 + ^в (Ф^ +
S~1	S~1
k	k
+ S X- (<k> Ф«’ *’ У’ ф) + ’S Ла (*ь) (2-43)
s=fe'+l	s**l
— сумма реактивных моментов, передающихся на тело В от
оснований двигателей в случае, если последние установлены
непосредственно на этом теле, а также тех моментов сил сопро-
тивления вращению роторов вибраторов, которые являются для
рассматриваемой системы в целом внутренними моментами, дей-
ствующими между роторами вибраторов и несущим телом В
(через q's в формуле (2.43) обозначено число, равное единице,
если момент Rsa внутренний, и равное нулю, если этот момент
внешний).
Заметим, что функция Q’, так же как и функции является
периодической по каждой из переменных tpi, ..., <рл и по ыг
с периодом 2л.
4. Уравнения движения. Составим теперь уравнения движе-
ния системы в форме уравнений Лагранжа второго рода
4-^-4^=qz	(s=1.........&+з),
dt dzs dzs ^zs	v	”
Где L = T — П — функция Лагранжа системы, a zs — ее обоб-
щенные координаты. В соответствии с равенствами (2.12),
(2.13), (2.27), (2.33), (2.40) и (2.42) эти уравнения могут быть
представлены в форме
k
I&s + ks (фа - orsco) = - 2 (о^Фз - СГ/Ф/ - ^ + «/) +
/“1
+ mses [х sin <ps + у cos <ps - <prs cos (<ps + 6£) + g cos (<ps - %)] +
+ hs$cs--------------- y + Ls (ors<o, tp.., <p, <p, crsco/) -
bs
- Rs (as®, <ps) x, у, ф) (s = 1, ..., k)t
§ 2]
УРАВНЕНИЯ ДВИЖЕНИЯ СИСТЕМЫ
393
k
Мх + kxX + СхХ + сХфф = 2 ms85 (фа sin <ps + ф* cos фД
k
My + kytj + cyy + cyф<р = 2 mses (<ps cos q>s - ф* sin q>s),
(2.44)
/ф 4* &фф Ч- £(р<р Ч' сХ(рХ Ч~ СууУ
k
? [ф2 sin (ф5 + Ss) - ф5 cos (ф5 Ч- fij] +
,e^^.+e^L +
cs l2 Ф$ '
S~1
S"1	6«
+ <2ф(Ф1> Фь‘> Ф|> •••» Фа.; У» Ф> Ф> ф, ®0-
Первые k уравнений (2.44) описывают движение роторов ви-
браторов, последние три — колебания вибрирующего органа ма-
шины (несущего твердого тела В).
В совокупности уравнения (2.44) представляют связанную
систему, состоящую из k + 3 нелинейных дифференциальных
уравнений достаточно сложного вида. Если, однако, предполо-
жить, что роторы вибраторов вращаются равномерно, то есть
Фз = crs(«Z + а5), где as — постоянные, то последние три урав-
нения (2.44) превратятся в обычные линейные уравнения малых
колебаний тела В под действием гармонических возмущающих
сил. Эти уравнения соответствуют предположению, что колеба-
ния тела В, на котором установлены роторы вибраторов, никак
не отражаются на движении самих вибраторов. При изучении
ряда вопросов такая упрощенная постановка задачи является
вполне приемлемой.
Однако при рассмотрении вопросов синхронизации вибрато-
ров нельзя игнорировать наличие связей между колебатель-
ными и вращательными координатами системы, ибо как раз
наличие этих связей и предопределяет картину движения. Адек-
ватные задаче уравнения движения системы при этом, есте-
ственно, оказываются значительно более сложными.
Отметим, что имеется также и ряд других вопросов, при ре-
шении которых обычная концепция заданных возмущающих сил
недостаточна, и требуется учет взаимодействия колебательной
части системы и возбудителей колебаний. Эти вопросы возни-
кают, в частности, и когда возбудитель всего один, то есть когда
проблемы синхронизации вибраторов не возникает.
Рассмотрению некоторых из таких задач, представляющих
простейшие частные случаи (k = 1) соответствующих задач о
синхронизации вибраторов, посвящена семнадцатая глава кни-
ги. Там же приведен краткий обзор достаточно многочисленных
394
ПЛОСКАЯ ЗАДАЧА О СИНХРОНИЗАЦИИ ВИБРАТОРОВ
[ГЛ. XIII
работ по изучению взаимодействия возбудителя с колеблю-
щейся системой.
В отличие от указанных работ, в задачах о синхронизации
вибраторов приходится изучать системы, в которых число вибра-
торов более единицы и в которых существенным является не
только взаимодействие каждого вибратора и колеблющихся тел,
но также (и даже главным образом) взаимодействие вибрато-
ров друг с другом через посредство этих тел.
Естественно, что отыскание общего решения системы нели-
нейных уравнений (2.44) в замкнутой форме не представляется
возможным. Этого, однако, и не требуется для решения задач
теории синхронизации механических вибраторов, перечисленных
в предыдущей главе и представляющих основной интерес для
исследователя и конструктора вибрационных машин.
§ 3.	Математическая постановка задачи.
Введение малого параметра
В соответствии со сказанным в п. 2 § 2 главы XII основной
задачей исследования является установление необходимых и
достаточных условий существования и устойчивости синхронных
движений системы, то есть движений, которым соответствуют
решения уравнений (2.44) вида *)
Ф, = [со/+ ф5 (со/)]	(s= 1, ..k),
,V = x(co/), y = y(®f), ф = ф((0/),	' ' '
где ffs = ± 1, со > О— абсолютная величина средней угловой
скорости синхронного вращения роторов, а ф.,(со/), х(со/),
у (at) и ф (со/) — периодические функции времени t с периодом
Т = 2л/со.
Помимо выяснения условий существования и устойчивости
синхронных движений, представляет интерес также отыскание,
хотя бы приближенное, закона движения вибраторов и несущего
твердого тела в устойчивом синхронном движении, а также ре-
шение обратной задачи («задачи синтеза»), состоящей в таком
выборе параметров системы, при котором обеспечивается суще-
ствование и устойчивость синхронного движения определенного
характера.
Как уже отмечалось, если хотя бы один из двигателей вибра-
торов является синхронным, то угловая скорость со есть вели-
чина заранее заданная, и правые части исходных уравнений
(2.44) содержат в явном виде время /; иными словами, система
(2.44) представляет неавтономную систему уравнений, и задача
*) Напомним, чго в данной главе мы ограничиваемся рассмотрением
задачи о синхронизации вибраторов с одинаковыми по абсолютной величине
средними угловыми скоростями, то есть задачи о простои синхронизации.
§ 3]
математическая постановка задачи
395
должна рассматриваться как задача о внешней синхронизации
(см. § 1 главы II).
Если же все двигатели вибраторов являются асинхронными,
как это имеет место, например, в случае задачи о самосинхро-
низации, то угловая скорость синхронного вращения вибрато-
ров со заранее не задана и подлежит определению. В уравне-
ния движения (2.44) при этом время явно не входит, то есть си-
стема является автономной, и мы имеем, таким образом, задачу
о внутренней синхронизации.
Задачу о синхронизации вибраторов будем рассматривать
в предположении, что вибраторы в изучаемых синхронных дви-
жениях вращаются почти равномерно и что связи между вибра-
торами являются слабыми. В соответствии с этим предположе-
нием введем в систему (2.44) малый параметр ц > 0, положив
цфДф1.......ф&; х, &’ ч>> Ф> ф> =
k
= csj<ys (щ.фз - СГ/Ф/ - xs + Xj) +
/=
4- msRs [x sin ф3 4- у cos ф: - фгх cos (ф3 4- 6S) + g cos (ф5 - %)] 4-
e X* (bs + esX )
4-	hs^cs----—j—г~“ Ф 4- Es(crsco, фз, ф, ф, ascof) -
bs
- Rs (crsco, Фз, x, if, ф) (s = 1...k),	(3.2)
kx =	ky =
hQ;(<Pp ...,фй; Фр -	ф&; у> ф, Ф. ®0 =
= <?ф(Фр Ф/е; фр ф*; х, у, ф, ф, ф, at).
Тогда уравнения (2.44) запишутся в форме
/,Ф,4-^(ф!-м) = 11Ф8(ф1, • ••> Фь х, у, ф, ф, ф, at)
(s = 1.......................k),
k
Mx 4- cxx 4- сХ(рФ = 2 rnse,s ((ps sin фх 4- ф2 cos ф5) - ц6'х,
S=1
k
Му 4- суу 4- Су^у = 2 msEs (ips cos ф., - ф2 sin ф5) - \xk'y,
s — 1
fe
/ф 4- СфФ + cX(fx 4- Cyvy = mse/s [ф2 sin (ф5 4- 6S) -
s=l
(3.3)
- (ps cos (фз 4- 6S)] 4
k
cs
S=“l
eX(&s + eX) ..
-----------m
-н^фф4-нРф(Ф1, •••. Ф*; Фр •••> ф&; x, у, Ф, ф, ф, со/),
396
ПЛОСКАЯ ЗАДАЧА О СИНХРОНИЗАЦИИ ВИБРАТОРОВ
[ГЛ. XIII
где функции цФ5 и u.Qr' являются периодическими функциями
времени t с периодом 2л/со и остаются таковыми после под-
становки (3.1).
Рассмотрим несколько подробнее принятый способ введения
малого параметра.
Отметим прежде всего, что предположение о малости выра-
жений
mses [х sin tps 4- у cos <ps - iprs cos (<ps 4- 6S) 4- g cos (<ps - %)] 4-
+ hs3cs----^2------ Ф 4- Ls (Gs®, qps, ф, Ф, crsco/) -
-/?s(ctsg>, ф51 x, у, ф), (3.4)
фигурирующих в правых частях первых k дифференциальных
уравнений (2.44), не означает, что малым считается каждое из
слагаемых в этих выражениях. По существу, делается более
слабое допущение — что в рассматриваемых движениях вибра-
торов модули угловых скоростей вращения последних изме-
няются вблизи некоторого постоянного значения. Как показы-
вает опыт (см. главу XIX настоящей книги), это допущение
в рассматриваемых системах всегда выполняется.
Далее, по своему смыслу выписанные выше члены представ-
ляют разности между вращающими моментами двигателей и
моментами сил сопротивления, сложенные с членами, отражаю-
щими влияние колебаний твердого тела В на движение вибрато-
ров. Как указывалось выше, всеми этими членами при рассмо-
трении задачи о вынужденных колебаниях в обычной поста-
новке вообще пренебрегают, считая вращение валов вибраторов
строго равномерным.
Остановимся на предположении о малости слагаемых
k	k
2 csias (огяфз - стуф/ - 4- X/) = S cstas Ok - Ф/ - xs 4- хД (3.5)
/=i	/=i
представляющих моменты, передаваемые на роторы вибраторов
синхронизирующими элементами.
В отличие от рассмотренных ранее членов, присутствие этих
слагаемых в соответствующих уравнениях (2.44) не препят-
ствует наличию у этих уравнений решений типа ф8= <ys(coZ 4- as),
где as — постоянные. Поэтому предположение о малости ука-
занных слагаемых не является необходимым для получения
движений, близких к равномерному вращению вибраторов. Это
предположение означает, по существу, что все частоты соб-
ственных колебаний роторов вибраторов, обусловленные нали-
чием упругих синхронизирующих элементов, считаются доста-
точно малыми по сравнению с угловой скоростью синхронного
§ 3]	МАТЕМАТИЧЕСКАЯ постановка ЗАДАЧИ	397
вращения со. Речь идет о собственных частотах, отвечающих
системе линейных дифференциальных уравнений
k
fsips + 2 cslas (cr4<ps - ajcpj) = 0 (s = 1, ..., k).	(3.6)
/=i
Изучение случая «мягких» синхронизирующих элементов,
когда Л, со, представляет наибольший интерес, ибо если не-
сколько частот Л; значительно больше со и прочие hi значительно
меньше со, то соответствующую часть системы синхронизации
можно считать абсолютно жесткой и уменьшить число враща-
тельных обобщенных координат системы <ps. Полученная после
указанного упрощения система уже будет удовлетворять приня-
тому выше предположению о малости частот Л,- по сравнению
с со. Лишь промежуточный случай, когда имеются собственные
частоты hi, близкие к со, требует специального рассмотрения.
Однако изучение этого случая может представить интерес лишь
применительно к весьма специальным машинам и устройствам,
в которых существенно используются резонансные явления в си-
стеме синхронизации. Обычно же такие явления крайне неже-
лательны.
Предположение о малости членов kxx, kyy и £фф, характери-
зующих вязкое сопротивление колебаниям твердого тела В,
всегда делается при традиционном подходе к решению задач
рассматриваемого типа, когда отдельно изучается движение си-
стемы вдали от резонанса и движения вблизи резонанса [275]*).
Такой традиционный подход при решении данной задачи яв-
ляется не обязательным, однако в настоящей главе мы все же
будем ему следовать, поскольку это позволит получить некото-
рые преимущества (по этому поводу см. § 17 настоящей главы).
Наконец, предположение о малости слагаемого Q* в послед-
нем уравнении (2.44) соответствует допущению о незначитель-
ности влияния на колебания несущего твердого тела В реактив-
ных моментов, передаваемых на это тело основаниями электро-
двигателей вибраторов, а также реактивных моментов, обуслов-
ленных силами сопротивления вращению роторов вибраторов.
Указанные моменты, как правило, действительно весьма малы
по сравнению с упругими и инерционными моментами, дей-
ствующими на тело В; они вызывают лишь небольшое (и при-
том несущественное) постоянное смещение тела из положения
*), Под резонансом в данном случае следует понимать совпадение по
крайней мере одной из частот собственных колебаний твердого тела на
опорных упругих элементах с величинами пш, где п — целое положительное
число или пуль. Указанные собственные частоты соответствуют системе
однородных уравнений, которые получаются путем приравнивания пулю пра-
вых частей трех последних уравнений (3.3).
398
ПЛОСКАЯ ЗАДАЧА О СИНХРОНИЗАЦИИ ВИБРАТОРОВ
(ГЛ. Xi И
статического равновесия и весьма малые дополнительные коле-
бания тела В.
Отметим, что приведенные выше соображения, разумеется,
не могут рассматриваться как строгое обоснование принятого
способа введения малого параметра — они представляют собой
лишь правдоподобные рассуждения, равно как только правдо-
подобным является предположение о возможности использо-
вания получаемого ниже решения математической задачи для
суждения о поведении рассматриваемой реальной системы*).
Поэтому одна из глав настоящей части книги посвящена экспе-
риментальной проверке некоторых основных результатов теоре-
тического исследования синхронизации вибраторов. Забегая впе-
ред, отметим, что эти результаты находят вполне удовлетвори-
тельное подтверждение. Заметим, далее, что принятый выше
способ введения малого параметра не является единственно воз-
можным. Так, например, можно дополнительно считать малыми
члены &s(<ps — см)) в первых k уравнениях (3.3). В этом случае
при н. = О движение вибраторов будет описываться уравне-
ниями
Др° = О (s = 1......k),	(3.7)
соответствующими простейшим чисто консервативным объектам
(см. главы VIII—X третьей части книги). Такую идеализацию
вибраторов будем в дальнейшем называть квазиконсерватив-
ной, в отличие от принятой выше неквазиконсервативной идеа-
лизации.
Исследование синхронизации квазиконсервативных вибрато-
ров более сложно, нежели решение задачи о синхронизации не-
квазиконсервативных вибраторов; в более сложном виде фор-
мулируется и окончательный результат. Между тем для широ-
кого класса задач эти результаты, по существу, совпадают или
приводят к одним и тем же практическим выводам. Поэтому
в дальнейшем изложении мы придерживаемся именно того спо-
соба введения малого параметра, о котором говорилось выше.
Результаты исследования синхронизации вибраторов при
квазиконсервативной идеализации будут кратко изложены и со-
поставлены с результатами, найденными для неквазиконсерва-
тивных вибраторов, в § 5 главы XIV. Для общего случая квази-
линейных объектов такое сопоставление сделано в § 6 главы IX.
Наиболее подробно в настоящей главе будет рассмотрен слу-
чай движения системы вдали от резонанса, ибо он представляет
основной интерес для приложений: подавляющее большинство
изучаемых здесь машин с плоским движением работает в после-
*) Подробному обсуждению этих вопросов посвящена глава IV настоя-
щей книги, а также статья [82].
§ 4]	УСЛОВИЯ СУЩЕСТВОВАНИЯ И УСТОЙЧИВОСТИ	399
резонансной области (см. пп. 5—10, 14—17 таблицы 2). По ре-
зонансной схеме осуществлены главным образом лишь те ма-
шины этого типа, вибрирующий орган которых имеет всего одну
степень свободы (см. пп. 1а и 16 таблицы 2). Исследованию
синхронизации вибраторов таких машин посвящен § 13 настоя-
щей главы.
§ 4. Условия существования и основные условия
устойчивости синхронных движений вдали от резонанса.
Уравнения для определения фаз вращения вибраторов
в синхронных движениях
Рассмотрим соответствующую дифференциальным уравне-
ниям (3.3) порождающую систему, то есть систему, получаю-
щуюся из указанных уравнений при ц = 0:
+ ks (яС “ <V°) = 0 (s = 1.....ft)>
k
Mx° + cxx° 4- cx <p° = 2 тд (ф° sin q>° + ф°2 cos <p°),
S==l
k
My° + cyy° + cw<p° = 2 tnses (ф° cos <p° - ф°2 sin <p°),
(4.1)
/ф 4" £фф 4~ "Ь £у^У
k
= S mArs (<Ps2 Sin (<Ps + M	C0S (<Ps + M +
S = 1
s-1	5
Несмотря на нелинейность, структура этой системы такова,
что ее синхронные решения могут быть легко найдены. Действи-
тельно, первые k уравнений (4.1) допускают относительно пере-
менных <р° семейство синхронных решений
=	+ O (s= 1, .... /г),	(4.2)
зависящее от k произвольных параметров as.
Подстановка выражений (4.2) в последние три уравнения
(4.1) при использовании очевидных соотношений
sincrsT = crssinT,
COSсг/г =-= cost, a^=l : о,	(4,3)
400
ПЛОСКАЯ ЗАДАЧА О СИНХРОНИЗАЦИИ ВИБРАТОРОВ
[ГЛ. XIII
приводит к следующей системе линейных дифференциальных
уравнений с постоянными коэффициентами:
k
Мх° + схх° +	= S cos (со/ + aj,
S = 1
k
Му° 4- cyy° + с^ф0 = - S vsmsesa2 sin (at + aj,	(4.4)
№ 1
k
Iф° + Сфф° + cX(fx° +	= s osmsesrsa2 sin (at + + or Д).
Частотное уравнение соответствующей уравнениям (4.4) од-
нородной системы может быть представлено в форме
D (р2) (р2х ~ Р2') (Р2 ~ Р2) (р£ - Р2) ~ Р^ (Р2Х ~ Р2} ~ Р^ (Ру - Р2) = 0,
(4.5)
где
2 _ Сх	2 _ C,J
рх~ м ’	РУ~~М~’
„ _ Сд-ф	„ _ С„ф
'хч Мр ’ руЧ Мр ’
Рассматривая вначале движение системы вдали от резо-
нанса, будем предполагать, что уравнение (4.5) имеет положи-
тельные корни pi, Рг и рз, в достаточной мере отличающиеся
от па, где п — целое положительное число или нуль.
В указанном предположении система уравнений (4.4)
допускает единственное периодическое (с периодом 2п/а)
решение
k
х° =	cos + аЛ + asBssin И + О]>
s==l
k
У° = ^л [Cs C0S И + “s) + a°D°° Sin + as)]>	(4-7)
№ 1
k
ф0 = S cos (ю/ + +аЛ°sin (®z + °QJ>
«•I
5 4]
УСЛОВИЯ СУЩЕСТВОВАНИЯ И УСТОЙЧИВОСТИ
401
где
л: = А° (®2) = Ьхх (®2) + bxv (Ф2) vs sin 6S,
B°s = B° (Ф2) = - bxy (ф2) + bxv (ф2) vs cos 6S,
C^Cas(^==bxy^) + by^)vsSinbs,
D°s = D° (ф2) = - byy (ф2) + byv (Ф2) vs cos
< = Al° (®2) = bx<p (®2) + &w (Ф2) vs sin 6S,
W° = №s (®2) = - byv (®2) +	(®2) vs cos 6/,
&x/«>2) =
Ьет(®2) =
Ьуу (®2) =
M®2b
Vs = /\/Р>
h /„2X _ W " °2) (4 “ °2) ~	„2
&xx (® )-------------Щм2)------------
Oxq> )	D (o2)	•
2	2	2
Pxtpf y<P°
D (co2) ’
P^(Px-“2)®2
D (co2)	’
(p2-CO2)(p2-CO2)-p4x(p
D (co2)
D (co2)
(4.8)
®2.
Равенства (4.2) и (4.7) в совокупности и представляют син-
хронное решение порождающей системы (4.1), зависящее от k
произвольных постоянных «1, ..., аь-
Первостепенное значение теперь имеет вопрос, может ли рас-
сматриваться это синхронное решение как первое приближение
к синхронному решению основной системы уравнений (3.3).
Иными словами, необходимо выяснить, соответствуют ли реше-
ниям (4.2) и (4.7) порождающей системы такие синхронные ре-
шения основной системы, которые при ц = 0 обращаются в ре-
шения (4.2) и (4.7). Условия, при выполнении которых будет
иметь место указанное соответствие, одновременно будут яв-
ляться искомыми условиями существования синхронных движе«
ний вибраторов. Далее необходимо исследовать устойчивость
этих движений.
Для решения поставленных вопросов в наших работах [44,
54] были непосредственно использованы методы А. Пуанкаре
и А. М. Ляпунова, Здесь мы воспользуемся для этой цели
432
ПЛОСКАЯ ЗАДАЧА О СИНХРОНИЗАЦИИ ВИБРАТОРОВ
[ГЛ. XIII
результатами исследования синхронизации слабо связанных ав-
токолебательных объектов с почти равномерными вращатель-
ными движениями; соответствующая задача была подробно
рассмотрена в девятой главе книги.
Заметим с этой целью, что дифференциальные уравнения
(3.3) представляют собой частный случай уравнений (1.4), (1.5)
указанной главы. Поэтому, в соответствии с формулами (2.5)
главы IX, соотношения для определения фаз вращения вибра-
торов в синхронных движениях as будут иметь вид
2я/<л
РДа,, .... aft, (о)^-^У [Ф5]^/ = 0 (s=l........k),	(4.9)
о
где квадратные скобки со значком «О», в которые заключены
функции Ф8, означают, что указанные функции вычисляются для
порождающего решения (4.2), (4.7). Эти основные в теории син-
хронизации механических вибраторов уравнения будут пред-
ставлены в развернутой форме и обсуждены в § 6 настоящей
главы. Здесь мы лишь напомним, что синхронные решения
основной системы уравнений (3.3), обращающиеся при р = 0
в решения (4.2), (4.7) порождающей системы (4.1), могут от-
вечать только тем значениям фаз ае, которые удовлетворяют
уравнениям (4.9).
Таким образом, наличие вещественных решений у уравнений
(4.9) является необходимым условием существования периоди-
ческих решений уравнений (3.3) рассматриваемого типа и тем
самым необходимым условием существования синхронных дви-
жений.
Далее из результатов § 2 главы девятой следует, что если для
определенной системы значений вещественных постоянных а, =
=а*,	= удовлетворяющих уравнениям (4.9), все корни
и алгебраического уравнения k-й степени
дР,	дР,	йР,	
X О(1|	да2		
дР2	дР2	дР2	
дщ	да2 Н •	dak	= 0
dPk	дРь	dPk м	
дй]	да2	dak	
(4.Ю)
отличны от нуля, то при достаточно малом р этой системе дей-
ствительно соответствует единственное аналитическое относи-
тельно р периодическое решение уравнений (3.3), обращаю-
щееся при р, = 0 в порождающее решение (4.2), (4.7).
§ 4J	УСЛОВИЯ СУЩЕСТВОВАНИЯ И УСТОЙЧИВОСТИ	403
Для асимптотической устойчивости указанного решения не-
обходимо, чтобы все корни уравнения (4.10) имели отрицатель-
ные вещественные части. Что же касается достаточных условий
устойчивости, то по этому поводу следует заметить, что харак-
теристическое уравнение системы в вариациях, отвечающее по-
рождающим уравнениям системы связи (см. последние три урав-
нения системы (4.1)), имеет в данном случае шесть корней:
р(0) —	р(0) — Q—2л/Х[	:=s
р(0) = e2na.,t Р® — _ g-2niXj (^ = /2^0)),	(4-Ш
равных по модулю единице (через р,, рг и рз обозначены корни
частотного уравнения (4.5), которые в силу известных положе-
ний непременно являются вещественными).
Поэтому сформулированные выше условия будут одновре-
менно и достаточными условиями асимптотической устойчивости,
если выполняются некоторые дополнительные условия, выра-
жающие требования, чтобы критические корни характеристиче-
ского уравнения системы в вариациях, отвечающего полной си-
стеме уравнений (3.3), обращающиеся при ц = 0 в корни (4.11),
при [1 ¥= 0 имели модули, меньшие единицы (см. сноску на
стр. 287).
Указанные условия будут получены ниже, в § 5 настоящей
главы. Однако, забегая вперед, заметим, что существенного зна-
чения эти условия не имеют, ибо они практически всегда выпол-
няются.
Таким образом, решение вопроса об устойчивости синхрон-
ных движений практически зависит только от знаков веществен-
ных частей корней уравнения (4.10): если все корни имеют от-
рицательные вещественные части, то движение асимптотически
устойчиво; при наличии хотя бы одного корня с положительной
вещественной частью движение неустойчиво; случай, когда
имеются нулевые или чисто мнимые корни, требует, вообще го-
воря, дополнительного исследования.
Сказанное выше относилось к задаче о внешней синхрониза-
ции, когда привод по крайней мере одного из вибраторов осу1
ществляется от двигателя синхронного типа. В случае задачи
о внутренней синхронизации, когда используются только двига-
тели асинхронного типа, согласно результатам главы девятой,
из уравнений (4.9) определяются разности фаз вращения вибра-
торов as — аь и неизвестное в этом случае значение исходного
приближения ы к угловой скорости синхронного движения*).
*) Перечисляемые здесь особенности задачи о внутренней синхронизации
вибраторов станут очевидными после того, как в § 6 настоящей главы основ-
ные уравнения (4.9) будут представлены в развернутой форме (см. также
§ 9 данной главы).
404
ПЛОСКАЯ ЗАДАЧА О СИНХРОНИЗАЦИИ ВИБРАТОРОВ
[ГЛ. XIII
В данном случае условием существования синхронных движе-
ний изучаемого типа является наличие у уравнений (4.9) веще-
ственных решений относительно разностей фаз as — ад и поло-
жительных относительно «. Уравнение же (4.10), от характера
корней которого зависит решение вопроса об устойчивости,
в случае задачи о внутренней синхронизации заменяется урав-
нением k— 1-й степени (см. равенство (2.7) главы IX, где сле-
дует положить ns = 1, s = 1, ..., k, так как здесь рассматри-
вается задача о простой синхронизации)
d(Pt-Pk)
да^
д (Р2 - Pk)
c?af
d(Pk-i-Pk)
да (
djPt-Pk)
5a2
d(P2~Pk)
da2
djPk-t-Pk)
<3a2
d(P,-Pk)
Ъ-i
д(Р2-Рк)
dak-l
d(Pk-t-Pk)
dak-i
= 0.	(4.12)
Отметим, что иногда с целью сохранения симметрии записи
бывает более удобно и в задаче о внутренней синхронизации
рассматривать не уравнение (4.12), а уравнение (4.10), имею-
щее k-ю степень, помня, однако, что один из корней этого урав-
нения непременно должен быть равен нулю и что решение во-
проса об устойчивости зависит от знаков вещественных частей
всех прочих корней.
§ 5.	Дополнительные условия устойчивости синхронных
движений вдали от резонанса
С целью получения упомянутых в конце предыдущего параграфа допол-
нительных условий устойчивости рассмотрим систему уравнений в вариациях,
отвечающую уравнениям (3.3) и взятую для рассматриваемого синхрон-
ного решения этих уравнений. Указанная система может быть записана
в форме
Er 4- ar^r = рСг (5. z, z, z, т) 4- ... (г = 1, ..., k),
k
+ *xZl + ХхфРгЗ = 3 [^1	+ 4si (T) L] + pD] (?, Z, Z, Z, T) + . . .,
s= 1
k
+ Чг2 + ^<рРгЗ = 2 [Ps2 (*) + <7s2 (*)	+ Z> Z> 2, T) 4- .... (5.1)
5= 1
z3 + ^q>z3 + у (^<₽zl + ^<ргг) “
k
“ \ [ps3 (1) k 4- qs3 (t)	+ pD3 (J, z, z, z, t) 4- ...
ДОПОЛНИТЕЛЬНЫЕ УСЛОВИЯ УСТОЙЧИВОСТИ
405
Здесь через t,r, zb z2 и г3 обозначены соответственно вариации функций <рг,
х, у и <р; точкой, в отличие от предыдущего, обозначено дифференцирование
по безразмерному времени т = a>t, а невыписанные члены в правых частях
уравнений имеют относительно р порядок выше первого. Кроме того, исполь-
зованы следующие обозначения:
,2 . .	Рх сх ,2	... Ру	__ CU ,2 ........... P<f>	_ СФ
х	со2	Л/со2	' у со2 Л/со2	’	<₽	со2 /со2	’
2	2
,2 = РхЧ> _ схЧ> , 2 _ РуФ _ СУФ
Х'Р СО2 Л/рСО2 ’ У® СО2 Л/рСО2 ’
/ = Л/р2, ar = kr/I ггл,
х Л/со У М<£> Ф /со
' k
Cs (£> z> zi z> т) —г—о"	/ j I “л--1	4" I	—H""— )	+
/sco2 1 dm,	/	/ I dx /	1
L/=1 1 4
k
Dt (£, z, z, г, t) = J] Cs (g, z, z, z, t) - 2n'xz{,
Scaj
(5.2)
k
(£, z, z, z, t) »	%* T") ~
s= 1
k
D3 (£, z, z, z, t) =	Cs (g, z, z, z, t) - 2n'z3 +
s==l
ffts&s	. . 2	\
(Фз sin Ф5 4- <PS cos Ф,),
k
x (ф, ф, ф, t) - 2
1
k
Y (ф, ф, ф, t) = J] -2^- (ф, cos <ps - ф® sin ф5),
s»»!
406
ПЛОСКАЯ ЗАДАЧА О СИНХРОНИЗАЦИИ ВИБРАТОРОВ
[гл. XIII
k
ф (ф, ф, ф, Т) = 2 -2к^£_.|ф2 sIn +	cos (ф* + 6s^
s==l
"•«-Ш’
. .	( дФ \	( дФ\
qsi (т) = -гг- - «а .
\d<fs) s\d<fs)
Здесь, как и выше, круглые скобки, в которые заключены производные функ-
ций Ф?, X, Y, Ф и <2ф, означают, что значения этих производных вычис-
ляются для порождающего решения (4.2), (4.7). Отметим, что функции С,,
Dj, paj и q31 являются периодическими функциями безразмерного времени
т = u>t с периодом 2л.
Уравнения в вариациях (5.1) даже при ц = 0 представляют систему
уравнений с периодическими коэффициентами. Особенности структуры этих
уравнений делают возможным их интегрирование в виде рядов по степе-
ням ц, однако построение характеристического уравнения и исследование его
корней непосредственно для системы (5.1) было бы все же связано с весьма
громоздкими выкладками.
Исследование устойчивости удается значительно облегчить, если, подобно
тому как это делалось в §§ 2 и 3 главы V, предварительно преобразовать
систему уравнений с периодическими коэффициентами (5.1) в такую систему
уравнений первого порядка (каноническую систему), которая при р = 0 об-
ращается в систему уравнений с постоянными коэффициентами, причем каж-
дое уравнение системы содержит только одну неизвестную функцию. Разу-
меется, такое преобразование находится достаточно простыми средствами
далеко не всегда. Однако для рассматриваемой системы это как раз удается
сделать.
С целью некоторого упрощения выкладок дальнейшее исследование про-
ведем для случая, когда оси координат хОу можно с достаточной точностью
считать «главными осями жесткости», то есть положить
сх<р = 0, су<р = 0,	= Xyq = 0.	(5.3)
Заметим, что во многих реальных системах такое условие выполняется,
ибо в них система опорных упругих элементов симметрична (или «почти
симметрична») относительно некоторых взаимно перпендикулярных осей, про-
ходящих через условный центр тяжести тела В. Изучение более общего слу-
чая, когда cx(f и Суф отличны от нуля, также может быть проведено исполь-
зуемым ниже способом, но оно связано с более громоздкими вычислениями.
Как нетрудно убедиться непосредственной проверкой, преобразование
уравнений в вариациях (5.1) к канонической форме в рассматриваемом слу-
чае осуществляется посредством соотношений
= Лг~ Лй+г> ir — агФ(+г (г““К •••> k),
2k
Z1 “ ~2 (T|2fe + 1 + T12fe+2) + "XJ
s= 1
2k
ZI = i	(П2й + 1 “ n2fe + 2) + S	Re (T)-
§ 5]
ДОПОЛНИТЕЛЬНЫЕ УСЛОВИЯ УСТОЙЧИВОСТИ
407
2fe
г2 "° ~2 (^2ft+3 "* ^2*4-4) Х~4—
^=1	(5.4)
2k
*2 “ у 'Ъ (Ъ+3 - Ъ+4) + 5 Ъ Re (Т),
s==l
2k
гз = у Cbfc+s + ’’Ъй+б)+ у S ^3>
ф 5=1
2k
У у *\р (^2fe+5 ~ ^гл+б) + S Re R® (Т)’
$== 1
Здесь T|i, ..., т)2л+б — новые переменные, введенные взамен £r, tr (г™ I,
.... k) и Zj, Zj (j = 1, 2, 3), a V(J} (t) (s = 1, ..., 2k; j = 1, 2, 3)— комплекс-
ные периодические функции т с периодом 2л, определяемые дифференциаль-
ными уравнениями
^” + (Ч-'Ч) = «<'’(?),
V<2) + (X,-ZXj/)V<2> = «®(t),	(5.5)
^3) + (^-'Ч) ^3) = 43)(т)
(s= 1.....2k),
где
, _ ( - as, s = 1........k,
0, s~k+ 1, .... 2k,
t .	. t	(5.6)
„'/)(T) = [ PsjM’ s=1> •••> k,
s I asqsj (t) — psj (t), s = k+ 1, .... 2k
(/=1, 2, 3).
Периодические функции V(s,} (т) существуют, если 1ж, и отличны
от целых чисел и от нуля; последнее условие, согласно равенствам (5.2),
выполняется, поскольку мы изучаем нерезонансный случай.
Нетрудно убедиться, что преобразование (5.4) при сделанных предполо-
жениях является неособенным, и поэтому исследование устойчивости по пе-
ременным г).......... равносильно исследованию устойчивости по исход-
ным переменным.
В переменных т|г уравнения (5.1) представятся в форме
•Пг = Мг + В^г(П1- •••> П2Й+6, Т)+	(г=1.....2й 4 «)	(5.7)
где в дополнение к (5.6) введены обозначения
1 —	^2Й + 2 = “	^2& + 3 “	(5 g}
Agfe-f- 4 ~	^2^4-5 ~ ^(р>	^2&+б =
408
ПЛОСКАЯ ЗАДАЧА О СИНХРОНИЗАЦИИ ВИБРАТОРОВ
[ГЛ. XIII
a Wr являются функциями, представляющими линейные комбинации функций
Ст и Dj с коэффициентами, зависящими от (т):
U7r = U7ft + r = _l-Cr
аг
^2 (* + /)-!
______1_____
^2 (fc + /)-l
1
(5-9)
1
К (k+j)
(k+j) —j-------~
A2 (k+j)
k
s== 1
(/=1, 2, 3).
Черта над буквой здесь, как обычно, является знаком комплексно-сопря-
женной величины.
Составим теперь характеристическое уравнение для системы в вариа-
циях (5.7).
Функции
т|г/(т) = т|°у (т) +	(т) 4- ...	(г,/=1........2Аг + 6),	(5.10)
где
о , .	.	7 т
Пг/(т) = бг/е г ,
т	(5.П)
^’(т)»/^ j ...............Пгм-б. /> ^)е~КтХ dx,
о
образуют фундаментальную систему решений уравнений (5.7), удовлетворяю-
щую начальным условиям
Пгу(О)=бг/ = { ’’	(5.12)
Поэтому характеристическое уравнение
I Т)г; (2л) - бг;р | = 0	(г, j'= 1..26	4-6)
может быть представлено в форме *)
Це2ЯХ'-р)бг/4-рПг/(2л)4- ... |==0	(г, j = 1.264-6). (5.13)
Как и следовало ожидать, уравнение (5.13) в силу (5.6) и (5.8) при
р = 0 имеет 6 корней р®-1 (s-1, ..., 6), 6 корней вида p$+s = е s
f.	w /л)	2л IK г	/о)
k) и, наконец, шесть корней	> •••’ P2fc+6“* ъ
модули которых равны единице.
*) См. сноску на стр. 168.
§ S]	ДОПОЛНИТЕЛЬНЫЙ УСЛОВИЯ УСТОЙЧИВОСТИ	40§
В силу непрерывности при достаточно малом р те k корней уравнения
(5.13), которые при ц = 0 обращаются в = е s, также будут иметь
модули, меньшие единицы. Поэтому вопрос об устойчивости при достаточно
малых р решается следующими приближениями к прочим k 4- 6 корням (то
есть к критическим корням).
Условия | р31 < 1 для первых k критических корней (то есть для кри-
тических корней ведущей группы) были получены выше: они сводятся к тре-
бованию отрицательности вещественных частей всех корней алгебраического
уравнения (4.10) (или (4.12) в случае задачи о внутренней синхронизации).
Здесь нашей целью является получение соответствующих условий для прочих
шести критических корней.
„	_ mi 2Л /Л г
Рассмотрим сначала корень, обращающийся при ц = О в Р24+1 = е •
Рассуждения, вполне аналогичные проведенным в §§ 2 и 3 главы V, пока-
зывают, что указанный корень можно искать в виде
р = е2яЛх[1 +px2j. + I 4-рХ2б+1 (р)],	(5.14)
где К2*+1(0)=0. Подстановка последнего выражения в уравнение (5.13)
дает
2fe+6
и[п2»+1, 24+1 (2я)-е2ла^+1] п (е2ЛХг-е2Лйх)+ =0. (5.15)
Г== 1
(г 24+1)
Здесь невыписанные слагаемые имеют относительно р порядок выше пер-
вого.
Если в дополнение к оговоренным выше условиям отсутствия резонанса
ни одно из чисел ±ЛУ и ±ХфНе равно Лх или не отличается от него на целое
число, а само Хх не равно нулю или целому числу с половиной (что мы и
будем предполагать), то произведение в равенстве (5.15) отлично от нуля и
из этого равенства при учете (5.3) и (5.11) следует:
*24+1 “ е2Я/Мй+1, 24+1 (2л) -
2л
= | ^24+1(41, 24 + 1» •••> 424+6, 24+1’ т) е Х^х‘ (®-16)
0
Точно таким же способом и при аналогичных предположениях найдем
выражения для поправок Хзл-н (/ = 2.......6)	к прочим пяти критическим
корням:
2л
*24+2= | ^24 + 2 (*11, 24+2»	424+6, 24 + 2» т) е Х^т»
0
• • • • .............................................. (5.17)
2л
Г XV7 / О	X
*24+6 = J "'24 + 6 (41, 24+6» •••> 424+6, 24+6» Х) е
0
Далее заметим, что при достаточно малом р условия | p24+j I < (
(/ = 1, .... 6), согласно равенствам (5.14) и им аналогичным, сводятся к
условиям Rex2ft+j<0. Но, как следует из формул (5.8), (5.9) и (5.17),
*2 (4+/)-1 *= х2 (4+у)	(/=1, 2, 3).	(5.18)
410
ПЛОСКАЯ ЗАДАЧА О СИНХРОНИЗАЦИИ ВИБРАТОРОВ
[ГЛ. Xttt
Поэтому искомые дополнительные условия устойчивости фактически сво-
дятся лишь к трем неравенствам
nRex2(ft+/)_,<0	(/»!, 2, 3).	(5.19)
Остается выразить последние неравенства непосредственно через исход-
ные параметры системы. С этой целью вычислим сначала функции V^f1.
Согласно соотношениям (5.6), (5.2), (4.2) и (4.3) имеем
Os^S^S
М~
sin (т -f- as),
$ = 1.......k,
( ЭХ \	2 / дХ \ ( дХ \_ 2asmsBs
°s \	/ а“ \ difs / \ д<Рз ) ~ М
as cos (т + cis) 4-
+	(1 — а^) sin (т + as), s — k + 1..........2k,
cos + «s)>	1......k,
mses
M
(5.20)
2mses . , , ч
----— as sin (т + as),
s = k + 1, .... 2k,
° - Ise/rs cos (t 4- as 4- os5s), s = l,
\ Ofl>S / I
k,
( дФ \	2 ( дФ\ ( дф\ 2msesrs
UqJ" /
as sin (t + as — as6s) —
- msefs 0 _ a2) CQS + + (s = fe + 1......2k).
Далее заметим, что периодические (с периодом 2л) решения уравнений
Vs — iXVs Т$ cos (т 4* Ps) 4- Sj sin (т 4- Ps)>
Vt+s - (as 4- iX) Vft+s= Tft+jcos (r 4-Ps) 4-Sft+jSin (t4-Ps)	(5.21)
(s= 1.....k),
где Ts, Ss, Tk+j, Sk+s и Ps — постоянные, имеют вид
Vs = Ms cos (t 4- Ps) 4- Ns sin (t 4- Ps).	(5.22)
Здесь введены обозначения:
u Ss4-iA.7’s Mr — 7’s4-iA.Ss
v-1 ’	-----’
м _	~ ^ ) (Sfe+s + as^ft+s) ^k+s _
«"ft + s8®	f n 2\2 9Я 0
(1 +a;-r)2+ 4ajX2
^fe+sf1 + gs~^2)~2as^('Sfe+s + as7’fe+s) 
(1 + а2_Л2)2 + 4а2Х2

§ 5]
ДОПОЛНИТЕЛЬНЫЕ УСЛОВИЯ УСТОЙЧИВОСТИ
411
(1 + а2 - X2) (Tk+s - asSk+s) — 2ask2Sk+s
(1 + а2 — X2)2-f-4а2Х2
2a?(^-aA+s) + x(i + a*-*2)^+s .
(1 + а2 — X2)2 + 4а2Х2	‘
(s = 1, ..., k).
В соответствии с формулами (5.20) в уравнениях (5.5) имеем (верхний
индекс при постоянных Т и S соответствует верхнему индексу функций F*/’)
Т’У)=О,
s М
7>(3)	ms£sr s
s I •
c(i) _
s М
s<2) = 0,
S(s3) = о,
<-2^4
(5.24)
^=-2-^.
(s= 1...k).
Подставив последние выражения в формулы (5.23), можно иайти соот-
ветствующие значения коэффициентов Ма и N, в выражениях (5.22) для
функций УДт), однако пока этого целесообразно не делать, поскольку не
все значения указанных коэффициентов окажутся необходимыми для полу-
чения окончательного результата.
Далее, согласно равенствам (5.9), для вычисления величин tizk+j по
формулам (5.16) и (5.17) понадобятся выражения функций D, и С,, соот-
ветствующие значениям аргументов н zs, отвечающих 2(fe-f-/)-My (/ =
= 1, 2, 3) решению фундаментальной системы (5.10). В соответствии с фор-
мулами (5.4), (5.6), (5.8) и (5.11)
£s, 2k+l ~ ’Is, 2k + j~ ’Ife + s, 2k + j- °	(s= 1, ..., fe; /- 1, ..6),
О	1 / О	О	\	1	0	О
zl, 2Й+1	2Й+1 + ^2k+2, 2k+l)°~2e	’ zl,2fe + 3= Zl, 2fc+5 = 0>
(5.25)
0	1 ( 0	, °	\ 1 'S’ °	° n
z2, 2fe + 3 = 2 '.’12fe+3> 2fe+3 + ’Ы-Н, 2k+3j = 2 6	’ Z2, 2fe + 1 = Z2, 2fe+5 =
о 1 / °	,	\	1 'S’ о о
z3, 2fe+5 = ‘2’(’12fe+5, 2й+5+Л24 + 6, 2й+5) = "2"е	> z3, 2k + 1 = z3, 2Й+3 = °'
Обозначим для краткости через С,, 2<i+j)-i и Dj, 2(4+д_[ (/=1, 2, 3) вы-
ражения (5.2) этих функций, соответствующие значениям аргументов
и z1i 2(fe+/)-r Тогда, в соответствии с формулами (5.2), (5.25),
412
ПЛОСКАЯ ЗАДАЧА О СИНХРОНИЗАЦИИ ВИБРАТОРОВ
[ГЛ. XIII
(3.2), (2.37), (2.38), (2.40), (2.42) и (2.43), будем иметь*)
И (d0>s\ до
НЧ, 2*+1 = yst02 Qx j 2I, 2fe+l
ЦТ 1 Г „	\ /^¥1
= “Те "	8’п(т + оМ^Л
,2
О'С/71С8„А4, г	*	1 ZA, Т
--------2Л-----[S'n (Т +	+ h^s C0S (тН as) ] е Х •
г	И ( d®s \
И S, 2Л+3	/5(02 \ ду ) I’
ЛиХ 1 Г 2 t ' Р'М!
= _¥е 7^rses“ cos(T+as)-hr/.r
------[cos (т + as) - hsfs sin (т + as)] е а ,
Г	ц [7 дФз W , (	л° , ( d®s \ о
НЧ, 2ft+5 - /sCd2 Ц-дф-J г3, 2Н-5+	Z3. 2fe + 5+ [ дф ) 23, 2fe+5
= 2^-^ [</0 + cos (т + as + <тД) - hsfs sin (т + Ч + аД)] е Ф ,
k
v 1 ldx\fda>s\.o п ,.о
gDi-2ft + i f* 2j /sm2 \дф?Д dx jzi. 2fe+i 2H42i,2fe+i
1 «2 t t \	a
= —zrKxd,{x)e	—iKxn,,e ,
>i Л I '	'	Л A
^•D2, 2k+3 =
k
SI (dY\(d®s\..o n ,.o
/s®21, <?$s; v dy )Z2- 2*+3 ~2gV2,2&+3 -
S’l
1 о	iK.,%
= - у Kyd2 (T) e - 'V&e ’
*
у i rpoy^y.o
3, 2fe + 5	Is(i>2 [\<?фз/ \ <?ф / г®> 2^+5
s-1
( 0Ф 'I ( d^s \	( дФ \ ( d®s \ о 1 Z .o
\ dips Д дф ) z3- 2*+5 + [,‘афГ) ["дф~) 23. 2*+5J “ 2|X^Z3, 2fe+5 +
Ц (dQfp \ о ( dQq \ ,o ( dQ<p \ о
/<02 ,\ dip / 3. 2Й + 5 у дф У 23, 2£ + 5	дф / 23, 2£ + 5
1	9	,	IK X
= “ ~2	<T) e ф “ ^<р«Фе Ф ~
k
1 >. • V V
2 ^1е A*
3-1
"Ws 4sks
I Is^>
1 Z4T
cos (r + as + as6s) - — K^ie
У
Is® '
s— 1
*)' Напомним, что в формулах данного параграфа точкой обозначается
дифференцирование по безразмерному времени т, между тем как во всеХ
прочих параграфах точка означает дифференцирование по t.
§ 5]	ДОПОЛНИТЕЛЬНЫЕ УСЛОВИЯ УСТОЙЧИВОСТИ	413
Здесь, в соответствии с равенствами (3.2) и (5.2), обозначено:
2/гл. = 2(хих = -^-, 2/гг/ = 2|хпг, = -^—,
(5.27)
/
2«<р = 2ц,!ч)=	,
di(t), d2(x) и б/3(т) — вещественные периодические функции т с периодом 2л,
a d0 — комплексная постоянная; конкретные выражения этих функций и по-
стоянной в дальнейшем роли не играют.
Обратимся, наконец, к непосредственному вычислению величин
ц Re x2(ft+j)-i (/’=1,2,3), через которые выражаются условия устойчивости
(5.19). В соответствии с формулами (5.16), (5.17), (5.8), (5.9), (5.22), (5.25)
и (5.26) получаем
И Re и2£ + ! =
Г Г k
= в Re J Тх- Dl, 2Й + 1 ~ S Cs, 2*+1 (^> + ^ft + s)
О	L	s_i
е х dx
= - 2-W + "НГ '1^' J [s!n (Т + “«) + h^'s cos (Т + “*)] Х
s«l	5 О
'k
х ta (Г/1 + Гй.) Л - - 2», +	2 ТГ *
S=I

И Re x2ft+3 =
k
D2, 2k + 3 ~ 2 "^7 Cs- 2*+3	' + +
S“1

dr —
k	2n
= - 2шгу + —	— —ц— J [cos (т + as) - hsfs sin (t + as)] X
s-l S 0
л
, / m ,91 ч	лли vt I mszs
Xlm(y^ + V^dx=-21Wy + ~24—-T—X	(5.28)
№=1
Xlm^+^’^-yXe + C.)].
nRex2fe+5 =
2Л
"""J-ir
0 T
k
D3, 2k + 3-^~CSt 2,+5(v[3) + ^t)
S=®1
e 4> dx
414
ПЛОСКАЯ ЗАДАЧА О СИНХРОНИЗАЦИИ ВИБРАТОРОВ
[ГЛ. XIII
„ v q& V 1 Г г / ,	. * ч
- - 2л«ф - п 2j -------Г- 2j "о? —1---J fcos + “s +	~
s-1	s-=l	5 О
- hsfs sin (т + “s + ’A)]Im (vi3) + Vfe+s) dx =
_v ЯЧ V 1 msesrs , г/.,13) , .ИЗ) 4
2ляф	/ю 2 as Is Im +Mk+S)~
S«»l	5"1
-yxe+43is)].
Здесь через и (s = 1.............2A;	j = 1, 2, 3) обозначены значения этих
постоянных, которые получаются по формулам (5.23) прн подстановке в них
вместо Ts и Ss значений и S^' в соответствии с (5.24), а вместо Л — ве-
личины Кх для /= 1, Ку для / = 2 и \р для / = 3.
Производя вычисления по указанным формулам, после простых, хотя и
громоздких преобразований получаем дополнительные условия устойчивости
(5.19) в следующей форме:
, 1 4 v (тл)2	(3 + 4 + 4)«s
4^-i£ «/, (i + a:-vj+4«x
. 4 k	9	1
Ч У h f' msBs
2 A sts Mls (l+a2-K2x)2 + 4asK2
, 1 4 у (mA)2 (з+4+Ч)^
M!s (1+a2-K2)2 + 4a2K2
, V «Л 2 V (msesrs)2 (3 + 4 + ^-ф) as	_
n<t zi ;® 44-1zj1 us (i + 4-4>)2+444
_ у h _________________!______
(i + ^-x^+4ax
Напомним, что величины nx, ny, «ф, a3< Kx, Ky и Хф, фигурирующие в
последних формулах, определяются равенствами (5.2) и (5.27); k' есть число
дебалансных вибраторов, k" — число планетарных вибраторов, a k = k'-\-k"—
общее число вибраторов.
Примечательно, что дополнительные условия устойчивости (5.29) не за-
висят от порождающих фаз ai....as, и поэтому они не влияют на отбор
устойчивых значений этих фаз из числа систем значений, удовлетворяющих
уравнениям (4.9).
§ 61	РАЗВЕРНУТАЯ ФОРМА ОСНОВНЫХ УРАВНЕНИЙ	415
Более детальный анализ неравенств (5.29) показывает, что вследствие
малости для реальных машин параметров	и (т,е,г,)21П, эти
неравенства практически всегда выполняются, если только машина или уста-
новка работает хотя бы на небольшом удалении от зон основного резонанса,
то есть от зон, где Хх = Дх/со « 1, = pvl<a ~ 1 или Аф =	« 1. (На-
помним, что коэффициенты kx, kv, fe<p, k, и ^существенно положительны.)
Таким образом, в нерезонансных режимах, для которых и было прове-
дено изложенное выше исследование, дополнительные условия устойчивости
движения (5.29) в подавляющем большинстве случаев выполняются.
§ 6. Развернутая форма основных уравнений теории
синхронизации вибраторов и их интерпретация.
Вибрационные моменты
1. Развернутая форма основных уравнений. Представим
уравнения (4.9), играющие основную роль в теории синхрони-
зации вибраторов, в развернутой форме, выразив их левые части
через параметры рассматриваемой системы. Подставив в ука-
занные уравнения выражения для функций цФ5 согласно фор-
мулам (3.2), запишем их в виде *)
Ps(a......... G))^-i-(L<m)-/?<m)-Ss-1F(sw)»0	(6.1)
(s= 1, ..., k).
Здесь обозначено:
Um) = -^-asJ Ls(ps®, q>°, q>°, q>°,
о
= ЯДоув, <P°, x°, y°, ip°)dt,
о
2Л/в> k
SS = °* J S A (CTX “ a/(P/ “ + X/) dt>	<6-2)
0 /-=1
2n/e>
=“ °* J [*°sfn <₽:+y° c°s <₽: -
0
- <f°rs cos (<p° + 6S) + g cos (q>° - %)] + hsSfls	фо | jt.
DS	j
♦) Здесь опущен несущественный положительный множитель 4лДю,
416
ПлоскАя задача о синхронизации вибраторов (Гл. хш
Вычислим вначале величины Выполнив интегрирова-
ние при учете равенств (4.2), (4.7) и с использованием соотно-
шений
2л/и
Jsj = — Jjs = J sin (ш/ + as) cos (ш/ + a/) dt = - sin (a5 — a/),
о
2Л/Щ
9 J S J	Г	Л
—^- =	sin (co/ + as) sin (co/ + a,) dt = — cos (as — ay), (6.3)
' о
2Л/Щ
dJ gt	P	jr
-Д—-=	cos (co/ + as) cos (at + a,) dt — — cos (as — ay),
OClj J	1	u)	1
0
находим
k
П7(Ю — — msBs®2 у m p г/д0 _ a гт Г)° I
“ 2 М ЛЛ т1Ъ1 К71/	+
/-1
+	cos Ss -I- VSM° sin Ss) sin (as - a,) +
+ (a.B° - a C° — M°a v cos 6 + cr.v № sin 6 ) cos (a - a.)].
Подставив в последнюю формулу вместо величин А°,
В°, ..., №j их значения согласно равенствам (4.8) и выполнив
несложные преобразования при учете соотношений (4.3), пред-
ставим выражение для F*/0 в форме
r«)=F<«>(ai........aA, со)»
k
=	injSj 1Д, sin	+ CQS _ a^j	(6
/-=1
(s = I, ..., k).
Здесь обозначено:
Psi = bxx + OsOjbyy + bxv (vj sin 5/ + vs sin fis) -
-	(V/ cos Sy + vs cos ds) + Swasa/vsvy cos (стД - стубу),
Qsl = (°5 - CT/) bXy + bX(f (OjVj cos Sy - asvs cos 6S) +
+ byq (<JsVj sin Sy - ayvs sin 6S) + S^aya^VyV^ sin (aД - оД)	(6.5)
(s, /=1......k).
Безразмерные величины Psj и Qsj играют существенную
роль в дальнейшем; заметим, что между ними имеют место
соотношения
Psi~Pls, Qsj^-Q (S,/=1, ...» k),	(6.6)
§ G]	РАЗВЕРНУТАЯ ФОРМА ОСНОВНЫХ УРАВНЕНИЙ	41/
то есть k X 6-матрица Р = ||Р5/11 является симметрической,
a k X 6-матрица Q = || Qsl || — кососимметрической.
Подставив, далее, в выражения (6.2) для величин Ss зна-
чения углов поворота вибраторов <р° в порождающем прибли-
жении согласно формулам (4.2), находим
k
Ss(a15 .... a*)=S cs/(“s~а/~«5 + »</)	(s=l, .... 6).	(6.7)
Остается развернуть выражения (6.2) для величин L(sm>
и R^}. Выполнив интегрирование при учете равенств (2.36),
(2.37), (4.2), (4.3), (4.7), (4.8) и (6.3), получим
I	(asco) для двигателя асин-
ZT = Ы (aS) as<0) =!	. о п донного типа,
asLs [as (as — |3S)] для двигателя син-
1	хронного типа,	д.
R!f = R(f («!...ak, а) = R’(a) + F«>(ap ..., ак, со).
Здесь
/?»=r°a (®)+/?:в(«)>
(“) = тЛ“2 [т fsds + hs - у f А)] “
у fsmsasdsa2 Для дебалансного вибратора,
f'т е2а2 для планетарного вибратора,
ь	(6.9)
(а,....ак, со) = у hsf's 2 /П/e, [Psl cos (as - a7) -
/=i
- Qsl sin (as - a/)],
причем величины Psl и Qsj по-прежнему определяются форму-
лами (6.5).
Таким образом, уравнения (6.1) для определения порождаю-
щих фаз ci].....а* можно представить в следующей форме:
Ps(ab .... aft, со) = j-[L(sm) (as, osa) - Rs (а) -
-Ss(a,, ..., at)-lF<w(a........ a)-
-^(a>........“)] = ° <6-10)
(s= 1, .... 6),
14 И. II. Блехман
418
ПЛОСКАЯ ЗАДАЧА О СИНХРОНИЗАЦИИ ВИБРАТОРОВ
[ГЛ. XIIt
или также в виде
^m)(as> ^®)=Л°(а>) + 5Да1. > <) +
+ W^(a........ а4,<о) + ^(а1( .... а,, со) (s = 1, ..., k). (6.11)
Полученные трансцендентные уравнения играют основную
роль в теории синхронизации вибраторов; как уже отмечалось
в § 4, наличие у этих уравнений вещественных решений относи-
тельно порождающих фаз а\, . .., ak является необходимым
условием существования синхронных движений изучаемого типа.
Уравнения (6.11) достаточно сложны. В общей форме их ре-
шение может быть просто получено лишь в случае двух вибра-
торов (см. § 16 настоящей главы). Однако и для систем со мно-
гими вибраторами, которые встречаются в приложениях, как
правило, удается найти решение, поскольку таким системам
свойственны тот или иной вид симметрии в расположении виб-
раторов, одинаковость отдельных параметров и т. п. Сказанное
будет ниже проиллюстрировано на ряде примеров. Кроме того,
как будет ясно из дальнейшего, при изучении ряда вопросов
вообще нет надобности прибегать к непосредственному решению
уравнений (6.11).
2. Интерпретация основных уравнений-, вибрационные мо-
менты. Рассмотрим подробнее смысл основных уравнений (6.11).
Прежде всего заметим, что эти уравнения могут быть фор-
мально получены, если предположить, что движение системы
происходит по закону
= =	+	х==х°> У = У°> Ф = Ф°,
определяемому равенствами (4.2), (4.7) и отвечающему порож-
дающему решению, а затем осреднить за период Т = 2п/а пер-
вые k исходных уравнений движения (2.44) (то есть уравнения
движения вибраторов), предварительно умножив их на as. Та-
ким образом, основные уравнения (6.11) являются приближен-
ными уравнениями равновесия средних моментов сил, действую-
щих на роторы вибраторов в установившемся синхронном дви-
жении.
Обращаясь к анализу отдельных членов уравнений (6.11),
отметим, что величина L^(as, asco) представляет среднее за пе-
риод Т — 2л/со значение вращающего момента двигателя, вы-
численное для порождающего решения <ps = <р°, х = х°, у~у°,
<р = ф°; при этом момент [№>, в отличие от момента Ls, отсчи-
тывается в направлении вращения s-ro вибратора.
Величина-/?^'(а,, ..., ak, со) = -7?°(со) —	.... ak, со)
представляет средний за период момент сил сопротивления дви-
жению вибратора, также вычисленный для порождающего
§ 6]	РАЗВЕРНУТАЯ ФОРМА ОСНОВНЫХ УРАВНЕНИЙ	419
решения и отсчитываемый в направлении вращения s-ro вибра-
тора. Указанный момент представлен в виде суммы двух сла-
гаемых: момента —(со), не зависящего от фаз а\, ak, и
момента — (ар ak, со), существенно зависящего от ука-
занных фаз. При этом момент — согласно равенствам
(6.9), отличен от нуля для планетарных вибраторов и равен
нулю для дебалансных вибраторов*). Последнее связано с тем
обстоятельством (см. § 2 настоящей главы), что в дебалансных
вибраторах можно не учитывать зависимость радиальной реак-
ции в подшипниках Ns от ускорения колебаний оси ротора виб-
ратора, между тем как в планетарных вибраторах эта зависи-
мость является более существенной и ею не всегда допустимо
пренебрегать. Слагаемое	•••, ak, со) как раз и учиты-
вает зависимость нормальной реакции а тем самым и мо-
мента сил сопротивления /?, в планетарных вибраторах от уско-
рения колебаний основания, на котором установлен вибратор.
Далее, величина Ss(ab ..., а/,), определяемая выражением
(6.7), является средним моментом, передаваемым s-му вибра-
тору от системы принудительной синхронизации. Эта величина
может быть представлена в виде суммы соответствующих «част-
ных» моментов:
k
Ss=Ss(ai, ..., aj= 3ss/ (s=l,	(6.12)
слагаемые которой
Ss/ S/s Cs j (щ. CCj Xs ~г X/)	(6.13)
характеризуют воздействие s-ro вибратора на /-й вибратор че-
рез систему синхронизации. При этом в силу свойства взаим-
ности частных моментов sSJ-= —s,s сумма всех моментов Ss
равна нулю:
к	к к
3Ss=3 3 ss/ = 0.	(6.14)
S=1	Jo] /Я]
Наконец, величины Ws= + W{SR\ фигурирующие в урав-
нениях (6.11), назовем вибрационными моментами. Эти моменты
можно трактовать как дополнительные средние моменты, дей-
ствующие на неуравновешенные роторы вибраторов вследствие
колебаний основания, на котором они установлены. Вибрацион-
ные моменты представляют для роторов вибраторов как бы до-
бавочные средние внешние нагрузки (в случае, если Ws > 0)
или добавочные вращающие моменты (в случае, если U7s<0).
Как следует из формул (6.4), вибрационные моменты
при прочих равных условиях увеличиваются с увеличением
*) См. первую сноску на стр. 390.
14*
420
ПЛОСКАЯ ЗАДАЧА О СИНХРОНИЗАЦИИ ВИБРАТОРОВ
[ГЛ. XIII
статических моментов вибраторов mses и квадрата угловой ско-
рости синхронного вращения и и уменьшаются при увеличении
массы системы М и ее момента инерции /. Можно сказать по-
этому, что вибрационные моменты возрастают при увеличении
интенсивности колебаний основания, на котором установлены ви-
браторы. В пределе при М —> оо и /—*оо, соответствующем не-
подвижному вибрирующему органу (несущему телу В), вибра-
ционные моменты равны нулю. Существуют, однако, условия,
при которых вибрационные моменты обращаются в нуль неза-
висимо от интенсивности колебаний вибрирующего органа.
Вибрационные моменты U7S состоят из двух частей — «кон-
сервативной» части WsK] и «неконсервативной» W's'1 (смысл по-
добных названий станет ясным из дальнейшего).
Согласно выражению (6.4) «консервативную» часть вибра-
ционного момента W(SK}, действующего на ротор s-ro вибратора,
можно рассматривать как сумму
k
.... ak,	(6.15)
слагаемые которой
1 mse.sm ,е/<о2 ,
wW = -	_-----------[ps/ Sin (as - a,) + Qsl cos (as - a,)]
(6.16)
представляют «частные» консервативные вибрационные мо-
менты, характеризующие воздействие /-го вибратора на s-й. При
этом, как и для частных моментов sSj, имеет место свойство
взаимности	w^} = Q, вследствие которого сумма
всех консервативных частей вибрационных моментов тождест-
венно равна нулю:
’г	k k
2	2 2	(6.17)
s=l	s=l j = l
Неконсервативные части вибрационных моментов, несмотря
на разложимость
k
W8 ~ 2j Wsj ,
/=|
подобным свойством не обладают, ибо
1	,е ;м2 г ,	,
= Т hJ'S----М-----cos (as “ “ Q°i Sin (a* “ “/)] ~ WT°>
§ 6]	РАЗВЕРНУТАЯ ФОРМА ОСНОВНЫХ УРАВНЕНИЙ	421
то есть соответствующие частные моменты, вообще говоря, не
удовлетворяют соотношениям взаимности.
Роль вибрационных моментов в уравнениях (6.11) для опре-
деления порождающих фаз и в условиях устойчивости синхрон-
ных движений будет подробно проанализирована ниже (см.
§§ 10 и 11 настоящей главы). Здесь укажем лишь, что нали-
чием этих моментов объясняется самосинхронизация вибрато-
ров, вибрационное поддержание вращения, а также ряд своеоб-
разных явлений, сопутствующих принудительной электрической
или механической синхронизации.
Физическое существо этих явлений состоит в наличии суще-
ственной связи между отдельными вибраторами, обусловленной
колебаниями общего основания, на котором они установлены.
Возникновение вибрационных моментов и является проявлением
этой связи. Иногда указанная связь носит такой характер, что
движение вибраторов с желательной комбинацией сдвигов фаз
существует и устойчиво «само по себе». При этом можно не
вводить искусственных связей между роторами. В других слу-
чаях для обеспечения существования и устойчивости требуе-
мого движения приходится либо изменять характер «естествен-
ных» вибрационных связей, либо вводить ту или иную искус-
ственную связь.
В завершение общего анализа уравнений (6.11) для опреде-
ления порождающих фаз аь . .., аЛ получим одно существенное
соотношение, вытекающее из этих уравнений. С этой целью, сло-
жив все уравнения (6.11), умножим затем обе части получен-
ного равенства на угловую скорость синхронного вращения со,
Тогда в силу (6.14) и (6.17) находим
k	k
СО 2 (as, <Tsco) == со 2 [М0) + М*’ (аь ..., а*, со)]. (6.18)
S = I	.5=1
Последнее соотношение представляет не что иное, как урав-
нение баланса энергии в системе: работа за один период сред-
них вращающих моментов L*.m)(as, щсо) равна работе за период
средних моментов сил сопротивления
> ak> “) = <> +^W(ai, .... ак, со).
Консервативные части вибрационных моментов (aj, ..ak, со)
и моменты системы синхронизации Ss(ai, • • •. «л) в равенство
(6.18) не входят. Эти моменты представляют как бы реактив-
ную нагрузку, они обусловливают лишь перераспределение на-
грузки между отдельными двигателями вибраторов, не вызывая,
однако, дополнительных затрат энергии.
422
ПЛОСКАЯ ЗАДАЧА О СИНХРОНИЗАЦИИ ВИБРАТОРОВ
[ГЛ. XIII
§ 7. Различные формы записи и способы вычисления
вибрационных моментов и моментов системы
принудительной синхронизации
Выше основные уравнения теории синхронизации вибраторов
были получены путем непосредственного вычисления интегра-
лов, входящих в выражения (4.9). Однако те же уравнения,
естественно, могут быть получены и из уравнений (3.11) и (3.12)
главы IX, которые отличаются от (4.9) тем, что в них выделены
специфические слагаемые в левой части. При этом пришлось бы
составить выражение для среднего за период значения функции
Лагранжа системы Л, найти его производные по as и вычислить
моменты неконсервативных сил 71s. Не останавливаясь здесь на
соответствующих выкладках, сопоставим уравнения (3.11) и
(3.12) главы IX с уравнениями (6.10) настоящей главы, что
позволит прийти к некоторым общим выражениям для вибра-
ционных моментов Ws и моментов системы принудительной син-
хронизации Ss.
Прежде всего, заметим, что в рассматриваемой задаче, со-
гласно последним четырем равенствам (3.2), немалые части не-
консервативных сил Q(0), отвечающих колебательным координа-
там, равны нулю. Поэтому, в соответствии с формулой (3.8)
главы IX, равны нулю также и соответствующие средние мо-
менты:
Gs = 0.	(7.1)
Далее, средние моменты неконсервативных сил, отвечающие
вращательным координатам, будут
Zs = (as, <tsco) — Rs (to) — W(SR} (ab ak, to). (7.2)
Поэтому общие средние моменты неконсервативных сил, отве-
чающих s-му объекту (вибратору),
Л = Gs 4-Zs =/.<< (as, asto)-Rs(co)-ITlR)(ai, •••> a*, co). (7.3)
Наконец, сопоставляя оставшиеся члены уравнений (3.11),
(3.12) главы IX и уравнений (6.10), находим
«.(»......“.)+ “ДД»,.......«.• »)-«.- -	(7.4)
Здесь Л = Л(«1, ... , ал, to) — среднее за период значение функ-
ции Лагранжа системы L — Т — П, вычисленное для порождаю-
щего решения (4.2) и (4.7). В соответствии с равенствами (2.4)
н (2.7) — (2.11) эта функция в рассматриваемой задаче может
быть представлена в форме
L = L' + L^ +	(7.5)
§ 7]	СПОСОБЫ ВЫЧИСЛЕНИЯ ВИБРАЦИОННЫХ МОМЕНТОВ .	423
где
k
+ Lj = ^Ij^l — mje,jg\\ - sin (ср; - х)],
/-I
k
AL* = —	m^jcp j (x sin ф; + i) cos фу) —
/-I
k
-ф^ Ф/
/=i
mjEj (v0] sin фу — uOj cos фу) + hj^cj
e.jkf (bs + ezXz)
(7.6)
L(I) = 1M (x2 + y2) + у /ф2 - у (cxx2 + суу2 + Сфф2 + 2СхфХф + 2сйфуф),
k k
L(II) = - Пс = - - Cqj (<T^„ - <Т;ФУ -	+ xz)2.
<7 = 1 /-I
Величина L* представляет собой функцию Лагранжа объек-
тов (вибраторов), вычисленную с учетом поправки, обусловлен-
ной подвижностью тела, на котором они установлены (то есть
наличием несущих связей; см. § 2 главы X). Выражение LW есть
функция Лагранжа собственно несущего тела (связей первого
рода), и, наконец, величина L<n> есть функция Лагранжа син-
хронизирующих элементов (связей второго рода), равная в дан-
ном случае взятой с противоположным знаком потенциальной
энергии этих элементов.
Из равенств (7.5) и (7.6) следует, что для рассматриваемой
системы выполняются все условия, оговоренные в § 4 главы IX;
поэтому оказываются справедливыми и полученные там соот-
ношения (4.5) и (4.9):
дХ _ д(Л(11>-Д(1)) _ 5(л(и)+у
das	да.
das
das
= - Ms = - Ss-W{^\ (7.7)
где
2JT/<o
A(I)=^J (LW)dt,
О ‘
2п/(0
AA* = -^J (AL*)d/,
О
2п/(о	2п/(0
л<11)=-^[ (LW)dt, Az=^f {Ls)dt,
l> fl	Л4 J I» ff
0	0
к	(7.8)
л’=S л/+дл‘
/-1
— средние за период значения соответствующих лагранжианов,
вычисленные в порождающем приближении. При этом, заметив,
424
ПЛОСКАЯ ЗАДАЧА О СИНХРОНИЗАЦИИ ВИБРАТОРОВ
If Л. Х111
что согласно равенства (4.2) и (7.6) величины Aj не зависят
от ai, , ah, будем иметь
™(К) = дА(1)   1_ дЛ*  ______1_ д(\Л*)
s	das	2 das	2 das ’
О = _ дА(11> = д (Пс)0	(7‘9)
s das das
Иными словами, консервативные части вибрационных мо-
ментов W(® могут быть подсчитаны, например, как частные
производные по as от среднего за период и вычисленного в по-
рождающем приближении лагранжиана несущего тела LW. Со-
ответственно средние моменты системы принудительной синхро-
низации представляют собой частные производные по as от
соответствующей потенциальной энергии, также вычисленной
в порождающем приближении.
Приведем, наконец, формулу для консервативных частей
вибрационных моментов в которой последние выражены
через так называемые гармонические коэффициенты влияния
второго рода (см. § 3 главы XIV):
k
= у msesa4	(as - a;) +
Ф^Г/К™ - asKu»)cos(as -ay)].	(7.10)
Здесь через Кш обозначен коэффициент при cos oV в выраже-
нии для проекции перемещения (в режиме установившихся ко-
лебаний) оси вращения s-го вибратора на ось Ощ при действии
на ось вращения /'-го вибратора гармонической силы cos at, на-
правленной вдоль оси О[М; величина Kuv есть коэффициент при
cos at в выражении для проекции перемещения оси вращения
s-го вибратора на ось OfV при действии на ось вращения /-го
вибратора гармонической силы cos at, направленной вдоль оси
О\и. Аналогичным образом определяются величины Kvv и Kvu-
В § 3 главы XIV соотношения типа (7.10) будут получены
для значительно более общего случая.
Сопоставление выражений (6.9) и (7.10) приводит к сле-
дующим соотношениям между введенными ранее безразмер-
ными величинами Рй, и Qsj, с одной стороны, и коэффициен-
тами Кии, Kuv И т. д. - с другой *):
Psl = М Ю + <T/<TSCS)) со2 = Pjs,
Qsj = М (vjKvu - CD2 = - Qjs.	‘11}
*) Заметим, что указанные коэффициенты удовлетворяют соотношениям
взаимности (см. равенства (3.20) главы XIV).
§ 8] ВИБРАЦИОННЫЕ МОМЕНТЫ В НЕКОТОРЫХ ЧАСТНЫХ СЛУЧАЯХ 425
Эти формулы позволяют дать величинам Psi и Qsj определен-
ную физическую интерпретацию.
Разумеется, выражения (7.10) и (7.11) могут быть получены
и путем непосредственного вычисления на основе использова-
ния определений величин Кии, Kuv и т. д., равенств (6.3) и
уравнений малых вынужденных колебаний несущего тела В.
В рассматриваемой задаче выражения (7.10) вряд ли имеют
особое значение, поскольку здесь для вибрационных моментов
удается получить их конкретные выражения через исходные
параметры системы (см. формулы (6.4), (6.5) и (4.8)). Однако
в более сложных случаях использование выражений (7.10), как
и отвечающий им способ нахождения вибрационных моментов,
может представить определенные преимущества (см. § 3 гла-
вы XIV).
§ 8.	Выражения для вибрационных моментов в некоторых
частных случаях
Из всех членов уравнений (6.11) наиболее сложную струк-
туру имеют выражения для вибрационных моментов Ws. К со-
ставлению указанных выражений, по существу, и сводится
теоретическая часть решения задач о синхронизации вибрато-
ров. Ниже, в главе XIV, будет изложена общая методика по-
лучения выражений для и W(SK} для различных, в том чис-
ле и для более сложных, чем изучаемая в настоящей главе,
систем. Здесь же мы рассмотрим ряд часто встречающихся
в приложениях частных случаев задачи о синхронизации вибра-
торов в машинах и установках с плоским движением вибрирую-
щего органа, для которых выражения моментов W(SK} и
существенно упрощаются.
а)	Вибрирующий орган машины (несущее твердое тело В)
имеет одну степень свободы, соответствующую поступательному
движению.
К этому простейшему частному случаю относятся некоторые
вибрационные машины и установки с направляющими элемен-
тами типа пластинчатых рессор или рычагов с шарнирами на
концах (см. пп. 1а и 16 таблицы 2).
В данном случае можно положить
с</=°°> сч>=°°.	= сйф = 0,	(8.1)
и тогда, в соответствии с формулами (4.5), (4.6) и (4.8), имеем
Ру=°°,	P<f=°°, Px^ = Py<f = 0,
ЬXX ~	> Ьуу =	= bXy = bXq = byq = 0.	)
Рг	
426
ПЛОСКАЯ ЗАДАЧА О СИНХРОНИЗАЦИИ ВИБРАТОРОВ
[ГЛ. XIII
Выражения для величин PSj и QSj, согласно равенствам
(6.5), примут вид
Ps/ = bxx = -^-T, Qs/ = 0,	(8.3)
Рх~а
и, таким образом, моменты и IFsW, в соответствии с фор-
мулами (6.4) и (6.9), представятся в следующей простой форме:
Г<К)(а1;
k
.	1 msesa4 V1  /	\
а., и) =------т,е; sin (а — а,),
’ k ’	2 М(щ-м2)	' s
\' X	J jej
k
= 7 Vs _a2j 1 cos К - “/)•
(8.4)
Моменты и WsR} в рассматриваемом случае не зависят
ни от направлений вращения роторов вибраторов (то есть от
чисел oj), ни от их расположения на вибрирующем органе
(то есть от координат Г) и 6, осей вращения роторов).
б)	Вибрирующий орган имеет одну степень свободы, отве-
чающую повороту вокруг оси, проходящей через условный
центр тяжести.
В данном случае можно положить
Су °°> ^хср=	0,	(8.5)
и тогда, аналогично предыдущему, по формулам (4.5), (4.6),
(4.8), (6.4) (6.5) и (6.9) последовательно находим
Рх = Ру=°°’ Рх^ = /7ф = 0-
^tpm =	2	2~ ’ XX ~~ bgg — bXg Ьу = byrf! = 0,
P<p - “
PSj = <wvsVj ——гcos (CTA -
(0^
Qsj = (W/VsV/—-----T sin (оД - Gjbj),
Ptf -®
^w(al’ •••’ ak> “) =
k
= T 771------27 °imieiri sin (as + aA -ay-ayay),
2
(8.6)
..., aft, co) =
k
= 7 Vs r( 2_ 2\ 2j	C0S (as +	” a/ ” a/a/)‘
1 (Pep “ ) , .
§ 8]
ВИБРАЦИОННЫЕ МОМЕНТЫ В НЕКОТОРЫХ ЧАСТНЫХ СЛУЧАЯХ
427
В данном случае моменты WsK) и зависят как от на-
правлений вращения роторов вибраторов, так и от их распо-
ложения на вибрирующем органе.
в)	Система опорных упругих элементов симметрична (или
«почти симметрична») относительно двух взаимно перпендику-
лярных плоскостей.
В широком классе вибрационных машин упругие опорные
элементы таковы, что существуют два взаимно перпендикуляр-
ных направления (их всегда можно принять за оси Ох и Оу),
для которых жесткости с.гф, cytf и сху допустимо считать рав-
ными нулю одновременно; выражения для моментов W(SK) и W1®
при этом существенно упрощаются.
По упоминавшимся выше, формулам получаем в данном
случае
Pxq> = Pytf
,	_	(О2 *	,	_	(О2	(О2
О XX	2	2~ >	® УУ 2	2~ > h = 2 Т" >
Рх~®	Ру ® w Рф-®
b ху = Xlf ~ Ь ytf ~
п	И2 I	а2 I	СО2	/ я X \
*	2	2	^-$^7 2	2	2	2 COS ((У$О5 (Тубу),
Рх ~(D	Рф —0	©
(0^
Qsj = <T^/Vsv/ 2 ' 2' sin (<тД - (Тубу),
Рф-И
rW(ai; ..., ak, со)=	’
k	Г/ ,	X
1 msesa4 VI ! 1	. GsGj \	,
kpv+7^/sin а‘“а/ (8.7)
/=1	L \ ' л	’У I
, OsOjVsV) . ,
+ —----2~ sin(as + оД — ay — Оубу) ,
№«) (a„...,aft,ra) =
, fe
I , ,, mse5to4 yi /	1	. сгзсг/ \
“ 2 h-!- ~1T %,ЛЛ U^+7F^rs(“-“°') +
y = l	L\ A	' У t
I CT*a/v*v/ /	, я	я /
H—2----г cos (“s +	- o’/бу) .
Pep й
г) Угловая скорость синхронного вращения вибраторов су-
щественно превышает частоты собственных колебаний вибри-
рующего органа (твердого тела В) на упругих опорах.
Случай, когда вибрационная машина работает далеко в по-
слерезонансной области, является весьма широко распростра-
ненным на практике (см. таблицу 2). В этом случае при
428
ПЛОСКАЯ ЗАДАЧА О СИНХРОНИЗАЦИИ ВИБРАТОРОВ
[ГЛ. XII1
вычислении моментов и WsR} можно пренебречь величинами
Рх’ Ру> Рч>’ Рхч> и Руч> по сРавнепию с и2 и тем самым суще-
ственно упростить выражения для указанных моментов. Анало-
гично предыдущему при сделанных предположениях находим
^ХХ ЬУУ	’ &ХУ ^Xtf Ь Уф О,
Psi = - (1 + °Д) - O’4.(T;VdV/ cos (оД - оД),
Qsj = - sin (СТЛ “ СТ/б/)>
яТ(ан •••’ а*’ и) =
.	, *	(8.8)
= - у —— Zj zn/e, [(1 + а4.а;) sin (а4 - ау) +
/=1
+ a.a/v^v/ sin (а4 + аД - а/ - стД)],
«Г (% ••• - “) =
k
= - у hsf's 2 mjei [(1 + cos (а,. - а;) +
/=1
+ asCT;vdv j cos (а4. + оД — а,- — аД)].
§ 9.	Потенциальная функция и интегральный критерий
устойчивости синхронных движений вибраторов
Конкретизируем результаты, изложенные в § 5 главы IX,
применительно к изучаемой задаче о синхронизации вибра-
торов.
С этой целью рассмотрим условия существования потен-
циальной функции Z) = Z)(«i, ..., ад, со). Заметим предвари-
тельно, что согласно равенствам (7.3) и (7.4) выражения для
порождающих функций Ps могут быть представлены в форме
РДа,, .... aft, co)^J-(a4 + ^) =
= ^[/.(m’(as, о*®) - Яз (со) - WsR}(ult ..., ak, со)+ (9.1)
($ = 1............................k),
соответствующей форме записи левых частей уравнений (3.12)
главы IX. Отсюда при учете положительности коэффициентов ks
следует, что для существования функции D достаточно, чтобы
существовала функция В, удовлетворяющая соотношениям
g- = Д = Zs = L(m) (a4., ст4со) - Rs (co) - W{R} (a„ .. ., ab co)
(s = 1, ..., k).	(9.2)
§ 9]
ПОТЕНЦИАЛЬНАЯ ФУНКЦИЯ И ИНТЕГРАЛЬНЫЙ КРИТЕРИЙ
429
Но для возможности последнего равенства необходимо и до-
статочно выполнение тождеств
d/ls dAj
даj das
(«, / = 1...........k),
(9.3)
выражающих условия равенства вторых смешанных производ-
ных от функции В по as и ajt вычисленных в различном по-
рядке. Нетрудно видеть, что выполнение последних равенств
в общем случае задачи невозможно, ибо в силу соотношений
(9.2) и (6.9)
_ dW^	______1	,	'»sesw/e/	[р. cos (as — a,) —
da j	da j	2	s's M
dW(R} dA,
- Qsj sin (as - a,)] ¥=	=	(9.4)
Таким образом, для существования потенциальной функ-
ции D в рассматриваемой задаче о синхронизации вибраторов
достаточно, чтобы моменты были тождественно равны
нулю. Последнее условие выполняется либо в случае, когда все
вибраторы дебалансные (hi = h2 = ... — hk = 0), либо когда в
планетарных вибраторах можно пренебречь зависимостью мо-
ментов сил сопротивления от ускорения колебаний их осей (см.
п. 3 § 2 настоящей главы).
Указанные условия, будучи достаточными для существова-
ния потенциальной функции D, практически являются также и
необходимыми в том смысле, что любые менее жесткие усло-
вия потребуют соблюдения некоторых равенств между парамет-
рами системы, что лишит эти условия практического значения.
При выполнении сформулированных условий за потенциаль-
ную функцию можно принять выражение
D=-(A + B),	(9.5)
где
k
в = J (as, щы) - Rs (co)] das	(9.6)
s=i о
есть, no существу, работа осредненных непотенциальных сил,
действующих на роторы вибраторов.
В соответствии с равенствами (7.7) и (7.9) функцию D
в рассматриваемой задаче можно взять также либо в виде
D = (Л(1) - Л(11> - В),	(9.7)
либо положить
£>= - (уАЛ’ + Л(,1) +в).	(9.8)
430	ПЛОСКАЯ ЗАДАЧА О СИНХРОНИЗАЦИИ ВИБРАТОРОВ [ГЛ. XIII
В соответствии с интегральным критерием устойчивости (см.
§ 8 главы V и § 5 главы IX) изучаемые синхронные движения
вибраторов могут отвечать лишь стационарным точкам
aft = a* функции D. При этом найденные из усло-
вий стационарности
дР  _ д(к + В)	д(А(1)- Л(11)- В) == _ (~2 Л + Л<П> + В) =
das	das	das	das
^-Ps(at, . . ., ak, w) = 0	(s=l, k) (9.9)
величины a;. = «’ являются одновременно (с точностью до зна-
ков) начальными фазами вращения вибраторов в соответствую-
щих движениях (порождающими фазами).
Точкам строгого минимума потенциальной функции D, нали-
чие которого обнаруживается путем анализа членов второго по-
рядка в разложении D по степеням cty —а’, действительно от-
вечают асимптотически устойчивые синхронные движения изу-
чаемого типа. При отсутствии минимума, обнаруженного тем
же путем, движение неустойчиво; неопределенный случай тре-
бует, вообще говоря, дополнительного исследования*).
Такой неопределенный случай, не вызывающий, однако, ка-
ких-либо осложнений, как раз имеет место в задачах о само-
синхронизации, а также о принудительной синхронизации по-
средством использования упругих синхронизирующих элементов.
Как уже отмечалось в § 4 настоящей главы, в этих задачах
одна из фаз aj может быть назначена произвольно, что является
следствием автономности исходных дифференциальных уравне-
ний движения системы.
При этом экстремумы функции D являются нестрогими: до-
бавление ко всем фазам а,- одной и той же постоянной а0 не
влечет за собой изменения значения функции D, которая в дан-
ных задачах зависит только от разностей а, — а;. Здесь должна
идти речь о стационарных точках и соответственно об экстре-
мумах функции D = —(Л + В) по k—1-й переменной, напри-
мер по со — ал, «2 — ссд., . . . , сел—1 — ah.
Несколько забегая вперед, отметим, что сформулированный
результат существенно упрощается в часто встречающемся па
практике случае задачи о самосинхронизации дебалансных ви-
браторов, обладающих одинаковыми положительными пар-
циальными скоростями. В таком случае
Л<И) = 0	(9.10)
и, кроме того, как будет показано в § 10 настоящей главы, воз-
*) См. сноску на стр. 434.
§ 9] ПОТЕНЦИАЛЬНАЯ ФУНКЦИЯ И ИНТЕГРАЛЬНЫЙ КРИТЕРИЙ 431
можно синхронное движение вибраторов с угловыми скоро-
стями, равными по модулю общей парциальной угловой скоро-
сти со*. При этом согласно формулам (10.9)
(as, osco ) = <ysL{sa} (o4-co ) — (co )
и в силу (9.6)
В = const.	(9.11)
В соответствии с равенством (9.7) в рассматриваемом слу-
чае за потенциальную функцию D может быть принято среднее
за период значение функции Лагранжа несущего тела, вычис-
ленное в порождающем приближении:
2л/щ
D = A(I) = -^- = J [7’<1)-П(1)]0Л.	(9.12)
о
Таким образом, отыскание порождающих фаз аь . . ., ал
в возможных синхронных движениях системы и исследование
устойчивости этих движений сводится в данном случае к изуче-
нию характера стационарных точек среднего за период 2л/со
значения функции Лагранжа Ls® = Г®— П®, вычисленного
только для несущего тела и для порождающего решения (4.2),
(4.7). Именно в таком виде последний результат был сформу-
лирован без доказательства, в качестве подтвержденной на ряде
примеров гипотезы, в совместной статье Б. П. Лаврова и ав-
тора [60].
В соответствии с формулой (9.8) за функцию D в рассмат-
риваемом случае можно также принять
2л/(0
£>= _ДА* = —J (AL’)dZ,	(9.13)
о
то есть взятое с противоположным знаком среднее за период
значение добавки к «собственным» лагранжианам вибраторов,
обусловленной колебаниями несущего тела; поправка при этом
вычисляется в порождающем приближении.
Эквивалентная формулировка интегрального критерия устой-
чивости, основанная на выражении (9.13) дана Б. П. Лавро-
вым [244].
Заметим в заключение, что при установке вибрирующего
органа машины на весьма мягких амортизирующих опорах
(случай, часто встречающийся на практике) потенциальной
энергией П® в равенстве (9.12) можно пренебречь, и тогда оно
принимает еще более простой вид:
2ntco
[r<I)Ur-	(9.14)
л
432
ПЛОСКАЯ ЗАДАЧА О СИНХРОНИЗАЦИИ ВИБРАТОРОВ
[ГЛ. XIII
Иными словами, устойчивым движениям таких машин могут
отвечать только точки минимума среднего за период значения
кинетической энергии вспомогательного тела.
Использование интегрального критерия устойчивости син-
хронных движений позволяет в ряде случаев существенно упро-
стить решение задач о синхронизации вибраторов и о синтезе
вибрационных машин с самосинхронизирующимися вибрато-
рами. В частности, при рассмотрении задач синтеза часто
удается на основе интуитивных энергетических соображений
сделать правдоподобные прогнозы о влиянии на фазировку ви-
браторов в устойчивом движении тех или иных конструктивных
изменений в системе и тем самым наметить направления поис-
ков решения. Примеры применения интегрального критерия
устойчивости при решении конкретных задач о самосинхрониза-
ции вибраторов приводятся в § 8 главы XIV и в §2 главы XXIII.
§ 10.	Основные соотношения и общий анализ задачи
о самосинхронизации вибраторов
1.	Основные уравнения в случае задачи о самосинхрониза-
ции. В общей форме основные результативные соотношения для
задачи о внутренней синхронизации вибраторов были рассмот-
рены в § 4 настоящей главы. Здесь мы конкретизируем эти
соотношения применительно к случаю задачи о самосинхрони-
зации.
В случае самосинхронизации вибраторы приводятся от асин-
хронных двигателей и электрические или механические связи
между роторами вибраторов отсутствуют. При этом моменты
Ss равны нулю и, согласно равенствам (6.8), L'"l> = asZ.(sa) (asco).
В результате уравнения (6.10) для определения порождающих
фаз ац . .. , ak принимают вид
Ps(a„ • • •> ak, w) =
=	(asco) - Rs (co) - W{SK} (ait . .., ak, co) -
- Wf} («!,..., ak, co)] = 0 (s=l.....k) (10.1)
или, при учете соотношений (6.4) и (6.9),
....ak, со) =-^-|asLla)(asco) - 7?s(co)-
k
- S miei	sin («s - «/) +
/=i
+ (QS/+VXjc°s(«s-Я/)][--0	(s= 1, .... k).	(10.2)
§ 10]	ЗАДАЧА О САМОСИНХРОНИЗАЦИИ ВИБРАТОРОВ	433
Для дебалансных вибраторов здесь должно быть положено
/;.ч = 0, а для планетарных h* = 1; для вибраторов, лишенных
двигателей или же работающих с отключенными двигателями,
следует положить asL{sa) (а3ы)	0.
Как и следовало ожидать, величины ац .... а* входят
в уравнения (10.1) и (10.2) только в виде разностей a.s— a,.
Очевидно, что среди таких разностей имеется лишь k—1 неза-
висимых, через которые легко выражаются все прочие. С дру-
гой стороны, в уравнения (10.1) и (10.2) входит угловая ско-
рость синхронного вращения со, которая в задаче о самосинхро-
низации является заранее неизвестной.
Таким образом, число независимых неизвестных в уравне-
ниях (10.1) и (10.2) как раз равно числу уравнений k, и поэтому
из этих уравнений, вообще говоря, определяются k—1 разно-
стей порождающих фаз, а также угловая скорость ю*). Что же
касается самих фаз ац . . . , ад, то они принципиально не могут
быть однозначно определены из уравнений (10.1) и (10.2), по-
скольку добавление ко всем фазам одной и той же произволь-
ной постоянной «о, в силу (4.2), эквивалентно изменению на-
чала отсчета времени t. Последнее же не меняет характера
решений исходной системы дифференциальных уравнений дви-
жения (2.44), так как в случае задачи о самосинхронизации они
являются автономными. Поэтому порождающие фазы опреде-
ляются из уравнений (10.1) или (10.2) только с точностью до
произвольной постоянной ао, или, что то же самое, из этих урав-„.
нений могут быть найдены лишь разности фаз as— aj.
При практическом решении уравнений всегда можно одну
из постоянных, например ад, положить равной нулю, а после
получения решения восстановить утраченную общность добав-
лением произвольной постоянной «о = ад ко всем as.
Таким образом, необходимым условием возможности само-
синхронизации вибраторов в случае движений рассматривае-
мого типа является наличие у уравнений (10.1) или (10.2)
решений, вещественных относительно фаз он,..., ад, определен-
ных с точностью до аддитивной произвольной постоянной, и по-
ложительных относительно угловой скорости и.
Окончательное решение вопроса о существовании изучаемых
синхронных движений, а также решение вопроса об их устой-
чивости, зависит от знаков вещественных частей алгебраиче-
ского уравнения k—1-й степени (4.12), где в соответствии
*) Напомним, что в задаче о самосинхронизации найденное таким обра-
зом со представляет ие точное, а приближенное значение модуля угловой
скорости синхронного вращения, вычисленное с точностью до членов первого
порядка относительно малого параметра ц включительно (см. § 3 главы VII
и § 2 главы IX).
434	ПЛОСКАЯ ЗАДАЧА О СИНХРОНИЗАЦИИ ВИБРАТОРОВ [ГЛ. XIII
с равенствами (10.1) и (10.2)
dPs	1 д (»'</' + W{sRr) __
dctj	ks daj
k
iw mrer l(Psr - hJsQsr) cos (as - ar) -
r=l
- (Qsr + hj'spsr) Sin (as - ar)] (S “ /)>
т,г> f- - cos -a/) -
-(Qs/ + W\/)sin (“«-«/)] <s^/)
(s, /=- 1, .... k),
(10.3)
причем штрих при знаке суммы указывает на пропуск слагае-
мого, соответствующего г = s.
Если для определенной системы значений угловой скорости и
и порождающих фаз at, . . . , ah, найденных из уравнений (10.1)
или (10.2), корни уравнения (4.12) имеют отрицательные веще-
ственные части, то соответствующее синхронное движение рас-
сматриваемого типа действительно существует и устойчиво
(асимптотически орбитально устойчиво) *). Если в числе кор-
ней имеется хотя бы один с положительной вещественной ча-
стью, то соответствующее синхронное движение неустойчиво-,
случай, когда среди k— 1 корней имеются нулевые или чисто
мнимые, требует дополнительного исследования как в отноше-
нии существования синхронного движения, так и в отношении
его устойчивости.
Как уже отмечалось в § 4 настоящей книги, вместо уравне-
ния (4.12) иногда удобнее рассматривать уравнение (4.10)
с пеотделенным нулевым корнем, который в таком случае не
принимается во внимание.
В случае задачи о самосинхронизации дебаланспых вибра-
торов (hi = /г2 = . . . = hh — 0) выражения (10.3) для элементов
определителя (4.10) резко упрощаются; кроме того, в силу из-
ложенного в § 8 главы V в этих выражениях могут быть без
всякого ущерба опущены положительные множители
msesa2/2Mks. Наконец, в указанном случае результаты решения
задачи о самосинхронизации вибраторов просто формулируют-
ся посредством интегрального критерия устойчивости синхрон-
ных движений (см. § 9 данной главы).
*) Напомним, что для устойчивости синхронных движений необходимо
также выполнение дополнительных условий устойчивости (5.29). Однако, как
уже отмечалось, эти условия обычно удовлетворяются автоматически,
§ 10]	ЗАДАЧА О САМОСИНХРОНИЗАЦИИ ВИБРАТОРОВ	43а
2. Общий анализ задачи о самосинхронизации. Парциаль-
ные угловые скорости. В дальнейшем уравнения (10.2) и (10.3)
будут использованы для решения различных прикладных задач
о самосинхронизации вибраторов. Здесь же мы остановимся
лишь на некоторых общих результатах, для получения которых
нет необходимости непосредственно решать трансцендентные
уравнения (10.2).
Рассмотрим сначала относительно более простой случай, ко-
гда все вибраторы являются дебалансными.
В этом случае (/г, = 1г% — . . . = Ilk = 0) основные уравнения
(10.1) и (10.2) приобретают вид
Ps(at, ..., ak, &) =
= ~ [щД0) (o-sco) — R° (со) — W(SK> (а,, ..., аА, со)] =
S osLsa} (asa) - Rs (со) -
k
- Т mfii lpsj sin (as - a/) + Qsj cos (as - ay)]| = 0 (10.4)
/=i
(s — 1, .. ., k).
Складывая эти уравнения и используя затем равенства
(6.17), приходим к соотношению
k	k
2 <ysI-Aa} (crsco) = 2 R°s (co).	(10.5)
S«1	S= I
Последнее уравнение, конечно, может быть получено также
и из общего уравнения баланса энергии (6.18). В данном слу-
чае это уравнение содержит только одно неизвестное — угловую
скорость синхронного вращения со, которая, таким образом,
определяется независимо от фаз cq, .. ., а&. Обычно уравнение
(10.5) при фиксированных значениях параметров имеет един-
ственное положительное решение; возможно, однако, что таких
решений несколько или они вовсе отсутствуют; в последнем
случае самосинхронизация невозможна.
Для дальнейшего удобно ввести в рассмотрение величины сщ,
которые равны угловым скоростям установившегося вращения
роторов вибраторов при условии, что последние установлены не
на вибрирующем теле В, а на неподвижном основании и что за
положительное направление угловой скорости принято направ-
ление, в котором вращается ротор s-ro вибратора в рассматри-
ваемом синхронном движении. Эти угловые скорости ws будем
в дальнейшем называть парциальными угловыми скоростями
вибраторов.
4зб	ПЛОСКАЯ ЗАДАЧА О СИНХРОНИЗАЦИИ ВИБРАТОРОВ [ГЛ. ХШ
Угловые скорости вращения роторов вибраторов, установ-
ленных на неподвижном основании ф80, определяются в данном
случае из уравнений
M^o) = 0<Ko|)sien<i,so>	U°-6)
а парциальные угловые скорости, согласно приведенному выше
определению, будут
®5 = ФЛ-	(Ю.7)
Таким образом, парциальная угловая скорость cos положи-
тельна, если s-й вибратор, будучи установлен на неподвижном
основании, вращается в том же направлении, что и в рассмат-
риваемом синхронном движении.
В случае, когда указанные направления вращения противо-
положны, то cos отрицательно; при этом двигатель асинхронного
типа работает в генераторном режиме*). Парциальные угловые
скорости вибраторов с выключенными двигателями или вообще
не имеющих двигателей равны нулю.
Допустим теперь, что все парциальные угловые скорости по-
ложительны и одинаковы:
coI = w2= ••• = сод, = со* > 0.	(10.8)
Тогда, в силу (10.6) и (10.7), справедливы соотношения
L{sa} (cTsto*) = (j3Rs (со*)	(s=l,	(10.9)
Складывая все эти равенства, умноженные предварительно
на o.s, получаем
k	k
2 <тДГ (<W) = 2 R°s (co*).	(10.10)
S=I	S—I
Последнее соотношение в точности совпадает с уравнением
(10.5) для определения угловой скорости синхронного враще-
ния cd. Таким образом, в случае одинаковых и положительных
парциальных угловых скоростей вращения дебалансных вибра-
торов одно из возможных значений угловой скорости синхрон-
ного вращения вибраторов cd равно общей парциальной угловой
скорости вращения вибраторов cd*:
со — - со*.	(10.11)
*) Напомним, что величины (>„ = ±1, входящие в равенства (3.1) и мно-
гие последующие соотношения, в задаче о самосинхронизации отнюдь не яв-
ляются параметрами рассматриваемой системы, а характеризуют лишь тип
исследуемого синхронного движения. Так, например, если о, = 1, о2 = 1,
Оз = —1 и т. д„ то это означает, что изучается синхронное движение, в кото-
ром роторы первого и второго вибраторов вращаются в положительном на-
правлении (то есть по ходу часовой стрелки), ротор третьего вибратора—
в отрицательном направлении и г. д.
§ iO]	ЗАДАЧА О САМОСИНХРОНИЗАЦИИ ВИБРАТОРОВ	43?
Если, как это часто бывает, уравнение (10.5) имеет един-
ственное решение, то синхронное вращение дебаланспых вибра-
торов может происходить только с угловой скоростью, равной
общей парциальной угловой скорости вибраторов со*.
Подобный вывод, вообще говоря, уже не будет справедлив
для системы с планетарными вибраторами, для которых соот-
ношение типа (10.5) имеет более сложную структуру.
Полученный результат легко понять, исходя из физических
соображений. Действительно, в дебаланспых вибраторах нали-
чие колебаний основания, на котором они установлены, прак-
тически не вызывает дополнительных потерь энергии на трение.
Поэтому естественно ожидать, что если такие вибраторы, бу-
дучи установленными на неподвижном основании, вращались
с одинаковыми по модулю угловыми скоростями, то при уста-
новке на колеблющемся теле эти вибраторы будут вращаться
с теми же средними угловыми скоростями. Положение, есте-
ственно, может измениться в случае планетарных вибраторов,
в которых затраты энергии на преодоление сопротивления ка-
чению роликов существенно зависят от характера колебаний
тела, на котором вибраторы установлены.
Заметим теперь, что при выполнении равенства (10.11) урав-
нения (10.4), в силу соотношений (10.9) и (7.9), приобретают
вид
n I	\	1 ,К/(Ю /	х	1 dA(I)
Ps(аь ..., аь со)= - Wls (а,, . . ., аА, со)	=
k
1? ~!1LJ^^,niedPsjsin(as-a!) + Qsicos(as--ai)] = 0 (10.12)
/=|
(s — 1, . .., k),
то есть порождающие фазы в данном случае определяются из
условия равенства нулю вибрационных моментов IES =• WsK> или,
что то же самое, из условий стационарности функции АО),
Нетрудно показать, что уравнения (10.12), по крайней
мере в большинстве случаев, допускают вещественные реше-
ния, то есть самосинхронизация вибраторов при одинаковых и
положительных парциальных угловых скоростях, как правило,
возможна. При этом во многих случаях указанные веществен-
ные решения могут быть достаточно просто найдены.
Пусть, например, вибрирующий орган машины (твердое
тело В) имеет одну поступательную степень свободы. Тогда ви-
брационные моменты F(SK) определяются формулой (8.4) и урав-
нения (10.12) допускают решения вида
ая=<7Л + ао	(10.13)
438
ПЛОСКАЯ ЗАДАЧА О СИНХРОНИЗАЦИИ ВИВРАТОРОВ
[ГЛ. XIII
где каждое из чисел q*s может быть равно нулю или единице,
а ао — произвольная постоянная.
В случае одной вращательной степени свободы вибрирую-
щего органа, когда вибрационные моменты WsK> определяются
по формуле (8.6), уравнения (10.12) также допускают веще-
ственные решения, в частности решения вида
as = — <тД + q*sn + а0 (s=l, ...,k).	(10.14)
Решения типа (10.13) уравнения (10.12) допускают и в слу-
чае, когда все вибраторы коаксиальны (то есть = г2 = ...
... — ru, Vi — v2 = ... = vit и 6| = бг = • • • = 6л) и вращаются
Рис. 31.
в одинаковых направле-
ниях (Щ = (Т2 = ... = щ).
При этом согласно фор-
мулам (6.5)
psI = р, Qsj = о
(s, j = i....k)
и уравнения (10.12) сво-
дятся к равенствам
k
2 ntjEj sin (щ —	— 0
(s = 1, ..., k).
(10.15)
Рассмотрим также случай, когда жесткости схЧ> и суч> равны
нулю, и допустим, что при этом
6S= оД±^“л,	(10.16)
где 6о — постоянная, а каждое из чисел q° может быть равно
нулю или единице. Иными словами, будем предполагать, что
оси вращения роторов всех вибраторов расположены на двух
прямых, пересекающихся в центре тяжести вспомогатель-
ного тела и образующих с осью соответственно углы 6о
и —б0; при этом па каждой из прямых располагаются оси ви-
браторов, вращающихся в одинаковых направлениях (рис. 31).
При этом согласно (8.7)
Wf (а,.....ак, а>) =
_ j_ mses^ у 1	. <WJ	(—1)	1 'OsOjVsVj
2 M ум
(s= 1, ..., k).	(10.17)
Отсюда следует, что в рассматриваемом случае уравнения
(10.12) также допускают систему решений типа (10.13).
sin (as — ay)
§ 10]	ЗАДАЧА О САМОСИНХРОНИЗАЦИИ ВИБРАТОРОВ	439
Простое вещественное решение уравнения (10.12) допускают
и для двух вибраторов (см. § 16 настоящей главы).
Итак, если все дебалансные вибраторы обладают одинако-
выми положительными парциальными скоростями, то их само-
синхронизация, как правило, возможна; при этом решения
основных уравнений (10.12) зачастую легко находятся.
Из соображений непрерывности отсюда следует, что и при
достаточно близких положительных парциальных скоростях cos
вибраторов самосинхронизация также возможна, по крайней
мере в большинстве случаев. Таким образом, близость пар-
циальных скоростей является одним из важнейших факторов,
обеспечивающих самосинхронизацию.
3.	О вибрационном поддержании вращения и «генератор-
ном» режиме работы вибраторов. Наличие самосинхронизации
вибраторов с одинаковыми или близкими положительными пар-
циальными скоростями не является неожиданным, поскольку
если вибраторы работали синхронно или почти синхронно, бу-
дучи установлены на неподвижном основании, то естественно
допустить, что и при установке их на вибрирующее тело будет
иметь место синхронное вращение этих вибраторов в тех же
направлениях.
Однако одинаковость и положительность парциальных ско-
ростей совсем не обязательны для возможности самосинхрони-
зации. Как мы убедимся ниже па конкретных примерах (см.,
в частности, § 16 данной главы), при определенных условиях
самосинхронизация имеет место даже и при очень большой
разности парциальных скоростей отдельных вибраторов. В част-
ности, двигатели одного или нескольких вибраторов могут быть
отключены или вообще отсутствовать, но, несмотря на это, та-
кие вибраторы будут работать синхронно с другими вибрато-
рами, снабженными двигателями. Между тем отключенные ви-
браторы, а также вибраторы, лишенные двигателей, обладают
нулевыми парциальными скоростями. Указанное весьма эффект-
ное явление, называемое вибрационным поддержанием вра-
щения, подробно рассматривается в главе XVIII настоящей
книги.
Заметим, что отнюдь не исключена и может быть эффек-
тивно использована самосинхронизация вибраторов, один или
несколько из которых имеют отрицательные парциальные ско-
рости. Двигатели таких вибраторов передают на вал вибратора
момент, направленный противоположно вращению вибраторов
в синхронном движении, и поэтому эти двигатели работают
в «генераторном» режиме*).
*) Термин «генераторный режим» обычно относится лишь к электриче-
ским или другим обратимым двигателям. Между тем в вибрационных маши-
нах могут использоваться и двигатели необратимого типа.
440
ПЛОСКАЯ ЗАДАЧА О СИНХРОНИЗАЦИИ ВИБРАТОРОВ
[ГЛ. XIII
Энергия, необходимая для преодолевания сил сопротивле-
ния в вибраторах с нулевыми и с отрицательными парциаль-
ными угловыми скоростями, передается, очевидно, от включен-
ных в сеть вибраторов благодаря колебаниям тела, на котором
они установлены. Вибрирующий орган представляет собой как
бы канал, передающий энергию, максимальная «пропускная спо-
собность» которого при прочих равных условиях имеет порядок
произведения массы вибрирующего органа па квадрат ампли-
туды вибраций и куб их частоты. Это вытекает из того обстоя-
тельства, что уравнения (6.11) после умножения обеих частей
на и приобретают смысл уравнений баланса мощности в каж-
дом вибраторе, причем слагаемые соWs = со (W[SK> + lEsW)
в этих уравнениях содержат, согласно (6.4), произведение
со3т58д.щ/-8; в качестве множителей во всех членах*).
Благодаря наличию этого «канала», мощности, подводимые
к отдельным вибраторам, перераспределяются между ними та-
ким образом, что происходит «выравнивание» угловых скоро-
стей вращения вибраторов — их самосинхронизация**).
§11. Основные соотношения и общий анализ задачи
о принудительной синхронизации вибраторов
1.	Принудительная синхронизация посредством использова-
ния двигателей синхронного типа. Если требуемый характер
движения вибраторов и вибрирующего органа (несущего твер-
дого тела В) не может быть обеспечен путем использования
явления самосинхронизации, то следует применить те или иные
способы принудительной синхронизации.
Рассмотрим сначала способ синхронизации и фазировки
вращения вибраторов, основанный на использовании синхрон-
ных электродвигателей. В этом случае, согласно формулам
(6.8),
=	(H-l)
Напомним, что здесь p.s — так называемые установочные
углы синхронных электродвигателей, определяющие ориенти-
ровку осей магнитных потоков их статоров, а синхронизирую-
щие моменты Ls (9S) при J0S|<OS удовлетворяют условиям
*)	Не следует забывать, конечно, что величины Prs и Q™ в выражениях
(6.4) также зависят от частоты о; однако эта зависимость при достаточном
удалении от зон резонанса является относительно слабой.
**	) Можно показать при достаточно общих предположениях, что угло-
вая скорость синхронного вращения о, по крайней мере в случае дебаланс-
пых вибраторов, не меньше, чем наименьшая, и не больше, чем наибольшая
из парциальных скоростей на доказательстве этого положения, однако,
не будем останавливаться.
§ 11]
ЗАДАЧА О ПРИНУДИТЁЛЬНОЙ СИНХРОНИЗАЦИЙ
441
(2.18)	и являются периодическими функциями угла 0S с пе-
риодом, равным 2л в случае использования для привода вибра-
торов двухполюсных синхронных двигателей без промежуточ-
ных редукторов, и периодическими функциями 0S с периодом
2л/1Рп в случае использования 2/г-полюсных двигателей и по-
нижающего обороты редуктора с передаточным отношением ip
(предполагается, что ip— целое число). Кроме того, синхрони-
зирующий момент LS(QS) обычно является нечетной функцией
угла 6S:
£s(-6s)=-М6Л	(И.2)
и тогда равенство (11.1) принимает вид
н”>(Ц.З)
Часто момент LS(QS) задают в виде
z^(os)- - (/I1 ’ sin zf M’es +/*2> sin 2z{,Ms)es),	(i 1.4)
где, согласно (2.18),
-&)	=-(/l1> + 2/<2))zf)n(s)>0.	(11.5)
\ “Os /0s= о
Иногда принимают LS(QS) еще в более простой форме:
LS(6S)- -/ssinz^<s)Os,	(Н.6)
где, аналогично неравенству (11.5), ls > 0.
Заметим также, что в случае вибраторов, приводимых от
синхронных электродвигателей, мы предполагаем, что направ-
ление вращения вибратора в изучаемом синхронном движении
совпадает с направлением его вращения при установке не-
уравновешенного ротора на неподвижном основании. Очевидно,
что в противном случае синхронный двигатель работает не-
нормально. Для вибраторов с двигателями асинхронного типа
такое предположение было необязательным (см. § 10 настоя-
щей главы).
При учете равенства (11.1), а также того обстоятельства,
что в рассматриваемом случае принудительной синхронизации
моменты Ss(ai, ..., а/,) системы синхронизации посредством
упругих элементов должны быть положены равными нулю,
уравнения (6.10) для определения порождающих фаз можно
представить в форме
Ps (а..... со) {°sLs [<Д (as - ₽.)] “	(®) -
-Г^(а„ ..., aft, Ю)-Г«>(а1, ..., ak, а>)] =- 0 (s = 1.k),
(Н.7)
442
ПЛОСКАЯ ЗАДАЧА О СИНХРОНИЗАЦИИ ВИБРАТОРОВ
[Гл. xtii
или, при учете соотношений (6.4) и (6.9), в виде
рДа1> •••> аР
k
- S [(Р5/ - hsf'sQsj) sin (as - а;.) +
/=i
+ (Qsj + hsf'PJ cos (as - И/)]] = 0 (s = 1, ..., k). (11.8)
Для существования синхронных движений изучаемого вида
необходимо, чтобы трансцендентные уравнения (11.8) допускали
вещественные решения относительно порождающих фаз аь ...
• • •, as-
Определенной системе значений а^а’, ..., aft —а*, удов-
летворяющих этим уравнениям, действительно отвечает един-
ственное и асимптотически устойчивое синхронное движение
указанного типа, если все корни алгебраического уравнения
(4.10) имеют отрицательные вещественные части*). При нали-
чии хотя бы одного корня с положительной вещественной
частью соответствующее синхронное движение неустойчиво-,
случай нулевых или чисто мнимых корней требует дополнитель-
ного исследования.
Элементы определителя, фигурирующего в уравнении (4.10),
в данном случае, согласно равенствам (11.7), (11.8), будут
daj ks rf0jOs=as(as_ps)	daj J
{/ , ♦ \	2
MUS P5/
- (Qsr + hsf'spsr) Sin (as - «г)]}	= /)>
=	\(psl - cos (“s - “/) -
- (Qsl + VZs/) Sin (as - a/)] (s /)
(s, /=1, . . ., k).
(11.9)
Штрих при знаке суммы здесь, как и выше, указывает на про-
пуск слагаемого, соответствующего г = s.
Рассмотрим уравнения (11.7), (11.8) и соотношения (11.9)
несколько подробнее. Заметим прежде всего, что если основа-
*) См. сноску на стр. 434.
§ П]
ЗАДАЧА О ПРИНУДИТЕЛЬНОЙ СИНХРОНИЗАЦИИ
443
ние, на котором установлены вибраторы, неподвижно, то мо-
менты Ws = WsK} + WsR' равны нулю, и уравнения (11.7) и (11.8)
обращаются в обычные уравнения установившегося режима
движения роторов синхронных электродвигателей при постоян-
ной внешней нагрузке:
•••> *)• (н.ю)
При этом уравнения движения отдельных вибраторов, есте-
ственно, оказываются совершенно независимыми. Обычные
условия устойчивости установившегося режима движения дви-
гателя
dLs \
Ms '0 =а
О
(И.Н)
получаются в случае неподвижного основания согласно (11.9)
и из уравнения (4.10). Эти условия в силу соотношений (2.181
всегда выполняются, если только значения сдвигов фаз as = а°,
определяемые из уравнений (11.10), таковы, что углы 6° =
= os(a° —Р5)не превосходят по модулю критических значений 0*.
Наличие вибраций основания, на котором установлены ви-
браторы, приводит к появлению дополнительных нагрузочных
моментов	..., ай, со) и	а&) м). Эти мо-
менты, как видно из уравнений (11.7) и (11.8), вообще говоря,
вызывают изменение углов ai, ..., aft по сравнению с их зна-
чениями а°, ..., а°к, соответствующими установившемуся ре-
жиму при условии установки вибраторов на неподвижное осно-
вание. Существенное изменение, согласно (11.9), претерпевают
и условия устойчивости движения.
В результате движение вибраторов, устойчивое в случае
установки последних на неподвижном основании, может ока-
заться неустойчивым в случае работы вибраторов на вибра-
ционной машине; и наоборот, движение, неустойчивое при не-
подвижной установке вибраторов, может оказаться устойчивым
при работе их па общем вибрирующем органе. Этот вывод,
подтвержденный экспериментальными исследованиями (см. гла-
вы XIX и XX настоящей книги), необходимо учитывать при про-
ектировании вибрационной машины с вибраторами, приводи-
мыми от синхронных электродвигателей.
Вместе с тем, как нетрудно видеть (см. также п. 5 § 16
настоящей главы, § 2 главы XV и §§ 3, 5 главы XX), путем
применения синхронных электродвигателей принципиально
всегда можно обеспечить существование и устойчивость син-
хронного движения вибраторов с любой наперед заданной ком-
бинацией порождающих фаз аь ..., а/(. Это достигается путем
444
ПЛОСКАЯ ЗАДАЧА О СИНХРОНИЗАЦИИ ВИБРАТОРОВ
(ГЛ. ХШ
надлежащего выбора установочных углов 01, Рл, а также
посредством выбора достаточно мощных двигателей, для кото-
рых модули производных dLsIdQs («жесткости» синхронизи-
рующих моментов) достаточно велики по сравнению с модулями
производных dWs/daj = д (Ws<! + W^/dap
2. Принудительная синхронизация посредством использова-
ния синхронизирующих элементов. Рассмотрим теперь способ
принудительной синхронизации посредством введения синхро-
низирующих элементов между роторами вибраторов в виде
упругих валов или систем типа электрического вала. Привод
вибраторов будем считать при этом осуществляющимся от дви-
гателей асинхронного типа.
Поскольку в данном случае время t не входит явно в урав-
нения движения системы, то данная задача имеет в точности
те же особенности, что и задача о самосинхронизации, подроб-
но рассмотренная в § 10 настоящей главы.
Основные уравнения (6.10) для рассматриваемого способа
синхронизации согласно формулам (6.8) представятся в виде
РДа,, аА, =	/?° («)-(а,, ..., а,, «>)-
-Г«>(а1( .... а,, ®)-Ss(a,, .... aj] = 0 (s = 1, k) (11.12)
или — при учете равенств (6.8) и (6.9) —в форме
Ps(ait ..., ak, w) = -^|osMa> (o5w) -/?° («) ~
- S "¥/	- hJ'sQsl)sin (as ~ а/) +
/-I
к	1
+ (Qsi + cos (as - «/)] - S cn (as - az - xs + X/) [ = 0 (11.13)
/»!	)
(5—1, . . . , k).
Как и в задаче о самосинхронизации, из уравнений (11.13)
определяются не только порождающие фазы аь ..., ай (с точ-
ностью до несущественной аддитивной произвольной постоян-
ной ао), но и приближенное значение модуля угловой скорости
синхронного вращения вибраторов ы.
Для возможности синхронных движений изучаемого типа
по-прежнему необходимо, чтобы уравнения (11.12) или (11.13)
допускали вещественные решения относительно ai, .... а/, и
положительное решение относительно а. Каждой системе зна-
чений = а*, . . ., ak = а’ и о = (о*, найденной из уравнений
(11.12) или (11.13), действительно отвечает единственное и
§ 12] О КОМБИНИРОВАНИИ РАЗЛИЧНЫХ СПОСОБОВ СИНХРОНИЗАЦИИ 445
асимптотически устойчивое синхронное движение рассматривае-
мого типа, если все корни уравнения (4.12) имеют отрицатель-
ные вещественные части*). При наличии среди указанных кор-
ней хотя бы одного корня с положительной вещественной
частью движение неустойчиво', в случае, когда у уравнения
(4.12) имеются нулевые или чисто мнимые корни, требуется
дополнительное исследование.
Выражения для производных от функций Ps, фигурирующих
в левой части уравнения (4.12), в соответствии с равенствами
(11.12) и (11.13) в рассматриваемом случае будут такими:
dPs	1 д (w™ + W{SR))
да,	k да,
1	s	I
г k '	k
i 2	2 Xе,- [(p.sr - hsf'QSry°$ («s - ar) -
Ir-1	r-l
- (Q,r + hsf'sPsr) Sin (“S - “,)] } (S = /).
CP +	[(ps/ - ЛЖ/) cos (as - %) ~
-(Q./ +V'Ps/)sin(ai.-a/)]}	(s^/)
(s, /=1, . . ., k).	(11.14)
Если все вибраторы, установленные па машине, являются
дебаланспыми, то модуль угловой скорости синхронного вра-
щения и определяется независимо от порождающих фаз
aj, ..., аь- Уравнение для определения ® при этом, естествен-
но, в точности совпадает с уравнением (10.5).
Как и при использовании соответствующих синхронных дви-
гателей, рассмотренным способом можно обеспечить существо-
вание и устойчивость движения вибраторов с любой наперед
заданной комбинацией фаз; это достигается путем надлежа-
щего выбора установочных углов и жесткостей csr (см., на-
пример, п. 6 § 16 настоящей главы и § 2 главы XV).
§ 12.	О комбинировании различных способов
синхронизации вибраторов
Выше различные способы синхронизации и фазировки вра-
щения вибраторов — самосинхронизация, электрическая и ме-
ханическая принудительная синхронизация — были рассмот-
рены в предположении, что они применяются в данной машине,
если так можно выразиться, в чистом виде. Между тем в ряде
случаев оказывается целесообразным использовать в пределах
*) См. сноску па стр. 434.
446
ПЛОСКАЯ ЗАДАЧА О СИНХРОНИЗАЦИИ ВИБРАТОРОВ
[ГЛ. XIII
одной машины или установки сразу несколько различных спо-
собов синхронизации и фазировки; иногда такой путь пред-
ставляется даже единственно возможным.
Так, например, в дробильно-измельчительных машинах, схе-
матически представленных в п. 16 таблицы 2, синхронность и
синфазность работы дебалапсных вибраторов (вибраторов-воз-
будителей) целесообразно обеспечивать путем использования
самосинхронизации или, если это не удается, путем применения
синхронных двигателей. Для обеспечения же синхронности ка-
чения дробящих тел (планетарных вибраторов) в машинах дан-
ного типа принципиально возможно только использование са-
мосинхронизации.
В вибрационных машинах и установках значительной дли-
ны, схемы которых изображены в пп. 10 и 256 таблицы 2, для
обеспечения синхронности и необходимой фазировки вращения
пары близлежащих вибраторов могут быть использованы меха-
нические синхронизирующие элементы, связывающие роторы
вибраторов; между тем для синхронизации и фазировки раз-
личных пар вибраторов, обычно удаленных друг от друга на
расстояние порядка 3—8 метров, можно использовать электри-
ческую синхронизацию.
С иной точки зрения машины и установки с комбинирован-
ной системой синхронизации вибраторов будут рассмотрены
в § 5 главы XV, в котором изучается задача синтеза машин
с несколькими механическими вибраторами.
Основные соотношения, необходимые для исследования раз-
личных комбинированных вариантов синхронизации вибрато-
ров, могут быть без труда получены как частные случаи из
общих уравнений (6.10) или (6.11). На анализе этих соотно-
шений можно не останавливаться, поскольку он подобен про-
веденному в §§ 10 и 11 настоящей главы для задач о само-
синхронизации и принудительной синхронизации.
§ 13.	Синхронизация вибраторов, установленных
на вибрирующем органе с одной степенью свободы,
в случае резонанса
1.	Описание системы и уравнения ее движения. Все пред-
шествующее исследование, проведенное в настоящей главе, от-
носилось к случаю движения машины вдали от резонанса, когда
модуль угловой скорости синхронного вращения вибраторов и
в достаточной мере отличается от частот собственных колебаний
вибрирующего органа машины' (несущего твердого тела В) на
упругих опорах; эти частоты определяются из уравнения (4.5).
В настоящем параграфе будет рассмотрено движение си-
стемы вблизи резонанса. При этом, поскольку по резонансной
СИНХРОНИЗАЦИЯ ВИБРАТОРОВ ВБЛИЗИ РЕЗОНАНСА
44'/
§ 13]
схеме обычно осуществляются лишь такие вибрационные ма-
шины изучаемого в настоящей главе тина, вибрирующий орган
которых имеет только одну степень свободы (см. таблицу 2),
мы ограничимся здесь исследованием именно этого случая.
Для конкретности предположим, что единственная степень
свободы вибрирующего органа (тела В) соответствует его по-
ступательному перемещению вдоль некоторой оси Ох (см. рис. 2
и п. 1 таблицы 2). Изучение более общего случая, соответ-
ствующего, например, схеме п. 2 таблицы 2, не представляет
каких-либо существенных особенностей.
Постановка задачи о самосинхронизации дебалансных ви-
браторов, установленных на вибрирующем органе с одной сте-
пенью свободы, была рассмотрена в качестве примера в § 1
главы I; решение этой задачи было дано в нашей работе [44].
Здесь мы изучим значительно более общий случай, когда ви-
браторы могут быть планетарными, а синхронизация — принуди-
тельной.
Уравнения движения рассматриваемой системы получаются
из первых k + 1 уравнений (2.44) и соответственно из первых
& + 1 уравнений (3.3), если положить в них у == 0 и <р = 0.
В результате последние из упомянутых уравнений запишутся
в форме
/& +	- as®) = Н'Т’ЛФь •••> Фь °> °, °> °, “0
Мх + схх = S mses (ф5 sin <ps + ф; cos <р 4 - ц/г'х.
S = 1
Здесь функция ц.Ф8 по-прежнему определяется формулой (3.2).
Рассматривая случай основного резонанса, будем предпола-
гать, что «относительная расстройка»
где р2х — сх/М — частота свободных колебаний тела В на упру-
гих элементах, есть величина порядка ц; тот же порядок при
этом следует приписать совокупности членов, фигурирующих
в последнем уравнении (13.1) под знаком суммы.
Тогда, заменяя в указанном уравнении величину p^ — cjM
ее выражением согласно (13.2), представим уравнения (13.1)
в форме
ls(fs + ks (<ps - <т5оэ) = p.<i»s (<p,, .. ,, <pb x, at)
(s=l.......k),	(13.3)
x -F co2x = цХ (ф, ф, ф, x, x, at),
448
ПЛОСКАЯ ЗАДАЧА О СИНХРОНИЗАЦИИ ВИБРАТОРОВ
[ГЛ. ХШ
где, в соответствии с (3.2),
цФз(ф........... Фь х, <о/) = р.ФДф|, • ••> Фь х, 0, 0, 0, 0, ©/) =
h
= - csjtys((j^s -O'/Ф/ -hs + %/) + mses [x sin <ps + g cos (<ps - %)]+
+ 6s(crsco, <ps, 0, 0, asat) — Rs (щсо, <ps, x, 0, 0), (13.4)
цХ (ф, ф, ф, x, x, co/) =
k
VI mses /..	.  ,	, kr . , г
= 2j ~~лГ (4 SH1 4 (₽sC0S ф«) ~ 7Й X + pw x-
s = l
2.	Уравнения для определения порождающих параметров и
их анализ. Квазилинейная система дифференциальных уравне-
ний (13.3) относится к тому же типу, что и изученная в § 4
главы VIII. Поэтому здесь можно было бы воспользоваться
полученными там результатами, считая только, что число син-
хронизируемых объектов (в обозначениях настоящего пара-
графа) равно k + 1, то есть считая тело, на котором установ-
лены вибраторы, одним из таких объектов. Можно, однако,
непосредственно применить теорему § 2 главы V, что и будет
сделано ниже.
Получающаяся из системы (13.3) линейная система с по-
стоянными коэффициентами имеет характеристические показа-
тели
О, s —	, k,
- Ф<0, s = k + 1, . . ., 26,
/со, s = 2k + 1,
— i(t>, s = 2k-\- 2,
(13.5)
причем элементарные делители, соответствующие 6-кратному
нулевому показателю, очевидно, будут линейными. Крити-
ческими характеристическими показателями являются в данном
случае X.s = 0 (s = 1, ..., k), Xzs+i = /со и ?^h+2 — —/со. Все эти
6 + 2 показателей образуют ведущую группу.
Как нетрудно видеть, в данном случае преобразование урав-
нений (13.3) к канонической форме может быть осуществлено
посредством соотношений
Фе Лз Л/s+s>	Фз 7 Л^ + s	($ ~ 1, • • • > 6),
1S
1 ,	ч .	1 .	(13.6)
х — 2 (Л2й+1 + Л2А+2), х — у /со (т|2& + [ — Л2й+г)>
§ 13]	СИНХРОНИЗАЦИЯ ВИБРАТОРОВ ВБЛИЗИ РЕЗОНАНСА	449
В новых переменных гц..........т]2*+2 система (13.3) предста-
вится в виде
T]S = CTSCO + p,J-(bs,	=_-^.T] -р^со + ц-кф^
«s	Js	Ks
(s=l,...,k),	(13.7)
'П2А + 1 ~ г’И112/г+1 —	Л24 + 2 = — r<arl2fe + 2 + И “ X.
Соответствующая уравнениям (13.7) порождающая система
допускает семейство синхронных решений
= as® + <rs + as), r)°fe+s = A
(s = 1, ..k),	(13.8)
C+l = ^toZ> n2ft+2 = Be-tor>
зависящее от k + 2 произвольных постоянных ai, ..., ал, A
и В. В исходных переменных то же решение имеет
<p° = as((o£+ as) (s=l, .... k),
x° = 1(Ле^ + Be~iat).
Поскольку x° должно быть вещественным, то
В — А.
Поэтому ПОЛОЖИМ
А = В — 1Ф, В = Р + 1Ф,
где F и Ф — вещественные постоянные. Тогда будем
х° = F cos со/ + Ф sin tut.
Теперь воспользуемся теоремой § 2 главы V с учетом ска-
занного в § 7 той же главы о возможности применения теоремы
также и к синхронным решениям соответствующих систем. Со-
гласно указанной теореме синхронные решения системы (13.3)
могут соответствовать лишь тем решениям (13.9) порождаю-
щей системы, для которых постоянные ai, .... ал, А и В
15 И. И. Блехман
ВИД
(13.9)
(13.10)
(13.11)
иметь
450
ПЛОСКАЯ ЗАДАЧА О СИНХРОНИЗАЦИИ ВИБРАТОРОВ
[ГЛ. ХП1
удовлетворяют уравнениям *)
2л/<о
W............
о
(« = 1....k),
Pk+i(ai, • • - , a*, A, В, oj) =
2Л/(о
CO / f
—----FT~ Ц -
2л co J
0
Лк+2(«1.....aft, А, В, &) =
X^°’ Ф0- <₽°- *°> x°' ^eiatdt = O.
. ., ф^, х°, <в/) dt = 0
(13.13)
, ф°, ф°, х°, х°, at)e~,<at di = Q,
Поскольку
Pk+^Pk+x,	(13.14)
то последние два уравнения (13.13) эквивалентны следующим
двум соотношениям, имеющим вещественную форму:
Re/\+1 = 0,	Im7\+1 = 0.
Производя интегрирование при учете равенств (13.4),
(13.12), (2.37) и (2.38), представим уравнения (13.13)
дующей развернутой форме:
Ps(«i> ..., <хА, A, B) = -£-[z,lm)((xs, cts<o) - R° (oj) -
-S,(O„ ....
- № («„ A+A,	J
(s = 1, . . . , k),
Pfe+i(ai, ..., aA, A, B, &) =
(13.15)
(13.9),
в сле-
as,

(13.16)
—> 2
-s=l
Рь+Лщ, ..., <хъ A, B, 0)) =
Г k
- I to S ТГ '“• + (P + 2n,0 В
= 0,
= 0.
-I/. 2
-s=l
*) В отличие от § 2 главы V, число переменных тц, соответствующих
ведущей критической группе характеристических показателей, равно k + 2.
Кроме того, в функции Р, здесь для удобства введен дополнительный поло-
жительный множитель ц(о/2л, что, конечно, не повлияет на результаты.
§ 13]	СИНХРОНИЗАЦИЯ ВИБРАТОРОВ ВБЛИЗИ РЕЗОНАНСА	451
Здесь, в соответствии с (13.11), обозначено:
I А + В В — А 1f/(G) ( А + В В — А \
ИТ’(as, -2-,	+ М ’(as,	<о) =
= (as, F, Ф, и) + Г10) (as, F, Ф, и) =
ms8c<t>2 [ А +В . В —А \ mse.sa>2 , „ .	,
= -Af— —2" 8111	---2Z- cos “s) = —f— (F sin as + Ф cos as),
(13.17)
Wf* (as,	<o) = (as, F, Ф, ®) =
= hsfs ~Н~ I ~2~ C0S -------2T~ Sin “J =
= /г^, «^(Fcos^-cDsina^ (13.18)
а моменты /Д'п) (as, cts<b) и Fs(<o) по-прежнему определяются
формулами (6.8) и (6.9) настоящей главы. При этом смысл
величин Lsm}, R°s, Ss и Ws = W'SK' +	+ Ws® здесь тот же са-
мый, что и смысл соответствующих величин, введенных в § 6
для нерезонансного случая *): все эти величины являются
средними моментами соответствующих сил, действующих на ро-
торы вибраторов, вычисленными в предположении, что дви-
жение системы происходит по закону
Ф? - Ф° = os (<о/+ as) (s = 1, ..., k),
.	(13.19)
х — х° = -^-(Ае1ш/ + Be~ia>t) = F cos <в/ + Ф sin <в/,
соответствующему порождающему решению. При этом каждый
из средних. моментов отсчитывается в направлении вращения
соответствующего вибратора в рассматриваемом синхронном
движении.
Первые k уравнений (13.16), как и уравнения (6.10), яв-
ляются уравнениями равновесия средних моментов, действую-
щих на роторы вибраторов при их движении по закону (13.19).
При решении уравнений (13.16) удобно освободиться от
комплексных величин; для этого достаточно перейти в указан-
ных уравнениях от комплексных амплитуд А и В = А к веще-
ственным амплитудам F и Ф по формулам (13.11), (13.17),
*) О дополнительно выделенном из W, слагаемом IF,0 будет сказано
ниже.
15*
452
ПЛОСКАЯ задача о синхронизации вибраторов
[ГЛ. XIII
(13.18) и представить последние два уравнения (13.16) в форме
(13.15). В результате получим систему
L'sm) (as, ctsoj) = Rs (<о) + Ss (ai, .. ., aft) +
+ r^(as, F, Ф, co) + W{SK} (as, F, Ф, <o) + W{sa) (as, F, Ф, <o)
(s = 1, .... k),
k
О r . V ms8s .	(13.20)
2nxF + рФ = 2j —Sin as,
s™ 1
k
pF - 2пхФ = - 2 cos czs.
Трансцендентные уравнения (13.20) (или, что то же самое,
уравнения (13.16)) просто решаются во многих практически
интересных случаях, в частности в случае задачи о самосин-
хронизации (см. ниже). При рассмотрении же других задач
зачастую вообще нет надобности прибегать к непосредствен-
ному решению этих уравнений (см. § 2 главы XV).
Заметим также, что полученные уравнения, как и уравне-
ния (6.10) для определения порождающих фаз при движении
вдали от резонанса, допускают простое физическое истолкова-
ние и могут быть формально легко получены из энергетических
соображений.
Последние два уравнения (13.20) легко разрешить относи-
тельно неизвестных F и Ф; при учете равенства (13.2) полу-
чаем
k
F / 2 ‘ л 2\ X (2/г* sin as — р cosas) =
М (Р +4«х) £
k
X mse,s cos (as + ys),
S = 1
k
ф = „ / 21 , 2\ X (p sin as + 2/гх cos as) =
AT (P +4nx) ZZ
(13.21)
1
S“1
k
X mse.s sin (as + yx),
§ 13]
СИНХРОНИЗАЦИЯ ВИБРАТОРОВ ВБЛИЗИ РЕЗОНАНСА
453
где обозначено:
(13.22)
В соответствии с (13.21) для амплитуды колебаний Н ви-
брирующего органа машины, соответствующей порождающему
решению (13.12), будем иметь формулу
Г k k
Н = /Р+Ф2 = — z- 1 === 1/ 2 S т°е°т!е!cos
(13.23)
Отметим, что последнее выражение в точности совпадает
с формулой для амплитуды установившихся вынужденных ко-
лебаний линейной системы с одной степенью свободы, описы-
ваемых последним из уравнений (13.1), при условии, что ро-
торы вибраторов вращаются равномерно по закону <ps ~ cps =
= cts (со/+ as). Различие состоит, однако, в том, что в данном
случае фазы а., слагающих возмущающего усилия не являются
заданными, а определяются из системы трансцендентных урав-
нений (13.20).
Заметим, что с помощью равенств (13.21) из первых k урав-
нений (13.20) можно исключить F и Ф и получить таким об-
разом, как и в нерезонансном случае, систему из k уравнений,
содержащих только порождающие фазы аь ..., aft. Для этого
достаточно исключить F и Ф из выражений (13.17) и (13.18)
для моментов 1Г.Ч с помощью равенств (13.21) и (13.22).
Тогда находим
=
k
= _ _^g>2	ntjEj [р sin (as - ay) - 2nx cos (as - a,)] =
2M (p + 4nx) "
k
_ _	--- I	(13.24)
V ('-$
454
ПЛОСКАЯ ЗАДАЧА О СИНХРОНИЗАЦИИ ВИБРАТОРОВ
[ГЛ. ХН1
k
W<R) = - hJ's	.. У m/e/ [p cos (a, - a,) +
2Л-1	|/(p2 + 4n2x)"
+ 2nx sin (as — a/)] =
i mses<£>2
J s 2Л4
k
J] m/e/cos(as-a/-Yx)- (13.25)
+ 4nx
/-I
1
Положим теперь, в соответствии с (13.24),
k
ИТ(а1- -> av	2+Р4№2 ^m/e/sin(a5-a/), (13.26)
Р х ja[
k
....»1’“)=2^7Г7Тт5'"Л“!! (»•-“<>	<13-27>
М Р TWX
и выясним смысл этих составляющих общего вибрационного
момента
= W{SK} +	+ Г'01.	i 13.28)
Прежде всего заметим, что согласно (13.23)
k
3^ю=о,	(13.29)
S = 1
к
3 ^ = пхМНг<л у=о,	(13.30)
то есть моменты связаны только с перераспределением
расхода энергии между отдельными вибраторами, но не
связаны непосредственно с дополнительными затратами энер-
гии в системе. Что же касается моментов , то они, так же
как и соответствующие моменты сопротивления WsK} связаны
не только с перераспределением нагрузки между отдельными
вибраторами, но и с затратами энергии в системе. Поэтому
составляющие вибрационного момента W'sKl можно назвать,
как и в § 6 настоящей главы, консервативными, а составляю-
щие и lTs0) — неконсервативными. Первая из этих состав-
ляющих обусловлена зависимостью сопротивления в пла-
нетарных вибраторах от движения несущего тела, а
вторая — сопротивлением при колебаниях этого тела.
Отметим, что выражения для Wf* и И^Л) аналогичны со-
ответствующим выражениям (8.4), полученным для нерезонанс-
§ 13]
СИНХРОНИЗАЦИЯ ВИБРАТОРОВ ВБЛИЗИ РЕЗОНАНСА
455
ного случая, и переходят в них, если пренебречь величиной 2пх
по сравнению cp=l- величины же W's°} при этом обра-
щаются в нуль. Указанное приближение означает не что иное,
как обычное пренебрежение влиянием сил сопротивления на
вынужденные колебания вдали от резонанса. Поэтому можно
сказать, что уравнения для определения порождающих фаз
ai, ..., ал, отвечающие нерезонансному движению, получаются
из уравнений (13.16) и (13.20) как частный случай.
Уравнение баланса энергии в системе в рассматриваемой
задаче получится, если сложить первые k уравнений (13.20) и
умножить обе части полученного равенства на со. Тогда будем
иметь
k	k
+	(13.31)
s=l	s-1
В силу равенств (13.29) и (13.30) это соотношение упрощается:
k	k
® 2 Um) = ® 2 (/?s + W(SR} + rl0)),	(13.32)
S"=»l
и может также быть представлено в форме
k	k
0) s L'sm} = 0) s (₽° + W{SR}) + ntMHW. (13.33)
S=1	s=»l
3. Условия существования и устойчивости синхронных дви-
жений вибраторов. В соответствии с теоремой § 2 главы V для
возможности синхронных движений необходимо, чтобы уравне-
ния (13.20) допускали вещественные решения относительно
ai, ..., as, F и Ф. Каждой системе величин a, = а,.......=
=а^, F = F* и Ф = Ф*, удовлечворяющей этим уравнениям, дей-
ствительно соответствует единственное и притом асимптотиче-
ски устойчивое синхронное движение изучаемого типа, если все
корни алгебраического уравнения k + 2-й степени
dp, L — х  • За(	dPt dak	dPt dA	dPt dB	
dPk	dPk „	dPk	dPk	
				
За!	duk	dA	dB	= 0 (13.34)
dPk+i	dPk + i	dPk+i	dPk + i	
За]	dak	—n	X dA	dB	
дР^+2	dPk+z	dPk+z	dPk+2	
да1	dak	dA	dB k	
456
ПЛОСКАЯ ЗАДАЧА О СИНХРОНИЗАЦИИ ВИБРАТОРОВ
[ГЛ. Х111
имеют отрицательные вещественные части. Если имеется хотя
бы один корень с положительной вещественной частью, то рас-
сматриваемое движение неустойчиво-, при наличии чисто мни-
мых или нулевых корней, вообще говоря, требуется дополни-
тельное исследование.
Вычисление элементов определителя, фигурирующего в ле-
вой части уравнения (13.34), не встречает затруднений. Как
следует из формул (13.16) для функций Ps, элементы последних
двух строк и столбцов этого определителя получаются ком-
плексными. Для удобства при проведении вычислений в про-
цессе решения конкретных задач целесообразно преобразовать
уравнение (13.34) к вещественной форме. С этой целью при-
бавим к k + 1-му столбцу определителя его k + 2-й столбец,
после чего вычтем k + 1-й столбец полученного определителя
из удвоенного k + 2-го. Те же операции затем проделаем
с k + 1-й и k + 2-й строкой.
Тогда после умножения k + 2-й строки и k + 2-го столбца
на i и сокращений при учете равенств (13.16) уравнение (13.34)
примет следующий вид:
dPi	дР, I mie,o2 ,	. .	.	\ I	.
-=-—x -j-—, -г---------s— (sin a + h f cos a I, —--------— (cos a -ft f, sin a,)
Sa,	oa/t ft 2	\	111 I/ ft 2	\	111	1/
1 mfteft(°2 /	Z \
-z’V^~(sin a*+v*cos “*>
dPk	dPk
da} .... da^
m.E]
—~ <o cos a.......——— о cos ab.
M	1	M	R
m.e.	mfteft
—ту2- o sin a.....- ,, K a> sin ah,
M	1 M	K
I тл<о!
-----— (cos ai sin a>.)
lb 2 k ft ft ft k)
(|)р
(Ор,
-о.
Здесь, в соответствии с формулами (6.7),
(13.35)
yi dL1^ tnsBM2
“ 2j °sr +	--------— [F (cos as - hjs sin as) -
r-l
- Ф (sin a, + hsf's cos as)] }	($ = /),	(13.36)
(s =# /),
причем штрих при знаке суммы указывает на пропуск слагае-
мого, отвечающего г = $.
Уравнение (13.35) уже не содержит комплексных коэффи-
циентов.
4. О случае, когда исследование устойчивости существенно
упрощается. Укажем на часто встречающийся в приложениях
§ 13]
СИНХРОНИЗАЦИЯ ВИБРАТОРОВ ВБЛИЗИ РЕЗОНАНСА
457
случай, когда в определителе (13.35) удается выделить ряд эле-
ментов, малых по сравнению с прочими, и в результате — су-
щественно упростить изучение знаков вещественных частей
корней этого уравнения.
С этой целью предварительно умножим два последних
столбца определителя (13.35) на Н, а две последние строки —
на 1/// и затем все элементы — на k\lmxzxHw?. Тогда уравне-
ние (13.35) представится в форме
аи —z ... а]А g, (sin а, + hxf'x cos а,) (cos а, — hxf\sin aj)
ат	akk~z	ik (sin ak + hkf'k cos ak) ik (cos ak ~ hJk sin ak)		= 0
£|dcosct| .	.. SA6cosafe	«*d + z	р’б	
sin а, .	E**sinat	p’d	-(n’d + z)	
(13.36')
где обозначено:
j _ V' 2с^	2	dL°m> _
ks	тхе,хН<л2	mxe,xH<s>2 das
г=»1
- 7f \F (C0S as - hJ's Sin О - °(Sin “s + Vs C0S as)])
(s = /),
ks тхг,хН<л2
(s, / = 1...........k),
kx mj^i	mle,j	^ia
kj mxex ’	mxex ’	& MST®2 *
z = 2x —, <6 = 2nr kZ , ,	(13.37)
* s	—.	Л? j CO
P P mxe.xH<n2
На практике часто встречаются машины и установки, в ко-
торых статические моменты неуравновешенных роторов mses и
коэффициенты ks имеют одинаковый порядок для всех вибра-
торов, моменты csr и dL^/das имеют тот же порядок, что и
моменты ms8sZ/co2, а моменты ksaj малы по сравнению с мо-
ментами МН2ы2. Тогда можно считать, что введенные выше
величины |s, |s и aSj имеют порядок единицы, а величина б
458
ПЛОСКАЯ ЗАДАЧА О СИНХРОНИЗАЦИИ ВИБРАТОРОВ
[ГЛ. ХШ
мала по сравнению с единицей. Малыми по сравнению с еди-
ницей следует считать, в соответствии с исходными предположе-
ниями настоящего параграфа, также и величины 2пх ^'^2 =
= п*6 и р—5-=р*6. Полагая, что эти величины имеют
порядок 6, заключаем в соответствии с (13.37), что пх и р’
имеют порядок единицы.
При указанных допущениях корни уравнения (13.36') можно
искать в виде рядов по целым степеням 61/А+2. При этом, по-
скольку нас интересуют лишь знаки вещественных частей кор-
ней, можно ограничиться нахождением лишь первых, не обла-
дающих нулевыми вещественными частями членов этих рядов.
При 6 = 0 уравнение (13.36') имеет два корня, равных нулю
(пусть это будут корни z°k+i и z°+2), и k корней г°, ..., z°k,
определяемых из уравнения
йц —	z°	а|2	...	а,*
Й21	а22	~ z°		• •	0,2k
Ok\	ak2	•	• •	dkk ~ z°
(13.38)
Корни Zfe+i и z/i+2 уравнения (13.36'), обращающиеся при
6 = 0 в нуль, как нетрудно заключить путем рассмотрения со-
ответствующего многоугольника Ньютона [418], можно разы-
скивать в виде
Zk+1, k+2 ~ ®Z*+1, k+2 + •••’	(13.39)
где невыписанные слагаемые имеют относительно 6 порядок
малости выше первого.
Подставив выражение (13.39) в уравнение (13.36') и при-
равнивая . нулю коэффициент при 62 в разложении определи-
теля по степеням 6, получаем для нахождения величин
и z^+2 следующее квадратное уравнение:
аи	... axk	g, (sin а, 4- fij, cos aj g, (cos a, - hj' sin
aki	••• akk	h (sin ak + hkf'k c°s ak) ^(cosaA-/i^sinaA) =Q
^cosa, ... gAcosaft	ra*+z(1)	p’
^sina, ... gfesinaft	p’	-(«’-i-z(1))
(13.40)
Если корни уравнений (13.38) и (13.40) имеют отличные от
нуля вещественные части, то для решения вопроса об устой-
§ 13]	СИНХРОНИЗАЦИЯ ВИБРАТОРОВ ВБЛИЗИ РЕЗОНАНСА	459
чивости при достаточно малых 6 можно ограничиться выясне-
нием знаков вещественных частей этих корней; в противном
случае следует искать дальнейшие приближения к корням с ну-
левыми вещественными частями.
Изучение знаков вещественных частей корней уравнений
(13.38) и (13.40) значительно проще соответствующей задачи
для уравнения (13.35).
Особенно существенные упрощения достигаются в случае за-
дач о самосинхронизации или о принудительной синхронизации
посредством использования синхронных двигателей, когда коэф-
фициенты cSj равны нулю и поэтому, согласно (13.37), обра-
щаются в нуль все недиагональные элементы определителя
(13.38). Тогда
о	*1 /	2 dLsm} . ’ ,Е/	, £, • Ч
- O(sin as + hsf's cos as)]|	(s = 1, ..., k), (13.41)
и поскольку все коэффициенты ks предполагаются существенно
положительными, то условия устойчивости, связанные с кор-
нями £1, .... £а, сводятся к неравенствам
dC™' т.ъ.а? . ,	,	.	,	, ,	,
___ < __— Р (cos a-hsrs sin as)-0> (sin as + hsfs cos as)] (13.42)
(s = 1, .... k).
5. Случай задачи о самосинхронизации. Рассмотрим теперь
более подробно случай задачи о самосинхронизации вибрато-
ров. Как уже неоднократно отмечалось (см., например, п. 5 § 3
главы V), результативные соотношения для этого случая могут
быть получены из соответствующих формул задачи о внешней
синхронизации.
А именно, если считать, что неизвестное в задаче о само-
синхронизации значение первого приближения к синхронной
угловой скорости определяется из условия обращения в нуль
линейного относительно ц члена поправки к периоду, то урав-
нения (13.16) (или, что то же, уравнения (13.20)) могут слу-
(	Рх\
жить для нахождения <в (или расстройки р=1-------и пара-
метров ai, ..., aj, А и В порождающего решения. При этом
одно из неизвестных ai,	А и В или же одно дополни-
тельное соотношение между ними вследствие автономности
исходной системы можно задать произвольно. В результате
число неизвестных в указанных уравнениях по-прежнему будет
равно числу уравнений.
460
ПЛОСКАЯ ЗАДАЧА О СИНХРОНИЗАЦИИ ВИБРАТОРОВ
[ГЛ. XIII
Положим, например, А = В. Тогда в силу равенств (13.11)
и (13.23) будем иметь
Я = В = ^ = /7,	(7 = 0.	(13.43)
Ограничимся рассмотрением машин с дебалансными вибра-
торами. Тогда при учете равенств (13.17) и (13.43) уравнения
(13.20) примут следующий простой вид*):
щДа> (щсо) = Rs (со) + mse2s0) И sin as
(s-1, ..., А:),	(1344)
k	k
2пхН = ’S sin as, pH = - cos as.
S“1	S«1
Наличие у последних уравнений решений, вещественных от-
носительно аь .... ак и Н и положительных относительно со,
является необходимым условием возможности самосинхрониза-
ции вибраторов, реализующейся при движениях изучаемого
типа. Эти необходимые условия, а также и сами решения урав-
нений (13.44), в данном случае могут быть легко получены
в явной форме.
Действительно, при выполнении условий
k
^Z°(as, ®)>0,	|Z°(as, со)|^^^ (s = 1, ..., k), (13.45)
S»1
где
Z°s(as, ®) = asLsa} (crsco) — /?s(co),	(13.46)
первые k + 1 уравнений (13.44) допускают относительно ампли-
туды Н и фаз ai, ..., аь вещественные решения вида**)
Н =
(13.47)
as = n^4-(-l)4“.
*) Напомним, что в задаче о самосинхронизации моменты Ss тожде-
ственно равны нулю, а моменты (as, 0sai), согласно (6.8), заменяются
их значениями для двигателей асинхронного типа.
**) Заметим, что то же самое выражение амплитуды Н получается для
данного случая из уравнения баланса энергии (13.29).
$ 13]	СИНХРОНИЗАЦИЯ ВИБРАТОРОВ ВБЛИЗИ РЕЗОНАНСА	461
Здесь
1 о . 2Z°(as, ®)	1
arcsin	< у л> <13’48)
а любое из чисел q*s может быть равно нулю или единице;
каждой комбинации из k таких чисел отвечает определенное
решение уравнений (13.44).
Заметим, что по своему смыслу величина Zs(as, ®) пред-
ставляет превышение среднего вращающего момента двигателя
s-ro вибратора над средним моментом сил сопротивления при
условии, что эти моменты отсчитываются в направлении вра-
щения вибратора в рассматриваемом движении. Поэтому ве-
личину Zs(as, со) можно назвать избыточным моментом на валу
s-го вибратора.
Подставив выражения (13.47) в последнее из уравнений
(13.44), приходим при учете обозначения (13.2) к следующему
уравнению для определения модуля угловой скорости*) син-
хронного вращения со:
со2 Н	М У	т2е2№со4
s»|	г	6 о
-------" V (-D’l Л.
1/ м 2	°)SD|	у ms8s“2 S ®)
r /=1	/_|
(13.49)
Определив из уравнения (13.49) величину со и подставив ее
в выражения (13.47), получим значения порождающей ампли-
туды Н и порождающих фаз 0ц, ..., ан-
Уравнение (13.49) имеет достаточно сложную структуру, од-
нако величина со из него легко определяется, если, как это
предполагалось выше, движение происходит вблизи резонанса,
. Рх
так что расстройка р=1—есть величина порядка мало-
сти pi.
Действительно, полагая р = pip' и обозначая через р(со) =
= цр'(со) правую часть равенства (13.49), находим по фор-
муле (13.2), с точностью до членов первого порядка малости
включительно,
со « рх[1 +урр' (Рх)] = ря[1 + у Р(Рх)]>	(13.50)
*) См. сноску на стр. 433.
462
ПЛОСКАЯ ЗАДАЧА о синхронизации впвраторов
[ГЛ. XIII
где, в соответствии с (13.49),
Р (Рх) =
(kx = 2пхМа>).
2kx\z°s(as, Рх)]2
k
2 Z/ (°i' Рх)
i-i
(13.51)
Таким образом, уравнения для определения порождающих
параметров в данном случае допускают решение в общей
форме.
Обратимся к рассмотрению вопроса об устойчивости син-
хронных движений, причем ограничимся изучением случая,
когда справедливы сформулированные выше предположения
о порядке величин gs, £s и 6, так что изучение корней уравне-
ния (13.35) (или, что то же самое, уравнения (13.36')) сво-
дится к рассмотрению знаков вещественных частей корней урав-
нений (13.39) и (13.40).
Поскольку в рассматриваемой задаче о самосинхронизации
дебалансных вибраторов cSj = 0, L'™’ = <JsL(s'(os, со), hs = О, F = И
и Ф = 0, то, в соответствии с (13.37), корни уравнения (13.38)
будут
17cos“s = ~ Lcos“s (s=I,..., fe), (13.52)
а уравнение (13.40) примет		вид			
-£i cos at	0	0	sin a.	cos a.	
0	-cosa2 ...	0	£2 sin a2	b cos a2	
0	0	...	~ cos	Asinas.	Ik cos aft	= 0.
С, cos a,	C2 cos a2 . . .	cos a .	nx + г(|)	P*	
t, sin a. ~1	1	?2sina2 ...	C* sin ak	P*		
(13.53)
Прибавив к последнему столбцу определителя в левой части
уравнения (13.53) все прочие столбцы и учитывая, что вели-
чины й|, ..., % и // удовлетворяют последним двум уравне-
ниям (13.44), получим столбец, все элементы которого, кроме
нижнего, равны нулю, а нижний элемент равен —г<'>. Отсюда
следует, что один из корней уравнения (13.53), как и следовало
ожидать, непременно равен нулю. Вопрос об устойчивости ре-
§ 13) СИНХРОНИЗАЦИЯ ВИБРАТОРОВ ВБЛИЗИ РЕЗОНАНСА 463
шается знаками вещественных частей прочих корней уравнений
(13.38) и (13.53).
Для завершения исследования устойчивости остается найти
второй корень уравнения (13.53); этот корень определяется из
уравнения, которое получается из (13.53) в результате прибав-
ления к последнему столбцу определителя всех прочих столб-
цов и последующего сокращения на zO);
-|i cos a,	0	. 0	£1 sin a.	
0	- £2 cos a, ..	. 0	&>sina2	
				= 0. (13.54)
0	0	•	COS Ct	Ik sin ak	
Cl cos a.	?2 cos a2 ..	Ik cos ak	П+Z1'1'!	
Прибавив к последней строке определителя в левой части
последнего уравнения все прочие строки, предварительно умно-
женные на (/ — номер строки), получим строку, все эле-
менты которой, кроме последнего, равны нулю. Таким обра-
зом, в предположении, что cosaj¥=0 (/= 1, ..., k) *), корнем
уравнения (13.54) будет
z(1) = — п' — 2 Zt sin а/.
Согласно равенствам (13.37) и предпоследнему уравнению
(13.44) отсюда получаем
z<D = -2n*<0.	(13.55)
Поскольку найденный корень существенно отрицателен, то
решение вопроса об устойчивости зависит только от знаков вы-
ражений (13.52). Сопоставление этих выражений с формулами
(13.47) и (13.48) показывает, что условия устойчивости
ReZy<0 (/ = 1, ..., k) выполняются только для того синхрон-
ного движения вибраторов, для которого все числа q*s в равен-
ствах (13.47) равны нулю, то есть для решения, которому от-
вечают значения порождающих фаз
.	2Z°(a_, ш)
as = X, = arcsin ---Я(д2-.	(13.56)
Все прочие синхронные движения являются неустойчивыми.
Согласно формулам (13.50) и (13.51) в устойчивом движе-
нии р^О, и поэтому ы-^-рх, то есть это движение является
*) Заметим, что согласно равенствам (13.47) и (13.48) величины cos а.<
могут обратиться в нуль только на границе области существования рассма-
триваемых движений, определяемой неравенствами (13.45).
464
ПЛОСКАЯ ЗАДАЧА О СИНХРОНИЗАЦИИ ВИБРАТОРОВ
1ГЛ. XIII
дорезонансным. Заметим также, что если параметры всех ви-
браторов и избыточные моменты Zs(as, со) одинаковы (или
почти одинаковы), то в устойчивом движении вибраторы вра-
щаются синфазно (или почти синфазно).
Полученный результат может оказаться несправедливым
лишь вблизи границы области существования синхронных дви-
жений, определяемой условиями (13.45), ибо на самой границе,
как уже отмечалось, по крайней мере одна из величин cosaj
(/= 1, ..., k) равна нулю. При этом решение вопроса об
устойчивости движения зависит от членов более высокого по-
рядка в разложениях корней уравнения (13.36') по степеням
параметра 6.
Подчеркнем также, что сформулированный результат отно-
сится к случаю, когда параметры и имеют порядок еди-
ницы, а параметр д мал по сравнению с единицей. В противном
случае картина может оказаться более сложной. В частности,
могут оказаться устойчивыми и послерезонансные синхронные
движения.
Заметим, что исследование, аналогичное проведенному, мо-
жет быть без особых затруднений выполнено и для систем
с вибраторами планетарного типа.
Полученные в настоящем параграфе общие результаты ниже
будут использованы для изучения систем более конкретного
вида (см. п. 4 § 16 настоящей главы, а также главу XX).
§ 14. О законе движения системы при установившемся
синхронном вращении вибраторов
В значительном числе прикладных задач о синхронизации
требования синхронности и определенной фазировки вращения
роторов вибраторов не являются самоцелью: определенный
закон движения вибраторов необходим для того, чтобы обеспе-
чить заданный технологическими требованиями закон колеба-
ний вибрирующего органа машины или установки (см. гла-
ву XV книги). Так, например, в машинах, схематически пред-
ставленных в пп. 3—5, 8, 10, 11, 13, 17, 23 и 25 таблицы 2,
приведенные в четвертом и пятом столбцах таблицы условия
вытекают из необходимости обеспечить (с определенной точ-
ностью) прямолинейные поступательные колебания рабочего
органа машины.
Таким образом, вопрос о нахождении закона движения эле-
ментов системы, в частности закона движения вибрирующего
органа (тела В), имеет существенное значение.
Как правило, при решении прикладных задач оказывается
достаточным определить движение роторов вибраторов и ви-
брирующего органа с точностью, отвечающей исходному при-
§ 141
О ЗАКОНЕ ДВИЖЕНИЯ СИСТЕМЫ
465
ближению. В случае вибрирующего органа с плоскопараллель-
ным движением вдали от резонанса указанное исходное при-
ближение определяется соотношениями (см. равенства (4.2)
и (4.7))
<р° = cr s (со/+ as)	(s=l,	(14.1)
k
x° = 2 [X cos (at + as) + GsBs sin (at + as)],
S=1
k
y° = 'S [Cs cos (at + as) + asD°s sin (at + as)]>	(14.2)
s«l
fe
<p° = 2 ~M~S' W cos (co/ + as) + asN°s sin (co/ + as)].
S“I
Здесь порождающие фазы as находятся из трансцендентных
уравнений (6.11) (или — в частных случаях — из уравнений (10.2),
(11.8), (11.13)), причем устойчивым синхронным движениям мо-
гут отвечать лишь те системы значений ai, ..., а*, удовлетво-
ряющие указанным уравнениям, для которых все (или все, за
исключением одного) корни алгебраического уравнения (4.10)
имеют отрицательные вещественные части. Постоянные вели-
чины As, Bs, , Ns в равенствах (14.2) связаны с исходными
параметрами системы соотношениями (4.8), (4.5) и (4.6).
В задаче о синхронизации вибраторов, установленных на
вибрирующем органе с одной степенью свободы, исходное при-
ближение для закона движения системы дается соотношениями
(см. равенства (13.19))
Фз = as(®z + as) (s=l, •••> k),	(14.3)
x° = F cos at + Ф sin at,	(14.4)
где порождающие фазы as и порождающие амплитуды F и Ф
определяются из трансцендентных уравнений (13.20). При этом
устойчивые синхронные движения отвечают лишь тем комби-
нациям постоянных ai, ..., ak, F и Ф, для которых все (или,
быть может, все, кроме одного) корни алгебраического урав-
нения (13.36х) имеют отрицательные вещественные части.
Заметим, что формулы (14.2) и (14.4) соответствуют пред-
положению, что вибрирующий орган машины (тело В) совер-
шает малые вынужденные колебания под действием возмущаю-
щих сил вибраторов, равномерно вращающихся по закону,
определяемому равенствами (14.1) и (14.3).
466
ПЛОСКАЯ ЗАДАЧА О СИНХРОНИЗАЦИИ ВИБРАТОРОВ
[ГЛ. XIII
Таким образом, можно сказать, что равенства (14.1) —(14.4)
определяют движения системы с точностью до колебаний фаз
вращения вибраторов вблизи средних значений as и с точно-
стью до соответствующих искажений, вносимых этими колеба-
ниями фаз в движение вибрирующего органа.
Вычисление последующих приближений в разложениях ко-
ординат ф8, х, у и ср в ряды
Ф5 = о Д®/+ as + цф*/’(ш/) + ...]	($=1...........k),
х = х° (м/) 4- цх(1) (tot) 4- ..., у = //°(м/) 4-	(со/) 4- ..., (14.5)
Ф = ф° (со/) 4- р.ф( ° (со/) + ...
по степеням малого параметра ц может представить интерес
лишь при оценке упомянутых выше искажений.
Как правило, присутствие искажений, о которых идет речь,
является нежелательным. Однако в некоторых случаях эти
искажения, связанные с появлением в движении вибрирующего
органа высших гармоник, могут оказаться полезными с тех-
нологической точки зрения.
Заметим также, что наличие колебаний фаз вращения ро-
торов вибраторов цфй’ (со/) 4- ... объясняет значительный шум
и интенсивный износ в зубчатых или цепных передачах, на-
блюдаемые при «жесткой» кинематической синхронизации и
фазировке вибраторов.
Процесс вычисления последовательных приближений в раз-
ложениях (14.5) был рассмотрен в § 9 главы V настоящей
книги. В изучаемой задаче о синхронизации вибраторов это вы-
числение не связано с принципиальными трудностями, посколь-
ку, несмотря на нелинейность порождающей системы уравнений
(4.1), общее решение уравнений в вариациях для этой системы
удается легко найти*). Поэтому на указанном вопросе можно
не останавливаться. Простейший пример вычисления приближе-
ния цф^1’ (со/) приводится в работе [48].
Приведем в заключение формулы, выражающие закон дви-
жения произвольной точки вибрирующего органа (тела В) че-
рез обобщенные координаты х, у и ф. Обозначая через и* и v*
координаты точки в системе осей uO\v, связанной с телом,
а через х* и у* — координаты той же точки в неподвижных
осях хОу, будем иметь (см. рис. 26)
х* = х 4- и* cos ф 4- v* sin ф,
у* — у — и* sin ф 4- v* cos ф.	(^4.6)
*) Разумеется, однако, что п здесь, как обычно, громоздкость вычисле-
ний быстро нарастает по мере увеличения номера приближения.
движение роликов без отрыва И СКОЛЬЖЕНИЯ
467
§ 15]
Сохраняя в последних равенствах лишь члены, линейные
относительно малого угла поворота ф, получаем
X = X + и + V ф,
.	.	(14.7)
у = у — и ф + V .
§ 15. Условия, при которых ролики или кольца планетарных
вибраторов движутся без отрыва и скольжения
При выводе уравнений движения рассматриваемой в настоя-
щей главе системы предполагалось, что движение ролика внут-
реннего планетарного вибратора (или кольца внешнего плане-
тарного вибратора) происходит без нарушения контакта между
роликом и стаканом (или между кольцом и осью) и без про-
скальзывания в точке контакта (см. § 2). Для того чтобы это
имело место, в любой момент времени рассматриваемого дви-
жения должны выполняться неравенства
^>0,	(15.1)
— f°Ns< Fs<f°Ns.	(15.2)
Здесь Ns, как и выше, — нормальная реакция, действующая на
тело качения в точке контакта со стаканом или с осью, Fs—
сила трения, приложенная в той же точке (см. рис. 30, б, в), и
— коэффициент трения покоя.
Нормальная реакция Ns, найденная из уравнения относи-
тельного движения центра тяжести тела качения в проекциях
на нормаль к траектории, согласно (2.31) определяется по фор-
муле
= ms Ms + g sin (<PS - %) - Xos COS ф8 + ijos sin ф8]. (15.3)
Выражение для силы трения Fs получим из того же урав-
нения в проекциях на касательную к траектории центра тя-
жести:
Fs = mJ -	4- g cos (ф5 - %) + xos sin ф5 4- yos cos ф4.].	(15.4)
Заменив в последней формуле ускорение ф., его значением со-
гласно первым k уравнениям движения (2.44), взятому для слу-
чая Z, = 1 (качение без скольжения), и воспользовавшись ра-
венствами (2.27) и (2.32), представим выражение для силы
трения Fs в виде
Fs = ms [g cos (ф5 - %) 4- xos sin ф8 + yos cos фх] -
k
~!~s	csias (<т5ф5 <tуф/ xs 4~ X/) ks (<p5 щ<л) 4“
/=i
+ mses [g cos (ф5 - %) 4- xos sin фх 4- yos cos Ф.,] 4-
4-Д„М~Ф + Ls(asto, <ps, ф, Ф, <Jsat) - Rs (а4.и, <ps, x, ij, ф)). (15.5)
bs	J
468
ПЛОСКАЯ ЗАДАЧА О СИНХРОНИЗАЦИИ ВИБРАТОРОВ
[ГЛ. xtn
В дальнейшем при вычислении сил Ns и Fs по формулам
(15.3) и (15.5) вместо обобщенных координат системы <р5, х, у
и <р будем подставлять их значения ф°, х°, у° и <р°, соответ-
ствующие исходному приближению (см. равенства (14.1) и
(14.2)).
Тогда условие (15.1) может быть записано в форме
еХ > - g sin (q>° - %) - Vx2os + ifts cos (q>° 4- xs).
Здесь Xs — углы, конкретные выражения которых для дальней-
шего несущественны.
Последнее неравенство наверняка выполняется, если
es®2 > g 4- ws,	(15.6)
где через ws обозначено наибольшее значение ускорения
Vx2os + yos оси вибратора.
Для вычисления ws заметим, что координаты xos и yos оси,
в соответствии с равенствами (2.32) и (14.2), могут быть пред-
ставлены в форме
X = и + Х^ COS (At 4- Xf sin (At,
z/os = nos 4-У<.” cos ш/4-У® sin
где обозначено:
k
ч" - s тг +v "i)cos °'+(s;+sin ° J 
/»!
k
=S T b &+V	cos “/ - (A°+V M°dsin a J ’
'=k'	(15.8)
=2 дг l(cr Hcos “/+«/	- v ^)sin a J ’
/=1
k
- S tt Ь (°; - т (ч - т «;) ^4
/“1
Воспользовавшись выражениями (15.7), после несложных
преобразований находим
“’s = (VC + ^S)max==
=	{(х<'>)2 4- (У10)2 + (Х<2))2 4- (у<2))2 +
4- [(/?)2 4- т2 - (х<2>)2 - т2]2 4- 4 (х№ 4- У^У<2))2}'\ (15.9)
§ 16]	ДВИЖЕНИЕ РОЛИКОВ БЁЗ ОТРЫВА И СКОЛЬЖЕНИЯ	469
Аналогичным образом, но в результате более сложных вы-
кладок с использованием формул (2.35), (2.37) и (6.8) полу-
чается следующее условие, обеспечивающее выполнение нера-
венств (15.2) в любой момент времени установившегося син-
хронного движения:
f°ey>Sup(X <)•	(15.Ю)
Здесь символом Sup (/С, As) обозначена наибольшая из вели-
чин А* и АГ, определяемых по формуле
АГ =(g+ ®s) j/^(1----+{—rf~asfs ± /s) *
Is
k
- S csl (“s - “/ - *s + */) - fsmses “2 - ^sA И +
^CS^sRs 9	/ dL
“^Гв+,1И
*\	I2
г +(?Ж<»)2.
s VSMS)-
(15.11)
причем Ф есть амплитуда колебаний угла ср0, которая в соот-
ветствии с (14.2) может быть представлена в виде
Ф = V (ф(|))2 + (ф(2,)2>	(15.12)
где
ф’1’ = J} (Ms COS as + оЖ Sin as),
'T	(15.13)
ф(2) = 'S (.°s№s cos as - M°s sin as).
/“i
Итак, для соблюдения условий (15.1) и (15.2), обеспечи-
вающих отсутствие отрыва и проскальзывания роликов или ко-
лец планетарных вибраторов, достаточно выполнения нера-
венств
es®2 > g + wst
f°es®2> Sup (A*, As~).
(15.14)
Заметим, что при достаточно большом ускорении едо2 эти усло-
вия всегда выполняются.
В случае задачи о синхронизации вибраторов, установлен-
ных на вибрирующем органе с одной степенью свободы, при
движении системы вблизи резонанса условия (15.14) сохраняют
470
ПЛОСКАЯ задача о синхронизации вибраторов
[ГЛ. XIи
свой вид, однако выражения для величин ws и Л* существенно
упрощаются; в этом случае, как нетрудно видеть,
ws = w = J/ F2 + Ф2 + ]/(F2 - Ф2)2 + 4А2Ф2 = со2 |/> + Ф2 ,
У2	(15.15)
Ф = 0.
§ 16. Случай двух вибраторов
1. Предварительное замечание. Применение общих резуль-
татов решения задачи о синхронизации может быть хорошо
проиллюстрировано на примере рассмотрения простейшего слу-
чая двух вибраторов. Этот случай представляет, однако, и са-
мостоятельный интерес, поскольку двухвибраторные машины
находят достаточно широкое практическое применение (см.
таблицу 2).
2. Самосинхронизация вдали от резонанса. Рассмотрим вна-
чале самосинхронизацию двух вибраторов вдали от резонанса.
Уравнения (10.1) для определения разности порождающих
фаз ai — о.2 = а и приближенного значения модуля угловой
скорости синхронного вращения вибраторов со в данном случае
могут быть представлены в форме
Р{ (а, соИ	[а1Л1а> (а1“)-	(и) -	(а, со) -	(а, со)] = 0,
/	(16.1)
Р2 (а, со)=	[а2А<а) (<т2со)- R° (со) +	(а, со) -	(а, со)] = 0,
где, в соответствии с формулами (6.4), (6.5) и (6.9), обозна-
чено:
(а, со) = Г(/° (а, со) = - W(2*} (а, со) =
= у -Л18''”28^ /р2 + Q2 sin (а +
1 m2e2co2
+ ^,f;	V'P?+Q5cos(« + T), "6-2)
2 2 2
1 т,е,со
(а, со) = 2 h2f'2-^-P22 +
+1	ургп^ cos (а + Y)>
Pss = Ьхх + Ьуу + 2Ьх^ Sin - 2byVVs C0S + bwv2s’ Qss = 0
(S= 1, 2),
СЛУЧАЙ ДВУХ ВИБРАТОРОВ
471
§ 161
р = Р12 =- Pzi = bxx + (Ji(j2byy + bX(f (v, sin 6, + v2 sin 62) -
- ЬУЧр^2 (vI cos d, + v2 cos 62) + ftq^cr^Va cos (стД - a262),
Q = Q12 = - Q21 = (<*1 - 02) bxy + bxrf> (<T2V2 cos d2 - OjVj cos 6,) +
+ byq (0^2 sin d2 - a2v1 sin 6,) + ЙФФСГ|СГ2У1У2 sin (сгД - a2d2),
cosy = p//P2 + Q2, sin у = Q/ V'P2 + Q2.	(16.3)
Если ввести далее обозначения
Zs (os, co) = asL^ (osco) - R° (co) - hsf's Pss
'	(s=l,2),	(16.41
W (CO) = l..i?18|'”2e?(0-. У p* + Q2 ;
то уравнения (16.1) можно записать также в виде
Pi = V {^i (ai’ “) “	(“) [sin (“ + Y) + hj\cos (a + y)]} = 0,
(16.5)
P2 (a, co) =	[Z2 (ct2, co) + IF (co) [sin (a + y) — h2f2 cos (a + y)]} = 0.
Если по крайней мере один из вибраторов планетарный,
то hj'y + h2f2 =£ 0, и из этих уравнений получаем соотношения
. /	, х	(ffp C0)'-ftj[Z2(ff2, СО)
sin (a + y) =----7s—/---к—=—'------- ,
coS(a + v)-^“>7?<°;'">,
(ftj^ + h2f2) F (co)
из которых легко исключается угол а и получается уравнение
для определения со:
[2,(0,, со) +Z2(a2, со)]2+ [^'2, (ст,, со) - Л,/[22(а2, со)]2 =
= Г2(со)(Л,/[ + Л2/')2. (16.7)
После решения уравнения (16.7) разность фаз а без труда
находится из равенств (16.6). Условием существования син-
хронных движений вибраторов является, таким образом, нали-
чие у уравнения (16.7) положительных решений относительно со.
Соответствующие необходимые условия существования мо-
гут быть легко получены следующим образом. Будем рассмат-
ривать равенство (16.7) как квадратное уравнение относитель-
но 2^01, со) или 22(о2, со). Если со, найденное из (16.7),
472
ПЛОСКАЯ ЗАДАЧА О СИНХРОНИЗАЦИИ ВИБРАТОРОВ
[ГЛ. ХП1
вещественно, то дискриминанты соответствующих квадратных
уравнений должны быть положительными, ибо в противном слу-
чае Zi(oi, со) или 2г(сг2, со) оказалось бы комплексным. Отсюда
вытекают неравенства
^if[ + h^f2
— h2f2
| Zs (as, со) К IF (со)
К1 +	(s=l, 2). (16.8)
Полученные соотношения, не являясь достаточными усло-
виями положительности со, все же играют важную роль при
решении вопроса о существовании синхронных движений ви-
браторов. Это обстоятельство будет проиллюстрировано в §§ 2
и 3 главы XXI. ,
Если оба вибратора дебалансные, то /ii = /i2 = 0, ZS = ZS —
=osL^} (asco)—/?s(co), и из уравнений (16.5) получаются следую-
щие соотношения для определения величин а и со:
sin (а + у) =
z° (qi> ю) = _
Г(со)
^2 (q2> ю)
W (со) ’
Z“(a„ co)+Z°(o„ со) = О.
(16.9)
(16.10)
При наличии у уравнения (16.10) положительных решений
и при выполнении неравенства
]z;(a„ co)| = |Z°((T2, со) | < Г (со)	(16.11)
каждому решению со = со* > 0 отвечают два существенно раз-
личных вещественных решения уравнения (16.9) *):
а — (а). = — у + arcsin [Z°(<r., <л\1№ (со)],
(16.12)
а = (а)2 = — y + л — arcsin [Z°(crp со)/W (со)],
где, под arcsin х понимается главное значение этой функции,
Г 1	1 1
заключенное в пределах — -% л, л .
В случае отсутствия у уравнения (16.10) положительных ре-
шений или невыполнения неравенства (16.11) самосинхрониза-
ция вибраторов невозможна. Заметим при этом, что условие
(16.11) допускает простую интерпретацию: оно означает, что
модули избыточных моментов на валах вибраторов |Zs(crs, со)| =
*) Можно не различать решения а, отличающиеся на 2лп, где п — лю-
бое целое положительное или отрицательное число, ибо таким решениям от-
вечают одни и те же синхронные движения вибраторов.
§ 16]	СЛУЧАЙ ДВУХ ВИБРАТОРОВ	473
= | оТ$а (asco) — R°s (со) | не должны превосходить некоторого пре-
дельного значения
W = у -'^г282 ]/р2 + Q2 ,
являющегося, согласно (16.2), максимальным значением вибра-
ционных моментов WsK)-
Если известны характеристики двигателей (<ps), то урав-
нения (16.7) и (16.10) могут быть достаточно просто решены
графическим способом. Кроме того, зачастую нет никакой на-
добности фактически решать эти уравнения. Важно лишь знать,
что они допускают положительное решение относительно св. Во
многих задачах заранее известно, что со мало отличается от
некоторого определенного значения соо, отвечающего номиналь-
ному числу оборотов двигателей машины. Тогда уравнения
(16.7) или (16.10) можно линеаризировать относительно со — соо,
тем более что характеристики двигателей асинхронного типа на
рабочих участках, как правило, весьма близки к линейным.
Обратимся к изучению вопроса об устойчивости синхрон-
ных движений вибраторов. Уравнение (4.12) в рассматривае-
мом случае является линейным, и его единственный корень мо-
жет быть, в силу (16.5), представлен в форме
д(Р{-Р2) d(Pi-P2} VF(со) Г/, , . .	, , . ,
х =	----=------Та---= ~ ~ТТТ + cos (“ + Y) +
+ (h2f2ki — sin (a + y)]. (16.13)
В случае, если хотя бы один из вибраторов планетарный, то
есть /г,/( + h2f2=p 0, из выражения (16.13) можно исключить
угол а с помощью равенства (16.6); тогда условие устойчиво-
сти синхронного движения х < 0 запишется в форме *)
(Z?1 + k2) [Zi (04, со) + Z2 (<т2, и)] +
+ (Wi - hlf'lk^\h2f2Zl(al, ю) - h{f\Z2^2, a>)]>0. (16.14)
Если оба вибратора дебалансные (Л1 = /г2 = 0), то выраже-
ние (16.13) существенно упрощается и условие устойчивости
сводится к неравенству
cos(a + Y)>0,	(16.15)
или, в соответствии с обозначениями (16.3), к соотношению
Р cos а — Q sin a> 0.	(16.16)
*) Напомним, что коэффициенты k, предполагаются положительными;
существенно положительна, согласно (16.4), также и величина W (®) (счи-
таем, что Р и Q не обращаются в нуль одновременно).
474
ПЛОСКАЯ ЗАДАЧА О СИНХРОНИЗАЦИИ ВИБРАТОРОВ
[ГЛ. XIII
Сопоставление неравенства (16.15) с формулами (16.12) по-
казывает, что устойчивому синхронному движению отвечает
значение угла a=(a)i=(ai— а2)г, углу же а=(а)2 =
= (ai — аг) 2 отвечает неустойчивое движение.
Приложения полученных выше результатов к исследованию
различных конкретных машин с двумя самосинхронизирующи-
мися вибраторами будут рассмотрены в пятой части настоящей
книги. Здесь мы остановимся лишь на анализе нескольких про-
стых, однако также имеющих прикладное значение случаев са-
мосинхронизации двух дебалансных вибраторов.
Предположим, что вибраторы имеют одинаковые и положи-
тельные парциальные угловые скорости ол = со2 = со* (см. § 10
настоящей главы), то есть каждое из уравнений
Zs(as, со) ^asAsa)(ascos) — /?°(cos) = 0 (s = 1, 2) (16.17)
имеет относительно cos одно и то же положительное решение
со, = со2 = со* > 0.	(16.18)
Тогда уравнение (16.10), в силу (16.4) и (16.17), допускает
решение относительно модуля угловой скорости синхронного
вращения со, равное общему значению со* парциальных скоро-
стей <01 И С02.
Поскольку при этом, согласно (16.17), Zs(as, со) = 0, то усло-
вие (16.11) непременно выполняется и разность порождающих
фаз а, определяемая по формулам (16.12), вещественна, причем
(a)i=-y, (а)2 = л-у.	(16.19)
Первому решению, как уже говорилось, отвечает устойчивое,
второму — неустойчивое синхронное движение вибраторов.
Таким образом, в случае одинаковых и положительных пар-
циальных угловых скоростей всегда существует по крайней
мере одно устойчивое синхронное движение вибраторов с угло-
вой скоростью со = coi = со2 = со*. Этот вывод согласуется с об-
щим заключением, сделанным в § 10 настоящей главы.
Рассмотрим теперь еще более частный, однако часто встре-
чающийся на практике случай двух одинаковых дебалансных
вибраторов, оси вращения которых о, и о2 лежат в плоскости,
проходящей через центр тяжести О] вибрирующего органа
(тела В), на одинаковых расстояниях г = O1O1 = o2Oi от центра
тяжести (рис. 32). При этом
т1е1 = т2е2 = те> ^1 = ^2 = ^0’ В°(со) = (со) = /?°(со),
б, = л, д2 = 0, Г\=Гг~г,	(16.20)
Vj = r1/p = r2/p = v2 = v (р = 1/1 /м).
§ 16] .
СЛУЧАЙ ДВУХ ВИБРАТОРОВ
475
Пусть, далее, упругая система симметрична относительно
осей координат, то есть жесткости*)
СхФ = 0, с,ф = 0.	(16.21)
В указанных предположениях по формулам (4.5), (4.6),
(4.8), (16.2)— (16.4) и (16.20) находим
Л (со2) = (р2 - (О2)(р2 - Ш2)(р2 - со2),
Рхф Руф 0,
,	СО2	.	__	(О2	к	(О2
°хх~ Р2Х-«Т D™~ pt-a2’
Р= -2ю2 2+g|g2H2(—2 1 -V Q = o, (16.22)
Рх ~ ®	\ Ру - ® I Р ^~ч> )
,Т„, ,	1 /и282<02 . di	( 0 при Р>0,
•'W-2—^1.	У-(л р<0.
При этом, согласно равенствам (16.19), устойчивому
нию отвечает
(а,)= - у =
I 0 при
( — л при
а неустойчивому —
(а)2 = л - у =
1 л при Р > 0,
-{о ПрИ Р<0.	"6-24’
сдвиг фаз
Р>0,
р<0, <16-23
У,и
реше-
MJ
К
х,и



Синхронное движение,	Рис. 32.
соответствующее сдвигу фаз
а = 0, условимся далее называть синфазным, а сдвигу фаз а =
= ±л — противофазным. Тогда можно сказать, что в рассмат-
риваемом случае при выполнении условия
г. <о2	,	9/	1 Mr2 1 Л
Р 2	2 4“ 04*^2® | 2	2	г	2	2 I > 0	(16.25)
РХ~®	\Ру~®	1 Рф“® J
устойчиво только синфазное синхронное движение вибраторов,
а при выполнении неравенства противоположного смысла —
только противофазное синхронное движение. Относительно
сложный характер расположения зон устойчивости синфазного
*) Указанный случай был рассмотрен автором в работе [68]; позднее
ИНЫМ способом он был изучен J1. Шперлингом [482].
476
ПЛОСКАЯ ЗАДАЧА О СИНХРОНИЗАЦИИ ВИБРАТОРОВ
[ГЛ. XIII
движения в плоскости параметров р2, w = pxlp2y виден из
рис. 33, а и б. Области устойчивости синфазного движения
(а = 0) на этих рисунках заштрихованы; в тех же областях про-
тивофазное движение неустойчиво. В незаштрихованных частях
плоскости устойчиво противофазное движение (а = —л), а син-
фазное— неустойчиво. Рис. 33, а соответствует случаю враще-
ния вибраторов в одинаковых направлениях (oio2 = 1),
Рис. 33.
а рис. 33,6 — вращению в противоположных направлениях
(СТ1О2 = —!)• При построении областей устойчивости принято
2	2
— = 0,856,	-^ =	2,25,
1	Ру
что отвечает параметрам экспериментальной установки, опи-
санной в § 2 главы XIX.
Нетрудно видеть, что противофазному вращению роторов
вибраторов в противоположных направлениях отвечают прямо-
линейные поступательные колебания несущего тела В вдоль
оси Оу, противофазному вращению в одинаковых направле-
ниях— поворотные колебания, а синфазному вращению в оди-
наковых направлениях — поступательные колебания с эллипти-
ческими траекториями.
§ 16]
СЛУЧАЙ ДВУХ ВИБРАТОРОВ
477
Будем далее предполагать, что жесткости сх, су, сф, cxtf
и суф упругих элементов , связывающих вибрирующий орган
с неподвижным основанием, достаточно малы, так что квадра-
тами частот рх = Усх/М, Ру=Усу/М, р^Ус^/I, = УЧ^/Мр,
pytf = УCyyjMp можно пренебречь по сравнению с квадратом
угловой скорости синхронного вращения ы. Иными сло-
вами, будем рассматривать случай мягкой амортизации вибри-
рующего органа.
В указанных предположениях, согласно формулам (16.22),
имеем
Z) (со2) со®, Ьхх Ьуу &фф 1, bXy bX(f> bО,
Р = — (1 + ЩСГ<) + СТЩ2 > Q = о,
tvz / \	1 т2е2<и2 I Mr2 . I
= 7----м~|°1СГ2—7--------(1 "Б СГ1СГ2) |.
Если роторы вибраторов вращаются в одинаковых направ-
лениях (стщг = 1), то при выполнении неравенства
Мг2/1>2	(16.26)
величина Р>0 и, в соответствии с равенствами (16.23) и
(16.24), устойчиво только синфазное движение вибраторов
(cc = (a)i=0), а при выполнении противоположного неравен-
ства— только противофазное движение (а = (а)г = —л).
Синфазному движению, очевидно, соответствуют поступа-
тельные круговые колебания вибрирующего органа машины
с амплитудой А = 2ти/М, а противофазному — чисто поворот-
ные колебания относительно оси, проходящей через центр тя-
жести вибрирующего органа (рис. 34, а).
Таким образом, характер движения системы существенно
зависит от выполнения условия (16.26).
Пусть теперь роторы вибраторов вращаются в противопо-
ложных направлениях (о|гт2 = —1). Тогда выражение Р отрица-
тельно*) и, согласно (16.23) и (16.24), условие устойчивости
выполняется только для противофазного движения (а = (а)г =
= —л); синфазное же движение (а = (а)| =0) всегда неустой-
чиво. Как нетрудно видеть, устойчивому противофазному движе-
нию отвечают прямолинейные поступательные колебания ви-
брирующего органа машины в направлении, перпендикулярном
) Предполагается, что г отлично от нуля.
478
ПЛОСКАЯ ЗАДАЧА О СИНХРОНИЗАЦИИ ВИБРАТОРОВ
[ГЛ. XIII
плоскости, проходящей через оси вращения вибраторов
(рис. 34, б).
Мы приходим, таким образом, к выводу, что при сформули-
рованных выше условиях для получения прямолинейных посту-
пательных колебаний имеется возможность не прибегать к при-
менению обычных двухроторных дебалансных вибраторов на-
правленного действия с шестеренной синхронизацией. Синхрон-
Рис. 34.
ность и необходимая фазиров-
ка вращения роторов могут
быть обеспечены автоматиче-
ски вследствие явления само-
синхронизации. Это обстоя-
тельство позволяет значитель-
но упростить конструкцию
привода ряда вибрационных
машин и установок (вибра-
ционных грохотов, конвейе-
ров, питателей и многих дру-
гих), в которых обычно при-
меняется кинематическая син-
хронизация (см. § 1 главы XX).
Разумеется, для возмож-
ности практического исполь-
зования самосинхронизую-
щихся вибраторов в указан-
ных выше машинах необходи-
мо убедиться в стабильности
эффектов самосинхрониза-
ции и автоматического под-
держания постоянства разно-
стей фаз вращения вибрато-
ров по отношению к возмож-
ным отклонениям параметров,
обусловленным неточностью изготовления. Этот вопрос рас-
сматривается в главе XVI и в § 2 главы XX настоящей книги.
3. Случай одного выключенного вибратора (вибрационное
поддержание вращения неуравновешенного ротора). В качестве
особого частного случая задачи о самосинхронизации двух
вибраторов рассмотрим эффект вибрационного поддержания
вращения неуравновешенного ротора, то есть случай, когда один
из вибраторов не приводится от какого-либо двигателя, а пред-
ставляет собой обычный неуравновешенный ротор (физический
маятник). О возможности такого явления уже говорилось в п. 3
§ 10 настоящей главы.
Пусть оба вибратора являются дебалансными (/ii = /i2 = 0).
Предположим для конкретности, что двигателем снабжен пер-
СЛУЧАЙ ДВУХ ВИБРАТОРОВ
479
§ 16]
вый вибратор, то есть aiL\a) (одсо) #= 0, a (щ®) •-= 0. Тогда,
согласно равенствам (16.4),
Z, (Ojco) = OjLi0’(о,®) —/?i (®), Z2(cr2co) =—	(16.27)
и уравнение (16.10) для определения модуля угловой скорости
синхронного вращения со принимает вид
а^>1ш) = /^(о) + Ш	(16.28)
Отсюда видно, что электродвигатель первого вибратора вос-
принимает момент сопротивления вращению обоих вибраторов.
Поскольку моменты R.s (и) существенно положительны, то
в рассматриваемом случае непременно должно быть
а1Т1(а1®)>0,	(16.29)
то есть направление вращения двигателя в синхронном движе-
нии должно совпадать с направлением вращающего момента
Т1(ст1Ш) в этом движении. При таком условии уравнение (16.28)
в случае достаточно мощного двигателя непременно допускает
положительное решение относительно со, и тогда вопрос о воз-
можности синхронного вращения сводится к изучению условий
выполнения неравенства (16.11). В соответствии с (16.4) и
(16.27) это неравенство может быть представлено в форме
/?2° (и) < '-1181™282- и2 |/P2 + Q2.	(16.30)
Полученное соотношение и представляет основное условие
вибрационного поддержания вращения неуравновешенного ро-
тора. Как и исходное неравенство (16.11), оно имеет простой
смысл: мощность со/?2 (и), расходуемая на преодоление со-
противления вращению ротора, не должна превышать некото-
^3	г 111 *
рого максимального значения т1е1т2е2 у Р2 + Q2, завися-
щего от параметров системы.
Если сопротивление вращению ротора обусловлено только
трением в его подшипниках, то согласно равенствам (6.9)
/?2л(®) = 0, /?г(м) =/?2в(со) = у/2"г2е2^2и2,	(16.31)
и условие (16.30) приобретает следующий вид:
^g-yp^Q2>f2.	(16.32)
Последнее неравенство еще более упрощается в случае, ко-
гда вибрирующий орган установлен на весьма мягких упругих
опорах, а оси вращения вибраторов расположены симметрично
480	ПЛОСКАЯ ЗАДАЧА О СИНХРОНИЗАЦИЙ ВИБРАТОРОВ [ГЛ. XII!
относительно центра тяжести Ot (рис. 34). Тогда величины Р
и Q определяются выражениями (16.25) и неравенство (16.32)
записывается в форме
»-|^.-(l+aia2)|>f2.	(16.33)
Заметим, что коэффициент сопротивления в подшипниках
качения /2 обычно не превышает 0,01. Отсюда нетрудно заклю-
чить, что неравенство (16.33) выполняется в достаточно широ-
кой области изменения параметров системы.
Примечательно также, что в значительной части этой обла-
сти выключение одного из двух первоначально включенных
двигателей вибраторов не приводит к существенному изменению
характера движения системы.
Для иллюстрации сказанного рассмотрим случай, отвечаю-
щий рис. 34, б, когда одинаковые симметрично расположенные
вибраторы вращаются в противоположных направлениях
(очаг = —1) со сдвигом по фазе а = —л, развивая вертикально
направленную возмущающую силу.
Пусть теперь двигатель одного из вибраторов выключается.
Тогда из (16.33) следует, что при выполнении неравенства
выключенный вибратор сможет по-прежнему вращаться син-
хронно с другим вибратором, двигатель которого включен
в сеть.
Выключение одного из двигателей, как вытекает из рассмот-
рения уравнения (16.10), приведет лишь к некоторому сниже-
нию модуля угловой скорости синхронного вращения со и к из-
менению угла сдвига фаз а по сравнению с его значением
а = —л. А именно, в соответствии с равенствами (16.10),
(16.12), (16.25), (16.27) и (16.31), будем иметь для устойчивого
движения
а =— л + Аа,	(16.35
где
Аа = —arcsin f 2	(16.36)
— изменение угла сдвига фаз, обусловленное выключением од-
ного из двигателей.
Для шариковых радиальных подшипников качения
/2-<0,004 [36]. Пусть, далее, //Mr2 412,	10, cf/e < 1; ука-
занные неравенства выполняются для широкого ряда вибра-
ционных машин. Тогда из равенства (16.36) следует, что
|Аа| <0,08~4°35/.
§ llil
СЛУЧАЙ ДВУХ ВИБРАТОРОВ
481
Столь незначительное изменение угла сдвига фаз, естествен-
но, не сказывается сколько-нибудь существенно иа законе дви-
жения вибрирующего органа.
В ряде случаев экспериментально наблюдался даже следую-
щий «парадокс»: выключение одного из двигателей приводило
к уменьшению «угла рассогласования» Да = а + л, имеющего
место при обоих работающих двигателях вследствие неодинако-
вости параметров вибраторов, обусловленной неточностями из-
готовления.
Следует подчеркнуть, что найденные выше условия вибра-
ционного поддержания вращения неуравновешенного ротора
сами по себе еще не обеспечивают возбуждения вращения ро-
тора из состояния покоя системы при включении только одного
из двигателей. Условия возбуждения, как и вообще условия
возникновения определенных установившихся движений в за-
висимости от начальных данных, получить аналитическим пу-
тем в более или менее общем случае чрезвычайно затруднитель-
но. Результаты соответствующего экспериментального иссле-
дования приводятся в главе XIX, а исследований, проведенных
с помощью вычислительных машин, — в § 6 главы XVIII.
В иной постановке задача о вибрационном поддержании вра-
щения неуравновешенного ротора рассматривается в главеXVIII
настоящей книги, где приводится также сопоставление получае-
мых в обоих случаях результатов и обзор литературы.
4. Самосинхронизация вблизи резонанса. Рассмотрим те-
перь задачу о самосинхронизации вибраторов, установленных
на вибрирующем органе с одной степенью свободы, вблизи ре-
зонанса. Поскольку этот случай был подробно изучен для про-
извольного числа вибраторов k в § 13 настоящей главы, то здесь
мы ограничимся лишь формулировкой результатов, относящих-
ся к двум дебалансным вибраторам с одинаковыми парамет-
рами и одинаковыми избыточными моментами
Zs{os, a) = CJsL(sa)(CTsM)-Ros(®) = Z(w) (s = l, 2). (16.37)
В соответствии с неравенствами (13.45) самосинхронизация
в данном случае возможна при условиях
Z(co)>0, Z (и) < те^а2 ,	(16.38)
где, согласно (13.47), амплитуда колебаний Н вычисляется по
формуле
Н = 1/	= 2 1/4^-,	(16.39)
Г пхМ& У kxa> ’	'	’
16 И. И. Блехман
482
ПЛОСКАЯ ЗАДАЧА О СИНХРОНИЗАЦИИ ВИБРАТОРОВ
[ГЛ. Xltl
а угловая скорость синхронного вращения о> в устойчивом дви-
жении, в соответствии с (13.50), определяется соотношениями
® = Рж[1 +ур(рх)],
п/_\_ V 2 те Г pxkx Г. Z(px)kx (16.40)
Из неравенств (16.38) вытекает, что для наличия самосин-
хронизации в данном случае необходима, прежде всего, поло-
жительность избыточных моментов Z(co). Отсюда следует, что
и моменты osLf (crsco) также должны быть положительны, то
есть двигатели вибраторов должны работать в обычном (а не
в генераторном) режиме. Во-вторых, необходимо, чтобы избы-
точные моменты Z(<o) не превосходили по модулю некоторого
предельного значения, зависящего от параметров системы.
Если условия (16.38) выполняются, то порождающие фазы
as в устойчивом синхронном движении одинаковы и опреде-
ляются, в соответствии с (13.47), следующим равенством:
• 2Z (а)	,, с .
а, = а2 = arcsin	(16.41)
Согласно (16.40) устойчивое движение вибраторов является
дорезонансным (ы<рх); устойчивые послерезонансные движе-
ния вибраторов вблизи резонанса при сделанных в § 13 пред-
положениях отсутствуют. Заметим, что заключение о синфазно-
сти и дорезонансном характере устойчивого синхронного дви-
жения одинаковых вибраторов остается справедливым и в
случае произвольного числа вибраторов.
Эти выводы интересно сопоставить с результатами, относя-
щимися к движению дебалансных вибраторов с одинаковыми
положительными парциальными скоростями вдали от резонан-
са, при условии, что вибрирующий орган имеет только одну сте-
пень свободы, отвечающую поступательному движению.
В данном случае, согласно (8.2) и (8.3), Р = Ьхх = со2/(р2 — со2),
Q — 0, и поэтому, в соответствии с (16.2),
(°,
У =
л,
(0<рх,
(0>рх.
Но устойчивому движению, в силу (16.15) и
ветствует сдвиг фаз a = (ct)i=(cti — а2) i — — у.
зом в устойчивом движении
( 0, а<рх,
а = а, — а2 =)
[ —л, со > рх.
(16.42)
(16.19), соот-
Таким обра-
(16.43)
Иными словами, и вдали от резонанса устойчивое синхрон-
ное движение вибраторов с одинаковыми парциальными скоро-
СЛУЧАЙ ДВУХ ВИБРАТОРОВ
483
§ 16]
стями является в дорезонансной области синфазным. Послере-
зонансное же устойчивое движение таких вибраторов является
противофазным. При этом, если статические моменты дебаланс-
ных грузов m.ses обоих вибраторов одинаковы, то в противо-
фазном движении вибрирующий орган остается (в первом при-
ближении) неподвижным, ибо соответствующие составляющие
возмущающих сил взаимно уничтожаются.
Подобная ситуация на первый взгляд представляется пара-
доксальной: определенное соотношение между фазами враще-
ния роторов вибраторов обеспечивается здесь, несмотря на то
что связь, казалось бы, не работает — платформа в установив-
шемся движении практически неподвижна. Объяснение состоит
в том, что при появлении возмущения (в частности, при откло-
нении вращения роторов вибраторов от противофазного) плат-
форма перестает быть неподвижной. Ее движения как раз та-
ковы, что и обеспечивают устойчивость указанного выше про-
тивофазного вращения.
Как и при движении вдали от резонанса, так и в случае
близости к резонансу, при определенных условиях возможна
самосинхронизация вибраторов с резко отличающимися пара-
метрами, в частности эффект вибрационного поддержания вра-
щения вибратора с выключенным из сети двигателем. Возможна
также и самосинхронизация двух вибраторов, один из которых
искусственно тормозится двигателем, работающим в генератор-
ном режиме (ffsLs(ffsa) <0). Подробно этот случай обсуждает-
ся в нашей работе [44] и в статье Л. Шперлинга [482]. В ука-
занных публикациях приведены также диаграммы областей
существования и устойчивости синхронных движений.
5. Синхронизация с применением синхронных электродвига-
телей. Обратимся к рассмотрению случая принудительной син-
хронизации с использованием синхронных электродвигателей;
по-прежнему изучим вначале движение вдали от резонанса.
Уравнения (11.8) для определения порождающих фаз а1 и а2
в данном случае могут быть представлены в форме
1	(	»	о	1	/ т|е?со2
Р1 (а,,	а2,	(0) = —{ null [ст,	(щ	-₽i)]	-	R\ (со)	-	у h\f i —Рп	-
_ г((о)---п(а|~а2+;+/г|р‘И=о,
COS р|	J ’
1	(	*	г	°	1	.г т^е|<в2
Р2 (аь	а,,	со) ss	{o2L2 [<т2	(аг	- ₽г)1	-	Rz (со)	-	у /г2/2 —Р22	+
+	+	Up.
COS р2	J
(16.44)
16*
484	ПЛОСКАЯ ЗАДАЧА О СИНХРОНИЗАЦИИ ВИБРАТОРОВ [ГЛ. XIII
Здесь р' = arctg f's и по-прежнему использованы некоторые из
обозначений (16.2) — (16.4).
Зная характеристики двигателей Ls (0S), из трансцендентных
уравнений (16.44) можно найти порождающие фазы и а2
в синхронных движениях вибраторов. Естественно, для суще-
ствования таких движений необходимо, чтобы фазы а\ и аг
были вещественными.
Уравнение (4.10) в рассматриваемом случае является квад-
ратным и имеет вид
dPt	дР{
-т-!— х ——
оси	оа2
дР2	дРг
дщ	да2
(16.45)
Каждому вещественному решению уравнений (16.44) дейст-
вительно отвечает единственное и асимптотически устойчивое
синхронное движение рассматриваемого типа, если для этого
решения корни уравнения (16.45) имеют отрицательные веще-
ственные части.
При рассмотрении наиболее важной с прикладной точки зре-
ния задачи о принудительной электрической синхронизации —
задачи синтеза системы возбуждения*) нет надобности непо-
средственно решать систему трансцендентных уравнений
(16.44). Действительно, зная фазы at и аг и направления вра-
щения вибраторов (числа од и н2) в требуемом синхронном дви-
жении вибраторов, можно из уравнений (16.44) найти устано-
вочные углы Pj и |32. Разумеется, характеристики двигателей
(0S) при этом должны быть такими, чтобы Pi и р2 оказались
вещественными. Определенные требования к характеристикам
получатся и из условий устойчивости синхронного движения.
Рассмотрим в качестве примера машину с двумя одинако-
выми дебалансными вибраторами (/ц = /г2 = 0), приводимыми
непосредственно (то есть без промежуточных редукторов) от
одинаковых синхронных двухполюсных двигателей с нечетными
характеристиками LS(QS). Предположим при этом, что оси вра-
щения вибраторов расположены симметрично по отношению
к центру тяжести вибрирующего органа, а упругие элементы,
которыми машина связана с основанием, являются достаточно
мягкими, так что можно пренебречь квадратами частот соб-
ственных колебаний системы на упругих опорах по сравнению
с квадратами угловой скорости синхронного вращения и. Ины-
ми словами, будем рассматривать ту же систему, что и в изу-
ченном в п. 2 настоящего параграфа частном случае задачи
) В обшей постановке эта задача рассматривается в главе XV.
СЛУЧАЙ ДВУХ ВИБРАТОРОВ
485
§ 16]
о самосинхронизации (рис. 34), но с вибраторами, приводимыми
от синхронных двигателей указанного выше типа.
Для параметров рассматриваемой системы, таким образом,
справедливы соотношения (16.20) и (16.25'), а также следую-
щие условия, которым удовлетворяет характеристика двига-
телей:
L\ (0) =	(0) = В* (0), L* (0 + 2л) = L* (9),
Г(—е) = — Г(0),	Г(0) = 0,	(16.46)
^-<0 при |0 |< 9’.
При использовании соотношений (16.4), (16.20), (16.25') и
(16.46) уравнения (16.44) представятся в форме
Pi(«i. а2, w) = -b[C(al-pl)-7?o(Q)-B(ra)sin(a|-a,)j = 0,
(16.47)
Р2 (a,, а2, со) -т-[£‘(а, — ft) — /?° (и) +В (и) sin (а,-а2)] = 0.
«о
Здесь обозначено:
В (ю) = m 26МЮ-	^1^2 ~ (1 + а,^)] •	(16.48)
Заметим, что величина В (и) sin (а, — а2), фигурирующая
в уравнениях (16.47), есть не что иное, как вибрационный мо-
мент Й7|Ю. Действительно, согласно (16.2), (16.20) и (16.25')
1Г(,Ю (а, со) = —	(а, со) = В (и) sin а (а = а,—а2). (16.49)
Величина | В (со) | = £Г((о) при этом, как и выше, есть наиболь-
шее значение вибрационного момента (см. равенства (16.25')).
Уравнение (16.45) в рассматриваемом случае может быть
представлено в форме
(<7п - к) (<?22 - к) - Q2 = 0,	(16.50)
где в соответствии с (16.47) обозначено:
dPs 1 17 dL'\	D , .	.	.1
= -557 - 77 (тг) - в <“> “s <“> - “J
(s=l, 2),	(16.51)
дР\ дР2 1 о / т i \
? = 3^=^~s(“)cos(ai"a2)‘
Рассмотрим теперь задачу синтеза для машины данного
типа.
Пусть, например, необходимо получить устойчивые круговые
поступательные колебания вибрирующего органа. Для этой
486
ПЛОСКАЯ ЗАДАЧА О СИНХРОНИЗАЦИИ ВИБРАТОРОВ
[ГЛ. XIII
цели, очевидно, следует обеспечить устойчивое синфазное вра-
щение обоих вибраторов в одинаковых направлениях (рис. 34, а),
то есть движение, соответствующее условиям:
ог1<Т2= 1»	О]--а2 = а0.	(16.52)
Тогда, как следует из уравнений (16.47), установочные углы
обмоток статоров fh и р2 также должны быть одинаковы и удов-
летворять уравнению
L(a0-₽) = /?°(fi>).	(16.53)
Отсюда видно, что либо значение ао, либо значение р может
быть выбрано совершенно произвольно: из уравнения (16.53)
определяется лишь разность а0 — р. Однако для того, чтобы
указанная разность была вещественной, то есть чтобы любому
заданному ао отвечало вещественное р, необходимо и достаточ-
но выполнение неравенства
7-max> R° (и),	(16.54)
где Rmax — наибольшее значение момента А*(0). Неравенство
(16.54) представляет одно из условий, налагаемых на характе-
ристику двигателей.
Пусть, например, выражение для L* (0) задано в виде
L* (0) = — / sin 0.	(16.55)
Тогда условие (16.54) сведется к требованию
/>/?°(й),	(16.56)
при выполнении которого уравнение (16.53) допускает, вообще
говоря, два существенно различных решения относительно
ao —Р:
(0)1 = (ao-p)i=-- —arcsinR°((o),
(0)2 = (а0 — р)2 = л + arcsin R° (и).
Обратимся теперь к получению условий устойчивости рас-
сматриваемого синхронного движения. Поскольку в данном слу-
чае ai = а2 = ао и Pi = р2 = р, то согласно (16.51)
(16-58)
и уравнение (16.50) имеет корни
. ,	1 ldL*\
ТЙГ’' ,	(16.59)
х = 4* _ Q	-2В(й) .
А 4	4 kn L\ dQ /0-а.-в v '.I
§ 161
СЛУЧАЙ ДВУХ ВИБРАТОРОВ
487
Условия устойчивости xs < 0 (s = 1,2) сводятся, в соответ-
ствии с (16.48) и (16.52), к неравенствам
dL* \
dQ /0=а«—₽
<0,
dL* \	m2e2<o2 / Mr2
dd )е=а0-р М \ I
(16.60)
Первое неравенство, в силу предположений (16.46) о типе
характеристики двигателя, выполняется, если только
I а-₽ 1<е*.
(16.61)
Второе же условие (16.60) при выполнении неравенства
Mr2
I >
(16.62)
и справедливости условия (16.61) выполняется вне зависимости
„ I dL I
от значения «жесткости» характеристики двигателей "jjj-
Заметим теперь, что условие (16.62) в точности совпадает
с'неравенством (16.26), обеспечивающим устойчивость синхрон-
ного движения рассматриваемого типа при использовании для
привода вибраторов одинаковых двигателей асинхронного типа.
Таким образом, при выполнении условия (16.62) для обеспече-
ния круговых поступательных колебаний вибрирующего органа
нет никакой надобности прибегать к использованию синхрон-
ных двигателей, необходимый эффект достигается за счет явле-
ния самосинхронизации. Этот результат вполне согласуется
с полученным в п. 2 настоящего параграфа.
При выполнении неравенства, противоположного неравен-
ству (16.62), второе условие (16.60) является существенным.
В этом случае самосинхронизация не может быть использована
для получения синфазного вращения вибраторов, а при приме-
нении синхронных двигателей необходимо, чтобы «жесткость»
их характеристики в рабочей точке 0 = а0 — Р превышала ве-
личину
т2е2ш2 I Mr2	п I
М I I	2Г
В случае, если характеристика двигателя задана выраже-
нием (16.55), критическое значение угла 0, при котором dL/db
обращается в нуль, равно у л, и неравенство (16.61) принимает
вид
| а0 —р |<4 л.	(16.63)
488
ПЛОСКАЯ ЗАДАЧА О СИНХРОНИЗАЦИИ ВИБРАТОРОВ
[ГЛ. Х111
При выполнении условия (16.56) этому неравенству удовлет-
воряет лишь первое из решений (16.57); второму решению от-
вечает положительное значение производной dL*/d^=—/ cos 0,
и поэтому, в силу (16.60), соответствующее движение неустой-
чиво.
Что же касается первого решения (16.57), то для него первое
условие устойчивости выполняется автоматически, а второе сво-
дится к неравенству
I ]/1-[Я° (®)]2 >	(2 ~	•	(16-64)
Соотношения (16.56) и (16.64) дают искомую совокупность
требований, которым должна удовлетворять в рассматриваемом
случае характеристика двигателей.
Заметим, что если, как это и предполагалось выше, синхрон-
ные двигатели являются двухполюсными, то есть наименьший
период функции L* (0) равен 2л, то при |3t = ₽2 = ₽ уравнения
(16.47) допускают лишь одно решение, отвечающее устойчивому
движению, а именно рассмотренное выше решение ai = a2 = ao-
В случае многополюсных двигателей или же при наличии сни-
жающих обороты редукторов между валами двигателей и ви-
браторов наименьший период функции L* (0) оказался бы рав-
ным 2л/п, где п — целое число. При этом могло бы существо-
вать несколько устойчивых синхронных движений при одних
и тех же параметрах системы и для обеспечения устойчивости
только одного требуемого по условиям задачи движения пона-
добились бы дополнительные устройства [240].
Как было установлено выше, для того чтобы получить
устойчивые прямолинейные поступательные колебания вибри-
рующего органа (рис. 34,6), можно использовать явление само-
синхронизации. Нетрудно видеть, что если мы все же будем
рассматривать для этого случая (слог = —1, «1 — «2 = —л) за-
дачу о синтезе машины с синхронными двигателями, то ока-
жется, что условия устойчивости не предъявляют какого-либо
дополнительного требования к «жесткости» характеристики
двигателей \dL*/dQ\ в рабочей точке, за исключением условия
dL*/dQ<0, автоматически выполняющегося при |0| <0*.
Решение задач синтеза вибрационных машин с синхронными
электродвигателями в случае вибрирующего органа с одной сте-
пенью свободы при движении системы вблизи резонанса более
просто, чем в нерезонансном случае. Это объясняется тем, что
условия устойчивости движения вблизи резонанса удается вы-
разить в достаточно простой форме для любого числа вибра-
торов k (см. неравенство (13.42)).
Не приводя соответствующих примеров, заметим, что и здесь
в случае, когда требуемое движение может быть обеспечено
§ 16]	СЛУЧАЙ ДВУХ ВИБРАТОРОВ	489
путем использования самосинхронизации, на величину жестко-
сти характеристики двигателей |с/Ея/с/05| в рабочей точке не
налагается никаких дополнительных требований. Если же при
асинхронных двигателях рассматриваемое движение неустой-
чиво, то для сообщения ему устойчивости жесткости характери-
стик в рабочих точках должны быть по модулю не меньше
некоторых величин, зависящих от параметров системы. Осо-
бенно большие значения жесткости требуются для обеспечения
синфазного движения вибраторов в послерезонансной области
в непосредственной близости от резонанса. Подобные движе-
ния, как уже было отмечено выше, в случае привода от двига-
телей асинхронного типа неустойчивы.
6. П ринудителъная синхронизация с использованием упругих
синхронизирующих элементов. Перейдем к рассмотрению за-
дачи о принудительной синлронизации посредством использова-
ния упругих синхронизирующих элементов или систем типа
электрического вала.
Как и в предыдущей задаче, ограничимся здесь изучением
движения вдали от резонанса, как наиболее сложного и наибо-
лее часто встречающегося случая.
Уравнения (11.13) при k = 2 могут быть представлены в
форме
Р, (а, и) = Zj (cTj, co) — с (а — й) — W (со) [sin (а + у) +
*1 (
+ /z,Kcos (а + у)|[ = 0,
! г~	- г	(16‘65)
Р2 (а, со) = -г- [Z-2 (а2, со) + с (а — й) + W (со) [sin (а + у) —
«2
- h2f'2 cos (а + у)]) = 0.
Последние уравнения отличаются от уравнений (16.5) за-
дачи о самосинхронизации лишь членами с(а— й), отражаю-
щими наличие связи между роторами вибраторов; в этих урав-
нениях по-прежнему использованы обозначения (16.3) и (16.4)
и, кроме того, положено
С = С|2 = С21, Й = %1 — Х2.	(16.66)
Из уравнений (16.65), как и в задаче о самосинхронизации,
должны быть определены разность порождающих фаз а и при-
ближенное значение модуля угловой скорости синхронного вра-
щения ы, причем наличие вещественных решений относительно а
и положительных решений относительно со является необходи-
мым условием возможности синхронных движений изучаемого
типа.
490
ПЛОСКАЯ ЗАДАЧА О СИНХРОНИЗАЦИИ ВИБРАТОРОВ
[ГЛ. XIII
Уравнение (4.12), от характера корней которого зависит ре-
шение вопроса об устойчивости, в случае k = 2 является линей-
ным, и его корнем, в силу (16.65), будет
д (Р, - Р2) = d (Р, - Р2)	_ с kx + k2 _
<3cti	da	k\k2
-Г(<о) cos (a + y) +	sin (a + y) • (16.67)
Условие устойчивости синхронных движений х < 0, таким
образом, может быть представлено в форме
с > — W (<о) cos (a + у) +
k\ + k2
sin (a + у)
(16.68)
Отсюда непосредственно следует, что устойчивость любого
синхронного движения вибраторов, если оно существует, мож-
но обеспечить путем выбора достаточно большого значения
жесткости с упругого элемента (или электрического вала).
В случае дебалансных вибраторов (hi = h2 = 0) уравнения
(16.65) и условие (16.68) существенно упрощаются, принимая
вид (см. формулы (16.4))
?! (а, <о)^Е	(О|Ш) — Ri (со) — с (а — х) — W (со) sin (а + у)] = 0,
Р2 (а, а>) =	[а2/Ла> (сг2со) — R2 (<о) + с (а — х) + W (<о) sin (а + y)] = 0,
(16.69)
с> — IF (со) cos (а + y)-	(16.70)
Из системы (16.69) получается следующее независимое урав-
нение для определения угловой скорости:
a^i*” (а,ы) + а2Ь(2} (ст2<о) = R° (со) + Рг (со).	(16.71)
Это уравнение, естественно, совпадает с уравнением (16.10),
полученным при рассмотрении самосинхронизации.
В качестве примера решения задачи синтеза вибрационной
машины с упругим синхронизирующим элементом по-прежнему
рассмотрим мягко амортизированную машину с двумя одинако-
выми симметрично расположенными дебалансными вибрато-
рами, обладающими одинаковыми положительными парциаль-
ными скоростями. Для параметров этой системы, представлен-
ной на рис. 34, справедливы соотношения (16.20) и (16.25').
Пусть необходимо получить устойчивые круговые поступа-
тельные колебания вибрирующего органа, то есть обеспечить
устойчивое синфазное вращение обоих вибраторов в одинако-
вых направлениях (рис. 34, а). Полагая в уравнениях (16.69)
§ 1Ь]
СЛУЧАЙ ДВУХ ВИБРАТОРОВ
491
а = ой — «2 = 0, <Т|<Т2 = 1 и учитывая равенства (16.20) и
(16.25х), получим
(<т,<о) - R° (со) - с (а - й) = 0,
t о	(16.72)
ст27Т*(<т2<о) — #2 (со) + с (а — й) = 0.
Первые два слагаемых в последних уравнениях обращаются
в нуль в силу предположения о равенстве парциальных угловых
скоростей (см. соотношения (16.17) и (16.18)), и поэтому из
(16.72) находим, что для обеспечения требуемого движения
разность установочных углов я = щ — х2 следует принять рав-
ной нулю.
Условие устойчивости движения (16.70) при а = 0 и СТ1СТ2=1,
согласно (16.25'), принимает вид
1 m2e2co2 (Mr2
С>-2~Л4—<16-73>
Отсюда следует вывод, аналогичный полученному в задаче
о синхронизации путем использования синхронных двигателей:
при выполнении неравенства Mr^/I > 2 условие устойчивости
(16.73^ выполняется автоматически, и необходимость в синхро-
низирующем элементе отсутствует. Эффект здесь может быть
достигнут, как было показано выше, путем использования само-
синхронизации.
Напротив, при Мг'2[1 < 2 для обеспечения требуемого дви-
жения синхронизирующий элемент необходим; его жесткость с
должна удовлетворять условию (16.73).
Заметим, что указанное условие получается из второго условия
устойчивости (16.60) задачи о синхронизации с помощью син-
хронных двигателей, если заменить жесткость характеристики
двигателей—(t//.7^O)o»aa-p в рабочей точке на жесткость с.
Предположим теперь, что необходимо получить прямоли-
нейные поступательные колебания рассмотренной только что
системы, то есть обеспечить устойчивое противофазное враще-
ние вибраторов в противоположных направлениях (рис. 34,6).
Из уравнений (16.69) в этом случае (а =	— а2 = —л, ою2 =
- —1) аналогично предыдущему получаем й = xj — х2 = —л,
а условие устойчивости (16.70), в силу равенств (16.25'), при-
нимает вид
Поскольку последнее условие при г¥=0 всегда выполняется, то
для обеспечения требуемого синхронного движения вибраторов
никакого синхронизирующего элемента не нужно. Как было
показано выше, в этом случае можно использовать явление
самосинхронизации.
492
ПЛОСКАЯ ЗАДАЧА О СИНХРОНИЗАЦИИ ВИБРАТОРОВ
[ГЛ. XIII
§ 17. Замечания о способе решения рассмотренной задачи
Как уже отмечалось в § 3 настоящей главы, принятый при
решении рассмотренной задачи способ введения малого пара-
метра не является единственно возможным. В частности, в диф-
ференциальных уравнениях (3.3) силы вязкого сопротивления,
отвечающие колебательным координатам х, у и <р, можно было
бы не относить к малым слагаемым. В результате для данной
задачи оказалось бы возможным получить единое решение, при-
годное как для резонансного, так и для нерезонансного случая.
Нетрудно показать, что при определенных условиях это ре-
шение совпало бы как с нерезонансным, так и с резонансным
решением. Некоторые упрощения были бы достигнуты при
исследовании устойчивости, ибо отпала бы надобность в ана-
лизе условий устойчивости, названных выше дополнительными
(см. § 5).
Вместе с тем учет сил вязкого сопротивления уже в поро-
ждающем решении усложнил бы промежуточные выкладки и
результативные соотношения для основного, нерезонансного
случая; в частности, оказался бы несправедливым (по крайней
мере в прежнем виде) интегральный критерий устойчивости
синхронных движений. Поэтому мы и предпочли здесь иную ме-
тодику решения, приводящую к необходимости раздельного изу-
чения резонансного и нерезонансного движений. Как уже отме-
чалось в § 3 настоящей главы, эта методика является тради-
ционной при изучении квазилинейных систем с помощью
методов Пуанкаре — Ляпунова.
Заметим, однако, что для определенных частных задач о син-
хронизации вибраторов такой традиционный подход может ока-
заться менее целесообразным. В таких случаях можно прибег-
нуть к указанному выше иному способу введения малого па-
раметра, позволяющему получить единое решение для всего
частотного диапазона.
Приведенные соображения развиты автором в работе [68].
Позднее эти вопросы были более подробно рассмотрены
К- Ш. Ходжаевым [408].
О возможности рассмотрения задачи в предположении о ма-
лости членов fes(<ps — Oslo) в уравнениях движения вибраторов
(3.3) говорилось в § 3. Результаты, получающиеся при этом бо-
лее сложном для решения «квазиконсервативном» варианте
идеализации вибраторов, будут рассмотрены в § 5 главы XIV.
ГЛАВА XIV
ОБОБЩЕНИЯ ЗАДАЧИ О СИНХРОНИЗАЦИИ
МЕХАНИЧЕСКИХ ВИБРАТОРОВ
§ 1. Предварительные замечания
В настоящей главе рассмотрен*ряд задач о синхронизации
механических вибраторов при значительно более общих пред-
положениях, чем принятые в главе XIII. Эти предположения
примерно отвечают общей постановке задачи, изложенной в
главе XII. Естественно, что окончательные результаты исследо-
вания здесь далеко не всегда представлены в столь конкретном
виде, как в главе XIII, то есть, по существу, выраженными не-
посредственно через параметры рассматриваемой системы. Од-
нако везде, где это представилось возможным, указанные ре-
зультаты выражены через некоторые характерные, допускающие
непосредственное физическое истолкование величины (энерге-
тические характеристики, коэффициенты влияния и т. п.). В та-
ких случаях рассмотрение конкретных систем сводится к четкой
стандартизированной методике, что весьма желательно с точки
зрения приложений.
Общее представление о механическом вибраторе как о фи-
зическом объекте было дано в § 1 главы XIII; там же указаны
основные технические реализации вибраторов, их главнейшие
типы.
Рассмотрение, проводимое в настоящей главе, охватывает
все эти типы вибраторов: как простейшие дебалансные, так и
планетарные вибраторы, вибраторы направленного действия,
моногармонические и полигармонические вибраторы (см.
рис. 23). Единственное существенное ограничение, принятое
в основной части исследования, состоит в предположении, что
состояние основного инерционного элемента вибратора — его
ротора, «поршня» и т. п. может быть описано посредством об-
общенной координаты, изменение которой в процессе интере-
сующего нас синхронного движения представляет собой почти
равномерное вращение:
+ +	|х)].	(1.1)
494
ОБОБЩЕНИЯ ЗАДАЧИ О СИНХРОНИЗАЦИИ ВИБРАТОРОВ [ГЛ. X1V
Здесь, как и ранее, со, и as — постоянные, о, = ±1, а
рдрДсщ/, ц)—слагаемое, характеризующее малые колебания от-
носительно равномерного движения.
Указанное предположение, с одной стороны, справедливо
в подавляющем большинстве практически интересных случаев,
а с другой — позволяет воспользоваться результатами, изло-
женными в девятой главе книги.
Отметим, что если в случае вибраторов с вращающимися
неуравновешенными массами имеется естественная координата,
обычно удовлетворяющая сформулированному требованию,—
угол поворота ротора, то, например, в случае поршневых вибра-
торов за такую кородинату, как правило, можно принять угол
поворота кривошипа действительно существующего или фиктив-
ного кривошипно-шатунного механизма, связанного с поступа-
тельно колеблющейся массой (см. рис. 25).
Во многих других случаях возможно осуществить преобразо-
вание от исходной координаты к «почти равномерно вращаю-
щейся» координате, например, так, как это было сделано в § 1
главы X при изучении синхронизации почти консервативных
объектов (переход к переменным фаза — частота).
В настоящей главе рассматриваются устройства как с несу-
щими, так и с несомыми связями между вибраторами; отдельно
изучается случай кратной синхронизации и синхронизации в ви-
броударных системах.
§ 2. Общая задача о простой (некратной) синхронизации
вибраторов
1. Описание системы и главные предположения. Рассмотрим
задачу о простой (некратной) синхронизации вибраторов, уста-
новленных на произвольной системе твердых тел Вх,.. ., Вп (не-
сущих тел), связанных между собою и с неподвижным основа-
нием упругими и демпфирующими элементами, а также некото-
рыми кинематическими связями (рис. 25). Колебательная часть
системы при этом не предполагается линейной, однако нелиней-
ные характеристики считаются достаточно гладкими — случай,
когда тела Bh . . . , Вп могут соударяться, здесь исключается.
Вибраторы могут быть как дебалансными, так и поршневыми,
моно- и полигармоническими, а также и планетарными; в по-
следнем случае, однако, предполагается, что в рассматриваемых
режимах движение роликов (колец) происходит без отрыва от
поверхности станков (осей). Между валами вибраторов могут
иметься (не показанные на рис. 25) несомые связи в виде уп-
ругих валов, муфт или связей типа электрического вала, а так-
же центробежно-инерционных связей или муфт [28, 353], пред-
ставленных на рис. 35 в нескольких вариантах.
§ 2]
ОБЩАЯ ЗАДАЧА О ПРОСТОЙ СИНХРОНИЗАЦИИ
495
На этом рисунке звенья 1 связаны с одним из валов, а
звенья 2 — с другим; на рис. 35, а— е, и изображены случаи
соосных валов, а на рис. 35, ж, з — случаи несоосных валов.
Рис. 35.
Варианты, представленные на рис. 35, а — д, отвечают связям
без «собственных степеней свободы», а варианты, изображенные
на рис. 35, е — и, — связям с «собственными степенями свободы».
Упругие элементы с показаны пунктиром или изображены
в виде пружин.
496
ОБОБЩЕНИЯ ЗАДАЧИ О СИНХРОНИЗАЦИИ ВИБРАТОРОВ [ГЛ. XIV
Центробежно-инерционные связи до последнего времени не
применялись в качестве синхронизирующих элементов вибрато-
ров; не исключено, однако, что они будут применяться в даль-
нейшем. К тому же обычный случай использования таких пере-
дач, отвечающих неподвижным осям синхронизируемых валов,
соответствует частному случаю рассматриваемой системы, когда
тела . , Вп являются неподвижными в пространстве. Отме-
тим, что несомые связи здесь не предполагаются линейными.
В соответствии со сказанным в § 1 будем предполагать, что
в изучаемых движениях изменение обобщенных координат ви-
браторов q>s (обычно это углы поворота соответствующих валов,
векторов-эксцентриситетов роторов и т. п.) близко к равномер-
ному вращению с общей средней угловой скоростью со (рассма-
триваем задачу о простой, то есть некратной, синхронизации;
случаю кратной синхронизации посвящен § 6 настоящей главы).
Как в главе XIII, в основном варианте решения задачи ви-
браторы будут рассматриваться в неквазиконсервативной идеа-
лизации (см. § 3 указанной главы). Сопоставление с решением,
получаемым при квазиконсервативной идеализации, дается в
§ 5 настоящей главы.
2. Основные результативные соотношения. В указанных выше
предположениях к рассматриваемой задаче оказывается пол-
ностью применимым все изложенное в главе IX книги, и здесь
остается лишь остановиться на истолковании и конкретизации
основных величин и результативных соотношений применительно
к случаю синхронизации механических вибраторов.
Прежде всего, заметим, что уравнения (1.4) главы IX в рас-
сматриваемой задаче являются уравнениями движения вибра-
торов, а уравнения (1.5)—уравнениями движения несомых и не-
сущих связей, состояние которых характеризуется обобщенными
координатами хь ..., xv.
Отметим, что уравнения (3.3) главы XIII как раз имели фор-
му уравнений (1.4) главы IX, хотя к первым из этих уравнений
мы пришли путем анализа порядков малости соответствующих
членов исходных дифференциальных уравнений движения.
Рассмотрим вначале задачу о внешней синхронизации.
Характер изучаемых синхронных движений определяется вы-
ражениями (1.1) при (Di = <02 = • • • = <оа, а в порождающем при-
ближении— равенствами (2.3) и (2.4) главы IX:
+ °Q	(s= 1.  > k),
x° = х°(и/, ap . . ., afe) (r — 1, . . ., v),	^-0
где x° — периодические no t (с периодом
уравнений
'	г cl ()L 0L _ (, 1
[ dt O.ir <)xr Ju 
T = 2jt/co) решения
(2.2)
§ 2]
ОБЩАЯ ЗАДАЧА О ПРОСТОЙ СИНХРОНИЗАЦИИ
497
Напомним, что квадратные скобки со значком «О», а иногда
и просто круглые скобки, здесь означают, что заключенное в них
выражение вычисляется для порождающего решения (2.1).
При этом значения порождающих параметров оц,. . . , ah
представляют собой (с точностью до знаков) начальные фазы
вращения вибраторов и определяются из уравнений (см. равен-
ства (3.10) и (3.11) главы IX)
Ps(at, ak, <o) = £(Z,-Gs-0 = 0 (s == 1, ..k). (2.3)
Последние уравнения, как и уравнения (6.11) главы ХШ, мо-
жно трактовать как уравнения равновесия средних моментов,
действующих на валы вибраторов. При этом величины
2л/о>
МДа(, . . ., ak, (й) = —= —f (L)dt (2.4)
’ das das 2л J ' ’ v ’
о
представляют собой средние потенциальные моменты, действую-
щие на вибраторы. Действительно, в рассматриваемой задаче
функцию Лагранжа системы L можно считать не зависящей
явным образом от времени t. Но тогда имеет место равенство
(3.7) главы IX:
2Х=-2^0’	<2-5)
5=1	5=1
то есть сумма всех моментов Ms равна нулю, и они, таким обра-
зом, не связаны непосредственно с притоком (или убылью) энер-
гии в системе; эти моменты лишь перераспределяют нагрузку
между отдельными вибраторами.
Рассмотрим подробнее структуру лагранжиана системы и тем
самым моментов Ms. В рассматриваемой задаче функция L мо-
жет быть представлена в виде
L^L+Lm + Lw.	(2.6)
Здесь
//=2Д + АД АЛ* =2 АЛ’	(2.7)
5=1	5=1
где Ls = Ls(cps, qps) — «собственные лагранжианы» вибраторов, а
ал; = ал; (фь„ <р,; х,,..., хт-, %,,..., хт} (2.8)
— добавки к этим лагранжианам, обусловленные подвижностью
тел, на которых установлены вибраторы (то есть подвижностью
«несущих» связей, или связей первого рода). Под х\,...,хт в
выражениях (2.8) и ниже понимаются обобщенные координаты,
определяющие положение несущих тел.
498
ОБОБЩЕНИЯ ЗАДАЧИ О СИНХРОНИЗАЦИИ ВИБРАТОРОВ [ГЛ. XIV
Через
L(!) = L(I)(xb хт; хь хт)	(2.9)
обозначен собственный лагранжиан несущих тел, а через
А<П) = А(п)(ф1, .... фА; Фи ф*; х1( ..., xv; xlf .... xv) (2.10)
— лагранжиан несомых связей (или связей второго рода). Как
отмечалось, таковыми могут быть упругие валы или муфты, со-
единяющие роторы вибраторов, устройства типа электрического
вала, а также центробежно-инерционные связи. Несомые связи,
в отличие от несущих, не приводят к появлению дополнительной
подвижности вибраторов. Эти связи, как правило, являются
средствами принудительной синхронизации, искусственно вводи-
мыми в систему для получения желаемого эффекта.
Напомним, что зависимость функций AL* и L<n> от фь ..., фд
предполагается такой, что при подстановке вида (2.1) они ста-
новятся периодическими функциями времени t с периодом
Т = 2л/(о.
Обозначим далее по аналогии с (2.4)
2л/ш
As = ^- [ (Ls)dt,
s 2л J v sf ’
о
2Л/(й	2n/(o
a’ = -£ f ^dt’ AA’ = ir f №dt> (2-H)
о	0
2Л/С0	2Л/С0
A(I) = ^ f (L’l'')dt,	A(I1)=^ [ (Lw)dt.
2л J 7	2л J '
о	о
Поскольку собственные лагранжианы каждого вибратора за-
висят только от обобщенных координат и скоростей этого вибра-
тора, то, очевидно,
^- = 0.	(2.12)
Поэтому
м	= _	-J^ = -/-AA’,	(2.13)
s das das das oas
где
2 л/и	2Л/И
Ло = ^ f ^dt = ^ f (AL + L(I) + L(II)) dt (2.14)
£ J V j/	J V 4/
о	0
— среднее значение лагранжиана системы связей, вычисленного
р порождающем приближении.
§ 2]
ОБЩАЯ ЗАДАЧА О ПРОСТОЙ СИНХРОНИЗАЦИИ
409
По своему смыслу (см., в частности, §§ 6 и 7 главы XIII)
момент A4S в задачах о синхронизации представляет собой сумму
консервативных частей К'1/''1 и Sw вибрационного момента и
момента системы принудительной синхронизации (то есть систе-
мы несомых связей)*):
A4S =	+ S(sK).	(2.15)
При этом в случае безынерционных несомых связей, когда
движение несущих тел не сказывается на кинетической энергии
элементов несомых связей, можно положить
W(K) =  д(дл +л(1))	=  ол™.	(
das ’	das	'	'
Для моментов и S(sK) справедливы равенства
£	k
2^ = 0,	2S<K) = 0,	(2.17)
S“l	s—l
получающиеся так же, как и (2.5), и имеющие тот же смысл.
Обратимся к рассмотрению прочих членов уравнений (2.3).
Величину
v 2л/и	о
°---(Л-fedt <2-18>
Г=1	1
в рассматриваемой задаче можно трактовать как средний мо-
мент неконсервативпых сил, связанных с колебательными коор-
динатами и учитываемых в порождающем приближении. Оче-
видно, можно положить
СДа,, .... afe, <о)=Г(0)(а„ .... aft> <о) + S<«> (а,.afel со), (2.19)
где
/П 2JT/C0
г«“ 1	О
V	2л/а>	(2.20)
•s“-- S •S-J’ [<Л#<«•
r»m+l	о
Как отмечалось в § 17 главы XIII, если рассматривается дви-
жение вдали от резонанса по колебательным координатам, то,
*) Напомним, что под вибрационными моментами понимаются дополни-
тельные слагаемые, которые возникают в уравнениях равновесия средних
моментов (2.3) вследствие колебаний.
500
ОБОБЩЕНИЯ ЗАДАЧИ О СИНХРОНИЗАЦИИ ВИБРАТОРОВ [ГЛ. XIV
как правило, неконсервативпые силы, соответствующие этим ко-
ординатам, в порождающем приближении можно не учитывать;
тогда
Q)°' = 0	(r=l,...,v) и W(sa> = S(G) = Gs = 0.
При этом основные уравнения (2.3) значительно упростятся не
только за счет обращения в нуль моментов Gs, но и за счет упро-
щения выражений для x°(cof, ар cQ, определяемых теперь
из уравнений (2.2) при Q,0' = 0. Однако при этом приходится от-
дельно рассматривать резонансный случай, а в перезонансном
случае — получать так называемые дополнительные условия
устойчивости, правда, видимо, малосущественные (см. § 5
главы ХШ).
Если же неконсервативные силы, отвечающие колебательным
координатам (в основном это силы сопротивления колебаниям),
учитываются уже в порождаемом приближении, то надобность
в отдельном рассмотрении резонансного случая отпадает. Отпа-
дает необходимость и в полученнии дополнительных условий
устойчивости, ибо число критических корней характеристиче-
ского уравнения системы в вариациях в точности равно числу
вибраторов k.
Наконец, величины
2л/(0
=	(s=l.....fe)	(2.21)
о
в рассматриваемых задачах представляют собой средние значе-
ния полных избыточных моментов, действующих на валы ви-
браторов:
Zs = L™ (ар as<o) -	(a........ co). (2.22)
Здесь Esm’—среднее значение момента, передаваемого от двига-
теля вибратора, а Rsm — среднее значение момента сил сопро-
тивления движению вибратора (см. § 6 главы ХШ).
Величины средних моментов L1™ (as, osco) в зависимости от
вида двигателя по-прежнему определяются формулами (6.8)
главы XIII.
Из величины Rsm> можно выделить слагаемое Rs, не зави-
сящее от колебаний несущих тел, и слагаемое зависящее
от указанных колебаний:
/?‘"”(ар ак, <л) = R° (со) +	(а,....ak, со). (2.23)
§2]	ОБЩАЯ ЗАДАЧА О ПРОСТОР! СИНХРОНИЗАЦИИ	501
Слагаемое ............. ctfe, со) естественно отнести к вибра-
ционному моменту W's, который, таким образом, представится
в виде суммы трех составляющих:
Ws =	+ W{sa}	(2.24)
— одной консервативной и двух неконсервативных. В аналогич-
ном виде представляется и момент Ss, обусловленный наличием
несущих связей:
Ss = S<*’ + S<°>.	(2.25)
Напомним, что выше (см. главу ХП1) часто применялось обо-
значение
Z°s = LT}{as, os®) - 7?Лсо).	(2.26)
Величина Z° при этом называлась просто избыточным мо-
ментом (в отличие от полных избыточных моментов Zs).
В результате выполненного анализа членов основных урав-
нений (2.3) можно представить их применительно к рассматри-
ваемой общей задаче о синхронизации в одной из следующих
эквивалентных форм:
РДа,, ..., a„ffl)^^(r-r;-Ss) = 0 (s = 1, ..., k), (2.27)
ps^......«*>	(4m) ~Ps- «Т -	-
-	- S'^' - S(s&) = 0	(s=l,...,fe), (2.28)
Ps(at....ak, W)^^(ZS-GS + 4“) = O (s=1, ..., k). (2.29)
Эти уравнения вполне аналогичны выведенным в §§ 6 и 7
главы ХШ для рассмотренного там частного случая задачи.
Они могут быть формально получены путем осреднения правых
частей уравнений движения вибраторов (см. уравнения (1.4)
главы IX), в которые вместо <ps и хг подставлены значения этих
величин, отвечающие порождающему решению (2.1) (см. фор-
мулы (2.5) главы IX).
Следует заметить, что выполненное выше разбиение момен-
тов A4S, Gs и Zs, фигурирующих в уравнениях (2.3), до некоторой
степени условно; фактически, например, ошибки не произойдет,
если отнести часть консервативных сил к неконсервативным.
Однако такое разделение отвечает физическому содержанию
задачи и удобно при рассмотрении прикладных вопросов.
Устойчивые синхронные движения могут отвечать лишь тем
решениям уравнений (2.27) — (2.29) относительно ои,..., «л, для
502
ОБОБЩЕНИЯ задачи о СИНХРОНИЗАЦИИ ВИБРАТОРОВ [ГЛ. XIV
которых все корни алгебраического уравнения k-й степени
|4^--6s/x| = 0	(s,/= 1, ..А)	(2.30)
имеют отрицательные вещественные части. При наличии хотя бы
одного корня с положительной вещественной частью соответ-
ствующее движение неустойчиво, а в случае присутствия нулевых
или чисто мнимых корней, вообще говоря, требуется дополни-
тельное исследование.
В ряде частных случаев уравнения (2.27) — (2.29) упрощают-
ся. Так, например, для дебалансных вибраторов
Г^ = 0, Zs = Z° = Z.'m)(as, asa)-/?°((o).	(2.31)
Если несомые связи, как это предполагалось в главе XIII,
являются безынерционными упругими элементами, демпфирова-
нием в которых можно пренебречь, то
о(0) а	е   е(Ю    дДИI)   д (Пс)„
-U,	Os-Os -	да$ - да° ,	(2.62)
где потенциальная энергия упругих элементов Пс определяется
выражением (7.6) указанной главы.
По поводу специфики задач о самосинхронизации и о прину-
дительной синхронизации здесь можно было бы повторить почти
дословно сказанное в §§ 10—12 главы XIII. Здесь мы напомним
лишь, что предшествующее изложение относилось к случаю за-
дачи о внешней синхронизации, когда хотя бы один из двигате-
лей вибраторов является синхронным; уравнения движения при
этом неавтономны и частота синхронного движения задана.
В случае же, когда все вибраторы приводятся от двигателей
синхронного типа, мы имеем задачу о внутренней (автономной)
синхронизации. В данном случае из уравнений (2.27) — (2.29)
фазы at, ..., o.k определяются лишь с точностью до произволь-
ной постоянной, но зато из тех же уравнений, вообще говоря,
находится также исходное приближение к модулю угловой ско-
рости синхронного вращения со.
Уравнение (2.30) при этом непременно имеет нулевой корень,
который, однако, не влияет на решение вопроса об устойчивости
и легко отделяется, после чего получается уравнение k— 1-й сте-
пени
~м| = °	(s,/=l,	й).	(2.33)
Приведем уравнение баланса энергии в системе
k	ь. k
2 Л = 2	+ 5<0)<о),	(2.34)
S“1	S“l
§ 2]	ОБЩАЯ ЗАДАЧА О ПРОСТОЙ СИНХРОНИЗАЦИИ	503
которое получается в результате сложения всех уравнений (2.28),
предварительно умноженных на aks, и учета равенств (2.17).
Отметим, далее, что в случае самосинхронизации дебаланс-
ных вибраторов с одинаковыми и положительными парциальны-
ми скоростями (см. п. 2 § 10 главы XIII) и когда силы сопро-
тивления в колебательной части системы не учитываются, имеем
L'm) = osMa)(osffl) = 7?s(ffl), Zs = Zs = 0,
и уравнения (2.27) —(2.29) и (2.33) существенно упрощаются:
- d(aAa„tA''’' "	.....<s - 1.................Ч,
—-—  + Ss/x =0	(s, / = 1, .. ., k).
3.	Синхронизация валов посредством центробежно-инерцион-
ных связей. О способе синхронизации валов с неподвижными в
пространстве осями посредством так называемых центробежно-
инерционных связей (см. рис. 35) уже говорилось в п. 1 настоя-
щего параграфа. Динамика таких синхронизирующих передач
явилась предметом ряда исследований К. М. Рагульскиса,
А.-П. К. Каволелиса и И. И. Виткуса [353], [354]. Основные урав-
нения, относящиеся к данному случаю, получаются из уравнений
(2.27) — (2.29), если положить в них
ДА* = Д(1) = 0, Ws = W(SK) =	= 0.	(2.35)
Тогда эти уравнения существенно упростятся и примут соответ-
ственно следующий вид:
РДа,, ..., afe, M)^£(Z“-Ss) = 0 (S-l...........k), (2.36)
РДа,,	- SW - S<°)) = 0	(2.37)
(s = 1....k),
P,(a„	~	(^ ~ S» + ^) - 0	(2.38)
(s= 1, ..., k).
Заметим, что данная задача не обязательно должна рассма-
триваться как задача о внутренней синхронизации. Если, напри-
мер, вращение одного из валов можно с достаточной точностью
считать заданным и не зависящим от движения прочих элемен-
тов системы, то задачу можно ставить и решать как задачу
о внешней синхронизации. По поводу устойчивости движений,
отвечающих определенным решениям уравнений (2.36) — (2.38),
остается в силе все сказанное выше относительно общего случая.
504
ОБОБЩЕНИЯ ЗАДАЧИ О СИНХРОНИЗАЦИИ ВИБРАТОРОВ [ГЛ. XIV
4.	О синхронизации вибраторов в системах с распределенны-
ми параметрами. Характер записи основных уравнений (2.27) —
(2.29) таков, что формально они могут быть составлены и для
систем, в которых несущие связи (тела, на которых установлены
вибраторы), а также и элементы несомых связей (например,
валы, соединяющие роторы вибраторов) рассматриваются как
тела с распределенными параметрами. Строго говоря, использо-
вание указанных уравнений в таких случаях требует обоснова-
ния. Однако для механика-прикладника здесь не возникает осо-
бых проблем, ибо все реальные элементы фактически обладают
распределенными параметрами. Вопрос о том, как схематизи-
ровать эти элементы при принятом в прикладной механике уров-
не строгости, решается, с одной стороны, на основе общих сооб-
ражений о допустимости той или иной идеализации, а с другой
стороны, исходя из соображений максимального удобства и про-
стоты решения задачи.
Ниже (см. п. 7 § 8 настоящей главы) приводится пример ре-
шения задачи о синхронизации вибраторов на упругой балке
с распределенными параметрами, основанного на формальном
использовании полученных выше соотношений, без обоснования
законности такого приема. Получающиеся при этом результаты
оказываются вполне правдоподобными, хотя, конечно, они точно
так же нуждаются в экспериментальном подтверждении, как и
все другие результаты теоретического исследования при исполь-
зовании их применительно к реальным системам (см. § 1 гла-
вы IV, а также § 1 главы XIX).
5.	Основные трудности и общий план решения задач о син-
хронизации вибраторов. Обычно при решении задач о синхрони-
зации вибраторов оказывается вполне достаточным найти значе-
ния фаз вращения вибраторов оц,...,^ из уравнений (2.27) —
(2.29), выяснить, каким из решений этих уравнений могут соот-
ветствовать устойчивые синхронные движения, и найти условия
существования таких движений; последние условия предста-
вляют собой не что иное, как условия существования веществен-
ных решений тех же основных уравнений (2.27) — (2.29).
Таким образом, одним из центральных моментов решения за-
дачи является реальное составление уравнений (2.27)—(2.29).
Главной же технической трудностью, которая может возникнуть
при этом, является отыскание периодического решения поро-
ждающих уравнений (2.2) относительно x°(a>t, ар ..., cQ при
<ps = <р° =• а, (со/+ as). Иными словами, речь идет о реальном на-
хождении порождающего решения (2.1). Но уравнения (2.2)
представляют собой не что иное, как уравнения вынужденных
колебаний системы в предположении, что движение вибраторов
происходит по простейшему закону <р, = <р° = ст,(со/ + «,)с некото-
§ 3J	КВАЗИЛИНЕЙНАЯ КОЛЕБАТЕЛЬНАЯ СИСТЕМА	505
рыми заранее неизвестными начальными фазами ац. . . , a,t и
что в уравнениях колебаний отброшены малые слагаемые. Таким
образом, можно сказать, что одним из главных элементов реше-
ния задачи о синхронизации является решение (вообще говоря,
приближенное) задачи об установившихся вынужденных колеба-
ниях системы при условии, что движение вибраторов происходит
по закону qps =	+ а.ч).
Наиболее просто указанная задача решается в случае, когда
колебательную систему, с которой связаны вибраторы, можно
считать линейной. Рассмотрению этого наиболее распространен-
ного на практике случая посвящен следующий параграф настоя-
щей главы.
Пусть, однако, порождающее решение (2.1) реально найдено.
Тогда можно прибегнуть к одному из двух способов составления
основных уравнений (2.27)—(2.29):
1. Подставить решение (2.1) в выражение (2.6) для лагран-
жиана системы (или в выражения (2.7) — (2.10) для его отдель-
ных слагающих), а также в выражения для обобщенных сил
iQ^'Ja и выполнить осреднение в соответствии с формулами
(2.11), (2.18), (2.20). После этого-легко определяются все члены
основных уравнений.
2. Осреднить в соответствии с формулой (2.5) главы IX за
период Т = 2л/(о правые части уравнений движения вибраторов
(см. уравнения (1.4) главы IX).
Выбор того или иного способа, естественно, является делом
вкуса исследователя. Как будет показано ниже, в случае квази-
линейной колебательной системы указанные выше выкладки,
связанные с осреднением, могут быть выполнены для определен-
ных классов систем раз навсегда, если ввести некоторую систему
коэффициентов; определить эти коэффициенты можно как тео-
ретическим, так и экспериментальным путем, причем в последнем
случае вообще отпадает надобность в составлении и решении
дифференциальных уравнений (2.2).
Подробнее методика решения задач о синхронизации вибра-
торов изложена в Добавлении 1.
§ 3. Синхронизация вибраторов, связанных с квазилинейной
колебательной системой
1. Некоторые общие соотношения. Пусть колебательная часть
рассматриваемой системы, то есть система, получающаяся из ис-
ходной при снятых вибраторах (или при зафиксированных в
определенном положении подвижных частях вибраторов), яв-
ляется линейной, по крайней мере в порождающем приближе-
нии. Предположим, далее, что несомые связи (элементы системы
принудительной синхронизации) безынерционны и не вносят
503
ОБОБЩЕНИЯ ЗАДАЧИ О СИНХРОНИЗАЦИИ ВИБРАТОРОВ [ГЛ. XIV
дополнительных степеней свободы. Тогда т = v и выражение
(2.10) для лагранжиана £<п> не будет содержать переменных
Xi,...,xv. Наконец, допустим, что рассматривается случай дви-
жения вдали от резонанса по колебательным координатам; при
этом, как отмечалось выше, неконсервативные обобщенные силы,
отвечающие колебательным координатам, в исходном прибли-
жении могут не учитываться, то есть можно принять
<QrC) = 0	(г=1.......v).	(3.1)
Тогда, согласно (2.20),
= W{sQ) = S'0).	(3.2)
Сформулированные предположения соответствуют принятым
в § 4 главы IX, и поэтому в рассматриваемом случае справед-
ливы соотношения
д (А + А(1) — А(11)) == д(А* + 2А(1)) = d(AA* + 2A(1))
das	das	da's '	' ‘ '
Последнее из этих равенств получается при учете формул
(2.13). Если принять теперь во внимание, что в данном случае
справедливы также формулы (2.16), то будем иметь при учете
(2.13) и (2.3)
= W{SK} + Sf'=- 4^- = - — = d(A(I/-A<I1))
das das	das ’
ц/(К) = _ d(AA* +A(1)) = 5A(1) __1_ д .д’	= _ dA(11)
s	das	das 2 das ’ s das "
(3.4)
Основые уравнения (2.28) — (2.29), в силу приведенных соот-
ношений, также упрощаются и могут быть записаны в одной из
следующих форм:
Ps(ap .... ак,	^’-5^) = °	(3-5)
(s = 1, ..., fe),
РД»,......•) = ^[ь“Ч-и»1 - d(A'k,A'">)]-° (3-б)
(s= 1, ..., fe).
2, Выражение вибрационных моментов через гармонические
коэффициенты влияния. Рассмотрим теперь более подробно син-
хронизацию вибраторов в системе, подобной описанной в п. 1
настоящего параграфа, однако для конкретности будем вначале
считать вибраторы обычными дебалансными (рис. 23, а), а несо-
мые связи — отсутствующими. С другой стороны, откажемся от
предположения о равенстве нулю неконсервативных сил Qr0),
§ 3]
квазилинейная колебательная система
507
отвечающих колебательным координатам, а также от предполо-
жения об отсутствии резонанса по этим координатам; будем счи-
тать при этом, что силы Q,G) являются силами вязкого трения.
В рассматриваемом случае
IVf’ = 0, S'fl = SlsGl = Ss = 0, ZS = Z° = L™ -R°s, (3.7)
где величины Z.(sm) и Rs определяются соответственно выраже-
ниями (6.8) и (6.9) главы ХШ. Чтобы составить основные урав-
нения (2.28), остается, таким образом, найти выражения для
вибрационного момента
Ws = W{SK) + W{s°\	(3.8)
то есть среднего момента, взятого с противоположным знаком,
действующего на ротор s-ro вибратора вследствие колебаний
его оси.
Для решения этой задачи * *) найдем вначале (с точностью до
величин более высокого порядка малости) мгновенное значение
указанного момента, а затем произведем усреднение согласно
формуле (2.5) главы IX.
Пусть osusvsws (s = I,..., k)—прямоугольная система коор-
динат, связанная с колеблющимся телом (рис. 36, а), причем
ось osws направлена вдоль оси вращения ротора s-ro вибратора,
Рис. 36.
а начало координат os выбрано так, чтобы центр тяжести этого
вибратора cs всегда находился в плоскости usosvs\ направления
осей и8 и vs могут быть произвольными. Положение ротора ви-
братора по отношению к указанным осям определяется углом
поворота фз между вектором-эксцентриситетом
 	OSCS ' &s&s (фз)	(3-9)
*) Здесь излагается в несколько видоизмененном и дополненном виде
соответствующий раздел работы К. Ш. Ходжаева [4071.
508
ОБОБЩЕНИЯ ЗАДАЧИ О СИНХРОНИЗАЦИИ ВИБРАТОРОВ [ГЛ. XIV
и осью osus. Здесь через es обозначен модуль, а через
es (<ps) = bcos <ps + js sin <ps
(3.10)
— орт вектора-эксцентриситета вибратора (is и /s— соответствен-
но орты осей osus и osvs).
Пусть, далее, rs = oso° — вектор смещения точки os из поло-
жения равновесия о° при колебаниях тела. Тогда момент, дейст-
вующий на ротор вибратора вследствие колебаний его оси, будет
Ts = - msesrs • rs (<ps).	(3.11)
Здесь точка, как обычно, является знаком скалярного произве-
дения векторов, а
тз(фз) = ~ is sin <ps + /s cos cps	(3.12)
есть орт, перпендикулярный вектору-эксцентриситету вибратора;
направление т., отвечает направлению отсчета угла q>s. Выраже-
ние (3.11), конечно, является приближенным: в нем, в частности,
не учтено влияние поворотов оси вращения дебаланса в процес-
се колебаний. Однако неучтенные слагаемые обычно имеют бо-
лее высокий порядок малости; это подробно показано в цитиро-
ванной выше работе К. Ш. Ходжаева [407].
Выразим теперь ускорения rs (в порождающем приближении)
через параметры вибраторов и колебательной части системы.
Отметим, что эти ускорения являются линейными функциями
ускорений xi,...,xv системы несущих тел; для частного случая,
рассмотренного в главе XIII, соответствующая связь, например,
определяется формулами (2.32) указанной главы. Но значения
обобщенных координат Xi,...,xv в порождающем приближении
определяются в данном случае как решение задачи об устано-
вившихся вынужденных колебаниях линейной системы под дей-
ствием возмущающих сил, развиваемых вибраторами при их
движении по закону
Фз = Фз = азИ + «з)-	(3.13)
где as — произвольные постоянные. Эти возмущающие силы
определяются выражениями
К = mses (ф°з)2 es (Фз) = Шзез®4 К (М/ + «з)] =
= msesco2[is cos (со/ + as) + js<ys sin (со/ + as)]. (3.14)
Введем в рассмотрение 8/е2 величин
О), ^’(со), Cs)(co), ^’(й),
С^(®)>	Cs)(®).
определяемых следующим образом.
КВАЗИЛИНЕЙНАЯ КОЛЕБАТЕЛЬНАЯ СИСТЕМА
509
§ 3]
Пусть к точке несущего тела о, в направлении оси OjUj при-
ложена гармоническая сила единичной амплитуды с периодом
2л/<о. Пусть, кроме этой силы, на колебательную систему не
действуют никакие другие задаваемые силы. Тогда амплитуда
проекции перемещения точки os на ось о.,м, при установившихся
вынужденных колебаниях и угол сдвига фаз между указанным
перемещением и силой*) будут соответственно равны величинам
и
Таким образом, если на колебательную систему в точке Oj
действует только одна задаваемая сила ij cos ott, то проекция пе-
ремещения точки o.s на ось osus в режиме установившихся коле-
баний будет
Suu = kuu C0S Н - CS) (®)J-	(3- 15)
Аналогичным образом величины /e'/J-1 (co) и ф^®’ (co) опреде-
ляются соответственно как амплитуда и сдвиг фаз проекции пе-
ремещения точки os на ось при действии единичной гармо-
нической силы периода 2л/со на точку Oj в направлении оси оцц
и т. д.
Введенные коэффициенты могут быть определены в резуль-
тате решения соответствующих линейных задач или даже экспе-
риментальным путем (см. ниже). В случае, когда трение в коле-
бательной части системы не учитывается, величины kuu (со), ...
..., kvv (со) представляют собой обычные гармонические коэф-
циенты влияния; мы сохраним этот термин также для систем
с трением и будем называть указанные коэффициенты гармони-
ческими коэффициентами первого рода.
Для гармонических коэффициентов влияния имеют место со-
отношения взаимности [406, 407]
kuu (<й) kuu (®), kvu (®) = k(uv (®), kvv (®) = k^v (®),
ф(Щ (со) = ф</®> (<о), фб/) (Ш) = ф(/®> (со), ф(Щ (со) = Ф^) (со). (ЗЛ6)
Отметим, что для определенности фаз ф^>, ..., ф^ можно
считать, что величины kuu, . k„l} существенно положительны.
Через введенные величины нетрудно выразить вектор смеще-
ния rs центра s-ro вибратора о., при установившихся вынужден-
ных колебаниях под действием возмущающих сил, определяемых
*) Напомним, что силы сопротивления колебаниям могут в рассматри-
ваемом случае учитываться в порождающем приближении.
510
ОБОБЩЕНИЯ ЗАДАЧИ О СИНХРОНИЗАЦИИ ВИБРАТОРОВ [ГЛ. XIV
выраженяими (3.14). Получаем
k
r°s = й2 2 mjej {[&</*> cos (at + О/ - ф<М) +
+ ЧиЧsin (®f + а/ “ Cs))] ls + [Ч'о’ cos И + а/ ~ Cs)) +
+ sin (at + ау - ф<^)] Js + [•••] 4} • (3.17)
Выражение для проекции перемещения rs на ось osws (ks есть
орт этой оси), которое здесь не выписано, в дальнейшем не пона-
добится.
Заметим теперь, что согласно формуле (2.5) главы IX и ра-
венствам (2.27) — (2.29) настоящего параграфа искомые вибра-
ционные моменты будут
2л/ш	2п/а>
(rs)df = -^/nAJ <.zs(^dt. (3.18)
о	о
Производя вычисления в соответствии с равенствами (3.12),
(3.13), (3.17) настоящего параграфа и формулами (6.3) гла-
вы XIII, приходим окончательно к следующему выражению для
вибрационных моментов через гармонические коэффициенты
влияния первого рода:
k
+ 1F<«> =	\k™ sin (as - a, + ф<£>) +
/=i
+ cos (as - a7 + ф(£>) - ask^ cos (as - a, + ф^) +
+ aiask^} Sin (as “ “/ + CS))]- (3- 19)
Отметим, что при as = aj = 1 последняя формула совпадает,
с точностью до обозначений, с соответствующей формулой рабо-
ты [407]. Отличие в знаке объясняется иным определением ви-
брационного момента, принятым в указанной работе.
Часто удобнее пользоваться не гармоническими коэффициен-
тами влияния первого рода k^, ..., k^\ ф^®\ ..., фО®>, а вели-
чинами
cos ф^х),	— k'ls> cos ф^5),
/((/j) = /(W) = COS Ф(/®',
Q(/s) = GW) = fe(/s) sin ф(/5), G</s) = G(s/) = &(/s) sin ф(/з), (3,2°)
(jds) = g(s/> — sin ф(/х\
w vv vv vv • vv 9
КВАЗИЛИНЕЙНАЯ КОЛЕБАТЕЛЬНАЯ СИСТЕМА
511
§ 3]
которые назовем гармоническими коэффициентами влияния вто-
рого рода*). Очевидно, что но своему физическому смыслу, на-
пример, величины Кии и Guu представляют собой коэффи-
циенты соответственно при cos at и при sin at в выражении
для проекции смещения точки os на ось osus при действии на
точку Oj гармонического возмущения единичной амплитуды, на-
правленного вдоль оси OjUp Иными словами, при действии ука-
занного возмущения проекция смещения точки os на ось
'osus представляется не в виде (3.15), а в форме
s«u = Кии cos at + Guu sin at.	(3.21)
Нетрудно видеть, что соотношения (3.20) непосредственно
вытекают из сопоставления равенств (3.15) и (3.21).
При использовании гармонических коэффициентов влияния
второго рода выражение (3.19) для вибрационных моментов
может быть представлено в форме
Ws= Г 1го + Г'0) =
k
= S [(«"» - »,G"? + <7,0"? + <7,0 Л"?) sin («, - «,) +
/-1
+ (Guu + а!^и ~ as^v + aiasG^ C0S (“s - «/)]. (3.22)
аналогичной форме записи выражений (6.4) главы XIII, полу-
ченных для рассмотренного там частного случая.
Как и в § 6 главы XIII, здесь можно ввести «.частные» вибра-
ционные моменты
wsi = ™s! (“s - «/> ®) = ^e^/e/M [feW sin (as - a/ ++
+ cos (as ~ af +	~ ask<ilv cos (as - “/ +	+
+ ajOsk^ sin (as - a, +	=
= —[(К™ ~ Oj + asG^ + ojGsKW} sin (as - a,) +
+ (Guu +	- °sKuv + °iasGvv)cos (as - “/)]> (3-23)
*) Подобные коэффициенты влияния были использованы при изучении
синхронизации вибраторов в работе Л. Шперлинга [482], появившейся почти
одновременно с цитированной выше статьей К.. Ш. Ходжаева [407]. Л. Шпер-
линг получил общее выражение вибрационных моментов W, через эти коэф-
фициенты и рассмотрел ряд конкретных примеров.
512
ОБОБЩЕНИЯ ЗАДАЧИ Cl СИНХРОНИЗАЦИИ BllliPA IОРОВ Н'.П XIV
удовлетворяющие равенству
/г
ws = 2 wsl(as-ah со)
/-1
(3.24)
и отражающие взаимодействие s-ro и /-го вибраторов.
Отметим, что в случае, когда силы трения в порождающем
приближении нс учитываются и рассматривается движение в не-
резонанспом режиме, все величины . .., равны либо О,
либо л (напомним, что коэффициенты k<№>, ..., считаются
существенно положительными). Поэтому в указанном случае
G(™^ G^> = g£> = G(v'vs> = О	(3.25)
и выражение (3.22) упрощается:
= U7(K) =	m.е.	+	sin (as - a,) +
/=1
+	- *MS)) cos (as - ay)] (UZ(G) = 0). (3.26)
Частные вибрационные моменты
mI.e<./n;ei<£>4 r
----[(K1^ - vMs>)sin (“s - a/) +
+ (oA(/u)-^))C0S(as-a/)] (3-27)
при этом удовлетворяют соотношениям взаимности
(3.28)
которые легко получаются при учете равенств (3.20). Из соот-
ношений (3.28) следует:
2 2 ^ = 2^°=о,	(з.29)
S=I /=|	$=»!
как это и должно быть в рассматриваемом случае.
Значение изложенных результатов состоит в том, что они
позволяют составлять основные уравнения задачи о синхрониза-
ции вибраторов, не прибегая к решению уравнений движения
колебательной части системы и даже не выписывая, этих урав-
нений. Действительно, гармонические коэффициенты влияния
можно найти экспериментальным путем, возбуждая колебания
конструкции в точках крепления вибраторов и измеряя возни-
кающие при этом колебания в соответствующих точках. Есте-
ственно, что такие измерения следует выполнить для определен-
ного диапазона частот оц со со2, в котором может лежать
§ 3]	квазилинейная колебательная система	513
угловая скорость синхронного вращения вибраторов. Обычно
этот диапазон достаточно узок.
Описанный полуэкспериментальный метод исследования син-
хронизации вибраторов приобретает особое значение в случаях,
когда колебательная система столь сложна, что трудность пред-
ставляет даже составление достаточно точных уравнений ее дви-
жения. Таким случаем является, например, исследование само-
синхронизации нескольких неуравновешенных машин, установ-
ленных на групповом фундаменте или на связанных между
собой фундаментах.
Отметим, что подобно тому, как это было сделано в цитиро-
ванной работе К. Ш. Ходжаева, выражения вибрационных мо-
ментов через коэффициенты влияния могут быть получены и для
систем с другими типами вибраторов.
Рассмотрим, в частности, случай поршневых вибраторов,
в которых колебания инерционной массы ms сообщаются от
центрального кривошипно-шатунного механизма (рис. 36,6).
Отношение радиуса кривошипа es к длине шатуна ls при этом
будем считать столь малым, чтобы движение массы tns при рав-
номерном вращении вала кривошипа можно было рассматри-
вать с достаточной точностью как простое гармоническое.
Мгновенное значение момента, передающегося на вал вибра-
тора вследствие колебаний тела, на котором этот вибратор
установлен, в данном случае будет
Ts= - msesls cos <ps,	(3.30)
где fs — проекция на ось osiis ускорения колебаний точки os не-
сущего тела, совпадающей со средним положением центра тя-
жести массы ш., при ее колебаниях относительно тела, а ср5 —
угол поворота вала кривошипа. Проекция на ось osus возму-
щающей силы, развиваемой вибратором при вращении вала
кривошипа по закону (3.13), будет
F°u = — msus = <jsmse.s(i)2 sin (и/ + as).	(3.31)
Проекция смещения точки os несущего тела при установив-
шихся колебаниях под действием указанных сил может быть
представлена в форме
k
С = 2	<Т/"г/8/®2 sin (®Z + “ Чи’)-	(3.32)
где, как и выше, через обозначен гармонический коэффи-
циент влияния первого рода, равный амплитуде проекции пере-
мещения при колебаниях точки о3- несущего тела на ось OjUj,
514
ОБОБЩЕНИЯ ЗАДАЧИ О СИНХРОНИЗАЦИИ ВИБРАТОРОВ [ГЛ. XIV
вызванных гармонической силой единичной амплитуды с перио-
дом 2л/(о, действующей на точку os вдоль оси os«s; ф^) есть
соответствующий угол сдвига фаз.
Произведя теперь осреднение по формуле
2п/о>	2л/а>
^coscp^Z, (3.33)
о	о
аналогичной формуле (3.18), в соответствии с равенствами (3.31)
и (3.32) приходим к искомому выражению для вибрационных
моментов:
k
Ws = W™ +	= CTsms2es-£	sin (as - a,. + <>). (3.34)
/-1
При использовании гармонических коэффициентов влияния
второго рода, определенных соотношениями
К™ =	cos е>,	= GW) = sin (3.35)
выражение (3.34) принимает следующий вид:
ws =	+ r(sG) =
k
= asnts2s-S Ю sin (as - O/) + G^ cos (as - ay)]. (3.36)
/-i
Отметим, что в отношении применимости полученных здесь
формул к колебательным системам с распределенными пара-
метрами справедливо все сказанное по этому поводу в п. 4 § 2
настоящей главы.
Заметим также, что для вибраторов, генерирующих возму-
щающие силы и моменты весьма общего характера, выражения
для вибрационных моментов через гармонические коэффи-
циенты влияния были получены Р. Ф. Нагаевым [317]. Однако
па изложении этой работы, послужившей основой для исследо-
вания синхронизации вибраторов гироскопического типа [10,
196, 213], мы не будем здесь останавливаться.
§ 4. Интегральный критерий устойчивости синхронных
движений механических вибраторов
1. Основные соотношения. По поводу интегрального крите-
рия устойчивости синхронных движений вибраторов примени-
тельно к рассмотренной в §§ 2 и 3 задаче можно было бы по-
вторить почти все сказанное в § 5 главы IX и в § 9 главы XIII.
интегральный критерий устойчивости
515
§ 4]
Поэтому здесь мы лишь перечислим основные факты и приве-
дем геометрическую форму интегрального критерия, о которой
выше еще не говорилось.
а) Для справедливости интегрального критерия устойчивости
синхронных движений вибраторов достаточно, чтобы существо-
вала функция В = В(а\, . . ., ай, ®) такая, что
< = г,-О„	(4.1)
Тогда за потенциальную функцию D, фигурирующую в форму-
лировке интегрального критерия, можно принять выражение
D = - (А + В).	(4.2)
Как было показано в § 9 главы ХШ, при наличии планетар-
ных вибраторов функция В, вообще говоря, не существует даже
в условиях плоского движения. В случае же вибраторов деба-
лансного типа и при условии, что неконсервативные силы в по-
рождающем приближении не учитываются (рассматривается
движение вдали от резонанса), эта функция определяется фор-
мулой (9.6) главы ХШ, которая остается справедливой и в об-
щем случае. Поскольку «собственные» лагранжианы вибраторов
не зависят от ац ..., ал (см. равенства (2.12)), то за функ-
цию D можно также принять выражение
D = - (Ао + В) = - (ДА* + А(1> + А(П) + В\	(4.3)
Изучаемые синхронные движения вибраторов могут отвечать
лишь стационарным точкам а( = а(, .. ., ak = ak функции D. При
этом точкам строгого минимума (в случае задачи о внешней
синхронизации), который обнаруживается путем анализа членов
второго порядка в разложении D по степеням as — а*, действи-
тельно отвечают асимптотически устойчивые синхронные дви-
жения. Отсутствие минимума, обнаруживаемое тем же путем,
свидетельствует о неустойчивости.
В случае задачи о внутренней синхронизации из условий
стационарности
-^(“ц •••. “ь®) = ° (s = l, ...,&)	(4.4)
определяются разности фаз ai — as, ..., ал-i — ak и исходное
приближение со к модулю угловой скорости синхронного дви-
жения.
Для устойчивости синхронного движения при этом требуется
наличие строгого минимума потенциальной функции В по
k — 1 переменным ai — ал, .., ccft-i —
516
ОБОБЩЕНИЯ ЗАДАЧИ О СИНХРОНИЗАЦИИ ВИБРАТОРОВ [ГЛ. XIV
б) В случае, когда вибраторы связаны с квазилинейной ко-
лебательной системой, а неконсервативные силы по колебатель-
ным координатам не учитываются (рассматривается движение
вдали от резонанса), справедливы соотношения (3.3), и поэтому
за потенциальную функцию может быть принято, кроме (4.3),
также и одно из следующих выражений:
£) = А(1) — А(11) — В,	(4.5)
£)= - (у АА’ + А(11) + В].	(4.6)
При этом в случае самосинхронизации вибраторов (А<п) == 0)
с одинаковыми и положительными парциальными угловыми ско-
ростями (см. п. 2 § 10 главы ХШ), как и в § 9 указанной главы,
В = const,	(4.7)
и поэтому можно положить
D = А(,) или D = - ДА*.	(4.8)
Иными словами, в этом случае за потенциальную функцию
можно принять либо осредненный за период лагранжиан си-
стемы несущих тел, либо взятую с противоположным знаком
добавку к лагранжиану вибраторов, обусловленную подвиж-
ностью несущих тел; при этом лагранжианы предполагаются
вычисленными в порождающем приближении.
Как уже упоминалось, второе из выражений (4.8) соответ-
ствует формулировке интегрального критерия устойчивости,
предложенной Б. П. Лавровым [242, 244].
В еще более частном, однако нередко встречающемся на
практике случае, когда несущие твердые тела связаны с непо-
движным основанием и одно с другим весьма мягкими упру-
гими элементами (кинематические связи между телами, однако,
могут присутствовать), потенциальной энергией П<9 несущей си-
стемы можно пренебречь, и тогда, согласно первому выраже-
нию (4.8),
2л/о>
(4.9)
о
Таким образом, в данном случае устойчивые синхронные дви-
жения отвечают минимумам осредненной за период кинетиче-
ской энергии несущих тел.
2. Геометрическая форма интегрального критерия устойчи-
вости. Величина — ДА*, фигурирующая в равенствах (4.3), (4.6)
и (4.8), по существу представляет собой в рассматриваемых за-
§ 5J	КВАЗИКОНСЕРВАТПВНАЯ ИДЕАЛИЗАЦИЯ ВИБРАТОРОВ	517
дачах «потерю» суммарной кинетической энергии вращающихся
дебалансов, обусловленную колебаниями их осей. Поэтому ука-
занную величину можно выразить через характеристики коле-
баний осей вибраторов. Оказывается, что минимуму выраже-
ния — АЛ* = — Д7* соответствует минимум суммы амплитуд
проекций перемещений точек os пересечения осей вращения ро-
тора s-ro вибратора с плоскостью вращения его вектора-эксцен-
триситета (рис. 36) на направление этого вектора-эксцентриси-
тета. Таким образом, в случае самосинхронизации вибраторов
с одинаковыми и положительными парциальными угловыми
скоростями устойчивым синхронным движениям отвечает мини-
мум упомянутой выше суммы амплитуд.
Соответствующая геометрическая форма интегрального кри-
терия устойчивости была предложена Б. П. Лавровым [242, 244];
эта форма может оказаться удобной при решении задач синтеза
вибрационных машин с самосинхронизирующимися вибраторами
(см. главу XV настоящей книги).
§ 5. Решение задачи о синхронизации при квазиконсервативной
идеализации вибраторов. Сравнение с «неквазиконсервативным»
решением
При решении задачи о синхронизации вибраторов во втором
и третьем параграфах настоящей главы предполагалось, что
вибраторы могут быть идеализированы в виде объектов, дви-
жение которых описывается дифференциальными уравнениями
вида
+ ks (<ps - сцш) = цФ, ($=1.....k).	(5.1)
Такая идеализация была названа неквазиконсервативной (см.
§ 3 главы XIII и § 6 главы IX), ибо в исходном приближении
(р = 0) вибраторы обращаются в объекты диссипативного типа.
Здесь мы приведем решение задачи в предположении, что
коэффициенты демпфирования ks малы, так что движение вибра-
торов описывается уравнениями
ЛФг =НФ4 (s= 1, • •k),	(5.2)
где обозначено
Ф5 = Ф5 — £s(<ps —а,о>), ks = n%s.	(5.3)
Подобную идеализацию естественно назвать квазиконсерва-
тивной, ибо вибраторы считаются близкими к простейшим кон-
сервативным объектам
(s==i....*)• (5-4)
Рассмотрение задачи в этой второй постановке было выпол-
нено К. Ш. Ходжаевым [407]. Оно представляет интерес, с одной
518
ОБОБЩЕНИЯ ЗАДАЧИ О СИНХРОНИЗАЦИИ ВИБРАТОРОВ [ГЛ. XIV
стороны, поскольку в ряде случаев силы трения и соответствую-
щие силы, связанные с «жесткостью» характеристик асинхрон-
ных моментов, естественно предположить малыми по сравнению
с силами инерции. С другой стороны, интересно изучение во-
проса об «устойчивости» результатов исследования по отноше-
нию к характеру идеализации вибраторов, то есть сравнение
обоих решений. В отношении системы связей будем считать, что
она является квазилинейной относительно колебательных коор-
динат и скоростей, так что уравнения (1.5) главы IX после соот-
ветствующего преобразования могут быть представлены в
форме
г» = Дг- + У(0) + |хУ(1).	(5.5)
Здесь v есть 2у-мерный вектор фазовых координат системы
связей, А — постоянная 2v X 2у-матрица, У(°) и — 2т-мерные
векторные функции, удовлетворяющие неоднократно упоминав-
шимся общим условиям, характерным для задач о синхрони-
зации.
Поставленная задача частично уже рассмотрена в § 6
главы IX, где изучался общий случай систем с почти равномер-
ными вращательными движениями, квазилинейных относительно
колебательных координат. Из сказанного в упомянутом пара-
графе следует, что основные уравнения задачи о синхронизации
квазиконсервативных вибраторов, связанных с линейной коле-
бательной системой
2л/о>	2я/ш
Ps(<xi....(Ф5)Л = -^-£-/ (^s)^ = 0. (5-6)
о	о
(s = 1....k),
оказываются равносильными уравнениям
2я/о>
РДа„ .... ak,	(Ф5)Л = 0 (s = 1, .... k), (5.7)
s о
отвечающим неквазиконсервативным вибраторам*).
Таким образом, возможные синхронные движения, по край-
ней мере в порождающем приближении, будут одинаковыми для
обоих моделей вибраторов. Различие может состоять лишь
в правиле отбора устойчивых движений.
*) В настоящем параграфе, как и в § 6 главы IX, постоянные величины
и функции со значком «~» (тильда) относятся только к случаю квазикон-
сервативной идеализации вибраторов, а так же обозначенные постоянные
или функции, но без этогр значка —к случаю неквазиконсервативной идеали-
зации. ...
<Эа, fis'Z
§ S]	КВАЗЙКОЙСЕРВАТИВНАЯ ИДЕАЛИЗАЦИЯ ВИБРАТОРОВ	519
Первая группа условий устойчивости квазиконсервативных
вибраторов состоит в требовании отрицательности всех корней й
алгебраического уравнения £-й степени (рассмотрим для кон-
кретности случай внешней синхронизации)
= 0	(s,/=l,..., k)t	(5.8)
При неквазиконсервативной же идеализации вибраторов доста-
точным условием устойчивости является требование отрица-
тельности вещественных частей корней уравнения
|-gi-ds/%| = 0	(s,j=l, .... k).	(5.9)
Поскольку согласно (5.6) и (5.7) функции Ps и Ps отличаются
лишь положительными множителями, то в силу сказанного в § 8
главы V указанные требования вполне равносильны.
Остается рассмотреть вторую группу условий устойчивости
движения квазиконсервативных вибраторов, выражаемую соот-
ношениями (5.57) главы VIII. Для получения этих условий в бо*
лее конкретной форме придется, однако, несколько конкретизи-
ровать также и рассматриваемую систему. Ограничимся, прежде
всего, изучением задачи о синхронизации дебалансных вибрато-
ров при отсутствии несомых связей. Заметим, далее, что в по-
рождающем приближении
v° = Аг>° + У	(5.10)
уравнения (5.5) описывают малые колебания несущих тел под
действием возмущающих сил, развиваемых вибраторами при
равномерном вращении по закону
Ts = as(at+“Л ф>ал>	(5-и)
удовлетворяющему уравнениям (5.4). Поэтому функцию У<°>
можно считать имеющей вид
k
У(0) = 2 g, (ср,, ф/, ср/),	(5.12)
где векторные функции gj таковы, что они становятся Т = 2л/<о-
периодическими функциями времени t при подстановке (5.11).
Будем предполагать также функции Ф5 в уравнениях движения
вибраторов (5.2) представимыми в форме
ф, = ф^(Фр •••> ФА; Ф1....ф*; ®9 +
+ф1”(Ф1......фа; Фр •••» ф*)-л (5.13)
520
ОБОБЩЕНИЯ ЗАДАЧИ О СИНХРОНИЗАЦИИ ВИБРАТОРОВ [ГЛ. XIV
где Ф® — скалярные, а Ф^ — векторные функции того же
типа, что и введенные выше функции gs.
Последние предположения не были необходимыми для об-
щего рассмотрения задачи при неквазиконсервативной идеали-
зации вибраторов; впрочем, они в большинстве случаев выпол-
няются.
В силу равенств (5.11) и (5.12) Т = 2л/и-периодическое ре-
шение уравнений (5.10) может быть представлено в форме
k
v°= 2 v°[v> °/(“z+ “/)];	(5-i4)
естественно, что, как и в § 5 главы VIII, предполагается, что та-
кое решение существует и является единственным.
При учете равенств (5.13) и (5.14) основные уравнения (5.6)
могут быть представлены в форме
k
^ = ^+2^ = 0,	(5.15)
S=»l
где обозначено:
2л/ш	2л/ш
М’М	(5.16)
J	I S
о	0
Теперь, согласно (5.11) и формуле (5.29) главы VIII,
д V]	dv ]
~ й да dttj ~ да '
Так что
dv\
= <5-17>
и, в соответствии с обозначением (5.61) главы VIII и форму-
лами (5.13) и (5.16) настоящего параграфа,
2Л/Ш	~	2Л/Ы	0	~
“ Is 2л J \	dv	I dt ~ Is 2л J (	’ ) да	dt да	‘
о	о
Заметим, что представление основных уравнений в форме
(5.15) в рассматриваемом случае задачи о синхронизации отве-
чает представлению
S
k
м - (“) - S(“s - ai> ®)
i=>I
(5.19)
§ 5]
КВАЗИКОПСЕРВАТИВНАЯ ИДЕАЛИЗАЦИЯ ВИБРАТОРОВ
521
где Цт1 и /?,—соответственно средний момент, передаваемый
от двигателя, и средний момент сил сопротивления, a — част-
ные вибрационные моменты, отражающие воздействие колеба-
ний, возбуждаемых /-м вибратором, на s-й вибратор; об этих
последних моментах говорилось в § 3 настоящей главы (см. фор-
мулу (3.23)).
Таким образом,
й 1
Psi = — —j— Wsi’
ls
rtPsl _______J_ dwsl
да	Is да
(5.20)
Далее согласно равенствам (5.3) и (5.6) и обозначениям,
принятым в § 5 главы VIII (см. стр. 273), имеем *)
k
ks К - Ю) + М"” (ffs> - P°s (“) - 2 W'sl
l~l
(5.21)
Если теперь учесть, что момент w'st зависит от <о,-, но не за-
висит от o)j, где j =# I (см., например, формулы (3.17), (3.18) и
(3.23)), то получим
(Й =	+	(5.22)
\ а“/ /. s \ а® )
где. как и выше, б.,, — символ Кронекера. Подставив теперь вы-
ражения (5.20) и (5.22) в формулу (5.60) главы VIII. запишем
второе условие устойчивости (5.57) той же главы в виде (напом-
ним, что = 1)
(5.23)
Напомним, что в последнем выражении величины Л4/ и М/
определяются для каждого корня уравнения (5.8) как решения
сопряженных систем линейных уравнений (5.45) и (5.54)
главы VIII.
Покажем теперь, что в случае, когда неконсервативные силы
по колебательным координатам в порождающем приближении
*) В рассматриваемом случае <?> = ...=<?), = 1, и поэтому Vi = <В|, ...
,.., Vk = он; в выражения для и Rs вместо w не нужно подставлять
и8, поскольку величины Ls и R, в уравнениях движения вибраторов предпо-
лагаются не зависящими от ф, (см., например, равенства (3.2) главы ЭДИ).
522
ОБОБЩЕНИЯ ЗАДАЧИ О СИНХРОНИЗАЦИИ ВИБРАТОРОВ [ГЛ. XIV
не учитываются (рассматривается движение вдали от резо-
нанса), условия (5.23) практически всегда выполняются*).
Действительно, при этом Gs = 0 и, аналогично (2.29), основные
уравнения (5.19) могут быть представлены в форме
рАа.......... ®) = -/7[^т)(а5’	= 0 (5-24)
(s = 1....k).
В результате уравнения (5.45) и (5.54) главы VIII приобретают
соответственно следующий вид:
Л Г 1 д2Ап / дк(!п) \1
Ум, ~г~я	=0	($=1, ...,£), (5.25)
ЛЛ ‘ / да да, SI \ да	v ’	’	”	'	'
y=I L s s 1	\	s /J
Г 1 з2л !	дь^ V
Ум, -f- я °	=0 (s=l............k). (5.26)
1 I, да, да ,s \ да, /	v ’	’ '	'	'
/=1 L /	/ s \	1 /J
Умножив каждое из уравнений (5.25) на /5 и преобразовав урав-
нения (5.26) с учетом равенства 6JSQj = 6sjQs, представим эти
уравнения в форме
Л Г 52Л„ f dMYl
Zj А д + M, й -	= 0,
' da da, sl s\ da I ’
L s /	\	s /J
V M’ Г d2A0	/ dL™ \1
1гИ7 + !./'.«"ТГ -°	(s-1......*) (5-27)
/.!	/ L s /	\	s /J
Сравнение последних уравнений приводит к следующему про-
стому соотношению между решениями взаимно сопряженных
систем:
A4/-A4///.	(5.28)
В результате неравенство (5.23) представится в форме
_	1 S = 1	1 S“1 /=1
'2 "	2T	T
2	2 's^s
S—l	S“1
Но двойная сумма в последнем равенстве, очевидно, обращается
в нуль в силу соотношений взаимности (3.28) для частных виб-
*) Отметим, что в указанном случае к рассматриваемым условиям устой-
чивости должны быть присоединены некоторые дополнительные соотношения,
которые, однако, частр не играют существенной роли (см., например, § 5
ГЛ. ХШ).
§61
О КРАТНОЙ СИНХРОНИЗАЦИИ ВИБРАТОРОВ
523
рационных моментов wSj = ws), справедливых в рассматривае-
мом случае. Поэтому условия (5.23) еще более упрощаются и
принимают вид
k	I k
(5-29>
s = l	I S = 1
Выполнение последнего неравенства обеспечивается положи-
тельностью коэффициентов сопротивления ks и моментов Is.
Таким образом, мы приходим к заключению, что результаты
исследования синхронизации вибраторов, по крайней мере в по-
рождающем приближении и при достаточно общих предположе-
ниях о характере системы, не зависят от способа идеализации
вибраторов. Вместе с тем за неквазиконсервативной идеализа-
цией остается преимущество значительно большей простоты ис-
следования.
Для конкретности приведенное выше рассмотрение было вы-
полнено применительно к задаче о внешней синхронизации.
В случае задачи о внутренней синхронизации сделанные вы-
воды, разумеется, остаются в силе, а о специфике этой задачи
можно было бы повторить все сказанное в п. 3 § 5 главы VIII.
§ 6. О кратной синхронизации вибраторов
Все предыдущее изложение велось применительно к задаче
о так называемой простой синхронизации механических вибрато-
ров. Как отмечалось, однако, в главе XII, для ряда приложений
представляет интерес задача о кратной синхронизации, когда
обобщенные координаты <ps в установившемся движении изме-
няются по закону
% =	+ а5 + нФ’(«/, и)]	($=1, ...» fe), (6.1)
где ns — целые положительные числа, а прочие обозначения сов-
падают с принятыми выше.
Как и в § 2 настоящей главы, целесообразно ограничиться
рассмотрением вибраторов в виде объектов с почти равномер-
ными вращательными движениями, то есть принять, что вели-
чина ц>0 в равенствах (6.1) является малым параметром и
что уравнения движения вибраторов могут быть представлены
в форме
ips + (ф5-<ТЛ®) = цФв (s= 1, ..k),	(6.2)
аналогичной форме уравнений (1.4) главы IX.
Нетрудно убедиться, что по отношению к решениям (6.1)
уравнений (6.2) вместе с соответствующей системой уравнений
для колебательных координат остается полностью справедли-
вым все сказанное в главе IX, а также в §§ 2—5 настоящей
S24
ОБОБЩЕНИЯ ЗАДАЧИ О СИНХРОНИЗАЦИИ ВИБРАТОРОВ [ГЛ. XIV
главы. Поэтому для решения задачи о кратной синхронизации
вибраторов можно непосредственно воспользоваться результа-
тами, полученными при изучении простой синхронизации. Сле-
дует лишь иметь в виду, что порождающее решение для пере-
менных ф., имеет в данном случае вид
Ф° = <ts(ns<f>t + “s)	(s=l, .... k),	(6.3)
а для колебательных координат представляет собой установив-
шиеся вынужденные колебания под действием возмущающих
сил, развиваемых вибраторами при их движении по закону
(6.3). Несколько иной вид имеет также уравнение, от характера
корней которого зависит решение вопроса об устойчивости дви-
жений в случае внутренней синхронизации (см. уравнение (2.7)
главы IX); оно отличается от соответствующего уравнения (2.33)
задачи о простой внутренней синхронизации множителями nslnh.
Специфика задач о кратной синхронизации вибраторов со-
стоит, однако, в том, что в определенном и притом достаточно
широком классе случаев (назовем их непростыми случаями) по-
рождающие фазы ai, . . . , а/, не определяются из уравнений
типа (2.27) — (2.29), выражающих условия периодичности пер-
вого приближения. В таких случаях для определения порождаю-
щих фаз следует составить условия периодичности следующих
приближений, как это было указано в § 10 главы V. Здесь при-
ходится также прибегать к некоторому изменению предположе-
ний о порядке малости сил сопротивления вращению вибрато-
ров и вращающих моментов.
Указанная ситуация возникает, в частности, в задаче о крат-
ной самосинхронизации моногармонических вибраторов, связан-
ных с линейной колебательной системой. Такие вибраторы, вра-
щающиеся с угловыми скоростями, отличающимися в целое
число раз, в первом приближении не взаимодействуют один
с другим: соответствующие частные вибрационные моменты (см.
§ 3), пропорциональные интегралам от тригонометрических
функций кратных периодов, обращаются в нуль. В результате
основные уравнения (2.27) — (2.29) не содержат разностей по-
рождающих фаз указанных вибраторов.
Отмеченные особенности непростого случая кратной синхро-
низации иллюстрируются ниже на примере исследования субро-
тационного режима стационарного вращения неуравновешенного
ротора с колеблющейся осью (см. § 4 главы XVIII).
Иное положение, вообще говоря, будет в случае кратной син-
хронизации полигармонических вибраторов, в случае принуди-
тельной синхронизации, а также при синхронизации вибраторов
в нелинейной колебательной системе. В таких случаях (назовем
их простыми) при определенных достаточно широких условиях
взаимодействие вибраторов будет учитываться уже в первом
§7]	О СИНХРОНИЗАЦИИ В СИСТЕМАХ С СОУДАРЕНИЯМИ	525
приближении, и фазы, вращения определятся из уравнений
(2.27) — (2.29) (см., например, п. 8 § 8 настоящей главы).
Как уже упоминалось, ряд задач о кратной синхронизации
вибраторов был изучен К. М. Рагульскисом и его сотрудниками
с помощью модифицированного метода усреднения [352—354].
§ 7. О синхронизации вибраторов в системах с соударениями
В случае, когда тела, па которых размещены вибраторы, мо-
гут в процессе колебаний соударяться одно с другим или с не-
подвижным основанием, решение задачи усложняется. Если,
как и выше, исходить из предположения, что вращение вибра-
торов, несмотря на соударения тел, на которых они установ-
лены, близко к равномерному, то уравнения движения системы
сохраняют вид уравнений (1.4), (1.5) главы IX. Особенность,
однако, заключается в том, что на некоторых поверхностях
69(х...... 0 = 0	(<?=1, .... щ)	(7.1)
скорости соударящихся тел xs претерпевают скачки, определяе-
мые законом сохранения импульса и обычными гипотезами
о частично или абсолютно упругом ударе.
В рассматриваемом случае, как правило, представляют инте-
рес кратно-синхронные решения вида
Фя =	+ “s + (т *)]
,	,	(7.2)
хг = Хг (тд	(г = 1, ..v),
где ф* и хг — периодические функции времени t с периодом
Т = 2лп/а> (/г = 1, 2, ...), в целое число раз превышающим
время одного оборота валов вибраторов То = 2л/о>. Средние за
период Т значения функций ф8 для определенности значений на-
чальных фаз as можно считать равными нулю. Производные
функций ф., и хг при этом, как отмечалось, вообще говоря,
имеют разрывы первого рода в точках, отвечающих моментам
соударений тел.
Выражения (7.2) являются более общими по сравнению с вы-
ражениями (1.1) главы IX, переходя в последние при п = 1.
Движения, определяемые равенствами (7.2), также можно на-
звать синхронными; о возможности такого обобщения уже го-
ворилось в § 1 главы II настоящей книги. Причины, по которым
в изучаемой задаче целесообразно рассматривать движения
типа (7.2), состоят в следующем.
В соответствии со сделанным выше предположением враще-
ние роторов вибраторов в порождающем приближении
q>: = as(a>Ma4.) (s=l, ..., fe)	(7.3)
526
ОБОБЩЕНИЯ ЗАДАЧИ О СИНХРОНИЗАЦИИ ВИБРАТОРОВ [ГЛ. XIV
есть равномерное вращение с одинаковыми по модулю угло-
выми скоростями ю, а движение несущих тел
Х° = Хг°(-М (Г=1......................<7-4>
определяемое уравнениями (2.2), есть установившиеся периоди-
ческие колебания (с соударениями) под действием возмущаю-
щих сил, развиваемых вибраторами при их движении по закону
(7.3). Как следует из теории виброударных систем (см., напри-
мер, [214]), таких периодических режимов колебаний при задан-
ных значениях начальных фаз ai, .. ., ал может быть несколько,
а их период Т может быть равен или кратен периоду То = 2л/со.
Под выражением (7.4) понимается какое-либо одно из указан-
ных выше устойчивых периодических движений. В настоящее
время методы нахождения установившихся режимов движения
виброударных систем и исследования их устойчивости доста-
точно хорошо разработаны.
Для решения вопроса о существовании и устойчивости син-
хронных решений системы в рассматриваемом случае можно
воспользоваться результатами исследований М. 3. Коловского,
изложенными в п. 2 § 6 главы V, а также методом точечных
отображений, разработанным для рассматриваемых задач
Ю. И. Ней марком и Л. П. Шильниковым [320]. Первому пути
следовал Р. Ф. Нагаев, рассмотревший самосинхронизацию виб-
раторов в сложной пространственной системе (см. [308], а также
§ 4 главы XXI), а второму-—Л. Б. Зарецкий, изучивший в об-
щей форме задачу о синхронизации вибраторов в системах
с разрывными характеристиками [192, 193] и рассмотревший не-
которые прикладные задачи. Еще раньше самосинхронизация
вибраторов в простейшей системе с одной степенью свободы
была рассмотрена К. М. Рагульскисом с помощью модифициро-
ванного метода осреднения [352].
Результат исследования может быть сформулирован в виде,
вполне аналогичном случаю непрерывных движений (рассма-
триваем задачу о внешней синхронизации') *): синхронные дви-
жения системы, обращающиеся при р = 0 в порождающее, мо-
гут соответствовать только тем значениям фаз at, ..., afe, ко-
торые удовлетворяют уравнениям
2л/ы
РДа,, .... а„ = [ФЛ^ = 0 (s = 1..................k).	(7.5)
о
*) Для случая задачи о самосинхронизации подобный результат получен
Л. Б. Зарецким [193].
§ 8]	НЕКОТОРЫЕ ВАЖНЫЕ ЧАСТНЫЕ СЛУЧАИ, ПРИМЕРЫ	527
Определенному решению этих уравнений а*, ..., ak дей-
ствительно отвечает единственное асимптотически устойчивое
синхронное движение, если для этого решения все корни х ал-
гебраического уравнения k-й степени
4^--6s/x| = O (s, / = 1......k)	(7.6)
имеют отрицательные вещественные части. Наличие хотя бы
одного корня с положительной вещественной частью свидетель-
ствует о неустойчивости, а случай, когда имеются нулевые или
чисто мнимые корни, вообще говоря, требует дополнительного
исследования. По поводу специфики задачи о внутренней син-
хронизации по-прежнему можно повторить все сказанное в § 2
настоящей главы.
Основные уравнения (7.5) по форме и смыслу совпадают
с уравнениями (2.5) главы IX: они получаются путем осредне-
ния за период движения Т = 2лл/со правых частей уравнений
движения вибраторов, вычисленных для порождающего прибли-
жения. Различие, однако, состоит в том, что интегрирование
в выражениях (7.5) следует понимать в обобщенном смысле,
ибо вследствие разрывности порождающего приближения по
отношению к колебательным скоростям ir и ввиду того, что
функции Фя зависят от ускорений хг, подынтегральные выраже-
ния содержат дельта-функции.
Пример задачи о синхронизации вибраторов в системе с со-
ударениями приводится в § 4 главы XXI.
§ 8. Некоторые важные частные случаи, примеры
1. Два одинаковых дебалансных вибратора на мягко амор-
тизированном плоско колеблющемся твердом теле при наличии
упругой несомой связи. В первых четырех пунктах настоящего
параграфа рассмотрим задачи синхронизации двух одинаковых
вибраторов в некоторых простейших системах. Все приводимые
примеры, с одной стороны, имеют целью проиллюстрировать
применение общих результатов, полученных в настоящей главе.
С другой стороны, соответствующие задачи представляют ин-
терес для ряда приложений, рассматриваемых в пятой части
книги.
В качестве простейшего примера изучим задачу о синхрони-
зации двух одинаковых дебалансных вибраторов с параллель-
ными осями вращения, расположенных на некотором твердом
теле. Тело может совершать движение, параллельное плоскости,
которая перпендикулярна осям вращения роторов вибраторов;
центр тяжести тела лежит в плоскости, проходящей через
528
ОБОБЩЕНИЯ ЗАДАЧИ О СИНХРОНИЗАЦИИ ВИБРАТОРОВ [ГЛ. XIV
указанные оси, и удален от них на одинаковые расстояния г
(рис. 37). Будем считать, что тело мягко амортизировано, то
есть что квадраты частот его свободных колебаний па пружин-
ных опорах достаточно малы по сравнению с квадратом угловой
скорости синхронного вращения роторов вибраторов.
Роторы предполагаются связанными пружиной жесткости с,
концы которой прикреплены к роторам на расстояниях а от
осей вращения. Пружина находится в недеформированном со-
стоянии, когда углы поворота роторов <pi и фг равны между
собой.
Поскольку вибраторы являются дебалансными, то
=	=	(8.1)
и уравнения (3.6) записываются в форме
Р (а., а,, со) е= -j- [/W -	- 5 (AU* А<П>) 1 = 0 (s=l, 2). (8.2)
s\ 1’ 2’ ) ks L s s oas J '	'
Для получения этих уравнений в явной форме необходимо
составить выражения для осредненных лагранжианов А<т> и А(п>
несущего твердого тела и
несомых связей.
Обратимся вначале к по-
лучению выражения для А*1).
Уравнения движения вибри-
рующего органа (несущего
тела В) при движении виб-
раторов по закону
<р° = ст, (со/ 4- а,),
□	, . , .	(8.3)
Ф2 = ст2 (со/4-а2)
имеют вид (вследствие пред-
положения о малости квад-
ратов частот собственных колебаний системы по сравнению
с квадратом угловой скорости синхронного вращения со, силами
упругости амортизирующих элементов пренебрегаем; по той
же причине можно не учитывать и силы сопротивления
колебаниям)
Мх = F [cos (со/ 4- О]) 4- cos (со/ 4- а2)],
Му° = — F [ст, sin (со/ + а,) 4- ст2 cos (со/ 4- а2)],	(8.4)
/ф° = Fr [ст, sin (со/ 4 а,) — а2 sin (со/ 4 а2)[.
§ 8]	НЕКОТОРЫЕ ВАЖНЫЕ ЧАСТНЫЕ СЛУЧАИ. ПРИМЕРЫ	529
Здесь Ми/ — соответственно масса и момент инерции вспомо-
гательного тела*), F = mew2— амплитуда возмущающей силы,
развиваемой каждым вибратором.
В связи с предположением о мягкости упругих элементов по-
тенциальную энергию ГВ1» можно считать пренебрежимо малой,
положив £(> = 7W. Поэтому, определив х°, у° и ф° в установив-
шемся движении непосредственным интегрированием равенств
(8.4), получим при учете формул (6.3) главы XIII
2л/(о	2л/<о
Л(1) = ^И = И*о2 + Л+/Фо2й =
о	о
F2 I	Mr2 \
= 2Л^ (1 4- ст 1CF2 — ст!сг2 —j cos (а! - а2) + Ct.	(8.5)
Здесь Ci — некоторая не зависящая от углов ai и а2 величина.
Вычислим теперь функцию A<n). Поскольку несомая связь
в рассматриваемом случае безынерционна, то
2я/и	2л/ш
=	(П<">)	= _ “ f ['еД2)Л1	(8.6)
о	0
где (см. рис. 37)
A = / — /0 = / — 2г a (cos ф| — cos <p2)	(8.7)
— относительное удлинение пружины (считаем, что величина afr
значительно меньше единицы, и пренебрегаем степенями этой
величины более высокими, чем первая). Производя вычисления
при учете равенств (8.7) и формул (6.3) главы XIII, находим
Л<”) = у са1 cos (а, — а2) + С2,	(8.8)
где С2 — постоянная, не зависящая от ai и а2. Как и следовало
ожидать, функции Л(|» и Л<п> оказались зависящими только от
разности фаз a = ai — a2, но не отдельно от а, и а2.
При учете выражений (8.5) и (8.8) уравнения (8.2) легко
записываются в явной форме, и с их помощью можно проанали-
зировать синхронные движения вибраторов в различных слу-
чаях. Мы остановимся лишь на случае синхронизации вибрато-
ров, приводимых от двигателей асинхронного типа и обладаю-
щих одинаковыми положительными парциальными скоростями.
Тогда В = С3 (С3 не зависит от а, и а2) и, согласно сказанному
*) Под вспомогательным телом здесь, как и в § 2 главы XIII (см.
стр. 378), понимается твердое тело, получающееся из исходного, если при-
соединить к нему неуравновешенные массы вибраторов, поместив их в сред-
ние положения при колебаниях относительно тела.
530
ОБОБЩЕНИЯ ЗАДАЧИ О СИНХРОНИЗАЦИИ ВИБРАТОРОВ [ГЛ. XIV
в § 4, можно не прибегать к рассмотрению уравнений (8.2),
а воспользоваться интегральным критерием устойчивости, при-
няв за потенциальную функцию величину
D = Л”) — Л(11) = - 	(1 + Ц|сг2 — О|Сг2 -—) cos а. (8.9)
244<о2 \	12	1 2 I т2е,2&2)	v
Приравняв нулю производную dD/da, приходим к следующему
уравнению для определения сдвига фаз а — он — аг в возмож-
ных синхронных движениях:
sina = 0.	(8.10)
Это уравнение имеет два существенно различных решения:
(а)] = (а, - а2), = 0,	(а)2 = (cq - а2)2 = л, (8.11)
первое из которых, как и в п. 2 § 16 главы XIII, назовем син-
фазным, а второе — противофазным. Если
1 + О|СГ2 — О|СГ2—j-„(2е2(й2 <0,	(8.12)
то функция D при a = (a) । = 0 имеет минимум, а при a = (а)г =
= л — максимум, и поэтому, в соответствии с интегральным кри-
терием, синфазное движение вибраторов является устойчивым,
а противофазное — неустойчивым.
Рассмотрим неравенство (8.12) несколько подробнее. Пусть
сначала щсгг = 1, то есть вибраторы вращаются в одинаковых
направлениях. Тогда условие устойчивости синфазного движе-
ния вибраторов принимает вид
Здесь
Mr2 п Мса2 ___________Q 4са2
I	1п2е2&2 Л4Лд<в2
(8.13)
Ао = 2т&1М
(8.14)
есть амплитуда (радиус круговых траекторий) поступательных
колебаний тела, которые оно совершает при синфазном враще-
нии вибраторов в одинаковых направлениях (см. формулы
(8.4) и рис. 34, а). При невыполнении условия (8.13) устойчиво
противофазное вращение вибраторов и тело совершает поворот-
ные колебания относительно центра тяжести О\.
Пусть теперь вибраторы вращаются в противоположных на-
правлениях. Тогда сг|сгг = — 1 и условием устойчивости проти-
вофазного синхронного вращения вибраторов будет неравен-
ство
(8.15)
I т2е.2а>2 Л4Лр(о2
§ 8]	НЕКОТОРЫЕ ВАЖНЫЕ ЧАСТНЫЕ СЛУЧАИ, ПРИМЕРЫ	531
Здесь величина Ло, по-прежнему определяемая равенством
(8.14), может рассматриваться как амплитуда прямолинейных
поступательных колебаний тела в направлении, перпендикуляр-
ном плоскости, в которой лежат оси вращения роторов вибра-
торов. Как следует из равенств (8.4) и рис. 34, б, именно такие
колебания происходят при ai<T2 =— 1 и противофазном вращении.
При выполнении неравенства, противоположного неравен-
ству (8.15), устойчивым является синфазное вращение.
Заметим, что при с = 0 неравенства (8.13) и (8.15) приводят
к результатам, полностью совпадающим с полученными в п. 2
§ 16 главы ХШ иным путем. Из упомянутых условий следует,
что наличие пружины, связывающей роторы вибраторов, облег-
чает выполнение условия устойчивости синфазного вращения
роторов в одинаковых направлениях. С другой стороны, для
обеспечения устойчивости противофазного вращения в противо-
положных направлениях пружина не нужна и даже, более того,
вредна, ибо может привести к неустойчивости этого режима.
Проиллюстрируем теперь па том же примере способ решения
задачи с использованием гармонических коэффициентов влия-
ния, изложенный в п. 2 § 3 настоящей главы. Нетрудно видеть,
что при составлении выражений (3.26) для вибрационных мо-
ментов в данном случае понадобятся лишь коэффициенты Кии,
Kvv, Kvu, Kvu, Kvu И Kvu (следует учитывать соотношения
взаимности (3.20), а также то обстоятельство, что коэффи-
циенты Кии, К™, Кии и Kvv в выражения (3.26) фактически
не войдут). Кроме того, для рассматриваемой системы
= о (/,/=1,2),
поскольку гармонические возмущающие силы, действующие на
оси вибраторов в направлении одной из осей О,ц или Охи, не
вызывают колебаний вдоль другой из этих осей. Таким образом,
необходимо найти лишь коэффициенты Кии и Ко?- С этой
целью рассмотрим уравнения*)
AIx = cosw/, Му = 0, /ф = 0
и
Мх = 0, Му = cos at, /ф = 0,
описывающие колебания тела при действии на ось первого
вибратора гармонических возмущающих сил единичной ампли-
туды соответственно в направлении осей Оул и Оул. Колебания
оси второго вибратора в направлении тех же осей в режиме
*) Значок «0», указывающий на то, что соответствующие координаты вы-
числяются в порождающем приближении, далее в настоящем параграфе нами
опускается.
532
ОБОБЩЕНИЯ ЗАДАЧИ О СИНХРОНИЗАЦИИ ВИБРАТОРОВ [ГЛ. XIV
установившихся вынужденных колебаний соответственно будут
%2 = х = “ АЙ4cos&t’	У2=:У~г(р = (-	+ cosco/.
Отсюда, согласно определению коэффициентов Кии и Kvv,
имеем
Ь-<12) _ iz(2l) _	1	^(12) _ ^(21) _	1	, Г2
1\ии-Лии~	Мсй2-ГТ^Г-
Теперь по формуле (3.20) настоящей главы находим
у, _ -	re> + O|„iK£,)sina =
=-----2М~ (1 + а'а2 ~ а1а2 ~Г") 51П а>
и основные уравнения (3.5) записываются в форме
Pt (<xj, а2,	=	4-ощ,~ca2]sina = 0,
•P2(ai, а2, w)s —Р](а,, а2, а>) = 0.
Здесь учтено, что парциальные угловые скорости вибраторов
одинаковы и поэтому Л<т) = 7?°, что	= 0, а моменты S1-®,
как и ранее, определяются выражениями (3.4) и (8.8).
Единственным корнем уравнения '(2-33) в данном случае
будет
d(Pt -Р2)	„ ЭР, 1 Гм282со2 /. ,	Мг2) ,1
х =---д-----= 2 -~-= — -г- —— 1 4-о,о2 — О|О2—т— — са2 cos а.
da, <9а, k L М \	1	/ ) J
Из полученных соотношений следует, что для определения
сдвига фаз а = ai — a2 в возможных синхронных движениях,
как и при использовании интегрального критерия устойчивости,
получится уравнение (8.10), а условие устойчивости х < 0 син-
фазного движения вибраторов (a = (a)i=0) совпадает с нера-
венством (8.12). Таким образом, результаты, получаемые обоими
способами, как это и должно быть, полностью совпадают.
2.	Два одинаковых инерционных вибратора направленного
действия на мягко амортизированном твердом теле [68]. Пусть
два одинаковых инерционных вибратора установлены на неко-
тором твердом теле так, как показано на рис. 38.
Пусть, далее, Oxyz — система неподвижных осей координат,
которые в положении статического равновесия совпадают
с главными центральными осями инерции Otuvw вспомогатель-
ного тела. Линии действия возмущающих сил вибраторов па-
раллельны плоскости tiOiW, равноудалены от нее и образуют
§ «]
НЕКОТОРЫЕ ВАЖНЫЕ ЧАСТНЫЕ СЛУЧАИ, ПРИМЕРЫ
533
с плоскостью uOxv некоторый угол р. Рассмотрим задачу о са-
мосинхронизации, то есть будем предполагать двигатели вибра-
торов асинхронными; что же касается самих вибраторов, то они
могут быть как двухвалентными дебалансными («самобаланс-
ными»), так и любыми другими инерционными вибраторами на-
правленного действия, например вибраторами поршневого типа
(см. § 1 главы XII). Пусть парциальные частоты обоих ви-
браторов одинаковы, поло-
жительны и равны с». Амор-
тизирующие пружины пред-
полагаются настолько мягки-
ми, что частоты собственных
колебаний тела значительно
меньше рабочей частоты и,
и поэтому жесткость пружин
при исследовании синхрониза-
ции можно считать равной
нулю.
Получим выражение для
осредненного лагранжиана А*1».
Уравнения малых колебаний тела под действием возмущающих
сил, развиваемых вибраторами, имеют вид
Mx = ~ F cos р [sin at + sin (со/ + а)],
Mij = О,
Mz = F sin р [sin at + sin (at + a)],
Ixax = Fr sin p[sin at — sin (at + a)],
Izaz = Fr cos p [sin at — sin (at + a)].
Здесь x, у и z—координаты центра тяжести вспомогательного
тела О, в неподвижных осях Oxyz-, ах, ау и az— проекции век-
тора мгновенной угловой скорости тела на те же оси, отожде-
ствляемые вследствие малости поворотов с проекциями угловой
скорости на оси Oxuvw, связанные с телом; М — масса и 1Х, 1У
и /г — главные центральные моменты инерции вспомогательного
тела; F— амплитуда возмущающих сил вибраторов; 2г — рас-
стояние между линиями действия возмущающих сил; а — не-
известный относительный сдвиг фаз возмущающих сил*).
*) Поскольку ясно, что искомое выражение для А<[\ как и в п. 1, долж-
но зависеть лишь от относительного сдвига фаз a = <Xi — <х2, то начальную
фазу вращения одного из вибраторов, не нарушая общности, можно поло-
жить равной нулю.
534
ОБОБЩЕНИЯ ЗАДАЧИ О СИНХРОНИЗАЦИИ ВИБРАТОРОВ [ГЛ. X1V
Так как потенциальной энергией пружин, согласно сказан-
ному выше, можно пренебречь, то
2Л/й>	2Л/И
Л(1,=-М	(7'ш)л=
о	о
2 л/w
[j«(i! + i;>+4>) + l(/X + /X + «)]<«• <8.17)
О
В результате непосредственного интегрирования равенств
(8.16) и последующего вычисления элементарных квадратур
в соответствии с формулами (6.3) главы ХШ находим
где С — не зависящая от а постоянная.
Но функция Л*1) в рассматриваемом случае может быть при-
нята за потенциальную функцию D. Поэтому синхронные дви-
жения изучаемого типа могут отвечать лишь значениям сдвига
фаз а, удовлетворяющим уравнению
dD <ЭЛ<!) р г 1	/ sin2 Р . cos2p\T . п ,о
-^Г = -^Г==-	ГлГ+-ОГ1па = 0- (8Д9)
Предполагая, что выражение в квадратных скобках послед-
него равенства отлично от нуля, заключаем, что возможно син-
фазное (а = 0) и противофазное (а = л) движение вибраторов.
Первому случаю, как нетрудно заключить из рассмотрения
рис. 38 или уравнений (8.16), отвечают прямолинейные посту-
пательные колебания тела в направлении действия возмущаю-
щих сил, второму — поворотные колебания вокруг некоторой
неподвижной оси, лежащей в плоскости xOz.
При выполнении условия
Мг2Ц'>\,	(8.20)
где
I' =	>	(8.21)
Ix COS2 Р + Iz sin2 Р	v '
величина в квадратных скобках выражения (8.19) отрицательна,
и поэтому значению а = 0 отвечает минимум, а значению
а = л — максимум функции Л*1). При выполнении неравенства
противоположного смысла углу а = 0 отвечает максимум,
а углу а = л — минимум.
Отсюда, в соответствии с интегральным критерием устойчи-
вости, следует, что при выполнении неравенства (8.20) устой-
чиво только синфазное синхронное движение роторов вибрато-
ров, а при выполнении противоположного неравенства — только
противофазное движение.
§ 8]
НЕКОТОРЫЕ ВАЖНЫЕ ЧАСТНЫЕ СЛУЧАИ, ПРИМЕРЫ
535
При [3 = 0, согласно (8.21), Г = Д а при |J = л/2 имеем
Г = 1Х, так что условие (8.20) существенно упрощается; заме-
тим, что получающиеся при этом неравенства, по существу, от-
личаются от условий устойчивости синфазного вращения в оди-
наковых направлениях обычных дебалансных вибраторов лишь
тем, что в правой части фигурирует не единица, а двойка (см.
формулу (16.26) главы XIII).
Отметим, что, используя выражение (8.18), можно составить
основные уравнения (3.6) и для задач о принудительной синхро-
низации вибраторов в рассматриваемом случае. Однако здесь
на изучении этих задач мы
останавливаться не будем.
3.	Два коаксиальных деба-
лансных вибратора на мягко
амортизированном твердом те-
ле [68]. Рассмотрим теперь за-
дачу о самосинхронизации двух
одинаковых коаксиальных де-
балансных вибраторов, приво-
димых от независимых асин-
хронных двигателей и обладаю-
щих одинаковыми и положи-
тельными парциальными ско-
ростями и. Оси вращения рото-
ров вибраторов предполагают-
ся совпадающими с одной из главных центральных осей инерции
Oiv твердого тела, на котором установлены вибраторы (рис. 39).
Плоскости вращения центров тяжести роторов вибраторов рас-
положены на одинаковых расстояниях г от центра тяжести
тела.
Для решения задачи может быть использован интегральный
критерий устойчивости, причем за потенциальную функцию D
можно принять среднее за период значение функции Лагранжа,
отвечающей координатам несущего тела.
Составим соответствующее выражение. Сохраняя те же пред-
положения о выборе осей координат и те же обозначения, что
и в предыдущем пункте, будем иметь следующие дифферен-
циальные уравнения малых колебаний тела под действием воз-
мущающих сил вибраторов (жесткостью амортизирующих пру-
жин по-прежнему пренебрегаем):
Mx = F [cos at + cos (со/ + a)], Mij = 0,
Mz = — Д' [sin со/ + sin (а>£ + а)],
Fr [sin coZ — sin (ш/4-а)], Iyay — 0,	(8'22)
/г<Ьг = — Fr [cos at — cos (at + a)],
536
ОБОБЩЕНИЯ ЗАДАЧИ О СИНХРОНИЗАЦИИ ВИБРАТОРОВ [ГЛ. XIV
Используя последние уравнения, после простых вычислений,
вполне аналогичных выполненным при рассмотрении предыду-
щей задачи, находим
2л/(О	2л/<а
О	о
+ | (7Х + Jy^y + W] dt =	[4 -г2 (т? + 7г)]cos а + с- (8-23>
где С — не зависящая от а постоянная.
Приравнивая нулю производную от Л<*> по а, получаем (при
условии отличия от нуля выражения в квадратной скобке) урав-
нение sin а = 0. Из этого уравнения находим два значения угла
сдвига фаз а, которым могут отвечать синхронные движения
вибраторов изучаемого типа. Первому значению (а = 0) соот-
ветствует синфазное вращение роторов вибраторов, при котором
твердое тело совершает поступательные колебания по круговым
траекториям. Второму значению (а = л) отвечает противофаз-
ное вращение роторов вибраторов, обусловливающее так назы-
ваемое «качателыюе» движение тела. Очевидно, что при выпол-
нении условия
Мг2/1" >2,	(8.24)
где
r	(825)
* X "Г *Z
функция ДО при а = 0 имеет минимум, а при а =л—макси-
мум; в случае выполнения противоположного неравенства
приходим к обратным заключениям.
Таким образом, если справедливо условие (8.24), то устой-
чиво только синфазное синхронное вращение роторов вибрато-
ров; в случае же, когда имеет место противоположное неравен-
ство, устойчиво только противофазное синхронное вращение.
Как и в п. 2, отметим сходство неравенства (8.24) с неравен-
ством (16.26) главы ХШ. Заметим также, что выражение (8.23)
для функции Л<4 может быть использовано и для решения за-
дачи о принудительной синхронизации вибраторов.
4.	Два одинаковых инерционных вибратора направленного
действия, развивающих коллинеарные возмущающие силы [68].
В качестве последнего из простейших примеров рассмотрим за-
дачу о самосинхронизации двух одинаковых инерционных вибра-
торов направленного действия, установленных па упруго опер-
том жестком основании (рис. 40).
Предполагается, что вибраторы приводятся от двигателей
асинхронного типа, причем линии действия возмущающих сил
вибраторов совпадают, а парциальные угловые скорости одина-
§ 8]
НЕКОТОРЫЕ ВАЖНЫЕ ЧАСТНЫЕ СЛУЧАИ, ПРИМЕРЫ
537
ковы, положительны и равны со. Вибраторы могут быть как
двухвальными дебалансными («самобалансными»), так и лю-
быми другими вибраторами направленного действия.
К рассмотрению описанной системы приводятся некоторые
задачи об исследовании работы динамически неуравновешенных
машин, установленных на групповом фундаменте (см. гла-
ву XXIII настоящей книги).
Уравнения малых колебаний основания как твердого тела
под действием возмущающих сил, развиваемых вибраторами,
имеют вид
Mx + схх = F [sin at + sin (со/ + a)], ЛЛ/= О,
/ф + сф(р = Fh [sin at + sin (at + а)].
(8.26)
Здесь x и у — координаты центра тяжести О, вспомогательного
тела в неподвижной системе осей хОу, совпадающей в поло-
жении статического равновесия с системой осей «Ощ, жестко
связанной с телом; ф — угол
поворота тела, отсчитывае-
мый по ходу часовой стрел-
ки; М и / — соответственно
масса и центральный момент
инерции вспомогательного
тела; сх и сФ — коэффициен-
ты, характеризующие жест-
кость основания*); F и а —
как и в предыдущих приме-
рах— амплитуда и относи-
тельный сдвиг фаз возму-
щающих сил вибраторов;
h — расстояние от центра тя-
жести вспомогательного тела
y,v
Рис. 40.
01 до линии действия возмущаю-
щих сил вибраторов.
Выражение для среднего за период колебаний значения
функции Лагранжа, отвечающей колебательным координатам
(несущим связям), имеет вид
2л/®	2л/и
о	о
2л/<й
= -^/ |[М(х2 + //2) + /ф2-схх2-С(рф2]Л.	(8.27)
о
*) Принимаем, что коэффициент cx,f, характеризующий взаимосвязь ко-
лебаний по координатам х и ф, равен нулю или пренебрежимо мал.
S38
ОБОБЩЕНИЯ ЗАДАЧИ О СИНХРОНИЗАЦИИ ВИБРАТОРОВ [ГЛ. X1V
Решением уравнении (8.26), соответствующим установив-
шимся вынужденным колебаниям частоты со, будет*)
х= F г, -к—[sin со/ + sin (at + а)], и —О,
-Им2 Л2-1
Р. 1	(8,28)
Ph 1 г • j. , • / j. , м	v '
Ф = —j- —2—~ Lsm at + sin (at + a)J,
/<В /ф — 1
где обозначено:
1 Г С,:	1 Г Ст
Кх = — У Л№ = — У	(8.29)
х со г М ’ ч> со t I	'
Подставив выражения (8.28) в равенство (8.27), после не-
сложного вычисления интегралов находим
Л<1) = -^-/'—+ kosa + C, (8.30)
а.мсо2 \ л2 -1 р2 л2 -1)	v ’
где р = УЦМ — радиус инерции вспомогательного тела и С —
постоянная, не зависящая от а.
Поскольку и в данной задаче функция Л<т> может быть при-
нята за потенциальную функцию D, то и здесь возможны два
случая: синфазное синхронное движение вибраторов, отвечаю-
щее корню а = 0 уравнения sin a = 0, и противофазное син-
хронное движение, соответствующее корню а = л.
При выполнении условия
+ ^_1_<0
Л2-1 + р2 Л2-1
(8.31)
функция Л(1) в точке а = л имеет минимум, а в точке а = 0 —
максимум, то есть, в соответствии с интегральным критерием,
npoi ивофазное движение устойчиво, а синфазное неустойчиво.
В случае выполнения неравенства противоположного смысла,
напротив, устойчиво синфазное и неустойчиво противофазное
движение.
Как следует из рис. 40, а также из равенств (8.28), при про-
тивофазном движении вибраторов (а = л) колебания основания
в рассматриваемом приближении отсутствуют. Это обстоятель-
ство имеет существенное значение, поскольку применительно
к задаче о двух машинах, установленных на групповом фунда-
менте, оно означает, что неуравновешенные силы, возникающие
*) Предполагается, что движение системы происходит вдали от резо-
нанса, то есть что частоты собственных колебаний тела Рх~ г Сх/М и
“ Ус<$!1 в достаточной мере отличаются от частоты <о.
§ 8]
НЕКОТОРЫЕ ВАЖНЫЕ ЧАСТНЫЕ СЛУЧАИ, ПРИМЕРЫ
539
при работе машин, автоматически взаимно уравновешиваются.
Условием взаимного уравновешивания, таким образом, и яв-
ляется неравенство (8.31).
Как нетрудно заметить, в послерезонансной области, то есть
при
Лх<1,	^ф<1,	(8.32)
неравенство (8.31) непременно выполняется, то есть всегда
имеет место противофазное движение вибраторов. Напротив,
в дорезонансной области, где X* и Хф больше единицы, это
условие никогда не выпол-
няется, и поэтому противо-
фазное движение вибраторов
неустойчиво.
На рис. 41 в плоскости
параметров и представ- ‘
лены области устойчивости и
неустойчивости противофаз-
ного движения вибраторов при
различных значениях пара-
метра г)2 = /г2/р2; области ус-
тойчивости показаны на фигу-
ре штриховкой границ внутрь
областей устойчивости.
5.	П роизвольное число «ка-
чающихся» дебалансных виб-
раторов на мягко амортизированном твердом теле {«простран-
ственный» случай}. Рассмотрим теперь значительно более слож-
ную и общую задачу — о синхронизации некоторого числа k виб-
раторов на мягко амортизированном твердом теле 1,которое мо-
жет совершать произвольные пространственные колебания
(рис. 42). При этом предположим, что вибраторы являются
«качающимися», то есть что их корпуса 2 могут поворачиваться
относительно некоторых осей Л8Л.?, расположенных в твердом
теле и лежащих в плоскостях вращения центров тяжести cs
роторов вибраторов 4. Корпус каждого вибратора связан с твер-
дым телом пружиной 3, определяющей положение оси вращения
ротора вибратора BSBS в состоянии статического равновесия.
Жесткость этих пружин, так же как и жесткость опорных упру-
гих элементов, считается столь малой, что частоты собствен-
ных колебаний системы малы по сравнению с угловой скоростью
синхронного вращения. Описанная схема вибраторов, предло-
женная Б. П. Лавровым [238], обладает, в частности, тем до-
стоинством, что позволяет располагать электродвигатель 5 на
значительном расстоянии от оси качаний Л.ЧЛ.Ч и тем самым
540
ОБОБЩЕНИЯ ЗАДАЧИ О СИНХРОНИЗАЦИИ ВИБРАТОРОВ (ГЛ. XIV
обеспечивать значительное снижение амплитуд его колебаний
по сравнению с амплитудами колебаний точек оси ASA,4.
На рис. 42 изображен лишь один из вибраторов, однако их
число k может быть произвольным. Произвольным (в пределах
некоторых естественных ограничений, оговариваемых ниже) мо-
жет быть и расположение осей ASAS и BSBS. Отметим, что обыч-
ный дебалансный вибратор является частным случаем качаю-
щегося вибратора; в другом частном случае, отвечающем нуле-
вому статическому моменту дебаланса, качающийся вибратор
вырождается в обычный физический маятник. Поэтому можно
сказать, что фактически рассматривается синхронизация обыч-
ных дебалансных вибраторов, размещенных в системе, состоя-
щей из твердого тела, к которому присоединен ряд других твер-
дых тел с одной степенью относительной подвижности (то есть
физических маятников).
Описанная система включает как частные случаи значи-
тельное число динамических схем вибрационных машин и
устройств. Ее рассмотрению была посвящена работа Б. П. Лав-
рова [241], результаты которой мы изложим ниже, опустив ряд
достаточно громоздких промежуточных вычислений.
§ 8]	НЕКОТОРЫЕ ВАЖНЫЕ ЧАСТНЫЕ СЛУЧАИ, ПРИМЕРЫ	541
Пусть O\iivw — главные центральные оси инерции вспомога-
тельного тела, совпадающие в положении равновесия с непод-
вижными в пространстве осями Oxyz. Свяжем, далее, с корпу-
сом s-ro вибратора систему осей osx'f/'z', в которой ось ost'
направлена по оси подвеса Д.ЧЛЛ., ось osz's — по оси вращения
ротора BSBS, а ось osy's — так, чтобы система координат была
«правой».
Координаты точки os в осях Oitivw, связанных со вспомо-
гательным телом, обозначим через ая, bs, cs, а угол наклона
оси oszs к плоскости uOiV — через у« — причем при-
мем, что в положении статического равновесия ips = 0. Через
л — ps обозначим угол между направлениями Ощ и osxs. Пусть,
далее, есть угол между направлением вектора-эксцентриси-
тета дебаланса oscs и осью osxs, отсчитываемый против хода
часовой стрелки, если смотреть со стороны оси osz's.
Положение вспомогательного тела в пространстве при его
малых колебаниях определяется координатами х, у, z цен-
тра инерции этого тела и проекциями 0Х, 0У, 0г вектора пово-
рота 0.
Величины х, у, г, 0Х, 0у и 0Z вместе с углами поворотов рото-
ров ф., и углами качаний образуют совокупность из 2^ + 6
обобщенных координат рассматриваемой системы (напомним,
что k есть число вибраторов).
В дальнейшем предполагается, что оси подвесов корпусов
вибраторов A.,AS параллельны одной из координатных плоско-
стей вспомогательного тела, оси системы osx'y'z' параллельны
главным центральным осям инерции корпуса вибратора, а пло-
скость z'soscs есть плоскость симметрии ротора вибратора. Эти
предположения почти всегда выполняются в существующих кон-
струкциях машин и поэтому практически не ограничивают
общность исследования.
Выражение для кинетической энергии системы, составленное
с точностью до членов второго порядка малости включительно,
имеет вид
k
т-Хм^+р + ^+Х^+Х	+ X 1& + V1	+
5= [
Й
4” Ips s^s [С*'	Sin ys SIП ps
s = l
+ (y +	- exwms) sin Ys cos Ps 4- (z + Qxvms - Qeums) cos yj +
+ /xMSin₽s"AC0S₽s)}
542
ОБОБЩЕНИЯ ЗАДАЧИ О СИНХРОНИЗАЦИИ ВИБРАТОРОВ [ГЛ. XIV
k
+ <ps {fnA [(cos sin cps — sin ys sin ps cos cps) (x 4- 0„cs - Qzbs) -
S>=1
- (sin sin cps 4- sin y,. cos cos cps) (y - Qxcs - Qzas) 4-
+ cos ys cos cps (z 4- Qxbs - 0ynj] +
+ ;zs (4 cos V, sir> ₽s + cos у cos p + 0 sin у J}. (8.33)
Здесь
k
М = Л + s (т + Л\ I" = 3" + т£,
\ О	О/	40	2о	л о
S=1
I XS “ XS Н” jK. U"s,
k
1Х = УХ+ 2 [ws(&2 + c2) + (y2ms + <s)4-$'xscos2Ps4-
4- (p'ys sin2 vs + Vzs cos2 ys) sin2 ps],
k
Iu = $y + 2 [ms (a2s 4- c2) 4- Jts (u2ms 4- <s) 4- 3'xs sin2 ps 4-	(8.34)
+ (?'ys sin2 Ys + 3'zs cos2 ys) cos2 Ps],
k
1=^г+Ъ К № 4- 62) 4- Jls (u2ms 4- V2ms) 4-
s=l
+ ^scos2ys4-^'ssin2Ys],
Ums = as + Is COS ys Sin Ps, Vms = bs + ls COS ys COS Ps,
ay№ = c54-/ssinys,
причем Л, Ль и ms являются соответственно массами основ-
ного твердого тела, корпусов вибраторов и их роторов, Л1 — мас-
са вспомогательного тела, Ух, 3у, 3z, S^'xs, ^'ys, 3'zs и 3"xs, 3"s>
3"zs— главные центральные моменты инерции соответственно
основного твердого тела, корпусов и роторов вибраторов, 1Х, 1У
и 1г — главные центральные моменты инерции вспомогательного
тела, es — эксцентриситеты вибраторов, ls — расстояния oscs от
центров тяжести корпусов вибраторов до осей Д848; ums, vms
и wms — координаты указанных центров тяжести в осях 0}uvw,
связанных со вспомогательным телом.
При составлении выражения (8.33) принято во внимание,
что начало системы координат Oxuvw совпадает с центром тя-
жести вспомогательного тела, а оси координат — главные цент-
J 8]	НЕКОТОРЫЕ ВАЖНЫЕ ЧАСТНЫЕ СЛУЧАЙ, ПРИМЕРЫ	543
ральные оси инерции этого тела, так что имеют место соотно-
шения
k
Ла + У {msas + Msum^ = О,
S=1
k
ЛЪ + ^ (msbs + Jtsvms} = 0,
S«j
k
J(c + 2 {tnscs 4- Mswm^ = 0,
s=i
fe
i$Clb “b	“h jit's^ms^ms)
s=l
+ (Jxs + ^us si°2 Ys + I'zs cos2 Ys) sin 0 cos pl = 0,
k
Лас + 2 f(mAcs + ^sumswms) + (f'us - J'ZS) sin Ps sin Ys COS у 1 = 0,
fe
ЛЬс + 2 \(msbSCs + ^sVmsWmS') + (J'us ~ C0S Ps sin Ys cos Y.1 = 0,
L ' ООО	О С C to Т/4О/ \ у о	«СО/	1 о	’О	• о Д
выражающие условия равенства нулю статических моментов
и центробежных моментов инерции относительно указанных
осей (через а, b и с обозначены координаты центра тяжести
основного твердого тела в осях Ощода),
Дифференциальные уравнения, описывающие изменение ко-
лебательных координат системы, составленные в предположе-
нии, что роторы вибраторов вращаются по закону
<Ps = gs (со/ + as),	(8.35)
имеют вид
k	fe
Мх + 2 ^Л^в sin Ys sin 0S 'Ь 2 mA°2 [cos ps cos (co/ + as) +
S=1	S-I
+ Gs sin Ys sin 0s sin (to/ 4- as)] = 0,
k	k
My + 2 sin Ys COS Ps — 2 msesw2 [sin Ps cos (co/ + as) —
s=l	S-I
— gs sin Ys cos Ps sin (co/ f- as)] = 0,
k	k
Mz + 2 <Ps-<s/s cos Ys — 2 Osmsesa2 cos Ys sin (со/ -I- as) = 0,
s—1	s—1
544
ОБОБЩЕНИЯ ЗАДАЧИ О СИНХРОНИЗАЦИИ ВИБРАТОРОВ [ГЛ. XIV
k
+ 2 ИЛ(- Wms Sin Ys cos ps + Vms cos ys) - rxs cos Ps] +
k
4- 2 "ise3.co2 [cs sin ps cos (co/ + as) — oscs sin ys cos ps sin (co/ + as) —
S=>1
— osbs cos Ys sin (co/ + as.)] = 0,
k
lfiu + 2 % Ws (ums cos Ys + ™ms sin Ys sin Ps) + rxs sin ps] +
k
+ 2 tn^sd)'2 [cs cos ps cos (со/ + as) + oscs sin Ys sin ps sin (co/ + ctj +
S=1
+ osas cos ys sin (co/ + as)] = 0,
..	* ..	.	.	(8.36)
4” 21 tys*^ s^sЩт! COS Ps	sill Ps) Sin Ys 4"
s=l
k
4-	2	~ bs cos Ps cos (co/ + cts) —
s = l
—	osbs sin Y.s sin р5 sin (co/ + as) — as sin ps cos (co/ 4- as) 4-
+ asas sin у5 cos р5 sin (co/ 4- cts)] = 0,
АЛ = “ Ws sin Ys sin Ps - yJ(sls sin Ys cos ps - zJlsls cos Ys -
-	A И A (Vms C0S Ys - ®ms Sin Ys COS ps) + I'xs COS ps] -
-	A W* W cos Ys + wms sin Ys sin Ps) - J'xs sin Ps] -
- ^sls (um, cos Ps - vms sin Ps) sin Ys (s = 1.........k).
С помощью последних k уравнений (8.36) из прочих урав-
нений легко исключаются величины i|:s и получается система из
шести уравнений, которая относительно х, ij, z, бх, Qy и 02
является линейной алгебраической. Из этой системы путем не-
посредственного двукратного интегрирования нетрудно найти
установившиеся вынужденные колебания основного твердого
тела. Нетрудно заметить, что выражения для закона этих коле-
баний могут быть представлены в форме
k
qr= - 2 mses [ Ars sin (со/ + as) 4- Brs cos (co/ 4- as)] (8.37)
s—1
•	(r=l, ..., 6),
где
Я1 = х, q2 = y, q3 = z, q4 = QX! q5 = Qy, qQ = Qz,
§ в]
НЕКОТОРЫЕ ВАЖНЫЕ ЧАСТНЫЕ СЛУЧАИ, ПРИМЕРЫ
545
a Ars и Brs — постоянные. Отметим, что получение выражений
для этих постоянных в общей форме вряд ли имеет смысл, по-
скольку в представляющих интерес конкретных случаях урав-
нения (8.36), как правило, резко упрощаются и вычисление <4ГЗ
и Brs не представляет труда.
Заметим теперь, что поскольку потенциальной энергией рас-
сматриваемой системы можно пренебречь, то
2л/а>
(T^)dt,	(8.38)
о
где (Л1)) — кинетическая энергия колеблющихся тел системы
(основного твердого тела и корпусов вибраторов), вычисленная
в порождающем приближении, то есть для закона колебаний
(8.37). Выражение для Л1) соответствует первым четырем строч-
кам формулы (8.33).
Располагая равенствами (8.37), нетрудно найти также и вы-
ражения для углов фч и выполнить интегрирование по формуле
(8.38).
В результате находим
k k
Л<1) = W	[Qs/ Sin (as - a/) - Psl cos (as - az)J, (8.39)
S=1 /=1
где
6	6
Qsi = - Qis = - 4 S S c‘r
|=i| faj
6 6	(8-40)
Ps! = Pis = - 4 S S C‘r (AisArj + BlsBrl),
l=i r=I
а штрих при знаке суммы указывает на пропуск слагаемого, со-
ответствующего j = s. Кроме того, приняты обозначения;
k
С1г = Сг1 = ar6ri - 2 KlqKrq,
4=1
JIJ.
Kiq = -7= sin yq sin p9,
г * xq
JLL
^2? = -T7=sinyflcosp?,
V i'
Г 1 xq
JLL
K3? = _^cosYe,
V ‘Xq
(8.41)
IQ M U Блехман
546
ОБОБЩЕНИЯ ЗАДАЧИ О СИНХРОНИЗАЦИИ ВИБРАТОРОВ (ГЛ. XIV
к<ч = ^тч cos Y" “ Wmq sin Y"sin cos
r ^xq
K5q = -j75~ (umq cos	Sin yq sin pfl) + I'xq sin ₽fl],
’ xq
Ла1а z	к •
KGq = —(umq cos - vmq sin P^) sin
' * xq
81 = 82 = 83 —M, 84 = Ix, 85 = Iy, 86 = 1г,
причем, как и ранее, бг, есть символ Кронекера.
В соответствии с равенством (3.4) для консервативных ча-
стей вибрационных моментов будем иметь выражения
k
П7(Ю = дЛ-т =
das 2М
S miEi lPsi Sin (as ~ “/) + Qsi C0S (a;
(8.42)
использованы для составления основных
задач о
которые могут быть
уравнений различных
(6.4)
записи выражений
синхронизации вибраторов в рас-
сматриваемой системе (см. § 3).
В частности, если изучается за-
дача о самосинхронизации виб-
раторов, то эти уравнения при
учете уже сделанных предполо-
жений запишутся в форме
1 д«т>	—
— U7W(a,, ... ,aft, и)] = 0 (8.43)
(s = 1, ..., k).
Заметим, что структура и фор-
ма записи выражений (8.42) для
вибрационных моментов вполне
аналогичны структуре и форме
главы XIII, полученных для частного
случая «плоской» задачи. Нетрудно убедиться, что последние
выражения получаются при соответствующих предположениях
из формул (8.42).
Если рассматривается задача о самосинхронизации вибра-
торов с одинаковыми и положительными парциальными скоро-
стями, то выражение А® можно принять за потенциальную
функцию D и воспользоваться для решения задачи интеграль-
ным критерием устойчивости.
§ 8]
НЕКОТОРЫЕ ВАЖНЫЕ ЧАСТНЫЕ СЛУЧАИ, ПРИМЕРЫ
547
Рассмотрим в качестве простейшего примера использования
полученных соотношений задачу о самосинхронизации двух
одинаковых вибраторов со скрещивающимися осями, симмет-
рично установленных на мягко амортизированном твердом теле
так, как показано на рис. 43. Вибраторы считаются обычными
дебалансными; предполагается, что их парциальные угловые
скорости одинаковы и положительны, а также что вращение
происходит в одинаковых направлениях [241]. Для рассматри-
ваемой системы
а, = — а2 — a, bx = b2 — Q, Ci = c2——c, Ц = 12 — 0,
Pt = л, р2 = 0, Yi=y2 = Y, а,а2=1,
=	=	I'=0.
11	Z Z	1	Z	хь
В данном случае уравнения (8.36) существенно упрощаются,
все величины Кяд обращаются в нуль и несложные вычисления
по формулам (8.39) и (8.40) дают
Q12 = 0, PI, = ^f/-2-4 + 4bin2Y--^4Y—
М |Д Рх Рг/	Ру
n A(I) 1 F2 Г/о с2 «2\ . 2	, a2cos2y + c2'
D = Л'! =---12 4- —у 5- ] sin Y 4---т---
2М М р2 p2J	р2
Здесь
F = теа2,	а — а, — а2,
px=VlJm, Ри^УЦм, pz=VTjm.
Приравнивание нулю
нению
производной dDIda приводит
к урав-
(8.46)
sin a = О,
откуда следует, что возможно как «синфазное» (а = 0), так и
«противофазное» (а = л) синхронное движение вибраторов.
Условием устойчивости синфазного движения, в соответствии
с интегральным критерием устойчивости, является условие ми-
нимума функции D = Л<т> при а = 0. Последнее требование при
учете обозначений (8.45) приводит к неравенству
+	+	.	(8.47)
Д ' Д Д sm2 у	v ’
Нетрудно убедиться, что синфазному движению соответствуют
«винтовые» колебания тела, то есть колебания по закону
х = ц = О, z=----------cos YSin at,
,,	(8-48)
= О, Q2=--------у!?- sin y sin at.
18*
548
ОБОБЩЕНИЯ ЗАДАЧИ О СИНХРОНИЗАЦИИ ВИБРАТОРОВ [ГЛ. XIV
Именно такие колебания необходимы для нормального проте-
кания процесса в ряде вибрационных машин (см. § 5 главы XX).
Условие (8.47) представляет собой, таким образом, необходи-
мые условия возможности использования самосинхронизирую-
щихся вибраторов в соответствующих машинах. Как и должно
Рис. 44.
быть, при с = 0иу = -^л, а = г и /г = I условие (8.47) пере-
ходит в условие устойчивости противофазного вращения вибра-
торов соответствующей плоской системы, вытекающее из най-
денного в п. 2 § !6 главы ХШ (см. также рис. 34, а). Иным
путем, с использованием гармонических коэффициентов влияния
(см. п. 2 § 3 настоящей главы), неравенство (8.47) было полу-
чено Л. Шперлингом [482].
6.	Произвольное число одинаковых дебалансных вибрато-
ров, связанных с «цепной» колебательной системой. Рассмотрим
систему, состоящую из п масс X», каждая из которых свд-
$ 8]	НЕКОТОРЫЕ ВАЖНЫЕ ЧАСТНЫЕ СЛУЧАИ. ПРИМЕРЫ	549
зана с остальными п — 1 массами, а также с неподвижным ос-
нованием линейными упругими элементами (рис. 44). Все массы
имеют лишь по одной степени свободы. На каждой массе Jts
может быть установлено любое число k<s> одинаковых дебаланс-
ных вибраторов, общее число которых
k = 2 k{s\	(8.49)
5=1
Задача о самосинхронизации вибраторов в описанной си-
стеме рассмотрена Л. Шперлингом [481], результат которого и
воспроизводится ниже.
Дифференциальные уравнения малых колебаний системы
при вращении роторов вибраторов по закону
<ps/ = osi(“/ +asl) (j=l.....s = l, n) (8.50)
имеют вид
n	kfo
Msxs + 2 Csq (xs-xq) = F 2 COS (co/ + as/) gj
(A4S = J(s + x0 = 0) (s = 1, ..., n).
Здесь q>Sj — угол поворота /-го вибратора, установленного на
s-й массе, — соответствующая начальная фаза, csq = cqs
(q, s = 1, . . ., n) —жесткости упругих элементов, связывающих
массы системы одну с другой (при этом, естественно, css = 0),
cso — жесткости элементов, связывающих массы с неподвижным
основанием, F = /песо2,— как и выше, возмущающая сила, раз-
виваемая каждым вибратором при отсутствии колебаний масс.
Через oSj обозначены числа, равные 1 или —1; впрочем, по-
следние в рассматриваемой задаче, очевидно, роли не играют.
Решение системы (8.51), отвечающее установившимся вы-
нужденным колебаниям, можно представить в форме
п /Л*
Xs =- 2 Xsq 2 cos (со/ + aql).	(8.52)
4 = 1	/'=1
Здесь Xsq — постоянные, удовлетворяющие неоднородным алге-
браическим уравнениям
п
2 asvXsq = 6vqF (v, q=l, n)	(8.53)
$»1
(6vg — символ Кронекера), коэффициенты которых
_ =l Scs?-co2Ms при s = v, _ .
	при 5$=^=v,
550
ОБОБЩЕНИЯ ЗАДАЧИ О СИНХРОНИЗАЦИИ ВИБРАТОРОВ [ГЛ. XIV
Решения системы (8.53) имеют вид
д
Y   SQ Е
XSq	д Л
(8.55)
где А—определитель системы (8.53), а — алгебраическое
дополнение элемента asq этого определителя. В результате вы-
ражения (8.52) представятся в форме
п
Xs = 4 S S cos •	(8.56)
4=1	/=1
Функция Лагранжа колебательной части системы (связей
первого рода) может быть представлена в форме
или также в виде
s = l	s=0 (? = s+l
Lw
(8.57)
В результате подстановки выражений (8.56) и интегрирова-
ния при учете формул (6.3) главы XIII и соотношений
п
&syAsq
s = l
вытекающих из (8.53) и (8.55), получается
2л/й)
0
kW
COS (apr - aas) +
S=1
n	fe(P) ft(P)	]
+	cos (apr — aps) I + C, (8.58)
p=l	r=l s = r+l	J
где C — постоянная, не зависящая от a7v.
Может представится более удобной «сквозная» нумерация
вибраторов и начальных фаз. Тогда выражение для ДФ запи-
шется в одной из следующих форм:
k k
A(I) = - 4 S 2 cos (as - ar) + Ct,
s=l r=s+I
k k
л(1)=- 4 S x*sr c°s +с?,
(8.59)
§ 8]	НЕКОТОРЫЕ ВАЖНЫЕ ЧАСТНЫЕ СЛУЧАИ, ПРИМЕРЫ	551
где X*sr —коэффициенты в представлениях
k
xs = 2 X*sr cos (и/ + al,	(8.60)
r = 1
аналогичных представлениям (8.52), a C; и C2 не зависят
от aj.
Нетрудно, наконец, выразить функцию А(1> через гармони-
ческие коэффициенты влияния. В соответствии с равенствами
(3.4) и (3.22) настоящей главы в данном случае имеем следую-
щее выражение для вибрационных моментов:
ч"  С' S к‘г"sin (“* - -
=^<rs)sin(«s	(8-61)
г
Здесь K(rs} — K(sr} — амплитуда установившихся колебаний оси
вращения s-ro вибратора при действии на систему гармониче-
ской силы Fr = cosat, приложенной к оси r-го вибратора и на-
правленной вдоль оси х; при этом величина /Сг“> берется с над-
лежащим знаком (см. стр. 511).
Из равенства (8.61) следует:
k k
А(,) = ~ 4 S 2 ^'Sr) cos - ai) + а <8-62)
s»lr=l
Сопоставление формул (8.59) и (8.62) приводит к соотношению
Xsr~FK(sr\ которое, конечно, могло быть установлено и непо-
средственно по смыслу величин Xsr-
В качестве простейшего примера рассмотрим случай двух
вибраторов [482]. При этом
Л(1)= - ^-Kcosa + C,	(8.63)
где
=	=	а = а1-а2.
Если парциальные угловые скорости вращения вибраторов
одинаковы и положительны, то функция AW может быть при-
нята за потенциальную функцию D. Поэтому в указанном слу-
чае, как следует из (8.63), при
А > 0	(8.64)
будет устойчивым только синфазное вращение роторов вибра-
торов (а = ai — «2 = 0), а при Л'<0 —только противофазное
вращение (а = cti — а2 = л).
552
ОБОБЩЕНИЯ ЗАДАЧИ О СИНХРОНИЗАЦИИ ВИБРАТОРОВ [ГЛ. XIV
Пусть для конкретности речь идет о двухмассной системе,
представленной на рис. 45. Вибраторы предполагаются установ-
ленными на массе Л1[, непосредственно связанной с неподвиж-
ным основанием. В данном слу-
Рис. 45.
чае, как нетрудно найти,
a pt и р2 — собственные частоты
системы, определяемые из урав-
нения
Р4~Р
с2
Mi
Ci Сг ___ а
Mi М2
(8.66)
График функции щ/<(а)2), построенный по формуле (8.65)
при
М, = 2кг, М2= 1,05 кг, ct = 405 кГ/см, с2 = 175 кГ/см,
представлен на рис. 46. На графике указаны значения фазового
сдвига а = ai — аг, отвечающие устойчивому синхронному вра-
к =
щению роторов вибраторов. Как видно, характер устойчивой
фазировки изменяется при переходе как через полюсы со2 = р\
и ш2 = р^, так и через нуль <а2 = /г функции Л (и2).
§ 8]
НЕКОТОРЫЕ ВАЖНЫЕ ЧАСТНЫЕ СЛУЧАИ. ПРИМЕРЫ
553
В качестве второго, более сложного примера, также заимст-
вованного из работы [482], рассмотрим два одинаковых деба-
лансных вибратора или два вибратора направленного действия,
установленных на шарнирно опертой балке длины I с постоян-
ной жесткостью на изгиб ЕУ и с равномерно распределенной
массой р (рис. 47). Вибраторы расположены в точках балки
EJ,p о,	ог	я
Мл-,—.	4^»^ »	ъл Л т	
			
	у		
			
та			
Рис. 47.
с координатами xt и х2; массы вибраторов предполагаются либо
пренебрежимо малыми, либо учитываются приближенно при
определении величины р.
Функция К(и2) в данном случае может быть представлена
в форме
со
(“2) = УУ S sin Ml sin/ng2. (8.67)
/=i
Здесь
(8-68)
причем значениям q — j (j =1, 2, .. .) отвечают частоты соб-
ственных колебаний балки без сосредоточенных масс
/лЕУ
(8.69)
График функции
, . R / 2 Р eV 1	• •	• • У
= q 7 sin sin /л£2,
/=>i
построенный для значений gi = 1/4 и g2 = 3/4, представлен на
рис. 48; там же указаны значения фазовых сдвигов, отвечающих
согласно формуле (8.63) (при одинаковых и положительных
парциальных скоростях) устойчивым движениям вибраторов*).
Как видно из рисунка, характер фазировки вибраторов в устой-
чивом движении изменяется при переходе через собственные ча-
стоты балки.
*) Отметим, что указанная формула, так же как и общее выражение
(8.62), применима и в рассматриваемом случае, когда несущее тело пред-
ставляет собой одномерную систему с распределенными параметрами (см.
п. 1 § 2 и п. 2 § 3 настоящей главы).
554
ОБОБЩЕНИЯ ЗАДАЧИ О СИНХРОНИЗАЦИИ ВИБРАТОРОВ [ГЛ. XIV
Задача о синхронизации вибраторов в своеобразной цепной
системе (рис. 49) возникает в связи с исследованием динамики
привода так называемых многомассных вибрационных машин.
Отдельные твердые тела Mi, ..., Мп, образующие такую си-
стему, могут перемещаться одно относительно другого лишь
Рис. 49.
в определенном направлении Ои, связанном с одним из тел (на
рис. 49 — с телом УЙ2). Вся система крепится к неподвижному
основанию посредством пружин пренебрежимо малой жестко-
сти и может совершать плоское движение. Колебательная часть
системы имеет, таким образом, п + 2 степеней свободы, где п
есть число масс. На одной из масс (обозначим ее номер че-
рез д)установлены два одинаковых дебалансных вибратора,
вращающихся в противоположных направлениях.
§ 8]
НЕКОТОРЫЕ ВАЖНЫЕ ЧАСТНЫЕ СЛУЧАИ, ПРИМЕРЫ
555
Выражения для кинетической и потенциальной энергии несу-
щих тел рассматриваемой системы соответственно имеют вид*)
(п	\
2 MsXs + м/ + /ф2 ,
5=1	'	(8.70)
Il("=2cs,s+1(xs-xs+1)2.
s = l
Здесь у— смещение центра тяжести системы в направлении,
перпендикулярном оси системы Ощ, ф — угол поворота, отсчи-
тываемый по ходу часовой стрелки, М—масса всей системы
(включая массы вибраторов), / — ее момент инерции относи-
тельно центра тяжести О], с.,, s+i — жесткости пружин, связы-
вающих массы Л4.ч и A4s+1. В массу М(, тела, па котором установ-
лены вибраторы, считается включенной и масса этих вибра-
торов.
Решение уравнений движения системы, отвечающее ее уста-
новившимся малым колебаниям при равномерном вращении ви-
браторов с некоторыми начальными фазами ai и аг, имеет вид
xs = FK^x [sin (w4 + cti) + sin (yat + а2)] (s = 1, . .., n),
у = —[cos (и/ + а,) — cos (со/ + а2)],
тег	(8.71)
Ф =----j— [cos (ы/ + а, + р) — cos (и/ + а2 + р)].
Здесь те — статический момент дебалансных грузов вибратора;
F — mew2— возмущающая сила; г — расстояние от осей враще-
ния роторов вибраторов до центра тяжести системы; р —
угол между линиями, соединяющими оси вращения роторов
вибраторов с центром тяжести Oi и осью Oi«; К'хх’ — взятая
с надлежащим знаком амплитуда установившихся колебаний
s-ro тела вдоль оси х под действием гармонической возмущаю-
щей силы единичной амплитуды, направленной вдоль той же оси.
Среднее за период значение функции Лагранжа несущей
системы
2 Л/б)	Г п
Л.П_» f (7.<.>_П>")Л = Г V
ZJL J	Z Жяя
О	LS = 1
cos а + С, (8.72)
где а = ai — а2, a С — не зависящая от а/ и а2 постоянная.
*) Исследование данной системы, результаты которого приводятся ниже,
выполнено А. Д. Рудиным [365].
556
ОБОБЩЕНИЯ ЗАДАЧИ О СИНХРОНИЗАЦИИ ВИБРАТОРОВ [ГЛ. XIV
В соответствии с интегральным критерием, условием устойчи-
вости синфазного вращения роторов дебалансных вибраторов,
приводимых от асинхронных двигателей и обладающих одинако-
выми парциальными скоростями, явится неравенство
£	(й? - в "7 - i (-Г+4) < 0.
(JJ \ Jvi	J j
5“I	5 = 1
(8.73)
При выполнении этого условия вибраторы будут развивать сум-
марную возмущающую силу, направленную вдоль оси системы
Ощ, а все массы — совершать колебания только в том же на-
правлении.
В частном случае, когда число масс п равно трем, условие
(8.73) может быть представлено в следующем виде:
а)	при установке вибраторов на теле Mi
] Мid)2 (х3ц2 + 1	)2 + М2в>2 (х3т)2 - 1 - й2)2 +
+ М3со2(1 -ft2 + T]2)2-c12f—+ 1V(1 - ft2)2-
- с23 h2 (х2 - 1) - 2 (1 - ft2)]2} -	(4- +	< 0; (8.74)
б)	при установке вибраторов на теле М2.
д2^20.4 { М1ю2(х3т]2 - 1 + ft2)2 + М2а>2 (х3ц2 + х, -	+
+ Л43<в2 (ft2 — т]2 + х2)2 — с[2 (ft2 + -^-1 — х,)2 —
-	(1 + X.) - (1 +	- 4 (4 + 4) <°- (8.75)
Здесь обозначено:
Д = И4 _ („^ + „2^ И2 + „2^	_ Н1НД
ft = —,	7] = ^,
/г23	^23
/ c,2(/n,+/n2)	_	/ с23 (т2 + т3)	(7 8-76)
12 Y mtm2 ’	23 V т2т3 ’
т,	т2	т3
т2 + т3’ л гщ+т3 ’ J mi+m2
7. Произвольное число одинаковых вибраторов направлен-
ного действия, установленных на мягко амортизированной упру-
гой балке с распределенной массой. Рассмотрим задачу о син-
хронизации некоторого числа k одинаковых вибраторов направ-
§ 81
НЕКОТОРЫЕ ВАЖНЫЕ ЧАСТНЫЕ СЛУЧАИ, ПРИМЕРЫ
657
ленного действия, размещенных на балке с распределенной
массой р и жесткостью на изгиб Е.7 (рис. 50).
Пусть линии действия возмущающих сил вибраторов лежат
в плоскости симметрии балки и образуют с ее осью Ох некото-
рый угол р, одинаковый для всех вибраторов. Вибраторы могут
быть как дебалансными вибраторами направленного действия
(именно такие изображены на рис. 50, см. также рис. 23, е),
так и «поршневыми» вибраторами (рис. 23,(5). Обозначим через
Рис. 50.
«1, Xk координаты точек пересечения линий действия возму-
щающих сил вибраторов с осью балки (назовем эти точки точ-
ками крепления вибраторов), через т\—массы вибраторов, че-
рез 2/И8 — их статические моменты.
Балка связана с неподвижным основанием амортизирую-
щими элементами пренебрежимо малой жесткости с. Общая
длина балки I предполагается ограниченной требованием,чтобы
наименьшая частота ее продольных собственных колебаний
была в достаточной мере выше угловой скорости синхронного
вращения вибраторов <о; при этом можно считать, что в про-
дольном направлении балка в процессе движения не дефор-
мируется.
Задача о самосинхронизации вибраторов в описанной системе
была решена Р. Ф. Нагаевым и И. А. Поповой [315], причем ви-
браторы рассматривались в квазиконсервативном приближении
(см. § 5).
Здесь мы рассмотрим вибраторы в более простой, неквази-
консервативной идеализации, причем для этого, естественно,
можно будет воспользоваться соответствующими соотношениями
цитированной выше работы. Отметим, что изучаемая задача
представляет интерес в связи с теорией ряда вибрационных
машин с протяженным рабочим органом, приводимых от не-
скольких вибраторов (см. § 5 главы XX).
558
ОБОБЩЕНИЯ ЗАДАЧИ О СИНХРОНИЗАЦИИ ВИБРАТОРОВ [ГЛ. XIV
Пусть роторы вибраторов вращаются равномерно по закону
<ps =	+ as (s = 1, ..., k).	(8.77)
Тогда уравнения малых колебаний балки соответственно в про-
дольном и в поперечном направлениях будут
d*v
дх*
ЕЗ
k
ЛГ = F cos р cos (и/ + as),
S = 1
k
р + (тх + 2m)	6 (х — xs)
S=I
d2v _
'7)tr~
k
= — F sin p 6 (x — xs) cos (и/ + as). (8.78)
Здесь u = u(t)—продольное и o = o(x, t)— поперечное смеще-
ния точек оси балки, М = pl + (тх + 2т) k— общая масса си-
стемы, F = 2mew2 — возмущающая сила, развиваемая вибрато-
ром, д(х)—дельта-функция Дирака. Поскольку мы ограничи-
ваемся изучением движения вдали от резонанса по колеба-
тельным координатам, то силы сопротивления в уравнениях
(8.78) не учитываются.
Поскольку концы балки свободны, то граничные условия
имеют вид (начало координат выбрано посередине балки)
Пусть 0Д£) — собственные функции рассматриваемой балки
с массами, удовлетворяющие уравнению
d'Q,
(i-Т) (/-0,1,2,...)
(8.80)
граничным условиям
~dtf
S-±
_1_
2
= 0,
(8.81)
d3Q;
= 0
и условиям нормировки
r‘ Г	-
-v, L	*-i
0М = «г/
(г, /= 1, 2, ...). (8.82)
§ 8]	НЕКОТОРЫЕ ВАЖНЫЕ ЧАСТНЫЕ СЛУЧАИ. ПРИМЕРЫ	559
Здесь обозначено:
7=-#. Y~	(? + Y=l), L =	(8.83)
бГ; — есть символ Кронекера, a vj— собственные числа, вводи-
мые посредством соотношений
+ '/г
v)= J l"dFJ	(8-84)
-/2
Функция 0j(g) в промежутке —	имеет / нулей
(узлов). Безузловая форма колебаний 6о(£) = 1 отвечает по-
ступательным, а одноузловая форма 0[ (g) = g ]/ЛТ/2//— поворот-
ным колебаниям балки как твердого тела; при этом соответ-
ствующие собственные числа vo = Vi = 0.
В случае симметричного расположения вибраторов на балке,
когда
xs=-xk^s+] (s=l, ...,fe),	(8.85)
выполняются соотношения
0/(-£) = 0/(£) (s = 0, 2, ...),	0/(-g)= -0;(g) (8.86)
(s=l, 3, ...).
При использовании функций 0,- решение уравнений (8.78), от-
вечающее установившимся вынужденным колебаниям, может
быть представлено в форме
k	k
u = «0-^~ У} cos (со/ + as), v = о0 у Г (gs, g) cos (&t + as). (8.87)
S = 1	S=>1
Здесь
2,/гей	o	2m ей . n	oo,
«о = ~M~C0S P’ V° =	sm 0	(8.88)
— амплитуды колебаний балки в идеальном случае, когда жест-
кость ее не только в продольном, но и в поперечном направле-
нии бесконечно велика и когда все вибраторы работают син-
хронно и синфазно («! = ... = aft);
T(l.n) = r4^£^>	=	(8,9)
— гармонический коэффициент влияния, равный безразмерной
амплитуде поперечных колебаний точки £ балки под действием
единичной гармонической силы частоты со, приложенной в точ-
ке Т].
560
ОБОБЩЕНИЯ ЗАДАЧИ О СИНХРОНИЗАЦИИ ВИБРАТОРОВ [ГЛ. XIV
Выражение для функции Лагранжа колебательной части си-
стемы (несущих связей) имеет вид
£“’-ТМ(-5г)! +
k
р +	+ 2т)	6 (х — xs)
S=>1
\ dt ) \дх2 )
dx.
(8.90)
Выполнив интегрирование при учете равенств (8.82), (8.88) и
соотношения
’/г
Г d20r d20,
J	= V (*,/ = 0,1,2,...),	(8.91)
-/»
получим
k k
A<1) = 2 2 [“° + r ^s’ °°-l C0S ~ + C’ (8-92)
S-I /-I
где C — не зависящая от a,, ..., a;{ постоянная.
Отметим, что к выражению вида (8.92) можно было бы
прийти также путем использования формулы (3.34), выражаю-
щей вибрационный момент через гармонический коэффициент
влияния*). Однако реальное вычисление этого коэффициента
все равно потребовало бы решения уравнений движения (8.78).
В случае задачи о самосинхронизации вибраторов с одина-
ковыми положительными парциальными скоростями устойчивые
синхронные движения вибраторов могут отвечать точкам стро-
гого минимума функции Л® по k—1-й фазе as. При этом наи-
больший интерес с точки зрения приложений представляет вы-
яснение условий устойчивости синфазного движения вибрато-
ров; такой режим, очевидно, непременно существует, ибо
уравнения
k
Л4ФГ =	+ Г ^s’ ^)«olsin(as-a/) = °	(s=l, ..., k)
s /-1
(8.93)
всегда допускают решение вида
(Х] = a2 = ... = ак.
(8.94)
*) Нетрудно видеть, что выражение в квадратных скобках формулы
(8.92) пропорционально проекции амплитуды колебаний точки балки xs на
ось вибратора под действием единичной гармонической силы частоты со, при-
ложенной в точке Xj и направленной по оси вибратора.
§ 8]
НЕКОТОРЫЕ ВАЖНЫЕ ЧАСТНЫЕ СЛУЧЛЦ, ПРИМЕРЫ
561
Условие устойчивости синфазного движения сводится к требо-		
ванию отрицательности k— 1-го корня уравнения		
	й - р12	...	- plk /-1	
	k ~Pl\	li'p-21-Я ...	~ p.2k	= 0,	(8.95)
	k ~ Pkl	~ Pk2 ••• 2 PkJ~^ /-I	
где		
	Ps/ = P/s = cos2p + r(^, £/)sin2p,	(8.96)
а штрих при знаках сумм указывает па пропуск слагаемого
вида ри.
Отметим, что при выполнении условий симметрии (8.85)
определитель в левой части уравнения (8.95) становится сим-
метричным относительно обеих своих диагоналей, и вследствие
этого исследование его корней значительно упрощается. Так, на-
пример, в случае четного числа вибраторов k указанный опре-
делитель распадается на произведение определителей &/2-го
порядка.
Балка, на которой установлены вибраторы, обычно является
рабочим органом вибрационной машины. Поэтому, наряду с ус-
ловием устойчивости синфазного движения вибраторов, часто
накладывается требование, чтобы при таком движении балка
совершала колебания, достаточно близкие к ее колебаниям как
твердого тела. Это требование приводит к неравенству
| (V - v0)/v0 К т].	(8.97,
Здесь ц— максимально допустимое относительное отклонение
формы поперечных колебаний балки V = V(x), определяемой
согласно равенствам (8.87) и (8.89) в случае синфазного вра-
щения вибраторов по формуле
k	°° fi’o
S=1	/-0
где
k
в;-т£9/(М	(8.99)
есть среднее «дискретное» значение /-й формы собственных ко-
лебаний балки. В случае симметричной машины
е; = о (s=i, з,...)	(8.1оо)
562
ОБОБЩЕНИЯ ЗАДАЧИ О СИНХРОНИЗАЦИИ ВИБРАТОРОВ [ГЛ. XIV
и выражение (8.98) можно представить в виде
V=v0
(8.101)
/ = 2, 4, ...
В излагаемом исследовании на электронной цифровой вы-
числительной машине была выполнена серия расчетов по выяв-
лению областей значений параметров, в которых одновременно
выполняется условие (8.97) и условие устойчивости синфазного
вращения вибраторов. Рассматривался случай балки без со-
средоточенных масс; считалось, что массы вибраторов либо пре-
небрежимо малы, либо могут быть учтены соответствующим
увеличением равномерно распределенной массы р. Равномерно
распределенными по длине балки предполагались и точки кре-
пления вибраторов xs.
Как показали вычисления, синфазный режим устойчив лишь
в частотном диапазоне
v2ft_I<v = |/-^<v2ft,	(8.102)
где собственные числа в рассматриваемом случае определяются
из уравнения
chv5cosv5=l,	(8.103)
причем значения vo = Vi = 0, как и выше, отвечают поступатель-
ным и поворотным колебаниям балки как твердого тела,
Рис. 51.
v2 = 4,73, V3 = 7,85, V4 = 11,0 и вообще vs ~ — (2s — 1) при s > 2.
В качестве примера графики корней х уравнения (8.95) для
случаев k = 2 и k = 3 представлены на рис. 51. Что касается
условия (8.97), то, как выяснилось, для ц = 1 оно выполняется,
если
v<v’,	(8.104)
§ 81
НЕКОТОРЫЕ ВАЖНЫЕ ЧАСТНЫЕ СЛУЧАИ, ПРИМЕРЫ
563
где У2 = 8, ^з=10, ^=15,5, vj = 21, Vg = 22. Такой результат
согласуется с полученным в статье [50] необходимым условием
нормальной работы многоприводных вибрационных машин *)
v 3fe,
(8.105)
найденным из условия (8.97) при т] = 0,25; естественно, что чис-
ла v* получились несколько большими, чем 3fe, ибо они были
найдены исходя из более мягкого ограничения, отвечающего
ц = 1.
Сопоставление неравенств (8.102) и (8.104) показывает, что
они одновременно выполняются лишь при k = 2 в узком диапа-
зоне **)
7,85 <v< 8.	(8.106)
При fe^>3 указанные неравенства не выполняются совместно ни
при каких значениях v. Отсюда следует, что использование само-
син.хронизирующихся вибраторов в рассматриваемой машине
возможно лишь при числе вибраторов k = 2. В случае большего
числа вибраторов необходимы либо изменения в динамической
схеме машины, либо использование тех или иных способов при-
нудительной синхронизации. Отметим, что требования к элемен-
там принудительной синхронизации при этом могут быть полу-
чены путем решения соответствующей задачи на основе исполь-
зования выражения (8.92) для функции Л®.
Заметим, что уравнения (8.93), помимо решения (8.94), до-
пускают также и другие решения вида
as = <7sn + a,	(8.107)
где числа qs равны нулю или единице, а а — произвольная по-
стоянная. Каждая такая фазировка полностью характеризуется
fe-значным двоичным числом <7i<?2 • • • общее число указанных
существенно различных фазировок (следуя [315], их можно на-
звать фазировками первого рода) быстро растет при увеличении
числа вибраторов fe; оно может быть подсчитано по фор-
муле [315]
nk — 2 . Q 2	г
2	+22	, если fe четное;
nk-2 . „4 I*-3)	,
2	+22	, если fe нечетное.
(8.108)
*) См. неравенство (2.22) цитированной статьи; следует учитывать, что
через I в настоящем параграфе обозначена общая длина балки, а в работе
[50] — расстояние между вибраторами.
**) Отметим, что этот диапазон может быть несколько расширен за счет
верхней границы при некотором смещении точек крепления вибраторов по
отношению к принятому в данных расчетах [242J
Б64
ОБОБЩЕНИЯ ЗАДАЧИ О СИНХРОНИЗАЦИИ ВИБРАТОРОВ [ГЛ. XIV
Вместе с тем при k > 2 уравнения (8.93) допускают и каче-
ственно иные решения (назовем их фазировками второго рода).
Так, например, при k = 3 система (8.93) допускает решение
cos cq = —, а2 = 0,	а3=—а|(	(8.109)
*Pl 3
которое отвечает устойчивому движению при выполнении условия
р13/2>|р12|.	(8.110)
Соответствующие нетривиальные фазировки существуют (и
притом в большом количестве) также и при числе вибраторов
k > 3, хотя их отыскание при этом существенно осложняется.
Рис. 52.
Изучение таких фазировок при неограниченно возрастающем
числе вибраторов k приводит к понятию о так называемой фазо-
вой волне — непрерывной функции а(х//), характеризующей рас-
пределение начальных фаз вращения. На относящихся сюда рас-
суждениях здесь, однако, мы не останавливаемся.
8. Два одинаковых бигармонических дебалансных вибратора,
расположенных на мягко амортизированном твердом теле. В ка-
честве простейшего примера задачи о синхронизации полигармо-
нических вибраторов рассмотрим самосинхронизацию двух оди-
наковых бигармонических вибраторов, каждый из которых
состоит из двух неуравновешенных роторов с параллельными
осями вращения, жестко связанных, например, посредством зуб-
чатой передачи с передаточным отношением j = plq4=\., где
р и q — произвольные целые положительные неодинаковые числа
(рис. 52). Пусть оси вращения роторов первого вибратора 1 и 1'
НЕКОТОРЫЕ ВАЖНЫЕ ЧАСТНЫЕ СЛУЧАИ, ПРИМЕРЫ
665
§ 8J
и второго вибратора 2 и 2' параллельны, а плоскости осей вра-
щения каждого вибратора равноудалены от центра тяжести
твердого тела, на котором размещены вибраторы. Будем считать
тело мягко амортизированным и пренебрегать влиянием жест-
кости опорных упругих элементов.
Выражение для кинетической энергии вспомогательного тела
имеет вид
Г(1) = уМ (х2 +//2) + у/<р2,	(8.111)
где х и у— координаты центра тяжести Oi вспомогательного тела
относительно неподвижных осей хОу, ф— угол поворота тела,
М и I — его масса и момент инерции относительно оси, проходя-
щей через точку Oh
Пусть роторы вибраторов равномерно вращаются по закону
1|)1 = /ф1+б = /(о/ + /а1 + б, (8 112)
ф2 = <о/ + а2, ф2 = /Фа + б = /со/ + /а2 + б, '	'
где б — угол сдвига фаз между вращениями роторов каждого
вибратора, а направления отсчета углов, соответствующие на-
правлениям вращения роторов, отвечают показанным на рис. 52.
Уравнения малых колебаний тела под действием возмущаю-
щих сил вибраторов, развиваемых при вращении по закону
(8.112), имеют вид
Mx — F [cos (<о/ + а,) + cos (и/ + а2)] +
+ F' [cos (/со/ + /а1 + б) + cos (/’со/ + /а2 + б)],
Му = F [sin (at + dj) — sin (at + а2)] +
+ F' [ — sin (jat + /а, + 6) + sin (jat + /«2 4- 6)],	( 1 )
/ф = Fr [ — sin (at 4- a1 — y) + sin (at + a2 — Y)] +
+ F'r' [sin (jat + jd! + 6 4- y') — sin (jat + jd-> + 6 + /)].
Здесь через F — mea2 и F' = m'ef'fa2 обозначены возмущающие
силы, развиваемые при вращении соответствующих роторов
(те и т'е' — статические моменты роторов); г и г' — расстояния
от осей вращения до центра тяжести вспомогательного тела Оу,
у и у' —углы между плоскостями, проходящими через оси вра-
щения роторов и центр тяжести Оь и осью Oi«, связанной с
телом.
Определив путем непосредственного интегрирования соотно-
шений (8.113) значения х, у и ф, отвечающие установившимся
вынужденным колебаниям, после осреднения выражения (8.111)
566
ОБОБЩЕНИЯ ЗАДАЧИ О СИНХРОНИЗАЦИИ ВИБРАТОРОВ [ГЛ. XIV
нетрудно прийти к следующему выражению для функции А<!):
А» =□-/’(£<»)./
О
1 *
J- Г (г(1))л =
* * J
о
= ~	I?7’7)2 cos “ + (yf cos И + с-	(8-114)
Здесь через Tt = —q обозначен общий наименьший период
возмущающих сил, развиваемых вибраторами, а = си— «2. а
С—не зависящая от а постоянная.
Пусть рассматривается задача о самосинхронизации одина-
ковых вибраторов с одинаковыми положительными парциальны-
ми скоростями. Тогда, в соответствии с интегральным критерием
устойчивости (справедливым и для случая полигармонических
вибраторов), устойчивые движения могут отвечать минимуму
функции А®.
Согласно равенству (8.114) функция Л<т) всегда имеет мини-
мум при а — (a)i = 0; нетрудно убедиться, что такому движению
отвечают поступательные бигармонические колебания несущего
тела вдоль оси Ох. Обычно именно такие колебания как раз и
являются желательными по технологическим соображениям.
Однако, как показывает несложное исследование, точка
а = (а)! = 0 не всегда является единственным минимумом функ-
ции А(1>, и поэтому кроме основного режима, отвечающего « = 0,
могут оказаться устойчивыми также и побочные (обычно неже-
лательные) режимы, которым соответствуют а=£0 и непосту-
пательные колебания твердого тела.
Рассмотрим для определенности случай, когда угловая ско-
рость вращения роторов Г и 2' превышает угловую скорость
вращения роторов / и 2 ровно в два раза, то есть когда / = 2.
В данном случае при выполнении неравенства
F'r'<Fr	(8.115)
или
4т'е'<те	(8.116)
точка a = (a)i = 0 является единственным минимумом функ-
ции А*1). При выполнении неравенств противоположного смысла
появляется также минимум в точке а = (а)г = л, отвечающий
устойчивому движению системы, при котором колебания тела не
являются поступательными и носят достаточно сложный харак-
тер (см. уравнения (8.113)).
Интересно отметить [1,2, 73], что равенство
4т'е = те	(8.117)
§ 8]	НЕКОТОРЫЕ ВАЖНЫЕ ЧАСТНЫЕ СЛУЧАИ, ПРИМЕРЫ	567
представляет собой оптимальное соотношение между статиче-
скими моментами роторов вибраторов для некоторого важного
класса машин с бигармоническими колебаниями рабочего орга-
на. Из изложенного следует, что в указанных машинах самосин-
хронизация вибраторов может быть использована при выборе
параметров, достаточно близком к оптимальному соотношению
(8.117).
Заметим также, что характер синхронных движений вибрато-
ров оказался не зависящим от угла сдвига фаз б между враще-
ниями роторов вибраторов. Наконец, нетрудно убедиться, что
при Fr = 0 или F'r' = 0 из формулы (8.114) получаются резуль-
таты, соответствующие найденным в п. 2 § 16 главы XIII для
пары обычных дебалансных вибраторов.
* * *
Как уже отмечалось, приведенные примеры были рассмотре-
ны не только с иллюстративной целью, но и в связи с практиче-
скими приложениями, о которых будет сказано ниже (см. пятую
часть настоящей книги). Исследование других конкретных си-
стем приводится в главах XV и XX—XXIII.
ГЛАВА XV
О СИНТЕЗЕ ВИБРАЦИОННЫХ МАШИН
С МЕХАНИЧЕСКИМИ ВИБРАТОРАМИ
§ 1.	Проблема синтеза вибрационного поля
В предыдущих главах настоящей части книги задача о син-
хронизации вибраторов ставилась и решалась как задача ана-
лиза: колебательная система с возбудителями считалась задан-
ной, и изучались возможные синхронные движения вибраторов
этой совокупной системы. Однако в связи с теорией и проектиро-
ванием вибрационных машин и ряда других устройств, в которых
механические колебания применяются для достижения полезных
целей, все большее значение приобретает следующая задача,
в известной мере обратная по отношению к первой:
Имеется некоторая упругая система, в виде которой идеали-
зируется рабочий орган (или рабочие органы) машины. Тре-
буется обеспечить с некоторой заданной точностью периодиче-
ские колебания ее точек по определенным законам, задаваемым
исходя из технологических соображений*).
Сформулированная задача возникает перед конструктором
после того, как ему становятся известны характеристики колеба-
ний, обеспечивающие оптимальное (или хотя бы приемлемое)
протекание рабочего процесса. Будем называть эту задачу зада-
чей синтеза вибрационного поля упругих систем и рассмотрим
в общих чертах ее особенности.
Пусть
и(х, у, z, t)^u(x, у, z, t+T)	(1.1)
есть Т-периодическая функция времени t и функция простран-
ственных координат х, у и z, описывающая колебания точек рас-
сматриваемой упругой системы или некоторой ее части. Пусть,
далее, условная запись
Lu = p(x, у, z, t), Qu\s = As	(1.2)
*)' Обычно задаются колебания не всех точек упругой системы, а, на-
пример, лишь точек некоторой поверхности, на которой осуществляется ра-
бочий процесс.
§ 1]	ПРОБЛЕМА СИНТЕЗА ВИБРАЦИОННОГО ПОЛЯ	569
означает соответственно систему уравнений движения упругой
системы под действием некоторых внешних сил р(х, y,z,t) и со-
вокупность граничных условий. Под L и Q понимаются некото-
рые дифференциальные операторы, под As— заданный вектор, а
S суть границы тел упругой системы.
В важном частном случае задачи требуется обеспечить коле-
бания свободной упругой балки, пластины или тела с распреде-
ленными и с сосредоточенными массами, близкие к их поступа-
тельным колебаниям как абсолютно твердых тел (см. работы
[50, 84, 85], а также главу XX настоящей книги). В этом слу-
чае вектор и = u(t) = u(t + Т) не зависит от координат точек
соответствующего тела, т. е. вибрационное поле однородно.
В вырожденном случае системы с конечным числом степеней
свободы соотношения (1.2) представляют собой систему обыкно-
венных дифференциальных уравнений.
Может показаться, что обсуждаемая задача не представляет
особых трудностей, ибо является так называемой первой задачей
динамики — задачей определения действующих на систему сил
по известному закону движения. В действительности, однако, это
не так по следующим двум причинам.
1) Подстановка выражения (1.1) для известного закона дви-
жения системы*) в уравнения (1.2) приводит к некоторому вы-
ражению для распределенного по объему и по поверхности си-
стемы (иногда — либо по объему, либо по поверхности) периоди-
ческого возмущения р. Между тем подавляющее большинство
известных в технике возбудителей развивает сосредоточенную
(распределенную по небольшому участку поверхности) возму-
щающую силу. Так, обычные дебалансные вибраторы передают
возмущающую силу через поверхности подшипников ротора.
Максимальное число возбудителей, которое можно разместить
на упругой системе конечных размеров, при этом всегда ограни-
чено вследствие конечных размеров возбудителей. Более того,
как правило, экономически выгоднее и с эксплуатационной точки
зрения удобнее применять по возможности меньшее число более
мощных возбудителей, нежели большое число менее мощных.
Таким образом, фактически мы имеем задачу о воспроизве-
дении определенного поля колебаний точек упругой системы
посредством минимального числа возбудителей, генерирующих
сосредоточенные усилия или моменты. Несколько облегчает дело
то обстоятельство, что допустимо ограничиться воспроизведением
этого поля колебаний с заданной точностью: можно считать,
что цель достигнута, если действительный закон колебаний
u*(x,y,z,t) удовлетворяет условию достаточной близости к
*) Отметим, что функция и должна удовлетворять очевидным условиям
«гладкости», на рассмотрении которых здесь можно не останавливаться.
570
О СИНТЕЗЕ ВИБРАЦИОННЫХ МАШИН
[ГЛ. XV
заданному закону и{х, у, z,t) \ например, можно поставить усло-
вие, чтобы выполнялось соотношение
| и — и | е,	(1.3)
где е — заданное положительное число.
2) Возбудители колебаний, присоединяемые к упругой си-
стеме, фактически образуют с ней единую систему, зачастую
значительно отличающуюся от исходной упругой системы. Дело
в том, что при решении большинства задач нельзя использовать
обычную концепцию теории вынужденных колебаний, при ко-
торой возмущающие силы считаются заданными и не зависящи-
ми от движения системы. Как правило, необходимо учитывать,
что силы, передаваемые упругой системе от вибраторов, суще-
ственно зависят от колебаний тех участков упругой системы, к ко-
торым присоединены вибраторы. Об указанном обстоятельстве
применительно к механическим вибраторам говорилось в конце
§ 2 главы XIII и более подробно говорится в главе XVII.
Более того, вибраторы вносят в систему дополнительные сте-
пени свободы — их состояние характеризуется «собственными»
обобщенными координатами (в случае механических дебаланс-
ных вибраторов — углом поворота ротора, в случае электромаг-
нитных вибраторов — магнитными потоками и т. п.), дифферен-
циальные уравнения движения для которых образуют вместе
с уравнениями колебаний упругой системы (1.2) единую совокуп-
ную систему с большим числом степеней свободы (см., например,
системы (2.44) главы XIII и (3.1) главы XXV). При этом, даже
если левая часть системы (1.2) линейна, то уравнения движения
расширенной системы, как правило, оказываются нелинейными
вследствие нелинейности уравнений движения вибраторов.
Иначе говоря, вместо (1.2) приходится рассматривать си-
стему вида
L« = p(q>i, .... <Pft, х, z/, z), Q« |s — As,
£>sfps = Bs (rps, u, t) (s=l,..., k),
где последние k соотношений представляют условную запись
уравнений движения возбудителей колебаний (Ds и Bs — некото-
рые дифференциальные операторы, a <р3— векторы, компонента-
ми которых являются «собственные» обобщенные координаты
вибраторов).
Редко встречающийся случай, когда в рассматриваемой зада-
че допустимо ограничиться концепцией возмущающих сил, соот-
ветствует пренебрежению в уравнениях (1.4) членами Bs(u, <ps, t)
характеризующими, в частности, обратное влияние колебаний
системы на движение вибраторов.
§ 2] ВИБРАЦИОННЫЕ МАШИНЫ С МЕХАНИЧЕСКИМИ ВИБРАТОРАМИ 571
Часто, однако, можно считать, что это обратное влияние отно-
сительно мало, то есть положить
Bs = yBs,
где ц— малый параметр. При этом уравнения (1.4) приобретают
вид
Dsq>s = pB*(q)s, и, /)	k),
(1.5)
£и = р(ф!, . .., <ръ х, у, г), Qu\s = As,
соответствующий уравнениям движения системы объектов со
слабыми взаимными связями (см. § 2 главы II настоящей
книги). Изучение таких систем значительно проще, чем систем
общего вида, ибо здесь удается воспользоваться аппаратом ме-
тода малого параметра. В наиболее распространенных случаях
возбуждения от механических и от электромагнитных вибрато-
ров, в частности, оказывается, что задача об удовлетворительном
воспроизведении заданного поля колебаний упругой системы
наименьшим числом заданных сосредоточенных сил, как правило,
может решаться независимо от задачи о создании этих сил,
предполагающей учет взаимодействия возбудителей через упру-
гую систему (см. § 2 настоящей главы, а также работы [409,
84, 85]).
Перечисленные особенности изучаемой проблемы и делают ее
нетривиальной. Из изложенного видно также, что речь идет о
своеобразном классе задач современной теории колебаний, имею-
щем существенное практическое значение.
Вопросы синтеза колебаний упругой системы имеют свою спе-
цифику в зависимости от вида вибраторов, используемых для
возбуждения колебаний. Поэтому, не останавливаясь более на
рассуждениях общего характера, перейдем к рассмотрению важ-
ного конкретного класса систем с механическими возбудителями.
§ 2. Синтез вибрационных машин с механическими вибраторами
Задачу о синтезе вибрационных устройств с механическими
возбудителями будем рассматривать в тех же предположениях,
что и общую задачу о синхронизации вибраторов, изученную в
главе XIV. Иными словами, допустим, что вибраторы, установ-
ленные па упругой системе, могут рассматриваться как слабо
связанные квазилинейные объекты с одной степенью свободы,
совершающие почти равномерные вращательные движения. До-
пустим, далее, что синтезируемый закон колебаний упругой си-
стемы таков, что он в принципе может быть осуществлен син-
хронно работающими механическими вибраторами. Напомним
(см. § 2 главы XIII), что именно такие законы движения, как
правило, представляют практический интерес.
572
О СИНТЕЗЕ ВИБРАЦИОННЫХ МАШИН
[ГЛ. XV
Тогда, в соответствии с изложенным в § 2 главы XIV, основ-
ными соотношениями для решения задачи синтеза вибрацион-
ной машины с механическими возбудителями будут:
1)	Формулы
и° = и°(х, у, z, t, аь аД	(2.1)
выражающие закон установившихся Т — 2л/и-периодических ко-
лебаний упругой системы под действием возмущающих сил, раз-
виваемых вибраторами при равномерном вращении их валов
по закону
<р° =--• ст5(со/ + aj (s=l, . .., k).	(2.2)
Здесь, как и ранее, k есть число выбраторов, ст., = ±1, a as —
начальные фазы; для некоторого упрощения рассматриваем слу-
чай простой (некратной) синхронизации.
2)	Уравнения
Ps (a,, ..., ak, со) = 0 (s = 1, ..., k),	(2.3)
как правило, трансцендентные, для определения фаз вращения
вибраторов ai,.. ., ал в возможных синхронных движениях. Кон-
кретный вид и способы составления этих уравнений для различ-
ных случаев были рассмотрены в предыдущей главе. Здесь же
существенно, что уравнения (2.3), отражающие взаимодействие
вибраторов через колебательную систему, требуют для своего
составления лишь знания закона колебаний (2.1), то есть част-
ного решения уравнений колебаний упругой системы под дей-
ствием заданных возмущающих сил.
3)	Алгебраическое уравнение
|^-6s7x| = 0	(s,/ = 1, ..., k),	(2.4)
от характера корней которого зависит решение вопроса об
устойчивости движения, отвечающего определенной комбинации
фазана*, ..., ak=®k, найденной из уравнений (2.3).
Рассмотрим теперь задачу о синтезе поля вынужденных
колебаний упругой системы, предполагая, что приближение (2.1),
получаемое указанным выше способом, с достаточной точностью
описывает действительный закон движения упругой системы.
Отметим, что в реальных задачах такое предположение почти
всегда выполняется, и вычисление более высоких приближений
не требуется.
Прежде всего, из приведенных выше соотношений следует,
что рассматриваемая задача в данном случае распадается на
две задачи, допускающие (с определенной оговоркой, см. ниже)
последовательное решение.
Первая задача состоит в определении минимально допусти-
мого чисда вибраторов k, их типа, расположения на упругой с,д-
5 2]
ВИБРАЦИОННЫЕ МАШИНЫ С МЕХАНИЧЕСКИМИ ВИБРАТОРАМИ 573
стеме, рабочей частоты со, направлений вращения основных ва-
лов (чисел Oi, ... , оь), начальных фаз вращения ai, .., , аь, ста-
тических моментов неуравновешенных масс вибраторов wiiei,.. .
. . . , mhe.h и других параметров, входящих в решение (2.1), при
которых обеспечивается (по крайней мере с некоторой заданной
точностью) поле колебаний упругой системы, требуемое по тех-
нологическим соображениям. Иными словами, первая задача
представляет собой задачу о синтезе заданного поля выну-
жденных колебаний посредством приложения к системе некото-
рого (по возможности, меньшего) числа сосредоточенных перио-
дических возмущающих сил Fs. Естественно, что характер ука-
занных сил Fs определяется типом вибратора: это силы,
развиваемые вибратором при равномерном вращении его основ-
ного вала и при «заторможенной» упругой системе. Так, напри-
мер (см. формулу (3.14) главы XIV), в случае обычных одноча-
стотных дебалансных вибраторов
F°s = msesa2[is cos (at + as) 4- Jsossin (at + as)],	(2.5)
где is и js — взаимно перпендикулярные неподвижные орты, ле-
жащие в плоскости вращения центра тяжести ротора вибратора,
причем предполагается, что угол поворота вектора-эксцентриси-
тета дебаланса отсчитывается от направления i к / «по кратчай-
шему пути».
Решение первой задачи во многих случаях не представляет
труда; в частности, это так, если поле однородно, а упругую
систему можно рассматривать как мягко амортизированное твер-
дое тело. Значительно сложнее случай, когда упругая система при
требуемых частотах возмущения является «гибкой»; здесь пока
имеются лишь некоторые результаты, относящиеся к одномер-
ным системам [50, 84, 85]. В общем же случае задача еще не
рассматривалась. Естественно, что решение первой задачи вооб-
ще не всегда возможно, особенно при ограничении числа вибра-
торов. Заметим также, что при решении первой задачи следует
считать, что вибраторы соответствующим образом присоединены
к исходной упругой системе, то есть что фактически мы имеем
задачу о возбуждении заданных колебаний сосредоточенными
силами несколько видоизмененной системы *).
Вторая задача (ее можно назвать задачей синтеза системы
возбуждения-, она, по существу, совпадает с поставленной в § 2
главы XII задачей синтеза) состоит в таком подборе оставшихся
*) Выше (см. главу XIII) соответствующие твердые тела этой видоиз-
мененной системы были названы вспомогательными; они получались из тел
исходной системы путем присоединения масс роторов вибраторов, сосредото-
ченных в точках пересечения осей с плоскостями вращения их пентрор tsp
?кести,
574
О СИНТЕЗЕ ВИБРАЦИОННЫХ МАШИН
[ГЛ. XV
«свободными» после решения первой задачи параметров системы
и параметров двигателей (или комбинации этих параметров),
чтобы требуемые значения начальных фаз а, = а* *.аА = а‘
были решением системы трансцендентных уравнений (2.3) и удо-
влетворяли условию устойчивости, связанному с уравне-
нием (2.4).
Прежде всего отметим, что задача принципиально всегда мо-
жет быть решена путем использования принудительной синхро-
низации с применением синхронных электродвигателей или
квазиупругих синхронизирующих элементов, связывающих валы
вибраторов. Действительно, в этом случае уравнения (2.3) имеют
соответственно вид соотношений (11.8) и (11.13) главы XIII.
Подставив в эти уравнения значения фаз а*, ..., а’, чисел
ai, . .., Ой и других величин, найденных из решения первой за-
дачи, можно практически всегда *) подобрать установочные углы
синхронных двигателей рь .. ., ₽/< или установочные углы квази-
упругих элементов хц. . ., хь, а также характеристики двигате-
лей таким образом, чтобы соответствующие значения углов
а’, . .., ак были решениями указанных уравнений. Затем путем
выбора достаточно больших значений «жесткостей» характери-
стик синхронных двигателей
( дЬ'Д	( dL*s \
—-4*)	; - \(2-6>
или жесткостей квазиупругих элементов cSJ- можно всегда до-
биться, чтобы уравнение (2.4) имело корни только с отрицатель-
ными вещественными частями, то есть чтобы соответствующее
движение было устойчивым.
Такой результат хорошо понятен из физических соображе-
ний: естественно, что путем надлежащей установки достаточно
жестких связей между валами вибраторов всегда можно добить-
ся их синхронного движения с заданными фазовыми сдвигами.
В заключение исследования надлежит убедиться, не превосхо-
дят ли в рассматриваемом движении углы | О.ч | = ] сс.ч — р.ч | (соот-
ветственно углы |ая — xs |) предельно допустимых значений. В от-
дельных случаях может также оказаться необходимым прове-
рить, не выходят ли отклонения <ps — cts (со/+ as) = a^s (®0 (s =
= !,...,&) вращения вибраторов от равномерного, а также соот-
ветствующие отклонения колебаний вибрирующего органа маши-
ны, из допускаемых по техническим условиям пределов.
*) Предполагается, что вибрационные моменты при заданных ар ...
*
,конечны.
§ 2] ВИБРАЦИОННЫЕ МАШИНЫ С МЕХАНИЧЕСКИМИ ВИБРАТОРАМИ 575
Поскольку мы ограничиваемся рассмотрением устойчивости
в малом, то после выполнения описанных операций в ряде слу-
чаев желательно убедиться в том, что при найденных значениях
параметров существует и устойчиво только’ данное синхронное
движение вибраторов. В противном случае при определенных на-
чальных условиях возможно возникновение устойчивого син-
хронного движения системы, отличающегося от требуемого по
условиям. Эта часть исследования сложнее, ибо здесь может
потребоваться прямое решение трансцендентных уравнений для
определения порождающих фаз ai,. . . , a&, отвечающих задан-
ным значениям параметров системы, а также соответствующее
исследование устойчивости.
В случаях, когда путем надлежащего выбора параметров
оказывается невозможным избежать наличия побочных устой-
чивых движении, для их предотвращения можно воспользоваться
устройствами, подобными упоминавшемуся в § 2 главы XII авто-
матическому устройству Б. П. Лаврова.
Заметим, что простейшие примеры решения задач о синтезе
машин с принудительно синхронизированными вибраторами уже
были рассмотрены в пп. 5 и 6 § 16 главы ХШ; другие примеры
даются в § 3 главы XX.
Принудительная синхронизация вибраторов является универ-
сальным, однако далеко не наилучшим способом обеспечения
требуемого синхронного режима вращения валов вибраторов.
Практически почти всегда желательно обойтись без усложняю-
щих систему элементов принудительной синхронизации и вос-
пользоваться явлением самосинхронизации, а в случае, если это
не удается, то установить между роторами вибраторов лишь ми-
минимально необходимое число связей с минимально допусти-
мыми «жесткостями».
В особых, однако реально встречающихся случаях может ока-
заться, что требуемая фазировка вращения роторов удовлетворяет
уравнениям (2.3) и условиям устойчивости, отвечающим случаю
самосинхронизации, непосредственно или после допустимых из-
менений значений свободных параметров. В большинстве же слу-
чаев это будет не так; тогда, прежде чем прибегать к средствам
принудительной синхронизации, следует попытаться добиться
возможности использования явления самосинхронизации путем
некоторых видоизменений рассматриваемой системы. Можно
указать два способа таких видоизменений; один из них состоит
в изменении колебательной части системы, а другой — в добавле-
нии одного или нескольких вибраторов, играющих роль стаби-
лизаторов требуемого режима. Эти способы рассматриваются
соответственно в §§ 3 и 4 настоящей главы.
Наконец, если все же оказывается необходимым использовать
средства принудительной синхронизации, например, квазиупругие
576
О СИНТЕЗЕ ВИБРАЦИОННЫХ МАШИН
[ГЛ. XV
или абсолютно жесткие кинематические связи между валами
вибраторов, то желательно, чтобы число этих связей было мини-
мальным. Соответствующая задача об оптимальном (в опреде-
ленном смысле) синтезе машин с жесткими связями между рото-
рами вибраторов рассматривается в § 5 данной главы.
Как уже частично отмечалось выше, если упругую систему
при решении первой из указанных задач не считать наперед за-
данной, а допустить возможность се изменений (не затрагиваю-
щих существенным образом рабочих элементов), то выбор этой
системы можно подчинить требованиям «оптимального» в опре-
деленном смысле решения как первой задачи, так и задачи син-
теза вынужденных колебаний в целом*).
Допустим, например, что упругую систему удается видо-
изменить таким образом, чтобы одна из форм ее свободных ко-
лебаний, отвечающая собственной частоте А = и, с определенной
точностью воспроизводила требуемое поле колебаний (как и
ранее, предполагается для упрощения рассуждений, что указан-
ное поле колебаний близко к монохроматичному, то есть со-
держит в основном лишь одну гармонику некоторой частоты и).
Тогда, как известно, при возбуждении колебаний с частотой
со ~ А форма вынужденных колебаний будет близка к соответ-
ствующей форме собственных колебаний и будет слабо зави-
сеть от распределения возмущающих сил и вообще от характера
возмущения. Естественно, что при этом можно вызвать нужные
колебания системы весьма небольшим числом и даже, быть мо-
жет, всего лишь одним возбудителем. Естественно, что в по-
следнем случае задача о взаимодействии вибраторов через
колебательную систему вообще отпадает (или крайне упро-
щается) .
По существу, мы изложили здесь в обобщенной форме идею
резонансных вибрационных машин, получившую воплощение в
ряде конструкций. Из сказанного вытекает важность решения
задачи о синтезе форм собственных колебаний упругих систем,
то есть о таком выборе упругой системы, чтобы некоторая ее
собственная форма V\(x, у, z), отвечающая заданной частоте А,
с определенной точностью аппроксимировала некоторую задан-
ную функцию U (х, у, z), удовлетворяющую тем же граничным
условиям, что и VK(x, у, 2).
Пусть, например, необходимо сообщить свободной (мягко
амортизированной) балке колебания некоторой частоты и, близ-
кие к прямолинейным поступательным колебаниям как абсолют-
но твердого тела (рис. 53, а). В продольном направлении будем
считать балку абсолютно жесткой. Если первая частота собствен-
*) Сказанное относится не только к системам с механическими возбуди-
телями.
§ 2] ВИБРАЦИОННЫЕ МАШИНЫ С МЕХАНИЧЕСКИМИ ВИБРАТОРАМИ 577
пых упругих колебаний *) балки Аз в достаточной мере превы-
шает частоту со, то балку можно рассматривать как абсолютно
жесткую, и задача становится тривиальной: для возбуждения
требуемых колебаний достаточен, например, один вибратор на-
правленного действия, возмущающая сила которого проходит
через центр тяжести балки Oi (рис. 53,6).
Дело значительно осложняется, если частота возбуждения ©
превышает частоту Аз, и поэтому балка должна рассматриваться
Рис. 53.
как упругая. В этом случае решение, отвечающее рис. 53,6, не-
пригодно: как нетрудно убедиться, вибратор будет возбуждать
интенсивные упругие колебания балки (рис. 53, а). Если задачу
требуется решить, не изменяя существенным образом упругой си-
стемы, то такое решение может состоять в том (рис. 53,г), чтобы
вместо одного относительно мощного возбудителя применить не-
которое число k менее мощных одинаковых возбудителей, распо-
ложенных на одинаковых расстояниях I = L/k один от другого
(L— длина балки). Как показывает исследование [50], если
— </
£ ‘max
4 <
= з-|/
рш2
(2.7)
*) Эта частота фактически является третьей собственной частотой, ибо
первые две частоты Ai = Аг = 0 отвечают поступательным и поворотным сво-
бодным колебаниям балки как твердого тела.
578
О СИНТЕЗЕ ВИБРАЦИОННЫХ МАШИН
[ГЛ. XV
(ЕЯ— жесткость на изгиб, а р — погонная масса балки), то
можно возбудить колебания балки, достаточно близкие к ее по-
ступательным колебаниям как абсолютно твердого тела.
Если, однако, считать допустимым видоизменение рассматри-
ваемой упругой системы, то напрашивается и иное решение, при
котором часто можно ограничиться лишь одним возбудителем
колебаний [379, 150]. Указанное решение, иногда являющееся бо-
лее предпочтительным, состоит в том (рис. 53, д), чтобы снабдить
балку некоторым числом k масс тг, связанных с нею пружинами
жесткости Ci и расположенных на расстояниях I, удовлетворяю-
щих условию (2.7). При этом, если жесткости с, выбрать соглас-
но соотношению
.. _ -1 С1	т___kniipL	д,
СО ~ I/	«	ИТ. —	. » «	(Z«o)
V	’	* т \ + pL	' J
то одна из частот собственных колебаний получившейся системы
будет близка к а>, а соответствующая собственная форма будет
характеризоваться колебаниями балки, близкими к ее посту-
пательным колебаниям как твердого тела. Естественно, что при
этом для возбуждения указанных колебаний в принципе*) мо-
жно будет ограничиться всего одним возбудителем.
Естественно, что описанный способ решения задачи синтеза
закона колебаний может быть применен и в случае упругих тел
более сложного вида, чем балка.
В качестве другого примера рассмотрим задачу о возбужде-
нии колебаний балки по закону
и (х, i) = V (х) sin (<nt + е),	(2.9)
где 8 — постоянная, а V(x)— заданная функция, удовлетворяю-
щая краевым условиям. Очевидно, что если можно подобрать
поперечную жесткость балки ЕУ(х), погонную плотность р(х)
или их сочетание таким образом, чтобы удовлетворялось урав-
нение
-^[EJ(x)^] = p(x)^V,	(2.10)
то функция У(х) совпадет с собственной формой колебаний
балки, отвечающей частоте возбуждения (». Вынужденные коле-
бания такой балки по закону (2.9) могут быть возбуждены наи-
более простым путем.
*) Если отвлечься от соображений стабильности рабочего режима колеба-
ний (см. ниже). Отметим также, что в цитированных работах говорится
лишь о возможности уменьшения числа возбудителей по сравнению с числом
добавочных масс на пружинах, а не об уменьшении числа возбудителен до
единицы.
§ 3]	ИЗМЕНЕНИЕ КОЛЕБАТЕЛЬНОЙ ЧАСТИ СИСТЕМЫ	579
Заметим в заключение, что способы синтеза законов колеба-
ний упругих систем, возбуждаемых от электромагнитных возбу-
дителей, предложенные в работе [85], при определенных условиях
могут быть применены и к случаю возбуждения от механических
вибраторов. Подчеркнем также, что если это представляется
возможным, то имеет смысл не расчленять решение задачи син-
теза заданного закона колебаний на две отдельные задачи,
а рассматривать задачу в целом. Такой, правда, более сложный
путь, как явствует из разобранных простых примеров, может
привести к получению лучшего решения.
Отметим, наконец, что выше мы не касались практически
важного вопроса о «стабильности» синтезированного закона ко-
лебаний и(х, у, z, t), то есть о его «устойчивости» по отношению
к отклонениям параметров системы. Этот вопрос будет рассмо-
трен в главе XVI настоящей книги.
§ 3. Обеспечение устойчивости требуемого режима синхронного
вращения вибраторов путем изменения колебательной части
системы
Как следует из рассмотренных примеров (см., в частности,
п. 2 § 16 главы XIII, а также § 8 главы XIV), иногда можно до-
биться устойчивости требуемой фазировки самосинхронизирую-
щихся вибраторов путем простого изменения параметров коле-
бательной системы, с которой они связаны, а также путем изме-
нения расположения осей их вращения. Направления таких из-
менений вытекают из анализа соответствующих условий устой-
чивости, если, конечно, эти условия получены в аналитической
форме. Указанный простейший способ стабилизации требуемого
синхронного режима движения особых пояснений не требует.
Другой способ состоит в изменении числа степеней свободы
колебательной системы или, точнее, в изменении интервала ме-
жду собственными частотами системы, в котором лежит задан-
ная рабочая частота колебаний (». Такое изменение можно осу-
ществить посредством наложения или устранения связей, при-
соединения к исходной системе дополнительных колебательных
систем (например, типа грузов на пружине, маятников и т. п.).
О том, что характер устойчивой фазировки может изменять-
ся при изменении числа степеней свободы системы или при пере-
ходе от одного диапазона между собственными частотами к дру-
гому в той же самой системе*), свидетельствуют примеры, рас-
смотренные в пп. 6 и 7 § 8 главы XIV. Приведем здесь еще два
примера, иллюстрирующих описываемый способ и представляю-
щих к тому же определенный самостоятельный интерес.
*) То есть, по существу, также при изменении «эффективного» числа сте-
пеней свободы.
580
О СИНТЕЗЕ ВИБРАЦИОННЫХ МАШИН
[ГЛ. XV
Вначале рассмотрим следующую задачу. Пусть необходимо
обеспечить прямолинейные поступательные колебания мягко
амортизированного твердого тела по закону, близкому к гармо-
ническому с амплитудой А и частотой со. Один из мыслимых пу-
тей решения этой задачи представлен на рис. 54, а. Движение
тела ограничивается жесткими направляющими, допускающими
Рис. 54.
перемещение только в нужном направлении. На теле размещены
два одинаковых, не связанных друг с другом дебалансных ви-
братора, роторы которых вращаются с одинаковой угловой ско-
ростью со в противоположных направлениях. Отметим, что ис-
пользование двух дебалансных вибраторов в рассматриваемом
случае позволяет исключить передачу неуравновешенных усилий
на неподвижное основание в направлении, перпендикулярном
направлению движения тела; если уравновешенность несуще-
ственна, то можно ограничиться одним дебалапсом и проблемы
не возникает.
Нетрудно видеть, что желаемое движение тела осуществляет-
ся при условии, что роторы вибраторов вращаются по закону
Ф) = at,	ф2 = —-со/,	(3.1)
§ 3]
ИЗМЕНЕНИЕ КОЛЕБАТЕЛЬНОЙ ЧАСТИ СИСТЕМЫ
581
а статические моменты
из условия *)
дебалансных грузов вибраторов выбраны
те = у М[А,
(3.2)
где М[ — масса тела и вибраторов.
Как следует из изложенного в п. 4 § 16 главы XIII (см. фор-
мулу (16.43) указанной главы), в описанной системе для реше-
ния поставленной задачи нельзя воспользоваться явлением само-
синхронизации, ибо в послерезонансной области
f с,
°»Р* = У мг
(3.3)
устойчиво не синфазное, а противофазное вращение роторов ви-
браторов
ср, = <о/, ф2 = — (со/+ я),	(3.4)
при котором тело практически остается неподвижным, а на осно-
вание передается неуравновешенная сила с амплитудой F =
— 2тесо2. Устойчивые фазировки на рис. 54 показаны сплошны-
ми, а неустойчивые — пунктирными линиями.
В соответствии с рассматриваемым способом синтеза возмож-
ны два варианта решения данной задачи, показанные на рис. 54,6
и 54, в. В первом варианте (рис. 54,6) к основной массе АД до-
бавляется еще одна масса М2, связанная с массой АД посред-
ством пружины жесткости су Тогда получается частный случай
системы, рассмотренный в п.6§ 8 главы XIV (см. также рис. 45),
соответствующий значению Ci ~ 0. При этом, согласно соотноше-
ниям (8.64) — (8.66) указанной главы,
Pl ~ 0,	~ у -дрг, м = М1 + М;
и в случае выполнения условия
Pi < со < р2
(3.5)
(3.6)
устойчивым будет именно желаемое синфазное вращение роторов
вибраторов по закону (3.1). Вне диапазона (3.6), то есть либо
при «слишком малой», либо при «слишком большой» частоте со,
будет устойчиво противофазное вращение по закону (3.4).
Другой вариант решения задачи более прост: он состоит в
устранении направляющих (рис. 54, в). Действительно, как было
показано в п. 2 § 16 главы XIII, при этом устойчивым всегда
*) Напомним, что жесткость опорных пружин Ci считается пренебрежимо
малой.
582	° СИНТЕЗЕ ВИБРАЦИОННЫХ МАШИН	[ГЛ. XV
будет вращение вибраторов, обеспечивающее прямолинейные по-
ступательные колебания тела в направлении, перпендикулярном
плоскости осей роторов вибраторов*). Заметим, что полученный
результат представляется с определенной точки зрения парадок-
сальным: при наличии связи, допускающей колебания системы
только в нужном направлении, система фактически не колеблет-
ся в этом направлении, оставаясь неподвижной (в рассматри-
ваемом приближении); при устранении же связи система «сама
по себе» совершает нужные колебания.
Отметим, что если при первом варианте решения задачи для
обеспечения необходимой амплитуды колебаний А нужна неко-
торая корректировка значений статических моментов дебаланс-
ных грузов вибраторов, то при втором варианте такой корректи-
ровки не требуется.
В качестве другого примера рассмотрим случай, когда не-
обходимо обеспечить круговые поступательные колебания мягко
амортизированного твердого тела. Как было показано в п. 2 § 16
главы ХШ, а также в п. 1 § 8 главы XIV, указанной цели можно
добиться, например, путем использования двух одинаковых сим-
метрично расположенных самосинхронизирующихся дебаланс-
ных вибраторов, роторы которых вращаются в одинаковых на-
правлениях (см. рис. 34, а). При этом, однако, должно выпол-
няться соотношение
где М и / — масса и момент инерции тела с вибраторами, г —
расстояние от центра тяжести до осей вращения роторов вибра-
торов. При невыполнении условия (3.7) устойчивым является
противофазное вращение роторов, и тело совершает не круговые
поступательные, а поворотные колебания.
В ряде случаев удовлетворить неравенству (3.7) либо вообще
не удается, либо представляется затруднительным. Возникает
задача — обеспечить устойчивость синфазного вращения вибрато-
ров в условиях, когда соотношение (3.7) несправедливо.
Один из возможных путей решения задачи состоит в при-
соединении к исходному твердому телу М, посредством упругих
и демпфирующих элементов некоторой дополнительной симме-
трично расположенной массы М2 (рис. 55, а). Чтобы показать
это, выведем условия устойчивости синфазного вращения рото-
ров вибраторов в получившейся системе, по-прежнему предпо-
лагая вибраторы одинаковыми и обладающими одинаковыми и
положительными парциальными угловыми скоростями [92].
*) То обстоятельство, что в § 16 главы ХШ говорится об устойчивости
противофазного, а не синфазного вращения, связано с иным способом выбора
начала отчета углов rpj и ср2 (сравните рис. 34 и 54).
§ 3]
ИЗМЕНЕНИЕ КОЛЕБАТЕЛЬНОЙ ЧАСТИ СИСТЕМЫ
583
Составим вначале выражения для вибрационных моментов
и W2, воспользовавшись формулой (3.22) главы XIV. С этой
целью найдем гармонические коэффициенты влияния второго
рода, фигурирующие в этой формуле.
У, v
6)
Рис. 55.
Заметим прежде всего, что в рассматриваемом случае имеют
место равенства
zz(I0_	_ к'^^ _ 1^(21) _ к"
Лии Лии —Лии —Лии —Ао>
ЩИ) __ г(22) _ „(12) _ „(21) _ „	(З-8)
и ии иии — иии — ^ии — ^о,
обусловленные тем, что установившиеся колебания точек тела
Mi не зависят от точки приложения силы, действующей вдоль
оси OiU. Коэффициенты влияния (3.8) определятся в результате
решения системы уравнений
+ с (%! — х2) + р(х1 — х2) = cos со/,
М2х2 — с (%! — х2) — 0(х, — х2) = 0,	(3-9)
584
О СИНТЕЗЕ ВИБРАЦИОННЫХ МАШИН
[ГЛ. XV
где %1 и х2— смещения тел Afi и М2 вдоль оси Ох, с — жест-
кость упругих элементов, связывающих тела и М2, а [3 — со-
ответствующий коэффициент вязкого сопротивления.
стемы (3.9), согласно определению величин К и G
главы XIV), находим
%! = K0cos at + Gosin at,
где
„	1 Г р2 — а>2 М2 11	„ _ 2/ш М2
Ко- дГ L А	М\ Mt •
Д = (р2 - а2)2 + 4nW, р2 = с/М“, 2п = $/М',
М* = М1М2/(М1 + Л/2), М = М1 + Л42.
Коэффициенты Коо’, Kvv==Kvv, Gvv И Ga„)=Gaa)
ляются в результате решения системы
+ с (t/i - у2) + р (у 1 - у2) = cos at,
М2у2 -с (у г- у2) - ₽ (г/i - у2) = О,
/ф = г cos at,
где у\ и у2 — смещения тел Mi и М2 вдоль оси Оу;
поворота тела ЛЬ, отсчитываемый по ходу часовой
г — расстояние от центра тяжести тела до осей
роторов вибраторов; / —момент инерции тела Afi относительно
центральной оси. Интегрируя последнее уравнение (3.13) и
замечая, что первые два уравнения совпадают с уравнениями
(3.9), находим
У1 = хь Ф = — cos at.	(3.14)
Смещения осей вибраторов Oi и о2 вдоль оси Оу соответственно
будут
Т11 = У1 + пр, П2 = У1 - пр,
и поэтому согласно (3.10) и (3.14)
i]i = (Ко — cos at + Gosin at,
Из .си-
(см. § 3
(3.10)
(3.11)
(3.12)
опреде-
ли 3)
Ф — угол
стрелки;
вращения
Таким образом,
г2 jc^2^____________________________________М-2^ — К -I- г
J\vv — Ao	> J\vv ~ Дао -«хо Т /и2 >
(Ш11) _ (7(|2' — /7<21' — С,
\J рр   и рр — \J РР
§ 3J	ИЗМЕНЕНИЕ КОЛЕБАТЕЛЬНОЙ ЧАСТИ СИСТЕМЫ	585
Нетрудно убедиться, далее, что и
G®2) = G^0 = Go,	(3.16)
а также что
= G^ =	= 0	(s, /=1, 2),	(3.17)
ибо колебания системы вдоль осей Ох и Оу независимы.
При учете равенств (3.11) и (3.15) — (3.17) по формулам
(3.22) главы XIV находим
W, = W, (а, со) =	[к0 (1 + а.аг) +	-<] sin а +
+ 2G0+ G0(l +<Т[а2) cos а к
2 2 4 f Г	2 1	(ЗЛ8)
Г2= «72(а, co) =----2—I - |tf0(l + ^2) + ^2 7^] sin а+
+ 2 Go + Go (1 + а^г) cos a j,
а = cq — a2.
Основные уравнения (см. равенства (2.28) главы XIV) в рас-
сматриваемом случае имеют вид
Р] (а, и) = ~ [c^L^ (04со) — Р (со) — U7t (а, со)] — О,
й	(3.19)
Р2 (а, со) ees j [<т2Р(а) (а2со) - Р° (со) - W2 (а, со)] = 0.
Складывая эти уравнения, получим соотношение для опре-
деления угловой скорости со, а вычитая — следующее уравнение
для нахождения разности фаз вращения вибраторов a = ai — аг
в возможных синхронных движениях (напомним, что вибраторы
имеют одинаковые и положительные парциальные угловые ско-
рости и поэтому cT[L<a) (cTtCo) = a3Lw (cr2co)):
= — j ш2е2со4 [p0 (1 + cT|Cr2) + cT|Cr2 sin a = 0.	(3.20)
Отсюда видно, что, как и в случае отсутствия массы М2, воз-
можно синфазное (а = 0) и противофазное (а = я) синхронное
вращение роторов вибраторов. Согласно уравнению (2.33)
главы XIV условием устойчивости синхронного движения яв-
ляется неравенство
_ с> (Р, — Р2) = д(Р,-Р2) =
Х дсп	да
= — ~ т2е2а* £Ро(1 + ^1^2) + 9i<t2 cos a < 0. (3.21)
586
О СИНТЕЗЕ ВИБРАЦИОННЫХ МАШИН
[ГЛ. XV
Из этого неравенства следует, что при вращении роторов
вибраторов в противоположных направлениях (ctict2 = — 1), как
и при М2 — 0, устойчивым является только противофазное дви-
жение (а = ai — а2 = л). В интересующем же нас здесь случае
роторов, вращающихся в одинаковом направлении (счстг = 1),
условием устойчивости синфазного вращения (а = 0) будет со-
отношение
2K0AW,
(3.22)
которое при учете обозначений (3.11) и (3.12) может быть пред-
ставлено в форме
Mr2 . „	2 (Л2-1) м2	. . ,о
> 2 - Л2 Л2,4я2 ТГ = Р!&’ "1 =	<3-23)
I	\Л — 1^ +	Л11
Отметим, что, как это и должно быть, при Х->оо, то есть
при жестком присоединении массы М2, неравенство (3.23) пере-
ходит в неравенство (3.7); при X —* 0, п —► 0, а также при Л42-»0
получается неравенство вида (3.7), в котором, однако, вместо
М =	+ М2 фигурирует Mt.
Величина
2(Л2—1) М2
(л2-1)2 + 4«1 М,
(3.24)
в соотношении (3.23) характеризует эффект, полученный в ре-
зультате упруго-вязкого присоединения к системе массы М2 по
сравнению с жестким присоединением указанной массы. Оче-
видно, что этот эффект является положительным лишь в дорезо-
нансной области, то есть при X = р/а > 1; он тем больше, чем
больше отношение масс М2/М[. В послерезонансной области
(Х = р/со-<1) коэффициент f всегда отрицателен, и наличие
упруго-вязкой связи между массами и А42 лишь ужесточает
условие устойчивости синфазного вращения роторов вибраторов.
Графики функции Л = f (X2, п2) представлены на
рис. 56, откуда видно, что наибольший положительный эффект
достигается в области, примерно соответствующей 1 <Х< 1,5.
Так, например, при nt = 0,1, X = 1,1 и М2/М{ = 0,4 имеем
f = fi = 5 • 0,4 = 2,0, и условие (3.22) выполняется при лю-
бых значениях массы М и момента инерции /. Отметим, что
функция fi имеет минимум, равный—при Х=|/1 — 2П[ и
максимум, равный при X =• |/1 + 2nj,
§ 3]
ИЗМЕНЕНИЕ КОЛЕБАТЕЛЬНОЙ ЧАСТИ СИСТЕМЫ
587
Разумеется, рассмотренный вариант способа стабилизации
синфазного вращения двух вибраторов путем изменений коле-
бательной части системы является далеко не единственным. Той
же цели можно достигнуть, например, путем присоединения
к исходному твердому телу колебательных систем более слож-
ного характера, виброударных элементов и т. п. Отметим в связи
со сказанным, что результативное соотношение (3.22), как легко
убедиться, сохраняет свою силу и в гораздо более общем слу-
чае, когда к основному телу Al, присоединена произвольная ли-
нейная колебательная система (с конечным или бесконечным
числом степеней свободы), «одинаково устроенная» вдоль осей
O[U и OiV и такая, что колебания системы вдоль этих осей не
связаны между собой и с поворотными колебаниями тела Mi.
Следует лишь под коэффициентом Ко понимать соответствую-
щим образом подсчитанный коэффициент влияния.
Так, например, в случае, когда к основному телу при-
соединены два одинаковых прямых призматических стержня
588
О СИНТЕЗЕ ВИБРАЦИОННЫХ МАШИН
[ГЛ. XV
с распределенной массой, несущих на концах сосредоточенные
массы Л12 (рис. 55, б), нетрудно найти *) [92]
М !<d
Мр - tg р
(%? + %2) Р + (Д’ДУ - 1) tg Р •
(3.25)
Здесь обозначено:
. 2 _ EF 1 _ с 1
(5=1, 2),
EF
а>1
а
(3.26)
причем Е, р, F и I есть соответственно модуль упругости и
объемная плотность материала, площадь поперечного сечения и
длина стержней, а — скорость распространения звука, с — про-
дольная жесткость стержней. Формула (3.25) получена путем
решения задачи об установившихся вынужденных продольных
колебаниях свободного стержня с массами ЛД и М2 на концах
под действием силы cosco/, приложенной к массе Afb
Для системы, отличающейся от изображенной на рис. 55, а
наличием запаздывания на время to в упругих и демпфирующих
элементах**), аналогичным образом можно найти [92]
А1а>2
' М2________V — 1 — V (1 — cos т) + 2»! sin т
М1 (Л2 — 1)2 + 4/г2 + 2Z2 (1 — cos т) — 4п{ sin т
- 1
(3.27)
Здесь т = со/о и использованы обозначения (3.12) и (3.23), при
учете которых видно, что в случае отсутствия запаздывания
(т = 0) выражение (3.27), как это и должно быть, совпадает
с выражением (3.11).
Рассмотренные системы представляют определенный интерес
в связи с теорией вибрационных мельниц, грохотов и конвейеров
(см. главы XX и XXI книги).
Метод синтеза вибрационных устройств, изложенный в на-
стоящем параграфе, был применен В. Э. Романовским,
Б. П. Лавровым, Р. Ф. Нагаевым, Н. Г. Тимофеевым и автором
в ряде изобретений, о которых будет сказано в пятой части
книги (см. также таблицу 5). В частности, Б. П. Лаврову,
Р. Ф. Нагаеву и Н. Г. Тимофееву принадлежит решение задачи
синтеза систем с четырьмя и большим числом вибраторов
(см. п. 2 § 1 главы XX и пп. 20 и 22 таблицы 5 Добавления 2).
*) Предполагается, что оси стержней параллельны осям О,и и О]О.
**) Имеется в виду система, описываемая уравнениями, которые
отличаются от уравнений (3.9) и (3.13) тем, что в них вместо членов
с[Х1(0-х2(0].....₽	[//, (о -1/2 (01 фигурируют члены c[xi(<~<o)-
- Х2 (/ - t0)], • • •, ₽ [(/1 (/ - t0) -y2(t- /о)]-
§ 4]
ИЗМЕНЕНИЕ ЧИСЛА ВИБРАТОРОВ
589
§ 4. Обеспечение устойчивости требуемого режима
синхронного вращения вибраторов путем изменения числа
вибраторов
В качестве простого примера использования способа стаби-
лизации требуемого режима синхронного вращения вибраторов
путем введения дополнительного вибратора рассмотрим ту же
задачу, что в конце предыдущего параграфа, — задачу обеспе-
чения устойчивости синфазного вращения двух одинаковых сим-
метрично расположенных дебалансных вибраторов в одинаковых
направлениях при условии, что неравенство (3.7) не выпол-
няется. Покажем, что желаемой цели можно добиться путем
присоединения к системе до-
полнительного вибратора с
ротором, вращающимся в том
же направлении, обладающим
той же парциальной угловой
скоростью, что и два основ-
ных вибратора, но имеющим,
вообще говоря, иной статиче-
ский момент дебалансныхгру-
зов тзбз (рис. 57).
Для получения необходи-
мых соотношений, относящих-
y,v
Рис. 57.
ся к рассматриваемой системе, можно воспользоваться резуль-
татами § 3 главы XXI. В указанной главе изучен случай,когда
центральный вибратор является планетарным; интересующий
нас здесь более простой случай дебалансного вибратора от-
вечает значению коэффициента f' = tg р' = 0. Следует учесть
к тому же следующее соответствие обозначений (сравните ри-
сунки 57 и 114):
тьеь = тле3, mded = me,, та = Mi + 2md,
kb=^k3, М — М, + 2md + т3.
(4.1)
Тогда уравнение (3.9) главы XXI для определения разности фаз
вращения а = ои — аз = «2 — а3 роторов основных (крайних)
вибраторов и ротора дополнительного (центрального) вибратора
примет вид
sina = 0.	(4.2)
Это уравнение допускает два существенно различных решения:
(а)! = 0,	(а)2 = п.	(4.3)
Из второго неравенства (3.14) главы XXI следует, что устойчи-
вое синхронное движение может отвечать только решению a =
= (a)2 = л. Но тогда первое из указанных неравенств при учете
590
О СИНТЕЗЕ ВИБРАЦИОННЫХ МАШИН
[ГЛ. XV
обозначений (3.8) главы XXI и соотношений (4.1) приводит
к следующему простому условию устойчивости интересующего
нас движения:
То же условие, естественно, получается как частный случай из
неравенств (3.15) и (3.16) главы XXI.
Итак, при выполнении соотношения (4.4) роторы основных
вибраторов вращаются синфазно, а дополнительный — в проти-
вофазе по отношению к ним; при этом тело М\ совершает кру-
говые поступательные колебания с амплитудой
Л= t (4>5)
несколько меньшей, чем амплитуда колебаний А* = 2те/М при
отсутствии дополнительного вибратора. Иными словами, «смяг-
чение» условия (3.7) при введении дополнительного вибратора
достигается ценой некоторого уменьшения амплитуды колеба-
ний тела Mj.
Отметим, что смягчение условия (3.7) получается и при вве-
дении дополнительного планетарного вибратора; соответствую-
щее этому случаю условие устойчивости дается упоминавшимися
выше формулами (3.15) и (3.16) главы XXI и иллюстрируется
рис. 115.
Идея использования дополнительного вибратора для обеспе-
чения устойчивости определенного синхронного движения дру-
гих вибраторов была высказана А. К. Рундквистом и автором
в 1961 г. Позднее она была реализована Б. П. Лавровым,
Г. А. Денисовым и Р. Ф. Нагаевым в их изобретениях [168, 169,
171]. На рассмотрении соответствующих значительно более
сложных, чем изученная выше, систем здесь мы не останавли-
ваемся.
Заметим далее, что устойчивость синфазного вращения ро-
торов вибраторов при <й>]/с/М достигается путем введения
дополнительного вибратора и в системе с одной степенью сво-
боды, представленной на рис. 54, а; здесь также, однако, при
этом несколько снижается амплитуда колебаний тела.
§ 5. Оптимальная система связей между роторами вибраторов,
обеспечивающая устойчивость заданного режима вращения
Рассмотренные выше способы обеспечения устойчивости тре-
буемой фазировки вращения роторов вибраторов открывают
возможности значительного расширения области использования
эффекта самосинхронизации в вибрационных устройствах. Вме-
§ 5]
ОПТИМАЛЬНАЯ СИСТЕМА СВЯЗЕЙ МЕЖДУ РОТОРАМИ
591
сте с тем в ряде случаев соответствующие принципиальные и
конструктивные решения могут оказаться нецелесообразными
или даже невозможными. В таких случаях можно прибегнуть
к тому или иному способу принудительной синхронизации и
фазировки. О решении задачи синтеза устройств с применением
средств принудительной синхронизации уже говорилось в § 2
настоящей главы. Там же было отмечено, что всегда желательно
ограничиться установлением минимально возможного числа свя-
зей между валами вибраторов, а «жесткости» этих связей вы-
брать минимально допустимыми.
Аналитическое решение такой задачи — задачи синтеза уст-
ройств с оптимальной (в указанном смысле) системой прину-
дительной синхронизации — в общем случае достаточно сложно;
можно указать лишь алгоритмы, рассчитанные на применение
вычислительных машин. Исключение составляют относительно
простые случаи, в частности, рассмотренные в пп. 5 и 6 § 16
главы ХШ, в п. 1 § 8 главы XIV, а также в § 3 главы XX.
Не останавливаясь на обсуждении сформулированной общей
задачи, изложим некоторые результаты, относящиеся к случаю,
когда связи между валами вибраторов являются абсолютно
жесткими. Эти результаты принадлежат Р. Ф. Нагаеву; они из-
ложены в докладе [86].
Будем предполагать, что вибраторы приводятся от двигате-
лей асинхронного типа и что выполняются условия, обеспечи-
вающие справедливость интегрального критерия устойчивости
синхронных движений (см. § 4 главы XIV и § 8 главы V); тогда
задача о выяснении характера возможных синхронных движе-
ний вибраторов при их самосинхронизации окажется вполне
аналогичной соответствующей задаче о положениях равновесия
консервативной системы со склерономными связями. А именно
возможные значения фаз вращения вибраторов в синхронных
движениях будут определяться (с точностью до постоянной) из
уравнений
ЗН «-1..............ад
где D = D(ai, ..., а/() — потенциальная функция, о правилах
составления которой в различных случаях говорилось в § 4
главы XIV. Определенному решению «, =«[......ak=za*k УРав‘
нений (5.1) действительно отвечает единственное асимптотиче-
ски устойчивое синхронное движение, если алгебраическое урав-
нение
=	J	(5.2)
7 аСа1
Б92
О СИНТЕЗЕ ВИБРАЦИОННЫХ МАШИН
[ГЛ. XV
имеет k — 1 положительный корень*). Один из корней уравне-
ния (обозначим его через %к) непременно равен нулю вслед-
ствие автономности исходных уравнений; все прочие корни ве-
щественны; будем предполагать их различными, так что можно
положить
Xi >Хг > • • • > Xfe-b
Иными словами, для устойчивости движения однородная
квадратичная форма
k k
=	(*i = ai1.............k) (5-3)
5=1 /=1
должна быть неотрицательной в окрестности точки Лц = .. . =
= xh = 0. На прямой Х\ = . . . = xh = а, где а — произвольная
вещественная постоянная, форма D2 тождественно равна нулю.
Как известно [138], в результате неособенной линейной под-
становки
k
xt = 5 aipyp,	(5.4)
р-1
где atp — нетривиальные решения линейных однородных систем
k
2 lsi@sp %p@ip (р 1 > • • • > ^)>	(5.5)
5=1
удовлетворяющие условиям
Л	(0, p¥=q,
^dipd!q — ^p4--yy^ p~q,	(5’6)
квадратичная форма (5.3) может быть представлена в виде
k
= Т S У*рУр'	(5-7)
р=1
Посредством некоторого иного линейного преобразования
форму (5.3) можно записать также в виде
^“i('12f + 772'!+ +тйггф <5-8)
где /ц ..., Ik — последовательные диагональные миноры мат-
рицы (Определитель этой матрицы Ik, в силу сказанного
*) Заметим, что величины которые часто называют коэффициен-
тами устойчивости А. Пуанкаре, отличаются знаком от использовавшихся ра-
нее величин и, (см., например, формулу (8.5) главы V и формулу (2.30)
главы XIV).
§ 5!	ОПТИМАЛЬНАЯ СИСТЕМА СВЯЗЕН МЕЖДУ РОТОРАМИ	593
выше, всегда равен нулю.) Из последнего равенства и вытекает
форма записи условий устойчивости движения
li>Q, /2>0, ..., lk^>Q,	(5.9)
о которой уже говорилось в § 8 главы V (так называемые ус-
ловия Сильвестра).
Предположим теперь, что некоторой комбинации фаз =
= а‘, ак — а’, удовлетворяющей уравнениям (5.1), отвечает
п отрицательных коэффициентов устойчивости
Xfc_„<0, ..Xfe-i <0	(5.10)
при прочих положительных коэффициентах. Иными словами,
синхронный режим, соответствующий фазировке вибраторов
а’, ..., а*, неустойчив, причем «степень неустойчивости» равна п.
Попытаемся сделать этот режим устойчивым путем наложе-
ния на вращения валов вибраторов п жестких кинематических
связей вида
/Ч(Ф1....фД = 0 (v = l, ...,п).	(5.11)
Предполагается, что
и поэтому задание углов поворота валов вибраторов с номерами
п + 1, ... , k полностью определяет углы поворота прочих ви-
браторов. Иными словами, число степеней свободы системы
уменьшается на п единиц. Естественно предположить, далее, что
связи (5.11) не препятствуют равномерным синхронным движе-
ниям вибраторов с фазами Ир ..., а*, то есть что выполняются
соотношения (рассматривается случай простой синхронизации)
+ aj), ..., ei(af-|-at)]sFv(ola;) ...,	(5ЛЗ)
(v --= 1, ..., /г).
Дифференцируя эти тождества по at, получаем
k
<5.14)
i=l ‘
При наличии связей (5.11) уравнения движения вибраторов
могут быть записаны в форме
п
/зф3 + ks (ф, - щи) = р,Ф5 + У}	(s= 1, ..., k). (5.15)
V=1
594
О СИНТЕЗЕ ВИБРАЦИОННЫХ МАШИН
[ГЛ. XV
Эти уравнения отличаются от уравнений движения несвязанных
вибраторов (см. равенство (1.4) главы IX и замечания в на-
чале § 2 главы XIV) наличием дополнительного слагаемого
в виде суммы, представляющей моменты, действующие на ро-
торы со стороны связей. Величины $v при этом представляют
собой неопределенные множители Лагранжа (множители свя-
зей). Функции цФ., в уравнениях (5.15) имеют тот же смысл,
что и в § 1 главы IX. Уравнения движения колебательной си-
стемы при наличии связей (5.11) не изменяются.
Исключив из уравнений (5.15) множители связей, можно по-
низить общий порядок системы на п единиц. Однако в данном
случае удобнее рассматривать непосредственно систему (5.15)
с дополнительными неизвестными — множителями $v.
Будем разыскивать эти множители в виде рядов
1% = <) + pOv) + p2Ov)+.. . ,	(5.16)
где
<’ = 0	(v= 1, .... /г),	(5.17)
поскольку, как указывалось, связи не препятствуют равномер-
ным синхронным вращениям вибраторов.
Порождающее решение для координат вибраторов в рас-
сматриваемой задаче, как и при отсутствии связей будет иметь
вид
<р° = os (a>t + as) (s=l, ..., k),	(5.18)
однако оно будет содержать лишь k — п произвольных фаз, ибо
эти фазы теперь связаны п конечными соотношениями
/^(сгщн ..., <зкак) = 0	(v= !,...,»).	(5.19)
Применение к системе (5.15) тех же теорем, которые были
использованы при изучении системы (1.4) в главе IX, и вполне
аналогичные последующие выкладки приводят к следующему
результату.
1) Фазы вращения вибраторов ai, .... ак при синхронном
движении и средние за период Т = 2л/ю значения коэффициен-
тов ,б'У) в разложениях (5.16) определяются из соотношений
(5.19) и из системы
-О (/ = 1, . . ., k),	(5.20)
где
2л/<а
№dt.	(5,21)
a

§ 5]
ОПТИМАЛЬНАЯ СИСТЕМА СВЯЗЕЙ МЕЖДУ РОТОРАМИ
595
2) Условием устойчивости синхронного движения является			
положительность всех (за исключением одного пулевого) кор-			
ней уравнения			
	Л1 — X •  •	fll • • • f In	
	^k\	• • • ^kk X	f kl • • • fkn	
				= 0,	(5.22)
	fn  • • hi	0	... 0	
	f In	• • • tkn	0 ... 0	
где			
	г _ dFv Isv ~ das	* *	(5.23)
		'V'/	
Как нетрудно видеть, система k + п уравнений (5.19), (5.20)
допускает решение
as = a* (s=l, ..., k),	$(!> = 0 (v = 1......n). (5.24)
Что же касается уравнения (5.22), то оно, очевидно, имеет
k — п корней; один из этих корней, в силу соотношений
п	k
= ^lsl = 0	(s= 1, ..., fe)> (5.25)
V-l	1-1
всегда равен нулю (первое из этих соотношений вытекает из
(5.14), а второе — из равенства (4.46) главы VIII при ttj = q> =
= 1, k' — k).
Таким образом, для устойчивости рассматриваемой системы
достаточно, чтобы потенциальная функция £>(ai, ..., а*) имела
условный минимум при наличии п ограничений (5.19).
Из сказанного следует также, что на устойчивость стабили-
зируемого режима существенное влияние оказывает лишь ли-
нейная форма разложения функций Fv вблизи точки а, = ар . ..
k
Fv(°iai’ • • • > аЛ) = 2 fsvxs + ... (xs = as - a;). (5.26)
s«= 1
Можно теперь указать частный вид коэффициентов fSv, обес-
печивающих устойчивость требуемого синхронного движения.
С этой целью просуммируем равенства (5.5) по индексу j от
1 до k. Тогда в силу соотношений (5.25) получим
k
Кр1^а1р = 0	(р=1, .... k),
/“1
596
О СИНТЕЗЕ ВИБРАЦИОННЫХ МАШИН
[ГЛ, XV
и поэтому для всех р, кроме р = k (ибо %k = 0),
k
^alp = Q.	(5.27)
Если теперь принять
fsv &s, k—ra+v—1	1 > • • • > ^)>	(5.28)
то, с одной стороны, будут выполнены условия (5.14), а с дру-
гой— все k — п—1 нулевых корней уравнения (5.22) будут
положительными, поскольку это уравнение может быть преоб-
разовано к виду
Х1~Х 0	0 Х&—гг—1 X	0	0	0		
		Х*-„-Х	0		1	0	
	0	о	Xfe-1-X	0	0	1	= 0.
0		0	-х	0		
		1	0				
	0	0	' 1	0	0		
					(5.29)	
Итак, оптимальная в указанном выше смысле стабилизация
требуемого синфазного режима движения вибраторов дости-
гается наложением связей между роторами вида
k
2 as,fe_„+v_1(<Ps-aA)+ ••• =°	(v=	п). (5.30)
S-I
Подчеркнем, что число этих связей п равно степени неустойчи-
вости изучаемого режима при отсутствии связей.
Заметим, что в наиболее общем случае вопрос о знаках кор-
ней уравнения (5.22) рассмотрен применительно к задаче о ста-
билизации положения равновесия консервативных систем в ра-
боте М. Ш. Косса [227]. По терминологии, принятой в этой ра-
боте, используемые здесь связи являются «дефектными» — их
положение не влияет на наличие нулевого корня уравнения
§ 5]
ОПТИМАЛЬНАЯ СИСТЕМА СВЯЗЕЙ МЕЖДУ РОТОРАМИ
597
(5.2). Введение недефектных связей означало бы передачу на
роторы вибраторов внешнего синхронного воздействия.
Общие условия устойчивости синхронного режима, обеспе-
чиваемой посредством связей типа (5.11), могут быть получены
вполне аналогично тому, как это сделано в работе [227] для
случая недефектных связей. Они состоят в выполнении соотно-
шений
k	k	k
sign 2 li = - sign 2 W = sign 2	•
i-1	i = l	i=l
k
... = ( —l)resign 2 № =(-!)"	(5.31)
i^l
Здесь /7* (v=l, .... n) — минор элемента 1ц определителя
/п ... /ц fn ... fiv
• //г/г fk\  •  f kv
fn fkx 0 ... 0
(5.32)
fiv fkv 0 ... 0
Условиям (5.31) и должны удовлетворять коэффициенты при
линейных членах в уравнениях связей (5.11), чтобы достига-
лась устойчивость нужного синхронного режима.
Отметим, что определенная система связей, для которой
условия (5.31) выполняются, может оказаться трудноосуществи-
мой практически; тогда можно попытаться выбрать новую си-
стему связей
п
=	= 0	(v=l, .... п),	(5.33)
Ц“1
— постоянные), эквивалентную старой, но более удачную
в определенном смысле.
Интересен и вопрос о возможности обеспечения устойчиво-
сти режима связями простейшего типа
Фа-V “ Фа = °k-vak-v - ° Л = 0 (v = 1......П).	(5.34)
Такие связи кинематически объединяют группу вибраторов с но-
мерами k — п, k — п + 1, ..., k. Для устойчивости рассматри-
ваемого режима при наложении указанных связей, согласно
сказанному выше, функция
Di(ffiai> ..., ok_n++	•••
• • • >	~ <Wk> °kak) (5-35)
593
О СИНТЕЗЕ ВИБРАЦИОННЫХ МАШИН
[ГЛ. XV
должна иметь минимум по переменным ац .... а/(-я+1, а* в точ-
ке aj, а^_п+р а*. Соответствующее условие минимума сво-
дится к требованию положительности всех (кроме одного) кор-
ней уравнения
п
^11 X • • •	l\,k—п— 1	S ^1, k —V
V= О
^k— п — 1, 1	• • • ^k—n — 1. к~П~1	X	Ik—n—X*k—v
V- 0
n	n	n	n
S Ik — V. 1	•  	S Ik — v, k — n— 1	2	S	Ik—Ц. k — V	X
v-U	v=0	H=o	V=
или, что то же самое, к требованию выполнения k — п — 1 не-
равенств Сильвестра 1\ > 0, . . .,	> 0.
Таким образом, обеспечение устойчивости путем наложения
связей простейшего типа (равенства (5.34)) осуществимо, если
удается указать такой порядок пересчета вибраторов, при ко-
тором первые k — п—1 слагаемых выражения (5.8) положи-
тельны. Остальные п «неустойчивых» слагаемых вследствие за-
кона инерции квадратичных форм должны быть отрицательны.
В указанном случае п + 1 вибраторов с номерами k — п, п
выделяются в локально неустойчивую группу. Естественно, что
в общем случае таких групп может быть несколько.
Отметим, что процесс выделения неустойчивых групп вибра-
торов может быть эффективно осуществлен с помощью вычис-
лительных машин.
ГЛАВА XVI
О СТАБИЛЬНОСТИ РЕЖИМА КОЛЕБАНИЙ
РАБОЧИХ ОРГАНОВ ВИБРАЦИОННЫХ МАШИН
С МЕХАНИЧЕСКИМИ ВИБРАТОРАМИ
§ 1. Понятие стабильности режима колебаний
вибрационной машины
Для практической реализации вибрационной машины еще
недостаточно решить задачу синтеза закона колебаний ее ра-
бочих органов. Необходимо также обеспечить, чтобы этот за-
кон существенным образом не искажался как вследствие всегда
возможных неточностей изготовления машины, так и вследствие
изменения нагрузки, характеристик подводимой энергии, «дрей-
фа» параметров системы, связанного с износом или приработ-
кой деталей или с другими причинами. Поэтому для вибрацион-
ных машин и устройств особое значение имеет свойство ста-
бильности режима колебаний рабочих органов, которое можно
определить следующим образом.
Пусть bi, b2, ...— параметры, определяемые полем коле-
баний рабочих органов машины u(x,y,z,t) и либо непосред-
ственно характеризующие технологические показатели работы
машины, либо существенно влияющие на эти показатели и
определяющие их. Параметры bt, b2, ..., которые ниже будем
называть контрольными параметрами, в общем случае являются
функционалами от и (х, у, z, t):
bt^bt{u(x, у, z, /)}.
Пусть, далее, а>, а2, ... — совокупность параметров машины
или обрабатываемой среды, от которых, с одной стороны, суще-
ственно зависят контрольные параметры bt, b2, ... и которые,
с другой стороны, могут либо варьировать в определенных пре-
делах вследствие неточности изготовления деталей машины и
ее сборки, либо по тем или ины.м причинам изменяться со вре-
менем в процессе эксплуатации машины.
В число параметров ai, а2, ... могут входить массы отдель-
ных частей машины, жесткости упругих элементов, параметры
600
О СТАБИЛЬНОСТИ РЕЖИМА КОЛЕБАНИЙ
[ГЛ. XVI
характеристик двигателей, частота и напряжение сети, масса
находящегося на машине материала и т. п.
Что же касается параметров Ь\, Ь2, ..., то за таковые, как
отмечалось, можно принять непосредственно технологические
показатели работы машины или отклонения этих показателей
от номинальных значений. Однако часто удобнее расчленить
задачу и понимать под контрольными параметрами Ь\, Ь2, ...
совокупность функционалов от закона колебаний, которыми
указанные технологические показатели определяются. В част-
ности, за bit b2, ... можно принять размахи (амплитуды) коле-
баний проекций на координатные оси определенных «контроль-
ных» точек рабочих органов машины, коэффициенты Фурье в
разложениях указанных проекций и т. п.
Как правило, изменение параметров а{, а2, ... можно счи-
тать достаточно медленным и предполагать, что за промежутки
времени порядка одного периода колебаний 2л/со эти параметры
практически не изменяются. Тогда функциональные связи
bi^b^ai, а2, ...)	(/=1,2,...)	(1.1)
определяются зависимостями, полученными для устойчивого,
установившегося режима колебаний рабочих органов машины.
Пусть, далее, по условиям эксплуатации машины ее работу
можно считать удовлетворительной, если конец вектора
b(bi, b2, ...) лежит в пределах некоторой области В простран-
ства контрольных параметров bi, b2, ..., и неудовлетворитель-
ной, если конец вектора b попадает за пределы этой области.
Тогда под стабильностью S режима колебаний рабочих ор-
ганов вибрационной машины будем понимать вероятность того,
что конец контрольного вектора b не выйдет за пределы задан-
ной области В в течение некоторого промежутка времени То.
Данное выше определение стабильности является некоторым
обобщением определения, предложенного в работе А. Д. Ру-
дина и автора [79]. Еще ранее соответствующее понятие было
использовано в статье автора [56], а затем в работе Б. П. Лав-
рова [242].
Необходимо отметить определенную связь введенного поня-
тия с понятием надежности, характеризующим способность си-
стемы к выполнению задания в некотором установленном объе-
ме. Методам исследования и повышения надежности различных
систем в последние годы уделяется все возрастающее внимание
(см., например, [27, 251]).
Заметим, что машина может считаться удовлетворительной,
если стабильность S не ниже некоторого допустимого уровня S*.
Подчеркнем также, что приведенное определение ставит оценку
стабильности машины в существенную зависимость от «чувстви-
тельности» технологического процесса к изменению поля коле-
§ и
ПОНЯТИЕ СТАБИЛЬНОСТИ РЕЖИМА КОЛЕБАНИЙ
601
баний рабочих органов. Так, например, определенная схема ма-
шины с конкретным выбором параметров может быть удовлетво-
рительной по стабильности при использовании этой схемы в
транспортирующей машине, но неудовлетворительной при ее
применении в устройстве для рассева сыпучих материалов.
Если известен закон распределения системы случайных вели-
чин «1, а2, •••> зависимости (1.1) и область В допустимых зна-
чений контрольных параметров Ь\, Ь2, то по известным фор-
мулам теории вероятностей можно вычислить и стабильность S.
Достаточно сложное в общем случае, такое вычисление часто
может быть упрощено вследствие допустимости линеаризации
зависимостей (1.1) вблизи номинальных значений параметров
«1, а2, ...; благодаря независимости этих параметров, как слу-
чайных величин; нормальности законов распределения и т. п.
Рассмотрим в качестве примера случай, когда число конт-
рольных параметров равно единице, причем известно, что рас-
пределение контрольного параметра b подчиняется нормально-
му закону с математическим ожиданием Ьт и дисперсией а2ь.
Пусть, далее, область допустимых значений параметра b оп-
ределяется неравенством
IЬ-bQ |	„
...ь~ <
(1.2)
где R.— максимально допустимое относительное отклонение па-
раметра b от его номинального значения Ьо. Тогда, согласно
определению стабильности, будем иметь
I & — &01
Ьо
b-ba
Ьо
— — ( ф Г ~ У>т ~ ^°) 1 I ф Г т 1^'» ~ ^д) 11 __ / boR_
21 L	J L аь J J I аь ’
Ьт ~ Ьр \
°ь Г
(1.3)
Здесь 1Е(...), как обычно, означает вероятность выполнения за-
ключенного в скобки неравенства, а
2
V 2л
Ф (х) =
х
J e~№dt
о
— интеграл вероятностей. График зависимости функции S от па-
раметров boR/оь и (Ьт — Ь0)/оь представлен на рис. 58.
Другой, более простой и требующий меньшей информации
подход к вопросу о стабильности возможен, если отказаться от
использования вероятностных соображений, по крайней мере
в явной форме. А именно можно считать, что режим колебаний
рабочих органов стабилен, если при изменении параметров
602
О СТАБИЛЬНОСТИ РЕЖИМА КОЛЕБАНИЙ
[ГЛ. XVI
а\, а2, ... в некоторой области А, содержащей точку ai0, «20, 
(эта точка отвечает номинальным значениям параметров), конец
контрольного вектора Ь(Ъ\, b2, ...) не покидает заданной обла-
сти В.
Область В при этом, как и ранее, определяется из условий
удовлетворительной работы машины, а область А—как область
возможных значений отклоняющихся параметров а1; а2, ...
Часто, например, можно
считать, что области А и
В суть параллелепипеды
(/=1, 2, ...),
(/=1, 2, ...),
где 6*. и 6" — соответст-
венно нижнее и верхнее
максимально возможные
отклонения параметра
от его номинального значения а,о, а е* и ej*—нижнее и верхнее
максимально допустимые отклонения контрольного параметра bi
от его номинального значения.
Для оценки стабильности режима колебаний рабочих органов
вибрационной машины могут быть использованы и величины
производных
,	(1.6)
\ да.)	’
as = aso
которые можно назвать коэффициентами чувствительности.
Иногда целесообразно пользоваться также величинами
|л&7ех _ |бУ-&УоС	с, 7\
~ I I “ Гы *	°
представляющими собой максимальные относительные измене-
ния контрольных параметров bj при изменении параметров
в пределах области А. Эти величины можно назвать чувствитель-
ностями параметров bj по отношению к изменениям параметров
ai, а2, ... Если линейное приближение является достаточно точ-
ным, то для вычисления величин R, достаточно знать коэффи-
циенты чувствительности (1.6) и интервалы (1.4) изменения
параметров ai. При вероятностном подходе можно принять
\^bl\^ = \blm-bl0\ + 3al>	(1.8)
§ 2) ВИБРАЦИОННЫЕ МАШИНЫ С НЕСКОЛЬКИМИ ВИБРАТОРАМИ 603
где bjm—математическое ожидание величины bj, a Oj — среднее
квадратичное отклонение этой величины, рассматриваемой как
функция случайных величин а\,	.
Понятно, что свойство чувствительности в определенном
смысле противоположно свойству стабильности.
Примеры использования сформулированных выше понятий
для исследования различных вибрационных машин содержатся
в работах [56, 68, 79, 83, 172, 242]. О примерах, относящихся
к машинам с самосинхронизирующимися вибраторами, будет
сказано в следующем параграфе.
Отметим в заключение, что для реального вычисления харак-
теристик стабильности и чувствительности часто целесообразно
использовать моделирующие или цифровые вычислительные
машины.
§ 2. О стабильности режима колебаний вибрационных машин
с несколькими механическими вибраторами
Существенная особенность вибрационных машин, приводи-
мых от нескольких самосинхронизирующихся или не абсолютно
жестко синхронизированных механических вибраторов, состоит
в том, что основную роль в числе параметров а\, а2, • • •, от кото-
рых зависит искажение режима колебаний, играют параметры,
характеризующие неодинаковость парциальных угловых скоро-
стей отдельных вибраторов.
Это обстоятельство легко уяснить на примерах систем с двумя
самосинхронизирующимися вибраторами, рассмотренных в п. 2
§ 16 главы ХШ, а также в § 8 главы XIV. Во всех этих примерах
парциальные угловые скорости вращения роторов вибраторов
предполагались одинаковыми, причем неизменно оказывался су-
ществующим и устойчивым режим движения, характеризую-
щийся либо синфазным (а = ai — а2 = 0), либо противофазным
(а = ai —аг = ±л) вращением роторов. Между тем парциаль-
ные угловые скорости вибраторов, даже если они номинально
одинаковы, в действительности всегда несколько отличаются
одна от другой вследствие неточностей изготовления и сборки
деталей двигателей и вибраторов.
Нетрудно проследить (и это будет действительно сделано в
§ 2 главы XX и в § 3 главы XXIII), что в таком случае устойчи-
вые стационарные значения сдвигов фаз а станут отличными отО
или от ±л, что в свою очередь приведет к искажению законов
колебаний вибрирующих тел.
Отсюда ясно, что для практической реализуемости машины
с самосинхронизирующимися (а также и с «нежестко» прину-
дительно синхронизированными) вибраторами еще недостаточ-
но, чтобы требуемый режим синхронного вращения вибраторов
604
О СТАБИЛЬНОСТИ РЕЖИМА КОЛЕБАНИЙ
[ГЛ. XVI
существовал и был устойчив при номинальных значениях пара-
метров вибраторов. Совершенно необходимо также, чтобы соот-
ветствующий режим колебаний тел, являющихся рабочими ор-
ганами машины, не слишком сильно искажался вследствие
всегда возможных отличий параметров вибраторов и системы
в целом от их номинальных значений. Иными словами, необхо-
димо, чтобы режим колебаний был стабилен по отношению
к указанным отклонениям. Разумеется, отклонения параметров,
влияющих на парциальные угловые скорости вращения вибра-
торов, являются не единственными факторами, которые могут
приводить к искажению закона колебаний рабочих органов
рассматриваемых машин. Эти отклонения, однако, в данном
случае являются основными: влиянием отклонений прочих па-
раметров часто оказывается возможным пренебречь.
Задача о стабильности колебаний вибрационных машин
с механическими вибраторами естественно расчленяется на две
части. Вначале с помощью основных уравнений теории синхро-
низации (см., например, уравнения (2.27) — (2.29) главы XIV)
определяются искажения начальных фаз вращения вибраторов
аь ..., аи (или законы распределения этих величин), обуслов-
ленные отклонениями входящих в указанные уравнения пара-
метров от номинальных значений. Затем с помощью соотноше-
ний типа приведенных в § 14 главы XIII находятся искажения
закона колебаний точек рабочего органа, обусловленные откло-
нениями начальных фаз си....ан, а также и других парамет-
ров системы.
Примеры исследования стабильности вибрационных машин
с самосинхронизирующимися вибраторами приводятся в § 2
главы XX и в § 3 главы XXIII настоящей книги.
ГЛАВА XVII
ВЗАИМОДЕЙСТВИЕ МЕХАНИЧЕСКОГО ВИБРАТОРА
С КОЛЕБАТЕЛЬНОЙ СИСТЕМОЙ
(СЛУЧАЙ ОДНОГО ВИБРАТОРА)
§ 1. О неприменимости концепции теории вынужденных
колебаний для объяснения некоторых явлений
в колебательных системах с механическими возбудителями.
Краткий обзор исследований
В § 2 главы XIII уже отмечалось, что обычная концепция
теории вынужденных колебаний, когда возмущающие силы
предполагаются заданными и не зависящими от движения коле-
бательной системы, является неприемлемой при изучении синхро-
низации механических вибраторов. Решение этой задачи воз-
можно лишь при учете взаимодействия колебательной системы
с источниками возбуждения. Здесь приходится рассматривать
совместно движение возбудителей и колебательной системы, в
результате чего порядок системы повышается на 2rk единиц,
где г — число степеней свободы возбудителя, a k-—число возбу-
дителей. Кроме того, получающаяся расширенная система ока-
зывается нелинейной.
Для изучения многих закономерностей, относящихся к взаи-
модействию возбудителей с колебательной системой, нет на-
добности рассматривать случай нескольких возбудителей, а до-
статочно остановиться на простейшем частном случае одного
вибратора (&=1); естественно, что в этом случае задачи
о синхронизации, как таковой, не возникает. Рассмотрению ука-
занного частного случая и посвящена настоящая глава книги.
К числу наиболее важных нелинейных явлений, наблюдае-
мых в системах с механическими возбудителями и необъясни-
мых в рамках обычной теории вынужденных колебаний, отно-
сится известный эффект стабилизации частоты колебаний вблизи
резонансной частоты Колебательной части системы и резкого
«срыва» колебаний с переходом на послерезонансный режим,
характеризующийся относительно высокой частотой. Этот эф-
фект, по-видимому, впервые был описан А. Зоммерфельдом еще
в 1902 г. [480] и поэтому часто связывается с его именем.
606
ВЗАПМОДЕЙСТ. ВИБРАТОРА С КОЛЕБАТЕЛЬНОЙ СИСТЕМОЙ [ГЛ. XVII
Другой примечательный факт, связанный с эффектом
Зоммерфельда, состоит в том, что ниспадающая ветвь класси-
ческой резонансной кривой линейной колебательной системы
оказывается практически нереализуемой.
Разумеется, перечисленные эффекты весьма существенны
для теории различных машин и устройств, и поэтому естествен-
но, что они привлекли внимание многих исследователей.
Экспериментальное изучение обсуждаемых явлений было
выполнено А. К. Калишуком [202] (1939 г.) и В. С. Мартышки-
ным [281] (1940 г.), которыми сделаны также первые попытки
теоретического исследования вопроса и установлен ряд инте-
ресных закономерностей. Однако полного объяснения наблю-
давшихся эффектов в цитированных работах получено не было,
ибо авторы фактически не рассматривали вопроса об устойчи-
вости движения.
В дальнейшем И. Рокар [473] (1949 г.) дал постановку за-
дачи об исследовании эффекта Зоммерфельда как задачи
о взаимодействии двигателя с колебательной системой. К сожа-
лению, вследствие допущенной ошибки в знаке одного из чле-
нов дифференциальных уравнений движения автор пришел
к неверному заключению об устойчивости движения системы.
Теоретическое исследование эффекта Зоммерфельда с ис-
пользованием методов А. Пуанкаре и А. М. Ляпунова было
выполнено в наших работах [44] (1953 г.) и [46] (1955 г.), а за-
тем, для иной системы, — в совместной статье с Г. Ю. Джане-
лидзе [48] (1955 г.).
Весьма удачная энергетическая интерпретация эффекта Зом-
мерфельда дана Г. И. Николаенко [324] (1954 г.). Укажем и на
появившуюся в 1955 г. монографию Р. Мазетта, в которой также
содержится исследование рассматриваемого вопроса [468].
Наиболее подробное и всестороннее изучение эффекта Зом-
мерфельда и ряда других нелинейных явлений, связанных со
взаимодействием колеблющейся системы с источником энергии
ограниченной мощности, было выполнено в цикле работ
В. О. Кононенко, его сотрудников и последователей: С. С. Ко-
раблева, К. В. Фролова, Л. Пуста, О. Вейводы, А. П. Субача,
В. К. Преснякова, 3. Е. Филера и других авторов. В указанных
исследованиях (1958 г. и позднее) рассмотрены системы, коле-
бательная часть которых нелинейна, и системы со многими
колебательными степенями свободы. Особое внимание уделено
изучению нестационарных процессов, в частности прохождению
через резонанс; последний вопрос подробно рассматривался
также Л. А. Растригиным [356] и Э. А. Аграновской [3].
Систематическое изложение результатов данного цикла ра-
бот и обзор исследований, выполненных до 1964 г., даны в мо-
нографии В. О. Кононенко [222].
§У	ОСНОВНЫЕ УРЛВНЁПИЯ В СЛУЧАЕ ОДНОГО ВЙБРАТОРЛ 607
В интересном исследовании В. М. Большакова, Е. С. Зель-
дина, Р. М. Минца и Н. А. Фуфаева [99] колебательная система
с одной степенью свободы, возбуждаемая одним механическим
вибратором, рассмотрена при помощи метода Ван-дер-Поля.
При этом изучение динамики системы удалось свести к рас-
смотрению поведения траекторий «а фазовой плоскости. Это
позволило, наряду с установившимися движениями системы,
исследовать также и режимы установления.
Особенности проявления эффекта Зоммерфельда в системе,
частота собственных колебаний которой изменяется по случай-
ному закону, рассмотрены в статье М. Ф. Диментберга и
К. В. Фролова [177].
Ряд вопросов, решение которых также потребовало учета в
той или иной мере взаимной связи вибратора и колебательной
системы, изучен в работах В. Д. Земскова [149], А. П. Бессонова
[42] и И. И. Быховского [ИЗ].
В статьях К. Ш. Ходжаева [404, 405] рассмотрена задача
о взаимодействии колебательной системы с вибратором электро-
магнитного типа и показано, что методы исследования и ряд
закономерностей поведения системы сохраняются и в этом слу-
чае. Общее рассмотрение проблемы взаимодействия возбуди-
телей с колебательной системой дано К. Ш. Ходжаевым в ра-
боте [409].
В настоящей главе результаты решения задачи о синхрони-
зации вибраторов используются для изучения взаимодействия
колебательной системы с одним механическим возбудителем.
При этом, наряду со случаем привода вибратора от двигателя
асинхронного типа (§§ 4 и 5), рассматривается случай привода
от синхронного двигателя (§ 3). Этот случай [68] имеет ряд
существенных особенностей; в частности, здесь, как правило,
оказывается нереализуемой не только ниспадающая часть, нои
вся «верхушка» пика резонансной кривой. Параграфы 4 и 5
представляют обобщение соответствующих результатов, полу-
ченных в наших работах [44, 46] для случая дебалансных виб-
раторов, на случай вибраторов планетарного типа [68].
§ 2. Основные уравнения в случае одного вибратора
Итак, рассмотрим систему, состоящую из механического виб-
ратора, связанного с подрессоренным твердым телом; для прос-
тоты предположим, что это тело может .смещаться только в од-
ном фиксированном направлении, то есть имеет всего лишь
одну степень свободы (см. рис. 2).
Такая система в случае произвольного числа вибраторов k
была рассмотрена в § 13 главы ХШ. В указанном параграфе
предполагалось, что движение происходит вблизи резонанса,
608
ВЗАИМОДЕЙСТ. ВИБРАТОРА С КОЛЕБАТЕЛЬНОЙ СИСТЕМОЙ [ГЛ. XVII
однако, как оказалось, полученный результат охватывает так-
же и случай движения вдали от резонанса.
В соответствии с формулами (13.9) и (13.12) главы XIII
установившиеся движения системы в исходном приближении
происходят по закону
Ф° = а(ю/ + а), х° = F cos®/ + Ф sin ®/,	(2.1)
причем, согласно равенствам (13.17), (13.18) и (13.20) той же
главы, величины F, Ф, а и м связаны соотношениями (на-
помним, что рассматривается случай k = 1)
£<m’ (а, аю) = R (®) + у /де®2 [F (sin а + hf' cos а) +
+ Ф (cos а — hf' sin а)],
рФ + 2nxF = sin а,
pF — 2пхФ = cos а.
Из последних двух уравнений находим
F =	(2пх sin а - р cos а),
А1(р +4пх)
Ф = ——тг (р sin а + 2пх cos а),
М(р2 + 4«2)
я = у/^ТФ2 - — —	 = —
м рр2 + 4л2
(2.3)
2
) + 4пх
что, естественно, вытекает также и из общих формул (13.21)
и (13.23) главы XIII.
Подставив выражения (2.3) в первое равенство (2.2), полу-
чаем уравнение для определения порождающей фазы а:
L(m} (а, а®) = Я* (®),	(2.4)
где
м I \ D° / \ । 1 «2е2®2 (2«.г - Л/'р)	in еч
Лн(®) = /? (®) + ------> \ /т. -	(2.5)
2 М (р + 4пх)
— величина, которую можно назвать нагрузочным моментом.
Этот последний момент обусловлен наличием сопротивлений
вращению вала вибратора и вязкого сопротивления колебаниям
платформы. Заметим, что по своему смыслу нагрузочный мо-
мент есть существенно положительная величина. Последнее
очевидно в случае дебалансного вибратора, когда h = 0. Для
§ 3J
СЛУЧАЙ СИНХРОННОГО ВИБРАТОРА
609
вибратора планетарного типа момент может стать отрица-
тельным лишь при нарушении условия безотрывной обкатки
ролика или кольца (см. § 15 главы XIII); такой случай, однако,
был с самого начала исключен из рассмотрения.
Отметим также, что при использовании введенных в § 13
главы XIII и в п. 2 § 2 главы XIV величин вибрационных мо-
ментов (см., например, формулы (13.25) главы XIII) выраже-
ние (2.5) для нагрузочного момента v#H(w) может быть пред-
ставлено в форме
Ж, = /?° (со) + W (со),
где
IV (со) = IV(0’(co) + Ww (со)
есть суммарный вибрационный момент, а
IV (со) = пх------------------
1
р2 + 4/г2 ’
IV(/?) (со)=- ±hf'
/?г2е2соа
М
Р
Р2 + 4«2
— соответственно составляющие вибрационного момента, обус-
ловленные наличием сил вязкого трения в колебательной си-
стеме и дополнительных сил сопротивления, возникающих в
случае, если вибратор является планетарным (то есть если
h V0; см. § 6 главы XIII). «Консервативная» составляющая
вибрационного момента IVW, связанная со взаимодействием
вибраторов, в данном случае, как это и должно быть, тож-
дественно равна нулю.
Подставив найденные из уравнения (2.4) значения а в ра-
венства (2.3), найдем порождающие амплитуды F и Ф. Ампли-
туда колебаний платформы И = ]/К2 + Ф2 не зависит от значе-
ния а и определяется по формуле (2.3), совпадающей с извест-
ной формулой для амплитуды установившихся вынужденных
колебаний линейной системы.
§ 3. Взаимодействие синхронного вибратора
с простейшей колебательной системой [68]
Рассмотрим сначала случай, когда вибратор приводится от
синхронного электродвигателя, так что согласно формуле (6.8)
главы XIII Z/m>(a, ст со) = oL*[o(a — |3)]. При этом будем пред-
полагать, что ZA(0) есть нечетная функция и, таким образом,
L(,n}(a. сгсо) = А*(а— |3). Установочный угол |3 в случае одного
вибратора без нарушения общности может быть положен рав-
ным нулю, и поэтому окончательно (а, оа>) = L* (а).
(ЗбЗ ТЯ ТЯ RnavMou
610
ЬзАИМодейст. вибратора с Колебательной системой [гл. xvii
Возможный вид графика функции L*(0) схематически пред-
ставлен на рис. 29; как отмечалось в § 2 главы ХШ, это перио-
дическая функция 0 с периодом 2n]ivn, где п — число пар по-
люсов двигателя и ip — передаточное отношение редуктора
(если таковой имеется); напомним, что в случае нескольких
вибраторов ip считалось целым числом, в рассматриваемой же
здесь задаче оно может быть любым.
Поскольку нагрузочный момент Л7Н не зависит от угла а,
то, как видно из графика на рис. 29, уравнение (2.4) имеет
вещественные решения лишь при условии
I Xi К Emax,	(3.1)
где Лтах — максимальное значение синхронизирующего момен-
та Е*(0). Если же неравенство (3.1) не выполняется, то урав-
нение (2.4) не имеет вещественных решений, и движения дан-
ного типа невозможны. Это означает, что при -заданной угловой
скорости вращения вала вибратора w расход энергии в рас-
сматриваемой системе превышает максимальную мощность,
которую может отдавать электродвигатель. Двигатель в такой
системе не может войти в синхронизм и будет работать в
асинхронном режиме, развивая угловую скорость, меньшую
чем со.
Далее, из рис. 29 видно, что при выполнении условия (3.1)
со знаком неравенства существуют два рода значений а = а*,
удовлетворяющих уравнению (2.4). Одним значениям соответ-
/ щг_(т) \	\
ствует d j ~ \~d9~/	> О, ДРУГИМ значениям отвечает
Рассмотрим вопрос об устойчивости движений, отвечающих
решениям уравнения (2.4). При этом примем предположение
о порядках величин, входящих в уравнение (13.36) главы ХШ,
сформулированное в § 13 указанной главы.
Уравнение (13.38) главы ХШ, согласно равенствам (13.41)
и (13.37) той же главы, имеет в данном случае единственный
корень
г° = an =	(cos a-/zf sin а)-Ф (sin а + hf' cos а)],
или, если учесть, что величины F, Ф, Н и а удовлетворяют ра-
венствам (2.3),
4-«п--------2	(3.2)
1	1 meHo>2\da 2М р2 + 4п2
§ 3]
СЛУЧАИ СИНХРОННОГО ВИБРАТОРА
611
Уравнение (13.40) главы XIII в данном случае принимает
вид
аи	sin a + hf' cos a	cos a — hf' sin a
cos a	nx + г(1)	P*
sin a	* p	-« + Л
(3.3)
и после раскрытия определителя может быть представлено в
форме
— ан [(«* + z(”)2 + р*2] + hf' (z(I) + n‘) + р* = 0.	(3.4)
Если выполняется условие устойчивости z° = a|]<0, то для
отрицательности вещественных частей корней уравнения (3.4)
достаточно, чтобы был положителен свободный член этого урав-
нения:
-«„(/Г + р^ + р' + ^Х >«•	(3.5)
После несложных преобразований с использованием формул
(3.2), (2.3) и формул (13.37) главы XIII неравенство (3.5) сво-
дится к требованию dL*lda<Q. Таким образом, условиями
устойчивости движения в рассматриваемом случае будут
IdL* \
\ da /а=а*
о,
’ dL* \	_ ш2е2ш2 2hf'nx + р _ МН2а>2
, da /a=a*	2М р2 + 4«2	2
(3.6)
Отсюда следует, что устойчивые движения могут соответ-
ствовать только тем значениям фаз а = а*, найденным из урав-
нения (2.4), которым соответствует отрицательное значение про-
изводной dL*fda. В тон части дорезонансной области, где
р=^1—< — 2hf'nx, отрицательность производной dL*fda
является при этом и достаточным условием устойчивости. При
0>р>—2nxhf', а также в послерезонансной области (р > 0)
необходимо выполнение более жесткого условия: dL*fda. дол-
жно быть меньше некоторого отрицательного числа, существен-
р2
но зависящего от расстройки р=1— то есть (при за-
данной скорости со) от частоты собственных колебаний си-
стемы рх = У сх/М .
Может оказаться, что в определенном интервале значений
расстройки
Pi < I -	< Р2	(3.7)
20:
612
ВЗАИМОДЕЙСТ. ВИБРАТОРА С КОЛЕБАТЕЛЬНОЙ СИСТЕМОЙ [ГЛ. XVII
второе неравенство (3.6) перестает выполняться, и поэтому не
существует устойчивых движений изучаемого типа.
Для иллюстрации изложенного рассмотрим случай, когда
момент L*(Q) определяется равенством
L* (а) = — Z sin а, 1>0,	(3.8)
что при определенных предположениях соответствует двухпо-
люсному синхронному двигателю.
Уравнение. (2.4) при этом имеет два существенно различных
решения *):
а(1) = _ arcsin , а(2) = л + arcsin.	(3.9)
Решению а = оД) соответствует отрицательное значение про-
изводной dL*/da, а решению а = а<2>— положительное значение.
Поэтому, согласно первому условию (3.6), решению а = а<2> от-
вечает неустойчивое движение.
Второе условие устойчивости (3.6) сводится для решения
а = а(|), в силу (3.8), к неравенству
которое при
I > 0), а при
m2e2co2 2hf'nx + р
2М р2 + 4п2 ’
(3.10)
р < —2hf'nx всегда выполняется (ибо
р > —2hf'nx сводится к требованию
1/	\ 2М I у р2 + 4пх I
по
условию
(З.Н)
Согласно (2.5) и (3.1) условие существования решений
в данном случае принимает вид
I > Яп = R° (а) +	2п‘ ~ hf'? .	(3.12)
2М р + 4пх
Предположим, что дополнительные сопротивления враще-
нию ротора вибратора отсутствуют, то есть /?а(ш) = 0. Тогда,
в соответствии с равенствами (6.9) главы ХШ,
R° (со) = R°B (ш) = теш2 [у fd + h (f'e - у fd ) ],
и условия (3.11) и (3.12) могут быть представлены в следую-
щей форме:
*) Прочие корни уравнения (2.4) отличаются от а(1> и а'2’ на 2л«, где
п — целое число; поэтому их можно не отличать от а(1) и а(Ч
§ 3]
СЛУЧАЙ СИНХРОННОГО ВИБРАТОРА
613
а)	для вибратора дебалансного типа (/г = 0)
, /м2е2соа . Г /г M d , ‘2пх V . р2
2А4 у у т в р2 + 4п2 /	(р2 + 4п2)2 ’
»г2е2<о'2 > I М d । 2nv
2Л4	me	р2 + 4/г2 ’
б)	для планетарного вибратора (/г = 1)
w2e2(°2 .	1 //9Г	М , 2nf-pr	V	,	/ 2/'лг + р	,2
2М	|/ \	т р2+4«2	)	у р2 + 4«2	)
т2е2а>г	of/ М ।	2n.v — pf
Г q	Q •
2М	т р + 4п2
(3.15)
(3.16)
На рис. 59 представлена область существования и устойчи-
вости движения, соответствующего значению а — aSl\ в плоско-
Рх
сти параметров р = 1 —и
т2е2(й2
I: —2лГ” ‘ Построение выпол-
нено для вибратора планетар-
ного типа, причем принято
f' = 0,2, 2пх = 0,2, т/М = 0,1.
В случае дебалансного вибра-
тора картина получается ана-
логичной.
Область существования
рассматриваемого движения,
определяемая условием (3.16),
лежит выше кривой У£ЪЖ
(область 4). Это движение
устойчиво всюду, кроме обла-
сти В, ограниченной линией
QLN. Часть границы LN этой
области построена в соответ-
ствии с условием (3.15). В по-
лосе С, заключенной между линиями
мое движение существует, однако оно
Предположим, что все параметры системы, кроме частоты
собственных колебаний рх, фиксированы, а частота рх медлен-
но изменяется от оо до 0, так что расстройка р пробегает зна-
чения от —сю до 1. Это соответствует движению изображающей
точки по прямой DE рис. 59 слева направо.
Могут представиться два случая. Если момент I больше мак-
симального значения нагрузочного момента Ж» (прямая DE
ЕМ и LN, рассматривае-
неустойчиво.
614
ВЗАИМОДЕПСТ. ВИБРАТОРА С КОЛЕБАТЕЛЬНОЙ СИСТЕМОЙ [ГЛ. XVII
не пересекает кривую ЖЬЛ], то рассматриваемое движение
может реализоваться при
колебаний рх. Если же I
любом значении частоты собственных
меньше максимального значения
то прямая DE дважды пересекает
кривую JtLN, как это показано на
рис. 59, и в диапазоне
Р~х
р < р = 1 -	< р"
движение рассматриваемого типа
невозможно. При этом нижнее гра-
ничное значение р = р' определяется
условием существования, а верхнее
граничное значение р = р"— усло-
вием устойчивости движения.
Из сказанного следует, что в слу-
чае I < (Лв) max «ПИКОВая» ЧЗСТЬ
классической резонансной кривой, определяемой последним ра-
венством (2.3), не может быть реализована; на рис. 60 эта часть
кривой изображена пунктиром.
§ 4. Случай асинхронного вибратора.
Эффект Зоммерфельда [44, 46]
Рассмотрим теперь случай, когда привод вибратора осуще-
ствляется от электродвигателя асинхронного типа, так что
согласно равенствам (6.8) главы XIII L{m} (а, ото) = <3L{a} (сив).
Поскольку при одном вибраторе, не нарушая общности, допу-
стимо считать, что вращение ротора происходит в положитель-
ном направлении, то можно принять ст = 1 и L<m) (а, ото) = L{ci} (со).
Далее, ввиду автономности рассматриваемой системы, как
и в задаче о самосинхронизации (см. п. 5 § 13 главы XIII),
можно положить
F = H, Ф = 0.	(4.1)
Тогда из уравнений (2.2) получаем соотношение
W-2)
2М р + 4пх
для определения угловой скорости со, а также формулы для
последующего вычисления порождающей амплитуды Н и поро-
ждающей фазы а:
л 11	•	и	/ л
2nxH = -jj- sin а,	pH = ~^ cos а.	(4.3)
§ 4]	СЛУЧАЙ АСИНХРОННОГО ВИБРАТОРА	615
Отсюда
м ]/p2+4^ ’ Sin“ /р2 + 4п2 ’
В-----
Рис. 61.
Для порождающей амплитуды колебаний Д, естественно,
по-прежнему получилась известная классическая формула; все
различие сводится к тому, что частота возмущающей силы в
данном случае не является заданной, а определяется из урав-
нения (4.2). Это уравнение представляет собой не что иное, как
уравнение баланса энер-
гии в системе при условии,
что ее движение происхо-
дит по закону, соответст-
вующему порождающему
решению.
Рассмотрим указанное
уравнение подробнее. Не-
смотря па то, что это
уравнение получено спе-
циально для резонансного
случая, оно остается спра-
ведливым и в нерезонанс-
ном случае. Действитель-
но, При (О рх и при
k
Ы рх, (0	= 2/1гС0
'	м х
рассматриваемое уравне-
ние переходит в уравне-
ние, получающееся из ра-
венства (6.11) главы XIII
той же главы. Поэтому уравнение (4.2) может служить для
определения со во всем диапазоне 0 < со < оо.
Уравнение (4.2) удобно решать графическим способом. Для
этого следует построить характеристику двигателя = L'al (со)
и график нагрузочного момента Лц(со) = Ro(co) + №(со), где
W (со) °= ~~2^М 2п2х+ 4%Р (рис. 61). При этом следует учиты-
вать, что величины р и 2пх зависят от со в соответствии с равен-
Рх
ствами р=1—и 2пх = ~м^-. Абсциссы точек пересечения
графиков L<“)(oj) и	и будут искомыми корнями уравне-
ния (4.2).
Отметим, что корни со уравнения (4.2), близкие к рх, то есть
отвечающие движению вблизи резонанса, для дебалансных ви-
браторов можно подсчитать по формуле (13.50) главы XIII.
k = 1 и при учете равенств (8.6)
(Ий ВЗАИМОДЕЙСТ. ВИБРАТОРА С КОЛЕБАТЕЛЬНОЙ СИСТЕМОЙ [ГЛ. XVIt
Условия, при которых значения ш, определяемые по этой фор-
муле, являются вещественными, имеют простой физический
смысл. Как нетрудно видеть, они сводятся к требованию, чтобы
мощность, отдаваемая электродвигателем при его вращении
с угловой скоростью и ~ рх, с одной стороны, превышала по-
тери энергии в вибраторе и, с другой стороны, была меньше
максимально возможного расхода энергии в системе при резо-
нансе [44, 46, 324].
Эти требования и являются необходимыми условиями нали-
чия движений вблизи резонанса. Если они не соблюдаются, то
кривые	и	на рис. 61 не могут пересечься вблизи
точки оз ~ рх.
Обычно имеют место либо три пересечения кривых L<a>(u)
и Лн(ш) и, следовательно, возможны три установившихся дви-
жения изучаемого типа, либо одно пересечение и соответственно
одно движение. При этом, если справедливо предположение
о малости момента ku> по сравнению с моментом МНга2, то,
в соответствии с изложенным в § 13 главы XIII, для значений ш,
близких к рх, дорезонансному значению со (то есть значению
со < рх) отвечает устойчивое движение, а послерезонансному
значению со (то есть значению со > рх)—неустойчивое движе-
ние.
Значениям же со, в достаточной мере отличающимся от рх,
всегда соответствует устойчивое движение рассматриваемого
типа, ибо уравнение (4.10) главы ХШ при k = 1 имеет един-
ственный корень х = 0, не влияющий, вследствие автономности
исходной системы, на решение вопроса об устойчивости*).
Точки пересечения кривых L(a*(w) и .//„(ш), отвечающие
устойчивым движениям, помечены на рис. 61 знаками « + »,
а точки пересечения, отвечающие неустойчивым движениям,—
знаками «—».
Изложенное позволяет объяснить неоднократно наблюдав-
шийся на опыте факт, заключающийся в том, что в системах,
подобных рассматриваемой, часть послерезонапспого участка
кривой // = /7(ш) оказывается невозможным реализовать. Эта
кривая, построенная по формуле (4.4), представлена на рис. 62,
причем нереализуемый участок, соответствующий неустойчи-
вому движению, изображен пунктиром. Заметим, что картина
здесь получается иной, чем в случае привода вибратора от син-
хронного электродвигателя (см. рис. 60).
*) Заметим, что сформулированные заключения об устойчивости движе-
ний, естественно, относятся к случаю, когда справедливо предположение о по-
ложительности коэффициента k = А’(со), равного сумме «коэффициентов жест-
кости» характеристики двигателя и характеристики сопротивления (см. фор-
мулы (2.38) и (2.41) главы ХШ). Отрицательным значениям коэффициента
/г = fe(co), как нетрудно заключить, отвечают неустойчивые движения.
§ 4]
СЛУЧАЛ АСИНХРОННОЮ ВИБРАТОРА
617
Точка JI, которая отвечает переходу от устойчивого после-
резонаиспого движения к неустойчивому, как правило, может
быть найдена из дополнительного условия устойчивости (5.29)
главы XIII.
В случае наличия при заданных значениях параметров систе-
мы двух устойчивых движений в зависимости от начальных
условий реализуется какое-либо одно движение.
Рассмотрение рис. 61 позволяет' объяснить некоторые свое-
образные нелинейные явления, наблюдаемые в вибрационных
машинах и установках.
Изучим, например, пове-
дение системы при медлен-
ном непрерывном изменении
характеристики двигателя
L<a>(w), соответствующем
последовательному переходу
от кривой 1 па рис. 61 к
кривым 2, 3, ...
Если в начале этого про-
цесса система совершала
устойчивое движение с угло-
вой скоростью и, соответ-
ствующей точке пересече-
ния А кривой 1 с кривой
то при переходе к
Рис. 62.
кривым 2,3, ... указанная угловая скорость будет медленно на-
растать до тех пор, пока соответствующая точка пересечения
не совпадает с точкой В на кривой	отвечающее этой
последней точке значение со лежит в непосредственной близости
от резонансного значения рх.
Дальнейшее небольшое изменение характеристики двига-
теля в том же направлении приведет к исчезновению околоре-
зонансных движений системы, и последняя совершит «перескок»
на нерезонансный режим, характеризующийся точкой пере-
сечения кривой 5 с кривой ..#,|((о); угловая скорость со при
этом резко возрастает, а амплитуда колебаний Н резко па-
дает.
Если теперь медленно изменять характеристику двигателя
в противоположном направлении, то есть переходить от кривой 5
последовательно к кривым 4, 3 и т. д., то угловая скорость бу-
дет непрерывно уменьшаться до значения, отвечающего точ-
ке Е, которая лежит на границе неустойчивого послерезонанс-
пого участка кривой	При дальнейшем «снижении» ха-
рактеристики двигателя L<a>(w) система совершит «перескок»
па режим, отвечающий исходной точке А, не «задерживаясь»
на режимах, близких к резонансному.
618
ВЗАИМОДЕЙСТ. ВИБРАТОРА С КОЛЕБАТЕЛЬНОЙ СИСТЕМОЙ [ГЛ. XVII
Как уже отмечалось в § 1, описанное явление в главных
своих чертах наблюдалось А. Зоммерфельдом еще в 1902 г. и
получило название эффекта Зоммерфельда [480].
Обращаясь к дальнейшему анализу рис. 61, заметим, что
в случае, когда имеются три точки пересечения кривых
и ^n(w) и при одних и тех же параметрах системы возможны
два устойчивых режима движения, «перескок» от одного ре-
жима на другой может быть осуществлен путем надлежащего
возмущения системы. Такие явления, по-видимому, впервые
экспериментально наблюдались С. П. Тимошенко [393], который
для осуществления «перескока» системы от низкочастотного ре-
зонансного режима на высокочастотный нерезонансный попро-
сту придерживал колеблющуюся рессору рукой.
Скачкообразный переход от резонансного режима на нере-
зонансный представляет неприятную особенность резонансных
вибрационных машин с дебалансными вибраторами, приводи-
мыми от двигателей асинхронного типа. Тот факт, что подобный
переход имеет место при превышении рабочей нагрузкой опре-
деленного предела, легко объясняется из рассмотрения кривых,
изображенных на рис. 61. Действительно, увеличение нагрузки
па машину связано с увеличением коэффициента сопротивления
kx. При этом, как нетрудно видеть, пиковое значение нагрузоч-
т2ъ~р:>х
ного момента [J(a (со)]тах ~ Л» (рх) = /?°(рх) 4-уменьшает-
ся, и может оказаться, что кривая £<“>(со) перестанет пересекать
кривую .#„(<») вблизи значения со = рх. Иными словами, резо-
нансное движение может при увеличении нагрузки перестать
существовать.
Другую противоположность представляют послерезонапсные
вибрационные машины с приводом от двигателей асинхронного
типа. В таких машинах при пуске может наблюдаться нежела-
тельное «застревание» в режиме, близком к резонансному, со-
провождающееся весьма интенсивными колебаниями вибри-
рующего органа. Изложенное выше показывает, что рассматри-
ваемые машины желательно проектировать таким образом,
чтобы кривые £<а>(со) и ^н(®) имели только одно пересечение,
отвечающее послерезонансному режиму работы (<о^рл).
Мерами, обеспечивающими расположение резонансного ника
кривой ../#,(((») ниже характеристики двигателя £<а>(со), могут
служить, например, резкое увеличение сопротивления вблизи
резонансной частоты путем использования специальных демп-
феров, включающихся при превышении амплитудой колебаний
определенного предела; использование дебалансных грузов,
автоматически включающихся после прохождения резонансного
числа оборотов: надлежащий выбор характеристики двигателя
§ 51	О ДИНАМИКЕ РЕГУЛЯТОРА БУАССА-САРДА	619
/АДо) и ее расположения относительно кривой ^„(со); исполь-
зование нелинейных упругих элементов.
Предотвратить «застревание» системы на резонансном ре-
жиме можно также путем выбора двигателя, характеристика
которого	вблизи со ~ рх имеет достаточно большую по-
ложительную производную dLldto, так что коэффициент k отри-
цателен. При этом оба околорезонансных движения, согласно
сказанному выше, будут неустойчивыми.
Не останавливаясь более подробно на обсуждении этих важ-
ных, по специфических вопросов, отошлем интересующегося
читателя к соответствующей литературе (см., в частности,
[3, ИЗ]).
§5.0 динамике регулятора Буасса — Сарда
Эффект Зоммерфельда и другие рассмотренные выше явле-
ния имеют много общего с процессами, характерными для свое-
образного регулятора, предназначенного для обеспечения рав-
номерности опускания подвешенного на канате груза, — регуля-
тора Буасса — Сарда. Этот регулятор описан в монографии
И. Рокара [473], где также составлены дифференциальные урав-
нения движения системы с регулятором и путем усреднения
нелинейных членов найдены условия, при выполнении которых
регулятор справляется со своей задачей.
Исследование регулятора Буасса — Сарда методами А. Пуан-
каре и А. М. Ляпунова было выполнено Г. Ю. Джанелидзе и
автором в работе [48], в которой обращено внимание на анало-
гию с задачей о взаимодействии асинхронного вибратора с ко-
лебательной системой, а также установлены некоторые особен-
ности динамики системы с регулятором, не отмеченные И. Ро-
каром. Здесь мы кратко остановимся лишь на результатах
указанной работы, уделив особое внимание аналогии с зада-
чей о вибраторе. Отметим, что позднее задача рассматривалась
также Р. Конти (см. [223]).
Схема системы, снабженной регулятором Буасса — Сарда,
представлена на рис. 63. Канат или трос, на котором подвешен
опускающийся груз I, сматывается с цилиндрического бара-
бана 2, насаженного на вал 3. Собственно регулятор состоит из
массы 4, подвешенной на пружине 5 к кривошипу 6, располо-
женному на валу 7, и катаракта 8 с неподвижным корпусом.
Вал 3 барабана и вал 7 кривошипа связаны между собой парой
шестерен *) с радиусами Г\ и г2-
*) В цитированной выше книге И. Рокара рассматривается схема, в ко-
торой барабан расположен непосредственно на валу кривошипа. Описанная
выше схема, как нам представляется, делает возможным более рациональный
выбор параметров регулятора.
620
ВЗАИМОДЕЙСТ. ВИБРАТОРА С КОЛЕБАТЕЛЬНОЙ СИСТЕМОЙ [ГЛ. XVII
Описанная система имеет две степени свободы. Примем за
ее обобщенные координаты угол поворота вала кривошипа <pi
и вертикальное перемещение массы регулятора х, отсчитывае-
мое от положения конца ненапряженной пружины при <pi = 0.
Рис. 63.
Тогда дифференциальные уравнения движения системы могут
быть записаны в форме
/ф + А,ф = Mgr + схе (х — е sin ф,) cos фь
тох + kxx -г схх = m,g + се sin ф!
(г = /?Г2/Г!).
Здесь /? — радиус барабана, е—плечо кривошипа, М — масса
груза, т0—масса регулятора, сх — жесткость пружины, / — при-
веденный к валу кривошипа момент инерции системы, k\ и kx —
коэффициенты вязкого сопротивления, g— ускорение силы тя-
жести.
Интерес представляет выяснение условий существования и
устойчивости решений уравнений (5.1) вида
Ф] = at + ф (at), x = x(at),	(5.2)
где tp(coZ) и x(at)— периодические функции времени t с перио-
дом Т = 2л/сй. Такие решения соответствуют опусканию груза
с постоянной средней за период скоростью V = аг. При этом
значение средней угловой скорости вала кривошипа |фСр| = <о
заранее неизвестно и подлежит определению в ходе решения.
О ДИНАМИКЕ РЕГУЛЯТОРА БУАССА-САРДА
621
Сформулированная задача вполне аналогична рассмотрен-
ной выше задаче об исследовании стационарных режимов дви-
жения вибратора, приводимого от двигателя асинхронного типа
и установленного на вибрирующем органе с одной степенью
свободы. Действительно, уравнения (5.1) весьма схожи с урав-
нениями (3.1) главы XIII при числе вибраторов k = 1, а вид
решений (5.2) совпадает с видом решений, изучавшихся в за-
даче о синхронизации вибраторов. При этом сходство диффе-
ренциальных уравнений движения и вида рассматриваемых ре-
шений в обоих задачах является не формальным, а обусловлено
близостью их физического содержания. Как в первом, так и во
втором случае рассматривается взаимодействие линейного ос-
циллятора с возбудителем колебаний. В задаче о регуляторе
Буасса — Сарда собственно регулятор соответствует колеблю-
щемуся телу S, а вал барабана с опускающимся грузом — меха-
ническому вибратору, причем роль вращающего момента L иг-
рает момент силы тяжести.
По изложенным причинам решение задачи о регуляторе
может быть проведено вполне аналогично решению задачи о ви-
браторе; эта задача также может рассматриваться как вырож-
денный частный случай задачи о самосинхронизации. Поэтому,
не останавливаясь на процессе решения, изложенном в цитиро-
ванной выше работе [48], приведем лишь окончательный ре-
зультат.
Движения системы, соответствующие опусканию груза с по-
стоянной средней скоростью V = юг, могут иметь место при ус-
ловии, что уравнение
Jf.gr =	(®),	(5.3)
где
о
= k^ + cxe9~-------2	,	Д;=-^,(5.4)
11 — Рх I + (— I
\	(о2 /	\ тоа>)
допускает положительные решения относительно величины ®,
представляющей приближенное значение средней угловой ско-
рости вращения вала кривошипа.
Уравнение (5.3) вполне аналогично уравнению (4.2) задачи
об асинхронном вибраторе: оно может быть формально полу-
чено в результате осреднения за период Т = 2л/® первого урав-
нения (5.1), если принять epi = <»t + а и х = Н cos ®/, причем
величину амплитуды Н найти из второго уравнения (5.1), в ко-
тором также положено ф| = ®? + а.
Заметим, что именно таким способом аналогичное уравнение
было найдено И. Рокаром, который, однако, не учел сопротив-
лений движению груза и вала, характеризуемых членом k\ ф.
622
ВЗАИМОДЕПСТ. ВИБРАТОРА С КОЛЕБАТЕЛЬНОЙ СИСТЕМОЙ [ГЛ. XVII
в уравнении (5.1). Как будет показано ниже, учет этих сопро-
тивлений необходим, ибо он предопределяет важные качествен-
ные особенности работы регулятора.
Для решения и исследования уравнения (5.3) можно вос-
пользоваться графическим представлением. С этой целью следует
построить график функции Мп(а>), определяемой равенством
(5.4). Абсциссы точек пересечения этого графика с прямой ли-
нией L = Mgr и будут искомыми значениями о>. Указанное по-
строение представлено на рис. 64, где, однако, вместо со отло-
жена пропорциональная ей величина V = сот— средняя скорость
опускания груза, а вместо Mgr—вес груза Mg.
Из рассмотрения рис. 64, который во многом аналогичен
рис. 61 для вибратора, следует, что могут иметь место либо
одно, либо три пересечения кривой Мп(У) и прямой t<g' = const.
Тем самым определенному значению веса груза Mg может со-
ответствовать либо одно, либо три значения скорости опуска-
ния V. При этом точкам пересечения, лежащим иа участках ОА
и CD кривой Мн(У), мало уклоняющимся от прямой линии OD,
отвечают движения вдали от резонанса*). Такие движения мо-
гут иметь место при достаточно малых и при достаточно боль-
ших значениях веса груза Mg, причем скорость опускания
в этих случаях примерно прямо пропорциональна Mg, то есть
существенно зависит от веса груза. Поэтому указанные «нере-
зонансные» участки не могут считаться рабочими.
Участки АВ и ВС кривой MH(V), соответствующие значениям
скорости опускания, близким к резонансной скорости Укр = рхг,
характеризуются тем, что на них скорость опускания мало за-
висит от веса груза Mg.
*) То есть движения со скоростью V = ыг, в достаточной мере отличной
от «резонансной» скорости VKp = Рхг.
§5]	О ДИНАМИКЕ РЕГУЛЯТОРА БУАССЛ-СЛРДЛ	623
Исследование устойчивости, вполне аналогичное проведен-
ному в задаче о вибраторе, показывает, что нерезонансные
движения всегда устойчивы, а из двух резонансных режимов
устойчив лишь дорезонансный, отвечающий участку АВ кривой
^П(К). Движение же, определяемое участком ВС (послерезо-
нанспое), является неустойчивым.
Итак, в диапазоне значений веса груза
JCg<Jtg<Jt2g,	(5.5)
где J(]g и Jtig — ординаты точек графика кривой Л'ц(К), в ко-
торых касательные горизонтальны, каждому значению веса
груза соответствуют два устойчивых установившихся движения:
одно отвечает рабочему участку АВ, а другое — нерабочему
участку CD, на котором, как нетрудно видеть, регулятор прак-
тически не работает. Таким образом, в диапазоне (5.5) суще-
ствует опасность скачкообразного увеличения скорости опуска-
ния с переходом от рабочего участка на нерабочий.
Наличие опасности перехода к нежелательному режиму не-
сколько затрудняет проектирование надежно работающего регу-
лятора, ибо после подбора его параметров и выбора рабочего
участка необходимо убедиться, что возможные в системе воз-
мущения не могут привести к «перескоку». Как и в задаче о ви-
браторе, решение этого вопроса требует изучения поведения
траекторий системы «в целом», а не только вблизи стационар-
ных режимов движения.
Ввиду того, что И. Рокаром [473] не учитывалось наличие
сопротивлений движению груза и вала, построенная им кривая
зависимости скорости опускания V от веса груза имеет другой
характер. На графике И. Рокара определенному весу груза
отвечают лишь два значения скорости опускания, из которых
одно соответствует устойчивому, а второе — неустойчивому дви-
жению. Вследствие этого нежелательный режим работы регуля-
тора, а также возможность перехода на него при наличии воз-
мущений И. Рокаром не были обнаружены.
Из рассмотрения рис. 64 следует также, что грузы, большие
M2g, при всех условиях выводят систему за пределы рабочего
участка; таким образом, нагрузка сверх M2g непременно при-
ведет к опусканию груза с недопустимо большой скоростью.
Значения Jft\g и Jt2g определяются из условия
d Wg)	А	/Г
—Г °’	(5-6)
в котором под J(g понимается функция от V = сог, определяе-
мая равенством (5.3).
В развернутом виде равенство (5.6) сводится к алгебраиче-
скому уравнению четвертой степени. В случае малости безраз-
624
ВЗЛИМОДЕЙСТ. ВИБРАТОРА С КОЛЕБАТЕЛЬНОЙ СИСТЕМОЙ [ГЛ. XVII
мерных коэффициентов сопротивления а = k/Iu и пх = kx/2in0(a
по сравнению с единицей из этого уравнения получается сле-
дующая приближенная формула для определения предельного
груза ./Cg:
k,px , торх _ kipx . 1	/с-
c.ve2 схе2 2kx схе2 4пх '	V • )
Последнее соотношение имеет простой смысл: оно пред-
ставляет условие равенства убыли потенциальной энергии груза
2z\rJ(g за один оборот вала кривошипа и максимальной энергии
2л (k]Px + m°P2AkC^e ) = 2л [klPx +	,
которая может поглотиться за то же время в резонансном ре-
жиме, то есть при со = Рх.
Приведем в заключение числовой пример. Пусть рассмат-
риваемая система имеет параметры г = 3 см, mog = 30 кГ,
сх = 300 кГ/см, е = 2 см, klPx = 200 кГ/см, Рх = 100 \/сек, пх = 0,\.
Тогда подсчет по формуле (5.7) дает значение предельного веса
груза Jt2g 1000 кГ. Такому значению веса соответствует кри-
тическая скорость опускания Vltp = Pxr = 100 • 3 = 300 см/сек =
= 3 м/сек. Заметим, что при грузе в 500 кг скорость опускания
груза в нормальном режиме всего лишь на 10% меньше кри-
тической.
С другой стороны, если произойдет срыв на послерезонанс-
ный нерабочий установившийся режим, то скорость опускания
V будет для груза весом 500 кг составлять Jtgr^/ki = 500 • 9/2 =
= 2250 см/сек = 22,5 м/сек, то есть окажется сравнительно боль-
шой (и вряд ли допустимой).
Сопоставляя изложенное с результатами исследования ра-
боты вибратора, приводимого от двигателя асинхронного типа,
нетрудно проследить почти полную аналогию между особенно-
стями динамики регулятора Буасса — Сарда и нелинейными
явлениями в системе с вибратором, в частности — эффектом
Зоммерфельда.
ГЛАВА XVIII
ВРАЩЕНИЕ НЕУРАВНОВЕШЕННОГО РОТОРА
ПОД ДЕЙСТВИЕМ КОЛЕБАНИЙ ЕГО ОСИ
§ 1. Предварительные замечания. Краткий обзор исследований
Колебания оси неуравновешенного ротора (физического ма-
ятника), происходящие с некоторой частотой <о, могут вызвать
его стационарное вращение со средней угловой скоростью
фср = ± со, где р и q— целые положительные числа. Это инте-
ресное явление, несомненно, связано с явлением синхрониза-
ции вибраторов, установленных на общей колебательной систе-
ме: в обоих случаях можно говорить, что эффект обусловлен
появлением так называемых вибрационных моментов — допол-
нительных средних моментов, действующих на вращающийся
ротор вследствие колебаний его оси (см. § 6 главы ХШ).
По отношению к задаче о синхронизации вибраторов задача
о движении неуравновешенного ротора под действием колеба-
ний его оси представляет вырожденный частный случай: это
задача о внешней синхронизации единственного объекта — за-
дача о захватывании (см. § 1 главы II). В некоторых случаях
задачу о синхронизации вибраторов допустимо рассматривать
как соответствующую задачу о вращении вибратора под дей-
ствием заданных колебаний его оси.
Явление вибрационного возбуждения и поддержания враще-
ния неуравновешенного ротора все более широко используется
в технике. Напомним, в частности, о специальных вибрационных
грохотах, вибрационных дробилках и истирателях руды, вибра-
ционных питающих устройствах *) и т. п. (см. § 1 главы XII
и пп. 6, 7, 15, 16, 22 и 23 таблицы 2). Теория рассматриваемого
явления существенна при изучении работы ударных демпферов
для снижения уровня колебаний брусьев круглого сечения, при-
меняемых, например, в качестве тяг проводки управления
*) Естественно, что теория этих устройств в расширенной постановке
может рассматриваться и в рамках теории синхронизации вибраторов (см. §5
настоящей главы, а также главу XXI).
626
ВРАЩЕНИЕ НЕУРАВНОВЕШЕННОГО РОТОРА
[ГЛ. XVIII
вертолетов*) [12, 13]. Эта теория лежит также в основе извест-
ной игры-упражнения «хула-хуп» [452].
Отметим также, что явление вибрационного возбуждения
и поддержания вращения имеет много общего с эффектами, ис-
пользуемыми в циклических ускорителях заряженных частиц
и в так называемых системах автоматической подстройки ча-
стоты (см., например, [100, 122—124, 160, 425]). Это родство явле-
ний находит свое отражение в сходстве соответствующих диффе-
ренциальных уравнений.
Насколько нам известно, впервые задача о вибрационном
поддержании вращения физического маятника рассматривалась
Н. Н. Боголюбовым [95] (1950 г.); соответствующее исследова-
ние, выполненное с помощью асимптотического метода, воспро-
изводится также в монографии [96]. Н. Н. Боголюбов получил
условия существования основного режима стационарного вра-
щения (|фср|= <о) в простейшем случае, когда ось маятника
горизонтальна и совершает прямолинейные гармонические ко-
лебания.
В нашей работе [45] (1954 г.) рассмотрен случай дебалапс-
пого и планетарного вибраторов, оси которых совершают сдви-
нутые по фазе гармонические колебания в двух взаимно пер-
пендикулярных направлениях, так что траектория колебаний
представляет собой эллипс. Условия существования и устойчи-
вости основного режима стационарного вращения получены в
работе с помощью метода малого параметра Пуанкаре — Ляпу-
нова. Связь явлений синхронизации вибраторов и вибрационного
поддержания вращения неуравновешенного ротора рассмотрена
в работах [44, 46, 68].
Д. Д. Баркан и О. Я- Шехтер наблюдали, а затем О. Я. Шех-
тер исследовала случай вращения ротора со средней угловой
скоростью фср, равной половине частоты колебаний осп ротора
[426] (1959 г.).
М. К. Бирюков в дипломной работе [43] (1962 г.), выполнен-
ной под нашим руководством, показал, что та же задача мо-
жет быть решена с помощью метода Пуанкаре, развитого для
особого случая.
Почти одновременно (1962—1963 гг.) К. М. Рагульскпс
[352] с помощью модифицированного метода осреднения рас-
смотрел стационарные режимы движения маятника, соответ-
ствующие фср = -j- (р == 1,2, 3).
Указанные режимы наблюдались
экспериментально и были воспроизведены на электронной моде-
лирующей установке.
*) Заметим, что в этом случае наступление режима стационарного вра-
щения является весьма нежелательным.
§ 1]	ПРЕДВАРИТЕЛЬНЫЕ ЗАМЕЧАНИЯ	627
В 1960 г. Т. К- Каучи, по-видимому, ие знакомый с предше-
ствующими исследованиями той же задачи, рассмотрел ее и
применил результат исследования для объяснения природы
вращения кольца («кольцевого планетарного вибратора») в уже
упоминавшейся игре-упражнении «хула-хуп» [452].
Наконец, имеется ряд исследований Л. Д. Акуленко,
В. М. Волосова, Н. Н. Моисеева, а также Б. И. Моргунова и
Ф. Л. Черпоусько (1963 г. и позднее), в которых рассматри-
ваются вращательные движения «обобщенного маятника», то
есть системы, описываемой уравнением вида
z + f (z) = щр(г, z, /),
где f(z)— периодическая функция z, ср — периодическая функ-
ция I, а [1 — малый параметр. В некоторых из указанных ра-
бот, основные результаты которых отражены в книге Н. Н. Мои-
сеева [302], рассмотрены также примеры, относящиеся к отдель-
ным частным случаям задачи о маятнике (в узком смысле этого
термина) с гармонически колеблющейся осью. Упомянутые ав-
торы также, по-видимому, не были знакомы с исследованиями
своих предшественников.
Интересный вопрос об «областях притяжения» определенных
стационарных режимов движения маятника был предметом
работ Э. А. Аграновской [2] (1963 г.), А. А. Митулнса [296]
(1965—1966 гг.) и 3. С. Баталовой [29] (1967 г.), А. Л. Кумпи-
каса и К- М. Рагульскпса [234] (1968 г.). В цитированной рабо-
те 3. С. Баталовой, выполненной с помощью цифровой вычисли-
тельной машины, рассмотрен также ряд сложных режимов
стационарного вращения и колебаний маятника; другие из
упомянутых исследований проведены с помощью электронных
моделирующих установок.
Вопросы, связанные с практическим использованием явле-
ния, рассмотрены в статьях В. В. Гортинского [155] (1959 г.),
Б. Н. Дубровина, А. Д. Рудина, А. К. Рундквиста и автора
[65* 182, 369, 370] (1959—1961 гг.), Г. Б. Вальца [118] (1966 г.).
Экспериментальное исследование режимов установления ста-
ционарного вращательного движения ролика планетарного ви-
братора под действием колебаний было выполнено автором
в 1960 г. с прйменением скоростной киносъемки [59]; результаты
этой работы изложены в главе XIX книги.
Весьма отчетливое изложение существа рассматриваемой за-
дачи дано в книге Я. Г. Пановко и И. И. Губановой [331].
Следует упомянуть также статьи японских авторов Иноуэ
Дзюнкити, Араки Иосиаки, Хаяси Сэцуко и Мияура Суга [198,
199] (1966—1967 гг.).
В настоящей главе излагаются в существенно видоизменен-
ном и дополненном виде соответствующие результаты работ
628
ВРАЩЕНИЕ НЕУРАВНОВЕШЕННОГО РОТОРА
[ГЛ. XVIII
автора [45, 68], а также результаты некоторых других упоми-
навшихся выше исследований. О приложениях теории вибра-
ционного возбуждения и поддержания вращения говорится
в главе XXI, некоторые экспериментальные результаты приво-
дятся в §§ 3 и 4 главы XIX.
§ 2. Уравнение движения и постановка задачи
Итак, рассмотрим механический вибратор (рис. 65), ось ко-
торого совершает гармонические колебания в двух взаимно пер-
пендикулярных направлениях по закону
х = Н sin at, у = G cos (at + ft),	(2.1)
где H и G — амплитуды, <о — частота колебаний, a ft —угол,
характеризующий сдвиг фаз между составляющими колебаний;
будем считать для определенности, что G 0 и Н 0.
Для конкретности предположим, что ось вибратора горизон-
тальна, а плоскость колебаний хОу перпендикулярна указанной
оси; переход к иным случаям, естественно, не представит каких-
либо затруднений. Ось Ох, очевидно, не нарушая общности
можно считать горизонтальной, а ось Оу — направленной вер-
тикально вверх. Относительно типов рассматриваемых вибрато-
ров сделаем те же предположения, что и в § 2 главы XIII.
Вместе с тем, в отличие от главы XIII, будем рассматривать
движения вибратора, близкие к равномерному вращению с уг-
„	.-I р
ловои скоростью |ф| = —го, где р и q — целые положительные
числа.
Тогда уравнение движения ротора вибратора может быть
формально получено из первого уравнения (2.44) главы XIII,
§ 2]	УРАВНЕНИЯ ДВИЖЕНИЯ И ПОСТАНОВКА ЗАДАЧИ	629
если положить в нем ф, = ср, ls — 1,	— Уks = k, = О,
mses = me, ср s= 0, х — 0, заменить os на -у ст и учесть равен-
ства (2.1) настоящего параграфа. Указанное уравнение, кото-
рое, конечно, можно легко вывести и непосредственно, будет
иметь вид
/ ф 4- k (ф — о	оз j =
— mge cos qp — теа2 [И sin at sin ф 4- G cos (оз/ + ft) cos ф] 4-
— со, ф, 0, 0, о — aft'j —
\ q ’ q J
— /? Го -у (О, ф, — На2 sin at, — Ga2 cos (at 4 ft), ol. (2.2)
L 4	J
Это уравнение справедливо как для дебалапсного
(рис. 65, а), так и для планетарных (рис. 65,6 и s) вибраторов;
в последнем случае предполагается, однако, что ролик или
кольцо не отрываются от поверхности стакана или оси.
В уравнении через ф обозначен угол поворота вектора-экс-
центриситета ротора вибратора, отсчитываемый от оси Ох в на-
правлении движения часовой стрелки; число ст = 1, если рас-
сматривается вращение ротора в положительном направлении,
и ст = —1, если изучается вращение в отрицательном направ-
лении. Как и в § 2 главы XIII, /г > О есть суммарный коэффи-
циент сопротивления, / — приведенный момент инерции, L —
вращающий момент, передаваемый от двигателя, R— момент
сил сопротивления; эти величины определяются соотношениями,
вполне аналогичными формулам (2.5), (2.35) — (2.39) и (2.41)
главы ХШ. В частности, для момента инерции / будем иметь
выражение
/ = Зс [1 4-/i(-^b - l)j 4-те2.	(2.3)
Напомним, что здесь J— момент инерции ротора вибратора
относительно его центра тяжести с, величина b в случае внут-
реннего (роликового) планетарного вибратора есть радиус ро-
лика (b — R — е), а в случае внешнего (кольцевого) планетар-
ного вибратора есть внутренний радиус кольца (b = R 4-е);
через R обозначен радиус стакана в случае внутреннего и ра-
диус оси в случае внешнего планетарного вибраторов
(рис. 65,6 и s). Величина h равна нулю для дебалансного ви-
братора и равна единице для планетарных вибраторов. Нако-
нец, параметр X* равен единице, если ролик или кольцо ка-
тятся без скольжения. Если же они скользят по соответствую-
щей поверхности, не поворачиваясь относительно стакана или
оси, то /.* = 0. Условия, при выполнении которых в установив-
630
ВРАЩЕНИЕ НЕУРАВНОВЕШЕННОГО РОТОРА
[ГЛ. XXIII
шемся режиме действительно осуществляется движение ролика
или кольца без отрыва и проскальзывания, могут быть полу-
чены аналогично тому, как это было сделано в § 15 главы XIII
(см. также [45]).
Для планетарного вибратора со сплошным цилиндрическим
роликом, катящимся без скольжения, имеем h = 1, А* = 1,
1	3
Ус = у mb2, и поэтому, согласно формуле (2.3), I =
В случае L = 0, то есть когда двигатель отсутствует (или вы-
ключен), рассматриваемые вибраторы, очевидно, превращаются
в соответствующие маятники.
Основная задача исследования состоит в установлении усло-
вий существования и устойчивости стационарных режимов дви-
жения вибратора по закону
Ф = о at + ф ,	(2.4)
где ф(т)— периодическая функция аргумента т с периодом 2л.
Представляет существенный интерес также более сложная за-
дача об установлении «областей притяжения» указанных режи-
мов в фазовом пространстве системы ф, ф, t.
§ 3. Основной режим стационарного вращения ротора
1. Условия существования и устойчивости основного режима
движения. Под основным режимом стационарного вращения
ротора вибратора будем понимать вращение со средней угло-
вой скоростью фср, равной по абсолютной величине частоте
колебаний и; этому случаю отвечает plq = 1. Указанный режим,
как правило, представляет наибольший практический интерес;
область его существования и устойчивости занимает обычно
наибольшую (по сравнению с другими режимами) часть обла-
сти возможных значений параметров системы; то же можно
сказать и об «области притяжения» в фазовом пространстве.
В настоящем параграфе рассмотрим именно основной режим
стационарного вращения.
Ограничиваясь рассмотрением движений ротора, близких
к равномерному вращению с угловой скоростью сив, запишем
уравнение (2.2) в виде (полагаем plq = 1)
/ф + k (ф — о<о) = рФ (ф, at),	(3.1)
где
цф (ф, at) =
— mge cos ф — /песо2 [Н sin at sin ф + G cos (at + ft) cos ф] +
4- L(aa, ф, 0, 0, aat) — R [стсо, ф, — Ha2 sin at, — Ga2cos(at + ft), 0],
(3.2)
ОСНОВНОЙ РЕЖИМ СТАЦИОНАРНОГО ВРАЩЕНИЯ РОТОРА
631
§ 3]
причем величину ц>0 будем толковать как малый параметр.
Здесь можно не останавливаться на доводах в пользу такого
способа введения малого параметра, поскольку они вполне ана-
логичны приведенным в § 3 главы XIII при рассмотрении за-
дачи о синхронизации вибраторов. Отметим лишь, что уравне-
ние (3.1) отвечает неквазиконсервативной идеализации вибра-
тора; при квазиконсервативной идеализации в данном случае
результаты исследования получаются в точности теми же (см.
ниже).
Уравнение (3.1) представляет собой простейший частный
случай системы (3.3) главы XIII. Поэтому здесь можно непо-
средственно воспользоваться результатами, полученными в § 4
указанной главы. Эти результаты сводятся к следующему.
Для существования решения уравнения (3.1), обращающе-
гося при ц = 0 в порождающее решение
Ф° = о (cot + а),
необходимо, чтобы постоянная а удовлетворяла уравнению*)
2.Т/Ы
Р (а, со) = ц -^- [ Ф(ф°, со/)с// = 0.	(3.3)
zJT J
о
Каждому решению этого уравнения а = а* действительно
отвечает единственное и асимптотически устойчивое решение
рассматриваемого типа, если выполняется условие
х = dP м) < 0.	(3.4)
При выполнении противоположного неравенства соответ-
ствующее движение неустойчиво, а случай х = 0 требует допол-
нительного исследования**).
Выполнив интегрирование при учете формулы (3.2) настоя-
щего параграфа и соотношений (2.36), (2.37) и (6.3) гла-
вы XIII, представим уравнение (3.3) в форме
Р (а, со) =	(а, стсо) - /?° (со) - W (а, со) = 0,	(3.5)
вполне аналогичной форме записи уравнений (6.10) главы XIII.
*) В выражение для функции Р(а, со), в отличие от выражения (4.9)
главы XIII, введен несущественный положительный множитель ц£(о/4л.
**) Напомним, что, как и соответствующие условия § 4 главы XIII, нера-
венство (3.4) выражает условие устойчивости в предположении, что суммар-
ный коэффициент сопротивления положителен. При этом, согласно формулам
(2.38),(2.39) и (2.41) главы XIII,
aoi
где для двигателя асинхронною типа k* = —4/[а£(,'>(сТ(о)J/dco, а для синхрон-
ного двигателя k* — положительная постоянная.
632
ВРАЩЕНИЕ НЕУРАВНОВЕШЕННОГО РОТОРА
(ГЛ. XVIII
В равенстве (3.5) величина
2л/ы
L('n) (а, асо) = -£-о f L [стсо, а (со/ + а), 0, 0, асо/] dt =
о
<rL(0) (стсо) для двигателя
асинхронного
типа,
crL’[а (а — р)] для двигателя
синхронного
типа,
как и в § 6 главы ХШ, представляет собой средний за период
2л/(!> вращающий момент двигателя, вычисленный для поро-
ждающего решения (3.2) и отсчитываемый, в отличие от мо-
мента L, в направлении вращения ротора.
Величина
-/?>)==-[Яа(<о) + Яв(й)]	(3.7)
есть не зависящая от угла а часть среднего за период момента
сил сопротивления вращению ротора вибратора, также вычис-
ленного для решения (3.2) и отсчитываемого в направлении
вращения ротора вибратора. Момент Rb (со) связан с сопротив-
лением в подшипниках ротора дебалансного вибратора или
с сопротивлением перекатыванию ролика (кольца) планетар-
ного вибратора, а момент /?д(со) —с прочими сопротивлениями
движению ротора. При этом, вполне аналогично соответствую-
щей формуле (6.9) главы ХШ,
/й(со) =
у fme ddy
f'те'(ji-
nn я дебалансного
вибратора,
для планетарного
вибратора.
(3.8)
Напомним, что здесь f есть коэффициент сопротивления в под-
шипниках качения дебалансного вибратора, d — диаметр внут-
реннего кольца подшипников, а f'—коэффициент сопротивле-
ния перекатыванию тела качения планетарного вибратора.
Наконец, величина
W (а, со) = у meco2{/7 (cos а — hf sin а) 1-
+ aG [cos (а — fl) — hf sin (a — fl)]} (3.9)
представляет собой «вибрационный момент», то есть дополни-
тельный средний момент, действующий на ротор вибратора
вследствие колебаний его оси. Своеобразное поведение ротора
3] ОСНОВНОЙ РЕЖИМ СТАЦИОНАРНОГО ВРАЩЕНИЯ РОТОРА 633
вибратора с колеблющейся осью, в частности его стационарное
вращение при отсутствии двигателя (£<т) = 0), может быть объ-
яснено появлением указанного момента.
В результате простейших преобразований выражение (3.9)
для вибрационного момента можно представить в форме
w = Xtlp'cos +Ар/ “	(3-10)
где обозначено:
Л = | У G2 + H2 + 2<rG/7cosfl = у (а + о'Ь),
п_____________GH I cos е I__________
y'G2 + Н2- К(G2 + Н2)2 - 4G2/72 cos2 о ’
ь =___________рТ GH I cos е I_______
|/g 2 + Н2 + /(G2 + Я2)2 - 4G2Я2 cos2 "О’ ’	(3 [
о* — a sign (cos ft) = ± 1,
A cos% = y (H + oG cos ft),
Л sin % = у <tG sin ft,
tg p' = f'
Эти обозначения требуют некоторых пояснений. Прежде
всего, нетрудно заметить, что величины а и b представляют со-
бой соответственно большую и малую оси эллиптической траек-
тории колебаний. Указанная траектория определяется равен-
ствами (2.1), из которых, в частности, следует, что значениям
cos 'О' > 0 отвечает движение оси вибратора по эллипсу в на-
правлении хода часовой стрелки, а значениям cos О'<0 — про-
тив хода часовой стрелки. Поэтому величина ст* = о sign (cos О')
равна 1, если рассматривается вращение ротора в направле-
нии, совпадающем с направлением движения оси вибратора по
эллиптической траектории (2.1), и равна —1 при несовпадении
указанных направлений. Величину Л, играющую определенную
роль в дальнейшем, можно назвать эффективной амплитудой
колебаний оси вибратора. В соответствии с равенствами (3.11),
эффективная амплитуда равна полусумме полуосей эллипса
(2.1), если рассматривается вращение вибратора в направле-
нии движения его оси по эллиптической траектории (ст* = 1),
и равна полуразности полуосей при несовпадении указанных
направлений (а* = —1).
В случае прямолинейных колебаний оси а = 0 и b = Н, то
есть эффективная амплитуда попросту равна половине ампли-
туды колебаний оси вибратора. При колебаниях оси вибратора
634
ВРАЩЕНИЕ НЕУРАВНОВЕШЕННОГО РОТОРА
[ГЛ. XVIII
по окружности радиуса г0 = а = b эффективная амплитуда
А = г0, если рассматривается вращение ротора вибратора в том
же направлении, что и движение оси по окружности. В случае
же, когда указанные направления противоположны, эффектив-
ная амплитуда, а вместе с нею и вибрационный момент W
равны нулю.
Подводя итог, подчеркнем, что условием существования
основного режима вращения ротора вибратора является нали-
чие вещественных решений относительно а у уравнения (3.5).
Условие устойчивости движения, отвечающего определенному
корню этого уравнения, дается неравенством (3.4).
Следует иметь в виду, что, обеспечивая возможность и
устойчивость в малом основного режима вращения ротора ви-
братора, указанные выше условия еще не гарантируют возник-
новения этого режима при произвольных начальных данных.
Соответствующий вопрос, связанный с определением «области
притяжения» режима в фазовом пространстве системы, будет
рассмотрен в § 6 настоящей главы.
Наконец, отметим, что при квазиконсервативной идеализа-
ции вибратора (см. § 3 главы XIII и § 5 главы XIV) результат
исследования получается в точности таким же, как и выше. Это
легко установить, рассматривая соответствующие частные слу-
чаи формул п. 2 § 5 главы VIII или § 5 главы XIV.
2. Случай физического маятника (вибрационное поддержание
стационарного вращения). Рассмотрим вначале простейший,
однако, быть может, наиболее интересный с принципиальной
точки зрения случай, когда двигатель у вибратора отсутствует
или выключен (L<m> = 0), то есть вибратор превращается в фи-
зический маятник. В этом случае уравнение (3.5) при учете
равенства (3.10) может быть представлено в форме
Р (а, Ю)	- R° (М) - 2^- cos (а + hp') = 0,	(3.12)
а условие устойчивости (3.4) — в виде
sin (а 4-/гр') < 0.	(3.13)
При выполнении неравенства *)
о (	тМ	(3.14) v ’ cos йр
уравнение (3.12) допускает два существенно различных ре-
шения:
cq = — /гр' 4-6, а2 = — /гр' — 6
(л	Г (<о) cos/гр'1	\	(3.15)
(т < 6 = arccos [--------теДсоЗ J < ’
*) Отметим, что величина	по своему смыслу существенно поло-
жительна.
ОСНОВНОЙ РЕЖИМ СТАЦИОНАРНОГО ВРАЩЕНИЯ РОТОРА
635
§ 31
первому из которых, согласно (3.13), отвечает устойчивое,
а второму — неустойчивое вращение маятника со средней угло-
вой скоростью (О.
Условие существования (3.14) основного режима вибрацион-
ного поддержания вращения неуравновешенного ротора имеет
простой физический смысл: составляющая R°(<j)) среднего мо-
мента сил сопротивления вращению ротора не должна превы-
шать некоторого предельного значения Rma*(a)> равного, как
легко видеть, максимальному значению вибрационного момента
lF(a, со). Домножив обе части того же соотношения на со,
можно выразить его в энергетических терминах: мощность, не-
обходимая для преодоления момента сопротивления R°(a), не
должна превышать некоторого предельного значения:
Л^(со) = /?°(со)со<Л'тах((о) = ^^-.	(3.16)
Отметим, что указанная мощность может реально достигать
довольно больших значений. Так, например, для обычного (не
планетарного) физического маятника (/гр' = 0) со статическим
моментом mge = 1000 кгсм при эффективной амплитуде А, рав-
ной 0,25 см, и частоте колебаний а = л/г/30 = л3000/30 =
= 314 1/сек получаем
Л/тах (со) =----ggj----» 8 • 10” кГсм сек 800 кет.
Условие (3.14) приобретает особенно простой вид, если со-
противление вращению ротора (маятника) обусловлено преиму-
щественно сопротивлением в подшипниках качения (для обыч-
ного физического маятника) или сопротивлением перекатыва-
нию ролика или кольца (для «планетарного» маятника), а про-
чие сопротивления пренебрежимо малы. Тогда вместо (3.7)
можно принять
R° (и) = Rb (со),
и при учете равенств (3.8) условие (3.14) приобретает вид:
а)	для обычного маятника
(3.17)
б)	для «планетарного» маятника
— > sin р' = /—.	(3.18)
е к К1 + (/')2	v ’
Иными словами, в первом случае отношение эффективной
амплитуды колебаний к диаметру внутреннего кольца, а во вто-
ром — к эксцентриситету должно быть больше некоторой вели-
чины, зависящей от характеристик сопротивления. Если учесть,
636
ВРАЩЕНИЕ НЕУРАВНОВЕШЕННОГО РОТОРА
[ГЛ. XVIII
что значение коэффициента f для подшипников качения лежит
в пределах 0,001—0,01 (см., например, [36]), а коэффициент f'
редко превышает 0,3, то можно заключить, что условия (3.17)
и (3.18) являются достаточно «мягкими».
Из неравенств (3.17) и (3.18), как, впрочем, и из более
общих соотношений (3.14) и (3.16), следует, что условие под-
держания вращения маятника в направлении движения его
оси по эллиптической траектории является более «мягким»,
чем соответствующее условие для случая, когда указанные на-
правления противоположны (в первом случае эффективная ам-
плитуда А больше, чем во втором). В случае колебаний оси
по окружности в определенном направлении вращение маят-
ника в противоположном направлении вообще невозможно
(/1 = 0). Исключение составляет случай прямолинейных коле-
баний оси маятника, когда оба направления вращения совер-
шенно равноправны. Такой результат вполне согласуется с фи-
зическими соображениями.
3. Случай асинхронного вибратора. Если вибратор приво-
дится во вращение двигателем асинхронного типа, то, в соот-
ветствии с выражениями (3.6) и (3.10), основное уравнение
(3.5) записывается в форме
Р(а, оз) = аТ<Л) (aw) — Р° (оз) —cos (а +/гр') = 0, (3.19)
а условие устойчивости (3.4) совпадает с неравенством (3.13).
При выполнении соотношения
|о£<а)(™)-/?°(М)|<-^^	(3.20)
уравнение (3.19) допускает два существенно различных реше-
ния, одно из которых, как и в п. 2, устойчиво, а другое не-
устойчиво.
Обозначим через
Z°(a, ®) = аТ<а>(ам)-р°(м)	(3.21)
избыточный момент на валу вибратора, то есть превышение
момента, развиваемого двигателем, над моментом сил сопро-
тивления, а через
№(а>) = -^^-	(3.22)
у ' cos яр	4	’
наибольшее возможное значение вибрационного момента. Тогда
соотношения (3.19) и (3.20) могут быть представлены в форме
Р (а, со) = Z0 (а, и) — W (со) cos (а + /гр') = 0,	(3.23)
| Z0 (а, и) | < Г (<о).	(3.24)
§ 3] ОСНОВНОЙ РЕЖИМ СТАЦИОНАРНОГО ВРАЩЕНИЯ РОТОРА 637
Смысл условия (3.24) весьма прост: для существования
изучаемого режима избыточный момент не должен превышать
по абсолютной величине наибольшего возможного значения
вибрационного момента.
Рассмотрим условие (3.20) или, что то же самое, неравен-
ство (3.24) несколько подробнее. Предположим сначала, что
ось вибратора не колеблется. Тогда, в соответствии с уравне-
нием движения (2.2), угловая скорость вращения ротора в уста-
новившемся режиме определится из условия равенства вра-
щающего момента и момента сил сопротивления:
£<*> (ф°) = А?°(1 Ф° l)sign ф°.	(3.25)
Введем теперь, как и в п. 2 § 10 главы XIII, парциальную (соб-
ственную) угловую скорость вращения вала вибратора со*, от-
личающуюся от ф° лишь тем, что со* отсчитывается в направле-
нии вращения ротора вибратора в рассматриваемом движении,
а не по ходу часовой стрелки, как ф°. Тогда, очевидно,
со* = <тф°.	(3.26)
Отметим, что колебания оси вибратора в принципе могут
вызвать вращение его ротора в направлении, противоположном
тому, в котором его стремится вращать двигатель. В этом слу-
чае, отвечающем работе двигателя в генераторном режиме, мо-
жет оказаться, что оф° = со* < 0, то есть что парциальная ско-
рость отрицательна.
Заметим, что парциальная угловая скорость со* по своему
смыслу вполне соответствует частоте автоколебаний системы.
Пусть со* > 0; тогда, в силу равенств (3.25) и (3.26), спра-
ведливо соотношение
<тЛ(0) (стсо‘) = R° (со*).	(3.27)
Отсюда следует, что если парциальная угловая скорость со*
положительна и частота колебаний оси вибратора со совпа-
дает с со*, то условие (3.20) (или (3.24)) непременно выпол-
няется. Иными словами, если при отсутствии колебаний оси ро-
тора последний вращался в установившемся режиме с угловой
скоростью ф° = асо*, то при наличии колебаний частоты со = со*
этот ротор также сможет вращаться с той же угловой скоро-
стью. Рассматриваемый режим, однако, будет существовать и
в случае, когда частота колебаний со не совпадает с парциаль-
ной скоростью со*, а не слишком сильно от нее отличается, так
что вибрационный момент может скомпенсировать избыточный
момент Z°(o, со), то есть разность между моментом двигателя
и моментом сил сопротивления. Таким образом, будет, вообще
говоря, существовать интервал изменения частоты колебаний со
— Aj < со — со* < Д2,	(3.28)
638
ВРАЩЕНИЕ НЕУРАВНОВЕШЕННОГО РОТОРА
[ГЛ. XVH1
внутри которого вращение ротора вибратора «захватывается»
частотой внешнего возмущения; ширину этого интервала
А = А] + Аг часто называют полосой захватывания.
Рис. 66.
г)
Отметим, что полоса захватывания для рассматриваемой си-
стемы может быть достаточно широкой; в частности, как явст-
вует из предыдущего пункта настоящего параграфа, парциаль-
ная угловая скорость может быть равной нулю, то есть
вибратор может являться физическим маятником и, несмотря
§ 3j ОСНОВНОЙ РЕЖИМ СТАЦИОНАРНОГО ЁРАЩЕЙЙЙ РОТОРА 639
на это, захватываться колебаниями достаточно высокой ча-
стоты. Следует заметить также, что помимо интервала (3.28),
содержащего со*, могут существовать и иные области измене-
ния частоты <0, в которых существует рассматриваемый режим
вращения ротора.
Графическое построение, позволяющее выявить все такие
области, иллюстрируется рис. 66, где изображено несколько ва-
риантов взаимного расположения графиков функций crL(0) (стсо),
/?°(со), Z°(o, и) и W (со) = meAco2/cos /гр', входящих в условия
(3.20) или (3.24). На рис. 66, а представлена несколько схе-
матизированная типичная статическая характеристика асин-
хронного двигателя (см., например, [423]). На рис. 66,6 для
случая положительной парциальной скорости со* изображены
графики моментов ctL<°)(ct<o) и /?°(со); разность этих моментов
определяет избыточный момент Z°(o, ш). На рис. 66, в одновре-
менно нанесены графики функций Z°(a, со), W (со) и — W (со);
в соответствии с неравенством (3.24) область существования
изучаемого режима отвечает тем значениям частоты <г», для
которых кривая Z°(o, ы) лежит между кривыми W (со) и
— W (со). На рис. 66, в кривые ± 1К(со) изображены для двух
различных случаев: в одном случае имеется относительно узкая
полоса захватывания со] < со < со', содержащая парциальную
угловую скорость; во втором случае, когда максимально воз-
можный вибрационный момент W (со) = W" (со) относительно
больше, чем в первом, рассматриваемый режим имеет место
при любых со>со".
Аналогичные построения для варианта, когда парциальная
угловая скорость со* отрицательна, приведены на рис. 66, г и д.
Кривая стЛ(°)(асо) на рис. 66, г соответствует участку характери-
стики £(°)(ф), отвечающему ф^СО (см. рис. 66,а).
В одном из случаев (W (со) = W' (со)), согласно рис. 66, д,
изучаемый режим не существует ни при каких значениях ча-
стоты со; в другом случае (№ (со) = W" (со)> W' (со)) этот режим
существует при со>со".
Отметим, что в тех частях областей существования режима,
где момент aL(“>(crco) отрицателен (см. рис. 66,6—г), двигатель
работает в генераторном режиме; энергия, необходимая для
компенсации потерь на трение и для вращения вала двигателя,
поставляется вибрационным моментом.
В наиболее типичном случае, отвечающем кривым ± W(со)
и Z°(o, со) на рис. 66, в, функции Z°(or, со) и И7(со) при значе-
ниях со, близких к со*, мало отличаются от линейных. Этим
обстоятельством можно воспользоваться для приближенного
аналитического определения полосы захватывания (3.28).
640
ВРАЩЕНИЕ НЕУРАВНОВЕШЕННОГО РОТОРА
[ГЛ. XVIII
Действительно, линеаризируя указанные функции вблизи со = со*,
то есть полагая
Z° (о, со) = — kz (со — со*),
2	~	(3.29)
№(со) = Г (со*) + (со - со’),
где
_ _ д [gZ.(Q) (geo) — R° (со)] I
z	до
<Ж I	2/пеЛсо* _ п
uz----а — г ? > 9
9(0 |м=м, cos/гр'
(3.30)
находим
А
= со* — со
W (со*)
/гг + kw
.	. W (со*) zqqix
А2 = со2 —со = ,	.	(3.31)
Из формул (3.31) отчетливо видно отсутствие порога за-
хватывания — такого значения эффективной амплитуды колеба-
ний, при котором полоса захватывания пропадает. Для случая
обычной автоколебательной системы этот факт был установлен
А. А. Андроновым и А. А. Виттом [15, 18].
4. Случай синхронного вибратора. Если вибратор приво-
дится во вращение от синхронного двигателя, то предпола-
гается, что синхронная угловая скорость в точности совпадает
с частотой колебаний оси вибратора. Такая ситуация возможна,
например, в случае, когда колебания возбуждаются электро-
магнитным или каким-нибудь другим вибратором синхрон-
ного типа.
Основное уравнение (3.5), согласно (3.6) и (3.10), прини-
мает вид
Р(а, со)-аЛ*[а(а-р)]-/?°(со)--^^-соз(а + /гр'-Х) = 0. (3.32)
vuo
Пусть момент, развиваемый двигателем, определяется выра-
жением
Z,* (0) = — / sin 0.	(3.33)
Тогда уравнение (3.32) может быть представлено в форме
Р (a, со) = Q (со) sin (ф — а) — Д° (со) = 0,	(3.34)
где принято
Q cos ф = I cos р — W (со) sin (/гр' — %),
Q sin ф = I sin р — W7 (со) cos (/гр' — %)	(3.35)
(q = V/2+ r2(co)-2/r(co)sin ф + /гр'-х))
и использовано обозначение (3 22).
§ 4]
СУБРОТЛЦИОПНЫЕ РЕЖИМЫ ВРАЩЕНИЯ РОТОРА
641
При выполнении условия
/?° (со) < Q (со)
(3.36)
уравнение (3.34) допускает два существенно различных ре-
шения:
a, =i|)-arcsin-Q^-, а2 = ф - л + arcsin(3.37)
первому из которых, согласно (3.4) и (3.34), отвечает устой-
чивое, а второму—неустойчивое вращение ротора вибратора
со средней угловой скоростью со.
Заметим теперь, что в случае, когда колебания оси вибра-
тора отсутствуют, W (о)) = 0, и Q (со) = Z. При наличии колеба-
ний, согласно (3.35), величина Q(co)/Z в зависимости от значе-
ния установочного угла может изменяться в пределах
Г (со) | Q (со) |	! Г (со) |
Отсюда следует, что колебания оси синхронного вибратора
могут существенно изменить начальную фазу вращения рото-
ра а в устойчивом режиме. Более того, колебания оси вибра-
тора могут привести к появлению рассматриваемого режима
вращения ротора в случае, когда при неподвижной оси он отсут-
ствует, и, наоборот, — к исчезновению этого режима, когда при
неподвижной оси он имеется.
1
§ 4. Субротационные режимы вращения ротора
1. Условия существования и устойчивости субротационных
режимов. Изучение стационарных режимов вращения ротора ви-
братора со средней угловой скоростью, в целое число раз мень-
шей частоты колебаний со, более сложно, чем изучение основ-
ного режима. Для этих режимов, соответствующих plq = l//i
(п — 2, 3, ...), принятый в § 3 способ введения малого пара-
метра оказывается неудовлетворительным.
Действительно, если представить уравнение (2.2) для этого
случая в форме
+ k (ф — о = цф (ф, со/) (п = 2, 3, ...),	(4.1)
аналогичной форме записи уравнения (3.2), то для определе-
ния постоянной а в порождающем решении
о / 0) > .	\
ф ==о(-/+а)
(4.2)
21 И. И Блехман
642
ВРАЩЕНИЕ НЕУРАВНОВЕШЕННОГО РОТОРА
[ГЛ. XVIII
вместо (3.3) получим уравнение
2пп/<л
Р(а,а)^^^- J ф(ф°, ю/) dt^ [}т} (а,	- R° (-2-) = 0. (4.3)
о
В этом соотношении никак не отражается влияние вибраций
оси на величину фазы; к тому же эта фаза определяется лишь
для случая синхронного вибратора (см. равенство (3.6)).
В случае асинхронного вибратора фаза а не входит в урав-
нение (4.3), а в случае маятника (Я™) = 0) из этого уравнения
следует, что изучаемые режимы вообще невозможны.
В связи со сказанным сделаем несколько иные предположе-
ния о малости членов уравнения движения (2.2); при этом рас-
смотрим вначале случай н = 2 для дебалансного вибратора*).
А именно, положив
(ф, <р, со/) = — k (ф —+ mge cos ф —
— mea2 [Я sin mt sin ф + G cos (mt + 0) cos ф],
ц2Ф2 (ф, mt) = -у, ф,0,0,а-у^ —
— R [а -у , ф, — Яш2 sin а/, — Gm2 cos (mt + О), о],
представим указанное уравнение в виде
7ф = фЗф (ф, ф, mt) + ц2Ф2 (ф, mt),	(4.5)
причем, как и ранее, под величиной у, > 0 будем понимать
малый параметр.
Уравнение (4.5) отвечает квазиконсервативной идеализации
вибратора; такая идеализация не обязательна, однако в дан-
ном случае она приводит к менее громоздким выкладкам.
Решение уравнения (4.5), отвечающее рассматриваемому ре-
жиму, будем искать в виде ряда
ф = О [-у t + а + Цф1 (-у + ц2ф2 (т + • • • ] ’	<4-6)
/ (В ,\	,	(0 ,
где фг l-g-1\ — периодические функции аргумента	с пе'
риодом 2л.
*) Краткий обзор работ, посвященных изучению рассматриваемого ре-
жима, был приведен в § 1 настоящей главы. Здесь мы следуем, в основном,
работе [43].
§ 4]
СУБРОТАЦИОППЫЕ РЕЖИМЫ ВРАЩЕНИЯ РОТОРА
643
Порождающее решение ф° определяется формулой (4.2) и
зависит от одной произвольной постоянной а; для определения
функций и фг имеем уравнения
Zxp! = aOj (ф°, ф°, со/),
=	"Ф1 + СГф2 (<Р°>	(4'7)
где круглые скобки, в которые заключены производные от функ-
ции Фь как и выше, указывают на то, что они вычисляются
для порождающего решения.
При учете обозначений (4.4) первое из уравнений (4.7) при-
нимает вид
7ф! =	cos (-у- + aj — тгы’Н sin со/ sin (-у + a^ —
— omew2G cos (со/+ •&) cos ^-у +	.	(4,8)
Это уравнение, вне зависимости от значения а, допускает
периодическое (периода 4л/ю) решение
, 4те Г <тф {at .	\	1 r, (at \ ,
Hi  -----— cos	+ aj - у Н cos	- aj +
Д-у Ясоэ (уу + а) - у oG cos (-у- + <> — а) —
- -у aG cos (-^ + а + а)]+Х	(4.9)
где Ж— произвольная постоянная.
Таким образом, мы имеем здесь особый случай, когда усло-
вие периодичности первого приближения
Р (а, ®) = уу / Ф. (Фо, Фо dt = 0	(4.10)
о
удовлетворяется тождественно, не позволяя определить вели-
чину а. В соответствии с результатом Г. А. Мермана [291],
изложенным в § 10 главы V, в этом случае следует пытаться
найти постоянную а из условия периодичности следующих при-
ближений.
Для того чтобы допускало периодическое решение второе
уравнение (4.7), должно выполняться условие
4л/со
Q(a,	[(^)ф1 + (^-)ф1 + оФ2(ф0,(о/)]л = 0, (4.11)
о
644
ВРАЩЕНИЕ НЕУРАВНОВЕШЕННОГО РОТОРА
[ГЛ. XVIII
которое после выполнения интегрирования при учете равенств
(4.2), (4.4), (4.9) настоящего параграфа и соотношений (2.36),
(2.37) и (6.3) главы XIII может быть представлено в форме
Q (а, и) L(m) (а,	- /?° (-£-) - W (а) = 0.	(4.12)
Здесь моменты L<m) и R° имеют тот же смысл, что и в § 3,
а вибрационный момент И7(а) определяется выражением
W (а) — 2 [аН sin 2а + G sin (2а — "&)].	(4.13)
Введя эффективную амплитуду колебаний оси вибратора А и
угол х п0 формулам (3.11), можно представить выражение
(4.13) в виде
IT (а) = о 4 ('"О 4g sjn (2а — ^).	(4.14)
Уравнение (4.12) по своей форме вполне аналогично урав-
нению (3.5), однако по существу эти уравнения существенно
отличаются из-за различия в выражениях для вибрационного
момента W.
А именно, если в выражение (3.10) ускорение силы тяже-
сти g и момент инерции ротора I не входят, то в формуле
(4.14) они играют существенную роль. Напротив, в выражение
(4.14) не входит фигурирующий в (3.10) квадрат частоты ко-
лебаний со. В соответствии с этим, если условия существования
основного режима стационарного вращения ротора в различных
случаях совершенно не зависели от направления силы тяже-
сти, то в данном случае они будут существенно зависеть от
этого направления (см. ниже). В частности, в изучаемом здесь
случае вибрационный момент W обратился бы в нуль при вер-
тикальном расположении оси вибратора, в то время как в пер-
вом случае он сохранил бы свое значение.
Отметим, далее, что максимальные (по а) значения вибра-
ционного момента, как правило, будут значительно больше для
основного режима, чем для изучаемого субротационного. Дей-
ствительно, отношение
I 1Гтах (а) I _ 4mge _ 4g е_
I ^тах (а, со) I /со2 рсо2 р
(тр2 — 1)
(4.15)
обычно значительно меньше единицы, ибо радиус инерции боль-
ше эксцентриситета е, а ускорение рсо2 значительно превышает
ускорение силы тяжести.
Обратимся теперь к рассмотрению вопроса об устойчивости
движения. Отвечающее уравнению (4.5) и решению (4.6) урав-
нение в вариациях можно представить в форме
V = И [pi (t) Y + Qi (0 y] + И2 [р-2 (0 Y + (0 yL (4-16)
§ 4]	СУБРОТАЦИОННЫЕ РЕЖИМЫ ВРАЩЕНИЯ РОТОРА	645
где обозначено:
(,) = 7 [(тЙ +	+ (wO ' (4'|7)
,л 1 г/д2Ф, \ , . I д2Ф, \ , 1
&=т LhH	1 •
При у. = О уравнение (4.16) имеет кратный нулевой характе-
ристический показатель, и поэтому для решения вопроса об
устойчивости необходимо найти следующие приближения к ха-
рактеристическим показателям. Эти показатели, в соответствии
с изложенным в п. 7 § 3 главы III, будем искать, используя
подстановку
y = e6ty,	(4.18)
из условия периодичности функции у. Согласно (4.16) и (4.17)
эта функция должна удовлетворять уравнению
у = - 2бу - 62г/ + у (qxy 4- q{ бу -,L щу) + у2 (p,y + qty + q2 бу). (4.19)
Поскольку при у = О двукратному характеристическому по-
казателю 6о — О отвечает одна группа решений уравнения
(4.16), то согласно сказанному в п. 3 § 3 главы III, вообще
говоря, характеристические показатели 6 могут быть аналити-
ческими функциями не от у., а от у1/2. Однако в рассматривае-
мой задаче вследствие равенства
4Л/И
-J-J Р1(/)Л = 0,	(4.20)
о
вытекающего из формул (4.4) и (4.17), как можно убедиться,
эти показатели будут разлагаться по целым степеням у, то есть
их можно разыскивать в виде рядов
6 = фу + фу2 + .. .	(4.21)
(см. также [275], § 15, гл. III).
Решение уравнения (4.19) будем искать также в виде раз-
ложения
У = Уо (0 + уг/1 (0 + у2у2 (0 + •••	(4.22)
с 4л/ю-периодическими коэффициентами. Подставив ряды
(4.21) и (4.22) в указанное уравнение, получим, приравнивая
выражения при одинаковых степенях у, уравнения для опреде-
ления этих коэффициентов. Прежде всего находим, что у0 — 0.
Отсюда следует, что величина у0 должна быть постоянной;
646
ВРАЩЕНИЕ НЕУРАВНОВЕШЕННОГО РОТОРА
[ГЛ. XVIII
поскольку же интересующее нас решение (4.22) в принципе
определяется лишь с точностью до произвольного множителя,
то можно, не нарушая общности, положить
7о=1-	(4.23)
Для определения функции yt(t) получаем уравнение
Z/! = P1(O,	(4.24)
которое в силу равенства (4.20) допускает периодическое ре-
шение. Далее для функции У2 при учете (4.23) получаем диф-
ференциальное уравнение
У2 = Ф71 (0 + 71 (0 У\(0 + Pi V) У\ (0 + Р-2 (f) ~ 251 г/! (0 - 6?. (4.25)
Для того чтобы последнее уравнение допускало 4л/и-перио-
дическое решение, необходимо и достаточно, чтобы выполня-
лось равенство
4л/и
f [6171 (0 + 71 (0 7. (0 + Pi (0 71 (0 + Pi (0 ~ 26,7! (0 - 6?] dt = 0.
»	(4.26)
Это соотношение представляет собою квадратное уравнение
для определения первых приближений 6, к харатеристическим
показателям (4.21). Если учесть, что среднее за период значе-
ние производной от периодической функции 7,(/) равно нулю,
а также что, согласно (4.17) и (4.4), функция 7,(/) фактически
не зависит от времени t, то оно запишется в форме
4л/о	4л/ш
б>-б'-М	[71^71(П + р2(0]^ = 0. (4.27)
о	о
Для асимптотической устойчивости рассматриваемых реше-
ний (по крайней мере, при малом ц) достаточно, чтобы веще-
ственные части величин 6, были отрицательны; последнее усло-
вие в свою очередь сводится к требованию положительности
коэффициентов уравнения (4.27), то есть к неравенствам
4л/и
7,(/)с//<0,	(4.28)
О
4Л/(о
[Pl(t)yi^ + p-2(t)]dt<Q.	(4.29)
о
Если хотя бы одно из этих неравенств заменить соответ-
ствующим равенством, то получаются необходимые условия
§ 4]
СУБРОТАЦПОННЫЕ РЕЖИМЫ ВРАЩЕНИЯ РОТОРА
647
устойчивости; при выполнении же неравенств противополож-
ного смысла движение неустойчиво. Отметим, что в частном
случае, когда <?)(/) = (), сформулированный результат переходит
в полученный для соответствующего уравнения в монографии
[275]; неравенство (4.29) является при этом лишь необходимым,
но не достаточным условием устойчивости.
Составим неравенства (4.28) и (4.29) для изучаемой кон-
кретной задачи. Поскольку согласно (4.4)
(4.30)
то неравенство (4.28) выполняется автоматически, если только
справедливо принятое выше предположение о положительно-
сти суммарного коэффициента сопротивления k.
Обратимся к рассмотрению неравенства (4.29). При учете
обозначений (4.17) и (4.4) это неравенство представится
в форме
4л/со
со 1 f Г/ <M>i \	, ( <52Ф1 \ , . (<ЭФ2 \"l п	/л о с \
477 J Цтг) (/) + (тД + (тг) Jdt < °-	(4,31)
о
Сопоставим левую часть последнего неравенства с выра-
жением для производной dQjda, где Q — функция, определяе-
мая равенством (4.11). Заметим предварительно, что интеграл
от первого слагаемого в выражении (4.11) обращается в нуль,
поскольку ф>1 есть периодическая функция t с периодом 4л/ю
и, согласно (4.4), производная (дФ1/дф) = —k = const. Поэтому
4Л/С0
dQ _ ta 2 f Г/ д2Ф1 \ дф°	, / д2Ф1 \ дф°
da ~~ 4л	J [Ддфдф/ да \ д2ф ) да
о
+	+ а рэф^и (4.32)
1 \ Лр ] да \ <Э<р ) да J '	’
Но в силу равенства (4.2)
^ = а,'	^ = 0,	(4.33)
да ’ да ’	'	’
и, так как с2 — 1, то выражение (4.32) может быть представ-
лено в виде
4Л/й)
*0. “Д	+	(4.34)
da 4л r J |_\ дф j да \ д2ф )	\ дф /J '	'
о
Таким образом, левая часть неравенства (4.31) отличается от
выражения (4.34) лишь положительным множителем у,2 и тем,
что в первом слагаемом подынтегрального выражения вместо
648
ВРАЩЕНИЕ НЕУРАВНОВЕШЕННОГО РОТОРА
[ГЛ. XVIII
функции yi(Z) фигурирует dtyi/da. Но в силу равенств (4.24),
(4.17), (4.7) и (4.33) указанные функции удовлетворяют одина-
ковым дифференциальным уравнениям
,7 - 1 PM	(^i У'	1 (<M>i)
1 \ дер )’	\ да )	I \ дер Г
(4.35)
Поскольку функции у\ и д^/да— периодические по t с пе-
риодом 4л/ю, то отсюда следует, что они могут отличаться лишь
на постоянную. Но эта постоянная в данном случае несуще-
ственна, ибо среднее за период значение функции (дффдер)
равно нулю, и соответствующее слагаемое не дает вклада в вы-
ражение (4.31) или (4.34).
Таким образом, условие устойчивости движения (4.31) мо-
жет быть представлено в форме
4г < °.	(«в)
аналогичной форме записи условия устойчивости (3.4) основ-
ного режима.
Согласно равенствам (4.12) и (4.14) условие (4.36) сво-
дится к требованию
-ц'р Т)
da
dW ah \а- 2 /	8 (me)2 Л# ,п ,
----Та-----o^-^cos(2a-X)<0.
(4.37)
В заключение пункта заметим, что изучение субротационных
движений, отвечающих значениям p/q — п>2, имеет те же осо-
бенности, что и в случае p/q = 2, однако связано с более гро-
моздкими выкладками. Нетрудно видеть, что при рассмотрении
таких движений потребуется предполагать избыточный момент
L — R пропорциональным ц”, а фаза а будет определяться из
условия периодичности п-го члена разложения (4.6). На соот-
ветствующем исследовании останавливаться не будем.
2. Случай физического маятника. Если двигатель вибратора
отсутствует или выключен, то L<m) = О и уравнение (4.12) при
учете равенства (4.14) может быть представлено в форме
Q (a, со) = - R° (-у) - 4а (m-e^Ag- sin (2а - %) = 0,	(4.38)
а условие устойчивости (4.36) — в виде
a cos (2а — х) > 0.	(4.39)
При а — 1 последнее условие совпадает с полученными в рабо-
тах [426, 352] иными методами.
§ 4]
СУБРОТАЦИОННЫЕ РЕЖИМЫ ВРАЩЕНИЯ РОТОРА
649
При выполнении условия
DO ( ю \	4 (me)2 Ag
* \ 2 ) <	/
(4.40)
уравнение (4.12) имеет четыре
ния *) относительно а:
«1 = тНу + х)’
«з = л + 4(Y + X),
где обозначено:
существенно различных
а2 = 4 (л - у + х),
а4 = 4 (-л-V + x),
реше-
(4.41)
л
у < у = arcsin
R'
4а (me)2 Ag _
(4.42)
л
2 '
Нетрудно заметить, что двум из четырех решений (4.41) всегда
отвечают устойчивые, а двум — неустойчивые движения маят-
ника. Действительно, в силу (4.41) и (4.42)
cos (2а, - X) = cos (2а3 - х) = cos у > 0,
cos (2а2 — х) = cos (2а4 — х) = — cos у < 0.	\	)
Сопоставляя эти соотношения с (4.39), заключаем, что при
о=1, то есть при вращении маятника в положительном на-
правлении, устойчивым движениям отвечают первое и третье,
а при о = —1, то есть при вращении маятника в отрицательном
направлении, — второе и четвертое решения.
Относительно физического смысла условия существования
рассматриваемых режимов (4.39) здесь можно было бы по-
вторить дословно сказанное в п. 2 § 3 настоящей главы по
поводу условия (3.14). Как и последнее условие, неравенство
(4.39) можно представить в форме
=	=	(4.44)
\^/ \ £ \ “ / *
Различие СОСТОИТ, однако, В ТОМ, ЧТО МОЩНОСТЬ Afmax (4")
обычно значительно меньше мощности Мпах(ю), соответствую-
щей основному режиму вращения маятника. Так, в условиях
примера, приведенного в п. 2 § 3, и при 7=10 кГсмсек.2 полу-
чаем
.,(2)	10002 • 0,5 • 314	1 с 1 л4 г -1	1 с
Лг,пах =--10^981-- “ ,6 ' ° кГсМСвК 1	1,6 КВТ,
в то время как для Wmax(to) было получено значение 800 кет.
*) Прочие решения отличаются от (4.41) на 2лп, где п = ±1, ±2, ...
650
ВРАЩЕНИЕ НЕУРАВНОВЕШЕННОГО РОТОРА
[ГЛ. XVIII
Если сопротивление вращению ротора обусловлено главным
образом сопротивлением в подшипниках качения, так что мож-
но принять в соответствии с (3.8)
Я° (у) = R°B (у) = fme da?,
то условие (4.37) приобретает следующий вид:
Л	f /и2
d	32 mge.
(4.45)
(4.46)
Это условие также является обычно более жестким, чем со-
ответствующее условие (3.17) для основного режима (как пра-
вило, 7(o2/16/nge >1).
3. О случаях асинхронного и синхронного вибраторов. Ана-
лиз случая асинхронного вибратора, выполненный в п. 3 § 3 на-
стоящей главы для основного режима вращения, полностью
сохраняет силу и для рассматриваемого субротационного дви-
жения, если заменить избыточный момент Z°(o, и) и макси-
мальный вибрационный момент IF(co) соответственно следую-
щими выражениями:
7° (о, у и) = (у оси) - R° (f),
Г(2) = 4(Т ^-eW.	(4’47)
Различие, таким образом, будет состоять только в том, что
теперь максимальный вибрационный момент 1К<2> не зависит
от ®; это вызовет некоторое видоизменение кривых, представ-
ленных на рис. 66, и соответствующее изменение областей за-
хватывания. Кроме того, в данном случае устойчивы два раз-
личных движения, в то время как в случае основного режима
устойчивым было лишь одно. Сказанное вытекает из того об-
стоятельства, что условие устойчивости (4.39) сохраняет силу
и для асинхронного вибратора.
В случае синхронного вибратора при синхронной угловой
скорости, равной ы/2, имеют место те же качественные законо-
мерности, что и для основного режима (см. п. 4 § 3 настоящей
главы); здесь, однако, также возможно появление нескольких
устойчивых движений. На специальном рассмотрении этого слу-
чая останавливаться не будем.
§ 5. Связь между задачей о движении вибратора
с колеблющейся осью и задачей о синхронизации вибраторов
Задачу о вращении неуравновешенного ротора под действием колебаний
его оси можно толковать как идеализированный случай задачи о синхрониза-
ции вибраторов, когда все вибраторы являются значительно более «мощ-
ными», чем рассматриваемый, так что их движение допустимо считать не за-
§ 5]
СВЯЗЬ С ЗАДАЧЕЙ О СИНХРОНИЗАЦИИ
651
висящим от движения рассматриваемого вибратора и предполагать закон ко-
лебаний оси этого вибратора полностью заданным, если известно движение
остальных вибраторов. Иными словами, если, например, вибраторы асинхрон-
ные, то переход от задачи о синхронизации к задаче о вибрационном поддер-
жании вращения представляет собой типичный пример перехода от задачи
о внутренней синхронизации к задаче о внешней синхронизации (см. § 1
главы II).
Нетрудно показать, что основные результативные соотношения задачи
о вращении неуравновешенного ротора под действием колебаний его оси
могут быть получены из соответствующих соотношений задачи о синхрониза-
ции вибраторов в предположении, что отношение статического момента рас-
сматриваемого вибратора к статическим моментам прочих вибраторов доста-
точно мало.
Рассмотрим для конкретности задачу о синхронизации дебалансных ви-
браторов, связанных с квазилинейной колебательной системой, в случае, когда
непосредственная связь между роторами вибраторов (элементы системы при-
нудительной синхронизации) отсутствует и движение происходит вдали от
резонанса. Тогда, в соответствии с формулами (2.27) и (3.19) главы XIV,
уравнения для определения фаз вращения вибраторов вц, ..., будут
иметь вид
РДа1( .... ak, W)=J-(Z°-U7S) = O	(s=l.....k).	(5.1)
причем вибрационные моменты определяются выражениями вида
к
rs = rs(«l- ak> 0)=™^ 2 mieifsj(as~al’ “)’	(5-2)
где f8j(as — a;, co) —функции разностей фаз as и aj, а также и, конкретный
вид которых в данном случае роли не играет.
Пусть теперь статический момент первого вибратора значительно
меньше статических моментов /и2е2.wue* всех прочих вибраторов. Что
же касается избыточных моментов Zs = Zs (as, и), то будем считать, что они
имеют не менее высокий порядок малости, чем соответствующий вибрацион-
ный момент Ws. Последнее предположение естественно, ибо в противном слу-
чае колебания оси s-ro вибратора будут слабо сказываться на движении этого
вибратора; подобный случай не представляет для нас интереса. Но тогда,
если пренебречь в последних k— 1 уравнениях (5.1) величинами, содержа-
щими «181, то система (5.1) распадется на одно уравнение
a,(5.3)
и систему из k— 1 уравнений
к
Р’(а2, .... ak,
as — ajt и) =0. (5.4)
После того как из системы (5.4) будут независимо определены *) по-
стоянные а2.....as, их можно подставить в уравнение (5.3) и, вообще го-
воря, найти фазу вращения первого вибратора ось Но уравнение (5.3), по
*) Мы не оговариваем здесь для краткости особенностей, относящихся
к задаче о самосинхронизации (см., например, п. 2 § 2 главы XIV).
652
ВРАЩЕНИЕ НЕУРАВНОВЕШЕННОГО РОТОРА
[ГЛ. XVIII
существу, совпадает с основным уравнением (3.5) задачи о движении вибра-
тора под действием заданных колебаний его оси; это следует хотя бы из спо-
соба получения выражений для вибрационных моментов через гармониче-
ские коэффициенты влияния (см. § 3 главы XIV).
Рассмотрим теперь уравнение
-^--б ,х =0
да^ si
(s, /= 1, .... k),
(5.5)
от знаков вещественных частей корней которого зависит решение вопроса об
устойчивости движения (см. формулу (2.30) главы XIV). Поскольку, согласно
(5.1) и (5.2), первая строка и первый столбец определителя (5.5) содержат
члены порядка тще,, то это уравнение с точностью до членов более высокого
порядка может быть представлено в форме
*
<?р2
3------X
да2
	* дР,
дР\ \	О
да,	
~ * _ *
дР2	дР2
да,	'' ‘ да.
О	к
дР3	дР*3
5а3	’ ‘ ‘ dak
= 0.	(5.6)
дР\ да2	* * dPk	dPk 		... -Т	К
Отсюда следует, что условия устойчивости в рассматриваемом случае сво-
дятся к неравенству
^=<г<0	(5-7)
и к требованию отрицательности вещественных частей корней уравнения
dPs
,x =0
daj si
(s, j = 2............k).
(5.8)
Но условие (5.7) совпадает с условием устойчивости (3.4) соответствую-
щей задачи о вращении неуравновешенного ротора, а уравнение (5.8) служит
для решения вопроса об устойчивости движения в задаче о синхронизации
вибраторов с номерами 2, 3, ..., k.
Таким образом, из соотношений (5.1) и (5.5) задачи о синхронизации k
вибраторов в случае, когда вибраторы с номерами 2, 3, .... k имеют значи-
тельно большие статические моменты, чем первый вибратор, мы получили со-
отношения (5.3) и (5.7), определяющие решение задачи о движении первого
вибратора под действием заданных колебаний его оси; указанные колебания
при этом отвечают устойчивым решениям задачи о синхронизации более мощ-
ных вибраторов, определяемым соотношениями (5.4) и (5.8). Тем самым и
устанавливается соответствие между двумя сопоставляемыми задачами*).
*) Приведенное выше рассмотрение легко обобщается на случай несколь-
ких вибраторов с относительно малыми статическими моментами: для ка-
ждого из таких вибраторов тем же путем получается независимая задача
о вибрационном поддержании вращения, если известно (также определяемое
независимо) устойчивое синхронное движение вибраторов с «немалыми» ста-
тическими моментами.
§ ы
СВЯЗЬ С ЗАДАЧЕЙ О СИНХРОНИЗАЦИЙ
653
Разумеется, вопрос о действительном нахождении предельных значений
отношений статических моментов т1е1//м282, ...,	при которых еще
допустимо «расщепление» системы с k вибраторами на две последовательно
рассматриваемые системы, состоящие из k—1 и одного вибратора, остается
открытым и каждый раз должен решаться особо. Впрочем, можно указать
случаи, когда имеется полное соответствие между задачами о синхронизации
п о движении вибратора с колеблющейся осью вне зависимости от соотно-
шения между статическими моментами вибраторов.
Рассмотрим, например, задачу о самосинхронизации двух асинхронных
дебалансных вибраторов в предположении, что силами сопротивления в коле-
бательной части системы можно пренебречь. Тогда, согласно соотношениям
(3.28) главы XIV,
Wi = — 31^2 = И>12 (а1 ~ а2’ ®)	(5.9)
и уравнения
p2^-L(z°2-w2) = o (5.10)
д И<2 \
доч /
1 \ дГ. I 1	1 \ дР
приведут в точности к тому же равенству для определения разности фаз
ai — «2 = а, что и уравнение
которое получилось бы, при рассмотрении движения первого вибратора под
действием колебаний его оси, возбуждаемых вторым вибратором, вращаю-
щимся с угловой скоростью со и с начальной фазой а2. Поскольку, далее, из-
быточные моменты Zl в рассматриваемом случае не зависят от а, и а2, то
= д(Р1-Р2) = _ /Д_	_ _L
да.1	\ й] доч k2
= - (-4- +-7—I |-£- + Т-|
\ k\ &2 / t'ttj \ k\ П2 / UCC(
и поэтому условие устойчивости синхронных движений х<0 также совпа-
дает с условием устойчивости (3.4).
Нетрудно показать, в частности, что условие возможности вибрационного
поддержания вращения маятника (выключенного вибратора) в системе, изо-
браженной на рис. 32, полученное из решения задачи о синхронизации (см.
неравенство (16.33) главы XIII), вполне эквивалентно неравенству (3.17) на-
стоящей главы в том смысле, что выражение
,	1 mte, I Mr2 ,,	,1
Л = у | -у----------(И-ОГ1ОГ2)	(5.13)
совпадает с выражением для эффективной амплитуды колебаний А оси вто-
рого вибратора, возбуждаемых первым вибратором.
Пусть, для конкретности, первый вибратор (см. рис. 32) вращается по
закону (pi — (dt, то есть оч = 1. Тогда, как нетрудно видеть, ось второго ви-
братора в режиме установившихся вынужденных колебаний будет двигаться
по закону
«181	.	«161 (, Mr2 \ .	.	. .,
х2=-----— cos ш/, у2 = —II-------------— I sin юЛ (5.14)
Отсюда следует, что при Мг'-!П < 1 ось второго вибратора будет пробе-
гать свою эллиптическую траекторию по ходу часовой стрелки, а при Мг2/1 >
> 1 —против часовой стрелки. Поэтому при <г2 = 1, то есть в случае 04СГ2 = 1>
654
ВРАЩЕНИЕ НЕУРАВНОВЕШЕННОГО РОТОРА
[ГЛ. XVIII
за эффективную' амплитуду Л следует принимать полусумму (а + 6) полу-
осей эллипса (5.14), если Мг2Ц < 1, и полуразность полуосей -~(а—Ь), если
Мг2/1 > 1. При <т2 = —1, то есть в случае о/Щг = —1, следует руководство-
ваться противоположным правилом. Но согласно (5.14)
и поэтому, в соответствии с (3.10), при ащ2 = 1
1 /77,81 Mr2 \
2 М {	1 )
1 777,81 С Mr2	\
2	М	\ 1	)
при
при
^>2
(5.16)
И при ОЩ2 = —1
.	1 /77 [8, Air2
Д — __ 1 1 ________
2 М I •
(5.17)
Но равенства (5.16) и (5.17) объединяются одной формулой, которая совпа-
дает с формулой (5.13), что и требовалось показать. Таким образом, условия
(16.33) главы XIII и (3.17) настоящей главы, полученные различным путем,
действительно являются эквивалентными в указанном выше смысле.
§ 6. Об условиях возбуждения стационарных
режимов вращения
Полученные выше условия существования и устойчивости
(в малом) стационарных режимов вращения ротора с колеб-
лющейся осью еще не обеспечивают возникновения этих режи-
мов при произвольных начальных условиях: такая ситуация
имела бы место лишь в случае устойчивости указанных режи-
мов «в большом». Поэтому представляет значительный при-
кладной интерес определение «областей притяжения» рассмот-
ренных режимов в фазовом пространстве системы. Последнее
для изучаемой системы трехмерно — за фазовые координаты
могут быть приняты, например, <р, ф и t. Это предопределяет
сложность задачи, ибо достаточно универсальные и эффектив-
ные методы исследования и построения фазовых траекторий
разработаны лишь для одно- и двумерных систем.
Укажем вначале один частный случай задачи, в котором
последняя сводится к двумерной и допускает аналитическое
решение. Пусть речь идет о роторе с вертикальной осью, совер-
шающей поперечные поступательные колебания по круговым
§6] О ВОЗБУЖДЕНИИ СТАЦИОНАРНЫХ РЕЖИМОВ ВРАЩЕНИЯ 655
траекториям радиуса г0; мгновенный избыточный момент L — R,
действующий на ротор, будем считать постоянным. Уравнение
движения ротора в данном случае получится из (2.2), если
принять
g = 0, С = Я = г0, Ф = 0.	(6.1)
Это уравнение будет иметь вид
/ф + /гф = — mer0co2 cos (ф — со/) + L — R -1  k	стсо.	(6.2)
Положив (см. рис. 65, а)
Ф = 0 + со/—L — R + k — стсо = Т = const, (6.3)
z	q
представим уравнение (6.2) в форме
/0 + kQ + mer0co2 sin 0 = Т.	(6.4)
Последнее уравнение представляет собой хорошо известное
уравнение движения «маятника с постоянным моментом», суще-
ственное в теории синхронных электрических машин [22, 442,
476, 491]. Вопрос об определении областей начальных условий по
углу 0, приводящих к колебательным и вращательным движе-
ниям по углу ф, рассмотрен, например, в работах [2, 296,
29, 234]. Особенно просто вопрос решается в случае k = 0,
Т = 0. Рассматривая интеграл энергии, нетрудно, например, за-
ключить, что при начальных условиях
0(О) = О (ф(0)=-|),
0 (0) < 0* - 2со ]/(6.5)
(ф (0) < ф* = 0* + со = со (1 + 2	}
имеет место колебательное, а при 0(0) = 0 и 0(О)>0* (то есть
при ф(О)>ф*)—вращательное движение ротора.
Ряд вариантов задачи, не сводящихся к двумерному
случаю, был решен с помощью электронных вычислительных
машин.
Э. А. Аграновская [2] рассмотрела уравнение (6.4) при
Т = 0, но при наличии в правой части члена —mgesinO, отра-
жающего влияние силы тяжести (рассматривался ротор с го-
ризонтальной осью). Для интегрирования уравнения исполь-
зовалась моделирующая установка МН-7 в сочетании с функ-
циональным устройством, позволяющим получать функции
sin 0 и cos0 в неограниченном диапазоне изменения 0. Было
656
ВРАЩЕНИЕ НЕУРАВНОВЕШЕННОГО РОТОРА
[ГЛ. XVIII
установлено, в частности, что при значениях параметра
с = тггй11, больших некоторого значения с*, то есть при доста-
точно больших амплитудах колебаний г0, захватывание ротора
в основной режим вращения происходит даже в случае нулевой
начальной угловой скорости. При с < с* захват осуществляется
лишь при сообщении некоторой начальной скорости, отличной от
нуля. С увеличением параметров ао = k/Ia и b0 = tngfJlM2 в из-
ученном диапазоне их изменения значение с* возрастает.
По более широкой программе изучение движения маятника
с горизонтальной осью, совершающей прямолинейные гармони-
ческие колебания, было выполнено А. А. Митулисом [296]; при
этом предполагалось, что помимо момента вязкого сопротивле-
ния па ротор действует также момент сил сухого трения, а вра-
щающий момент L отсутствует. Изучение процесса установления
проводилось графо-аналитическим методом, а также с по-
мощью моделирующей установки МНБ-1. Автор пришел к вы-
воду, что если движение маятника возбуждается сообщением
ему начальной скорости, то вращение легче всего возникает
в случае, когда величина начальной скорости близка к средней
скорости его вращения в стационарном режиме. Изменение
частоты, амплитуды и начальной фазы колебаний оси меняет
предельные значения начальной скорости, при которых воз-
буждается вращательное движение.
Гораздо труднее возбудить вращение маятника приданием
ему некоторого начального отклонения при нулевой начальной
скорости. Начальное отклонение чаще всего возбуждает только
колебательный процесс, и для того, чтобы последний переходил
во вращение, амплитуда колебаний оси должна быть относи-
тельно велика.
Условие возбуждения вращения маятника в большой сте-
пени зависит также от величины сил сопротивления, от частоты
и амплитуды колебаний точки подвеса.
Силы сопротивления затрудняют возбуждение вращения
маятника. С увеличением сил сопротивления увеличиваются
минимально необходимые значения начальной скорости, при
которых возбуждается вращение. В случае придания маятнику
начального отклонения увеличение сил сопротивления приводит
к увеличению значения амплитуды колебаний оси, при котором
колебательный процесс переходит во вращение. Однако силы
сопротивления уменьшают длительность переходного процесса.
Увеличение частоты колебаний точки подвеса расширяет
диапазон значений начальной скорости, в котором возбуждается
вращение маятника; если же вращение возбуждается приданием
маятнику начального отклонения, то увеличение частоты коле-
баний точки подвеса затрудняет условия возбуждения вра-
щения.
const,
(6.7)
§6] о возбуждении стационарных режимов ВРАЩЕНИЯ 657
Увеличение амплитуды колебаний точки подвеса облегчает
условия возбуждения вращательного движения независимо от
того, какие начальные условия маятнику сообщаются.
Если амплитуда колебаний точки подвеса превышает опре-
деленную величину, то наступает «мягкое» возбуждение вра-
щения, то есть вращение возбуждается при любых начальных
условиях.
В работе 3. С. Баталовой [29] рассматривался случай ротора
с вертикальной осью вращения, совершающей прямолинейные
гармонические колебания; помимо момента сил вязкого сопро-
тивления предполагалось наличие постоянного крутящего мо-
мента. В указанных предположениях уравнение движения ро-
тора (2.2) может быть приведено к виду
+ ^!-4^-= Afj — XsinTsintp,	(6.6)
dx2 1 dx 1	'	'
где
L — R+ k~ no
T = co/, hx =	, Mi =
. mzH
причем H есть амплитуда колебаний оси ротора.
Исследование проводилось путем сведения задачи к точеч-
ному преобразованию плоскости в плоскость с применением для
построения этого преобразования цифровой электронной вы-
числительной машины М-20. Особое внимание было уделено
вопросам, связанным с ограниченной точностью вычислитель-
ной машины, с ограниченным временем, в течение которого
можно реально вести интегрирование, а также с тем обстоя-
тельством, что при изучении поведения траекторий в фазовом
пространстве практически всегда можно «перебрать» лишь ко-
нечное число начальных точек. Все эти обстоятельства приво-
дят к тому, что результаты исследования режимов движения
динамических систем с помощью цифровых вычислительных
машин являются лишь правдоподобными [30]. Степень точности
и достоверности результатов определяется заданием некоторых
постоянных, характеризующих время интегрирования, расстоя-
ние между «пробными» точками в фазовом пространстве, пре-
дельную «сложность» изучаемых режимов и т. п.
В цитируемой работе поведение системы изучалось в обла-
сти пространства параметров, определяемой неравенствами
Л>0, 0<Л1<3, 0<М1<2,5.
658
ВРАЩЕНИЕ НЕУРАВНОВЕШЕННОГО РОТОРА
[ГЛ. XVIII
Было, в частности, установлено, что при <М( = 0 в области
h\ (1,8 -0,4/ii) + 0,5 <л<
Ml + 0,85^)+ 1,1
при 0</i! < 1,65,
0,9/?! + 3,4
при 1,6 </?i< 2,25
(6.8)
при любых начальных значениях <р(0) и ф(0) устанавливается
основной режим вращения ротора в положительном или отри-
цательном направлении (|фср| = со).
При Mi > 0 основной режим вращения существует в области
2Mi + 0,2+ hi (^V2j-3,7)>Z>
2,35 (hi-Mi)
при hi Mh
2hrl(Mt-hi)
(6-9)
при hi < Mi.
3, С. Баталовой были обнаружены и частично изучены
также и более сложные движения ротора.
ГЛАВА XIX
ЭКСПЕРИМЕНТАЛЬНЫЕ ИССЛЕДОВАНИЯ
СИНХРОНИЗАЦИИ ВИБРАТОРОВ
§ 1.	Предварительные замечания. Цели экспериментального
исследования
Как уже отмечалось, явление самосинхронизации механиче-
ских вибраторов было впервые экспериментально обнаружено
в Советском Союзе в 1947—1948 гг. в процессе работ по созда-
нию вибрационных устройств, проводившихся в институте
«Механобр» под руководством Д. А. Плисса. В дальнейшем,
после разработки теории синхронизации вибраторов автором и
его сотрудниками, в том же институте были выполнены спе-
циальные эксперименты по сравнительно широкой программе.
Изложение результатов этих экспериментов и составляет основ-
ное содержание §§ 2—4 настоящей главы. Краткий обзор дру-
гих экспериментальных работ приведен в заключительном, пя-
том параграфе.
Проводившиеся в институте «Механобр» опыты преследо-
вали в основном две цели:
1)	Проверку некоторых выводов теории и в особенности
тех, которые могут быть эффективно использованы для усовер-
шенствования существующих и для создания новых вибрацион-
ных машин и установок*).
2)	Изучение вопросов, существенных при проектировании
вибрационных машин, но не получивших полного разрешения
в рамках теоретического исследования.
Важнейшим из таких вопросов является вопрос об условиях
установления синхронных движений. Дело в том, что выполне-
ние теоретически найденных условий существования и устойчи-
вости (в малом) синхронных движений вибраторов обеспечи-
вает наличие и устойчивость этих режимов при достаточно
малых возмущениях, однако еще не гарантирует возникновения
*) Причины, по которым указанные теоретические результаты требуют
експериментальной проверки, подробно обсуждены в четвертой главе книги.
660
ЭКСПЕРИМЕНТАЛЬНЫЕ ИССЛЕДОВАНИЯ СИНХРОНИЗАЦИИ [ГЛ. XIX
этих синхронных движений при реально встречающихся в кон-
кретной системе начальных условиях.
Между тем для возможности использования синхронизации
в вибрационных машинах необходимо быть уверенным не
только в том, что необходимое синхронное движение вибраторов
будет устойчиво поддерживаться, однажды возникнув, но также
и в том, что именно это, а не какое-либо иное движение действи-
тельно установится в результате включения двигателей.
Иными словами, для выяснения возможности практического
применения того или иного способа синхронизации вибраторов
и особенно самосинхронизации большое значение имеет изуче-
ние условий захвата системы в требуемый синхронный режим.
С математической точки зрения мы сталкиваемся здесь с за-
дачей о поведении системы «в большом», а именно с задачей
выделения в расширенном фазовом пространстве системы та-
ких областей начальных значений фазовых координат и вре-
мени, которые приводят к установлению требуемого синхронного
движения. Эта весьма трудная задача в настоящее время исчер-
пывающе решена лишь для некоторых простейших систем, и
поэтому в подавляющем большинстве случаев, в том числе и
при рассмотрении явлений синхронизации, приходится прибе-
гать либо к экспериментальному исследованию, либо к изуче-
нию системы с помощью вычислительных машин (см. § 2
главы VI, а также § 6 главы XVIII).
§ 2.	Описание экспериментальных установок
и техники экспериментов
Для решения поставленных выше вопросов в институте
«Механобр» было разработано и изготовлено несколько спе-
циальных экспериментальных стендов и установок, а также
создан ряд моделей вибрационных машин с самосинхронизи-
рующимися и электрически синхронизированными вибраторами.
Помимо опытов, поставленных на этих устройствах, большой
цикл экспериментов проведен на реальных машинах и установ-
ках лабораторного и промышленного типа. Описания указан-
ных устройств и сведения о результатах соответствующих экс-
периментов приводятся в пятой части книги.
Основными средствами эксперимента были скоростная кино-
съемка, фотографирование быстро движущихся объектов с ма-
лыми экспозициями и наблюдение за такими объектами при
стробоскопическом освещении с регулируемой частотой вспы-
шек лампы.
Общий вид одной из экспериментальных установок приво-
дится на рис. 67; эта установка была рассчитана и спроекти-
рована А. И. Макаровым и автором.
Рис. 67.
662
ЭКСПЕРИМЕНТАЛЬНЫЕ ИССЛЕДОВАНИЯ СИНХРОНИЗАЦИИ [ГЛ. XIX
Основной частью установки является жесткий вибрирующий
орган 1 (несущее тело), выполненный в виде трубы с наруж-
ным диаметром около 100 мм и длиной около 600 мм. В трубе
размещены три дебалансных вибратора 2 с горизонтальными
осями (рис. 67, а). При этом средний дебалапсиый вибратор
может быть легко заменен планетарным вибратором того или
иного типа; рис. 67, б отвечает случаю, когда такой планетарный
вибратор образуют два симметрично расположенных стакана 9,
в которые могут свободно вкладываться цилиндрические ро-
лики. Ось среднего вибратора проходит через центр тяжести
вибрирующего органа, а оси крайних лежат в одной плоскости
с осью среднего и равноудалены от нее.
Дебалансные вибраторы приводятся во вращение от уста-
новленных на раме двигателей 3 через гибкие резиновые ва-
лики 10. Неуравновешенные грузы вибраторов выполнены
в виде круглых шайб 11, имеющих в центральной части отвер-
стия с резьбой. Меняя расположение шайб на радиальных
стержнях — винтах, укрепленных на роторах вибраторов, можно
легко изменять в широких пределах их статические моменты.
Каждый из дебалансных вибраторов снабжен специальными
тормозами 4, посредством которых можно изменять момент
сопротивления вращению вибратора и тем самым его парциаль-
ную угловую скорость (см. п. 2 § 10 главы XIII).
Вибрирующий орган (несущее тело) подвешен к раме 8 на
двух мягких пружинах 5, жесткость которых выбрана настолько
малой, чтобы частоты собственных колебаний вибрирующего
органа не превышали 1/8 от угловой скорости вращения ви-
браторов. Кроме того, вибрирующий орган может связываться
с рамой системой упругих стержней 6 круглого поперечного
сечения. Активную длину стержней можно легко изменять, пе-
ремещая кронштейн 7 вдоль рамы. Это позволяет варьировать
жесткость упругой системы и тем самым частоты собственных ко-
лебаний вибрирующего органа в достаточно широких пределах.
При горизонтальном расположении осей упругих стержней,
показанном на рис. 67, а, вибрирующий орган имеет три суще-
ственные степени свободы, так как он может произвольным
образом перемещаться в вертикальной плоскости. Установка
допускает, однако, возможность вертикального расположения
осей стержней; при этом вибрирующий орган, ввиду горизон-
тального расположения осей вибраторов, имеет всего лишь
одну существенную степень свободы, отвечающую перемещению
вдоль оси трубы, то есть в направлении, перпендикулярном
осям стержней.
Жесткость вибрирующего органа обеспечена достаточно
большой, чтобы исключить возможность возникновения в нем
существенных упругих колебаний.
§ 2]	ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНЫХ УСТАНОВОК	663
В установке могли быть использованы для привода вибра-
торов любые двигатели, однако все описываемые ниже экспери-
менты проводились с обычными асинхронными короткозамкну-
тыми электродвигателями типа АОЛ 12/4 (пСипхр = 1500 об/мин,
Ниом = 1400 об/мин, Nnntt = 0,18 кет).
Ряд результатов теории самосинхронизации вибраторов был
проверен на универсальном вибрационном стенде, предложен-
ном Б. П. Лавровым и автором [66] и также изготовленном
в институте [Механобр»; фото этого стенда приведено на
рис. 106, а описание — в § 8 главы XX.
Конструкция стенда позволяет произвольным образом варьи-
ровать углы наклона осей вибраторов в вертикальных плоско-
стях, а также закреплять в вибрирующем органе дополнитель-
ные планетарные вибраторы или колебательные системы. Это
дало возможность проверить на стенде результаты решения
задач о самосинхронизации вибраторов в «пространственном»
случае, а также выводы, относящиеся к самосинхронизации ви-
браторов, связанных со сложными колебательными системами.
Для исследования самосинхронизации моно- и полигармони-
ческих дебалансных вибраторов и механических вибраторов
направленного действия, а также для изучения вопросов
использования явления самосинхронизации при установке не-
скольких неуравновешенных машин на групповом фундаменте
в институте «Механобр» был спроектирован*) и изготовлен
специальный вибрационный стенд.
Схема стенда представлена на рис. 68, а, а его фото — па
рис. 68, е. Стенд состоит из жесткого стола 1, связанного с не-
подвижной рамой системой пружин 2 и демпфирующих элемен-
тов 3\ параметры тех и других можно менять в относительно
широких пределах. К столу может крепиться до четырех и бо-
лее универсальных моделирующих вибраторов 4. Каждый та-
кой вибратор включает несколько кинематически связанных
валов с изменяемым передаточным отношением между ними.
На концы валов могут быть установлены неуравновешенные
грузы с легко варьируемым статическим моментом, а также
эксцентрики кривошипно-шатунных механизмов; «поршни» этих
механизмов играют роль возбудителей направленных возму-
щающих сил; амплитуды сил могут изменяться путем изменения
масс «поршней». Схемы вибраторов, которые могут моделиро-
ваться универсальными вибраторами стенда, представлены па
рис. 68,6—д; рис. 68,6 отвечает простому дебалансвому вибра-
тору, рис. 68,s — бигармоническому дебалапсному, рис. 68, г—•
моногармопическому поршневому и рис. 68,6 — бигармониче-
*) Разработка конструкции стенда выполнена Л. Г. Троицкой ц
Я. А. Гольдштейном под руководством Б. П. Лаврова п автора.
664
ЭКСПЕРИМЕНТАЛЬНЫЕ ИССЛЕДОВАНИЯ СИНХРОНИЗАЦИИ [ГЛ. XIX
скому поршневому. Головки, в которых смонтированы универ-
сальные вибраторы, могут быть закреплены на раме в различ-
ных положениях; в частности, осям вибраторов можно прида-
вать не только горизонтальное, но и вертикальное положение.
Рис. 68.
Наибольшее значение возмущающей силы, развиваемой
одним вибратором, может достигать 200 кГ. Привод вибраторов
осуществляется от универсальных коллекторных электродвига-
телей или от двигателей постоянного тока, с тем чтобы обеспе-
чивалось легкое регулирование числа оборотов.
Для проведения серии опытов по изучению условий уста-
новления основного режима стационарного вращения планетар-
§ 31	ПРОВЕРКА ВЫВОДОВ ТЕОРИИ САМОСИНХРОНИЗАЦИИ	665
кого вибратора с колеблющейся заданным образом осью был
использован лабораторный истиратель проб руды, разработан-
ный в институте «Механобр» А. И. Макаровым. Основной
частью истирателя (рис. 69) является стакан 1, со внутренним
диаметром 2R = 60 мм, которому сообщаются круговые посту-
пательные колебания с помощью эксцентрикового механизма,
заключенного внутри корпуса 2. Механизм допускает плавное
изменение амплитуды круговых колебаний от нуля до 10 мм.
Рис. 69.
В стакан истирателя свободно вложен цилиндрический ро-
лик 3, который под воздействием колебаний может обкаты-
ваться внутри стакана. Крышка стакана 4 выполнена в виде не-
полного кругового кольца, через отверстие которого ролик в
процессе опытов может наблюдаться при стробоскопическом
освещении.
Привод установки осуществляется через клиноременную пе-
редачу от асинхронного электродвигателя 5; частота колебаний
стакана изменяется путем замены шкивов передачи.
§ 3.	Проверка некоторых выводов теории
самосинхронизации вибраторов
Экспериментальной проверке на описанной в § 2 настоящей
главы установке (рис. 67) был подвергнут ряд выводов теоре-
тического исследования, существенных для разработки новых
вибрационных машин.
Вращающиеся роторы вибраторов наблюдались при стробо-
скопическом освещении с регулируемой частотой вспышек. При
совпадении числа вспышек в минуту с числом оборотов вала
вибратора последний казался неподвижным. Такой метод по-
зволял не только следить за одинаковостью средних скоростей
see ЭКСПЕРИМЕНТАЛЬНЫЕ ИССЛЕДОВАНИЯ СИНХРОНИЗАЦИИ [ГЛ. XIX
вращения роторов (то есть констатировать самосинхронизацию
или ее отсутствие), но и наблюдать за средними значениями
фаз вращения вибраторов. Кроме того, для получения более
точных и объективных данных работающая установка фотогра-
фировалась с весьма малыми экспозициями (1/1250 и
1/2500 секунды); при этом на снимках получалось почти не
«размытое» изображение небалансов.
Одна из серий опытов относилась к случаю самосинхрони-
зации двух одинаковых дебалансных вибраторов, симметрично
расположенных на мягко амортизированном вибрирующем
органе.
Теоретически этот случай был подробно рассмотрен в п. 2
§ 16 главы ХШ, где установлено (см. формулу (16.26)), что
при вращении обоих вибраторов в одинаковых направлениях
в случае выполнения неравенства
устойчивым является синфазное вращение вибраторов, приво-
дящее к круговым поступательным колебаниям вибрирующего
органа, а при выполнении противоположного неравенства —
противофазное вращение, которому отвечают чисто поворотные
колебания вибрирующего органа. В случае вращения вибрато-
ров в противоположных направлениях устойчивым всегда яв-
ляется только противофазное вращение, обусловливающее пря-
молинейные поступательные колебания вибрирующего органа
в направлении, перпендикулярном плоскости осей вращения
вибраторов.
Все упомянутые результаты полностью подтвердились экс-
периментально.
На рис. 70 и 71 представлены фотоснимки работающей уста-
новки с двумя вибраторами, полученные при экспозиции
1/2500 секунды.
Рис. 70, а— в соответствуют случаю вращения вибраторов
в одинаковых направлениях (aia2=l). При этом в условиях
рис. 70, а и б соотношение (3.1) выполняется, а в условиях
рис. 71—не выполняется; рис. 70, а отвечает обоим включен-
ным в сеть двигателям вибраторов, а рис. 70, б — только од-
ному включенному двигателю: вращение вибратора с выклю-
ченным двигателем в данном случае устойчиво поддержи-
вается благодаря колебаниям вибрирующего органа установки
(см. ниже).
В условиях рис. 71 вибраторы вращаются в различных на-
правлениях (щетг =—1), причем рис. 71,а соответствует обоим
включенным в сеть двигателям, а рис. 71,6 — одному выклю-
ченному двигателю.
§ 3]
ПРОВЕРКА ВЫВОДОВ ТЕОРИИ САМОСИНХРОНИЗАЦИИ
667
Как видно из приведенных фотоснимков, фазировка враще-
ния вибраторов во всех случаях полностью соответствует най-
денной теоретическим путем. Выключение двигателя одного из
двух работающих вибрато-
ров из сети в условиях опы-
Рис. 70.
тов, как это и должно было
получаться согласно теории,
приводило лишь к неболь-
шому уменьшению угловой
скорости синхронного вра-
щения вибраторов и к весь-
ма небольшому нарушению
синфазности (или проти-
вофазности) вращения.
Рис. 71.
Синхронное вращение вибратора с выключенным двигателем
могло продолжаться неограниченно долго.
Отметим, что в условиях опытов при отключенных тормоз-
ных устройствах и весьма близких парциальных угловых ско-
ростях вибраторов наблюдался весьма резкий переход от
устойчивого синфазного вращения вибраторов к устойчивому
противофазному вращению при нарушении неравенства (3.1).
Так, если при Мг2!21 — 1,03 наблюдалось (с точностью до по-
грешностей измерений) синфазное вращение вибраторов, то уже
668
ЭКСПЕРИМЕНТАЛЬНЫЕ ИССЛЕДОВАНИЯ СИНХРОНИЗАЦИИ [ГЛ. XIX
при Мг2121 = 0,97 имело место (с той же степенью точности)
противофазное вращение. И лишь достаточно узкому диапа-
зону 1,03 > Мг2/21 > 0,97 соответствовала переходная область
от синфазного вращения к противофазному.
Вместе с тем было обнаружено увеличение ширины переход-
ного диапазона по мере возрастания неодинаковости парциаль-
ных угловых скоростей вращения вибраторов. Нетрудно видеть,
что этот экспериментальный факт полностью объясняется тео-
ретическими зависимостями, полученными в п. 2 § 16 главы XIII
(см. формулы (16.9), (16.2) — (16.4) и (16.25) указанной главы).
Другая серия опытов*) имела своей целью проверку резуль-
татов теоретического исследования вибрационного поддержания
вращения неуравновешенного ротора, приведенных в п. 3 § 16
главы XIII.
Установка была собрана по той же двухвибраторной схеме,
что и в описанной выше серии опытов, однако жесткость упру-
гих элементов подвески была несколько повышена, что позво-
лило проверить также характер зависимости наблюдавшегося
эффекта от частот собственных колебаний вибрирующего ор-
гана (несущего тела) на подвеске.
Опыты проводились следующим образом. Первоначально
включались оба вибратора. Затем через промежуток времени,
достаточный для установления стационарного режима синхрон-
ного вращения, электродвигатель одного из вибраторов выклю-
чался. При некоторых сочетаниях параметров вибратор с выклю-
ченным двигателем продолжал работать синхронно с другим
вибратором, включенным в сеть, в других случаях — останав-
ливался. Путем непрерывного изменения параметров фиксиро-
валась граница области существования эффекта синхронизации
(вибрационного поддержания вращения).
Согласно формуле (16.30) главы XIII критическое значение
момента сопротивления вращению выключенного вибратора
R°2 (со) — (/?2)max’ ПРИ КОТОРОМ эффект вибрационного поддержа-
ния вращения исчезает, будет**)
(^)max = Wiege2(°2 VP^+Q2-	(3.2)
Для рассматриваемой системы жесткости сх, сх<1, и суЧ> упру-
гой подвески можно было считать пренебрежимо малыми по
сравнению с жесткостями су и сф. При этом, согласно форму-
*) В проведении этой серии экспериментов участвовали Р. Ф. Нагаев и
К. Ш. Ходжаев.
**) Индексом 2 здесь снабжены величины, относящиеся к выключаемому
вибратору.
§ 3]
ПРОВЕРКА ВЫВОДОВ ТЕОРИИ САМОСИНХРОНИЗАЦИИ
669
лам (4.5), (4.6), (4.8) главы ХШ,
^ху ~ ^х<р = УЧ ~ 0, Ьхх = — 1
, _ и2 , со2	v3-'3'
"УУ 2	2 > 0<РФ - „2	, 2 ’
Ру ~ Ш	Рф - ®
Учитывая, далее, что для рассматриваемой установки
= 0, б2 = л, Vi = v2 = v = j, v2 = -^- = -^-,	(3.4)
получим по формулам (16.3) главы ХШ
Р = bxx + <Ti<t2Z>w, Q = 0.	(3.5)
Тогда формула (3.2) для критического момента сопротивления
примет вид
I - -Т М -11 • <3-«>
В процессе экспериментов были практически фиксированы
масса М и момент инерции / вибрирующего органа установки,
расстояние между осями вращения вибраторов 2г, частоты соб-
ственных вертикальных и поворотных колебаний вибрирующего
органа ру и угловая скорость синхронного вращения со. При
этом путем непосредственных измерений было найдено
44 = 0,0368 кГ сек2/см, / = 5,21 кГ см сек2,
г = 20 см,	Мг2/1 = 2,82,
ру =27,2 \/сек, рф = 54,2 \1сек,
1490 ,ес ,.
со = л —хт— = 156 1/сек.
ои
Таким образом, из числа фигурирующих в формуле (3.6)
параметров варьировались лишь величины т\, т2, ei, е2 и пара-
метр стщг, характеризующий взаимное направление вращения
роторов вибраторов.
Эксперименты проводились при нескольких дискретных зна-
чениях статического момента т2е,2 дебалансных грузов выклю-
чаемого вибратора (см. таблицу. 3). Для каждого такого зна-
чения ставился цикл опытов, в процессе которых определялось
критическое значение статического момента дебалансных гру-
зов включенного вибратора (miei)*, которое отвечало исчезно-
вению эффекта вибрационного поддержания вращения: при
OTiei <(miei)* выключаемый вибратор останавливался.
Полученные таким путем величины (miCi), и соответствую-
щие значения (/?|)тах, найденные по формуле (3.6) при учете
равенств (3.3) и (3.7) отдельно для случаев вращения вибрато-
ров в одинаковых (<ткт2=1) и в различных (<Tio2 =—1) на-
правлениях, приведены в таблице 3.
670
ЭКСПЕРИМЕНТАЛЬНЫЕ ИССЛЕДОВАНИЯ СИНХРОНИЗАЦИИ [ГЛ. XIX
Таблица 3
maEa’ltr (кГ сек2)	F2 - m2e2<o2 (кГ)	а,аг — 1		СГ|СГ? «и — 1	
		(mtEi), • 103 (кГ сек2)	О^гпах (кГ см)	(miEi)„ • 103 (кГ сек2)	О^тах (кГ см)
1,77	42,9			1,23	2,33
2,16	52,3	2,97	2,51	—	—
2,68	65,0	—	—	0,804	2,31
2,71	65,6	2,26	2,40	—	—
4,06	98,7	2,02	3,21	0,66	2,86
5,32	129	1,91	3,98	—	—
6,27	152	1,91	4,69	—	—
Соответствующие графики зависимости критического мо-
мента (^г)тах от иентР°бежной силы, развиваемой выключае-
мым вибратором, приведены
на рис. 72.
Примерное совпадение
(с точностью до погрешно-
сти экспериментов, состав-
лявшей для величины
(Сх ПРИ = 1 около
15% И При <Ti<J2 = —1 око-
ло 4%) кривых, отвечающих
вращению вибраторов в оди-
наковых и в противополож-
ных направлениях, может
рассматриваться как косвен-
ное подтверждение теорети-
ческой формулы (3.2) (и тем самым условия (16.30) гла-
вы XIII), ибо очевидно, что момент сопротивления вращению
ротора вибратора не должен ощутимо зависеть от направления
его вращения*). Одновременно этот результат служит про-
веркой условия (3.17) главы XVIII (см. также § 5 указанной
главы).
На описанной в § 2 установке и на специальных малых мо-
делях машин были проведены и другие довольно многочислен-
ные эксперименты, имевшие целью проверку основных теорети-
ческих результатов. Не останавливаясь здесь на подробном опи-
сании этих опытов, охарактеризуем коротко их содержание.
а)	На экспериментальной установке изучались различные
случаи самосинхронизации трех дебалансных вибраторов,
*) С точностью до влияния характера колебаний осп вибратора, которое
для дебалансных вибраторов незначительно (см. § 2 главы ХП1).
§ 3]
ПРОВЕРКА ВЫВОДОВ ТЕОРИИ САМОСИНХРОНИЗАЦИИ
671
в частности определялась граница области устойчивости такого
синхронного вращения вибраторов в одинаковых направлениях
(oi = о2 = Из), при котором фаза вращения среднего вибратора
противоположна фазам вращения двух крайних вибраторов
(рис. 73). Опыты полностью подтвердили теоретическую фор-
мулу, вытекающую из соотношения (4.4) главы XV.
Кроме того, определялась граница области существования
эффекта вибрационного поддержания вращения отключенного
Рис, 73.
среднего вибратора при включенных крайних и отключенных
крайних при включенном среднем.
Полученные результаты находятся в полном согласии с тео-
ретическими.
б)	Проводилась киносъемка вращающихся дебалансных гру-
зов вибраторов установки (в случае двух вибраторов) со ско-
ростью до 2000 кадров в секунду*). Благодаря такой скорости
можно было следить не только за изменениями фаз вращения
вибраторов, протекавшими с основной частотой (около
1500 кол!мин, или 25 гц), но и за второй и даже третьей гар-
мониками колебаний фаз. В частности, на одно полное колеба-
ние с частотой 3 X 25 гц = 75 гц приходилось около 27 кадров
(2000:75).
Наличие в стационарных синхронных движениях упомяну-
тых колебаний фаз вращения вибраторов, происходящих с ча-
стотами, кратными угловой скорости синхронного вращения со,
согласуется с результатами теоретического исследования (см.
§ 14 главы XIII). Этими колебаниями объясняется значитель-
*) Съемка производилась камерой СКС-1 с объективом f = 20 мм по ме-
тодике, разработанной Я. И. Шпильбергом и В. Г. Концевым.
672
ЭКСПЕРИМЕНТАЛЬНЫЕ ИССЛЕДОВАНИЯ СИНХРОНИЗАЦИЙ [ГЛ. XIX
ный шум, производимый зубчатыми колесами и цепями при
кинематической синхронизации и фазировке, а также бы-
Машины с самосинхронизирую-
щимися вибраторами лишены
этих недостатков.
Более подробно результаты
опытов, проведенных с помо-
щью скоростной киносъемки,
описаны в следующем пара-
графе.
в) Большой цикл опытов
был проведен на варианте
установки с центральным ви-
братором планетарного типа.
На рис. 74, а изображена
установка с синхронно рабо-
тающими вибраторами в слу-
чае, когда роторы дебаланс-
ных вибраторов вращаются в
одинаковых направлениях;
рис. 74, б отвечает вращению
роторов дебалансных вибрато-
ров в противоположных на-
правлениях. Поскольку значи-
тельная часть этих опытов от-
носилась к изучению режимов
стрый износ колес и цепей.
Рис. 74.
установления синхронных движений, то о них также подробно
говорится в следующем параграфе.
г) Ряд опытов был проведен на универсальном вибрацион-
ном стенде, изображенном па рис. 106. В частности, на этом
стенде было проверено условие устойчивости фазировки враще-
ния двух вибраторов, обеспечивающее винтовые колебания тела
(см. неравенство (8.47) главы XIV)). Фото, относящееся к од-
ному из соответствующих экспериментов, приведено на рис. 106, в.
Результаты экспериментов, проведенных на лабораторных
моделях и промышленных образцах машин, в том числе на ма-
шинах с синхронными двухполюсными электродвигателями, бу-
дут изложены в главах XX и XXI настоящей книги.
§ 4. Исследование режимов установления
синхронного вращения вибраторов [59]
1. Дебалансные вибраторы. Как отмечалось в § 1 настоящей
главы, одной из основных целей экспериментального исследова-
ния было изучение режимов установления синхронного враще-
ния и получение условий, при выполнении которых обеспечи-
§ 4] Установление сйнхропного вращения вибраторов 673
вается установление требуемых синхронных движений вибрато-
ров в результате включения двигателей.
Основной результат многочисленных экспериментов, прове-
денных как на экспериментальных установках, так и на вибра-
ционных машинах с дебалансными вибраторами, приводимыми
от серийных, асинхронных короткозамкнутых электродвигателей,
состоит в том, что самосинхронизация всегда устанавливалась
через весьма непродолжительный промежуток времени после
включения двигателей, если только выполнялись условия суще-
ствования и устойчивости установившегося синхронного дви-
жения, вытекающие из результатов теоретического иссле-
дования.
Таким образом, условия самовозбуждения синхронных дви-
жений в данном случае оказались не «жестче», чем соответ-
ствующие условия существования и устойчивости установив-
шихся режимов. Этот весьма существенный с точки зрения воз-
можностей практического использования самосинхронизации
результат, по-видимому, связан с тем обстоятельством, что от-
носительные разбросы угловых скоростей вращения роторов
однотипных асинхронных электродвигателей 2<?° при номи-
нальной нагрузке довольно малы. Так, согласно ГОСТ 183—55,
п. 30, эти отклонения не должны превышать 25% номинального
скольжения двигателей, то есть
21^о>|<4 иС11пхр - TShom’	(4Л)
где sH0M — номинальное относительное скольжение, пСипхр —
синхронное, а ппом — номинальное число оборотов вала электро-
двигателя в минуту. Поскольку номинальное скольжение для
асинхронных двигателей sHOm редко превышает 0,1—0,2, то пар-
циальные угловые скорости вращения роторов отдельных вибра-
торов мало отличаются одна от другой, что и обеспечивает «за-
хват» вибраторов в режим синхронного вращения в случаях,
когда такой режим существует и устойчив (в малом).
Другой существенный экспериментальный факт состоит
в том, что в случае дебалансных вибраторов эффект вибрацион-
ного поддержания вращения неуравновешенного ротора, как
правило, не является самовозбуждающимся. Иными словами,
если включить двигатели некоторых вибраторов машины или
установки, то прочие (не включенные) вибраторы обычно не за-
тягиваются в режим синхронного вращения, несмотря на то что
он существует и устойчив (в малом): после установления син-
хронного вращения всех вибраторов, например, в результате
включения на некоторое время их двигателей или надлежащего
«толчка» ротора один или несколько двигателей могут быть от-
ключены и, несмотря на это, не выйдут из синхронизма. Таким
22 И. И. Блехман
6?4
ЭКСПЕРИМЕНТАЛЬНЫЕ ИССЛЕДОВАНИЯ СИНХРОНИЗАЦИЙ [ГЛ. XlX
образом, в случае дебалансных вибраторов выполнение условий
существования и устойчивости (в малом) вибрационного под-
держания вращения неуравновешенного ротора, как правило,
еще не обеспечивает установления вращения при произвольных
начальных условиях.
Исключение составляют лишь случаи, когда амплитуда ста-
ционарных колебаний оси вибратора имеет примерно тот же по-
рядок, чго и приведенная длина соответствующего неуравнове-
шенному ротору физического маятника. Однако такие случаи на
практике могут встретиться крайне редко: обычно амплитуды
колебаний вибрирующего органа машины не менее чем в 5—
10 раз меньше эксцентриситетов вибраторов.
Для изучения деталей быстропротекающего процесса уста-
новления синхронного движения вибраторов был использован
метод скоростной киносъемки.
На рис. 75 представлены кадры, относящиеся к процессу
установления синхронного противофазного вращения двух оди-
наковых дебалансных вибраторов в противоположных направ-
лениях. В процессе экспериментов, проводившихся на установке,
описанной в § 2 настоящей главы, вначале включался один ви-
братор и после установления его вращения с постоянной угловой
скоростью — другой вибратор. Первый кадр из серии, представ-
ленной на рис. 75, а, примерно соответствует моменту включе-
ния второго (правого) вибратора; промежутки времени А/, про-
текшие между последовательными кадрами, составляют 0,01 сек;
за это время в установившемся режиме вибратор успевает сде-
лать около четверти оборота. Как следует из рассмотрения кад-
ров, угловые скорости вращения роторов вибраторов постепенно
сближаются, однако остаются различными.
Первый кадр второй серии (рис. 75, б) относится к моменту
времени, отстоящему от момента пуска двигателя второго вибра-
тора на 0,43 сек, а все последующие кадры сняты через проме-
жутки времени Kt = 0,01 сек. Как видно, вращение роторов ви-
браторов происходит уже с весьма близкими средними угловыми
скоростями, однако сдвиг фаз вращения еще заметно отличен
от значения а — 180°, отвечающего установившемуся движению.
Изучение кадров для более продолжительного интервала вре-
мени позволяет установить полное выравнивание средних скоро-
стей вращения, сопровождающееся, однако, значительными по
амплитуде постепенно затухающими колебаниями разности фаз
вращения относительно а = 180°. Эти колебания, происходящие
со сравнительно низкой частотой, отчетливо видны из серии
кадров, представленных на рис. 75, в (0,7—0,8 сек после вклю-
чения второго вибратора); последовательные кадры здесь сняты
через промежутки времени А/ ~ 0,04 сек, отвечающие одному
обороту вала вибратора, движение которого установилось.
Рис. 75.
22'
676
ЭКСПЕРИМЕНТАЛЬНЫЕ ИССЛЕДОВАНИЯ СИНХРОНИЗАЦИИ [ГЛ. XIX
Наконец, рис. 75, г (1,3 сек после включения второго вибра-
тора; время между последовательными кадрами М = 0,01 сек)
отвечает полностью установившемуся режиму синхронного про-
тивофазного вращения роторов вибраторов. Как нетрудно ви-
деть, вращение роторов весьма близко к равномерному; неболь-
шие колебания угловой скорости объясняются здесь, во-первых,
действием силы тяжести и, во-вторых, обратным влиянием ко-
лебаний осей вибраторов; наличие таких колебаний, как уже
отмечалось в предыдущем параграфе, устанавливается также и
теоретическим путем.
Вполне аналогичная картина получается и в случае процесса
установления синхронного вращения вибраторов в одинаковых
направлениях.
2. Планетарные вибраторы. Для теории ряда дробильно-из-
мельчительных и классифицирующих машин, а также некоторых
дозирующих устройств (см. пп. 6, 7, 15, 16, 22 таблицы 2) пер-
востепенное значение имеет выяснение условий самовозбужде-
ния из состояния покоя основного стационарного режима дви-
жения вибраторов планетарного типа, лишенных «собственных»
двигателей (то есть возбуждения обкатки роликов, вложенных
в стаканы, или колец, сидящих с зазором на осях).
Как выяснилось после первых же опытов, существенные осо-
бенности режимов установления для вибраторов планетарного
типа определяются наличием в этих вибраторах неудерживаю-
щей связи между роликом и стаканом (или осью и кольцом):
в процессе установления синхронного движения, как правило,
имеет место нарушение связи, то есть отрыв ролика от стакана
(кольца от оси) с последующими соударениями.
Одна из серий опытов была проведена на истирателе проб
руды, фото которого представлено на рис. 69 и который описан
в § 2 настоящей главы.
Эксперименты проводились при трех значениях частот коле-
баний стакана (1200, 1520 и 1820 кол/мин) и со стальными
роликами четырех различных диаметров (25, 40, 50 и 55 мм).
При установке достаточно малой амплитуды круговых коле-
баний стакана Ао обкатка ролика внутри стакана (то есть основ-
ной режим вибрационного поддержания вращения) не возбуж-
далась, что фиксировалось с помощью стробоскопа. Увеличение
амплитуды колебаний приводило к самовозбуждению обкатки,
причем переход от отсутствия самовозбуждения к его наличию
почти всегда был относительно резким. Это позволило устано-
вить критические значения амплитуд Л*, соответствующие гра-
нице области самовозбуждения обкатки.
Результаты опытов графически представлены на рис. 76, где
по оси абсцисс отложен относительный эксцентриситет ролика
е/7? = (R — b)/R (b — радиус ролика, R — радиус стакана), а по
§ 4J
УСТАНОВЛЕНИЕ СИНХРОННОГО ВРАЩЕНИЯ ВИБРАТОРОВ
677
оси ординат — отношение
Т)* = е/ Д’.
В соответствии со сказанным выше, при
И0>Л’ = е/п или я = еМо<п’
(4.2)
(4.3)
обкатка самовозбуждается, а при выполнении противоположных
неравенств — не самовозбуждается. Величина if, очевидно, ука-
зывает, во сколько раз эксцентриситет е может превышать
амплитуду колебаний До, чтобы обкатка ролика еще самовоз-
буждалась.
Из графиков, представленных на рис. 76, видно, что в широ-
ком диапазоне изменения относительного эксцентриситета e/R
коэффициент 1]* увеличивается при возрастании e/R и с увели-
чением частоты колебаний ы — лм/30.
Помимо опытов со сплошными роликами, ряд экспериментов
был проведен с полыми роликами, имеющими те же наружные
диаметры. Оказалось, что расхождение между значениями ко-
эффициента ц* для более легких полых роликов и соответствую-
щими значениями для сплошных роликов лежит в пределах точ-
ности эксперимента. Таким образом, было установлено, что
в изученной области изменения параметров if не зависит от
веса ролика.
Неравенства (4.3) интересно сопоставить с условием суще-
ствования и устойчивости (в малом) основного стационарного
режима обкатки ролика, найденным теоретическим путем, то
есть с соотношением (3.18) главы XVIII. В данном случае, оче-
видно, следует положить А = До (см. определение эффективной
678
ЭКСПЕРИМЕНТАЛЬНЫЕ ИССЛЕДОВАНИЯ СИНХРОНИЗАЦИИ [ГЛ. XIX
амплитуды А в п. 1 § 3 главы XVIII), и упомянутое соотноше-
ние может быть представлено в форме
Ц = е/Л0 < т}’(,	(4.4)
где обозначено:
а f' есть так называемый коэффициент сопротивления перека-
тыванию. Значения этого коэффициента, найденные в различ-
ных экспериментах, проводившихся в институте «Механобр», ле-
жат в пределах
0,15<fz<0,35;	(4.6)
примерно такие же значения приводятся для соответствующих
случаев в справочной литературе. Интервалу (4.6) отвечает сле-
дующий диапазон изменения коэффициента r|*t:
3,0 <^<6.7.	(4.7)
Но этот диапазон очень близок к промежутку
3,0 < л* <5,3,	(4.8)
в котором, согласно нашим опытам (см. рис. 76), оказались за-
ключенными значения коэффициента г]*, входящего в условие
самовозбуждения обкатки. Это наводит на мысль, что условия
самовозбуждения основного режима стационарного движения
(обкатки) ролика являются (с точностью до погрешностей про-
веденных до сих пор экспериментов) не более «жесткими», чем
условия существования и устойчивости (в малом) этого режима,
найденные теоретическим путем. Иными словами, имеются
основания считать, что основной режим стационарного движе-
ния ролика практически самовозбуждается во всей области
своего существования*). Здесь мы имеем, таким образом, суще-
ственное отличие от случая неуравновешенного ротора (обыч-
ного физического маятника), рассмотренного в п. 1 настоящего
параграфа.
Другая серия опытов проводилась на описанной в § 2 на-
стоящей главы экспериментальной установке, которая была
собрана по схеме, представленной на рис. 67, б, то есть с цен-
тральным планетарным вибратором. Существенное отличие этих
опытов от опытов первой серии состояло в том, что амплитуда
колебаний не была заданной кинематически, а зависела от ре*
жима работы установки.
*) Отметим, что для случая инерционной дробилки (см. § 2 главы XXI)
подобное утверждение впервые было высказано А. К- Рундквистом.
§ 4] УСТАНОВЛЁНИЕ СИНХРОННОГО ВРАЩЕНИЯ ВИБРАТОРОВ Н7<3
Диаметр стакана 2R во всех опытах оставался неизменным
и равным НО мм. Опыты проводились при трех различных зна-
чениях веса вибрирующего органа Ра = mag (27,1.0; 33,62 и
39,98 кГ).
Применялись сплошные стальные ролики с диаметрами 2Ь,
равными 80, 86, 92 и 98 мм. Вес роликов был равен соответ-
ственно 1,410; 1,635; 1,885 и 2,150 кГ. Специальные опыты, про-
веденные с полым роликом, имеющим наружный диаметр 98 мм
и вес 0,920 кГ, дали те же результаты, что и для сплошного
ролика того же диаметра.
Опыты ставились как для случая прямолинейных поступа-
тельных колебаний вибрирующего органа, соответствующего
вращению роторов вибраторов в противоположных направле-
ниях (рис. 71), так и для случая круговых поступательных
колебаний, которые получались при вращении роторов в одина-
ковых направлениях (рис. 70, й), поскольку выполнялось усло-
вие (3.1).
Как показали эксперименты, обкатка ролика по стакану воз-
буждается и устойчиво поддерживается при выполнении условия
8 'Г 8	«	f A f\\
(4.9)
А; Ai
где
2mded для случая круговых
та колебаний,
Ло =	(4.10)
для случая прямоли-
та нейных колебаний,
— эффективная амплитуда колебаний вибрирующего органа
установки, подсчитанная в предположении, что ролики в стака-
нах отсутствуют (mded — суммарный статический момент деба-
лансных грузов одного вибратора, та — масса вибрирующего
органа с вибраторами).
В ходе опытов, путем подбора дебалансных грузов; для
каждой комбинации значений диаметра ролика и веса вибри-
рующего органа находились три значения статического момента
дебалансных грузов: значение (mded)’_, определяемое как наи-
большая величина статического момента, при которой движение
ролика с обкаткой не самовозбуждается; значение (mdeay ,
являющееся наименьшим, при котором движение с обкаткой
устанавливается практически сразу (не более чем через 2 сек)
после включения электродвигателей вибраторов, и, наконец, зна-
чение (гпаеа)'о, соответствующее возникновению обкатки в сред-
нем через 10 сек после включения двигателей.
680 ЭКСПЕРИМЕНТАЛЬНЫЕ ИССЛЕДОВАНИЯ СИНХРОНЙЗАЦЙИ [ГЛ.xik
Далее по формулам (4.9) и (4.10) подсчитывались ампли-
туды колебаний Ад, Aq и X и коэффициенты if., ц"). и г^,
отвечающие найденным значениям (mded)'_, (mded)'+ и (mdsd)g.
Результаты подсчетов представлены графически на рис. 77.
Как видно, ширина полосы if_ — ц'+, характеризующая пере-
ходную область, не очень велика, особенно в случае прямо-
линейных колебаний.
Из графиков следует также, что значения коэффициента г|^,
которые следует принимать за расчетные, лежат для прямоли-
нейных колебаний в пределах от 5,50 до 6,6, а для круговых
колебаний *) — в пределах от 3,3 до 5,2; последние две цифры
весьма хорошо согласуются с пределами изменения коэффи-
циента ц* (3,0 < я* < 5,3), полученными в первой серии опытов
для случая круговых колебаний стакана, задаваемых кинема-
тически (рис. 76). Таким образом, есть основания полагать, что
роль эффективной амплитуды А в случае колебаний мягко амор-
тизированного тела, возбуждаемых двумя симметрично распо-
ложенными вибраторами, играет введенная выше условная эф-
фективная амплитуда Aq.
*) Говоря здесь условно о круговых и прямолинейных колебаниях вибри-
рующего органа установки, мы имеем в виду колебания при отсутствии роли-
ков в планетарных вибраторах.
$ 4]	УСТАНОВЛЕНИЕ СИНХРОННОГО ВРАЩЕНИЯ ВИБРАТОРОВ 681
Такое же вполне естественное соответствие имеет место и
в теоретически найденных условиях существования рассматри-
ваемого установившегося режима. Чтобы убедиться в этом, сле-
дует сопоставить неравенства (3.18) главы XVIII и (3.10)
главы XXI. При учете указанного соответствия и после выпол-
нения несложного анализа условия устойчивости рассматривае-
мого режима применительно к параметрам экспериментальной
установки можно сделать тот же вывод, что и при анализе дан-
ных первой серии опытов: с точностью до погрешностей экспери-
мента условия самовозбуждения основного режима движения
ролика оказываются выполняющимися во всей области, опреде-
ляемой теоретически найденными условиями существования и
устойчивости (в малом) этого режима.
Тот же вывод, по-видимому, справедлив и в случае прямо-
линейных колебаний. Чтобы убедиться в этом, следовало бы
получить условия существования и устойчивости рассматривае-
мого синхронного движения в случае, когда роторы дебаланс-
ных вибраторов вращаются в противоположных направлениях.
Соответствующее несложное исследование, выполняемое так же,
как и для случая круговых колебаний (см. § 3 главы XXI), нами
не приводится, поскольку случай прямолинейных колебаний ме-
нее интересен с точки зрения приложений.
Заметим лишь, что из графиков рис. 77 и соотношений (4.9),
(4.10) следует, что при прямолинейных колебаниях для воз-
буждения обкатки необходимы примерно в два раза большие
амплитуды колебаний, нежели при круговых. Напомним, что
в точности двукратное отношение соответствующих амплитуд
получается и из условия (3.18) главы XVIII, выражающего тре-
бования, необходимые для поддержания основного режима ста-
ционарного движения ролика (эффективная амплитуда колеба-
ний при заданных круговых колебаниях с действительной ам-
плитудой .40 в два раза больше, чем при прямолинейных
колебаниях с той же действительной амплитудой).
Результаты, вполне аналогичные приведенным выше, были
получены также на лабораторных и промышленных образцах
инерционных дробилок [182, 368—370]. Эти результаты, послу-
жившие экспериментальной основой для разработки так назы-
ваемой теории критической щели инерционных дробильно-из-
мельчительных машин, а также и собственно теория критической
щели будут изложены в главе XXI настоящей книги.
Как и для дебалансного вибратора, с целью детального
изучения процесса самовозбуждения стационарного режима дви-
жения ролика планетарного вибратора была использована ско-
ростная киносъемка.
На рис. 78, а представлены кадры, относящиеся к случаю
круговых поступательных колебаний вибрирующего органа
682
ЭКСПЕРИМЕНТАЛЬНЫЕ ИССЛЕДОВАНИЯ СИНХРОНИЗАЦИИ [ГЛ. XIX
установки. Последовательные снимки сделаны через промежу-
ток времени А/ = 0,01 сек, причем первый кадр отвечает мо-
менту включения дебалансных вибраторов, возбуждающих ко-
лебания вибрирующего органа.
Рис. 78.
Из рассмотрения рис. 78, а явствует, что начальный период
процесса установления сопровождается систематическим нару-
шением неудерживающей связи, то есть отрывом ролика и уда-
рам-и его по стакану. Такая картина наблюдалась во всех опы-
тах с вибрационным возбуждением синхронного движения ро-
лика вибратора планетарного типа.
На рис. 78, б представлены кадры, относящиеся к основному
установившемуся режиму движения ролика с обкаткой по ста-
кану. Снимки сделаны через 1,4 сек после включения вибрато-
§ 5] ОБЗОР ДРУГИХ ЭКСПЕРИМЕНТАЛЬНЫХ ИССЛЕДОВАНИИ 683
ров, причем интервалы времени А/ между последовательными
кадрами, как и выше, равны 0,01 сек. Как видно, за эти про-
межутки времени вектор-эксцентриситет ролика успевает сделать
около 1/4 оборота, что соответствует частоте около 1500 кол/мин-,
именно с такой угловой скоростью, как отмечалось выше, вра-
щались роторы дебалансных вибраторов.
§ 5. Краткий обзор других экспериментальных исследований.
Заключение
Из общего обзора исследований в области синхронизации
вибраторов, приведенного в § 3 главы XII, явствует, что экспе-
риментальные работы проводились параллельно с развитием
теории. Помимо упоминавшихся экспериментов Д. А. Плисса и
описанных в настоящей главе опытов автора, ряд специальных
экспериментальных работ был выполнен другими исследовате-
лями как в СССР, так и за рубежом.
Ряд экспериментальных работ был посвящен изучению эф-
фекта вибрационного возбуждения и поддержания вращения
неуравновешенного ротора; об этих работах уже говорилось
в § 1 главы XVIII. Значительная часть исследований собственно
эффектов самосинхронизации и принудительной синхронизации
была выполнена на моделях или промышленных образцах ви-
брационных машин и устройств [56, 170, 173, 178, 242, 246, 250,
327, 328, 415]; работы этой группы кратко рассматриваются в со-
ответствующих параграфах глав XX и XXI. И наконец, относи-
тельно небольшая часть экспериментальных исследований была
выполнена на специально спроектированных установках, допу-
скающих регулировку основных параметров и предоставляющих
определенные удобства при проведении измерений и записи про-
цессов. Такие установки были использованы в работах В. Бо-
гуша и 3. Энгеля [447] и Л. Шперлинга [482].
Из рассмотрения всей совокупности перечисленных работ
вытекает, что изложенная в данной части книги теория синхро-
низации механических вибраторов хорошо подтверждается экс-
периментом и является достаточно надежной основой техниче-
ских расчетов при проектировании вибрационных машин и
устройств.
Автору не известно ни одного экспериментального факта,
который не укладывался бы в рамки разработанной теории*).
*) Отметим, что иногда экспериментальные результаты неправильно срав-
ниваются с результатами теории, полученными для случая, когда несущие
тела имеют иное число существенных степеней свободы. Недопустимость по-
добного сопоставления явствует, например, из сказанного в § 3 главы XV.
На разборе соответствующих (весьма немногочисленных) работ мы здесь не
останавливаемся.
684 ЭКСПЕРИМЕНТАЛЬНЫЕ ИССЛЕДОВАНИЯ СИНХРОНИЗАЦИИ [ГЛ. XIX
Это не значит, однако, что такие факты не могут встретиться
в дальнейшем при проведении более тонких опытов, а также
опытов, поставленных в условиях, при которых заведомо не-
справедливы основные теоретические допущения.
Осуществление подобных экспериментов представляет суще-
ственный методический и прикладной интерес. Не лишено инте-
реса также построение границ областей существования и устой-
чивости синхронных режимов в пространстве параметров
системы и сопоставление этих границ с теоретическими для бо-
лее сложных случаев, чем это было выполнено до сих пор (па-
пример, для случая многих вибраторов).
ЧАСТЬ V
ПРИЛОЖЕНИЯ ТЕОРИИ СИНХРОНИЗАЦИИ
МЕХАНИЧЕСКИХ ВИБРАТОРОВ
В данной части книги рассматриваются некоторые приложе-
ния развитой в четвертой части теории синхронизации механи-
ческих вибраторов.
Первые три из четырех глав части посвящены использованию
теории синхронизации вибраторов для усовершенствования су-
ществующих и разработки новых вибрационных машин. Идеи
создания почти всех этих машин возникли именно в результате
развития указанной теории, ибо основные соотношения между
параметрами, обеспечивающие устойчивую и стабильную работу
вибраторов в нужном режиме, вряд ли могли быть найдены
только путем интуитивного конструирования или пробных экс-
периментов. Многие из таких закономерностей вообще пред-
ставляются парадоксальными — достаточно вспомнить, напри-
мер, о существенной зависимости характера устойчивой фази-
ровки вибраторов при их самосинхронизации от числа степеней
свободы колебательной системы, с которой они связаны.
Особое значение при создании вибрационных машин с не-
сколькими механическими вибраторами имеют методы синтеза
таких устройств, рассмотренные в главе XV книги. Вместе
с тем, несмотря на наличие этих методов, процесс синтеза ди-
намической схемы вибрационной машины пока еще включает
ряд эвристических элементов. В сущности, теория в настоящее
время позволяет лишь находить решения в простейших случаях,
указать направление поиска для более сложных систем, убе-
диться в пригодности или непригодности намеченного решения,
а в случае пригодности — осуществить оптимальный или прием-
лемый выбор параметров устройства. При этом следует иметь
в виду, что для реальной осуществимости машины с самосин-
хронизирующимися (а также и с электрически синхронизиро-
ванными) вибраторами еще недостаточно обеспечить существо-
вание и устойчивость требуемого режима колебаний, а необ-
ходимо убедиться также в стабильности этого режима по
отношению к отклонениям параметров системы. Для некоторых
распространенных типов вибрационных машин и устройств
686
ВИБРАЦИОННЫЕ ГРОХОТЫ, КОНВЕЙЕРЫ, ПИТАТЕЛИ
[ГЛ. XX
условия стабильности получены в § 2 главы XX и в § 2 гла-
вы XXIII данной части книги.
С тем чтобы облегчить конструктору или расчетчику практи-
ческое использование конкретных результатов, нашедших отра-
жение в книге, эти результаты сведены в обширную таблицу
(Добавление 2). Для тех же читателей предназначена и мето-
дика исследования синхронизации вибраторов, приведенная
в Добавлении 1. Пользование указанной методикой не предпо-
лагает владения теорией синхронизации в полном объеме.
В настоящее время насчитывается несколько десятков изо-
бретений, основанных на применении эффекта самосинхрониза-
ции или электрической синхронизации вибраторов в различных
машинах; многие из этих машин серийно изготовляются и
успешно эксплуатируются в промышленности как в СССР, так
и за рубежом. Ссылки на авторские свидетельства и патенты
приводятся в соответствующих разделах настоящей части книги,
а также в § 3 главы XII. Следует, однако, заметить, что воз-
можности использования явлений синхронизации вибраторов
еще далеко не исчерпаны, и можно ожидать появления в бли-
жайшее время новых усовершенствований и изобретений. Одна
из задач книги как раз и состоит в том, чтобы этому способ-
ствовать.
Глава XXIII посвящена приложению теории синхронизации
вибраторов к проектированию групповых фундаментов под не-
уравновешенные машины. Возможности в этой области, выте-
кающие из теоретического анализа, также еще ждут своей прак-
тической реализации.
ГЛАВА XX
ВИБРАЦИОННЫЕ ГРОХОТЫ, КОНВЕЙЕРЫ, ПИТАТЕЛИ
И ДОЗАТОРЫ; ВИБРАЦИОННЫЕ ПЛОЩАДКИ
И НЕКОТОРЫЕ ДРУГИЕ МАШИНЫ
§1.0 возможностях использования эффекта
самосинхронизации для получения прямолинейных, круговых,
эллиптических, винтовых и поворотных колебаний
рабочего органа вибрационной машины
1. Предварительные замечания. Прямолинейные и круговые
поступательные, а также эллиптические, поворотные и винто-
вые колебания рабочего органа характерны, для большинства
транспортных, транспортно-технологических и других вибрацион-
ных машин, в особенности для машин, перечисленных в назва-
нии данной главы (см. таблицу 2 на стр. 340—358). Причины,
§ I]	ИСПОЛЬЗОВАНИЕ ЭФФЕКТА САМОСИНХРОНИЗАЦИИ	687
по которым в таких машинах часто бывает желательным или
даже необходимым использование нескольких механических ви-
браторов, были подробно обсуждены в § 2 главы XII.
Из примеров, рассмотренных в четвертой части книги, видно,
что здесь имеются широкие возможности для использования
явления самосинхронизации, позволяющего избежать примене-
ния каких-либо связей между роторами вибраторов. В настоя-
щей главе будут изучены также и другие системы с несколь-
кими вибраторами, которые могут представить практический ин-
терес. Для удобства обозрения соответствующих результатов,
полученных в различных разделах книги, они сведены в таб-
лицу 5 (Добавление 2), о которой уже говорилось выше.
Ниже рассматриваются по отдельности схемы, позволяющие
получить каждый из основных типов колебаний рабочих орга-
нов машин.
2. Прямолинейные поступательные колебания. Некоторые
способы получения прямолинейных поступательных колебаний
твердого тела с применением нескольких (преимущественно
двух) самосинхронизирующихся вибраторов представлены
в пп. 1, 3, 6—12, 14—17, 19 и 22 таблицы 5 (Добавление 2).
Здесь мы остановимся лишь на системах пп. 8, 9 и 14, кото-
рые находят применение в машинах, рассматриваемых в настоя-
щем параграфе, и не были изучены ранее.
О схеме, представленной в п. 8 таблицы 5, можно сказать
следующее. В п. 2 § 16 главы XIII было показано, что два оди-
наковых дебалансных вибратора, обладающих одинаковыми по-
ложительными парциальными скоростями, установленных на
мягко амортизированном жестком вибрирующем органе с пло-
ским движением таким образом, что оси вращения роторов ле-
жат в одной плоскости с центром тяжести тела и па равных
расстояниях г от центра тяжести, в устойчивом движении обес-
печивают (при вращении в различных направлениях) прямо-
линейные поступательные колебания вибрирующего органа (см.
п. 3 таблицы 5).
В ряде случаев, однако, оси вращения роторов по конструк-
тивным соображениям не могут быть расположены в одной пло-
скости с центром тяжести вибрирующего органа. Поэтому и
представляет интерес изучение более общей системы, изобра-
женной на рис. 79, а и в п. 8 таблицы 5. В данной системе
предполагается лишь одинаковость расстояний О]О| = г и
О\О2 — г между осями вращения роторов вибраторов и центром
тяжести О] вспомогательного тела*); вместе с тем по-преж-
нему считается, что вибраторы вращаются в противоположных
направлениях, обладают одинаковыми положительными пар-
*) Определение вспомогательного тела см. на стр. 378 и 529.
688
ВИБРАЦИОННЫЕ ГРОХОТЫ, КОНВЕЙЕРЫ, ПИТАТЕЛИ
[ГЛ. XX
циальными угловыми скоростями и что жесткости опорных упру-
гих элементов достаточно малы. В связи с последним предполо-
жением ориентация осей uO\V является произвольной, ибо вне
зависимости от этой ориентации считается, что жесткость сху~0.
Рие. 79.
Из соображений удобства допустим, что ось направлена
вдоль биссектрисы угла 0i<9|02.
В силу сказанного для рассматриваемой системы справед-
(16.10) и первые три равенства
(16.25х) главы XIII, с той лишь
разницей, что теперь
6, = 6, д2 = я-д. (1.1)
Легко видеть, что, несмотря
на указанное различие, при
0102 = —1> то есть для случая
вращения роторов вибраторов
в различных направлениях, по-
следние три равенства (16.25х)
главы XIII сохраняют силу. По-
этому, как и в более простом
случае, изученном в п. 2 § 16
указанной главы, устойчивым яв-
ливы соотношения (16.17),
F^Fsiniat Fz=Fsin(ii)t+ix)
Рис. 80.
ляется только противофазное вращение вибраторов (а=(а)2 =
= —л), которому по-прежнему отвечают прямолинейные посту-
пательные колебания вибрирующего органа машины. Направле-
ние этих колебаний совпадает с направлением биссектрисы
угла 01<Э|02 между прямыми, проходящими через оси вращения
вибраторов и центр тяжести Oj вспомогательного тела.
Система, представленная в п. 9 таблицы 5, а также на
рис. 80, отличается от системы п. 3 той же таблицы наличием
не простейших дебалансных вибраторов, а вибраторов направ-
ленного действия.
§ I]
ИСПОЛЬЗОВАНИЕ ЭФФЕКТА САМОСИНХРОНИЗАЦИИ
689
В сущности, эта система представляет собой частный случай
рассмотренной в п. 2 § 3 главы XIV пространственной системы
(см. рис. 38, а также п. 15 таблицы 5), отвечающий 0 = 0 или
0 = л/2. При учете этого обстоятельства в силу соотношения
(8.20) главы XIV получаем, что синфазное движение вибраторов
(а значит, и прямолинейные поступательные колебания вибри-
рующего органа) устой-
чиво лишь при выполне-
нии неравенства
где М и / — соответствен-
но масса и момент инер-
ции вспомогательного
тела относительно оси,
проходящей через его
центр тяжести О\. При
невыполнении этого усло-
вия устойчиво не синфаз-
ное, а противофазное дви-
жение вибраторов, приво-
дящее к поворотным ко-
лебаниям вибрирующего
органа.
Рассмотрим, наконец,
систему, изображенную
на рис. 81 и в п. 14 таб-
лицы 5, которая пред-
ставляет собой пространственный вариант рассмотренной выше
системы п. 8 той же таблицы (см. также рис. 79, а). Для ряда
машин, в частности для грохотов, обрабатывающих горячие
материалы (см. § 5 настоящей главы), такое боковое располо-
жение вибраторов является предпочтительным.
С целью изучения вопроса об устойчивости противофазного
вращения вибраторов в противоположных направлениях, не-
обходимого для получения прямолинейных поступательных ко-
лебаний твердого тела, можно воспользоваться интегральным
критерием устойчивости*).
Уравнения малых колебаний тела при вращении вибраторов
по закону
<р, = со/, <р2 = —(со/ + а)	(1.3)
*) Иным способом — путем использования результатов статьи [241], изло-
женных в п. 5 § 8 главы XIV настоящей книги, — данная система была ра-
нее рассмотрена Б. П. Лавровым в работах [242, 245]; в этих работах изучен
также случай, когда к телу М присоединен физический маятник.
690
ВИБРАЦИОННЫЕ ГРОХОТЫ, КОНВЕЙЕРЫ, ПИТАТЕЛИ
[ГЛ. XX
имеют вид (см. рис. 81)
Мх = F [sin со/ — sin (<о/ + a)] cos р,
Му = — F [cos со/ + cos (со/ + а)],
Mz — — F [sin со/ — sin (со/ + а)] sin р,
1хйх = ?r sin б sin р [cos со/ + cos (со/ + а)] —
— Fr cos б sin р [sin со/ + sin (со/ + а)],
7^ = 0,
/гйг = Fr sin б cos р [cos со/ + cos (со/ + а)] —
— Fr cos б cos р [sin со/ + sin (со/ + а)].
Здесь М, 1Х, 1У и Iz — соответственно масса и моменты инерции
вспомогательного тела относительно главных осей инерции
Oxyz (O\uvw) \ F = mew2; величины б и р —углы, смысл которых
ясен из рис. 81 (угол р обычно называют углом вибраций);
г — расстояния от центра тяжести вспомогательного тела О, до
осей вращения вибраторов.
Проинтегрировав выражения (1.4), подставив значения ско-
ростей Д..., wz, отвечающие установившимся вынужденным ко-
лебаниям, в выражение для кинетической энергии тела *) и,
произведя осреднение, найдем после несложных выкладок
2л/(о	2л/й
=	[ (7’(1))л =
2Л J	2Л J 7
О	О
2л/о)
= £ f + + + + +
XJL J L
0
1 F2r2
= TWcosa + C’ <L5)
где
1 = lx cos2 p + Д sin2 p ’	(1>6)
а С есть величина, не зависящая от фазового сдвига а. Таким
образом, при а = л функция А<г> всегда имеет минимум, и поэто-
му желательное противофазное вращение вибраторов устойчиво
при любых значениях параметров (если только г =#0). Отме-
тим, что такая ситуация характерна для многих систем,
обеспечивающих прямолинейные поступательные колебания тел
(см. пп. 3, 8, 14 и 19 таблицы 5 Добавления 2). В других
*) Потенциальная энергия считается пренебрежимо малой в силу предпо-
ложения о мягкости амортизирующих пружин.
$ И
ИСПОЛЬЗОВАНИЕ ЭФФЕКТА САМОСИНХРОНИЗАЦИИ
691
случаях, однако, получаются некоторые ограничения на пара-
метры системы (см. пп. 9 и 15 таблицы 5). В этих случаях, если
выполнение указанных ограничений почему-либо затруднитель-
но, можно прибегнуть к тому или иному способу смягчения этих
ограничений (см. § 3 главы XV, а также п. 3 настоящего пара-
графа).
Из числа схем, пригодных для использования двух самосип-
хронизирующихся вибраторов с целью получения прямолиней-
ных поступательных колебаний рабочего органа, отметим схемы,
представленные в пп. 19, 10 и 11 таблицы 5. Первая из этих
схем позволяет получить бигармонические колебания, а две дру-
гие — гармонические колебания в тех случаях, когда этого
нельзя добиться при двух одинаковых вибраторах, установлен-
ных на одном твердом теле с одной или двумя степенями сво-
боды (см. § 3 главы XV и § 3 главы XXII). Из схем, не по-
мещенных в таблицу 5, упомянем рассмотренную в п. 6 § 8
главы XIV и изображенную на рис. 49 трехмассную систему,
изученную А. Д. Рудиным.
Если в случае двух одинаковых вибраторов, установленных
на мягко амортизированном вибрирующем органе с плоским
движением, явление самосинхронизации может быть эффективно
использовано для получения устойчивых прямолинейных посту-
пательных колебаний, то в случае четырех одинаковых симме-
трично расположенных дебалансных вибраторов, обладающих
одинаковыми положительными парциальными угловыми скоро-
стями, это невозможно Схема системы, о которой идет речь,
Рис. 82.
представлена на рис. Ь2, а и в п. 21 таблицы 5. В данном случае
при направлениях вращения роторов, показанных на рисунке,
устойчивым оказывается вращение роторов с такими фазовыми
соотношениями, при которых вибрирующий орган в первом при-
ближении остается неподвижным. Соответствующее этому дви-
жению расположение роторов вибраторов изображено на
692
ВИБРАЦИОННЫЕ ГРОХОТЫ, КОНВЕЙЕРЫ, ПИТАТЕЛИ
[ГЛ. XX
рис. 82, а сплошными линиями; очевидно, что центробежные
силы, развиваемые вибраторами, здесь взаимно уравновеши-
ваются.
Можно не останавливаться на доказательстве сформулиро-
ванного утверждения, так как устойчивость описанного движе-
ния непосредственно вытекает из интегрального критерия устой-
чивости. Действительно, для такого движения среднее за период
значение кинетической энергии вибрирующего органа в исход-
ном приближении равно нулю, а в близких движениях — отлично
от нуля и положительно. Иными словами, в рассматриваемом
движении средняя кинетическая энергия минимальна, и поэтому,
в соответствии с интегральным критерием, это движение устой-
чиво (подробнее о подобных случаях см. § 2 главы XXIII).
Вместе с тем, как будет показано в § 3, движение, при ко-
тором тело совершает поступательные колебания вдоль оси Ох,
оказывается неустойчивым (соответствующее этому движению
положение роторов второго и третьего вибраторов при заданном
положении роторов первого и четвертого вибраторов показано
на рис. 82, « пунктиром). Для обеспечения устойчивости такого
движения необходима принудительная синхронизация вибрато-
ров (см. § 3 настоящей главы).
Заметим, что вывод о невозможности использования четырех
самосинхронизирующихся вибраторов для получения прямоли-
нейных поступательных колебаний вибрирующего органа отно-
сится только к случаю мягко амортизированного абсолютно
жесткого вибрирующего органа, совершающего плоское движе-
ние. Этот вывод перестает быть справедливым в случаях, когда
опорные упругие элементы обладают конечной жесткостью*),
когда вибрирующий орган должен рассматриваться как упругое
тело или тело, совершающее пространственные колебания,
а также если имеется не одно, а несколько связанных между со-
бой колеблющихся твердых тел.
Яркой иллюстрацией этого обстоятельства является, напри-
мер, следующий факт, установленный Б. П. Лавровым [242].
Оказывается, что фазировка четырех самосинхронизирующихся
вибраторов, требующаяся для обеспечения прямолинейных по-
ступательных колебаний тела в рассмотренной выше схеме
рис. 82, а (п. 21 таблицы 5 Добавления 2), может быть сделана
устойчивой путем превращения этой схемы в простран-
ственную: следует лишь повернуть плоскости вращения центров
тяжести роторов каждой пары вибраторов 1 и 4, 2 и 3 на неко-
торый угол р таким образом, как это показано на чертеже
*) В частности, как уже указывалось выше, четыре и более одинаковых
вибраторов работают синхронно и синфазно в случае установки на платформе
с одной степенью свободы при условии, что движение происходит в дорезо-
нансной области (см. п. 1 таблицы 5).
§ 1]	ИСПОЛЬЗОВАНИЕ ЭФФЕКТА САМОСИНХРОНИЗАЦИИ	693
в п. 23 таблицы 5; там же приведены найденные Б. П. Лавровым
условия устойчивости требуемого движения*). Естественно, что
этим условиям нельзя удовлетворить при [3 = 0, то есть в слу-
чае плоской схемы.
Можно было бы показать, что желаемый эффект достигается
и другими перечисленными выше способами (см., в частности,
[169, 246]). Иначе говоря, и в данном случае можно воспользо-
ваться методами синтеза систем с самосинхронизирующимися
вибраторами, изложенными в главе XV книги.
3.	Круговые и эллиптические поступательные колебания. Ряд
схем, позволяющих использовать два самосинхронизирующихся
вибратора для получения круговых поступательных колебаний
твердого тела, представлен в пп. 3, 7, 13, 20 и 27 таблицы 5
Добавления 2; все эти схемы, за исключением схемы п. 27, рас-
сматриваемой в главе XXI, были изучены ранее, и поэтому на
их обосновании здесь можно не останавливаться.
Согласно схеме п. 3 два одинаковых дебалансных вибра-
тора, обладающих одинаковыми положительными парциальными
угловыми скоростями и установленных на мягко амортизирован-
ном вибрирующем органе с плоским движением таким образом,
что оси вращения роторов лежат в одной плоскости с центром
тяжести вспомогательного тела и на равных расстояниях г от
центра тяжести, при вращении в одинаковых направлениях обес-
печивают устойчивые круговые поступательные колебания ви-
брирующего органа, если выполняется неравенство
где М и 1 — масса и момент инерции вспомогательного тела от-
носительно его центра тяжести.
Иногда удовлетворение неравенства (1.7) вызывает затруд-
нения по тем или иным причинам. Тогда можно воспользоваться
одним из способов его «смягчения», вытекающих из рассмотре-
ния схем, которые представлены в пп. 7, 20, 27 таблицы 5.
В первом случае эффект достигается изменением числа степеней
свободы колебательной части системы, в двух других — при по-
мощи дополнительного вибратора. Аналогичным образом может
быть смягчено и условие устойчивости требуемого режима для
схемы п. 13 таблицы. Наконец, иногда может оказаться целе-
сообразным использование того или иного способа принудитель-
ной синхронизации (см. пп. 4 и 5 таблицы 5).
Сказанное выше относилось к схемам с двумя вибраторами.
Используя интегральный критерий устойчивости синхронных
движений, нетрудно показать, что четыре одинаковых самосин-
*) На получении этих условий, которые вытекают из результатов работы
[241], изложенной в п. 5 § 8 главы XIV, здесь мы не останавливаемся.
694
ВИБРАЦИОННЫЕ ГРОХОТЫ, КОНВЕЙЕРЫ, ПИТАТЕЛИ
[ГЛ. XX
хронпзирующихся дебалансных вибратора, обладающих одина-
ковыми положительными парциальными скоростями и симме-
трично установленных на мягко амортизированном твердом теле
с плоским движением (см. рис. 82,6 и п. 21 таблицы 5), не мо-
гут быть применены для получения круговых поступательных
движений тела. Рассуждения здесь вполне аналогичны прове-
денным в п. 2 настоящего параграфа. Мгновенное положение
роторов вибраторов, отвечающее устойчивому синхронному вра-
щению, представлено на рис. 82,6 сплошными линиями; при
этом твердое тело остается неподвижным, ибо возмущающие
силы вибраторов взаимно уравновешиваются.
Синфазное же вращение роторов (см. пунктирные линии на
рис. 82,6), необходимое для обеспечения круговых поступатель-
ных колебаний, в данном случае при использовании эффекта
самосинхронизации не обеспечивается. Как и в предыдущем
пункте, подчеркнем, однако, что этот отрицательный результат
относится только к рассмотренной «плоской» схеме.
Одна из возможных схем, позволяющих использовать два
одинаковых самосинхронизирующихся вибратора для возбужде-
ния поступательных колебаний твердого тела по эллиптическим
траекториям, представлена в п. 6 таблицы 5. Следует, однако,
заметить, что любая из упоминавшихся выше схем, пригодных
для возбуждения круговых колебаний, может быть весьма про-
сто видоизменена с целью получения эллиптических колебаний.
Так, например, в схемах пп. 3—7, 13, 20 и 27 таблицы 5 для
этого достаточно шарнирно присоединить к основному телу одно
или несколько дополнительных тел (физических маятников).
Очевидно, что «присоединенная масса» таких маятников при
колебаниях оси подвеса в направлении, совпадающем с направ-
лением вектора-эксцентриситета маятника, будет равна массе
маятника, а при колебаниях в перпендикулярном направлении —
составлять лишь часть этой массы. Поэтому, если векторы-экс-
центриситеты маятников в положении равновесия будут парал-
лельны осям координат, то, вообще говоря, колебания тел из
круговых (при отсутствии маятников) превратятся в эллипти-
ческие.
В схеме, представленной в п. 7 таблицы 5, кроме того, можно
достигнуть цели, выбрав жесткости упругих элементов, посред-
ством которых дополнительная масса связана с основной, раз-
личными в направлениях Ох и Оу.
Разумеется, во всех рассмотренных случаях изменения
колебательной части системы необходимо убедиться в том,
что синфазное движение вибраторов продолжает оставаться
устойчивым.
4.	Винтовые и поворотные колебания. Два способа использо-
вания самосинхронизирующихся вибраторов для получения вин-
§2]	О СТАБИЛЬНОСТИ КОЛЕБАНИЙ РАБОЧИХ ОРГАНОВ	695
товых колебаний твердого тела представлены в пп. 2 и 18 таб-
лицы 5 Добавления 2. Отметим, что обеспечение выполнения
условия устойчивости требуемого движения вибраторов в случае
наиболее интересной для приложений схемы п. 18 обычно не вы-
зывает каких-либо затруднений.
О способах смягчения этого условия, а также о способах
обеспечения требуемого режима вращения более чем двух ви-
браторов при получении винтовых колебаний здесь можно по-
вторить сказанное по этому поводу в пп. 2 и 3 настоящего
параграфа. Эти способы были применены Б. П. Лавровым,
Г. А. Денисовым и Р. Ф. Нагаевым в их изобретении [168].
Поворотные колебания тела можно рассматривать как ча-
стный случай винтовых; для их получения с использованием двух
самосинхронизирующихся вибраторов пригодны схемы, пред-
ставленные в пп. 2, 3, 6, 7, 9, 15 и 17 таблицы 5. Все указанные
схемы, кроме схемы п. 17, были обоснованы выше и не нуж-
даются в особых пояснениях; о последней же схеме подробно
говорится в § 4 главы XXII.
5.	Заключение. Подводя итог, следует подчеркнуть, что в на-
стоящем параграфе были рассмотрены лишь некоторые простей-
шие способы использования самосинхронизирующихся вибрато-
ров для получения прямолинейных и круговых поступательных,
а также винтовых и поворотных колебаний. Что же касается
приведенных схем, то выбор какой-либо из них определяется
главным образом конструктивными и эксплуатационными сооб-
ражениями при разработке конкретной вибрационной машины.
§ 2. О стабильности колебаний рабочих органов
некоторых вибрационных машин с самосинхронизирующимися
вибраторами
1.	Предварительные замечания. Как было указано в гла-
ве XVI настоящей книги, для возможности практического ис-
пользования эффекта самосинхронизации вибраторов еще недо-
статочно выполнения условий существования и устойчивости
требуемого по технологическим соображениям движения си-
стемы. Необходимо, чтобы это движение было «устойчиво» (ста-
бильно) также и в ином смысле, а именно чтобы искажения
траекторий колебаний точек вибрирующего органа вследствие
всегда возможных на практике неточностей изготовления кон-
струкции и несимметрии нагрузки не превышали допустимых по
технологическим требованиям пределов, по крайней мере для по-
давляющего большинства машин определенной серии. Это усло-
вие накладывает дополнительные, иногда весьма существенные
требования на параметры машин, в которых используется эф-
фект самосинхронизации вибраторов.
696
ВИБРАЦИОННЫЕ ГРОХОТЫ, КОНВЕЙЕРЫ. ПИТАТЕЛИ
[ГЛ. XX
В главе XVI были сформулированы в общей форме основные
понятия и намечены пути изучения стабильности колебаний ви-
брационных машин. В настоящем параграфе, в основном пред-
ставляющем собой развитие работ автора [56, 68], условия ста-
бильности будут получены для одной из распространенных схем
изучаемого в данной главе класса машин с прямолинейными
поступательными колебаниями мягко амортизированного вибри-
рующего органа, привод которой осуществляется от двух само-
синхронизирующихся вибраторов (см. рис. 79, а и п. 8 таб-
лицы 5). Будет указан также простой способ получения упрощен-
ных соотношений для оценки стабильности режима колебаний
машин с двумя одинаковыми самосинхронизирующимися вибра-
торами в общем случае и приведены такие соотношения для
конкретных систем.
Читатель, интересующийся лишь расчетными формулами, мо-
жет обратиться непосредственно к п. 6 настоящего параграфа.
2.	Колебания тела при наличии отклонений параметров си-
стемы и неодинаковости вибраторов. Рассмотрим систему, отли-
чающуюся от представленной на рис. 79, а тем, что соответ-
ствующие параметры вибраторов, а также расстояния Г\ и
отличаются друг от друга (см. рис. 79,6). В данном случае
по-прежнему справедлива первая группа равенств (16.25') гла-
вы XIII и соотношения (1.1) настоящей главы*). Поэтому по
формулам (16.3) и (16.4) главы XIII при ctict2 = —1 находим
Р =	Q = О,
Г (со) = -W1?.me^.^2, v = o.	(2.1)
Далее с целью упрощения вычислений линеаризируем выра-
жения для моментов (ст4со) и R°s (со) вблизи определенного
значения со = соо, за которое можно принять номинальное зна-
чение угловой скорости вращения вибраторов. А именно
положим
<JsL(sa) (crsco) = Ls (со0) — zLs (со - со0),
Rs (к>) = Rs (соо) + Zf{s (со — соо),
Zs (ffs<n) = Z°s (<Js, co) = L°s (coo) - R°s (co0) — (zLs + Zrs) (co - Wo) (2.2)
(5=1, 2).
Тогда, в силу равенств (16.4), (16.10) и (16.7) главы XIII, угло-
вая скорость синхронного вращения вибраторов со определится
*) Напомним, что ось 0,4 всегда может быть направлена вдоль биссек-
трисы угла o^jOj.
§ 2]
О стабильности Колебаний рабочих органов
697
по формуле
А, (<оо) + L2 (<оо) — Л) (<оо) — R2 (<о0)
Q) 83 (On “Г".....  •	"	.......... ... '**' '	' "
zLl+zL2 + zRl+zR2
(2.3)
а парциальные угловые скорости вибраторов будут
<ns = <о0
+ zLs + ZRS
(•$=1,2).
(2.4)
Положительность величины со, определяемой по формуле
(2.3), является одним из необходимых условий существования
синхронного движения вибраторов. Заметим, что это условие
наверняка выполняется, если обе парциальные угловые скорости
положительны, ибо, как нетрудно видеть, со не меньше наимень-
шей и не больше наибольшей из парциальных скоростей cos.
Другое условие (см. неравенство (16.11) главы XIII) после
несложных преобразований с использованием формул (2.1) —
(2.4) может быть представлено в виде
<м>
где
^(М) (Z£l + Z£2 + Zj?l +Zj?2) _t
W 2w0 (ZLl + ZR1) (ZL2 + ZR2)
= 1	^+2^ + 2^+^)
4	f(00	(2Д1+Z£l)(ZI2 + Zfl2)
Таким образом, изучаемое синхронное вращение вибраторов
наверняка существует, если парциальные угловые скорости
и иг положительны и не слишком значительно отличаются друг
от друга. При этом величина фигурирующая в формуле (2.5),
представляет не что иное, как максимальное относительное от-
клонение парциальных скоростей от номинального значения, при
котором еще возможна самосинхронизация вибраторов.
Согласно равенствам (2.1) и (2.2), а также соотношениям
(16.12). и (16.15) главы XIII разность фаз вращения вибраторов,
отвечающая устойчивому синхронному движению, будет
где
а = а, — а2 = — л + Да,
(2.7)
Да = arc sin (-~/ри
(2.8)
—дополнительный сдвиг фаз, обусловленный неодинаковостью
-парциальных скоростей вибраторов.
698
Вибрационные грохоты, конвейеры, питатели
(ГЛ, хх
Запишем теперь закон движения системы в устойчивом син-
хронном движении. Замечая, что без нарушения общности мож-
но положить «1 = а, аг = 0, в соответствии с формулами (14. 1),
(14.2), (4.8), первой группой равенств (16.25') главы ХШ и
при учете соотношений (1.1) и (2.7) настоящей главы находим
(напомним, что щог = —1)
<р° — (at — л + Да, q>£ = (at,
х° = —	sin Да sin (at +	cos Да —	cos (at,
М	\ М	М/
у° — —	sin Да cos (at —	cos Да +	sin (at, (2.9)
<p° =	sin (б + Да) — sjn cos
+OTi^ri cos (6 + Да) — -2^2-2 cos sin (at.
Из равенств (2.8) и (2.9) непосредственно видно, что если
параметры вибраторов mses, расстояния rs и парциальные угло-
вые скорости <о5 одинаковы, то
f = 0, (р°=0, у° = — sin (at.	(2.10)
Иными словами, вибрирующий орган в этом случае совершает
прямолинейные поступательные колебания в направлении, пер-
пендикулярном плоскости, в которой лежат оси вращения виб-
раторов. Этот результат, естественно, соответствует получен-
ному в п. 2 § 1 настоящей главы.
Предположим теперь, что параметры вибраторов, их пар-
циальные угловые скорости и расстояния rs, будучи обуслов-
лены неточностями изготовления, мало отличаются друг от дру-
га, то есть можно положить
nile1 = me = m2e2+Д(те), г1 = г = г2 + Дг,
(0[ = (0 = (02 + Д®>
£1(ы0)~Л°(ю0)~Л2(о>о)-М£°(й)о),
2д1 ~ ZL~ ZL2 "I"
/?1 (®о) ~ R (®о) = %2 (®о) + &R (wo),
zRi ~ ZR~ zR2 + &ZR
и считать, что относительные разбросы параметров Д(те)/те,
Дг/r и Дю/w, а также величина Да = arc sin (’/гДы/иоРю) малы
По сравнению с единицей. Тогда, записанные с точностью до
§21
О СТАБИЛЬНОСТИ КОЛЕБАНИЙ РАБОЧИХ ОРГАНОВ
699
величин первого порядка малости включительно, последние три
равенства (2.9) примут вид
х° = 4 4> fcos _ да sjn
2 и L те	J
и° = — До sin at + 4 Да Г sin — Да cos ,
17 и	2 L we	J
0 тег Г. х , / А (те) . \г \ . .1	, .	(2.12)
Ф =—г- Да coso + —1—- Н--sin б cos at -+
/ L	\ те г ) J
. тег Г .	. » . / А (те) , Ar \	,
Н—г- — Да sin б + —'—-ч cos б sin <ог.
1 I L	\ те 1 г / J
Здесь, согласно (2.6) и (2.8) и с учетом принятой точности вы-
числений,
. 2те .	1 Асо 1
До = ——,	Да =  -----о-
М	2 “о Ри
О _ (тег)2 а>о
1 (ZL + zr)
(2.13)
причем До есть амплитуда прямолинейных поступательных ко-
лебаний вибрирующего органа при отсутствии отклонений па-
раметров.
В соответствии с (2.12) и равенствами (14.7) главы XIII за-
кон движения точки вибрирующего органа с координатами и*
и v* может быть представлен в форме
х* = и‘ + х° + и'ф° = и* + До (gj cos at + g2 sin соЛ,
y' = v* -I- y° + п‘ф° = v* — До (г]| cos at + ц2 sin at).
Здесь
1 f A (me) , Mrv* ff\(me) . Ar \ .	1 Асо ,1 |
g, -L—_L__H------------sin6 + —5- — cos6 !,
2 j me I [\ me r /	2pa co0 j
„	1(	1 Аю . Mrv* Г/ h (me) , Ar\ .	1 Affl . ,11
g,2= —(-у---1--—---H---COS 6----------г -Sill 6 I,
2 ( ®o Z me r )	2pa co0 J|
(2.15)
a r]i и г]2 — малые по сравнению с единицей величины, конкрет-
ные выражения которых в дальнейшем не понадобятся.
Из формул (2.14) нетрудно усмотреть, что неодинаковости
вибраторов и расстояний г\ и г2 приводят к превращению траек-
торий колебаний точек вибрирующего органа из прямых линий
в «вытянутые» эллипсы, различные для различных точек
(рис. 83). Уравнение этих эллипсов легко получить путем ис-
ключения времени t из уравнений (2.14):
(х* - Ц‘)2 +	(х* - «’) (/ - о*) +	+ $ (у" - v*)2 - Д2 = 0. (2.16)
Здесь отброшены члены, имеющие относительно £2, rji и т|2
порядок выше второго.
700
ВИБРАЦИОННЫЕ ГРОХОТЫ, КОНВЕЙЕРЫ, ПИТАТЕЛИ
[ГЛ. XX
Используя хорошо известные формулы для элементов эл-
липса, нетрудно убедиться, что с принятой выше степенью точ-
ности вычислений величина |gi| представляет собой отношение
длины малой полуоси эллипса В к его большой полуоси, при-
близительно равной амплитуде Ло (рис. 83). Точно так же уста-
навливается, что £2 есть угол
наклона большой оси эллипса
к направлению оси у*, то есть
к направлению неискаженных
колебаний вибрирующего ор-
гана.
3. Контрольные параметры
и их зависимость от отклоне-
ний параметров системы. Со-
гласно изложенному, величи-
ны gi и £2 вполне характери-
зуют отклонения колебаний то-
чек рабочего органа рассмат-
риваемой вибрационной маши-
ны вследствие неточностей
изготовления и несимметрии
нагрузки. Поэтому за кон-
трольные параметры закона
колебаний рабочего органа (см. главу XVI настоящей книги),
исходя из вида формул (2.15), примем значения величин gi и
в точке К рабочей поверхности, которой отвечает максимальное
по модулю значение координаты V* (рис. 79,6), эту точку, то
есть точку, наиболее удаленную от оси Ощ, также назовем
контрольной. Иными словами, положим
bi — (&1)к — 2 (
Д(те) MrvK
me “I Г
^2 = fe)# — ~
&(me) Дг\
--------1---I Sin 6 +
me r /
,	1 Дш
H----5----cos 0
2/’<o “o
1 Дш MrvK Г/ Д (me) Ar\
—о-------1------------------1---COS 6 -
2ри 0>o	1 IA me r /
(2.17)
1	A co
2p« “о
sin 6 I
4, Условия стабильности. Для обеспечения нормальной ра-
боты устройства следует потребовать, чтобы величины |&i| и
| Ь21 не превосходили некоторых максимально допустимых зна-
чений ры и ры- Выбор этих значений зависит от технологиче-
ских задач, решаемых машиной. В вибрационных конвейерах,
судя по имеющимся данным, технологический процесс не нару-
§ 2]
О СТАБИЛЬНОСТИ КОЛЕБАНИЙ РАБОЧИХ ОРГАНОВ
701
цгается, если |&i| и рг| не превосходят 0,2—0,25; при |&i|
и 1621, не больших 0,15, заметные отклонения от нормального
режима работы практически отсутствуют. Отметим, что изобра-
женный на рис. 83 эллипс как раз отвечает значениям gi =
= Ь = 0,15.
В соответствии с определением, приведенным в § 1 главы XVI,
стабильность рабочего режима есть вероятность одновременного
выполнения неравенств	'
\b1\<pbi,	\b2\<pb2	(2.18)
в течение некоторого достаточно длительного промежутка вре-
мени Т. Получим условия выполнения этих неравенств с доста-
точно высокой вероятностью, то есть достаточные условия ста-
бильности.
„	1 А (те)
С этой целью заметим, что относительные отклонения-^--,
•	2 те
1 Ar 1 Аса	, ..	,
— — и -z—представляют собой величины, зависящие от боль-
2 Г 2 (О0
того числа случайных факторов. Будем считать эти отклонения
независимыми случайными величинами, распределенными по
нормальным законам с математическими ожиданиями, равными
нулю, и с некоторыми средними квадратическими отклонениями
оте, щ и ом. Тогда величины bi и Ь2 также будут подчиняться
несмещенному нормальному закону распределения со средними
квадратическими отклонениями
Если воспользоваться известным «правилом трех сигма-»,
приняв *)
Qbl I Ь[ Imax 3^61, 7*2 — I Ь2 |п1ах — 3(Tft2,
*) Напомним (см., например, [125]), что согласно этому правилу за мак-
симальное значение модуля случайной величины х с нулевым математическим
ожиданием можно принять утроенное среднее квадратическое отклонение этой
величины <tx; значения |х|, большие Зстх, будут встречаться достаточно редко
(при нормальном законе —не чаще чем в 0,3% случаев).
702
ВИБРАЦИОННЫЕ ГРОХОТЫ, КОНВЕЙЕРЫ, ПИТАТЕЛИ
[ГЛ. XX
где qme, qr, q,m, qbi и qb2—максимально возможные значения
соответствующих относительных отклонений, то формулам (2.19)
можно придать также следующий вид *):
= |/ (1 + vK sin 6)2C + (vksin ^q2r + fecos6>) q^,
tfb2 “
1Z (yK cos 6)2 (q2mE+q2) + p.1+^osin6)
V	zPm
(2.21)
Результаты вычислений по последним формулам и надлежит
сравнивать с максимально допустимыми значениями ры и рЬ2
величин bi и Ь2. А именно, для гарантии нормальной работы ма-
шины должно быть
qbi<Pbi, qbi<Pb2-	(2.22)
Отметим, что удовлетворение этих условий обычно влечет за
собой автоматическое выполнение условия сохранения эффекта
самосинхронизации, состоящего, согласно (2.5) и (2.20), в вы-
полнении неравенства
qa<P°a-	(2.23)
Заметим, что невыполнение условий (2.22) еще не означает,
что каждая из нескольких изготовленных машин действительно
будет плохо работать: реальные отклонения параметров в конк-
ретном экземпляре машины, естественно, могут быть меньше,
нежели предельно возможные. Поэтому представляет интерес
оценить вероятности Pi и Р2 непоявления недопустимых откло-
нений величин bi и Ь2 в случае, когда предельно возможные от-
клонения qbi и qb2 превосходят максимально допустимые откло-
нения ры и рь2 этих величин.
В соответствии с принятым нормальным законом распределе-
ния и обозначениями (2.20) имеем
Ps = Ps(I bJ<pbs) = Ps{\bs\<3absKbs) = Ф(3ofe) (s = 1, 2). (2.24)
Здесь
<2-25>
2
2 Г
а Ф (z) =	- j e~tm dt — интеграл вероятности.
Аналогичным образом, если условие (2.22) не выполнено, то
это свидетельствует не о невозможности самосинхронизации, а

б СТАБИЛЬНОСТИ КОЛЕБАНИЙ РАБОЧИХ ОРГАНОВ
703
Лишь о том, что самосинхронизация может наступить с некото-
рой вероятностью Р,ю < 1. При этом
- ₽» (т I-S71 < ^ = ₽. (41VI < З'’-’1-)= ф (3и-> (2'26’
и, согласно (2.13) и (2.20),
0 । 0
х	= —J______ = -^-
w Ча> I Imax 3<ги
(2.27)
Величины кь, и хм естественно назвать коэффициентами за-
паса соответственно по стабильности траектории и по самосин-
хронизации.
График функции Р|М — Ф(3хщ) представлен на рис. 122 сплош-
ной линией. В качестве примера найдем вероятности непревыше-
ния максимально допустимых отклонений в случае, когда х = 0,5,
то есть когда максимально возможные отклонения вдвое больше
предельно допустимых. Пользуясь графиком, находим
Р = Ф (3 • 0,5) = Ф (1,5) ~ 0,9 = 90%.
Таким образом, вероятность удовлетворительной работы ма-
шины даже и при этих достаточно неблагоприятных условиях
все же довольно велика.
В большом числе вибрационных устройств с самосинхронизи-
рующимися вибраторами максимально возможное отклонение
сдвига фаз | Да |тах = значительно превышает максимально
возможные относительные отклонения qme и qr (см. п. 5 настоя-
щего параграфа). В этом случае формулы (2.19) и (2.20) зна-
чительно упрощаются, принимая вид
| v„ cos б |	| 1 + sin б |
~ о о	®Ь2 ~	~о	<7И,
2РИ	2ри
I cos б I	I 1 + sin б I	(2.28)
---?<»>	“------Л-------qa.
2Р<Л
Последние две формулы становятся еще более простыми, если
ввести коэффициент запаса по самосинхронизации хм = p°a[q^
согласно равенству (2.27):
I v „ cos б I
__ | 1 + sin б |
qbi ~
(2.29)
Соотношения (2.29) позволяют обосновать применяемый в
настоящее время при конструировании машин с двумя самосин-
хронизирующимися вибраторами принцип, согласно которому
/04	ВИБРАЦИОННЫЕ ГРОХОТЫ, КОНВЕЙЕРЫ, ПИТАТЕЛИ [ГЛ. XX
рабочий режим является достаточно стабильным, если коэффи-
циент запаса по самосинхронизации хм = выбран доста-
точно большим [56, 245].
Так, Б. П. Лавров [245] рекомендует для виброконвейеров
принимать хщ не ниже 3,54-5, для вибропитателей в зависимости
от их назначения — от 5 до 12 и выше и для грохотов — от
12 до 20.
Если учесть, что величина v/( = |A4rv^/| имеет порядок еди-
ницы, то из равенств (2.29) следует, что при хш = 34-5 макси-
мально возможные значения отклонений параметров траекторий
Ь\ и в контрольной точке К. будут величинами порядка 0,1 —
0,15. Напомним, что примерно такие и несколько большие значе-
ния указывались в начале данного пункта в качестве допустимых
для вибрационных конвейеров. Иными словами, условия ста-
бильности (2.22) в рассматриваемом случае выполняются.
Разумеется, приведенные выше цифровые значения коэффи-
циентов запаса хщ нуждаются в уточнении и конкретизации, од-
нако ими вполне можно пользоваться как ориентировочными.
5.	Оценка максимально возможных отклонений параметров
системы. Для завершения исследования остается оценить вели-
чины максимально возможных отклонений qme, qr и qU).
Отклонения в значениях статических моментов могут быть
обусловлены неточностью изготовления дебалансных грузов в
пределах допусков, а также наличием раковин в отливках и >не-
одинаковостью удельного веса различных частей деталей.
Неодинаковость расстояний /ц и Гг может иметь место как
вследствие неточностей изготовления и сборки машины, так и
вследствие несимметрии загрузки машины обрабатываемым ма-
териалом. Оставляя пока в стороне вопрос об учете последнего
фактора*), заметим, что, исходя из допусков на изготовление
деталей машин, можно ориентировочно принять, что максималь-
ные относительные отклонения qme и qr не превышают двух про-
центов, то есть
Qme ~ Яг ~ 0,020 — 2,0%.
Значительно сложнее оценить максимально возможное откло-
нение парциальных угловых скоростей q^ = ± | Асо/(оа |тах. Это от-
клонение в наиболее общем случае зависит от отклонений в ха-
рактеристиках электродвигателей, от отклонений в передаточных
отношениях и к. п.д. передач от валов двигателей к валам ви-
браторов, а также от отклонений сил сопротивления вращению
роторов вибраторов. Как показывают расчеты, оно во многих
машинах значительно превышает отклонения qme и qr.
) Этот вопрос рассматривается в п. 7 настоящего параграфа.
§ 2]
О СТАБИЛЬНОСТИ КОЛЕБАНИЙ РАБОЧИХ ОРГАНОВ
705
Пусть вибраторы приводятся во вращение от электродвига-
телей асинхронного типа. Обозначим через L<e>(®<р>) момент на
валу такого двигателя и представим его вблизи номинального
значения угловой скорости двигателя со(е> — со<е) в виде
£(е)	= А(е>	_ tf Це)) (tf _	(2.30)
Обозначим через
передаточное отношение, а через ц— коэффициент полезного
действия передачи от вала двигателя к валу вибратора. Тогда
из условия баланса энергии получим следующее соотношение
между величинами L(<?) и Zl} и введенными выше соответ-
ствующими величинами L° и zL для вала вибратора:
L°(®o) — zl (®о) (® —	= [^<е>(г®о) — Zt’(zcoj) i (и — соа)] /г). (2.32)
Отсюда находим
L° (со0) = й]£(е) (zco0), z£ (<»о) i2t)Zl ’ (zco0).	(2.33)
Заметим при этом, что величины /Je)(zco0) и z/f'fzcoo) легко
находятся по каталожным данным электродвигателей: А(<?) (/со0)
есть номинальный момент двигателя, а коэффициент z<.e>(z'a>0)
может быть с достаточной точностью подсчитан по формуле
(!т ч = (top) = 30 (top)
L ' °'	а//1 — Це> л п(се) — п<ое> ’
(2.34)
где == 30(в(е)/л и = ЗОи^/л — соответственно синхронное
и номинальное число оборотов вала электродвигателя в минуту.
Пусть, далее, дополнительные сопротивления вращению ро-
торов вибраторов отсутствуют, так что согласно формулам (6.9)
главы XIII и соотношениям (2.2) настоящего параграфа
/?°(со0) =	d(o%, zR = fmeda)0.	(2.35)
При учете равенств (2.33) и (2.35) формула (2.4) для опреде-
ления парциальной угловой скорости вибратора принимает вид
(za0) — -у fme ztojj
© = ®0 Н-----5-----------------------•
i r\zL 1 (to0) + f me zto0
(2.36)
Используя последнее равенство, нетрудно выразить относитель-
ное отклонение парциальной угловой скорости м от номиналь-
ного значения через относительные отклонения величин z, т],
23 И. И. Блехман
706
ВИБРАЦИОННЫЕ ГРОХОТЫ, КОНВЕЙЕРЫ, ПИТАТЕЛИ
[ГЛ. XX
//е>, Zl\ f и med. С точностью до величин первого порядка от-
носительно указанных отклонений находим
1 A®	ди> 1 А//е) , z)e> [ da 1
2 а0 “ а0	2 L(e) а() ( дАе} ) Т z<e)
и	и	О \ L /	L
I / da \ 1 Аг
®0 \ di ) 2 z
! т] / da \ 1 Ад . f i да \ 1 Af . med
' а0 \ <Эт) / 2 г] о0 \ df ) 2 f ' w
да \ 1 A (med)
. d (med) ) 2 med
(2.37)
He выписывая здесь легко вычисляемых выражений для част-
ных производных функции со, заметим, что они должны быть
взяты для номинальных значений параметров.
Величина
1 Да(0>	£(е) / да \ 1 AL(e) z(,e) / da \ 1 Az(e)
(2,38)
как нетрудно видеть, представляет относительное отклонение
парциальных скоростей вибраторов, обусловленное только не-
точностями изготовления двигателей. Поэтому, считая все фи-
гурирующие в формулах (2.37) и (2.38) отклонения случай-
ными величинами, распределенными по нормальному закону,
получим, аналогично равенствам (2.21),
’ /ю!
+ [^(‘3г)1?<] Г («<sd)J	> (2*39)
где обозначено:
о 1 / Аа(0) \	_ 1 ( Ат1)
2 \ ®о /max’	2 \ i /max’	2 \ Г] /max’ /п
„ =J_ ( Af \	_ 1 / A (med) \
4f 2(fJmax’ Чтг“ 2( med Jmax’
Приведем ориентировочные значения максимальных откло-
нений. Согласно ГОСТ 183—55, п. 30, максимальное отклонение
угловых скоростей асинхронных двигателей общего применения
при номинальной нагрузке не должно превосходить 25% от но-
минального скольжения. Поэтому
о _ . 1 Не)-»ое>)
8
(2.41)
§2]	О СТАБИЛЬНОСТИ КОЛЕБАНИЙ РАБОЧИХ ОРГАНОВ	707
где, как и выше, и — соответственно синхронное и но-
минальное число оборотов электродвигателя в минуту*).
Для клиноременной передачи, в соответствии с данными,
приводимыми в справочниках, можно принять
qt ~ q-n ~ 0.05 = 5%.
Отклонения коэффициента трения f в подшипниках качения
достигают значительных величин. Учитывая справочные данные
и результаты экспериментов, проведенных в институте «Меха-
нобр», можно принять для часто применяемых в вибрационных
машинах радиальных сферических роликоподшипников
qf ~ 0,3 = 30%.
Наконец, величину qme.d можно считать равной максималь-
ному отклонению qme, то есть примерно 2% (см. выше).
6.	Результативные соотношения для проверки стабильности.
Обобщение на случаи, отличные от рассмотренного. Для удоб-
ства практического использования приведем сводку полученных
выше окончательных расчетных формул, повторив также и ос-
новные обозначения. Укажем также способ ориентировочного
расчета схем с двумя самосинхронизирующимися вибраторами,
отличных от изученной выше.
В соответствии с изложенным стабильность рабочего ре-
жима вибрационных машин изученного выше типа (см. рис. 79)
может считаться достаточно высокой, если одновременно вы-
полняются неравенства (см. соотношения (2.21) — (2.23))
Яы<Рьо Яъ2<Рь2> qw<po^	(2-42)
где qb\, qi>2 и qa> — максимально возможные, a pbi, pb2 и —
максимально допустимые относительные отклонения парамет-
ров траекторий колебаний контрольной точки рабочего органа
и парциальных угловых скоростей вибраторов.
При этом величины ры и pi>2 задаются исходя из техноло-
гических соображений (см. п. 4 настоящего параграфа), а ве-
личина определяется, согласно (2.13), по формуле
в которой «о есть номинальное значение угловой скорости вра-
щения роторов вибраторов, те — статический момент дебаланс-
ных грузов вибраторов, г — расстояние от осей вращения виб-
раторов до центра тяжести (% корпуса машины с вибраторами,
*) Заметим, что величина qa может быть значительно снижена, если спе-
циально подбирать пары электродвигателей (см. п. 9 настоящего параграфа).
23'
708
ВИБРАЦИОННЫЕ ГРОХОТЫ, КОНВЕЙЕРЫ, ПИТАТЕЛИ
[ГЛ. XX
/ — центральный момент инерции корпуса с вибраторами, а
коэффициенты zL и zR определяются, в соответствии с (2.32) —
(2.35), равенствами
•2	30
zL = z2n
4е)
л п<е) - ntf ’
ZR = fme
(2.44)
Здесь i = п^/по — передаточное отношение, ц— к. п.д. пере-
дачи от вала двигателя к валу вибратора, L»\ и п(ое) — со-
ответственно номинальный момент, синхронное и номинальное
число оборотов в минуту вала электродвигателя (значения этих
величин находятся по каталожным данным двигателей), f —
коэффициент трения и d — диаметр внутреннего кольца под-
шипников вибраторов.
Величины qbi и qi>2 определяются, согласно (2.21), равен-
ствами
/	/ V
0 + ^sin6)2^e + (vKsin6)2?2 + [-4-cos6 ql,
^Й2
(vkcos6)2(^e + <72) +	' (1 + sin 6) 2Р»	2 fl2 "(0
(2.45)
Mrv^
Здесь М — масса вибрирующего органа машины с вибраторами,
v*K — координата точки рабочей поверхности, наиболее удален-
ной от оси О\и (контрольной точки; см. рис. 79), 6 — угол меж-
ду прямыми OiOi, OiO2 и осью Ощ. Величины qme и qr имеют
порядок 2,0%, а величина qm определяется по формулам
(2.37) —(2.41).
Для ориентировочных расчетов на стабильность можно ре-
комендовать соотношение [56, 245]
О
х = —>х*	(2.46)
где минимально допустимое значение коэффициента запаса по
синхронизации х*, можно, при отсутствии более точных дан-
ных, принимать для виброконвейеров в пределах от 3,5 до 5,0,
для вибропитателей — от 5 до 12 и для грохотов — от 12 до 20.
Заметим теперь, что основная формула ориентировочного
расчета на стабильность (2.46) является справедливой и для
любых других систем с двумя номинально одинаковыми само-
синхронизирующимися вибраторами. При этом формулы для
вычисления величины q:£t и принципы задания минимально до-
§ 2]
О СТАБИЛЬНОСТИ КОЛЕБАНИЙ РАБОЧИХ ОРГАНОВ
709
пустимого коэффициента запаса %* остаются прежними, а изме-
няется лишь выражение для максимально допустимого откло-
нения парциальных скоростей вибраторов р°. Нетрудно прове-
рить (см. формулы (16.4), (16.5) главы ХШ и (2.1), (2.5), (2.6)
и (2.13) данного параграфа), что
=	Г°(<оо)
<*0(zl + zR)'
(2.47)
где 1Г(«0) есть максимальное (по сдвигу фаз а) значение
вибрационного момента, вычисленное для случая в точности
одинаковых вибраторов и для номинальных значений парамет-
ров системы.
Учитывая это обстоятельство, легко найти, что, например,
для пространственного варианта основной схемы, рассмотрен-
ной в настоящем параграфе (см. п. 14 таблицы 5), расчет мож-
но вести, пользуясь в точности теми же соотношениями, если
заменить момент инерции / в формуле (2.43) «приведенным»
моментом инерции
/' = ----2	(2.48)
COS2 Р +/у sin2 р	'	’
(см. формулу (1.6) § 1 настоящей главы; обозначения расшиф-
рованы в упомянутой таблице).
Для схемы п. 18 таблицы 5, обеспечивающей при определен-
ных условиях получение винтовых колебаний твердого тела,
о 1 (те)2 а0 a2 sin2 у 2 sin2 у а2 cos2 у + с2 с2 sin2 у I
(2.49)
Последняя формула была получена Г. А. Денисовым [172].
Наконец, для «плоской» схемы, представленной в п. 16 таб-
лицы 5, имеем (см. § 3 главы ХХШ)
о _ 1	(те)2 <0р
2	+
1	. Mh 1
I Л2-1
(2.50)
Случай, отвечающий п. 3, б таблицы 5, рассмотрен в § 5
главы XXI.
Заметим в заключение, что невыполнение неравенств (2.42)
и (2.46) еще не означает, что отклонения, превышающие допу-
стимые, будут наблюдаться во всех изготовленных экземплярах
изучаемых машин. Вероятности непревышения фактическими
отклонениями допустимых значений могут быть в этих случаях
оценены по формулам (2.24) и (2.26) настоящего параграфа.
7.	О случаях, когда имеются детерминированные отклоне-
ния. Формулы (2.21) и (2.39) перестают быть справедливыми^
710
ВИБРАЦИОННЫЕ ГРОХОТЫ, КОНВЕЙЕРЫ, ПИТАТЕЛИ
[ГЛ. XX
если какие-либо из отклонений или какие-либо их составные
части известны заранее. В этом случае можно в исходных ра-
венствах (2.15) и (2.37) расчленить отклонения Ди/w, Д(те)/те,
Дг/г и т. д. на детерминированные (заранее известные или до-
статочно точно вычисляемые) и на случайные составляющие и
перенести члены с детерминированными составляющими в ле-
вые части формул. После этого для максимального отклонения
правых частей полученных равенств можно будет написать
формулы, аналогичные (2.21) и (2.39), поскольку эти равенства
опять будут являться соотношениями между случайными откло-
нениями со средними значениями, равными нулю.
Естественно, что в таком случае вопрос о максимально до-
пустимых отклонениях ры и ры величии pj и | Ь21 может ста-
виться иначе. Здесь целесообразно регламентировать не сум-
марные отклонения |&i| и |62| от прямолинейных поступатель-
ных колебаний, а лишь случайные составляющие отклонений.
Сказанное относится, например, к машинам с преднамеренными
«искажениями» траекторий колебаний точек вибрирующего ор-
гана для достижения того или иного полезного эффекта (см. §6
настоящей главы).
С наличием детерминированных составляющих отклонений
приходится сталкиваться и при оценке искажений траекторий,
обусловленных изменением расположения условного центра тя-
жести системы (и тем самым расстояний Г] и г2) вследствие
несимметрии загрузки машины материалом. Соответствующую
составляющую отклонения целесообразно выделить как детер-
минированную, приписав ей при оценках максимально возмож-
ных отклонений наиболее неблагоприятное значение. Следует,
конечно, при этом иметь в виду, что максимально допустимые
отклонения ры и ръ2 при возникновении несимметрии нагрузки
могут зачастую приниматься большими, нежели те же отклоне-
ния при нормальном режиме работы. Здесь обычно важно обес-
печить лишь достаточно быстрое «рассасывание» несимметрии
нагрузки.
С детерминированными отклонениями параметров вибрато-
ров приходится оперировать и при расчете машин, в которых
двигатель одного из вибраторов после пуска машины отклю-
чается. В этом случае заранее известно, что одна из каждой
пары величин L°(co0) и zLs равна нулю, и поэтому главная часть
отклонения Дш/со0 известна заранее.
8.	О стабильности режима колебаний системы по отношению
к отклонениям, изменяющим структуру системы. Выше речь шла
лишь о стабильности колебаний по отношению к отклонениям
параметров системы, не изменяющим ее качественного харак-
тера. Между тем не лишен, в частности, интереса и вопрос
о стабильности по отношению к погрешностям, вносящим новые
§ 2]
О СТАБИЛЬНОСТИ КОЛЕБАНИЙ РАБОЧИХ ОРГАНОВ
711
(«паразитные») степени свободы, не учтенные при исходной
идеализации.
Предположим, например (рис. 84), что вследствие неточно-
сти изготовления или несимметрии загрузки машины, осуще-
ствленной по схеме *) п. 3 таблицы 5, плоскость вращения цент-
ров тяжести роторов вибраторов, оставаясь параллельной пло-
скости uOtV (Оу и Оу— главные центральные оси инерции
тела), оказалась удаленной на некоторое расстояние с от центра
тяжести 01 вспомогательного тела. Такая ситуация была рас-
смотрена в качестве примера
общие результаты которой из-
ложены в п. 5 § 8 главы XIV.
Как показано в цитирован-
ной работе, условием устойчи-
вости противофазного враще-
ния роторов вибраторов в раз-
личных направлениях является
неравенство
где Ix, Iv и /2 — главные цент-
ральные моменты инерции тела.
Из неравенства (2.51) сле-
дует, что если /у < !х, как
это часто бывает в рассматриваемых машинах, то опасности
выхода из требуемого режима не существует: как и при отсут-
ствии отклонения с, этот режим устойчив при любых комби-
нациях параметров (если г^О). В случае же, когда 1У>1Х,
неравенство (2.51) накладывает определенное условие на макси-
мально допустимую величину погрешности с. Следует, однако,
иметь в виду, что наличие этой погрешности приводит к откло-
нению колебаний тела от прямолинейных поступательных коле-
баний вдоль оси Оу, на легко выполняемой оценке величины
указанных отклонений здесь мы останавливаться не будем.
При вращении роторов вибраторов в одинаковых направле-
ниях условием устойчивости синфазного вращения является не-
равенство
(2.52)
которое «более жестко», чем неоднократно приводившееся усло-
вие Mr2/! > 2, отвечающее отсутствию отклонения с. При
*) Отметим, что изучаемая здесь схема (при отсутствии отклонений)
представляет собой частный случай основной схемы, рассматриваемой в на-
стоящем параграфе (рис. 79, а), отвечающий 6 = 0.
712
ВИБРАЦИОННЫЕ ГРОХОТЫ, КОНВЕЙЕРЫ, ПИТАТЕЛИ
{ГЛ. XX
невыполнении неравенства (2.52) устойчиво противофазное вра-
щение роторов.
9.	Заключение. Как показали расчеты, выполненные при
конструировании машин рассматриваемого типа, удовлетворе-
ние условиям стабильности (2.42) или (2.46) обычно не вызы-
вает особых затруднений. Лишь в некоторых случаях, когда
вибрации рабочего органа машины недостаточно интенсивны
и синхронизирующее воздействие колебаний общего основания,
на котором установлены вибраторы, недостаточно, неравенства
(2.42) или (2.46) не удовлетворяются и приходится либо видо-
изменять динамическую схему машины, либо искусственно по-
вышать интенсивность колебаний, либо снижать степень неоди-
наковости параметров вибраторов путем увеличения точности
изготовления или же путем специального подбора пар электро-
двигателей*) с целью снижения величины отклонения пар-
циальных скоростей	либо, наконец, вообще отказаться
от применения самосинхронизирующихся вибраторов.
§ 3. О необходимых условиях нормальной работы
некоторых вибрационных машин со многими вибраторами,
приводимыми от синхронных электродвигателей [68]
1.	Предварительные замечания. Выше мы уже неоднократно
встречались с системами, в которых требуемая фазировка вра-
щения роторов вибраторов неустойчива в случае использования
для привода асинхронных двигателей. В подобных системах сле-
дует или видоизменить систему, воспользовавшись одним из
способов синтеза, изложенных в главе XV, или использовать
тот или иной вид принудительной синхронизации.
Простейшие примеры задач о принудительной синхрониза-
ции вибраторов были рассмотрены в § 16 главы ХШ. Здесь мы
разберем более сложные случаи, представляющие определенный
интерес с точки зрения приложений к теории ряда машин, рас-
сматриваемых в настоящей главе.
2.	Четыре вибратора на мягко амортизированном твердом
теле. Рассмотрим сначала мягко амортизированное твердое
тело с четырьмя симметрично расположенными одинаковыми
дебалансными вибраторами (см. рис. 82, а и п. 22 таблицы 5
Добавления 2). Как указывалось в п. 2 § 1, в такой системе
для обеспечения прямолинейных поступательных колебаний
твердого тела эффект самосинхронизации вибраторов не мо-
жет быть использован. Попытаемся решить ту же задачу по-
средством синхронизации с помощью синхронных двигателей
*) Как уже отмечалось, последний способ, предложенный Б. П. Лавровым,
дал положительные практические результаты.
§ 3]	О НЕОБХОДИМЫХ УСЛОВИЯХ НОРМАЛЬНОЙ РАБОТЫ	713
и получим условия, которым должны удовлетворять установоч-
ные углы и характеристики двигателей, чтобы требуемое дви-
жение обеспечивалось.
Речь идет, очевидно, о движении, в котором роторы первого
и второго вибраторов вращаются в одном направлении, а
третьего и четвертого — в противоположном, причем фазы вра-
щения as для всех вибраторов одинаковы. Иными словами, сле-
дует изучить условия существования и устойчивости движения,
для которого
оч = а2 — 1, а3 = а4 = — 1,
.	(3.1)
а, = а2 = а3 = а4 = 0.
Положение роторов второго и третьего вибраторов в указанном
движении при заданном, положении роторов первого и четвер-
того вибраторов показано на рис. 82, а пунктирными линиями;
этому движению отвечают поступательные колебания тела
вдоль оси 01 и.
Для решения поставленной задачи синтеза вибрационной
машины рассмотрим уравнения (11.7) и (4.10) главы ХШ, от
характера корней которых зависит существование и устойчи-
вость синхронных движений.
Составим сначала выражения вибрационных моментов Ws.
Согласно формулам (8.8) главы ХШ, для мягко амортизиро-
ванного вибрирующего органа
Дц = - О + «Д) - ffsff/v4vy cos (аД - ofij),
Qsj = W5V/ Sin (<уД - оД),
4
= - 4 S miei K1 + sin “ a/>+	(3-2)
/=i
+ as<JjVsvi sin (as + аД - a; - оД)]
(s= 1, 2, 3, 4).
Учитывая, что в рассматриваемом случае (см. рис. 82, а)
Г1 = г2 = г3 = r4, 6j=6, 62 = л - 6, б3 = л + б, б4=-б,
Vj = v2 = v3 = v4 = r/p (р=///М),
путем непосредственной подстановки значений величин crs, as,
бз и vs согласно равенствам (3.1) и (3.3) в выражения (3.2) не-
трудно убедиться, что для изучаемого движения все вибрацион-
ные моменты равны нулю. При этом уравнения (11.7)
главы ХШ дают (учитываем, что для дебалансных вибраторов
ft, = 0 и W{SR) = 0)
ДЛ;(-*А) = Я» (5=1,2, 3,4),	(3.4)
714
ВИБРАЦИОННЫЕ ГРОХОТЫ, КОНВЕЙЕРЫ. ПИТАТЕЛИ
]ГЛ. XX
Таким образом, для обеспечения данного движения обмотки
статоров двигателей нужно ориентировать в точности таким же
образом, как и при отсутствии колебаний основания, на котором
размещены вибраторы. Из факта равенства нулю вибрацион-
ных моментов вытекает также, что соотношению фаз а> = аг =
— аз = «4 = 0 отвечает определенное синхронное движение и
при использовании для привода вибраторов обычных асинхрон-
ных двигателей. Как уже, однако, отмечалось, в таком случае
это движение неустойчиво.
Будем предполагать, что Ls, как обычно, есть нечетная функ-
ция своего аргумента; напомним, кроме того, что в силу пред-
положения об одинаковости вибраторов
б;(6)=... =л;(е)==лф(е),
к°(<о)=... =/?:(«)=/?°((о).
Тогда уравнения (3.4) принимают вид
-Г(р5.) = /Л®)	($=1,2, 3,4).	(3.6)
Если выполняется условие (см. рис. 29)
Ттах >	(®),
(3.7)
что мы и будем предполагать, то уравнения (3.6) допускают
решение
Р. = Р ($=1,2, 3, 4),	(3.8)
для которого
/ dL* (6) \
\ dQ /e=ps_p
(3.9)
Если асинхронные двигатели являются двухполюсными, а
передача от валов двигателей к валам вибраторов осуществ-
ляется «напрямую», то имеется только одно решение*), обла-
дающее свойством (3.9); в противном случае таких решений
может быть несколько.
Обратимся к исследованию устойчивости рассматриваемого
движения, считая, что установочные углы ps взяты одинако-
выми в соответствии с равенствами (3.8). При учете соотноше-
ний (11.9) главы XIII и формул (3.2) — (3.9) настоящего пара-
*) Не говоря, конечно, о решениях, отличающихся на 2ям, где п — целое
число.
§ 3]
О НЕОБХОДИМЫХ УСЛОВИЯХ НОРМАЛЬНОЙ РАБОТЫ
715
графа алгебраическое уравнение (4.10) главы XIII после прос-
тых преобразований может быть представлено в форме
— а + 2 — z	а cos 26 — 2	а cos 26	а	
a cos 26 — 2	— а + 2 — z	а	— а cos 26	= 0,
— а cos 26	а	— а + 2 — г	а cos 26 — 2	
а	— а cos 26	а cos 26 —2	— а + 2 — z	
(3.10)
где обозначено:
z ~	117 о I ( dQ )0=6	k°* I ’	kQ-k\-k2=-k3-^ kit
Корни уравнения (3.10) легко найти, не раскрывая опреде-
лителя. Прибавив к первой строке определителя все прочие,
представим это уравнение в виде
1111
a cos26 — 2 — а + 2 — z a	—a cos26
2 •	—— 0
— a cos 26 а	— а + 2 — z a cos 26 — 2
a	—a cos 26 a cos 26 — 2 — а + 2 — z
(3.12)
Таким образом, одним из корней будет z = zi = 0.
Прибавим теперь к последнему столбцу определителя в ле-
вой части уравнения (3.12) первый, к третьему — второй, затем
ко второй строке полученного определителя — третью его строку,
а к третьей строке — четвертую. Тогда придем к уравнению
1	1	2	2	
— 2	2-z	2 (2 - z)	— 4	
а — а cos 6	a — a cos 26	— z	— z	= 0.	(3.13)
а	— а cos 26	-2	2-z	
При г = 22 = 4иг = гз = —2а (1 — cos 26) определитель (3.13)
обращается в нуль, поскольку в первом случае его вторая
строка, а во втором случае третья строка становятся пропор-
циональными первой строке. Таким образом, z2 = 4 и z3 =
= —2а(1—cos 26)—корни уравнения (3.13). Отделив эти кор-
ни путем прибавления ко второй строке удвоенной первой, а
к третьей строке — первой, умноженной на —а(1—cos 26),
716
ВИБРАЦИОННЫЕ ГРОХОТЫ, КОНВЕЙЕРЫ, ПИТАТЕЛИ
(ГЛ. XX
приходим к следующему уравнению для определения послед-
него, четвертого корня уравнения (3.10):
1	1	2	2	
0	1	2	0	= 0.
0	0	1	1	
0	— a cos 26	— 2	-2г	
Отсюда легко находим
z = z4 = — 2 [2 — а (1 + cos 26)].
Согласно (3.11) корнями и уравнения (4.10) главы XIII,
соответствующими полученным выше значениям корней z урав-
нения (3.10), будут
1 ldL*\	1 Г.,„ , ('dL*\	]
*0 ( de Vp’ “2 k0 |_4Го+ I de VpJ’
i ~ 2“	- “s 26> +	] •	(3.14)
»< - i {- 2B7«[2 - °(1+25>1+НЦ. J 
Поскольку величины 1Е0 и а существенно положительны, то ус-
ловия устойчивости zs< 0, согласно (3.11), сводятся к требо-
ванию
( dL"\ 2mleV	.
ЬоЧм?—Г-	<3-15)
Таким образом, для обеспечения устойчивости рассматри-
ваемого синхронного движения вибраторов необходимо, чтобы
характеристика синхронных двигателей была достаточно «жест-
кой». Из полученного результата следует также, что при ис-
пользовании для привода вибраторов асинхронных двигателей
данное движение неустойчиво. Как уже отмечалось в п. 2 § 1,
в этом случае устойчиво движение, для которого
а! = 0, а2=— л, а3 = — л, а4 = 0	(3.16)
и вибрирующий орган практически не колеблется.
Если ввести обозначения
F = 2me®2’	(3.17)
где Ао — амплитуда колебаний вибрирующего органа, a F —
амплитуда возмущающей силы, развиваемой парой вибраторов,
§ 31
О НЕОБХОДИМЫХ УСЛОВИЯХ НОРМАЛЬНОЙ РАБОТЫ
717
то условие (3.15) можно представить в форме
A0F
4 '
(3.18)
3. Шесть вибраторов на мягко амортизированном, твердом
теле. Рассмотрим теперь систему в виде мягко амортизирован-
ного твердого тела, которое может совершать плоские колеба-
ния и на котором установлено шесть одинаковых дебалансных
вибраторов, приводимых от синхронных электродвигателей (см.
рис. 85 и п. 23 таблицы 5 Добавления 2). Оси роторов каждой
пары вибраторов, вращающихся в противоположных направле-
ниях, предположим совпадающими, причем общая ось вращения
Рис. 85.
средней пары вибраторов пусть проходит через центр тяжести
01 вспомогательного тела, а оси крайних вибраторов располо-
жены симметрично относительно оси средних вибраторов на рас-
стоянии г от этой осй.
Как и выше, найдем условия существования и устойчивости
движения, при котором вибрирующий орган совершает прямо-
линейные поступательные колебания вдоль оси Орг. Очевидно,
что такое движение будет иметь место при нулевых значениях
всех фаз as.
Значения параметров rs, <ys, 6S и as для рассматриваемого
случая сведены в таблицу 4; принятая нумерация вибраторов
ясна из рис. 85.
Таблица 4
S	1	2	3	4	5	6
rS	0	0	г	Г	Г	г
6s	—	—	0	0	Л	л
	-1	1	-1	1	-1	1
Os	0	0	0	0	0	0
718
ВИБРАЦИОННЫЕ ГРОХОТЫ, КОНВЕЙЕРЫ, ПИТАТЕЛИ
[ГЛ. XX
Дальнейшее исследование вполне аналогично проведенному
в п. 2 настоящего параграфа. Как и выше, оказывается, что
все вибрационные моменты Ws, определяемые равенствами (8.8)
главы ХШ, для рассматриваемого движения равны нулю, и по-
этому обмотки статоров двигателей следует ориентировать
точно таким же образом, как и при отсутствии колебаний осно-
вания, на котором размещены вибраторы. Отсюда следует так-
же, что изучаемое движение является возможным (однако, как
мы убедимся ниже, неустойчивым) и в случае использования
для привода вибраторов асинхронных двигателей.
Для установочных углов ps получаются соотношения, впол-
не аналогичные формулам (3.6), (3.8) и (3.9); сохраняет силу
и условие (3.7).
При учете равенств (8.8) и (11.9) главы ХШ, а также дан-
ных таблицы 4 алгебраическое уравнение (4.10) упомянутой
главы	после	несложных преобразований может		быть представ-	
лено в	виде				
4-	z 0	— 2	0	—2	0	
0	4	-г 0	— 2	0	— 2	
— 2	0	4 —	a — z а	а —2	— а	
0	— 2	а	4 — а — z —а	а—2	= 0,
— 2	0	а —	2 —а	4—a—z	а	
0	— 2	— а	а~2	а	4 — a — z	
(3.19)
где по-прежнему использованы обозначения (3.11).
Прибавим все четные строки определителя к предшествую-
щим нечетным, а затем вычтем из первой строки третью, а из
третьей пятую. В результате уравнение (3.19) примет вид
	1	1	-1	-1	0	0	
	0	4-z	0	— 2	0	2	
	0	0	1	1 -1	-1	
(6 - г)2 •	0 -	2	а	4 — а — z ~а	а — 2	= 0.
	— 2 -	2	— 2	-2	4-г	4-г	
	0 -	2	— а	а — 2	а	4 — а — г	
					(3.20)	
Таким образом,		два	корня,	г[ = г2 — 6, найдены. Для опреде-		
ления других корней прибавим последнюю строку определителя
(3.20) к четвертой, а затем четвертую строку полученного опре-
делителя — к его последней строке. Тогда вторая строка будет
§ 3]
О НЕОБХОДИМЫХ УСЛОВИЯХ НОРМАЛЬНОЙ РАБОТЫ
719
содержать множитель —г. Вынесем этот множитель за знак
определителя и прибавим после этого к четвертой строке учет-
веренную вторую. В результате придем к уравнению
	1	1	-1	-1	0	0	
	0	1	0	1	0	0	
	0	0	1	1	-1	-1	
1 1	0	0	0	1	0	1	= 0.
	--2	— 2	— 2	— 2	4-z	1	
	0	— 2	а	а — 2	а	4 — а — z	
(3.21)
Таким образом, найдены еще два корня: гз = 6 и г4 = 0.
Прибавим теперь к пятой строке определителя (3.21) удвоен-
ную первую и учетверенную третью, а затем пятую строку по-
лученного определителя сократим на —z и прибавим к его
третьей строке. Тогда получим уравнение
	1	0	1	0	1	
	0	1	1	0	0	
— z •	0	0	1	0	1	= 0.
	0	0	0	1	1	
	— 2	— а	а — 2	а	4 — а — z	
(3.22)
Отсюда легко находим: zs = 0, zg = 2(3 — 2а).
В соответствии с (3.11) корнями и уравнения (4.10) гла-
вы XIII, отвечающими найденным выше корням z, будут
“•-’•==v(cs-L’	<3-23>
Отсюда при учете обозначений (3.11) следует, что условия
устойчивости рассматриваемого движения zj < 0 сводятся к не-
равенству
<з-24>
Если, как и выше, ввести обозначения для амплитуды коле-
баний Ло, равной в данном случае 6me/A4, и для возмущающей
силы, развиваемой парой вибраторов F2 = 2meio2, то условие
720
ВИБРАЦИОННЫЕ ГРОХОТЫ, КОНВЕЙЕРЫ, ПИТАТЕЛИ
[ГЛ. XX
(3.24) в точности совпадет с неравенством (3.18), полученным
для четырехвибраторной машины.
Можно ожидать, что условие (3.18) останется справедливым
и для аналогичной машины с произвольным числом пар вибра-
торов. Соответствующее исследование, однако, вряд ли может
представить особый интерес, поскольку, как правило, большое
число вибраторов не применяется в машинах с единым рабочим
органом, который еще допустимо рассматривать как абсолютно
твердое тело.
§ 4. Вибрационные грохоты с самосинхронизирующимися
вибраторами
Вибрационный грохот представляет собой машину с основ-
ным рабочим элементом в виде сита, решетки или колосников.
Распространенный, спасай согласования-
вращения вибраторов
Рис. 86.
Этому элементу сообщаются ко-
лебания, под действием которых
поступающий на грохот сыпучий
материал перемещается вдоль
рабочей поверхности, рассеи-
ваясь одновременно на два клас-
са. Если просеивающих поверх-
ностей не одна, а несколько, то
происходит разделение материа-
ла более чем па два класса
крупности. Вибрационные грохо-
ты находят широкое применение
в обогатительной технике и в
промышленности стоительных
материалов.
В течение нескольких десяти-
летий для привода инерционных
«послерезонансных» грохотов с
прямолинейными поступатель-
ными колебаниями короба приме-
нялся двухвальный вибратор на-
правленного действия с синхрони-
зацией посредством зубчатых ко-
лес, иногда называемый самоба-
лансным вибратором или вибра-
тором типа Бюллера (рис. 86, а),
недавно было обращено внимание на
Лишь сравнительно
возможность отказаться во многих случаях от зубчатой пере-
дачи. В частности, результаты теоретического исследования,
изложенные в п. 2 § 2 настоящей главы, а также эксперименты,
описанные в главе XIX, явились основой для создания грохота’
§ 4]	ВИБРАЦИОННЫЕ ГРОХОТЫ	721
приводимого от двух одинаковых самосинхронизирующихся де-
балансных вибраторов, вращающихся в противоположных на-
правлениях (рис. 86, б) [44, 51, 56].
Некоторые из схем грохотов с самосинхронизирующимися
вибраторами представлены в п. 5 таблицы 5 Добавления 2;
о возможностях (далеко еще не исчерпанных) использования
явления самосинхронизации в приводе грохотов свидетельствуют
многие схемы, представленные в таблице 5 и рассмотренные
в §§ I и 3 настоящей главы.
Применение в грохотах явления самосинхронизации вибра-
торов позволяет получить ряд конструктивных и эксплуата-
ционных преимуществ, на перечислении которых мы не будем
здесь подробно останавливаться *). Заметим лишь, что ряд этих
преимуществ обусловлен возможностью помещать валы само-
синхронизирующихся вибраторов на значительных расстояниях
друг от друга и, в частности, крепить вибраторы у бортов ко-
роба грохота, как это показано, например, на схеме, представ-
ленной в п. 5, в таблицы 2 (стр. 343). Такая схема особенно
предпочтительна в грохотах, предназначенных для обработки
горячих материалов. Естественно, что в случае кинематической
синхронизации вращения валов вибраторов подобные конструк-
ции либо неосуществимы, либо нецелесообразны.
Ряд ‘грохотов с самосинхронизирующимися вибраторами
спроектирован, изготовлен и испытан в институте «Механобр».
В этих работах, помимо автора, принимали участие К. А. Рунд-
квист, Б. П. Лавров, В. В. Дубровин, Г. П. Шей, Е. П. Капра-
лов, И. С. Квашнин, А. Д. Рудин, Г. Б. Букаты, С. Н. Горшков
и другие конструкторы и исследователи.
Лабораторная модель грохота с площадью сита 0,4 X
X 0,8 м2 и производительностью около 10 т)час представлена
на рис. 87. В этом грохоте, осуществленном по схеме п. 5, а
таблицы 2 (п. 3 таблицы 5), использованы вибраторы со
встроенными асинхронными электродвигателями (мотор-виб-
раторы).
На рис. 88 изображена установка, состоящая из работаю-
щих в замкнутом цикле грохота и двух конвейеров с самосин-
хронизирующимися вибраторами. Эта установка, спроектиро-
ванная и изготовленная в институте «Механобр», демонстриро-
валась на Выставке достижений народного хозяйства в Москве,
а также на ряде международных промышленных выставок
(Лондон, Брно, Рио-де-Жанейро). Производительность каждой
из машин установки составляет около 10 т/час, длина лотков
виброконвейеров — более двух метров.
♦) Общая .характеристика достоинств и недостатков различных способов
синхронизации вибраторов дана в § 2 главы XII.
722	ВИБРАЦИОННЫЕ ГРОХОТЫ, КОНВЕЙЕРЫ, ПИТАТЕЛИ [ГЛ. XX
В институте «Механобр» разработан также проект промыш-
ленного грохота тяжелого типа с двумя самосинхронизирующи-
мися вибраторами (площадь сита 1,8 X 5,5 м2); схема машины
Рис. 87.
также отвечает п. 5, а таблицы 2. С целью всесторонней экспе-
риментальной проверки возможности создания такого грохота
вначале были изготовлены и испытаны на специальной баласт-
ной раме его вибраторы. Вес, момент инерции и основные
Рис. 88.
размеры рамы могли изменяться в пределах, включающих зна-
чения этих величин для короба спроектированного грохота.
Общий вид рамы с вибраторами, представляющей, таким
образом, натурную модель грохота, показан на рис. 89, а. Как
видно на фото, вибраторы снабжены автоматически регулирую-
щимися дебалансными грузами (см., например, [2, 149]), приме-
§ 4J
ВИБРАЦИОННЫЕ ГРОХОТЫ
723
некие которых позволило практически полностью избежать на-
растания колебаний вибрирующего органа при прохождении
через резонанс в процессе пуска и выбега. При вращении виб-
ратора с угловыми скоростями, меньшими некоторого заранее
Рнс. 89.
задаваемого критического значения со*, лежащего выше частот
собственных колебаний конструкции на амортизирующих опо-
рах, дебалансные грузы вибратора отжаты пружинами к оси
вращения, так что статический момент вибратора имеет доста-
точно малую величину (рис. 89, а). При скоростях, превышаю-
щих критическую, развивается центробежная сила, достаточная
724
ВИБРАЦИОННЫЕ ГРОХОТЫ, КОНВЕЙЕРЫ, ПИТАТЕЛИ
[ГЛ. XX
для преодоления восстанавливающей силы пружины, в резуль-
тате чего дебаланс отжимается к периферии шкива, и при этом
его статический момент достигает номинального значения
(рис. 89,6). Фото, представленное на последнем рисунке, полу-
чено при работе вибраторов в установившемся режиме; экспо-
зиция составляла около 1/2000 сек. Как видно, соотношение фаз
вращения как раз таково, что обеспечиваются прямолинейные
поступательные колебания вибрирующего органа.
Длительные испытания описанной натурной модели промыш-
ленного грохота подтвердили весьма высокую стабильность эф-
фекта самосинхронизации по отношению к неточностям изготов-
ления и несимметрии нагрузки. При этом в результате специаль-
ных экспериментов с записью траекторий колебаний точек
вибрирующего органа с помощью «светящейся точки» были
подтверждены теоретические соотношения, полученные в § 2 на-
стоящей главы.
Так, например, в результате одного из опытов с использова-
нием стробоскопического освещения было найдено, что факти-
ческое относительное отклонение парциальных угловых скоро-
стей вращения вибраторов 4- — составляет 0,50% ±0,04%.
2 I С00 |
С другой стороны, для максимально возможного теоретиче-
ски отклонения qa = ~ —-	по формуле (2.39) было найдено
2 | Ш0 |тах
значение 0,60%, а по формуле (2.43) для максимально допусти-
мого по условию сохранения самосинхронизации отклонения
р°—значение 1,06%. Коэффициент запаса по самосинхрониза-
ции хю, таким образом, в данной серии опытов был равен всего
лишь p^/q^ = 1,06/0,60 ~ 1,8. Для отклонений траекторий од-
ной из крайних точек рамы от прямолинейных были экспери-
ментально найдены значения ^ = 0,14 и g2 = 0,16. По фор-
мулам же (2.45) для максимально возможных значений тех
же величин было получено | gi |max = qbi = 0,22 и |g2 max =
= qb2 = 0,23.
Была установлена также весьма значительная стабильность
режима синхронного движения и траекторий колебаний рамы по
отношению к неодинаковости натяжения ремней клиноременной
передачи.
На рис. 90, а приведено фото грохота института «Механобр»
(ведущий конструктор Б. П. Лавров), осуществленного по схе-
ме рис. 79, а (см. также п. 8 таблицы 5 Добавления 2).
Изложенные результаты теоретического и эксперименталь-
ного исследования, а также опыт конструирования в институте
«Механобр» грохотов с самосинхронизирующимися вибраторами
были использованы институтом «Гипромашобогащеиие» (веду-
щий конструктор Б. П. Прянишников) для разработки промыш-
§ 4]
ВИБРАЦИОННЫЕ ГРОХОТЫ
725
ленного грохота с площадью сита 2 X 5 м2. Фото этого грохота
приведено на рис. 90, б.
Другой вариант промышленного грохота примерно тех же
размеров был разработан в институте «Механобр» примени-
тельно к условиям грохочения горячего агломерата. Этот гро-
хот, в отличие от описанных выше, выполнен по схеме п. 5, в
Рис. 90.
таблицы 2 (п. 14 таблицы 5), то есть с боковым расположением
вибраторов; привод последних осуществляется от встроенных
вибростойких электродвигателей. Фото вибраторов грохота,
установленных на натурном испытательном стенде, приведено
на рис. 91,а.
По аналогичной схеме, но с рядом конструктивных отличий
выполнен грохот института «Гипроникель», имеющий примерно
те же размеры и назначение (ведущий конструктор В. Н. Ста-
ростин). Электродвигатели вибраторов установлены в этом гро-
хоте на неподвижной раме (рис. 91,6). Вибраторы снабжены
особым механизмом, позволяющим на ходу изменять статиче-
ский момент дебалансных грузов от нуля до максимального
726
ВИБРАЦИОННЫЕ ГРОХОТЫ, КОНВЕЙЕРЫ, ПИТАТЕЛИ
[ГЛ. XX
значения. Такое устройство позволяет, в частности, избежать
интенсивных колебаний при проходе через резонанс в процессе
пуска и выбега машины.
Рис. 91.
Многодечный вибрационный грохот с двумя самосинхронизи-
рующимися вибраторами, предназначенный для рассева шлиф-
порошков и шлифзерна (рис. 92), был предложен и разработан
в институте «Механобр» С. Н. Горшковым и Б> П. Лавровым
[157, 245]. Этот грохот, весьма успешно эксплуатируемый в про-
мышленности, осуществлен по оригинальной схеме. Дебаланс-
§ 4]
ВИБРАЦИОННЫЕ ГРОХОТЫ
727
ные вибраторы (на фото рис. 92 они не видны) размещены на
мягко амортизированной раме симметрично снизу по бокам, так
что образуется система типа представленной в п. 8 таблицы 5.
Вместе с тем каждое из двенадцати решет грохота крепится к
раме посредством наклонных плоских рессор, «мягких» в попе-
речном направлении. Эти рессоры задают декам определенные
Рис. 92.
направления колебаний, тогда как рама под действием вибра-
торов совершает вертикальные колебания: как было установле-
но, в этой системе с 3 + 12 = 15 существенными степенями сво-
боды устойчив тот же режим вращения роторов, что и в системе
п. 8 таблицы 5, то есть при отсутствии решет-маятников.
В институте «Механобр» предложен и разработан также дру-
гой своеобразный грохот — так называемый гранулометр [104].
Он предназначен для автоматического контроля крупности дроб-
леной руды (рис. 93). В корпусе 1 этого грохота размещены два
сита 2 и 3, выполненные в виде полувитков винтовой поверхно-
сти с вертикальной осью. По краям сит имеются щели для про-
хода материала. На корпусе гранулометра, установленного на
мягких амортизирующих пружинах, размещены две пары де-
балансных вибраторов 4, которые приводятся от независимых
асинхронных электродвигателей 5. Одновременно включаются
двигатели вибраторов только одной пары, то есть двух вибрато-
ров, расположенных на противоположных сторонах короба по
схеме рис. 43 (см. также п. 18 таблицы 5). При этом вибраторы
самосинхронизируются и обеспечивают винтовые колебания ко-
роба, приводящие к движению материала вверх по ситам при
728
ВИБРАЦИОННЫЕ ГРОХОТЫ, КОНВЕЙЕРЫ, ПИТАТЕЛИ
[ГЛ. XX
работе одной пары вибраторов и вниз по ситам при работе дру-
гой пары (различное направление движения обеспечивается со-
ответствующим наклоном скрещивающихся осей пар вибрато-
ров). Выключение одной и включение другой пары вибраторов
производится специальным автоматическим устройством.
Работа прибора происходит следующим образом. После по-
ступления пробы руды включается пара вибраторов, обеспечи-
вающая движение материала вверх по винтовым поверхностям
сит. При этом, покидая одно
сито, материал попадает на
другое и т. д. По истечении
определенного промежутка
времени, необходимого для до-
статочно полного просеивания
мелкой фракции, эта фракция,
попавшая в специальный бун-
кер, автоматически взвеши-
вается, а ее вес запоминается
логическим устойством. Затем
первая пара вибраторов вы-
ключается и включается вто-
рая пара, обеспечивающая дви-
жение оставшегося на ситах
крупного материала в противо-
Рис. 93.	положном направлении, то есть
вниз. При этом, достигая краев
сит, материал сквозь радиальные щели ссыпается в бункер, после
чего взвешивается вся проба в целом. Сигнал, пропорциональный
весу пробы, также поступает в логическое устройство, которое
выдает сигнал, пропорциональный отношению веса мелкой фрак-
ции к весу всей пробы. Этот сигнал подается затем на вторичный
прибор, шкала которого отградуирована в процентах содержа-
ния контролируемого класса крупности материала.
Многочисленные расчеты показали, что обычно применяемые
на практике основные параметры вибрационных грохотов тако-
вы, что условия стабильности по отношению к неточностям из-
готовления и асимметрии нагрузки, приведенные в § 2 настоя-
щей главы, выполняются и притом с надлежащим запасом.
Более того, во многих случаях даже выключение двигателя од-
ного из вибраторов не приводит к его остановке, а также к за-
метному искажению траекторий колебаний точек рабочего орга-
на грохота. Иными словами, имеет место эффект вибрационного
поддержания вращения неуравновешенного ротора, рассмотрен-
ный в п. 3 § 16 главы XIII, а также в главе XVIII книги.
Ряд грохотов с двумя самосинхронизирующимися дебаланс-
ными вибраторами, выполненными по тем же схемам, что и опи-
ВИБРАЦИОННЫЕ КОНВЕЙЕРЫ
729
§ 6]
санные грохоты отечественных конструкций, выпускается в
настоящее время многими зарубежными фирмами, в частности,
в ФРГ — фирмами «Jost», «Siebtechnik» и «НопегЬ, в США —
фирмой «Link-Belt», во Франции — фирмой «Атесо», в Велико-
британии— фирмой «OWZ engineering supplies limited» [499,
503, 504, 505, 506]. Фото грохота фирмы «Link-Belt» и разреза
узла его вибраторов представлены на рис. 94. Напомним также
о грохотах оригинальной конструкции, схемы которых приведены
в пп. 6 и 7 таблицы 2. В этих машинах, принцип работы которых
Рис, 94.
был пояснен в § 1 главы XII, используется в той или иной мере
эффект вибрационного поддержания вращения.
Подводя итог, следует подчеркнуть, что возможности исполь-
зования явления самосинхронизации вибраторов для усовершен-
ствования вибрационных грохотов далеко не исчерпываются кон-
кретными машинами такого рода, рассмотренными в настоящем
параграфе. Осуществимость других типов грохотов с самосин-
хронизирующимися вибраторами вытекает, в частности, из крат-
кого обзора схем, приведенного в пп. 2—4 § 1 настоящей главы
(см. также таблицу 5). Между тем в грохотах, отвечающих мно-
гим из описанных схем, в настоящее время применяется прину-
дительная кинематическая синхронизация вибраторов.
§ 5.	Вибрационные конвейеры с самосинхронизирующимися
и с принудительно синхронизированными вибраторами
Подавляющее большинство способов возбуждения прямоли-
нейных и круговых поступательных, а также винтовых колебаний,
которые были рассмотрены в § 1 настоящей главы, пригодны
также для создания некоторых новых типов вибрационных
730
ВИБРАЦИОННЫЕ ГРОХОТЫ, КОНВЕЙЕРЫ. ПИТАТЕЛИ
[гл. хх
конвейеров, предназначенных для транспортировки сыпучих ма-
териалов.
Схемы простейших конвейеров с двумя самосинхронизирую-
щимися вибраторами представлены в п. 5 таблицы 2 стр. 343.
Рис. 95.
Рис. 96.
Фото работающей простейшей модели конвейера, осуществлен-
ной по схеме п. 5,а таблицы 2 (п. 3 таблицы 5 Добавления 2),
приведено на рис. 95, а. Снимок выполнен с экспозицией
1/2500 секунды при числе оборотов валов вибраторов около
2700 в минуту. Поэтому на фото видно, что фазы вращения ро-
торов соответствуют результатам теоретического исследования
(см. п. 3 таблицы 5) и обеспечивают прямолинейные поступа-
тельные колебания лотка конвейера.
Вибрационные конвейеры того же типа входят в описанную
выше установку (рис. 88).
§ 5]
ВИБРАЦИОННЫЕ КОНВЕЙЕРЫ
731
Первый образец вибрационного конвейера с самосинхрони-
зирующимися вибраторами был испытан в институте «Меха-
нобр» Д. А. Плиссом еще в 1947—1948 гг., то есть задолго до
выдачи первых зарубежных патентов на грохоты и конвейеры
такого рода (1950 г. — в США и 1956 г. — во Франции) и до их
появления в каталогах иностранных фирм (см. § 3 главы XII).
В институте предложен, разработан и испытан ряд вибрацион-
ных конвейеров с самосинхронизирующимися и электрически
синхронизированными вибраторами [52, 56, 68, 72, 81, 169, 239,
242, 245, 246]; работы по созданию конвейеров проводились в
основном под руководством Б. П. Лаврова и автора.
Рис. 97.
На рис. 96, а изображена секция вибрационного конвейера
с двумя самосинхронизирующимися вибраторами, установлен-
ными по схеме п. 5, в таблицы 2 (п. 14 таблицы 5). В этом кон-
вейере, предложенном Б. П. Лавровым и автором [72], приме-
нены специально разработанные удобные в промышленной
эксплуатации вибраторы. Электродвигатели вибраторов уста-
новлены на упругой подвеске, на которую вибрации трубы не
передаются. Это позволяет улучшить условия работы двигате-
лей и применять двигатели в обычном (не вибростойком) испол-
нении. Конструкция конвейера делает его пригодным для пере-
мещения горячих материалов.
Наибольшая длина одной двухвибраторной секции конвейера
(см. ниже) составляет около 7,5 м, внутренний диаметр транс-
портирующей трубы — 305 мм, производительность — 60 мР/час.
Отдельные секции конвейера могут быть соединены переррузоч-
1ными патрубками (рис. 96, б).
Фото другого секционированного вибрационного конвейера, в
котором использованы так называемые качающиеся вибраторы.
732
ВИБРАЦИОННЫЕ ГРОХОТЫ, КОНВЕЙЕРЫ, ПИТАТЕЛИ
[ГЛ. XX
представлено на рис. 97. Схема установки этих вибраторов,
также отличающихся пониженным уровнем вибраций электро-
двигателей, ясна из рисунка в п. 17,6 таблицы 2. Конвейер пред-
ложен, разработан и испытан Б. П. Лавровым [239]; им же рас-
смотрена теория вибрационных устройств с качающимися
вибраторами, изложенная в п 5 § 8 главы XIV.
Помимо вибрационных конвейеров, осуществляющих прямо-
линейное перемещение сыпучих материалов, находят применение
вертикальные виброконвейеры (виброподъемники), в которых
материал движется вверх или вниз по винтовому желобу. Схе-
мы таких машин приведены в пп. 2, 19, 20 таблицы 2. В качестве
привода вертикальных конвейеров (как отмечалось в п. 4 § 1;
см. также пп. 2 и 19 таблицы 5) могут быть использованы
два самосинхронизирующихся дебалансных вибратора. Фото
работающей малой модели такого конвейера представлено
на рис. 98.
Фото вибрационного подъемника института «Механобр» с
двумя самосинхронизирующимися вибраторами дано на рис. 99;
в этой машине также использована виброизолирующая упругая
подвеска электродвигателей. Подъемник хорошо зарекомендо-
вал себя в промышленной эксплуатации. Работы по теории, рас-
чету и испытаниям подъемника выполнены Г. А. Денисовым
[167, 172, 173].
Необходимо отметить, что, как и в случае грохотов, основ-
ные параметры вибрационных конвейеров, как правило, таковы,
что условия стабильности их работы, приведенные в п. 6 § 2,
либо выполняются автоматически, либо могут быть удовлетво-
рены без особых затруднений.
Некоторым недостатком описанных выше вибрационных кон-
вейеров с самосинхронизирующимися вибраторами является
ограниченная длина одной двухвибраторной секции, определяе-
мая из условия, чтобы частота упругих колебаний трубы или
лотка была в достаточной мере выше рабочей частоты колеба-
ний. В противном случае труба или винтовой желоб являются
нежесткими; траектории колебаний их отдельных точек различ-
ны, и процесс направленной транспортировки происходит нерав-
номерно или вообще нарушается. Для вибрационных конвейе-
ров (а также и других машин), рабочий орган которых пред-
ставляет собой мягко амортизированную балку однородного
сечения, указанное условие приводит к следующей формуле для
предельно допустимой длины [242, 307]:
/max = 0,75	₽ = ₽(^)-	(5Д)
Здесь ЕЗ — изгибная жесткость балки, р — ее погонная, а М —
общая масса, Мо— масса вибраторов, принимаемая за сосредо-
§ 5]
ВИБРАЦИОННЫЕ КОНВЕЙЕРЫ
733
точенную посередине балки, со — рабочая частота колебаний,
Р = р(Л1о/Л4)—функция отношения указанных масс, график
которой представлен на рис. 100.
Аналогичное соотношение получа-
ется и для наибольшей высоты двухви-
браторной секции виброподъемников.
Рис. 99.
Рис. 98.
Расчеты по формуле (5.1) приводят к выводу, что макси-
мальная длина трубы или лотка одной секции вибрационных
конвейеров изучаемого типа
обычных промышленных
размеров практически не
может превышать 8—10 м.
Поэтому в конвейерных
установках значительной
протяженности и приходит-
ся применять несколько
двухвибраторных секций с
перегрузкой материала из
одной секции в другую
(рис. 96). Наличие таких
перегрузочных узлов созда-
ет определенные эксплуата-
ционные неудобства.
Стремление осуществить
брационный конвейер с цельным
рабочим органом неограниченной длины привело к идее
734
ВИБРАЦИОННЫЕ ГРОХОТЫ, КОНВЕЙЕРЫ, ПИТАТЕЛИ
[ГЛ. XX
использования для его привода не одной, а большего числа рав-
номерно распределенных по длине пар дебалансных вибрато-
ров*); при этом, однако, возникает проблема обеспечения син-
хронизации и надлежащей фазировки вращения их роторов.
Как отмечалось в п. 2 § 1, в случае, когда вибрирующий
орган является абсолютно твердым телом, а вибраторы располо-
жены по «плоской» схеме (см. пп. 21 и 24 таблицы 5 Добавле-
ния 2), эффектом самосинхронизации здесь удается восполь-
зоваться лишь при одной паре дебалансных вибраторов. Две и
три пары вибраторов в устойчивом движении фазируются таким
образом, что их возмущающие силы взаимно уравновешиваются,
и колебания рабочего органа отсутствуют. Указанный вывод
иллюстрируется рис. 95, а—в, на котором приведены фото рабо-
тающих моделей конвейеров. Снимки сделаны при столь малой
экспозиции, что можно четко различить положение неуравнове-
шенных грузов вибраторов.
Можно добиться устойчивости нужной фазировки четырех
самосинхронизирующихся вибраторов путем перехода к про-
странственной схеме (п. 23 таблицы 5). Однако существенного
увеличения максимальной длины конвейеров в пределах этой
схемы добиться нельзя вследствие требования, наложенного на
жесткость колеблющегося тела. Таким образом, наибольший
прикладной интерес рассматриваемая задача представляет для
случая упругого тела, то есть тела, ряд частот собственных ко-
лебаний которого ниже рабочей частоты со.
В п. 7 § 8 главы XIV было показано, однако, что для плоской
схемы при вибрирующем органе балочного типа эта задача ре-
шается положительно лишь в случае двух самосинхронизирую-
щихся вибраторов. Иными словами, максимальная длина цель-
ного конвейера, выполненного по такой схеме, в лучшем случае
может быть равна 2/тах (практически не более 16—18 л). По-
этому следует либо обратиться к иным схемам, воспользовав-
шись методами синтеза, изложенными в главе XV, либо прибег-
нуть к электрической синхронизации**).
Вибрационный конвейер с вибраторами, приводимыми от
синхронных двухполюсных электродвигателей, был предложен
А. В. Ватсон, А. И. Кириченко, Б. П. Лавровым и автором [52],
а виброподъемники с такими двигателями — Г. А. Денисовым и
*) Как было показано Г. Ю. Джанелидзе и автором [50, 55], для воз-
можности реализации этой идеи необходимо, чтобы расстояние между вибра-
торами I не превышало так называемого предельного шага вибраторов
4
1*пах = 3 ф^ДУ/ри2 (обозначения здесь те же, что и в формуле (5.1); кроме
того, lmsx близко по величине к 1тах, что, конечно, не случайно).
**) Кинематическая синхронизация в этом случае вряд ли применима
из-за значительного расстояния между вибраторами.
§ 5]
ВИБРАЦИОННЫЕ КОНВЕЙЕРЫ
735
Б. П. Лавровым [166, 170]. Благодаря другому, уже упоминав-
шемуся предложению Б. П. Лаврова [240] в таких машинах
Рис. 101.
могут быть использованы также серийно выпускаемые многопо-
люсные синхронные двигатели. При этом можно, не прибегая
к преобразователям, снизить рабочую
величину предельного шага вибра-
торов и скорость транспортировки
материала.
Снимок работающей малой мо-
дели конвейера с шестью синхрон-
ными двухполюсными электродви-
частоту машины, повысив
Рис. 103.
Рис. 102.
гателями представлен на рис. 101. В институте «Механобр»
Б. П. Лавровым и автором была испытана также и модель этого
конвейера промышленных размеров (диаметр трубы 426 мм,
производительность около 25 т/час). Привод вибраторов
736
вибрационные грохоты, конвейеры, питатели
(ГЛ. XX
осуществлялся от двухполюсных синхронных мотор-генераторов
типа DE GETS-302, выпускаемых фирмой «Kaiserwerke» (За-
падный Берлин). Как и опыты на малой модели, проведенные
эксперименты подтвердили необходимость наличия достаточной
«жесткости» характеристики синхронного двигателя \dL*/dQ\ для
обеспечения требуемой фазировки колебаний (см., например,
пп. 5, 22 и 24 таблицы 5 Добавления 2). При этом критическое
Рис. 104.
значение жесткости, как и предсказывается теорией, при прочих
равных условиях увеличивается с ростом статического момента
роторов вибраторов те.
Как уже отмечалось, добиться устойчивости требуемой фази-
ровки синхронного вращения роторов многих вибраторов можно
и не прибегая к принудительной синхронизации, а воспользовав-
шись способами синтеза систем возбуждения колебаний, изло-
женными в §§ 3 и 4 главы XV. На этой основе Б. П. Лаврову,
Г. А. Денисову, Р. Ф. Нагаеву и Н. Г. Тимофееву удалось пред-
ложить ряд схем вертикальных и горизонтальных виброконвейе-
ров [162, 169, 171, 173, 246].
Вибрационные конвейеры различных типов и размеров, при-
водимые от двух самосинхронизирующихся вибраторов, серийно
выпускаются несколькими зарубежными фирмами *). На рис. 102
и 103 представлены в качестве примеров трубчатый виброкон-
вейер и вибрационные подъемники фирмы «Uhde» (ФРГ).
*) В частности, фирмами «Jost», «Beumer-Maschinenfabrik, «НопегЬ, «Uh-
de», «Becker-Priinte» — в ФРГ [500—504]; «АМЕСО», «Sinex» — во Франции
[499, 507]; «Venanzetti» — в Италии [508]; «OWL engineering supplies limi-
ted» — в Великобритании [506].
§ 6]
ВИБРАЦИОННЫЕ ПИТАТЕЛИ
73?
В этих машинах, осуществленных соответственно по схемам
пп. 14 и 18 таблицы 5, использованы вибростойкие электродвига-
тели, непосредственно связанные с корпусами вибраторов [465].
Другой вибрационный конвейер, также выпускаемый в ФРГ,
изображен на рис. 104. Этот конвейер приводится от двух само-
синхронизирующихся дебалансных вибраторов маятникового
типа (см. п. 17, а таблицы 2). При некоторых очевидных упро-
щающих предположениях схема конвейера отвечает представ-
ленной в п. 9 таблицы 5.
Подводя итог, отметим, что возможности использования эф-
фекта самосинхронизации, а также средств электрической син-
хронизации механических вибраторов в приводе вибрационных
конвейеров, как и в приводе грохотов, еще далеко не исчерпаны.
§ 6.	Вибрационные питатели с самосинхронизирующимися
вибраторами
Вибрационные питатели отличаются от вибрационных кон-
вейеров в основном тем, что в первых, как правило, должна
обеспечиваться возможность изменения на ходу основных пара-
метров колебаний рабочего органа (частоты, амплитуды и т. п.),
в результате чего изменяет-
ся скорость транспортиров-
ки материала и тем са-
мым — производительность
питателя. Питатели обычно
значительно короче конвейе-
ров, и поэтому для них про-
блема жесткости рабочего
органа не является столь
острой.
Вибрационные питатели,
в которых регулирование
производительности осу-
ществляется путем измене-
ния частоты колебаний, мо-
Рис. 105.
гут быть осуществлены по любой из двухвибраторных
схем, представленных в пп. 5, а—а, 8, 17 и 19 таблицы 2
(стр. 340—358) и также в пп. 3, 8, 11, 13—16 и 18 таблицы 5
(Добавление 2), если для привода вибраторов использовать
электродвигатели с регулируемой скоростью вращения ротора.
На рис. 105 приведено фото такого вибрационного питателя,
осуществленного по схеме п. 3, в таблицы 2 (п. 14 таблицы 5);
этот питатель, предложенный Б. П. Лавровым и автором [67],
был сконструирован Б. П. Лавровым, изготовлен и испытан в
институте «Механобр».
738
ВПЬРЛЦШНШЫЕ ГРОХОТЫ, КОНВЕЙЕРЫ, ПИТАТЕЛИ
[ГЛ. хх
Принцип регулирования производительности питателя по-
средством изменения частоты колебаний, однако, далеко не все-
гда приводит к рациональным с практической точки зрения
решениям. Другая идея, также предложенная и разработанная
автором совместно с Б. П. Лавровым, состоит в использовании
эффекта, описанного в п. 2 § 2 настоящей главы как нежела-
тельного. Речь идет об искажении траекторий колебаний ма-
шины с двумя самосинхронизирующимися вибраторами при на-
личии неодинаковости параметров вибраторов, в частности
неодинаковости парциальных угловых скоростей coi и о>о. Изме-
нение одной из парциальных скоростей достаточно просто осу-
ществляется посредством изменения напряжения питания соот-
ветствующего двигателя или даже перевода этого двигателя на
работу в генераторном режиме. В результате, как явствует из
формул (2.7), (2.8), (2.15) и рис. 83, изменяется сдвиг фаз вра-
щения роторов вибраторов в синхронном движении, и траекто-
рии колебаний точек транспортирующей поверхности превра-
щаются из прямых линий в эллипсы. Это в свою очередь при-
водит к изменению средней скорости движения материала, то
есть производительности питателя.
Для экспериментальной проверки изложенного выше прин-
ципа регулирования производительности питателя авторами был
использован лабораторный грохот с самосинхронизирующимися
вибраторами, описанный в § 4 настоящей главы и представлен-
ный на рис. 87. Опыты показали, что таким путем можно легко
изменять производительность машины от максимального зна-
чения примерно до 50% от этого значения. В специально скон-
струированном питателе пределы регулирования производитель-
ности, естественно, могут быть значительно расширены.
Практическое значение изложенных выше способов регули-
рования производительности, как нам представляется, состоит
в том, что они открывают один из возможных путей создания
экономичных питателей с механическими дебалансными вибра-
торами взамен значительно более тяжелых и дорогостоящих
питателей с электромагнитными вибраторами, применяемых в
настоящее время.
Вибрационные питатели с самосинхронизирующимися вибра-
торами выпускаются, как правило, теми же фирмами, которые
производят вибрационные конвейеры с таким типом привода
(см. сноску па стр. 736); изготовляет их также фирма «AEG»
(ФРГ) и ряд других. Отметим, однако, что в большинстве вы-
пускаемых питателей с механическими вибраторами возможность
плавной регулировки производительности на ходу не предусмат-
ривается: питатель выдает материал «релейно» — либо с номи-
нальной, либо с нулевой производительностью. В ряде случаев
такие питатели вполне удовлетворяют требованиям производства.
§ 7]	ВИБРАЦИОННЫЕ ПЛОЩАДКИ	739
§ 7.	Вибрационные площадки с самосинхронизирующимися
и принудительно синхронизированными вибраторами
Рассмотренные в § 1 настоящей главы способы получения
прямолинейных и круговых поступательных колебаний с по-
мощью самосинхронизирующихся дебалансных вибраторов мо-
гут быть использованы и в вибрационных площадках для уплот-
нения бетона и других материалов. Насколько нам известно,
первые работы в этом направлении были проведены во
ВНИИСтройдормаш (Москва), затем появились статьи
К. А. Олехновича [327] и И. И. Долицкого [178], в которых сооб-
щалось о положительном опыте применения эффекта самосин-
хронизации в вибрационных площадках и в других машинах
аналогичного типа. В последующих работах К. А. Олехновича
идея использования этого эффекта получила дальнейшее кон-
структивное развитие и практическое воплощение [328].
Следует отметить, что если параметры колебаний вибрацион-
ных грохотов и конвейеров в большинстве случаев обеспечивают
автоматическое выполнение условий стабильности работы ука-
занных машин по отношению к неточностям изготовления и к
асимметрии нагрузки (см. § 2 настоящей главы), то, как пока-
зывают выполненные нами расчеты, в виброплощадках это
имеет место далеко не всегда. Причина состоит в том, что для
этих машин характерны сравнительно низкие амплитуды коле-
баний вибрирующего органа, имеющего к тому же в ряде слу-
чаев относительно малую жесткость.
Указанными обстоятельствами отчасти и объясняется тот
факт, что в существующей литературе встречаются весьма про-
тиворечивые высказывания о возможности использования эф-
фекта самосинхронизации в вибрационных площадках. Те же
причины побудили, по-видимому, к поискам эффективных спосо-
бов принудительной синхронизации и фазировки вращения виб-
раторов в рассматриваемых машинах (см. цитированную выше
работу П. И. Новосельского, А. Б. Борщевского и В. Н. Силь-
вановича [326]).
По-видимому, стабильность рабочего режима колебаний виб-
роплощадок с самосинхронизирующимися вибраторами значи-
тельно повышается в случае использования нелинейных упругих
элементов, подобных примененным К. А. Олехновичем упругим
прокладкам: колебания площадки в этом случае происходят
как бы в смягченном виброударном режиме.
Результаты, сведенные в таблицу 5 (Добавление 2) и изло-
женные в п. 6 § 2, позволяют ответить на вопрос, когда в внбро-
площадках, осуществленных по соответствующей схеме, может
быть использован эффект самосинхронизации и когда необхо-
димо прибегнуть к тому или иному способу принудительной
24;
740
ВИБРАЦИОННЫЕ ГРОХОТЫ, КОНВЕЙЕРЫ, ПИТАТЕЛИ
[ГЛ. XX
синхронизации. В последнем случае можно подсчитать также
необходимую «жесткость» характеристики синхронизирующих
элементов (синхронных двигателей, системы электрического
вала, обычного вала).
§ 8.	Универсальный вибрационный стенд
с самосинхронизирующимися вибраторами
Рассмотрим схему машины с двумя одинаковыми дебаланс-
ными вибраторами и мягко амортизированным вибрирующим ор-
ганом, представленную в п. 18 таблицы 5 (Добавление 2). Пред-
положим, что оси вращения роторов вибраторов могут быть
произвольным образом повернуты вокруг перпендикулярной им
прямой АВ и затем зафиксированы. Тогда, очевидно, путем над-
лежащей установки осей вращения роторов вибраторов, выбора
соответствующих направлений вращения роторов и, возможно,
некоторого перераспределения масс твердого тела можно будет
легко перейти от схемы и. 18 таблицы 5 к схеме п.п. 3 и 8. В ре-
зультате окажется возможным получать на одной и той же уста-
новке колебания весьма разнообразного вида, в том числе:
а)	прямолинейные поступательные колебания, направленные
под любым углом к горизонту;
б)	круговые поступательные колебания, параллельные про-
извольным образом ориентированной плоскости;
в)	поворотные колебания относительно оси, наклоненной под
любым углом к горизонту;
г)	винтовые колебания, ось которых может иметь произволь-
ное направление в пространстве, а «шаг» изменяться в широких
пределах;
д)	сложные колебания, при которых траекториями точек яв-
ляются произвольным образом ориентированные эллипсы.
Таким образом, мы получаем вибрационный стенд (рис. 106),
который является почти универсальным с точки зрения получе-
ния колебаний различной формы и ориентации. Добавим к тому
же, что к поворотному столу стенда можно присоединять пла-
нетарные вибраторы, а также различные колебательные систе-
мы, получая таким образом схемы, подобные изображенным в
пп. 7 и 27 таблицы 5. Изменение частоты и амплитуд колебаний
стола стенда может быть достигнуто обычными средствами.
Подобный стенд с самосинхронизирующимися вибраторами
был предложен Б. П. Лавровым и автором [66]. Конструкция
стенда разработана в институте «Механобр» под руководством
Б. П. Лаврова. Серия стендов изготовлена институтом; они
успешно используются в исследовательских лабораториях раз-
личных учреждений и предприятий.
Стенд оказался особенно удобным для изучения различных
вибрационных процессов, в частности вибротранспортировки,
§ 8]
УНИВЕРСАЛЬНЫЙ ВИБРАЦИОННЫЙ СТЕНД
741
грохочения, вибросепарации, виброуплотнения, вибробункериза-
ции и многих других. На нем были проведены также исследова-
ния ряда моделей машин с самосинхронизирующимися деба-
лансными и планетарными вибраторами, например транспорт-
ных и транспортно-технологических машин, рассмотренных в
настоящей главе, а также дробильно-измельчительных машин,
изучаемых в следующей главе.
Фото стенда с пультом управления представлено на
рис. 106, а. На рис. 106, б и в показаны установленные на стенде
модели горизонтального и винтового конвейеров или питателей,
а на рис. 106,г—инерционной конусной дробилки с двумя са-
мосинхронизирующимися вибраторами.
ГЛАВА XXI
ВИБРАЦИОННЫЕ ДРОБИЛЬНО-ИЗМЕЛЬЧИТЕЛЬНЫЕ
МАШИНЫ
§ 1. Инерционная дробилка и вибрационные измельчители
института «Механобр». Связь их теории с теорией
самосинхронизации вибраторов
В институте «Механобр» разработана конусная дробилка для
руды, конус которой приводится в движение не посредством
эксцентрика, как в обычных дробилках этого типа, а с помощью
размещенного в конусе дебалансного вибратора*) [212, 367].
Схема такой дробилки, называемой инерционной дробилкой,
представлена на рис. 107 (см. также п. 22 таблицы 2 на
стр. 355). Дробящий конус машины 1 заключает в себе де-
балансный вибратор «3. Вращающий момент передается на вал
вибратора от электродвигателя 5, установленного на опорной
раме 6, через карданный вал 4. Корпус дробилки 2 подвешен к
раме на мягких пружино-тросовых подвесках 7, 8, благодаря
чему машина является практически полностью уравновешенной.
Дробление руды осуществляется в кольцевой полости между
рабочей частью наружной поверхности конуса и соответствую-
щей частью внутренней поверхности корпуса.
В нормальном установившемся режиме работы дробилки ось
конуса вращается вокруг оси корпуса с угловой скоростью, рав-
ной угловой скорости вращения вала дебаланса; при этом конус
контактирует с корпусом либо непосредственно, либо через слой
руды в рабочей полости. Направление отклонения оси конуса
от оси корпуса в установившемся режиме совпадает (с точ-
ностью до некоторого, обычно острого, угла) с направлением
вектора-эксцентриситета дебаланса (см.ниже). Поэтому сум-
марное дробящее усилие развивается не только за счет центро-
*) В работах по созданию инерционных дробилок принимали участие
К. А. Рундквист, Б. Н. Дубровин, А. И. Кириченко, А. К. Рундквист,
И. Л. Успенский, А. Я. Иваненко, Н. А. Иванов, Б. Г. Иванов, Л. П. Зарогатс-
кий и другие конструкторы и исследователи. Участие автора книги состояло
в проведении ряда теоретических и экспериментальных исследований.
§ 1)
Инерционная дробилка
743
бежной силы инерции вращающегося дебаланса, ио также и за
счет центробежной силы, возникающей при прецессионном дви-
жении конуса.
Дробилка работает при числе оборотов в минуту вала де-
баланса, значительно превышающем число качаний конуса в
обычных конусных дробилках, в которых движение конуса обес-
печивается не дебалансным
вибратором, а эксцентриковым
механизмом. Это обстоятель-
ство в сочетании со значитель-
ными дробящими усилиями и
особенностями конструктивной
схемы машины обеспечивает
получение в данной дробилке
весьма высоких степеней из-
мельчения (порядка тридца-
ти — сорока).
Фото общего вида промыш-
ленного образца дробилки с
диаметром конуса у основания
600 мм и производительностью
около 20 т/час представлено
на рис. 108. На рис. 109
приведено фото опытного об-
разца значительно более
крупной машины (диаметр
конуса у основания 1650 мм,
производительность около
200 т!час).
Более подробное описание
конструкции и технологиче-
ских особенностей дробилки
можно найти в работах
А. К. Рундквиста [368, 369].
Вначале теория инерционной
дробилки развивалась незави-
симо от теории синхронизации вибраторов [369]; однако после
обобщения последней теории на вибраторы планетарного типа
[45, 68] стало ясно, что задача об исследовании динамики дро-
билки может рассматриваться как своеобразный частный слу-
чай задачи о синхронизации.
Для того чтобы установить указанную связь между теорией
дробилки и теорией самосинхронизации вибраторов, достаточно
заметить, что конус дробилки можно рассматривать как несу-
щее твердое тело, а корпус — как кольцо внешнего планетар-
ного вибратора, лишенного приводного электродвигателя. То
обстоятельство, что роль корпуса вибратора играет внутреннее
744
ВИБРАЦИОННЫЕ ДРОБИЛЬНО-ИЗМЕЛЬЧИТЕЛЬНЫЕ МАШИНЫ [ГЛ. XXI
тело (конус дробилки), а место ролика занимает корпус, не
имеет в данном случае решающего значения. В соответствии со
сказанным условиями существования и устойчивости нормаль-
ного режима работы дробилки являются условия существования
и устойчивости синхронного движения обоих «вибраторов» маши-
ны—дебалансного и планетарного или, поскольку последний
Рис. 108.
лишен двигателя, — условия вибрационного поддержания дви-
жения планетарного вибратора.
Покажем [68], что последние условия, вытекающие из полу-
ченных в главе XIII общих результатов, совпадают с соответ-
ствующими соотношениями, специально найденными для дро-
билки иными методами.
Ограничимся изучением плоской схемы дробилки, представ-
ленной в п. 15 таблицы 2 на стр. 349 (см. также п. 26 таб-
лицы 5 Добавления 2); рассмотрение такой схемы достаточно
для решения многих важных вопросов динамики дробилки
[369]. Тело с массой Л отвечает конусу дробилки (вибрирую-
щему органу машины), тело массы т\ = md — ротору дебаланс-
ного вибратора, тело с массой т2 — ть — корпусу дробилки
(«ролику» планетарного вибратора). Для рассматриваемой си-
стемы в соответствии с обозначениями, принятыми в главе XIII,
§ I]
ИНЕРЦИОННАЯ ДРОБИЛКА
745
МОЖНО положить
Л, = О, Л2 = 1, ст1=ст2=1, f'2 =
L\a} (со) = л (со), (со) = О
и, поскольку дробилка предполагается мягко амортизирован-
ной,— считать справедливыми первую группу равенств (16.25')
указанной главы. Тогда, согласно формулам (16.2) — (16.4) той
же главы, будем иметь
Р — Ри — Рц~ 2, Q — О,
т.е.т.е.а2
Г(соН	>
у — л,
u^ = o,
,, т.е..т.е.<о2
-	cos а.
М
Далее, в силу формул (6.9) и (16.4) главы XIII,
R2 (со) = f'
Zi (со) =-- L (со) —	(со),
Z2 (со) = -
(1.2)
(1-3)
Ща -ф- Ж	о
2~^М---- "W11’
где в соответствии с обозначениями, принятыми в указанной
главе, М = .Ж + ш, + т2 — масса вспомогательного тела, а
.Ж — масса конуса дробилки (несущего тела).
Уравнения (16.6) главы XIII для определения разности фаз
а = ой — сс2 и угловой скорости синхронного движения элемен-
тов машины со в данном случае принимают вид
L (со) - 7?] (со)
— sin а =-----------~-------—
Г (со)
о	л о + Ж „
Д (со) — /?! (со) — f mbe2b---------со
— cos а =----------------------=--------------------
f’W (со)
(1-4)
Исключив отсюда L (со) — /?|(со), находим
sin (а — р') =—sin pz,	(1.5)
•^0
где обозначено:
та = md + Ж = М — ть,
тл. т.е.
p' = arctgf, До = —(1.6)
d	a
746
ВИБРАЦИОННЫЕ ДРОБИЛЫЮ-ИЗМЕЛЬЧИТЕЛЬПЫЕ МАШИНЫ [ГЛ. XXI
причем, очевидно, Ао есть амплитуда колебаний тела М (кону-
са) под действием возмущающей силы, развиваемой дебалан-
сом при условии, что тело ть (корпус) отсутствует.
Необходимым и достаточным условием наличия у уравнения
(1.5) вещественных решений относительно а является неравен-
ство
>sinp'<l	(1.7)
Ао
или, согласно (1.6), соотношение
(1.8)
^0	I
Заметим, что полученное условие по форме в точности совпа-
дает с условием существования основного режима движения
«планетарного» маятника, возбуждаемого заданными колеба-
ниями его оси по круговой траектории радиуса г0 (см. неравен-
ство (4.4) главы XIX). Естественно, что такое совпадение не
случайно.
Исключив а из системы (1.4), приходим к следующему урав-
нению для определения угловой скорости со:
(Г)2 [А (со) - Я° (со)]2 + [L (со) - (со) - f'mbh	со2]2 = [/'W (со)]2.
(1-9)
Не останавливаясь здесь на выяснении условий существо-
вания у уравнения (1.9) вещественного решения относительно
со, лежащего на рабочем (устойчивом) участке характеристики
асинхронного двигателя (см. рис. 27), будем предполагать эти
условия выполненными*); но тогда единственным условием су-
ществования изучаемого режима работы дробилки будет нера-
венство (1.8). При его выполнении уравнение (1.5) допускает
два существенно различных решения относительно угла а:
(a)i = р' — arcsin sin p'l,
,	Л°/е \	И-Ю)
(а)2 = р + л + arcsin (-J- sin р').
kA, /
В соответствии с равенством (16.13) главы ХШ и формула-
ми (1.2) настоящего параграфа условие устойчивости движения
% < 0 в данном случае может быть представлено в форме
cos (а — р') + ф-соэ р' cosa< 0.	(1.11)
К]	'	'
*) Можно показать, что они выполняются, если двигатель обладает до-
статочной мощностью.
§ I]	ИНЕРЦИОННАЯ ДРОБИЛКА	747
Как показывают расчеты, для дробилки коэффициент демп-
фирования /г2 значительно меньше коэффициента /гц тогда, пре-
небрегая вторым слагаемым в левой части неравенства (1.11)
по сравнению с первым, приходим к заключению, что устойчи-
вым является только движение, отвечающее второму из реше-
ний (1.10); движение же, отвечающее первому решению, не-
устойчиво.
В заключение исследования заметим, что первое из уравне-
ний (1.4) при учете (1.2) может быть представлено в виде
~	о	ii.t’ii.e.iu1
Zl(co) = L(co)-7?,(co)=--	.	(1.12)
Отсюда следует, что для изучаемого синхронного движения
непременно должно быть справедливым неравенство
т .е.чг.е.со2
|Z,(«>)|<IF(«>)= ddMbb 	(1.13)
Полученные соотношения полностью согласуются с найден-
ными А. К. Рундквистом и автором для пространственной
схемы инерционной дробилки совершенно иными методами
[368—370].
Не останавливаясь здесь на изложении цитированных иссле-
дований, заметим лишь, что все приведенные выше соотношения
остаются справедливыми и в случае, когда вибратор размещен
не в конусе дробилки, как предполагалось первоначально, а в ее
корпусе. В последнем случае под несущим телом Л (вибрирую-
щим органом) следует понимать не конус, а корпус дробилки,
а под «роликом» теперь уже внутреннего планетарного вибрато-
ра— дробящий конус машины.
Отсюда следует, что сформулированные выше результаты
непосредственно относятся также к одной из схем вибрацион-
ных роликовых измельчителей, разработанных в институте «Ме-
ханобр»*). Принципиальная схема этих машин представлена
в п. 16 таблицы 2 (стр. 350). В цилиндрических полостях
мягко амортизированного корпуса машины Л размещено п из-
мельчающих роликов (внутренних планетарных вибраторов).
Вследствие колебаний корпуса, возбуждаемых дебалансными
вибраторами (их может быть несколько), ролики обкатываются
по стаканам, измельчая поступающую в них руду. Как и в дро-
билке, при нормальном режиме работы машины измельчающие
*) В разработке и испытаниях роликовых измельчительных устройств
принимали участие К. А. Рундквист, А. И. Макаров, В. В. Дубровин,
Б. Н. Федоров, В. А. Олевский, А. Д. Рудин, Г. А. Денисов и автор настоя-
щей работы.
748
ВИБРАЦИОННЫЕ ДРОБИЛЫЮ-ИЗМЕЛЬЧПТЕЛЬНЫЕ МАШИНЫ [ГЛ. XXI

тела обкатываются внутри стаканов с угловой скоростью со,
равной угловой скорости вращения роторов вибраторов. Таким
образом, основная задача динамики измельчителей данного
типа сводится к установлению условий существования и устой-
чивости синхронных движений нескольких дебалансных и плане-
тарных вибраторов. При этом, поскольку планетарные вибра-
торы в данном случае лишены двигателей, то по отношению к
ним мы имеем задачу о вибрационном поддержании вращения.
Как следует из изложенного, полученные в настоящем пара-
графе соотношения могут быть весьма просто трансформирова-
ны применительно к измельчителю с одним центрально распо-
ложенным вибратором и с одним
стаканом, ось которого совпа-
дает с осью дебалансного вибра-
тора. Схема такого измельчителя,
разработанная В. А. Олевским и
А. Д. Рудиным, представлена на
рис. 110. Для быстрого измель-
чения лабораторных проб руды
в институте «Механобр» создана
установка, также отвечающая
схеме п. 16 таблицы 2, но с че-
тырьмя симметрично расположен-
ными стаканами при одном де-
ановка используется в лаборато-
риях ряда институтов и предприятий.
Заметим в заключение, что приведенные выше результаты
(а также результаты § 3 главы XVIII) непосредственно при-
ложимы к теории дозирующих и питающих устройств институ-
тов ВНИИНСМ и ВНИИЗ, краткое описание которых было
приведено в § 1 главы XII.
Таким образом, обобщение понятия о механическом вибра-
торе позволяет рассмотреть в рамках единой теории не только
динамику вибрационных машин с вибраторами-возбудителями
(грохоты, конвейеры, мельницы и т. п.), но и динамику таких
машин, как вибрационные и инерционные дробилки, мельницы
и дозаторы, в которых ролики «планетарных вибраторов» вы-
полняют функции рабочих тел.
§ 2. Критическая щель инерционной дробилки
и некоторых других машин
Из соотношения (1.8) следует, что нормальная работа дро-
билки или другой аналогичной машины возможна лишь при ус-
ловии, что «щель» S = 2еь, то есть двойной эксцентриситет пла-
нетарного вибратора (см. рис. 107 и схему п. 22 таблицы 2 на

Рис. 110.
балансном вибраторе. Эта
§ 21
КРИТИЧЕСКАЯ ЩЕЛЬ ИНЕРЦИОННОЙ ДРОБИЛКИ
749
стр. 355), не превышает некоторого значения S’ = 2r]*tA0, назван-
ного критической щелью:
S<S*, S’ = 2r)st^0. 5 = 2ей.	(2.1)
Наличие в рассматриваемых машинах критической щели
впервые было обнаружено Б. Н. Дубровиным в результате тех-
нологических испытаний дробилки*). Позднее автором на осно-
ве экспериментального исследования лабораторных моделей
дробилок и мельниц было показано, что наличие критической
щели связано с нарушением синхронного движения рассмотрен-
ного выше типа (режима обкатки дробящих тел) [182]. Для вы-
числения критической щели была предложена формула (2.1), в
которой коэффициент r)*t рассматривался как эмпирический. Об
этих экспериментах уже говорилось в п. 2 § 4 главы XIX.
Наиболее удачное с нашей точки зрения теоретическое объяс-
нение наличия критической щели (для случая дробилки) было
дано А. К- Рундквистом, который на основе простых энергети-
ческих соображений**) впервые получил формулу (1.8) для вы-
числения коэффициента T]’t и предположил, что стационарный
режим движения самовозбуждается во всей области своего су-
ществования и устойчивости, определяемой условием (1.8). На-
помним, что как эта формула, выведенная здесь нами из общих
результатов теории синхронизации ви-
браторов, так и указанная гипотеза по-
лучили экспериментальное подтвержде-
ние (см. п. 2 § 4 главы XIX).
Подробное изложение перечисленных
выше, а также и некоторых других ре-
зультатов, относящихся к теории крити-
ческой щели, дано в работах Б. Н. Дубровина, А. Д. Рудина,
А. К- Рундквиста и автора [182, 64, 65, 370]. Здесь мы отметим
лишь одно любопытное обстоятельство, состоящее в следующем.
Изучая поведение шарика, помещенного в запаянную по кон-
цам трубку, совершающую продольные гармонические колеба-
ния с амплитудой До (рис. Ill), А. Е. Кобринский получил
условие существования стационарного режима движения ша-
рика, при котором происходит по одному соударению шарика
с противоположными концами трубки за каждый период ее ко-
лебаний [214]. Указанному условию можно придать вид
2 1—/?
Р л 1 + R ’
А. К. Рундквист, частично изложив-
2е
Рис. 111.
е К1 + Р2
_________________До Р ’
*)	В этих опытах принимал участие
ший их результаты в работах [368, 369].
**	) О возможности энергетической трактовки условий существования син-
хронных движений см. § 6 главы XIII и п. 2 § 3 главы XVIII.
(2.14)
750
ВИБРАЦИОННЫЕ ДРОБИЛЬНО ИЗМЕЛЬЧИТЕЛЬНЫЕ МАШИНЫ (ГЛ. XXI
где е — половина длины хода шарика в трубке, a R — коэффи-
циент восстановления при ударе.
Таким образом, роль коэффициента сопротивления перекаты-
ванию, фигурирующего в формуле (1.8), в соотношении (2.14)
играет величина р, связанная с коэффициентом восстановления
R. Более того, значения величины р при изменении R в наиболее
широких пределах 0,2 < R < 0,55, приводимых для систем, по-
добных рассматриваемой, в справочной литературе, лежат в
диапазоне 0,2 < р < 0,4, весьма близком к диапазону для коэф-
фициента f' (0,15 < f < 0,35; см. неравенство (4.6) главы XIX).
На анализе отмеченного факта мы здесь, однако, останавливать-
ся не можем.
§ 3. Инерционные дробилки, приводимые от двух
самосинхронизирующихся вибраторов
В развитие идеи, лежащей в основе описанной в § 1 инер-
ционной дробилки «Механобра», автором совместно с К. А. Рунд-
квистом, А. К. Рувдквистом, И. Л. Успенским и А. Я- Иваненко
Рис. 112.
была предложена дробилка,
приводимая от двух само-
синхронизирующихся деба-
лансных вибраторов, разме-
щенных в корпусе [69].
Схематический разрез
дробилки представлен на
рис. 112; можно не останав-
ливаться на характеристике
отдельных элементов ма-
шины, изображенных на
схеме, ибо они вполне ана-
логичны элементам дробил-
ки, описанной в § 1 (и обо-
значены на схеме теми же
цифрами).
Дробилка с самосинхронизирующимися вибраторами, разме-
щенными в корпусе, обладает рядом достоинств по сравнению
с инерционной дробилкой, осуществленной по рассмотренной
выше схеме, однако на их перечислении мы также здесь не бу-
дем останавливаться.
Принципиальная возможность создания дробилки с самосин-
хронизирующимися вибраторами вначале была установлена чи-
сто теоретическим путем, а затем проверена на специальной
экспериментальной установке (см. §§ 3 и 4 главы XIX настоя-
щей книги, а также рис. 74, а и 78). После этого в институте
«Механобр» была сконструирована, изготовлена и прошла испы-
§ 3]
ДРОБИЛКИ, ПРИВОДИМЫЕ ОТ ДВУХ ВИБРАТОРОВ
751
тания лабораторная дробилка с самосинхронизирующимися
вибраторами (диаметр основания дробящего конуса 250 мм);
общий вид этой дробилки пред- .
ставлен на рис. 113.
Для нормальной работы ма-
шины необходимо обеспечить
синхронное и синфазное враще-
ние роторов обоих дебалансных
вибраторов в одинаковых направ-
лениях и синхронное движение
конуса дробилки (ролика внут-
реннего «планетарного вибрато-
ра») в том же направлении.
Получим условия существова-
ния и устойчивости такого дви-
жения, ограничившись рассмот-
рением плоской схемы машины,
представленной на рис. 114; за-
метим, что эта схема относится
одновременно и к вибрационному
измельчителю, имеющему два де-
балансных вибратора и один
ролик (см. схемы п. 16 табли-	Рис 113
цы 2 и п. 27 таблицы 5).
Для решения задачи [68] воспользуемся общими результа-
тами, изложенными в § 8 главы XIII. В изучаемом случае, при-
писав дебалансным вибраторам индексы 1 и 2, а «планетарному
y,v
Рис. 114.
вибратору» индекс 3, в соответствии со схемой рис. 114 можно
положить (дебалансные вибраторы считаются одинаковыми)
= m2 = md, т3 = mb; = е2 = ed, е3 = eb; d{ = d2 = dd;
ki = k2 = kd, k3 = kb; O| = o2 = o3=l;	(3-1)
H = f'; /; /г =o, /г=1;
* и *	14	9
752
ВИБРАЦИОННЫЕ ДРОБИЛЬНО ИЗМЕЛЬЧИТЕЛЬНЫЕ МАШИНЫ [ГЛ. XXI
(со) = R° (со) = R (со), (со) == fmbe2 со2;
£1°'(со) = L2a) (со) = £ (со), £3a)(co) = 0;	(3.1)
ri = r2 = r, г3 = 0; 6|=л, 62 = 0.
Поскольку корпус рассматриваемой дробилки мягко аморти-
зирован, то для вычисления вибрационных моментов Ws® и
Ws® можно воспользоваться формулами (8.8) главы XIII. То-
гда при учете равенств (3.1) настоящего параграфа уравнения
(10.1) указанной главы для определения порождающих фаз at,
а,2 и а3 и угловой скорости синхронного вращения со могут быть
представлены в форме
Pi (аь а2, аз, со) = ~\zd (со) + у Wd (со) (2 - v2) sin (а, - а2) +
кд L	z
Pi («1,
+ W (со) sin (а, — a3)j = 0,
а2, а3, со) е= -b[zd(co) - у Wd (со) (2 - v2)sin(a, -а2) +
4 W (со) sin (а, — а3)1 = 0,
Ря (аь а2, а3, со) == ~ {Zb (со) + W (со) [sin (а3 — at) + sin (а3 — а2) +
+ f' cos (а3 — аО + f' cos (а3 — а2)]} = 0.	(3.2)
Здесь обозначено:
Zd (со) = £ (со) —/?° (со),
причем та представляет массу корпуса дробилки с вибраторами.
Получим теперь условия, при которых уравнения (3.2) допу-
скают относительно ai и аг вещественные решения вида
«1 = a2 = «>	(3.4)
соответствующие синхронному и синфазному вращению обоих
дебалансных вибраторов. При этом, поскольку рассматривается
задача о самосинхронизации, фазу аз, согласно сказанному
в § 10 главы XIII, можно, не нарушая общности, положить рав-
ной нулю:
а3 = 0,
(3.5)
§ 3]
ДРОБИЛКИ. ПРИВОДИМЫЕ ОТ ДВУХ ВИБРАТОРОВ
753
Подставив выражения (3.4) и (3.5) в (3.2), приходим к сле-
дующим двум уравнениям для определения угла а и угловой
скорости синхронного вращения со:
Zd (со) + W (со) sin а = О,
Zb(co) + 2W (со) (/' cos а — sin а) = 0.
Первое из этих уравнений сразу же дает соотношение, кото-
рому должен удовлетворять избыточный момент на валу ка-
ждого из дебалансных вибраторов 2д(со) в синхронном дви-
жении:
"1,е .ог.е.со2
| Zd(co) I < Г (со) =	.	(3.7)
Величина W (со), фигурирующая также и в неравенстве (1.12),
по своему смыслу в точности совпадает с известным выраже-
нием для максимального момента, передаваемого дебалансным
вибратором в синхронном движении; последнее выражение для
одновибраторной дробилки было получено иным путем
А. К. Рундквистом [368, 369].
Второе уравнение (3.6) нетрудно разрешить относительно
угла а. Вводя обозначения
p' = arctgf', А0 = 2-^-,	(3.8)
tna
вполне аналогичные обозначениям (1.6), при учете (3.3) на-
ходим
е.
sin (а — р)=----— sinp.	(3.9)
А
Отсюда следует, что необходимым условием существования рас-
сматриваемого синхронного движения, как и для дробилки с од-
ним дебалансным вибратором, является неравенство
Если ввести щель S = 2еь и критическую щель S* = 2ii*tA0, то
последнее условие в точности совпадет с соотношением (2.1).
При выполнении неравенства (3.10) уравнение (3.9) допу-
скает два существенно различных вещественных решения отно-
сительно угла а:
(3.11)
(а)2 = р' + л + arcsin I -4- sin р'I.
\ Tin /
(а), — p' — arcsin I ~ sinp'
\ 710
754
ВИБРАЦИОННЫЕ ДРОБИЛЬНО-ИЗМЕЛЬЧИТЕЛЬНЫЕ МАШИНЫ [ГЛ. XXI
Для получения второго условия существования изучаемого
режима следует подставить выражения (3.11) в первое равен-
ство (3.6) и потребовать, чтобы получившееся уравнение допу-
скало положительные решения относительно угловой скоро-
сти и, отвечающие устойчивым ветвям характеристики двигате-
лей. Для достаточно мощных двигателей это условие всегда
выполняется, и поэтому мы не будем его рассматривать.
Обратимся к изучению вопроса об устойчивости синхронных
движений. С этой целью вычислим предварительно значения
производных dPsfdaj при ai = аг = а и аз = 0. Согласно ра-
венствам (3.2) имеем
'3-|2>
-ЖГ = 45-“ “ ST W (cos « +/'sin «) = с.
Отсюда следует, что уравнение (4.12) главы ХШ в рассматри-
ваемом случае имеет вид
(а — с — х)2 — (Ь — с)2 = 0,
и поэтому его корни
[	~	2	—
xt = а + b — 2с = -г- W (со) cos а + -г- W (со) (cos a + f' sin а),
,	"	’	(3.13)
х2 = а - b = -f- [ Wd (со) (2 - V2) + W (со) cos а].
«б/
Таким образом, условия устойчивости xs < 0 сводятся к нера-
венствам
Wd (со) (2 - v2) + W (со) cos а < 0,
,	1 k„ ,	(3-14)
cos (а — р ) + -у -т2- cos р cos а < 0.
Здесь использовано обозначение (3.8).
Обычно отношение kb]kd значительно меньше единицы; в част-
ности, для изготовленной модели дробилки с диаметром конуса
250 мм (рис. 113) оно имеет порядок 0,01. Поэтому последним
слагаемым в левой части второго неравенства (3.14) можно
пренебречь. Тогда из этого неравенства следует, что устойчивым
может быть только движение, соответствующее значению угла
а = (а)г, определяемому второй формулой (3.11). Подставив
указанное значение в первое из условий устойчивости (3.14),
§ 3]
ДРОБИЛКИ, ПРИВОДИМЫЕ ОТ ДВУХ ВИБРАТОРОВ
755
после простых преобразований при учете обозначений (3.3) и
(3.8)	представим это условие в форме
т.
__D _О
ma До
Mr2
I
или в виде
(3.15)
2
Последние неравенства и представляют искомое условие
устойчивости рассматриваемого синхронного движения машины.
Для его анализа рассмотрим несколько характерных частных
случаев.
а)	Работа при критической щели S — S*. При этом соотно-
шение (3.10) выполняется со знаком равенства, и условие (3.16)
приобретает вид
-^>2.	(3.17)
При выполнении неравенства (3.17) устойчивость рассматри-
ваемого движения обеспечивается при всех щелях, вплоть до
критической.
б)	Работа при щели, равной двойной амплитуде колебаний
корпуса при отсутствии конуса. В этом случае еь = До и условие
(3.15) переходит в соотношение
Т >2 (• - S“s2p') -2 ['ТТ$Ч- <ЗЛ8>
в)	Работа при весьма малой щели или в условиях, близких
к «завалу» полости дробилки рудой. При этом можно положить
ео/До ~ 0, и неравенства (3.15) и (3.16), как и следовало ожи-
дать, сводятся к условию устойчивости синфазного вращения
двух дебалансных вибраторов в системе, представленной в п. 3
таблицы 5 (Добавление 2):
-^>2.	(3.19)
Поскольку Mlma > 1, то очевидно, что выполнение этого усло-
вия еще не обеспечивает справедливости неравенства (3.17),
гарантирующего устойчивость изучаемого режима при всех ще-
лях, вплоть до критической. Вместе с тем выполнение условия
(3.19) со знаком равенства гарантирует устойчивость движения
при щелях, весьма близких к критической. Сказанное следует
756
ВИБРАЦИОННЫЕ ДРОБИЛИ 10 ИЗМЕЛЬЧИТЕЛЬНЫЕ МАШИНЫ [ГЛ. XXI
из того обстоятельства, что выражения в квадратных скобках
правых частей неравенств (3.15) и (3.16) обращаются в нуль
при
^ = —.	(3.20)
Ло f'
Поскольку обычно f'^0,3, то \/f' отличается от V1 + (Г)2/Г
не более чем иа 5°/о, и поэтому можно считать, что при выпол-
нении условия (3.19) практически гарантируется устойчивость
синфазного вращения роторов
Мгг	дебалансных вибраторов
“ I	вплоть до значения критиче-
ской щели.
\f=0,2 На рис. 115 представлены
области устойчивости рассмат-
риваемого режима работы ма-
шины в плоскости параметров
еь/Ло и v2 = Mr2)! (штриховка
направлена внутрь этих обла-
стей). При построении границ
областей принято ть/пга=0,85,
что примерно соответствует
Аа упоминавшейся выше лабора-
торной дробилке.
Заметим также в заключе-
ние, что полученные выше со-
отношения пригодны и для
дробилки с двумя самосинхро-
низирующимися вибраторами,
размещенными в конусе; такой случай отвечает внешнему
(кольцевому) планетарному вибратору.
Как уже отмечалось, эти результаты получили подтвержде-
ние в ходе экспериментов, проведенных на лабораторной мо-
дели дробилки и на специальной установке (см. §§ 3 и 4
главы XIX).
§ 4. Виброударная щековая дробилка, приводимая от двух
самосинхронизирующихся вибраторов
С. Н. Горшковым предложена виброударная щековая дро-
билка с двумя самосинхронизирующимися вибраторами [156].
Опытный образец машины был осуществлен и испытан ее ав-
тором и Б. П. Лавровым в институте «Механобр». Позднее были
изобретены и другие дробилки подобного типа [158, 395а].
Схема машины по предложению [156] представлена на
рис. 116, а и б, а фото — на рис. 116, в (см. также п. 28 таб-
§ 4]
В11БРОУДАРНАЯ щековая дробилка
757
лицы 5 Добавления 2). Она состоит из двух твердых тел / и 2,
связанных шарниром или сайлент-втулкой 3, обеспечивающими
телам одну относительную
степень свободы (поворот
относительно оси шарнира).
На одном из тел (пусть это
будет для конкретности
внутреннее тело следуя
К. А. Рундквисту, назовем
Рис. 116.
его условно «молотом») установлено два одинаковых дебаланс-
ных вибратора 4, приводимых от независимых асинхронных
758
ВИБРАЦИОННЫЕ ДРОБИЛЬНО-ИЗМЕЛЬЧИТЕЛЬНЫЕ МАШИНЫ [ГЛ, XXI
электродвигателей, роторы которых вращаются в противополож-
ных направлениях.
В нормальном режиме работы роторы вибраторов должны
вращаться синхронно и (при выбранном на рис. 116,6 способе
отсчета углов <pi и <рг) противофазно, развивая возмущающую
силу, направленную перпендикулярно оси шарнира и лежащую
в плоскости вращения их центров тяжести. При этом молот
колеблется внутри внешнего тела (используя по-прежнему тер-
минологию К. А. Рундквиста, назовем это тело «наковаль-
ней»), производя поочередные удары по руде, подаваемой в две
рабочие полости: удары следуют через половину периода коле-
баний молота, равного времени одного полного оборота валов
вибраторов *).
Наковальня связана с неподвижным основанием посред-
ством мягких амортизирующих пружин 5, не оказывающих за-
метного влияния на установившееся движение тел и предотвра-
щающих передачу динамических воздействий на основание.
Естественно, что оба тела в описанной схеме динамически
совершенно «равноправны» — вибраторы могут быть установ-
лены на любом из них.
Динамика виброударпой дробилки, в том числе и вопрос
о существовании и устойчивости синхронного и синфазного дви-
жения вибраторов при описанном выше «номинальном» режиме
колебаний рабочих тел, рассмотрена Р. Ф. Нагаевым в статье
[308], основные результаты которой здесь и воспроизводятся
в несколько иных обозначениях.
Пусть Oxyz — неподвижная в пространстве система прямо-
угольных координат, с которой в положении статического равно-
весия совпадают главные центральные осн вспомогательного
тело Oi«, v, w, отвечающего молоту, то есть тела, получающе-
гося из молота, если присоединить к нему массы роторов вибра-
торов, сосредоточенные на их осях в точках пересечения с пло-
скостями вращения центров тяжести, а также массу наковальни,
сосредоточенную на оси шарнира АА в точке Q0, лежащей в од-
ной из плоскостей симметрии системы. Предполагается, что си-
стема имеет две плоскости симметрии: одна (плоскость vOtw)
содержит ось шарнира и оси вибраторов, а другая (плоскость
uOiw) —перпендикулярна оси АА.
Положение системы определяется смещениями х, у и z цен-
тра тяжести вспомогательного тела малыми поворотами
фх, фу и Фг вокруг этих осей, углом поворота ср молота относи-
тельно наковальни и углами поворота роторов вибраторов <pi и
ера, отсчитываемыми от направлений, параллельных оси Oyi.
*) Разумеется в данной системе возможны также и иные режимы
(см. § 7 главы XIV).
§ 4]	ВИБРОУДАРНАЯ ЩЕКОВАЯ ДРОБИЛКА	759
Таким образом, система имеет семь колебательных степеней сво-
боды.
Угол относительного поворота тел ср не может превышать по
абсолютной величине некоторого заданного значения у:
(4.1)
При достижении равенства |ф| = у происходит соударение
тел, которое считается абсолютно неупругим и внецентренным;
точки соударения К+ и К- лежат в плоскости uOtw и имеют
координаты
I ик i = R sin 0, wK = — R cos0 + b,	(4.2)
где R — расстояние от точек соударения до центра тяжести на-
ковальни ть; b — расстояние от центра тяжести наковальни до
точки Оц |3 — угол между прямыми тьК+ и тьК- и отрицатель-
ным направлением оси OiW.
Удар считается абсолютно неупругим, и поэтому после со-
ударения тела могут двигаться слитно (ср = ±у, ф = 0) до тех
пор, пока не произойдет нарушения неудерживающей связи.
Уравнения движения роторов вибраторов могут быть запи-
саны в форме
/ф1 = L (ф,) - R (ф,) - ^фг +
+ те [(х — гф2 + афу) sin Ф1 — (г/ + cos ф^,
/ф2 = Л(ф2)-/?(ф2)-.Я’г+	(4’3)
+ те [(х + гф2 — дфй) sin ф2 — (у + дф^) cos ф2],
а уравнения малых колебаний молота и наковальни — в форме
Му — — те (sin ф! + sin ф2)“,
/хфх = ~ mea (sin ф, + sin ф2)”,
Мг = 0,
/гф2 = ~ mer (COS ф, — COS ф2)”,
Мх + ртй/гф = — те (cos ф! + cos ф2)",
1У^У — рВф = теа (cos ф[ -I- cos ф2)‘‘,
р (7фф + mbhx — В$у) = 0.
Здесь М = JC + ть + 2т, Ж, try, и т — соответственно массы
всей системы, молота, наковальни и роторов вибраторов; е—
эксцентриситет роторов; .У и / — соответственно моменты инер-
ции роторов относительно осей, проходящих через их центры
тяжести параллельно оси Oiw, и относительно осей вращения;
/х, Rj и /z—моменты инерции всей системы в положении отно-
сительного равновесия относительно главных центральных осей
(4.4)
(4.5)
760
ВИБРАЦИОННЫЕ ДРОБИЛЬПО ИЗМЕЛЬЧИТЕЛЬПЫЕ МАШИНЫ [ГЛ. XXI
вспомогательного тела; h — расстояние от центра тяжести нако-
вальни ть до оси шарнира АА; г — расстояние от осей вращения
роторов вибраторов до оси Otw; а — расстояние от плоскостей
вращения центров тяжести вибраторов до точки Оц В — /ф —
— rribbh; ht — момент инерции наковальни относительно оси
шарнира АА; число р равно единице при |ф| < у и равно нулю
при |<р| = у, то есть при слитном движении молота и нако-
вальни; £(ф)—вращающие моменты, передаваемые от асин-
хронных электродвигателей на валы вибраторов; /?(ф) —момен-
ты сил сопротивления вращению валов.
В связи с предположением о выборе начала системы коор-
динат в центре тяжести вспомогательного тела справедливо со-
отношение
сЛ — 2апг + (b — h) tnb = 0.	(4.6)
В уравнениях (4.3) — (4.5), как и в уравнениях ранее рас-
сматривавшихся задач о синхронизации вибраторов, опущены
члены, имеющие по сравнению с выписанными более высокий
порядок малости. Линеаризировав, как и в § 2 главы ХШ, вы-
ражения для А(ф) и /?(ф) вблизи значения синхронной угловой
скорости со и положив
L (ф) « L (со) — k* (ф — со), R (ф) = R° (со) + k° (ф — со),
k = k* + k° > 0,
ЦФ1(<Р1, х, у, z, фу, фг) = ше[(х — гфг +афу) sin ф! —
— (у + афл.) cos ф,] + L (со) — R (со),
цф2(ф2, X, у, 2, фх, фу, фг) = те [(х + гфг — афу) sin ф2—
-(& + афх)со8ф2],
где ц > 0—малый параметр, представим уравнения движения
вибраторов (4.3) в форме
/ф5+й(ф5-со) = цф5(ф5, X, у, 2, фх, фу, ф2)	($=1, 2). (4.8)
Система (4.8), (4.4), (4.5) и является исходной при иссле-
довании синхронных движений. При ц = 0, как и в задачах
о синхронизации вибраторов в системах без ударов, уравнения
(4.8) допускают «непрерывное» синхронное порождающее ре-
шение вида
ф10 = со/ + а1,	ф20 = — (со/ + а2),	(4.9)
то есть решение, отвечающее равномерному вращению роторов
вибраторов. Существенная особенность рассматриваемого слу-
чая состоит, однако, в том, что уравнения (4.4), (4.5) дают, во-
обще говоря, разрывные решения относительно скоростей
х, ..., фг уже в порождающем приближении; разрыв имеет ме-
ВНБРОУДАРНАЯ ЩЕКОВАЯ ДРОБИЛКА
761
§ 4]
сто при достижении углом |<р| значения у. Разрывными будут
также первые приближения к угловым скоростям вращения ро-
торов вибраторов ф8-
Пусть соударение тел происходит в некоторый момент вре-
мени t = ti. При этом все координаты системы останутся непре-
рывными функциями t, а скачки скоростей изменения координат
определятся путем почленного интегрирования уравнений дви-
жения (4.4), (4.5) в пределах от Ц — kt до h + kt и последую-
щего перехода к пределу при kt—>0. Тогда, в соответствии
с предположением об абсолютной неупругости удара, угловая
скорость ф0 после удара фо"= 0 и
= ^-ф^+),	~^-Фэ+)- (4.Ю)
Что же касается скоростей у, z, фх и ф2, то в исходном прибли-
жении они будут непрерывными. Здесь и ниже знак (—) отно-
сится к значениям скоростей после удара, а знак ( + ) —к зна-
чениям до удара. Аналогичным образом из уравнений (4.8)
определятся скачки первых приближений к угловым скоростям
вращения роторов вибраторов:
Н (Фн ’ - Фи’) = ™ К’ “ С’ “ а (С - Чо’)] sin(c,Zi + ai)>
(4.П)
О (?2i ’ - ФгГ) =	1*о ’ - С’ - а (Ч? “ Чо’)] sin (Ч + аг)‘
К изучаемой системе применима теорема М. 3. Коловского,
изложенная в п. 2 § 6 главы V. Не останавливаясь здесь на по-
дробностях вычислений, заметим лишь, что получение основных
уравнений
Ps(aj — a2, со) = 0	(s~ 1, 2)	(4.12)
в данном случае, так же как и в ранее рассмотренных задачах
о синхронизации, сводится к осреднению за период правых ча-
стей уравнений движения вибраторов (4.8); правда, интегриро-
вание теперь следует выполнять в обобщенном смысле. Уравне-
ниям (4.12) по-прежнему можно дать отчетливую энергетиче-
скую интерпретацию.
Вычисления показывают, что уравнения (4.12) всегда допу-
скают решение ai = ai — <хг = 0, отвечающее желаемому син-
фазному движению роторов вибраторов. Условие устойчивости
этого движения получается из требования отрицательности ве-
личины х = d(Pi — P2)/dai и имеет вид
„/ 1	1 \ г2 1 /ф ,
a2 -j---т-1+-7— >-------тг (у + ft cost]),	(4.13)
\/х	1у! 1г	л meQ '	'
762 ВИБРАЦИОННЫЕ ДРОЁИЛЬНО-ИЗМЕЛЬЧИТЕЛЬНЫЁ МАШИНЫ [ГЛ. XXI
где
а 1 2те ,,	.	.
л. 1 F("W , Д21
/Ф L м
1
Лр
/ mi,h
\ М
аВ \
‘у Г
(4.14)
1
Q
а величина ti = со Л (фаза, отвечающая моменту удара it) опре-
деляется как корень трансцендентного уравнения
,	л , Q (1 — d)	, .
n + cost^y + у—(4.15)
лежащий в промежутке уп^г^п. Последнее неравенство
для ti дает условие существования рассматриваемого режима
работы дробилки, которое приводит к следующему ограничению
на максимальный угол относительного отклонения молота и на-
ковальни:
Y<Y* =
л те
(4.16)
или, что то же
наковальней:
самое, — на щель S = 2Ry между молотом и
S<S* =
2 л/? те
1 -d "О' *
(4.17)
Соотношение (4.17) вполне аналогично неравенству (2.1), по-
лученному для конусных дробилок, а величина S* играет для
щековой дробилки роль критической щели.
Рассмотрим несколько подробнее условие устойчивости
(4.13). Прежде всего, заметим, что правая часть этого неравен-
ства связана с наличием в системе ударов и дополнительной сте-
пени свободы. Действительно, при отсутствии щели между мо-
лотом и наковальней, то есть при у = О, из (4-15) получаем
Т1 = |я, COSTCO, и соотношение (4.13) принимает вид
“2(т7-Т7)+£>0-	(4-18>
Как и следовало ожидать, это неравенство (если учесть разли-
чие в выборе осей координат и способе отсчета углов cpi и <рг)
совпадает с условием (2.51) главы XX, полученным для случая
одного мягко амортизированного тела.
Заметим, далее, что, как показывают простые вычисления,
выражение в правой части неравенства (4.13) при изменении
угла y в промежутке
О < Y < 1 >3-	(4.19)
отрицательно, и поэтому в данном случае условие (4.13) навер-
няка выполняется, если 1Х < 1У. При дальнейшем увеличении у
§ 5]	ВИБРАЦИОННЫЕ ШАРОВЫЕ МЕЛЬНИЦЫ	763
вплоть до критического значения у* правая часть неравенства
(4.13) монотонно увеличивается; поэтому при заданной левой
части «запас устойчивости» рассматриваемого режима пони-
жается. Максимальный запас устойчивости в этом смысле полу-
чается при
Y = Y = 0.57-j4y-^,	(4.20)
что соответствует значению ti = л.
Приведем в заключение формулу для мощности, потребляе-
мой при работе дробилки каждым электродвигателем:
N = aR°(a) +^(1 ~d)I4W,	(4.21)
для величины ударного импульса в точках соударения К±:
SK = ± [4&) I1 ~ 77) + mbh2 f1 -	~ mohb (4-22)
и для проекций реактивного ударного импульса в шарнире АА:
^ = <(1	— cospjsx, s!?’= - SKsinp. (4.23)
Здесь через обозначен момент инерции наковальни относи-
тельно оси, проходящей через ее центр тяжести и параллельной
оси Оу, обозначения R и р были расшифрованы выше (см. так-
же рис. 116, б).
Заметим, что помимо рассмотренного основного режима ра-
боты дробилки при синфазном вращении роторов вибраторов
могут существовать и иные режимы. Так, например, при
у >J возможен безударный режим колебаний. Возмож-
ны также режимы, в которых период движения молота и на-
ковальни в целое число раз превышает время одного оборота
валов вибраторов. Однако такие режимы особого практического
значения не имеют.
§ 5.	Вибрационные шаровые мельницы
с самосинхронизирующимися или принудительно
синхронизированными вибраторами *)
Вибрационные шаровые мельницы успешно применяются для
тонкого измельчения ряда материалов [250]. Рабочий процесс
в этих машинах осуществляется в камерах, наполненных шаро-
вой загрузкой; как правило, камеры устанавливаются на мягко
*) Автор благодарен А. Д. Лесину за интересное обсуждение ряда во-
просов, изложенных в настоящем параграфе.
764
ВИБРАЦИОННЫЕ ДРОБИЛЬНО-ИЗМЕЛЬЧИТЕЛЬНЫЕ МАШИНЫ (ГЛ. XXI
амортизированных твердых телах, которым сообщаются колеба-
ния посредством дебалансных вибраторов. Наиболее часто встре-
чаются мельницы с круговыми (или близкими к круговым) по-
ступательными колебаниями камер.
Явление самосинхронизации механических вибраторов может
быть использовано и в приводе вибрационных мельниц.
Предложенная автором мельница с двумя самосинхронизи-
рующимися вибраторами [53] представлена в п. 14 таблицы 2.
Преимущество такой машины по сравнению с мельницей, приво-
димой от одного центрально расположенного вибратора, состоит
в том, что ее камера не загромождена вибратором; кроме того,
появляется возможность снижения
нагрузки на подшипники ви-
браторов. При условии, что
корпус мельницы вместе с
камерой и загрузкой допу-
стимо идеализировать в ви-
де твердого тела, рассмат-
риваемой мелышце будет
соответствовать система,
изображенная в п. 3 табли-
цы 5 (Добавление 2). При
выполнении неравенства
-^—>2	(5.1)
Рис. 117.	вибраторы, роторы которых
вращаются в одинаковых
направлениях, будут двигаться синфазно, обеспечивая круговые
поступательные колебания корпуса. Если же роторы вращаются
в противоположных направлениях, то корпус будет совершать
прямолинейные поступательные колебания перпендикулярно
плоскости осей роторов. Таким образом, изменение режима ра-
боты может быть достигнуто путем простого изменения направ-
ления вращения ротора одного из вибраторов.
Малая модель описанной мельницы была изготовлена и ис-
пытана в институте «Механобр», а машина более крупных раз-
меров (рис. 117) сконструирована и испытана во ВНИИНСМ
под руководством А. Д. Лесина [250]. В процессе этих последних
значительно более полных экспериментов, в частности, опреде-
лялся сдвиг фаз вращения роторов вибраторов. Последний ока-
зался несколько отличным от нуля, причем отличие существенно
зависело от отношения Мг2/2/ и от других параметров системы.
Указанные отклонения, несомненно, объясняются главным
образом неодинаковостью парциальных угловых скоростей вра-
щения вибраторов и тем, что данные неодинаковости по-разному
влияют на угол сдвига фаз при различных значениях парамет-
§ 5]
ВИБРАЦИОННЫЕ ШАРОВЫЕ МЕЛЬНИЦЫ
765
ров. Для случая прямолинейных поступательных колебаний изу-
чаемой системы это было показано в § 2 главы XX; нетрудно
провести соответствующее исследование на стабильность и в дан-
ном случае, когда колебания являются круговыми. Согласно
формулам (2.46), (2.47), (2.27) главы XX и (16.25') главы XIII
находим, учитывая, что для рассматриваемой системы ощг = 1
и Мг2/1 > 2:

m2e2w2 / Mr2
М \ 2/
„о _______^'°
шо(2д + ^)’
1
А<Х Itnax ~	п~
Ио P.O
V°o (zl + zr)
w° (%)
M(ZL+ZR>
22 ( Мг2	,) ’
т 2е2соо 1-^-11
(5.2)
Из последнего соотношения и вытекает существенная зависи-
мость максимально возможного угла рассогласования фаз вра-
щения вибраторов от параметров системы и в особенности от
отношения Mr2!?!-, эта зависимость становится особенно резкой
при Мг2121, близком к единице, то есть при небольшом «запасе»,
с которым выполняется условие устойчивости (5.1). Сказанное и
объясняет в значительной мере результаты опытов А. Д. Лесина.
Иногда удовлетворение условия (5.1), особенно с определен-
ным запасом, вызывает конструктивные затруднения. В таких
случаях можно прибегнуть к способам смягчения указанного
условия, рассмотренным в § 3 главы XV и вытекающим из пп. 7,
20 и 27 таблицы 5 (Добавление 2). Наконец, можно обратиться
к способам принудительной синхронизации, представленным
в пп. 4 и 5 таблицы 5.
Следует заметить, что рассмотренная схема вибрационной
мельницы с самосинхронизирующимися вибраторами является
далеко не единственно возможной; укажем, например, на си-
стему с двумя коаксиальными вибраторами, изображенную
в п. 13 таблицы 5. Такая схема может оказаться более пред-
почтительной, так как в ней удовлетворение соответствующего
условия устойчивости менее затруднительно.
При работе вибрационных мельниц некоторые затруднения
вызывает моделирование загрузки, составляющей ощутимую
долю от веса корпуса машины. Чаще всего загрузку учитывают
лишь в виде некоторой «присоединенной массы», добавляемой
к массе корпуса. В этой связи заметим, что результаты иссле-
дования, изложенные в § 3 главы XV, позволяют проследить
влияние на самосинхронизацию вибраторов более сложного
характера взаимодействия загрузки с корпусом машины в про-
цессе се работы.
ГЛАВА XXII
ВИБРАЦИОННЫЕ ПОГРУЖАТЕЛИ СВАЙ,
ШПУНТА И ОБОЛОЧЕК
§ 1.	Об особенностях использования самосинхронизирующихся
или принудительно синхронизированных вибраторов
в изучаемом классе машин
Как явствует из таблицы 2 (стр. 340—358; см. пп. 3, 4, 13
и 21), вопрос о синхронизации дебалансных вибраторов пред-
ставляет интерес также и применительно к вибрационным по-
гружателям свай, шпунта и оболочек.
Существенная особенность этого класса машин состоит в том,
что при исследовании синхронизации здесь нельзя игнорировать
упругость грунта, которая может оказывать значительное влия-
ние на характер устойчивого движения вибраторов. Определен-
ный способ синхронизации является приемлемым лишь при усло-
вии, что синхронность и требуемая фазировка вращения обес-
печиваются в течение всего процесса вибропогружения.
Первое известное нам исследование самосинхронизации ви-
браторов при погружении оболочек принадлежит О. Я. Шехтер
[427] (см. § 4). В данной главе, основанной на работе автора
[68], рассматриваются некоторые возможности использования яв-
ления самосинхронизации при обычном (безударном) вибропо-
гружении. Некоторые экспериментальные факты, относящиеся
к виброударным погружателям (вибромолотам), изложены
в книге С. А. Цаплина [415], а теоретическое исследование ряда
схем с ударами выполнено Л. Б. Зарецким [192, 193], а также
Е. Л. Браверман и Л. Б. Зарецким [101].
§ 2.	О невозможности использования двух
самосинхронизирующихся вибраторов в простейшем
вибропогружателе с продольными колебаниями
Простейший вибропогружатель представлен в п. 3 таблицы 2
и в идеализированном виде в п. 12 таблицы 5 (Добавление 2).
Предположим, что свая или шпунт при колебаниях не могут
перемещаться поступательно в направлении, перпендикулярном
их оси, и представляют собой твердое тело, обладающее двумя
§ 4
!ii>UC.l 1.И111ИЯ ВИБРОПОГРУЖАТЕЛЬ
767
степенями свободы: одна степень свободы соответствует про-
дольному перемещению погружаемого элемента у, а другая —
повороту вокруг некоторой точки Оь лежащей на оси элемента.
Вибраторы будем считать одинаковыми, приводимыми от асин-
хронных двигателей и обладающими одинаковыми и положи-
тельными парциальными скоростями; направления вращения
роторов вибраторов предполагаются противоположными.
Используя интегральный критерий устойчивости (см. §§ 4
и 8 главы XIV), нетрудно получить следующее условие устойчи-
вости синфазного синхронного вращения вибраторов, приводя-
щего (см. схему в п. 12 таблицы 5) к прямолинейным поступа-
тельным колебаниям погружаемого элемента:
Здесь
^Х = Рх/“>,
-------Ь Я2 7г-----< О-
А2 - 1 Ч “ 1
\ = Р<р/“. П2 = Mh2/I! = /г2/р2,
(2.1)
(2.2)
причем рх=Усх/М и рч>= Ус^Ц—соответственно частоты соб-
ственных продольных и поворотных колебаний системы; М —
масса и /1 — момент инерции вспомогательного тела относи-
тельно прямой, перпендикуляр-
ной оси погружаемого элемен-
та и проходящей через точку
Of, h — расстояние от точки
Oi до плоскости, в которой ле-
жат оси вращения роторов
вибраторов.
Области устойчивости син-
фазного вращения роторов ви-
браторов представлены на
рис. 118 (эти области заштри-
хованы) .
В процессе вибропогруже-
ния величины и /,х моно-
тонно возрастают, причем в
начальный период ~ 0; из-
меняется в процессе погруже-
Рис. 118.
ния и величина тр
Для нормальной работы погружателя необходимо, чтобы ка-
ждая точка кривой АВС, характеризующей изменение величин
Z2 и Z2, по мере увеличения глубины погружения s, лежала
внутри областей устойчивости движения. Как явствует из
рис. 118, такая ситуация крайне маловероятна, и поэтому в рас-
смотренном вибропогружателе самосинхронизирующиеся вибра-
торы вряд ли могут быть использованы.
768
ВИБРАЦИОННЫЕ ПОГРУЖАТЕЛИ
(ГЛ. XXII
§ 3.	Вибропогружатель с самосинхронизирующимися
вибраторами, установленными на мягко амортизированной
платформе
В. Э. Романовским был предложен вибрационный погружа-
тель с двумя самосинхронизирующимися дебалансными вибра-
торами, установленными на платформе, которая связана с по-
гружаемым элементом плоскими рессорами, оси которых парал-
лельны оси элемента [361] (см. п. 4 таблицы 2, стр. 342). Плат-
форма с вибраторами может свободно смещаться перпендику-
лярно осям рессор, жесткость которых в поперечном направлении
относительно мала. С другой стороны, рессоры нерастяжимы и
полностью передают на погружаемый элемент продольные со-
ставляющие возмущающих сил вибраторов.
Как мы сейчас покажем, в описанной схеме погружателя,
в отличие от рассмотренной в предыдущем параграфе, эффект
самосинхронизации вибраторов может быть использован.
Рассматриваемая система, представляющая интерес не толь-
ко применительно к вибропогружателям, имеет две степени сво-
боды— одна отвечает продольному смещению всей системы,
а другая — поперечному смещению платформы; схема этой си-
стемы представлена в п. 11 таблицы 5 (Добавление 2).
Вопрос о самосинхронизации вибраторов в данной системе
в предположении о малости жесткости t>i был рассмотрен в на-
шей работе [68] и позднее при более общих предположениях --
в статье Л. Шперлинга [482]. Результат, полученный в этой
последней работе, сводится к следующему. При выполнении
условия *)
устойчиво синфазное вращение роторов вибраторов, то есть дви-
жение по закону
<Pi = aiwZ, ф2 = <т2«/	(3.2)
(каждое из чисел oi и ста может быть равно 1 или —1); при вы-
полнении неравенства противоположного смысла устойчиво про-
тивофазное вращение роторов:
Ф1 = а,со/, ф2 = о2 («/+ л).	(3.3)
В формуле (3.1) величина есть масса тела, на котором
установлены вибраторы (включающая также массы вибрато-
*) На выводе этого соотношения, вполне аналогичном неоднократно воС'
производившимся выше, мы не останавливаемся,
усовершенствованный вибропогружатель
769
§ 3|
ров), Л12 — масса второго тела, М = Mt + М2, сх и су— жестко-
сти упругих элементов,
со,
Из
воды:
СО, р1 = сх[М, Р2у~су/М. (3.4)
приведенного результата можно сделать следующие вы-
(3.5)
а)	При вращении роторов вибраторов в одинаковых направ-
лениях (ощ2 = 1) в случае выполнения неравенства
Z2 — 1~ Af2 X2 - 1
А	4 у
устойчиво синфазное движение (3.2), при котором масса М2 со-
вершает колебания как в направлении от оси х, так и в направ-
лении оси у, а масса Mi— в направлении оси х. Если справед-
ливо неравенство, противоположное (3.5), то устойчиво проти-
вофазное вращение (3.3), при котором колебания в системе
(в рассматриваемом приближении) отсутствуют.
б)	При вращении роторов вибраторов в противоположных
направлениях (снег = —1) в случае справедливости неравенства
устойчиво синфазное вращение (3.2), приводящее теперь к коле-
баниям массы Mi в условиях отсутствия колебаний массы М2;
если же выполняется противоположное неравенство, то устой-
чиво противофазное вращение (3.3), обусловливающее колеба-
ния массы М2 в направлении оси у при отсутствии колебаний
массы Mi.
В случае вибропогружателя необходимо гарантировать вы-
полнение неравенства (3.6), обеспечивающего синфазное враще-
ние роторов вибраторов в противоположных направлениях: при
этом вибраторы развивают продольное возмущающее усилие,
а колебания платформы М2 в поперечном направлении отсут-
ствуют. Если жесткость упругих элементов су выбрать относи-
тельно малой, то можно будет положить X2 ~ О, и неравенство
(3.6) примет вид
М >____1
М2 1 - X2 '
Поскольку М М2, то условие (3.7) всегда выполняется,
если только движение происходит не в непосредственной близо-
сти от зоны резонанса, точнее — если X2 не лежит в пределах
достаточно узкого интервала
1	12 . । М2
(3.7)
(3.8)
770
ВИБРАЦИОННЫЕ ПОГРУЖЛТЕЛИ
[ГЛ. ХХП
Впрочем, не исключено, что если учесть наличие значитель-
ного сопротивления колебаниям по координате х, то рассматри-
ваемый режим окажется устойчивым при любых значениях
Читатель может легко выполнить соответствующие выкладки,
воспользовавшись методом гармонических коэффициентов влия-
ния (см. п. 2 § 3 главы XIV и § 3 главы XV).
§ 4. О некоторых возможностях использования
самосинхронизирующихся вибраторов при погружении оболочек
Использование самосинхронизации и электрической синхро-
низации вибраторов при погружении оболочек большого диа-
метра представляет особый интерес ввиду значительных расстоя-
ний между вибраторами и неудобства применения кинематиче-
ской синхронизации. Этим объясняется определенный интерес,
Рис. 119.
проявляемый исследователями к данному вопросу. На рис. 119
представлено в качестве примера фото установки для изучения
возможности использования самосинхронизации и систем элек-
трической синхронизации, разработанной во ВНИИГС под руко-
водством М. Г. Цейтлина [415а]. На установке можно иссле-
довать совместную работу до десяти дебалансных вибраторов.
Здесь мы рассмотрим более простую систему — круговую ци-
линдрическую оболочку, погружаемую в грунт всего двумя оди-
наковыми вибраторами, приводимыми от асинхронных электро-
двигателей и обладающими одинаковыми положительными пар-
циальными скоростями (см. рис. 120 и п. 17 таблицы 5 Добавле-
ния 2). Вибраторы будем считать коаксиальными, причем
§ 4]
погружение оболочек
771
Рис. 120.
предположим, что их оси перпендикулярны оси оболочки. До-
пустим, что оболочка уже погружена в грунт на некоторую глу-
бину, и поэтому можно считать, что она имеет две степени сво-
боды: одна соответствует перемещению х оболочки вдоль ее
оси О\Х, а другая — повороту ср вокруг той же оси.
Выясним характер устойчивого синхронного движения ви-
браторов [68], для чего воспользуемся интегральным критерием
устойчивости. Рассмотрим колебания оболочки при вращении
вибраторов по закону
<Р1 = Oj (и/ + dj, ф2 = сг2(<й/+ d2), (4.1)
где ф1 и ф2 — углы поворота роторов ви-
браторов, отсчитываемые от касательных
к боковой поверхности оболочки, перпен-
дикулярных ее оси, в . направлении хода
часовой стрелки при наблюдении со сто-
роны внешней нормали к боковой по-
верхности.
Уравнения малых колебаний оболочки
имеют вид
Мх + схх = — F [оу sin (at + d]) +
+ a2sin(a>/ + a2)],
/ф + сфф = — Fr [cos (<о/ + a,) + ' ’
+ cos (at + a2)].
Здесь M — масса вспомогательного тела, I — его момент инер-
ции относительно оси х, F—возмущающая сила, развиваемая
каждым из вибраторов, сх и с,р — соответственно продольная и
поворотная жесткости грунта, г — расстояние от плоскостей
вращения центров тяжести роторов вибраторов до оси обо-
лочки.
Решением уравнений (4.2), отвечающим установившимся вы-
нужденным колебаниям с частотой возмущающих сил, будет
х =-----5——5 — [erI sin (at + dj) + cr2 sin (at + d,)],
- or M
1 Fr	(4.3)
Ф =-------s----5----[cos (at + d]) + cos (at + d2)],
Рф - ® I
где
Рх = V cx/M > Др = Vc<flM	(4.4)
— соответствующие частоты собственных колебаний оболочки.
Выполнив интегрирование, находим среднее за период 2л/ю
значение функции Лагранжа вспомогательного тела, отвечающее
772
ВИБРАЦИОННЫЕ ПОГРУЖАТЕЛИ
[ГЛ. ХХП
Ми 1 -	1 -
Ч = Р<р/®>	=	(4.6)
а постоянная.
решению (4.3):
2л/о>
[Т<’)-Па)]0Л =
О
2л/й)
= ^/ 4[^2 + /ф2-сл.х2-сф<р2]Л =
о
1 F2 Г О'! °2	,	9	1	1 ~ I Г>
= —-----о  --А- -I- п2 -—— COS а + С.
Здесь
= Рх/со,
а С есть не зависящая от
Из условия dA^/da = 0 находим, что возможны два суще-
ственно различных синхронных движения вибраторов: синфаз-
ное, которому отвечает а= (a)i~ 0, и противофазное, для ко-
торого а = (а) 2 = л.
Пусть сначала вибраторы вращаются в одинаковых (в ука-
занном выше смысле) направлениях, так что сгцтг = 1. Тогда
при выполнении неравенства
синфазное движение будет устойчивым, так как ему соответ-
ствует минимум функции Л*1), а противффазное движение — не-
устойчивым. При невыполнении неравенства (4.7), наоборот,
синфазное движение неустойчиво, а противофазное — устойчиво.
Синфазному движению при этом, как следует из формул (4.3),
отвечают продольно-поворотные колебания оболочки, при кото-
рых траекториями точек ее боковой поверхности являются эл-
липсы; при противофазном же движении колебания оболочки
вообще отсутствуют (в рассматриваемом приближении).
Для выяснения областей устойчивости синфазного вращения
вибраторов можно воспользоваться диаграммой, представленной
на рис. 41, если величину ц определять по формуле (4.6). Из
диаграммы, а также и непосредственно из неравенства (4.7)
следует, что синфазное движение устойчиво в дорезонансной
области (со < Рх, со < Рч>) и неустойчиво в послерезонансной об-
ласти (со > Рх, со > Р<р). В промежуточных областях (рх > со > р,Р
или ptf > со > Рх) может быть устойчиво как синфазное, так и
противофазное движение.
Полученный результат согласуется с найденным иным мето-
дом в цитированной выше статье О. Я. Шехтер [427].
§ 4]	ПОГРУЖЕНИЕ ОБОЛОЧЕК	773
Пусть теперь вибраторы вращаются в противоположных на-
правлениях, так что 0102 = —1. Тогда условием устойчивости
синфазного движения и одновременно условием неустойчивости
противофазного движения будет соотношение *)
При выполнении противоположного неравенства устойчиво
противофазное и неустойчиво синфазное движение. Синфазному
движению при шог = —1 отвечают чисто поворотные, а противо-
фазному— чисто продольные колебания оболочки (см. фор-
мулы (4.3)).
Подчеркнем в заключение, что приведенные здесь результаты
справедливы лишь в случае, когда оболочка действительно мо-
жет рассматриваться как твердое тело с двумя степенями сво-
боды. Картина существенно изменяется, если, например, допу-
стить возможность поворота оболочки относительно осей, пер-
пендикулярных оси х. Получение соответствующего результата,
естественно, не вызывает каких-либо затруднений.
*) Отметим, что это неравенство совпадает с неравенством (2.1) на-
стоящей главы, и поэтому в данном случае также пригодна диаграмма обла-
стей устойчивости, изображенная на рис. 118.
ГЛАВА XXIII
ГРУППОВЫЕ ФУНДАМЕНТЫ
ПОД НЕУРАВНОВЕШЕННЫЕ МАШИНЫ
§ 1.	Проблема групповых фундаментов с точки зрения теории
синхронизации вибраторов. Общий план теоретического
исследования
В последнее время обнаруживается тенденция к проектиро-
ванию единых (групповых) фундаментов под несколько номи-
нально одинаковых неуравновешенных машин или устройств.
При известных условиях такие машины можно рассматривать
как почти одинаковые механические вибраторы, расположенные
на упруго опертом твердом или упругом теле (см. рис. 25 и п. 24
таблицы 2 на стр. 357) или на нескольких связанных между
собой телах.
В проблеме групповых фундаментов тенденция вибраторов
(неуравновешенных машин) к синхронному вращению и к опре-
деленной фазировке в одних случаях может оказаться полез-
ной, а в других случаях — вредной и даже опасной. А именно,
если валы машин стремятся синхронно вращаться таким обра-
зом, что эффект от воздействия их неуравновешенностей скла-
дывается, то синхронизация играет отрицательную роль. Если
же машины обнаруживают тенденцию к движению с такими
комбинациями фаз, что воздействия неуравновешенностей от-
дельных машин частично или полностью взаимно компенси-
руются, то налицо положительное явление, которое может зна-
чительно усилить технический эффект от применения группо-
вых фундаментов.
Если бы отдельные машины не взаимодействовали через
вибрирующий фундамент (или фундаменты), то можно было бы
считать, что вследствие естественного разброса параметров от-
дельных машин частоты и фазы развиваемых ими возмущаю-
щих сил носят случайный характер [376, 191а]. Однако при на-
личии взаимодействия такой способ расчета верен, лишь когда
влияние случайного разброса параметров более сильно, нежели
тенденция к синхронному вращению и к определенной фази-
ровке.
§ I]	ПРОБЛЕМА ГРУППОВЫХ ФУНДАМЕНТОВ	775
Рассмотрим этот вопрос несколько подробнее. Как было
установлено выше на многочисленных примерах, наличие или
отсутствие самосинхронизации наиболее существенным образом
зависит от того, насколько отличаются одна от другой пар-
циальные угловые скорости вращения валов отдельных ма-
шин (o.s. Если указанные скорости одинаковы, то есть если валы
машин, установленных па неподвижном основании, вращаются
с одинаковой угловой скоростью, то самосинхронизация прак-
тически всегда имеет место (вне зависимости от значений дру-
гих параметров) и при установке машин на групповом фунда-
менте.
Однако самосинхронизация может иметь место даже и в слу-
чае, когда парциальные угловые скорости значительно отли-
чаются одна от другой. Грубо говоря, величина предельно воз-
можных отклонений парциальных скоростей, при которых еще
имеет место самосинхронизация, определяется максимально
возможными значениями вибрационных моментов, которые, как
уже указывалось, играют роль перераспределителей энергии
в системе, выравнивая угловые скорости валов отдельных
машин.
Эти предельные значения вибрационных моментов при про-
чих равных условиях пропорциональны квадратам статических
моментов неуравновешенных масс и квадрату угловой скорости
синхронного вращения (см., например, п. 2 § 6 главы XIII и
п. 6 § 2 главы XX). Вместе с тем эти моменты, вообще говоря,
уменьшаются при увеличении массы фундамента и его момента
инерции. Можно сказать поэтому, что вибрационные моменты
возрастают при увеличении интенсивности колебаний фунда-
мента, на котором установлены вибраторы; в пределе при не-
ограниченно возрастающих массе и моментах инерции фунда-
ментов (то есть при переходе к неподвижным фундаментам)
вибрационные моменты равны нулю. Общее вибрирующее тело
или связанные между собой тела, на которые установлены не-
уравновешенные машины, играют как бы роль каналов, пере-
дающих энергию от одной машины к другой, в результате чего
угловые скорости машин могут выравниваться.
Итак, если параметры машин, в особенности их парциальные
угловые скорости, одинаковы, то самосинхронизация и опреде-
ленная фазировка непременно осуществляются. Однако па прак-
тике указанные параметры более или менее значительно откло-
няются один от другого для различных машин. При этом в од-
ном случае (когда «вибрационная связь» слаба) может
оказаться, что даже незначительные отклонения приводят к не-
возможности самосинхронизации, и тогда угловые скорости и
фазы вращения носят случайный характер; в другом случае
(когда налицо сильная «вибрационная связь»), напротив,
776
ГРУППОВЫЕ ФУНДАМЕНТЫ ПОД МАШИНЫ
[ГЛ. XXIII
оказывается, что даже при существенных отклонениях самосин-
хронизация и определенная фазировка имеют место.
Допустим, что известны законы распределения отклонений
параметров, входящих в основные уравнения задачи о само-
синхронизации (см. равенства (10.2) главы XIII и (2.27) —
(2.29) главы XIV), как величин, носящих случайный характер.
Тогда в принципе всегда можно найти вероятность самосинхро-
низации Ра (см., например, п. 4 § 2 главы XX). Если эта
вероятность окажется близкой к нулю, то проектирование груп-
повых фундаментов можно производить без учета явления са-
мосинхронизации; если же указанная вероятность будет зна-
чительной, то явление самосинхронизации может оказать суще-
ственное влияние на всю картину, и его необходимо учитывать.
В последнем случае прежде всего надлежит найти значения
фаз вращения валов совершенно одинаковых машин в устойчи-
вых установившихся синхронных движениях; эти значения фаз
будут являться центрами распределения фаз вращения при на-
личии случайных отклонений параметров. Если окажется, что
в определенном устойчивом синхронном движении фазы вра-
щения валов машин таковы, что неуравновешенности отдельных
машин складываются, то явление самосинхронизации, в случае
установления этого режима, играет отрицательную роль, ибо
и при наличии отклонений параметров более вероятными ока-
жутся неблагоприятные сочетания фаз вращения. Если же для
установившегося устойчивого синхронного движения окажется
характерной такая комбинация фаз, при которой неуравнове-
шенности отдельных машин взаимно компенсируются, то само-
синхронизация будет иметь положительное значение. Именно
к такой ситуации и следует стремиться при проектировании
групповых фундаментов под неуравновешенные машины. Здесь
могут представить интерес методы синтеза законов колебаний
в машинах с самосинхронизирующимися вибраторами, рассмот-
ренные в главе XV настоящей книги.
При благоприятном сочетании фаз в устойчивом синхронном
движении математическое ожидание максимальной амплитуды
колебаний фундамента Л1(Лтах) снижается по сравнению со
значением, определяемым в предположении об отсутствии
взаимодействия машин через фундамент, а при неблагоприят-
ном сочетании — увеличивается. Точно так же соответственно
уменьшаются или увеличиваются вероятности появления недо-
пустимо больших амплитуд колебаний фундамента. Указанные
математические ожидания и вероятности могут быть найдены
по известным законам распределения параметров на основе
анализа упоминавшихся выше основных уравнений теории само-
синхронизации, а также уравнений, описывающих колебания
фундаментов при заданных законах движения валов машин.
§ 2]	ОДНО СЛЕДСТВИЕ ИЗ ИНТЕГРАЛЬНОГО КРИТЕРИЯ	777
При этом в практических расчетах часто могут приниматься во
внимание лишь отклонения параметров, влияющих на величины
парциальных угловых скоростей машин.
Практически эффективный способ выяснения характера
устойчивых синхронных движений дает интегральный критерий
устойчивости, изложенный в § 9 главы XIII и в § 4 главы XIV;
особенно полезным может оказаться следствие из этого кри-
терия, приводимое в § 2 настоящей главы. В сложных случаях
с целью получения выражений для вибрационных моментов
может быть применен полуэкспериментальный метод (см. п. 2
§ 3 главы XIV).
Намеченная выше методика исследования и общие пред-
ставления иллюстрируются в § 3 данной главы на простом кон-
кретном примере.
Приведенные соображения о связи проблемы групповых
фундаментов с теорией синхронизации механических вибрато-
ров были развиты в наших работах [46, 77, 68, 83], на этих ра-
ботах и основано содержание главы. Мы не останавливаемся
здесь па изложении исследования А. Л. Кумпикаса и К- М. Ра-
гульскиса [233], в котором рассмотрена задача о самосинхро-
низации неуравновешенных машин, развивающих полигармони-
ческую возмущающую силу и установленных на фундаменте
с одной степенью свободы, к которому присоединены динами-
ческие поглотители колебаний.
Автор благодарен О. А. Савинову за советы и интерес, про-
явленный к содержанию главы.
§ 2.	Одно следствие из интегрального критерия устойчивости
синхронных движений вибраторов
При проектировании групповых фундаментов под неурав-
новешенные машины и в некоторых других случаях может ока-
заться полезным следующее простое следствие из интегрального
критерия устойчивости синхронных движений механических дс-
балансных вибраторов и вибраторов направленного действия
(см. § 9 главы XIII и § 4 главы XIV):
Если несколько механических вибраторов, обладающих оди-
наковыми парциальными угловыми скоростями, установлено на
мягко амортизированном твердом теле*) таким образом, что
при равномерном синхронном вращении их валов существует
фазировка вращения, при которой развиваемые вибраторами
возмущающие силы взаимно уравновешиваются, то такая
фазировка отвечает устойчивому установившемуся режиму
*) Напомним, что под мягко амортизированным твердым телом мы пони-
маем такое твердое тело, частоты собственных колебаний которого на упругих
опорах значительно ниже частот возмущающего воздействия.
778
ГРУППОВЫЕ ФУНДАМЕНТЫ ПОД МАШИНЫ
[ГЛ. XXIII
синхронного вращения роторов. Тело, несущее вибраторы, в ука-
занном режиме остается неподвижным (в исходном прибли-
жении) .
Иными словами, вибраторы с одинаковыми парциальными
скоростями, установленные на мягко амортизированном твер-
дом теле, взаимно уравновешивают развиваемые ими возму-
щающие силы, если только такое уравновешивание в принципе
возможно. При невозможности полного уравновешивания устой-
чивым оказывается движение, отвечающее наибольшему воз-
можному уравновешиванию в том смысле, что кинетическая
энергия тела в указанном движении является минимальной.
Действительно, согласно интегральному критерию комбина-
ции фаз вращения валов вибраторов, при которой среднее за
период значение функции Лагранжа, отвечающей несущему телу,
имеет минимум*), соответствует устойчивое синхронное движе-
ние валов вибраторов. Но если несущее тело мягко амортизиро-
вано, то потенциальной энергией можно пренебречь, и среднее
значение лагранжиана оказывается совпадающим со средним
значением кинетической энергии тела. Если при этом суще-
ствует фазировка, приводящая к уравновешиванию, то именно
этой фазировке и соответствует минимум кинетической энергии
тела, равный нулю. Если полное уравновешивание невозможно,
то устойчивым оказывается движение, отвечающее минимуму
средней за период кинетической энергии тела; часто такое дви-
жение по понятным причинам соответствует наилучшему (или
близкому к нему) уравновешиванию также и в смысле мини-
мизации наибольших амплитуд колебаний точек тела.
Заметим, чго при формулировке приведенного положения
мы не оговорили здесь некоторые особые случаи, так как они
вряд ли имеют серьезное практическое значение.
Отметим также, что это положение иллюстрируется пп. 1, 2,
10, 11, 16, 17 и 21 таблицы 5 (Добавление 2).
§ 3.	Пример: фундамент под две машины, развивающие
неуравновешенные силы постоянного направления
С целью иллюстрации изложенного рассмотрим относи-
тельно простой конкретный пример, имеющий, однако, и само-
стоятельное значение. Пусть две машины с поступательно дви-
жущимися по гармоническому закону**) неуравновешенными
массами установлены на едином фундаменте (рис. 121), при-
чем движение масс происходит вдоль прямых, не проходящих
*) Обнаруживаемый путем анализа членов второго порядка в соответ-
ствующих разложениях.
**) Обобщение на случай произвольных периодических сил не представ-
ляет особых затруднений.
§ 3]
ПРИМЕР: ФУНДАМЕНТ ПОД ДВЕ МАШИНЫ
779
в общем случае через центр тяжести фундамента. Будем считать,
что машины приводятся от двигателей асинхронного типа, так
что колебания масс могут быть сдвинуты по фазе. Вследствие не-
точностей изготовления машин и их двигателей, а также из-за
неодинаковости полезных сопротивлений основные параметры, от
которых зависит движение машин, также могут различаться.
Та же система, по с одинаковыми и одинаково расположен-
ными вибраторами рассматривалась в п. 4 § 8 главы XIV
(рис. 40). Было установле-
но, что при выполнении не-
равенства (8.31) указанной
главы (см. также рис. 41)
устойчиво противофазное
вращение валов машин, при
котором колебания фунда-
мента отсутствуют. Рас-
смотрим теперь поведение
системы при наличии откло-
нений параметров. Рассуж-
дая в точности так же, как
и в п. 4 § 8 главы XIV,
и (8.30) следующие выражения,
получим вместо равенств (8.28)
определяющие закон колебаний фундамента в установившемся
движении, и соответствующее среднее значение функции Ла-
гранжа:
х =-------зпД-------г [Fi sin at 4- F2 sin (at + a)],
Alio2 (A2 - 1)
(3-1)
sin at + /Х/г2 sin (at + a)];
z/ = 0,
^2(a2-i)
д(1) = _ J_ FiF2 2 Afco2	1	. hih2	1 X-i p2 Ч-1.	cos a + C
(3.2)
Здесь, аналогично п. 4 § 8 главы XIV, х и у — координаты
центра тяжести Oi фундамента с машинами в неподвижной
системе координат хОу, совпадающей в положении статического
равновесия с системой осей uOv, жестко связанной с фундамен-
том; <р — угол поворота фундамента, отсчитываемый по ходу
часовой стрелки; М и / — соответственно масса и центральный
момент инерции фундамента с машинами; сх и с,р — коэффи-
циенты, характеризующие жесткость основания*); F\ = mieiw2 и
F2 = т2&2<х>2 — амплитуды неуравновешенных сил, развиваемых
машинами; m^ei и т2е2— максимальные значения статических
) См. сноску на стр. 537.
780
ГРУППОВЫЕ ФУНДАМЕНТЫ ПОД МАШИНЫ
[ГЛ. XXIII
моментов неуравновешенных масс; h\ и /г2 — расстояния от
центра тяжести фундамента с машинами до линий действия не-
уравновешенных сил; р = у7/М — радиус инерции фундамента
с машинами; С — постоянная, не зависящая от а;
\ = Ч = РФ/®, Р2х = сх/М, p^c^I, (3.3)
причем рх и р.р — частоты малых колебаний фундамента.
Составим теперь основные уравнения теории самосинхрони-
зации. В рассматриваемом случае W{sR) = 0, Lsm} =	(co),
/?s = /?«(©) и Л(И) = 0, и поэтому уравнения (3.6) гла-
вы XIV при учете формул (3.2) принимают вид
Ps(a, <й) = ^-[Л<а)(<й)-7?°(<й)- Г (со) (-l)s“* sin а] = 0
(s=l,2),	(3.4)
где
W (со) = -	-уЦ =
2 Л! и2 Z2 - 1 р2 Л2 - 1 /
_ 1 mie1m2e2a>2 / 1	. hth2 1 \
2 М	\Л2-ГЬ р2 Z2 — 1 у ’
| IF(со) | есть максимальное значение вибрационных мо-
IF.,. Дальнейшие рассуждения и выкладки вполне анало-
гичны проведенным в § 2 главы XX. Линеаризировав моменты
Л1а)(со) и 7?s(®) вблизи номинального значения угловой скоро-
сти ио, представим их в форме
Л<а)(и) = Л“((Оо)-гм(и-и0),	/?°(co) = /?°(co0) + zR^co-co0), (3.6)
и тогда угловая скорость синхронного вращения валов ма-
шин ио и их парциальные угловые скорости будут определяться
выражениями (2.3) и (2.4) указанной главы.
После несложных преобразований с использованием этих
выражений и равенств (3.6) из уравнений (3.4) находим
sina^y-^/po»	(3.7)
где через
_	ZIA + Z L2 +	+ Z R2	/о о\
“	2ю0 (ZL\ + ZRl) (ZL2 + ZRs)
обозначено максимальное значение относительного отклонения
парциальных угловых скоростей Ди/2и0, при котором еще воз-
можна самосинхронизация машин. Действительно, уравнение
причем
ментов
§ 3]
ПРИМЕР: ФУНДАМЕНТ ПОД ДВЕ МАШИНЫ
781
(3.7)	имеет вещественные решения относительно разности фаз а
при выполнении условия
1 Лео
2 со
IpJ =
Ю1 Ю2 (2Z,1 + 2Д|) (ZZ,2 + гда)
(®)	(г£1 +гД2 + гй1 +гД2)
<1,	(3.9)
то есть в случае, когда относительное отклонение парциальных
угловых скоростей меньше величины |дм|.
Из равенств (3.5) и (3.8) следует, что если параметры zL,
zR, h, Л°(ыо) и (?°(ыо) остаются неизменными, то величина
|р|М| прямо пропорциональна квадрату статических момен-
тов те, квадрату угловой скорости со и обратно пропорцио-
нальна массе фундамента М. Это согласуется со сказанным
в § 1 о зависимости тенденции к синхронному вращению от па-
раметров системы.
Если условие (3.9) выполняется, то уравнение (3.7) допу-
скает два существенно различных решения (прочие решения
отличаются от указанных на числа, кратные 2л):
а = (а), = arcsin (у ^-/ра\', а = (а)2 = л - (а)Р (3.10)
Если парциальные угловые скорости машин одинаковы, то
Ды = 0, условие (3.9) непременно выполняется, а решения (3.10)
принимают вид
а = (а)° = 0, а = (а)° = л,	(3.11)
то есть первому решению отвечает нежелательное синфазное,
а второму — благоприятное противофазное движение машин.
При Д<>) ¥= 0 фазы вращения могут отличаться от нуля или л
на некоторый угол
-уЛ^Да= arcsin (у <у л.	(3.12)
Для краткости будем и в случае Ды ¥= 0 первое решение
условно называть синфазным, а второе- противофазным.
Обратимся к изучению вопроса об устойчивости синхронных
движений. Уравнение (2.33) главы XIV в данном случае яв-
ляется линейным, и в соответствии с (3.4), его корень
Для устойчивости движения х должно быть отрицательным;
отсюда при учете соотношений (3.5), (3.10) и (3.12) и положи-
тельности коэффициентов ki и k2 следует, что при выполнении
неравенства
782
ГРУППОВЫЕ ФУНДАМЕНТЫ ПОД МАШИНЫ
[ГЛ. XXI11
противофазное движение устойчиво, а синфазное — неустойчиво;
при выполнении неравенства противоположного смысла, напро-
тив, устойчиво синфазное движение и неустойчиво противофаз-
ное движение. Соотношение (3.14) является, таким образом,
условием наличия благоприятной ситуации, когда при установке
на едином фундаменте машины обнаруживают тенденцию
к взаимному уравновешиванию. Естественно, что при До» = 0 и
hi = h2 полученные результаты переходят в найденные в п. 4
§ 8 главы XIV. Для нахождения областей устойчивости проти-
вофазного движения, определяемых условием (3.14), оказы-
вается, очевидно, по-прежнему пригодной диаграмма, изобра-
женная на рис. 41, если под величиной ц2 понимать AiA2/p2.
Допустим теперь, что соответствующие параметры машин и
расстояния hi и h2 отличаются друг от друга, вследствие неточ-
ностей изготовления и монтажа, на некоторые малые величины.
Тогда записанное с точностью до малых первого порядка вклю-
чительно условие (3.9) примет вид
где
Ра
(со,))	~	1 (те)2сод 1 h2 1
<Мгт + гД	2 М Л2-1 р2 Л2-1
(3.16)
Здесь через zL, zR, h и те обозначены поминальные значения
соответствующих величин.
Согласно изложенному в § 1 настоящей главы нас прежде
всего интересует оценка вероятности выполнения неравенства
(3.15), то есть вероятности наступления самосинхронизации.
С этой целью, так же как и в п. 3 § 2 главы XX, будем предпо-
лагать, что отклонение парциальных угловых скоростей у Д(о/Мо
обусловлено большим числом случайных факторов и поэтому
может считаться распределенным по несмещенному нормаль-
ному закону со средним квадратическим отклонением
1
з Яа’
(3.17)
где
— 1 I Асо I
2 I ©о |тах
(3.18)
— максимальное возможное значение рассматриваемого относи-
тельного отклонения. Об оценке этой величины подробно ска-
зано в п. 5 § 2 главы XX, и мы будем считать ее известной.
§ 3]
ПРИМЕР: ФУНДАМЕНТ ПОД ДВЕ МАШИНЫ
783
При сделанных предположениях вероятность выполнения
условия самосинхронизации (3.15) будет
р.=М41 тт I < ₽:) - М41 тт | < М=ф (ю-	is»
Здесь Ф(х) — интеграл вероятности Гаусса и, согласно
(3.17),
(3.20)
(7<о 3erffl
Рис.
122.
ии мала.
В этом
есть отношение максимально допустимого по условию самосин-
хронизации относительного отклонения парциальных скоростей
к максимально возможному
значению этого отклонения;
указанная величина была
в § 2 главы XX названа ко-
эффициентом запаса по са-
мосинхронизации.
График зависимости Р11Я
от 1/хщ представлен на
рис. 122 сплошной линией.
Из рассмотрения графика
видно, что даже при хш~0, 1
вероятность самосинхрони-
зации несколько более 20%,
а при х,а = 0,5 имеем
Рт ~ 90°.
Как отмечалось в § 1,
могут представиться следу-
ющие характерные случаи:
а) Вероятность самосин:
можно считать, что машины практически независимы, то есть
угловые скорости вращения их валов равны соответствующим
парциальным скоростям кц и ыг. Колебания фундамента при
этом будут носить характер биений, в процессе которых, неза-
висимо от разброса скоростей (>ц и иг, максимальная амплитуда
колебаний фундамента периодически будет достигать значения
А*, примерно соответствующего синфазному движению машин.
Нетрудно вычислить это значение амплитуды. Для модуля
малого смещения точки фундамента с координатами и, v
(рис. 121) имеем
S (t) = ]/(х + V(f>)2 + u2(f>2.	(3.21)
Для получения приближенного значения /1* в это выражение
достаточно подставить амплитудные значения координат х и ср
в соответствии с равенствами (3.1), взятые в предположении,
что параметры машин одинаковы, а сдвиг фаз а = 0. После
784
ГРУППОВЫЕ ФУНДАМЕНТЫ ПОД МАШИНЫ
[ГЛ. XXIII
этого в получившееся выражение надлежит подставить коорди-
наты точки фундамента и = ик и v — vK, колебания которой
представляют наибольший интерес. Такой контрольной точкой
может служить та точка верхнего края фундамента, в которой
амплитуда колебаний имеет наибольшее значение. В результате
найдем
2F
=—-
Afw
1	o„h	1 р u ft 1	2
_____ | А _______ | А __________
^-1	р2	- i J Я р2 Z2-l_
(3.22)
Здесь множитель 2F/Mcr представляет собой максимальную ам-
плитуду колебаний центра тяжести фундамента как свободного
твердого тела, а квадратный корень — коэффициент усиления.
Среднее за период биений значение амплитуды колебаний
в той же точке будет
Л
(А.ах)т =	j* Sin т dx ~ 0,64Д*.
о
б) Вероятность самосинхронизации относительно велика.
В этом случае связь между машинами игнорировать нельзя, ибо,
несмотря на отличие парциальных угловых скоростей, как пра-
вило, будет устанавливаться синхронное движение. При наличии
такого движения максимальная амплитуда колебаний фунда-
мента определится по формуле (3.21), если подставить в нее
амплитудные значения координат х, у и <р, вытекающие
из формул (3.1), а также и = ик и v = Vk. При этом будем счи-
тать, что параметры машин Ft и F2, /ii и h2 одинаковы и разли-
чаются лишь парциальные угловые скорости вращения машин
Mi и иг, предопределяющие, согласно (3.12), наличие дополни-
тельного сдвига фаз Да. Учет также и иных отклонений пара-
метров проводится без особых затруднений (см. п. 2 § 2 гла-
вы XX), однако, как показывают простейшие подсчеты, практи-
ческое значение в рассматриваемой задаче имеет только разброс
скоростей (01 и иг (см. п. 4 § 2 главы XX).
В результате вычисления получим
Лщах = | cos У а | Д*,	(3.23)
где А* — по-прежнему наибольшая возможная амплитуда коле-
баний точек фундамента, вычисляемая по формуле (3.22),
Подставив в формулу (3.23) значения разности фаз в устой-
чивом движении согласно формулам (3.10), находим
“ И/' + 7^/'’- ± /' -	А‘- <3-24)
§ 3]
ПРИМЕР: ФУНДАМЕНТ ПОД ДВЕ МАШИНЫ
785
Здесь верхние знаки соответствуют нежелательному синфазному
движению машин, а нижние — желательному противофазному
движению, имеющему место при выполнении условия (3.14).
Равенство (3.24) имеет смысл лишь при выполнении условия
самосинхронизации (3.15), что, по предположению, имеет место
с вероятностью, близкой к единице. Но в таком случае с доста-
точно большой вероятностью выполняется и несколько более
жесткое требование
1ту№|«°-8-	(3-25)
При выполнении же последнего условия формулу (3.24)
можно (с погрешностью, не превышающей 10%) заменить ее
линейным приближением.
В случаях синфазного и противофазного движений получаем
соответственно
(41„)+~-г,	(3.26)
Таким образом, если устойчиво синфазное движение машин,
го максимальная амплитуда колебаний практически оказывается
неслучайной величиной, равной наибольшему значению А*, то
есть ситуация получается в известном смысле даже худшей, не-
жели при отсутствии самосинхронизации, ибо в режиме биений
амплитуда А* достигается лишь в отдельные моменты времени,
а среднее значение (Лтах)т = 0,64Д*.
В случае же, когда обеспечена устойчивость противофазного
движения, математическое ожидание максимального значения
амплитуды резко снижается. Действительно,
М [(Дщах)_] —
1 Доз 1
2 ®0 Ро
_1_
2
1	/	1 (Дю)2\ ,/1 Лш\ д’ат
----7=- ехр	W НЧ-----= -у— -о •
ои V 2л	\	4-/ \ 2 ш0) р2л Ра
Отсюда при учете равенства (3.20) получаем
М [(Дтах)_] = —= —4=-— = 0,133 —. (3.27)
1	3 У 2л рю 3 У 2л
Даже при коэффициенте запаса хш= 0,5 имеем М [(Дтах)_] =
= 0,266Д*, то есть почти четырехкратное снижение ожидаемой
максимальной амплитуды по сравнению с наибольшим значе-
нием Л*.
Нетрудно подсчитать и вероятность пепревышения макси-
мальной амплитудой (Дтах)- заданной доли I от Д*. При учете
786
ГРУППОВЫЕ ФУНДАМЕНТЫ ПОД МАШИНЫ
[ГЛ. XXIII
соотношений (3.26) и (3.20) находим
“ (I т ТГI <	- ф (х?) - ф (3-28>
где Ф(х) —по-прежнему интеграл вероятности Гаусса. Графики
функции = Ф(б£хю) представлены на рис. 122 пунктирными
линиями. Из их рассмотрения, в частности, следует, что при
хи = 0,5 вероятность непревышения величиной (Лтах)_ значе-
ния 0,ЗЛ* составляет около 65%; в случае же хю = 1 эта вероят-
ность практически равна единице.
Из рассмотрения формул (3.26) — (3.28) вытекает, что в дан-
ном случае, как и при изучении стабильности (см. п. 6 § 2
главы XX), практические расчеты можно вести, не прибегая
к прямым вероятностным оценкам, а исходя из определенного
минимально допустимого значения коэффициента запаса по са-
мосинхронизации Так, в условиях рассматриваемой задачи
для эффективного снижения амплитуды колебаний фундамента
достаточно принять
О
~	(3.29)
Действительно, в этом случае величина (Лтах)-, согласно фор-
муле (3.26), будет удовлетворять неравенству
(71тах)_ <
4
О
Рш
Л’<- А*.
8
(3.30)
Приведем в заключение параграфа конкретный пример рас-
чета.
Пусть вес неуравновешенных частей каждой машины
mg = 1600 кГ, полуразмах колебаний этих частей е = 1,2 см,
число колебаний в минуту п0 = 30 (о0/л = 300, номинальная мощ-
ность электродвигателей 2,8 кет, номинальное число оборотов
двигателей nff = 1420 об/мин. Вес фундамента с установленными
на нем машинами Mg = 8000 кГ, отношения частот собственных
колебаний к частоте вынужденных колебаний = А,ф = !/з,
hi = h2 = h, /г2/р2 = ’Д. В данном случае
—1----.ДА —!— =--------!----1_1_____!__= - 1 41 <0
р2 Z2-l (>/з)2-1	(>/з)2-1	’	’
то есть условие (3.14) выполняется, и устойчивым является про-
тивофазное движение.
§ 3]
ПРИМЕР: ФУНДАМЕНТ ПОД ДВЕ МАШИНЫ
787
Согласно формуле (3.16) настоящего параграфа и соотноше-
ниям (2.31), (2,33) и (2.34) главы XX находим (полагаем т] = 1)
.у, , ,	1 (1600 х 1,2)2 х 31,42 I 1	,1	1 I	г
И'о W = у 8000 X 981 I (1/з)2 — 1 + 1 (7з)2 - 1 I	’
Z = W=4’73’ “о =	31-4 1/сек, =	149 1/сек,
L° (ЫО) = L° (ы0) ~ (ЫО) = 2.8Х1О2 Х91О2Х Д73 =
905 X 4,73 X 30 с, г
zl zli ~ ZL2- (1500 — 1420)л	3 7 кГсмсек.
Предположим, далее,- что момент сопротивления /?(ы) про-
порционален квадрату угловой скорости <» и что при номиналь-
ной скорости ио он составляет 75% от момента электродвига-
теля L°. Тогда А (со) = йы2, где k — постоянная, которая опреде-
лится из условия /?(о)0) = 0,75 L°, и находим
,	0,757,°	0,75 X 905 п „„„	„	2
k — —5— = —-------5— = 0,688 кГсм сек2,
<о2	(31,4)2
ZR ~ ZR\ ~ ZR2
= 2ka0 = 2 X 0,688 X 31,4 = 43,2 кГсм сек.
Теперь по формуле (3.16) нетрудно подсчитать максимально
допустимое по условию самосинхронизации (3.15) значение от-
носительного разброса парциальных угловых скоростей:
31,4 (SIX 43,2) = °-°183 - 1,83%.
Примем, что максимально возможное отклонение парциаль-
ных угловых скоростей (см. соотношение (2.41) главы XX)
„	1 п‘е)-/Фе)	1,5 (1500- 1420)
п = 1W = 1,5 X - - ,е,— = —-------------------- = 0,01 = 1 %.
Ча 1а	8	«7	8 X 1500
Таким образом, xft) = |	|/| qa ] = 1,83, то есть условие само-
синхронизации (3.15) выполняется практически всегда. Согласно
формуле (3.25) имеем (контрольной точкой фундамента будет
точка К на рис. 121, координаты которой приняты равными
ик = 1,5 р и vK ~ h = 0,5 р)
,, 2 X 1600 X 1,2 /Г 1	“1	1 Т~Г 0,75	_
8000 V 1(‘/з)2-1+ 4 С/з)2-и +L(73)2-d
= 0,768 см = 7,68 мм.
788
ГРУППОВЫЕ ФУНДАМЕНТЫ ПОД МАШИНЫ
[ГЛ. XXIII
Такой была бы амплитуда колебаний точки К, если бы устой-
чивым оказалось не противофазное, а синфазное движение; не-
трудно видеть (рис. 41), что последнее имело бы место, напри-
мер, при /х = Px/tit = 2 и неизменных прочих параметрах си-
стемы, то есть при чрезмерно большой жесткости сх.
В рассматриваемом же случае математическое ожидание
амплитуды колебаний точки /С, согласно (3.27), будет
Л4[(Дтах)_] = -2^ = 0,0725Д*.
При этом, в соответствии с
того, что (Л1Пах)- не превысит
Рис. 123.
на роликовые опоры (рис. 123)
статочно гибкими стойками. А
рис. 122, например, вероятность
20% от А*, то есть не превысит
значения 0 786 см X 0,2 =
= 0,157 см = 1,57 мм, составит
около 97%.
Заметим, что результаты
расчета получаются даже не-
сколько лучшими, если предпо-
ложить, что при прочих рав-
ных условиях Л* ~ 0 и А<р—»оо.
Такой случай соответствует
установке жесткой рамы, на
которой размещены машины,
или на портальную раму с до-
именно получается
Wz0(w0) = 323/1,41 =229, р°а = 1,83/1,41 = 1,3%, нш=1,3,
А’= 0,48 см, М[(Атах)_] = °-133^0-48 = 0,0491 см = 0,491 мм.
Вероятность того, что (Атах)_ не превысит значения 0,157 см
(см. окончание предыдущего примера), то есть будет составлять
не более (0,157/0,48) X 100% =32,7% от А*, окажется теперь
равной 99%.
§ 4. О случае, когда машины приводятся от синхронных -
двигателей
Все сказанное выше относилось преимущественно к машинам,
приводимым от двигателей асинхронного типа. В случае, когда
привод осуществляется от синхронных электродвигателей (непо-
средственно или через передачу без скольжения), вращение ва-
лов всех машин происходит с одинаковой угловой скоростью.
Предположим сначала, что фундамент неподвижен. Тогда
сдвиги фаз вращения валов в случае двухполюсных нереактив-
ных двигателей могут быть заданы (с точностью до отклонений,
§ 4]	МАШИНЫ, ПРИВОДИМЫЕ ОТ СИНХРОННЫХ ДВИГАТЕЛЕЙ 789
обусловленных неодинаковостями полезных сопротивлений) пу-
тем определенной ориентации полюсов статоров двигателей.
В случае 2и-полюсных двигателей эти сдвиги фаз могут отли-
чаться на 360° mln, где т — 1, . , п.
При подвижности общего фундамента, на котором установ-
лены машины, на их валы действуют те же ,амые вибрацион-
ные моменты Ws, о которых говорилось в § 1. Наличие этих
дополнительных моментов может привести к существенному из-
менению устойчивых значений фаз вращения валов, ибо и в дан-
ном случае возникают новые или смещаются прежние «центры
притяжения» фаз. Соответствующие указанным центрам комби-
нации фаз опять-таки могут оказаться благоприятными, то есть
приводящими к взаимной компенсации неуравновешенных сил,
или же неблагоприятными.
Таким образом, эффекты, возникающие вследствие подвиж-
ности фундамента, может оказаться необходимым учитывать
также и в случае привода от синхронных двигателей. Соответ-
ствующие расчетные формулы могут быть получены по аналогии
с тем, как это было сделано выше для двигателей асинхронного
типа.
ЧАСТЬ \п
НЕКОТОРЫЕ ДРУГИЕ ПРИЛОЖЕНИЯ ТЕОРИИ
СИНХРОНИЗАЦИИ ДИНАМИЧЕСКИХ СИСТЕМ
В данной части книги будут рассмотрены некоторые задачи
динамики систем, содержащих однотипные объекты. Все эти за-
дачи более или менее естественным образом сводятся к задаче
о синхронизации слабо связанных объектов, и поэтому для их
решения оказываются применимыми методы, развитые в третьей
части книги.
В главе XXIV изучаются системы, в которых удается выде-
лить слабо взаимодействующие объекты с почти равномерными
вращательными движениями — два типа балансировочных уст-
ройств и вращающиеся гибкие валы с неуравновешенными ди-
сками. Дифференциальные уравнения движения указанных си-
стем весьма похожи на уравнения задач о синхронизации
механических вибраторов, и поэтому сходен также процесс ре-
шения этих задач. Вместе с тем в рассматриваемых физических
системах далеко не всегда удается выделить физические
объекты, подобные механическим вибраторам.
В главе XXV рассматриваются объекты типа слабо связан-
ных квазилинейных осцилляторов, в том числе маятниковые
часы, синхронизирующиеся при подвеске на общее подвижное
основание (задача Гюйгенса). Здесь же изучается важная
в практическом отношении задача о движении колебательной
системы со многими электромагнитными возбудителями.
В отличие от подробно изученной в четвертой и пятой частях
книги синхронизации механических вибраторов, при рассмотре-
нии задач в данной части мы не ставили целью сколько-нибудь
полное изучение соответствующих вопросов. Здесь лишь иллю-
стрируется применимость общих методов и результатов теории
синхронизации динамических систем к рассмотрению сравни-
тельно широкого круга прикладных задач. Ряд важных проблем,
о связи которых с проблемой синхронизации говорилось в пер-
вой части книги, нами вообще не рассматривается (проблемы
параллельной работы электрических машин, задачи о синхро-
низации в биологических системах и др.). Это объясняется вовсе
не тем, что методы теории синхронизации динамических систем
здесь не могут быть эффективно использованы, а лишь тем, что
даже конспективное изложение соответствующих вопросов по-
требовало бы привлечения весьма обширного специального ма-
териала.
ГЛАВА XXIV
СИСТЕМЫ С ВРАЩАЮЩИМИСЯ РОТОРАМИ
§ 1. Автоматический балансир для уравновешивания
вращающихся роторов
Рассматриваемый балансир, предложенный Сирлем [488, 489]
и применяемый для автоматической компенсации неуравнове-
шенности роторов, сидящих на быстро вращающемся гибком
валу, изображен па рис. 7 и 8. Его описание и постановка соот-
ветствующей задачи исследования приведены в § 2 первой главы
книги, там же упомянуты основные публикации.
Дифференциальные уравнения движения системы (см. урав-
нения (2.1) и (2.2) главы I) могут быть представлены в форме
Фх + Ро (<Ps - “) = Е«2Ф (<ps, х, ij) (s=l.k),	(1.1)
k
Мх + ex = tnR S sin <ps + <p2 cos <ps) 4- JHre? cos co/ — pP'x,
s;‘	(i-2)
My + cy = tnR S cos фв — ф2 sin ф5) — Яге? sin со/ — ц|У«/.
Здесь
р,Ф (ф5, X, у) = (х sin ф4. + у cos фД	(1.3)
а прочие обозначения расшифрованы в § 2 главы I.
Задача заключается в исследовании решений уравнений (1.1),
(1.2) типа
Ф5 = со/+ as + цф* (со/), х = х(со/), г/ = «/(со/),	(1.4)
где ф’, х и «/ — периодические функции времени / с периодом
2л/со, a as — постоянные.
Поставленная задача, очевидно, представляет частный слу-
чай задачи о синхронизации объектов с почти равномерными
вращательными движениями, рассмотренной в главе IX книги:
в указанной главе речь идет как раз об изучении синхронных
движений типа (1.1), причем уравнения движения (1.1) и (1.2)
относятся к категории уравнений (1.4) и (1.5) главы IX.
Соответствующая уравнениям (1.1) и (1.2) порождающая
система при р2 = с/М ¥= со2 (рассматривается нерезопапсный
случай) допускает следующее семейство решений вида (2.3),
(2.4) главы IX:
Ф° = и/ + as,
k
x°=wR T]cosa>/+ S cos(a>/-t аЛ ,
/=i
k
y° — — wR T] sin co/+ S sin (co/-F a/) .
(1.5)
792
СИСТЕМЫ С ВРАЩАЮЩИМИСЯ РОТОРАМИ
[ГЛ. XXIV
Здесь обозначено:
Mr	т и2	о с
*1 = 7^’ w=-m7^’ р Т1
(1.6)
Составим уравнения (2.5) главы IX для определения значе-
ний параметров аь . .., ал, которым могут отвечать решения
уравнений (1.1) и (1.2) вида (1.4), обращающиеся при ц = О
в порождающее решение (1.5). В соответствии с равенствами
(1.3) и (1.5) указанные уравнения запишутся в форме
P^(ai- aft) со)
2л/(0
~ j (<р°,	У°)dt =
О
2л/о)
(x°sin<p° + y°sinq)°)d/ =
о
k
4лсо .	, V • /	\
-----р— w 1] sin as + 2j sin (as — v-j)
(s=l.........k). (1.7)
Заметим, что уравнения (1.7) непременно допускают реше-
ния относительно ai, . . ., ал, удовлетворяющие условиям
k	k
т| + 2 cosa, = 0, 2sinaz = 0,	(1.8)
/=i	/=i
при выполнении которых, как следует из (1.5), колебания вала,
в первом приближении, отсутствуют, то есть
х° (со/) = у° = 0.	(1.9)
Поэтому основной интерес представляет, во-первых, установ-
ление условий устойчивости движений, отвечающих решениям
типа (1.8), и, во-вторых, выяснение вопроса, не будут ли одно-
временно с указанными движениями устойчивы также и другие
движения, которым отвечают решения уравнений (1.7), не удо-
влетворяющие условиям (1-8). Как нетрудно видеть, эти послед-
ние решения всегда имеются.
Решения уравнений (1.7), удовлетворяющие условиям (1.8),
а также соответствующие движения для краткости назовем ос-
новными, а все прочие решения (и движения) — побочными.
Ответ на вопрос о действительном существовании и об устой-
чивости решений, соответствующих какому-либо решению урав-
нений (1-7), зависит от знаков вещественных частей корней
алгебраического уравнения (2.6) главы IX.
§ П
АВТОМАТИЧЕСКИЙ БАЛАНСИР
793
Рассмотрим сначала случай двух шариков в полости диска.
При k = 2 уравнения (1.7) принимают вид
ц?! (аь а2, со) = — 4jTtOffll [т| sin а, + sin (а, — а2)] = О,
Ро
рР2 («I > «2, со) ss — 4ЯдЮа1 [л sin а2 — sin (а, — а>)] = 0.
Ро
(1.10)
Как нетрудно видеть, эти уравнения допускают, вообще го-
воря, четыре следующих существенно различных решения*):
1)	а)1* = л — у,
2)	а<2> = 0,
3)	а<3* = л,
4)	а<4> = О,
(п ,	.	(	п	Лг \
а^*=-(л-у) (у = arccos= arccos-g^J;
а22) = °;	(1,11)
а!>!) = л;
а!,4* = л.
Как нетрудно видеть, только первое из указанных решений
удовлетворяет условиям отсутствия колебаний вала (1.8). Иначе
говоря, лишь первое решение является основным; прочие реше-
ния суть побочные. Условием существования основного решения
является выполнение неравенства
Ч __ Лг .
2 2mR ~~~
(1-12)
которое выражает очевидное требование, чтобы статический мо-
мент обоих шариков относительно оси вала был не менее ста-
тического момента диска относительно той же оси.
Взаимное расположение центров шариков c'i и с2, центра
вала в недеформированном состоянии О и при движении Оь
а также центра тяжести диска для каждого из четырех реше-
ний (1.П) представлено на рис. 124. Построение выполнено в со-
ответствии с формулами (1.11) и (1.5) для момента времени
t = 0; произвольному моменту времени отвечает поворот диска
с шариками и связанной с диском системы координат иОхи на
угол фо = со Л
Обратимся к исследованию устойчивости решений (1.11).
Уравнение (2.6) главы IX в данном случае может быть пред-
ставлено в форме
х24-Лх + В = 0,	(1.13)
*) Очевидно, можно не различать решения, в которых соответствующие
а8 отличаются на 2лн, где п — целое число, а также, поскольку шарики счи-
таются одинаковыми,—решения, в которых значения и ag меняются ме-
стами.
794
СИСТЕМЫ С ВРАЩАЮЩИМИСЯ РОТОРАМИ
[ГЛ. XXIV
где в силу (1.10)
дах
4лсои)
Рой
[г] (cos at + cos a2) -г 2 cos (at — a2)],
' dPi dP2 _ dPt dP2'
dat да2 <Эа2 <?CZ|
16«2CO2ffi)2T| r
-----r-5—1 h cos at cos a2 +
py
(1-14)
4 (cos a, + cos a2) cos (at — a2)].
Достаточными условиями существования и асимптотической
Рис. 124.
устойчивости движений рассматриваемого типа, отвечающих ре-
шениям (1.Н), являются неравенства *)
Л>0,	В>0.
(1.15)
*) Строго говоря, к неравенствам (1.15), обеспечивающим отрицатель-
ность вещественных частей корней уравнения (1.13), следует присоединить
также некоторые дополнительные условия устойчивости, аналогичные усло-
виям (5.29) главы XIII. Нетрудно, однако, показать, что, как и в задаче
о синхронизации вибраторов, эти условия существенного значения при до-
статочном удалении от резонанса не имеют. Об этом см. также в конце
настоящего параграфа.
§ 11
АВТОМАТИЧЕСКИЙ БАЛАНСИР
795
Для первого, основного решения (1.11) по формулам (1.14) на-
ходим
.	.(1) 8лсои) /	. о \ 8лаи0
Л== Л =~ТйН~ ц cos у + cos 2у) = --5—,
РоН	РоН
г, _(И	16л2(О2И)2П /9 г,	О \
В = Д' =----^~2—- (n cos- у — 2 cos у cos 2у) =
(1.16)
16гт2со2ау 2г)2 /.	Т]2 \
’ РУ \ ~~Тг
Согласно (1.12) величина В всегда положительна внутри обла-
сти существования рассматриваемого решения; что же касается
величины А, то условие ее положительности приводит к требо-
ванию w <0 или, согласно (1.6), к неравенству
<в > р = У с/М .
(1.17)
Таким образом, основное движение, то есть движение, при
котором вал не колеблется вследствие компенсации неуравно-
вешенности диска воздействием шариков, устойчиво в закрити-
ческой области.
Для трех побочных движений (1.11) по формулам (1.14) на-
ходим
д(2> = -^(Щ), РоН л<з)= 8жо^(1_п); РоН	в(2) = Д6л»ч РоН2 Д'3) = а1^1(п_2);	(1.18) РоН
л<4)		8лши) РоМ	„(4)	16л2(О2И)2Т]2 D	=	П 9 РоН
Отсюда следует, что второе решение устойчиво лишь в докри-
тической области (w > 0, то есть со < р) ; третье решение устой-
чиво только в закритической области (to < 0, то есть со > р), и
притом лишь в случае, если т] > 2; последнее, четвертое решение
вообще неустойчиво. Таким образом, при выполнении условия
(1.12), гарантирующего существование основного решения, это
решение в закритической зоне (и > р) является единственным
устойчивым решением рассматриваемого типа. При докритиче-
ских же скоростях вращения вала это решение неустойчиво.
Сказанное предопределяет область эффективного применения
изученных автобалапспров.
Таким образом, мы имеем здесь совпадение с широко из-
рестным результатом решения классической задачи (задачи
796
СИСТЕМЫ С ВРАЩАЮЩИМИСЯ РОТОРАМИ
[ГЛ. XXIV
Стодолы) о самоуравновешивании несбалансированного диска
без шариков (см., например, [332]).
Заметим, что, как и в задаче о синхронизации вибраторов,
в данном случае возможен учет затухания по колебательным
координатам уже в исходном приближении (см. § 17 главы XIII).
Не приводя здесь соответствующего исследования, отличающе-
гося несколько более сложными выкладками, укажем, что глав-
ный результат исследования устойчивости получается таким же,
как и в предположении о малости сопротивлений [Ji и |3г/: основ-
ное решение устойчиво в области закритических и неустойчиво
в области докритических угловых скоростей и. Сказанное еще
раз подтверждает несущественность в данном случае дополни-
тельных условий устойчивости движения, о которых говорилось
выше (см. сноску на стр. 794), ибо если не считать сопротивле-
ния pi и (Зг/ малыми порядка р,, то эти условия вообще отпа-
дают.
Полученные выше выводы [68] согласуются с результатами,
найденными Ф. М. Детинко иными методами [174], и в опреде-
ленном смысле дополняют эти результаты *).
Поскольку автобалансир справляется со своей задачей уже
при числе шариков, равном двум, то нет надобности прибегать
к использованию большего числа шариков. С другой стороны,
при k > 2 исследование существенно усложняется, ибо в этом
случае решения уравнений (1.8) (а значит, и уравнений (1.7))
перестают быть изолированными. Это является отражением того
обстоятельства, что при числе шариков k, большем двух, и вы-
полнении условия, аналогичного неравенству (1.12), уравнове-
шивание диска возможно при любом фиксированном положе-
нии k — 2 шариков за счет выбора положений двух прочих ша-
риков.
Заметим также в заключение, что и в рассматриваемой за-
даче из общих соотношений §§ 4 и 5 главы IX может быть легко
получен простой интегральный признак устойчивости движений,
вполне аналогичный соответствующему признаку в задаче о син-
хронизации вибраторов. Нетрудно усмотреть в частности, что
факт устойчивости основного движения системы в закритической
области согласуется со следствием из интегрального критерия
устойчивости, изложенным в § 2 главы XXIII. На соответствую-
щих рассуждениях и выкладках, однако, мы не останавли-
ваемся, ибо они почти полностью совпадают с проведенными
в главах XIII и XIV.
*) Ф. М. Детинко не рассматривал вопроса об устойчивости побочных ре-
шений, а устойчивость основного решения изучал при трех конкретных зна-
чениях параметра ц (О, У2, 2). Вместе с тем Ф. М. Детинко решена также и
более сложная задача о вале с распределенным по длине небалансом.
§ 21
ВРАЩАЮЩИЙСЯ РОТОР С МАЯТНИКОВЫМИ ПОДВЕСКАМИ
797
§ 2. Вращающийся ротор с маятниковыми подвесками
1. Постановка задачи и уравнения движения. Для теории
ряда устройств представляет интерес задача о стационарном
движении сидящего на вертикальном валу диска, к которому
присоединены два физических маятника с осями вращения, пер-
пендикулярными плоскости диска (рис. 125,а). Особый интерес
при этом представляет отыскание условий существования и
устойчивости такого движения системы диск — маятники, при
котором маятники взаимно уравновешивают друг друга, так что
центр диска остается неподвижным в пространстве и, таким об-
разом, на подшипники вала и на неподвижное основание не пе-
редается неуравновешенных усилий.
Задача о движении ротора с двумя маятниковыми подве-
сками была рассмотрена Л. И. Мачабели [290] путем сведения
ее к задаче о синхронизации объектов с почти равномерными
вращательными движениями. Результаты цитированной работы
и воспроизводятся нами ниже с несущественными видоизмене-
ниями *).
Динамическая схема системы показана на рис. 125, б. Пред-
полагается, что диск сам по себе статически и динамически
уравновешен и закреплен посередине вала, так что центр диска
О| может совершать колебания только в плоскости диска. Тогда
в предположении, что вращение диска является равномерным,
*) Мы исправляем здесь также ряд опечаток, вкравшихся в указанную
публикацию.
798
СИСТЕМЫ С ВРАЩАЮЩИМИСЯ РОТОРАМИ
[ГЛ. XXIV
рассматриваемая система имеет четыре степени свободы, и ее
движение может быть описано в неподвижной системе коорди-
нат хОу двумя уравнениями колебаний маятников с учетом под-
вижности их осей и двумя уравнениями малых колебаний диска
с учетом реакций, возникающих от наличия маятников:
Iitfl + &1Ф! — (х sin <р, + у cos ф,) 4- m|8|Z[(B2 sin (ф, — <»Z) = 0,
/2фг 4- &2Ф2 — w2Z2(*sin Ф2 + У c°s Ф2) — m2e2Z2tti2 sin (ф2 — coZ) =0,
Mx + ex — s<»2 cos at — ш,/, (ф, sin ф] 4- ф2 cos ф,) —
—	m2l2 (ф2 sin ф2 + ф2 cos ф2) = 0,
My 4- cy + s<»2 sin at — m,/, (ф, cos ф, — ф2 sin ф^ —
—	tn2l2 (cp2 cos ф2 — ф2 sin ф2) = 0.
Здесь x и «/ — координаты центра тяжести диска; ф! и ф2 — углы
поворота маятников, отсчитываемые от положительного направ-
ления оси Ох по ходу часовой стрелки; т и 3— соответственно
масса и момент инерции диска; щ1 и т2— массы маятников;
.71 и — моменты инерции маятников относительно их осей;
1\ и Z2 — расстояния от осей маятников до их центров тяжести;
8i и е2 — расстояния от центра диска до осей маятников (экс-
центриситеты подвески маятников); k\ и k2— коэффициенты
вязкого сопротивления вращению маятников; с — изгибная жест-
кость вала; и — угловая скорость вращения диска; М = т +.
4- tni + т2 — масса всей системы,
I. = 7, 4- т.е2 /9 = 794-т.,е2
г ' Д 2	(2-3)
I = 3 4-	4- m2e2, s = mtel — m2e9,
Введя обозначения
ц<в2Ф[(ф1, х, ij, <bZ) = [miZ, (х sin ф, 4-//cos ф^ —
— tn^ilia2 sin (ф, — at) —
(2.4)
р<в2Ф2 (ф2, x, ij, at) = [m2l2 (x sin ф2 + ij cos ф2) —
— m2e2Z2<B2 sin (ф2 — at) — &2<b],
где p — положительный малый параметр*), можно представить
уравнения движения маятников (2.1) в форме
/,5ф.5 4-Zys (ф9 - оз) =-цш2Ф, (фх, х, ij, at) (s=l,2),	(2.5)
*) Мы не останавливаемся здесь на обосновании способа введения ма-
лого параметра, ибо он вполне аналогичен многократно использовавшемуся
тише,
§ 2] ВРАЩАЮЩИЙСЯ РОТОР С МАЯТНИКОВЫМИ ПОДВЕСКАМИ 7QQ
совпадающей с формой записи уравнений (1.4) главы IX. Инте-
рес при этом представляют решения вида
<Ps = ®Has + Hj(®0	(s=l, 2),
(2.6)
X = x(at), y = y(at),
где ф*(со/), x(w/), У (at) —периодические функции времени t
с периодом 2л/<в. Поэтому, как и в предыдущем параграфе, здесь
можно воспользоваться результатами исследования синхрониза-
ции в системах с почти равномерными вращательными движе-
ниями.
Отвечающая уравнениям (2.5) и (2.2) порождающая система
допускает семейство синхронных решений вида
ф° = at + (Zj,	<р° = at + <х2,
х° = w [a cos at + b< cos (at + a,) + b2 cos (at + a2)],	(2.7)
y° = xa/a = — w [a sin at + bx sin (at + cq) + b2 sin (at + a2)],
зависящее от двух произвольных постоянных ai и a2; по своему
смыслу эти постоянные, очевидно, представляют собой углы от-
клонения маятников от прямой охо2, равномерно вращающейся
с угловой скоростью со.
В равенствах (2.7) обозначено:
СО3	о С	S
™ =	а=М~’
2. Уравнения для определения параметров порождающего
решения. Условия самоуравновешивания системы. Составим те-
перь уравнения (2.5) главы IX для определения значений пара-
метров си и а2, которым могут отвечать решения уравнений (2.5)
и (2.2) вида (2.6), обращающиеся при ц = 0 в порождающее
решение (2.7). В соответствии с равенствами (2.4) и (2.7) эти
уравнения могут быть представлены в форме
2Л/ш
a2,	J	x°, у3, (bf)dtz=i
1 о
2л/со
^y~j" {/«/i sin (®^ + aj 4- ij° cos (at + aj] —	(2.9)
1	о
—	sin a( — k j co J dt s
e= —(m^a2 [(доя + e,) sin cq + b2w sin (a, — a2)] — k{a} = 0,
800	СИСТЕМЫ С ВРАЩАЮЩИМИСЯ РОТОРАМИ	(ГЛ. XXIV
2л/о)
Н^2(ар а2’	=	(фр *°» У°> ®t)dt =
о
2Л/(О
= -^-J {m2l2 [х° sin (at + а2) + у° cos (at + а2)] +	(2.9)
2	о
+ т2/2е2а>2 sin а2 — k2(£>} dt =
ss — {fn2t2a2 [(иш — е2) sin а2 — b\W sin (ctj — а2)] — k2a} — 0.
Каждому решению а = а*, а2 = а* последних уравнений дей-
ствительно отвечает единственное и асимптотически устойчивое
решение, если корни уравнения (см. уравнение (2.6) главы IX)
дР{	dPt
«Эа, Х да2
дР2	дР2
dat	да2
(2.10)
имеют отрицательные вещественные части.
При наличии хотя бы одного корня с положительной веще-
ственной частью рассматриваемое движение неустойчиво; при
наличии нулевых или чисто мнимых корней требуется допол-
нительное исследование*).
Для упрощения исследования заметим, что в реальных си-
стемах моменты сопротивления йц» и k2a малы по сравнению
с прочими осредненными моментами, фигурирующими в урав-
нениях (2.9). Поэтому можно ограничиться решением этих урав-
нений с точностью до членов, содержащих /гцо и k2a в степенях
не выше первой.
Нетрудно установить, что существует (с точностью до несу-
щественной постояной 2лп, где п — любое целое число) шесть
следующих решений системы (2.9):
1) а',0 0 4- АциЛ) ' + k2aB\ \
2) a(i1 2) 3 « 0 + /с,<оzl!i2) 4- k2aBa,
3) aj ' « л 4- k[(i>Л) ’ + k2a>B\ \
4) а<4) ~ л 4 АциЛ’4' + k2a>B{\\
5) а® « Р -I- АцснЛ)5’ + k2aB{\\
6) а)6' ~ — (54- k\aЛ(,6) + k2aBf\
а2'	0 4- k[(i>Л2' 4- k2a>B2^‘,
а2 ’ «« л + k\<£> Л2) 4- k2ti>B2^',
а2) л + kiC£>Л2+ k2aB2\
а24)	0 + ^1<»Л24) + ^2<вВ24);
а25) ss у + k\<i>Л® + k2aB2^\
а{2	— y + ki(»A2} + k2aB[2\
) См. сноску на стр. 794.
§ 2)
ВРАЩАЮЩИЙСЯ РОТОР С МАЯТНИКОВЫМИ ПОДВЕСКАМИ
801
Здесь
.	, ,ц	.	wa-e,
у = a rccos---1 — — 1 —	, Hi =----------->
1 (П1 .	2'
П, + — — - 1 - П2
2тц \П2
____________ > . -
I —--------л
2ТЦ \Т12
wa — е2
гр =----------, Р = arccos
Ь]И>
Па
П1 .
(2.12)
Постоянные и B'f1 (/=1, 2; й=1,	6) легко находятся
из уравнений (2.9) путем подстановки в них соответствующих
выражений (2.11) и пренебрежения членами kja в степенях
выше первой.
Нетрудно видеть, что из всех решений (2.11) наибольший ин-
терес в изучаемой задаче представляет второе решение. Дей-
ствительно, если параметры системы выбраны таким образом,
что выполняется соотношение
/И] (е, +/,) = т2 (е2 + /2)
или, в обозначениях (2.8),
а + 6] — 62 = 0,
(2.13)
(2.14)
то для указанного решения отклонения центра диска х и у в со-
ответствующем движении с точностью до малых членов порядка
kjV> равны нулю, то есть имеет место практическое самоуравно-
вешивание системы.
В самом деле, согласно (2.7), (2.11) и (2.14) при aj=a<2) и
= а® имеем
x°/w ~ a cos at + bi cos (at + йцв Л<2) + kzaB?) +
+ b2 cos ((£>/ + л + Й1<оЛ22) + &2®B22)) ~ (a + b\ — b2) cos at —
— bi (&i<o A(2) + &2®B<2)) sin at + bi (^шЛг2' + fe®5^2)) sin at =	(2 15)
=	+ k2aB2}) — bi (й1<оЛ(2) + й2<оВ12))] sin at 0,
y°/w = x°/wa ~
—(bi(й1<оA2) + k2aB2^— 61 (/jig)Л[2^ +/j2wBi2^)] cos o)/ «0.
Для всех прочих решений (2.11) величины х и у будут со-
держать в своих разложениях по kia и k2a свободные члены,
то есть самоуравновешивание (в изучаемом приближении) не
будет иметь места. Поэтому рассмотрим вопрос об устойчивости
именно решения, отвечающего aj=a(2) и a2 = a®.
С точностью до членов, содержащих неотрицательные сте-
пени k{a и k2a, для указанного решения при учете равенств
802	СИСТЕМЫ С ВРАЩАЮЩИМИСЯ РОТОРАМИ	[ГЛ. XXIV
(2.9) и (2.14) находим
дРх	4л	1	,	9,	.	,
дР2	4л	1	,
,D	л	,	(2.16)
dPt	4л	I	,	,,	v '
дРъ	4 л	I	f	<y z	t	\
Таким образом, условия отрицательности вещественных ча-
стей корней квадратного уравнения (2.10), совпадающие с усло-
вием положительности коэффициентов этого уравнения, могут
быть представлены в форме
/ дР, . дР2\ а
— Н -a-L+-S-^' “Г~ =
\ 00] <Эа2 / 4л
zn./.a2 , ,	,	m2/2a2 , ,	п
=------1^— (wbx - е,)------g— (wb2 - e2) > 0,
1.2 f др1 dP2 _ dpi dP2 \ g>2 =	/9 171
Iх \ <3a1 3a2	<3a2 da, / 16л2	' ‘ '
=	[(иуЙ! - 8]) (wb2 - e2) - bxb2w2] =
л-1 n-2
= - -	' [eie2 - w (bxe2 + 62ej)] > 0.
После преобразований с учетом (2.8) последние неравенства
принимают вид
а2 (т^^^г + m2Z2e2/j]) Л1 ~
2	9~	2»2«	.	2»2»	Al,
р -а2 mxlxk^m2l^x
а2	A4eie2 _ „
р2 — а2 mi/^г + т2/2е1	/'2‘
Условия (2.18) выполняются при
а<р VR/(R+ 1) <р,
где R — Inf (Ал, /?г) — наименьшее из двух положительных чисел
Rx и R2, определяемых по формулам (2.18). Кроме того, вне
зависимости от значений прочих параметров системы, условия
устойчивости (2.18) выполняются, если
со > р = У с/лГ,	(2.19)
то есть если угловая скорость вращения вала со превышает ча-
стоту собственных колебаний диска с жестко закрепленными на
нем маятниками, то есть так называемую первую критическую
ВРАЩАЮЩИЙСЯ ГИБКИЙ ВАЛ
803
§ 3]
скорость. Поэтому можно считать, что основное условие само-
балансировки системы, так же как и системы, рассмотренной
в § 1 настоящей главы, совпадает с соответствующим условием
для классического случая — неуравновешенного диска без маят-
ников [332].
§ 3.	Вращающийся гибкий вал с неуравновешенными дисками
Постановка задачи об изгибно-крутильных колебаниях вра-
щающегося вала с неуравновешенными дисками (рис. 4) была
дана в § 3 главы I. Здесь мы рассмотрим эту задачу в предпо-
ложении, что все частоты собственных крутильных колебаний
вала с полностью уравновешенными дисками существенно ниже
угловой скорости вращения ы, а частоты изгибных колебаний
в достаточной мере отличаются от поз, где п — целое положи-
тельное число [68].
Допустим, далее, что вал приводится во вращение от двига-
телей асинхронного типа, и положим Ls = Ls(<ps), Rs = Rs(<p5);
будем считать также, что отношения msesrs//s и [Д(ы) —
— Rs(<o)]//s®2, где rs — величина порядка амплитуды колебаний
центра s-ro диска, малы по сравнению с единицей.
Тогда дифференциальные уравнения (3.3) главы I, описы-
вающие движение системы, естественно представить в форме
/,Фз + МФз - “) =	(Фз-1, Фз, Фз, xs, ijs),
msxs + S (c^xi + cTai) = mses (Фз cos Фз “ Фзsin Фз) 4
msijs + 2 (c(sy>/ + СП) = m383 (Фз sin Фз + Фз C0S Фз) + HQ*/’,
*	~	(3.1)
л A + 2 (<“% + СЧ) =
k
лд + 2№ + ^Ч) = ^
(s = 1, . .	k),
где положено:
цФз = m^s cos <p5 + ys sin <ps) - os_i, s (<ps - <ps_j -xs + %,_,) +
+ Сз+I, 3 (фз+J - Фз ~ *s + i + xs) + Ls (<o) - Rs (co),
Q<*> = PQW, Q'yl = Q‘a) = !<a), Q<₽) = pQ*₽),	(3’2)
Ls (Фз) ~ Ls (“) - К (Фз - “) ^3 (Фз) ~ A (®) + k°s (Фз - “)>
а ц — по-прежнему положительный малый параметр.
804	СИСТЕМЫ С ВРАЩАЮЩИМИСЯ РОТОРАМИ	[ГЛ. XXIV
Уравнения (3.1), очевидно, также относятся к классу систем
(1.4), (1.5) главы IX. Как и в главе IX, при этом интерес пред-
ставляют решения системы (3.1), имеющие вид выражений (1.1)
указанной главы.
Отвечающая уравнениям (3.1) порождающая система при
указанных выше условиях допускает семейство решений
<р° = at + as,
k	k
х° = — 2 Msl sin (at + a;), a° = - 2 ^s/ sin + ay),
,<3.3)
y\ - S cos(w( + a,),	₽° - - 3 rs/ cos (ш/ + a,),
(s = 1, . . ., k),
зависящее от k произвольных постоянных a.,. В равенствах (3.3)
через Afsj, USj, Nsj и обозначены постоянные, определяемые
путем решения линейных алгебраических уравнений, получаю-
щихся при ц = 0 из последних k уравнений (3.1) в результате
подстановки выражений (3.3) и сокращения на sin at и cos at.
Составим уравнения (2.5) главы IX для определения значе-
ний параметров аь .. ., a/t, которым могут отвечать решения
уравнений (3.1) рассматриваемого типа, обращающиеся при
р = 0 в порождающее решение (3.3). Согласно (3.2) и (3.3)
этими уравнениями будут *)
2л/а>
Ря(а„ ..., ak,	<P°S+1, Ф°, С y°^)dt =
о
Г k
= 1? - Z ^Msi + Sin ~ Cs-I, s(as ~ a3-l ~
L	,_i
- xs + xs+l) + cs, S+1 (as+1 - as - xs+I 4- %s) + Ls (a) - Rs (и)] = 0 (3.4)
(s= 1, ..., k).
Об интерпретации последних уравнений можно почти до-
словно повторить сказанное в § 3 главы IX и в § 2 главы XIV.
Так, величины
k
U7S (ab ..., оц, ш) =	(Ms/ + Nsi) sin (as - a,) (3.5)
/=|
*) Здесь для удобства в функции введен несущественный положи-
тельный множитель [хю/4л.
ВРАЩАЮЩИЙСЯ ГИБКИЙ ВАЛ
805
§ 3]
по аналогии с задачей о синхронизации вибраторов могут быть
названы вибрационными моментами; величины
(as_i, as+1)
= Cs— и s (®s as-i 4” i) Cs, s+i (as+! as %s+i 4~ ^s)	(3.6)
являются средними за период 2л/со значениями упругих крутя-
щих моментов, а L.,(w) и Rs(a>)—средние значения вращаю-
щего момента двигателя и момента сил сопротивления, дей-
ствующих на s-й диск. Часто вращающий момент приложен
только к крайнему диску; тогда
L1(<o)y=0, 12(®)= ••• =^ft(®) = 0.
Сопоставляя уравнения (3.4) с уравнениями (3.4) главы IX
и принимая во внимание, что в рассматриваемой задаче Q<°> = 0
(г = 1, ..., v = 4й) и Qs =	заключаем, что должны
быть справедливы соотношения
-^-= - U7s(ab ..., ak, со) - Ss(as_1; as, as+1) =
k
= -	(Ms/+ Nsl) sin (as -a.j) - cs_b s (a, - as_! - xs + xs_ +
/=i
+ cs,s+i(as+i-as-xs+l + xs) (s = l,	(3.7)
Здесь, как и выше, через А обозначено среднее за период зна-
чение функции Лагранжа системы, вычисленное для порождаю-
щего решения (3.3) в соответствии с равенствами (3.1) и (3.2)
главы I и формулой (3.2) главы IX.
При учете соотношений (3.7) уравнения (3.4) могут быть
представлены в форме
Ps(a,, ..., ak, со) = j- [Ls (и) - Rs (ы) -
- Ss(as_i, a,, as+j) - ^(a,, ..., aft, co)] = 0	(3.8)
(s = 1....k)
или в виде
Ps(ab .... ak, co) ee= J- + Ls (co) - Rs (w)] = 0	(3.9)
(s = 1, .... k).
Последние уравнения вполне аналогичны уравнениям (2.28)
и (2.29) главы XIV, относящимся к задаче о синхронизации ви-
браторов.
806
СИСТЕМЫ С ВРАЩАЮЩИМИСЯ РОТОРАМИ
(ГЛ. XXIV
Из тождеств (3.7) и из условия независимости от порядка
дифференцирования значений вторых смешанных производных
функций А по ая получаем
mses (Ms] + As/) cos (as - a,) =	(Mfs + Nls) cos (a, - as). (3.10)
Сложив все уравнения (3.4), предварительно умноженные на
aks, находим, используя последние соотношения, равенство
k	k
со 2 Ls (<о) = 2	(со) со,
S-I	S-1
которое представляет уравнение баланса энергии в системе
(в исходном приближении) и служит для определения угловой
скорости синхронного вращения со. Порождающие фазы as на-
ходятся из уравнений (3.4) (или, что то же самое, из уравнений
(3.8) или (3.9)) лишь с точностью до аддитивной произвольной
Тюстоянной. Все это, как уже неоднократно отмечалось, является
следствием автономности исходной системы уравнений.
Определенному решению с^ = а*, ..., ak = a*k трансцендент-
ных уравнений (3.4) действительно отвечает единственное, ана-
литическое относительно ц при достаточно малых его значениях,
решение рассматриваемого типа, обращающееся при р, = 0 в по-
рождающее решение (3.8), если k—1 корней алгебраического
уравнения (2.7) главы IX имеют отрицательные вещественные
части; при наличии корней с положительной вещественной
частью соответствующее решение неустойчиво; случаи, когда
указанное уравнение имеет более одного нулевого корня или
чисто мнимые корни, требуют дополнительного исследования*).
Совершенно аналогично тому, как это было сделано в § 9
главы ХШ и в § 4 главы XIV, в рассматриваемом случае может
быть сформулирован интегральный критерий устойчивости дви-
жения, причем за потенциальную функцию можно принять вы-
ражение
D=-(A + B),	(3.11)
где
k
B = B(ab ..., ak, и)= 2 {Lj (co)] a,.	(3.12)
Мы здесь не имеем целью подробное изучение задачи об из-
гибно-крутильных колебаниях вращающегося вала с неуравно-
вешенными дисками и поэтому ограничимся приведенными выше
основными соотношениями и коротко остановимся на главных
качественных выводах.
*) Здесь необходимо сделать огоровку о дополнительных условиях устой-
чивости, подобную приведенной в сноске на стр. 794,
§ 3]	ВРАЩАЮЩИЙСЯ ГИБКИЙ ВАЛ	807
Один из выводов состоит в том, что вследствие неуравнове-
шенности дисков изгибные и крутильные колебания вала ока-
зываются взаимно связанными, причем может оказаться, что
эту связь игнорировать нельзя, и тогда следует рассматривать
задачу в описанной выше нелинейной постановке. Конкретное
проявление указанной взаимной связи между изгибными и
крутильными колебаниями состоит в появлении в уравнениях
(3.8) вибрационных моментов В результате при определен-
ных условиях в процессе движения участки вала могут ока-
заться закрученными на значительные дополнительные углы,
так что крутильные колебания будут происходить относительно
иных средних положений. При этом в сечениях вала могут воз-
никнуть значительные напряжения, а характер воздействия вала
на опоры — существенно измениться.
Указанные эффекты проявляются тем сильнее, чем больше
максимальные значения вибрационных моментов Ws по сравне-
нию с наибольшими упругими крутящими моментами Ss, то есть
чем меньше жесткости участков вала на кручение cs,s+I, чем
больше неуравновешенности mses и чем выше угловая скорость
со. Разумеется, эти эффекты можно как угодно ослабить путем
выбора достаточно больших жесткостей.
ГЛАВА XXV
СИСТЕМЫ СО СЛАБО СВЯЗАННЫМИ
КВАЗИЛИНЕЙНЫМИ ОСЦИЛЛЯТОРАМИ
§ 1. Взаимная синхронизация слабо связанных
осцилляторов Ван-дер-Поля
1. Уравнения движения. Поставленная в § 6 первой главы
настоящей книги задача о синхронизации осцилляторов Ван-дер-
Поля с близкими парциальными частотами автоколебаний сво-
дится к исследованию периодических решений автономной си-
стемы квазилинейных дифференциальных уравнений
xs + 62xs = p0)s(xs> xs; хь хк) ($=1,	k),	(1.1)
где
k
= “st1 - *s)+ Xs«4 + 2 bsjXj,	(1.2)
w, as, y_s и bSj — постоянные, а ц>0— малый параметр.
He нарушая общности, можно положить
3 = 1,	(1.3)
поскольку для обращения в единицу коэффициента при xs в ле-
вых частях уравнений (1.1) достаточно лишь изменить масштаб
времени. Тогда в результате замены переменных
%s Us Ук+st	%s i (.У* Ук+s)	(1 -4)
система уравнений (1.1) преобразуется к канонической форме
Уз^ЪУг + чЛ	(«=1......2й),	(1.5)
соответствующей форме уравнений (3.3) главы V. При этом по-
ложено
K =	Ffe+s = 4®s («=1.......k). (1.6)
2. Уравнения для определения параметров порождающего ре-
шения и условия устойчивости. Система (1.3) является квази-
линейной и почти консервативной, поэтому для решения задачи
можно было бы воспользоваться результатами § 4 главы VIII,
§ и
ВЗАИМНАЯ СИНХРОНИЗАЦИЯ ОСЦИЛЛЯТОРОВ
809
а также в п. 4 § 2 главы X. Однако в данном случае удобнее
непосредственно применить теорему, доказанную в § 3 главы V.
С этой целью заметим, что характеристические показатели по-
рождающей системы
(S=i,..., 2k),
отвечающей уравнениям (1.5), являются критическими и
зуют ведущую особую группу, причем указанная система
скает семейство периодических решений (с периодом 2л)
aselt, s=l, ..., k,
ase~“, s = k + i, ..., 2k,
зависящее от 2k произвольных постоянных ои, ..., а2д-
Составим выражения функций Ps(ai, ..., агь), фигурирую-
щие в уравнениях для определения порождающих фаз си, ..., а2/г.
В соответствии с формулами (3.50) главы V и равенствами
(1.2) — (1.6) настоящего параграфа находим*)
/ k Y
= Л CLS (1	^s^k+s) «s I ^Xs^s bs j&j ,
&	Y
- 2 bsIak+l] .
(1.7)
обра-
допу-
У° = ase S'
(1-8)
P-Ps
(1-9)
fe+s	(1 ^s^fe+s) ®k + s “1“ I Xs^fe +
Уравнения (3.49) главы V, из которых определяются пара-
метры порождающего решения, таким образом, имеют вид
pQs ss - OikiiPs - a^iP2k =
I	k \
=Е-ла2й — i xsa,
ОА+Д +
k),
I \	/=i	/
[/	k	\
1 I Xfca2fe ~ S bhjak+l I + ak (1 — а^а2/г) a2i. = 0
\	/=i	1
(8=1, ...
^Qfc + s =	^Pk+s 4" (^k + sl^Pik —
k \
^4 bsiak + ! j 4” nis (1 cti.<X/e.LS)
(1-Ю)
--- ЛШ^. i I Xs^fe + s
+ ™fe + s
' /	k	\	1
i ^«2^ - 5 bsiak+jj + ak(l- aka,k) a24 j = 0
(s = 1,	k-\).
*) Следует иметь в виду, что в § 3 главы V число критических корней,
образующих особую ведущую группу, было обозначено через k, в то время
как здесь это число обозначается через 2k.
810
СИСТЕМЫ СО СЛАБО СВЯЗАННЫМИ ОСЦИЛЛЯТОРАМИ
[ГЛ. XXV
Из равенств (1.4), (1.6) и (1.8) следует, что для веществен-
ности исходных переменных х° должны быть выполнены равен-
ства ak+s = as; кроме того, как указывалось в § 3 главы V, не
нарушая общности, можно положить аы = си = а, причем а,
в силу указанных равенств, вещественно. Но тогда, согласно
^-му уравнению (1.10), Ph = —Ргн и из (1.9) и (1.10) вытекают
соотношения
Pk+s = Ps, Qk+s = Qs (s=l, ...,£).	(1.11)
Отсюда следует, что для определения 2/г—1 комплексных
постоянных ои, ..., a,h-i, cu+ь •  •, и а = ак = агь, которые
вследствие равенств cu+s =a<i (s = 1, ..., k) можно заменить
2k—1 вещественными постоянными
0 = 1 asl	(s= 1, •••> k),
	/1 t, n (1.12)
T|)s = argas= - argaft+s (s= 1,	1),
достаточно рассмотреть 2k—1 уравнений, получающихся в ре-
зультате приравнивания нулю вещественных и мнимых частей
первых k выражений (1.10). Заметим, что этих уравнений полу-
чается именно 2k— 1, а не 2k, поскольку из условия
а2й =	= ak — йь = а
и соотношений (1.11) следует тождество
ImQft = 0.	(1.13)
Для возможности синхронных колебаний изучаемого типа,
в силу теоремы § 3 главы V, необходимо, чтобы указанные урав-
нения допускали решения, вещественные относительно ф8 и по-
ложительные относительно rs.
Определенному решению этого рода действительно отвечает
единственное асимптотически устойчивое синхронное движение
изучаемого типа, если для этого решения все корни % алгебраи-
ческого уравнения 2k— 1-й степени*)
dQi ।	dQ,	
dat 1 a>c •	^Gt2fe —i	
		= 0	(1.14)
dQih — i	dQzk-i ।	
dai	• aa2ft_. 1 a’“	
имеют отрицательные вещественные части. При наличии хотя
бы одного корня с положительной вещественной частью соот-
ветствующее движение неустойчиво; случай чисто мнимых или
нулевых корней требует дополнительного исследования.
*) В данном случае величина пк, фигурирующая в уравнении (3.51) гла-
вы V, должна быть заменена на —1 (см. равенства (1.6) и сноску на
стр. 809).
$ 1]
ВЗАИМНАЯ СИНХРОНИЗАЦИЯ ОСЦИЛЛЯТОРОВ
811
Ниже мы не будем заниматься детальным изучением данной
задачи, а ограничимся рассмотрением простейших частных слу-
чаев и формулировкой некоторых качественных заключений [68].
3. Случай почти одинаковых и одинаково связанных осцилля-
торов. Предположим сначала, что все осцилляторы одинаковы
и одинаково связаны, то есть
as = a, ь = х, bsj — b (s, j = 1, ..k).	(1.15)
Тогда первые k уравнений (1.10) в переменных rs = |as| =
= | ak+s |. 4>« = argas = —arga*+a могут быть представлены
в форме
lxQs = -nrfte /ф*
/	k \
-	- b 2 г/е'ф/у + а (1 -
— nrse
I	к \
i \/rke~^k - b 2	+
(1.16)

(s= 1....k).
Рассмотрим те решения уравнений (1.16), которые соответ-
ствуют колебаниям всех осцилляторов с одинаковыми амплиту-
дами
г,= ...=гь	(1.17)
совпадающими, как нетрудно видеть, со значениями амплитуд
при отсутствии связи между осцилляторами (Ь = 0). Для ука-
занного случая, отделяя в уравнениях (1.16) вещественные и
мнимые части, получаем следующие 2k равенств, которым дол-
жны одновременно удовлетворять k постоянных ф1, ..., ф&:
k	k
2 COS Ф/ = 2 COS (фа — фу),
/-1	/-1
k	k	(1.18)
2 Sin ф/ = 2 sin (Фа - Ф/)
/-1	/-1
(s = 1...k).
При этом одна из постоянных фз, а именно фь, в силу условия
аь = «гл = azh = а должна быть заранее положена равной нулю.
Уравнения (1.18) удовлетворяются, в частности, если
ф,= ... =ф, = 0,	(1.19)
что соответствует колебаниям всех осцилляторов с одинаковыми
фазами. Таким образом, уравнения (1.16) имеют по крайней
мере одно решение, определяемое равенствами (1.17), (1.19);
этому решению отвечают значения постоянных as = 1. Однако
уравнения (1.18), вообще говоря, могут иметь и иные решения.
812
СИСТЕМЫ СО СЛАБО СВЯЗАННЫМИ ОСЦИЛЛЯТОРАМИ
[ГЛ, XXV
'Гак, например, в случае четного числа осцилляторов существуют
решения вида
rs=l,	(s=l, •••, k = 2k'),	(1-20)
,, k	., k
где qs — числа, из которых k =y равны нулю, а другие « — у
равны единице. Иными словами, имеются решения, соответ-
ствующие колебаниям одной половины всего числа осциллято-
ров в противофазе по отношению к другой половине осциллято-
ров. Возможны, конечно, и решения более сложного характера,
чем указанные выше (см., например, [292, 364а]).
Нетрудно показать, что положительные относительно rs и ве-
щественные относительно ф8 решения уравнений (1.10) непре-
менно существуют не только для осцилляторов с одинаковыми
параметрами, по также и при наличии достаточно малых откло-
нений этих параметров. Таким образом, синхронизация осцил-
ляторов всегда возможна, если их одноименные параметры
достаточно мало отличаются один от другого. Последнее утвер-
ждение на основе физических соображений было высказано
А. А. Андроновым и А. А. Виттом в статье [17]; для случая двух
осцилляторов оно было проиллюстрировано конкретными рас-
четами в работах В. П. Рубаника [362, 364а] (см. также ниже).
4. Случай двух осцилляторов. Изучим подробнее синхронные
колебания системы двух осцилляторов.
При k = 2 первые два уравнения (1.10) приводят к трем ве-
щественным соотношениям (напомним, что фг = 0):
rt sin ф] = й2г2(1 - г%),
(У2	+ &п ~ М cos +
+ [a, (1 — r^) + a2 (1 — r^)] 51пф, = 21 1r-1^,
(%2“X1 +	- &22)з1пф1 + [a,(l -f2) + a2(l -r|)] соэф, = 0,
(1.21)
которые служат для определения постоянных и, г2 и фь Иссле-
дование системы (1.21) в общем случае довольно громоздко,
поэтому мы ограничимся решением задачи в двух частных слу-
чаях.
Допустим сначала, что имеют место соотношения
%2-Xi + Ьц -	= bl2- b2h а1 = а2 = а. (1.22)
Заметим, что такие равенства выполняются в некоторых кон-
кретных системах, в частности в индуктивно связанных лампо-
вых генераторах, для которых изучаемая задача была рассмот-
рена иным методом Н. Минорским в уже упоминавшейся ра-
боте [292].
§ I)
ВЗАИМНАЯ СИНХРОНИЗАЦИЯ ОСЦИЛЛЯТОРОВ
813
При выполнении первого из равенств (1.22) система уравне-
ний (1.21) допускает решение
Г1==г2=1,	-ф1 = л,	(1.23)
отвечающее противофазным синхронным колебаниям осциллято-
ров с одинаковыми амплитудами.
Рассмотрим вопрос об устойчивости этого решения. Согласно
равенствам (1.10), (1.12) и (1.22) при k = 2 имеем
dQi	• < ^--ib da, ~	Z&21> ДОз. = а да,	Д ~ а tbi2’	ib2i’ ^ = 2a~ib^ ^ = ib^	П-24) =	Д' = а + г(Ь12 + Ь21); Qs ^Qs/цл	(s= 1, 2, 3).
Уравнение (1.14), таким образом, в данном случае может
быть представлено в форме
a — ibl2 + z	— a — ibl2	a — ib2.	
- zT>21	2a — ib2t + z	ib2i	= 0, (1.25)
a	a	a + i(bi2 + b2i) + z	
где z — к/л. В результате несложных преобразований опреде-
лителя находим следующие значения корней уравнения (1.25):
Zj=— 2а,	z2, з = — а ± /а2 — (Ь12 + Ь21)2.	(1.26)
Отсюда видно, что единственным условием устойчивости рас-
сматриваемого решения является положительность коэффи-
циента а:
а>0.	(1.27)
Для генерирующих осцилляторов изучаемого типа это условие
всегда выполняется, и поэтому противофазные синхронные коле-
бания осцилляторов асимптотически устойчивы. Этот результат
совпадает с полученным Н. Минорским с помощью предложен-
ного им так называемого стробоскопического метода.
Изучим теперь более частный случай, когда все параметры
обоих осцилляторов одинаковы, то есть имеют место равенства
(1.15). При этом для 6 » 2 уравнения (1.16) допускают два су-
щественно различных решения:
r(11) = r(D= 1, ф(1> = 0, ф<‘> = 0;
Г(2) = Г(2)=1, ф(2) = П> ф(2> = 0,	(L28)
814
СИСТЕМЫ СО СЛАБО СВЯЗАННЫМИ ОСЦИЛЛЯТОРАМИ
[ГЛ. XXV
Первому из этих решений соответствуют синфазные, второму —
противофазные синхронные колебания осцилляторов.
Рассмотрим вопрос об устойчивости таких колебалий. Со-
гласно равенствам (1.10), (1.12) и (1.15) при k = 2, n = r2 = 1
и фг — 0 имеем
4^- = а + ibe-W', (70 j	3Q, да2	— ае^' — ib,	?Qi <?а3	— ае2‘^' + ibe1^1;
^- = — lb, (70]	dQi да2	= 2а + ibe~1^',	dQt да3	= ib’,	(1.29)
За,	’	dQ3 да2	= — ае-2*,	dQ3 да3	= а — 2ibe~i'h,
где, как и выше, Qs = Qs/pn (s = 1, 2, 3).
Для первого из решений (1.28) уравнение (1.14) может быть
представлено в форме
а + ib + z a — ib
— ib 2а + ib + z
a	—a
a + ib
ib
a — 2ib + z
(1.30)
где z = х/рл. В результате несложных преобразований опреде-
лителя находим следующие значения корней последнего урав-
нения:	_____
= — 2а,	z2>з = — а ± /а2 — 462.	(1-31)
Отсюда следует, что необходимым и достаточным условием
устойчивости рассмотренного решения по-прежнему является
условие (1.27).
Для второго решения (1.28), вместо (1.30), получим, со-
гласно (1.29) и (1.14), следующее уравнение;
а — ib + z —a — ib a—ib
— ib 2а — ib + z ib
= 0.
(1.32)
a	a	a + 2ib +z
Корни этого уравнения также легко находятся путем простых
преобразований определителя, причем эти корни оказываются
в точности совпадающими с корнями (1.31) уравнения (1.30).
Таким образом, в случае двух одинаковых индуктивно свя-
занных осцилляторов рассмотренного типа могут существовать
и являются устойчивыми как синфазные, так и противофазные
синхронные колебания; к такому заключению ранее пришел
также В. П. Рубаник в цитированной выше работе [362]. В ука-
занной работе путем подробного численного анализа уравнений,
§ 2]
ВЗАИМНАЯ СИНХРОНИЗАЦИЯ МАЯТНИКОВЫХ ЧАСОВ
815
отвечающих уравнениям (1.21) настоящего параграфа, изучен
также случай осцилляторов с одинаковыми параметрами. При
этом найдены зависимости границ областей существования и
устойчивости синхронных режимов, а также амплитуд и сдвига
фаз колебаний осцилляторов от параметров системы (в том
числе от величины запаздывания в элементе связи). Установ-
лено, что режимы колебаний, близкие к указанным выше син-
фазному и противофазному режимам, существуют и устойчивы,
если отклонения параметров осцилляторов и запаздывание не
слишком велики. При наличии значительного по сравнению с пе-
риодом колебаний запаздывания противофазный режим может
стать неустойчивым для любых значений параметров.
§ 2. Взаимная синхронизация маятниковых часов
(задача Гюйгенса)
Рассмотрим поставленную в § 4 главы I задачу Гюйгенса
о взаимной синхронизации маятниковых часов, висящих на
упруго опертой платформе (рис. 11).
После приведения к безразмерной форме уравнения движе-
ния системы (см. уравнения (4.4) главы I) принимают вид
+	Ф«. »	(S-1......*).
<2Л)
dx2 и ' dx2 r dx
/=1
где обозначено:
x — &t, х0 = х/А, 2n' = k'IMG>,
»о р2	mszsA	ntsRs
~	’ Ps Ts cos^> Ps ЛЙГ C0SX>
л. I dtys d2xa \ d2Xo .	.	(2.2)
’ <Ps! ~dxr) ~ Ps ~dxr Zs<₽s +
/sco2 L s\ dx ^s! s\ dx )J
Здесь через А обозначена произвольная величина с размерно-
стью длины; удобно считать, что А имеет порядок хюах.
Задача заключается в изучении условий существования и
устойчивости периодических решений уравнений (2.1), имеющих
при ji = 0 период 2л.
Будем рассматривать нерезонансный случай, то есть предпо-
ложим, что частоты собственных колебаний маятников па не-
подвижном основании G>s ~ & в достаточной мере отличаются от
816
СИСТЕМЫ СО СЛАБО СВЯЗАННЫМИ ОСЦИЛЛЯТОРАМИ
[ГЛ. XXV
р/п, где р — частота собственных колебаний платформы, ап —
целое число; в указанном предположении величина к = р/а от-
лична от целого числа. Далее примем, что безразмерный избы-
точный момент (Ls — Rs)/IsS>2 задан выражением
(2-3)
где as и vs — положительные постоянные. Иными словами, вме-
сто модели с импульсным притоком энергии к маятнику часов
будем рассматривать модель с непрерывным притоком энергии,
подобную осциллятору Ван-дер-Поля.
Соображения в пользу возможности такой идеализации были
высказаны в цитированном выше докладе Н. Минорского [292],
который, однако, по существу не рассматривал задачу Гюйгенса,
как таковую, а ограничился изучением разобранной в конце § 1
настоящей главы задачи о двух индуктивно связанных электрон-
ных генераторах (осцилляторах Ван-дер-Поля). Вместе с тем,
несмотря на существенное различие систем уравнений (2.1) и
(1.1), как мы убедимся ниже, соображения Н. Минорского об
аналогии между указанными задачами являются справедли-
выми, правда, при выполнении некоторого соотношения между
параметрами более сложной системы, отвечающей задаче Гюй-
генса.
Приводимое ниже исследование воспроизводит один из раз-
делов нашей работы [68].
Как нетрудно убедиться, в результате неособенного линей-
ного преобразования переменных
<ps = Ds “Г Pk+s> Ф« i (Уз Уь+s) ($	1 > • •  > ^)>
k
х0= y^k+i “Ь y^k+2	12 _ । Яз (Уз “Ь Уь+з)>
(2.4)
k
= ^(ytk+i y^k+i} ^2 _ [ Уз (У s Ук+s)
s=I
система уравнений (2.1) приводится к канонической форме
du
-^- = ^зУз + рРз («= 1,  • •, 2k),
+	'	(2-5)
= - iKy2k+2 + pF2k+2,
§ 2]
ВЗАИМНАЯ СИНХРОНИЗАЦИЯ МАЯТНИКОВЫХ ЧАСОВ
817
соответствующей форме уравнений (3.3) главы V. В уравнениях
(2.5) при этом приняты следующие обозначения:
Ks = i, h+s=~P	Pk+s^j-^s (s=l, ..., k),
P2k+1-----P2fe + 2 ~ Z
n' dxa 1 К
T "diT ~ "2 V - 1
k
S=1
(2.6)
Как и в предыдущем параграфе, применим к системе (2.5)
теорему § 3 главы V о существовании и устойчивости периоди-
ческих решений квазилинейных автономных систем.
Отвечающая уравнениям (2.5) порождающая система
=	(s=l,	2k),
я о	.°	<2-7)
аУ2к + 1	.. о	alhk+2 ., о
dx	lMJ2k+l’	dx ~ -Pk + 2
допускает семейство периодических (с периодом 2л) решений
°= MJ"5*"	(s=\,...,k),
а*е I ase~ix (s = k + 1,	2k),	(2.8)
H2k+\ ~ lJ2k + 2 ~ U’
зависящее от 2k произвольных постоянных as. Эти постоянные,
как и соответствующие Х8, можно, не нарушая общности, счи-
тать попарно комплексно-сопряженными, то есть положить
S>	a& + s as rs6 S,	(2 g)
rs = I as 1 = I ak+s 1	(s= 1.k).
Кроме того, вследствие автономности системы (2.5) опять-
таки, не нарушая общности, допустимо считать, что
a* = a2j. = = а, ф* = 0.	(2.10)
Характеристические показатели Xs = ±i системы (2.7), в со-
ответствии с терминологией, принятой в § 3 главы V, являются
критическими и образуют особую ведущую группу. Критиче-
скими являются также и остальные два показателя Z.2/H-1 = &
и %2h+2 — —ih, однако при X ¥= п/2, где п — целое число, они не
входят в число особых, в том числе и ведущих особых, пока-
зателей.
В результате несложных вычислений в соответствии с фор-
мулами (3.49) и (3.50) главы V, а также равенствами (2.2) —
818
СИСТЕМЫ СО СЛАБО СВЯЗАННЫМИ ОСЦИЛЛЯТОРАМИ
[ГЛ. XXV
(2.4), (2.6) и (2.8) настоящего параграфа, получаем следующие
выражения для функций Ре:
p
[1PS Jit ^ 2 Z-" |
liPk+s = ni %sak+s +
Ps
V - 1
k
- Ъ <7/а/ + ias (1 - W4+s) а4. ,
7	(2.11)
^/О4+/-й«(* - vsa4a&+s)a&+s
/=1
(s= 1,	k),
и следующие уравнения для
ждающего решения *):
pQs = ~ a2kp.Ps -	=
определения параметров as nopo-
JTCC2&
— ла
, Ps
I %s®s "Е 2,2 — 1
\ /=1
' / k
	, pk V
I Xfe^-2fe ~Ь 2,2_।
k \
J} <?/“/ H- as (1 - vsasa&+s) a;
+ ай(1-vsa&a2J а2й =0
(s= 1, . . ., k),
PQfe + s ==	^2kl^Pk + s б- O'k+ sV'P2k ==
fe	-,
2,2__] Q+ «s (1 vsctsci£-|.s) ct^^_s
/ = i
fe	V
2,2 _ [ Qi^k+1 j "b ^-fe (1 ^fe^fe^fe) ®2fe
l-i	/
(s — 1, . . ., k).
— Jta2fe I (Xs&k + s “6
+ na&+s i i%ka2k -
Если в последней
(2.12)
системе уравнений ввести обозначения
.	Ps4/	as
bsl —-----— >	«s — ~""r— >
sl	V-l	s /vs ’
(s, /=1, . . ., k),
то она совпадет с системой (1.10) задачи о синхронизации
осцилляторов Ван-дер-Поля (см. § 1 настоящей главы).
га _ ab+s
uk + s — л/-
V Vs
(2.13)
*) Как и в § 1 настоящей главы, число критических корней ведущей осо-
бой группы здесь обозначено через 2k, в то время как в § 3 главы V это
число обозначалось через k.
= 0
§ 2]
ВЗАИМНАЯ СИНХРОНИЗАЦИЯ МАЯТНИКОВЫХ ЧАСОВ
819
Поэтому о существовании и устойчивости синхронных движе-
ний часов далее можно было бы повторить почти все, сказанное
в предыдущем параграфе о существовании и устойчивости син-
хронных колебаний осцилляторов.
Некоторое различие состоит в том, что отрицательность ве-
щественных частей корней уравнения (1.14) теперь дает лишь
необходимые условия устойчивости движения. Для получения
достаточных условий, как следует из теоремы § 3 главы V,
необходимо рассмотреть корни уравнений (3.53) указанной
главы. Таких уравнений в данном случае будет всего одно, при-
чем оно будет линейным относительно х. Дополнительное усло-
вие устойчивости движения, таким образом, сводится к нера-
венству
Re х = Re
2я
J \ dy2k +1 )
0
P 2fe
Ct2fe^2fe
(2.14)
В результате несложных вычислений при учете равенств
(2.2) — (2.4), (2.6) и (2.9) —(2.11) последнее условие принимает
ВИД
k
2«	2 ?/г/ sin Ф/ + Kak С1 ~ Vs) > °-	(2- !5)
7-1
Заметим, что для всех решений уравнений (2.12) вида
rs = 4=, ^s = qsn,	(2.16)
V vs
где каждое из чисел qs равно нулю или единице (то есть для
решений, отвечающих решениям (1.20) предыдущего парагра-
фа), условие (2.15) реально всегда выполняется, так как оно
сводится к требованию 2п > 0, иначе говоря, к условию положи-
тельности затухания.
Из сказанного выше следует, что с точностью до условия
(2.15) упоминавшиеся выше соображения Н. Минорского об
аналогии между задачей об осцилляторах Ван-дер-Поля и зада-
чей Гюйгенса являются справедливыми. Следует, конечно, иметь
в виду, что это условие может и не выполняться. Вместе с тем,
поскольку указанное условие, как легко проверить, справедливо
для всех систем, отвечающих разобранным в § 1 настоящей
главы примерам, то результаты упомянутого параграфа после
простой перефразировки могут быть отнесены и к соответствую-
щим случаям задачи Гюйгенса. Сформулируем некоторые из
этих результатов.
а)	Некоторое число k одинаковых маятниковых часов, ви-
сящих на подвижном основании с одной степенью свободы, мо-
гут ходить синхронно и синфазно, а при k четном — синхронно
820
СИСТЕМЫ СО СЛАБО СВЯЗАННЫМИ ОСЦИЛЛЯТОРАМИ
[ГЛ. XXV
и таким образом, что колебания одной половины всех часов на-
ходятся в противофазе к колебаниям другой половины часов.
б)	Часы, параметры которых достаточно мало отличаются,
всегда синхронизируются.
в)	Двое часов, обладающих одинаковыми парциальными ча-
стотами <i>s= Vmsges//s и одинаковыми параметрами as и vs, но
имеющих различные статические моменты msges и моменты
инерции ls, синхронизируются с частотой, близкой к 6, причем
колебания маятников происходят в противофазах. Сказанное
следует из того, что в рассматриваемом случае, в соответствии
с обозначениями (4.3) главы I и (2.2) настоящего параграфа,
~ А 1 / т‘£81 - 1 / ш2^е2 - А	7-7-0
Ю] = О>2 = |/  — — |/  — — (О,	Л1 — А2 —
т.е.Л v т2г2А
Pl = Р> = г cos Х = г cos %’
* 1	'2
miei , m2e2
<71=-^C0SX¥=<72 = -^rC0S%,
и поэтому, согласно (2.13), справедливы соотношения (1.22).
Нетрудно было бы показать, что при наличии малых откло-
нений парциальных частот и других параметров часов послед-
ние также синхронизируются, причем колебания маятников
близки к противофазным.
Изложенное позволяет объяснить наблюдения Гюйгенса,
описание которых мы привели в § 1 введения к настоящей книге
(см. стр. 15 и 16, а также рис. 11,6 и в).
§ 3. Синхронные колебания в системе со многими
электромагнитными возбудителями
1. Предварительные замечания. Уравнения движения. В ря-
де вибрационных устройств с электромагнитными возбудителями
колебаний приходится использовать несколько возбудителей,
тем или иным образом размещенных на колебательной системе
(рис. 6). Причины, по которым во многих случаях нельзя огра-
ничиться одним более мощным возбудителем вместо нескольких
менее мощных, примерно те же, по которым используют не-
сколько однотипных механических возбудителей (см. п. 1 § 2
главы XII, § 1 главы XV и § 5 главы XX); эти причины рас-
сматриваются также в работах [50, 84, 85]. Постановка рас-
сматриваемой задачи была приведена в § 1 первой главы книги.
Задача о взаимодействии одного электромагнитного возбу-
дителя с линейной колебательной системой, а также более слож-
ная задача о совместной работе нескольких таких возбудителей
на общую линейную нагрузку рассмотрены К. Ш. Ходжаевым
§ 3]	СИСТЕМА С ЭЛЕКТРОМАГНИТНЫМИ ВОЗБУДИТЕЛЯМИ	821
в статьях [404—406, 410]. Здесь мы и воспроизведем результаты
работы [406].
Уравнения, описывающие изменения магнитных потоков в
зазорах двухзазорных возбудителей, схематически изображен-
ных на рис. 6,6, имеют вид (см. равенства (1.1) и (1.2) главы!)
-7r-^-7r==sinT + ^((PS’	(М
-rfT - -rfT = sin т + pFs (<ps, (ps> -es) (3.2)
(s = 1,	k),
где
<₽;> V’ 0 =
- - тс К1 + M ч- ”. (1 - M <p;i - p, (I + У ч>, + ». (3-3)
Здесь <ps и <p’— безразмерные магнитные потоки в зазорах
s-ro вибратора; gs — безразмерное перемещение якоря s-ro виб-
ратора относительно сердечника из положения статического рав-
новесия, отсчитываемое в направлении увеличения того из за-
зоров, который пронизывает поток <ps; т = со/— безразмерное
время; ц — малый параметр, xs, 6S, ps и es — безразмерные пара-
метры.
К уравнениям (3.1) и (3.2) необходимо присоединить урав-
нения колебаний механической системы, с которой связаны воз-
будители. Однако эти уравнения в случае линейной колебатель-
ной системы можно не выписывать в явной форме, если считать
известными так называемые гармонические коэффициенты влия-
ния и Последние коэффициенты, уже использовав-
шиеся при решении задач о синхронизации механических вибра-
торов (см. §§ 3 и 8 главы XIV) в данном случае определим сле-
дующим образом.
Пусть в зазорах r-го вибратора к его якорю и сердечнику
приложены равные по величине и противоположные по направ-
лению заданные синфазные гармонические силы частоты v (пот)
таким образом, что сумма безразмерных амплитуд сил, прило-
женных к якорю, равна единице; пусть кроме указанных сил,
на колебательную систему не действуют никакие другие зада-
ваемые силы. Тогда безразмерная амплитуда перемещения яко-
ря s-ro вибратора относительно его сердечника при установи-
вшихся вынужденных колебаниях и угол сдвига фаз между ука-
занным перемещением и силами будут соответственно	и
Величины	(г, s = 1,..., k) определяются, оче-
видно, из решения линейной задачи; будем считать, что они
известны для всех встречающихся ниже значений v. Механиче-
822
СИСТЕМЫ СО СЛАБО СВЯЗАННЫМИ ОСЦИЛЛЯТОРАМИ
[ГЛ. XXV
скую колебательную систему будем считать в достаточной сте-
пени отстроенной от резонанса или достаточно демпфированной.
Заметим, что в приведенной выше записи уравнения движе-
ния электромагнитных возбудителей мало похожи на уравнения
квазилинейных осцилляторов. Однако если учесть, что обычно
«якорь» электромагнитного возбудителя связан с его «сердеч-
ником» системой упругих элементов, подобранных из условий
резонанса [252, 253], то в системе могут быть выделены объекты
(последние называют электромагнитными вибраторами), со-
стоящие из электромагнитного возбудителя, масс, на которых
размещены его якорь и сердечник, и связывающих их упругих
элементов. Иными словами, окажется, что мы как раз имеем
дело с системой своеобразных квазилинейных осцилляторов.
В некоторых случаях подобное подразделение более удобно,
чем принятое выше разделение системы на электромагнитную
и механическую части. Сказанное оправдывает отнесение рас-
сматриваемых систем к классу систем со слабо связанными ква-
зилинейными осцилляторами.
По своему характеру данная задача в определенном смысле
близка к задаче о движении колебательной системы с механи-
ческими вибраторами, приводимыми от синхронных электродви-
гателей (см. главу ХШ настоящей книги), — в обоих случаях
речь идет о внешней синхронизации объектов. Существенно раз-
личными, однако, являются уравнения движения объектов (воз-
будителей).
2.	У равнения для определения параметров порождающего
решения. Условия устойчивости. При сделанных предположе-
ниях отвечающая уравнениям движения порождающая система
допускает 2л-периодическое (по т) решение
о	1	*	1
^ = as~7^C0ST> % =a.-T^C0ST>
k	(3.4)
=S fr № k«:)2 - w2] - « - “,) krs) c°s - «} >
r-1
зависящее от 2k произвольных постоянных as и a*.
Для определения значений этих постоянных, которым могут
отвечать 2л-периодические решения полной системы уравнений,
обращающиеся при ц = 0 в порождающее решение (3.4), а так-
же для выяснения вопроса об устойчивости периодических ре-
шений можно воспользоваться теоремой, доказанной в § 2
главы V.
Вычисление функций Ps, фигурирующих в равенствах (2.41)
главы V, в данном случае сводится к простому осреднению пра-
вых частей уравнений (3.1) при учете (3.4). После простых
преобразований получается следующая система алгебраических
§ 3]
СИСТЕМА С ЭЛЕКТРОМАГНИТНЫМИ ВОЗБУДИТЕЛЯМИ
823
уравнений для определения постоянных а,, и а*:
ВДа,, .... ай; <
cos
1 — r.r
Г=1
+ es = 0
,	(s= 1, • • k),
где es = es/ps.
Что же касается уравнения (2.42) главы V, то оно приводит-
ся к алгебраическому уравнению 26-й степени
+ br6rsK das	dBr	t <> a st" и	gA/ das
dB*r das	dB* —-ТГ + br6rsK das
(г, s — 1, ..., 6). (3.6)
Здесь, как и ранее, 6rs — символ Кронекера, а Ьт = р/рг, где за
величину р можно принять один из параметров ps. Для устойчи-
вости периодического движения, отвечающего определенному
решению системы (3.5), достаточно, чтобы для этого решения
все корни уравнения (3.6) имели отрицательные вещественные
части; при наличии хотя бы одного корня с положительной ве-
щественной частью соответствующий режим неустойчив, а слу-
чай, когда имеются нулевые или чисто мнимые корни, требует
дополнительного исследования.
3.	Симметричный режим работы возбудителей. Нетрудно за-
метить, что уравнения (3.5) допускают решение, для которого
справедливы соотношения
а'= -as (s = 1, ..6);	(3.7)
соответствующий этому решению режим был назван К. Ш. Ход-
жаевым симметричным. Постоянные as, отвечающие симметрич-
ному режиму, определяются из системы линейных алгебраиче-
ских уравнений
2 Л frk\rs) cos
Cs (a)( ..., aft) = -O1 + -j—- У.... ,	----ar + es = 0 (3.8)
1	1 zCf
Г=1
(s = 1, .... 6),
324	СИСТЕМЫ СО СЛАБО СВЯЗАННЫМИ ОСЦИЛЛЯТОРАМИ [ГЛ. XXV
и поэтому их нахождение значительно проще, чем отыскание
иных решений системы (3.5).
Как установлено в излагаемой работе, исследование устой-
чивости симметричного режима также значительно упрощается,
ибо в данном случае уравнение 26-й степени (3.6) распадается
на два уравнения 6-й степени:
f6<rs> cos
(1"^(1-х,) -[I + г>г(1 +xr)x]6rs =0	(г,s=i,..., 6),
l4fr6("'aA-[l + 6r(l-xr)X]6rs = 0	(г, 5=1, ..., 6).	(3.9)
Корни первого из выписанных уравнений не зависят от зна-
чений as. Вследствие этого, если при определенных параметрах
системы симметричный режим оказывается неустойчивым из-за
того, что не все указанные корни имеют отрицательную веще-
ственную часть, то такой режим будет неустойчив независимо
от величин амплитуд колебаний. В частности, в данном случае
будет неустойчивым и положение равновесия, отвечающее нуле-
вым значениям напряжений, приложенных к обмоткам подмаг-
ничивания (щ = ... = eh = 0). Если же все корни первого урав-
нения (3.9) имеют отрицательные вещественные части, то, как
следует из рассмотрения второго уравнения (3.9) и равенств
(3.8), устойчивость симметричного режима всегда может быть
обеспечена путем уменьшения величин es.
Относительно несимметричных режимов в работе [406] вы-
сказывается предположение, что они практически всегда не-
устойчивы, ибо эти режимы всегда неустойчивы в устройствах
всего лишь с одним возбудителем.
4.	Случай одинаковых возбудителей. Интегральный критерий
устойчивости. В важном частном случае, когда все возбудители
одинаковы и различны лишь величины постоянных напряжений,
приложенных к их обмоткам подмагничивания, исследование
устойчивости симметричного режима еще более облегчается
благодаря вещественности корней уравнения (3.9). Действи-
тельно, учитывая, что в этом случае
[,= ... =Д==[,	«!= ... =Xfe=X,
и принимая во внимание соотношения взаимности k'"' — k^r\
— ^(sr), которым удовлетворяют гармонические коэффи-
циенты влияния (см. равенства (3.16) главы XIV), заключаем,
что элементы определителей (3.9) будут симметричными.
Из равенств (3.10) и (3.8) следуют также соотношения
(г, 5= 1, .... 6),	(3.11)
даг 3a., v ’	’	”		'
§ 3]	СИСТЕМА С ЭЛЕКТРОМАГНИТНЫМИ ВОЗБУДИТЕЛЯМИ	825
из которых вытекает существование функции D0(ai, ..., аь) та-
кой, что
-СДа,. .... «*)= ^°(ai— ak} (s=l, ..., k). (3.12)
Функция Do при этом легко находится из равенств (3.8) и
(3.12):
V V	cos	е а„	k
£>0 = /j Zj 77--77!---42— aras-ь— + 771----17 • (3.13)
и Л*	2k	2(1—z)2 r '	k J 2(1—z)2 v '
r=ls=i
Несущественная в принципиальном отношении постоянная
здесь выбрана так, что выполняется соотношение
к Т Г k
+ So +£)(<-(!-ШМ (з.н)
о Ls=l
где функции ф°, ф*° и определяются равенствами (3.4).
Из изложенного следует, что в рассматриваемом случае ус-
ловия стационарности функции Do совпадают с уравнениями
(3.8), а условия отрицательности корней первого уравнения
(3.9) совпадают с условием минимума функции Do (множитель
1 + и всегда положителен).
Таким образом, в случае одинаковых электромагнитных воз-
будителей справедлив интегральный критерий устойчивости,
дающий, однако, лишь необходимые условия устойчивости
(в том смысле, что он не касается условий отрицательности
корней второго уравнения (3.9)).
Как и в задачах о синхронизации вибраторов (см. § 9 гла-
вы ХШ и § 4 главы XIV), этот критерий можно выразить через
осредненные физические величины. С этой целью в формуле
(3.14) следует перейти к размерным переменным. Тогда при
использовании соотношений, приведенных в работе [406], полу-
чается выражение
k
Do (Ф)(0>.Ф^) = у №(0) (Ф(10), ..., Ф/°’) -	Г«®ф(<».
№ 1
Здесь Ф®, и — вычисленные в порождающем при-
ближении средние за период значения магнитных потоков, маг-
нитодвижущих сил подмагничивания в одной половине возбу-
дителя и энергии магнитного поля в системе. Иными словами,
при устойчивом симметричном режиме средние за период зна-
чения магнитных потоков Ф«о> (совпадающие с постоянными со-
ставляющими этих потоков) сообщают минимум функции Dq.
Добавление 1
МЕТОДИКА ИССЛЕДОВАНИЯ СИНХРОНИЗАЦИИ
МЕХАНИЧЕСКИХ ВИБРАТОРОВ
§ 1. Основной случай
Чтобы облегчить использование главных результатов теории
синхронизации вибраторов конструкторами и исследователями
вибрационных устройств, приведем краткую сводку этих резуль-
татов в форме методики исследования синхронизации. При этом
вначале остановимся подробно на наиболее часто встречающем-
ся случае простой (некратной) самосинхронизации дебалансных
вибраторов или инерционных вибраторов направленного дей-
ствия, связанных с линейной колебательной системой и обладаю-
щих номинально одинаковыми положительными парциальными
скоростями. Иными словами, будем считать, что мы имеем си-
стему, состоящую из твердых или упругих тел Bi, . . ., Вп (не-
сущих тел), связанных одно с другим и с неподвижным основа-
нием линейными упругими и демпфирующими элементами; на
телах установлено некоторое число k дебалансных вибраторов
или вибраторов направленного действия, приводимых от двига-
телей асинхронного типа; вибраторы и двигатели таковы, что
при установке вибраторов на неподвижном основании их валы
вращаются с номинально одинаковыми *) по абсолютной вели-
чине угловыми скоростями; при этом рассматриваются только
такие режимы, когда при установке на несущих телах все валы
вращаются в тех же направлениях, что и при «затвердевших»
(неподвижных) несущих телах.
С достаточной для подавляющего большинства приложений
точностью движение несущих тел можно определять как малые
(линейные) вынужденные колебания под действием возмущаю-
щих сил, развиваемых вибраторами при равномерном вращении
их валов по закону
+ (1.1)
где и > 0 — угловая скорость синхронного вращения, щ == ±1,
a as—неизвестные заранее постоянные (начальные фазы
*) То есть одинаковыми, если не учитывать влияния неточностей изготов-
ления вибраторов и их двигателей.
ОСНОВНОЙ СЛУЧАЙ
827
§ 1]
вращения). Обозначим соответствующий закон колебаний не-
сущих тел через
«° = а°(со/, dj, ak),	(1.2)
понимая под 2л/и-периодическим вектором «° всю совокупность
обобщенных координат этих тел.
Нахождение указанных вынужденных колебаний не пред-
ставляет принципиальных трудностей; о составлении и решении
соответствующих дифференциальных уравнений подробно гово-
рится в курсах теории колебаний.
Дело сводится, таким образом, лишь к определению началь-
ных фаз ai, ..., аь, что не может быть осуществлено в рамках
линейной теории колебаний. Правила нахождения этих фаз, со-
ответствующих устойчивым синхронным движениям, как раз и
даются теорией синхронизации механических вибраторов. В со-
ответствии с результатами, изложенными в четвертой части
книги, здесь можно воспользоваться одним из следующих спо-
собов *).
1. Интегральный критерий устойчивости синхронных движе-
ний. Этот критерий применим в случаях, когда рассматривается
движение вдали от резонанса, то есть угловая скорость синхрон-
ного вращения со в достаточной мере отличается от частот соб-
ственных колебаний несущей системы, и когда силами сопро-
тивления колебаниям можно пренебречь. Исследование здесь
проводится в такой последовательности:
а)	Составляются уравнения малых колебаний несущих тел
в предположении, что валы вибраторов равномерно вращаются
по закону (1.1). Из этих уравнений определяется закон движе-
ния несущих тел и° (со/, ai, ..., аь), соответствующий установи-
вшимся вынужденным колебаниям.
б)	Составляются выражения для потенциальной П<т> и кине-
тической Л1) энергии несущей системы, причем неуравновешен-
ные массы вибраторов считаются сосредоточенными на осях
вращения их валов.
в)	Вычисляется среднее за период значение функции Ла-
гранжа несущих тел в предположении, что эти тела движутся
по закону и° = и° (at, at, ..., ал), найденному согласно сказан-
*) Прежде чем приступать к исследованию, необходимо убедиться, что
изучаемая система не была рассмотрена ранее. В частности, следует просмот-
реть таблицу 5 (Добавление 2), в которой перечислен ряд известных резуль-
татов и даны ссылки на источники, где рассмотрены некоторые другие системы.
Необходимо также иметь в виду, что ряд классов систем рассмотрен в общей
форме (см. главу XIII и пп. 5 и 6 § 8 главы XIV настоящей книги).
Отметим также, что при решении задач о синхронизации необходимо об-
ращать особое внимание на правильность идеализации системы несущих тел:
неучет существенных степеней свободы этих тел может привести к грубым
ошибкам (см., в частности, § 3 главы XV и § 5 главы XIX).
828
МЕТОДИКА ИССЛЕДОВАНИЯ СИНХРОНИЗАЦИИ ВИБРАТОРОВ
ному в пункте а). Иными словами, находится функция
2л/<о
£>(а„ .... аА) = Ла> (а,..aA) = ^J (T(»-ri<i))0^. (1.3)
о
Фактически функция D всегда оказывается зависящей лишь
от разностей фаз as — a;-, и поэтому одну из фаз, например а/;,
можно назначить произвольно. Согласно интегральному крите-
рию устойчивые синхронные движения вибраторов соответствуют
тем значениям прочих постоянных а,—а], ..., afe_l==a‘_1, ко-
торые сообщают минимум функции D. После того как значения
а*, ..., а*_! найдены, не представляет затруднений и определе-
ние закона колебаний несущих тел w° = w°(gV, a*, ..., а^, от-
вечающего устойчивым синхронным движениям.
Примеры исследования самосинхронизации вибраторов с
применением интегрального критерия устойчивости приведены
в § 8 главы XIV, в § 1 главы XX, в § 4 главы XXII, а также в
§ 2 главы XXIII.
2. Выражения для вибрационных моментов через гармони-
ческие коэффициенты влияния. Этот способ, вытекающий из ре-
зультатов работ [407, 482], в отличие от предыдущего, применим
также и в случае, когда рассматривается движение вблизи ре-
зонанса и когда учитываются силы сопротивления колебаниям
несущих тел.
Способ основан на использовании выражений (3.19) или
(3.22) главы XIV для вибрационных моментов Ws(a,i,..., а*) и
характеризуется следующей последовательностью действий:
а)	Находятся гармонические коэффициенты влияния kuu («)>
kUV (“)’ kVU (®)> kVV} И; (®)>	(®)> Ч»’ (®) и	или
<s>), ^(<0); G^(<o), G^((0), G^(<o)
и G^^co), которые определяются следующим образом.
Пусть osusvsws — прямоугольная система координат, локаль-
но связанная с несущим телом (рис. 36, а), причем ось osws на-
правлена вдоль оси вращения s-ro вибратора (предполагаем
вначале, что вибраторы дебалансные), а начало координат os
выбрано так, чтобы центр тяжести ротора этого вибратора cs
всегда находился в плоскости uso„vs; направления осей us и vs
могут быть произвольными. Пусть, далее, к точке несущего тела
о, в направлении оси о,«; приложена гармоническая сила еди-
ничной амплитуды с перидом 2л/со и, кроме этой силы, на коле-
бательную систему не действуют никакие другие задаваемые
силы. Тогда амплитуда проекции перемещения точки os на ось
при установившихся вынужденных колебаниях и угол
ОСНОВНОЙ СЛУЧАЙ
829
§ I]
сдвига фаз между указанным перемещением и силой будут со-
ответственно равны	и ф/'*' (а).
Иными словами, если да несущую систему в точке о, дей-
ствует только одна задаваемая сила ij cos a>t (ij — единичный
вектор оси OjUj), то проекция перемещения точки os на os«s
в режиме установившихся колебаний будет
= kuu (“) C0S № - № (“)]•
Аналогичным образом величины (и) и ф^> (а) — соответствен-
но амплитуда и сдвиг фазы проекции перемещения точки os на
ось osvs при действии единичной гармонической силы периода
2л/а на точку Oj в направлении OjU и т. д.
Вместо введенных коэффициентов часто удобно пользовать-
ся величинами	и G^, .... G^\ связанными с
ними посредством соотношений
((d) = kuu (a) cos ф<£> (а),	((d) =	(«) cos ф<£> (а),
G^) (и) =	(a) sin ф^> (а), . . .,	(а) =	(a) sin ф^> (а).
По своему физическому смыслу величины |/С| и | G | пред-
ставляют собой амплитуды соответствующих «косинусных» и
«синусных» составляющих перемещения. Величины	.
k1-^ неотрицательны, а	и G^ и G^ могут
быть любыми действительными числами. Все введенные коэф-
фициенты влияния связаны соотношениями взаимности вида
W (®) =	((d), • • •, G^ (а) = G^ (a)>
G(£> (®) =	(a), G^ (a) = G^ (a),
что, естественно, значительно облегчает их вычисление.
В соответствии с определением, для нахождения гармониче-
ских коэффициентов влияния прежде всего необходимо соста-
вить дифференциальные уравнения малых колебаний несущих
тел под действием соответствующих сил, а затем найти решения
этих уравнений, отвечающие установившимся вынужденным ко-
лебаниям. После этого гармонические коэффициенты влияния
несложно вычисляются при использовании кинематических соот-
ношений, связывающих смещения осей вибраторов с обобщен-
ными координатами несущих тел.
В случаях, когда рассматривается движение вдали от резо-
нанса и когда силы сопротивления колебаниям не учитываются,
число подлежащих определению гармонических коэффициентов
влияния уменьшается в два раза, так как при этом все коэффи-
830
МЕТОДИКА ИССЛЕДОВАНИЯ СИНХРОНИЗАЦИИ ВИБРАТОРОВ
циенты G равны нулю; значительные упрощения вносятся так-
же при наличии «симметрии» рассматриваемой системы и при
независимости колебаний по некоторым группам обобщенных
координат от колебаний по другим группам координат.
В случае «поршневых» вибраторов (рис. 36,6) играют роль
лишь коэффициенты и или и соответствую-
щие направлениям действия возмущающих сил этих вибраторов.
Для сложных систем гармонические коэффициенты влияния мо-
гут быть найдены экспериментальным путем, на основе их опре-
делений как «откликов» системы на действие соответствующих
возмущающих сил.
б)	Составляются выражения для вибрационных моментов
в одной из следующих двух форм:
1)	для дебалансных вибраторов
k
Ws =	[kuu Sin (“s - “/ + CO +
/=1
+ cos (as - a, +	- ask^ cos (as - a, +	+
+ a!ask№ sin К - “/ + 'Ф(Л]>
k	(1.4)
Ws =	[«> - a, G^ +
+ °М5) + sin (as - “/) +
+ (Gi/US) +	- °	+ °l°sG^) C0S (“s - “/)]•
где msEs — статические моменты неуравновешенных роторов;
2)	для поршневых вибраторов
*
sin (“s - “/ + 'Фй))>
J;1	(i.5)
= aslns^— 2 mi^i [C? Sin (“s - “/) + G(uu C0S (“S - “/)]>
/=1
где ms — массы, 2es — ходы поршней, а числа as указывают на
направления вращения соответствующих реальных или фиктив-
ных кривошипов вибраторов (см. § 3 главы XIV).
в)	Составляются уравнения
a^a)(<^) = W+^(“i............а*)	= ° (s=1> d-б)
где и Д° —средние значения соответственно вращающих
моментов двигателей и моментов сил сопротивления на валах
§ 1]
ОСНОВНОЙ СЛУЧАЙ
831
вибраторов (см. формулы (6.8) и (6.9) главы XIII). Из этих
уравнений определяются значения начальных фаз ai, ..., ал, ко-
торым могут отвечать синхронные движения вибраторов. Значе-
ния фаз находятся из указанных уравнений лишь с точностью до
произвольной постоянной, или, что то же самое, одна из фаз, на-
пример ait, может быть взята произвольно.
Если силы сопротивления в колебательной части системы не
учитываются, то для вибраторов с одинаковыми парциальными
скоростями
<rsL(“' (crsco) = Rs (co) (s = 1.k),
и уравнения (1.6) существенно упрощаются:
№s(a,.....aft) = 0 (s = 1, ..., k).
г)	Для каждой системы значений фазана*, .... aft_1 =
найденных из уравнений (1.6), рассматривается алгебраическое
уравнение k— 1-й степени
d(Wx-Wk) ,
dat
d(W2~Wk)
да{
djWi-Vf'k)
da2
d(W2-Wk)
da2 '
d(Wt-Wk)
dah-t
d(W2-Wk)
dak-i
= 0. (1.7)
3a,	delj	' ‘ ’ дсц_,
Устойчивые синхронные движения отвечают тем решениям а, =
= а*, ..., ak_I=a'k_i уравнений (1.6), для которых все корни
уравнения (1.7) имеют отрицательные вещественные части; при
наличии хотя бы одного корня с положительной вещественной
частью соответствующее движение неустойчиво, а в случае нуле-
вых или чисто мнимых корней необходимо дополнительное, обы-
чно достаточно сложное исследование.
д)	После того как отобраны значения фазана*, .	—
=а*_!, отвечающие устойчивым синхронным движениям вибра-
торов, можно составить уравнения малых колебаний несущих
тел под действием возмущающих сил, развиваемых вибраторами
в этих движениях, а затем найти и соответствующие вынужден-
ные колебания несущих тел.
Как видно из изложенного, при использовании данного спо-
соба в его аналитическом варианте приходится решать несколь-
ко систем линейных дифференциальных уравнений, тогда как
при использовании интегрального критерия устойчивости необ-
ходимо решить всего одну, хотя и несколько более сложную
систему таких уравнений. В конкретных случаях, по-видимому,
832
МЕТОДИКА ИССЛЕДОВАНИЯ СИНХРОНИЗАЦИИ ВИБРАТОРОВ
следует отдавать предпочтение одному из этих способов, в зави-
симости от особенностей рассматриваемой системы.
Примеры использования данного способа приведены в п. 1
§ 8 главы XIV и в § 3 главы XV.
3. Непосредственное осреднение дифференциальных уравне-
ний движения вибраторов. Этот способ является наиболее уни-
версальным; он, в частности, пригоден и в случае, когда в числе
вибраторов имеются планетарные. Однако, в отличие от двух
предшествующих способов, рассматриваемый здесь способ тре-
бует составления не только уравнений вынужденных колебаний
несущих тел под действием заданных (с точностью до фазовых
сдвигов) возмущающих сил, но и полных уравнений движения
вибраторов с учетом обратного воздействия колебаний несущих
тел на движение вибраторов.
Рассматриваемый способ заключается в следующем*).
а)	Составляются уравнения движения системы «несущие
тела + вибраторы» в целом. Обычно эти уравнения удобно со-
ставлять в форме уравнений Лагранжа второго рода, как это
сделано, например, в § 2 главы XIII.
б)	Уравнения движения несущих тел решаются в предполо-
жении, что валы вибраторов вращаются по закону (1.1) с зара-
нее неизвестными начальными фазами oti, ..., а&. При этом на-
ходится лишь периодическое решение указанных уравнений с пе-
риодом Т = 2л/и, отвечающее установившимся вынужденным
колебаниям несущей системы, то есть решение (1.2).
в)	Уравнения движения вибраторов записываются в форме
;Л + ^(ф5-ал) = фХч’1- Фй’ “> “> “> “О (Ь8)
(s=l, ..., k)
(см., например, первые k уравнений (2.44) главы XIII), после
чет о их правые части осредняются за период Т = 2л/ш в пред-
положении, что координаты <ps и и изменяются по закону (1.1) и
(1.2), отвечающему исходному приближению <р° и и°. При этом
образуются функции
2л/о>
Л(«1.....J ФХФ1> •••’ Фй’ “°’	(L9)
о
(s *= 1, . . ., k).
г)	Из уравнений
Ps(a1; ..., aft) = О (s=l....k)	(1.10)
*) Здесь для упрощения излагается вариант способа, относящийся к слу-
чаю, когда движение происходит вдали от резонанса.
§ 21
КОЛЕЕ СЛОЖНЫЕ СЛУЧАЙ
833
находятся значения фаз а, — а*, ..., ак — a*k, которым могут от-
вечать синхронные движения вибраторов.
д)	Составляется алгебраическое уравнение /г-й степени
дРх -ч-*— V. ОИ] дРг дсп	dPj да2 дР2 	К иССр	dPi dah дР2 dah	= 0,	(1.11)
dPk	dPk	dPk %		
да\	да2	dak ’°		
по характеру корней которого судят об устойчивости синхрон-
ных движений. В случае задачи о внешней синхронизации опре-
деленной комбинации фаз = а*, .ak — a*k отвечает устойчи-
вое синхронное движение, если все корни уравнения (1.11)
имеют отрицательные вещественные части. В случае задачи о
внутренней синхронизации (в том числе и в задаче о самосин-
хронизации) для устойчивости достаточна отрицательность ве-
щественных частей лишь k— 1-го корня уравнения (1.11): один
из корней этого уравнения в указанном случае непременно ра-
вен нулю.
В рассматриваемом случае задачи о самосинхронизации де-
балансных вибраторов или инерционных вибраторов направлен-
ного действия с одинаковыми парциальными угловыми скоро-
стями выражения (1.9) упрощаются: в них отсутствуют разности
осредненных моментов, развиваемых двигателями, и моментов
сил сопротивления движению вибраторов; кроме того, в указан-
ных выражениях могут быть опущены коэффициенты ks.
е)	Значения фаз «, = «’, afe = а^, отвечающие устойчивым
синхронным движениям вибраторов, подставляются в выраже-
ния (1.2), и тем самым определяются (в исходном приближе-
нии) соответствующие законы колебаний несущих тел.
Описанная процедура исследования фактически выполнена
в §§ 4 и 6 главы ХШ и для более частной системы, но с соуда-
ряющимися несущими телами — в § 4 главы XXI; в последнем
случае интегрирование при осреднении по формуле (1.9) следует
понимать в обобщенном смысле.
§ 2.	Более сложные случаи
В случаях, отличных от рассматриваемого в § 1, по-прежнему
важнейшим этапом является составление уравнений
.....«j = 0	(з=1.....k)	(2.1)
27 И. И. Блехмав
834
МЕТОДИКА ИССЛЕДОВАНИЯ СИНХРОНИЗАЦИИ ВИБРАТОРОВ
для определения начальных фаз вращения вибраторов ац ..аь
в выражениях (1.1) и (1.2). После того как решения этих урав-
нений найдены, для отбора тех решений, которым отвечают ус-
тойчивые синхронные движения вибраторов, как и выше, служит
алгебраическое уравнение (1.11). Поэтому остановимся лишь
на особенностях составления уравнений (2.1). Отметим прежде
всего, что в случае, когда справедливы все ограничения, указан-
ные в начале § 1, за исключением предположения об одинако-
вости парциальных скоростей вибраторов и о том, что двигатели
вибраторов — асинхронного типа, уравнения (2.1) имеют вид
Л(«1................(а*>	^м)-^(®)- ^(«1.......«л)]	= 0
(s=l,	(2.2)
где и ^ — соответственно средние значения моментов, пе-
редаваемых от двигателей, и моментов сил сопротивления дви-
жению вибратора, легко вычисляемые по формулам (6.8) и (6.9)
главы XIII. Выражения же для вибрационных моментов IVS, фи-
гурирующие в уравнениях (2.2), совершенно не зависят от пар-
циальных скоростей вибраторов и от характера двигателей. По-
этому для нахождения Ws может быть применен любой из пер-
вых двух способов, указанных в предыдущем параграфе. При
этом следует иметь в виду, что в случае использования инте-
грального критерия устойчивости эти моменты можно найти по
В случае же, когда используется способ непосредственного
осреднения уравнений движения вибраторов, уравнения (2.2)
получаются автоматически (см. равенства (1.9)). Заметим, далее,
что этот способ пригоден также, если несущая система нели-
нейна*). В этом случае, однако, отыскание закона колебаний
несущих тел (1.2) является более затруднительным; к тому же
каждой определенной системе значений начальных фаз oti, ..., аь
здесь могут отвечать несколько различных законов движения
несущей системы.
В других случаях при составлении уравнений (2.1) следует
руководствоваться изложенным в главах XIII и XIV настоящей
книги, где приведены также соответствующие примеры (см. § 8
главы XIV).
*) Для изучения синхронизации вибраторов, связанных с нелинейной си-
стемой, при соблюдении прочих ограничений § 1 может быть использован
также и интегральный критерий устойчивости, однако «потенциальная функ-
ция» D в этом случае вычисляется несколько более сложным образом (см.
§ 4 главы XIV).
§ 3] ОБ ИССЛЕДОВАНИИ СТАБИЛЬНОСТИ РАБОЧЕГО РЕЖИМА 835
§ 3.	Об исследовании стабильности рабочего режима
колебаний
Для возможности практического использования самосинхро-
низирующихся или «нежестко» принудительно синхронизирован-
ных вибраторов еще недостаточно существования и устойчивости
требуемого синхронного режима движения системы при номи-
нальных значениях параметров вибраторов и их двигателей. Не-
обходимо также, чтобы этот режим был в достаточной мере
слабочувствителен («стабилен») по отношению к разбросу одно-
именных параметров вибраторов и двигателей вследствие неточ-
ностей их изготовления. Методика соответствующего исследова-
ния и расчетные формулы для ряда частных случаев приведены
в главе XVI, а также в п. 6 § 2 главы XX.
УСЛОВИЯ УСТОЙЧИВОСТИ важнейших
№
п/п
Краткое описание системы *)
Динамическая схема, обозначения **)
1	Произвольное число одинако-
вых дебалансных вибраторов,
установленных на абсолютно
твердом теле с одной «поступа-
тельной» степенью свободы
2	Такие же вибраторы, одина-
ковым образом установленные
па абсолютно твердом теле
с одной «винтовой» илн «пово-
ротной» степенью свободы
Два одинаковых дебалансных
вибратора, симметрично уста-
новленные на мягко амортизи-
рованном твердом теле, которое
может совершать плоские коле-
бания; осн вибраторов парал-
') О применении приведенных схем в различных устройствах см. таблицу 2 на стр.
Добавление
СИНХРОННЫХ ДВИЖЕНИЙ ВИБРАТОРОВ В НЕКОТОРЫХ
КОЛЕБАТЕЛЬНЫХ СИСТЕМАХ1)
Таблица 5
	Характер синхронного движения (в первом приближении)		Условия устой- чивости синхрон- ного движе- ния ****)	Разделы данной книги или публика- ции, в ко- торых рас- смотрена система	Примечания
	вибраторов ***)	несущих тел			
	а> 1ЧР11 = Гчр2 1 = • • • ••• = К1 = М/	Гармониче- ские посту- пательные колебания	со < р = Vс/М (р — частота собственных колебаний системы)	Глава XIII, § 8; § 13, п. 5, § 16, пп. 2 и 4; [44, 46, Ю]	1.	Результат справедлив и для вибраторов на- правленного дей- ствия (спаренных дебаланспых и «поршневых»), 2.	При числе вибраторов k> 2 в системе могут существовать и другие синхрон- ные движения. 3.	О более об- щих системах данного типа см. § 13 главы XIII, примечание к п. 10, а также работы [44, 46, 482, 483]
	б) |Ф1| = |<Р2|=--- • • • = 1 Ф*/2 1 = = | ф/г'2+l + л I = ... = |	+ л | = со/ (k четное)	Отсутствие колебаний	со > р = Vс/М		
	То же, что и в п. 1, а	Г армониче- ские винто- вые колеба- ния относи- тельно оси Z	со < р = У с/М (р — частота собственных колебаний системы)		
	То же, что и в п. 1,6	Отсутствие колебаний	со > р		
	а) <р, = ± и/, q>2 = + (<о/ + л) (роторы вибраторов вращаются в про- тивоположных на- правлениях) 340-358 и главы ХХ-ХХ	Прямоли- нейные по- ступатель- ные гармо- нические ко- лебания в направлении оси Оу с ам- плитудой До = 2гпе/М III книги; сно	Режим устойчив при любых соче- таниях пара- метров, если г=>0 гкп *), *»), ***) п	>***) иомеще	1. О более об- щих системах с плоскими коле- баниями несу- щего твердого тела см. главы XIII и работы [54, 57] ны на стр. 862 и 863.
838
УСЛОВИЯ УСТОЙЧИВОСТИ
№ п/п	Краткое описание системы *)	Динамическая схема, обозначения **)
3
лельны, лежат в одной плоско-
сти с центром тяжести тела О
и удалены от него на одинако-
вые расстояния г
4
Та же система, что и в п. 3,
но роторы вибраторов связаны
пружиной жесткости с, присо-
единенной иа расстояниях а от
осей вибраторов
5
Та же система, что и в п. 3,
ио роторы вибраторов либо свя-
заны упругим или электриче-
ским валом, либо приводятся
во вращение от одинаковых и
одинаково установленных син-
хронных двухполосных электро-
двигателей с жесткостью харак-
теристики в рабочей точке
d£*/d6= - с
УСЛОВИЯ УСТОЙЧИВОСТИ
839
Таблица 5 (продолжение)
	Характер синхронного движения (в первом приближении)		Условия устой- чивости синхрон- ного движе- ния **•*)	Разделы дайной КИНГИ или публика- ции, в ко- торых рас- смотрена система	Примечания
	вибраторов ***)	несущих тел			
	б) ф] == ± со/, ф2 = ± СО/ (роторы вибраторов вращаются в оди- наковых направле- ниях)	Круговые поступатель- ные колеба- ния с ампли- тудой г0 = 2те!М	Mr2 I	Глава ХШ, § 16, п. 2; [54, 57]	2. О системе, в которой пло- скость вращения центров тяжести роторов не сов- падает с плоско- стью главных цен- тральных осей инерции хОу, а сдвинута па- раллельно этой плоскости на рас- стояние с, при- чем твердое тело совершает про- странственные колебания, см. п. 8 § 2 главы XX и работу [241]
	В) ф| = ± со/, Фз = ± (а/ + Л) (роторы вибраторов вращаются в оди- наковых направле- ниях)	Поворотные гармониче- ские коле- бания с угловой амплитудой 2mer Фо = j	-^<2		
	а) То же, что и в п. 3, а		Mr2 Мса2	Глава XIV, § 8, п. 1	
			I	m2e2co2		
	б) То же, что и в п. 3, б		Mr2 „ I > __ Mca2 m2e2co2		
	в) То же, что и в п. 3, в		—y—<2 — Mca2 m2e2co2		
	а) То же, что и в п. 3, б		c> — 1 m2e2(o2 2 M X x(T-2)	Глава ХШ, § 16, п. 6; [68]	
	б) То же, что и в п. 3, в		c< - 1 m2e2co2 2 M X x(T-)		
840
УСЛОВИЯ УСТОЙЧИВОСТИ
№
п/п
Краткое описание системы *)	Динамическая схема, обозначения
6
Та же система, что и в п. 3,
но твердое тело связано с непо-
движным основанием симме-
тричной системой упругих эле-
ментов с жесткостями сх>
Су И Сф (Слф я Суф я 0)
Рх“ М ’ ру = М ’ P'f= I ’
_ Рх _ Ру	Рф
7
Та же система, что и в п. 3,
но с твердым телом связана
посредством упругих элементов
жесткости с и демпфирующих
элементов с коэффициентом
сопротивления 0 дополнитель-
ная симметрично расположен-
ная масса
М',1
•У
со^О
р2 = М* -= м1^2— 2п = -2-
Р М* ’	Л4, + Л42 ’ Z М*
УСЛОВИЯ УСТОЙЧИВОСТИ
841
Таблица 5 (продолжение)
	Характер синхронного движения (в первом приближении)	Условия устойчивости синхронного Движе- ния ****)	Разделы данной книги или публика- ции, в ко- торых рас- смотрена система	Примечания
	вибраторов ***)	несущих тел			
	а) То же, что и в п. 3, а, но амплитуда поступательных колебаний вдоль оси Оу . 2те.	1 X к-||	_!	+ ^-i i2-i Mr2 1 +	х	<0 / Ч-i	Глава XIII, § 16, п. 2; [68]	
	б) То же, что и в п. 3, б, но траекторией поступатель- ных колебаний является эл- липс с полуосями . 2me	1 Лх =	гтч	г> М |Л2-1| _ 2me	1 М |%2-1|	_—J	 %2 - 1	Л2 - 1 Л	У '	>0 /	Л2-1		
	в) То же, что и в п. 3, в, но угловая амплитуда пово- ротных колебаний 2тег	1 Фо ' К-1|	_ V — 1	— <м а, —	1 о> е- + ~ 7 Ц	1 с<	1		
	а) То же, что и в п. 3, а (кроме формул для амплитуд)	То же, что и в п, 3, а	Г лава XV, § 3; [92]	О системах, в которых к телу Л11 при- соединены бо- лее сложные колебательные системы, см. § 3 главы XV, а также [92]
	б) То же, что и в п. 3, б (кроме формул для амплитуд)	^>2- / 2(%2—1) М2		
		(Z2-l)2 + 4nf (Л = p/со, П] = п/со)		
	в) То же, что и в п. 3, в (кроме формул для амплитуд)	^-<2- I 2(Л2—1) М2		
		(Л2 — 1)2 + 4n2 М,		
842
УСЛОВИЯ УСТОЙЧИВОСТИ
№
п/п
Краткое описание системы *)
Динамическая схема, обозначения *•)
8
Та же система, что и в п. 3,
но оси вибраторов не лежат
в одной плоскости с центром
тяжести тела О
9 Та же система, что и в п. 3,
но вибраторы не простейшие
дебалансные, а моногармониче-
ски# вибраторы направленного
действия; линии действия воз-
мущающих сил лежат в одной
плоскости с центром тяжести
тела О и равноудалены от него
УСЛОВИЯ УСТОЙЧИВОСТИ
843
Таблица 5 (продолжение)
Характер синхронного движения (в первом приближении)		Условия устойчивости синхронного движе- ния ****)	Разделы данной книги или публика- ции, в ко- торых рас- смотрена система	Примечания
вибраторов ***)	несущих тел			
ф1 = ± со/, <р2 “ + (®/ + я) (роторы ви- браторов вра- щаются в про- тивоположных направлениях)	Прямоли- нейные посту- пательные гар- монические ко- лебания с ам- плитудой Ло = 2те/М, направленные вдоль оси Оу (перпендику- лярно плоско- сти осей ви- браторов 0i02)	Режим устойчив при любых сочета- ниях параметров, если г Ф 0	Глава XX, § 1. п. 2; [56. 68]	О стабиль- ности колеба- ний тела см. § 2 главы XX, а также [56]
a) qpi == ± со/, ф2 “ ± со/	Прямоли- нейные посту- пательные гар- монические ко- лебания с ам- плитудой . 2тг направленные вдоль оси Оу (перпендику- лярно плоско- сти осей ви- браторов)	^->1	Глава XX, § 1, п. 2; [68]	
б) q>t = ± со/, ф2 “ ± (®/ + л)	Поворотные гармонические колебания с угловой ам- плитудой 2т ег Фо — J	^-<1		
844
УСЛОВИЯ УСТОЙЧИВОСТИ
№
п/п
Краткое описание системы *)
Динамическая схема, обозначения **)
10
Два одинаковых дебалансных
вибратора, установленных на
одной из масс цепной двухмас-
сной колебательной системы
11
Та же система, что и в п. 10,
ио массы могут перемещаться
во взаимно перпендикулярных
направлениях и вибраторы уста-
новлены на «внешней» массе
УСЛОВИЯ УСТОЙЧИВОСТИ
845
Таблица 5 (продолжение)
	Характер синхронного движения (в первом приближении)		Условия устойчивости синхронного движе- ния ****)	Разделы данной книги или публика- ции, в ко- торых рас- смотрена система	Примечания
	вибраторов ***)	несущих тел			
	а) | ср, | = = | ф2 | = ш/	Г армопиче- ские колеба- ния обеих масс	(p2-<o2)/(pf-co2) X X (^2 — W2) > 0, где р = с2/М2, a pj и р2 — корни уравнения р4 _ „2 |'_О_ +	+. р И \МХ _С2_\	_e,i:2 М2 к А1,Л12	Г лава XIV, § 8, п. 6; глава XV, § 3; [481]	О более об- щих цепных системах с произвольным числом масс и произвольным числом любым образом раз- мещенных де- балансных ви- браторов см. п. 6 § 8 главы XIV, а также [481, 366]
	б) 1 <₽! 1 = = | фг + Я| = СО/	Отсутствие колебаний			<0		
	а) ф| = ± со/, ф2 = ± со/ (роторы ви- браторов вра- щаются в оди- наковых на- правлениях)	Г армониче- ские колеба- ния массы Af2 в направлении осей х и у и массы М[ — в направлении оси X	А + - - - 1 - 1 +	Г лава XXII, § 3; [361, 68, 482]	
	б) ф, = ± со/, ф2 = ± (со/ 4-л) (роторы ви- браторов вра- щаются в оди- наковых на- правлениях)	Отсутствие колебаний	1 9 Л2 — 1 М 1 +	9	< 0 %2-1		
	В) ф| = ± со/, ф2 -- + со/ (роторы ви- браторов вра- щаются в про- тивоположных направлениях)	Г армониче- ские колебания обеих масс только в на- правлении оси X	1 Л2 - 1 М2 %2-1		
	г) ф! = ± со/, ф2= + (со/ +л) (роторы ви- браторов вра- щаются в про- тивоположных направлениях)	Масса Alj неподвижна, масса М2 ко- леблется толь- ко в направле- нии оси у	1 Л2 - 1 М2 Х2-1		
846
УСЛОВИЯ УСТОЙЧИВОСТИ
№
п/п
Краткое описание системы *)
Динамическая схема, обозиачеиия •*)
12
Два одинаковых дебалансных
вибратора, установленных на
твердом теле с одной «посту-
пательной» и одной «поворот-
ной» степенями свободы; тело
связано с неподвижным осно-
ванием системой упругих эле-
ментов с жесткостями сх и
10 — момент инерции тела относительно
«оси поворотов» Оь
Рх-ех/М, P^c^/Iq,
hx~Px/{^>	~ Рф/®
13
Два одинаковых дебалансных
вибратора, установленных на
мягко амортизированном твер-
дом теле с шестью степенями
свободы; оси роторов вибрато-
ров совпадают с одной из глав-
ных центральных осей инерции
тела; плоскости вращения цен-
тров тяжести роторов равно-
удалены от центра тяжести
тела
УСЛОВИЯ УСТОЙЧИВОСТИ
847
Таблица 5 (продолжение)
-	Характер синхронного движения (в первом приближении)		Условия устойчивости синхронного движе- ния **♦*)	Разделы данной книги или публика- ции, в ко- торых рас- смотрена система	Примечания
	вибраторов ***)	несущих тел			
	<pt — ± со/, (р2 = Ч" СО/ (роторы ви- браторов вра- щаются в про- тивоположных направлениях)	Прямолиней- ные поступатель- ные гармониче- ские колебания вдоль оси Ох с амплитудой . 2те, 1	+ - >>	V - е ьэ 1 1 ~ - “ + А	Г лава XXII, §2; [68]	
	ф|’= ± со/, <f>2 = ± СО/ (роторы ви- браторов вра- щаются в оди- наковых на- правлениях)	Круговые по- ступательные ко- лебания парал- лельно плоско- сти xOz с ампли- тудой 2те г°—лГ	Мг2 2 — >2 1г"ш„ 1х1г ) \ Ix + Iz)	Глава XIV, § 8, п. 3; [68]	О более общем слу- чае произ- вольного числа деба- лансных или «качаю- щихся» ви- браторов см. п, 5 § 8 главы XIV и работы [242, 245]
848
УСЛОВИЯ УСТОЙЧИВОСТИ
№
п/п
Краткое описание системы *)
Динамическая схема, обозначения **)
14
Та же система, что и в п. 13,
но оси вибраторов параллельны
плоскости xOz, равноудалены
от нее и наклонены под углом
К плоскости хОу (с^Оог —
плоскость вращения центров
тяжести роторов; оси Oxyz—
главные центральные оси инер-
ции тела)
Вид А (повернуто)
15
Та же система, что и в п. 13,
но вибраторы не простейшие,
дебаланспые, а моногармони-
ческие вибраторы направлен-
ного действия; линии действия
возмущающих сил вибраторов
oiOj и о2о2 параллельны плоско-
сти xOz, равноудалены от нее
и наклонены под углом 0 к пло-
скости хОу
УСЛОВИЯ УСТОЙЧИВОСТИ
849
Таблица 5 (продолжение)
	Характер синхронного движения (в первом приближении)		Условия устойчивости синхронного движения ****)	Разделы данной книги или публика- ции, в ко- торых рас- смотрена система	Примечания
	вибраторов ***)	несущих тел			
	<р, = ± со/, ф2= + (со/ + л) (роторы ви- браторов вра- щаются в про- тивоположных направлениях)	Прямоли- нейные посту- пательныегар- монические ко- лебания с ам- плитудой „ 2те Ао==~м~' параллельные линии 00*	Режим устойчив при любых сочетаниях па- раметров (если г=^=0)	Г лава XX, § 1, п. 2; [242, 245]	1. Данная система предста- вляет собой простран- ственный вариант си- стемы п. 8. 2. О той же системе с присоеди- ненным к телу маят- ником см. работы [242, 245]
	а) |<р, | = = 1 ф2 | = (О/	Прямоли- нейные посту- пательные гар- монические ко- лебания с ам- плитудой „ 2пгъ параллельные линиям дей- ствиям возму- щающих сил вибраторов И O2O2	Mr2 I,.		) \	Ix cos2 р + ly sin2 р/	Г лава XIV, § 8, п. 2; [68]	Данная система предста- вляет собой простран- ственный вариант системы п. 9
	б) |ср, 1 = = | ф2 + Л I = со/	Поворотные гармонические колебания от- носительно не- которой оси, лежащей в плоскости xOz	Mr2		
850
УСЛОВИЯ УСТОЙЧИВОСТИ
№
п/п
Краткое описание системы *)
Динамическая схема, обозначения **)
17
Два одинаковых моногармони-
ческих вибратора направлен-
ного действия, установленных
на твердом теле, которое свя-
зано с неподвижным основанием
симметричной системой упругих
элементов и может совершать
плоские колебания; линии дей-
ствия возмущающих сил вибра-
торов совпадают и удалены от
центра тяжести тела на рас-
стояние h
2 Сх 2 _ СФ
рх “ м ’ P<f м
. _Р* т _
A.v- ю , Аф- ю
Два одинаковых коаксиаль-
ных вибратора, установленных
на твердом теле, которое может
поворачиваться и поступательно
смещаться относительно осн,
параллельной плоскостям вра-
сх — жесткость при смещении тела
вдоль оси X,
Сф — жесткость при повороте тела
относительно той же оси,
2 Сх 2 СФ
Рх^ М ’ I 1
, _ Р* , Р<Р
УСЛОВИЯ УСТОЙЧИВОСТИ
851
Таблица 5 (продолжение)
	Характер синхронного движения (в первом приближении)		Условия устойчи- вости синхронного движения ****)	Разделы данной книги или публика- ции, в ко- торых рас- смотрена система	Примечания
	вибраторов ***)	несущих тел			
	а) |<Р1 | = = 1 ф2 + Л 1 = b>l	Отсутствие ко- лебаний	^-1 + + ^_L_<0 1 4-'	Глава XIV, § 8, п, 4; [68, 83]	О стабиль- ности дан- ного режима см. § 3 главы XXIII, а также [68, 83]
	б) |Ф11 = — 1 <р2 | = со/	Плоские непо- ступательные ко- лебании	+ । ~ । - - - + V о		
	а) (р; = ± (at, <р2 = ± (at (роторы вибра- торов вращаются в одинаковых направлениях при наблюдении со стороны внешних нормалей к ци- линдру)	Поступатель- ные и поворот- ные гармониче- ские колебания по закону 2m е ,, Х= ± —гр X М X	—тг sin со/, 1 -% 2те.г ,, Ф =	! X X	—5- cos со/ 1-^	+ - _ ” 1 - 1 — + А о	Глава XXII, § 4; [427, 68]	
	б) <р, = ± со/, ф2 = ±	+ л) (направления вращения рото- ров такие же, как в и. а)	Отсутствие ко- лебаний	+ - ~ 1 ~ 1 — 6ЬЭ	“Г V О		
852
УСЛОВИЯ УСТОЙЧИВОСТИ
№ п/п	Краткое описание системы *)	Динамическая схема, обозначения **)	
17	щения центров тяжести рото- ров вибраторов и равноудален- ной от этих плоскостей		
18	Два одинаковых дебалансных вибратора, установленных на мягко амортизированном твер- дом теле с шестью степенями свободы; оси Охуг — главные центральные; оси вибраторов на- клонены под углом у к плоско- сти хОу	с,. 4- '< со~0\	1	i:» u / 1	\ А е	
УСЛОВИЯ УСТОЙЧИВОСТИ
853
Таблица 5 (продолжение)
	Характер синхронного движения (в первом приближении)		Условия устойчи- вости синхронного движения ****)	Разделы данной книги илн публика- ции, в ко- торых рас- смотрена система	Примечания
	вибраторов ***)	несущих тел			
	В) <Pi = ± (й/, (р2 :=: 4— 65/ (направления вращения рото- ров противопо- ложны в смысле, указанном в п. а)	Поворотные гармонические колебания с ам- плитудой _ 2/пег j	X х ||-ЧГ колебания вдоль оси х отсут- ствуют	V + с') 9- — << —	1	1 +		
	г) ф! = ± со/, ф2 = + (со/ + л) (направления вращения рото- ров противопо- ложны в смысле, указанном в п. а)	Поступатель- ные гармониче- ские колебания вдоль оси х с ам- плитудой М Х X I	9 1’ |1-^| поворотные ко- лебания отсут- ствуют	i	4- is 1 7	1 - 1 — е		
	ф, = ± со/, ф, = ± со/	Винтовые гар- монические коле- бания относи- тельно оси z; ам- плитуда верти- кальной соста- вляющей Л 2/necosv - м = угловая ампли- туда . 2/neasiny ф = 12.	Ма2 п Мс2 , <2 + ~Г~ + * z	‘х М (с2 + a2 cos2 у) ly sin2 у	Глава XIV, § 8, п. 5; [241, 242, 482]	Об анало- гичных системах с произ- вольным числом вибраторов см. работы [170, 171]; о стабиль- ности ре- жима см. [172, 173]
854
УСЛОВИЯ УСТОЙЧИВОСТИ
№
п/п
Краткое описание системы *)
Динамическая схема, обозначения •*)
19
Два одинаковых бигармони-
ческих дебалансных вибратора,
симметрично расположенных на
мягко амортизированном твер-
дом теле, которое может совер-
шать плоские колебания. Пло-
скости 1—1' и 2—2' осей ка-
ждого вибратора параллельны
и равноудалены от центра тя-
жести тела О
j — передаточное отношение между
валами каждого вибратора
20
21
Три дебалансных вибратора,
симметрично расположенных на
мягко амортизированном твер-
дом теле, которое может совер-
шать плоские колебания; пло-
скость осей вращения всех ви-
браторов проходит через центр
тяжести тела; крайние вибра-
торы одинаковы
Четыре одинаковых дебаланс-
ных вибратора, симметрично
расположенных на мягко амор-
тизированном твердом теле, ко-
торое может совершать плоские
колебания
УСЛОВИЯ УСТОЙЧИВОСТИ
855
Таблица 5 (продолжение)
	Характер синхронного движения (в первом приближении)		Условия устойчи- вости синхронного движения ****)	Разделы данной книги или публика- ции, в ко- торых рас- смотрена система	Примечания
	вибраторов ***)	несущих тел			
	Ф1 = ± (at, ф2 =® ± (Of	Прямолинейные поступательные бигармоиические колебании парал- лельно осн Ох по закону 2/пе	, , х = —гг— cos со/ + м , 2т'е'	. . + м cos'“z	Режим устой- чив п|)И любых сочетаниях пара- метров, однако могут быть устой- чивыми также и иные синхронные режимы. При j = 2 такие побочные режимы отсутствуют, если 4т'е'< тг	Глава XIV, § 8, п. 8; [68]	
	Ф1 = фз = ± юЛ фз = ± (со/ + л) (роторы всех ви- браторов вра- щаются в одина- ковых направле- ниях)	Круговые по- ступательные ко- лебания с ампли- тудой 2те — т3г3 г°	М	Mr2 г. тЗвЗ 1	те.	Глава XV, § 4	
	а)	ф1 = ± (at, Ф2 == ± ((at 4- л), Фз= + ((at 4- л), ср4 =~ -+- (at (роторы третьего и четвертого ви- браторов вра- щаются в напра- влении, противо- положном напра- влению враще- ния роторов пер- вого и второго вибраторов) б)	ф! = ± со/, Фз = ± (со/ + л), Фз = ± at, Ф<= ± (со/ + л) (роторы всех ви- браторов вра- щаются в одина- ковых направле- ниях) .	Отсутствие ко- лебаний	Режимы устой- чивы при любых сочетаниях пара- метров	Г лава XX, § 3, п. 2; [68]	Об устойчи- вости режи- мов, в кото- рых отсут- ствуют ко- лебания несущего тела, для систем более общего вида см. § 2 главы XXIII
856
УСЛОВИЯ УСТОЙЧИВОСТИ
N9
л/л
Краткое описание системы *)
Динамическая схема, обозначения **)
22
Та же система, что и в п. 21,
ио привод осуществляется от
одинаковых синхронных элек-
тродвигателей с соответствую-
щим образом ориентированными
обмотками статоров
23
Та же система, что в и. 21,
но плоскости вращения центров
тяжести роторов каждой пары
вибраторов 1 и 4, 2 и 3 накло-
нены под углом р к плоскости
главных центральных осей инер-
ции хОу
24
Шесть одинаковых попарно ко-
аксиальных дебалансных вибра-
торов, приводимых от синхрон-
ных электродвигателей с соот-
ветствующим образом ориенти-
рованными обмотками статоров
и симметрично установленных
на мягко амортизированном
твердом теле, которое может
совершать плоские колебания
УСЛОВИЯ УСТОЙЧИВОСТИ
85?
Таблица 5 (продолжение)
	Характер синхронного движения (в первом приближении)		Условия устойчи- вости синхронного движения •*♦•)	Разделы данной книги нли публика- ции, в ко- торых рас- смотрена система	Примечания
	вибраторов ***)	несущих тел			
	Ф1 = ± ю/, ф2 “ ± Фз ~ -ь со/, ф4 == “+ Сй/ (роторы третьего и четвертого ви- браторов вра- щаются в напра- влении» противо- положном напра- влению вращения роторов первого и второго вибра- торов)	Прямолинейные поступательные гармонические колебания в на- правлении оси Ох с амплитудой , 4те	Л0Г. ивГ 4 ’ ~ “ <ЖесТ- кость» характе- ристики двигате- лей в рабочей точке, F = 2тесо2, ,	4 те л°—лГ	Глава XX, § 3, п, 2; [68]	В случае привода вибраторов от асинхрон- ных двига- телей дан- ный режим всегда неустойчив
	<Р1 = ± at, Ф2 = ± а/, фз = + (at + л), ф4 = Т (at + л) (роторы третьего и четвертого ви- браторов вра- щаются в напра- влении, противо- положном напра- влению вращении роторов первого и второго вибра- торов)	Прямолинейные поступательные гармонические колебания с ам- плитудой Ай~~м~ в направлении, параллельном плоскости xOz и составляющем угол р с плоско- стью хОу	1 &г sin2 fi М	1и 1 a2 sin2 р _ Af	1х a2 cos2 р + Ь2 1г	<	Глава XX, § 1, п. 2; [242, 245]	
	Ф1 = фз = Фб = = ± at, ф2 = ф4 = фв = = + at (роторы вибрато- ров с нечетными номерами вра- щаются в напра- влениях, проти- воположных на- правлению вра- щения роторов вибраторов с чет- ными номерами)	Прямолинейные поступательные гармонические колебания в на- правлении оси Ох с амплитудой „ 6/пе 4 = —гг- М	_ (dL*\ 1 de)> 4 ; “ \Гм) ~<жест’ кость» характе- ристики двигате- лей в рабочей точке, F = 2me<as, , 6me л“ = -лГ	Глава XX, § з, п. 3; [68]	То же, что и в п. 22
858
Условия устойчивости
№ п/п	Краткое описание системы •)	Динамическая схема, обозначения **)
25
Два одинаковых дебалансных
вибратора или вибратора на-
правленного действия, устано-
вленных на шарнирно опертой
балке однородного сечения
с равномерно распределенной
массой
ЕУ — изгибная жесткость,
р — погонная плотность балки
УСЛОВИЯ УСТОЙЧИВОСТИ
859
Таблица 5 (продолжение)
	Характер синхронного движе- ния (в первом приближении)		Условия устойчивости синхронного движения ***•)	Разделы данной книги или публика- ции, в ко* торых рас- смотрена система	Примечания
	вибраторов ***)	несущих тел			
	а) 1 ф1 I — со/, | ф21 = со/	Упругие колеба- ния под действи- ем син- фазных гармони- ческих возмуща- ющих сил с ампли- тудой F—теа)2, прило- женных в точках 01 и о2	k (со2) > 0; 2 /3 оо Х S - q* Sin sln уЯ®2’ £1 = Xi/l, Ь = Х2/1, q* = р1*сог1лЕУ	Г лава XIV, § 8, п. 6; [482]	0 случае мягко амор- тизирован- ной балки с произволь- ным числом одинаковых вибраторов направлен- ного дей- ствии см. п. 7 § 8 главы XIV
	б) I Ч>11 = 1 ф2 | = СО/ + Л	Упругие колеба- ния под действи- ем про- тивофаз- ных гар- мониче- ских воз- мущаю- щих сил с ампли- тудой F— /песо2, прило- женных в точках 01 и о2	k(^)<0		
860
УСЛОВИЯ УСТОЙЧИВОСТИ
№
п/п
Краткое описание системы ****)
Динамическая схема, обозначения **)
26
27
Один дебалансный (/) и один
«пассивный» (лишенный двига-
теля) внешний планетарный ви-
братор (2), коаксиально уста-
новленные на свободном твер-
дом теле (3), которое может со-
вершать плоские колебания
Два одинаковых дебалансных
вибратора и один пассивный
внутренний планетарный вибра-
тор, симметрично установлен-
ные па мягко амортизирован-
ном твердом теле, которое может
совершать плоские колебания
УСЛОВИЯ УСТОЙЧИВОСТИ
861
Таблица 5 (продолжение)
	Характер син> движения (в пе ближен вибраторов ***)	ройного рвом При- 4И) несущих тел	Условия устойчивости синхронного движения ****)	Разделы данной книги или публика- ции, в ко- торых рас- смотрена система	Примечания
	ф1 = zt ,  (е + р +arcsin 1 — \ Л фг = ± л0 = -^А '"а p' = arctgf (/' — коэффи- циент сопро- тивления пере- катыванию), та = М-ть	- л 4- • А “ Sin p l , 0	/. at; Круго- вые по- ступа- тельные колеба- ния	Режим устойчив во всей области своего существо- вания, определяемой не- равенством Г1+(П2 Ло	f если ki/ki С 1 (ks — суммарные коэффи- циенты сопротивления)	Г лава XXI, § 1; (369, 65, 68, 370]	Результат остается спра- ведливым и в случае, когда планетарный вибратор яв- ляется вну- тренним
	Ср, = ± (£>/, ф2 = ± фз = « ± [<0/ + р? +Л+ / е. + arcsin —Sr \ A) = 2mded/«a> p'=arctgf ({'- коэффи- циент сопро- тивления пере- катыванию), та==М~тЬ	sin р'^ , Круго- вые по- ступа- тельные колеба- ния	Afr2	(	m.s. 	>21	1	 /	1	таА0 Х	1	+	(/Т Х х |/ ! + (/') -ат 4^1}, Ло J если kb!kd < 1 (kb и ka - соответствующие суммар- ные коэффициенты сопро- тивления) ।	Глава XXI, § 3; [68]	1. Режим существует при Ло < V 1 + (ГУ г 2. Результат остается спра- ведливым и в случае, когда планетарный вибратор яв- ляется внеш- ним
862
УСЛОВИЯ УСТОЙЧИВОСТИ
Mi
п/п
Краткое описание системы *)
Динамическая схема, обозначения ** ***))
28
Два одинаковых деба-
лансных вибратора с парал-
лельными осями, симметрично
установленных на твердом
теле. Тело шарнирно связано
с другим мягко амортизиро-
ванным твердым телом, с ко-
торым может двухсторонне
соударяться; ось шарнира
перпендикулярна осям вра-
щения роторов вибраторов
и лежит с ними в одной пло-
скости
AI, IXt /у,	—масса и моменты инерции
всей системы; — масса тела /; /ф —мо-
мент инерции тела 2 относительно осн
шарнира АА; Са — центр тяжести тела 2;
О — центр тяжести всей системы
*) 1. В случаях, когда это не оговаривается особо, предполагается, что привод
всех вибраторов одинаковы н положительны.
2. Термин «мягко амортизированное твердое тело» означает, что частоты собственных
вибраторов (о (на схемах соответствующие амортизаторы снабжены надписью со~О). Об уело
абсолютно твердого, см., например, § 5 главы XX.
•♦) 1. При отнесении реальной системы к одной из представленных схем следует обра
2. В таблице приняты следующие общие обозначения:
Л4, 1Х, /у,	—масса и главные центральные моменты инерции относительно соответ
точить массы всех дебалансных и планетарных вибраторов в центрах вращения их векто
иих положениях);
О — центр тяжести вспомогательного тела;
т, е—масса и эксцентриситет вибратора;
оо — ось вращения ротора вибратора.
***) При наличии двойных знаков в формулах столбца 4 таблицы следует принимать
***♦) Для возможности практического применения большинства приводимых схем
рабочего режима колебаний (см. главу XVI, а также § 2 главы XX и § 3 главы XXIII).
УСЛОВИЯ УСТОЙЧИВОСТИ
863
Таблица 5 (продолжение)
	Характер синхронного дви- жения (в первом прибли- жении)		Условия устойчивости синхронного движения ****)	Разделы данной книги или публика- ции, в ко- торых рас- смотрена система	Примечания
	вибрато- ров ***)	несущих тел			
	<Р1 = ± <в/, ф2 = ± ш/	Колебания тела 1 отно- сительно те- ла 2 с соуда- рениями через каждую поло- вину периода	2 ( 1	1 \ Г2 . U Iy) Iz 1	/ф >	7Г (Y + ^cos т,); л meQ 1 Л	1	2 те	. й= 1-d Q (1 S,nT1)' 1	1	/ mbh	aB \ Q	/ф	\ Al	I у / 1 /	m2bh2	B2\ d	\	M	1уГ B = l — m.b, ф	b 2y — максимальный угол относительного пово- рота тел 1 и 2, т( — корень уравнения л Т( +COS Т! = ~ + + vQ(1-rfL, 1 me лежащий в пределах 1 -- Л	л	Глава XXI, § 4; [308]	1. Режим существует при Y<Y*~ л те “ 1-d Q ’ 2. О синхро- низации ви- браторов в других систе- мах с соуда- ряющимися несущими те- лами см. ра- боты [352, 192, 193, 101]
вибраторов осуществляется от двигателей асинхронного типа, причем парциальные скорости
колебаний тела на амортизаторах значительно ниже наименьшей скорости вращения валов
виях, при которых мягко амортизированное упругое тело может быть идеализировано в виде
щать особое внимание на правильность учета существенных степеней свободы несущих тел.
ствующих осей вспомогательных тел (то есть тел, получающихся из исходных, если сосредо-
ров эксцентриситетов, а массы всех вибраторов направленного действия —в их сред-
либо только верхние, либо только нижние знаки.
необходимо, наряду с условиями устойчивости, также выполнение условий стабильности
литература
1.	Аграновская Э. А. иБлехман И. И., Четырехвальный дебаланс-
ный вибратор. Авторское свидетельство № 157917 с приоритетом от
16 июля 1962 г. Бюллетень изобретений, 1963, № 19.
2.	А г р а н о в с к а я Э. А., Решение на аналоговых вычислительных маши-
нах нелинейных дифференциальных уравнений, содержащих периодиче-
ские функции зависимой переменной. Изв. АН СССР. ОТН, Механика и
машиностроение, 1963, № 4.
3.	А г р а н о в с к а я Э. А., Исследование процессов прохождения через ре-
зонанс в устройствах с инерционными возбудителями. Изв. АН СССР,
Механика, 1965, № 4.
• 4. Аграновская Э. А. иДенисов Г. А., Экспериментальное исследо-
вание работы вибрационных машин с бигармоническим приводом. «Обо-
гащение руд». Изд. ин-та «Механобр», Ленинград, 1965, № 1.
5.	А й з е р м а и М. А., Физические основы применения методов малого па-
раметра. Автоматика и телемеханика, 1953, № 5.
6.	Айзерман М. А. и Смирнова И. М., О применении метода ма-
лого параметра для исследования периодических режимов в системах
автоматического регулирования, не содержащих малого параметра. В сб.
«Памяти А. А. Андронова». Изд-во АН СССР, Москва, 1955.
7.	А к а л о в с к и й И. В., Исследование взаимной синхронизации двух
автогенераторов методом обобщенных частотно-фазовых диаграмм. Ра-
диотехника, 1950, 17, № 3.
8.	Аксельрод 3. М., Часовые механизмы. Теория, расчет и проектиро-
вание. Машгиз, Москва, 1947.
9.	Аксельрод 3. М., Электромеханические часы. Машгиз, Москва, 1952.
9а. Алабу же в П. М., Зуев А. К. иКирнарский М. Ш., Самосин-
хронизация вращательной пары. Труды по теории и применению явления
синхронизации в машинах и устройствах. Изд-во «Минтис», Вильнюс,
1966.
10.	А лабужев П. М., Зуев А. К., И в а н о в Е. Н. и К и р н а р-
ский М. Ш., О самосинхронизации гироскопических вибраторов. В сб.
«Машины и механизмы виброударного действия». Труды Новосибир-
ского электротехнического ин-та, вып. 1, Новосибирск, 1969.
И. Альтшуль Б. А. и Рубаник В. П., О взаимодействии нелинейных
колебательных систем при наличии линейных сил связи с малым запазды-
ванием. Изв. вузов, Радиофизика, 1963, 6, № 1.
12.	Ананьев И. В. и Колбин Н. М., Исследование параметров ударного
демпфера. Труды ЦАГИ, вып. 991, Москва, 1966.
13.	Ананьев И. В. и Кол б ни Н. М., Экспериментальное исследование
ударного демпферирования изгибных и крутильных колебаний брусьев
круглого сечения. Труды ЦАГИ, вып. 1059, Москва, 1967.
14.	Ан др ею к В. А., Вывод достаточных условий устойчивости «в боль-
шом» системы синхронных машин. Изв. НИИ постоянного тока, 1957,
№ 2.
15.	Андронов А. А. и Витт А. А., К математической теории захваты-
вания. Журнал прикл. физ. 1930, 7, вып. 4.
ЛИТЕРАТУРА
865
16	Андронов А. А. и Витт А. А., Об устойчивости по Ляпунову.
ЖЭТФ, 1933, 3, вып. 5.
17.	Андропов А. А. и В и т т А. А., К математической теории автоколе-
бательных систем с двумя степенями свободы. Журнал техн. физ. 1934,
4, вып. 1.
18.	Андронов А. А., Собрание трудов, Изд-во АН СССР, Москва, 1956.
19.	Андропов А. А., В и т т А. А. и X а й к и и С. Э., Теория колебаний.
Физматгнз, Москва, 1959.
20.	А р к а д ь е в В., Об электромагнитной гипотезе передачи мысленного
внушения. Журнал прикл. физ., 1924, 1, вып. 1—4.
21.	Аронович Г. В., К определению достаточных условий динамической
устойчивости сложной энергосистемы при переменной э. д. с. Изв. вузов,
Радиофизика, 1959, № 3.
22.	Аронович Г. В., Белюстииа Л. Н., К а р т в е л и ш в и л и II. А.
иЛюбиыцев Я. К., Применение методов теории колебаний к задачам
устойчивости стационарных режимов гидроэлектрических станций и энер-
гетических систем. Труды Международного симпозиума по нелинейным
колебаниям, т. III, Изд-во АН УССР, Киев, 1963.
23.	А р т е м ь е в Н. А., Метод определения характеристических показателен
и приложение его к двум задачам небесной механики. Изв. АН СССР,
серия матем., 1944, 3, № 2.
24.	Артоболевский И. И., Основные проблемы современной теории ди-
намики машин. Труды Ин-та машиноведения АН СССР. Семинар по
теории машин и механизмов, 1961, 21, вып. 83—84 (Доклад на Всесоюз-
ном съезде по теорет. и прикл. механике, 1960).
25.	А р т о б о л е в с к и й И. И. и Боголюбов А. Н., Теория механизмов
и машин. В сб. «Механика в СССР за 50 лет», т. 1. Общая и приклад-
ная механика. «Наука», Москва, 1968.
26.	Б а б с к и й Е. Б. и У л ь я н и и с к и й Л. С., Электрическая стимуляция
сердца. Изд-во АН СССР, Москва, 1961.
27.	Б а з о в с к и й И., Надежность. Теория и практика. Перев. с англ.,
«Мир», Москва, 1965.
28.	Б а л ж и М. Ф. и Е с и н Г. Д., Соединительная муфта с упругими ди-
намическими связями и ее антивибрационные свойства. Челябинское
книжное изд-во, 1959.
29.	Баталова 3. С., О движении ротора под влиянием внешней гармони-
ческой силы. Инженерный журнал, Механика твердого тела, 1967, № 2.
30.	Б а т а л о в а 3. С., К численному исследованию динамических систем
с помощью ЭВМ. Изв. вузов, Радиофизика, 1967, 10, № 3.
31.	Баутин Н. И., К теории синхронизации. Журнал техн, физ., 1939, 9,
вып. 6.
32.	Б а у т и н И. И., Поведение динамических систем вблизи границ области
устойчивости. Гостехиздат, Ленинград, 1949.
33.	Баутин И. Н., Динамические модели свободных часовых ходов. Сб.
«Памяти А. А. Андронова». Изд-во АН СССР, Москва, 1955.
34.	Баутин Н. Н., Теория точечных преобразований и динамическая тео-
рия часов. Труды Международного симпозиума по нелинейным колеба-
ниям, т. И, Изд-во АН УССР, Киев, 1963.
35.	Б а р б а ш и и Е. А. Введение в теорию устойчивости. «Наука», Москва,
1967.
36.	Бейзельмап Р. Д. и Цыпкин Б. В., Подшипники качения (спра-
вочник). Машгиз, Москва, 1959.
37.	Б е л е н о в Э. М. и Ораевский А. Н., Молекулярный генератор с
двумя последовательными резонаторами. Радиотехника и электроника,
1963, 8, № 1.
38.	Беллмаи Р., Теория устойчивости решений дифференциальных уравне-
ний. Перев. с англ., ИЛ, Москва, 1964,
28 И- И- Блехман
866
ЛИТЕРАТУРА
39.	Бел л юстин С. В., К теории двух слабо связанных коптурон. Ученые
записки Горьковского ун-та, 1939, вып. 12.
40.	Беляковский Н. Г., Конструктивная амортизация механизмов, при-
боров и аппаратуры на судах. «Судостроение», Ленинград, 1965.
41.	Берштейн И. и Иконников Е., К математической теории выну-
жденных колебаний в автоколебательных системах с двумя степенями
свободы, Журнал техн, физ., 1934, 4, вып. 1.
- 42. Б е с с о н о в А. П., Исследование по динамике дебалансного вибратора.
«Acta Technica» (Чехословакия), 1960, № 6.
43.	Бирюков М. К., Вибрационное поддержание субротационного движе-
ния. Дппл. работа. Ленингр. политехи, ип-т им. М. И. Калинина, 1962.
43а. Блакьер О., Анализ нелинейных систем. Перев. с англ., «Мир», Москва
1969.
44.	Б л е х м а и И. И., Самосинхронизация вибраторов некоторых вибра-
ционных машин. Инженерный сб., 1953, 16.
45.	Б л е х м а и И. И., Вращение неуравновешенного ротора, обусловленное
гармоническими колебаниями его оси. Изв. АН СССР, ОТН, 1954, № 8.
46.	Блехман И. И., Нелинейные задачи динамики вибрационных машин,
Капд. диссертация. Ленингр. политехи, ин-т им. М. И. Калинина, 1955.
47.	Б л е х м а п И. И., К вопросу об устойчивости периодических решений
квазилинейных неавтономных систем со многими степенями свободы.
Докл. АН СССР, 1955, 104, № 6.
48.	Б л е х м а н И. И. иДжанелидзе Г. Ю., Динамика регулятора Буас-
са—Сарда. Изв. АН СССР, ОТН, 1955, № 10.
49.	Блехмап И. И., Об устойчивости периодических решений квазилиней-
ных автономных систем со многими степенями свободы. Докл. АН СССР,
1957, 112, № 2.
50.	Б л е х м а н И. И. и Джанелидзе Г. Ю., Исследование вынужден-
ных колебаний некоторых вибрационных машин со многими вибрато-
рами. Изв. АН СССР, ОТН, 1958, № 3.
51.	Блехман И. И., Инерционный грохот. Авторское свидетельство
№ 112448 с приоритетом от 13 мая 1957 г. Бюллетень изобретений, 1958,
№ 4.
52.	Б л е х м а н И. И., Ватсон А. В., К и р и ч е п к о А. И. и Л а в-
ров Б. П., Вибрационный конвейер. Авторское свидетельство № 118283
с приоритетом от 2 апреля 1958 г. Бюллетень изобретений, 1959, № 4.
53.	Б л е х м а н И. И., Шаровая вибромельница. Авторское свидетельство
№ 125117 с приоритетом от 11 июля 1958 г. Бюллетень изобретений, 1959,
№ 24.
54.	Блехман И. И., О самосинхронизации механических вибраторов. Изв.
АН СССР, ОТН, 1958, № 6.
 55. Б л е х м а н И. И., О выборе основных рабочих параметров вибрацион-
ных конвейеров. «Обогащение руд». Изд. ин-та «Механобр», Ленинград,
1959, № 2.
• 56. Блехмап И. И., Вибрационные машины с механическими возбудите-
лями колебаний. Применение вибротехники в горном деле. Сборник ста-
тей. Госгортехиздат, Москва, 1960.
57.	Б л е х м а п И. И., Теория самосинхронизации механических вибраторов
и ее приложения. Труды второго Всесоюзного совещания по основным
проблемам теории машин и механизмов. Динамика машин. Машгиз, Мо-
сква, 1960.
58.	Блехман И. И., Динамика привода вибрационных машин со многими
синхронными механическими вибраторами. Изв. АН СССР, ОТН, Меха-
ника и машиностроение, 1960, № 1.
59.	Блехман И. И., Исследование режимов установления самосинхрони-
зации механических вибраторов методом скоростной киносъемки. Научно-
технич. информац. бюллетень Ленингр. политехи, пн-та им. М. И. Кали-
ЛИТЕРАТУРА
867
нина, (Применение специальных видов киносъемки в научных исследо-
ваниях). Ленинград, 1960, ,М» 2.
60.	Б л е х м а н И. И. и Л а в р о в Б. П., Об одном интегральном признаке
устойчивости движения. Прикл. матем. и мех., 1960, 24, № 5.
61.	Блехман И. И., Обоснование интегрального признака устойчивости
движения в задачах о самосинхронизации вибраторов. Прикл. матем. и
мех., 1960, 24, № 6.
62.	Б л е х м а н И. И., Иптиральный критерий устойчивости периодических
движений некоторых нелинейных систем и его приложения. Труды Ме-
ждународного симпозиума по нелинейным колебаниям, т. И, Изд-во АН
УССР, Киев, 1963.
63.	Б л е х м а н И. И., Совместная работа нескольких синхронных механиче-
ских вибраторов. Труды Ин-та машиноведения АН СССР. Семинар по
теории машин и механизмов, 1961, 21, вып. 83—84.
64.	Блехман И. И., О критической щели вибрационной роликовой мель-
ницы. «Обогащение руд». Изд. ин-та «Механобр», Ленинград, 1961, № 1.
65.	Б л е х м а н И. И., Рудин А. Д. и Р у и д к в и с т А. К-, Об условиях
движения с обкаткой дробящих тел в вибрационных дробильно-измельчи-
тельпых машинах. «Обогащение руд». Изд. ин-та «Механобр», Ленинград,
1961, № 3.
66.	Б л е х м а и И. И. и Лавров Б. П., Механический вибрационный стенд.
Авторское свидетельство № 243923 с приоритетом от 19 сентября 1961 г.
Бюллетень изобретений 1969, № 17.
67.	Б л е х м а п И. И. и Л а в р о в Б. П., Вибрационный питатель. Автор-
ское свидетельство № 152407 с приоритетом от 19 сентября 1961 г. Бюл-
летень изобретений, 1962, № 24.
68.	Б л е х м а н И. И., Синхронизация динамических систем. Докторская дис-
сертация. Ленингр. политехи, ип-т им. М. И. Калинина, 1962.
69.	Б л е х м а н И. И., Иванов Б. Г., Иванов И. А., Р у н д-
квист А. К. иРундквист К. А., Конусная инерционная дробилка.
Авторское свидетельство № 184125 с приоритетом от 16 апреля 1962 г.
Изобретения, промышленные образцы, товарные знаки, 1966, № 14.
70.	Б л е х м а и И. И., Вибрационные машины, применяемые при обогаще-
нии и окусковании. Сб. «Современное дробильно-измельчнтельное и агло-
мерационное оборудование за рубежом». Изд. ЦИНТИАМ, Москва, 1963.
71.	Блехман И. И., Об условиях нормальной работы мпоговибраторных
вибрационных машин. Труды третьего Всесоюзного совещания по основ-
ным проблемам теории машин и механизмов. Машгиз, Москва, 1963.
72.	Блехман И. И. и Лавров Б. П., Вибрационный конвейер. Авторское
свидетельство № 163524 с приоритетом от 24 июля 1963 г. Бюллетень
изобретений и товарных знаков, 1964, № 12.
73.	Блехман И. И. и Джанелидзе Г. Ю., Вибрационное перемеще-
ние. «Наука», Москва, 1964.
74.	1? ле хм ан И. И., Проблема синхронизации динамических систем.
Прикл. матем. и мех., 1964, 28, вып. 2.
75.	Блехман И. И., Поляков В. И. и X о д ж а е в К. Ш., Способ на-
стройки многоприводных электровибромашин. Авторское свидетельство
№ 185386 с приоритетом от 5 марта 1965 г. Изобретения, промышленные
образцы, товарные знаки, 1966, № 17.
76.	Б л е х м а н И. И., Проблемы динамики вибрационных машин. Сб. докла-
дов Международной конференции по механизмам и машинам, т. 3, Бол-
гария, Варна, 1965.
77.	Блехман И. И., Проблема синхронизации колебательных и вращатель-
ных движений. Труды по теории и применению явления синхройЙации
в машинах и устройствах. Изд-во «Мннтис», Вильнюс, 1966.
78.	Б л е х м а н И. И., Работы института «Механобр» в области теории ви-
брационных процессов и машин. Сб. «Вибрационная техника». Материалы
868
ЛИТЕРАТУРА
научно-технической конференции. Изд. НИИИНФСТРОЙДОРКОММУН-
МАШ, Москва, 1966.
79.	Блехман И. И. и Рудин А. Д., Стабильность рабочего режима ви-
брационных машин. Сб. «Вибрационная техника». Материалы научно-тех-
нической конференции. Изд. НИИИНФСТРОЙДОРКОММУНМАШ, Мос-
ква, 1966.
80.	Б л е х м а и И. И., Математические вопросы теории синхронизации дина-
мических систем. Международный конгресс математиков. Тезисы кратких
научных сообщений, секция 12, Москва, 1966.
81.	Б л е х м а и И. И., Д е н и с о в Г. А. и Л а в р о в Б. П., Вибрационный
конвейер конструкции «Механобра» с самосинхронизирующимися меха-
ническими вибраторами «Обогащение руд». Изд. ин-та «Механобр», Ле-
нинград, 1966, № 5.
82.	Блехман И. И., Мышкис А. Д. и П а п о в к о Я. Г., Правдоподоб-
ность и доказательность в прикладной математике. Инженерный журнал.
Механика твердого тела, 1967, № 2.
83.	Блехман И. И., К динамике групповых фундаментов под неуравнове-
шенные машины. Инженерный журнал. Механика твердого тела, 1967,
№ 1.
84.	Блехман И. И., Ладыженский Л. А., Поляков В. И., По-
пова И. А. и Ходжаев К. Ш., Колебания резонансных многопривод-
ных вибрационных устройств, Инженерный журнал. Механика твердого
тела, 1967, № 5.
* 85. Б л е х м а и И. И., П о л я к о в В. И. и X о д ж а е в К. Ш., Синтез форм
вынужденных колебаний и настройка многоприводных резонансных ви-
брационных машин. Инженерный журнал. Механика твердого тела, 1967,
№ 6.
86.	Б л е х м а п И. И. и Нагаев Р. Ф., Оптимальная стабилизация син-
хронных движений механических вибраторов. Тезисы докладов и сооб-
щений па Всесоюзном межвузовском симпозиуме по прикладной матема-
тике и кибернетике. Горький, 1967.
87.	Блехман И. И., Проблема синтеза форм колебаний упругих систем.
Третий Всесоюзный съезд по теоретической и прикладной механике. Ан-
нотации докладов. Изд-во АН СССР, Москва, 1968.
88.	Б л е х м а и И. И., О понятиях вибрационной силы в момента в некото-
рых задачах теории нелинейных колебаний. Конференция по проблеме
колебаний механических систем. Тезисы докладов. «Наукова думка»,
Киев, 1968.
 89. Б л е х м а п П. И., Синтез машин и устройств с самосинхронизирующи-
мися вибраторами. «Обогащение руд». Изд. ин-та «Механобр», Ленин-
град, 1968, № 4.
90.	Блехман И. И., Метод малого параметра. Сб. «Механика в СССР
за 50 лет», т. I, «Наука», Москва, 1968.
91.	Блехман И. И. и Пановко Я. Г., Прикладные проблемы теории
колебаний. Сб. «Механика в СССР за 50 лет», т. I, «Наука», Москва,
1968.
92.	Б л е х м а н И. И. н М а р ч е н к о Ю. И., Влияние реологических свойств
рабочей среды на самосинхронизацию механических вибраторов, Изв. АН
СССР, Механика твердого тела, 1969, № 5.
93.	Б л е х м а н И. И. и Н а г а е в Р. Ф., Синхронизация слабо связанных
динамических объектов и интегральный критерий устойчивости синхрон-
ных движений. Пятая международная конференция по нелинейным коле-
баниям. Тезисы докладов, Киев, 1969.
94.	Боголюбов Н. Н., О некоторых статистических методах в матема-
тической физике. Изд-во АН УССР, Киев, 1945.
95.	Б о г о л ю б о в Н. Н., Теория возмущений в нелинейной механике. Сб.
трудов Ин-та строительной механики АН СССР, 1950, № 14.
ЛИТЕРАТУРА
869
96.	Б о г о л ю б о в Н. Н. и Митропольский Ю. А., Асимптотические
методы в теории нелинейных колебаний. Физматгиз, Москва, 1958.
97.	Боголюбов Н. Н. и Митропольский Ю. А., Метод интеграль-
ных многообразий в нелинейной механике. Труды Международного сим-
позиума по нелинейным колебаниям, т. 1, Изд-во АН УССР, Киев, 1963.
98.	Боголюбов Н. Н. (мл.) и Садовников Б. И., О периодических
решениях дифференциального уравнения и-го порядка с малым парамет-
ром. Украинский матем. журнал, 1961, 13, № 3.
99.	Бо л ь ш а к о в В. М., Зельдин Е. С., М и н ц Р. М. и Ф у ф а е в Н. А.,
К динамике системы осциллятор — ротатор. Изв. вузов, Радиофизика,
1965, 8, № 2.
100.	Бом Д. и Фолди Л., Теория фазотрона. Сб. «Резонансные цикличе-
ские ускорители заряженных частиц». ИЛ, Москва, 1950.
101.	Бравермап Е. Л. п Зарецкий Л. Б., Математическое моделиро-
вание задачи о самосинхронизации центробежных вибровозбудителей. Сб.
«Исследование строительных и дорожных машин с применением вычис-
лительной техники». ВНИИСТРОЙДОРМАШ, Москва, 1968.
102.	Бремзен А. С. и Ф а й п б е р г И. С., Анализ работы двух связанных
релаксационных генераторов. Журнал теорет. физ., 1941, 11, вып. 10.
103.	Бруевич А. И., Асинхронные колебания в автогенераторе с двумя сте-
пенями свободы. Радиотехника и электроника, 1960, 5, № 10.
104.	Б у к а т ы Г. Б., 3 а к р ы т н о й О. С., И т к и и Г. Е., П у п л я е в И. М.,
Р ю л ь м а и А. Ф., Сыпчепко Б. А. и Шей Г. П., Устройство для
контроля гранулометрического состава дробленой руды. Авторское сви-
детельство № 189218 с приоритетом от 28 октября 1965 г. Бюллетень
изобретений и товарных знаков, 1967, № 23.
105.	Булгаков Б. В., О применении метода Пуанкаре к свободным псевдо-
линейным колебательным системам. Прикл. матем. и мех., 1942, 4, вып. 4.
106.	Булгаков Б. В., Колебания. Гостехиздат, Москва, 1954.
107.	Булгаков Н. Г., Колебания квазилинейных автономных систем со
многими степенями свободы и иеаналитической характеристикой нелиней-
ности. Прикл. матем. и мех., 1965, 19, вып. 3.
108.	Бу те ниц Н. В., Об одной задаче Кельвина, относящейся к теории ча-
сов. ЖЭТФ, 1940, 10, вып. 11.
109.	Б утенин II. В., К теории вынужденных колебаний в нелинейной меха-
нической системе с двумя степенями свободы. Прикл. матем. и мех. 1949,
13, № 4.
НО. Б утенин Н. В., К теории «резонанса» в механической автоколебатель-
ной системе с гироскопическими членами. Прикл. матем. и мех., 1950, 14,
вып. I.
111.	Б у тенин Н. В., К теории принудительной синхронизации. Сб. «Памяти
А. А. Андронова», Изд-во АН СССР, Москва, 1955.
112.	Б ы с т р и ц к и й Д. И., Вопросы синхронизации генераторов сельских
ветроэлектрических станций, работающих в энергосистеме. Автореферат
кандидатской диссертации. Москва, 1952.
113.	Б ы х о в с к и н И. И., Основы теории вибрационной техники. «Машино-
строение», Москва, 1969.
114.	Б ы х о в с к и й М. Л., К вопросу о динамике машин с электроприводом.
Труды Ин-та машиноведения АН СССР. Семинар по теории машин и ме-
ханизмов, 1958, 18, вып. 71.
115.	Б ы х о в с к и й М. Л., 3 и н о в ь е в В. А. и П а в л о в а Т. Т., Экспери-
ментальные исследования динамических систем с электроприводом. Тру-
ды Ин-та машиноведения АН СССР. Семинар по теории машин и меха-
низмов, 1960, 20, вып. 78.
116.	Валеев К. Г., К методу Хилла в теории линейных дифференциальных
уравнений с периодическими коэффициентами. Определение характеристи-
ческих показателей. Прикл. матем. и мех., 1961, 25, вып. 2.
870
ЛИТЕРАТУРА
117.	Валеев К. Г. и Г а н и е в Р. Ф., Исследование колебаний нелинейных
систем. Прикл. матем. и мех., 1969, 33, вып. 3.
118.	Вальц Г. Б., Передача крутящего момента на расстояние и в герме-
тическое пространство без проницания стенок. Труды по теории и приме-
нению явления синхронизации в машинах и устройствах. Изд-во «Мип-
тис», Вильнюс, 1966.
119.	В а и - д е р - П о л ь Б., Нелинейная теория электрических колебаний.
Связьиздат, Москва, 1935.
120.	Васильев Л. Л., Таинственные явления человеческой техники. Гос-
политиздат, Москва, 1963.
121.	В ей вод а О., Заметка по поводу статьи Ладислава Пуста «Влияние
свойств источника переменной силы на колебания механической системы».
Aplikace Matematiky, 1958, Svazek 3, cislo 6, Praha.
122.	Векслер В. И., Публикация об открытии. Бюллетень изобретений,
1961, № 3.
123.	Векслер В. И., Новый метод ускорения релятивистских частиц. ДАН
СССР, 1944, 43, № 8.
124.	Векслер В. 14. Ускорители атомных частиц, Изд-во АН СССР, Москва,
1956.
125.	Вентце ль Е. С., Теория вероятности. Физматгиз, Москва, 1958.
126.	Випер И., Кибернетика и общество. ИЛ, Москва, 1958.
127.	Винер Н., Нелинейные задачи в теории случайных процессов. Перев.
с англ. ИЛ, Москва, 1961.
128.	Винер Н., Динамические системы в физике и биологии. Вестник АН
СССР, 1964, № 7.
129.	Винер Н., Новые главы кибернетики. «Советское радио», Москва,
1963.
130.	Витек В., Устойчивость в малом регулирования турбин в условиях
параллельной работы электростанций. Научн. доклады высш, школы.
Энергетика, 1958, № 2.
131.	Воз и юк Л. Л., Исследование устойчивости периодических решений
уравнений высокого порядка. Украинский матем. журнал, 1957, 9, № 3.
132.	Волк И. М., Некоторые обобщения метода малого параметра в теории
периодических решений неавтономных систем. Прикл. матем. и мех., 1947,
11, № 4.
133.	Волк И. М., О периодических решениях неавтономных систем, завися-
щих от малого параметра. Прикл. матем. и мех., 1948, 12, вып. 1.
134.	Волк И. М., Об одном классе автоколебательных систем. Докл. АН
СССР, 1956, ПО, № 2.
135.	Волосов В. М., Моисеев Н. Н., Моргунов Б. И. и Черно-
усько Ф. Л., Асимптотические методы нелинейной механики, связан-
ные с осреднением. Труды второго Всесоюзного съезда по теоретической
и прикладной механике, вып. 2, «Наука», Москва, 1965.
136.	Волосов В. М., Метод осреднения в теории нелинейных колебаний.
Сб. «Механика в СССР за 50 лет», т. I, «Наука», М., 1968.
137.	Волосов В. М. и Моргунов Б. И., Методы расчета стационарных
резонансных колебательных и вращательных движений некоторых нели-
нейных систем. Журнал вычислит, матем. и матем. физ., 1968, 8, № 2.
138.	Г а н т м а х е р Ф. Р. и К р е й п М. Г., Осцилляционные матрицы и ядра
н малые колебания механических систем. Гостехиздат, Москва, 1950.
139.	Гапонов В. И., Два связанных генератора с мягкими самовозбужде-
ниями. Журнал техн, физ., 1936, 6, вып. 5.
140.	Гапонов А. В., Электромеханические системы со скользящими кон-
тактами и динамическая теория электрических машин. Сб. «Памяти
А. А. Андронова». Изд-во АН СССР, 1955.
141.	Г а узе Г. Ф. и В и т т А. А., О периодических колебаниях численности
популяции. Изд-во АН СССР, сер. 7, 1551, 1934.
ЛИТЕРАТУРА
871
142.	Гельман А. Е., Метод малого параметра для операторных уравнений.
Докл. АН СССР, 1958, 123, А» 4.
142а. Г е ц я в и ч у с 10. Ю. и Р а г у л ь с к и с К. М., Самосинхронизация
пневмовнбраторов вибростевда трех направлений. Труды по теории и
применению явления синхронизации в машинах и устройствах. Изд-во
«Минтис», Вильнюс, 1966.
143.	Гладков С. Н., Промышленные вибраторы. Сб. статей «Применение
вибротехники в горном деле». Госгортехиздат, Москва, 1960.
144.	Гогенемзер К. и П р а г е р В., Динамика сооружении. ОНТИ, 1936.
145.	Голдстейн Г., Классическая механика. Гостехнздат, Москва, 1957.
<	146. Гольдштейн Б. Г., Пневматические планетарные вибраторы. Строй-
издат, Москва, 1964.
	•147. Гольдштейн Б. Г. и Петрунькии Л. П., Глубинные вибраторы
для уплотнения бетона. Конструкция, теория, расчет. «Машиностроение»,
Москва, 1966.
	148. Гольдштейн Я. А., Стенд для исследования самосинхронизации объ-
ектов типа механических вибраторов. Труды по теории и применению яв-
ления синхронизации в машинах и устройствах. Изд-во «Минтис», Виль-
нюс, 1966.
149.	Г о и ч а р е в и ч И. Ф., Земсков В. Д. и Корешков В. И., Вибра^
циоиные грохоты и конвейеры. Госгортехиздат, Москва, 1960.
150.	Гончаревич И. Ф. и Сергеев П. А., Вибрационные машины
в строительстве. Машгиз, Москва, 1963.
151.	Горев А. А., Переходные процессы синхронной машины. Госэнергоиз-
дат, Москва, 1950.
152.	Горев А. А., Избранные труды по вопросам устойчивости электриче-
ских систем. Госэнергоиздат, Москва, 1960.
153.	Горелик Г. С., Жизнь и труды А. А. Андронова Сб «Памяти
А. А. Андропова». Изд-во АН СССР, Москва, 1955.
154.	Горнштейн В. М., Предотвращение нарушений устойчивости энергети-
ческих систем со слабыми связями при любых возмущениях. Труды
ВНИИЭ, 1959, 9.
154а. Г о р о ж а н к и и Б. Н., О взаимном захватывании на расстоянии. Изв.
АН СССР, сер. физ., 1947, 11, № 2.
155.	Г о р т и и с к и й В. В., Об условиях вращения инерционного распредели-
теля мельничных рассевов. Труды Ии-та машиноведения АН СССР. Се-
минар по теории машин и механизмов, 1959, 18, вып. 72.
156.	Горшков С. II., Двухсторонняя вибрационная щековая дробилка. Ав-
торское свидетельство № 149667 с приоритетом от 26 августа 1961 г. Бюл-
летень изобретении, 1962, № 16.
157.	Горшков С. Н. и Лавров Б. П., Вибрационный грохот. Авторское
свидетельство № 155391 с приоритетом от 21 мая 1962 г. Бюллетень изо-
бретений и товарных знаков, 1963, № 12.
158.	Горшков С. Н, Лавров Б. П. и Т у р к и и В. Я., Вибрационная
щековая дробилка. Авторское свидетельство № 208425 с приоритетом от
21 июля 1965 г. Изобретения, промышленные образцы, товарные знаки,
1968, № 3.
159.	Горшков С. Н., Л а в р о в Б. П. и Т и м о ф е е в Н. Г., Вибрацион-
ный грохот. Авторское свидетельство № 212046 с приоритетом от 19 ав-
густа 1964 г. Изобретения, промышленные образцы, товарные знаки,
1968, № 8.
160.	Гринберг А. П., Методы ускорения заряженных частиц. Гостехнздат,
Москва, 1950.
161.	Гробов В. А., Асимптотические методы расчета изгибных колебаний
валов турбомашии. Изд-во АП СССР, Москва, 1961.
162.	Гурса Э., Курс математического анализа, т. II, Гостехнздат, Москва,
1936.
872
ЛИТЕРАТУРА
163.	Гущин М. Н., Об устойчивости колебательных компонент в автоколе-
бательной сисюме со многими степенями свободы при асинхронном соот-
ношении частот. Вестник МГУ, сер. 3, Финика и астрономия, 1960, № 2.
164.	Гюйгенс X., Три мемуара по механике. Перев. с латин. Изд-во АН
СССР, Москва, 1951.
165.	Ден-Гартог Дж. И., Механические колебания, перев. с англ., Физ-
матгиз, Москва, 1960.
166.	Денисов Г. А. и Лавров Б. П., Вертикально-винтовой вибрацион-
ный конвейер. Авторское свидетельство № 152408 с приоритетом от 11 ок-
тября 1961 г. Бюллетень изобретений, 1962, № 24.
167.	Денисов Г. А. и Л а в р о в Б. II., Расчет вертикально-винтового ви-
броконвейера. «Обогащение руд». Изд. ин-та «Механобр», Ленинград,
1963, № 6.
168.	Денисов Г. А., Лавров Б. П. и Нагаев Р. Ф., Вертикальный ви-
броконвейер. Авторское свидетельство As 232105 с приоритетом от 2 сен-
тября 1967 г. Изобретения, промышленные образцы, товарные знаки, 1968,
№ 36.
169.	Денисов Г. А., Л а в р о в Б. П. и Н а г а е в Р. Ф., Привод для гори-
зонтального виброкопвейера. Авторское свидетельство № 233523 с прио-
ритетом от 2 сентября 1967 г. Открытия, изобретения, промышленные об-
разцы, товарные знаки, 1969, № 2.
170.	Денисов Г. А. и Л а в р о в Б. П., Применение миоговибраторного
привода для винтового виброподъемника. «Обогащение руд». Изд. ин-та
«Механобр», Ленинград, 1968, As 2.
171.	Денисов Г. А., Л а в р о в Б. П. и Н а г а е в Р. Ф., Динамика много-
вибраторного виброподъемника с синхронизатором. Тезисы докладов
Всесоюзной конференции по колебаниям механических систем. Киев, 1968.
172.	Денисов Г. А., О стабильности рабочего режима вертикально-винто-
вого вибрационного конвейера с самосинхронизирующимися вибраторами.
Машиноведение, 1969, № 1.
173.	Денисов Г. А., Исследование вибрационных подъемников с синхронно
работающими дебалансными вибраторами. Кандидатская диссертация, Ле-
нинград, 1969.
174.	Детинко Ф. М., Об устойчивости работы автобалансира для динами-
ческой балансировки. Изв. АН СССР, ОТН, Механика и машиностроение,
1959, № 4.
175.	Джанелидзе Г. Ю. и Лурье А. И., О применении интегральных и
вариационных принципов механики в задачах колебаний. Прикл. матем.
и мех., 1960, 24, вып. 1.
176.	Диментберг Ф. М., Изгибные колебания вращающихся валов. Изд-
во АН СССР, Москва, 1959.
177.	Диментберг М. Ф. и Фролов К. В., Эффект Зоммерфельда в си-
стеме со случайно изменяющейся собственной частотой. Докл. АН СССР,
1966, 171, Ns 6.
178.	Долицкий И. И., Экспериментальное исследование модели рабочего
органа бетоноукладчика — вибрирующей рамы. Сб. трудов ин-та ВНИИ-
СТРОЙМАШ, Ленинград, 1958.
179.	Дородницын А. А., Асимтотическое поведение решения уравнения
Ван-дер-Поля. Прикл. матем. и мех., 1947, И.
180.	Дроздов Ю. М., Вынужденные колебания нелинейных систем с одной
степенью свободы, близких к консервативным (примеры). Прикл. матем.
и мех., 1955, 19, вып. 1.
181.	Дубошин Г. Н., Небесная механика. Основные задачи и методы.
«Наука», Москва, 1968.
182.	Дубровин Б. Н. и Б л е х м а п И. И., О критической щели инерцион-
ных дробилок. «Обогащение руд». Изд. ин-та «Механобр», Ленинград,
1960, jVs 6.
ЛИТЕРАТУРА
873
183.	Ерофеев Л. В., Вибромолот для погружения и извлечения металли-
ческих труб малого диаметра. Строительное и дорожное машиностроение,
I960, № 10.
184.	Еругин Н. П., Приводимые системы. Труды Математического ин-та
им. Стеклова, 1946, 13.
185.	Еругин Н. П., Об асимптотической устойчивости решения некоторой
системы дифференциальных уравнений. Прикл. матем. и мех., 1948, 12, Ns 2.
186.	Еругин Н. П., Первый метод Ляпунова. Сб. «Механика в СССР за
50 лет», т. 1, «Наука», Москва, 1968.
187.	Е с а ф о в Н. И., Экспериментальное исследование взаимной синхрони-
зации двух связанных томсоновских генераторов. Журнал техн. физ. 1947,
17, вып. 7.
188.	Жданов П. С., О статической устойчивости сложных электрических
систем. (В сб.: Лебедев С. А., Жданов П. С., Городский Д. А.
и Кантор Р. М., Устойчивость электрических систем). Труды ВЭИ,
1940, вып. 40.
189.	Жданов П. С., Устойчивость электрических систем. Госэнергоиздат,
1948.
190.	Жуков Л. А. и Хачатуров А. А., Расчет длительности асинхрон-
ного режима гидрогенераторов и качественное исследование условий син-
хронизации. Труды ВНИИЭ, 195, 9.
191.	Жуковский Н. Е., О прочности движения (1882). Полное собрание
сочинений, т. 1, ОНТИ, 1937.
191а. За бы л ин М. И., Интерференция колебаний отдельно стоящих фунда-
ментов при одновременной работе группы машин. Труды по теории и
применению явления синхронизации в машинах и устройствах. Изд-во
«Минтис», Вильнюс, 1966.
192.	Зарецкий Л. Б., О самосинхронизации центробежных вибровозбуди-
телей виброударного механизма. Машиноведение, 1967, № 1.
193.	Зарецкий Л. Б., Синхронизация центробежных вибровозбудителей в
системах с разрывными характеристиками. Инженерный журнал. Меха-
ника твердого тела, 1968, Ns 1.
194.	Зубов В. И., Методы А. М. Ляпунова и их применение. Изд-во ЛГУ,
1957.
195.	Зубов В. И., Математические методы исследования систем автомати-
ческого регулирования. Судпромгиз, Ленинград, 1959.
196.	Зуев А. К., Иванов Е. Н. и Кир царский М. Ш., Гироскопиче-
ский генератор полигармонических колебаний. Сб. «Машины и меха-
низмы виброударного действия». Труды Новосибирского электротехниче-
ского ин-та, вып. 1, Новосибирск, 1959.
197.	Иноземцев Б. С., Исследование параллельной работы синхронных
генераторов с поршневыми двигателями па малых сельскохозяйственных
электростанциях. Кандидатская диссертация, Киев, 1955.
198.	Ин оу э Дзюнкити, Араки Йоси аки и Хаяси Сэцуко,
О самосинхронизации вибраторов. Часть 1. Вращение неуравновешенного
ротора, зависящее от гармонических колебаний его оси. «Нихон кикай
гаккай ромбунсю», Trans. Japan. Soc. Meeh., Engrs., 1966, 32, № 234 (на
японском языке).
199.	Иноуэ Дз ю пк ит п, Араки йосиаки и Мияура Суга,
О самосинхронизации механических вибраторов. Часть 2. Механизм с дву-
мя самосинхронизирующимися вибраторами и автоматическим балансиром.
«Нихон кикай гаккай ромбунсю», Trans. Japan Soc. Meeh. Engrs., 1967,
33, Ns 246 (на японском языке).
200.	К а ж и н с к и й Б. Б., Передача мыслей. Москва, 1923.
201.	К а ж и в с к п й Б. Б., Биологическая радиосвязь. Киев, 1962.
202.	К а л и ш у к А. К., Элементарный способ изучения динамических свойств
систем. Журнал техн, физ., 1939, 4, вып. 8.
874
ЛИТЕРАТУРА
203.	Каннингхэм В., Введение в теорию нелинейных систем. Госэперго-
издат, Москва, 1962.
204.	Карпов Н. А., Легкие вибрационные путевые машины. Труды ВНИИ
железнодорожного транспорта, вып. 245. Трансжелдорнздат, Москва, 1962.
205.	Картвел и швили Н. А., Влияние взаимодействия гидравлических,
механических и электрических процессов иа устойчивость работы элек-
тростанций. Изв. АН СССР, ОТН, 1958, № 2.
206.	К а р т в е л н ш в и л н Н. А., Методы исследования статической устой-
чивости энергетических систем при сильном регулировании. Труды НИИ
электроэнергетики, 1959, 9.
207.	Картвелишвили Н. А., Континуальные модели и устойчивость в
малом динамических систем, состоящих из множества однотипных эле-
ментов. Изв. АН СССР, ОТН. Механика и машиностроение, 1964, Ns 3.
208.	Каудерер Г., Нелинейная механика. ИЛ, Москва, 1961.
209.	Кац А. М., Вынужденные колебания нелинейных систем с одной сте-
пенью свободы, близких к консервативным. Прикл. матем. и мех., 1955,
19, № 1.
210.	Кац М., Вероятность и смежные вопросы в физике. «Мир», Москва,
1965.
211.	Ким барк Э., Синхронные машины и устойчивость электрических си-
стем. Госэпергоиздат, Москва, 1960.
212	Кириченко А. И. и Рундквист К. А., Инерционная конусная дро-
билка. Авторское свидетельство Ns 88805 с приоритетом от 5 сентября
1949 г. Бюллетень изобретений, 1951, Ns 1.
213.	К н р н а р с к и п М. Ш., Синхронизация гироскопических генераторов
«динамы». Сб. «Машины и механизмы виброудариого действия». Труды
Новосибирского электротехнического ип-та, вып. 1, Новосибирск, 1969.
214.	Кобринский А. Е., Механизмы с упругими связями. «Наука», Моск-
ва, 1964.
215.	Коддингтон Э. А. и Л е в и н с о и Н., Теория обыкновенных диффе-
ренциальных уравнений. Перев. с англ., ИЛ, Москва, 1958.
216.	Колов ск ин М. 3., Об условиях существования периодических реше-
ний системы дифференциальных уравнений с разрывными правыми ча-
стями, содержащими малый параметр. Прикл. матем. и мех., 1960, 24,
Ns 4.
217.	Колонский М. 3., О применении метода малого параметра для опре-
деления разрывных периодических решений. Труды Международного сим-
позиума по нелинейным колебаниям, т. I, Изд-во АН УССР, Киев, 1963.
218.	Коловский М. 3., Нелинейная теория виброзащитных систем. «Нау-
ка», Москва, 1966.
219.	Кононенко В. О., Резонансные колебания вращающегося вала с ди-
ском. Изв. АН СССР, ОТН, 1958, № 7.
220.	Кононенко В. О., Резонансные свойства центробежного вибратора.
Труды Ин-та машиноведения АН СССР, 1958, вып. 71.
221.	Кононенко В. О., Некоторые автономные задачи теории нелинейных
колебаний. Труды Международного симпозиума по нелинейным колеба-
ниям, т. ПТ, Изд-во АН УССР, Киев, 1963.
222.	Кононенко В. О., Колебательные системы с ограниченным возбужде-
нием. «Наука», Москва, 1964.
223.	Конти Р., Г р а ф ф и Д. и С а н с о н е Дж., Вклад итальянских мате-
матиков в теорию нелинейных обыкновенных дифференциальных уравне-
ний и в нелинейную механику в течение 1951—61 годов. Труды Между-
народного симпозиума по нелинейным колебаниям, т. И, Изд-во АН
УССР, Киев, 1963.
224	К о п н и н Ю. М., Периодические колебания нелинейных неавтономных
систем со многими степенями свободы. Инженерный журнал. Механика
твердого тела, 1965, 5, Ns 2.
ЛИ ГЕРЛТУРА
875
225.	Кораблев С. С., Исследование резонансных свойств механических си-
стем. Труды Ин-та машиноведения АН СССР, 1959, т. I.
226.	Кораблев С. С., Об особенностях резонансных колебаний двух меха-
нических систем. Изв. АН СССР, ОТН, Механика и машиностроение,
1959, № 6.
227.	Косс М. Ш., Исследование структуры линейных связей, обуславливаю-
щих малые колебания консервативных систем. Научные труды Ташкент-
ского политехи, ин-та 1965, вып. 29.
228.	Костенко М. П., Электрические машины. Специальная часть. Гос-
энергоиздат, 1948.
229.	Красовский Н. Н., Некоторые задачи теории устойчивости движе-
ния. Физматгиз, Москва, 1959.
230.	Креп дел л С. (редактор), Случайные колебания. Перев. с англ., «Мир»,
1967.
231.	Крылов Н. М. и Б о г о л ю б о в Н. Н., I. О колебаниях синхронных
машин. II. Об устойчивости параллельной работы п синхронных машин.
ОНТВУ —ЕНЕРГОВИДАВ, Харьков, 1932.
232.	Крылов Н. М. и Боголюбов Н. Н., Введение в нелинейную меха-
нику, Изд-во АН УССР, Киев, 1937.
233.	Кум пик а с А. Л. и Р а г у л ь с к и с К. М., Самосинхронизация и ди-
намическое гашение колебаний фундаментов машин. Труды по теории и
применению явления синхронизации в машинах и устройствах. Изд-во
«Минтис», Вильнюс, 1966.
234.	Кумпикас А. Л. и Рагульскис К. М., Об областях захвата син-
хронных вращений маятника с вибрирующей точкой подвеса. Вибротех-
ника 2(2). Научные труды вузов Литовской ССР. Изд-во «Минтис»,
Вильнюс, 1968.
235.	Кушу ль М. Я., О квазигармонических системах, близких к системам
с постоянными коэффициентами, у которых чисто мнимые корпи фунда-
ментального уравнения имеют непростые элементарные делители. Прикл.
матем. и мех., 1958, 22, № 4.
236.	К ушу ль М. Я., О почти-пернодических решениях квазилинейных си-
стем при многократном резонансе. К теории автоколебаний роторов. Изв.
АН СССР, ОТН, Механика и машиностроение, 1960, № 1.
237.	Кушу ль М. Я., Почти-периодическпе колебания нелинейных систем,
содержащих квазициклические координаты. Инженерный журнал. Меха-
ника твердого тела, 1966, № 1.
238.	Лавров Б. П., Дебалансный вибратор. Авторское свидетельство
№ 121375 с приоритетом от 24 октября 1958 г. Бюллетень изобретений,
1959, № 14.
239.	Лавров Б. П., Вибрационный конвейер. Авторское свидетельство
№ 135401 с приоритетом от 20 июня 1960 г. Бюллетень изобретений, 1961,
№ 2.
240.	Лавров Б. П., Способ изменения углового положения ротора вра-
щающегося электрического двигателя. Авторское свидетельство
№ 141210 с приоритетом от 20 июня 1960 г. Бюллетень изобретений, 1961,
№ 18.
241.	Лавров Б. П., Пространственная задача о синхронизации механиче-
ских вибраторов. Изв. АН СССР, ОТН, Механика и машиностроение,
1961, № 5.
242.	Лавров Б. П., Использование явления самосинхронизации при созда-
нии некоторых новых типов вибрационных транспортных машин. Док-
торская диссертация. Ленипгр. горный ии-т им. Г. В. Плеханова, 1966.
243.	Лавров Б. П., Вибратор направленных колебаний, преимущественно
для уплотнения бетонных смесей. Авторское свидетельство № 147497
с приоритетом от 19 сентября 1961 г. Бюллетень изобретений, 1962,
№ 10.
876
ЛИТЕРАТУРА
244.	Лавров Б. П., Новая формулировка интегрального критерия устойчи-
вости синхронных движений механических вибраторов и ее приложения.
Сб. «Вибрационная техника» (материалы научно-технической конферен-
ции). Изд. НИИИНФСТРОЙДОРКОММУНМАШ, Москва, 1966.
245.	Лавров Б. П., Вибрационные машины с самосинхронизирующимися
вибраторами (конструктивные схемы и специфические особенности рас-
чета). Труды по теории и приложению явления синхронизации в маши-
нах и устройствах. Изд-во «Миитис», Вильнюс, 1966.
246.	Лавров Б. П., Нагаев Р. Ф. и Тимофеев Н. Г., Протяжен-
ный герметизированный виброконвейер для горячих материалов.
Труды научно-технической конференции ин-та «Механобр», Ленинград,
1969.
247.	Л а - С а л л ь Ж. и Л е ф ш е ц С., Исследование устойчивости прямым
методом Ляпунова. Перев. с англ. «Мир», Москва, 1964.
248.	Л а - С а л л ь Ж- П., Критерий асимптотической устойчивости. В
сб. «Гидродинамическая неустойчивость». Перев. с англ. «Мир», Москва,
1964.
249.	Лауд В. С., Синхронизация в возмущенных автономных системах.
Труды Международного симпозиума по нелинейным колебаниям, т. II,
Изд-во АН УССР, Киев, 1963.
250.	Лесин А. Д., Экспериментальное исследование самосинхронизации ме-
ханических вибраторов в вибрационных мельницах. Труды по теории и
применению явления синхронизации в машинах и устройствах. Изд-во
«Минтис», Вильнюс, 1966.
251.	Левин Б. Р. и Ушаков И. А., Некоторые аспекты современного со-
стояния проблемы надежности. Радиотехника, 1965, № 4.
252.	Левин Л. П., Вопросы теории и расчета электровнбрационных машин.
Сб. «Механика и расчет машин вибрационного типа» под ред. И. И. Ар-
тоболевского, Изд-во АН СССР, Москва, 1957.
253.	Левин Л. П., Вопросы теории и расчета электровнбрационных машин.
Труды ин-та «Механобр», вып. 125, Ленинград, 1960.
254.	Левин Л., Методы решения технических задач с использованием ана-
логовых вычислительных машин. «Мир», Москва, 1966.
255.	Лефшец С., Геометрическая теория дифференциальных уравнений. Пе-
рев. с англ., ИЛ, Москва, 1961.
256.	Лойцяиский Л. Г. и Лурье А. И., Курс теоретической механики,
т. II. Гостехиздат, 1948.
257.	Лурье А. И., Некоторые нелинейные задачи теории автоматического
регулирования. Гостехиздат, 1951.
258.	Лурье А. И., О неустановившихся движениях в квазилинейных авто-
номных колебательных системах. Труды Ленингр. политехи, ин-та, Ns 192,
Машгиз, Москва, 1958.
259.	Лурье А. И., Аналитическая механика. Физматгиз, Москва, 1961.
260.	Любимов Г. П. и Хохлов Р. В., О поляризации молекулярного
пучка переменным полем с изменяющейся амплитудой и фазой. ЖЭТФ,
1957, 33, вып. 6/12.
261.	Ляпунов А. М., Общая задача об устойчивости движения. Гостехиз-
дат, 1950.
262.	М а й е р А. Г., К теории вынужденных колебаний в сложном генераторе.
Уч. записки Горьковского ун-та, 1937, вып. 6.
263.	М а к - М и л л а н В. Д., Динамика твердого тела, перев. с англ., ИЛ,.
Москва, 1951.
264.	Малахов А. Н., Максимов А. С. и Нефедов Ю. Я., Об элек-
тромагнитной гипотезе биологической связи. Бионика. «Наука», Москва,.
1965.
265.	Малахов А. Н., Флуктуации в автоколебательных системах, «Наука»,.
Москва, 1968.
ЛИТЕРАТУРА
877
266.	Малкин И. Г., Об устойчивости периодических решений динамических
систем. Прикл. матем. и мех., 1944, 8, № 4.
267.	Малкин И. Г., К теории периодических решений Пуанкаре. Принт,
матем. и мех., 1949, 12, № 6.
268.	Мал кии И. Г., Методы Ляпунова и Пуанкаре в теории нелинейных
колебаний. Гостехиздат, 1949.
269.	Малкин И. Г., К теории колебаний квазилинейных систем со многими
степенями свободы. Прикл. матем. и мех., 1950, 14, № 4.
270.	Мал кип И. Г., Колебания квазилинейных систем с неаиа.титической
характеристикой нелинейности. Прикл. матем и мех., 1950, 14, № 1.
271.	Малкин И. Г., Теория устойчивости движения. Гостехиздат, 1952.
272.	М а л к и и И. Г., О резонансе в квазпгармонических системах. Прикл.
матем. и мех., 1954, 18, № 4.
273.	Малкин И. Г., О почти периодических колебаниях нелинейных не-
автономных систем. Прикл. матем. и мех., 1954, 18, № 6.
274.	М а л к н и И. Г., Современное состояние метода Пуанкаре и возмож-
ность его использования. Труды 2-го Всесоюзного совещания по теории
автоматического регулирования, т. I, Изд-во АН СССР, 1955.
275.	Малкин И. Г., Некоторые задачи теории нелинейных колебаний. Гос-
техиздат, Москва, 1956.
276.	Мандельштам Л. И. и Папалекси Н. Д., О явлениях резонанса
n-го рода. Журнал техн, физ., 1932, 2, вып. 7—8.
277.	Мандельштам Л. И. и Папалекси Н. Д., Об обосновании одно-
го метода приближенного решения дифференциальных уравнений. ЖЭТФ,
1934, 4, вып. 2.
278.	Мандельштам Л. И. и Папалекси Н. Д., Обоснование одного
метода приближенного решения дифференциальных уравнений. Л. И. Ман-
дельштам, Поли. собр. трудов. Изд-во АН СССР, Москва, 1947.
279.	Мандельштам Л. Й.. Папалекси Н. Д., Андронов А. А.,
Витт А. А., Горелик Г. С. и X айкни С. Э., Новые исследования
нелинейных колебаний. Поли. собр. трудов акад. Л. И. Мандельштама,
т. III. Изд-во АН СССР, 1950.
280.	М а и е ш и н П. К. и Хохлов Р. В., Взаимная синхронизация двух
молекулярных генераторов при малой связи. Научные доклады высшей
школы, Радиотехника и электроника, 1958, № 3.
281.	Мартышкин В. С., Установка для изучения динамических характе-
ристик строительных материалов. Сб. «Динамические свойства строи-
тельных материалов» под ред. Ю. А. Нилеидера. Изд. ЦНИИПС, Мо-
сква, 1960.
282.	Марченко Ю. И. и Рубаник В. П., Взаимная синхронизация моле-
кулярных генераторов в случае значительных сил связи. Тезисы докла-
дов XX научной сессии Черновицкого ун-та. Секция матем. наук. Чер-
новцы, 1964.
283.	Марченко Ю. И., Взаимная синхронизация трех автогенераторов, свя-
занных звездой на общую емкость. Тезисы докладов XXI научной сессии
Черновицкого ун-та. Черновцы, 1965.
284.	Марченко Ю. И. и Рубаник В. П., О взаимной синхронизации
молекулярных генераторов. Изв. вузов, Радиофизика, 1965, 8, № 4.
285.	Марченко Ю. И. и Р у б а и и к В. П., О взаимодействии колебатель-
ных систем при наличии между ними волновой связи. Инженерный жур-
нал. Механика твердого тела, 1966, Ns 2.
286.	Марченко Ю. И. и Рубаник В. П., О взаимной синхронизации
автоколебательных систем с учетом волновых связей. Труды по теории
и применению явления синхронизации в машинах и устройствах. Изд-во
«Минтае», Вильнюс, 1966.
287.	Марченко Ю. И., Взаимная синхронизация автоколебательных системе
учетом запаздывания сил связи. Изв. вузов, Радиофизика, 1967, 10, № 11.
878
ЛИТЕРАТУРА
288.	Матюхин В. М., О статической устойчивости электропередачи в связи
с наличием нескольких генераторов на передающей станции. Изв. АН
СССР, ОТН, 1957, № 7.
289.	Матюхин В. М., Об устойчивости сложных энергосистем. Изв. АН
СССР, ОТН, 1958, № И.
290.	Мачабели Л. И., О движении диска с двумя маятниками. Изв. АН
СССР, Механика, 1965, № 2.
291.	Мерцав Г. А., Новый класс периодических решений в ограниченной
задаче трех тел и в задаче Хилла. Труды Ин-та теорет. астрономии,
вып. 1, 1952.
292.	М и н о р с к и й Н., О синхронизации. Труды Международного симпо-
зиума по нелинейным колебаниям, т. I, Изд-во АН УССР, Киев, 1961.
293.	Митропольский Ю. А., Нестационарные процессы в нелинейных
колебательных системах. Изд-во АН УССР, Киев, 1955.
294.	Митропольский Ю. А., Проблемы асимптотической теории неста-
ционарных колебаний. «Наука», Москва, 1964.
295.	Митропольский Ю. А. и Лыкова О. Б., Лекции по методу инте-
гральных многообразий. Изд-во АН УССР, Киев, 1968.
296.	Митулис А. А., Характер стационарного движения математического
маятника с вибрирующей точкой подвеса в зависимости от выбора на-
чальных условий. Труды по теории и применению явления синхрониза-
ции в машинах и устройствах. Изд-во «Минтис», Вильнюс, 1966.
297.	Митюшкин В. М., Лит и иска я Л. Л. и Камипир Л. Б., О син-
хронном изменении клеточных ядер. Сб. «Колебательные процессы в
биологических и химических системах». «Наука», Москва, 1967.
298.	Михневич Г. В., Регулирование возбуждения группы параллельно
работающих синхронных генераторов электростанций. Изв. АН СССР,
ОТН, 1957, № 6.
299.	Михневич Г. В. и Козловский Г. Ф., Устойчивость и качество
переходных процессов системы регулирования возбуждения многоагре-
гатной электростанции. Изд. АН СССР, 1960.
300.	Могильников В. С., Резонанс в асинхронных электроприводах при
пульсирующей нагрузке. Электричество, 1956, № 8.
301.	Моисеев Н. Д., Количественный аспект теории устойчивости. Записки
семинара по теории устойчивости движения, вып. I. Изд. Военно-воз-
душной академии им. Н. Е. Жуковского, Москва, 1946.
302.	Моисеев Н. Н., Асимптотические методы нелинейной механики. «Нау-
ка», Москва, 1969.
303.	Молчанов А. М., Возможная роль колебательных процессов в эволю-
ции. Сб. «Колебательные процессы в биологических и химических систе-
мах». «Наука», Москва, 1967.
304.	Молчанов А. М., Термодинамика и эволюция. Сб. «Колебательные
процессы в биологических и химических системах». «Наука», Москва, 1967.
305.	М о р о з о в с к и й В. Т., Об устойчивости работы однотипных синхронных
генераторов. Изв. АН СССР, Энергетика и автоматика, 1959, № 2.
306.	М у й ж п и е к А. И., Исследование устойчивости автоматического дина-
мического балансировщика. Уч. записки Рижского политехи, ин-та, т. I,
Рига, 1959.
307.	Нагаев Р. Ф., Динамика вибрационной машины с рабочим органом
балочного типа. Изв. АН СССР, ОТН, Механика и машиностроение,
1963, № 1.
308.	Нагаев Р. Ф., Динамика виброударной дробилки с парой самосинхро-
низирующцхея вибраторов. Изв. АН СССР, ОТН, Механика и машино-
строение, 1963, № 5.
309.	Нагаев Р. Ф., О внутренней синхронизации почти одинаковых дина-
мических объектов под действием слабых линейных связей. Прикл. ма-
тем. и мех., 1964, 28, вып. 2.
ЛИТЕРАТУРА
879
310.	Нагаев Р. Ф., О синхронизации почти одинаковых динамических си-
стем, близких к системам Ляпунова. Прикл. матем. и мех., 1964, 28,
вып. 3.
311.	Нагаев Р. Ф., Синхронизация в системе существенно нелинейных объ-
ектов с одной степенью свободы. Прикл. матем. и мех., 1965, 29, вып. 2.
312.	II а г а е в Р. Ф., Общая задача о синхронизации в почти консервативной
системе. Прикл. матем. и мех., 1965, 29, вып. 5.
313.	Нагаев Р. Ф. и Н а х а м к и и Л. А., От разнобоя к унисону. Знание —
сила, 1966, №11.
314.	Нагаев Р. Ф., Типы связей между объектами и критерии устойчивости
синхронных режимов. Труды по теории и применению явления синхро-
низации в машинах и устройствах. Изд-во «Минтис», Вильнюс, 1966.
315.	Нагаев Р. Ф. и Попов а И. А., Самосинхронизация нескольких ме-
ханических вибраторов, установленных иа едином рабочем органе балоч-
ного типа. Инженерный журнал Механика твердого тела, 1967, № 1.
316.	Нагаев Р. Ф. и Ходжаев К. Ш., Синхронные движения в системе
объектов с несущими связями. Прикл. матем. и мех., 1967, 31, вып. 2.
317.	Нагаев Р. Ф., Синхронизация генераторов конечномерных «сил».
Прикл. матем. и мех., 1968, 32, вып. 5.
318.	Н а л и м о в В. В. и Ч е р п о в а Н. А., Статистические методы планиро-
вания экстремальных экспериментов. «Наука», Физматгиз, Москва, 1965.
319.	Н е й м а р к Ю. И., Метод точечных отображении в теории нелинейных
колебаний, I, II, III. Изв. высших учебн. завед., Радиофизика, №№ 1, 2,
5, 6, 1958.
320.	Неймар к Ю. И. н Шильников Л. П., О применении метода малого
параметра к системам дифференциальных уравнений с разрывными пра-
выми частями. Изв. АН СССР, ОТН, Механика и машиностроение, 1959, № 6.
321.	Неймарк 10. И., Метод точечных отображений в теории нелинейных
колебаний. Труды Международного симпозиума по нелинейным колеба-
ниям, т. II, Изд-во АН УССР, Киев, 1963.
322.	Неймарк 10. И., Метод точечных отображений в теории нелинейных
колебании. В сб. «Механика в СССР за 50 лет», т. I, Общая и приклад-
ная механика. «Наука», Москва, 1968.
323.	Немыцкин В. В. и Степанов В. В., Качественная теория диффе-
ренциальных уравнений. Гостехнздат, 1949.
324.	Николенко Г. И., Теория расчета амортизаторов вибрационных ма-
шин. Кандидатская диссертация. Ин-т машиноведения АН СССР, Москва,
1954.
325.	Николенко Г. И., Колебания первоначально напряженных упругих
систем. Инженерный сборник, 1950, 11.
326.	Новосельский П. И., Борщевский А. В. и Сильвано-
вич В. Н., Синхронпо-сипфазпый привод дебалансных виброплощадок.
Строительное и дорожное машиностроение, 1956, № 5.
327.	О л е х п о в и ч К. А., Виброплощадкп иа упругих прокладках. Механи-
зация строительства, 1956, № 5.
328.	О л е х п о в и ч К. А., Использование эффекта самосинхронизации в
крупных вибрационных установках с виброударными колебаниями на
упругих прокладках. Труды по теории и применению явления синхрони-
зации в машинах и устройствах. Изд-во «Минтис», Вильнюс, 1966.
329.	О раевский А. Н., Молекулярные генераторы. «Наука», Москва, 1964.
330.	Отроков Н. Ф., К устойчивости периодических интегралов. Уч. за-
писки Горьковского ун-та, 1938, 6.
331.	Паповко Я. Г. и Губанова И. И., Устойчивость и колебания упру-
гих систем. Изд. второе, дополненное, «Наука». Москва, 1967.
332.	П ановко Я. Г.. Основы прикладной теории упругих колебаний. «Ма
шиностроение». М.. 1967.
333.	Папкович П. Ф., Труды по вибрации корабля. Судпромгиз,-1960,
880
ЛИТЕРАТУРА
334.	П а р ы г и и В. Н., Взаимная синхронизация трех связанных автоколеба-
тельных генераторов в случае слабой связи. Радиотехника н электро-
ника, 1956, 1, вып. 2.
335.	П а р ы г и н В. Н., Уточнение теории взаимной синхронизации двух авто-
генераторов. Вестник Московского ун-та, сер. матем., мех., астр., физ.,
хим., 1957, № 2.
336.	Пинчук И. С., Переходные процессы в асинхронных двигателях при
периодической нагрузке. Электричество, 1957, № 9.
337.	Пищиков В. И. и Соколов Н. И., Влияние сильного регулирования
возбуждения на устойчивость параллельной работы синхронных генера-
торов. Труды ВНИИЭ, 1959, 9.
338.	Плис с В. А., Нелокальные проблемы теории колебаний. «Наука», 1964.
339.	П л и с с Д. А., Сепарация сыпучих материалов па вибрирующих поверх-
ностях. Кандидатская диссертация. Рижский политехи, ин-т, Рига, 1968.
340.	Попа Д., Математика и правдоподобные рассуждения, перев. с англ.
ИЛ, Москва, 1957.
341.	Понтрягин Л. С., О динамических системах, близких к гамильтоно-
вым. Журнал экспериментальной и теоретической физики, 1934, 4, вып. 9.
342.	Попов Е. П., О малом параметре в методе гармонической линеариза-
ции. Изв. АН СССР, ОТН, 1955, № 2.
343.	Попов Е. П., К вопросу о применении метода гармонической линеари-
зации в теории регулирования. Докл. АН СССР. 1956, 106, № 2.
344.	Попов Е. П. и П альтов И. П., Приближенные методы исследования
нелинейных автоматических систем. Физматгиз, Москва, 1960.
345.	Попов Е. П., Об особенностях введения малого параметра при иссле-
довании нелинейных колебаний в автоматических системах. Прикл. ма-
тем. и мех., 1962, 26, № 1.
346.	Потураев В. Н., Фр анчук В. П. и Червоненко А. Г., Вибра-
ционные транспортирующие машины. «Машиностроение», Москва, 1964.
347.	Проскуряков А. П., О способе введения малого параметра в урав-
нения нелинейных колебаний. Прикл. матем. и мех., 1958, 22, № 5.
348.	Проскуряков А. П., Колебания квазилинейных неавтономных си-
стем с одной степенью свободы вблизи резонанса. Докл. на Всесоюзном
съезде по теоретич. и прикладп. механике, Москва, 1960.
349.	Проскуряков А. П., Периодические решения квазилинейных авто-
номных систем с одной степенью свободы в виде рядов по целым и
дробным степеням параметра. Труды Международного симпозиума по
нелинейным колебаниям, т. I, Киев, 1961.
350.	Проскуряков А. П., Метод малого параметра Пуанкаре в теории
нелинейных колебаний. Труды II Всесоюзного съезда по теоретич. и
приклад, механике, вын. 2, «Наука», Москва. 1965.
351.	Пуанкаре А., О кривых, определяемых дифференциальными уравне-
ниями. Перев. с франн. Е. Леонтович и А. Майер под ред. А. А. Андро-
нова. Гостехиздат, 1947.
352.	Ра тульские К. М„ Механизмы на вибрирующем основании (вопросы
динамики и устойчивости). Изд. Ип-та энергетики и электротехники АН
Литовской ССР, Каунас, 1963.
353.	Рагульскис К. М., Виткус И. И. и Рагульскене В. Л., Само-
синхронизация механических систем (1. Самосинхропиые и виброудар-
пые системы). Изд-во «Миитнс», Вильнюс, 1965.
354.	Рагульскис К. М., Каволелис А.-П. К., В а л т р у ш а й т и с И. Д.
и С а тк я вич у с Э. Б., Самосинхронизация механических систем
(2. Самосинхронизация, моделирование). Изд-во «Минтис», Вильнюс, 1967.
355.	Рапопорт Г. Н., К вопросу о взаимной синхронизации автогенерато-
ров сравнимой мощности. Радиотехника, 1951, 6, № 4.
356.	Р а с т р и г и н Л. А.. Некоторые особенности нестационарного движе-
ния гибкого вала е двигателем как автономной системы вблизи крити-
ЛИТЕРАТУРА
881
ческой скорости. Изв. АН СССР, ОТН, Механика и машиностроение,
1959, № 5.
357.	Родионов А. М., Квазилинейные системы с отклоняющимся аргумен-
том нейтрального типа,-Прикл. матем. и мех., 1960, 24, А" 6.
358.	Р о д ы г и и Л. В., К теории связанных релаксационных генераторов.
Сб. «Памяти А. А. Андропова», Изд. АН СССР, 1955.
359.	Розанов М. Н., Расчет режимов ресинхронизации и самосинхронизации
гидрогенераторов. Изв. высш, учебн. завед., Энергетика, 1956, № 4.
360.	Розенвассер Е. Н., О применении интегральных уравнений в теории
нелинейных колебаний. Труды II Всесоюзного съезда по теоретич. и
приклад, механике, вып. 2, «Наука», Москва, 1965.
360а. Розо М„ Нелинейные колебания и теория устойчивости, перев. с франц.,
«Наука», Москва, 1971.
361.	Романовский В. Э. К расчету поминальной мощности и механиче-
ских характеристик привода вибропогружателя. Кандидатская диссерта-
ция. Сталинградский сельскохозяйств. ин-т, Сталинград, 1958.
362.	Рубаник В. П., О взаимной синхронизации автоколебательных си-
стем. Радиотехника и электроника, 1962, 7, № 10.
363.	Рубаник В. П., О взаимодействии двух нелинейных колебательных
систем при наличии малых запаздывающих енл связи. Труды семинара
по теории дифференциальных уравнений с отклоняющимся аргументом,
т. П, Москва, 1963.
364.	Рубаник В. П., О взаимной синхронизации автоколебательных систем
при кратном отношении частот колебаний. Изв. высш, учебн. завед.,
Радиотехника, 1963, 6, № 3. 
364а. Рубаник В. П., Колебания квазилинейных систем с запаздыванием.
«Наука», Москва, 1969.
365.	Рудин А. Д., Исследование вибрационных машин трехмассной системы.
Кандидатская диссертация. Рижский политехи, ин-т, Рига, 1966.
366.	Рудин А. Д., Динамические свойства и перспективы развития машин
трехмасспой системы. Сб. «Вибрационная техника» (материалы научно-
технической конференции). Изд. НИИИНФСТРОЙДОРКОММУНМАШ,
Москва, 1966.
366а. Румянцев В. В., Метод функций Ляпунова в теории устойчивости дви-
жения. Сб. «Механика в СССР за 50 лет», т. I. «Наука», Москва, 1968.
367.	Рундквист К. А. и Кириченко А. И., Гирациопная дробилка. Ав-
торское свидетельство № 76141 с приоритетом от 8 марта 1948 г. Бюл-
летень изобретений, 1949, № 8.
368,	Рундквист А. К., Механико-технологическое исследование инерцион-
ной дробилки «Механобра». Кандидатская диссертация. Ленингр. горный
пн-т им. В. Г. Плеханова, 1954.
369.	Руидкист А. К., Механика инерционной дробилки «Механобра». Сб.
«Механика и расчет машин вибрационного типа» под ред. акад. И. И. Ар-
тоболевского. Изд-во АН СССР, 1957.
370.	Рундквист А. К., Блехман И. И. и Рудин А. Д., К теории кри-
тической щели инерционных дробильно-измельчптельных машин. «Обога-
щение руд». Изд. ин-та «Механобр», Ленинград, 1961, № 2.
371.	Риденберг Р., Переходные процессы в электроэнергетических систе-
мах. Перев. с первого амерпкаи. издания под ред. В. Ю. Ломоносова.
ИЛ, Москва, 1955.
372.	Рябов Ю. А., Обобщение одной теоремы А. М. Ляпунова. Уч. за-
писки Московского yn-та, Математика, 1957, вып. 165.
373.	Рябов Ю. А., Оценка области сходимости периодических рядов реше-
ний дифференциальных уравнений с малым параметром. Докл. АН СССР,
1958, 118, № 3.
374.	Рябов Ю. А., Об оценке области применимости метода малого пара-
метра в задачах теории нелинейных колебаний. Труды Международного
882
ЛИТЕРАТУРА
симпозиума по нелинейным колебаниям, т. II, Изд-во АН УССР, Киев,
1963.
375.	Савинов О. А., Цейтлин М. Г. и Л у с к и и А. Я., Вибрационные
машины продольно-вращательного действия для погружения свай-обо-
лочек и тонкостенных цилиндров. Труды совещания по применению виб-
раций при устройстве оснований сооружений и бурения скважин в
строительных целях. Изд. НТО строительной индустрии СССР, Ленин-
град, 1959.
376.	Савинов О. А., Современные конструкции фундаментов под машины и
их расчет. Сгройнздат, 1964.
376а. С а д о в с к и й И. М., Согласованное вращение асинхронных двигателей
(электрический вал). Госэнергоиздат, Москва, — Ленинград, 1948.
377.	Самойлов В. Ф.. Синхронизация генераторов телевизионной разверт-
ки. Госэнергоиздат, 1961.
377а. Сан дл ер А. С. и Богач ко в Б. Г., Следящая система электриче-
ского вала. Электричество, 1968, № 4.
378.	С а тк я впч у с Э. Б., Применение аналоговых вычислительных машин
для исследования явлений синхронизации. Труды по теории и примене-
нию явления синхронизации в машинах и устройствах. Изд-во «Минтис»,
Вильнюс, 1966.
379.	Сергеев П. А., Исследование рабочего процесса вибрационных транс-
портирующих машин. Кандидатская диссертация. Ин-т горного дела АН
СССР, Москва, 1960.
380.	Скнбарко А. П. и Стрелков С. П., Качественное исследование
процессов в генераторе по сложной схеме. Журнал техн, физ., 1934, 4,
вып. 1.
381.	Соколов В. М., О периодических колебаниях систем Ляпунова в од-
ном особом случае. Труды Уральского политехи, ин-та, 1954.
382.	Спиваковский А. О. и Тонча ревич И. Ф., Горнотранспортные
вибрационные машины. Углетехиздат, Москва, 1959.
383.	Старжииский В. М., Обзор работ по условиям устойчивости три-
виального решения системы линейных дифференциальных уравнений с
периодическими коэффициентами. Прикл. матем. и мех., 1954, 18,
№ 4.
384.	Стокер Дж., Нелинейные колебания в механических и электрических
системах, перев. с англ. ИЛ, 1952.
385.	Стрелков С. П., Введение в теорию колебаний. «Наука», Москва,
1964.
386.	Стретт Дж. (лорд Рэлей), Теория звука, т. II, перев. с англ., Гостех-
издат, 1944.
387.	Страбл Р., Колебания маятника при параметрическом возбуждении.
Сб. переводов н обзоров иностранной литературы. 1964, № 5 (87).
388.	Страхов С. В., Переходные процессы в электрических цепях, содер-
жащих машины переменного тока. Госэнергоиздат, Москва, 1960.
389.	Сыромятников И. А.. Режимы работы синхронных генераторов.
Госэнергоиздат, Москва, 1952.
390.	Теодорчик К. Ф. и Хайкин С. Э., Акустическое захватывание.
Журнал техн. физ.. 1932, 2, вып. 1.
391.	Т е о д о р ч и к К. Ф., Томпсоновские колебательные системы с двумя сте-
пенями свободы. Радиотехника, 1946, 1, № 3—4.
392	Теодорчик К. Ф.. Автоколебательные системы. Гостехиздат, Москва,
1952.
393	Тимошенко С. П., Теория колебаний в инженерном деле. Гостехиздат,
1934.
394.	Тондл А., Об устойчивости движения ротора с учетом влияния жест-
кости на кручение вала и муфты и податливости стоек подшипников.
Изв. АН СССР, ОТН, 1957, № 4.
ЛИТЕРАТУРА
883
395.	Т р и б е л е в а Т. Н., Об устойчивости периодических движений. Докл.
АН СССР, 1960, 133, № 2.
395а. Т у р к и и В. Я., Хечанов Ю. С. и Шульц П. П., Вибрационная
щековая дробилка. Авторское свидетельство № 202724 с приоритетом от
21 декабря 1966 г. Изобретения, промышленные образцы, товарные знаки,
1967, Ns 19.
396.	Уайлд Д. Дж., Методы поиска экстремума, перев. с англ., «Наука»,
Москва, 1967.
396а. У л а м С., Нерешенные математические задачи. Из серии «Современные
проблемы математики», перев. с англ., «Наука», Москва, 1964.
397.	Уткин Г. М., Исследование двухконтурпого генератора при кратности
частот 1 : 2. Научные доклады высшей школы, Радиотехника и электро-
ника, 1958, № 1.
398.	Файн В. М., Об уравнениях колебаний молекулярного генератора.
ЖЭТФ, 1957, 33, вып. 4 (10).
399.	Франк-Каменецкий Д. А., Механизм двухстадиального воспламе-
нения. Журнал физич. химии, 1940, 14, вып. 1.
400.	Фрезер Р., Дункан В. и Коллар А., Теория матриц и ее прило-
жения к дифференциальным уравнениям и динамике. ИЛ, Москва, 1950.
401.	Фролов К. В., О моделировании резонансных свойств некоторых авто-
номных нелинейных колебательных систем. Труды Международного сим-
позиума по нелинейным колебаниям, т. III, Изд-во АН УССР, Киев, 1963.
402.	Хая си Т., Нелинейные колебания в физических системах. «Мир», Мо-
сква, 1968.
403.	Хейл Дж., Колебания в нелинейных системах, перев. с англ., «Мир»,
Москва, 1966.
404.	Ходжаев К. Ш., Динамика вибрационных устройств с однозазориыми
электромагнитными вибраторами. Изв. АН СССР, Механика, 1965, Ns 3.
405.	Ходжаев К. Ш., Динамика электровибрационных устройств с двух-
зазорными вибраторами. Инженерный журнал. Механика твердого тела,
1966, № 1.
406.	Ходжаев К. Ш., Колебания в системе со многими электромагнитными
возбудителями. Инженерный журнал. Механика твердого тела, 1966, № 2.
407.	Ходжаев К. Ш., Синхронизация механических вибраторов, связанных
с линейной колебательной системой. Инженерный журнал. Механика
твердого тела, 1967, № 4.
408.	Ходжаев К. Ш., Резонансный и нерезонансный случаи в задаче о воз-
буждении механических колебаний. Прикл. матем. и мех., 1968, 32, вып. 1.
409.	Ходжаев К. Ш., О возбуждении вибраций. Инженерный журнал. Ме-
ханика твердого тела, 1968, № 2.
410.	Ходжаев К. Ш., Колебания, возбуждаемые электромагнитами в ли-
нейных колебательных системах. Инженерный журнал. Механика твер-
дого тела, 1968, № 5.
411.	Ходжаев К. Ш., Интегральный критерий устойчивости для систем с
квазициклическими координатами и энергетические соотношения при коле-
баниях проводников с токами. Прикл. матем и мех., 1969, 33, вып. 1.
412.	Холоденко Л. П., К теории синхронизации разрывных автоколеба-
ний. Журнал техн, физ., 1940, 10, вып. 2.
413.	Хохлов Р. В., К теории захватывания при малой амплитуде внешней
силы. Докл. АН СССР, 1954, 97, № 3.
414.	Хохлов Р. В., Об одном случае взаимной синхронизации отражатель-
ных клистронов. Радиотехника п электроника, 1956, 1, № 1.
414а. Хэнзел Ч., Парапсихология, перев. с англ., «Мир», Москва, 1970.
415.	Цаплин С. А., Виброударные механизмы. Автотрансизд., Москва, 1953.
415а. Ц е й т л и н М. Г., Совков Г. В., Бал абашквп Ю. В., Погружение
экспериментальной крепи вибромеханизмами продольно-вращательного
действия. Шахтное строительство, 1969, № 11.
884
ЛИТЕРАТУРА
416.	Цу кер ник Л. В., Обобщение уравнений динамики сложной энергоси-
стемы п применение электронной счетной машины для анализа ее устой-
чивости. Автоматика и телемеханика, 1957, № 1.
417.	Цу кер ник Л. В., Устойчивость связанной системы автоматического
регулирования при внутригрупповой симметрии. Изв. АН СССР, ОТН,
Энергетика и автоматика, 1959, № 4.
418.	Чеботарев Н. Г., «Многоугольник Ньютона» и его роль в развитии
математики. Собр. соч., т. III. Изд-во АН СССР, 1950.
419.	Чезари Л., Асимптотическое поведение и устойчивость решений обык-
новенных дифференциальных уравнений. «Мир», Москва, 1964.
420.	Чет а ев Н. Г., Устойчивость движения. Гостехиздат, Москва, 1955.
421.	Чижевский А. Л., Солнце и мы. «Знание», Москва, 1963.
422.	Чижевский А. Л. и Ш а шин а Ю. Г., В ритме Солнца. «Наука»,
Москва, 1969.
423.	Ч и л и к и п М. Г., Общий курс электропривода. Госэнергоиздат, 1951.
424.	Шалеа Р., Синхронизация пеизохронного осциллятора. Труды Между-
народного симпозиума по нелинейным колебаниям, т. II, Изд-во АН
УССР, Киев, 1963.
425.	Ш а х г и л ь д я и В. В. и Л я х о в к и и А. А., Фазовая автоподстройка
частоты. «Связь», Москва, 1966.
425а. Ш е п л и X., От атомов до Млечных Путей. ГТТИ, 1934.
4256. Шепл и X., Звезды и люди. ИЛ, Москва, 1962.
426.	Ill е х т е р О. Я., Об одном примере субгармонических колебаний. Труды
совещания ио применению вибраций при устройстве оснований сооруже-
ний и бурения скважин в строительных целях. Изд. НТО строительной
индустрии СССР, Ленинград, 1959.
427.	Шехтер О. Я., О погружении тяжелых железобетонных оболочек. Ди-
намика грунтов. Сборник № 44, Госстройиздат, 1961.
428.	Шиманов С. Н., К теории квазигармонических колебаний. Прикл.
матем. и мех., 1952, 16, № 2.
429.	Шиманов С. Н., К теории колебаний квазилинейных систем. Прикл.
матем. и мех., 1954, 16, № 2.
430.	Шиманов С. Н., Об одном способе получения условий существования
периодических решений нелинейных систем. Прикл. матем. и мех., 1955,
19, № 2.
431.	Шиманов С. Н., К вопросу об отыскании характеристических пока-
зателей систем линейных дифференциальных уравнений с периодическими
коэффициентами. Докл. АН СССР, 1956, 109, № 6.
432.	Шиманов С. Н., Об отыскании характеристических показателей систем
линейных дифференциальных уравнений с периодическими коэффициен-
тами. Прикл. матем. и мех., 1958, 22, № 3.
433.	Шиманов С. Н., К теории колебаний квазилинейных систем с запаз-
дыванием. Прикл. матем. и мех., 1959, 23, № 5.
434.	Шиманов С. Н., О почти-периодических колебаниях квазилинейных
систем с запаздыванием времени в случае вырождения. Докл. АН СССР,
1960, 133, № 1.
435.	Шноль С. Э., Конформационные колебания молекул. Сб. «Колебательные
процессы в биологических и химических системах». «Наука», Москва, 1967.
436.	Штейнберг Т. С., О периодических решениях дифференциального
уравнения нелинейных колебаний при наличии сил «сухого» и «вязкого»
трения. Изв. АН СССР, ОТН, 1954, № 4.
437.	Штейнберг Т. С., Метод малого параметра при исследовании перио-
дических движений систем с трением. Труды Уральского политехи, ин-та,
1958, сб. 74.
438.	Штейнберг Т. С., Метод малого параметра для дифференциальных
уравнений второго порядка с разрывными членами. Изв. АН СССР, ОТН,
Механика и машиностроение, 1960, № 1.
ЛИТЕРАТУРА
885
439.	Ш’т окало И. 3., Критерий устойчивости и неустойчивости. Математи-
ческий сборник, 1946, т. 3/45, № 2.
440.	Якубович В. А., Метод малою параметра для канонических систем
с периодическими коэффициентами. Прикл. матем. и мех., 1959, 23, вып. 1.
441.	Я н к о - Т р и и и ц к н й А. А., Новый метод анализа работы синхронных
двигателей при резко-переменных нагрузках. Госэнергоиздат, 1958.
442.	Amerio L., Determinazione delle condizione di stabilita per gli integral!
di un’equazione interessante 1’electrotecnica. Ann. mat. рига appL, 1949,
4, 30.
443.	A p p I e t о n E. V., The automatic synchronization of triode oscillator.
Proc. Cambridge Philos. Soc. (Math, and Phys. Sci.), 1922, 21.
444.	Bailey H. R. and Gambill R. A., On Stability of Periodic Solutions
of Weakly Nonlinear Differential Systems. J. Math. Meeh., 1957, 6.
445.	Baltz W. E., Zur Frage des Gleichlaufs bei Mehrmotorenantrieben.
Technische Mitteilungen Conz. Elektrizitats-Gesellschaft, Hamburg, Okt.
1955, H. 7.
446.	В lech man 1., Die Selbstsynchronisation nieclianischer Vibratoren und
das Problem der Gruppenfundamente fiir unbalancierte Maschinen (Ma-
schinen init Llnwuehten). Internationale Tagung «Verfahren Geriite der
mechanischen Schwingungstechnik», Teil II. Technische Hochschule Otto
von Guerike Magdeburg, Sept. 1965.
447.	Bogusz W„ Engel Z., Badania doswiadczalne urzadzen samosynchro-
niz.ujacych. Przeglad mechaniczny, 1965, № 8.
448.	Cesari L., Sulla stabilita delle soluzioni dei sistenii di equazioni diffe-
renziali linear! a coefficienti periodici. Atti acad. Italia, Mem. Cl. Sci. Fis.
Mat. Nat., 1940, 6, 11.
449.	Cesari L., Asymptotic behavior and stability problems in ordinary diffe-
rential equations. Ergebn. Math., 1959, № 116.
450.	Coddington E. A. and Levinson N., Perturbations of linear systems
with constant coefficients possessing periodic solutions. Contributions to
the theory of non-linear oscillations, 1952, 2, Princeton.
451.	«Comessa». Perfectionnements aux appareils vibratoires de distribution,
transport ou criblage. Republique Franpaise. Brevet d’invention № 1.107.703.
Gr. 5-C1. 6. Demande le 25 Juin 1954, publie le 4 Janvier 1956.
452.	Cough ey T. K-, Hula-hoop: one example of heteroparametric excitation.
Amer. J. Phys., 1960, 28, № 2.
453.	Diliberto S. P., Hufford G., Perturbation theorems for non-linear
ordinary differential equations. Contributions to the theory of non-linear
oscillations, HI, Princeton, 1956.
454.	Fagerberg B., New vibrating screen improves iron ore processing.
Engr. and Min. Journal, July, 1960.
455.	Faure R., Sur les systemes d’equations differentielles non lineaires a
coefficients periodiques. Etude d’un cas particulier. C. r. Acad. Sci., 1957,
245, Ns 19.
456.	Faure R., Sur la synchronisation des systemes oscillants. Solutions
voisines de points singuliers. C. r. Acad. Sci., 1958, 247, № 15.
457.	Friedrichs K. G., Fundamentals of Poincare’s theory. Proc. Sympos.
Non-linear Circuit Analysis, 1953, 2.
458.	Gambill R. A., Stability criteria for linear differential systems with
periodic coefficients. Riv. Mat. Univ. Parma, 1954, 5, №№ 1—3.
459.	Gambill R. A., Criteria for parametric instability for linear differential
systems with periodic coefficients. Riv. Mat. Univ. Parma, 1955, 6,
№№ 1—2.
460.	G о 1 d a c r e R., The control of rhythm and homeostasis in biology and
medicine. Cibernetica, 1960, № 2.
461.	Haag J., Etude asyniptotique des oscillations de relaxation. Ann. Sci.,
Ec. Norm., 1943, Sup. 60.
886
ЛИТЕРАТУРА
462.	Haag J., Sur la synchronisation des systemes oscillants non lin£aires.
Ann. Sci. Ecole Norm. Sup., Paris, 1950, 67, 321—322.
463.	Haag J., Les movements vibratoires. Collection Euclide. Presses univer-
sltaires de France, 1952, Chap. 6, 7, 8, Paris.
464.	Hale J. K., On the stability of periodic solutions of weakly non-linear
periodic and autonomous differential systems. Contributions to the Theory
of Non-linear Oscillations, vol. 5, pp. 91 — 113. Ann. Math. Studies, Prin-
ceton University Press, Princeton, New York, 1960.
465.	Heidemeyer H. und Schweinfurth H., Der Unwuchtmotor als
Schwingantrieb und seine Anwendungsmoglichkeiten. Erdol und Kolile
1956, № 3.
466.	Jordan H., Uber den stationaren Betrieb und die Auslegung von elektri-
schen Ausgleichswellen. Elektrotechnische Zeitschrift, 1952, 73, 2.
467.	MacMillan W. D., An existence theorem for periodic solutions. Trans.
Amer. Math. Soc., 1912, 13.
468.	Mazett R., Mecanique vibratoire. Paris — Liege, Libr. politechn. ch. Be-
ranger, 1955.
469.	Mayer A-, On the theory of coupled vibrations on two self-excited gene-
rators. Technical physics of the USSR, 1935, 11, № 5.
470.	Noh el J. A., Stability of perturbed periodic motions. Journ. reine und
angew. Math., 1960, 203, FI. 1/2.
471.	О 11 с n d о r f F., Peters W., Schwingungstabilitat parallelarbeiten der
Synchronmaschinen. Wissenschaftliche Veroffentlichungen aus dem Sie-
mens-Konzern. VI, S. 7—26. Springer, 1925—1926.
472.	Poincare H., Les methodes nouvelles de la mecanique celeste. Paris,
1892, t. 1; 1893, t. II; 1899, t. 111.
473.	R о c a r d Y., Dijiamique Generale des vibrations. Masson, Paris, 1949.
474.	Rod er L, Stoff F., Material Handling Vibrating Machine. United States
Patent Office, № 3, 053, 379. Claims priority, application Germany June 21,
1956. Patented Sept. 11, 1962.
475.	Schur L, Uber Potenzreihen, die im Innern des Einheitkreises beschriinkt
sind. Zeitschr. reine und angew. Math., 1918, 148.
476.	Seifert G., On the existence of certain solutions of a non-linear
differential equation. Zeitschr. angew. Math, und Phys., 1952, 3,
Fasc 6.
477.	Si buy a Y., On perturbation of periodic solutions. Journ. Math. Meeh.,
1960, 5, 771—782.
478.	Signeul R. A O., Apparat for behandling av ett objekt medelst riktade
vibrationer. Sverige, patent № 163270, KI. 80a : 49. Patenttid fran den
6 Augusti 1946, pablicerat den 13 Maj 1950.
479.	Signeul R. A. O., Vibrating device for a directed vibratory effect by
means of rotatable vibratory members. United States Patent Office, № 2,
531, 706. Application May 25, 1948, in Sweden August 6, 1946. Patented
Nov. 28, 1950.
480.	Sommerfeld A., Beitrage zum dynamischen Ausbau der Festigkeits-
lehre. Zeitschr. VDI, 1902, XXXXVI, № 11, Berlin.
481.	Sperling L., Selbstsynchronisation unwuchtbehafteter Rotoren an ela-
stischen Ketten. Internationale Tagung «Verfahren und Gerate der mecha-
nischen Schwingungstechnik», Teil II, Techn. Hochschule Otto von Guericke,
Magdeburg, Sept. 1965.
482.	Sperling L., Beitrag zur allgemeinen Theorie der Selbstsynchronisation
umlaufender Unwuchtmassen im Nichtresonanzfall. Wissenschaftliche Zeit-
schrift der Tcchnischen Hochschule Otto von Guericke Magdeburg, 1967,
11, H. 1.
483.	Spurlin W. V., Dual eccentric weight vibratory generator for circular
feeder. United States Patent Office № 3, 053, 380 Filed Febr. 15, 1960,
Patented Sept. 11, 1962.
ЛИТЕРАТУРА
887
484.	Stellmacher К. L., Ober erzwungene nichtlineare Schwingungen hoher
Erregerfrequenz und ihre Stabilitat. Zeitschr. angew. Math, und Meeh.,
1954, 34, № 3
485.	Stoff F., Ro der 1., Schwingfordcrer oder-sieb. Bundesrepublik Deut-
schland, Patentschrift № 972488, KI. 81e, Gr. 51. Patentiert von 29. April
1951, ausgegeben am 12. November 1959.
486.	Stoker J. J., Periodic oscillations of non-linear systems with infinitely
many degrees of freedom. Publ. Sci. tech. Min. Air., 1953, № 281, Paris.
487.	Suezaki Teruo, Mori Shiusaku, Mutual synchronization of
two oscillators. Summaries papers Internat. conf, microwaves. Circuit
Theory and Inform. Theory, Tokyo, 1964, Part 2. Tokyo, Inst. Electr.,
Common Engrs. Japan, s. a. Ill —112.
488.	Thearle E. I.., A new type of dinamic balancing machine. Trans.
A. S. M. E. 1932, 54, № 12.
489.	Thearle E. L., Automatic dinamic balancers. Mashine Design, 1950, 22,
№№9,10,11.
490.	Thomson W., Tait P. G., Treating on Natural Philosophy, 1879,
vol. 1, p. 1.
491.	Tri comi F., Integrazione di un’equazione differenziale presantatasi in
electrotecnica. Annali della R. Scuola Normale Superiore di Pisa, 1933,
Ser. II, 2.
492.	Ungruh F., Gleichlaufantriebe mit elektrischen Wellen. Elektro-Technik,
1960, № 8/9.
493.	Van der P о 1 B., On relaxation oscillation. Philos. Mag., 1926, (7) 2,
p. 978.
494.	Van der Pol B., Uber Relaxationschwingungen. Zeitschr. Hochfre-
quenztechnik, 1926, 28, S. 178; 1927, 29, S. 114.
495.	VanderPol B„ Van der Mark M., Le battement du coeur considers
comme oscillation de relaxation et un modele electrique du coeur. L’Onde
electrique, 1928, № 7.
496.	Veyvoda O., On the existence and stability of the periodic solution of
the second kind of a certain mechanical system. Чехословацкий матема-
тический журнал, 1959, 9 (84).
497.	Vol terra V., Lecons sur la Theorie Mathematique de la Lutte pour la
Vie. Paris, Gauthier-Villars, 1931.
При составлении обзора п. 3 § 3 главы XII и §§ 4 и 5 главы XX исполь-
зованы каталоги и рекламные заметки следующих иностранных фирм:
498. AEG (DBR) Fachgebiet Vibrationstechnik.
499.	АМЕСО (France) Departement de vibration.
500.	Becker-Priinte Gmb H (DBR).
501.	Beumer-Maschinenfabrik (DBR).
502 Friedrich Uhde Gmb H (DBR)'.
503.	Honert W. (DBR) Maschinen- und Apparatebau.
504.	Jost GmbH (DBR) Schwingungstechnik.
505.	Link-Belt (USA).
506.	OWL Engineering Supplies Limited (England).
507.	Sinex E. Damond s. a. (France).
508.	Venanzetti Vibrazione s. a. (Italia)',
509.	Bixby Zimmer engineering (USA).
510.	«Сопсепсо» (USA).
ИМЕННОЙ УКАЗАТЕЛЬ
Аграновская Э, А. 14, 235, 345, 566, 606, 619,
626, 655, 722, 864
Айзерман М. А. 141, 864
Акаловский И. В. 80, 864
Аксельрод 3. М. 72, 864
Акуленко Л. Д. 627
Алабужев П. М. 360, 369, 370, 514, 837, 864
Альтшуль В. А. 81, 864
Америо (Amerio L.) 655, 885
Ананьев И. В. 626, 864
Андреюк В. А. 19, 79, 864
Андронов А. А. 20, 32, 33, 72, 79, 81, 85, 89,
107, 128. 129, 139, 149, 180, 186, 219, 640,
812, 864, 865, 871, 877
Аракн Иосиаки (Arakl Josiaki) 370, 627, 873
Аркадьев В. 94, 865
Аронович Г. В. 19, 79, 655, 865
Артемьев Н. А. 133, 138, 189, 196, 208, 275.
330, 865
Артоболевский И. И. 865, 881
Бабский Е. Б. 89, 865
Базовский (Bazovsky I.) 600, 865
Балабашкин Ю. В. 770, 883
Балжн М. Ф. 494, 865
Балтрушайтис И. Д. 233, 525, 880
Бальтц (Baltz W. Е.) 78, 885
Барбашнн Е. А. 115, 149, 865
Баркан Д. Д. 626
Басов Н. Г. 86
Баталова 3. С. 235, 627, 655, 657, 658, 865
Баутин Н. Н. 20, 32, 72, 145, 152, 865
Бейзельман Р. Д. 385, 386, 480, 636, 865
Бейли (Bailey Н. R.) 138, 885
Беленов Э.М. 87, 865
Беллман (Bellman R.) 115, 865
Беллюстин С. В. 81, 86, 866
Белюстина Л. Н. 79, 655. 805
Беликовский II. Г. 377, 866
Берштейн И. 20, 866
Бессонов А. П. 607. 866
Бине (Binet J. Ph. М.) 164, 178, 201
Бирюков М. К.' 626, 642, 866
Блакьер (Blaquire А.) 866
Блехман И. И. 16, 17, 21, 32, 58. 61, 75, 108,
137—145, 154. 167, 169, 177, 182, 184, 219
224, 252, 283, 309, 343—362, 368—373, 398,
401,	431,	447, 466.	475,	483,	492,	532. 535,
563,	566,	569—573,	577,	579,	582,	588—591,
6QQ.	603,	606—609,	614,	619,	621,	626-630,
659,	660,	663 , 672 ,	681,	683 ,	696,	704, 708,
712,	721,	731—751,	764,	766,	768,	771, 777,
796, 803, 811, 816, 820, 837—861, 864, 866—
868, 872, 881, 885
Богачков Б. Г. 78, 882
Боголюбов А. Н, 865
Боголюбов Н. Н. 19, 20, 171, 212, 233, 234,
626, 8ё§, 869, 875
Боголюбов Н. Н. (младший) 138, 869
Богуш (Bogusz W.) 3/0, 683, 885
Большаков В. М. 607, 869
Бом (Bohm D.) 17, 626, 869
Бор Г. (Bohr Н.) 210
Борщевский А. В. 17, 78, 346, 358, 362, 371,
739 879
Браверман Е. Л. 235, 766, 863, 869
Брсмзен А. С. 20, 80, 84, 91, 869
Бруевич А. Н. 869
Буасс (Boisse) 55, 619, 621, 624
Букаты Г. Б. 371. 721, 727, 869
Булгаков Б. В. 99, 107, 164, 184, 201, 300,
302, 869
Булгаков Н. Г. 136, 170, 177, 869
Бутенип Н. В. 20, 75, 82, 769
Быстрицкий Д. Н. 19, 869
Быховскмй И. И. 14, 607, 619, 869
Быховский М. Л. 380, 869
Валеев К. Г. 138, 224, 318, 869, 870
Вальц Г. Б. 627, 870
Ваи-дер-Марк (Van der Mark М.) 21, 89,
233, 887
Ван-дер-Поль (Van der Pol В.) 20, 21, 59,
79, 81, 85, 86, 89, 607, 808, 816, 818, 819,
870, 872, 887
Васильев Л. Л. 93, 870
Ватсон А. В. 346, 358, 362, 734, 866
Вейвода (Veyvoda О.) 219, 606, 870, 887
Векслер В. И. 17, 626, 870
Вентцель Е. С. 151, 701, 870
Винер (Wiener N.) 17, 88, 92—96, 870
Внтек В. 19, 870
Виткус И. И. 233, 494, 503, 525. 880
Витт А. А. 17, 20, 21, 33, 72, 79, 81, 85, 89,
107, 128, 129. 149, 180, 184, 219, 640, 812,
864, 865, 870, 877
Вознюк Л. Л. 138, 870
Волк И. М. 136, 870
Волосов В. М. 136, 233, 234, 269, 627, 870
Вольтерра (Volterra V.) 17, 21, 89—91, 887
Гамбилл (Gambill R. А.) 138, 885
Гамильтон (Hamilton W. R.) 295, 296, 313
Ганиев Р. Ф. 224, 318, 870
Гантмахер Ф. Р. 220—223, 592, 870
Гапонов А. В. 78, 870
Гапонов В. И. 20, 80, 870
Гаузе Г. Ф. 17, 21, 89, 870
Гаусс (Gauss К- F.) 783, 786
Гельман А. Е. 107, 871
Гецявичус Ю. 1О. 370. 871
Гладков С. Н. 871
Готенемзср К. (Ilohcnemser К.) 671
Гольдстейн (Goldstine IIJ 99, 300, 302, 871
Гольдштейн Б. Г. 338, 871
Гольдштейн Я. А. 663, 871
Гольдэкр (Goldacre R.) 17, 88, 89, 885
Гончаревич И. Ф. 578, 722, 871, 882
Горев А. А. 19, 79, 871
Горелик Г. С. 32, 871. 877
Горнштейн В. М. 19, 79, 871
Городский Д. А. 873
Горожанкнн В, Н. 81, 871
ИМЕННОЙ УКАЗАТЕЛЬ
889
Гортииский В. В. 339, 627, 871
Горшков С. Н. 356, 371, 721, 726, 756, 871
Граффи (Graffi D.) 80, 619, 874
Гринберг А. П. 17, 626, 871
Гробов В. А. 71, 871
Губанова И. И. 370, 627. 879
Гурвиц (Hurwitz А.) 132, 137, 167, 168, 182,
184
Гурса (Goursat Е.) 132, 201, 871
Гущин М. Н. 81, 872
Гюйгенс (Huygens II.) II, 15, 16,45, 59 72,
86, 103, 248, 790, 815, 816, 819, 820, 872
Делоне (Delaunay С.) 303
Ден-Гартог (Den Gartog .1. Р.) 67, 872
Денисов Г. А. 14, 353, 369, 371, 590, 603, 683,
693, 709, 731—736, 747, 853 , 864, 867, 868,
872
Детинко Ф. М. 67, 68, 796, 872
Джанелидзе Г. Ю. 14, 58, 61, 296, 345, 346,
360, 466, 563, 566, 569—573, 577, 606, 619,
621, 695 , 734, 820, 866 , 867, 872
Джиоваинини (Glovannini G.) 80
Дилиберто (Diliberto S. Р.) 107, 885
Диментберг М. Ф. 607
Диментберг Ф. М. 71, 872
Дирихле (Dirichlet Р. G. L.) 221, 224
Долнцкий И. И. 370, 683, 739, 872
Дородницын А. А. 872
Дроздов Ю. М. 308, 872
Дубошин Г. Н. 107, 872
Дубровин Б. Н. 14, 627, 681, 742, 749, 872
Дубровин В. В. 14, 721, 747
Дуикаи (Duncan W. J.) 122, 883
Дуффииг (Duffing Н.) 320
Есафов Н. И. 20, 80, 873
Есин Г. Д. 494, 865
Ерофеев Л. В. 347, 873
Еругин Н. П. 115, 138, 873
Жданов П. С. 19, 873
Жуков Л. А. 19, 873
Жуковский Н. Е. 296, 873
Забылии М. И. 370, 873
Закрытной О. С. 371, 727, 869
Зарагатский Л. П. 742
Зарецкий Л. Б. 216, 235, 369, 526, 766, 863,
869, 873
Зельдин Е. С. 607, 869
Земсков В. Д. 607, 722, 871
Зиновьев В. А. 380, 869
Зубов В. И. 127, 873
Зуев А. К. 360, 369. 370, 514 , 837, 864, 873
Зойферт (Seifert G.) 655, 886
Зоммерфельд A. (Sommerfeld А.) 55 302
605—607, 614-619, 624, 886
Иваненко А. Я- 742, 750
Иванов Б, Г. 350, 742, 867
Иванов Е. Н. 360, 370, 514, 837, 864, 873
Иванов И. А, 350. 742, 867
Иконников Е. 20. 866
Иноземцев Б. С. 19, 873
Ииоуэ Дзюнкитн (Inoue Dzunkiti) 370, 627,
873
Иордан (Jordan Н.) 78, 886
Иткии Г. Е. 371, 727, 869
Каволелнс А. П. К. 233, 503, 525, 880
Кажинский Б. Б. 93, 873
Калишук А. К. 606, 873
Каминир Л. Б. 88, 878
Каннннгхем (Cunningham W. J.) 874
Кантор Р. М. 873
Капралов Е. П. 721
Карпов Н. А. 370, 874
Картвелпшвили Н. А. 19, 20, 78, 79 655,
865, 874
Кауги (Coughey Т. К.) 626, 627, 885
Каудерер (Kanderer Н.) 874
Кац. А, М. 308. 874
Кац М. (Кос М.) 210, 874
Квашнин И. С. 721
Кельвин (Kelvin, Thomson W.) 75, 82, 296,
887
Кимбарк (Kimbark Е.) 19, 20, 874
Кириченко А. И. 346, 349, 355, 358, 362, 371,
734, 742, 866, 874, 881
Кириарский М. Ш. 360, 369, 370, 514 , 837,
864, 873, 874
Кобринский А. Е. 143 , 526, 749, 874
Коддингтои (Coddlngton Е. А.) 107, 136,
170, 177, 213, 874, 885
Козловский Г. Ф. 19, 878
Колбин Н. М. 626, 864
Коллар (Collar A. R.) 122, 883
Коловский М. 3. 14, 137, 213—216, 226 , 295,
526, 761, 874
Коломбо (Colombo G.) 80
Кононенко В. О. 72, 606, 874
Конти (Conti R.) 80, 619, 874
Концевой В. Г, 671
Копнин Ю. М. 137, 231, 874
Кораблев С. С. 606, 875
Корешков В. И. 722, 871
Косс М. Ш. 596, 597 , 875
Костенко М. П. 19, 875
Коши (Cauchy A. L.) 164, 178, 201, 210
Красовский Н. Н. 115, 875
Крейн М. Г. 220—223, 592, 870
Креиделл (Crandall St. Н.) 875
Крылов Н. М. 19, 171, 212, 233 , 234 , 875
Кумпикас А. Л. 369, 627 , 655, 777 , 875
Кушуль М. Я. 137, 138, 232, 269, 875
Лавров Б. П. 13, 14, 17, 224, 343, 346, 351,
353,	358,	362,	368—371, 383,	431,	488,	516
517,	539,	540,	547,	563, 573,	588,	590,	600,
603,	663,	683,	689,	692—695,	704,	708,	711,
712,	721,	724,	726,	731—740,	756,	839	847,
849, 853, 857, 866—868, 871, 872, 875
Лагранж (Lagrange J. L.) 30, 34. 71, 78,
142,	221,	224,	284,	288—296,	299,	302,	304,
313,	316,	392,	422—424,	431,	497,	498,	535,
537 ,	550,	555,	560,	594,	771,	778,	779,	805,
832
Ладыженский Л. А.	360,	569—573,	820,	868
Лауд (Loud W. S.) 20, 876
Ла-Салль (La Salle J.) 115, 128, 149, 152, 876
Лебедев С. А. 19, 876
Левин Б. Р. 600, 876
Левин (Levine L.) 224, 876
Левин Л. П. 63, 822, 876
Левинсон (Levinson N.) 107, 136, 170, 177,
213, 874, 885
Лесин А. Д. 370, 683, 763—765, 876
Лефшец (Lefschetz S.)	115,	128,	149,
152, 876
Липшиц (Lipschitz R.) 210
Литииская Л. Л. 88, 878
Лойцянский Л, Г. 876
Лурье А. И. 14, 70, 234, 296, 300, 302, 312,
313, 377, 872, 876
Лускин А. Я- 354, 371, 882
Лыкова О. Б. 234, 878
Любимов Г, П. 87, 876
890
ИМЕННОЙ УКАЗАТЕЛЬ
Любимцев Я. К. 79, 655, 865
Ляпунов А. М. 21, 25—27, 31, 32, 60, 103
105—154, 171, 221, 324—332, 401, 492, 606
619, 626, 876, 881
Ляховкин А. А. 21, 626, 884
Мазет (Mazett R.) 606, 886
Майер А. Г. 80, 876, 886
Макаров А. И. 14, 660, 665, 747
Мак-Миллан (Mac Millan W. В). 107, 876,
886
Максвелл (Maxwell J. С.) 78
Максимов А. С. 94, 876
Малахов А. Н. 13, 20, 33, 80, 81, 94, 876
Малкин И. Г. 20, 107, ПО—И5, 121, 125—128,
133, 136, 137, 153, 163, 187—190, 195 196
204—213, 219, 221, 224—230, 269, 272 325*
397, 645, 647, 877
' Мандельштам Л. И. 107, 877
Манешин П. К. 21, 87, 877
Мартышкин В. С. 606, 877
Марченко Ю. И. 81, 87, 370, 582, 588, 841
868, 877
Матюхни В. М. 19, 878
Мачабели Л. И. 69, 797, 878
Мерман Г. А. 136, 137, 231, 643, 878
Минорский (Minorsky N.) 20, 75, 81, 86,
812, 813, 816, 819, 878
Минц Р. М, 607, 869
Митропольский IO. А. 20, 212, 233, 234, 626,
869, 878
Митулис А. А. 627, 655—657, 878
Митюшкин В. М. 88, 878
Михневич Г. В. 19, 878
Мияуро Суга (Mijauro Suga) 370, 627, 873
Могильников В. С. 384, 878
Моисеев Н. Д. 149, 878
Моисеев Н. Н. 234, 627, 870, 878
Молчанов А. М. 61, 88, 878
Моргунов Б. И. 234, 627, 870
Мори Шиузаки (Mori Shiuzaki) 81, 887
Морозовский В. Т. 19, 878
Муйжииек А. И. 67, 878
Мышкис А. Д. 32, 139, 145, 398, 868
Нагаев Р.	Ф.	13, 14, 21, 31,	34,	207,	208,
216, 222, 224, 244, 247, 269, 299, 309, 316—
319,	322,	325,	346,	358,	368—371,	514,	526,
557,	563,	588,	590,	591,	668,	683,	693,	695,
731,	732,	736,	758,	853,	863,	868,	872,	876,
878, 879
Налимов В. В. 224, 879
Нахамкин Л. А. 879
Неймарк Ю. И. 136, 167, 213, 526, 879
Немыцкий В. В. 98, 879
Нефедов Ю. Я- 94 , 876
Николенко Г. И. 14, 377, 606, 616, 879
Новосельский П. И. 17, 78, 346, 358, 371,
739, 879
Ноэль (Nohel J. А.) 138, 886
Ньютон (Newton I.) 132, 165, 232, 458
Олевский В. А. 14, 747, 748
Олохнович к. А. 370, 683, 739, 879
Оллендорф (Ollendorf F.) 19, 886
Ораевский А. Н. 86, 87, 865, 879
Остроградский М. В. 295
Отроков Н. Ф. 128, 219, 879
Павлова Т. Т. 380, 869
Пальтов И. П. 141, 880
Пановко Я- Г. 14, 32, 67, 139, 145, 370, 398,
627, 797, 803, 868, 879
Папалекси Н. Д. 107, 877
Папкович П. Ф. 377, 879
Парыгин В. Н. 80, 880
Паста (Pasta J.) 97
Петерс (Peters VV.) 19, 886
Нетрунькин Л. П. 338, 871
Пинчук И. С. 384, 880
Пищиков В. И. 19, 880
Плисс В. А. 880
Плисс Д. А. 14. 16, 367, 371, 659, 683, 731
880
Плотникова Г. В. 137, 231
Пойа (Polya G.) 140, 147, 880
Поляков В. Н. 360, 569—573, 579, 820, 867
868
Понтрягин Л. С. 880
Попов Е. П. 141, 880
Попова И. А. 358, 360, 369, 557, 563, 569—
573, 820, 868, 879
Потураев В. Н. 880
Прагер (Prager W.) 871
Пресняков В. К. 606
Прохоров А. М. 87
Проскуряков А. П. 108, 137, 141, 231, 880
Прянишников Б. П. 724
Пуанкаре (Poincare Н.) 21, 25—27, 31, 32,
60, 81, 86, 103—154, 159, 163, 177, 195, 234,
251, 252, 401, 492, 592, 606, 619, 626, 880,
886
Пуплясв И. М. 371, 727, 869
Пуст (Post L.) 606
Рагульскене В. Л. 233, 494, 525, 880
Рагульскис К. М. 143, 233 , 235, 368—370, 494,
503, 525, 526, 626, 627. 648, 655, 777, 863,
871, 875, 880
Рапопорт Г. Н. 81, 880
Растригии Л. А. 72, 606, 880
Раус (Routh Е. J.) 312, 313
Рёдер (Roder I.) 16, 371, 886, 887
Родионов А. М. 137, 881
Родыгии Л. В. 80, 82—85, 881
Розеивассер Е. Н. 141, 360, <381
Розо (Roseau М.) 108, 137, 881
Розеивассер Е. Н. 360, 881
Рокар (Rocard J.) 606, 619, 621, 623, 886
Романовский В. Э. 341, 342, 371, 588, 768,
845, 881
Рубаник В. П. 81, 87, 812, 814, 864, 877, 881
Рудин А. Д. 14, 555, 600, 603, 627, 681, 691,
721, 747—749, 845, 861, 867, 868, 881
Румянцев В. В. 115, 881
Рундквист А. К. 14, 349, 350, 355, 371, 590,
627 678, 681, 742—744, 747, 749, 750, 753,
861, 867, 881
Рундквист К. А. 14, 349, 350, 355, 371, 721,
742 747, 750, 756, 867, 874, 881
Рэлей (Rayleigh, Strutt J. W.) 16, 149, 882
Рюденберг (Rudenberg R.) 19, 20, 881
Рюльмаи А. Ф. 371, 727, 869
Рябов Ю, A. 144, 881
Савинов О. А. 14, 347, 354, 371, 774, 777, 882
Садовников Б. И. 138, 869
Садовский И. М. 78, 882
Самойлов В. Ф. 79, 882
Сэндлер А. С. 78, 882
Сансоне (Sansone G.) 80, 619, 874
Сарда (Sarda) 55, 619. 621, 624
Саткявичус Э. Б. 233, 525, 880, 882
Сергеев П. А. 578, 871, 882
Сибуйя (Sibuya Y.) 138, 886
Сигнул (Signeul R. А. О.) 16, 367, 371, 88С
Сильванович В, Н. 17, 78, 346, 358, 371, 739,
879
ИМЕННОЙ УКАЗАТЕЛЬ
891
Сильвестр (Sylvester J. J.) 30, 223, 593
Сирль (Thcarle Е. L.) 58, 67, 791. 887
Скибарко А. П. 81, 882
Смирнова И. М. 141, 864
Совков Г. В. 770, 883
Соколов В. М. 325, 882
Соколов Н. И. 19, 880
Спиваковский А. О. 882
Спурлин (Spyrlin W. V.) 16, 371, 837, 886
Старжинский В. М. 882
Старостин В. Н. 725
Степанов В. В. 98, 879
Стодола (Stodola) 796
Стокер (Stoker J. J.) 107, 882, 887
Страбл (Struble R. А.) 143, 882
Страхов С. В. 384, 882
Стрелков С. П. 81. 882
Стретт (Strutt J. W., Rayleigh) 16, 149, 882
Субач А. П. 606
Суезаки Теруо (Suezakt Teruo) 81, 887
Сыпченко Б. А. 371, 727, 869
Сыромятников И. А. 19, 882
Хааг (Haag J.) 20, 108, 136, 886
Хайденмайер (Heidenmever Н.) 737, 886
Хайкин С. Э. 20, 72, 85, 149, 865, 877, 882
Хачатуров А. А. 19, 873
Хаяси Сецуко (Hayashi Sezuko) 370, 627,
873
Хаяси Тихнро (Hayashi Chihiro) 883
Хейл (Hale J. К.) 108, 138, 883, 886
Хечанов Ю. С. 371, 756, 883
Ходжаев К. Ш. 13, 14. 21, 31, 44, 59, 65, 66,
222, 224, 269, 309, 317, 360, 368, 369. 492,
507—513, 517, 569—573, 579, 607, 668. 820—
826, 829, 867, 868, 879, 883
Холоденко Л. П. 20, 81, 883
Хохлов Р. В. 21,80, 81, 87, 876. 877, 883
Хуффорд (Hnfford G.) 107, 885
Хэнзел (Hansel С. Е.) 93, 883
Цаплии С. А. 347, 370, 683, 766, 883
Цейтлин М. Г. 347, 354, 371, 770, 882, 883
Цукерник Л. В. 19, 884
Цыпкнн Б. В. 385, 386, 480, 636, 865
Талицких Н. А. 14
Таунс (Townes С. Н.) 86
Тейлор (Taylor В.) 220
Теодорчик К. Ф. 20, 80, 882
Тимофеев Н. Г. 346, 358, 371, 388, 683, 693,
731, 736, 871, 876
Тимошенко С. П. 618, 882
Тондл (Tondl А.) 72, 882
Томсон (Thomson W., Kelvin) 75, 82, 296,
887
Трибелева Т. Н. 128, 883
Трикоми (Tricoml В.) 655, 887
Троицкая Л. Г. 663
Туркин В. Я. 371, 756, 871, 883
Тэт (Tait Р, G.) 296, 887
Уайлд (Wilde D. J.) 224, 883
Улам (Ulam S. М.) 97, 883
Ульяиннский Л. С. 89, 865
У игру (Ungruh F.) 78, 887
Успенский И. Л. 742, 750
У|гкии Г. М. 81, 883
Ушаков И. А. 600, 876
Фагерберг (Fagerberg В.) 339, 344, 885
Файн В. М. 87, 883
Файиберг И. С. 20, 80, 84, 91, 869
Федоров Б. Н. 747
Ферми (Fermi Е.) 97
Филер 3. Е. 606
Финкельштейн Г. А. 14
Фолди (Foldy L.) 17, 626, 869
Фор (Faure R.) 20, 107, 136, 885
Франк-Каменецкий Д. А. 89, 883
Франчук В. П. 880
Фрезер (Fraser R. А.) 122, 883
Фрндрихс (Friedrichs К. G.) 108, 885
Фролов К. В. 606, 607, 872, 883
Фурье (Fourrier J.) 600
Фуфаев Н. А. 607, 869
Чеботарев Н. Г. 132. 165, 232, 458, 884
Чезари (Cesari L.) 20, 107, 127, 138, 149, 232,
884, 885
Червоненко А. Г. 880
Чернова Н. А. 224, 879
Черноусько Ф. Л. 234, 627, 870
Четаев Н. Г. 115, 122, 123, 138, 8Р1
Чижевский А. Л. 89, 884
Чнликин М. Г. 639, 884
Шалеа (Chalet R.) 20, 884
Шахгильдян В. В. 21, 626, 884
Шашина Ю. Г. 89. 884
Швайнфурт (Schweinfurth Н.) 737, 886
Шей Г. П. 371, 721, 727. 869
Шейли (Shapley Н.) 17, 884
Шехгер О. Я. 233, 354, 368, 626, 648, 766,
772, 851, 884
Шильников Л. П. 136, 213 , 526, 879
Шиманов С. Н. 133, 136—138, 216, 232, 884
Шноль С. Э. 88, 884
Шперлннг (Sperling L.) 369, 475, 483, 511.
548—554, 683, 768, 829, 837, 841, 845, 853,
859. 886
Шпильберг Я.И. 671
Штейнберг Т. С. 216, 884
Штельмахер (Stellmacher К. L.) 269, 887
Штокало И. 3, 138, 885
Штофф (Stoff F.) 16, 371, 886, 887
Шульц П. П. 371, 756, 883
Шур (Schur I.) 132, 886
Эйиштейи (Einstein А.) 86
Энгель (Engel Z.) 370, 683, 885
Эпплтон (Appleton Е. V.) 20, 79, 885
Якубович В. А. 138, 885
Янко-Триницкий А. А. 20, 79, 384, 885
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Альфа-ритм 92
Амплитуда колебаний эффективная 57, 633,
634
Анизохронизм мягкий, жесткий 34, 321
Балансир автоматический 66, 791—796
Захватывание 14, 20, 56
— (вибрационное поддержание) вращения
17, 41, 55—58, 478—481, 625—650, 667—670
---------, основной и субротационный ре-
жимы 630, 641
—, полоса 638—640
—, порог 57, 640
Вал электрический 78, 362
«Вероятность-один» и «вероятность-два» 147
Вибраторы (возбудители) механические 34,
63, 336—339
-------Бюллера 720
— — — гироскопические 359
-------двухчастотные (бигармонические)
359, 564—567
-------дебалансные 34, 336, 373
-------качающиеся 539—540
-------, квазиконсервативная и неквази-
консервативная идеализации 398,517—523
---— многочастотныс (полигармониче-
ские) 359
-------одночастотные (моногармониче-
ские) 359
-------планетарные внешние (кольцевые)
и внутренние (катковые) 338, 373
-------поршневые 339
— — — самобалансные 359, 720
— электромагнитные 59, 63, 820—825
Генераторы квантовые 86, 87
— релаксационные 82—85
Гранулометр 727, 728
Движение асимптотически устойчивое по
Ляпунову 117
—	возмущенное 116
—	кратно-синхрониое 99
—	либрациоиное 99, 301
—	невозмущеииое 116
—	неустойчивое по Ляпунову 116
—	орбнтально устойчивое 128
—	простое синхронное 99
—	ротационное 99, 301
—	устойчивое по Ляпунову 116
Действие по Гамильтону 296
Действия интеграл 301
Делители элементарные характеристиче
ской матрицы 122—124
Диапазон частотный консервативного объ-
екта 302, 314
Задача Гюйгенса 72—75, 815—820
—	Кельвина 75
—	синтеза вибрационного поля системой
сосредоточенных периодических сил 573
---системы возбуждения 573—575
Иерархичность систем слабо связанных
объектов 60
Изохронизм 34, 321
Координаты вращательные 23, 99, 301, 374
— колебательные 23, 99, 301, 374
—	объектов собственные 24
—	системы связи 23, 24, 98
—	фазовые 23, 98
Корни характеристического уравнения 119
------критические 132, 135, 155, 156
Коэффициенты влияния гармонические
508-511, 531, 532, 551—553, 555-556, 559,
821
—	демпфирования суммарные 391
— запаса по самосинхронизации 52, 703, 783
—	— по стабильности траектории колеба-
ний 703
— сопротивления перекатыванию 387, 388
—	устойчивости Пуанкаре 592
—	чувствительности 602
Критерий Сильвестра 223
— устойчивости синхронных движений ин-
тегральный 30, 219—224
-----------в задаче о гибком вале с не-
уравновешенными дисками 806, 807
---------------- о групповых фундамен-
тах под машины 777, 778
-----------квазиконсервативных объек-
тов 305, 318-323
----------- _ механических вибраторов 44,
428-432, 514-517, 827, 828
-----------систем с почти равномерными
вращениями 294 —296
— --------- электромагнитных вибраторов
825
Маятник физический (неуравновешенный
ротор), вибрационное возбуждение и
поддержание вращения 41, 55—58, 439—
440, 478—481, 634—636, 648—650, 654—658,
667—670, 744, 748
— —------, характер анизохронизма 320
Метод Лагранжа вариации произвольных
постоянных 302
Многоугольник Ньютона 132
Моменты вибрационные 40, 58—60, 419—
421, 499-501, 506-514, 609, 632-633, 804,
805, 828-831
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
393
Моменты вибрационные, выражения через
гармонические коэффициенты влияния
506—514, 828—831
---, способы вычисления 43—44, 422—428
— избыточные на валах вибраторов 461,
500, 501, 636
—	нагрузочные 609
Область захвата («притяжения») синхрон-
ного режима 24, 101, 634, 654—660
Объекты аиизохронныс 319—321
—	изохронные 319
— слабо связанные 24, 25, 103, 237
------, близкие к произвольным нелиней-
ным 238—247
— ----, - - к системам Ляпунова 324—333
------квазпкоисерватпвные 240, 299—323
------квазилинейные с одной степенью
свободы 248—251
-------------------, с малым демпфиро-
ванием и с малыми частотами свобод-
ных колебаний 248—250, 267—282
-----------— — —,-------— или с малы-
ми частотами свободных колебаний
248-250, 252—267
—	— — — —------—, с немалым демпфи-
рованием или с немалыми частотами
свободных колебаний 248—252
---— одинаковые и почти одинаковые 104
------с почти равномерными вращениями
283
Определитель Пуанкаре ПО
Осцилляторы Ван-дер-Поля 59
—	квазилинейные 808—825
—	нелинейные 20, 59, 96
«Парадокс» изменения устойчивости фази-
ровки при устранении связи 47, 48, 581,
582
— неработающей связи (неподвижного не-
сущего тела) 13, 45, 483, 692, 694, 777, 778
Параметры контрольные 50, 599, 700
—	порождающие 162
Переменные «действие — угол» 302
—	«фаза — частота» 301
Периоды обращения астероидов 96
--- Земли и Венеры вокруг Солнца 96
Подвески маятниковые 797
Поддержание вращения вибрационное 17,
41, 55—58, 478—481, 625—650, 667—670
— — —, связь с явлением синхронизации
вибраторов 650—654
Подстановка Артемьева 133
Показатели характеристические 119
---критические 132, 135, 155, 156
Полоса захватывания вращения ротора
638-640
Порог захватывания 57, 640
— синхронизации 32, 94, 95
Потенциал кинетический Рауса 313
Правдоподобность
— при «нелокальном применении результа-
тов локального исследования» 31, 32,
146-153
—	рассуждения 139
—	результата исследования 140
Правило трех сигм 701
Преобразования матрицы элементарные 122
Проблема синтеза вибрационного поля 45,
568—571 (см. также «Задача синтеза...»)
— -------машин с механическими возбу-
дителями 571- 598
--- в задаче о синхронизации механиче-
ских вибраторов 366—367
Проблема синтеза в общей задаче о син-
хронизации 22, 101
---форм собственных колебаний 576
Расстройка относительная 447
Регулятор Баусса — Сарда 55, 619—624
Режим генераторный работы двигателей
механических вибраторов 439, 637—639.
738
— синхронный, жестко возбуждаемый («не-
самоустанавливающийся») 34
---, мягко возбуждаемый («самоустанав-
ливающнйся») 34
Самосинхронизация 16—18
— маятниковых часов 15, 72, 815—820
— механических вибраторов 35, 40—45, 363.
432—440
------ —. коэффициент запаса 52, 703, 783
— электрических машин 76—79
Связи биологические 93—96
— несомые (второго рода) 291, 309, 310
— несущие (первого рода) 291, 309, 310
—	сильные 11
—	, система 99
—	слабые 11, 25
—	центробежно-инерционные 494—496
Символ Кронекера 240
Синхронизация акустических объектов 16
—	биологических объектов 16, 17, 21, 88—
96
—	валов посредством центробежно-инерци-
онных связей 322, 323, 503
—	внутренняя, взаимная (автономная) и
внешняя (неавтономная) 14, 24, 39, 101
	, взаимоотношение задач
247
—	возбудителей механических колебаний
16, 34, 63—66, 360—367
—	как проблема кибернетики И, 17
—	квазилинейных объектов с одной сте-
пенью свободы 248—267
—	квантовых генераторов 21, 86, 87
—	кратная 22, 99, 100
—	ламповых генераторов 16. 20, 79
—	маятниковых часов 15, 72, 815—820
—	механических вибраторов бнгармониче-
скнх 546—567
------вблизи резонаиса 446—464, 481—483
—-----в системах с распределенными па-
раметрами 504
-----------с соударениями 525—527, 756—
763
---—, иитегральный критерий устойчиво-
сти и потенциальная функция 428—432,
514—517
------, задача синтеза 366
--- — кинематическая 362
------кратная 366, 523—525
------, методика исследования 827—835
-------1	обобщенная задача 491—503
------, общая постановка задачи 360—367
------, общий план решения задач 504—
505
------, основные уравнения теории 415—
421, 450-456, 496—503
------принудительная 363, 440—445, 483—
492
---— простая 365
------, связанных с квазилинейной коле-
бательной системой 505—514
.. ---t_ с цепной колебательной систе-
мой 548—556
------условия существования и устойчи-
вости режимов 402—404
894
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Синхронизация механических вибраторов,
экспериментальная проверка результатов
теории 665—672
------электрическая 362, 483—489
— нелинейных осцилляторов 20, 59, 96
— объектов, близких к произвольным нели-
нейным 238, 247
----, — к системам Ляпунова 324—333
---с почти равномерными вращениями
283—298
—, общая постановка задачи 22, 98—102
—.определение 11, 13, 15
—, о расширении понятия 62, 102
—,основная задача теории 99
основные закономерности 32—34
— осцилляторов Ван-дер-Поля 59, 808—815
— принудительная 18, 50
— простая 22, 99, 100
— электрических машин 16, 19, 76—79
Синхронно-синфазное и синхронно-проти-
вофазное движения двух механических
вибраторов 475
Скорости угловые парциальные механиче-
ских вибраторов 22, 41, 435—437
— — электрических генераторов 77
Скорость угловая (частота) синхронная 23,
100
Система тел несомая 38
----несущая 38
— уравнений порождающая 26, 108, 112
----сопряженная 124—126
Системы Ляпунова 324, 325
Способ, подстановка Артемьева 133
Стабильность режима колебаний 50—52,
599—604, 695—712
Тело вспомогательное 378, 863
— несомое 38
— несущее 38, 336, 365
— упругое, мягко амортизированное 862—
863
Теорема Андронова и Витта об устойчиво-
сти автономиях систем 127—129
— Ляпунова об аналитичности коэффици-
ентов характеристического уравнения 129
----об устойчивости по первому прибли-
жению 126, 127
---- о корнях характеристического уравне-
ния сопряженных систем 125
— о минимуме кинетической энергии мягко
амортизированного тела при синхронных
движениях вибраторов 44, 777, 778
— Пуанкаре о решениях дифференциаль-
ных уравнений, содержащих малый па-
раметр 110
--------- уравнений в вариациях 118
— Сильвестра 30, 223, 295
Точки контрольные 600, 700, 708, 784
Уравнения в вариациях 118
— дифференциальные с многомерной быст-
ро вращающейся фазой 233, 269
— основные задачи о синхронизации меха-
нических вибраторов 39—44, 415—421,
450—456, 496—503
----общей задачи о синхронизации 29, 219
Ускорители циклические заряженных ча-
стиц 17, 626
Устойчивость орбитальная 128
— периодических решений 119—136
— по Ляпунову асимптотическая 117
— — —.определение 116
Фазировки первого и второго рода при са-
мосинхронизации механических вибрато-
ров 563, 564
Фазы порождающие, начальные 38
Фокусы кинетические 295
Форма каноническая квазилинейных диф-
ференциальных уравнений 157, 158, 170
----- (нормальная) системы линейных од-
нородных дифференциальных уравнений
124
Фундаментальная система решений линей-
ных однородных дифференциальных
уравнений 119
Функции порождающие 29, 111, 219
— связей 23, 98
Функция Лагранжа 284
— потенциальная 30, 219, 220
— почти периодическая по Г, Бору 210
— Рауса 312
Характеристика скелетная консервативного
объекта 319
Хула-хуп, игра-упражнение 56
Центр тяжести условный (вспомогательного
тела) 378
Частота (угловая скорость) синхронная 23,
100
Частота (угловые скорости) парциальные
22
---------автоколебательных объектов 22,
101
---------- маятниковых	часов 74
---------- механических	вибраторов	41,
435—437
---------осцилляторов Ван-дер-Поля 85
--------- электрических генераторов 77
Чувствительность контрольных параметров
602
«Чудо большого ц» 32, 145
Углы установочные при принудительной
синхронизации механических вибраторов
378, 381, 440, 444, 574
Уравнение Дуффинга 320
*- характеристическое системы в вариациях
119, 128
Щель критическая вибрационных дробиль-
но-измельчительиых машин 748—750, 762
Электроэнцефалограмма 92
Эффект Зоммерфельда 605, 617—618
Илья Израилевич Блехман
СИНХРОНИЗАЦИЯ ДИНАМИЧЕСКИХ СИСТЕМ
М., 1971 г., 896 стр. с илл.
Редактор М. 3. Коловский,
Техн, редактор С. Я. Шкляр.
Корректор Г С. Смоликова.
Сдано в набор 29/XII 1970 г. Подписано к печати
20/V 1971 г. Бумага 60X90*/ie Физ. печ. л. 56.
Условн. печ. л. 56. Уч.-изд. л. 59,41. Тираж 4350 экз.
Т-06591. Цена книги 3 р. 70 к. Заказ № 914.
Издательство «Наука».
Главная редакция
физико-математической литературы.
Москва, В-71, Ленинский проспект, 15.
Ордена Трудового Красного Знамени
Ленинградская типография № 2
имени Евгении Соколовой Главполиграфпрома
Комитета по печати при Совете
Министров СССР. Измайловский проспект, 29.
ИЗДАТЕЛЬСТВО «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
Москва, В-71, Ленинский проспект, 15
ГОТОВЯТСЯ К ПЕЧАТИ:
Александров А. Я-, Ахметзянов М. X., Поляриза-
ционно-оптические методы механики деформируемого
тела.
Бугаков И. И., Ползучесть полимерных материалов (тео-
рия и приложения).
Вильямс Ф. А., Теория горения (основы теории течений
с химическими реакциями), перев. с англ.
Механика в СССР за 50 лет, под общей ред. акад. Л. И. Се-
дова, т. III, Механика твердого деформируемого тела.
Парс Л. А., Аналитическая динамика, перев. с англ.
Лунц Я- Л., Введение в теорию гироскопов.
Мер кин Д. Р., Введение в теорию устойчивости движения.
Предварительные заказы на печатающиеся книги прини-
маются без ограничения всеми магазинами Книготорга и
Академкниги, распространяющими литературу данной те-
матики.