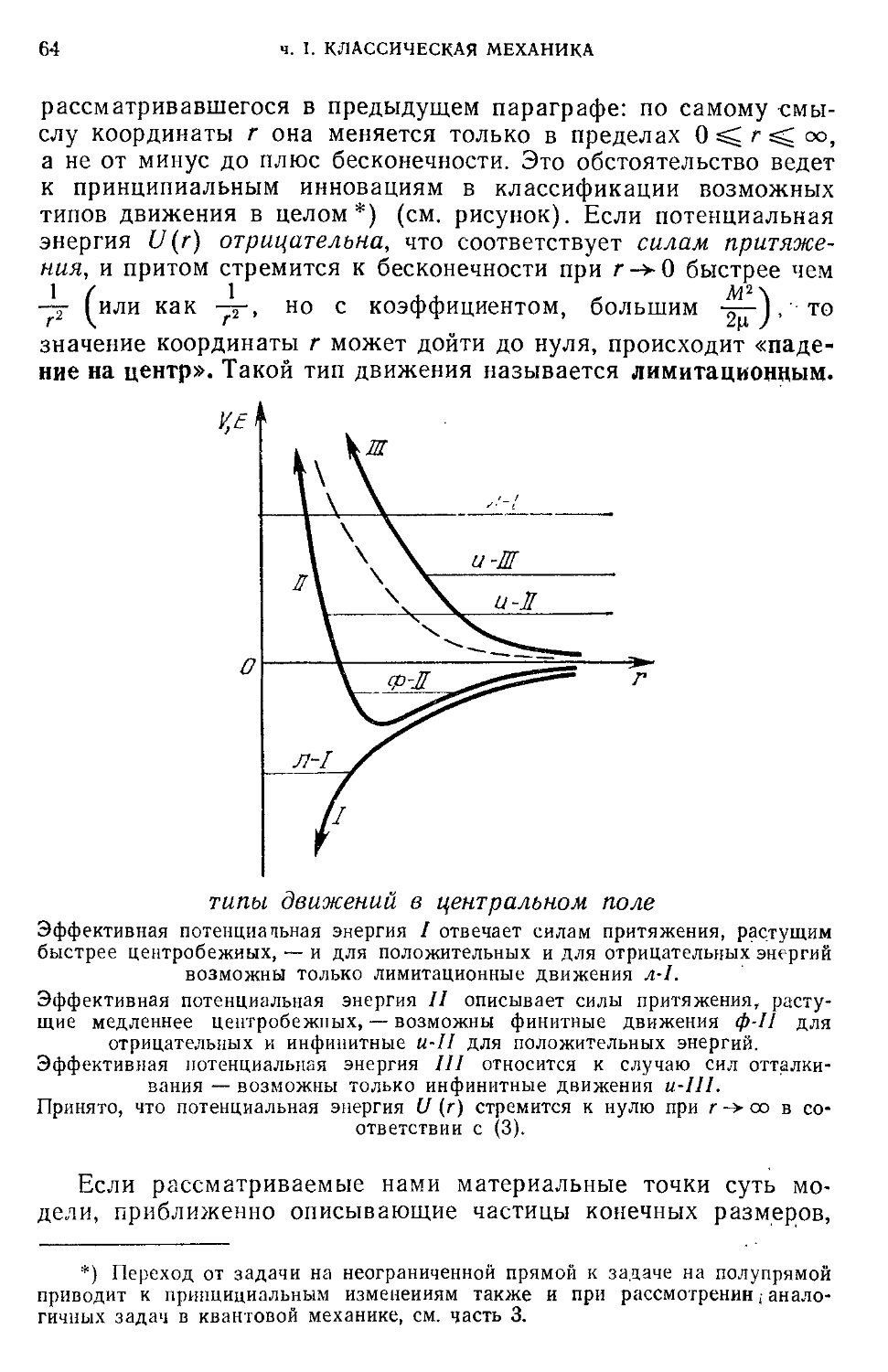
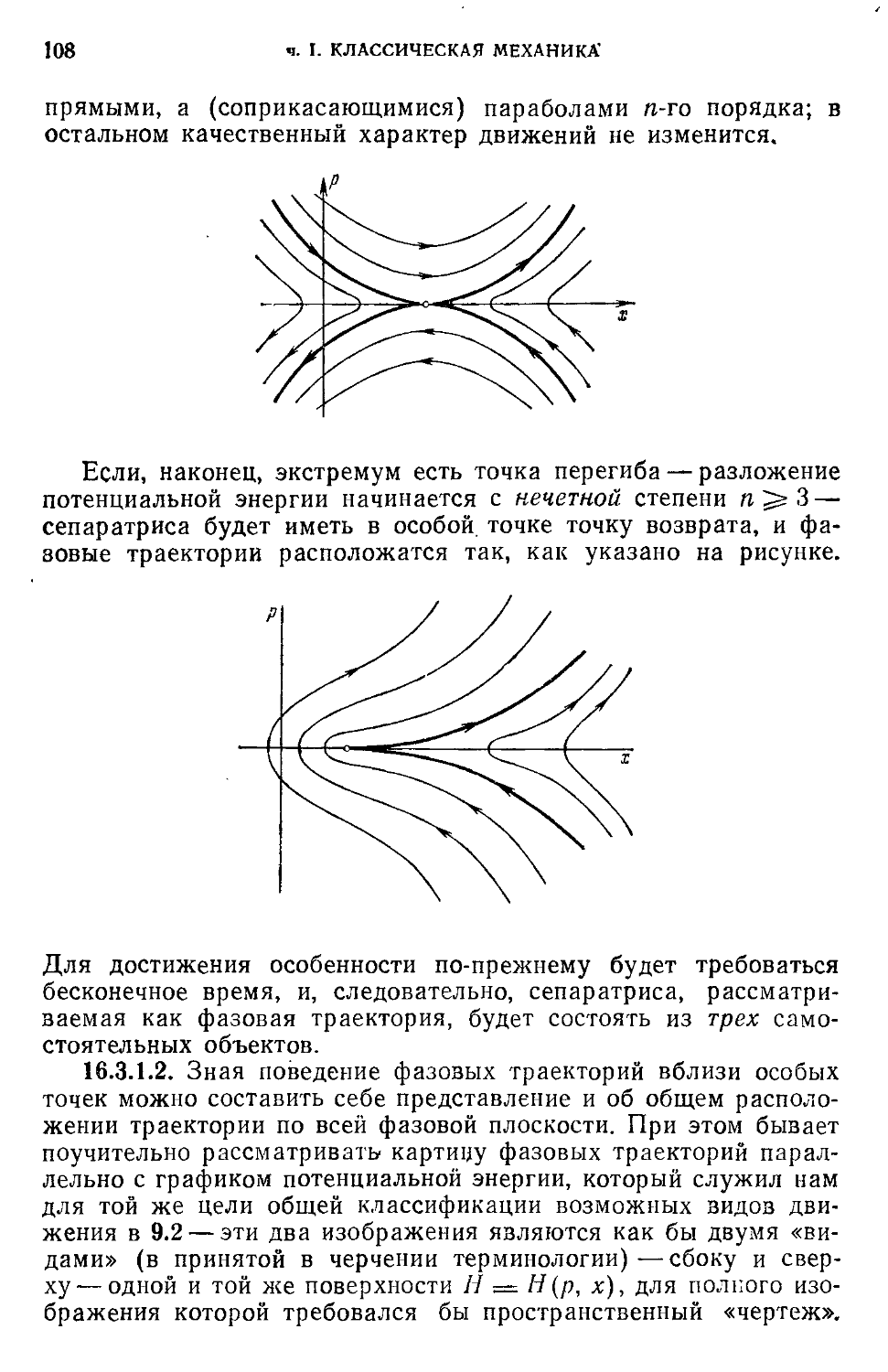
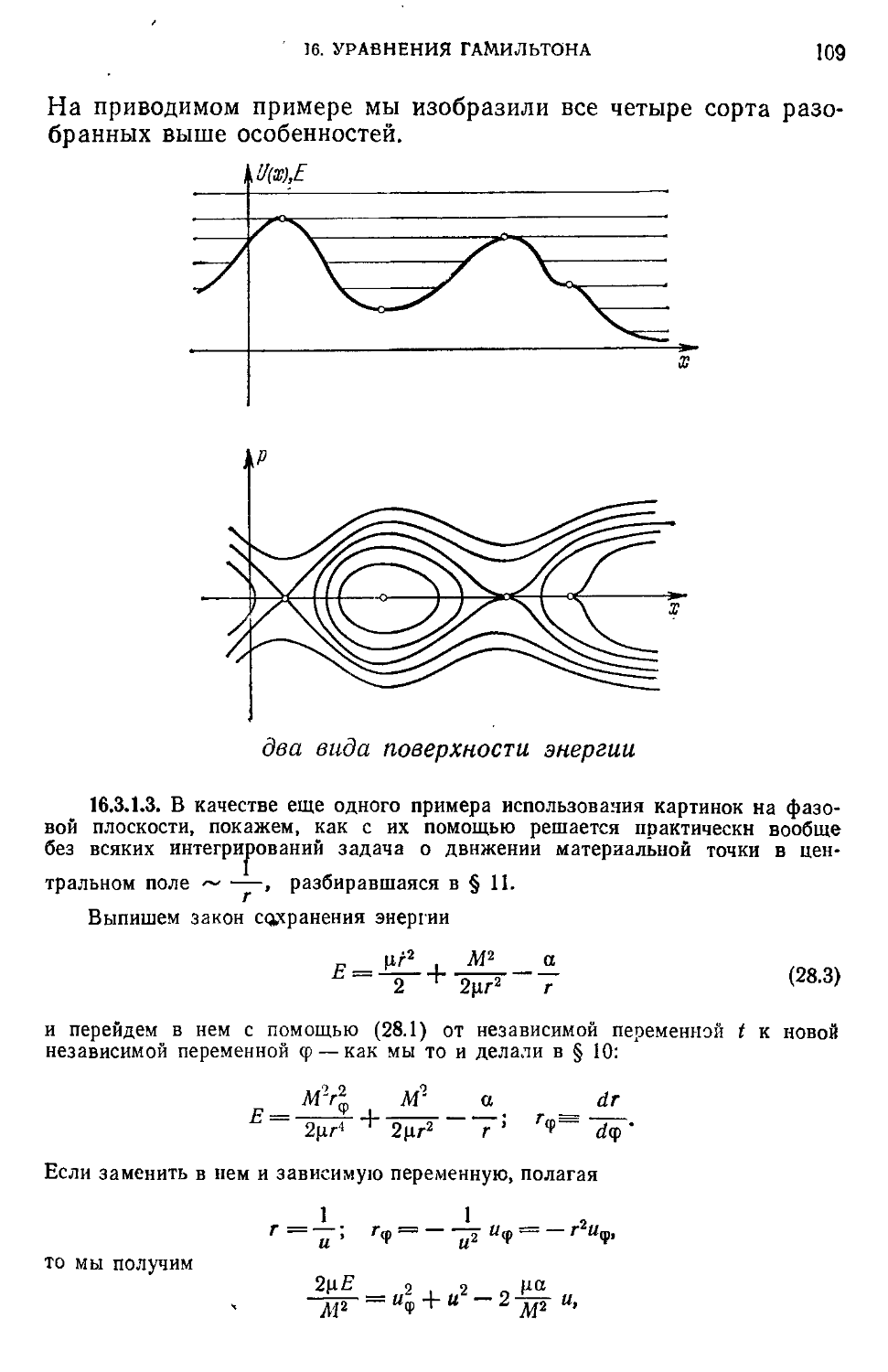
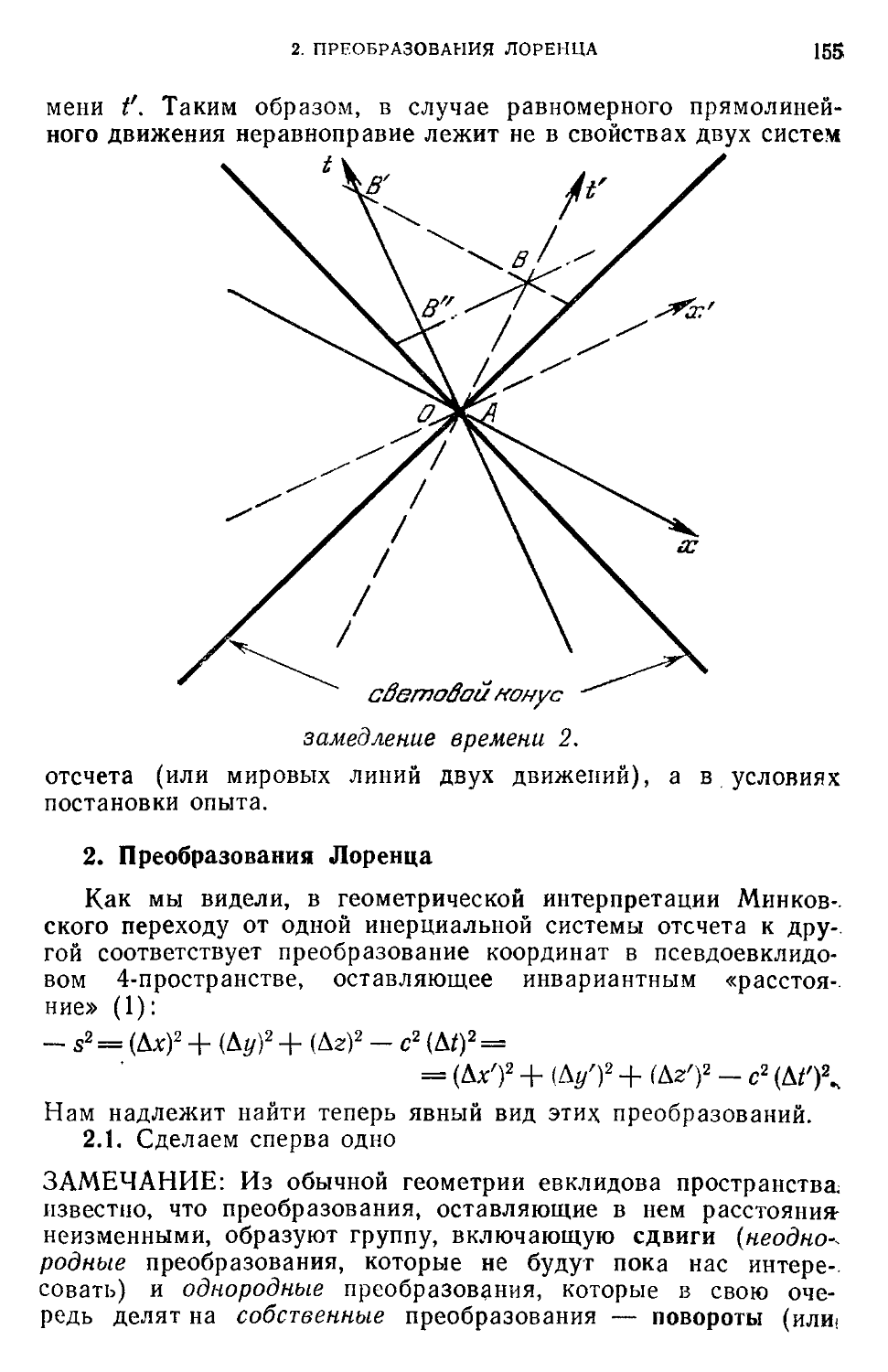
Текст
Б. В. Медведев
НАЧАЛА
ТЕОРЕТИЧЕСКОЙ
ФИЗИКИ
МЕХАНИКА
ТЕОРИЯ ПОЛЯ
ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
Допущено Министерством высшего
и среднего специального образования СССР
в качестве учебного пособия
для студентов физических специальностей
высших учебных заведений
ИЗДАТЕЛЬСТВО «НАУКА>
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
Москва 1977
530.1
M 42
УДК 539.1E30.1)
Начала теоретической физики. Б. В. Медве-
Медведев, Главная редакция физико-математической ли-
литературы изд-ва «Наука», 1977.
Книга представляет собой краткое изложение
начал теоретической физики: механики, теории поля,
квантовой механики. Главное внимание уделяется
при этом логически последовательному изложению
узловых фундаментальных вопросов с современной
точки зрения. Книга будет полезна всем изучающим
теоретическую физику, ио ие обязательно выбравшим
ее своей основной специальностью: студентам физ-
физтехов, физикам-экспериментаторам, а также интере-
интересующимся физикой инженерам, математикам, хими-
химикам, биологам и др. Книга даст также возможность
лицам, получившим физическое образование в пре-
предыдущие десятилетия, получить представление о со-
современном состоянии науки.
Борис Валентинович Медведев
НАЧАЛА ТЕОРЕТИЧЕСКОЙ ФИЗИКИ
М., 1977 г., 496 стр., с илл.
Редактор А. Д. Суханоа
Технический редактор В. Я. Кондакова
Корректоры О. А. Сигал, Н. Д. Дорохова
Сдано в набор 9.08.1976 г. Подписано к печати 26.01.1977 г.
Бумага 60X90'/ie тип. № 3. Физ. печ. л. 31. Усл. печ. л. 31.
Уч.-изд. л. 31,5. Тираж 25 000 экз. Цена книги 1р. 36 к.
Заказ № 267.
Издательство «Наука>
Главная редакция физико-математической
литературы, 117071, Москва, В-71,
Ленинский проспект, 15
Ордена Трудового Красного Знамени
Ленинградская типография № 2
имени Евгении Соколовой Союзполиграфпрома
при Государственном комитете Совета Министров СССР
по делам издательств, полиграфии и книжной торговли,
193052, Ленинград, Л-52. Измайловский проспект, 29.
20402 026 © Главная редакция
М ¦ 83-77 физико-математической литер
053@2)-77 издательства «Наука». 1977
ОГЛАВЛЕНИЕ
Предисловие . 5
Введение. Предмет и метод теоретической физики . 7
Часть I. КЛАССИЧЕСКАЯ МЕХАНИКА 10
1. Место механики в физике 10
2. Основные понятия механики 12
3. Принцип наименьшего действия 16
4. Принцип относительности Галилея 19
5. Законы сохранения 27
6. Преобразования сохраняющихся величин 3S
7. Инвариантность относительно преобразований Галилея .... 41
8. Рассеяние частиц . 51
9. Одномерное движение 59
10. Движение в центральном поле 62
11. Движение в кулоновом поле 67
12. Эффективное сечение 7J
13. Формула Резерфорда 81
14. Малые колебания . 83
15. Функции Грииа . . Ш
16. Уравнения Гамильтона 103
17. Вариационный принцип для уравнений Гамильтона .112
18. Скобки Пуассона 115
19. Канонические преобразования 126
20. Пример иа канонические преобразования: осциллятор ..... 135
Часть П. МЕХАНИКА ТЕОРИИ ОТНОСИТЕЛЬНОСТИ 140
1. Принцип относительности и принцип постоянства скорости света 140
1а. Одновременность и пространство 148
16. Замедление времени 152
2. Преобразования Лоренца 155
3. Четырехмерные векторы и тензоры 162
4. Динамика свободной материальной точки 174
5. Десять фундаментальных величин 181
6. Взаимодействие в теории относительности. Неизбежность поня-
понятия поля . .¦ 190
7. Лагранжев формализм для поля 194
8. Законы сохранения 198
9. Электромагнитное поле 207
10. Уравнения электромагнитного поля 211
11. Энергия и импульс электромагнитного поля 215
12. Трехмерная формулировка 219-
4 % ОГЛАВЛЕНИЕ
13. Решение уравнений поля 228
а. Однородное уравнение 230
б. Уравнения с правой частью 237
14. Электростатика 246
15. Электростатическое поле вне системы зарядов 253
16. Стационарное поле. Магнетостатика 258
17. Излучение электромагнитного поля 270
18. Дипольные и квадрупольное излучения 278
19. Старшие мультипольные излучения 285
20. Рассеяние света на свободных зарядах 310
Часть III. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ 315
1. Историческое введение 315
2. Состояния. Сюперпознция 327
. . 3. Векторы состояния и операторы 332
4. Проблема собственных значений 341
5. Функции наблюдаемых . 350
6. Спектральные представления и вероятности 355
7. Коммутирующие наблюдаемые 362
8. Представления 372
9. Квантование 375
10. Система с одной степенью свободы 378
11. Соотношение неопределенностей Гайзенберга 409
12. Волновая функция 417
13. Сдвиги и повороты системы отсчета 422
14. Квантование момента . 429
15. Реализации момента 437
16. Уравнения движения 457
17. Первый пример. Осциллятор 471
18. Дальнейшие примеры динамических задач 477
19. Движение в центральном поле 484
20. Кулоиово поле 490
ПРЕДИСЛОВИЕ
За последние три-четыре десятилетия теоретическая физика,
как и вся физика вообще, испытала период необычайно бы-
быстрого роста. Возникли новые физические представления, была
разработана масса методов, использующих самые разнообраз-
разнообразные математические средства, было успешно решено совершен-
совершенно невероятное количество задач. Неизбежным следствием этого
процесса явился весьма значительный рост объема науки — так,
известный курс Ландау и Лифшица, задуманный в свое время
как собрание того минимума сведений, который необходимо
знать всякому теоретику, разросся сейчас более чем до 250 пе-
печатных листов. Изучение такого количества материала требует
нескольких лет упорного труда; ясно, что такая роскошь до-
доступна лишь решившим избрать теоретическую физику своей
основной специальностью. Между тем все расширяется круг лиц,
не претендующих на профессиональную работу в теоретической
физике, которым тем не менее регулярно приходится пользо-
пользоваться ее результатами и методами, — это, в первую очередь,
•физики-экспериментаторы и воспитываемые физико-техниче-
физико-техническими и инженерно-физическими факультетами физики с инже-
инженерным уклоном, затем математики, которым хотелось бы по-
понимать смысл физических задач, которые их просят помочь
решить, далее химики, биологи и представители других есте-
естественных наук, в самые основы которых все сильнее вторгаются
физические методы и т. п. С другой стороны, даже для профес-
профессионалов-теоретиков возникает реальная опасность потерять об-
общую перспективу за деталями хитроумных методов решения ча-
частных задач.
Эти обстоятельства побудили автора предпринять попытку
краткого изложения начал теоретической физики — той основ-
основной схемы физических идей в их взаимной связи и логической
последовательности, которая образует каркас или, если можно
так выразиться, скелет, обрастающий в дальнейшем «мясом»
бесчисленных конкретных задач. Если угодно, автор поставил
себе целью написать научно-популярную книгу на научном
уровне, без каких-либо пропусков в логике или математике —
6 ПРЕДИСЛОВИЕ
судить о том, насколько удалась эта попытка, дело чита-
читателей.
Идея написать книгу такого рода зародилась у автора в про-
процессе чтения курса теоретической физики, который он ряд лет
вел в Московском институте электронного машиностроения.
Автор благодарен заведующему кафедрой прикладной матема-
математики МИЭМ В. П. Маслову, который предоставил ему такую
возможность; автор также благодарен В. А. Гордину, конспек-
конспекты которого были использованы при составлении первого ва-
варианта рукописи.
Автор пользуется случаем, чтобы выразить свою благодар-
благодарность всем лицам, читавшим рукопись и сделавшим ряд ценных
замечаний: В. Л. Бонч-Бруевичу, О. И. Завьялову, Г. Ф. Дру-
кареву, В. А. Франке, М. Г. Веселову, рецензенту издательства
Д. В. Ширкову, редактору книги А. Д. Суханову, а также всем
моим коллегам, советами которых я имел случай воспользо-
воспользоваться.
ВВЕДЕНИЕ. ПРЕДМЕТ И МЕТОД
ТЕОРЕТИЧЕСКОЙ ФИЗИКИ
0.1. Теоретическая физика выделилась как самостоятельная
наука в первых десятилетиях нашего века. Ее двоякого рода за-
задача состоит в том, чтобы, во-первых, открывать — исходя из ре-
результатов отдельных, частных опытов — общие законы, управ-
управляющие какой-либо областью физических явлений, и, во-вторых,
указывать, каким образом, исходя из этих общих законов, мо-
можно заранее описать ожидаемое поведение тех или иных физи-
физических систем, предсказать результаты определенных конкрет-
конкретных экспериментов.
Обе эти задачи на достигнутом нами теперь уровне понима-
понимания природы оказываются настолько сложными и требуют
обычно построения столь длинных цепочек логических умоза-
умозаключений, что в них вряд ли можно было бы продвинуться
сколько-нибудь далеко, не прибегая к техническим средствам,
позволяющим формализовать и в какой-то степени автоматизи-
автоматизировать процесс получения логических выводов.
0.2. Такие средства предоставляет нам математика, поэтому
в обеих своих частях — и в индуктивной и, особено, в дедуктив-
дедуктивной— теоретическая физика широко пользуется средствами ма-
математики, и эта непривычно высокая для любого естествоиспы-
естествоиспытателя— включая сюда и физика-экспериментатора — степень
математизации является, по-видимому, первой бросающейся в
глаза характерной чертой теоретической физики. Для многих
она может казаться—-и оказывается — трудно преодолимым по-
порогом, но тем не менее через него ведет самый простой путь к
пониманию того, как устроена природа.
0.3. Однако в способах использования математических
средств, в самом характере рассуждений теоретической физики
имеются некоторые специфические особенности, которые не
только препятствуют тому, чтобы рассматривать ее просто как
один из разделов математики, но и делают иногда ее методы
в каком-то смысле прямо противоположными математическим.
Один известный советский теоретик любил формулировать это
8 • ВВЕДЕНИЕ
отличие словами: «Математик доказывает, а физик убеждает
слушателей».
Различие это обусловлено, конечно, не различным складом
ума математиков и физиков-теоретиков, а различием предмета
их исследования — в то время как математик в известном смысле
сам конструирует объекты своего исследования по собствен-
собственному произволу и ограничен лишь требованиями логической оп-
определенности и непротиворечивости, физик изучает независимо
от нас существующую природу, которая «выдана» нам в одном
единственном экземпляре, и ему волей-неволей приходится
больше заботиться о соответствии вводимых понятий этому един-
единственному объекту, чем о соображениях удобства рассмотрения
или логической стройности.
Иными словами, теоретическая физика, будучи по используе-
используемым в ней методам наукой точной, остается в то же время нау-
наукой par excellence естественной по предмету и цели своего иссле-
исследования.
Такая двойственность предопределяет другую — так сказать»
оборотную — особенность теоретической физики, отношение к
математике не более как к вспомогательному средству, которое
«подобно жернову перемалывает то, что под него засыпают»,
средству, от которого не следует требовать точности большей,
чем точность исходных предпосылок.
0.4. Что же до этих предпосылок, то единственный объект
исследований теоретической физики — природа — настолько
сложен, что полное рассмотрение по существу любого явления,
с учетом всех его сторон и особенностей, практически невозмо-
невозможно средствами современной математики. Поэтому то, чем на
самом деле занимается теоретическая физика, это не столько
непосредственно природные объекты и их отношения, сколько
искусственно конструируемые модели, которые получаются иа
природных объектов, если абстрагироваться от всех деталей, не
существенных для рассматриваемого явления, и сохранить толь-
только его основные, определяющие черты. Так входят в физику та-
такие абстрактные понятия, как абсолютно твердые тела, несжи-
несжимаемые жидкости, материальные точки и т. п. Естественно, что
выбор подходящей модели — а это есть действие не логическое,
а интуитивное — играет при этом чрезвычайно существенную
роль, чем и предрешается значение интуитивного мышления в
теоретической физике.
0.5. Вообще, постоянная аппеляция к интуиции составляет
неотъемлемую особенность теоретической физики. Не только
установление общих законов, но и получение следствий из них
оказывается обычно невозможным без создания наглядных
образов протекающих явлений — на чисто формальном пут»
трудно избегнуть грубейших ошибок. Особенно опасно поддать-
ВВЕДЕНИЕ 9
ся тут соблазну искать для всех входящих в теорию понятий и
объектов определения, исчерпывающие в математическом смыс-
смысле, — при этом приходится обычно принимать ряд допущений,
которые могут выглядеть достаточно невинно, но физический
смысл которых совершенно темен; в результате легко прийти
к заключениям, логическая обоснованность которых безукориз-
безукоризненна, но которые тем не менее могут не иметь никакого отно-
отношения к изучаемой физической проблеме.
0.6. Особо следует сказать о месте, которое занимает в те-
теоретической физике приближенное рассмотрение.
Прежде всего, все численные значения физических величин
суть результаты измерений и, значит, могут быть найдены лишь
с некоторыми погрешностями.
С другой стороны, и математические задачи, которые прихо-
приходится решать, чтобы сделать физические предсказания, бывают—
кроме самых простейших случаев — столь сложными, что речь
может идти только о приближенном, а не о точном решении
(причем проверить оправданность совершаемых приближений
удается далеко не всегда, часто для этого требовалось бы обла-
обладать точным решением).
Гораздо существенней, однако, то обстоятельство, что не-
нередко мы не можем неограниченно увеличивать (хотя бы в прин-
принципе) точность измерений или вычислений — может оказаться,
что при чрезмерном увеличении точности рассматриваемые ве-
величины или закономерности вообще исчезнут, подобно тому как
изображение на газетном клише вовсе исчезает при попытке
лучше рассмотреть его детали под лупой (для математика, на-
наверно, нагляднее пример асимптотического ряда, члены кото-
которого сперва убывают, а затем начинают возрастать). Это зна-
значит, что само существование подобных величин или функцио-
функциональных зависимостей имеет приближенный характер.
Ч а с т ь I
КЛАССИЧЕСКАЯ МЕХАНИКА
1. Место механики в физике
Как уже говорилось во введении, в теоретической физике
само существование тех или иных «законов» может возникать
лишь в определенном приближении. Характерным примером этой
ситуации может служить классическая механика.
1.1. Классическая механика возникла из обобщения тех све-
сведений о движении материальных тел, которые можно было по-
почерпнуть из нашего повседневного опыта. При этом в резуль-
результате многовековых стараний пришли к тому выводу, что при
построении законов механики следует абстрагироваться от неко-
некоторого круга явлений, играющих в повседневном опыте весьма
существенную роль, — именно, от явлений, связанных с тре-
трением, — или, во всяком случае, отказаться от описания их ме-
механизма и точных законов *).
1.2. К концу прошлого века в результате создания кинетиче-
кинетической теории этому обстоятельству возникло то объяснение, что
«на самом деле» законы механики в точности применимы только
к микрочастицам, из которых построены все материальные тела,—
к молекулам и атомам. Применимость же — приближенная —
механики к поведению «больших» тел не прямая, а опосред-
опосредствованная. Она возникает лишь за счет статистического усред-
усреднения, причем и сами динамические величины для макроскопи-
макроскопических тел — координаты, импульсы, энергия — не есть собст-
собственно динамические переменные, а лишь некоторые средние
значения (полученные в результате усреднения по микроскопи-
микроскопическим движениям) некоторых настоящих динамических пере-
переменных. Сама же точность, с которой выполняются макроскопи-
макроскопические уравнения движения, есть лишь следствие громадного
числа молекул во всяком макроскопическом теле, почему флук-
флуктуации—отклонения от средних — оказываются поразительно
малыми.
Таким образом, для макроскопической механики ее законы
возникают способом, для которого Э. Шредингер предложил
очень меткое название «порядок из беспорядка», и при доста-
*) Поэтому наилучшее поле для приложения классической механики мы
находим в астрономии.
1. МЕСТО МЕХАНИКИ В ФИЗИКЕ Ц
точном увеличении точности измерений перестают выполняться
(известным примером служит броуново движение). Что же ка-
касается сил трения, то нам приходится отказаться от их описа-
описания или вводить их извне как некий чужеродный механике
объект.
1.3. Однако полная парадоксальность ситуации проявилась
лишь в XX веке, когда выяснилось, что как раз для составляю-
составляющих большие тела микрочастиц классическая механика в боль-
большинстве случаев вообще неприменима, что их движения управ-
управляются совсем другими законами, законами квантовой механики.
Кроме того, при больших скоростях вступают в силу изменения,
связанные с теорией относительности.
Таким образом, строго говоря, классическая механика вовсе
не имеет области применимости. Она оказывается как раз та-
такой теорией, само существование которой обязано лишь прибли-
приближенности описания.
Зачем же изучать классическую механику?
Не стоит повторять того, что хотя и нет никакой области
явлений, точно описываемой классической механикой, есть очень
обширные области, описываемые ею в очень хорошем прибли-
приближении.
Не менее существенно другое обстоятельство. Именно в клас-
классической механике были очень подробно развиты чрезвычайно
удобные общие математические методы, составляющие предмет
аналитической механики, которые достигли такого совершенства,
что именно «по их образу и подобию» строятся сейчас почти
все физические теории*). Поэтому знакомство с теоретической
*) Это обстоятельство может служить замечательной иллюстрацией ин-
интуитивной консервативности человеческого мышления. Более двух с полови-
половиной веков, от времен Ньютона до конца прошлого столетия, механика рас-
рассматривалась как прямая и единственная основа всей физики. Под словами
понять или объяснить какое-либо физическое явление имели в виду построе-
построение его механической модели, причем выражение «модель» понималось бук-
буквально, в смысле какой-либо реальной конструкции из предметов, подчиняю-
подчиняющихся законам классической механики. Так для объяснения распространения
световых волн была придумана специальная заполняющая все пространство
упругая среда — «мировой эфир», — в котором световые колебания распро-
распространялись так же, как звук в твердых телах. Создатель современной элек-
электродинамики Максвелл потратил немало сил на попытки так «оборудовать»
эту среду, чтобы она описывалась бы выведенными им уравнениями: дело
доходило до напоминающих часовой механизм моделей с колесами и зубча-
зубчатыми передачами. Только к концу прошлого века физикам пришлось прими-
примириться с тем, что новые области физических явлений — тогда в первую оче-
очередь шла речь об электродинамике — принципиально несводимы к механике.
В связи с этим место реальных механических моделей начали занимать в
физике модели математические, от которых уже требовалось ие конструкцион-
конструкционное тождество с объектом, а только математически аналогичное описание —
и что же, в качестве материала для построения таких моделей мы опять ис-
используем механические уравнения!
12 ч. I. КЛАССИЧЕСКАЯ МЕХАНИКА
физикой приходится начинать с методов аналитической меха-
кики.
Однако основы аналитической механики мы будем излагать
не с математической, а с физической точки зрения, и во главу
угла мы будем все время ставить не строгость доказательств,
а связи с нашими физическими представлениями о природе.
2. Основные понятия механики
2.1. В соответствии с известным положением философии диа-
диалектического материализма, что пространство и время суть
формы существования материи, понятия пространства и времени
относятся к основным понятиям теоретической физики. Введе-
Введение этих понятий, как и любых физических понятий, должно
опираться на данные опыта, основываться на некоторой про-
процедуре, позволяющей сопоставлять соответствующим понятиям
физическим величинам определенные числа, получаемые в ре-
результате измерений.
2.1.1. Не существует, однако, опытов, которые позволяли бы
измерить положение тела в пространстве или момент времени,
когда происходит некоторое событие, — экспериментально мы
можем измерять только расстояния между телами или проме-
промежутки времени между событиями.
Таким образом, чтобы сопоставлять пространству и времени
какие-либо физические величины, мы должны выбрать некото-
некоторое тело в качестве начала отсчета расстояний и некоторый мо-
момент в качестве начала отсчета промежутков времени.
2.1.2. Для измерения расстояний пользуются масштабами —
т. е. сравнивают измеряемое расстояние с размерами некоторого
тела — масштаба, — принимаемого за эталон.
Для измерения времени пользуются часами. Часами может
служить любой периодический процесс, т. е. такой процесс, в ко-
котором многократно повторяется одно и то же состояние.
2.1.2.1. Какими соображениями надо руководствоваться при
выборе каких-либо масштабов и часов в качестве эталонов длины
и времени? Единственным решающим доводом служит тут тре-
требование воспроизводимости: если мы рассмотрим какую-то
большую группу масштабов (или часов) и будем многократно
сравнивать все их друг с другом, то среди этой группы начнет
выделяться подгруппа, повторные сравнения внутри которой
приводят к наименьшим расхождениям — какой-либо из членов
этой подгруппы и будет рационально принять за эталон. Если
в последующих сравнениях (в которых могут участвовать и мас-
масштабы (часы), не входившие в первоначальную группу) выде-
выделится более узкая (а может быть — другая) подгруппа, дающая
2. ОСНОВНЫЕ ПОНЯТИЯ МЕХАНИКИ 13
лучшую воспроизводимость, то естественно перейти к новому
эталону.
Именно таким образом шел процесс отбора «наилучших»
эталонов длины и времени в реальной истории науки. При этом
долгое время в качестве наилучших эталонов длины служили
специальным образом подобранные твердые тела макроскопиче-
макроскопических размеров, а в качестве наилучших часов — астрономические
периодические процессы — вращение планет и их обращение во-
вокруг Солнца. В последнее время в связи с успехами микрофи-
микрофизики обнаружилось, что эталоны лучшего качества можно найти
среди атомных процессов, — сейчас за международный эталон
принимают длину волны в вакууме определенной спектральной
линии *).
2.1.3. Опыт показывает, что для того, чтобы определить по-
положение одного тела относительно другого, надо произвести
с помощью некоторого масштаба три независимых измерения.
Таким образом наше пространство трехмерно. Дальнейшее со-
сопоставление опытных фактов, относящихся к измерениям рас-
расстояний между различными телами, приводит к тому выводу, что
наше пространство евклидово, а, следовательно, обладает свой-
свойствами однородности и изотропности.
2.2.1. Как уже говорилось, мы можем измерять на опыте
только расстояния между какими-то парами тел, т. е. определять
только относительное положение тел по отношению к какому-то
другому телу. То тело, относительно которого мы определяем
положения остальных тел, называют телом отсчета (его, в прин-
принципе, можно выбрать совершенно произвольно), а совокупность
связанной с этим телом системы координат в пространстве и
некоторых часов называют системой отсчета.
2.2.2. Для классической механики характерно представление
об абсолютности пространства и времени — принимается, что
расстояния между телами и промежутки времени не зависят от
движения системы отсчета, в которой они рассматриваются.
*) Тут стоит отметить два любопытных момента:
С одной стороны, примечательно, что в качестве эталона длины выбран
не предмет, а процесс (колебаний электрона в атоме)—в соответствии со
сказанным непосредственно он осуществляет эталон не длины, а времени.
Эталон длины получается отсюда опосредствованным образом, умножением
на фундаментальную постоянную природы — скорость света в вакууме.
С другой стороны, однако, используя этот эталон косвенным образом
для измерения длины, мы, на современном уровне техники, не можем ис-
использовать его прямым путем в качестве эталона времени — трудность лежит
просто в том, что хотя мы сейчас можем практически сосчитать, сколько све-
световых волн приходится, скажем, на метр, мы не умеем сосчитать, сколько
колебаний атомной системы происходит в секунду. Обратному же пересчету
длины световой волиы в частоту колебаний мешает то, что хотя скорость
света, как фундаментальная постоянная природы, есть величина абсолютно
точная, мы знаем ее сейчас еще недостаточно точно.
14 ч. I. КЛАССИЧЕСКАЯ МЕХАНИКА
2.3. Выше уже говорилось о роли упрощенных моделей в тео-
теоретической физике. Очень важным модельным понятием в ме-
механике, понятием, без использования которого, строго говоря,
невозможно сформулировать основные законы механики, яв-
является понятие материальной точки. Материальной точкой на-
называется тело столь малое, что его размерами и внутренней
структурой можно пренебречь, и единственно существенным яв-
является лишь его положение в пространстве*).
2.3.1. Согласно классическим (в смысле — неквантовым) пред-
представлениям материальная точка имеет в каждый момент вре-
времени точно определенное место в пространстве, которое можно
характеризовать заданием ее трех координат или радиус-век-
радиус-вектора, как функции времени:
г = {х, у, z} = r(t)^{ra(t)}, a=l,2, 3.
Заметим, что это есть физическое допущение (в квантовой ме-
механике оно не выполняется). Будем считать, что зависимость
радиус-вектора от времени (или координат от времени) описы-
описывается достаточно гладкими функциями, так что существуют их
первые и достаточное число высших производных (это — опять
физическое допущение, несправедливое для квантового описа-
описания).
2.3.2. Тогда можно определить скорость материальной точки
как производную ее радиус-вектора по времени
rfr
V : —- Г
v dt T
я ускорение как производную скорости, т. е. вторую производ-
производную радиус-вектора по времени:
w dt dt2 v r
(в дальнейшем мы будем обозначать обычно дифференцирова-
дифференцирование по времени точкой над знаком функции). Векторы г, v и w
•суть основные кинематические характеристики' материальной
точки.
2.4.1. Чтобы задать вектор г(^), надо задать три скалярные
функции. Говорят, что система из одной материальной точки
имеет три степени свободы. Вообще, число независимых скаляр-
скалярных функций времени, которые нужно задать, чтобы полностью
*) Для макроскопической механики материальная точка — это некоторая
идеализирующая модель. В микромире, однако, выясняется, что мы должны
рассматривать элементарные частицы как, в несколько ограниченном смысле,
настоящие материальные точки. Таким образом, понятие материальной точки
оказывается первичным по сравнению с понятием протяженного тела не
только с точки зрения логического удобства изложения, но и с точки зрения
устройства природы.
2. ОСНОВНЫЕ ПОНЯТИЯ МЕХАНИКИ 15
описать движение системы, называется ее числом степеней сво-
свободы.
Ниже в основном будет излагаться механика систем материальных точек.
Случаи наличия связей будут нас интересовать очень редко, и если они
будут упоминаться в каких-либо примерах, то только идеальные, конечные и
удерживающие.
2.4.2. В качестве описывающих движение системы независи-
независимых функций не обязательно, конечно, выбирать декартовы ко-
координаты составляющих систему материальных точек. Для этой
цели можно взять любые п функций
<7i@. •••. Qn(t)
(если п — число степеней свободы), полностью характеризую-
характеризующих движение. Они называются тогда обобщенными координа-
координатами, а их производные по времени
A _i?jJO. л — d-Яп (О
Я\ — dt > •¦¦> Чп — -~af-
— обобщенными скоростями. Итак, для одной материальной
точки потребуются 3 обобщенные координаты, а для системы
из N материальных точек без связей — п = 3N.
2.5. Для дальнейшего нам будет важно понятие состояния
системы. В классической теории, которой мы пока занимаемся,
задать состояние системы в некоторый момент времени — зна-
значит задать в этот момент времени значения стольких динамиче-
динамических переменных, что значения всех динамических переменных
в остальные моменты времени смогут быть однозначно предска-
предсказаны. Опыт приводит нас к тому выводу, что для задания со-
состояния механической системы достаточно задать значения всех
ее обобщенных координат и обобщенных скоростей в некоторый
момент времени *). Это утверждение составляет с чисто матема-
математической стороны некоторое дополнительное допущение, которое
можно было бы и ослабить,— тогда мы пришли бы к теориям,
которые объединяются именем механики с высшими производ-
производными. Рассмотрение таких теорий оказывается полезным в не-
некоторых специальных разделах физики. Принимая, однако, это
допущение, мы приходим к тому выводу, что значения ускоре-
ускорений должны определяться однозначно, коль скоро задано со-
состояние, то есть значения координат и скоростей в некоторый
момент. Следовательно, ускорения в некоторый момент должны
выражаться через координаты и скорости в тот же момент вре-
времени.
*) Задания одних значений координат — как говорят, конфигурации —
в некоторый момент времени недостаточно для фиксации состояния — скоро-
скоростям в тот же момент можно приписать произвольные значения.
16 ч. I. КЛАССИЧЕСКАЯ МЕХАНИКА
2.6. Соотношения (специфичные для рассматриваемой си-
системы), выражающие ускорения через координаты и скорости,
называются уравнениями движения рассматриваемой системы.
Основная задача механики состоит в том, чтобы
A) Устанавливать вид уравнений движения для механических
систем и
B) Интегрировать найденные уравнения, чтобы найти в явном
виде «движение» системы, т. е. зависимость обобщенных коор-
координат от времени.
3. Принцип наименьшего действия
В рассмотрении первой половины основной задачи механики
мы не будем повторять исторического пути, который шел через
последовательные обобщения постепенно накоплявшихся опыт-
опытных фактов (заметим только, что основные заслуги в установ-
установлении физических основ механики принадлежат Галилею и Нью-
Ньютону, а в разработке ее математической формы — Лагранжу и
Гамильтону), а сразу сформулируем чрезвычайно общий прин-
принцип, который называется принципом наименьшего действия и
позволяет очень изящным и компактным образом выяснять, ка-
какие именно ограничения на вид уравнений движения налагают
определенные физические требования.
Сопоставим каждой механической системе характеризующую
ее функцию всех обобщенных координат, обобщенных скоростей
и, вообще говоря, времени,
L=L(qh qu t)\ i = \, ..., n,
которая называется функцией Лагранжа этой системы, и по-
построим с ее помощью функционал
{ququt)dt, A)
называемый действием. Этот функционал имеет своими аргумен-
аргументами функции qi(t), определенные в интервале t\ ^ t ^ t2 и
принимающие на концах этого интервала заданные значения
qi{U) nqi(t2).
Принцип наименьшего действия утверждает тогда, что
действительные движения выделяются из всех мыслимых тем
условием, что для них действие принимает экстремальное (для
достаточно малых t2 — ^i — минимальной) значение.
Сохраняя обозначение <7t@ для действительного движения,
обозначая близкое к действительному движение через
3. ПРИНЦИП НАИМЕНЬШЕГО ДЕЙСТВИЯ 17
и пользуясь тем, что
L (q't (t), q\ (t), t) = L (qt + bqt, qt + -|- 6qt, i) ,
получим известным способом для вариации функционала A):
Первый член обращается здесь в нуль в силу закрепленности
концов, а во втором в силу произвольности вариации б^,(/) надо
¦будет потребовать обращения в нуль подинтегрального выраже-
выражения. Тем самым требование принципа наименьшего действия
приводит нас к уравнениям Лагранжа — Эйлера:
A. Mi <1L — о ii\
dt dqt dq.-V- U)
Так как функция Лагранжа зависит от обобщенных скоро-
скоростей с/и а уравнения B) содержат дополнительное дифференци-
дифференцирование по времени, то уравнения B) будут, вообще говоря,
уравнениями второго порядка. Число их равно числу п степеней
свободы. Решения такой системы уравнений будут, следова-
следовательно, содержать 2п произвольных постоянных, например зна-
значения всех координат и скоростей в некоторый начальный мо-
момент времени to'.
Qi (to), gi (to),
т. е. будут как раз однозначно определяться заданием состояния
системы в момент to.
ЗАМЕЧАНИЕ 1: На самом деле, конечно, аргументация разви-
развивается в противоположном направлении: мы потому и допустили
в функцию Лагранжа только q и q, но не q, q, ..., что хотели
добиться, чтобы состояние системы определялось только коорди-
координатами и их первыми производными. Для теорий с высшими
производными, о которых мы кратко упомянули, в функцию
Лагранжа, естественно, входят и более высокие производные
координат. |
ЗАМЕЧАНИЕ 2: Если вторые производные входят в функцию
Лагранжа линейно с коэффициентами, зависящими лишь от ко-
координат (но не от скоростей), то уравнения B) окажутся все
равно второго порядка. Поэтому такие функции Лагранжа тоже
не выведут нас за пределы обычной механики. I
ЗАМЕЧАНИЕ 3: Для левой части уравнений B) используют иногда специ-
специальное название гамильтоновой производной и пишут
18 ч. I. КЛАССИЧЕСКАЯ МЕХАНИКА
С ее помощью уравнения Лагранжа — Эйлера принимают совсем простой вндг
ег
^- = 0; /=1,2, ...,«. | Bа>
ЗАМЕЧАНИЕ 4: Мы сформулировали принцип наименьшего-
действия в каких-то обобщенных координатах qt. Поскольку их
выбор ничем не предопределен, принцип будет иметь физиче-
физическую ценность, только если его следствия не зависят от этого
выбора, т. е. если при переходе от обобщенных координат qi
к другим Qj с помощью преобразования
Qi = fi(Qi,tY, L(Q,, Ql,t) = L(fi,fht)
уравнения движения сохранят в новых координатах форму B):
JL^2L 0. Bb>
Убедимся, что это действительно так.
В самом деле, если
dL _y dL dfk . у dL { у d*(k ¦ ,_дЪ_)
dQi Li dqk dQ. """ Lt dqk ) Li dQ, dQ v/ "*" dt dQ \ '
dL _ у dL dqk _ V* dL dfk
rlCi Li ЯЛ r)Q
^l k v« "« k
Таким образом интересующая нас комбинация
dtdQi dQi V dtydq.) dQ. V дЯь
ft N Я I fc К
у dL dfk __ydL fy
L, dqk dQt L,dqk{Li
Вторая и последняя суммы здесь взаимно уничтожаются, и мы получаем, что
d dL _ _dL_^ у ( _d_ / dL \ _ dL ^ d>k
dt dQt dQt Y { dt \ dqk ) dqk J dQ{
— т. е. из выполнения B) действительно следует выполнение Bb):
уравнения Лагранжа — Эйлера инвариантны относительно про-
произвольной (конечно, однозначной, обратимой и т. п.) замены
одних обобщенных координат другими. |
ЗАМЕЧАНИЕ 5: Если рассмотреть две функции Лагранжа
L {q, q, t) и к' {q, q, t) = L (q, q, t)+^rF ?> *)>
4. ПРИНЦИП ОТНОСИТЕЛЬНОСТИ ГАЛИЛЕЯ 19
отличающиеся друг от друга на полную производную некоторой
произвольной функции F(q,t) координат (но не скоростей!) и
времени, то соответствующие вариации действия будут совпа-
совпадать, поскольку член с полной производной проинтегрируется
по времени и приведет к разности значений F на концах времен-
временного интервала, где вариации 6^ = 0- Таким образом функция
Лагранжа определена лишп с точностью до полной производ-
производной от произвольной функции координат и времени. Это обстоя-
обстоятельство очень часто используется как в общих вопросах, так и
для упрощения вида функции Лагранжа для частных систем. ]
ЗАМЕЧАНИЕ 6: Так как для уравнений движения существенна
не сама вариация 6S, а только факт равенства ее нулю, 8S = О,
то умножение L на произвольную константу также не меняет
вида уравнений движения. Поэтому казалось бы, что можно счи-
считать, что функция Лагранжа определяется также и с точностью
до мультипликативной константы. Этому, однако, препятствует
одно физическое соображение. |
Если рассмотреть две системы, находящиеся очень далеко
друг от друга, то физически очевидно, что процессы в одной си-
системе совсем никак не должны влиять на движение другой. По-
Поскольку, с другой стороны, ничто не мешает нам рассматривать
две такие системы как две части, I и II, единой общей системы,
то мы приходим к условию асимптотической аддитивности:
Если некоторая система (I + II) разделяется на две подси-
подсистемы I и II таким образом, что минимум расстояния между
материальными точками разных подсистем гщ—*-°°, то ее
функция Лагранжа распадается' в сумму функций Лагранжа
обеих подсистем:
^ + " и „¦>¦.' *•! + *•"• C)
При умножении функций Лагранжа разных систем на произволь-
произвольные множители это равенство разрушилось бы. Таким образом,
у нас остается только возможность одновременного умножения
всех функций Лагранжа на одну и ту же константу — но такая
операция сводится по существу к изменению системы единиц.
4. Принцип относительности Галилея
4.1. Выше уже говорилось, что для описания механических
движений нужно выбрать систему отсчета, связанную с каким-
либо материальным телом. В принципе можно пользоваться
системой отсчета, связанной с любым, как угодно движущимся
телом, или даже любыми, не имеющими прямого физико-гео-
физико-геометрического смысла обобщенными координатами qf. Однако
20 ч. i. КЛАССИЧЕСКАЯ МЕХАНИКА
такая, наудачу выбранная, система не будет обладать свой-
свойствами ни однородности, ни изотропии. Так, например, покоив-
покоившаяся в некоторый момент времени в такой системе отсчета сво-
свободная материальная точка в следующие моменты придет, во-
вообще говоря, в движение в некотором направлении.
Можно определить инерциальиые системы отсчета как такие-
системы, в которых первоначально покоившаяся свободная ма-
материальная точка продолжает покоиться сколь угодно долго.
С чисто логической точки зрения такое определение инер-
циальных систем связано с большими трудностями, так как не-
неизвестно, что такое «свободная материальная точка» — под этим
надо понимать материальную точку, на которую не действуют
никакие силы, а о действии сил мы узнаем по изменениям, ко-
которые они вносят в движение материальной точки — т. е. мы
оказываемся в порочном кругу. Однако физически обычно всегда
бывает можно различить, испытывает ли материальная точка
посторонние воздействия или нет, хотя полный анализ этого
обстоятельства может быть весьма сложным.
4.2. Поэтому, если угодно, можно принять как опытный факт
существование инерциальных систем отсчета, в которых про-
пространство и время однородно и изотропно. Более того, оказы-
оказывается, что существует не одна, а сколько угодно инерциальных
систем отсчета. Именно:
если К—некоторая инерциальная система отсчета, положе-
положение материальной точки в которой оисывается радиус-век-
радиус-вектором г в каждый момент времени t, & К' — система, в ко-
которой то же событие имеет координаты г' и время t', причем
штрихованные и нештрихованные величины связаны преоб-
преобразованием
г == г' + \f;
ts=t, (V = const), D).
то система К' будет по всем своим физическим свойствам
эквивалентна системе К, т. е., в частности, будет тоже инер-
циальна.
Сформулированное утверждение называется принципом от-
относительности Галилея, а преобразования D) называют преоб-
преобразованиями Галилея.
4.2.1. ЗАМЕЧАНИЕ 1: Если в системе К' радиус-вектор
r'(t')=R — постоянному вектору, то в системе К для той же точ-
точки будет r(^)= R + V/, т. е. система К' движется относительно
системы К равномерно и прямолинейно со скоростью V. |
Таким образом преобразования Галилея суть преобразования,
выполняющие переход от одной инерциальной системы отсчета
4. ПРИНЦИП ОТНОСИТЕЛЬНОСТИ ГАЛИЛЕЯ 21
к другой (согласно принципу относительности Галилея — тоже
инерциальной), движущейся относительно первой прямолинейно
и равномерно.
4.2.2. ИСТОРИЧЕСКОЕ ОТСТУПЛЕНИЕ: Здесь, по-види-
по-видимому, надо сказать несколько слов о той многовековой эволю-
эволюции представлений, которая привела к нашему — достаточно
абстрактному — способу введения инерциальных систем и пре-
преобразований Галилея.
Основное положение первой, приписываемой Аристотелю, по-
попытки построить общую логическую схему механики, попытки,
которая, опираясь на его авторитет, подавляла умы почти две
тысячи лет, можно, несколько модернизируя терминологию,
сформулировать как:
«Все тела пребывают в состоянии покоя (относительно абсо-
абсолютного пространства), пока и поскольку действующие на них
силы не выведут их из этого состояния».
Таким образом аристотелева механика принимала существова-
существование преимущественной системы отсчета, движение или покой
относительно которой имели абсолютное значение.
Фундаментальное открытие Галилея, — к которому он при-
пришел, комбинируя простые опыты с рассуждениями, послужив-
послужившими образцом для дальнейшего развития «новой» науки,—
состояло в том, что удалось объяснить этот житейски очевидный
факт самопроизвольной остановки всякого тела по прекращении
поддерживавших его движение усилий тем, что на него, кроме
сознательно учитываемых нами сил, всегда действуют и направ-
направленные против движения силы трения — в идеальном предель-
предельном случае исчезающе-малого трения однажды приведенное
в движение тело должно было бы двигаться сколь угодно долго.
Этот логический вывод был сформулирован Ньютоном в виде
его первой аксиомы о законах движения:
«Все тела пребывают в состоянии покоя или равномерно-
прямолинейного движения (относительно абсолютного про-
пространства), пока и поскольку действующие на них силы не вы-
выведут их из этого состояния».
Таким образом понятие преимущественной системы отсчета и
абсолютного различия покоя и движения относительно ее со-
сохранялось в оригинальной формулировке ньютоновой механики.
Однако из нее логически следовало, что все инерциальные
системы, определяемые как движущиеся прямолинейно и равно-
равномерно относительно преимущественной «абсолютно неподвиж-
неподвижной», совершенно эквивалентны по своим механическим свой-
свойствам— утверждение, которое мы называем теперь принципом
относительности Галилея. Но это означает, что положенную
•22 ч. I- КЛАССИЧЕСКАЯ МЕХАНИКА
в основу преимущественную систему отсчета никак нельзя вы-
выделить из числа других инерциальных систем — абсолютное про-
пространство Ньютона ненаблюдаемо в чисто механических опытах.
Если бы такая ситуация сложилась в наши дни, то сразу
было бы четко осознано, что мы стоим перед дилеммой: либо
примириться с тем, что классическая механика не есть логи-
логически замкнутая теория, либо принять, что абсолютное про-
пространство не имеет смысла и подлежит изгнанию из формули-
формулировки основ механики. Однако такой отваге в выявлении конф-
конфликтов между логикой и здравым смыслом нас научил только
Эйнштейн (проследивший все парадоксальные следствия из не-
ненаблюдаемости абсолютного пространства в любых физических
опытах), наши научные предки были не так придирчивы к ло-
логике и больше полагались на самоочевидный здравый смысл,
так что только немногие испытывали неудовлетворенность ньюто-
ньютоновым механически-ненаблюдаемым абсолютным пространством.
В результате, как это часто случается, реальное развитие науки
не пошло логически прямолинейным путем, и современный взгляд
на основы классической механики выработался только после
создания и под влиянием теории относительности. |
4.2.3. Сейчас мы безусловно опираемся на вторую альтерна-
альтернативу и считаем, что все —связанные друг с другом преобразова-
преобразования Галилея —- инерциальные системы равноправны, и, поэтому,
механику следует формулировать так, чтобы она обладала свой-
свойством инвариантности относительно таких преобразований*).
4.2.4. Из формул D) видно, что преобразования Галилея
фактически захватывают только пространство; время, как уже
говорилось, считается в классической механике абсолютным, не
зависящим от движения системы отсчета.
4.2.5. Согласно принципу относительности Галилея всякая
система отсчета, связанная с инерциальной преобразова-
преобразованиями D), инерциальна. Чтобы можно было утверждать и об-
обратное, что всякие две инерциальные системы связаны преобра-
преобразованием Галилея, надо несколько расширить совокупность
галилеевых преобразований. В самом деле, ясно, что временные
сдвиги (изменения начала отсчета времени)
t = t'-\-r; т = const,
пространственные сдвиги
r = r'-fa; a = const
*) Трудно не увидеть иронии природы в том, что как раз теперь мы
можем выделить преимущественную систему отсчета, как такую, в которой
материя в среднем — в космологических масштабах — покоится, по наблюде-
наблюдениям реликтового излучения, сохранившегося с ранних стадий расширения
Вселенной.
4. ПРИНЦИП ОТНОСИТЕЛЬНОСТИ ГАЛИЛЕЯ 23
и повороты пространственных осей
где Саа' — постоянная ортогональная матрица, также не выво-
выводят нас за пределы инерциальных систем. Поэтому принято
включать такие преобразования в число преобразований Гали*
лея и говорить в этом случае о преобразованиях Галилея в ши-
широком смысле; преобразования D) называют тогда преобразо-
преобразованиями Галилея в узком смысле.
4.2.6. Если продифференцировать первое из равенств D) по
времени, то мы придем к закону сложения скоростей
v = v'-fV, Da)
из которого видно, что в разных инерциальных системах одна
и та же материальная точка обладает разными скоростями —
понятия «абсолютной» скорости и «абсолютного» покоя не имеют
смысла. В отличие от скоростей, ускорения — абсолютны: при
двукратном дифференцировании D) мы получим
w = w', Db)
т. е. ускорения не зависят от выбора инерциальной системы
отсчета.
4.3. Теперь можно перейти от довольно абстрактных рас-
рассуждений к более конкретным вещам и вывести вид функции
Лагранжа для свободной материальной точки. Конечно, «вы-
«вывести» можно только потому, что в наших физических допуще-
допущениях уже заложено все для этого необходимое — изотропия и
однородность пространства и времени в инерциальных системах
отсчета и принцип относительности Галилея.
Для одной материальной точки функция Лагранжа может
зависеть только от ее радиус-вектора г, скорости v и времени t,
т. е. L = L(r, v, /). Однако в силу однородности времени L не
должна зависеть от времени явно; в силу однородности про-
пространства— не должна зависеть от радиус-вектора г и, наконец,
в силу изотропии пространства не должна зависеть от направ-
направления скорости. Таким образом функция Лагранжа должна
иметь вид
L = L(v2).
Чтобы найти вид зависимости L от квадрата скорости, обра-
обратимся к принципу относительности Галилея. Лучше всего было
бы, конечно, найти такую зависимость L от v2, чтобы L остава-
оставалась бы инвариантной при преобразованиях Галилея D). Легко,
однако, сообразить, что это невозможно. Поэтому приходится
обратиться к замечанию 4 к принципу наименьшего действия
и постараться, чтобы при переходе от одной инерциальной
24 ч.. I. КЛАССИЧЕСКАЯ МЕХАНИКА
системы отсчета к другой функция Лагранжа менялась бы не
более чем на полную производную, — тогда, по крайней мере,
уравнения движения в обеих системах отсчета будут одинаковы.
Потребуем этого сперва для бесконечно малого преобразо-
преобразования Галилея. Пусть система К движется относительно си-
системы К' с бесконечно малой скоростью е
v' = v + e.
Тогда
L (v'2) = L (v2 + 2ve + e2) = L (v2) + ¦— • 2ve + О (е2),
и для удовлетворения нашего требования второй- член справа
должен быть полной производной некоторой функции г и /.
Легко видеть, что последнее возможно, только если 4~т не за-
ВИСИТ ОТ V2.
Итак, в силу принципа относительности Галилея функция
Лагранжа для свободной материальной точки должна иметь вид
L = av* = ^v\ E)
где постоянная m > О, так как иначе действие не могло бы иметь
минимума и для близких t\ и t%. Постоянную m называют, как
известно из элементарного изложения механики, массой ча-
частицы.
Легко проверить, что функция Лагранжа E) меняется только
на полную производную и для конечных преобразований D).
Часто приходится преобразовывать функцию Лагранжа к криволинейным
координатам. Для такого преобразования достаточно заметить, что, поскольку
rfr . (rfrJ rf/2 , ,
v = -tt, то vz = (dM'"" (dt\* ' И для пРе°бразования v2 к криволинейным
координатам достаточно выписать в этих координатах выражение для квад-
квадрата линейного элемента и поделить его на (dtJ. Так, например, в цилин-
цилиндрических координатах, в которых
dl2 = dp2 + P2 rf<P2 + dz\
функция Лагранжа будет иметь вид
а в сферических, в которых
rf/2 = dr2 + r2 dW + r2 sin2 # d(f2,
— вид:
I = 1JL {f2 + гг? + r2 sin2 ©ф2}.
4.4. Перейдем теперь к системам материальных точек. Будем
опять считать, что все материальные точки системы настолько
удалены от всех остальных тел, что не взаимодействуют ни
4. ПРИНЦИП ОТНОСИТЕЛЬНОСТИ ГАЛИЛЕЯ 25
с чем, не входящим в систему (про такую систему говорят не
свободная, как в случае одной материальной точки, а замкнутая)
Если можно пренебречь и взаимодействием внутри системы,
то ее функция Лагранжа получится просто сложением функ-
функций Лагранжа для каждой материальной точки — действи-
действительно, тогда уравнения движения для каждой материальной
точки будут содержать только ее координаты и скорости. Итак,
в силу E) функцией Лагранжа замкнутой системы невзаимо-
невзаимодействующих частиц будет
4.5. Для того, чтобы учесть взаимодействие внутри системы,
оказывается достаточным добавить к F) функцию, зависящую
лишь от взаимного расположения частиц (как говорят, только
от конфигурации системы):
= 2^^—c/(r" •••' r^ G)
(индекс а в формулах F) и G) —это номер частицы).
ЗАМЕЧАНИЕ 1: Форма G)—это есть некоторое допущение,
которое должно оправдываться опытом. Сколько-нибудь хорошо
оно выполняется обычно только в «настоящей» механике микро-
микрочастиц— для макроскопических тел обычно присутствуют силы
трения, которые вообще не находят себе места в лагранжевом
формализме. Но и тогда допущение G) не будет выполняться,
например, в неинерциальных системах отсчета, или в случае
присутствия магнитных сил, или при приближенном учете по-
поправок, связанных с теорией относительности. |
ЗАМЕЧАНИЕ 2: Первый член в G) называют обычно кине-
кинетической энергией и обозначают буквой Т; как мы видим, в инер-
циальной системе отсчета в декартовых координатах кинетиче-
кинетическая энергия есть квадратичная форма скоростей, и притом при-
приведенная к главным осям. Если перейти для описания системы
материальных точек к каким-то обобщенным координатам q%
с помощью преобразования, не зависящего от времени, то кине-
кинетическая энергия останется квадратичной формой скоростей, но
теперь — квадратичной формой общего вида (но положительно
определенной!) с коэффициентами, зависящими от обобщенных
координат;
i, к
26 ч: I. КЛАССИЧЕСКАЯ МЕХАНИКА
¦Функция U называется потенциальной энергией; в силу одно-
однородности пространства она может зависеть не от всех N радиус-
векторов частиц, но только от их (N—1) независимых разно-
разностей Га — Г6. |
ЗАМЕЧАНИЕ 3: В выражении G) уже содержится представле-
представление о мгновенности распространения взаимодействий — всякое
изменение положения какой-либо одной частицы в тот же мо-
момент времени сказывается на силах, действующих на все осталь-
остальные, ведь координаты всех частиц входят в U в один и тот же
момент времени. Впрочем, существование какой-либо скорости
распространения взаимодействий несовместимо с принципом от-
относительности Галилея: для нее, как и для всех скоростей, дей-
действовал бы закон сложения Dа), а это нарушило бы физиче-
физическую эквивалентность всех кнерциальных систем отсчета. |
ЗАМЕЧАНИЕ 4: Формулируя физические требования к описа-
описанию механических систем, мы не налагали явно условия изотро-
изотропии времени. Поскольку, однако, функция Лагранжа G) содер-
содержит только четные комбинации производных по времени, то она
не меняется при замене t—*¦—t. Следовательно, уравнения ме-
механики обратимы: если для системы возможно какое-либо дви-
движение, то возможно и обратное движение. |
4.6. О виде функции Лагранжа для незамкнутой системы
в общем случае трудно сделать какие-либо утверждения. Однако
тут имеется один важный частный случай, когда интересующая
нас незамкнутая система (обозначим ее I) взаимодействует
только с другой системой (II), движение которой можно считать
заданным (т. е. не зависящим от движения системы I), — гово-
говорят о движении системы I во внешнем поле. Тогда можно вы-
выписать функцию Лагранжа полной системы I + II (она уже бу-
будет замкнутой), отмечая в ней координаты первой и второй под-
подсистем соответствующими индексами, в виде
Lt+u = Ti{qh qu qu) + Tn{qn, qu) — U{qu qu).
Координаты и скорости второй подсистемы можно считать здесь
заданными функциями времени, поэтому второй член можно
отбросить. Остающееся выражение
L = T(ququqn(t))-U(qu qn(t))
имеет такой же вид, как и функция Лагранжа замкнутой си-
системы, с тем только отличием, что и кинетическая и потенциаль-
потенциальная энергия могут теперь явно зависеть от времени. Если для
описания материальных точек системы используются декартовы
координаты, то то же справедливо и относительно явной зави-
5. ЗАКОНЫ СОХРАНЕНИЯ 27"
симости потенциальной энергии от координат (а не только от
их разностей, как для замкнутой системы).
В частности, если находящаяся во внешнем поле система
состоит из одной материальной точки, то мы получим для ее
функции Лагранжа
mv2
Функция U(r,t) называется потенциальной энергией во внеш-
внешнем поле.
5. Законы сохранения
Всякое равенство вида {(qt, qi) = const называется интегра-
интегралом движения. Для замкнутой системы с п степенями свободы
всего существует Bя—1) независимых интегралов движения.
В самом деле, если считать q{ в уравнениях движения новыми
переменными, не зависимыми от qj, то полный набор уравнении
движения запишется в виде
d / dL \ dL dq{
~dl\Tfi)~~~dq'l' ЧГ^Ч"
причем для замкнутой системы время войдет здесь только в виде
явно выписанных дифференциалов. Поэтому исключая из этих
уравнений dt, мы получим Bя— 1) уравнений, не содержащих
времени. Их интегрирование и приведет к Bл — 1) соотноше-
соотношениям, которые мы назвали интегралами движения.
5.1. Среди всех интегралов движения особое значение имеют
(асимптотически) аддитивные интегралы движения (в смысле
формулы C)), для которых существует специальное название
законы сохранения. Законы сохранения имеют весьма глубокое
происхождение, связанное с инвариантностью описания механи-
механической системы относительно некоторой группы преобразовании
времени и координат. Именно, существует весьма общая теорема
Нётер, утверждающая, что для системы дифференциальных урав-
уравнений, которые могут быть получены как уравнения Эйлера из
некоторого вариационного принципа, из инвариантности вариа-
вариационного функционала относительно однопараметрической не-
непрерывной группы преобразований следует существование одного
закона сохранения. Если группа содержит / параметров, то из
инвариантности функционала будет следовать существование I
законов сохранения.
Чрезвычайно существенно, что теорема Нётер позволяет, при
заданном виде функции Лагранжа, найти аддитивные интегралы
движения в виде явных функций координат и скоростей, не ин-
интегрируя никаких уравнений, — ведь в общем случае каждый и»
28 ч. I. КЛАССИЧЕСКАЯ МЕХАНИКА
интегралов движения находится лишь интегрированием системы,
число уравнений которой лишь на одно меньше полной системы
уравнений движения.
Наличие входящих в требуемую теоремой Нётер группу пре-
сбразований симметрии зависит, конечно, от природы физиче-
физической системы. Однако уже сделанные выше общие допущения
позволяют утверждать, что для рассматриваемых нами (замкну-
(замкнутых!) механических систем действие должно быть инвариантным
относительно семипараметрической группы преобразований —
зависящего от одного параметра сдвига по времени, завися-
зависящих от трех параметров пространственных сдвигов и зави-
зависящих от трех параметров вращений пространства. В соответ-
соответствии с этим у всякой замкнутой системы должны существовать
7 сохраняющихся величин, отвечающих указанным преобразо-
преобразованиям. Если система такова, что она допускает еще и другие
преобразования симметрии, то сохраняющихся величин может
оказаться больше — с одним таким примером мы встретимся во
второй части курса при рассмотрении электромагнитного поля.
5.2. Теорема Нётер. Начнем с точной формулировки и до-
доказательства теоремы Нётер. Мы рассмотрим при этом самый
общий случай и проведем рассуждения во всей полноте, чтобы
затем можно было бы применить результаты ко всем частным
случаям, которые нам понадобятся.
Рассмотрим некоторую систему, описываемую функцией Ла-
гранжа
L = L(qh qu t).
Мы знаем, что форма уравнений Лагранжа — Эйлера, получае-
получаемых из вариационного принципа с такой функцией Лагранжа,
инвариантна относительно преобразований вида qfi = ft{qj, i)
и также, как легко понять, и относительно более общих преоб-
преобразований
включающих замену независимой переменной. Однако конкрет-
конкретный вид нового выражения для действия, как функционала но-
новых координат, зависящих от нового времени, может, конечно,
претерпеть при таком преобразовании любые изменения.
Теорема Нётер интересуется тем — исключительным — слу-
случаем, когда таких изменений не происходит.
Итак, будем считать, что мы ввели совокупность зависящих
от (для простоты) одного параметра X преобразований обоб-
обобщенных координат и времени
[f, ?,(')}=Ф
5, ЗАКОНЫ СОХРАНЕНИЯ 29
таких что
Л (к2) Л (А.,) = Л (А-з (А,,, А,2)), Л @) = 1,
т. е. образующих однопараметрическую группу. Рассмотрим бес-
бесконечно малое преобразование, отвечающее параметру А-»0.
Тогда
дп | (8>0)
Собственно вариации обобщенных координат, происходящие при
рассматриваемом преобразовании, — это разности значений q't(f)
новых координат в некоторый момент нового времени и значе-
значений старых координат q^t) в соответствующий момент старого
времени
Наряду с ними удобно ввести в рассмотрение вариации формы
зависимости координат от времени, которые отличны от нуля,
даже если наше преобразование затрагивает только время, а не
координаты. Между двумя введенными видами вариаций есть
очевидное соотношение
dV* = a«7f + U«. (8.3)
Ясно, что вариации без звездочек, относящиеся к одному зна-
значению аргумента, перестановочны с дифференцированием по
времени:
(мы этим уже пользовались при выводе уравнений Лагранжа-
Эйлера), в то время как для вариаций со звездочками это,
вообще говоря, неверно.
Соответствующие два вида вариаций можно ввести и для
любой динамической переменной. Например, для функции Ла-
гранжа
6*L = L[q'(t\ q'{f),t'\-L[q{t), q (t), t] = V (... t') - L(... t);
6L = L [tf {t), q' (t), t]-L[q (t), q (t), /] = V (... t) - L(... /),
причем
30 ч. I. КЛАССИЧЕСКАЯ МЕХАНИКА
где-jj включает дифференцирование как по явно входящему
времени, так и по времени, входящему неявно, через координаты
и скорости.
Потребуем теперь, чтобы интеграл действия не менялся бы
при нашем преобразовании, — это и есть тот исключительный
случай, который требуется условием теоремы, — т. е., чтобы
было
6*5 = J dt'L'(. .-t')-\ dtL (... 0 = 0,
г т
где V — та же область интегрирования, что и Г во втором инте-
интеграле, но выраженная через новые переменные*). Тогда:
6*5= J<ft' [/.(.. Л) + b*L\
г т
Выражая здесь б*/, через 6L и переходя в первом интеграле к интегри-
интегрированию no t вместо t', причем «якобиан» преобразования будет равен
йГ . . d .,
—г— = 1 + —тг Ot, получим:
±
Но
dL
Под знаком первой суммы здесь стоят гамильтоновы производные от функ-
функции Лагранжа по обобщенным координатам; для действительных движений
они обращаются в нуль в силу уравнений Bа). Поэтому для действительных
движений
Остается еще выразить eq, с помощью (8.3) через б*^ и Ы
*) Мы приняли здесь одинаковую функциональную зависимость действия
от старых и новых переменных и потребовали равенства их численных зна-
чевий, в то время как из логики наших рассуждений следовало равенство
значений, а одинаковой зависимости надо было потребовать, — ио это, ко-
конечно, одно и то же.
5. ЗАКОНЫ СОХРАНЕНИЯ 31
после чего мы приходим к окончательному выражению для вариации дей-
действия
H^[(ii0?^H (8-4)
Мы должны потребовать равенства этой вариации нулю. В силу
произвольности области интегрирования Т из равенства нулю
интеграла следует равенство нулю подинтегрального выражения,
и мы приходим к тому, что необходимым и достаточным усло-
условием инвариантности действия относительно преобразова-
преобразования (8.0) служит удовлетворение уравнения
Иными словами, из инвариантности действия относитель-
относительно (8.0) мы получили то следствие, что величина
dL dh -"-' (8.6)
сохраняется во времени. Это и есть точное утверждение тео-
теоремы Нётер.
ЗАМЕЧАНИЕ 1: Величина (8.6) еще не есть сохраняющаяся динамическая
величина — кроме обобщенных координат, скоростей и времени она зависит
еще и от задающих преобразование функций f, fu (8.6) станет динамическим
законом сохранения лишь тогда, когда сами задающие (8.0) функции будут
(помимо параметров к) зависеть лишь от q, q и t. |
ЗАМЕЧАНИЕ 2: Обратим внимание на разный характер двух
членов в (8.6). Первый из них включает саму функцию Лагран-
жа, поэтому обязательно *) перепутывает все степени свободы
системы и поэтому может обладать самое большее лишь асимп-
асимптотической аддитивностью C). Напротив, второй имеет явную
форму суммы по отдельным степеням свободы. Таким образом,
если преобразование, относительно которого действие инва-
инвариантно, затрагивает время, то мы можем надеяться на сохра-
сохранение лишь асимптотически аддитивной величины, если же пре-
преобразование меняет лишь координаты, то сохраняться будет
точно аддитивная величина. |
5.3. Закон сохранения энергии. Начнем применение теоремы
Нётер к обсужденным выше универсальным преобразованиям
симметрии с рассмотрения сдвига во времени. Чтобы получить
это преобразование надо, очевидно, положить в общих форму-
*) Кроме совершенно исключительных случаев.
32 ч. I. КЛАССИЧЕСКАЯ МЕХАНИКА
лах (8.0) й7 = 0, ^=1> т" е' считать 6/ за независимый (и
постоянный) параметр преобразования, а 8*qf положить рав-
равными нулю.
Уравнение (8.5) превратится тогда в
Ц'-'Ещ ¦-]-«¦ «»>
Оно означает, что как следствие инвариантности действия отно-
относительно временного сдвига сохраняется динамическая величина
Эта величина называется энергией системы. Согласно замеча-
замечанию 2 предыдущего раздела энергия асимптотически аддитивна,
если, конечно, условию асимптотической аддитивности удовлет-
удовлетворяет функция Лагранжа.
ЗАМЕЧАНИЕ: Если раскрыть полную производную по времени в (9.1), учи-
учитывая, что мы рассматриваем только действительные движения, то получим
dL ¦ Л _ dL -i_ V \dL л j_ dL ¦¦ dL ¦¦ d fdL
ЕЛЬ dL dL
l
— т. е. из теоремы Нётер следует, что если действие инвариантно относи-
относительно временного сдвига, то функция Лагранжа просто не может зависеть
от времени явно. Последнее обстоятельство не самоочевидно, поскольку при
сдвиге времени меняется не только функция Лагранжа, но и область инте-
интегрирования. В
5.3.1. Если функцию Лагранжа можно представить в виде G)
разности Т—U кинетической и потенциальной энергий, то для
энергии получится
т. е. она представится в виде суммы кинетической и потенциаль-
потенциальной энергии. В частности, энергия системы материальных точек
в декартовых координатах з инерциальной системе отсчета по-
получает вид
^^ф- + и(га-гь). (9.2а)
5.4. Сохранение импульса. Найдем теперь аддитивный закон
сохранения, вытекающий из однородности пространства, т. е. вы-
5. ЗАКОНЫ СОХРАНЕНИЯ . 33
берем в качестве преобразования (8.0) пространственный сдвиг.
Прежде всего (если пользоваться инерциальной системой от-
отсчета) такое преобразование не затрагивает времени, следова-
следовательно, Tjjr^O и пеРвые члены в (8.5,6) пропадут. Что же ка-
касается вариаций координат, то ясно, что проще всего они запи-
запишутся, если использовать для описания системы материальных
точек их декартовы координаты — тогда бесконечно малый па-
параллельный сдвиг сведется к преобразованию всех радиус-век-
радиус-векторов точек системы одинаковым образом: гд =Фт'а = та -\- X;
X — постоянный вектор; -^^- = 1. Поэтому уравнение (8.5) при-
примет в этом случае вид
dt Lt д\а
а
Величина
называется импульсом а-ой материальной точки. Поэтому из (8.6)
мы получаем, что вектор
называемый импульсом системы материальных точек, сохраняет
во время движения постоянное значение.
Если, как для системы материальных точек в декартовых
координатах, функция Лагранжа имеет специальный вид G),то,
Pa — tnaVa И Р = ? tttaVa. A1)
а
(Подчеркнем, что A1) дает определение импульсов только для
частного случая; общим определением служит формула A0).
Формула A1) не будет справедливой, например, при наличии
магнитных взаимодействий.)
5.4.1. С помощью введенного понятия импульса материаль-
материальной точки можно записать уравнения Лагранжа — Эйлера в де-
декартовых координатах как
^Ра__р F _
dt ~Га> где а~~
р F
dt ~Га> где а~~ дта
называется силой, действующей на а-ю материальную точку.
Так записанные уравнения называются уравнениями движения
в форме Ньютона.
2 Б. В.. Медведев
34 ч. I. КЛАССИЧЕСКАЯ МЕХАНИКА
Суммируя эти уравнения по всем материальным точкам, по-
получим, что в силу закона сохранения импульса:
— в замкнутой системе сумма сил равна нулю. Для двух ча-
частиц это дает
г 1 — г2
— третий закон Ньютона.
5.4.2. При использования для описания системы произволь-
произвольных обобщенных координат удобно ввести по аналогии названия
обобщенные импульсы: обобщенные силы:
(хотя эти «импульсы» и не имеют, конечно, никакого отношения
ни к сдвигам, ни — вообще говоря — к каким бы то ни было за-
законам сохранения), с помощью которых уравнения движения
записываются в «квазиньютоновой» форме
5.5. Момент. Чтобы найти аддитивную величину, сохра-
сохраняющуюся в силу изотропии пространства, опять удобно рабо-
работать в декартовой системе координат; тогда, как легко сообра-
сообразить, бесконечно малый поворот (в отличие от конечных вра-
вращений) можно параметризовать, выбирая в качестве параметра Л
составляющие бесконечно малого вектора 6ф, направленного по
оси вращения по правилу правого винта, и записывая преобра-
преобразование (8.0) как
Га = fа (ТЬ, 6ф) = Га + [6ф • Га].
Теорема Нётер будет тогда утверждать, что
Векторную величину
ma=[ra-pa] A3.1)
называют моментом *) материальной точки. Таким образом тео-
теорема Нётер учит нас, что из инвариантности относительно про-
*) Говорят также «момент импульса» и даже еще длиннее «момент ко-
количества движения».
6. ПРЕОБРАЗОВАНИЯ СОХРАНЯЮЩИХСЯ ВЕЛИЧИН 35
странственных поворотов следует сохранение вектора
л.Рл]=const; ^г^0' A3-2«3)
называемого моментом системы.
Поскольку сдвиги и повороты пространства суть преобразо-
преобразования, не затрагивающие времени, импульс и момент не только
асимптотически, но и точно аддитивны — они и получились у нас
в выражениях A0,13.2) прямо как суммы по частицам.
ЗАМЕЧАНИЕ: Надо, однако, сказать, что эта аддитивность — если только
функция Лагранжа не имеет специального вида G) — имеет несколько фор-
формальный характер. Дело в том, что хотя импульс A0.2) и представляется в
виде суммы импульсов A0.1) отдельных частиц, ио каждый из этих послед-
последних может, вообще говоря, зависеть не только от скорости «своей> частицы,
но н от «чужих» скоростей (и координат). То же справедливо н для мо-
момента. |
5.6. Итак, мы установили, что для всякой замкнутой механи-
механической системы сохраняются
Е, Р и М
— скаляр и два вектора — всего семь величин.
Для незамкнутой системы законов сохранения, вообще го-
говоря, не будет. Однако в важном случае движения системы во
внешнем поле — в том случае, если само поле обладает некото-
некоторой симметрией, — может остаться справедливой и часть зако-
законов сохранения. Так, если поле не зависит от времени, то у на-
находящейся в нем системы будет сохраняться энергия; если поле
допускает не меняющие его сдвиги, — соответствующие компо-
компоненты импульса; если вращения вокруг некоторых осей, — то
соответствующие компоненты момента. Внешнее поле может
обладать и более сложной симметрией, например оставаться
инвариантным только относительно одновременно производимых
вращения и сдвига — тогда будут сохраняться определенные
комбинации компонент импульса и момента.
6. Преобразования сохраняющихся величин
Зададимся вопросом, что произойдет с сохраняющимися ве-
величинами при преобразовании Галилея D), т. е. при переходе
от «нештрихованной» системы отсчета К к движущейся относи-
относительно нее прямолинейно и равномерно со скоростью Vo «штри-
«штрихованной» системе К':
2»
36 ч. I. КЛАССИЧЕСКАЯ МЕХАНИКА
(Vo — здесь, конечно, постоянный вектор). Ради простоты в этом
параграфе мы будем все время считать, что функция Лагранжа
имеет специальный вид G), т. е. представляется в виде разности
кинетической и потенциальной энергии.
6.1. Начнем с преобразования импульса. Поскольку при сде-
сделанном допущении справедливы соотношения A1), то формулу
для преобразования импульса а-оя частицы можно получить,
просто умножая закон преобразования ее скорости на ее массу:
Ра = Ра + Voma.
Суммированием по всем частицам системы найдем отсюда для
полного импульса
2>
6.1.1. Теперь можно ввести понятия пэкоя и движения си-
системы материальных точек как целого. Именно, примем, что
система материальных точек покоится как целое в той системе
отсчета, в которой ее полный импульс равен нулю.
Далее,
под скоростью V системы материальных точек в произвольной
системе отсчета понимается скорость относительно нее той
специальной системы отсчета, в которой система материальных
точек покоится.
6.1.2. Выберем в преобразовании Галилея, которое мы начали
рассматривать, специальным образом V0=V так, чтобы в си-
системе К' интересующая нас система материальных точек покои-
покоилась бы (в К она будет иметь тогда как раз скорость V). Тогда
импульс в системе К примет вид
г — v 2^t ma.
а
Сравнивая эту формулу с выражением A1) для импульса
одной.материальной точки, видим, что естественно определить
массу М всей системы как
а
С этим определением соотношение между импульсом, массой
и скоростью всей системы
P = MV A5.1)
оказывается в точности таким же, как соотношение A1) для
одной материальной точки.
ЗАМЕЧАНИЕ: Устанавливая эту аналогию, мы руководствова-
руководствовались, конечно, не соображениями красоты и легкой запоминае-
6. ПРЕОБРАЗОВАНИЯ СОХРАНЯЮЩИХСЯ ВЕЛИЧИН 37
мости формул. Совпадение соотношений A5.1) и A1) позволяет
нам трактовать систему материальных точек — в тех случаях,
когда внутренние движения в ней нас не интересуют — как одну
материальную точку, т. е. по существу оправдывает введение
самого' модельного понятия материальной точки, i
1.6.3. Разрешая A5.1) относительно V и подставляя выра-
выражения A4) и A1) для массы и импульсов, представим скорость
V движения системы как целого через скорости и массы состав-
составляющих ее материальных точек
Проинтегрируем эту формулу по времени:
=K- A6)
2.. т°
Точка с так определенным радиус-вектором R называется
центром инерции системы материальных точек.
Итак, мы нашли, что в силу закона сохранения импульса
центр инерции замкнутой системы материальных точек движется
прямолинейно и равномерно со скоростью V (опять в полной ана-
аналогии с радиус-вектором одной свободной материальной точки).
Это движение в высокой степени тривиально, поэтому есте-
естественно вовсе исключить его из рассмотрения. Того ради вер-
вернемся к преобразованию Галилея и посмотрим, как будет пре-
преобразовываться энергия системы (рассуждение для функции
Лагранжа совершенно тождественно).
6.2. Подставляя в действующее в принятых допущениях вы-
выражение (9.2а) Е = Т -\- U выписанное в начале параграфа пре-
преобразование скоростей (подставлять преобразования радус-век-
торрд .нет нужды, так как разности радиус-векторов, единствен-
единственно входящие в потенциальную энергию, этим преобразованием
не затрагиваются), получим
Е=т Е m" (v«+V°)Z+и=
Таким образом, при произвольном преобразовании Галилея
энергия преобразуется по закону
Е = Е'+?'Уо + -^г. A7.2)
38 ч. I. КЛАССИЧЕСКАЯ МЕХАНИКА
Выпишем здесь же полученное ранее преобразование для им-
импульса:
р = Р'+ MV0. A7.1)
6.2.1. Если выбрать теперь в качестве К' опять ту систему
отсчета, в которой система материальных точек как целое по-
покоится, т. е. взять Vo = V, то второй член справа в A7.2) исчез-
исчезнет и останется
^f A5.2)
Второй член в правой части — это энергия движения системы
как целого, опять совершенно аналогичный выражению для
энергии одной свободной материальной точки. Первый член
справа принято называть внутренней энергией системы (в со-
соответствие с чем мы и обозначили его через ?*п); он зависит не
только лишь от разностей координат, но и лишь от разностей
скоростей*). Таким образом, в качестве обобщенных координат
описываемой этим членом системы можно принять (N— 1) неза-
независимую разность радиус-векторов (га — г^), т. е. число степеней
свободы уменьшается на три.
Для выпавших из «внутренних» движений трех степеней сво-
свободы первоначальной системы можно принять в качестве обоб-
обобщенных координат координаты радиус-вектора центра инерции
A6). Таким образом формула A5.2) действительно осуще-
осуществляет разбиение задачи о движении замкнутой системы N ма-
материальных точек на две независимые задачи: задачу о вну-
внутренних движениях н (тривиальную) задачу о равномерном и
прямолинейном движении системы как целого.
6.3. Осталось еще посмотреть, что делается при преобразо-
преобразованиях Галилея с моментом
В этом случае интересно исследовать результат действия общего
преобразования Галилея, включающего пространственный сдвиг:
Подставляя это преобразование ( и получающееся иэ него
умножением на массы преобразование импульсов отдельных
*) В этом утверждении проще всего убедиться, если заметить (что про-
вернется прямой выкладкой), что комбинация Е -— инвариантна отно-
относительно добавления ко всем скоростям одного и того же вектора. Отсюда,
в частности, следует инваряаитность внутренней энергии относительно пре-
преобразований Галилея.
6. ПРЕОБРАЗОВАНИЯ СОХРАНЯЮЩИХСЯ ВЕЛИЧИН 39
частиц
Ра = Ра + та\0)
в выражение для момента, получим сперва
M = M' + <[Vo-P/] + [Ro-P'] +
+ М [R' • Vo] + Ш [Vo • Vo] + М [Ro • Vo].
Члены правой части удобно сгруппировать здесь в три группы,
записывая
М = М' + [(Ro + Wo) • Р'] + М [R • Vo]. A7.3)
6.3.1. Обсудим полученное выражение. Прежде всего, не-
нетрудно видеть, что, в отличие от энергии и импульса, момент
меняется при трансляции. Действительно, если рассмотреть чи-
чистую трансляцию, положив Vo = 0, то получим из A7.3)
трансляция: М = М' + [Ro • Р'].
Исключение составляют трансляции в той системе отсчета, в
которой система материальных точек покоится как целое, т. е.
Р = Р' = 0 (Такую систему отсчета принято называть системой
центра инерции или системой центра масс, обозначая ее со-
сокращенно буквами ЦИ или ЦМ),— тогда второй член обра-
обращается в нуль и момент не зависит от выбора начала отсчета.
6.3.2. Если выбрать теперь в качестве системы К произволь-
произвольную систему отсчета, а в качестве системы К' систему ЦИ, так
что будет
Р' = 0, a Vo = V — скорости (в К\) системы как целого,
то произведение A1V = P — импульсу в системе /С,аМ'=Мци —
независящему от выбора начала отсчета моменту в системе
ЦИ. Поэтому мы получим тогда из A7.3)
M = MUH+[R-P] A5.3)
— т. е. момент системы в произвольной системе отсчета рав-
равняется сумме ее момента в системе центра инерции Мци (этот
момент часто называют собственным моментом системы) и век-
векторного произведения радиус-вектора центра инерции на им-
импульс. Этот последний член опять имеет форму момента одной
материальной точки, обладающей координатой R и импульсом
Р*). Таким образом совокупность формул A5.1), A5.2) и A5.3)
*) Заметим, что только формула A5.3) окончательно оправдывает при-
принятое выше определение R A6)—ведь по смыслу вывода A6) радиус-вектор
центра инерции определялся лишь с точностью до постоянной интегрирова-
интегрирования, которую мы там произвольно положили равной нулю. Теперь видно, что
прн другом распоряжении этой постоянной нельзя было бы трактовать доба-
добавок к собственному моменту в A5.3) как момент одной материальной точки.
40 ч.' I. КЛАССИЧЕСКАЯ МЕХАНИКА'
составляет доказательство того, что систему материальных то-
точек— коль скоро не интересуются внутренними движениями в
ней — можно рассматривать как одну материальную точку с
массой A4) и радиус-вектором A6).
6.4. Обсудим еще, как преобразуются основные динамические
переменные системы при бесконечно малых поворотах
— ведь такие преобразования тоже входят в число преобразо-
преобразований Галилея в широком смысле. Поскольку преобразования
скоростей получаются отсюда дифференцированием, преобразо-
преобразования импульсов отдельных частиц —умножением на массы, и
преобразования полного импульса — суммированием по веем
частицам системы, а все эти операции в данном случае линейны»
то импульс системы будет преобразовываться при поворотах
так же, как и радиус-вектор каждой частицы.
Менее тривиально обстоит дело с преобразованием момента,
являющегося квадратичной функцией линейно преобразующихся
радиус-вектора и импульса. Для одной частицы приращение ее
момента бта при бесконечно-малом повороте сложится по фор-
формуле Лейбница из приращений радиус-вектора и импульса:
бта = [бга • ра] + [га • бра] = [[бгр • г«] • р«] + [го • [6ф • ра]].
Переставляя во втором члене порядок множителей в обоих век-
векторных произведениях
6та= [[6Ф • rj • pj + [[рв • 6ф] • гв],
мы сможем прибегнуть для объединения двух членов к имею-
имеющему для двойных векторных произведений место тождеству
Якоби
[[А • В] • С] + [[С • А] • В] + [[В • С] • А] = 0.
Тогда приращение момента примет вид
бта = - [[гв • ра] • &ч>] = [&ф • [гв • pj] = [6ф • та],
совпадающий с выражениями для приращений радиус-вектора
или импульса. Переход к полному моменту системы требует
опять только тривиального суммирования по частицам.
Заметим, что полученный вывод об одинаковости закона пре-
преобразования радиус-векторов, импульсов и моментов при прост-
пространственных поворотах является совершенно очевидным и есте-
естественным. Ведь он означает просто, что все эти величины' суть
векторы — а это уже сразу было видно из полученных для них
выражений. По тем же причинам скалярные величины — энер-
энергия и функция Лагранжа — вовсе не должны преобразовываться
при поворотах.
7. СЛЕДСТВИЯ ГАЛИЛЕЕВОЙ ИНВАРИАНТНОСТИ 41
Итак, при бесконечно малых поворотах системы отсчета
основные динамические переменные преобразуются по форму-
формулам:,
6.5. Роль законов сохранения в физике чрезвычайно велика.
Основная их ценность состоит в том, что они позволяют выя-
выявить некоторые основные черты явления, совершенно не вникая
в его детальный механизм, который может быть и неизвестен —
либо из-за сложности интегрирования уравнений, либо потому,
что мы не знаем в подробностях устройства системы и управ-
управляющих ею законов.
В этом последнем случае законы сохранения часто служат
единственным источником информации о проистекающих в си-
системе процессах. Особенно плодотворным оказывается такой
подход, если интересующая нас система инвариантна еще и
относительно каких-то дополнительных преобразований — как
говорят, обладает дополнительной симметрией, — тогда сведе-
сведения, которые можно почерпнуть из одних законов сохранения
могут оказаться весьма детальными*).
При переходе к квантовому описанию значения сохраняю-
сохраняющихся величин служат основой классификации состояний си-
системы квантовыми числами.
По этим причинам энергию, импульс и момент, сохраняю-
сохраняющиеся всегда для всякой замкнутой системы, называют часто
основными или фундаментальными динамическими величи-
величинами:
Наконец в более простых случаях, когда уравнения движе-
движения системы нам известны и речь идет только об их интегриро-
интегрировании, законы сохранения могут послужить вспомогательным
средством, упрощающим эту процедуру за счет снижения числа
переменных, их разделения или даже сведения интересующей
задачи к одномерной — с примерами этого мы познакомимся в
следующих параграфах.
7. Инвариантность относительно преобразований Галилея**)
7.1. При рассмотрении в предыдущих двух параграфах след-
следствий, которые можно извлечь из инвариантности описания
*) Именно с таким положением мы столкнулись сейчас в теории элемен-
элементарных'частиц и их сильных взаимодействий, где единственным надежно уста-
установленным фактом является существование многочисленных свойств сим-
симметрии.
**) Этот параграф может быть опущен при первом чтении без ущерба
Для дальнейшего.
42 ч. I. КЛАССИЧЕСКАЯ МЕХАНИКА
замкнутой механической системы относительно определенных
непрерывных преобразований, были обойдены молчанием пре-
преобразования Галилея в узком смысле D). Причина этого была
двоякой. Во-первых, хотя уравнения движения и инвариантны
относительно таких преобразований, но функция Лагранжа —
а, следовательно, и действие — не обладает, как было показано
в § 4, этим свойством. Поэтому общая техника получения зако-
законов сохранения, содержащаяся в теоремах Нётер, не может быть
приложена к этому случаю.
Во-вторых, для того специального класса динамических си-
систем, которые описываются функциями Лагранжа типа G), ин-
инвариантность уравнений относительно преобразований Галилея
вообще не ведет ни к каким новым следствиям. Дело в том, что
при преобразовании Галилея, как уже отмечалось при обсужде-
обсуждении преобразования энергии, второй член в выражении G) вовсе
не испытывает никаких изменений, и все сводится к изменению
кинетической энергии, которая при выполнении допущения G)
есть просто сумма кинетических энергий отдельных материаль-
материальных точек системы. А вид кинетической энергии одной свободной
материальной точки как раз и устанавливался в § 4 исходя из
требования максимально допустимого изменения при преобра-
преобразовании Галилея — т. е. изменения на полную производную.
Таким образом требование инвариантности уравнений дви-
движения уже учтено в специальной форме G) функции Лагранжа,
и те следствия, которые были получены с использованием этой
формы в предыдущем параграфе, фактически уже основыва-
основывались на этой инвариантности. Если проследить внимательно рас-
рассуждения предыдущего параграфа с этой точки зрения, то
можно заметить, что это касалось в первую очередь закона пре-
преобразования импульса при переходе от одной инерциальной си-
системы к другой и основанного на нем- утверждения о равномер-
равномерном и прямолинейном движении центра инерции A6); как мы
сейчас увидим, как раз эти утверждения и являются собственно
следствиями галилеевой инвариантности уравнений движения.
7.2. Итак, рассмотрим замкнутую механическую систему, описывающуюся
в некоторой инерциальиой системе отсчета К функцией Лагранжа L (га, ve)
не имеющей частного вида G). В другой инерциальной системе К', связанной
с К (пусть — бесконечно-малым) преобразованием Галилея D), та же меха-
механическая система будет описываться функцией Лагранжа L (r'a, v^) (с той
же функциональной зависимостью!).
Требование галнлеевой инвариантности уравнений движения рассматри-
рассматриваемой системы означает, что эти две функции Лагранжа должны разли-
различаться не более чем иа полную производную некоторой функции Ф только
координат, но не скоростей:
7. СЛЕДСТВИЯ ГАЛИЛЕЕВОЙ ИНВАРИАНТНОСТИ 43
Мы написали здесь Ф (ra, Vo), поскольку функция Ф должна, конечно,
зависеть от параметра преобразования D), причем так, что Ф(га, 0) = 0 —
в системе К никакой добавочной функции нет. Поэтому, разлагая Ф в ряд
по Vo и оставляя только первый член, можем записать ее как
Ф (г«, Vo) = Vo«D (re),
где Ф — новая (векторная) функция опять только от координат.
С другой стороны, приращения координат и скоростей частиц системы
при бесконечно-малом преобразовании D) составляют
- V0-
и, следовательно,
L(r'. v') = L(ra,
Таким образом требование (*) галилеевой инвариантности приводит к
тому, что должно (при произвольных малых Vo) выполняться равенство:
Воспользовавшись здесь произвольностью Vo и вспоминая (общее!) опреде-
определение A0) импульсов отдельных частиц и полного импульса, заключаем от-
отсюда о необходимости выполнения условия
т. е.
-^-(Р<-Ф(га))=0 или Р<-Ф(га)= const. A9)
Это и есть тот закон сохранения, выполнение которого следует из требования
инвариаитности относительно преобразований Галилея.
7.3. На первый взгляд кажется, что закон сохранения A9) содержит
очень мало информации, — ведь вид входящей в сохраняющуюся комбинацию
функции Ф (ra) совершенно произволен. Тем не менее оказывается, что из
него можно извлечь довольно существенные физические следствия.
Вспомним того ради, что входящий в левую часть A9) полный импульс
сам тоже должен сохраняться для замкнутой системы, —гг = 0. Воспользо-
Воспользовавшись этим обстоятельством при выполнении дифференцирования в первом
из равенств A9), мы получим из него, что
Но функция Ф есть функция только координат, поэтому и ее частные произ-
производные, стоящие в качестве коэффициентов при скоростях в сумме по части-
частицам, также суть функции только координат, но не скоростей. Следовательно,
правая часть A9а) есть однородная линейная функция скоростей; значит, то
чсе должно быть и для левой части. Итак,
44 ч: I. КЛАССИЧЕСКАЯ МЕХАНИКА
Импульс замкнутой системы есть, как следствие инвариантности относи-
относительно преобразований Галилея,' линейная однородная функция скоростей
всех материальных точек системы.
7.4. ЗАМЕЧАНИЕ: Для одной материальной точки мы получаем отсюда
одним интегрированием по скорости выражение E) для функции Лаграижа,
которое мы получили в § 4 рассуждениями.
В самом деле, для одной материальной точки в силу линейности и одно-
однородности
3L . .
р = —v = /га (г) • v,
дг
где /га (г)—пока произвольная функция единственного радиус-вектора г. Ин-
Интегрируя, получаем отсюда
где Ь(т) опять может пока быть произвольной функцией г. Поэтому уравне-
уравнениями Лагранжа-Эйлера для нашей системы будут
dp
dt
dL
dr
V2
dm
~dF^
db
' dr '
Но в силу однородности пространства импульс р должен сохраняться, т. е.
должно быть
dp v2 dm , db .
чг=0 или -t-w+sf-0'
откуда благодаря произвольности v2 следует
i2—о и 41 = 0,
rfr rfr
т. е. обе произвольные функции оказываются константами. Вторую из них
в функции Лагранжа можно просто отброснть, и мы приходим к
. /rav2
2 '
что в точности совпадает с нашей старой формулой E). Щ
7.5. Вернемся теперь к общему случаю JV материальных точек и сравним
полные импульсы в системе К и К'- По общему определению они будут равны
в/С:
Но функции Лагранжа в этих двух системах отсчета связаны соотношением
(*). Поэтому:
a
в силу A9.а)
а, Ь
7. СЛЕДСТВИЯ ГАЛИЛЕЕВОЙ ИНВАРИАНТНОСТИ 45
Итак, импульсы в системах К я К' связаны соотношением
Pa = P; + aKapFop> , B0a)
в котором тензор 2йар> который можно назвать «тензором масс» системы,
определяется как
gftag=y „ д^ B1а)
a, b
Подчеркнем, что использованные до сих пор соображения ни в коей мере не
требуют, чтобы его компоненты были постоянными, они с равным правом
могут оказаться произвольными функциями координат (но не скоростей!).
Мы видим, что полученное соотношение весьма существенно отличается
от найденного ранее для специальных функций Лагранжа вида G) соотно-
соотношения A7.1) и что рассматриваемые нами сейчас общие системы могут об-
обладать весьма парадоксальными свойствами. Вместо скалярной массы у них
появляется тензор масс, который к тому же может зависеть от координат,
импульс может не совпадать по направлению со скоростью и т. д.
7.6. Дело в том, что пока мы использовали еще не все физические тре-
требования, которые следует предъявлять к описанию системы материальных
точек. Как уже отмечалось в § 3, кроме требований инвариантности относи-
относительно преобразований Галилея в широком смысле, следует еще наложить на
функцию Лагранжа требование асимптотической аддитивности C).
Будем считать, что энергия системы достаточно велика (вид функции
Лагранжа не зависит от численного значения энергии), чтобы для достаточно
большого момента времени Т все материальные точки системы разошлись бы
сколь угодно далеко друг от друга. Тогда в момент времени Т и при боль-
больших временах в силу асимптотической аддитивности в функции Лагранжа
системы будут существенны только члены, отвечающие свободному движению
составляющих ее материальных точек, которые образуют комбинацию F).
Следовательно, для достаточно больших времен тензор Ш!ар примет вид
^аз Ь>:Г = 6аз ? та = &а^М, где как и в A4) М= ? пга.
а а
Но тогда соотношение B0а) примет (опять для больших времен) прежнюю
форму A7.1) .
для t^5T: P=P'-fvMV0.
Однако полный импульс системы материальных точек должен сохранять-
сохраняться как в системе отсчета К, так и в К', Р = const, Р' = const, т. е. в по-
последнем равенстве все величины, кроме М, не зависят от времени. Следова-
Следовательно, то же равенство должно иметь место в любой момент времени, т. е.
должно быть
p=P' + V0Af B0b)
i?ki^ !> B1b)
а, Ь
Подчеркнем еще раз, что это восстановление простых формул шестого па-
параграфа произошло только как следствие лсимптотическои аддитивности, свой-
свойства, которое, как и правильное поведение при преобразованиях Галилея, изна-
изначально присуще функциям Лагранжа ранее рассматривавшегося класса G).
Второе замечание, которое полезно здесь сделать, состоит в том, что
отмеченное постоянство относится только к полной массе. До суммирования
46 «• I. КЛАССИЧЕСКАЯ МЕХАНИКА
d2L
отдельные производные -т-—т могут произвольным образом зависеть ие
ovaa 0Dbg
только от координат, но и от скоростей.
Дальнейшие рассуждения идут так же, как и в предыдущем параграфе.
Определяем скорость системы как целого V условием A5.1) как
»-i*
и, интегрируя это равенство
1
М v 1Г1> ' •*• TN> "¦ VI» •••> тц>' \ll>d>
обнаруживаем, что точка с радиус-вектором R (i-j г^) движется прямо-
прямолинейно и равномерно.
Таким образом выясняется физический смысл входящей в A9) или A9а)
величины Ф (Tj, ..., г^) — будучи поделенной на полную массу, она дает нам
радиус-вектор центра инерции системы.
Подчеркнем, что равенства A6а) являются теперь единственным опреде-
определением радиус-вектора центра инерции; фигурировавшее в A6) определе-
определение R как взвешенного (с массами) среднего радиус-векторов всех точек си-
системы теперь, вообще говоря, не обязано иметь место.
7.7. Перейдем теперь, повторяя программу § 6, к рассмотрению того, как
преобразуется момент при преобразовании Галилея со сдвигом
Правило для преобразования импульсов отдельных частиц теперь уже
нельзя будет получить отсюда умножением второй строки на массы, и мы
сможем только написать, что
Чтобы выяснить смысл стоящей здесь суммы, обратимся снова к нашему
«закону сохранения» A9а) и перепишем его в тензорном виде
ЕдФ
Введенные здесь обозначения Саа1ресть, в силу A9а), с одной стороны част-
частные производные Ф по радиус-векторам, а с другой в то же время — частные
производные полного импульса по скоростям. Вспоминая еще определение
импульса
У у dL
видим, что
<5Фй дРл ^~у д L
=д Сап о =я ¦ =я / A9Ь)
дгаа аа'* dvaa L, dvaadvb? KV>
(t. е. «тензор масс» B1а) есть 9Kog
c
ao,
7. СЛЕДСТВИЯ ГАЛИЛЕЕВОЙ ИНВАРИАНТНОСТИ 47
Эти следующие из A9а) тождества являются чрезвычайно плодотвор-
плодотворными. В частности, для интересующего нас сейчас преобразования импульсов
частиц при повороте мы получаем из A9Ь)
или Ра = Ра + (?«Vo)'
если воспользоваться полуснмволической прямой записью.
Теперь можно заняться вычислением преобразования момента
o< + Ro • p'a + (CaV0)] =
? Ь'а ¦ P'a] + [V + Ro • S P'J + E К ¦ (eaVo)l-
a u a J a
Суммирование во втором члене дает полный импульс, и, значит,
М = М' -f [(Ro + VoO • P'l + X [ra • (CaV0)]. B2а)
a
Рассмотрим опять два наиболее интересных частных случая. Если рас-
рассматриваемое преобразование есть чистый сдвиг, Vo = 0, то третий член и
половина второго пропадают, и остается
трансляция: М = М' + [Ro • Р'] B2Ь)
— выражение, в точности совпадающее с полученным в прошлом параграфе.
Если теперь штрихованная система есть система центра инерции, т. е.
Р'=О и V0 = V = -J-,
то пропадает второй член, и мы приходим к
На первый взгляд это выражение ие имеет ничего общего с аналогичной
формулой A5.3). Вернемся, однако, к определяющим Са формулам A9Ь) и
A6а) —
J_ 1 $
М Саа- В — М дгаа - дгаа •
Поэтому добавок к моменту при переходе от ЦИ-системы к произвольной
системе К можно записать как
где крышечка над Р означает, что этот вектор ие следует дифференцировать.
Далее, пока мы еще никак не сформулировали то требование, что
R(rj Где) должен быть действительно зектором (если не считать того,
что изображали его полужирным шрифтом). Математическое условие век-
ториости R состоит, естественно, в том, что его изменение при произвольном
бесконечио-малом повороте 6<р,
(
а а \ а
должно выражаться общей для всех векторов формулой A8):
6R = [6<р ¦ R]. A8.4)
48 ч. I. КЛАССИЧЕСКАЯ МЕХАНИКА
Таким образом, после скалярного умножения на Р, должно быть
a
откуда, в силу произвольности 6q>,
Благодаря этому тождеству добавок к моменту принимает вид вектор-
векторного произведения радиус-вектора центра инерции н импульса т. е. мы полу-
получаем, для преобразования момента из ЦИ-системы в произвольную, формулу
М = Мци + [R • Р], B2с)
идентичную по виду формуле A5.3). (Следует, конечно, все время помнить,
что смысл этих двух формул может быть и различным, поскольку старое
определение A6) для R теперь, вообще говоря, не имеет места.)
7.8. Итак, эксплуатируя только требование инвариантности описания ме-
механической системы относительно преобразований Галилея в широком смысле
(т. е. — принцип относительности) и условие асимптотической аддитивности
и не используя специальное допущение G) относительно вида функции Лаг-
ранжа, удалось привести все формулы для сохраняющихся величин к виду,
полученному ранее в рамках этого специального допущения. Поэтому все
отличие настоящего более общего рассмотрения сосредоточилось в свободе
выбрать для зависимости радиус-вектора центра инерции от координат,
R (г;, ..., г„), выражение, более общее, чем следовавшая из G) простая фор-
формула A6) *). Чтобы разобраться в том, какие дополнительные возможности
при этом открываются, посмотрим, как происходит тепеоь отделение трансля-
трансляционного движения от внутренних.
7.9. Для этой цели введем для описания рассматриваемой механической
системы вместо радиус-векторов rv ..., г^ ее материальных точек обобщен-
обобщенные координаты:
_ определяемый A6а) радиус-вектор центра инерции R,
и
(N—1) линейно независимую разность гд — гл радиус-векторов
отдельных точек; будем обозначать эти разности через
р,,.... р#_,; Ре=тв-г6.
Вид зависимости R от гь неизвестен; однако нз соображений трансляционной
и ротационной инвариантности можно утверждать, что самым общим выра-
выражением для R будет линейная комбинация
всех векторов Ть, коэффициенты Fb которой суть произвольные ротационно-
инвариантные функции г1?..., г^. Тогда мы получим для введенных в A9Ь)
*) Конечно, одного совпадения выражений для фундаментальных сохра-
сохраняющихся величин еще недостаточно для совпадения всей динамики двух
систем. Поэтому, даже если R будет задаваться формулой A6), функция
Лагранжа все еще может не иметь вида G).
7. СЛЕДСТВИЯ ГАЛИЛЕЕВОЙ ИНВАРИАНТНОСТИ 49
коэффициентов Саа, у:
1 _ dRy _ y1 dF"
ь
Асимптотическая аддитивность B1Ь) требует, чтобы суммирование этих
коэффициентов по а приводило бы к единичному тензору; при принятом ан-
заце для R это приводит к
В силу независимости всех векторов Ть для выполнения последнего условия
необходимо и достаточно, чтобы было сразу
Вторая группа требовании означает, что все функции Fb долж:
свойством F" (та + с) = F° (ra), т. е. должны быть (ротационно-г
должны обладать
-инвариантны-
-инвариантными) функциями не самих радиус-векторов гя, а только их (независимых)
разностей г^ — г^. Таким образом требование асимптотической аддитивности
ограничивает принятый анзац зависимости R от та формой
Ra=E/ra(Pc)Ta. где ^f=l.
Однако мы еще ие использовали это требование до конца. Поскольку
асимптотическая аддитивность требует, чтобы для больших взаимных рас-
расстояний функция Лагранжа принимала вид F), а для таких функций Лаг-
ранжа радиус-вектор центра инерции выражается формулой A6), то пре-
предельные значения каждой из функций Fa при всех разностях ть — г , стремя-
стремящихся по модулю к бесконечности, должны составлять просто—¦—, где ша —
масса (по асимптотическим измерениям) а-й частицы. Иными словами, мы
можем записать
где
lim fa=0 и У/а(Рс)=О. A6с)
¦ ' BCelrb-rcl->-°° a
Итак, наиболее общая форма зависимости R от г1 г^, допускаемая
из соображений трансляционной и ротационной инвариантности и требования
асимптотической аддитивности, есть
где /„ подчинены условиям A6с). Заметим еще, что в силу второго из этих
условий второй член { }п в A6b) обладает свойством { }п (ra + с) = { }и (га),
1. е. является в целом опять функцией не самих га, а только их разностей.
50 ч. I. КЛАССИЧЕСКАЯ МЕХАНИКА
Поскольку Рс не меняются при сдвиге, то полный импульс системы есть
—г-, и в силу A6а)
Интегрируя это соотношение по R, приходим к функции Лагранжа:
L (R, R, ре> рс) = JZf- + L, (рс> ре). B3)
(От координаты R второй член здесь зависеть не может, так как иначе урав-
уравнение Лагранжа — Эйлера по этой степени свободы приводило бы к измене-
изменению полного импульса со временем.) Это и есть наиболее общая функция
Лагранжа, удовлетворяющая требованиям принципа относительности Галилея
и асимптотической аддитивности.
Естественно, что для полного импульса эта функция Лагранжа возвра-
возвращает нас к исходному выражению P = AfR, что же касается полного мо-
момента, то, поскольку «обобщенные координаты» R и рс преобразуются при
повороте по общему векторному правилу A8), то для него получается
N-1
М= X [рс • пс] + [R • Р], B2d)
с= I
если обозначить через лс (обобщенные) импульсы, сопряженные координа-
координатам рс,
JT -: dL = dLl
дрс дрс
Формула B2d) совпадает, конечно, с ранее полученным выражением B2с),
в ней только явно учитывается, что собственный момент, обозначенный в
B2с) через МцИ, зависит только от координат и импульсов относительного
движения.
7.10. Можно ли еще сильнее сузить найденный класс допустимых зависи-
зависимостей B3), A6Ь)?
Введем в B3) и A6Ь) вместо радиус-векторов частиц го новые коорди-
координаты Ro с помощью соотношения
Это преобразование не затрагивает разности координат, поэтому векторы рс
будут выражаться через Ro так же, как н через г„; что же до радиус-век-
радиус-вектора R центра инерции, то ои выразится через Ro как
1
М М ' MLj 'аУа М
а
— т.е. в точности по старой формуле A6).
Таким образом, мы нашли такие новые координаты для частиц, в терми-
терминах которых выражение для радиус-вектора центра инерции возвращается
к «простой> форме A6). Эти новые координаты Ra ведут себя по отношению
ко всем фундаментальным для нашего способа изложения преобразованиям
8. РАССЕЯНИЕ ЧАСТИЦ 5!
симметрии — по отношению к сдвигам, поворотам и преобразованиям Гали-
Галилея в узком смысле — точно так же, как и «старые» координаты г»:
Поэтому из соображений поведения при преобразованиях симметрии нельзя
будет сказать, какие нз ннх «лучше», какие более заслуживают названия
«настоящих радиус-векторов материальных точек системы». Нельзя выяснить
это и на основании анализа асимптотического поведения — при стремлении
всех разностей | rfl — rft | к бесконечности дополнительный член в (•) обра-
обратится в нуль, н Го не будут отличаться от Ro. Наконец, условие «соприкосно-
«соприкосновения» какой-либо пары частиц га — г& = 0 выражается только через раз-
разности координат, т. е. опять выглядит в терминах ra и Ra одинаковым об-
образом.
Иными словами, координаты материальных точек системы определяются
введенными физическими требованиями лишь с точностью до преобразования
(*), и не видно никаких препятствий тому их выбору, при котором восста-
восстанавливается простая формула A6) для центра инерции, которая вместе с B3)
определяет функцию Лагранжа через координаты Ro отдельных материаль-
материальных точек. Вид отвечающей относительным движениям части L\ (р, р) оста-
остается при этом произвольным; ограничения на него налагает лишь необходи-
мбсть выполнения асимптотической аддитивности при любом разбиении си-
системы на удаленные подсистемы.
8. Рассеяние частиц
Хорошим примером того, какую пользу могут сослужить
законы сохранения, может быть задача двух тел, т. е. задача
о поведении замкнутой системы, состоящей всего из двух мате-
материальных точек.
В § 6 уже было показано, что формулы A5) осуществляют
отделение движения системы как целого от внутренних движе-
движений в системе. В случае двух материальных точек эти последние
будут движением одной материальной точки во внешнем поле,
и всю программу разделения переменных, относящихся к транс-
трансляционному и к внутреннему движениям, удобно полностью
провести въявь.
8.1. Итак, пусть изучаемая система состоит из двух мате-
материальных точек с массами Ш\ и т2 и координатами г{ и г2:
ти Г[Г т2, г2.
В рамках допущения G) ее функция Лагранжа будет иметь вид
'2 '2
7711Г i ГПлТ о
z ^L + |JLt/(||)
8.1.1. Введем в качестве новых координат радиус-вектор
центра инерции R и радиус-вектор первой материальной точки
относительно второй г:
52 ч. I. КЛАССИЧЕСКАЯ МЕХАНИКА'
Скорость центра инерции V = R и относительная скорости v*= r
будут выражаться через скорости V! и \.2 обеих частиц в точ-
точности теми же формулами. Разрешая эти сотношения относи-
относительно г, и г2, получим для обратного преобразования
Поэтому в новых переменных R и г функция Лагранжа ока-
окажется равной
где мы воспользовались полной массой A4) М = т\т\-тъ и
ввели приведенную массу
8.1.2. Итак, в соответствии с A5.2) функция Лагранжа раз-
разбилась у нас в сумму
L = Ltr(R, R) + /-m(r, Г)
членов, описывающих трансляционное и внутреннее движения,
причем каждый из членов зависит лишь от «своих» координат
и скоростей, т. е. переменные, относящиеся к каждому виду дви-
движения, полностью разделились.
Трансляционное движение является свободным, полностью
задается формулой A6) из 6.1.3 и не представляет поэтому даль-
дальнейшего интереса, внутреннее же движение оказывается описы-
описываемым такой же функцией Лагранжа Цт как для движения
одной материальной точки с приведенной массой \i во внешнем
поле U(r).
8.1.3. Для импульсов каждой материальной точки в новых
переменных мы получим
р и p2 = m2R — цг = т2\ — р, (**)
если ввести относительный импульс
р = цГ = —г- = A (V, — V2) ,
дг
а для полного импульса —
Р = р, + р2 = MR + \ir — \ir = MV
— т. е., как и должно было быть в силу A5.1), в него вносит
вклад только трансляционное движение.
8. РАССЕЯНИЕ ЧАСТИЦ 5*
8.1.4. Несколько сложнее выкладка для момента:
М = тх [г, • г,] + т2 ['г • Ы =
2
= т, [R • R] + A [R • г] + (х [R • г] + ^ _^ ^J [г • г] +
то есть
М = [R • МЩ + [г • (xr] = [R ¦ Р] + [г • р]
в полном соответствии с A5.3).
8.2. ЗАМЕЧАНИЕ: Выше преобразование (*) трактовалось
как переход к новым (обобщенным) координатам. Однако срав-
сравнение выведенных формул с полученными в § 6 показывает, что
то же преобразование можно трактовать как преобразование
Галилея, переводящее произвольную первоначальную систему
отсчета в систему центра инерции — тогда первый член R в пра-
правых частях обеих формул (*) будет осуществляющим преобра-
преобразование сдвигом, а вторые члены — радиус-векторами ri0 и г2о.
в системе ЦИ первой и второй частиц соответственно. Радиус-
вектор центра инерции в системе центра инерции Ro = —-JiL-1.——^-
till 1 Wl%
по определению равен нулю, и поэтому для определения конфи-
конфигурации частиц в системе ЦИ достаточно разности их радиус-
векторов г10 — Г2О = Г[ — г2 = г, т. е. относительной координаты
г. Аналогично формулы (**) можно понимать как преобразова-
преобразование импульсов каждой частицы к той же системе — вторые чле-
члены в правых частях этих равенств, р и —р, суть импульсы р|о,
и р20 первой и второй частицы в системе ЦИ; они равны по вели-
величине и противоположны по направлению. |
8.3. Проведенное разделение трансляционных и внутренних
переменных в задаче двух тел позволяет вместе с законами
сохранения получить ряд важных результатов, не зависящих
от конкретного вида потенциальной энергии взаимодействия
U(г), в задаче о рассеянии или столкновении частиц.
Под этими словами имеется в виду следующая специальная
постановка задачи в проблеме двух тел. Будем считать, что в
проблеме двух тел начальные условия ставятся в далеком прош-
прошлом, в момент времени ?_->— оо, и что в это время составляю-
составляющие систему частицы находятся сколь угодно далеко друг от
друга. Тогда согласно условию асимптотической аддитивности
каждая из них является свободной и движется с постоянным
импульсом pi и, соответственно, р2, т. ,е. равномерно и прямоли-
прямолинейно. Именно эти равномерные и прямолинейные движения.
54 ч. I. КЛАССИЧЕСКАЯ МЕХАНИКА
каждой из частиц задаются в качестве начальных условий;
иными словами в качестве начального условия задается асимп-
асимптотическое поведение радиус-векторов обеих частиц.
Далее, с течением времени, частицы могут сблизиться, так
что взаимодействие U(r) окажется уже существенным и движе-
движение станет и криволинейным, и неравномерным. Детали этого
движения не будут нас интересовать, мы зададимся только во-
вопросом: что произойдет при t = t+-*- +00, когда частицы снова
разлетятся далеко друг от друга и опять будут двигаться рав-
равномерно и прямолинейно с посто-
постоянными импульсами р, и р? *).
Иными словами, задача о рассе-
рассеянии состоит в том, что считается
заданной асимптотика движения
при t-*¦—с» и ищется асимпто-
тг<Ргтика движения при t-*--\-oo.
Описанная задача о рассеянии
занимает центральное место во
всей физике атомных или ядер-
ядерных явлений и в физике элемен-
рассеяние частиц тарных частиц. Причина этого
состоит в том, что мы не слу-
случайно сосредотачиваем свой интерес на асимптотиках, оставляя
без внимания детали движения во время сближения частиц —
когда мы имеем дело с частицами атомных или еще меньших
размеров, то имеющиеся у нас экспериментальные средства
просто недостаточны, чтобы проследить за этими деталями. По-
этому практически все грандиозные успехи, которые нам уда-
удалось достичь в XX веке в понимании микромира, основаны на
изучении процессов упругого или неупругого рассеяния, захвата
или распада.
8.3.1. При рассмотрении задачи о рассеянии приходится вс.е
время пользоваться двумя системами отсчета: одной, в которой
задаются начальные асимптотические значения рь р2 и ищутся
конечные асимптотические значения р, и р'2> и другой — системой
ЦИ, в которой удобнее вести теоретическое рассмотрение. Пре-
••) Такой процесс называют упругим рассеянием частиц. Может, конечно,
случиться, что в результате взаимодействия частицы образуют столь тесную
систему, что уже не разойдутся иа большие расстояния ни при каких време-
временах— тогда мы будем говорить о процессе захвата частиц. Может быть и
так, что в процессе рассеяния частицы изменят свою природу — например,
изменится внутренняя энергия тех материальных тел, которые входят в наше
рассмотрение в виде ндеализироваиной модели точечных частиц — тогда го-
говорят об неупругом рассеянии. Строго говоря, однако, процессы захвата нлн
неупругого рассеяния — пока ие сделано более детальных допущений об нх
механизме — находятся за пределами возможностей настоящего механиче-
механического рассмотрения.
8. РАССЕЯНИЕ ЧАСТИЦ
Б5
образование импульсов от системы ЦИ к произвольной системе
описывалось (ср. замечание 8.2) формулами (*) из 8.1.3
Pi ~~м~
где мы не поставили штрихов, считая что все величины относятся
к асимптотике до рассеяния.
После рассеяния полный импульс Р должен остаться тем же
по закону сохранения импульса, что же касается импульса р
относительного движения, то — поскольку в силу отсутствия
взаимодействия на асимптотике внутренняя энергия ?*„ сво-
сводится к одной кинетической энергии Tin, которая в силу сохра-
сохранения энергии должна быть одной и той же до и после рассея-
рассеяния,— должен сохраняться его квадрат
ИЛИ р = р = A | V| — V2 |.
Итак, импульс относительного движения при рассеянии
только поворачивается:
р' = п-р, п2=1.
Поэтому те же самые формулы (*) дадут нам для асимпто-
асимптотических величин после рассеяния
I »»1 г» I т\ I I \ I I I
Pi = -гг- Н ¦+• П • О = —гт- (р[ "Г" Pv ~Г П(Х | Vi — V2 I,
B5)
Итак, одни лишь законы сохранения позволяют выразить
асимптотические импульсы обеих частиц после рассеяния через
асимптотические величины до рассея- ^_
ния и один единичный вектор л, т. е. р
через два угла. Описываемые форму-
формулами B5) соотношения становятся
очень наглядными, если изобразить их
на графике.
8.3.1.1. Выберем ось абсцисс парал-
параллельно вектору Р и отложим (равные
в сумме ему) векторы -?*- Р и —- Р
так, чтобы первый из них кончался, а
второй начинался в начале координат.
Проведем далее вокруг начала коорди-
координат окружность радиуса р. Тогда эта окружность будет геометри-
геометрическим местом концов всех возможных векторов пр, начинающих-
начинающихся в начале координат. (На самом деле следовало бы, конечно,
S6 ч. I. КЛАССИЧЕСКАЯ МЕХАНИКА
устроить трехмерный «чертеж», в котором роль окружности иг-
играла бы соответствующая сфера; однако соотношения B5) сим-
симметричны относительно вращений вокруг Р, и мы реально изо-
изображаем сечение трехмерного чертежа проходящей через Р
плоскостью). Как легко видеть, определяемые B5) импульсы
частиц после рассеяния будут изображаться векторами, идущими
(для первой частицы) от начала ^~ Р к концу пр и (для второй
частицы) от конца пр к концу -^~ Р. Если двигать теперь конец
вектора пр по всей окружности (на самом деле — по всей по-
поверхности сферы), то мы нолучим все возможные пары значений
импульсов частиц после рассеяния.
Практически особенно важен тот случай, когда одна из ча-
частиц— скажем, вторая — до рассеяния покоилась:
"Именно этот случай отвечает большинству опытов, реально ста-
ставящихся в лабораториях, когда искусственно ускоренным ча-
частицам дают рассеяться на неподвижной «мишени»*). Поэтому
ту систему отсчета, в которой рг = 0, называют обычно лабора-
лабораторной системой.
8.3.1.1.1. В лабораторной системе
ИГ Р = ~м (р' + р2» = ИГ Р'= -ИГ v'= ~м~(v' ~ v*) = Р.
т. е. конец вектора -—¦ Р попадает на нашем графике на окруж-
окружность. Что же касается положения начала вектора 4т-Р, то
юно зависит от соотношения масс частиц -^-. Если т,\ < щ, то
начало вектора -п- Р лежит внутри окружности, если пг{ > щ,
то.вне ее.
/ 8.3.2. Определим углы рассеяния частиц. Углом- рассеяния
X в системе ТДИ называется угол между направлениями относи-
л
тельного импульса до и после рассеяния, угол р'р, т. е. один из
*) Опыты, в которых разгоняются обе сталкивающиеся частицы — опыты
со встречными пучками — начинают ставиться только в самые последние годы.
Причина этого лежит в том, что реально достижимые плотности частиц в
искусственно ускоряемых пучках несравненно меньше «естественных» плотно-
плотностей в материальных телах. Поэтому вероятности того, что две частицы из
разных пучков пролетят настолько близко друг к другу, что испытают за-
заметное отклонение, оказываются очень малыми.
8. РАССЕЯНИЕ ЧАСТИЦ
ЪТ
углов, определяющих положение единичного вектора п. Углом
рассеяния ¦&! первой частицы в лабораторной системе назы-
называется угол между направлениями ее импульса в этой системе
А
до и после рассеяния, т. е. угол pfpt. Наконец в лабораторной
системе можно ввести угол рассеяния второй частицы Ф2 как
угол между векторами р[ и р'2.
Для интерпретации результатов опытов по рассеянию при-
приходится выражать одни углы рассеяния через другие; поэтому
выведем соответствующие формулы, несмотря на их громозд-
громоздкость.
8.3.2.2. Связь угла дг с углом х устанавливается просто. Из
наших графиков видно, что треугольник, образуемый векторами
р, р' и рг, всегда равнобедренный, поэтому
^2 = iLiJL- B6.2)
Угол х рассеяния в ЦИ-системе может меняться от 0 (отсутст-
(отсутствие рассеяния) до я (рассеяние назад). Из B6.2) видно, что при
этом угол ®2 рассеяния второй частицы в Л-системе меняется
от -j до нуля.
8.3.2.1. Сложнее обстоит дело с уголом $i рассеяния первой
частицы. Из наших графиков видно, что случай mx < m2 и
гп\ > т2 ведут здесь к существенно разным картинам.
8.3.2.1.1. В первом случае Ot равняется нулю для х = 0, мо-
монотонно растет по мере роста х — будучи, однако, все время
меньше %— вплоть до значения ¦&[ — я, которое достигается для
X = п. При этом отличие угла ¦&{ от угла х тем меньше, чем
/Ml
/Ml
меньше отношение —, и при
от.
О угол Ф, ->/.
8.3.2.1.2. Совершенно по-иному обстоит дело для т\ > т2.
Угол ¦&! для малых % также начинает расти вместе с %, однако-
58 ч. I. КЛАССИЧЕСКАЯ МЕХАНИКА
этот рост продолжается лишь до того значения х. Для которого
вектор р[ касается окружности; при дальнейшем росте х угол
-&1 убывает и при х — я обращается в нуль. Таким образом при
Щ\ ~> пг2 зависимость х от ¦&[ дву-
двузначна. Кроме того, при рассея-
рассеянии более тяжелой частицы на
более легкой ее угол отклоне-
отклонения не может быть сколь угодно
велик; как видно из графика,
всегда fli < ftimax, где
8.3.2.1.3. Чтобы связать 0ч с углом х. опустим нз конца вектора р' пер-
перпендикуляр на вектор р: тогда образуется два прямоугольных треугольника,
из сопоставления которых видно, что
— p + pcosx
то есть
8.3.2.3. Что же до длин импульсов р, и р2 после рассеяния, то нз тех
же прямоугольных треугольников видим, что
г Sin Y ,
Pl^P-^ЖГ' ' = 1.2,
то есть, что
', 1 . Vт\ + ml + 2m{m2 cos х
2т{т2 cos /
Выражая еще все через импульс pi первой частицы до рассея-
рассеяния, получаем окончательно
2miт2cos 1 Г, 4ц . „ X
Р^Д/1 ~!TSin
Г, 4ц . „ X
^Д/1 ~!TSin 2
М pi V ill 2 ^' B6.3,4)
8.3.2.4. Формулы B6) существенно упрощаются в том спе-
специальном случае, когда массы обеих частиц равны, т{ = т2 —
9. ОДНОМЕРНОЕ ДВИЖЕНИЕ 69
= т, и, следовательно,
Тогда
¦ „А — sin X _ t- X
то есть
*i—f: ^2 = -f — f; jt?( = cosx-Pi; P2 = sinx-p,. B6a)
Заметим, что из этих формул видно, что pi-p2 = 0, т. е. в слу-
случае равных масс в Л-системе частицы всегда разлетаются после
рассеяния под прямым углом.
Итак, законы сохранения позволили нам выразить все асимп-
асимптотические величины после рассеяния через начальную асимпто-
асимптотику и единственный параметр — угол рассеяния % в ЦИ-систе-
ме. Найти этот угол можно, только реально решая соответствую-
соответствующую динамическую задачу.
9. Одномерное движение
9.1. Другим примером использования законов сохранения,
примером, в котором за этот счет удается вовсе обойти интегри-
интегрирование уравнений движения, может служить случай системы
с одной степенью свободы — случай одномерного движения во
внешнем поле, не зависящем от времени.
Функция Лагранжа для такой системы может (в рамках
допущения G)) иметь наиболее общую форму
причем, поскольку U не зависит от /, энергия
Е ——• * ~~l~ LJ (о) ~tf~ const
должна сохраняться. Разрешая это соотношение относительно <J,
мы приходим для определения зависимости q от времени к диф-
дифференциальному уравнению первого порядка
которое для любого U(q) интегрируется в квадратурах
ч. I. КЛАССИЧЕСКАЯ МЕХАНИКА
ЗАМЕЧАНИЕ. Попытка непосредственно проинтегрировать в
квадратурах уравнения движения смогла бы здесь привести к
успеху лишь при привлечении искусственных приемов, в дейст-
тельности эквивалентных использованию сохранения энергии. |
Если координата q — это декартова координата, скажем х,
материальной точки, которая может двигаться только вдоль по
прямой, то коэффициент a(q)= m, массе частицы, и закон дви-
движения принимает вид
B7.2)
-triE-U(x))
9.2. Единственный вопрос, который требует теперь еще до-
дополнительного исследования — это вопрос о выборе знаков кор-
корня и пределов интегрирования по х (или по q). Того ради заме-
заметим, что под корнем в B7) стоит фактически кинетическая энер-
энергия, которая существенно положительна. Таким образом движе-
движение возможно только для тех значений х, для которых
?/(*)<?.
(Как раз там, где интеграл B7) дает вещественное решение.)
Разумно проиллюстрировать это обстоятельство графически,
изобразив на одном и том же чертеже кривую потенциальной
точки остановки
энергии U(x) и «прямую» полной энергии Е, не зависящей от х.
Области, где — при выбранном значении полной энергии Е —
движение запрещено, отмечены на рисунке крестиками. Грани-
Границей допустимых и запрещенных для движения областей яв-
являются точки, в которых
они называются точками остановки или точками поворота.
В них кинетическая энергия — а, следовательно, и скорость —
обращаются в нуль.
9. ОДНОМЕРНОЕ ДВИЖЕНИЕ 61
Относительно скорости можно утверждать и больше: вообще
говоря в точке остановки скорость меняет знак. Действительно,
если в точке остановки производная —— Ф 0, то отлична от
О X
нуля и —-. Следовательно, значения х в моменты ? + Д.' и
1—-At, где t — момент остановки, будут разных знаков*), при-
причем обоим этим значениям скорости будут соответствовать ко-
координаты х, лежащие с одной стороны от точки остановки —
ведь с другой стороны движение невозможно. А интегралы B7)
как раз и дают нам для каждого значения координаты два воз-
возможных движения, отличающихся знаком скорости.
Таким образом пределами интегрирования в B7) служат
точки остановки, и при прохождении такой точки движение пе-
переходит с одной ветви корня на другую.
9.3. Наличие точек остановки может служить для классифи-
классификации движения в целом. Если допустимая область движения
ограничена точками остановки с обеих сторон (как для значе-
значения энергии, равного Еи между точками хх и х2 на рисунке), т. е.
движение может происходить только в конечной области прост-
пространства, то такое движение называют финитным. Если имеется
только одна точка остановки (как для движений справа от х$
при энергии Еи или справа от xi при энергии Е2 на рисунке), то
материальная точка может прийти из бесконечности, дойти до
точки остановки, переменить там знак скорости и снова уйти в
бесконечность. Если точек остановки нет вовсе (как при энергии
?3 на рисунке), то материальная точка проходит из одной бес-
бесконечности в другую, сохраняя знак скорости неизменным.
В обоих этих случаях движение называют инфинитным.
В случае финитного движения встает вопрос о его перио-
периоде— о промежутке времени, по истечении которого состояния
системы, т. е. значения х и х, повторяются. Поскольку движение
между ограничивающими финитное движение точками остановки
Xi и Х2 требует одинакового времени в прямом и обратном на-
направлении, то период будет равен удвоенному времени движения
от одной точки остановки до другой:
dx =. B7.3)
'_ , ' dU
) Оговорка «вообще говоря» относится как раз к случаю равенства —^—
в точке" остановки нулю. Тогда может оказаться — н наверняка окажется,
если U{x) аналитична в окрестности точки остановки, — что для достижения
точки остановки необходимо бесконечное время, поэтому вопрос о знаке ско-
скорости после достижения точки остановки теряет смысл.
62 ч. t. КЛАССИЧЕСКАЯ МЕХАНИКА
Период системы является функцией ее энергии; вид этой
функциональной зависимости определяется с помощью B7.3)
видом потенциальной энергии U(x). Может быть поставлена об-
обратная задача выяснения того, какая потенциальная энергия
приведет к заданной зависимости периода от энергии Е. Ответ
(который можно выразить в квадратурах) гласит, что предпи-
предписание функции Т(Е) однозначно определяет симметричную от-
относительно точки минимума часть функции U(x); антисиммет-
антисимметричная часть остается произвольной.
ПРАКТИЧЕСКОЕ ЗАМЕЧАНИЕ: При реальном вычислении периода но фор-
формуле B7.3) часто приходится делать запутанные замены переменных. При
этом нет нужды следить, как будут преобразовываться точки остановки —
онн всегда определяются обращением подкоренного выражения в нуль; по-
поэтому их проще находить из этого условия сразу в окончательных перемен-
переменных. 1
10. Движение в центральном поле
10.1. Вернемся теперь к задаче двух тел. В § 8 мы отделили
в ней движение центра инерции и установили некоторые асимп-
асимптотические соотношения. Теперь нам надлежит заняться остав-
оставшейся задачей об относительном движении. Она эквивалентна
задаче о движении одной частицы с приведенной массой ц в цент-
центрально-симметричном поле U(г), или, как кратко выражаются,
задаче о движении в центральном поле. Соответствующая функ-
функция Лагранжа имеет, согласно § 8, вид
Поскольку она не зависит явно от времени и обладает сфериче-
сферической симметрией, то должны сохраняться энергия
? =-!?- + {/(г) = const
и момент
М = [г • р] = coast.
Помножив последнее равенство скалярно на г, получим
Mr=[r-p]-r = (r-p-r) = O.
Но это (при постоянном М) есть уравнение плоскости, проходя-
проходящей через начало координат. Поэтому A-е следствие иэ сохра-
сохранения момента).
Движение в центральном поле происходит в одной пло-
плоскости.
Выберем эту плоскость за плоскость ху; тогда момент будет
направлен по оси г, т. е. будет
] М | = Af г = iW
10. ДВИЖЕНИЕ В ЦЕНТРАЛЬНОМ ПОЛЕ 63
мы будем в оставшейся части параграфа обозначать буквой
М без дополнительных значков не полную массу, которая нам
нигде не встречается, а численное (сохраняющееся) значение
момента. Для дальнейшего использования симметрии задачи
естественно ввести на плоскости движения полярные коорди-
координаты. В них
М — Mz = хру — урх = ц(ху — ух) = 11г2ф = const
или
а функция Лагранжа и энергия приобретают вид:
L = -%-(r2 + r2q>2)-U(r) B8.2)
Если выразить в последнем из этих равенств ф через сохра-
сохраняющийся момент с помощью B8.1), то мы получим для энергии
f ^. B8.3)
Таким образом B-е следствие из сохранения момента).
Задача о движении в центральном поле сводится к задаче
об одномерном движении с «эффективной» потенциальной энер-
энергией V(r):
V(r) = -^r + U(r)**). B8.4)
ЗАМЕЧАНИЕ 1: «Эффективной» функцией Лагранжа будет
~V(r).
Она отнюдь не получается подстановкой B8.1) в первоначальную функцию
Лагранжа B8.2). Причина этого состоит в том, что для функции Лагранжа
существенно ее выражение не только и не столько для реальных движений
q(t), сколько для виртуальных движений q(t)+6q(t), для которых B8.1) не
имеет места. I
ЗАМЕЧАНИЕ 2: «Эффективное одномерное» движение в цент-
центральном поле имеет одно отличие от одномерного движения,
*) Поскольку — r2d<p = -jr dt есть площадь, «заметаемая» радиус-век-
радиус-вектором за время dt, то закон сохранения B8.1) утверждает, что раднус-век-
тор описывает за равные времена равные площади. Поэтому его называют
интегралом площадей, или — по нменн первооткрывателя — вторым законом
Кеплера.
М2
*) Член -g—J- здесь называют центробежной энергией.
**\
64
ч. I. КЛАССИЧЕСКАЯ МЕХАНИКА
рассматривавшегося в предыдущем параграфе: по самому смы-
смыслу координаты г она меняется только в пределах 0 ^ г ^ оо,
а не от минус до плюс бесконечности. Это обстоятельство ведет
к принципиальным инновациям в классификации возможных
типов движения в целом*) (см. рисунок). Если потенциальная
энергия U (г) отрицательна, что соответствует силам притяже-
притяжения, и притом стремится к бесконечности при г->0 быстрее чем
—5" (или как -J-, но с коэффициентом, большим -д—), то
значение координаты г может дойти до нуля, происходит «паде-
«падение на центр». Такой тип движения называется лимитационным.
V,E\
0
V
\
\
л-1
fl
\
и-Ш
и-Л
типы движений в центральном поле
Эффективная потенциальная энергия / отвечает силам притяжения, растущим
быстрее центробежных, — и для положительных и для отрицательных энергий
возможны только лимитационные движения л-1.
Эффективная потенциальная энергия // описывает силы притяжения, расту-
растущие медленнее центробежных, — возможны финитные движения ф-II для
отрицательных и инфинитные и-П для положительных энергий.
Эффективная потенциальная энергия 111 относится к случаю сил отталки-
отталкивания — возможны только инфинитные движения и-Ш.
Принято, что потенциальная энергия U (г) стремится к нулю при г -> оо в со-
соответствии с C).
Если рассматриваемые нами материальные точки суть мо-
модели, приближенно описывающие частицы конечных размеров,
*) Переход от задачи на неограниченной прямой к задаче на полупрямой
приводит к принципиальным изменениям также и при рассмотрении,- анало-
аналогичных задач в квантовой механике, см. часть 3.
10. ДВИЖЕНИЕ В ЦЕНТРАЛЬНОМ ПОЛЕ 65
то возможность падения на центр означает физически, что части-
частицы могут прийти в соприкосновение. Тогда потенциальную энер-
энергию U(г), описывавшую взаимодействие несоприкасающихся ча-
частиц, надо будет заменить другим выражением, учитывающим, что
частицы пришли в непосредственный контакт. С точки зрения
механических модельных представлений о частицах как о «твер-
«твердых шариках» новая потенциальная энергия должна очень бы-
быстро расти для г, меньших суммы «радиусов» частиц; для «абсо-
«абсолютно твердых» шариков — просто обращаться при г, равном
сумме радиусов, в -j-oo. «Падение на центр» тем самым исклю-
исключается.
Мы уже упоминали, однако, что в современной теории эле-
элементарных частиц приходится считать эти частицы настоящими
материальными точками. В этом случае возникновение лимита-
ционной ситуации оказывается тяжелым ударом, указывающим
на физическую несостоятельность или неполноту используемой
теории. В третьей части курса мы увидим, что как раз возникно-
возникновение такого положения в задаче об атоме заставило нас отка-
отказаться от классической механики и перейти к квантовому описа-
описанию. 1
10.2. С учетом сделанных замечаний можно применить
развитую для одномерного движения технику и записать диф-
дифференциальное уравнение первого порядка:
dr
±^j-(E-V(r))
определяющее зависимость / от г.
Однако рассматриваемая теперь задача богаче одномерной —
кроме переменных г и t в ней участвует еще и угловая перемен-
переменная ф, связанная с ними дифференциальным уравнением B8.1).
Правая часть этого уравнения существенно положительна, т. е.
Ф монотонно возрастает с ростом времени. Это позволяет толко-
толковать ф как некоторое фиктивное «угловое время» и получить
с помощью B8.1) из предыдущего уравнения дифференциальное
уравнение (опять первого порядка)
dr
М г2
определяющее зависимость «углового времени» от г. Формаль-
Формально оно совершенно подобно первому дифференциальному урав-
уравнению, физически же является уравнением, определяющим тра-
траектории движения. (Заметим себе, что в силу отсутствия в
3 В. В, Медведев
66 ч. I. КЛАССИЧЕСКАЯ МЕХАНИКА
последнем уравнении обычного времени, траектории могут быть
найдены без отыскания закона движения.) Интегрирование
этих двух уравнений дает
dr
dr . _ =JMf г2
2 \i \ / 2
г))
B9)
10.3. Как и в одномерном случае, допустимая область движе-
движения— область интегрирования по г в B9)—находится из ус-
условия
знак равенства в котором определяет точки поворота г0. В соот-
соответствии с новой классификацией возможных типов движения
(см. рисунок в 10.1)
для лимитационного движения может быть только одна точка
поворота го = rmax или же их нет вовсе;
для инфинитного движения есть одна точка поворота r0 = rmin;
для финитного движения есть две точки поворота r0 = rmfn и
г0 = ''maxi И Гт1п ^ г ^г rmax-
Как и в одномерном случае, оба решения B9) переходят при
прохождении точки поворота с одной ветви корня на другую;
так как эти ветви отличаются только знаком, то время движения
между заданными г в обоих направлениях одинаково, а траекто-
траектории симметричны относительно точек поворота.
Остановимся подробнее на возможном виде траекторий.
В случае финитного движения rmln s^ r ^ rmax, поэтому траекто-
траектории могут размещаться только в соответствующем кольце.
И. ДВИЖЕНИЕ В КУЛОНОВОМ ПОЛЕ
«Период» по «угловому времени» ф очевидно равен
67
rmax dr
rmin
Вообще говоря, этот «угловой период» Ф не будет рациональ-
рациональным кратным 2л,
и траектория образует незамкнутую кривую, заполняющую все
кольцо между rmin и rmax- Важные исключения составляют U{r),
пропорциональные — и г2, когда угловой пе-
период оказывается кратным 2л, и траектории
образуют эллипсы.
Для инфинитного (нелимитационного) дви-
движения вместо углового периода естественно
ввести полный угол отклонения
м
dr
C0)
rmin
испытываемого частицей за все движение, на- полный угол
чинающееся при бесконечном г и заканчиваю- отклонения
щееся уходом частицы на бесконечность. Этот
угол равен углу между асимптотами, проведенными из притяги-
притягивающего центра к траектории частицы.
11. Движение в кулоновом поле
11.1. Наибольший интерес, представляет движение в цент-
центральном поле сил, убывающих обратно пропорционально квад-
квадрату расстояния, — именно так ведут себя силы ньютонова за-
закона всемирного тяготения или силы между двумя электрически
заряженными частицами, взаимодействующими по закону Ку-
Кулона.
Потенциальная энергия в этом случае имеет вид
причем а >> 0 соответствует силам притяжения, а а < 0 — от-
отталкивания.
68
ч. I. КЛАССИЧЕСКАЯ МЕХАНИКА
Из общей формулы B9.2) (в ней удобно сделать подстановку — = и J
получаем тогда для траекторий:
и dr
и
f M~ f
<Р — фо = \ — = — \
J л ЛцЕ + iEL _ if. J
Mdu
— d Гми —
V
4т
М
где
Таким образом,
М
то есть
ф
\ — dy
= \ —, - = arccos у,
м
г; у = cos (ф — фо).
2EM2
М2
ца
^ 1+есоз(ф-ф0)
. C1.1)
Здесь решение нарочно сформулировано таким образом, что
оно оказалось совпадающим с известным из аналитической гео-
геометрии уравнением для конических сечений в полярных коорди-
координатах с началом координат в фокусе. Напомним, что длина р
называется параметром кривой, а безразмерное число е — ее
эксцентриситетом (точнее — численным эксцентриситетом).
Итак, траектория движения в центральном поле есть плоская
кривая второго порядка, один из фокусов которой совпадает с
силовым центром, а параметр и эксцентриситет равны, соответ-
соответственно,
11.2. Рассмотрим теперь подробнее возникающие здесь от-
отдельные частные случаи. Начнем со случая сил притяжения и
•финитного движения:
<1) а>0; ?<0, точнее: -|^-
11. ДВИЖЕНИЕ В КУЛОНОВОМ ПОЛЕ 69
В этом случае подкоренное выражение в C1.3) меньше 1,
т. е.
р>0; 0<е<1,
« C1.1) описывает эллипс, большая и малая полуоси которого
суть, соответственно,
и Ь = —====¦.
1-е2
В случае минимально возможной при данном моменте энергии
эксцентриситет обращается в нуль, и эллипс вырождается в ок-
окружность.
Подставляя значения параметра и эксцентриситета, получаем
для большой полуоси
д
а~ ца (. 2ЕМ2\ ~ 2Е ~ 2\Е\ ^л>
V ца2 /
— т. е. большая полуось зависит только от энергии, но не от
момента, и обратно — энергия эллиптического движения в задан-
заданном кулоновом поле зависит только от большой полуоси. По-
Поэтому большая полуось равна радиусу той окружности, в кото-
которую вырождается траектория при максимально возможном для
заданном энергии моменте.
Мы никак не аргументировали выбор положительного знака
перед корнем в C1.1). Легко видеть, однако, что перемена этого
знака эквивалентна добавлению я к постоянной интегрирования
<р. Сделанный выбор соответствует тому, что при ф — ф0 = О
— принимает максимальное, следовательно, г — минимальное
значение. Максимальное значение г получается при ф — ф0 = я.
Зти значения
rmin = -f^7 = a(l — е) и rmaIE==yzre-==a(l +e)
называют часто, следуя астрономической традиции, перигелием
и афелием.
Найдем период рассматриваемого финитного движения.
Согласно второму закону Кеплера B8.1)
2ц
и, следовательно, период равен
2Л
т
J 2 '
о
70 ч. I. КЛАССИЧЕСКАЯ МЕХАНИКА
Но в силу сноски к B8.1) стоящий здесь интеграл — это не что иное как
площадь эллипса
Поэтом-у
M A — е2)/2 Урца A — е2)% V a V. 1 — е2
то есть
T = 2ny\J^ ct1*. C2.2)
Если, наконец, рассматриваемое кулоново поле создано гра-
гравитационными силами, то постоянная а сама пропорциональна
массе обращающейся частицы (если она много меньше массы
тела, создающего поле), зависимость от массы в C2.2) пропа-
пропадает, и мы приходим к утверждению третьего закона Кеплера
Т2~а\
11.3. Перейдем теперь к инфинитному движению под дейст-
действием сил притяжения, т. е. к случаю
B) а>0; ?>0.
Тогда подкоренное выражение в C1.3) больше 1, и
р > 0; е> 1
— уравнение C1.1) описывает (ближнюю к фокусу) ветвь
гиперболы с полуосями
и о = -
е2 - 1 Уе2 - 1
(Граничный случай е = 1 соответствует движению по параболе.
Физически он отвечает тому, что скорость частицы на бесконеч-
бесконечности равна нулю.) Для большой полуоси получим теперь
е2 — 1 2Е '
т. е. она опять зависит лишь от энергии. Расстояние перигелия
получается из C1.1) при положении ф — фо = 0:
Новое, сравнительно с эллиптическим случаем, обстоятель-
обстоятельство состоит в том, что теперь надо специально позабо-
позаботиться чтобы правая часть C1.1) не оказалась бы отрицатель-
11. ДВИЖЕНИЕ В КУЛОНОВОМ ПОЛЕ
71
ной, — ведь левая есть существенно положительная величина.
Это приводит к условию
1+ecosqiI^O, т. е. cosq)I> ,
или
— arccos ( ) ^m ^arccos ( )
(мы положили фо = 0, т. е. отсчитываем угол ф от направления
на перигелий). При граничных значениях ф = ± arccos Г J
траектория уходит на бесконечность в соответствии с инфинит-
ностью движения — движение происходит по незамкнутой траек-
траектории, по которой частица сперва приближается из бесконечно-
бесконечности к притягивающему центру вплоть до расстояния rmln, а затем
снова уходит на бесконечность. «Полный угол отклонения» Ф
составит очевидно
Ф = 2 arccos Г J = 2 arccos f ~
то
в соответствии с на-
наПоскольку в рассматриваемом случае —
у ^ arccos (—-)^я, т. е.
глядным впечатлением от рисунка
Если записать аргумент арккосинуса в виде
Ф = 2 arccos |
то есть
,Ф,_ -I . *_« /и
в—^ ; ?= Л/- .
М V 2Е
COS-
•; 1 =
и положить — = -5- + Р, то будет
Zt ?i
sinP = -7==; с
72 ч. I. КЛАССИЧЕСКАЯ МЕХАНИКА
то есть
Поэтому получаем удобное выражение для полного угла откло-
отклонения
J/-. C2.3>
где для арктангенса берется главная ветвь.
11.4. Последний случай, который следует рассмотреть, — это
случай сил отталкивания, когда возможны только инфинитные
движения с положительной энергией:
C) а < 0; Е > 0.
Подкоренное выражение в C1.3) опять будет больше 1, а пара-
параметр, получаемый при формальном использовании C1.2), оказы-
оказывается отрицательным
р<0, е>1.
В этом случае удобно выбрать
перед корнем C1.3) знак минус.
Тогда уравнение траектории C1.1)
примет форму
J 1 — е cos (ф — ф0)
г ~ ~\Р\
совпадающую с уравнением дальней от фокуса ветви гиперболы,
а точка перигелия будет обладать координатами ср — <р0 = (>
(в дальнейшем опять положим ф0 = 0, т. е. будем отсчитывать
угловую координату от направления на перигелий) и
Как и в случае сил притяжения, здесь возникнет условие
положительности правой части C1.1), условие того, «чтобы г
оставалось бы ближе бесконечности». Оно будет теперь требо-
требовать
1— ecosqp^O, т. е. coscp:>—,
или
— arccos^t— sCqp^arccos^-.
Поэтому «полный угол отклонения» составит
Ф = 2 arccos
12. ЭФФЕКТИВНОЕ СЕЧЕНИЕ
73
Совершенно аналогичными предыдущему случаю тригономет-
тригонометрическими преобразованиями это выражение приводится к
форме
М/^^д/^, C2.4)
отличающейся от C2.3) лишь знаком а.
Заметим, наконец, что физически безразлично, отсчитываем
ли мы полный угол отклонения по или против часовой стрелки.
Это значит, что углы отклонения Ф и 2я —Ф физически эквива-
эквивалентны.
С учетом этого замечания C2.4) дает тот же угол отклоне-
отклонения, что и C2.3). Значит, угол отклонения в кулоновом поле не
зависит от знака потенциала, от того, имеет ли место притяже-
притяжение или отталкивание.
12. Эффективное сечение
12.1. Когда мы говорили в § 8 о соотношениях, возникающих
в задаче о рассеянии частиц, то подчеркивали, что речь в ней
идет об асимптотических величинах, поскольку лишь такие под-
поддаются непосредственному наблюдению на опыте. В применении
к величинам, характери-
характеризующим частицы, совер-
совершающие инфинитное дви-
движение, ясно, что асимпто-
асимптотические характеристики
могут включать лишь ско-
скорости и направления, но
не сами координаты, стре-
стремящиеся к бесконечным
пределам. Однако по от-
ношению к этому утверж-
дению надо сделать одну
весьма существенную ого-
оговорку— могут существовать такие комбинации динамических
переменных, включающие координаты, которые — если можно
так выразиться — «выносятся на асимптотику» законами сохра-
сохранения.
В самом деле, рассмотрим частицу, двигавшуюся на беско-
бесконечности равномерно и прямолинейно с импульсом р, так что
-если бы она не испытывала сил со стороны рассеивающего цен-
центра О, то пролетела бы мимо него по штрихованной прямой
(см. рисунок) на минимальном расстоянии р. В действительно-
действительности из-за взаимодействия она двигается вблизи центра по неко-
некоторой кривой, изображенной на рисунке сплошной линией. Чему
прицельное расстояние
74
Ч. Т. КЛАССИЧЕСКАЯ МЕХАНИКА
будет равен момент этой частицы? В центральном поле он сохра-
сохраняется, поэтому его можно вычислять на еще не возмущенной
асимптотической части траектории как произведение [г-р]^. Из
рисунка видно, что это произведение даст нам:
C3)
Итак, в явно асимптотическую величину М входит некоторое
конечное расстояние р, которое называется прицельным расстоя-
расстоянием. Как же избавиться от прицельного расстояния — ведь
измерить его в опытах с микрочастицами невозможно?
12.2. Физики прибегают для этого к чрезвычайно остроумно-
остроумному приему, состоящему в том, что переходят от (не поддаю-
поддающихся измерению) характеристик одного индивидуального акта
рассеяния к статистическим характеристикам, описывающим ве-
вероятностные свойства целого класса таких индивидуальных
процессов. Именно, от рассмотрения
задачи с точно заданным прицельным
расстоянием переходят к рассмотре-
рассмотрению совокупности задач, в которых
прицельные расстояния распределены
по некоторому заданному закону. Вы-
Выгода состоит в том, что один такой за-
закон может быть очень легко осущест-
осуществлен экспериментально, в каком-то
смысле даже осуществляется на опыте
сам собой. Дело в том, что с точки зрения экспериментальных
возможностей было бы весьма затруднительно направить на рас-
рассеивающий центр одну единственную частицу; реально всегда
имеют дело с пучком частиц, который за счет соответствующих
экспериментальных предосторожностей можно сделать в жела-
желательной степени монохроматическим и однородным — т. е. до-
добиться, чтобы все частицы имели — с некоторой степенью точно-
точности— скорости, одинаковые как по величине, так и по направле-
направлению, и чтобы через любую площадку, поставленную поперек
пучка, проходило по одинаковому числу частиц в единицу вре-
времени через единицу площади, скажем
п
частиц
см2•сек
Тогда можно утверждать, что среднее в единицу времени
число частиц, испытывающих на силовом центре рассеяние с
прицельным расстоянием, лежащим в интервале (р, p-j-dp),
будет равно среднему числу частиц, которые при отсутствии
взаимодействия с центром пролетели бы в единицу времени
через построенное в проходящей через центр перпендикулярной
пучку плоскости S кольцо, ограниченное окружностями радиуса
12. ЭФФЕКТИВНОЕ СЕЧЕНИЕ 75
р и р -j- dp, т. е. составит
2лр dp • п.
Все эти частицы обладают, в силу монохроматичности пучка,
одинаковой скоростью v^ и одинаковым (с точностью до dp)
прицельным расстоянием р. Следовательно, все они будут обла-
обладать одинаковой энергией и, согласно C3), одинаковым момен-
моментом — поэтому, в силу результатов § 10, все они отклонятся
на одинаковый угол %.
12.3.1. Величина, которую будет тогда рационально опреде-
определять на опыте, есть отношение числа частиц, рассеянных в
определенном направлении, к плотно- счетчик^
сти потока падающих частиц. Первое
из этих чисел измеряют с помощью
счетчика, обладающего некоторой пло- АоЪльшоеЯ
щадью dS и расположенного на (боль-
(большом) расстоянии R от рассеивающего
центра. (Расстояние R должно быть
велико по сравнению с радиусом дей-
ствия сил — это всегда так для любого
макроскопического Я-но кроме того, оШТ по Рассе™»ю
R должно быть еще достаточно велико,
чтобы в счетчик не попадали частицы прямого пучка — это тре-
требует определенных предосторожностей.)
Ясно, что число частиц, рассеиваемых в площадь dS, будет
убывать как -^¦ поэтому разумно рассматривать отношение
к плотности потока падающих частиц числа частицы dN, рассеи-
рассеиваемых в единицу времени в элемент телесного угла dO.
Эффективным сечением (дифференциальным) называется
отношение
da= —. C4.1)
Оно имеет размерность площади.
12.3.2. Как мы только что напоминали, при движении в цент-
центральном поле угол рассеяния х зависит только от энергии и мо-
момента. Энергия всех частиц фиксирована заданием асимп-
асимптотической скорости vx, момент же при этом будет зависеть еще
от прицельного расстояния р. Таким образом, при фиксированной
v<x угол рассеяния х будет функцией только от р или, что то же
самое, прицельное расстояние р будет функцией только угла %.
Поэтому 2npdp-n частиц, нацеленных в кольцо (р, p + dp), от-
отклонятся на угол х и попадут в интервал углов (х, %-\-d%), где
dx^^f-dp, или dp^^fdt.
76
ч. I. КЛАССИЧЕСКАЯ МЕХАНИКА
Итак,
или
dN =
da = 2яр (х)
dX
d%-n,
dO,
C4.2>
поскольку dO — йф sin x ^X = 2л sin X ^X (ПРИ аксиальной сим-
симметрии). Знак модуля введен в C4.2) по той причине, что обыч-
обычно р падает с ростом х (рассеяние на большой угол требует
более тесного приближения частицы к рассеивающему центру).
Если р — неоднозначная функция х. то в формуле C4.2) надо-
сложить все ветви.
12.3.3. Вид зависимости р(х) прицельного расстояния от угла
рассеяния надо, конечно, извлекать из решения динамической
задачи о движении частицы в поле рас-
рассеивающего центра. Мы получили при
ее рассмотрении в § 10 формулу C0)
для «полного угла отклонения» ф.
При этом угол Ф определялся как
угол между асимптотами к траектории,,
понимаемыми как лучи, одинаково на-
направленные от центра. Угол же рас-
рассеяния % был определен нами в § 8 как
угол между асимптотами, понимаемыми в смысле лучей, направ-
направленных по скоростям. Поскольку при рассеянии скорость па
отношению к центру меняет знак (см. рисунок), то видно, что-
Х = я — Ф. C0а)
Формулы C4.2), C0а) и C0) решают задачу о нахождении
эффективного сечения по заданному закону зависимости потен-
потенциальной энергии от расстояния.
12.3.4. Перепишем формулу C0) еще раз, выражая энергик>
Ц.СГ
и момент через скорость и прицельное расстояние Е = —^- >
dr
rmin
VU2
dr
¦2ц?/
12. ЭФФЕКТИВНОЕ СЕЧЕНИЕ 77
Иными словами,
/ 1
'mln У г2 »vl
В этой форме наглядно видно, что все определяется двумя без-
безразмерными отношениями
г И Тх '
равно как и то обстоятельство, что для U = О угол Ф обра-
обращается в я, т. е. угол х— в нуль.
12.4. Полное сечение рассеяния а определяется как отно-
отношение числа частиц ./V, как бы то ни было рассеянных в единицу
времени, к плотности потока падающих частиц:
а = ^-. C5.1)
Очевидно, что
\\^d%, C5.2)
где интегрирование распространяется по всем возможным углам
рассеяния.
Но согласно C4.2)
где теперь интегрирование распространяется на все прицельные
расстояния, при которых происходит хоть какое-либо рассеяние.
Таким образом, если потенциальная энергия U(r) хотя и спа-
спадает с г сколь угодно быстро, но не обращается точно в нуль,
начиная с некоторого г0, то полное эффективное сечение в клас-
классической механике расходится.
ЗАМЕЧАНИЕ: Физически этот результат парадоксален: не-
невероятно, чтобы в науке, основанной на измерениях, сколь
угодно малая величина могла бы вести к результатам, принци-
принципиально отличным от получаемых для точного нуля. В поисках
выхода из этой трудности привлекалось то рассуждение, что для
достаточно быстро убывающих потенциалов большие прицель-
прицельные расстояния будут обуславливать рассеяние на столь малые
углы, что рассеянные частицы нельзя будет экспериментально
отличить от частиц падающего пучка, и поэтому измеренное на
опыте полное сечение окажется конечным. Однако то обстоя-
обстоятельство, что при этом значение физической величины должно
78
ч. I. КЛАССИЧЕСКАЯ МЕХАНИКА
было существенно зависеть от достигнутого прогресса в точности
эксперимента, выглядело в равной степени неудовлетворительно.
Лишь после создания квантовой механики выяснилось, что упо-
упомянутое ограничение на возможность различить рассеянные ча-
частицы от нерассеянных носит не приборный, а фундаментальный
характер — грубо говоря, достаточно мало отклоненные частицы
принципиально неотличимы от нерассеянных. Поэтому в кван-
квантовой механике мы увидим, что для U(r), не слишком медленно
убывающих с ростом г, вычисление полного сечения рассеяния
приводит к конечному результату. I
12.5. Аналогично сечению рассеяния можно ввести и эффек-
эффективные еечения каких-либо других процессов. При этом, если
процесс зависит от непрерывного параметра, то удобно вводить
дифференциальные сечения, если же нет — то только полные.
Например для потенциалов, допускающих лимитационные дви-
движения, бывает интересно ввести эффективное сечение падения
на центр (сечение захвата).
12.6. В качестве практически не требующего вычислений
ПРИМЕРА: найдем эффективное сечение для взаимного рассеяния частиц,
описываемых моделью непроницаемых абсолютно твердых шаров радиуса -^-,
в остальном не взаимодействующих друг с другом. Представление об непро-
непроницаемости означает, что частицы никоим образом нельзя сблизить больше
чем до поверхностного соприкосновения, т. е. нельзя сделать расстояние ме-
между их центрами меньшим а. С точки зрения потенциальной энергии это
означает, что для г < a U(r) должна обращаться в оо. Для г > а взаимо-
взаимодействия нет, и U(г) должна равняться нулю (см. рисунок). Относительные
О
г
траектории частиц для прицельных расстояний р <; а имеют (см. рисунок)
вид двух лучей с угловой точкой, лежащей на окружности радиуса а. Прн
этом в силу симметрии траекторий относительно точки поворота оба луча
расположены симметрично относительно нормали к этой окружности. По-
Поэтому (для р sZ а)
Ф . п — %
р = a sin — = a sin —г—— = a cos %,
.для больших же а прицельных расстояний траектории суть прямые и угоя
рассеяния х = 0.
12. ЭФФЕКТИВНОЕ СЕЧЕНИЕ
79
Итак,
da = 2л
dp_
d% = 2яа2 —cos-|- sin-? d% = -— sin % d%,
то есть
— рассеяние изотропно,
не зависит от углов.
В рассматриваемой модели потенциальная энергия U(r) локализована
в ограниченной области; поэтому должно существовать полное сечение. Дей-
Действительно, интегрируя по углам, получаем
сг = & da = & -j- dO
12.7. Эффективное сечение непосредственно связано с дина-
динамикой в системе ЦИ, наблюдения же обычно проводятся в ла-
лабораторной системе. Поэтому надо вывести формулы для пере-
пересчета сечений из одной системы в другую.
12.7.1. Будем исходить из формулы B6.1) § 8:
sin0,_ misinx B6I)
Для пересчета из системы ЦИ в Л-снстему надо разрешить это соотношение
относительно %. Имеем последовательно
т2 sin х cos fr[ ~ mi cos % sin d[ = m.\ sin ftu
то есть
-di) = — sin *i = sin I];,
v = ft, + ф = ft, + arcsin f-^i-
V т.ч.
- arcsm
C6.1)
C6.1a)
если мы не позабудем о многозначности арксинуса и выпишем также и вто-
вторую существенную ветвь, считая что знак
arcsin обозначает все время главную ветвь.
12.7.2. Чтобы разобраться в нужных нам
ветвях, проще всего вернуться к геометриче-
геометрическим соображениям раздела 8.3.2.1.3. Если
mi < т2, то связь между % и fti однозначна;
следует пользоваться только главной ветвью
арксинуса C6.1) (области значений главной и ¦
второй B6.1а) ветвей арксинуса в этом случае
не пересекаются). Если же mi > m% то зави-
зависимость % от 01 двузначна; оиа выражается
1
п
обеими ветвями арксинуса, приЪ\ = arcsin
главная ветвь C6.1) переходит во вторую
ветвь C6.1а); большие <h физически невозможны. В граничном случае
пц = tf*2 мы также находимся все время на главной ветви; зависимость % ог
¦©1 линейна.
80
ч. I. КЛАССИЧЕСКАЯ МЕХАНИКА
Поэтому в выражении для косинуса %
cos х = cos ft, cos ф — sin ft, sin ф =
= --^±-sin2 ft,
«2
-C-^LVsin»», -cosft, C6.2)
надлежит брать перед корнем знак + для главной ветвн и знак — для
ветви C6.1а).
12.7.3. Формулы C6.1, 1а, 2) объясняют, как пересчитывать -тту- Пере-
Пересчет элемента телесного угла
dCx = 2я sin х dx = ~ 2nd (cos x)
можно выполнить въявь. Дифференцируя C6.2), получаем
— d (cos x) = 2 ¦— sin ft, cos fri dft, ±
-2
1 \ sin2 d, I sin ft, + I -± I sin A, cos ft, • cos *,
«2 / V m2 I
sfnJ
то есть
--isin2*,
t}%2
В соответствии со сказанным о выборе ветвей, для mi < тг здесь сле-
следует выбирать знак +:
l + —l cos:
/Иг
Vm2
sin2 ft,
dObc C6.3.1)
Для пц > ni2, когда дают вклад обе ветви, мы наблюдаем в Л-системе под
некоторым углом ft, < arcsin—- частицы, рассеянные в ЦИ-системе как под
углом C6.1), так и под углом C6.1а); поэтому для получения сечения в Л-си-
Л-системе надо сложить оба ЦИ-сечения
da
do
C6.1)
do*.
da\
IC6.U)
13. ФОРМУЛА РЕЗЕРФОРЛА
При этом (ср. рисунок) для основной ветви
dOn
т
= 2—-cosO, +
т,
а для ветви C6.1а)
dO»
m;
1 4 ~ cos 2ft,
1 i- sin2 ft,
Щ
m:
1 4 5-cos 20,
2
V1-
sin2 ft.
81
•; tnt> m2, C6.3.2)
m2, C6.3.3)
поскольку для нее производная . * отрицательна. Наконец, в случае равных
масс преобразование телесного угла речко упрощается
C6.3.4)
т. =
dO% = 4 cos Ьх
13. Формула Резерфорда
13.1. Важнейшим случаем вычисления эффективного сечения
в классической механике является тот, когда взаимодействие
частиц происходит по закону Кулона. Особое внимание к этому
случаю определяется совмещением трех обстоятельств. Во-пер-
Во-первых, само кулоново взаимодействие занимает среди взаимодей-
взаимодействий микрочастиц очень видное место. Во-вторых, это один из
немногих случаев, когда потребные для получения эффективного
сечения квадратуры вычисляются в элементарных функциях.
В-третьих, случай кулонова взаимодействия преподносит нам
очень приятный сюрприз — оказывается, что в этом случае вы-
вычисленные в классической механике сечения сохраняют свой вид
и при переходе к квантовомеханическому описанию (если толь-
только рассеиваемая и рассеивающая частицы не тождественны).
Наконец будет вполне уместным упомянуть, что именно в этой
задаче, в работе Резерфорда 1911 года, возник тот подход к
проблеме рассеяния, который излагался в предыдущем разделе.
13.2. Все нужные для получения эффективного сечения в ку-
лоновом поле вычисления у нас фактически уже проведены.
Подставляя в формулу C0а) для угла рассеяния вычисленные
нами в параграфе 11 выражения C2.3,4) для полного угла от-
отклонения, видим, что
82 ч. I. КЛАССИЧЕСКАЯ МЕХАНИКА
то есть
а
~М
Переходя здесь от энергии и момента к асимптотической скоро-
скорости и прицельному расстоянию, получаем отсюда
, 1
В2"'
или — прямо в удобном для вычисления эффективного сечения
виде —
Остается только выполнить дифференцирование по %
da = — л—*— =л|—я- 1 2
sinf sin^f 2
и мы приходим к формуле Резерфорда:
а V
полученной им в уже упоминавшейся работе 1911 года.
13.3. Формула C7) дает нам эффективное сечение рассея-
рассеяния на кулоновом потенциале в системе центра инерции, или, что
то же самое, сечение рассеяния частицы на неподвижном рас-
рассеивающем центре. Последний случай осуществляется физиче-
физически, если масса рассеивающего центра много больше массы рас-
рассеивающейся частицы — например, для рассеяния электронов
на атомных ядрах.
Если массы рассеиваемой и рассеивающей частиц соизмери-
соизмеримы, то для сравнения с опытом надо еще пересчитывать фор-
формулу Резерфорда в Л-систему. Чтобы избежать громоздких вы-
выкладок, посмотрим, как производится этот пересчет в простом—-
но самом по себе важном — случае одинаковых масс
Ш] = m<i = Ш.
Тогда [х = -?- и, согласно B6а), углы рассеяния первой и вто-
второй частиц ¦&1 = -|-, ®2 = Y~~ \~ Т ~~ *1- ПоэтомУ
= 2я sin % d% = 2я • 4 sin fy cos ft, dbx =
= 4 cos #i dOo = 4 cos O2! dO», |.
14. МАЛЫЕ КОЛЕБАНИЯ . 83
Таким образом мы получаем для сечения рассеяния падающих
частиц в Л-системе
а для сечения рассеяния первоначально покоившихся частиц
м'* C7л-2)
Если, наконец, падающие и первоначально покоившиеся ча-
частицы не только обладают одинаковой массой, но и тождествен-
тождественны по всем своим свойствам, то на опыте невозможно отличить,
какую из частиц мы наблюдаем. Тогда имеет смысл лишь
эффективное сечение рассеяния какой-либо частицы под некото-
некоторым направлением, выражение для которого получится сложе-
сложением обеих формул C7Л):
Тождественные частицы: da = ( -^-) ( . ... -\ rs- j
V ?лаб / V sin4 V ' cos1 Ь )
C7Л.З)
Именно эта формула не сохраняется в неизменном виде при пе-
переходе к квантовой механике, в ней появляется дополнительный
член, связанный с принципиальными отличиями статистики со-
совокупностей одинаковых квантовых объектов от статистики
классических совокупностей.
14. Малые колебания
Вернемся к рассмотрению системы с одной степенью сво-
свободы. В § 9 мы установили, что для финитного движения
такая система совершает колебания
между двумя точками поворота.
Особенно простым оказывается изу-
изучение такого движения в случае,
когда амплитуда колебаний очень
(в пределе — бесконечно) мала.
Остановимся на нем несколько под-
подробнее.
14.1. Колебания с малой амплитудой могут происходить
вблизи минимума потенциальной энергии U(q), пусть этот ми-
минимум имеет место в точке q = q0. Тогда
dU ,-. d2U . ,-.
= <?0: -d7 = 0 и Ж>0
84 ч. I. КЛАССИЧЕСКАЯ МЕХАНИКА
— второе условие есть условие устойчивости равновесия в точке
q = <7о- Разложим оба члена функции Лагранжа
системы с одной степенью свободы в ряды вблизи точки q =
и обозначим разность q — qo = x. Мы получим тогда
(a (go) + стар, члены) i2 тн„\
. — ¦ „ х — и \qQ) —
X
dU
dq
<7о
чл-
Нулевой член разложения потенциальной энергии U(qo) есть
константа, которую из функции Лагранжа можно выбросить,
первый член —-г— равен нулю в точке минимума. Поэтому
разложение U(q) эффективно начнется с квадратичного члена;
более старшие члены мы отбросим. В разложении кинетической
энергии первым существенным членом будет нулевой, поскольку
он умножается на q2 = х2; мы опять ограничимся им одним..
Тогда, если ввести обозначения
т = а(</0)>0; /- <^
dq2
<7о
функция Лагранжа примет вид
тхг Ьх2
Систему, описываемую такой функцией Лагранжа, в физике
называют обычно (гармоническим) осциллятором. Уравнением
движения будет
тх + kx = О
или
х + (й2х = 0, где <й = д/-|-. C9)
называется (собственнной) частотой осциллятора. Мы видим,,
что гармонический осциллятор описывается линейным уравне-
уравнением.
Это обстоятельство является чрезвычайно важным. Дело в
том, что линейные дифференциальные уравнения — это практи-
практически единственный класс дифференциальных уравнений, для
рассмотрения которых — рассмотрения в смысле нахождения
решений, а не в смысле доказательства теорем существования —
математика выработала общие и единые методы. Это побуждает
физиков при рассмотрении очень многих задач стараться исполь-
использовать такие приближения, которые сводили бы уравнения проб-
проблемы к линейным — линеаризовали бы задачу. Если это удается,.
14. МАЛЫЕ КОЛЕБАНИЯ 85"
то исходная проблема сводится к рассмотрению набора гармо-
гармонических осцилляторов.
В самом деле, чтобы уравнения движения системы были линейными, ее-
фуикция Лаграижа должна быть квадратичной функцией координат и скоро-
скоростей в совокупности. Поэтому кинетическая энергия, всегда являющаяся квад-
квадратичной функцией скоростей, должна быть квадратичной функцией скоростей
(по общим свойствам — положительно определенной) с коэффициентами, не
зависящими от координат. Потенциальная же энергия всегда может быть
освобождена от линейных по координатам членов их (координат) линейным
преобразованием, а постоянный член в ней несуществен. Поэтому она так-
также должна быть квадратичной формой — теперь координат — и притом поло-
положительно определенной, если мы интересуемся финитными движениями. Итак,
общий вид функции Лагранжа для системы, описываемой линейными уравне-
уравнениями, есть
i I
^, ? ltxtxr C8а>
i, 1 i. I
где обе квадратичные формы Г и U — положительно определенны. Линейным
однородным преобразованием координат можно, как то показывается в ли-
линейной алгебре, привести обе эти формы одновременно к главным осям, после
чего в новых нормальных координатах Qi функция Лагранжа примет вид
суммы
?(?Ф?) C8Ь).
функций Лагранжа C8) для каждой степени свободы, т. е. движение све-
сведется к движению независимых гармонических осцилляторов в числе, равном
числу степеней свободы.
Изложенные соображения побуждают нас заняться гармони-
гармоническим осциллятором гораздо подробнее, чем казалось бы заслу-
заслуживает эта достаточно тривиальная задача, и разработать на ее
простом примере методы, истинная плодотворность которых вы-
выяснится в применении к наборам большого (особенно — беско-
бесконечно большого) числа подобных систем.
Вторая причина внимания к гармоническому осциллятору
опять связана с тем, что уравнения движения для него решаются
въявь, — он оказывается хорошим модельным примером, на ко-
котором можно «пощупать руками», как конкретно проявляются
те или иные общие соображения, детальный механизм действия
которых в более сложных случаях проследить затруднительно.
14.2. Общая теория предписывает искать решение уравнения
движения C9) в экспоненциальном виде, именно, поскольку кор-
корнями характеристического уравнения будут ±йо, в виде
где а и b — постоянные интегрирования. Выполняя здесь комп-
комплексное сопряжение:
-86 ч. 1. КЛАССИЧЕСКАЯ МЕХАНИКА
видим, что для того, чтобы решение было вещественным, надо
потребовать
Ь = а*.
Кроме того, бывает_удобно выделить из произвольных постоян-
постоянных множитель ^2® и записать, таким образом, общее реше-
решение C9) в виде
*"'-+Г'-' . ,40.1)
»@- Г .
Характеризующую решение (комплексную) произвольную по-
постоянную а называют (комплексной) амплитудой. Ее модуль
дает нам обычную вещественную амплитуду, а аргумент — фазу
колебаний.
14.3. Выразим энергию через амплитуду. Заметим для этого
сперва, что соответствующая решению D0.1) скорость
х = -^{еа-
представляется через разность тех же комплексных экспонент,
сумма которых образует решение D0.1). Поэтому при подста-
подстановке в
квадратов скорости и координаты
я2 = =~- {ё>ша*а* - 2а* а + е~2Шаа),
ш2х2 = -^ {ё>ша*а* + 2а* а + е-*'«аа)
обе группы членов, зависящих (с удвоенной частотой) от вре-
времени, взаимно уничтожаются, и остается только не зависящая от
времени часть:
Итак, энергия
Е = ш(аа*а D0.2)
(а) не зависит от времени;
(б) есть билинейная форма амплитуд а* и а.
14.4.1. Бывает удобно ввести вместо х и х новые, более тесно
««вязанные с амплитудами переменные A*(t) и A(t), положив:
x(t)= A*(t) + A(t) , x(f: = -^=(A*(t)-A(t)). D0.1a)
14. МАЛЫЕ КОЛЕБАНИЯ 87
Обратное преобразование будет иметь вид
«*,,-, __ х (t) + fax (t) ox — ix
д ,д __ x(t) — ia>x(t) __ ax
— i -\/2<a
Выписав преобразование переменных D0.1а), мы' Предпи--
сали независимые выражения через новые переменные и коорди-
координате х, и скорости х. Поэтому надо еще ограничить его тем усло-
условием, что скорость есть действительно производная от коорди-
координаты по времени, -jjx = x. Это условие дает нам А*-\-А =
= ia(A* — Л), т. е. должно тождественно выполняться:
(Л* - ш/Г) + (Л + шА) = 0. D1.3)
14.4.2. Найдем теперь уравнения движения для новых пере-
переменных. Дифференцируя второе равенство D0.1а) по времени^,
находим, что
Поэтому
= —==- (А — тА +—7=^(А + тАУ
д/2ш V2o)
и уравнение движения C9) утверждает, что сумма этих двух
членов должна равняться нулю. Но благодаря тождеству D1.3)
эти члены равны друг другу, поэтому нулю должен равняться
каждый из них.
Итак, уравнениями движения в новых переменных будут
= 0 D1.1)
или
— i V2g> (Л + шЛ) = 0. D1.2)
Только одно из этих уравнений независимо, поскольку другое
получается из него комплексным сопряжением.
Теперь видно, в чем состоял смысл проведенного преобразо-
преобразования переменных D0.1а) —с его помощью мы перешли от урав-
уравнения второго порядка C9) к уравнению первого порядка, прав-
правда — комплексному.
14.4.3. Решением этого уравнения будет, конечно,
А*Н) — еша* или A(t) = e~iata,
ч. I. КЛАССИЧЕСКАЯ МЕХАНИКА'
где а* и а — взаимно комплексно-сопряженные постоянные, со-
совпадающие с введенными выше амплитудами. Действительно,
подставляя это решение в D0.1а), получим в точности старое
решение D0.1) уравнения C9).
14.4.4 Заметим еще, что
т. е. энергия выражается через переменные A*(t) и A(t) в точ-
точности так же
E = m(nA*(t)A(t), D0.2а)
как и через не зависящие от времени амплитуды а*, а.
14.5. Конечно, для свободного осциллятора польза от преоб-
преобразования D0.1а) невелика — мы и без того проинтегрировали
C9) без каких-либо затруднений. Однако предложенная замена
переменных оказывается очень удобной, если на осциллятор дей-
действует произвольная внешняя сила F(l), т. е. уравнение движе-
движения C9) заменяется на
x + «>*x = ±.F(t).
Тут уже иметь дело с уравнением первого порядка гораздо удоб-
удобнее, чем второго.
14.5.1. Действительно, соответствующее уравнение первого по-
порядка
А* Ц) - юА* (t) = f(l-L Гили A (t) + шА (t) = Щ=
im -у2(о \ — im V2»
D2)
можно интегрировать методом вариации произвольной постоян-
постоянной, полагая
А*{г) = аЦг)еш. (*)
ЗАМЕЧАНИЕ: В старых переменных эта подстановка имела бы вид
еша* @ + е~ша (t)
X
т.е. означала бы, что мы ищем решение в форме D0.1), но с амплитудами,
зависящими от времени. Таким образом подстановка («) приводит к отделе-
отделению тривиальной экспоненциальной зависнмостн от времени, характерной для
свободного осциллятора, от дополнительной зависимости, обусловленной
внешней силой. В переменных А*, А эта процедура совершенно естественна;
в первоначальных переменных х, х об ней было бы не так легко дога-
догадаться. Щ
Подстановка (*) приводит для а*A) к уравнению
12Ж ' F(t)e-™,
dt im V2o> '¦
14. МАЛЫЕ КОЛЕБАНИЯ 89
которое интегрируется непосредственно, приводя к
J
im
V2co J int
где мы обозначили новую постоянную интегрирования опять че-
через а* без аргумента. Таким образом, общее решение D2) для
A*(t) имеет вид
t
dte ,— /=" (Г) + е'«*а*, D3.А)
tra V"co
где первый член есть частное решение неоднородного уравнения,
а второй—общее решение однородного.
14.5.2. Для самой же координаты x(t) получится
х (t) = *0 (/) + _L J df sin со [t -1') F {t% D3)
о
где xo(t) есть общее решение D0.1) однородного уравнения, а
второй, интегральный член ¦— частное решение неоднородного
уравнения. Легко видеть, что это частное решение обладает тем
специальным свойством, что обращается в нуль вместе со своей
первой производной при t = 0. Для самого решения это оче-
очевидно из выбранных пределов интеграла, а для производной сле-
следует еще и из того, что под интегралом стоит синус, также об-
обращающийся для малых аргументов в нуль. Поэтому решение
D3) —это такое решение неоднородного уравнения, которое при
t = 0 совпадает, вместе со своей первой производной, с реше-
решением xo(t), т. е. есть решение задачи Коши с начальными усло-
условиями:
при f = 0: x{t) = xo(t) и x{t) = xo(t). D3а)
ЗАМЕЧАНИЕ: Следует обратить внимание на не совсем обыч-
обычную формулировку начального условия D3а): мы не просто за-
задаем численные значения функции x(t) и ее производной в
начальный момент времени t = 0, а требуем в этот момент вре-
времени совпадения x(t) и x(t) с другой функцией — решением сво-
свободного уравнения xQ(t) — и ее производной. При таком подходе
можно определить для всякого решения неоднородного уравне-
уравнения целое однопараметрическое семейство «касательных» к нему
решений однородного уравнения-—решений, совпадающих с ним
(вместе с первой производной) в различные моменты времени
^о- Либо напротив — для всякого решения xQ(t) свободного
уравнения можно определить однопараметрическое семейство
90
ч.1. КЛАССИЧЕСКАЯ МЕХАНИКА
решений неоднородного уравнения, совпадающего с xo(t) (вме-
(вместе с первой производной) в различные моменты времени to. Та-
Такой способ установления соответствия между решениями одно-
однородного и неоднородного уравнений (или — в более общем слу-
случае— между решениями невозмущенной и возмущенной задачи)
оказывается полезным во многих физических проблемах. |
14.5.3. Рассмотрим теперь такой случай, когда для t < 0 ос-
осциллятор находится в покое, x(t) =x(t) = 0 для t < 0, а начи-
начиная с момента t = 0 на него начинает действовать внешняя сила
F(t), и зададимся вопросом о том, какую энергию приобретет
осциллятор за счет действия этой силы к некоторому моменту
времени t.
Рассматриваемым начальным условиям соответствует, оче-
очевидно, выбор а* в D3а) равным нулю; поэтому в D0.2а) нужно
подставлять только интегральный член из D3а), члены с t в по-
показателях уничтожаются, и в результате мы получаем
D4.1)
В частности, если мы хотим найти энергию, накопляемую ос-
осциллятором за все время действия внешней силы, то верхний
предел интеграла в D4.1) следует устремить к +°°; нижний же
предел интегрирования можно опустить до — оо, поскольку для
t <С 0 сила F(t) все равно равна нулю. Итак, энергия, получае-
получаемая первоначально покоившимся осциллятором за все время дей-
действия внешней силы F(t), есть
E =
2га
dte-l<i>tF{t)
D4.2)
т. е. пропорциональна квадрату модуля компоненты Фурье внеш-
внешней силы с основной частотой осциллятора.
14.6. Теперь наступило самое время приостановить выкладки
и задаться вопросом о том, что мы, собственно говоря, вычис-
вычисляли в обеих формулах D4)? На первый взгляд в этом вычис-
вычислении мы провели довольно странную операцию — найдя из
D3а) значение переменной A*{t) для удовлетворяющего вы-
выбранным начальным условиям решения неоднородного уравне-
уравнения D2), мы подставили это значение в выражение D0.2а) для
энергии, выведенное для решений однородных уравнений D1).
Или, выражаясь физически, решение для осциллятора с внеш-
внешней силой подставили в выражение для энергии свободного ос-
осциллятора.
14. МАЛЫЕ КОЛЕБАНИЯ 9f
Чтобы разобраться в возникшей ситуации, полезно вернуться
к вопросу о том, что же собственно имеют в виду, когда говорят
об энергии осциллятора, на который действует внешняя сила,
или, более общим образом, об энергии системы, находящейся
во внешнем иоле.
14.6.1. Согласно § 4 функцию Лагранжа для системы, находящейся во
внешнем поле, можно записать в виде
где Lo — та часть функции Лагранжа, которая зависит только от координат
н скоростей, Цг и </(, интересующей нас незамкнутой системы I (ср. 4.6.):
a Uext — та часть потенциальной энергии, которая зависит как от коорди-
координат <?(, так и от координат qu большой системы, которые можно считать яв-
явными заданными функциями времени:
Уравнениями движения будут
где перенесенные в правую часть производные —-z игрэют роль внешних-
сил, действующих на t'-ю степень свободы.
Наряду с системой во внешнем поле можно рассматривать соответствую-
соответствующую ей замкнутую, будем говорить свободную систему, функция Лагранжа
которой есть просто Lo. Уравнениями движения свободной системы будут
уравнения (*) с правыми частями, равными нулю. Если образовать для сво-
свободной системы комбинацию
Z. dLa
. 11-оТ{
то
d /V • <?L0 , \ V«f . dL0
-V л f d dL
L qi \ dt dq
dL° dLo
dqt
т. е. в силу свободных уравнений движения
dE0
dt
= 0
— энергия ?о свободной системы сохраняется.
14.6.1.1. Дли системы во внешнем поле полная производная энергии Е&
по времени будет в силу той же выкладки равна
V • ext О
-W — Lq—ЪТ
•92 ч. I. КЛАССИЧЕСКАЯ МЕХАНИКА
Мы можем записать здесь правую часть как
н, перенося полную производную —тг налево, привести (••) к форме
— (E0 + Uext(q,t))-
Если теперь энергия взаимодействия с внешним полем ?/ext не зависит
dUext
от времени явно, ——— = 0, то стоящая в левой части последнего равенства
комбинация Ео + ?/e*t будет сохраниться. Поэтому разумно ввести для иее
специальное обозначение, назвав
энергией системы во внешнем поле. Именно с такой энергией мы имели дело
например в задаче о движении частицы во внешнем центральном поле.
dU xi
14.6.1.2. Если, однако, —-гг—ф 0, то энергия системы во внешнем
поле Е все равно не будет сохраниться, и ее введение не иесет с собой ни-
никакой выгоды. Единственная энергия, о которой имеет смысл говорить в этом
случае, это энергия Ео. Она, конечно, не сохраняется, но в силу (»•) и (•) ее
изменение во времени можно представить в форме
r^.o, (...)
т.е. как сумму работ Fjxidq[, производимых всеми внешними силами за еди-
единичное время. Именно так понимаемая энергия и выражается формулами D4).
14.6.2. Физическое значение энергии Ео можно пояснить сле-
следующим рассуждением. Предположим, что в некоторый момент
времени t = t мы сразу выключаем действовавшее на систему
внешнее поле. Тогда система превращается в свободную систе-
систему, дальнейшая эволюция которой определяется значениями ко-
координат и скоростей qi и qu которые имела система в поле в мо-
момент t = t — для возникшей свободной системы эти значения
будут начальными условиями. В терминах замечания после фор-
формулы D3а) это будет свободная система, «касательная» к си-
системе в поле в момент t = 1. Для этой свободной системы энер-
энергия Ео будет точно сохраняться, численно же она будет равна
энергии Ео, вычисленной для системы в поле в момент 1.
Итак, под энергией в некоторый момент времени 7 системы,
находящейся в зависящем от времени внешнем поле, разумно
понимать энергию -соответствующей свободной системы, каса-
касательной к системе в поле в момент t = 1.
После этого несколько затянувшегося отступления вернемся
снова к формуле D4,2) и сделаем относительно нее еще одно
замечание.
15. ФУНКЦИИ ГРИНА 93
Согласно D4.2) энергия, переданная внешней силой гармони-
гармоническому осциллятору, пропорциональна квадрату модуля ком-
компоненты Фурье внешней силы с собственной частотой осцилля-
осциллятора (о. Спрашивается, а как же будет обстоять дело, если на
осциллятор действует периодическая внешняя сила с некоторой
частотой &' ф © — ведь в ее фурье-разложении будет присут-
присутствовать только ее частота о/, а в то же время известно, что под
действием такой силы осциллятор приходит в состояние колеба-
колебаний с той же частотой <о'?
Объяснение.состоит в том, что мы должны каким-то образом
включить внешнюю силу; за счет включения она уже не будет
строго периодической, в ее фурье-разложении появятся все час-
частоты, в том числе и собственная частота осциллятора со.
15. Функции Грина
Мы проинтегрировали уравнения движения осциллятора, на-
находящегося под действием произвольной внешней силы, с по-
помощью несколько искусственного приема сведения к (комплекс-
(комплексному) уравнению первого порядка. В этом разделе для той же
•самой задачи будет развита другая, пожалуй — более естествен-
естественная, техника, основанная на построении и использовании
функций Грина. Такая техника чрезвычайно широко применяет-
применяется и в теории поля, и в квантовой механике, поэтому будет
уместным не пожалеть места, чтобы разработать ее на этом про-
простом примере во всех подробностях.
15.1. Итак, пусть нам задано уравнение движения для осцил-
осциллятора, находящегося под действием внешней силы:
x + o>lx = F(t) D5)
(массу ради простоты кладем равной единице).
Будем искать решение этого уравнения в форме интеграла
Фурье
оо
k \ ш*(«>) D6.1)
и таким же образом представим внешнюю силу*)
F @ = -~ J dae-^F (со). D6.2)
*) Ниже будет много интегрирований в бесконечных пределах, поэтому
ради краткости мы не будем эти пределы выписывать, подразумевая именно
такое интегрирование, коль скоро не оговорено что-либо иное. В физических
статьях такое сокращение обычно и, как правило, не оговаривается.
94 ч. I. КЛАССИЧЕСКАЯ МЕХАНИКА'
Обратное преобразование будет иметь вид
F (со) = J dt'e^'F (/'), Dб.3>
Уравнение движения D5), переписанное для фурье-образов
jc (со) и F ((й), станет алгебраическим:
(со2, — со2) х (со) = F(a>) + const (со2 — со2) б (со2 — со2). D5а>
Разрешая его относительно х(и>), получим
*(<")= Jl"^ +С6(со02-со2). D5Ь>
15.1.1. При переходе от D5а) к D5Ь) мы поделили обе части
уравнения на множитель (со2 — со2), который может обращаться
в нуль. Чтобы не потерять возникающий из-за этого дополни-
дополнительный произвол, мы прибегли здесь к часто употребляемому
формальному приему. Именно, мы добавили к правой части
D5а) (члены, подчеркнутые угловой скобкой) произведение б-
функций от «подозрительного» множителя (со2 — со2) на сам этот
множитель и на произвольную константу. Произведение б-функ-
ции на ее аргумент есть нуль, поэтому дополнительный член в
D5а) тождественно равен нулю и его всегда можно добавить.
В D56), однако, множителя (со2 — Ю2) у дополнительного члена
уже нет, и поэтому член этот дает конечную добавку к фурье-
образу х(а). Что это за добавка? Из-за б-функции она даст в
решение x(t) только вклады с частотами ±со0 —но это как раз
частоты свободного решения соответствующего уравнения без
правой части. Таким образом, дополнительный член в D5Ь) дает
нам решение свободного уравнения (и притом общее решение:
поскольку аргумент б-функции в D5а) имеет два корня, то
можно выбрать произвольные константы для каждого из этих
корней независимо; тем самым вклад дополнительного члена за-
зависит от двух произвольных констант, как то и должно быть
для общего решения уравнения второго порядка). Главный же,
пропорциональный ^(со) член в D5Ь) дает частное решение не-
неоднородного уравнения D5); таким образом все выражение
D5Ь) приводит к общему решению D5).
15.2. Займемся частным решением неоднородного уравнения.
Подстановка D5Ь) и D6.1) с использованием D6.3) дает
Для *(*) ^ _^{
x(t) = -±-\da> -f^-j- \ dt'e^'F (П,
2л J иг, -ш' J
15. ФУНКЦИИ ГРИНА 95
что можно, поменяв порядок интегрирования, записать в виде
x{t)=\dt'G{t,t')F{t'), D7.1)
если ввести функцию от двух аргументов:
1 Г -ia(t-t')
G(f,/') = — Wco— — D7.2)
— функцию Грина уравнения D5).
15.2.1. Функция Грина, как легко убедиться, удовлетворяет
уравнению
®
т. е. уравнению D5) с б-образной внешней силой. Таким обра-
образом, с наглядной точки зрения представление решения в форме
D7) можно понять как представление решения уравнения D5)
с произвольной правой частью в виде сюперпозиции решений
того же уравнения с внешними силами в виде кратких импуль-
импульсов, действующих в различные моменты времени.
Формулами D7) заканчивается формальная теория интег-
интегрирования уравнения D5) с помощью функции Грина. Однако
настоящая наука о функциях Грина — вся еще впереди.
15.2.2. Дело в том, что подинтегральное выражение в D7.2)
имеет полюса в точках со = ±соо. Поэтому безоговорочное вычи-
вычисление интеграла в пределах от —с»
до +оо, т. е. вдоль вещественной оси
в комплексной плоскости со, бессмыс-
бессмысленно— интеграл в обычном смысле не
существует. Чтобы придать ему смысл, ^
надо сперва исключить из области ин-
интегрирования особенности, а затем из-
избавиться от этого исключения с помо- полюса 8 ппоскооти ы
щью какого-либо предельного перехода.
В качестве такой операции удобно применять деформацию
контура интегрирования, выводящего его в комплексную пло-
плоскость, с последующим предельным
возвратом на вещественную ось. Тем
самым возникает вопрос, как именно
деформировать контур интегрирова-
интегрирования, т. е. как обходить полюса?
15.2.3. Чтобы выяснить это, посмот-
^л-шо С Рим> чт0 произойдет, если изменить об-
обход полюса, т. е. обойти вокруг него.
Посмотрим, например, что даст интегрирование по контуру (см.
рисунок), обходящему оба полюса в отрицательном смысле,—
это отвечает разности интегралов, вычисленных по контурам,
96
ч. I. КЛАССИЧЕСКАЯ МЕХАНИКА
проходящим из —с» в +оо над и под вещественной осью. Для
изображенного на рисунке контура с помощью теоремы о вы-
вычетах:
2я
то есть
, T
(со — ш0) (со + со0)
„-'tot
2 2
On — CO
1
где
= t — i'.
Но получившаяся функция — sin co0 (t — t') есть решение одно-
однородного уравнения. Следовательно,
изменение правила обхода сводится к добавлению к D7) ре-
решения однородного уравнения.
15.2.4. Это значит, что принципиально выбор обхода безраз-
безразличен —ведь мы сейчас ищем частное решение неоднородного
уравнения, и для получения общего все равно будем добавлять
к нему общее решение однородного. Практически, однако, выбор
конкретного обхода может составить заметное преимущество —
удачным выбором обхода можно вообще избавиться от необхо-
необходимости добавлять общее решение однородного уравнения или
придать добавляемому общему решению более прозрачный фи-
физический смысл. Поэтому остановимся сейчас на детальном рас-
рассмотрении нескольких возможностей в выборе контура интегри-
интегрирования, которые оказываются физически интересными.
15.3. Запаздывающая функция Грина получается, если про-
провести путь интегрирования над вещественной осью, т. е. обойти
оба полюса сверху. В показателе экс-
экспоненты в подинтегральном выражении
стоит —icoT, поэтому при т>0 можно
замкнуть контур снизу, добавив к не-
нему (равный нулю!) интеграл по ниж-
нижней половине большого круга—оба по-
полюса окажутся при этом внутри кон-
контура, и получится тот же результат,
что для контура С. Если же т < 0, то
замыкать контур надо сверху, оба по-
полюса оказываются вне контура и интеграл — равным нулю.
Итак, для контура Cret
контур С
¦ret
2я J
cret
(On — (О
.__ I —-sinco0T для
о
•для
т>0,
т<0.
Полученная при таком выборе контура функция Грина назы-
называется запаздывающей и обозначается обычно буквой D с ин-
15. ФУНКЦИИ ГРИНА 97
дексом ret (или просто г)—первыми буквами слова retarded.
Чтобы компактно записать ее, удобно воспользоваться ступен-
ступенчатой функцией, которую в физике обычно обозначают симво-
символом О:
+1 для т>0,
0 для т<0;
с ее помощью
ret ^ D8г)
15.3.1. Физический смысл запаздывающей функции Грина ста-
становится ясным, если заметить, что в выраженном с ее помощью
частном решении
xret (t) = J dt'DIet {t-t')F{f)
в силу обращения Z)ret в нуль для отрицательных аргументов
интегрирование выполняется только по — с» < f < /, т. е. функ-
функция эта выражает запаздывающее влияние на решение в неко-
некоторый момент времени внешней силы, действовавшей в преды-
предыдущие времена. Ею естественно пользоваться, если начальные
условия задаются в бесконечно-прошлом.
15.3.2. Вместо того, чтобы смещать (вверх) контур интегри-
интегрирования, можно оставить его проходящим по вещественной оси,
но сместить (бесконечно мало) особенности в противоположную
сторону (вниз). Такое смещение достигается добавлением к ко-
координатам обоих полюсов ±соо бесконечно малой мнимой до-
добавки —is, e > 0, которая должна быть устремлена к нулю после
выполнения интегрирования по со. Тогда дробь —5 5~ перехо-
<а„ — ш
дит в
-1 -1
[со — (со0 •- »е)] [со — (— соа — ie)] со2 — со2, + «в (со + со0) + 1г (со — соо)
— 1
со2 — cog + ('еш
Таким образом, для фурье-образа запаздывающей функции
Грина можно написать символическое выражение, включающее
указание о способе обхода особенностей:
3\
cog — со — teco
D9г)
в котором необходимость выполнить предельный переход е
после интегрирования по со держится в уме.
4 Б. В. Медведев
98 ч. I. КЛАССИЧЕСКАЯ МЕХАНИКА
15.4. Опережающая функция i рина получается, если про-
провести путь интегрирования под вещественной осью. Тогда при
замыкании контура снизу для % > 0 внутри него не окажется
особенностей и интеграл будет равен нулю, а при замыкании
сверху для т < О обе особенности окажутся внутри контура, ко-
который, однако, будет теперь обходиться в положительном смыс-
смысле, так что результат будет отличаться
от найденного для контура Cret знаком.
-а0
*
Итак,
Л 2. «.dv,_x Л/ л 1 ., D8а)
Для обозначения опережающей функции
ado используется индекс adv (или просто а) —
mmyp с первые буквы слова advanced. Она
отлична от нуля только для отрицательных аргументов, т. е.
приводит к частному решению, зависящему, в некоторый момент
времени, от действия внешней силы в последующие моменты.
Поэтому опережающая функция Грина находит себе применение
в таких задачах, в которых предписывается «конечное» условие
при t = +°°-
15.4.2. Если заменить, как то делалось для запаздывающей
функции, смещение контура интегрирования смещением полюсов,
то оба полюса должны быть смещены вверх, и мы получим для
фурье-образа опережающей функции символическое выраже-
выражение
Dadv(m) = -2 1—-, D9а)
«о — со + /ею
которое следует понимать в том же смысле, что и D9г).
15.5. D-функция Паули. Найденное выше специальное ре-
решение свободного уравнения, получавшееся при интегрировании
по контуру С, также имеет особое название — его называют
D-функцией Паули по имени одного из крупнейших тебретиков
первой половины нашего века, который ввел это решение в за-
задачах релятивистской теории полей, и обозначают
^ D8)
15.5.1. Сравнивая D8г) и D8а), легко заметить, что
D(T) = Oret(T)-Dadv(T). E0)
15.5.2. В силу линейности фурье-преобразования такое же со-
соотношение должно существовать и между соответствующими
фурье-образами. Поатому, пользуясь символическими выраже-
15. ФУНКЦИИ ГРИНА 99
ниями D9г) и D9а), можно написать для фурье-образа /5(со):
1 1 2<еш
со2 — /еш со2 — со2 + /еш (со2 — со2J + е2ш2
О, если со2, ф со2,
Z>(co) = -
__ 2j _ z
|ю| (со2, - ш2J + е'2 у оо, если со* =
Обнаруженные свойства Л(ш) заставляют заподозрить, что оно содержит
б-фуикцию от (со2 — со,2). Чтобы проверить такое предположение, проинте.ри-
B 2\
ш — ш0^:
dy t ,°°
-T—r =arctgy|_oo= я.
Поскольку для б-функции такой интеграл должен равняться 1, то наше пред-
предположение подтверждается; попутно мы иашли полезное символическое вы-
выражение для б-функции
6(|)=7Г^ + е2'
которое следует понимать в том же смысле стремления е к нулю после инте-
интегрирования, как и все формулы D9). Итак, если ввести еще знаковую функ-
функцию, которую в физике обозначают символом е (не путать с бесконечно-ма-
бесконечно-малым е, фигурирующим в наших символических формулах! Перенасыщенность
обозначений освящена традицией),
то мы получим для фурье-образа /)-функции:
б (со) = 2те (о) • 6 (со2 — со2,)- D9)
15.6. Для обычной постановки задачи Коши, когда началь-
начальные значения задаются в некоторый не бесконечный момент вре-
времени / = t0, удобной функцией Грина будет
t\ t0) = [&{t-t')-&,t0- f)] sin Юва(в' ~ П =
= [f>(t-t')-b(to-f)]D(t-t'). D8o)
Легко видеть, что G(t,t'\U) обращается при t — t® в нуль вме-
вместе со своей производной. Для функции это видно сразу, а для
производной
+ b(t-t')
получается за счет того, что
4*
100 ч. I. КЛАССИЧЕСКАЯ МЕХАНИКА'
15.6.1. Поэтому решение, записанное в виде
х @ = хи @ + \ G (t, f | /0) F (П dt', D3')
где xta(t) — решение однородного уравнения, будет обладать
тем свойством, что
при t = t0: x{t) = xu{t), i(/) = i,t@, D3а')
т. е. будет решением, касательным к свободному решению xh(t)
в момент времени t0 в смысле замечания после формул D3)
предыдущего параграфа. Легко видеть и то, что решение D3')
буквально совпадает с найденным там решением D3) —для
этого достаточно перенести заключенные в О-функции в D8о)
неравенства в пределы интегрирования.
15.6.2. Чтобы перейти отсюда к решению собственно задачи
Коши с начальными значениями
x(t) — fi и x(t) = f2 в момент / = /0, (*)
надо еще выразить решение xu(t) однородного уравнения в
произвольный момент времени через значения его и его произ-
производной в момент t0
15.6.2.1. Заметим для этого, что рассматривавшееся выше
специальное решение свободного уравнения D(t — to) обладает
свойствами:
при / = /0: ?>(/ —/о) = О; D{t — to)=U D{t-to) = O. E1)
15.6.2.2. Поэтому, если построить выражение
то оно
(а) будет решением однородного уравнения;
(б) при t = t0
Xt.it) = ft *u@ = fr
15.6.3. Итак, решением задачи Коши с начальными значе-
значениями («) является
x{t) = D{t-10) fl + D(t-t0)f2+\G (t, t' | *0) F (f) dt'. D3")
Кроме уже рассмотренных, бывает полезно ввести еще не-
некоторые специальные функции Грина.
15.7. Симметричная функция Грииа D определяется тем, что полюса в
D7.2) обходятся в смысле главного значения. Очевидным образом она рай-
15. ФУНКЦИИ ГРИНА 101
няется полусумме опережающей и запаздывающей функций:
5 (т) =1 [D'« (т) + />*<* (тI = ^fl(r)=Sin;;T|, D8)
и то же самое справедливо для ее фурье-образа:
Д (со) = l[5ret(<D) + Dadv («>)]=/> ' 2. D9)
2 (Oq "~ ®
Комбинируя E0) и D8), получим, что
Dret (т) = D(t)+jD(т) или 5ret (со) = 5 (со) + ~ D (<o). E0a)
В развернутом виде второе из этих равенств гласит:
\' ~ Р '
—г, м ' ~ Р г 2
о «Oq — © — »е (©) • е % — а>
Отсюда получается полезное символическое тождество:
+ 'Яе («•> 6 (®0 - О2)-
т
e'>o У'-y-iaz' у'-У
e'->0
(предельный переход подразумевается, конечно, быть выполненным после ин-
интегрирования по у' или у), которое находит себе богатые приложения при
вычислениях с обобщенными функциями.
15.8. В задачах о рассеянии в квантовой механике часто бывает полезно
вводить причинную функцию Грина D", определяемую обходом по контуру С0
контур Сс
(см. рисунок), который можно, по развитому выше образцу, заменить смеще-
смещением полюсов в точки
— (ю0 — »е) и + (о);, — »е).
Мы получаем тогда для фурье-образа
" к > [со - (со„ - /в)] [со + (со„ - /в)] со2 - (со„ - /вJ '
то есть
бс (со) =-2 ^ • D9с)
©О — СО — (8
Вычисление интегралов (его приходится теперь делать заново) дает ,
для т > 0: D (т) = —— (•
для т < 0: Dc (т) = — -х- 2:
102 ч. I. КЛАССИЧЕСКАЯ МЕХАНИКА
Таким образом:
В отличие от других, введенных ранее, причинная функция Грина — ком-
комплексна. Поэтому основное применение она находит себе в квантовой меха-
механике. Ее вещественная часть
l
равииется симметричной функции Грина.
* 15.9. ЗАМЕЧАНИЕ: Стоит обратить внимание на то обстоя-
обстоятельство, что функции Грина получаются из решений однород-
однородного уравнения домножением на разрывные функции Ф(т) (или
е(т)). Покажем, что именно за этот счет они и становятся функ-
функциями Грина.
Рассуждение проведем на примере функции /)ге'(т). По определению
), где
Подействуем дифференциальным оператором ("Х~Г
-^г + m*) D (т) = 6 (т) D (т) + 26 (т) Ь (т)
— поскольку производная О-функции равна б-функцни, а третий член обра-
обращается в нуль. Смысл производных, сидящих на б-функции, состоит в том,
что их надо снимать интегрированием по частям. Следовательно,
6 (т) D (т) = - б (т) Ь(х)-й (т.) D (т) ¦— *),
где «свободный оператор —г— будет действовать на другие функции от т, на
которые нам возможно будет благоугодно умножить это тождество. Впрочем,
в нашем конкретном случае б(т)О(т)=0, так что член со свободным опера-
оператором исчезает.
*) Более аккуратно это рассуждение проводится следующим образом.
Умножая 60 на какую-либо основную функцию <р(т) и интегрируя по т, на-
находим
йт.6 (т) D (т) <р (т) = - J dxb (т) -|L [D (Т) ф (Т)] =
= - J dxb (х) Ь (т) Ф (т) - J dxb (т) D (т)
откуда и следует выписанное в тексте символическое равенство.
16. УРАВНЕНИЯ ГАМИЛЬТОНА ЮЗ
Итак,
(-^т+ a>l)ft(T)D(%) = d{T)D{%) = 6(%)
в силу E1), т. е. O(t)Z)(t) действительно образует функцию
Грина. |
16. Уравнения Гамильтона
В составлявшем до сих пор наш основной метод лагранжевом
формализме система с п степенями свободы описывалась п
уравнениями второго порядка. Иногда бывает удобнее перейти
от них к 2п уравнениям первого порядка. Такие уравнения ока-
оказываются более красивыми и симметричными, если в качестве
основных переменных выбрать не координаты и скорости, а ко-
координаты и импульсы
„ I • 4\ dL (q, q, t) /i о i\
Pi=zPi\Qi Qi *) == ^p • \llb.lj
16.1. Преобразование переменных, описываемое формулой
A2.1), когда новые переменные рь ..., рп суть частные произ-
производные по старым переменным qu ..., qn от некоторой одной
функции, называется преобразованием Лежандра, а эта функ-
функция называется производящей функцией по отношению к пре-
преобразуемым переменным. Итак, импульсы получаются из скоро-
скоростей преобразованием Лежандра, причем производящей функ-
функцией является функция Лагранжа системы. Координаты qu ..., qn
и время t играют в этом преобразовании роль параметров.
Если детерминант
0, что мы будем предполагать
(в противном случае возникают существенные осложнения), то
такое преобразование обратимо.
Тогда
A) Обратное преобразование тоже будет обладать производя-
производящей функцией.
В самом деле, в силу A2.1) ? pidqi = (dL(q, q, t))q t —
полному дифференциалу функции Лагранжа при постоянных
«параметрах» qu t. Если предположить теперь, что соответствую-
соответствующее выражение для обратного преобразования также образует
полный дифференциал некоторой новой функции H(q, p, t),—
т. е. что
ii = j^-> 02.1а)
(Я, Р, t) dPi = (dH (q, p, t))qtt t,
104 ч. I. КЛАССИЧЕСКАЯ МЕХАНИКА
— то, складывая два последних равенства
увидим, что это действительно так, поскольку разность двух
полных дифференциалов есть полный дифференциал.
Выпишем теперь выражения для полных дифференциалов L
и Н без предположения о постоянстве «параметров» qu t
(производные по qi и t берутся у L при постоянных qu а у Я
при постоянных рг!) и сложим эти два выражения
Отсюда видно, что
есть некоторая функция только координат и времени. Положим
эту функцию равной нулю.
Тогда производящая функция для обратного преобразования
от импульсов к скоростям будет равна
Я (<?, р, 0 = S рьсц (р, q,t)-L (q, q (p, q, t), t). E2)
Она называется функцией Гамильтона. Далее:
B) Частные производные функций Лагранжа и Гамильтона по
играющим в преобразовании Лежандра роль параметров коор-
координатам и времени будут связаны соотношениями
(Такова же и связь частных производных функций Лагранжа и
Гамильтона по каким-либо иным параметрам, не являющимся
динамическими переменными.) Утверждения A) и B) носят имя
теорем Донкина.
16.2. Обратное преобразование A2.1а), соотношения E2а) и
воспоминание о том, что в силу уравнений Лагранжа ¦^-=Рг,
16. УРАВНЕНИЯ ГАМИЛЬТОНА 105
позволяют выписать полный дифференциал функции Гамиль-
Гамильтона в виде
Y Ydpi + ^rdt. E2b)
Эта форма уже содержит в себе систему основных уравнений
механики, записанных как уравнения первого порядка в пере-
переменных q и р, — уравнения Гамильтона:
dqs дН dp, дН
dt ~ dpt ' ~dt dqt • ^й>
В силу красоты и симметрии этих уравнений их называют также
каноническими уравнениями механики, а переменные — коорди-
координаты и импульсы — в терминах которых выписываются эти урав-
уравнения, — каноническими переменными. Для дальнейшего
имеет особое значение то обстоятельство, что именно такой вы-
выбор уравнений и переменных оказывается наиболее удобным при
переходе от классического описания к квантовому.
16.3. В лагранжезом формализме состояние механической си-
системы (в некоторый момент времени) фиксировалось B.5, 2.4.2)
заданием значений всех обобщенных координат и всех обобщен-
обобщенных скоростей. При использовании для описания системы кано-
канонических уравнений естественно фиксировать состояние зада-
заданием (в некоторый момент времени) значений всех координат
и импульсов. Поэтому, если построить (для системы с п степе-
степенями свободы) 2«-мерное пространство, координатами которого
служат обобщенные координаты и импульсы системы, то каж-
каждая точка в нем будет отвечать определенному состоянию
системы. Такое пространство называют обычно фазовым прост-
пространством^ его точки, изображающие состояния системы в неко-
некоторый момент времени, — изображающими точками. Совокуп-
фазовая траектория
ность точек, изображающих состояния системы в различные мо-
моменты времени, образует в фазовом пространстве некоторую
кривую. Ее называют фазовой траекторией системы.
Поскольку, по самому смыслу понятия состояние, задание
состояния системы в некоторый момент t = t0 предопределяет ее
106 ч. I. КЛАССИЧЕСКАЯ МЕХАНИКА
состояния во все другие моменты времени, то задание изобра-
изображающей точки в некоторый момент t = t0 предопределяет всю
фазовую траекторию (в отличие от задания положения системы
в конфигурационном пространстве, оставляющего широкий про-
простор для возможных конфигурационных траекторий). Таким об-
образом, через каждую точку фазового пространства проходит
только одна фазовая траектория.
16.3.1. Даже самая общая — топологическая — картина рас-
расположения фазовых траекторий в фазовом пространстве позво-
позволяет сделать ряд заключений о характере возможных движений
системы. Чтобы составить себе такую картину, удобно исследо-
исследовать E3) с помощью качественной теории дифференциальных
уравнений. Особенно успешно оказывается такое исследование
в простейшем случае одной степени свободы.
16.3.1.1. Если система, как в 9.2, описывается функцией Лаг-
ранжа
то особыми точками уравнений E3) будут те, в которых одно-
одновременно
dp дх
Первое условие выполняется при р = 0; второе означает, что по-
потенциальная энергия в особой точке должна иметь экстремум.
Если этот экстремум есть минимум, то в окрестности экстре-
экстремальной изображающей точки @, л'о) функции Лагранжа и Га-
Гамильтона будут иметь вид, изучавшийся в § 14:
Поскольку энергия сохраняется, то фазовыми траекториями бу-
будут линии постоянной энергии — эляипсы с центром в особой
точке @, х0). В частности, сама особая точка будет образовы-
образовывать фазовую траекторию. В теории дифференциальных уравне-
уравнений такую особую точку называют центром. Если экстремум есть
минимум, но такой, в котором разложение U по (х — лг0) начи-
начинается не со второй, а с более высокой (четной) степени, то
конкретный вид фазовых траекторий изменится, однако качест-
качественная картина однопараметрической совокупности замкнутых
кривых, окружающих особенность, сохранится.
Если экстремум есть максимум, то в окрестности экстремаль-
экстремальной изображающей точки @, х0) функция Гамильтона запи*
шется как
Н (р, х) = Е = -z s— h Ео
16. УРАВНЕНИЯ ГАМИЛЬТОНА
107
и фазовыми траекториями будут гиперболы с центром в особой
точке @, х0).
Изображающая точка движется по фазовым траекториям в
направлениях, указанных стрелками; они определяются из того
соображения, что для р > 0 координата х должна расти с рос-
ростом времени. Видим, что траектории разбиваются на четыре
класса: когда х меняется от —оо до + оо; от + оо до —оо
(этим классам движений отвечает Е— ?10>0); когда х ме-
меняется от — оо до некоторого конечного значения, а затем снова
центр
убывает до — оо; когда х меняется от + оо до некоторого конеч-
конечного значения, а затем снова возрастает до + оо (этим классам
отвечает Е — ?0 < 0) *).
Траектории разных классов разделяются на фазовой плоско-
плоскости парой пересекающихся прямых, называемых сепаратрисами;
находящаяся в некоторый момент времени на сепаратрисе изо-
изображающая точка движется вдоль по ней. Поэтому в том, что
сепаратрисы пересекаются, можно было бы заподозрить проти-
противоречие со сделанным выше утверждением, что через каждую
точку проходит лишь одна фазовая траектория. В действитель-
действительности, однако, противоречие отсутствует благодаря тому, что
для достижения особой точки по сепаратрисе потребно бесконеч-
бесконечное время (ср. пример в § 9) и сепаратрисы, рассматриваемые
как фазовые траектории, состоят из пяти объектов—четырех лу-
лучей и одной изолированной точки @, х0) — каждый из которых
сам по себе есть отдельная целая фазовая траектория. Такая
особая точка называется седлом.
Если экстремум есть такой максимум, в котором разложение
потенциальной энергии по (х — х0) начинается с более высо-
высокой чем вторая (четной) степени 2п, то сепаратрисы будут не
*) Упоминание о ±оо надо, конечно, понимать в «пиквикском» смысле,
поскольку наше рассмотрение относится лишь к окрестности особой точки
108
ч. I. КЛАССИЧЕСКАЯ МЕХАНИКА"
прямыми, а (соприкасающимися) параболами п-го порядка; в
остальном качественный характер движений не изменится.
Если, наконец, экстремум есть точка перегиба — разложение
потенциальной энергии начинается с нечетной степени п^З —
сепаратриса будет иметь в особой точке точку возврата, и фа-
фазовые траектории расположатся так, как указано на рисунке.
Для достижения особенности по-прежнему будет требоваться
бесконечное время, и, следовательно, сепаратриса, рассматри-
рассматриваемая как фазовая траектория, будет состоять из трех само-
самостоятельных объектов.
16.3.1.2. Зная поведение фазовых траекторий вблизи особых
точек можно составить себе представление и об общем располо-
расположении траектории по всей фазовой плоскости. При этом бывает
поучительно рассматривать картицу фазовых траекторий парал-
параллельно с графиком потенциальной энергии, который служил нам
для той же цели общей классификации возможных видов дви-
движения в 9.2 — эти два изображения являются как бы двумя «ви-
«видами» (в принятой в черчении терминологии)-—сбоку и свер-
сверху— одной и той же поверхности И = Н(р, х), для полного изо-
изображения которой требовался бы пространственный «чертеж».
16. УРАВНЕНИЯ ГАМИЛЬТОНА
109
На приводимом примере мы изобразили все четыре сорта разо-
разобранных выше особенностей.
два вида поверхности энергии
16.3.1.3. В качестве еще одного примера использования картинок на фазо-
фазовой плоскости, покажем, как с их помощью решается практически вообще
без всяких интегрирований задача о движении материальной точки в цен-
центральном поле ~ —, разбиравшаяся в § 11.
Выпишем закон сохранения энергии
M2
2ц/-2
B8.3)
и перейдем в нем с помощью B8.1) от независимой переменной t к новой
независимой переменной ф — как мы то и делали в § 10:
+
м-
1^
а
г '
dr
Если заменить в нем и зависимую переменную, полагая
то мы получим
— — г2
ф|
но
ч. I. КЛАССИЧЕСКАЯ МЕХАНИКА
и еще одной — теперь лииейиой — заменой
приведем закон сохранения энергии на фазовой плоскости новых переменных
»ф, v к совершенно простому виду
где обозначено
Таким образом, кривая U(v) потенциальной энергии в новых перемен-
переменных есть парабола, а фазовые траектории на фазовой плоскости v^, v суть
окружности «радиуса» е.
Такая картина фазовых траекторий
соответствует осциллятору единичной
частоты (по отношению к «времени» ф1);
поэтому закон движения можно сразу
выписать как
о (ф) = 8 cos ф,
или, возвращаясь к переменной и, в виде
1
и (ф)
cos Ф :
М2
ца
который буквально совпадает с форму-
формулой C1) из § 11.
При ее интерпретации надо, конечно
учесть, что переменная v отличается от
координаты осциллятора в том весьма существенном смысле, что не все
ее значения допустимы. Действительно, переменная и должна была быть
существенно положительной, почему допустимые значения о ограничены не-
неравенством
кулонова фазовая плоскость
В соответствии с этим все наши фазовые траектории — окружности — разби-
разбиваются на два класса: лежащих целиком в допустимой области v, и выходя-
выходящих за ее пределы — для траекторий второго класса мы вправе рассматри-
рассматривать не всю окружность, а только ту ее часть, которая лежит в разрешеииой
фазовой полуплоскости*). При переходе к «настоящей» переменной г траек-
*) Легко убедиться, что изображающая точка не может покинуть разре-
разрешенную часть фазовой плоскости, поскольку для этого было бы потребно
бесконечное время.
16., УРАВНЕНИЯ ГАМИЛЬТОНА 11 ]
ториям первого класса будут соответствовать замкнутые кривые иа плоско-
плоскости (г, ср)—эллипсы, а траекториям второго — разомкнутые гиперболы. Легко
видеть, что критерием попадания движения в первый или второй класс яв-
является знак энергии: для Е <С 0 мы получаем эллипс, а для Ё > 0 —гипер-
—гиперболу. Граничному случаю Е = 0, когда на фазовой плоскости Оф, v окруж-
окружность касается границы разрешенной части, соответствует на «обыкновенной»
плоскости (г, <р) парабола.
16.4. Вычислим полную производную функции Гамильтона по
времени:
dH
Таким образом,
dH _ дН _ dL
dt ~ dt ~~ dt "
Значит, если функция Гамильтона не зависит от времени явно —
а в силу E2а) это равносильно тому, что не зависит от времени
явно функция Лагранжа, — то она сохраняется. Вспоминая оп-
определение (9.2) энергии системы, видим, что
если функция Гамильтона не зависит от времени явно, то ее
численное значение совпадает с энергией системы.
ЗАМЕЧАНИЕ: Оговорка «если не зависит от времени явно»
весьма существенна. В § 14 мы убедились, что для системы, на-
находящейся в зависящем от времени внешнем поле, введение по-
понятия энергии не является самоочевидным, и физически разум-
разумное определение (несохраняющейся!) энергии не совпадает
с (9.2).
Следует упомянуть, что такая неприятность с определением
физически разумной энергии может случиться и тогда, когда И
не зависит от времени явно. Именно, такое может произойти,
если используемые обобщенные координаты получены из декар-
декартовых преобразованием, зависящим от времени. Конечно, функ-
функция Я будет и в этом случае сохраняться, буде она не зависит
от времени явно, но ее значение может оказаться отличным от
того, что физически естественно называть энергией системы.
В конце этой части мы приведем пример, иллюстрирующий та-
такую ситуацию. Ее полное прояснение проистекает, парадоксаль-
парадоксальным образом, только в квантовой теории. I
16.5. Как уже подчеркивалось, гамильтонова форма теории пожалуй даже
важнее лагранжевой; поэтому вид функции Гамильтона для простейших си-
систем надо держать в памяти не менее твердо, чем вид соответствующих
функций Лагранжа. Выпишем его для важнейших частных случаев.
Если
L (q, q) - Т (q, q) - U (q),
TO
H (q, p) = Г (q, q (p, q)) + U(q) = T (q, p) + U (q).
112 ч. I. КЛАССИЧЕСКАЯ МЕХАНИКА
Если
ТО
а
Для одной материальной точки во внешнем поле
в
2т 2т
В цилиндрической системе координат, в которой
получаем для функции Гамильтона
9 О О
н- рё м Р* м р;
~2"**
Наконец, в сферических полярных координатах, когда
l^-^1+?»L»»+ mr2siф Ф2 _
функция Гамильтона имеет вид
2т ^ 2mr2 ^ 2mr2sm2'& ^
17. Вариационный принцип для уравнений Гамильтона
Уравнения движения в форме Лагранжа мы получали из
вариационного принципа, именно из требования экстремально-
экстремальности функционала
и
6S = 0; S= J dtL{q,q,t) (*)
относительно произвольных вариаций переменных qi с условием
6<7г = 0 на границах области интегрирования, т. е. независи-
независимыми считались вариации координат, а вариации скоростей
были их следствием:
bqt незав.; б#? = 0 на границах, bqi = -jjbqi.
Теперь мы хотим так преобразовать этот вариационный прин-
принцип, чтобы он непосредственно давал нам уравнения в форме
Гамильтона.
17. ВАРИАЦИОННЫЙ ПРИНЦИП ИЗ
Перейдем того ради к независимому варьированию а% н qi, и в знак
этого будем обозначать </,¦ особыми буквами vt, записывая действие в виде
S=[dtL{q, v, t).
Будем варьировать здесь н qi н vt\ чтобы так формулнруемый новый вариа-
вариационный принцип был бы равносилен старому, надо, чтобы все время выпол-
выполнялись дополнительные условия
v. = q{ или v{ — <7j = 0,
т. е. мы приходим к задаче об условном экстремуме.
По известным из вариационного нечисления правилам нахождения услов-
условного экстремума будем искать вместо него безусловный экстремум функцио-
функционала, получаемого нз первоначального добавлением дополнительных условий,
умноженных на неопределенные множители Лагранжа (которые нам будет
удобно обозначить через Pi(t)), т. е. потребуем безусловного экстремума вы-
выражения
по отношению к независимому варьированию координат qt, скоростей о* и
множителей Лагранжа pi. Вариации кординат должны обращаться в нуль на
границах; то же условие можно наложить и на вариации множителей Лаг-
Лагранжа. Итак, в (»*)
bqt, bv{, bpt независимы; б<7г=0, др( = О иа границах.
Выполняя варьирование, получаем, что
Таким образом, уравнениями Лагранжа — Эйлера будут:
dL _ .
'" дР{ с'
при б».: р.=——; B)
1 l OV.
при 6р.: о. = qv C)
Вторая группа этих уравнений объясняет, почему мы обозначали множители
Лагранжа буквами р,-.
Перейдем теперь от задачи на безусловный экстремум (**) снова к за-
задаче на условный экстремум, но с другим дополнительным условием. Именно,
выберем в качестве дополнительного условия уравнения B). Поскольку эти
условия возникли у нас в качестве множителей при бО(, то в новой задаче
скорости Vi уже не надо подвергать независимому варьированию, но следует
выразить их в виде функций q и р
»; = О, (<7> Р).
114 ч. I. КЛАССИЧЕСКАЯ МЕХАНИКА'
разрешая уравнения B) относительно »« (предположенное в § 16 отличие де-
термиианта
dv.
от нуля позволяет это сделать!). Мы приходим тогда
к вариационному принципу в форме:
6S" = 0; S"= J dt Г \L {q, v (q, p), *) - ? Pft (<!> P>1 + ? Pt4t ]. (•••>
где независимо варьируются Pi и ^j:
6G., бр. независимы; 6qi=0, 6p. = 0 на границах,
a ui суть функции от q и р.
Стоящая в (»••) в квадратных скобках величина — это как раз (взятая
с обратным знаком) функция Гамильтона H(p,q,i). Поэтому вариация функ-
функционала dS" запишется в виде
Г V Г
)dtL[
дИ (Р. ?• 0 dPil f d
dH{p,q.t) dqt
и требование 65" = 0 даст в качестве уравнений Эйлера
dq{ дН dPi дН
~W==i~dp~t ~Ж~^ dq~'
т. е. как раз уравнения Гамильтона E3).
Итак, поставленная задача выполнена, и вариационный прин-
принцип (***), приводящий непосредственно к уравнениям Гамиль-
Гамильтона, можно записать, опуская теперь штрихи, в виде
i^-H{p, q,t)) =
\tYiH{p,q,t)dt\, • E5)
где независимо варьируются
Pi и qu a 6<7; = -Ji;bqi, причем dqi = O, Sp; = O на границах,
E5а)
а интегрирование выполняется вдоль траекторий системы в фа-
фазовом пространстве.
В силу E5а) сформулированный вариационный принцип не
изменится, если добавить к подинтегральному выражению пол-
полный дифференциал произвольной функции координат и импуль-
18. СКОБКИ ПУАССОНА
сов. В частности, добавляя d (— EpiqA, этим обстоятельством
можно воспользоваться, чтобы привести E5) к другому виду:
E5')
сопоставление которого с E5) показывает, что и в вариацион-
вариационной формулировке гамильтонова формализма соблюдается пол-
полная симметрия координат и импульсов.
18. Скобки Пуассона
Механику в форме Гамильтона (часто говорят гамильтонов
формализм для механики) можно привести к очень красивому
виду, если ввести одно специальное образование, которое будет
играть в дальнейшем очень существенную роль.
18.1. Пусть / и g— две функции (какие-то) координат, им-
импульсов и времени
f = f(q,P,t) и g = g{q,p,t).
Скобкой Пуассона (СП) величин fug называется выражение:
Скобки Пуассона обладают следующими свойствами:
A) антисимметрии:
If, *) = -(*,-fM E7.1)
(отсюда, в частности, следует, что
if, f) = 0); E7.1a)
B) равенства нулю скобки с константой:
(f, с) = 0; E7.2)
C) линейности по каждому аргументу:
*) = (fi. g) + (h, g),
и аналогично для g; (в частности, отсюда получается равенство
нулю СП двух линейно зависимых величин (f, cf) = 0);
D) распределительным свойством по отношению к умножению,
аналогичным правилу Лейбница для дифференцирования произ»
ведений:
(flf2, g) = (f,, ?)f2 + fl(f2, g),
if, 8182) = (f, 8i) g2 + 8i (f, &)
\
116 ч. I. КЛАССИЧЕСКАЯ МЕХАНИКА
E) выполнением правила Лейбница для частного дифферен-
дифференцирования по времени и вообще по параметру:
( Ж)"' E7'5>
F) выполнением тождества Якоби:
if, iS. h)) + (g, (h, f)) + (ft, (f, g)) = 0. E7.6)
Первые пять свойств — тривиальны, доказательство же по-
последнего тождества довольно громоздко; поэтому мы не будем
проводить его целиком, а укажем лишь «скелетную схему» рас-
рассуждения.
Исходный пункт состоит в том наблюдении, что каждый член разверну-
развернутого выражения двойной скобки Пуассона содержит вторые производные од-
одного (и только одного) из множителей внутренней скобки. Поэтому, если же-
желать собрать все вторые производные, скажем, функции / в левой части
E7.6), то надо будет вычислять комбинацию
(g, (h, П) + (h, (I, g)),
считая при вычислении внешней скобки второй элемент внутренней скобки по-
постоянным. Это обстоятельство можно записать, отмечая не подлежащий вто-
второму дифференцированию элемент, например, чертой снизу:
(g. (A. f)) + (*. (Г.*))-
Тогда, согласно свойству C), можно будет вынести не подлежащий диф-
дифференцированию элемент за знак внешней скобки, т. е. внести операцию
{g, ...) под знак внутренней скобки. При этом, однако, первый элемент внеш-
внешней скобки (которая теперь становится внутренней) попадает под знак вну-
внутренней скобки (которая становится внешней), но не должен, конечно, этой
скобкой дифференцироваться, что и надлежит отметить нашим значком
В применении к первому члену выписанного выражения это рассуждение
выглядит как преобразование
(8. (А. П) = (*. (?, /)),
после которого этот член тождественно уничтожается со вторым в силу свой-
свойства A).
Таким образом оказывается, что все члены, содержащие вторые произ-
производные функции f, в сумме обращаются в нуль. Поскольку то же рассужде-
нне проходит и по отношению к членам левой части E7.6), содержащим вто-
вторые производные функции g или функции h, а членов без вторых производ-
производных левая часть E7.6) не содержит, то отсюда следует равенство ее нулю,
т.е. выполнение тождества E7.6).
Заметим еще, что тождество Якоби может быть интерпрети-
интерпретировано как применимость правила Лейбница при вычислении
скобки Пуассона со скобкой Пуассона
(/, (g, А)) = ((/, g), h) + (g, (f, A)). E7.6'>
18.2. Установим теперь значения некоторых важных специ-
специальных скобок Пуассона. Прежде всего
(f'^—Щ и </.Р<>~ ^. E8)
18. СКОБКИ ПУАССОНЖ \\Т
Затем, еще более специальные скобки,
(<7ь<7/) = 0; (pi><7/) = 6«/; (pt,Pi) = O- (Щ
18.3. Эти специальные значения сразу подсказывают нам, как"
использовать скобки Пуассона для усовершенствования записи
гамильтонова формализма.
18.3.1. В самом деле, с помощью E8) уравнения Гамильтона
E3) принимают вид
<7< = (Я, <?;); Р1 = (Н,р{), E3а>
замечательный симметрией, с которой в него входят координаты
и импульсы. Однако в действительности эта симметрия еще
шире.
18.3.2. В самом деле, возьмем любую динамическую вели-
величину— т. е. любую функцию f координат, импульсов и времени —
и вычислим ее полную производную по времени:
dt ~ dt ^ Li dqt 4l ^ L, dp{ Pi dt TL^(j( dp{ 6pt dqj'
Сумма в правой части — это как раз скобка Пуассона.
Таким образом, для любой динамической величины /:
¦7t=Jt+(H>f) F0>
— полная производная по времени равна частной производной
плюс скобка Пуассона функции Гамильтона с этой величиной.
Если же, в частности, динамическая величина / не зависит
от времени явно, то
-57 = (Я, f), если -|- = 0, F0а)
ее полная производная по времени равняется скобке Пуассона
функции Гамильтона с ней.
Уравнения F0) представляют собой замечательно компакт-
компактную и симметричную форму записи всей механики. Сами урав-
уравнения Гамильтона (в форме E3а)) получаются теперь из F0)
в качестве частного случая.
18.4. Однако формализм скобок Пуассона позволяет не толь-
ко элегантно записать уравнения механики, но и выписать их
общее решение, конечно в виде разложения в ряд, параметром
малости которого является время, протекшее с начала движе-
движения. Чтобы показать это, ограничимся сперва случаем, когда
функция Гамильтона не зависит от времени явно, и будем ис-
искать зависимость от времени произвольной динамической пере-
переменной f(p, q), также не зависящей явно от времени, т. е. опи-
описываемой уравнением движения F0а).
118 я. I. КЛАССИЧЕСКАЯ МЕХАНИКА!
Перепишем это уравнение в интегральном виде
t
f (р (t), q (t)) ^f(t) = f (to) + J df (H (f), f (f)), F0b)
и будем решать его итерациями, считая интегральный член ма-
малым. Для нулевой итерации получим, полностью пренебрегая
интегральным членом,
fo. @)
Чтобы найти первую итерацию, заменим стоящую под интегра-
интегралом скобку Пуассона ее нулевой итерацией
что приведет нас к
t
П @ = f Со) + S df (H (t0), f (/о)) = U + (t - to) (//о, fo). A)
Продолжая этот процесс, получим для второй итерации f
h (t) = U + (t - t0) (Я0) f0) + -%¦«- to? (Ho, (#o, f)). B)
^Мы воспользовались здесь при нахождении первой итерации
скобки Пуассона тем, что, согласно E9), у нас H(t')—H(to)
и так далее.)
Таким образом мы приходим для зависимости / от времени,
т. е. для движения, к разложению
to)H0, fo)M-^{{t-to)Ho,((t-to)Ho, fo))+..., F0c)
о сходимости которого, конечно, нельзя сделать общих утверж-
утверждений. Тем не менее это формальное решение основной задачи
механики оказывается очень полезным в различных случаях.
18.5. В общем случае, когда как гамильтониан Н —
— H(p(t), q(t), t), так и рассматриваемая динамическая пере-
переменная f(p(t), q(t), t) могут зависеть от времени явно, тре-
требуются заметно более громоздкие и тонкие рассуждения.
18.5.1. Уравнение движения F0) для зависящей явно от времени дина-
динамической переменной f[p(t), q(i)', i] гласит
df [p {t),j (t); t] _ {H [p {tl q (<); t]> f {p {tl q (f); (])p (<) qit)+M.t F0)
где мы прибегли к более подробной записи, в которой отмечено, по каким
переменным вычисляется скобка Пуассоиа; ниже мы будем отмечать это —
привносящее с собой основные осложнения — обстоятельство просто индек-
индексом t. Как и в рассмотренном выше случае, его можно переписать в инте-
интегральной форме, что, однако, несколько осложнено двойной зависимостью —
18. СКОБКИ ПУАССОНА Ц91
неявной и явной — / от t. Поэтому мы расцепим эти две зависимости и вве-
введем в рассмотрение динамическую переменную f, у которой неявное и явное-
времена различны:
f\p{t),q(t);T]^f(t;r),
установив заодно сокращенное обозначение. Ясно, что
~di -^I'-'nfttjb dx = ^ ,
где вторая производная определяется явной зависимостью f от времени и ие
имеет отношения к динамике.
18.5.2. Первое же уравнение приводится к интегральной форме сразу:
t
! (/; т) = / (t0; х) + J dt' (H (/'; Г), f (/'; %))t,. F0b'>
Мы видим, что под интегралом складываются скобки Пуассона, вычисляемые-
по разным переменным. Поэтому, если принять, как и в предыдущем рассу-
рассуждении, что произведение (t— k)H содержит в себе параметр малости и ис-
искать / в виде ряда итераций
/ (/; т) = /@) (t; х) + f{l) (/; т) + fB) (/; т) + ....
то просто найдутся только нулевая итерация
и первая
f"> (/; т) = J dt' (H {t0; П f №, x))tt. (V)
Прямое вычисление всех следующих итераций потребовало бы преобразования
скобок Пуассона от одних переменных к другим, а этого мы как раз и хотим
избежать, ибо пока не умеем это делать.
18.5.3. Вместо этого займемся обещанными нагромождениями, и введем,
динамические переменные, зависящие от нескольких явных времен /(/; п, ...
..., Тщ). Конкретно нам понадобятся из величин такого рода т-кратные
мультискобки Пуассона:
Mm(t;t' *<т);т.) =
= U(ft *(m>), (Я (/; /&-»>), .... (H(t; f). fit; x))t ...),)
(аргумент т мы будем при ненадобности опускать). Легко видеть, что инте-
интегральные уравнения движения для этих мультнскобок будут иметь вид:
*„(/;/', ...,»<¦»>) ~Af„(<„;/' *"">) +
t
<+i)Ui+1h f
Заметим теперь, что в определении Mm уже имеется m-кратная малость
(в дальнейшем войдут лишь интегралы от них по всем явным временам по-
областям, меньшим / — to); поэтому итерационный ряд для Мт будет начи-
начинаться с ш-го члена, именно:
= О для k<m; М™ Ц; f, ..., <(m)) = Мт (t0; f. ....
120 ч. I. КЛАССИЧЕСКАЯ МЕХАНИКА' .
18.5.4. Мы, конечно, не случайно построили последовательность перемен-
переменных М. С их помощью основное уравнение F0b') преобразуется к виду
t
fV; г)-/(/0;т)+ J Л'А1, (/';/'; т),
аналогичному интегральным уравнениям для Мт, если ввести естественное
теперь обозначение f{t;x) =M0(t,t). Мы видим, что каждая следующая
переменная Mm+i есть подинтегральное выражение в правой части уравнения
для предыдущей Мт, причем последовательность начинается с Mo = f.
Такая цепочка уравнений очень удобна для решения по теории возмуще-
лий. Для приближения порядка п>0 в основном уравнении для / мы имеем
i
/(«) (t; т) =» J dt'M[n) (t'\ t'; т).
Далее, последовательно,
v t' f
M[n)(t'; П = \ dt"Mf\t"; f, t") = \ dt" \ dt'"M^(t'"; t', t", <"')=¦
t> t(n-\)
U U
Ho Af^'('*"'; ...) = Af„ (<0; ...), а для следующих Мт с т > ге и-е прибли-
приближение равно нулю. Таким образом построенная цепочка уравнений обры-
обрывается, и мы получаем явное выражение re-го приближения для динамической
переменной f(t; т)
fn) (t; т) = \ dt' ... ^ dtM • Мп (fa f №; т).
18.5.4.1. Теперь становится ясной суть той хитрости, к которой мы при-
<бегли. Вместо того чтобы находить старшие приближения для интересующей
нас динамической переменной f, непосредственно решая уравнение F0Ь'), мы
построили такую последовательность новых динамических переменных, что
приближение каждого порядка к / выражается через младшее неисчезающее
приближение переменной того же номера. Для вычисления же последнего
нужны лишь скобки Пуассона по координатам и импульсам в один момент
"времени to — тем самым удалось избежать пугавшего нас преобразования
скобок от одних переменных к другим.
18.5.5. Вспоминая теперь определение переменных Мт, можем выписать
»есь ряд для интересующей нас f(t) (и, кстати, положить в ием t = т)
/@= \
n-0 U
tin-1)
J (t0; <<">), (Я (fa <<*-')), ... (ff(/„ П f(t0;
n раз
18. СКОБКИ ПУАССОНА 12Г
Мы видим, что все динамические переменные р и q во всех стоящих под ин-
интегралом гамильтонианах, равно как и в /(/о; t), берутся в этом разложении
в начальный момент времени to, по тем же самым переменным вычисляются
и все скобки Пуассона. Таким образом найденная формула действительно-
дает явное решение уравнений движения.
18.5.6. Принято считать, что мы получаем эстетическое преи-
преимущество, если выражаем в этой формуле пределы интегрирова-
интегрирования с помощью ¦б-функций и относим их к подинтегральному
выражению, т. е. пишем
= Z \ dt' '' • dt(n) • * С — О * С - И ¦ ¦ • * tf("~" - iw) X
F0с0
(в аргументах всех гамильтонианов стоят p(t0), q(t0), в смысле
тех же переменных берутся все скобки Пуассона). Все подин-
тегральное выражение здесь называют запаздывающеймульти-
скобкой Пуассона.
Если явная зависимость от времени и у f и у гамильтониана
отсутствует, то это выражение должно переходить в F0с). Легка
видеть, что это в самом деле так — мультискобку Пуассона
можно вывести тогда из-под знака интеграла, и оставшийся ин-
интеграл по ««-мерному треугольнику» даст как раз стоящую в.
F0с) м-ю степень (t — /0), деленную на п\.
18.6. Итак, мы познакомились с одним из плодотворных при-
применений понятия пуассоновых скобок. Другое важное примене-
применение скобок Пуассона открывается тем обстоятельством, что
скобки Пуассона являются эффективным инструментом образо-
образования одних динамических переменных из других.
18.6.1. С этой точки зрения важно найти полную производную-
по времени от скобки Пуассона. Имеем последовательно
+ ((Я, f), g) + (f, (Я, g)) = (|f + (Я, f), g) + (f, -|f + (Я, g)),
т. е. для взятия полной производной по времени от скобки Пуас-
Пуассона применимо то же правило Лейбница
что и для частного дифференцирования (свойство E)),
122 ч. I. КЛАССИЧЕСКАЯ МЕХАНИКА
18.6.2. Если, в частности, обе рассматриваемые динамические
величины I и g суть интегралы движения, -J- = Q, -^- = 0, то и
величина (/, g) будет интегралом движения:
(f, g) = const, если /== const и g — const. F1 a)
Последнее утверждение носит название теоремы Пуассона.
18.6.3. Теорема Пуассона может иногда дать возможность
найти новые интегралы движения. Именно, если мы уже знаем
несколько (>1) интегралов движения системы, то, вычисляя их
•скобки Пуассона, мы опять получим по F1а) интегралы движе-
движения. Может, конечно, случиться, что так вычисленные интегралы
движения окажутся функциями уже известных, или тождест-
тождественно обратятся в нуль — такие случаи не представляют инте-
интереса. Но возможен и третий случай, когда скобка Пуассона ока-
окажется существенно новым интегралом движения.
18.7. Напомним, что для замкнутой системы имеют место
¦семь законов сохранения: законы сохранения энергии, трех ком-
компонент импульса и трех компонент момента,
Е, Р и М.
Для системы, находящейся во внешнем поле, их будет мень-
меньше (или вообще не будет). Теорема Пуассона позволяет легко
установить, какие именно комбинации компонент импульса и
момента могут сохраняться одновременно.
18.7.1. Чтобы выяснить это, найдем скобки Пуассона компо-
компонент импульса и момента. Будем, для простоты вычисления,
считать, что система материальных точек описывается декарто-
декартовыми координатами, и, следовательно,
P = Zpa; М = Ц[га-ра] или Afa = ea(lVv- "
а
Тогда сразу ясно, что
(/»„, Рр) = 0. . F2.1)
18.7.2. Вычисляя теперь скобку Пуассона компонент момента
и импульса, получим последовательно*)
а
еацу 2] @ —
*) При проведении подобных выкладок сперва появляются три суммы по
частицам ?, У\ У*. • • • > первая из которых возникает из первого элемента
a b с
скобки Пуассона, третья — нз второго, а вторая — из суммирования в опреде-
определении скобки. В силу аддитивности импульса и момента, однако, при выпол-
выполнении предписываемых E6) дифференцирований возникают б„ь и бьс. по-
поэтому всюду остается только по одной сумме.
18. СКОБКИ ПУАССОНА 12?
Таким образом скобка Пуассона компонент момента и импульса
дает нам другую компоненту импульса, номер которой опреде-
определяется антикруговой перестановкой
(Ма, Pp) = -eaf3YPY. F2.2)
18.7.3. Несколько более громоздко проходит вычисление скоб-
скобки Пуассона двух компонент момента:
Маа Ша* дМ*а дМа»\
у
дгау дгау драу ) i-t дра„ дгау
а
vfivy6pyPaa = (?(ацуе31 V» ?_, Га»Раа ~ •••
a>
~ e|anve3| pa
a
Заметим теперь, что
где первое произведение б-символов обратится в нуль при антисимметрирова-
антисимметрировании по а и р. Поэтому, продолжая цепочку равенств, можем написать, вы-
выполняя антисимметрирование въявь,
• • • — — (*ац5Cа — 6аа^йц) 2j гацРаа = — ^аррвцар 2j raiiPao = ~ еаррМр.
а а
Итак, скобка Пуассона двух компонент момента дает нам era
третью компоненту, причем знак опять определяется правилом
антикруговой перестановки:
(Ма, VW3) = -ea3YyWY. F2.3>
Формулы F2) содержат ответ на поставленный вопрос о воз-
возможных комбинациях сохраняющихся величин. Из них видно,
что если сохраняются две разные компоненты момента, то обя-
обязательно будет сохраняться и третья; если сохраняется весь мо-
момент и одна составляющая импульса, то сохраняется и весь им-
импульс; если сохраняется одна компонента импульса и одна пер-
перпендикулярная ей составляющая момента, то будет сохраняться
и другая составляющая импульса, перпендикулярная сохраняю-
сохраняющейся компоненте момента.
18.8. Однако действительное значение этих формул гораздо-
больше. Вспомним, что возникновение законов сохранения было
следствием инвариантности описания изучаемой системы отно-
относительно тех или иных преобразований из группы движений
трехмерного пространства. Поэтому на самом деле соотношения
F2) не связаны с конкретными свойствами рассматриваемой
системы, а выражают собой структуру самой группы трехмер-
трехмерных движений.
18.8.1. В этой связи весьма поучительно вычислить скобки
Пуассона полных импульса Р и момента М с координатой а-к
частицы ra и ее импульсом ра. Удобнее при этом взять не сами
124 ч. I. КЛАССИЧЕСКАЯ МЕХАНИКА'
Р и М, а их скалярные произведения а • Р и 6ф • WI с беско-
бесконечно малыми постоянными векторами а и бф.Имеем:
(a.P,ra)=>;(^f--^.f4 = a
opj оть оть ay
b. с "
и аналогично для импульса:
g(a-P) дра _Q
EФ • М, р.) - -
&, с Ь
18.8.2. Легко видеть, что в правых частях этих равенств у нас
получились как раз изменения координат и импульсов отдель-
отдельных материальных точек при бесконечно-малых сдвигах и пово-
поворотах. (Ср. замечания в 6.4 перед формулой A8).). По-
Поэтому, если прочесть их справа налево, то эти равенства будут
товорить нам, что изменения как координат, так и импульсов
частиц при бесконечно малых сдвигах и поворотах выражаются
скобками Пуассона с величинами (а • Р) и Fф • М), соответст-
соответственно,
баг6=(а-Р,г&); бар6 = (а.Р, р„), F3.1)
В дополнение к этим соотношениям можно выписать еще и
изменения при бесконечно-малом временном сдвиге на т, кото-
которые получаются из уравнений Гамильтона в форме E3а):
6*ь = (тН,ть) и бгРь = (тЯ, р6). F3.3)
18.8.3. В чем преимущество новой формы F3) для бесконечно
малых изменений координат и импульсов при движениях по
сравнению с выписывавшимися в § 6 явными выражениями? Оно
той же природы, что преимущество формы E3а) для уравнений
Гамильтона: как легко сообразить, рассуждения, совершенно
аналогичные приведшим нас от E3а) к F0), ведут от выраже-
выражений F3) для декартовых координат и импульсов к в точности
таким же выражениям для изменений при бесконечно-малых
движениях для любой динамической переменной, не зависящей
явно от координат или углов.
Можно сказать, что бесконечно малая динамическая пере-
переменная
6G = a-P + 6v./ft F4)
18. СКОБКИ ПУАССОНА 125
осуществляет по закону
S/ = (SG, f) F3a)
преобразование любой другой динамической переменной /, вы-
вызываемое сдвигом пространства на а и поворотом на бф, точно
так же, как функция Гамильтона И осуществляет преобразо-
преобразование, вызванное сдвигом по времени, т. е. движение.
18.8.3.1. В частности, из общей формулы F3а) можно теперь сразу полу-
получить все правила, которые мы выводили в § 6 для преобразования полных
импульсов и момента при сдвигах и вращениях. Например, при сдвиге, когда
6ф = 0,
ЬМа — ар (Рр, Ма) = ареаруРу, т. е. 6М = [а • Р] и т. п.
18.8.4. Рассмотрим теперь две величины F4) 8Gt и 6G2, отличающиеся
значениями параметров а и 6ф, которые соответственно осуществляют два
преобразования динамических переменных, 7\ и 7V
Применим к системе сперва преобразование Ти а потом — Т2. Существенно
не упустить, что преобразование Ti преобразует все динамические величины
системы, в том числе и величину 6G2:
r,6G2 = 6G2 + FGb 6G2).
Поэтому результатом применения к некоторой величине / двух преобразова-
преобразований, сперва Т\, а потом Т2, будет
T*TJ = / + FGb f) + FG2 + FGb 6G2), f + FG,, {)) =
= f + (SGb /) + FG2, f) + FG2, FG,, f)) + (FG,, «G2), f) =
= / + «.f + 62f + FGb FG2, f)) = A + 6, + 62 + 626,) /.
Применение же тех же самых двух преобразований в обратном порядке даст
нам
Г,7У = f + 62/ + 6,/ + FG2, FG,, /)).
Вычитая эти результаты друг из друга, мы получим, что
{T2T, - TJ2) f = FGb FG2, /)) - FG2, FG,, f)),
то есть, что
(T2Ti - TXT2) f = (FGb 6G2), f). (C4a)
Но такая разность двух пар последовательных преобразований пространства,
выполненных в разном порядке, должна опять быть движением в трехмерном
пространстве, которому должна соответствовать своя динамическая перемен-
переменная 6Оз, осуществляющая преобразование всех динамических переменных по
общему правилу F3а). Значения параметров а3 и 6ф3 этой динамической пе-
переменной должны выражаться через параметры а!, бф, и а2, 6qp2 двух перво-
первоначальных движений, и притом чисто геометрическим образом, совершенно
независимым от природы динамической системы, которой мы интересуемся.
Сравнение этого замечания с формулой F4а) показывает, что полученный
в 18.7 вывод, что скобки Пуассона компонент импульса и момента выра-
выражаются через них самих, можно было предсказать заранее, и что значения
коэффициентов могут зависеть только от природы группы трехмерных враще-
вращений. Их называют структурными константами этой группы.
126 ч. I. КЛАССИЧЕСКАЯ МЕХАНИКА
19. Канонические преобразования
19.1. Общая форма B) лагранжевых уравнений движения,
согласно замечанию 4 в § 3, не менялась при любом переходе от
одних обобщенных координат к другим, т. е. при произвольном
(но разумеется — невырожденном) преобразовании вида
Ясно, что то же должно быть справедливым и для уравнений
Гамильтона E3). Оказывается, однако, что последние уравне-
уравнения инвариантны и относительно более широкого класса преоб-
преобразований, именно, относительно некоторых (но не всех!) пре-
преобразований, перемешивающих координаты и импульсы.
Введем новые координаты и новые импульсы
Qi = Qt (q, Р, t); Pi = Pi (q, P, t) F5)
как (пока — произвольные, с единственным условием обрати-
обратимости:
, Qn, Рь •¦-, Рп
функции старых координат, старых импульсов и (вообще го-
говоря) времени.
Если такое преобразование сохраняет форму E3) уравнений
Гамильтона, то оно называется каноническим преобразованием.
19.2.1. Чтобы выделить канонические преобразования из всех
преобразований F5), естественно обратиться к вариационному
принципу E5), из которого непосредственнЪ получались урав-
уравнения Гамильтона —каноническими будут те из преобразований
F5), для которых действие, выраженное через новые перемен-
переменные, сохраняет форму E5), т. е. для которых
S=\r?jPidQi-H'{P,Q,t)dt\.
ЗАМЕЧАНИЕ: Выражаясь более точно, для сохранения формы
уравнений Эйлера требуется инвариантность не самого функцио-
функционала E5), а только его вариаций. Поэтому, — если, как то имеет
место в нашем вариационном принципе E5), независимые ва-
вариации обращаются в нуль на границе области интегрирова-
интегрирования,— подинтегральные выражения в старых и новых перемен-
19. КАНОНИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ 127
ных вполне могут отличаться на полный дифференциал любой
функции координат, импульсов и времени*). |
19.2.2. Таким образом, достаточное условие каноничности
преобразования F5) можно записать как
или же в виде требования
df = Zpi dqL - ? Р, dQi + (Я' - Я) dt, F6)
чтобы стоящая в левой части комбинация образовывала бы пол-'
ный дифференциал некоторой функции /. Функция f есть функ-
функция 2/г переменных (кроме времени); в качестве этих ее аргу-
аргументов можно выбрать любую группу 2м независимых величин
из числа 4/г переменных qit p{, Qt и Pi. Однако из F6) видно,
что если выразить / (с помощью F5)) как функцию старых и
новых координат qt и Q,-, то она окажется по отношению к этим
переменным производящей функцией для преобразования Ле-
жандра от {qu Q,} к {pit Pi}. Таким образом условием канонич-
каноничности преобразования F5) от старых координат и импульсов к
новым координатам и импульсам,
оказывается то требование, чтобы переход от старых и новых
координат к старым и новым импульсам,
был бы преобразованием Лежандра.
Производящая функция этого преобразования Лежандра
f(q, Q, t) называется производящей функцией канонического
преобразования F5).
19.2.3. Как и для всякого преобразования Лежандра, новые
и старые переменные связаны с производящей функцией соот-
соотношениями
Pi- ц , Pi "-щ1 , H—H + -^, F7)
*) Это замечание совершенно аналогично отмеченной в замечании 4
к принципу наименьшего действия в § 3 возможности добавлять к функции
Лагранжа полную производную любой функции координат (и времени)
"/77 f (if 0' Стоит обратить внимание иа то обстоятельство, что такое пре-
преобразование индуцирует в гамильтоиовом формализме (не самое общее) пре-
преобразование
типа F5).
128 ч. I. КЛАССИЧЕСКАЯ МЕХАНИКА
в понимании которых возможны две точки зрения: или можно
считать заданными явно выражающие преобразование формулы
F5) (или хотя бы часть из них) и искать производящую функ-
функцию, или же считать заданной производящую функцию и полу-
получать из F7) выражающие каноническое преобразование фор-
формулы F5).
19.2.4. Если стоять на первой точке зрения, то, прежде всего,
надо выразить из уравнений F5.1) старые импульсы /?,• в виде
функций pi = pi(qj, Qj, t) старых и новых координат (и вре-
времени). Условием возможности этого является отличие от нуля
'функционального детерминанта
д«?ь •¦-, Qn) . 0
Если это условие не выполнено, то производящей функции по
отношению к старым и новым координатам не существует, что,
однако, еще не означает, что соответствующее преобразование
не может быть каноническим.
19.2.5. Действительно, из § 17 мы знаем, что формулировка
вариационного принципа для каждой совокупности перемен-
переменных— новых или старых — допускает произвол, связанный с до-
добавлением полного дифференциала и позволяющий преобразо-
преобразовывать функционал E5) к виду E5'). Если воспользоваться
этим произволом, скажем, для новых переменных, то к правой
части F6) добавится d X QiPt, и мы придем к другому доста-
достаточному условию каноничности преобразования F5)
<*Ф = Е Pi dqt + Z Qi dP{ + (Я' - Я) dt F6a)
с другой производящей функцией ср. Если выбрать в качестве ар-
аргументов ф старые координаты и новые импульсы, полагая
Ф = ф (q, P, t), .
то F6а) будет утверждать, что преобразование F5) окажется
каноническим, коль скоро переход от старых координат и новых
импульсов к новым координатам и старым импульсам есть пре-
преобразование Лежандра, и приведет вместо F7) к соотношениям
pt = Ql.= ^ H>=H+<*L. F7a)
Для нахождения производящей функции по заданным связям
F5) теперь надо будет находить р^ = pi(q, P, t), разрешая вто-
вторую группу F5) относительно старых импульсов, условием воз-
возможности чего теперь будет отличие от нуля якобиана
д{Р 'Рп)ф0. F8а)
d(Pi Рп)
19. КАНОНИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ 129
19.2.5.1. Отмеченным произволом в формулировке вариацион-
вариационного принципа можно воспользоваться не только для новых пе-
переменных, но и для старых. Кроме того, этот произвол можно
эксплуатировать независимо для каждой степени свободы — для
каждой степени свободы можно произвольным образом выби-
выбирать в качестве аргументов производящей функции одну ста-
старую и одну новую переменную, каждая из которых может быть
либо координатой, либо импульсом. Соответственно будет варьи-
варьироваться и вид выражающего разрешимость якобиана, и хотя
бы один из них будет отличен от нуля — иначе обратился бы
в нуль полный якобиан всего преобразования F5.3).
19.2.5.2. ЗАМЕЧАНИЕ: На самом деле,- только что обсуждавшееся за-
затруднение вообще не является существенным. Практически, если якобиан F8)
обращается в нуль, то оказывается возможным рассмотреть вместо одного
преобразования некоторое семейство, зависящее от параметра, такое, что F8)
обращается в нуль только для некоторого критического значения этого пара-
параметра— тогда окончательные формулы для критического значения параметра
можно восстановить по непрерывности. |
Поясним сказанное
ПРИМЕРОМ: Пусть система имеет одну степень свободы и преобразование
E) не меняет координату: Q = q. Это уравнение совсем не содержит им-
импульса, почему его, очевидно, и нельзя разрешить относительно р.
Построим, однако, семейство преобразований, имеющих вид поворота на
угол а в фазовом пространстве:
Q = cos а • q + sin а • р; Р = — sin а • q + cos а • р.
Тогда из F5.1)
Q cos a д! (q, Q)
sin а sin а dq
Интегрируя по q, находим
, / - ~s Qq cos а о2 , , , Л.
где произвольная /i(Q)—постоянная интегрирования. Тогда из F7.2)'новый
импульс будет равен
dQ~ sin a '< K4)t
а из обоих уравнений F5) —
cos2a , cosa 1 cosa .
Я = — sin a ¦ о ; q -\ : Q = : q A Q.
4 sin a 4 sin a ^ sin a 4 sin a 4
Приравнивая эти два выражения, найдем, что
fin)- cosa о f in) cosa Q2
' >(W) ~ sin a У> ' i W} ~ sin a 2 '
и, следовательно,
f(q,Q)~- cosaV-2gQ + Q»
V4 ^' 2 sin a
Ъ Б. В. Медведев
130 ч. I. КЛАССИЧЕСКАЯ МЕХАНИКА
Для а = 0 это выражение, конечно, расходится, но все остальные формулы
сохраняют смысл. Q
19.2.6. Более существенно другое обстоятельство — наудачу
взятое преобразование F5), вообще говоря, не будет канониче-
каноническим, т. е. для него нельзя будет подобрать никакой функции /,
полным дифференциалом которой стала бы правая часть F6).
Действительно, производящая функция находится, как было про-
продемонстрировано на примере, интегрированием уравнений F7.1),
которое в случае более чем одной степени свободы, вообще го-
говоря, невозможно, так как уравнения не обязаны быть совмест-
совместными. Далее возникающие при интегрировании произвольные
функции от Qi, вообще говоря, нельзя подобрать так, чтобы
удовлетворить уравнениям F5.2). Эти трудности не меняются
при переходе к другой форме вариационного принципа. Поэтому,
если стоять на той точке зрения, что исходными являются пре-
преобразования F5), то только в виде исключения можно найти ка-
каноническое преобразование, общим же результатом не слишком
краткого исследования будет тот вывод, что заданное преобразо-
преобразование неканонично.
19.3. Другой подход к соотношениям F7) состоит, как уже
упоминалось, в том, чтобы считать заданной производящую
функцию f(q, Q, t). Тогда, разрешая F7.1) относительно Qj, мы
получим F5.1) и, подставляя найденные зависимости в F7.2),
найдем выражения F5.2) для новых импульсов.
Неудобство этого подхода состоит в том, что из-за условия
F8) ограничиться лишь рассмотрением производящих функций
вида f(q, Q, t) нельзя — мы не получим при этом всех канониче-
канонических преобразований. Если же ввести в рассмотрение обсуждав-
обсуждавшиеся выше производящие функции от любых комбинаций ста-
старых и новых переменных, то, как можно показать, мы действи-
действительно получим все канонические преобразования. Однако при
этом каждое преобразование встретится нам по многу раз, воз-
возникая из разных производящих функций.
Другое, менее принципиальное неудобство состоит в том, что
при таком подходе трудно догадаться, какую производящую
функцию нужно брать, чтобы получить каноническое преобразо-
преобразование желательной формы.
19.4. Поэтому иногда оказывается удобел несколько иной
подход, не использующий вовсе производящих функций.
19.4.1. Рассмотрим снова все преобразования вида F5) и вы-
выделим из них специальный класс таких преобразований, кото-
которые оставляют скобки Пуассона инвариантными:
(t, g)pq = Kt, g)pq Для любых функций f и g. F9)
19. КАНОНИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ 131
19.4.2. Займемся левой частью этого равенства и преобразуем ее так,
чтобы ввести промежуточные дифференцирования по новым импульсам и ко-
координатам:
и
t dqt
dqt dpj
m , - P, <>Pi Щ dPi)\dPl dq. -r dQt
df dPj dj dQj \ / dg dPt dg dQi
)P, dq, dQ, dq- J\dP, dpl dQ, dp.
de dQl\--
n n
it
В третьем члене здесь удобно поменять индексы /' и I, а затем воспользо-
воспользоваться свойством антисимметрии скобок Пуассона:
"Wi ~дР7(Q/> Pl)pq=~Zw4"{Р}' Qt)pq
Wi 7
11 И
— тогда становится ясным, что если скобки Пуассона новых им-
импульсов и координат, вычисленные по отношению к старым, суть
(Pi, Pi)n = (Qi, Q«)w = 0, (Ph Qi)pq = bn, G0)
TO
т. е. равенства G0) составляют достаточное условие того, чтобы
преобразование F5) относилось бы к специальному классу,
удовлетворяющему F9).
19.4.3. Легко видеть, что это условие является и необходи-
необходимым— для этого надо только подставить в F9) последовательно
в качестве / и g все пары Pj, Pi, Qj, Qr, P$, Qi и вспомнить, что
скобки Пуассона всякого набора импульсов и координат, вычис-
вычисленные по отношению к ним самим, имеют (см. E9)) как раз
форму G0).
Итак, характерным признаком специального класса преобра-
преобразований F5), сохраняющих скобки Пуассона, является выпол-
выполнение условий G0), которое легко проверяется для всякого кон-
конкретного преобразования.
19.5; Покажем, что этот класс преобразований, сохраняющих
скобки Пуассона, совпадает с введенным выше классом канони-
канонических преобразований. Рассмотрим сперва преобразования F5),
не содержащие времени, и удовлетворяющие условиям G0).
5*
132 ч. I. КЛАССИЧЕСКАЯ МЕХАНИКА1
Тогда для новых координат и импульсов их производные по вре-
времени будут, по общей формуле F0а) равняться
Qt = (H, Q,)M = {H, Qt)PQ= дН?\ Q) ,
Pi = (Я, Pt)Pq = (Я, Pt)PQ = - дН?®
PQ ?
— т. е. для новых координат и импульсов будут выполняться
уравнения Гамильтона E3), и, следовательно, рассматриваемое
преобразование будет каноническим.
Пусть теперь (сохраняющее скобки Пуассона!) преобразова-
преобразование F5) содержит время. Повторяя предыдущую выкладку, по-
получаем
Если можно построить такую новую функцию Гамильтона
Н'(Р, Q, 0, что
/ая'ч _ (МЛ 4- ( dQi)
\ dPi )pqt V. dPi Jpqt \ dt ) pq
i) :
то уравнения движения для новых координат и импульсов опять
примут гамильтонову форму
Qi = (H',Qi), Pi = {H',Pi),
т. е. рассматриваемое преобразование опять окажется канони-
каноническим.
Естественно, что уравнения G1) только тогда, действительно
определяют новую Н'{Р, Q, t), когда будут выполнены соответ-
соответствующие условия интегрируемости. Однако тут можно пока-
показать—мы не будем проводить этой довольно громоздкой, хотя
и совершенно прямолинейно идущей выкладки, — что условиями
интегрируемости уравнений G1) будут как раз равенства G0),
необходимые и достаточные, чтобы рассматриваемое преобра-
преобразование сохраняло бы скобки Пуассона.
Таким образом, всякое преобразование F5), сохраняющее
скобки Пуассона, есть каноническое преобразование. Справед-
Справедливо и обратное утверждение, которое мы опять-таки не будем
доказывать.
Итак, мы видим, что формализм скобок Пуассона предостав-
предоставляет нам простой критерий G0), позволяющий сразу выяснить,
19. КАНОНИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ 133
является ли преобразование вида F5) каноническим или нет.
Оказывается, однако, что из этого формализма можно извлечь и
большую пользу, именно, построить способ записи канонических
преобразований, альтернативный методу производящих функций.
19.6. Чтобы показать это, нам придется установить несколько
дополнительных свойств скобок Пуассона. Выберем некоторую
динамическую переменную (т. е. функцию координат, импульсов
и, быть может, времени) К, которую будем считать на протя-
протяжении следующих рассуждений фиксированной. Для всякой дру-
другой динамической переменной / = f{p, q, t) определим преобра-
преобразованную с помощью К динамическую переменную f по правилу
= ? -jj- (/С, (/С, .... (К, f)...)) = fi«- - f G2)
n=0 /t раз
(последнее выражение в цепочке равенств есть просто символи-
символическая запись предыдущего ряда).
Тогда
если fug — преобразованные с помощью К динамические переменные
/ и g,
J "f + {к. п + -^-(к. (к. т + •••.
g — g + (К, g) + -rjr (К. СС. ff)) + • • •.
то все алгебраические связи между / и g остаются неизменными:
G3)
C) G?*) = (f, g) + (/С, (/, г)) + ^г (/С, (/С, (f, в))) + • • ¦ = 0, g).
B) fg^Jg + (/С, te) + ^j- (/С, (/С, fg)) + ... =fg,
2!
ДОКАЗАТЕЛЬСТВО: A) тривиально.
B) Перемибжая разложения для J и §, получаем
f §=fg + (K.f)g+f (к, в) + -jj- w> w. /
H
134 я. I. КЛАССИЧЕСКАЯ МЕХАНИКА
С другой стороны преобразуем разложение для fg с помощью распредели
тельного свойства СП E7.4):
(К, fg) — (K,f)e + f W> e)>
у (К, (К, fg)) = у (К, {(К, f)g + f (К, g)}) =
= у {(К, (К, f)) g + {К, f) (К, 8) + (К, П (К, g) + f (К, (К, в))}.
после чего видим, что младшие члены обеих частей G3.2) соответственно
совпадают. Далее доказательство.легко может быть продолжено по индукции.
C) Заметим, что тождество Якоби в форме
(/. (ft. ?*)) = ((>г. gi). 82) + (ft, (h ft)) E7.6')
алгебраически изоморфно распределительному свойству E7.4) по отношению
к умножению. Поэтому доказательство C) изоморфно доказательству B). Д .
ЗАМЕЧАНИЕ: Именно такая форма тождества Якоби обычно удобна в при-
приложениях, я
СЛЕДСТВИЕ 1: Если СП динамических переменных / и g есть константа,
(f. g) = С,
то она ие меняется при преобразовании с помощью К (любого!),
0. i) = (f,g).
В самом деле, по C)
(/. е) = (П) = (/, е) + (К, (/, *))+...= (/, 8),
поскольку СП любого К с константой тождественно равны нулю. |
СЛЕДСТВИЕ 2: Скобки Пуассоиа преобразованных с помощью К координат
и импульсов qt и pi (взятые относительно непреобразованных координат и
импульсов) сохраняют свои значения E9). |
СЛЕДСТВИЕ 3: Преобразование с помощью К G2) в применении к коорди-
координатам и импульсам
Q,-?, = *, + (*.ffi) + yr(*. (K'Qt))+ •••>
, G4)
pi - Pi = Pt + (*. Pi) + if (^ (*. p,)) + • • •
осуществляет над ними преобразовние F5), сохраняющее скобки Пуассона,
т. е. каноническое преобразование. Щ
Итак, мы действительно указали другой способ построения
канонических преобразований—с помощью разложений G4).
Этот способ особенно существен в связи с его переносом в
квантовую теорию, где в его формулировке удается избавиться
от неуклюжего разложения в ряд.
Отметим еще одно следствие, которое получается из найден-
найденных свойств преобразования G2).
20. ПРИМЕР: ОСЦИЛЛЯТОР 135
СЛЕДСТВИЕ 4: Применим преобразование G2) с помощью од-
одного и того же К ко всем входящим в теорию динамическим пе-
переменным. Тогда, если СП каких-то двух динамических перемен-
переменных / и g имела вид
где буква F характеризует не значение величины, а форму за-
зависимости от координат и импульсов, то свойство G3), C) дает
нам
где второе равенство написано на основании сохранения (G3),
A), B)) при преобразовании G2) всех алгебраических соотно-
соотношений. Поскольку, однако, в применении к координатам и им-
импульсам G2) осуществляет каноническое преобразование, то
(I u)pq = Cf, ё)№
и, следовательно,
если (f,g)n = F(p,q), то (J, §)„„== F ф, q), G5)
— т. е. при одновременном преобразовании с помощью G2) всех
динамических переменных сохраняются не только все алгебраи-
алгебраические соотношения, но и все соотношения в скобках Пуассона,
т. е. преобразованная теория оказывается полностью изоморф-
изоморфной первоначальной. I
Если теперь сравнить преобразование с помощью К G2) с
полученным в предыдущем параграфе общим решением F0с)
уравнений движения, то нетрудно видеть, что второе совпадает
с первым, если выбрать в нем
K = {t-to)Ho.
Таким образом:
движение есть каноническое преобразование.
Мы доказали это утверждение для систем с функцией Га-
Гамильтона, не зависящей от времени явно; оно сохраняет свою
справедливость и в общем случае.
20. Пример на канонические преобразования: осциллятор
Проиллюстрируем применение канонических преобразований
на чрезвычайно подробно разбиравшемся выше примере гармо*
нического осциллятора:
? = ^ ; q = x, р = — = х, Я = х .
136 ч. I. КЛАССИЧЕСКАЯ МЕХАНИКА
20.1. Введем новые импульс и координату (преобразование
F5)) по формулам:
Р — .-л* —,- p + fog n—I— p-ie>q
•V2co V2(o
Вычисляя единственную скобку Пуассона, найдем что
~toi^
2ш У 2ш
то есть
(Л*, Л) = -/; 'Р, Л)=1
— предлагаемое преобразование является каноническим.
В новых переменных
то есть
и, следовательно, уравнениями движения будут
р = iA* = - U = |(вР = /вмЛ'; Л* = /©Л'.
Решение уравнений движения есть
А = ае~ш, А* = а*еш (а, а* — константы).
Для функции Гамильтона -^т- = 0, следовательно, Н сохра-
сохраняется:
20.2. Постоянные интегрирования а* и а можно, однако, рас-
рассматривать и как динамические переменные, как функции Л*,
Л и явно входящего времени t:
а* — е-шА*г а = ешА. (*)
В таком аспекте можно вычислить скобку Пуассона динамиче-
динамических переменных а* и а:
Таким образом, две пары динамических переменных — а*, а,
с одной стороны, и Л*, Л — с другой — обладают одинаково за-
зависящими от них функциями Гамильтона и одинаковыми скоб-
скобками Пуассона. Тем не менее их движения совершенно различны,
например
-jjr= УН, а) + -^ = — и»а+ i&a = 0.
20. ПРИМЕР: ОСЦИЛЛЯТОР 137
Дело в том, что:
«большие» А не зависят от времени явно, и потому зависят от
времени,
в то время как
«малые» а зависят от времени явно, и потому не зависят от
времени!
20.3. Но разве нельзя «забыть» про явную зависимость «ма-
«малых» а от времени? Можно, но это будет означать, что мы хотим
ввести их в качестве основных канонических переменных — ко-
координаты и импульса (с точностью до /), а это можно сделать
лишь с помощью канонического преобразования, зависящего от
времени.
Иными словами, соотношения (*) надо будет для этого рас-
рассматривать как вводящие каноническое преобразование урав-
уравнения F5). Поскольку эти уравнения явно содержат время, то
новая функция Гамильтона Н' не будет более совпадать со ста-
старой, ее надо будет искать из уравнений G1), которые примут вид
\ дп )a.t~\dn Ja'T'Vdt )р,А' \ да )n,t Кда)„ \dt)p,A'
п = ia*.
Отсюда
(!?) $ + f (а).
В то же время
Я' = Я_ J (**.} da=*H —\(— i<an)da = H + шая + g{n).
Следовательно, f(a) = g(n) =0 и
Н' = Я -+- iema = coa*a — ma*a = 0.
Итак, если рассматривать «малые» а как канонические коор-
координату и импульс, то новая функция Гамильтона тождественно
обращается в нуль, и уравнения движения для (теперь не зави-
зависящих от времени явно\) а и а* по-прежнему дадут
d = @, a); d* = @, a*), т.е. а = const; a* = const.
20.4. Проведенное в рассмотренном примере преобразование
к новым каноническим переменным а, п —такое, что новая
функция Гамильтона В' (я, а) = 0 и, следовательно, новые ка-
канонические переменные постоянны во времени, — не является
138 ч. I. КЛАССИЧЕСКАЯ МЕХАНИКА
каким-либо монстром, но составляет основу одного из самых
могучих методов интегрирования уравнений движения.
Именно, рассматривая теперь уже произвольную механиче-
механическую систему, сделаем каноническое преобразование с произво-
производящей функцией ф =ф(<7, Р, t), так что
причем постараемся выбрать производящую функцию так, чтобы
новая функция Гамильтона
Н' (Р, Q,t) = H (p, q) + -Ц- обратилась бы в нуль: Н' = 0. G6)
Записанное через производящую функцию ф это требование
приобретает форму
"(?• «.')+$¦-<•. «")
— т. е. является по отношению к ф дифференциальным уравне-
уравнением в частных производных первого порядка и степеней:
первой — по отношению ко времени,
второй — по отношению к остальным переменным, если функ-
функция Гамильтона имеет вид суммы кинетической и потенциаль-
потенциальной энергии.
Это уравнение называется уравнением Гамильтона — Якоби.
В новых переменных Р,- и Qi динамическая задача тривиаль-
тривиальна, поскольку Pi = const и Qi = const и все сводится к уста-
установлению связи новых переменных со старыми, т. е. к интегри-
интегрированию уравнения G7).
Для наших целей интересен так называемый полный интег-
интеграл уравнения Гамильтона — Якоби, зависящий от п произволь-
произвольных постоянных Pi, ..., Рп
Ф = Ф(<7„ ..., qn; t; Pu ..., Рп).
Если полный интеграл известен, то можно принять фигурирую-
фигурирующие в нем п произвольных постоянных за новые (постоянные
в силу Н' = 0) импульсы, а частные производные по ним — за
новые (постоянные!) координаты Q,-: тогда 2п уравнений (*)
позволят нам выразить старые координаты и импульсы в виде
функций времени и новых (постоянных) импульсов и координат.
20.5. Как в рассмотренном примере, так и в общем случае
преобразования Гамильтона — Якоби мы сталкиваемся с ситуа-
ситуацией, описанной в замечании после формулы E4) в § 16: новая
20. ПРИМЕР: ОСЦИЛЛЯТОР 139
функция Гамильтона Н' не зависит от времени явно, но, тем не
менее, не совпадает с физической энергией системы.
Этот парадокс находит себе исчерпывающее объяснение
лишь в квантовой механике, где выясняется, что рассмотрен-
рассмотренному нами зависящему от времени каноническому преобразо-
преобразованию Гамильтона — Якоби отвечает переход от представления
Гайзенберга к представлению Шредингера, в котором появляет-
появляется «другая» функция Гамильтона, управляющая изменением во
времени состояния системы — концепции, не имеющей себе в
классической механике прямого аналога. Тогда оказывается, что
роль физической энергии играет, грубо говоря, сумма этих двух
гамильтоновых функций — она-то и сохраняется или не сохра-
сохраняется, судя по тому, замкнута ли физическая система или нет.
Часть II
МЕХАНИКА ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
1. Принцип относительности
и принцип постоянства скорости света
1.1. Классическая механика, излагавшаяся в первой части,
основывалась по существу на двух фундаментальных физических
допущениях: принималось, что
A) справедлив принцип относительности, т. е. все инерциаль-
ные системы отсчета равноправны*);
B) состояние системы — следовательно, в частности, и силы,
действующие на некоторую частицу, — в какой-либо момент вре-
времени определяется полностью координатами и скоростями всех
частиц системы в тот же момент времени — т. е. принималось
представление о мгновенности распространения взаимодей-
взаимодействий.
(Кроме этих двух постулатов требовалось еще и допущение
об однородности и изотропии пространства и времени в инерци-
альных системах. Это допущение полностью сохраняется в тео-
теории относительности, однако сейчас нет нужды концентрировать
на нем свое внимание.)
1.2. При переходе от чисто механических явлений к области
оптики и электродинамики — а эти два раздела физики бурно
развивались во второй половине XIX века —выяснилось**),что
в природе существует процесс — распространение света или
электромагнитных волн — обладающий парадоксальными свой-
свойствами. Именно, с одной стороны, для явлений, включающих этот
процесс,
A) принцип относительности сохраняется,
*) Это утверждение часто формулируют в виде «принципа невозможно-
невозможности»: Никакими механическими опытами нельзя установить выделенное поло-
положение какой-либо одной инерциальной системы отсчета относительно всех
остальных. Такие принципы невозможности удобны для формулировки фунда-
фундаментальных физических положений — можно напомнить читателю формули-
формулировку закона сохранения энергии в форме принципа невозможности построе-
построения вечного двигателя первого рода.
**) Мы не будем здесь вдаваться ии в историю экспериментальных от-
открытий, ни в изложение последовательной эволюции теоретических представ-
представлений, а ограничимся формулировкой основных выводов из накопившихся
к началу XX века опытных фактов.
1. ДВА ПРИНЦИПА 141
— т. е. оптические или электромагнитные эффекты также не позволяют пре-
преимущественно выделить какую-либо частную инерциальную систему отсчета;
но в то же время
B) скорость света не зависит от движения источника
— под этим имеется в виду, что в некоторой инерциальной системе отсчета К
скорость света, испускаемого движущимся в этой системе источником S', та
же, что и для испускаемого покоящимся (в К) источником S*).
Чтобы понять, почему эти свойства света парадоксальны, за-
заметим, что первое из утверждений представлялось бы совер-
совершенно естественным в рг.мках корпускулярной теории света:
если испускание света есть просто испускание некоторых — очень
легких и быстрых — частиц, то это есть типичный механический
процесс, и неудивительно, если для него сохраняется справедли-
справедливый для всех механических процессов принцип относительности.
Однако в такой теории следовало бы ожидать, что источник,
движущийся со скоростью v, испускал бы — в соответствии с ме-
механическим законом сложения скоростей A.4а)—в направле-
направлении своего движения свет со скоростью с -\- v, а в противопо-
противоположном— со скоростью с — v, если с есть скорость распростра-
распространения света от неподвижного источника.
Напротив, второе утверждение самоочевидно с точки зрения
волновой теории света, которая представляет себе свет в виде
возмущений, волн, распростаняющихся, подобно звуковым вол-
волнам в упругух средах, в некоторой гипотетической мировой сре-
среде — эфире — последовательно от одной точки к соседней со ско-
скоростью, которая может зависеть лишь от свойств среды, но ни-
никак не от природы первоначального возмущения. Однако тогда
с этой универсальной мировой средой — с эфиром — можно было
бы связать (инерциальную) систему отсчета, которая была бы
выделена из всех прочих — т. е. первое утверждение было бы
нарушено.
Мы видим, таким образом, что утверждения A) и B) ка-
кажутся противоречащими друг другу. Противоречие это не свя-
связано с рассматривавшимися конкретными механизмами распро-
распространения света. В самом деле, рассмотрим две системы отсчета,
«неподвижную» систему К и движущуюся относительно нее си-
систему К', и пусть в момент времени t = О качала отсчета этих
двух систем совпадают (см. рисунок). Тогда спустя некоторое
время т эти две системы сдвинутся относительно друг друга.
Пусть теперь в момент времени ( = 0 в точке с координатами
*) То, что скорость света в К, испускаемого покоящимся в ней источни-
источником 5, совпадает со скоростью света, испускаемого источником 5', в той
(инерциальной) системе отсчета К', в которой источник S' покоится, — это не
есть новое утверждение, но часть утверждения A)! Мы специально подчер-
подчеркиваем это обстоятельство, поскольку во многих (даже хороших!) книгах
утверждение B) формулируется небрежно, что ведет к недоразумениям.
142 ч. II. МЕХАНИКА' ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
х = х' источник S (б силу утверждения B) состояние его дви-
движения для нас безразлично!) испускает световой сигнал. К мо-
моменту т этот сигнал достигнет в системе К точек А и В с коор-
координатами х — сх и х-\-сх. Однако в силу утверждения A) этот
сигнал должен достигнуть в тот же момент в системе К' точек
А' и В' с координатами х' — сх и х' + сх. Поскольку система К'
движется относительно К, то в момент х А' не будет совпа-
совпадать с А, а В' — с В. Но световой сигнал приходит в момент т
в какие-то определенные точки вне зависимости от того, в какой
системе отсчета мы описываем его распространение — т. е. мы
приходим к противоречию.
1.3. Научный подвиг Эйнштейна, подвиг, потребовавший ис-
исключительной отваги мысли, состоял в том, чтобы пойти в раз-
разрешении образовавшегося парадокса по самому простому пути,—
коль скоро оба утверждения A) и B) суть прямые обобщения
опытных фактов, то они не могут находиться в логическом про-
противоречии друг с другом. Поэтому оба эти утверждения следует
постулировать как основные физические принципы — принцип
относительности A) и принцип постоянства скорости света B).
Источник же только что проиллюстрированного противоре-
противоречия следует искать не в неверности одного из этих принципов,
а в некритическом использовании представлений, основанных на
обычном «здравом смысле».
Если пересмотреть проведенное рассуждение с такой точки
зрения, то можно заметить, что мы неявно допустили в нем, что
время течет в движущихся друг относительно друга системах
отсчета К. и К' одинаковым образом, т. е. допустили абсолют-
абсолютность времени C). Таким образом в логическом противоречии
оказываются не два утверждения A) и B), а три—A), B) и C).
Одно из них должно быть неверным, и поскольку только третье,
как показал проведенный Эйнштейном анализ, не имело на са-
самом деле никакого опытного подтверждения, то именно им и
приходится пожертвовать.
Таким образом за логическую совместность принципов отно-
относительности и постоянства скорости света приходится распла-
1. ДВА ПРИНЦИПА 143
чиваться отказом от «очевидного» представления об абсолютно-
сти времени, приходится принимать, что каждой инерциальной
системе отсчета К' соответствуют не только свои координаты
х', у', z', но и свое время f. В дальнейшем построении вытекаю-
вытекающей из принципов A) и B) теории — такая теория называется
специальной теорией относительности, а в качестве притяжа-
притяжательного прилагательного употребляют слово релятивистский —
мы не будем — в соответствии с общей нашей методической
установкой — точно следовать оригинальным рассуждениям
Эйнштейна, но в целях упрощения изложения сразу восполь-
воспользуемся предложенной Минковским в 1908 году геометрической
интерпретацией.
1.4. Основным понятием этой интерпретации является поня-
понятие события, которое характеризуется местом, где и временем,
когда оно происходит. Это место и время может быть указано
только по отношению к некоторой (инерциальной! другие пока
вовсе исключаются из рассмотрения) системе отсчета К—в
ней событие характеризуется четверкой чисел (координат со-
события)
{t, х, у, z) = {t, r}.
Таким образом в каждой системе отсчета координаты событий
образуют некоторое четырехмерное многообразие. В другой си-
системе К' координаты событий
образуют другое четырехмерное многообразие.
Чтобы установить связь между 4-многообразиями, изобра-
изображающими события в двух системах отсчета, обратимся к основ-
основным принципам A) и B).
1.4.1. Рассмотрим два события: 5i ¦—состоящее в испускании
светового сигнала в некотором месте в некоторый момент, и
S2 — состоящее в регистрации того же сигнала в другой момент
в другом месте. Будем рассматривать эту пару событий с точки
зрения двух разных инерциальных систем К и К'. Тогда:
В системе отсчета: К
координатами S, будут {t{, xv у{, z,}
координатами S2 будут {tv х2, у2, г2}
К'
*!• У[> z\)
\'2>
В силу A) и B) распространение света в обеих системах от-
отсчета происходит с одной и той же скоростью с, т. е.
с (t2 -1{) = У(*2 - хх? + (у2 - г/,J + (г2 - г,J
144 ч. И. МЕХАНИКА ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
причем можно утверждать, что из выполнения одного из этих
равенств должно следовать выполнение другого.
1.4.2. Высказанное утверждение можно сформулировать в
красивой геометрической форме, если соотнести каждой паре
координат событий — число s, называемое интервалом, по фор-
формуле
- «S, = (*» - *iJ + (У* ~ УгГ + (*» - *iJ - с* ('« - W. (О
Тогда то обстоятельство, что события Si и S^ могут состоять
в испускании и регистрации одного и того же светового сигнала,
можно записать — в силу только что приведенной аргументации
в любой системе отсчета — в форме требования:
в К: s21 = 0; в К': s'2l = 0 и т. д.
Итак, в силу принципов A) и B) факт обращения интер-
интервала между двумя событиями в нуль не зависит от системы от-
отсчета; это обстоятельство характеризуют словами, что нулевые
интервалы инвариантны, или суть инварианты.
1.4.3. Бывает удобно рассматривать интервал между двумя
бесконечно близкими событиями
ds2 = с2 dt2 - dx2 - dy2 - dz2. (la)
Для таких интервалов, конечно, тоже сохраняется выражающее
принципы A) и B) основное свойство, что из обращения интер-
интервала между двумя событиями в нуль в одной системе отсчета
следует его обращение в нуль в другой и наоборот:
ds2 = 0&ds'2 = 0. Ba)
Не составляет труда показать, что это свойство может быть
выполнено только в том случае, если бесконечно-малые (не
равные нулю!) интервалы в разных системах отсчета пропорцио-
пропорциональны:
с коэффициентом пропорциональности, в принципе зависящем от
координат, времени и относительной скорости рассматриваемых
систем отсчета. Однако зависимость у от координат или времени
противоречила бы (ср. I, § 4) однородности пространства и вре-
времени в инерциальной системе отсчета, а зависимость от направ-
направления относительной скорости двух систем — изотропии прост-
пространства, и остается только зависимость от квадрата относитель-
относительной скорости V2. Однако и такая возможность исключается, если
рассмотреть два последовательных преобразования, сперва от
системы К и К', а затем от К' к К, — при этом интервал ds при-
приобрел бы множитель у2 и в то же время должен был бы рав-
равняться первоначальному значению.
I. ДВА ПРИНЦИПА 145
Таким образом, мы пришли от Bа) к значительно более
сильному утверждению
ds2 = ds'2 (За)
об инвариантности не только нулевых, но и произвольных беско-
бесконечно-малых интервалов.
1.4.4. Чтобы перейти от бесконечно-малых интервалов к ко-
конечным, надо использовать еще то обстоятельство, что при пе-
переходе от одной инерциальной системы к другой равномерно-
прямолинейное движение остается равномерно-прямолиней-
равномерно-прямолинейным—в комбинации с (За) оно приведет нас к выводу, что
координаты и время одной системы должны выражаться через
координаты и время другой линейно, из чего и будет сразу сле-
следовать перенос утверждения (За) на конечные интервалы
*?2 = 4 C)
1.4.5. Итак, основные физические принципы A) и B) позво-
позволяют установить в многообразии координат событий квадратич-
квадратичную форму A), значение которой не зависит от выбора системы.
отсчета. Пользуясь этим можно, продолжая построение намечен-
намеченной геометрической интерпретации, ввести в многообразии со-
событий метрику, полагая «квадрат расстояния» между событиями
равным значению формы A), и превратить тем самым многооб-
многообразие событий в пространство, точками которого эти события
являются. Выбор частной инерциальной системы отсчета К будет
отвечать тогда введению в этом пространстве частной (ортого-
(ортогональной) системы координат. Таким образом в нашей геометри-
геометрической интерпретации обычное трехмерное пространство и время
объединяются в одно четырехмерное пространство (далее будем
говорить для краткости 4-пространство), которое называют
пространством Минковского или (постепенно выходящий из
употребления термин) — миром Минковского *).
1.5. Метрика A) мира Минковского содержит (как и в ев-
евклидовом пространстве) только квадраты разностей координат,
но один из них входит со знаком «+», а три другие — со знаком
«—»; такое пространство принято называть псевдоевклидовым
(точнее, псевдоевклидовым с сигнатурой (+, —, —, —,)). Бла-
Благодаря индефинитное™ метрики псевдоевклидова пространства
его геометрия в некотором смысле богаче содержанием, чем
евклидова. В то время как пары точек евклидова пространства
могут качественно находиться (если они не совпадают) только
в одном соотношении друг с другом, квадрат псевдоевклидова
*) В соответствии с последним термином, события, являющиеся точками
мира Мннковского, называют мировыми точками (термин, постепенно выходя-
выходящий из употребления; чаще говорят 4-точка), а линии в этом пространстве —
(термин вполне живой) мировыми линиими.
146
ч. II. МЕХАНИКА TFOPHH ОТНОСИТЕЛЬНОСТИ
«расстояния»
s2 — с2 (AtJ — (А/J, (А/J = (АхJ ¦
может быть как положительным, так и отрицательным или (для
несовпадающих точек!) равным нулю. В соответствии с этим
возникают три качественно разные возможности взаимного рас-
расположения двух мировых точек:
если квадрат разделяющего их интервала:
s2 > 0, то интервал называют времени-подобным;
s2=0, — свето-подобным;
s2 < 0, — пространственно-подобным.
Те же термины употребляют и по отношению к самой паре: го-
говорят «точка А пространственно-подобна точке В» и т. п.
1.5.1. Если фиксировать одну из точек пары, — скажем при-
принять ее за начало отсчета некоторой системы координат, — то
все остальные мировые точки разобьются в смысле этого отно-
отношения на три класса, т. е. все 4-пространство разобьется (по
отношению к началу координат) на три области. Такое разбие-
разбиение поучительно проиллюстрировать на чертеже*). Поскольку
условие s2= 0 есть уравнение, то
размерность области, занятой точ-
точками, свето-подобными началу коор-
координат, будучи на единицу меньше
размерности пространства, будет
образовывать в нем 3-мерную (на
чертеже — одномерную) гиперпо-
гиперповерхность. Эта гиперповерхность
называется световым конусом (на
чертеже виден только след, образо-
образовавшийся при сечении светового ко-
конуса плоскостью у = z = 0: две
прямые x—±ct). Световой конус
служит границей областей, просг-
ранственно-подобных и времени-по-
добных началу координат. На черте-
чертеже каждая из этих областей выгля-
выглядит в свою очередь разбитой на две
несвязные подобласти; однако в реальном 4-случае, как легко
сообразить, пространственно-подобная область связна (хотя и
не односвязна); времени же подобная область действительно
*) Естественно, что на листе бумаги нельзя изобразить 4-простраиство,
поэтому иам придется ограничиться осью времени и одной из пространствен-
пространственных осей; но и с этим ограничением псевдоевклидову плоскость нельзя метри-
метрически точно наложить на евклидову; поэтому предлагаемый чертеж, как и
все дальнейшие графики, будет давать иам только аффинное соответствие.
структура псевдоевклидо-
псевдоевклидова пространства
1. ДВА ПРИНЦИПУ 147
распадается на две несвязные подобласти соответственно зна-
знаку разности временной координаты. Таким образом фактически
все 4-пространство разбивается даже не на три, а на четыре
различные области.
1.6. Чтобы установить физический смысл проведенной клас-
классификации возможных взаимных расположений точек псевдо-
псевдоевклидова пространства, будем, как и при ее иллюстрации на
графике, рассуждать сперва в' рамках какой-то определенной
системы координаты в 4-пространстве Минковского. С обыч-
обычной трехмерной точки зрения выбор системы 4-координат — это
выбор некоторой инерциальной системы отсчета, а инерциаль-
ная система отсчета фиксируется, как мы знаем, заданием ка-
каких-либо материальных тел (или материального тела), кото-
которые принимаются в этой системе за неподвижные.
1.6.1. Но материальное тело занимает в каждый момент вре-
времени некоторое определенное положение в пространстве; по-
поэтому, если отвлечься от его размеров, то оно представляется
в геометрической интерпретации Минковского непрерывной це-
цепочкой событий — мировой линией. В частности, материальное
тело, олицетворяющее начало координат обычного 3-простран-
ства в выбранной системе отсчета, есть совокупность событий,
образующих в 4-пространстве прямую линию — ось времени си-
системы координат в 4-мире.
Интервал между любой парой принадлежащих этой линии
событий, поскольку для них А1 = 0, всегда времени-подобен:
•As2 > 0. Это свойство, будучи инвариантным, не может зави-
зависеть от того, связали ли мы с телом систему отсчета или нет.
Один из старейших прозелитов релятивизма, известный англий-
английский астроном А. С. Эддингтон, характеризует его в своей
превосходной книге «Теория относительности» словами: «Ма-
«Материальная частица, понимаемая как совокупность событий, яв-
является системой, у которой линейное протяжение обладает вре-
временным характером» — в переводе на менее изысканный способ
выражения это означает, что мировая линия, изображающая
материальную частицу, всюду времени-подобна, т. е. любая
пара ее точек разделена времени-подобным интервалом.
Итак, пары событий, разделенных времени-подобными ин-
интервалами, могут физически соответствовать двум разным мо-
моментам «жизни» одной и той же материальной частицы или —
выражаясь более абстрактно — лежать на оси времени некото-
некоторой (инерциальной) системы отсчета — этим и объясняется при-
принятый в их отношении термин.
ЗАМЕЧАНИЕ: Отсюда мы видим, в частности, что материаль-
материальное тело в теории относительности не может ни в какой системе
отсчета К двигаться со скоростью, большей скорости света с.
148 ч. 11. МЕХАНИКА ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
•В самом деле, если некоторое материальное тело двигалось бы
со скоростью, большей с, то оно изображалось бы на нашем
графике (стр. 146) мировой линией, лежащей вне светового ко-
конуса; пары событий на такой линии были бы разделены (в си-
системе К) пространственно-подобными интервалами. Однако
с этим телом можно было бы, как и с каждым материальным
телом, связать систему отсчета К', в которой оно покоится, —-
в ней та же мировая линия была бы осью времени, т. е. интер-
интервалы между лежащими на ней событиями были бы времени-
подобны. Таким образом знак интервала зависел бы от системы
отсчета, что в силу инвариантности интервала невозможно.
1.6.2. Физический смысл свето-подобного расположения двух
событий нам уже известен — это события, которые могут быть
связаны световым сигналом, а световой конус есть просто гео-
геометрическое место траекторий таких сигналов, испускаемых из
одной 4-точки (или принимаемых в ней).
1а. Одновременность и пространство *)
Прежде чем перейти к физическому смыслу пространствен-
пространственно-подобного расположения двух событий, уточним, что, соб-
собственно, имеют в виду, когда говорят о пространстве. С четы-
четырехмерной точки зрения под пространством (в некоторый
момент времени) естественно понимать совокупность всех одно-
одновременных друг другу событий. Таким образом пространство
оказывается определяемым через понятие одновременности. Од-
Однако как раз с понятием одновременности в теории относитель-
относительности дело обстоит совсем не просто — мы уже видели, что два
основных принципа несовместны с интуитивным представле-
представлением о независимости одновременности от выбора системы
отсчета.
la.l. Поэтому будем сперва рассуждать в рамках некото-
некоторой фиксированной инерциальной системы отсчета К и допу-
допустим, что одновременность событий, происходящих в ней в раз-
разных местах, как-то установлена, т. е. что мы каким-то способом
(неизвестно — хорошим или плохим) умеем синхронизовать
часы, покоящиеся в разных точках, скажем в точках Х\ и х2**).
*) Он же, по логической классификации, 1.6.3.
**) Заметим, что в классической (иерелятивистской) теории в специаль-
специальном определении одновременности нет надобности, поскольку в принципе она
может быть установлена с помощью допускаемых в ней мгновенно распро-
распространяющихся взаимодействий. Реальная же измерительная практика исполь-
использует для этой цели два способа: (а) перевозку хоонометров и (р) синхрони-
синхронизацию с помощью световых (или радио-, что то же самое) сигналов. Подроб-
Подробный анализ показывает, что в теории относительности оба способа ведут к
тождественным результатам, а поскольку второй из них принципиально про-
проще, то именно его рассмотрением мы и ограничиваемся ниже.
'la. ОДНОВРЕМЕННОСТЬ И ПРОСТРАНСТВО
149-
На рисунке изображены мировые линии (/) и B) этих часов
и «одновременные» события @, Xj) и @,лг2).
1а. 1.1. Произведем теперь два (мысленных) опыта. Во-пер-
Во-первых, испустим в пространственной точке хх в момент времени О
(событие @,хх)~) световой сигнал и зарегистрируем его приход
в пространственную точку лг2 в момент t2 (событие (t2,x2)). Во-
вторых, одновременно с регистрацией сигна- ,
ла направим из точки х2 (то же событие ™ ''Xf
(t2,x2)) ответный сигнал в точку Х\. Пусть
его прибытие в Х\ будет зарегистрировано
в момент t\ (событие t\,X\)).
Каждый из этих опытов может служить
для определения скорости света, причем из
первого опыта мы получим для нее зна-
значение
1*2 —
а из второго с = ^Щ-—^
«I — «2
(tz,xz)-
B)
синхронизация
часов
Однако из-за изотропии пространства
скорость света не может зависеть от на-
направления распространения сигнала, т. е.
оба опыта должны (при правильной синхро-
синхронизации часов в разных местах!) дать один и тот же результат,,
т. е. должно быть:
ti — t.2 — t2 или к = \-
Иными словами, событием в пространственной точке хь~одно-
хь~одновременным событию (t2>x2), должно быть событие (-?-, хЛ .
1а.1.2. Рассмотренные мысленные опыты позволяют теперь
сформулировать определение одновременности:
Назовем событие О' одновременным событию О, имеющему ко-
координаты t = 0, х = 0 (и !/ = 0, г = 0), если световой сигнал,
испущенный в момент t =.—т по часам, покоящимся (в си-
системе К) в пространственной точке х = 0 (и у = 0, z = 0), вер-
вернется после отражения (событие О') в то же место х = О
(и у = 0, z = 0) в момент t = -f-т по тем же часам.
На рисунке изображены две пары таких одновременных О
событий О\, С'\ и (У2, 0*, отличающиеся направлением испу-
испущенного сигнала (внутри пары) и временем распространения
сигнала 2т.
ЗАМЕЧАНИЕ 1: Нетрудно показать, что сформулириованное
определение обладает свойствами рефлексивности и транзи-
транзитивности. ¦
150
ч. И. МЕХАНИКА ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
1а.2. Поэтому можно дать дальнейшее определение:
Для всех т и всех направлений распространения события С
образуют в совокупности гиперплоскость / = 0, называемую
пространством в момент t = 0.
В силу сделанного замечания 1 пространство не будет зависеть
от того, относительно какой его точки его начали строить.
ЗАМЕЧАНИЕ 2: Принятая процедура определения одновре-
одновременности позволяет, в частности, установить также и способ
измерения пространственных расстояний без использования
масштабов, с помощью лишь одних
часов. В самом деле, поскольку свет
всегда распространяется со скоро-
скоростью с, то событие О' потребо-
потребовавшее время 2т для распростра-
распространения светового сигнала от начала
координат в пространстве до О' и
х обратно, должно быть расположе-
2т
но на расстоянии -^-с=сх от нача-
начала координат, т. е. иметь коор-
координату х = сх (или х = —сх, судя
по направлению посылки сигна-
сигнала). I
определение
одновременности ЗАМЕЧАНИЕ 3: Определения одно-
одновременности и пространства основы-
основывались на использовании часов, покоящихся в некоторой частной
инерциальной системе К. Поэтому может случиться (и — в силу
рассуждений начала параграфа — следует ожидать), что опре-
определенные понятия относятся к этой частной системе. Покажем,
что это действительно так. В
1а.З. Рассмотрим вторые часы, движущиеся в системе К
равномерно и прямолинейно со скоростью V. В мире Минков-
ского их изображением будет прямая мировая линия х = Vt,
и если связать с этими часами новую инерциальную систему
.отсчета К', то эта прямая будет осью времени Of системы К'.
Повторяя со вторыми часами предписанную определением од-
одновременности процедуру посылки световых сигналов, получим
в качестве совокупности мировых точек, одновременных точке О
в системе К', т. е. в качестве пространства в системе К!, гипер-
гиперплоскость (Ух'.
Итак, пространство в системе отсчета К' не совпадает с про-
пространством в системе отсчета К; понятие одновременности двух
событий оказывается — в полном соответствии с рассуждениями
1а. ОДНОВРЕМЕННОСТЬ И ПРОСТРАНСТВО
151
в начале параграфа 1 — не абсолютным, а относительным, за-
зависящим от выбора инерциальной системы отсчета: события О
и О', одновременные в К.', неодновременны в К*).
ЗАМЕЧАНИЕ 1 (не принципиальное): На чертеже системы отсчета К и К'
выглядят неравноправно — координатные оси системы К' кажутся неортого-
неортогональными. В действительности это — чисто кажущийся эффект лишь аффин-
аффинного соответствия евклидовых рисун-
рисунков псевдоевклидову объекту: в псе-
псевдоевклидовом мире Минковского си-
системы К а К' совершенно равно-
flpocmpoHCTffo
6Nr
нравны. 3
1а.4. ЗАМЕЧАНИЕ 2 (очень
важное): Временной порядок
пары событий, разделенных
времени-подобным (или свето-
подобным) интервалом, не за-
зависит от выбранной системы
отсчета. Напротив, порядок
следования во времени двух
событий, которые разделены
пространственно - подобным
интервалом, может быть уста-
установлен выбором системы от-
отсчета по произволу (например, на чертеже событие О" происхо-
происходит позже О в системе К, но раньше О в системе К'). В частно-
частности, для любой пары событий, разделенных пространственно-
подобным интервалом, всегда можно найти систему отсчета, в
которой они одновременны. !
пространство ч
ей'
одновременность в разных
системах отсчета
Поскольку общефилософский принцип причинности требует,
чтобы причина всегда предшествовала бы следствию во вре-
времени, то из замечания 2 видно, что причинно-следственные со-
соотношения могут связывать лишь пары событий, интервал
между которыми времени-подобен. Но о всякой паре событий
А и В, связанных соотношениями причины — следствия, всегда
можно сказать, что из 4-точки А посылался сигнал, принятый
в 4-точке В. Такими образом, оказывается, что в теории отно-
относительности любой сигнал из некоторой 4-точки А может быть
послан лишь в 4-точки, отделенные от А времени-подобным ин-
*) Напомним, что уже в классической механике следствием' равноправия
всех инерциальных систем отсчета была «относительность одноместное™»:
события, происходящие в системе отсчета К' в одном месте, скажем О и Тг
иа чертеже, в системе /С происходили в разных местах.
152 ч. II. МЕХАНИКА ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
тервалом*). Но этому всегда будет соответствовать скорость
распространения сигнала, меньшая скорости света с (или,
в крайнем случае свето-подобного интервала, равная ей). Та-
Таким образом выясняется, что в теории относительности ско-
скорость света есть максимально возможная скорость сигнала или
максимально возможная скорость распространения взаимо-
взаимодействий**).
Итак,
механика теории относительности отличается от классической
механики тем, что в ней существует максимальная скорость
распространения взаимодействий.
16. Замедление времени ***)
16.1. Вернемся к рассмотрению часов, покоящихся в неко-
некоторой инерциальной системе отсчета /С; в четырехмерной кар-
картине они будут изображаться прямой мировой линией, парал-
параллельной оси времени системы К. Пусть То, Т\, Т%, ... — события,
состоящие в том, что часы показывают время 0, ть тг, ... соот-
соответственно, тогда события 7\ будут отделены от То, поскольку
для покоящихся часов А/= О, интервалами s* = с(А0* = ex,.
Но—аргументация, к которой мы прибегаем уже не первый
раз — значение интервалов между событиями не зависит от си-
системы отсчета, те же самые интервалы будут разделять события
Ti и Го и в такой системе отсчета, в которой часы движутся.
Мы приходим, таким образом, к важному выводу:
Показания покоящихся или движущихся равномерно и прямо-
прямолинейно часов пропорциональны интервалу между прочтением
показаний и установлением нуля на часах.
*) Точнее, в 4-точки, лежащие в или на верхней половине светового ко-
конуса. В немецкой литературе для этой половины существует образный тер-
термин «Nachkegel», что можно было бы перевести как послеконус. Аналогично,
нижнюю половину конуса, объединяющую события, могущие служить источ-
источниками, сигналов, принимаемых в А, по-немецки называют предконусом —
«Vorkegel».
Ниже мы будем использовать обозначение А > В (читается: А позже В)
чтобы отметить, что 4-точка А лежит в послеконусе В (или — что то же са-
самое— 4-точка В лежит в предконусе А). Для пары же просгранственно-по-
добных событий будем применять значок Л ~ В (читается: пространственно
подобно). Удобство этих — предложенных Н. Н. Боголюбовым — обозначений
состоит в том, что для всякой пары 4-точек А и В всегда имеет место точно)
одна- из четырех возможностей: А > В, А < В (читается: А раньше В),
А ~ В или А = В (т. е. точки А и В просто совпадают).
**) Скорости, не могущие служить для передачи сигнала, не ограничены
этим пределом. Так — популярный пример — если поворачивать источник
остронаправленного светового пучка, то на достаточно удаленном «экране»
образуемый этим пучком «зайчик» может двигаться сколь угодно быстро.
***) Он же формально 1.7.
16. ЗАМЕДЛЕНИЕ ВРЕМЕНИ 153
Иными словами, с четырехмерной точки зрения часы есть при-
прибор для измерения (времени-подобных) интервалов; лишь в той
частной системе отсчета, где они покоятся, они измеряют одно-
одновременно и временную координату.
Для неравномерно движущихся часов их показания могут
зависеть от деталей конструкции — от того, насколько она чув-
чувствительна к ускорениям. Часы считаются хорошими, если они
и в этих условиях продолжают измерять интервалы. Ставшие
в последние годы практически доступными атомные часы очень
хороши с этой точки зрения.
16.2. Рассмотрим теперь материальное тело, движущееся по
отношению к некоторой инерциальной системе отсчета К про-
произвольным образом (не обязательно равномерно и прямоли-
прямолинейно). Время т, измеренное с помощью «хороших» часов, по-
постоянно связанных с телом, называют собственным временем
для данного материального тела.
Определим дифференциал собственного времени dr. «Xopo-
шие» часы измеряют (разделенный на с) интервал. Следова-
Следовательно,
dx = -ds = -^c2df-dl2=dt^\\ — -5- , Dа)
где v(t)—скорость материального тела в системе К в момент t.
Конечный промежуток собственного времени получается отсюда
интегрированием
Поскольку
V
1
С
_
2
то Ат всегда ^А?, т. е.:
Собственное время всегда течет не быстрее, чем координатное
время в какой-либо системе отсчета.
Этот эффект носит название эйнштейнова замедления времени.
16.3. Может возникнуть опасение, не находится ли эффект
замедления времени в противоречии с принципом равноправия
всех инерциальных систем отсчета — разве мы не можем свя-
связать с рассматриваемым телом (хотя бы в том случае, когда
его движение равномерно и прямолинейно) систему отсчета К',
относительно которой должно было бы замедляться координат-
координатное время t — собственное время тех материальных тел, кото-
которые реализуют систему отсчета /С?
Чтобы разобраться в этом кажущемся парадоксе, разбе-
разберемся подробнее в условиях, в которых может наблюдаться.
154
ч. II. МЕХАНИКА ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
t
эффект замедления времени. Оказывается, что тут возможны
две принципиально разные ситуации.
16.3.1. Первая возможность состоит в том, что мы хотим из-
измерять начало и конец промежутка А^ координатного времени
в одном месте системы К. Но для этого движение материаль-
материального тела обязательно должно быть неравномерным, его миро-
мировая линия не может быть прямой. В этом случае речь идет,
следовательно, о сравнении длин (в 4-смысле, конечно) пря-
прямой G и кривой С, имеющих общие концы, — ясно, что эти
длины должны быть разными; то что длина кривой оказывается
меньше длины прямой, объясняется
псевдоевклидовостью 4-мира. Итак,
первая возможность явно несиммет-
несимметрична по отношению к замене рассмат-
рассматриваемого материального тела на тела,
осуществляющие систему К.
16.3.2. Вторая возможность состоит
в наблюдении эффекта замедления
времени для равномерно (и прямоли-
прямолинейно) движущегося тела. С таким те-
телом действительно можно будет свя-
связать другую инерциальную систему К',
саму по себе равноправную с К. Одна-
Однако тогда начало и конец промежутка
А* координатного времени обязатель-
и
At
О
мировая линия
тела •
замедление времени 1.
но придется измерять в разнрсх пространственных точках системы
К. (См. рисунок на стр. 155, где 4-точки начала и конца рас-
рассматриваемого отрезка движения тела обозначены через А и В.
Координатные оси системы К нанесены сплошными, а К' — пунк-
пунктирными линиями; мы расположили их евклидово-симметричио
относительно конуса, тогда вдоль них сохраняется и метрическое
соответствие с псевдоевклидовой картиной). Для измерения этой
разности в одном месте («одними часами»), надо будет
сперва построить на оси времени системы К событие, одновре-
одновременное событию В. Но ведь одновременность различна в К и Л'';
к какой из них надо прибегнуть? Если речь идет о наблю-
наблюдении движения тела в системе К, то мы должны строить
событие В', одновременное В в этой системе — тут-то и нару-
нарушается равноправие обеих систем отсчета и возникает замед-
замедление времени f относительно времени t. Если бы мы строили
на оси t событие В", одновременное В в системе К' — а это
отвечало бы наблюдению движения тел, осуществляющих си-
систему К, в системе К', — то пришли бы не к замедлению, а к
ускорению времени f относительно времени t (на тот же самый
множитель), т. е. к замедлению времени t относительно вре-
2. ПРЕОБРАЗОВАНИЯ ЛОРЕНЦА 155
мени f. Таким образом, в случае равномерного прямолиней-
прямолинейного движения неравноправие лежит не в свойствах двух систем
световой' нонус
замедление времени 2.
отсчета (или мировых линий двух движений), а в условиях
постановки опыта.
2. Преобразования Лоренца
Как мы видели, в геометрической интерпретации Минков-.
ского переходу от одной инерциальной системы отсчета к дру-
другой соответствует преобразование координат в псевдоевклидо-
псевдоевклидовом 4-пространстве, оставляющее инвариантным «расстоя-.
ние» A):
- s2 = (АхJ + (АуJ + (АгJ - с2 (AtJ =
= (Ax'f + (Ay'J + (Az'J - с2 (At')\
Нам надлежит найти теперь явный вид этих преобразований.
2.1. Сделаем сперва одно
ЗАМЕЧАНИЕ: Из обычной геометрии евклидова пространства
известно, что преобразования, оставляющие в нем расстояния-
неизменными, образуют группу, включающую сдвиги (неодно--
родные преобразования, которые не будут пока нас интере-
интересовать) и однородные преобразования, которые в свою оче-
очередь делят на собственные преобразования — повороты (или*
156 ч. П. МЕХАНИКА ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
вращения), детерминант матрицы которых равен +1, и
несобственные преобразования — отражения, с детерминантом
— 1 (сдвиги также являются собственными преобразованиями).
При этом число независимых сдвигов равно я— числу измере-
/''« — ])
нии пространства, число независимых поворотов -г—,
а независимое отражение существует только одно — например,
преобразование, меняющее знак нечетного числа координат.
Преобразование, состоящее в последовательном проведении
двух таких отражений — т. е. преобразование, меняющее знаки
четного числа координат, — оказывается уже вращением. 1
Новый момент, возникающий при переходе к псевдоевкли-
псевдоевклидову пространству, обусловлен тем, что в нем мы должны раз-
различать «времени-подобные» и «пространственно-подобные» ко-
координаты. Поэтому появляются два независимых отражения—•
изменение знака единственной временной координаты и изме-
изменение знака нечетного числа пространственных координат, при-
причем последовательное проведение двух отражений разных сор-
сортов уже не оказывается более вращением*).
В свою очередь из вращений можно выделить преобразова-
преобразования, затрагивающие только х, у и г, но не t, — это будут обыч-
обычные пространственные повороты (напомним, что независимых
среди них три), действие которых на трехмерный радиус-вектор
г = (х, у, z) определено общей формулой (I, 18).
Нетривиальными являются три остальных независимых вра-
вращения— повороты в плоскостях (х, t), (у, t) или (г, t). Чтобы
получить аналитическую форму этих преобразований, восполь-
воспользуемся удобным формальным приемом, позволяющим сводить
псевдоевклидову метрику к евклидовой.
2.2. Будем для (как мы увидим ниже — очень существенного)
сокращения письма обозначать пространственные координаты
х, у, z одной буквой х с индексами 1, 2, 3 соответственно, а вме-
вместо времени t введем четвертую чисто мнимую координату
х4 = ict, E)
так что выражение для интервала примет формально евклидов
*) Отражение времени, т. е. преобразование
/ = — /'; х = х'; у—у'; г = г',
принято обозначать символом Г: T{t, х, у, г) = {—/, х, у, г}. В качестве неза-
независимого пространственного отражения выбирают обычно инверсию — одно-
одновременное изменение знака всех трех пространственных координат; это
преобразование принято обозначать символом Р: Р{1, x,y,z}={t,—х,—у,—г}.
В этих обозначениях только что сделанное утверждение гласит: &РТ не есть
вращение». В классической (в смысле неквантовой) теории, которой мы пока
занимаемся, его значение не очень существенно, но в релятивистской кванто-
квантовой теории оно играет важную роль.
2. ПРЕОБРАЗОВАНИЯ ЛОРЕНЦА 157
ВИД
2 2 2 2 2
2.2.1. Тогда линейные преобразования, оставляющие Eа) ин-
инвариантным и затрагивающие только координаты х\ = х и х4 =
= ic^, запишутся в хорошо знакомой форме
хх = cos -ф х[ — sin ty х'4,
где г|) — параметр поворота. Чтобы выяснить его физический
смысл, будем считать, что рассматриваемый поворот соответст-
соответствует переходу от некоторой инерциальной системы отсчета К.
к другой инерциальной системе К', движущейся относительно К
вдоль оси х с (постоянной!) скоростью V. Тогда движение ма-
материальной точки, имеющей в К' во все моменты «времени» x't
постоянную координату х' = 0, должно изображаться в системе
у
К уравнением х = Vt, т. е.х{= — х4. Из выписанных же формул
мы получаем
Следовательно, угол -ф «евклидова поворота» оказывается чисто
мнимым, причем
. V
.V 1 . , 1Т
) = i —, cos ib = —, , sin гЬ
V-
2.2.2.1. Как следует поступить здесь с выбором знака у кор-
корня? Если выбрать в обоих случаях знак «+», то мы придем к
формулам
V , .V
—х4 i —
X x' 4 x' х
Fa)
Эти преобразования называют специальными преобразования-
преобразованиями Лоренца или преобразованиями Лоренца в узком смысле
по имени голландского физика Гендрика Антоона Лоренца,
впервые их написавшего. (Надо отметить, что смысл, который
придавал Лоренц этим преобразованиям, существенно отличался
от того, который, следуя Эйнштейну, придаем им мы.)
Общими же преобразованиями Лоренца называют любые
преобразования, оставляющие инвариантным A) (впрочем, в по-
последние годы возникла тенденция сохранить этот термин только
для однородных преобразований, привлекая для обозначения
158 ч. II. МЕХАНИКА ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
неоднородных имя французского математика Пуанкарэ). Они мо-
могут быть получены путем последовательного применения («пе-
(«перемножения») специальных преобразований Лоренца в плоско-
плоскостях (х, t), (у, t) и (z, t), пространственных поворотов и отра-
отражений Р и Т. Преобразования Лоренца, не включающие отра-
отражений, называют часто собственными преобразованиями Ло-
Лоренца.
2.2.2.2. Выбор знака «—» у корня в выражении для синуса
не даст нам ничего нового, так как это сведется к замене знака
скорости V. Если же, однако, выбрать знак «—» в выражениях
и для синуса и для косинуса, то мы придем к преобразованиям
нового рода, не связывающихся непрерывно с преобразованиями
Fа) ни при каких значениях параметра V. В частности, при зна-
значении параметра V = О мы придем при таком выборе не к тож-
тождественному преобразованию, а к преобразованию
меняющему знаки времени и одной пространственной коорди-
координаты,— это есть пример декларированного выше рода преобра-
преобразований, которые, будучи произведением двух отражений, не
суть вращения.
ЗАМЕЧАНИЕ: Любопытно проследить, в каком именно месте проявляется
здесь отличие псевдоевклидова случая от евклидова. В последнем выражения
синуса и косинуса угла поворота через тангенс также содержат иррациональ-
иррациональность и ставят вопрос о знаках. Однако для вещественного угла, с которым
мы имеем дело в евклидовом случае, и синус и косинус могут иметь оба
знака, поэтому изменение знака корня для обеих функций можно интерпрети-
интерпретировать как изменение аргумента. В псевдоевклндовом же случае, когда угол
чисто мним, т. е. в обличье тригонометрических функций выступают на самом
деле гиперболические, гиперболический косинус существенно положителен и
изменение его знака никакой заменой аргумента скомпенсировано быть не
может. Щ
2.2.3. Мы записали специальное преобразование Лоренца в
плоскости (х, t) через формальное мнимое «время» х4. Перепи-
Переписанное через настоящее время t, оно будет выглядеть как
x\ + Vt' _ , _ , _ *'+-^х'\
у2 ' • Х2—Х2' Х3 Х3' '
2.2.3.1. Если перейти в преобразовании Лоренца к случаю
скоростей V, малых по сравнению со скоростью света, выполняя
формальный предельный переход с->оо, то мы получим из FЬ)
xl=x[ + Vt, х2 = 4> хг = х'у t = i> Fс)
— хорошо знакомое по первой части преобразование Галилея
2. ПРЕОБРАЗОВАНИЯ ЛОРЕНЦА'
159
гA.4). Таким образом, для кинематики теории относительности
выполняется принцип соответствия: в той области физических
явлений, в которой все скорости малы по сравнению со ско-
скоростью света, релятивистское описание совпадает с описанием
классической механики. Обратим внимание на то обстоятельство,
что в Fс) t=zt' —при предельном переходе к малым скоро-
скоростям время становится абсолютным.
Преобразования Лоренца F) определяют все кинематиче-
кинематические соотношения к теории относительности. Рассмотрим два
важных их применения.
2.3. Лоренцево сокращение. Пусть в системе К расположено
некоторое неподвижное твердое тело — по историческим причи-
причинам обычно говорят о «стержне» или «масштабе», — длина кото-
которого (в направлении х) есть Iq. Какую длину припишет тому
лоренцево сокращение
же телу наблюдатель, проводящий измерения в системе К',
жущейся относительно К со скоростью V?
В (двумерном на нашем чертеже) мире Минковского непод-
неподвижное в К тело изобразится полосой, ограниченной мировыми
линиями его концов — прямыми, параллельными оси t. Под
длиной тела мы понима-ем разность пространственных коорди-
координат х одновременных друг другу 4-точек этих мировых линий.
Поскольку, однако, одновременность зависит от системы отсчета,
то оказывается, что под длинами тела в разных системах К и
К' мы понимаем разность пространственных координат разных
пар 4-точек: на нашем чертеже это будут 4-точки Л и Р2 в си-
системе К и 4-точки Р\ и Р'2 в системе К', причем пара (Рь Р2),
160 ч. II. МЕХАНИКА ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
имеет одинаковую координату t, пара (Р'и Р'г) — одинаковую
координату f, а пары (Яь Я{) и (Р2, Я2) — соответственно одина-
одинаковые координаты х: х = хх и х = х2.
Выразим с помощью FЬ) пространственные координаты
4'точек Р{ и Я2 в системе К через их координаты в К':
х\ + W' х'9 + Vt'
и вычтем эти выражения друг из друга
.. „ _ Х1 - *2
V
1--?
В левой части полученного равенства оказывается тогда как раз
длина х2 — Xi тела в системе Л", в которой она покоится; ее на-
называют собственной длиной и обозначают через /0. В числителе
же правой стоит длина V = х'2 — х\ того же тела в системе К!.
Итак,
-1Г, G)
то есть
В той системе отсчета, относительно которой материальное
тело движется, его длина в направлении движения / сокра-
сокращается сравнительно с собственной длиной /0.
Этот эффект называется лоренцевым сокращением длины *).
ЗАМЕЧАНИЕ: Подчеркнем, что этот результат получился только за счет
того, что под длинами стержня в К и в К' мы понимаем разности простран-
пространственных координат разных пар точек. Если бы речь шла о сравнении разно-
разностей пространственных координат фиксированной пары точек, скажем, собы-
событий Pj и Рг одновременных в К, то мы получили бы, совершая преобразова-
преобразование Лоренца от К. к К':
,__ хг—Vh - / . Xi — УU __
Х2 — I— у2 ' ' Х — ¦— ~: *" — *'
ЧТО
t I Х2 — Х\
Хп X1 — ¦
— т.е. эффект был бы прямо противоположным G). Это замечание суще-
существенно для правильного преобразования пределов интегрирования, выпол-
выполняемого вдоль по фиксированной гиперповерхности, при переходе от одной
системы отсчета к другой. Я
*) Некоторые говорят: сокращение Фицджеральда.
2. ПРЕОБРАЗОВАНИЕ ЛОРЕНЦА 161
Поскольку поперечные (к направлению движения) измерения
тела не затрагиваются преобразованием F), то его объем Т
в движущейся системе сокращается по тому же закону G):
r = ro^/l-^-. Ga)
2.4. Сложение скоростей. В качестве второго важного при-
примера применения преобразований Лоренца, посмотрим, как скла-
складываются в релятивистской кинематике скорости, т. е. выясним,
с какой скоростью v будет двигаться относительно системы К
материальное тело, которое движется со скоростью v' относи-
относительно системы К', в свою очередь движущейся относительно К
со скоростью V. Напомним, что классические преобразования
Галилея приводили к простому ответу
на этот вопрос; теперь такой результат явно невозможен, так как
при сложении двух скоростей у < v', V < с он приводил бы к
v > с.
Перепишем преобразование FЬ) для дифференциалов:
X
и поделим почленно первые три равенства на четвертое. Вспоминая опреде-
определение скорости как производной координаты по времени, получим тогда
dx\ + V dt
тТ , О2 = -
или
V2 I V2"
c2 c2
Мы видим таким образом, что — в отличие от координат —
при переходе к другой системе отсчета преобразуются не только
составляющая V\ скорости по оси Х\, но и составляющие v2 и v$,
и притом различным способом. Поэтому чтобы переписать полу-
полученные формулы в векторном виде, приходится выделять у v и v'
продольные (вдоль V) и поперечные составляющие:
с2
6 В. В. Медведев
+ / v2
162 ч. П. МЕХАНИКА ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
Формула (8) и есть искомый релятивистский закон сложения
скоростей, заменяющий простое галилеево правило (*).
ЗАМЕЧАНИЕ 1: Если обе складываемые скорости v' и V парал-
параллельны друг другу, то закон (8), который можно записать тогда
в скалярной форме, значительно упрощается:
В частности, из него видно, что если обе складываемые скорости
у' и V меньше скорости света, то такой же будет и результирую-
результирующая скорость v. Можно показать, что это утверждение тем более
справедливо в общем случае (8). |
ЗАМЕЧАНИЕ 2: В случае непараллельных скоростей v' и V обе
эти скорости входят в (8) несимметрично. Это значит, что ре-
результат сложения двух скоростей в теории относительности за-
зависит от порядка. Поскольку всякую скорость (меньшую с!)
можно рассматривать как параметр преобразования Лоренца от
одной инерциальной системы к другой, то отсюда следует, что
и результат двух последовательных специальных преобразова-
преобразований Лоренца, выполняемых в несовпадающих плоскостях, зави-
зависит от порядка их выполнения. |
3. Четырехмерные векторы и тензоры
Как мы видели, интерпретация Минковского позволяет пере-
перевести кинематические соотношения на геометрический язык. По-
Поэтому полезно познакомиться с наиболее удобным геометриче-
геометрическим аппаратом — векторным и тензорным исчислением в четы-
четырехмерном псевдоевклидовом пространстве.
3.1. Совокупность четырех координат Х\, х2, Хз, х* мировой
точки можно рассматривать как компоненты проведенного из
начала координат в эту точку 4-радиус-вектора
х1 = {*,, х2, х3, х4), i = 1,2, 3,4
(в дальнейшем мы будем всегда считать, что латинские индексы
пробегают четыре значения 1, 2, 3, 4, а греческие по-прежнему
три: 1, 2, 3). При переходе от одной системы отсчета к другой
эти компоненты преобразовываются в соответствии с формулами
Fа) или аналогичными общеизвестными формулами для чисто
пространственных поворотов. Совокупность компонент радиус-
вектора во всех системах отсчета образует сам радиус-вектор; в
четырехмерной геометрии трудно развить символику прямого
исчисления, аналогичного трехмерным векторным обозначениям,
3. ЧЕТЫРЕХМЕРНЫЕ ВЕКТОРЫ И ТЕНЗОРЫ 163
поэтому прибегают к аналогу трехмерного тензорного исчисле-
исчисления и не делают в записи различия между радиус-вектором и
его компонентами в какой-то системе отсчета, обозначая его тем
же символом х\. В последнее время, впрочем, входит в моду опу-
опускать индекс и писать просто х, предоставляя читателю догады-
догадываться, о какой величине идет речь.
3.1.1. В аналогии с радиус-вектором любой набор заданных
в каждой системе отсчета упорядоченных четверок чисел Alt Лг,
А3, Ац называют 4-вектором
А{ = {Аи А2, А3, Л4} = {А, Л4} = А,
если при переходе от одной системы отсчета к другой они пре-
преобразуются по тем же формулам
что и радиус-вектор, т. е. с помощью матрицы ац —задаваемой
Fа) для специальных преобразований Лоренца и имеющей
обычный вид для пространственных поворотов.
В формуле (9.1) подразумевается суммирование по повто-
повторяющемуся индексу / от 1 до 4; мы будем систематически поль-
пользоваться этим соглашением о суммировании, подразумевающим,
что по каждому дважды входящему в один член латинскому
индексу должно быть проведено суммирование от 1 до 4.
3.1.2. 4-тензором s-ro ранга
называют совокупность заданных в каждой системе отсчета 4*
чисел, преобразующихся при переходе от одной системы отсчета
к другой с помощью произведений матриц а,.,-:
At t =аи ... at , А] ,*). (9.2)
М 's MM ls's М >s '
3.2. Как и в трехмерном тензорном исчислении, основными
алгебраическими операциями являются:
сложение тензоров одинакового ранга,
умножение, в результате которого образуется тензор, ранг
которого равен сумме рангов сомножителей, и
свертывание по паре индексов, в результате которого обра-
образуется тензор на две единицы меньшего ранга.
Удобно, особенно для двух векторов, рассматривать операцию,
состоящую в последовательном проведении умножения и свер-
свертывания; ее называют скалярным умножением. Если два век-
*) Из этого определения видно, что вектор есть тензор первого ранга»
а тензором нулевого ранга можно считать инвариант — число, не меняющееся
при изменении системы отсчета.
6*
164 '• "• МЕХАНИКА ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
тора в сокращенной записи (без индексов) записаны рядом, то
это всегда означает их скалярное произведение:
А ¦ В = АВ = AtBt = AtBkblk = AiBi + А2В2 + А3В3 + А^ —
= АВ + Л4В4*). A0.1)
Скалярное произведение вектора на самого себя образует
его квадрат
Л2 = Л? = А2 + 4 = А2-^. A0.2)
В частности, квадрат радиус-вектора равен
x? = x2-c42 = -s2. A0.3)
3.3. В нашем определении временная часть радиус-вектора входит в его
квадрат со знаком минус {а пространственная — со знаком плюс); о таком
определении говорят как о выборе отрицательной сигнатуры. Не менее часто
используется и положительная сигнатура, при выборе которой квадрат ра-
радиус-вектора определяется с противоположным знаком
Х2 = C2t2 _ Х2 = S2 (+ сИгнаТура!). A0.3')
4-радиус-вектор выбран у нас так, что его пространственные составляю-
составляющие вещественны, а временная xi — чисто мнима. Очевидно, что тем же свой-
свойством должны обладать н любые другие векторы, изображающие веществен-
вещественные физические величины. Что же касается (изображающих вещественные
физические величины) 4-тензоров, то те их компоненты, номер которых содер-
содержит нечетное число четверок, должны быть чисто мнимы, все же остальные —
вещественны. Поскольку ниже мы будем интересоваться только веществен-
вещественными величинами в вещественном псевдоевклидовом пространстве, то мы
ограничим (с одним тривиальным исключением, которое будет вскоре опи-
описано) класс допустимых тензоров обладающими этим свойством.
Появление мнимых составляющих векторов и тензоров обусловлено толь-
только тем, что мы для внешней аналогии с евклидовым пространством ввели
вместо времени мнимую четвертую координату *4; как говорят, мы поль-
пользуемся мнимой системой координат. В этом нет необходимости; не менее ча-
часто пользуются вещественной системой координат, вводя вместо времени ве-
вещественную координату размерности длины
хо = ct (Xi = i,fl) E')
и поступая аналогичным образом для всех векторов:
Ai = iA"
и тензоров.
Если пользоваться вещественной системой координат, то для скалярного
произведения приходится писать
А ¦ В = АВ - А*В° = gikAlBk,
и метрический тензор gik не будет уже единичным, но будет иметь на глав-
главной диагонали три плюса и один минус или три минуса и один плюс, судя
по выбираемой сигнатуре. Поэтому приходится различать ко- и контрава-
риантные (нижние и верхние) индексы; например при положительной сигна-
сигнатуре, для контраварнантного вектора А* = (А°, А1, А\ А3} соответствующим
ему ковариантным будет
At = {Ао. Аи А2, А3} = {А", - А\ - А\ - А').
*) Где, как обычно, 6<а = 1 при I = k и =0 прн I ф k.
3. ЧЕТЫРЕХМЕРНЫЕ ВЕКТОРЫ И ТЕНЗОРЫ 165
Суммирование (от 0 до 3) надо будет выполнять только по паре совпадаю-
совпадающих индексов, один из которых ко-, а другой — контравариантен, появление
же- пары одинаковых верхних или нижних индексов в одном члене служит
указанием на бессмысленность выписанного выражения. Квадрат вектора за-
запишется в этом случае как скалярное произведение контравариантного век-
вектора на соответствующий ему ковариантный
Л2 = ЛМ,=(Л0J-(АJ, A0.2')
если ие привлекать явно метрический теизор go,-
Как мы видим, избавление от мнимых составляющих достигается при
выборе вещественной системы не слишком дешево; поэтому мы будем ис-
использовать в дальнейшем мнимую систему, однако в некоторых случаях бу-
будем располагать индексы и внизу и вверху (в мнимой системе положение
индекса безразлично), так чтобы формулы сохранили бы смысл и прн -пере-
-переходе к вещественной системе координат*).
3.4. Кроме перечисленных выше алгебраических операций в
тензорном исчислении играет важную роль операция переста-
перестановки индексов. С ее помощью можно выделить из числа тензо-
тензоров второго ранга симметричные тензоры, обладающие свойством
Tlk = Tkl, A1.1)
и антисимметричные, удовлетворяющие
Aik—Akt. A1.2)
Произвольный тензор второго ранга может быть однозначно
представлен в виде суммы симметричного и антисимметричного.
Свертывая симметричный тензор Tih по двум его индексам,
получаем инвариант
Spur Tik = Tlh A1.3)
называемый следом тензора 7\ft (говорят также шпур). Всякий
симметричный тензор второго ранга однозначно представим в
виде суммы
¦единичного тензора и тензора со следом, равным нулю.
С разложением тензоров высших рангов на составляющие,
•обладающие определенной симметрией, дело обстоит значи-
значительно сложнее.
ЗАМЕЧАНИЕ: Легко понять, что преобразования (9.2) не ме-
меняют свойств симметрии тензоров. Иными словами, наличие оп-
определенной симметрии у тензора есть свойство, инвариантное
*) Читатель может быть несколько оглушен изобилием соописываемых
систем обозначений. Беда, однако, в том, что все они реально сосуществуют
в распространенной литературе — сравнимая анархия царит, пожалуй, только
в нормировке преобразований Фурье или каких-либо популярных специальных
функций.
166 ч. II. МЕХАНИКА ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
относительно выбора системы координат. Поэтому, если мы раз-
разбиваем тензор на части, обладающие противоположной симмет-
симметрией, то компоненты. каждой из этих частей в новой системе
координат будут выражаться с помощью (Э.2) только через ком-
компоненты той же части в старой системе. |
Особую роль играют тензоры с постоянными компонентами,
т. е. такие, компоненты которых не меняются при преобразова-
преобразованиях (9.2). В существенном существует только один такой тен-
тензор— тензор второго ранга 6,vi, совпадающий с символом Кро-
иекера; его называют единичным тензором. Все остальные тен-
тензоры с постоянными компонентами получаются из единичного
применением алгебраических операций, перечисленных выше.
3.5. До сих пор мы определили поведение компонент тензо-
тензоров только по отношению к собственным преобразованиям Ло-
Лоренца. Поскольку квадрат всякого отражения есть собственное
преобразование, то принятое определение предписывает поведе-
поведение тензора при отражении с точностью до множителя ±1: тен-
тензор может либо преобразовываться и при отражениях так же
(9.2), как произведение соответствующего числа радиус-векто-
радиус-векторов, либо испытывать дополнительную перемену знака. В пер-
первом случае его называют истинным тензором или просто тензо-
тензором, а во втором — псевдотензором*).
3.5.1. При включении в рассмотрение псевдотензоров, сово-
совокупность возможных объектов с постоянными компонентами рас-
расширяется. Действительно, рассмотрим (псевдо)тензор четвер-
четвертого ранга, антисимметричный относительно перестановки любой
пары индексов. Такой тензор имеет только одну не равную нулю
существенную компоненту — все его компоненты, имеющие со-
совпадающие индексы, равны нулю, а компоненты с четырьмя раз-
разными индексами равны ± компоненте с индексами 1, 2, 3, 4,
судя по тому, образуют ли индексы четную или нечетную пере-
перестановку этого набора. Полагая единственную существенную
компоненту равной единице, мы приходим к дискриминантному
тензору
etktms=± !.°»
судя по сформулированному выше правилу. Мы определили зна-
значения компонент дискриминантного тензора сразу во всех систе-
системах отсчета. Поэтому следует проверить, будут ли они преобра-
преобразовываться по закону (9.2). Легко увидеть, что по отношению
*) Строго говоря, в псевдоевклидовом пространстве тензор может вести
себя по-разному относительно временных и пространственных отражений.
В соответствии с этим можно было бы рассматривать, кроме истинных тен-
тензоров, псевдотеизоры трех разных сортов. Однако в классической (некванто-
(неквантовой) теории в этом не встречается нужды.
3. ЧЕТЫРЕХМЕРНЫЕ ВЕКТОРЫ И ТЕНЗОРЫ 167
к собственным преобразованиям Лоренца это действительно так,
при отражении же какой-либо координатой оси ешт остается
неизменным, в то время как истинный тензор должен был бы пе-
переменить знак. Таким образом дискриминантный тензор есть
псевдотензор *).
3.5.2. В трехмерном пространстве с помощью дискриминаит-
ного тензора можно было построить из всякого антисимметрич-
антисимметричного тензора второго ранга псевдотензор первого ранга — псев-
псевдовектор (или аксиальный вектор). В четырехмерном простран-
пространстве мы приходим на этом пути к тому, что всякому антисим-
антисимметричному тензору второго ранга Aim можно сопоставить
дуальный ему антисимметричный псевдотензор второго ранга
а* еЛ
так что задание дуального псевдотензора полностью определяет
первоначальный тензор. Полностью антисимметричному тензору
третьего ранга Akim можно таким же образом сопоставить ду-
дуальный ему псевдовектор:
a* eA
Наконец, полностью антисимметричному тензору четвертого
ранга АШт, имеющему только одну существенную компоненту,
можно сопоставить дуальный псевдотензор нулевого ранга —
как говорят, псевдоскаляр, величину, не меняющуюся при соб-
собственных преобразованиях Лоренца, но меняющую знак при от-
отражении, —
°* —f ештАшт\ АШт = еШта*. A2.3)
Поскольку псевдовектор или псевдоскаляр менее громоздки, чем
антисимметричные тензоры соответственно третьего или четвер-
четвертого ранга, то последними обычно и не пользуются.
ЗАМЕЧАНИЕ: Мы назначили не равным нулю компонентам дискриминант-
ного тензора значения ±1, между тем номер каждой такой компоненты со-
содержит одну четверку — т. е. мы нарушили наше правило о распределении
вещественных и мнимых компонент в тензорах. Из-за этого все дуальные
величины будут иметь распределение вещественных и мнимых компонент, про-
противоположное нормальному — т. е. будут включать лишний множитель
, про
«'• I
*) В некотором смысле дискриминантный тензор есть объект более эле-
элементарный, чем единичный, поскольку последний можно получить из него
средствами тензорной алгебры:
. 1_
** ~ 31
_
31 еЧтпеМтп-
168
ч. II. МЕХАНИКА ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
3.6. В четырехмерном пространстве можно интегрировать по
линии, по 2-поверхности, по трехмерной гиперповерхности и по
4-объему.
3.6.1. Для линейного интеграла элементом интегрирования
является бесконечно-малое смещение dxt вдоль линии; если ли-
линия задана в параметрической форме Xi — Xi(K), то это смеще-
dx,
ние можно записать как dxt —тзт""^-
3.6.2. Элемент площади двумерной поверхности есть, как известно из диф-
дифференциальной геометрии, антисимметричный тензор второго ранга dan, об-
образуемый в форме детерминанта из двух независимых смещений dixi и d2Xi
вдоль поверхности:
!"*, d*x,
da
if
d2x, d2x
¦¦dlx.d2xj-dlxjd2x..
Если поверхность задана в параметрической форме Xi == Xi (Xi Д2), то эти
д д
дх.
дх.
дх, дх,
независимые смещения можно записать как d[x, = _. dX,, d2x, — -rr— dXo.
Иногда удобно использовать вместо элемента интегрирования
ему «ортогональный» поверхности элемеит
* 1 дхь дх.
4 ^
rr
дуальный
3.6.3. Элемент площади трехмерной гиперповерхности есть детерминант,
образованный из трех независимых смещений:
dS
ilk'
dl*i dl*i dlxk
d2x. d2x, d2xk
d3x,
*/
+ {еще 5 членов, получающихся
перестановками индексов i, /,
k с соответствующими измене-
изменениями знаков). A3.2)
Если гиперповерхность задана параметрически
Вместо антисимметричного тензора третьего ранга всегда удобнее использо-
использовать дуальный ему (звездочку здесь писать не принято)
1
Рассмотрим составляющую dS\\
Выберем в качестве параметров Xi, %г, Яз координаты Хг, Хз, х!к (этого нельзя
сделать только в том случае, когда рассматриваемый элемент гиперповерх-
гиперповерхности ортогонален гиперплоскости (xi, хз, лч), но тогда нормальный элементу
3. ЧЕТЫРЕХМЕРНЫЕ ВЕКТОРЫ И ТЕНЗОРЫ 169
поверхности вектор dSi лежит в этой гиперплоскости, и, следовательно, его
составляющая dSi равна нулю). Тогда
Поэтому
dSt = dx2 dx3 dx4. A3.2')
Такое же рассуждение дает для остальных компонент dSf.
dS2 = dxi dx3 dxit dS3 — dx{ dx2 dxk> rfS4 = — dx{ dx2 dx3 = — dT.
A3.2')
Именно элементом гиперповерхности в виде A3.2') единсткенно
и пользуются при реальных интегрированиях.
3.6.4. Элементом интегрирования по четырехмерному много-
многообразию— 4-объему — будет по общему правилу антисиммет-
антисимметричный тензор четвертого ранга dunM, образованный в виде ана-
аналогичного A3.1) и A3.2) детерминанта четвертого порядка из
компонент четырех независимых смещений. При его раскрытии
мы получили бы 4! = 24 члена, отличающихся лишь порядком
расстановки индексов и соответствующими знаками. При обра-
образовании дуального элемента число этих членов опять сократится
с нормирующим множителем из A2.3), и мы получим
du = -?- emi duijkl = dPx^XfiPxkfPxt • ецы. A3.3*)
Повторяя рассуждение с рациональным выбором параметриче-
параметрического представления (теперь удобно выбрать в качестве четырех
параметров ки ..., Я4 четыре координаты дгь ..., х4), придем
для элемента 4-объема к единственно употребляемому выраже-
выражению
dQ = dxx dx2 dxz dx4 = ic dT dt. A3.3')
ЗАМЕЧАНИЕ 1: Поскольку dS, и du получились свертыванием
с дискриминантным тензором, то они содержат «лишний множи-
множитель 1»; никаких неудобств это не приносит. |
ЗАМЕЧАНИЕ 2: Формально dS{ и dQ суть nceedo-вектор и
пс?в<Эо-скаляр; однако фактически лишние перемены знака при
отражении всегда бессознательно компенсируются изменением
порядка пределов интегрирования. Поэтому можно считать их
вектором и скаляром. |
170 ч. П. МЕХАНИКА ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
ЗАМЕЧАНИЕ 3: Для трехмерного элемента объема dT упот-
употребляют еще и обозначения {d\)% или (dr). Аналогично, для
элемента 4-объема кроме d?l пишут еще и (dx)i, (dxi) или даже
dx. I
ЗАМЕЧАНИЕ 4: В формуле A3.2) используется разная параметризация для
разных компонент dS,-. Если гиперповерхность а, по которой производят ин-
интегрирование, пространственно-подобна (т. е. пространственио-подобна любая
пара точек этой гиперповерхности), то dSi никогда не равно нулю, и пара-
параметризацию для всех четырех компонент можно выбрать единообразно, при-
приняв за независимые параметры три пространственные координаты Xi, Хг, х$
и описывая гиперповерхность уравнением Xi. = f(xt, x2, x3). Тогда
0/. + »,4 ЖГ) 0/2 + »|4 ¦?) 0/3 + *Н ¦?
то есть
ОХг
что можно записать как
где я;, tti = — I, — единичный вектор (направленной в будущее) нормали
к a, a dx — инвариантный элемент интегрирования:
Выбор знака у кория соответствует здесь выбору направления нормали
V'+Ш"
Единичный вектор л;(х) определяет*) в каждой точке (х, f(x)) гиперпо-
гиперповерхности новую систему отсчета К': (х', t'), движущуюся относительно пер-
первоначальной системы К со скоростью
*) Вместе с условием, чтобы проекции пространственных осей системы К'
на гиперплоскость t = const были бы соответственно параллельны простран-
пространственным осям системы К.
3. ЧЕТЫРЕХМЕРНЫЕ ВЕКТОРЫ И ТЕНЗОРЫ
171
Через эту скорость:
{т.'}
A3.2")
*• V1-(*)'
В системе К' имеет место
я- = @, г), ^ = 0, dS4 = — dr' = ~ dx,
я формулы A3.2") суть просто результат преобразования 4-векторов «; и
из системы К' в систему К согласно формулам преобразования Лоренца Fа):
dS' V dS'.
Несколько неожидан другой наш вывод — то что «элемент объема» гипер-
гиперповерхности а испытывает вместо лоренцева сокращения Gа) — растяжение
Причину этого обстоятельства мы уже обсуждали в замечании к сокращению
Лоренца — при проектировании элемента гиперповерхности из К' в К речь
172 ч. II. МЕХАНИКА ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
идет о сравнении разностей пространственных координат фиксированной пары
точек («концов» элемента dS[^, а не о сравнении пространственных «ши-
«ширин» полосы, которая получилась бы из этого элемента, если сдвигать его
в направлении xv |
3.7. Как и в привычном случае векторного анализа в трех-
трехмерном евклидовом пространстве, в пространстве Минковского
имеют место интегральные теоремы, позволяющие преобразо-
преобразовывать интеграл по замкнутому многообразию т измерений в-
интеграл по заключенному в нем многообразию (m-f-1) изме-
измерения. В 4-мерном случае т может, очевидно, принимать значе-
значения 3, 2 и 1. Если обозначить временно элемент интегрирования
для любого т одним значком df с равным т числом индексов,,
то все такие интегральные теоремы можно записать единооб-
единообразно как
где интегрирование справа выполняется по (т + 1)-мерному
многообразию, а слева по «ограничивающему» его замкнутому
m-мерному многообразию, многоточие же означает остальную
часть подинтегрального выражения, которая может иметь лю-
любую тензорную размерность. Придавая теперь т значения 1, 2,
3, получим отсюда для
т=\, &dx, ... = \dolt-?- .... A3.4.1)
теорему Стокса: J , J i
т = 2: §do,h...-=\dSllk-?r ..., A3.4.2)
m-3, & dSm ... = \dQlw -§- ... A3.4.3)
теорему Гаусса: J J i
— последняя встретится нам особенно часто. В двух последних
формулах надо, конечно, перейти к дуальным элементам интег-
интегрирования, в результате чего они примут форму
^L-rfS, JL) .... A3.4.2*)
т-3, &dSt ... =\dQ-?-..., A3.4.3*)
теоремы Гаусса: J J i
в которой их обычно и выписывают в книгах.
3.8. Из линейных интегралов чаще всего приходится встре-
встречаться с интегрированием вдоль мировой линии материальной
точки.
3. ЧЕТЫРЕХМЕРНЫЕ ВЕКТОРЫ И ТЕНЗОРЫ 173
В нерелятивистской теории при рассмотрении интегралов
вдоль траектории частиц мы использовали в качестве незави-
независимого параметра время t, записывая движение как ха = xa(t)'r
координаты и время входили в эту запись совершенно неравно-
неравноправным образом. Теперь такой выбор (хотя и всегда возможен)
не всегда удобен, поскольку, не говоря уже о нарушении четы-
четырехмерной симметрии, время не есть инвариант.
Чтобы восстановить симметрию, напишем четыре уравнения
вместо трех:
— тем самым мы привлекаем для описания движения одной ма-
материальной точки четыре функции вместо трех, но зато у нас по-
появляется свобода в выборе параметра X, который мы пока оста-
оставили произвольным.
Иногда бывает удобно некоторое время сохранять этот про-
произвол, иногда оказывается все-таки полезной 4-несимметричная
запись через Я = t (четвертое уравнение оказывается тогда тож-
тождеством). Однако чаще всего прибегают к непосредственной ин-
вариантизации нерелятивистского способа записи, выбирая в ка-
качестве независимого параметра введенное формулой D) соб-
собственное время т или отличающуюся от него лишь множителем
с 4-длину мировой линии s = с% и записывая *)
Эта запись напоминает движение нерелятивистской системы
с четырьмя степенями свободы. Не надо, однако, упускать из
виду два существенных отличия:
A) в отличие от dt, ds (или dx) не есть полный дифференциал,
B) из четырех выписанных уравнений только три — незави-
независимы; причем связь формулируется в неявной интегральной
форме D), служащей для определения s.
3.8.1. Элемент смещения вдоль мировой линии, dxi, запишется
dx.
тогда как dxt = -^- ds.
4-вектор
( dx . \
и -dxJ = dx' = X~dT'lci
1 ds Vc2^2
оказывающийся при таком выборе параметризации аналогом
скорости, называют 4-скоростью. Через обычную трехмерную
*) Такой выбор обычен в дифференциальной ггометрии.
174 ч. II. МЕХАНИКА ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
скорость y = ~jf он выражается в форме
(И)
Не все компоненты 4-скорости независимы. Действительно, воз-
возводя A4) в скалярный квадрат, убеждаемся что
и] = ~\, A4а)
т. е 4-скорость есть (времени-подобный) единичный вектор.
Выполняя еще одно дифференцирование по ds, приходим к
к 4-ускорению
du,
»i—ЗГ- A5)
В силу тождества A4а) 4-ускорение всегда ортогонально 4-ско-
4-скорости
ulwi = 0. A5а)
4. Динамика свободной материальной точки
4.1. В нерелятивистской механике нам не удалось построить
для свободной материальной точки действие, инвариантное от-
относительно преобразований Галилея,—этим свойством обладала
лишь его вариация. Выражение для действия одной свободной
материальной точки, инвариантное относительно преобразований
Лоренца, построить можно. Умножая (векторный) элемент dxf
мировой линии частицы скалярно на единственный локальный
dxt
вектор Ui — —i—.который можно построить из характеристики
мировой линии Xi = Xi(s), не прибегая к производным старше
первого порядка, придем к пригодному для роли действия ин-
инвариантному интегралу
Р, Рг , Р>
С С dx\ Г
S = aJ uidxl = a } -57 = — aj ds, A6)
pt p. л
где a —постоянная, которая должна быть положительной, так
как в псевдоевклидовом пространстве можно, как мы видели,
Рг
удлинением траектории сделать \ ds между времени-подоб-
pL
ными Рг > Р\ сколь угодно малым.
Действие в форме A6) приводит, однако, при использовании его в ва-
вариационном принципе к одному неудобству: поскольку ds не есть полный
дифференциал, то при выполнении интегрирования в A6) между фиксирован-
4. ДИНАМИКА СВОБОДНОЙ МАТЕРИАЛЬНОЙ ТОЧКИ
175
ными 4-точками Pi и Рг, пределы интегрирования по s сами будут изменяться
при варьировании траектории. Поэтому удобно ввести временно вместо длины
дуги s другой (в остальном — произвольный) независимый параметр X, зна-
значения которого в точках Pi н Р2 можно было бы, однако, держать фиксиро-
фиксированными. Мы придем тогда к
Г> ft
С , f
*=== ct \ ы dx • '==: ct \
j i i j
Pi Pi
dxt
~Ts Ik
d\-
л,
-dx\
dk;
A6')
К
В таком виде действие имеет уже привычную нам по первой части фор-
форму, н к нему можно применить развитый там общий формализм. Роль вре-
времени в A6') играет параметр к, поэтому «функцией Лагранжа» будет
A7)
«Импульсом» будет теперь производная от функции Лагранжа по «скорости»
dL
О
dx,
L
dk
dx.
L_
d%
V-hr) V-(-ar)
A8)
Уравнения движения будут по общему правилу гласить
dx,
d
dk
dL
dx
¦¦ 0, т. e.
d\
A9)
т. е. «импульс» pi будет сохраняться
pt = const,
как то и должно было быть в силу D-мерной) трансляционной инвариантно-
инвариантности действия, ради обеспечения которой мы приняли, что функция Лагранжз
не может зависеть от самих координат частицы Xi(X).
*) Поскольку мы не требовали инвариантности X, то н скорость
dk
или
импульс pi не обязаны быть 4-векторами, хотя и несут один тензорный ин-
индекс. Правда, конкретный импульс A8) есть 4-вектор: поскольку dk в чис-
числителе и знаменателе сокращаются, то он не зависит от выбора к, а при
инвариантном X обязан быть 4-вектором.
176 ч. II. МЕХАНИКА ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
Наконец, построение формального аналога функции Гамильтона
dx.
(сумма по четырем степеням свободы) приводит к тождеству
dx, dx.
4.2. Теперь можно заняться рациональной конкретизацией %.
Подчеркнем, что конкретный выбор А, не влияет на существо
полученных результатов, а затрагивает только форму их записи.
¦Форма, наиболее близкая к нерелятивистской теории, получается,
если выбрать Я = t. Тогда
=-«у- DгJ - № = -ас Vi -
тде v = -ji обычная 3-скорость. В предельном случае малых
¦скоростей получаем отсюда
или, поскольку постоянный член в функции Лагранжа несущест-
несуществен,
, a v2
L
Отсюда видно, что для соблюдения принципа соответствия
характеризующая частицу постоянная а должна равняться
а —/яс,
где m — масса частицы. Следовательно,
A70
Для «импульса» pt мы получаем теперь из A8)
{v, ic)
4. ДИНАМИКА СВОБОДНОЙ МАТЕРИАЛЬНОЙ ТОЧКИ 177
Пространственные компоненты дают нам здесь релятивистское
выражение обычного импульса
Р= Г , , A8.1)
четвертая же компонента
imc
Тождество B0) удобно записать теперь в форме
откуда видно, что (умноженная на -^- = —ic\ компонента р4
есть энергия материальной точки:
«¦=Pv-i=—==-• A8.2)
Для скорости v = 0 энергии & не обращается в нуль, а стре-
стремится к константе
при v = 0 Ж = 80 = тс2, A8.3)
называемой энергией покоя.
Для малых, но не равных нулю, скоростей выражение A8.2)
для энергии превращается в
при v->0; v^O Ж = тс2 + -~,
отличающееся лишь постоянной <ЁГ0 от обычного нерелятй&ист-
ского вида кинетической энергии.
Наконец, для v-*-c энергия Устремится к бесконечности
Отсюда видно, что для того, чтобы разогнать материальную час-
частицу любой конечной массы до скорости, равной скорости света,
потребовалось бы затратить бесконечно много энергии*).
Из A8.1) и A8.2) получается важная формула
р = -^. A8.4)
*) Поэтому состояние движения быстрых частиц практически неудобно
задавать значением их скорости; гораздо рациональнее пользоваться для
этого отношением их энергии к энергии покоя (или импульса к энергии по-
покоя, деленной на скорость света).
178 ч II. МЕХАНИКА ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
Из нее, в частности, можно усмотреть, что теория относитель-
относительности не противоречит существованию частиц, постоянно дви-
движущихся со скоростью света, для них соотношение A8.4) пре-
превращается в р = —. Масса покоя таких частиц должна, естест-
естественно, равняться нулю. Такие частицы на самом деле сущест-
существуют в природе — их примером могут служить кванты света
(фотоны).
В силу аналогии A8.4) с нерелятивистской формулой р = тч,
иногда называют Л- — т полной массой или массой,.
зависящей от скорости.
Вообще надо сказать, что слову «масса» очень не повезло в теории отно-
относительности. В ее ранние годы почему-то представлялось большим облегче-
облегчением для понимания существа теории сохранить это слово для релятивист-
релятивистских аналогов всех многочисленных ипостасей, в которых выступает масса
в классической механике. А так как каждая «ипостась» обобщалась при пере-
переходе к теории относительности по-разному, то возникло детое семейство раз-
разных релятивистских «масс». Так, например, желая придать релятивистским,
уравнениям движения
# = 0 (свобо7ва) "ЛИ 4Г = f ("«a"" подТйс
at v свооодва / dt \ внешних сил f
привычный вид th—7—=f, приходили к очень громоздкому выражению для т.
Оно упрощалось, если «сила» f была направлена перпендикулярно или парал-
параллельно скорости v. В первом случае, когда сила меняет скорость только по
направлению, получалось
rfv rip т dv_
ЧГ 1Г Ж
/ V2
V с2
и величина . г называлась «поперечной массой» (она совпадала
с «массой, зависящей от скорости»). Во втором случае, когда скорость меня-
менялась только по величине, приходилось дифференцировать и корень, приходя,
к результату
d\ .. dp т dv_
¦rfFl|v: dt ~ ( v2 \'h dt
V c2 )
и величину — 2 3/ называли «продольной массой». Сейчас вся эта>
терминология, равно как и развивавшаяся по ее поводу «философия», имеют
лить исторический интерес.
Выразим энергию через импульс. Из A8.1)
г!
с'-т'- + р:
2 Х> V go V2 pz
i —!—— = mrv1. т. е. —х- = —т,—г?—.—к-
4. ДИНАМИКА СВОБОДНОЙ МАТЕРИАЛЬНОЙ ТОЧКИ 179
Поэтому
тс2
V
с2т2 + р2 — р2
= с -\1т2с2 + р2.
Энергия, выраженная через импульс, есть функция Гамиль-
Гамильтона. Итак, для свободной материальной точки в теории отно-
относительности функция Гамильтона (три степени свободы!) есть
Ж(Р, r) = cVm2c2 + p2. A9)
Для импульсов, много меньших характерного импульса тс,
|р|-С тс, отсюда получается Ж = тс2 + -~ сумма энергии
покоя и обычной нерелятивистской функции Гамильтона.
Для импульсов, удовлетворяющих противоположному силь-
сильному неравенству |р| ^> тс, можно пренебречь под корнем чле-
членом с массой, и мы получаем Ж « ср — как раз формулу A8.4)
для безмассовых частиц. Результат вполне естественный — для
энергий, много больших энергии покоя, эта последняя перестает
быть существенной.
4.3. Другая разумная возможность выбора параметра К со-
состоит в том, чтобы после проведения вариационной программы *)
положить его равным инвариантному параметру s.
dx.
Тогда «скорость» -^г = «г есть 4-вектор A4), и в силу тож-
тождества A4а)
благодаря чему из A8) и A9) получаем уравнения движения:
dmcu, du,
-5^ = 0, т.е. ^- = 0, B0)
и выражение для сохраняющегося 4-вектора импульса:
Pi = mcu{ = const. B1)
Подставляя в B1) выражение A4) для 4-скорости и сравни-
сравнивая с формулами A8.1) и A8.2), находим, что
/о i \
*) До этого полагать l = s в силу сделанного выше замечания нельзя.
.Действительно, при такой попытке выясняется, что формально Ls = —me,
т. е. константе!
180
ч. П. МЕХАНИКА ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
Таким образом, импульс A8.1) и энергия A8.2) образуют один
4-вектор*)—он называется 4-импульс.
Как и всякий 4-вектор, 4-импульс преобразуется при преоб-
преобразованиях Лоренца с помощью формул Fа). Отсюда полу-
получается правило для преобразования трехмерного импульса и
энергии:
V1-*1
=-• 08.5)
Возводя B1) в квадрат, получаем, в силу тождества A4а) для 4-скоро*
сти, связь между энергией и импульсом, выраженную в 4-симметричной форме::
Pi тс . (,1у у
Если выразить здесь компоненты 4-импульса через трехмерные импульс и
энергию, то получим
ЗАМЕЧАНИЕ 1: Если извлечь из A9") почленно квадратный
корень, то мы опять придем к формуле A9), но с одной сущест-
существенной оговоркой: при извлече-
извлечении корня возникает двойной
знак. Таким образом формаль-
формально в теории относительности
энергия частицы может быть
не только положительной, но и.
отрицательной.
Поучительно изобразить эту
зависимость & от р в виде по-
поверхности в псевдоевклидовом
4-пространстве, координатами
которого
служат i —, ри р2у
поверхность энергии
р3 — в импульсном пространст-
пространстве. Она имеет вид двуполого
гиперболоида, лежащего внут-
внутри светового конуса, к кото-
которому приближается асимптотически при <??->±°o.
Эту поверхность называют поверхностью энергии; ее верхняя
пола отвечает функции Гамильтона A9).
Для знака минус (нижняя пола гиперболоида)
S (р) < S (р = 0) = - тс2 < 0,
*) Поэтому нельзя выбросить из A8.2) энергию покоя — мы не получили
бы тогда 4-вектора.
5. ДЕСЯТЬ ФУНДАМЕНТАЛЬНЫХ ВЕЛИЧИН 181
т. е. с ростом импульса — по мере ускорения частицы — ее энер-
энергия уменьшалась бы, а энергия покоя была бы отрицательна.
Это значит, что нижняя пола поверхности энергии соответство-
соответствовала бы частицам отрицательной массы\
В неквантовой теории эта трудность не имеет существенного
значения, ибо непрерывный переход из положительных энергий
в отрицательные невозможен, поскольку они разделены энерге-
энергетической «щелью» ширины 2тс2. В квантовой теории, однако, это
обстоятельство доставляло много неприятностей, пока не было
выяснено, что эта двузначность действительно реализуется в при-
природе, хотя и совсем не прямым образом, и проявляется в том, что
каждой элементарной частице соответствует «античастица». |
ЗАМЕЧАНИЕ 2: В нерелятивистской теории функции Лагранжа и Гамиль-
Гамильтона находились в соотношении определенной симметрии друг к другу (ср.
I, 16). В релятивистской теории эта симметрия нарушается ых различным тен-
тензорным характером. Действительно, функция Лагранжа является скаляром
(правда, в несколько «пиквикском» смысле, поскольку для иеинвариантной
параметризации это не так, а для инвариантной ее нельзя варьировать). Функ-
Функция же Гамильтона есть, как мы теперь видим, четвертая компонента вектора.
Это обстоятельство приводит к тому следствию, что гамильтонова формули-
формулировка уравнений всегда оказывается не обладающей явной релятивистской
инвариантностью. 1
5. Десять фундаментальных величин
5.1. Рассмотрим теперь систему не взаимодействующих друг
о другом свободных материальных точек. Действие для нее пред-
представится суммой по номеру а частицы выражений A6)
5.1.1. Что следует выбрать здесь за независимый параметр,
за формальное «время»? Ведь для того, чтобы с действием A6")
можно было обращаться, как с целым, оно должно быть пред-
представлено одним интегралом, значит, надо выражать координаты
мировых линий всех частиц в функции одного общего параметра.
Пока у нас была одна частица, мы могли выбирать незави-
независимый параметр для параметрического представления ее миро-
мировой линии совершенно произвольным образом, с тем единствен-
единственным ограничением, чтобы он монотонно возрастал вдоль миро-
мировой линии в направлении от прошлого к будущему. (Тут было
182 ч. И. МЕХАНИКА ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
бы неплохо объяснить, чем отличается будущее от прошлого, но
это-то как раз мы и не умеем делать, хотя считаем, что все это
и так понимают!). Коль скоро, однако, у нас есть несколько —
хотя бы и не взаимодействующих друг с другом — частиц, то
если мы хотим трактовать какие-либо их совокупные свойства,
желательно выбрать параметризацию таким образом, чтобы вся-
всякий раз, когда мировые линии (хотя бы) пары частиц пересе-
пересекаются (т. е. две частицы оказываются в одном месте в один и
тот же момент времени (с точки зрения любой инерциальной
системы отсчета!)), значения параметров, служащих для описа-
описания движения каждой из частиц, совпадали бы. (Мы уже знаем,
что собственное время т или взятый вдоль мировой линии интер-
интервал s не удовлетворяют этому пожеланию!)
Поскольку мировыми линиями частиц могут быть в принципе
любые (достаточно гладкие, конечно) времени-подобные кривые
в пространстве Минковского, то
сформулированное пожелание озна-
означает, что в каждой 4-точке прост-
пространства Минковского значение неза-
b-) висимого параметра на любой про-
ходящей через нее времени-подоб-
ной линии должно зависеть только от
точки, но не от конкретной линии.
А поскольку мировая линия какой-
либо частицы может оказаться про-
проходящей через любую 4-точку, то
всякой 4-точке Р следует приписать свое значение параметра, ко-
который мы будем называть X. Естественно принять, что параметр
1 непрерывно (и достаточно гладко) зависит от 4-точки Р.
Рассмотрим какую-либо мировую точку Р и будем считать,
что мы приписали этой точке некоторое значение параметра,
скажем X. В любую близкую к ней точку Р', расположенную в
«послеконусе» точки Р (Р'~>Р), из Р может направиться ми-
мировая линия какой-либо частицы — значит, значение X' нашего
параметра в такой 4-точке Р' должно быть больше значения X,
X' > X. Точно так же всякой точке Р" из окрестности Р, лежа-
лежащей в ее «предконусе», Р > Р", необходимо приписать значение
X" < X.
Таким образом, те точки Р'" из окрестности Р, которым со-
соответствуют значения Х(Р"') =Х(Р), могут быть расположены
только пространственно-подобно Р: Р'" ~ Р. Продолжая это
рассуждение, приходим к выводу, что совокупность 4-точек, ко-
которым мы можем приписать то же значение параметра X, что
и выбранное для точки Р, должны образовывать в мире Мин-
Минковского некоторую пространственно-подобную гиперповерх-
гиперповерхность, которую будем обозначать символом а(Р). Те же аргу-
5. ДЕСЯТЬ ФУНДАМЕНТАЛЬНЫХ ВЕЛИЧИН 183
менты применимы, очевидно, ко всякой 4-точке и ко всякому зна-
значению параметра. Итак:
рациональная параметризация 4-пространства состоит в том, что
в нем выбирается произвольное однопараметрическое семейство
пространственно-подобных гиперповерхностей, такое, что через
каждую 4-точку проходит одна и только одна поверхность се-
семейства.
Такая операция может быть проведена бесчисленно различ-
различными способами, и любой из них представит нам независимый
параметр, «время», для построения лагранжева формализма для
системы материальных точек. С точки зрения выполнения реля-
релятивистской инвариантности и причинности все эти времена рав-
равноправны. Чтобы сузить класс «времен», удобных для физики,
уместно вспомнить, что лагранжев формализм служит основой
для получения по теореме Нётер сохраняющихся величин, и что
согласно замечанию 2 в 1.5.2 эти величины приобретают осо-
особенно простую—аддитивную — форму для тех преобразований
симметрии, которые не затрагивают независимой переменной.
Чтобы не упустить эту возможную выгоду, надо, очевидно, нало-
наложить на выбор семейства гиперповерхностей а то ограничение,
чтобы — хотя бы для некоторых преобразований симметрии
4-пространства (т. е. — элементов неоднородной группы Лорен-
Лоренца)— соответствующие преобразования координат xai(X) частиц
не затрагивали бы независимую переменную X.
На геометрическом языке это значит, что мы хотим, чтобы
некоторые (чем больше — тем лучше) преобразования Лоренца
не смещали бы гиперповерхностей or, но двигали бы их самих по-
себе, осуществляли бы на них внутренние движения. Такое воз-
возможно лишь для поверхностей постоянной кривизны — простран-
пространственно-подобных гиперплоскостей или «сфер» (пространственно-
подобная сфера в псевдоевклидовом пространстве скорее похо-
походит— во всяком случае, на наших чертежах — на двуполый
гиперболоид, см. в виде примера чертеж «поверхности энергии»
на стр. 180) или — предельный случай — световых конусов, либо
наконец, — другой особый случай — гиперплоскостей, касающих-
касающихся светового конуса. В соответствии с этим оказывается, что
релятивистскую динамику можно строить в трех различных фор-
формах: мгновенной, когда за гиперповерхности а принимается се-
семейство параллельных гиперплоскостей — такая форма представ-
представляется наиболее обычной с точки.зрения аналогии с нереляти-
нерелятивистской теорией, точечной, когда за а выбираются гиперсферы,
и фронтальной, когда гиперповерхностями являются гиперпло-
гиперплоскости, касающиеся светового конуса.
ЗАМЕЧАНИЕ: Эти соображения о существовании различных форм реляти-
релятивистской динамики были впервые развиты Дираком в работе: P. A. M. D i-
rac, Rev. Mod. Phys., 21, 392 A949). Их упоминание здесь есть некоторо
184 ч. II. МЕХАНИКА ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
излишество, поскольку в рассматриваемом случае системы невзаимодействую-
невзаимодействующих материальных точек все сохраняющиеся величины аддитивны уже бла-
благодаря аддитивности лагранжиана. Когда же мы включим ниже в рассмотре-
рассмотрение взаимодействие, то явным образом будем использовать только гиперпло-
гиперплоскости, и при том вида х4 = Я. |
5.1. Итак, проведя параметризацию всего 4-мира с помощью
зависящего от одного параметра к семейства пространственно-
подобных гиперповерхностей, мы сможем выразить и четверки
координат каждой материальной точки в функции того же па-
параметра, т. е. записать действие A6") для системы материаль-
материальных точек в виде одного интеграла
При такой форме записи любые преобразования координат не
будут затрагивать независимой переменной X и, согласно теоре-
теореме Нётер, из инвариантности действия относительно преобразо-
преобразования
будет следовать закон сохранения (удобно исходить из A.8.4))
вида
dk
5.1.2. Выбирая в качестве преобразования, относительно ко-
которого действие должно остаться инвариантным, 4-сдвиг
придем к закону сохранения 4-импульса системы
pi = Т, РТ= Т, tn си° == const. B2)
а а
Т n с
а а
В силу аддитивности действия он равен сумме 4-импульсов от-
отдельных частиц.
5.1.3. Выберем теперь в качестве преобразования симметрии
бесконечно малое однородное (общее) преобразование Лоренца.
Такое преобразование можно записать как
х? -+ x'i = *? + 6х?> 6х? = xi 6Qki> гДе ши = ~ mik B3)
бесконечно-малые параметры. Действительно, тогда
5. ДЕСЯТЬ ФУНДАМЕНТАЛЬНЫХ ВЕЛИЧИН , 185
в силу антисимметрии dQa. (Антисимметричный тензор 6Qift
имеет б независимых компонент — как раз столько, сколько не-
независимых поворотов в 4-пространстве.)
Из инвариантности действия относительно B3) будет тогда
следовать, что
d
~d% Lj^i'-k^ki)— d% 'У~и>к ~ьни о — °.
a a
т. е. что для системы свободных материальных точек сохраняет-
сохраняется антисимметричный тензор второго ранга
?*=const-
Этот тензор называется 4-момент.
ЗАМЕЧАНИЕ: Мы отнормировали 4-момеит так, чтобы было
Тогда пространственная часть дает
6S = -^ Мор бйар = у еаруеорцЛ1 Y бфц = (М ¦ 6<р)
в полном согласии с нормировкой, избранной нами в формулах A3) нереля-
нерелятивистской теории. |
5.1.3.1. Как всякий антисимметричный тензор, 4-момент
имеет шесть независимых компонент. Три из них получаются,
если придавать индексам i, k только значения а, р = 1, 2, 3. Эта
пространственная часть 4-момента образует трехмерный анти-
антисимметричный тензор второго ранга
в трехмерном пространстве его можно заменить дуальным псев-
псевдовектором
М еМ е
Итак, пространственная часть 4-момента есть та величина, ко-
которую мы называли просто моментом; выраженный через коор-
координаты и импульсы он записывается точно так же, как и в нере-
нерелятивистском случае (конечно, при выражении через коорди-
координаты и скорости мы не получим простой нерелятивистской
формулы, так как для импульсов войдут выражения A8.1)).
5.1.3.2. Остальные три компоненты момента получатся, если
придать первому индексу значение 4, а второму а = 1, 2, 3. Эти
компоненты образуют 3-вектор относительно чисто пространст-
186 ч. II. МЕХАНИКА ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
венных вращений, а так как в числе 4-индексов все они содер-
содержат одну четверку, то чтобы сделать этот вектор вещественным,
надо выделить из него множитель /. Итак, полагая
4a = ic ? (tapt - S-^r-) = icNa = const, B4b)
М,
видим, что три смешанные компоненты закона сохранения 4-мо-
мента приводят с трехмерной точки зрения к сохранению век-
вектора:
?(i^l) B5)
Вектор N не имеет твердо установившегося названия. Мы будем
называть его лоренцев момент (поскольку он сохраняется вслед-
вследствие инвариантности относительно специальных преобразова-
преобразований Лоренца F)).
5.1.4. Чтобы выяснить физический смысл лоренцева момента,
выберем прежде всего в качестве параметра X время t, которое
вынесется из под суммы
J
и поделим это равенство на -^ > &. Мы получим тогда
i?- = c2=^-/ + Ro; Ro = const. B50
В таком виде это равенство утверждает, что точка с радиус-век-
радиус-вектором
движется равномерно и прямолинейно со скоростью
V = c2-^-: R = V^+R0. B5". 2)
Векторы R и V суть, конечно, релятивистское обобщение ра-
радиус-вектора и скорости центра инерции системы. Таким образом,
закон сохранения лоренцева момента устанавливает тот физиче-
физический факг, что у замкнутой системы материальных точек суще-
существует центр инерции, движущийся равномерно и прямолинейно.
Как мы видим, в релятивистской механике — в отличие от клас-
классической, где получение аналогичного результата из инвариант-
инвариантности вариации действия относительно преобразований Галилея
5. ДЕСЯТБ ФУНДАМЕНТАЛЬНЫХ ВЕЛИЧИН 187"
потребовало довольно тонких рассуждений — этот вывод совер-
совершается совершенно непринужденно.
5.1.5. ЗАМЕЧАНИЕ 1: Хотя для свободных частиц и сохра-
сохраняются их импульсы р° и моменты Щк по отдельности, а как
описывать взаимодействие, мы пока не знаем, тем не менее за-
законы сохранения для системы частиц имеют свое дополнительное
содержание. В самом деле, предположим, что в некоторый на-
начальный момент мы имеем дело с системой невзаимодействую-
невзаимодействующих частиц, затем эти частицы сближаются, как-то—мы не знаем
как — взаимодействуют друг с другом, и наконец расходятся на-
набольшие расстояния и становятся опять свободными. Тогда
можно утверждать, что значения полных 4-импульса Pi и 4-мо-
мента Mik для системы после взаимодействия будут равны их
исходным значениям до него, в то время как для 4-импульсов
и 4-моментов отдельных частиц такого, конечно, утверждать
нельзя. На основе этого замечания можно было бы провести
аналогичное сделанному в 1,8. исследование поведения частиц,
при рассеянии; мы не будем этим заниматься. |
5.1.6. ЗАМЕЧАНИЕ 2: Запишем выражение для (сохраняющегося) век-
вектора лореицева момента п для одной свободной частицы и продифференци-
продифференцируем его по времени:
<*n dp _ .gfv _ I dS
dt~p + t4f ~W !5"r"dT~a
Но импульс и энергия свободной частицы сохраняются сами по себе (как
следствие инвариантности относительно пространственных и временных сдви-
сдвигов),
Поэтому в качестве следствия сохранения лоренцева момента остается соот-
соотношение
Р- —= 0 или р = -р- (•>
— т.е. как раз формула A8.4). А из этой формулы легко восстанавливается
вид функции Лагранжа или функции Гамильтона.
В самом деле, функция Гамильтона равна энергии (если выразить ее че~
рез импульс), а с другой стороны v = —r—. Поэтому (*) приводит к диффе-
дифференциальному уравнению
гт дЖ п
Поскольку —г— = 0 из-за сохранения р, то отсюда следует
т. е. р2 = \X* + const
с
или
const.
188 ч. II. МЕХАНИКА ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
Но это и есть как раз полученный выше вид A9) релятивистской функции
Гамильтона (естественно, с неопределенной постоянной вместо массы). С по-
помощью соотношения L = pv — Ж отсюда сейчас же получается и выражение
для функции Лагранжа. |
Таким образом, наша исходная формула A70, постулирован-
постулированная выше на основе полуинтуитивных рассуждений, теперь по-
получается как точное следствие требования инвариантности от-
относительно специальных преобразований Лоренца.
5.1.7. Итак, мы установили что для системы невзаимодей-
невзаимодействующих материальных точек сохраняется 10 динамических ве-
величин: 4 компоненты 4-импульса и 6 компонент 4-момента. По-
Поскольку основой этого вывода было требование инвариантности
действия относительно преобразований полной группы Лоренца,
то эти 10 величин должны сохраняться и для любой системы.
Поэтому их называют фундаментальные динамические величи-
величины системы.
5.2. Установим соотношения в скобках Пуассона между фун-
фундаментальными динамическими величинами
М=?[г.р] и N =
5.2.1. Заметим для этого прежде всего, что выражения для
Р и М остались у нас в точности теми же, что и в классической
механике. Поэтому:
2. (Ма, Aip) = -eapvM6; B6)
Не переменятся и скобки Пуассона импульса и момента с га-
гамильтонианом:
4. (*,/>¦> = <>;
5. («,М„) = 0;
Новыми будут все скобки Пуассона, включающие лоренцев мо-
момент N. Для их вычисления полезно заметить, что, дифференци-
дифференцируя A9"), мы получаем
pdp, т. е. ^- —= А.
5. ДЕСЯТЬ ФУНДАМЕНТАЛЬНЫХ ВЕЛИЧИН 189
Поэтому
6. (*, N,) = ? Т (- 07 V= - pt> *>
7- (Р«, ^)
Далее
— -^ *р )
Последний член здесь равен нулю по симметрии, а первые два как раз вос-
восстанавливают лоренцев момент, и мы получаем
8. (Ма, ATp)==-eapYyvY; B6)
Наконец,
9. (Na, NJ = ±ea}yMT B6)
5.2.2. Мы уже имели случай отмечать, что СП-соотношения
между сохраняющимися величинами характеризуют ту группу
преобразований, из-за инвариантности действия относительно ко-
которых эти сохраняющиеся величины возникают, а не механиче-
механическую систему, для которой они конкретно находятся. Поэтому
найденные выше соотношения в скобках Пуассона B6) между
десятью фундаментальными динамическими величинами должны
выполняться для любой системы, инвариантной относительно
преобразований полной группы Лоренца. Это есть условия ре-
релятивистской инвариантности теории, записанной в гамильтоно-
вой форме.
5.2.3. Условия B6) записаны у нас в трехмерных обозначе-
обозначениях. Перепишем их в четырехмерном виде, как соотношения
между 4-вектором ^г = | Ра, i — \ и 4-тензором
Ми: Ма? = еЧУМу; M^ = icN^, Mai = — icNa.
Соотношения 1. и 4. объединятся тогда в одно соотношение
A) {Pt,Pk) = 0; A. и 4.). B7)
Перейдем в соотношении 3. от компонент аксиального вектора
к компонентам антисимметричного 3-тензора
190 ч. II. МЕХАНИКА TFOPHH ОТНОСИТЕЛЬНОСТИ
Четырехмерным обобщением этого соотношения будет
B) (Ми, Рк) = - (bik6n - 6nbik) Pi = ~y еЦтпеЫтпРй
C., 5., 7., 6.) B7>
Проверим, что B) действительно содержит в себе 3., 5., 7. и 6. Если все
индексы в B) пространственны: Ц = оф, k = у, то непосредственно полу-
получается 3. в только что приданной ему форме 3'. Если ij = ар1; k = 4, то все
символы Кронекера равны нулю и мы получаем соотношение 5. Пусть
Ц = 4р. Тогда из B):
ic (ЛГр, Рк) = — (fyfcOp/ — 64;6|3fc) P,\
если здесь к = у, то U (Л/а, PY) = 5BY ; (Ра. Л'р) = г— • т- е- 7-<-
" ^ С С
если здесь k = 4, то je — (Л/р, Х) = (У6, N$) = — Рр, т. е. 6.
Проверка завершена.
Точно так же, переходя от аксиальных векторов к антисим-
антисимметричным тензорам в 2., получим
то есть
Четырехмерным обобщением этого будет
C) (Mth Mkl) = — -^j eijmseklnsMmn =
= -в«Л«/, + вдЛ1„ + в„Л1д-в//Л1<* B., 8. н 9.). B7)
Предоставляем читателю убедиться в том, что это соотношение
действительно содержит в себе кроме 2. еще и 8. и 9.
6. Взаимодействие в теории относительности.
Неизбежность понятия поля
6.1. В нерелятивистской механике мы описывали взаимодей-
взаимодействие частиц с помощью понятия потенциальной энергии. На-
Например, для системы заряженных материальных точек, взаимо-
взаимодействующих по закону Кулона, мы должны были ввести в
функцию Лагранжа L кроме их кинетической энергии еще и по-
потенциальную энергию
а, Ь
6. ВЗАИМОДЕЙСТВИЕ В ТЕОРИИ ОТНОСИТЕЛЬНОСТИ 191
Мы уже говорили, что введение потенциальной энергии, зави-
зависящей только от координат частиц, соответствует представлению
о мгновенном распространении взаимодействия на любое рас-
расстояние— изменение координаты какой-то, скажем с-ой, частицы
в некоторый момент времени t в тот же момент времени сказы-
сказывается на силах, действующих на какую-либо другую, скажем
d-ую, частицу, как бы далеко ни были расположены друг от
друга частицы с номерами end. Такое, введенное — для грави-
гравитационных сил — еще Ньютоном, представление о непосредствен-
непосредственном действии частиц друг на друга через расстояние, actio in
distans, с самого начала вызывало недоумение с физической
точки зрения.
Однако в классической механике оно по крайней мере не
вело к логическим противоречиям. Теперь же оно недопустимо,
поскольку позволяет устроить сигнал со скоростью, большей ско-
скорости света. Поэтому в теории относительности мы должны ис-
искать другие способы описания взаимодействия. Чтобы получить
к тому наводящие соображения, подвергнем (*) некоторым,
сперва чисто формальным, преобразованиям.
6.2. Введем прежде всего понятие электростатического потен-
потенциала ф(г) некоторой системы зарядов:
—е±—- (**)
г ~ х I
— в нем сидит пока то же самое действие на расстоянии. Тогда
из (*) получится
Теперь мы хотим заменить оставшуюся сумму объемным ин-
интегралом. Для того введем плотность распределения зарядов
l^(r-g, B8)
а
с помощью которой получим
Заметим еще, что в силу известного соотношения
д1=-4п6(г)
для нашего потенциала ф(г):
Дф(г) = — 4я Yj eb б (г — ть) = — 4я р (г),
192 ч. II. МЕХАНИКА ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
т. е. введенный с помощью (**) потенциал удовлетворяет урав-
уравнению Пуассона. Поэтому плотность заряда можно выразить
через него
и переписать тем самым U через один лишь потенциал:
[/= - JL J dT (Аф (г)) • <р (г) «= - -L J dF div (grad ф) ¦ ф ==
= — -g- \ dT div (ф • grad ф) + ^ \ dT grad ф • grad ф.
Первый член преобразуется здесь с помощью теоремы Гаусса
в поверхностный интеграл
—g- ф dS (ф grad ф)
по бесконечно-удаленной поверхности, который обращается в
нуль, и остается только второй.
Вводя еще вектор
Е = — gradф,
приводим (*) к окончательной форме
а, Ь
Таким образом мы представили потенциальную энергию взаи-
взаимодействия на расстоянии в виде интеграла от плотности энер-
Е2 • „,
гии -g—, распределенной по всему пространству. Тем самым мы
ввели новый физический объект — поле вектора Е, который
нигде не локализован, а распределен по всему пространству, и,
главное, ввели новое представление о природе взаимодействия
частиц.
В то время как раньше мы стояли на той точке зрения, что
Частица непосредственно взаимодействует с другой путем actio
in distance, теперь мы хотим принять, что непосредственным,
Элементарным является лишь взаимодействие каждой частицы
с полем Е(г) в окрестности той точки г, где расположена час-
частица,— частицы возбуждают поле согласно уравнению div E =
ч= 4яр и, в свою очередь, поле возмущает движение частицы
а
dt дта а дтп Е 1Га) е*'
— перенос же взаимодействия из одной точки в другую совер-
совершается полем в соответствии с его «законами движения», кото-
6. ВЗАИМОДЕЙСТВИЕ В ТЕОРИИ ОТНОСИТЕЛЬНОСТИ 193
эые нам еще предстоит открыть. Иными словами, мы хотим
считать элементарным актом взаимодействия взаимодействие
частицы с полем, а само взаимодействие частиц трактовать как
вытекающий из этого элементарного взаимодействия вторичный
эффект.
6.3. Естественно, что эта новая точка зрения будет обоснована
лишь в том случае, если нам удастся обнаружить такие прояв-
проявления поля, которые не сводятся к простому actio in distance —
ведь пока поле
ь
по-прежнему полностью определяется координатами частиц (или
видом плотности р) в данный момент времени! Ясно, что таких
новых эффектов поля можно ждать лишь в области явлений,
связанных с быстрыми движениями частиц — ведь для медлен-
медленных движений, которыми мы занимались в классической меха-
механике, представление о непосредственном действии на расстоя-
расстоянии великолепно объясняло все опытные факты.
Итак, уже само понятие поля подсказывает нам направление
возможного обобщения: естественно заподозрить, что поле оп-
определяется координатами источников в тот же момент времени
лишь для достаточно медленных движений зарядов, — подоб-
подобно тому, как координаты осциллятора определяются внешней
силой в тот же момент времени лишь для внешних сил, меняю-
меняющихся достаточно медленно сравнительно с его периодом, —
для быстрых же движений следовало бы принять во внимание
возможное запаздывание поля.
Чтобы реально продвинуться по такому пути, нам надо
ввести уравнения движения для поля. Мы попробуем строить
такие уравнения, следуя той общей схеме механики, которая
была развита в первой части.
6.4. Будем считать, что поле описывается одной или несколь-
несколькими функциями координат и времени, определенными во всем
4-мире:
ф<«> = ф(а) (х); X = {хи Х2, Х3, ХА).
При формулировке лаеранжева формализма удобно сохранять
4-мерную симметрию и рассматривать все четыре координаты
*i. Х2, х3, Х4 как равноправные аргументы, т. е. рассматривать
поле как механическую систему с конечным числом степеней
свободы (определяемых значением индекса (а)) над многомер-
многомерным временем.
При формулировке гамильтонова формализма 4-мерная сим-
симметрия все равно теряется *) и удобнее сохранять в качестве
*) Ср. замечание в конце § 4.
7 К R 1IИ»П.1>
194 ч. П. МЕХАНИКА ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
аргумента только одно время х4. Пространственные координаты
х выступают тогда в роли параметра, своеобразного непрерыв-
непрерывного номера степени свободы. Таким образом, в гамильтоновом
формализме поле рассматривается как
как система с бесконечным числом степеней свободы, но над
обычным временем.
Никакой принципиальной разницы между этими двумя спо-
способами описания нет, и выбор какого-либо одного определяется
лишь соображениями удобства. Мы прибегнем к первому и бу-
будем строить
7. Лагранжев формализм для поля
В лагранжевом формализме действие для поля надо, оче-
очевидно, записать в виде 4-кратного интеграла «по всем време-
временам Х\, Х2, х3, Хь» т. е. по 4-объему
S = ^ duL !ф° (х), фа, i (х), х); 6S = О B9)
R
от «плотности функции Лагранжа» или лагранжиана L, зави-
зависящего от функций поля <ра(х) (мы обозначаем номер компо-
компоненты поля, который не обязан быть тензорным индексом, пер-
первыми буквами латинского алфавита), их первых произродных
—^Г~^Ф /(*> C0)
(такое сокращенное обозначение производных является обыч-
обычным и мы будем им пользоваться) и, может быть, явно от коор-
координат (времен) хи Дальнейшие рассуждения будем строить так,
чтобы одни и те же выкладки послужили и для получения урав-
уравнений движения и для нахождения законов сохранения с по-
помощью теоремы Нётер.
7.1. Будем считать, что при бесконечно-малом преобразова-
преобразовании координат
х* -* x'k = xk + 6x*; 6xk = AkaCa, C1.1)
где Са — независимые параметры преобразования, функции
поля фа(х) преобразуются по тому или иному линейному пред-
представлению группы Лоренца:
<Ра ,х) -+ ф'в кх') = Фа (х) + 6V (х); 6V (х) = Л З7"V (х) С». C1.2)
b
7. ЛАГРАНЖЕВ ФОРМАЛИЗМ ДЛЯ ПОЛЯ 195
ЗАМЕЧАНИЕ: Индекс а нумерует независимые параметры рас-
рассматриваемой группы преобразований, он не должен ни быть
тензорным, ни иметь какое-либо отношение к индексам а, Ь, ну-
нумерующим функции поля. В качестве рассматриваемой группы
преобразований можно выбрать какую-либо подгруппу полной
группы Лоренца, но можно ввести в рассмотрение и какие-либо
другие непрерывные преобразования, не связанные с выбором
системы отсчета, — для таких преобразований матрицы Aha бу-
будут равны нулю. I t
Вариации б*фа непереставимы с дифференцированием по х{;
с ним переставимы вариации формы
Описанные вариации понадобятся нам для доказательства тео-
теоремы Нётер; чтобы вывести уравнения Лагранжа — Эйлера, надо
будет добавить в вариации формы C1.3) к членам, вызываемым
параметрами С™, еще и произвольные вариации б1фа, т. е. напи-
написать вместо C1.3)
бфа (*) = 6V (*) - Фа, k (x) bxk + б1фа (х), C1.3')
где первые два члена управляются независимыми параметрами
О, а вариации б1фа последнего члена сами являются независи-
независимыми. Чтобы получить уравнения движения, надо будет поло-
положить параметры Са равными нулю и потребовать равенства
нулю вариации действия при произвольных вариациях б1фа, рав-
равных нулю на границах области R. Чтобы вывести законы сохра-
сохранения, нужно положить равными нулю вариации б1фа и потре-
потребовать неизменности действия 65 = 0 по отношению к произ-
произвольным изменениям параметров Са.
7.2. Вычислим вариацию интеграла B9); вычисление это совершенно ана-
аналогично выполненному в I, 5, поэтому теперь можно проводить его с меньшей
подробностью.
as= \ L'(x') dQ'— \L(x)dQ*= \ (L(..., x) + 6*L) dQ' — \ L dQ =
Здесь
дх'
дх'
дх*
якобиан для перехода от пе-
d
ременных х к переменным х, а —— означает «полную частную производ-
dx"
ную», которая имеет в виду дифференцирование не только по явно входящнм
7*
196 ч. II. МЕХАНИКА ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
в лагранжиан координатам хк, но и по неявной зависимости L от них через
функции поля. Продолжая выкладку, получаем
н.
Но
oS = J (bL + -ij (L Ьхк)Л dQ.
^ \д<ра dxk d<?atk) dxk
Поэтому окончательно
dxk ^
J ^ ( J] ^ C2)
7.3. Займемся сперва уравнениями движения. Тогда незави-
независимые вариации суть
6фа = 61<ра(х); б!фа(х) = 0 на границах области R; 6х* = 0.
Второй интеграл в C2) можно преобразовать с помощью тео-
теоремы Гаусса
в интеграл по C-мерной) гиперповерхности, ограничивающей
область R; на ней по условию 6if" = 0 и этот интеграл пропа-
пропадает. Из требования же равенства нулю первого интеграла за-
заключаем, в силу произвольности и независимости б1фа(лг), что
должно быть
&Lrf dL _ л
Это и есть уравнения движения для поля. Поскольку L зави-
зависит от функций поля и их первых производных, а C3) включает
еще одно дополнительное дифференцирование, то это суть урав-
уравнения в частных производных второго порядка. Следовательно,
состояние поля определяется полностью, если задать на какой-
либо пространственно-подобной гиперповерхности все функции
поля и их первые производные. Именно для этого мы требовали,
чтобы лагранжиан содержал только первые производные полей.
Как и в механике, последнее свойство не нарушится, если вклю-
включить в лагранжиан вторые производные линейно.
7. ЛАГРАНЖЕВ ФОРМАЛИЗЯ ДЛЯ ПОЛЯ 197
7.4. ПРИМЕР: Рассмотрим в качестве примера простейший случай, когда поле
имеет только одну компоненту ф<°> ¦¦ ф. При преобразованиях Лореица эта
компонента может преобразовываться только сама через себя, т. е., в силу
.допущения о линейности, только умножаться на некоторый множитель, кото-
который может зависеть лишь от якобиана преобразования, т. е. детерминанта
матрицы |]а<,||. Но этот детерминант равен +1 для всех непрерывных пре-
преобразований и —1 для отражений •*» таким образом для поведения одиоком-
понентного поля при преобразованиях Лоренца остаются лишь две возмож-
возможности: оно может или вообще быть инвариантным нли испытывать дополни-
дополнительную перемену знака прн отражениях (ср. тут примечание в 3.5). В пер-
первом случае говорят о скалярном поле, Для него всегда
Ф' (*') - Ф (х);
во втором — о псевдоскалярном.
И в том и в другом случае лагранжиан может зависеть лишь от двух
¦инвариантных комбинаций ф и ф t *), вид этой зависимости нз общих со-
соображений установить нельзя. Если, однако, желать еще, чтобы уравнения
движения C3) были бы линейны, то лагранжиан однозначно с точностью до
одной константы должен иметь вид
2 V •' '
гт dL , дЬ
Поэтому -д— = х^ф; -г = Ф, k и, следовательно, уравнением движения бу-
.дет
2-6 = 0 или
(л ~1?~Ж -х2) ф = °-
д2 1 д2
Оператор —9~ = А 5"—гг^П, обобщающий оператор Лапласа на
дхк с дг
C+ 1)-пространство, называют оператором д'Аламбера, а отличающийся от
него на константу К = О —к* — оператором Клейиа — Гордона. С их по-
помощью уравнение движения для скалярного поля записывается как
(?-и2)ф = 0 или Лф = О;
его тоже называют уравнением Клейна — Гордона.
Если искать частное решение этого уравнения в форме плоской волны
(а из теоремы об интеграле Фурье следует, что общее решение можно полу-
получить в виде сюперпознции таких частных), то уравнение даст нам связь
между частотой со и волновым вектором к:
JL оJ = к2+ х2 или со(к)=± Vk24-*2-
Мы видим таким образом, что для уравнения Клейна—Гордона всегда
|w(k) | ^ |ск|, т. е. нормаль к поверхности волнового фронта всегда времени-
¦подобна, следовательно, сам волновой фронт образует пространственно-подоб-
лую гиперповерхность, а фазовая скорость волны
1 к |
*) А в скалярном случае — еще и от самого ф, но такая зависимость
устраняется тривиальной заменой ф->-ф + а. ГДе о — постоянная.
198 ч. II. МЕХАНИКА ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
зависит от волнового вектора н всегда больше скорости света. Напротив,
групповая скорость
у _ dw (k) _ ck
gr dk Vk2 + x2
всегда меньше скорости света.
Все перечисленные свойства решений уравнения Клейна — Гордона суше7
ственно зависят от того, что мы приписали единственной входящей в лагран-
лагранжиан скалярного поля постоянной определенный знак, записав ее в виде
х2 > 0. При другом выборе знака интерпретация решений вступила бы в кон-
конфликт с требованиями причинности. |
8. Законы сохранения
8.1. Будем рассматривать теперь только действительные дви-
движения, для которых выполняются C3), и потребуем равенства
нулю вариации действия, 65 = 0, для таких вариаций коорди-
координат C1.1) и функций поля C1.3), которые обусловлены только
описываемыми параметрами О преобразованиями симметрии.
Тогда в C2) будет равен нулю первый член, во втором же мож-
можно будет переписать подинтегральное выражение в виде
или, выражая все вариации через независимые параметры С*,
как
Определяя теперь величины
видим, что условие инвариантности действия относительно рас-
рассматриваемого преобразования свелось к
Здесь опять приходится прибегнуть к аргументу о произвольно-
произвольности области R, позволяющему из равенства нулю интеграла за-
заключить о равенстве нулю подинтегрального выражения, с по-
помощью которого мы приходим к выводу, что величины Nah удов-
удовлетворяют дифференциальному закону сохранения
-^- = 0. C4.2)
dx*
8. ЗАКОНЫ СОХРАНЕНИЯ
199
8.2. Если проинтегрировать теперь C4.2) по 4-области, имею-
имеющей форму (не обязательно — правильного) 4-цилиндра, основа-
основания которого образованы двумя пространственно-подобными ги-
гиперповерхностями ai и аг, а боковая гиперповерхность включает
времени-подобное направление, и преобразо-
преобразовать объемный интеграл с помощью теоремы
Гаусса в интеграл по ограничивающим цилиндр
гиперповерхностям, то, удаляя неограниченно
боковую гиперповерхность на пространствен-
пространственную бесконечность, где нет поля, сведем ре-
результат к разности интегралов по простран-
пространственно-подобным гиперповерхностям oi и <т2 (разности, по-
поскольку меняется знак одной нормали). Итак,
\dSkNak=\dShNka.
Oi at
Определим теперь динамические величины (интегральные):
ЗДЛ C5.1)
Тогда результат только что проведенного рассуждения озна-
означает, что интегральные динамические величины Jfa не зависят
от выбора пространственно-подобной гиперповерхности а:
.^Ы = ^Ы C5.2)
лли, в дифференциальной форме,
bjfa [а]
&а(х)
= 0.
C5.3)
ЗАМЕЧАНИЕ: Стоит обратить внимание на то, каким чрезвы-
чрезвычайно любопытным способом тут фактически восстановилась
выделенная роль времени. В удовлетворяющем требованию че-
четырехмерной симметрии лагранжевом формализме мы все вре-
время трактовали три пространственные координаты и время на
равных правах, и дифференциальный закон сохранения C4.2)
блюл эту симметрию. Теперь, однако, мы вспоминаем, что в
псевдоевклидовом пространстве есть выделенный класс — прост-
пространственно-подобных— гиперповерхностей, и интегрируем имен-
именно по ним. Тем самым восстанавливается особая роль — но не
времени, а времени-подобных направлений, без выделения ка-
какой-либо частной системы отсчета. Мы можем даже, как видим,
вернуться обратно к дифференциальной формулировке C5.3)!
Поэтому можно сказать, что рассмотрение класса произволь-
произвольных пространственно-подобных гиперповерхностей а в каком-то
200 ч. П. МЕХАНИКА ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
смысле позволяет вновь ввести в теорию относительности инва-
инвариантное описание времени. Эти соображения сыграли очень,
важную роль в квантовой теории поля. |
В частности, если выбрать в качестве поверхностей а семей-
семейство всевозможных пространственно-подобных гиперплоскостей.
то из C5.5) воспоследует, что интегральные величины
A) сохраняются во времени (интегральный закон сохранения):
Jfa(t) = const; C5.4)
B) преобразуются при преобразованиях Лоренца как пара-
параметры Са (точнее — контравариантно им, но в мнимой системе
координат это безразлично).
Последнее утверждение следует из того замечания, что интеграл
dSkNak • Са,
взятый по фиксированной гиперповерхности а, должен быть инвариантен, аг
значит, интеграл C5.1) \dSkNa по фиксированной гиперповерхности а —
а
вести себя по отношению к преобразованиям Лоренца контравариантно пара-
параметрам Са. В силу же C5.2) значение интегралов C5.1) от выбора а н&
зависит; поэтому, преобразуя C5.1') в другую систему отсчета, мы вправе-
заменить интегрирование по гиперплоскости а: х,, = const на интегрирование-
по о': #4== const. Отсюда следует, что тем же законам преобразования бу-
будут удовлетворять и величины C5.1'), в которых подразумевается интегриро-
интегрирование в каждой системе отсчета по своей гиперплоскости — 3-пространству
в этой системе.
8.3. Тензор энергии-импульса. Выберем в качестве преобра-
преобразования C1) сдвиг. Этому должен отвечать выбор
а^/ = {1, 2, 3,4}; Са = а>;
Л*а = бД т. е. bxk = ak и ^а6а=0.
Соответствующая величина Nah = Nih называется тогда тензор
энергии-импульса и обозначается буквой Т:
8. ЗАКОНЫ СОХРАНЕНИЯ 201
Согласно C4.2) тензор энергии-импульса удовлетворяет диффе-
дифференциальному закону сохранения
""*• = <); C7.2)
дхк
интегрированием по пространству получаем из него полный
-4-импульс поля
Pt(f)~ 5 йУТ? = const, C7.3)
f=const
сохраняющийся во времени.
8.4. Момент. Чтобы получить закон сохранения момента, рас-
рассмотрим в качестве преобразований C1) пространственные и
лоренцевы повороты.
8.4.1. Такие повороты описываются шестью независимыми
параметрами 8Qhj, поэтому нужно положить:
— действительно, тогда
6xl = Alkl 6Q*' = хф\ №ki = xk 6Qfti
в согласии с B3). Что же до матрицы 3?abhj, по которой преоб-
преобразуются компоненты поля, то ее вид определяется поведением
поля относительно преобразований Лоренца (или, лучше, наобо-
наоборот: задание этой матрицы определяет поведение поля при пре-
преобразованиях Лоренца): если, например, поле описывается од-
нокомпонентной скалярной (или псевдоскалярной) функцией, то
матрица Skj равна нулю; если компоненты поля образуют 4-век-
тор, фа = фга, то матрица будет такой же, как и матрица Л для
координат:
. п. C8V)
АтДп 4- fimfin
{Из C8V) легко сообразить, что для тензора ранга s:
smx ... m,; я,... п. = ? ^т,*, ^ _ _ SmO%kt . . . g*"*, C8T)
1<<
где 2nfi>kf берутся из C8V)).
8.4.2. Соответствующая величина Nak = -j Мцк (напоминаем
замечание в 5.1.3, что bS = -^МцЬп'1) называется теперь
202 ч. П. МЕХАНИКА ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
тензор плотности момента:
М„* = 2ЦЫ-У -^- ср*. Л Л'„ + 2 У -^- 2аЬфЪ =- Мпк.
а, 6
Он складывается из двух разнородных членов: в первом в скобке
стоит тензор энергии-импульса C7.1), поэтому он имеет одина-
одинаковую форму для всех полей и обязан своим происхождением
тому, что при 4-повороте смещается точка, в которой рассмат-
рассматривается поле; второй же специфичен для поля каждой тензор-
тензорной природы и проистекает из-за того, что при повороте проис-
происходит перемешивание полевых компонент. Относительно этого
второго члена нельзя более сделать никаких общих утвержде-
утверждений, мы обозначим его через
Л *' = - **; И = 2 ? -^ <?<* ,Ф\ C9.2)
a, b
В первый же член можно подставить C8) и воспользоваться
обозначением ГД Мы находим тогда
Мцк = XiT," - x,Ttk + Л у. C9.1)
Согласно C4.2) этот тензор удовлетворяет дифференциаль-
дифференциальному закону сохранения (начиная с этого места, будет удобнее
писать все тензорные индексы снизу, что позволительно в мни-
мнимой системе)
-^ = ^-7-,,+ -?-?-0, C9.3>
где мы воспользовались тем, что 7\-j уже удовлетворяет закону
сохранения C7.2). Тензор энергии импульса Тц не обязан быть
симметричным; мы видим, что закон сохранения момента свя-
связывает его симметризацию со вторым — специальным — членом
тензора плотности момента C9.1). Эту связь можно сделать бо-
более непосредственной, если удастся представить 1^, ц в виде раз-
разности двух тензоров, также антисимметричных по второй паре
индексов:
h\U = fi\ik—fl;tk\ fi;ik = — fi\ki- D0.1)
8.4.3. Легко убедиться, что это возможно. В самом деле, мы можем
переписать D0.1) в виде
lk;il + fi;ik + fl;ki=°- <•>
Поэтому естественно искать f{. jk в форме
с неопределенным коэффициентом Я. Подстановка в (•) дает
A + 2Я) (/,. ,к + I,. м + lk. tl) = 0, т. е. Я = -1/2.
8. ЗАКОНЫ СОХРАНЕНИЯ 203
Итак, ft. jk можно найти:
8.3.1. Теперь мы можем ввести вместо Тц новый теизор
который в силу закона сохранения момента C9.3) будет сим-
симметричен:
Вц=*Вц. C7.4а)
Покажем, что тензор 9jj можно использовать вместо тензора
Т,-;. Во-первых, он удовлетворяет тому же закону сохранения
C7.2)
дх( дх} ^ дх{дхк~"> К6'-г)
поскольку первый член исчезает в силу C7.2), а второй — в силу
антисимметрии D0.1) тензора /*;д. Во-вторых, при подстановке
в C7.3) Bij приведет к тому же самому полному 4-импульсу,
поскольку вклад второго члена можно будет преобразовать
с помощью 3-мерной теоремы Гаусса в интеграл по бесконечно-
удаленной (обычной) поверхности, где нет поля. (Заметим, что
для обоих выводов была существенна только антисимметрия
/i;jh по второй паре индексов).
Тензор энергии-импульса Эг;- называют симметричный тензор
энергии-импульса (иногда говорят — метрический, поскольку
в общей теории относительности показывают, что его можно по-
получить варьированием действия по метрическому тензору gij);
наш первоначальный Тц, в отличие от него, называют канони-
канонический тензор энергии-импульса.
8.4.4. Основное преимущество симметричного тензора энер-
энергии-импульса состоит в том, что из него можно построить — ав-
автоматически сохраняющийся в силу C7.2') и C7.4а) — тензор
0- C9>4)
Подставим в него выражение C7.4) для в;,-:
xiTlk ~ *,Tik ~ fti ы + fti ki + -Щ [*iU: kl ~ *,ft; ki) ¦
Таким образом
I**/; * = Мц: k + -?- [Xtf,.t M - XjU; ki], C9.4')
204 ч. II. МЕХАНИКА ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
и, в силу таких же соображений, которые только что приводились
при сравнении 9<j и Тц, тензор ]Hj-t \ может на равных правах
с Мц; k служить в качестве тензора плотности момента. Спе-
Специального названия у него нет; тензор Мц- \ называют иногда
канонический.
8.4. Полный 4-тензор момента получается по общему пра-
правилу интегрированием четвертых по последнему индексу компо-
компонент тензора плотности момента (по сказанному — все равна
какого) по 3-пространству:
М{,= \ dTMlhi= J dy>|i//!4 = const. C9.5).
Как и 4-импульс, он сохраняется во времени.
8.5. ЗАМЕЧАНИЕ 1: Мы выяснили, что, в отличие от пол-
полных фундаментальных динамических величин, локализация их
в пространстве, занимаемом полем, не устанавливается лагран-
жевым формализмом однозначно. Однозначным образом лока-
локализация энергии, импульса и момента находится только в реля-
релятивистской теории тяготения — общей теории относительности.
При этом выясняется, что правильное распределение в прост-
пространстве описывается симметричным тензором энергии импульса
9jj и тензором цц-h- Это распределение обладает еще и той до-
добавочной особенностью, что восстанавливает для плотностей.
имевшееся в теории частиц соотношение B4) между моментом
и импульсом: если записать QudT как dP{, то выражение пол-
полного момента через щ^ 4 можно представить как
Mlf— J {xidPj—XjdPi) (н 4-импульс Pt = J d
f-const \ <=const
C9.6)
С каноническим тензором плотности момента такая интерпре-
интерпретация невозможна. |
ЗАМЕЧАНИЕ 2: Мы использовали для перехода от канониче-
канонического тензора энергии-импульса к симметричному соображения
сохранения момента и структуру канонического тензора его
плотности, выразив «добавок» f*; ^ через /,; )ъ.. Практически ча-
часто удобнее другой путь: пользуясь тем, что от тензора /ч;;л фак-
фактически требуется лишь антисимметрия по последним индексам
и что он должен, очевидно, быть построен только из функций,
поля и их первых производных, бывает проще догадаться, ка-
какую величину fi; jk надо выбрать, чтобы она симметризовала
тензор энергии-импульса. Если это удается, то тензор плотности
8. ЗАКОНЫ СОХРАНЕНИЯ 205
момента \щ,к строится по C9.4), и всю длинную процедуру с ис-
исследованием трансформационных свойств поля удается обойти. 1
ЗАМЕЧАНИЕ 3: Мы применили технику теоремы Нётер, чтобы
найти величины, сохраняющиеся в силу инвариантности действия
относительно преобразований полной группы Лоренца. Та же
техника применима и для случая каких-либо других непрерыв-
непрерывных преобразований, относительно которых есть основания тре-
требовать инвариантности действия. Вычисления даже упрощаются,
поскольку преобразование не затрагивает координаты. |
ЗАМЕЧАНИЕ 4: Могло бы показаться, что симметричный тензор 0jj опре-
определяется однозначно. В самом деле, чтобы заменить симметричный 0,j на
другой симметричный 9^:
надо добавить к нему симметричный в i и / '' . Между тем, если \\.
симметричен в i, /, то это значит согласно D0.1), что соответствующий
и, поскольку f и I однозначно выражаются один через другой, что nfj. ,k =
Однако в действительности рассуждение это несостоятельно: симметрия
- 'df'i;ik
//»/fc есть Достаточное, но не необходимое условие симметрии г» -, и сим-
ОХ
df'i- Ik
метричные в i и \ выражения ' — могут быть отличны от нуля. ¦
axk
Чтобы убедиться в этом, рассмотрим интересный и сам по себе
ПРИМЕР: однокомпонентного (скалярного или псевдоскалярного) поля
<р"(х)= <р(х) с лагранжианом L = ~(ф,\ + х2ср2), к которому мы уже
обращались (см. 7.4) для иллюстрации уравнений движения.
В этом случае канонический тензор Tij сразу симметричен:
тч = y дч (ф- ? + XV) ~ Ъ г<Р-1-
Вычислим его след:
Spur T(j = Тн = 2ф j + 2«V - Ф. ? = 2х2ф2 + Ф_ \
— ои, вообще говоря, не равен нулю. Более того, он не равен нулю и для
того случая, когда само поле <р не входит в лагранжиан, х = 0,:
Spur Гц I =ф ?.
Этот результат физически неприемлем. Чтобы пояснить природу возни-
возникающей трудности, приходится, к сожалению, обратиться к квантовомехаии-
ческим аргументам. В квантовой теории каждому полю сопоставляются
206
ч. II. МЕХАНИКА ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
частицы, и притом таким способом, что групповая скорость волны равна
скорости частицы. Как мы видели в 7.4, при х2 = 0 все решения уравнения
Клейна — Гордона обладают одной и той же групповой скоростью, равной с.
Но частицы, движущиеся со скоростью света, должны обладать нулевой мас-
массой покоя, а вычисление тензора энергии-импульса для совокупности класси-
классических (невзаимодействующих) частиц показывает, что если масса покоя ча-
частиц равна нулю, то должен быть равен нулю и след этого тензора.
Чтобы исправить дело, попробуем подобрать такую ft; jk; производная
которой не испортила бы симметрии канонического Тц и в то же время из-
изменила бы его след. В нашем случае выбор невелик: чтобы не испортить ли-
линейности теории, нельзя привлекать степени поля выше второй и в то же
время надо набрать три тензорных индекса. Единственная возможность —
это образование типа 6,-jCp, ьср; чтобы достичь требуемой для ft-jk антисим-
антисимметрии, его надо антисимметризовать по двум индексам, что можно выпол-
выполнить единственным способом. В результате приходим к «кандидату»
h; jk = x E<7<P. fe<P - 5«ft4>, /Ф),
где Я — пока неопределенная постоянная. Дифференцирование (с учетом
уравнения движения) дает
; jk
-¦ Я (х2ф2 + Ф, *ф, k) bij — Яф, гф, / — Яф, j, уф,
т. е. действительно симметричное выражение.
Итак, «исправленный» тензор энергии-импульса в»-j будет равен
1 + 2Я
ьа (ф, I + *V) - A + я) ф ,ф_ у - яф и ,ф.
Сравнительно с 7\,- он обладает одним недостатком — в него явно входят
вторые производные поля; однако чисто пространственные или смешанные —
пространственно-временные —вторые производные еще не составляют нетер-
нетерпимого дефекта, а производную ср44 можно исключить, пользуясь уравнением
движения.
Вычисляя след %а, находим, что
еп = A + зя) ф J + B+зя) *У.
Поэтому для нашей цели следует выбрать Я = ——; тогда
о
или
у=т ("г ф- * ~ ф- 'ф- /)+т \~г
= Х2ф2.
Любопытно отметить (мы не будем приводить соответствующих формул),
что «исправленный» тензор 6(j можно получить в качестве канонического из
измененного лагранжиана, приводящего к тому же самому уравнению дви-
движения. Этот лагранжиан содержит, конечно, вторые производные (линейно!)
и отличается от первоначального на полную дивергенцию. I
9. ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ 207
9. Электромагнитное поле
9.1. В обычной — макроскопической и атомной — физике ос-
основную роль агента, переносящего взаимодействие между части-
частицами, берет на себя электромагнитное поле. Электромагнитное
поле характеризуется задаваемым в каждой мировой точке Xt
4-вектором
At = At{x, = {\,iq>}, D0)
который называется 4-потенциал (электромагнитного поля).
Его пространственная и временная составляющие, А и qp, назы-
называются, соответственно, векторным и скалярным потенциалами.
9.2. Лагранжиан для электромагнитного поля должен со-
состоять из двух частей — лагранжиана свободного электромаг-
электромагнитного поля Z-ph и лагранжиана, описывающего взаимодействие
этого поля с заряженными частицами — Lint. (Кроме того, в
действии должен быть, конечно, еще и «кинетический» член, от-
отвечающий свободным частицам — мы его уже знаем, он выра-
выражается формулой A6") из § 5.)
«Вывести» форму обоих членов действия для электромагнит-
электромагнитного поля с помощью какой-либо умозрительной аргументации,
конечно, невозможно — выбор определенной формы лагранжиа-
лагранжианов оправдывается только согласием с опытом. Тем не менее
полезно сформулировать те полученные из опытных фактов об-
общие свойства электромагнитного поля, которые оказываются
для этого выбора определяющими.
9.2.1. Таких основных свойств — три: электромагнитное поле
A) распространяется со скоростью, точно равной скорости
света с (свет — это и есть свободное электромагнитное поле);
B) удовлетворяет принципу сюперпозиции — поведение нового
электромагнитного поля в какой-либо области пространства не
зависит от того, было ли уже там какое-нибудь другое электро-
электромагнитное поле или нет;
C) обладает свойством градиентной инвариантности.
Последнее утверждение означает, что поля, описываемые по-
потенциалами Ai(x) и А\ (х), связанными соотношением
A'i(x=Al(x) + ~, D1)
где к(х) — произвольная функция 4-точки, по своим физическим
свойствам тождественны.
К сформулированным трем физическим требованиям можно
добавить еще наше стандартное условие:
1 D) описывающие поле уравнения должны быть не старше вто-
I рого порядка.
208 ч. II. МЕХАНИКА ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
Кроме того, мы хотим, конечно, чтобы описание электромаг-
электромагнитного поля было релятивистски-инвариантным, — и это, пожа-
пожалуй, самое сильное ограничение.
9.3.1. В силу B) лагранжиан LPh должен быть квадратичен
по полевым величинам (чтобы уравнения оказались линейными),
в силу A)—не должен содержать самого потенциала Л**), в
силу D) должен содержать только первые производные поля и
притом, в силу C), лишь в комбинации
Fik = Ak.i-Ai.k\ Fik = -Fki. D2)
Эта комбинация имеет специальное имя — тензор электромаг-
электромагнитного поля.
Легко сообразить, что из тензора поля Ftu можно образовать
лишь две квадратичные комбинации без индексов
Flm.Flm = Flm И eiklmF'tkF\m
и что только первая из них есть скаляр, в то время как вторая —
псевдоскаляр. Поэтому для привлечения в лагранжиан остается
единственная возможность — он должен быть ~ FimFim. Коэффи-
Коэффициент пропорциональности зависит от выбора единиц; мы при-
примем, что
L f *ml Sph = 1Ш7 \ йпр\ш. D3)
9.3.2. Что же касается лагранжиана взаимодействия поля с
частицами, то мы примем, что соответствующий член в действии
имеет вид:
Y\ D4)
где еа есть скалярная характеристика а-й частицы, определяю-
определяющая ее отношение к электромагнитному полю, называемая за-
зарядом частицы (еа может быть и положительным и отрицатель-
отрицательным), йх\— элементарное смещение вдоль мировой линии а-ой
частицы, а интегрирование производится вдоль мировых ли-
линий всех частиц.
9.3.2.1. Выбор для действия именно выражения D4) представ-
представляет собой определенную гипотезу о характере взаимодействия
(что взаимодействие частицы с полем определяется одной и ска-
скалярной характеристикой), которая, строго говоря, ниоткуда не
следует. Если рассматривать взаимодействие с электромагнит-
электромагнитным полем макроскопических тел, то опыт показывает, что они
*) Аргументация этого утверждения станет очевидной ниже, когда мы
займемся решениями уравнений поля, пока же можно только сослаться на
пример 7.4, в котором мы видели, что групповая скорость обращается в с
для'х2 = 0, т. е. если само поле <р не входит в лагранжиан.
9. ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ 209
могут кроме заряда обладать еще и моментами *) возрастаю-
возрастающих порядков; если же говорить об элементарных частицах, то
взаимодействие такого рода опять оказывается гипотезой, назы-
называемой тогда гипотезой минимальности электромагнитного взаи-
взаимодействия. Непонятным образом пока не найдено случаев на-
нарушения этой гипотезы — точнее, все случаи отступления от нее
находят рациональное объяснение в своего рода неэлементарно-
неэлементарности рассматриваемой частицы.
Выбор константы в D4) опять определяется, конечно, изби-
избираемой системой единиц, прежде всего — единицами измерения
заряда.Наш выбор соответствует использованию гауссовой сим-
симметричной системы CGS.
9.3.2.2. В свете сказанного выше при взгляде на D4) возни-
возникает естественный вопрос: как же быть с градиентной инвари-
инвариантностью?— ведь в D4) мы ввели сам потенциал. Легко ви-
видеть, однако, что при проведении преобразования D1) дополни-
дополнительный член в действии будет иметь вид
, dx\ dk(x)
дх:
т. е. к функции Лагранжа добавится полный дифференциал, а
к действию — константа, не влияющая на вариации.
Можно добиться и того, чтобы действие вовсе не менялось, если одно-
одновременно с D1) провести над действием для каждой частицы преобразование
Sa = - mac J dsa => - mac J dsa —ef J dsa -?- (k (*?)), D1')
добавляющее к нему не меняющую уравнений движения производную по s
функции X\xi) только от координат х". Именно такой путь избирают обык-
обыкновенно в квантовой механике.
9.3.3. Итак, полное выражение для действия системы матери-
материальных точек, находящихся во взаимодействии с электромагнит-
электромагнитным полем, есть сумма выражений A6") + D3) + D4^.
dSa + ? A. \ dxfA, (xa) - -JL- \ dQFL. D5)
Чтобы получить полный набор уравнений движения этой си-
системы, мы должны проварьировать D5) по координатам частиц
х<1 и по «координатам» поля Л,-(ж).
*) Смысл термина будет разъяснен ниже в подходящем месте.
210 ч. II. МЕХАНИКА ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
9.4. Уравнения движения для частиц в поле получаются варь-
варьированием по координатам частиц х?; поскольку они входят
лишь в два первых члена D5), то достаточно варьировать эти
члены, которые того ради удобно переписать (ср. § 4), выражая
координаты мировых линий частиц в функции одного произволь-
произвольного параметра К (не путать с Я, в D1)!)
- mac V- Йг) + ^At (**))• D6)
9.4.1. Для 4-импульса а-ой частицы в поле Р? мы получаем
тогда
dx, г. . c -.. -. D7.1)
d~dT
(в правой части можно уже положить А, = s0), где pf =
импульс свободной о-й частицы, а для полного А-импульса си-
системы частиц в поле —
/>, = ?/>?. D7.2)
а
ЗАМЕЧАНИЕ: Импульс Pi — это обобщенный импульс, ка-
канонически сопряженный координате xf, именно он должен фигу-
фигурировать в таких образованиях, как функция Гамильтона, скоб-
скобки Пуассона и т. п., и, если частица находится во внешнем поле„
не должен, конечно, сохраняться. Однако наши координаты*? —
декартовы: поэтому если мы дополняем систему частиц в поле,,
описываемую лагранжианом D6), до замкнутой системы D5),.
добавляя к ней действие поля SPh, то Р? будет как раз вкла-
вкладом а-ой частицы в полный сохраняющийся 4-импульс, а Р{~
вкладом в этот 4-импульс от всех частиц; поэтому, чтобы полу-
получить сохраняющийся 4-импульс полной системы D5), надо до-
добавить к D7.2) только 4-импульс, извлекаемый по теореме Нс-
тер из одного лишь 5рь. Мы используем ниже это обстоятель-
обстоятельство. |
9.4.2. В уравнениях движения
d ра dL e d) dA
a
d% dxf с ds dxf
тоже полагаем к = s° и, замечая что
<Ь4г|*а) ^ g^j dxf dxf ^
10. УРАВНЕНИЯ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ 211
находим окончательно
duf е./дА, дА/,
-r1
дх,
D8)
Таким образом, изменение скорости ы? — а как раз в этом и
состоит физически наблюдаемый эффект — зависит только от
градиентно-инвариантной комбинации F^.
10. Уравнения электромагнитного поля
Прежде чем переходить к варьированию действия D5) по
полю, чтобы получить уравнения движения поля в присутствии
зарядов, удобно будет преобразовать 5int D4) к другой форме,
так, чтобы в нем, так же как и в SPh, вошло бы интегрирование
по 4-объему, а не по мировым линиям частиц.
10.1. Того ради заметим, что интеграл (или сумму интегра-
интегралов), берущихся вдоль мировых линий частиц, можно преобра-
преобразовать следующим образом:
10.1.1. Поэтому
если определить 4-вектор тока или 4-ток (так как действие и
элемент объема — инварианты, а Аг — 4-вектор, то и /,(х) есть
4-вектор) выражением:
212 ч. II. МЕХАНИКА ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
С трехмерными величинами 4-ток связан с помощью соотноше-
соотношения
/* = {J;/cp}, D9a>
где
Е
есть (трехмерная) плотность заряда, а
Lra(t)) B8.2)
— трехмерный вектор, который называется плотность тока (го-
(говорят и просто ток, что не совсем точно).
ЗАМЕЧАНИЕ 1: Так как и( есть 4-вектор, то из D9) видно, что-
V
1 2. б (г — га) есть инвариант. |
С
dx, dxf
ЗАМЕЧАНИЕ 2. Комбинация {v; 'С}==~Л~< Следовательно, о (г — га) —тт-
есть 4-вектор. |
ЗАМЕЧАНИЕ 3. Поскольку заряды еа были определены как инвариантные
характеристики частицы, то из B8), D9а) видно, что трехмерная плотность,
инварианта не есть инвариант, а ведет себя как четвертая компонента век-
dt
тора, как —г- |.
10.2. С помощью 4-вектора тока можно переписать действие
взаимодействия Sint в виде интеграла по 4-объему:
= Е Т- \
a
10.1.2. Если предпринять здесь над потенциалом градиентное
преобразование D1), то Sint получит дополнительный член:
Первый интеграл здесь может быть преобразован по теореме
Гаусса в интеграл по границам рассматриваемой пространствен-
пространственно-временной области, где он добавит к действию только не ме-
меняющуюся при варьировании константу. Требование же обра-
обращения в нуль второго интеграла для произвольных К дает
уравнение непрерывности: ~aZ~~® E0.1)>
°xi
•—новый дифференциальный закон сохранения.
10. УРАВНЕНИЯ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ 213
Интегрируя его по такой же области, что и в 8.2, найдем, что
соответствующая интегральная динамическая величина — пол-
полный заряд Q —
Q Н = ~У \ dStJt = const E0.2)
о
не зависит от выбора пространственно-подобной гиперповерхно-
гиперповерхности а, т. е. удовлетворяет интегральному закону сохранения, что,
как мы знаем, можно выразить и в виде
Ш-°- <50-3>
Любопытно, что в этом рассуждении мы выяснили некоторое
свойство системы зарядов (ведь к ним относился 4-ток, через
который определен полный заряд) на основании свойства гра-
градиентной инвариантности электромагнитного поля.
10.1.3. Проверим, что ток D9) действительно сохраняется. Имеем:
Ж = Лл.-!?.Т р дЬ (г-г°V» -
<3л:. (Эг "^ ic Z-. а а/
а
йЛ(г-гв@) , йв(г-гв(О) йга
а
dra д , , . д * , .
если заметить, что —тг = ча и -?— 0 (г — га) = ^— 0 (г — га), так что
at с"*д от
два члена в скобках взаимно уничтожаются.
ЗАМЕЧАНИЕ: Заряды еа отдельных частиц были введены как
инвариантные характеристики каждой частицы. Не могли они
меняться и с ходом собственного времени sa частицы, так как
иначе их нельзя было бы считать постоянными при получении
уравнений Лагранжа — Эйлера. Поэтому новое утверждение, ко-
которое мы можем извлечь из E0), состоит в том, что если в ходе
взаимодействия одни частицы превращаются в другие, то всегда
Z еа = Z во' .
о а'
до взаимод. после взаимод.
Это утверждение нетривиально. Например, для другой инва-
инвариантной характеристики частицы, не меняющейся с ходом соб-
собственного времени, — для массы — при превращениях одних час-
частиц в другие полная масса не обязана сохраняться;
Z ma ?= T, tTla' • |
о о'
до взаимод. после взаимод.
-214 т. и. Механика теории относительности
10.3. После всех этих приготовлений, теперь можно перейти4
к выводу уравнений движения для электромагнитного поля, ис-
используя в качестве лагранжиана сумму подинтегральных выра-
выражений в D3) и D4'):
10.3.1. Для вычисления производной от F"\m проще всего вычислить его
вариацию:
dF2lm
6F?m = 2Flm bFlm = 2F.JS (Am .-A. \ = AFlm 6Am_ .; ^SL- = AFU.
"lm'=zrlmorlm==*rtm'}\'nm,t — 'nt,m)=^i'tm
Поэтому уравнения движения C3) примут теперь внд
1 1 d
с 16п ахк
илн
dFjk __ An . вторая пара /ci 2)
dxk с ll' уравнений Максвелла v ' '
Это уравнение называется вторая пара уравнений Макс-
Максвелла (пара потому, что в трехмерной записи оно распадается
на два уравнения).
10.3.2. Первая же пара уравнений Максвелла фактически уже
была неявно введена нами, когда мы определили тензор поля
(иногда говорят просто поле) Fih как 4-ротор потенциала Л*.
В самом деле, введем псевдотензор F'k, дуальный Fik\
* 1
Fik==-2eikimFim-==eikim^m,f D2*)
Его дивергенция будет тождественным нулем по соображениям
симметрии:
dP*ik
-fa- = etktmAm,i,k = O. E1.1*)
Возвращаясь к Flm, получаем отсюда
elklmFlm, k = 0
или, снова переходя к дуальному— теперь всей левой части —¦
тензору 3-го ранга, находим
р. .о... Р, .—п
^irst^iklm1 lm, k — "•
Но стоящая теперь перед F;m, k комбинация дискриминантных
тензоров есть, как легко видеть, просто оператор суммирования
по всем перестановкам индексов Imk, причем четные переста-
перестановки берутся со знаком +, а нечетные со знаком —. Эти ми-
минусы устранятся перестановкой индексов тензора поля. Поэтому
11. ЭНЕРГИЯ И ИМПУЛЬС ЭЛЕКТРОМАГНИТНОГО ПОЛЯ 215
окончательно получим сумму трех членов
^ + ^ + 4 0- первая пара E1.1)
°xl ax{ °xk уравнений Максвелла
Это и есть первая пара уравнений Максвелла. Как видно из
проведенного вывода, это не столько уравнение движения, сколь-
сколько своеобразное условие интегрируемости — если быть совсем
точным, это есть условие того, что антисимметричный тензор
поля Fih может быть представлен в виде D2) 4-ротора некото-
некоторого 4-вектора.
ЗАМЕЧАНИЕ: В обычном трехмерном виде обе пары уравнений
Максвелла очень похожи по форме. В нашей записи E1.1) не
имеет внешне ничего общего с E1.2), однако эта симметрия
формы восстанавливается, если перейти в одном из уравнений
к дуальному тензору поля D2*): E1.1*) очень напоминает E1.2). §
11. Энергия и импульс электромагнитного пэля
11.1. Займемся теперь законами сохранения для электромаг-
электромагнитного поля. Наша система состоит из взаимодействующих друг
с другом частиц и поля; ее действие представляется суммой трех
членов в D5). 4-импульс, возникающий из двух первых членов
действия, мы уже нашли в § 9 (формулы D7)), нам осталось
заняться поэтому только сохраняющимися величинами, получае-
получаемыми из действия 5Ph для одного поля. Канонический тензор
энергии — импульса из лагранжиана LPh получается по общей
формуле C7.1), которая в применении к нашему случаю гласит
Подставляя сюда LPh из D3) и используя только что найденное
-, i
г
-1 /-». -Al.t4Fu).
дрт
значение AFM для -ч лтп , получаем
ОЛ1, к
то есть
канонический тензор E2а)
энгргии-импульса
эл.-маг. поля
11.2. Этот канонический тензор не симметричен. Кроме
того, — и это гораздо хуже — он градиентно не инвариантен.
Чтобы перейти от него к симметричному тензору 0,-й, восполь-
воспользуемся приемом, упомянутым в замечании 2 в 8.5.: попробуем
ПОДОбратЬ fi;kl = —fi;lA-
216 ч. II. МЕХАНИКА ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
Имеющиеся в нашем распоряжении величины — 4-потенциал А{ и тензор
поля Fhi подсказывают нам форму fi; kl =——— AiFki, где а — постоянная,
которую надо подобрать. Тогда
с )
a / dF..
nic \ dxt
Тг1 А'. f" + Ai I ( Ai> 'Fkl +
Anic \ dxt ) Anic \ с
откуда видно, что нужно выбрать а = —1, т. е. положить
f п AtF!k'
С таким выбором f{. fk мы получаем для Q
h- E2b)
В этом выражении симметризована часть, относящаяся к
чистому электромагнитному полю, но зато появился несиммет-
несимметричный член Aijh. Этот член относится не к чистому полю, а к
взаимодействию поля с зарядами: если бы зарядов вообще не
было (т. е. правая часть уравнения движения E1.2) была бы
равна нулю), то тензор E26) был бы симметричен.
11.3. Однако с вкладом взаимодействия в энергию и импульс
мы уже имели дело — соответствующий член, происшедший из
Sint, входил в выражение D7) для полного 4-импульса системы
частиц в поле. Реальный смысл сохраняющейся величины имеет
только полный 4-импульс всей системы зарядов и поля, взаимо-
взаимодействующих друг с другом; он получится, если сложить D7)
с интегралом от E26) по пространству. Мы получим тогда
—— \ dT Aiji + (интеграл от первого члена в E2Ь)). (*)
Преобразуем третий член этой суммы. Четвертая компонента
4-тока есть icp = lc ? eab (г — та). Поэтому интеграл по dT вы-
вычисляется, приводя к результату
а
Таким образом третий член в (*), происшедший из огорчив-
огорчившего нас несимметричного добавка в E26), уничтожается со
11. ЭНЕРГИЯ И ИМПУЛЬС ЭЛЕКТРОМАГНИТНОГО ПОЛЯ 217
вторым. Значит, если ввести симметричный тензор энергии-им-
энергии-импульса «как бы для поля без зарядов» *)
9,k = -—г- FaFkt lk.lm , симметричный тензор E2с)
4Я'С L 4 j энергни-импульса
эл.-магн. поля
то мы получим для полного 4-импульса зарядов и поля, взаи-
взаимодействующих друг с другом,
Pi = Y pa, + \dT 9l4. полный 4-импульс E2d)
*—' J зарядов и поля
И поле и все заряженные частицы нужно брать при вычислении
E2d) в один и тот же момент времени t.
11.4. Итак, полный 4-импульс системы заряженных частиц,
взаимодействующих с электромагнитным полем, любопытным
образом представляется суммой 4-импульсов свободных частиц
и 4-импульса поля, также вычисленного в предположении, что
это поле свободно. Это обстоятельство, конечно, ни в коей мере
не служит указанием на то, что взаимодействие зарядов с полем
исчезло — оно просто служит иллюстрацией того, насколько ус-
условно подразделение энергии (и импульса) на «кинетические»
части и части взаимодействия; реальный смысл такое разделе-
разделение имеет только для величин, определяющих динамику, — для
функций Лагранжа или Гамильтона. (Если мы попытаемся пре-
превратить энергию E2) в функцию Гамильтона, заменивши ско-
скорости на обобщенные импульсы (что для электромагнитного
поля не тривиально, то распадение на два независимых члена,
один из которых зависит только от переменных частиц, а дру-
другой— только от переменных поля, сейчас же исчезнет!).
11.5. Тот же результат E2) можно получить и несколько
иным способом, представляющим самостоятельный интерес.
11.5.1. Введем по аналогии с плотностью заряда р B8)
плотности массы и 4-импульса для частиц, т. е. запишем
а а
т ^ . E3)
Pi = 2_, maCU° = \ dT } maCUaib (Г — Га).
Следовательно, если ввести формально тензор энергии-им-
m
пульса частиц Tik, то E3.2) должна будет представляться
*) В отличие от Тц,, тензор 0,* градиентно инвариантен. Кроме того, его
след 0н = 0 ср. обсуждение в 8.5,
i8 ч. II. МЕХАНИКА ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
в форме \йТТц, т. е. должно будет быть:
Ic
где мы представили правую часть в виде произведения трех
множителей, первый из которых есть 4-вектор ии второй (ср. за-
замечание 1 в связи с формулой D9))—скаляр, а третий — чет-
четвертая компонента щ того же 4-вектора ы;. Следовательно, весь
m
Tik будет иметь вид
/ V5"
aU<\ulN X -¦^б(Г~Г")- «нзор энергии - E4)
а й у с импульса свобод-
1
i / а й у с импульса свобод-
ных частиц
11.5.2. Теперь можно провести такое же рассуждение для
плотности 4-импульса частиц в поле D7) и записать для него
m + int
Второй член здесь — это 4-импульс, получившийся из 5int; как
преобразовать его в интеграл по объему (от величины, которую
lnt
естественно назвать Ti4), мы уже знаем (см. 11.3). Итак, можно
положить
lnt j
я, следовательно,
a
nt 1 _, / v2 1
l -^6(r-ra) + -nTAi(x) jk(x) E5)
тензор энергии-импульса «частицы + взаимодействие»
есть тензор энергии-импульса, построенный из двух первых чле-
членов Sm-f-Sint действия D5).
11.5.3. Поэтому полный канонический тензор энергии-импуль-
энергии-импульса получится, если прибавить к E5) канонический тензор энер-
энергии-импульса E2а), образованный из третьего члена 5Ph дей-
действия D5)
m+lnt+ph m+int
Tik = Tik + ТП- E5.2)
12. ТРЕХМЕРНАЯ ФОРМУЛИРОВКА
Симметризуя этот полный тензор с помощью того же /,-;ы, мы-
сразу придем к полному симметричному тензору энергии-им~
пульса:
m + int+ph
Из этого тензора энергии-импульса, конечно, опять получает-
получается то же выражение E2d) для полного вектора 4-импульса и
(раньше мы не могли этого утверждать!) аналогичная формула
для 4-момента в виде суммы 4-моментов «свободных» частиц.
и поля.
12. Трехмерная формулировка
Мы развили теорию электромагнитного поля, взаимодей-
взаимодействующего с заряженными частицами, в четырехмерных тензор-
тензорных обозначениях. Такая символика позволила получать и запи-
записывать результаты наиболее компактным образом. Из сообра-
соображений наглядности, однако, полезно представить всю теорию и:
в более привычных терминах трехмерного векторного анализа.
12.1. Мы уже отмечали, что с такой точки зрения 4-потенциал.
есть объединение
А( = {\, Ар} D0)
трехмерных вектора и скаляра.
Выразим через трехмерные величины компоненты тензора
поля Fik D2). Полагая ik = а$, получаем для его чисто прост-
пространственных компонент
Но вместо трехмерного антисимметричного тензора второго
ранга всегда пользуются дуальным ему аксиальным вектором
Fan = ea^Fy; F*a = — еа^Р^у = ea&Y j— Ay — (rot A)e.
Этот аксиальный вектор называют напряженностью магнитного
поля или, короче, просто магнитным полем Н:
H = rotA; /^v = е^цЯц. магнитное поле D2.1)
(Мы обозначаем трехмерные формулы теми же номерами, что
и соответствующие четырехмерные, с дополнительными цифрами
1, 2 и т. д.).
220
ч. II. МЕХАНИКА ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
Смешанные компоненты тензора поля Fia = —Fai образуют
с трехмерной точки зрения (настоящий) вектор
Этот вектор называют напряженностью электрического поля
или просто электрическим полем и обозначают буквой Е:
= -gradcp--A, Fia = -Fai =
электрическое
поле
D2.2)
В статическом случае электрическое поле Е сводится к (взятому
со знаком минус) градиенту скалярного потенциала ф.
Если записать компоненты тензора Fih в виде матрицы, в
которой индекс i нумерует строки, а индекс k — столбцы, то
она будет иметь вид
о
-Иг
Ну
iEx
0
-нх
iEy
- Ни - iE.
О
IE,
-1Ег
0
D2.3)
Выпишем еще и матрицу дуального тензора поля F$k (D2*)):
О
IEZ
-iEu
-IE,
О
iEx
— Нх —Ну
iEy
-iEx
О
-H,
Ну
Hz
о
D2.3*)
•она (с точностью до множителя) получается из D2.3) переста-
перестановкой электрического и магнитного полей Е и Н.
12.1.1. ЗАМЕЧАНИЕ: В евклидовом 4-пространстве мы могли бы обра-
образовать из Fik и Fik и линейные комбинации Fik ± F*ik — самодуальный и ан-
тисаиодуальный антисимметричные тензоры второго ранга, каждый из кото-
которых имел бы только три существенные компоненты (соответствовал бы одно-
одному 3-вектору).При любых поворотах эти два тензора преобразовывались бы
независимо друг от друга (но переходили бы один в другой при отражениях).
В псевдоевклидовом пространстве, однако, тензор Fik содержит лишний мно-
множитель L Поэтому самодуальный (антисамодуальный) антисимметричный тен-
тензор второго ранга будет иметь лишь три существенные компоненты, но три
комплексные (и будет соответствовать одному комплексному 3-вектору — в
.нашем случае вектору Н =F iE), так что число существенных вещественных
компонент не изменится.
Этот множитель i в Fih не случаен. Если прибегнуть к вещественной
системе координат, та он скажется в том, что квадрат операции образования
дуального тензора той же вариантности будет равен —1.
В самом деле, в вещественной системе координат надо различать два
дискриминантных псевдотензора: контравариантный eilhl и ковариантный
12. ТРЕХИЕРНАЯ ФОРМУЛИРОВКА 221
ijki- Один из них мы можем отнормнровать по произволу, положив, напри-
например, е0123 = +1; но тогда
«0123
= (-) (+) (+) (+) е°ш (или = (+) (-) (-) (-) е»123).
т.е. обязательно eOi23 = —1.
Операция * образования дуальной величины превращает коварнантный
тензор в контравариантный (псевдо) тензор и наоборот; поэтому при двойном
проведении этой операции приходится один раз использовать eiiM и один
раз ецк1'-
(Flm)'lk = -j еШтРш = G'ft; (G% = j enpikGik.
Таким образом в силу противоположной нормировки eilhl и eijki'.
т. е. действительно
((FT = -F. (.)
Таким образом, если бы мы захотели построить из антисимметричного
тензора второго ранга F самодуальиую и антисамодуальную величину в виде
линейной комбинации aF + bF*, то нам надо было бы найти решение урав-
уравнения
(aF + bF')* = X(aF + bF'), X = ± 1.
Однако в силу (*) это уравнение свелось бы к системе
Ха + Ъ = 0; а — ХЬ = О,
условие разрешимости которой дало бы иам К2 + 1 = 0; X = ±i, т. е. для
К = ±1 решений не было бы:
IB вещественном псевдоевклндовом пространстве не существует самодуаль-
самодуальных (аитисамодуальиых) тензоров.
Положение можно было бы исправить, введя вместо * новую операцию +:
(F)+ = ±i(F)*. Требование самодуальности (антисамодулльности) относи-
относительно новой операции
(aF + bF+)=(± i) (aF ± ibF'Y = X' (aF ± ibF*)=%r {a + bF+)
привело бы тогда к системе
X'a—b = 0; а — X'b = 0
с характеристическим уравнением —X'2 + 1 = 0; К' = ±1, все оказалось бы
в порядке — но эта новая операция + и есть как раз операция перехода к
дуальной величине в мнимой системе координат!
К сему два пояснения:
A) Неудача с построением самодуальной (аитисамодуальной) величины
в вещественной системе самоочевидна: рассматривая * как оператор в про-
пространстве «векторов» — антисимметричных тензоров второго ранга, виднм из
(*), что его квадрат (*J = —1 обладает единственным собственным значе-
значением— 1, следовательно, сам оператор * может обладать лишь собственными
значениями ±/.
B) Построение операции + также не искусственно. Дело в том, что если
быть совсем ригоричным, то в вещественной системе тензором надо считать
не е ' .а л/ge ' где gr=|g'iA| есть детерминант метрического тензора,
как раз и равный —1. |
222 ч. II. МЕХАНИКА ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
12.2.1. Для инварианта Fim получим через трехмерные поля
Е и Н
Flm — Fa^afi + ^4p^4p + Fa4Fa4 = еа^еа^Н^Нч — 2Е2 ==
= 2 (Н2 - Е2).
Поэтому действие для поля запишется теперь как
5ph = ~ J dt J dT (E2 - Н2), D3.1>
т. е. в трехмерной нормировке плотность функции Лагранжа
Е2-Н2
Равна ы ¦
12.2.2. Для действия взаимодействия в первой форме D4)
= J ^ Е (т- V°A -
то есть
Поэтому описывающая взаимодействие частиц с полем часть
функции Лагранжа есть
?(^) D4.2)
Первый член здесь совершенно аналогичен нерелятивистской
«потенциальной энергии во внешнем поле», второй же приводит
к силам, зависящим от скорости.
12.3.1. Займемся теперь поведением частицы в электромаг-
dp, e
нитном поле. Полагая в уравнениях движения D8)-^- = — Fikuk
индекс i равным а, имеем
1dPa е 1
e cEa
с
то есть
-jL = еЕ + ¦— [v • Н]. сила Лореица D8.1)
12.3.1.1. Стоящее здесь в правой части выражение есть
с трехмерной точки зрения сила, ее называют сила Лореица.
Лоренцева сила состоит из двух частей, первая не зависит от
12. ТРЕХМЕРНАЯ ФОРМУЛИРОВКА 223
скорости, а вторая (честь открытия которой собственно и при-
принадлежит Лоренцу) пропорциональна скорости частицы и на-
направлена перпендикулярно к ней. С точки зрения изучения
электромагнитного поля по поведению заряженных частиц в нем
именно это отличие служит основанием для разделения поля на
электрическое и магнитное.
12.3.2. Временная составляющая D8) даст нам
1 dT e 1
VV2
dt С
где, впрочем, было бы логичнее писать не <В', а &~, поскольку pt
есть 4-ая компонента 4-импульса свободной частицы и должна
быть пропорциональна кинетической энергии, Р\=-——. Итак,
при i == 4 мы получаем из D8)
~ = e(E-v), D8.2)
т. е. закон изменения кинетической энергии частицы под дей-
действием поля. Но увеличение кинетической энергии частицы есть
работа, совершаемая над нею силами поля. Мы видим, что ра-
работу совершает только электрическое поле. Поэтому действие
магнитного поля является хорошим способом изменить направ-
направление движения заряженной частицы, не меняя ее энергии.
12.3.3. Выпишем еще в 3-виде выражения D7.1) для полных
•импульса и энергии частицы в поле:
Р^Р + ^А; #—#" + «р. D7.1.1)
Здесь 3"— кинетическая энергия, а р — импульс без учета поля,
его иногда называют кинетический импульс:
Г-. ^=; р =
V1--^' V1--
12.3.3.1. Перенеся в D7.1) член с 4-потенциалом в левую
часть и возведя все соотношение в квадрат, мы получим
(Р, - у Л,J = р\ = m2c2u\ = - т2с2
или, переходя к трехмерным обозначениям,
224 ч- »• МЕХАНИКА ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
Если разрешить это соотношение относительно <? (напоминаем
замечание 1 в конце § 4 относительно знака корня), то, по-
поскольку каноническим импульсом в смысле гамильтонова фор-
формализма является именно Р, а не р, мы получим функцию Га-
Гамильтона
г, /) = ^ = ^mV + c2(P-JAfr, t)J +ap<r, t). E6)
функция Гамильтона для частицы в поле
12.4. Вектор тока через 3-величины мы уже выписывали D9а),
перепишем в трехмерном виде уравнение непрерывности E0.1):
^=O. E0.1.1)
12.5.1. Перейдем к уравнениям Максвелла. Начнем со второй
,,. г>\ dFiu 4я .
пары E1.2) -j~ = — 1с-
к
Полагая индекс i равным а, находим
3Fар д (— iEa) 4я д \ дЕа _ 4п
а полагая i = 4,
дЕа 4я
i -^-= /ср.
<Э*3 с
Итак, в трехмерных векторных обозначениях мы получаем
действительно пару уравнений:
н 1 дЕ Ьп_. I
п с dt — с J' \ р р
! уравнений Максвелла
J E1.2.2)
rot »• . jj — . j) i вторая пара
12.5.2. Чтобы получить трехмерный вид первой пары, проще
всего обратиться к трехмерным выражениям D2.1,2) полей че-
через потенциалы. Применяя к D2.2) операцию rot, находим, по-
поскольку rotgrad = 0, rotE = —^--^-H. В применении же к
D2.1) даст нуль операция div. Итак,
rot Е + 7 V = 0; | пераая пара E1.1.1)
| й М
V 0; | р р
| уравнгний Максвелла
ivH = 0. J
| уравнгний Максвелла .
divH = 0. J E1.1.2)
Тот же самый результат можно было бы получить, повторяя
рассуждения, использованные при выводе трехмерного вида вто-
второй пары, в применении к дуальному тензору поля FU D2*).
12.5.3. ЗАМЕЧАНИЕ 1: Мы видим, что — если абстрагироваться от источ-
источников— обе пары уравнений чрезвычайно сходны: одна получается из дру-
12. ТРЕХМЕРНАЯ ФОРМУЛИРОВКА 225
гой заменой Е?±Н н изменением знака одного из полей. Поэтому, если вве-
ввести комплексную лниейную комбинацию F=H — (Е, то, складывая E1.2.1)
и E1.1.1), мы получим
rot (Н -/Е)+1А(_Е- /Н) = ~ J,
то есть
, _. . 1 (9F 4я
rotF + 77^r==—j> (oL31>
а складывая E1.2.2) и E1.2.1) —
div(H-/E) = -—/ср,
С
то есть
divF = ^-p E1.3.2>
— обе пары уравиеннй Максвелла объединяются.
При собственных преобразованиях Лоренца компоненты вектора F пре-
преобразуются только через себя, но при отражениях вектор F переходит в ком-
комплексно-сопряженный вектор F.
С четырехмерной точки зрения образование величин F и F означает пере-
переход от взаимно дуальных тензоров F ik и Fik к самодуальному и антисамоду-
альному, каждому из которых соответствует один трехмерный вектор, — мы
уже говорили, что в псевдоевклидовом случае он обязательно комплексен. Щ
ЗАМЕЧАНИЕ 2: Главное отличие первой пары уравнений Макс-
Максвелла от второй состоит в том, что она не содержит в правой
части источников поля. Это не случайно. В самом деле, в отли-
отличие от Е магнитное поле Н есть аксиальный вектор. Поэтому,
будь в правой части первой пары источники, они должны были
бы быть аксиальным вектором и (трехмерным) псевдоскаляром.
Классический способ описания материальных частиц во всяком
случае не дает возможности построить из динамических пере-
переменных частицы величины такого рода. И
12.6. Теперь осталось только записать через трехмерные ве-
величины составляющие тензора E2с) энергии-импульса и выяс-
выяснить их наглядный смысл.
12.6.1. Начнем с компоненты 944 = ——т— ( F\t — — FJm J. Квадрат тен-
тензора поля мы уже считали: F2lm = 2 (Н2 — Е ). Поэтому
и, так как
P4 = l
то плотность энергии поля W есть
W = 11±Л1;
W = 11±Л1;
oJX
8 Б. В, Медведев
= \ W dT. энергия поля E2.1)
J
226 ". II. МЕХАНИКА ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
Плотность импульса получится нз смешанных компонент 9а4:
ва* = ~ШЛ F«з^в= 1Ш е°е
Итак, импульс поля равен
Л F«з^в= 1Ш е°еу?Ряу = -?г • -^ № • н]а = -jr-
^ импульс поля E2.2)
если ввести вектор
S = -^-[E-H], вектор Пойитинга E2.3)
называемый вектором Пойнтннга. Итак,
плотность импульса поля равна вектору Пойнтинга, деленному
на квадрат скорости света.
12.6.2. Займемся теперь вопросом о перемещении электромаг-
электромагнитной энергии из одних мест пространства в другие. Рассмот-
Рассмотрим для этой цели дифференциальный закон сохранения
dxk dxk
для полного тензора энергии-импульса E2с) поля и зарядов Qi!t
(для простоты мы опускаем указание m-f-int + ph), для опре-
определенности его четвертую компоненту, и проинтегрируем это
равенство по конечному 4-цилиндру, образованному двумя ги-
гиперплоскостями t = t\ и t = t% и боковой гиперповерхностью,
параллельной оси t
Разделяя интегралы по основаниям цилиндра и по боковым поверхностям,
получаем отсюда
J Q4idT- J
v, t"-t, r, t-t,
по боков.
поверхн.
где последний интеграл берется по (обычной) поверхности f, которая ограни-
ограничивает трехмерный объем У, вырезаемый 4-цилиндром из гиперплоскостей
t = const.
Будем теперь считать, что на границе f объема У есть только
чистое электромагнитное поле, но не заряды. Тогда на этой
12. ТРЕХМЕРНАЯ ФОРМУЛИРОВКА 227
границе 64а = Э?о — -^г Sa и
то есть
и
&2 — &i = —[dt&diS. поток анергии E7.1)
J J из объема
Но слева стоит разность полных энергий частиц+ поле в объ-
объеме У в моменты времени U и t\. Поэтому, в силу элементар-
элементарного понимания закона сохранения энергии в правой части
должна стоять (со знаком минус) энер-
энергия, вытекшая из этого объема за время
t2 — tu а под интегралом по t—полный
поток энергии, вытекающий из рассмат-
рассматриваемого объема. Однако на границах
объема f у нас есть только электромаг-
электромагнитное поле. Следовательно, интеграл в
правой части E7) дает нам полный поток
энергии электромагнитного поля, пересекающий (в единицу вре-
времени) поверхность f. Поскольку форма этой поверхности ничем
не выделена, то подинтегральное выражение в правой части E7)
должно описывать плотность потока энергии электромагнитного
поля. Итак,
плотность потока энергии в электромагнитном поле равна век-
вектору Пойнтинга.
12.6.2.1. Если принять теперь, что и внутри рассматриваемого
объема нет зарядов, и устремить сам объем к нулю, то мы полу-
получим из E7.1)
-^ = -divS E7.2)
— закон сохранения энергии для одного электромагнитного поля
в дифференциальной форме. Естественно, что мы могли бы по-
получить то же самое прямо из дифференциального закона сохра-
сохранения энергии-импульса для свободного электромагнитного поля
= 0, полагая в нем i = 4 и переходя к трехмерным вели-
я
чинам.
12.6.3. Все последние рассуждения мы провели для временной
компоненты дифференциального закона сохранения для полного
тензора энергии-импульса. Точно так же они проходят для про-
странственных составляющих — мы пришли бы тогда к понятию
плотности потока импульса электромагнитного поля, которая
8*
228 ч. II. МЕХАНИКА ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
выражалась бы чисто пространственной частью 9?р тензора
энергии-импульса. Следуя Максвеллу, ее называют иногда
(трехмерным) тензором натяжений электромагнитного поля.
13. Решение уравнений поля
13.1.1. Вернемся ко второй паре уравнений Максвелла E1.2).
Выразим в них (что возможно в силу E1.1)!) поле Fik через
4-потенциал At с помощью D2). (Решать уравнения второго
порядка чаще проще, чем первого!). Мы получим тогда уравне-
уравнение для 4-потенциала
aMft ам, _ 4л
dXidxk дх\ ~ с ;" (Ь9'
равносильное системе уравнений Максвелла.
Второй член в его левой части содержит оператор
дх\ дх\ с2 dt2 с2 dt2 д'Аламбера
который называется оператором д'Аламбера *); содержащие его
уравнения хорошо изучены. Первый же член в левой части E9')
неудобен.
13.2. Чтобы избавиться от него, воспользуемся произволом
в выборе потенциала, связанным с градиентным преобразова-
преобразованием D1), и, как говорят, выберем калибровку так, чтобы было
¦тг*- = 0, т. e. divA + -^ = 0 условие E8)
dxk c dt Лоренца. V '
Это условие называют условием Лореица; легко видеть, что
всегда можно подобрать градиентное преобразование, переводя-
переводящее произвольный потенциал А{ в удовлетворяющий этому ус-
условию. О 4-потенциале, удовлетворяющем E8), говорят как о
потенциале в лоренцевой калибровке. Можно выбирать и другие
калибровки потенциала — иногда это бывает удобно, — но ло-
ренцева калибровка есть единственная, налагаемая релятивист-
релятивистски инвариантным способом, т. е. не зависящая от выбора си-
системы отсчета.
13.2.1. ЗАМЕЧАНИЕ: Условие Лоренца не фиксирует 4-по-
4-потенциал однозначным образом: остается еще возможность изме-
изменять потенциал за счет специальных градиентных преобразова-
преобразований:
где ПА = 0. 1 D1а)
*) Оператор д'Аламбера можно рассматривать как обобщение оператора
Лапласа Д на 4-пространство. Существенно, однако, что в силу псевдоевкли-
довости он оказывается уже не эллиптическим, а гиперболическим.
13. РЕШЕНИЕ УРАВНЕНИЙ ПОЛЯ 229
13.1.2. Условие Лоренца уничтожает первый член в E9'), и
-мы приходим к основному уравнению электродинамики, выра-
выраженному через потенциалы
гJД j 4 тс
——1-=?2А{ = ——/;. основное уравнение E9)
dxj с поля (только в лорен-
цевой калибровке!)
Его называют волновым уравнением или уравнением д'Алам-
бера с правой частью.
Займемся решением этого уравнения.
13.3. Будем поступать с ним так же, как мы обошлись в 1.15.
с уравнением для осциллятора с произвольной правой частью.
Разложим искомое поле А\ и заданный ток jt в четырехмерные
интегралы Фурье
F0>
.Мы обозначили здесь четыре фурье-переменных через ku k% k3,
k4 и требуем, чтобы они образовывали бы 4-вектор
F1)
— тогда переход к фурье-образам будет релятивистски инвари-
инвариантным. Элемент 4-объема в «/г-пространстве» мы обозначаем
через
= dkx dk2 dk3 dk4 = :dk) - dco.
С
Вектор ki называется волновым 4-вектором, его пространствен-
пространственная часть к — просто волновым вектором.
Обратное фурье-преобразование в избранной нормировке бу-
будет иметь форму (выпишем его для тока)
jt (k) = — \ dQ e I iji 'x). F0')
13.1.3. Во введенных фурье-образах уравнение движения E9)
перепишется как
с
Mi (k) = ~ h (k) + ?t (k) k)b (kf) E9a)
— мы здесь опять прибегаем к тому же приему, что и в 1,15.,
добавляя в правую часть тождественный нуль k)b(kf), умножен-
умноженный— теперь уже не на произвольную константу, а на произ-
230 ч. II. МЕХАНИКА ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
вольную функцию переменных ku регулярную на световом ко-
конусе /г/ = 0. После того как мы поделим обе части E9а) на/г/.
kj
F2>
добавленный член уже не будет нулем, а будет описывать произ-
произвольное решение Л? свободного волнового уравнения:
Ш,= 0. E9.0>
а. Однородное уравнение
13а.1. Займемся сперва этим свободным решением. Оно удов-
удовлетворяет (в координатном представлении) волновому уравне-
уравнению nA°i(x) = 0 и условию Лоренца -j~~ = ^, тем не менее в
нем еще сохраняется произвол в выборе потенциала, связанный
с возможностью провести специальное градиентное преобразо-
преобразование D1а). Поскольку каждая компонента Аг сама удовлетво-
удовлетворяет волновому уравнению, то этим произволом можно восполь-
воспользоваться, чтобы обратить какую-нибудь одну компоненту 4-по-
тенциала в нуль; потребуем, чтобы нулю равнялась четвертая
компонента Л4 = щ = 0. Заметим, что это требование уже не-
неинвариантно; поэтому дальнейшее будет относиться к какой-
либо одной системе отсчета, а при переходе к другой систе-
системе надо будет, чтобы сохранить формулы неизменными, совер-
совершать каждый раз еще и градиентное преобразование типа
D1а).
13а.2. Итак, произвольное свободное решение имеет форму
2ТЧ + 2Т?|
f (F (к. с | к |) 6 (и - с | к |) + F (k, - с | к |) 6 (со + > | к |)) =
(F(-» (Ю 6 (И - c I k I) + F(+) (k) 6 (ш + с I k I)),
где мы явно учли, что б-функция бf f — J —k2j приводит, при:.
заданном векторе к, к двум возможным значениям для <о, в со-
соответствии с чем произвольная функция F(&) четырех аргумен-
аргументов сводится реально к двум произвольным функциям F'^k) ог
трех аргументов каждая.
13а. ОДНОРОДНОЕ УРАВНЕНИЕ 231
Условие Лоренца E8) при сделанном дополнительном уточ-
уточнении калибровки сводится к равенству
кА°F) = 0, т. е. к kF(")(k) = 0 и kF(+)(k) = 0. E8')
Таким образом каждая из двух векторных функций F<T> имеет
только две независимые компоненты, т. е. ее можно разложить
по двум единичным и взаимно-перпендикулярным векторам ei и
удобно принять, что векторы еь ег и угу
образуют правый единичный репер, местный или локальный ре-
репер в ^-пространстве:
kea(k) = 0; е,е2 = 0; е? = е|=1; [е, • е2] = у^- = п (к)) . F3)
Поэтому об условии E8') говорят как об условии попсречности
свободного электромагнитного поля.
Итак, многообразие решений свободного уравнения E9) опи-
описывается четырьмя скалярными функциями волнового вектора
к, в соответствии с возможностью для каждого к двояким об-
образом выбрать как знак частоты со, так и направление векторов
F<T> по ei или е2 — как говорят, направление поляризации. Ока-
Оказывается, что две из этих функций комплексно сопряжены двум
другим. В самом деле, 4-потенциал F0) должен быть вещест-
вещественным; это налагает на фурье-образ Лг(&) условие
В применении к свободному решению оно переносится на
дает
F<-> (- k) = (F!+) (к))*; F(+) (- к) = (F<-> (к))*.
С учетом этого обстоятельства удобно переменить нормировку
и выразить F через новые произвольные амплитуды аа(к) и
а* (к) (а=1,2)
F(-} (к) = V2co (к) BяУ/!е„а„ (к);
Bn)'h еаа'а (к).
13а.З. Через эти произвольные амплитуды общее свободное
решение уравнения E9) запишется в обычно используемой
форме:
F4.1)
a = l, 2.
232 ч. И. МЕХАНИКА ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
(Обратите внимание на аналогию с решением в форме A.40.1)
для координаты гармонического осциллятора!)
Найдем выражения для электрического и магнитного полей,.
соответствующие решению F4). Поскольку скалярный потен-
потенциал ф в нашей калибровке равен нулю, то электрическое поле
Е получится дифференцированием А по времени:
-.. Лк|.еа(к){... - ...}. F4.2)
(В силу аналогии с выражением F4.1) мы выписали здесь в ос-
основном лишь те детали, которые отличают эту форму от преды-
предыдущей.) Аналогично, чтобы получить магнитное поле, надо вы-
вычислить ротор вектор-потенциала, что дает
..t|k|[n(k)-ea(k)H... -...}. F4.3)
Мы видим таким образом, что общее решение для свободного
электромагнитного поля оказывается сюперпозицией плоских
волн со всеми возможными длинами и направлениями распро-
распространения (задаваемыми волновым вектором к), причем группою
da (к) . _
вая скорость .... всех волн одинакова, совпадает с фазовой
скоростью ?. | и равна скорости света с*). При заданном вол-
новом векторе имеется 4 независимых амплитуды а* (к); значки
± отвечают двум независимым фазам — косинусу и синусу, а
значения сс=1, 2 — двум поляризациям.
В последнем пункте стоит разобраться подробнее.
Ш.З.1. В формулах F4) коэффициентом при определенной экспоненте
е-»и (k) t+ikx является сумма (ej (к) aj (к) + Сг (к) а2 (к)). Поскольку ампли-
амплитуды aa(k) комплексны, то эта сумма зависит от четырех параметров — ве-
вещественных частей амплитуд aa(k) и мнимых—Pa (к); эти параметры удобно-
/а, а2\
записать в виде матрицы I I. Легко сообразить, однако, что не все.
V Pi P2/
эти параметры физически существенны. Действительно, в нашей записи коэф-
коэффициента при экспоненте присутствуют два произвольных момента.
Во-первых, местный репер (ei (k), е2 (к), п (к)} можно, не меняя никаких
использованных его свойств, поворачивать вокруг направления к; такие пово-
*) Когда мы перечисляли в § 9 основные физические свойства электро-
электромагнитного поля, определяющие выбор его лагранжиана, мы сослались на
это обстоятельство как на опытный факт и связали его с отсутствием в лаг-
лагранжиане 4-потенциала Л;. Теперь можно пояснить эту связь. Если бы 4-по-
тенциал At входил в лагранжиан электромагнитного поля, то, как и в при-
примере 7.4, в уравнении E9) появился бы еще и член, пропорциональный потен-
потенциалу, скажем х2Л,-, где у.2 — константа. Тогда мы получили бы при проведе-
проведении фурье-преобразования в качестве выражения для частоты ие со = ±с|к|*
а а = ± Vс2к2 + х2 — групповая и фазовая скорости были бы различны и за-
зависели бы от длины волиы.
13а. ОДНОРОДНОЕ УРАВНЕНИЕ 233
роты образуют однопараметрическое семейство, переводящее матрицу
р2/ ¦ vp;
справа на матрицу ортогонального поворота на плоскости:
J в новую матрицу I I, которая получается из нее умножением
2/ " V В^ В„/
a[ v'2\_ fa\ «2 V cos<p в1пф\
Pi P2/VP1 h A-sin4) *<**'
Во-вторых, из обеих амплитуд ai(k), аг (к) можно выделить общий фазовый
множитель е!* и отнести его к экспоненте. Такое, тоже однопараметрическое,
преобразоваиие соответствует повороту иа угол ^ в комплексной плоскости;
легко убедиться что его действие иа матрицу параметров сводится к умно-
умножению ее слева опять-таки на матрицу ортогонального поворота:
(
cosi|)
К
(cos ф sini^N/a, a2\f совф sin qA
— sin ф cos -ф/ V Pi P2/V — sin ф совф/
Таким образом, преобразования, ие меняющие физического смысла
матрицы параметров, оказываются аналогичными тем преобразованиям кото-
которые используются обычно для приведения квадратичной формы к главным
осям за счет ортогонального поворота системы координат; разница состоит
лишь в том, что в последнем случае обе ортогональные матрицы были бы
взаимно обратны: г|) =¦ —ф. Зато наша матрица параметров отличается от
матрицы квадратичной формы тем, что ие обязана быть симметричной,
Pi = аг. Лишняя степень произвола в допустимых преобразованиях идет как
раз на уничтожение лишнего коэффициента первоначальной матрицы, и ре-
результат оказывается тем же самым — описанные допустимые преобразова-
преобразования всегда позволяют привести матрицу параметров к виду
[ О
13а.3.2. Итак, векторный потенциал для волны с фиксиро-
фиксированным волновым вектором к всегда можно привести к виду
Ак (х, t) — e-"lrf+lta+'*(eIa1 + /е2р2) + в""'-"»-'* (е,а, - /е
= ei • 2а! cos М — кх — г|з) + е2 • 2р2 sin (at — кх — ip)
— при фиксированном х (в фиксированном месте пространства)
конец вектора Ак@ описывает эллипс с полуосями а\ и 02, на-
направленными по направлениям е, и е2. Такая волна называется
эллиптически поляризованной. В частности, один из параметров
ai или Рг может равняться нулю, тогда эллипс вырождается
в отрезок прямой; в этом случае говорят о плоско поляризова-
иой волне. Мы видим, что эллиптически поляризованную волну
можно рассматривать как сюперпозицию Двух волн, плоско по-
поляризованных в направлении главных осей эллипса, фазы кото-
234 ч П. МЕХЛНИКА ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
рых сдвинуты одна относительно другой на -%*). Другой важ-
важный частный случай получается, когда ai = fb, т. е. эллипс вы-
вырождается в круг; тогда говорят о циркулярной или круговой
поляризации.
Вектор электрического поля в монохроматической эллипти-
эллиптически поляризованной волне вращается (как видно из F4.2)
или просто из Е = -зт-] по тому же (точнее — подобному).
эллипсу, что и А, но отстает от него на у;
Ек(х, 0 =
= е, • 21 к | a! sin (<о/ — кх — ф) — е2 • 2 | к | р2 cos (at — кх —1|))..
Что же касается магнитного поля монохроматической волны
Hk(*, t), то из F4.3) видно, что оно получается из Ек(х, t) век-
векторным умножением на n(k); но в плоскости (еь е2) такая опе-
операция просто поворачивает вектор на прямой угол. Поэтому маг-
магнитное поле во всякий момент времени ортогонально электри-
электрическому и конец вектора Нк вращается по эллипсу, такому же*
как у электрического поля, но повернутому относительно его на
прямой угол:
Нк(х,/) =
= е2 • 21 к | at sin {at — кх — if) + е, • 21 к | р2 cos (at — кх — if)..
13а.4. Итак, в монохроматической плоской электромагнитной',
волне, т. е. в частном решении свободного уравнения E9), отно-
относящемся к определенному волновому вектору к,
A) и электрическое и магнитное поля лежат в плоскости
(ei, e2), т. е. всегда направлены поперек направления распро-
распространения волны n(k). Поэтому свободная электромагнитная
волна поперечна (когда мы отметили в E8') аналогичное об-
обстоятельство для вектор-потенциала, ему нельзя было придавать
много значения, поскольку потенциал неоднозначен).
B) Электрическое и магнитное поля перпендикулярны друг
другу.
C) Электрическое и магнитное поля равны друг другу по ве-
величине.
Все три свойства можно записать в виде двух векторных
формул:
H(k)=[n(k)-E(k)] и E(k) = -[n(k)-H(k)]. F4.4)
*) Если сдвиг фаз отличен от —, то сюперпозиция двух плоско поляри-
поляризованных воли приводит к волне, поляризованной по эллипсу, главные ос»
которого ие совпадают с направлениями поляризации первоначальных волн»
13а. ОДНОРОДНОЕ УРАВНЕНИЕ 235
13а.5. Поучительно вычислить, как выражаются через ампли-
амплитуды fla(k) и aa(k) фундаментальные динамические величины
поля, например энергия. Оставляя проведение довольно громозд-
громоздкого вычисления читателю (ленивый читатель может попытаться
заглянуть в конец параграфа), приведем прямо результат:
?>Ph = J йГ ЕЩЦ _ _L J (Л) ffl (к) д. (к) aa (к). F5)
Мы видим, что энергия свободного электромагнитного поля
представляется в виде суммы энергий отдельных (парциальных)
монохроматических волн, — интерференционные члены отсут-
отсутствуют^. — причем для каждой парциальной волны получается
в точности то же самое выражение A.40.2), которое мы полу-
получили в механике для осциллятора (единичной массы). Если при-
принять (ср. 1.20.) амплитуды аа(к) за обобщенные координаты
поля, то обобщенными импульсами окажутся (с точностью до
множителя /) а*а(к), а F5) станет функцией Гамильтона; по-
поэтому распадение F5) в сумму (интеграл) функций Гамильтона
для парциальных степеней свободы означает, что движение каж-
каждой степени свободы происходит независимо от остальных.
В этом смысле часто говорят о разложении поля на независи-
независимые осцилляторы.
Аналогичные F5) выражения получаются и для остальных
фундаментальных динамических величин; мы не будем их выпи-
выписывать.
13а.6. Итак, мы выяснили, что свободное уравнение электро-
электромагнитного поля E9.0) допускает нетривиальные (т. е. приводя-
приводящие к неравным нулю энергии, электрическому и магнитному
полям) решения. Это значит, что в природе может существо-
существовать электромагнитное поле, не связанное с зарядами, как со-
совершенно автономный физический объект, распространяющийся
в пространстве со скоростью света. Тем самым поле, введенное
сперва со сравнительно скромной целью описать необходимое
в теории относительности запаздывание взаимодействия частиц,
приобретает самостоятельное, не зависимое от этих частиц
бытие.
Чтобы окончательно убедиться, что этот новый вид материи
с неотвратимостью должен занять подобающее ему место в на-
нашей общей картине физического мира, остается еще обнару-
обнаружить, что он не отгорожен от привычного нам мира частиц ни-
никакой китайской стеной, что в процессе взаимодействия элект-
электромагнитного поля с заряженными частицами они действительно
могут обмениваться с ним своими динамическими характеристи-
характеристиками— энергией, импульсом, моментом —, т. е. что в природе
.действительно может иметь место процесс излучения (и погло-
поглощения) электромагнитного поля движущимися зарядами.
236 ч. II. МЕХАНИКА ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
Этой задаче будет посвящен следующий раздел.
13а.3.3. ДОПОЛНЕНИЕ 1: Восстановление амплитуда^' (к) по полям *).
Формулы F4) очень похожи на трехмерное преобразование Фурье, в кото-
котором время выступает в роли параметра. Дело осложняется, однако, тем, что
они выражают, скажем, электрическое поле через два трехмерных фурье-
образа— аа(к) и а* (к) (для краткости— а^ (к)). Поэтому ясно, что для
восстановления этих фурье-образов задания одной функции Е(х, t) при фик-
фиксированном t недостаточно, нужна еще и другая, в качестве которой естест-
естественно призвать Е(х,/) (при том же фиксированном t).
Попробуем построить линейную комбинацию обратных фурье-преобразо-
ваний этих двух функций, именно, вычислим интеграл вида
V2a.(q)
С помощью прямого фурье-разложения F4.2) получим для него
Г = -J- \ -Лак) Ш «, (к) еа (к) ( е* ** <>* (± 1 + !°Щ аа (к)
BяK J V2« (к) • 2а> (q) I V (oD)j
В этом выражении есть три интегрирования по dx, которые превратят три
экипоненты в б-функции, однако экспонент здесь четыре. Поскольку, однако,
ш (к) = и (q), если k=±q, то при верхнем знаке в первом и нижнем — во'
втором члене фигурных скобок временная экспонента превращается в еди-
единицу. При двух же других знаках обращаются в нуль круглые скобки! По-
Поэтому наша линейная комбинация дает иам
Но это значит, что
„W (к) = —V [ ,Ш) е* ikxta (к) (* Д> (х, 0 + -J— Ё (х, /Л. |
а BяK/г J V2m (к) Ч и (к) ) "
F4.5К
ЗАМЕЧАНИЕ 1: Левая часть F4.5) не зависит от времени. Сле-
Следовательно, и значение интеграла в правой части, вычисляемого
по пространству в некоторый момент времени t, от выбора этого
момента не зависит. |
ЗАМЕЧАНИЕ 2: Мы выяснили, что амплитуды а* (к) однозначно,
определяются заданием Е и Е в один момент времени. Но со-
согласно первому уравнению второй максвелловой пары, в отсут-
отсутствие зарядов E = crotH. Поэтому для определения амплитуд
а&Цк) достаточно задать лишь сами электрическое и магнитное
поля Е и Н в один момент времени.
*) или «Полезные маленькие хитрости. 1.»
ТЗб. УРАВНЕНИЯ С ПРАВОЙ ЧАСТЬЮ 237
Но если амплитуды а(±'(к) известны, то формулы F4.2,3) дают
нам поляЕ и Н во все моменты времени; поэтому задание по-
полей при t = t0 определяет их для всех /, т. е. фиксирует задачу
Коши для свободного электромагнитного поля. Мы могли бы,
пользуясь этими соображениями, построить и ее явное реше-
решение, однако это будет гораздо проще сделать, опираясь на не-
некоторые понятия, которые появятся в следующем разделе в свя-
связи с неоднородными уравнениями. |
13а.5.1. ДОПОЛНЕНИЕ 2: Вычисление энергии свободного поля*). При
подстановке разложений F4.2,3) для электрического и магнитного полей в
формулу E2.1) для энергии поля мы сталкиваемся с тем же затруднением,
что и в Дополнении 1, — число интегрирований по х-пространству меньше
числа экспонент. В половине членов — тех, которые содержат произведения
амплитуд типа а*а — лишняя временная экспонента опять обратится в еди-
единицу, ио в другой половине — в которой стоят а*а* и аа — останутся вре-
временные экспоненты с двойной частотой:
X О; (к) а3 (к) + аа (к) al (к)) +
J ?^у № {еа (к) ер (- к) + [п (к) • еа (к)] • [п (- к) ¦ ер (- к)]} X
X O2''m(k) laa (к) а\ (- к) + е-21*™ *аа (к) ^ (- к)).
Кроме того, коэффициенты при произведениях амплитуд выглядят очень гро-
громоздко.
Обе болезни лечатся одним лекарством: мы замечаем, что операция
[п (к) • еа] просто поворачивает еа на — в плоскости, ортогональной к. По-
Поэтому второе скалярное произведение в первой фигурной скобке — это про-
произведение тех же векторов еа и ер, что и в первом скалярном произведении,
только повернутых оба на один и тот же угол; значит оно, как и первое, рав-
равно просто бар. Во второй фигурной скобке оба сомножителя второго скаляр-
скалярного произведения тоже получаются из сомножителей первого — еа (к) и
ер (—к) —поворотом иа -=¦, ио поскольку п (— к) = — п (к), поворотом в
противоположных направлениях — поэтому эти два произведения взаимно
уничтожаются и второй интеграл, содержащий двойные частоты, исчезает.
Чтобы получить стоящую в основном тексте формулу F5) остается только
учесть, что с2к2 = ш2(к). |
б. Уравнения с правой частью
136.1. Вернемся к частному решению неоднородного уравне-
уравнения. Как и в случае разобранной в части I задаче для осцилля-
осциллятора, будем выписывать решение через функцию Грина. Из
*) или «Полезные маленькие хитрости. 2.»
238 ч. И- МЕХАНИКА ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
фурье-разложений F0) и уравнения F2) следует:
л /((у)
где
At М = ^г т \ (dyL G{x-y) и (у), F6.1
i Г ikl (x-V)i
G(x — y)= 4 . \ (dkL j функция Грина F6.2)
— функция Грина.
136.1.1. Разделяя здесь интегрирование по волновому вектору к и часто-
частоте и, получаем последовательно
e-te>{t-n
с2
(rfk)
«Чисто временная» функция Грина
A'47-2>
— это в точности тот же объект, который мы изучали в § 15 первой части.
Поэтому можно сразу заимствовать оттуда нужный нам результат, причем
нам удобно будет избрать запаздывающую функцию Грииа
DT« (t - t') = °(J(~n sin [<a (k) (/ - /')]. (I. 48r)
Ее подстановка в F6) дает четырехмерную запаздывающую
функцию Грина
sin ^ W т); 2 ев {R, /ст} = х - у,
F6т)
и нам остается только выполнить трехмерное фурье-преобразо-
вание.
136.1.2. Перейдем к сферическим координатам в k-просгранстве, и обозна-
обозначим ради простоты письма
|R| = ?, I fe | ===== Jfe,
136. УРАВНЕНИЯ С ПРАВОЙ ЧАСТЬЮ 239
так что это будут не 4-векторы, а длины 3-векторов. Тогда и (k) = ck и
оо I
О -1
2 ль о s'n ^ ^ (т) sin ckx
dk sin ?# sin ckx = " v2p \ dk [cos ? (# — ex) — cos k (R + ex)] тт.
о о
Ho \ dk cos kX = яб (X). Поэтому
О
Dret(z) = т~Т"р"* (т) № (^ — ст) — 6 (# + ст)].
Обратим здесь внимание на ступенчатую функцию ¦&(т). Она
отлична от нуля только для т > 0. Но R > 0 по своему опреде-
определению. Поэтому аргумент второй б-функции существенно поло-
положителен и ее можно выбросить. А в качестве множителя при
первой б-функции функция Ф(т) не нужна — эта б-функция мо-
может отличаться от нуля только для положительных т.
Итак, в нашей функции Грина остался только член, в кото-
котором расстояние R растет с ростом времени т. Далее, функция
Грина не зависит от углов. Таким образом найденная функция
Грина изображает сферически-симметричную волну, причем вол-
волну, расходящуюся. Последнее обусловлено тем, что мы выбрали
в качестве временной функции Грина запаздывающую функцию.
Если бы мы избрали опережающее решение, то б-функции поме-
поменялись бы своей судьбой — выжила бы только вторая, и мы по-
получили бы вместо расходящейся волны — волну сходящуюся.
С учетом этих замечаний можем выписать окончательное вы-
выражение для запаздывающей функции Грина
F7г)
136.1.3. Соответствующая формула для опережающей функ-
функции имела бы вид
Dadv (х - х') = -L TFJ-FT 6 (| г - г' | + с (t - О). F7а)
136.1.4. Выбросивши в предыдущей выкладке одну из 6-функ-
ций и опустив «ненужную» О-функцию, мы упростили выражения
F7), но зато потеряли релятивистскую инвариантность, кото-
которой, по-видимому, обладала форма F6.2), — мы говорим «по-
240 ч. II. МЕХАНИКА ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
видимому», поскольку пока неясно, не теряется ли инвариант-
инвариантность уже в момент выбора конкретного контура интегриро-
интегрирования.
Чтобы разобраться в этом, восстановим в F7г) ненужную
Это выражение можно последовательно преобразовать как
=i *(т) б w - ст> (* +ст))=^г *(т) б (*2 - (ст>2)-
Мы получаем тем самым для Drct(z) новую форму:
F7r')
обладающую тем преимуществом, что из нее сразу видна инва-
инвариантность Dret(z) относительно ортохронных преобразований
Лоренца. Действительно, под знаком б-функции стоит инвариант-
инвариантный интервал z2, что же до знаковой функции ®(т), то она могла
бы меняться при ортохронных преобразованиях Лоренца только
для пространственно-подобных z, а для них 6(z2) обращается
в нуль.
В полной аналогии опережающую функцию Грина можно
записать в явно инвариантной форме
^(-T.N(z2). F7а')
Что же касается инвариантности относительно обращения
времени, то она действительно потерялась при конкретизации
контура интегрирования в F6.2)—запаздывающая функция пе-
переходит при таком преобразовании в опережающую и наоборот.
136.2.1. Разность запаздывающей и опережающей функций
Грина
Drst(z)-Dadv(z) = D(z) = ^-6(z2) F7 ')
должна быть решением свободного уравнения E9.0). Это реше-
решение— мы поторопились ввести его еще в механике для одного
осциллятора и знаем, что его зовут D-функция Паули — выде-
выделяется своими особыми свойствами, поэтому его стоит изучить
подробнее.
Прежде всего, из (§7 ') явствует, что D(z) — функция, ин-
инвариантная относительно ортохронных преобразований Лоренца,
а при изменении знака времени она меняет знак— D-функция
136. УРАВНЕНИЯ С ПРАВОЙ ЧАСТЬЮ 241
Паули есть «антисимметричное инвариантное решение» свобод-
свободного уравнения E9.0):
? D(z) = 0; D(R, -T) = -D(R, t). F7 М)
Можно показать, что это — единственное решение с такими
свойствами и вместе с «симметричным инвариантным решением»
D^(z), которое нам пока не понадобится, — одно из двух инва-
инвариантных решений.
Из свойств антисимметрии при замене т->—т следует, в ча-
частности, что для совпадающих времен
D(R, 0) = 0. F7 '.2)
Еще одно важное свойство D-функции найдется, если вер-
вернуться к формулам F6), подставляя в них вместо «чисто времен-
временной» запаздывающей функции A.48г) «чисто временную» D-
функциго
Мы найдем тогда для трехмерного фурье-разложения функции
Паули
J*^ <ад.
Дифференцируя его по времени, выясняем, что
дР (R, icx) с К , „ > ;кр , ,. , у rf\ln\ (R7 ' Ч\
ОТ l^^7 J T = 0
tH—= —7^—73- \ (cfk)e'kR(»(k)sin((a(k)T)
to = 0. F7 'A)
Покажем, что найденные свойства F7. 1—4) функции Паули
позволяют с ее помощью решить задачу Коши для свободного
уравнения д'Аламбера.
136.2.2. Пусть нам заданы значения вектор-потенциала А0
свободного поля и его первой производной А0 в некоторый фик-
фиксированный момент времени t =.t' = const.
Сконструируем образование;
\
/'=const
- [ (dr')D{x-xr)dt'Kf>{xr). F8 0)
t
j
г =const
Тогда
242 ч. II. МЕХАНИКА ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
(а) ? А0 (х) = 0, поскольку D и D суть решения свободного-
уравнения д'Аламбера;
(Р) А0 (г, П = 1 J (Ж-') сб (г - г') А° (г', t') = А" (г, П;
г, 0
1 I / j \ с / /\ Crt \л I C/rt (I , ( I
'' = const
— т. е. построенное выражение есть такое решение свободного
волнового уравнения, которое имеет на гиперплоскости t = tr
заданные значения функции и нормальной производной, т. е.
есть решение задачи Коши.
Легко видеть, что если начальные условия заданы не на пло-
плоскости, а на произвольной пространственно-подобной гиперпо-
гиперповерхности а, то решением задачи Коши будет естественно обоб-
обобщающее F8 0) образование:
А° (х) - i \ dStD (х - х') -?- А» (*')• F8 Оа)
Решение задачи Коши, поставленной для полей, а не для по-
потенциала, получается из этих формул дифференцированием.
136.3. С помощью запаздывающей функции Грина мы можем
получить теперь явную форму частного решения неоднородного
уравнения E9):
Используя 6-функцию, здесь можно проинтегрировать по t', при-
причем временной аргумент стоящего под интегралом тока заме-
заменится на запаздывающее время
t' = t- — , где опять Я = |г —гЧ F8а г>
Таким образом частное решение примет форму
запаздывающие ffiSrY
потенциалы Vй01/
Это решение неоднородных уравнений поля называют решением
в форме запаздывающих потенциалов или просто запаздываю-
запаздывающими потенциалами.
Общее решение уравнений E9) запишется тогда как
At (x) = A°i (x) + A\et (x). общее решение F9г>
136.4. Решение F9г) в форме запаздывающих потенциалов
занимает в теории поля особое место. Чтобы пояснить, почему
136. УРАВНЕНИЯ С ПРАВОЙ ЧАСТЬЮ 243
это происходит, сделаем сперва несколько замечаний относи-
относительно смысла выраженного через посредство какой-то функции
Грина G'{x— х') общего решения
At (х) = A? W + ¦§¦ J dx'G' (x - *') й (х) F9')
уравнения E9).
136.4.1. Если мы интересуемся только численным значением
решения, т. е. тем, каким числам будут равны компоненты 4-по-
тенциала в каждой точке хк, то ничего не изменится, если мы
перейдем в F9') от G' к какой-либо другой функции Грина G"
(скажем, от DTet — к Z)adv): поскольку разность двух функций
Грина есть решение свободного уравнения (см. 1,15),
то тот же самый 4-потенциал запишется в аналогичной F9')
форме
Ai (х) = А7°(*) + ?$ dx'G" (х - х')U (*'), F9*),
где другое свободное решение А (х) будет связано со старым
соотношением
А? (х) = А? (х) + —¦ \ dx'D (х - х>) U (х'). (*}
В соответствии с этим и говорят обычно, что конкретный выбор
частной функции Грина в решении типа F9) несуществен.
136.4.2.1. Действительно существенный момент выбора реше-
решения состоит не в том, через какую функцию Грина его записать,
а в том, чтобы решить, какое свободное решение мы считаем не
зависящим от тока ji(x')l Сама постановка такого вопроса озна-
означает, что мы хотим взглянуть на решение F9) с новой точки
зрения, рассматривая его как (неоднородный) линейный функ-
функционал Aj(x,Ц(х')]) от тока ji(x') и интересуясь не только "чис-
"численным значением 4-потенциала, но и видом его функциональ-
функциональной зависимости от тока.
Из соотношения («) видно, что если мы хотим, чтобы F9')
и F9") определяли бы одно и то же решение и в этом новом
понимании, то не зависеть от /* может только одно свободное
поле — или А? (х) или А"°(х). Решить, какое именно, — это зна-
значит сделать физический выбор, эквивалентный выбору началь-
начального условия для уравнения E9).
136.4.2.2. Можно стать и на иную точку зрения, и согласиться,
что всякий раз, когда мы'пишем решение в форме F9) — с какой
бы то ни было функцией Грина — свободное поле A'i(x) всегда
не зависит от j(x'). При таком соглашении переход от F9') к
F9") уже не есть тождественное преобразование, поскольку два
244 ч. И. МЕХАНИКА ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
решения — обозначим их как А\ (х, [/]) или А'{ (х, [/]), — будучи
численно равными, по-разному зависят (функционально) от /,
и разные функции Грина становятся неэквивалентными.
136.4.3. С этими разъяснениями мы можем теперь сделать
выбор преимущественной функции Грина. Мы знаем, что в силу
принципа причинности в теории относительности в некоторую
4-точку х могут приходить сигналы только из 4-точек х', лежа-
лежащих в нижней половине построенного в х светового конуса
(только из предконуса точки х)—для такого взаимного распо-
расположения точек х и х? используют обозначение х > х' (читается —
х позже х'). Но влияние тока / в точке х' на 4-потенциал А
в точке х есть частный вид сигнала, получаемого в х из 4-точки
х'\ следовательно, условие причинности для поля состоит в том,,
что 4-потенциал А (х) может зависеть от 4-токов /(*') только в
тех точках х'', которые лежат в предконусе точки х, х > х'. Ана-
Аналитически это условие можно записать в виде равенства
~С$~ = 0' если xf^x*), G0)
где запись х' ^ х означает или х' > х или х' пространственно-
подобно х (х' ~ х).
136.4.3.1. Применение G0) к решению в форме F9) дает нам.
6Л,- (х) An х п . ,.
т. е. приводит к условию причинности для функции Грина:
G{x — x') = Q, если х'^х. GО'>
Это требование выполнено для запаздывающей функции Грина
Dret(x — х'). Можно показать, что Dret есть единственная реля-
релятивистски инвариантная функция Грина, обладающая этим свой-
свойством.
136.4.4. Итак, при использовании в F9) в качестве функции
Грина запаздывающей функции Dret достигаются одновременно
две цели: выполняется условие причинности, и в то же время
полное решение А{(х), записанное в форме F9г), явным обра-
образом разделяется на два члена, из которых второй описывает
электромагнитное поле, создаваемое зарядами системы, а пер-
первый не имеет к этим зарядам никакого отношения и есть суще-
существующее само по себе свободное электромагнитное поле, как го-
говорят, падающее на систему излучение.
136.5. ЗАМЕЧАНИЕ: Во всем этом параграфе, решая уравне-
уравнения E9), мы считали 4-ток ji(x') заданной функцией координат
х' и времени V. Реально, однако, 4-ток определяется, как мы
*) Такая форма условия причинности принадлежит Н. Н. Боголюбову.
136. УРАВНЕНИЯ С ПРАВОЙ ЧАСТЬЮ 24S
знаем (D9)), движением зарядов, а оно — в свою очередь —
электромагнитным полем согласно уравнениям движения D8).
Поэтому может показаться, что мы занялись не слишком ос-
осмысленным делом, выделивши совершенно произвольно из су-
существенно нелинейной проблемы лишь одну линейную стадию *)
и сможем на этом пути достигнуть, самое большее, преобразо-
преобразования уравнений движения поля из дифференциальной формы
в интегральную**).
В действительности, однако, дело обстоит гораздо хитрее, и
с такой полной нелинейной проблемой очень редко приходится
сталкиваться. В большинстве случаев в самой физической по-
постановке задачи обнаруживается некоторый параметр малости,
позволяющий прибегнуть к методу последовательных прибли-
приближений. Параметр этот в разных задачах может быть различным,,
но в конечном счете смысл его всегда сводится к малости об-
обмена энергией между полем и зарядами сравнительно с их пол-
полной энергией.
Прежде всего, в правой части уравнений движения зарядов
D8) кроме силы Лоренца могут стоять еще и другие силы, дей-
действующие на заряды—сторонние силы, и если эти последние
превосходят силу Лоренца, то найденные выражения F9) для
поля при заданном движении зарядов приобретают ясный смысл
в рамках теории возмущений — решения полной задачи после-
последовательными приближениями.
Правда, в релятивистской динамике сторонние силы тоже
должны быть силами, действующими на заряды со стороны ка-
каких-то полей, а пока мы не спускаемся до масштабов, сущест-
существенно меньших размеров атомов, в природе не существует ни-
никаких других полей, которые могли бы переносить взаимодей-
взаимодействие между заряженными частицами, кроме электромагнитного
поля (другое поле классической физики — поле тяготения — ста-
становится существенным только для очень больших —астрономи-
—астрономических — размеров).
Тем не менее бывает удобно исключить из явного рассмотре-
рассмотрения большую часть электромагнитных взаимодействий, связан-
связанную с поддержанием атомной и молекулярной структуры веще-
вещества или с обеспечением наблюдаемой стабильности твердых
тел, — их адекватное описание все равно возможно лишь в
квантовой механике — и считать поэтому движение зарядов
заданным через некоторые феноменологические параметры —
с точностью до малых возмущений, вызываемых явно рассмат-
рассматриваемой частью электромагнитного поля.
*) Оправданием этому мог бы служить лишь принцип пьяного, искав-
искавшего потерянную в темном проулке трешку под фонарем, ибо там светлее.
**) В квантовой теории поля эту последнюю называют уравнениями
Яага — Фелдмана.
46 ч. II. МЕХАНИКА ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
Далее, малым параметром разложения теории возмущений
часто может служить малое отношение скорости зарядов к ско-
скорости света — с задачами в такой постановке мы познакомимся
ниже.
Могут встретиться и другие источники появления малого па-
параметра. Если же никакого малого параметра нет, то «теорети-
«теоретический опыт» показывает, что уже в самой постановке задачи —
в формулировке начальных условий — возникают большие труд-
трудности. |
14. Электростатика
14.1. Займемся обсуждением найденных решений уравнений
поля и начнем с того частного случая, когда все заряды по-
покоятся, т. е. /, не зависит от времени, — случая электростатики.
Тогда не зависит от времени и потенциал F8):
At(r) = -jydrf)-^-. F8stat)
Поэтому естественно требовать того же и от общего решения
F9). Но добавляемое в последнем к частному решению F8)
общее решение для свободного поля обязательно зависит от вре-
времени. Следовательно, в классе статических решений решение
F8) оказывается общим и определяется в то же время заря-
зарядами единственным образом. Это существенная особенность ста-
статического случая объясняется тем, что в статическом случае
уравнение д'Аламбера E9) превращается в уравнение Лап-
Лапласа— эллиптическое уравнение, не обладающее — при гранич-
граничных условиях убывания на бесконечности — нетривиальными од-
однородными реше'ниями.
Подставляя в подинтегральное выражение статического по-
потенциала выражение D9) для 4-вектора тока
/г (г, О = Ееаб(г —ra){va; ic},
а
надо учесть, что для покоящихся зарядов все va = 0. Таким об-
образом, не равной нулю остается только четвертая компонента
4-тока /4 = icp. Следовательно, исчезает и векторный потенциал
А; для скалярного же потенциала ф получаем теперь
; А(г) = 0. G1)
Взятое для одного заряда это выражение для потенциала
называют законом Кулона.
14. ЭЛЕКТРОСТАТИКА 247
ЗАМЕЧАНИЕ: Итак, мы видим, что в статическом случае мы
возвращаемся к тому самому выражению (**) (стр. 191) для
потенциала в классической механике, которое послужило нам
в § 6 исходным пунктом обобщения, приведшего в конце концов
к понятию поля. Теперь мы можем утверждать, что это выраже-
выражение является хорошим приближением для описания взаимодей-
взаимодействия зарядов только в предельном случае, когда все скорости
va исчезающе малы сравнительно со скоростью света. |
14.2. Найдем энергию поля, создаваемого зарядами в стати-
статическом случае— электростатическую энергию системы зарядов.
Общее выражение E2.1) даст нам, поскольку магнитное поле Н
равно нулю,
& = ±\(dr)E2(r). G2 Е>
Выражая здесь электрическое поле Е через градиент потенциала, выделяя
полную дивергенцию и прибегая к теореме Гаусса (причем интеграл по по-
поверхности даст нуль, поскольку поверхность растет как г2, потенциал убывает
1 Э IN
р д у,
1 <Эф IN
как—, а -— как —I,
получим
Таким образом, если воспользоваться еще для потенциала фор-
формулой G1), мы придем к выражению электростатической энер-
энергии через распределение плотности зарядов
S = 1 J № Ф (г) р (г) = 1 J (rfr) W) *?№%-. G2 р)
Хотя подинтегральное выражение в G2 р) и имеет особен-
особенность при г=г', для непрерывного распределения зарядов со всю-
всюду конечной плотностью р (г) электростатическая энергия конечна.
Не составляет труда убедиться, что энергия остается конечной и в слу-
случае, когда плотность заряда имеет изолированные особенности не более силь-
сильные, чем
В нашем изложении, однако, мы последовательно развивали
представление о точечных зарядах; для таких зарядов плот-
плотность B8) содержит более сильные 6-образные особенности, и
в электростатической энергии появляются бесконечные члены.
В самом деле, подстановка B8) в G2р) преобразует энергию
электростатического поля в двойную сумму по зарядам
248 ч. "• МЕХАНИКА ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
В диагональных членах этой суммы знаменатель |га — гь| об-
обращается при а = Ъ в нуль, т. е. все они бесконечны. Каждый
такой (бесконечный) член
возникающий как энергия взаимодействия заряда со своим соб-
собственным электростатическим полем, называют собственной
энергией соответствующего заряда.
14.3. История борьбы физиков с бесконечностью собственной
энергии заряженных элементарных частиц столь же стара, как
само применение максвелловой электродинамики — которая са-
самим автором строилась как существенно макроскопическая тео-
теория— к первой найденной в природе элементарной частице—•
электрону.
14.3.1.1. Простейшая идея состояла, конечно, в том, чтобы
принять в качестве модели элементарной частицы («электрона»)
не точку, а некоторое протяженное распределение заряда, на-
например, по шару малого радиуса а. Тогда электростатическая
энергия сразу становилась конечной, равной по порядку вели-
е2
чины —.
В самом деле, если принять для распределения заряда по «шарику»,
скажем, степенную функцию с неопределенным показателем
( =— г < а,
р (/¦)«-< г»
<¦ =0, г > а,
то заряд внутри объема радиуса г составит
°
о
[ = е,
Требование совпадения обоих выражений при г = а определит нам констан-
ту С:
( / . \3-о
3 —а I =
^ = е, /¦ ^ а.
Для сферически симметричного распределения заряда из второго уравне-
уравнения E1.2.2) второй максвелловой пары ШуЕ=4лр интегрированием по шару
радиуса г получается
4л \ (dtr) р (/¦') = I (dtr) -^r Е (г') = Ф г2 d&E = 4лг2Е (г),
г'-г
14. ЭЛЕКТРОСТАТИКА 249
Т. е. Е (г) = —^—• Следовательно, электростатическая энергия нашего рас-
распределения составит
2 (О е* { f dr , f dr /г
*• а о
— первый член представляет здесь энергию электрического поля вне шарика
и не зависит от внутреннего распределения заряда, а второй — зависящую от
распределения заряда энергию внутреннего поля. Итак, электростатическая
энергия действительно оказывается равной —, умноженному на безразмер-
безразмерный численный множитель F(a), зависящий от распределения заряда «внутри
частицы». Интегрирование дает
значит, для конечности F иа показатель а надо наложить ограничение
а < —, уже упоминавшееся выше. Тогда
_ . . 3 —а
т.е. для допустимых значений показателя —со < a < —, множитель F мо-
может меняться в довольно широких пределах от — до оо. Можно отметить,
что значению а = —оо отвечает шарик, равномерно заряженный по поверх-
поверхности, этой модели соответствует F = —; равномерно заряженному по объ-
ему шару (м = 0) соответствует .F = -g-; значению a = 2, когда одинако-
одинаковый заряд содержится в каждом сферическом слое одинаковой толщины dr,
соответствует F = 1 и т. п.
Итак, протяженная модель электрона решает вопрос о ко-
конечности собственной энергии его электростатического поля.
В релятивистской теории этой энергии ё?0 должна отвечать
ср
масса те\ = —?-, составляющая часть массы покоя электрона.
Чрезвычайно соблазнительной представляется та идея, что
«электрическая» масса mei составляет всю массу электрона —
эту идею называют гипотезой полевой массы.
14.3.2.1. Если принять эту гипотезу, то можно — с точностью
до неопределенности, вносимой структурным множителем F,—
определить порядок величины ^о размеров электрона. Действи-
250 Ч. II. МЕХАНИКА ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
тельно, приравнивая электростатическую энергию <?§ умножен-
умноженной на с2 экспериментальной массе т электрона:
получаем для % выражение
Ч = -^- G3)
Эта длина называется классическим радиусом электрона и
составляет по последним данным (апрель 1976 г.)
*о = B,817938±0,000007) • 103 см> 2,8 • 10~13 см. G3а)
Накопившиеся к настоящему времени сведения об элемен-
элементарных частицах дали очень большое число фактов, косвенно
говорящих в пользу гипотезы полевой массы. Прежде всего,
в природе существует частица — нейтрино, — отличающаяся от
электрона только отсутствием электрического заряда, и ее масса
равна нулю. Затем, все элементарные частицы с массами, зна-
значительно большими электронной, способны и к иным (и при
том более сильным!) взаимодействиям, кроме взаимодействия
с электромагнитным полем; поэтому их большие массы есте-
естественно объясняются в рамках той же гипотезы, как происходя-
происходящие от этих иных взаимодействий. (Правда, тут есть единствен-
единственное исключение: в природе существует частица — ц-мезон или
мюон — которая примерно в 200 раз тяжелее электрона, но тем
не менее ведет себя относительно всех взаимодействий совер-
совершенно тождественно электрону; многие теоретики сохраняют
надежду, что будут обнаружены взаимодействия, в которых
участвуют ц-мезоны, но не электроны.) Наконец, многие эле-
элементарные частицы объединяются в группы, члены которых
различаются лишь электрическим зарядом (наиболее известный
пример — группа, объединяющая протон и нейтрон) — разности
масс членов группы, которые естественно отнести за счет энер-
энергии электромагнитного поля, оказываются того же порядка, что
и масса электрона.
14.3.1.2. Тем не менее простейшее осуществление гипотезы
полевой массы — классическая модель протяженного электрона,
с которой мы только что познакомились, — оказывается внут-
внутренне противоречивой. Противоречие обнаруживается, если
кроме энергии электрического поля заряженной частицы вычис-
вычислить также и импульс, который будет нести электромагнитное
поле, если привести частицу в движение со скоростью v. В этом
вычислении можно избежать выхода за рамки электростатики
и необходимости каких-либо новых гипотез о том, что случится
с распределением заряда, когда весь заряд приводится в дай-
14. ЭЛЕКТРОСТАТИКА 25f
жение, если заметить, что покоящийся в какой-либо системе от-
отсчета К заряд движется равномерно и прямолинейно в другой,
движущейся относительно К со скоростью —v, инерциальной
системе К', которая в силу принципа относительности физически
равноправна К. В силу этого замечания чтобы найти импульс
электромагнитного поля движущегося заряда, достаточно пре-
преобразовать его электростатическое поле в другую систему от-
отсчета и проинтегрировать в ней соответствующие компоненты
тензора энергии-импульса. В результате (для малых скоростей)
для импульса получается выражение
P=4^v, G4>
4
отличающееся множителем -я- от правильного выражения для
импульса частицы с массой т = —§-.
14.3.2.2. Итак, энергия и импульс электромагнитного поля,,
создаваемого распределением заряда, статическим и сферически
симметричным в одной системе отсчета (системе покоя час-
частицы), не образуют компонент 4-вектора. Физическая причина
этого понятна — такое распределение заряда не будет устойчи-
устойчивым и, поэтому, не сможет поддерживаться более чем в началь-
начальный момент времени, если только заряд не сдерживается каки-
какими-то дополнительными силами неэлектромагнитной природы,
вклад которых в энергию и импульс не учитывается этим вычис-
вычислением. Не менее существенным возражением против протяжен-
протяженных моделей элементарных частиц служит и то замечание, что
внутри такой частицы, если она является жестким образова-
образованием, происходило бы мгновенное распространение сигналов,
что означало бы, с релятивистской точки зрения, нарушение
причинности. Правда, такое нарушение происходило бы в об-
области пространственно-временных масштабов, в которой у нас
нет прямой возможности экспериментальной проверки причин-
причинности, однако можно опасаться, что и такие «нарушения при-
причинности в малом» могут сказаться на наблюдаемых эффектах,
например на процессах рассеяния.
14.3.3. Наконец замечание, которое имеет для обсуждаемой
проблемы в некотором смысле технический характер. Мы знаем
теперь, что для расстояний порядка G3) (и даже много боль-
больших!) и соответствующих промежутков времени классическое
описание неприменимо и следует использовать квантовую меха-
механику. Поэтому с количественной стороны приведенные выкладки
имеют чисто исторический интерес, однако лежащая в их основе
физическая идея, равно как и отмеченные принципиальные
трудности, переходит в квантовую теорию без изменений. Труд-
252 ч. II. МЕХАНИКА ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
ность с бесконечностью собственной энергии точечной частицы,
взаимодействующей с (не обязательно — электромагнитным)
полем остается и в квантовомеханическом рассмотрении. До сих
пор предпринимаются попытки найти выход на пути, физически
аналогичном введению представления о протяженных частицах,
и эти попытки сталкиваются с нарушением причинности в ма-
малом (с нарушением релятивистской ковариантности научились
бороться) или (и) с появлением объектов — полей или частиц —
не наблюдаемых в природе. Заметного успеха до сих пор не до-
достигнуто, и общепринятым, ортодоксальным представлением со-
современной теории является представление о точечных элемен-
элементарных частицах.
14.4. Но что же тогда делать с входящими в сумму G2 е)
бесконечностями? В теории с точечными частицами разрубают
гордиев узел — грубо говоря, просто вычитают из суммы бес-
бесконечные диагональные члены и заменяют G2 е) выражением
У = 1у , е<А ,. «72 еО
2 Lu г — г. '
Разумеется, такая процедура вычитания двух бесконечностей
с целью получить конечный результат не является слишком
хорошо определенной математической операцией, и следы до-
допущенной вольности сказываются в некоторых выводах тео-
теории — например, попытка последовательного учета взаимодей-
взаимодействия точечного заряда с его собственным полем приводит,
даже после вычитания бесконечной собственной энергии, к по-
появлению таких решений, в которых скорость заряда неограни-
неограниченно нарастает со временем.
В последовательном для элементарных частиц квантовом
рассмотрении идея, в принципе аналогичная переходу от G2 е)
к G2 е'), была развита около 30 лет назад релятивистски инва-
инвариантным образом в виде так называемого метода перенор-
перенормировок, который до сих пор не приводил ни к каким явным
противоречиям и позволил предсказать в электродинамике эле-
элементарных частиц много тонких эффектов с совершенно пора-
поразительной точностью. Надо, однако, подчеркнуть, что, во-пер-
во-первых, все результаты метода перенормировок получаются только
способом последовательных приближений, а проблема самого
существования точных решений остается открытой, и, во-вторых,
что, исключая величины типа собственной энергии из выраже-
выражений для наблюдаемых величин, метод перенормировок в прин-
принципе отказывается от вычисления собственных энергий, а, зна-
значит, и от возможности объяснить упоминавшиеся выше законо-
закономерности в массах элементарных частиц за счет полевой ги-
гипотезы.
15. ЭЛЕКТРОСТАТИЧЕСКОЕ ПОЛЕ ВНЕ СИСТЕМЫ ЗАРЯДОВ
253
15. Электростатическое поле вне системы зарядов
15.1. Рассмотрим определяемое G1) поле системы зарядов
для того случая, когда все они сосредоточены в конечной обла-
области пространства, скажем внутри некоторой сферы радиуса Ь,
центр которой мы выберем в качестве начала отсчета радиус-
векторов. Интересоваться же мы будем полем в точках R, рас-
расположенные вне сферы, так что ра-
радиус-векторы зарядов го (или г', ес-
если пользоваться плотностью заряда
р) и точки наблюдения R будут ог-
ограничены неравенствами
ra<b <R (или г' < b < R).
G5а)
(Мы обозначаем теперь радиус-век-
радиус-вектор точки наблюдения R большой
буквой, а не малой, как в G1), чтобы подчеркнуть, что он
велик.) Специальное же обозначение для знаменателя нам не
понадобится, поскольку мы сразу разложим его в ряд
I R - г' 1
n f*
1 , 1 ,, d2 1 ¦
a <J#a i? "*" 2! Гагр ^/?a а^„ ;? "T-
Ho
d J_
"^ R
Поэтому
<p(R) = 4-
-1 Ra
R2 ~R~
d2
R~ R3'1' *a R* R ~
if
Здесь в третьем члене стоящий вне интеграла тензор
з/га/?р
имеет след, равный нулю. Поэтому и под интегралом можно ос-
оставить только бесследовый тензор, поскольку произведение бес-
следового тензора на единичный дает при полном свертывании
нуль. Мы воспользовались этим замечанием, заменив тензор
на
15.2. Таким образом явно выписанные три младших члена
разложения потенциала зависят от свойств системы зарядов
254 ч. II. МЕХАНИКА ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
только через интегральные константы, называемые моментами.
*. G5-0)
ra, G5.1>
р (г) = ? еа (гП - 6а/а). G5.2>
а
Момент нулевого порядка Q есть просто полный заряд системы.
Момент первого порядка da есть 3-вектор, который называют
дипольным моментом системы. Момент второго порядка Da$
есть симметричный тензор второго ранга со следом нуль; его
называют квадрупольным моментом.
Аналогично определяются моменты высших порядков, /-кратные произ-
производные -„- должны образовывать совершенно симметричный тензор /-го ран-
К
га, и при том такой, что его свертывание по любой паре индексов дает нуль-
(последнее — из-за того, что -тр удовлетворяет уравнению Лапласа). По-
Поэтому и коэффициент при этой производной в разложении потенциала дол-
должен быть тензором той же симметрии (добавки другой симметрии дадут нуль-
при полном свертывании, ср. аргументацию при выводе квадрупольного мо-
момента), образованным из компонент га, с дальнейшим умножением на р и
интегрированием по объему:
где символом SP обозначена операция образования тензора должной симмет-
симметрии, что достигается, как и в квадрупольном случае, вычитанием из произве-
произведения /"„j ... га[ соответственно подобранной комбинации его следов, умио-
жеииых на единичные тензоры. Мы не будем заниматься явным выписыва-
выписыванием этих моментов /-го порядка, которые принято называть 2г-п6лями,
а ограничимся тремя замечаииями:
ЗАМЕЧАНИЕ I: поскольку совершенно симметричный тензор ранга / в п-мер-
' U+l)...(l + (n- 1))
иом пространстве имеет -.—— ... независимых компонент,
(/+ 1)(/ + 2)
следовательно в 3-мерном пространстве „ , а условие обраще-
обращения в нуль при свертывании по паре индексов есть требование обращения
в нуль тензора ранга (/—2), т. е. совокупность ¦ условий, то-
(/+!)(/+ 2) Ц1~\) ... .
2'-поль обладает ^ 2 = ¦« + 1 независимыми компонен-
компоненЗАМЕЧАНИЕ 2: Найденное число независимых компонент 2'-поля совпадает
с числом независимых сферических функций 1-го порядка; поэтому возникает
подозрение, что они должны быть связаны друг с другом. Подозрение это
15. ЭЛЕКТРОСТАТИЧЕСКОЕ ПОЛЕ ВНЕ СИСТЕМЫ ЗАРЯДОВ 255
оправдывается: если выделить нз подинтегральиого выражения 2'-поля мно-
множитель р(г)г', то независимые компоненты остающегося после этого безраз-
безразмерного тензора линейно выражаются через 2/ + 1 сферическую функцию
порядка /. Проще всего это обстоятельство усматривается из следующего рас-
рассуждения. Выделенные нами в разложении <p(R) в отдельные множители без-
безразмерные тензоры, зависящие от R,
I* п *
R ' R*
суть решения уравнения Лапласа, и при том зависящие от углов, а не от R;
а в классе таких решений сферические функции образуют полную систему. Щ
ЗАМЕЧАНИЕ 3: Согласно своим определениям G5) мульти-
польные моменты не независимы от выбора начала отсчета.
Легко сообразить, однако, что первый неисчезающий момент не
зависит от этого выбора, т. е., например, для системы с нуле-
нулевым полным зарядом не зависит от выбора начала отсчета ди-
польный момент, для систем с равными нулю зарядом и диполь-
ным моментом — квадрупольный и т. п. 1
15.3. Итак, потенциал системы зарядов вне области, зани-
занимаемой ими, можно представить разложением:
dR , ' П М^Р-У?' ! ,
~ L, П \dRa....dRa, R) "<»i •••"/• V°>
которое обычно называют разложением поля по мультипэлям.
15.3.1. Легко сообразить, что ряд G5) сходится для всех
R> b. Таким образом потенциал всякой системы зарядов
вне ее полностью определяется последовательностью мульти-
польных моментов системы, т. е. мы видим, что для фиксации
потенциала вне системы существен не весь ход функциональной
зависимости р(г), а только значения счетного набора чисел —
мультипольных моментов. Набор этот зависит от двух парамет-
параметров — номера момента и номера компоненты в нем — в то время
как распределение плотности заряда имеет три степени свободы:
описывается функцией р от трех переменных, скажем г, д и <р.
Таким образом при переходе от плотности заряда к создавае-
создаваемому ей потенциалу электростатического поля вне системы про-
происходит уменьшение числа степеней свободы. Это обстоятель-
обстоятельство связано, конечно, с тем, что зависимость потенциала от
трех переменных г, д, <р не произвольна, а ограничена вне си-
системы уравнением Лапласа Д<р (г, Ь, ф) = 0, т. е. потенциал
в пустоте есть — эффективно — функция только двух перемен-
переменных, например * и <р.
256 ч. II. МЕХАНИКА ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
Итак, два разных распределения плотности зарядов внутри
системы, pi (г) и рг(г), будут приводить к одному и тому же
полю вне ее, если только все их мультипольные моменты совпа-
совпадают. В частности, электростатическое поле произвольной си-
системы вне ее совпадает с суммой полей, создаваемых помещен-
помещенными в начало отсчета точечными полным зарядом, дипольным
моментом, квадрупольным моментом и т. д. Внутри системы
такая эквивалентность, естественно, не может иметь места, по-
поскольку по потенциалу G1) плотность заряда восстанавли-
восстанавливается однозначно как p(R) —¦ Ф4л , а для ряда G5) Дф = О
всюду, кроме точки R = 0. Следовательно, внутри системы, для
R <С Ь, ряд G5) не может сходиться к функции ф^).
Практически интересным разложение G5) будет, как
всегда в физике, только для тех R, для которых ряд не только
сходится, но и сходится достаточно быстро, так что можно
ограничиться в нем одним, в крайнем случае двумя членами.
Так, в частности, будет обстоять дело, если мы интересуемся
асимптотикой потенциала при R-^oo— тогда достаточно оста-
оставить в G5) первый неисчезающий член (напомним, что соот-
соответствующий момент не зависит от выбора начала отсчета).
15.3.2. Электрическое поле вне системы получается диффе-
дифференцированием G5) по радиус-вектору точки наблюдения R.
Вычислим в качестве примера электрическое поле дипольного
члена G5). Имеем последовательно
то есть
Это выражение часто встречается в практических задачах.
15.4. Перейдем теперь к задаче, в некотором смысле обрат-
обратной рассмотренной — пусть система зарядов сконцентрирована
вблизи точки с радиус-вектором R (скажем, внутри сферы ра-
радиуса Ь, описанной вокруг точки R), так что если написать
та = R + Ра. то будет | ра |< b < R G6a)
(ро—не плотность!). Если эта система находится во внешнем
электрическом поле с потенциалом фвн(г), то ее потенциальная
энергия в этом внешнем поле составит
15. ЭЛЕКТРОСТАТИЧЕСКОЕ ПОЛЕ ВНЕ СИСТЕМЫ ЗАРЯДОВ 257
Будем теперь считать, что внешнее поле медленно меняется на
протяжении размеров системы 26, так что можно написать:
(второй член в фигурных скобках в третьем члене разложения
добавлен на том основании, что внешний потенциал удовлетво-
удовлетворяет уравнению Лапласа и потому его вторые производные
образуют симметричный тензор со следом нуль). Тогда суммиро-
суммирование в выражении для потенциальной энергии будет распро-
распространяться только на множители при производных внешнего
потенциала, т. е. опять приведет к последовательным мультиполь-
ным моментам G5), только теперь к моментам системы, нахо-
находящейся в поле, а не системы, создающей поле; будем для опре-
определенности отмечать величины этой системы индексом 2. Итак,
мы приходим для потенциальной энергии системы зарядов в
медленно меняющемся внешнем поле (системы 2) к выражению:
которое очень напоминает формулу G5).
15.5. Пусть теперь внешнее поле с потенциалом фвн «вблизи
R» само создается некоторой системой зарядов 1, расположен-
расположенных «вблизи нуля», так что точка R находится вне некоторой
сферы, вмещающей все заряды системы 1. Тогда для этого по-
потенциала можно будет прибегнуть к разложению G5). Тем са-
самым мы придем к выражению для потенциальной энергии вза-
взаимодействия систем 1 и 2 в виде двойного ряда по их мульти-
польным моментам:
и _ Q'Q2 , ^2 di*i2 Qi <№2 1 Q2 3/?a/?9 - 6a94, n
i2
'9|ОарЗЦУB , ' drd2^23(drRi2)№R12)
' О P3 R1 P4 D1 '
J. «j2 «!2 Aj2 «12
(i)' G7)
где явно выписаны все члены вплоть до третьей обратной сте-
степени расстояния |R12| = |R| между системами 1 и 2. Как и пре-
предыдущие, эта формула практически интересна, когда расстоя-
расстояние Ru между системами много больше размеров Ьх и Ъ2 обеих
систем; тогда члены ряда быстро убывают и наибольшее значе-
значение имеет первый неисчезающий член. Из G7) видно, что если
9 Б. В. Медведев
258 ч. II. МЕХАНИКА ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
первыми не равными нулю моментами систем 1 и 2 будут
2/рполь и 2/г-поль, то потенциальная энергия взаимодействия
обеих систем будет убывать как \IR\tu+h.
ЗАМЕЧАНИЕ: Сила, действующая на систему 1 со стороны си-
системы 2, получается дифференцированием потенциальной энергии
по RI2. Мы видим из G7), что все члены, кроме первого, дадут
в эту силу и составляющие, не направленные по Ri2. Таким
образом, если материальная частица обладает кроме заряда еще
и электрическими мультипольными моментами, то силы взаимо-
взаимодействия между такими материальными частицами не будут
центральными. |
16. Стационарное поле. Магнетостатика
Если создающие поле заряды движутся, т. е. j ФО, то, во-
вообще говоря, надо учитывать запаздывание, т. е. пользоваться
общим решением F8), F9). Существует, однако, один важный
частный случай, когда, несмотря на движение зарядов, запаз-
запаздывание учитывать не надо — случай стационарного поля.
16.1. Пусть заряды, взаимодействующие с полем, совершают
финитное движение. Тогда все координаты (и скорости) зарядов
остаются все время конечными, и имеет смысл образовать из
каждой динамической переменной l(t) среднее по времени
+т
I = lim 4г [ dt l{t).
Г-»оо 2> _J,
Нам будет важно то их свойство, что среднее полной производ-
производной по времени любой динамической переменной равно нулю.
Действительно,
в силу ограниченности 1(Т) и /(—7").
Проведем усреднение по времени уравнений Максвелла.
Первой паре уравнений равносильны выражения полей через
потенциалы; при их усреднении по времени получается
H = rotA; E = -gradf—j-^- = -gradf, D2.1,2)
т. е. магнитное поле выражается только через векторный, а элек-
электрическое— только через скалярный потенциал. Аналогично, во
второй паре уравнений Максвелла E1.2.1,2) при усреднении по
16. СТАЦИОНАРНОЕ ПОЛЕ. МАГНИТОСТАТИКА 259
Ш
времени пропадает член с -^-, и мы получаем для усреднен-
усредненных полей
divl = 4np; rotH = — J. E1.2. Ш
С
В условии Лоренца E8) при усреднении по времени пропадает
dtp
член с —тг
divA = 0, E8)
и, наконец, в уравнении непрерывности E0.1.1)—производная
по времени от плотности заряда —
divj~=O. E0.1.1)
Если рассмотреть теперь оставшиеся уравнения для усред-
усредненных по времени величин, то легко заметить, что все харак-
характеризующие электромагнитное поле величины распались на две
группы, не связанные более между собой уравнениями. В пер-
первую группу входят скалярный потенциал, электрическое поле
и плотность заряда; они связаны уравнениями
Е = — gradqj; divE = 4jip, G8)
эквивалентными, как легко понять, уравнениями электроста-
электростатики, изучавшимся в двух предыдущих параграфах в инте-
интегральной форме.
Вторую группу образуют векторный потенциал, магнитное
поле и плотность тока; для них остается система уравнений
И = rot A; rotH= — j и divA = 0; div] = 0, G9)
которую называют уравнениями магнетостатики.
16.2. Итак, в стационарном случае средние по времени от
единого электромагнитного поля разбиваются на два отдельных
поля — электростатическое и магнетостатическое*). Историче-
Исторически именно этот случай очень долгое время единственно состав-
составлял предмет опытов (или, скорее, наблюдений); поэтому созда-
создалось представление о существовании двух самостоятельных об-
областей физических явлений — электричества и магнетизма —
представление, следы которого можно и до сих пор заметить
в построении школьных программ.
*) Следует подчеркнуть, что разбиение на электрические н магнитные ве-
величины происходит лишь в той мере, в какой^мы рассматриваем поля, созда-
создаваемые заданными распределениями и движениями зарядов. В полной задаче,
включающей рассмотрение движения зарядов под действием сил электромаг-
электромагнитного поля, такого разделения не происходит; средние по времени плот-
плотность заряда и ток не определяются только средними по времени полями.
9*
260 ч. П. МЕХАНИКА ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
Как мы уже видели, описываемая уравнениями G8) электро-
электростатика осуществляется и для не усредненного по времени поля,
если все создающие поле заряды неподвижны ra(t) = ra, va = 0.
Стационарный случай не дает здесь ничего нового.
Напротив, описываемая уравнениями G9) магнетостатика
может реализоваться в классической (в смысле — неквантовой)
микроскопической электродинамике, которой мы занимаемся,
только для временных средних, так как не усредненный по вре-
времени ток D9) не может не зависеть от времени.
ЗАМЕЧАНИЕ: В макроскопической электродинамике (полу-
(получающейся из микроскопической усреднением всех величин по
объемам, включающим много атомов и молекул), которая мо-
может пренебрегать дискретным строением вещества, не завися-
зависящие от времени токи могут существовать. Соответственно в ней
может осуществляться и магнетостатика не усредненных по
времени полей и токов. Любопытным образом случай «статиче-
«статической магнетостатики» оказывается реализуемым и в «противо-
«противоположном» предельном случае квантового рассмотрения микро-
микрочастиц— в квантовой механике не зависящие от времени токи
опять могут осуществляться. I
16.3. Общее решение уравнений магнетостатики G9) проще
всего получить, усредняя F8) повремени*):
(80)
16.4.1. Изучим, как мы то сделали в предыдущем параграфе
для электростатики, более подробно структуру этого решения
вне области, занятой зарядами и токами.
Записывая опять
1 _ 1 , Rr' ,
IR-r'l ~~ R "Т" R3 "Г" ••¦'
получим из (80)
A(R) = ^
16.4.1.1. Для дальнейших преобразований этого разложения
чрезвычайно существенно, что (см. G9.4)) дивергенция тока
в стационарном случае обращается в нуль; из этого следует
последовательность тождеств, из которых сейчас нам понадо-
понадобятся два. Дифференцируя по г~ произведение r'J'^ (мы поло-
*) Как и в электростатике, добавлять к F8) решение однородного урав-
уравнения не надо. Впрочем легко видеть, что такое решение F4) при усреднении
исчезает — при усреднении экспонент остается лишь член с нулевой частотой
и нулевым волновым вектором, не несущий ни энергии, ни импульса.
16. СТАЦИОНАРНОЕ ПОЛЕ. МАГНИТОСТАТИКА 261
жили здесь и далее j (r') = j'), получаем
-ir(r'aQ = ra + r'adiv>y = j>a, т.е. У = -цП). (а,
Аналогично
V
т. е. (Р)
Поэтому, если разбить г'^'а на два члена и оставить один из
них в первозданном виде, а другой преобразовать по только
что полученному тождеству, то окажется, что
Тождества (а) и (у) понадобятся ниже для преобразования
выражений, стоящих под знаком интегрирования по г'; поэтому
полные производные в их правых частях можно будет проинте-
проинтегрировать по теореме Гаусса, преобразуя их в интегралы по по-
поверхности, охватывающей все заряды и токи (например, по
сфере радиуса Ь), интегралы, равные нулю, поскольку токов на
этой поверхности нет.
16.4.2. Итак, нулевой член в выписанном разложении вектор-
потенциала равен нулю, а из первого остается
16.4.3. Выполним здесь антисимметризацию подинтеграль-
ного выражения въявь:
Va ~~ rah = ^PaiAeuVe = еРац 1Г * J V
Поэтому, если определить магнитный момент системы стацио-
стационарных токов как
т-~~2? \ &У \х ' j (г)]> магнитный момент, (81.1)
то первый (и в отличие от электрического поля — главный!)
член разложения векторного потенциала вне области, занимае-
занимаемой токами, запишется в виде
имеющем, хотя и неполную, аналогию с видом соответствую-
соответствующего члена в G5),
262 ч. II. МЕХАНИКА ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
Оказывается, что аналогия становится полной, если перейти
от вектор-потенциала к магнитному полю. В самом деле,
rot A = rot-^I - [grad -L. [m ¦ R]] + Jj. (at div R - ( m —^ r) =
то есть
„ __ 3R (Rnt) - R2m ,_, (i) .
ti ^5 , (81. a)
— что уже в точности совпадает с выражением дипольной части
электрического поля G5.1а) через электрический дипольный
момент.
16.5. Определение высршх магнитных моментов, через которые записы-
записываются старшие члены разложения поля, опирается на эту только что вскры-
вскрытую нами тесную аналогию магнитного и электрического случаев.
16.5.1. Разложим, как и при построении высших электрических мульти-
польных моментов, в выражении (80) для векторов-потенциала функцию Грина
-= тт в ряд по степеням -„-:
К — Г | А
| R - г' | Li П \dRai...dRat R ) «I '"" <V
Соответствующий ряд для вектор-потенциала запишется тогда как
где мы обозначили ради краткости совершенно симметричные тензоры 1-го
ранга со следом нуль:
<5/?ai • • • dRai R a\ ¦ • ¦ I
16.5.1.1. Теперь настало время прибегнуть к старшим тождествам, следую-
следующим из равенства нулю дивергенции тока. Вычисляя
•7-Г ('а, ¦ • • 'а/о/э) = га, • • • 'в,/а +
получаем, поскольку полную производную можно обратить в нуль с помощью
теоремы Гаусса, что под интегралом выполняются тождества
(О
без i
где в последнем равенстве мы воспользовались тем обстоятельством, что все
рассматриваемое выражение будет далее свертываться с симметричным тен-
16. СТАЦИОНАРНОЕ ПОЛЕ. МАГНЕТОСТАТИКА 263
зором Ra 0 , почему все равно существенна только его симметричная
часть.
Далее, как и прн получении дипольного магнитного момента, нам будет
удобно разбить /а . ¦. ra ja на две части с неопределенными пока весами
A — X) и к, и, оставив первую нз них неприкосновенной, преобразовать вто-
вторую с помощью (/), т.е. написать
«¦о, • • • ra,lo = 0 - Л) rOi
Произвольный множитель X мы выберем теперь так, чтобы правая часть ока-
оказалась бы антисимметричной в а; и 0, т. е. потребуем, чтобы было
1—л = hi; Я =
. . ;
Тем самым мы приходим к тому выводу, что в подннтегральных выражениях
в разложении вектор-потенциала можно сделать замены
га, • • ' гаг/а=?7+Т Ч '"' S-1 V al!a ~ r"'al) ~
16.5.2. Итак, эксплуатируя вытекающие из равенства нулю дивергенции
тока тождества, можно преобразовать разложение вектор-потенциала к форме
Чтобы вскрыть аналогию этого выражения с соответствующим электростати-
электростатическим разложением, запишем его, как то мы уже_делали для первого члена,
не для вектор-потеициала, а для магнитного поля Н. Имеем
дА°
(/ + 1)! *va,... a/nv
1 = 1
Но e№vaea^at = — 6m6v% + 6№t6V0/, и второй член справа даст нуль при
умножении на (бесследовый!) Rva ,.,„. Поэтому все тензорные множители
перед интегралом дают
16.5.3. Но это значит, что мы представили магнитное поле Н, которое
было определено как ротор векторного потенциала, в форме градиента неко-
некоторой скалярной функции точки qpm(R), т.е. можем написать
!Щ) = - grad <fm (R), G9.5)
264 ч. II. МЕХАНИКА ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
где скалярная функция q>m(R) представляется выражением
без i
в записи которого мы восстановили явную симметрию интеграла в индексах
ai cti. Эту симметрию можно сделать еще очевиднее, если заметить, что
1 = 1 без i "' ^
т. е. что под интегралом
I _ _
r«i ¦ • • s1г ¦j Ц=~ ч • • • s ¦ v 1г ¦3 J
Поэтому:
Найденная новая форма для Н теперь уже совершенно аналогична пред-
представлению электрического поля через градиент скалярного потенциала (р.
Функция фт называется скалярным магнитным потенциалом.
ЗАМЕЧАНИЕ: Подчеркнем, что описание магнитного поля с помощью ска-
скалярного магнитного потенциала возможно только в стационарном случае и
только вне области, занятой зарядами и токами. Прн этом, если свободная
от зарядов область неодносвязна (в наших разложениях это невозможно, но
при использовании точных выражений (80), G9.1) для поля такая возмож-
возможность может встретиться), то скалярный магнитный потенциал, вообще го-
говоря, оказывается бесконечнозначным, в соответствии с тем, что во всем про-
пространстве «силовые линии» безнсточникового (div H = 0) магнитного поля
всегда замкнуты. |
Сама возможность представить магнитное поле в области, где нет токов,
во второй форме G9.5) объясняется, конечно, тем, что в такой области одно-
одновременно и rot Н = 0 (условие существования векторного потенциала) н
div H = 0 (условие существования скалярного потенциала).
16.5.4. Теперь ясно, что в поисках точной аналогии магнетостатического
и электростатического разложений надо сравнить только что выпнсанное раз-
разложение для скалярного магнитного потенциала грт с полученным в преды-
предыдущем параграфе разложением G5) электростатического потенциала. Эти раз-
разложения действительно оказываются совершенно аналогичными, если на месте
электрических мультипольных моментов
16. СТАЦИОНАРНОЕ ПОЛЕ. МАГНИТОСТАТИКА 265
поставить интегральные характеристики распределения токов системы
без i
называемые магнитными моментами 1-го порядка или магнитными 2'-полями.
В силу бесследовости тензоров Ra _ >0 магнитные моменты всегда можно
определять удовлетворяющими тому же свойству; как и в электрическом
случае, этого можно достичь, вычитая из подынтегрального выражения в
(81. /) некоторую линейную комбинацию его следов, умноженных на единич-
единичные тензоры. Мы опять не будем формулировать эту операцию явно, а про-
просто укажем иа нее символом У.
16.5.5. С помощью введенного понятия магнитных моментов выражение
для скалярного магнитного потенциала записывается в виде
qpm(R) =
i=i
уже совершенно тождественном электростатическому разложению G5): един-
единственное отличие состоит в том, что в (81. ф) суммирование начинается ие
с нуля, а с единицы, в соответствии с тем, что аналогичный электрическому
заряду магнитный момент нулевого порядка тождественно равен нулю.
16.6. ЗАМЕЧАНИЕ:!} трехмерном пространстве векторное поле,
скажем В (г), имеет три компоненты: Вх(г), Ву(г) и Bz(r). По-
Поэтому естественно ожидать, что такое поле можно фиксировать
заданием трех инвариантных функций точки, т. е. трех скаляр-
скалярных полей.
Действительно, оказывается, что произвольное векторное
поле В (г) полностью определяется тремя скалярными полями
фo(r) = divB(r); Ф!(г) = Г'В(г) и Ф2 (г) = div [г • В] =
= - г • rot В (г)
в том смысле, что всякое векторное поле, для которого все эти
три инвариантные функции тождественно равны нулю, само
есть тождественный нуль.
Для того случая, когда векторным полем является магнето-
статическое поле усредненного по времени тока, В (г) = j (r),
первая инвариантная функция Фо(г, Ш) равна нулю тожде-
тождественно. Найденная нами форма (81./) для магнитных момен-
моментов показывает, что магнетостатическое поле вне системы ста-
стационарных токов зависит не от всего векторного поля j(r),
266 ч. И. МЕХАНИКА ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
а только от одного из двух фиксирующих такое поле скаляр-
скалярных полей, от
Ф2 (г) = div [г • J] = — г ¦ rot],
в то время как значение второго инварианта
никак не сказывается на магнитном поле вне системы.
Итак, если для электростатического поля вне системы были,
грубо говоря, существенны только две степени свободы из трех,
которыми обладала функция р(г) распределения зарядов, то
для магнетостатического поля опять существенны только две
степени свободы, но теперь из шести, присущих стационарному
распределению токов j (г) с divj = O. Иными словами, если
распределение электрических зарядов сохраняло при фиксиро-
фиксированном внешнем поле одну степень свободы, то распределение
стационарных токов сохраняет при фиксированном внешнем
магнитном поле целых четыре степени свободы. В частности,
никак не сказывается на внешнем магнитном поле системы опи-
описываемое вторым инвариантом Ф[(г) = г-] распределение ра-
радиальных составляющих тока.
Поэтому отсутствие внешнего магнитного поля у какой-либо
системы еще в меньшей степени, чем в электростатике, может
служить указанием на отсутствие внутри системы токов j(r).
Простейшим «макроскопическим» примером служит тороидаль-
тороидальный соленоид, все магнитное поле которого сосредоточено вну-
внутри тора. |
16.5.6. Конечно, «отнормированиые» по скалярному магнитному потенциа-
потенциалу магнитные моменты можно ввести теперь и в разложение векторного по-
потенциала. Мы получим тогда
A(R) =
i-i
Именно этим выражением и пользуются обычно в магнетостатике в качестве
основного; однако без промежуточного обращения к скалярному потенциалу
рациональные определения магнитных мультнполей было бы трудно уста-
установить.
16.5.7. Выражение для магнитною поля можно получить теперь, или вы-
вычисляя (—grad) от (81. (р), или ротор от (81. А). В первом случае получаем
сразу
-О' **»¦.-«,„. \М-1)г+1„
p
16. СТАЦИОНАРНОЕ ПОЛЕ. МАГНИТОСТАТИКА 267
во втором же дифференцирование дает
со
(* и4 * ^Ч )
Z Т
что сводится к предыдущему в силу симметрии и «бесследовости» Ra a
Итак,
со
Естественно, что относительно сходимости разложений (81) можно бук-
буквально повторить то же самое, что говорилось относительно сходимости раз-
разложения G5) в электростатике. Физически опять, конечно, интересно разло-
разложение в той области, где оно сходится быстро, так что можно удовлетво-
удовлетвориться первым неисчезающим членом — в большинстве случаев дипольным
членом (81<'>).
16.7. Перейдем теперь, опять следуя примеру электростатики,
к рассмотрению «обратной» задачи: найдем энергию системы
стационарно движущихся зарядов (системы 2) в медленно ме-
меняющемся в пространстве внешнем магнитном поле.
16.7.1. Для одной частицы функция Гамильтона во внешнем
электромагнитном поле имеет вид E6)
Будем считать здесь внешнее поле малым, так что можно будет
оставить только первую степень А.
Тогда
л/
тЧ* + с2Р2 - 2с2— РА + вф « Жв - — -^^- + «р.
С С &&Q
Но с той же точностью,
аж 2c*(p-fA)
V = r=="dP"== 2 (Э(? — еф) ^Ж"'
Значит,
Второй, подчеркнутый, член здесь и есть энергия взаимодей-
взаимодействия заряженной частицы с внешним магнитным полем.
16.7.2. Для среднего по времени значения этой дополнитель-
дополнительной энергии для всей системы 2 мы получим, суммируя по час-
частицам,
Z evA (г) $ dFj (г) А (г) = - |
268 ч. II. МЕХАНИКА ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
Здесь мы прибегли к тому допущению, что движение зарядов
в системе 2 и изменение со временем внешнего магнитного поля
происходят совершенно несогласованно, так что среднее по
времени от произведения jA, j (r) А (г), будет равняться произ-
произведению средних значений тока и потенциала. О таком допу-
допущении говорят как о допущении некогерентности тока и потен-
потенциала. Если только само движение зарядов не определяется
существенно внешним полем (ср. замечания в конце § 13), то
допущение о некогерентности выполнятся очень хорошо.
16.7.3. Как и в электростатическом случае, будем считать,
что все заряды системы 2 постоянно сконцентрированы вблизи
точки с радиус-вектором R, так что (буквальное повторение)
rfl = R + Pfl; lPel<6<R. G6a)
Поэтому для векторного потенциала медленно меняющегося
внешнего поля можно будет написать, ограничиваясь лишь
двумя членами разложения,
Подставляя это разложение в выражение для магнитной
энергии и принимая, что в описании распределения токов си-
системы 2 начало отсчета принято в точке с радиус-вектором R,
получим
ии = - ± aTrJ \ (Ф)ПЫ - ^р-1 \ (dp) 9J~a.
С помощью тождеств (а) и (у) первый интеграл здесь обра-
обращается в нуль применением теоремы Гаусса, а второй сводится
к магнитному моменту системы 2:
дАа
'flan V
Итак, энергия взаимодействия системы зарядов с медленно ме-
меняющимся внешним магнитным полем составляет в первом при-
приближении
П„ = - Н (R) • гп (82)
— выражение, совершенно тождественное дипольному члену со-
соответствующей электростатической формулы G6).
16.8. Теперь мы в состоянии выписать дипольный член (самый
важный) и для энергии магнитного взаимодействия двух си-
систем 1 и 2:
fitti • иг») /??<> — 3 (т. • R12) (nto • R12)
{J jn ==- e \OOf
•—он опять совершенно подобен члену взаимодействия двух
электрических диполей в G7),
16. СТАЦИОНАРНОЕ ПОЛЕ. МАГНИТОСТАТИКА 269
ЗАМЕЧАНИЕ: Любопытно сравнить относительную силу элек-
электростатического G7) и магнетостатического (83) взаимодей-
взаимодействия двух пространственно ограниченных систем зарядов. Во-
Вообще говоря, магнитное взаимодействие должно быть гораздо
слабее электрического: прежде всего, в (83) вовсе отсутствует
главный в G7) зарядовый член, это приводит к ослаблению вза-
-„-) , где Ь — размеры систем, a R —
расстояние между ними. Затем в определение магнитного мо-
момента входит дополнительный (сравнительно с электрическим
V
диполем) множитель —, где v — порядок скоростей зарядов
системы, — это ведет к уменьшению энергии взаимодействия
— J . Для всех обычных движений — как макро-
скопических, так и внутриатомных — отношение (—J очень
мало, порядка 10~4 для атомных электронов. В результате маг-
магнитное взаимодействие должно было бы составлять лишь ни-
ничтожную поправку к электростатическому.
Повседневный опыт общения с электротехникой учит нас
прямо противоположному — магнитные взаимодействия оказы-
оказываются достаточно сильными, чтобы на их использовании зиж-
зиждилась вся электротехника сильных токов, в то время как элек-
электростатическое притяжение проявляет себя лишь в лаборатор-
лабораторных демонстрациях с «электрической машиной» да в том, что
в современных пересушенных помещениях синтетические ткани,
а иногда даже и листы бумаги слипаются друг с другом. В чем
же тут дело?
Объяснение этого кажущегося парадокса лежит в невероят-
невероятной огромности числа Авогадро, выражающего количество мо-
молекул во всяком макроскопическом теле. Поскольку всякая
молекула содержит по меньшей мере десятки или сотни заряжен-
заряженных частиц, то столь же невероятно велики и полные положи-
положительный и отрицательный заряды каждого макроскопического
тела. Но в состав молекул входят положительные и отрицатель-
отрицательные заряды в равном количестве, поэтому огромные положи-
положительные и отрицательные заряды макроскопического тела всегда
скомпенсированы, причем с такой тщательностью, что не ос-
остается и нескомпенсированных мультипольных моментов.
Когда мы пытаемся с помощью каких-либо воздействий на-
нарушить эту компенсацию, то такое нарушение удается провести
лишь в ничтожной мере — в «заряженном» с макроскопической
точки зрения теле избыток зарядов одного знака составляет ни-
ничтожную долю суммарного заряда. Современными средствами
мы просто не умеем макроскопически разделить заметную часть
содержащихся в веществе зарядов.
270 ч- "• МЕХАНИКА ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
Напротив, привести в макроскопический порядок магнитные
моменты если не всех, то заметной доли внутримолекулярных
движений удается сравнительно легко — существует специаль-
специальный класс веществ — ферромагнетики — в которых заметная
макроскопическая ориентация магнитных моментов молекул до-
достигается воздействием уже сравнительно слабого внешнего
поля.
Итак, макроскопические магнитные силы оказываются силь-
сильнее электрических только за счет того, что для них мы умеем
поднимать на макроуровень большую часть того «запаса», что
хранится в «молекулярном подвале». В
17. Излучение электромагнитного поля
17.1.1. Вернемся теперь снова к общему случаю, когда ре-
решение уравнений поля представляется запаздывающими потен-
потенциалами F8). Как и в двух последних разделах, будем спе-
специально интересоваться полем на расстояниях, больших по
сравнению с размерами системы зарядов, и, соответственно, ис-
использовать введенные в § 15 обозначения, т. е. писать R вместо
г (значит, 4-точка х будет теперь иметь координаты
x={R, id})
и |R — г'| вместо R. В этих обозначениях F8) запишется как
Далее, мы опять можем написать
где п = -|-.
В дальнейшем использовании этого разложения в примене-
применении к запаздывающим потенциалам F8) возникает, однако,
существенно новый момент. Дело в том, что |R — г'| входит
в F8) дважды: в знаменатель и в выражение для запаздываю-
запаздывающего времени. Разложение |R — г'| в знаменателе ведет к со-
совершенно таким же результатам, что и в рассмотренных стати-
статическом и стационарном случаях — последовательные члены по-
получают лишние степени -ъ-~"б- и при #->оо не только стре-
стремятся к нулю, но и становятся исчезающе малыми сравнительно
с главным членом порядка -„¦.
17.1.2. С разложением запаздывающего времени дело об-
обстоит гораздо более тонко. Основным членом в нем является
17. ИЗЛУЧЕНИЕ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ 271
р
на первый взгляд для растущих R он стремится к беско-
нечности. Хитрость состоит однако в том, что для системы заря-
зарядов, совершающих финитное движение в конечной области про-
пространства, поле которой мы рассматриваем, зависимость j от
времени обязательно имеет периодический или приближенно
периодический характер, поэтому существенны только измене-
п
ния времени «по модулю периода», и член , сколь бы ве-
лико ни было R, не будет эффективно большим, чем характер-
характерный период системы Т. Если выделить в аргументе тока множи-
множитель —
то роль отдельных членов в нем можно охарактеризовать сле-
следующим образом. Главным членом всегда будет сумма (ct — R),
но эффективно она будет всегда лишь порядка Я, длины излу-
излучаемых системой волн. Следующий член г'п будет порядка раз-
размеров Ъ системы. Поэтому взаимная величина двух первых чле-
членов будет определяться совсем не значением R, а относительной
величиной размеров системы, и длины излучаемых ею волн*).
Наконец, все старшие члены будут порядка размеров системы,
ь
умноженных минимум на одну степень отношения -„-.
Итак, если мы интересуемся только асимптотикой создавае-
создаваемого системой зарядов электромагнитного поля, т. е. только
членами, убывающими по мере роста R медленнее всего, как
-я- (ниже мы покажем, что для системы движущихся зарядов
к
члены такого порядка никогда не обращаются в нуль), то мы
должны сохранить в разложении |R — r'| только один член
в знаменателе, но два члена в аргументе 4-тока, т. е. для век-
векторного потенциала асимптотическое выражение будет иметь
вид
Я» 6:
Совершенно аналогично будет выглядеть и асимптотика для ср.
17.1.3. Самое интересное обстоятельство выясняется, однако,
если мы начнем дифференцировать асимптотические потенци-
*) Если движение зарядов системы достаточно сложно, так что его
спектральное разложение включает сильно различающиеся частоты, то может
случиться, что для одних излучаемых волн главным будет первый член, а
для других — второй.
A (R, 0 = -^-$(*")j (г', F + 41)- * = *--7
272 ч. П. МЕХАНИКА ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
алы, чтобы получить поля Е и Н. В статическом и стационарном
случае мы могли дифференцировать только знаменатель анало-
аналогичного (84) выражения, и при этом возникали дополнительные
степени -„-, т. е. поля убывали быстрее потенциалов. В выра-
выражении (84) R входит не только в знаменатель, но и в аргумент
тока. При дифференцировании знаменателя возникает допол-
дополнительный множитель -„-, но при дифференцировании тока
= д\ di _ Ra d] _ na d\
dRa di dRa cR di с di '
значит,
dR ~ с di ~ Тс *~ X
т. е. возникает не —, a -r- !
Поэтому на расстояниях R > к главными членами в произ-
производных потенциалов окажутся те, в которых дифференциро-
дифференцировался ток, и эти члены будут убывать лишь как -„-. Итак, при
вычислении полей из асимптотических потенциалов (84) поля
убывают не быстрее потенциалов, но по тому же закону -^-.
Та (асимптотическая) область, в которой члены порядка -=¦
в полях оказываются основными, называется волновой зоной;
мы видим из проведенного сравнения, что волновая зона опре-
определяется не только условием R ;> Ь, но и требованием:
R ^$>к. волнэвая зона (85)
При выполнении пространственных дифференцирований в вол-
волновой зоне нужно, как мы убедились, дифференцировать только
по R, входящему неявно, через запаздывающее время
" с '
т. е. в ней имеет место операторное равенство
— =--^¦-4. (85а)
dRa с dt
17.1.4. Если, как то бывает во многих важных случаях,
длина излучаемых системой волн много больше размеров си-
системы, Ь <с X, то в области R > Ъ, в которой вообще применимы
разложения по степеням —, кроме волновой зоны существует
R
17. ИЗЛУЧЕНИЕ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ 273
еще одна, характеризуемая неравенствами
В этой зоне одинаковые степени т и "F будут одного порядка
величины. Поэтому и в потенциалах и в полях уже нельзя бу-
будет ограничиться членами ~-тг, а нужно будет и при разложе-
разложении в ряд и при выполнении дифференцирований учитывать от-
отличие |R — г'| от R как в знаменателе, так и в аргументе тока.
Наконец, на расстояниях R: Ъ <; R -С X время запаздывания
становится малым сравнительно с характерным временем Т си-
системы и можно вернуться к статическим разложениям предыду-
предыдущих параграфов, в которых время останется лишь в роли пара-
параметра.
Условие Ь <с %. можно сформулировать и иначе. Для зарядов,
совершающих приблизительно периодическое движение, их ско-
скорости
4W
Таким образом, -%~—, и наше условие 6<Я принимает вид
»<с — движение всех зарядов совершается со скоростями,
много меньшими скорости света. Это условие
b <С А. или 5<С условие квазистационарности (86)
называется условием квазистационариости.
Его физический смысл состоит в том, что энергия, излучае-
излучаемая системой зарядов за характерное для нее время, мала
сравнительно с запасенными системой — кинетической или по-
потенциальной — энергиями. Поэтому, если условие квазистацио-
квазистационарности выполнено, то при изучении движения зарядов си-
системы можно пренебрегать влиянием, которое оказывает на это
движение потеря энергии на излучение, т. е. сперва искать дви-
движение зарядов, а потом находить поле, излучаемое зарядами,
движущимися уже известным образом*).
17.1.5. Существование волновой зоны имеет решающее зна-
значение для всей теории электромагнитного поля. В самом деле,
поток энергии электромагнитного поля описывается, как мы
знаем, вектором Пойнтинга E2.3). Поскольку поля в волновой
зоне убывают лишь как-„-, то вектор Пойнтинга будет убывать
как -5J-, а значит, поток вектора Пойнтинга через окружающую
*) Ср. замечание 136, 5.
274 ч. II. МЕХАНИКА ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
систему сферу радиуса R совсем не будет зависеть от этого ра-
радиуса. Но это значит, что будет существовать отличный от нуля
поток энергии, вовсе покидающей систему зарядов, — энергия
системы зарядов переходит в энергию свободного электромаг-
электромагнитного поля. Происходит излучение энергии.
Итак, существование волновой зоны показывает, что заряды
могут передавать свою энергию электромагнитному полю, кото-
которое распространяется далее в пространстве совершенно незави-
независимо от «породившей» его системы зарядов. Именно этот факт
заставляет нас считать электромагнитное поле самостоятельным
физическим объектом, а не просто элегантным способом описа-
описания (запаздывающего) взаимодействия зарядов.
Нам надо еще, конечно, проверить качественные оценки вы-
вычислением, равно как и исследовать поле в волновой зоне более
подробно.
17.2. Заметим прежде всего, что нет необходимости исследо-
исследовать все четыре компоненты решения F8) — в нестатическом
случае скалярный потенциал не является независимым. В са-
самом деле, на потенциалы наложено дополнительное условие
Лоренца E8)
div A-\—ф = 0.
Проинтегрируем это соотношение по времени, причем будем счи-
считать, что знак неопределенного интеграла \dt... означает то
его частное значение, для которого средние по времени
Тогда
Ф (R, t) = - с \ dt div A + Фсои1 (R), (87)
где постоянная интегрирования 9coui(R) будет как раз статиче-
статическим потенциалом параграфов 14, 15.
Таким образом переменная (во времени) часть скалярного
потенциала однозначно определяется векторным (причем опять
переменной его частью, поскольку divA = 0). Поэтому при вы-
вычислении электрического поля мы получим
Е = - grad фсои1 (R) - -j А + с J grad div A • dt.
Но grad div A = rot rot A + ДА; стало быть, если ввести под
, „ 1 »
интеграл по г и второй член ~~уА> то мы получим под
17. ИЗЛУЧЕНИЕ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ 275
интегралом
rot rot А + Га —-^ ~эр) А = rot rot A,
поскольку поле в пустоте удовлетворяет уравнению д'Аламбера.
Итак,
Е = Ecoui + с ^ dt rot rot A = ECoui + с jj dt rot H (87.E)
(эту формулу можно, конечно, получить и непосредственно, ин-
интегрируя по времени первое уравнение второй максвелловой
пары). В (87. Е) безразлично, что писать под интегралом, rot H
или rot(H— Н), поскольку вне зарядов rot H ='0.
ЗАМЕЧАНИЕ: Ненезависимость <р не случайна — его можно вообще убрать
с помощью не меняющего условия Лоренца E8) специального градиентного
преобразования D1а) *). Действительно, выберем в градиентном преобразо-
преобразовании
% так, чтобы в новом скалярном потенциале остался только статический член
<р' = <pcoul(R). Для этого нужно, чтобы было
div A dt,
с J
то есть
dtdtdivA
—А, = — с \ div
с J
(постоянную интегрирования можно положить равной нулю, так как она не
повлияет ни на скалярный, ни на векторный потенциал). Тогда
А' = А - с2 [[ dtdt grad div A
и, если опять преобразовать здесь grad div,
А' = А - [ [ dt dt A - с2 [[ rot ret A dt dt.
Поскольку для наших интегралов
то в разности двух первых членов остается только А(Д), т. е. мы получаем
*) Ср. аналогичную операцию, примененную при изучении общего реше-
решения свободного уравнения в 13а. 1.
276 ч. И. МЕХАНИКА ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
в качестве новых скалярного и векторного потенциалов
ф'(R,0-«Pcoui W; A'(R, /) = MR)~cl\\dtdtrotrotA- <87'>
Дифференцирование (87') возвращает нас, конечно, к формуле (87. Е). g
17.3. В волновой зоне выражения переменной части скаляр-
скалярного потенциала и полей через A(R,/) претерпевают дальней-
дальнейшие упрощения. (Мы будем ниже заниматься только перемен-
переменными частями и не будем выписывать фСОи1 и А.) Правила
(85а) дифференцирования в волновой зоне сразу дают нам
(88)
= |[[A.n].n]=[H-n].
17.3.1. Мы видим, что для фиксированного R электромагнит-
электромагнитное поле в волновой зоне устроено так же, как в распространяю-
распространяющейся в направлении п плоской волне:
A) Электрическое и магнитное поля Е и Н перпендикулярны
направлению распространения п, перпендикулярны друг другу,
Е • Н = О, и равны по величине, | Е | = | Н |.
B) Существенна только поперечная часть вектор-потенциала;
часть вектор-потенциала ~п не дает никакого вклада в поля.
ЗАМЕЧАНИЕ: Из (87') мы знаем, что такую часть А всегда
можно убрать градиентным преобразованием. Практически
удобнее, однако, не выполнять такого преобразования явно,
а держать эту возможность про запас в качестве аргумента,
позволяющего выбрасывать из A(R, t) (или добавлять в него)
любые пропорциональные п члены. В
17.3.2. Электрическое и магнитное поля позволяют найти
вектор Пойнтинга:
S = ^[E.H]=-?[[H.n]-H]=^n = ^n. (88.4)
Он направлен по п (с существенно положительным коэффи-
коэффициентом!)— значит, во всякой точке R волновой зоны, если
только электромагнитное поле в ней не равно нулю, существует
поток энергии, направленный от системы зарядов в направле-
направлении п. Наше главное утверждение относительно поля в волно-
волновой зоне подтверждено.
17.3.3. Поток энергии через элемент dor поверхности сферы
радиуса R, видный из начала отсчета под телесным углом йС,
17. ИЗЛУЧЕНИЕ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ 277
будет равен
т. е.
^ = сН2#2-^- = сЕ2#2-^-. (88.5)
Поскольку в волновой зоне Н ~ /?-', он не зависит от R,
а только от направления п и угла dO. Полный поток энергии
через сферу большого (все равно какого!) радиуса получится
отсюда интегрированием по углам; в силу закона сохранения
этот поток должен равняться энергии, теряемой системой
в единицу времени. Итак,
^ = cR2W2 = cR2?2, (88.6)
где теперь черта сверху означает усреднение не по времени,
а по углам, фиксирующим направление п.
Формулы (88.6), (88.5) и (88.2) решают вопрос о полной
потере энергии системой и о распределении излучаемой энергии
по направлениям; чтобы воспользоваться ими, осталось только
найти выражения для вектор-потенциала в волновой зоне, более
детальные, чем общая формула (84). Мы посвятим этому два
следующих параграфа, но сперва сделаем еще одно
17.4. ЗАМЕЧАНИЕ: Мы только что убедились, что поле излучения в вол-
волновой зоне локально, вблизи какого-либо фиксированного R, есть плоская
волна, распространяющаяся в направлении п. Эта оговорка «локально» су-
существенна; для волны в целом не только аналогия с плоской волной не ока-
оказывается полной, но и сама концепция волновой зоны — вполне последова-
последовательной.
Оставляя подробное обсуждение этого обстоятельства до параграфа 19,.
скажем пока только, что источник трудностей лежит в том, что хотя связь ска-
скалярных полей Ф< (см. 16.6) с А и локальна, само сопоставление векторному
полю над некоторым пространством скалярных полей существенно зависит от
свойств пространства как целого, что проявляется хотя бы в том, что обрат-
обратные выражения векторного поля А через Ф< интегральны. В частности, в до-
доказательстве теоремы об обращении в нуль векторного поля, все трн инва-
инварианта которого суть нули, существенно использовалось то обстоятельство,
что после обращения Ф\ в нуль задача о построении ненулевого А с равны-
равными нулю Фо и Фг сводится к нахождению нетривиального векторного (дву-
(двумерного) поля, удовлетворяющего уравнению Лапласа на всюду ортогональ-
ортогональной R поверхности. На сфере таких решений не существует, но на касатель-
касательной к сфере плоскости, которую мы получаем, заменяя поле в волновой зоне
плоской волной, такие нетривиальные решения есть. Поэтому, если мы хо-
хотим сопоставлять векторному потенциалу инвариантные скалярные поля, то
мы должны (даже в волновой зоне!) учитывать кривизну сферы — волнового
фронта излучаемой системой волны — что сводится к учету возникающих при
дифференцированиях старших членов в разложении по -5-, выбрасываемых
правилами (85а). Если восстановить эти члены, то парадокс исчезает—.-
хотя бы одно из полей Фо и Фг оказывается отличным от нуля, g
278 ч. II. МЕХАНИКА ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
18. Дипэльные и квадрупольное излучения
18.1. Разложим, пользуясь условием квазистационарности,
аргумент тока под интегралом в (84) в ряд по степеням
(т. е. по малому параметру -т-) и выпишем пока в этом ряду
два первых члена:
живо напоминающие по строению первые члены разложения
вектор-потенциала в магнетостатическом случае в 16.4.1.
18.1.1. В § 16 мы использовали для преобразования подинте-
гральных выражений в этих членах тождества (а) — (у), при
выводе которых использовалось то обстоятельство, что в ста-
стационарном случае div j = 0. Теперь, согласно уравнению непре-
непрерывности, divj =—~ и в правых частях тождеств появляются
дополнительные члены, в результате чего тождества принимают
вид
и
При подстановке под интеграл полные производные можно бу-
будет обратить в нуль, используя теорему Гаусса; тем самым два
младших члена разложения вектор-потенциала дадут нам
— т. е. мы получаем сумму производных по времени от трех
интегралов по распределению токов и зарядов.
18.1.2. В первом из этих интегралов сразу узнается электри-
электрический дипольный момент системы зарядов G5.1). Второй ин-
интеграл приводится к магнитному дшгольному моменту (81.1),
вычисляемому, однако, для истинной плотности тока j(r',7),
а не для усредненной по времени j. С третьим интегралом си-
ситуация уже несколько сложнее. Он напоминает электрический
квадрупольный момент G5.2), с тем, однако, отличием, что
подинтегральное выражение содержит образованный из г' про-
18. ДИПОЛЬНЫЕ И КВАДРУПОЛЬНОЕ ИЗЛУЧЕНИЯ 279
стейший симметричный тензор второго ранга r'ari, а не сим-
симметричный тензор второго ранга со следом нуль г'аг'^ — -%r'2ba^r
фигурирующий в G5.2); мы будем называть такое образование
приводимым электрическим квадрупольным моментом. В ста-
статическом случае мы тоже получили при непосредственном вы-
/ Ь \
полнении разложения (там—-по степеням -= I сперва приводи-
приводимый квадрупольный момент, но могли заменить его на неприво-
неприводимый G5.2), прибегая к тому аргументу, что там квадруполь-
квадрупольный момент свертывался с симметричным тензором, след кото-
которого равнялся нулю благодаря тому, что потенциал вне системы
зарядов удовлетворял в статике уравнению Лапласа. Теперь
эта аргументация неприменима, и при замене приводимого
квадрупольного момента на неприводимый в разложении век-
вектор-потенциала появится дополнительный член:
Для электрического квадрупольного момента этот член оказы-
оказывается направленным по п; поэтому, согласно сделанному в пре-
предыдущем параграфе замечанию этот член можно убрать гради-
градиентным преобразованием, и оставлять его в выражении для А
нет нужды.
ЗАМЕЧАНИЕ 1: Фигурирующая в этом члене интегральная ха-
характеристика распределения заряда зависит только от изотроп-
изотропной части плотности; поэтому она должна была бы служить
поправкой к нулевому электрическому моменту G5.0)—пол-
G5.0)—полному заряду системы. Но полный заряд системы не зависит от
времени (как раз вследствие инвариантности относительно гра-
градиентных преобразований!) и, значит, не может давать вклада
в нестатическую часть поля. В
ЗАМЕЧАНИЕ 2: В статическом случае электрические и маг-
магнитные мультипольные моменты были константами. Если р и j
зависят от времени, то они становятся функциями времени.
В нашем разложении все они берутся в момент времени
р
t = t , учитывающий запаздывание на пути от центра си-
С
стемы 0 до точки наблюдения R. |
18.1.3. С учетом этих замечаний младшие члены разложения
вектор-потенциала можно теперь записать в компактной форме
A(R, t)e=±±d(i)+±-±[m(i)-n]+±-±r(Dn) + ..., (89>
280 ч. II. МЕХАНИКА ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
где (Dn)a есть краткое обозначение для Da^n^. Отдельные члены
этой формулы называют, соответственно, электрическим ди-
польным, магнитным дипольным и электрическим квадруполь-
ным членами в излучении.
18.2.1. Для электрического дипэльного излучения, А1в =
= -й— d, электрическое и магнитное поля и вектор Пойнтинга
находятся по общим формулам (88.2—4) в виде:
§le== n [d-np
(90. IE)
AnR2
Подставляя эти значения в (88.5), получим для потока энер-
тии, излучаемой в единицу времени в элемент телесного
угла dO,
Jd^W dl^d)^ (91ЛЕ)
An
Если дипольный момент меняется только по величине, то удобно
ввести полярную систему координат с осью, направленной по
единственному выделенному направлению d || d; в ней выраже-
выражение для энергии, излучаемой в направлении ¦&, ф, примет вид
1 о* I d . п п isv d sin3 О d'b ,„ t t „,.
dy = ln~~^sm ®d0 = 2? • (91.IE')
18.2.2. Полная энергия, теряемая системой на дипольное
¦излучение в единицу времени, получается, согласно (88.6),
усреднением (91.IE) по углам. Поскольку единственной завися-
зависящей от направления величиной в (91.IE) является единичный
вектор п, то задача сводится к усреднению произведений пап$
компонент единичного вектора.
Результат такого усреднения должен быть единичным тензором второго
ранга — а такой тензор может отличаться лишь множителем от тензора 6ag.
Итак, должно быть
пап$ = ^-^ар-
Значение числового множителя установим, свертывая это выражение по а и E;
1 = 1 = папа = Ябаа = Я • 3;
1
¦значит, Я = — и
о
«о«р = у боз *)•
*) Те же самые рассуждения применимы и к усреднению произведений
большего числа векторов п. При этом усреднение нечетного числа векторов п
дает нуль, поскольку единичных тензоров нечетного ранга не существует, а
средние от произведений четного числа векторов выражаются через соответ*
ствующим образом симметризованные произведения тензоров бад.
18. ДИПОЛЬНЫЕ И КВАДРУПОЛЬНОЕ ИЗЛУЧЕНИЯ 281
Итак,
__ «х. _
d2 — <iin) d2-
dt " c3 c3 3c3 ' v"'
т. е. мы видим, что дипольное излучение системы пропорцио-
пропорционально второй производной ее дипольного момента.
В частности, если система состоит из одного единственного
заряда е, расположенного в точке г(^), то d = er, значит d =
= ew, и
.g^^Jflw^ (92. IE')
т. е. дипольное излучение одного заряда пропорционально квад-
квадрату его ускорения — чтобы заряд излучал, необходимо, чтобы
он двигался ускоренно*). Это условие совершенно понятно:
если заряд не испытывает ускорения, то он движется равно-
равномерно и прямолинейно, и можно выбрать инерциальную систему
отсчета, в которой он неподвижен и, следовательно, создает
лишь статическое кулоново поле.
18.2.3. Оценим порядок величины энергии, теряемой систе-
системой на излучение согласно (92.IE). Заметим для этого, что ди-
польный момент системы есть величина порядка ее размеров Ь,
умноженных на заряд е, d ~ eb, а дифференцирование по вре-
времени приводит к вхождению в знаменатель характерного вре-
времени системы Т. Поэтому &ie ~\~т2) Т ¦ что удобно записать,
комбинируя множители, как \~г) '\~f) ' ~^з—f- Но первый
множитель здесь -г- есть величина порядка электростатической
энергии взаимодействия зарядов системы, значит, вообще го-
говоря, порядка полной энергии ё" системы. Отношение же у
размеров системы к характерному времени порядка скорости v
зарядов в системе. Итак, потеря энергии на дипольное излуче-
, dJTle ар ( V \3 1 -
ние в единицу времени Щ~~ '\Т) Т' "олее показа-
показательна, конечно, потеря энергии за характерное время системы
*) Справедливо и обратное — всякий движущийся ускоренно заряд излу-
излучает. Для одного заряда это следует из (92.1Е'); если заряд входит в си-
систему зарядов, совершающих когерентное (ускоренное) движение, то диполь-
дипольное излучение разных зарядов системы может взаимно скомпенсироваться,
однако для старших членов разложения вектор-потенциала это невозможно —
для системы из конечного числа зарядов в результате компенсации может
обратиться в нуль лишь конечное число членов разложения вектор-потен»
Циала.
282 ч. П. МЕХАНИКА ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
Г; мы получаем для нее
C
8. (93.1E)
Итак, относительная потеря энергии на дипольное излучение
за характерное время системы порядка третьей степени отноше-
отношения скоростей зарядов системы к скорости света. Тем самым
мы подтвердили сделанное после формулы (86) предыдущего
параграфа утверждение о смысле условия квазистационарности.
Теперь мы можем и уточнить это утверждение: поскольку по-
f » \3
тери энергии на излучение пропорциональны I —I , то с точно-
точностью (—J этими потерями можно пренебрегать и рассматри-
рассматривать систему зарядов как изолированную, движение которой
описывается некоторой функцией Лагранжа, зависящей от ко-
координат и скоростей только зарядов, но не поля. Такую функ-
функцию Лагранжа действительно можно построить.
18.2.4. Дипольный член является главным в ряду (89), и
если он отличен от нуля, то следующие члены играют, обычно,
роль малых поправок. Если, однако, дипольный момент системы
есть нуль, то они могут стать основными.
18.3.1. Для магнитного дипэльнэго излучения А"" =
= —[m-n], формулы (88.2—4) приводят нас к выражениям
,- 12 (90.1М)
[mn]2
все отличие которых от электрического дипольного случая со-
состоит в том, что электрическое и магнитное поля поменялись
местами. Поэтому формулы (91) и (92) для излучения по направ-
направлению п и полного излучения вообще не претерпят никаких из-
изменений, и мы сможем просто переписать их (заменяя, конечно,
электрический дипольный момент на магнитный) в неизменном
виде:
йО _ m'-(mnJ dO /Q
7 (y
И
-^-. (92.1М)
18.3.2. С физической точки зрения, однако, в них имеется
существенное отличие от электрического дипольного случая.
В определении (81.1) магнитного момента фигурирует лишний
множитель с в знаменателе; кроме того, в нем участвует плот-
18. ДИПОЛЬНЫЕ И КВАДРУПОЛЬНОЕ ИЗЛУЧЕНИЯ 283
ность тока j вместо плотности заряда р в электрическом случае,
т. е. лишний множитель v. Итак, магнитный момент отличается
от электрического лишним множителем Г—j (ср. дискуссию
в конце § 16), что приводит при оценке порядка величины (91)
и (92) к лишнему множителю ( —J . Итак, по порядку вели-
величины магнитное дипольное излучение составляет
&, (93.
т. е. оно в Г —J раз слабее электрического.
18.4.1. Перейдем к элехтрическому квадрупольному излуче-
излучению. Согласно (89) для него А = -^-—(Dn), поэтому выраже-
выражения для магнитного и электрического поля и вектора Пойнтинга
получатся из электрических дипольных формул заменой d ->¦
<90-2Е>
Поток энергии, излучаемой в направлении п, составит
d?2e = -±г t(Bn) • п? % = -^ {(БпJ - (nSny} %¦ =
= -^г Фа^ауП^Пу - D^D^n^n^} 4fL. (91.2Е)
18.4.2. В нем появился член с четырьмя единичными векторами п, по-
поэтому для вычисления полного квадрупольного излучения надо научиться
усреднять произведения четырех па. Из соображений симметрии
Свертывая по a = E и ц = v, находим
j j 2
т.е. A, = -j-jp Далее, Da^D^ -^- (барб^ + ба|лб^ + 6av6|5li) = — (?>арJ,
1 = «оЯоПцЯц => Я, C-3 + 3 + 3)= 15>,
j
лее, Da^D^ -
поскольку Spur Z)ap = 0. Поэтому
?>ap
Итак,
284 ч. II. МЕХАНИКА ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
— т. е. квадрупольное излучение определяется уже не второй, а
третьей производной электрического квадрупольного момента.
18.4.3. Это обстоятельство приводит при оценке порядка ве-
величины (92.2Е) к появлению в знаменателе лишнего множителя
Г2; далее, сам квадрупольный момент пропорционален второй,
а не первой степени размеров Ъ системы — это вносит в (92.2Е)
лишний Ь2 в числитель; наконец, в знаменателе (92.2Е) явно
стоит на две степени скорости света больше, чем в дипольных
формулах. Все это вместе взятое вносит в порядок величины
квадрупольного излучения лишний множитель I — I , и мы по-
получаем
(MГ (93.2Е)
— суммарное электрическое квадрупольное излучение оказы-
оказывается того же пятого порядка по параметру квазистационарно-
квазистационарности —, что и дипольное магнитное.
18.5. ЗАМЕЧАНИЕ: Мы вычисляли вектор Пойнтинга и из-
излучаемую энергию для каждого члена в (89) по отдельности. Но
вектор Пойнтинга квадратичен по полям, поэтому в нем должны
появиться интерференционные члены Sle-lm, Sle>2e и Slm>2e. Легко
проверить, что такие члены действительно появляются. Оказы-
Оказывается, однако, что при интегрировании по углам все они обра-
обращаются в нуль, и суммарное излучение системы, излучающей
сразу электрическим дипольным, магнитным дипольным и элек-
электрическим квадрупольным образом, тем не менее представляется
простой суммой трех формул (92).
Для интерференционных членов Slelm и Sle2e это утверждение следует из
простого подсчета степеней единичного вектора п. Действительно, в 1е-члене
магнитное поле содержит нечетное, а электрическое — четное число множите-
множителей п, а в lm- и в 2е-членах — наоборот. Поэтому векторы Пойнтинга
Slelm и Sle2e будут содержать лишь четные степени п, а, значит, соответ-
соответствующие члены в dSf — только нечетные, которые обязательно дадут нуль
при усреднении по углам.
Менее очевидно исчезновение lm— 2е интерференции. Из (90.1М.2Е):
S«w«~ {_ [ [ty,n]. [(Sa) n] ] + [ [ [фп) п] п] • [ [ш] п] ]}.
Оба вектора второго векторного произведения получены из векторов первого
произведения поворотом на —90° вокруг п, поэтому оба произведения равны
друг другу, и можно рассматривать только первое
[ [(бп) п] • [шп] ] = n {{Dn) тп).
Таким образом,
19. СТАРШИЕ МУЛЬТИПОЛЬНЫЕ ИЗЛУЧЕНИЯ 285
При усреднении по углам мы получим п^п = —¦ 6. и, следовательно,
благодаря симметрии тензора ?>av. g
19. Старшие мультипольные излучения
В предыдущем параграфе мы подробно исследовали нулевой
и первый члены разложения асимптотического вектор-потен-
вектор-потенциала (84) в ряд по степеням запаздывания внутри системы
f-^-J. При дальнейшем непосредственном продолжении этого
разложения возникают некоторые особенности, новые как срав-
сравнительно с первыми членами, так и по сравнению с рассмотрен-
рассмотренными выше статическими разложениями, и появляются довольно
существенные осложнения. Осложнения эти обусловлены в ко-
конечном счете тем, что основные величины, с помощью которых
мы описываем электромагнитное поле, — поля Е и Н или вектор-
потенциал А — суть векторы. Дело сильно упростилось бы, если
бы можно было иметь вместо них дело со скалярами.
19.1. Способ, позволяющий сопоставить всякому векторному
полю — скажем полю вектора А — три эквивалентных ему ска-
скалярных поля Фо(А), <Di(A) и Фг(А), нам уже известен — мы
познакомились с ним в 16.6. при рассмотрении магнетостатики.
Если, однако, прибегнуть к этой процедуре в волновой зоне,
когда вектор-потенциал задается формулой (84), а пространст-
пространственные дифференцирования выполняются с помощью равенства
(85а), то мы наткнемся на одну неприятность.
Именно, вычисляя таким способом три связанных с вектор-
потенциалом скалярных поля и выбирая притом «поперечную»
калибровку (87'), мы получим:
для вектор-потенциала
A'(R, 0 = -[n-[n-A]]_Ln;
для скалярных полей
[А'] = RA' = - Rn • [п • [п • А] ] = 0;
т. е. все три связанных с полем вектор-потенциала инварианта
тождественно обращаются в нуль. По теореме, на которую мы
ссылались в 16.6, это должно было бы означать тождественное
обращение в нуль и самого векторного поля A'(R,/)!
286 ч. II. МЕХАНИКА ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
Хитрость состоит тут в том, что для вычисления связанных
с вектор-потенциалом А (или полями Е и Н) скалярных полей
Фг правила дифференцирования в волновой зоне (85а) (а может
быть и асимптотическое выражение (84)?) оказываются слиш-
слишком грубыми. Действительно, в определение полей Ф] и Ф2 вхо-
входит умножение на R; поэтому, чтобы получить результат, пра-
правильный вплоть до членов ~-п-, который нас интересует в
волновой зоне, надо было бы вычислять А (или Е и Н) вплоть
до членов —кг". Напротив члены —^- в векторном потенциале
(которые привели бы в Ф{ к членам порядка R0) при вычисле-
вычислении скалярных полей — как мы только что убедились — полно-
полностью сокращаются и не дают никакого вклада в результат.
Взаимно уничтожается и большая часть членов ~-sr (например,
все -й2--поправки к формуле (84)), так что реальное вычис-
вычисление действительно существенных для фi членов не очень тру-
трудоемко, однако аккуратное выяснение того, какие именно члены
единственно нужно вычислять, оказывается довольно гро-
громоздким.
Поэтому оказывается проще не вычислять Ф,- из решения
F8) для А и ф, а преобразовать сами уравнения Максвелла
таким образом, чтобы соответствующие скаляры Ф прямо вошли
бы в уравнения — тогда они найдутся непосредственным инте-
интегрированием.
19.2. Будем исходить из уравнений Максвелла в трехмерной
форме E1.1,2.1,2):
div H = 0;
, «I 1 dE |^ 4зт •
ГОТ П — ^т" 1 \ iui ы — -..
с dt с ¦" с dt
и введем скалярные поля, ассоциированные с магнитными и
электрическими полями Н и Е:
O0[E]=divE; a>,[E]=R.E; (94)
Тогда первая строка максвелловых уравнений даст нам
сразу
Ф0[Н] = 0; Ф0[Е] =
19. СТАРШИЕ МУЛЬТИПОЛЬНЫЕ ИЗЛУЧЕНИЯ 287
— первую пару уравнений для скалярных полей. Умножая ска-
лярно на —R вторую максвеллову строку, получим вторую пару
уравнений:
Чтобы получить еще одну пару (всего для шести функций Ф([Н/Е],
нужны, очевидно, шесть уравнений), применим ко второй максвелловой строке
оператор -[
.^.rotE —1Аф11Н].
Для преобразования левых частей этих уравнений научимся вычислять
—| R • -тр- IrotB = Ф2 [rot В] где В — произвольный вектор. Имеем:
^1 rot В = — R rot rot В = — R grad div В + R ДВ =
^r
= - R • — Фо [В] + ДФ, [В] - 2Ф0 [В],
д (RB) — -2L- ?аВ„ = -J- f5apBa + Ra~ \ = div В + div В + R ДВ.
поскольку
- ?аВ„ = -J- f5apBa + Ra
Итак,
Ф2 [rot В] = ДФ! [В] - B + R • -^) Фо [В]. {*)
С помощью этого тождества приводим, поскольку div Н = О,
магнитное уравнение третьей пары к виду
Соответствующее электрическое оказывается чуть сложнее:
Как видим, нам действительно удалось преобразовать урав-
уравнения Максвелла в систему шести уравнений для шести скаляр-
скалярных функций, ассоциированных с полями Е и Н. Более того,
источники поля — плотности заряда и тока, вошли в эту систему
опять-таки лишь в виде трех скаляров, ассоциированных с век-
векторным полем j — это становится ясным, если вспомнить, что
плотность заряда р связана с ФоШ уравнением непрерывности
р=-Ф0Ц].
Удобно слегка преобразовать эту систему. Введем, прежде
всего, для двух из шести скалярных полей специальные
288 ч. II. МЕХАНИКА ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
обозначения, положив
H = R.H = O1[H] и e = R-E = cp1[E]) (94')
и выразим, далее Фг[Е] и Ф2[Н] в первом и втором уравнении
третьей пары с помощью второго и первого уравнений второй
пары, соответственно. Тогда в каждом из уравнений третьей
пары образуется полный оператор д'Аламбера, т. е. они примут
вид неоднородных волновых уравнений для скалярных полей
е и ц, правые части которых содержат только инвариантные
функции источников:
Что же касается остальных четырех уравнений,
Ф0[Н] = 0; Ф0[Е] = 4яр; (95а)
Ф2[Н]^-Ц--^Ф,Ш; ФьИ-4-f, ОБЬ)
то они оказываются не уравнениями, а дополнительными усло-
условиями, поскольку не содержат производных остальных четырех
функций ни по координатам, ни по времени, но явно выражают
эти четыре функции Фо[Н], Фг{Н], Фо[Е] и Фг[Е] в какой-либо
точке R, t либо через остальные две скалярные функции ц и е,
либо через значения источников — р и j — в той же точке.
Итак, в новой системе переменных электромагнитное поле
исчерпывающе описывается всего лишь двумя функциями—[х
и е — удовлетворяющими неоднородным "уравнениям д'Алам-
д'Аламбера. Этот результат совершенно естествен — так и должно
быть для векторного поля «без массы» (т. е. для поля, у кото-
которого и в уравнения и в лагранжиан входят только производные,
но не сама функция) согласно общей теории представлений
группы Лоренца (см., например книги Гельфанда или Наймар-
ка). При обычном описании, однако, для электромагнитного
поля используются целых шесть функций — если работать с по-
полями— или четыре функции — если работать с потенциалами.
Дополнительное условие Лоренца уменьшает в последнем слу-
случае число потребных функций до трех, дальнейшая же редукция
оказывается затруднительной: для свободного поля три функции
А'х, А'у, А'г связаны одним дифференциальным условием div А'=
= 0, поэтому выделение независимых компонент легко совер-
совершается лишь для фурье-образов (ср. соответствующие рассуж-
рассуждения в § 13а); для поля в присутствии источников не удается
и это
19. СТАРШИЕ МУЛЬТИПОЛЬНЫЕ ИЗЛУЧЕНИЯ 289
ЗАМЕЧАНИЕ: Основной принцип «научной бухгалтерии» утвер-
утверждает, что никакой результат не дается даром — за всякий успех
приходится чем-то расплачиваться, «Jeder Vorteil bringt seinen
Nachteil rait». Что же теряем мы, выбирая в качестве перемен-
переменных поля |х и е? Не так мало — трансляционную инвариант-
инвариантность— ведь в их определение явно входит радиус-вектор R.
Поэтому использование таких переменных удобно лишь в зада-
задачах, в которых все равно нет трансляционной инвариантности,
т. е. есть выделенное место в пространстве. Как раз так обстоит
дело для занимающей нас задачи об излучении пространственно
ограниченной системой зарядов. |
19.3. Займемся следствиями, которые можно получить из
системы (95—95Ь).
19.3.1. В вакууме (95) превращаются в однородные уравне-
уравнения д'Аламбера
? ц = 0; Пе = 0, (95. V)
обе функции Фо согласно (95а) обращаются в нуль, а функции
Ф2 оказываются в силу (95Ь) просто производными е и ц, по
времени. В статическом случае в отсутствии зарядов не равными
нулю остаются, поэтому, только ц, и е, каждая из которых удов-
удовлетворяет однородному уравнению Лапласа.
19.3.2. При наличии зарядов в статическом случае система
уравнений распадается на две отдельные системы электроста-
электростатики и магнетостатики
Фо[Н] = 0; Дц = ^-
Ф2[Н]^--^Ф,[Я (95.ESt)
~)p; Ф2[Е]=0. (95.MSt)
19.3.2.1. Решением электростатической системы будет
8 = - \ Т^Т B + г'' ~) Р (г')- (96.ESt)
Совершая в нем во втором члене под интегралом интегрирование по ча-
частям, получим для электростатического решения последовательно:
— т. е. (96. ESt) действительно ведет для е к тому же результату, что и по-
полученная интегрированием уравнений для потенциалов формула G1).
Ю Б. В. Медведев
290 ч. II. МЕХАНИКА ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
19.3.2.2. Магнетостатическая система (95.MSt) имеет решением
- 1 Г (rfr')q>2[j(r'I I Г (dr')div'[r'-}'} ,адМоП
^ = -7J—\W=T\ T) рГПИ • (96-MSt>
Из него сразу очевидно то, установленное нами в § 16 не без сложностей,
обстоятельство, что вне системы стационарных токов ее магнитное поле за-
зависит только от ФгШ =div[r-j]. Разложение (96. MSt) по степеням r'/R
прямо приводит к последовательности стационарных магнитных моментов,
которые мы уже строили в § 16.
19.3.3. Совершенно неожиданным оказывается, однако, то
обстоятельство, что и в общем нестационарном случае в присут-
присутствии зарядов система (95—95Ь) также распадается на две неза-
независимые подсистемы. Одна из них включает полевые величины
ц, Фо[Н], Фг[Е] и источники d>2[j]. Ее составляют уравнения
(95.1), (95а.1) и (95Ь.2). Другая подсистема — уравнения (95.2),
(95а.2) и (95Ь.1)— налагается только на полевые величины е,
Фо[Е] и Ф2[Н]. Ее источниками служат р и Oi[j].
19.3.3.1. Таким образом мы видим, что все электромагнитное
поле распадается на две совершенно независимые друг от друга
части; иногда говорят (особенно вне источников) о разбиении
поля на электрические (е ф 0, ц = 0) и магнитные (е = 0,
ц Ф 0) волны *).
19.3.3.2. Как обычно, физически интересно (ср. § 13) запа-
запаздывающее решение (95):
*--S ' ' ' IR-'г-М ' ' <96-M>
— J-
|R-r'
j. (ат )т ¦} 1Г ,
ЗАМЕЧАНИЕ: г' входит в аргументы источников в (96. М, Е) дважды: непо-
непосредственно и через запаздывающее время; поэтому прихрдится различать
частные и полные производные по г'. В обеих формулах (95) участвует только
частное дифференцирование по явному г', что мы отметили круглыми д.
Частные производные по г' связаны с полным очевидным соотношением
А д 1 г'-r а
йт' ~ дг' с |r'-R| df ( '
Это тождество позволяет с помощью серии интегрирований по частям, по-
*) Подчеркнем условность этих названий. При описании поля с помощью
векторов Е и Н, а не скаляров е и ц, и «электрические» и «магнитные» волны
обладают ненулевыми электрическим Е и магнитным Н полями (подробнее
см, ниже 19.7).
19. СТАРШИЕ МУЛЬТИПОЛЬНЫЕ ИЗЛУЧЕНИЯ 291
добных подробно проведенным для электростатики, убедиться в том, что ре-
решения (96) эквивалентны обычным нашим решениям через запаздывающие
потенциалы А и ф. |
19.3.4. Нас будет в дальнейшем интересовать в основном по-
поле, создаваемое системой зарядов и токов, вне этой системы, там
где р и j равны нулю. Специальная форма (95—95Ь), которую
мы придали системе максвелловых уравненией, разделив их на
уравнения (95) и дополнительные условия (95а, Ь), позволяет
нам теперь утверждать, что в такой области два скаляра Фо[Н]
и Ф0[Е] будут тождественными нулями, а другие два Ф2[Е] и
Фг [Н] окажутся просто производными по времени от последней
пары Ф1{Н] = ц и Ф1 [E] = е. Таким образом, единственно су-
существенными будут задаваемые формулами (96) цие. Задание
этих двух величин полностью определяет электромагнитное поле
системы вне ее.
19.3.4.1. Скаляр ц, зависит при этом, как и в магнетостати-
ческом случае (96.MSt), только от ассоциированного с током
скаляра ФгШ = div[r-j]. Поэтому при его разложении в вол-
волновой зоне по степеням запаздывания войдут, как мы ниже
убедимся, только магнитные моменты системы.
19.3.4.2. Напротив, скаляр е зависит не только от р (т. е.
в существенном от ФоШ = div j), но и от третьего ассоциирован-
ассоциированного с током скаляра <Di[j] = r-j. Поэтому при его разложении
в волновой зоне, если поступать попросту, кроме электрических
моментов системы появятся моменты еще одного семейства, мо-
моменты от <Di [j], которые называют иногда анапольными момен-
моментами. Существенно, однако, что электрические и анапольные
моменты входят в характеризующее поле вне системы величины
не независимым образом, а только в определенной, предписывае-
предписываемой (96.Е) комбинации. Поэтому для поля излучения сущест-
существенны не сами электрические и анапольные моменты, а только
эти их комбинации, и если мы задаем, чтобы определить излу-
излучение системы, и ее электрические и ее анапольные моменты, то
мы сообщаем о системе больше сведений, чем это действительно
нужно—можно было бы ограничиться меньшим. Ниже мы пока-
покажем, что это действительно можно сделать, вводя для излучаю-
излучающей системы вместо электрических и анапольных только одну
последовательность моментов — их можно назвать обобщенными
электрическими моментами*).
*) Заметим, что такое любопытное положение возникло не случайно. Оио
обусловлено тем, что мы выражаем электромагнитное поле, имеющее, как мы
выяснили, только две существенные компоненты, через вектор тока, все тра
компоненты которого независимы. Если бы вместо электродинамики мы зани-
занимались бы задачей об излучении «поля с массой», которое обладало бы тремя
существенными компонентами, то все три семейства моментов вошли бы не-
независимо.
10*
292 ч. II. МЕХАНИКА ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
Описанное «не вполне полноправное» появление третьего се-
семейства моментов составляет наиболее существенное отличие
старших членов разложения излучения системы по мультипо-
лям, как от статических разложений, так и от рассмотренных
в предыдущем параграфе младших членов излучения, в которых
анапольные моменты не появлялись.
19.4М. Займемся сперва более подробным изучением маг-
магнитной части поля вне системы. В волновой зоне в общем выра-
выражении (96.М) можно пренебречь г' в знаменателе и написать
(Иногда удобно сперва преобразовать (96.М) с помощью (97) к виду
f (rfr'H(R-r')-r'-i) , С №')((R-r').r'-J)
Ц~3 |R-r'Pc2 +J |R-r'|3-c ' (96'М)
где второй член вообще несущественен в волновой зоне, а первый дает в ней
) (96-MW'>
*0 с
(т'п\
Разлагая это выражение в ряд по степеням запаздывания I I, приходим к
(член с 1 = 0 в этой сумме можно обратить в нуль интегрированием по ча-
частям; поэтому реально суммирование начинается с единицы!).
Если вынести здесь еще из-под интегралов по г' и единичные
векторы п, то в качестве параметров, характеризующих свойства
излучающей системы, останутся образования
Й'К, •• • г^[г'. Л, (SU.red)
которые мы назовем приводимыми магнитными моментами.
19.4М.1. Мы встречаемся тем самым еще с одной особенно-
особенностью, отличающей разложения по мультиполям в проблеме
излучения от аналогичной статической задачи — в § 16 мы мог-
могли, пользуясь тем, что скалярный магнитный потенциал удов-
удовлетворял уравнению Лапласа, оставить в разложении лишь
тензоры пц ... а[ со следом, равным нулю, — неприводимые маг-
магнитные моменты (81./) (см. 16.5.4), отличавшиеся от введенных
теперь приводимых тем, что к произведению г'а :.. г'а под ин-
интегралом применялась обращающая все следы в нуль «операция
^». Теперь такая редукция невозможна, поскольку она изме-
изменила бы электромагнитное поле. Мы вернемся ниже к обсужде-
обсуждению этого обстоятельства.
19. СТАРШИЕ МУЛЬТИПОЛЬНЫЕ ИЗЛУЧЕНИЯ 293
Множитель A+1)с, введенный в определение приводимых моментов, не
имеет особого смысла и объясняется соответствием с определением (81.0
неприводимых, которые были отнормироваиы в § 16 по разложению скаляр-
скалярного магнитного потенциала (81. ф). Удобно ввести еще специальное обозна-
обозначение ш'г) для магнитного 2'-польного момента, скалярио умноженного на
(/— 1) единичный вектор п
(О (Ored red
ша, =«, ... a/S ••• \ и ша, ««««, ... «,««, — \ <81-' >
19.4М.2. С помощью понятия приводимых магнитных момен-
моментов разложение для ц, в волновой зоне принимает форму:
(/+1>сп. ^ /98 м^
Rc „у n> d?« • (98-м>
19.4Е. Перейдем к изучению скаляра е.
Воспользуемся для преобразования (96.Е) соотношением I 2 + г' %-^-т 1=
=(-г-т-*г/ —1 J и перейдем с помощью (97) от частного дифференцирова-
дифференцирования по г' к полному, после чего можно будет проинтегрировать по частям,
причем проинтегрированный член обратится в нуль. Мы придем тогда для е
к выражению:
r') (R - г') • г'р (г', t - |К7ГЧ) Г (*') р (г', / -
|R-r'|2c + J |R-r'
r') г'-j (r'( t-\^~ I ) г (Л') (R-f) т'р (V, t-
- J
|R-r'|cJ + J | R - r' |3 '
(96E')
Последний член здесь ведет себя как 1/#2 и поэтому в волновой зоне несу-
несущественен*); из первых же трех получаем обычным образом
Разложение по степеням запаздывания дает:
в первом члене:
m=0
2-1
*) В статическом разложении по мультиполям как раз он играет главную
роль.
294 ч. II. МЕХАНИКА ТЕОРИИ 'ОТНОСИТЕЛЬНОСТИ
во втором:
и в третьем
^Поэтому, объединяя две первые однородные суммы в одну, можем написать
для е
R
jLy±4rUd,')(j^)l(s±-\
Re f^~o l\ dt' J \ с J \ c2 J
Мы выделили здесь в первой сумме нулевой член, поскольку стоящий в нем
интеграл есть просто полный заряд системы, который не зависит от времени.
Поэтому этот нулевой член для переменной части поля несущественен.
19.4E.I. В остальных интегралах первой суммы легко угадать
приводимые 2'-польные электрические моменты:
<С... а, (?) = J (АО г;, ... /а[р (г', t), G5.1.red)
после введения которых она принимает вид, совершенно анало-
аналогичный «магнитной» формуле (98.М)*). В виде же интегралов,
стоящих во второй сумме, появляются как раз те моменты тре-
третьего семейства, о которых мы уже говорили.
Мы определим приводимые анапольные моменты как
опять оставляя читателю построение формул (99./) и (99./').
19.4Е.2. Таким образом, разложение для е в волновой зоне
принимает вид:
_ Q , 1 у1 (*+»с - <*'d<»red , 1 viL+ii?- d'all)red
R R ^ lie1 dtl Re
R Re ^ lie1 dtl Re *-< l\ cl dtl
(98.E)
I9.4E.3. Мы видим, что, как мы уже говорили, электрические
и анапольные моменты входят сюда не независимо, а только.
*) Если восстановление невыписанных формул G5. /') вызывает у чи-
читателя затруднения, то, значит, он читает слишком быстро.
19. СТАРШИЕ МУЛЬТИПОЛЬНЫЕ ИЗЛУЧЕНИЯ 295
фактически, в виде комбинаций
dl red + al red_ (t)
Эти комбинации нельзя, однако, непосредственно записать в
форме моментов какой-либо функции от Фо [j] и Ф1 [j], поскольку
G5./) и (99./) нормированы у нас различным образом («само-
(«самоочевидная» функция выглядела бы как р—ггтгтт ~^-') • По-
этому, желая объединить электрические и анапольные моменты,
приходится прибегать к некоторой хитрости, результат приме-
применения которой, впрочем, тоже слегка противоестественен, хотя
и позволяет — в случае, когда мы интересуемся только перемен-
переменной частью поля — придать выражению для е более изящную
форму.
19.5.1. Вернемся к системе (95—95Ь), и рассмотрим уравнение (95.2).
Для переменных полей, для которых
-$*¦
де
dt
мы ничего ие потеряем, если продифференцируем это уравнение по времени:
что можно записать и как
Пе = 4я{-B + г--^г)фоШ + АФ1Ш-АФ|Ш+-^--^-Ф|Ш }•
Два первых члена можно теперь объдинить с помощью тождества (*) из
19.2, а два последних образуют как раз оператор д'Аламбера, применяемый
к Ф1 [j]. Поэтому его рационально перенести в левую часть, и мы получаем
таким образом вместо (95.2):
П.(в + 4яФ, Ц]) = 4лФ2 [rot j]. (95.2)
В левой части этого уравнения возникла комбинация
«Н-4лФ, Ц]. Та же комбинация уже стоит в правой части (95Ь.I)
Фа[Н] = —4-(в + 4яФ,Щ). (95Ь.1)
Наконец, дифференцируя (95а.2) по времени и вспоминая, что
в силу уравнения непрерывности р = —ФоЦ] получаем вместо
Него
0. (95а.2)
19.5.2. Итак, «электрическая» система уравнений, записанная
для новых*функций
в: ё==ё + 4яФ,Ц] и Фо (Е): Фо (Е) = Фо [Ё + 4nj], (**)
становится —для переменных полей — совершенно аналогичной
«магнитной» системе (95.1), (95а.1), (95Ь.2), в которой только
296 ч. II. МЕХАНИКА ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
источники Ф2 Ш магнитной системы заменяются — для е — на
cO2[rotj] или —для е —на с \ d/O2[rot j]. Заметим, что в силу
определения Ф] замена (**) эквивалентна замене электрического-
вектора Е на новый вектор
Ё: E = E + 4nj или Ё = Е +4л jj j d/. (***)
В силу аналогии новой электрической системы с магнитной,
решение будет фактически повторять формулу (96.М):
', t- lR~r l
19.5.3. Замена (***) любопытна тем, что вне системы заря-
зарядов ее нет: Е = Е. Поэтому вне области занятой зарядами и.
интересуясь только переменной частью поля, мы можем напи-
написать:
r'- \ dt 4ot}\ ~
Rjr4 J. 96.E>
(t + ^)]. (96.EW)
и, соответственно, в волновой зоне
8 = - ±
Разложение по степеням запаздывания проводится в точности
так же, как в магнитном случае, и приводит, если определить
обобщенные электрические приводимые моменты равенствами
?>#•• «чФ =7ТТ \ (dr')r«. • • * rH ' div ff' * *°1Я, (ЮО./.red)
к результату
1 у U+Jlc_ J> . И) red gg
Re Lj i\ci at1
19.5.4. Итак, мы достигли поставленной цели — выразили.
скаляр е в виде разложения по (новым) моментам одного рода.
Посмотрим, однако, как связаны эти новые обобщенные элек-
электрические моменты с входившими ранее в разложение той же
величины е обычными электрическими и анапольными момен-
моментами.
Удобнее сразу рассматривать входящую в (98. Е) комбинацию
-L п6(г) red = -=^- [ (dt') Г—V div [r' • -tot i'h
с / + 1 J V с /
19. СТАРШИЕ МУЛЬТИПОЛЬНЫЕ ИЗЛУЧЕНИЯ 297
и воспользоваться тождеством
[г'. rot Л = у + rot [г' • у] - г' • div У + grad (r'. J').
При подстановке под интеграл первого члена правой части этого тождества
сразу образуются моменты от плотности заряда р; во втором члене дивер-
дивергенция ротора даст нуль; в третьем члене надо будет сделать одно интегри-
интегрирование по частям, после чего опять возникнут моменты от р; наконец, в чет-
четвертом, где образуется оператор Лапласа, интегрировать по частям придется
дважды, после чего там возникнут анапольные моменты порядка (/ — 2).
В конечном результате мы придем к формуле
n-D(')red n-d«)red , I (/-IJ С JA n-a"-2>red
Если переписать полученное соотношение для самих тензоров?)а ,..а.
то оно будет гласить
22 (I I) f red
- «I-»'
nred _ Jred , 2C2 (I— I) . f
>al...al-\...al+ (/+i) P \-fy }
где буква Р означает, что нужно взять сумму по всем . . . способам,
выделяющим из индексов ai aj какую-либо фиксированную пару в каче-
качестве индексов у символа Кронекера. Из последней записи ясно видно то лю-
любопытное обстоятельство, что аиапольная составляющая тензора ^^¦..а
не имеет неприводимой части и является на самом деле комбинацией (ана-
польных) моментов порядка (I — 2).
В этом и состоит прокламированная выше «противоестествен-
«противоестественность» объединения электрических и анапольных моментов в
единые обобщенные электрические моменты. Хотя и можно най-
найти такую величину — d>2[rotj], — моменты которой объединяют
электрические и анапольные свойства излучающей системы как
раз в той комбинации, которая определяет излучение, но эти
моменты будут тогда объединять электрические и анапольные
моменты разной мультипольности.
ЗАМЕЧАНИЕ: С чисто формальной стороны это обстоятельство
довольно очевидно уже из того, что, при одинаковых значениях
/, анапольные моменты включают, сравнительно с электриче-
г' д _
скими, две лишние степени малого параметра тт—. |
19.6.1. Как мы^уже подчеркивали, в построенные пока разложения
{98. М), (98. Е), (98. Е) скаляров ц и 8 входят приводимые моменты
(81. /.red), G5./.red), (99. /. red) или A00./.red). Поэтому иногда говорят,
что определяющие излучение мультипольные моменты имеют больше компо-
компонент, чем статические — такая позиция в какой-то мере естественна, если
смотреть на излучение с точки зрения излучающей системы.
19.6.2. Можно однако, как и в только что обсужденной проблеме объеди-
объединения электрических и анапольных моментов, занять и другую позицию, рас-
рассматривая излучение только с точки зрения строения излучаемой волны, т. е.
зависимости ц и е от вектора п. Тогда естественно разложить, например в
298 ч. II. МЕХАНИКА TFOPHH ОТНОСИТЕЛЬНОСТИ
(81. I red) симметричные тензоры г'а ...г'а по бесследовым симметричным
тензорам убывающих рангов, записывая
ч • • • ч - <¦ • • • ч+с</2 ¦р ¦ *\ • ¦ ¦ v, ¦ V,«,+
где Си, s = 0, 1, ...; Сю = 1 — надлежаще подобранные численные коэффн-
коэффнциенты, а Р — операторы перестановок индексов, которые необходимо выпол-
выполнить, дабы не потерять свойства полной симметрии. Подставив это разложе-
разложение под интеграл в (81./. red) и свертывая, как то потребно для разложения
(98. М), с I векторами п, заметим, что — поскольку папа Ьа а =п2 = 1 —
1-й член правой части (+) даст в
-5 г-nm" ra вклад
(,_2,Л
который ведет себя в смысле зависимости от п совершенно так же, как и
1 d1' ,п „ " .
—77- —=тгпш — главный, неприводимый, вклад приводимого момента
с dv
m(l') red c ,, = , _ 2s_
19.6.3. Естественно, поэтому, собрать все такие вклады, проистекающие от
всех I > /', вместе для каждого /'. Мы придем тогда для ц к разложению
вида
где d[fi, dj/2> ... —некоторые новые численные коэффнциенты. Оно содержит
уже только неприводимые моменты, но построенные не из самого ассоцииро-
ассоциированного с током скаляра Ф2 [j'] = div [r'-j'J, а из некоторого эффективного
скаляра
, г'2 д* Г , -
<$12 [j'] = Ф2 [j'] + dtl ^-*Фг^'1+ ••• — \ dtK1 (r',t — т)Ф2[\(т', t)]
c2 dt2 J
A01. M>
учитывающего фактически некоторую долю запаздывания внутри системы.
19.6.4. Итак, второе усложнение, с которым мы встречаемся
при исследовании мультипольного разложения в задаче об излу-
излучении, связано с необходимостью различать приводимые
(81./. red) и эффективные неприводимые
мультипольные моменты, в чем в статических разложениях не
было нужды. Первые непосредственно выражаются через харак-
характеризующие распределение зарядов и токов излучающей систе-
19. СТАРШИЕ МУЛЬТИПОЛЬНЫЕ ИЗЛУЧЕНИЯ 299
мы скаляры Ф2[Л (или — в электрическом случае — Oajrotj']),
но содержат в себе больше информации о системе, чем то дей-
действительно нужно знать для однозначного определения ее поля
излучения. Вторые олицетворяют как раз тот набор сведений
о свойствах излучающей системы, который необходимо и доста-
достаточно знать для однозначного определения ее излучения — но
зато их надо строить не из действительных скаляров ФгО'] (или
O2[rot j']), а из эффективных скаляров ср^, своих для всякого /.
Попытка построить явное выражение для этих эффективных ска-
скаляров ф2' (т. е. найти значения коэффициентов d!s или вид функ-
функции К в A01.М)) элементарными тензорными методами, кото-
которыми мы здесь пользуемся, приводит к громоздкой комбинато-
комбинаторике. С другой стороны, оно довольно непринужденно находится,
если прибегнуть к аппарату сферических функций, изучаемых
обычно в курсах математической физики. Поэтому мы не будем
вдаваться здесь в такое решение этой задачи, подробности кото-
которого можно посмотреть, например, в книгах Джексона или
Блатта и Вайскопфа.
19.6.5. Характеризующий магнитную часть излучаемого поля
скаляр ц запишется теперь в виде разложения по эффективным
неприводимым магнитным моментам как
г «а, -.,('")• A03.М)
19.6Е. Мы подробно обсудили переход от приводимых к эф-
эффективным неприводимым моментам для магнитной части поля.
Для электрической части все рассуждения — в применении к
обобщенным электрическим моментам (lOO./.red)—проходят
совершенно аналогично и приводят к определению эффективных
обобщенных неприводимых электрических моментов
7/TTT$V ^П (Ю2.Е)
и разложению для е
оо
1^4 ^ A03.E)
Как и ранее, будет удобно использовать обозначения т<0
и D(;) для результатов свертывания A02) с (/—1) единичным
вектором п.
19.7. Введение двух скалярных характеристик электромагнит-
электромагнитного поля1 — [I и е — позволило прийти к простым и симмет-
симметричным формулам A03) для разложения поля системы зарядов
300 ч- "• МЕХАНИКА ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
по мультиполям; но эти разложения построены пока только для
скаляров A и е. Нам надо теперь научиться, как восстанавли-
восстанавливать по известным ц и е величины, имеющие непосредственный
физический смысл, — сами поля Е и Н, вектор Пойнтинга S и
полный поток 3 излучаемой системой энергии.
19.7.1. Вернемся того ради к основной системе максвелловых
уравнений E1.1,2.1,2) и разобьем в ней источники на две груп-
группы согласно схеме:
P = P* + Pm; i = ie + lm; р'=р; Рт = о;
Фо[Л = ФоШ; Фо[Л=О; Ф,[Л = Ф,Ш; Ф,[Л = 0;
Тогда и поля (мы ведь все время занимаемся только частным —
запаздывающим — решением неоднородных уравнений) разо-
разобьются на
Е = Е' + Ет; Н = Не+Нт,
причем каждая пара (Ев, Не) и (Ет, Нт) будет сама по себе
удовлетворять уравнения Максвелла с источниками (рв, )е) и
(pm, jm) соответственно.
19.7.2. При переходе к скалярной системе (95) (в видоизме-
видоизменении (95)),
? |i = ¦?¦ Ф2 Ш s-?- Ф2 Ц]; DS = 4яФ, [rot j] s 4яФ2 [rot Л,
выяснится прежде всего, что благодаря принятому разбиению
источников
\1т = ц; \ie = 0 и ет = 0; ее = е.
Потому остальные уравнения (94'), (95а,Ь) системы для «маг-
«магнитной» части поля будут содержать только ц:
Ф0[Нт] = 0; Ф0[Ет] = 0;
Ф,[Нт] = ц; Ф,[Ет] = 0; A04.M)
а для «электрической» части — только е:
Ф0[Не] = 0;
A04.E)
19.7.3. Рассмотрим «электрическую половину» системы
[A04.М) для магнитной части поля. Последнее из ее уравнений
19. СТАРШИЕ МУЛЬТИПОЛЬНЫЕ ИЗЛУЧЕНИЯ 30 Г
гласит
Попробуем «решить» его чисто формально, разделив обе части
на оператор IR • -^\ и не задумываясь пока о смысле такого
действия, т. е. написать
см __ 1 J_ d}i_
* " с dt
или, чтобы не иметь все-таки вектора в знаменателе,
1 ду.
с dt '
Em = — IR • —1 ——I—— — -^H-
Легко видеть, что такое решение формально удовлетворяет всем
трем уравнениям «электрической половины» A04.М).
Действительно,
ж[*ж]
° ¦
Далее, вектор Нт можно восстановить по формальному найденному Ет с
помощью первого уравнения E1.1.1) первой максвелловой пары, что дает:
Hm = rot -p -r^- ц.
[•¦¦агГ
Для такого Hm скаляр Фо [Hm] = 0 как дивергенция ротора,
— поскольку
г' ж]R=г' ж\ 'ж=0>
"dR
'dR
т.е. выполняются и все уравнения «магнитной половины» системы A04.М).
302 ч- П. МЕХАНИКА ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
19.7.4. Итак, если образовать из скаляра (х новый скаляр ц
с помощью пока чисто формальной операции деления на опе-
оператор
? ^ 12 ¦ A05.М.1)
то уравнения A04.М) для «магнитной» части векторов Е и Н бу-
будут удовлетворены выражениями
*"•—Ш*'7йг]Ь Н« - rot [R •¦?¦]?. (Ю5.М.2.3)
которые, следовательно, решают задачу о восстановлении маг-
магнитной части полей по известному ц, коль скоро формальной
операции A05.М.1) удастся придать реальный смысл.
19.7.5. Совершенно аналогично проходит и рассмотрение системы A04. Е)
для «электрической» части поля. Ее «магнитная половина» формально удовле-
удовлетворяется образованием
[
Электрическая часть Е" электрического поля восстаиовливается по нему с по-
помощью первого уравнения E1.2.1) второй максвелловой пары в форме
Ee = i
и подстановка этого выражения в «электрическую половину» A04. Е) пока-
показывает, что эти уравнения также удовлетворяются.
19.7.6. Найденные выражения для «электрической» части век-
векторов Ее и Не упрощаются и становятся совершенно анало-
аналогичными выражениям A05. М) для магнитной части, если рас-
рассмотреть их вне системы зарядов, где ё = е, а \е = 0. Производя
опять формальное построение нового электрического скаляра
получим в такой области для Es и Не:
]
— выражения, решающие (формально) задачу восстановления
электрической части полей по известному е.
19.8. Зная поля, мы можем теперь найти по общим формулам
(88.4—6) 17-го параграфа излучение системы.
19.8.1. При вычислении вектора Пойнтинга и полного излучения магнит-
магнитной части поля удобно выражать все величины в формулах (88) через элек-
19. СТАРШИЕ МУЛЬТИПОЛЬНЫЕ ИЗЛУЧЕНИЯ
трическое поле Ет (т. е. пользоваться тем, что в волновой зоне Hm = [n-Em]).
Мы получим тогда для полной потери энергии на излучение магнитных волн
сут с
Но
Поэтому
Первый член здесь обращается в нуль в силу теоремы Стокса
как поток ротора через замкнутую поверхность, второй же дает
нам результат:
3 — с ) An Г d V ¦ ¦ A06-М>
19.8.2. При вычислении излучения электрической части поля
удобно выражать все через магнитное поле Не (т. е. пользовать-
пользоваться тем, что в волновой зоне Ее = —[п-Не]); тогда совершенно
тождественные рассуждения ведут к результату
Ы Г_ d f •
~LrrJ
Поскольку излучение & квадратично по полям, то, если поле
содержит и электрическую и магнитную части, могут возникнуть
интерференционные члены Sem-f-Sme и j«™.[. j™«. В § 18 мы
убедились, что для младших мультиполей такие члены в полном
излучении & исчезают. Покажем, что эта особенность сохра-
сохраняется и в общем случае.
19.8.3. Смешанные члены в полном излучении задаются выражением
Эте + дет = cR2 (f) *&_ (|=т . Ее + Ее . Ет) = !&_ (Ь 6(у (Ега . Ее)_
В волновой зоне и в силу A05) здесь можно написать
304 ч. II. МЕХАНИКА ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
Во втором члене
[«"ЯГ]-[-"'l— !(.-Н-)-.[[*.Х.].Н']-
поскольку (п-Не) = 0. Однако легко видеть, что
поэтому второй член равен
Что же касается первого члена в скалярном произведении Ет-Е", то после
подстановки под интеграл его можно будет проинтегрировать с помощью
теоремы Стокса; следовательно, его вклад в полное проинтегрированное по
всем направлениям излучение тоже будет равно нулю. Таким образом
згет = згте==0> A06.ЕМ)
— т. е. электрическая и магнитная часть полного излучения действительно не
интерферируют.
19.8.4. Итак, мы нашли изящные формальные выражения
A06) для энергии, излучаемой системой в виде магнитных и
электрических волн. Пока, однако, эти выражения не имеют ни-
никакого смысла, поскольку неизвестно, что означает помещение
оператора в знаменатель: наша запись, например A05.М.1),
|Х==
говорит нам не более того, что \i должно быть решением урав-
уравнения
решением, которое еще предстоит найти (убедившись сперва в
его существовании и единственности).
19.9. Оказывается, однако, что эта проблема очень легко ре-
решается, если воспользоваться для ц и е построенными выше раз-
разложениями A03) по неприводимым (эффективным) моментам,
отдельные члены которых, как мы сейчас выясним, очень просто
ведут себя по отношению к действию оператора R • ^iF • Од-
Одновременно мы придем и к явным выражениям для электриче-
электрического и магнитного полей излучающей системы.
19. СТАРШИЕ МУЛЬТИПОЛЬНЫЕ ИЗЛУЧЕНИЯ 305
ЗАМЕЧАНИЕ: Забегая вперед в область квантовой механики, поясним, в чем
причина упрощения. Оператор R ¦ -Тр-1 есть, с точностью до множителя i,
квантовомеханический оператор момента, а бесследовые произведения
3"па ... па единичных векторов суть, как уже отмечалось в § 15, линейные
комбинации сферических функций — собственных функций квадрата этого опе-
оператора. При действии на иих I R • -т=г-1 превращается — мы сейчас в этом
убедимся — в число, не равное нулю, которое, следовательно, можно переве-
перевести в знаменатель, не вызывая недоумения. Щ
ЗАМЕЧАНИЕ К ЗАМЕЧАНИЮ: По существу это тот же метод Фурье, ко-
которым мы воспользовались, чтобы найти решение уравнений электромагнит-
электромагнитного поля. Только теперь положение упрощается тем, что среди собственных
значений нет нуля, поэтому однородное уравнение не имеет решений, а ре-
решение неоднородного — единственно. |
19.9.1. Существенная часть общего члена разложения A03.М)
для (i есть
#4., • • • nutria, ... в/ з= дц . . . П^ТОа, ... a, = (n • Ю<").
19.9.1.1. Подействуем на него оператором |R--7k-|.
L "К J
Замечая сперва, что
[rf I дпа
и, следовательно, что, если С — постоянный вектор,
.C) = [n-C] и
получаем без труда:
[R.-^] (п •&'>)==/[и-Л<»]. A07.1)
19.9.1.2. Далее
'"' ' без I
= - 2 (n ¦ ntw) - (/ - 1) (n • m@),
то есть
[R • -^-] [п • тО] = - (I + 1)(п • т<«). A07.2)
19.9.1.3. Комбинируя эти два правила действий, получим, в
частности,
~[R • ikf(n * ™A)>= l{l + l} [n ' ™(l)) A07>3)
306 "• II. МЕХАНИКА ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
— результат, который мы уже прокламировали: действие опера-
R • -^-1 на каждый из членов разложения (ЮЗ.М) (или
A03.Е)) сводится к умножению на число /(/+1) (не равное
нулю, поскольку суммирование в A03) начинается с /= 1).
19.9.2. Требуемое соотношениями A05.М, Е.1) деление не вы-
вызывает теперь затруднений, и мы можем записать мультиполь-
ные разложения для скаляров ц и е:
2 A08)
е=—У ^^
Re fa I-И-с'-1 dtl
Правило A07.1) позволяет перейти от этих разложений к
мультипольным разложениям для полей (при вычислении ротора
в выражениях для Нт и Ее следует, конечно, использовать упро-
упрощение (85а) волновой зоны). Находим:
Е« _ J ?
Re ?-> ll-c1
Г AО9.М>
(Ю9.Е).
Re fa /!-c' dil+1
19.10. Эти выражения можно привести к форме, внешне со-
совершенно аналогичной выражениям для полей электрического №
магнитного диполя из § 18 (ЭОЛЕ) и (90.1М). Для этой цели
надо ввести для системы зарядов единые характеристики, опре-
определяющие излучение системы по данному направлению (зави-
(зависящие не только от свойств системы, но и от выбранного в про-
пространстве направления п!), два вектора
19. СТАРШИЕ МУЛЬТИПОЛЬНЫЕ ИЗЛУЧЕНИЯ 307
Я
ЗАМЕЧАНИЕ 1: Первые, главные в разложении по малому па-
параметру квазистационарности, члены этих двух векторов совпа-
совпадают соответственно с магнитным и электрическим дипольиыми
моментами системы:
m(n,i)=m(t)+ -..; D(n,?)==d(?)+... A10a)
ЗАМЕЧАНИЕ 2: Исходя из скаляров \i и е, эти векторы можно
определить как
1 дШ _ rfjl . 1 да rf? . . ш
_ —-— __ ¦ f —*• — --~ — —— * {11UD)
Re dt rfn Re dt da
ненезависимость компонент па (папа = \) не должна нас сму-
смущать при выполнении дифференцирований в правых частях этих
равенств, поскольку произведения па[ ... па входят в A08)
лишь в виде полных сверток с бесследными моментами ЗЯ или
D. |
Поля выражаются через эти два вектора совершенно так же,
как для электрического или магнитного диполя:
(90М)
но аналогия эта, конечно, чисто внешняя, поскольку Ш1 и D
сами зависят от п, почему действительная зависимость полей
(90.Е) и (90.М) от направления может быть сколь угодно
сложной.
Это обстоятельство, однако, ни в коей мере не препятствует
получить из (90.Е, М) совершенно аналогичные (ЭОЛЕ, М.З) и
(91.IE, M) выражения для вектора Пойнтинга и полного излу-
излучения:
(90.Е.З) S'№ J^
308 ч. II. МЕХАНИКА ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
19.11. Единственное, что нам еще осталось сделать, это—ис-
это—используя разложения A08) или A10) по неприводимым момен-
моментам— реально выполнить фигурирующие в формулах для
полного излучения интегрирования по dO, т. е. провести ту опе-
операцию, которую мы назвали в § 18 усреднением произведений
единичных векторов по углам. В случае дипольных и квадруполь-
ного излучения мы провели эту операцию непосредственным вы-
вычислением, использующим лишь соображения симметрии. Рас-
Распространение этого способа на старшие моменты хотя и было
бы возможно, но привело бы к весьма громоздкой комбинато-
комбинаторике. Счастливым образом оказывается, что ее можно избежать
за счет искусственного приема.
Действительно, в ходе последних рассуждений мы получили
два выражения для суммарного излучения: формулы A06) и
(91); оба эти выражения должны, конечно, давать одинаковый
результат. Оказывается, как раз этого требования достаточно
для нахождения самого результата. Однако сперва несколько
предварительных замечаний и простых выкладок.
19.11.1. Когда мы подставим.например в A06), разложения A03), то при-
придем к двойной сумме интегралов (все численные множители пока несуще-
несущественны) типа
\ <^% ... nanh ... Яр//шв1 ... e/mPi... Э|/.
При интегрировании («усреднении по углам») векторы п объединяются (ср.
подробное рассуждение в § 18) во всевозможные пары — образуют «сверт-
«свертки», — каждая из которых дает кронекеров символ с теми же индексами.
Легко видеть, что ненулевой результат дадут лишь те члены, в которых «свер-
«свертываются» исключительно пары па и Пр —иначе получилась бы оа а , нли
бр р ,, которая дала бы нуль при внутреннем умножении на неприводимый
момент. Следовательно, — первый вывод — в двойной сумме по I и /' оста-
останутся после интегрирования лишь диагональные члены с 1 = 1', т. е. она пре-
превратится в одинарную.
19.11.2. Выпишем теперь со всеми коэффициентами выражение, скажем
для полного магнитного излучения, которое получается, исходя из A06. М).
Подставляя A03. М), имеем:
dV+i l(l+l) dil+i
1 /+1 &dl+i(n.mW)
1 /+1 &
^
С другой стороны, то же полное излучение должно получаться из (91. М)
19. СТАРШИЕ МУЛЬТИПОЛЬНЫЕ ИЗЛУЧЕНИЯ 309
в виде
Чтобы эти два выражения совпадали, надо, чтобы было тождественно
dO (m"> • m»> - (n • m<'>J) = i±l ^> dC (nnt'»J *).
Тождество (*) — это наш второй вывод.
19.11.3. Рассмотрим теперь интеграл
В результате интегрирования все векторы па_ и По в ием объединятся
в пары, которые дадут кроиекеровы ба а , и после свертывания с обоими
моментами 1-го порядка может остаться только квадрат момента (шЛ2 =»
= ^1а ...аша ...а с некоторым зависящим лишь от / численным коэффи-
коэффициентом С/, который пока неизвестен:
/, = С,(т,J
— наш третий вывод.
19.11.4. Во второй форме выражения для Эт кроме U участвуют еще и
интегралы вида
дающие на один fi-символ меньше, чем /i. Легко сообразить, что
С учетом этого замечания, тождество (*) принимает вид
или
2Ш-с-с ¦ с -г / с
— т. е. ведет к рекуррентной формуле для коэффициентов Си
С учетом очевидного граничного условия Со = 4я это рекуррентное соот-
соотношение немедленно решается и приводит к
Г Л . ЛЛ2*
» B/+1I1 4JI = 4}1 B/+1)!
*) Не составляет труда и прямая проверка этого тождества, опираю*
щаяся на теорему Стокса и тождество A07.1).
Г310
ч. II. МЕХАНИКА ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
и, следовательно, к выражению
-Е-
л/12'
(-i llilc2l+l l
для полного магнитного излучения 3fm.
19.11.5. Итак,
ОО 00
1=1 1=1
B/+ 1)! c
2/ + 1
(92М)
Рассуждения для полного электрического излучения совершенно
аналогичны; поэтому мы не будем их повторять, а сразу выпи-
выпишем результат:
Легко проверить, что, выбирая из этих формул члены с / = 1
и с / = 2, мы снова вернемся к формулам (92.1Е), (92.1М) и
(92.2Е) предыдущего параграфа.
20. Рассеяние света на свободных зарядах
20.1. В качестве — представляющего и самостоятельный ин-
интерес— примера на вычисление излучения системой зарядов,
рассмотрим задачу о свободном заряде, находящемся в (задан-
(заданном) поле плоской монохромати-
монохроматической электромагнитной волны.
Под действием этого поля заряд
придет в (неравномерно-прямо-
(неравномерно-прямолинейное) движение и в резуль-
результате этого начнет излучать вто-
вторичные электромагнитные вол-
волны— с точки зрения асимптоти-
асимптотического наблюдателя будет про-
происходить рассеяние первоначаль-
первоначальной волны.
Если падающая волна с волновым вектором к обладает плот-
плотностью потока энергии З'о = |S0|, а поток энергии, уносимый
вторичной — рассеянной — волной в направлении п в телесный
угол dO есть, согласно (88.5), dSf — Sda== \S\R2dO, то диф-
дифференциальным эффективным сечением рассеяния естественно
Тут следует только сделать одно заме-
замеРассеянные Волны
назвать отношение
ло
о
чание. Поля и в падающей и в рассеянной волне суть периоди-
20. РАССЕЯНИЕ СВЕТА НА СВОБОДНЫХ ЗАРЯДАХ 311
ческие функции времени, а обычные приборы для обнаружения
электромагнитных волн обладают инерционностью, большой
сравнительно с периодом — колебаний. Поэтому реально изме-
измеряются всегда лишь энергетические величины, усредненные по
промежутку времени, много большему периода колебаний. По-
Поэтому и эффективное сечение рассеяния разумно определить как
отношение таких средних, т. е. как
. ПИ)
9o
В падающей плоской монохроматической волне
&о — I So I = -^ | [Ео • Но] | = -^ | [Ео • [п • Ео]] | = -г— | п | Ео f \,
т. е.
В рассеянной волне будем учитывать только электрическую-
дипольную часть — как мы знаем, эта часть, если она только не
обращается в нуль (в чем мы сейчас убедимся), составляет ос-
основную часть излучения системы, а все остальные мультиполи
дают лишь поправки, меньшие по крайней мере в отношении
Г—V. Поэтому, согласно ,(91.IE'),
Следовательно,
dCT==-4=-sin2f>.d<?
и остается только установить связь между d и Ео.
20.2. Для этой цели надо обратиться к уравнению движения
нашего свободного заряда
Принятое дипольное приближение для излучения будет хорошим,
если для заряда v <; с, т. е. если его движение можно считать
нерелятивистским*). Тогда в левой части уравнения движения
можно заменить импульс заряда р на произведение т\, а в пра-
правой— пренебречь силой Лоренца — [v • Но]'сравнительно с элек-
*) Это предположение содержит в себе и то требование, что амплитуда
падающей волны должна быть не слишком велика.
312 ч. II. МЕХАНИКА ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
тростатической силой еЕо. Мы получаем
mr = eE0(r, t).
Но для одного заряда дипольный момент d = ег, поэтому можно
записать уравнение движения прямо для дипольного момента
Как видим, его даже не нужно решать — в левой части стоит
как раз та вторая производная, которую надо подставлять в вы-
выражение для сечения. Не требуется исследовать и усреднение
по времени — средние по времени от квадрата поля в числителе
и знаменателе формулы для эффективного сечения просто со-
сокращаются*), и мы приходим к искомому результату:
itfb-d0, A12)
по поводу которого уместно сделать несколько замечаний.
20.3. Прежде всего обратим внимание на то обстоятельство,
что в формуле A12) из характеризующих частицу массы т и
заряде е образовалась константа размерности длины. Если час-
частица, на которой происходит рассеяние, есть электрон, то эта
константа
есть как раз та величина, которую мы назвали в § 14 классиче-
классическим радиусом электрона и которая определяла порядок разме-
размеров протяженных моделей элементар-
элементарных частиц. Сейчас, однако, вычисляя
рассеяние электромагнитной волны,
мы исходили из представления о то-
точечной заряженной частице; формула
A12) показывает, что и такая части-
частица демонстрирует в своем взаимодей-
взаимодействии с электромагнитным полем не-
некоторый размер, и притом как раз
равный классическому радиусу.
Второе замечание относится к тому, что входящий в A12)
угол $ есть угол между направлением рассеяния п и направле-
р
нием поляризации у^у падающей волны, но не направлением
*) То есть сечение не зависит от интенсивности падающей волны. Это
есть, конечно, следствие линейности уравнений Максвелла.
20. РАССЕЯНИЕ СВЕТА НА СВОБОДНЫХ ЗАРЯДАХ 313
ее распространения по||к. Если принять, что падающая волна, рас-
распространяется вдоль оси z, рассеяние происходит в плоскости
(xz), а направление поляризации (лежащее в (ху)) отклонено
от оси Ох на угол q>, и обозначить угол рассеяния буквой %, то:
cos ¦& = (п • j± J; cos % = (n • n0);
no = {O; 0; 1}; n = {sinx; 0;
En d / Л\
— = -т- = {со8ф; smq>; 0}
t |d|
и, следовательно,
cosifr = sin% • соэф, значит, sin2'fr= 1 — cos^sin2%.
Подставляя это значение sin2ifr в A12), получаем эффектив-
эффективное сечение, выраженное через углы % и ф, определяющие на-
направление рассеяния п относительно направления п0 распростра-
распространения падающей волны и ее плоскости поляризации (п0, Ео):
A12а)
Обратим внимание на то обстоятельство, что эффективное
сечение рассеяния плоско-поляризованной волны не обладает
аксиальной симметрией, — мы впервые встречаемся с таким яв-
явлением.
20.4. Свет от естественных источников редко обладает опре-
определенной поляризацией; обычно он бывает смесью плоско-поля-
плоско-поляризованных волн со всевозможными направлениями поляриза-
поляризации, не когерентных между собой. Поэтому при вычислении
эффективного сечения для рассеяния такого света складываются
энергии, а не поля, т. е. следует просто усреднить A12а) по
всем направлениям ф поляризации. Такое усреднение дает
I + COS2 Y
—
1 — sin^xcos^ = 1 — зш^хсо82ф= 1 2 ==2
Поэтому для неполяризованной волны сечение рассеяния есть:
3 + cos2x ,^ /,,ft,\
4 dOr 012b)
В классической механике полное сечение рассеяния почти
всегда оказывалось бесконечным; случай конечного полного
сечения был в каком-то смысле исключительным. Полное
314 ч. П. МЕХАНИКА ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
эффективное сечение рассеяния света на свободном заряде ко-
конечно: интегрированием по углам получаем — равным образом
из A12) или A12Ь) —
0= 1у йо=—хг I —7Г I полное сечение (ИЗ)
Эту формулу называют формулой Томсона.
ЗАМЕЧАНИЕ: Томсоново сечение не зависит от длины волны
падающего света. В квантовой теории выясняется, что это об-
обстоятельство справедливо только для достаточно длинных волн;
.для коротких волн сечение начинает падать. |
Часть III
ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
1. Историческое введение
В первой части, начиная рассмотрение классической меха-
механики, мы подчеркивали, что эта теория, строго говоря, вообще
не имеет области применимости — для элементарных частиц^
когда уже нет необходимости в статистическом усреднении,
вступают в игру квантовые эффекты. Теперь как раз настало
время заняться рассмотрением квантовомеханического описания.
При изложении мы не будем следовать историческому пути —
это заняло бы слишком много времени и хотя и было бы поучи-
поучительно, но, пожалуй, не только не помогало бы преодолению
трудностей в восприятии новых понятий, но, наоборот, способ-
способствовало бы их нагромождению. Тем не менее не будет лишним
привести краткий перечень главнейших трудностей, непреодоли-
непреодолимых для классического описания, и напомнить о времени воз-
возникновения важнейших новых идей, приведших нас к квантовой
картине.
1.1. В конце прошлого века у физиков господствовало то
впечатление, что их наука близка к исчерпанию своего пред-
предмета— все главные законы природы уже открыты, и осталась
лишь чисто техническая работа — применять их к конкретным
задачам и повышать точность экспериментального определения
различных констант. Один из крупнейших английских физиков
сказал тогда, что в физике остались, собственно, три нерешен-
нерешенные задачи: вывести формулу для равновесного теплового из-
излучения, узнать, что такое шаровая молния, и объяснить, по-
почему гудят провода.
Первая из этих задач оказалась как раз тем орехом, на ко-
котором классическая физика сломала себе зубы.
1.1.1. Суть проблемы состояла в следующем: Статистическая
физика учит, что для всякой системы, находящейся в термоди-
термодинамическом равновесии, энергия распределяется равномерно по
всем степеням свободы (мы не даем сейчас точной формули-
формулировки этой теоремы). Поскольку у электромагнитного поля, как
мы выяснили, например в И. 13а., число степеней свободы бес-
бесконечно велико, то отсюда следовал парадоксальный и не отве-
отвечающий опыту вывод, что система частиц (имеющая всегда
316 '. III. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
конечное число степеней свободы) не может находиться в равно-
равновесии с электромагнитным полем — вся энергия должна была
бы переходить в излучение.
За 17 дней до начала XX века Макс ПЛАНК предложил ре-
решение этой проблемы, но достиг его ценой того совершенно
«ортогонального» всей классической физике предположения, что
энергия осцилляторов (которые он выбрал в качестве модели со-
состоящего из конечного числа частиц материального тела) может
принимать не любые значения, а лишь значения, кратные неко-
некоторому наименьшему «кванту» ef
Е = п8, n<=N, A.1)
который в свою очередь надо было считать пропорциональным
частоте осциллятора
^ = Йю = Лу, A.2)
где Ь — фундаментальная мировая постоянная, по современным
данным
Й= 1,05459 • КГ27 эрг • сек. B)
Величина Ъ была названа квантом действия.
1.1.2. Следующий шаг по расшатыванию здания классической
физики был сделан в 1905 году Альбертом ЭЙНШТЕЙНОМ.
«Слабым местом» оказался теперь фотоэффект — явление выби-
выбивания электронов из вещества под действием света. Поразитель-
Поразительным с точки зрения классической электродинамики образом
энергия электронов не зависела при этом от интенсивности света
(т. е. от амплитуды электрического вектора в световой волне),
но решительно зависела от его частоты. Эйнштейн показал, что
это парадоксальное поведение можно объяснить, если принять,
что свет определенной частоты состоит из отдельных частиц —
фотонов, — обладающих энергией
Е = Й(о,
и что при взаимодействии с веществом могут поглощаться пооди-
поодиночке лишь целые фотоны. Тогда для энергии фотоэлектронов
получалась естественная формула
где W — работа выхода, связанная с преодолением сил, удер-
удерживающих электрон в металле.
1.1.2.1. Введение представления о фотонах в какой-то сте-
степени возрождало корпускулярную теорию света. Оно получило
дальнейшие подкрепления при рассмотрении еще ряда оптиче-
оптических явлений; особенно наглядно это проявилось в 1923 году,
1. ИСТОРИЧЕСКОЕ ВВЕДЕНИЕ 317
когда КОМПТОНОМ был открыт эффект, показывающий, что
при рассеянии на электронах свет достаточно малой длины
волны, сравнимой с (или меньшей) так называемой комптоно-
вой длиной волны
(длины волн такого порядка величины имеют рентгеновы лучи),
ведет себя так, как будто происходят индивидуальные акты
соударения фотонов с электронами, в которых выполняются все
механические законы сохранения, причем фотонам оказывается
необходимым приписать не только
энергию fico, но и импульс
Р = Йк, C) м
где к — волновой вектор, к = —п.
1.1.2.2. Однако в то же время оста-
оставались непоколебленными результаты
многочисленных оптических опытов, фотон, рассеивающийся
связанных с явлениями интерференции на электроне
и дифракции, поддававшиеся истолко-
истолкованию только на основе волновой теории. Таким образом воз-
возникло то странное положение вещей, что все оптические явления
разбивались на две группы, одна из которых поддавалась ин-
интерпретации в терминах корпускул, в то время как другая —
лишь в терминах волн. Такая конфронтация двух казалось бы
взаимно исключающих друг друга точек зрения получила имя
корпускулярно-волнового дуализма и нашла себе объяснение
лишь в квантовой механике.
1.1.3. Упомянем еще о проблеме теплоемкостей твердых тел.
Согласно уже упоминавшейся теореме о равнораспределении по
степеням свободы, теплоемкость должна была бы определяться
числом степеней свободы. Для твердых тел получалось при этом,
что если учитывать только степени свободы, описывающие дви-
движение атомов как целого, то для всех тел атомная теплоемкость
должна была бы быть одинаковой -и составить примерно
6 -^ это так называемый закон ДЮЛОНГА и ПТИ. Оста-
моль
валось, однако, неясным, почему у-некоторых веществ — а при
низких температурах практически у всех — теплоемкость оказы-
оказывалась меньше этого значения, и почему, во-вторых, при под-
подсчете теплоемкостей не следовало принимать во внимание внут-
внутренние степени свободы атомов — к тому времени было ясно,
что они есть. В 1907 году Эйнштейн показал, что здесь мы стал-
сталкиваемся по существу с той же проблемой, что и рассмотренная
Планком проблема «теплоемкости электромагнитного поля», и
318 ч. III ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
что принятие планковской гипотезы о «квантованности» энергий
осцилляторов приводит к тому, что для температур, малых по
сравнению с энергией осциллятора A), соответствующая степень
свободы перестает возбуждаться, «вымораживается».
Эйнштейн выбрал в качестве модели твердого тела совокуп-
совокупность осцилляторов с одной единственной частотой, и получил
одну универсальную кривую (с одним параметром) для всех
тел. Вскоре ДЕБАЙ уточнил это рассмотрение и связал отступ-
отступления от закона Дюлонга и Пти с упругими константами ве^
щества.
Все описанное находилось, конечно, в разительном противо-
противоречии с классической физикой, однако все еще имело характер
мелких поправок и заплаток, харак-
характер «некоторых дополнительных
правил в отдельных частных вопро-
вопросах». Настоящее крушение класси-
классические механика и электродинамика
потерпели, столкнувшись с пробле-
проблемой описания строения атома и
, объяснения атомных спектров.
теплоемкость твердого тела , 2, R н века бы?0
по Дюлонгу и Пти и по стт> цт0 атомьДюбого вешества
Эйнштейну электрически нейтральны и совер-
совершенно стабильны — т. е. с не под-
подвергающимся внешним воздействиям атомом сколько угодно
долго ничего не происходит (интригующее явление естествен-
естественной радиоактивности по-видимому не имело к «обычным» ато-
атомам никакого отношения). В то же время было известно, что>
атому можно разнообразными способами сообщить дополни-
дополнительную энергию — «возбудить» его — и что возбужденный атом
отдает свою лишнюю энергию в виде электромагнитных волн —
света. Частота света, испускаемого атомом каждого сорта, не
может быть произвольной, а только равной некоторым избран-
избранным дискретным значениям — атом может испускать только от-
отдельные «линии», которых может быть и весьма много.
В то же время было известно, что при еще большем возбуж-
возбуждении из атомов начинают вылетать электроны, заряженные от-
отрицательно и имеющие ничтожную (~10~4 от массы атома)
массу, оставляя положительно заряженный «атомный остаток».
Таким образом, можно было думать, что атом состоит из поло-
положительно заряженного «атомного остатка», несущего всю массу,,
и вкрапленных в него, как изюм в калорийную булочку, отрица-
отрицательно заряженных электронов, и было бы вполне естественно
допустить, что электроны связаны с остатком квазиупругим об-
образом и при возбуждении атома начинают совершать колеба-
колебания, что и приводит к излучению света по формулам, получен-
1. ИСТОРИЧЕСКОЕ ВВЕДЕНИЕ 319
иым нами в конце второй части. Однако по классической теории
частота света должна равняться частоте колебаний или быть
кратной ей, а частоты, испускаемые атомами, не оказывались
целочисленными кратными не слишком большого числа фунда-
фундаментальных частот. Таким образом, практически требовалось
ввести столько же степеней свободы, сколько спектральных линий
испускает атом. Это число степеней свободы даже для простей-
простейшего атома водорода оказывалось уже совершенно необозри-
необозримым.
Подход к более разумной модели атома совершался истори-
исторически с двух совершенно независимых сторон.
1.2.2. С одной стороны, РИТЦ в 1908 году выдвинул «комби-
«комбинационный принцип», согласно которому все многообразие испу-
испускаемых атомом частот можно получить в виде разностей неко-
некоторых величин, «термов», последовательность которых может
быть очень простым образом выражена через целые числа. Так,
для водорода термы образуют одну последовательность, «серию»
^(rt)^-^-, R'— константа D.1)
и частоты равны
) D.2)
л= 1, 2, ...; т> п.
Ритц опирался при формулировке своего принципа на формулу,
описывающую длины волн четырех последовательных линий во-
водорода, которую еще в 1885 году нашел БАЛЬМЕР, учитель
средней школы в Базеле, обессмертивший этой гениальной до-
догадкой свое имя.
1.2.3. С другой стороны, в 1912 г. РЕЗЕРФОРД, проводя
опыты по расеянию ос-частиц на атомах и сравнивая их резуль-
результаты с выведенной им «формулой Резерфорда» для эффективного
сечения рассеяния в кулоновом поле, установил, что атомный
остаток» отнюдь не занимает всего атома (~ 10~8 см), а сосредо-
сосредоточен в области, не большей 10~12—1О~13 см, т.е. не большей, чем
«размеры электрона». В заключение своей работы Резерфорд вы-
выдвинул для объяснения очень больших (~10~8см), с точки зре-
зрения этих результатов размеров всего атома ту гипотезу, что,
возможно, атом устроен аналогично планетной системе, в кото-
которой электроны обращаются вокруг ядра подобно планетам, об-
обращающимся вокруг солнца, и все «материальные» составные
•части занимают еще меньшую долю совокупного пространства
320
ч. III. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
системы, чем даже в «практически совершенно пустой» системе
Солнца *).
1.2.4. Гипотеза Резерфорда не облегчила дела с атомными
спектрами. Действительно, если электрон в атоме вращается во-
вокруг ядра, то атом должен обладать диполь-
ным моментом, зависящим от времени. В са-
самом деле, если движение совершается в куло-
новом поле ядра с зарядом Ze (e — заряд
электрона), пусть, для простоты, по круговой
орбите, то
* = r0cos(p; y = rQs'm<f>; z — Q
и
е d = — rGe{cosop, sincp, 0}.
круговая орби-
та Согласно выводившимся в первой части кур-
курса формулам при этом (радиус орбиты г0 бу-
будет сразу большой полуосью эллипса а и его параметром р)
будет
М2 а М , ,
Р г; г ; ф * ©*;
@2 =
м2
М2 = (хал0; со2
If.-
Zp2
I E 1= •
d = — тф(cosat, sinat, 0}
откуда
и
Но система с зависящим от времени дипольным моментом те-
теряет за счет дипольного излучения в единицу времени (формула
F5) второй части курса) энергию gg3 ¦¦ Таким образом энер-
энергия такой системы не может оставаться постоянной, а будет убы-
убывать со временем:
dE ^ d \ E | = 2 (dJ
dt ~
dt
Зс3
*) Мы уже имели случай указывать на беспримерную идейную насыщен-
насыщенность этой работы, в которой автор не только экспериментально установил
действительные размеры «атомного остатка», но и впервые поставил проблему
макроскопического исследования мнкросоударений, и решил ее для кулонова
потенциала, да еще сформулировал модель атома, сохранившуюся практиче-
практически до наших дней!
1. ИСТОРИЧЕСКОЕ ВВЕДЕНИЕ 321
откуда, переходя от энергии к однозначно с ней связанному ра-
радиусу орбиты, получаем
dt 2r0 ~ Зе3 ^ ° ' ~ Зс3
то есть
d I 4Ze4 I
dt г0
или
Л 3 V гп ) '
Стоящая в числителе последней дроби длина —?-»—5- уже
встречалась нам в электродинамике — через ее квадрат выража-
выражалось эффективное сечение рассеяния света свободными элект-
электронами, и мы назвали ее «классическим радиусом электрона»
¦fj. Она составляет приблизительно (сейчас она известна с ше-
шестью надежными значащими цифрами) 2,8-10~13см. С другой
стороны, радиус г0 орбиты электрона должен быть в резерфор-
довой модели порядка размеров атомов, т. е. порядка 10~8 см.
Таким образом квадрат фигурирующего в последней формуле
отношения составляет по порядку величины
Так как скорость света с есть 3-Ю10 см/сек, то «скорость» —р-
убывания радиуса электронной орбиты за счет потери энергии
на излучение имеет порядок одного (или, если обратить вни-
внимание и на небольшие численные множители даже 101) см/сек.
Поскольку размеры атома составляют Ю~8 см, то этот резуль-
результат означает, что атомы не только не могли бы быть совершен-
совершенно стабильны, но вообще не могли бы существовать макроскопи-
макроскопически заметное время — через 10~8 сек электроны атомов должны
были бы упасть на ядро.
Итак, с точки зрения классической физики в модели Резер-
форда
A) атом не только не мог бы быть стабильным, но и пол-
полностью терял бы свою энергию на излучение за время порядка
10~8 сек;
B) частота этого излучения, обратно пропорциональна ра-
радиусу орбиты в степени 3/2 (третий закон Кеплера), непрерывно
изменялась бы, и никаких дискретных линий в спектре атома
не было бы.
1.3. В следующем 1913 году Нильс БОР сделал в каком-то
смысле решающий шаг, объединивший два указанных подступа
к проблеме строения атома: он применил к модели Резерфорда
идею Планка о квантовании.
1 1 К_ R Мрпйрпри
322 ч. III. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
Именно, Бор допустил, что в планетарной модели возможны
не любые «орбиты», а лишь некоторые избранные, для которых
момент (его размерность совпадает с размерностью действия)
имеет значения, кратные планковской постоянной h:
М = пН. квантовое условие
Находясь на этих избранных орбитах, электрон не излучает,
вопреки классическим представлениям, хотя и движется с уско-
ускорением. Этим объясняется стабильность атома, если электрон
занимает низшую допустимую орбиту с М = Ь.
С «высших» же орбит электрон может переходить на низшие,
совершая «квантовый скачок» и испуская один квант света.
При этом частота испускаемого света определяется не частотой
движения электрона, а фактически планковским условием A),
которое записывается теперь как
<3 п — в т = Й@. условие частот E)
Если мы посмотрим на связь энергии с моментом, которая
получается из только что приводившихся формул кеплеровой
uZ2e4
задачи, \Е\= 2М2 , то увидим, что эта связь вместе с кванто-
квантовым условием и условием частот сразу приведет нас к сериаль-
сериальной формуле D), причем теперь можно будет вычислить и зна-
значение R' (или R) постоянной Ридберга:
^' = Ж^; ^"IF т~масса электрона,
(мы положили для водорода Z = 1), которое оказывается в пре-
превосходном согласии с опытом.
1.4. Здесь уместно сделать несколько замечаний относительно
натуральных единиц, которые определяют масштабы основных
физических величин в атомной области.
1.4.1. В предыдущей части, в классической электродинамике,
обсуждая вопрос об энергии собственного кулонова поля заря-
заряженной частицы, мы пришли к выводу, что для частицы с мас-
массой т и зарядом е помимо естественной единицы энергии — энер-
энергии покоя <ff0 = тс2 существует и естественная единица длины
&o тс*
Если рассматриваемая частица — это электрон, то соответ-
соответствующие величины называют собственной энергией электрона
??0 = тс2т0,5\ МэВ
и его классическим радиусом
1. ИСТОРИЧЕСКОЕ ВВЕДЕНИЕ 323
Привлечение квантовых представлений добавляет нам новую
фундаментальную постоянную — постоянную Планка B), — за
счет чего оказывается возможным сопоставить частице массы
т еще одну длину—комптонову длину волны, уже упоминав-
упоминавшуюся в 1.1.2.1.
Легко понять, как образуется эта величина. Из массы т
электрона мы получаем по соотношению Эйштейна его собствен-
собственную энергию &q = тс2. Этой энергии по основной гипотезе
Планка A) отвечает некоторая частота
ffa тс2
из которой в свою очередь можно получить длину волны, поде-
поделив на нее универсальную скорость с:
см-
1.4.2. Но коль скоро в нашем распоряжении есть две длины,
связанные с одной и той же частицей, то, поделив их друг на
друга, мы получим безразмерное отношение
—.?¦ —о
~~ hc~a
тс2 )'\тс )~~ hc
— т. е. число, которое не зависит от выбора единиц измерения
и про которое можно поэтому спросить, почему оно имеет имен-
именно такое значение, а не какое-нибудь иное.
Полученное нами сейчас число а называется (по историче-
историческим причинам) постоянной тонкой структуры. Как видно, она
пропорциональна квадрату заряда электрона и тем самым, по-
поскольку заряд всех (заряженных) элементарных частиц (с точ-
точностью до знака) одинаков (поэтому говорят просто об элемен-
элементарном заряде е), характеризует «силу» самого электромагнит-
электромагнитного взаимодействия.
Опыт показывает, что постоянная тонкой структуры с до-
довольно высокой точностью равна
_ 1
а~ 137
— обратному целому числу 137 (точное современное значение —
137,0360). Таким образом электромагнитное взаимодействие
оказывается взаимодействием довольно слабым. Это обстоятель-
обстоятельство является весьма отрадным для теоретиков, так как позво-
позволяет вычислять многие эффекты этого взаимодействия прибли-
приближенным образом, разлагая их в ряды по степеням малого пара-
параметра а, члены которых весьма стремительно убывают (правда
относительно сходимости таких рядов существуют настолько вес-
веские сомнения, что противоположная точка зрения представляется
более обоснованной).
324 ч. III ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
Почему именно постоянная тонкой структуры равна 1/137, а
не какой-либо другой величине, современная физика сказать не
может. Особенно провоцирующим вызовом человеческой изобре-
изобретательности лредставляется то обстоятельство, что обратное зна-
значение постоянной тонкой структуры есть целое число — это по-
побуждает искать объяснение его значения на пути подсчета числа
каких-то комбинаций.
Собственно говоря, способ получить такое большое число из числа мень-
меньшего и имеющего физический смысл известен уже около полувека. Число 137
можно представить в форме
]з7= D-4) D-4+1) +>>
где «исходное» число 4 есть число измерений пространства-времени, произве-
произведение D-4) можно осмыслить как число компонент какого-либо билинейного
объекта в этом пространстве, образование дроби — как подсчет числа ком-
компонент симметричного билинейного объекта в пространстве билинейных объ-
объектов, а добавляемую единицу представить себе как происходящую из-за иа-
лнчия некоторой дополнительной дискретной степени свободы. Дело остается
за малым — заставить поверить — даже не в убедительность, а хотя бы в ве-
вероятность — спекуляций подобного рода других лиц, не являющихся их авто-
авторами. В этом направлении еще никому не удалось достичь успеха, хотя ему
отдали дань такие исследователи, как известный английский астрофизик
Зддингтон и один из создателей квантовой механики Гайзенберг.
Возвращаясь на более реальную почву, примиримся с тем
значением, которое имеет постоянная тонкой структуры в нашем
мире, и посмотрим, какие следствия можно извлечь из этого
для интересующего нас вопроса о масштабах атомных явлений.
1.4.3. Начнем с характерных длин. Две такие длины — клас-
классический радиус электрона и его комптонову длину волны — мы
уже ввели. Найдем теперь радиус первой разрешенной в модели
Бора орбиты, соответствующей числу л= 1. Обращаясь опять
к выписанным в 1.2.4 формулам кеплеровой задачи, найдем,
что этот радиус — его принято называть просто боровским ра-
радиусом и обозначать а-в — равен
_ е2 _ е2 2/гЧ2 _ /г2 _ Й2с2 е2 _ 1
ав ~~ 2 | Ei | ~~ 2 me4 me2 ei тс2 ~~ а2 4°'
Следующую масштабную ступеньку мы получим, если оценим
длину волны света, который может излучаться атомом при пере-
переходе электрона с одной орбиты на другую. Выписанная нами
в 1.3 постоянная Ридберга R выражена в энергетических едини-
единицах и представляет собой (взятую по модулю) энергию элек-
электрона на первой разрешенной орбите. Соответствующая этой
энергии по формуле E) частота (конечно, чтобы получить по
E) частоту, надо брать разность энергий на двух орбитах, но
поскольку мы интересуемся сейчас только порядками величин,
то можем взять просто энергию) будет равна © = -т-, и, следо-
1. ИСТОРИЧЕСКОЕ ВВЕДЕНИЕ 326
вательно, длина излучаемой электромагнитной волны составит
2пс 2псН Anh3 с . he Л2 . _1_ An
<в R оте1 е2 те2 а а3
В числах это дает
% ж 12- 137ав=1600ав = 800- 10"8 см = 800А;
это соответствует далекому ультрафиолету. Длины волн види-
видимого света еще примерно на порядок больше; это происходит
за счет того, что видимому свету отвечают переходы не на пер-
первую орбиту.
Таким образом мы пришли к целой шкале характерных для
микромира размеров, величина (одинаковых в логарифмическом
масштабе) «ступеней» которой определяется умножением на
обратные ступени постоянной тонкой структуры а:
~т~^2== •*о==2,8- 10 СМ. классический радиус электрона
лг- = —— = ^"*о = >*>у ' IV см- комптонова длина волиы электрона
aB = ~iruF = ~а? ^° == ^'^ ' ^ СМ- Боровский радиус
Я-~ — = —j- *o == J~ ав=== 0.8 • 10 СМ. длины волн испускае-
те мого атомами света
Третья ступень этой шкалы — боровский радиус — опреде-
определяет порядок размеров атомов и, следовательно, расстояние
между ними в твердых и жидких телах, где взаимное располо-
расположение атомов всегда близко к плотной упаковке.
Сравнивая теперь с третьей ступенью — четвертую, видим,
что длины испускаемых атомами волн много больше атомных
размеров. Выполнение такого неравенства было в электродина-
электродинамике условием применимости квазистационарного приближения.
Теперь мы можем сказать, что применимость условия квазиста-
квазистационарности — а, значит, и таких вещей, как разложение по
мультипольным моментам и т. п. — обусловлено малостью по-
постоянной тонкой структуры а, т. е. слабостью электродинамиче-
электродинамического взаимодействия.
1.4.4. Скажем еще несколько слов о характерных энергиях.
Первая характерная единица на шкале энергий — это собствен-
собственная энергия электрона тс2. Характерная энергия атома — по-
постоянная Ридберга в энергетических единицах R, связана с ней
соотношением
.. _9 I 9 9 1 л г» v»
326 ч. III. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
т. е. опять сравнительная малость атомной энергии связи обус-
обусловлена малым значением постоянной а.
1.5. Крушение классических представлений. Предложенный
Бором способ рассмотрения атомной модели составил основу
того, что называли потом «старой квантовой механикой». Как
мы видим, она представляла собой довольно своеобразную смесь
классической теории и дополнительных чисто рецептурных пра-
правил. В последующие 12 лет эта теория усиленно развивалась »
усложнялась. Были выработаны специальные рецепты о том, как
следует проводить квантование в случае многих степеней сво-
свободы («квантовать» полагалось все степени свободы, отвечаю-
отвечающие финитным движениям), проводилось обобщение на сложные
системы типа молекул, вводились релятивистские поправки
и т. д.
Однако теория в такой форме явно была логически не завер-
завершена. Не всегда хорошо обстояло дело и в смысле сравнения
с опытом: некоторые системы упорно не поддавались расчету,,
иногда приходилось вводить вместо целых квантовых чисел —
полуцелые и т. п. Тем не менее роль этой теории в развитии
представлений, приведших нас от классического описания к со-
современной квантовой механике, трудно переоценить. Сейчас,
оглядываясь назад, мы знаем, что теория Бора осуществила наи-
наилучшее из возможных описаний квантовых объектов на клас-
классическом языке.
1.6. Следующий шаг был сделан в 1924 году де БРОЙЛЕМ.
Действуя по аналогии с электромагнитным излучением, для
которого, как мы уже упоминали, была выяснена необходимость
двойного — корпускулярного и волнового — описания, и исполь-
используя давно развитую ГАМИЛЬТОНОМ оптико-механическую
аналогию, де Бройль пришел к тому, чтобы сопоставить каждой
материальной частице — волну, частота и волновой вектор кото-
которой были бы связаны с энергией и импульсом частицы соотно-
соотношением
Й© = Е; Йк = р, F)
i-(?*-pr)
т. е. волну, которая описывалась бы выражением вида еп
Принимая для Е релятивистское выражение Е = с д/р2 + (rncf%
де Бройль получил, что фазовая скорость такой волны
JL
iPi
mc
всегда больше с, однако групповая скорость
da __ dE ср с2р
dk ~~ dp ~~ Vp2 W ~ ~Ё
2. СОСТОЯНИЯ. СЮПЕРПОЗИЦИЯ 327
как раз равняется скорости частицы v. Ему принадлежит также
замечание, что на «разрешенных» боровых орбитах уклады-
укладывается как раз целое число его волн. Однако ни уравнений для
его волн — т. е. динамики, ни выяснения того, какое отношение
эти волны имеют к частицам, у де Бройля еще не было.
1.7. Чуть позже, в 1925—26 годах, была открыта новая кван-
квантовая механика. Знаменательно, что открытие это было совершено
одновременно в двух формах:
Эрвином ШРЕДИНГЕРОМ в виде волновой механики
и
Вернером ГАЙЗЕНБЕРГОМ, Максом БОРНОМ и Паскуа-
лем ИОРДАНОМ в виде матричной механики.
Последующие два-три года были «героическим временем»
квантовой механики, периодом, в ходе которого она приняла
фактически уже современную форму. В этой работе чрезвычайно
велика была опять-таки роль Нильса БОРА, который нашел
правильную (вероятностную) физическую интерпретацию тео-
теории, в частности вопросов, связанных с процедурой измерения, а
также роль Поля Адриана Мориса ДИРАКА, придавшего мате-
математической форме теории весьма законченный и элегантный вид
(с точки зрения физика, а не математика).
2. Состояния. Сюперпозиция
2.1. Механическое описание какой-либо системы имеет два
аспекта:
во-первых, надо как-то описывать состояния системы в дан-
данный фиксированный момент времени и,
во-вторых, описывать изменение состояния со временем, то, что
мы собственно называем движением системы.
Классическая механика занимается по существу только вто-
вторым аспектом проблемы — именно изменения состояний во вре-
времени составляют предмет и кинематики и динамики. Что же
касается первого аспекта, то в классической механике он не
представляется подающим повод для размышлений, и от него
в лучшем случае отделываются замечанием, что состояние си-
системы полностью характеризуется заданием значений обобщен-
обобщенных координат и их первых производных по времени —обобщен-
—обобщенных скоростей — в некоторый момент.
Все новое, что привносит с собой квантовомеханическое опи-
описание, относится по существу к первому аспекту проблемы —
описанию состояний системы в фиксированный момент времени.
Наоборот, вся динамика может быть перенесена из классической
теории практически без сколько-нибудь существенных измене-
изменений. Впрочем, как мы увидим ниже, как раз динамические
328 ч. III. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
проблемы оказываются в квантовом описании в каком-то смы-
смысле тривиальными.
2.2. Откуда же берутся те новые моменты, которые возни-
возникают при переходе от классического описания к квантовому? Их
источником является логический анализ тех способов, которыми
мы устанавливаем соответствие между математической теорией
и существующими в природе объектами. Значения координат и
скоростей, фигурирующие в классическом описании состояния,
надо измерить. Спрашивается, можно ли, хотя бы в принципе,
провести сколь угодно точное измерение так, чтобы'сам процесс
измерения не изменил измеряемой величины?
В классической механике на этот вопрос неявно отвечали
положительно. Поэтому утверждения:
(а) Мы измерили (в каком-то порядке) у некоторой системы
все координаты и импульсы и получили для них некоторые зна-
значения {с};
(Р) Координаты и импульсы системы имеют некоторые зна-
значения {с};
и (у) Если мы измерим у системы ее координаты и импульсы
(в каком бы то ни было порядке), то наверняка получим для
них некоторые значения {с}
в классической механике эквивалентны*).
Проведенный в 20-х годах подробный логический анализ этой
проблемы, в детали которого мы не будем вдаваться, привел к
тому выводу, что на самом деле это не так: измерение всегда
возмущает измеряемую величину **). Поэтому в квантовой меха-
механике утверждения (а) и (у) оказываются, как правило, различ-
различными, а утверждение (Р) без дальнейших пояснений — вообще
непонятным.
*) Во всех трех утверждениях речь идет, разумеется, об одном и том
же фиксированном наборе значений {с} в одни и тот же момент времени.
**) Суть дела состоит в том, что у нас нет достаточно «нежных» агентов
для наблюдения за частицами. С житейской точки зрения, при рассмотрении
макроскопических тел мы всегда можем сказать: «Мы совсем ничего не будем
делать с интересующим нас объектом, мы только посмотрим на него». Но
«посмотреть» — это значит дать рассеяться на интересующем нас объекте
какому-то числу световых квантов, а у иих есть энергия и импульс (A),
C)), которыми оии могут неконтролируемо обмениваться с измеряемым объ-
объектом, возмущая тем самым значения его динамических переменных.
Тут существует некоторая аналогия с теорией относительности. Подобно-
тому, как все ее логическое здание возведено на том допущении, что суще-
существует максимальная скорость любых взаимодействий, и достаточно допустить
существование хоть одного сигнала, распространяющегося быстрее, чтобы все
оно рухнуло, так и для квантовой механики существенно, что все объекты
в природе подчиняются квантовым условиям A), C). Достаточно было бы
одного не подчиняющегося им объекта, чтобы для всех оказались бы воз-
возможными сколь угодно мало возмущающие измерения.
2. СОСТОЯНИЯ. СЮПЕРПОЗИЦИЯ 329
В дальнейшем мы будем понимать под (Р), т. е. под словами:
«некоторая величина имеет определенное значение» утвержде-
утверждение (у), точнее, что при измерении этой величины, выполненном
до всякого другого измерения, мы наверняка получим интере-
интересующее нас значение. Поэтому, в частности, для проверки
утверждения (р) для п величин нам необходимо иметь не менее
я экземпляров рассматриваемой системы — ведь после первого
измерения всякий экземпляр уже портится.
Итак, в том, что касается проблемы описания состояний, из
ряда мысленных экспериментов, обобщающих накопленный к
20-м годам experience о поведении атомных частиц, можно было
только сделать вывод негативного характера: состояния в кван-
квантовой механике нельзя описывать заданием значений всех коор-
координат и импульсов (или скоростей) в некоторый момент вре-
времени. Более того, можно было утверждать, что отвечающие
одной степени свободы координата и импульс либо вообще не
существуют одновременно, либо — во всяком случае — не могут
быть одновременно измерены. Это утверждение известно под
именем принципа неопределенности. Он был сформулирован
Гайзенбергом в 1927 году.
ЗАМЕЧАНИЕ: Дополнительность корпускулярно-волнового опи-
описания — «корпускулярно-волновой дуализм» — есть, конечно, то-
тоже проявление приниципа неопределенности. При квантовомеха-
ническом описании света мы можем выбрать в качестве канони-
канонически сопряженных переменных «числа заполнения» (грубо
говоря — число фотонов) и фазу волны, — а как раз от разно-
разностей фаз и зависит критическое для волновой картины явление
интерференции. Поэтому интерференцию можно наблюдать
лишь тогда, когда число фотонов неопределенно, а при извест-
известном числе фотонов нет интерференции. |
2.3. Итак, согласно принципу неопределенности мы никогда
не можем знать о системе столько, сколько мы знаем о ней в
классической теории, мы никогда не можем однозначно предска-
предсказать результаты всех измерений, которые можно провести над
системой.
В квантовой теории задать состояние системы — это значит
знать о ней столько, что любые дополнительные сведения мо-
могут быть включены лишь ценой потери некоторых из уже
включенных,
т. е. уметь однозначно предсказать результаты стольких изме-
измерений, что возможность предсказать однозначно результат изме-
измерения еще какой-либо физической величины, не являющейся
функцией первых, может быть достигнута лишь ценой отказа
330 ч. III. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
от однозначности каких-либо из уже сделанных предска-
предсказаний *).
Итак, для системы, находящейся в некотором известном со-
состоянии, мы можем однозначно предсказать результаты изме-
измерений лишь некоторых динамических переменных; результаты
измерения остальных динамических переменных в том же со-
состоянии не могут быть предсказаны однозначно: если мы будем
проводить одно и то же измерение несколько раз (для этого,
конечно, необходимо несколько идентичных экземпляров систе-
системы, находящихся каждый в том же состоянии), то будем полу-
получать разные результаты. Поэтому приходится говорить о вероят-
вероятности получить при такого рода измерениях тот или иной ре-
результат. Эти вероятности, как мы увидим ниже, теория действи-
действительно позволит определить.
2.4. Важнейшей отличительной чертой состояний квантовой
теории является то, что система, находящаяся в некотором со-
состоянии, может в то же время частично находиться и в других.
Чтобы понять, о чем идет речь в этом утверждении, рассмотрим класси-
классический пример с поляризацией колебаний.
ПРИМЕР: Пусть у нас есть колебания, допускающие поляризацию, — все-
равно какие: может быть, чистая механика, например шарнк, подвешенный5
иа нити, или же электромагнитная система — свето-
световая волна, в которой электрический вектор можег
колебаться в двух направлениях, — и пусть «изобра-
«изображающая точка» движется по кругу, т. е. пусть
х = л0 cos at, у = г0 sin at,
то есть
г = {r0 cos at, rosinat}.
Это движение можно записать в виде суммы двух.
разложение цир- Движений: =
кцлярно поляри-
поляризованных КОЛеба- т- е- состояние круговой поляризации можно предста-
„ вить в виде суммы, сюперпозиции двух состояний,.
HUU на ПЛОСКО плоско поляризованных вдоль осей х и у. Эти состоя-
состояло ляризованные ния реально существуют, их можно выделить под-
подходящим анализатором (например, поляроидом»
в случае света) — после прохождения анализатора останется только одно,
плоско поляризованное состояние.
*) Так, например, из принципа неопределенности прямо следует, что если-
система с одной степенью свободы находится в таком состоянии, когда мы
можем точно предсказать результат измерения ее координаты, то мы не мо-
можем однозначно предсказать результат измерения импульса; если же переве-
перевести ее в такое состояние, в котором измерение импульса наверняка приведен-
к определенному результату, то в этом новом состоянии в результате измере-
измерения координаты нельзя будет сделать никаких определенных утверждений..
Равным образом, поскольку энергия есть, вообще говоря, функция и коорди-
координаты и импульса, то в состоянии, в котором можно точно предсказать резуль-
результат измерения координаты, нельзя сделать однозначных предсказаний о. зна-
значении энергии.
2. СОСТОЯНИЯ. СЮПЕРПОЗИЦИЯ 331
Но неправильно было бы считать, что циркулярно поляризованное со-
состояние «состоит» из двух состояний, плоско поляризованных по осям х и у,
в том, скажем, смысле, в котором стол состоит из столешницы и ножек или
атом водорода — из протона и электрона. С равным правом можно было бы
рассматривать циркулярно поляризованное колебание как сюперпозицию по-
поляризованных плоско в других направлениях, скажем по ^ и Ч^. Более того,
циркулярно поляризованное состояние ничем не менее элементарно, чем пло-
>ско поляризованные: можно, наоборот, считать, что плоско поляризованное
состояние есть сюперпозиция двух состояний, поляризованных по кругу
{rocosco/, 0} = — {го cosat, r0 sin <?>t}r + -х- {ra cos со/, — r0 sin co^Ji- I
ЗАМЕЧАНИЕ: В классической теории, с которой мы имели
дело в этом примере, можно было считать, что циркулярно
поляризованный свет частично проходит через «плоский» анали-
анализатор, а плоско поляризованный — частично проходит сквозь
«циркулярный» анализатор. В квантовой теории имеется очень
существенное отличие. В этом случае написанные соотношения
надо относить к одному фотону. Но один фотон может только
либо пройти «целиком» через анализатор, либо не пройти. По-
Поэтому наши формулы будут относиться теперь к вероятностям
того, что циркулярно поляризованный фотон пройдет через пло-
плоский анализатор или наоборот. |
При сюперпозиции двух квантовомеханических состояний об-
образуется такое состояние, что промежуточными для него будут
не рззультаты наблюдения, а вероятности определенных ре-
результатов.
Принцип сюперпозиции: Если измерение некоторой вели-
величины в состоянии А всегда дает результат а, а в состоянии В —
результат Ь, то сюперпозиция А п В даст состояние, в котором
в результате измерения той же величины может быть получено
либо а, либо Ъ с некоторыми вероятностями.
Итак, мы видим, что при переходе к квантовому описанию
физической системы придется оперировать с совершенно но-
новыми для классической теории понятиями: состояниями, удов-
удовлетворяющими принципу сюперпозиции, измерениями динами-
динамических величин, не приводящими к одному определенному ре-
результату, вероятностями частных результатов измерений. Для
дальнейшего развития этого описания надо поставить физиче-
физической теории в соответствие некоторую математическую схему,
придумать некоторую математическую модель, в которой этим
новым физическим понятиям будут соответствовать какие-то
математические объекты. Эта работа, в которой наша воспитан-
воспитанная на макроскопическом опыте интуиция не сможет нам по-
помочь, займет еще и несколько следующих параграфов.
332 ч- "'¦ ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
3. Векторы состояния и операторы
3.1. Попробуем ставить состояниям системы в соответствие
векторы | ) *) некоторого (пока неизвестно какого) линейного
пространства над полем комплексных чисел, причем каждому
вектору будем ставить в соответствие одно состояние, и состоя-
состояниям, которые физически нельзя различить и которые, поэтому,
надо считать одним и тем же состоянием, будем (с одной ого-
оговоркой, которая сейчас будет сделана) ставить с соответствие
один вектор. Внутри символа | ) вектора мы будем при необхо-
необходимости располагать значки, отличающие один вектор от другого.
Мы сознательно не хотим пока детализировать дальнейшие свой-
свойства вводимого векторного пространства, пока то не будут
заставлять нас делать какие-либо физические требования, кото-
которые будут возникать по мере дальнейшего установления соответ-
соответствий математической модели с физическими объектами**).
Итак, мы приняли, что отвечающие состояниям векторы | )
(мы будем иногда говорить «кет-векторы») можно складывать и
умножать на комплексные числа. Мы примем далее, что сюпер-
позиции двух состояний А и В отвечает образование линейной
комбинации отвечающих этим состояниям векторов:
\R) = Cl\A)+c2\B). ¦ G.1)
Нам придется рассматривать не только конечные суммы, но и
ряды:
|/?) = с1|Л1) + с2|Л2>+с3|Лз)+ ... G.2)
или даже, если состояния зависят от непрерывного параметра,
интегралы:
$ G.3)
вопросов сходимости или существования которых мы пока не
затрагиваем.
*) Мы будем последовательно использовать терминологию и обозначе-
обозначения, разработанные Дираком (P. A. M. Dirac) в его классической книге
«Принципы квантовой механики», вышедшей в свет в 1930 году. Последний
русский перевод (с 4-го английского издания) был опубликован в 1960 г.
**) Тут сказывается коренное различие физического и математического
подходов. Математик всегда может начать рассмотрение теории с набора
аксиом, из которых остается затем лишь выводить строгие логические след-
следствия. Физик лишен такой свободы, он не может назначать аксиомы своей
теории по произволу — ведь их следствия должны соответствовать обнаружи-
обнаруживаемым на опь1те свойствам реального мира — и он не может знать заранее,
какая именно математика для этого нужна. В физических теориях индук-
индуктивная часть составляет не менее важную долю, чем дедуктивная, и эта пер-
первая, естественно, никогда ие может быть проведена с той строгостью, что>
вторая.
3. ВЕКТОРЫ СОСТОЯНИЯ И ОПЕРАТОРЫ 333
Соотношение, скажем, G.1) симметрично во всех трех век-
векторах— если состояние R есть сюперпозиция состояний А и В,
то В есть сюперпозиция состояний А и R и т. д.
3.1.1. Если провести сюперпозицию состояния с ним самим,
то согласно G) такому состоянию будет отвечать вектор
с1\А) + с2\А) = (с1 + с2)\А).
Но в образующемся при такой сюперпозиции состоянии значе-
значения всех динамических величин будут теми же, что и в исход-
исходном. Поэтому надо принять, что вектор
с | А); с ф 0 описывает то же состояние, что и | А).
ЗАМЕЧАНИЕ 1: В этом пункте квантовомеханическая сюпер-
сюперпозиция отличается от классической сюперпозиции, например,
электромагнитных волн. |
ЗАМЕЧАНИЕ 2: Поэтому иногда говорят, что состояниям отве-
отвечают не векторы, а лучи. Последнее, однако, не совсем удобно:
хотя векторы
\ А) и а\А) или, соответственно, \ В) и Ь\ В)
и описывают соответственно одни и те же состояния, но линей-
линейная комбинация
не будет, конечно, отвечать тому же состоянию, что и комби-
комбинация
сх • а | А) + с2 • Ь | В)
с теми же самыми С\ и с2, если только афЪ. Таким образом,
чтобы не нарушать соотношений линейной зависимости, можно
помножить все векторы состояния только на одинаковое ком-
комплексное число. Поэтому, например, конкретная сюперпозиция
состояний А и В определяется двумя вещественными парамет-
параметрами. 1
Теперь следовало бы ввести в нашем пространстве метрику,
т. е. скалярное произведение. Оказывается, однако, что это удоб-
удобнее делать не непосредственно, а обходным путем.
3.2. Введем сперва линейные скалярные функции векто-
векторов | ):
Ф(|Л», такие, что <р(с,| А) + с2\ й» = с,ф([ А)) + с2ср(| В». (8)
Сумму и произведение на число этих функций определим обыч-
обычными условиями
Ф2)(|» ф1(!» + ф2(|)), |
(Сф)(М» = с.фAЛ» Ь.ля любого | Л). (9)
334 ч. III. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
Тогда ф тоже будут образовывать линейное векторное простран-
пространство, сопряженное (иногда говорят — дуальное) исходному. Бу-
Будем называть векторы этого пространства со-векторами *) или
«бра-векторами», употреблять для их обозначения значок ( |,
зеркально симметричный обозначению кет-вектора (внутри него
могут помещаться индексы, служащие, чтобы отличить один
со-вектор от другого) и писать
Ф(|Л)) = E|Л), ¦ (8а)
рассматривая значение функции ф как скалярное произведение
со-вектора на вектор. Для этого произведения, очевидно,
(9а)
Мы примем, кроме того, что
если (В\Р) = 0 для любого | Р), "|
то <й| = 0. ) '10)
ЗАМЕЧАНИЕ-. Участвующие в этих определениях слова «для любого |Я>»
нуждаются, строго говоря, в пояснениях. Вопросов не возникало бы, если
бы в нашем пространстве {| )} было бы не более конечного числа линейно
независимых кет-векторов. В большинстве задач квантовой механики это не
Так — число линейно независимых векторов бесконечно. При этом вместо
слов «любой вектор» следовало бы говорить о полной системе, разрешенных
свойствах коэффициентов разложения по ней и т. п. Дело осложняется еще
и тем, что в квантовой механике вопрос полноты — это вопрос не чисто ма-
математический, а иногда и физический: система, полная в одной постановке
задачи, может не оказаться таковой в другой. |
3.3.1. Итак, мы ввели скалярные произведения со-вектора
на вектор (бра-вектор слева, кет-вектор— справа!). Скалярных
же произведений двух кет-векторов или двух бра-векторов у нас
нет. Вместо этого будем теперь считать, что между пространст-
пространствами векторов и со-векторов установлено взаимно однозначное
антилинейное соответствие ( ] = .F(| )), такое что
= c'F{\A)).
J
Мы будем отмечать наличие этого соответствия, используя в
обозначении вектора и соответствующего ему со-вектора одну
и ту же букву (или группу букв) внутри значка:
F(\A)) = (A\. A1.3)
*) Термин предложен В. А. Фоком.
3- ВЕКТОРЫ СОСТОЯНИЯ И ОПЕРАТОРЫ 335
3.3.2. Теперь мы можем сопоставить каждому состоянию А
не только вектор \А), но и соответствующий ему со-вектор
(А\ *). Поэтому для описания двух состояний А и В можно
теперь привлечь
векторы: | А) и [ В), со-векторы: (Л | и (В |,
из которых можно образовать смешанные скалярные произве-
произведения:
(В | А) линейное в | Л) и антилинейное в | В),
(Л | В) антилинейное в | Л) и линейное в | В),
((Л | В))* линейное в | Л) и антилинейное в | В),
— т. е. мы можем связать с двумя состояниями целых два
числа, линейные в первом и антилинейные во втором. Это, как
мы увидим ниже, слишком много для физических целей, что>
побуждает нас наложить на вводимое соответствие F между
векторами и со-векторами условие
(В\А) = ({А\В))*. !12.1>
Из него следует, что для \В) = \А) : ((Л |Л))* = (Л |Л), т. е.
(Л|Л) вещественно. Мы потребуем еще большего, наложив вто-
второе условие
<Л|Л}>0 для \А)=фО. A2.2)
ЗАМЕЧАНИЕ 1: Естественно, что мы могли бы с тем же успе-
успехом и не прибегать к обходной конструкции с сопряженным про-
пространством, а прямо ввести в пространстве кет-векторов мет-
метрику. Условия A2) означали бы тогда: ( .1) эрмитовость этой
метрики и ( .2) ее положительную определенность. |
ЗАМЕЧАНИЕ 2: Зачем же нам понадобилась обходная кон-
конструкция с сопряженным пространством? Дело в том, что, каза-
казалось бы излишняя с точки зрения математики, она совершенно
естественна физически. При сопоставлении квантовой механики
с опытом состояния выступают как бы в двух «ипостасях» — с
точки зрения их наблюдения и с точки зрения их «приготовле-
«приготовления». Этим двум сторонам физического проявления состояний
как нельзя лучше отвечает двойная математическая модель бра-
и кет-векторов, связанных соответствием A1). Следует еще под-
подчеркнуть, что физически описание с помощью бра- и кет-векто-
*) Такую пару вектора \А) и со-вектора (Л| называют (взаимно) адъ-
юнгированными или сопряженными.
336 ч. III. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
ров должно быть совершенно симметричным *) (Это есть прояв-
проявление изотропии времени.)—как раз это требование находит
себе выражение в условии A2.1) эрмитовости метрики. Что же
до условия A2.2) положительной определенности метрики, то,
как мы увидим ниже, оно необходимо для возможности вероят-
вероятностной интерпретации теории. |
3.3.3. Скалярное произведение сопряженных векторов позво-
позволяет ввести — в обоих, бра- и кет-, пространствах— норму,
полагая
^ША>. A2а)
С ее помощью можно уменьшить произвол, который был у нас
в сопоставлении векторов состояниям. Именно, мы можем сопо-
сопоставлять всем состояниям только нормированные векторы \А)
такие, для которых || |Л)||= 1, после чего останется лишь про-
произвол в выборе фазового множителя:
\А)-+\А)е1\ y<=R. A2b)
Впрочем, пользоваться только нормированными векторами со-
состояния не всегда удобно и, главное, не всегда возможно. Как
мы увидим, нам придется включить в рассмотрение и ненорми-
руемые состояния, которым отвечают векторы с бесконечной
нормой.
3.4.1. Следующий объект, который (математически) естест-
естественно ввести в нашем векторном пространстве, это линейные
*) Поэтому «сопряженное» пространство — это не -совсем то, что имеют
в виду под этим словом в функциональном анализе, где между простран-
пространством функций определенного рода н «сопряженным» пространством функ-
функционалов на этих функциях нет однозначного соответствия. Так, например,
если пространство кет-векторов реализуется в форме пространства функций
/(дг) одной вещественной переменной, то можно ввести функционал
которому будет соответствовать бра-вектор (ядро функционала) 6(дг — дг0):
Ф [/ (*)] = \ dx б (х - дс°) / (*) = / (*„).
Значит, аналогичном объект, б(х— х<>), должен входить и в пространство
кет-векторов.
В этой связи соотношение между взаимно сопряженными кет- и бра-век-
торамн гораздо ближе соотношениям между контра- и коварнантными век-
векторами в аффинной геометрии пространства конечного числа измерений.
3. ВЕКТОРЫ СОСТОЯНИЯ И ОПЕРАТОРЫ 337
рфу, значение \G) которых можно рас
как действие на аргумент \А) линейного оператора:
причем
вектор-функции, значение \G) которых можно рассматривать
\А) й
и
а {с, | Ах) + с21 А,}} = с,а | Л,) + с& \ А2)
а = 0, если а|Я) = 0 для любого \Р).
A3)
Назовем, по определению, суммой и произведением операторов
операторы, удовлетворяющие
для любого | Р);
A4)
для любого | Р).
Хорошо известно, что такие определения не приводят к комму-
коммутативной алгебре, т. е. что, вообще говоря, ар Ф Ра.
Если ар = ра, то а и р коммутативны.
Отметим еще, что в качестве частного случая оператора можно
рассматривать умножение на комплексное число, поэтому комп-
комплексные числа можно при желании считать операторами.
3.4.2. Чтобы определить действие оператора на со-вектор,
рассмотрим скалярное произведение (В\ -а]/!). Оно является ли-
линейной скалярной функцией вектора \А), следовательно, равно
скалярному произведению на \А) некоторого со-вектора F'|
(В\{а\А)} (В\А).
Но со-вектор {В'\ должен быть линейной со-вектор-функцией
со-вектора (В\, (В'\-=(В\а'. Естественно положить а' = а. *)
Итак, мы пришли к тому, чтобы определить действие оператора
на со-вектор равенством
{(В\а}\А) = (В\{а\А)} для любого \А). A5)
Таким образом мы по сути допустили, что произведение бра-
векторов, операторов и кет-векторов ассоциативно и что, следо-
следовательно, тройное произведение может быть записано просто
как (В|а|Л). Последнее образование часто называют — по при-
причинам, которые станут ясны ниже, — матричным элементом опе-
оператора а между состояниями А и В. .
ЗАМЕЧАНИЕ к определениям A4.2) и A5): Мы фактически
определили и произведение операторов и произведение опера-
оператора на со-вектор по свойству ассоциативности. Такой путь
*) Разумеется, при этом (В\а ф F(a\B)) (f из A1)).
338 ч- 1!! ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
обладает тем недостатком, что нарушает симметрию векторов
и со-векторов, но в общей теории у нас просто не было иного
выбора. В частных задачах бывает, что можно определить про-
произведение оператора на со-вектор или операторов друг с другом
непосредственным и естественным образом, притом сохраняю-
сохраняющим желаемую симметрию. При этом может случиться, правда
в довольно экстравагантных ситуациях, что независимо опреде-
определенные произведения не оказываются ассоциативными, т. е. два
возможных определения оказываются различными. Каким из них
пользоваться — приходится тогда решать в каждом случае за-
заново*) . |
3.4.3. Введем теперь понятие сопряженного оператора. Век-
Вектор \Q), сопряженный со-вектору (Р|а = (<2|, зависит антили-
нейно от (Р\, значит линейно от \Р), поэтому получается из
\Р) действием некоторого линейного оператора. Обозначим этот
оператор через а+ и будем называть оператором, сопряженным.
оператору а. Итак, а+ определяется условием:
a+|P) = |Q>, если <Q | = <Р | а для любого \Р). A6)
1зовать скалярное произведение (В\{а+\Р)},
I) будет
(В | (а+ | Р)} = (В | Q> = «Q | В)У = «Р | а | В))*,
Если образовать скалярное произведение (В\{а+\Р)}, то в силу
A6) и A2) будет
то есть
Это соотношение с равным правом может служить в качестве
определения а+. Легко получить, что (а+)+ = а.
3.4.4. Если
а+=а, A7)
то оператор а называется эрмитовым или самосопряженным.
ЗАМЕЧАНИЕ: Строго говоря, здесь надо проводить различие между эрми-
эрмитовыми операторами, для которых достаточно A7), и самосопряженными,
определение которых требует еще дополнительных свойств областей опреде-
определения и значений операторов, но мы здесь не будем вдаваться в эти тон-
тонкости, изложение которых можно найти, например, в книге фон Неймана
«Математические основы квантовой механики». I
*) Указанной трудность может возникнуть только для векторов, не вме-
вдающихся в гильбертово пространство и неограниченных операторов, напри-
например для векторов и операторов, представляемых бесконечно-рядными матри-
матрицами (с неубывающими по мере роста номера элементами!)—тогда есть и
«естественное» определение произведения по правилу матричного умножения.
Ср. замечание в книге Бремермана, «Распределения, комплексные переменные
и преобразования Фурье», «Мир», 1968, дополнение.
3. ВЕКТОРЫ СОСТОЯНИЯ И ОПЕРАТОРЫ 339
Ясно, что оператор, сопряженный сумме, есть сумма сопря-
сопряженных операторов
!а+р)+ = а+ + р+.
Что есть оператор, сопряженный произведению? Для этого рас-
рассмотрим скалярное произведение
{В | р+а+ | А) = {(В | р+} | {а+1 А)} = (Q | Р) = ((Р | Q»* -
= ((Л | ар | В»* = (В |(ар)+| Л).
Итак,
+ + + + = Р+а+. Ц8)
Отсюда видно, что если | = |+ и т) = т)+ эрмитовы, то их произ-
произведение (|т])+ = г)| ф |г), вообще говоря, не будет таким. Од-
Однако можно утверждать, что
если Г = |; „+-„ |
то (grj + r|S)+ = (Ел + лБ); (Ел - п?) = - Aл - л!)- J
СЛЕДСТВИЕ: степень |™ эрмитова оператора \ эрмитова. 1
Докажем
ЛЕММУ 1: Если | = |+ и |m|P) = 0, | P) — фиксирован
то 11 Я> = 0.
ДОКАЗАТЕЛЬСТВО: Помножим равенство из условия слева на
(РЦт-2.
Следовательно, по A2.2), |т-1|Р) = 0. Далее по индукции. |
3.4.5. Специальный вид линейного оператора получится, если
образовать произведение кет-и бра-векторов, в котором кет-
вектор стоит слева:
\А){В\,
и считать, что действие такого образования на векторы и со-
векторы определяется сочетательным законом:
{! А)(В |}| Р> = | А){(В\ Р)}; (Q\ {| А)(В \) = {(Q\A))(B |.
Для такого оператора, по определению сопряжения в A6), {| А) (В \}+ | Я) =
= | Q), если (Q | = (Я | А) (В |. Но в силу антилинейности A1.2) соответствия
бра-векторов кет-векторам | Q) = {(Я | А)}* \ В) — {{А | Я)} | В) = | В) (А | Я).
Следовательно,
(+ < A9)
340 ч. in. элементы квантовой механики
3.4.6. В дальнейшем нам часто придется иметь дело с поня-
понятием проекционного оператора. Оператор Р называется проек-
проекционным оператором (или оператором проектирования, или,
совсем коротко, проекторам), если
Р+ = Р и Р2 = Р. B0).
Перечислим некоторые свойства проекционных операторов:
A) A-РJ=1-2Р + Р2=1 -Р, т.е.
A — Р) — проектор.
B) Для любого вектора \А):
C) Действуя на вектор, проектор может только уменьшить
его норму:
Для произвольного вектора |.4)
<Л|Л) = (Л|Р|Л) + (Л|1-Р|Л) = ]|Р|Л)|Р + ||A -Р)\А)Р,
где мы использовали свойства A) и B). Следовательно,
Комбинируя B) и C), полезно выписать двойное неравенство:
D) Пусть у нас имеется несколько проекционных операторов
Рг, г— 1, 2, ..., га, и пусть TiPr — Q, где Q —опять проекци-
г
онный оператор, Q2=Q.
Тогда
/W = 0 (гфг%
ДОКАЗАТЕЛЬСТВО: Рассмотрим норму произвольного вектора | Л). Для нее
можно написать:
= Е <Л I рг I л> > (А I рг I Л> + (А I рг> I Л) = || Рг \ А) |р + || Яг, 1 Л> f,
г
Выберем теперь в качестве \ А) вектор РГ\В), где \В)— опять произвольный
вектор. Тогда крайние элементы предыдущей цепочки дадут неравенство-
\Pr\B)f>\Pr\B)f + \Pr,Pr\B)f, из которого следует, что РГ,РГ\В) = О,
а значит, в силу произвольности \В), и PrPr, — 0. |
Справедливо, как легко видеть, и обратное утверждение:
Dа) Если проекционные операторы некоторого набора {Рг\
взаимно-ортогональны, РГРГ' — О, то ^j Pr — Q будет опять про-
г
екционным оператором.
4. ПРОБЛЕМА СОБСТВЕННЫХ ЗНАЧЕНИЙ 341
Если выбрать теперь в A9) | В) = \ А), то оператор |Л)(Л| будет эрми-
эрмитовым, (| Л)(Л|)+ = |Л)(Л|. Далее (| А){А |J = | А) (А | -(А | А). Поэтому, если
| Л) нормирован, то |Л)(Л| будет частным случаем проекционного оператора:
РА = \ А) (А | есть оператор проектирования в состояние | Л). B1)
Эти операторы будут играть ниже очень важную роль.
3.5. Мы ввели операторы в пространствах векторов состоя-
состояния, следуя естественному ходу математической, а не физиче-
физической мысли.
Действительно, физически казалось бы трудно найти какой-
либо смысл в соотнесении одному состоянию — другого, найти
какое-либо место операции, которая преобразует состояние си-
системы в некоторое новое состояние (Какие-либо аналогии можно
протянуть только к изменениям системы под действием преобра-
преобразований симметрии.).
Тем не менее мы сделаем теперь физическое допущение:
Динамическим переменным классической теории соответ-
соответствуют в квантовом описании линейные операторы в простран-
пространстве векторов состояния. При этом вещественным динамиче-
динамическим переменным отвечают эрмитовы операторы.
— допущение, физически еще менее естественное, так как трудно
себе представить, как это динамическая переменная, «действуя»
на состояние системы, может перевести его в другое состояние.
Однако, как мы сейчас увидим, оказывается возможным найти
совершенно убедительные точки соприкосновения так вводимых
динамических переменных с тем, что имеют в виду под этим
словом в классической теории.
Заметим еще, что с чисто алгебраической стороны основное
отличие «новых» динамических переменных от классических —
это их некоммутативность. Ниже мы увидим, что как раз это
отличие приведет нас к принципу неопределенности.
4. Проблема собственных значений
4.1. Когда мы говорили о состояниях, то отмечали, что вся-
всякая квантовомеханическая система может, в частности, нахо-
находиться в состоянии, в котором какая-либо динамическая пере-
переменная имеет совершенно определенное значение —т. е. можно
предсказать, что ее измерение наверняка приведет к одному
фиксированному результату. Естественно допустить, что в таком
состоянии изображающий эту переменную оператор ведет себя
в каком-то смысле подобно соответствующей классической ди-
динамической переменной. Но динамические переменные класси-
классической механики ничего не делают с состояниями. Поэтому ин-
интересно найти такие случаи, когда действие квантовой динами-
динамической переменной на какое-то избранное состояние системы
342 ч. III. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
состоит в «недействии» на него. Поскольку векторы сопостав-
сопоставляются состояниям с точностью до числового множителя, то
изображающий динамическую переменную оператор не будет
«действовать» на состояние, если действие этого оператора на
соответствующий состоянию вектор сведется к умножению этого
вектора на число.
4.2. Такие соображения приводят нас к рассмотрению урав-
уравнения
а\Р) = а\Р). B2)
Это уравнение, часто встречающееся во многих разделах мате-
математики, имеет специальное название — уравнения проблемы соб-
собственных значений (иногда, особенно в устной речи, употреб-
употребляют и принятый в других языках термин «Eigenwertproblem»;
мы будем иногда использовать сокращение EWP). Напомним,
что постановка EWP состоит в том, что оператор а считается
заданным и ищутся такое число а и ненулевой вектор \Р) (или
числа и векторы), которые удовлетворяли бы B2). Число а
называется тогда собственным значением («Eigenwert», EW)
оператора а, а вектор \Р) —собственным вектором («Eigen-
vektor») оператора а, принадлежащим собственному значению
а (или «относящимся» к собственному значению а). Наряду с
B2) бывает удобно рассматривать и EWP-y для со-вектора:
(Q\a = b{Q\. B2а)
Если одному собственному значению принадлежит несколько
линейно независимых собственных векторов
|Р1>, |Р2>, ..., \Рп),
то собственным вектором, отвечающим тому же EW-y, будет
и любая их линейная комбинация
Ci\Pi) + c2\P2)+ ... +сп\Рп).
Если оператор а есть число, а = k, то у него будет единст-
единственный EW a = k и любой вектор будет собственным, принад-
принадлежащим этому собственному значению.
4.3. В дальнейшем нас будет интересовать EWP практиче-
практически только для эрмитовых операторов \ = |+. В таком случае:
A) все собственные значения вещественны.
.ДОКАЗАТЕЛЬСТВО: В самом деле, тогда из B2) следует
В правой части здесь (Р\Р) вещественно и больше нуля, как норма, левая
же часть вещественна по правилу сопряжения матричных элементов A6а) и
эрмитовости g. Следовательно, вещественно и а. И
4. ПРОБЛЕМА СОБСТВЕННЫХ ЗНАЧЕНИЙ 343'
B) Co-вектор, сопряженный собственному вектору, есть соб-
собственный со-вектор, относящийся к тому же EW-y*).
ДОКАЗАТЕЛЬСТВО: Из
Эти два свойства позволяют провести:
УСОВЕРШЕНСТВОВАНИЕ ОБОЗНАЧЕНИЙ: Будем обозна-
обозначать собственные значения эрмитова оператора g той же буквой
в сопровождении какого-либо индекса или номера: ?', |п, \г и
т. п.; тем же самым числом будем отмечать и собственные век-
векторы, помещая его внутри символа кет- или бра-: ||') и т. п.
Если одному EW-y принадлежат несколько собственных векто-
векторов, то будем, при нужде, различать их, добавляя дополнитель-
дополнительные значки: |?'1), ... . В
Рассмотрим два собственных вектора оператора |, принадле-
принадлежащих разным EW-м.
Пусть: тогда:
и пусть
111") = I" 11") => (П111") = I" (Г 11").
Поэтому (Г -1") (Г ! ГО = 0 и, поскольку Г -1" Ф О, (Г I И = О-
Итак,
(ПГ') = 0 Для Г=^Е", т. е. B3)
C) Два собственных вектора, принадлежащих различным
собственным значениям одного оператора, ортогональны.
На вопрос о существовании решения проблемы собственных
значений для эрмитова оператора к сожалению нельзя дать
исчерпывающего ответа. Можно, правда, указать классы опера-
операторов, для которых EWP всегда имеет решения и притом доста-
достаточно много решений, чтобы из собственных векторов можно
было построить полную систему, однако эти классы оказы-
оказываются для квантовой механики слишком узкими.
4.4. Теперь настало время наполнить физическим содержа-
содержанием наш пока чисто формальный постулат о сопоставлении
динамическим переменным эрмитовых операторов. Отталкиваясь
от замечаний, сделанных в начале параграфа, мы потребуем для
этого, чтобы:
*) В общем случае неэрмитова оператора а этот со-вектор будет соб-
собственным со-вектором, принадлежащим сопряженному EW-y a'*.
344 ч- ш- ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
A) Если система находится в таком состоянии, что при
измерении некоторой динамической переменной | мы наверняка
получаем один определенный результат |', то это состояние
описывается собственным вектором оператора ? с собствен-
собственным значением ?'.
B) Обратно, если состояние системы описывается собствен-
собственным вектором эрмитова оператора |, принадлежащим EW-y ?',
то в результате измерения динамической величины ? обяза-
обязательно получится значение ?'.
C) Если система находится в произвольном состоянии, то
в силу принципа сюперпозиции мы можем рассматривать
это состояние как сюперпозицию различных собственных
состояний некоторого ?. Измерение извлекает тогда из этой
сюперпозиции какое-либо одно определенное состояние, систе-
система скачком переходит в него, и мы опять получаем в качестве
результата измерения одно из собственных значений ?', только
теперь мы уже не сможем заранее сказать, какое именно.
ЗАМЕЧАНИЕ: Поскольку мы можем измерять любую динами-
динамическую величину в каком угодно состоянии и всегда должны
получить при измерении какой-то результат, а в силу сделанных
допущений этот результат может быть только одним из EW-ob
соответствующего оператора, то это значит, что любое состояние
должно быть представимо в виде сюперпозиции собственных
состояний каждой физической величины, которую хотя бы з
принципе можно измерять. Но для этого надо, чтобы собствен-
собственные векторы отвечающего такой динамической переменной опе-
оператора образовывали бы полную систему. |
Динамические переменные, собственные состояния которых
образуют полную систему, мы будем называть наблюдаемыми.
4.5. Как записать утверждение о полноте набора собствен-
собственных векторов математически? Если наблюдаемая ? обладает
только дискретным спектром собственных значений, то полнота
требует, чтобы любой вектор \Р) мог бы быть записан в виде
\Р)=Т.\1')- Дискр. спектр B4.1)
г
Если спектр | непрерывен, то сумма заменяется интегралом:
1 Р) = J | Г) dl'. Непрер. спектр B4.2)
Если, наконец, у ? есть и дискретный и непрерывный спектр, то
= J I I'c) dl' + ? | I'd), Дискр. и непр. спектр B4.3)
4. ПРОБЛЕМА СОБСТВЕННЫХ ЗНАЧЕНИЙ 345
где индексы с и d указывают на принадлежность к непрерыв-
непрерывному или дискретному спектру. Заметим, что в разложении типа
B4.3) .непрерывный и дискретный спектры могут и перекры-
перекрываться. Мы не пишем в B4) никаких коэффициентов Сг, фигури-
фигурировавших, например, в формулах G). Дело в том, что всякая
линейная комбинация собственных векторов, принадлежащих
одному и тому же собственному значению gr, тоже будет соб-
собственным вектором, принадлежащим тому же EW-y. Поэтому
мы можем считать, что в правых частях B4) стоят как раз те
линейные комбинации, которые нужны, чтобы получить век-
вектор \Р).
4.5.1. Когда в разложении вектора по собственным векторам
есть непрерывный спектр, то встает вопрос о разумной норми-
нормировке. Пусть \Р) и \Q)—два вектора с разложением B4.2). Их
скалярное произведение будет тогда равно
Рассмотрим интеграл
Для |' Ф g" (!'р|!"<7) = 0 по свойству ортогональности. Следо-
Следовательно надо, чтобы {l'p\l"q) равнялось бы бесконечности —
иначе весь интеграл просто обратится в нуль. Поэтому норми-
нормируемые собственные векторы, принадлежащие EW-м непрерыв-
непрерывного спектра, нам совершенно бесполезны — их вклад в боль-
большинство интересующих нас выражений будет равен нулю. Мы
видим, что в таком случае приходится вводить собственные век-
векторы, не нормируемые в обычном смысле, и нормировать их
так, чтобы
&'р I Ъ"я) было бы ~ б (?' - I").
Постулируем, обобщая требование A2.2), что для векторов не-
непрерывного спектра всегда
\ dl" (I'p I Vp) > О, коль скоро V$Zt °' B5)
Дальнейшие подробности нормировки зависят от того, что за
векторы сами \Р) и \Q) и относятся ли они к дискретному или
непрерывному спектру какого-либо оператора.
4.6. Оглядывая два последних раздела, мы видим теперь,
каким нетривиальным и неожиданным образом вторгается по-
понятие линейного оператора в физическое описание явлений в
квантовой области.
Физически первичным оказывается не понятие самого опера-
оператора, а скорее понятие совокупности его собственных векторов
•346 ч. III. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
||') с принадлежащими им собственными значениями g', как
совокупности специальных состояний системы, в которых измере-
измерение величины | приводит всякий раз к определенным резуль-
результатам |'. Оператор, выражаясь геометрическим языком, возни-
возникает в обличье своих главных направлений и характеристиче-
характеристических чисел, его общая форма появляется только как вторичное
понятие при переходе в описании состояний физической системы
к их классификации по значениям какой-либо другой динамиче-
динамической переменной. Это отличие представляется столь сильным,
что иногда отказываются от проводимой в нашем изложении
тесной идентификации физической величины с отвечающим ей
оператором, предпочитая скорее идентифицировать ее с EW-ми
возникающих при измерении собственных состояний, так что при-
приходится считать, что физические величины не присущи изначаль-
изначально квантовым системам, а лишь возникают в процессе измерения.
Более того, в отличие от привычного в математике подхода,
вторичным представляется физику и понятие пространства век-
векторов состояния, в котором действуют операторы, — оно возни-
возникает для него просто как совокупность векторов, растягиваемых
всеми собственными векторами какой-либо наблюдаемой. Имен-
Именно последнее соображение удерживает нас от того, чтобы точно
оговорить свойства рассматриваемого пространства, прежде чем
начать изучение операторов, действующих в нем.
4.7. Мы уже говорили, что в общем случае затруднительно
сказать, можно ли набрать из собственных векторов того или
иного линейного эрмитова оператора полную систему, то есть
установить, является ли он наблюдаемой. Мы заключим этот
параграф разбором одного частного примера, в котором указан-
указанный вопрос можно исследовать до конца. Это случай, когда
эрмитов оператор удовлетворяет целому алгебраическому урав-
уравнению степени п.
4.7.1. Именно, докажем:
.ЛЕММУ 2: Если эрмитов оператор | удовлетворяет целому ал-
алгебраическому уравнению степени п:
М?-Ы(Б-Ы ••• (?-!») = о, B6)
т. е. если Qn(z)\A) = 0 для любого \А) и если
это — простейшее уравнение, которому он удовле-
удовлетворяет, т. е. не существует никакого Qn'(?) = 0 с
п' <п,
то
(а) оператор ? имеет точно п собственных значе-
значений;
4. ПРОБЛЕМА СОБСТВЕННЫХ ЗНАЧЕНИЙ 347'
(Р) все они различны (и вещественны)*);
(у) собственные-векторы ? образуют полную си-
систему.
ДОКАЗАТЕЛЬСТВО:
A) Собственными значениями могут быть только числа
sii • • • i Sn:
Для любого EW-a g' и собственного вектора ||') должно быть
О I V) = Qn F) I Г) = Qn (Г) I Г), т. е. Qn (Г) = О,
значит, Sj' есть одно из чисел |i, ..., §„.
Для дальнейшего запишем Qn(?) в одной из п форм
Qn(S) = (S-Ir)tfr(l); r=l, 2 п.
B) Каждое из чисел |г есть EW:
В самом деле, поскольку Rr(%) есть полином степени <п, то должеи
существовать вектор \А) такой, что Rr\A) Ф О, но (| — 1г)йг(?)|Л) =0.
Следовательно, все векторы #г(|)|.Л) ^=0 суть собственные векторы, при*
надлежащие EW-y tr**).
C) Все ?г различны:
В самом деле, если ?s — кратный корень B6), (? — |i)mSi (|) | Л) = &
для всех | Л), то для \ B) = SS\A) мы получим по лемме 1 нз (| — ls)m | В) =
= 0 =ф (| - ls) | В) = 0, откуда (? — Ы Ss (|) |Л> = 0 для всех | Л), т. е. %
удовлетворял бы уравнению степени ниже га.
D) Все !г вещественны: как собственные значения эрми-
эрмитова |.
E) Собственные векторы | образуют полную систему:
Введем операторы
r(S)~ Rri.tr)'
Поскольку (см. B)) RT переводит произвольный вектор в собственный век-
вектор | gr), то то же справедливо и для Pr (g). Рассмотрим теперь Р, (|). Для
любого | Л)
Следовательно, Р2Г — РГ. Следовательно, Рг — оператор про-
проектирования, точнее, оператор проектирования на собственное
подпространство, отвечающее EW-y |r.
*) То есть эрмитов оператор не может удовлетворять алгебраическому
уравнению, которое, будучи рассматриваемо как уравнение для чисел, имело
бы комплексные корни.
**) Заметим, что отсюда все A — \г) н RT(\) суть делители нуля в коль-
кольце полиномов оператора %.
348 ч- "I- ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
Вычислим 2] Рг (|). Рассмотрим для этого ^ Рг (z). где г не оператор,
г г
а (комплексное) число:
L Pr {Z) ~L Rr (lr) <* - lr) ~ Qn {Z) L («-|р)й,у
Г Г г
Но
1 1 у11
QnH (г-h) .-. (г-6») Zj г-g, Fr-Ei) ••¦ Fг —6»).'
без г
(В последнем равенстве проще всего убедиться, заметив, что обе его части —
аналитические функции с одинаковыми вычетами в совпадающих полюсах).
Следовательно, ^jPr(z) ^ 1. н0 поскольку эта функция — полином, то то же
г
справедливо и для аргумента |.
Итак:
2>,(S) = i- w
.r-l
Поскольку 1 есть проектор, то в силу свойства D) из 3.4.6 про-
проекционных операторов (*) означает, что все Рг ортогональны,
PrPf — 0 и, следовательно, осуществляют разбиение всего про-
пространства в прямую сумму ортогональных подпространств, каж-
каждое из которых составлено только из собственных векторов
оператора |, относящихся к одному EW-y. Итак:
Любой вектор \А) можно записать как
)tr)
т. е. в виде суммы собственных векторов ||г). Полнота дока-
доказана *). 1
Приведем еще представление для самого оператора |. По-
Поскольку для любого \А)
*) Простота, с которой в нашем примере удалось достичь исчерпываю-
исчерпывающих результатов, объясняется тем, что он соответствовал по существу слу-
случаю конечномерного пространства. В самом деле, размерность собственных
подпространств каждого EW-та нигде не входила в наше рассмотрение, и
все доказательство проходило бы точно так же, если бы мы рассматривали
вместо самого векторного пространства его представление, в котором каж-
каждому собственному подпространству соотносился бы единственный (с точ-
точностью до числового множителя) собственный вектор — а это и был бы, в
силу конечности п, случай эрмтова оператора в конечномерном пространстве.
Уравнение B6) было бы тогда уравнением Гамильтона — Кэли с только ве-
вещественными корнями, которому удовлетворяет каждый эрмитов оператор в
конечномерном пространстве, а условие отсутствия уравнения низшей степени
для рассматриваемого оператора означало бы исключение случая кратных
корней, в котором эффективная размерность могла бы быть еще уменьшена.
4. ПРОБЛЕМА СОБСТВЕННЫХ ЗНАЧЕНИЙ 349
ТО
l=tlrPtr> если 5>sr=l, B7)
r-l г
где мы написали Р% вместо Рг, чтобы подчеркнуть смысл про-
проектирования в подпространство, отвечающее собственному зна-
значению |г.
4.7.2. Справедлива и обратная теорема:
ЛЕММА 2а: Если
A) эрмитов оператор обладает лишь конечным
числом собственных значений ||, .... ?„ и
B) является наблюдаемой (т. е. обладает полной
системой),
то он удовлетворяет уравнению
(i-i,) ... (|-у=о. (*)
Действительно, любой вектор можно разложить по полной
системе собственных векторов оператора |, поэтому, после при-
применения к этому разложению левой части (•), в каждом члене
разложения хотя бы один из множителей в (*) обратится в нуль.
4.7.3. Лемма 2 дает еще одно свойство проекционных опера-
операторов. Поскольку всякий проектор удовлетврряет уравнению
то
E) Каждый проекционный оператор имеет полную систему
собственных векторов, отвечающих EW-ам О и 1, т. е. он есть
наблюдаемая.
4.8. ЗАМЕЧАНИЕ: Разобранные примеры указывают на
естественную иерархию, существующую среди объектов — кото-
которые мы называем наблюдаемыми или линейными эрмитовыми
операторами с полной системой собственных векторов—, при-
призванных описывать в квантовой механике физические величины.
Низшую — простейшую — ступень в ней занимают вещественные
числа, которые можно, как мы видели, рассматривать как эрми-
эрмитовы операторы, все (образующие полную систему) собственные
векторы которых относятся к единственному EW-y. Вторую сту-
ступень занимают проекторы — наблюдаемые, обладающие двумя
собственными значениями; можно сказать, что это — простей-
простейший квантовый объект, выходящий за рамки классики, где все
динамические переменные изображались числами. На третьей
ступени мы находим объекты, изучавшиеся в лемме 2: эрмитовы
операторы, удовлетворяющие целому алгебраическому уравне-
уравнению конечной степени. Согласно лемме они всегда обладают
350 ч. III. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
полной системой собственных векторов, распределяющихся по
точно п собственным значениям. Отметим, что объекты первых',
трех ступеней можно реализовать как эрмитовы операторы в
пространстве конечного числа измерений, поэтому для обраще*
ния с ними было бы достаточно привлечь средства обычной век^
торной и тензорной алгебры. Естественным — и необходимым
для физики — обобщением объектов третьей ступени являются
наблюдаемые, обладающие счетной последовательностью EW-ob/;
т. е. наблюдаемые с чисто дискретным спектром. Для реализа-т
ции этих, занимающих четвертую ступень иерархии, объектов,;
приходится прибегать к построению гильбертова пространства.*
Однако и этого оказывается недостаточно — поскольку в природа
существуют физические величины, при измерении которых может]
быть, найдено любое вещественное число из некоторого интер-i
вала, то нашу иерархическую лестницу приходится дополнить^
пятой ступенью, наблюдаемыми с непрерывным спектром, обла-j
дающими континуумом собственных значений. |
5. Функции наблюдаемых
5.1. В нашем примере мы уже имели дело с функцией Qn{\)\
наблюдаемой \ — полиномом, определявшимся чисто алгебраи-j
ческими действиями сложения и умножения. Из определения^
этих действий следовало, что всякий собственный вектор наблю-
наблюдаемой Ъ, есть в то же время и собственный вектор Qn(E) и при!
том отвечающий собственному значению Qn(?')> если он отве-ч
чал EW-y I' наблюдаемой |, т. е. что '.¦
каждый | Г) есть | (Qn (?))'> и (Qn (?))' = Qn (Г). B8?:
ЗАМЕЧАНИЕ: Обратное, вообще говоря, неверно. Действи-
Действительно, рассмотрим, например,
где l\W = ll\h); l\h) = h\h). \
Тогда собственными векторами Q(|) будут не только \li) и;
\12), но и \а) = ai||i) + агЦг) с произвольными а{ и а2 — по-;
следние векторы не суть собственные векторы \. Все эти век-5
торы будут относиться к одному EW-y Q(l), равному X. |
Если Q(l) имеет одинаковые EW-ы для двух или несколь^
ких собственных векторов оператора |, то линейные комбинаь
ции этих векторов также будут собственными векторами Q(g)f
Ясно, что прямое рассуждение непосредственно переносится
не сходящиеся (как?!) ряды по %.:
/Ш = со+С1Е + с262+ .. B9>
-для них тоже |Г)Ф|/(Г)> и (/(б)O = /(!')•
5. ФУНКЦИИ НАБЛЮДАЕМЫХ
351
5.2. Желательно, однако, не быть привязанным к сходимости
ряда и вообще к разложению в ряд. Того ради можно дать
другое определение функции от наблюдаемой.
Пусть f(x)—некоторая функция вещественного перемен-
переменного х, определенная для х, равного любым собственным зна-
значениям %' некоторой наблюдаемой | и однозначная. Тогда мы
определим \{?) как такой линейный оператор, для которого
f (I) \l') = f &') 11') Для всех 1?'> наблюдаемой g. C0)
Действие же f(|) на произвольный вектор \Р) определится раз-
разложением B4)
f(l) | Р) = J dl' f (Г) I I'c) + ? / (У | lTd). C0a)
ЗАМЕЧАНИЕ: Функция f(x) не обязательно должна быть вещественно-знач-
на, она может принимать и комплексные значения. В последнем случае со-
сопряженный оператор (f(t))+ естественно' 'определить уравнением, сопряжен-
сопряженным к C0)
+
где i*(x)—функция, комплексно-сопряженная f(x). С другой стороны, по
общему правилу (i'l (/(§))+ есть бра-вектор, сопряженный кет-вектору
/(i)IS') ==ftl') II'). и мы опять приходим к тому же выражению
Требование однозначности f(x) весьма существенно. При его
нарушении возможны разнообразнейшие парадоксы.
5.3. Чтобы разобраться в трудностях, которые могут при этом возникнуть,
рассмотрим один простейший пример, который естественно возникает из по-
подробно рассмотренного случая, когда некоторая наблюдаемая \ удовлетворяет
целому алгебраическому уравнению. Пер- .
вая существенная нетривиальное™ полу- 11-
чается, если i удовлетворяет уравнению
3-ей степени, скажем
Мы можем тогда ввести три проекционных
оператора (ср. 4.7.1) п\, Па и Лз'-
- h) (ii - Ь) '
(••) О
%h%% f
Каждый из этих операторов является функцией | в определенном выше
смысле, причем никаких вопросов пока не возникает, поскольку Ki(x)—одно-
Ki(x)—однозначные функции х. Кроме того, я;(|) являются наблюдаемыми, поскольку
fti{x) — вещественны.
5.3.1. Вопросы начнутся, если мы захотим построить обратные функции,
выражающие, скажем, | в виде функции от nt, — эта функция, рассматри-
352 ч. III. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
ваемая как функция числового аргумента, неоднозначна. Действительно, из
(**) мы имеем для ?
> h +1» ± Vfe - ЬУ + 4 A, - Ь) A. - Ь) я,
ь— 2 ¦ '"г*
Поэтому, если обозначить буквой S совокупность всех «ветвей» |, то
для я,=О | 2 -\ltt
для n'=l=j (g2 + 6з) ± Bgi - (Ь +Ы) '*
Собственному значению я,' = 1 принадлежит единственный собственный
вектор *) — тот самый, который первоначально был собственным вектором %
с EW-ом |i — будем обозначать его |1). Поэтому ясно, что появившиеся
в ( + +) Два разных значения для EW-a В в этом состоянии могут отвечать
только образованию двух ветвей функции в том же смысле, что и для функ-
функции обычного непрерывного числового аргумента. Это еще сравнительно без-
безобидно.
5.4.2. Гораздо сложнее ситуация с собственным значением п'{ = 0—этому
собственному значению отвечают два собственных вектора ?, будем их назы-
называть |2) и |3). Возникает вопрос, можем ли мы выбирать различные ветви
числовой функции для разных собственных векторов, относящихся к одному
EW-y?
5.3.2.1. Если ответить на него отрицательно, то все опять сведется к вы-
выбору ветви (конечно, для, например, двузначной в обычном смысле функции
оператора, имеющего п различных EW-ов, при этом получится 2П ветвей!).
Однако при таком определении мы вообще не сможем обратить функцию
Jii(?) — ни одна из ветвей S не даст старой наблюдаемой ?: ведь состояния
|2) и |3) относятся к одному собственному значению оператора Ль а для ?
они имели разные EW-ы |4 и |г-
5.3.2.2. Если же разрешить брать различные ветви числовой функции для
разных собственных векторов, принадлежащих одному EW-y, то «число вет-
ветвей» функции от оператора поразительно возрастает, но зато среди них най-
найдется и та ветвь 5. которая обращает функцию Я|(|).
В самом деле, эта ветвь получится, если выбрать для вектора |2) соб-
собственное значение |2, а для |3) —13-
Казалось бы, теперь все слава богу. Посмотрим, однако, повнимательней,
насколько возрастает число ветвей при таком определении.
Вспомним для этого, что собственными векторами Л\, принадлежащими
EW-y 0, будут не только |2) и |3), но и любые их линейные комбинации,
например
| Ц> = cos 9 12> + sin 9 13>;
|Ш) = — sin е 12) + cos e | з>.
(Исключительно ради простоты мы выбрали здесь матрицу поворота веще-
вещественной, тогда она зависит от одного параметра. На самом дел« из требо-
требования ортогональности и нормируемости новых состояний она должна быть
только унитарной, и значит, зависеть от трех вещественных параметров).
*) Мы принимаем минимальную реализацию, т. е. считаем, что все |' не-
невырождены, т. е. все пространство растягивается тремя линейно-независимыми
векторами.
5. ФУНКЦИИ НАБЛЮДАЕМЫХ 353
Операторами проектирования в новые состояния будут по общему правилу
B1)
яП1 = | ш) <ш I = sin* e • n2 + cos2 e • л3 - i!l?? 12><з i - ^~- \ з> B [.
При сделанном соглашении мы можем теперь выбрать разные ветви функции
E(jii) для состояний |П) и |1П) и тем самым получить для частной ветви
оператора S, скажем |, выражение:
I = li«i + ?2яп + 1злш =Ь\Щ + (l2cos2 е + h sin2 е) Л2 +
+ (|, sin2 6 + |3 cos2 6) т+ h~b sin26{|3)B| + |2)Cl} (...)
— таким образом уже из одного выбора значений функции мы получаем се-
семейство операторов, зависящих от одного непрерывного параметра G (а если
бы мы совершили унитарный поворот — то от трех непрерывных параметров) 1
Итак, принятие правила, разрешающего выбирать различные значения функ-
функций для разных собственных векторов одного EW-та, приводит к тому, что
фуикция от оператора получает континуум ветвей — только при таком их оби-
обилии в их число попадает и «правильное» обращение |!
Более того, разные «ветви» оператора могут и не коммутировать друг
с другом. В самом деле, вычисляя коммутатор (***) с «правильным» | =
l + | + |зя3, найдем
II - ll = I* ^fl- sin 26 | 3) B | + Ь Ь~Ь sin 26 | 2) C | -
- |з ^=^-sin 26 | 3) B | - |2 i^li sin 26 | 2) C [,
то есть
[I, II- = (|2~Ы2 sin26{|3)B|-|2)C|}^0, 2?=l3>
2 2.6 Ф 0.
Мы видим теперь, насколько «излишне жестко» или, наоборот, «излишне
мягко» определяют операторные уравнения «значения» операторов — ведь то,
чем мы только что занимались, можно было рассматривать как решение урав-
уравнения
F-6») F-6а) __„
Fi-6»)Fi-6s)
(где |ь %2, |з — заданные числа, a iti — заданный оператор) относительно 1-
Поэтому, как правило, решение операторных уравнений требует каждый раз
особого исследования *).
5.4. Рассмотрим два важных примера операторных уравне-
уравнений— обратный оператор и квадратный корень.
*) Читатель, не прошедший мимо примечания в 4.7.1, заметит, конечно,
что все трудности рассмотренного примера связаны по существу с тем, что
мы обращали переход от оператора |, имеющего трехрядное «минимальное»
представление, «к менее богатому» оператору ni, минимальное представление
которого двурядно. Однако в более реалистических примерах функций от опе-
операторов, обладающих бесконечным числом EW-ов, заранее заметить подобную
«потерю информации» нелегко.
12 Б, В. Медведев
354 ч. III. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
5.4.1. Итак, рассмотрим уравнение
Е-*=1, *)
где \ — заданная наблюдаемая, такая, что среди ее собственных
значений нет нуля, а х — искомый оператор. Как наблюдаемая,
\ обладает полной системой собственных векторов
11Г> = ПГ), Ъ'чьо.
Определим теперь оператор f (g) условием
1Г)
Тогда, при действии на произвольный вектор )Р),
то есть
Умножая теперь (*) слева на f(?), получаем
как естественно назвать введенную функцию. В этом примере
и прямая и обратная функции от числовых аргументов одно-
однозначны, и никаких вопросов после исключения значения ?' = О
не возникает.
Часто приходится находить оператор, обратный произведе-
произведению двух или нескольких (не обязательно коммутирующих)
операторов. При этом порядок множителей меняется на проти-
противоположный, например,
(бтО-'-тГТ1.
В самом деле, имеем
если Ц~1 = 1 и х\х\-1 = 1.
5.4.2. Что же касается квадратного корня из наблюдаемой
а, т. е. решения уравнения
|2 = <х, а—задано; ? = д/а =а1/!>
то тут мы можем столкнуться со всеми трудностями, отмечен-
отмеченными в предыдущем примере, — можно произвольным образом
выбирать ветвь корня для каждого собственного значения ди-
6. СПЕКТРАЛЬНЫЕ ПРЕДСТАВЛЕНИЯ И ВЕРОЯТНОСТИ 355
скретного спектра и, даже, иногда бывает целесообразно вы-
выбирать разные ветви для разных векторов, принадлежащих
одному EW-y а. (Например, в релятивистском случае, когда
энергия выражается через импульс как ё — ± с Vp2 + (тс)'2.)
Практически, однако, из всего бесконечного числа ветвей корпя
используются лишь некоторые избранные, в первую очередь
арифметическая ветвь + д/^*
5.4.3. Решение уравнения для обратного оператора позво-
позволяет нам ввести еще один класс операторов, играющих, наряду
с эрмитовыми, важную роль в теории. Мы имеем в виду
унитарные операторы, определяемые уравнением
U+U = UU+ = \ илн U~l = U+. C1)
Здесь опять возникают вопросы относительно областей опреде-
определения и значений, которых мы не будем касаться. Отметим толь-
только две часто встречающиеся формы представления унитарного
оператора в виде функции какого-то эрмитова оператора:
±±&. C1a, b)
Обе формы гарантируют унитарность U, если I эрмитов.
ЗАМЕЧАНИЕ: Вторую из этих формул называют преобразованием Кэли;
если среди EW-ов О отсутствует —1, U' ф —1, то она допускает недвусмыс-
недвусмысленное обращение
# <31с)
6. Спектральные представления и вероятности
В примере, который мы рассматривали выше в § 4, мы уста-
установили, что всякий эрмитов оператор, удовлетворяющий целому
алгебраическому уравнению конечной степени, обладает ровно п
собственными значениями, и построили операторы проектирова-
проектирования на отвечающие этим EW-ам собственные подпространства —
операторы Р\ , образующие полную и ортогональную систему,
2Я{,= 1, PlrPlr>sssQ- Далее, мы получили для самого опера-
оператора | спектральное представление B7):
выражающее этот оператор через его EW-ты и операторы проек-
проектирования в собственные подпространства. Мы хотим теперь
12»
356 ч. Ш. ЭЛЕМЕНТЫ КВАНТОВОЙ СТЕХЖНИКИ
обобщить эти результаты на произвольный эрмитов оператор 1 *),
нам придется только допустить, что | является наблюдаемой,
чтобы его собственные векторы образовывали бы полную си-
систему, так что согласно принципу сюперпозиции любое состояние
можно было бы разложить по его собственным векторам
в виде B4):
М> = ?|6Г, A)+\dl'\\', A), (B4))
г
причем это разложение единственно.
6.1. Фигурирующие в правой части B4) конкретные собствен-
собственные векторы должны быть линейными вектор-функциями век-
вектора \А), т. е. получаться из него действием некоторого линей-
линейного оператора.
Будем сперва для простоты считать, что спектр ? чисто дис-
дискретен, и обозначим оператор, образующий из вектора \А) его
составляющую, отвечающую EW-y ln через Р$ :
\Ь, А) = Р1г\А).
6.1.1. Убедимся, что оператор Р| —эрмитов.
В самом деле, для эрмитовости должно для любых векторов \А) и (В|
выполняться равенство
{В | Ptf \Л)-(В\ Р? | А), т. е. {В | ?г, А) = AГ, В | А).
Подставляя здесь для (В\ в левой части и \А) в правой разложения B4),
приведем это условие к виду
^ В\%т„ А).
Но (!г/, В | |г> А} = 0 для г' Ф г, как скалярное произведение собственных
векторов, относящихся к разным EW-ам. Следовательно, условие эрмитовости
сводится к требованию
{%r,B\lr, А) = {ЪГ, В Mr, A),
выполняющемуся тождественно.
*) Здесь, вероятно, следует пояснить задачу несколько громоздких рас-
рассуждений, соствляющих основное содержание этого и следующего параграфов.
Дело в том, что пока в рассмотрение введена только единственная наблю-
наблюдаемая %, то у нас, как уже отмечалось, нет никаких средств, чтобы разли-
различить разные (если их несколько) собственные векторы ||') этой наблюдае-
наблюдаемой, относящиеся к одному EW-y |' — ведь, как мы говорили вначале, задать
состояние, это означает физически сказать, какие динамические величины
имеют определенные значения и какие именно значения, а в наше рассмотре-
рассмотрение включена пока единственная динамическая величина |. Мы даже ие мо-
можем узнать, отвечает ли некоторому EW-y i' одно состояние или целое соб-
собственное подпространство. Тем менее можем мы теперь сказать что-либо
о полном пространстве векторов состояния или ортоиормироваииом базисе
в нем — поэтому иам и приходится вместо разложения по базису — его еще
только предстоит построить — прибегать к разложениям по операторам проек-
проектирования в собственные подпространства.
6. СПЕКТРАЛЬНЫЕ ПРЕДСТАВЛЕНИЯ И ВЕРОЯТНОСТИ 357
6.1.2. Если, в частности, )А) является собственным вектором
г(или одним из собственных векторов) оператора ?, принадле-
принадлежащим 1г, то из единственности разложения B4) должно быть
любого \%г),
т. е. в собственном подпространстве {|?г)} оператор Р| должен
сводиться к единичному. Рассмотрим теперь (Р|гJ. Для него
(Plry\A) = Plr.Plr\A) = Plr\lr, A) = \lr, A) = Plf \A),
откуда, в силу произвольности | А), следует (PirJ — Р\г, т. е. Р$г
есть проектор.
6.1.3. С другой стороны, для любого \А)
rZ\lr, А) = \А), т.е. 5>5г=
6.1.4. Итак, операторы Pg обладают свойствами:
(Р?гJ = Р5г; ZP|r=l; PiPir. = PiTbrr'.
проектор полнота по свойству D)
Записывая еще
C2)
получаем опять представление самого оператора \ через, как го-
говорят, принадлежащие ему проекционные операторы *)
l=ZlrPir. C3)
Это — обобщающее формулы B7) —спектральное представление
относится теперь к произвольной эрмитовой наблюдаемой и от-
отличается от B7) тем, что индекс г пробегает в нем бесконечное
число значений.
6.1.5. Функция f(l) наблюдаемой \ в смысле определения
{30),
Е/'(&¦)! Ег, А),
*) Семейство проекционных операторов со свойствами C2), C3) назы-
называют часто разложением единицы, принадлежащим наблюдаемой ?. Иногда,
впрочем, (например, в книге фон Неймаиа) разложением единицы называют
семейство проекционных операторов
ег = ? V
что хотя и менее удобно для вычислений, но разрешает более единообразную
трактовку дискретного и непрерывного спектра.
358 ч. III. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
может быть записана через проекторы также в спектральной
форме
Z C3а)
6.2. Посмотрим, какие изменения надо будет внести в полу-
полученные формулы, если спектр оператора \ непрерывен. Эти изме-
изменения будут, конечно, касаться способа нормировки, поскольку
мы знаем, что в непрерывном спектре нормировать собственные
векторы условием (|'|!;') = 1 нельзя. Поэтому придется изме-
изменить и нормировку проекционных операторов, прибегая к таким
операторам, для которых вместо C2.1) имеет место
P\' = Pi'P\', где pi—некоторое число.
6.2.1. Конкретно удобно искать правильную нормировку, рас-
рассматривая сперва тот специальный случай, когда все EW-ы опе-
оператора 1 невырождены и рольР|' будет играть уже вводившийся
нами (см. B1)) оператор проектирования в определенное со-
состояние.
Итак, примем, что в таком случае
Векторы непрерывного спектра будем считать нормированными
условием
(Б'Щ-в№' -?")*). B3а)
Вычислим произведение двух проекторов:
6.2.2. Таким образом вместо формул C2.1.3) мы получаем
Pr/V = 6(?'-r')/Y- C4.1)
Это есть условие того, что зависящие от непрерывного параметра
операторы Р\- образуют систему взаимно ортогональных проек-
проекторов. Выбор нормировки с весом (B3Ь)) не меняет формулы
C4.1). Можно показать, что вид этой формулы не зависит и от
сделанного предположения о невырожденности собственных зна-
значений оператора |.
*) Можно было бы использовать (что иногда делают) и более общую
«нормировку с весок»
<ПП--^у*(Г-Г). B3Ь>
где р(?')—некоторая дефинитная весовая функция. Проекционные операторы
определяются тогда как
6. СПЕКТРАЛЬНЫЕ ПРЕДСТАВЛЕНИЯ И ВЕРОЯТНОСТИ 359
В самом деле, чтобы модифицировать рассуждения, которые мы вели
для дискретного спектра, надо было бы заметить просто, что для любого
(фиксированного) собственного вектора 11 ) должно было бы быть
т. е. вместо условия
Plf I Ъг) = I \г) появилось бы Рг ||'> = б (|" - I') | |'>
— все остальные рассуждения прошли бы без всяких изменений.
Наконец, совершенно так же как и для дискретного спектра,
показывается, что
условие полноты Г , , _ .
в непрерывном спектре J 5 * — 'OTiZ'
6.2.3. Спектральное представление оператора \ будет отли-
отличаться от C3) только заменой суммы интегралом:
vl'. C5)
ЗАМЕЧАНИЕ: Если пользоваться в качестве принадлежащего g разложения
единицы не семейством {Р%>}, а семейством {?g'}, то при включении непре-
непрерывного спектра удается обойтись без привлечения обобщенных функций
(так же, как можно избежать функции S (х), образуя каждый раз Ф (х) =
X
= \ 6(х — х') dx'). Такая программа проводится фон Нейманом, g
— ОО
6.2.4. Если, наконец, у оператора | есть и дискретный и не-
непрерывный спектр, то вводятся проекционные операторы обоих
родов:
PlrPlr' = brr'Pir\ PvPY = b{l'-l")Pv\ /yV = 0; C6.1)
условие полноты записывается теперь как
С2 = С, D + C==l; DC = 0,
C6.2)
а спектральное представление наблюдаемой \ принимает вид:
l'-l'-Pv' C6.3)
6.3. Теперь у нас заготовлено достаточно формального мате-
материала, чтобы сформулировать еще один, в некотором смысле ре-
решающий, постулат, устанавливающий физическую интерпрета-
интерпретацию развитой математической теории.
6.3.1. Рассмотрим некоторую наблюдаемую % и принадлежа-
принадлежащие ей проекционные операторы Р\г (опять принимаем сперва,
360 ч. III. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
что есть только дискретный спектр). Пусть, далее, рассматри-
рассматриваемая система находится в некотором фиксированном состоя-
состоянии \х), описывающий которое вектор мы будем считать норми-
нормированным: (#|л:) = 1.
Построим числа (являющиеся квадратичными формами со-
состояния)
Wlr/x = (x\Plr\x); л=1, 2, ...
По свойствам проекционных операторов для этих чисел имеет
место
1): Wlr
B): Wrif/*<1,
а в силу полноты системы Р| , принадлежащих наблюдаемой ?,.
C): У. W* = У! (х\Рг I х) = (х\ У. Р% \х) = (х \х)= 1
г г г т г т
Но свойства A) —C)—это как раз те свойства, которыми
должны обладать вероятности альтернативных суждений.
6.3.2. Поэтому представляется естественным интерпретиро-
интерпретировать эти числа таким образом, а именно, ввести физический по-
постулат:
Вероятность найти для физической величины % при измере-
измерении этой величины у системы, находящейся в состоянии \х),
точно значение \г есть
СЛЕДСТВИЕ: Если до измерения система находилась в соб-
собственном состоянии | %г>) наблюдаемой |, то
т. е. эта вероятность равна единице или нулю, судя по тому, со-
совпадает ли собственное значение, вероятностью найти которое
мы интересуемся, с тем, к которому относится состояние си-
системы, или нет. |
Новый постулат C7) есть обобщение физических постулатов-
A) — C) из 4.4. Действительно, только что сформулированное
следствие совпадает с постулатом B) из 4.4, утверждавшим*
что «при измерении в собственном состоянии всегда получается
соответствующее собственное значение».
6.3.3. Если, теперь, система находится в таком состоянии
Ю> 111011 = 1» что ПРИ измерении | мы наверняка получим
значение |Г', то это значит, с нашей новой точки зрения, что
(r' I Pi Ir') = &гг' Для всех г.
6. СПЕКТРАЛЬНЫЕ ПРЕДСТАВЛЕНИЯ И ВЕРОЯТНОСТИ 361
Но тогда оператор Р^ , действуя на \г'), должен переводить его в неко-
некоторый вектор
являющийся суммой | г') н вектора | г, г'), ортогонального | г'). Записывая
(г' | Р%г | г') = (г' | Р%г ¦ РЪг | г') = Ц Р^ | г') |Р,
получим, что
в„, = || Ьгг, | г') + | Гг'> |р = Ьгг, || | г') f + \\ | гУ) |р,
то есть
|| | ГО IP =0; значит, | г~') = 0.
Следовательно,
РЪГ\Г') = ЬГГ'\Г'),
т. е. \г') является собственным вектором наблюдаемой | с EW-m
\г', а это и есть содержание A) из 4.4.
6.3.4. Что же касается постулата C) из 4.4., то теперь мы
уточнили его нашим новым утверждением, что при измерении
величины | в произвольном состоянии \х) ее различные соб-
собственные значения {¦' встретятся с вероятностями C7).
6.4. Среднее значение, которое мы получим для величины |,
производя многократные измерения этой величины (в различ-
различных, конечно, экземплярах системы), найдется теперь по стан-
стандартным правилам теории вероятностей как
!«= Z lrWlr/x= Е ?г<*| Pir\x) = (x\Z %rPlr\x).
Но стоящая здесь сумма — это не что иное, как спектральное
представление C3) самой наблюдаемой |. Следовательно,
среднее значение наблюдаемой | 5 =/е\ /visiv\ ая\
в состоянии | х) ё* — W* — V* I 6 I *;• I**}
Утверждение C8) можно использовать (что иногда и делают)
вместо C7) в качестве основного постулата статистической ин-
интерпретации квантовой механики.
ЗАМЕЧАНИЕ: В дальнейшем мы будем всегда называть обра-
образования типа (jt|ajjc), т. е. диагональные матричные элементы
оператора а, средними значениями оператора а в состоянии
\х), независимо от того, является ли а эрмитовым, наблюдаемой
и т. д. Говорят также «ожидаемое значение», «Expectation value»
с сокращенной записью EV или «Erwartungswert» с сокращен-
сокращенной записью Er. |
6.5. Включение непрерывного спектра не сталкивается здесь
ни с какими трудностями. Надо только не забыть, что в случае
362 ч. III. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
непрерывного спектра не имеет смысла говорить о вероятности
найти при измерении величины | точное значение %', а лишь о ве-
вероятности найти значение из интервала d\' вблизи %'. Такая ве-
вероятность задается выражением
= Pfdl', |37.c>
причем опять будут выполняться свойства A) — C):
О < dWVfs < 1; \ dWvlx = \{х\ dPr | х) =
и, как легко видеть, будет
если интервалы dg' и а%" не пересекаются. Формула C8) для
среднего значения величины % преобразуется тогда в
t = $ Г dWvlx = \ d%' -|'<*1 Ъ U) = {x |g \x).
C8.С)
Если, наконец, у наблюдаемой 1 есть и дискретный и непре-
непрерывный спектр, то мы получим, в соответствии с формулами C6),
?' I' <* I *V I *> = <*1 * 1*>. C8. d + с)
Мы выписали все формулы для того случая, когда само
состояние \х) относится к дискретному спектру (х\х)= 1.
Если само |jc) принадлежит непрерывному спектру и нормиро-
нормировано условием {х'\х) = 8(х' — я), то и матричный элемент
(х'\Ръ'\х) будет пропорционален б(х' — х), а вероятность будет
получаться из коэффициента при ней.
7. Коммутирующие наблюдаемые
7.1.1. Может случиться, что какое-нибудь состояние |Л) ока-
окажется одновременно собственным состоянием двух разных на-
наблюдаемых | и г):
Тогда в таком состоянии сумма и произведение этих наблюдае-
наблюдаемых также будут иметь определенные значения %' + ц' и %ц'.
Для суммы это очевидно, а для произведения получаем последо-
последовательно:
|Л \А) = Ы \А) = |У | А) = пТ | А) = пГ I А) = т,| \А).
7. КОММУТИРУЮЩИЕ НАБЛЮДАЕМЫЕ 363
Следовательно, в таком состоянии будет также
\1ц — Til) | Л) = 0; для фиксированного |Л)!
7.1. Отсюда ясно, что
если два оператора | и ц обладают столькими совместными
собственными состояниями, что из них можно выбрать
полную систему,
то | и г) коммутируют
5л-чЕ = О. C9)
Обратная теорема гласит:
если две наблюдаемые ? и т] коммутируют,
го можно построить полную систему, все векторы которой
будут общими собственными векторами 1 и т|.
7.2.1. Для доказательства обратной теоремы, которое будет
содержать не безразличный для нас способ построения такой
полной системы, докажем сперва
ЛЕММУ 3: Если для | и т) выполнено C9),
то все принадлежащие | проекционные операторы Р?
коммутируют с г).
ДОКАЗАТЕЛЬСТВО: Имеем последовательно:
= 0
Следовательно, оператор Р^цР^, должен быть пропорционален
br'r'i /\.Л]^\"== ('П)г' Ьг'г", где (ri)r, — некоторый новый оператор.
Поэтому, умножая вторую строчку проведенной выкладки
только на Pj^ слева и используя обозначение (г))г„ получим
К' - (р1г>ч - D0=°; *Vi - Wr-=о.
Умножая здесь на 6r'v и суммируя по г":
и, поскольку 2Л-"=1,
0- ¦ C9а)
364 ч- ш- ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
7.2.2. Применяя теперь эту лемму к коммутирующим опе-
операторам Р\г и т), получим, что
plrp% ~ Р%\ = °» * 39Ь>
т. е. все проекторы, принадлежащие коммутирующим операто-
операторам, коммутируют друг с другом.
7.2.3. Поэтому можно ввести совместные проекторы
ptrr\s = plrpi\s = PnsPlr D0.1)
со свойствами:
уР -р Уур L* Г> D0-2~5>
Действием этих проекторов все пространство векторов \А) раз-
разбивается в двойную сумму ортогональных подпространств,
г, s г s
и притом так, что всякий вектор из подпространства с номерами
(г, s): P\i\s\A) (| Л)—произвольный вектор) является собст-
собственным вектором обеих наблюдаемых {¦ и ц с собственными зна-
значениями |г и tis:
7.2.4. Для самих же операторов | и г\ можно теперь написать
двойное спектральное представление
r,s т s г, s r s
ЗАМЕЧАНИЕ 1: Мы провели все рассуждения для дискретного
спектра. Для непрерывного спектра все проводится совершенно
аналогично, единственным отличием будет замена сумм интегра-
интегралами и кронекеровых б-символов дираковыми б-функциями. |
ЗАМЕЧАНИЕ 2: Некоторые из входящих в двойную сумму под-
подпространств могут оказаться пустыми, т. е. соответствующие про-
проекторы Pi ns — тождественно равными нулю: из того, что для Е
существует собственный вектор, принадлежащий |г> а для rj —
принадлежащий ц8, не следует, что существует вектор, являю-
являющийся собственным для обоих операторов | и ц с собственными
значениями |г и t|s- Можно утверждать лишь, что из всех под-
подпространств с фиксированным |г и произвольным ц8 хотя бы
7. КОММУТИРУЮЩИЕ НАБЛЮДАЕМЫЕ 365
одно будет не пусто; то же самое для фиксированного r\s и ме-
меняющегося !г—иначе не могли бы выполниться формулы
D0.3,4). I
7.3.1. В соответствии с последним замечанием добавление к
наблюдаемой | коммутирующей с ней наблюдаемой х\ может
оказаться тривиального характера — когда осуществляется ука-
указанный предельный случай и при соответствующей нумерации
не пусты лишь подпространства с совпадающими номерами г и
s, т. е. когда P| ns = brsPir = 6rsAis- Ясно, что тогда наблюдаемая
т) оказывается функцией наблюдаемой {¦ (и наблюдаемая 6—
функцией наблюдаемой г\) в смысле определения C0) (или
C3а)) —такая возможность не будет нас сейчас интересовать *).
Во всех других случаях хотя бы некоторые совместные EW-ы
Ъг, Tls будут иметь меньшую кратность, чем |г или r\s.
Продолжая этот процесс, можно искать дальнейшие опера-
операторы, коммутирующие со всеми предыдущими, пока мы не дой-
дойдем до некоторого набора (мы будем теперь обозначать нижним
индексом номер наблюдаемой, номера же собственных значе-
значений— верхними индексами) наблюдаемых:
Ui,.... U; Б<&#-1/Ь = о (i, /=i,.... п) D2.1)
такого, что каждому набору собственных значений [l[l, lr22, ...
..., |J»} принадлежит (если вообще принадлежит) единствен-
единственный (конечно — с точностью до множителя) собственный вектор
, • • •, 5„ /•
Соответствующие проекционные операторы
5i'*2 g« si S2 s« «i -«« D2.2)
P / , , .p „ „ » =б '»б '»... б' -Р'
будут тогда разбивать все пространство в сумму взаимно-орто-
взаимно-ортогональных одномерных подпространств.
7.3.2. Установим критерий одномерности подпространств, от-
отвечающих проекционным операторам D2.2). Применяя такой
(фиксированный) оператор к произвольному вектору \А), мы
сможем найти (если соответствующее подпространство не пусто)
такой \А), что IР ' ' | Л) 11= 1 (считаем сперва спектр дискрет-
дискретным). Тогда Ць ..., ln) = P%' ,'\А) будет нормированным
*1 " • • *п
*) Противоположный предельный случай состоит в том, что все подпро-
подпространства вида Р| ,, \А) не пусты — т.е. любое собственное значение |»
можно комбинировать с любым собственным значением т)«.
366 ч. III. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
собственным вектором всех операторов ?ь ..., ?п> отвечающим
собственным значениям ?{, ..., %'п, определенным по допущен-
допущенному с точностью до унимодулярного множителя, и оператор
проектирования в соответствующее подпространство будет вы-
выражаться через него с помощью формулы B1), т. е. в виде
.' .'=1б1 Sn)\5b • ••. 6я I (III 61. • • •. 5n)ll = !)•
Это и есть критерий одномерности. Для случая, когда некоторые
из наблюдаемых |i, ..., |„ имеют непрерывный спектр, ре-
результат сохранится тем же, надо будет только нормировать
I И, • • • > In) по соответствующим переменным не на единицу,
а на 6-функцию.
7.3.3. Совокупность векторов | 5i, •... in) образует тогда ор-
тонормированный базис во всем пространстве. Через проекцион-
проекционные операторы его можно определить условиями:
l" I SI» - • -, 6e) = 0EY • • • Olbf "" Se)l fib • • м S/t))
461, • • •. Sn I li, • • •, In) = <55y ... о (|„ — !„);
n |?' 6'\ /6' ?' I.
^i' p' — I 61» • • • > Ъп) \il, • • • , 6n l>
D2.3)
предпоследнее из которых выражает требование одномерности
всех совокупно-собственных подпространств.
7.4. О системе наблюдаемых, удовлетворяющих всем требо-
требованиям D2), говорят как о полном наборе или о полной системе
коммутирующих наблюдаемых*).
7.4.1. Каждая из наблюдаемых полного набора представима,
конечно, в аналогичной D1) форме спектрального разложения
по совокупным проекционным операторам
..dln.\'m.P, . . D1а)
sl "' i
Можно ввести, в полной аналогии с C0) или C3а), функции
от совокупности наблюдаемых полного набора, определяя их
*) Слово «полный» употреблено здесь не в том смысле, что хватит век-
векторов, чтобы растянуть все пространство, а в том, что хватит проекторов,
чтобы расщепить каждое собственное пространство на одномерные!
7. КОММУТИРУЮЩИЕ НАБЛЮДАЕМЫЕ 367
равенством
I Ifei, ..., fee) 2., J • * • °en ' *fel» < • •• fed
;
, ТОЛЬКО ОДНО-
.. %'n значные /!
i;,.-
D3)
7.4.2. Для систем с конечным числом степеней свободы долж-
должно быть возможным выбрать полный набор так, чтобы число
наблюдаемых в нем было конечным. В самом деле, при класси-
классическом описании состояние такой системы фиксируется зада-
заданием всех ее координат и импульсов — т. е. конечного числа 2п
чисел. Задать квантовое состояние — значит сказать о системе
все, что мы можем о ней знать; но в квантовом описании можно
знать только меньше, чем в классическом. Стало быть, должно
быть возможным фиксировать квантовое состояние заданием
меньшего чем 2п числа чисел — т. е. выбрать число переменных
полного набора меньшим 2п.
Такой выбор должен быть возможен, но он не обязателен:
даже для системы с одной степенью свободы можно вместо ха-
характеризующей ее некоторой наблюдаемой | — которая сама по
себе образует полный набор — выбрать принадлежащие ей про-
проекторы Р\,. Они также образуют полный набор, но число их —
если | имеет бесконечно много EW-ob — будет бесконечным!*)
7.4.3. Мы использовали для определения понятия полного на-
набора и операторы, и векторы. В действительности можно опреде-
определить полный набор, не выходя за пределы алгебры операторов.
7.4.3.1. Для этой цели докажем сперва важную
ТЕОРЕМУ: Если линейный оператор ш коммутирует со всеми
наблюдаемыми полного набора,
то о является функцией этих наблюдаемых.
ДОКАЗАТЕЛЬСТВО: Оператор со можно записать как
со = 1 • со • 1 = ( dg'd!"Ps,w/>r, (*)
(мы пишем для краткости одну букву | вместо \\, ..., |„ и, аналогично, |'
вместо \[ |^), т. е. в виде двойного интеграла (суммы) по операторам
Р|,<»/>?«•, каждый из которых переводит векторы из собственного подпро-
подпространства |" в векторы из собственного подпространства |'.
Используем коммутативность со с наблюдаемыми полного набора,
[со, |]_=0; согласно доказательству леммы 3, из этого свойства следует,
*) В нашем примере из 5-го параграфа наблюдаемая | сама по себе
могла образовывать полный набор, а наблюдаемая я» — нет. Полный набор
могла образовывать только совокупность {яь лг, Яз} (точнее — совокупность
{щ, Пг), поскольку л3 — 1 — Л[ — яз).
368 ч. "I. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
ЧТО
где (ш)^ — некие новые операторы. Существенный момент состоит в том,
что операторы P^atP^, оказываются пропорциональными в-фуякцин (или —
для дискретного спектра — кронекерову в-символу), т. е. операторами, дей-
действующими внутри каждого нз собственных подпространств %'. Поэтому
двойной интеграл в (*) превращается в однократный:
a> =
Если теперь | образуют полный набор, то в силу D2.3.3)
Pt.uPv -110 <!' I »I i'O <Г I = <!' I»I ГО • 110 (Г I,
где мы вынесли численный множитель перед операторной частью. Так как
из-за коммутативности ю и | все это выражение должно быть пропорцио-
пропорциональным в-функцин, а операторная часть не имеет отношения к ю, то содер-
содержать в-функцию должен именно численный множитель:
где о>|/|« — не оператор, а число\ (Иными словами, (а>)^ = а>|,|, • Р^„ и это
есть характерное свойство полного набора: в подпространстве, выделяемом
Pj/, — а Р^,а>Р^, есть проекция оператора со в это подпространство — не
может существовать операторов, отличных от числа, — оно одномерно!)
Следовательно,
PjHdPj. - «>|Г • о A' - I") | Г) (ИГ I - «sT • V * в' ~ Е*)«
и, значит, (*) превращается в
т. е. приобретает форму D3) функции наблюдаемых |. |
7.4.3.2. Справедливо и обратное утверждение:
Если система взаимно коммутирующих наблюдаемых |ь ..., in
такова, что любой новый оператор, коммутирующий со
всеми наблюдаемыми |ь ..., |п, есть их функция,
то наблюдаемые |ь ..., |п образуют полный набор.
В самом деле, условием полноты набора является требование D2.3.3).
Предположим, что хотя бы для одной совокупности in ..., ij, оно не выпол-
выполнено, скажем
6i • ¦ • ы
Но тогда линейный оператор
очевидным образом коммутирующий со всеми |i %п, не сможет быть
представлен в виде D3). Щ х
Т. КОММУТИРУЮЩИЕ НАБЛЮДАЕМЫЕ 369
7.4.3.3. Итак, мы можем дать новое определение:
Набор взаимно коммутирующих наблюдаемых называется пол-
полным, если любой новый оператор, коммутирующий со всеми
наблюдаемыми набора, есть их функция.
ЗАМЕЧАНИЕ 1: В этой формулировке становится особенно яс-
ясным, что полнота набора коммутирующих наблюдаемых есть
вопрос в значительной степени физический: в определении фигу-
фигурирует слово «любой», но, конечно, «любой из числа вообще рас-
рассматриваемых операторов», а объем совокупности рассматри-
рассматриваемых операторов определяется физической постановкой за-
задачи. |
ЗАМЕЧАНИЕ 2: Теперь мы можем, наконец, описать способ по-
построения пространства, векторы которого призваны отображать
состояния квантовой механики. Мы находим полный набор ком-
коммутирующих наблюдаемых и строим их совместные проекторы
Р' '. Собственные векторы этих проекторов с EW-ми +1,
т. е. ненулевые векторы, удовлетворяющие D2.3), суть тогда
векторы базиса, а порождаемое этим базисом линейное про-
пространство и есть нужное нам пространство кет-векторов (бра-
векторов).
При этом физически задать входящее в базис состояние —
это значит указать полный набор проекционных операторов, сов-
совместным собственным вектором которых с EW-om +1 оно яв-
является, т. е. указать численные значения динамических перемен-
переменных полного набора, которые наверняка будут получены при из-
измерении в этом состоянии. |
7.5. Можно получить ряд теорем, трактующих свойства функ-
функций коммутирующих наблюдаемых,
7.5.1. Приведем одну из них:
Если I и т]—две коммутирующие наблюдаемые,
то всякая функция /(?) коммутирует со всякой функцией
()
Доказательство непосредственно следует из леммы 3 и пред-
представления функций от наблюдаемых в форме C3а).
ЗАМЕЧАНИЕ: Обобщение этого утверждения приводит нас к
тому, что множество функций п коммутирующих наблюдаемых
образует коммутативную алгебру с единицей. |
СЛЕДСТВИЕ 1: Всякая функция наблюдаемой коммутирует
с самой наблюдаемой. I
370 ч. Ш. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
СЛЕДСТВИЕ 2: Всякие две функции /i(|) и /2(|) одной и той
же наблюдаемой перестановочны. |
ЗАМЕЧАНИЕ: Мы видели на примере, что с неоднозначными
функциями дело обстояло совсем не так! |
7.5.2. Формально справедливо и утверждение, обратное след-
следствию 2, которое, записанное в несколько более общей форме,
гласит:
Если задан некоторый набор ?ь ..., |„ коммутирующих
наблюдаемых,
го существует такая наблюдаемая ?, что все ?ь ..., |„ бу-
будут функциями /ь ..., /„ наблюдаемой ?.
ДОКАЗАТЕЛЬСТВО для случая чисто дискретного спектра
совсем просто. В самом деле, коммутирующие наблюдаемые
%и .... |„ обладают совместными проекционными операторами
«1 • •¦•• «я
которые нумеруются набором номеров {г,, ..., г„}, нумерующих
собственные значения каждого оператора ?,-. Мы можем сде-
сделать произвольную перенумерацию этих наборов, нумеруя каж-
каждый набор {/¦], ..., /¦„} одним натуральным числом R, R= 1,2, ...,
так, чтобы каждому значению # отвечал только один набор,
{г(-} = {ф^ (/?)}. Введем теперь наблюдаемую ?, скажем определив
Тогда наши совместные проекционные операторы наблюдаемых
li будут операторами проектирования в собственные подпрост-
подпространства наблюдаемой ?, принадлежащие ее EW-ам С/?=='
^ <р, (Я) <р„ («) = ¦PjR,
sl s»
а сами наблюдаемые ?» (г = 1, ..., п) представятся в форме
г, ... г„ 1 • « Я
совпадающей с формой C3а). |
7.5.3. ЗАМЕЧАНИЕ 1: Почему мы предпослали доказанному
утверждению эпитет «формально»? Дело в том, что как наблю-
наблюдаемая ?, так и функциональные зависимости, выражающие че-
через нее наблюдаемые ?ь ..., |„, не будут в большинстве слу-
7. КОММУТИРУЮЩИЕ НАБЛЮДАЕМЫЕ 371
чаев i!.%ieib никакого физического смысла. Ведь коммутирующие
наблюдаемые могут описывать физические величины, не имею-
имеющие совсем никакого отношения друг к другу — например, коор-
координаты, отвечающие разным степеням свободы, или, даже, ка-
какие-либо динамические величины, относящиеся к разным систе-
системам, вовсе не взаимодействующим друг с другом. Ясно, что в
таких случаях навязывание каких бы то ни было функциональ-
функциональных зависимостей не может отвечать никаким физическим свя-
связям — такие просто отсутствуют.
Особенно ярко это обстоятельство проявляется в случае не-
непрерывного спектра (теорема, с соответствующими оговорками,
остается справедливой и в этом случае), когда, например, для
применения обсуждаемого утверждения к двум декартовым ко-
координатам материальной точки приходится, для проведения пе-
перенумерации, привлекать такие построения, как известная кри-
кривая Пэано — образование, совершенно чуждое математическим
средствам, действительно потребным для описания природы. |
ЗАМЕЧАНИЕ 2: Вернемся к вопросу о числе наблюдаемых в
полном наборе для некоторой определенной системы. Проведен-
Проведенное обсуждение показывает, что формально математически та-
такой вопрос бессмыслен — согласно доказанной теореме всегда
можно редуцировать число наблюдаемых в наборе до одной.
Если, однако, ограничиваться лишь наблюдаемыми, обладаю-
обладающими очевидным физическим смыслом, то тогда их число обычно
равняется числу степеней свободы материальной системы. |
7.6. Скажем еще несколько слов о физической интерпретации
наборов коммутирующих наблюдаемых. Поскольку наблюдае-
наблюдаемые набора обладают общими собственными векторами, то со-
согласно постулату B) из 4.4 они одновременно измеримы, — т. е.
система может находиться в таком состоянии, когда все наблю-
наблюдаемые рассматриваемого набора имеют одновременно опреде-
определенные значения.
ЗАМЕЧАНИЕ: «Одновременно измеримы» значит, по нашему со-
соглашению, что мы можем одновременно предсказать точные зна-
значения всех этих наблюдаемых, если каждая из них будет изме-
измеряться первой, — т. е. вообще говоря нам нужно по меньшей мере
п экземпляров системы. Однако относительно коммутирующих
наблюдаемых можно утверждать и больше: что, хотя бы в ирин
ципе, всегда можно придумать такую постановку опыта, что все
они будут измерены реально одновременно — в одном экспери-
эксперименте. |
Что же касается вероятности найти какой-то набор значений
?ji, .... l^n таких наблюдаемых при измерении, совершаемом
372 ч. III. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
над системой, находящейся в произвольном состоянии \х), то
обобщая постулат C7) из 6.3.2, мы примем, что
Вероятность найти для набора физических величин ?ь ... ,!=„,
которым отвечают коммутирующие наблюдаемые, при изме-
измерении (одновременном) этих величин у системы, находя-
находящейся в состоянии \х), точно значения g'J1 g^S соответст-
соответственно, есть
г<. t./.-<"V,.<;.i* l44>
Обобщение на непрерывный спектр очевидно.
ЗАМЕЧАНИЕ: Последние абзацы показывают, что с физической
точки зрения тоже может представиться естественным рассмат-
рассматривать набор коммутирующих наблюдаемых как одну «слож-
«сложную» наблюдаемую, «значения» которой суть не одно число, а
(упорядоченный) набор нескольких чисел. Таким образом в ка-
каком-то смысле можно сказать, что математический и физический
подход к интерпретации набора коммутирующих наблюдаемых
различает только отношение к нумерации собственных векто-
векторов— математик может предпочесть «более простую» одномер-
одномерную нумерацию, в то время как физик не может отказаться от
может быть более громоздкой, но зато связанной с природой
изучаемой системы. |
8. Представления
Итак, всякий полный набор коммутирующих наблюдаемых
определяет полную ортонормированную систему состояний D2.3)
в пространстве векторов состояния \А). В квантовой механике
о выборе определенного базиса говорят обычно, как о выборе
представления *).
8.1. Для произвольного вектора \А) можно написать:
6,...
— X \ Hi' ! ?' ?'\/?{ ?' I A\ /&\
Возникшее здесь выражение ^$^'1^' •••» l«)Ei> •••» ^»l
— т. е. фактически разложение единицы, принадлежащее полному
*) Не следует отождествлять это использование термина «представление»
с идентичным словоупотреблением в математической теории представлений
групп, хотя эти два словоупотребления и имеют точки соприкосновения.
8. ПРЕДСТАВЛЕНИЯ 373
набору |ь ..., |n. — в котором имеется в виду суммирование
по всем дискретным и интегрирование по всем непрерывным
индексам, называют обычно суммой по полной системе, а о пе-
переходе от левой части выкладки (*) к правой говорят иногда:
«вставим сумму по полной системе».
8.1.1. Совокупность фигурирующих в (*) чисел
\А) — {Ъ\, ..., Vn\A) D5.1)
полностью определяет (при фиксированном базисе) вектор \А).
Она называется представителем*) вектора \А) в рассматривае-
рассматриваемом представлении.
8.1.2. Представителем со-вектора {А\ будет совокупность его
скалярных произведений с базисными векторами:
(А\ 041Й, .... tn). D5.2)
Поскольку, в силу A2.1),
(А\Ъ'и ..., ?» = «& ..., %'п\А)Г,
то представители вектора и сопряженного ему со-вектора в од-
одном представлении комплексно сопряжены друг другу.
8.1.3. Рассмотрим теперь некоторый линейный оператор а,
который характеризуется уравнением
Умножая это уравнение слева на произвольный базисный со-
вектор и вставляя сумму по полной системе между а и |А), по-
получим
1%"(?] ... 1'п| а| Е7> • • •» En)(?7, ••>. I»I A) = (l'i, ..., l'n\B).
Отсюда видно, что представителем линейного оператора являет-
является матрица **)
а <Й, .... &|а|Е7, .... In), D5.3)
у которой левый индекс (или индексы) нумерует строки, а пра-
правый— столбцы, причем действие операторов на векторы или со-
векторы происходит по правилу матричного умножения, в кото-
котором принимается, что представитель вектора D5.1) есть матрица
с всего лишь одним ненулевым столбцом, а представитель со-
вектора D5.2)—матрица с одной ненулевой строкой***). Эта
*) Математик сказал бы — координатами.
•*) Этот термин используют в квантовой механике, невзирая на то, ну-
нумеруются ли здесь строки и столбцы дискретными или непрерывными индек-
индексами.
***) Легко заметить, что при таком, матричном, понимании представите-
представителей векторов и со-векторов, представителями сопряженных вектора и со-век-
со-вектора будут матрицы, эрмитово сопряженные друг другу.
.¦374 ч. III. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
терминология поясняет, почему мы назвали в § 3 образования
типа {А\а\В) матричными элементами (иногда добавляют —
перехода) оператора а между состояниями \А) и \В).
Такое же рассуждение с вставлением полной системы пока-
показывает, что представитель произведения двух операторов есть
матрица, получаемая из матриц, представляющих сомножители,
по правилу матричного перемножения.
8.1.4. Легко сообразить, что:
A) Представителем эрмитова оператора будет эрмитова мат-
матрица.
B) Представителем любого из операторов полного набора,
определяющего базис, будет диагональная матрица:
h — arV...a'-г--#*).
Поэтому о выборе представления, базисные векторы которого
суть собственные векторы некоторой наблюдаемой ?, часто гово-
говорят, как о выборе представления, в котором наблюдаемая %
диагоиальна.
C) Представителем единичного оператора является единич-
единичная матрица
1 ( S
D) Представителем проекционного оператора Р •» »> будет
матрица, имеющая единственный (диагональный) не равный
нулю элемент:
in'
E) Представителем линейного оператора, коммутирующего
со всеми наблюдаемыми полного набора (и являющегося, сле-
следовательно, их функцией), будет диагональная матрица.
8.2. Выбор представления может быть, конечно, совершен бес-
бесконечно разнообразными способами. Как совершается переход
от одного представления к другому?
Пусть, кроме полного набора {?}, у нас есть другой полный
набор коммутирующих наблюдаемых {г\и ¦¦¦, r\w), которому
*) Если спектр непрерывен, то матрица называется диагональной, если
она имеет вид
(l'\a\l") = i(l'N(l'~l")
-—т. е. пропорциональна 6-функции (а не ее производным!)
9. КВАНТОВАНИЕ 375
будут соответствовать базисные со-векторы (ч\'\, ..., r\'w\. Напи-
Напишем тогда («вставляя полную систему»):
Эта формула дает нам разложение новых базисных со-векторов.
по старым*). Если писать в дальнейшем для краткости просто
| и т) вместо {|i In} и {t)i, ... .т)»}. то правило преобразо-
преобразования базисных со-векторов запишется в виде
(Tl'l=Z(^ir>-(ri. D6.1)
Аналогично, для базисных векторов:
IV>=Zir>-<riV>, D6.2).
причем, конечно,
(riV> = (^'ir»*. D6.3)
Тогда
ZW\t){r\) (IOZ(|>ri^> D7)
— т. е. представитель вектора преобразуется как базисные со-
векторы, а представитель со-вектора — как базисные векторы.
Наконец, для линейного оператора
WI«I п"> = ? WI Г> • <Г I <х | ГО • <Г I л">. D8)
Если, в частности, а = 1, то получаем из D8)
Е (л' I Г) <Г I л") =ZW\ Г) (WIГ)^ = а,,-* D9)
— т. е. переход от представителей в одном ортонормированием
базисе к представителям в другом совершается с помощью уни-
унитарной матрицы.
9. Квантование
Как мы видели, одной из основных особенностей квантово-
механического описания, отличающей его от классического, осо-
особенностью, обеспечивающей возможность осуществления прин-
*) Подчеркнем, что числа наблюдаемых в двух наборах п и до, могут
быть и различными. Можно было бы успокоить себя тем, что неизменным
остается полное число базисных векторов 2j = ^ . В случае ко-
иечномерных пространств это действительно так. В бесконечномерном про-
пространстве мы можем даже, однако, перейти от полного набора наблюдаемых
с дискретным спектром к полному набору с непрерывным.
376 ч- !"¦ ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
ципа неопределенности Гайзенберга, является то, что динами-
динамическим переменным |, ц, ... физической системы сопоставляют-
сопоставляются величины («наблюдаемые»), которые, вообще говоря, не ком-
коммутируют:
II, Л]_ = ?4-41^0.
Однако это следующее из принципа неопределенности утвержде-
утверждение [?, г\]_ ф 0 имеет чисто негативный характер. Чтобы разви-
развивать теорию дальше, потребно позитивное утверждение, нам
надо установить, чему же именно равен коммутатор пары дина-
динамических переменных— надо установить перестановочные соот-
соотношения или, как говорят,— ибо именно здесь квантовая меха-
механика ответвляется от классической, — установитьправилакван-
установитьправилаквантования.
Для этой цели мы обратимся к принципу соответствия с
классической теорией, именно, будем стараться строить даль-
дальнейшее квантовомеханическое описание так, чтобы оно примы-
примыкало к классическому столь тесно, сколь это возможно. При
этом удобно отталкиваться от классической механики, записан-
записанной в гамильтоновой форме.
Из первой части курса мы уже знаем, что механика в га-
гамильтоновой форме наиболее удобно и красиво формулируется
с помощью скобок Пуассона. Мы хотим поэтому перенести по-
понятие скобок Пуассона (кратко — СП) в квантовую теорию—•
т. е. соотнести всякой паре квантовых динамических перемен-
переменных*) (наблюдаемых), взятых в определенном порядке, новуК>
наблюдаемую, которую мы будем называть квантовой СП этих
наблюдаемых, и притом так, чтобы при этом сохранились все
свойства классических СП:
A) антисимметрии;
B) равенства нулю скобки с константой;
C) линейности по каждой переменной;
D) выполнения тождества Якоби и
E) свойства, аналогичного правилу дифференцирования про-
произведения:
(щи2, v) = (и,, о) «2 + и, («2, v); (и, viv2) = (и, w,) v2 + о, (и, о2).
(Подчеркнем, что в равенствах, выражающих свойства E) уже
нельзя будет, разумеется, изменять порядок множителей.)
Оказывается, что если мы хотим сохранить все свойства A) —
E) для некоммутирующих величин, то мы получим очень жест-
жесткое ограничение на возможный способ нарушения коммутатив-
коммутативности.
*) При кваитовомеханическом описании мы ведь ие можем пользоваться
классическим определением СП через дифференцирования по координатам и
импульсам.
9. КВАНТОВАНИЕ 377
Именно, вычислим квантовую СП двух произведений uiU2 и
ViV2. Это вычисление можно вести двумя способами — или при-
применяя свойство E) сперва к произведению щи2, а затем к произ-
произведению »i»2, или же наоборот. На первом пути получим:
(И,И2, V1V2) = (UU
= («,, О,) О2И2 + Oj (И,, 02) И2 + И, (Иг, О,) 02 + «if 1 («2. О2),
а на втором:
= {U1U2, 0iH2+0, (ЩЫ2, 02) =
= ("if i) «2»2 + «1 («2» »l) «2 + Щ (И,, 02) «2 + Ol«, («г, 02)-
Надо, конечно, потребовать, чтобы результаты обеих выкладок
совпадали, т. е. чтобы было
{U\, V\){U2V2—V2U2) = (tliVi — 0iU()(u2, V2),
или
(tt|Ol — V{Ui) (U2t>2 — УгЩ) / ч
(«1, »l) («2, Vi) ' ' " *¦*'
где цепочку равенств можно продолжить, добавляя такие же
выражения для новых пар наблюдаемых, скажем и3, о3; uit
04; ..., так что выражение (*) не зависит от той пары наблю-
наблюдаемых, из которых оно образовано.
Итак, с СП-формализмом может быть совместна не любая
некоммутативность динамических переменных, а только такая,
когда коммутатор пропорционален квантовой СП:
uv — vu = [и, v]_ = -lh- (и, v), E0>
где коэффициент пропорциональности Ь — универсальная по-
постоянная— как выясняется, та самая постоянная Планка B),
которую мы уже вводили в историческом введении.
Вспомним теперь, что в классической теории особенно про-
просты были СП канонически сопряженных координат и импульсов:
(Р;> <7/) = fy/; ^Рь Р/)==(<7<> <7/) = 0- E1.1)
Примем в качестве постулата, что
I Квантовые СП канонически сопряженных координат и импуль-
I сов сохраняют вид E1.1).
В силу E0) отсюда сейчас же получится, что канонически
сопряженные координаты и импульсы должны удовлетворять
перестановочным соотношениям
' — QjPt — \Pi> Qi\- — — *'Й0Ф
Г 1 Л Г 1 П E1.2)
378 ч. III ЭЛЕЖЕНТЫ КВАНТОВОЙ МЕХАНИКИ
Перестановочные соотношения E1) отвечают на поставлен-
поставленный в начале параграфа вопрос, как именно не коммутируют
квантовые динамические переменные. Их часто называют усло-
условиями квантования.
Для случая одной степени свободы, когда есть только одна
обобщенная координата и один обобщенный импульс, условия
квантования сводятся к одному равенству
pq — qp = — ih. E2)
Как быть с СП других динамических переменных, не являю-
являющихся координатами и импульсами? В классической теории
принимается, что всякая динамическая переменная какой-либо
системы есть функция ее обобщенных координат и импульсов.
На пути переноса этого допущения в квантовую теорию лежит
та трудность, что в ней приходится вводить в рассмотрение
функции от некоммутирующих наблюдаемых. Особых вопросов
не возникает, пока эти функции являются полиномами — имею-
имеющаяся алгебра операторов позволит нам выразить коммутаторы
этих функций и, v, ... через канонические коммутаторы E1),
после чего мы найдем СП функций ы, о, ... из E0), считая те-
теперь, что СП любых динамических переменных определяются
этим равенством через их коммутатор.
Это рассуждение можно, с определенными оговорками, рас-
распространить и на функции обобщенных координат и импульсов,
разложимые в степенные ряды. Как правило, мы приходим при
таком вычислении к тому же самому выражению для квантовой
скобки Пуассона, выраженной через квантовые динамические
переменные, что и получаемое в классической теории, при выра-
выражении классической скобки Пуассона через классические пере-
переменные, с той единственной оговоркой, что порядок множителей
в произведениях, который в классическом случае был безраз-
безразличен, оказывается теперь фиксированным. (Эта оговорка в дей-
действительности весьма существенна: при проведении вычислений
через ряды мы часто приходим к таким результатам, которые
(в классике) удается обратно просуммировать в известные
¦функции только за счет произвольного распоряжения порядком
множителей. В квантовом случае такое суммирование может
оказаться невыполнимым.)
10. Система с одной степенью свободы
Займемся теперь исследованием тех следствий, которые
можно извлечь для операторов координаты q и импульса р из
правил .кватования. Начнем с рассмотрения простейшего случая
одной степени свободы, когда эти правила задаются перестано-
перестановочным соотношением E2), и будем при этом считать, что на
10. СИСТЕМА С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ 3/9
эти операторы не наложено никаких дополнительных условий,,
которые могли бы ограничивать допустимые значения EW-ob
операторов q и р*). Наша цель будет состоять в том, чтобы
найти конкретную реализацию операторов р и q, т. е., на мате-
математическом языке, построить представление алгебры Ли E2).
Как мы вскоре увидим, оба эти оператора окажутся обла-
обладающими непрерывным спектром. Отчасти по этой причине бу-
будет удобнее исследовать E2) не непосредственно, а обходным
путем, введя в виде промежуточного шага некоторые новые
операторы, спектр которых будет дискретен. Впрочем, мы полу-
получим на этом пути ряд результатов, которые и сами по себе
пригодятся в дальнейшем.
10.1. Итак, введем вместо q и р новые операторы
.». р ± iaq I h a+ — а / ah , + , » /t-o\
а Jm'' q==y^—i—' р = Л/-2-(й +а)- E3>
где а — некоторая константа, и а означает то же самое, что
и а~ (Подобные динамические переменные мы уже вводили
в классическом случае при изучении осциллятора, см. 1.14**).).
Операторы а и а+ не являются наблюдаемыми, они даже неэр-
неэрмитовы (но эрмитово сопряжены друг другу)***). Найдем их
перестановки. Согласно E3) получаем
aa+-a+fl = J^(m[p, q)_-ia[q, р]_)=^-/й= 1. E4>
10.1.1. Построим теперь еще один оператор а+а. Он эрми-
эрмитов и положительно дефинитен: для любого \А):
(A\a+a\A)=Z{A\a+\t')(t'\a\A) =
Е|<1|
следовательно, все EW-ы оператора а+а — будем обозначать
их п — п :> 0. Поставим для него проблему собственных зна-
значений
а+а\п) = п\п) E4а)
*) Тем исключаются такие случаи, когда q — скажем радиальная коор-
координата г, собственные значения которой по самому своему смыслу могут быть
только положительными, или же угловая переменная типа углов Ь и <р, EW-ы,
которых должны восприниматься по модулю я или 2л.
**) Мы изучаем пока систему в один фиксированный момент времени.
Поэтому делать различие между переменными а (малыми) и А (большими)
нет нужды.
***) Об области определения операторов а и а+ мы пока ничего не можем
говорить, так как у нас есть только их алгебра, но нет пространства, в кото-
котором они действуют — его еще предстоит построить.
380 ч. HI. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
и допустим, что она имеет хотя бы одно нетривиальное решение,
которому отвечает собственный вектор |«). Тогда
а • а+а | п) = а - п | п) а+ • а+а | п) = а+ • п \ п)
или, по E4),
(а+а + 1) а | п) = п • а \ п) {а+а — 1) а+1 п) = п ¦ а+1 п),
то есть
а+а{а\п)} = (п — 1){а\п)} а+а{а+\ п)} = (п+ 1){а+\п)}.
Таким образом, действуя на собственный вектор |«) опера-
оператора а+а операторами а или а+, мы опять получаем собственные
векторы оператора а+а, отвечающие EW-ам («—1) и (га+1)
соответственно:
(Мы пока не считаем собственные векторы нормированными.)*).
Повторяя эту операцию многократно, приходим к тому, что из
каждого одного собственного вектора возникает целая последо-
последовательность собственных векторов, отвечающих EW-ам, расту-
растущим или убывающим от члена к члену на единицу. Но эта по-
последовательность собственных значений обязательно должна
оборваться снизу — ведь все они должны быть неотрицательны.
Поэтому в этой последовательности обязательно должен суще-
существовать собственный вектор |0), такой что
а| 0> = 01 0> == 0; |||0>||=1. E5)
Такой вектор называется вектором вакуума. Мы будем счи-
считать его нормированным на единицу.
Вакуум является собственным вектором оператора а+а
с собственным значением 0. Так как все остальные EW-ы от-
отличаются от него на целые числа, то, следовательно,
1 Все EW-ы оператора а+а суть целые числа n^N.
Других EW-ов (образующих какую-либо другую последова-
последовательность с другим «исходным» собственным вектором) у а+а
быть не может, так как, не содержа вакуума, другая последо-
*) Надо еще, конечно, показать, что найденные таким образом новые ре-
решения проблемы собственных значений нетривиальны — т.е. что собственные
векторы .а\п) н а+\п) не суть нули. Однако из а\п) =0 следовало бы
а+ {а | и» = а+а \ п) = п\ й>=*=0,
и, поскольку мы допустили, что \п) #0, п = 0. Аналогично, из а+\п) =0
следовало бы .
00+ | п) = (а+а + 1) | л> = (п + 1) | «> = О,
т. е. п = —1, что невозможно для EW-та положительно дефинитного а+Л,
Итак, а+\п) всегда #iO, а а|л) = 0 тогда и только тогда, когда, я =.0.
10. СИСТЕМА С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ 381
вательность не оборвалась бы снизу, а содержа — совпала бы
с первой.
ДОПУЩЕНИЕ: Вакуум невырожден. |
Это — физическое допущение: ведь могли бы быть другие, ком-
коммутирующие с а+, а операторы Ь+, Ъ; с+,с; ..., и вакуум по а+, а
мог бы быть любым состоянием по этим операторам.
10.1.2. Итак, все собственные векторы оператора а+а будут
получаться из вакуума последовательными действиями опера-
оператора а+
\п) = сп(а+Г\0),
где сп — нормировочные множители. Мы выберем их так, чтобы
все состояния |га) были бы теперь нормированы на единицу.
Вычисляя квадрат нормы |га):
видим, что эта нормировка будет достигнута, если выбрать
с„ = —т=г и, следовательно, положить
V"!
i „\ _J_/,,+yti л\. /„ i /л!„" 1 . mi-mi 1 нормированные
' ' "V^P ' ' '' \ral = \°la 7/rf; lllra)ll=1 собственные
»ni ¦ "П| векторы.
E6)
Кроме того, все векторы E6) с разными п — взаимно ортого-
ортогональны:
{п'\п") = ЬП'П'>. E6.4)
Действие операторов о+иана эти векторы запишется тогда
как
а+ | п) = -L- (a+)n+i | 0> = V^+TI п + 1);
а\п)=—р=- (а+)п '|0) = л/~п\ п— 1),
E7а)
т. е. оператор а+ переводит каждое собственное состояние |га)
в следующее старшее состояние, а оператор а —в предыдущее
младшее.
ЗАМЕЧАНИЕ 1: Мы впервые сталкиваемся здесь с операто-
операторами, для которых нам интересно их действие на векторы, а не
поиск тех состояний, которые не меняются под их влиянием. |
ЗАМЕЧАНИЕ 2: Оператор а+а, который мы здесь ввели, на-
называют обычно оператором числа частиц, его собственные ,зна-
382 ч. III. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
чения « — числами заполнения, а операторы а+ и а —операто-
—операторами рождения и, соответственно, уничтожения частиц. Смысл
этих названий становится ясным в так называемом «методе вто-
вторичного квантования», в котором выясняется, что переход кван-
квантовой системы из одного состояния в другое можно трактовать
как «рождение» в системе некоторых новых частиц и, возможно*
«уничтожение» других. |
10.2. Итак, совокупность векторов
|я>, я = 0, 1, ....
образует базис в пространстве векторов состояния квантовоме-
ханической системы с одной степенью свободы. Согласно
D5.3) представителем всякого линейного оператора а в этом
я-представлении служит матрица
через посредство которой а можно записать в виде двойной
бесконечной суммы по диадным произведениям A9): | п')(п"\
базисных векторов и совекторов *)
а= ? <«'| а \п")-\ п')(п"\**). <•>
«', »">о
В частности, представителями самих основных операторов
а+ и а будут согласно E7а) матрицы
(п'\а+ |rt")=V«"+ 16»', в-+1 — <sfn' Ьп; „*+,;
(пг | а | п") — V«" бц'+i. »* = V«' + 1 б»'+1. л*
и, следовательно,
a+= Z Vnr4rl\n'+l)(nr\; a= Z V«"+ 11 «"><«"+ 11.
»'>0 lt»>0
10.2.1.1. Возводя первое из этих соотношений в квадрат
*) Мы надеемся, что читатель достаточно освоился со словом «совек-
тор», чтобы не нуждаться далее в подчеркивающем его новизну дефисе.
**) Таким образом, можво сказать, что совокупность днадных произведе-
произведений \п') (п"\ играет роль базиса в «пространстве линейных операторов».
10. СИСТЕМА С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ 383
и, повторением этой процедуры,
п'>0
V
п">0
Поэтому произвольный моном по операторам рождения и уничтожения
о+иа запишется через базисные диадные произведения как:
п\ п">0
т. е. как
(a + )v'(a)v"= ]T -p~{ V(n' + v')! («' + v")! I «' + \'){п' + v" |.
10.2.1.2. В классической механике всякая динамическая переменная для
системы с одной степенью свободы должна была быть функцией ее коорди-
координаты q и импульса р — в этом собственно и состоял смысл утверждения, что
система обладает именно одной степенью свободы. Если мы хотим сохранить
то же понимание числа степеней свободы системы и в квантовой теории, то
мы должны ожидать, что для квантовой системы с одной степенью свободы
всякий линейный оператор а должен быть функцией ее операторов q и р,
или — что конечно то же самое — функцией операторов а> и а. Вспоминая
сказанное в конце предыдущего параграфа относительно возможного пони-
понимания функции от иекоммутирующих операторов, легко сообразить, что эти
замечания сводятся к требованию, что
Для системы с одной степенью свободы всякий оператор а представим в виде
двойной суммы элементарных мономов (a+)v оУ *), т. е. в виде
V, v" > О
Таким образом в пространстве линейных операторов для системы с од-
одной степенью свободы у нас возникли естественным образом две разные, пол-
полные системы элементарных объектов — система диадных произведений и си-
система мономов (a+)v av — по каждым из которых может быть разложен
произвольный оператор а — в форме (*) или в форме (**). Ясно, что при
этом каждый из объектов одной системы должен разлагаться по объектам
другой.
10.2.1.3. Одно из этих разложений — выражение монома (а+У аУ" через
сумму диад —мы уже получили ( + ). Чтобы получить второе, рассмотрим
представление в форме (•*) простейшего из диадных произведений — опера-
оператора проектирования в состояние вакуума
Яо = |0><0|= ? 4'v"(a + )V'-flV"-
V, V">0
•)• Моиомы, образуемые перемножением того же количества операторов
а+ и а в другом порядке разлагаются по мономам выписанного вида с по-
помощью перестановочных соотношений E4); например, aa+= a+a + 1.
384 ч. Ш. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
По определению этого проектора
и это дает нам условие
V'. V">0
Вычислим типичный матричный элемент правой части:
и' | <*+?' ¦ „у 1 п») _,_J— <о 1 <*"'• («+)v< • «v" • (<*+)"" I о)-
Переводя здесь v' операторов а+ последовательно налево с помощью пере-
перестановочных соотношений E4), пока оии, действуя на совектор вакуума, не
дадут нуль, a v" операторов а — таким же образом направо, увидим, что он
равен
п' (п' - \) ... (п' - у' + I) ¦ п" ... (п" -у" + \)
Vn'ln"!
я' I п"! ,. „
<„ _ v | п - v >
__________ <„ _ v | п - v > = —-——j- о„,_„. „._,.,
если л' — v'^ 0 (и л" — v"^0); в противном же случае матричный эле-
элемент равен нулю.
Таким образом наши условия на коэффициенты C°'V» принимают вид
"' "" /
(п' | Ро | п") = 6п'п»&п,0 = 2_j _, 6/i'-v'. n"-v" (n/_v'
v'=o v"=0
Легко сообразить, что в силу этих условий отличны от нуля лишь диагональ-
диагональные коэффициенты:
(любитель педантизма может доказать равенство нулю всех коэффициентов
вида cy/+fti k, v'= 0, 1, ..., по индукции от к к fe+ 1), для которых оста-
остаются условия
п'
— V П'1
o- _ (B'_v')l Су/<
V'=0
Полагая здесь «'=0, получаем, что со=1; Для п' = \ получаем с0 +
+ П • Ci = 0, т. е. ci —¦ -г . Допустим теперь, что вплоть до fe ^ п' — 1 вы-
(— 1)*
полняется ск = ' . Тогда
п'-\
п'Хсп'- _ (n'-v')lv'! (
(n'-v')l'
V'=0
V' = 0
10. СИСТЕМА С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ 385
т. е. и для k = п' выполняется
и наша гипотеза доказана по индукции.
Итак, оператор Ро проектирования в вакуум выражается через произве-
произведения операторов рождения н уничтожения рядом
V'>0
Если бы а+ и а ие были некоммутативны, мы сразу узнали бы в этом ряду
экспоненту от —а+а. Иными словами, мы сталкиваемся здесь с простейшим
примером тех очень нередких (и очень огорчительных) случаев, иа которые
указывалось в конце предыдущего параграфа, когда некоммутативиость опе-
операторов мешает представить полученный в виде ряда результат в компактной
форме элементарной функции.
10.2.2. В рассматриваемом конкретном случае последняя цель представ-
представляется настолько притягательной, что ради ее достижения идут на введение
нового понятия. Когда мы выписывали выше мономы, которые можно по-
построить из v' операторов рождения а+ и v" операторов уничтожения а, мы
выбрали те, в которых все операторы рождения а+ стоят слева от всех опе-
операторов уничтожения а — про такие моиомы говорят, что в иих а+ н а стоят
в нормальном порядке. В каждом члене полученного ряда для Ро опера-
операторы а+ и а стоят в нормальном порядке, ио если мы свернем ряд в экспо-
экспоненту, то этот порядок потеряется. Чтобы воспрепятствовать этому, вводят
понятие нормального произведения некоторого числа операторов а+ и а, ко-
которое обозначается двоеточиями вокруг перемножаемых операторов : ... : и
означает, что стоящие внутри этого знака операторы должны пониматься
расположенными в нормальном порядке вне зависимости от того, в каком
порядке они реально выписаны, например:
:а+а: = а+а; :аа+: = а+а; :аа+а: = а+аа н т. п.
Рассматриваются и нормальные многочлены нли ряды, под которыми пони-
понимаются (конечные или бесконечные) суммы нормальных одночленов.
ЗАМЕЧАНИЕ 1: Из определения нормального произведения следует, что под
его знаком любые операторы коммутативны: например
:аа+: = :а+а:. |
ЗАМЕЧАНИЕ 2: Поэтому из
отнюдь не следует
а = р\
Труднее примириться с тем, что из
не следует
:а: = :(}:.
Например,
аа+ =а+а + 1.
Но
:аа+: Ф :(а+а-\- 1):,
поскольку
:аа+: = :а
ЗАМЕЧАНИЕ 3. Мы уже обращали внимание иа то, что моном нз а+ и а,
перемножаемых в произвольном порядке, можно с помощью перестановочных
Fi R Мрпкрпр
386 ч. Ш. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
соотношений E4) представить в виде суммы моиомов, в которых а+ и а
стоят в нормальном порядке. Теперь это замечание будет звучать как утвер-
утверждение, что любое обычное произведение операторов а+ и а можно предста-
представить в виде суммы нормальных произведений, например,
а+аа=* :а+аа:\ аа+а = :аа+а: + :а:; ааа+ = :ааа+: + 2:а:,
пр-ичем в силу замечания 1
10.2.3. С помощью понятия нормального произведения можно свернуть
полученный для Ро ряд в нормальную экспоненту:
,а><0|-Р0-
Построение остальных проекционных операторов не составляет теперь
труда. В самом деле, по определению
Pn = \n)(n\=(a)\0){0\a = ±
Но все не входящие в нормальную экспоненту операторы а+ стоят здесь на
самом левом месте, а операторы а — на самом правом. Поэтому ничего не
изменится, если включить и их в нормальное произведение. Под знаком же
нормального произведения операторы можно писать в произвольном порядке,
и нам будет удобно записать Р„ в форме
которая подсказывает, что можно ввести общую для всех Р„ производящую
функцию (точнее, конечно, производящий оператор), записывая их в элегант-
элегантном виде
Р _ (-1)" f d у -Afl+g.
" п\ \dk )
В качестве примера использования последней формулы продемонстрируем
с ее помощью, что ^ Рп = 1. Имеем:
п>0
п>0 п>0
Но в силу теоремы Тейлора, для любого
*) Заметим, что, выполняя формальное суммирование ряда слева, можно
представить эту теорему в красивой форме
п>4
— оператор е а сдвигает аргумент к на |; это замечание понадобится нам
в дальнейшем.
10. СИСТЕМА С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ
387
Поэтому
п>0
Аналогично проекционным операторам выражаются через нормальные
произведения а+ и а и недиагоиальные диады:
¦Ла+)
П'е-а+а
(а)п
(+
+>
10.3.1. Вернемся к представляющим в «-представлении опе-
операторы рождения и уничтожения матрицам E7Ь). Эти пред-
представители очень важны, поэтому мы не поленимся переписать
их еще раз в развернутой матричной форме:
О УТ о ~
0 0 V2
о
0
0
о
0
0
о
0
Уз"
0
0
0 ...
0 ...
о ...
л/4 ...
0 ...
0
0
0
0
0
0
У2-
0
0
0
0
0
Уз
0
0
0
0
0
л/Т
0..
0 ..
0..
0..
0..
E7с)
10.3.2. Теперь можно опять заняться собственно интересую-
интересующими нас операторами координаты q и импульса рис помощью
формул E3) получить для их представителей в «-представ-
«-представлении:
(n'\q\ п") = д/A-
{п'\р\ п") = д/-^-
1. „*
E8.
+ 1б„', „»_! + л/п'Ьп', п*+\]' E8.2)
Один из них, например представитель координаты, выпишем
в виде явной матрицы:
0 /VI
— I л/Т 0 i л/2
-1л/2 0
О . Г.1*
О
58а>
13*
388
ч. III. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
Представитель оператора
Vir
р получается отсюда заменой
ЗАМЕЧАНИЕ: Матричные элементы операторов координаты
и импульса растут с ростом номера! Это обстоятельство весьма
поучительно для вопроса о том, какие операторы следует до-
допускать в теорию. Если бы мы решили ограничиться лишь теми,
матричные элементы которых с-ростом номера убывают, то, как
видно, в нашей схеме не нашлось бы места даже для операто-
операторов р и q системы с одной степенью свободы. I
10.4. Как мы видим, в «-представлении оператор q (и р) не
диагоналей. Попробуем привести его к диагональному виду,
т. е. решить для него проблему собственных значений. Удобнее
всего делать это в явной матричной форме.
Проблема собственных значений для операторов координаты
{или импульса)
= р'\р') E9а)
E9Ь)
запишется в представителях как
п">0
{п'\р\п"){п"\р') = рг{п'\р'),
или, если ввести временно обозначения
/1гсГ , /~Т~ ,
как
V W
п">0
т. е. в развернутом виде как
0 *л/Г
— i л/Г о
о
-;л/з" о
о
о
Со'
с2
С}
,, ,
ХСо
хс2
хс3
10. СИСТЕМА С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ
389
о
VT
О
Мы записали здесь представители собственных векторов {n'lq')
и {п'\рг) в виде матриц-столбцов с неопределенными элемен-
элементами Ci = Ci{x) и di = di(y), которые, конечно, могут зависеть
от EW-ов хну. Выполняя матричное перемножение в левых
частях, получим
0
V2
V2-
0
V3"
л/з
0
V4
0
V4
0
d2
dz
yd\
yd2
yd%
yd.
+ i
— i л/3с2 + ' л/А со
—
1
xc0
хс.
xc2
XCj
t
л/Tdi
Vlrfo
yd0
yd.
yd2
откуда будут следовать рекуррентные формулы:
n — 1
— 1
E.9c)
(Можно было бы, конечно, получить E9с) и прямо из E9Ь),
не «расписывая» матриц въявь, однако практический опыт по-
показывает, что в выкладках такого рода обычно бывает разум-
разумнее не пожалеть бумаги, чем тщиться не запутаться в пределах
суммирований.).
Полагая в первой группе формул E9с)
приводим ее к виду
п — 1
совпадающему со второй группой E9с), поэтому дальнейшие преобразования
можно проводить для координаты и импульса совместно. Рекуррентные фор-
формулы, очевидно, допускают последовательное решение, которое выражает все
390 ч. III. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
сп как некоторые полиномы от х, умноженные на Со. Чтобы избавиться от
корней, сделаем дальнейшую подстановку:
сп=~7к\ или d«
которая приведет наши рекуррентные формулы (для определенности пишем х,
имея в виду координату) к виду
еп = хеп-1 — (п— 1)е„-2. E9d)
Из математической физики известно, что полиномы Эрмнта *)
(?)«li F0)
tfo (I) = i;
#,(?)=2|;
удовлетворяют рекуррентным соотношениям
#„ (|) = 2|Я„_, (|) - 2 (« - 1) Я„-2 (|), F0а)
которые отличаются от E9d) только лишними двойками. Легко сообразить,
что для того, чтобы «подогнать» эти двойки, надо сделать в E9d) последнюю
подстановку
1 ( х \
после которой рекуррентные соотношения для hn:
кШ-^'Ш-21'-"h-Ш E9е>
уже не будет отличаться от F0а).
Таким образом, собирая все наши подстановки, видим, что
рекуррентные соотношения E9а) будут удовлетворены, если по-
положить
E9f)
где нулевые элементы cq и d0 остаются пока произвольными.
*) См., например, известные справочники Рыжика или Янке — Эмде.
Впрочем, нужные результаты нетрудно получить н кустарным способом; см.
дополнение в конце параграфа.
10. СИСТЕМА С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ 391
Итак, мы получили, что представителями собственных векто-
векторов координаты и импульса в n-представлении будут
<„<I ,<> = <- if -ф= Я,-(д/i ,') „„ (,');
причем EW-ами q' и р', которым принадлежат эти собственные
функции, могут служить любые вещественные числа. Подчерк-
Подчеркнем, что нулевые элементы этих представителей й> и d0 могут
еще произвольным образом зависеть от собственных значений
q' и р'.
10.5. Чтобы найти эту зависимость, потребуем выполнения
условий нормировки. Поскольку собственными значениями, ска-
скажем q, могут быть любые числа, т. е. спектр непрерывен, то
нормировать надо на б-функцию, т. е. потребовать, чтобы
было бы
<<Я?'> = I (q"\ n'){n' \q') = б fo" -<?'), F2.1)
rt'>0
и аналогично для импульса. Форма F1) приводит это условие
к виду
= b(q"-qr). F2.2)
10.5.1. Чтобы вычислить стоящую здесь сумму, воспользуемся для поли-
полиномов Эрмита известным интегральным представлением:
F0b)
С его помощью стоящая в F2.2) сумма сразу вычисляется:
¦?$Л'«Е
392 4. III. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
и остается взять гауссов интеграл
Я
— оо
10.5.1.1. С помощью естественной подстановки
. __v + w о — w д (t, и) .
W' "~~W; 7{^Г)-1 F3а>
этот интеграл
оо
л
—оо
распадается в произведении двух интегралов
оо
1
[ dwe [ dvе
первый из которых, не содержащий вторых степеней, есть просто ннтеграль-
ное представление б-функции. Для вычисления второго
делаем для уничтожения линейного члена подстановку
о == т + d,
благодаря которой
показатель = — 2т2 — 4 dx — 2d2 + « V2"(i + ц) т + / V2 (| + n)d + 2 ;п,
откуда
(I + )
2V2" '
показатель - - 2т2 + 2 « + ")' - ^^- + 2Бч
Следовательно, весь интеграл /г равен
ате
—оо
= а/ —- е
поскольку из-за получающейся из первого интеграла б-функции % = ц.
10. СИСТЕМА С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ 393
10.5.1. Таким образом, мы получаем для вычислявшейся суммы S зна-
значение
то есть
/_i nrt'. „'I п' п' \>
п'>0
10.5.2. Поэтому
— <7'2 ( /~а
^ко^ОРд/^6 W-<7') F2а)
и, значит, для правильной нормировки надо выбрать
\e~^. F2b)
Подставляя это значение в F1.1), получаем окончательное
выражение для представителя нормированного собственного
вектора оператора координаты в п-представлении
где фод — фаза нормировочного множителя, остающаяся произ-
произвольной согласно A2Ь).
ЗАМЕЧАНИЕ: Мы построили F1.1а) как представитель век-
гора \q') в базисе {п'\. Но то же самое выражение будет и
представителем совектора (п'| в базисе \q') — представителем
(нормированного на единицу*)) собственного совектора опе-
*) Действительно, из F2.1);
J] (q"\n')(n'\q') = b(q"-q')
п'>0
уже автоматически следует соотношение ортонормнрованности для представи-
представителей собственных векторов оператора числа частиц в д'-представлении.
В самом деле, рассмотрим
dq'{n'\q'){q' | п"> = /(«', п"),
394 ч. III. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
ратора числа частиц в координатном представлении. Наконец,
то же выражение есть и матрица преобразования от п- к q-ба-
зису. В том, что мы сразу видим из F1.1а) эти обстоятельства,
сказывается чрезвычайное удобство используемых нами обозна-
обозначений Дирака. В
10.5.3. Совершенно аналогично проводится нормировка соб-
собственных векторов оператора импульса, которая приводит нас
к результату
{п'\р') =
,2
5
^'
У2" -я'!
где фор — опять неопределенная фаза. Подчеркнем, что мы не
обязаны выбирать фазы в F1.1а) и F1.2а) равными, хотя
и можем это сделать.
10.6. ^-представление. Перейдем теперь в ^-представление.
10.6.1. Согласно общим правилам D7), представитель век-
вектора |<7о) в ^-представлении получится из представителя (п'|<70)
того же вектора в n-представлении по формуле
(qr \Qo) = Z tf I n') <n' | <7o> = б W - ?o), F4)
n'
где последнее равенство написано на основании нормировки
F2.1). Следовательно, представителем собственного вектора
оператора q в ^-представлении будет диракова б-функция. (За-
(Заметим, что то же обозначение (^'l^o). которое имело в F2.1)
смысл скалярного произведения бра- и кет-векторов базиса,
можно понять и как представитель совектора (q'\ в базисе
где f{n',n") пока не более чем обозначение. Тогда
<<?"К> J dq' {n'\q') (<7'|«">= ? (<?" I «')
n'>0 rt'>0
откуда, в силу F2.1),
| dq' б (q" - q') (q' | n") = J] (<?" | n') / («', «");
n'>0
<<?"!«')= ? (<?"|«'>f(«', n"),
и, поскольку «" произвольно,
f(ra', n") = 6(n' — n").
Отсюда вытекает искомое утверждение
q'{n'\q'){q'\n") = bn,na.
10. СИСТЕМА С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ 395
|<7о) — это не может дать повода к недоразумениям, поскольку
все эти величины совпадают.)
10.6.2. Найдем в том же представлении представитель опе-
оператора q. Имеем по общему правилу D8) преобразования от
одного базиса к другому,
W\q\<T)= I {q'\n'){n'\q\n"){n"\q")=...
п', п." > 0
если подставить сюда E8.1) для (n'\q\n"),
= i д/-^ ? W I "'> [У^+Тб^,»-,-, - У^У»^,] <п" | q") =
Суммирование в первой сумме можно распространить и на
п" = 0, так как корень все равно даст нуль. Объединим суммы
и подставим значения {n'\q') из F1.1):
12 п* { . , . I
Но по рекуррентной формуле F0.а)
и, следовательно, квадратная скобка в F5*) равна2л/^q'Hn"{...').
Поэтому продолжаем цепочку равенств:
.. = /J4VW). /а у ^,.(...0^(..Л
V а 2 V fi ^ 2"" • я"!
га >0
где последнее равенство установлено на основании условия
нормировки F2.2).
396 ч. III. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
Итак, представителем оператора q в ^-представлении яв-
является
{q'\q\q") = q'b{q'-q"). F5)
Совершенно аналогичная выкладка приведет нас к выраже-
выражению для представителя оператора импульса в р-представлении:
{р'\р\р") = р'Ь{р'-р"). F6>
ЗАМЕЧАНИЕ: Сами формулы F5) и F6) являются, конечно,
тривиальными — их можно было бы сразу выписать на осно-
основании общего свойства B) представителей из § 8. Цель по-
подробно проведенной выкладки состояла поэтому в том, чтобы
продемонстрировать на этом простом примере, как конкретно
производится переход от одного представления к другому (при-
(притом от дискретного — к непрерывному). |
10.6.3. Займемся теперь менее тривиальной задачей, именно,,
получим представитель собственного вектора \р') импульса
в q-представлении.
Начиная опять с D7) и используя F1), получаем последовательно:
п'
rt' ^ О
10.6.3.1. Прибегая, как и при установлении нормировки, к интегральному
представлению F0Ь), мы снова свернем сумму по п' в экспоненту:
,-n'
n'>0
oo
<]-2T]t-2lu-(P+u'+2ttuY
и придем к гауссову интегралу, отличающемуся от F3*) только лишними
множителями и Подстановка F3а) приводит квадратичную часть показа-
показателя к
_A + 0 о2— A — i)w2,
а линейную — к _ _
- V2 (| + Ti) v - V2 (т! - |) w,
10. СИСТЕМА С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ 397
после чего двойной интеграл опять распадается в произведение двух инте-
интегралов
00 СО
— ОО — ОО
однако, в отличие от вывода F3), теперь оба интеграла сохраняют квадра-
квадратичную часть показателя.
Для вычисления первого из этих интегралов
— ОО
делаем подстановку
/i = [ dvt
Э
л_ A+4)
V2 A + i)
которая приводит его к виду
(?+ч)' ,, .,
Второй интеграл вычислять нет нужды, так как он получается из первого
одновременной заменой i-*-—i, §-»¦—|. Таким образом, получаем для сум-
суммы Si
V2 V2
_
2
10.6.3. Возвращаясь к нашей задаче вычисления координатного предста-
представителя собственного вектора импульса, получаем с использованием F1Ь),
F1.2а), что
2ft ф
¦у/пЛа
то есть
e^-e4v"%)> F7>
где фор и cpog — фазовые множители, которые все еще нахо-
находятся в нашем распоряжении.
Итак, представителями собственных векторов импульса
в координатном представлении являются функции F7), т. е.
состояния с определенным значением импульса описываются
в координатном представлении одномерными плоскими вол-
волнами.
398 ч. III. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
10.6.4. Последняя выкладка, которую нам еще осталось про-
провести с помощью развитой в этом параграфе техники, — это
найти представитель оператора р в q-представлении. В п-пред-
ставлении (E8)) представитель импульса отличается от пред-
представителя координаты только тем, что в обоих членах стоит
одинаковый знак -f и отсутствует множитель i.
10.6.4.1. Поэтому сперва выкладка пойдет точно так же, как и при вы-
выводе формулы F5) для представителя q, но вместо F5*) возникнет выра-
выражение
Воспользоваться рекуррентной формулой для полиномов Эрмита теперь уже
не удастся, и придется непосредственно прибегнуть к интегральному пред-
представлению F0Ь). Мы получим тогда для суммы:
л/2 1 4^Q 2nnl
ОО
= -U [
si 2 я, J
-+ У Я"'-ь'[Е)^'(т|)).
^ ' " Z ' Л ! I
dt du
т. е. получим в этом случае в каждой из сумм по одному «лишнему» множи-
множителю 2(т] + iu) или 2(% + it). Свертывая суммы, найдем
—
1
\.
Первый интеграл здесь мы уже считали (F3*)), он пропорционален 6(s — ц)
и в силу наличия множителя (| — г\) даст теперь нуль. Второй интеграл сво-
сводится подстановкой F3а) к произведению
оо
= -^L — —)=r \
V2 я V2 J
ОО
X
первый множитель которого есть интегральное представление для функции
б'(| — ц), а второй — интеграл /г, вычисленный в 10.5.1.1 (мы не вправе,
10. СИСТЕМА С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ 399
конечно, полагать теперь в выражении для последнего интеграла | = ц).
Итак,
и, следовательно,
<Ч'\р\ q") / -Vnah cl (<?') c0 (q") 6' (I - n) e
e 2<Г2 *
- - / a e 4 6' (| - ,) e (%•" V) = Ai6'(«'- <?") e' (V-V).
10.6.4. Таким образом получаем окончательно
W\P\Я") = 4б'(<?' - q")e (Фо»""V') «=
F8)
10.6.4.2. ЗАМЕЧАНИЕ 1: Последнюю формулу мы могли бы, уже имея
выражение F7), получить другим, более простым способом: сперва выписать
представитель F6) оператора импульса в его собственном представлении, а
затем перевести его в координатное представление с помощью F7), которая
играла бы теперь роль функции преобразования. В самом деле, по общему
правилу D8)
<<?' I Р ! <?"> = \ dp' dp" (q' | p') (p'\p\ p") <p" | <T> =
dp. dp" _i_ e*в1 (%' -%')p'd (p' - p") е^е (%"-V
VOq" 40q qq h
^'' = у 6' (<?' - <
q') Г
J
что, конечно, опять приводит к F8). В
10.7. ЗАМЕЧАНИЕ 2: Во всех полученных выше формулах
сохранились произвольные фазы фод и фор. Они не должны быть
существенными, поскольку векторы сопоставляются состоя-
состояниям — которые фиксируются результатами измерений — лишь
с точностью до этих фазовых множителей, т. е. с точностью до
преобразований
Наши результаты говорят, однако, что такие преобразо-
преобразования (будем для определенности иметь в виду первое из
них) изменяют (формула F8)) выражение для представителя
400 ч. III. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
оператора импульса в координатном представлении, добавляя
к нему второй член 6 (q' — q") дУ . Это наблюдение можно
интерпретировать как изменение самого оператора импульса,
претерпевающего преобразование
где (foq — произвольная (вещественная) функция оператора ко-
координаты q, и сделать, следовательно, из него тот вывод, что
оператор р определяется при известном q перестановочными со-
соотношениями E2) не однозначно, а лишь с точностью до пре-
преобразования (•), — последний вывод совершенно очевиден, по-
поскольку второй член в (*) коммутирует с q n поэтому ничего
не вносит в E2). I
О связи преобразований (+) и (*) стоит поговорить более
подробно.
10.7.1. Собственные векторы всякого оператора, скажем опе-
оператора координаты q, определены у нас исключительно урав-
уравнением проблемы собственных значений
q\q') = q'W) (а)
и условием нормировки {q'\q") = 8(q — q"). Поэтому, если
умножить (а) слева на произвольный унитарный оператор V,
коммутирующий с 9,
V: VV+ = U [V,q]_ = O,
то будет
q.
т. е. векторы
\q')=V\q') (P)
смогут на тех же основаниях, что и \qr), претендовать на имя
собственных векторов q. В том частном случае, когда V=V(q) =
= е'% (этот случай обязательно осуществляется для си-
системы с одной степенью свободы, для которой q сам по себе
образует полную систему коммутирующих наблюдаемых), пре-
преобразование (Р) и есть преобразование (+)•
10.7.2. Сделаем теперь очень существенное для понимания
структуры математического описания квантовой механики за-
замечание. Подвергнем все операторы, векторы и совекторы од-
одновременному преобразованию
10. СИСТЕМА С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ 401
с помощью произвольного унитарного оператора U, UU+=l.
Замечание, которое мы хотели сделать, состоит в том, что пре-
преобразование (y) не меняет ни одного из чисел, которые можно
построить в нашей математической схеме. Действительно, един-
единственные числа, которые мы умеем строить из векторов, совек-
торов и операторов — это скалярные произведения A2) или
матричные элементы A5), а для них:
Таким образом унитарное преобразование (у) не меняет ника-
никаких проверяемых предсказаний квантовой механики — ведь все
такие предсказания могут быть сделаны только в терминах чи-
чисел. В частности, (у) не меняет ни одного представителя. По-
Поэтому можно сказать, что унитарный поворот (y) затрагивает
лишь принципиально ненаблюдаемые детали той математиче-
математической схемы, которую мы привлекли для описания квантовых
явлений, и его проведение никогда не влечет никаких наблю-
наблюдаемых следствий.
10.7.3. Используя отмеченное обстоятельство, выполним
вслед за преобразованием (Р) преобразование (y), в котором
выберем в качестве унитарного U
Тогда новые векторы будут | А) = е~ "V \а) и, в частности, но-
новые собственные векторы оператора координаты:
т. е. выполняемое после преобразования (р) преобразование
(y) возвращает собственные векторы оператора q к их перво-
первоначальному виду, убирая «произвольную фазу» 6%.
10.7.3.1. Однако (у) преобразует не только векторы, но и
операторы, переводя любой не коммутирующий с координатой
оператор | в
*) Исключение составляет только сам оператор q (или коммутирующие
с ним операторы), для которого
т. е. последовательное выполнение преобразований (($) и (у) не меняет ии
оператора q, ни его собственных векторов.
402 '¦ Ш- ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
В частности, оператор импульса
р =ф р = е~ "p°7peiq>0</ =
-\dq'dq"dq"'dqlv\ q') {q'U^" \q") {q" \p\ q"'){q'" |e'%| ,
Ho
1 6' (/ -
6 (/ _ (
(/ ,) (, ,) +
i i dq
где первый чяен есть представитель (<7 | р I <г / оператора р, а второй —
прекставитель \<7 I h —ц—\q ) оператора п —-г—.
10.7.3.2. Итак, последовательное проведение преобразова-
преобразований (|3) и (у) оставляет собственные векторы |^') оператора
координаты без произвольной фазы, но зато переводит импульс
Р в
т. е. осуществляет преобразование (*).
В более общей форме результат проведенного рассуждения
можно резюмировать как утверждение:
Умножение собственных векторов какого-либо оператора
(или набора коммутирующих операторов) | на унимодуляр-
ный (зависящий от собственных значений!) множитель можно
(с помощью физически ненаблюдаемого ^-преобразования)
реинтерпретировать как унитарный поворот всех операторов,
кроме коммутирующих с |, и всех векторов (и совекторов),
кроме собственных векторов (и совекторов) ||').
10.7.4. Таким образом, мы видим, что в квантовой теории
принятые нами соотношения между состояниями и векторами
допускают преобразования типа (+) (или (*)), приводящие
к появлению в таких формулах, как F7) или F8), дополни-
дополнительных членов. Такие преобразования суть некоторые преоб-
преобразования симметрии; их смысл становится ясным, если заме-
заметить, что (*) в точности аналогично преобразованию импульсов
10. СИСТЕМА С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ 403
в классической механике, индуцируемому добавлением к функ-
функции Лагранжа полной производной
В первой части мы выяснили, что такое преобразование есть
каноническое преобразование с производящей функцией
10.7.4.1. Во второй части (П. 9) мы уже указывали, что преобразования
(*•) тесно связаны с введением взаимодействия системы с электромагнитным
полем и обеспечивают инвариантность уравнений при изменении калибровки
последнего. Действительно, вспоминая выражение для импульса частицы во
внешнем электромагнитном поле
видим, что при градиентном преобразовании электромагнитного поля
е d% , . _
импульс частицы в поле получает как раз добавку -z— типа (**). Поэтому,
чтобы импульс частицы не менялся при градиентном преобразовании, надо
одновременно с изменением калибровки электромагнитного поля делать и пре-
преобразование
| q')-> \q') е~а
типа (+).
По этой причине преобразования (+) называют калибровоч-
калибровочными преобразованиями первого рода.
10.7.4.2. Итак, с помощью подходящего калибровочного пре-
преобразования первого рода полученные нами выражения F8)
и F7) для представителей в ^-представлении оператора им-
импульса и его собственных векторов могут быть приведены
к простому виду
i ч'р'
; F7a)
-</")¦ F8а)
10.8. Сделаем еще несколько замечаний относительно рас-
распространения полученных результатов на системы со многими
степенями свободы. Если все эти степени свободы кинематиче-
кинематически независимы, т. е. кроме перестановочных соотношений
E1.2) не существует никаких дополнительных условий, огра-
ограничивающих возможные наборы собственных значений коорди-
координат и импульсов, то, используя коммутативность E1.2) пере-
переменных, относящихся к разным степеням свободы, мы можем
прибегнуть к следующей процедуре:
404 ч. III. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
10.8.1. Рассмотрим сперва по отдельности каждую пару ка-
канонически сопряженных переменных qt и р{, образуем из них
с помощью E3) отвечающие дайной степени свободы опера-
операторы рождения и уничтожения af и ai и, повторяя рассужде-
рассуждения начала параграфа, построим ортонормированный базис:
= @1,@,)"'—;=. F9>
Этот базис будет растягивать векторное пространство
в котором действуют относящиеся к t-й степени свободы опе-
операторы af, ait qt, ...
10.8.1.1. Введем теперь прямое (говорят также внешнее
или тензорное) произведение векторов, взятых по одному иа
каждого такого пространства,
| А\ | АJ ... | A)N
(N — число степеней свободы), такое что
= cl\A)l...\A)t...\A)N + c2\A)i... |5>г...|Л>„ G0).
для любого 1 ^ / ^ N.
Тогда можно рассматривать такие произведения
как элементы некоторого нового векторного пространства, об-
образуемого как линейная оболочка этих произведений, которое
называется прямым произведением {1Л)]}® ... <8>{\A)N) про-
пространств {| A)i), {\АJ), ..., {| A)N}. Конечно, не всякий элемент
{\A)i}<8> ... ®{l^)w} может быть представлен в форме
| А)\ | ЛJ ... | A)N, но, вообще говоря, лишь в виде линейной
комбинации некоторого (возможно — бесконечного) числа та-
таких специальных форм (полиад)*). Скалярное произведение
в «большом» пространстве {|Л\} ® ... <8){\A)N} определяется
*) Мы фактически уже сталкивались с примером произведений такого
типа, когда рассматривали специальный линейный оператор, образованный
произведением кет- и бра-векторов, с кет-вектором слева (|Л) (В(), и даже
представляли любую наблюдаемую в форме линейных комбинаций таких про-
произведений
Совокупность линейных операторов можно рассматривать как линейное про-
пространство, образованное прямым произведением пространств кет- и бра-век-
бра-векторов.
10. СИСТЕМА С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ 405
сперва для пары векторов и совекторов специального вида G1)
как
<*i Bn\A\ AN) = (Bl\l\Al)l...(BN\N\AN)N, G1 а>
а затем расиространяется на произвольные векторы по свойству
линейности по каждому аргументу.
10.8.1.2. Полную ортонормированную систему в «большом
пространстве» можно получить, рассматривая в нем совокуп-
совокупность векторов, являющихся прямыми произведениями всевоз-
всевозможных комбинаций базисных векторов каждого пространства,
относящегося к t-ой степени свободы:
1«1, «2 «Л/> = |Л.>1«2> ••• \1ц). G2)
10.8.1.3. Чтобы построить операторы в «большом простран-
пространстве», переведем сперва в него операторы ?,-, действующие в
f-ом «малом пространстве», полагая по определению, что та-
таким операторам сопоставляются в «большом пространстве»
операторы
Зг: El\A1,...,AN) = \A)l...h\A)i...\A)N, G3)
что можно записать символически как
В, = / ® / ® ... ® Ь ® ... ® /. G4)
на ?-м месте
Суммы и произведения таких операторов образуют произволь-
произвольные операторы в IX {I А)}.
®
ЗАМЕЧАНИЕ: Физически между операторами |,- и Е,-, между
«большими» и «малыми» операторами, нет никакой разницы —
и тот и другой служит представителем одной и той же физиче-
физической величины. Поэтому в физических книгах обычно обозна-
обозначают их одной и той же буквой и ничего не говорят о переходе
от одного к другому.
Математически же это конечно совсем разные операторы —
они действуют в разных пространствах.
Особенно ярко эта ситуация проявляется, если рассматри-
рассматривать для каждой степени свободы однородные физические ве-
величины и при том такие, которые из физических соображений
должны быть аддитивны. Так, например, исходя из «чисел час-
частиц» п*, относящихся к отдельным степеням свободы, можно по-
построить физическую величину, равную их сумме, «полное число
частиц» (К сожалению, на изложенном до сих пор материале
трудно построить более наглядный пример.). Полный способ
рассуждения должен был бы гласить, что мы образуем сперва
из операторов Ai = afal, действующих в частных пространствах,
406 ч- ш- ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
с помощью G4) соответствующие операторы JV,- в большом
пространстве:
NN = I®I® ... ® nN, G5)
и после этого для образования оператора полного числа частиц
складываем уже эти, действующие все в одном и том же про-
странстве, конструкции:
N=NX + N2 + ... +NN. 76)
В физике же, однако, не различая «малых» и «больших» опе-
операторов, пишут обыкновенно вместо G6) просто
JV = й, + п2 + ... + hN. I G6а)
10.8.2. Теперь уже ясно, как распространяются результаты '
этого параграфа на случай N степеней свободы. Прямое произ-. \
ведение собственных векторов операторов каждой координаты \
(или импульса) в своем «малом» пространстве будет общим ]
собственным вектором «больших» операторов всех координат 1
в «большом» пространстве. Его представителем в базисе G2) ¦
будет обыкновенное произведение одномерных представителей,
F1.1а):
v
к77)
EW-ы q\ каждой координаты пробегают непрерывную область
значений —оо < q't<_ + oo. Совокупность этих EW-ов можно рас-
рассматривать как координаты в некотором конечномерном (Af-мер-
ном) вещественном пространстве.
10.8.2.1. Это пространство называется конфигурационным
пространством системы. Для одной материальной точки конфи-
конфигурационное пространство совпадает с обычным трехмерным
физическим пространством, с которым мы имели дело в класси-
классической теории. Однако во всех остальных случаях это не так;
например, для системы п материальных точек конфигурацион-
конфигурационное пространство имеет размерность N = Зл.
10. СИСТЕМА С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ 407
Аналогично напишется представитель общего собственного
вектора операторов импульса.
10.8.2.2. Функции G7) могут служить для перехода к пред-
представлению, в котором все координаты диагональны. В этом
представлении представителем того же вектора будет произве-
произведение б-функций F4), а представителем оператора /-ой коор-
координаты— произведение б-функций, умноженное на EW этой
координаты:
-?;4tf-#)*)¦ F5а>
Совершенно таким же будет и выражение для представителя
1-го импульса в импульсном представлении.
Весьма часто (особенно—когда наши N обобщенных ко-
координат суть 3 декартовы координаты одной материальной
точки) используется представитель в координатном представ-
представлении общего собственного вектора импульсов. Мы выпишем
его для этого специального случая **):
**"'"'- <78>
Наконец, представителем /-го импульса в координатном
представлении будет производная произведения б-функций по
/-ой разности EW-ов координат:
"(Мы выбрали во всех предыдущих формулах произвольные
фазы равными нулю.)
10.4.1. ДОПОЛНЕНИЕ: Введем для фигурирующих в E9d) коэффициен-
коэффициентов еп(х) производящую функцию
Л=0
так что
*) Мы привели здесь обычный способ сокращенной записи, в котором-
под первым множителем понимается одии EW, а под вторым — произведение
iV б-функций.
**) В общем случае таким представителем будет монохроматическая
плоская волиа в УУ-мерном конфигурационном пространстве.
408 ч- ш- ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
дФ
Вычислим , , заменяя еп(х) с помощью E9d):
дФA,х) 1
lF ()
= - (х + Я) Ф (X, х)
Таким образом производящая функция удовлетворяет дифференциальному
уравнению
с разделяющимися переменными, интегрирование которого дает:
In Ф (X, x) — — I -%- + "Xx J + In ф (я), т. е. Ф (?
где «постоянная интегрироваиия» ф(х) есть
Ф (*) = Ф @, х) = е0 (х).
Поэтому можно написать
еп (х) = е„ (д;) • е0 (х),
где
и, тем самым,
Полиномы еп(*) отличаются от полиномов Эрмита в общепринятой норми-
нормировке F0) только лишней половиной в производящей функции и приводятся
к ним очевидной подстановкой ArV2i, после чего получается
— как раз та формула, которая используется в тексте.
Выведем еще интегральное представление F0Ь), которое потребовалось
нам в 10.5.1. Перейдем в F0) от дифференцирования по % снова к дифферен-
дифференцированию по X:
Но
ОО
1_
-»-И,
II- СООТНОШЕНИЕ НЕОПРЕДЕЛЕННОСТЕЙ ГАИЗЕНБЕРГА 409
где мы ввели новую переменную интегрирования, положив т = t + i'K. От
интегрирования от —оо — й. до оо — i% можно, сдвинув контур, перейти к ин-
интегрированию от —оо до оо, т. е. продолжить цепочку равенств:
__1
Поэтому
оо
»п (I) = Hm f- -*-)* -L \ dt e
oo
то есть
оо
— мы приходим к желательному интегральному представлению.
11, Соотношение неопределенностей Гайзенберга
11.1.1. Рассмотрим некоторую квантовую систему, находя-
находящуюся в произвольном состоянии, описываемом вектором \А),
который мы будем считать нормированным,
и зададимся целью узнать, какие ограничения накладывают ус-
условия квантования E2) на возможные результаты измерений
координаты q и сопряженного ей импульса р (это может быть
или единственная координата одномерной системы, или одна
из координат системы со многими степенями свободы — все
равно).
Мы уже знаем, что сопряженные координата и импульс не
могут иметь одновременно точных значений, поэтому речь пой-
пойдет о средних значениях.
На средние значения самих величин q и р условия кванто-
квантования не налагают никаких ограничений. Поэтому для удоб-
удобства мы будем сперва считать, что в рассматриваемом состоя-
состоянии средние значения координаты и импульса равны нулю:
Какова может быть наименьшая неопределенность этих
значений, т. е. как велик будет разброс при многократных из-
410 ч. III. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
мерениях? Эту неопределенность удобно характеризовать сред-
средними квадратичными отклонениями
(Л?J = (Л?J = (q - qJ = q2 - 2qq + ? = q2
в силу предположения q = 0, и такой же величиной для р.
Построим вектор
и рассмотрим его норму:
Таким образом для неотрицательности нормы \В) должно вы-
выполняться неравенство
при любых значениях а > 0. Условием этого будет неположи-
неположительность дискриминанта:
или
Aq - Ар ~^-z • 79)
Это условие и есть знаменитое соотношение неопределенностей
Гайзенберга. Оно утверждает, как мы видим, что произведе-
произведение неопределенностей в значениях координаты и импульса
(т. е. по существу в значениях любой пары канонически сопря-
сопряженных переменных) может быть только больше—или, в край-
крайнем случае, равно—половине постоянной Планка.
11.1.2. Знак равенства достигается в G9), как легко сообра-
сообразить только если (для некоторого значения а)
||| в)||= 0, т. е. |В> = 0.
Но это значит, что |Л) есть вектор |0) (для того же значения
параметра а), который мы назвали выше вакуумом (в «-пред-
«-представлении). В координатном представлении его представите-
представителем будет
aq'2
-j-e 2h (формула F2b)),
а. в импульсном
(р' | о> = d0 (/>')= ~—е~ 35*" (согласно F1.2а)).
11. СООТНОШЕНИЕ НЕОПРЕДЕЛЕННОСТЕЙ ГАЙЗЕНБЕРГА 41Г
Таким образом оказывается, что есть целое семейство «со-
«состояний наименьшей неопределенности», зависящее от одного
параметра ос, в зависимости от значений которого мы получаем,,
как легко видеть,
Д<7 = д/-2^-; Ар = л/-~, причем для всех a: &q-&.p = Y-
ЗАМЕЧАНИЕ: Поскольку переход от координатного представ-
представления к импульсному есть в силу формул F7), G8) просто
преобразование Фурье, то можно заметить, что «состояния наи-
наименьшей неопределенности» отличаются той особенностью, что-
форма их представителей не меняется при преобразовании
Фурье. Иными словами, эти состояния симметричны относи-
относительно замены координат на импульсы. I
11.2. Итак, мы выяснили, что состояния \А), (А\А)=1, об-
обладающие свойствами:
^ (А \р | Л) = 0;
= (А\(р -рJ\А),
суть состояния вакуума,
| А) = | 0), по отношению к а = ,
для какого-либо одного любого а > 0.
Зададимся теперь вопросом, как построить аналогичные
состояния минимальной неопределенности, несущие не нулевые,
а некоторые заданные конечные средние значения координаты
и импульса, т. е. состояния \А) со свойствами:
где р и q — заданные числа.
11.2.1. Того ради заметим, что из перестановочных соотно-
соотношений E2) следует, что
_ t gp * qp _ 1 аР г ар
е h qe h =e h e h (— а + q•'. = (q — a);
up . ctp
e * p e H = =p;
. btj . bq
e * qe h = =<75
bq . bg
e * p e h = = (p — b).
412 ч. III. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
Поэтому
е н е н qe н е н = C/i^C/Г1 = (<7 — a); UlPUrl = (p-b), A)
а равно также и
е *е *?е fte * =U2qU2l=:{q-ay, U2pU2l = (p-b). {2)
11.3. Чтобы понять, что две выпираиные группы формул взаимносогласо-
ваны, займемся подробнее экспонентой от некоммутирующих операторов, ска-
скажем i и t). Если бы | и t) коммутировали, то для них, как и для чисел,
было бы
е?+ч = е6еч = ечД если ^ г,] _ = о.
В общем случае [|, т]]_ >#= 0 простых соотношений между е^+т), е? и е4 ие
получается; если, однако, коммутатор [|, t)]_ хоть и отличен от нуля, ио есть
с-число (точнее, если он коммутирует как с 5. так и с t)), то можно получить
достаточно обозримые формулы.
Итак, рассмотрим экспоненту
^Г [|,Т1]_=с; [|, с\_ = \% с]_ = 0,
rt>0
определением которой служит приведенное разложение в ряд. Для однознач-
однозначности записи такого разложения нам, как н в 10.2.2 надо избрать какой-либо
порядок операторов | и t) в качестве нормального. Будем считать нормаль-
нормальным (и обозначать тремя точками) такой порядок, когда все t) стоят слева
от всех %, т. е. порядок r)v4V!. При таком соглашении обычные произведения
операторов | и г\ можно будет, как и в 10.2.2, разложить по нормальным,
в частности произведения пар операторов будут суммами нормального произ-
произведения н с-числа:
14 = 41+ с= : |п! + с; Ц= Hi; +0;
Ч1 = : nl: + 0; тщ = : чч
Эти числа называют свертками соответствующей пары операторов и записы-
записывают:
|Ч==с; ч1 = 0; 1|_=0; чч,= 0.
С помощью понятия свертки произведение любой пары линейных в 1 и Ц
операторов А и В записывается единообразно как
АВ=\АВ\ +АВ,
где только свертки АВ — свои для каждой пары А, В. В частности,
Для разложения по нормальным произведениям обычного произведения
более чем двух линейных в 1 и ч операторов Аи ..., А„ имеет место
ТЕОРЕМА ВИКА:
i п
без U. /„ <„ /,
11. СООТНОШЕНИЕ НЕОПРЕДЕЛЕННОСТЕЙ ГАЙЗЕНБЕРГА 413
где суммирование в правой части выполняется по всем возможным комбина-
комбинациям всех возможных чисел сверток, причем каждая комбинация сверток
берется ровно один раз.
Легко видеть, что в силу теоремы Вика
s\2s (re-2s)!
2s.
Действительно, ————— есть число возможных выборов одной пары
, - v (л — 2) (я — 3)
(с безразличным порядком) из п элементов, - ^ число воз-
возможных выборов второй пары из (и — 2) оставшихся и т. д.; множитель же
—г- возникает из-за того, что каждая группа из s сверток появляется в на-
нашем подсчете в si различных несущественных порядках сверток внутри
группы.
Применяя последнюю формулу к разложению экспоненты е^+11, полу-
получаем
n! Lj si \2j (n-
и! Lj n! Lj s\ \2) (n-2s)! '
n—0 n-0
(n - 2s)!
n—2s—0
—-/>2 teE+Ti: —-„2
с
2 .
или
[6. 41-
и, заменой ?<^л»
11.2.2. Возвращаясь к нашим формулам A) н B), видим,
что в первой из них преобразование q и р проводится с по-
помощью оператора
п -<jt-'-t- т(-0"+»«> w(-'A) и -'is-
Ul = e e * = е * е2Л = с/е г ,
414 ч- ш- ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
а во второй — с помощью оператора
отличающегося от первого лишь численным (и унимодулярным)
. _аЬ_
множителем е л , исчезающим из всех комбинаций ULU-*
с любым L.
11.4.1. Итак, в рассматриваемом состоянии |Л), (А\А) = Н
причем под U можно понимать любой из унитарных операторов
U, Ui или С/г. Поэтому, если выбрать теперь постоянные
|Л>
то будет
(A\UqU~l\A) — 0 и
Те же равенства можно прочесть и иначе, в форме утверж-
утверждения, что в состоянии
средние значения координаты и импульса q ъ и р.ъ равны
нулю.
Но для такого состояния мы уже знаем из 11.1.2, что тре-
требуется, чтобы неравенство соотношения неопределенностей пре-
превратилось бы в нем в равенство — для этого необходимо и до-
достаточно, чтобы | А) было вакуумом для некоторого а,
Соответствующее состояние |Л) есть тогда
|Л)-С/|О)в.
11.4.2. Найдем Aq2 в состоянии |Л).
Поскольку Д<72 = q2 — (qJ, то мы вндим, что
] (A\q2\A)- (*,д>)*-<0| U~lq2U |
Но U~lqU = q + a = q + щ Ау а
П. СООТНОШЕНИЕ НЕОПРЕДЕЛЕННОСТЕЙ ГАЙЗЕНБЕРГА 415
Поэтому средний квадрат неопределенности значения координаты в состоянии
| Л) есть
Д<7?л> = (О I <J2 + 2qq{ А) + (<?u)J I 0) - ($, А) J =
Таким образом
Ща) = Щ0) и Д<7|Л)=А?ю>
— неопределенность значения координаты в состоянии |Л) та
же, что и в состоянии |0).
11.4.3, Вычисление неопределенности значения импульса про-
проистекает совершенно так же, и, значит, — поскольку состояние
|0) было состоянием вакуума, в котором произведение A.q-&p
принимало наименьшее значение—, —то же самое выпол-
выполняется и для построенного с помощью унитарного преобразова-
преобразования U состояния \А), которое теперь естественно обозначить
относящимися к нему средними значениями q и р (и, может
быть, еще и значением а):
|Л> = |<7, p)s3|<7, р; а).
Итак, в состояниях \q,p) выполнены все сформулирован-
сформулированные в 11.2 пожелания:
Поэтому эти состояния суть такие квантовые состояния, кото-
которые осуществляют наибольшее возможное приближение к клас-
классическому состоянию, в котором сразу q — q и р = р. Их при-
принято называть когерентными состояниями.
11.5.1. Выразим унитарный оператор U, образующий коге-
когерентное состояние из вакуума, через операторы рождения
и уничтожения E3). Простая выкладка показывает, что
j(—qp + pq) = aa+ — а* а,
где а и а* — средние значения операторов а и а+, т. е.
- р — iaq т _* р + iuC}
Таким образом [/ = ейо+~й*а; его удобно переписать в нор-
нормальной форме (теперь в обычном смысле 10.2.2), опять
416 ч. 111. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
прибегнув к результату 11.3 о преобразовании экспоненты от
суммы в произведение экспонент. Имеем
U = ^а+-а'а = еТ [~й'а- йа*]~еаа+е-а*а==
В?а а*а
— е 2 gao+g~a*a = e 2 • gaa+-a*a^
При действии на вакуум все — стоящие теперь справа — сте-
степени а кроме нулевой, уничтожатся, и мы получим, что
¦ а*а
и, если учесть, что "J а а ^ 2й" V 2сГ + Т <ГJ'
\q,p) = e 2h ^2а г ;eVV2aft V 2ft |o).
11.5.2. Мы определили когерентные состояния как состоя-
состояния наименьшей неопределенности в значениях координаты и
импульса при заданных средних значениях. Но из выписанных
явных формул видно, что они обладают также и свойством
a\q, p) — a\q, р),
т. е. когерентные состояния суть собственные состояния опера-
оператора уничтожения а; это свойство в равной степени может слу-
служить их определением.
Мы выяснили таким образом, что неэрмитов оператор а
имеет своими собственными значениями любые комплексные
числа. Его собственные векторы — найденные нами когерентные'
состояния — образуют нормированную, но не ортогональную
систему — простая выкладка показывает, что
а*а+а' а'
{q',p'\q,p) = e~ 2 <0|e*'V«+10> =
L Г(р-р')' a ($-?
— е 2Й L 2a 2
е g 2й .
разлагая их по собственным векторам оператора а+а, мы найдем
а*а
a Ю)
(n\q,p) =
Система собственных векторов неэрмитова оператора а яв-
является также и полной. Проще всего убедиться в этом, проде-
продемонстрировав, что из операторов проектирования в когерентные
12. ВОЛНОВАЯ ФУНКЦИЯ 417
состояния \q,p)(q,р\ можно построить единичный оператор.
Действительно, образуя
\dpdq\q,p)(q,p
т, п>0
убеждаемся, что интеграл легко вычисляется после перехода
к полярным координатам на плоскости х = л/-^г q, у —
= a/*~ Р> оказывается диагональным по т, п, что и ведет к
результату
^, p)(q, р| =
В действительности система когерентных состояний с фикси-
фиксированным а и произвольными q и р является даже сверхполной,
и для построения полной системы достаточно использовать
лишь некоторые из них. Можно даже найти всего лишь счет-
счетную последовательность когерентных состояний, являющуюся
полной.
11.5.3. Весьма поучительно, что, в то время как мы нашли громадное (го-
(гораздо большее, чем потребно для образования полной системы) многообразие
собственных состояний оператора уничтожения а, оператор рождения о+
вообще не имеет собственных состояний. Последнее обстоятельство очевидно
из следующего рассуждения: Предположим, что такое собственное состояние
существует, и будем представлять его себе записанным в виде суммы по со-
состояниям |и). Поскольку re ^ 0, должно существовать наименьшее п, скажем
«о, входящее в эту сумму. Под действием я+ состояние |«о) перейдет в
|«о + 1) i т. е. после действия оператора рождения его гипотетическое соб-
собственное состояние будет иметь наименьшим и ие «о, а по + 1 и, значит, не
сможет оказаться коллинеарным исходному.
12. Волновая функция
Как мы убедились в конце раздела 10, можно выбрать такое
представление, в котором все координаты диагональны. Такое
представление, называемое координатным представлением,
часто используют в квантовой механике преимущественным
образом.
Но если мы преимущественно работаем в одном фиксиро-
фиксированном представлении, то обозначения для представителей век-
векторов и операторов можно упростить способом, который осо-
особенно удобен, если диагональные в избранном представлении
наблюдаемые имеют непрерывный спектр.
12.1.1. Будем, для краткости, обозначать полный набор ком-
коммутирующих наблюдаемых, определяющий избранное представ-
14 Б, В, Медведев
418 ч. III. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
ление, одной буквой |. Представитель Ц'\Р) какого-то вектора
\Р) в этом представлении есть функция от ?'— скажем, \|>(|')—
и она однозначно определяет вектор |Я). Поэтому ее разумно
использовать вместо Р в качестве значка, отличающего вектор
JP) от всех прочих, т. е. принять, что
если <|/|Я> = Ф(Е/), то |/>> = | Ч> (S)>. (80.1)
(Вектор определяется всей функцией ч|э(?)!)
Далее, если рассмотреть оператор специального вида а =
= /F), то
<Г \f(l)\P>=f (Г) <П />>=f <? ¦ (Б'),
значит,
т. е. мы видим, что черту слева можно не писать, и остано-
остановиться на том, что
если <Б'1Р) = ¦*(!'), то |/>) = о|)<|)), или, кратко, = а|>>. (80. Г)
Эту запись можно рассматривать при желании как произ-
произведение коммутирующего со всеми операторами полного набора
оператора тр(|) (ср. § 7) на некоторый стандартный (для дан-
данного представления) вектор ), который имеет одинаковые со-
составляющие по всем базисным векторам ||'): (Б'|= 1-
Можно, наконец, вообще держать ) постоянно в уме (или не
держать его там) и выписывать только ¦§(%), памятуя, что эту
волновую функцию можно умножать на операторы только сле-
слева. Именно так и поступают в большинстве изложений кванто-
квантовой механики.
12.1.2. Совершенно таким же образом можно условиться,
что для совекторов
если <<Э|Г> = ф(Г), то <Q| = (cp(i)| или (Q | = (Ф Ц) = <Ф (|).
(80.2)
Заметим теперь, что в силу A2.1),
если |Р> = ф(|)>. то {P\ = Wd),
— т. е. совектор представляется волновой функцией, комплекс-
комплексно-сопряженной функции, представляющей сопряженный ему
вектор *).
*) Это казалось бы нарушает наше общее правило, что вектор и сопря-
сопряженный ему совектор всегда обозначаются одинаковыми значками. Однако до
сих пор значки, отмечавшие векторы, всегда были у нас вещественны. По-
Поэтому мы не придем в конфликт со старым прлзилом, если будем читать
в нем вместо одинаковыми — комплексно-сопряженными.
12. ВОЛНОВАЯ ФУНКЦИЯ 419
12.1.3. Согласно формуле C7с) из 6.5 вероятность найти для наблюдае-
наблюдаемой | значения, лежащие в интервале (!', |' + d\') при измерении, произво-
производимом над системой, находящейся в состоянии |Л>, есть
Поскольку наблюдаемые | образуют полный набор, то проекционные опера-
операторы Рг> будут выражаться формулой B1):
и, следовательно, мы получим для вероятности
Если теперь состояние А записывается в упрощенных обозначениях как
М) = яН1)>.
то по (80.1')
<ГМ> = <ГЖ1)> = *КГ)
<Л|6'>-+•№').
Итак, вероятность найти для наблюдаемой ? значения, ле-
лежащие в интервале (?', t' + d|') для системы, находящейся в со-
состоянии с волновой функцией ij)(l), есть
dWm = tf <t')ty(Z') df. (81.1)
Если, в частности, ? есть координата х, то
dW = ty'(x)q>(x)dx, (81.2),
а если | есть радиус-вектор материальной точки г (совокупность
трех ее координат х, у и г), то
— т. е. вероятность того, что частица будет обнаружена при из-
измерении в некоторой точке пространства, пропорциональна
квадрату модуля волновой функции в этой точке.
12.1.4. Перейдем теперь к скалярным произведениям. Так
как в полной записи скалярное произведение совектора (Q\
и вектора \Р), выраженное через их представители в ?-пред-
ставлении, записывается как
если представители совектора и вектора есть, соответственно,
ф(|') и i|)(|') (мы выписали эту формулу в самом общем виде,
когда среди наблюдаемых | есть обладающие и непрерывным,
и дискретным спектром), то и в краткой записи под произведе-
произведением (ф(?И(|)) следует всегда разуметь
(ф (е; ф а»)=J] S <*Гф (|/) *(|/)- (82Л>
14*
420 ч. III. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
Поэтому вообще примем то определение, что для любой f(Q
выражение (f(|)) всегда будет обозначать сумму по всем дис-
дискретным и интеграл по всем непрерывным EW-ам:
?$) (82.2)
V
•— комбинации (82) являются пожалуй единственными, для ко-
которых выписывание или невыписывание сохраняемого в уме
стандартного вектора ) имеет значение для смысла формулы.
12.2. Остановимся еще на так подробно разобранном нами
случае одной степени свободы.
12.2.1. Согласно формулам F5) и F8) из предыдущего па-
параграфа представителями операторов координаты и импульса
в координатном представлении являются
-q") и
Переведем их в сокращенную запись, выбирая в качестве стан-
стандартного ^-представления координатное представление.
Если представитель вектора \Р) в этом представлении есть
{q'\P) = ^(я'), т. е. если \Р) = ty(g)), то представителем век-
вектора а|Я), где а — некоторый линейный оператор, будет
V | а | Р) = J dq" fa' | о | q11) {q" \P)=\ dq" {q' | а | q") * (</").
Следовательно,
если | P) = ф(<7)> и {q'\a\q") = KaW,q"),
то a}P)=\dqKa(q,q)q(q)), (83.0)
— т. е. произвольный линейный оператор приобретает в сокра-
сокращенной записи вид линейного интегрального оператора; выгода
от этого невелика.
12.2.2. Преимущество сокращенной записи оказывается, од-
однако, весьма существенным, если ядро интегрального опера-
оператора— т. е. его представитель в ^-представлении — выражается
через б-функцию или конечное число ее производных. В самом
деле, если оператор а есть оператор координаты q, то
Kq{q',q")= 6(q'' — q"), интегрирование по q в (83.0) выпол-
выполняется, и, следовательно,
если \P) = $(q)), то q | Р) = q ф (q)). (83.1)
Иными словами, в сокращенной записи оператору q отвечает
просто оператор умножения на число q:
q = q (83.1a)
!-- обстоятельство, с установления которого даже для произ-
12. ВОЛНОВАЯ ФУНКЦИЯ 421
вольной функции f(q) мы как раз и начали вводить сокращен-
сокращенные обозначения.
12.2.3. Аналогичное упрощение происходит и для оператора
импульса, для которого Kp(qr, q") = — 6r {q* — q"). Освобождаясь
в (83.0) от производной интегрированием по частям и снимая за-
затем б-функцию, получаем, что
если |Р>«Ч>(<7)>, то p\P)=*L*±jf-)=l-L.q(q). (83.2)
Иными словами, оператором импульса в сокращенной записи
оказывается (с точностью до множителя) оператор дифферен-
дифференцирования по qi
Р = Т1ГЦ' <83-2а>
12.2.4. Итак, мы видим, что такие важные наблюдаемые, как
импульс и координата, изображаются в сокращенной записи
дифференциальным оператором или даже просто оператором
умножения иа число. Именно это обстоятельство и составляет
ее главное преимущество; оно сохраняется, конечно, и для на-
наблюдаемых, являющихся целыми алгебраическими функциями
импульса (и произвольными функциями координаты). Ниже мы
убедимся, что в очень многих задачах только с такими наблю-
наблюдаемыми и приходится иметь дело — тогда в формализме сокра-
сокращенной записи удается вообще избегнуть введения математи-
математически более сложных объектов типа (83.0).
ЗАМЕЧАНИЕ 1: Калибровочное преобразование первого рода
{ср. замечание 2 к F8)) может, конечно, добавить к (83.2а)
член
ЗАМЕЧАНИЕ 2: Реализации (83.1,2.а) конечно снова приво-
приводят нас к перестановке E2):
ЗАМЕЧАНИЕ 3: Следует специально остановиться на действии
(83.2а) на совектор. Если (Q| = (q>(<7), то
{Q\p\qrr)=\dq'{Q\q')(q'\p\q")
*) Итак, мы пришли еще к одной — очень важной и полезной — реализа*
дни алгебры Ли E2)*
422 ч. III. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
т. е. мы должны принять, что
т. е. что в записи — -т— имеется в виду дифференцирование
вправо. Если действовать этим оператором на — стоящий от
него слева\ — совектор, то надо перейти к дифференцированию
влево; при этом переменится знак. Поэтому именно оператор
\-r-j— ) эрмитов, в то время как
dci) dq dg • "
12.3. Отметим еще, как записываются в сокращенной записи
собственные векторы координаты и импульса. Согласно F4)
собственный вектор оператора q с собственным значением q&
имеет своим представителем
qq)
Следовательно,
(84.1)
Собственный вектор импульса, отвечающий EW-y po, имеет по
F7) своим представителем
Поэтому
-¦»<«>>• (84>2)
Мы видим отсюда, что сокращенные обозначения связаны
и с епределенными неудобствами — в них не заготовлено места
для EW-ов оператора, собственным вектором которого является
рассматриваемый вектор — поэтому приходится такие уточнения
вводить в виде дополнительных подстрочных (или надстрочных)
индексов.
13. Сдвиги и повороты системы отсчета
13.1. В первой части курса мы вывели формулы (формулы
F3а), F4) первой части), выражающие изменение любой дина-
динамической переменной классической механики при (бесконечно-
малом) изменении системы отсчета — сдвиге или повороте, когда
декартовы координаты каждой частицы (Ь — ее номер) претер-
претерпевают одновременно преобразование
r6; 6ri, = 6a+[6q)Td]; (85)
13. СДВИГИ И ПОВОРОТЫ СИСТЕМЫ ОТСЧЕТА 423
изменение любой динамической переменной а при таком преоб-
преобразовании записывалось с помощью СП в виде (A.64) и A.63а)).
М, а),
где Р и М — полный импульс и момент системы.
Поскольку мы хотим сохранить при переходе от классиче-
классической механики к квантовой весь формализм СП по возможности
в неизменном виде, то нам надо будет потребовать, чтобы со-
сохранилась и эта формула, которую будет теперь удобнее пере-
переписать—с помощью соотношения E0)—через коммутаторы:
6а = у [6а- Р + Ч •№,«]_. (86)
Символы Р и М в этой формуле должны теперь означать опе-
операторы полного импульса и полного момента и нам надо еще
их определить. Примем, что как и в классике они суть суммы
импульсов и моментов отдельных частиц:
P = Zp*; М = ?тй, (86а)
ь ь
причем сложение операторов надо понимать в смысле конструк-
конструкции, поясненной в конце § 10 (формулы G5) —G6а)), — тогда
вопрос сведется к определению импульса и момента для си-
системы, состоящей из одной материальной точки.
13.2. Рассмотрим для такой системы сперва сдвиг, для оп-
определенности сдвиг по одной оси, скажем по оси х. Тогда со-
согласно (85) должно быть б* = 6a.t, a согласно (86), если из-
избрать в качестве наблюдаемой а. координату х,
Значит, фигурирующая в (86) ^-компонента импульса должна
удовлетворять перестановочному соотношению
[р*,*]_ = у
с координатой х. С другой стороны, сдвиг вдоль оси х вовсе не
должен менять координат у и г; выбирая эти наблюдаемые
в качестве а в (86), приходим к тому, что
[рх, г/]_ = 0; [рл>2]_=0.
Проведя такое же рассуждение со сдвигами вдоль осей у и z,
придем к системе перестановочных соотношений
[Pa, *P]=TSap.
Но это как раз те перестановочные соотношения E1.2), кото-
которым должны удовлетворять координаты и канонически сопря-
424 ч. III. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
женные им импульсы. Итак, в качестве компонент оператора
импульса (в смысле оператора, выполняющего бесконечно ма-
малый сдвиг согласно (86)) одной материальной точки можно
принять обобщенные импульсы, канонически сопряженные ее
декартовым координатам, после чего оператор импульса си-
системы определится из (86а).
13.3.1. В результате преобразования (86) из первоначальной
наблюдаемой а возникает новая, «сдвинутая» наблюдаемая а;
поскольку мы считаем параметр сдвига 8ах малым и пренебре-
пренебрегаем его старшими степенями, то новую наблюдаемую а можно
записать как
Применим теперь это преобразование п раз, обозначая
и перейдем к пределу п-*-оо, притом так, чтобы ах было бы
фиксировано, а 8ах стремилось бы к нулю. Мы получим тогда»
что
ахРх
a = Uax-a-U^, где Uax = e~; Utx = Ualx, (87)
т.е. Uax—унитарный оператор.
13.3.2. Совершенно аналогично при произвольном сдвиге,,
описываемом вектором а, имеющим составляющие по всем
трем осям:
a^Ua-a-U;1; Ua = e *; Vt = VZl (87a>
(разные составляющие импульса коммутируют друг с другом,,
и поэтому вопроса о смысле экспоненты, содержащей в показа-
показателе различные операторы, не возникает).
13.3.3. Таким образом, мы построили выражения для пре-
преобразования любой наблюдаемой при сдвиге на конечный век-
вектор а, т. е. проинтегрировали дифференциальные уравнения Ли
(86). Проверим, что найденное преобразование (87) есть дей-
действительно сдвиг, т. е. что в применении к радиус-вектору любой
частицы, скажем с номером Ъ, оно дает
h
rbe h =r6 + a. (87b)
13. СДВИГИ И ПОВОРОТЫ СИСТЕМЕ! ОТСЧЕТА 425
Проверка совершается проще всего, если заметить, что в со-
сокращенных обозначениях (§ 12) в фиксированном импульсном
представлении rb = iti-j—, после чего остается лишь выполнить
дифференцирование.
13.4.1. Пока полученные результаты совершенно аналогичны
классическим — вследствие сдвига или поворота системы коор-
координат все динамические величины переходят в новые динамиче-
динамические величины по закону, имеющему весьма тесный классиче-
классический аналог. Однако в квантовой механике возможна и иная
точка зрения. Действительно, ведь система в квантовой меха-
механике описывается не только относящимися к ней динамическими
переменными, но и описывающими ее векторами состояния.
С физической точки зрения систему характеризуют не сами ее
динамические переменные а (а,, i = 1, 2, ...), но их средние
значения в том состоянии \Р), в котором находится система:
а = (Р\а\Р) ((Р\а{\Р), /=1,2,...),
или же матричные элементы перехода между двумя состояниями
<Q|ct|P>.
В результате сдвига все эти средние значения перейдут в
причем весьма существенно, что унитарный оператор Ua зави-
зависит здесь только от рода преобразования (и рассматриваемой
системы, конечно), но не от оператора а или от состояний
\Р), IQ).
13.4.2. Вспомним теперь, что развитая нами алгебраическая
схема описания состояний и динамических переменных допус-
допускает определенный класс преобразований, которые вообще ни-
ничего не меняют в физической интерпретации. Мы имеем в виду
обсуждавшиеся в 10.7.2 одновременные преобразования всех
векторов, совекторов и операторов
(B\ = (B\U; |1>=?Г'|Л>; I^U^IU; U~l = U+, (88)
которые никак не влияют на физическую интерпретацию тео-
теории просто потому, что они — как мы убедились в 10.7.2 — не
затрагивают ни одного из чисел, которые можно построить
в нашей математической схеме. Чтобы преобразование (88) пре-
преобразовывало бы эрмитовы операторы в эрмитовы и не меняло
бы соотношений сопряжения, надо только, как мы то и сделали,
потребовать унитарности оператора U, который в остальном
может быть произвольным. Итак,
426 ч. III. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
унитарное преобразование (88) ничего не меняет в существе
физического содержания теории.
Пользуясь этим обстоятельством, мы можем совершить после
преобразования (87а) еще и унитарное преобразование типа
(88), записывая
й = (Р |UaaU:x \P) = (P\U • (/-'[/аСхС/а 'С/ • СГ1 | Р) = {Р I(S) |Р>.
Выберем теперь оператор унитарного преобразования ?/ так,
чтобы было
(а) = а для всякого а. (89.1)
В силу независимости ?/а от а это как раз и можно сделать,
полагая просто
U = Ua. (89.2)
В результате мы получаем новую форму для выражения преоб-
преобразования сдвига в квантовой механике:
„_>?; g = (P|a|P); <P| = <P|t/a; ify^UI^P). (89.3)
13.4.3. ЗАМЕЧАНИЕ: Необходимо четко различать три вида
преобразований, особенно когда все они производятся с по-
помощью одного и того же унитарного оператора:
(87)—когда преобразуются динамические переменные, но не
меняются векторы состояния;
(89)—когда не меняются динамические переменные, но преоб-
преобразуются векторы состояния;
— оба эти преобразования меняют физику — осуществляют
сдвиг — и
(88)—когда преобразуются и динамические переменные, и век-
векторы состояния, но не меняется физическое содержание
теории. |
13.5. Аналогично обстоит дело и с преобразованиями пово-
поворота системы отсчета. Как и для сдвигов, мы можем написать
для динамических переменных после совершения бесконечно-
малого поворота бф вокруг некоторой оси, направление которой
задается (фиксированным!) единичным вектором п, так что
бф = бф-п,:
а для динамических переменных после поворота на конечный
угол ф вокруг того же фиксированного направления п — в пол-
полной аналогии с (87)—
ф
а == С/„. „ а и^п; U9,n = ejnn; U*, '„ = U? „• (90)
13. СДВИГИ И ПОВОРОТЫ СИСТЕМЫ ОТСЧЕТА 427
Дальше, однако, возникает существенное осложнение. Дело
в том, что — в отличие от группы трансляций — группа враще-
вращений трехмерного пространства —это группа неабелева. Поэтому
нельзя ожидать, что унитарные операторы (90), соответствую-
соответствующие поворотам вокруг различных осей, будут коммутировать.
13.5.1. Первый пункт, на который в связи с этим надо обра-
обратить внимание, это вопрос, как следует записать последователь-
последовательное действие двух поворотов: сперва поворота на угол ф] вокруг
оси rii, а потом поворота на угол ф2 вокруг оси пг. Тут надо не
упустить из виду (ср. I, 18.8.4) то обстоятельство, что первый
поворот на Ф1П1 = фь преобразуя все динамические переменные
по (90), делает то же и с оператором U9l второго поворота,
преобразуя его в
Поэтому результат последовательного совершения двух поворо-
поворотов в указанном выше порядке будет равен
<х = UV2aU^ = U4lUV2U^1 • UVlaUVl ¦ U,,U*U*,
то есть
а = и,Уъ • а • U,,lU,.1. (90a)
Так как проведенное рассуждение никак не было связано с тем,
что операторы U4i и ?/Ф, выполняют унитарное преобразова-
преобразование, отвечающее именно повороту, то мы получаем из (90а)
общее правило:
При последовательном выполнении двух унитарных преоб-
преобразований соответствующие унитарные операторы действуют
на динамические переменные системы в порядке, обратном по-
порядку выполнения преобразований.
То же правило справедливо и для последовательного выполне-
выполнения более длинной серии унитарных преобразований.
Легко сообразить, что при использовании другой эквивалентной картины
действия унитарных преобразований — картины (89), когда преобразуются не
операторы, а векторы состояния, — только что отмеченное обстоятельство ие
имеет места.
13.5.2. После этого предварительного замечания займемся
опять бесконечно-малыми поворотами.
Если мы совершим сперва поворот на угол 6q>i потом поворот на
угол бфг, затем «обратный поворот на —6q>i и, наконец, обратный поворот
на —бфг, то в силу только что установленного правила такая последователь-
последовательность поворотов преобразует любую динамическую переменную а в
428 ч. III. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
причем в силу (90)
Поэтому, полагая еще ради краткости Uiv = Uit имеем
D
а = UflJJ^Uz1 ¦a-UJJ]U2XUXl.
Рассмотрим суммарный унитарный оператор преобразования U = i/]f/2f/f '?/?"'.
Для абелевой группы ои был бы тождественной единицей, но для неабеле-
вой группы, в которой Ui и i/г не коммутируют, это ие так. Обозначая ком-
коммутатор
и1и2-и2и1 = ф,
получим
Записывая теперь
и^еН (/ = 1,2),
где \i{~ = |ij и суть бесконечно-малые первого порядка по 6ф;, найдем, что
с точностью до второго порядка
и2 \ / и2 М
1*1 1 I г*2 1 1
+- /lii г- 1,11 + *|Аа 7Г- ) I = // [Щ, W2]_+O (°ф )»
Поэтому с точностью до членов второго порядка по бф
или, с той же степенью точности,
13.5.3. Но суммарное преобразование U, получившееся в ре-
результате нашей серии вращений, должно быть опять некоторым
поворотом в 3-пространстве, т. е. иметь форму (90) с некото-
некоторыми новыми параметрами, определяемыми параметрами пер-
первоначальных поворотов и структурой группы вращений в R3. Но
это значит, что возникшие в показателе в выражении для U
коммутаторы
{[Afv, Ma)_
должны линейно выражаться через компоненты оператора мо-
момента.
13.6. Сравнение с преобразованием (85) радиус-вектора поз-
позволяет установить, что коэффициенты должны иметь вид ihevaYr
т. е. что компоненты оператора момента должны удовлетворять
перестановочным соотношениям:
Ша, Мй] _ = ifieakyMy. (91)
14. КВХНТОВАНИЕ МОМЕНТА' 429
13.6.1. Совершенно аналогично, выполняя последовательно
в разных порядках преобразования поворота и сдвига, мы при-
придем к перестановочным соотношениям между моментом и им-
импульсом:
[Ма, Pp]_ = meagYPY. (92)
13.6.2. Перестановочные соотношения (91), (92) имеют фи-
физически тот же смысл, что и соотношения в скобках Пуассона
между компонентами импульса и момента, которые мы выписы-
выписывали в классической механике.
Перестановочные соотношения (92) можно трактовать и
иначе—как выражение для изменения импульса при бесконеч-
бесконечно-малом повороте системы отсчета. Действительно, полагая
в (86) ба = 0, a = Яр и подставляя значение коммутатора (92),
находим для изменения импульса при бесконечно-малом по-
повороте
iWfyM п 1 _ / (бф)а ¦,-/}„ р
то есть
6P = [6tp.P]. (92а)
13.6.3. Поскольку, однако, последняя формула должна иметь
место не только для импульса, но и для любого векторного опе-
оператора (ср., например, выражение (85) для изменения радиус-
вектора), то столь же универсальной должна обернуться и пер-
первоначальная формула (92): Для любого векторного оператора
А его коммутатор с оператором момента должен равняться
[Ma,A^]_ = ihe4yAy. (92')
ЗАМЕЧАНИЕ: Мы провели обсуждение поворотов в той кар-
картине, в которой меняются операторы, а векторы состояния ос-
остаются постоянными. Можно было бы, конечно, перенести пре-
преобразование, как то было проделано в случае сдвигов, с опера-
операторов на векторы и совекторы. |
14. Квантование момента
Большая сложность группы вращений сравнительно с группой
параллельных переносов имеет, однако, и свою положительную
сторону. Оказывается, что дополнительные связи, налагаемые
на три оператора Мх, Му и Mz перестановочными соотноше-
соотношениями (91), являются столь сильными, что позволяют — по-
подобно тому, как то мы делали в § 10 для операторов а и а+,—
найти спектр собственных значений оператора момента и по-
построить систему его собственных векторов — т. е. решить соот-
соответствующую проблему собственных значений.
430 ?• •»• ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
14.1. Того ради введем, прежде всего, оператор квадрата мо-
момента:
т2 = м1 + М2у + М2г. ,93.1)
Вычисляя коммутатор какой-либо компоненты момента, скажем Мх, с
этим оператором
[Мх, М*]_ = [Мх, Му\_ Му + My [Мх, МУ\_+[МХ, Мг}_ Мг+Мг [Мх, Мг\_ =
= лмгму + тМуМг — шМуМг — лмгму = о,
видим, что
[Ма, М2]_ = 0, (93.2)
— т. е. каждая из компонент момента коммутирует с его квад-
квадратом и, следовательно, обладает общей с ним полной системой
собственных векторов. (Эта система общих собственных векто-
векторов, конечно, своя для каждой компоненты — две разные ком-
компоненты момента в силу (91) не коммутируют, и, следовательно,
полной системы общих собственных векторов иметь не могут.)
Заметим, что равенство нулю коммутатора (93.2) можно было
бы предсказать и до вычисления: ведь квадрат момента — это
скаляр в обычном 3-пространстве, поэтому при поворотах он
должен оставаться неизменным, следовательно, —коммутиро-
—коммутировать с моментом.
Итак, мы имеем дело с четырьмя операторами
Мх, Му, Мг и М2*),
связанными перестановками (91), (93.2):
Шх, Му]_ = ЯМг; [My, Мг)_ = ШМх; [Мг, Мх] = ШМУ;
и желаем найти EW-ы и общие собственные векторы двух из
этих операторов, скажем Мг и М2**).
14.2.1. Для решения этой задачи мы воспользуемся следую-
следующим искусственным приемом. Введем две пары операторов а,
а+ и р, р+, подчиняющихся (каждая) перестановочным соотно-
соотношениям C4) и коммутирующих между собой:
<т+-а+а=1; рр+-р+р=1; [а*, р±]_ = 0. (94.1)
Тогда, повторяя рассуждения § 10, мы можем построить для
каждой пары операторов базисы E6) пространств, в которых
*) Иногда вводят вместо Мх и Му операторы
М+ = Мх + Шу и М~ = Мх — Шу.
**) С математической точки зрения рассматриваемая задача состоит в
отыскании неприводимых представлений алгебры Ли (91).
14. КВАНТОВАНИЕ МОМЕНТА 43!
они действуют (будем обозначать числа заполнения, отвечаю-
отвечающие паре а, а+ через р, a nape р, р+— через г). Построим, да-
далее, прямое произведение этих двух пространств и переведем
в него операторы а, а+ и р, р+ в соответствии с процедурой, опи-
описанной в 10.8.1.3, причем будем следовать «физической» манере
записи, не различающей операторы в «большом» и «малом»
пространствах.
Мы придем таким образом к полной системе векторов со-
состояния \р, г), р, г = 0, 1, ..., таких, что:
<x+ct\p,r) = p\p, r); tp', r'\р,г) = 6РР'6ГГ';
P+Plp,r) = r|p,r); |р,г)=(а+^1+)'|0, 0); | 0, 0' =| 0), (94'2)
причем
а+1 р, г) = л/рТГ| р + I, г); р+ \р,г) = л/7ТТ \ р, г+1);
/- г- <94-3)
а\р, r) = VP \P — l.r); Р!р, г) = -\/г\р, г — 1);
•—векторов, которые мы обозначили'—в исключение из общего
правила — круглыми скобками для отличия от другой системы,
которую придется ввести.
14.2.2. Цель этого вспомогательного построения состоит в том,
чтобы выразить интересующие нас компоненты момента в виде
функций введенных операторов рождения и уничтожения. Чтобы
сообразить, каким путем надобно к ней стремиться, заметим,
что билинейные функции операторов рождения и уничтожения
обладают тем замечательным свойством, что их коммутаторы
тоже являются билинейными функциями этих операторов*) —
при коммутировании «съедается» один оператор рождения
и один уничтожения, следовательно, остается опять били-
билинейное выражение. Поэтому, поскольку коммутаторы компонент
момента должны в силу (91) выражаться опять через них са-
самих, естественно пытаться выразить Мх, Му иМ,в виде именно
билинейных форм, а, а+, р, р+. Далее мы хотим, чтобы М, был
бы диагоналей, поэтому его следует искать в виде комбинации
диагональных в базисе (94) билинейных выражений а+а и р+р.
На долю же операторов Му и Мх, которые не могут быть диа-
диагональными, остаются недиагональные комбинации а+р и р+а
После этих кратких пояснений произнесем какое-нибудь ма-
магическое слово и вытащим из-под черного покрывала готовый
*) Можно утверждать и больше — что коммутирование любого монома
в операторах рождения и уничтожения, (а+)т(а)п, с билинейной функций
а+, а опять даст моном тех же степеней. Это свойство характеризуют обычно
тем утверждением, что «коммутирование любого выражения с билинейной
функцией <х+, а не меняет его операторной структуры».
432 ч. III. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
результат:
M fi
2/ ' — 2 '
(95.1-3)
M+ = Mx + iMy = ha+fl; M~ = Мх — iMy = /ф+а. (95.1', 2')
В самом деле, при таком выборе все перестановки (91) удовлетворяются:
[Мх, Му]_ = ~{[р+а, а+р]_ - [а+Р, Р+а]_} = /Й-| (а+а - р+р) = Ш
[Му. Мг}_ = -g {[<х+р, <х+а]_-[<х+р, р+р]_-[р+а, а+а]_ + [р+а, р
[Afz мх)_=~{а+р - р+а + а+р - р+а} = i> • h
14.2.3. Но это еще только половина фокуса — главное впе-
впереди. В (95.1—3) мы использовали только три линейные комби-
комбинации четырех независимых билинейных выражений. Включим
в рассмотрение и четвертую — введем (эрмитов) оператор
—'» [МаД]_ = 0. (95.4)
Этот оператор коммутирует со всеми компонентами момента.
В самом деле, в базисе (94) он диагоналей и поэтому комму-
коммутирует с диагональным Mz. Кроме того, он равен в этом базисе
полусумме чисел р и г, а каждый из операторов М± меняет, как
легко видеть, одно из этих чисел на +1> а другое на —1, остав-
оставляя полусумму неизменной.
Обозначим теперь временно четыре основных билинейных комбинации
a+a = a, fJ+P = b, a+fj = с и fJ+a = a и вычислим
= %¦ (cd + dc~ab- ba) = ^-(a+pp+a + p+aa+p - a+ap+p - p+pa+a) =
= -y-(a+a+p+p) = U.
Таким образом
М2==А2+ЙА, (95.5)
т. е. нам удалось выразить квадрат момента, квадратичный
в его компонентах и, следовательно, биквадратичный во вспо-
вспомогательных операторах рождения и уничтожения, в виде функ-
функции одного оператора Я, билинейного в операторах рождения
14. КВАНТОВАНИЕ МОМЕНТА
433
и уничтожения, — мы в некотором смысле линеаризовали стоя-
стоящую перед нами задачу о спектре момента.
14.3. Задача эта, собственно, теперь уже решена. Оба же-
желаемых оператора, Мг и заменяющий теперь М2 оператор Я,
диагональны в базисе (94), их собственные значения — эти соб-
собственные значения принято обозначать буквами т и I, соответ-
соответственно, — равны
(96.1)
и нам осталось только перенумеровать векторы уже имеюще-
имеющегося базиса новыми квантовыми числами. Положим для этого:
г), (r = t — т)); \р,г) —
— как раз для векторов в новой нумерации мы и сохраняли
наши обычные обозначения через угловые скобки. Для «новых»
векторов, как сразу устанавливается из (94):
p| I, т) = {1 — т)\ I, т) (97.2)
а+а|
, т) = (I + т)\ I, m)\
a\l,m) =
I — j, т — j
(97.3)
Г* I
PI/, m) = '\/T^7fi\t--j, m
14.3.1. Какие значения могут принимать новые квантовые
числа I и т? Старые квантовые числа р и г менялись незави-
независимо друг от друга, принимая все возмож-
возможные целочисленные неотрицательные значе-
значения, т. е. на плоскости (р, г) допустимые
значения заполняли все целочисленные точ-
точки первого квадранта. Преобразование
(96.1) к новым квантовым числам состоит
в повороте координатных осей на 45°; как чч
видно из рисунка, квантовые числа I и т
не будут теперь меняться независимым об-
образом.
Возможные значения квантового числа I
распадаются на два существенно различ-
различных класса: все неотрицательные целые числа и неотрицатель-
неотрицательные, как говорят, «полуцелые»: равные неотрицательному
434
ч. Ш. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
целому числу плюс половина. Квантовое число т может прини-
принимать как положительные, так и отрицательные значения, лежа-
лежащие в интервале —/ ^ т ^ -\-1 и меняющиеся при переходе от
одного разрешенного значения к соседнему на единицу
Таким образом, для целого / все совместные с ним значе-
значения т тоже целы, а для полуцелого — полуцелы. Каждому зна-
значению / отвечает B/+ 1) совместных с ним значений числа т:.
целые I
(96.2а)
1 = 1 1 A
2 ' 2 ' 2 ' Ф
полу целые I
= 0,1,2,...;
т = -1, -A-1), ..., A-1), г,
число различных т
нечетно четно
есть m = 0 нет m = 0
(96.2b)
14.3.2. Итак, мы установили, что из перестановочных соот-
соотношений (91) следует, что можно построить общую систему
собственных векторов, определяемых формулами (97.1), (94.2)г
квадрата и одной из компонент, скажем М2, момента со спек-
спектром собственных значений
М2| /, т) = ПЧ (I + 1)| /, т);
т.е.
(96.3)
> = Am|/, m); m = —/,—/+1, ...,/ —
Как действуют на эти собственные векторы два оставшихся
недиагональных оператора (удобнее воспользоваться операто-
операторами М±, а не Мх, My), сразу устанавливается из их выражения
(95.Г.2') через а и р и формул (97.3):
М+ \l,m) =
= h
M~ \l,m) = W+a \l,m) = P+
= h <\/(t + m)(l —
I /, m + 1);
m t —-, m —
l)|/,m-l)
(98)
— эти операторы изменяют число m на ±1 (т. е. значение Мг
на ±Ь), оставляя число / неизменным.
14.3.3. Итак, мы видим, что совокупность собственных век-
векторов (97) с фиксированным / и меняющимся т. образует под-
подпространство, инвариантное относительно действия любого из
операторов момента. Таким образом, в каждом из этих подпро-
14 КВАНТОВАНИЕ МОМЕНТА 435
странств реализуется представление алгебры Ли (91). Все эти
представления неприводимы. (Последовательным действием
оператора М+ можно, согласно (98), получить из вектора |/,—/)
все остальные векторы подпространства вплоть до |/, /):
I
V
2/1 (/ + „)»
Точно так же
(99)
мы не будем доказывать, что они исчерпывают все неприводи-
неприводимые представления (91).
14.3.4. Найденные формулы позволяют без всяких хитростей выписать
выражения для матричных элементов компонент момента между состояниями
[/, т) —«представители» этих операторов в представлении, в котором диаго-
.«альны М2 и Мг
(I, m'\M-\ U т") = А У(/ - т" + 1) (I + т") 6т, „._, =
т') (l + m' + \Nm,t „,._,,
(I, т'\М+\ I, т") = Й V(/-/я'+1) (/+«')*„'. „.+, =
= A V(/-
m">= A01)
я»*)
14.4. Важнейший результат проведенного рассмотрения —
это то, что из перестановочных соотношений (91) следует спектр
(96.3).
В частности, отсюда получается важное
СЛЕДСТВИЕ: Вектор момента нельзя направить точно по ка-
какому-то направлению. |
Действительно,
Ml + МI = М2 - М2г = ft2 (/(/ +1) - m-)> h2l,
т. е. если стремиться направить момент по одной оси, то в наилучшем слу-
случае, когда т = ±1, все равно остается перпендикулярная составляющая
436 ч. III. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
Af j_ = д/Af| + Мх = Й V' • Только при больших числах /, что соответствует
предельному переходу к классической теории, отношение этой перпендику-
перпендикулярной составляющей к составляющей вдоль изобранного направления
lMxk ti-s/T 1 .
I '->°°
стремится к нулю, и момент снова начинает вести себя как «порядочный»
классический вектор.
Напротив, в некоторой плоскости момент можно точно уста-
установить, если он целый. Для целого / есть EW m = 0 и состояние
|/, 0) отвечает тому, что весь вектор момента лежит в плос-
плоскости х, у.
14.5. Посмотрим теперь, как будут действовать на собствен-
собственные векторы момента повороты системы отсчета вокруг оси г
(Другие вращения будут действовать сложнее, и мы не будем
в это углубляться.). Будем пользоваться той картиной, в кото-
которой операторы неподвижны, а преобразуются векторы состоя-
состояния. Тогда, согласно (89.3), (90), при повороте вокруг оси z на
угол ф
то есть
\ltfn)==e h \iyrn) = e-im^\l,m). A02)
СЛЕДСТВИЕ 1: Если собственные векторы \1,пг) можно запи-
записать в координатном представлении, то они зависят от угла q>
как eim>. I
СЛЕДСТВИЕ 2: Если сделать поворот на угол 2я, то
| On) = e~™m\l, tn)=±\l, m),
судя по тому, цело m или полуцело. Но целость/полуцелость m
определяется по (96.2) целостью/полуцелостью /. Следова-
Следовательно, отмеченным нами в (96.2) двум сортам квантовых чи-
чисел / отвечают два класса представлений группы вращений —
однозначные и двузначные.
Описываемым целыми / однозначным представлениям отве-
отвечают объекты, рассматриваемые в обычном тензорном исчисле-
исчислении: одномерному представлению с I = 0 отвечают скаляры,
трехмерным представлениям с / = 1 — векторы, 5-мерным.
1Б. РЕАЛИЗАЦИИ МОМЕНТА 437"
с 1 = 2 — симметричные тензоры 2-го ранга со следом, равным
нулю, и т. д.
Двузначным представлениям с полуцелым / отвечают новые
объекты—спиноры и симметричные спинтензоры — которые
изучаются в спинорном исчислении. |
15. Реализации момента
15.1. Мы ввели оператор момента чисто абстрактным обра-
образом, как совокупноеть (деленных на —ih) генераторов группы
вращений обычного трехмерного пространства. Не менее абст-
абстрактной была и найденная в предыдущем параграфе реализа-
реализация этих операторов — операторы рождения и уничтожения
а+, р+ и а, {5 не имели никакой связи с динамическими перемен-
переменными физической системы, к которой относится рассматривае-
рассматриваемый момент. Возникает естественный вопрос о существовании
физических реализаций этого оператора, т. е. вопрос о том,
можно ли построить операторы со свойствами (91) из основных
динамических переменных физической системы, скажем из ее
координат и импульсов со свойствами E1).
Простейшая реализация момента находится на основе много
раз уже приходившей нам на помощь аналогии с классической
механикой. Именно, если написать для момента одной матери-
материальной точки аналог классического выражения
ma = [ra-pa] A03.1)'
(Прямые скобки с точкой между множителями означают здесь
векторное произведение, а не коммутатор, в котором элементы
всегда разделяются у нас запятой, а скобка снабжается индек-
индексом «—». Вопрос о порядке расположения некоммутирующих
операторов здесь вообще не возникает, поскольку в каждом
члене векторного произведения участвуют только разные со-
составляющие координаты и импульса), а для момента системы
материальных точек — в соответствии с (86а) сумму таких вы-
выражений:
М = Z ma = Е [га • Ра\, (Ю3.2>
a a
то легко проверить, что для так определенных моментов будут
выполняться перестановочные соотношения (91). Оказывается,,
однако, что на этом пути получаются (мы вскоре это увидим)
лишь целые значения /, т. е. только тензорные представления
группы вращений.
Поэтому можно было бы заподозрить, что двузначные пред-
представления с полуцелыми / не имеют отношения к физике. Опыт,
однако, показал, что это не так, что объекты, описываемые по-
полуцелыми представлениями, реально существуют в природе..
438 ч. III. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
Поскольку из классической аналогии для системы материаль-
материальных точек такие представления получить нельзя*), то это зна-
значит, что квантовомеханическая частица есть более богатое обра-
образование, чем материальная точка, что кроме координат частицы
у нее есть некоторые внутренние степени свободы.
Тут казалось бы очень соблазнительным рассматривать квантовые ча-
частицы если не как классические материальные точки, то как аналог класси-
классических твердых тел — как волчки. Оказывается, однако, что такая модель
тоже не проходит для элементарных частиц. Не вдаваясь в подробности,
скажем только, что момент волчка можно было бы менять, а собственные
моменты элементарных частиц постоянны. Кроме того, попытки разрабаты-
разрабатывать модели такого рода приводили к скоростям, большим скорости света.
Поэтому приходится принять, что элементарные частицы мо-
могут обладать внутренними степенями свободы—собственным
моментом или спином,—не допускающими классического ана-
аналога. Такие степени свободы не допускают и наглядного описа-
описания, и нам не остается ничего иного, как принять, что сами
чисто абстрактные построения предыдущего параграфа имеют
физический смысл, хотя мы и не можем построить сколько-ни-
сколько-нибудь точно передающей свойства новых степеней свободы на-
наглядной модели. Именно на этом пути появляются полуцелые
моменты.
ЗАМЕЧАНИЕ: Тем самым мы — на этот раз особенно нагляд-
наглядным образом — знакомимся с весьма знаменательной чертой со-
современной теоретической физики: перейдя к изучению явлений
природы при условиях, существенно отличных от привычно вос-
воспринимаемых нашими органами чувств, ей приходится отка-
отказаться от использования наглядных — т. е. в конечном счете ме-
механических— моделей и прибегать вместо этого к моделям ма-
математическим— логическим построениям чисто абстрактного
свойства. |
15.2. Спин у. Простейшим (и важнейшим) случаем полу-
полуцелого момента является случай 1=-^, —как раз половине
равен собственный момент самых «обычных» элементарных
частиц — электрона, протона и нейтрона. Построим для него не
только алгебру Ли (93.3), но и всю обычную алгебру наблю-
наблюдаемых.
*) Невозможность существования прямых классических аналогов для
объектов, описываемых представлениями с полуцелыми /, видиа уже из того,
что <величины» таких объектов принципиально определены лишь с точностью
до знака. В квантовом описании, напротив, мы все время имеем дело с та-
такими объектами, как векторы состояния, определенные с точностью даже до
умножения на унимодулярный множитель.
15. РЕАЛИЗАЦИИ МОМЕНТА 439*
Того ради удобно положить
где о — новый оператор, удовлетворяющий в силу (91) переста-
перестановочным соотношениям
a a —a a =2ie а П04 2V
Oft ft О *^ttft V V" \ \J**&/
Так как в рассматриваемом случае оператор Мг имеет только
два EW-a ±ip то опеРатоР аг имеет только два собствен-
собственных значения ±1, а, значит, а\ — единственный EW + 1. Сле-
Следовательно, а\ есть число; то же самое, конечно, должно быть-
и для а| и а? (ср. лемму 2а, § 4):
О2 = а2 = а2 = 1. A04.3)
Вычислим теперь выражение
4- — — i ( — L-( — ) )==
к силу A04.3). Следовательно, разные операторы оа антиком-
мутируют:
ааа3+араа = 0, а ф р\ A04.4)
Свойство антикоммутации позволяет объединить в A04.2)
вторые члены слева с первыми, после чего оказывается, что
A04.2) и A04.4) объединяются в компактную и красивую
запись:
а о =6 4-ie а П04 5>
Oft OS IttftVV* ^ I v *• *-*/
выражающую декларированное выше обстоятельство, что опе-
операторы ах, оу и вг образуют алгебру не только относительно
коммутирований (алгебру Ли), но и (вместе с единицей) отно-
относительно обычного умножения.
Все три оператора оа являются, разумеется, эрмитовыми
(таковы компоненты момента); кроме того, они являются,
в силу свойства A04.3), одновременно и унитарными:
v? — va', аааа =' (не суммир. по а!). A04.6)
Поскольку каждый оператор оа имеет лишь два EW-та, то
естественно попробовать представить оа двурядными мат-
матрицами.
Построим такое представление для случая, когда аг диагональна, т. е.
/1 04 „
имеет представителем <TZ = I n ,1. Тогда, если написать для ох матрицу
-440 ч "I ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
(а Ь\ (а —Ь\ fa Ь\
общего вида Ох = \ , I, то оглогг = 1 I и ог2ог* = 1 I, сле-
\с dj \с —dj \—c —dj
довательно, в силу A04.4) а = d = 0. В силу эрмитовости должно быть
,, _ 2 (ЬЪ* 0 \ (\ 0\
с = Ь . Далее, вычисляя <** = ( „ ,, ) = I , видим, что должно
\0 о о J \0 1/
быть b = eta, т. е. <JX = I I. То же рассуждение буквально спра-
Ve а 0/
/ 0 е^\
ведливо и для матрицы, представляющей ог«, т. е. <уи = I I
\ е 0 /
— с другой, разумеется, фазой р\ Наконец ог^ст^ = /ст2 дает СТдгСТ^
е1 (а-р) 0 ^ / в 2 0 1 я
1= , т. е. а—р = —. Одна фаза а
0 e-'ta-fV I _, ? I 2
^0 е 2 /
¦ -остается произвольной *). Обычный выбор состоит в том, что полагаем а = 0,
после чего три матрицы приобретают вид:
/1 0\ /01\ /0 —/Л**)
Чо -i) °* = U о> ^ = (/ о) •
A04.7)
Векторный оператор в называют обычно оператором спина,
а представляющие его матрицы — их принято, когда нет опас-
опасности недоразумения, обозначать теми же буквами ах, av и аг —
матрицами Паули, по имени знаменитого швейцарского тео-
теоретика Вольфганга Паули, который впервые ввел их в физику.
Как мы увидим ниже, совокупность этих трех матриц представ-
. ляет собой объект, в некотором смысле основной для всей тео-
теории полуцелого спина.
15.3. Спиноры. Займемся изучением того, как ведут себя
состояния «системы со спином у» при пространственных пово-
поворотах.
15.3.1. Если система описывается вектором состояния \W)
то, согласно общим формулам (89.3), (90), при повороте (в кар-
картине, в которой преобразуются векторы состояния) этот вектор
перейдет в
-I 4- <п-М)
, Для спина -т- М = -т-а, поэтому
*) Этот произвол отвечает тому, что репер (М*, М„) на плоскости (х, у)
неотличим с точки зрения алгебры A04.5) от такого же репера, повернутого
иа произвольный угол вокруг оси Ог.
**) Естественно, что эти матрицы можно было бы получить и из общих
формул A01).
15. РЕАЛИЗАЦИИ МОМЕНТА 44t
Теперь мы можем использовать то отмеченное выше (алгебра
A04.5)) замечательное свойство операторов а, что все их сте-
степени выражаются через первые и единицу. Именно,
(паJ = п„ИрОга(Тр = иаир (бвр + ieaSiyay) = п2 = 1.
Но в разложении косинуса участвуют только четные степени;
поэтому в его аргументе можно заменить (па) единицей. В раз-
разложение же синуса входят только нечетные; поэтому из нега
выделяется общий множитель (па), все же остальные степени:
опять дадут единицу. Итак:
=|cos-| — i(nor)sin|-}|W)*). A05.
Для дальнейших рассуждений удобно перейти от векторов-
состояния к их представителям в, скажем, Мг-представлении,.
используя в качестве полной системы «в спиновом простран-
пространстве» векторы |т = +'/2) и |т = —'/г) (или совекторы
(m = +V2I и (т = —У2|) и обозначая
ЗАМЕТИМ то своеобразие этого перехода, что величины i|>*y
будучи представителем вектора в пространстве спиновых со-
состояний, вполне могут оставаться вектором (или — волновой
функцией) в пространстве, в котором действуют наблюдаемые,,
отвечающие остальным динамическим переменным системы —
координатам и импульсам — имеющим классический аналог.
Поскольку спиновые динамические переменные аа описываюг
новые внутренние степени свободы, то они коммутируют*
с «классическими» координатами и импульсами, и полное про-
пространство векторов состояния системы можно считать прямым
произведением «обычного квантовомеханического» простран-
пространства, в котором действуют операторы координат и импульсов,,
и «спинового» пространства, в котором действуют аа. I
В представителях A05.1) запишется как
T-e- ^=Уг|)Ч-бф2 A051а>
*) Бросается в глаза аналогия этого выделения множителя (па) выде-
выделению мнимой единицы в формуле Эйлера ei<f = cos q> + i sin ф. Эта анало-
аналогия не случайна — алгебра ах, ov, аг изоморфна алгебре кватернионов с тре-
тремя мнимыми единицами i, j, k
442
еде матрица
ч. III. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
6 I
есть представитель оператора < cos -|—•
5L
2
2
inx) sin -I
A05.3)
В силу унитарности U<p,n эта матрица унитарна:
0053а)
Кроме того из A05.3) видно, что она обладает еще и тем свой-
свойством, что ее детерминант равен единице:
ad - pY = cos2 f- + п\ sin21 + (n2 + n2) sin2-| = 1 A05.3b)
— такие матрицы называют специальными унитарными матри-
матрицами. В силу A05.3Ь), A05.3а) дает нам
6 = а* и -Р = у*, A05.3с)
т. е. эрмитово-сопряженной матрицей будет
(у 0 =(-Y а)" A053d)
ЗАМЕЧАНИЕ: Двурядная матрица (а *^\ фиксировалась за-
заданием четырех комплексных — т. е. восьми вещественных чи-
чисел; условия A05.3с) уменьшают число свободных параметров
до четырех, а условие A05.ЗЬ) — до трех — как раз столькими
параметрами и определяется поворот в вещественном 3-про-
странстве. |
Итак, мы установили отображение вращений веществен-
вещественного 3-пространства на специальные унитарные преобразова-
преобразования A05.1а) (с условиями A05.3Ь,с)) некоторого комплексного
векторного 2-пространства. Векторы этого пространства \р^ на-
называют (контравариантными) спинорами.
В этой терминологии представитель квантовомеханического
вектора, описывающего спиновое состояние системы со спином
1/2, есть контравариантный спинор.
15.3.2. Как будет преобразовываться при поворотах трехмер-
трехмерного пространства представитель совектора? Вводя для пред-
представителя совектора обозначения
«Ф 172>, (ФI - 72» = (Ф„ Ф2) = (*', ^) (Ю5.2Ь)
15. РЕАЛИЗАЦИИ МОМЕНТА 443-
и подвергая A05.1а) эрмитову сопряжению, придем к
/а' у*
(Фь Ф2) = ( )^
или, в силу A05.3d), к
что можно переписать, записывая <рх также в виде столбца, как
:)(:;)•
:;
Мы видим тем самым, что представитель совектора преобра-
преобразуется при поворотах по представлению A05.1Ь), отличному от
представления A05.1а), по которому преобразуются представи-
представители векторов, хотя и имеющему аналогичную структуру —
в нашем спинорном пространстве имеются векторы двух родов.
Двумерные комплексные векторы, преобразующиеся по
A05.1b'), называются ковариантными спинорами.
Как и в нашей общей схеме пространств состояний, мы не
будем вводить для двух контравариантных или двух ковариант-
ных спиноров скалярного произведения в обычном смысле, но
введем скалярное произведение одного ко- и одного контрава-
риантного спинора
/'\ *)
«по образу и подобию» скалярного произведения совектора на
вектор. Существенно, что такое скалярное произведение ведет
себя при вращениях как инвариант:
-К ~ f^\ ( Ь — РЧ/арч/
<м> =(фьФ2)^2;=(фь <P2)UY «.Ay <JU
1 0\/ф'
чем оправдывается как его название, так и сделанное выше
утверждение, что представители вектора и совектора образуют
величины, контраградиентные друг другу.
15.3.3. Для дальнейшего развития спинорной алгебры ре-
решающим оказывается следующее замечание. Перепишем фор-
*) Мы будем использовать для спинорных индексов, пробегающих два
значения 1, 2, средине буквы греческого алфавита X, \i, ... и подразумевать
суммирование по повторяющимся (верхнему и нижнему) индексам от 1 до 2.
Первые же греческие буквы а, Р, ... мы сохраним для пробегающих три
значения тензорных индексов обычного 3-пространства.
-444 ч Ш- ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
гмулы A05.1Ь) для преобразования ковариантного спинора (мы
нарочно выписали их и в развернутом виде) в форме
Ф^ = Y (—ф2) + бф! (Ю5.1Ь")
-—тогда из них становится ясным, что из ковариантного спи-
спинора можно «перетасовкой компонент» образовать величину,
преобразующуюся по матрице ( flJ, т. е. контравариантный
-спинор:
ф' = — ф2; Ф2 = ф1 и обратно ф,=ф2; ф2 = —ф1. A05.4а)
Эти соотношения можно записать в тензорной форме
Ф* = еЧрц. A05.4Ь)
если ввести два — ко- и контравариантный — единичных спин-
тензора (т. е. два тензора в спинорном 2-пространстве)
еХ(г = -е^; е,2=1 и e^ = -e^; е12 = -1. A05.4с)
Компоненты этих тензоров не меняются при вращениях, как
•компоненты антисимметричных тензоров ранга, равного размер-
-ности пространства. Кроме того, как легко видеть,
= б?, (I05.4d)
ЗАМЕЧАНИЕ: Иногда о введении этих тензоров говорят как о введении,
«антисимметричной» метрики н даже обозначают их как g^ и g •*. Действи-
Действительная их природа совершенно другая; они суть дискриминантные тензоры в
нашем двумерном пространстве. Необычность ситуации состоит лишь в том.
что, в то время как в трехмерном пространстве с помощью дискримннантного
тензора можно было сопоставить новый вектор (векторное произведение)
паре векторов, в 4-пространстве — тройке*), теперь же в пространстве двух
измерений дискриминантныи тензор сопоставляет новый вектор—одному век-
вектору. Эта последняя особенность позволяет поднимать и опускать индексы
< помощью дискриминантного тензора «как бы с помощью метрического»,
В «порядочном» метрическом 2-пространстве из каждого коитравариантного
вектора можно было бы образовать (инвариантным способом) целых два ко-
«ариантных: опуская индекс один раз с помощью метрического тензора, а
другой раз — с помощью днскриминантного, и это были бы существенно раз-
разные векторы — в евклидовом случае, когда ко- и коитравариантные векторы
совпадают, это были бы два вектора, повернутых один относительно другого
на 90°. |
В интересующем нас спииорном случае указанное обстоя-
обстоятельство присутствует в слегка завуалированной форме: хотя
из-за отсутствия явно введенной метрики мы можем казалось
45ы поднимать и опускать индексы, лишь прибегая к дискрими-
*) Напомним, что как раз на примере псевдоевклидова 4-пространитва
мы видели, что дискриминаитный тензор сопоставляет тройке векторов — век-
вектор другой вариантности.
15. РЕАЛИЗАЦИИ МОМЕНТА 445
нантному тензору A05.4с), фактически в нашем распоряжении
всегда есть и другой способ, опирающийся на квантовомехани-
ческое сопряжение.
В самом деле, исходя из некоторого совектора (Ф| мы образовали ко-
варнантный спинор <рх компоненты которого суть
Ф1=<ф|'/2>; <P2 = <O|-V2>.
Поднимая в нем индексы с помощью г**1, получим контравариаитный спинор
<р = е ^ф^ с компонентами
ф1 = — Фг = — <фI — 72>; ф2 = Ф1=(Ф|'/2>. (•)
С другой стороны, мы можем образовать из совектора (Ф| кваитовомехани-
ческим сопряжением вектор, который по общему правилу должен называться
|Ф>, а из него — контравариантный спинор с компонентами
(Чг | Ф> И (— '/г I Ф>, равными ф* И ф^.
По логике вещей этот спинор следовало бы обозначить через ф^ (нли
(ф) ?)—но он, как видим, совсем не равен уже введенному спинору («) (и
не сопряжен ему).
Поэтому мы условимся — в соответствии с традицией — обо-
обозначать всегда одной и той же буквой пару спиноров, связан-
связанных тензором е^ц, а для обозначения представителей отвечаю-
отвечающих одному состоянию вектора и совектора нам придется ис-
использовать разные буквы.
15.3.3.1. Тензоры в спинорном пространстве (их называют
спинтензорами или спинорами высшего ранга) вводятся в пол-
полной аналогии с обычной тензорной алгеброй— к раз кова-
риантным н s раз контравариантным спинтензором (спинором)
называют величину, преобразующуюся как произведение k ко-
вариантных и s контравариантных спиноров. Индексы спинтен-
зоров можно поднимать или опускать с помощью дискрими-
иантиых тензоров е^ или е^.
По двум индексам спинтензора — одному верхнему и одному
нижнему— можно провести суммирование; ранг спинтензора
понижается тогда на два. Если все индексы спинтензора пере-
переведены в одно — скажем, верхнее — положение, то его ранг
можно понизить на два свертыванием по двум индексам с дис-
криминантным тензором ехц. Существенно, что при этом сим-
симметричный в % и ц спинтензор даст нуль. Поэтому спинтензор,
симметричный во всех индексах (кратко говорят просто сим~
метричныи спинтензор или симметричный спинор), нельзя упро-
упростить никаким способом — симметричные спиноры неприво-
димы. Все компоненты симметричного спинора, индексы кото-
которых имеют равное количество единиц и двоек, равны между
446 ч. Ш. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
собой; поэтому симметричный спинор ранга р имеет {р-\-\) раз-
различную компоненту. Что же касается антисимметричных спин-
тензоров, то в двумерном пространстве может существовать
такой тензор только второго ранга, и притом равный дискри-
минантному тензору, умноженному на скаляр.
15.3.4. Рассмотрим матричный элемент оператора а, взятый
между двумя какими-либо состояниями (Ф| и l^)
а = <Ф | а] 40 = «Ф | 72>, <Ф I - 72» (о) ((_(!д ] *)) = «fcoVP, A05.5a)
где мы перешли к представителям в спинорной записи, в кото-
которой матрицы (а) будут объектами с двумя — верхним и ниж-
нижним— спинорными индексами. Совершим в этом матричном
элементе над \р^ и q^ преобразования A05.1а) и A05.1Ь), не
меняя о\*).
Тогда мы получим, что
или, в силу A05.3), A05.1),
в = (ф) (cos-|-+ i (nff) sin -|-) (о) (cos-|- - i (nff) sin -|) (ф).
Для дальнейших упрощений заметим, что из алгебры сигм A04.5) следует,
что
«(«п) = п + (|п-»] и (<гп)<г = п— i(n <г).
Поэтому
(cos-| + / sin -|- • (пот)) (or) (cos-|- - / sin -|-. (nff)
= cos2-^ "a + ' sin T cosy ((nff) ff — a (nff)) + sin2 -|- (nff) a (nff)
= cos2 |-« + 2 sin |-cos-|-[n ¦ or] + sin2-|- ((nor) n + i [n • (nff)o"])
C0S Ф • в + sin Ф [n • ff] + -C°S(P ((nff) n + [n • [n •«]]) =
Итак,
2
= cos ф • ff + sin ф [n • ff] + A — cos ф) п (n • ff).
Ss. _ _ _
a = cosq>'or+sin<p[n-or]-|-(l — cos ф) n (n • a). A05.5)
Легко сообразить, что полученная формула есть не что иное,
как закон преобразования вектора при конечных поворотах
в обычном 3-пространстве. Проще всего усмотреть это обстоя-
обстоятельство, если перейти к бесконечно-малому повороту фп->6<р.
*) Мы принимаем таким образом, что числа а^ одни и те же во всякой
системе отсчета.
15. РЕАЛИЗАЦИИ МОМЕНТА 447
Косинус превращается тогда в единицу, синус в свой аргумент,
и A05.5) вырождается в формулу
а = а + [6ф.а], A05.5Ь)
которой мы многократно пользовались, начиная с классической
механики.
ЗАМЕЧАНИЕ: В качестве «полезного побочного продукта» мы
получили удобную формулу для записи преобразования любого
вектора 3-пространства при конечном повороте:
А = cos ф А + sin ф [п • А] + A — cos ф) n (n • А). A05.5с)
Она поддается простой геометрической интерпретации. Если
разложить А на продольную и поперечную (относительно п)
составляющие:
А = А|| + А±; Ац = п(пА); А± = А — п(пА) = — [п • [п • А]],
то A05.5с) перепишется как
А± = coscp A± + sin<P [n • Ах]; Аи = Ац. I A05.5с')
Таким образом, назначив числам ст/ц быть одними и теми
же во всех системах отсчета, мы получили, что да = фл<тал-мг|;М|
есть вектор; отсюда следует, что сами числа аа1^ образуют
смешанный спинтензор второго ранга с векторными ком-
компонентами (или вектор со спинтензорными компонентами)
и при том такой, что его компоненты не меняются при поворо-
поворотах*). Понятно, что этот спинтензор играет фундаментальную
роль в физической интерпретации любых фактов спинорной гео-
геометрии— ведь сами спиноры, как мы уже отмечали, ненаблю-
даемы хотя бы из-за своей двузначности, а спинтензор (а) уста-
устанавливает связи между объектами спинорного и нашего обыч-
обычного 3-мерного пространства, позволяя переходить от спино-
спиноров— к векторам, и от векторов — к спинорам.
15.3.5. Перепишем еще раз формулы A05.5а), образующие
компоненты вектора из двух — ко- и контравариантного — спи-
спиноров, в развернутом виде, присоединив к ним и выражение
*) Это рассуждение можно было бы, конечно, провести и в обратном
направлении: Допустив, что A04.7) определяют (Гахц лишь в одной фикси-
фиксированной системе отсчета, мы могли бы назначить нх значения в остальных
системах по «спннтензор-векторному» закону преобразования (т.е. по A05.1а)
по к, A05.1Ь) по A и A05.5с) по а)—из чего уже следовала бы вектор-
ность 0а — и обнаружили бы тогда, что они остаются неизменными в любой
системе отсчета.
448 ч. III. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
для образованного из тех же спиноров скаляра — их скалярного
произведения:
A05.5а) < _ kJ ., _ 2., . ,., > A05.5а")
В правом столбце мы выписали те же формулы, заменив в них
ковариантные компоненты спинора ф контравариантными со-
согласно A05.4а). Поучительность последней формы записи со-
состоит в том, что из нее сразу видно, что компоненты вектора а
образуются только из симметричного спинтензора 2-го ранга
. A056Л)
а единственная компонента скаляра совпадает с (единствен-
(единственной!) компонентой антисимметричного спинтензора
ОТСТУПЛЕНИЕ A5.3.5.1.): Остановимся еще специально на том случае,
когда (Ф| не описывает нового состояния, а есть совектор, квантовомехани-
чески сопряженный вектору \*?) (т. е. в обозначениях § 12 (Ф = (??*).
Тогда (ср. A05.2Ь)) ф1=ф', ф2 == ф2, и, следовательно, <р' == — ф2, ф2 = 'ф1.
Таким образом в этом случае (черта сверху означает теперь среднее по со-
состоянию Ф):
A055aW)
|
обычное условие нормировки состояло бы в требовании 1 = 1.
Итак, образовав средние по состоянию V значения скаляра 1 и вектора О,
мы образовали из характеризующих состояние двух пар комплексно-сопря-
комплексно-сопряженных — т. е. четырех вещественных — чисел (или функций)
четыре (тоже вещественных, как средние эрмитовых операторов) числа (функ-
(функции) 1, дх> о у, дг. Поэтому можно было бы ожидать, что эти две четверки
связаны взаимно-однозначным образом. Легко, однако, видеть, что все числа
A05.5а"') не меняются, если подвергнуть ф1 н ф2 одновременному умножению
иа общий фазовый множитель: ^ -*¦ еia^; ф -> e"~'ai|> . Поэтому четыре
числа A05.5а'") не могут быть независимыми, но между ними должно быть
минимум одно соотношение.
15. РЕАЛИЗАЦИИ МОМЕНТА 449
Чтобы найтя его, запишем
Тогда
Г=р2 + р2; а2 = p'f — pf; aJ. = 2p,p2cosp; a4 = 2р,р2 sin f5.
Отсюда уже ясно, что если образовать
КJ + (а,J + (агJ = 4Р2р2 (cos2 р + sin2 р) + (р2 - р2J = (р* + р|J,
то мы получим как раз (IJ. Итак, искомое соотношение есть
илн, если перейти к физическим средним, которые для ненормированного со-
состояния с 1 ф 1 суть, конечно,
4
то
Итак, нельзя найти такого состояния, в котором все трн ога сразу будут иметь
нулевые средние. |
СЛЕДСТВИЕ: Если в некотором состоянии (ах) — {ау) = 0, то
\о2) = ±1, т. е. это состояние есть собственное для az. I
ЗАМЕЧАНИЕ: С точки зрения привычной тензорной алгебры
удивительно, как из одного вектора \р*- можно образовать не-
невырожденный (с | ^ | ф 0) тензор 2-го ранга \pAtl. Разъяснение
s s
связано с подчеркивавшимся выше фактом, что в двумерном
пространстве всякому вектору однозначно сопоставляется дру-
другой, ему «ортогональный» — а из пары ортогональных векторов
конечно можно построить невырожденный тензор 2-го ранга. |
Вернемся к тому, что вектор а образуется только из симмет-
симметричного спинтензора A05.6.1),а скаляр — из антисимметричного
A05.6.2). С точки зрения представлений группы вращений (реа-
(реализаций алгебры, Ли для момента) это обстоятельство должно
означать, что «симметрированное» произведение представлений
с /=-2-дает нам представление с /= 1, а «антисимметрирован-
«антисимметрированное» — с / = 0. В силу важности этого утверждения (в нем со-
содержится, фактически, и уже прокламировавшееся более ши-
широкое утверждение, что из представлений cl=-^ можно по-
построить представления со всеми /) стоит остановиться на нем
поподробнее.
15.3.6. Рассмотрим две разные (и независимые) «подсистемы»,
обладающие спином у каждая, и объединим их в общую
16 В. В. Медведев
450 ". "I ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
систему с помощью процедуры, описанной в конце § 10. Пусть
первая система описывается вектором состояния | Ч^}, предста-
( .<т| Л
вителем которого в базисе I , I —1( I будет спинор ф\
а вторая —вектором состояния | W2) с представителем фл в ба-
2
зисе 2{к |, т. е. пусть
Тогда состояния всей системы будут описываться прямым
произведением
в пространстве, базис которого можно образовать из прямых
произведений базисных векторов пространств 1 и 2: i{k\®^\.
Представителем \W) в этом базисе будет
!<"¦ I ® 2(» I • I v ,> 01 ?2>=,<»¦ | ч',> • ^ | ?2>=фч^,
1 2
где ф* и ф пока — спиноры в двух разных спинорных прост-
1 2
ранствах 1 и 2. При повороте эти спиноры преобразуются со-
согласно A05.1а):
с совпадающей матрицей f , J (ее параметры определяются,
как мы знаем, параметрами <р, п поворота в обычном 3-прост-
ранстве); поэтому мы вправе отождествить оба спинорных про-
пространства и считать, что представители ф*- и гр векторов со-
1 2
стояния обеих подсистем суть два спинора в одном и том же
спинорном пространстве, а представитель ф* гр состояния
1 2
всей системы есть спинтензор 2-го ранга в том же пространстве.
15.3.6.1. Как записать представитель оператора момента?
Согласно нашим допущениям момент всей системы есть сумма
моментов подсистем
М = Mi -f M2 = m, 0 /2 + /, ® ш2 = у (от, 0 /2 + /, ® о2);
поэтому его представитель есть
2<Р IЛ ц>2
15. РЕАЛИЗАЦИИ МОМЕНТА 451
где мы обозначили через \h)i векторы базиса, квантовомехани-
чески сопряженного базису i^| (при этом, конечно, U)i =5^'
?='е,хц iD0 и аналогично для ]цJ. Итак,
Но матрицы (cri) и (огг) в первом и втором пространствах
одинаковы. Поэтому у них можно опустить индекс, указываю-
указывающий на номер подсистемы (у операторов а\ и о2 сделать это
было, конечно, нельзя!) и записать
MVV =|(<Л • С + Ы • ог°Д (Ю5.7.1)
Итак, для оператора момента — так же как и для векторов со-
состояния— при переходе от самого оператора к представителям
прямые произведения объектов из разных пространств превра-
превращаются в произведения тензоров одного пространства*).
Действие оператора момента на состояние системы запи-
запишется поэтому как
<М | %> <Я> | ЩГ = М^фЧ" = 4 {«Л.ФЧ0 + №\^}'
12 Z 12 12
В частности,
(м21 ?,> ® | ?2»vo = А {(- 1Г' фЧр + (-1Г' * V}
^ 12 12
-т- т. е. все фЧР суть собственные состояния Мг, причем относя-
1 2
щиеся к EW-ам:
к т = +1, A05.7.3.1)
1 2
ф'ф2 и ф2ф' к т = 0, A05.7.3.2)
12 1 2
ф2ф2 к т = -\. A05.7.3.3)
1 2
15.3.6.2. Найдем представитель оператора М2:
-т KV<:+б^-;,) (^«ц- +
*) Именно поэтому прямое произведение называют теперь часто тен-
тендерным.
15*
452 ". "I- ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
Но свернутое по векторному индексу выражение оаА к-оа*"^ = 1^ есть
спинтензор с постоянными компонентами, а такой тензор в спинорном про-
пространстве должен — как и во всяком другом — выражаться только через еди-
единичный спинтензор б?' или дискриминантные тензоры е^ или ек"^ . Инте-
Интересующий нас спинтензор обладает симметрией
легко видеть, что единственные комбинации бие, обладающие той же сим-
симметрией, суть б?"б?' и б^'б^ (третья комбинация той же симметрии еАAеЛ|1"
выражается через первые две). Поэтому должно быть
Для определения коэффициентов а и Ь воспользуемся тем, что для лю-
любого a: ejva^'ji = 0 (Spuraa=0). Имеем:
6$> O(f = Spur 0 • а^ = 0 = 2абЦ" + ЬЬ*' = Bа + Ь) 6|j", т. е. 2а + Ь = 0.
С другой стороны,
2\ ^" *", т. е. а + 26 = 3.
б
Отсюда
а = —1; 6 = 2,
то есть
и
(М2Г^ = 2Й2-^Ц^^ ==2й2б^. A05.8.1)
Таким образом представитель М2 содержит оператор сим-
симметризации по Я, и \i и, следовательно, ведет себя различно по
отношению к состояниям, симметричным и антисимметричным
в подсистемах
Именно:
,„ S S A05.8.2)
A
А это значит, что как раз эти комбинации суть собственные со-
состояния М2 для всей системы, причем симметричное есть со-
состояние с I — I, а антисимметричное — с./ = 0 в полном соот-
соответствии с полученными выше формулами (Ю5.6), согласно
15. РЕАЛИЗАЦИИ МОМЕНТА 453
которым из симметричных комбинаций фиф для одной частицы
можно было построить вектор, а из антисимметричной — ска-
скаляр. Все они — согласно A05.7.3)—при фиксированных индек-
индексах л и (а суть также и собственные векторы Mz.
Что же касается несимметрированных произведений -ф^-ф1*,
1 2
описывающих систему, подсистемы которой находятся в со-
состояниях с определенными tniz и т22, то они вообще говоря не
суть представители собственных векторов М2, т. е. не отвечают
определенным значениям (квадрата) полного момента системы.
Итак, мы подтвердили утверждение, что симметричный спин-
тензор 2-го ранга описывает состояние с /= 1; а симметричный
спинтензор ранга 0 — т. е. скаляр — состояние с / = 0. Анало-
Аналогично устанавливается, что симметричный спинтензор ранга р
описывает состояние с / = -§•*).
15.3.7. Действительно, ситуация, в таких подробностях исследованная
нами сейчас для случая объединения в одну систему двух независимых под-
подсистем с /i = k = —, остается в основных чертах той же самой и для объ-
объединения подсистем с произвольными 1[ н k. Состояние каждой из таких под-
подсистем представляется в «ее» спииорном пространстве симметрическим спин-
тензором ранга pi == 2/<. Представителями прямых произведений состояний
подсистем будут произведения
^i-V/i-'V* A05.9.1)
I 2
симметричных спиитеизоров фиф, которые можно считать вложенными в
1 2
одно спинориое пространство; они не будут относиться к определенным зна-
значениям / (хотя будут отвечать определенным т). Определенным значениям I
будут принадлежать только полиостью симметричные спиитеизоры, которые
можно образовать из A05.9.1).
Простейший такой спинтензор получается при симметризации A05.9.1)
во всех индексах Я,, .... Яр|, fi, \ipj он будет отвечать моменту
*) Для этого надо сперва установить — путем совершенно аналогичных
рассуждений, — что действие оператора М2 на спинор ранга р описывается
формулой
)
i<i</<p
A05.8.р)
где P(i,i)—оператор перестановки индексов X* и kj. В применении к совер-
совершенно симметричному спинору все P(i,j) = 1, и правая часть A05.8.р) при-
принимает вид
если р
454 ч. Ш. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
системы с / = /i -f- W.
v'li + li — I 1' ""' Pi* "l* *'¦' ^Рг/ ™ ™
A05.9.2)
(здесь через Р (Х.^ ...,Я,р; "Xj, ..., ц ) обозначен оператор симметризации).
Дальнейшие состояния с определенными / получается, если до симметриза-
симметризации свернуть A05.9.1) по какой-либо паре индексов с дискриминаитным тен-
тензором е;ц,. В силу симметрии обоих спиноров гЬ и ¦ф можно свертывать
1 2
только по паре индексов, взятых один у if), а второй у ф; благодаря той же
1 2
симметрии несущественно, какой именно индекс выбирается у каждого спи-
спинора, и результат зависит лишь от числа свертываемых пар. Мы приходим
таким образом к последовательности совершенно симметричных спинтензоров.
с убывающим от одного к другому иа 2 рангом
Ф/,'+/2_1 = Р (^i • • • ^p,-i '• Мч ••• Цр2_1)
A05.9.3)
отвечающих определенным квантовым числам полного момента системы
Такой способ построения совершенно симметричных спинтензоров можно-
будет продолжать до тех пор, пока на свертки не исчерпаются все индексы
того i|), у которого их меньше, т. е. можно будет сделать всего mm(pi, рг)
шагов, а ранг последнего симметричного спинтензора будет равен
Pi + Pi — 2 min (/>,, р2) = | Pi — рч. I,
т. е. ои будет описывать состояние системы с / =|/i — h\.
Итак, объединяя в одну систему две независимые подсистемы с момен-
моментами U и /г, мы можем выделить у полной системы состояния со значения-
значениями /, меняющимися от h + h до |/i — h\:
l=-\li-h\; Mi - hI + l; ..•; (h + h- D; (h + h). A06.3)
Подсистемы в этих состояниях ие будут обладать определенными т.\ и mi
(но будут обладать определенным т = mi + m2).
15.4. В чем состоит физический смысл преобразований и рас-
рассуждений, которыми мы занимались в разделах 15.3.6,7? Со-
Состояние двух квантовых систем с точки зрения их поведения
при пространственных поворотах характеризовалось, пока мы
рассматриваем их независимо друг от друга, заданием (квад-
(квадрата) момента каждой системы и его проекции на выделенную
ось — т. е. набором квантовых чисел
/ь /2, /я, и т2. A06.1)
Проведенные в предыдущих разделах рассуждения показывают,
что, рассматривая эти две системы как подсистемы одной об-
общей системы, мы можем перейти для ее описания к другому
15. РЕАЛИЗАЦИИ МОМЕНТА 455
набору коммутирующих наблюдаемых и характеризовать ее
состояние заданием (квадратов) моментов каждой из подси-
подсистем и суммарными наблюдаемыми всей системы — квадратом
полного момента JW2 и его проекцией на выделенное направле-
направление Mz, т. е. перейти от набора квантовых чисел A06.1) к дру-
другому набору
1и 12, т = т{-\-т2 и /. A0Р.2)
Наблюдаемые нового набора действительно коммутируют друг с другом.
В самом деле, Мг коммутирует с М2 как проекция момента со своим квадра-
квадратом (93.2), а с Mj и М|— поскольку в коммутировании каждый раз будет
участвовать только «своя» слагающая Miz или M2z- To же справедливо и для
Мх или Му, откуда следует и коммутативность М2 с М( и М2.
Такой переход от индивидуальных наблюдаемых подсистем
к суммарным наблюдаемым полной системы называют обычно
сложением моментов *).
15.4.1. Если не ставить себе целью полностью разрешить за-
задачу сложения моментов, т. е. найти собственные векторы, от-
отвечающие набору квантовых чисел A06.2) в виде явных линей-
линейных комбинаций собственных векторов, отвечающих набору
A06.1) (Ее решение потребовало бы довольно громоздких вы-
выкладок. Коэффициенты таких разложений одних собственных
векторов по другим называются коэффициентами Клебша —
Гордана; их значения для небольших квантовых чисел приво-
приводятся в книгах по квантовой механике или по теории групп),
а желать лишь получить формулы A06.3), указывающие, ка-
какие значения A06.2) получатся при комбинировании A06.1)
с фиксированными 1Х и /2, то результата можно достичь совсем
просто, если исходить из подсчета числа состояний.
Нарисуем прямоугольную таблицу, столбцы которой будем
нумеровать значениями т2, а строки*—т.\. В клетках таблицы
расположатся состояния — прямые произведения состояний под-
подсистем с определенными т2 и т,\, имеющие, следовательно, и
определенное значение т = тх -f- tn2, которое мы и будем един-
единственно отмечать. Тогда на каждой линии, параллельной побоч-
побочной диагонали, расположатся состояния с одним и тем же т,
из линейных комбинаций которых надо строить состояния с оп-
определенными /.
Первая такая линия, содержащая единственный элемент
|..., l\ -f- /2) = |/i) I/2), будет отвечать значению т = lx -f-12.
Это значение может относиться только к квантовому числу
*) С математической точки зрения задача состоит, как легко видеть»
в разложении прямого произведения неприводимых представлений алгебры
Ли (91) (которое образует, вообще говоря, приводимое представление этой
алгебры) в прямую сумму неприводимых.
456
ч. III. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
/ = l\ + h- Но тогда должны присутствовать все B/+1) со-
состояний, соответствующие всем значениям —/ ^ т ^С +/, отве-
отвечающим полному моменту /] + h, т. е. значениям т = lt + h,
(h + h—1), (/1 + h — 2), ..., (—/i — /2). Первое из них мы
уже нашли, следующие должны получаться линейными комби-
комбинациями состояний, лежащих на одной побочной диагонали.
. На второй побочной диагонали лежат два состояния
|/i — 1)| 4) и |/i)|/2—1). Одна их линейная комбинация вой-
войдет, согласно сказанному, в число состояний, относящихся
к полному моменту /=/,-(- /2, вторая независимая комбинация
может относиться только к полному моменту {1\ + /2—1) и его
ZI2+1
h-г
к
h-1
li-z
-k
проекции на ось г, характеризуемой числом т = A{ -\-12—1).
Повторяя приведенное рассуждение, заключаем, что должны
присутствовать и остальные состояния, отвечающие полному
моменту / = /i + /2—1 и всем допустимым значениям т.
Продолжение этих рассуждений приводит нас к тому, что
состояния на каждой норой побочной диагонали должны до-
допускать линейные комбинации, отвечающие всем уже найден-
найденным значениям /, и еще одну линейную комбинацию, относя-
относящуюся к значению I, на единицу меньшему последнего найден-
найденного. Так будет продолжаться до тех пор, пока мы не выйдем
за «квадратную» часть таблицы, т. е. не достигнем ближайшего
из углов — левого нижнего или правого верхнего. После про-
прохода угла число состояний с данным т перестанет нарастать,
и поэтому новых значений / более вводить не понадобится.
Ближайший угол введет для / последнее значение I =
= Ui — h\. Таким образом, образуя подходящие линейные ком-
комбинации состояний с квантовыми числами A06.1), мы построим
16. УРАВНЕНИЯ ДВИЖЕНИЯ
457
состояния с параметризацией A06.2) со значениями
l=li + h, h + k-h ••¦, \h~k\
A05.3)
и всеми соответствующими значениями т.
Проверим, что мы приходим при этом к правильному полному числу не-
независимых состояний. Каждому / соответствует B/+1) различных состоя-
состояний; поэтому всему набору A06.3) будет соответствовать число состояний,
равное сумме 2 min(/i, /2)+ 1 членов:
= у [2 (/, + 1г + | U -
D] [2 min (/„ t2) + 1] =
177/- If Ь
= [2 max (/„ h) + П [2 min (/„ h) + \\ = B/, + 1) B/2 + 1),
— что как раз соответствует числу различных состояний в параметризации
A06.1).
Итак, при сложении моментов U и 12 двух независимых си-
систем мы получаем для полного момента все значения A06.3) от
суммы до модуля разности складываемых мо-
моментов.
15.4.2. Заметим, что найденное правило сло-
сложения моментов допускает очень простое (хо-
(хотя и нестрогое) наглядное истолкование. Бу-
Будем рассматривать направление, по которому
«направлен» один из моментов, скажем ть как
выделенное направление, проекция второго
момента т2 на которое определяется числом
т.ч.. Тогда «векторная сумма» обоих моментов
будет равна / = /, + т2, т. е. будет принимать
как раз требуемые формулой A06.3) значения
от l = U + l2 до l = h — l2 (считаем, что векторная
h ^ h)- Дефект этого рассуждения лежит, ко- оель
нечно, в том, что момент нельзя, как мы
знаем, направить целиком по одному направлению (ср. 14.4).
Последовательное использование такой картины привело бы для
квадрата момента к значению М2 = ЬЧ2 вместо правильного вы-
выражения М2 = Ь21A-\- I); тем не менее эта векторная модель
сослужила немалую пользу на начальных этапах развития тео-
теории квант.
16. Уравнения движения
До сих пор все наше описание относилось к одному мо-
моменту времени — к описанию состояний и динамических пере-
переменных в этот фиксированный момент. Теперь нам надлежит
установить связь между описанием системы в различные мо-
моменты времени — т. е. ввести динамику.
мо-
458 ч. III ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
16.1.1. Чтобы описать поведение системы при временном
сдвиге, мы опять, как и для пространственных сдвигов и пово-
поворотов, будем исходить из принципа соответствия, требуя, чтобы
в квантовую теорию можно было бы перенести из классической
соответствующие соотношения в скобках Пуассона.
В классической механике зависимость любой (не зависящей
явно от времени) динамической переменной от времени описы-
описывалась скобкой Пуассона с фундаментальной для данной дина-
динамической системы динамической величиной — функцией Га-
Гамильтона
а = (Я(р, q), а). A.60а)
Поэтому теперь мы, совершенно так же как для сдвигов
и вращений, потребуем, чтобы временная зависимость любой
(не зависящей от времени явно) динамической переменной а
задавалась бы уравнением
a(t) = ^[H(t),a(t)], A07)
где Н — некоторый, основной для характеристики рассматри-
рассматриваемой системы, оператор, который называется оператор Га-
Гамильтона или, кратко, гамильтониан.
Переходя к изменению операторов за конечный промежуток
времени, мы можем, как и для пространственных сдвигов, про-
проинтегрировать это уравнение*), и получим тогда
a(t) = U(t,to)a(to)U-1(t,to); )
где
. A-ця \ (Ю8)
U(t,to) = e * ; U+(t, to) = U1
состояния не зависят от времени.
Уравнения A07) и A08) показывают, что и как меняется в рас-
рассматриваемой системе с течением времени, т. е. являются дина-
динамическими уравнениями или уравнениями движения системы.
Использованная в этих уравнениях форма описания движе-
движения системы называется Гайзенберговой картиной, говорят
также и о Гайзенберговом представлении.
Эта картина наиболее близка к классическому способу опи-
описания движения — в ней зависят от времени динамические пе-
переменные, а описывающие состояние системы векторы — по-
постоянны. Так построенные динамические переменные также
называют гайзенберговыми динамическими переменными.
*) Мы принимаем здесь, что сам гамильтониан Н не зависит от времени
явно. В противном случае в выписанных формулах возникают осложнения,
в природу которых мы пока не будем вдаваться.
16. УРАВНЕНИЯ ДВИЖЕНИЯ 459
16.1.2. Мы уже знаем, однако, из § 13, что в квантовой ме-
механике такой способ описания — это не единственный способ
описания изменения системы при каком-либо преобразовании
симметрии. Точно так же, как и для пространственных движе-
движений, мы можем подвергнуть теперь все операторы, векторы и
совекторы общему унитарному преобразованию типа (88), вы-
выбирая в качестве унитарного оператора
зависящий от времени оператор U(t,t0),
так что
|Л>=#|Л, t) = U-'(t, to)\A); (Bi#(fi, t\ = (B\U(t, t0);
a (f) # a @ = ?/"'(', to)a(t)U(t, tu) = U~lUaU~'U = a.
Итак, мы пришли к другой картине, в которой динамические
переменные не зависят от времени (если только не зависят от
времени явно),
о (<) = о, A09.1)
а векторы и совекторы состояния зависят от времени *):
\A,t) = e * \A,t0); A09.2>
(B,t\ = (B,to\e * . A09.3)
Дифференцируя второе из уравнений A09) по времени, по-
получим уравнение движения в дифференциальной форме
Это уравнение часто рассматривается как основное уравнение
квантовой механики и называется уравнение Шредиигера или,
точнее, временное уравнение Шредингера.
Та картина, к которой мы пришли для описания движения
с помощью A09), называется Шредингеровой картиной или
представлением Шредингера. Соответственно, динамические
переменные этой картины, не зависящие от времени, называют
шредингеровыми динамическими переменными, а зависящие от
времени векторы состояния — шредингеровыми векторами со-
состояния.
*) Мы опять считаем, что Н не зависит от времени явно.
-460 ч. III. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
16.1.2.1. Если перейти теперь (в рамках шредингеровой кар-
картины) к конкретному фиксированному представлению, в кото-
котором диагональны некоторые наблюдаемые I, образующие полный
«абор, то можно перейти к сокращенным обозначениям формул
<80) — (82), т. е. вместо \A,t) писать — $(U)) или просто
-i|>(g, /), если (l'\A, t) = г|з(|', t) *). В этих обозначениях времен-
временное уравнение Шредингера запишется в форме
iH**fJ±=H^(Z,A (ПОа)
я которой его и пишут в большинстве книг по квантовой меха-
механике. Это уравнение называют еще иногда волновым уравне-
уравнением, а его решение— (зависящей от времени) волновой функ-
функцией системы. Основанием такой терминологии является то об-
обстоятельство, что для системы, состоящей из одной свободной
материальной точки, решением этого уравнения будут, как мы
вскоре убедимся, плоские волны, распространяющиеся в обыч-
обычном трехмерном пространстве (ср. замечание о конфигурацион-
конфигурационном пространстве в 10.8.3)**).
16.2. Изложенная схема возможных способов описания за-
зависимости поведения квантовомеханической системы от време-
времени является — в двух отношениях — простейшей, и в ней воз-
возможны осложнения двоякого рода.
16.2.1. Первое усложнение возникает при желании включить
в рассмотрение системы, гамильтониан которых может явно
зависеть от времени. Уравнения движения A07) сохранят при
этом свою форму; можно будет и искать их решение в форме
A08.1) преобразования посредством некоторого унитарного опе-
оператора U{t,tb); однако выражение A08.2) этого унитарного опе-
оператора через не зависевший от времени гамильтониан не оста-
останется, конечно, более справедливым, и из формы A08.1) можно
<5удет получить только дифференциальную связь между U и
4A).
*) Полная система состояний (§'|, определяющая представление, не
обязана иметь никакого отношения не только к зависимости от времени, но
« вообще к рассматриваемой динамической системе — это просто некоторый
базис в пространстве состояний.
**) Уравнение A10а) формально относитси к параболическому типу,
однако нз-за стоящей слева мнимой единицы оно на самом деле ближе к ги-
гиперболическим. В самом деле, как раз такое уравнение получится, если для
аналогичного гиперболического уравнения
искать решение в виде ф = еш<р и заменить при подстановке в уравнение
множителем ih только одну производную по времени.
16. УРАВНЕНИЯ ДВИЖЕНИЯ 4611
В самом деле, дифференцируя A08.1) по времени, полу-
получаем *)
и, поскольку это уравнение должно совпадать с A07), заклю-
заключаем отсюда, что зависящий от времени гамильтониан H(t)
должен выражаться через U(t, t0) как.
Н (t) = - ih dU(J;io) U+ (t, t0). A08.5).
Соотношение A08.5) можно рассматривать как дифферен-
дифференциальное уравнение для нахождения U(t,t0) по известному
H(t)\ если бы оно было не операторным, а численным, то мы
сразу выписали бы его унимодулярный интеграл как
t
U(t,to) = e v . (¦)¦
В нашем операторном случае дело, однако, существенно ослож-
осложняется тем обстоятельством, что операторы H(t) для разных t
не только не равны друг другу, но и не обязаны друг с другом,
коммутировать, поэтому наивное использование решения (*)
привело бы нас к экспоненте от некоммутирующих операторов,,
смысл которой надо было бы еще уточнять. Оказывается, что:
такое уточнение можно совершить очень изящным способом,,
с помощью понятия, введенного американским физиком Фриме-
ном ДАЙСОНОМ в 1949 году.
Пусть имеется несколько операторов, относящихся каждый,
к какому-то определенному моменту времени: L\(ti), L2(ts),.
Lz(t3), ••• • Тогда их упорядоченным по времени или хроноло-
хронологическим произведением называют такое их произведение, в
котором подразумевается, что сомножители должны быть рас-
расположены слева направо в порядке убывания времен, к кото-
которым они относятся. Для обозначения хронологических произве-
произведений пользуются помещаемым перед произведением символом
Т (поэтому кратко говорят и «7"-произведение>); таким образом
Т {Ц (/,) ... Ln (tn)} = Lix (th) ,,. Lin Qin),
. если th>ti2> ... >tin..
*) Мы пользуемся здесь тем, что из UU+ = 1 следует
-462 ч. "!¦ ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
Рассмотрим теперь интеграл (*) уравнения A08.5), в кото-
котором порядок действия стоящих в показателе операторов H(t)
определен условием хронологического упорядочения, как гово-
говорят,— Г-экспоиеиту от интеграла гамильтониана
Т Jtf(T)dT
Т{е *' }. (**)
Если заменить в ней стоящий в показателе интеграл римановой
-суммой
t п
\ dxH (т) = litn У At ¦ Н (tk)\ tn = t; t0 = t0,
то в силу определения Г-произведения экспонента превратится
в (бесконечное в пределе) произведение экспонент
T{e
(иногда говорят о фейнмановом мультипликативном интеграле)
от гамильтонианов в моменты времени, убывающие слева
направо. Если выполнить теперь эрмитово сопряжение (***), то
порядок перемножения экспонент изменится на противополож-
противоположный, т. е. при умножении (***) на эрмитово-сопряженное выра-
выражение рядом окажутся (сопряженные) экспоненты, относящиеся
к одному t, которое при перемножении дадут единицу, после
•чего рядом опять окажутся множители, относящиеся к одно-
одному— следующему — моменту времени, и этот процесс про-
продлится, пока каждая из участвующих в (***) экспонент не «по-
тасится» сопряженной. Таким образом определяемый (***) —•
¦т. е. (**) —оператор унитарен.
Чтобы его можно было принять за решение
} A08.6)
уравнения A08.5), осталось еще убедиться, удовлетворяет ли он
уравнению. Но последнее почти самоочевидно: при дифференци-
дифференцировании A08.6) под знаком Г-произведения появляется новый
множитель -jH(t), который по смыслу Г-произведения должен
«стоять слева от всех остальных, т. е.
dU (t, ta) _ г И(ЛТ,., м
16. УРАВНЕНИЯ ДВИЖЕНИЯ 463
откуда, благодаря унитарности U(t,to), немедленно следует
A08.5). Итак,
если гамильтониан системы может зависеть от времени, то
решением гайзенбергова уравнения движения A07) является
Г-экспонента A08.6).
16.2.2. Второе усложнение связано с различными возможно-
возможностями, которые открываются в выборе служащего для перехода
от одной картины к другой унитарного преобразования типа
(88). В 16.1.2 мы выбрали зависящий от времени унитарный
оператор, осуществляющий такое преобразование, равным опе-
оператору эволюции A08.2). Что получится, если выполнить это
преобразование с помощью какого-то произвольного унитарного
оператора V(t, 4), т. е. положить
\Ab=V+(t,t0)\A); {IU\ = (B\V{t,tJ;
d(t)=V+(t,t0)a(t)V(t,t0) ?
Дифференцируя эти определения по времени, мы получим:
dt
da {t) __ ,.+ i ,„ „ .... .. ,.+ dV
V+ ± [H, a (t)]_ V-V+-~V+a (t) V + V+a (t) ^- V+V ¦.
ji ¦ * I** ¦ w \"/J— r r jjj
(мы рассматриваем случай, когда гамильтониан в гайзенберговой картине
¦может зависеть от времени явно, Я = H{t)). Введем теперь оператор
h (t) = - ih dVi^to) V+ (t, t0), A08.5')
связанный с V(t, to) так же, как гамильтониан H(t) был связан с оператором
эволюции U(t,to); по смыслу своего определения оператор h(t) есть динами-
динамическая переменная в гайзенберговой картине. В нашей новой картине, опре-
определяемой преобразованием (•). та же переменная будет изображаться по
общему правилу оператором
h (t) = V+ (t, <„) h (t) V (t, to). A08.5")
С его помощью уравнения, выражающие временную зависимость векторов,
совекторов и операторов в новой — тильдованной — картине, запишутся как
— т. е. в тильдованной картине вообще говоря зависят от времени и векторы,
и операторы.
464 ч- 1П- ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИК!
Третье из этих уравнений, выражающее зависимость опера-
операторов от времени, совершенно аналогично по своей форме урав-
уравнению движения A07) в гайзенберговой картине, отличаясь от
него лишь заменой гамильтониана H(t) на «эффективный гай-
зенбергов гамильтониан»
Hr(t) = H(t)-h(t). (Ш7а)
Первое же (второе не является независимым), выражающее за-
зависимость от времени векторов состояния, совершенно анало-
аналогично уравнению Шредингера (ПО) с «эффективным шредин-
геровым гамильтонианом»
Нш(г)= +h(t). (ПОа)
Итак, в тильдованной картине полная система уравнений дви-
движения содержит как уравнение Гайзенберга для операторов
-^ = |[Яг@,«@Ь A07)
так и уравнения Шредингера для векторов и совекторов
(iTo>
и временная эволюция (т. е. — динамика) определяется не од-
одним гамильтонианом, а двумя Яг if) и Яш@-
При переходе от одной тильдованной картины к другой с по-
помощью преобразования (-*) эти гамильтонианы преобразуются
двояким образом: во-первых, они получают аддитивные до-
добавки (противоположных знаков) A08.5'), а затем преобра-
преобразуются как все прочие операторы с помощью унитарного V(t, f)
согласно третьей формуле (*). Что же касается их суммы
Нт ¦+¦ Яш, то она испытывает лишь унитарное преобразование
подобно «сем остальным операторам. Ее средние значения не
зависят поэтому от выбора картины; как раз они имеют физи-
физический смысл энергии.
Рассмотренные в 16.1.1 и 16.1.2 гайзенбергова и шредингерова
картины оказываются теперь предельными частными случаями
общей тильдованной картины, выделенными той особенностью,
что в каждой из них один из гамильтонианов—шредингеров'
в гайзенберговой и гайзербергов в шредингеровой — обращается
в нуль. Таким образом в них — и только в них — временная
эволюция описывается одним гамильтонианом. В гайзенбер-
гайзенберговой картине это первоначальный гамильтониан H(t), кото-
который логично обозначить как Н (t) = Яр (t), где верхний латин-
латинский индекс указывает на гайзенбергову картину,- а нижний"
16. УРАВНЕНИЯ ДВИЖЕНИЯ 465
русский — на то, что это гайзенбергов гамильтониан, стоящий в
уравнении A07).
В шредингеровой картине — если первоначальный гамильтониан H(t) за-
зависит от времени, векторы состояния суть
| A, t)Sch = U+ (t, t0) | Af,
с оператором U(t,to), задаваемым A08.6). Поэтому (при операции эрмитова
сопряжения порядок операторов меняется на обратный; следовательно, хро-
хронологическое произведение Т переходит в антнхронологическое Т, в котором
операторы идут слева направо в порядке возрастания времен!)
t
—1 \
t
Я (т) dx
t. to)H(t)\A)H =
= U+ [t, t0) H (t) U (t, t0) | A, t)Sch.
Таким образом в случае, когда первоначальный гамильтониан
зависит от времени, уравнение Шредингера в шредингеровой
картине имеет форму
d]AfCh )Sch
= Я^сЬ(t)\A, t)Sch A10t)
с шредингеровым гамильтонианом в шредингеровой картине
(t) = U+ {t, t0) H @ U(t, t0) = U+ (t, t0) Я?(t) U(t, to). A lOt. a)
Если же зависимость H(t) отсутствует, H(t) = H, то U(t,tQ) в
(HOt. а) будет задаваться простым выражением A08.2), комму-
коммутирующим с не зависящим от времени Я, благодаря чему
окажется просто
Таким образом, если мы — как то делалось в 16.1 —ограничи-
—ограничиваем себя рассмотрением только гайзенберговой и шредингеро-
шредингеровой картин и при том для систем, гамильтониан которых не за-
зависит от t, то нам оказывается достаточным всего лишь два
гамильтониана, и при том равных друг другу. Для понимания
общей структуры квантовой динамики, однако, необходимо толь-
только что проведенное рассмотрение общего случая.
ЗАМЕЧАНИЕ 1: Заканчивая первую часть этого курса — клас-
классическую механику, — мы отметили парадоксальную ситуацию,
которая возникает там при использовании метода Гамильтона—
16 Б. В. Медведев
466 ч. III. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
Якоби, в котором ищут такое каноническое преобразование,
которое обращало бы функцию Гамильтона системы в нуль —
такая функция Гамильтона не зависит от времени явно, сохра-
сохраняется, но не имеет никакого отношения к энергии системы. Те-
Теперь мы видим, в чем тут дело — в классической механике из
двух гамильтонианов Яг и Яш остается аналог только гайзен-
бергова гамильтониана Нг — он-то и обращается в нуль в про-
процедуре Гамильтона — Якоби, которая аналогична переходу к
шредингеровой картине. В квантовой теории в этой картине воз-
возникает другой гамильтониан Яш, который управляет временной
зависимостью векторов состояния, — но векторы состояния не
имеют классического аналога, и поэтому в классическом рас-
рассмотрении этот новый объект исчезает из виду. Впрочем, это
исчезновение не совсем бесследно: в классическом описании
сохраняется величина, связанная с квантомеханическим опера-
оператором эволюции U(t, to) (мы не будем сейчас устанавливать
характер этой связи)—это производящая функция <р канониче-
канонического преобразования Гамильтона — Якоби, которая удовлетво-
удовлетворяла там уравнению Гамильтона — Якоби A.77). Поэтому
именно это уравнение оказывается «классическим следом» урав-
уравнения Шредингера и может быть получено из него соответст-
соответствующим предельным переходом. I
ЗАМЕЧАНИЕ 2: Поскольку в шредингеровой или гайзенберго-
вой картине уравнения квантовой динамики выглядят проще,
чем уравнения A07), (ПО) «тильдованной» картины, то возни-
возникает естественный вопрос, а зачем вообще вовлекать в рассмот-
рассмотрение ведущий казалось бы лишь к дополнительным осложне-
осложнениям общий случай произвольной картины? Ответ состоит в
том, что очень часто приходится сталкиваться со случаями, когда
временная эволюция квантовой системы состоит — если можно
так выразиться — из двух составляющих, одна из которых три-
тривиальна в том смысле, что мы хорошо умеем с ней обращаться,
а другая составляет истинную проблему. Так вот, чтобы «три-
«тривиальная» составляющая временной эволюции не усложняла
дополнительно «нетривиальную» часть, их удобно разделить,
выбрав такую картину, в которой Яг содержит только «триви-
«тривиальные» члены, а все нетривиальные сосредоточены в Нш. Тогда
при отсутствии нетривиального взаимодействия эта картина
оказалась бы гайзенберговой картиной, в которой векторы со-
состояния не зависят от времени, и, следовательно, все изменение
векторов состояния со временем связано только с нетривиальной
частью взаимодействия. Такую картину называют картиной Ди-
Дирака или —пожалуй чаще—представлением взаимодействия.
Техника использования представления взаимодействия была
разработана в конце 40-х годов в связи с релятивистской кван-
16. УРАВНЕНИЯ ДВИЖЕНИЯ 467
товой теорией, но оказалась очень удобной и для нерелятивист-
нерелятивистских квантовомеханических задач. 1
16.3.1. Вернемся к рассмотрению систем, гамильтониан ко-
которых не зависит от времени явно. Для них формулы A09) в
шредингеровой или A08) в гайзенберговой картине дают реше-
решение основной задачи динамики — нахождения движения. Однако
практической пользы от этих «решений» пока еще очень мало
вследствие трудности каких-либо реальных вычислений с экспо-
кентой от оператора — в нашем случае — от гамильтониана.
Действительно, даже если выбрать конкретное фиксированное
представление, то представителем гамильтониана будет, вооб-
вообще говоря — бесконечно-рядная матрица, и речь будет идти о
практическом вычислении (и суммировании!) всех ее степеней.
Делу, однако, можно в сильной степени помочь, если выбрать
представление, в котором рассматриваются векторы и операторы,
специальным рациональным образом. Мы уже знаем, что вы-
выбрать представление — это значит выбрать некоторый полный
набор коммутирующих наблюдаемых, которые будут в этом
представлении диагональны. Выберем такой набор коммутирую-
коммутирующих наблюдаемых, чтобы одной из них был бы гамильтониан.
Что за наблюдаемые коммутируют с гамильтонианом?
Если какая-либо динамическая переменная а коммутирует
с гамильтонианом, то в силу уравнения A07) в гайзенберговой
картине
из [Я,а]_-0 следует ^-={|Я, а(*)]_ = 0, A11)
то есть такая переменная а является интегралом движения.
Итак, выберем в качестве определяющих представление опе-
операторов полный набор из гамильтониана и взаимно коммути-
коммутирующих интегралов движения, и обозначим совокупность опера-
операторов этого полного набора одной буквой а*). Соответствующие
базисные векторы и совекторы можно будет тогда записать как
\а") и (а'|; все они будут собственными состояниями гамиль-
гамильтониана Н, т. е. будет
Н | а") = Е (а") | а"); (а' | Я = (а' | Е (а'),
где через Е' = Е(а') обозначено собственное значение гамиль-
гамильтониана в состоянии |а'). (Собственные значения гамильто-
гамильтониана принято обозначать буквой Е, в аналогии с тем, как в
классической механике численные значения сохраняющейся
функции Гамильтона принято называть энергией системы.)
*) Не обязательно, конечно, требовать, чтобы сам гамильтониан Н был
одной из наблюдаемых полного набора а. Достаточно, чтобы он был их
функцией, как то наверняка и будет, если все наблюдаемые набора суть
интегралы движения, согласно теореме (нз 7.4) об операторе, коммутирующем
со всеми наблюдаемыми полного набора.
16*
468 ч. »!• ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
Выписывая теперь представитель (в а-представлении) какой-
либо динамической переменной Р@> получаем в силу A08):
. Я <<-<„) .HU-t,)
= е h (а'| ро| а"), если Н\а") = Е"\а"), A12)
— т. е. в выбранном нами представлении представители всех
зависящих от времени наблюдаемых зависят от времени гармо-
гармонически, с амплитудой, равной представителю той же наблюдае-
наблюдаемой в начальный момент времени*).
Выбранное нами представление называют специальным пред-
представлением Гайзенберга. Именно в этом представлении была
сформулирована первоначальная форма квантовой (или мат-
матричной) механики, открытая ГАЙЗЕНБЕРГОМ в 1925 году.
16.3.2. В шредингеровой картине аналогичное упрощение
возникает, если рассмотреть зависимость от времени не произ-
произвольных состояний, а таких, которые являются собственными со-
состояниями гамильтониана (и, может быть, еще каких-то наблю-
наблюдаемых у, образующих вместе с ним полный набор **)). Для та-
таких состояний мы опять (теперь из A09)) получим:
\E,Y,t) = e * \E,y',to) = e h \E,y',t0), A13)
если
H\E,y',to) = E\E,y',t0).
Таким образом собственный вектор гамильтониана в начальный
момент времени tQ остается собственным вектором Я и в другие
моменты времени и лишь умножается на гармонический фазо-
фазовый множитель. Само же состояние, следовательно, вовсе не
меняется. Такие состояния называются стаиционарными.
Переходя теперь к представителям в каком-то фиксирован-
фиксированном --представлении, получим, что волновая функция ф?(|, <))
стационарного состояния зависит от времени как
iBt
а уравнение Шредингера упростится до
*) Существо перехода'от общей формы временной зависимости A08)
к специальной форме A12) состоит, конечно, в том, что, столкнувшись с не-
необходимостью вычислять экспоненты от матрицы, мы заметили, что задача
сведется к вычислению численных экспонент, если предварительно привести
матрицу к диагональному виду.
**) И в этом случае, конечно, достаточно, чтобы гамильтониан был
функцией полного набора, определяющего состояния.
16. УРАВНЕНИЯ ДВИЖЕНИЯ 469
— уравнения Шредингера, не зависящего от времени, или про-
просто уравнения Шредингера (Говорят также станциоиарное
уравнение Шредингера).
Уравнения A10а) и (ПОЬ) были найдены Шредингером в
1926 году и составили основу его волновой механики.
16.3.3. Как же можно теперь сформулировать основную за-
задачу квантовой механики?
В классической механике основная задача состояла в том,
чтобы найти движение системы, функция Гамильтона которой
задана. В квантовой механике, как мы теперь видим, аналогич-
аналогичная проблема существенно упрощается — и в гайзенберговой и
в шредингеровой картине, — если найти предварительно соб-
собственные значения и собственные векторы гамильтониана, т. е.
решить EWP-y для Я:
(АЛ) Н\Е) = Е\Е).
Но собственные значения гамильтониана обычно вырождены;
чтобы снять это вырождение, надо достроить к гамильтониану
полный набор взаимно коммутирующих интегралов движения а:
(А.2) [Я, а]_ = 0; [а„ а/]_ = 0,
я решить совокупную EWP-y:
Г а|а') = а' |а'>,
(А-3) 1Я|а') = ?(а')|а').
Коль скоро (А.1—3) выполнено, то будет найден спектр энергии
системы Е(а') и построен такой базис |а') в пространстве со-
состояний, что либо его векторы зависят от времени гармониче-
Е(а') . .
чжи с частотами «> = —-г-2- (в шредингеровой картине), либо
представители любых наблюдаемых в нем зависят от времени
гармонически согласно A12) (в гайзенберговой картине).
Тем самым формально задача определения временной зави-
зависимости наблюдаемых и состояний решена, но физически это
еще далеко не все: наблюдаемые а могут быть не теми наблю-
наблюдаемыми, которые нас интересуют, не теми наблюдаемыми, ко-
которым можно придать ясный физический смысл на основе прин-
принципа соответствия. Будем называть эти последние — с ясным
физическим смыслом — наблюдаемые \\ очень часто это — ко-
координаты системы, иногда — ее импульсы. Будем считать, что
мы знаем решение EWP-ы для них:
470 ч. III. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
т. е. их спектр и собственные векторы. Тогда физически под
решением квантовомеханической задачи имеют в виду не только
ее формальное решение, т. е. выполнение программы (АЛ—3),
но и возможность интерпретировать это решение в терминах
II') и I' (т- е. в терминах гр(|)). А для этого надо еще найти
матрицу преобразования от а-представления к ^представлению:
(В.2) <П«'>-
Эта матрица есть совокупность
(I) представителей (|'|в а-представлении,
и в то же время совокупность
(II) нредставителей |ос') в ^представлении.
Если мы исходим при ее определении из понимания (I), то
такой подход отвечает работе в специальном представлении
Гайзенберга. Если из понимания (II), — то работе в специаль-
специальном представлении Шредингера.
Итак, решение основной задачи квантовой динамики, задачи
о «движении» системы сводится к тому, чтобы
в гайзенберговой картине:
Найти полный набор интегралов движения, решить для
них EWP-y, а затем найти представители интересующих
нас динамических переменных — скажем, координат или
импульсов — в том представлении, в котором этот набор
диагоналей.
в шредингеровой картине:
Найти собственные состояния (собственные волновые
функции) некоторого полного набора интегралов движения
в том представлении, в котором диагональны интересую-
интересующие нас переменные — скажем, координаты или импульсы.
Мы видим, что решение и той и другой задачи сводится к проб-
проблемам собственных значений, причем к проблемам собственных
значений, формулируемых в терминах операторов и векторов,
относящихся к одному фиксированному моменту времени. Коль
скоро же эта EWP разрешена, то сама временная зависимость
выписывается в виде тривиальных формул A12) или A13).
Именно это обстоятельство мы имели в виду в самом на-
начале, в 2.1, когда говорили, что все существо квантовой меха-
механики связано с описанием состояний (и динамических перемен-
переменных) в фиксированный момент времени, в то время как соб-
собственно динамические проблемы, проблемы зависимости от вре-
времени, являются в пояснённом выше смысле тривиальными.
16.4. Откуда следует брать выражение для гамильтониана —
вид его зависимости от координат и импульсов? Строго го-
17. ПЕРВЫЙ ПРИМЕР. ОСЦИЛЛЯТОР 471
воря, — как то мы уже несколько раз отмечали, — ниоткуда: за-
задать гамильтониан — это и значит специфицировать систему,
которую мы желаем изучать. В этом обстоятельстве, впрочем,
нет ничего особенного для квантовой механики — в класси-
классической теории, когда опыт приводит нас к потребности описывать
какую-либо совсем новую систему, у нас тоже может не ока-
оказаться другого выбора, как подбирать для нее вид функции
Гамильтона методом проб и ошибок, добиваясь согласования
динамических предсказаний с наблюдениями.
Новый момент возникает, однако, если мы хотим, как то
часто бывает, строить квантовое описание не какой-то системы,
а такой, классическое описание которой нам известно. В этом
случае руководящим соображением должен, как всегда, послу-
послужить принцип соответствия: в качестве первой попытки по-
построить квантовое описание следует взять классическую функ-
функцию Гамильтона и попробовать заменить в ней классические
координаты и импульсы на соответствующие операторы кван-
квантовой теории.
Действие это неоднозначно, поскольку квантовые операторы
координат и импульсов не коммутируют друг с другом, и из
одной классической функции Гамильтона можно построить не-
несколько квантовых гамильтонианов, различающихся порядком
следования операторов в произведениях. В действительности
такая неоднозначность появляется даже и в тех случаях, когда
классическая функция Гамильтона не содержит произведений
некоммутирующих величин —ведь к ней всегда можно приба-
прибавить члены, пропорциональные i[pj,Qj]-, равные в классическом
пределе й->0 нулю.
Детали возникающей ситуации проще всего пояснить на кон-
конкретных примерах, к рассмотрению которых мы сейчас и пе-
перейдем.
17. Первый пример. Осциллятор
В качестве первого примера, на котором очень удобно про-
проследить в деталях процесс перехода от классического описания
к квантовому, поскольку в нем все что нужно без труда вычис-
вычисляется в явном виде, рассмотрим линейный гармонический ос-
осциллятор.
17.1. В классической механике осциллятор описывался функ-
функцией Гамильтона
Первое замечание в связи с переходом к квантовому опи-
описанию связано с вопросом об однозначности. Не нарушая прин-
472 ч. III. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
ципа соответствия, можно добавить к (*) выражение вида*)
ica>[p, q]_,
где — если мы не хотим нарушать квадратичной зависимости:
гамильтониана (*) от координат и импульхов, с которой связана
линейность уравнений, — с есть произвольная вещественная
константа**). Правда, на первый взгляд такая добавка выгля-
выглядит совершенно искусственной. Покажем, что при более внима-
внимательном подходе это не так.
17.1.1. Итак, запишем гамильтониан, призванный описывать квантовый
гармонический осциллятор, в виде I
где с — постоянная.
Введем теперь вместо р и q динамические переменные а+, а, которыми
мы пользовались в § 10, по формулам E3):
Тогда в новых переменных
р2 + (mcoJ q2 =
aft /
— (a
+
2\гл м j^l*i* i 1л и \ им j у — \ м u UU [^ I* I* ^^ 1*1* / "^t"
если положить а = та,
= «©А (а+а + аа+)>
и, следовательно,
„ тан ,д + д , дд+^ ,
ч 2m
A14а)'
— т. е. мы видим, что добавление постоянной с эквивалентно изменению по-
порядка некоммутирующих операторов а+ и а, т. е. как раз тому произволу,,
который автоматически возникает при переходе от классического описания
к квантовому.
17.1.2. Как же все-таки следует поступить с постоянной с?
Оказывается, что для соответствия с опытом в разных случаях
приходится выбирать с по-разному. Если осциллятор образован.
*) Можно, конечно, «портить» гамильтониан н другими способами. Но
тогда о выполнении принципа соответствия надо будет специально забо-
заботиться.
**) В этом сказывается особая простота рассматриваемого примера. В об-
шем случае с в этом рассуждении могло бы быть произвольной функцией
координат и импульсов, и произвол, связанный с построением «квантового»
аналога классической системы», невероятно вырос бы.
17. ПЕРВЫЙ ПРИМЕР. ОСЦИЛЛЯТОР 473
"системой материальных точек, то надо полагать с = О, т. е.
записывать гамильтониан в виде
) (П4Ь)
Бели же осциллятор — это, например, один из осцилляторов, на
которые мы разлагали свободное электромагнитное поле (фор-
(формула F4) из второй части курса), то надо положить с = —к
и писать для гамильтониана
ft (©(k) = e|k|). (H4c)
17.2.1. Посмотрим теперь, как описывается квантовая дина-
•мика осциллятора. Прибегнем сперва к гайзенберговой кар-
картине. Для одномерного осциллятора полный набор коммути-
коммутирующих наблюдаемых насчитывает только одну величину; вы-
выберем в качестве такой величины рассмотренный нами в § 10
•оператор числа частиц а+а, собствен-
собственными значениями которого п были це-
целые числа п = 0, 1,2, ..., а собствен-
собственные векторы обозначались нами как
\п). Гамильтониан Н является в си-
силу A14Ь) функцией этой наблюдае-
наблюдаемой, поэтому те же векторы \п) будут
и собственными векторами Н:
Н\п) = Еп\п) с EW-ми
. | . потенциальная энергия
En = h(u(п +")• (И5) и спектр осциллятора
Полученное таким образом выражение для энергетического
ч:пектра осциллятора — это и есть первоначальная формула
Планка A), положившая начало созданию квантовой теории.
Единственное отличие нашего нового выражения A15) состоит
в том, что планковы целые числа п заменились полуцелыми
17.3. Замена эта весьма существенна — она означает, что
ъ состоянии наинизшей возможной энергии — в основном состо-
состоянии — движение в системе не прекращается; вместо того
чтобы прийти (как то можно было бы ожидать на основании
классических представлений), когда у нее отнята вся возмож-
возможная энергия, в статическое состояние устойчивого равновесия,
•система продолжает находиться в движении — в ней происхо-
происходят так называемые нулевые колебания. В реальности суще-
существования этих нулевых колебаний можно убедиться на опы-
474 ч. Ш. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
те — они проявляются, например, в рассеянии света в кристал-
кристаллах при достаточно низких температурах. Эффект существова-
существования нулевых колебаний не явля'ется специальным свойством
гармонического осциллятора — кривую потенциальной энергии
вблизи регулярного минимума всегда можно приблизить пара-
параболой; поэтому всякая система вблизи минимума потенциальной
энергии ведет себя подобно гармоническому осциллятору — т. е.
будет испытывать нулевые колебания. Отличия от гармониче-
гармонического осциллятора будут сказываться только на высших уров-
уровнях энергии — спектр не будет более, как в гармоническом слу-
случае— эквидистантен*). Более того, как мы увидим в § 18, та
же качественно картина сохраняется и тогда, когда потенци-
потенциальная энергия имеет в минимуме (не слишком сильную) осо-
особенность!
Специфическую квантовомеханическую природу нулевых ко-
колебаний можно качественно усмотреть из того соображения,
что их появление можно рассматривать как следствие принципа
неопределенности — для системы, находящейся в покое в точке
устойчивого равновесия и координата, и импульс имели бы
определенные значения, что принципом неопределенности за-
запрещено. Более того, описывающий состояние нулевых колеба-
колебаний вектор |0) есть как раз один из векторов (см. § 11), для
которых неравенство в соотношении неопределенностей G9)
превращается в равенство. С этой точки зрения нулевые коле-
колебания являются состоянием «наименьшего движения, совмест-
совместного с принципом неопределенностей».
Для большинства систем эффект нулевых колебаний есть
тонкое микроскопическое явление, которое можно наблюдать
лишь в специально подобранных условиях. Есть, однако, редкие
случаи, когда по существу то же самое явление складывается
для системы из очень большого, макроскопического, числа N
частиц таким образом, что само «нулевое движение» приобре-
приобретает в некотором смысле макроскопические масштабы. Приме-
Примером может служить система, состоящая из макроскопического
количества атомов Не — такое «вещество» в макроскопическом
смысле обладает той особенностью, что (при не очень больших
давлениях) остается жидким вплоть до абсолютного нуля: ну-
нулевые колебания оказываются в этом случае столь сильны срав-
сравнительно с силами взаимодействия между атомами, что не дают
им выстроить атомы в кристаллическую решетку.
17.2.2. Вернемся к обсуждению осциллятора. Коль скоро
энергетический спектр A15) найден, то для любой динамиче-
*) Качественное отличие может произойти только тогда, когда образуе-
образуемая потенциальной энергией вблизи минимума «потенциальная яма» настоль-
настолько мелка, что в ней ие помещается даже основной уровень.
17. ПЕРВЫЙ ПРИМЕР. ОСЦИЛЛЯТОР 475
ской переменной р будет, согласно A12),
е1 <»'-*> »*<л'| {Jo|«"> A16.1)
— т. е. представители всех динамических переменных будут за-
зависеть от времени гармонически с помощью целочисленных гар-
гармоник классической собственной частоты осциллятора со.
В частности, матричные элементы оператора координаты —
это есть специфическая особенность гармонического осцилля-
осциллятора—
<n' \q{t)\ п") = i д/^- У^ТТЬП<, „»_, е-'»« - V^ в»'. »'+i ^af}
A16.2)
содержат только основную частоту со — в полном соответствии
с тем фактом, что координаты классического линейного осцил-
осциллятора зависели от времени гармонически с его собственной
частотой.
То же самое будет, конечно, и для матричных элементов
оператора импульса p(t). (Легко сообразить, что в силу той
специальной особенности q и р, что их матричные представи-
представители содержат лишь элементы на диагоналях, соседних с глав-
главной, временная зависимость любой динамической переменной,
выражающейся через q и р полиномом степени не выше N®, бу-
будет содержать гармоники основной частоты с номерами, не
большими No — опять в точном соответствии с результатом
классической механики.)
17.2.3. Напомним теперь, что в электродинамике мы выяс-
выяснили, что взаимодействие заряженного нерелятивистского ос-
осциллятора с электромагнитным нолем определяется в главном
приближении его дипольным моментом, который, в свою оче-
очередь, пропорционален координате осциллятора q(t). Отсюда
следует, что заряженный осциллятор может поглощать и испус-
испускать свет только одной частоты — его собственной частоты оз.
При этом поглощению света соответствует переход осциллятора
из состояния \п) в состояние |я+ 1), энергия осциллятора воз-
возрастает на йсо, а испусканию — переход из состояния \п) в со-
состояние \п—1), энергия осциллятора уменьшается на йо>.
Это — как раз те соотношения, которые приходилось постули-
постулировать на первоначальных этапах теории квант, о чем шла
речь в § 1.
Подчеркнем еще раз, что для того, чтобы прийти к резуль-
результатам A15), A16), нам сперва понадобилось найти спектр
полного набора коммутирующих интегралов движения (в дан-
данном случае — единственного оператора а+а), а затем решить
476 ч. III. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
EWP-y для оператора q в «-представлении — вся эта «чернаяг
работа» была проделана нами заранее в § 10.
17.4.1. Как решается та же задача об осцилляторе в шре-
дингеровой картине? В этом случае нам надо было бы перейти
с самого начала к координатному представлению и искать
в нем собственные функции и собственные значения гамильто-
гамильтониана, т. е. решать проблему собственных значений
(q) = E^n(q) 0 17)
(мы пользуемся сокращенными обозначениями § 12, в которых
действию оператора координаты соответствует умножение на
ее значение, а импульсу — оператор дифференцирования
(83.1,2а)), которая свелась бы в этом случае к EWP-e для
уравнения Шредингера — дифференциального уравнения в пе-
переменном q. При решении этой проблемы собственных значений
средствами математической физики мы опять нашли бы в каче-
качестве собственных функций A17) те же самые функции
(формула F1.1а)), которые уже были найдены нами в § 10
«с другой стороны», и, конечно, те же самые EW-ы A15)
для оператора Н.
17.4.2. «Волновые функции, зависящие от времени» 'tyn(q,t),.
получились бы затем по A13а) равными
*Ля.Ъ = е-'?-*я(я) = е-Ш№)*я{<1). (И8>
а для матричных элементов произвольного оператора между
такими состояниями мы получили бы, в точной аналогии:
с A16.1),
«- (<7. О P4V (Я. 0) = в' <"'-""> а<<<- (Я) №п (Я)). (П9.1)
17.4.3. Для вычисления оставшегося «не зависящего от вре-
времени матричного элемента» (ty*n,(q) P^lv (<?)) надо явным обра-
образом выразить оператор р через координату q и импульс р, т, е.
через координату и оператор дифференцирования по ней. В ча-
частности, если оператор р есть сама координата q, то, в соответ-
соответствии с (82),
«, (q) q V (q)) = \dq • q • ^ (q) ^ (q). A19.2>
— oo
Вычисление этого интеграла с полиномами Эрмита F1.1а)>
опять привело бы нас, конечно, к выражениям E8) и A16.2).
18. ДАЛЬНЕЙШИЕ ПРИМЕРЫ ДИНАМИЧЕСКИХ ЗАДАЧ 477
17.5. Таким образом мы видим, что и в гайзенберговой и в
шредингеровои картине, приходится решать одну и ту же по суще-
существу EWP-y — только в разных представлениях и, в каком-то
смысле, проводить одни и те же вычисления в разном порядке.
18. Дальнейшие примеры динамических задач
18.1. В качестве следующего простого примера рассмотрим
свободное движение, когда в классическом описании потенци-
потенциальная энергия отсутствует и функция Гамильтона
)=уА
а
вовсе не зависит от координат. Примем, что то же справедливо
и в квантовом случае для гамильтониана, который, следова-
следовательно, есть функция только импульсов, для одной степени сво-
свободы— единственного импульса:
Н = Н(р) = 1?г. A20)
18.1.1. Таким образом всякий собственный вектор импульса
\р') будет в то же время и собственным вектором гамильто-
гамильтониана и притом с собственным значением -|— :
Н\р') = Е(р')\р'У, Е(р') = ^. A20.1)
Обратное утверждение неверно — из A20.1) следует, что соб-
собственные значения импульса выражаются через EW-ы гамиль-
гамильтониана в иррациональной форме
р' = ± <\/2тЕ. A20.2)
и, следовательно, мы не можем использовать зависимость
A20.2) для определения импульса как операторной функции
гамильтониана в смысле определения C0) или C3а). Поэтому
собственный вектор гамильтониана, вообще говоря, не будет
собственным для импульса, а будет линейной комбинацией
двух собственных векторов импульса с двумя значениями A20.2)
I Е) = С[ | + л/2тЕ) + с21 — л/2тЕ)
*) Мы сталкиваемся здесь с тем любопытным положением, что, в то
время как оператор импульса сам по себе образует полный набор коммути-
коммутирующих наблюдаемых, его функция — гамильтониан — сам по себе полного
набора ие образует и для этой цели к нему надо добавить еще какой-либо
коммутирующий с ним оператор. Этот пример показывает, насколько неопре-
неопределенными могут быть в квантовой механике предсказания о числе операто-
операторов полного набора.
478 ч. III. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
'— все собственные значения гамильтониана двукратно вырож-
вырождены *).
Вычисляя квадрат нормы этой линейной комбинации, мы по-
получим
<?¦' \E") = c\cfi(<^2nuF—')/2mE")+c*2c26(— л/2тЕ/
Последние два члена обращаются в нуль, поскольку под знаком
б-функции в них стоят дефинитные выражения, в двух же пер-
первых членах можно перейти к 6-функциям от разности энергий.
Таким образом
/
(Е' IЕ") = (| с, р + ! с2 Р) д/^- 6 (?' - Е").
Итак, если принять, что коэффициенты линейной комбинации
подчинены условию |ci|2-(-|с2|2 = 1, то «нормированное на
энергию» (т. е. на 6-функцию от разности энергий) собственное
состояние гамильтониана запишется через «нормированные на
импульс» собственные векторы импульса с EW-ами A20.2) как
= -!=, {с, |
л/ х)
A20.3)
L |p + |pl
т
Если, в частности, вектор \Е) является собственным и для им-
импульса (т. е. если из двух коэффициентов с только один отли-
отличен от нуля (и равен единице)), то он отличается от соответ-
соответствующего \р') только множителем 7="> выражающим отли-
отличие нормировки, — этим часто приходится пользоваться.
18.1.1.2. Чем отличаются физически два состояния, входя-
входящие в комбинацию A20.3)? Чтобы получить тут наиболее на-
наглядное истолкование, «включим зависимость от времени», при-
причем воспользуемся гайзенберговой картиной, и посмотрим, как
зависят от времени матричные элементы оператора координаты
q(t), вибирая в качестве полной системы собственные векторы
\р') импульса.
В силу A12) имеем
( Е{р')-Е{р")
(p'\d(t)\p") = e h
*) В силу непрерывности спектра импульса отсюда следует, что гамиль-
гамильтониан будет обладать непрерывным спектром, занимающим всю положитель-
положительную полуось 0 ^ Е ^ оо.
IS. ДАЛЬНЕЙШИЕ ПРИМЕРЫ ДИНАМИЧЕСКИХ ЗАДАЧ 479
где мы воспользовались тем, что в силу симметрии (точнее — антисимметрии)
перестановочных соотношений E2) в р и q представитель координаты в им-
импульсном представлении должен отличаться лишь знаком от представителя
F8) импульса в координатном. Освобождаясь теперь от экспоненты за счет
использования свойств б-функцни, мы получим, что
<р' I Q (О I Р"> = Й *' (Р' - Р") + I» (- ^ t-?) в (/>' - Р").
т. е. — если заметить, что справа стоят как раз выражения для матричных
элементов д и р в начальный момент времени — что
(р' \q(t)\p") = {p' \qo\p")+ (P']PJP"} t- A20.4)
Соотношение A20.4) получено нами для произвольных {р'\
и \р")\ поэтому, в силу линейности формул D7) для перехода
от одного представления к другому, оно будет справедливо для
матричных элементов, взятых между произвольными состоя-
состояниями. Выбирая, в частности, эти произвольные состояния оди-
одинаковыми и вспоминая основную форму C8) для среднего зна-
значения наблюдаемой в произвольном состоянии, приходим
к тому, что зависимость от времени среднего значения коорди-
координаты в произвольном состоянии |Л) описывается выражением
При классическом описании свободного движения мы полу-
получили бы вместо (*)
Поэтому, если мы хотим чтобы (*¦*) сохранилось в квантовой
теории для средних значений, надо определить оператор ско-
скорости как оператор импульса, деленный на массу. Тогда мы по-
получим для среднего значения координаты
W) = Qo + vt; © = ¦?-. A20.5)
Мы видим теперь, что два состояния A20.3), различающиеся
знаком импульса при одинаковой его абсолютной величине, бу-
будут различаться и знаками средней скорости в этих состоя-
состояниях— т. е. первое из них будет соответствовать движению
вправо, а второе — влево.
18.1.2.1. В шредингеровой картине в координатном пред-
представлении задача о свободном движении сведется к уравнению
Шредингера
480 ч. III. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
Для каждого Е > 0 это уравнение имеет два линейно незави-
независимых решения, которые можно записать в форме
iq iJ2mE _ iq
A21.1)
Нормированное «на б-функцию от энергии» общее решение бу-
будет тогда, в полной аналогии с A20.3), иметь вид
^ = 1. A21.2)
Для отрицательных Е решения A21) содержали бы экспоненту
с вещественным показателем, которая неограниченно нарастала
бы или при ^->+°° яли при q-*—оо. Такие решения нельзя
было бы нормировать не только в собственном смысле A2), но
и в несобственном смысле B3а, Ь). Тем самым для них оказа-
оказалась бы невозможной вероятностная интерпретация; поэтому
следует считать, что такие решения не имеют никакого физиче-
физического смысла и должны быть исключены из числа допустимых
решений EWP-ы.
Таким образом мы снова приходим к тому результату, что
спектр рассматриваемого гамильтониана непрерывен и зани-
занимает положительную полуось, все EW-ы дважды вырождены
и связаны с собственными значениями импульса соотношением
A20.1) — ведь два решения A21.1) — это как раз собственные
функции импульса (84.2) для двух собственных значений
A20.2).
18.1.2.2. С помощью A13а) можем выписать «зависящие от
времени» волновые функции; двум решениям A21.1) будут от-
отвечать
1 --j-(Ei-*/mBq)
% в (<у, 0 = nrs-
A21.3)
Эти функции действительно имеют вид плоских волн (отсюда
и происходит название «волновая функция»), причем верхнему
знаку в A20.2) отвечает волна, распространяющаяся вправо,
а нижнему — влево, с фазовыми скоростями
18. ДАЛЬНЕЙШИЕ ПРИМЕРЫ ДИНАМИЧЕСКИХ ЗАДАЧ 481
Такие фазовые скорости не имеют никакой прямой физиче-
физической интерпретации; если, однако, вычислить групповую ско-
скорость решений A21.3)
v d@ dE = dE{p) — j_ p — i v
gr dk d (± V2m? ) d (± p) m ~ '
то она как раз будет равна скорости частицы, оператор которой
A20.5) диагоналей в состоянии с определенным импульсом
A21.3.1 или 2). Полученный результат — это как раз предполо-
предположение де Бройля, о котором мы говорили- в § 1 (формула F)
и далее).
18.2. Разобранные примеры показывают, что при использо-
использовании шредингеровой картины в координатном представлении
(говорят иногда о шредингеровом представлении в узком
смысле этого слова) уравнение проблемы собственных значе-
значений принимает вид линейного дифференциального уравнения
в частных производных второго порядка.
В самом деле, в классической механике мы принимали
в большинстве случаев, что функция Гамильтона есть сумма
кинетической и потенциальной энергий, в декартовых коорди-
координатах
1
Поэтому при переходе по принципу соответствия к квантовоме-
ханическому описанию «той же системы» в координатном пред-
представлении остается только заменить в каждом члене кинетиче-
кинетической энергии
о
ра -а I (Ь д У_ Л!_ Л П99э\
и мы приходим к гамильтониану*)
A22.1)
а уравнение Шредингера «без времени* принимает вид
•i, .... г„). A22.2)
Поскольку линейные дифференциальные уравнения второго
порядка уже давно очень подробно изучены в математике, то
такая форма основной задачи на собственные значения оказы-
*) Дополнительные члены — такого типа, как мы обсуждали для осцил-
осциллятора,—в декартовых координатах приходится прибавлять редко.
482 ч. Ш. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
вается весьма удобной. Именно по этой причине специальное
представление Шредингера используется в квантовой механике
настолько часто, что может даже создаться ложное впечатление
о наличии каких-то причин, принципиально выделяющих его из
всех прочих, — таких не существует.
ЗАМЕЧАНИЕ 1: Если искать какие-либо особенности, действи-
действительно выделяющие это представление из всех прочих, то можно
отметить только то, что для решения EWP-ы в форме A22.2)
существуют некоторые регулярные приемы, в то время как при
работе в других представлениях приходится каждый раз изо-
изобретать какие-либо искусственные способы, как то можно было
видеть на примере рассмотрения осциллятора и момента*).!
ЗАМЕЧАНИЕ 2: Подчеркнем, что для системы из п частиц
уравнение A22.2) записывается в конфигурационном простран-
пространстве, а не в обычном физическом трехмерном. Поэтому степень
наглядности решений A22.2) невелика. |
ЗАМЕЧАНИЕ 3: Переход к обобщенным (например — криволи-
криволинейным) координатам вызывает в квантовой механике большие
осложнения. В самом деле, при этом уже классическая кине-
кинетическая энергия становится квадратичной формой общего вида
от импульсов, с коэффициентами, зависящими от координат.
Поэтому при замене типа A22а) встает во весь рост проблема
порядка расположения операторов. По этой причине наиболее
рациональный путь состоит в том, чтобы сперва «прокванто-
вать» систему (т. е. сделать замену A22.2)) в декартовых ко-
координатах, а уже затем переходить к обобщенным по обычным
правилам замены переменных в дифференциальных выраже-
выражениях второго порядка. 1
ЗАМЕЧАНИЕ 4. Можно объяснить, почему именно координат-
координатное представление получает несколько выделенную роль. При-
Причина лежит конечно в том, что классическая функция Гамиль-
Гамильтона, будучи произвольной функцией координат, есть квадра-
квадратичная функция сопряженных им импульсов — поэтому при
переходе к координатному представлению порядок дифференци-
дифференцирований будет всегда равен двум. Если бы мы перешли к про-
противоположному— импульсному — представлению, то потенци-
потенциальная энергия оказалась бы дифференциальным оператором
произвольно высокого порядка — вообще говоря — интеграль-
*) Можно сказать, что при работе в абстрактном гайзенберговом пред-
представлении задача иногда решается гораздо красивее, зато представление
Шредиигера наверняка приведет к цели.
18. ДАЛЬНЕЙШИЕ ПРИМЕРЫ ДИНАМИЧЕСКИХ ЗАДАЧ 483
ным оператором. Поэтому использование импульсного пред-
представления оказывается рациональным лишь в специальных слу-
случаях «простой» потенциальной энергии. 1
18.3. В (чрезвычайно важном) случае одной единственной
частицы, движущейся во внешнем поле, уравнение Шредингера
A22) упрощается до
)»(«¦) = ?»*«(«•), A23)
и, главное, оказывается записанным уже в обычном трехмерном
пространстве. Это обстоятельство позволяет связать с рассмат-
рассматриваемой задачей определенные наглядные представления.
Выпишем того ради соответствующее A23) временное урав-
уравнение Шредингера, равно как и уравнение для сопряженной
волновой функции
умножим первое из них на ф*(г, t), второе на o|)(r, t), и вычтем
первое из этих произведений из второго.
Получим:
то есть
2т \ dr \ dr т) dr dr d\
что можно записать как
d in d { и ib u*ib \
dt 2m dr \ dr dr )
Смысл величины, стоящей в первом члене под знаком произ-
производной по времени, мы уже знаем — это (ср. (81)) есть плот-
плотность вероятности (обнаружить частицу в точке г) p(r, t).
С другой стороны, само полученное нами соотношение имеет
типичную форму уравнения непрерывности (ср., например, элек-
электродинамическое уравнение непрерывности (II.50.1.1)). Поэтому,
если ввести вектор
A24.1.2)
484 ч. III. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
то j (r, t) будет иметь смысл плотности потока вероятности
(говорят иногда и короче: вектор плотности тока или проста
ток), и этот вектор вместе с плотностью вероятности p(r, t) бу-
будут удовлетворять уравнению непрерывности:
iip ,O = O. A24.3)
ЗАМЕЧАНИЕ: С чисто формальной стороны уравнение непре-
непрерывности выражает, конечно, просто то обстоятельство, что
нормировка волновой функции сохраняется в ходе временной
эволюции системы.
Физически формулы A24) открывают перед нами возмож-
возможность чрезвычайно наглядно (для случая одной частицы!) пред-
представить себе решение квантовомеханической задачи в виде рас-
распределения «облака вероятности» p(r, t), которая может «пере-
«перетекать» в ходе временной эволюции из одних точек в другие
в соответствии со значениями j(r, t). Надо, однако, подчеркнуть,
что такие наглядные представления ни в коем случае нельзя
воспринимать слишком серьезно — попытки представить себе
квантовомеханическую частицу «составленной» из некоторой
непрерывной субстанции, «текущей» в соответствии с A24), ве-
ведут к противоречиям. 1
19. Движение в центральном поле
В качестве последнего примера рассмотрим весьма важную
задачу двух тел, взаимодействующих с помощью сил, завися-
зависящих только от их относительного расстояния. Согласно прин-
принципу соответствия эта задача описывается гамильтонианом
ke2Jru^-^)- <125>
19.1. В классической механике мы сводили соответствую-
соответствующую задачу к задаче одного тела (движущегося во внешнем
поле), вводя вместо rt и г2 относительный радиус-вектор г и ра-
радиус-вектор центра инерции R
г г . п win + m2r2
r-r,-r2) R- m] + m2 •
Поскольку это преобразование линейно, то никаких осложне-
осложнений не произойдет и при переносе его на квантовый случай.
В результате гамильтониан A25) приведется к сумме гамильто-
гамильтонианов, отвечающих переносному и относительному движениям:
Я,г = —^-Дл; яГе1 = -~Ar-hU(r)t A26)
19. ДВИЖЕНИЕ В ЦЕНТРАЛЬНОМ ПОЛЕ 485
каждый из которых зависит только от «своих» координат и им-
импульсов. Следовательно, можно будет искать собственные век-
векторы гамильтониана A26) в виде прямого произведения соб-
собственных векторов гамильтонианов #tr и #rei и, значит, соб-
собственные волновые функции 4f(R, r) в виде произведений
Ч*"(R)ip(г) собственных функций каждого из гамильтонианов.
Задачу о собственных функциях свободного движения мы
уже рассмотрели в предыдущем разделе. Таким образом, все
дело сводится к нахождению собственных функций -ф (г), т. е.
к решению задачи о движении одной частицы в центральном
внешнем поле. Этой задаче соответствует уравнение Шредин-
гера без времени
? ] , A26а)
которым нам и надлежит теперь заняться.
19.2.1. Для решения этой задачи удобно прежде всго перейти к поляр-
полярным координатам г, ¦&, ср, воспользовавшись известным выражением для опе-
оператора Лапласа в полярных координатах
1 д ( 2 д \ 1 Г1 д ( . д \ 1 д2
которое иам" будет удобнее переписать в форме
. 1 д2 1 Г 1 <Э/<Э\ 1 <Э2
19.2.2. Далее, в классической механике для решения тон же задачи о дви-
движении в центральном поле мы пользовались тем, что кроме энергии в этом1
случае сохраняется и момент. Чтобы сделать то же самое и теперь, заметим
сперва, что
V дг Je, ф "
/ дга\ д т d \ Ь d 1,чйа
I —;— I "з— = j— , т. е. что — г -г —г- = — (гр) = —
V дг /е, ф дга г dr r t dt г *' i дг
илн
Вьмнслим теперь квадрат оператора орбитального момента:
М2 = MaMq. = еарувацуГрруГцру = ГрруГ^ру — Г^руГуР^ =
, , . й , . , Ь . ,, Й2 д д И2 д
= r. ._ _ d2
To есть:
(y)^rr. A27Ь>
Следовательно,
485 ч. III. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
и сравнение A26а) со A27с) и (*) показывает, что уравнение
Шредингера для нашей задачи можно записать в форме
0, A28а)
где оператор квадрата орбитального момента есть
A28Ь)
т. е. зависит только от угловых переменных 8 и <р.
19.2.3. Поэтому, как и в классическом рассмотрении, опера-
оператор М2 коммутирует с гамильтонианом, если потенциальная
энергия U есть функция только от г: U = U(r). Но это значит,
что можно искать общие собственные функции EWP-ы A28а)
и задач на собственные значения *)
М2гр (г) = ПЧ (I + 1) ф (г); МгЪ (г) = ft/m|> (r). A28с)
В такой постановке задачи можно переписать A28а) в виде
19.2.4. Тем самым мы достигли того результата, что опера-
операторы в A28с) зависят только от углов 8 и <р, а в A28d) —
только от радиальной координаты г. Поэтому естественно дей-
действовать методом разделения переменных, т. е. искать решение
нашей задачи \|)(г) в виде
*(r) = IW8,qj)-*i....(r), A28e)
где YUm — решение системы A28с), зависящее только от углов,
a Ri,... — решение A28), зависящее только от г**).
*) Ср., например, изложение у Зоммерфельда в книге «Дифференциаль-
«Дифференциальные уравнения в частных производных физики», ИЛ, 1950.
**) Заметим, что, в отличие от разделения переменных в A26), теперь
было бы, конечно, неверным сказать, что пространство, растягиваемое ре-
решениями A28а), есть прямое произведение пространств, растягиваемых ре-
решениями A28A) и A28с)—ведь в A28d) в качестве параметра входят
собственные значения I первого из уравнений A28с); поэтому произведение
любой пары решений A28с) и A28d) (при, может, быть, разных значениях/)
не будет, вообще говоря, решением A28а). Именно поэтому решения A28d)
приходится нумеровать двумя группами индексов — индексом (или индекса-
индексами), нумерующим собственные значения A28d) — мы обозначаем его пока
многоточием — и индексом I, который входит в само уравнение A28d) как
параметр. Заметим в связи с этим и то, что квантовое число т не входит (па-
(параметром) в A28d). Это значит, что любое решение Ri, ... A28d) может ком-
комбинировать с любым (совместным с его /) значением ш. Так как таких зна-
значений имеется 21 + 1, то мы заключаем, что все группы собственных значений
(/,...) B/ + 1)-кратио вырождены.
19. ДВИЖЕНИЕ В ЦЕНТРАЛЬНОМ ПОЛЕ 487'
Угловая часть нашей задачи — уравнения A28с) — это хо-
хорошо известные уравнения для сферических функций; их реше-
решения записываются известным образом как
л тер
У() ^1.Я1(в), A29)
где в;, т выражаются через присоединенные полиномы Ле-
жандра. В науке о сферических функциях показывается, что
разумные квадратично интегрируемые решения получаются при
этом только для целых значений / и т; именно для
/ = 0, 1, 2, ..., )
«—«.-1+1 1-1./I A29а)'
— как мы уже упоминали ранее, орбитальное движение может
привести только к целым, а не к полуцелым значениям мо-
момента. Подробности рассмотрения угловой части задачи можно
посмотреть в любой книге по квантовой механике, напр, в книге
Ландау и Лифшица (см. § 28 и дополнение «с» по изданию
1974 года).
19.3. Перейдем теперь к радиальной части задачи — т. е.
к уравнению A28d) для функции /?(i...(r). Для этой функции
делают обычно подстановку
Д(г) = -^, A30а)
приводящую радиальное уравнение к виду
](r) = 0. A30b)
Мы видим, что это уравнение имеет вид уравнения Шредин-
гера для одномерного движения с эффективной потенциальной
энергией (ср. A.28.4))
m{^+l) . A30с)
ЗАМЕЧАНИЕ: Эта эффективная потенциальная энергия зави-
зависит только от квантового числа / угловой части задачи, т. е.,
как мы уже отмечали, не зависит от т. Поэтому каждому
EW-y энергии соответствует B1 + 1) собственный вектор, отли-
отличающийся лишь ориентацией в (физическом трехмерном) про-
пространстве.
Более существенное отличие A30Ь) от уравнения для одно-
одномерного движения связано с тем, что по самому своему смыслу
координата г в нем меняется только в полупространстве
0 ^ г < оо. Поэтому, если бы мы желали трактовать A30Ь)
как одномерное уравнение Шредингера, то нам пришлось бы
488 ч- !"¦ ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
считать, что «потенциальная энергия» равна выражению A30с)'
только в правом полупространстве г ^ 0, в левом же полупро-
полупространстве надо было бы положить V(г) = -f-oo, г ¦< 0. Щ
19.4. Теперь уместно поговорить о граничных условиях, ко-
которые следует наложить на функцию R(r). Основное условие,
выполнения которого надо требовать от решений всякого урав-
уравнения Шредингера, — это то, чтобы соответствующие векторы
состояния были бы нормируемы, или в собственном смысле A2)
для дискретных EW-ов, или хотя бы в несобственном смысле
B3а, Ь) для состояний непрерывного спектра. Для уравнения
A30Ь), если потенциал U(r) регулярен (допустимы конечные
разрывы) для всех г Ф 0, следует специально позаботиться
лишь об интегрируемости при г->0 (особой точке A30Ь))
и при г-»-оо.
19.4.1. При г->0 условие нормируемости означает требова-
требование существования интеграла \ dVty* (r) ¦$ (г) по любой области,
включающей начало координат, т. е. существования интеграла
r2R2 ... (г) dr.
Если принять, что при г->-0 функция R(r) ведет себя как rs, то
для существования этого интеграла надо, чтобы было 2(s-f-l)>
>—1, т. е. s>—z/2. Практически во всех нерелятивистских
задачах оказывается возможным удовлетворить даже требова-
требованию s^— '/г- Для функции %(г) этому соответствует показа-
показатель ^ + '/2. т. е. для функции %(г) имеет место граничное
условие
X(r)-+0. A30d)
г->0
19.4.2. При г->-оо условие квадратичной интегрируемости
оо
\ %2(r)dr необходимо только для функций дискретного спектра.
Для функций непрерывного спектра достаточно, чтобы такой
интеграл можно было бы определить как обобщенную функцию.
Такие, ненормируемые в собственном смысле A2), состояния
аналогичны инфинитным движениям классической теории,
когда частица может уходить на бесконечность или приходить
оттуда.
19.4.3. Рассмотрим подробнее поведение решения A30Ь)
при г->0. Допустим, что потенциальная энергия U(r) такова,
что
г2 С/(г)-* о; A31а)
19. ДВИЖЕНИЕ В ЦЕНТРАЛЬНОМ ПОЛЕ 489
тогда при г->0 в A30Ь) можно пренебречь членами U и Еу
и у нас остается
0
Это уравнение имеет решения степенного вида
причем для показателя (s + 1) (*) приводит к условию
s(s+ !) = /(/+ 1),
которое допускает два решения
s = l или s = — (/+1),
соответственно тому, что уравнение второго порядка должно
иметь два независимых решения. Второе из этих решений, с по-
показателем s = —(/+!)' не удовлетворяет условию A30d), по-
поэтому его следует отбросить, и у нас остается единственное до-
допустимое решение
при r->0 %(r)~Crt+1, т.е. Ri,...(r)~ Crl. A31)
19.4.4. Перейдем теперь к определению вида допустимых
решений при больших г, г->-оо. Предположим, что потенциаль-
потенциальная энергия нормирована обычным условием
U(r)->0.
/¦->¦«>
Тогда то же справедливо и для V(r) и при больших г в A30Ь)
достаточно будет оставить только члены с производной и с Е
¦#—?¦*¦ «>
откуда сразу следует
%(r)-*Cie-^ + C^, A32)
/•-*¦<»
где
k==
19.4.4.1. При Е>0 оба значения корня в A32а) чисто
мнимы, и мы получаем решения осциллирующего типа. Оба ре-
решения ненормируемы в собственном смысле, но нормируемы
в обобщенном, т. е. оба — допустимы. Единственное допустимое
решение A31) при г->0 продолжится при г->оо в некоторую
линейную комбинацию двух решений A32), и, поскольку оба
эти решения допустимы, то будет допустимой и эта специаль-
специальная их комбинация. Следовательно, при всяком значении Е > О
будет существовать одно решение, удовлетворяющее сразу
•490 ч. III. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
обоим граничным условиям при г->0 и при г->-оо: мы будем
иметь дело с непрерывным спектром.
19.4.4.2. При Е <С О оба значения корня в A32а) веще-
вещественны, при этом одно из них положительно, а другое отрица-
отрицательно. Положительный вещественный корень ведет к решению,
экспоненциально растущему на бесконечности — такое решение
нельзя нормировать даже в обобщенном смысле и, следова-
следовательно, оно должно быть отброшено. Таким образом из двух
решений, входящих в A32), допустимым будет только одно;
постоянную С2 следует положить равной нулю. Поэтому, когда
мы будем продолжать в область больших г единственное до-
допустимое в области г->-0 решение, то мы, вообще говоря, при-
придем к недопустимой линейной комбинации, включающей запре-
запрещенную константу С2, — т. е. вообще говоря, при произвольных
?, решений, удовлетворяющих обоим граничным условиям
сразу, не будет. Лишь для некоторых избранных значений Е
может случиться, что при продолжении допустимого в области
малых г решения на большие г мы придем как раз к един-
единственно допустимому там решению с С^ = 0. Эти избранные
значения ЕПг будут собственными значениями дискретного
спектра. Поскольку соответствующие волновые функции на бес-
бесконечности будут экспоненциально убывать, то для них будет
о
т. е. они будут нормируемыми в собственном смысле A2).
20. Кулонов о поле
Важнейший случай квантовомеханического движения час-
частицы в центральном поле составляет, конечно, движение элек-
электрона в кулоновом поле атомного ядра.
20.1.1. Тогда, если заряд ядра равен Ze, то
я радиальное уравнение A30Ь) принимает вид
Мы будем рассматривать наиболее интересный случай Е < 0,
и поэтому положили здесь в соответствии с A32а)
A34а)
20. КУЛОНОВО ПОЛЕ 491
Асимптотическая форма A32) побуждает нас сделать под-
подстановку
%(r) = e-4(r), A34b)
которая приводит уравнение A33а) к виду
]1-о. оззь).
При малых г функция f(r) должна, как и %{г), иметь асимпто-
асимптотику A31), поэтому разумно сделать вторую подстановку:
f(r) = r'^w(r), A34с)
приводящую к
^[Щ?]==0. A33с)
Последнее уравнение сразу напоминает известное уравнение
для конфлюэнтнои гипергеометрической функции *)
Ясно, что для того, чтобы привести A33с) к виДу A35.1),.
следует сделать замену независимого переменного, положив
2kr = x. A34d>
Тогда A33с) примет вид
)-х]% -[/+1 —Sgf.]w = O, A33d)
х
который совпадет с A35.1), коль скоро выбрать
и Y = 2(/+l). A34e>
20.1.2. При больших г гипергеометрический ряд A35.2) рас-
растет, как известно, как ех = e2hr. Следовательно, в общем слу-
случае получаемая подстановками A34) из A35.2) функция %{г)
будет при больших г экспоненциально расти (в соответствии с»
сделанными выше общими замечаниями) и не даст нам удов-
удовлетворяющего граничным условиям решения уравнения Шре-
дингера.
Особый случай произойдет, только если ряд A35.2) обо-
оборвется на конечном члене. Из его структуры видно, что для
*) См., например, Рыжик, 1948, стр. 138; Яяке —Эмде, 1948, стр. 373.
492 ч. III. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
этого нужно, чтобы а оказалось бы целым неположительным
числом. Итак, условие обрыва ряда записывается как
а = — пг; пг = 0, 1, ...., A36а)
или, если ввести другое целое число
-а = /+1 + «г, A36Ь)
в виде
п = 1+1, 1 + 2, ... (всегда п>1). A36с)
Если условие A36) выполнено, то w растет при больших г
лишь степенным образом, а, следовательно, %(г) в силу A34Ь)
экспоненциально убывает. Таким образом условие A36) выде-
выделяет нам те значения параметра а, "при которых наша EWP
для уравнения Шредингера имеет нормируемые решения, а чис-
числа пг (или п) нумеруют эти собственные функции. Число п,
принято называть радиальным квантовым числом, а число
п — главным квантовым числом.
20.1.3. Подставляя эти квантовые числа в A34е), находим,
что собственными значениями определяющего, согласно A34Ь),
скорость убывания волновой функции мнимого «волнового век-
вектора» k будут
20.1.4. При движении электрона в поле атомного ядра масса
электрона даже в самом легком атоме — в водороде — при-
примерно в 2000 раз меньше массы ядра, поэтому в хорошем при-
приближении можно считать, что приведенная масса ц равна про-
просто массе электрона т. Тогда полученная формула примет вид
, mZe2 I Z
где ав — характерная для определения атомных масштабов
длина, которую в честь Нильса Бора называют боровским
радиусом. Мы уже встречались с этой, определяющей порядок
размеров атомов, — а, следовательно, и привычные нам плот-
плотности (точнее — числа атомов в кубическом сантиметре) жид-
жидких и твердых макроскопических тел, — длиной в историческом
введении и отмечали тогда ее связь с другой фундаментальной
для физики элементарных частиц постоянной размерности
длины классическим радиусом электрона -s0 = —г" (см. И, § 14).
trie
Именно
«в =^ = ^" = 0.529. Ю-8 см; а-^-^. A37.1а)
20. КУЛОНОВО ПОЛЕ 493
Безразмерная постоянная a = -j^- —так называемая по-
постоянная тонкой структуры —характеризует, независимо от
применяемой системы единиц, силу электромагнитного взаимо-
взаимодействия. Поэтому формула A37.1а) показывает, что сравни-
сравнительно (с классическим радиусом электрона) очень большие
«размеры» атомов объясняются слабостью электромагнитного
взаимодействия — другое известное нам в природе взаимодей-
взаимодействие— сильное или ядерное взаимодействие, для которого со-
соответствующая константа велика (порядка 15-ти), — приводит
к связанным системам (атомным ядрам), размеры которых по
порядку величины не отличаются от классического радиуса
электрона. Таким образом можно сказать, что привычные нам
плотности макроскопических тел определяются слабостью элек-
электромагнитного взаимодействия — будь это взаимодействие силь-
сильным, все окружающие нас тела были бы в а~6, т. е. примерно
в миллион миллионов раз «тяжелее»*).
• 20.1.5. Обратимся теперь к энергии собственных состояний.
Ее значения через волновой вектор k задаются формулой
A34а). Подставляя в нее k из A37.1), получаем
Сп~ 2\i ~ 2т ~ 2 Й2 п2 ~ п2 '
где мы опять заменили приведенную массу ц на массу элек-
электрона т. Введенная здесь постоянная Ридберга R опять-таки
уже фигурировала в историческом введении и выражалась —
способом, очень похожим на A37.1а), — через «естественную»
единицу энергии — собственную энергию или энергию покоя
электрона тс2 — и постоянную тонкой структуры a
/?=s^.B=lmc2.a» = l.0,511 МэВ-а2 = 1- 27,21 эВ A37.2а)
(Ее значение известно сейчас с семью значащими цифрами!).
Это — та самая постоянная, которая фигурировала в эмпири-
эмпирически найденных «термах» водородного атома. Таким образом
*) Внимательный читатель мог бы возразить здесь, что проводимое срав-
сравнение с ядерными системами не совсем правомерно — при его проведении мы
почему-то отвлеклись от того обстоятельства, что массы М ядерных частиц —
протонов и нейтронов— как только что указывалось, примерно в 2000 раз
больше массы т электрона. Оказывается, однако, что хотя протоны или ней-
нейтроны и гораздо тяжелее электронов, но их «классический радиус», получае-
получаемый при замене в \ =—Ц- массы электрона т на Af и электромагнитного
заряда е на «постоянную сильных взаимодействий» g, т. е. величина /?о =
S2
= /: 2 , практически совпадает с электронным -to-
Этот поразительный факт до сих пор не нашел себе никакого теоретиче-
теоретического объяснения.
494
ч. III. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
теоретическое получение формул A37.2) сразу указывает, что-
теория правильно описывает результаты опыта. Именно эти
формулы были получены в работе Шредингера 1926 года и под-
поддерживали надежду, что поиски правильной «микромеханики»
направились по нужному пути.
20.2.1. Однако главный смысл полученного результата со-
состоит, конечно, не в количественных совпадениях чисел. Основ-
Основное принципиальное значение имеет качественный характер по-
полученного спектра энергии (см. рисунок).
Согласно A37.2) энергия зависит только от главного кван-
квантового числа п, которое A36с) принимает значения 1, 2, ...
уровни энергии в кулоновом поле
Таким образом для Е < 0 спектр возможных значений энергии
дискретен, причем имеется наинизший уровень энергии, отве-
отвечающий значению я = 1. Более подробный анализ показывает,
что эта последняя особенность является общей для всех потен-
потенциалов, удовлетворяющих A31а). Далее, по мере роста п, сле-
следующие уровни располагаются все выше, и при и->оо дискрет-
дискретный спектр обладает точкой сгущения при ?->0. При Е > О
начинается непрерывный спектр. Бесконечность числа уровней
дискретного спектра является специальной особенностью куло-
нова потенциала, связанной с его сравнительно медленным
убыванием при больших г. Для потенциалов, которые быстро-
стремятся к нулю с ростом г, число уровней может быть ко-
конечным.
Главный, наиболее важный вывод из этих результатов кван-
квантовой механики состоит, конечно, в том, что энергетический
спектр ограничен снизу, что существует наинизший уровень
энергии, которому соответствует основное состояние системы.
20.2.2. Почему этот вывод представляется таким существен-
существенным? Почему при изучении всякой системы нас прежде всего
интересуют ее состояния с самой малой энергией?
20. КУЛинОВО ПОЛЕ 495
То представление, что всякая система всегда «стремится»
к наинизшему возможному энергетическому состоянию, осно-
основано на молчаливо принимаемом допущении, что всегда есть
некоторый механизм «потери» энергии. Это есть по существу
неявный перенос в «точную» микромеханику обыденных макро-
макроскопических представлений, что всегда есть диссипирующие
энергию силы типа сил трения.
Более ученым образом такую систему взглядов можно ха-
характеризовать тем утверждением, что «в природе нет действи-
действительно изолированных систем с конечным числом степеней
свободы» (взаимодействие с другой системой с конечным чис-
числом степеней свободы не могло бы предоставить возможности
для неограниченной передачи энергии).
Если присоединиться к такой точке зрения, — а для атомных
систем она обосновывается тем, что можно, как то мы делали
во введении, указать явный механизм диссипации за счет по-
потери энергии на электромагнитное излучение, — то возникает
проблема наинизших состояний: за счет чего можно обеспечить
такое положение вещей, что у всякой системы (между части-
частицами которой могут действовать силы притяжения) всегда есть
состояние самой низшей и при том конечной энергии?
20.2.3. В наивно-механическом понимании этого можно было
добиться за счет «непроницаемости» частиц, наглядно пред-
представляемых как что-то вроде твердых биллиардных шариков.
Более утонченной формулировкой того же представления могут
быть слова об изменении сил взаимодействия на малых рас-
расстояниях, о введении потенциалов, приводящих на малых рас-
расстояниях к силам отталкивания. Однако в связи с проблемой
устойчивости атомов, где этот вопрос впервые встал во весь
рост перед физиками, такие модельные попытки не привели,
как мы уже говорили, ни к каким успехам.
20.2.4. Квантовая механика предлагает решение этой проб-
проблемы на совершенно другом пути. Силы, вид потенциальной
энергии, оставляются такими же, как в классической теории.
Однако другая «кинематика», точнее, другой подход к описанию
состояний системы, не позволяют частице проваливаться в по-
потенциальную яму сколь угодно глубоко.
В самом деле, легко показать качественным рассуждением,
что достигнутый нами вывод об ограниченности возможных
значений энергии снизу есть прямое следствие принципа неоп-
неопределенности, точнее, соотношения неопределенностей G9).
20.2.4.1. Рассмотрим частицу, находящуюся в образованной
кулоновым полем потенциальной яме, и предположим, что она
все время находится в области с размерами порядка некото-
некоторого а; тогда ее средняя потенциальная энергия будет порядка
493 ч- HI. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
. Того же порядка а будет и неопределенность значения
координаты частицы; значит, по соотношению неопределенно-
неопределенностей, неопределенность ее импульса будет порядка —. Такого
же порядка (во всяком случае — не меньше) будет и сам им-
импульс, он привнесет с собой кинетическую энергию порядка
¦?—= 2 q2 . Поэтому полная энергия частицы (имеющая в ста-
стационарном состоянии определенное значение) будет равна
с _51_
L ~ 2ma2 ~ а •
Полученная зависимость полной энергии от параметра а
имеет (абсолютный) минимум при
А2 1
а а
равный
i = E(a0) = -^r=E1
— т. е. в точности равный низшему уровню найденного нами
спектра A37.2) (при Z= 1).
20.2.4. Таким образом получаемый из решения квантовоме-
ханической задачи самый низший «основной» уровень энер-
энергии— это просто минимальная энергия, которую может иметь
система в силу соотношения неопределенностей (напомним ана-
аналогичный результат для осциллятора в 17.3.). Образно выра-
выражаясь, можно сказать, что по мере приближения частицы к син-
сингулярной точке потенциала она начинает испытывать столь
сильные нулевые колебания, что (для потенциалов, удовлетво-
удовлетворяющих A31а)) прирост кинетической энергии оказывается
больше убыли потенциальной, и суммарная энергия оказы-
оказывается ограниченной снизу. Корень нашего макроскопического
представления о «непроницаемых» телах оказывается лежащим
в том, что при слишком сильном сближении микрочастицы на-
начинают двигаться «слишком быстро»!