Теория расчета железобетонных конструкций на прочность и устойчивость - Беглов А.Д., Санджаровский Р.С.

Автор: Беглов А.Д. Санджаровский Р.С.

Теги: строительство конструкции строительные конструкции железобетонные конструкции сопротивление материалов предел прочности

Год: 2004

Похожие

Расчеты железобетонных конструкций по предельным состояниям и предельному равновесию

Трещиноустойчивость, жесткость и прочность железобетона

Деформационные критерии разрушения и расчет элементов конструкций на прочность

Расчет железобетонных конструкций из тяжелого бетона по прочности, трещиностойкости и деформациям

Текст

Л. 1ЫПОВ ИС. слнжлкпк кий
ТЕОРИЯ РАСЧЕТА ЖЕЛЕЮБЕ1ОННЫХ
КОНСТРУКЦИЙ НА 11ГОЧ1ККП 1>
и устойчивость. современные
НОРМЫ И ЕВРОСТЛНДЛР1 ы
Л. 1ЫПОВ ИС. слнжлкпк кий
ТЕОРИЯ РАСЧЕТА ЖЕЛЕЮБЕ1ОННЫХ
КОНСТРУКЦИЙ НА 11РОЧ1КМЧ 1>
и устойчивость. современные
НОРМЫ И ЕВРОСТЛНДЛР1 ы
Л. 1ЫПОВ ИС. слнжлкпк кий
ТЕОРИЯ РАСЧЕТА ЖЕЛЕЮБЕ1ОННЫХ
КОНСТРУКЦИЙ НА 11РОЧ1КМЧ 1>
и устойчивость. современные
НОРМЫ И ЕВРОСТЛНДЛР1 ы
Л. 1ЫПОВ ИС. слнжлкпк кий
ТЕОРИЯ РАСЧЕТА ЖЕЛЕЮБЕ! ОННЫХ
КОНСТРУКЦИЙ НА ПРОЧПСМЧ 1>
и устойчивость. современные
НОРМЫ И ЕВРОСТЛНДЛР1 ы
ВВЕДЕНИЕ
Развитие теории железобетона неуклонно двигалось в сторону создания деформа-
ционной модели сечения Евростандартов [197]. Первоначальная «классическая теория
железобетона» [147] использовала три гипотезы:
- бетон в растянутой зоне не работает, растягивающие напряжения восприни-
маются арматурой;
- нормальные напряжения в бетоне и арматуре распределены по линейному
закону;
нейтральная ось поперечного сечения элемента проходит посредине высоты
х - О,5йо *.
Классическая теория неоднократно подвергалась критике, однако, первые попыт-
ки построить расчет железобетонных конструкций, исходя из стадии разрушения, бла-
годаря чисто эмпирическому направлению не являлись конкурентом теории упругого
бетона. Вместе с тем, ученые отмечали, что будущая теория железобетона будет постро-
ена на базе упругопластических деформаций бетона и арматуры. Указывались три ста-
дии работы железобетонного сечения при изгибе [166].
Стадия 1. Растягивающие напряжения в бетоне не достигли предела прочности,
и трещин в сечении нет.
Стадия 2. С появлением трещины в растянутой зоне бетона работает только ар-
матура. Трещина увеличивается с ростом нагрузки; сжатая зона бетона уменьшается,
напряжения в бетоне растут.
Стадия 3. За стадией 2 наступает период, ведущий к моменту разрушения. Напря-
жения в бетоне <5Ь и арматуре as возрастают и приближаются к предельным Rb и Rs.
Как только достигается одна из этих величин, либо обе вместе, сечение разрушается.
Гипотезы «деформационной модели сечения» Евростандартов отрабатывались в
течение десятилетий, поэтому не удивительно, что каждая из них вызывала оживленное
обсуждение в научной литературе прошлых лет. Наибольшие дискуссии вызывали две
из них: форма очертания эпюры напряжений по сечению и гипотеза Навье (плоских
сечений).
Распределение напряжений по сечению железобетонного элемента в ранних ис-
следованиях рассматривалось формально и не связывалось с общей картиной напря-
женно-деформированного состояния конструкции, что приводило к противоречивым
выводам при оценке стадии разрушения. Например, в своих работах Лолейт А.Ф. дока-
зывал, что закон распределения напряжений в сжатой зоне (будет ли это прямая или
какая-либо кривая) не отражается на результатах расчета [88]. К тому времени предла-
галось много различных законов распределения напряжений по сечению: линейный -
в соответствии с законом Гука; билинейный - с различными модулями упругости в сжа-
той и растянутой зонах (Мелан, Мёрш, Остенфельд, Штаерман); билинейный - в сжатой
зоне бетона (Мурашёв, Тюлье) и наличие трещин в растянутой зоне; параболический -
* Эта теория, предложенная Куанье, Тедеско, Кристофом, Мёршем и другими учеными,
применялась первоначально в нормах почти всех стран.
5
в сжатой зоне бетона (Залигер, Риттер, Фрайфельд, Лолейт, Столяров, Подольский)
и наличие трещин в растянутой зоне; прямоугольная эпюра напряжений в сжатой зоне
бетона (Гвоздев, Эмпер1ер, Мурашёв); эпюра в сжатой зоне имеет вид трапепии,
а в растянутой зоне напряжения равномерно распределены по этой зоне (Гебауэр, Ста-
филевский).
Мурашёв В.И. [101] в этой связи отмечал, что с точки зрения простоты расчета
могут быть приняты либо треугольная, либо прямоугольная эпюры напряжений по вы-
соте сжатой зоны. Всякий другой более сложный закон изменения напряжений в сече-
нии, по его мнению, неприемлем, так как ни одно сечение, кроме прямоугольного, прак-
тически нельзя было бы рассчитать.
Использование в нормах по железобетону модели пластического шарнира [43] (во
многих странах) позволяло не учитывать форму распределения напряжений в сжатой
зоне и существенно упростило практические расчет. Однако такая модель удаляла те-
орию железобетона от методов строительной механики. На это удаление, как на неесте-
ственное, указывали неоднократно известные ученые теории железобетона.
В 1959 году Гвоздев Л А. [44] выступил с идеей о развитии строительной механики
железобетонных конструкций, в которой учитывались бы все особенности работы желе-
зобетона пол нагрузкой. Здесь же он указал на необходимость учета в расчетах железобе-
тонных конструкций диаграммы аь - £ь с ниспадающим участком для бетона.
Являясь автором метода предельного равновесия, внедренного им же в нормагив-
ные расчеты, Гвоздев А А. ясно видел ограниченность этого метода, сдерживающего раз-
витие теории железобетона, как строительной меха!гики железобетона. Ещё в 1949 году
Гвоздев А.А указывал [50, стр. 14]: «Метод предельного равновесия, как известно, был
создан ещё в XVIII веке... Он применим только... при соблюдении следующих условий:
...Вплоть до исчерпания несущей способности деформации должны быть настолько
малыми, чтобы можно было пренебречь изменением всех геометрических величин, вхо-
дящих в уравнения равновесия». Наличие ниспадающего участка на диаграмме аь - £ь,
указывал Гвоздев А. А., обнаруживается в ряде экспериментов, создающих условия для
проявления особенностей деформирования сжатого бетона: нисходящий участок не об-
наруживается, если нагрузка Р на бетонный образец (с достижением призменной проч-
р
кости Rb = - - ) не начинает уменьшаться после значения Р = Рь, либо уменьшается
Fb
слишком медленно. В обычных экспериментах по сжатию бетонных призм на участке
деформирования Р > Р^, трудно подобрать закон уменьшения силы Р, соответствую-
щий ниспадающему участку аь - £ь (заложенному в свойствах структуры бетона), а
также соответствующий работе бетонною волокна, находящегося в массиве окружаю-
щих бетонных волокон конструкции. Это можно видеть в экспериментах Уитнея К.,
испытывавшего бетонные цилиндры на прессе со специальной жесткостью (рост де-
формации образца ведет к уменьшению усилий пресса)
Таль К.Э. остроумно и просто выявил реальную диаграмму бетона аь - £ь (соот-
ветствующую структуре бетона) путем центрального сжатия железобетонных призм
размером 10 х 10 х 30 см, армированных высокопрочной проволокой (12 стержней ди-
6
аметром 5 мм) с пределом текучести 5000 кг/см2, работающей в упругой стадии [152].
С помощью измеренных деформаций е находились усилия, воспринимаемые сталью
• £ • Es* Остальная часть нагрузки, подаваемой на призму, позволяла найти
напряжения бетона
Na-N°
=
Схема работы железобетонной призмы показана на рис. В.1,а.
В этих экспериментах установлено, что сила сжатия воспринимаемая бето-
ном, сначала возрастает с ростом деформаций, потом убывает с их же ростом.
Таль К.Э. указывает, что обнаруженное им явление объясняется плавным перерас-
пределением усилий с бетона на арматуру и отсутствием резкого нарастания напряже-
ний (перераспределение усилий с более слабых мест на места с ненарушенной структу-
рой), которое происходит в неармированном бетоне.
Аналогичный результат получил Михайлов В.В. при испытании на изгиб балки в
виде обоймы, составленной из двух швеллеров и заполненной бетоном [107].
Изгибающий момент в бетонной балке определялся разностью
Mb=M-Ms,
где Л/ - экспериментальный момент всей балки;
М s- момент, воспринимаемый упругими швеллерами и рассчитанный по изме-
ренным деформациям.
Михайлов В.В. для бетонного сечения не использовал гипотезу плоских сечений
(ввиду специальной конструкции балки) и получил ниспадающий участок кривой <ть - еь
при работе бетона на растяжение.
В экспериментах Дегтярёва В.В. [61] применялся высокопрочный бетон
(до Rb =814 кг/см2) и высокопрочная сталь (диаметр до 18 мм, предел текучести до
6000 кг/см2) с большими процентами армирования (ju = 0,077), и также выявлен нис-
падающий участок в работе бетона. В этих экспериментах проявилась (при централь-
ном сжатии) большая неравномерность распределения деформаций по сечению и по
длине призмы, вызванная относительно большими диаметрами арматуры
(d 18 d 18^
“ уд» ~ J5о > большими процентами армирования и конструктивно неравномер-
ной передачей усилий на торцах призм. Дегтярёв В.В. утверждал, что параметры диаг-
раммы сгЛ — еь бетона существенно зависят от количества арматуры и её свойств.
Е. Хогнестед с соавторами [207] испытывали внецетггренно сжатые стержни и для
анализа напряжений в бетоне использовали гипотезу плоских сечений. Они также получи-
ли нисходящий участок кривой <ть — Еь. Это вызвало критику ученых, не признававших
выполнимость гипотезы плоских сечений в бетоне, а также сомнение в достоверности по-
лученных результатов. Однако, большое число опытов Е. Хогнестеда, без сомнения, ука-
зывало на наличие ниспадающего участка диаграммы при внецентренном сжатии.
7
------------------ соедние д&Ьоомаиии аомиоованных поизм
-----------------соедние де&оомаиии бетонных поизм
Рис. ВЛ
8
Косвенным подтверждением существования нисходящего участка диаграммы
<УЬ — £ь бетона явились значения деформаций крайних сжатых волокон сечения, заме-
ренные при испытаниях железобетонных конструкций. Эти деформации имеют гораз-
до большие величины, чем аналогичные деформации при центральном сжатии.
В последующие годы уделялось большое внимание уточнению и аналитическому
описанию диаграммы сгь — £ь с ниспадающим участком. Укажем на работы Байкова
В.Н., Бигера А., Бачинского ВЛ., Бамбуры А.И., Горбатова С.В., Димитрова З.А., Кар-
пенко Н.И., Мухамедиева ТА., Петрова А.П., Сарджина М. и других ученых. В Евроко-
дах [201] рекомендована к использованию модель аь -£ь Сарджина М. [218], в кото-
рой нормированы координаты характерных точек диаграммы с ниспадающим участ-
ком.
Применение гипотезы плоских сечений в теории железобетона имеет неоднознач-
ные оценки. Многие ученые полностью отрицают возможность использования этой ги-
потезы в третьей стадии работы сечения, предшествующей моменту разрушения. Некото-
рые из них, отрицая эту гипотезу якобы за её условный характер, вынуждены соглашать-
ся, что она дает хорошие расчетные результаты, согласуемые с данными опытов.
Приведем в качестве примера типичное высказывание в литературе последних лет
по этому поводу: «...гипотеза Бернулли о сохранении плоского сечения в данном случае
не отвечает действительности». Профессор Фрайфельд С.Е. раньше высказывался
более категорично: «Если... до момента, предшествующего разрушению, мы имели право
с достаточной достоверностью применять гипотезу Бернулли, то для момента, со-
ответствующего разрушению, применение этой гипотезы следует считать серьез-
ной ошибкой». Отрицание гипотезы плоских сечений в теории железобетона оживлен-
но осуществлялось и в последние годы; в наших нормах [148] по расчету несущей спо-
собности изгибаемых и сжатых железобетонных элементов эта гипотеза не использова-
лась. Последнее обстоятельство вызывало неоднократные дискуссии между сторонни-
ками и противниками гипотезы плоских сечений. Такая дискуссия между А.А. Гвозде-
вым и К.Э.Талем в соё время была опубликована в журнале «Бетон и Железобетон».
Однако, следует подчеркнугь, что такие полезные дискуссии по нормативным моделям
не должны препятствовать развитию научных исследований в различных направлениях
теории железобетона.
В теории железобетона, посвященной расчету сжатых стержней, исторически сло-
жилась противоречивая ситуация, вызванная желанием использовать единую модель
пластического шарнира для расчетов изгибаемых и сжатых конструкций. В первых нор-
мативных методах расчета сжатых железобетонных конструкций использовались ли-
нейные модели
М N
— + — ,
W F
либо
М N
W* (pF*
где W - момагг сопротивления сечения;
<р - коэффициент продольного изгиба при центральном сжатии.
9
Гвоздев А. А и Мурашёв В И. [43], используя опыты Боришанского М С. и Кузне-
цова А А., предложили взамен этих моделей способ учета гибкости внецентреино сжа-
тых железобетонных колонн, вытекающих из таких соображений: «Благодаря эксцент-
риситету нагрузки элемент к моменту разрушения прогнется. В связи с этим эксцен-
триситет продольной силы возрастет И если будет введен в расчет эксцентриси-
тет силы не начальной, а соответствующей моменту разрушения, то, очевидно, раз-
рушающую нагрузку можно будет определить по формулам указанным в предыдущих
параграфах (изгиб) Однако, определить эксцентриситет сипы к моменту разрушения
по понятным причинам нелегко. Сейчас можно предложить очень грубое решение».
В 1938 году эта теория вошла в нормы (ОСТ 90 003-38) В этой теории эксцентриситет
вр силы N находился с учетом прогиба колонны f:
gp — ео + f gp + 2-,г
л ы
llN
gp
,_лч2
л2 El’
где е0 - эксцентриситет силы N.
Откуда
*0+/^ 1 = 1______
е» 1 12ЛГ fzoY
п‘Е! x2Ebh\h
_________1 = 1_
”, 12Им/г„р0у________________л, |4Y'
Ел bh h 400^й J
лгЕ
-----= 400; b,h - размеры сечения.
N
где п. =----
1 bhR.
Гибкость элементов учитывалась при ~ > Ю
В последующие годы структура данной формулы не изменялась, а уточнялись в
ней отдельные коэффициенты. При этом в научной литературе устойчиво сохранялось
неудачное мнение, что при сжатии схема работы элемента подобна чистому изгибу, что
«точная форма эпюры напряжений в сжатом бетоне неизвестна, но, как и при изгибе,
принятие той или иной криволинейной эпюры практически не имеет большого значе-
ния. Поэтому для упрощения расчетов здесь также принята прямоугольная эпюра на-
пряжений».
Расчет центрально сжатых железобетонных стержней производился при этом на
устойчивость с учетом продольного изгиба, который оценивали коэффициентом <р
В свете использования гипотез «деформационной модели сечения» Евростандар-
тов заметим, что форма распределения напряжений по поперечному сечению имеет су-
щественное значение как для расчета изгибаемых, так и для расчета сжатоизогнутых
железобетонных конструкций
10
В теории сооружений неоднократно указывались сложность аналитического на-
хождения изогнутой оси упругопластических балок. В работах Безухова Н.И. [28] неуп-
ругая балка заменяется упругой балкой переменного сечения, но якобы находящейся
в упругом состоянии при той же нагрузке; либо сохраняется упругая балка постоянного
сечения, но вводятся специальные фиктивные нагрузки для учета пластических дефор-
маций; при этом используется обычная форма метода начальных параметров.
В работах Качанова Л.М. [77] и Филина А.П. [164] упрощенная степенная зависи-
мость
<j-Asn
применялась к расчету балок.
Неразрезные балки предложено рассчитывать при помощи уравнений трех момен-
тов методом последовательных приближений. В общем случае лишние неизвестные
определяются в виде
dR„
—— -0
» Де Rm = Е
1*1
JV + loJ du
dx - дополнительная работа, обусловленная изгибом;
Xi - / - я лишняя неизвестная;
Du = у Л dF - изгибная жесткость.
Указывается на затруднительность решения задачи для произвольных показателей
степени N. В простейших случаях нелинейность не сильно изменяет величины лиш-
них неизвестных.
Однако, при учете диаграммы а - £ в виде диаграммы Прандтля, результаты не-
линейного расчета существенно отличаются от расчетов по линейной модели. Напри-
мер, по данным Яценко В.Ф. упругопластический прогиб превышал в 2,26 раза анало-
гичный прогиб упругой балки; здесь [191] использована громоздкая графо-аналитичес-
кая процедура расчета.
Теория ползучести бетона имеет существенное значение для расчетов длительно-
го сопротивления железобетонных конструкций. В этой теории полные деформации
бетона представляются в виде суммы мгновенных (кратковременных) деформаций
и деформаций ползучести. Подавляющее большинство работ в теории ползучести бето-
на учитывает лишь мгновенно линейные модели. Деформации ползучести разделяются
на линейные и нелинейные. Наибольшее развитие получила линейная теория ползучес-
ти, наблюдаемая при относительно невысоких напряжениях. При постоянных напряже-
ниях умножение величины напряжения на постоянный множитель изменяет величины
деформаций ползучести на тог же множитель.
Ползучести бетона и железобетонных конструкций посвящены фундаментальные
работы Работнова Ю.Н., Арутюняна Н.Х., Гвоздева А.А., Дэвиса Р.Е., Гленвиля В.Х.,
Васильева П.И., Александровского С.В., Качанова Л.М., Бондаренко В.М., Ржаницына А.Р.,
Прокоповича И.Е., Улицкого И.И., Фрайфельда С.Е., Фройденталя А. и других отече-
ственных и зарубежных ученых.
11
Нелинейная теория ползучести бетона в рамках мгновенно упругих моделей полу-
чила развитие в трудах Арутюняна Н.Х., Васильева ПЛ., Улицкого И.И. и их учеников.
Бондаренко В.М. и Бондаренко С.В. впервые учли нелинейность мгновенного дефор-
мирования бетона в рамках гипотез наследственной теории старения бетона
В научной литературе по ползучести бетона и железобетона идея Бондаренко В.М.
не нашла должного практического развития для расчетов конструкций Это аргументиро-
валось зачастую не очень корректным утверждением о том, что в экспериментах мгновен-
ные деформации бетона «даже при высоких напряжениях линейно зависят от напряже-
ний». Такая аргументация, а также сложная математическая запись нелинейных дефор-
маций сдержали внедрение таких общих теорий в научные разработки по железобетону.
В данной работе рассматриваются вопросы нелинейной теории железобетона.
В рамках гипотез Евростандаргов деформирование железобетонных элементов, имею-
щих трещины в растянутой зоне даже при крат ковременном действии нагрузки эксплу-
атационного уровня, является нелинейным Эта нелинейность деформирования конст-
рукции существенно увеличивается в области линейной ползучести бетона а особенно
в области нелинейной ползучести. Разрабатываемая теория в рамках гипотез линейной
и нелинейной ползучести бетона учитывает модель мгновенного нелинейного дефор-
мирования Евростандартов и формулируется в дифференциальной форме. На основе
полученных нелинейных законов ползучести разрабатывается теория длительного со-
противления железобетонных конструкций. Устраняется разрыв между теориями мгно-
венного и длительного сопротивления конструкций, существующий вследствие исполь-
зованной ранее в уравнениях ползучести модели мгновенного линейного материала.
Предложена новая модель описания напряженно-деформированного состояния произ-
вольного сечения железобетонного элемента при длительном загружении, характеризу-
емая нормальной системой дифференциальных уравнений третьего порядка. При крат-
ковременном загружении система уравнений имеет второй порядок.
Функциональная связь этих систем дифференциальных уравнений позволяет пос-
ледовательно переходить от кратковременного загружения к длительному, и наоборот
В современной теории ползучести бетона имеется несколько моделей, различных
по уровню разработки и по использованию в реальных расчетах.
Прежде всего это основополагающая нелинейная теория ползучести Арутюняна Н.Х.
[3] с мгаовенными линейными свойствами, применяемая в расчетах железобетонных
конструкций. К недостаткам этой теории, отмеченным Гвоздевым А. А еще в 1955 году
на основании опытов Боришанского М С., относится то обстоятельство, что она «резко
занижает, почти стирает эффект напряжений, действующих непосредственно пе-
ред моментом наблюдения деформаций». Эта теория не отображаег наблюдаемое
в опытах быстрое натекание деформаций ползучести к моменту наблюдения, близкому
к моменту загружения образцов. Начальные участки кривых ползучести, построенные
на основе теории Арутюняна Н X., не имеют характерного подъемистого очертания (кру-
то восходящих ветвей при т близком к t), которое наблюдается не только над молодым,
но и над старым бетоном. Гвоздев А. А. [45] указывает; что они неприменимы для реше-
ния задач с быстро изменяющимися во времени процессами.
Яшин А В. [188] предложил меру ползучести бетона, объединяющую особенности
теории наследственности и теории старения бетона и исправляющую недостатки меры
ползучести Арутюняна Н.Х. [3]. К сожалению, модель Яшина А.В. не получила долж-
ного развития из-за неоднозначной оценки её, высказанной в научной литературе: мо-
12
дель сложна, и построенные на её основе интегральные уравнения ползучести нельзя
привести к соответствующим дифференциальным уравнениям. Однако, наши ученики
построили на основе модели Яшина А.В. дифференциальное уравнение ползучести тре-
тьего порядка, реализуемое в расчетах конструкций
Катин Н.И. [75] усложнил модель Яшина А В., дополнив её сингулярной функци-
ей, аналогичной функции Фройденталя А.М. И для этого случая нашими учениками
построена дифференциальная модель ползучести. С использованием понятия условно-
го времени эта модель имеет в дифференциальном виде третий порядок.
Прокопович И.Е. и Улицкий И.И. [123] упростили модель ползучести бетона Яши-
на А.В. Эту упрощенную модель успешно использовал в интегральной форме Яценко
Е.А. для решения некоторых практических задач [192].
Александровский С.В. [2] и его ученики в рамках мгновенно упругого материала и
гипотез Арутюняна Н.Х. построили интегральные уравнения нелинейной ползучести,
учитывающие явления быстронатекающей ползучести. В случае линейной ползучести
наши сотрудники построили для меры ползучести Александровского С.В. дифференци-
альное уравнение третьего порядка; в общем случае это уравнение имеет пятый порядок
На основе предложенного нами подхода [22] по учету мгновенной нелинейности,
а также новой модели сечения [23], все перечисленные выше уравнения можно реали-
зовать для решения практических задач длительного сопротивления железобетонных
конструкций
Разработанная теория [26] позволяет учитывать совместно шесть типов нелиней-
ности. Первый - нелинейность кратковременного деформирования бетона всего сече-
ния или (чаще) бетона сжатой зоны Второй - нелинейность упругопластических де-
формаций стальной арматуры. Третий - нелинейность, обусловленная наличием тре-
щин в бетоне растянутой зоны. Четвертый ~ нелинейная (либо линейная) ползучесть
бетона, существенно изменяющая характер распределения напряжений по сечению,
обусловленный кратковременным загружением. Пятый тип нелинейности может про-
являться при использовании специальных видов арматуры (канатов, стеклопластиков),
обладающих свойством ползучести. Шестой йш - геометрическая нелинейность, име-
ющая большое значение для сжатоизогнутых элементов и статически неопределимых
систем. Здесь различают два вида геометрической нелинейности: учет прогибов на ос-
нове приближенного выражения для кривизны, предполагающего малость прогибов
([у'(х «1); учет прогибов с использованием точного выражения для кривизны
На основе предложенной теории приведены численные эксперименты, позволяю-
щие изучить влияние различных типов нелинейностей на значения несущей способно-
сти элементов. Изучено влияние вида диаграмм <jb - £ь Евростандартов (нелинейная,
диаграмма Прандтля с ограниченной площадкой текучести) на несущую способность
кратковременно нагруженных железобетонных колонн. При малых и средних эксцент-
риситетах сжимающих сил наблюдается завышение несущей способности при приме-
нении диаграммы Прандтля. Сравнение несущей способности колонн по данным Евро-
кодов и моделям СНиП показывает, что для малых и средних эксцентриситетов несу-
щая способность по СНиП выше. Экспериментальные данные Чистякова Е.А. [176] по
центральному сжатию железобетонных колонн лежат выше теоретической кривой
еЮ1 = 0 Еврокодов, так как она учитывает случайные эксцентриситеты и различные не-
совершенства
13
Выявлено существенное влияние вида действительной диаграммы с упрочнением
<т, - £s арматуры на несущую способность железобетонных элементов в области не-
больших эксцентриситетов и малых гибкостей. Наличие указанной зоны упрочнения
арматуры для некоторых типов железобетонных балок приводит к тому, что эксплуата-
ционные свойства их утрачиваются раньше наступления неограниченного роста проги-
бов Поэтому несущую способность этих балок следует оценивать по деформационным
критериям, например, по критерию достижения прогибом некоторой допустимой вели-
чины, а не значения пластического шарнира
При оценке несущей способности сжатоизогнутых элементов следует учитывать
на диаграмме состояний «момент-кривизна» наличие изломов и пиковых экстремумов.
При ползучести коэффициент длительного сопротивления железобетонных балок
и колонн можно найти только расчетным путем. Из экспериментов определяется лишь
интервал в котором находится этот коэффициент Экспериментально-расчетным путем
установлено, что коэффициент длительного сопротивления зависит от ряда следующих
факторов: формы поперечного сечения, условий сочетания кратковременной и длитель-
ной нагрузок, коэффициента армирования элемента; эксцентриситета приложения сжи-
мающей силы; диаграммы мгновенного деформирования бетона суь — еь и диаграм-
мы — 85 арматуры, характеристик ползучести бетона; длины колонны и других фак
торов.
Евростандарты учитывают только предельную характерисгику ползучести бето-
на; в расчетах она дополнительно умножается на отношение уровней кратковременно-
го и длительного загружений. В этой модели ползучести бетон считается упругим, нео-
граниченно работающим на растяжение-сжатие. Численные характеристики этой моде-
ли, полученные для случая центрального сжатия бетонного стержня [133], распростра-
няются на другие случаи работы сжатоизогнутых железобетонных элементов. Прибли-
женность этого подхода, реализованного при длительном загружении, существенно от-
личается от строгости деформационной модели, заложенной в основу расчетов крат-
ковременного загружения железобетона. Вместе с тем укажем, что результагы расчетов
длительного загружения колонн в Еврокодах дают запас несущей способности, величи-
на которого никак не оценивается.
Модель расчета ползучести железобетона, предложенная нами, более точна, но
требует использования в практических расчетах для отыскания значений коэффициен-
тов длительного сопротивления дополнительных табличных или графических материа-
лов Например, для расчета центрально сжатых колонн значения коэффициента дли-
тельного сопротивления приведены в таблице
Значения коэффициентов Г]дл
Л 0 50 75 100 150 200 250 300
лдя 1,0 0,84 0,72 0,63 0,56 0,54 0,52 0,45
СЕВ 0,45 0,45 0,45 0,45 0,45 0,45 0,45 0,45
14
Кратковременная критическая нагрузка стержней рассчитывалась с учетом упру-
[ластических деформаций.
Значения коэффициента т]дй в табл.1 соответствуют бетонам, у которых предсль-
I характеристика ползучести (р{^>Л0 ) = 1,2. Меняя последнюю, в соответствии с дан-
ми Евростандаргов, мы получим иные значения коэффициента г]дл.
15
Глава 1. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ НОРМАТИВНЫХ МЕТОДОВ
РАСЧЕТА ЖЕЛЕЗОБЕТОННЫХ КОНСТРУКЦИЙ
§ 1.1. Нелинейные проблемы механики в задачах расчетов
железобетонных конструкций
Современная теория расчетов строительных конструкций, в том числе норматив-
ные модели, в основном опирается на три раздела строительной механики: линейная
механика, нелинейная механика, теория ползучести.
Принцип малости перемещений Навье, используемый совместно с законом Гука,
создали методы линейной теории. На основании общих методов линейной строитель-
ной механики производится первый этап расчета практически всех статически неопре-
делимых стержневых конструкций, определение лишних неизвестных Нормативные
методы большинства стран в этой части мало отличаются друг от друха.
Некоторые нормативные методики (в рамках закона Гука) отказываются от пред-
посылки расчета по недеформированному состоянию, которая опирается на малые зна-
чения перемещений конструкций. В расчетах учитывается наличие прогибов элемен-
тов В рамках использования приближенного выражения для кривизны возникает и учи-
тывается нелинейность, называемая геометрической нелинейностью первого рода. Ис-
пользуется также геометрическая нелинейность, учитывающая точное выражение для
кривизны (геометрическая нелинейность второго рода).
Замена закона Гука нелинейными зависимостями между напряжениями и дефор-
мациями приводит к учету физической нелинейности в теории нелинейной упругости и
теории пластичности. Общие методы расчета статически неопределимых систем в ус-
ловиях физической нелинейности разработаны недостаточно. Вследствие этого в нор-
мах некоторых стран имеются лишь декларативные соображения о возможном расчете
с учетом физической нелинейности
Совместное рассмотрение физической и геометрической нелинейности позво.хяет
дать исчерпывающую информацию о работе конструкции на всех этапах её существо-
вания: от момента захружения до момента потери несущей способности. К сожалению,
учет этих нелинейностей существешхо усложняет решение задачи. Энергия деформа-
ции физически нелинейной системы не является квадратичной формой. Вследствие этого
не выполняется принцип независимости действия сил и фундаментальные теоремы ли-
нейной механики С большой наглядностью эта проблема проявляется в области устой-
чивости сложных статически неопределимых стержневых систем. В решении таких за-
дач обычно ограничиваются рассмотрением плоских упругих рам, испытывающих до
потери устойчивости лишь безмоментное напряженное состояние (нагрузка приклады-
вается в узлах, все стержни идеально прямые).
Часто для расчета физически нелинейных стержневых систем используется гипо-
теза нелинейно-упругого материала, когда диаграмма а — е для разгрузки совпадает с
диаграммой -Е для загружения. Дополнительно заметим, что в условиях активной
деформации поведение нелинейного упругого тела и упругопластического тела неотли
чимы. Сильным упрощением решения физически нелинейных задач является примене-
ние гхшотез метода предельного равновесия, здесь не учитываются этапы деформиро
вания, предшествующие развитию и образованию пластических шарниров. Существу-
16
ют две особенности, характеризующие условность пластического шарнира: в месте по-
явления пластического шарнира кривизна изогнутой оси элемента равна бесконечнос-
ти; при совместном действии сжатия и изгиба пластический шарнир может образовать-
ся только у стержней нулевой длины - если длина стержня не равна нулю, происходит
потеря его несущей способности задолго до момента образования пластического шар-
нира Эти две важные условности необходимо иметь в виду при применении модели
пластического шарнира в реальном проектировании, особенно при знакопеременных
нагрузках.
В железобетонных конструкциях под нагрузкой возникают трещины, в процессе
развития которых повышается деформативность их. Появление трещин в бетоне обус-
ловлено малой прочностью его на растяжение Наличие трещин в растянутой зоне же-
лезобетонных конструкций является дополнительным специфическим проявлением
нелинейности этих конструкций, создающим дополнительные специфические пробле-
мы в теории их расчета.
В теории ползучести математические методы решения задач сильно отличаются
от методов линейной теории и теории пластичности.
Ползучесть существенно проявляется в расчетах железобетонных конструкций.
В условиях линейной ползучести, когда все стержни изготовлены из одного материала
и одинаково работают па растяжсние-сжатие, стагически неопределимую систему рас-
считывают как обычную упругую. Если же ползучесть разных стержней описывается
различными линейными операторами, то раскрытие статической неопределимости осу-
ществляется решением системы интегральных уравнений, и в общем случае чрезвы-
чайно громоздко. Наличие трещин даже в условиях линейной ползучести требует со-
здания специальных методов расчета стержневых систем. Для систем, составленных из
элементов, подчиняющихся различным линейным законам деформирования общего вида,
но инвариантным во времени, можно применять символический метод; последний нельзя
применять в случае неинвариантных во времени уравнений деформирования отдель-
ных стержней, так как в этом случае не выполняется условие коммутативности произ-
ведения операторов.
В решениях нелинейных задач теории ползучести следует с осторожностью отно-
ситься к методу конечных элементов, который эффективен при квадратичных формах
функционала энергии. При учете физической и геометрической нелинейности необхо-
димо интегрировать степенные или тригонометрические зависимости от взаимных про-
изведений сплайн-функций. Это весьма трудоемкая и не всегда реализуемая в замкну-
том виде процедура. Кроме этого, свою погрешность в результаты расчета вносит по-
шаговая процедура на временных интервалах Дту = ту+1 - Tj, на которых фиксируют-
ся напряжения и вычисляются деформации ползучести. Следовательно, условия равно-
весия, существовавшие в момент времени , разрушаются к моменту времени гу+1 за
счет деформаций ползучести. В момент времени тусловия равновесия восстанавли-
ваются, но уже за счет другого типа деформаций - упругих Другими словами, парал-
лельно используются две противоположные предпосылки отказ от условий равновесия
при расчете деформаций ползучести, а также отказ от принципа суперпозиции; затем
восстановление условий равновесия упругими деформациями и использование прин-
ципа суперпозиции при декларировании его невыполнимости. Перечисленные обстоя-
17
тельства дают погрешность в вычислениях, не имеющих опоры на действительные урав-
нения равновесия
Вместе с тем, следует указать что метод конечных элементов (МКЭ) является вы-
сокоэффективным методом решения нелинейных задач строительной механики и тео-
рии упругости. Он нашел применение в отдельных методиках расчета железобетонных
конструкций, реализованных в последние годы в трудах Сегалова А.Е., Брусенцова Г.Н.,
Балана Т.А, Ерышева В.А., Клованич С.Ф , Петрова А.Н., Ярина Л.И., Крылова С.Б.,
Ngo D., Scordelis А.С Ю Bazant Z Р. и других ученых. Опыт указанных исследователей
показывает целый ряд особенностей и трудностей использования МКЭ в нелинейных
расчетах железобетонных конструкций. При шагово-итерационной процедуре вычис-
лений сходимость процесса ухудшается с ростом напряженно-деформированного со-
стояния конструкций Это является следствием развития трещин и нелинейных свойств
бетона и арматуры даже при кратковременных нагрузках. При высоких уровнях загру-
жений простой итерационный процесс сходится плохо; проявляются скачкообразное
снижение жесткости конечных элементов, неучет передачи сдвига через трещину, плас-
тические деформации арматуры. После образования трещин часто используется услов-
ный прием, состоящий в определении модуля сдвига (G' = J3G; (3 = 0,125 4- 0,5) воле-
вым порядком
Известно также, что в общем случае на границах конечного элемента производные
искомой функции в направлении перпендикулярном границе имеют разрывы; сама фун-
кция имеет изломы, либо разрывы. Это является одним из главных источников погреш-
ностей МКЭ Способы устранения этих недостатков имеют ограничения При ползуче-
сти эффективность использования МКЭ в задачах расчета железобетона существенно
уменьшается.
Из вышесказанного вытекает естественный вывод, что развитие теории расчета
железобетонных конструкций должно осуществляться параллельно с развитием МКЭ.
Теория железобетона должна использовать в перспективе все преимущества метода ко-
нечных элементов; последний оперирует с рационально подобранными структурами
данных, которые автоматически могут формироваться из базы данных о механических
свойствах конструкций и их геометрии.
Специальные модели нелинейного деформирования железобетона должны сфор-
мировать базу физико-механических данных для различных типов конструкций. Эта
база данных может быть получена на основе интегрального модуля деформаций, экви-
валентного модуля деформаций других моделей получения жесткосгных характерис-
тик сечений и отдельных конструкций.
В перспективе развития методов расчета статически неопределимых сложных же-
лезобетонных конструкций можно будет получить ясные ответы на два вопроса: пер-
вый - о несущей способности конструкции, рассчитанной нелинейно; второй - об отли-
чии параметров расчета, даваемых широко используемой линейной моделью, в сравне-
нии с данными нелинейного расчета.
В последние годы интенсивно разрабатываются методы расчета нелинейных кон-
струкций на основе конечно-разностной (сеточной) аппроксимации дифференциальных
уравнений равновесия с последующим использованием процедур шагового нагруже-
ния; метод сеточной аппроксимации позволяег учитывать переменность геометрии се-
чения в процессе нагружения. Сравнение результатов (кратковременное загружение)
нелинейных расчетов с аналогичными, полученными с помощью метода конечных эле-
18
ментов, показывает значительные расхождения в перемещениях конструкций 1184]: рас-
чет с использованием прохраммы «ЛИРА» уже на первом, по сути линейном таге, уво-
дит расчет в направлении секущего модуля, а не касательного модуля (как установлено
процедурой расчета).
На втором этапе нормативных расчетов конструкция расчленяется на отдельные
элементы на основании принципа освобождаемости от связей, и производится расчет
каждого элемента конструкции. В большинстве своем нормативные методы расчетов
отдельных элементов считаются нелинейными, и в этом выявляется противоречие пер-
вого и второго этапов расчета.
В теоретических моделях второго этапа расчетов можно выделить пять основных
типов моделей:
1 - линейные;
2 - нелинейные, упругопластические, с трещинами;
3 - основанные на методе предельного равновесия;
4 - эмпирические;
5 - смешанные, основанные на совместном использовании некоторых предыду-
щих пунктов.
В нижеследующих парахрафах приводятся примеры использования указанных
моделей в нормативных расчетах.
§ 1.2. Некоторые линейные нормативные модели
Линейные модели применяются в нормативных методиках как самостоятельно,
так и в совместном использовании с другими моделями. Нормы некоторых стран ранее
были основаны на линейных моделях, вытекающих из применения законов Гука. В на-
ших нормах расчета устойчивости деревянных конструкций используются известные
решения из сопротивления материалов.
Линейная модель заложена в основу расчетов устойчивости каменных конструк-
ций. Основная теоретическая модель устойчивости кирпичной кладки вытекает из фор-
мулы Эйлера
= (1-20
рассматривающей случай центрального сжатия элемента. Профессор Онищик Л.И. ввел
в эту формулу значение переменного модуля упругости для кирпичной кладки. Он ис-
пользовал формулу касательного модуля деформаций:
„ da
(1-2.2)
as
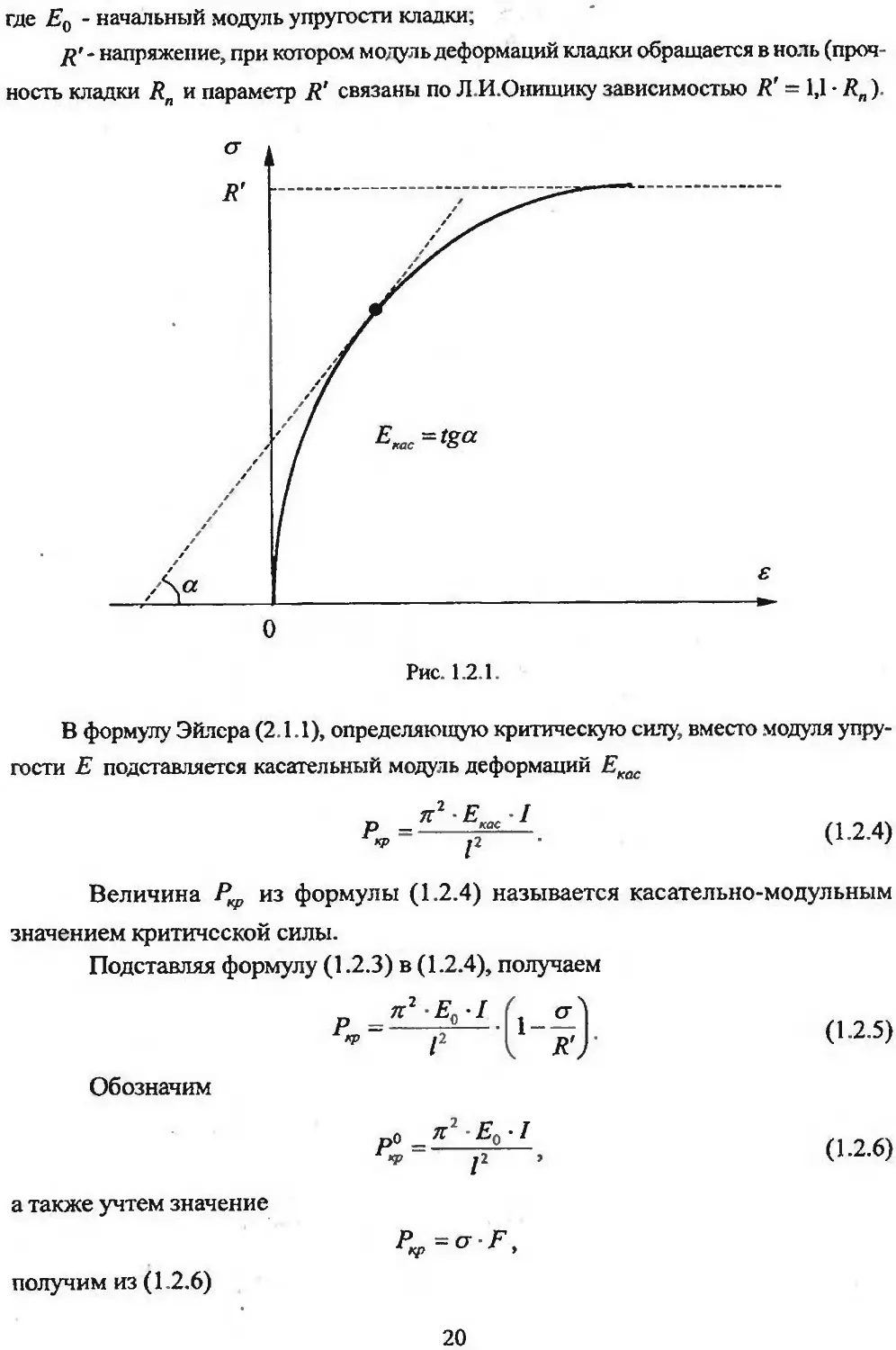
где Екас - касательный модуль деформации, определяемый с помощью диаграммы ст - s
(рис.1.2.1)
На основании обширных экспериментальных исследований Л.И.Онищик предло-
жил следующую формулу для касательного модуля
1
Екас
о
К ’
(1.2.3)
19
где Eq - начальный модуль упругости кладки,
7^'- напряжение, при котором модуль деформаций кладки обращается в ноль (проч-
ность кладки Rn и параметр R' связаны по Л.И.Онищику зависимостью R' = 1,1 • Rn).
В формулу Эйлера (2 1.1), определяющую критическую силу, вместо модуля упру-
гости Е подставляется касательный модуль деформаций Екас
Pv = n2'EtT : l (1-2.4)
Величина из формулы (1.2.4) называется касательно-модульным
значением критической силы.
Подставляя формулу (1.2.3) в (1.2.4), получаем
Обозначим
р° _ ‘
*Р р i
(1.2.5)
(1-2.6)
а также учтем значение
получим из (1.2.6)
20
(1-2.7)
Введем понятие коэффициента продольного изгиба с помощью выражения
где произведение F R' являегся величиной, характеризующей прочность сечения кир-
пичной кладки.
Разделим выражение (1 2 7) на прочность сечения F R , получим
откуда
<Ро
ср = —-—
1 + ^0
(1.2.9)
На основании формулы Онищика Л.И (12 9) получены численные значения коэф-
фициента продольного изгиба <р, приведенные в табл 18 СНиП П-2-81 «Каменные
и армокаменныс конструкции».
Внсцентрснное сжатие является основным видом загружения каменных конструк-
ций. На внецентренное сжатие работают стены, столбы, своды, карнизы и т. п Экспери-
ментальные исследования показывают, что внецентрепно сжатые элементы разруша-
ются при значительно более высоких нагрузках, чем это получается по расчетным фор-
мулам сопротивления материалов. Эти расхождения доходят до 1,5-2,0 раз против вы-
численных теоретических величин. С одной стороны, это расхождение объясняется
криволинейностью эпюры напряжений, тогда как формулы сопротивления материалов
основаны на линейной эпюре напряжений с постоянным модулем упругости С другой
стороны, эксперименты показали, что при разрушении деформации кладки значитель-
но больше таковых при разрушении от центрального сжатия. Это объясняется неодно-
родностью напряженного состояния сечения; менее напряженная часть сечения помо-
гаег работе более напряженной части.
Расчет внецентренно сжатых каменных конструкций весьма сложен, поэтому их
рассчитывают по эмпирическим формулам, основанным на ряде допущений Растяну-
тая зона кладки исключается из работы сечения. В сжатой зоне, по аналогии с теорией
железобетона, принимается прямоугольная эпюра напряжений. Центр тяжести сжатой
зоны сечения и прямоугольной эпюры напряжений совпадают с осью действия внеш-
ней расчетной нагрузки
N = mg (р} R Ас-а, (1.2.10)
где mg коэффициент, учитывающий влияние прогиба сжатых элементов на их несущую
способность при длительной нагрузке вследствие ползучести,
- коэффициент продольного изгиба,
R - расчетное сопротивление кладки сжатию;
Ас - площадь поперечного сечения сжатой кладки элемента,
со- коэффициент, учитывающий возможность повышения расчетною сопротивле-
21
ния сжатой части сечения за счет влияния менее напряженной части сечения (зачастую
6) ~ 1)
Остановимся более подробно на способе получения коэффициента . Коэффици-
ент <р} должен учитывать снижение несущей способности кирпичного элемента вслед-
ствие двух факторов: наличие эксцентриситета е0 приложения силы //; влияния гибко-
сти элемента.
В нормах используется иной прием Коэффициент определяется как среднее
арифметическое между коэффициентом продольного изгиба (р для стержня с высотой
сечения h (все сечений) и ^для стержня, имеющего сечение равное сжатой части сече-
ния
(1.2 11)
2
Такой расчет является весьма условным
Для прямоугольного сечения внецентренно сжатого элемента формула (1.2.10) за-
писывается в виде
где е0 - эксцентриситет приложения сжимающей силы относительно центра тяжести
сечения,
А - площадь сечения элемента.
Если принять А = b • h >то площадь сжатой части сечения
Ле = лГ1-^"|
I h )'
Коэффициент со в этом случае записывается в виде

< 1,45.
Некоторые линейные модели сопротивления материалов используются в качестве
частных методик Евростандартов. Например, задача о деформировании сжатого стерж-
ня, имеющего начальную погибь, рис. 1.2.2. Исследуемый стержень шарнирно оперт по
концам и в ненагруженном состоянии искривлен. Начальное искривление задается в
виде некоторой известной функции
Л X
У о =foSin—
(1.2 12)
где /0 - прогиб в середине незагруженного стержня, рис. 1.2.2, а). Сам вид функции
(1.2 12) для последующего исследования не имеет большого значения.
К точке М первоначально искривленного стержня прикладывается сжимающая
продольная сила, линия действия которой совпадает с осью Ох (рис. 1.2.2,б). Под дей-
22
станем этой силы стержень получает дополнительный прогиб у(х). Дифференциаль-
ное уравнение изгиба упругого стержня

записывая для значения момента
ЛГ = Р(уо + у),
получим
ЕУ = -Р(у04-у).
Рис. 1.2.2.
После преобразования имеем
Вводя обозначение
EJ'
имеем основное разрешающее дифференциальное уравнение задачи
r + Vy = -i2y„. (1.2.13)
23
Решение неоднородного дифференциального уравнения (1.2.13) записываем в виде
У = У1 +У2’
где у, - общее решение однородного дифференциального уравнения, а у2- частное ре-
шение уравнения (1.2.13). Решение yt записываем в виде
У] = С, coskx + С2 sinkx
частное решение у2 равно:
Л X
y2=f sin—.
Отсюда
Л X
У-У1+У1=^1 coskx + С2 sinkx + f sin-j-. (1.2.14)
Для нахождения констант Сх и С2 запишем граничные условия
У = 0 ; при х = 0, х=/-
С учетом этого получаем два уравнения
л о
О = С. cos ко + С, sinko + f sin--
1 2 / ’
О = Cj coskl + C2 sink! + f зтл.
Из первого уравнения имеем С] — 0.
Второе уравнение
С2 sin к! = 0
показывает, что общее решение
У] -С2 sinkx
существует только при значении Р — Рэ. Если же Р < Рэ, то общее решение у, отсут-
ствует. При этом в формуле 1.2.14 остается только последнее слагаемое
Л X
y = fsin—. (1.2.15)
Для нахождения константы f подставляем (1.2.15) в дифференциальное уравне-
ние задачи (1.2.13) и получаем
.л2 . ях . лх . лх
-f^sm-p + k fsm— = ~k fQsin—,
откуда находим дополнительный прогиб f под действием сжимающей силы Р
24
или
(1.2.16)
5--1
Полный прогиб в среднем сечении при Х = Т равен
(1.2.17)
J ср J р
На рис. 1.2 3 показан график зависимости между прогибом f и силой Р
в безразмерных величинах —------, где г - радиус инерции сечения
Рэ г
F - площадь поперечного сечения
г =
Кривые построены для различных значений начального прогиба —.
р
Обратим внимание, что все кривые асимптотически устремляются к величине —- = 1.
Иными словами, когда сжимающая сила Р приближается к силе Рэ, прогиб f стремится
к оо. При малых значениях начальной погиби 2Р. кривые располагаются вблизи оси
ординат. Все стержни с разными значениями — имеют одну критическую силу Рэ.
25
Формулы (1 2 16) и (1.2.17), соответствующие принятой модели стержня, показан-
ной на рис. 1.2.2, нашли широкое применение в нормативной практике. Вместе с тем,
следует указать, что именно с практической точки зрения они имеют три существенных
дефекта.
Первый дефект. Материал стержня предполагается нешраниченно упругим, хотя
таких материалов в строительной практике не применяют
Второй дефект Модель имеет внутреннее противоречие, заключающееся в том,
что она построена на приближенном выражении для кривизны (геометрическая линеа-
ризация), предполагающем наличие только малых прогибов В то же время на рис. 1.2.3
прогибы показаны стремящимися к бесконечности, что противоречит приближенному
выражению для кривизны При малых значениях — кривые сначала тесно расположе-
ны вблизи оси ординат
а затем резко устремляются к горизонтальной линии
— = 1. Это создает следующие неудобства при численной реализации. Незначительное
^3
увеличение сжимающей силы вызывает значительное приращение прогибов стержня
что приводит к неустойчивости вычислительной процедуры, основанной на использо-
вании формулы (1.1.17).
Рис 1 2.4.
Третий дефект Сжато-изогнутый
упругий стержень не имеет критичес-
кой силы и никогда не теряет устойчи-
вость Действительный характер диаг-
раммы «сила-прогиб» имеет иной вид,
чем показанный на рис. 1.2.3. Решение,
полученное на основе точного прибли-
жения для кривизны показывает отсут-
ствие критической силы у сжато-изог-
нутого упругого стержня, а также отсут-
ствие бесконечного нарастания проги-
бов, рис. 1.2.4. В любой точке кривых
1, 2, 3 может действовать возмущаю-
щая сила, приводящая к дополнитель-
ному перемещению точки В в положе-
ние (рис. 1.2.4). Однако это переме-
щение исчезнет после окончания дей-
ствия возмущающей силы. Если же воз-
мущающую силу не убирать, то новая
кривая состояний 3' будет находиться
вблизи кривой 3, рис. 1.2.4.
26
§ 1.3. О модели предельного равновесия. Смешанные модели
При расчете железобетонных конструкций по методу предельного равновесия счи-
тается, что в сечении изгибаемого элемента образуется пластический шарнир («прин-
цип пластического разрушения»); напряжения в бетоне и арматуре достигают предель-
ных значений одновременно, рис. 1.3.1.
Рис. 1.3.1.
Бегон растянутой зоны не работает, его сопротивление на растяжение принимает •
ся равным нулю; напряжения в бетоне сжатой зоны принимается равным сопротивле-
нию бетона сжатию Rb; напряжения в арматуре достигают предела текучести Rs и R's.
При использовании такой модели нет необходимости использовать гипотезу плоских
сечений и диаграммы <з — £ для бетона и стали Модель пластического шарнира зало-
жена в нормативные методики расчета изгибаемых и сжатых железобетонных элемен-
тов Для этой модели составляются два уравнения равновесия
M = Rb b-x^-O.S-x^R^A^^-a'),
где М - внешний момент.
Момент внутренних сил определяется относительно центра тяжести растянутой
арматуры.
Как уже отмечалось, кривизна оси элемента в таком сечении равна бесконечности.
Заметим также, что данная модель сечения в качестве пластического шарнира противо-
речит «деформационной модели сечения».
Для расчетов сжатых колонн помимо модели пластического шарнира дополнитель-
но привлекается линейная модель предыдущего параграфа, с помощью которой нахо-
дится прогиб середины колонны сжато-изогнутого стержня, рис. 1.3.2 В нормах эта рас-
четная схема сжато-изогнутого стержня заменяется другой расчетной схемой - внецен-
тренно сжатого стержня шарнирно опертого по концам, рис. 1.3.3.
27
Сила W приложена с равными эксцентриситетами е0 по концам
М
е0 = —,
0 N
где М - максимальный изгибающий момент по длине I сжато-изогнутого стержня,
рис. 1.3.2.
Замена расчетной схемы сжатоизогнутого стержня другой расчетной схемой вне-
центренно-сжатого стержня проведена без должного обоснования; критические силы
таких стержней существенно могут различаться в упругопластической стадии.
Основным расчетным сечением внецентренно сжатого железобетонного элемен-
та, определяющим его несущую способность, принимается сечение в середине расчет-
ной длины /0, точка О. Предполагается, что в сечении образуется пластический шар-
нир, рис.1.3.1.
Расчег устойчивости сжатого железобетонного элемента осуществляется путем
увеличения эксцентриситета е0 с помощью коэффициента т]. То есть продольная сила
N прикладывается к среднему сечению элемента с эксцентриситетом е0 • т]. Величину
коэффициента т/, учитывающего влияние прогиба на увеличение значения эксцентри-
ситета продольного усилия е0, рекомендуется определять по формуле
(13.2)
Ncr
где Ncr - критическая сила.
28
Следовательно, полный прогиб в среднем сечении О, рис. 1.3.3, равен
ео
е°'77=1
хсг
Для анализа этой формулы обратимся к выражению (1.2.16)
(1.3.3)
(1.3.4)
1-------
полученному для прогиба в среднем сечении упругого стержня, имеющего начальную
погибь f0, рис. 1.2.2,а.
Сравнивая правые части формул (1.3.3) и (1.3.4), выявляем их полную тождествен-
ность. Но формула (1.3.3) в нормах записана для внецентренно сжатого стержня, а со-
ответствует расчетной схеме стержня, имеющею начальную погибь, рис. 1.2.2,а. Други-
ми словами, происходит- новая замена расчетных схем пугем замены начальной погиби
/0 эксцщггриситетом е0 и введением гипотезы, что эта начальная погибь совпадает по
величине с эксцентриситетом приложения силы N. Критические силы, соответствую-
щие отмеченным расчетным схемам стержней, существенно различаются в упругопла-
стической стадии работы материала.
Критическая сила Эйлера формулы (1.3.3) в нормах
называется условной критической силой. Напомним, что
критическая сила Эйлера для центрально сжатого упругого
стержня (рис. 1.3.4) определяется выражением
„ „ n2-EJ
P, = N,=------2---. (1.3.5)
*0
Проанализируем структуру сил, определяющих [148]
критическую силу Ncr. В железобетонном стержне совме-
стно работают два материала, что позволяет написать
^cr = Mh + Ns= + . (1.3.6)
‘0 A)
Критическая сила бетонной части сечения равна
Nb = *—Ef--±. (1.3.7)
*0
Для учета физической нелинейности бетона, его пол-
зучести и других факторов в формуле Эйлера (1.3.7) (упру-
гий стержень) принимается
Рис. 1.3.4.
29
тг2=0,9-
1
h
где h - высота поперечного сечения железобетонной колонны.
ео
Затем отношение ~ заменяется коэффициентом 8е
-J-+1,
0,1 + 5, J’
а критическая сила бетонной части сечения (1.3.7) записывается в виде
п2 = 0,9-
—!— + 11-0,9.
0,1 + <5е )
Критическая сила арматурного каркаса равна
It
В этой формуле предложено значение заменигь цифрой 8
Л7 ~-ь.-ь
1УЬ ,2
10
N =-- s
I2
Подставляя формулы (1.3.10) и (1.3.12)
в
$
(1.3.6), записываем
(1-3.8)
(1.3.9)
(1.3.10)
(1.3.11)
(1.3.12)
N =^Ъ 'ь
Сг г2
10
ОД + 8е
1 0,9 +
8E,-JS
%
(1.3.13)
Обозначая отношение модулей упругости стали и бетона
а^.
Еь
а также вынося цифру 8 за скобки и проводя некоторые округления, имеем
N
СГ .2
‘0
0,11
(1.3.14)
ь
€
Для учета влияния ползучести в последнюю формулу вводится коэффициент <pg
1 П Ме
+ (1.3.15)
м
где Р - коэффициент;
Л/ - момент от действия постоянных, длительных и кратковременных нагрузок;
30
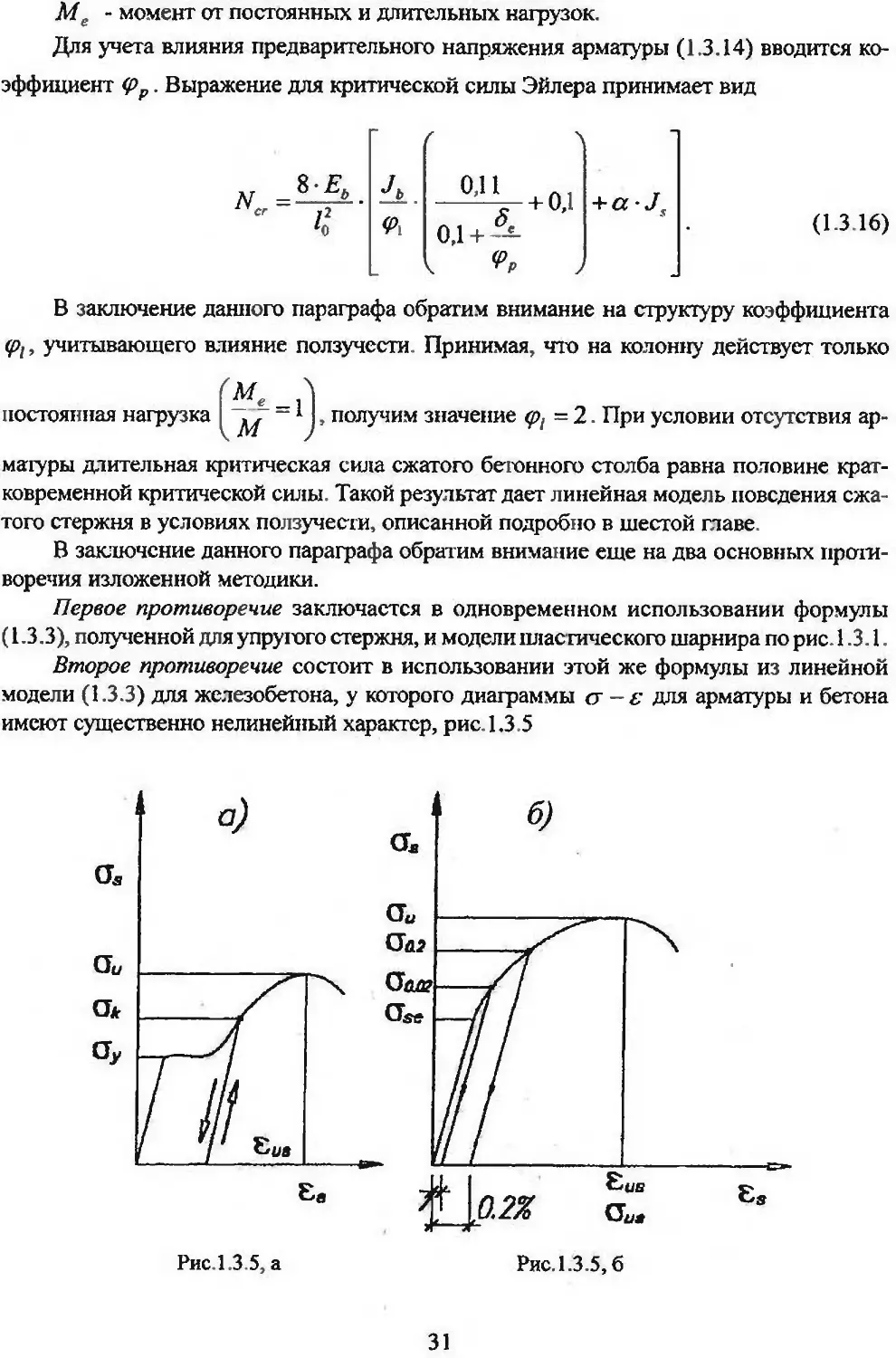
Ме - момент от постоянных и длительных нагрузок.
Для учета влияния предварительного напряжения арматуры (1.3.14) вводится ко-
эффициент <рр. Выражение для критической силы Эйлера принимает вид
0,11
0,1+ i
г 0,1
(1.3.16)
Л
В заключение данного параграфа обрагим внимание на структуру коэффициента
<рх, учитывающего влияние ползучести. Принимая, что на колонну действует только
постоянная нагрузка
(М
— — = I I
, получим значение = 2. При условии отсутствия ар-
магуры длительная критическая сила сжатого бетонного столба равна половине крат-
ковременной критической силы. Такой результат дает линейная модель поведения сжа-
того стержня в условиях ползучееги, описанной подробно в шестой главе.
В заключение данного параграфа обратим внимание еще на два основных проти-
воречия изложенной методики.
Первое противоречие заключается в одновременном использовании формулы
(1.3.3), полученной для упругого стержня, и модели пластического шарнира по рис. 1.3.1.
Второе противоречие состоит в использовании этой же формулы из линейной
модели (1.3.3) для железобетона, у которого диаграммы <у -е для арматуры и бетона
имеют существенно нелинейный характер, рис. 1.3.5
31
растяжение
сжатие
Rbt
&ubt
&Ы
Рис.1.3.5, с
§ 1.4. Упругопластические модели
Упругопластические нелинейные модели расчетов сжатых железобетонных колонн
использовались ранее в нормах некоторых стран. Теоретической основой таких моде-
лей является предложение Е.Хвалла, реализованное до уровня практического использо-
вания К.Ежеком для идеального упругопластического материала, рис. 1.4.1. Впослед-
ствии эта модель реализовалась в работах Никитина Г.В., Ржаницына А.Р., Гениева Г.Н.,
А.Хабеля и О.Баумана с учетом трещин в растянутой зоне сечения.
Лолейт А.Ф. и Мурашев В.И. учитывали диаграмму Прандтля для сжагой зоны
бетона в расчетах изгибаемых элементов, а также наличие трещин в растянутой зоне.
Эти работы заложили предпосылки «деформационной модели сечения», принятой
сейчас в Евростандартах. Рассмотрение отмеченных теоретических решений задачи
выявляет ряд особенностей поведения железобетонных элементов под нагрузкой, под-
тверждаемых экспериментами и важных д ля развития нелинейной теории железобетона.
Ниже приводится схематичное решение для сжатоизогнутого элемента, являюще-
еся основным для нормативных построений. Внецентренное сжатие колонны является
базовой моделью нормативных методов, к которой приводится ряд других расчетных
схем сжатых конструкций, позволяющей учитывать главные факторы расчета и отбра-
сывать второстепенные факторы. Эго имеет также дальнейшее значение для учета ве-
роятностного характера факторов в нормативных моделях.
32
Итак, рассмотрим внецентренно сжатый стержень; сжимающие силы р приложе-
ны с одинаковыми эксцентриситетами е Концы ст ержня могут свободно перемещать-
ся и поворачиваться при деформировании под нагрузкой, рис 1.4.1 Прогиб в середине
длины стержня обозначен через f.
Рис. 1.4.1
Рассмотрим сначала напряженно-деформированное сечение упруго-пластическо-
го стержня постоянного прямоугольного сечения Оказывается необходимым рассмат-
ривать пять случаев распределения зон пластичности по длине стержня, рис. 14.1, удов-
летворяющих диаграмме Прандгля. В случае I материал стержня удовлетворяет закону
Гука. Потеря устойчивости стержня в этом случае произойти не может В случае II зона
пластичности развивается с вогнутой стороны на средней части длины стержня. В слу-
33
чае Ш пластические деформации развиваются с двух сторон на средней части длины
стержня. В случае IV зона пластичности развивается по всей длине стержня со стороны
наиболее сжатых волокон. В случае V пластические деформации распространяются на
зсю длину стержня с вогнутой стороны и на среднюю часть стержня с выпуклой сторо-
ны. Наконец, в случае VI происходит развитие пластических деформаций с выпуклой и
вогнутой сторон стержня по всей его длине.
На поле критических зависимостей «длина-сила-эксцентриситет» каждый случай
соответствует определенному соотношению указанных величин Р,1,е.
Аналитическое решение задачи устойчивости стержня в упруго-пластической ста-
дии для случаев И-VI является сложным в математическом отношении ввиду необходи-
мости интегрировать дифференциальное уравнение на каждом участке пластичности и
учитывать условия стыковки участков между собой. Поэтому в задачах упруго-пласти-
ческой устойчивости широко используется приближенное представление (аппроксима-
ция) уравнения изогнутой оси стержня какой-либо подходящей кривой, а также произ-
водится обоснование этого приближенного представления.
Ниже приводится одно из таких приближенных решений, используемых в практи-
ке составления норм расчета устойчивости конструкций. В приближенном решении
оказывается возможным рассматривать напряженно-деформированное состояние толь-
ко одного среднею сечения. 11усть это сечение является прямоугольным.
Рассмотрим случай односторонней текучести в среднем сечении стержня, рис. 1.4.2.
Рис. 1.4.2.
На основании принципа освобождаемости от связей отбрасываем сначала связи,
рис. 1.4.3. Из трех уравнений равновесия находим, что опорные реакции Л15 R2, R3
равны нулю. Далее разрезаем стержень по сечению С пополам и отбрасываем верхнюю
часть.
34
Рис. 1.4.3.
Сила Р1 является главным вектором эпюры нормальных напряжений; момент Л/1
является главным моментом эпюры нормальных напряжений. Поперечная сила Q1
в среднем сечении равна нулю.
При анализе напряженно-деформированного состояния сечения используются две
гипотезы: во-первых, гипотеза плоских сечений; во-вторых, каждое волокно в сечении
считается имеющим диаграмму ст - £ в виде диаграммы Прандтля. На основе этих двух
гипотез находятся величины главного вектора Р1 и главного момента Л/1.
Модуль главного вектора Р1 эпюры нормальных напряжений равен
Р' =b-h-vm-^b\a2 + am)\h-a\ (1.4.1)
Из подобия треугольников на рис. (1.4.2) записываем
(h-a) с ’
откуда
h-a
°2+°т=°т--------. (1.4.2)
с
35
Окончательно находим
(1 4.3)
гдеРт=& h-am.
Главный момент эпюры нормальных напряжений равен
М*
h 1
2 3
где
- плечо равнодействующей силы треугольника напряжений а{, а2,
относительно центра тяжести сечения 0, рис. 1.4.2.
Записываем два уравнения равновесия половины стержня, отделенной средним
сечением
(14 5)
(1 4.6)
где
Р = Р -L.b.a
/П гъ гп
2 с
Из первого уравнения равновесия найдем значение упругой зоны с
12
(1-4.7)
1
2 “ (Р„~Р)’
(1.4.8)
которое подставим во второе уравнение равновесия
р.(е+/)=1.Л.(Р„-/>)-!.(
откуда
(1.4.9)
P-(e+f)=(Pm-P)~^
О
В уравнение равновесия (1.4.9) входит прогиб f стержня в среднем сечении; этот
прогиб выразим через параметры деформированного состояния среднего сечения Для
этого используем две гипотезы. Одна из них - гипотеза плоских сечений, отмечалась
выше С ее помощью кривизна стержня в рассматриваемом сечении записывается в виде
1 £у + £9
(£=- = ---=
р h с
(1 4 10)
где се - кривизна, р - радиус кривизны.
Формула (1.4.10) получается на основе геометрических соотношений. Вторая ги-
потеза заключается в аппроксимации уравнения изогнутой оси стержня синусоидой
36
j = . (1.4.11)
С помощью уравнения (1.4.11) находится кривизна изогнугой оси, причем исполь-
зуется приближенное выражение для кривизны
d'y
ГО “ ““ “—-----------------------------------
2 ‘
(1 4.12)
В упругопластической стадии работы стержня потеря устойчивости происходит
при малых значениях прогибов, поэтому использование приближенного выражения для
кривизны является обоснованным.
На основании (1.4.11) и (1.4.12) кривизна изогнутой оси равна
я2 я-х
(1.4.13)
I '
I
В среднем сечении при х = — имеем
2
2 •
(1.4.14)
Сравнивая выражения (1.4.10) и (1.4.14), получаем
f
}' I1 с
откуда находим значение прогиба
Я С
Эту величину подставляем в уравнение равновесия (1.4.9)
h + 2-а
6 ’
(1.4.15)
V я с
откуда находим длину стержня, удовлетворяющую условиям равновесия
(1 4.16)
Z2 (Р„~Р h + 2-а У е
I Р 6 J
Подставляем в (1.4.17) значение с из (1.4.8), Ихмеем
2
(1.4.17)
2-1
2
Р-Р
т__
р
h + 2-а
--------е
6
(1.4.18)
т
1
Вводим обозначения
, 1 , я2
к - b- Е• т---
2 (Рм-
^1=(Л-а) ;
(1.4 19)
\ Рт~Р (, \
<°2=6--F (Л + 2а)"е-
37
Отсюда
I2 =k<px{a)-<p2(d).
(1.4.20)
Выражением (1.4.20) определяют равновесные состояния стержня. Задача состоит
в отыскании условия потери несущей способности. На рис. 1.4.4. линией 1 представлена
диаграмма «нагрузка-прогиб» для упруго-пластического стержня.
Точка максимума кривой 1 соответствует критическому состоянию упругопласти-
ческого стержня - моменту потери устойчивости. Линия 2 на рис. 1.4.4. характеризует
поведение упругого внеценгренносжатого стержня, не имеющего потери устойчивос-
ти. В точке у, характеризуемой силой Ру, у упругого стержня в наиболее нагруженном
волокне напряжения достигают предела текучести сут (устойчивая прочность). Отли-
чие значений сил Ру и Р^ является существенным. При использовании силы Ру в каче-
стве предельной происходит существенное недоиспользование несущей способности
элемента.
Рассмотрение кривой 1 в научной литературе носит название «теории устойчивос-
ти второго рода». Критическая сила Р^ характеризуется критическим прогибом f^>.
Величина этого прогиба мала в сравнении с длиной I, и при нахождении обоснова-
но использование приближенного выражения для кривизны.
Кривая / на рис. 1.4.4 называется кривой состояний стержня. При загружении стер-
жня по линии OYK он находится в устойчивом состоянии. В максимальной точке К
происходит потеря несущей способности упруго-пластического стержня. После точки
К стержень является неустойчивым.
38
Аналитический критерий потери устойчивости записывается в виде
dP
~=0
df
(1.4.21)
При этом длина / стержня считается фиксированной.
Задачу отыскания критического состояния
стержня можно поставить иначе. Фиксируется ве-
личина силы Р. В этом случае кривая «длина-про-
гиб» имеет вид, показанный на рис 1 4 5
Для этого случая условие потери устойчивос-
ти имеет вид
<и _п
^-0. (1.4.22)
Заметим, что применение условий критичес-
кого состояния в виде (1 4 21) и (1.4.22) приводит
к тождественным результатам
Если длина стержня выражена через некото-
рый параметр а, то условие потери устойчивости
записывается в виде
da
(1.4 23)
Па основании (1.4.23) и выражения для длины / из (1.4.20) записываем
2J ~ = К -<р2+(р\-(р^ (1.4 24)
da
Отсюда условие критического состояния имеет вид
<р\ '<Рг + Pi 'Ч>\ =0- (1-4.25)
Производные (р\ и (р\ находим из (1.4.19)
р,(а) = (й-а)2;
^’(а) = -2-(й-а);
1 Р —Р
Ыд)=7 т '(h + 2-a)-e-t (1.4.26)
о Р
,/ ч 1 Рт -Р
^2^~з Р '
Окончательно условие критического состояния запишем в виде
Lfyf.(A + 2.a)-e =0. (1.4.27)
При значении величин силы р и эксцентриситета еиз уравнения (1.4.27) находит-
39
ся значение критического параметра а^. Эти значения а*?, Р у. е - подставляются
в (1.4.18), и находится критическая длина стержня .
Критическое состояние стержня характеризуют три связанные между собой вели-
чины: е - эксцентриситет приложения нагрузки; Р - величина сжимающей силы; -
длина.
Аналогичным образом выводятся аналитические зависимости для других случаев.
Для стержня прямоугольного поперечного сечения эти зависимое™ на рис. 1.4.6
представлены в относительных величинах в трафической форме.
, I
По оси абсцисс отложена гибкость л = -, где г - радиус инерции прямоугольного
г
сечения в плоскости наибольшей жесткости
где Jz - момент инерции сечения относительно оси z;
F - площадь поперечного сечения.
По оси ординат отложен коэффициент продольного изгиба
где Рт - прочность центрально сжатого стержня.
Рв=М-(гя.
Вводится понятие относительного эксцентриситета формулой
е
m~k’
где к- ядровое расстояние сечения,
Wz- осевой момент сопротивления сечения
J, b-h3 2 b-h2
1 h/ 12 Л 6 •
Отсюда ядровое расстояние для прямоугольного сечения равно
k_Wt b-h2 1 Л
F 6 b-h 6‘
Проанализируем данные графика на рис. 1.4.6. На поле критических зависимостей
<ф-Л», рис. 1.4.6 каждому случаю распределения зон пластичности (1.4.1) соответ-
ствует определенное соотношение гибкостей и эксцентриситетов. Случаю I соотвст-
40
ствует кривая Эйлера для центрального сжатия. Случай II охватывает основную группу
средних и больших гибкостей. При больших эксцентриситетах располагается область
III. Случай IV находится в области малых гибкостей и эксцентриситетов. При больших
эксцентриситетах располагаются области V и VI случаев.
Обратим внимание натри особенности поведения кривых на рис. 1.4.6.
1. По мере увеличения эксцентриситета т кривые критических зависимостей
становятся не сильно зависимыми от гибкости.
2. При малых гибкостях и малых эксцентриситетах значения <р также не сильно
зависят от гибкости.
3. В начале графика при Л = 0 пластические зоны растяжения-сжатия смыкаются,
и образуется пластический шарнир (рис. 1.4.7); наступает исчерпание несущей способ-
ности элемента (нулевой длины) по прочности; кривизна элемента становится равной
бесконечности.
Следовательно, исчерпание несущей способности по прочности совпадает с поте-
рей устойчивости только для стержней нулевой длины. Если же длина стержня не равна
нулю, то его потеря несущей способности происходит только от потери устойчивости
в упругопластическои стадии.
Заметим, что в научных исследованиях по теории сооружений для расчета стати-
чески неопределимых конструкций зачастую используется понятие пластического шар-
41
нира по рис 1.4.7, при этом не учитываются его особенности, указанные в пункте 3. Тем
более недопустимым является использование модели пластического шарнира в задачах
исследования колебаний строительных конструкций. Возвращаясь к рассмотрению гра-
фика на рис. 1.4.6, отметим следующее обстоятельство, вытекающее из особенностей
2 и 3. Для стержней небольшой гибкости предельные силы по устойчивости мало отли-
чаются от предельных сил по прочности для стержней с нулевой гибкостью Естествен-
но, это отличие трудно заметить при проведении экспериментальных исследований.
Например, для железобетонных конструкций это отличие мало заметно при гибкостях
7 = 10 Эти обстоятельства вызывали в научней литературе оживленные дискуссии по
h
проблемам прочности и устойчивости строительных конструкций.
Рассмотрим еще два случая поведения упругопластических сжато-изогнутых стер-
жней. Первый случай учитывает влияние поперечной нагрузки, рис. 1.4 8.
Рис. 1.4.8.
42
Второй - наличие начального прогиба /0, рис 1.4.9. Методика решения задачи
данных случаях не сильно отличается от методики исследования внецентренно сжа-
эго стержня, поэтому опустим аналитические выкладки и остановимся лишь на основ-
ых результатах.
Кривые критических зависимостей (рис. 1 4 8 - рис.1 4.9) существенно отличают-
i от аналогичных для внецентренного сжатия тем важным обстоятельством, что при
16кости А = О они все сходятся в одной точке (р = 1. В этой точке в сечении элемента
аракгерна продольная эпюра продольных напряжений, равных пределу текучести,
ис.1.4.10, характеризуемая отсутствием изгиба.
Рис. 1.4.10.
43
В области малых и средних гибкостей критическая сила внецентренно сжатого
стержня существенно отличается от критической силы аналогичного, но сжатоизогну-
того стержня. В области малых гибкостей отличие составляет несколько раз.
Поэтому замена расчетной схемы внецентренно сжатого стержня расчетной схе-
мой сжатоизогнутого стержня должна производится с большой осторожностью в нели-
нейной стадии. Это обстоятельство должно учитываться также при проведении экспе-
риментов по сжатию колонн, имеющих начальные погиби.
Форма поперечного сечения оказывает существенное влияние на расположение
кривых (р - Л на поле критических зависимостей.
Для двутаврового сечения кривые лежат значительно ниже, чем для прямоуголь-
ника. Этого и следовало ожидать, так как прямоугольное сечение лучите приспособлено
для восприятия развивающихся по сечению пластических деформаций.
Кривые критических зависимостей «(р-т -Л», показанные на рис. 1.4 6, явля-
ются моделью для построения нормативных таблиц.
В заключении данного параграфа сделаем некоторые выводы.
Кривые критических зависимостей в упругопластической стадии, показанные на
рис. 1.4.6, позволяют сделать важные выводы о применимости подхода Эйлера в зада-
чах устойчивости. Рассмотрим нижнюю кривую трафика, характеризуемую эксцентри-
ситетом m = 4,0. Для гибкости Л - 50 коэффициент (р в предположении упругой ста-
дии работы стержня оказывается завышенным в 13 раз, по сравнению с упругопласти-
ческой стадией работы.
Для гибкости Я = 20 это завышение составляет 72 раза, для гибкости Я = 10 - 261 раз.
Эти сравнения оказываются целесообразными для анализа устойчивости сложных
стержневых систем, где в качестве основной модели устойчивости рассматривается
бифуркационная задача в смысле Эйлера, в которой рассматриваются плоские упругие
рамы, испытывающие до потери устойчивости лишь безмоментное напряженное со-
стояние. Причем в этой бифуркационной задаче, как правило, разыскиваегся лишь пер-
вое собственное значение.
Большая условность такого расчета устойчивости упругих сложных стержневых
систем не должна вызывать у проектировщиков иллюзии достоверности полученных
результатов по значению критических сил для системы в целом. Особенно эти сообра-
жения важны для расчетов устойчивости высотных зданий с их сложными технологи-
ческими нагрузками.
Высказанное замечание относится к любым строительным конструкциям, выпол-
ненным из материалов, не подчиняющихся закону Гука и имеющих нелинейные диаг-
раммы (7 - е .
§ 1.5. Теория ползучести бетона и длительное загружение
железобетонных конструкций
В теории ползучести железобетонных конструкций последовательно рассматри-
ваются три основных проблемы. Первая проблема состоит в построении уравнений
ползучести бетона при переменных (режимных) нагружениях. Вторая - в получении
решения уравнения ползучести. Третья проблема заключается в расчете железобетон-
ных конструкций при длительном загружении.
44
Первая проблема обстоятельно рассмотрена в трудах отечественных и зарубеж-
ных ученых. В последних работах Александровского С.В., Арутюняна Н.Х., Бондарен-
ко В.М., Васильева НИ., Гвоздева А.А., Прокоповича И.Е., Улицкого И.И., Щербакова
Е.Н. и их учеников построены уравнения ползучести бетона при различных режимах
загружения. Эти уравнения учитывают особенности длительного деформирования бе-
тона, в частности, явления быстронатекающей ползучести.
В работах Александровского С.В. и его учеников предложено и обосновано урав-
нение нелинейной ползучести
£(= + 'к(t,T)'dT + ’к^t,T> dT’ (L5 l)
где к(1,т) и kH(t,T) - специально сконструированные линейные и нелинейные ядра
ползучести;
/[о-(^)] =
- нелинейная функция напряжений;
т - константа;
ст0 - некоторое постоянное напряжение, например, Rh.
Уравнение (1.5.1) является развитием уравнения нелинейной ползучести Арутю-
няна Н.Х.
= dT (1.5.2)
E(t) i дт E(t) dr
где С(/,г) -мера ползучести;
t - момент наблюдения;
т - возраст бетона;
tQ - момент загружения.
Ядра интегрального уравнения (1.5.2) имеют аналогичную структуру с (1.5.1)
л((>Г)=-ад.А.[_]_+с(г,г)];
*,О,г)=-£(г) ^-С,(лг).
ОТ
Существенным достижением Александровского С.В. является предложенные им
меры ползучести C(f,r) и Ch(Z,t), записанные в тождественном виде, но с различны-
ми константами
С(/,г) = 9?(г) - ^(/) • —^2. - А(т) • е~а^т\
е* -А2
(1.5.3)
где - заданные функции;
ууАг,а - константы.
45
ервые слагаемые этого уравнения характеризуют долговременную ползучесть
бетона; последнее слагаемое представляет быстронатекающую компоненту деформа-
ций ползучести в виде вертикальных отрезков.
Уравнение (1.5.3) позволяет весьма хорошо аппроксимировать различные опыт-
ные данные.
Уравнение (1.5.1) и его мера ползучести (1.5.3) проверялись в экспериментах Баг-
рия В.Я., Багрия ЭЛ., Колесникова Н.А., Когана Е.А., Попковой О.М., Соломонова В.В.,
Сюч Ференца, Черноярова В.А.
В наших исследованиях с учениками выведено соответствующее интегральному
уравнению (1.5.1) дифференциальное уравнение пятого порядка. Интегральному урав-
нению (1.5.2) соответствует дифференциальное уравнение второго порядка. Мера пол-
зучести (1.5.3)хорошо описывает экспериментальные данные, например, известный факт,
что скорость деформаций ползучести образцов, загруженных в различных, но близких
друг к другу возрастах (не слишком большими напряжениями), спустя некоторое время
после загружения сравнительно быстро становятся почти одинаковыми. Мера (1.5.3)
хорошо отражает наблюдаемое в опытах быстрое натекание деформаций ползучести
вслед за загруженном образцов.
В рекомендациях Евростандартов мера ползучести записывается в следующем виде:
(1.5.4)
где A,aj,a2,a3 - константы.
Первые слагаемые этого уравнения характеризуют долговременные составляющие
деформации ползучести: обратимые и необратимые. Последнее слагаемое характеризу-
ет значения быстронатекающей ползучести в виде вертикального отрезка. Уравнение
(1.5.4) представлено суммой степенных функций гиперболического типа. В нем содер-
жатся 6 параметров, нормируемых по специальным методикам.
Укажем еще на одну запись меры ползучести, предложенную Щербаковым Е.Н.
и использующую понятие приведенного времени (похожее на введение Будановым П.А.
и Ржаницыным А.Р. условного масштаба времени)
C(F,f) = С(28)[С + g • е* ]• [1 - к • ], (1.5.5)
где t = t • 1 +-
< 8 +1
C(28),C,g,/,fc,60,<!> - опытные константы.
Мера ползучести (1.5.5) отличается от меры ползучести Бондаренко В.М., Проко-
46
новина И Е. двумя дополнительными константами, а также использованием приведен-
ного времени.
Щербаков Е.А в своей работе установил важный результат путем численного ана-
лиза мер ползучести (1.5.3) - (1.5.5). Получено, что при всем различии математической
формы соответствующих уравнений наблюдается полное качественное и близкое коли-
чественное совпадение расчетных ординат кривых ползучести в возрасте наблюдений
до 720 суток, найденных по этим уравнениям (при простой ползучести).
Мера ползучести в форме (1.5.5), но с использованием обычного времени (z,r),
предложена в работах Бондаренко В.М., Прокоповича И.Е., Зедгенидзе В.А., Мехадде-
на Р, в развитие меры ползучести Арутюняна Н X.
C(/,r) = fc0 +-1(1-£?Л'-г))
\ т )
Параметр к < 1 в уравнении (1 5.5) учитывает быстронатекающую ползучесть
в виде вертикального отрезка на кривых ползучести; первые два сомножителя характе-
ризуют функцию старения бетона, последний сомножитель характеризует наследствен-
ную функцию действия
Большинство уравнений ползучести бетона, предложенных к настоящему време-
ни, рассматривают только мгновенные упругие свойства его ((1.5.1), (1.5.2)). Обосно-
вывается это обстоятельство не совсем удачным утверждением о том, что в эксперимен-
тах мгновенные деформации бетона даже при высоких уровнях загружений линейно
зависят от напряжений. Такая аргументация, а также сложная математическая запись
нелинейных деформаций, сдерживали внедрение их в научные разработки по железобе-
тону. Ситуацию изменили научные разработки В.М.Бондаренко и С.В Бондаренко Раз-
вивая теорию пластической наследственности металлов Ю.Н.Работнова и уравнение
нелинейной ползучести Арутюняна Н.Х. и стремясь получить уравнения теории ползу-
чести, пригодное для описания деформаций в области высоких уровней напряжений,
близких к призменной прочности бетона, В М Бондаренко обощил уравнение (1.5.2) на
случай нелинейных мгновенных деформаций и предложил его в форме
= ^(^ ^[^(г)]. 5 С*(/,т) dr (156)
МО
^0
где FM [сг(г)] и Fn [сг(т)] - нелинейные функции напряжений соответственно для упруго-
мгновенных и деформаций ползучести;
С*(Т,г) - мера ползучести в форме, предложенной С.В.Александровским.
С В Бондаренко записывает его в следующем виде
^(Л^о) = ^о[°’(0] )0-(0-
Наличие функции 5о[<т(0] согласуется с предложением Ю.Н.Работнова о квази-
линйном представлении неравновесного деформирования твердых тел.
Вместе с тем, В.М.Бондаренко указывает, что применение таких уравнений «при-
водит к математическим трудностям, неприемлемым для прикладного расчетно-кон-
структорского использования».
47
Кратко остановимся на проблеме получения решения уравнения ползучести. Здесь
выделим четыре различных подхода. Первый подход следует из общей теории интег-
ральных уравнений г(0=£Ю + 'г£Ю.5( ).л E(t)
сг(£)
£(/)
-£•(7)+p(r) 7?(/,r)Jr
1о
и состоит в отыскании резольвенты Я(Г,г) по заданному ядру S(t,T) из решения урав-
нения
Я(/,г)-$(Лг) = )ед,г) £(«,<) </£
т
(1.5 7)
При общих структурах ядер решение строится с помощью метода последователь-
ных приближений и представимо в виде ряда Неймана. Такое решение в принципе (ма-
тематически) всегда приводит к цели. При определенных ограничениях на функцию
ядра решение сходится в среднем, либо равномерно. Однако, практика показала [128J,
что ряд Неймана сходится очень медленно, и для получения необходимой точности нужно
удерживать очень большое число членов ряда (до 400). Следовательно, в этой ситуации
нужно пользоваться предложением Ю Н Работнова. При выборе функций, аппроксими-
рующих ядра, всегда имеется известий произвол, так как экспериментальные данные
обнаруживают разброс. Аппроксимирующая функция должна не проходить через экс-
периментальные точки, а в некотором смысле укладываться в пределы полосы разбро-
са. Естественно поэтому выбирать для ядер такие аппроксимирующие функции, для
которых решение интегрального уравнения может быть получено достаточно простым
способом.
Второй подход состоит в численном решении интегрального уравнения ползучес-
ти методом Крылова-Боголюбова. Процедура метода Крылова IIМ и Боголюбова П.Н.,
примененная впервые для расчета ползучести бетона А.В.Швецовым, состоит в после-
довательном определении из уравнения ползучести
ЕМ
значений напряжений заключающихся в интервале интегрирования
Давая верхнему пределу интеграла последовательно возрастающие значения
,t2>-^j> и применяя к интегралам теорему о среднем
dr =
Е(г)
• dr,
(15 8)

можно найти для произвольного момента времени
48
Отсюда можно получить формулу для нахождения напряжений

+ С(/,4’’)
(1-5.9)

Изложенный численный метод часто применяется также для нахождения резоль-
венты интегрального уравнения 7?(/,т) по заданному ядру S(t,т), сводящемуся к ре-
шению интегрального уравнения (1.5.7). Эго уравнение такого же типа, как и исходное
интегральное уравнение. Отличие состоит в том, что в исходном уравнении напряже-
ние сг(г) является функцией одной переменной, а резольвента R(t,r) является функ-
цией двух независимых переменных. При сложных ядрах 5(/,г) аналитическое реше-
ние для резольвенты 1?(/,г) получить не удается, и применяется существенно громозд-
кая и многодельная процедура замены интегралов конечной суммой
Smn
ГПуП
[|9_ _ • R„ _ + 2 - (S'- । _ Rm __i
+ ... + Sm_l n • Rm m.i [ J + Sm n Rm m J;
д = Ь»—
m - n
где Si k и Ritk - значения ядра и резольвенты для значений переменных и ик.
Шаг интетрирования существенно зависит от характера изменения функций S
и R-
Третий подход состоит в интегрировании дифференциального уравнения (при воз-
можном его построении), соответствующего интегральному уравнению ползучести.
В некоторых простейших случаях можно получить аналитическое решение уравнения
при заданных законах (режимах) изменения напряжений либо деформаций с течением
времени. В общем случае решение задачи ползучести здесь сводится к решению задачи
Коши (например, методом Рунге-Кутта).
Ввиду математической сложности и затруднительности решения задач теории пол-
зучести в научной литературе имеется труппа работ (четвертый подход), использующих
законы ползучести не в строгой интегральной или дифференциальной записи, а в виде
49
некоторого алгебраического выражения С Е Фраифельд еще в 1941 году ввел понятие
временного модуля деформаций
/ ч <г(0
(к510)
В линейной постановке выражение для временного модуля деформаций имеет вид
В теории старения бетона интегральное уравнение ползучести на основании тео-
ремы о среднем сводится к алгебраическому
e(0=F
^0
(1.5.11)
где использована гипотеза о линейной зависимости между сгг и (рг [162]. Использова-
ние гипотезы о параболической зависимости между сгг и (рт дает [87]
£0 3
Современный вариант такого упрощения [ 9] записывается в виде
£б(О = '~тт + сг£(^о) (^о)> (1.5.12)
где <J^(/,f0) - условное «среднее эквивалентное напряжение бетона» за промежуток
времени t -/0, вызывающее такие же деформации ползучести как и переменное на-
пряжение
сг*(Г0)£сгь(т)<сг*(О.
Рассмотрим теоретическую основу использования алгебраических законов ползу-
чести на примере модели Арутюняна Н X. для мгновенно упругого бетона
Полная деформация бетона, находящегося под действием постоянного напряже-
ния, приложенного в момент времени tQ, равна
*(М0) = а(Г0)
+ C(t,t^)
где С(?,/о) - мера ползучести.
Выносим E(tQ) за скобку, получим

50
Знаменатель этого выражения Арутюнян Н.Х. называет модулем полной дефор-
мации
£М,т) -------------------= £(7) • ub(t,T)
(1.5.13)
где иь((,т)
----—----------, (у - возраст бетона; 7 = /0 - время загружения, совпада-
1 + С(г,т) -£(т)
ющее с возрастом) в методе изохронных кривых называют коэффициентом изменения
секущего модуля.
В случае нелинейной ползучести и мгновенно упругого материала записываем
где £(сг) = f (ст) = а + /? - <т2 записываем по Арутюняну Н.Х.
В этом случае полную деформацию можно представить в виде
Д'о)*
Здесь модуль полной деформации равен знаменателю
£(7)
£О,т) =
Полагая меру ползучести не зависящей от возраста бетона С(/,7) = y/(t), а функ-
цию, характеризующую нелинейную зависимость между напряжениями и деформация-
ми ползучести, степенной функцией f (<т) = <ут, имеем
^(0 = ~ + ат ИО =-------------------------
£о £ 1
1 + сг"^1 • £0 • ИО
____________1____________
1 + о-'""1 • £0 • ИО
(1.5.14)
где =
1

1
Арутюнян Н.Х. указывает, что последнее «соотношение... справедливо при посто-
янных напряжениях, однако часто некоторые авторы распространяют его на случай
нагрузок, изменяющихся во времени. Такая ошибочная трактовка уравнения ... может
привести к ложным результатам»*.
Высказанное утверждение обосновывается тем обстоятельством, что теория пол-
зучести бетона Арутюняна Н.Х., даже в рамках использования ограничительных гипо-
тез афинного подобия кривых ползучести и принципа наложения, связывает между со-
бой (помимо напряжений а и деформаций £ ) четыре характеристики деформирова-
ния - ё,<т,£,сг.
‘ (3], стр.291
51
Нашими учениками показано, что учет деформаций быстронатекающей ползучес-
ти в уравнении деформирования бетона по Александровскому С.В. приводит к необхо-
димости учитывать также производные пятого порядка - £,6,ё,ё,£,&,£,&,£,ё. Эти
условия требуют более обстоятельных процедур получения изохронных кривых.
Рассмотрим дальше учет мгновенного деформирования и нелинейной ползучести
при фиксированных напряжениях.
Полная деформация бетона равна
, , , , 1
1
' ь>0
где и0- коэффициент начального изменения мгновенного секущего модуля. После эле-
ментарных преобразований имеем
Ц> a{t )
(1.5.15)
сгОо)
Дробь, стоящая в знаменателе уравнения (1.5.15), является теоретической основой
построения метода диаграмм-изохрон, нашедшего достаточно широкое применение
в последние годы в расчетах ползучести железобетонных конструкций
*>(Мо) =----- ------------------------ 0-5.16)
<т(<0)+р0.£(Г0).'Щ^.С(<Л)
<7('о)
В общей теории ползучести материалов уравнения вида (1.5.15) называются пер-
выми типами теории старения (классическая теория старения бетона [ 162] к этому от-
ношения не имеет) В некоторых теориях старения мгновенными деформациями мате-
риала пренебрегают.
Существуют три эмпирических варианта использования уравнений вида (1.5.15)
в практических расчетах. Первый подход заключается в непосредственном нахождении
полной деформации бетона по заданному времени t (не обращая внимания на требова-
ние постоянства напряжений).
Второй вариант заключается в построении набора изохронных кривых ст - £ для
фиксированных моментов времени tx ,..Jn. Третий вариант состоит в построении кри-
вых ст -1 для ряда фиксированных значений деформации £1}..£„; построенные таким
образом кривые должны совпадать с опытными кривыми релаксации. Как указывает
Ю.Н. Работнов уравнение (1.5.15) по сути является законом нелинейной упругости ма-
териала, у которого свойства меняются со временем; он также показывает простейшие
задачи, иллюстрирующие непригодность уравнения (1.5.15) для описания деформа-
ций при переменных напряжениях. Теория, удовлетворительно описывающая кривые
релаксации, построенные по кривым ползучести (третий подход), вероятно, будет при-
годна и для условий переменных напряжений. В общей теории старения (ползучести)
существует мнение, что она плохо предсказывает кривые релаксации. Однако при сда-
ст
бых изменениях напряжений применение теории старения может быть целесообразно
как приближенный прием. Вместе с тем, Качанов Л.М. [76] указывает на отрицатель-
ные оценки теории старения для решения практических задач.
В работах Яшина А.В. [188] показывается, что даже линейная теория ползучести
бетона, учитывающая переменность напряжений, дает отклонения до 30% в значениях
деформаций, определенных по непосредственным кривым релаксации. Эта погрешность
существенно увеличивается при использовании кривых простой ползучести для рас-
смотрения условий релаксации.
Однако, существуют классы специальных задач, в которых возможно применение
упрощенных законов ползучести (типа теории старения). Ю.Н.Работнов относит к та-
ким задачам построение теории длительного разрушения при неодномерном сложном
напряженном состоянии (для нахождения условного времени до разрушения по схеме
установившейся ползучести, когда при постоянном напряжении скорость ползучести
постоянна)
Рассмотрим подробнее метод изохронных кривых. Напомним, что алгебраическая,
в том числе и нелинейная, связь между напряжениями и деформациями простой ползуче-
сти наблюдается только при постоянных напряжениях. С целью наиболее полного, но
алгебраического использования простых кривых ползучести Ф.Шенли в 1947 году сфор-
мулировал метод изохронных кривых, основанный на построении диаграмм ст - £ для
последовательно фиксируемых моментов времени ,. .tr. Применение данного
метода к решению задач ползучести металлов дает противоречивые результаты; многие
авторы склоняются к отрицательной оценке применения этого метода для ползучести
металлов, так как для получения изохронных кривых используются только данные ис-
пытаний при постоянных напряжениях. Вместе с тем, в квазилинейной интегральной
теории ползучести Ю.Н.Работнова используется идея метода изохронных кривых.
В последние годы метод изохронных кривых стал использоваться для бетона
в следующем виде. Диаграмма-изохрона описывается зависимостями
«до— -
что аналогично по структуре временному модулю деформаций.
Здесь нелогично используется переменный модуль E(t,tQ) вместо постоянного
модуля £(/0), характеризующего величину мгновенной деформации в момент загруже-
на f0; то же самое относится к переменному напряжению cr(f) вместо фиксированно-
го ст(/0).
Модуль деформации £г>(/,/0)предла1ается определять различными приемами:
1 - Eb (f0) - модуль деформации в начале загружения; 2 - Еь (Г) - модуль деформации для
текущего времени t; 3 - усредненный модуль деформации в интервале действия напря-
жения.
Коэффициент L>fc(f,/0) характеризует приближенное уравнение изохронной кри-
вой, с помощью которой учитываются нелинейные мгновенные и нелинейные длитель-
ные деформации и который записывается в эмпирическом виде
53

^•Д£Оо)
a£(t0) + ub fc
(1.5.17)
где fc - функция нелинейности
fc = 1 + к • vc •
д/1 - О,8е/,('~'о)
(1.5.18)
При этом полная деформация бетона первоначально равна сумме
^(О = сГбОо)
2_4
ЕМ 4
Ес С(/,/о)
Знаменатель в коэффициенте fc, отвечающий за деформации ползучести, являет-
ст
ся функцией старения Фрайфельда С Е. Максимальный уровень напряжений при-
нимасгся равным 1.
В современном методе изохронных кривых для бетона предлагается выделить пред-
варительно несколько фиксированных вспомогательных режимов, чтобы применять для
решения конкретных задач один или несколько из них. В качестве таких вспомогатель-
ных режимов рекомендуется фиксировать либо постоянную скорость деформирования,
либо постоянную скорость загружения. Однако это, по В.М.Бондаренко, затруднитель-
но, поскольку «любое режимное стесненное деформирование переводит вопрос в класс
релаксационных задач, а режим постоянной скорости силового напряжения приводит
к незатухающей ползучести и одновременно к независимости модуля деформаций от
самой скорости».
Дополнительно к замечаниям В М.Бондаренко укажем, что используемые меры
ползучести С(//о) накладывают требования не только на скорости, но и на ускорения
процессов деформирования.
Уже в рамках теории ползучести Арутюняна Н.Х. «вспомогательные режимы» дол-
жны содержать четыре основных набора скоростей и ускорений:
1) для
2) для ст;
3) для ё;
4) для &,
что является довольно проблематичным.
54
Глава 2. МОДЕЛИ ДЕФОРМИРОВАНИЯ ПРИ КРАТКОВРЕМЕННОМ
ЗАГРУЖЕНИИ
§ 2.1. Некоторые модели Евростандаргов и СНиП по бетону и железобетону
Расчетные модели и гипотезы, заложенные в основу норм проектирования бетон-
ных и железобетонных конструкций, развиваются естественным образом. Первоначально
нормы использовали линейную «классическую» модель, основанную на законе Гука.
В тридцатые годы прошлого столетия А.А.Гвоздев внедрил в нормативные методы но-
вую и уникальную модель для расчета несущей способности, основанную на понятии
пластического шарнира. Введению этой модели предшествовали жесткие научные дис-
куссии по моделям Консидера, Мёрша, Лолейта, Николаи, Геннибека, Штаермана и др.
Тем самым А.А.Гвоздев остроумно разделил отдельные расчетные задачи теории желе-
зобетона: определение разрушающей нагрузки; расчет появления трещин и их разви-
тия; определение деформаций и т.д. Модель пластического шарнира целенаправленно
позволила в последующие годы существенно продвинуть теорию расчета железобетона
и получить целый ряд важных результатов.
Одновременно за эти годы шло накопление экспериментальных данных о работе
железобетона в конструкциях, что позволило разработчикам Евростандаргов обосновать
внедрение в нормы «деформационной модели сечения» железобетонного элемента.
«Деформационная модель сечения» железобетонных балок и колонн европейских
стандартов основывается на четырех гипотезах.
Согласно первой из них деформации бетона и арматуры в плоскости и из плоско-
сти изгиба определяются с использованием гипотезы плоских сечений. Эта гипотеза
дает существенное геометрическое упрощение задачи и является условием совместнос-
ти деформаций бетона и стали железобетонного элемента. Она также широко использу-
ется в теории расчета металлических, деревянных конструкций и кирпичной кладки.
Приближенная теория, основанная на гипотезе плоских сечений, позволяет избежать
бесполезных дискуссий и неоправданной работы.
При использовании модели пластического шарнира для оценки несущей способ-
ности надобность гипотезы плоских сечений отсутствовала. По этой причине возникла
большая серия научных работ, отрицавших возможность применения этой гипотезы
со ссылкой на экспериментальные данные. При этом не учитывалось, что гипотеза плос-
ких сечений не включает в себя никаких предположений о свойствах материала конст-
рукции. В этой гипотезе важно было, только чтобы выполнялось основное условие её
применимости - малость сдвигов по сравнению с углами поворота
Согласно второй гипотезе считаются известными для случая неоднородного на-
пряженного состояния при изгибе зависимости «напряжение-деформация» для бетона и
армазуры, позволяющие по известным относительным деформациям рассчитать напря-
жения бетона и арматуры в различных точках сечения. Для обоснования этой гипотезы в
последние годы появилось достаточное количество экспериментально-теоретических
работ. Более ранние попытки уточнить эпюру бетона в сжатой зоне следует считать преж-
девременными, так как для этого не было достаточных экспериментальных данных
Третья гипотеза считает возможным указанные выше диаграммы «напряжение-
деформация» при неоднородном напряженном состоянии (вследствие изгиба) получать
из опытов по однородному напряженному состоянию простого сжатия или растяжения
55
В частности, для бетона используется криволинейная диаграмма с ниспадающей вет-
вью, и предлагается аналитическое описание этой диаграммы.
Деформация в бетонных образцах, находящихся в условиях одноосного равномер-
ного сжатия (безградиентного, однородного), может развиваться с отличиями от дефор-
маций сжатых волокон, находящихся в сжатой зоне изгибаемого элемента (градиентно-
го, неоднородного). Однако не существует экспериментальной техники, позволяющей
только экспериментальным путем построить зависимость ст - £ для бетонного волок-
на изгибаемого элемента. Вследствие этого и используется в расчетах изгибаемых эле-
ментов для бетона дишрамма <? - £, полученная для других условий - одноосное, од-
нородное сжатие.
Коэффициенты (а, Ь, с, d, е) этой модели [218]
= W*
Ь + С€У
d + сг\
(2.1.1)
представляющей неправильную дробно рациональную функцию (произведение линей-
ной функции на дробно линейную функцию), в Евростандартах преднамеренно жестко
связаны с прочностными и деформативными характеристиками бетонного тела (при-
зменная прочность, предельная деформация и т.д.). Такая жесткая привязка не позволя-
ет в нормативном проектировании заниматься уточнением значений этих коэффициен-
тов, хотя такие попытки уже имеются.
Расчеты конструкций показывают, что запись диаграммы бетона ст - £ в форме
(2.1.1) не дает существенных результативных отличий в сравнении с другими формами
записи. С другой стороны, жесткая форма записи (2.1.1) позволяет на основе практи-
ческих расчетов конструкций наметить пути дальнейшего совершенствования Еврос-
тандартов.
Четвертая гипотеза позволяет считать совпадающими нейтральные оси напря-
жений и деформаций при длительном загружении.
На основании изложенной выше «деформационной модели сечения» рассмотрим
некоторые модели современного СНиП по бетону и железобетону и предложения по его
совершенствованию.
Из анализа «деформационной модели» следует частный предельный случай плас-
тического шарнира. В нем зоны пластического растяжения - сжатия смыкаются; эпюра
напряжений в сжатой зоне бетона достигает прямоугольного очертания; кривизна про-
гнутой оси элемента в этом сечении становится равной бесконечности. Такому пре-
дельному частному случаю соответствуют стержни нулевой гибкости ( — = 0; I - дли-
h
на; h - высота).
Указанный выше частный предельный случай «деформационной модели» соот-
ветствует методу предельного равновесия, принятому в наших нормах, модели теории
разрушающих нагрузок. Характеризуя её, А.А.Гвоздев пишет [50]: «Вплоть до исчерпа-
ния несущей способности деформации должны быть настолько малыми, чтобы можно
было пренебречь изменением всех геометрических величин, входящих в условия рав-
новесия». Такое требование выполняется только для стержней небольшой гибкости
/
— So. Для внецентренно сжатых элементов ситуация усугубляется тем обстоятельством,
b
56
что при г > 8 замена криволинейной эпюры напряжений - прямоугольной - недопус-
b
тима. В наиболее нагруженном сечении внецентренно сжатого элемента (в момент по-
тери несущей способности) эпюра напряжений в бетоне может принимать различные
очертания: треугольное (со слабой нелинейностью); криволинейное трапецеидальное;
криволинейное. Напряжения в арматуре могут быть при этом различны. Заметим, что
погрешность применения прямоугольной эпюры напряжений в бетоне нелинейно уве-
личивается с ростом гибкости 7. Причем этот результат не меняют ни учет отклонения
о
распределения деформаций от гипотезы плоских сечений, ни видоизменение очерта-
ний диаграммы сг - £ для бетона в сравнении с (2.1.1).
В наших нормах используется условная модель учета гибкости внецентренно сжа-
тых элементов, предложенная ещё в тридцатые годы прошлого столетия Гвоздевым А. А.,
Боришанским М.С., Кузнецовым А.А. Для того времени, когда свойства железобетона
были мало изучены, применение этой модели совместно с моделью пластического шар-
нира являлось удачной находкой. Краткая суть этой модели в следующем. На основе
приближенной линейной теории прогиб внецентренно сжатого прямоугольного стерж-
ня f записывается в виде:
1 ____L
1-^2
я El Е F
(2.1.2)
2 »
£
где 77 = 400/?а; Ru = l,25/?v- модуль упругости бетона Е выражается через призмен-
ную прочность бетона Лпр.
В последующие годы вводились и уточнялись коэффициенты в выражении (2.1.2)
[174].
Использование (2.1.2) в практике проектирования вызывало острые дискуссии в
научной лигерагуре [62], [175J, [137]. Причина этих дискуссий кроется в методических
несовершенствах модели (2.1.2), неверно описывающей прогиб колонны f, особенно
при приближении сжимающей силы р к силе Рэ (Эйлера). Заметим, что применение
деформационной модели сечения и формулы (2.1.2) является несовместимым.
Необходимо обратить внимание па проблему учета фактора времени в расчетах
железобетонных конструкций. Для её решения вместо уравнения (2.1.1) должны ис-
пользоваться объединенные уравнения пластичности и ползучести. Многие современ-
ные теории ползучести бетона этому требованию не удовлетворяют, так как используют
для мгновенных деформаций закон Гука, а не криволинейную зависимость (2.1.1).
В современной теории ползучести имеются достаточно точные модели решения задач
расчета конструкций с учетом фактора времени, позволяющие отказаться от различных
условных приемов: метода изохронных кривых; метода временного модуля деформа-
ций; метода, изложенного в [9] и других.
57
§ 2.2. Кратковременная нелинейность деформирования бетона
В рекомендациях ЕКБ-ФИП диаграммы ст - £ бетона для однократного кратков-
ременного загружения принимаются с ниспадающим участком [201]. Известно, что эти
диаграммы имеют большой разброс, обусловленный многокомпонентностью структу-
ры бетона. Однако, при использовании безразмерных напряжений и безразмерных де-
формаций разброс в диаграммах а - £ существенно уменьшается. На основании изу-
чения обширного экспериментального материала, накопленного исследователями для
бетона в возрасте 28 дней, аналитическая зависимость, аппроксимирующая криволи-
нейную диаграмму ст - £ с ниспадающей ветвью (рис. 2.2.1), принята в виде
ас = krj-T]1
fc 1 + (к-2)?]^
(2.2.1)
£ 1 IF • £
где т] = —; £с1 = 0,002; к = -—у—-.
Таблица 2.2.1
26 27,5 29 30,5 32 33,5 35 36 37 GPa
Л 12 16 20 25 30 35 40 45 50 MPa
£си -3,8 -3,7 -3,6 -3,5 -3,4 -3,3 -3,2 -3,1 -3,0 •10’3
58
В обозначениях, принятых в наших нормах уравнение (2.2.1) записывается в виде
(2.2.2)
где Rb = fc - максимальное напряжение на диаграмме;
£ьч ~ £d ~ 0,002 - относительная деформация, соответствующая напряжению Rb;
£ы ~£си _ максимальная относительная деформация, соответствующая напряже-
нию сгь = 0,57?t и определяемая по эмпирической формуле
Еь = 1,1 Ес_ - начальный модуль упругости.
Указанные параметры диаграммы сгь — £ь характеризуют работу тяжелого бетона
при кратковременном статическом действии нагрузки и нормальных условиях эксплуа-
тации.
В абсолютных величинах диаграмму аь - еь запишем в виде

a + Seh
£ъ------~
c + g£b
(2.2.3)
или

R.
O = £b;5 = -4:c=l;g=к.
Rb £ьо)
Функцию (2.2.3), разлагая её в ряд, можно представить после некоторых преобра-
зовании в виде полинома четвертой степени, что часто удобно при решении конкрет-
ных задач нелинейной теории железобетона:
= 4£ь + А£ь + аз£ь +
где
£ьо
(2.2.3*)
где А, = Еь;
Л
—--—— Р

£А_ 2
Rb £ы>
Л3=2-4р-—+2|^-
"2 Ч ^0 1 1 D
£ьо
Е„ Ji
Rb £ьо )
59
(Е 2 R (Е 2 Y
л=-б^-А 4-6 .
£ьо) £Ь0 Х^Ъ £Ьй J
Дальнейшее повышение степени полинома (2.2.3’) не имеет особого значения.
В нелинейной теории железобетона помимо прямой зависимости (2.2.3) часто при-
дется использовать обратную зависимость
(2-2.4)
Для получения обратной функции (2.2.4) по заданной прямой функции (2.2.3) вос-
пользуемся рядом Лагранжа, в котором ограничимся четырьмя членами ряда. Сначала
запишем обратную функцию в виде
(2-2-5)
c + g£b
/ ч а + Зеь
где у/{£ь) =-------
c + g£b
Тогда ряд Лагранжа записывается в таком виде

(2.2.6)
В теории железобетона известно, что полином четвертой степени достаточно хо-
рошо аппроксимирует диаграмму сгь - £ь с ниспадающим учаегком. Из (2.2.6) находим
четыре члена ряда, характеризующие обратную зависимость (2.2.4)
еЬ ~ fl(°7>)~ + + ^заь + ^4аь ’ (2.2.7)
где коэффициенты В ,В.,В3,В4 получены в следующем виде:
2 21 а3
с2
60
1 2а eg2 - badge1 + 45 с3
/>, = -5 ----------
3 3!
а5
->2
Ег
Вь £ьо
R.
Ек 2

b^\Rb
2
ьо J
•5
Ь
_ 1 . 6a3g3c - 34a2dg2c2 + 48ag52c3 - 2053c4
°4 ~ Л1 7
4! a
l3^
3~
b 2
Rb
R {E
+ 17E2^
Gb(J £bO
£,__2_
Rb £ьс _
E7
^b
2
+ 24£„
A.
^o>
Eb 2
Rb £ьо
( n у
+Ю 4-
V^fcO /
Обратим внимание, что коэффициенты а,8, g, входящие в прямую (2.2.3) и обрат-
ную (2 2.7) зависимости, могут изменяться с течением времени, если меняются с тече-
нием времени Eb = Еь(i),Rb = Rb(t); £м - £b0(t)
В этом случае
= (2.2.8)
£b^£b{<Jb>t)=B\(t)^b + ^(t)(j2b + B3(t)al + B4(t)a* = f2(ab,t)> (2-2-9)
где cb - мгновенные деформации бетона, суммарно учитывающие упругие (линейные) и
пластические (нелинейные) свойства бетона.
Время t, входящее в уравнения (2.2 8) и (2.2.9), характеризует только изменение с
течением времени мгновенных свойств бетона.
Помимо криволинейной диаграммы <jb — £ь Евростандарты также разрешают ис-
пользовать ещё два варианта более простых нелинейных диаграмм, не имеющих ниспа-
дающих участков, а имеющих ограниченные площадки текучести.
Во-первых, рекомендована к использованию ломаная диаграмма, состоящая из трех
расчетных прямолинейных участков (рис.2.2.2).
Угол наклона первого участка А характеризуется модулем Еь (tga = Еь), совпада-
ющим с Еь = 1,1 на криволинейной диаграмме, рис.2.1 1. Точка Л диаграммы имеет
_ 0,6Яь
координаты а { = 0,62?,,; £ь\ ~ 7, • Точка В диаграммы характеризуется максималь-
вь
ным напряжением Rb и деформацией £ьо =0,002, соответствующей максимальной точке
В на криволинейной диаграмме, рис.2.2 1 (fh0 —£с1) Третий В горизонтальный учас-
ток ВС диаграммы характеризует пластическое состояние бетона, деформирующегося
61
при постоянном параметре текучести, равном Rb. Предельная деформация (.е?62 = £л),
при которой происходит разрушение бетона в точке С, принимает значение еЬ2 = 0,035.
Скорость деформирования бетона на горизонтальном участке диаграммы предполага-
ется весьма малой и соответствующей понятию статического загружения.
Во-вторых, рекомендована к применению диахрамма идеального упругопласти-
ческого материала - диаграмма Прандтля, рис.2.2.3, характеризуемая наличием двух
расчетных участков: упругого OAt и пластического А(С.
Расчетный модуль упругости Еь (соответствующий некоторому осредненному
секущему модулю) является тангенсом угла at и определяется отношением
62
£ _ ^b _____Л
bred 0,0015’
(2.2.10)
где £b\.red ~ 0,0015- условная расчетная деформация, соответствующая началу площад-
ки текучести бетона.
На горизонтальном участке диаграммы AtC рост деформации еь происходит при
постоянном напряжении Rb. Когда деформация £h достигает значения еь , = 0,0035,
бетон разрушается в точке С.
Все три модели диаграмм ст - е для бетона (рис.2.2.1 - 2.2.3), принятые в Еврос-
тандартах, имеют ограниченную протяженность площадки текучести.
Эта конечная протяженность площадки текучести накладывает жесткое условие на
теорию железобетона — невозможность использования модели пластического шарнира в
расчетах железобетонных конструкций. Модель пластического шарнира является след-
ствием неограниченной протяженности диаграмм ст - £ для бетона и стали, рис 2.2.4.
д Момент
Рис.2.2.4.
Пластический шарнир М(1. по рис.2.2.4 характеризуется кривизной равной беско-
нечности и нулевой длиной элемента; кривая Ф асимптотически в бесконечности при-
ближается к линии ®, характеризующей пластический шарнир. Па самом деле, при ог-
раниченной протяженности зоны текучести материалов разрушение сечения произой-
дет в точке Р, соответствующей либо началу текучести арматуры в растянутой зоне,
тибо достижению фибровой деформации бетона в сжатой зоне величины еь2 (либо од-
новременному выполнению этих условий)
У сжатоизогнутых элементов точка Р может быть и не достигнута. в точке У, достигае-
мой ранее точки Р (рис.2.2.4), может произойти потеря устойчивости элемента.
В точках У и Р, характеризующих предельное состояние конструкции, сечение железобетон-
63
ной конструкции находится в упругопластическом состоянии (содержи! упругую и пласти-
ческую зоны), а не в пластическом состоянии, соответствующем линии @ Для некоторых
сжатоизогнутых элементов точки У и Р могут совпадать (разрушение наиболее нагружен-
ного состояния и потеря устойчивости элемента в целом происходят одновременно) Кроме
того, для некоторых сжатоитогнутых элементов разрушение сечения (точка Р) может пред-
шествовать моменту потери устойчивости (точка У на кривой ОР не существует); зависи-
мость «нагрузка - прогиб» (рис.2.2 5) таких элементов имеет пиковый экстремум в точке Р.
Рис.2.2.5
В вышеприведенных рассуждениях использованы свойства модели Евростандартов
для диаграммы crs - £s арматуры, рис.2.2 6, являющейся также диаграммой Прандтля.
Тангенс угла а соответствует модулю упругости Е арматуры Относительная
деформация в точке Ai, соответствующей началу площадки текучести арматуры, нахо-
дится из закона Гука
S =
* Е,-
Предельная относительная деформация площадки текучести es2 , характеризую-
щая разрыв арматуры в точке С, принимается равной esl = 0,025.
64
Глава 3. УРАВНЕНИЯ ДЛИТЕЛЬНОГО ДЕФОРМИРОВАНИЯ БЕТОНА,
УЧИТЫВАЮЩИЕ МГНОВЕННУЮ НЕЛИНЕЙНОСТЬ
И НЕЛИНЕЙНУЮ ПОЛЗУЧЕСТЬ
§ 3.1. Некоторые упрощенные модели ползучести бетона
Исследования данной главы являются развитием идей Работнова Ю.Н., Бондарен-
ко В.М., Качанова Л.М. в области нелинейного длительного деформирования, а также
основываются на фундаментальных исследованиях по линейной теории ползучести бе-
тона
Рассмотрение упрощенных моделей ползучести в данном параграфе позволяет
выявить основные закономерности деформирования бетона с течением времени, а так-
же использовать многочисленные эксперименты различных авторов по ползучести бе-
тона для построения достаточно надежных и простых моделей, учитывающих нели-
нейность мгновенного деформирования, а также нелинейные деформации ползучести.
В теории ползучести обычно раздельно (первая гипотеза) рассматриваются дефор-
мации мгновенные £м и деформации ползучести £п.
Затем используется вторая хипотеза, заключающаяся в сложении указанных выше
деформаций для нахождения величины полной деформации £:
* = (3-1-1)
Из этой гипотезы следует, что каждая деформация (£м и £п) возникает под дей-
ствием одного и того же напряжения <т.
Рассмотрим сначала мгновенно линейный материал, удовлетворяющий закону Гука:
a = £ME(f), (3 12)
где E(t) - изменяющийся с течением времени модуль упругости бетона ( E(t) - извест-
ная функция от времени t).
Для деформаций ползучест бетона £п (f) запишем линейный закон вязкого тела
а = Х(0 (3 13)
где K(f) - переменный во времени коэффициент вязкости, называемый иногда коэффи-
циентом внутреннего сопротивления деформации элемента. В простейшем случае при-
нимают значение коэффициента K(f) постоянным X = const-
а = К-Еп. (3.1.4)
В механике такие силы называют диссипативными; вектор диссипативной силы
пропорционален скорости движущейся точки (рис 3.1.1).
Сила сопротивления Fconp равна
Fconp=-<*V, (3.1.5)
где а - константа, коэффициент пропорциональности;
V - скорость движения точки Л/, на которую действует сила сопротивления Fconp.
Дифференцируем уравнения (3.1.1) и (3.1.2) по времени
65
£ = Ёи+£п\ (3.1.6)
d(04(0-*(0+M0M (3-1.7)
В (3.1.6) подставляем (3.1.7) и (3.1.3), получаем
E(t) E2(t)
cr(t) + —- cr(t)
K(t)
откуда записываем основной линейный закон ползучести бетона в виде
1 £(Г) '
£(/) =
£(0=—- • <7(6 + ,
е(о [ад *2(oJ
•сг(О.
(3.1.8)
В простейших моделях ползучести коэффициенты k и Е постоянны, что позволя-
ет записать
1
£ = —
Е
Качанов Л.М. [76] ввел предположение для ползучести металлов о зависимости
коэффициента вязкости К от времени: К = K(f), а также нелинейную от напряжения
связь (3.1.1)

где = В,(t) - положительная
АГ(О
убывающая функция времени, от-
считываемая от момента начала
ползучести и асимптотически стре-
мящаяся к предельному значению
Bj(oo) (на основании опытных
данных).
66
Следовательно для модели линейных упругих деформаций и нелинейных вязких
деформаций уравнение, обобщающее модель Максвелла, Качанов Л.М. записал в виде
£ = Bl(t)am
Е
Это уравнение имеет ряд ограничений, выявленных обработкой эксперименталь-
ных данных:
1. Оно справедливо при не слишком малых скоростях ползучести.
2 Напряжения ст должны изменяться медленно и монотонно
3. Начало процесса ползучести должно протекать при достаточно больших на-
пряжениях (см. случай изгиба).
4. Уравнение неинвариантно относительно изменения начала отсчета времени.
Для удобства обработки экспериментальных данных вместо времени г предложе-
на новая переменная £2] (/)
Hi(t)=Bx(t)dt>
приводящая уравнение ползучести к следующему дифференциальному виду
de _ 1 da
----= а +---------
dQ Е dQ '
Из нелинейной теории Максвелла-Качанова просматривается гипотеза простого
сложения мгновенных деформаций и деформаций ползучести, находящая широкое при-
менение в построении моделей ползучести различных конструкционных материалов
в дифференциальной форме. Например, Содерберг К.Р. записывает основной закон пол-
зучести в виде
г = 1.<7 + Г(О-,П,
Е
где функция V(а, Г) характеризует скорость деформаций ползучести, зависящей от
напряжений а и температуры Т.
Одквист Ф.К и Хофф Н.И. учли дополнительно необратимую пластическую де-
формацию
£ = — -a + N - g\a) - a + V(a)-,
где из функции V(a Т) исключена температура Т
В теории упрочнения металлов (теория ползучести) приведены различные анали-
тические выражения для описания скорости деформаций ползучести (с учетом темпе-
ратуры Т и без учета температуры Г):
£в = S(a) F

67
Существуют материалы, у которых проявляется влияние больших пластических
деформаций на деформации ползучести Однако, картина экспериментальных резуль-
татов здесь является достаточно сложной и запутанной.
Мгновенная нелинейность деформаций проявляется у ряда материалов при высо-
ких уровнях загружения, поэтому модель .мгновенно неупругого материала широко ис-
пользуется в теории ползучести металлов в гипотезе уравнения состояния.
Линейное мгновенное деформирование явилось привлекательным с точки зрения
математического применения общей теории наследственно-упругого тела
£ = — (? + (3.1.9)
& —со
а = Е-£- 'jr(t-T) £(T) dvt (3.110)
где функции K(t - г), Г(1 - т) представляют собой некоторые ядра интегральных урав-
нений (3.1.9), (3.1.10), являющиеся произвольной функцией аргумента (t-т) и удов-
летворяющие лишь некоторым достаточно общим условиям, а также способные опи-
сать ползучесть многих конструкционных материалов.
Аргумент (t - г) ядра ползучести указывает на неизменность свойств материала
во времени; начало отсчета времени является инвариантным.
В теории интегральных уравнений известен тот факт, что если ядро интегрального
уравнения является вырожденным, то оно сводится к линейному дифференциальному
уравнению и наоборот
Простота использования линейных интегральных и дифференциальных уравне-
ний оказалась привлекательной и в теории ползучести бетона, что дало толчок для
широкого использования модели мгновенного упругого материала в этой теории, а
также различных экспоненциальных функций для аналитического описания кривых
ползучести.
§ 3.2. Количественные меры ползучести бетона
Ползучесть бетона (в линейной теории) обычно характеризуется двумя количествен-
ными мерами, наиболее исследованными для случаев одноосного сжатия бетонных
призм характеристикой ползучести и мерой ползучести.
Характеристикой ползучести бетона называется отношение деформации ползуче-
сти £п (t, т,) в произвольно рассматриваемый момент времени t к упругой деформа-
ции £у(т1), возникшей от напряжения tr(r,), приложенного в момент времени т1:
(3-21)
Мерой ползучести (или удельной относительной деформацией ползучести) назы-
вается отношение деформации ползучести £п (t, т}) к величине напряжения <т(т|), при-
ложенного в момент времени т}:
68
(3.2.2)
Другими словами, характеристика ползучести С(/,7,) может рассматриваться как
значение ползучести к моменту времени t, вызванной действием единичного напряже-
ния гг(г() = 1 кг/см2, приложенного в момент времени Г].
Для бетонов естественного твердения нормирование кривой ползучести часто на-
чинают от момента времени - 28 сут. В некоторых теориях ползучести [162] вре-
мя Г] = 28 сут. называют нулевым моментом времени, при этом считается, чго на-
грузка прикладывается в нулевой момент времени, а характеристика ползучести запи-
сывается в виде
т
— , (3.2 3)
*0
где Eq - упругая деформация бетона в момент времени / = 0 - Из формул (3.2 1) и (3.2 2)
видно, что характеристики ползучести или <Рг величина безразмерная, мера
ползучести же C(f,r) имеет обычно размерность
I кг /
, либо {МПа} Характеристика
ползучести связана с мерой ползучести (как это следует из (1) и (2) выражением
' а(г, )/£(,,) " £(1|)' (” > Р-2-4»
Величина деформации ползучести (очевидно) определяется выражением
^(^^i) = cr(7i)-C(/,Ti), (3.2.5)
что позволяет- говорить о гипотезе подобия кривых ползучести при разных уровнях
напряжений.
Следует заметить, что при экспериментальном определении характеристики пол-
зучести обязательно должна быть известна упругая деформация бетона, точное опреде-
ление которой связано с определенными трудностями. Для получения деформации пол-
зучести в любой момент времени следует из полной измеренной деформации вычесть
упругую деформацию и деформацию усадки При нахождении же меры ползучести мож-
но обойтись без нахождения упругой деформации. Поэтому проще экспериментально
определить меру ползучести. Однако, в расчетной практике удобнее применять безраз-
мерную характеристику ползучести Для аналитического описания выражения характе-
ристики ползучести C(t,Tx} в научной литературе предложено много различных фор-
мул. Наибольшее распространение получила форма записи, предложенная Н.Х.Арутю-
няном [3]
С(/,г1) = 0(т)./(/-т), (3.2.6)
где 0(г) называется функцией старения
69
0(т) = Со+4-; (3.2.7)
г
f(t - г) называют функцией продолжительности действия нагрузки
/(/-г) = 1-е“х('-г); (3.2.8)
Cg,Ax,y - опытные константы.
Для модуля упругости Н X Арутюнян предложил следующую формулу
£(г)=£0-(1-Д-е-от), (3.2.9)
где Е0,(3,а- опытные константы.
Теория ползучести бетона, использующая эти формулы в своей основе, называет-
ся наследственной теорией старения или теорией упруго-ползучего тела.
Для описания ползучести тел, не обладающих старением, и тел, нагруженных в
старом возрасте, применяется теория упругой наследственности, получившая развитие
в работах Работнова Ю.Н., Ржаницына А.Р., Малмейстера А.К., Скудры А.М и других
ученых. В этой теории ползучести принимаются дополнительные допущения о посто-
янстве модуля упругости
Е(т) = Eq= const, (3.2.10)
а также постоянное значение для функции старения
@(г)=С0. (3.2.11)
Следует заметить, что теория упруго-ползучего тела описывает частичную обра-
тимость деформации ползучести.
Теория же упругой наследственности игнорирует процесс старения бетона, в ре-
зультате чего вся деформация ползучести оказывается обратимой.
Мера ползучести по теории упругой наследственности зависит только от времени,
прошедшего с момента загружения до рассматриваемого момента t Кривая деформа-
ций ползучести бетона, нагруженного в возрасте T{,T2t... целиком повторяет кривую
деформаций ползучести, соответствующую нагружению в начальный момент времени,
но сдвинутую вправо на отрезок т{,г2,—
В линейной теории ползучести, созданной специально для расчетов бетонных и
железобетонных конструкций [34], названной теорией старения, используется допол-
нительная и существенная гипотеза о параллельности кривых ползучести. Эту гипотезу
сформулировали независимо друг от друга В США - Уитни Ц., а в СССР - Буданов Н. А
Значительное развитие и экспериментальное обоснование теория старения полу-
чила в капитальных трудах Улицкого И.И., Столярова Я.В., Голышева А.Б., Чжан Чжун-
Яо, Лившица Я. Д и других ученых.
Гипотеза о параллельности кривых ползучести позволяет получить кривую ползу-
чести бетона, загруженного в возрасте т, из кривой ползучести бетона, загруженного в
начальном возрасте,
С(/,т)=С(/)-С(г), либо
1^(0“ «’(«')], (3.2.12)
где ?>(?), ^(г) - характеристика ползучести, аппроксимируемая подходящей кривой.
70
Используемая таким образом параллельность кривых ползучести выявляется
в экспериментах целого ряда авторов, исследовавших ползучесть бетона. Теоретически
формула (3.2.12) означает, что кривые ползучести различных бетонных образцов, заг-
руженных одним и тем же постоянным напряжением ту, но в разные моменты времени
Т1 ,г2,...г„, совпадают всеми точками (конгруэнтны) при их поступательном перемеще-
нии по вертикали (вдоль оси деформаций). Это экспериментальное свойство параллель-
ности кривых ползучести нельзя считать общей закономерностью в теории ползучести
бетона. Однако, это свойство параллельности вносит упрощения в расчеты железобе-
тонных конструкций на ползучесть. Здесь же следует обратить внимание, что использо-
вание гипотезы параллельности кривых ползучести приводит к полной необратимости
деформаций ползучести. Последнее обстоятельство не имеет существенного значения
для случаев монотонного увеличения, либо монотонного уменьшения напряжений в
загруженном волокне, что важно в расчетах напряженно-деформированного состояния
сечений железобетонных элементов.
С математической точки зрения условие параллельности кривых ползучести со-
стоит в удержании только некоторых членов ряда Тейлора при разложении функции
С(/,г)
С(/, г) = С(0,0) + - • ?C(t’r) t + -
7 v 7 1/ dt 0 1/
^£2 r +
дт 0
1 д2
2!
Z2+1.2.^^
0 2/ dt дт
1 &с(*’г
у dt2dr
tr +-------—
2/ дт2
t2T+L з
У dtd2T
tT2
0
1 д^С^'
3/’ дт3
<3.2.13;
3/ 5?
0
0
2
0
0
0
3
Из анализа (3.2.13) видно, что применение гипотезы параллельных кривых (3.2 12)
игнорирует члены ряда, содержащие смешанные производные по t и т.
С целью приближенного учета обратимости деформаций по тзучести Александ-
ровский С.В [2] предложил идею использования «вертикальных отрезков». Суть её со-
стоит в следующем. Мера ползучести записывается в виде
С(/,т) = р(г) - Г(0 - Л2)- Д(г)е'а('-Г).
Вергикальные отрезки Д(т) отражают весьма быстро натекающую деформацию
ползучести.
Прокопович И Е и Улицкий И.И. [123] с этой же целью записывают характеристи-
ку ползучести в виде
^(Z,r) = (р} [1 - е-п('“т)]+ (р2 [е~Г2Т - е~Г2‘ ],
что является удобным в математическом отношении для решения простейших задач
теории, например, при фиксированных режимах изменения напряжений во времени
(cr=cr0(l + sin<y/)) Наибольшее отклонение от параллельности кривых ползучести
наблюдается вблизи времени т. Вследствие этого ученые предложили приближенно
71
компенсировать это отклонение с помощью отрезка аах =аС{т). Другими словами,
кривая ползучести в момент нагружения г выходит не от оси времен (Z,r), а из точки
С, отстоящей от этой оси на расстоянии отрезка (г, с), равного по длине аС(т). Коэф-
фициент а считается постоянным и определяемым из опыта.
В этом случае мера ползучести бетона в рамках теории старения равна
С(/,т) = С(0 - ОД + а • ОД = С(0 -(!-«)• ОД. (3.2.14)
§ 3.3. Мгновенно нелинейные законы ползучести бетона
Рассматриваем бетон, обладающий свойствами мгновенно нелинейного материа-
ла и удовлетворяющий уравнениям Евростандаргов (2.2.3) и (2.2.4). Сначала будем рас-
сматривать бетон, мгновенные свойства которого с течением времени не меняются.
Пусть диаграмма or - е аппроксимируется выражениями вида
(3-зл)
^=^(°’)=:Л(СГ)’ 3-3-2)
1де ем - мгновенные деформации бетона.
Выражения (3.3.1) и (3.3.2) дифференцируем по времени

да
да
(3.3.4^
В этих выражениях фигурирует значение касательного модуля деформаций бетонг
Е'кас'^м' ^кас д J
д£м ОЕМ
Г ( x_F 1 1
ксД<Т' ™ дЕм(а) df2{g)
да да
который характеризуется на рис.3.3.1 углом а (Екас = (gtz)-
На основании (3.3.5) и (3.3.6) из (2.3) и (2.7) получаем
Екас(ем)
ас + (28с) £м+ 8g(2c -1)
(c + g£M)2
(3.3.5;
(3.3.6;
(3.3.7;
Екас(<У)
______________1_____________
Вх + 2В2а + ЗВ3а2 + 4£4ст3 ’
(3.3.8;
72
Рис.З 3.1.
Из выражений (3 3.3) и (3.3 4) записываем
<3-3’)
да
<^=е««(^) (3.310)
Полная скорость деформации находится из (3.1.6) как сумма скорости мгновенной
деформации и скорости деформаций ползучести.
^ = ^+£и-
Отсюда получаем вид основного закона ползучести
<3-312>
где К - коэффициент вязкости из (3.1.3) либо (3.1 4).
Основной закон линейной ползучести можно записать также через функции ft )
и /2(сг):
(з-злз)
ЭЕм
73
либо
3f2(a) . 1
f = ^_Z.cr + — а. (3.3.14)
ОСУ К
В рамках моделей, основанных на простом суммировании относительных дефор-
маций ползучести и мгновенных нелинейных деформаций, основной закон линейной
ползучести будем записывать в виде (3.3.13), либо (3.3.14).
Задача состоит в нахождении экспериментально обоснованных значений коэффи-
циента вязкости бетона К, имеющих в различных теориях ползучести различные вы-
ражения.
§ 3.4. Мгновенный нелинейный закон деформирования в рамках
линейной ползучести бетона
В интегральной форме основное уравнение для линейной теории старения бетона
имеет вид
(3.4.1)
где сг0 - напряжение бетонного волокна в момент загружения t0 = 0;
Eq - модуль упругости бетона в момент загружения.
Сначала уравнение (3.4.1) сведем к дифференциальному
(ЗЛ2)
В случае использования модели с неизменным модулем упругости бетона диффе-
ренциальное уравнение линейной теории старения имеет вид:
(3.4.2*)
Из (3.4.2) видно, что коэффициент вязкости К для бетона с неизменным модулем
упругости Eq является функцией времени
<pl
Рассмотрим случай переменного модуля упругости бетона, изменяющегося по за-
кону
Е =----------
Найдем производную Е в виде
74
®о ' & о * &t
С учетом (3.1.8) записываем
1
/:(/)
ДОЪ 1 «
F2(r)J £о й
откуда уточненный коэффициент вязкости
K(Z) = ^
<pt
1
(1 + *0)
Представляя уравнение (3.1.8) в виде
1
E(t)
_<Pt
о г
Eq)
1
замечаем, что первое слагаемое • <7 характеризует скорость мгновенных деформа-
£(/)
ций, вызванную скоростью изменения напряжений а; второе слагаемое характеризует
скорость мгновенных деформаций, вызванную увеличением модуля мгновенных дефор-
маций E(t), третье слагаемое характеризует чисто вязкую составляющую скорости
деформаций. Структура двух последних слагаемых позволяет их объединить в одно сла-
гаемое и считать процесс увеличения модуля мгновенных деформаций проявлением
вязких свойств бетона
Ео)
Характеристика ползучести бетона
где en(t) - относительная деформация ползучести к моменту времени (;
£0 - относительная упругая деформация £м в момент загружения t0 = 0
Для мгновенно упругого материала эта деформация рассчитывается
ст а
£« =------= - -
£Г«о> Ео'
но в эксперименте £0 — £м . Обратим внимание, что функция характеристики ползучес-
ти (p(t) учитывает фактически мгновенные свойства материала в момент за!ружения
р(<)=р.(1-е"6'), О-4-3>
75
где (р и Ь - коэффициенты, определяемые из опытов
Деформация ползучести выражается через характеристику <pt
0-4.3)
где £м0 - мгновенная деформация в момент загружения /0 ~ 0; для мгновенно
упругого материала £м0 = е0.
Для мгновенно нелинейного материала деформацию ел0 запишем теперь в виде

^0
^к(о-0)
(3.4.4)
где Ес“ (сг0) - секущий модуль бетона в момент загружения /0 = О
Формулы для нахождения секущего модуля определяем из (2.2.3) и (2.2.4)
Е ~ £t(0 + B2(t)a + Вэ(/)<72 + В4(/)<73 ;
EceK(^t)
l + g0X< ‘
В частности, при неизменяемых свойствах бетона
£0'“(о-о) =----------------1-----5---------Т
в,(0) + В2(0)ао + В3(0)ао2+ B4(0>’’
<т0 - напряжение в бетоне в момент загружения tQ = 0.
Скорость деформаций линейной ползучести в теории старения бетона равна
= — <Д0, (345)
^0 ^0 £,м0
где £п<р - скорость деформаций ползучести, отнесенная к характеристике ползучести
<pt. Тогда связь между скоростями £п и £п(р определяется соотношением
<Тл £п<р 1 .. сг
—. (346)
°0 ^.мО ^0
Обратим внимание на особенность характеристики ползучести <pt (заложенной в
основу теории старения), вытекающей из (3.4.6). Скорость деформаций ползучести бе-
тона Еп пропорциональна скорости деформации £n(f, выраженной через характеристи-
сг(/)
ку ползучести Коэффициент пропорциональности-------изменяется по тому же закону,
что и функция <т(/); при выполнении условия сг(/) = <70 = const скорости £п и £п<р
совпадают
76
В условиях учета мгновенной нелинейности скорость деформаций ползучести равна

£п
(3.4.7)
либо
1 £п<Р z. J . a(t)
Eq (<7q) EmQ <То
Формула (3.4.6) показывает своеобразность трактовки характеристики нолзучесги
<pt в теории старения бетона, а также своеобразность нахождения с её помощью скоро-
стей ползучести. Причем, эта трактовка не зависит от способа учета мгновенных де-
формаций (упругие, неупругие).
Итак, основной закон ползучести бетона в условиях учета мгновенных нелинейно-
стей имеет вид:
1 • Г 1 - 'I
£ - ---- . 0- +----ф . ст .
№(<><,)
де.
либо
. sf2(o) . ( i Л
е--^—-а +-----------(р. -а
да [Е™(а0)
Коэффициент вязкости Кх в данных уравнениях - величина переменная и зависит
от времени
<3-4-8>
Eq Eq (а0)
Далее рассмотрим случай, когда диаграмма мгновенного загружения бетона изме-
няется с течением времени; другими словами, переменными являются коэффициенты в
уравнениях (2.2.8) и (2.2.9)
cr = cr(fM,Z) = /1(^,r);
(3.4.9)
=^(^) = Л(^,0-
В этом случае скорости мгновенных деформаций будут равны
• ^(^,0 - . ^2(^0
да dt ’
либо
. =____1_______. dfx(eM,t) 1
£м а dt dfi(£M,t)
дем д£»
(3.4.10)
77
Последние слагаемые в (3.4.10) равны
_о „ . О ~2 , о _3 , о ^.4
^2 * ^3 * ^4 * & ?
(3.4.11)
dfx(£M,t)=d f а + 8£м'
dt dt { м c + gEM;
Основной закон линейной ползучести бетона в условиях изменения мгновенной
диаграммы с течением времени имеет вид
do |_д/
(3.4.12)
= л,(() + 2В2(0 • О- + ЗВ3 (/) • аг + 4B4(Z) • а3;
до
ut \Е J
Либо
1 . _ dt 1
а а.^1(£^) + К
д£м L д£м
(3.4.13)
где
36 <£M,t) Q(0 + 28(f) • £м 4- 8(f) • g(Z) • E2m
d£„ (1 +
a{t) • em + [<£(/) + g(Q • g(z) - g(z) • д(р]. £2m + [<?(0 • g(Q - 8(f) • g(p]-
0 + g(O £m)2
£M=^-£n-
Выражения, стоящие в квадратных скобках (3.4.12) и (3.4.13) зависят от способа
экспериментального нахождения характеристики ползучести. Последняя - величина
безразмерная. Для получения только деформаций ползучести £п (в любой момент вре-
мени t) из полной деформации бетонного образца £3 вычитают упругую мгновенную
деформацию £у (иногда вместе с деформацией усадки)
78
Мгновенная деформация экспериментально определяется в момент загружения
t0 = 0. В произвольный момент времени / на замеренную полную деформацию Е ока-
зывает влияние изменение модуля упругости E(f) , изменение с течением времени проч-
ности бетона Rb и другие параметры. Все они интегрально учитываются в измеренной
полной деформации еэ и, следовательно, в характеристике ползучести <pt. Последняя
экспериментально определялась в многочисленных экспериментах научных школ Улиц-
кого И.И., Голышева А.Б., Лившица Я.Д., Dischinger F. и других. Поэтому выражение,
стоящее в квадратных скобках (3 4.12) и (3.4 13), для практического использования за-
писываем в виде
1
.£Г(<7„)'₽ •
удовлетворяющим понятию характеристики ползучести (pf, принятому в теории старе-
ния бетона.
Окончательно основной закон, учитывающий фактические мгновенные свойства
бетона и линейную ползучесть бетона, записываем в следующем виде
Ё = [5 (Z) + 2В2 (Г) ст + ЗВ3 (/) - <т2 + 4/?4 (/)] • а +
(3.4.14)
1
'<Pt
(Ло^о)
либо
[i+g(O -sj2_________
a{t) + 26 (t) em + d (0 • g(0 • e2m
(3 4 15)
причем форма (3.4.14) является менее громоздкой.
Рассмотрим далее применение идеи Александровского С.В. (из предыдущего па-
раграфа) о приближенном учете обратимости деформаций ползучести с помощью «вер-
тикальных отрезков». На основе записи меры ползучести в виде (3.2.14) интегральное
уравнение линейной теории старения бетона представим в виде [87]
•cda(r)
о dr Ео
(3 4.16)
о Ео
где а характеризует «вертикальный отрезок»
а-С(т) (3.4.17)
в промежуточный момент нагружения т.
79
Дифференцируя интегральное уравнение (3.4 16) по параметру t и производя не-
которые упрощения, имеем
1
£ ------
E(t)
f 1 b f1
•а+ a — -<Pt О-+ — -<р,
к ^0 ) 1^0 )
(3.4.18)
В этом уравнении первое слагаемое характеризует скорость мгновенных дефор-
маций; второе слагаемое приближенно учитывает влияние обратимости деформаций
ползучести; третье слагаемое учитывает вязкую составляющую деформаций ползучес-
ти.
Учтем далее в уравнении (3.4.18)мгновенные нелинейные свойства бетона Окон-
чательно результат записывается в виде
I . f 1
£ = ---------г • ст + а------------------------
(3.4.19)
(3.4.20)
§ 3.5. Совместный учет нелинейной ползучести и мгновенного
нелинейного деформирования
В современной нелинейной теории ползучести бетона учитывается тот факт, что
зависимость между напряжениями и деформациями ползучести нелинейная Причем
эта нелинейность ползучести никак не связывается с мгновенными линейными (упру-
гими) деформациями или мгновенными нелинейными.
В нелинейной теории ползучести [39] вводится дополнительная гипотеза о суще-
ствовании афинною подобия кривых деформаций простой ползучести, соответствую-
щих напряжениям различных уровней:
^„(cr,Z,r1) = /(cr) C(/,r1) , (3.5.1)
где £п(ст,Z,T|)- деформация ползучести волокна, загруженного напряжением ст;
/(ст) - некоторая нелинейная функция, называемая функцией напряжений,
C(t, Г]) - значение деформации ползучести при единичном нагружении в волокне
(мера ползучести)
Гипотеза (3.5.1) означает, что кривую деформаций ползучести вызванных напря-
жением ст, можно получить умножением ординат кривой деформаций ползучести, выз-
ванных единичным напряжением, на некоторую функцию напряжений.
Положив функцию напряжений /(ст) = ст, получают уравнение линейной теории
ползучести. Арутюнян Н.Х. предлагает принимать при ст < — • Rb - а. При боль-
ших напряжениях ст > — он предлагает принимать функцию /(ст) в виде полинома
/(ст) = ст +Дет2,
80
где р - эмпирический коэффициент. Обстоятельные исследования по эксперименталь-
ному обоснованию функции нелинейности f (а) проведены Улицким И И.
Интегральное уравнение нелинейной ползучести на основе гипотезы параллель-
ности кривых ползучести и мгновенно упругого материала имеет вид
. Л^о) т
ь ~ г- v W j ,
^0 о
(г) J dr
^-dr-
(3.5.2)
Х(<0(1-а)
О ^0
'<р?
где коэффициент а учитывает обратимость деформаций ползучести; /(<т) - функция
напряжений.
Дифференцируя интегральное уравнение (3.5.2) по параметру /, получаем
1 . <У(сг) . 1 0, ч
£.=-----а + ~----а------<p-a+—f(a)
Е(/) да Ео 1 Eq (
Вводя в рассмотрение мгновенно нелинейные свойства бетона (2.3) либо (2.4) и
делая преобразования, сходные с проведенными ранее в (3 4 12) и (3.4 13), записываем
£
до-
<Pt-a
да
0г
(3-5.4)
L^(<r0)J
либо
£ =
(р^а
да
___<PL
ЕГ(г
(3.5.5)
О£.
Подставляя, например, в (3.5.4) функции f2(a,t) и f (а), найдем основной нели-
нейный закон ползучести, учитывающий и мгновенную нелинейность бетона и его не-
линейную ползучесть.
£ = [в1(0 + 2Е2(0*о' + 3B3(t)-a2 +4Д4(/)<73]-<т +
(3-5 6)
Отметим важные свойства объединенного уравнения пластичности и ползучести
бетона (3.5.6):
- дифференциальное уравнение первого порядка является линейным относи-
тельно производных £, о, что позволяет эффективно решать различные слож-
ные задачи нелинейной теории железобетона;
81
- дифференциальное уравнение содержит переменные коэффициенты, являю-
щиеся нелинейными функциями напряжения ст и времени t у это позволяет с
наибольшей полнотой учитывать нелинейные свойства бетона, в частности,
установленные Евростандартами;
- параметры ползучести бетона, заложенные в уравнение (3.5.6), достаточно
глубоко и тщательно обоснованы экспериментами, проведенными солидны-
ми научными школами;
- уравнение (3.5.6) позволяет исследовать нелинейную ползучесть бетона на
всем диапазоне мгновенных напряжений нелинейной диаграммы ст - е , в том
числе и на ниспадающем участке её;
зависимости нелинейной ползучасти можно применять не только для случая
загружения, но и при разгрузке, если, начиная с некоторого значения ст в точ-
ке диаграммы, напряжения начинают убывать; можно принимать, что разгрузка
MOt следует прямой параллельной первоначальному прямолинейному учас-
тку, рис.3.5.1
§ 3.6. Нелинейное уравнение ползучести бетона,
основанное на использовании схемы Кельвина
В теории ползучести бетона широкое распространение получила линейная модель,
основанная на схеме Кельвина и получившая название теории упругой наследственнос-
ти, основоположниками которой являются Л.Больцман и В.Вольтерра. Широко исполь-
зуют её в своих трудах Ю.Н.Работнов, А.Р.Ржаницын, А.М.Скудра, А.К.Малмейстср
и другие ученые. В этой теории принимается, что модуль упругости бетона - величина
постоянная и равная £0; деформация ползучести считается функцией только продол-
82
жительности действия нагрузки, т.е. игнорируется процесс старения бетона. Интеграль-
ное уравнение теории упругой наследственности бетона записано в виде
f(/)=

(3.6.1)
В этой теории кривая деформаций ползучести, соответствующая нагружению бе-
тона,загруженного в начальный момент (она сдвинута по горизонтали на величину т);
в этом случае вся деформация ползучести оказывается обратимой.
Интегральное уравнение (3.6.1) дифференцированием по времени t сводится к
следующему дифференциальному уравнению
£0 Ео 1
______У------- £ 4---У----£ =--------------о- +
у • (1 + £0 • Со) 1 + Eq • Со у • (1 + Eq • Со)
где Со - постоянное значение функции старения бетона в выражении для меры ползу-
чести.
Уравнение (3.6.2) можно получить из известной схемы Кельвина путем параллель-
ною соединения комплексного волокна с мгновенно упругим волокном М;; комплекс-
ное волокно является последовательным соединением вязкого волокна ещё с одним
мгновенно упругим волокном М2
Комплексное волокно подробно описано в § 3.3. Рассмотрим сначала линейный
вариант модели. Деформация комплексного волокна является одновременно полной
деформацией всей модели:
(3.6.3)
где £в - деформация вязкого волокна с напряжением сгк = К • ёв;
К - коэффициент вязкости.
Дифференцируем (3.6.3) по времени
ё = ё^ + ёв,
либо
1 . 1
e = E~i'<7k + K'aki (3-64)
где Ех - модуль упругости волокна Мj.
Полное напряжение модели
сг = ак + сг2 = сгк + Е2 е,
откуда
<т = + ст2,
либо
сгА = ст - сг2 = ст - £2 • f;
(3.6.5)
&к = & - <т2 = & - Е2 • ё.
83
Значения (3.6.5) подставляем в (3.6.4), получаем
Сравнивая уравнение (3.6.2) с (3.6.6), получаем, что они тождественны при усло-
виях
- р . Со F =Е
0 iif z^* > "* 2 0 । f z^ э
1 + Eq ' Cq 1 + Eq ‘ Cq
(3.6.7)
(3.6.8)
где Ео - модуль упругости бетона.
Численные значения констант для бетона, по данным Арупоняна Н.Х., таковы
Eq = (2 - 3,73) • 105 кг 1см2; в среднем Eq = 2,86 • \05 кг/см2;
Со = (0,9 4- 0,975) • \0~5см2/кг; в среднем Со = 0,938 • 10"5сл? /кг;
у = (0,026 -г-0,03) • 10~5сл/2 /кг; в среднем у - 0,028.
Обозначим соотношения модулей упругости
^0=еГ^=е2‘£2»
где в; и е2 - коэффициенты из (3.6.8):
1+ Д)' О) , , ч
1 Е 'С ’ е2 = О + ’О))-
^0 '“'0
Подставляя численные значения Ео и Со из Н.Х.Арутюняна, можно получить:
1 + Eq • Cq — 3,683 -
Тогда значение % становится равным
2,683
У (3,683)2 ’ (З А9)
Напомним, что в теории старения бетона коэффициент вязкости равен
к=-т-, (3.6.10)
'Kt
либо
Eq 1
(3-610)
где kG = 0,09.
Рассмотрим далее мгновенно нелинейную модель в рамках схемы Кельвина.
Для элемента Мх считаем известной диаграмму мгновенного деформирования
84
Её производная

а = ^L
5аА
(3.6.12)
(3.6.13)
Для элемента М2 также известны диаграмма мгновенного деформирования
= сг2 (£2 ) = сг2 00 = <р2 G0 (3.6.14)
4 её производная
дет, . Эси .
о2^—^-е = ~±'£. (3.6.15)
О£ О£
Уравнение (3.6.4) в данной модели принимает вид
• • 1
е = ~8^'^ + к'^- (3-616>
Напряжение в комплексном волокне из (3.6.5) записываем в виде
ак - <7 - сг2 = ° ~ ^г(60» (3.6.17)
1 также его производная
5^2 .
сг*=сг—p--f. (3.6.18)
О£
Значения (Ук и &к подставляем в (3.6.18), получаем
_ /С
(3.6.19)
После упрощений имеем
£• 1 +
^i(^) д<Р2(£)
д<ук д£
•К + ф2(£) = &
Зег*
К + сг
(3.6.19)
Обратим внимание на одну существенную особенность исследуемых моделей, по-
строенных по классической схеме Кельвина. Учет мгновенных нелинейных свойств
эетона в элементах Мj и М2 меняет их диаграммы сг - £•, по сравнению с (2.3) и (2.4),
тго существенно усложняет получение окончательной модели. Вместе с тем, задачу эту
иожно однозначно разрешить, привлекая существующие в теории железобетона экспе-
риментально обоснованные уравнения связи (между собой) параметров диаграмм а - £ -
Например, по Скрамтаеву Б.Г. призменная прочность Rb связана с начальным модулем
/крутости бетона Еь уравнением
R _ 360 д,
‘ 1106-£tl,7-
Из него записываем для элементов Мj и М2 соответственно
85
36ОЕо-
et
1-106-£0 —-1,7’
ei
36O£o- —
е2
ЫОб-£о--1,7’
и так далее.
Можно также связь между параметрами Rb,Ebieb0 устанавливать на основании
нормативных табличных данных, используя осредненные численные значения.
В случае принятия линейной зависимости между Rb и Еь

где £ь - константа.
На основании (3.6.8) записываем
-/(о-*);
е2
В этих формулах номера 1 и 2 относятся к номерам элементов Ма и М2 соответ-
ственно).
Окончагельное уравнение ползучести записываем в виде

%(£)
де
К+-/2(с)-
«2
(3.6.20)
дак
где коэффициент вязкости находим из (3.6.7).
В более короткой записи
-е^К + сг,
\ At
S--/2'U) -К +
е2 J
-•/2w=
(•)
86
В уравнении (*) рассматривается линейная ползучесть. Для учета нелинейной пол-
зучести будем считать вязкий элемент удовлетворяющим следующему закону деформи-
рования
^•^ = /(ст), (3.6.21)
где К определяется уравнением (3.6.7);
/(ст)- функция нелинейности, имеющая вид
/(а)=сг + Д-ст2; (3.6 22)
, ,Д-Е0 С,
' 1 + Е0-С0;
(3 6.23)
ft - коэффициент в функции нелинейности Арупоняна Н.Х.
Учет нелинейной ползучести в (3 6.2) (мгновенно упругий бетон) дает
Е Е \ ( \
Z (l + £0-C0) 1 + Ео-Со Z-(1 + EOC<,) ' я, / . (3.6.24)
Учет нелинейности мгновенного деформирования и нелинейной ползучести дает
из (3.6.16)
ЭстА
•°-*
1
ч---
К
fM.
(3.6.25)
Учет в нем (3.6.18) и (3 6.19) дает
dcrk е2 де
К + -Ш—
е2 е2
(**)
= ofe/ifoЖ ч- ст ч- Дст2 - Дqf2{e) • —
е2
Уравнение (**) представляет объединенное уравнение пластичности и ползучести
бетона, учитывающее произвольный закон мгновенного деформирования ам - е „,
а также нелинейную ползучесть в гипотезах теории упругой наследственности бетона.
Сопоставим полученные уравнения (*) и (*♦) с теорией упругой наследственности, при-
нимая в ней нижний предел интегрирования /0 = 0 (до этого момента времени в мате-
риале не было никаких напряжений)
^(r) = -J-- ct(Z)+ jcy(r)-K(t-T)-dT
Eq L О
(3 6.26)
Для описания нелинейной ползучести оказалось эффективным предложение
Ю.Н. Работнова заменить в левой части (3.6.26) произведение e(t) Ео функцией де-
формаций <р(е) - ординатой кривой мгновенного деформирования:
87
I
<р(£-)=сг(/)+K(t -r)-d -t
0
(3.6.27)
Применяя для ядра K(t - t) функцию в форме (3.6.1) и дифференцируя (3.6.27) по
времени, получим соответствующее интегральному уравнение линейное дифференци-
альное уравнение - <рх • )
Ео д(р} . Ео ( ч 1
—А * + 1а. Р "Л"' = а. г 'а + а- (3.6.28)
X • (1 + Eq Cq ) ^£ 1 + Eq Cq У * (1 + Eq ' Cq )
Сопоставляя (3.6.28) и (♦), видим, что применение для бетона подхода, реализо-
ванного в (3.6 27), возможно только при выполнении следующих тождеств-
Eq
\+ Eq ’ Cq
Pi GO;
(3 6.29)

/1' * I “ 2 • /2 (*)J = const. (3.6 30)
Левая сторона тождества (3 6 29) является функцией от напряжения и деформации
0 = 0(ст, £), а правая сторона - функцией только от деформации <р} (г) Их совпадение
возможно только при постоянных напряжениях <jk, то есть при фиксированном значе-
нии касательного модуля бетона, в общем случае такое совпадение отыскать трудно, так
как касательный модуль деформаций постоянно меняется с изменением сгм.
Если же сравнивать уравнение (3.6.28) с общим уравнением ползучести (♦♦), то
необходимо учитывать дополнительно равенство нулю двух последних слагаемых в (♦.♦),
что весьма проблемагично, (е &£м)
/?, • ст2 - Д • а • /2(^)— = 0 {3 6 31)
е2
Даже в рамках мгновенно упругого бетона с нелинейной ползучестью (3.6.24) при-
менение (3.6.28) вызывает определенные трудности. Действительно, сопоставляя
z.(I + E0-C0)-(1 + A-o-)‘6 + (1 + £о СоМ1 + Д cr) f“-
(3.6.32)
Eq
/•(1 + £0«С0)‘(1 + Д сг)
с (3.6 28), видим, чго необходимо найти обратные функции для двух первых коэффици-
ентов в (3.6.32), а также выполнить условие постоянства коэффициента в предпослед-
нем слагаемом (3 6 32).
1 1
/ (1 + Е„ Со)' (1 + Д а) " ’ при №Рема“ом значении а.
88
Рассмотрим также вторую схему Кельвина, представляющую последовагельное
соединение комплексного элемента с мгновенно нелинейным волокном М2комплек-
сное волокно состоит из параллельного соединения вязкого волокна с мгновенно нели-
нейным волокном М
Полная деформация модели является суммой
£-£х+Е2, (3.6.33)
где £x=£r.
Скорость полной деформации
£ = £х + е2 , (3.6.34)
Величина и скорость деформации волокна Мх равны
-г -е2 = £-Е2(а)', (3.6 35)
. д£2
£^£-£г^е--^.а (3.6.36)
да
Напряжение в модели
а = <т2 -ах + а£, (3.6.37)
где сг2 - напряжение волокна М2;
crj = сг, (£]) - напряжение волокна Мх,
ав - напряжение вязкого волокна.
Учитывая формулу для ав, из (3.6.37) записываем
a = <Tj(£][) + К-es =сг|(б'1) + /С (3 638)
Подставляем (3.6.35), (3.6.36) в (3.6.38), получаем
сг = сТ1 \e-e2(v))+K-e-K^-(j. (3.6.38)
да
Применяя уравнения мгновенного деформирования
= = = (3.6.39)
<Рг =(р2(а)=Е2(а}, (3.6.40)
имеем
a = ^i(£, =£-<p2(aj)+K-£-K —--а (36.41)
оа
Функции (рх и (р2 связаны с функциями f и f2 соотношениями
= ; (3 6.42)
ei
<p2(cr) = f,(p), (3.6.43)
где ех = 2,683.
89
Окончательно для второй модели Кельвина основной закон пластичности и ли-
нейной ползучести записываем в виде
сг = — ЛОч (***)
е{ ост * 4 '
где К = —-—.
Г'Со
Тождественность уравнений (♦♦♦) и (3.6.28) трудно выполнить, так как для этого
необходимо выполнение условий
Z^const-, ^const-
За де 1 + £0-С0
причем из левой части последнего условия требуется исключить напряжения ст -
§ 3.7. Основные соотношения нелинейной теории ползучести бетона
В современной теории ползучести можно выделить два основных направления
построения уравнений ползучести: в интегральной форме и в дифференциальной фор-
ме. Для металлов первое направление теории ползучести формировалось в работах
ЮЛ.Работнова и ею учеников; второе направление развивалось в работах Л.М.Кача-
нова и ряда других ученых, причем второе направление развивалось интенсивнее пер-
вого.
В работах первого направления широко используется интегральный принцип Воль-
терра, состоящий в следующем. При решении статических задач теории наследствен-
ной упругости основные уравнения теории упругости сохраняют свою форму, только
упругие константы заменяются упругими операторами. Поэтому для получения реше-
ния задачи ползучести сначала решают соответствующую задачу теории упругости, а в
окончательном результате решения упругие константы заменяются упругими операто-
рами. Общая теория линейной вязкоупругости строится по образцу обычной теории
упругости, для нее доказываются интегральные теоремы.
Вследствие рассмотрения скоростей в работах второго направления широко ис-
пользуется дифференциальный принцип возможных мощностей (что существенно для
нелинейных задач)
Ё(ЛА + + ZA)=0, (3.7.1)
1=1
являющийся следствием принципа возможных перемещений
±(Xi&i + Y,.Sy,+Zl-&i)=0.
i=l
Тогда же возникла дискуссия о точности указанных направлений.
Для ползучести бетона первое направление развивалось интенсивно, а второе на-
правление являлось следствием первого.
90
При построении интегральных уравнений использовались две основные гипоте-
зы. Первая гипотеза заключалась в раздельном рассмотрении упругих деформаций и
деформаций ползучести, складываемых между собой для нахождения полных дефор-
маций
Е = £м+£п- (3-7.2)
Вторая гипотеза носит название принципа наложения и предполагает для дефор-
маций ползучести, что каждое приращение напряжений а, приложенное в момент вре-
мени -г,, вызывает деформации, которые зависят от времени общего напряжения
(ст0 + ст,), но не зависят от характера загружения до этого момента. Для упругих де-
формаций справедлив общий принцип независимости действия сил.
В частных случаях удается сводить интегральные уравнения ползучести к эквива-
лентным дифференциальным.
Например Интегральному уравнению (3 6.1) соответствует дифференциальное
уравнение (3 6.2), которое запишем в виде
ё=а^ + а2а+а3е, (3.7.3)
где й,,а2,а3 - постоянные величины
Из (3.7.3) формулируем для линейной теории ползучести бетона важный принцип
независимости скорости полных деформаций от различных параметров скорости на-
пряжения, величины напряжения, величины деформации.
В линейной теории старения бетона скорость полных деформаций равна
£ = a}(t)-& + a2(f)-cr, (3.7.4)
где а},а2 - известные функции времени t.
Здесь скорость £ не зависит от самого относительного перемещения £.
В уравнении (3.6.24), характеризующем нелинейную ползучесть теории упругой
наследственности скорость деформации
£ = а}& + a2f (ст) -к а3£
является линейной комбинацией скоростей, но параметр напряжений входит во второе
слагаемое нелинейно; существенным является линейность скорости напряжений ст
В уравнении теории старения бетона с нелинейной ползучестью (3.5.3) скорость
полной деформации равна
ё = а, (0 • ст + ап (t) • а12(а) -<т + а3(t)f (ст). (3.7.5)
Здесь скорость полной деформации линейна только отаосительно скорости на-
пряжений ст, но уже нелинейна относительно самих напряжений ст. Учет мгновенной
нелинейности бетона усложняет выражение коэффициента at в уравнении (3.7.5)
£ = щ(сг,1)-& + аи (t) ax2(v) -& + a3(t)f (ст) (3.7.6)
но сама скорость ст входит нелинейно.
Наследственная теория старения бетона, описывающая мгновенно упругий мате-
риал с нелинейной ползучестью в дифференциальной форме, записывается в виде уско-
рения деформаций
£(0 = (t)a(t) + b2(a ,0^(0 + b3£(t).
91
Ускорение ё линейно зависит от трех параметров ускорения напряжении & ско-
рости напряжений <7, скорости деформаций ё. Коэффициент Ъх - нелинейная функция
времени t, Коэффициент Ь2 - нелинейная функция времени t и линейная функция на-
пряжений (У .
Подводя итог исследованиям, проведенным в данной главе, авторы данной книги
и их ученики предложили эффективный практический метод совместного учета мгно-
венных нелинейных деформаций и деформаций нелинейной ползучести. Он позволяет
использовать аналитические зависимости ползучести бетона, обоснованные фундамен-
тальными трудами ученых-экспериментаторов. Этот метод развивает одновременно идеи
Работнова Ю Н., Бондаренко В.М., Качанова Л М, Ржаницына А Р. Он добавляет к об-
щеизвестным гипотезам теории ползучести две мало используемые в научной литера-
туре идеи: использование функции нелинейности напряжений ф в качестве новой не-
ременной вместо напряжения аь; использование условного времени z в качестве аргу-
мента интегрального уравнения вместо реального времени t
Использование общеизвестных гипотез в дальнейшем специально нс подчеркива-
ется, ввиду общеизвестной формы записи уравнений.
В четвертой главе мы введем дополнительно еще одну новую идею, позволяющую
успешно и достаточно точно решать задачи длительного сопротивления железобетон-
ных конструкций в дифференциальной форме.
Ранее были записаны диаграммы мгновенного деформирования бетона по Ьврос-
тандартам в виде (2.2.3) и (2.2.4)
= ^=^(^b) = /2(°’fc) (3-7-7)
Введем на их основе в рассмотрение функцию нелинейности в виде
Ф(<т5,/) = sbEb(t) = f2{ab )Eb(t), (3.7.8)
где Eb(t) - начальный модуль упругости бетона, изменяющийся с течением времени по
любому ранее предложенному закону, например [3]
£ь(О = £л(0)[1-ДГ“],
либо [162]
^(0=
^(0)
£ь - мгновенная деформация бетона.
Функцию нелинейности O(crfc,f) записываем в виде
Ф(сг^, 0 = b} (t)crb + b2 (t)crb + b3 (0<Ть + b4 (t)a^, (3.7.9)
где коэффициенты Ь: получаем из (2 2.7)
6,=1;
Eb(f) 2
^(/)
. £»(oj' 4(0.
t>2 (0 —
92
^2(0-
*з(0 =-----
+ 3ад)^^-
[RbW ^o(Oj
ад) 2
£Ь0 (О *Ь (0 £ьо (0
E2b(t)
(ад)
<^2о(О
2
и так далее.
Заметим, что принимая функцию (3.7.11), мы вводим в рассмотрение новую пере-
менную Ф(сгг> ), обладающую вместе с тем всеми свойствами напряжения сь; она имеет
размерность напряжения и позволяет эффективно учитывать в задачах ползучести мгно-
венные нелинейные деформации совместно с деформациями нелинейной ползучести.
Введение новой переменной Ф(сг^) требует видоизменения ядра интегрального
уравнения, а также другого масштаба меры ползучести бетона, либо масштаба характе-
ристики ползучести бетона. Схема этого видоизменения достаточно прозрачна.
В связи с использованием функции Ф(сгь) вместо напряжения сгь, введем в рас-
смотрение меру ползучести Сф(/,т), удовлетворяющую следующему уравнению, оче-
видно вытекающему из условия равенства деформаций ползучести
ф(ад»сф(лг)=ад)С(г,т).
Отсюда находим
СФМ - . (3.7.10)
Аналогично записываем из условия афишюго подобия кривых нелинейной ползу-
чести
Сф('’г)=с('’т)Лф(^ю]- (1711)
Записывая, например, меры ползучести в виде функций
С(/,т) = f Со + -1(1 -
V т)
+ AVi-e-r-C”)
V т J
можно записать
Сф + А = со-^А_ + --^—
° т Ф(о>,) т Ф(аь)‘
Для случая нелинейной ползучести
Г*4.^1 = г ,А
‘ * ° Дф(^)) г/(Ф(а,))-
Аналогично можно записать уравнения для характеристики ползучести (p{ttT).
В пятом параграфе первой главы мы привели три выражения для меры ползучести
(1.5.3-1.5.5), дающие близкие между собой результаты по описанию ползучести бетона.
93
Для случая переменных напряжений, который мы рассматриваем здесь в дальней-
шем, было нами установлено, что наиболее простые результаты получаются при ис-
пользовании меры ползучести в виде, предложенном Арутюняном Н.Х., Бондаренко
В.М., Прокоповичем И.Е. и усовершенствованным Щербаковым Е.Н.
Сф(г.&) = С("28>|сф + [1 - <3-712)
где z — z(t); 0 = 0(т) - условное время.
Условное время в расчетах ползучести введено в работах Буданова Н.А. и Ржани-
цына А.Р.
Буданов Н.А. (1940 г.) вводит условное время, пропорциональное деформациям
ползучести при постоянном напряжении. При этом деформации приняты независящи-
ми от возраста бетона, в таком случае условие ползучести является инвариантным в
абсолютном времени. Здесь использование условного времени не дает принципиально
новых результатов в сравнении с теорией ползучести, не учитывающей изменения
свойств бетона во времени. Однако, данный первый опыт по введению условною вре-
мени в виде гиперболической функции Фройденталя А
at
Z~l + bt’
использованный при постоянных напряжениях на основании опытов Дэвиса Р.Е. и Глен-
виля В.Х., уже учитывает в значении условного времени синулярность. А.Р.Ржаницын
использует для условного времени функции, не имеющие особенностей, но позволяю-
щие решать новые задачи теории ползучести.
Е.Н.Щербаков развил идею Буданова Н.А. и предложил использовать более слож-
ную функцию
для обработки экспериментов с деформациями быстронатекающей ползучести (а>,8 -
опытные константы) также при постоянных напряжениях
Рассмотрим подробнее метод Ржаницына А.Р., заключающийся в том, что отсчет
времени берется не в абсолютной шкале, а в некоторой условной, зависящей от харак-
теристики состояния материала t
z- Jy/(0)t/0
о
где 5/(0 - некоторая функция состояния, отображающая изменение деформативных
характеристик материала под влиянием возраста, влажности, температуры и т.д.
Большим преимуществом предложения Ржаницына А.Р. является сформулирован-
ная им остроумная идея эквивалентного преобразования уравнений ползучести. Диф-
ференциальное уравнение с переменными коэффициентами
£«(/)£• + Ас = а + n(t)&,
путем введения условного времени в виде
94
оЧо’
Ржаницын А.Р. сводит к уравнению с постоянными коэффициентами
„tte ,, da
Е— + Не = оч------
dt df
К сожалению, эта идея эквивалентных преобразований уравнений ползучести не
нашла широкого применения в решениях задач теории ползучести.
В условном времени уравнение наследственной ползучести записывается в виде
«(г)=-^-- рг(е)Ф(г>е)<«э
г0
Укажем на некоторые особенности применения метода Ржаницына А.Р, основан-
ного на введении понятия условного времени. Этот метод даег упрощенный прием уче-
та изменения состояния бетона и его влияния на деформации ползучести. Основное
требование к функции условного времени состоит в том, чтобы в условной шкале вре-
мени по возможности соблюдалось условие инвариантности уравнения деформирова-
ния материала
Решение уравнения ползучести в условном времени проводится обычными мето-
дами. Окончательный результат, выраженный в функции условного времени, перево-
дится в реальное время путем подстановки в него функции абсолютного времени. Дру-
гими словами, в интегральном уравнении ползучести с условным временем можно ис-
пользовать известные ядра; корректировка же реальных ядер, записанных абсолют-
ном времени, производится за счет конструирования функции условного времени.
Если ядро K(z,&) имеет более простое аналитическое выражение, чем первона-
чальное ядро K(t,r), то введение условного времени оказывается целесообразным.
Таким путем можно преобразовать ядра с особенностью к более простым ядрам
Особенность ядра ползучести молодого бетона состоит в том, что при значениях
т близких к t деформации ползучести резко увеличиваются, они несколько менее резко
увеличиваются при малых значениях т. Это означает, что наибольшее влияние на де-
формацию в момент времени t оказывают захружения в моменты времени т, непос-
редственно предшествующие t, а также загружаемые в самые ранние сроки после из-
готовления бетона. Загружения же в периоды, удаленные от момента наблюдения, срав-
нительно мало сказываются на величинах деформации ползучести. Подбор подходящих
функций для К(/,г) затруднен сложностью интегрирования уравнения ползучести с яд-
ром общего вида. В ряде случаев подходящую аналитическую функцию для ядра удается
получить из другого, уже изученного ядра путем изменения шкал времени t и т [134J.
Выбор функции состояния у/(О) должен осуществляться путем метода проб и
являться, в определенной степени, искусством Сам Ржаницын А.Р. в своих задачах ис-
пользует преобразования вида
4 — ~ _ „О©
t = е > т = е
для ядра, описывающего свойства бетона раннего возраста
95
которое сводится к инвариантному во времени ядру
tf(z-0) =
Tg(z-&)p
где A,A'tj3,g,p = l- g - безразмерные коэффициенты; Т - постоянная, имеющая раз-
мерность условного времени z;
А
(ату-
Пользуясь структурой ядра Ржаницына и развивая его идею, запишем шкалу ус-
ловного времени в виде выражений
z(0
_ аеа - а
~ (b + t)p ;
0(г) =
аеаг - а
(Ь + тУ
(3.7.13)
ще а,а,р- константы; постоянная b имеет размерность времени и вводится для смяг-
чения сильной особенности ядра; показатель степени 0 < р < 1.
Введенное условное время содержит два важных свойства, в отличие от времени
Ржаницынв А.Р. (z = ле01). Первое свойство заключается в совпадении нулевых значе-
ний фактического и условного времени (z = t = О). Второе свойство состоит в наличии
особенности в знаменателе; этим достигается присутствие особенности в фактическим
ядре ползучести. Действительно, мера ползучести бетона по Бондаренко В.М., которую
запишем в условном времени, равна
C(z, 0) = (с„ + Ае* )=₽(0)/(z - 0).
Ей соответствует простое ядро в условном времени
K(z,&) = ™С(2,0) = <i>(0)/(z - 0) + ?(0)^-/(z - 0).
50 50
Переходя к реальному времени, будем иметь сишулярное ядро ползучести
K(t,T)=U(0=0(r))/[z(O - 0(r)]+- ®«) • •
Производные от условного времени z(t) равны
VA dZ е<а \еа-Ч
z(t) = — = аа----ар-*---V -
dt (b + ty (b + ty"'
96
,ч d2z 2 еа е* t ,ч -1
dt2 (b + tY (b + ty+x (Ь + Г/
Схема решения задачи для учета переменных напряжений становится следующей
Сначала для простого ядра в условном времени построим дифференциальное уравне-
ние ползучести, в котором перейдем затем к реальному времени
Выражение удельных деформаций в виде (3.7.12) позволяет получить основное
уравнение нелинейной ползучести (с учетом мгновенных нелинейных деформаций бе-
тона) в виде дифференциального уравнения второго порядка.
Воспользовавшись общеизвестными гипотезами нелинейной теории ползучести
бетона, основное уравнение ползучести запишем сначала в интегральном виде
= . (3-7.14)
где f - функция, характеризующая нелинейность деформаций ползучести; индексы Ф
в мере ползучести ниже для удобства записи опущены.
Па основании (3.7.12) находим ядро интегрального уравнения
Дг,0)=—C(z,e)=-c^gr^ [i-fe-*-0’]-
50
-c(28)(c+ge-?0^-z(2r-e)
Ядро (3.7.15) подставляем в интегральное уравнение (3.7 14)
(3.7.15)
^(z)
Ф[^^]
Eb(z)
Z
г0
5 1

% г ч
- f/[o-(,,0]{-c(28)ge ,е [1-Ае-Иг-0>]-с(28)(с + ge-7®^)®-*-®^©.
го
Производная по z интирального уравнения (3.7 16) позволяет записать
^(*) =
1 дФ[од,,*]
£fc(*)|_ даь
дФ[о7»*1
dz

- ку )/[Ф(аь,0)]- {- c(28)g?t? 70 + ?с(28)(с + ge"70)}-
«о
e~^~G) d@ + у[ф(а6,0)] • ^(28)[с + ge~^ ]- (1 - *)[- g^(28)e^ ]},
где Eb(z) = — -,<yb(z) = -у-.
dz az
Вторая производная равна
97
£b(z)
,2ф[сгь,г] 2
aJdt(2)+^®hdl
bdz ‘ az2 J
4(z)|’a®[<^.d.i ,.s. Эф(сг»>-г]],
£fc2(z)L d<Tfc(z) dz J
+ ку2 |/[ф(от,,©)]{- с(28)£7€_7в + ?c(28) • (c + ge"7®)}•
*0
.-/U-e)d0 _ к^[ф(аь , z)|_ C(28)g^-” + jc(28) • (c + sev )
(3.7.18)
e
дФ |_ dafc(z) dz J
• [“ g^(28)e-?e ]+ /[Ф(от, ,z)] • [ky - (c(28))g^-;
v -(1- *)c(28)g/2e
.. z . d2£b .. . . d2ub x dEb
где £b(z) - —; <7fc(z) = ; Eb(z) = —-.
dz dz oz
Исключая из (3.7.18) интегральный член с помощью (3.7.17), записываем основ-
ное дифференциальное уравнение ползучести относительно приведенного времени
^(^) + ^(z) = crfc(z)
1 аф[^,г]
^(z)
~2,_s 1 dMcrfc,z]
+ CTl (Z )--------:
’Eb(z) Sa2b(z)
J 1 2d2<tfab,z] ! ai>[o-t,z]r у
7[rh(z) dabdz dub{z) [£j(z)
£2(z) ЭФ
•ky-
• c(28)(c + ge

, ea>k,z] r_r_______ад+^[Ф]
9z |_£t(z) £2(z) 5Ф
•C(28)(C + - 4- +
С/Ф J о
После некоторых упрощений
98
1 д2Ф crb,z
£b(z) + y£b(z) = ab(z) *’ + a?(z)
Eb(z) dab(z) Eb(z) olab(z)
+<jb(z)
——.2 1
Eb(z) dabdz
ao-fc(z) |_£fc(z) Efc)
Z Ёь(г) , у[ф)
" ' ' £?(z) 0Ф

' v " & |_Efc(z) E2b(z)
^2S)r(kc + ge-^+ ‘.......а2ф^’^.
V ' Eb(z) dz2
При практическом решении задач с помощью (3.7.19) необходимо, с целью мас-
штабирования меры ползучести, вместо константы с(28) подставлять величину
(3.7.19)
c(28) < L/v- <bj
Лф(^(о)]-
Для упрощения закона ползучести (3.7.19) будем считать диаграмму мгновенного
деформирования с течением времени неизменной. Из (3.7.19) запишем
I . лг(л 1 32Ф[СТ4]
i да, "'’Б, да2,
^(z) + z^(H) = crfc(z)
+07,^)—^
дет*
+ ge
(3.7 20)
ь J
Учитывая значение приведенного времени из (3.7.13), находим значения перемен-
ных в действительном времени t:
d(z) = О-(0— = o-(f)- (fe + Z)j> ,-у
z(t) aae (b + t)- ар\р -1)»
e(z) = ОД— = ОД------„ + ( а---X;
z(0 aae (b + t)-ар[е№ -1)’
cr(z) = сг(О= &(')---------------m “
z(<) z (t) aae (b + t)-ap[e -1)
. z 4[aa^(b + 02 “ 2aoeat(b + t)- ap(p + l)(e* - l)fe + tp) (3.7.21)
~ a W-------------f--------------7~^—№ -------- ------’
[aa(Z> + 0e“ -cqAe* -
ад=ад^ _ =ЭД
z(f) z (t) aae (b + t) -aple
[aa2e<a(b +1)2 -laae0*(b + t)-ap(p + 1)(еш -l)J/> + )
[aa(Z> + r)e“ - ар(ра - 1)P
99
Подставляя (3.7.21) в дифференциальные уравнения (3 7 19) и (3 7.20), мы получа-
ем основные уравнения нелинейной теории ползучести, учитывающие как мгновенные
деформации бетона, так и наличие быстронатекающих деформаций ползучести в рам-
ках модели, использующей условное время.
Учет мгновенных нелинейных деформаций в рамках модели нелинейной упругости
Арутюняна Н.Х позволяет записать интегральное уравнение в виде (обычное время t)

(3 7.22)
'о
где /[ф] - функция нелинейной ползучести;
е
- мера ползучести
Соответствующее ему дифференциальное уравнение имеет вид
: ^(<W) . • 2 Г д2ф((Уь,1)
(У,-------F <7. ---—— + (У, 2---------Т
дсгь dal [ dtdab
^(0 . v F /ЛГгф . Лф 1Мф(сгл^)]^ф(^»0
т. ^(77) гаГ
а2Ф(ог,,*) + дФ(оу) дФ(<^)^(0 +
dt2 dt dt Eb(t)
УФЕЬ(О
гф , Л ](У[ф(оу)]дФ(аь,0
0 t J сФ(^,/) dab
= ёьЕь(0 + £ьуфЕь^),
где
5Ф £2/3/4
-^-=Ь2аь + Ь3аь +Ь4аь;
dt
о Ч7 ;• 2 L 3 г 4
—г = Ь2аь +Ь3аь + Ь4аь-
ot
~ = by + 2Ь2суь + 3>Ь3(У I + 4Ь4&1.
а<ть
^ = 2b2vb+3b3vl+Ab4vlt
dtdab
= 2b2 + 6Ь3аь + 12/>4о*2
юо
Если принять модуль упругости Еь постоянным, а также принять постоянными
остальные параметры (sbQ,Rb\ то уравнение (3.7.23) существенно упрощается
~ d<J?(ab) а2Ф(аь)
ь ,2
асгь
+ °ь Гф
<Ю(<?Ь)
dab
. ГСФ , ^Ф(о-д)
\ 0 t JdO dab
~Wb ^ь^ь-
(3.7.24)
Функцию нелинейности деформаций ползучести принимаем в виде
/[ф] = Ф + /№2 =Ь,аь + <6, +Л2Н +
+ (б, + 2РЬ. Ь2)а3ь + (i4 + flbl + 2^)r44 + 2P(b,bt + +
+ p(b2bt + 262*4>‘ + + p(b2)a‘,
(3.7.24)
где р - опытный коэффициент.
Производная от функции нелинейности имеет вид
= I + 2рФ = 1 + 2РЬХ<УЬ + 20Ь2<у2ь + 2Д>3сг^ + .
сФ
(3.7.25)
Упростим эти выражения, используя аналогию с теорией Арутюняна Н.Х. и Улиц-
кого И.И. Ограничимся рассмотрениехМ только первых двух степеней напряжений аь в
рассматриваемых функциях /(ф) и
3/[Ф]
получим
/[ф(^)]=*|ст<>+(b2+/2>i2)^;
^1 = 1+ 2^ + 2^,
где Ь} =1.
В.М.Бондаренко и С.В. Бондаренко рассматривают мгновенные нелинейные де-
формации и нелинейную ползучесть путем использования интегрального уравнения в
виде
b^~ 1аъ(т)5Л°ь>Ч-^с (3.7.26)
где
S°(cr*.z)=l +
vk
- функция нелинейности мгновенных деформаций;

R(t)
- функция нелинейности деформаций ползучести;
101
R(t) - прочность бетона;
£® (f) - начальный модуль мгновенных деформаций;
- мера ползучести.
Параметры нелинейности vk,mk>vc,mc нормированы в зависимости от класса бе-
тона.
Для учета отклонения от афинноподобия семейства кривых ползучести параметр
нелинейности vc умножается на коэффициент
= е-170йй(/о)0,778б+ВС(лг<>)}
где С(Г,/0) вычисляют, исходя из предельного значения меры линейной ползучести
с"^).
К достоинствам уравнения (3.7.26), помимо использования двух нелинейных фун-
кций, относится также солидное экспериментальное обоснование этих функций (3.7.27)
и (3.7.28).
Функция мгновенной нелинейности (3.7.27) записана в форме, предложенной Тер-
цаги [147],
которая впоследствии использована Хоффом Н.

°ь
Последнее выражение преобразуем к виду
£ь
(3.7.29)
В.М.Бондаренко и С.В.Бондаренко распространили (3.7.29) на случай перемен-
ных во времени t величин, и обосновали на основании многочисленных эксперимен-
тов значения Eb,a,(m -1).
При использовании интегрального уравнения (3.7.26) функцию ф[сгЛ(/)] следует
записать в виде

Ф[оъ(0] = сгДО + v*crfc(0
(3.7.30)
L*(Oj '
Сравнивая (3.7.30) и функции нелинейности Евростандартов (3.7.11) (более гро-
моздкую), получаем необходимое условие их близости

(3.7.31)
102
С использованием функции нелинейности (3.7.30) интегральное уравнение (3.7.26)
имеет вид
(3 7 32)
который трудно использовать в практических расчетах, что требует преобразования ею
к дифференциальному уравнению. Функция нелинейной ползучести при этом имеет вид
Теперь рассмотрим более простые уравнения ползучести, основанные на ядрах
вида
dr|_£fc(r) J’
и на их основе проведем анализ особенностей предложенного метода учета мгновенной
нелинейности’.
Интегральное уравнение нелинейной ползучести запишем в виде
(О = - Ж(г)]А-1-Л + С*Гф . (3.7.34)
ЕЬЦ) 0 ст ЕЬ{Т) 0
Производная по времени от (3.7.34) дает
^(0 = - “(СоФ/фУф (г)ЖФ Г^т + /[Ф(ст*(т))]С0ФгФ, (3 735)
V ) о
Вторая производная равна

—------+ --------------------
i't(') ЗстЛО Eb(f) 8af(t)

£Д0 dcrb(t)dt Eb(t) dab(t)
i 4(')зфЬ,.'],
^ь(0 +
(3.7.36
Eb(t) St2 Eb(f)
-
о
- C?rlf№tSjl+f
дФ cc b(t) dt
* В выполнении данного анализа принимал участие Кузнецов С В.
103
Находя из (3.7.35) интегральный член и подставляя его в (3.7.36), найдем основ-
ное уравнение ползучести
^(0+/Ф^(0
—-----£^Лтй(/) +
^(0 ^(0
1 1Г»’Ч2(0 + 2
Eb(t) da2b(t) [ Eb(t) dub{t)dt
£fe(QdO[<7fc,z] । Гф ЭФ[<М1 +
£*(0 дстДО Eb(t) dcrb(t) j
(3.7.37)
Eb(t) dt) Eb(t) dt Eb(t)
df ГдФ[<^]д. ! Me.
дФ d<jb(t) b dt
J СФУ
'“'О /ф-
dt2
Уравнение (3.7.37), имеющее второй порядок, можно упростить и получить диф-
ференциальное уравнение первого порядка. Для этого нужно положить, что параметры
диаграммы мгновенною деформирования с течением времени не изменяются. Опуская
промежуточные выкладки, запишем окончагельное дифференциальное уравнение пол-
зучести первою порядка, учитывающее мгновенные нелинейные свойства и нелиней-
ную ползучесть
(3.7.38)
Еь dcrb Еь 4 ’
11одставляя значения функции нелинейности Ф(стл ) в эго уравнение, можно получить
4(0 + /ф^(0
1 + 2b2ab(t) + 3b,a2b(t) + 4bta}b(t)
=---------------------------М0+
Еь
, v °b (f) + b2°b (0 + b3°b (0 + b*°b (0 .
+ / Ф r, *"
Eb
+ СО°/ф/кь + b2°b + b&b + b^b ] •
(3.7.39)
В правой части уравнения (3.7.39) стоят касательный и секущий модуль с диаграм-
мы <ть-£ь
dsb 1 + 2Ь2аь + ЪЬ3а1 + 4Z?4ct^ ’
104
Учитывая особенности меры ползучести Co(f,r), вытекающие из (3 7.11), запи-
сываем основной закон нелинейной ползучести (3.7.39) в виде
Еь
<*ь(0 +
, v <?ь (0 + bzoj (0 + b3a3 (0 + b^b (/)
’/ф ~
Еь
(3.7.40)
где функция, характеризующая нелинейность ползучести, принята по предложению
(3 7.28) Бондаренко В.М.
Уравнение (3 7.40) учитывает также нелинейность мгновенных деформаций в рам-
ках модели Евростандартов.
Для случая линейной ползучести и одновременного учета м1новенной нелинейно-
сти уравнение (3 7 40) упрощается
(0 + ГфЪ = (<)-----------------------------1 — Сто (0 +
Еь
+ (0^. + СФ (0 <3-741>
Еь
Следует обратить внимание на два важных обстоятельства. Первое обстоятель-
ство состоит в том, что полученные уравнения ползучести применимы при возрастаю
щих напряжениях. При постоянных напряжениях <уь = const имеем, что скорость
ab(t) = 0; правые части уравнений (3.7.40) и (3.7.41) постоянны, а сами дифференци-
альные уравнения дают известные решения.
При убывающих напряжениях разгрузка происходит по линейному закону с моду-
лем упругости Еь; дифференциальные уравнения ползучести приобретают известный
вид. Например, для случая (3.7.40) записываем
£Ь(0 + МО = + Г + CQy[ab ) (3 7 42)
Еь Еь
Указанное первое обстоятельство необходимо учитывать при ступенчатых и ре-
жимных загружениях. Даже в простом гармоническом загружении, рис.3.7.1, при за-
данной функции аь(/)на участке 0-1 необходимо использовать уравнение (3.7.40), а на
участке 1-2 деформации вычисляются с помощью уравнения (3.7.42) Другими слова-
ми, на участке 0-1 полные деформации еь находятся с учетом мгновенной нелинейнос-
ти, а на участке 1-2 полные деформации вычисляются по мгновенной линейной модели.
Второе обстоятельство состоит в том, что значения параметров мгновенного не-
линейного деформирования бетона должны приниматься по данным Евростандартов
105
лишь при реальном проектировании. В научных же исследованиях эти параметры дол-
жны уточняться в соответствии со скоростями используемых загружений, особенно в
динамических задачах теории ползучести.
Рис.3.7.1.
В заключении данного параграфа выведем с помощью функции ф основной за-
кон ползучести в рамках гипотез теории старения бетона Здесь можно учесть перемен-
ность во времени диаграммы мгновенного нелинейного деформирования бетона, со-
хранив первый порядок дифференциального уравнения основного закона ползучести.
Интегральное уравнение ползучести записываем в виде
1 dT+
‘ Ею Ек I dr Е„(т)
о о dz Еьо
Ему соответствует следующее дифференциальное уравнение первого порядка
1

+
£b(t)
Eb(t)
&b(t) +
dt
(3.7.43)
Eb0
где функция Ф[егд,т] и ее производные определены выражением (3.7 9)
106
ГЛАВА 4. ИЗГИБ ЖЕЛЕЗОБЕТОННЫХ БАЛОК ПРИ КРАТКОВРЕМЕННОМ
ЗАГРУЖЕНИИ
§ 4.1. Деформации и прочность балок
Гипотезы моделей Евростандартов, изложенные в § 2.1., позволяют исследовать
напряженно-деформированное состояние изгибаемых железобетонных балок на всех
стадиях их загружения, а также четко зафиксировать момент их разрушения
Следует обратить внимание на многовариантность характера распределения на-
пряжений и деформаций по поперечному сечению, которую нужно прослеживать пос-
ледовательно. В отличие от модели пластического шарнира метода предельного равно-
весия, в рамках гипотез Евростандартов необходимо учитывать очередность достиже-
ния различными сталями и бетоном состояния текучести (£j0, £b} reJ), рис 4 1 1
Оказывается необходимым рассматривать четыре последовательных варианта на-
пряженно-деформированного состояния сечения, образующихся с ростом изгибающе-
го момента М
I. Бетон и арматура работают в упругой стадии; бетон на растяжение не работает.
II. Бетон работает в упругой стадии; в сжатой зоне арматура течет; растянутая
арматура работает в упругой стадии
III. В сжатой зоне армагура течет; бетон работает в упругопластической стадии,
растянутая арматура работает в упругой стадии.
IV. Бегон находится в упругопластической стадии, сжатая и растянутая арматура
находятся в упругой стадии
Рассмотрим сначала процесс нагружения сечения в стадии I, рис.4.1.2.
Напряженно-деформированное состояние сечения будем характеризовать двумя
параметрами -с, сгь, рис.4.1 2 Остальные величины определяются на основании ги-
потезы плоских сечений:
h с
На основании (4.1.1) можно переходить от одних параметров к другим
Продольная сила N в сечении изгибаемого сечения равна нулю-
ЛГ = Е°‘/’Л =0. (4.1.2)
>1
Изгибающий момент в сечении равен моменту от внешней нагрузки
п
(4.1.3)
где , Aj - напряжение и площадь любого элемента; - расстояние от элемента j до
моментной точки (выбирается произвольно)
107
Рис 4.1.1.
108
Для изгибаемых элементов, ввиду отсутствия продольной силы yV , удобно за мо-
ментную точку принимать точку Л > находящуюся на уровне растянутой арматуры. Тог-
да из уравнений (4.1.2) и (4.1.3) находим
-•6.С.<7‘+ЛГ,-М,=0; (4.1.4)
~Ь с <Гг ГА-т1+^ (Ао-я')”ЛТ». (4.1.5)
Усилия в арматуре равны
N' = А', • Е' .
S 5 5 S г* £,
*^b,red
Аг Л & As-Es h-a-c b
N=A-£-E= ——-------------------cr2
л J -j jp X _
E'bjtd &
где Es ,E'S - модули упругости арматуры;
As , A's - площади поперечных сечений растянутой и сжатой арматуры;
1
^b red
с-а'
(4.1.6)
1
^b red
h-a-c b
‘ <^2 ;
Г’ ’
(4-1.7)
tjj - максимальное напряжение в бетоне.
109
Для рассмотрения процесса изменения напряжений и деформаций сечения диф-
ференцируем (4.1.4) и (4.1.5) по времени t, считая уравнение изменения изгибающего
момента Мх -Mx{t) заданным,
.ь 1 ,
<т2 - - • b С +
4'%
Ebjred
c-a' As-Es
b.red
£j
h-a-c
c
1 h +
— О’СУ-) Т----------
2 Ebsed
а' гтЬ л
2 ‘а2 4
С
As'Es
Eb,red
h-a
c2
b
= 0.
J'-j?' c-a'
Ebjed C
. 1 ъ . (. 2
+ с • — а, о• Л-с
2 2 { 3
1
2
ь а
е2
= M-
откуда получаем систему двух дифференциальных уравнений для нахождения гг2 и с •
/>
-Мх -Ьсгь +
2
AgEs h а ь
- -Ь-
2
Eb,red C2
c-Д' AsE, h-a-c>
Eb^red Ebjed )
Ebjed C2
1 *,(, Y
(TjD- h — c +
2 1 3 J
a
Eb,red c
(4.1.8)
, с
ch-----+
3
A^E^ c-a
Eb,red C
1
• —Ь<т£ +
2 2
№
Ebtred
c2 Eb,ed
h~a ь .
—-CT2 ’
-Mx\-bc+^ - a -AsEs
2
C = ----------------
। a;Es c-a' ASES h-a-c
^2 Ebred c Ebreci
Ebjed С ^b,red
h-a-c
c
1
с
1 bk (< 2 )
• -crjh i h—c +
2 I 3 J
2
4 E's b a'
~ «2 ’“T
Eb,red C
(4.1.9)
c
1 с
- -b- ch-—- +
2
3
s ;
Eb,red
с-а'
1
2 2
A'E' a' bAsEs
" ’ * CT n “Г
Eb,red C Eb,red
h-a ь
v-4
110
Интегрирование уравнений (4 1.8) и (4 1.9) легко осуществляется по стандартным
программам методом Рунге-Кутта.
При использовании в сжатой зоне арматуры класса A-I или А-П интегрирование
проводится до момента достижения деформации
I с-а ь
£s - г а2
^bjed С
значений £ 0 =107-10 5 либо £50 =133-10 5- Далее необходимо рассматривать ста-
дию II.
Система дифференциальных уравнений для этой стадии получается из(4.1.8) и
(4.1.9) путем приравнивания нулю вторых слагаемых во всех скобках:
-Мг -М +
-ь
1, h ASES h-a ь
0 * 2 F J- 2
2 ^b,red C
1, AS
-Ьс+- ~
2 Ebfed
с
I (.А f. 2 1 1 f с2'] (1 ,
•- a2b- я—с —b ch-------------- ~a2b +
2 ( 3 ) 2 3 2 2
п-а ь
Z " СТ2
' _2 *
'b,red с
2
2
3
2
(4.1.10)
-Мх-Ьс-
x 2
AS
&bred
,\
c-a
1 AE h-a
-bc+ — ----------
2 ^b,red c
-11 l
' --(T^b-i h—c —b- ch
j 2 2 I 3 J 2
-a2b+—sE-
2 ^ed
h-a b
2
2
3
c
Если деформация растянутой арматуры
(4.1.11)
£s
1
^b.red
h-a-с
с
ь
2
при интегрировании станет равной значению £sG, то сечение разрушается, необходимо
увеличить площадь растянутой арматуры As, и проводить расчет повторно.
После достижения деформацией £2 значения £м red = 150 • 10 5 в сжатой зоне бе-
тона на основании диаграммы Прандтля развивается пластическая зона (рис 4 1 3) раз-
мером X]; упругая зона характеризуется расстоянием с.
Деформация s^red характеризует переход от упругой зоны бетона к пластичес-
кой. Обратим также внимание, что для изгибаемых балок без сжатой арматуры размер
«а'» равен нулю, и при достижении деформацией £2 величины £ь , происходит разру-
шение сечения Обозначим изгибающий момент в плоскости величиной Мх. При
111
напряжении в растянутой арматуре равном величине (характеризуется деформа-
цией £\0) также происходит разрушение сечения балки.
Рис. 4.1.3.
Напряженно-деформированное состояние сечения в этой стадии (рис.4.1.3) ха-
рактеризуется двумя независимыми параметрами, которыми могут считаться и £2,
либо г, и с. Связь между ними устанавливается (на основании гипотезы плоских сече-
ний) из подобия треугольников:
£\ + е2 £b\,red
h с ’
f 2 _ £b ,red
h h-xx
Из уравнений (4.1.2) и (4.1.3) находим
б-Х^-Д-б-С-^+^-Л^О; (4.1.12)
— b-C'Rb- Л0-х, -
Усилия в арматуре равны
N's = At, • < • Е’„ = А', • Е', еы^ “
С
А Г h- с - X.
s * £b\,red
С
S
112
Дифференцируем (4 1 12) и (4.1.13) по времени, получаем
Xj •[ bRb + AsEstbX d + AsEs£bx
V c c
1 , a - x, . _ ha - x,
+ c • —bRb + AsEs£bx >red —+ AE£bxd —-j—
12 c
= 0 ;
xt • bRb • (Ao - Xj)- ~bRbc + (Ao - a')• A'E'ebi>>
1 ( 2 1 (
+ с- -bRb\h0-xx--c + (^-<
2 V 3 J

bl,red '
C_
a' -
bi,red 2
C
откуда записываем систему дифференциальных уравнений задачи для стадии IV:
1 11(11 2
+ А'$Е^£ЬХ^ - + AsEs£hXred - - bRb Цо -X, - с
с с) \ 2 \ 3
fl ,п a -х, , . _ -X!
Мх JbRf)+A!.E,c£b} d 2 +AsEs£h]j
\2 с с* 2 J
+ (ЛЬ -^) ’ ~
(4.1.14)
1
-fe -xx)-\bRbc+(hfi -^)^£ь^-
2 с

• I , 1 1
• bRb +AsEs£bXred- + AsEs£bVed-
_________________________k_____________£_________CJ__________
[^ + 4ГА,^--+4£5ем^,Л ^/<,к-х1-?С'|+(Л0-а')-4£”£ы,га(‘?Цй -
к с cJ |_2 к 3 J с
(4.1.15)
1
ЬЦ,-X,)-‘ ft^c+fe -а')-4£-£ы^1
2 С
[1, Л _ a'-x. hn-x,
~bRb +-^s^s£b\xed ~ 2 2
2 С С
Если сжатая арматура течет, то в системе (4.1.14) и (4.1.15) следует положить рав-
ными пулю все вторые слагаемые в скобках Получается система дифференциальных
уравнений для сгадии III:
113
1
-Af/I^+^^W^5
<2 С
1
(4.1.16)
2
cj 2 к 3 ,
2
2
3
J-* \ JW
• ( 1
Л/j. bfy +^^6^^ •
к С
( 1
+Л&£Ъ1ге<Г
к С
1,- , 2
-Ь^-х^-с
bfy'fa-xj—bfy
~ ЬЦ> + As^s£tA/-ed ‘
4>~^
с2
(4.1.17)
Интегрирование системы уравнений останавливается в момент достижения крае-
вой деформацией £2 значения еЬ2 = 350 • 10-5, либо в момент достижения деформации
es величины fs0 (текучесть растянутой арматуры). В каждый из этих моментов време-
ни сечение разрушается. При оптимальном армировании сечения эти моменты времени
совпадают.
Рассмотрим далее использование общей диаграммы бетона, записанной в виде
(2.2.3)
а £х + 8 • £2
Ci+g£x
(4.1.18)
Распределение напряжений и деформаций по сечению в этом случае показано на
114
Напряжение сгх и деформацию £х выражаем через текущую координату х
_ g2 £ £2
х с ’ с
(4.1.19)
£2 с £2 2
а- — -х + ё-~\ -х
с с
= (4.1.20)
ct + g~-x
С
Продольная сила в сечении
W = + (4.1.21)
о
Изгибающий момент относительно нейтральной оси Ну
М? =Cfax-x-dx + N's-(Ло - а'). (4.1.22)
о
Подставляя (4.1.20) в (4.1.21) и (4.1.22), получаем (после интегрирования по сече-
нию и упрощений)
= [g£2 -ln(\+g-£2)] +
g ^2
Ь S С 1 2 2 rzi »
• ~g -^-g-^+W + g-th) +
g3 ^2
(4.1.23)
с
с
1 з з 1 2 2 , ,, \
~'g £2~^g +g-f2-lH(l + g£2)
•J At
b-a
г_
£2
~-g1 2 4~g ^2+ln(l + g-f2)
(4.1.24)
c c
В выражениях (4.1.23) и (4.1.24) сжагая и растянутая арматура работают в упругой
ти. Если сжагая арматура находится в состоянии текучести, то следует положить
ЛГ' = Л' • £' • £s.o = const.
Если же растянутая арматура достигает состояния текучести, то наступает прс-
тое состояние сечения (исчерпание прочности сечения).
115
Для исследования изменения напряженно-де ормированного состояния сечения
дифференцируем (4.1.23) и (4.1.24) но времени
Ь-а
—-(g-z-2 -ln(l + g-£2))+
£2
+ ^ —-fi-g2 -6’2-g-£2 +ln(l + g-f2)| +
g £2 U )
+ A's-E’s-£2-^ + As-Es-£2-^-
c c
1
c'4
(4.1.25)
• S 2c (1 3 3 1 2 2 in
"4 ~ ,'g '£2~^-S ‘£2 + g-^“Hl + g £2) +
Г £2 u 2 J
2
g3
. g4
Ъ-а 2
s
• -g-f2+ln(l + g-^2) +
c
c2
1 3 4
- g -£2-g-£2

„.P2
2----*---2_ + 2 • £2 ln(l + g • £2)
^2
£42
')2
£2
>2

C
(4.1.26)
116
Отсюда получаем два дифференциальных уравнения, позволяющих проследить
изменение напряженно-деформированного состояния сечения от начала загружения его
до момента разрушения сечения.
Система дифференциальных уравнений (4.1.25) и (4.1.26) сводится к нормальной
форме
? 1
С 2
g £2 k
ba 1
_g2 £2
g£2
l + gs2>
6£_1_
g3 £2
b§
g3
~g2e} ~ g£2 + lnG + g*2) +
If 1 2 g£2
C—r ~g£2+ ~—
£2\2 1+gf2
+ а;е’л^+а,еа^-
С с
b8 2
Г
1Ж— -a- + AsEs^
____c________c
-S2£4-££2__S£1
og fc2 5fc2 ,
3 i + gg2
*2
Ьа 2
Vе
l+gg2
4
-MH ba
1
+лж(с--^£
с

с
bS 2c
{ g3^2 - |g^2 + g£2 - ln(l + g£l) J +
-J 1
_______________________________J_____________________________
ba 2c (1 22 л X A,-, c2-(af Av c2-h2
+ -5 ‘ - g£2 + ln(! + g£2) + AsEs£2-F^“ + АЛ£2----2—
g ^2 \ 2 J C • C
ba 1
1 2 g£2
~-g£, +
2 2 1 + g£2
____________1___________
, , c - a' h0-c
AsEs + AsEs£2 ~ 2
C C
117
£г
м"
^—(g^-Hi+g^))
g ^2
| g£2 “ g£2 + ln(l + g£2 ) ] +
g £2 u J
^7—(g£2 -ln0 + 2*2))+ ^T“f|g2*2 - g£2 + W + g£2) +
,g £2 g M2
+ A'E's£2 + AfE,£2
c c
(4.1.27)
_____________________________1___________________________
b& 2v f 1 1 *1 1 ? 2 » л b(^ 2x7 (1^22 x I
---4 ~ ’ £2~^g £\\+gE2-W\+g£2} + — ~‘kg £1 -g^+H+g^) +
Lg £2 13 2 ) g e2 \2 J
____________1___________
+4£>2^ф£+лА^£-:г^ •
5 5 Z ^2 S S 4. ^2
1
1 (1 г g£2 1 л \Y
4-— C-^- ^g£t+~-2 -ln(l + g£2) +
g £2 I2 1+^2 J
1
C~- ln(l + gg2)- £g; 1
г? I 1+g^J
c c
Аналогичные зависимости легко получить для других случаев поперечных сече'
ний железобетонных балок.
118
§ 4.2. Упрощенная модель кратковременного деформирования
железобетонной балки
Уравнение нелинейного деформирования бетона (4.1.18) можно разложить в ряд,
ограничиться пятью членами ряда (4.2.1) и существенно упростить решение задачи.
При этом коэффициенты А, В, С, D, F получаются нс экспериментальным путем (4.2.1),
а соответствуют параметрам диаграммы Евростандаргов (2.2.3). Таким образом, не ак-
центируется внимание на разногласиях среди исследователей, связанные с различием
факторов, определяющих вид кривой деформирования бетона при сжатии и изгибе: раз-
ной скоростью нагружения волокон по высоте сечения, влиянием сдвига, формы сече-
ния и других.
б)
а)
14
1,3
1,2
1,1
1,0
0,9
0,8
0,7
0,6
0,5

= 10 Л (Па
/>Rb = 20 . 4Па
2 к =з0 1 4Па
L 0.2 =^1,0 23 = 40 , 4Па>
50 М Па
Rb- 60 м 1а

Рис.4.2.1. Кривые напряжение-деформация различных классов бетона
а) - в относительных величинах; б) - функции подобия:
1Т7 ст
I =----; <зср - напряжения средней кривой.
119
Расчетные схемы продольных напряжений и деформаций в поперечном сечении
железобетонной балки приведены на рис.4.2.2.
Составляем уравнения равновесия части балки, отделенной средним сечением
р
F
где Л/(/) = ^- - главный момент относительно центра тяжести сжатой арматуры
и главный вектор эпюры нормальных напряжений
**
рв„ (£н Ч )=b Jаь dx + as • As - а' • Л' = 0;
о
Рис. 4.2.2. Расчетная схема железобетонной балки.
120
Пусть пока арматура работает в упругой стадии; для аппроксимации диаграммы
а - е бетона записываем полином пятой степени
о-ь^Аеь + Веь +C-£b+D-£b +F-E5b
(4.2.1)
Учитывая гипотезу плоских сечений, главный вектор и главный момент записыва-
ем в виде
n f \ rx b'h (А 2 3 С 4 5 F
вгЛ 1 27 ^-^2 (2 1 3 1 4 1 5 1 2 U
V h J h \ hj
где As, А* - площади сечения растянутой и сжатой арматуры;
Es - модуль упругости арматуры;
Еь - начальный модуль упругости бетона;
£], £2 - краевые деформации волокон сечения.
Далее предполагаем, что закон изменения силы р известен:
Р = Р(О.
Принимается такая скорость возрастания P(z), при которой можно пренебречь
силами инерции.
Дтя исследования процесса изменения напряженно-деформированного состояния
балки на всех этапах загружения дифференцируем систему уравнений (4.2.2), получаем
арем -
——•£,
дЕх
+ =0,
д£2 2
1
(4-2.3)
дМвн .
о» Л
О ।
дЕ}
оМ
121
где М (t) —------ известная функция (в случае линейного изменения р - константа).
Частные производные здесь равны
ти12 =
дРен= ь-h (а г
fc-^2)2 v2
ГТ* А1 1 Е* Л
+ -- Е- Л + 1— -Е -Л •
h ' s I h)
Выведенные закономерности позволяют проследить изменение напряженно-дефор-
мированного состояния железобетонной балки от момента загружения до момента ис-
черпания несущей способности по прочности Задача сведена к интегрированию систе-
мы двух линейных диференциальных уравнений
122
7?1| j " 4“ * ^2 “ »
(4.2.4)
W21 -^1 + т22 £2 =Ф(0.
где Ф(/) = М(/).
Приводим систему дифференциальных уравнений (4.2.4) к нормальному виду
-Ш12-Ф(0
1 тп'т22 ~т\2 -™21 ’
(4 2.5)
ffln -Ф(0
т22 -м12-т2| '
Интегрируя систему дифференциальных уравнений, получим величины, характе-
ризующие напряженно-деформированное состояние балки, вызванные воздействием на
неё поперечной силы P(t).
Изложенная методика позволяет найти аналитическое выражение для экстремаль-
ного критерия исчерпания прочности сечения железобетонного элемента. Этот крите-
рий соответствует максимальному значению момента
где х * кривизна изогнутой оси балки
Так как изгибающий момент является функцией двух переменных М = Мвн (s, ,е2),
то будем исследовать его на условный экстремум. В качестве дополнительного уравне-
ния связи используем первое уравнение равновесия Рвн (fуе2) = 0.
Составляем функцию Ла1ранжа
F(£j ,f2) = Мен ,£2 ) + 2 • Рвн (£, ,Е2),
где 2 - неопределенный множитель Лагранжа.
Записываем условия экстремума
^ = 0. ^ = 0
’ де2
Получаем
дМ дРвн
де} С’£2
дМт о п
де2 де{
Исключая неопределенный множитель 2 > получаем уравнение, связывающее пе-
ременные в момент исчерпания прочности
123
дмви
дМвн dsx дРвн
6f2 д?т де2
сех
(4.2.7)
где частные производные получены выше.
Сопоставляя (4.2.3) и (4.2.7), видим, что критерии исчерпания прочности (4 2.7)
тождественны условию совместности системы дифференциальных уравнений (4.2.3),
условию существования решений £] = E] (t) и s2 = е2 (О После этого момента време-
ни система уравнений, полученная из статических условий равновесия, становится не-
совместной. Дальнейший характер перемещений балки следуег рассматривать уже с
учетом сил инерции, то есть в динамической постановке.
Рассмотрим графическую интерпретацию полученных результатов
На рис.4.2.4 приведены зависимости «изгибающий момент - кривизна» ( М - х),
постоенные для различных диаграмм деформирования бетона (рис.4 2.3): 1 - упругая
модель; 2 - диаграмма Прандтля с неограниченной текучестью; 3 - полином, не имею-
щий ограничений па предельную деформацию, 4 - диаграмма Прандтля с ограничен-
ной площадкой деформаций £пр текучести; 5 - полином, ограниченный предельной
деформацией (Евростандарты).
Кривая 1 соответствует упругой стадии работы бетона (бетон работает на растяже-
ние). Кривая 2 на этом же рисунке соответствует диаграмме Прандтля с неограничен-
ной площадкой текучести Здесь момент
М = Л/2
д ь у
£ J
где М 2 - предельный момент, соответствующий шарниру пластичности (бетон работа-
ет на растяжение, арматуры нет);
е - удлинение крайней фибры сечения;
(ех+е2 2-е _ % h
- удлинение при фибровой текучести.
Таким образом, изгибающий момент М в пределах упруго-пластической области
работы сечения является гиперболической функцией удлинения крайней фибры е , имея
своей асимптотой момент М2 Отсюда следует, что величине М2 отвечает бесконечно
большое удлинение крайней фибры (либо кривизны), так что фактически предельный
момент и шарнир пластичности полностью проявиться нс могут. Однако на протяже-
нии площадки текучести пластичность может проявиться в достаточной мере.
Кривая 3 на рис 4 2-4 соответствует диаграмме бетона в виде полинома (бетон ра-
ботает на растяжение, арматуры нет). Точка М3 на этой кривой соответствует уравне-
нию (4.2.7), после этой точки система уравнений равновесия становится несовместной.
124
Рели диаграмма <у - е бетона ограничена деформацией (4,5 на рис.4 2.3), то кри-
вые 4, 5 на диаграмме М - % обрываются в точках Л/4 и М5 на рис. 4.2.5.
Если же бетон работает на растяжение, а арматура имеется в растянутой и сжатой
частях сечения то вид кривых на диаграмме М - % видоизменяется Математическая
же сущность процесса деформирования, описанная выше, не изменяется
Рис.4.2.4. Диаграммы
«момент-кривизна:
1 - упругая модель,
2 - диаграмма Прандтля;
3 — полином.
X
125
Допустим, что в некоторый момент времени арматура в сжатой зоне бетона поте-
ряла несущую способность (точка Л на рис.4.2.6). Кривая 3W (М — %) в точке А' приоб-
ретает излом (рис.4.2.6). Усилия в сжатой зоне воспринимаются бетоном, и, за счет это-
го, кривая 3” достигает максимума. Однако, если в некоторой предшествующей точке
Ав сжатия зона бетона разрушается, то кривая 3* имеет в точке Ав пиковый экстре-
мум. Последний будет наблюдаться и в случае разрушения растянутой арматуры.
Рис.4.2.5. Диаграмма «момент-кривизна» для бетонов
с ограниченной площадкой текучести.
Проведенный анализ показывает, что для оценки момента разрушения железобе-
тонною элемента необходимо одновременно прослеживать три критерия исчерпания
прочности сечения:
dM п
1 - экстремальный
2 - прочность сжатой зоны бетона;
3 - прочность растянутой арматуры.
Это позволяет избежать многих противоречий и дискуссий при оценке несущей
способности сечения.
Заметим также, что аналитическая методика построения зависимости «момент-
кривизна» проста в численной реализации и позволяет избегать применения различных
известных эмпирических зависимостей, широко используемых в научной литературе.
Известны, например, билинеарные функции А.А.Гвоздева, А.Л.Бекера и Х.Сойера, А.Ти-
126
хоро и И.Раскосника, трилинеарные функции Ф.Леви, тригонометрические функции
И В.Грищенко и другие.
Рис. 4 2.6. Диаграмма «момент-кривизна»
с учетом разрушения сжатой зоны бетона
§ 4.3. Некоторые экспериментальные данные и диаграмма <уь — £ь бетона при
градиентном (неоднородном) напряженном состоянии
В последние годы появились научные работы [177], [72], в которых анализируют-
ся параметры диаграмм сгь - £ь бетона, работающего в изгибаемых и внецентренно
сжатых железобетонных конструкциях Такой подход является перспективным, но он
ограничен рядом гипотез, которые нужно тщательно оговаривать при обработке экспе-
риментов Строгая модель, предложенная нами в § 4 1, показывает, что в анализе напря-
женно-деформированного состояния сечения при кратковременном загружении участву-
ют следующие гипотезы и параметры бетона и стали*
1. Гипотеза плоских сечений; её четко нужно указывать в проводимых рассужде-
ниях.
2 Гипотеза о совпадении нейтральных осей деформаций и напряжений, либо нуж-
но указывать закон, связывающий положения нейтральных осей деформаций и напря-
жений Н = Н(ех , £г ).
127
&s 1 7')
------1.7 (4.3.Г)
7
3. Диаграмма <rb - еь работы сжатого бетона, у которой модель Евростандаргов
нормирует шесть констант , Rbl, £ьо, Rb, £b2, Rbi.
4 Диаграмма abt - £bl работы растянутого бетона и её параметры; либо использо-
вание гипотезы о пренебрежении работой растянутого бетона.
5. Диаграммы as — £s и <т51 - £ । растянутой и сжатой арматуры, каждая из кото-
рых имеет часто три участка: линейный до уровня напряжений <rf = 0,7 Rs (предел про-
порциональности); кривотинейный представляемый кривой (до начала текучести)
-рА-оУ} -рл-од!
— = 0,953 + 0,265 е Uo }-0,289 е }-0,229 с1*’0
Rs
на участке 0,7 Rs < crs < Rs;
зону линейного упрочнения после предела текучести R (ст >7?^)
— = 1 + 0,015
Параметры, характеризующие два последних участка нелинейного деформирова-
ния арматуры, существенно сказываются на работе бетона в околопределыюй и запре-
дельной стадиях испытаний балки
5 Скорость загружения, зависящая от методики испытаний балок или колонн.
6. Начальные напряжения в арматуре, вызванные усадкой бетона.
7. Различные критерии предельного состояния балок, среди которых максималь-
ная нагрузка на балку, либо разрушающая нагрузка на балку, особенно это важно для
тех ситуаций, когда зависимость “момент-кривизна” имеет ниспадающий участок.
Неучст перечисленных выше обстоятельств при проведении эксперимента и его
обработке приводит к сомнительным результатам. Например, некоторые авторы полу-
чают значение предела прочности бетона при изгибе, в два раза превышающее его при-
зменную прочность. Более тщательная постановка экспериментов опровергает такие
результаты.
Остановимся также на сущности метода Фере, широко использующегося в после-
дние годы для оценки опытов над железобетонными балками и колоннами [177]. Этот
метод был предложен для экспериментального построения кратковременных диаграмм
суь — £ь и основывается на испытании бетонных (не железобетонных) балок на изгиб
до появления трещин в растянутой зоне. В теоретическую основу метода Фере положе-
ны только две первые гипотезы, указанные выше. Составляются два уравнения равно-
весия части балки, отделенной произвольным сечением
joiZF = 0. fazdF = Мх
F ’ F
где Мх - изгибающий момент.
С использованием гипотезы плоских сечений записываем (используем обозначе-
ния размеров по рис.4.1.2)
128
g2 ^2
с h-c h
и, подставляя в (4.3.1), имеем
~~ 'a,de ~777 &=0• <4 3-2>
И *2 0 fcI + fc2 О
Гл Г л лл (£1+£,2)2
Мds + V \ . 2 . (4.3.3)
оо bh
Первое слагаемое в этих выражениях характеризует рабогу растянутого бетона,
второе - сжатого Зоны изменения напряжений в бетоне ст] и <т2 по сечению неизвест-
ны. С целью нахождения этих напряжений записываем приращения величин в (4.3.2)
и (4.3.3)
O’f'Jg) -0-2^2
+СГ2Ч^2 dMx + ^2'Уг~-^(£| +^),
bh bh
где о-] , ст ’ - крайние напряжения в растянутой и сжатой частях сечения.
Из последних уравнений находим значения этих напряжений
b
= fe+f2)
1 dMx
bh2 d£x
+ 2Л/Х
1 fZ(gi+g2)
bh2 d£}
(4 3 4)
ъ
2
=fa+*2)
1 dMx
bh2 de2
+ 2mA-(£'^
bh2 de2
Проводим эксперимент по постепенному загружению бетонной балки на изгаб,
в котором измеряются деформации £х и £г, соответствующие каждому значению М
Составляется таблица измеренных в эксперименте величин Мх, £{, £г, (f| + £2), по
которым табличным способом находятся приближенные значения производных на каж-
дом этапе загружения i
М1 - М‘х~' М‘х - М'-’ Й - )+ Й - £‘~1) (г* - )+ Й - £‘~1)
’ 4-^Г1 ’ ’ 4-^Г1
Таким экспериментально-расчетным путем можно получить значения напряжений
erf в растянутой зоне бетона до начала разрыва волокон. Значения напряжений
в сжатой зоне бетона при этом соответствуют начальному незначительному участку' кри-
вой аь - £ь. Следует подчеркнуть, что значения напряжений а2 с помощью метода
Фере нельзя получить для основной части кривой <уь - £ь сжатого бетона; при этом
129
значения напряжений зависят от двух краевых деформаций и f2; никакой анали-
тической зависимости для диаграммы сгь - еь не используется. Для железобетонных
балок и колонн оказывается необходимым использовать еще ряд гипотез и особеннос-
тей деформирования, перечисленных выше в пунктах 1-7 данного параграфа. Свою по-
грешность в результаты вносит также приближенное вычисление производных. Напри-
мер. Для железобетонного элемента с одиночной арматурой, и не учитывая работу бето-
на на растяжение, можно получить весьма громоздкое выражение для напряжения ст*
ь ESAS d(E} + g2)
°2 ~
bh de2
2 1 dM;
bh2 dex
M
bh
41 ' bh
ESAS
de
„ \2
E~A~
bh
bh
ESAS
bh
dex
de2 ’
ЕЛ d(ei +g2)
в котором все производные находятся приближенным способом по эксперименталь-
ным данным.
В научной литературе неоднократно указывается на весьма большую сложность,
громоздкость и приближенность метода Фере, основанного на численном дифференци-
ровании экспериментальных данных.
Рассмотрим обработку экспериментальных данных, полученных в НИИЖБе Фи-
гаровским В.В. [165] при испытании железобетонных балок сечением 18 х 25 см крат-
ковременной нагрузкой. Балка ПО-2Пк имела процент армирования ц = 0,16% и проч-
ность бетона, равную 340 кг/см2; арматура периодического профиля диаметром 7 мм
выполнена из стали 25Г2С. Балка П1-2Пк, армированная такой же арматурой
с /л = 0,25%, имела прочность бетона 210 кг/см2.
На рис.4.3.1 приведены опытные кривые (сплошная линия) средних деформаций
крайнего волокна бетона сжатой зоны.
При значениях момента М~570 кгм наблюдается перелом кривой деформаций в
момент начала образования трещин в растянутой зоне (ПО-2Пк) экспериментальные
деформации сжатого бетона при этом равны 12 • 10"5 • При значениях момента 660 кгм
деформация сжатого волокна увеличилась почти в два раза. Резкое увеличение относи-
тельной деформации е2 после образования трещины приводит к уменьшению высоты
сжатой зоны балки и росту напряжений в бетоне.
Теоретические кривые (пунктирная линия) имеют более плавный характер, что
объясняется пренебрежением работы растянутого бетона на всех этапах загруже-
ния. В целом теоретические и опытные кривые удовлетворительно согласуются меж-
ду собой.
130
м
Рис 43.1. Деформации крайнего волокна бетона сжатой зоны балок
На рис.4 3 2 показаны экспериментальные (сплошная линия) и теоретические (пун-
линия) значения относительных деформаций растянутой армагуры.
£210~5
Рис.4.3.2. Средние деформации растянутой арматуры балок
131
Здесь также наблюдается резкое нарастание деформаций в момент образования
трещин в растянутой зоне бетона. 'Гак в балке П0-2Пк при моменте М = 570 кгм де-
формация es равнялась 15 • 10“5, а при моменте М = 660 кгм деформация es увеличи-
лась более чем в четыре раза: £s =65 • 10-5. Имеется удовлетворительное согласование
теоретических и экспериментальных значений деформаций растянутой арматуры (между
трещин).
Аналогичные результаты получены по величинам кривизн опытных балок; эти
результаты представлены на рис.4 3 3 (опытные данные - сплошная линия, расчетные -
пунктирная).
Рис.4.3.3 Нарастание кривизны балок
Дополнительно теоретически обработаны экспериментальные данные НИИЖБа,
тщательно обобщенные Ю.П.Гущсй и Л.Л.Лемышем [58] для балок с арматурой класса
А-Ш из бетона марки МЗОО (сохранена старая классификация)
Опытная диаграмма сгь -£ь представлена на рис.4.3.4; она получена из испыта-
ния центрально сжатых бетонных призм, выполненных из бетона с прочностью
Rb = 25МПа и Rb— ЗОМПа.
Опытные параметры этой диаграммы несколько отличаются от параметров соот-
ветствующей диа1раммы Евростацдартов. Поэтому в теоретических расчетах приняты
параметры диаграммы по рис.4 3.4
На рис.4.3.5 представлены зависимости «момент-кривизна», полученные экспери-
ментально (сплошные линии) и теоретически (пунктирные линии) для балок с различ-
ными процентами армирования. Они согласуются между собой Опытные линии имеют
ниспадающий участок, получаемый вследствие статической неопределимости балок.
В своих более ранних экспериментах А.Д.Беглов [19] также получил удов-
летворительное согласование опытных результатов с теоретическими для случая крат-
ковременного загружения железобетонных балок.
132

Глава 5. РАСЧЕТ ЖЕЛЕЗОБЕТОННЫХ КОЛОНН ПРИ КРАТКОВРЕМЕННОМ
ЗАГРУЖЕНИИ
§ 5.1. Гипотезы Евростандартов и некоторые модели для расчета сжатых
железобетонных колонн
В данной главе используются все гипотезы расчета сечений, изложенные в § 2.1
и § 4.1. Здесь следует заметить, что расчетные модели сечения для изгибаемых и сжа-
тых элементов вообще отличаются (в модели пластического шарнира такого отличия
нет). Для колонн необходимо рассмотреть дополнительно случай полностью сжатого
железобетонного сечения. Кроме этого, необходимо для сжатых колонн учитывать гео-
метрическую нелинейность, заключающуюся в учете прогибов колонн. Критерии ис-
черпания несущей способности колонн отличаются от критериев исчерпания прочнос-
ти изт-ибаемых балок: в момент исчерпания несущей способности сжатых колонн появ-
ление текучести в растянутой арматуре может не наблюдаться (в расчетной же модели
пластического шарнира текучесть растянутой арматуры характеризует исчерпание не-
сущей способности колонны); этим обстоятельством увеличивается число вариантов
(I-IV) напряженно-деформированного состояния сечения. Для сжатых колонн оказыва-
ется необходимым дополнительно рассматривать условие потери устойчивости в каче-
стве критерия исчерпания несущей способности.
Расчет сжатых железобетонных колонн производится по схеме (рис.5.1.1) плоско-
го изгиба внецентренно-сжатых элементов (в плоскости действия момента М). Рассто-
яние между линией действия сжимающих сил и продольной осью колонны называют
М
эксцентриситетом ео - ~, где величина изгибающего момента д/ принимается по дан-
ным статического расчета конструкций.
Из теории упругопластического изгиба сжатых стержней известно, что изогнутую
ось стержня удобно аппроксимировать полуволной синусоиды, рис.5.1.1, в осях
OQ,ZVXX.
Прогиб колонны в точке Л/, определяется уравнением
(5.1.1)
где f -
прогиб середины колонны в точке С, при zx =
4.
2’
- расчетная длина колонны;
ео
Мх
- эксцентриситет приложения сжимающей силы N (эксцентриситет от-
считывается от центра О сечения колонны, рис.4.1.2, 4.1.3, 4.1.4).
Для нахождения расчетных параметров (Zo и е0) сжатой колонны производится
сначала расчет статически неопределимой конструкции с учетом её деформированного
состояния при наиболее невыгодном (для рассматриваемой колонны) расположения
134
нагрузки, принимая во внимание неупругие деформации бетона, арматуры и наличие
трещин в бетоне. На основании этого достаточно сложного расчета находится наиболь-
ший момент Мх по длине рассматриваемой колонны.
Рис.5.1.1.

С целью некоторого упрощения расчета Евростандарты позволяют использовать
приближенные значения приведенной расчетной длины /0, полученные в классической
теории устойчивости центрально сжатых упруги колонн.
При шарнирном опирании концов
^=1.0,
где / - фактическая длина сжатой зоны колонны.
Для консольных колонн справедливо соотношение
— = 2,0
/
Если один конец колонны жестко заделан, а второй конец имеет шарнирно под-
вижную опору, то
~ = 7,0
I
Если один конец стержня защемлен и неподвижен, а второй конец защемлен в под-
вижной опоре, то расчетная длина равна
135
Zo=O,5Z.
В общем случае в Евростандаргах влияние продольного изгиба учитывают расче-
том сжагоизогнутого стержня по деформированной схеме на основе рекомендованных
выше диатрамм о - £ работы бетона и арматуры.
Отклонение точки Л/, от её первоначального положения Л/10 (при нулевых значе-
ниях сил 77,77') является учетом геометрической нелинейности в расчетах сжатых же-
лезобетонных колонн.
В Евростандаргах кривизна изогнутой оси колонны в плоскости действия момен-
та М определяется на основании приближенного выражения
_ =-----= j sm__L
rx k k ’
(5.1.2)
где гх - радиус кривизны изогнутой оси колонны в произвольном сечении [ ], характе-
ризуемом координатой Zj.
В середине колонны находится максимальная кривизна
1II- <513>
1 2
Изгибающий момент Мх в произвольном сечении находится с учетом прогиба Tj
M^N^ + x.), (5.1.4)
то есть с учетом геометрической нелинейности. В среднем сечении элемента
К=М«о+/)- (5.1.5)
Общей тенденцией мирового развития напрягаемой арматуры является замена всех
классов арматурной стали для обычного железобетона на один класс. Все страны Евро-
пы перешли на применение в строительстве только одного класса свариваемой армату-
ры для ненапрягаемого бетона: А500С (B500W) в соответствии с Евростандартом
EN10080, CEN. Для изготовления горячекатаной арматуры класса А500С в России раз-
работана новая марка арматурной стали 20ГСФ. Ранее свариваемая арматура класса
А500С выпускалась с помощью термомеханического упрочнения (ТМУ) в потоке про-
ката с применением метода прерванной закалки (из сталей марок СтЗсп, СтЗпс, СтЗГпс).
В Москве организовано производство арматуры класса А500С метолом холодной
деформации периодического профиля горячекатаной заготовки (катанки) с привлече-
нием специального оборудования из Германии. В качестве первоначальной заготовки
может также использоваться термомеханическая упрощенная катанка. Диаграммы рас-
тяжения таких сталей показаны на рис.5.1.3.
Помимо этого в России широко применяются арматурные стали от А240 (A-I) до
А400 (А-Ш). Последняя изготавливается из сталей марок 25Г2С и 35ГС. Сталь 35ГС
склонна к хрупким разрушениям по местам дуговой сварки, а также при изгибе из-за
образования закалочных структур.
136
деформации, %
•ТМУ арматура класса А500С т/r арматура класса А500С
Рис.5.1.2.
Из приведенных материалов можно видеть, что диаграммы <js-e растяжения
арматурной стали имеют большое разнообразие, что затрудняет их прямое использова-
ние в расчетах сжатых железобетонных колонн.
Диаграммы распекания
1. 2 - аортаквтаноО и терыомвхоиичаски упрочмоиноО катанки, 3, 4 - холодяодеформироввяноА арматуры класса АЗООС,
ижтоаланиоО из аор»лкатаноа и тврмоыахатчоски упрочненное катанки
Рис 5.1.3
Диаграммы (уь - £ь бетонов различных классов по материалам научных исследо-
ваний и данным Евростандартов также имеют большой разброс, рис.5.1.4
137
Можно заметить, что даже определенный класс материалов имеет достаточно боль-
шое количество применяемых марок, обладающих разными механическими свойства-
ми.
Вследствие указанного, не удается при разработке нормативных документов обой-
тись без объединения нескольких близких по деформационным свойствам материалов
в особые группы и выбора для каждой такой группы некоторой усредненной кривой.
Очевидно, что такая группировка должна производиться с использованием безразмер-
ных параметров: относительного напряжения ~ и относительной деформации
bs~ , где - деформация, соответствующая началу площадки текучести стали
*50
(или условному пределу текучести) Учитывая разброс величин £s{i в криволинейных
диаграммах, оказывается удобным (по аналогии с диаграммой Прандтля) рассматри-
вать условную деформацию начала текучести £0 - --, которая определялась точно.
^5
* £ £ Е
Тогда величина относительной деформации £5 - , где Rs - условный предел
^0
текучести
Вероятно, впервые для статического изучения разброса диаграмм сг - £ понятие
условной деформации использовал Вейнхольд И
Из рис.5.1 5 и 5 1.6 видно по данным Бельского Г.Е [18], что таким образом суще-
ственно уменьшается разброс диаграмм as - £s дня стали.
138
Рис.5.1.5. Диаграммы as — £s различных классов сталей
в абсолютных величинах
Рис 5.1.6 Диаграммы (Уs — £s различных классов сталей
в относительных (условных) величинах
♦ *
Аналогичные диаграммы os - £s, построенные для бетона, показаны на рис.5.1.7.
139
Рис 5.1 7.
Приведенные данные показывают, что материалы с близкими (подобными) диаг-
раммами встречаются сравнительно редко даже в рамках относительных ве 1ичин. Учи-
тывать действительный вид диаграмм для бетона и стали при их многообразии, да ещё
при их сочетании, сложно. Поэтому для расчета сжато-изогнутых стержней можно при-
♦ * ♦ •
нять некоторые унифицированные осреднснные диаграммы q- _£ и <? -£ , Па
раметры этой диаграммы для бетона равны
кН Н
Еь = 35---2 ; R = 40--2 '> 4) = 0,002; 4 = 0,0032, а сама дишрамма име-
ЛШ мм ™ oz
ет вид
-h h
ЬЬЬО
Кь
ph
\£ьо J
(Ehrh
^ЬеЬИ 9
ph
k Rb 7
$
1 +
Унифицированная диаграмма для арматуры имеет вид, показанный на рис.5.1.8.
Аналитическая запись диаграммы esh принимается в виде (4 3 1), который
удовлетворительно согласуется с обобщающими экспериментальными данными Бельс-
кого Г.Е., приведенными в табл.5.1.1.
Влияние разброса диаграмм crs — es и <jb - еь на окончательные данные расчета
существенно будет проявляться при весьма малых эксцентриситетах когда железобе-
тонные колонны работают вблизи центрального сжатия.
140
Рис.5.1.8
Таблица 5.1.1.
* Es • <JS Со • ♦ ♦ о\, Бельский Г.Е. • Es *
0 0 0,8 0,7865 0,66 (2,2%) 1,8 1,0015
0,9 0,8506 0,825 (3,1) 1,9 1,003
0,2 0,2 1,0 0,8976 0,870 (3,2) 2,0 1,0045
1,1 0,9318 0,907 (2,7) 3,0 1,0195
0,4 0,4 1,2 0,9563 0,937 (2,1) 4,0 1,0345
1,3 0,9735 0,961 (1,3) 5,0 1,0495
0,6 0,6 1,4 0,9853 0,976 (0,7) 6,0 1,0645
1,5 0,993 0,99 (0,3) 7,0 1,0795
0,7 0,7 1,6 0,9976 0,997 (0,06) 8,0 1,0945
1,7 1 1 10,0 1,1245
Вследствие этого в теории расчета строительных конструкций сознательно разде-
ляют методику расчета внецентренно сжатых стержней с методикой расчета централь-
но сжатых стержней. В последней одновременно могут присутствовать две расчетные
модели- первая - внецентреннос сжатие, с использованием некоторых эмпирических
значений случайных эксцентриситетов; вторая - касагельная (либо приведенно-модуль-
ная) критическая сила Эйлера, разделенная на некоторый коэффициент запаса (1,3),
с помощью которого учитываются возможные несовершенства. Например, использует-
ся эмпирическая зависимость случайных эксцентриситетов от гибкости показанная на
рис.5.1.9
141
Рис.5.1.9 Случайные эксцентриситеты в сжатых элементах
Наконец, обратим
внимание на некоторые
неточности, используе-
мые в расчетах сжатых
железобетонных колонн.
В научной литературе ча-
сто описываются экспе-
риментальные зависимо-
сти «момент-кривизна» с
ниспадающими участка-
ми, иллюстрирующими
работу внецентренно сжа-
тых колонн. На рис.5.1.10
приведена диаграмма за-
висимости «момент-кри-
визна (прогиб) -• сила».
142
Линия /’ характеризует внешний момент Л/ = N(e + /); линия 1 - характеризует
внешний момент при потере несущей способности (устойчивости), характеризуемой
точкой RKp Линия 2 - характеризует внутренний М3 момент; линия 3 - характеризует
рост прогибов под действием силы jV.
В точке Яф происходит потеря устойчивости (несущей способности) железобе-
тонной колонны. В этой точке, являющейся предельной точкой равновесия выполняет-
ся условие равенства приращений моментов внешних и внутренних сил
ДМ = ДЛ/®,
а линия 1 является касательной к линии 2. Очевидно, что в этом предельном равновесии
выполняется условие
--А>0
а линия 2 не имеет гладкого экстремума
df
и, следовательно, ниспадающего
учащка. При меньшей силе N < приращение момента внутренних сил превосхо-
дит приращение момента внешних сил (дм < ДМ* ). В запредельной стадии, характе-
ризуемой точкой R3, происходит динамическое увеличение прогибов при уменьшаю-
щейся силе N3 и, возможно, при ниспадающей зависимости “момент-кривизна”. Пос-
ледняя также может проявиться в статически неопределимой системе, но не при испы-
тании одиночной шарнирно опертой железобетонной колоны
Зависимость «момент-кривизна» может иметь изломы, вызванные появлением тре-
щин в растянутой зоне бетона, текучестью арматуры, разрушением сжатой зоны бетона.
§ 5.2. Внецентренное сжатие железобетонных колонн
Расчетная схема внецентренно сжатой колонны является основной в моделях сжа-
то-изогнутых колонн Евросгандартов, равно как и в нормах многих стран.
К ней различными способами приводятся другие расчетные схемы железобетон-
ных колонн.
В соответствии с данными параграфов (1.4) и (4.1) записываем уравнения равно-
весия половины колонны, отделенной средним сечением (рис 5.1 1, 4.1 4) Учитывая,
что в Евростандаргах эксцентриситет отсчитывается от центра тяжести сечения, при-
водим сжимающую силу NH и момент М * к центру о сечения; при этом величина силы
Nq не меняется, а для нахождения М* к момету М" добавляется момент главного
вектора NH относительно нового центра приведения 0, рис.4 1.4.
Окончательно записываем
143
N(t) = No(£2ic) = ~ — [gf2 - ln(l + g£2)] +
g £2
bS c |gM-g^2+ln(l+g^) +4-<(<)-я/г;к)
(5.2.1 )
g' £2 -
MO-[e+/ta»c)l
b8c2 '
л 4 2 o
g £2 L3
1 3 3 1
3g£^2
ba c1
~3 Д Э
g £2 L2
1 2 2
-g4-g*2 +
(5-2.2)
s s
h
c —
2
где N(t)- заданная внешняя сжимающая сила.
М* - равен правой части уравнения (5.2.2);
£ 1
/[£2»с)~^ ~т~ - прогиб середины колонны (см. (1.4.15)); (5.2 3)
7Г с
^=—(Ло-с); £s=—(c-a'). (5.2.4)
с с
Для функции ст" записывается три последовательно сменяющих друг друга выра-
жения’

0,953 + 0,265 е
-0,289 е
-0,229 е
es0
; (5.2.5)
= RS 1 + 0,015 -^--1,7
L
Уравнения (5.2.1) и (5.2.2) характеризуют произвольную точку на диаграмме
состояния «N - f ». Для нахождения условия потери несущей способности колонны
в точке Кф (потеря устойчивости) исследуем (5.2.1) на условный экстремум
Составляется функция
U(e2,c)=Nq(£2,c)+A [е + /(£2>с)]-^(£2»с)}>
и записываются условия экстремума
144
dU(c2,c) _dN^{c2,c)
дс2 де2
M^[e+yfeic)]
2
+
dz?2
5K0fa.c)'
dc2
du(c2,c) _dN(c2,c)
- ----------1_ y^
de de
ОС
’ g)a/(g2^) ^(g2,c)
0 X 29 / *4 -n,
de de
где 2 - неопределенный множитель, который можно найти из первого уравнения, а
затем подставим его во второе уравнение; записываем
(W0(g2,c)
дс
.^z£)[e+/fe,c)]+Wofe,c)^
(?^2 ^^2
дЛ^(с2,с)
^2
д/У0(с2,с)
дс2
• + /fe,c)] + ^(г2,с)^- - ^“М
ос дс дс
После упрощений получаем условие критического состояния сжатой железобетон-
ной колонны
dV0(g2,c) N , c\df(c2,c) _ dTV0(g2,c)_ дМ^с2,с)
дс 2’ дс2 дс дс2
йЛ/0(с2,с) дг/. г\^2>с) dN0(c2,с) дМх(е2,с)
de^ de
Производные, стоящие в (5.2 6), получены в следующем виде
(5.2.6)
(W0(£2,c) ba 1 ( , Z1 .ч
-ln(l + g£2)) +
ОС g £2
, &r;(g;)dg; a<(g5)ags
5 дс' дс s dcs дс ’
_R Г 0365 . 0.289 fe-”-7) .
L £so eso
0,687 -3fe"0-7)
145
ds' a' dss h0
de c2 ’ de c2 ’
8jV0(g2,c) _ ba 1
te2 g1C £2 _
bs i Гi 2
+
ln(l + ge2)--^
2 , g«2
g}
sa:(g;)a< л da’;{Et)des,
ds's O£2 tes ds2 ’
dss hG-£ ds^ c~a'
ds2 c * ds2 c *
df(s2,c)_l2 1 1. df(£2,c)_ 2£^ 1 .
d£2 я2 с’ де я2 c2 ’
dM*(s2 ,c)_bb 3 £1 g*2
dg2 g4 c
+ 1£2 ln(l + gg2)
-------------------4
ba 2
Vе
2g2ln(l + gg2)
g2
A. s^0<{c_a.}+A
d£’s ds 2 dss d£2 te2 к 2)
tes = ds's = c-a'.
ds2 c ’ ds2 c
dM^{s2,c} £><t> 2сГ1 з з 1 2 2 , „ ч
- —-----4 -2- -g «2 --Zg cji + ge2 - '"(1 + g«2> +
g c2L3 2 J
де г4
ba 2 2c 1 2 2 \
—C2— -g ls\f-gg2+ln(l+gg2) +
g ^2 L2 J
[r . 5 \ / s
te's d£2
.W
s
a<(gjag,
de de
+ wo(g2,c) +
(WoCgj.c) c h
de 2
146
Вычислительную процедуру построения практических зависимостей можно про-
изводить двумя способами Первый способ более точный, при котором уравнения рав-
новесия дифференцируются по времени. Дифференцируя (5.2 1) и (5.2.2), находим
д£2 де
ЛГ(0-[е+/(г2,с)]+^0
ff(£2>ch , У(£2-С),.
дс С£2
dMQx . дМ°х .
= -С 4-
дс д£2
Разрешаем эту' систему относительно производных х
£2(0 =
dN0(£2,c)
с£2 дс дс
ОС
дЛГ0(£2,с) дМ°(£2,с) df(s2ic)
дс дс2 д£2
(5 2.7)
c(t) =
_________tej___________________________
aTv0(g2,c) aA/f(g2>c) N^df(£2,c)
дс2 дс дс
ак°(£2.£)
ds2
дЛГ0(*2,с) дМ°(£2,с) tf(s2,c)
дс дс2 дс2
Интегрирование системы дифференциальных уравнений (5.2.7) на каждом шаге
дает значения £2(/,) и с(1/), которые подставляются в условие потери устойчивости
(5.2.6). Обращение последнего в ноль дает критические значения и с(^>) •
В своих исследованиях мы также применяли второй метод вычислений - более
простой, но менее точный обратный метод. Суть этого метода состоит в следующем.
147
Последовательно перебираются значения переменных е2 и с; по заданным значениям
рассчитываются три величины: N0,l,e. Из уравнения (5.2.1) находим величину про-
дольной силы No (е2»с) • Из условия критического состояния (5.2.6) находим длину стер-
жня 1/1, входящую сомножителем в первое и третье слагаемые:
1 <У(£2,с)_ .2 ^2
де2 л2с ’ дс п2с2
Наконец, из второго уравнения равновесия (5.2.2) находим эксцентриситет е при-
ложения силы N, отсчитываемый от середины высоты Л сечения.
Найденные величины представляют в виде номотраммы N0-e-l. Пересекая эту
номограмму прямой е = const, получаем критическую зависимость Nq-1 для любого
интересующего нас значения эксцентриситета. Абсолютные величины NQieyl далее
переводятся в любой интересующий нас масштаб относительных величин.
§ 5.3. Результаты численных экспериментов и практические рекомендации
Общие зависимости исследования устойчивости сжато-изогнутых железобетон-
ных колонн предыдущего параграфа, выведенные дифференциальные уравнения реше-
ния задачи охватывают всё многообразие различных классов бетонов и сталей, схем
армирования, а также частные теоретические методики, имеющиеся в научной литера-
туре (линейные модели с трещиной, упругопластические с диаграммой Прандтля, раз-
личные параболические зависимости); нет необходимости различать первые и вторые
случаи внецентренного сжатия, случаи граничного армирования.
Рассмотрим кривые критических зависимостей, предлагаемых в Еврокодах для
расчета гибких сжатых элементов, рис.5.1.1 [201].
Рис.5.3.1. Коэффициент продольного изгиба в функции
относительного эксцентриситета и относительной гибкости.
148
Коэффициент продольною изгиба
= N.
Хпч bhRb)
находится в функции отно-
сительного эксцентриситета и относительной гибкости:
где
яД1+<жУ
(5.3.1)
(5.3.2)
к
h ’
h у/a ’
h - размер колонны в плоскости изгиба;
(р - коэффициент ползучести ((р = 1,2 для обычного бетона)
П — ~ „
ч — ~~~ - отношение длительной составляющей силы к её полной величине.
N
В теории расчета сооружений рекомендуется вместо относительного эксцентри-
е
ситета ~ использовать приведенный эксцентриситет
W
где
- ядровое расстояние;
е
т — —
Р
W - момент сопротивления сечения;
F - площадь.
Для прямоугольного сечения
bh2
1
г 6 bh~ Ь
Таким образом, нормы Евростандартов не учитывают сильного влияния геомет-
рических размеров сечения на величины коэффициентов продольного изгиба. Исполь-
е
зование не приведенного, а относительного эксцентриситета ~ требует построения за-
висимостей типа 5.1.1 для каждого типа поперечного сечения (прямоугольное, квадрат-
ное, тавровое, двутавровое, круглое, кольцевое и др.)
Численные эксперименты, проведенные нами, показали, что даже для случая сплош-
ных сечений - прямоугольного и круглого — имеется заметное различие критических
сил, наблюдаемых в области средних и больших гибкостей: критическая сила прямоу-
I в
гольного сечения на 33% выше критической силы круглого сечения при ~ — 29 — = 0,5.
h h
149
С уменьшением гибкости различие уменьшается; при нулевых гибкостях оно составля-
в
ет до 11%; такая тенденция наблюдается с уменьшением эксцентриситетов до — = 0,17.
Рассмотрим далее выражение приведенной гибкости (5.3.1).
Оно следует из отношения напряжений
Rb
— =«!
э Rb _ я2Еь
где аь ~ - критическое напряжение из формулы Эйлера;
л
I
- - гибкосгь колонны;
г
up радиус инерции.
С учетом этого, получаем
а = Ъ =
Рь
Для прямоугольного сечения
2

—
Принимая с целью упрощений — «1, имеем

I2 1

называя X относительной гибкостью, записываем
Считая далее, что модуль упругости Еь зависит от ползучести, Евростандарты
уменьшают его с помощью эмпирической формулы (5.3.2)
150
F
г» полз _
Ь 4
1 + фТ]
Относительная гибкость (5.3.1) Евростандартов (равно как и относительный экс-
центриситет) не учитывает геометрических особенностей различных типов попереч-
ных сечений железобетонных колонн, что также вносит погрешность в вычисление ко-
эффициента продольного изгиба £. К достоинствам (5.3.1) следует отнести факт, что с
помощью коэффициента
учитываются влияния различных марок бетонов на ве-
личины расчетных усилий. Учет ползучести с помощью коэффициента (рт] достаточно
условен, о чем будет подробно сказано несколько ниже
Ниже также будет использовано понятие условной гибкости, учитывающей гео-
метрические и физические особенности сечений
I 1
где г - радиус инерции сечения
Рассмотрим теперь влияние класса бетона на величины критических сил. Расчеты
по разработанной теории с использованием диаграмм Еврокодов показали, что лаже в
__. g —
параметрах «к - m - А »(т = — - приведенный эксцентриситет; А
Р г №
1
=^=) наблю-
дается существенное расхождение значений коэффициента к При малых эксцентриси-
тетах
£
7 = 0,05
п
I
это расхождение сначала мало (при соотношениях — < 12); затем рас-
хождение возрастает и достигает при — = 30 значений 21,3 %.
п
Меньшие значения имеет бетон с /?л=10 МПа в сравнении с бетоном
е
Rb - 60 МПа С увеличением эксцентриситетов ситуация меняется, и при — = 0,42
h
наибольшие расхождения возникают при малых и средних гибкостях* 40% - при — = 20;
п
62% - при - 0 • Выявленные расхождения свидетельствуют, что в пракгических рас-
четах для бетонов низких классов и бетонов высоких классов следует использовать раз-
личные зависимости «к - тп - А ».
151
Обратим внимание на тот факт, что если в координатах 2 кривые критических
зависимостей малопрочного бетона (j?fc=10 МПа) и высокопрочного бетона
= 60 МПа) совпали, то в координатах Л кривые высокопрочного бетона лежат
ниже: 2j0 = 1,832^.
Проведены численные эксперименты, позволяющие изучить влияние вида диаг-
рамм аь - £ь Евростандартов на величины критических зависимостей. В этом анализе
использованы для бетона криволинейная диа1рамма но рис.2.2.1 и билинейная диаг-
рамма (упругопластическая) по рис.2.2.3.
При малых и средних эксцентриситетах приложения сжимающих сил наблюдает-
ся заметное расхождение критических сил; завышенные значения дает применение би-
линейной диаграммы. С увеличением эксцентриситета расхождение становится менее
заметным.
Рис.5.3.2. Изменение критических сил железобетонных стержней, вызванное изменением
вида диаграммы — £ь бетона:
билинейной - 1; криволинейной с ниспадающим участком.
Этим обстоятельством вызвано желание в ряде национальных норм раздельно рас-
сматривать центральное и внецентреиное сжатие. Именно при центральном сжатии с
наибольшей величиной проявляется влияние характера диаграмм аь - еь и crs - es.
152
сила центрально сжатого железобетонного стержня определяется по фор-
муле Эйлера, с использованием значений касательных модулей
° I2 I2 '
Отсюда рассчитывается длина колонны
/2= ^(еД>+е,7,)
(5.3.3)
где Е*ь, Е’ - касательные модули деформаций бетона и арматуры;
Ес“ ,Е™ - секущие модули деформаций бетона и арматуры.
Критическая сила (5 3.3) делится на коэффициент = 1,3 4-1,4 с целью учета на-
чальных несовершенств и учитывается в нормативных расчетах.
Если же для низкопрочных и высокопрочных бетонов использовать только упру-
гопластическую диаграмму по рис.2.2.3, то различие между критическими силами при
малых и средних эксцентриситетах можно признать малым, рис.5.3.3.
Рис.5.3.3. Использование идеализированной упругопластической диаграммы для
различных классов бетонов (= 10 МПа ,Rb =50 МПа )
153
Таким образом, численные эксперименты показали, что для расчетов сжато-изог-
нутых стержней предпочтение следует отдавать криволинейной диаграмме бетона
сь — с ниспадающим участком. Дополнительно установлено, что сам вид функции,
аппроксимирующей криволинейную диаграмму бетона, не имеет существенного значе-
ния для расчетов сжато-изогнутых железобетонных колонн.
Критические силы железобетонных колонн существенно зависят также от диаг-
раммы сгу - £s арматуры, имеющей нелинейный вид при cs > 0,7Rs. Однако, исполь-
зование условия линейности диаграммы as - £s арматуры до достижения предела те-
кучести Rs показало, что изменение коэффициента армирования Ц от 0,001 до 0,03
мало сказывается на величинах критических сил, рис.5.3.4.
Сравнение значений коэффициентов Л по данным Еврокодов и рассчитанных по
модели СНиП показывает, что кривая СНиП лежит несколько выше (рис.5.3.5), что впол-
не объяснимо.
Модель СНиП эмпирическая, но она обоснована значительным числом экспери-
ментальных данных по испытанию железобетонных колонн. Эти экспериментальные
данные из испытаний колонн, в которых применялась арматура различных классов
и различных свойств.
Зачастую арматура железобетонных колонн имела условный предел текучести, что
существенно влияло на результаты экспериментов; специальной оценки нелинейного
участия диаграммы trs - £s арматуры в этих экспериментах не производилось.
154
Остановимся теперь на практических модстях расчета сжато-изогнутых железо-
бетонных колонн. По аналогии с Еврокодами, использующими понятие эффективной
гибкости бетонных колонн, введем для железобетонных колонн эффективную гибкость,
для чего рассмотрим отношение
а = = AbRh + AsRs+A'sR's
1 Р* EX .
z2 z2 z2
где Psb - сила, характеризующая прочность железобетонной колонны при центральном
сжатии;
РД - критическая сила Эйлера
Вводя очевидные обозначения
S
А
— i' = -
записываем
4 . 4 . Я, Я' Е, , Е', .
д = —. и . к = —. Л-~-. п = —. п = — . i
4 ’ Я6 Еь> Е„-
(5 3 4)
ь
Отсюда находим выражение для эффективной гибкости прямоугольной колонны
155
г ffj- IK IK + +
1 h у Eb X л:2 V l + ni + n'i' ’
где h - размер в плоскости изгиба.
Учитывая применение одного класса арматуры в колонне (к = к', п = п' \ имеем
- / ^2 |1+* (ц + ц’)
h^£b\^2lj 1 + п (i + i') ’ (535)
Введем некоторые упрощения, связанные с геометрическими характеристиками
прямоугольного сечения с двойной арматурой,
/=у- = 3^(1-3 )2; Г = ^ = 3//'(1-з ),
h 1ь
а а
где з ~~к!2 ’ 3' ~ " относительный защитный слой бетона.
Константа
для прямоугольных и квадратных сечений не зависит от физико-
механических характеристик сечения; принимаем её равной единице, какого принято в
Евростандартах.
Асимметрию сечения арматурного каркаса в формуле X можно не учитывать; из
теории сооружений известно, что критические зависимости несимметричною и сим-
метричного двутавра в координате Л различаются несущественно.
На основании этого формулу для расчета эффективной гибкости прямоугольной
колонны
+ п 3/Л1 -
1 + А (ля-Х)
записываем в упрощенном виде
|К 11+^
(5.3.6)
где /л,к,п - общие коэффициенты всего сечения
А + А^ , R Е
и=—------- к = — . п = —
А ’ А’ Еь-
По аналогии вводим общие коэффициенты в формулу (5.3.4) для произвольного
типа сечений
1К Е [1+&
ИММ 1+ni ’
156
(5.3.7)
где i = —, IstIb - моменты инерции арматуры и бетона относительно оси, проходящей
Л
через центр тяжести бетонного сечения.
Для неармированного произвольного сечения эффективная гибкость равна
для неармированного прямоугольного сечения
я^Еь
Для армированной колонны произвольного сечения находим значение безразмер-
ного эффективного эксцентриситета с помощью ядрового расстояния всего железобе-
тонного сечения
е h}Ah\ + ku
т= — = е - °------—
Р 1Ь 1 + w’’
(5.3.9)
где Л] - расстояние от центра тяжести всего бетонного сечения до наиболее сжагого
волокна.
Для армированной колонны прямоугольного сечения
е \ + к[л
, (5 3 9)
Л1 + Ъпц 4 7
где величина тэ уменьшена в шесть раз с целью сохранения общего подхода Евростан-
дартов.
Для неармированной колонны
тэ
е
Г
Приводимые ниже упрощенные модели разработаны для железобетонных колонн
прямоугольного сечения в координатах (5.3.6) и (5.3.9). Значения коэффициентов к даны
на рис.5.3.5-5.3.6.
Коэффициент к на рис.3.5.6 предназначен для железобетонных колонн, изготов-
ленных из бетона класса fc — 12 МПа; на рис 3 5.7 — из бетона класса fc = 50 МПа
(см. таблицу 2.2.1).
Несущая способность сжато-изогнугой железобетонной колонны при кратковре-
менном загружении определяется по аналогии с предложением Еврокодов по формуле
N = (AbRb+A,Rs+A',R't) к. (53.10)
Значения коэффициентов А: для промежуточных классов бетона
(12 МПа< fc <50 МПа] следует определять по линейной интерполяции из данных
1 + к/л
рисунков 5.3 6-5 3.7 Безразмерный коэффициент । +
учитывает влияние следую-
щих параметров: прочности бетона и прочности арматуры, соответствующих их клас-
сам, начальных модулей деформаций бетона и арматуры; коэффициента армирования.
157
Рис. 5.3.7.
158

Влияние формы поперечного сечения колонны учитывается в двух коэффициен-
тах формул (5.3.7) и (5.3.9), предназначенных для колонн произвольной (не прямоу-
гольной) формы сечения
Л i=L
h' h'
В заключение данного параграфа приведем некоторые экспериментальные резуль-
таты по устойчивости железобетонных колонн, полученные в НИИЖБе под руковод-
ством Чистякова Е.А. [176].
В таблицах 5.3.1-5.3.3 указаны основные параметры и величины критических сил
колонн, имеющих только случайные несовершенства и случайные эксцентриситеты.
В таблице 5.3.4 приведены результаты испытаний. Иа рис.5.3.8 точками показаны экс-
периментальные данные: кривая 1 соответствует данным Евростандартов для случая
etoi = 0 [201]; кривая 2 — характеризует значения касательно-модульной критической
силы. Негрудно заметить, что кривая 1 учитывает наличие случайных эксцентрисите-
тов и различных несовершенств у реальных колонн.
Таблица 5.3.1.
Шифр О 2 h, СМ ь, см МПа 4=Л> см2 МПа а~а , см кН
1 2 3 4 5 6 7 8 9
КГ-9-1 3,75 11,9 24,3 20 1 54 325 1,6 460
КГ-9-2 3,75 11,8 24 20 1,46 335 1.6 460
КГ-9-3 3,75 12 24 22,5 1,46 330 1.6 440
КГ-9-4 3,75 12 24 22,5 1,54 330 1.6 400
КГ-12-1 4,55 15,2 24,1 12,6 2,18 380 !,.* __ 440
КГ-12-6 4,55 15 24 12,5 2,2. 378 1,8 400
КГ-14-1 4,55 15 24 20 2,25 375 1,6 640
КГ-14-2 4,55 15 24 20,5 2,26 372 1,6 620
КГ-20-5 3,1 15 24,4 40 1 485 1,5 1303
КГ-20-6 3,1 15,1 24,7 40 1 489 1,4 1303
КГ-21-3 2,35 15,3 24 31,5 0,98 387 1,5 1204
КГ-21-4 2,35 153 24,3 31,5 0,99 401 1,4 1103
КГ-22-3 4,58 15 24,4 34 3,02 435 1,7 899
КГ-22-4 4,58 15 24,6 34 3,08 411 1,7 862
КГ-24-1 4,6 15,2 24,2 26,3 3,17 366 V 757
КГ-24-2 4,6 15 5 25,1 26,3 3,1 338 1,7 800
КГ-27-1 4,58 15,2 24,3 24 3,07 431 1,7 795
КГ-27-2 4,58 15 24,6 24 3 05 428 1,7 824
КГ-28-4 4,58 10,2 24.4 32 1,4 421 1,5 280
КГ-28-6 4,58 10 24,3 32 1,41 420 1,5 300
КГ-29-1 13 12,4 24,6 22 0,25(ц) 540 6,2 700
КГ-29-2 1,3 12,1 24,1 22 0,25(ц) 540 6.1 750
КГ-29-3 2,5 12,4 24,4 25 0,2 5 (ц) 540 6,2 643
КГ-29-4 2,5 12,1 24,2 24,5 0,25(ц) 540 6,1 690
КГ-29-5 3,7 12 24,6 23,5 0,25(ц) 540 6 520
КГ-29-6 3,7 12,2 24,7 24,5 0^5(ц) 540 6,1 559
КГ-30-1 1.3 12,2 24,5 20,5 0,25(ц) 540 6,1 625
КГ-30-2 У 12,1 24,2 20,5 0,25(ц) 540 649
160
Окончание табл. 5.3.1
I 2 3 4 5 6 7 8 9
КГ-ЗО-З 2,5 12 24,3 19.5 0,25(и) 540 6,1 527
КГ-30-4 2,5 12,1 24,5 19 0,25(и) 540 6 499
КГ-30-5 3,7 12,1 24,6 19 0,25(ц) 540 6,1 401
КГ-30-6 3,7 12,2 23,9 18,5 0,25(ц) 540 6,1 401
КГ-34-1 4,6 15,1 24,7 22 О,25(ц) 540 7,5 550
КГ-34-2 4,6 15 24,4 22 0,25(ц) 540 7,5 550
КГ-36-1 4,6 15 24,7 39 0Д5(ц) 540 7,5 874
КГ-37-3 4,6 15 24,2 39 0.25(h) 540 7,5 860
КГ-37-4 4,6 15 23,9 37 0 25(ц) 540 7.5 719
КГ-ЗО-6 4,6 14,9 23,9 37 О^25(п) 540 7,5 646
КГ-ЗО-6 4,6 15 24 37 <\25(ц) 540 7,5 685
КГ-ЗО-6 4,6 15 24 31 3,05 353 1,7 800
Обозначения:
/о- расстояние между опорными шарнирами колонны;
a, d- расстояние от грани колонны до оси растянутой и сжатой арматуры;
h - высота сечения колонны;
b - ширина сечения колонны;
Rt, - призменная прочность бетона;
А„ А,' - площадь арматуры, соответственно растянутой и сжатой;
R} - предел текучести арматуры.
Таблица 5.3.2.
. Шифр Ль м h9 см ь, см Дь МПа а - а\ см см2 МПа кН
1 2 3 4 5 6 7 8 9
КПГ-ЗБ 3,78 23,5 22,6 28,2 3,1 2,26 317 940
КПГ-1А 4,17 21,9 21,8 22,6 2,6 2,26 287 666
КПГ-1Б 4,17 22,3 21,7 22,8 3 2,26 319 666
КПГ-1Г 4,18 23 21,4 28 3 2,26 318 877
КПГ-2А 4,67 22,8 21,4 29 3 2,26 311 839
КПГ-2Б 4,67 23,4 23 29,2 3,5 2,26 281 1044
КГТГ-1 4,92 23,4 21,7 27,2 3,5 2 26 300 801
КГТГ-2 5,35 23,5 22,4 26 5 3 2,26 294 793
КПГ-1 5,37 22,6 22,6 34,2 3 2,26 299 883
КПГ-П 5,42 23 21,6 29,2 3 2,26 290 872
КПГ-1-1 5,57 24,3 21,7 28,6 3,7 3,95 320 730
К11Г-1-2 5,55 24 22 28,6 3,6 3,95 322 1044
• Таблица 5.3.3.
Шифр 4, м Д,. см б, см см2 &ь> МПа Л, см2 Ъ МПа кН
/ 2 3 4 5 6 7 8 9
К-1А-1 1065 26,2 5,2 342 43,8 4,02 240 80
К-1А-2 1065 26,2 4,7 317 45 4 4,02 250 84
К-1А-3 1065 26,2 5,4 354 37,3 4,02 247 500
К-1А-6 1065 26,2 4,7 318 57 4,09 240 600
К-1А-7 1065 26,2 4,9 327 46 4,02 240 600
К-2А-7 647 26,3 5.5 366 50 4,1 241 1200
К-2А-8 646 26,2 5,6 362 44 4,02 240 1270
К2Б-3 648 26,1 4,8 323 48,6 15,3 339 1420
К-2Б-6 648 26,3 47 319 48,6 15,1 344 1480
Обозначения:
Dn - наружный диаметр колонны; &- толщина стенки.
161
Таблица 5.3.4
Шифр lo/h, см Кь, МПа Р % кН кН Ф
/ 2 3 4 5 6 7 8
КГ-9-1 31,5 109 20 1,06 460 678 0,68
КГ-9-2 31,6 109 20 1,03 460 664 0,69
КГ-9-3 31,2 1-8 22,5 1,03 440 745 0,6
КГ-9-4 31,2 108 22,5 1,06 400 749 0,54
КГ-12-1 30,0 104 12,6 U 440 622 0,7
КГ-12-6 30,2 104 12,5 1,22 400 619 0,64
КГ-14-1 30,3 105 20 1,24 640 889 0,72
КГ-14-2 30,3 105 20,5 1,26 620 907 0,68
КГ-20-5 20,7 72 40 0,54 1303 1562 0,83
КГ-20-6 20,5 71 41 0,54 1303 1626 0,8
1 2 3 4 5 6 7 8
КГ-21-3 15,3 53 31,5 0,54 1204 1233 0,97
КГ-21-4 15,4 53 31,5 0,44 1103 1243 0,89
КГ-22-3 30,5 105 34 1,65 899 1507 0,6
КГ-22-4 30 104 34 862 1505 0,57
КГ-24-1 30,2 104 26,3 1,72 757 1200 0,63
КГ-24-2 30 104 26,3 1,6 800 1233 0,65
КГ-27-1 30,1 104 24 1,66 795 1151 0,69
КГ-27-2 30,3 105 24 1,65 824 1147 0,72
КГ-29-1 10,5 36 22 0,08 700 670 1,05
КГ-29-2 10,8 37 22 0,08 750 642 1,12
КГ-29-3 20,2 70 25 0,08 643 756 0,85
КГ-29-4 20.6 71 24,5 0,08 690 717 0,96
КГ-29-5 31,6 109 23,5 0,08 520 673 0,78
КГ-29-6 30,22 104 24,5 0,08 559 738 0,76
КГ-30-1 10,7 37 20,5 0,08 625 612 1,02
КГ-30-2 10,8 37 20,5 0,08 649 601 1,08
КГ-ЗО-З 20,8 72 19,5 0,08 527 568 0,92
КГ-30-4 20,6 71 19 0,08 499 563 0,88
КГ-ЗО-5 30,6 106 19 0,08 401 566 0.71
КГ-30-6 30,3 105 18,5 0,08 401 539 0,75
КГ-34-1 30,5 105 22 0,7 550 834 0,66
КГ-34-2 30,5 105 22 0,7 550 830 0,66
КГ-36-1 30,7 106 39 0,7 874 1458 0,6
КГ-36-2 30,7 106 39 0,7 860 1430 0,6
КГ-37-3 30,7 106 37 0,7 719 1340 0,54
КГ-37-4 30,7 106 37 0,7 646 1330 0,49
КГ-37-5 30,7 106 37 0,7 685 1345 0,51
КГ-39-1 30,7 106 31 1,7 800 1331 0,6
КГ-2А-7 24,7 86 50,0 1,13 1200 2015 0,6
КГ-2А-8 24,7 86 44,0 1,12 1270 1667 0,76
К-2Б-3 24,7 84 48,6 5 1420 2062 0,69
К-2Б-6 24,7 83 48,6 5 1480 1998 0,74
КПГ-ЗБ 15,9 51 28,2 1,6 940 942 1,0
КПГ-1А 19 56 22,6 1,65 666 763 0,87
КПГ-1Б 18,7 56 22,8 1,62 666 784 0,85
КПГ-1Г 18,2 55 28,0 1,6 877 928 0,95
КПГ-2А 20,5 62 29,0 1,65 839 952 0,88
162
Окончание табл. 5.3.4.
J 2 3 4 5 6 7 8
КПГ-2Б 20 62 29,2 1,62 1044 1022 1,02
КПГ-1 21 63 27,2 1,57 801 910 0,88
КПГ-2 22,8 69 26,5 1,5 793 902 0,88
КПГ-1 23,8 70 34,2 1,66 883 1058 0,84
КПГ-П 23,6 69 29 .2 1,62 872 948 0,92
КПГ-1-1 23 70 28,6 2,7 730 1080 0,68
КПГ-1-2 23,1 7! 28,6 2,7 1044 1084 0.96
Обозначения:
^и4 * прочность колонны;
В заключении данной главы укажем, что различным аспектам экспериментальных
и теоретических вопросов кратковременной устойчивости железобетонных колонн по-
священы работы Боришанского М.С., Кузнецова А.Н., Ржаницына А.Р., Никитина Г.В.,
Манжаловского В.П., Гениева Г.А., Бондаренко В.М., Гусакова В.Н., Романова П.П.,
Махновского А.И., Таля К.Э., Чистякова Е.А., Каюмова Р.Х., Бамбуры А.Н., Подобенко
Т.Н., Попеско А.И., Мунира А., Роша М., Баумана О., Хогнестада Е., Хансона Р., Розен-
строма А., Хабеля А., Джекобсона А, Геллера В., Хоттера К., Бромса Б. и других уче-
ных.
За рубежом в последние годы указанную проблему рассматривали Foster S.I., Fttard
М.М. (1997), Chuang Р.Н., Kong F.K. (1997), Kim I.,Jang I. (1995), Ibrahim H.H.H.,
Mac Gregor LG. (1994), Held M., Konig G., Simsch G. (1993), Bjerkeli L., Tomaszewics A.
(1992) и другие; краткий анализ этих работ проводит Claeson С. [200].
Обратим внимание, что в зарубежных исследованиях для высокопрочных бетонов
учитывается различие прочностных свойств бетона, находящегося внутри арматурного
каркаса и вне ею, рис.5.3.9.
£со £сс
Рис.5.3.9. Различие диаграмм <уь — еь
работы сжатого высокопрочного бетона в колоннах.
163
Для связи прочностей бетона и fcc предложено несколько эмпирических фор-
мул Г.Кёниг и Г.Ситш рекомендуюг для величин fc0 зависимость
где fc^yi - прочность бетонного цилиндра диаметром 15 см и высотой 30 см;
а - эмпирический коэффициент:
е 1
а — 0,85 при малых эксцентриситетах Т < т; а = 1 - в остальных случаях.
п б
Куссон Д. и Паултре П. эмпирически представляют диаграмму сгь - £h бетона за-
висящей от прочности защитного слоя fco.
Нетрудно видеть, что такое влияние прочности fco на конечные результаты чис-
ленно будет- заметным при достаточно малых размерах поперечных сечений колонн.
Для высокопрочных бетонов сжатых колонн за рубежом получены специальные
рекомендации [200J по размерам толщины защитного слоя бетона (из условия его от-
слоения), рис.5.3.10
Рис.5.3.10
164
Глава 6. РАСЧЕТ ЖЕЛЕЗОБЕТОННЫХ БАЛОК И КОЛОНН С УЧЕТОМ
СОВМЕСТНОЙ НЕЛИНЕЙНОСТИ МГНОВЕННОГО И ДЛИТЕЛЬНОГО
ЗАГРУЖЕНИЙ
§ 6.1. Модель нелинейного деформирования бетонного волокна
При расчете балок в условиях нелинейного длительного загружения существует
трудность, заключающаяся в неизвестном характере распределения напряжений по по-
перечному сечению бетона [129], [33], [46]. Вследствие этой трудности некоторые ис-
следователи заменяют реальное сечение балки идеальным двухполосным, а величина
разрушающей нагрузки железобетонной балки зависит именно от распределения на-
пряжений но её поперечному сечению В работе [33] Брызжатого Э П., Мирвиса Я.Г,
Петровой К В. указывается, что вычислительная процедура является весьма громозд-
кой и затруднительной даже для одного сечения. В работе [46] Гвоздева А. А., Чистяко-
ва Е. А., Шубика А.В отмечается, что реализация предложенного авторами способа рас-
чета встречает серьезные затруднения, связанные с необходимостью удерживать в про-
цессе вычисления значительный объем информации, что заставляет существенно огра-
ничивать количество точек во времени tt, для которых может быть определено напря-
женно-деформированное состояние На сложность данной проблемы указывал и Работ-
ной Ю.Н., Шестериков С.А., Качанов Л М., Вишневецкии Г Д. и другие ученые.
В данной работе предлагается новый метод позволяющий эффективно рассчиты-
вать напряженно-деформированное состояние сечения при ползучести и при этом ис-
пользовать систему дифференциальных уравнений третьего порядка Суть метода реа-
лизуется в следующем обстоятельстве. На диаграмме аь - £, бетона с ниспадающим
участком выделяем опорные точки рис.6.1.1. В этих точках величины
напряжений известны 0, RU), Rh, Rib.
165
Пусть сечение балки находится в той ситуации, когда крайнее волокно, имеющее
напряжение о>2, находится в стадии между опорными точками Л2 и А'3, рис.6.1.2 В
отличие от деформаций, показанных на диа1рамме по рис 6 11, деформации волокон в
сечении (/), £2 (/) на рис.6.1.2 по величине не совпадают с фиксированными дефор-
мациями Ehl,£bQ,£2.
Эти деформации волокон сечения изменяются с течением времени / и удовлетво-
ряют выбранным уравнениям ползучести см ниже, а также гипотезе плоских сечений.
Через точки АО,АХ,А2,А3 проводим полином Лагранжа
o-b=ao + ai£b+ а2£ь + аз£ь- <6Л -1)
Значения полинома (6.1.1) в опорных точках дает систему уравнений для нахожде-
ния коэффициентов а0,а1,п2,«з:
=0;
&Ъ\ = а1 £Ь1 (0 + а2 ' £Ь\ (О + ai (О *
RbO = а\ ’ £ЬС (0 + “2 • £bcW + ai • £ыЮ ’ <6-1 -2)
сг2 = П] • £2(t) + а2 £2(i) + а3 • г2(Г)-
Из решения системы алгебраических уравнений (6.1.2) находим значения коэффи-
циентов полинома (6.1.1)
166
П _ Rib- £М (0 • 4 (О - RU> • 4 (О • £ЬО (О + £Ь1 (О £ЬО (О <4 ~
- £bl (О 4 (О • Rb + 41 (О • Rb • 4 (О - 41 (О • <4 £Ь0 (О.
д ?
п Rb'£i(t) £ы(^' £ы>(1) +R\b ' £ы>(1)' £г(^)
2 2
--4бо• W+4.f• £m(4i(t)-e2(t)-Rb. <6-13>
4
_ £bl (*) ' gfco(O ^2 ” £b\ (0 ' g2 (0 ' Rb + £b\ (0 ’ Rb ' g2 (0 —
U 1 — -----
Д
~ gfrl (0 ' ^2 ‘ g6o(O + Rjb ‘ gbO<0 ' g2 (0 ~ R\b ' £2 (*) ' g6o(O
Д
где
д=£ы (o • 4o (0-4 (0 - g6i (0 • £2 (o • 4o (0+4i (0 • 4o (0 • g2 (0 -
- 4i (0 • 4 (0 • £ьо(*)+4i (0 • gbo(o • g2 (0 ~ 4i (0 g2 (0 4o(O-
В случае, когда напряжение крайнего волокна сечения (рис.6.1.4) находится
между опорными точками А, и А2, рис.6.1.3, степень полинома(6.1.1) можно снизить.
Рис. 6.1.3.
167
Полином проводится через точки А$, At ,А3
ab =а0 +at £ь + п2 -е%. (6.1.4)
Значение его в точках , At, А3 дает систему уравнений
= 0;
= «1 • £Ы (0 + «2 • £Ь1 (0 > (6-1 5)
сг| =ах -E2(f) + a2 -£2(0-
Коэффициенты этого полинома равны
а _R\b [£г(?)~^2 ‘ £b\ (?)
£Ь\(?)'£1(?)~£1\(?)£2(?)'
(6.1.6)
а £ы(?)^2-£2(?)^1Ь
2 £ы(?)£2(?)-£Ь1(?)£2(?)'
Применение полиномов (6.1.1) и (6.1.4) позволяет избежать громоздкой процеду-
ры разбиения поперечного сечения балки на части и существенно снизить порядок си-
стемы дифференциальных уравнений для исследования напряженно-деформированно-
го состояния железобетонного сечения при ползучести. Такое снижение особенно важ-
но при рассмотрении статически неопределимых балок.
Рис.6.1.4.
168
Данный подход можно применять и для исследования кратковременного загруже-
ния. Это является весьма важным при изучении поочередных воздействий кратковре-
менного и длительного загружения Проводя полином через точки АО,А1>А2,А3
(рис.6.1.1), можно записать для кратковременного загружения:
аь = ахеь + аге^ + , (6.1.7)
где коэффициенты а1?а2,а3 этой кубической параболы - суть константы.
а R\b ' £ЬУ ' £Ь2 ~ *1Ь • £Ь2 £Ь0 + £Ь\ ' £Ь0 ’ R b ~ _____
£Ы ' £Ь0 £Ь2 ~ £М ' £Ь2 ' £Ь0 + £Ь\ £ЬО £Ь2 ~ £Ь\ ' £Ь2 ’ £Ь0 +
~ £Ы ' £Ь2 • Rb + £Ы ‘ Rb ' £Ь2 ~ £Ы ' • £ьь.
+ £Ы ‘ £Ь0 ’ £Ь2 ~ £Ы ‘ £Ь2 ’ £Ь0
а __________£Ы ' Rb ‘ £Ь2 ~ £Ы ' R$b ' £io + R\b • £Ь0 • £Ь2 ~_
Eb\ * £Ъ0 ‘ £Ь2 ~ £Ь\ £Ь2 £60 ” £b\ ' £bQ ' £Ь2 ~ £Ь\ £Ь2 ' £Ь0 +
” R\b • £Ь2 ' £Ь0 + £Ы £Ь0 ’ Rlb ~ £Ь1 • £Ь2 ' Rb 8)
+ £Ь\ ' £Ь0 ' £Ь2 ~ £Ь1 * £Ь2 ‘ £Ь0
а _ £Ы ' £Ь0 ‘ Rjb ~ £\Ъ ' £Ъ2 ’ Rb + £b\ ' Rb ' £Ь2 ~ £bl ' R$b ‘ £Ь0
£Ь1 ' £Ь0 £Ь2 ~ £Ь\ ‘ £Ь2 ' £Ь<> + £Ь\ ’ £Ь0 ' £Ь2 ~ £Ы ' £Ь2 ' £Ь0 +
+ R\b ' £ЬС ’ £Ь2 ~ R\b ' £Ь2 ' £Ь0
+ £Ы £Ь0 ' £Ь2 ~ £Ь\ ' £Ъ2 ’ £Ь0
где Rb - максимальное напряжение;
_0,6 Rb
Rlb = 0,6 - Rb; Rib = 0,5 • Rb, £ы ~ ; £fc0 = 200 • 10"5; eb2 = 350 • 10‘5.
Обратная функция к (6 1.7) записывается в виде
£ь=Ь\-аь+Ь2‘(т2+Ь3суь, (61.9)
где коэффициенты bx,b2,by находят из следующих выражений:
_ £Ы • Rb ' Rjb ~ £Ы • R^b ' Rb + Rbl • Rb • £Ь2 ~ Rb ' Rjb ‘ £b0 +
R\b' Rb R-lb ~ R\b Rm ‘ Rb + R\b Rb * Rib ~ R?b R& Rb +
+ R\b ' g£>0 ' Rib ~ R]b ' Cb2 ' Rb .
, pl p r>2 pl p p2 ’
+ К\ь ‘ кь ' Ry> Rib ' Rib ' Rb
169
£ ^61 ~£Ь0 • ~ ^1* ‘g62 + £fel '^36 £Я • ^lb Rb +
2 R,b • Rl R]b - Rlb 4 Rf + R?b R3b Ry, - R?b -R^ Rb +
+ 4^-gt2~4-«3t-gto. <61-10)
+^-Rb-R,t-Ru-R№-Rb'
. ^Ib ' • £f.2 ~ Rlb ' ^3b ~ £60 + -^16 ' £60 * Rib Rib '_^Ь2^Ль +
’ Rlb • Rl Rl„ - Rxb Rih Rl + Rl„ Rl R,„ -R?b R^ R„ +
+ g6i' ~ £ы' ^36'
+ Rlb-Rb-Rlb-Rlb-R3b-Rl'
Обратим внимание, что эти коэффициенты fy,Z)2,Z>3, строго говоря, несколько от-
личаются от коэффициентов Вх.,Вг,В3 из уравнения (2.7). Например, коэффициент
А = ТГ; в коэффициенте же Ь} начальный модуль упругости бетона в явном виде не
присутствует. Если принимать, что известны законы изменения Rbl,Rb,£bi,£b0 с тече-
нием времени из-за старения бетона, то в вычислении каждого из коэффициентов
5i ,b2,b3 участвует большее число функций.
§ 6.2. Напряженно-деформированное состояние железобетонного сечения
в условиях нелинейного длительного загружения
Характер распределения напряжений и деформаций по сечению показан на
рис.6.1.2. Положение произвольного волокна сечения будем характеризовать координа-
той х, отсчитываемой от нейтральной оси Ну. Напряжение произвольного волокна
бетона <ух представим в виде кубической параболы (6.1.1)
2 3
<т_ = а, • £_ + аг • + а, • £t.
Из подобия треугольников деформаций по рис.6.1.2 имеем
£х = g2(0
х С ’
откуда находим деформацию произвольного волокна
Из (6.2.1) находим напряжение произвольного волокна
(6.2.1)
(6.2.2)
(6.2.3)
(6.2.4)
170
Далее находим продольную силу бетонной части сечения
Nb = Jcr dF = h jcrx dx -
о
. . 2 , £г(О з
i Z— x + a2 —— x + a,-----— • x
c 2 c2 c3
С
а.
-dx.
о
После интегрирования и упрощений получаем
Г1
° - 2 -
Nt=b-c(t) 1 • a,(l,tt2,<^) e2(t) + |-a2(t,e2,o-^) e2(t) +
~a3(f,£2,<72)«2(0
(6 2 5)
Момент в бетонной части сечения находится относительно нейтральной оси Ny
Мь = fa-x-dF = b-c\ty - ax(t,c2,a2}-£2(t) +
F Lp
3
+ 2 a2(t,£2,cr2) • £2 (0 +1' a3(tf£2,a2) • £2(0
*т Э
Продольная сила в сечении всего элемента равна нулю
W = А' • Е- • • [с(0 - о']- А, Е, • • [Ло - с(0] +
с(/) с(0
+ ь • с(0 • | • а} (t,£ 2 ,СГ2 ) • е2 (/) +1 • a2{t,£2ia2 ) е} (t) +
1
+ —
4

Изгибающий момент сечения
М" = 4 Е'- ’ "eft) (С(,)" °')2 + А- Е‘ (h° ’С(,))2
. , 2/.\ Г1
4 z [з
+ |-^з(^^2,^2)-^(О •
+ b-c2(t)- - a}(t,£2iab2)-E2(t) + --a2(t,£2>(y^-£l(t) +
(6.2.7)
(6.2.8)
Дифференцируя уравнение (6.2.7) по времени, получаем
4-£2(t) + B} -^(О + С, -c(0 = Z>p (6-2.9)
171
где
4=4.£;.£2)г£:_л.£,.м)+
1 5 5 c(t) c(t}
. .. 1 да, . . 1 да2 2.. 1 даъ 3/
+ ь-с(О- -•-"-•^2(0 + --^--^(0+--т-2-^2(0 +
2 ^^2 0^*2 vZT‘7
— • a2(£,g2,CT2 ) • 2 g2(/) + — • Й3(£,£2,<Т2) ’ 3 • Е2 (0 ’
1 / ь
+ --а,(7,£2,<т2
B^b-cft}-
1 да}
2'да}
zx 1
•г2(0+--
дД2
6сг2
2, ч 1 да, 3,
^2(0+-----т‘£2(0
2 4 да} 2
с,-л;^- e2(t) с2(1) + л, • Е, • ег(1) > +
_ , , ч 1 да, .. 1 да, 2 z х 1 да3 з,.
D, = -Ь • c(t) ---1 • E2(t) +---~ • £2(f) +--1 - е2 (t)
1 L2 & 2 3 dt 2 4 dt J-
Дифференцируем второе уравнение равновесия (6.2.8) по t, считая закон измене-
ния внешнего момента М* известным (в частности, Л/" = const},
Л *^2(0 + ^2 ^(O + Q с(/) = d2,
(6.2.10)
где
£
л2 = л;-£;--^^—
2 5 5 c(i)
- г 1 даг
---------
3 de2
~а2(/,£2,сг|)-2 ^2(0 + 7-«3(Л^2,сг2)-3-^2(0 ;
4 5
+ b-c2(t}- -
1 z ь
• O[ (Z,^2,cr2
5 5 c(0
1 da2 2.. 1 da,
4 ds2 5 dc2
4
B2^b-c2(t}- -
1 da, .. 1 da2 2.. 1 da-, 3..
-----г' ^2(0 +--------It'£2(0+--------a ' £i(0 J
3 dab2 4 d<jb2 2 5 d<jb2 2
2 , , 2< 7 c2(t)
+ 2 • b-c(t)'
A5-Es-£2(t)-^r-^~4
5 s 2 c2(t)
172
гч >VИ , 2/. 1 Эй, , . 1 Эй j . , 1 Эй J , .
D2=MX -b e (t)- -‘~ £г(1) +-------------~---£2(t) +------y- ei(t)
2 л 3 dt 2 4 dt 21 5 dt 2
В качестве третьего уравнения связи переменных воспользуемся уравнением (3.7.43)
третьей главы
А3 - e2(t) + В3 <т2 (/) + С3 • с(Г) = Z>3, (6.2.11)
где
А = 1;
В - 1 а/ дф&-‘Ъ*а
3 Eb(t) dcrb(t) дФ dab(t) Ф’
С3=0;
В рамках нелинейной наследственной теории старения основное уравнение ползу-
чести стареющего бетона также запишем в форме (6 2 11), но коэффициенты А3, В3,
С3 и D3 имеют вид
Л3=1;
В, = 4 + 2 • Ь2 • <г ‘ + 3 Ь} (atf + 4 • Ь, • (<г‘) ] • ’ .
С3 = 0;
Линейная неоднородная система дифференциальных уравнений (6.2.9) - (6.2.11)
решается относительно скоростей ё2 (t), &2 (0> <Х0'
^1(0“тт /, \’[“ (^2’^*2О' ^2» )"
Д^2,сг2,с,^
+ >С»0" ^2 (^2’0’ (^*2’0^" (^2’^2 ,^>0' ^2(^2>^>0'
^3(^2»0~^1(^2’^2’^’0’^з^г’О'’
Э’г (/) т ?1](£2>^2’^'’0 '^3c2»0 ^''2v2’®'2»£’0"‘”
Д(£2,о-2,с,^
+ ,С,0* Ог (^2 »0^ ^1(^2’^2 ’^>0 ^2 (^2 >^2 >£>0" (6 2.12)
" ^3(^'2 »0— »С>0' ^2 (^2»^2 ’^’0] ’
173
<?(/) =
7 7 Ч ' [/^1 (^2’&2 ^2^2’^2 ^3 \Р*2
А|^2,2-/
где
- Л1(?2>СГ2 »С»0* ^з(СГ2>Ч'^)2(^2’СГ2’С>/)+
' D2 (^2’^2 ^1 (^2’^*2 ^з(р'2 >0' ^2 (^2’^*2
^(^2’^2 ’£’— —^1 \^2»^2 9^»^)" -^з(р"2 >^/'
* ^2(^2’^2 ^1(^2>^2 >^»^)’ ^-'2^2>^2 э^»0
~~ С] (^2 ’ &2 ’ С> 0' ^2 (^2 ’ &2 > ^1 (^2 ’ &2 >
Л2(£2,а2,с,?)-В3(сг£,/) •
В полученной системе дифференциальных уравнений считаются известными фун-
кции еЬ} (t) и sM (?), которые находятся из основного уравнения ползучести путем под-
становки в него постоянных значений Rbx = const и /?h = const (Rbx =0; Rb = 0):
£bl (0 = bl ‘ [(^1 + ^2 ‘ ^bl + ЗД1 + ^4^bl )+ Q (1 ~ x )]’
fbo(0 ~ Ъ ’ [(#1 + &2 ' ^b + + ^4^-b )+ G)(l ~ e )]
В этих выражениях мгновенная деформация найдена с помощью секущего модуля
деформаций (<7ft = RbX; ab = Rb2)
£“K +
Минимальный третий порядок система дифференциальных уравнений имеет только
в том случае, когда основной закон ползучести имеет первый порядок. Если же основ-
ной закон ползучести имеет второй порядок, то система разрешающих уравнений зада-
чи будет иметь шестой порядок. Наконец, если основное уравнение ползучести будет
иметь третий порядок, то система дифференциальных уравнений задачи принимает де-
вятый порядок.
Важным достоинством предложенного метода исследования напряженно-дефор-
мированного состояния при ползучести является то, что для любых поперечных сече-
ний система разрешающих дифференциальных уравнений имеет только третий поря-
док. Вычислительные процедуры решения таких систем тщательно математически изу-
чены. Результаты численного интегрирования их имеют надежные оценки сходимости
и точности. Процедуры построения функций, стоящих в правых частях системы диф-
ференциальных уравнений (6.2.12), прозрачны и не содержат в себе никаких упрощаю-
щих вычислительных допущений.
Другим важным достоинством предложенного метода является одновременный учет
трех типов нелинейности: наличие трещин в растянутой зоне бетона; мгновенную не-
174
линейность деформирования сжатой зоны бетона с учетом ниспадающего участка; не-
линейную ползучесть бетона. Оценка прочности сечения производится в процессе ин-
тегрирования дифференциальных уравнений с помощью трех критериев исчерпания
прочности: появления текучести в растянутой арматуре; достижения предельных де-
формаций в сжатой зоне бетона = £м); начало снижения величины изгибающею
момента fa Последний критерий не является обязательным при рассмотрении ста-
тически неопределимых железобетонных систем.
§ 6.3. Нелинейное длительное деформирование железобетонной колонны
в условиях модели Евростандартов
Учет ползучести бетона в Евростандартах при расчете сжатых стержней осуще-
ствляется в рамках классического теоретического подхода, предложенного впервые
Ржаницыным А Р. [133] при осевом сжатии и использованного впоследствии Работно-
вым Ю.Н., Шестериковым С.А., Арутюняном Н.Х., Бунятяном Л.Б., Колмановским В.Б.,
Прокоповичем И.Е., Яценко Е.А. и Улицким И.И. для задач линейной ползучести бето-
на. Дистефано И.Н., Прокопович И.Е и Линник В.С. применили этот метод, используя
уравнение нелинейной ползучести Арутюняна Н.Х. и два существенно упрощающих
допущения: идеализированное сечение в виде двух тонких полос; в функции нелиней-
ной ползучести бетона напряжение считалось одинаковым для обеих полос (при изгибе
сечения)
Бетон считался одинаково работающим при сжатии и растяжении (без трещин),
а также мгновенно упругим
В данном параграфе мы сделаем существенное развитие данного подхода на учет
мгновенно нелинейных деформаций. В сравнении с точной моделью § 6.6, которая тре-
бует численной реализации, упрощенная модель в узком диапазоне позволяет получить
качественные нелинейные оценки предела длительной устойчивости в конечном виде.
Пределом длительной устойчивости железобетонной колонны будем называть по
аналогии с Еврокодами коэффициент
где " критическая сила, при которой железобетонная колонна теряет устойчивость
за существенно большое время (время существования конструкции, время эксплуата-
ции сооружения, бесконечность);
- кратковременная критическая сила, соответствующая понятию кратковре-
менного испытания бетона (условию получения диаграммы <уь — £ь).
Уравнение ползучести бетона примем в виде уравнения (3 7.23), ограничившись
пока случаем линейной ползучести, для чего полагаем /[ф(<т6,г)]= Ф(сг^,/).
На основании этого записываем
175
<RM 1 ,
Л2 £t(0
_^\(О . v d£b(t)
—^~+u^T
1
ЗД)/
(6.3.2)
- Eb(t) • f2(crb,t}- нелинейная функция:
Ф(а4,Г) = о* + b2(t)a2b +b3(t)crl +b4(t)ab.
Осевая сила, сжимающая железобетонную колонну, равна
Nsb=Nb+Ns=Abab+Asas. (6.3.3)
Учитывая работу арматуры в упругой стадии, из (6.3.3) имеем
=^[1 + А«(1 + Е„(0 • С(Г,т)], (6.3.4)
либо
o-sZ> = = сгД1 + /zn(l + Eb(t) • С(/,т)]
Ab
Критические зависимости также должны удовлетворять уравнению (6.3.4).
В соответствии с определением устойчивости, изложенным в первой главе, анали-
зируем характер поведения центрально сжатого стержня, отклоненного незначитель-
ной возмущающей силой от первоначально прямолинейного положения. При изгибе
используется гипотеза плоских сечений
£ь=Цх{+£Ь0,
где £ьо - деформация сжатия;
К - кривизна изогнутой оси;
х, - расстояние волокна от центральной оси.
Выражение (6.5.3) дважды дифференцируем по времени t
£ь = к Xj, £ь = к х,. (6.3.6)
Значения производных (6.3.6) подставляем в основное уравнение ползучести (6.3.2)
dt2 Eb(t) dt E„(f) V ‘ * J dt £i(0|
d2 К d к (6.3.7)
=~dF'x' +r°~dTx'-
Для получения интегральных характеристик сечения умножаем последнее выра-
жение на х, и на величину элементарной площадки
dSb — bdxx ,
где Ь - ширина прямоугольной колонны, а затем интегрируем по всей площади сечения
Sb, вынося за знак интеграла производные от кривизны по времени
176
1 г^ФК<)
dt2
1
x,aSh +--
EM
/ф [1+ £»(<)«’»(')]-
dEM
dt
1 ]
£>(') '
. с^Ф(аь,1)
s dt
. , co
j*i dSh + ~г~Уф f*i dSb.
s> dt
(6.3.8)

Вводим обозначение для эквивалентного момента
|ф(сг/; д) x}dSb =Л/ф (639)
%
где имеет размерность момента, а также для эквивалентной продольной силы
dSb (ь jQ)
$b
где имеет размерность силы.
Между эквивалентными силой (6.3.10) и моментом (6.3.9) имеется такая же связь,
как между фактическими силой и моментом фактический момент в сече-
нии равен
™ ф
Меняя порядок дифференцирования по t и интегрирования по Sb с учетом (6.3.9),
записываем
1 d2M* 1
Eb(t) dt2 + Eb(t)

1 dM^ _
Eb(t)\ dt
(6 3.11)
где I = fx2dSb - момент инерции сечения относительно центральной Оси.
Таким образом, напряженно-деформированное состояние произвольного сечения
сжатой колонны характеризуется вспомогательными величинами (6 3.9) и (6.3.10),
в которых нелинейная функция Ф(сгь, г) линейно связана с деформацией £ь произволь-
ного волокна, воспринимающего напряжения ст .
Расчетная схема центрально сжатой колонны при длительном загружении показа-
на на рис 6.3.1 К центрально сжатому силой N стержню (рис 6.3.1,а) прикладывается
возмущающая сила Q (рис.6.3.2,б). Под действием этой силы колонна получит мгно-
венный прогиб f0; в течение некоторого времени Af н возмущающая сила Q и про-
177
дольная сила N увеличивает прогиб на величину д (рис.6.3.1,в) вследствие проявле-
ния ползучести бетона. В конце интервала Д/я (этот момент времени принимается да-
лее за начало отсчета t = /0) возмущающая сила исчезает (рис.6.3.1,г), и вместе с ней
исчезает мгновенный против (статическое перемещение) /0. При этом стержень еще
искривлен. Оставшийся прогиб Ao(to) середины сгержня и его скорость Aq(i0) опре-
деляют поведение колонны в условиях линейной ползучести.
Рис.6.3.1.
Это обстоятельство существенно отличает данную задачу от задачи сжатия стерж-
ня, имеющего при /V — О начальный прогиб (см. первую главу).
Сформулированный способ происхождения величины начального прогиба Aq со-
ответствует строгому определению устойчивости и позволяет избежать туманных фор-
мулировок, имеющихся в литературе, о причинах его появления.
В уравнении (6.3.11) учтем, что кривизна определяется приближенным выражением
К = -У,
а эквивалентная сила ДГ* постоянна во времени. Это следует из выражения
_ ( Ы дг2 /V3
N®—Sb-& = Nb l + b2^ + b3^ + b4^-
\ ьь ъь
178
и условия незначительного изменения Z>2,b3,h4 с течением времени.
На основании этого подставляем в уравнение (6 3.11) значения Л/ф и К, получаем
• /Л+Еь(,)(рф( О] - -!-L;xx,o=
Eb(t) Eb(t) [ dt Eb(t)j
Далее воспользуемся методом разделения переменных, и представим решение урав-
нения (6.3.12) в виде
y(x,t) = f(ty У(х), (6.3.13)
где функция У(х) удовлетворяет тряпичным условиям стержня, рис.6.3.1.
Подстановка (6.3.13) в (6.3.12) даст
-— N*f(f)Y(x) + --— /ф [I + Еь (Г )<рф (/)] - — -----
Eb(t) ь J \ j \ ' ^(0 1 dt
• = -[//(Г) + уф//(0]- у\х\
что позволяет разделить переменные по х и t вследствие линейности исходного
дифференциального уравнения
+777' Ul1+Еь(‘М)У ' 777,1' N^(l)
Eb(t)________Eb(t)______________________dt Eb(t)\_________=
if(t)+v^f(t)
_ УМ = С
У(х)
В результате получаем два дифференциальных уравнения относительно х и t
у”(х) + Су(х) = 0; (6.3.14)
1
Лб(0
1
-</ф[1 + Eb (0Рф(0]
dEb(t} 1
dt Eb(t)
Nf -CI f(t} +
J £»(<) С
Уравнение (6 3 14) для простейшего случая шарнирно опертого стержня дает
„2
(6.3.15)
I2'
С учетом этого вводим обозначение си ты Эйлера
«г-’-У
и записываем два интеграла уравнения (6.3.15)
179
f(t) = Aq(i0) jexpj - /ф (t - tQ) +
f0
Г ЕЬФф
J ЫЭ - д/ф
VV£>
dr -
/(0 = AAW ’ /ф(* “ *o) + /ф^ь ’
h -*4
-^rdt-
,ф
VTz> ”b
t
Ebdr
Из последней формулы можно делать выводы о поведении стержня при увеличе-
нии t > t0; в величине начальной скорости Д)(?о) важное значение имеет знак её.
Рассмотрим характер изменения экспоненты
Ijmexp. -/ф(/-<„) + /ф^ • . (бз 16)
Так как модуль Eb(t) с течением времени нс убывает, то в анализе (6.3.16) поло-
жим Еь (/) = const; Ёь(/) = 0. От этого условия суть анализа (6.3.16) не изменится.
Функция <рф записывается с учетом её масштаба в виде
<Рф

(6.3.17)
где ф(оо,/0) - предельная характеристика ползучести бетона по Евростандартам;
Ак - константа.
В этом случае предел (6.3.16) имеет вид
Пт ехр< - (t -10) + Мь ф • I + Ak < е~ГфГ dr ► f6 3 i r-j
— q Nt-N? ILeMctJ *<p(<7,,) j j- (6318)
При устойчивом деформировании предел (6.3.18) должен стремиться к нулю, сле-
довательно

Итехр
f-XX>
(6.3.19)
Ввиду малости последнего слагаемого, его можно отбросить; получаем условие,
при котором скорость прогиба стремится к нулю
180
N° <------------------ (6.3.20)
1 -Kp(coj) б -
w,)
В этом выражении величина ф(х,/) аналогична предельной характеристике пол-
зучести бетона , принятой в теории ползучести бетона.
В Еврокодах эта величина нормируется, и её данные приведены в табл.6.3.1.
В этой таблице Аь - площадь сечения бетона; и - периметр сечения; данные табли-
цы относятся к средней консистенции пластичности бетона в момент его укладки (при
жесткой консистенции бетона все значения умножаются на коэффициент 0,7; при плас-
тичной консистенции - на коэффициент 1,2).
Таблица 6.3.1.
Значения коэффициента Ф (со, t) по данным Евростацдартов
Возраст бетона /о при нагружении (сутки) Соотношения AJu (мм)
50 150 600 50 150 600
Сухая среда (ЯЯ= 50%) Влажная среда
(1 Ш=80%)
1 5,4 4,4 3,6 3,5 3,0 2,6
7 3,9 2,5 2,0 1,9 1,7 1,5
28 3,2 2,5 2,0 1,9 1,7 1,5
90 2,6 2,1 1,6 1,6 1,4 1,2
365 2,0 1,6 1,2 1 U 1,0 1,0
Анализ изменения самого прогиба /(/) показывает, чго при условии выполнения
(6.3.20) он уменьшается и стремится к некоторому предельному значению .
Если выполняется условие
,+ф(со’/)ф(ст)
то прогиб середины стержня с течением времени может стать большой величиной.
Естественно, весь этот анализ справедлив только при малых прогибах, ввиду ис-
пользования гипотезы приближенного выражения для кривизны. Однако, в рамках из-
ложенной модели и при отсутствии трещин в растянутой зоне бетона, критическая сила
может определяться из условия (6.3.20). Переходя в не.м к фактической критической
силе Nb, имеем
(6.3.21)
181
Можно показать, что первый сомножитель в (6.3.21) представляет собой (мгно-
венную упругопластическую) приведенно-модульную критическую силу . Для про-
стоты рассуждений ограничимся в выражении /2(^2») Д»УМЯ слагаемыми
/г(сгь) = В'Сгь+В2<г}.
Касательный модуль деформаций равен
Е =^- =---------!---
d£b В. + 2В2аь ’
Приведенный модуль деформаций в этом случае равен
Е ^касЕь 1
1X3 Вкас + Еь В1+В2сгь'
или в обозначениях (6.3.21)
£ =___&ь__
р*3 •
1 + Ь,^
Sb
Второй сомножитель в (6.3.21) учитывает влияние ползучести; его можно преоб-
разовать к виду
1 1
(6.3.22)
N1^3
Отношение fe — = 1 при значениях к =0,5 (соответствует напряжению
Nt
сгь = 0,5/?fc на диаграмме аь - еь и характеризует мгновенно упругий бетон).
Далее с развитием пластических деформаций на диаграмме оь - еь отношение
„э убывает и становится равным нулю при к = 1 (.Я = О), рис.6.3.2.
"ъ
Кривая 1 на рис.6.3.2 характеризует кратковременную устойчивость сжатой ко-
лонны в рамках модели Евростандартов. Кривая 2 (рис.6.3.2) характеризует длитель-
ную критическую силу, построенную на основе зависимости (6.3.21).
Известно, что различие между приведенно-модульной и касательно-модульной
критическими силами мало; вследствие этого в формуле (6.3.22) можно использовать
^.2 j
вместо N^3 величину Nbac ------— для простоты вычислений.
Участок л-л кривой 2 на рис.6.3.2 соответствует центральному сжатию для случая
линейной ползучести и линейного мгновенного деформирования бетона (на диаграмме
сгь — £ь Евр о стандартов соответственно - это участок до величин напряжений
crb<0,5Rb).
182
Рис 6 3.2.
Ему соответствует длительная критическая сила
N? =-----
(6.3.23)
получаемая из формулы (6.3.21) при значениях b2 = b3 = Д4 = 0.
Соотношениям между силами и показаны на рис.6.3.3.
Рис.6.3.3.
Линейной модели, описываемой формулой (6.3.23), соответствует линия л-л. Не-
линейная модель представлена пунктирной линией 2.
Соотношения условной линейной модели (6.3.23) заложены в Евростандаргах в
формулах, учитывающих длительную устойчивость железобетонных стержней.
Диаграмма <уь - £ь кратковременного реального загружения бетона имеет откло-
нения от линейной зависимости уже при напряжениях сгь = 0,27?fc. При центральном
сжатии таким напряжениям соответствуют гибкости равные А = 300- Нами рассчита-
ны коэффициенты т]дд для гибкостей 0 < А < 300» приведенных в таблице 6.3.2 для бе-
тона с предельной характеристикой ползучести Ф(со,г0) = 1»2, рекомендуемой Еврос-
тандаргами для нормального бетона (см. также табл.6.3.1).
Кратковременная критическая нагрузка стержней рассчитывалась с учетом упру-
гопластических (нелинейных) деформаций.
184
Таблица 6.3.2.
Значения коэффициентов Т]д,
X 0 50 75 100 150 200 250 300
Пал 1,0 0,84 0,72 0,63 0,56 0,54 0,52 0,45
Напомним, что значения коэффициента т]дл в табл.6.3.2 соответствуют бетонам,
у которых предельная характеристика ползучести ф(оэ,/0)= 1,2. Меняя последнюю,
в соответствии с таблицей 6.3.1, мы получим иные значения коэффициента т]дя.
§ 6.4. Нелинейное длительное деформирование железобетонных балок
с трещиной
Применение нелинейной функции Ф(сг^,?) позволяет в ряде случаев изгиба желе-
зобетонных балок в условиях линейной ползучести бетона получить решение в замкну-
той аналитической форме, без привлечения специальных вычислительных процедур.
Основной закон ползучести с учетом мгаовенных нелинейных деформаций запи
шем в виде
<?2Ф(оУ) 1 ! <№(crb,t) 1
dt2 Eb(t) dt Eb(f)
. deb(t)
-2 + ' Ф
- Гф[1+£ь(*>ф(О]
dEb(t) 1 =
dt Eb(t)
(6.4.1)
Используя в качестве переменной Ф(сг^,?), запишем уравнения равновесия про-
извольного сечения в виде
=0;
(6.4.2)
-^Ьхф(<ть,^ -+ Мф = 0,
где - напряжение в растянутой арматуре, соответствующее переменной ф(сгь,/);
момент в сечении относительно растянутой арматуры (в переменной
Ь,х- ширина и высота сжатой зоны сечения;
Л - расстояние от растянутой арматуры до крайнего сжатого волокна с деформаци-
ей
185
В рассматриваемом случае удается переменную и деформации растяну-
той арматуры £ и бетона еь, с привлечением гипотезы плоских сечений выразить че-
рез высоту сжатой зоны х. Действительно,
„ф „ф
£ь = £
х h-x’
откуда
ф ф л
£h -------------
О S j
h — x
Далее находим из (6.4.2)
Мф
—о h — х
2 I 3
.ф
S
S
МФ
л(, х¥
А.\п —
A 3J
Разделим второе уравнение (6.4.4) на первое, получим
<аф .
2 Л
Из (6.4.3) с учетом (6.4.5) и закона Гука для арматуры имеем крайшою деформа-
цию бетона сжатой зоны
(6.4.6)
ф 1 b 1 х
f =----------
2 As Es h-x‘
(6.4.7)
Выражения (6.4.4) и (6.4.7) позволяют в основном законе ползучести (6.4.1) перей-
ти к одной переменной x(t). Для этого находим производные, учитывая постоянство
нагрузки,
dt
•x(f)=ai(x)x(O;
(6.4.8)

186
= at (x)x(O + «2 (x) • x(f) >
dEb(t) _ 1 b 1 h
dt ~2TsE~(h-x)2
ад = Д(х)х(О
d\(t) = b 1_1
dt2 A^th-xf
(t) + Pi(x)x(t) =
=д(х)ад+/?2да2(0-
Найденные из (6.4.8) производные подставляем в (6.4.1), имеем
1
ХО «1W-T77 “ А & + а2<»
L ЕьЮ J L
1 _ Z
+ х а. (х)
L 4<ос
—------Д(х) +
Eb(t) Р1У 'J
dEb(t) 1
dt Eb(t)
'~7<МХ) =0.
(6.4.9)
Мы получили нелинейное однородное дифференциальное уравнение второго по-
рядка с переменными коэффициентами.
Для стареющего бетона дифференциальное уравнение задачи существенно упрос-
тится. Принимая Eb = const и ^?ф = const, запишем основной закон ползучести в виде
d<P(crb) 1
----———7------7----+ ф( ) =
dt /ф(1 + Ф(со,г0))
=; Е + е Е> (6-41°)
^/ф(1 + Ф(ооЛ)) *1 + Ф(оо,/0)’
Подставляем в (6.4.10) значения (6.4.8), имеем
1 Е
x(t) &\(х)-т---7----Р\(х)----7--~г---+
/ф(1+ф(°°а)) г^С+^л)).
+ 1 2Л/ф _ х b Еь = 0
Гл--\ Ь ^-х)2АхЕ^ + Ф(^,1й)
I 3J
(6.4.11)
Для случая нелинейной ползучести решение можно получить, если положить вы-
полнимость условия (6.4.4) и в этом случае.
Основной закон нелинейной ползучести запишем в виде
d&(Vb) 1 + Рф-ф^>^)ф2(ст
dt уф (1 + Ф(оо,/0 )) 1 + Ф(°°До )
+ Ф(<уь ) = Ёь-7-^7---гг + £ь--ф----г,
Гф С + )) 1 + )
(6.4.12)
187
где /?ф - коэффициент в функции нелинейной ползучести.
Подставляя в (6-4.12) значения ф(<ть), £ь и их производных, получаем дифферен-
циальное уравнение для нахождения высоты сжатой зоны бетона
1 Е
x(t) аЛх)—7------7----Ъ~Р\(Х)----7 Ь.-----тг +
/ф(1 + ф(оо,г0)) /ф(1+#(°°А)).
Г I2
= 2МФ 1
1 + Ф(оо,Г0) b L
_ I 3 JJ
(6.4.13)
, 1 2Л/Ф х_______L__A_ = 0
(, хА b h- х2А.ЕЛ + Ф(<х),10}
h — х * хи/
I 3J
Наконец, будем использовать нелинейный закон в рамках гипотез теории старения
бетона
(6.4.14)
£/Ф(о\,0 1 1 . ... . ...
—Л ТТа + 77т<Рф(Г)Ф(о'ь,/) =
dt Eh(f) Eb(0)
С его помощью дифференциальное уравнение для нахождения x(t) получено в
виде
x(t)
ах(х)
Eb(t)
о, t 1 . z . 2МФ
р'(х) +Т7о]<1>ф( ° 7 х\
J Е„(°) b-h--x
= 0.
(6.4.15)
В этом уравнении переменные нельзя разделить из-за величины Eb(t) Можно
использовать осредненное во времени значение Еьр; для такого случая переменные
в (6.4.15) разделяются, и можно записать уравнение с разделенными переменными
<b^ix(x)-EcpPx(x)\ ГА_ А.
Е? Л 3J
2МФ
ЬЕь(0)
фМ-Уф-С-^
Отсюда, после интегрирования, получаем алгебраическую связь между искомыми
величинами в замкнутом виде
2(ft2 + Ах-х2)
h(h - х)
л As
+ 4—-—-
Е? bh
и
ln- + ln
h
h-x
~~h~
4 As
Ecbp bh
4-9 In
3h-x
_ 4 As
Ecp bh
Ф(оод0)(1-е ,
(6.4.16)
h
*o
+
188
где х0 - высота сжатой зоны бетона в момент загружения / = 0 •
Дальнейшая процедура нелинейных расчетов строится следующим образом.
В начальный момент загружения / = О решается мгновенная нелинейная задача. Мо-
мент д/, действующий на сечение, является величиной постоянной. С его помощью
рассчитывается начальная высота сжатой зоны х0. Для произвольного момента време-
ни tk из (6.4.16) находится высота x(tk ), значение которой позволяет определить вели-
чины Ф(1к) и £b(tk ). Из уравнения
) = °ь + Ь2^ь + + Ь4&ь
находится значение напряжения <Jb(tk) крайнего волокна сечения.
Далее можно найти кривизну балки в этом сечении
x(tk
и другие необходимые величины.
Само решение, построенное изложенным способом, является аналитическим, свя-
зывающим искомые параметры алгебраическими зависимостями.
§ 6.5. Экспериментальные н практические данные по ползучести балок
В работе А.Д.Беглова [19] получены экспериментальные данные по ползучести
железобетонных балок, в том числе испытанных на устойчивость из плоскости изгиба;
там же эти эксперименты обработаны теоретически.
Здесь мы рассмотрим основательные эксперименты Мурашёва В.И. и Фигаровс-
кого В.В. [65], в которых развиваются идеи Гвоздева А.А. и Мурашёва В.И. об опреде-
лении кривизны и трещиностойкости элемента по деформациям бетона и арматуры.
В этих экспериментах учитывались температура и влажность окружающей среды, кото-
рые влияют на характеристики ползучести бетона.
В этих экспериментах также варьировались классы бетонов, коэффициенты арми-
рования и уровни длительной нагрузки. Например, у балок ГН-2 и П2-2 уровень нагруз-
ки составлял 0,42 и 0,75 от кратковременной соответственно; коэффициенты армирова-
ния у них различались в два раза.
Особенно тщательно замерялись средние деформации £ь крайнего волокна сжа-
той зоны бетона, а также средние деформации £s растянутой арматуры, прогибы балок.
На рис.6.5.1- 6.5.4 показаны экспериментальные и теоретические деформации бетона и
арматуры.
Наиболее интенсивное развитие деформаций балок происходило в первые 20 су-
ток; далее скорость нарастания деформаций уменьшается, однако, и после 250 суток
деформации бетона продолжали нарастать.
Рост деформаций растянутой арматуры затухает примерно к 50 суткам выдержки
балок под нагрузкой.
189
Сравнение теоретических и экспериментальных данных, показанное на рис.6.5.1 -
6.5.4, показывает их согласованность на всех этапах длительного деформирования ба-
лок.
t - время в сутках
Рис.6.5.1. Нарастание продольных деформаций еь крайнего волокна сжатой зоны бетона у
балок с коэффициентом армирования ц. — 0,0055, прочностью бетона 2?. = 220кг/ 2
/ см
1 - балка Т1-Шд, £bQ = 57 • 10 5; 2 - балка Т1-2Пд, sbQ = 86 • 10“5;
—---- - экспериментальные кривые;
t - время в сутках
Рис.6.5.2. Нарастание продольных деформаций растянутой арматуры при начальных
значениях этих деформаций: 1 - 105-10’5, балка Т1-1Пд; 2- 105-1(У5, балка Т1-2Пд.
190
t - время в сутках
Рис.6.5.3. Нарастание продольных деформаций еь крайнего волокна сжатой зоны бетона
у балок с различными коэффициентами армирования и одинаковой прочностью бетона
^ = 155*/ 2.
/ см
3 - балка П1-2, // = 0,0052, £60 = 45 • 10"5;
4 - балка П2 2, // = 0,0105, еь = 85-10S.
------ - экспериментальные кривые;
Ss - расчетные кривые.
150- 105 4

У?
50 10'5 3
0 50 100 150
t - время в сутках
Рис.6.5.4 Нарастание продольных деформаций растянутой арматуры при начальных
значениях этих деформаций-
3-балка П1-2, ^0 = 78 10’5;
4-балкаП2-2, es0 = 110-Ю’5.
191
На основании проведения численных экспериментов по предельной модели рас-
чета авторами впервые получены значения коэффициентов длительного сопротивления
железобетонных балок, табл.1.
Таблица 6.5.1
Значения коэффициентов длительного сопротивления
железобетонных балок при различных значениях
коэффициентов армирования /д
характеристика ползучести Ф (°о, /о) принята равной 2
Значения коэффициента армирования ц 0,005 0,01 0,025 0,05 0,075 0,1
Значения коэффициента длительного сопротивления тЛ1 0,677 0,735 0,795 0,83 0,870 0,895
В заключении отметим, что впервые в научной литературе получены практичес-
кие рекомендации по расчету длительного сопротивления изгибаемых железобетонных
элементов на основе моделей Евростандартов и нового объединенного уравнения плас-
тичности и ползучести бетона.
§ 6.6. Нелинейная ползучесть сжатых железобетонных колонн,
работающих с трещиной в растянутой зоне сечения
В параграфе 6.3 данной главы исследована устойчивость сжатых колонн, нс имею-
щих трещин. Этот частный случай, занимающий на поле практических зависимостей
малое место и, несмотря на это. положенный в основу модели Евростандартов, не явля-
ется основным для внецентренно сжатых железобетонных стержней. I чавное место
в работе сжатых железобетонных колонн занимает случай нелинейной работы сечения
с трещиной в растянутой зоне, рис.6.1.2. В таком сечении приходится учитывать совме-
стно четыре вида физической нелинейности: нелинейность мт новенного деформирова-
ния бетона всего сечения или (чаще) бетона сжатой зоны размером с; нелинейность
упругопластических деформаций стальной арматуры с площадями As и А^; нелиней-
ную (либо линейную) ползучесть бетона сжатой зоны, существенно изменяющую вид
кривой AqA^Aj (рис.6.1.2), в сравнении с мгновенной кривой по рис.5.1.1; нелиней-
ность, обусловленную наличием трещины глубиной (й - с) в бетоне растянутой зоны.
При использовании специальных видов арматуры (канатов, стеклопластиков) мо-
жет проявляться пятый тип нелинейности, вызванный ползучестью арматуры.
Нужно подчеркнуть, что в Евростандартах для учета ползучести сжатых колонн
используется только третий тип нелинейности, в виде модели линейной ползучести
сплошного бетонного сечения. В параграфе 6.3 было показано, что совместный учет
только двух видов нелинейности (первой и третьей - линейной ползучести и мгновен-
ной нелинейности) значительно меняет' численные значения критических сил сжатых
колонн, по сравнению с данными модели линейной ползучести. Это отличие критичес-
ких сил существенно возрастает при совместном учете всех видов нелинейности, а осо-
бенно - четвертого вида.
192
Помимо физической нелинейности в расчетах сжатых колонн должна учитывать-
ся одновременно геометрическая нелинейность. Различают два типа геометрической
нелинейности первым типом геометрической нелинейности в научной литературе на-
зывают учет прогибов на основе приближенного выражения для кривизны; вторым ти-
пом геометрической нелинейносги называют учет прогибов на основе точного выраже-
ния для кривизны. Следует иметь в виду что в большинстве случаев приближенное
выражение для кривизны, предполагающее малость прогибов колонн ([/(х)]2 «1),
дает при решении задач с учетом физической нелинейности вполне приемлемые для
практики результаты
Однако, в задачах ползучести при исследовании развития прогибов тина f(t) -> ос,
либо /(г) —> со, следует иметь в виду условность получаемых результатов
В рамках физически линейных моделей в первой главе мы обсуждали данную про-
блему; здесь рассмотрим ее аспекты в условиях физической нелинейности Напомним
результат Шенли Ф.Р, представленный на рис 6 6.1. и полученный на основе прибли-
женного выражения для кривизны для возрастающей нагрузки [182]. Сила Pk соответ-
ствует касательно-модульной нагрузке, сила Рп - приведенно-модульная нагрузка.
Рис 6 6 1.
I
Сила Рк - наименьшая, при которой возможно существование прогиба централь-
но сжатого стержня; при значениях силы Рп - прогиб обращается в бесконечность, что
является условным вследствие использования приближенного выражения для кривиз-
ны. На самом деле, поведение кривой 1 зависит от соотношений физической и геомет-
рической нелинейностей При слабой физической нелинейности материала стержня по
рис.6.6.2 (например, = 0,6£') и учете точного выражения для кривизны, кривая Г не
имеет горизонтальной асимшготы 2, рис 6 6.3.
193
Рис.6.6 3.
Кривые Г и 1* соответствуют случаям, когда боковое возмущение действует
на сжатый стержень при силах Р> Рк.
При использовании материала с сильной физической нелинейностью (например,
Е - 0,01Д [126] по Пинаджану В.В.) асимптота 2 также отсутствует, рис.6.6.4.
В критическом состоянии в точке кц (центральное сжатие) и в точке к (внецент-
ренное сжатие) достаточно строго выполняется гипотеза о приближенном выражении
для кривизны; точное выражение для кривизны можно использовать для анализа нис-
падающих участков кривых состояний Г и 1J,, имеющих значение в статически неопре-
делимых задачах.
194
р.
%
pt
рь
Рис. 6.6.4.
В случае ползучести бетона ситуация усложняется, появляется новое понятие для
сжатого стержня - критическое время потери устойчивости. Однако, недочеты, осно-
ванные на использовании гипотезы приближенного выражения для кривизны, при этом
увеличиваются Рассмотрим для примера поведение стержня, бетон которого удовлет-
воряет нелинейной модели Максвелла (нелинейность относится к вязкому элементу
модели)
(6.6 1)
где п обычно принимается нечетным ( п = 3 )•
Учитывая нелинейность , решение в аналитическом виде приходится записы-
вать для идеального двутавра высотой h по аналогии с решением Хоффа Н. [170].
Применяя обычные [40] и общеизвестные гипотезы, помимо (6.6.1), получено диф-
ференциальное уравнение с разделяющимися переменными для нахождения прогиба
f среднего сечения
УМ Et h [7 + £?
F2(N,-N)\h h3,
(6.6.2)
где к =
у(1-Ф(<о,оо))
Еь
F - площадь поперечного сечения, или в общем виде
/=Н/л),
(6 6.3)
195
где #>(/,?/) - нелинейная функция.
Решение дифференциального уравнения записываем в виде
4 df
(66-4)
Если прогиб f —> со при t, стремящемся к величине , то стержень считается
имеющим критическое время (кривая 3, рис.6.6.5)
» df
(66-5)
После упрощений критическое время сжатого бетонного стержня запишем в виде
. , (*,-*0 „2 J<Y
* б(1-ф(оо,*0))№
(6.6.6)
При нахождении этого выражения прогиб f(f) полагается бесконечно большим,
а изначально в выводе дифференциального уравнения (6.6.2) он полагался малым -
В момент t = скорость прогиба
Для линейной модели Максвелла п -1 прогиб сжатого стержня равен (рис.6.3.1)
Ему соответствует кривая 1 на рис.6.6.5; она характеризует бесконечное нараста-
ние прогибов. Там же кривые 2(л1==1)и4(л = 3) построены с учетом точного выраже-
ния для кривизны [221].
Рис.6.6.5. Изменение прогибов в условиях геометрической линейности (1,3)
и геометрической нелинейности (2,4)
196
Из сопоставления между собой кривых 1 и 2, а также кривых 3 и 4 можно видеть,
что условие о бесконечном прогибе и бесконечной скорости прогиба не реализуются.
Такое условие вызвано использованием приближенного выражения для кривизны и свой-
ствами мгновенно упругого материала, заложенными в вязкоупругой модели Максвел-
ла. В практических расчетах железобетонных конструкций к указанным условным кри-
териям потери устойчивости при ползучести следует относиться с осторожностью.
Обратим внимание еще на один недостаток изложенных моделей. Для нелинейной
модели Максвелла (6.6.6) имеем, что при любой силе Ng > 0 колонна должна всегда
потерять устойчивость. А из линейной модели (6.6.7) следует, что такая колонна не имеет
длительной критической силы К сожалению, описанные условные критерии поте-
ри устойчивости сжатых колонн при ползучести широко применяются в научной и прак-
тической литературе
Использование модели Кельвина для описания ползучести бетона привело
Л.Р.Ржаницына (1946 г.) [133] к понятию предела длительной устойчивости
„ я2 HI
Ps=—j2-, (6.6 8)
€
где Н - константа, названная длительным модулем упругости материала ( Е - мгновен-
ный модуль упругости: Е> II).
При значениях сил центрального сжатия стержня Р> Р1, прогиб стержня увели-
о
чивастся; при Р < Р прогиб уменьшается; при Р = Р - прогаб сохраняет с течением
"45 45
времени постоянное значение.
Последующие исследователи усложняли постановку задачи о центральном сжа-
тии путем применения более точных и сложных ядер ползучести, иногда при достаточ-
но произвольном их виде. Применялись более тонкие математические методы анализа
поведения центрального сжатого стержня при ползучести. Однако, величина длитель-
ной критической силы практически всегда, равно как и в Евростандартах [201], оцени-
валась выражением типа (6.6.8).
Работнов Ю.П. и Шестериков С.А. [129] рассмотрели поведение сжато-изогнуто-
го стержня, удовлетворяющего модели Кельвина. Получено, что при Р < Pg прогибы
стержня увеличиваются с затуханием, асимптотически стремясь к конечному пределу
(при t = со ); при Р = Pg и Р> Pg прогибы неограниченно увеличиваются (в рамках
приближенного выражения для кривизны) В двух последних случаях скорость проги-
бов не убывает
Сознавая условность отмеченных подходов о бесконечных прогибах сжатых ко-
лонн при ползучести, многие авторы используют различные условные критерии для
решения конкретных задач по аналогии с методом «устойчивой прочности» Корноухо-
ва Н.В. [137].
Арутюнян Н.Х. и Колмановский ВБ. предлагают граничить прогиб колонны не-
которым наперед заданным значением. Хилтон X. предлагает ограничить величину из-
гибающего момента в среднем сечении. Самуэльсон Л.А. считает критическим момен-
том достижение наибольшего напряжения в сечении. Веубек Ф. ограничивает прогиб
197
при ползучести величиной, полученной из задачи об упругопластическом стержне.
На основе анализа существующих теоретических моделей расчетов сжато-изогну-
тых колонн при ползучести построены зависимости «сила-прогиб», показанные на
рис.6.6.6. Линия 1 характеризует поведение упругой (без ползучести) сжато-изогнутой
колонны; точка д/ характеризует момент сближения её концов; здесь учитывается точ-
ное выражение для кривизны изогнутой оси колонны. Линии 1g и 1g' характеризуют
развитие прогибов вязкоупругой колонны при силах N = Ng и N> Ng. Линии
l'g и l'g показывают затухание прогибов вязкоупругих колонн в условиях точного вы-
ражения для кривизны при силах сжатия N <Ng.
Линия 2 характеризует диаграмму состояния сжатой железобетонной колонны при
кратковременном загружении; учитываются все типы физической нелинейности и вы-
является достаточность использования приближенного выражения для кривизны. Ли-
ния 2g характеризует работу сжатой колонны с учетом всех типов нелинейностей;
точка Н показывает момент загружения колонны длительной силой и начало процесса
ползучести бетона, точка К характеризует момент разрушения колонны вследствие
исчерпания прочности наиболее нагруженного сечения, либо вследствие потери устой-
чивости.
Рис.6 6 6 Поведение сжато-изогнутого стержня
при кратковременном и длительном загруженных
198
Рассмотрим характеристику точки к подробнее. После точки К зависимость
«N — f >> имеет ниспадающий участок; развитие его происходит либо с учетом сил
инерции, либо с учетом поддерживающего влияния остальных элементов в статически
неопределимой системе. Разрушение сечения оценивается двумя факторами: достиже-
нием наиболее сжатым волокном сечения напряжений Rib (рис.6.1.1); достижением де-
формацией es растянутой арматуры (рис.6.1.2) значений характеризующих теку-
честь арматуры.
Аналитическое условие потери устойчивости в точке к формулируется следую-
щим образом. Линия характеризует невозмущенное перемещение колонны вслед-
ствие ползучести. Рассматривая в точке /у достаточно малые отклонения f* от невоз-
мущенного состояния, и принимая линейную зависимость приращений внутренних сил
от этих малых отклонений, мы получаем аналог выполнения условий теоремы Лагран-
жа-Дирихле [85] на малых отклонениях у*, рис.6.6.7,а. Здесь величина А является
суммарной работой внешних и внутренних сил.
Рис. 6.6.7
По мере продвижения по горизонтальной линии ЦК кривая 2 становится более
пологой, по сравнению с кривой 1, рис.6.6.7,б. В этом проявляется увеличение физи-
ческой нелинейности: уменьшение касательных модулей деформаций бетона; увеличе-
ние трещины в растянутой зоне бетона; увеличение пластических деформаций армату-
ры. В точке К (рис.6.6.6) кривая A — f*становится прямой линией, рис.6.6.7,в; мы
получаем аналог первой теоремы Ляпунова А.М. [90] о неустойчивости равновесия кон-
сервативной системы; точка К является предельной точкой, точкой бифуркации по А.Пу-
анкаре. Математически условие критического состояния сжатой колонны при ползуче-
сти можно сформулировать следующим образом: алгебраическая система линейных
однородных уравнений, получаемая путем варьирования уравнений равновесия сжатой
колонны в точке К имеет решение (в предыдущие моменты времени эта система была
неоднородной).
На ниспадающем участке кривой после точки К мы получаем аналог второй тео-
ремы Ляпунова А.М. о неустойчивости равновесия, рис.6.6.7,г.
199
Применение указанных аналогий с теоремами Ляпунова А.М. и Лагранжа-Дирих-
ле позволяет успешно решать задачи устойчивости вязкоупругопластических колонн,
ввиду того, что силовой функции для таких конструкций не существует.
Решение задачи об устойчивости сжатых вязкоупругопластических колонн осуще-
ствляется следующим образом. На начальном участке QJY кривой 2 (рис.6.6.6) рас-
сматривается кратковременное загружсние упругопластической железобетонной колон-
ны с помощью уравнений, приведенных в параграфе 5.2. На участке (рис.6.6.6)
решение осуществляется следующим образом. Напряженно-деформированное состоя-
ние сечения в условиях ползучести показано на рис.6.1.2. Продольная сила и изгибаю-
щий момент эпюры нормальных напряжений отыскиваются по аналогии с данными
§ 6.2; однако, здесь приведение осуществляегся к центральной оси Оу, а нс к нейтраль-
ной оси деформаций.
С учетом сказанного уравнение равновесия для половины колонны записываем в
виде
N = bc(t)
-al(t,£2ta2)£2<t)+-a2(ti£2ia2)el(t) +
+ |a3(W2><72)4(0 + A'sE^[c(t)-a']-AsEs^[h<,-c{l)} (6А9)
4 J c(t) c(t)
+ f^2>d=be1 (?) ax(t,e2to2)E2{t)+^a2{t,£2,cr2)c2(?) +
^[c(?) - a']2 + ASES ^[Ao - c
c(t) L J " 5 c(?) L 0
1 ,. . 1
a3 &2 > )^2 (0 ^Es
+ fМО + + +
1
2
MO
"J c(f)
. _£2^)
s c(t)
+4E;%Q[c(t)
s S / -X L \ /
c(0
f _g2«) '2 £
:J c(t)rr2’ 1 e(t)
Дифференцируем уравнения равновесия по времени
W+Z>i = Ax£2(t)+Bx62(t)+C}c(t)'t
N(t]{e+f(et,c)]+N(ti^^c+^^i1 =
de de2
= Л2Ё2( 1) + B2&2( О + C2C( t) + D2 +
+ cN(e2,ctab)+ (с - t) + Bx&b2(t) + Cxc(t) - Д J
(6.6.10)
200
где функции приведены в параграфе 6.2; при этом следует положить
М* =0.
Дифференцируем последние два уравнения еще раз по t, получаем
A,£2(t) + Bxab(t) + Cxc(t) = N + Dl-Al£2(t)~Bxab2(t)-Cxc(t); (6.6.11)
д£2 I ‘
+ +?v(j
^2^2
B2+B.lc-—
2 4 2
-W
2/ J
(6.6.12)
dt d- 2
- A2s2 (t)-B2ab (t)- C2c( t)-fy2-c(t)N( £2rcfab)-
=N(e+f)+2N
de2
dt d£2
-c
Третье уравнение, связывающее переменные между собой, получим из основного
закона ползучести (3.7.23)
£2(t)Eb(t)-ab(t)
72,CT2,£2,£2,tY
(6.6.13)
где D3(&b,o>2,£2,£2,t) - обозначены все остальные слагаемые уравнения (3.7.23).
Система дифференциальных уравнений (6.6.11)-(6.6.13) линейна относительно
вторых производных неизвестных s2(t),&2 (t),c(t) • Разрешая её по аналогии с (6.2.12)
и вводя новые переменные, получаем систему дифференциальных уравнений шестого
порядка в нормальной форме Коша
0*2 (0 ^2 > *^*2 = У2(^2»^2 ’»^25^3’ (6.6.14)
^(0 — > ^3 ~ Уз v 2 >^2 >> %2 >Х3 *
Применяя основной закон нелинейной ползучести первого порядка(3.7.38) и запи-
сывая ею в виде
4г2(О+в;<72\г)+с;с(о=д,
„ .. , о-.. 1 ‘«’ta) « п
гае 4=1, с3=о,
Еь
(6.6.15)
201
В аналогичной форме запишем уравнения (6.6.10)
A^2 (0 + Вха2 (0 + С/(0 = D\;
(6.6.16)
А2ё2 (0 + B'dj(0 + qc(0 = Z>2 ’
где -D{ = N(t) + Dl’>
a^a2-n^>c>+
^2
c —
I 2)
Ax.
b'2=b2
C2 = C2-N+ ctob2) + fc- -
oc \ 2)
Z>2 = МФ + /(*2,d - £>2 +
остальные обозначения по § 6.2.
Решение системы дифференциальных уравнений третьего порядка (6.6.15), (6.6.16)
записывается в форме, аналогичной (6.2.12).
Система дифференциальных уравнений (6.6.15), (6.6.16) учитывает переменность
продольной силы N(t) (при М0 = const система упрощается). Другими словами, сис-
тема дифференциальных уравнений (6.6.15), (6.6.16) одновременно описывает мгно-
венное и длительное загружение железобетонной колонны.
Для получения условия критическою состояния колонны варьируем уравнения
равновесия (6.6.9). В результате получаем
AxSs2 + BxSa2 + Схдс = 0;
N—Sc + N~~d£2 = А2де2 + B2Sab2 + С26с + N8c +
дс де2 2 2
Сх3с)\
(6.6.17)
е Ь ёо2
да2 =—-д£.
дс2
Условие существования решений системы уравнений (6.6.15) является уравнени-
ем критического состояния колонны в точке К (рис.6.6.6)
2.
С2-^ + ^2,с,а2‘) + |с-^|
ОС \ 2J
д€2
+в(с-
I Г>2 + ЯЛ С
^2 \ V
(6.6.18)
Л,+В,^1
1 1 0s2
л2

202
Можно обратить внимание, что определитель систем уравнений (6.6.11-6.6.13)
и (6.6.15-6.6.16) одинаковы. Обращение этого определителя в ноль по-разному характе-
ризует состояние этих систем.
Для систем (6.6.11 -6.6.13) и (6.6.15-6.6.16) момент обращения определителя в ноль
не свидетельствует о достижении ускорениями или скоростями бесконечности (хотя
такие утверждения часто встречаются в научной литературе); в этот момент времени
системы дифференциальных уравнений движения становятся несовместимыми. Для
системы же (6.6.17) равенство нулю определителя свидетельствует, что исчезающе ма-
лые возмущающие воздействия приводят к появлению конечных возмущенных движе-
ний, или к потере устойчивости.
§ 6.7. Некоторые экспериментальные и практические результаты по расчету
длительного загружения колонн
Экспериментальные исследования по длительному загружению сжатых железобе-
тонных колонн, проведенные в различных странах, выявляют зависимость длительного
сопротивления колонн от коэффициента армирования, предела текучести арматуры и
от относительного эксцентриситета. В центрально сжатых колоннах влияние коэффи-
циента армирования и предела текучести Rs проявляется четко.
В таблице 6.7.1 приведены результаты испытаний центрально сжатых колонн [ 176].
Экспериментальные колонны,
испытанные в НИИЖБе на центральное сжатие
Таблица 6.7.1
Шифр колонны Uh NMp Н бу, сут. Срок наблюдения, сут.
1 KF-V-4(2) 31,4 0,582 0,0097 - 2602
2 КГ-1Х-5 31,4 0,565 0,0107 - 2602
3 КГ-1Х-6 31,4 0,579 0,0107 - 2602
4 KT-XXIV-3 30,6 0,65 0,017 278 278
5 KF-XXIV-4 30,6 0,735 0,017 92 . 92
6 KT-XXTV-5 30,6 0,732 0,017 95 95
7 KT-XXIV-6 30,6 0,656 0,017 136 136
8 кг-хх\п-з 30,6 0,724 0,017 - 2602
9 КГ-ХХП-4 30,6 0,715 0,017 - 2602
Основной расчетный интерес представляет величины ?]дл предела длительной ус-
тойчивости: уровень нагрузки, при котором колонна теряет несущую способность за
время 100-150 лет (^
Т^-.ПрИ ,„=«>).
л кр
203
Расчетным путем эта величина определяется из выполнимости условия (6.6.17)
при внецентренном сжатии, либо из данных формулы (6.3.21) параграфа 6.3. Экспери-
ментально можно определить только интервал, в котором находится величина предела
длительности.
Для колонн 1-3 (табл.6.7.1) с коэффициентом армирования // = 0,01, коэффици-
ент длительного сопротивления т]дя > 0,582; см. также рис.6.7.1. У колонн 8-9 коэффи-
циент армирования больше на 59%, чем у колонн 1-3; предел текучести арматуры Rs
также больше на 30%, экспериментальное значение т]дя повысилось до величины 0,724
(табл.6.7.1).
Эксцентричность приложения нагрузки изменяет значение предела длительной
устойчивости, что иллюстрируется данными табл.6.7.2 и рис.6.7.2.
Таблица 6.7.2
Экспериментальные колонны,
испытанные в НИИЖБе на внецентренное сжатие
и по данным Гэде К.
Шифр колонны V dh Uh сут.
1 КГ-ХХУ-З 0,77 0,0227 0,166 30,3 129
2 KT-XXV-4 0,772 0,0227 0,166 30,3 115
3 КГ-ХХУ-5 0,633 0,0227 0,166 30,3 -
4 KT-XXV-6 0,633 0,0227 0,166 30,3 -
5 KT-XXVI-3 0,777 0,017 0,5 30,3 -
6 КГ-ХХУ1-4 0,777 0,017 0,5 30,3 -
Опыты К.Гэде
7 1/2 0,807 0,014 0,2 29,4 17
8 1/3 0,745 0,014 0,2 29,4 7
9 11/2 0,705 0,014 0,5 29,4
10 11/3 0,775 0,014 0,5 29,4 -
£ Колонны 1-2, имеющие величину эксцентриситета ~ = 0,1 66 и уровень нагрузки
0,77, теряют устойчивость за конечное время. Предел длительной устойчивости этих
колонн находится в интервале 0,633 < < 0,77, что видно из сопоставления с анало-
гичными данными по колоннам 3-4; теоретическая величина коэффициента длительно-
го сопротивления, рассчитанная по формулам § 6.6.6, равняется = 0,72.
204
При значениях эксцентриситета — — 0,5 у колонн 5-6 получено, что эти колонны
устойчивости не теряют при
= 0,777. Такие же результаты следуют из экспе-
риментов К. Гэде, представленных колоннами 7-10 в табл.6.7.2 и на рис.6.7.2.
1,0

10 1 1 । ।
20 40 100 200 400 1000 2000 5000 t сут
Рис.6.7.1. Длительность существования центрально сжатых колонн под нагрузкой:
(•) - нет потери несущей способности; * - потеря устойчивости.
Нужно обратить внимание на малое число экспериментальных данных по опреде-
лению длительной устойчивости железобетонных колонн. Некоторые эксперименты
проводились на образцах малых размеров; например, в опытах Пекус-Сахновского Д.Н.
сечение колонн составляло 12 х 5 см при длине колонны 137 см.
Численные эксперименты показали, что на значения предела длительной устой-
чивости существенно влияют форма поперечного сечения колонны; применяемый класс
бетона; диаграмма <js - £s арматуры и коэффициент армирования; величина и знак эк-
сцентриситета приложения нагрузки; условия сочетания кратковременной и длитель-
ной нагрузок и другие факторы.
Слабая изученность указанных факторов, а также сложность и малая разработан-
ность теоретического решения задачи вынудили разработчиков Евростандартов пойти
по достаточно условному пути в расчетах длительной устойчивости железобетонных
205

0,9
® -3,4
—• - расчетные значения
• - потери устойчивости нет
* - потеря устойчивости
0,1 0,2 0,3 0,4 0,5
е
Рис.6,7 2.3начения коэффициента Т} при различных значениях эксцентриситета —
п
и коэффициента армирования (Л
колонн. В основу модели Евростандартов, равно как и моделей других стран, в частно-
сти, модели СНиП, положено теоретическое решение А.Р.Ржаницына, полученное им
при рассмотрении центрально сжатого стержня, ползучесть которого описывается ли-
нейной моделью Кельвина [133]. Учитывая большую практическую значимость про-
блемы, рассмотрим её подробнее. В рамках приближенного выражения для кривизны
найдено значение критической силы
я2 HI
(6.7.1)
где Н - параметр в модели Кельвина, рис.6.7.3, равный: для варианта а) - Н = ——~~;
Е} + Е2
для варианта б) - Н -Ех.
Если ползучесть бетона удается приближенно описать с помощью линейной
модели Кельвина, то в ней длительный модуль равен
р
Н=--------ь----
l + <Pf/„,co>’
206
а длительная критическая сила центрально сжатого бетонного стержня находится
из выражения
Рис.6.7.3.
Схемы соединения упругих и вязких элементов, соответствующие линейно
модели Кельвина:
а) - упругие элементы; 6) - вязкие элементы.
(6.7.2)
Изменение прогиба середины центрально сжатой колонны в решении Ржаницына
А.Р. имеет вид (рис.6.7.4)
Nf-N
Hy-N н
(6.7.3)
где Мм
tc2EI
I2
(E мгновенный модуль упругости); п
к___
+ &2
- для модели а),
п р - для модели б), к - коэффициент вязкости; Л - прогиб в начальный момент
времени.
Причина возникновения прогиба fQ не оговаривается, но указывается, что началь-
ный прогиб имеег место “по той или иной причине”.
Формула (6.7.2) является базовой при построении различных нормативных мето-
дик в том числе Евростандартов. В СНиП 2.03.01-84* вводится коэффициент заме-
няющий выражение, стоящее в (6.7.2) в скобках,
При постоянной сжимающей силе на колонну принято
207
Отсюда коэффициент длительного сопротивления сжатой колонны равен
Г) =—1— = о,5
\ + р
В Евросгандартах ползучесть сжатых колонн учитывается путем изменения фак-
тической длины их
^=^1+^0.^. (6-7-4)
где <J(/0,oo)= 1,2 для обычного тяжелого бетона. В этом случае коэффициент длитель-
ного сопротивления равен
n>,=----—----= 0,45
По данным экспериментов [162] для тяжелою бетона Ф(1й,<х>) = 2; коэффициент
длительного сопротивления равен т]Ля =0,333.
Формула (6.7.2) получена на основе модели Кельвина, у которой для бетона мера
ползучести записывается в виде
Еъ
(6.7.5)
Эго уравнение, заложенное в Евросгандартах как базовое для расчетов колонн,
путем использования в (6.7.2), существенно отличается от уравнения семейства кривых
ползучести, разработанного ЕКБ в развитие Евростандартов. Последнее представлено
суммой степенных функций гиперболического вида
С(Мо) = Д(О) 1-
(6.7.6)
где Д(0) - значение быстронатекающей ползучести в виде вертикального отрезка;
у/а(0) и предельное (при t = оо) значения обратимой и необратимой со-
ставляющих деформации ползучести бетона.
Вторым недостатком подхода Евростандартов является распространение модели
(6.7.4) (центрально сжатые колонны) на расчет внецентренно-сжагых колонн.
При внецентренном сжатии колонны, удовлетворяющие модели Кельвина, разви-
тие прогибов отличается от данных рис.6.7.4.
Прогибы сжато-изогнутого стержня в условиях линейной ползучести при различ-
ных уровнях сжимающей силы показаны на рис.6.7.5. При сжимающей силе N < Ng
прогибы увеличиваются с затухающей скоростью = 0 „р„ , = оо).
208
Рис.6.7.5.
При сжимающих силах N = Ng и N > Ng прогибы неограниченно увеличивают-
ся (в рамках приближенного выражения для кривизны (см. также рис.6.6.5). В этих мо-
делях бетон считается упругим, неограниченно работающим на растяжение и сжатие.
Перечисленные недостатки указывают на условность подхода Евростандартов
в расчете длительной устойчивости железобетонных колонн. Приближенность этого
подхода существенно отличается от строгости деформационной модели, залаженной
в основу кратковременной устойчивости железобетонных колонн.
Вместе с тем, укажем, что результаты расчета здесь дают запас несущей способно-
сти, величина которого никак не оценивается. Модель расчета, предложенная нами
в предыдущем параграфе, более точна, но требует использования в практических расче-
тах дополнительных табличных данных.
209
Вторым недостатком подхода Евростандартов является распространение модели
(6.7.4) (центрально сжатые колонны) на расчет внецентренно сжатых колонн. При вне-
центренном сжатии колонны, удовлетворяющей модели Кельвина, развитее прогибов
отличается от данных рис.6.7.4 Прогибы сжато-изогнутого стержня в условиях линей-
ной ползучести при различных уровнях сжимающей силы показаны на рис 6.7 5
При сжимающей силе N<Ng прогибы увеличиваются с затухающей скоростью
Л“°>п₽и
При сжимающих силах N = Ng и N > Ng прогибы неограниченно увеличивают-
ся (в рамках приближенного выражения для кривизны, см. также рис.6.6.5). В этих мо-
делях бетон считается упругим, неограниченно работающим на растяжение и сжатие
Перечисленные недостатки указывают на условность подхода Евростандартов
в расчете длительной устойчивости железобетонных колонн.
Приближенность этого подхода существенно отличается от строгости деформаци-
онной модели, заложенной в основу расчета кратковременной устойчивости железобе-
тонных колонн.
210
Библиография
1. Абрамов Л.М. Прочность и устойчивость П-образных статически неопреде-
лимых железобетонных рам при нелинейной ползучести бетона. Дисс. канд. тех. наук.
ЛИСИ, 1983. - 106 с.
2. Александровский С.В. Расчет бетонных и железобетонных конструкций на
изменение температуры и влажности с учетом ползучести. М., 1973. - 432 с.
3. Арупонян Н.Х. Некоторые вопросы теории ползучести. М.-Л., 1952. - 323 с.
4. Арутюнян Н.Х., Колмановский В.Б. Теория ползучести неоднородных тел.
М., 1983.-336 с.
5. Арупонян Р.А. Модели неупругого деформирования и разрушения среды со
старением. Автореф. докт. дисс. ЛГУ, 1990, - 29 с.
6. Астафьев Д.О. Теория и расчет реконструируемых железобетонных конст-
рукций. Дисс. доктора техн. наук. СПбГАСУ, 1995. - 435 с.
7. Анцыгин О.И. Прочность и устойчивость усиленных под нагрузкой железобе-
тонных стержней с коррозионными повреждениями. Дисс. канд. техн. наук. СПбГАСУ,
1998 г. - 168 с.
8. Бадалов Ф.Б. Метод степенных рядов в нелинейной наследственной теории
вязкоупругости. Ташкент, 1980. - 221 с.
9. Балявичус Р., Дулинскас Е. Учет линейной ползучести в расчетах железобе-
тонных элементов. - Бетон и железобетон. №1, 2002. С. 27-30.
10. Бабенко Д.В. Длительное сопротивление железобетонных стержней с высо-
ким коэффициентом армирования. Автореф. канд. дисс. Одесса, 1981. - 19 с.
11. Байков В.Н., Поздеев В.М. Определение напряженно-деформированного со-
стояния железобетонных балок в предельной стадии по неупругим зависимостям. -
Изв. ВУЗов. Стр-во и архитектура. №1, 1985. С. 1-5.
12. Байков В.Н., Сигалов Э.Е. Железобетонные конструкции. М., 1991. - 767 с.
13. Байков В.Н., Сигалов Э.Е. Железобетонные конструкции. Специальный курс.
М., 1981.-767 с.
14. Бамбура А.Н. Диа1рамма <7 - е для бетона при центральном сжатии. - Воп-
росы прочности, деформативности и трещиностойкости железобетона. Вып.8, Ростов-
на-Дону, 1988. С. 19-22.
15. Барашиков АЛ. Расчет железобетонных конструкций на действие длитель-
ных переменных нагрузок. Киев, 1977. - 155 с.
16. Барановский В.И. Разработка способов расчета элементов железобетонных
конструкций при высоких длительно действующих воздействиях. Автореф. канд.дисс.
Одесса, 1982. - 24 с.
17. Бачинский В.Я. Устойчивость длительно загруженных железобетонных стер-
жней при различном загружении концов. Автореф. канд.дисс. Киев, 1970. - 26 с.
18. Бельский ЕЕ. О расчете сжатоизогнутых стержней с учетом неоднородности
механических свойств материалов. - Строительные конструкции. Киев, вып.УП, 1968 г.
С. 170-182.
19. Беглов АД. Устойчивость железобетонных элементов из плоскости изгиба при
кратковременном и длительном загружениях. Дисс. канд. тех. наук. СПбГАСУ, 1993. -115 с.
20. Беглов А.Д. Некоторые проблемы устойчивости железобетонных конструк-
ций. СПбГАСУ, 2000. - 106 с.
211
21. Беглов А.Д., Санжаровский Р.С., Бондаренко В.М. К вопросу о моделях Евро-
стандартов и СНиП по железобетону. - Бетон и железобетон. №3, 2004.- с.30-31.
22. Беглов А.Д., Санжаровский Р.С., Бондаренко В.М. Ползучесть бетона и моде-
ли Евростандаргов. - Бетон и железобетон. №2, 2005.- с.29-30.
23. Беглов А.Д., Санжаровский Р.С., Кузнецов С.В., Бондаренко В.М. Нелиней-
ная ползучесть железобетонных балок. - Бетон и железобетон. №3, 2005. С.26-29.
24. Беглов А.Д., Санжаровский Р.С., Бондаренко В.М. Нелинейное длительное
деформирование железобетонной колонны в условиях модели Евростандаргов. - Вест-
ник отделения строительных наук. РААСН, 2005. С. 76-81.
25. Беглов Л.Д., Санжаровский Р.С., Бондаренко В.М. Нелинейная теория ползу-
чести бетона. Вестник отделения строительных наук. РААСН, 2005. С. 82-98.
26. Беглов А.Д., Санжаровский Р.С., Бондаренко В.М. Евростандаргы и нелиней-
ная теория железобетона. -Бетон и железобетон - пути развития. II Всероссийская (Меж-
дународная) конференция по бетону и железобетону. Том.1. Пленарные доклады. М.,
2005. С. 119-125.
27. Беккиев М.Ю., Маилян Л.Р. Расчет изгибаемых железобетонных элементов
различной формы поперечного сечения с учетом нисходящей ветви деформирования.
Нальчик, 1985. - 132 с.
28. Безухов Н.И. Теория пластичности в приложении к расчету сооружений. -
Строительная механика в СССР. М., 1957. С. 233-263.
29. Бондаренко В.М. Некоторые вопросы нелинейной теории железобетона. Харь-
ков, 1968. - 323 с.
30. Бондаренко В.М., Бондаренко С.В. Инженерные методы нелинейной теории
железобетона. М., 1982. - 287 с.
31. Бондаренко В.М. Диалектика механики железобетона. - Бетон и железобе-
тон. №1, 2002 . С. 24-27.
32. Бондаренко С.В., Санжаровский Р.С. Усиление железобетонных конструкций
при реконструкции зданий. М., 1990. - 352 с.
33. Брызжагый Э.П., Мирвис Я.Г., Петрова К.В. О перераспределении напряже-
ний в сечении внецентренно сжатого бетонного элемента с учетом нелинейной ползу-
чести. - Ползучесть и усадка бетона. М., 1969. С. 148-157.
34. Буданов Н.А. Расчет железобетонных конструкций с учетом ползучести бето-
на. М„ 1949.- 116 с.
35. Буданов Н.А. Влияние ползучести бегона на работу железобетонных арок.
ДИСИ, сообщение 30, 1940. - 160 с.
36. Баловнев Г.Г. Графоаналитический способ расчета на поперечный пластичес-
кий изгиб. - Вестник машиностроения. №7, 1954. С. 12-15.
37. Бунятян Л.Б. Устойчивость тонкостенных стержней с учетом ползучести ма-
териала. - Изв. АН Арм.ССР. т.6, №2, 1953. С. 43-53.
38. Вареник А.С. Устойчивость сжатых элементов деревянных конструкций. Дисс.
кацд. техн. наук. Новгород, 1994. - 108 с.
39. Васильев П.И. Связь между напряжениями и деформациями в бетоне при
сжатии с учетом влияния времени. - Известия ВПИИГ. 1951. т.45. С. 78-92.
40. Вольмир А.С. Устойчивость деформируемых систем. М., 1967. - 984 с.
41. Веселов А.А. Нелинейная теория сцепления арматуры с бетоном и её прило-
жения. Дисс. докт. техн. наук. СПбГАСУ, 2000. - 320 с.
212
42. Гвоздев А.А. О пересмотре способов расчета железобетонных конструкций
и о первых его результатах. М.,- Л., 1934. - 51 с.
43. Гвоздев А.А., Мурашёв В.И. О пересмотре технических условий и норм на
проектирование железобетонных конструкций. - Проекг и стандарт. №7, 1936. С. 2-9.
44. Гвоздев А.А. Некоторые механические свойства бетона, существенно важ-
ные для строительной механики железобетонных конструкций. - Исследование свойств
бетона и железобетонных конструкций. М., 1959. С. 5-17.
45. Гвоздев А.А. Ползучесть бетона и пути её исследования. -Исследование проч-
ности, пластичности и ползучести строительных материалов. М.» 1955. С. 126-137.
46. Гвоздев А.А. Чистяков Е.А., Шубик А.В. Исследование деформаций и несу-
щей способности габких сжатых железобетонных элементов с учетом длительного воз-
действия нагрузки. - Прочность и жесткость железобетонных конструкций. НИИЖБ,
1971.С. 5-13.
47. Гвоздев А.А. К вопросу о состоянии бетона при высоких сжимающих напря-
жениях. - Строительная механика и расчет сооружений. №5, 1977. С. 14-16.
48. Гвоздев А.А. Расчет несущей способности конструкций но методу предель-
ного равновесия. М., 1949. — 280 с.
49. Гвоздев А.А. Обоснование §33 Норм проектирования железобетонных кон-
струкций. - Строительная промышленность. №3, 1939. С. 51-59.
50. Гвоздев А.А. О развитии теории расчета железобетонных конструкций в СССР.
- Теория расчета бетонных и железобетонных конструкций. М., 1949. С. 3-18.
51. Гениев Г.А., Колчунов В.И., Клюева Н.В., Никулин А.И., Пятикрестовский
К.П. Прочность и деформативность железобетонных конструкций при запроектных
воздействиях. АСВ, М., 2004. - 216 с.
52. Георгиевский Д.В. Устойчивость процессов деформирования вязкопластичес-
ких тел. М., 1998. - 175 с.
53. Голышев А.Б. Расчет железобетонных стержневых систем с учетом фактора
времени. М.» 1984. - 127 с.
54. Горнов В.Н. Прочность и устойчивость бетонных конструкций. М., 1957. -
120 с.
55. Городецкий А.С. Применение метода конечных элементов к физически нели-
нейным задачам строительной механики. Дисс. докт. техн. наук. Киев, 1978. - 330 с.
56. Геммерлинг А.В. Расчет стержневых систем. М., 1974. - 207 с.
57. Гуща Ю.П. Предложения по нормированию диаграмм растяжения высоко-
прочной стержневой арматуры. - Бетон и железобетон. №7, 1989. С. ‘26-28.
58. Гуща Ю.П., Лсмыш Л Л. Расчет деформаций конструкций на всех стадиях
при кратковременном и длительном нагружениях. - Бетон и железобетон. №11, 1985.
С. 18-20.
59. Гусаков В.Н. Исследование и разработка методов расчета по деформациям и
несущей способности изгибаемых и внецентренво сжатых железобетонных элементов
из плотного силикатного бетона при статических нагрузках. Автореф. докт. дисс. М.,
1980.-48 с.
60. Давидов И.В. Определение перемещений в сжато-изотугых элементах при
их работе за пределами упругости. - Труды ХИСИ. вып.4, 1995. С. 167-182.
61. Дегтярев В.В., Крестников Ю.Н. Некоторые особенности деформирования
и разрушения центрально сжатых железобетонных колонн. - Исследование деформа-
213
ций, прочности и долговечного бетона транспортных сооружений М., 1969 С. 148-155
62. Дроздов П Ф О расчете гибких железобетонных колонн - Бетон и железобе-
тон. №12, 1979. С. 30-31.
63. Ерхов М.И. Теория идеально пластических тел и конструкций. М., 1978. -
352 с.
64. Европейский комитет по бетону. Международные рекомендации для расче-
тов и осуществления обычных и предварительно напряженных конструкций. М., 1970.
- 235 с.
65. Жаданова К.Ф. Исследование устойчивости сжатых стержней из сплавов алю-
миния с учетом ползучести материала Дисс. канд техн, наук ЛИСИ, 1978. - 157 с.
66. Зеленченков С А. Об устойчивости элементов металлических конструкций,
сжатых с двухосным эксцентриситетом. Дисс. канд. техн. наук. ЛИСИ, 1982. - 187 с.
67. Зибер Ф. Строительная отрасль крупного региона в переходный период
(на примере федеральной земли Саксонии). Дисс. доктора техн. наук. СПбГАСУ, 1995.
-301 с.
68 Залесов А.С., Чистяков Е.А., Ларичева И Ю. Деформационная расчетная мо-
дель железобетонных элементов при действии изгибающих моментов и продольных
сил. - Бетон и железобетон. №5, 1996. С. 16-18.
69. Звездов А И, Залесов А.С., Мухамедиев Т А., Чистяков Е.А. Расчет прочнос-
ти железобетонных конструкций при действии изгибающих моментов и продольных
сил по новым нормагивным документам. - Бетон и железобетон. №2, 2002. С. 21-25.
70. Ишлинский А.Ю. Прикладные задачи механики. Механика вязкопластичес-
ких и не вполне упругих тел. М., 1986. - 360 с.
71. Кадашевич Ю И., Новожилов В.В. Теория пластичности и ползучести, учи-
тывающая наследственные свойства и влияние скорости пластического деформирова-
ния на локальный предел текучести материала. - Докл. АН СССР, т.238, №1, 1978. С.
36-38.
72. Карпенко Н И., Мухамедиев Т.А., Петров А.Н. Диаграммы деформирования
бетона, их трансформации в зависимости от различных факторов и использование в
расчетах конструкций. - Предельные состояния бетонных и железобетонных конструк-
ций гидротехнических сооружений. Энергоатомиздат, 1986. С. 170-180.
73. Карпенко Н.И., Мухамедиев Т.А., Сапожников М.А. Об учете различных фак-
торов в аналитической зависимости для диаграммы деформирования бетона. - Перс-
пективы развития строительных конструкций Мат всесоюзн. конференции (Под ред
РС.Санжаровского). ЛДНТП, 1987 С 72-76.
74. Карпенко Н.П. Общие модели механики железобетона. М., 1996. - 409 с.
75. Катин Н.И. Исследование ползучести бетона при высоких напряжениях. -
Исследование свойств бетона и железобеюнных конструкций. Труды НИИЖБ, вып.4,
1959. С. 74-153.
76. Качанов Л.М Некоторые вопросы теории ползучести. Гостехиздат; 1949. -164 с.
77. Качанов Л.М. Устойчивость тонкостенных стержней при упругопластичес-
ких деформациях. - ДАН СССР. Вып 107, №6, 1956. С. 803-806
78. Каюмов Р.Х. Устойчивость гибких железобетонных стержней из высокопроч-
ных бетонов Автореф. канд. дисс. Киев, 1972. - 22 с.
79. Коршунов Д.А. Об Об актуальных вопросах теории железобетона. - Бетон
и железобетон. №3, 1998. С. 21-23.
214
80. Крылов А.Н О формах равновесия вертикально нагруженных элементов Изв.
АН СССР. 1931.-963 с.
81. Крылов С.Б. Численное исследование ползучести бетона в стержневых изги-
баемых конструкциях с трещинами. - Бетон и железобетон. 2003, №4. С. 19-20.
82. Крылов С.М. Физическая и геометрическая нелинейность железобетонных
конструкций и её учет в расчетах и проектировании. - Напряженно-деформированное
состояние бетонных и железобетонных конструкций. -М., 1986. С.4-6.
83. Кодекс - образец ЕКБ-ФИП для норм по железобетонным конструкциям Том
второй. М., 1984.
84 Кузнецов А А Экспериментальная проверка формул проекта НиТУ 1938 г
для расчета гибких колонн на внецентренное сжатие в условиях длительного действия
нагрузки. - Ученые труды ЦНИПС за 25 лег. 1952. С. 12-16
85. Лагранж Ж.Л. Аналитическая механика, 1950. - 594 с.
86. Лейтес С.Д. Устойчивость сжатых стальных стержней. М., 1954. - 308 с.
87 Лившиц Я Д. Расчет железобетонных конструкций с учетом влияния усадки
и ползучести бетона Киев, 1976. - 280 с
88. Лолейт А.Ф. Инструкция для подбора сечений железобетонных элементов по
критическим усилиям. М , 1933. С. 5-43.
89. Лукаш 11.А. Основы нелинейной строительной механики. М., 1978. - 208 с.
90. Ляпунов А.М. Общая задача об устойчивости движения. М., 1950. - 472 с.
91. Майер Г.Г. Система европейских стандартов на бетон и составляющие мате-
риалы. - Бетон и железобетон. №1, 2002. С. 2-4.
92. Мамуров М М. Нелинейная ползучесть железобетонных стержневых конст-
рукций Дисс. канд. техн наук ЛИСИ, 1983. - 179 с.
93 Маух С., Холли М.Д. Потеря устойчивости железобетонных колонн при пол-
зучести - Расчет строительных конструкций с применением электронных машин. М.,
1967. С. 96-104.
94. Мазур В.Ф. Особенности влияния длительных нагрузок на напряженно-де-
формированное состояние железобетонных элементов и предложения по их учету при
определении прочности Дисс. канд. техн наук. Одесса, 1987. -214 с.
95 Манукян М М. Деформация и напряжение в изгибаемой железобетонной балке
с учетом ползучести сжатой и частично растянутой зон бетона - Известия АН АССР.
Физ -матем., естеств. и техн науки, т.1Х, выл 9, 1956. С. 27-45.
96. Магевосян Р.Р. Устойчивость сложных стержневых систем. М., 1961. - 252 с
97. Мельник Р.А. Исследование нелинейной ползучести бетона и её влияние на
потери предварительного напряжения. Автореф. канд. дисс. Киев, 1964. - 21 с.
98. Митасов В.М., Емельянов М.П., Пирожков Г.И. Расчет изгибаемых железо-
бетонных конструкций с использованием действительных диаграмм арматуры и бето-
на. - Строительные конструкции зданий и сооружений транспорта Новосибирск, 1985
С. 39-43.
99. Мунир А Расчет железобетонных стержневых систем с учетом физической и
геометрической нелинейности. Дисс. канд. техн. наук. СПбГАСУ, 1992. - 116 с.
100. Мурашёв В.И. Трещиноустойчивость, жесткость и прочность железобетона.
М., 1950.-268 с.
101. Мурашёв В.И. Принципы построения теории сопротивления железобетона.
Теория расчета бетонных и железобетонных конструкций. М, 1949. С. 47-58.
215
102 Мусабаев ТТ Нелинейная теория расчета железобетонных оболочек и плас-
тин. Дисс докт. техн. наук. СПбГАСУ, 1999. - 422 с.
103. Мухамедиев Т.А. Методы расчета статически неопределимых железобетон-
ных стержневых и плоскостных конструкций с учетом нелинейных диаграмм деформи-
рования материалов и режимов на1ружения Дисс докт. техн, наук М., 1990 -343 с.
104 Менее Ж.И. Зависимость несущей способности изгибаемых железобетонных
элементов от псупругих деформаций. - Исследования по бетону и железобетону. Рига,
вып.2, 1956.
105 Методические рекомендации по уточненному расчету железобетонных эле-
ментов с учетом полной диаграммы сжатия бетона. Киев, 1987. - 25 с.
106 Методы расчета строительных конструкций на прочность и устойчивость. М.,
ЦНИИСК, 1989. - 202 с.
107. Михайлов В.В. Растяжимость бетона в условиях свободной и связанной де-
формаций. Исследование прочности, пластичности и ползучести строительных мате-
риалов М, 1955. С 116-125.
108 Мизернюк Б Н Исследование железобетонных изгибаемых и внецентренно
сжатых элементов, распалубливаемых и загружаемых в молодом возрасте. Дисс. канд.
техн. наук. М , 1954. - 148 с.
109. Мухидинова М.Х Расчеты элемен тов конструкций с учетом ползучести. Ав-
тореф. канд дисс. Ташкент, 1974. - 21 с
НО Николаи Е.Л Труды по механике. М., 1955. - 584 с
111. Никитин Г.В. О несущей способности центрально и внецентренно сжатых
гибких железобетонных стержней. - Теория расчета бетонных и железобетонных кон-
струкций М., 1949 С 59-66
112 Назарук А. В Исследование устойчивости сжатых стержней, работающих в
упругоплас! ической стадии при динамических нагрузках. Дисс. канд. техн. наук. ЛИСИ,
1977.- 156 с.
113. Немцев А.В. Напряженно-деформированное состояние толстостенных сосу-
дов с учетом ползучести материала при сложных режимах изменения давления и темпе-
ратуры Дисс. канд. техн наук. ЛИСИ, 1983. - 146 с
114. Оплачко В.М. Изгиб железобетонной балки с обычной арматурой при дли-
тельном действии нагрузки и нелинейной зависимости между напряжениями и дефор-
мациями бетона. - Известия ВУЗов Строительство и архитектура №4, 1968 С 21-28.
115. Подольский И.С. Расчет железобетонных конструкций с учетом некоторых
физических факторов М -Л., 1938. - 108 с.
116. Петров А.Н. Деформационная модель нелинейной ползучести железобетона
и её приложения к расчету плосконапряженных элементов и систем из них. Автореф
докт. дисс М., 2001. - 36 с
117 Половец В И Исследование несущей способности железобетонных балок
с обычной арматурой при длительно действующих нагрузках. Дисс. канд. техн. наук.
Одесса, 1975. - 158 с.
118. Паньшин Л.Л Крашенинников М.В. Оценка эффективности неупругой де-
формационной модели при расчете нормальных сечений. - Бетон и железобетон. 2003,
№3. С. 19-22.
119. Ползучесть и усадка бетона и и железобетонных конструкций. М., 1976. -
351 с.
216
120. Попеско А.И. Расчет железобетонных конструкций, подверженных коррозии.
Дисс. доктора техн. наук. СПбГАСУ, 1996. - 448 с.
121. Прокопович И.Е., Щербанов Е.Н О концепции приведенного времени в урав-
нениях семейств кривых ползучести бетона. - Бетон и железобетон. 1995, №6. С 19-24.
122. Прокопович И.Е. Влияние длительных процессов на напряженное и дефор-
мированное состояние сооружений. Госстройиздат, М., 1963. - 260 с.
123. Прокопович И.Е., Улицкий И.И. О теориях ползучести бетона. - Известия
ВУЗов. Строительсгво и архитектура. №10, 1963. С. 23-27
124. Педаховский И.И. Матричная теория упруго-ползучего тела. - Тезисы докла-
дов IV Всесоюзной конференции по применению электронных вычислительных ма-
шин в строительной механике, машиностроении и строительном производстве Киев,
1965. С 44
125. Проблемы устойчивости в строительной механике Труды Всесоюзной кон-
ференции. М., 1965. - 487 с.
126 Пинаджан В.В Некоторые вопросы предельного состояния сжатых элемен-
тов стальных конструкций. Ереван 1956. - 202 с.
127 Попов Е.П. Нелинейные задачи статики тонких стержней Л -М., 1948. - 170 с
128. Работнов Ю.Н. Элементы наследственной механики твердых тел. М., 1977. -
384 с.
129 Работнов Ю.Н. Ползучесть элементов конструкций М., 1966. - 607 с
130 Рафиев А.К. Расчет стержневых железобетонных конструкций на основе объеди-
ненных уравнений пластичности и ползучести. Дисс. канд. техн, наук, ЛИСИ, 1989. - 170 с.
131. Рочев А.А. Исследование работы внецентренно сжатых перфорированных
стержней в упругопластической стадии Дисс. канд. техн, наук, ЛИСИ, 1979. - 135 с.
132 Розовский М.И. О нелинейных уравнениях ползучести и релаксации матери-
алов при сложном напряженном состоянии. - ЖТФ. Том XXV, вып.13,1955. С. 153-158
133. Ржаницын А.Р. Процессы деформирования конструкций из упруговязких эле-
ментов. - Доклады АН СССР 1946, т.52, №1. С. 25-28
134 Ржаницын А.Р Теория ползучести М., 1968. - 416 с.
135. Ржаницын А.Р. Температурно-влажностная задача ползучести. -Исследова-
ния по вопросам теории пластичности и прочности строительных конструкций. М., 1958.
С. 36-49
136. Ржаницын А.Р. Внецентренное сжатие стоек из материала, не работающего
на растяжение. - Строительная механика. Труды МИСИ, №2, 1939. С. 3-18
137. Санжаровский Р.С. Устойчивость элементов строительных конструкций при
ползучесги ЛГУ, 1978. - 216 с.
138. Санжаровский Р.С. Усиления при реконструкции зданий и сооружений. Уст-
ройство и расчеты усилений зданий при реконструкции (Р.С.Санжаровский, Д.О.Аста-
фьсв, В.М.Улицкий, Ф.Зибер). СПбГАСУ, 1998. - 637 с.
139 Санжаровский Р.С. К теории устойчивости сжатых стержней, в частности
трубобетонных, при статическом и динамическом загружениях с учетом получести. -
Механика стержневых систем и сплошных сред. Труды ЛИСИ, №63, 1970. С. 216-243.
140. Санжаровский Р.С. О критериях потери устойчивости и методах исследова-
ния работы сжатых стержней в условиях ползучести. - Исследования по строительным
конструкциям Материалы IV научной конференции молодых ученых-строителей ЛИСИ,
1972. С.31-48.
217
141. Санжаровский Р.С. Исследование устойчивости сжатоизогнутых стержней
в условиях нелинейной ползучести материала. — Исследования по расчету и проектиро-
ванию сооружений Л., 1975, С. 164-171.
142. Санжаровский Р.С К вопросу расчета устойчивости сжатоизогнутых элемен-
тов с использованием приближенного выражения для кривизны - Исследования по стро-
ительным конструкциям и испытанию сооружений. Л., 1968, С. 23-27.
143. Санжаровский Р.С., Веселов А.А. Теория расчета строительных конструкций
на устойчивость и современные нормы Издательство АСВ, Санкт-Петербург, Москва,
2002 -128 с
144. Страхов Д А. Статический расчет стержневых железобетонных конструкций
с трещинами в растянутой зоне при нелинейной ползучести бетона. Автореф. канд.
дисс. Л., 1978. - 18 с.
145. Сегалов А.Е. О применении метода конечных элементов к расчету железобе-
тона с трещинами. - Исследование стержневых и плитных железобетонных статически
неопределимых конструкций М.» 1979 С 90-106
146. Состояние научных исследований по расчету несущих конструкций зданий
с учетом неупругих свойств материалов. М., 1974. - 52 с.
147. Столяров Я.В. Введение в теорию железобетона М., 1941. -447 с.
148. СНиП 2.03.01-84*. Бетонные и железобетонные конструкции М., 1985. - 79 с.
149. СНиП 52-01-2003 Бетонные и железобетонные конструкции. М, 2004. - 24 с.
150. Стрелецкий Н.С. Работа сжатых стоек М., 1959. - 283 с.
151. Тентиев Ж. Исследование прочности и устойчивости конструкций из винип-
ластовых труб при кратковременном и длительном загружениях. Дисс. доктора техн,
наук Алма-Ата, 1999. - 331 с.
152. Таль К.Э. О деформативности бетона при сжатии - Исследование прочнос-
ти, пластичности и ползучести строительных материалов. М., 1955. С. 202-207.
153. Таль К.Э. Расчет бетонных и железобетонных конструкций по расчетным
предельным состояниям. М., 1955. - 84 с.
154. Таль К.Э., Чистяков Е А. Экспериментальное исследование гибких железо-
бетонных стержней при длительном нагружении. — Исследование прочности, жесткос-
ти и трещиностойкости железобетонных конструкций. М., 1962. С 30-58
155. Теория расчета и конструирования железобетонных конструкций. М., 1958.-
214 с.
156. Тер-Эммануилян TH Применение метода полной дискретизации к расчету
пластан и стержней при ползучести Дисс. канд техн, наук ЛИСИ, 1989. - 149 с.
157. Тимошенко С.П. Устойчивость упругих систем. М., 1955. - 568 с.
158. Товстик П.Е. Асимптотические методы в механике тонкостенных конструк-
ций. СПбГУ, 1995. - 188 с.
159. Трулль В.А. Металлические конструкции Л, 1980. - 74 с.
160. Токмуратов А.М. Напряженно-деформированное состояние и устойчивость
пологих оболочек при нелинейной ползучести материала Дисс. канд. техн. наук. М.,
1988. - 138 с.
161. Узун И.Д. Диаграммы деформирования бетона при сжатии Одесский ЦНТИ,
1986 -68 с.
162. Улицкий И.И Теория и расчет железобетонных стержневых конструкций
с учетом длительных процессов. Киев, 1967. - 347 с.
218
163. Уначев А.Х. Устойчивость железобетонных колонн, сжатых с двухосным экс-
центриситетом, в условиях нелинейной ползучести. Дисс. канд. техн, наук ЛИСИ, 1987. -146 с.
164. Филин А.П. Определение лишних неизвестных в физически нелинейных ста-
тически неопределимых стержневых системах. - ДАН СССР. №4, 1953. С. 639-642.
165. Фигаровский В.В. Экспериментальное исследование жесткости и трещинос-
тойкости изгибаемых элементов при кратковременном и длительном действии нагруз-
ки. Дисс. канд. техн. наук. М., 1962. - 127 с.
166. Фрайфельд С.Е. Теория железобетона и его расчет. Харьков, 1934. - 85 с.
167. Фрайфельд С.Е., Рабинович Е.А. Определение напряжений во внецентренно
сжатых и изгибаемых армированных элементах методом прямой итерации. - Динамика
и прочность сооружений. Киев, 1965. С. 38-42.
168. Фрайфельд С.Е. Основные вопросы теории деформаций бетона. - Теория
расчета и конструирования железобетонных конструкций. М., 1958. С. 23-34.
169. Харлаб В.Д. Расчет статически неопределимых железобетонных конструк-
ций с учетом ползучести и твердения бетона. ВНИИГ, 1961, т.68. - 120 с.
170. Хофф Н. Продольный изгиб и устойчивость. ИЛ, 1955. - 155 с.
171. Цай В.Г. Деформации изгибаемых железобетонных элементов при длитель-
ном нагружении с учетом влияния формы поперечного сечения, неупругих свойств бе-
тона и арматуры. Дисс. канд. техн. наук. М., 1990. - 170 с.
172. Чжао-Цзу-У К вопросу о нелинейной теории ползучести. Acta mechanica sinica.
Т.3, №4, 1959.
173. Чижик В.А. Исследование напряженно-деформированного состояния желе-
зобетонных строительных конструкций с учетом трещинообразования, ползучести
и усадки бетона. Автореф. канд. дисс. Киев, 1978. — 18 с.
174. Чистяков Е.А. Беликов В.А. Изгиб и внецентренное сжатие коротких и гиб-
ких элементов. - Бетон и железобетон. 1971, №5. С. 10-14.
175. Чистяков Е.А. Учет прогибов при расчете сжатых элементов. - Бетон и желе-
зобетон. 1980, №1. С.36.
176. Чистяков Е.А. Основы теории, методы расчета и экспериментальные иссле-
дования несущей способности сжатых железобетонных элементов при статическом заг-
ружении. Дисс. докт. техн. наук. М., 1988. - 320 с.
177. Чайка В.П. Резервы прочности нормальных сечений крупноразмерных желе-
зобетонных изгибаемых элементов с высокопрочной сжатой арматурой. — Исследова-
ние прочности и деформаций бетона и железобетонных конструкций для транспортно-
го строительства. М., 1990. С. 25-43.
178. Шарипов X. Расчет железобетонных стержневых конструкций при импуль-
сивном нагружении. Дисс. канд. техн. наук. ЛИСИ, 1990. - 240 с.
179. Шеховцов В.А. Экспериментально-теоретическое исследование устойчивос-
ти сжатоизогнутых комплексных стержневых элементов конструкций в упругопласти-
ческой стадии. Дисс. канд. техн. наук. ЛИСИ, 1981. - 171 с.
180. Швецов А.В. Приближенный способ определения собственных напряжений
в бетоне с учетом переменности его деформативных свойств. — Гидротехническое стро-
ительство. №8, 1952.
181. Шубик А.В. Предложения по расчету железобетонных конструкций при дей-
ствии изгибающих моментов и продольных сил с учетом фактора времени. - Бетон
и железобетон. №1,2002. С. 16-19.
219
182. Шенли Ф.Р. Анализ веса и прочности самолетных конструкций. М., 1957. -
428 с.
183. Щербаков Е.Н. Физические и феноменологические основы прогнозирования
механических свойств бетона для расчетов железобетонных конструкций. Автореф. докт.
дисс. М., 1987. - 49 с.
184. Шеин А.И. Метод сеточной аппроксимации элементов в задачах строитель-
ной механики нелинейных стержневых систем. Автореф. докг. дисс. М., 2004. - 33 с.
185. Шура Мухамед. Определение напряженно- деформированного состояния ста-
тически неопределимых железобетонных балок в условиях нелинейной ползучести ма-
териала. Дисс. канд. техн. наук. ЛИСИ, 1988. — 158 с.
186. Эйлер Л. Метод нахождения кривых линий, обладающих свойствами макси-
мума, либо минимума. Приложение 1: Об упругих кривых. М., 1934.
187. Ярцев Б. А. Напряженно-деформированное состояние и устойчивость арок при
нелинейной ползучести материала. Дисс. канд. техн. наук. ЛИСИ, 1982. - 137 с.
188. Яшин А.В. Ползучесть бетона в ранеем возрасте. - Исследование свойств
бетона и железобетонных конструкций. М., 1959. С. 18-73.
189. Яшин А.В. Прочность и деформации бетона при различных скоростях нагру-
жения. - Воздействия статических, динамических и многократно повторяющихся на-
грузок на бетон и элементы железобетонных конструкций. М., 1972. С. 23-39.
190. Яшин А.В. Теория прочности и деформаций бетона с учетом его структур-
ных изменений и длительности нагружения. - Новые исследования элементов железо-
бетонных конструкций при различных предельных состояниях. М., 1982. С. 3-24.
191. Яценко В.Ф. Графоаналитический метод определения деформаций деревян-
ных балок при изгибе за пределом пропорциональности. - Труды АН УССР. №19, 1954.
С. 49-59.
192. Яценко Е.А. Методы расчета железобетонных конструкций на длительные
воздействия с учетом ползучести бетона. Автореф. докт. дисс. М., 1988. - 32 с.
193. Bazant Z.P. Stability States and Paths of Structures with Plasticity and Damage. -
Journal of Engineering Mechanics Division. ASCE, Vol.114, №12, 1988. P. 2013-2034.
194. Baumann O. Die Knicking der Eisenbeton Saulen. -EMPA. Bericht №89, 1934.
195. Beglov A.D., Sangarovski R.S. Construction calculation non-linear theory and
European codes. - XXXII Summer School-Conference “Advanced Problems in Mechanics”.
2004, St-Petersburg, Russia.
196. Broms B., Viest S. Ultimate Strength Analysis of Long Hinged Reinforced Concrete
Columns. - Journal of the Structural Division. V.84, №ST1, 1958.
197. CEB-FJP MODEL CODE, 1990.
198. Chang W.F., Ferguson P.M. Long Hinged Reinforced Concrete Columns. - ACJ
Journal. №1, 1963. P.1-25.
199. Chuang P.H., Kong F.K. Large-Scale Tests on Slender, Reinforced Concrete
Columns. - The Structural Engineer. Vol.75, №23-24, 1997. P. 410-416.
200. Claeson C. Structural behavior of reinforced high-strength Concrete Columns.
Gdteborg, 1998. — 221 s.
201. Commission of the European Communities. Eurocode №2. Common Unified Rules
for Concrete structures. 1984.
202. Grauers M. Composite Columns of Hollow Steel Sections Filled with High Strength
Concrete. Chalmers Universitu of Technology, Sweden, 1993. - 236 p.
220
203. ENV 1992-1. Eurokode 2. Design of concrete structures. Part 1, General rules and
rules for buildings, CEN, 1993.
204. Ezek K. Die Festigkeit von Driickstaben aus StahL - Wien, 1937. - 326 s.
205. Emperger F. Der Beiwert n=15 und die zulassigen Biegungs-spannungen. - Beton
und Eisen. 1931, №19.
206. Habel A. Berechnung fiir mittig gedruckte Stahlbetonsaiilcn. - Beton und
Stahlebetonbau. №11, 1955.
207. E. I lognestad, N.W.Hamson, D.Mc.Hcnry. Concrete Stress Distribution in Ultimate
Strength Design. - Journal of the Concrete Institute. XII, №4, vol. 27, 1955.
208. HofTN.J. Creep bucklihg. - Aeron. Quarterly. 7, 1956. p. 1-120.
209. Leaderman H. Elastic and creep properties of filamentous and other high polymers.
Textile Foundation. Washington, 1943.
210. Ngo D., Scordelis A.C. Finite Element Analysis of Reinforced Concrete Beams. -
ACJ Journal. Vol.64, №3, 1967. P. 152-163.
211. Rasch Chr. Spannungs-Dehnungs-Linien des Betons und Spannungs-verteilen in
der Biegerdruckzone bei konstanter Dehngeschwindigkeit. - Deutscher Ausschuss fur
Stahlbcton. Heft 154. 1962.
212. Rusch H., Sell R., Rasch Chr. Festigkeit und Verformung von unbewehrten Beton
unter konstanter Dauerlast. - Deutscher Ausschuss fiir Stahlbeton. Heft 198, 1968.
213. Sangarovski R.S., Astafiev D.O. Mechanics of Constructions and Technology of
Their Erection. - Applied Mechanics in the Americas. Pacam IV, 1999. S. 1006-1010.
214. Sangarovski R.S., Musabaev T.T. Calculation of Reinforced Concrete Envelopes
and Plates with craks. - Applied Mechanics in the Americas. Pacam IV, 1999. S. 939-942.
215. Sheikh S.A., Uzumcri S.M. Analytic Model for Concrete Confinement in Tied
Columns. - Journal of the Structural Division. ASCE. Vol. 108, №12, 1982. P. 2703-2722.
216. Shpak M., Stasuk M. On the Influence of Creep in Concrete on Crack Resistance
Concrete Structures. — Konstrukcjc betonowe. T.5, Krakow-Krynica, 1995. S. 189-196.
217. Shanley F.K. Inelastic columns theory - JAC. T.5, 14. 1947.
218. Sargin M. Stress-strain relations hips for concrete and the analysis of structural
concrete sections. - SM Study, №4, Solid Mechanics Division, University of Waterloo, Ontario,
Canada, 1971.
219. Taerve L. Codes and Regulations. Utilization of High Strength. High Performance
Concrete. - 4-th Int. Symp. Paris, 1996. P. 93-100.
220. Whitney C. Plastic Theory of Reinforced Concrete. Design Proceedings ASCE,
1940.
221. Zyczkowski M. Geometrically nonlinear creep buckling of bars. - Arch. Meeh.
Vol. 12, №3, 1960. P. 379-411.
222. Uppal I.Y., Kemp K.O. The effect of longitudional gradients of compressive stress
upon the failure of concrete. - Magasine of Concrete Research. Vol.23. №74, 1971.
221