Автор: Булдык Г.М.
Теги: теория вероятностей и математическая статистика теория вероятностей математическая статистика комбинаторный анализ теория графов математика задачи по математике
ISBN: 978-985-6868-18-7
Год: 2009
Похожие
Текст
РУКОВОДСТВО К РЕШЕНИЮ
ЗАДАЧ И УПРАЖНЕНИЙ ПО
ТЕОРИИ
ВЕРОЯТНОСТЕЙ
И МАТЕМАТИЧЕСКОЙ
СТАТИСТИКЕ
! Ж Ж. . ДКГ ж. Ж Ж _ х . Ж1*
Г. М. Ьу (лык
Руководство к решению задач
и упражнений по теории вероятностей
и математической статистике
Для практической и самостоятельной работы
стуленгов экономических специальностей
Минск
«ФУАинформ»
2009
УДК 519.21(075 8)
ББК 22.17я73
Б90
Рецензенты:
доктор физико-математических наук, профессор
Л.11.Садовский;
кандидат физике математических наук, допент Ю Л. Бон-
дарь.
Булдык, Г.М.
Б90 Руководство к решению ^адач и упражнений по теории ве-
роятностей и математической статистике Дли практической
и самостоятельной работы студентов экономических специ-
альностей. - Минск : ФУАинформ. 2009. - 228 с
ISBN 978-985-6868-18-7
Пособие написано в соответствии с программен курса
«Теория вероятностей и математическая статистика» для ву
зон Рассмотрены <кионные теоретические понятия и опреде-
ления теории вероятностей и математической статистики,
приведены примеры решения задач и сформулированы зада-
чи для самостоятельного решения.
Для студентов вузов.
УДК 519.2 Ц075.8)
ББК 22.17h7J
ISBN 978 985-6868 18-7
Сс> Будды к Г.М., 2009
<)(Хформпсине
(Х)О «ФУАинформ». 2009
СОДЕРЖАНИЕ
ПРЕДИСЛОВИЕ»
I ГЕОРИЯ ВЕРОЯТНО ГЕЙ S
1.1. Случайныесобытия Вероятность.................. 5
1.2. Свойства вероятностей!. Условная вероятность.
Независимость событий. Теоремы слежения
н умножения верояпюсгей...................... IS
13. Формула полной вероятности. Формулы Байеса
(теорема гипотез)............................ 28
14 Дискретные случайные величины ................ 36
I 5. Законы распределения дискретных случайных вс (ичин ...42
I 6. Непрерывные случайны величины...... ....54
I Законы распределения непрерывной случайной величины .60
I 8. Предельные теоремы и закон больших чисел ..... 7|
I 9 Двумерные случайные величины...... .. .. .......87
I 10. Случайные функции Цепи Маркова .......... 105
МАТЕМАТИЧ! I MI СТАТИСТИКА.. .........................ИЗ
2.1 Выборочная с гатис и*ил. 113
2.2 С гатистическое оценивание ..................... 126
23. С гатистические решения..........................145
2.3 I ( 1згистическая I ипогеза Проверка i ипотсты
о среднем значении при известной
и неизвестной дисперсиях... .........~...... 145
? 3.2 Проверка гипотез о дисперсиях............... 155
2 3.3 11роясрка гипотезы о равенстве значений двух
средних из нормально распределенных
генеральных совокупностей..................... . 160
2 4 Kpi крип согласия |де
ПРИЛОЖЕНИЕ |о-
ТаблицаЛ! г
Тебаина П2 ........ |<»>
падаПЗ 1<>-
Габлииа П4 ........................................ Р
Табпица П5......... . ......... .... .......... |<>q
аб :inia 116 ... 201
1аблм1ы1Г ч
। пм Ц8
1ИТБРАТУРА
СП RFTH, УКАЗАНИЯ И РЕШЕНИЯ ................ ... 210
ПРЕДИСЛОВИЕ
Студент, начиная шакомиться с теорией вероятностей, сразу
сталкивается со mhoihmh новыми понятиями. необходимыми для
описания изучаемых ситуаций г>гн поня1ия. а также термины и ве-
личины. используемые при их определении, должны бьыь усвоены,
прежде всего Только в пом случае станет доступной для понима-
ния вся теория вероятностей и математическая статистика, се зна-
чение в экономических приложениях. I* дине (венная причина, по
которой студент прекращает изучение предмета, не понимает, о
чем идет речь, или проело не в состоянии учиться — это пропущен-
ное слово, значение которою нс ясно. Поэтому никогда нс пропус-
кайте не осмысленных понятий Простоя истина о том. что нельзя
пропускать непонятные слова, является наиболее важной во всем
обучении, в том числе и в самостоятельном.
Во многих доступных для студентов учебных изданиях по
теории вероятное гей и математической статистики основные поня-
тия либо даются без строго математического обоснования, либо
теряются в обилии формул и символом Так. например у сгудентов
понятие вероятности часто ассоциируется только с классическим
определением, хотя известно, что современные определения веро-
ятностей основаны на аксиоматическом подходе Колмогорова
Цель настоящего издания заключается в закрешжнии основ-
ных понятии и определений. используемых в экономических при-
ложениях теории вероятное!ей и математической статистики при
проведении практических и самостоягельчых занятий
4
РАЗДЕЛ I. ТЕОРИЯ ВЕРОЯТНОСТЕЙ
Прсдмсюм ।серии вероятноеiей является анализ явлений,
наблюдения над которыми нс всегда приводят к одним и гем же
исходам и в то же время обладающими некоторой статистической
регулярностью. которая проявляется в статистической устойчиво-
сти частот исходов явлений.
Ста гис ги чес кая устойчивость частот делает весьма правдо-
подобной гипотезу о возможности количественной оценки случай-
ности гиги или иного события появляющегося в резулыазс экспе-
римента Как правило, эксперимент предпринимается для изучения
некоторых свойств интересующих нас экономического процесса
или явления При этом прэизводнгся построение математической
модели эксперимента, которое включает описание
- возможных исходов (элементарных событий),
класса рассматриваемых событий;
- вероятностей наступления этих событий
Современная теория вероятностей основана на аксиоматиче-
ском подходе Колмогорова, позволяющем охватить все классиче-
ские разделы теории вероятностей и дать основу для развития се
новых разделов, вызванных запросами практики
Одной из важных сфер приложения теории вероятностей яп
ляется экономика, так как при исследовании и прогнозировании
экономических показателей используется эконометрика, опираю-
щаяся на теорию вероятностей Практическое значение вероятно-
стных метадон сос тою в том. что они позволяют по известным ха
раыеристикам простых случайных явлений прогнозировать харак-
теристики более сложных ян тении
1.1. СI) чайные событии. Всрочкшкть
Пространством элементарных ct/бытии называют множе-
ство Q взаимоисключающих исходов эксперимента акос, чло каж-
дый интересующий результат эксперимента может быть однознач-
но описан с помощью элементов noio множества. Клементы £2 на-
зываются .элементарными событиями и обозначаются т О {г»}
Событием называют любое подмножество 11, элементов
из Q С ооытие Л произойдет, если прои эойдст какое-лнбю и < элемен-
тарных собыгий г» в А. Множества С нс содержащее ни одного
элементарного события. называется швашаисяылс событием. Мни-
жество Q. содержащее все элементарные собы i ня называется дсп -
товерным событием, i с. но событие, которое всегда происходит
Суммой двух собы । ии А и В называется событие
t * В(ЛоЛ). состоящее из элементарных событий, принадлежа-
щих ХО1Я бы одному из собы ГИЙ А или В.
Произведением двух событий А и В называется событие
ЛВ( АгI#), СОС1ОЯШИХ из элементарных событий, прима, (лежащих
одновременно А и В.
Противоположным собы гнем событию 4 называю, событие
Л. состоящее из элементарных событий, не припаял ежащих А
Разностью двух событий А и В называют событие 4\ Я. со-
стоящее из элементарных событий, принадлежащих событию Л, но
не принадлежащих событию В
События 4 и В называются несовматнычи. если у них нет
общих элементарных событий.
Пусть F поле собы i ни для данного эксперимента. Вероят-
ностью Р(Л) называется числовая неотрицательная функция, опре-
деленная на всех Ас Г и \ довлелвиряюшая трем аксиомам вероят-
ностей (аксиомам Колмогорова):
1 Вероятность любого события заключается в пределах от 0 до
I: 0< Р( Л)< I.
2 Вероятность дос говерно! о события равна единице /’(12)- I.
3 . Вероятность объединения побей конечной или бесконечной
последовательности попарно несовместимых собы i ий
(А,А; = 0 при г ху) равна сумме вероятностей
них событий:
p[E4»j=L'’(4).
R час । носта для твух сс бы гни 4 и Л: Л А -Ч)}- Р(А)•» Г(Н)
( утес । в) ни 4 способа задании чистовой неотрицательной
функции Р(лу.
1. Классический способ задания всроя i пост и
При данном спо» обе i .рост ранетве элементарных событий
яв дне гея конечным и все элемен гарные события раянонерои i ны
То. да вероятен, гь события определяется равенством:
(1.Л
п
6
|дс т число иемснгарных событий, благоприятствующих появ-
лению события Л, п общее число элементарных событий про-
орана ва 12
2.1 сомстричсский способ задания вероятное!и.
При данном способе пространство элементарных событий
ЯН.1ЯСТСН бесконечным, но все элементарные события, входящие в
это пространство, являются равновозможными
Если отождествлять ирсктранство элементарных событий с
некоторой замкнутой областью пространства из то верояп
ность события А будет вычисляться ио формуле:
ри=4?г ,,2>
1 дс gc6 и Да7) Ж G) меры областей
длина (если рассматривается прост рани во /?1);
- площадь (если расе м а грнвасАсм врос гранство Яз),
- объем (если рассматривается пространство /?,).
3. Дискретный способ задания вероятности.
При данном способе пространство элементарных событии
является бесконечным счетным множеством. Числовая нссприца-
тельная функция Р определяется таким образом, чтобы вероятность
каждого элементарней о события была равна некоторому числу
р., 0 < рж <!,/>,= Р\ (t)t) Toi да вероятное! ь любого события А вы-
числяется по формуле:
'Vh Хг. (1.3)
4. Статистический способ задания верой гности.
При данном способе рассматривается случайный экспери-
мент. для которого построить лространс!во элементарных событий
невозможно. ioi ла эксперимент проводится А ра< при неизменном
комплексе условий протекания и подсчитывается число экс пери-
мем гг в М*. в которых появилось некоторое собы те А. Вероятное ib
собьння оценивается относительной частотой (частостью) появле-
ния события Л, I с В!чЧИСЛЯСТСЯ по формуле
М
4-. (|41
/V
( oi ласно закону больших чисел, относительная частпга (час-
тость! почвления события сходится по вероятное jm к вероятности
появления события в каждом эксперименте:
7
Ila практике, при вычислении вероятностей а классической
схеме, при подсчете числа элементарных событий, принадлежащих
пространству П или некоторому событию, часто приходиться
пользоваться форму гами комбинаторики (соединений). Каждая из
комбинаторных формул определяет общее число элементарных со
бытии в некотором чкспериметгте. состоящем в выборе наудачу т
элементов из п различных элементов исходною множества Суще-
ствую! две принципиально различные схемы выбора
а) без возращения элементов (это значит, что отбираются либо
сразу все т элементов, либо последовательно по одному эле-
менту. причем каждый отобранный элемент исключается из
исходного множества).
б) с возвращением (выбор осуществляется поэлементно с обяза-
тельным возвращением отобранного элемента на каждом ша-
ге и тщательном перемешиванием исходного множсс1ва пе-
ред следующим выбором).
В результате получаются различные постановки эксперимен-
та по выСюру наудачу т элементов из общею числа п различных
элементов исходного множества.
1. Перестановки. Возьмем т различных элементов
будем перестав зять эти элементы всевозможными спо-
собами. оставляя геи змеиным их число и меняя лишь их порядок
Каждая из полученных таким образом комбинаций (в том числе и
первоначальная) носит название перестановки. Общее число пере-
становок из т элементов обозначается и равно т!:
/!>Ь2 3...(м-1) т = т!
С имвол ш! чи гается «эм факториал» С ледует огмез итъ, что 0!*1.
2. Размещения. Булем составлять из п различных элементов
множества по т элементов в каждом. отличающихся либо набором
элементов, либо порядком их следования Полученные при этом
комбинации элементов называются размещениями из п элементов
по т и иСюзначакнся < Их общее число равно.
А\ -л(и —1)(я-2) ..(и —(т —!)).
Замечать Перестановки можно считать частным случаем разме-
на чий (именно: размещениями из т элементов по т).
3. Сочетания. Из п различных элементов будем составлять
множества по т элементов, имеющих рахтичный состав По тучен
я
uuc при этом комбинации элементов называются сочетайиями из
п элементов по т Общее число различных между собой сочетаний
обозначается с 7 и вычисляется по следующим форму-
нам:
Выше прение laia/iocL, чтс нее п элементов различны. Если
же некоторые элементы повторяются то в этом случае число мио
жсствс покорениями вычне 1яюгся п< прут им формулам Так, если
срели п элементов есть П| элементов одного вила, п2 элементов дру-
гого вида, И| элементов третьего вида и т.п , то число перестановок
с повторениями определяется формулой
где л и. + г, + я, - и
Число размещений по т элементов с повторениями из л эле-
ментов равно л”, тс
(<) =л”.
\ 9 С nref
Число сочетаний с повторениями из и элементов по т эле-
ментов равно числу сочетаний без повторений из /Нпт-1 элементов
но т элементов, т.е.
(с;) ..
Задачи.
II. Плановое задание рабочие строительной фирмы могут
выполнить в срок или увеличив производите тьность Iсобытие ы
и ли увеличив продолжительность рабочего дня (событие о ), или
применив новую гехнпло|ию (событие м ). Любые действия рабо-
чих фирмы приводят к выполнению планового задания (событие
1) I рсбуется описать пространство элсменггрных событий D и за-
нисатьЯ в а небрс событий и через элементарные собы-
тия
Рсшстн Данный эксперимент состоит в выполнении плане
вою задания рабочими строительной фирмы. Все интересующие
нас в данном эксперименте элементарные собы, ня состоят в peiи-
с-грации выполнено или не выполнено планов*ч* стданис в срок. По-
этому пространство ♦тементарных событии состоит из следу юпгих
элементарных событий
9
fiA - co иРси - плановое задание не выполнено в срок;
лл со со1 со' плановое задание выполнено в срок увеличением
производительности груда рабочих;
ла со'со1 ш плановое задание выполнено в срок у нс л» чением
продолжи ic.ibHuci н рабоче । о дня,
соя си со'со плановое задание выполнено в срок применением
НОВОЙ ТСХНОЛО1'ИИ,
со< = со со со' плановое задание выполнено в ерик увеличением
производительности труда рабочих н увеличением
продолжительности рабочего дня;
бсА - со со' а? - плановое задание выполнено в срок увеличением
продолж!дельности рабочего дня и применением
новой технологии,
со, со со со - плановое задание выполнено в срок увеличением
производительности труда рабочих и применением
повой технологии.
о\-со'со<о' - плановое задание выполнено в срок увеличением
производительности труда рабочих, продолжи-
тельности рабочего дня и применением новой тех-
нологии.
Итак, Q«(tu.,j = l,8|.
Так как любые действия рабочих приводят к выполнению пла-
нового задания. то Л - л? г со1 ч л/ = оа + соу + г?>4 з сок з со* з- со + соя.
1.2. С ала и Маша договорились о встрече в определенном
месте между 17 и 18 часами Каждый приходи! в случайный момент
времени указанного промежутка и ждет другою до истечения часа,
но не более 10 минут, после чего ухолит Построить пространство
элементарных событии, взяв в качестве злемешарного события паре
чисел (хл-Х где х время прихо та Саши, а у - время прихода Маши
(время исчисляется в минутах, начиная с 17 часов) Выраз;пь событие
4 - встреча состоялась, через эд сменгарные собы гня,
13. Из ящика, содержащего 5 деталей, из которых 2 брако-
ванные. наудачу последовательно и без возвращения извлекается
по одной детали до появления бракованной, после' чего экспери
меш прекращается. Построить пространство элементарных собы
тин данного эксперимента
1.4. Взятая наудачу деталь может оказаться либо первого
(событие Л). либо второю (событие Я). либо третьего (событие С)
сорта Что представляют собой следующие события:
4* Я. Л+С,ЛЯ. ЛЯ + С?
Решение.
• 4-Я - эю событие, которое состоит при паст) пленив хотя
бы одного из событий /1 или В С тс ювагильно, Л + Я в на-
шем случае - деталь первого или второго сорта.
• так как Л+С - деталь первого или третьего сорта, то проти-
воположное этому событие А ¥ ( -деталь второю сори
• ЛЯ - невозможное событие, поскольку деталь одновре-
менно нс может быть и первого и второго сорта
• ЛЯ ♦ (’сумма невозможного события и события С равно С ,
т.е. АВ+С' -деталь третьего сорта
1.5. В урне 5 красных, 2 синих и 3 белых шара Все они про-
нумерованы цифрами ’.2...,10. Из урны берется нах дачу I шар
( обытие - шар с четным номером — обозначим через А. с номерам,
кратным 3, череэ Я. шар красного цвета - через С. синсз о - через
D и, наконец, белого - через L Что представляют собой следующие
события А+В: OE\Al\ А\В\ВЕ\ AD-L?
1.6. Очередной зритель входит в фойе театра, где уже собра-
лось 2л человек и начинает отыскивать знакомых среди собрав-
шихся. Пусть событие А состоит в том, что среди собравшихся
найдется л человек. знакомых вошедшему зрителю, а событие В
среди собравшихся найдется л человек незнакомых зрителю. Пока-
зать. что А ♦/? и Л \ Я з Я - достоверные события
1Л. Собрание, па котором присутствует 25 человек, в том
чиспе 5 женщин, выбирает делегацию их ipcx человек, (’читая, что
каждый из присутствующих с одинаковой вероятностью может
оыть избран, найти вероязноегь того, что в де iciзцпю войдут две
женщины и один мужчина.
Решение Рассмотренный в задаче эксперимент coctohi в вы-
боре *1 человек и < 2$ присутству ющих на собрании.
Выбор производится без возвращения и без у поря точения
ipex «теменtor hi множества, состоящего из 25 цементов Пусть
(о, выбор грех человек m 25 Тогда число элеме!гтарных собьпий
ространет на £2 определяется числом сочетаний и з 25 пл 3;
to
It
Событие А - наудачу составленная лелеганмя и< ipcx человек
состою из 2 женщин и одного мужчины. Число элементарных со-
бытии события Л равно числу способов выбрать 2 женщин из 5 и
одного мужчину нз 20.
m = C/Cl = — 20=200.
• 12
Вииюльювашиись формулой (1.1.). определим вероятность
того, чю в делегацию войд> i две женщины и один мужчина
и СД 3450 69
Ответ: Р[А)' 0.06
1.8. Брошены 2 тральные кости. Найти вероятность того,
что сумма очков на выпавших гранях равна 7.
1.9. В коробке 6 одинаковых пронумерованных кубиков Из
коробки наудачу по одному извлекают все кубики без возвращения.
Найти вероятность того, что номера извлекаемых кубиков появятся
в возрастающем порядке.
1.10. В коробке среди 40 лампочек 5 бракованных. Студент
покупает пять лампочек. Найти вероятность того, что среди 5 куп-
ленных лампочек 2 бракованные.
1.11. В магазин поступило 30 новых цветных телевизоров,
среди которых 5 имеют скрытые дефекты. Наудачу отбирается
один телевизор для проверки. Какова вероятность, что он нс имеет
скрытых цес}>ектов?
1.12. Ревизору нужно за определенный период времени про-
верять 100 предприятии Известно, что одно из предприятий со-
ставляет неправильные бухгалтерские отчетности, имеет скрытые
доходы. За первый квартал ревизор осуществил проверку на 10
предприятиях. Найти вероятность того, что среди 10 проверенных
предприятий окажется предприятие, которое ведет неправильные
бухгалтерские отчетности, имеет скрытые доходы.
1.13- И< 15 строительных рабочих 10 штукатуры, а 5 ма-
ляры Наудачу отбирается бригада нз 5 рабочих Какова вероят-
ность гою. ’по (.рели них будет 1 маляра и 2 штукатура0
1.14. Фирма <актю« ица 30 сделок по продаже товара У шести
из покупателей есть нарушения в регистрационных документах
П редставитс ль налоговой инспекции извлекает наудачу 5 логово
ров о про лаже товара. Найти вероятность того, «гго рсгис грацион-
ные документы у покупателем окажу гея правильно оформленными
12
1.15 .11а столе в беспорядки находя ся 15 ведомостей, среди
которых 10 непроверенных Бухгалтер наудачу извлекаем 3 ведомо-
сти Найти вероятность того, что извлеченные документы окажутся
непроверенными
1.16. В трех из 15 составленных кассиром счетов имеются
ошибки Ревизор решил проверить два счета Какова вероятность
юге. что а) ни в одном из проверяемых счетов нс окажется ошиб
ки. б) в каждом из двух проверяемых счетов будут обнаружены
ошибки?
1.17. В денежно-вещевой лагерес выпущено 1СЮОС» билетов В
лотерее рапагрываегся 120 денежных и 80 вещевых выигрышен
Определить вероятность тоге чю на приобретенный билет выпаде?
либо денежный либо вещевой вышрыш.
1.18. Среди 600 пошитых на фабрике женских пальто 16 шту к
оказались с дефектами Определить вероятность того, что взятое
наудачу для проверки новое пошитое пальто окажется с дефектом
1.19. В условиях подписки на Государственный грехлроцеш
ный выигрышный заем 1966 года сказано, что заем выпускается в
облигациях ДОСТОМНС1НОМ но 20 руб на 20 лет. Ежегодно произво-
дится 8 тиражей На каждый разряд займа в 100 млн.руб. ежегодно
падают выи)рыши на следующее количество облигаций
Рапкр выигрыша на 20 тн рублевую облигацию (руб.). включая царица тельную Стоимость облигации количсонс йьгггры шей в одном тираже
5000 >
2500 ! 1 5
I 1000 20
500 109
100 ’ i 750
40 8514
Всего
Определи ь вероятность выигрыша на одну облигацию а) в
нервом тираже 1966 юда б) и последнем тираже 198б юла
1.20. Набирая номер телефона абонент забыл последние 3
цифры Помня лишь то. что эти цифры различны, абонент набрал
их наудачу Найти вероятность того. что набраны нужные цифры
1.21. Двадцать юрювых фирм, заре! ис грированных в налог о-
вой инспекции, среди которых 4 имеют юварооборот свыше 10
мн пионов денежных единиц. для проверки налоювым ннспекто
ром случайно рагбиваюня на 4 пронумерованные группы по 5
фирм Найти верой । несть событий'
в
- А {в первую и вторую группу не попадет пн одна фирма,
имеющая товарооборот свыше 10 млн.дсн.ед.};
- Я3 {в каждую । рунцу попадет одна из фирм, имеющая това-
рооборог свыше 10 млн ден.сд.}.
1.22. Каждая из 8 фирм проверяется одним найм оным ин-
спектором. В штатом составе налоговом инспекции имеется 6 ин-
спекторов. Назначение инспектора на проверку данной фирмы
производится наудачу. Найти вероятность того, что первые шесть
фирм будут проверены налоговым инспектором
1.23. Ьу к пенный замок содержит на оси пять тисков, каждый
из ко орых разделен на шесть секторов с различными нанесенными
на них буквами. Замок открывается только н том случае, если каж-
дый диск занимает одно определенное положение относительно
корпуса замка Определить вероятность открытия замка, если уста-
новлена произвольная комбинация букв.
1.24. 3 подьезде лома установлен замок с кодом. Дверь авто-
матически открывается, если в определенной последовательности
набраны три кифрь из имеющихся десяти Некто вошел в полъетд
и. не зная кода, стал наудачу подбирать различные комбинации из
трех цифр. На каждую попытку он тратил 20 секунд Какова веро-
ятность события, состоящего в том, что вошедшему удастся от-
кры гь дверь за один час9
1.25. Пять человек вошли в лифт на первом этаже дсвяти-
этажиого дома. Любой пассажир может с равней вероятностью
выйти на 2-м, 3-м,..., 9-м пажах. Найти вероятность событий: а) пи
один из пассажиров нс выйдет на втором, третьем и чел вертом эта-
жах; б) трое пассажиров выйдут на девятом этаже: в) все пассажи-
ры выйду г на одиом этаже
1.26. Два парохода должны подойти к одному и тому же прича-
лу. Время прихода обоих пароходов независимо и равнонозможио в
течение суток. Определить вероятность того, что одном) нт парохо-
дов придется ожидать освобождения причала, се ти время раирузки
перного парохода Один час. а второ!о - два часа
Решение Пусть л время прихо.та к причалу пирвотт» парохо-
да. а V время прихода к причалу второю парохода. Гак как время
прихода обоих пароходов независимо и равнояозможло в течение
суток, то 0<r<24. OS>*<24 Тогда множество элементарных
событий Q определяется парой чисел (х г). т е
О~{(х,у) 0< х< 24, 0syS24).
Геометрически по множество точек квалрапт со с гор<нтой 24
>4
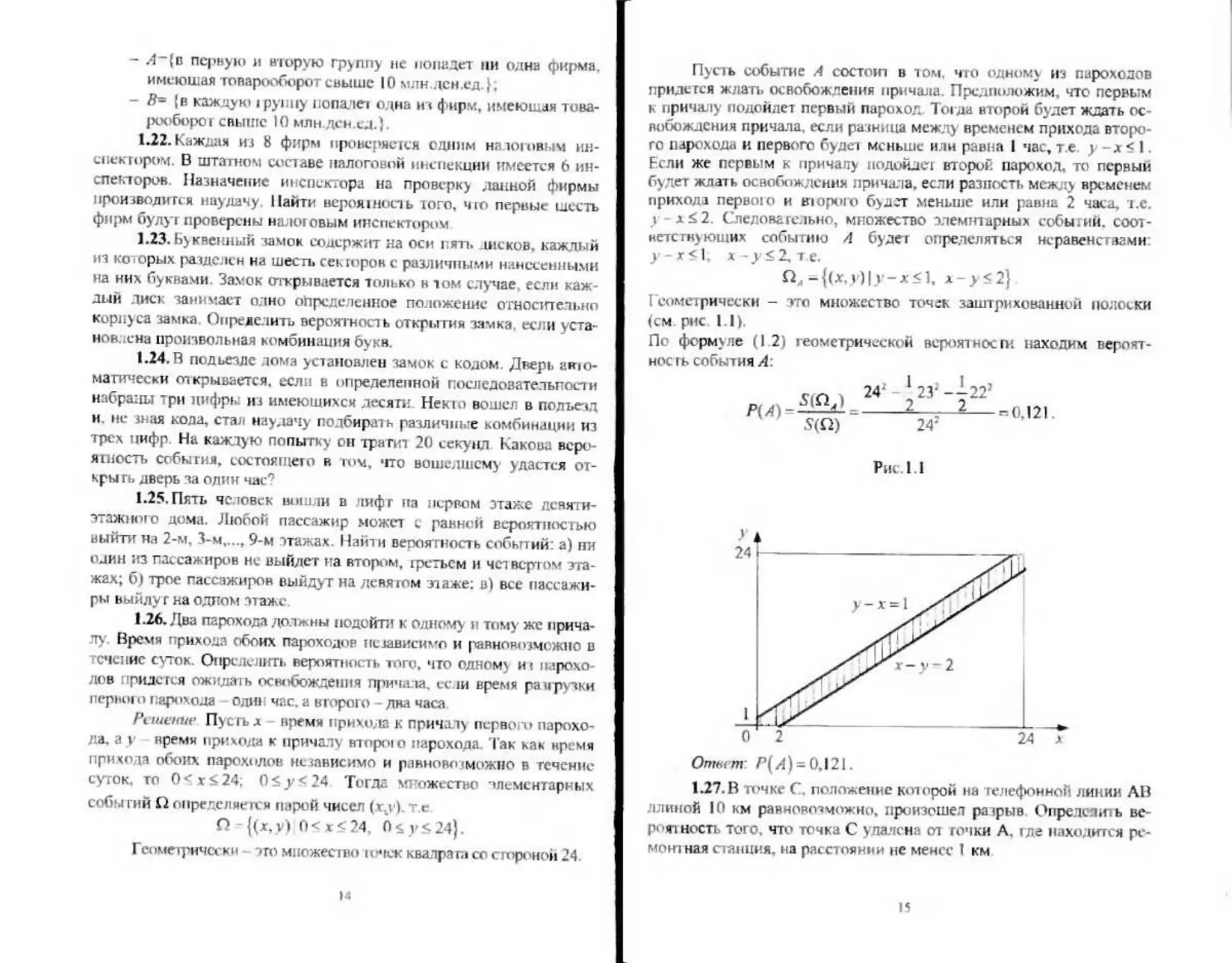
Пусть событие A состоит в том, чш одному из пароходов
придется ждать освобождения причала. Предположим, что первым
я причалу подойдет первый пароход Тогда второй будет ждать ос-
вобождения причала, если ра<ница между временем прихода второ-
го парохода и первого будет меньше или равна 1 час, т е ) - л < I.
Fenn же первым к причалу подойдет второй пароход, то первый
будет жлать освобождения причала. если разность между временем
прихода первою и tnoporo будет меньше или равна 2 часа, т.с.
у - х<2. Следовательно, множество элемнтарных собьний. соот-
ветствующих событию А будет определяться неравенствами
>--х<1, х-у<2,те.
_{(х,у)|у-х<1, л-у<2}
Геометрически - это множество точек заштрихованной полоски
(см рис. 1.1}.
По формуле (I 2) геометрической вероятности находим вероят-
ное 1ь события А:
Р(А)~
24’
23’ —22’
1___2__
24’
= 0.121.
Рис. 1 1
Отнепг Р(Л) = 0,121.
I.27. B точке С, положение которой на телес^юнноЙ линии ЛВ
длиной 10 км равневозможно, произошел расрыв Определить ве-
роятность того, что точка С удалена от точки А. где находится ре-
монтная станция, на расстоянии не менее I км
15
1.28. Определить вероятность события, состоящего в гом, что
студенту придется ждать поезда мсгро не более IU секунд при ус-
.швин,, что интернат движения поездов составляет 3 минуты
1.29. Два поставщика должны привести товар в Mai азин, у ко-
торого для разгрузки товара имеется одна рампа. Время поставки
товара поставщиками независимо и равновозможно в течение су
ток. Определить вероятность того, что одному из поставщиков
придется ждать освобождения рампы если время раирузки перво-
го поставщика один час, а второго два часа
130. В случайный момент времени к перекрестку. на котором
установлен автомаггичесюпт светофор. подъезжает автомобиль В све-
офоре олнх минуту торит зеленый свет и пплминуя ы красный, затем
снова одну минуту зеленый и по 1минуты красный и т.д. Какова вс
роятностъ тою, что автомобиль проедет перекресток без осгановки
131. К остановке через каждые 6 минут подходит автобус и
через каждые 7 минут троллейбус Интервал времени между мо-
ментами прихода автобуса и ближайшею следующего троллейбуса
равновозможен в пределах от 0 до 6 минут. Определить веройi-
нисть юго, что. а) первым подошедшим транспортом окажется ав-
тобус; б) автобус игк троллейбус подойдет через 3 минуты.
1.32. [Парик брошен наудачу внутрь круга радиуса R, Вероят-
ность попадания шарика (точки касания п юскости крута) в любую об-
ласть, расположенную внутри круга, пропорциональна плошали этой
области Найти вероятность тою. что точка прикосновения шарика к
плоскости круга находится от центра на расстоянии, меньше нг < К)
1.33. Случайная точка л равномерно распределена в правиль-
ном треут ельнике с вершинами (щ0).(-а,0),н).<г>/з ) Найти веро-
ятность того, что квадрат с центром г и сторонами пины Ь. парал-
лельными осям координат, целиком содержится в этом треугольнике.
1.34. Наудачу втять два положительных числа гну. каждое нт
которых не превышает I Найти вероятность юго. что сумма д не
превышает I. а произведение ту нс меньше 0.09
1.35. Быстро вращающийся дис к разделен на четное число сск-
горпя, попеременно окрашенных в красный и синий цвета. I In диску
произведен выстрел. Найти вероятность того, что пуля попадет в
один из красных секторов. Предполагается. что вероятность попада-
ния пули в плоскую фигуру пронорционатьма площади этой фи: уры
1-36. В шар вписан куб. Точка наудачу <афиксмрована в шаре
Найти вероятность того, чю точка попадет в куб.
16
1.37. Дяя предвари тельного опроса населения некоторого го-
рода в связи с избирательной компанией была произведена случай-
ная выборка 1000 участников 320 человек заявили, что они прош-
лосуюг за кандидата от партии «зеленых» Определите вероятность
того. что случайный избиратель будет голосовать за кандидата от
партии «зеленых».
Решение В эксперименте рассматриваемой задачи нет осно-
вании считать, что все элементарные события раваовозможны и
следовательно, нет возможности построить пространство элемен-
тарных событий.
Пусть событие А состоит r том что случайный избиратель
будет голосовать за кандидата от партии «зеленых» Дтя опрс юле*
ния вероятности злого события воспользуемся форм\ той (1.4)
/9М) =
320
КЮ0
= 0,32
1.38. Контролер, проверяя качество 500 деталей, изготовлен-
ных на автоматическом станке определил что И из них не удовле-
творяет стандарту Определите вероятность изготовления нестан-
дартной летали. 4
1.39. Среди 1000 новорожденных некоторого города оказа-
ккь 495 девочек. Чему равна вероятность рождения девочки в этом
городе0
1.40. При обследовании 1000 семей некоторого юрода оказа-
юсь что в 120 семьях имеются три ребенка Какова ожидаемая
частость семьи, имеющей 3 ребенка, в этом юроде?
1.41. Опре золите относительную частоту роста солдат равною
1м 80см, если среди НХХ) солдат сказатось 7J5O имеют ркт 1м 80см
1.42. На фондовую биржу на продажу поступи ю 30 акций, из
них 3 принадлежа г нефтяной компании Вес акции случайным об-
раюм распределитн поровну между' 3 брокерами Определи ib ве-
роятное гъ того, что каждому брокеру достанется по одной акиии
нефтяной компании.
1.43. Дворцовый чеканщик ктаде! к каждый ящик вместимо-
с!ы<» 100 мане! одну фальшивую. Король подозревает чеканщика и
подвергает проверке монеты, взятые наудачу пг одной и< каждою
из 100 ящиков Какова вероятное гь того, что чеканщик нс бу ici ра-
зоблачен.
1.44. Найти вероятность тою. что в номере сч< iu сберкнижки
стучайно гнягого кассиром я банке сумма дв\х первых цифр равна
сумме двух последних.
17
1.45. Вес некоторых пачек печенья оказывается заниженным.
Число таких паче* составляет 1% ел i>6u;ero числа пачек в большой
партии. Наугад из партии выбрали дне пачки печенья. Какова веро-
ятное! ь тою. что обе дачки имеют заниженным вес9
1.46. На отрезок ОА длины L числовой оси ОХ наудачу по-
ставлена точка В(Х). Наши вероятность тою, что меньший из от-
резков ОН и НА будет иметь длину, большую, чем 1/3. Предполага-
ется. что вероятность попадания точки да отрезок пропорциональна
тине отрезка и нс зависит от его расположения на числовой оси.
1.47. На плоскость, разграфленную параисльнь ми прямыми,
отстоящими дру! от npyia на расстоянии 6 см. наудачу брошен
круг радиуса I см Найти вероятность тою, что круг нс пересечет
ни одной из прямых.. Предполагается, что исход попадания круга на
плоскость определяется центром упавшего круга.
1.48. Имеются 300 претендентов на бухгалтерские должности.
Вероятность того, чго претендент имеет диплом равна 0,30, что он
располагает опытом бухгалтерской работы 0,70 и чго он имеет
диплом и опыт г л кой рабогы 0,20. Построить диаграмму Венна,
подьзчясь обозначениями: G - наличие лиги ома, И - наличие опы-
та бухгалтерской работы.
1.49. В 10 из 1000 собранных компонентов был обнаружен
монтажный, а в шли конструктивный брак. Имеются основания
полагатт, что ни один из ком пинен гон не имеет одновременно обо-
их браков. Постройте диаграмму Венна, показывающую различные
возможные исходы, при зтом пользуйтесь следующими обозначе-
ниями WO наличие монтажного брака, 5D - наличие конструк-
тивного брака, А7Э - отсутствие брака.
1.50. При обследовании потребителей была составлена выбор-
ка. включающая 100 человек. Возраст 60 из них превышает 30 лез
Я0 человек живут в городе, возраст 48 из 80 горожан превышает 30
лет. Постройте диаграмму Венна, отражающую состав выборки При
зтом пользуйтесь следующими обозначениями. ^30 - липа. возраст
которых превышает 30 лет. < 30 липа, возраст которых равен 30
Iодам или менее; Л - i орожнне, R сельские жители
1.51. Из множества претендентов па должность 'кономисза.
зарегистрированных на бирже труда, наудачу выбирают одного
Пусть событие А состоит н том что выбранный претендент закон-
чит ну < с красным дипломом. событие R - выбранный претендент
закончи । вуз без красного диплома, Г выбранный претендент за-
кончил техникум. Описать события, а) А НС, б) А ' АВ
18
1.52. Относите тьно каждой из группы событий ответьте па
следующие вопросы: образую! ли они полную группу, являются ли
несовместимыми, яв ляются ли равнонозможными Опыт результат
сбыта продукции Ач - {фирма не имеет прибыли}; Г = {фирма
имеет прибыль}.
1.53. Пусть «эксперимент состоит в проведении голосования по
ciparcrwi развития акционерного общества собранием из т членов
Каждый участник может юлосовать «за» и «пропив» или воздержаться
ст юлосования Каково число элементарных событий в 11 ес_ и голо-
сование является I) открытым. 2) тайным Если в процессе обсужде-
ния акционеры могут менял» свое мнение, то сколько элементов со
держит £2,если голосование проводжея жажды (двумя способами)
1.54. Акционер имеет и ценных бума! (акций). Пусть событие
J. (i। - 1,я) состоит в том, что r-я приобретенная нм акция обссцеии
ласы Описать события, заключающиеся в том. что: а) ни одна из акций
нс обесценилась. б) хотя бы одна акция упала в цене; в) только одна
акция обесценилась; г) только две акции обесценились; л) пи крайней
мере, две акции принесут прибы :ь; el только две акции обесценились.
1.55. Событие А, означает, чго данная прибыль получена от
i-го источника дохода С помощью событий А, и А описать собтт-
1им: а) прибыль получена, б) прибы и. полечена только от одною
источника дохода; в) прибыль нс получена
1.56. 11устъ события At = {трактор изготовлен на /-ом заводе}.
Я = {грактор, изготовленный на ьом заводе, дсфеюный}. f=L2
Выразить при помощи событий А и В и им противоположных сле-
дующие события а) получен доброкачественный трактор с первого
завода, 6) получен один доброкачественный трактор.
1.2. Свойства вероятностей. Условная вероятность.
Независимость событии.
Теоремы сложения н умножения вероятностен
Пусть язя некоторого случайного эксперимента постремно
вероятностное пространство 11 / ,Р).
Случайным событием А называется любое подмножество
пространства нкменгарных событий £1 Событие А 12 А называ-
ется событию А: событие А означает, что со-
бытие А не произошло События 4 и В называются
и.ч. если их ссвмсс нос появление (произведение) невозможное
событие: AB 0 События образуют полную группу собы-
зий. если они попарно несовместны и их объединение является
достоверным событием;
Числовая неотрицательная функция Р. определен! ая на Л,
удовлетворяет следующим свойствам:
1. Если события А Л?..- .Аг. образуют полную группу событии,
то вероятность объединения этих собьпии равна единице:
т
2. Вероятность противоположного события Р{ А)= 1 Р(А)
3. Если событие А влечет за собой событие В, то вероятность со-
бытия А Нс превосходит вероятности события В, т.с. Р(А)<Р(В\
11усть А и В - наблюдаемые события в эксперименте, причем
/Х^)>0 (Р(В)>0). Условной вероятное тъю Р(2?|Л) (Р(Л В)) осущест-
вления собы । ия В (А) при условии, что собьыис А (В) произошло в
результате данного эксперимента, называется величина, опреде-
ляемая равенством:
= р(л)>ОилиЛ^|Я) = -у^2. Р(5)>0(21)
Из этих формул следует, что
ИЛИ Р\АВ)~Р[В)Р(4|Я). (2 2)
Теорема сложения:
Пусть Л/Л?. <Лг - совместные события Toina вероятность
их объединения вычисляется по формуле:
т
I
\»«1 74 Ы •J* \/я
Для двух событий зга формула > мест вид:
Р(Л4 Я)-Р(Л) ♦ Р(В)-Р(АВ).
Событие А называется независимым от события
творяющего условию если выполняется
Р(А\ВУР(А).
События А и В называются шзависимыми, если:
P{ABVP(A}I\BY
А„ называются ненипн имыми в
сти, если для любого набора из т событий (п/ 2.3.
ся равенство:
fi. удовле-
равенство:
События A
совокупно-
и} выполняет-
20
P(A,A.S \J = P<A> )Р<А4 > *A,J. к„б{1 2...,п). (2.6)
Теорема умножения :
Вероятность произведения событий АЬА^.^1„, равна произ-
ведению вероятностей этих событий, причем вероятность каждого
следующего по порядку события вычисляется в предположении,
чю все предыдущие имели место
= р(4)ПА|л,)/’(Л14Л) •/’ 41Г14 • (2 7)
Дли нсмвииимых событий в совокупности формула (2 7)
принимает вид:
(2.8)
Заметим, что при использовании свойств и теорем теории ве-
рояпюстей пространство элементарных событий строшь нс обяза-
1СЛЬН0
Задачи.
2.1. Вероятность заключил, контракт с некотором фирмой
равна 0,5, а вероятность заключить контракт на сумму 1млн.ден.ед
равна ОД Найти вероятность тою. что при заключении контракта
его сумма I млн.ден.сл.
Решение: Для описания эксперимент, рассматриваемо!о в
задаче инсдсм следующие события: 4-{заключен контрам с неко-
торой фирмой). Я={сумма контракта равна I млн.лен ед ). Событие
ЛЯ={заключен контракт на сумму Iмлн.дел ед.}. Событие
А I "{сумма контракта при условии, что он заключен, равна
1млн.ленел }. Вероятность событий Я и 1R Р{А)-0,5; Р(АВ)=(Р
1 oi да по форму 1е (2 1) вероятность искомого собы гня равна:
«д
ГИ) 0.5 5
Отмен Вероятность того, чго сумма контракта при его за
к точении 1 млндсн.ед. равна 0.4.
2.2. В семье двое дней Считая, что рождение мальчика и
Девочки независимые и равновероятные события, вычислить ве-
роятность тою, что оба ребенка девочки, сети известно, чго в се
мы еегь девочка
2.3. Пусть события А и В ивисимы Следует из этого, что
они несовместимы? Независимы'
2.4, Пусть события А и R несовместимы Будут ди они зави-
симыми 1 Нс «ависимыми?
21
2.5. Из ИЮ претендентов на должность менеджера внешне-
горговой фирмы 50 человек шают английский язык, 40 француз-
ский и 35 - немецкий. Английский и французский языки шают 20
। рстендентов. ан/ шйский и немецким — R, французским и немец-
кий - 10 Вее три языка знака 5 претендентов Один из претенден-
тов зашел на собеседование Рассмотрим события: X-{вошедший
знает английским язык}; /^{вошедший знает французский язык};
С {вошедший 3naei немецкий язык}; /2-(вошедший знает англий-
ский или французский языки}; £-{ вошедший нс знает ни одного
языкаf. Требуется: а) указать вес пары независимых событий; б)
установить, являются ли события Л,Я.С независимыми в совокуп-
ности; в) вычислить вероятности событий D н Е.
Решение\Так как рассматриваемый эксперимен> состоит в
случайном выборе претендента, то пространство элементарных ис-
ходов £2 .можно записать в виде: £2 = \ ц | / - 1,10С J, и; выбор од-
ного /го прстендентх Отсюда следует, что и(12^100 События,
приведенные в задаче, имеют следующий состав
*’ " {м\ IJ - . В - j иа | к - Ц4о|; С • м; |е - 1:35}, индексы j\ к е
- изменяются независимо друг ст друга. D=A+B; Е - А В С Вос-
пользовая цись классическим определением всроя кости, опреде-
лим вероятности событ ии А. В, ('. AR, АС, ВС'
100 2 100 5
Р(4С) = - --2. —= ’ . Р{.АВС}——
100 25 100 10 100 20
а) Для отве.а на вопрос проверим ранено!на (2.2):
I) Р[АВ^Р(Л) Р{В},
”^7- Р(.ЧЯ),?£
100 20 100
С ледова 1ельно события А
и В независимы;
2) /1ЯС) ИЯ)ЛС). -
т — С дсдовяте/ ьмо собы-
10 50
гля В и С не являются независимыми
• Следоваггльно со-
2 20 25 40
бытия А и ( не являются независимыми.
6) I Тз приведенных вычис лепим следует. что для любых двух собы гни
и । совокупности событий A.RX нс выполнятся равенство (2.6), го
события А. В и (’нс являются независимыми в совокупное ти.
22
в) Поскольку события А и В совместны и D-A+B, то, воспользо-
вавшись формулой (2.4), получим:
P(D) ~ Г\ 4) Ч\В)-Р{АЬ) - - +
10
Легко показать, что А В C—AiB+C. Тогда, воспользовав-
шись свойством 2 и формулой (2.3) для трех событий будем
иметь.
P(L) = Р(ЛВС)= Р( 1+ В+ОЫ^М+С) l-(/’i4)+P(f)+ ПС)-
Р{АВ)-Р(АС)-Р(В( )» Р(АВС))-}
2*5*20*5 25 10*20/
, 50 + 40 + 35 20-8 + 5-10 г
-1------------------------=0,08.
100
2.6. В читальном зале имеется 6 учебников но теории веро-
ятностей, из которых 3 в твердом переплете Библиотекарь наудачу
взял 2 учебника. Найш вероятность тою, что оба учебника окажут-
ся в твердом переплете
Решение: Пусть А первый взявый учебник имеет твердый
переплет, В - второй учебник имеет твердый переплет. Вероят-
ное гь того, что первый учебник имеет переплет Г( . Ве-
роятность того, что второй учебник имеет твердый переплет, при
условии, что первый взятый учебник был в персптстс, т.с. условная
2
вероятност ь собы гия В равна Г( В | А) = —.
Искомая вероятность гою, что оба учебника имеют переплет,
но теореме умножения вероятностей зависимых событий равна
Р(Я5) = Р(/|)-Р(/?|4)= * ^-=0.2.
Ответ: Р’0,2.
2.7. 11айти вероятность того, что наудачу взятое двухзначное
число окажется кратным 2. либо 5, либо в ому и другому одновре-
менно.
2.8. Н продукции часового завода брак сослали яе- 5% от об-
щего количества выпускаемых часов Для контроля отобрано 20
часов. Какова вероятность того, что среди них имеются хотя бы
один часы с браком9
2.9. О цехе работают 7 мужчин и 3 женщины По табельным
номергм наудачу отобраны 3 человека. Найти вероятное! ь гою. что
все отобранные липа окажутся мужчинами
2.10. Бухгалтер составил два варнаша годового баланса пред-
приятия. Вероятность гоп», чго и первом варианте баланса содер-
жится ошибка 0,85, а во втором 0,99. Найт вероятность того, что
баланс предпрнягия cot гав ген с ошибкой.
2.11. Вероятности попадания в цель при стрельбе ил трех ору-
дий соответственно равны: р, -0,8. />2 =0,85: ру -0.9. Какова веро-
ятность хотя бы одного попадания при одном залпе из трех ору-
дий?
Решение: Введем следующие события: Л-{хотя бы одно по-
падание при одном залпе). А,= {попадание / го орудия}, г 1,2,3.
Л {промах i-го орудия). События AltArA> независимы в сово-
купности, но совместны Вероятности противоположных событий
раины.
J-1-0.8 0.2; Р(Я?)-,-г(л.')- 1 <>.«5 = 0.15;
Р(л) = 1-/>(А)’г1-0.9 -0,1
1ак как событие А противоположно событию, состоящему в
том, что все три орудия промахнулись, го
Р(Я|-1-Р(л) = 1 Р(д)-Р(л) />(4) = 1-0,2 0,15 0.1-
-1-0.003 = 0,997.
Ответ: р^0.997.
2.12. Студент Иванов подписал поздрав1ггслып>1с открытки
трем девушкам, запечатав их в конверты и случайным образом
подписал адреса. Определил вероятность того, чго xoih бы одна
открытка попадет по назначению.
2.13. В коробке гежит 3 буквы ратрешоЙ азбуки буква «М»,
две буквы «И», четыпе буквы «Р». Извлекаем подряд 3 карточки из
коробки без возвращения. Определить вероятность того, что в ре-
зультате извлечения букв образуется слово «МИР».
2.14. Студент знает 20 из 25 вонр<чнв программы Найти вс
роят пост ь того, что студент знает предложенные ему экзаменато-
ром гри вопроса
2.15. Hix производит кинескопы для телевизоров, причем
30% всех кинескопов имени диагональ Ч см. а 70% 72 см Из
всстно, чго 50% всей продукции отправляется на экспорт, причем
24
из общего числа кинескопов с диагональю 72 ем 40% отпранлясгся
на экспорт. Найти вероятное 1Ь того, что наудачу взятый кинескоп
имеет диагональ 51 см и будет отправлен на экспорт.
2.16. ( гудент может уехать в университет или автобусом, ин-
тервал движения которого 20 минус, или троллейбусом, интервал
движения которого 10 минут. Найти вероятность того, что с гулею,
подошедший к остановке, уедет в течение ближайших пяти минут
2.17. На распродаже к некотором} моменту времени осталось
1 пара мужской обуви. 2 пары доской и 3 пары женской обуви.
Каждый очередной покупатель с равной вероятностью покупает
лишь одну пару обуви Два человека из очереди последовательно
приобрели обувь. Найти вероятность юго. что а) куплена разная
обуть, б) куплена детская или женская обувь
2.18. Вероятность того, что в течение полугола цены на iсва-
ры народного потребления увеличатся, равна 0.95. а р.ер<эятносгь
того, что за -пот же промежуток времени изменится (увеличится)
минимальная заработная плата, равна 0,9 Найти вероятность появ-
ления только одного из этих событий, если они независимы
2.19. На рынке 7 фирм продают средства производства, а 3
фирмы - предметы потребления Покупатель наудачу заключает
сделки с гремя фирмами. Найти вероятность того, что вес отобран-
ные фирмы представляют средства производства
2.20. Определить вероятность того, что выбранное наудачу
изделие является первосортным, если известно, что 5% всей про-
дукции является бракованной, а 85% не бракованных изделий
>довлсгворяеттребонапиям первого сорта
2.21. Бухгалтер обслуживает 5 отделов. 20% рабочего време-
ни он проводит в нервом отделе, 10% - во втором 15% в гретым,
25% - в четвергом и наконец .30% - в пятом Найти вероятность
того, что в наудачу выбранный момент времени бухт'алтер нахо-
дился. а) в нервом или третьем отделе; б& во втором или пятом; в) в
первом или четвертом; г) в первом или втором, или третьем; л) в
четвертом или пятом
2.22. Акционерное общество состоит н< грех независимо ра-
ботающих заводов Эти заводы работают в течение времени 7 без
убытков соответственно с вероятностями 0.85 1. 0.75 I и 0,701. Най-
ти вероятность того, что за время 7 с убытками будет работать:
а) только один завод, б) хотя бы один завод.
2.23. Завод содержи! 2 одинаковых параллельных неча, дуб-
лирующих лри Друга. Ворон»жх'тъ безотказной работы каждого
пеха равна 0,9 При выходе из строя первого цеха хкущсствляется
мгновенное переключение с вероятностью, равной I. на второй цех.
Определить вероятность работы завода.
2.24. Завод состоит из трех цехов. Для юго. чтобы завод ос-
тановился. необходимо и дос cat очно, чтобы ос тиснились и пер-
вый и второй цеха или только третий цех. Цеха останавливаются
независимо друт от друга причем вероятности остановки цехов за
определенный промежуток времени соответственно равны
Опре.лелзггь вероятноеib гою. чго завод не выйдет из
строя за указанный промежуток времени
2.25. Вероятность снижения Hanoi а на корпорации н тюм го-
лу оценивают в 0,5. а вероятность зою чю наш основной конку-
рент не внесет изменений в важнейшее изделие - к 0.3, причем оба
эти события рассматриванием как независимые 4pyi oi друга. Оп-
ределит» nepoHVHocib появления обоих исходов.
2.26. Известны следующие значения вероятности допо шигс ib-
ных потребностей фирмы в инженерах на предстоящие два юда
Число инженеров <100 100-199 200 299 - 00-399 400-499 >500
ГЗсрояпюсп» 0.1 С.15 0,3 1 — ° 1 0,1 0,05
а) Какова вероятность того, что на нр<няжении двух предстоящих
лет фирме дополнительно требуется 400 и более инженеров.
б) Какова вероятность того, что фирме потребуется по меньшей
мере, 200, но не более 399 инженеров?
2.27. На протяжении некоторого периода пени двух третей
котирующихся па бирже акций повышались или оставались неиз-
мененными, а цены одной трети акции падали Предположим, что
проводится исследование цен грех наугад выбранных акции.
а) Обозначая повышение цены акции или ее неизменность через
Л. а падение пены через В. постройте древовидную диаграмму
вероятностей повышения или падения цен для выборки из трех
акций (диаграмма должна быть трсхступснчатой).
б) Пользуясь этой диаграммой, определите верояпюс.ъ падения
цен всех грех акций.
в) Какова вероятность паления цепы, по крайней мере, одной акции.
(Только ош а ветвь диаграммы нс удовлетворяет ггому условию;
поэтому для получения ответа из I (• можно вычесть вероятность
грех последовательных исходов представленных на этой ветви)
2.28.Вероятность увеличения потребительского спроса на из-
делия нашей фирмы в будущем году оценивают в 0,7 Гели эта
опенка оправдается, то с вероятностью с 0.8 возрастет объем нро-
26
лаж фирмы Гели же она не оправтасгся, го вероятность расшире-
ния продаж составит 0,5.
а) Какова вероятмехггъ роста по греб» геликого спроса и объема
продаж?
6) Какова вероятность ситуации, при которой нет одновременного
увеличения, как потребительского спроса, 1ак и объема продаж
2. 29.3л некоторый промежуток времени юрговая фирма мо-
жет бьп ь ликвидирована с вероятностью 0,25, работать с прибылью
с вероятностью 0,25 и разделиться на две фирмы по группам това-
ров с вероггностьк» 0,5. П следующий такой же промежуток време-
ни с каждой торговой фирмой независимо от ее регистрации про-
исходит то же самое. Сколько фирм и с какими вероятностями мо-
гут работать к концу второго промежутка времени'’
230. Пу с it собы гие А в каждом испытании появляется с ве-
роятностью р и проитволи1ся л испытаний. Как вычислить вероят
носатого, чго событие А появится хо1я бы один раз в и испытани-
ях (ответ обосновать).
Решение- Искомая вероятность Р( Л) - I1 - р]", «Хитя бы
один раз» это «начит, чго событие нс произойдет ни разу (1-р)"
Тогда искомая вероятность - эго вероятность противоположного
события.
231. R продукции завода брак сосзавтяет 3% ог общею ко-
личества выпускаемых деталей. Дтя контроля отобрано 10 деталей.
Определить вероятность тою, чю среди отобранных деталей име-
емся хотя бы одна бракованная.
232. На ярмарке л предпринима гелей пролают одну и гу же
продукцию. Вероя1ностъ продать всю продукцию любым прелнри-
|* имя гелем равна 0.8. Панги вероятность того, чю котя бы о дин из
них продаст всю продукцию
233. На бирже два брокера соревнуются кто на большую
скмму заключи» сдс>юк. Причем л я згою необходимо первому за
м.ючить т сделок, а второму п сделок (пг>л) Вероятность оклю-
чи1 ь следующую сделку для первою брокера равна р а для второю
7" I-р Определигь вероятное^ победить в этом соревновании пер
ним брокером
1.3. Формула полной вероятности. Формулы Байеса
(теорема i ипогез)
Пусть случайный эксперимент можно описать событиями
// Л2. -Л^ которые являются попарно несовместными
Н Г\Н ,-0, и их объединение достоверное событие
•н
|1Н, -Q. Такие соГнлия Н, называют гипотезачи. Предполагает-
гМ
ся, что событие А может произойти с одной из гипотез /4
Вероятность любого события /1. которое может произойти с
одной из гипотез И„ будет равна сумме про» {ведений вероятностей
гипотез на условную вероятность события Л. т.е. вычисляется по
формуле.
Р(А)^Р(Н,)Р(А\Н,). (3.1)
которая называется фо/нплсш полной вероятности.
Безусловные вероятности Р\Н ). i~\.m, рассматриваются
как априорные (доонышые) верой гнести гипотез.
Предположим, чтп эксперимент произведен и в результате
произошло событие А. Как изменится при лом апостериорная (но-
слеопнтная) вероятность 1 ипотез
Условные вероятности гипотез Н^Нъ--Лт при условии, что
собы iис А имело место, вычисляются по формулам Байеса:
ЖН.1Л). (3.2)
£р|«,)ЛЛ|И.)
ы
Задачи
3.1. В некоторую торговую точку поступает определенною
вида го вар or двух производителей. Известно . чти первый произ-
водитель поставляет 40% этого товара а второй - 60%. Опыт пока
зынает, что, как правило, 2% изделий перво» о производителя со-
держат брак, а для второго производителя брак составляет 3%. Оп-
ределить вероятность того, что случайно отобранием^ изделие со-
держит брак.
Решение, Из условия <и зячи следует, »ло рассматриваемое
событие Л -{случайно отобранное изделие содержит брак} может
произойти с одной из гипотез Н;, / -1.2. //; (изделие поставлено /-
ым производителем I.
ZK
Безусловные априорные вероятности этих гипотез легко вы-
числяются по классической формуле (II):
40 60
Р(Н,) = - = 0,4: Р(Н I- — -0,6
НЮ 100
Условные вероятности событий А\Н, ={бракованное изделие
составлено i-ым производителем}. /-^1.2, гак же определяется по
формуле! 1.1):
Р(Л|Н,) = —= 0,02; Р(А\Н- )= — = 0.03.
Применив формулу полной вероятности (3 I). получим иско-
мую вероятность:
РМЬ ХР(И,)Р(АЛ,)^Р(Н,)Р(А Я,)4
= 0,4 0,02 + 0,6 0,03 = 0,008 + 0.018 = 0,026.
Находясь в условия?, этой же задачи, предположим, чзо вы
бранное изделие содержи! брак Тогда определим вероятность то
го. что это изделие поставил первый поставщик, воспользовавшись
формулой Байеса:
и । п_ Pdii^AiHj 0,4 0,02 0,008 4
ПА) 0.026 0,026 13
Ответ: Л(Л)-0,026; Р(Н, | Л)-
3.2. Партия транзисторов, среди которых 10% дефектных,
пос гу ни ia на проверку Схема проверки такова, что с вероя гное тъю
0,9S обнаруживают дефект (если он есть), и существует ненулевая
вероятность 0.03 того, что исправный транзистор Суде! признан
1гфекгным. Какова вероятность того, что случайно выбранный из
партии транзисюр будет признан дефектным?
33. В продажу поступают телевизоры трех заводов. Продух
пия первого завода содержит 20% телевизоров со скрытым дефск-
। ом, второго !(*%. третьего 5% Какова вероятность пр кобра т и
неисправный телевизор, если в магазин поступило 30% те 1евизо»
рон с перво! о заел да, 20% со второго, 50% с третьего?
3.4. В ящике лежит 20 генннсных мячей в гом числе 15 но-
вых и 5 использованных r hi ре. Для игры наудачу выбирается 2
мяча и после игры возвращаются обратно Затем для второй игры
также наудачу навлекав пя ешс 2 мяча. Какова вероятность того,
что вторая игра будет проводиться новыми мячами*
29
3.5. Из деся и студентов, пришедн их сдава(ь экзамен по
теории вероятностей и взявших билеты. Иванов и Петров знаки 20
билетов из 30, Сидоров успел повторить только 15 билетов, осталь-
ные студенты знаки вес 30 би ютов. Ио прошествии отведенного
времени на подгоговку экзаменатор наудачу вызывает отвечать од-
ного из студентов Какова вероятность того, чго студет сдает эк-
замен, если знание билета гарантирует сдачу экзамена с вероятно-
стью 0,85, а при незнании билета, можно сдать экзамен лишь с ве-
роятностью 0,1?
3.6. Для контроля продукции иэ грех партий деталей взята
для испытаний одна деталь Как вс шка вероятность обнаружения
бракованной продукции, если в одной партии 2/3 де алей брако-
ванные, а о лру। их - Вес доброкачес!венные0
3.7. Число бракованных микросхем на I000 априори (цо
опыта) считается равповозможным ат 0 до 3. Наудачу протестиро-
ваны 100 микросхем, оказавшиеся исправными. Какова вероят-
ность того, что все схемы исправны?
3.8. Определить вероятность того, что 100 лампочек, взятых
наудачу из 1000, окажутся исправными, если известно, что число
HcnopMemiux лампочек на 1000 штук равново «можно от 0 до 5.
3.9. Известно, что 06% выпускаемой продукции удовлетво-
ряю- стандарту. Упрошенная схема контроля признает пригодность
стандартной продукции с нерол нос 1ью 0,98 и нестандартной — с
вероятноегыо 0,05. Определить вероятность того, что изделие,
прошедшее упрощенный контроль, удовлетворяет стандарту*.
3.10. 11а фирме работает два бухгалтера - опытный и начи-
нающий Опытный бухгалтер оформимет 75% документов, а начи-
нающий 25% V опытного 6ух1влтсра наличие ошибок в доку-
ментах составляет 0.5%, у начинающего - 8%. Какова вероятность
(ого, *гго взятий наудачу документ окажется с ошибкой?
3.11. Рабочий обслуживает 3 станка, па которых обрабатыва-
ются однотипные де а ш. Вероятное * брака для первого станка
равна 0,03. для второго - 0 05, для третьего - 0.06 Обработанные
детали складываются в один ящик Производительность второго
станка в дна раза больше, чем первого, а третьего в два раза мень-
ше, чем первого Какова вероятность того, чго В1ятдя наудачу де-
таль из ящика будет бракованной?
Ртеине, Введем события: 4= {взятая наудачу деталь брако
ванная}. Нг {лететь изготовлена ни /-ом станке}. / 1.2.3 Пусть г
производительность первого станка, toi да производите л ьнечть
10
н горою и — - производительность |ретьсю. Общая производи-
leibifocib трех станков равна х + 2х к —--х.
2 2
Вероятности i ипотсз Ht равны:
х 2 2г 4
2л г г у-» •
Вероятность события А находим по формуле (3 1):
Г(.П = -2 0.03+4 0.05+1-0.06 1(0.06 + 0,20 + 0.06) = —=-8
7 7 " ' 700 1‘
Ответ'. п-----
175
3.12. Фирма совершает сделки, 80% из которых прибыльные,
а 20% — неприбыльные. Вероятность банкротства фирмы за время г
в случае, когда она заключает прибыльные сделки, равна 0,01, а в
случае заключения нс прибыльных сделок равна 0,7. Определить
вероятность банкротства фирмы за врс мя /
3.13. При наступлении кризиса сбыта продукции фирма нс
терпи* убытков С ВероятностьюР/, полностью терпит банкрс гствос
вероятностью р_- и имеет серьезные издержки с вероятностью
= I -(р р-) Две серии серьезных издержек приводя] к полно-
му банкротству фирмы. Найти вероятность того, что при наступле-
нии и кризисов сбыта продукции фирма нс обанкротится.
3.14. В группу, состоящею из 20 студентов, добавили отлич-
ники после чего из нес наудачу перевели в другую группу cry лен-
ча. Определить вероятность того, что переведенный студет ска-
жемся отличником. если все предположения о первоначальном co-
Ci анс ipynnw равновозможны
3.15. Д1Я поиска самолета, потерпевшего аварию выделено 5
вертолетов. каждый из которых может быть использован для а пис-
ков ь одном из двух возможных районов, где самолет можс! нахо-
диться с верояпюстями 0.7 и 0.3 Как следует распреле шть верю ае-
•н по районам поисков, чтобы вероятность обнаружения самолета
была наибольшей ес аи каждый вертолет обнаруживает находящий-
ся н районе поисков само лет с вероятностью ОД а поиска осу шест н-
пяются каждым вертолетом независимо от других? Найти вероят-
ность обнаружения самолета при отимальной процедуре поисков
3.16. Два предпринимателя занимаются реализацией одинако
Boit продукции, которая поставляется ими в один и тот же магазин.
Первый предприниматель посганлцет продукции к 2 ра<а больше,
чем второй, причем продукция высшего качества у нею составляет
60 %, а у второго Н4% Случайный покупатель приобретает про-
дукцию высшего качества Определи к вероятность того, что она
поставлена первым предпринимателем.
Решение Рассматриваемое событие А “{приобретена про-
дукция высшего качества} может произойти из одном из ишотез //„
Нг {продукция посган!сна /-ым предпринимателем С / 1.2 Безус-
ловные неопытные вероятности гипотез вычисляются по классиче-
ской формуле (1.1):
Р(Н,) = |,
гак, как первый предприниматель шчлав ihct в 2 раза больше про-
дукции.
Условные вероятности событий А\Н. {/-ым предпринимате-
лем поставлена продукция высшего качества], так же находятся по
формуле (1.1):
Р(Л|Н,) — = 0,6; Р( Л |//,)«-- = 0,84.
100 ' 1Г 100
Далее находим вероятность того, что случайный покупатель
приобрел продукцию высшего качества, т.с. вероятность события
А Поскольку событие А может протгзойти с одной из imuotci Н\
или //2, то для нахождения вероятности события .1 воспользуемся
формулой полной вероятности
Р(Л)-Р(/7()Р(4|Н)+Г(//?)РМ /Л) =
--0.6 I --О.Ш-0,4 4 0,28=0.68.
3 3
Событие Л нроиюшло. тс. покупатель приобрел продукцию
нысшсго качества, тоша вероятность события А И\- (продукция
нысшего качества поставлена первым предпринимателем) вычис-
лим по формуле Байеса:
2
/•(// Я) 3 °-6 0.4 10
I 1 ' л 4) 0.68 0.68 17
3.17. Возбуждено деле» о банкроте! ве фирмы. Основанием для
Этого мог ли быть с 1едуюшис положения
I. Заявление предприятия о своем банкротстве.
2. Решение суда о возбуждении дела о банкротстве
12
3 Заявление кредитора. поданное после определенней о
срока
Вероятности использования каждого из положений соответ-
ственно равны 0.9: 0.96, 0.99. Найти вере <1носгь того, чго дело о
банкротстве фирмы возбуждено на основе второго положения
3.(8.Число трузовых автомобиле! проезжающих по шоссе,
па котором стоит бензоколонка, относится к числу легковых авто-
мобилей. проезжающих по тому же шоссе как 3:2. Вероятность to-
о. что будет заправляться ipy юной автомобиль, равна 01. для лег-
ковых автомобилей зга вероятность равна 0.2 К бензоколонке
подъезжает для заправки автомобиль 11айти пероя~нисть лого, чго
это грузовой автомобиль.
3.19.Изделие проверяется на стандартность одним ит двух
товароведов Вероятность того, что изделие попадет к первому то-
вароведу, равна 0,55. а ко второму 0.45. Вероятность того, что
стандартное изделие будет признано стандартным первым товаро
ведом, равна 0,9, а вторым - 0.98. Стандартное изделие при про-
верке было признано стандартным. Нагггн вероятность inio, что эго
изделие проверил второй товаровед
ЗЛО.Расследуются причины банкротства фирмы, о котором
можно высказа/ь четыре предположения (гипотезы) Н , /А, II3 //4
По статистическим паяным } 0.2, Р(/АНд4:
Л/А)=0.1. В ходе анализа обнаружено что фирма обанкротилась в
связи с неудачной маркетин]свое политикой (событие Л). Услов-
ные вероятности события согласно той же статистики равны:
/5 4 //0=0,9; Р(Л1//5)=0; Р(А Н ) 0,2, ЛХЛ1/74> <1,3. Какал из гипотез
наиболее вероятна при данных условиях?
3.21. Два из трех работающих гслсвиэоров. которые работают
независимо труг ел труга, отказали Harm верояпюстъ того, что от-
казали первый и второй телевизоры, если вероятность отказа гь рвого.
нторого н третьего телевизоров соответ*. гвенно равны 0.2 0,4 и 03
3.22.Ко» этильные студентов заочников попадают для провср-
•и к одному из двух прсподшгпегек Вероятность того, чго кон
Трольная попадет ь первому прт.ощиатс по равна 0.6. а ко второму
( 4 Вероятность того, что работа бу гст зачтен.» первым преподавате-
лем. рани; 0.94, 2 вторым 0.98 Работа при проверке была зачтена
Найти вероятность того, что ее проверил первый преподаватель.
3.23.Чис ю с удентов, изучающих французский язык, о»по
Сигся к числу студентов, изучающих ашлийскин жык как V7. Вс
реятпоегь того что за границу на практику отправят студентов.
тз
изучающих французский жык, равна 0,2. Для студентов, изучаю-
щих английский язык, эта вероятность равна 0,5. За границу отпра-
ВИ-HI студентов. Найти вероятность того, что эти студенты изучают
французский язык.
3.24. Имеются дне партии обуви, причем известно, что в од-
ной партии вся обувь доброкачественная, а но шорой % имеет
брак. Пара обчни. взятая из наудачу выбранной партии, оказалась
доброкачественной. Определить вероятность того, что вюрая пара
обуви из этой же партии будет иметь брак, если первая пара обуян
после проверки возвращена в партию.
3.25. Исследуется динамика курсов валют А и В (по отноше-
нию к некоторой валюте С) с целью прогнозирования. Статистика
валютных торгов показывает, что курс В возрастает в 90% случаев,
если иыр<к курс .4; в 60% случаев, если курс А не изменился. 11ред-
полагая. что все три исходные гипотезы об изменении курса А рав-
новозможны, оценил» вероятность этих гипотез, если извешно, что
на последних торгах курс В вырос.
3.26.В филиале панка А (в банке два филиала) проводят 40%
всех операций этого банка, а в филиале банка В 60%. В среднем 9
операций из 1000 проведенных в филиале банка А оказываются нс
прибыльными а в филиале В 2 операции из 500 Некоторая опе-
рация, выбранная случайным образом, оказалась не прибыльной
для этого банка Какова нс рояли осхь того, что она производилась в
филиале В9
3.27.Количество банкнот, поступивших r отделение банка из
четырех магазинов, соотносится как 4:3:2:1 Среди поступивших
банкнот из первого магазина 0,1% банкнот в силу изношенности
подлежат замене, из второго магазина таких банкнот 0,2%, из
гретьего 0,25%, из четвертого 0,5%. Нау» ал взятая контролером
банкнота не подлежит замене. Какова вероятноеib того, что кон-
тролер в<яп банкноту, поступившую из первого маха 1ина‘
3.28.В филиале Сбербанка клиенты срочных вкладов распреде-
ляются по трем категориям: первая срок сбережения от I до 3 лег.
вторая срок сбережения от 3 до 5 лет. третья срок сбережения
снышс 5 лет На 100 срочных вкладов к первой категории относится
55 вкладчиков, ко второй 35, к третьей 10. В среднем 8 вкладчи-
ков из 1000 первой категории эакрывакгт вклады, нарушив условия
договора размещения денег, т.с. снимают деньги раньше пбуегюннеп-
ного срока 1 года, средн вкладчиков второй категории нарушите хей
2 из 100, н третьей категории каждый пятый. Вкладчик закрыл вклад,
нарушив условия договора размещения денег. Какова вероятность то-
го. что вкладчик относится к клиентам третьей категории?
3.29.Число 1раж>|<1Н. имеющих высшее образование, обра-
тившихся на биржу труда с тем, чтобы найти работу, относится к
числу граждан, имеющих среднее специальное образование, так же
обратившихся на биржу труда, как 2:3. Вероятность того, что рабо-
ту получит гражданин со средним специальным образованием
равна 0.1; а для гражданина с высшим образованием эта всроян
ноезъ равна 0.2. Человек получил работу Найти вероятность того,
что это человек со средним специальным образованием.
3.30.11а распродажу поступает в среднем 50% продукции
фирмы К. 30% фирмы Н н 20% фирмы Л/. Вероятность полной
продажи товаров фирмы К раина 0,7, для фирм П и Л/эти вероя шв-
еи соответственно равны 0.8 и 0,9. Покупатель, попавший на рас-
продажу. покупает товар Найти вероятность того, что этот человек
купил товар фирмы К.
Случайные величины
Пусть (П. F Р)~ произвольное вероятностное пространство.
( лучайной величиной А называется измеримая функция А' - Л'(гм),
отображающая Q в множество действительных чисел R. и закая,
чю при любом д е К множество тех м, для которых А'(й>)<х,
при надлежит бт-алгебре событии данного эксперимента (множества
{X(гу) < х) - это события).
Функцией распределения случайной величины А называется
функция Л О деист нительною переменного х, определяющая вероят-
ность юго, чio случайная величина X примет в результате реализации
эксперимента значение. меньшее некоторою фиксированною числа х:
Г(х) г \ х;-Г{Л с(-тдц
Функция распределения имеет следующие свойства:
I. 0^F(r)£l.
2. Л’(х) неубывающая функция
3. lim/(x)-0; hm/(i)-1;
• **
4. /*(л) непрерывна слева, т.с. lim Г(л) - /♦’( rf)
Для любых Г| и х« вероятность неравенства х( < А <х вы-
числяется по формуле:
Г(л, £Х <х2) = Л’(х;) F(Х|).
Различают дискретные и непрерывные случайные нс гнчины.
1.4. Дискретные случайные величины
Случайная величина, обозначаемая Л. называется дискрет-
ном, если она принимает конечное либо счетное множество значе-
ний, т с. множество Qx - конечное, либо счетное.
Законом распределения дискретной случайной величины
называется совокупность пар чисел (ло где х, возможные зна-
чения случайной величины, а р^р, >0, яероязносчи. с которыми
она принимает зги значения, причем £ р 1,
t
Закон распределения дискретной случайной величины зада-
ют. как правило, в виде ряда распределения:
Х| Xj • •• xt — ••• 1
Jk Pl Я* • •• » »♦ J
Za-'-
4
I рафичсскос изображение ряда распределения называю!
многоугольником, т е. многоугольник распределения это ломаная
линия, соединяющая точки (х;рг). i 1.2, ...
РА
Рис.4.1
Зная закон распределения случайной величины, можно вы-
чис.1И1ь функцию распределения:
(4 1)
<1 %<•
где суммирование распространяется на псе значения индекса i, для
которых т, < х.
Малемшическим ожиданием \f(X) дискретной случайной
величины А наливается сумма произведений всех ее возможных
значений и соответствующих им вероятностей:
<4-2)
.'•1
Модой дискрс<ной случайной величины, обозначаемой М,„
называется се наиболее вероятное значение:
Л/=тах ЛА=л,). (4.3)
Медианой случайной величины X называется такое ее значе-
ние Mr. для которого одинаково вероятно, окажется ли случайная
вс 1ичина меньше или больше Мг, т.е /'(А < М) = /НА > Л/,.).
Дисперсией случайной величины называется математическое
ожидание квадрата ее отклонения: D(X) = М(Х- М Г))?
Дисперсия декретной случайной величины вычисляется по
формуле:
л( А ) Е(Х -М(А ))1 Д или £>( А )« р, (Л/(Л ))\ (4 4)
Средним квадратическим отклонением (стандартом) случай-
ной величины А называется арифметический корень из дисперсии, т е.
a(X)^D(X). (4.5)
Начальным моментом порядка к случайной величины А на-
зывасгся математическое ожидание А-й степени этой случайной ве-
личины. т е. А*).
Д 1Я дискретной случайной величины
«»(*)=£*? А- (4.6)
Центральным моментом порядка к случайной величины Л
называется математическое ожидание А-й степени отклонения X
.ИА), те д(-ЛЛА-Ж'))‘
Для дискретной случайной величины
А = £( - М( Л’))‘ р,. (4.7)
Задачи
Вероятность изготовления нсстод
тного изделия
при
1UL
некотором технологическом процессе ранка 0.02. Контролер наудачу
и-тлекас1 из партии изделия и проверяет их качество. Партия задер-
живается. если проверяемое изделие является бракованным. Если из-
делие стандартное го проверяется следующее и т.д. но нсегл пр же-
рястся i е баюс 5 изделий. 1 locijxHirb закон распределения случайной
величины А числа проверяемых изделий, многоугольник распреде-
ления Вычислить функцию распределения, моду, медиану, матема-
тическое ожидание, дисперсию, среднее квадратическое отклонение.
Решение Случайная ветчина А число проверяемых изде-
лий— тто дискретная случайная величина. I с множество значений
Qr {1.2,3:4^| конечное множество С лучайная величина А примет
значение ^-1, если первое проверенное контролером изделие ока-
жегся бракованным Вероятность такого исхода равна 0,02. тс.
P(A-/hO,02. Ьсли первое изделие сшндаргно, то пронсряекя второе
изделие и если оно содержит брак, го партия задерживается и. значит,
случайная величина А может принясь значение равное 2, т е А’ 2. Вс-
роятность исхода равна произведению вероятное!и тою, что первое-
изделие является стандартным на вероятность того, что второе изде-
лие является бракованным: P[X~-2Y 0.98 0,02=0,0196 (0,98-1 -0,02).
Контролер проверяет гри изделия, если первые два ока-
жутся стандартными, a ipcibe - бракованное. По теореме ум-
ножения вероятностен, вероятность такою исхода равна:
ЛА-3) 0.98 0.9Х4).02*0.0192 Аналогично. 1\.\=4>О.98ч•0.02*0.01X8,
Пячъ изделий проверяются вссыа, но при пом может оказать-
ся, чго пятое изделие станлар!Но или это пятое изделие содержит
брак. Вероятность такого исхода rto теореме сложения будет ранни
n9S4iO. ' М '2рО.984^О9?24
Итак, закон распределения.рассматриваемой случайной вели-
чины X можно представить в следующем виде
*1 1 *> 3 4 5
0.02 1 0.0196 0,0192 ' 0.0188 0.9224
Сумма вероятностей равна единице:
£р,-0.02 4 0.0196 ( 0 0192 + 0.0188 0 9224 I.
Значит, данная таблица <адаст икон распределения дискрет
ной с iy чайной величины.
Д «и построения мно! оу1ольника распределения на оси абс-
цисс откладываются значения случайной величины V, и из каждой
точки л, восстанавливаются перпендикуляры высотой получен-
ные точки (д„р#) соединяем отрезками прямой и получаем ломаную
линию, которая и является многоугольником распределения
(рис.4.2).
Вычислим функцию распределения по формуле (4 I):
0. если х < 1;
0.02, если 1 < х £ 2;
0,02*0,01 %-0.0396, если 2 < л 5 3;
0,0396+0.0192 0.05X8. если 3 < г < 4.
0.0588+0.0188 0.0776. если 4 < х £ 5.
0,0776+0.9224-1.0. если 5 < х
График функции распределения представлен на рис.4 3
зо
0,0776 - -----------◄-------j
0.058Я -----|
0,0196 -- - ;
0,02 - ;
I I • •
----p__i------------1 ----1-----
I 1 2 3 4 5
Рис.4.3
Из табл.4.1 следует что наиболее вероятное значение дис-
кретной случайной величины равно 0,9224 Поэтому Мг =5.
Медианы данное распределение нс имеет.
Математическое ожидание вычислим по формуле (4.2):
WV) 1-0.D2 + 2 0.0196-3 0,0192 ь 4 0.0188 5 0,9224 = 4.804
Для вычисления дисперсии воспользуемся форму .той (4.4);
D(x) = £ <р, -(М(х)Г = I • 0,02 + 21 • 0.0196 ♦ 3* • 0,0192 •
^4<0.01 КН » 5" 0,9224-(4.804)' = 23.632 - 23.078-0.554
Среднее квадратическое отклонение равно:
о^Л^в^/0,554 * 0,744.
4.2. В течение юла некоторая фирма трижды обращается та
кредитом в «Бсларусбанк» Вероятность получения кредита для
фирмы равна 0,R. Случайная величина А число кредитов фирмы
за юд Описать закон распределения данной с |учайной величины,
вычислить функцию распределения и числовые характеристики
D(X). сг[Х) Построить мнемлупмтьник и график функции рас
преиедения.
43. Проводятся независимые испытания приборов на на-
дежность Вероятность для каждою прибери пройти испытание
равна 0.Я Испытания заканчиваются после первого прибора, не
выдержавшего испытания, при ггом проверяется не бо ice * прибо-
40
ров Описать закон распределения случайной величины А числа
испытанных приборов; построить многоугольник распределения;
вычислить функцию распределения и числовые характеристики
АЛЛ). £ХЛ), о(А) Построить i рафик функции распределения.
4.4. Независимые испытания радиоаппаратуры проводятся до
тех пор. пока нс произойдет отказ. Вероятность отказа от испытания к
испытанию не меняется и равна 0.1 Найти математическое ожидание
и дисперсию чис ла безотказных испытаний.
4.5 На пут движения автомобиля четыре светофора Каждый
из них с вероятностью 0.5 либо разрешает, либо запрещает дальнейшее
движение автомобиля Построить закон распределения, многоуголь-
ник распределения случайной величины А характеризующей число
светофоров, пройденных автомобилем без остановки. Вычислить чи-
словые характеристики АДА) и /\ХУ функцию распределения
4.6. Из иаржи, содержащей 100 изделии, среди которых
имеется 10 дефектных, выбираются случайным образом (с возвра
том) 5 изделий для проверки их качества. Постройгь ряд распреде-
ления случайной величины А - числа дефектных изделий.
4.7. Продавец мороженого r солнечный день может зарабо-
тать 100 ден единиц, а в дождливый - 30 ден. ед. Чему равна ожи-
даемая дневная выручка, если вероятность того, что день окажется
дождливым. равна 0,35?
4.8. В ящики 20 деталей, среди которых 4 имеют скрытый
дефект Из этого ящика наудачу извлекают 3 летали. Описать <якон
распределения случайной величины А - число деталей, нс имею-
щих скрытого дефекта средн извлеченных, построить многоуголь-
ник распределения. Вычислить функцию распределения и число-
вые характеристики - моду, медиану, АДА). ZXA). гХА). Построить
график функции распределения.
4.9. Прибор состоит из четырех независимо работающих
блоков Б\, Б1, Б и Би каждый из которых выходит из строя с веро-
ятностями /ч 0.4 pi ру р4 0J соответственно. Ппи(м>р выходи! и<
строя как при отказе блока /», так и при одновременном отказе
блоков Ь|, Б} и Би Вычислить.
а) функцию распределения случайной величины А число испыта-
ний, при которых прибор выйдет из строя, и построить ее график.
6) числовые характеристики случайной величины X Л/(Л). /ХА).
гт(А).
410. Исследуются о дни торги на бирже, при которых изучается
повышение курса акций двух компаний Вероятность повышения
41
курса акций для одной компании равнаpt, для торон /а. Пусть слу-
чайная величина А суммарное число повышений акции, изучаемых
компанией на данных тортах. Найт и М(Х), М А), <КА)
4.11. В .клерсе, в которой выпущено 100 билетов. разыгрывает-
ся мотоцикл, слоимоелью 250 дсн ед, 2 велосипеда, стоимостью 70
ден. ед и четверо часов, стоимостью 40 дсн. ед. Некто покупает один
лотерейный билет Oiuicaib закон распределения случайной величи-
ны X величины выигрыша. Вычислить математическое ожидание,
дисперсию и среднее квадратическое отклонение выжрышв
4.12.Имеется 5 ключей, нз которых только один подходит к
замку Описать закон распределения случайной величины А’ харак-
теризующей число попыток открыть замок каждым ключом при
условии, что опробованный ключ в последующих попытках нс уча-
ствует. Найт и функцию распределения. Вычислить математическое
ожидание М{Х} и Дисперсию Л(А}.
4.13.В республике действуют 1000 банков. Из них 150 с го-
сударственной формой собственности. Налоговая инспекция про-
верила 100 банков Какова вероятность того, что среди них нет с
юсудар^твенной формой собственноеги Хотя бы один с негосу-
дарственной формой собственности? Найти среднее число банков с
государственной формой собственное™ среди 100 проверенных и
его вероятность Вычислить среднее квадрат ичсское отклонение
случайной величины Л число банков с государственной формой
собственности среди 100 проверенных.
4.14. Иванов держит пари о появлении (или не нояв »снии) со-
бытия Л, шанс наблюдения которого равен 25%. Иванов шапп I
ден. ед. в случае, если событие А появится и получает 2 лен. сд., ес-
ли оно не появился. Найти ожидаемый выигрыш Иванова
4.1 S.В партии нз 12 деталей имеется 10 иандартных. Из этой
партии наудачу взяты 2 детали. Описать закон респредс юння слу-
чайной величины А' число стандартных деталей среди отобран-
ных; вычислить функцию распределения, Л4(А\ ЩХ), nt АЗ и по-
строил, график Нт)
1.5. Законы распределения дискретных случайных величин
Производятся испытания, в каждом из которых может поя-
вился событие А или событие А.
Биномиальным (законом распределения Ьсрнуплн) называ-
ют закон распределения дискретной случайной величины А числа
появлений события А в п независимых испытаниях, в каждом из
которых нер'Ятшхпь появлена я события равна/?. Вероятность ьоз-
42
можного значения X - m (’шел а т появлений события) вычисляют
по формуле Берну ляп.
* /Л
?,(*} = W = • - ~/>V ’. (5.1)
тЦп т)
где 1-р - тто мс[мжгность ле наступления события Л (появления
событий А), Ряг. распределили случайной вслнчшш А* распреде-
ленной по биномиальному закону (закону распределения Бернулли)
имеет вид
п» 1>
Функция распределения: Г(л) - AV-' < к)- VC. р' q" ‘.
<1
Математическое ожидание и дисперсия случайной величины,
рае предо лент и по биномиальному закону, соотвстс гвенно равны:
ЛДАЭ=пр. D(X)=npq
Наивероятнсйшсс число т появлении событий в п нсшвиси-
мых испытаниях определяется по формуле
np-q£m(> <пр+р (5.2)
Если число испытании велико, г вероятность появления со
бытия р н каждом испытании мала, то вероятность тою. что неко-
торое событие появитьс я m раз в л испытаниях» приближенно вы-
числяется по формуле Пуассона:
(5.3)
т!
где т - число появлений событии в и независимых нспыtаниях.
п-лр-среднее число появлений события в п испытаниях
Ряд распределения случайной величины Х\ распределен той
но закону Пуассона имсеэ bi л
Если известно среднее число событий Я. которые нояв шюг-
ся в единицу времени, то вероятность почтения т событий про-
стейшего потока событий за время /, вычисляется по формуле
1Э \ (^0 .Ду
Функция пуассоновскою распределения; /•(*) Р(Х<х)-
Математическое ожидание и дисперсия случайной величины,
распределенной по закону Пуассона равны одному и тому же числу
a: M(X)~D(X)- а, а-пр.
Геометрическое распределение возникает в том случае, ко-
гда производится серия испытаний до первого появления события
А. Тогда распределение случайной величины А имеет вид:
X, 1 2 3 • • • т — • ••
Р‘ р ЯР Ч2Р - Я^Р ' ' ” 1
Вероятность появления события А в каждом иены гании по-
стоянна и равна р, i.c. р-Р(А), и Л |-1 - р - q.
Функция юометрического распределения: F(<)-P(A <х)-
<:<»
Математическое ожидание, дисперсия и ере (нее квадра-
тическое отклонение с туманной величины X, распределенной
по геометрическому закону, соответственно равны
A/(JT)=1; О(АГ)=4-; о(Х^^-.
Р Р Р
Гнпергеометрическин закон распредетения используется при
проверке качества продукции. 11усп, проверяется N изделий, и извест-
но, что среди этих изделий имеется М изделий, которые обладают не-
которым при «каком А. а остальные (Л/ М) признаком А Для про-
верки производится ныборка, со;«ержа1ная л изделий. Для определения
вероятности того, что среди этих изделий т изде тин облачают некото-
рым признаком А (событие А), используется классический способ за-
дания вероятности. Число злемешарных событии пространсгио ъте
ментзрных событий Q и события А определятся числом сочетаний
С . а искомая вероятное ib вычисляется по форму ле:
,и ,У м
ГМ) =
где А - событие, состоящее в том, что в выборке т объектов обка-
та нп признаком Л.
Закон распределения лискре:ной случайной величины А. ха-
рактеризующей число появлений события А т раз в N испытаниях
имеет вид
- если п £ М
Функция гипергеоме1рического распределения:
[0. х<0;
О < х < min(n,M)
х > min(n.M)
Гипергеометрический такой стреми ich к биномиальному за-
М
кону распределения, при Л—м®, если — = р = const, fcro числовые
Л’
равны:
характеристики
М . М „ N-n
М(Х}-пр, , Л(Л)-и/х/-—
/V /V N -I
Задачи
5.1. Вероятности рождения мальчика и девочки можно счи-
тать равными 0,5 Какова вероятность того, что средн 6 наудачу
отобранных новорожденных будет, а) хотя бы один мальчик - со-
бытие 4; б) число мальчиков и девочек одинаково событие R; в)
мальчиков болынс, чем девочек - событие С?
Решение Введем случайную величину V - чис ю мальчиков
среди 6 новорожденных. Так как при каждом рождении вероят-
ность рождения мальчика постоянна то эта случайная величина
подчиняется биномиальному закону распределения, л.е согласно
45
формуле (5.1) вероятность того, что случайная величина X примет
значение т будет равна:
р(Х*фс; - 4-1 -сг - .
UJ Чг;
I обьпию Л {средн б новорожденных будет хогя бы один маль-
чик! 11ротмшм|аюж1ю событию .4 - {среди 6 i ^порожденных нс будет
ни одного мальчика) Веройгность события Л найти проще. поэтому
р(Л) = 1-Р(Л)=1-р(т=0)=1-с;|-I-ill =1—L_63.
42J uJ 64 64
Вероятность события Р вычислим по формуле (5.1):
ШМЪ-З)-
16
Событие С произойдет, ес ли среди 6 новорожденных будет 4
мальчика или 5 или 6, г е. {А’>3} Нетрудно } виде it. что
/>(Л>3)-Р(Х<3)-1(|-Р(Л-=3)).
1аким образом.
-1 H-1L
X Z \ I о /
2 16 32
Ответ:
(4 16 32
5.2. Два равносильных niaxMaiiicra дш сворились стлрать 4
результативных партий. Ничьи нс учитываются и считается, что
каждый из участников может выиграть очередную партию с веро-
ятностью 0.5. Определить веропность выигрыша одного из шахма-
тистов (выигравшим матч считается гои кто победит в большем
числе партий).
Peiuryue Во всех партиях вероятность выигрыша постоянна и
Гч.тратлич1Юэ в какой пек лшопагельности бу луч выжраны партии,
юэтому случайная величина А - чис ло выжранных партий, подчиня-
ется биномиачыюму закону распределения. Олин из шахматистов
победит, если выиграет 3 или 4 партии. Воспользуемся г|юрмулой
(5.1) и вычистим вероятности /\(3) и Р4(4):
16
46
16
Тогда, применив
теорем>
• •
16
сложения,
летучим
P4(3)*F4(4)-1 + ^
4 16
16
Ответ: вероятность выигрыша одного из шахматистов рав-
на: л - —
16
5.3. В партии 10% нестандартных деталей Наудачу отобра-
ны 4 детали. Написать биномиальный закон распределения дис-
кретной случайной величины X - числа нестандартных деталей
среди 4-х отобранных и построить многоугольник полученного
распределения. Вычислить М(Х}\ 1ХХ); о(А'). Л'(х).
5.4. R банк подано 5 заявок фирм на получение кредита. Ве-
роятность получить кредит для каждой из фирм равна 2/3. Найти
вероятность того, что из пяти фирм кредит получит а) ровно I
фирма; б) по крайней мере 2; в) ровно 3; г) больше чем 3 фирмы.
5.5. Десять осветительных лампочек для елки включены в
цинь последовательно Вероятность перегореть для любой лампоч-
ки при повышении напряжения в сети равна 0,1. Определить веро-
ятность разрыва цепи при повышении напряжения в сети.
5.6. Вероятность того, что покупателю потребуется обувь
43-го размера, равна 0.4. В обувной мат азин вошли трое покупате-
лей. Найти функцию распределении случайной величины X числа
тех покупателей, которым потребовалась обувь 43-го размера Вы-
числить Р(х >2).
5.7. В некотором цехе брак составляет 5% всех изделий Со-
ставить закон распределения числа бракованных изделий из 6 нау-
дачу взятых изделии Найти математическое ожидание и диспер-
сию этой случайной величины.
5.8. Изделия некоторого производства содержат 5% брака
Взято 5 изделий. Построить ряд распределения числа бракованных
изделии и среднее квадратичное отклонение згой случайной вели-
чины,
5.9. В течение года может обанкротиться примерно одни
банк из 50. Определить, какова вероятность того, что из 200 банков
обанкротятся: a) Tie более двух банков, б) нс менее восьми.
5.10. Акционерное общество вытгустило очередной пакет акций
по номинал той стоимости за акцию 100000 и 10000 рублей Причем
47
я пакете 80% акций по пене 1О1ХХЮ и 20% по цене 10000 рублей. Ка-
кова нсрояптость гою. что из наудачу взятых по схеме возвратной
выборки восьми акций пят», окажутся но цене 100000 рублей?
5.11. Всроя гност ь того, что покупатель войдет н Mai азин в те-
чение часа, равна 0,005. Магазин обслуживает 6UU покупателей.
Какова вероятность того, что в течение часа войдет 5 покупателей?
5.12. Из 20 изделий цеха 25% изделия высшего copra, ОТК
проверяс! 8 изделий. Какова нс1ЮЯ1ность того, что из них 6 изде-
лий будут высшего сорта?
5.13. Ьапк в течение дня принимает 200 денежных вкладов от
населения. Определить с тремя десятичными знаками вероятность
того, что среди них окажется 100 валютные, если вероятность
принятия вклада в расчетных билетах РБ равна 0,515.
5.14. Работники коммерческого банка производят 2 вила опе-
раций. депозитные и кредитные счета Ироперка обнаружила, что
вероятноегн допущения ошибок при оформлении депозитных и
кредигных счетов соответственно равны 0.1 и 0,15. Найти вероят-
ность следующих исходов: а) в пяти проверенных депозитных сче-
тах обнаружено не менее двух неправильных; б) в трех проверен-
ных кредитных счетах обнаружены 2 ошибки.
5.15. Какое чинима 1ыюе число и испытании нужно пронести,
чтобы с вероятностью нс меньшей, чем 0,95, можно было бы ожи-
дать наступление события А хотя бы один раз, если вероятность
собыл ия А в одном испытании равна 0,3.
Решение. Наступление события Л хотя бы один раз в п испы-
таниях обозначает, что собы юс А наступит или один раз или два
раза или... во всех испытаниях. Поэтому проще вычислить вероят-
iiocib противоположного события Л, состоящего в том. что собы-
тие А не наступи! ни в одном испытании. Так как испытания неза-
висимы, го но теореме умножения для независимых событий будем
иметь. Р(/1)-0,7'0,7...0,7 = 0,7", где 0,7=1 0,3.
Гог да вероятность события А вычисляется но формую:
Г<.А) I 0,7 . По1ребусм. чюбы ла вероятность была не меньше,
чем 0,95: 1-0,7" 20.95.
Решив зго неравенство последовательно относительно л. по-
лучим: 1 0,95>0,7", или 0.7’50.05. или п In 0.7 * In 0.05, или
In 0.05 , л, л
пг . гак как 1п0,7<0.
1п0.7
48
Отсюда заключаем что минимальное число испытаний опре-
деляемся формуле)! ц -
In 0,05
In 0.7
Вычислив In 0,05- -2,996; In
0.7—0357, получим лп- 9
Ответ: максимальное число испытаний равно 9
5.16. На контроль поступила партия легален из цеха. Изнеез-
по. что 5% всех изделий не удон л створяют стандарту. Сколько
нужно испытать деталей, чтобы с вероятностью 0.96 обнаружить
хотя бы одну нестандартную деталь?
5.17. Всхожесть семян состав тяст в среднем 90%. Найти паи-
нсроятнейшее число всхожих семян среди 20 семян
Решение Воспользуемся формулой (5.2), так как число всхо-
жих семян подчиняется биномиальному закон) распределения
Подставив п = 20, р-0.9, q = |-0,9-0,1 потупим
20 0.9-0,1 < w< 20*0.9 + 0,9 или 17,9 < т <1Я,9-
Из последнею неравенства следует, что =1К.
5.18. Из практики известно, что в среднем 3% отчетов нред-
С1авляемых фирмами r налоговую инспекцию имеет ошибки. Оп-
рсде зить наивероятнейшее число отчетов, нс содержащих ошибок,
грели 100 сданных отчетов
5.19. На предприятии рабепаез 1000 рабочих. Какова вероят-
ность того, чю 1 января является днем рождения одновременно т
рабочих данного предприятия? Вычислить вероятность для значе-
ний т ранных 0, 1,5.
Решение Рассмотрим случайную величину А число рабочих.
1ЛПЛ
родившихся I января. Эта случайная величина А* = * где ~ 1.
если рабочий родился 1 января и А' = 0, если рабочий родится нс I
гннаря. Вероятность события 4 =" X - (рабочий родится 1 января)
I
равна-----, т.е. небольшая, а число л достаточно большое, то можно
считать, чго случайная величина X подчиняется закону распределе-
ния Пуассона с параметром а ~ лр = 1000*—*2,74^10. Поэтому
для вычисления искомых вероятностей применим формулу (5J):
2 74'
если т = О. то (О) - Р( А - 0) -- ’ /> 74 * 0,065;
НДЖ» ' Г * ' <
*
-Л
есшт = 1.ТО POftl(|)-P(A =l) = —е ?,4₽О,17К,
I I
49
если т-5, то р (5)= /’(Д' = 5)=—-р*’ * *0.084.
I
5.20. Число регистрируемых заявок в телеателье случайно и
образует пуассоновскую случайную величину Д'со средним значе-
нием 500 заявок и день. Каждая регистрируемая заявка может быть
выполнена с вероятностью 0,99. Описать закон распределения чис-
ла не выполненных заяэок, pei итерируемых диспетчером Вычис-
лить МД ) и АДГ).
Решение Рассмотрим случайную величину Л чис то не вы-
полненных заявок за день. Так как число заявок п — 500 велико, а
вероятность события 4 = (заявка не выполнена) мала. Р(.4)=0,01,
то закон распределения случайной величины Д’задается в виде:
0 1 2 • • • 500 1
л е’’ 11 52 —е 2! • • • 5*® ’ 500!С
где а=чф=500 0.01=5.
Математическое ожидание равно дисперсии для случайной
величины X, подчиняющейся закону распределения Пуассона, те.
M(X) = D(X) = 5.
5.21. Установлено, что численность обрывов нити за некоторой
промежуток времени следует закону Пуассона. Прядильщица обслу-
живает 800 веретен Наблюдения показали. что в течение I минуты в
среднем происходит 5 обрывов. Определить вероятность тою, что в
течение 1 минуты произойдет: а) 5 обрывов; б) не .менее пяти обрывов.
5.22. Среднее число вызовов, поступающих на АТС в минуту
равно 120. Найти вероятност ь следующих событий
А = {за две секунды на А ГС нс поступит ни одного вызова).
В {за две секунды на АТС поступит менее двух вызовов).
5.23. Корректура в 500 страниц содержит 1300 опечаток. Най-
ти наиболее вероятное число опечаток на одной станине текста и
вероятность этого числа.
5.24. При испытании легированной стаж па содержание уг-
лерода вероятность того, что в случайно взятой пробе процент уг-
лерода превысит допустимый уровень, равна 0,01 Счи(зя приме-
нимым закон Пуассона, вычислить, сколько в среднем необходимо
испытать образцов, чтобы с вероятностью р 0,95 указанный м|>-
фект наблюдался по крайней мере I раз.
5.25. Отдел по обмену валюты Сбербанка производит к тече-
ние рабочею дня 300 операций. Верой i нос и» совершить ошибку
при обмене валюты равна 0,01 Н^йти вероятности следующих ис-
ходов: а) не более трех операций из 300 будет произведено с ошиб-
ками; б) пять операций из 300 будет произведено с ошибками.
5.26. Вероятность того, чю к концу года акционерное обще-
ство банкротится, равна 0,004. Найти вероятность того, что из 1000
акционерных обществ к концу юла обанкротится не более пяти.
5.27. Вероятность тою. что стеклянное изделие повредится
при перевозке по железной дороге. равна 0.001. Какова вероятность
того, 'по из 1000 стеклянных изделий при перевозке повредится' а)
три изделия? б) больше трех изделий?
5.28. R геего, подготовленное для выпечки 500 булочек, за-
сыпают 5000 изюминок и тщательно перемешивают Какова веро-
ятность того, что в случайно выбранной булочке будет, а) 10 изю-
минок? б) больше 10 изюминок?
5.29. Производится ряд попыток реализации некоторою това-
ра по фиксированной пене Каждая попытка длитетьшктью 7 ча-
сов заканчивается реализацией товара по цене г© независимо от
других попыток с вероятностью />~0.095. Описать распределение
общею времени 7, которое требуется для реализации некоторого
товара. Вычислить функцию распределения. математическое ожи-
дание и среднее квадратическое отклонение случайной величины
7— времени, необходимого зля реализации товара.
Решение Введем случайную величину Л - число попыток реа-
лизовать товар по фиксированной цене г0. Эта случайная величина
распределена по геометрическому закону распределения. Общее вре-
мя 7, необходимое для реализации товара, связано со случайной ве-
личиной А но формуле 7 - tX, где / 7ч и имеет распределение вида:
W . --1--~------1 'Т
Р(Х *j) £ <Ц>5 ЧГо 05-0 . П.П475 </r O.Q52 O 9S
1
tf' р-О.ПГО 95 .
Функция распре имения общего времени Т необходимого
для реализации токари
5!
0. IS 7;
0.95. 7 </<14;
0.95 + 0,0475 = 0.9975, 14</<2I.
F(/)= ...
£(0.05* 0.95), 7m < / < 7(ш + 1).
I «1
Математическое ожидание и среднее квадратическое откло-
нение случайной величины Травны:
Л/(Г) = / - Л/( X) -/ 1 = 7-^ * 737(4);
<r(f) = /^- = 7.3/S21 3 |.б5(ч).
р 0,95
Отчет'. Л/(Т)* 7.37 ч.; а\Т)^ 1.65ч.
5.30. Вероятность того, что стрелок попадет в мишень при
одном выстреле, равна 0.8. Стрелку выдаются патроны до тех пор.
пока он не промахнется. Требуется: а) составить чакон распределе-
ния дискретной случайной величины А числа патронов, выдан-
ных стрелку; б) найти наивероятнейшее число выданных стрелку
патронов
531.Эк заменатор задает студенту’ дополнительные вопросы.
Вероятность того, что студент ответит на любой заданный вопрос,
равна 0,9, Преподаватель прекращает экзамен, как только студент
не отвечает на заданный вопрос Требуется а) составить закон рас-
пределения дискретной случайной величины А числа дополни-
те льнкх вопросов, которые задаст преподаватель студенту; б) май-
ги наивсроятнсйшсс число заданных студенту дополнительных во-
просов.
5.32. Из ящика, содержащего 4 изделия, содержащих скрнтый
дефект, и 6 стандартных изделий, слу'шйным образом и без воз-
вращения извлекают три изделия Описать закон распределения
случайной вс 1ичины А* - число изделий в выборке, содержащих
скрытый дефект. Вычислить функцию распределения математиче-
ское ожидание и дисперсию случайной величины А'.
Решение- Hi 10 изделий 4 и шелия содержат скрытый дефект
и 6 стандартных изделий Следовательно. случайная величина X
число изделий в выборке, содержащих скрытый дефект, подчиня-
ется I ипсргсомстричсскому закону распределения. Вероятность то-
го, чти случайная величина Л может принимать значение, ранное
т 0.1.2,3, вычисляется на основании классического определения
вероятности. 1 е. по формуле:
Р(А' mi-
ni = 0,1,2.3.
Закон распре ле лен и я случайной величины АГ задается н виде:
Функция распределения:
0.
1
6’
2 2.-2?
з ‘ ю зо ’
30 30
при х <, 0;
при 0 < д <1;
при 1 < х £ 2;
при 2 < х < 3;
при 3 < х.
Числовые характеристики случайной величины, распреде-
ленной но гипергеометрическому закону распределения равны:
4 12
М(Х)~пГ 3 — = — = 1,2;
10 10
D(X)-npq^-^3
4 6 10- 1 2 3 714
10 10 10 1 5 5 Q 25
Отпет Л4А>1,2; D(X)-0,5<>.
5.33. На станции технического обслуживания устраняется
один дефект автомобилей. На одну рабочую смену требуется 5 од-
нотипных деталей. Было закуплено 16 деталей, из которых 12 не
имеют дефектов Мастер на складе получает 6 детален, которые от-
бираются наудачу, на одну рабочую смене (одну Деталь «про за-
пас», учитывая наличие бракованных) Найти вероятность того, что
1а смену будут устранены все дефекты
5.34.Н а контроль поступила партия деталей. Известно, что
для данных И1ДС.1ИЙ брак составляет 7.5%. Сколько нужно испы-
53
тать деталей, чтобы с вероятностью нс менее 0.95 обнаружив хотя
бы одну нестандартную деталь?
5.35. На факультете обучается 500 студентов, 20 из которых
систематически занимается научной работой. На конференцию
случайным образом отбирают 5 студентов. Описать закон распре-
деления случайной не тимины Y число студент он в выборке, кото-
рые занимаются научной работой Вычислить функцию распреде-
ления, математическое ожидание и среднее квадратическое откло-
нение случайной величины Л. Построить график функции распре-
деления.
1.6. Непрерывные случайны величины.
Случайная величина .¥, которая может принимать все значе-
ния из некоторого промежутка, называется непрерывной случай-
ной величиной.
Множество значений QL непрерывной случайной величины
X— некоторый числовой интервал.
Плотностью распреде 1ения вероятностей /<г) непрерыв-
ной случайной величины X называют предел, если он существует,
отношения вероятности попадания случайной величины А'на отре-
зок х.х+Дх], примыкающий к точке х, к длине этого отрезка, когда
последний стремится к 0. г.с.
, . , Р(х £ X $ х + Дх)
л(г) hm -------- —
Свойства плотности распредетения вероятностей:
1 .р(х| неотри(атепы1ая функция,т е р(л)^0, Vxc(-oc;4oc).
2 . Вероятность достоверного события jA'c(-^ j с )} равна 1,
Т.С. р(х)Ж=1.
1. р(х) непрерывная или кусочно-непрерывная функция
Функция распределения случайной вс жчины А то <|уик-
ция Мх) действитс шной переменной г. определяющая всроя1ность
гою. что случайная величина i рннимаст, значение меньше некото-
рого фиксированного числа х, т.е. Д' (-оо.д):
F(x)-P( (6.1)
Болес строгое определение непрерывной случайной величи-
ны формулируется следующим образом.
Случайная величина Л называется непрерывной, если суще-
ствует такая неотрицательная. hhiciрирусмая но Риману функция
p(v). называемая плотностью распределения вероятностей, что при
всех хс R выполняется равенство (6.1)
Зная функцию раст ределенин Г(х) непрерывной случайной
величины, плотность распределения в точках непрерывности F(x)
можно вычистггь по формуле:
р(х) = Г(х). (6.2)
Если X непрерывная случайная величина, то вероятность
гою, что она принимает значения из полуинтервала [х|Л) вычис-
ляется по формуле:
Р(х, <%<xj = £(«,)-Г(х,). (6.3)
или через плеггность распределения вероятностей:
/’(«I < X < х2) = Jp(x)tfr. (6.4)
ч
Математическое ожидание и шсперсия непрерывной случайной
величины.
W(A') - j »р( rkfr; D(A') = |х’р(х)Л (Л/(Л))2. су(х) - X} (6.5)
Модой непрерывной случайной величины А называется дей-
ствительное число И„ определяемое как точка максимума плотно-
сти распределения вероятностей р(х).
Медианой непрерывном случайной величины А называется
действительное число Мс, удовлетворяющее условию Р[Х<М.) =
Р(Х>М„}. т.с. корень уравнения /• (х)~ .
Начальный момент 4-го порядка:
X
а,(У)-Л/(АГ‘)- Jx>(x)Jx.
Центральный момент к го порядка.
/ Jх) - ЛУ( А Л/( A ))*- j(»- М( X ))* р{ x)dx
Из определения моментов следует. что а(, = р(| -1;
W(X) = a,(X); D(.\ )-//,(Л')-а?(А')-(Л/( А))’.
Коэффициент асимметрии иди «скошенности» распределения:
Д ./'’О)
** ~ СТ}(Х)
55
Коэффициент эксцессы или островершинности распределения;
р__ Д<(<) 3
<т‘(х)
Случайная величина Л называется центрированной, если
MiXy-O Если же для случайной величины Л': *ЯЛ5-*О. е(х)=1. то она
называется центрированной и нормированной (стандартизованной)
случайной величиной.
Задачи
6.1. Случайная вс личина Л’ имеет плотность распределения
( (4 2x1 0<х<2;
вероятностей: Найти параметр С и
функцию распределения F(r) Построить график функции распре-
деления.
Решение. Для нахождения С воспользуемся свойством 2
от
плотности распределения веройгностей: jp( <)dx - I, г.с.
05
?
jC(4 2х)Л-1,
О
\ <1
<bn-?41oVc(S 4)=4С.
L *-
4С - I, откуда С -1/4.
, . I—(4-2х), 0<х<2;
ледова!ельно. р(х)=<4
It), х<0;х>2.
Значение функции распре имения Г(г) зависит от значения
дсйс1нительного числах, поэтому если.
I х^О.ти F(x)- jor/f-O.
2. 0<х<2,то
l ", х о » < | • *
И») | /ол J (4 J(4-2/)tfr
. . .<• П 4 4 g
56
О
График функции раслрслеления состою из двух лучей j^O,
х1
v- I и отрезка параболы j - х-и изображен на рис 6.1:
4
А(х)‘
Рис. 6.1
6.2. Случайная величина А задана функцией распределения:
О, х < О,
О < v S 4,
I, х > 4.
11айти плотность распределения вероятностей р(х) и вычислить ве-
роятность того, что случайная величина А'примет значение и.< ин-
тервала (0:2).
Решение Так как в точках непрерывности /•’(*) /’(г) “—“ •
dr
см (6.2), то
5”
Коэффициент эксцесса или островершинности распределения:
Случайная величина Л называется центрированной, если
MiX)~0 Если же для случайной величины .V \ЛЛ')ЯО. ofxjH, то она
называется центрированной и нормированной (стандартизованной)
случайной величиной.
Задачи
6.1. Случайная величина Л имеет плотность распределения
С(4-2х), 0<х<2;
вероятностей: р(т)-Х Найти параметр С и
,0. х<0, х£2.
функцию распределения F(r). Построить график функции распре-
деления.
Решение. Для нахождения С воспользуемся свойством 2
плотности распределения верой iкостей: I р( x)dx - I, г.е.
j
JG4 2х>Лг-1,
о
4 - 2x)dx = С
4С -1. откуда С=1/4
. . 1^(4-2х), 0<х<2;
ледова i е.тьно: р(л) = • 4
10. х <0; х > 2.
Значение функции распре деления Fix) зависит от значения
дсйс (вительною числа л. позтому если:
I х£0,то F(x)- J p(t)dt - jodf —0.
«г ««:
$6
3. V > 2. то
о,
о
а
С
о
Итак, Е(х) -
График функции распределения coctohi из двух лучей у^О,
_ х2
г-1 и отрезка параболы у = х--и изображен на рис. 6 1 :
6.2. Случайная величина Л задана функцией распределения
(О
16
Найти плотность распределения вероятностей /<») и вычислить ве-
роятность тою. что случайная вс личина X примет значение из ин-
тервала (0t2).
Решение: Так как в точках непрерывности f(i) />{ v)
dr
см (6.2), то
. ч *
•5
[о-
л <0;
О£ х < 4.
х > 4.
Искомую вероятность вычиашем но формуле (6.4):
1 2
Р(0<х<2) = jp(x)clx - j\x/8)dv = l/4
о о
Эту вероятность можно вычислить с помощью функции рас-
пределения по формуле (6.3):
Л0<л<2) = Г(2)-Г(0) = ^-0»}/.
63. Дана функция рас и реле кнпя непрерывной случайной
величины X:
Г(х) = <
0.
sin х.
х<0;
0< л <я’/2;
л > л/2.
Найти плотность распределения Построить! рафикир(х} и Fix).
6.4. Дана функция распределения непрерывной случайной
величины X.
О,
F(*) = < sin 1 г.
х<0;
0< x<rtf4\
х >л/^.
Найти плотность распре деления. Построить графики р(х) и F(x).
6.5. Случайная величина задана плотностью распределения
вероятностей’
ГО. х<0;
р(х) = - sinx.
0.
О < х < л/2.
г > к/2.
Определить магема1ическое ожидание и дисперсию ггой случай-
ной величины
6.6. Найти дисперсию случайно!! величины X, заданной
функцией распределения:
(0. х < -2;
(*/4) + (1/2), -2<х<2;
I. х>2.
5Я
6.7. С лучайная величина А распределена по закону» опреде-
лимому плотностью распределения вероятностей вила:
C- COS JI,
О
определить /•'(л). вычислить
Найти константу с,
Г(|х|< ^/4). М(Х). D(X).
6.8. Пусть функция распределения головых доходов лиц. об-
лагаемых наделом равна:
О’
О»
I0’
। де .г© — минимальный доход
Определить размер годового дохода, который для случайно
выбранного налогоплательщика может превзойти с вероятностью
6.9. Случайная величина эксцентриситета детали характери-
зуется функцией распределения Рэлея:
г л
ж
10, при х < 0.
Найти: I) плотность распределения/>(х) 2) медиану распределения;
3) моду распределения.
6.10. Функция распределения Всйбулла
Г(х) < 1-е г , при х^О;
0. прих<0.
в ряде случаев характеризует срок службы электронной аппарату-
ры. Найти 1) плотность распределения всроятостсй; 2) молу рас-
пределения.
6.11. Случайная величина К непрерывною чипа имеет плот-
ность распределения вероятностей изображенную на рис. 6.2
Написать анагиличсское выражение для плотности р(л). вы-
числи! ь функцию распределения, математическое ожидание, дис-
персию, моду, медиану. Нарисовать график функции распределе-
ния
SQ
Рис.6.2
1.7. Законы распределения непрерывной случайном величины
Равномерное распределение. Пусть плотность вероятности
равна нулю всюду, кроме отрезка [cr./Jj. на котором вес значения
случайной величины X одинаково возможны. Тогда выражение
плотное:и распределения вероятностей /О) имеет следующий вид:
0.
р(х) = -
0.
Функция равномерного распределения задастся формулой:
0. х < а:
Математическое ожидание, дисперсия и среднее ква.дратиче-
ское отклонение соответственно равны:
Р, . 1ZL2LI; (73,
Нормальное распределение. Распреде генис непрерывной
случайной величины на<ывается нормальным, если пши кость рас
пре деления вероятностей описывается формулой
где гт > О; т параметры распределения
Функция распределения случайной величины X. распреде
лепной но нормальному закону:
(7.5)
Полученный HHicipa.1 нельзя выразить через элементарные
функции, но ею можно вычислить через специальную функцию:
1 1 1 *
Ф *(л) - I [«• ' dr, (или Ф( г) = f= L
v2/r >J2k I
Jdt),
называемую нормальной функцией распределения (функцией Лап-
ласа*. Эта функция неубывающая, непрерывная слева и
Ф’(-д) -1-Ф’| О. ф‘(-.<)=(* и Ф'и * »-1
Математическое ожидание и дисперсия нормально распреде-
ленной случайной величины X соответственно равны М(Х)=т:
П(Х)=^..
Центральные моменты случайной величины с нормальным
законом распределения вычисляются при помощи следующих ре-
куррентных соотношений: = (q- 1кт2/^_г Поскольку /ц-0, то
нечетные центральные моменты равны нулю, а четные централь-
ные моменты равны: = о, щ = Зо4 - 15а6 Коэффициенты
асимметрии и эксцесса для нормального закона распределения рав-
ны нулю, так как они характеризуют «скошенность» и «крутизну»
исследуемого закона распределения по сравнению с нормальным
Вероятность попадания случайной величины X, подчиненной нор-
мальному закону распределения, на заданный интервал (а. Д). оп-
ределяется следующим образом:
Р|<Г< У </?)-/(/?)
или Pta < X < fl)
‘ Jz) - функция Лапласа.
(7.6)
6!
Функция Лапласа удон, ic ширяет свойствам функции распрс-
| I
деления и Ф(0>=0; Ф(-®) - Ф( М- Ф(-х)- -Ф(х).
Вероячпость шлаиного отклонения вычислмс1см но формуле:
' / с\
f Х| А' т' < Л) - Р( т 8<Х < т + А’) - 2Ф* | -1, или
Р(|Х-/я1<<У) = Р(т-<т + ^)-2Ф — |. (7.7)
\ а /
Интервалом практически возможных значений случайной ве-
личины X, распределенном по нормальному такому, будет интервал
I (оказательнос распределение. Показательным (экспонен-
циальным) называют распределение вероятностей непрерывной
случайной величины X, которое описывается функцией плотности
вероятности:
(7.8)
' (О,
»де X > О постоянная и называется параметром экспоненциального
распределения.
Функция распределения случайной величины, распределен-
ной по показательному закону, имеет вид:
О,
(7.9)
Математическое
ожидание М ( Л ) - —
Дисперсия
Л )- —.среднее ква>фатичсскосотклонение: <т(х) = —.
Задачи
7.1. Шкала секундомера имеет пену деления 0,2 сек Считая,
что случайная величина Л - ошибка окру» »ения, записать ее плот
Hocib рас преле гения функцию распределения. Вычислить ИА),
/XV) ^А*) случайной величины X какова вероятность следа с ь по
ному секундомеру отсчет времени с ошибкой более 0.05 сек , сс 1И
отсчет делается с округлением в ближайшую сторону9
Рсшенеие. Так как стрелка секундомера двигается скачмюбрашо
и цена лелсиия равна 07 сек, то случайная величина А ошибка ок-
ругления. распределена равномерно в ннгсрвалс (0. 0,2). Восполъзуем-
62
ся формулой (7.1). Тогда плотность распределения вероятностей для
случайной величины Л - ошибка окрут ления, запишется в виде:
1 0. х < 0;
/Хх)-^(
xi 0,2.
Функция распределения, согласно (7.2), задается формулой:
0, х<0:
Г(х)-|-^- 5х. 0<х<0,2;
0,2-0
1, xi 0,2.
Математическое ожидание, дисперсия и среднее кналратиче-
скос отклонение, согласно формулам (73), равны:
Л/(АГ)-°—°-2-0.1; D(X) =
0.2-0 I
12 ‘300’
Юх/З
Ошибка в отсчете времени будет больше 0,05 сек., если
стрелка секундомера будет «находится» на интервале (0,05; 0,15). А
вероятность того, что значения случайной величины Л принадле-
жат интервалу (0,05; 0,15) вычислим по
муле (6.3):
Р(0,05 < X < 0,15) = Г(0,15)- Г(0,05) =
= 5 0,15-5 0,05=5 (0,15-0,05)-0,5.в
Ответ: вероятность сделать ошибку более 0,05 равна 0.5.
7.2. Автобусы некоторого маршрута идут строго по расписа-
нию, интервал движения 5 минут. Считая, что случайная величина
А - время ожидания автобуса на остановке - распределена равномер-
но. найти верояпюегь toi о, что пассажир, подошедший на остановку,
будет ожидать очередной автобус менее 2 минут.
7.3. Цена деления шкалы амперметра равна 0.1 А. Показания
округляют ло ближайшего целою деления Найти вероятность того,
что при отсчете будет сделана ошибка, превышающая 0,02 А.
7,4. Шкала рычажных весов, установленных в торговой точ
ке, имеет цену деления 100г. При измерении массы товара отсчет
делается с точностью до целого деления с округлением в ближай-
шую сторону. Какова вероятность, что абсолютная ошибка опреде-
ления массы I) нс превысит величины среднеквадратического от
клонения возможных ошибок определения массы: 2) будет заклю-
чена в пределах от П до МА’)0
63
73. Пациснгы заходят в кабинет врача каждые 10 минут.
Пусть время ожидания пациентом посещения врача случайная ве-
личина А' которая имеет равномерное распределение Найти плот-
ность распределения, функцию распределения, математическое
ожидание, среднее квадратическое отклонение этой случайной ве-
личины V. Вычислить вероятность того, что пациент будет ожидать
посещения врача меньше 3 минут.
7.6. Определить закон распределения случайной величины
А, если ее плотность распределения вероятностей «адана функцией:
• I . 1 _ (*♦»>*
а)р(х)^—е к ; б) р(х)т=—72 .
4V2/T у1Т1л
Определить математическое ожидание, дисперсию и функцию рас-
пределения
1 -
Решение а) Поскольку р(х)~—12 , то, сравнив эту
4<2лг
функцию с формулой (7 4), заключаем, что случайная величина X
распределена по норматьному закону с параметрами тп~1\ сг 4. Так
как параметр т это математическое ожидание, а п - среднее квад
ратическое отклонение нормально распределенной случайной ве-
личины. то М(Х) = 2, />Р0 = 16.
( о) ласно формуле (7.5) определяем функцию распределения:
л-2
F(x) = Г е ~dt - Ф *' -Ж— ,
у/2гг ' I 4 J
I <x-2)
или F(x) = — + Ф — . гдсФСг)- функция Лапласа.
2 4
7.7. Записать плотность распределения вероятностей и
функцию распределения нормально рас пре де л сплои случаГшой не-
личины А; если: у) М(Х) = 5; D(X) - 9; б) МХ) ~ -3; D(X} = 16.
Гсшснис aj) Так как параметры т и л в форму ic плотности
распределения вероятностей являются математическим ожиданием
и средним квадратическим отклонением нормально распределен-
ной случайном величины V, то плотность определяется функцией:
р(ж)=—!— е
3V27 3Vbr
Coi ласно формуле (7 S) чанисываем функцию распределения:
, или F(x)= — 4 Ф
7.8. Известны числовые характеристики ЛДХ)=6; D(A)“25
нормально распрсдс шиной случайной величины А Вычислить ве-
роятность того, что значения случайной величины X принадлежи!
полуинтервалу (7;12).
Решение Для вычисления искомой вероятности воспользу-
емся формулой (7.6). учитывая, что т = 6. ст = V'D(X) - 5:
» 0,8849 - 0,5793 • 0,3056.
7.9. Математическое ожидание случайной величины А' рас-
пределенной по нормальному закону равно 5 Вычислить
ДО < А’< 5), если извссiно, что Р(0 <Х< 10) = 0.1.
Решение Воспользуемся формулой (7.6):
Ф’
-Ф’(О)-Ф’|-
i,5- (I -0t6) = 0,5 -0,4- 0,1 (при вычнсле-
ним
воспользова лись формулой Ф’ (-х) = I Ф*(х)).
Ответ Р(0^ х< 5)-0.1,
7.10. Станок-автомат изготавливает втулки, которые удовле-
творяют стандарту, сели отклонение величины диаметра А от про-
ектного размера по модулю не превышает 0,35 мм Каково нлибо
пес вероятное число стандартных втулок и| 200. если случайная ве-
тчина А распределена норма льно с параметром л 0,2 мм
Решение Вначале вычислим вероятность отклонения А от
проектного размера по формуле (7 7). учитывая, что Л 0.35. а
= 2 • 0,9599 - I - 0.9198 * 0,92
Для определения наиболее вероятного числа m0 стандартных
втулок воспользуемся формулой (5.2). в которой р = 0,92;
7 I -0.920.08. 17-200: 200 0.92 0,08 /л., < 200 -0.92 ч 0.92;
183,92 < тп0 S 184.92. откуда mo - 184.
Ответ: mt = 184,
7.11. Коробки с шоколадом упаковываются автоматически:
средняя масса одной коробки - 1,06 кг Известно, что только 5%
коробок имеют массу меньше I кг. Найти стандартен, отклонение,
(грелполагая, что масса коробок распределена нормально
Аъырнис Пусть случайная величина X масса коробки с шо-
коладом Из условия задачи следует, что случайная величина X
распределена нормально и что hf(X) - 1,06. Тогда стандартное от-
клонение ст
( а* ) = у/О( V ) найдем, из формулы, используя раяен-
г । _ । Q6 \
стьо Р( 1S А < -кс) - Ф i +х) Ф —-— Так как только 5% коробок
имеют массу меньше I кг и. следовательно, масса осчатьных коро-
бок больше 1 кг. то можно записать:
0.95 = 1 Ф'
1.645, откуда <т-
По габлиие 1 находим
0.П6
L645
*0.0365.
Отчет: <т(х) * 0,0365.
7.12. На авюматичсском токарном станке изготавливаются
болты, номинальная длина которых 30 мм. Наблюдаются случай-
ные отклонения от этого размера, распределенные по нормальному
закону с математическим ожизанием т 0 и средним квадратиче-
ским отклонением а - 1мм При контроле бракуются все болты,
размеры которых отличаются о» номинального больше, чем на до-
пуск Д *= 3 мм Найти вероятность гою, что наудачу выбранный
болт будет бракованный
7.13. ( ’лучинная величина X подчинена нормальному закону с
математическим ожиданием т 0 и средним кна фатичес ким от
кнонснием а При каком значении о вероятность попадания слу-
чайной величины Xв интервал (?; 4) достигает максимума?
66
7.14. В нормально распределенной совокупности 15% значе-
ний А меньше 12 и 40% «качений А больше 16.2. Найти среднее
«качение и стандартное отклонение данною распределения.
7.15. Химический «анод изготавливает серную кислоту' номи-
нальной плотности 1.84 г/см В результате статистических испы-
таний обнаружено, чго практически 99.9% всех выпускаемых реак-
тивов имеют плотность в интервале (1,82; 1.86). Найти вероятность
того, чго кислота удовлетворяет стандарту, если для этою досга-
точно, чтобы ее «ыотноегь не отклонялась oi номинальной более,
чем на 0,01 г/см , предполагая, что значение плотности распреде-
лено по нормальному закону.
7.16. В пакете 5% всех акций отклоняется от средней цепы в
I20S бопее чем на 2$. Считая, чго распределение иены акций под-
чиняется нормальному чакону, найти, какой процент акций имеет
цену и пределах от 1 19 до 121 $
7.17. Вероя!ность банкротства отдельной фирмы равна 0.75.
Основываясь на нормальном законе распределения, определить ка-
кова вероятность того, что из 200 фирм обанкротятся не менее 140
и не более 180.
7.18. Станок-автомат изготавливает цилиндры, номинальный
диаметр которых равен т - 10 мм. Случайная величина Л- вели-
чина диаметра, распределена нормально со средним квадратиче-
ским отклонением а- 0.1. Найти интервал, я котором с пероягно-
с гью 0,9973 будут заключены диаметры изготовленных цилиндров
7.19 .1 СИ» фирм одной отрасли работают независимо друл оз
друга. Известно, что каж^шя фирма обеспечена работой в течение
рабочего времени с вероятностью равной 0.8. Определить вероят-
ность гого, что в произвольно взятый момент времени будут рабо-
тать от 70 до 86 фирм, если распределение занятости работой под-
чиняется нормальному закону
7.20. Средний процент выполнения плана некоторыми предпри-
ми иями составляет ИХ)%, среднее кштдратнческос отклонение - 9°о По-
лл!ая. что выполнение плана «той i рунной предприятий подчиняются
шкону нормального распределения, определить процент предприятий:
а) не выпо-1нию111нх циан; б) выполняющих план от 110 до 150%.
7.21 .Дна небольших завода /зи/> производят некоторый то-
вар. Количество товара Л'| и А? производимого соответственно за-
водами / и 1 х за неделю, распределены независимо и можно счи-
1ать. что они имеют приближенно нормальное распределение Ко
шчество товара А*| имеет среднее значение, равное 6000 и диспер-
сию, рапную 900. Х> имеем среднее значение, равное 15000 и дис-
персию. равную 3600 1онар, производимый на заводе I ь приноси!
67
прибыль 3 ден. ел. в расчете ни 1 единицу шмара, а товар, произво-
димый на Г2 - 2 ден. ед. 11редполагая. что сумма издержек произ-
водства заводов составляет 10000 ден ед. в неделю, найти вероят-
ность того, чло за некоторую неделю суммарная чистая прибыль
завода будет больше 38500 ден. ед.
7.22. В среднем брак составляет 3% Какова вероятность того,
что в партии из 500 изделии число бракованных нс превышает 20?
Будем исходить из предложения, что число бракованных изделий в
определенных партиях подчиняется нормальному закону' распреде-
ления
7.23. При определении доли прибыли допускают случайные
ошибки, подчиненные нормальному закону распределения со сред-
ним отклонением 10 ден. ед Найти вероятность тою. что опреде-
ление прибыли будет проведено с ошибкой, не превосходящей 15
лен. ед., если систематические ошибки отсутствуют.
7.24. Деталь, изготовленная станком автомаюм. считается
годной, если отклонение сс контролируемого размера от проектно-
го пе превышает 1 мм Случайные отклонения контролируемого
размера от проектного подчинены нормальному распределению со
средним квадратическим отклонением ст*0,5мм и математическим
ожиданием т=0. Сколько процентов годных aeiaiefi изготавливает
станок-автомат?
7.25. Изделие считается высшего качества, если отклонение
сто размеров от номинала не превосходит по абсолютной величине
3,45 мм. Случайные отклонения размера изделия от номинала под-
чиняются нормальному закону распределения со средним квадра-
тическим отклонением равным 3 мм, а систематические отклоне-
ния отсутствуют. Определить среднее число изделий высшего сор-
та, если изготавливаются четыре изделия.
7.26. Как, зная среднее квадратическое отклонение а и мате-
матическое ожидание т случайной величины Х\ распределенной по
нормальному закону, ориентировочно указать интервал ее практи-
чески возможных значений?
7.27. Как изменяется ордината кривой нормального распреде-
I
ления для (Г = — и ст = 2 при х - m :
7.28. Непрерывная случайная вс личина распределена по пока-
зательному закону, заданному плотностью распределения вероят-
костей’
10 прих<0;
p(x) = < .
[Зе1 при 1 > О.
Вычислить функцию распределения, математическое ожидание
и дисперсию заданной случайной величины А. Найти вероятность то-
го, что значение случайной величины принадлежит интервалу (I. 3).
Решение. Воспользовавшись формулой (7.9) запишем функ-
цию распределения
при л < 0:
при х > 0.
Так как параметр показательного распределения Х=3, то
д/(Л)=у=Ь р(Л')
Л *
Вероятность попадания А в ни-
гер нал (I, 3) равна разности значений функции распределения на
концах интервала, т.е.
Л(1 < X < 3) = F(3)-F(I) = (1 -е ”) (1 - е*м)=е ’ - е* *
* 0,0498 - 0,0001 = 0,0497.
Отпет; Р(| < А' < 3) ~ 0.0497.
7.29. Функция распределения случайной величины Т времени
безотказной рабозы радиоаппаратуры имеет вид: F{l)~ 1-е"
12 0 Какому закону распределения подчиняется эта случайная ве-
личина Г? Вычислить: а) вероятность безоткатной работы радиоап-
паратуры в течение времени t 100 ч.; б) вероятность того, что ра-
диоаппараiypa откажет в течение времени Г-100 ч.
Решение Воспользовавшись формулой (6.2) определим плот-
ность распределения вероятностей случайной величины Т;
p(x)-(fir>>'-(l , |’-0ДОе4* i ।
которая совпадает с функцией (7.8). Следовательно, с туманная ве-
личина Г распределена по показательному закону.
Функция распределения F(/)-l е "v, /£0, определяет
вероятность отказа ралиоаппара гуры за время длительностью г с
интенсивностью отказов (среднее число отказов в единицу време-
ни) равной 0.01
а) Вероятность безотказной работы радиоаппаратуры в течение
эремсни /» 100 ч. равна
Р, 1 - ЛГ)|, «,= 1 - (i -1 00,,f°) = 1-1 + г"’= * 0.0498
6М
6) Так как функция распределения F{f) определяет вероятность
отката <а время длительностью г. то. иоде швин г—100 н функцию
распре печения, получим вероятней» очката радиоаппаратуры <а
время длительностью гМОО ч,:
Р, - F( 100) = I - - I _ е-’ . 1 _ 0.0498 = 0.9502
Ответ- Р, -0.0498; Г--0.9502.
7.30. Время ожидания у бензоколонки автозаправочной стан-
ции является случайной величиной X. распределенной по показа-
тельному закону со средним временем ожидания, равным 10 мину-
там. Найти вероятности следующих событии. А - {5 <Х< 15). В
= {Л>20).
7.31. На шоссе установлен контрольный пункт для проверки
технического состояния автомобилей Найти математическое ожи-
дание и среднее квадратическое отклонение случайной величины
/ времени ожидания очередной машины контролером, если ноток
машин простейший и время (в часах) между прохождениями ма-
шин через контрольный пункт распределено по показательному за-
кону
7.32. Студент помнит, что плотность распределения вероят-
ностей показательного распределения имеет вил;
f0, прнх<0;
PW = \r
( е , при х 2 О.
Однако он забыл, чему равна постоянная С. 11айти постоянную С.
7.33. Производится испытание двух приборов, работающих нс-
мвиси.мо друг от трута. Длительность безотказной работы приборов
распределена по показательному закону с плотностями распределе-
ния p,(t)-0,5-e п'', т>0; р,(/)= 0,4 е t >0. соответственно.
Найти вероязмость тою. что в ингервалс (0; 5) часов откажут 1) оба
прибора. 2) только один прибор; 3) хотя бы один прибор.
7.34. Искусе (венный спутник земли, движущийся по своей ор-
бите я течение л суток, может случайным образом С1Ш1кинатыя с Мс
тефритами Метеориты. пересекающие орбиту и сталкивающиеся со
спутником, образуют пуассоновский поток с плотностью Л (метеори-
тов в сутки к Метеорит, попавший в спутник, пробивает его оболочку
с нероязностыо /• ,. Метеорит, гробивший оболочку с вероятностью
Pi вынодиз hi строя аппаратуру спутника Найти вероятность еле
дующих событий’ а) за время полета его оболочка будет пробита; б)
за время полета его аппаратура будет выведена и« строя; в) за время
полета будет пробита обо ючка. а аппаратура будс) действовать.
7.35. При работе некоторого прибора в случайные моменты
времени возникают неисправности. Время Г работы прибора оз его
включения до возникновения неисправности распределено по пока-
тельному закону:
р(0*
Г>0;
0. 1 < 0.
При возникновении неисправности она мгновенно обнаружи-
вается, и прибор поступает и ремонт Ремонт продолжается время
т(:. после чего прибор снова включается в работу. Найти плотность
распределения р*(0 и функцию распределения г (г> промежутка
времени Т между двумя последовательными неисправностями
Найти его математическое ожидание и дисперсию. Найти вероят-
ность того, что время Т будез больше 2/0.
736. Время / между двумя сбоями в работе вычислительной
машины распределено по показательному закону с параметром
Р<0 =
Ле ", т£0;
0, /<0.
Решение задачи требует безотказной работы машины в тече-
ние времени т. Нели за время т произошел сбой, то задачу прихо-
дится решать заново, ( бон обнаруживается только через время т
после начгьпа решения задачи Найти закон распределения случай-
ной величины Т времени, за которое задача будет решена
1.8. ^Предельные теоремы и закон больших чисел
Все законы теории вероятностей получены из практики, то
есть из наблюдений за массовыми случайными явлениями. Массо-
вые случайные явления проявляются в статистической совокупно-
сти. Было шмечсно, что при определенных условиях массовые слу-
чайные явления порождают величину неслучайную, которая под-
чиняется вполне опоеделепным закономерностям. Все полученные
аютвстствующис теоремы и образуют зсорсмы закона больших
чисел, в которых приведены условия, когда среднее значение слу
чайных величин стремится к величине не случайной. Таким обра
юм закон больших чисел - это совокупность зеорем. в которых
приведены условия при которых последовательность случайных
величин подчиняется опрсде^нным закономерностям го есть
стремится к величине неслучайной.
Неравенство Чебышева: Вероятность тою, чго случайная
величина X отклоняется от своего математического ожидания на
71
.. D(X)
величину не мсныис к. ог раничена сверчу величиной ——, где
€
с - положительное действительное число:
или ГЦх-Л/И) <с}>1 (81)
£ ' £
В частности, если А* >0 н существует ЛДЛ\ то
Р(Х >£)<—— или Р(Х££)>}-М(Х-. (R.2)
£ е
Ес in существует Afl.V), то при любом £>0 справедливо не-
равенство:
Р(Л>Г)<
(83)
Теорема Чебышева (закон больших чисел): Если Л.А,... по-
следовательность независимы' случайных величин, которые имеют
конечные математические ожидания и ограни ленные дисперсии
>, то при возрастиии п среднее арифметическое наблюден-
injx значении случайных величин сходи гея по вероятности к средне-
му арифметическому их математических ожиданий
limP
г
£
п
Отсюда следует, что для больших п справедливо неравенство:
р ’£л, ’х.шх)
V «Т? л м
П£
Закон больших чисел справедлив к для швисимых случайных
величин, то есть справедлива теорема Маркова:
Если для случайных величин A'i^A*— выполняется условие
=0, то при вочрастапии л среднее арифметическое
lim—
_ ». -__ _ - *
наблюденных значений случайных величин сходится по вероятно-
сти к среднему арифметическому их математических ожиданий
ЯТГ
Гео!н:ма Бернулли: Если производится и испытаний, в каж-
дом из которых некоторое событие А может появиться с вероятно-
стью />. то относительная частота появления события в п испыгани
7?
ЯХ СХОДИТСЯ ПО вероятности К Bupow iHCK. I и появления события в
каждом испытании: lim Г
В час i нос 1 и д 1Я больших и
Теорема Пуассона: Пусть производится п независимых ис-
пытаний, я каждом их которых событие А появляется с всрояiки-
стями ..р* Тогда при неограниченном увеличении числа ис-
пытаний относительная частота появления события А сходится по
вероятности к среднему арифметическому вероятностей появления
события в различных испытаниях:
Теорема Линдеберга-Леви: Пусть АбЛь— независимые одина
коно распределенные случайные величины с математическими ожи-
даниями т и дисперсиями гЛ то при неограниченном увеличении и,
закон распределения нормированной случайной величины Zr стре-
мится к нормальному закону распределения с плотностью расстреле-
1 --
лс1птя вероятностей равной <р(7) - -е 2, для которого тМ), о ~ I,
V2/r
«де z _ ii!— -! - нормированная случайная величина.
Эго центральная предельная теорема для одинаково распре-
деленных независимых случайных вс шчин.
Теорема Ляпунова: Исли А'|Д?Г. независимые случайные ве
тичины, имеющие конечные математические ожидания т. диспер-
сии г/ и конечные абсолютные центральные моменты третьего по-
ш
рядка, удов;етж ряышис условиям: lim-.-.'Г . -O.io «акон
к - у
J
Ж «н /
распределения величины 7Г сходится к нормальному <акону paenpt
73
деления с плотностью распре.телсния вероятностей <р(г) = —г=^е 1 ,
J2rr
для Koropoi о т 0, tr-1.
Эта теорема имеет большое практическое значение, так как,
используя ее, можно вычислить вероятное гь того, что сумма неза-
висимых случайных величин принимает значение, принадлежащее
интервалу. Условие lim । ' 1 — - 0, характеризует тот факт.
ft- 1 «
что все случайные величины сравнимы между собой, го есть ни од-
на из случайных величин не имеет преимущества перед другими
случайными величинами.
Рассмотрим дискретную с лучайную величину А', которая ха-
рактеризует число появлений события А в п независимых испыта-
ниях Эту случайную величину можно представить в виде суммы
случайной величины Xh каждая из которых характеризует число
появлений события А в /-ом испытании. X - ^ Х
Нормированная сумма случайных величин А", / = 1,л будет
_ т-пр
иметь вид: Z„ -—и- , л де т - число появлений события А в ис-
пытаниях, р- вероятность появления события А в каждом испыта-
нии; п - число испьпаний;
Если случайная величина X подчиняется биномиальному за-
кону распределения, то вычисление вероятности того, что некото-
рое событие 4 появиться т раз в п испытаниях ио формуле Бернул-
ли затруднительно, ес ли п достаточно большое. а р ма ло В этом
случае можно воспользоваться следующими теоремами:
Теорема Myaepa-JIатаса (локальная): Пусть ироизволится
п испытаний, в каждом из которых некоторое событие А может
появиться с вероятностью р (0<р<). Тогда для всех т. удонлетво-
т - пр . .
ряюших условию а<—= < л, (где и, п произво льные числа)
Vnpg
выполняется соотношение;
74
Р„<гг) =0.
Локальная теорема используется при больших значениях п
тля вычисления вероятности Р(Л) гого, чго некоторое событие Л
наступает т раз в п испызаниях по формуле;
n , 1 ч , , I —г т — пп
СН’д--------yHz); (P(z) = -J=e . 7-~f=^~ (8.4)
yjnp<l <2я \ пРЧ
Теорема Маувра-Лапласа (интегральная): Пусчь произво-
дится л нс зависим их испытаний, в каждом из которых событие А
может появиться с вероятностью р. Тогда для любых я и Л справед-
ливо соотношение:
limP а<
т-пр
Из предельною равенства теоремы следует формула.
РОл, < ) * ntj) а Ф’
глеФ’(з)-
я
> - /. АЛ' - число появлений события А в т ом испытании.
Используя теорему Муавра-Лапласи, вычисляется
верояг-
ность неравенства
т
--Р
п
< 4,1 е. справедлива формула
1, гдеФ’(х) =
(8.6)
р|< 4) *2Ф’
• t1
|сЧ (8.7)
В отличие от теорем Бернулли и Пуассона последние дне
форму, гы дают более точную опенку вероятности отклонении час-
юты поян 1сния событий ci сю математического ожидания и час
тости события от вероятности появления события R каждом испы
танин.
Задачи
8.1. Средний вес яблока равен НО i Используя неравенство
Чебышева, оценить вероятность юго, чго наудачу взятое яблоко
весит не более 180 г.
75
Решение, С чайная величина X вес случайно выбранного
яблока. По условию гадачи М(Х) - 110. Тогда искомую вероятность
оценим ио второй формуле (8.2). где € будет равно 180 Подставив
значения М(Х) и с. получим:
PfA" <1Х0)>1 - —.
180 18
Отпет: п - —
18
8.2. Средняя скорсктъ движения автомобилей на одном из
>час1кон автомобильной дороги равно 85 км час. Используя нера-
венство Чебышева, оценить вероятность того, что у наудачу вы-
бранного автомобиля его скорость нс меньше 100 км/час.
Решение. Случайная величина А* скорость на>дач> выбран-
ного автомобиля на данном участке автомобильной дороги. По ус-
ловию задачи МА>=85 км/час. Искомую вероятность оценим, ис-
пользуя первую формулу (8 2), где с-100 км/час. Подставив значе-
85
ния и г= I(X), получим: Р(Х £ 100)< у— - 0,85
Отпет' р=О,85.
8.3. Средняя скорость вегра в одном из районов Земли 15
км час. Используя неравенство Чебышева, оценить вероятность io-
го, чго н наудачу выбранный день скорость вегра в этом районе бу-
дет не менее 100 км/час.
8.4. Для некоторого автопарка среднее число автобусов, от-
правляемых в ремонт после месяца эксплуатации на городских ли-
ниях, равно 5 Оценить вероятность события соегоящего в том, что
по истечении месяца в данном автопарке будет отправлено в ре-
монт меньше 15 автобусов, если нет информации о дисперсии.
8.5. Число фирм уклонякмцихся ог полной уплаты налогов для
города N является случайной величиной со средним значением КМ)
фирм и средним квадратичным отклонением равным 20 фирмам
Оценить сверху вероятность событий: Л - {А’> 150), В = (Д'>200).
8.6. Вероятность появления события А в каждом испытании
равна 0,5. Используя неравенство Чебышева оценить вероятность
того, что число А появлений события А будег заключено н пределах
от 40 до 60. если будет произведено 100 независимых испытаний
Решение А*- число гюян ними события А в 100 независимых ис-
пытаниях Найдем математическое ожидание Л /( V) и .икперсию £АА):
М(Х) пР 100- 0,5 - 50; ЩХ) « npq « 100 - 0.5 • 0.5 = 25.
76
Наилем максимальную разность между заданным числим по-
явлений события и математическим ожиданием ЛЛА) 50: с -60
• 5U - 10. Воспользуемся неравенством Чебышева н форме:
Подставляя VAA) 50t D(A)~25t £”10, получим:
p(|X-5«|<t0)M-^=0.75.
Ответ: Р(40 < X < 60)> 0.75.
8.7. Вероятность появления события в каждом испытании
равна 0.25. Используя неравенство Чебышева, оценить вероятность
тою, что число Л появлений события заключено в пределах от 150
до 250, если будет произведено 800 испытаний.
8.8. Вероятность производства нестандартного изделия при
данных технологических условиях равна 0.05. Оценить вероятность
того, что число нестандартных изделий среди 1000 будет заключе-
но в пределах от 85 до 95 включительно.
8.9. Дискретная случайная величина X задана законом рас-
пределения
х, 4 "У" S - 6 7 1
0.2 0.1 1 0.4 0,3 _
Пользуясь неравенством Чебышева, оценить вероятность ю-
го. что случайная величина Л’ примет значение, удовлетворяющее
неравенству |У - Л/( X )| < 3.
Решение. Вычислим математическое ожидание и дисперсию
случайной ве нчинн А": Л/( А') = 4 0,2* 5- 0,1 +6 0,4* 7 0,3- 5,8;
ZX*)=42 0,2+ 52-0.1+61-0,4 г 72 0.3-(5.8)’ -1.16.
Век пользу емся неравенством Чебышева в форме:
Р(| X Л/(А)|<г)2-1-^~.
£
Подставив значения ГЦХ) 1.16 и г = 3, получим:
Р(|А' Л/( X )| < г) 1> 1 - - 1 - -^6 » 0,87.
Ответ Г(|Л - Л/( X )| < £) > 0.87.
8.10. Дискретная случайная величина А'задана законом рас
прсде тения
а) I г, Т 0.3 1 0.6
UZL®-2 °.®
6)
Используя nepaitciiciBo Чебышева, оцепить всрояпюшь того, что
a) X - М(А' >| < 0. 2; б) |А - М( А ) < 4.
8.11. Заданы законы распределения попарно независимых
случайных величин, образующих случайную последова1ель-
Hocib{YJt
Выяснить, применима ли к этим последовательностям теорема Че-
бышева?
Решение а) Дея того, чтобы к последовательности случайных
величин была применима теорема Чебышева, достаточно, чтобы лги
случайные величины бы ш попарно независимы, имели конечные ма-
тематические ожидания и равномерно ограниченные дисперсии.
По условию задачи случайные величины Хп. п=1.2Д..., по-
парно независимы, т.с. первое условие теоремы Чебышева выпол-
нено.
Дзя проверки других >словим вычислим математические
ожидания и дисперсии тгих случайных величин. Математические
ожидания раины.
Л/(У.) ^л--+0 I -\+Jn--.O.
п \ п J п
Значит, случайные величины Х„ имеет конечные математические
ожидания
Для вычисления дисперсии составим «аноны распределения X*.
Л 0 I л 1
II Us, - £ л 1-1 п £ л
(сила дисперсии равны.
= и
Следовательно, дисперсии заданных случайных величии рав-
номерно ограничены числом 2. т.с. третье условие выполнено. По-
скольку все требования выполняются, то к случайно!! последова-
тельности {А'/} теорема Чебышева применима
8.12. Последовательность независимых случайных величин
Аь Л?,..., А„.... задана законом распределения
Применима ли к данной последовательности теорема Чебы-
шева?
8.13. При изготовлении деталей на с танке-автомате брак со
ставляст 2%. Найти вероятное!к того, что при проверке партии из
1000 деталей выявится отклонение от установленного процента
брака меньше, чем на 1%.
Решение. Пусть событие А состоит в изготовлении бракован-
ной детали. Всроя!нос1ь сю появления при каждом из1 отоплении
(испытании) летали постоянна и равна 0*02, г.с.р=0»02. По условию
<адачи нам нужно установить, что относительная частота появле-
ния бракованной детали отклонится от вероятности появления бра-
кованной детали в каждом испытании меньше, чем на 1%. г с.
меньше, чем на 0,01.
Воспользуемся теоремой Бернулли, т.е. неравенством
Поскольку л-1000, с=0,01; р~0.03, q~\ р=\ 0,02-0,98, то
подставив эти значения, получим:
р(±-Р<о.о|
л J 1000 (0,01) 0,1
79
I аким образом, искомая перон пюсть Р > 0,804
8.14. Всхожесть семян иски юрт о растения cociawwcr 80%.
Найти вероятное! ь тою, чю при посеве 10000 семян отклонение
относительной частоты (доли) изошедших семян от вероятности
гою, что взойдет каждое из них, не прсвюйдет по модулю 0,03.
8.15. Для определения средней продолжите л ьнехгги жизни жи-
телей некоторого города, численность которого равна 100000 чело-
век. взяли на выборку по одному человеку из каждой тысячи. Из-
вестно, что для каждой тысячи жителей дисперсия не превышает 3,5
года. Оценить вероятность того, чго отклонение средней выбороч-
ной продолжительности жизни отличае1ся от средней продолжи-
тельности жизни жителей для всего города не более чем на 0.5 лет.
Решение. Введем случайные величины X, - продолжитель-
ность жизни /-го жителя города /-1.100000 Эти случайные вели-
чины независимы, имеют конечные математические ожидания и
ограниченные дисперсии Следовательно, для оценки искомой ве-
роятности применим теорему Чебышева в форме:
>i-A-
п 77 л , J не .
Подставив значения с 0,5; с 3.5 и п 100. определенные в ус-
с 3,5
г.овии задачи, получим Р > I-- = 1---------- = 0,86.
ы2 100.(0.5)
Отпет. Р>0,8б.
8.16. Для определения средней продолжительности горения
элсы ролами, И31ОТОВЛСННЫХ за некоторое время, r партии из 500
коробок было изъято по одной лампе из каждой коробки. Оценить
вероятность того, что средняя продолжительность горения ото-
бранных 500 ламп отличается от средней продолжидельности горе-
ния во всей партии но модулю меньше, чем на 6 часов, если и>
песню, чго среднее квадратическое отклонение продолжительно-
сти । прения ламп в каждой коробке меньше 3 часов.
8.17. На станке изготавливаются цилиндрические детали. Оп-
ределить. сколько нужно произвести замеров, чтобы средний диаметр
цилиндрической ютали омичатся от номинального значения т не
более чем на 0,02 мм с вероятностью 0.98 Среднее квадратическое
отклонение диаметров изгптав тннаемых ди «индричсских деталей не
превышает 0,03 мм и измерения производятся без погрешности.
Решение Предположим что выСюр цилиндрической делали
для чамера диаметра. проводится наудачу Тогда случайные вели-
чины А, результаты измерения /-ой цилиндрической детали ян-
оякпся независимыми случайными величинами. Они имеют конеч-
ные математические ожидания и ограниченные дисперсии, так как
по условию задачи XD(X,) < 0.03 и, следовательно.
/ДА',) <0,0009.
11одстан.тяя
неравенство
с
-т <£ >1--------значения с~0.0009 и ь=0.02, получаем
НЕ
>0,98.
Поскольку I
1- — >0.98. то, решив «то нсравен-
л-0.02" 4Я г
ство, найдем л: I - 0,98 , 0,02^—, п>—-— = 112,5.
4л 4п 4 • 0,02
Таким образом, поскольку п натура тьное число, то доста-
точно выполнить 11 3 замеров диаметров цилиндрических деталей
Ответ п= 113.
8.18. Сколько pai нужно измерить данную величину, истин-
ное «качение которой равно т, чтобы с вероятностью, не меньшей,
чем 0.95, можно было утверждать, что среднее арифметической
«тих измерений отличается от т по модулю меньше, чем на 2, если
среднее квадратическое отклонение каждого измерения меньше 5.
8.19. При каких значениях пир биномиальный закон распре-
деления вероятностей аппроксимируе«ся пуассоновским? При ка-
ких условиях из биномиального и пуассоновского распределений
получаем нормальное распределение?
8.20. Вероятность поражения мишени при одном выстреле
равна 0,8. Нан и вероятность того, чю при 100 ньн тредах мишень
будет поражена 75 раз.
Решение. Рассмотрим случайную величину, характеризую-
щую число поражений мишени при 100 выс грезах-
и
А * ДА,, -{();!}, Г1С А/ число поражении мишени при од-
ном выстреле.
Гяи как п «елико, воспользуемся локальной теоремой Лапласа
(формулой (Я 4)) Pjm) *
(ГЧл), глс Н ')
”РЧ
Ы
Определяем значение х:
т~пр 75 —100 0.8 -5 , ..
л = , Л = } = -т= = -1.25.
yjnp4 <100 0,8-0,2 <16
По таблице функции р(л) найдем
у»(-1,25) = р( 1,25) = 0,1826. Подставив значения л-100, р~0,8, q~\
0,8~0.2, 1,25)-0,182б п формулу (8 4», найдем искомую ьеро-
ятность: Л, ,(75) = - • 0.1826 = 0.04565.
4
‘ Ответ P[w(15) - 0.04565.
8.21. Найти вероятность ют, чго событие А наступит 1400
раз в 2400 испытаниях, если вероятность появления лого события
в каждом испытании равно 0,6.
8.22. Веройзное 1ь рождения мальчика равна 0,512 Найти ве-
роятное/ь того, что среди 100 новорожденных окажется: 1) 50
мальчиков: 2) больше мальчиков, чем девочек.
8.23. Вероятность появления собы.ня А в каждом из 2100 не-
зависимых испытании равна 0," Найти верой шость того, что собы-
тие появился: а) не менее 1470 и более 1500 раз, б) не менее 1470
раз; в) не более 1496 раз.
Решение. а) Рассмотрим случайную величину Ад число по-
злю
явлений события А в 2100 испытаниях, которая равна X => V Л ,
где X, число появлений события А в /-ом испытании. Случайные
величины V, имеют одинаковые математические ожидания
Л/(Л) = р и дисперсии D(X)-pq Следовательно, для вычисле-
ния искомой всроя шести можно применив интегральную теорему
Муавра-Ланласа. г с. формулу (8.5)
По условию задачи п =2100, Ш|=1470, иь~15(Х), />”0,7,
p=0J Находим вначале х. — —-0; и
//W /2100.0,7-0,1
г i500^2-100 0 7 30 i зз
/w /2100 (Г,7 0,3 21 '
По таблице значений функции Ф*(г). находим Ф(0) - 0,5 и
Ф (1.43) 0,9236. Затем по формуле (8 5) находим искомою веро-
ятность:
Люо(1470;1500)-Фе(1,43) Ф*(0) 0.9236 0,5 0,4236.
Ответ Р.|о/Л470.1500) = 0,4236.
82
8.24. Проводятся последовательные испытания ио схеме Ьер-
не.тли Вероятность осуществления события А в одном испытании
равна 0,6 Считая применимыми предельные теоремы Муавра-
Запласа, вычислить вероятность следующих событий: Н {событие
•I произойдет н большинстве из 60 испытаний}: С -{число успеш-
ных осуществлений событий Л в 60 испытаниях будет заключено
между 30 и 42}.
8.25. Вероятность того, что деталь стандарта, равна 0,9. Слу-
чайная величина А - число стандартных деталей. Сколько нужно
проверить деталей, чтобы с вероятностью 0.95 можно было ожи-
дать. что не менее 150 деталей будут стандартными.
Решение. Случайная величина А =^А'. где А', число по-
явлений события А в /-ом испытании; .4={при проверке оказалось,
что деталь стандартна}; М(Х ) = р \ Г>(Х pq
Воспользуемся формулой (8.5). Согласно условия задачи
р-0.9. </ I р I 0.9 0,1. т, 150. тг^п неизвестная величина, ко-
торую нужно определить. Подставив эти значения в (8.5). получим:
Р„(150.л) = Ф*
' п 0,9» _ .( 150 - 0.9»
kV» 0.9-0.1) ~ 0.9 0,1
И III
/
0.95 = Ф’
0,)л
о.з7»
.1 150 0,9л
Ф “~г~ •
ч 0.3-7» )
или
0,95 - Ф’
Ф*
150-0.9»
i 0.3-7»
Из условия задачи следуег, что л>150. поэтому
1 д4.0Х. Поскольку Ф*(л) функция возрастающая и
Ф*(3,9) 1.0, то можно
положить
Следовательно.
0.05
0.95 -1 Ф’
ISO 0.9»
0.1 \[п
'150 0.9»
I оЗТя
По таблице значений функции Ф*(г) находим Ф(-1 645) 0 05
- 150 0.9» ,.л<
lot ia ершниная аргументы, получим: . --1.645:
150 0.9»= 0.40357». 0.0»-0.4935^ 150 = 0
Решая полученное квадратное уравнение огносигсльно
находим значение п: yfn ~ 13,19; и=1 4 (с учетом тою, что и - на-
туральное число).
Ответ ат=174.
8.26. Верой! ность появления события в каждом из независи-
мых испытаний равна 0,8. Сколько нужно произвести испытаний,
чтобы с вероятностью 0,9 можно было ожидать, что событие поя-
вится не менее 75 раз?
8.27. Вероятность появления положительного результата в
каждом из аа опытов равна 0,9 Сколько нужно произвести опытов,
чтобы с вероятностью 0.98 можно было ожидать, что нс менее 150
опытов дадут положительный результат?
8.28. Отдел технического кон грозя проверил качество науда-
чу отобранных 900 деталей. Вероятность р гою, что деталь стан-
лар» на равна 0,9. Случайная величина Л число стандартных дета-
ли в партии Найти наименьший интервал симметричный относи-
тельно ЛАЙТ), в котором с вероятностью, не меньше 0,9544 будет за-
ключено число стандартных деталей.
Решение. Воспо льзуемся форму пой (8.7):
в которую подставим значения №900; /г*0,9; д=1 />- I -0.9--0.1;
Р 0,9544 из условия задачи. Получим равенство:
' 900
= 0.9544: 2Ф’(100г)
= 0.9544;
2Ф’(10Ог) = 1,9544; Ф’(100г) = 0.9772
По laOjiiiue значений функции Ф*(х) находим Ф*(2)-0.9772.
Сравнивая аргументы, получим l00f = 2, откуда г = 0.02.
Ночнрлпмяе». к формуле (8.7), запишем неравенство
< 0.0? речная которое, находим интервал, в котором за-
900
ключено чис по стандартных деталей:
-0.02S— -0,9<0,02; 0.8Х< т <0.92; 792<w<829.
900 900
Оттт [792; R29]
8.2 9. Обе подуются 500 нар обуви тготов ленной на предпри-
ятии, где брак составляет ?% (нучайная величина Л число пар
84
обуви, нс содержащей брак Найзи наименьший интервал. в кото-
ром с вероятностью 0,99 будит заключено обследованное число пар
обуви, не содержащей брак.
8.30. Ежедневно в городе Л/ автобусами перевози ня 500000
пассажиров. 10% из которых не оплачивает проезд, Случайная ве-
личина А число пассажиров, нс оплативших преччл Найти ишер-
вал, в котором с вероятностью 0,95 будет заключено число пасса-
жиров, не оплативших проезд.
8.31. От дел технического контроля проверяет вес 500 коробок
с шоколадными конфетами. Их масса должна ровняться I ю. Из-
вестно, что масса 5% коробок не соответствует стандарту Найти
такое положительное число £, чтобы с вероятностью 0.95 модуль
отклонения частости появления коробки с массой, не соответст-
вующей стандарту, от его вероятности/М),05 нс превышал г.
8.32. В страховой компании застраховано 1СКМЮ автомобилей
Вероятность поломки любого автомобиля в результате аварии рав
на 0,006. Каждый владелец застрахованной) автомобиля платит в
год I ?0 ден.сл страховых взносов и в случае поломки автомобиля в
резу пьгатс аварии получает от компании 3000 ден ед. Найти веро-
ятность того, что 1) А - {по истечении года работы страховая ком-
пания потерпит убытки}, 2) Р {страховая компания получит при-
быль не менее Кден.ед.}, если К 30000; 40000; 50000
Решение. I) Сграховая компания потерпит убыток, если при-
дется выплатить потерпевшим сумму, большую страховых взносов
(сумма страховых взносов равна 120 • 10000 - 1200000). Сумма вы-
плат определяется числом автомобилей т, попавших в аварию и
равна т- 3000 - 1000m. Пусть случайная величина А число авто-
мобилей, попавших в аварию. Введем обозначения: М предельное
число автомобилей, попавших в аварию, .9- сумма, выплачиваемая
пострадавшему; с страховоГт взнос; п количество застрахован-
ных автомобилей
Страховая компания потерпит убыток, если т<Л <п Тогда,
воспользовавшись формулой (8 определим вероятность события А
Р|т< А < п}
Подставив данные из условия задачи л-10000, р- 0,006,
Q • I - р ~ I - 0.006 - 0.994 и значение /л, вычисленное ич равенства
гл 120-10000
ли си; т = — =----------« 4<К), получим
Я 3000
85
M v . I GOOD - 1OOOO • 0,00(1 •
r(m<\ Sm =Ф
, Jl 0000-0,006 0.994
400 10000 0.006
Ф --------
I J 0000 0.006 0.994
-Ф
10000 - 60) .(400-60
-------- - Ф -------
Ответ: I ) P-0
8.33. С конвейера сходи! 85% автомобилем, нс содержащих не-
исправнОк гей. Ckoikko автомобилей следует проверить, чтобы с ве-
роя1нос1ью 0,997 отклонение частости исправных автомобилей сре ди
сошедших с конвейера от вероятности р = 0.85 тою. чю случайно
выбранный автомобиль исправен, по модулю не превосходило 0,01?
8.34. Всхожесть семян моркови равна 0,95 Нам i и верой i ноегь
того, что из 1000 посаженных семян моркови число проросших за-
ключено межу 870 и 920.
8.35. Опредсли1ь, сколько нужно i роизвес1н замеров попе-
речного сечения сосен, пре ^назначенных для вырубки, на большом
участке, чтобы средний диаметр сосен отличался от заданного т не
более чем на 4 см с вероятностью не меньшей 0,95. Среднее квад-
ратическое отклонение поперечного сечения сосен на данном уча-
стке не превышает 9 см и измерения проводятся без погрешнос ти
836. ( головая, вмещающая 850 человек. имеет два разных входа.
Около каждою из входов имеется свой гардероб. Сколько мест должно
Гы ь в каждом и т i ардеробов. доя того, чтобы в среднем в 95 случаях из
100 все посети гели могли раздеться в гардеробе того входа, через кото
рын они вошли ’ Предполагается. »гто посепггели приходят парами и
каждая пара независимо от других выбирает с вероятностью 0,5 любой
ш входов. Насколько можно будет сократить число мест в lapacpoGc,
если посетители будут приходить по одиночке и также независимо друг
от друга с равной верояпкхзьм1 выбирать любой из входов
8.37. Известно, что в среднем 7% студентов носят очки. Како-
ва вероятность того, что из 250 студентов некоторого факультета
окажется нс менее 10% носящих очки?
8.38. Оценить вероятность события:
т I
500 5
<0.01.
8.39. Среднее число вызовов на \ IC ta I минуту равно
Л 40 Л/(Л), где случайная величина А - число вызовов, посту-
пивших на Л ГС Какова вероятность событий: /1-{А >40 .
ft = {30SA'<50}?
8.40. В яшике содержатся изделия, изготовленные ня лнух га-
водах в отношении V2 Проводятся последовательные извлечения
одною изделия с возвращением. причем каждый раз фиксируется
кь
па каким занодс изготовлена и «Денис. Каково минимальное чис «о
изв 1счсний, при котором с вероятностью не меньшей 0,9948 можно
ожидать, что отклонение относительной частоты появления изде-
лия завода Nc I or всроя1ностн его появления в одном извлечении
нс превысит величины /7 = 0,05?
1.9. Двумерные случайные величины
Совокупное*! ь случайных величин Ah AS,..., А„, определенных
па вероятностном пространстве (Г2,Г,Г) образует /ьмерную слу-
чайную величину (А\. AS,.... ¥„). Если экономический процесс опи-
сывается при помощи двух случайных величин А\ и AS, то опреде-
ляется двумерная случайная величина (Аь Аг)или (А'. У).
Функцией распределения системы двух случайных величин
(АЛ, рассматриваемой как функция переменных х,уе£2уу, налы
настся вероятность появления события {(X < х)r \ Y < у )|:
F(xty) = P{(Z<x)ri(y<^)}.
Значения функции распределения удовлетворяют неравенству
0<F(x,y)^'l.
С «гомерической точки зрения функция распределения
F(x, ;) определяем вероятность того, что случайная точка (A', F) по-
падет в бесконечный квадрат с вершиной в точке (х. у), «ак как
точка (А”, У) будет ниже и левее укачанной вершины (рис.9 I).
Рис 9 I
Ворся»кость попадания случайной точки < \ . У ) в полуполосу
{Г, < А < х21 п {) < г} (рис. 9.2) или н иолуполосу
j А < г} Г){ у, < ) < г,} (рис. 9.3) ныражистсв формулами:
Р(( г, < X < * )Г( > <>’))- Г(лл>)- F(r(,) ),
S7
р(( Л' < хIГ (V < ) <>,))= F( г,у})- Г (х,у,),
couibcictbchiio. Вероятность попадания значении двумерной слу-
чайной нсличины (.V, У) в прямоугольник
{г. < Л' < х,} п { (рис.9 4) можно найти по формуле
Г((ж,<Л<х,)П(.>,<Г<у,)|-
Дискретной называют двухмерную величину, составляющие
которой дискретны.
Законом распределения двумерной дискретной случайной ве-
личины (А,У) называется множество всевозможных значений (л„ у),
i,j’ = 1.*^ . дискретных случайных величин X и У и соответствующих
им вероятностей p(v , vj. i хараклсризутоших вероятность
того, чго составляющая А'примет значение х, и одновременно с этим
« X
сск ган.1яю1цдя Y примет значение » причем Г, “ • •
Закон распределения двумерной дискретной случайной вели-
чины (А,У') задавгг в виде табл. 9.1.
Непрерывно!! называю! двумерную случайную величину,
составляющие которой непрерывны. Функция pfr.y), равная преде-
лу отношения вероягное™ попадания двумерной случайной вели-
ЕЯ
чвшы GY. К) R прямоугольник со сторонами Дд и Av к площади это*
•о прямоугольника, когда обе стороны прямоугольника стремятся к
ну по. называемся плотностью распределения вероятностей:
Р<гЛ- Нт
м л
Зная плотность распределения, можно найти функцию рас-
1 >
прсделения по формуле: F( г.))
-в —X
Во всех точках, где существует смешанная производная вкк
рого порядка функции распределения /• (х. г), плотность распредс-
1сиия вероятностей р(х,у)
можно найти по формуле:
Вероятность попадания случайной н>чки (хд) в облаегь I)
определяется равенством, Р((ж,у)с Л) = J Р<х.yjdxdy.
и >
Вероятность того, что случайная величина X приняла значе-
ние V<x при условии, что случайная величина ) приняла фикенро
ванное значение У-у, вычисляется ио формуле:
ЛГ J
j p(£,y)dx£y
Г(х|>) = Р(Х<л)|(У-у) = ^----------.
J р(&у№ Р1^У
Ahxioi ично,
X >
jp(x,rj)dq \р(х,1]Мч
b (у | х) - Р((У < у )| (Х - х)) - .
|р(х./7)с/»7
Формулы для вычисления условных п ютностей распределе-
иия всрояпюстей составля>о1цих А’и Y:
р(х || ,Л(2_21-£Ц’У\ р(И j/M<
* р2(у) 1
р(* у)- Pi(f)“ fp(r.f7)dr}
•У Р,(х) J
К9
Совокупность условных вероятностей р(хцъ). р(хД)Л ....
рОФЖ ... отвечающих условию } у„ называется условным распре-
делением составляющей Г при У=), дискрс гной двумерной случай-
I , \ rfWl) РЧ
нои величины (л,?), iде /Ял |v )- -
₽(>',) А/
Аналот ично условное распределение составляющей У при
X х, дискрстой двумерной случайной величины (А’, У) это сово-
купность условных вероятностей
PO'il*.)» fO’jl ’f.). Р(У, I*,)• -. отвечающих условию А’=г, ,
/ , \ Р(^У,) Ptf
где р(у, к ) = ——— = —.
Р(*) А.
Начальным моментом порядка к+ч двумерной ста чайной
величины (А, >~) называется математическое ожидание произведе-
ний А‘ и У*, т.е. а, ,= М( А‘,У').
Если А' и > дискретные случайные величины, то
А,-
= 1
Если X и Y - непрерывные случайные величины, то
—т —i
Центральным моментом порядка к • v двумерной случай-
ной величины (А', К) называется маюматическое ожидание произ-
ведений (Х - М( Х)) и (У - Л/(У))’. т.с
Л, = Л/[(А--Л/(А'))‘(У-Л/(У))).
Если составляющие величины являются дискретными, то
р»> "ХХ(х-
Ьсли составляющие величины являются непрерывными, то
Л. “ f f (» Л/( X))' (у М( > ))’ p(x,y)dxdy,
где p(r, v) плотность распределения двумерной случайной вели
чины (X У).
Условным математическим ожиданием l (Vi при А' - г (при
У ву) называется выражение вида;
90
Л/(> I A'= *) = £>,/»() |х),
- для дискретной случайной всличи-
V/(A ') - 1 иУл.ри, | у) ,
V м >
ны Ц*),
Л^(У|Л=л)= Jyp(j.x)</>;
- - для непрерывной случайной вели-
| М(Л F = >)- kZx);
чины >( ¥).
Математические ожидания составляющие Л и > двумерной
т туманной величины вычисляются но форму лам
/ у р - для дискретной случайной величины.
ЛЯ X) -
J jxp(x.y)dxd\
—. «с
- Air непрерывной случайней величины.
или
<*. -WI
Л/(А )- J |*/>,(.».y)dxJ\
-се о
- для непрерывной случайной величины.
У.гр, - для дискретной случайной величины.
М(Г) = <
Л> I*.
J J »р(х. I Wxdv
- для непрерывней случайной величины.
или
WiJ )- I Г >р । > ! кМЛ - для iiciipi.гывной случайной величины
Корреляционным моментом независимых случайных ве хичин
А и ). входящих н двумерную случайную величину (\.У), называют
математическое ожидание ироизвихеннй отклонений чих яс|нчин*
Л., -/./(I \ -М( ) -М(У)))=М| • > М(А )
Л(Х 1 )-
УУ»Л /'. ) Л*(Г) - лля диофстных случайных величин;
[ [ К>Г<’ >>А</| Л*Л7 Л/<> ‘ непрерывных случайны* во-нчич
Q!
Корреляционный момег.i двух независимых случайных вели-
чин А' и Y. входящих в двумерную случайную вс шчину (A, У). ра-
вен нулю.
Коэффициентом корреляции с iy чайных нс шчии X и Y,
входящих в двумерную случайною величину (А', У). называют от-
ношение корреляционного момента к произведению средних квад-
ратических отклонений этих величин:
‘ а(х)сг(у)
Коэффициент корреляции характеризуют слепень Оесноту) ли-
нейной корреляционной зависимости между ¥ и Y. Случайные ве-
личины, для которых рп - 0, называются некоррелированными
Коэффициент корреляции удовлетворяет свойствам:
1, Коэффициент корреляции не зависит от единиц измерения
случайных величин
2. Абсолютная величина коэффициента корреляции не превы-
шает единицу: (рЛГ| < L
3. Если Рг, = ±1, то между составляющими А и Y случайной
величины (Л Y) существует линейная функциональная за-
висимость: У = ДА' ♦ Д.
4. Если рг, -0, то составляющие Л и У двумерной случайной
величины нскоррелированы.
5. Если рЛТ # 0, то составляющие А' и У двумерной случайной
величины зависимы.
Уравнения М(Х Y ~ у) - <p(i) и Л К) А я) у (л ) называют у рав-
нениями регрессии, а линии, определяемые ими. линиями регрессии
Задачи
9.1. Двумерная дискретная случайная величина (А' У) задана
законом распределения:
1 111k: 9 2 ______________
1 2 3 4
0 0,2 Г 0,15 0.08 0.05
1 0,1 0,05 ох* <м
* 0.05 0.07 1 0.0 0.02
Найти- а) «аконн распределения составляющих А и У.
б) условный закон распределения величины Y при Л «I;
в) функцию распреде 1сния.
92
Выяснить, являются ли независимыми величины А и )
Вычислить вероятность Р(Х > >) и основные числовые характе-
ристики Л/(Л), М Г), /А(Л). П(Г), ЖА'.П. р(ЛЛ ).
Решение, а) Случайные величины А’ и Y определены на
множестве Г}п , состоящем из элементарных исходов, которое
имеет вид:
Событию {Л-1) соответствует множество таких исходов.
> которых первая компонента равна 1: (1:0), (1:1). (1,2). Эти ис-
ходы несовместимы Вероятность тою, что А примет значение
л„ coi ласно аксиоме 3 Колмогорова. равна:
Г(Л=Ь=Г(1;0)+р(1;1)4 р(1,2) = О.2О + 0,10- 0.05 = 0.35.
Аналогично
А Л = 2)-/>(2.0) I />(2.1)+-/>(2;2)-0.15 + 0,05 + 0,07 = 0,27;
А V ~ 3) = р(3;0) * р(3.1) ♦ р( 3.2) = 0.08 + 0,05 -г 0.08 = 0.21;
/’(А - 4) - р(4;0) > /7(4 IН г(4.2)-0.05 + 0,10 + 0,02 = 0,17.
С ледовательно, vapi нналыюс распределение составляющей
Л", может быть задано в виде табл, 9.3.
Таблица 9.3
Z ^_АЛ' = л.)-0.35+ 0.274 0.214 0.17 = 1
Т' ’
Чтобы найти вероятность /’(>-+,) необходимо сложить веро
ятносзи с греки у, в табл. 9.2:
А) - 0) - /<Г(1) + />( 2 о: 4 р(3;2) + /44.0) = 0.20 + 0.15 + 0.08 + 0.05 - 0 48
А> ))= р(1.1)+/>{2.Ь +р(3,1) +/Ч4.1) -0,10 + 0.05 - 0,05 + 0,10 - 0.30,
А) = 2) - р(1.2) 4 2;2) + рО:2) + р(4.2) - 0,05 + 0.07 ♦ 0.0S + 0 02 - 0.22
Тогда Mapiиннльнос распределение составляющей ). дву-
мерной случайной величины, имеет вид
Таблица 9.4
£/’() - । ) - 0.48 ♦ 0.30 + 0.22-1
/
6) Совокупность усповнь|х вероятностей г( 1 ;0), г( IJ). /41.2)
отвечающих условию Л I, называется условным распределением
составляющей } ггпи X I. Вероятность значений величины ) при
V4 найдём при помощи формулы:
93
Поскольку Р(Х I)-0.2-^0.10 + 0,05-0.35 . го. подставив
значения соответствующих вероятностей, получаем
Р((У = 2)|( X = 1))== —= —.
" '•* '' 0,35 35 7
Итак, условнее распределение составляющей Y при Л-1 име-
ет вид:
Таблица 9.5
Так как условный и безусловный законы распределения нс
совпадают (см табл 94 и 9 5), то величины А и У зависимы. Этот
вывод подтверждается гем. что не выполняется равенство
для любой пары возможных значений А'и Y
Например.
Р((Х - 1)П(Г = 0)) = 0.2, Р(Л -1) = 0,35; Р(Г = 0) = 0,48;
Р((>Г-1)П(Г = 0))*/,(Л'=1) Р(} -О). т.к 0.2 + 0.35 0,48
и) Функция распределения /•(х,г) двумерной случайной вели-
чины (X Y) имеет вид:
r(r.r)~ X Г(<А'-А<Ю(> =rj)^ X Hw,)•
где суммирование выполняется по всем точкам (ж у ). для которых
одновременно выполняются неравенства х<г и ,Ц<У- (огла для <а-
данного закона рас г ре деления, получим:
' о
0.20
0.2U- 0.15-0.35
0.35 • 0.08 = 0.43
0,43 + 0.05 - 0.48
0.20 + 0.10 = 0.30
0,30 + 0.05 - 0,35
0.20+ 0,10 + 0,15 + 0.05 = 05
0,5 + 0,05+0.07=0,62
0,5 + 0,08 + 0,05 = 0,63
0.63 + 0,05 + 0,07 * 0.08 =0,83
0,63 ч 0.05 ♦ 0,10 = 0,78
0.78 + 0,05 । 0.07 । 0.08 + 0.02 = I
при х < I или j £ 0;
при I <д < 2 и 0< 1;
при 2<д ьЗ и U<
при 3<х < 4 и 0< 1 S 1;
при 4< д иО<1 < 1,
при I < х < 2 и 2 < у;
при 2 < i < 3 и I < । <2,
при 2 < х < 3 и 2 < у;
при 3 < v 4 и 1 < у < 2:
при 3 < > S 4 и
при 4 < х и I < у 2,
при 4 < д и 2 < у
Результат удобнее представлять в виде табл 9.6
Таблица 9.6
м
1 < 2<а<3 Г*- 1 ' " 11 1 : 3< XS4 4 < х
> 5(1 0 0 с 0 0
0 < ) < 1 0 0.20 0.35 0.43 0.4Я
J< > <2 0 0.30 ОЛ 0,63 0/^
0 1 0,35 0.62 1 , | 0.83 1
Воспользуемся формулами для начальных моментов и ре-
зультатами таблиц 9 3 и 94 и вычислим математические ожидания
составляющих У и Y:
4 з
М(А)-&|0 A, =l 0 3512 0.27,3 0.2! 4 0.17*2.2.
л=1 /Н
Mi У) - tr01
-О 0 4‘ ♦
O.V> . ? 0. V _ 0. 74.
Дисперсии вычислим через второй начальный момент и ре-
зультаты табл. 9.3 и 9 4.
0(A).//,„ (M(jr)f = lT 0.35.2' 0,27 + 3’ 021+4 0.17 4М 12
П(Г)-р,.-а„ (Л/|>))'-0: 0.48 Г 0.30 2: 0.22 (0.'4)’-0.(324
95
Для вычислении ковариации К(Х. У) используем аналогичную
формулу через начальный момент:
А'(А'.Г) -«,,-Л/О )• А/(> ) = ГС 0.2 Г 2 0-0.15 + 3 0 0.08 . 4 •()•().05 + 1 +
И 0,10 + 2 10.05 + 3 1-0.05 + 4-1-0.10+I 2-0.05 • 2 2-0.7 •
+ 3 2 0.08 + 4-2-0.02 - 2.2-0,74 = 0.142.
Коэффициент корреляции определяется по формуле.
„ К(А.У) 0,142
~Гй—77— = I I 3 0,163.
> а(Х )с(}) 7U-7o,6324
Искомая верожи+осп. /^>1) определяется как версии нос гь
попадания и область па плоскости, определяемую соответствую-
щим неравенством:
Р1ХИ г.* р^р. р.л р„.р„>р., Р»'Ра рк Ра =
<=: JA
= 0,2 + 0.15-0.08-0.05 + 0.10 + 0.05 J 0,05 +0.10 + 0.07 т 0,08 + 0.02 0,95,
гле рч . г((х чУХг-ку)).
9.2. Кораблем передается сообщение «SOS», которое может
быть принято двумя радиостанциями Этот сигнал может быть
принял одной радиостанцией независимо от другой. Вероятное гъ
того, чю ситал принят первой радиостанцией, составляет 0,95; ве-
роятность того, что сигнал принят (порой радиосташ^ией, равна
0,85. Найти закон распределения диммерной случайной величины,
характеризующей прием сигнала двумя радиостанциями Написагь
функцию распределения.
Решение. Пусть X — событие, состоящее в том, что сигнал
принимает первая радиостанция } событие состоит в том. что
сигнал принимает вторая радиостанция.
Множество значений П, = {0,1[ •
Л=1 -сигнат принят первой радиостанцией,
А 0 сигнал нс принят первой радиостанцией.
Множество «качений fl
К-1 - chi на । принят второй радиостанцией.
УМ) сигнал не приляг второй радиостанцией.
Вероятноеть того, «по сиг нал не принят ни первой, ни второй
радиостанциями равна:
/»{(.¥ П)г>(У = 0); = Р(Х = 0) /’(> 0)-= 0.05 0.15 0.0075
Вероятность принятия сигнала первой радиостанцией:
Р{(Л = 1)п(У-0)}-0,95 0,15-0.1425.
Вероятность того, что сигнал принят второй радиостанцией
/’{(Ж = 0) у = 1)} = 0.05-0,85=0,0425.
Вероятность тою, что сигнал принят и первой и второй ра-
диостанциями, раина /'{(А' ~1)п(У 1)| -=-0,95-0,85 = 0,8075.
Тогда закон распределения двумерной случайной величины
(А. Г) равен
* X 0 1
0 0,007 ‘ 0,142
d 0.042 0,И07
При каждом фиксированном значении точки с координатами
(x,i) значение /(x,v) равно сумме вероятностей тех возможных значе-
ний случайной величины (А.)), которые ноиаданп внутрь указанного
прямоугольника.
Тогда функция распределения будет иметь вид
0. х < 0.) £ О;
,, 0.0075, 0<х$1,у>1;
г(.» у)-<
0,15, *х>1; 0<>£1;
1. х>1;у>1.
93. Две фирмы выпускают оцииаковуто продукцию Каждая
независимо от другой может принять решение о модернизации произ-
водства Вероятность того, что первая форма приняла такое решение,
равна 0,6 Верояшость принятия такого решения второй фирмой равна
0,65 Написать закон распределения двумерной случайной величины,
характеризующей принятие решения о модернизации производства
двух фирм. Написан, функцию распределения.
Ответ: Закон распределения:
п 0 1
QJ 4 Oil
1 0,26 035
При каждом фиксированном значении точки с координатами
значение Г(х.у) равно сумме вероятностей тех возможных
тначений ( * ,_>,) которые попадают внутрь указанного прямо-
У1 ольника {А < х| гт {Y < у |.
9.4. На токарном станкс-автомат с и <плав швакнся поршневые
кольца для двигателей автомобиля. Измеряюзся толщина кольца
(случайная величина АА) и диаметр отверстия (случайная величина У).
Hircctho. чго около 5% всех поршневых колец бракованные При-
чем, 3% брака обусловлены нестандартными диаметрами отверстий»
1% - нестандартной толщиной и 1 % бракуют по обоим признакам.
Найти: совместное распределение двумерной случайной величины
(ХУ); одномерные распределения составляющих А и У; математиче-
ские ожидания составляющих А и У, корреляционный момент и ко-
эффициент корреляции между составляющими Л и У двумерной слу-
чайной величины (А\У).
Ответ: Закон распределения
\х‘ 0 1
0 0.01 0.03
1 0.01 0,95
Л/(Аг) = 0,98; Л/(> ) = 0»96; <т(А ) = 0,14;
<т(У)-0.196; -0,019; р„-0.692
9.5. В продукции завода брак вследствие дефекта А состав-
ляв i 4%, а вследствие дефекта В 3,5% Стандартная продукция
составляет 96%. Определить какой процент всей продукции обла-
дает дефектами обоих типов
9.6. Случайная величина (А',>) распределена с постоянной
плотностью г. у) - const - С внутри квадрата R, вершины кото-
рого имеют координаты (-2,0), (0,2), (2.0), (0,-2). Определить
плотность распределения случайной величины (А, У) и условные
плотности распределения р(х\г), рОМ-
Решение Посгроим на плоскости х0) заданный квадрат
(рис.9.5) и определим уравнения сторон квадрата ABCD. восполь-
зовавшись уравнением прямой, проходящей через две заданные
х — х у — v
точки: ---- - -——. Подставив координаты вершин А и В полу-
к- 2 у-0
чим последовательно уравнение (.тороны АВ < или
Рис 9.5
Аналогично находим уравнение стороны ВС : v -хч2, его-
роны CD: \ --1-2 и стороны DA у -1 - 2.
Согласно условия чадами, плотность распределения вероят-
ностей двумерной случайной величины имеет вид:
'0 при (х,у)е R-, [О при |х|>-|у|;
р(х, у) = < = <
I с при (xty)G R. [с при |л| Ь1у| < 2.
Констант} С находим, воспользовавшись свойством плотности
распределения:
JJ Cdxdy = 1.
(*)
♦
Так как область интегрирования является симметричной от-
носитсльно начала координат. то интеграл, стоящий в левой части
равенства, будет равен*
-4С(4-2)-8С
for а 8С I. слсловагельно С - — и плотность рас пре ле лени я
8
ятносчей чапишется в виде:
99
при )«| ♦ | v| 5 2.
при |л| > 2 - г|.
Услозпые плотное! и вычислим ио формулам:
Р< Х|У)
рМ
предвари гельно
вычислив
Pi (*) И Р: (у):
А(*)= J/4*.'7X*7-
о
0
100
Гш ла
о
%
At» *)-
о
Л2-х)
242-W
О
"Г-н Н • |1}>2
Отлет:
[0. |д|>2.
ПРК Н<2,
Р(х\ у)=
Н>: 1»1
1 I
При | г| < 2; р( )• | г) - • ?(2 - |х|)
°* М>2-Н
9.7. Плотнсхпь распределения двумерной случайной величи-
ны (Л.)) имеет нил
р( М’)-!
е( 1
О
♦ у) при 0 < х < 2.0 < у < 2;
в остальных случаях.
()1гредели1Ь конслангу С и вычислить математические ожича-
чня с<х (являющих А и >. коэффиииеж корреляции.
^'eiuchut Константу С найдем жх?1юлы*лнав1иись свойством
плотности распределения вероятности
101
p(x.y}dxdv -I или
r 4 ) }dxdy - I.
(НП2
Mr* 2
Область интегрирования ограничена прямыми х-0 х-2иуЧ),
У~2 Поэтому, переходя к повторному интегралу, получим:
2 т
С |Ж J( х Д y)dv - I.
о п
Вычистим инчрал в левой част ранено из:
-С(О4)-8С.
и
Тогда 8С~1, откуда находим С = —. Плотность распределения
двумерной
случайной ве.ти«шны
х ♦ у) при 0 < х < 2. О < у < 2,
примет
вид:
в остальных случаях.
Математические ожидания составляющих вычислим по фор-
мулам
« г©
Л/(Л')- | |лр(х, гк&<л ; M(Y)~ | jyp(x.y)dxdy.
чс
Подставив шачения плотности и учитывая область интегрирования,
получим:
Л/(Х)=^ Jdr j(A y)d) = 1 pi ху т у I Л = ^|(2x,*2r)dr =
Д гя выполнения коэфф ициента корре ишии, вычислим в на-
чале дисперсии MAX ZM }*) и корреляционный момент Л*(Л, К):
102
* । » / V' 2
/ДЛ')» f f(x-W(A))’rn.i)duA' -f x~- , dxf(A i i КЛ •
i *'o\ *
|'jr‘ 4 »’ 35 x’ 44 У’ 2/4 32 }\49|-----
4 T~3 3 36 2*3б’1„ 4 9 ~ 19 + 18 ' 4 18 36
P(H= f f()-Л/(Г)) p(x,) )dxcfy =| jfj-- лГ(х+rjc/x-^-.
J * a O . JO
поскольку no4Ninvipaльные выражения и пределы интегрирования
такие же, как и при вычислении D{XТ
г
8V 49 Г2? 8/')
- ас----- ---*----
3} 36 3 3 2)
1
£^ 8 8 49 1
8 < 3 3 J 36 ~ 36
Тогда коэффициент корреляции р(> равен:
9.8. Двх мерная случайная величина (А’. У"| распре челена с по-
стоянной плотностью внутри квадрата R. вершины которого имеют
координаты (О; О). (0; 2). (2. 0). (2: 2). Найти плотность вероятно-
стей р(х, у) и функцию распределения F(x, т ).
ю>
Omem p(*. )> =
0.
< *
о. I
при а < 0;
при R,
*7 *.>') = 4
9.9. Поверхность распределения системы случайных вели-
чин (X Г) предо авляет собой полушар с центром в начале коорди-
нат радиуса R. Найти плотность распределения вероятностей
Ответ:
♦1' i виу-ри «руга с центром в начале координат радиуса R.
вне этого круга.
9.10. Задана дискргптая двумерная случайная величина:
э 6
10 €.25 0.10 I
14 С. И (‘.05
18 032_ 0.13
Панги а) условнь й закон распределения А, при условии, что г= 10,
б) условный закон распределения 1, при условии, что х ~10;
в) математическое ожидание, лиснсрсию, коэффициент
корреляции
9.11. Непрерывная двумерная случайная величина (АГ, К) рав-
номерно распределена внутрг прямоугольного греугольника с
вершинами 0(0.0), /4(О;8), Н(К,0>.
Найти: а) плотшктъ распределения вероятностей;
6) аютностъ распределения вероятное гей сосгая-
лякнцих
104
Onteem a)
32
-----х при
4 32
32
К
при 0<x<F, ннс указанных шггерва.юь функции
ранни пулю.
9.12. В продукции завода брак вследствие дефема Л/состав
лясг 3%, а вследствие дефекта К - 4,5% Годная продукция сослан
ляег 95%. Определить, какой процент всей продукции обладает де-
фектами обоих чипов Вычислить коэффициент корреляции дефек
тов Л/ и К.
Ответ' 2.5%: рд/Л -0,669
1.10. Случайные функции. Цепи \1аркова
Пусть Т - некоторое множество действительных чисел. Если
каждому значению t сТ поставлена в соответствие случайная вс
личина А(/), то на множестве Тзадана случайная функция А(Г).
Если t - время, то случайная функция называется случайным
г ропессом Значение случайной функции А(/о) при /-/и. где < с Г.
называется сечением Каждое испытание дает конкретную функ-
цию x(t}. которая называсгся реализацией (траекторией) случайной
функции
При зафиксированном значении аргумента t случайная функ-
ция Л'(0 превращается в случайную величину - сечение случайной
функции или процесса Toiaa Л1Н в данный момент времени / оп-
ределяется плотностью распределения Однакг одномерные
законы распределения и их числовые характеристики, вычислен-
ные для одною момента времени (лям одною сечения семейства
рса (нзаций) не могут оценивать характер изменения процесса во
вГ**мсни Для этой цели используют характеристики связи между
ординатами, взятыми в различные моменты времени Наиболее
полно эти связи характеризуются многомерной плотностью р.ч-
предслс1!ияд.. л произвольных сечений процесса
Однако многомерная плотность распределения нс всегда известна,
Поэтому 1ля практических приложений случайные процессы харак
черизуются математическим ожиданием, дисперсией и коррсляци*
‘пгной функцией
105
Математическим ожиданием случайной функции А'(г) назы-
вают неслучайную функцию /лДг). кагорам при каждом значении
аргумента / равна математическому ожиданию соответствующего
сечения семейства реализаций случайной функции:
/л,(Т)® м[X(i)] и является средней траекторией для всех возмож-
ных реализаций.
Дисперсией с iy чайной функции А'(/) называют неслучайную
функцию /9Я</), значение ко горой для каждою t равно дисперс ии
соответствующего сечения случайной функции: = D[A'(f)] и
характеризующей возможный разброс реализаций случайной
функции относительно средней траектории.
Корреляционной функцией случайной функции АО) назы-
вают неслучайную функцию двух аргументов Kx(f.t\ которая при
каждой паре значении /. С равна корреляционному моменту соот-
ветствующих сечений случайной функции:
’о 11
о
X(6 = X(0-mt(a
Корреляционная функция характеризует степень зависимости
между сечениями случайной функции, относящихся к различным г.
Положительное значение корреляционной функции свидетельству-
ет о том, что при увеличении (уменьшении) ординат процесса в се-
чении / в среднем увеличиваются (уменьшаются) ординаты при (*.
Отрицательная корреляция означает увеличение (уменьшение) в
среднем ординат в сечении / при их уменьшении (увеличении) в
сечении Л
Корреляционная функция является симметричной функцией
своих аргументов, а ее ординаты по абсолютному значению не мо-
гут быть больше произведений среднеквадратичных отклонений в
моменты времени / и С:
|к(м')|<а(/) сг(/3.
Процесс считается стационарным, если ею многомерная
плотность распределения нс изменяется при сдвиге соответствую-
щих моментов времени на любую величину. В рамках корреляци-
онной георми. процесс считается стационарным, ее ш ctxi ковариа-
ционная функция Л/[А1/)Х(Л] нс зависит от времени, а швнеит
только от разности г = t' -t,
т (П~/и(г^г) тж-const, K(f.t г r) = A*(r).
юе>
Корреляционная функция стационарного процесса по моду-
лю не превосходит дисперсию: |A(r)|<A(O) = D -а\
Стационарный процесс у которою корреляционная функция
стремится к нулю А (г)—>0 при г—>сс называют эртоцичным. Эр
(одические процессы представляют наибо 1ьший интерес для прак-
1нческих приложений поскольку их характеристики, определяе-
мые по семейству и по одной реализации совпадают;
1г I г ° °
m —>—|Л(Гк7/; А ( г I —|А'(ОА (/- гцй.
* i • о
Марковскими случайными процессами называют такие про
цесса, у которык плотность совместною распределения произволь-
ных двух сечений полностью определяют характер процессов, те.
дальнейшее поведение процесса зависит только от значений, при-
нятых процессам в настоящий момент времени, и не зависит от ра-
нее принятых Марковский случайный процесс, в котором сама
функция принимает счел нос множеешо возможных состояний
(дискретные состояния) Х|.х2дь..лг,. м переход из одного состояния
в друпн: происходит скачком пол влиянием случайных факюров,
называют цепями Маркова Если переход из состояния в состоя-
ние происходит в дискретные моменты времени НЛЛ» /л. , то та-
кой процесс называют дискретными цепями Маркова Если пе-
реходы возможны в любой момент времени, то процесс н;иынаю1
непрерывными целими Маркова.
Вероятность того, что дискретная цепь Маркова в мемент
времени /.примет значение хг при условии, что в момент времени tf.
ина имела значение хт. называют вероятностью перехода из со-
стояния в состояние /I Если па вероятность зависит от
длины промсжу|ка времени г — г — и не зависит ел начала от-
счета времени, т е нс зависит от номера iiiaia. тс такую цепь Мар
кона называют однородной: (г)
Дискретные цепи Маркова однозначно определяются жбо
матрицей переходов
01
10
Р.п
P.I
те
л - m “ 1. т
107
/ = 0.т.
или графом состояний
Вектором вероя i костей (безусловной верой костью) со-
стояния цепи Маркова называют вероятности ря(Л) того, что в мо-
мент времени ti цепь примет значение г„, которая представляет со-
бой матрицу-строку:
ЛС) = [ Рс(С). Pi(t,). р>(1.),. г„(г,)]. где £/>„(/,) = 1.
Вектор вероятностей состояния однородной цепи Маркова
после I этапов однозначно определяется вектором вероя гнехл ей
) в начальный момент времени и матрицей переходов Р{ г):
ЛО^Л/J Р'(т).
Если в цепи Маркова / —»х, го вектор вероятностей состоя-
ния превращается в вектор финальной (стационарной) вероятност
[/’hPn—/>/:]» определяемый из однородной системы (п+1)-ги уравне-
ния:
Ро = РоГио + АРю * Р,Рп + -A, AhU
Pl = Р.Р.1 * AAi * Р.Р.1 < -р„р^
1 Р1 ~ РпЛпз * АА? ♦ Р2Р22 * - P'Pri*
I Рп РсРОл * PiPi, + Р2Р2” * Рг.Р.<
Учитывая. чгорп<р,1 *р„ - | и заменяя этим соотношением
одно из вышеприведенных уравнении в системе, находим искомые
финальные (стационарные) вероятности однородной цепи Маркова
108
Для непрерывных цепей Маркова возможности перехода из
состояния хП1 к состояние x/t за время Лг оценивается плотностью
вероятностен перехода Л*»
. Р^(Лл}
Лгжи - lim----; при условии, чтс
Л. 4) дг
Если нс зависит от времени, то непрерывная цепь Марко-
ва называется однородной.
Для непрерывных испей Маркова вектор вероятностей со-
стояния есть функция времени и определяется путем решения сис-
темы дифференциальных уравнений, кот орые составляются по
графу состояния цепи Маркова по следующим правилам:
в левой части каждого )равнения стоят производные по вре-
мени вероятностей состояния цени;
- правая часть этих уравнений содержит столько членов, сколь-
ко переходов (стрелок на графе) связанно с данным состояни-
ем,
- каждый член правой части уравнений равен произведению
плотности вероятностей перехода, сот встс гву ющей данной
стрелки 1рафа состояния, умноженной на вероятность тою со-
стояния из которого исходит стрелка;
- каждый член правой части уравнений имеет знак «минус», ес-
ли стрелка |рафа состояния входит в данное состояния и знак
«плюс», если стрелка выходит из данного состояния
Например: Имеем граф состояния однородной непрерывной
цепи Маркова:
Д 1я этого графа составляем систему уравнений по вышеука «анным
правилам:
109
Учитывая, что (O-pU/) I. известными метлами находят
Р<1), РзО). Рз(О-
В случае, koi ла нас интересуют вероятности состояния не-
прерывных цепей Маркова по истечению длительного промежутка
времени (установившейся процесс /—►ио), го решение системы по-
лучают путем записи в юной части системы дифферен11мальных
вместо прог.нюдных нулей, т е.---- = 0.
dt
Задачи
10.1. Имеются три конкурирующих изделия гьхзДз. Для опре-
деления спроса на эти изделия произведен r некоторый момент
времени /0 опрос 1000 человек. Оказалось, чтох» покупают 500 че-
ловек, х2 ~ 200, л, - 300 По истечению месяца ока шлось, что из 500
человек, покупавших изделие х;, 450 человек продолжали покупать
это изделие, 40 человек стали покупать изделие х2, Ю человек из-
делие Xi. Из 200 человек, покупавших изделие х2. 80 стали покупать
изделие хь 60 - изделие х3, 60 продолжали покупать изделие х2 Из
300 человек, покупавших ищелие х3, 60 продолжали покупать это
изделие, 210 стали покупать изделие Х|. а 30 - изделие л2. Опре де-
1итъ какое изделие по истечению месяца, двух и пяти лет будет
пользоваться наибольшим спросом.
Решение' Предположим. что поведение покупателей в каж-
дый следующий месяц обусловлено их поведением в предыдущий
месяц, то мы можем представить эту задачу в виде дискретной од-
нородной цепи Маркова с тремя состояниями.
В момент времени to (проведение опроса! вероятности со-
стояния системы (вероятности спроса на изделия* имели следую
щие значения:
ГМ'
|0.5;0.2:0.3|.
Определим параметры матрицы переходов (вероятности пе-
рехода из состояния в сос гоянис):
450 ЛЛ 40 Ю
ПО
60 210
р,,= -0.2. А1.-—=0.7,
за) КХ'
30
/>,.=— 0,3.
300
Ра
Рп
Рп
pti 0.9 0,08
/^=0,4 0,3
Ач О)7 0.1
0.02
ОЗ
0.2
Найлам вектор вероятностей состояния цепи по истечению одного
месяца
0.9
Р(/1)=Р(/о)хР,(г)-|0.5;О.2;0.3|х 0.4
0,7
0.08
0.3
0.1
0.02
0,3 = |0,74.0,110.13!
0.2
Т е. наибольшим спросом по истечению одного месяца будет поль-
зоваться изделие »|, (pH А) = 0,74), изделия *2, *з одинаковым спро-
сом (рА) = pAh) - 0,13).
По истечению двух месяцев
10,9 0,08
Р(/г) = Щ)х Лг) = |0.74;0.13;0,13|х 0,4 0,3
0.7 0.1
0.02
0,3 ;0 809;0.1112;0.(П<)8|
наибольшим спросом так же будет подьзсва.ься изделие л |. По ис-
течению более длительного срока оценку спроса можно произве-
С1и исходя из того, что для данной цепи условия эргодичности вы-
поли яется. При г -► ос получаем слелующ\ ю сис гему у равнении:
Pl =0,9 Pl +0.4р;+0,7рз;
pi =0.08/>| + 0.3р?+0.1р>;
Рг 0,07/7,+O.3p3+O,2pi.
Заменив одно из уравнений вышеуказанной системы уравне-
нием р\ +р- *рз“1, получим искомые финишные (стационарные) ве-
рея гности нашей цепи Маркова pi -0.84, р? 0,1, p,=0,06.
10.2.В городе N три местных супермаркета А, В, < , конкури-
руют между собой и относительно их фирма по изучения рынка
выявила следующие факты. На I января каждый магазин имел рав-
ное число покупателей За предыдущие 1? месяцев в среднем за
месяц
- Магазин А сохрани i 80% своих цоку пате 1сй и получил 10%
покупателей магазина В и 2% покупателей магазина С;
Магазин В сохранил 70% своих покупателей и получил 14%
покупателей магазина А и 8% покупателей магазина (;
ill
- Mai азин С сохранил 90% своих покупателей, получил 6%
покупателей Mai азина А и 20% покупателей магазина В
Составьте матриц} перехода для средних ежемесячных изме-
нений Если предположить, что общее число покупателей в юроде
Л постоянно, то какую долю от их числа имеет каждый магазин с I
февраля, учитывая, что состав теплая матрица переходов верна в
течение января
103. Компания по прокату автомобилей выдаст автомобили в
ipex аэропортах. Клиенты возвращают автомобизи в чти аэропорты
в состтвсгст вии с таблицей вероятностей:
а) Вычистить вектор X1 Марковской пспи. удовлетворяющий
1
равенству Х'-Х'Р, /Л -1. Представляет ли этот вектор ста-
ы 1
циопарпие вероятности9
б) В каком аэропорту следует иостронть авторемонтную стан-
цию?
10.4. Некоторая фирма находиться в одном из двух состоя-
нии: «получает прибыль» или «нуждается в диверсификации своей
деятельности». Если фирма получает прибыль сегодня, вероятность
того, чго она будет получать прибыль зан!ра, равна 0.7. а вероят-
ность того, что она завтра будет >гуждаться Ь диверсификации сво-
ей деятельности, равна 0J Если же фирма нуждается в тивсрсифи-
кации своей деятельности сегодня, то вероятность того, что она бу-
дет работать с прибы ью завтра ранга 0.6. а вероятность того, что
она будет пуж,татъся в диверсификации своей дсятс ihhocth. равна
0.4 Определить вероятность работы фирмы с прибылью через гри
дня.
РАЗДЕЛ 2. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА.
В основе законов распределения случайных величин, событий,
основных теорем теории вероятностей лежит эксперимент, тс. каждое
исследование случайных явлений, выполняемое методами теории ве-
роягностей, прямо или косвенно опирается на экспериментальные
данные. Поэтому математическая статистика занимается разработкой
методов сбора, описания и анализа экспериментальных данных, полу-
чаемых в результате наблюдений массовых случайных явлении При
пом можно выделить три этапа. присутствующие в любом приложе-
нии статистических методов:
I )сбор данных;
2 ) обработка данных;
3 )статистические выводы прогнозы и решения
2.1. Выборочные статистики
Статистические распределения. Исходным материалом ма-
тсмагмческого исследования является ст атлетическая совокуп-
ность. которая образует выборку. Если А изучаемая случайная ве-
личина, то возможное множество значений случайной величины
П, составляют генеральную совокупность, а наблюдаемые значе-
ния случайной величины {* .*.. выборку.
Распределение выборки, задаваемое ишервальным статистиче-
ским рядом (табл. 11) или таблицей относительных частот (табл.
I 2), называется мтиричсским распределением случайной величи-
на
Интервальный статистический ряд распределения пред-
ставленный графически, называется гистограммой (рис. 1.1):
Рис. 1.1
Площадь каждою прямоугольника равна соответствующем от-
носительной частоте. А площадь всей гистограммы равна единице
_______________________________________________Т абл ица 1 2
Наблюденные шачения дне кретной слу- чайном эеш- ЧШ1Ы, Kf С/ • • • Xk
Относительные частоты. п. •*. -г и И’. » — п nt, п п • • • Г1\ и; х п
Ломаная линия с вершинами в очках или точках
f т \ ___
гL/ = |Д, называется частотным многоугольником (полигоном
к я /
часта;) или полигоном относительных частое (рис.I 2):
114
'Эмпирической функцией [ни -пред*ченин начинается относи-
тельная частота события {Х<д ) в данной выборке значений слу-
чайной величины X, I.C.
где т, - число значений х„ меньших л. п объем выборки Значе-
ния эмпирической функции распределения принадлежат отрез
ку[о,1],т.е. 0£F(x)£l.
Эмпирическая функция распределения удовлетворяет сле-
ду ющим свойствам'
I. FU) - неубывающая функция;
2 I (д) кусочно-постоянная непрерывная слева функция;
3. Если х<л, го F(x) = 0 несли г>т*,тх> F(x)=l.
Эмпирическая функция распределения И») сходится по ве-
роятности к функции распределения F(x) генеральной совокупно-
сти, т.с. |,где оО.
Основные числовые характерно ики
распределения. Среднее арифметическое:
п 1-1
Медиана
эмпирическою
(И)
Me - х.
ИЛИ Mt.
где г„ средняя варианта, если
число вариант нечспю; средние вариаты, если число ва-
_ -s~-• *
риан! четно, или AA =xw ♦/ *' . £»».•»». 2)
| ас iri — нижняя граница интервала. в котором лежит медиана 1
длина интервала. 5^ -сумма частот во всех интерна.iax прение
ствунпцих медианному частота медианного интервала
Мода:
Л** - г,, где варианта ц имеет наибольшую частоту;
или .4. -< : - (1J)
(и«. -нж.,|
115
где - нижняя граница интервала, в котором лежит мода: / -
длина интервала; относительные частоты, соответ-
ствующие модальному, предшествующему и последующему' ин-
тервалам
Статистическая дисперсия;
s.* =<*' s-E(*«-*) X'” ®л; (1-4)
Среднее статистическое квадратическое отклонение (стан-
дартная ошибка):
Вариационный размах
К = - Х.шп • (1.6)
Среднее абсолютное (линейное) отклонение:
Коэффициенты вариации:
К-4 100%; Г,-4 100%, г =4-100%. (1.8)
' X г X * X
Начальный момент А-го порядка:
м, --2».. -п- <* 9>
Л /•! Ы
Центральный момек! (-1 о порядка
Асимметрия: Эксцесс: я* Е(МО) н 1.1 4,^^. (Ill) F. §--3 (112) «э
116
Задачи
1.1. Для статистической совокупности данных, характери-
зующих эаграты на I денежную единицу продукции (работ. уедут)
за год по 100 предприятиям г. Минска
61.55 61,59 62.09 61.08 63.97 64.74 65.07
67,12 68.10 69.38 70.21 70.21 70.36 71.25
71.86 72,00 72.39 72,41 72.46 72,50 72.80
72.84 73.44 74. 91 75.46 75.65 77.13 77J7
77.64 77.86 90.93 78.01 78.28 78.74 78,97
79.07 79.10 79.34 79.34 19.39 79,40 79,49
79.70 80.02 80,26 80.56 80.65 80.69 81,13
81.32 81.40 81.54 81.85 82,2 7 82.71 82.74
82.78 83.03 83.05 83,59 83.68 83.74 8338
83.% 84.98 85.18 85.32 85.64 85.71 85Х>4
86,01 86.03 86.11 86.11 86.48 86,94 86.98
87.38 87,47 87,59 87,89 88,03 88.04 88.11
88.24 88.89 90,34 90.40 90.58 90.73 90.76
92,51 96.34 92.72 96.55 92.94 94.58 95.06 95.73 96,11
построить эмпирическое распределение, эмпирическую функцию
распределения. Вычислить числовые характеристики.
Решение. Составим ряд распределения, характеризующий
затраты в денежных единицах на I лен ед продукции (работ, ус-
ну ।) по 100 предприятиям.
Каждое индивидуальное измерение затрат предсгавлено от-
дельно, поэтому ли данные называют несгру ниированнымм дис-
кретными данными Следовательно, исследуемая случайная вели-
чина X является дискретной случайной величиной. Дискретные
данные также могут быть подвергнуты (руппировке В результате
группировки данных облегчается их инюрпре^ация. хотя при этом
частично теряется точность.
Определим длину интервала по формуле:
/ _ " *- >- 9635 6135 _ s
♦ 33221g л 14 33221g ИЮ '
Вычислим частоты т и относительные частоты и, вари-
ант, принадлежащих каждому интерва iy. Результат сведем в
таб типу 1.3
117
Таблица 1 3
| Затрать: на 1 лен ед. копнчсспю < )тнос и тельная Накопленная Ж” *
продукции, ДСН сд предлрня! мн. т, часто! а, и, частота, /Л
[б!.55. 66,55) 7 !(. 7 0,07 ’
[66.55. 71,55) 7 0.07 0,14
1 (71.55; 76,55) 1 12 0,12 (^6
[76,55; 81,55) 26 0Д6 п,52
[81.55,86,55) 2?_ 0.23 1 0,75 1
[86.55,91,55) 16 0,16 0.9!
1 [•>! is S5J 1 9 1 й«2 1,00
Затрап,। по предприятиям, составляющие интервальный ряд
распределения, представим графически. Построим гистограмму и
Рис. 1.4
Используя накопленные относительные частоты, составляем
кумулянту (гмлиричсску ю фу нкник* распределения):
0. при л £61,55
0.07, при 61.55<х£66.55
0.7 ♦ 0.7 = 0,14, при 66,55 < л £ 1.55
0.14 + 0.12 =С,26.цр+71.55<х£76 55
1/ 0 0.26 к 0.26-0.52. при 76,55< л <М,55
0.52 + 0.23 = 0.75 при 81.55 < л <86.55
0.75+0,16 «0,91, при 86,55 < л £ 91,55
, 0.91 + 0,09 = 1.00. при 91,55 < л
I раф>ик эмпирической функции распределения показан на рис
1.5. _
11V 4
1.00
0.91
0.75 ........
0.14
0.07
' 61.65 6/.55 TL55
7п,55
«1.55 «6.55 91,55 06.55
Рис 1.5
Вычислим числовые характеристики загра' (в денежных еди-
ницах) на I лен. сд. продукции траСог, услуг) по данным 100 пред-
приятий г. Минска.
( релнее арифметическое для нес группированных данных
X -Ум —(61,55 + 6159 + -96.55) 8O.82R
п“ 100
Ес 1и данные представлены в вилс ингервальногс стагистмче-
ского ряда pai прелечения. то среднюю точку \ каждого интервала
выбирают в качестве представите ш всех вариант, входящих в со-
сгав HinupBaia Значение средней точки каждою ннгерната уммо-
119
жают па частоту инт ерзала суммируют эти произведения и делят
на объем выборки:
Г » ХА-Ш' - —(^.05 7 + 69.05 7-. . .4 94.05 9)= 80.80
л 100
Как уже отмечалось, группировка вист та сопровождается по-
терей точности, что и подтверждает вычисление среднего арифме-
тического Поэтому остальные числовые характеристики вычислим
по нс сгруппированным данным.
Не сгруппированные данные образую! дискретный вариаци-
онный ряд. содержащий четное число вариант, поэтому медиана
равна полусумме средних вариант
Me . л<* 4 *> = 8-32* * 40 ж g j 36
2 2
Такие исходные нс группированные данные не имеют моды.
Но если рассмотрен» интервальный статистический ряд распреде-
ления (таблица 1.3), то модальным интервалом будет интервал
(76,55;81.55Х имеющий наибольшую частоту и тогда моду вычис-
лим по формуле (1.3):
№ - 76,55*5-
— — =80.55.
C.I6 ♦ 0,04
С теоретической точки зрения наиболее подходящей мерой
колеблемости ряда распределения служит статистическая диспер-
сия:
I г
$’= У(х,-Л)----------------(171.641+ * 247.181) = 70,16491'.
л" tOO
Среднее статистическое квадратичное отклонение - величи-
на абсолютная, она ныражаеня в тех же единицах, что и сами за-
траты:
S-JF -/70.16498-К37645
Пределы изменения затрат характеризует ра ямах;
R = 96,55 61,55-35.0.
Вычисгяим безразмерные показатели вариации - коэффици
енты вариации*
г, _ Л 100*4,« 35,°- 100% - 41,30%;
F X 80.828
К-Г 100%«€ W,74K 100*4 8.25%,
’ X 80,828
120
i' = i 100% -—,tA- 100% = io.3O%.
A W.»28
Значение коэффициента вариации J’, показываст, чю сово-
купностъ исходных данных однородна.
Выяснение общего характера распределения npennonaiacr
вычисление показателей асимметрии и эксцесса Асимметрия
3373,145 4
100 5К7.7329О
=-II.ОМ 19*
игрицатсльна. слсдован-льни. распределение характеризуется не-
значительной левосторонней асимметрией
Эксцесс:
1317212,245
492311.4
-0.3 2443
отрицательный, следовательно, распределение затрат более плос-
ковершииное по с равнению с нормальным.
Ошибки асимметрии и эксцесса $4,-0.23774, $г,=0.45475
> довлстворяют неравен; тва м:
1^1 = 0.27 <3, ’£л =0.71 <3.
st,
откуда следует, что асимметрия и эксцесс незначительны в распре-
делении затрат
В задачах 1.2 - 1.4 построить эмпирическое распределение,
его графическое представление, эмпирическую функцию распреде-
ления и вычислить числовые характеристики выборки: среднее
арифметическое* моду, медиану, статистическую дисперсию, сред-
нее статистическое квадратическое отклонение, вариационный
размах, среднее абсолютное (линейное) отклонение коэффициенты
вариации, асимметрию и эксцесс
1.2. Число построенных квартир (тысяч) ра шинными органи-
зациями приводятся в таблице IА
121
I > ’ типа I !
Г осуларсгвенн ым и предприятиями и организациями Жилищно- с^роитеты’ыми кооперативами Индивидуальными застройщиками 1 X I 1 Кооперативными, арендными, обще- ственными органи- зациями и другими организациями
50/1 8.0 28.2 2,9 0,2
52.5 8.2 21,9 j 2,9 0,4
. 513 _ 9-’ 21,6 3? 0.4
58,8 8,5 -. > 3,5 0,4
53.2 _ 7,5 20,4 4.2 оз
5 : 7 6 4 18,7 5,0 j 0,4
50,1 6,5 15? 4.1 1 03
s 5 7 6,5 j 1,1,1 4.6 «3 I
54.8 1.6 5,0 03
54,6 L 6,1 11,0 6.0 о?
58.3 6.5 8.9 6.2 0.5
59 7 8.1 8.0 7.0 0.3
59.4 7.4 7.6 73 0?
59,4 9.6 6,9 73 03
61.0 10,2 6.4 03
61.1 11.1 <8 9,9 0,е
61.7 ПЛ 63 11.8 оз
710 13.8 5,7 8.9 03
673 П.4 5.7 25 _ 0?
69.7 12,0 55_ . 6 5 0 J
63? 10> 8,3 5,4 1.3
66? 52. 73 4.4 3.9 3.9 .1
70 3.3 4.1
36.0 П? 4? 3.0 Г 4,7
зол 15Л «,3 3,5 5,’ 4? 1,6 0.9 4 9 2.4
[ >3,4 15,1 5,9 0,6 3?
1.3. Поезда метро идут строю по расписанию с интервалом в
' минут В р< зулктате измерения птучсна выборка времени (н сс
куклах) ожидания поезда тля 15 студенток каждый из которых
выходит на перрон в случайный момент времени
38 61 66 4? 52. Я . т 72 Я0.0? 00. IM; 102,79
39; 60: 61.40;41.42. 50. 70. 71. 72. 73; 74. 75; 77. 80; 81. 84; 85;
40. 42.
1.4. Число автомобилей, подъезжающих на заправку в тече-
нии часа в различное время суток характеризуется выборкой
6-7; 7-8; 8-9; 9-10; 10-11; 11-12 12-13; 13-14; 14-15; 15-16.
12 20 40 37 28 15 21 17 18 II
16-17; 17-18; 18-19; 19-20,20-21; 21-22: 22-23
8 25 30 20 II 10 10
В задачах 1.5-1.14 построить интервальный статистический
ряд распределения (если он нс затаи), ьистсмрамму. полигон отно-
сительных частот, эмпирическую функцию распределения, вычис-
лить числовые характеристики выборки: среднее арифметическое,
медиану, моду, статистическую дисперсию и среднее квадратиче-
ское отклонение, вариационный размах, среднее абсолютное (ли-
нейное) отклонение, коэффициенты вариации
1.5. Интервальный ряд распределения:
Таблица 1.5
Границы интервалов. ) 10-20 20-30 30-40 40 50 50-60 60-70 70-80
Частоты, m 10 20 7Q L 1R0 120 ' 80 20
1.6. Интервальный ряд распре ния
Таблица 1.6
1ранины интервалов, । • ) 18 20 20-22 22-24 24-26 26-28 28-30 30-32 32 34
Частоты, го. 10 1 20 70 180 120 80 20 50
1.7. Результаты измерения емкости затвор сток у 96 поле-
вых транзисторов:
1.9 3.1 1.3 0.7 3.2 1.1 2,9 2.7 2.7 4.С 3.1 3.9
• 1.7 3.2 0.0 0.8 3.1 U 2 fa 1.9 2.3 3.2 1.3 2.8
4,1 и 2.4 4^5 2.5 0.9 1.4 1.6 2.2 3.1 2.1 2.5
1.5 1.1 2.3 4.3 2.1 0.7 12 1.5 1.8 2Л 2.5 2.1
0,8 0.9 1.7 4.1 4.3 2.6 0.9 0.8 12 2.1 1.8 3.1
У2 29 1.» л ? • 4S 2.1 3.1 5.1 1.1 1.9 и 2.6
0.9 3.1 0.9 3,1 3,3 2.8 2.5 4.0 4.3 1.1 т м
2.1 3.8 4.6 3.8 2.3 3.9 2.4 4.1 4.2 0.9 3.7 3.9
123
1.8. Распределение скорости автомобилей на одном из участ-
ков автома! негра, ih:
64 66 90 101 10 120 102 90 101 КИ1
65 67 91 104 101 117 106 95 100 95
63 69 89 103 109 118 107 94 HO 97
61 72 89 102 111 119 110 93 100 99
62 77 94 102 115 120 109 95 100 99
67 81 94 103 117 120 110 100 90 105
71 81 95 ПО 119 115 111 100 90 107
72 91 99 111 120 116 112 too 90 101
67 94 99 115 120 117 105 100 105 104
65 95 100 120 117 118 107 100 107 105
1.9. Распределение общего времени (в минутах) на ожидание
и обслуживание ав гомобилей на «правочной сганции
8 7 7 8 10 II 9 12 10 12 15 15 14 16 20 19 17 16 20 15
8 6 1 9 10 II 9 10 13 14 15 14 15 20 18 19 16 18 19 16
7 6 8 9 10 II 9 12 13 14 15 13 15 19 18 18 17 17 20 15
7 6 8 10 10 10 12 12 13 14 15 14 15 19 18 17 18 17 20 15
6 6 7 Ю 10 9 12 12 12 15 15 14 15 19 18 17 19 17 19 15
1.10. Как изменятся чистовые характеристики выборки, если ре-
зультаты наблюдения увеличить или уменьшить одновременно в т рал9
1.11. Распределение времени наработки ia откат приборов
некоторого типа:
1.31 0.48 0.76 1.71 1JC 0,54 0,20 0,67
0.62 0,15 0.05 0,78 0,24 0,29 1.47 1,11
0.67 0.99 1.02 0.51 0.65 1.56 0.16 0,49
1.12. Производство кожапой обуви в Республике Беларусь (в
млн. пар).
____ Таблица 1.7
t, годы V ।. nap l, годы У,,млм нар 45.3
1977 42 1989
1978 41,8 1990 46.8
1979 41Д 1991 453
1980 415 i 37.2
1981 41,3 1W - ’7 4 1
1982 42 1004 2£4
1983 42.2 1995 13
1984 43,1 1996 пл
1985 447 1997 15.6 1
124
1, годы Yg млн пир 1, ГОЛЫ nan
1986 44.8 19 16Л
1987 45 3 ' 1999 >6,5
19ЯЯ 469
1.13. Динамический ряд, характеризующий изменение значе-
ния денежных агрегатов (в условных денежных единицах):
_______ ______Т аблица 1 .Я
Гол Л| Гс v 1
01 01 97 । 5109.5 01.08.9 26459.0 j
01 02 97 , 5261,7 01.09 98 278033
0103 97 7553.0 01 10 98 285633
01.04 97 I 9223,8 01 1] 08 2N
01.05 97 10031.4 01.12.98 29837,7
01 06 97 12 W ,4 01.01.99 11483,2
01 07 97 : 3032,5 01.02.99 3938 К
О| 08 9“ 12676.1 01 03.99 39995,3
01 09 97 12981,8 01 04 99 40343,7
01.10 97 13351,2 01 05 99 47337.7
01 11 97 ' 12054,2 CI Ск>.99 48812,8
01 12 97 IV к 01.07.99 60232,4
01 01 98 ' 14454 8 01.08.99 65328,2
01 02 98 ! 5610.4 С 1.09.99 67134.1
01 (В 98 f 16883.2 01 1099 ~ 72487,2
01 <И Q8 1981 1 01.11 99 66044.1
01.05.98 20484 1 01.12.99 73073,0
01 06 98 24 ЖЯ ,2 01.01.00 74311 1
01 0^ 98 | 27196,9
1.14. Динамические ряды, харам ери <ующие урожайность
зерна (таблица 1 О) и валовой сСч*»р шрна (таблица 1 10) н Республи-
ке Беларусь.
__________ Габлмца 1.9
Год Урожайность черна г РЬ Год • • • • • я** ♦ Я 1 ( >..u » <М II ЭфНВ И Г1
(центнеров с 1 гектара) '’icimiepon с 1 гектара)
1990 26.6 1997 23,6
1991 212 1998 18,3
1992 26.8 1999
1993 I9J ।
2?.7 2000
1994 22.4 1 2001 !»<» J
_ 1995 20.4 2002 ?4.7
|09б 21,7 ММ
Таблица 1.10
Год Валовой сбор зерна В PK (TTJT ТОНН) Год Ва зовой сбор зер- на иРБ(гыс гони)
1990 7035 1997 6120
1991 6295 | 199Н_ 4830
1992 7230 1999 3645
1993 7508 2000 4856
1994 60)7 2 1 5153
1995 5502 2002 5990
1996 5792 2(иЛ I 5448.8
2.2. Статистическое оценивание
Основной задачей математическом статистики является зада-
ча определения закона распределения наблюдаемой случайной ве-
личины X по данным выборки.
Числовые характеристики выборки {х(.х7. . *.) называются
статистическими и яи 1яюгся величинами случайными Оми имеют
законы распределения, зависящие от законов распределения слу-
чайной ве Шинны X в генеральной совокупности.
Выборочная числовая характеристика, применяемая для по-
лучения оценки неизвестного параметра а генеральной совокупно-
сти, называется точечной оценкой а . Оценка а - это значение не-
которой функции элсмснгов выборки, ю есть а =й(х,.х2# . ,\Д.
Наилучшую точечную оценку определяют при г.омоши усло-
вий: нес неценно mie эффективности и состоятельности
Оценка а называется несмещенной оценкой параметра а. если
се математическое ожидание равно оцениваемому параметру, то
есть М(а) = а. Разность М(и)-а называется смешением.
Несмещенной оценкой математического ожидания гспсральной
совокупности с !ужиг среднее арифметическое выборки
где t, - вариаша выборки, т частота варианты >рлгУт, объ
ем выборки.
Для оценки парамегра а может быть предложено несколько
несмещенных оценок. Мерой точности несмещенной оценки и счи-
тают ее дисперсию СИ а). Если а । и а: две различные несметцен-
126
ныс опенки параметра а и D(«51)< D (а ). то оценка а । более эф-
фективна, чем опенка и .
Несмещенная оценка а параметра п, дисперсия которой дос-
тигает своего наименьшего возможного значения —-—. называется
Л(<0
эффективной: Р(а) =——. где - информация Фишера, содер-
жшпаяем в выборке об ьсма л относительно неизвестного параметра
а. Для непрерывной случайной величины А с плотностью распре
деления р (х, а) информация Фишера равна:
Л(а) ” "М f (~fn /Хх;<0) |, (2.1)
\ се )
Для дискретной стучаттпой величины
(4-I» где Г(г;п)- Р( А = х).
I да )
(2.2)
Оценка с, называется состоятельной оценкой параметра а.
если а сходится по вероятности ко, при и ->а.;hniFi|a а
Если Л/(а) и D(e)->0 при п->х, то а - состоятельная
оценка параметра а.
Для отыскания оценок параметров генеральной совокупности
но данным выборки применяют метод наибольшего правдоподобия
и метод моментов Согласно методу наибольшего правдоподобия,
оценку л неизвестно! о параметра распределения случайной вели-
чины X находят, решая уравнение:
сL(a) _ гL( ГрЛд
йа Fa
или систему уравнение?
(cJpO,. ..,лп;гД|,а^.) s о j - |
’ dat Fa,
если требуется оцени ib m неизвестных параметрон, i;ie
Ца) = /ДТрХ1. и /(гр*,. .х,.£ГрО: 4у*<К1ПО<иравлоподк’бчя
£<</) = П * еели А' непрерывная случайная величина и
127
L(a>~ П ;<3)’ CCJIH — дискретная случайная всли-
|»l
чипа, а вероятность /*(.¥ = jt) = p(x.g) функция неизвестного пара-
метра а.
Метод моментов заключается в том, что статистические мо-
менты выборки принимаются в качестве опенок для моментов рас-
пределения случайной нс 1ичины X и из построенных равенств ста-
тистических и теоретических моментов находят значение оценки
параметра.
Точность и нале ясность оценки а тля napavcipa а определя-
ют рассматривая вероятность неравенства
|о—<э| < 8: Р(3—(У < а<а +£).
Случайный интервал, определяемый розу платами наблюде-
ний, который с заданной вероятностью а = |-л накрывает неиз-
вестный параметр а. называется доверительным интервалом для
параметра о, соответствующим доверительной вероятности
а=I-г.
Доверительные интерва 1Ы для математического ожидания т
нормально распрелсленной случайной величины X имеют вид:
а) при неизвестном среднем квадратическом отклонении о:
*-•.-уЦ-<т<X+t, S = , (2.3)
где /э - квантиль распределения Сгьюдента (приложение 3) для за-
данной доверительной вероятности ан числа степеней свободы
v л-1 находят из равенства Р(Г>г.,) - Р(Т< /э, )=1 у*. S - ис-
правленная стандартная ошибка
6) при известном среднем квадратическом отклонении с
где А среднее арифметическое (несмещенная, эффективная и со-
стоятельная опенка математическою ожидания), г,- значение ар-
гумента функции Ф’Ы (приложения I), гаходят из равенства
Ф’ i л - объем выборки.
12*
Доверительные ипервалы разности математических ожида-
ний mi и т2двух генеральных совокупностей, распределенных по
нормальному закону. опредслякпся формулами
а) если дисперсии <т и а, известны, то
(V । -л . (2.5)
где га - квантиль нормального закона распределения для заданной
W 1 • <’
доверительней вероятности а находят из равенства Ф (Q« ;
б)если дисперсии о -о/ = <г, величина о' неизвестна,те
. - - . Ч"»-OS,’)(»».♦ л) - _
J-------------------------<т-т2<1А.-Л2 ‘
((л,-р£ +(»,-!)$/)( л,-п;)
/п \ +
1де /„ квантиль распределения Стьюдентд с числом степеней сво-
боды »=«,♦»> 2 находят из равенства P(T>f )-Р(Т< /о
п .п - обьсмы выборок; 52». S? исправленные статистические
дисперсии; £,.А, - средние арифметче-скис выборок
Доверительный интервал для дисперс ии а выражается фор-
мулой
(2 7)
где $’ - исправленная статистическая дисперсия,
I I " я I
квантили распрелелсния / с i п-1 степенями свободы для дове-
рите тьной вероятности а. л объем выборки; Л среднее ариф
мстическос
Д |я оценки среднего квадратическое о отклонения о нор-
мально распрсде юннон случайной величины Л применяется гак же
доверительный интервал
(1 -< о < (l-r-qXS (лри 9<l)t (2.8)
12ч
или
0<е <(! + «/(при ^>1), (2.9)
где значения g находя! ио таблице 8 (приложение 8)по за-
данной доверительной вероятности а и объеме выборки л
Если распределение генеральной совокупности нс является
нормальным, то в некоторых случаях по выборкам большего объе-
ма можно построить довсри 1сльные интервалы для неизвестных
параметров приближенно, используя предельные теоремы теории
вероятностей. Так доверительный интервал для вероятности р по-
явления события в одном испытании имеет вид
• , 1И4^. (2.10)
где И' относительная частота появления события в л испытаниях,
л объем выборки. ta - квантиль нормального закона распределе-
ния, находят из равенства Ф*(гв)-
. поскольку относительная
частота по теореме Муавра-Лапласа имеет асимптотически нор-
мальное распределение, а - доверительная вероятность.
Задачи
2.1. Пусть {ж,.*,»
выборка из нормально распределен-
ной генеральной совокупности с конечными математическим ожи-
данием т и дисперсией ст*, и пусть в качестве оценки матемазиче-
ского ожидания nj генеральной совоку пнехгти предполагается взять
среднее арифметическое Л выборки. Проверить несмещенность,
эффективность и состоятельность этой оценки.
Решение. Среднее арифметическое выборки |xPxr ..xj вы-
числялся г.о формуле:
Чтобы проверить несмещенность, эффективность и состоя
дельность среднего арифметического как оценки математического
ожидания т генеральной совокупности, рассмотрим ну статисти-
ку как функцию п- мерной случай нои величины
5 = ofA’,, Л\... А.),
составляющие которой имеют тол же закон распределения, той
изучаемая случайная величина X. го есть: АЛ А ) - т и
130
j 12 и, причем X. независимые случайные величины
я совокупности. Тогда
Л/(>) Л/ lVx -Л/ —У* А - V М(А’,) » — пт « гя.
' ) V tS / " п
Поскольку АН Al-т. то по определению получаем, что сред-
нее арифметическое Л - несмещенная опенка т. и 1ак Как
£НХ) ->0 при л->сг. го V - состоятельная оценка математического
ожидания гл генеральной совокупности.
^1я проверки эффективности опенки X вычислим информацию
Фишера по формуле (2 I) Платность распределения веройтио
стен нормально распределенной случайной величины имеет вид*
11рологарифмировав. получаем:
1лр(х.г0 -1п(гт>/2л)-——~-
2а
Частная прои вводная по т равна
с In р(г.гт) т-т
дт а2
Ма гемагическое ожидание случайной величины I ~ равно
= -^-Л/((А -т) )“7Г‘
а ' 'г
Подсинив шачепие математическою ожидания в (2 I). получим
= nAf
- 1 п
Поскольку. Г(А )--------— и днсисрч ия jMeHHiiaciCfl с рос-
п п
том п. то для нормально распределенной генеральной совокупности
срсднеи арифметическое А является эффективной оценкой матема-
тического ожи тания т.
OiBcr: среднее арифметичссмч: - несмещенная, эффективная и
состоятельная оценка математического ожидания
2.2. Пусть задана выборка {х ,хп...л J наблюдении случайной
величины X, распределенной по нормальному закону, и пусть в ка-
честве оценки математического ожидания т генеральной совокуп-
ности гредла(ается втять медиану: Me, Проверить несмещенность,
к| (|юк1ивность и состоятельное гь этой опенки
2.3. В результате про ведения N независимых жспсриментов
при одних и тех же условиях с случайное событие А произошло М
раз. Показать, что относительная частота — появления события А
в N экспериментах, является несмещенной, эффективной и состоя-
тельной оценкой вероятности Л Л) появлении события А в каждом
эксперименте
2.4. Пусть в качестве опенки математического ожидания ги
генеральной совокупности предлагается взять моду Afo , вычислен-
ную по выборке {г I . Проверить несмещенное)ь, эффектив-
ность и состоя принос ь этой оценки.
2.5. Предположим, что проигведены две случайные выборки
и П} из генеральной совокупности, распределенной но нормаль-
ному закону И пусть вычислены средние арифметические А', п А и
исправленные стглис гическнс дисперсии 5/ ь S,2 этих выборок.
Показать, что объединенные оценки, вычисляемые по формулам:
7 - г *1 \ - (f! ~ 11ч* jiLzlzLLL-
л 4 П, Л| * и, -2
буду г несмещенными, эффективными и состоятельными опенками
математического ожидания пи дисперсии гт генеральной сово-
купности
2.6. Методом наиГюльшего правдоподобии найш оценку ма
тематического ожидания m и дисперсии а1 по выборке . tj,
извлеченной из нормально распределенной генеральной совокуп-
ности
132
Решение. Пусть [x.xn xj выборка наблюдений из гене-
ральной совокупности нормально распределенной случайной вели-
чины X с плотностью распределения вероятностей
Z . 1
р(л,т.а)а yr r ,
Составим функцию правдоподобия £(л?,с’| по формуле:
Прологарифмировав но равенство, получим
ln/|m гт ) = 1по*'- у 1п(2г) 2п7Ё(х. ”
Применив необходимые условия экстремума функции
In/Jm.o ) составим систему уравнений для нахождения опенок па-
раметре^ т и а2'.
Последовательно преобразовывая первое уравнение системы,
находим оценку для m:
-п»)-О о г п;-0ГЛ--У г - ) ТО CCTI,
л -»
оценкой математического ожитания генеральной совокупности яв-
|яется среднее арифмсгичссксч- выбора ' Подставляя это значе-
ние т во второе уравнение системы, получим
или
л I
2^Ж2^
О »ку ла находим оценку для дисперсии генеральной совокуп-
ности:
' I PI V)
л , I
133
Отменим, ‘по среднее арифметическое Л является несмещен-
ной, эффективной и состоя i ел ьн ой оценкой математического ожи-
дания нормально распределенной 1снсральной совокупности, а ста-
тистическая дисперсия /ЛА') яв 1яется состоятельной и смещенной
оценкой nnenepew <т Поэтому, чтобы получить несмещенную
оценку дисперсии, умножают дисперсию на множитель
2.7. Методом наибольшего правдоподобия найти оценку пара-
метра а распределения Пуассона по выборке {л .л,. ..л„|.
2.8. Пусть р -вероятность появления события л-{А'-л }. а
А - дискретная случайная величина, заданная частотным рядом
распределения (таблица 2.1). Методом наибольшего правдоподобия
найти опенку параметра р и вычислить сс значение по выборке:
заданной в таблице 2.1:
Таблица 2.1
X 1 3 7 10 15
20 25 50 5
Решение. Случайная величина А' яв 1яется дискретной слу
чайной величиной, имеющей биномиальный закон распределения
Тогда вероятность того, что случайная величина V приняла значе-
ние х, равна Р{Х = г) = Сяр'(1-р), где А' может принимать нс-
отрицательные целочисленные значения от Одо л: А-С.1.2, .л.
Составим функцию правлопод(»б|!я для выборки:
। » *1 ’ " т =» г 1 1_J • • •
т. • • - Ь _ 4
м
((1-рГ '‘)'' (С Г (л г ((1-рГ‘Р-
•••• (Q)” (г- г- ((> р)” '•) Г (Q)’ ...(с,- )"* х
134
Прологарифмируем функцию
1пДр) = И(С; г(С’)’ (С?Г )+Х’т . |'"0 г»
4 1*4 в
Применяя необходимое условие экстремума, получим урав-
нение
di.{p\ 1 X
-------- ~ X X
<*Р Г
решив которое, последовательно найдем оценку р
Тогда для заданной выборки оценка вероятности появления
события Л»|Х»д,) равна
3 2С + 7 25->10 50-15 5
-О.ОМ.
Они i: /’-0.081
2.9. Предположим, чго число автомашин, подъезжающих на
заправку в течение п часов, описывается случайной величиной,
имеющей закон раснрсдс вен ня 11уассона с параметром лЛ. где /
возможное число автомашин подъезжающих на заправку в лечении
одного часа. Молодом наибольшею правдоподобия найти опенку
параметра А.
2.10. Производится и независимых испытаний. в каж юм из
которых событие А может произойти с вероятностьюр. Предполо-
жим. что событие Л может произойти в m испытаниях. Методом
наибольшего правдоподобия найти оиснк\ вероятное!и р появле-
ния события А в каждом испытании
2.11. Методом наибольшего прандоподоСн я найти оценку па-
раметра X по выборке {х,,л.. .1 ) из генеральной совокупности,
распределенной по показательному закону
. . ]Ле4\л^О.
f(х)=<
|C. л<0, гскА>0.
2.12. Пусть {< ,л,.. .д.) выборка наблюдений случайной ве ш-
чины X, имеющей распределение Пуассона с неизвестным пара-
метром а:
Методом наибольшее о правдоподобия найти оценку параметра а .
2.13. Пусть случайная величина X распределена по показа-
тельному закону с плотностью вероятностей
и неизвестным параметром X, Х>0
Метолом моментов найти оценку неизвестного параметра X но вы-
борке
Решение. Вычислим начальный момент первого порядка,
применив (| ормулу интегрирования по частям
Ц(х) - |= Л jxc~*'dx Л lim
0-4
А * - A
u —x.du * dx
|ir' kldx - e k*di = d*\
Поскольку С13ГИСТМ теский натальный момент первою порядка равен
то приравнивая значения этих двух моментов. получим.
I _ I
— А’ Откуда находим > = - .
л
Ответ: А = Х.
2.14. В п независимых испытаниях событие Л проитош ю тп
раз Метилом моментов найти оценку вероятности v появпения со-
бытия А в одном испытании
ие
2.15. Методом моментов по выборке .л.| объема п
найти оценку параметров m и ег* нормально распределенной слу-
чайной величины X.
2.16. Методом моментов по выборке {д(.д2. .1.) объема п
пай гм опенку параметра случайной величины X. имеющей Пуассо-
новское распределение: /V = х) = —г“*.
хг
2.17. Выборка из большей партии электроламп содержит
п 49 ламп. Средняя продолжительность горения зампы выборки
оказалась равной Л'= 500 ч. Haiti и с надежностью а=0.95 довери-
тельный интервал для средней продолжительности m горения лам-
пы всей партии, если известно, что среднее квадратическое откло
нение продолжительности iпрения лампы ст -14
Решение. Воспользуемся доверительным интервалом для
средней продолжительности m горения лампы при известном сред-
нем квадратическом отклонении о (форму за 2.4)
Средняя продолжительность горения лампы выборки Л-5<Юч,
объем выборки л~50 ламп. По заданной доверительной вероятно-
сти а=0,95. из равенства Ф‘ц )= —^21 Фф(/в)^0.975, по таблице
(приложение 1), находим /л«1.9е. Подставив значения У = 500,
I* =196, о = 14, дг-49 в (2.4), получим:
14 14
400-1,96-7=. < гл <500-1.96 ’
V49 <49
Вычислив, окончательно находим доверительный интервал.
4<ЯхО8 < w < 503.92
Ответ: 496.0b < /л < 503.92.
2.18. Для проверки износоус гойчмвекти шин фирмы «Ье тши-
иа» из большой партии было отобрано 100 шин. Средняя продоь
житсльность эксплуатации одной шины оказалась равной 81 тыс
км Найти с надежностью п • 0.Q5 доверительный интервал для
средней продолжительноети m эксплуатации шин всей партии ес ти
известно, что среднее квадратическое отклонение продолжил, лкно-
сти жсплуа1апии одной шины о ^9 тыс км.
137
2.19. Для проверки средней дневной выработки рабочих
строительном организации было проведено обследование выра-
ботки 50 рабочих Средняя выработка одного рабочею оказа-
лась равной 3 95 м , а среднее квадрашчсскос отклонение
гт =0,75 м‘, Найти с надежностью а = 0,95 доверительный ин-
тервал для средней выработки одною рабочею всей строитель-
ной организации.
2.20. Из партии поршневых колеи изготовленных за смену,
и<влечена выборка объема п - 100 и вычислено среднее арифмети-
ческое диаметров изготовленных поршневых колец, равное 120 мм.
Найти с надежностью а = 0.95 доверительный интервал для мате-
матического ожидания диаметра поршневых колец ичоювленных
за смен}, если среднее квадрагическос отклонение г = 0,2 мм
2.21. На;пи минимальный объем выборки, при котором с на-
дежностью а - 0,99 точность оценки математического ожидания т
генеральном совокупноеги времени безотказной работы электрон-
ной лампы по известному среднему арифметическому, будет равно
6 - 0,5, если известно среднее квадратическое отклонение, <7 = 10
часов, нормально распределенной гене|лальной совокупности
Решение. Воспользуемся формулой, определяющей точ-
ность оценки математического ожидания, нормально распреде-
ленной генеральной совокупности по известному среднему квад-
ратическому:
г (7
ел куда следует, что л
3
Из условия задачи известно, и 10, 8 0,5. Найдем t . Пользуясь
таблицей (приложение I). по доверительной вероя мости а = 0.99
из равенсгваФ*(/. i - -
+ а
2
• Ф*(М-
I 4-0,94
2
0.99«
находим 1Л -2.58.
Подставив / 2.58, гт
10,6 0,5, получим
• 2663.
Ответ: и 266V
2.22. Наити минимальный объем выборки, при котором с на-
дежностью а - 0,95 точность оценки математического ожидания
нормально распредс денной тснсра !ьмой совокупности емкостей
конденсаторов по известному среднему арифметическому выборки.
пя
будет равно 0,3. если известно среднее квадратическое отклонение,
а = 5 мкФ. нормально распределенной генеральной совокупности
2.23. Д я обследования средней урожайности ячменя с одного
гектара по области крове лево выборочное обследование участков
посевных площадей, результаты которого приведены в таблице 2.2:
Таблица 2.2
УрожаГгиос-ь пшеницы, х • • 38 40 45 г* "1 47 50 .
Число участ- ков. 3 12 20 9 i * 6
Оцени гь с надежностью п=0.95 математическое ожидание т и дис-
персию <т: нормально распределенной генеральной совокупности
по среднему арифметическому и статистической дисперсии при
помощи доверительного интервала.
Решение. Вычислим среднее арифметическое и исправление
ерспнее статистическое квадратическое отклонение соответственно
по формулам:
1 • , 7?17
А--Улт.—-(38 3 + 40 12-4? 20ч 47 9+50 Н~—— ₽4»,34.
’ 50 50
, 1 . , , , . .\Х
I *(40-44 34)’*(45-44 14)' *(47 - 44,34 > *(50-44,38) | | =
( 98.2132 У
\ 40 J
*1.42
По ловерг'тетьной вероятности а-=0,95 и числу степеней сво-
боды v = n-l = 5C-l=49 находим квантиль распределения Стьюден
та (приложение 6) / =1,68. Доверительный интервал д if математи-
ческого ожидания найдем по формуле.
• а
— S . « 5
А / —< т < А ♦ L 7 rw .
Vr-1 < п -1
ПО/Лставив значения А-44,34: 5 = 1,42. п -50; / = 1.68. после-
довательно находим доверительный интервал
44.34 I 68 ЬД^<ш<44,34*-т1£ 1.68. 40.40 < w 47.74 .
J49 V40
содержащий математическое ожидание т генеральной сонокупно-
сги с надежностью а-0.95. Для построения доверительного инн р-
вала для дисперсии с воспользуемся формулой (2 7) Для лове-
139
рительной вероятное।и а=0.95 и числа степеней свободы v п-1
по таблице (приложение 4) находим квантили хн квадрат распре-
деления
i а
Подставив значения 5 1.42; я-1=49 и ~ <2.4,
4,Гим - 71.4 в формулу доверительного интерва та (2.7.), получим
1.42 49 ч 1,42 49
--------<сг <----------
71.4
32.4
ИЛИ 0.97 < ст* <2,15.
Доверительный интерва-i для среднего квадратического от-
клонения (2 8) после подстановки д-|Да,>)=^(0,95;49) = (].21 Най-
денного по таблице (приложение 5), принимает вид
(1-0.21) 1.42<ст<(1 + 0.20-1,42 или 1.12<ег<|,71
Ответ: 40,49 < m < 47.74; 1.12 < с < 1,71.
2.24. Для исследования времени средней продолжительности
безотказной работы тслевияионных трубок, произведенных на за-
воде «Горизонт» было проведено выборочное обследование 100 те-
левизионных трубок Оказалось, чго среднее время безотказной ра-
боты равно 36 месяцев со среднем квадратическом отклонении
равным 4 месяца Постройте 95%-ные и 99% ные доверительные
интервалы для среднего времени безотказной работы телевизион-
ных трубок, произведенных на заводе «1 орнзонт».
2.25. Предельная нагрузка для выборки из 50 стальных
стержней характеризуется выборкой:
Н 13 14 16 17
4 5 30 7 4
----- — 11 4
Постройте доверите тьныс интервалы для опенки с надежностью
а~0,95 средней предельной нагрузки и среднего ква, трагического
отклонения прелельной нагрузки стальных стержней партии, из ко
торой произведена выборка
2.26. Для наблюдений каждой из пяти случайны* выСюрок
постройте с надежностью а-0.95 доверительные интервалы для
оценки математическою ожидания генеральной совокупности и
дисперсии
1) Выборка сопротивлений:
X 27 0.28 0,2° 030 | 031 0Д2
/и 1 5 17 2< 18 1 10 5
140
2) Диаметры шаров в шарикополтипнлках
£ 1.97 । 1.98 1.99 2.00 2.0] 2,02
гл • ] 3 1 4 13 30 10 — 4 1 1
3) Увеличение частоты пульса студентов после занятий физ-
культурой:
6 7 к 10 12 —П— 13 14
”, 13 28 32 40 1 25 L— - 10 1 12
-------------- - _ ----------U- -----
4) Процентное содержание витамина С в выборке витамин-
ных драже:
X 1 ( 12,9 14.3 14.8 15.2 16.3
10 17 23 1 12 6 1
5) Рос г студентов 1-го и 2-го курсов университета
Л. 1.63 1,68 1,70 1.71 1.73 1.80 1.87
1 2 4 20 43 21 5 5
2.27. Из большой партии микросхем одною типа были слу-
чайно отобраны и проверены 100 штук У 16 .микросхем обнаружи-
мся отклонения технических характерно!ик. Найти 95%-ный до-
верительный интервал для вероятности тою. что микросхема будет
бракованной ио всей партии Какой минимальный объем выборки
следует взять, для того, чтобы с вероятностью 0,95 можно было ут-
верждать. что вероятность появления бракованных микросхем в
выборке не более чем 1%.
Решение. Эффекзивной оценкой вероятности появления со-
бытия в одном испытании является относительная частота и' = —
Л
появления события в п испытаниях По теиремс М>авра-Лапласа
относительная частота W имеет асимптотически нормальное рас
предетение потому доверительный интервал для вероятности го
го, что некоторая микр<к*хсма во всей партии будет бракованной
имеет вил (2.10). Вычислив относительную час юту
16
и - = —-0,16 и |,а”ля по таблице I (приложение 1) квантиль
нормального распределения из равенства Ф’ц )*- ’1 " ,/вг>. по
л.
строим доверительный интервал:
tojxi о.i6)
\ loo V ioo
или
(1.088<р< 0.232.
|4|
Для определения минимального объема выборки представим
доверительный интервал (2.10) в виде неравенства
И'О-И7)
♦
л
|И -Г£1я-
которое выполняется с вероятностью п 0,95. Так как ио условию
задачи И' p|sO,cl, то для определения л получим неравенство
/И’(|-И)
"’V л
<0.01.
Последовательно преобрази неравенство, находим л
/0,160-0.16)
1*96 J <0,01.
\ п
/0.16-0,84 0.01
V п 1.96*
0.I60.R4 < , I Y
п 1*н I
w г 0, i 6 0,84 • 196' = 0.1344 I %’ = 3819.1004 л « 3820
Ответ: Доверительный интервал 0,08К<р<0.232;минималь-
ным объем выборки п =3820.
2.28. С произволе!венной линии* производящей часы, было
отобрано 100 часов, 10 из которых содержали брак. Найти 95% до-
верительным интервал для вероятности того, что случайно ото-
бранные часы с производственной линии будр содержать брак
Какой минимальный объем выборки следует взять для того, чтобы
с вероятностью 0.95 можно было утверждать, чго вероятность по-
явления бракованных часов на производственной линии отличается
от частоты появления бракованных часов в выборке не богее чем
на 5%?
2.29. Длз определения всхожести семян н пар!ни пшеницы
было отобрано 1000 зерен, из которых взошло 980. Найти 99% до-
верительный интернат для вероятности того, что случайно спо
бранное зерно пшеницы из партии взойдет. Найти минимальный
объем выборки, на основании которого можно утверждать, чго ве-
роятность torn. чго случайно отобранное зерно пшеницы из партии
взойдет, ол шчаегся от частоты всхожести семян пшеницы не более
чем на 3%.
2.30. Для предварительного опроса населения города N в свя
и с избиратель» й мнанией бы is произведена выборка 1000 из-
бирателей hi которых 350 заяви im. чго они проголосуют за канди-
дата от оппозиции. Найти 95% доверительным интервал для веро
язностм тою, чго случайно отобранный избиратель юрода N про-
голосует за кандидата от оппозиции. Какой минимальный объем
выборки следует взять, для того, чтобы с вероятностью 0,99 можно
было утверждать, что вероятность того, что избиратель в юроде N
проголосует за кандидата от оппозиции отличается от частоты из-
бирателей в выборке которые проголосуют за кандидата от оппози-
ции, не более чем на 2%.
2.31. При осмотре 50 изделий из парши обнаружено 5 содер-
жащих дефект. Найти 99% доверительный интервал для вероятно-
сти того, что случайно взятое изделие из партии будет дефектно
2.32. Предположим, что число сбоев компьютеров за месяц
имеет распределение Пуассона с параметром а Исследование раСхь
ты ИХ) компьютеров показало, что среднее число сбоев за месяц
равно 1,7 Найти 95% довери тельный интервал для параметра Л
Указание Воспользоваться формулой
где tf- квантиль нормального распределения N(O.I), находят из ра-
венства Ф’(/Л)-
, а -доверительная вероятность
2.33. Изучается работа фирмы на двух рынках. Среднее зна-
чение объемов продаж по 10 наблюдениям на первом рынке соста-
вила А -8 единиц продукции в месяц, а на втором по 15 наблюде-
ниям среднее значение объемов продаж i - 84 единиц продукции
Предположим, что дисперсии значений объемов продаж известны и
раины rrlt |б и сг{ -18 для первого и второго рынков соответствен-
но Найти 95% доверительный интервал для разности средних объ-
емов продаж М(Х) и МЦУ) на первом и втором рынках Можно лк
считать, что результаты объемов продаж случайны или действи-
тельно различны?
Решение. 11оскопьк\ дисперсии обегх совокупностей наблю-
дений известны, то доверительный интервал для разности средних
М( X) и М(\) определяются формулой
(Л - <MiA •> j|-r >а’ .
— \ п, п, -у \ п ч.
где
квантиль норма гьного распределения N(0:h для заданной
доверительной вероятности </ находим из равенства ——
Подставив в формулу доверительного интервала значения
143
-* w = A =8!; > -84, oj = 16; a2 — 18; Л|-10; л2-15, полу-
i
чим:
(81-64)-L96^ »^ < Л/<Л)- W(n<(RI И)
HIM
-3-3.2732 < Л/(А')- .tf(F)< -3-r 3.2732
или
-6,2732 < Л/(X) - АДУ) < о 2732.
Поскольку разность А - У - 81 - 84 - -3 принадлежи г доверительному
интервалу, то можно считать, что средние значения объемов про-
даж фирмы на двух рынках приблизительно равны.
Ответ: -62732< А/(А >-Л/(У)< 0.2732. Расхождение результа-
тов объемов продаж случайно.
2.34. Проводятся измерения диаметра однотипных валов, из-
готавливаемых на двух станках автоматах. По 20 измерениям ва-
лов. изготовленных на первом с ганке получено среднее значение
А—61 мм, а по 25 измерениям валов, и гготовленных на втором
станке, среднее значение > =65мм. Предположим, чго дисперсии
измерений известны и равны: гт; = 36 мм и ст2 -18 мм для первою и
второго станков Найти 99% доверительный интервал для разности
средних диаметров М(Х1 и M(Y) валов, изготовленных на первом и
втором станках. Можно ли считать, что результаты средних значе-
ний валов различаются?
2.35. Автопокрышки, произведенные на шинных комбинатах
N* I и № 2, исследовались на износ (в километрах пройденного пу-
ти) При этом оказалось, что средний пробил по 25 измерениям на
шинном комбинате №1 равен X = 95000 км. а на комбинате №2
средний пробег равен Y 105000 км при 15 измерениях. Дисперсии
измерений соответственно раины A’J. *блоо км, S =9000 к.м. Найти
95% доверительный интервал разности средних пробеюв М (X) и
М (Y) шин на шинных комбинатах N 1 и N* 2.
144
2.3 Статистические решения
Информация, полученная при обработке выборки из некото-
рой генеральной совокупности, может быть использована 1ыя по-
лучения выводов (решений) обо всей совокупности.
2.3.1. Статистическая гипотеза. Проверка гипотезы
о среднем значении при известной и неизвестной
дисперсиях.
Гипотеза тго предположение о том, что эмпирическое рас-
пределение описывается некоторым теоретическим распредезением.
или о принадлежности выборочных данных к одной генеральной со-
вокупности, или относительно одного или нескольких параметров
совокупности и т. л., по. вер! аемос статист и ческой проверке
Статистической гипотезой, обозначаемой /У, называется
любое предпо ложение относительно лида или параметров распре-
деления случайной величины X. которое может быть проверено по
результатам выборки.
Статистическим критерием для проверки гипотез 11^ Hf, ....
Нт называют случайную величину <5 принимающую значения
H,(i = 0,m)t т.е.
Критической областью для данного статистическою крите-
рия <5 гипотезы Нп налы вас с я множество значений статистической
характеристики гипотезы, которые, ссылаемо правилу д, приводят к
отвержению гипотезы Но.
Проверка гипотез проводится по следу юшей схеме
1 . Формулировка основной и альтернативной гипотез
2 Выбоп соответствующего уровня значимости критерия
0,05; 0,01; 0.001.
3 Определение объема выборки п (если выборки нет).
4 Определение статистической характеристики критерия.
5 Вычисление критической области и об !асти принятия гм
питезы.
6 Формулировка правила проверки гипотезы гипотеза //.
принимается при заданном уровне шачимости о если вы
бирочное значение статистическом характеристики попа
ласт н область принятия гипотезы. 1ипотеза 1Г отвернет-
ся. если выборочное шачсние статистической характери-
стики попадает в критическую Область
Если критические облас ти располагаются слева и справа от
математического ожидания случайной величины А го критическая
область называется а критерий д двусторонним
критерием значимости. Если же критическая область распо.татаег-
ся слева или справа от математического ожидания случайной вели-
чины <5. то критическая обгасть называется односторонней. а кри-
терий — односторонним.
Рассмотрим нормально рас пределе иную случайную величину
Л с неизвестным математическим ожиданием, среднее квадратиче-
ское отклонение которой п известно. Чтобы про верить гипотезу //«;
т-гъ 1. е. проверить предположение о равенстве математического
ожидания всей совокупности значению /и, при альтернативной ги-
потезе Н : т-т нужно воспользоваться статистической характе-
ристикой
г-*^Гп.
".
Если т, > %,то критическая область [г„ ;♦<») определяется из
равенства P(Z i z^) = at.
По таблице значений функции
фЧг)—[е,,а<Л
находим значение z„ , такое, что Ф*(г, ) I
Тогда, сс 1И . .. > то. т ипотеза отвергается, в против-
ном случае нет оснований отвергать нулевую гипотезу.
Если т, < %. то критическая область ( ] определяется из
равенства Г(Л<.?^)=Ф*( <)~\ щ Если то типотеза Нп
отвергается; в противном случае нет основании отвергать нулевую
гипотезу.
Если же алюернапивная тииогеза Н> определена не одно-
значно. то критическая область определяется так, чтобы ей принад-
лежали нее значения стаз истической характеристики Z, которые не
больше и не меньше . тле опречкняется из равенства
Ал
г е Ф*(г I I — . При выполнении нерансгстна Zs г или Z< г
типотеза атвергаегся; в противном случае нет оснований отвер-
1 азъ ну тсную гипотезу.
В случаи, koi да наблюдаемая случайная величина X полчипя
стся нормальному закону распределения с неизвестным средним
квадратическим отклонением, с гатмстической характерна икон
служит величина
(31)
У
имеющая закон распределения Стьюдеша с v- и - 1 степенями
свободы.
Для тою чтобы при заданном уровне значимости о прове-
рить нулевую гипотез} Нп т т., при альтернативной гипотезе
гл>ти, по таблице распределения Стъюдснга находят квантиль
। и3 равенег ва Р{Т > .) - а0.
Если Тгсгч >7 ,то нулевая гипотеза /Уо отверг аегся на уровне
значимости а, в противном случае (если ГЛЛГ^< /г » Л *<ст оснований
отвергать нулевую гипотезу Нп.
При альтернативной гипотезе Н, по таблице распре-
деления Сгьюдснга находят квантиль , из равенства
Если < /а . то нулевая гипотеза отвергается на уровне
значимости а , в противном случае (Т^Лг^нет оснований от-
вергать нулевую гипотезу.
При альтернат йеной гипотезе Hr. сравнивают модуль
ст а । мсти ческой характеристики Т с квакш гем te । распределения
/ х / \
Стьюдеята, найденным из равенства / ‘I Т < г - P\Tbt. । = —.
l -*♦ l -*> l
\ a / \ a / x
Если |7r). fH то нет оснований отвергать нулевую гипотсту /Л.
1 **
в противном случае (|ТЛ. ч / ) нулевая гипотеза //оотвер' асгся
а *
Задачи
3.1. Пре гельная сила натяжения прядильной нити в среднем
равна 20 г. Выборку нити из 64 мотков обработали некоторым хи-
мическим составом Пекле просушки быта заново измерена пре
дельная сила натяжения нити В среднем она оказалась равной 21г.
Предгюла ая. hi о среднее квадратичное отклонение с предельной
си 1Ы натяжения нити равно 2 г до и после обработки химическим
составам, проверить гипотезу о том. что зта обрабчика не увеличг
ла предельной силы нагяжения ниги
147
Решение. Обозначим среднюю предельную силу натяжения
прядильной ниги через АДА) = ж.
Решение задачи разобьем на ряд палов.
1. Формулировка нулевой и альтернативной гипотез. Сфор-
мулируем следующие гипотезы основная типигеза //<_•: т-20, аль-
тернативная гипотеза Hi : т >20 (односторонняя проверка, так как
нас интересует, увеличится ш предельная сила натяжения нити в
среднем после обработки химическим составом).
2. Выбор соответствующего уровня значимости а$. Возьмем
<Z/r=O,05.
3. Определение объема выборки. В условии выборка опреде-
лена (я=64)
4. Выбор статистики критерия. В качестве статистики
возьмем величину
<7
имеющую приближенное стандартное нормальное распределение
при условии, что гипотеза Н<, верна.
5. Вычисление критической области и облас ти принятия ги-
потезы При 5%-м уровне значимости для односторонней проверки
наибольшее значение величины Z, при котором //п еще не отверга-
ется, будет равно -1,65. 4то наибольшее значение определяется
из таблицы 3.1. Таким образом. область принятия гипотезы - полу
интервал (-«;!,65), а критическая область интервал U,65;+co).
6. Формулировка привили проверки гипотезы
Предельная сила натяжения прядильной нити в среднем уве-
личится, если значение статистики Z. вычисленное но выборке,
больше 1.65 В других случаях считаем, что предельная сила катя
жения нити в среднем не увеличится.
7 Проверка гипотезы По выборочным данным находим, что
Предельная сипа натяжения прядильной ни1н н среднем увс
дичится, так как ч-4>1,6 zt Этот вывод будет неверным ме-
нее чем для 5% всех случаев.
Ответ предельная сипа натяжения ниш в среднем увеличи-
вается.
3.2. Для анализа выпуска химической смеем производится
случайная выборка из дневной партии и определяется процентное
содержание воды двумя способами. Результаты, полученные в те-
чение b дней, указаны в таблице 3.2.
1 аблицв 3.2
( пособ определен г* ripvucHiHuro содержания воды Дни
1 2 3 4 5 6 £
А 53 .46 55 53 4S 45 50
L В 50 ' 47 53 J3 47 < - - —" *0 45 Й
Необходимо проверить гипотезу о том. чго методы анализа суще
стненно различаются между собой
Решение. Как видно из таблицы 3.2, имеется заметное разли-
чие в процентном содержании воды в химической смеси Эти кол
баиия нс дани возможности определи! ь различие р способах опре
деления процентного содержания воды.
Наблюдения, в которых результаты экспериментов объеди-
нены в царь и каждая пара представляет собой самостоя!ельнук
экспериментальную единицу, исследуем, применив критерии срав
нения Каждая пара дает олпо сравнение, которое опрелеляет меру
эффекта некоторого действия.
Обозначим через d разность результатов каждой пары. Оно бу-
дет иметь нормальное распределение со средним т и средним квад-
ратичным отклонением S. Значения величины d дгя дней 1, 2» .... Я
будут равны соотвстст венно: - Я 11—2.0.— I; 1; —5; -2.
Сформулируем следующие гипотезы основная гипотеза//, :
т - 0 (способ определения процентного содержания воды не имеет
значения); альтернативная гипотеза Ht л?>0 (способ В пре вое хо-
дит способ А дня спреде гения процентного содержания воды)
Гипотеза Н\ односторонняя, поэтому определяем односто-
роннюю критическую область при и л-А’.
Статистикой является величина (3 1)
имеющая! распределение С гьюлсигас г-л I степенями свободы
Так как критическое значение /я „, л ж 7 степеней свободы
равна 1,89. областью принятия гипотезы является интервал (-ес; 1,89)
Если значение Г, вычисленное по данным выборки, не мень-
ше 1,89. io можно сделать вывод о том. чго способ В имеет пре-
имущество перед способом А Если 7fMrv< /,Л9, то гипотеза Нс при-
нимается, т. с способы А иВ равнозначны.
По данным выборки имеем:
II, j»45-
Отсюда
8 ft— 1 7
Так как 1,76 < 1.89. то можно утверждать, что при 5%-м
уровне значимости методы анализа процензною содержания воды
равносильны. Таким образом, различия между способами А и В не
установлено.
Ответ: методы анализа не различаются.
3.3. По паспортным данным автомобильного двигателя рас-
ход топлива на 100 км пробега составляет 8 л В результате изме-
нения конструкции двигателя ожидается, что расход топлива
уменьшится Для проверки проноля гея испытания 50 случайно ото-
бранных автомобилей с модернизированным двшвведем. Среднее
арифметическое расходи топгнва на 100 км пробега, у отобранных
автомобилей, по резулыатам испытании составило А =7.6 i. Пред-
положим что случайная величина А характеризующая расход топ-
лива на !00 км пробега подчиняется нормальному закону распреде-
ления со средним т и дисперсией а' -2.?. Проверить гипотезу о
том, что модернизация двигателя нс повлияла на расход топлива.
Решение. В данной задаче нужно проверить гипотезу о ма-
тематическом ожидании т нормального распределения генераль-
ной совокупности. Проверку гипотезы проведем по трапам:
1. Проверяемая основная гипотеза Нс состоит в том, что матема-
ическое ожидание m нормального распределения случайной
величины X составляет 8 т. i е Н^ : т 8л. при альтернатив-
ной гипотезе /7 т < Ял (односторонняя проверка, нас интере-
сует. будет ли среднее меньше lapaHi ированлого минимума)
2. Выбираем уровень значимости а, - 0,05.
3 Объем выборки задан, л®50
4 В качестве статистической характеристики выбираем cj у-
чайную величину:
ГТ
имеющую нормальное распределение с параметрами т О, <т-1:
5. Так как альтернативная гипотеза Н : т<8, то критическая об-
ласть определяется неравенством Z,^s<z^. По таблице I (в
приложении I) находим m равенства Ф"(г > = 0.05, z. =-1 64х.
1 аким образом, область принятая i ипотезы интервал (-ос;
1.645> Критическая область полуинтервал [-1.645;-» «)
6. Правило проверки гипотезы По выборочным данным нахо-
дим значение статистической характеристики
Поскольку Z^xx= —2.0с = - I .645, тп гишмеэа Яс отвергается и при-
нимается альтернативная 1ипотеза Н : следует считать. что изменения
конструкции двигателя привело к уменьшению расхода топлива.
Ответ: Изменение конструкции двигателя привлекло к
уменьшению расхода топлива
3.4. Известно, что при некотором гс>.ноло1 ическим процессе за
смену (и » Л часов) выпускается в среднем 350 единиц изделия По-
сле некоторых изменений в производственном процессе за смену ста-
ло выпускал»ся в среднем 355 изделий Предположим, что случайная
величина X характеризующая число выпускаемых изделий за cmchv
(п ~ А часов) подчиняется нормальному закон) распределения со
средним ш и дисперсией сг = 12сдиниц Проверить 1ипотезу о том,
ыо модернизация производственного процесса не повлияла на уве-
личение производства изделий при уровне значимости af 0,05
3.5. В соот ест с твии с техническими условиями среднее время
безотказной работы приборов из партии, содержащей 10000 прибо
ров равно 1000 часам. При контрольной проверке 36 приборов из
/тиной партии среднее время безотказной работы составило ^50
часов Предположим, чзо случайная величина X характеризующая
время безотказной работы прибора подчиняется нормальному за-
кону распределения со средним т и дисперсией 100 часов. Прове-
рить гипотезу о том, что вся партия приборов не удовлетворяет
техническим ус ловиям при уровне значимости По=0.05
151
3.6. Технология производства некоторого вещества даст в
среднем 640 кг вещества в сутки (и-8 часов) После некоторых из-
менений в производственном процессе стхтн получать в среднем н
сутки 700 кд вещества Предполагается, что случайная величина X.
характеризующая производство вещества, подчиняется нормаль-
ному закону распределения со средним т и дисперсией 100 кг.
Проверить гипотезу о том, чю изменения в технологическом про-
цессе привели к повышению производительности.
3.7. Из статистическою сборника известно, что 7% всех за-
страховавших свою жизнь умирает по достижении 60 лег. В группе
из 1000 человек этого возраста, работающих в сфере обслуживания,
умерло 85 человек. Проверить гипотезу о том. что застрахованные
люди, работающие в сфере обслуживания, чаше умирают в 60 лет,
чем вес остальные застрахованные. Принять п.г-ОД)5.
Решение. В данной задаче нужно сравнить вероятность появле-
ния собы гия в каждом испытании с заданной вероятностью рз=0.07.
1 . Сформулируем основную гипотезу Н<, состоящую в том, чго
вероятность застрахованного человека умереть но достиже-
нии 60 лет равна 0,07. у.е Ht): р-0.07; при альтернативной
гипотезе состоящей в том, чго застрахованные люди, ра-
ботающие в сфере обслуживания чаще умирают в 60 ier. чем
все остальные, т.с. Hr: р>0,07.
2 . Выбираем уровень значимости: ар *0.65
3 Объем выборки задан: л-НИХ).
4 В качестве статистической характеристики выбираем слу-
чайную величину:
f Ш А г~
"Р Ып
у т /
имеющую распределение, близкое к нормальному распределе-
нию N(0J).
5 . Так как альтернативная гипотеза Н\ : р -0.7, то критическая
область при уровне значимости Ол определяется неравенст-
вом F(Z )-а,. квантиль находим по таблице I (прило-
жение I) из равенств;! Ф*(**) !-о.. I 64*. Слеповато ль
но, область принятия гипотезы интервал (-«;!,645), а кри-
т нчсская область полуинтервал [ 1.615/ ог>у.
6 По выборочным данным накопим значение статистической
характеристики
85 -0,07|-Л000
(1000 J
^7(1-0,07)
-1.869.
Поскольку ZH.... 1.869 > zOr;5 « 1.645 лежит в критической об-
ласти. ю с вероятностью 0,95 принимается альтернативная тиноте-
<а /Л. Следовательно, застрахованные люди, работающие в сфере
обслуживания, чаще умирают в 60 лет. чем все остальные застра-
хованные.
Ответ: Застрахованные люди, работающие в сфере обслужи-
вания. чаще умирают в 60 лет, чем все остальные застрахованные
3.8. Количество бракованных деталей в партии нс должно
превышать 3%. В результате контроля 100 деталей из этой пар1ии
обнаружено 5 бракованных Можно ли считать, что процент брака
превосходит допустимый при ао~0л)У!
3.9. При исследовании 100 корпусов упаковки стеклянных
изделии, случайным образом выбранных из большой партии этих
изделий, оказались, чго 8-см из них не имеют необходимой проч-
ности Согласуются ли эти данные с утверждением о том. что дав
пая партия содержит более чем 90е о прочных корпусов, если
а^0.05
3.10. Из суточной продукции кондитерскою цеха с iy чайным
образом отобрано и проверено 20 кондитерских продукта. При
зггом 5 единиц продукта признаны нс соответствующими госту
Можно ли считать, что годная продукция кон питерского цеха со-
ставляет 99%, если ао-0.05?
3.11. Д; и исследования на прочность волокон некоторою ви-
ла после химической обработки было отобрано и пронумеровано
шесть мотков волокон. Каждый отобранный моток был разделен
пополам, одна половина подверглась химической обработке, дру-
гая нет Затем с помощью прибора, измеряющего прочность во
локон, была намерена прочность (в %) двенадцати кусков волокон.
Результаты представлены в таблице 3.3.
Таблица 3 3
Номер исс тедуемт о куска 1 2 * 3 - А L*J
Обработанная половина 18.1 17 J L IO.I 18.4 г.2 16.7
Необработанная половина 16.4 17.(1 р IR.4 17.6 17.0
Увеличила ли химическая обработка прочность волокна
3.12. Обследование выпушенных видсомш нит о фонов покача-
ло, что 5% и < них имеют брак. Проверить гипотезу H,t: вероятность
того, что ма1тштофон бракованный, равна 0,05, взяв в качестве
уровня значимост критерия 0.01. Объем производимой вы-
борки п принять равным 400 видеомшнитофонов. Какое нужно
принять решение относительно гипотезы 11<если в произведенной
выборке окажется 26 бракованных видеомагнитофонов?
3.13. Считается, что завод, производящий за неделю 1000 те
ревизоров, работает удовлетворительно, если в среднем часк»сгь
бракованных телевизоров при контроле качества нс превышает 3%
Допустим, что в течение некоторой недели было забраковано 38
телевизоров. Необходимо ли директору завода провести более пол-
ную проверку качества изготовления телевизоров на производст-
венной линии или же следует отнести высокий процент дефектной
продукции этой недели за счет случайных изменений в условиях
произволе । на ? Воспользоваться односторонней проверкой гипоте-
зы с 5%-м уровнем значимости.
3.14. По утверждению фирмы, средним размер дебиторского
счета 187,5 гыс. р Реви юр составляет случайную выборку из 50 сче-
тов и обнаруживает, что средняя арифметическая выборки равна 175
тыс р при среднем квадратичном отклонении 35 гыс. р Может ли
оказаться в действительности правильным объявленный размер лепи
торского счета' Уровень значимости принять равным 0,05 и 0.01.
3.15. Но техническим условиям средняя прочность на разрыв
роса составляет 2000 кг. В результате испытаний 20 кусков гроса
было установлено, что средняя прочное in на разрыв равна 1955 ki
при средней ошибке 25 кг. Удовлетворяет ли образец трека техни
ческим условиям' Уровень значимости принять равным 0,05.
3.16. В фирме, производящей пек греческие лампочки, ут-
верждают, что среднее время безотказной работы лампочек мощ-
ностью ГО В । равно по меньшей мере 800 ч со средним квадра
тичным отк лонением 120 ч. Ph некоторой партии 120-ваггных лам
ночек производится выборка 25 лампочек, для которой выборочное
среднее времени работы лампочек оказалось равным 750 ч Можно
ли на основании этого сказать, что исс <едуемдя партия ым почек не
удовлетворяет i практик?
3.17. Поставщик трехпроходных ламп накаливания утвержда-
ет, что их средний срок службы равен 2500 ч. Для выСюрки из 37
ламп средний срок службы равен 2325 ч при среднем квадратичном
отклонении 600 ч. Можно ли считать, что при уровне значимости
IM
ао-0,05 срок службы ламп оказался значительно ниже japainкро-
панного поставщиком9
3.18. Предельная сила натяжения прядильной шерстяной ни-
ти в среднем раина 8 г. Выборку нити из 64 мотков обработали не-
которым химическим составом После просушки была заново из-
мерена предельная сила натяжения нити. В среднем она оказалась
равной 8,5 г. Предполагая, что среднее квадратичное отклонение
предельной силы натяжения нити равно 2 г до и после обработки
химическим составом, проверить гипотезу о том, что эта обработка
не увеличила предельной силы натяжения ниги Сделать проверку
при уровне значимости 0,05 и 0,01.
23.2. Проверка гипотез о дисперсии.
А. Рассматривается нормально распределенная случайная ве-
личина X Для А' получена выборка из п независимых наблюде-
ний, где и достаточно велико. Чтобы при заданном уровне значи-
мости On проверить основную гипотезу //, о равенстве неизвест-
ной генеральной дисперсии о' значению при альгерна гивной
гипотезе //, :г а; применяется статистика
• ' "! * =-!( •)
!Де 52 _ исправленная статистическая дисперсия, вычисленная по
выборке Случайная величина F2 имеет хи-квалрат распределение с
числом степенен свободы » =л-1. для заданного уровня значимо-
сти аг.
Построение области принятие гипотезы Н зависит от аль-
тернативной гипотезы Н Можно выделить следующие случаи:
1 Если алыеонативная гипотеза имеет вид //, :г, >л,, то об-
ластью принятия 1ипоте<ы является интервал ( -<г, Д а полуин-
тервал [ z, v . ♦ *) критической областью Вычиспиз по выборке
расчетное значение статистики Г/ сравниваем I с квашилем
z’ т , и если < х/ г то нет оснований для отвержения основ-
ной гипотезы н , если же > х , , то основная гипотеза отвер-
гается.
2 Если альтернативная гипотеза Н, г <<т; го гД, сравни
нанп с квантилем z; Если 1Д,,> /О( . то нет оснований твср1ать
15<
основную гипотезу //0; если же I то основную гипотезу
Н6 отвергают
3 . Ясли альтернаты ая гипотеза Н^ст' хс,', то областью при-
нятия гипотезы является интервал
полуинтервалов
Если /
< * Д* < z2 , то пег оснований
i * »•
2
, а объединение
1
критической областью.
отвергать основную ги-
потезу Н .
Б. Рассматриваются лис нормально распределённые случай-
ные величины X и Для X и Y получены независимые выборки
объемов п и nt. По зтим выборкам вычислены исправленные ста-
тистические дисперсии У, и S*. Нужно сравнить эти дисперсии
Чтобы при заданном уровне значимости стп проверить основ-
ную гипотезу /7Г:Р(Л ) = £>(>')< 0 равенстве генеральных дисперсии
нормально распределенных случайных величин А и К. применяет-
ся статистика
F = . г де S’ > S:. S’ - -L £,ч - Jу,
S, И~1 Г’
имеющая F-распределение ФишераЧ нслокора с »,-л.-1 и
1,=ч,-I степенями свободы при доданном уровне значимости а{.
F, сравнивают с квантилем Л'- распределения , (г,-чис-
ло степеней свободы большей исправленной дисперсии), или
F _ . в зависимости от пьгернап»вной гипотезы.
I. Если альтернат иннам гипотеза 1/ : ZXA) > £ЧЛ. и
F'„<F. . , го нет оснований для О1нсржсним основной гипотезы
//(. Если F|e>, > Л; u , ? , то основную г ипелчлу Н, отвергают
2. Если альтернативная гипотеза //, /)(А)<О(Г). и
о . то нет оснований для отвержения основной гипотезы
II,у \ если > F г , то основную гипотезу Нг игвергают.
156
Задачи
3. 19. В loo<bcicihhh с техническими условиями среднее время
безотказной работы для приборов определенного класса должно
составлять в среднем 10000 часом со средним квадратическим от-
клонением <тп--50 часов Время безотказной работы приборов под-
чиняется нормальному закону распределения Из некоторой партии
извлечена выборка объема л = 36 приборов и по ней найдена ис-
правленная выборочная дисперсия времени безотказной работы
приборов S -300 часов Можно ли считать, чю вся пария прибо-
ров не удовлетворяет техническим условиям, если а =0,05?
Решение. Для того чтобы ответить на поставленный вопрос
сформулируем основную i иитезу /?в а »= 250 и альтернатив-
ную 1Н1Ютезу Н с >с. =250. Уровень значимости =0.05 задан.
Объем выборки п 36.
Дпя проверки гипотезы Н6 воспользуемся статистикой
J‘4 ~1 *5 Подставим значения л « 36, S’ 300, а/ = 250 найдем
И .0*7!>”S.42.
гчх> 250
По таблице (при тожение № 5 к по уровню значимости at 0,05
и числу степеней свободы 1-36-1-35 находим квантиль
/:п> = Z iv =<4QТогда интервал (or,49.8), определяет область
принятия гипотезы, а полуинтервал, *49,8. *ап) критическую об-
ласть. поскольку 1о нет основании для утверждения основной
гипотезы Н, Это значит, что партия приборов удовлетворяет тех-
ническим условиям.
Ответ: партия приборов удовлет воряет техническим условиям
2. Известно, что добавление специальных веществ умеш.шает же-
ciKoc ь ноды Дисперсия измерении опенки жесткости воды по 50 нро-
бам пос ле добавления специальных веществ равна 4,0.»ряг*' Требуется
при уровне значимости а -0.05 проверить гипотезу о гом. что гене-
ральная днеперс ия гг измерений равна прелин за: аемому значению
а) - 5 град; 6) гу’ « з град1.
3.20. Точность наладки некоторого класса приборок характе-
ризуется лиспсреисч пек знания прибора Гели эта величина бу тс г
больше 120 чкч3. то прибор переналаживает*, я. Исправленная вы-
борочная дисперсия 25 случайны' измерений прибором оказалось
равной: a) S -200,чхм . б)$? »200 чкм’
157
Нужно ли производить напалку прибора, если уровень значи-
мости -0,01 ?
3.22. Из нормально распределенной генеральной совокупности
извлечена выборка значений коэффициента трения шины по ас-
фа л му:
«нччепия коэфф и цис н та грсния. \ 0,16 0.1/ 0,1 к 0,19 020 0Д1
Часнла шипений ко- лффициенча «рения. т 2 7 10 6 ' 4 1
Согласно технологии изготовления шины при определенной
процедуре проверки коэффициента зрения установлено, что дис-
персия г результатов измерений этого коэффициента равна 0,1.
Требуется, при уровне значимости л„ = 0.05. проверить гипотезу о
том, что дисперсия результатов измерений коэффициента трения
равна 0.1.
3.23. Точность наладки станка - автомата, производящего де-
тали, харакгеризуется дисперсией длины деталей. Из нормально
распределенной генеральной совокупности извлечена выборка:
Длина деталей, х зл зд 33 ЗЛ
Чаете а т 4» J) 7 12 9 4 1
грсбус1ся, при уровне значимости «„-0,05, проверить, обес-
печивает ли с ганок требуемую точность, если дисперсия длины де-
талей не должна превышать сг0? -0.1.
3.24. Фирма работает «устойчиво», если дисперсия величины
прибыли нс превосходит 600 лен.ед/. Неправ юнная выборочная
дисперсия |5 случайно отобранных фирм оказалась равной
720 денет. . Требуется, при уровне «начимосгн ап=Л).0), проверить
гипотезу о гом. что отобранные фирмы работают неустойчиво.
3.25. 11о дну м независ имым выборкам, объемов ц - 21 и - 25,
извлеченных из нормально распределенных генеральных совокуп
костей X и У. вычислены исправленные выборочные дисперсии
5 -1.45 и 5 1.21. Требуется, при уровне значимое!и «, -0.05,
проверить основную гипотезу о равенстве генеральных дисперсий.
Решение: (формулируем основную гипотезу Н - Р() X
и альтерна гивнуто //. • Щ V) > D(>).
Уровень значимости «алан а( 0.05
Объемы выборок известны п - 21 и н - 25
1 5К
Для про верки гипотезы Н, применим статистику
По таблице / распределения (приложение 7) находим кван-
тиль ! 7| л = Гп ч • 1.73. Поскольку альтернативная г ипенсза
// £>(>’) >/ХГ), тс критическая область правосторонняя
[1.73; + ос). а областью принятия :нпотсзы яв тяетсг интервал
(0.1.73)Лак как IJ98< / „ «1.73. то нет оснований лчя от-
вержения основной гипотезы Н . Значит, генеральные дисперсии
D(X) и £НГ) равны
Ответ: D<AZ)=D(>>.
3.26. На предприятии разработаны лла метода изготовления
изделия и вычис юны исправленные дисперсии раскола сырья на
единицу ютовой продукции S/^5.9 кг; $/=6.3 кг по выборкам
объемов й«П изделий и и. = 15 изделии. Требуется, при уровне
значимости лп = 0.05, проверить гипотезу о равенстве генеральных
дисперсий нормально распределенных совокупностей расхода сь -
рья на единицу изделия
3.27. Д1Я проверки эффективности новою лекарства были
отобраны две случайные группы больных по 30 человек Одной
группе давали таблетки с прежним проверенным лекарством, а
другой с новым. В первой ipyiinc исправленная дисперсия выздо-
ровления S* 5 дней, а во второй -$2 = 3 дня Требуется, при уров-
не значимости ап 0,(^, проверить гипотезу о том. что повое ле
карст во не более эффективное, чем прежнее.
3.28. При исследовании работы стабилизатора напряжения в
самолс ле на стенде проведено Р не завис имых испытаний:
Выходное напряжение с . F 0.21 0.24 OJ28 оло
Частота значений выходя <о напряжения, м 1 3 6 2
В полете проведено ёше И испытаний стабилизатора напря-
жения в самолете:
Выходное ил пряжение । , Я 0.3? 0.34 | 036 037 0.40
MiKTOlU. т 7 3
|<о
Требуется, при уровне зтгачимости а, =0.05. сравнив исправ-
ленные дисперсии, ответить, есть ли основания полагать, что фак-
торы. воздействующие на стабилизатор в полете, оказывали суще-
ственное влияние на точность его работы.
5.29. Результаты независимых измерений производительности
двух агрегатов приведены в таблице:
16.0
16.1
16.3 16,6
м.7
Можно ли считать, что производительности обоих агрегатов
равны? Требуется проверить гипотезу о равенстве генеральных
дисперсии нормально распределенных совокупностей при уровне
значимости а* = 0,01.
3.30. Для сравнения качества консервов двух заводов взяты
две выборки продукции этих заволок. Качество каждой банки кон-
сервов оценено в баллах при помощи органолептических показа ге-
гей. Результаты оценок приведены в таблице: ______
Завод №. 1 71 1 73 74 75 77 КО КЗ
Завод № 2 69_ 1 70 72 74 75 79 80
Можно ли считать, что качество продукции одинаковое на за-
водах №1 и №2, сравнив исправленные дисперсии выборок при
уровне значимости ао~0.05. Предполагается. что результаты оце-
нок ;\аспреде тепы нормально и выборки независимы.
2 3.3. Проверка гипотезы о равенстве значений двух средних из
нормально распределенных генеральных совокупностей
Рассмотрим нормально распределенные случайные величины
X и У Пусть я результате наблюдения получены две независимые
выборки объемами л, и Проверим гипотезу Но о равенстве ма-
тематических ожидании случайных величин X и У: М(Х) = M('Y)
при альтернативной гипотезе Нс M(X)*MiY)
Ес in а(Х) и а(} i известны, го в качестве статистической харак-
теристики принимаем величину
Z* -*-* (3 3)
Гсг’(Х),о’(П
имеющую нормальный закон распределения с параметрами Он Г
Л/(0;1).
16/»
Критическая область (-о.. -z. ] и +х) определяется та-
ким образом, чтобы Z a ze . где zA находят из условия P(\Z\ г г =
- u , т.е. Ф*( z, )- I —-, для уровня значимости а<
При алыернагивной ппклече Н : М(Х) > M(Y), нахолю тп из
условия Р(/< -г, /и е Ф*(г<ч/^ст0, для уровня значимости о<
Тогда, если Z/v.. < 2^ то, нулевую гипотезу К, отвергают; г про-
тивном случае (/глл, >-z, I нет основании отвергать нулевую гипо-
При альтернативной гипотезе Н| : М(Х) < M(Y). z% находят из
условия Р(7 > х ) — m е Ф*(га) -/-аг для уровня значимости
0Q) (по таблице значении функции Ф*(г)К Если Z^., > . то ну-
левую гипотезу отвергают, в противном случае (Zr,7 s < ze) нет ос-
нований отвергать пулевую гипотезу
Пусть для нормально распределенных случайных величин X и
Y дисперсии с2(Х) и o2(Y’) неизвестны. Тогда в качестве статисти-
ческой характеристики принимаем величину
Т - , to»,4wt-2) (3 4)
V л>*л»
имеющую распределение Стыодента с » = л < л7 2 степенями сво-
боды.
При альтернативном гипотезе Н« M(X)*M(Y). критическою
облас ть (-ос; - fn ] [/ ; >ос) определяют таким образом, чтобы
? 3
|Т „где 1Л находят из условия Р(|Т|2 / ) = о</2 для уровня
1 1*
значимости «т<,по таблице значений распредетения Стьюдеита с
v - л, тч. -2 степенями свободы (приложение 6).
Тогда, если \ТГС ч нулевую гипотезу отвергают; в про
гивном сну час (|7^V4’ <r ) нсг основании отвергать нулевую гипо-
j ’
тезу.
При апысрма'|явной гипотезе Нг M(X)>M(Y) (гни М(Х^<МЛ))
находят / , из условия Р< Ггt . ) On (или Р(Т < t ) аЛ для
уровня значимости По по таблице значений распределения Стью-
демта с к - г 4 г; 2 степенями свободы.
Lain
(или л ). то нулевую i ипшсзу uibcpia-
юг. к противном случае (*Г^у<га или 7}ЛЧ> t I пет оснований
отвергать нулевую гипотезу.
Ьсли объемы выборок щ и и2 достаточно ьеликг. го в качестве
ста।истичес,кой характеристики дли проверки пулевой 1ип(ггсзы
используется величина
Ветчина (3.5) имеет нормальный закон распределения с па-
раметрами 0 и 1: ,V(O;I).
Задачи
3.31. В двух фирмах, выпускающих детское питание, прото
водилась оценка качества продукции. В фирме Л. где проверялось
30 единиц продукции, средняя сумма баллов оказалась равной 52
По второй фирме В проверялось 36 единиц продукции, и их сред-
няя сумма баллов оказалась равной 47 Среднее квадратичное от-
клонение суммы баллов, вычисленное д я нескольких тысяч еди-
ниц продукции, гт 12, Определюь, лучшее ли питание выпускает-
ся фирмой А. чем фирмой В.
Решение. Из условия следует, чю проверенная продукция
фирмы А лучше, чем продукция фирмы В, Можно ли утверждать,
что фирма А вы лускаст ту mi jy ю продукцию, чем фирма R?
Сформх пируем гипотезы. Основная гипотеза Н<, ; Л, * А\, где
Хл и хь средние совокупностей балльных оценок детского пита-
ния, производимого фирмами А и В соответственно. Альтернатив-
ная гипотеза Яг А«>Ав.
Поскольку пас интересует лучшее ш детское питание выпус-
кается фирмой А . чем фирмой В. воспо 1ьзусмсь односторонней
альтернативной гипо тезой. Возьмем уровень <начимости а( ~ 0 05.
Из условия тазами известно, что “ 30, п# - J6.
R данной задаче нет другой информации. кроме двух выбо-
рочных средних. Полому разность средних А 4 представляет
собой меру сравнения качества стекою питания фирм А и В Эга
величина распределена приближенно нормально со средним А 4
А, и стандартным отклонением
В качестве статистики возьмем стандартную нормальную ве-
личину
(А - V 1
z4 '-1 (3.7)
Критическое значение ?. при 5%-м уровне значимости для од-
носторонней проверки гипотез равно 1.65 (см таблицу 3 1) По по
му областью прннятя нулевой гипотезы Ht будет множество зна-
чений Z. не превосходящих 1,65. т.е. интервал (-<х I 65).
Если выборочное значение Z,.„ £ 1,65. то делаем вывод, чю
фирмой Л выпускается детское питание лучшего качества, чем
фирмой В
Если 7. . < 1.65, то заключаем, что в общем фирмы А и В вы-
пускают детское питание одинакового качет гва.
Гак как по формуле (3.6) имеем
сг' г 2_*2_ = |2 i-L-J-г З.С27,
Vb л. \зо 36
Л
то выборочное значения статистики (3.7) равно.
Значение статистики Z - 1,6515 >< = 1.65. Поэтому при
5%-м уровне значимости можно утверждать, что фирма А выпуска-
ет лучшее детское питание, чем фирма В
Ответ: фирма А выпускает детское питание лучшего качества,
чем фирма В
3.32. Покрышки автомобиля были исследованы на износ после
10 000 км пути Каждая покрышка сделана наполовину из ретины
сорта А. наполовину - ит ретины сорта В Все колеса вращаются с
одинаковой ткорчгтью поэтому можно считать, что они находятся
в одинаковых условиях. Ре «у тьтаты исследования (в баллах) при
ведены в габл 3 4.
Сделать проверку односторонней гипотезы о том. что резина
сорта В больше изнашивается, чем резина copia Л. при уровне зна-
чимости критерия 0.05
3.33. В мадонне отобрали случайным образом по 40 банок
«Солянки» производства двух заводов Каждая из банок была оце-
нена в баллах с помощью органолептических пока jaic.icii. Резуль-
таты оценки приведены в табл. 3.5.
Таблица 3 5
Завод №.• 1 Завод 2
Средний балл 71 76
Стандартное отклонение Е 5 6
Проверить при уровне значимости 0,05 гипотезу о том. что
консервы завода № 2 лучшего качес ina, чем завода № 1.
334. На некотором поле выбрали 100 участков зем хи; 50 уча-
стков засеяли одним сорюм ячменя. 50 другим сортом. На первых
50 участках получили урожаи в среднем 60 ц'га со стандартным от-
клонением 3 цга Средний урожай на участках, засеянных ячменем
другого сорта, оказался равным 65 ц га со стандартным отклонением
3,5 цга. Будет ли средним урожай этою сорта ячменя значимо пре-
восходил ь средний урожай ячменя первою сорта? 11рипять ап «= 0.05
3.35. Длз проверки эффективное! и нового лекарства были
отобраны две случайные ipynnw по 50 человек, сградающих хрип-
лом. Одной группе давали таблетки, не содержащие никакого ле-
карства, другой группе дакали такие же по внешнему виду’ таблет-
ки, по содержащие новый вил лекарства оз гриппа В первой груп-
пе люди выздоровели в среднем через 7 дней, а во второй — через 6
дней. Стандартное отклонение продолжительности лечения одною
человека от тришта независимо от того, принимал или не принимал
он лекарства, можно положить равным двум дням. Можно ли на
основании полученных результатов сказать, что новое лекарство
существенно ускоряет выздоровление?
336. Было произведено 12 измерений диаметра вала. При этом
оказалось, 'гго среднее * — 10,?0 мм, а стандартное отклонение 0,05
мм. ’Затем вал поместили в условия с высокой температурой и про
извели еще 8 измерений диаметра ею оси. Среднее на этот раз ока-
залось равным 10.25 мм. а стандартное отклонение 0,05. Можно ди
сделать вывод, что диаметр нала существенно увеличивается в про-
странстве с высокой температурой при ^%-м уровне шачимости?
337. Студенты экономического и гуманитарного уни-
верситетов сдави in экзамен по математике В экономическом уни-
верситете. । дс экзаменова imcj 30 студентов. средняя оценка оказа-
IM
ласъ 4,52 В гуманитрном университете сдавали экзамен 36 сгу-
денгон. их средняя опенка оказалась равной 4.47. Среднее квадра-
тичное отклонение оценок по ма1ематике, вычисленное для не-
скольких студентов, а 0.12. Лучше ли подготовлены ио матема-
тике студенты экономического университета, чем студенты гума-
нитарного университета? Принять а, - 0,05
3.38. С целью ускорения производства интегральных схем про-
и зводет венная линия была модифицирована Дтя исследования эф-
фекта от этой модификации было зафиксировано время изготовле-
ния каждой из 50 интегральных схем при старом и новом процессах.
Л 1я нсмодифицированного процесса среднее время изготовления
одной интегральной схемы оказалось равным 35 с, а для процесса,
подвергшегося модификации - 33 с Стандартные отклонения вре-
мени изготовления митральном схемы для первою и второго про-
цессов можно считать приблизительно одинаковыми Вычисленное
значение объединенной оценки среднего квадратичного отклонения
равно 1.5 с Можно ли сделать вывод, что скорость изготовления ин-
тегральной схемы при модифицированном процессе больше?
339. Месячная терабитная плата для выборки из 50 рабочих оп-
ределенной фирмы сое являет 910 тыс р при среднем квадратич-
ном отклонении 1,44 тыс р., а заработная плата для выборки из 40
рабочих друюй фирмы равна 905 тыс р. при среднем кватратичном
отклонении 1,50 тыс р Выше ли заработная плата в первой фирме,
чем во второй? VpoeeHb значимости о, принять равным 0.01.
3.40. Средний диаметр для случайной выборки из 65 подшип-
ников. обработанных на каком-либо станке, равен 0,24 см при
среднем квадратичном отклонении о 0 02 см. На следующий день
из числа обработанных на этом станке подшипников вновь отби-
рают 65 штук и устанавливают, что их средний диаметр равен 0.25
см при среднем квадратичном отклонении 0,04 см. Требуется ли
переналадки станок? Уровень значимости принять равным 0,05
2.4. Критерии согласия.
Критерии согласия применяются дтя проверки гипотез о том.
чго распределение изучаемой случайной величины ¥ подчиняется
некоторому известному распределению р(х). например, нормаль-
ному. биномиальному или другому закону распределения
Критерий । о.чагик Пирсона основан ня выборке определенной
меры расхождения между теоретическим и эмпирическим распрслс-
1Ь5
пениями. В качестве такой меры берегся величина = ^П]> nf —.
м ПР.
которая имеет х - распределение < • =А-г-1 степенями свободы,
где к- чисго интервалов или групп, на которые разбито все множе-
ство наблюденных данных, г - число параметрон пнютстического
распределения вероятностей Р оцениваемых по выборке.
Применение критерия Пирсона основано на том, что сумма
квадратов случайных величин Л - ‘ . имеет распределение
V'v7.
X* -хи, а случайные величины X, асим! логически нормально рас-
пределены Чтобы по утверждение выполнилось, нужно чтобы для
всех интервалов выполни юсь условие пр >5. Если в некоторых ин-
тервалах это условно нс выполняется, го их следует объединить с
соседними.
А. Алгоритм применения критерия Пирсона:
1 Формируется выборка и< наблюденных данных случайной
величины X. Исходя из качественного анализа изучаемого
социально экономического явления определяется тин слу-
чайной величины: дискретная или непрерывная.
2. Строя гея эмпирические распределения:
- если /V дискретная случайная величина, то составляется
статистический ряд распределения относительных частот;
- если X непрерывная случайная вс шчина, то составляется
интервальный статистический ряд распределения относи-
тельных частей.
3. Строится графическое представление эмпирических распреде-
лений. По виду полигона (многоугольника) относительных
частот, или гистограммы визуально определяется вид теоре-
тического распределения Р, которому подчиняется выборка
4. Вычисляются оценки параметров закона распределения Р
Форм\ шруклся основная //в и альтернативная //, 1игютезы.
6 . Задаёюя уровень значимости аг, (*0,5; 0.01).
7 Вычисляется значение с ratистики /.
8 Для заданного уровня <начимости о и числа степеней сво-
боды v^-r-l но таблице - распределения находится
квантиль /, v> и < троится область принятия гипотезы Яп и
критическая область
9 Формулируется правило принятая гипотезы /Л,; если
• тс нсз оснований для отвержения гипотезы /Л;
се ли . 2 г,1 . ., то гипотеза Н отклоняется
О i мстим. чго если объем выборки большой и изучается дис-
кретная случайная величина X . ю ннборка также разбивается на
группы (интервалы).
Задачи
4.1 В налоговой инспекции проведено 100 проверок за юл о
правильности уплаты налогов частными предпринимателями. При
каждой проверке проверялось 10 частных предпринимателей.
Пусть дискретная случайная величина А’—число предпринимателей
неправильно уплативших налоги. Результаты проверок сведены в
таблицу 4.1:
Таблица 4 1
X. 1- 0 1 1 2 3 ; X 4 5 6 7 8
Lw2_ 2 3 II 20 1 25 19 16 3 1
1ле л - число предпринимателей неправильно уплативших налоги,
при одной проверке; т количество проверок, содержащих х,
предпринимателя Требуется, при уровне значимости /тл Ц05.
проверить гипотезу о том, что случайная величина А распределена
по биномиальному закону.
Решение. Поскольку изучаемая случайная величина А явля-
ется дискретной, то составим ряд распределения относительных
часто ц таблица 4.2
Таблица 4 2
Л. 0 1 2 4 5 6 7 6
Г” п 2 100 0.02 3 100 С. 03 I) 100* 0.11 20 100 0.20 25 100 * 0,25 14 100 0,19 16 и-’ 0.16 3 100 ~ 0.03 100 С 01
и пос троим полигон относите 1ЬНЫХ ЧИСТО!
16“
По виду полигона относительных частот можно предполо-
жить, чтЛ изучаемая случайная величина X распределена по бино-
миальному закону.
Неизвестны параметром является вероятнсхггь появления собы-
тия а - (случайно выбранный предприниматель неправильно уплатил
налоги}. Оценкой р вероятности появления события Л. р * р(А). бу-
дет относительная частота появления события в выборке.
г’ = —J^-rO-2 . J 3 • 2 11*3-20 + 4 25 + 5 19*6 16+7 3+8-1)*0.405.
ТОО
Сформулируем основную гипотезу Н,: случайная величина X
распределена по биномиальному закону и а тьгернагивн^ю гипоте-
зу //,: случайная величина X распределена не по биномиальному
закону. Уровень значимое ги шдан о, -0,05.
Вычислим значение ci a i истеки / У - где г? зм-
лирические, а пр - теоретические частоты Для вычисления теоре-
тических частот, по формуле Бернуллй найдем вначале вероятно-
сти того, что событие А появится i pai в 10 испытаниях:
w X,) —С|Л р Q •
гдер=0,405; <?=1 0.405-0.595
Подставив значения, получим:
Ло( V « 0) « С 0.405 0.595* * 0.006;
г-D-C 0.405 0.595 |0 0.405«0.00<*3• 0.038;
р, < х -- 2)« (П 40< О, SQS* « 0.1641 -0.0157 « 0.116;
I6S
10 Qk
/>0(Х»3) = С1 0.405’ 0.595’* — — 0.0664 0,0264 *C.2I I;
1-2 3
9-8 7
Pf (X - 4) - C;f 0,405* 0,595 *----0.0269 0.0 U4 * 0.251;
1*2-3 4
fn(Z-5)-C’n 0.405* 0,595* **—— — 0.0109 0,0746 * 0.205,
12 3 4 5
10*
pyr(X =6) = Cr 0,405* *0.595* *-0.0044 0.1253 » 0.116.
6M1
/:,<> = 7) = C.; 0,405' 0,595'*—-0 0018 0.2106 * 0,046;
> I* w | g
, in»
ft (Д- =8) = C 0,405’ 0.595* * — 0,0007 0,3540 * 0,011 .
JI Л r <<• ▼ ▼ g | ’
Составим расчетную таблицу 4 3, в которой объединим значе-
ния часто! меныпис 5
Таблица 4.3
т nf4 * НЮ * "А - ПР, («, ~ ДР,)’ (т, - лр.):
А - V. >
0.6 5 4.4 0.6 0J6 0.0Я 1 $
3 з.в
и 11.6 и 11.6 -0.6 0,36 0.0310
20 21.1 2(1 21.1 -1.1 1.21 0.4*573
25 25.1 25 25.1 -0.1 !’.(И 5.0004
19 20.5 19 20.5 -13 2Д5 0,1098
16 П.6 16 11.6 4.4 1936 1.6690
3 4.6 *4 ' * 5.8 1.8 324 0,5586
1 1.2 1
Х-1ГИ 100 10(1 100 ? 4261
В таблице находим расчетное значение статистики
Х^ ’2.4261.
Для заданного уровня значимости at 0,05 и числа степей сво-
боды ♦ -*•-» - I-6-1-1 4 (чис io ipynn, после объединения двух и
jpex групп, стало (>. один параметр оценивался поэтому г-/). на-
копим квантиль
z -распределения: г: „_, =9,49.
Область принятия ) иноте «ы //, интернам а,9,49); критиче-
ская область полуинтервал [9.49;*оо).
Так как „ «2.4261 < /С\М=Ч49, то нет основании для отвер-
жения гипотезы //..о биномиальном распределении случайной ве-
личины X
Ответ изучаемая случайная вс тмина А’ распределена по би-
номиальному чакону.
4.2 Л я проверки качества производимой продукции в течении
года проводилось 200 проверок При каждой проверке изучалось
качество 7 изделий. В итоге получено эмпирическое распределение
числа д, изделий содержащих дефекты в одной выборке; табл. 4 4:
Таблица 4.4
Число изделий в одной выборке, А. 0 1 2 4
Количество выборок, содержании х, дефект- ных мзде. нй. гч, * - — 45 68 41 35 10
Требуется, используя критерий Пирсона, при уровне значимо-
сти а =0,05. проверить 13<потезу о том, что дискретная случайная
величинах характеризующая число дефектных иислий. распреде-
лена но биномиальному закону.
4.3. Для оценки всхожести семян ячменя посеяно 100 выборок
по 50 семян в каждой В итоге получено эмпирическое распределе-
ние числа не взошедших семян в каждой выборке и число выбо-
рок, содержат и к х, не взошедших семян:
Требуется, используя критерии Пирсона, при уровне значимо-
сти гг t ,05. проверить гипотезу о том. то тиск|хг1ная случайная
величина X. характеризующая число не взошедших семян ячменя,
распределена по биномиальному закону.
4.4 Данные об отказе 400 шеырнчесьих приборов ia 1 (МММ) ча-
сов работы приведены в таблице 4.6;
170
Таблица 4.6
Число еггкаюв, ж. 0 1 2 3 4 ?5 1
Количество случае а. в которых наблюдалось г отказов, т, 236 56 2 1 С
Tpe6yci€«. используя критерий Пирсона при уровне значимо-
сти сгс-о.О5, проверить гипотезу о зим. чго дискретная случайная
величина А, характеризующая число отказов, распределена по за-
кону Пуассона.
Решение Поскольку изучаемая случайная величина Л являет-
ся дискретной, то составим ряд распределения относительных час-
тот, табл 4.6.
Таблица 4 7
к ° 1 2 3 4 £5
л 236 — =0.50 400 — = 0,2625 400 —-=0.14 400 2 400 1 4(К; 0
22IF I, и построим полигон относительных частот, рис 4.2:
/
171
По виду поли! она относительных частот можно предполо-
жпзь» что изучаемая случайная величина подчиняется закону рас-
пределения Пуассона Р(Х - к.)- — е \ (дс а н р. Неизвестным
г !
параметром закона распределения Пуассона является параметр
а-п-р. Согласно мстила наибольшего правдоподобия оценкой па-
раметра а является среднее чис ю отказов:
а- -Ух. т,-- '-(0 236-1 105 -2 56 < 3 2*4 1)- —= 0.5675.
п 400 400
Сформулируем основную гипотезу Н.: изучаемая случайная
величина X подчиняется закону распределения Пуассона: при аль-
тернативной гипотезы // : случайная величина Л'подчиняется дру-
гому закону распределения
Уровень значимости задан, ас =0,05.
Для вычисления значения статистики ^‘пайлем вероятности
числа отказов по формуле:
11одстанляя значения получим:
X, - 0: (X - 0) - (1-*7< • е"*” = 0.5669;
л,-I />дА=1) = ^^ е ,5Л” =0.3217;
д-2:Рк,(Х = 2)=—^^--е ’'“аО.ОРИ;
*,-3 С. (А' = 3)=1' $ г=0,0173;
А ж4;Р.„(А' = 4)-' t “”=0.0024;
г, >5 Г,.1Х 25)-1 <Pw(A'-0)4A =n»/’ .(A' 2)+/’Л,(А 3) +
♦Лп,(А =4)= 1-0.9996-0.0004
Составим расчетную таблицу 4.Я в которой объединим значе-
ния частей (Гд) меньшие 5.
172
Таблица 4.8
236 105 лг - 4('0> >Р(Л г 1 _ 226.76 12b,6S j 236 105 226.76 128.68 w Щ 9.74 -23.68 - 85 37 - 560.7424 (tn -лр V 25 0.37о5 4.3576
56 36.52 56 36.52 19.48 379,4704 103908
2 6.92 ] 3 8 04 5.04 25.4016 3J 594
1 Г 96
0 11.16
22:400 40(1 400 400 1ЯДЯ43
В таблице 4.8 находим расчетное значение статистики.
=18.2843.
Для затаппого уровня значимости а =0,05 и числа степеней
свободы и Дг-г-1 = 3—1 — 1— 1 (число । рули после объединения че-
тырех последних групп стало 3. к=3. один параметр оценивался,
поэтому г / находим квантиль - распределения = 3,84
Область принятия гипотезы Яп- интервал (-х,3,84): критиче-
ская область - полуинтервал [3.84; 4 х).
Так как = 18.2843 > =3,84, то гипотеза Н отклоняется
и принимается гипотеза //.
Ответ изучаемая случайная величина Я* подчиняется другому
закону распределения
4.5. О пел техническою контрою проверил точность хода
произведенных часов в 200 партиях, и получил следующие данные
укатанные в таблице 4.9
Таблица 4.9
Количестве часов с ненпным ХОДОМ в ОДНОЙ IIHpIHH. л 0 j 2 4 5 *
Количество парлп». годержитих х ча^ои с неточным хо,юм. м 111 52 24 7 1 4
Требуется при уровне значимости а, -0.01, проверить гипо-
тезу о том. что число часов с неточным ходом распределено по за-
кону Пуассона
I71
4.6. Отдел сбыта шнода. по производству стеклянных изде-
лий изучал количество поврежденных изделий н результате транс-
портировки в 400 отправленных партиях. Количество поврежден-
ных изделий в одной парши приведено в таблице 4.10
Таблица 4 10
Количество поврежденных стек личных изделий я одной партии. х, 0 1 •> •• 3 4 5 6
Количество партий, содержащих v поврежденных изделий, т 189 165 84 33 14 1 9 6
Требуется при уровне значимости </л=0.05 проверить гипотезу
о том что распределение количества поврежденных стеклянных
изделий в результате 1ранспорзирооки подчиняется закон) распре-
деления Пуассона.
4.7, В автопарке регистрировалось число автобусов нс вы-
шедших на маршруты Всего было проведено 400 наблюдений, ре-
зультаты которых приведены в таблице 4.Н;
Число ашобусов не н». шедших на мар- шруты. 1 2 | 3 4 5 6 7 8 9 10 И » ♦ • 12
Число зарегистриро- ванных случаев. т 106 95 i 67 42 30 21 6 4 2 1 1
1ребустся при помощи критерия Пирсона при уровне значимо-
сти сг0 = 0.05, проверить гипотезу о том, число автобусов не вышед-
ших на маршруты подчиняется закону распределения Пуассона.
4.8 В результате взвешивания 500 упаковок расфасов«знных
Требуется при уровне значимости 0.05, проверить гипоте-
зу о том, чго пес упаковок А распределен равномерно.
174
Решение Поскольку изучаемая случайная величина А'яв: чст-
ся непрерывной, то составим ингерва ъный статистический ряд
распределения, таб ища 4 13:
По виду гистограммы можно предположить, что изучаемая
непрерывная случайная величина X подчиняется равномерному за
кону распределения. т.е. распределена по закону:
1 ।
----.если х? сг ./П
/>(*)»< fl-а 1
0. если > * [ а, /1]
Неизвестными параметрами являются ан Поскольку лтя
равномерного распределения М{.\) — - и <т(А )= —. а оценка-
ми математическою ожидания М(Х> и среднего ква ратического
отклонения лр) являются, среднее арифметическое А и исправ-
ленное среднее статистическое квадратическое отклонение S. то
для нахождения оценок параметров « и // получим систему двух
линейных уравнений:
По эмпирическим данным выборки, вычислим среднее ариф-
метическое:
Д’- —У'.’ >»» —(475-91 -485-85 г 495-80 + 505 78 + 515 84 + 525 82) "494,5
п 50*)
(где <- середины ладанных интервалов), и исправленное среднее
статистическое квадратическое отклонение:
- «У-
' (475' "lines’ 85-4*15’ 80 + 505’ 78-515'+4-
499
I
-499,5:); *28,294.
Составим систему
а+ 3 = 2 499.5.
fl-n = 2-Ji 28.294
U.1U ‘ -
/«-а -98.0)3.
решив которую, найдем а » 450.49: //« 548.51 Тогда птотность рав-
номерного распределения будет иметь вид:
----- --------------- «0,0)02 «гад »₽ 450,49,548.5) ;
а 548/1 450.49----------- Г--* 1 1
• 0. если х «|450.4‘Л 548.51 ]
( формулируем основную гипотезу Н„: вес упаковок расфасо-
ванных продуктов, подчиняется равномерному закону распределе-
ния. и альтернативную гипотезу //,; вег упаковок не подчиняется
равномерному закону распределения.
Уровень значимости ак задан. а„*0.01.
Для вычисления значения статистики найдем вероятности
того, что значение веса упаковки принадлежит конкретному интер-
валу по формуле:
Р<х _, < X <л.)~ /Д о и х.|).
Р(а< X* < ж.) -/\450.49<Л < 480) —0.0102 (480-450.49) "0.3010.
Р(48С < X <490)-0 0102 (490-480) -0.102.
176
/(липы второго, треплю, меигерюю н тлею инк*рва.юв рав-
ны. поэтому вероятности также будут равны, т.е
Г(480< А < 490) - Р( 490 < А * 500) г И5ЫК А <510» Г(510< А <52<))-0.102.
Р\ *.<.<< /?> - Pi 520 < АГ < 548.51) • 0.0102(548.51 520) «0.2910
Составляем расчетную таблицу 4.14.
Таблица 4.14
- . • л/ - 500 Р( г|ш| < А < х | (">, пр.)’ 1' 'Г. L
450.49.481») 91 150.8 -59.8 3576.04 23.7138
[480. 490) KS 51.0 34.0 1156.0 22,6667
[49ft 500) 80 51.(1 29 Л 841.0 16.4902
(500,510) 78 51.< 27.С 729,0 14.2941
[510; 520) 84 51Л 33,0 1089,0 | 213529
[520.548,52] 82 145.2 -63.2 399424 27.5085
_ 1 МО 500.0 126 (Й62
В таблице находим расчетное значение статистики
а’ =126.0262.
Для запанного уровня значимости и. = 0.01 и числа степеней
свободы т А-» -) 6-2-1 3 по таблице/* - распределения нахо-
дим квантиль '11.3. Так как г’ «12е 0262 >113. го
гипотеза Н* отклоняется и принимается гипотеза К,
Ответ, изучаемая случайная величина А не подчиняется рав-
номерном) закону распределения
4.0 В течение с\ток регистрировалось прибытие отдыхающих
в дом отдыха Полученные данные свспсны в таблицу 4 15!
Таблица 4 15
Время суток в часах. |», Кочичсгтпо ПТЛЫХП1Л ших прибывших в jtom шперпалг, т Вро<ч суток в часах Кпличестпг ПТ 1ЫХВХ* шил прибывших в Vf ом ннтерна1е. пг
0-2 12 12-14
2 4 15 14- 16 16
4 6 14 16- 18 21
6 - 8 18 20 18
8 - 1( 18 20 22 21
10- 12 19 22 - 24 [ 16 J
Требуется при уровне значимости иг 05 проверить гипотезу
о том. что время прибытия отдыхающих в лом отдыха распределе-
но равномерно.
4.10 В результате исследования уровня заработной платы учи-
телей средних школ получены результаты, приведенные в таблице
4 16:
Таблица 4 16
Требуется при уровне значимости а =0.05 проверить гипотезу
о равномерном распределении уровня «работной платы учителей
4.11 Данные об износе основных производственных фондов по
60 предприятиям г. Минска прелегавлены н виде простейшей ста*
тпстнческой совокупности:
15.4 20.3 19.2 17.2 18.1 23.3 21.9
16.8 15.3 20,4 13.2 16,5 20,5 19.7
20 J 14.3 16.8 Н.7 19,5 20,8 15,3
17.8 19,3 15,7 163 22.9 21,8 12.6
10.2 21.1 18.4 15.8 14.6 18.2 18,3
15.8 19,2 18.6 20.3 23.7 16.6 20.2
19.4 17.1 195 •7.7 21Д 17Л 19.3
17.8 ИЗ 17,7 • 2,1 18,5 14,0 13.4
15.2 16.4 17.1 112
Требуется при уровне значимости #„-0.05. проверить 1ипотс-
зу о том, что износ основных прои<водсз венных фондов описыва-
ется нормальным законам распределения.
Решение Рассматриваемая случайная величина X. описываю-
щая износ произведет венных фондов, является непрерывной слу-
чайной величиной. Разобьем проС1Сйшую статистическую сова
куп ноет ь на интервалы одинаковой длины /, |де
--21,7 ",0—*1.95, (1в 60» 1,7782)
I ь3.322 Ign 1 - 3.3221р6О 1
17Я
Тогда число А интервалов равно.
д ж ***** ~ ***** = 2^* ~ Ю, 2
/ 1,95
Построим интервальный статистический ряд распределения в
таблице 4. И
Таблица 4. Р
т
HirrcpBX’U 1ГШОСЗ произвол ствснных фондов, [т, (,Л.) Относ ктельнля частоте тнэче ний износа производственных фондов, которые принадлежат данному интервалу. и» ж ГЧ • » СМ О *— 1 30 Ж • » гч •— 1 12 о • • • • 6 о 00 • • Ч> — 7 30 V о • » о ос - - ' 2 4 » гч * Г1 О' £ 6 ос •» гч • • О' • 1 15
По виду гистограммы можно предположить, чго исследуемая
случайная величина А распределена по нормальному закону рас-
пре ле пения, т.е по закону
Неизвестными параметрами являются математическое ожида-
ние т и дисперсия с’. В соответствии с методом наибольшего
правдоподобия. оценками параметров нормальною распределения
т и <т’ являются среднее арифметическое А и неправленная стэтц-
п«
стическая дисперсия 5’. Из таблицы интервального ряда распреде-
ления находим
- 1 (11.175-2 < 13.125 5 г
Ч*- 60
15,075 10 <17.025 14- 18.975 15.20,925 К) t 22,875 4)-
= 17.7075» 17.71;
<*= —У(х') «. (А I -—(11.175 -2*13 125 5-15.075’-10 +
>|-177 59
♦ 17.025’ 14-18.975’ -15 + 20.925’ 10 +
-22,875’ 4) 17,7075’«327,355 - 313.555-13.80.
S-4F -713,80 ч 3,71,
(в формулах л," - центры интервалов).
Подставив в плотность нормального распределения вместо па-
раметров т и а: их оценки, получим;
х-17.71 I > --
Г(.Н = Ф -- - . ГЛС ф«(т> |е »<fc.
I 3.71 / 777 1
Сформулируем основную гипотезу А/,: коэффициенты износа
производственных фондов подчиняются нормальному закону рас-
пределения, и альтернативную iииспезу /Т,; износ производствен-
ных фондов подчиняется другому закону распределения.
Уровеш» значимости за зап. г/о-0,01.
Для вычисления значения стаз истине / найдем всроя1нос1н
тот о, чз о значения коэффициензов износа производственных фон-
дов принадлежат конкретному интервалу по формуле:
Mr ,
при пом наименьшее «качение - левую границ) первою ин серва-
ла. заменяем а «с». а наибольшее значение правую !раницу седь-
мого интервала заменяем « ».
Л о^А'<12.15)-Ф’ 12,15 17,7 | Ф’( «)«Ф'(-1.5) Ф'(«)»
\ 71 j
0.066Х-П = 0 П66Я
180
/>(12.15< Л <|4.1) = Ф*
14,1-17,71
3,71
-Ф’(-0.97)-Ф’(-1,50) = О.1660 - 0,0668 = 0.0992,
/414.1 -Г Л <16.05)- Ф‘\ ---Ф*(-0.97)
\ 3,71
= Ф* (-0.4 5) Ф* ( С. 97) = 07 3264 - 0.1660 = 0.1604.
Г(1(>.05 s А'< 18.0; =Ф’1 *Л' ' |-<Г
I 3.71 7
(16,05-17.71 ,
I 3.71 )
Ф’ (0.08) - Ф’ (-0.45) = 0.5319 -0.3 264 0.2055;
«19.95 < Л <21.9) Ф’(1.13)-Ф‘(С 60) - 0.8708-0.7257 - 0.1451;
Р(21.9«А <(«)=<Г( ») Ф'(1.13)=1 0.8708 = 0.1292
Составляем расчетную таблицу 4 18:
Таблица 4 18
/л ЧГ ' | ' /х,-17.71') • 'ф, (w, -гу.Г
1 з — Y • .71 )
ф* 1 3,71
<-«;12.15) * 4,008] 9.96 -2.96 0.8797
[12,15.) 4.1) 5 5.952
[14.1; 16,05) 10 9,624 0,376 0.С147
[16.05; 18.0) 14 ( I2.33C 1.67 02262
118.0.19.95) 15 11.628 W7 0.9778
119 95; 21.9) |( 8.706 1294 0,1923
(21.9.-г*) 4 7,75602 -3.752 1,8160
I- Z 6С L- -- 4.1067
В таблице находим расчетное значение статистики
/' =4.1067
Для заданного уровня значимости «г-о.о5 и числа степеней
свободы I ( - г —I 5-2-1 ? (об1€ДИНН 1И ПСрВЫЙ И ВЧЮрОЙ ИНГСр-
валы, гак как теоретически частота пр 4.00Я в первом интервале
181
меньше 5) в 1аблице П5 (приложение 5) находим квантиль
Жом >=5.99.
Так как -4.1067< / “5.99. то нег оснований для отвер
же и ия основной гипотезы //„.
От не к изучаемая случайная величина А подчиняется нор-
мальному закону распределения
4.12 Используя критерий Пирсона, при уровне значимости
ап = 0.01, проверить гипотезу о нормальном распределении изучае-
мой случайной величины А по заданным выборкам
а) отк гонения диаметров валов от номинального размера.
Интервалы отклонений, k i;*,> [25; 27) рт-.аэд ♦ > [31; 33) [33.35) [35; 37) [37;39) • •
Число ва- лов, m 5 22 23 29 28 17 i 11 5
6) прочность нити волокна:
Прочность нити, г [х.-1 «А») (081 ‘091J - J [ 180; 200) [200; 220) [220; 240) [240; 260) (260; 280) [280; 300) (300; 320]
Число ни- тей, ПТ 36 70 105 129 | 128 115 1 87 30 1
в) диаметр стволов деревьев на учас1же теса:
Диаметр спина, см к | [Ю; 12) • [12; 14) (14; 16) (81 !9|] (ог-811 ’ 1 [20; 22) 1 [22. 24) J [24, 26) [26; 28]
Кплнчсс тип дс рсвьсв П1 10 25 51 66 87 147 120 80 39
182
4.13 При исследовании времени безотказной работы приборов
Требуется при уровне значимости а =0.05, проверить гипоте-
зу то том. что время безотказной работы приборов распределено по
показательному закону
Решение. Изучаемая случайная величина А'. характеризующая
время безотказной работы приборов, як inertя непрерывной слу-
чайной величиной Вычислим интервальный статистический ряд
распределения в таблице 4 19
Таблица 4 19
и пос гронм । не гограмму:
Но виду гистограммы можно предположить, что изучаемая
случайная величина подчиняется показательному закону распреде-
ления:
Ле J' .при г > 0;
г(д) = <
[0, при л <0.
где Л>о-нарамитр показательною закона распределения Найдем
оценку параметра А. В соответствии с методом наибольшего прав-
доподобия. оценкой параметра Л служи! среднее арифметическое
выборки, те Л -4г. Вычислим А’- среднее время безотказной ра-
боты приборов по формуле:
Х-^Ух’ т —ПО 258*30 125 + 50-65 + 70 35+90 I9+IJ0-17 +
я 11 500
1130 9 + 150 6)-35.2
Тогда А = 1 = — » 0,03.
А' 35,2
Таким образом. плотное 1ь /Ях) предполагаемого показатель-
ного распределения имеет вид
[0,03е "*1,при х20,
О, при х < 0
Сформулируем основную гипотезу Н{. изучаемая случайная
величина подчиняется показательному закону распределения. гои
альтернат явной гипотезе //, изучаемая случайная величина под-
чиняемся другому чакону распре дел сип я.
Уровень значимости о задан, =0,05.
Для вычисления статистики х найдем вероятности погалания
значений А'в каж пай из интервалов по формуле:
• •<
Р F(x , < А < х.) - | p(xV/x - 0,03 р "Jx-0.03
С • K.I
Получим /» /fO<A<20) «#п -I « '-I 0,5488-0.4512,
Г. = P(20S А'<40) = ,. ”» г 1 =0.5488 С.3012-0.2476.
Р, - Р140 i А' < 60) - »-и - г - 0.3012 -0.1653 0, И54
С - Р [60 < А < 80) - е ' * е ’ * - 0.1653 - 0.0907 - О.ГЦб;
Р.-P[80SA <100)-с() 0407-0.(И98-0.0409;
1X4
F = PflOOS У <120> = r ’ « ’'=0.0498 0.0273 = 0.0225.
P, - P1120 S A' < 140)« e ' * - - 0.0273 - 0.0150 « 0,0123.
P, - P|I4C< X -0,0150-0 = 0,0150.
(правую |раницу восьмою интервала заменим «*«»)
(оставляем расчетную таблицу 4.20:
Таблица 4 20
ГО, пГ -500(еч,т‘ е пт го, - пр, (ГН - ГЦ ,У
228 225,6 2.4 0.0255
120 1 1 123.8 3,8 0,1166
Й65 ' -.'>5 2.95 (Ц2В1
36 37Л -1,3 0.0453
19 20.45 1,45 0.1028
17 11.25 SJS 2.9389
9 6,15 2£5 13207
6 7.5 -1.5 0.3000
Х:50Г к — 500 4.9779
П таблице находим расчетное значение статистики
- 4.9779.
Для заданного уровня значимости ^ = 0.05 и числа степеней
свободы । =А г-1=8 1-1 = 6 в таблице П4 (приложение 41 нахо-
дим квантиль -12.6
Пак как , = 4 9779h -12.6, то нет оснований для отвер-
жения основной гипотезы //0.
Ответ: изучаемая случайная величина X подчиняется показа-
тельному закону распределения
4.14 В резулыате регистрации времени прикола пику нагелей в
супермаркет с момента открытия получены данные приведенные в
таблице 4 21
1Я5
(аблица 4 21
Требуется при уровне чначимисги ас=С,0! проверить гипотез}
о том, что время прихода покупателей в супермаркет распределено
по показательному закону.
4.15. В результате испытания на прочность нового разработан-
ного синтетического волокна получены данные, приведенные в
таблице 4.22:
Таблица 4.22
Требуется при уровне значимости аов0,05 проверить гипотезу
о том, что сила натяжения волокон распределена по показательно-
му закону
Б Критерии согласия Колмогорова основывается, по мере от-
клонения эмпирической функции распределения А(х) выборки
1^,1.... jrJ си гипотетической функции распределения F(>изу-
чаемой случайной величины \ В качестве такой меры рассматри-
вается величина Л-тах/Хд) Лх)Мй, |де Г(х>- непрерывная
функция распределения
IR6
Алгоритм применения крнюрия Колмогорова:
1 Из эмпирических данных составляется интервальным ряд
распределения.
2 Строится гистограмма »мпири чес кого распределения. По ви-
ду гистограммы визуально оценивается вид теоретического
распределения Т\ которому подчиняется выборка
3 Вычисляются оценки параметров закона распределения Г.
4 . Форму л ир> с ic-я основная Н(, и альтернат ивг. де //, гипотезы
5 Задастся уровень значимое! и - 0.05.0.01).
6 . Вычисляется значение статистики где
D * max |F(x) - F(x)|;
а) вычисляются значения эмпирической функции распреде-
ления
F(x)-—.
п
б) вычисляются значение гипотетической функции распреде-
ления Fix).
7 . Для заданного уровня значимости а по таблице П9 (прило-
жение 9) находя г критическое значение А, распределения
Колмогорова и строится область принятия гипотезы Н и
критическая область
8 Формулируется правило принятия гипотезы Н, если
» |О нет оснований для отвержения гипотезы нс. если
> > *10 1 ипотеза Н, отклоняется.
Г*1» «V V
Подчеркнем, что критерий Колмогорова примеряется для про-
верю гипотез о законах распределения только непрерывных слу-
чайных величин
4.16 В результате обследования средней урожайности зерновых
на площадях района получены данные, с веденные в таб »ицу 4.23
Таблица 4 23
1Я?
Требуется, используя критерий согласия Колмогорова, прове-
рить пшотезу о том, что средняя урожайность горновых распреде-
лена по нормальному закону. Принять уровень значимости
а, =0.05.
Решение Поскольку изучаемая случайная величина X являет-
ся непрерывной, то составим интервальный ряд распределения в
таблице 4.24.
Урожайность зерновых, [*• |»^|) m • • (38:41) (41:44) L (44;47) - j [47;50) 1 (50; 53) - [53; 55) [55; 59) (59:62)
'Относительная часки а колнчсс г- ва ус лонных уча- CTKOR. И( - —L п ю 3 о 1 8 > гч □е 9 II ос г 1 о II 8 § гч огьг но= .. и<т ?• 4 g|8 - ** ! гч 350 А,Л -Л, 14 от с» О И F 3 * Я 120 -0.04Х 2500 70 «0.028 2500
и построим гистограмму
По виду гистп| рам мы можно предположить. что и гучасмая
случайная величина V, подчиняется нормальному закону распреде-
ления который описывается функцией распределения
IF8
Г(л) = <7>’ -'—I, где f. :dl
\ о / V2jf
Неизвестными параметрами являются математическое ожцда
иис w и дисперсия с‘ Согласно метода наибольшею правдоподо-
бия. оценками т и а являются среднее арифметическое X и ис-
правленная статистическая дисперсия Л”. Вычислим их значения
по эмпирическим данным:
лДУл- - .5 12' +39.5 21 42 5 32( 1+43,3 13 1*48.5 600- 3 5 35G
яfT 250С
+54,5-270 ♦ 57.5 120 ♦ 60,5 701 = 47.732. (г* -середины w/rqpeaw).
У = —У (с ) (А X -Д— V 1Л » К с 200 42 5 320* 4S.5 4»-4Ъ,5*‘ 600 ►
л 1*Г 2499
♦ 51.5' 350- 54 .5-270*57.5 120 ♦ 60.5 70} <47.732)’* 33.02. У» \F = v6j.W • 5.75
Тогда функция распределения предполагаемого нормального
распределения будет и меть вид
. ..i г-47.73 ]
/ г) = ф ------
I 5.75 J
Сформулируем основную гипотезу //< изучаемая случайная
величина распределена по нормальному закону распределения; при
альтернат явной гипотезе //: изучаемая случайная величина рас-
пределена по другому чакону
Уровень значимости а. задан, а* =0,05.
Для вычисления статистики А^ =dVJj = лшл|Лг) F(.i)|
вычислим значения функции распределения Т(х); заменив левую
границу первою интервала «-х», а правую границу последнего ин-
тервала «+Х»; если ецЗЯЦ ТО
*'(М) I —— I * ^'(-1.60) = 0.0455;
Г(4П Ф’|41 47,73 1.17)^0.1210,
, [4144)™ Л(44)-ФЧ 1 ] ,<;>•(0.2578;
\ 5.75 )
147 -47 73
’ ’ 0.13)₽0.448\
г 5.75
» [47 50).»no F(50) фф 50-4^.73 s<t,-(o W)= () 6S|7
1К«
г с [50; 53). то Г(53) = Ф*
53 47.7 Г
5.75 ,
Ф*(0Л2> ~ 0.8212.
х ^(53; 56),гпи Г(5б|-Ф*
*6-47.73'
5.75 ,
» Ф*(|.44) = 0,9251.
хе[56; 59).та Г(59) = Ф*| * Ф’( 1.96) - 0.9750.
I 5.75 )
л с [59,-нс )»/w F( hjo) = I
Составляем расчетную таблицу 4.25.
Интерваты урожайно- сти зерно- вых. Количе- ство ус- ловных участков. Fhl-^ л Г(х) = Ф’ f х-47,73) 1 5.75 J |Лх)-Г(»)|
35 38 120 0,048 0,0455 0.0025
38-41 200 0,128 1 0,1210 1 0,007
41 44 320 0.256 J 0,2578 -0.0018
44 47 450 0.436 0,4483 -0.0123
47 50 600 0,627 0,6517 0.0243
50-53 350 0,816 0.8212 -0,0052
53 - 56 270 0,924 0,9251 -0,0011
56 59 120 0.972 0.9750 _-О,003
59 62 70 1,0 1 ,0 0
X 2500 - 1
Наибольший модуль рачнекти между соответствующими зна-
чениями эмпирической и i ипотетической функциями распределе-
ния выбираем и последнем столбце таблицы 4.25;
Г) тач|р(х) F(a)| = 0.0243 Тогда расчетное значение статистики
^0,0243*725ГЙ» 1 215 По таблице (приложение 9) крити-
ческих значений распределения Колмогорова для заданного уровня
чначимскпи ов 0 05 находим квантиль Л ,.-1.358 Так как
И.21 35К, то нет оснований для отклонения'нулевой
гипотезы нп о нормальном законе распределения средний урожаи
пости зерновых
190
Oieei: средняя урожайность зерновых в районе распределена
по норма шному закону
4.17 В результате испытаний 1000 элементен системы сигна-
лизации на время бекпказной работы получены данные, приведен-
ные в таблице 4.26
(рсбуется при уровне значимости а 0,01 при помоши крите-
рия Колмогорова, проверить гипотезу о том. что время безоткатной
работы элементов сигнализации распределено по показа тельному
закону
4.18 Результат»?! взвешивания валов, произведенных за смену
на станке автомате, приведены в таблице 4.27
рия Колмогорова проверить гипотезу о том. что вес на юн Д рас-
пределен равномерно
191
Таблица П1. Функция распределения Ф (х)
нормального закона ЛЧО.Щ
Ф*(-х) = 1-Ф'(х),
поп 0.01 0.02 i 0.03 0.04 0.05 0.06 0,07 0,08 0.09
0.0 0 5000 0.5040 0,5080 0,5120 0,5160 0,5 J 09 0,5239 0.5279 0,5319 0.5359 * — ◄
0.1 0.5398 0,5438 1 0,5478 0.5517 0.5557 0,5596 0,6636 >675 0,5714 0,5753 —
0.2^ 0.5793 0.5832 0.5871 0.5910 0Л94К 0,5987 0,6026 0.6064 0,6103 0,6141 — — 1
0,3 ] 0.6179 0,6217 0,6255 0.6293 0.6331 0,6368 0.6406 0 6443 0.6480 0,6517
0.4 06554 0.6591 0.662S 0,6664 0.6700 0,6736 0.6772 0.6808 0.6844 0.6879
0,5 0.6915 0,6950 0,6985 0,7019 1 0,7054 0,7088 0.7123 0.7157 0.7190 0.7224
0.6 07257 0,7291 0,7324 0,7357 0,7389 0. /422 0,7454 0,7486 0.7517 0.7549
и» —- 0.7 1 0.7580 _0,7611 0,7642 (V673 0.7704 0.7734_ 0,7764 0,7794 0.7823 0,7852
0.8 । 17881 0,7910 0.7939 0,7967 0.7995 0.8023 0,8051 0.8078 0.8106 -- — О.Х 133
0.9 0.8159 " 0.8186 0,8212 0.8238 0X264 0.8289 0,8315 0.8340 0,8365 0.8389
1.0 '.84В ’ 0.8438 0.8461 0,8485 0,8508 0.8531 0 Х524 0.8577 0,8599 0,8621
1.1 о.кмз 0.8665 0,8686 0.8708 0.8729 0,8749 0,8770 0,8790 О.Х810 0.8830
1.2 0,8849 08869 0.ХХХ8 0.8907 0,8925 0,8944 0.8962 0.8980 0.8997 0.9015
1.3 0.9012 0.9049 0.9066 0.9032 0,9099 0.9115 0,9131 0.9147 0,9162 0,9177
1 1.4 0,9192 09207 0.9222 0.9236 0,9251 0.9265 0,9279 0,9292 0.9306 - — — 0.9319
1.5 0.9 3 '2 0.9345 0.9357 0.9370 0.9382 0,9394 0 9406 0.941X 0.9429 0,9441
1.6 0.9452 0.9463 6.9474 0.9484 0.9495 0,9505 0,9515 0,952s 0 9535 0,9545
1.7 05554 П.9564 0 95X2 0.95X2 U.9591 0,9599 0,9608 0.9616 0.9625 0,9633
1.x 0.9641 0.9649 0.9656 0.9664 0.9671 0,9678 0,95X6 0,9693 0.9699 0.9706
Таблица III (продолжение)
X i 0.00 0.01 0.02 0,03 0.04 0.05 006 0,07 0,08 ' 0.09
1.9 0.9713 _0.9/19 1 0,9726 0.9732 0.9738 । 0.9744 0,9750 0,9 56 0.9 '61 0.976'/
2.0 0.9772 0,9778 0.9783 0,9788 0.9797 0,9798 0.9803 0.9808 0 0812 0.9817_
2.1 0.9821 0,9826 Г 0.98Ю 0.0R14 0,9838 0,9842 0,9846 0,9850 Г 0 9854 0.9857
2.2 __ 0.9861 0,9864 0,9868 0.9871 0.9875 0,9878 0.9881 0.9884 0.9887_ 0,9890 ]
Г 2.3 0.9893 0.9896 0.9898 0,9901 0,9904 0,9906 0.9909 0,9911 0.9913 а — . mi и 0.9916
2.4 9Ч18_ O.992U 0,9922 0.9925 0.9927 0.9929 0.9931 0,99.32 1 0,9934 ь. ... . 0,9936 —— — — и
Г 2.5 0.9938 0.994Л 0.9941 0.9943 0.9945 0.9940 0,9948 0.9949 0.9951 0.9952J]
2,6 0.9953 0,9955 0,9956 0.9957 0,9959 0.9960 0,9961 0,9962 0,9963 0.9964
2.7 0.9965 0,9966 0.9967 0,9968 0.9969 0,9970 0.9971 0.9972 _0.9973 0.9074
2.8 0.99 ’4 0,9975 0,9976 0.9977 0.9977 0.9978 0,9979 0.9979 0.9980 0.9981
2.9 0 9981 0,9982 09082 0,9983 0,9984 0.9984 0,9985 0,9985 0.9986 0.9986
3.0 0.9987 0.9987 0.9987 0.9988 0,9988 0.9989 0,9980 0,9989 0.9990 0,9990
3.1 0.9990 0.9991 0.9991 0,9991 6,9992 0,9992 0,9992 0,9992 0.9993 0,9993
3.2 0.9993 0.9993 0.9994 0.9994 0,9994 0.9994 0.9994 0,9995 0.9995 0,9995
1ЛЗ 3.4 0.9995 0.9997 0.9995 0.9997 __0.9995 0.9997 0,9996 0.9997 0,9995 0,9997 0,9995 0,9997 0,9995 0.9997 0,9995 0.9997 0,9995 0.9997 - - . 0,9997 0,9998
3,5 0.9998 0.9998 0.9998 0,9998 0,9998 6.9998 0.9998 0.9998 0,9998 0.9998
3.6 0,9998 0.9998 | 0,9998 0.9998 0.9998 6,9998 0.9998 0.9998 0.9998 0.9998
3,7 0.9999 0.9999 0,9999 0,9999 0,9999 0,9999 0,9999 0,9999 П 0,9999 0,9999
3.8 _ 0.9999 | 0.9999 0.9999 0.9999 0,9999 0.9999 0.9999 0,9999 1 0.9999 | 6.9999
3,9 | 1.0UU0 1.0000 1,0000 1.0000 1.0000 1,0000 | 1.0000 ] 1,0000 J 1.0000
Таблица П2 Значения функции плотности нормального распределения
1 --
<V(0.1)
196
Таблица ПЗ. Распределение Пуассона Р[А **]
6
0.1
0.6
0.90484
0.09048
0.00452
0.00015
од 0.3 0,4 0.5
0.81873 (.74082 0.67032 0.60653
O.I6J75 0.22223 0.26813 0,30327
0,01638 (,03334 0.05363 0.07582
0.00109 С.ООЗЗЗ 0.00715 0.01204
0.00СЮ6 0,00025 0.00072 0.00158
0.00003 0.00006 0.00016
0.00001
0.7 0.8 0.9 '
0,54881 G,49659 0,44933 0,40657
0.32929 0,34761 0.35916 0.36591
0.09879 0.12166 0,14379 0.16466
0.01976 0.02839 0.03834 0.049 U)
0.00296 0,00497 0.00767 0.01112
0.00036 0,(ХХ)70 0,00123 0,00200
О.ОООС4 0.00008 0.00016 0.00030
0.00001 0,00002 0,00004
2.0
Я
0,36768
036788
0.18394
0.06131
0.01533
0.00307
<)ДХ)051
0.00007
0,00001
10
12
14
16
0.13534
О27067
0.2706?
0.18045
0.09022
0.03609
0.01703
0.00344
0.00086
0.00019
0.00004
0,00001
0.04979
0,149*6
0.22404
0.22404
0.16863
0,10082
0.05041
0.02160
0.00810
0.00270
0.00081
0.СО022
0.0000
0.00001
0.CJ832
0,(7326
0.146
0.19537
0.19537
0.15629
0.10419
0.05954
0.02977
0.01323
0.00529
Q | I
0.00064
0.00020
0.00006
0.00002
0.00674
0,03369
0.08427
0.14037
0.17547
0.14622
O.K44S
0.06528
0,03627
< 1813
О.ООК2 1
0.00343
0.00132
(1,00047
0.00016
0.00005
0.00001
|О7
I аблнца П4 Суммарные вероятности для распределения
I(уассона: P[.V iл, = у' — <•3
\ л к 0.1 0.2 0.3 0.4 0.5 0.6 0.7
0 1.00000 1,00000 1.00000 ! ( । (мимо 1.00000 1.00000
1 0.09516 0.18127 0.25918 0.32968 079347 0.45119 0.50341
2 0046Х 01752 03694 06155 09020 12190 15580
ч 00016 00115 осзоо 00793 01439 023 2 03414
А 0 00006 00027 00С78 00175 00336 00575
Г- V*. sD Г 0 00002 00006 00017 00001 00039 00004 00079 00009 СОЮ1
Я * 0,8 0,9 1.0 2,0 4.0 6.0 8,0
0 1,00000 1 t <0000 100000 1.00000 1,00000 1.00000 1.00000
1 0.55067 0 59343 0.63212 0,86466 0.98168 0,99752 0.99966
2 19121 22752 26424 59399 90842 98265 99698
(М742 06286 08030 I233J 76190 93803 98625
* 00908 01346 01899 14288 56653 84880 96762
5 00141 00234 00366 Q3265 37116 71494 90037
6 00018 00034 00059 01656 21487 55432 80876
7 00002 00004 00008 00453 1 i 067 39370 68663
8 9 10 11 12 13 14 15 1 16 17 18 19 20 21 22 24 00001 00002 (ЮНО 00005 00001 05113 02136 00823 О0284 0Й192 00027 00008 0000? 00001 1- . 25602 15276 08392 04262 02009 00883 00363 U0I40 00051 00017 00006 0000? 00001 54704 40745 28338 1x411 11192 06380 03418 01726 00823 00372 00159 00065 00025 00009 00001 00О01
ия
6.26 7 01 8.23 9.39 109 12 9 14.4 20 6 22 8 26 0 28 9 31.5 34 8 37 2 42 3
6.84 7 63 8 91 101 117 13.7 15 4 21.7 23 9 27.2 30.1 32 9 36.2 38 6 43 8
7 43 8 26 9 59 10.9 I 12.4 14.6 16 3 32.8 25 0 28.4 31.4 34.2 37.6 40.0 45.3
199
2<Ю
Таблица П6. Квантили распределения С гьюдетла, удовлетворяющие
«* •
начальному условию ру < i,. 1 • j /-a.i )<* «> - a, a, -
уровень значимости (a, = 0,25; 0,1; 0,05, 0,025; 0.01: 0.005, 0.00!)
\ p 1' 0,750 1 0,900 0.950 0.975 0.990 0.995 0.999
1 1 000 3 678 6 314 1 12 706 II 821 63 657 318
5 C 816 1 886 2 920 4 303 6.965 9 925 22.3
3 0765 1.638 2 353 3 182 4.511 5 841 10 2
4 0 741 1533 2.132 j 2 776 3 747 4604 7173
5 0.727 J 476 ’ 2015 2.571 3.365 4.032 5.893
6 0718 1 440 1 943 2.447 43 , 3.707 5 208
7 07|| 1415 1 895 2 365 2 998 3.499 4.785
Я 0706 1.397 1 860 2.306 2 986 3 355 4 501
9 0 703 1 383 1 833 2.262 2 821 1 3 250 4 297
10 b—1 d 0700 J 372 1 812 2 228 2.764 3 169 4 144
JI 0 697 0 645 1 M 1.796 2.201 2.718 3 106 4.025
J2 1 356 1 782 2 179 2 681 3 055 3.930
Ji 0 694 1350 1 77| 2.160 2 650 3 012 1852
14 0.692 1 345 1.761 2.145 2.624 2.977 3.787
15 0.691 1 341 1.753 2.131 2.602 2 947 3.733 j
16 0.690 1337 1 746 2 120 2583 2 971 3.686
r 1 f 0.6Я9 I 333 1 740 2 не 2 567 2 898 3.646
18 0.688 1 330 1.734 2.101 2 552 2 878 3 610
19 0.688 1 328 1.729 2.093 J 2 539 2 861 3579
[20 —j 0.687 1.325 1.725 2 086 2 528 2 845 3 552
21 0.686 1.323 1 721 2080 2.518 2 831 3 527
22 0 686 1 321 1 717 2 074 2 508 2 819 3 505
1 5 1.319 1.714 2 069 2.500 2.807 3.485
24 0.685 1.318 1.711 2.054 2.492 2.797 3.467
25 0 684 1.316 1 708 2 060 2.485 2.787 3.450
26 0 684 L3J5 1 706 2.056 2 479 2.779 3 435
27 0 684 1 44 — — 1 703 к 2.052 2.473 2 771 3 42)
l28 0683 1 313 1 701 2.048 2 467 2.763 3.408
129 0 683 1 1.311 | ь .< 2.045 2 462 2 736 3 396
30 0 682 I 40 1 697 2.042 2 457 2.750 3 385
40 6 681 [ 1 303 1 684 2021 2 423 2 704 3307
60 0679 : 1 296 I 671 2.000 । 2.390 1 2.660 , 1232
120 . 0.67? 1 289 1.658 1.980 2.358 2.617 [ 3.160 ‘
bl — ! — 0 674 1252 1 J .645 I960 2326 1 2.576 [ 3.090 1
201
ТаблицаП? Квантили распределения Фишера Frlk,k.)
'У 1 |_ 1 2 J 3 I 4 ! 5 J Г‘ 7 в 9 10 12 1 р 20 24 W [ 4П ,_60 120
VL р - с, 9: «¥=0.1
' 39.86 40.50 53_59 55 83 57 24 5820 5891 ?9.44 59.86 6019 60.71 6172 61.74 62 00 62.26 62 53 62 79 63 06
4» 4.53 900 9.16 '24 9 29 9.33 935 9.37 9 38 9.39 941 9 4? 944 945 946 9 47 9 47 9 48
3 $.54 546 5J9 5.34 5.31 5.28 5J7 5.25 5 24 5.23 5 22 5 20 5 18 5.18 5 17 5 16 5.15 5.14
434 4 32 4 :о 4.11 405 4.01 198 195 3 94 192 390 3 87 3.84 383 3 82 3 80 119 1 7Я
5 406 3 7» 3 62 3.52 -145 3 40 3J7 1.34 332 110 32? 1 1 21 3.19 3.17 116 114 112
6 ЗЛ1 346 3.29 3.18 3.11 2 05 3.0! 2.98 2.96 2.94 190 217 2.84 2.82 2.80 178 276 2?4
7 1<9 3 26 307 296 2 88 183 2.78 275 272 2.70 167 2.63 159 2.58 2Л6 24 251 2 49
1.46 1 И 29? 2 В! 273 2.67 2.62 2.59 2 56 254 150 246 142 140 2J8 2 Mi 234 2 32
9 1 36 1.0) 281 2 69 261 255 151 2 47 2U 242 138 2 34 2 30 228 2-25 223 2 21 2 18
10 .3 29 2-92 2 73 7 61 2 ^2 2 46 241 2 38 2 35 2 32 2.28 ? 24 220 2.’.8 2.16 2.13 ХП 2.08
н 3-23 2.86 266 2.54 2.45 2 v> 2 14 7 Ш 2 27 2 25 221 2 17 2 12 210 208 205 2 03 200
12 Л18 2Л1 261 2.48 Z39 2 33 128 2.24 121 119 2 15 2 10 2.06 204 101 199 1 ’* 1 9J
п 3 14 176 2 56 2 43 135 2 28 2 23 2.20 2 16 114 2.10 2.05 2 01 1 «я 1 ‘Л 193 1 90 1 88
14 3 ю 173 2 52 2 39 2.31 224 2 19 2.15 212 2.10 2.05 101 1 96 1 94 1 91 1 89 1 86 ИЗ
15 3.07 2.70 2 49 2 36 Х2? 121 2 16 2.1? 109 2.06 102 197 1 92 ! ал 1 87 1 85 1 Я? 1 79
.6 3 05 2/7 14« 2 33 124 2 18 2 13 2 09 2 ГЛ 2 03 1 99 1 94 1 89 1 87 1 84 1.81 1 78 1 75
303 264 2.44 2 31 *»» 115 2 10 206 20.1 2 00 1 96 1 91 1.86 1 М 1 81 1 78 175 1 7?
ini 3 0! 2.62 2.42 229 120 111 2 08 2.04 200 1 98 193 1 89 1.Я4 I 81 178 1.75 1.72 1.69
19 *х> 2.61 2.40 2 2.18 111 206 102 1.98 1 96 1 9| 1.86 1 81 1 79 1 76 1 1.70 1.67
20 297 2.59 138 225 116 209 2 04 200 196 1 94 1 89 1.84 179 1 77 1 74 1.71 1 68 1.64
21 2.06 :.57 136 2 23 114 108 202 I.9R 2.95 1 92 1 Я? 1.83 1.78 1 75 1.72 1.69 1 66 1 62
22 295 256 135 222 2.13 106 201 1.9? 193 1.90 1 86 1.81 1.76 1.73 1 70 1 67 1 64 1 60
23 294 155 134 111 105 1 99 1 95 1.92 :.89 1 84 1 80 1.74 1 72 169 1 66 162 1 59
24 * М 2.33 2 19 2 10 104 1.98 1 94 1.91 1.88 1.83 1.18 1.73 1.70 167 164 1 61 157
25 137 2 18 2 то 102 1.97 1.93 1.89 1.87 1.82 1 1.72 1 69 1 66 1 61 1 59 1 56
2.9! 2 5? ? 1 2 Р 208 2 01 196 1 92 1.Я8 1.86 1 Я! 1 ?6 1.71 1.68 1 65 161 1 58 1 54
27 2 90 2.51 2 Ю 2 17 207 2 (XI 1.95 1 91 1 87 I.K 1 ко 175 1.70 1.67 1 64 160 1 57 1 53
2.89 ?Ч) 2 29 2 16 706 7 00 194 1 90 1 87 1 84 1.79 1.74 1.69 166 1.63 1 59 1 56 1 52
29 289 150 2.28 115 2 06 199 193 1 89 1 86 1 83 1.71 173 1 68 1.65 1.62 1 58 1 5< 1 <1
30 2.88 ’49 228 2 14 205 1 94 1 93 1 88 185 1.82 1.77 1.72 1.67 1.64 1.61 1 $7 1 54 1 50
40 2.84 2 44 223 2.09 200 1 91 1.87 1 81 1.79 1 76 171 1 66 1 61 157 1.54 1 51 147 1 4^
60 170 139 2 18 2 04 1 95 1 87 1 82 1 77 1 *»4 1 71 1 66 1 60 1 54 1.51 1.48 1.44 140 1 35
120 2.75 2Л5 113 199 190 1 82 1.77 1 72 1 68 1 65 1 60 1 5$ 1 48 1.45 | 4' I.J7 1 32 1 26
ПО 271 130 2М 1.94 1 85 1.77 1 1 67 1 63 1 Ml 1.55 1 49 1 42 1 18 I.M 1.30 124 1 17
Таблица П7 \ продолжения*
-
z’\ LiJ 2 | 3_ L4 J 5 [ 6 L 7 1 1 О БП L nJ 15 Г20 |_24 30 40 60 120
Р = О,95; (ХожО.СК
г 2 .61 4 ;оо 5 1157 224 6 230.2 2S4 0 2345* ТТ9 240* 241 9 243 9 2«*ч ?4Я 0 249 1 250 1 251 1 2522 251 ♦
18.51 19 ос 19 16 19 25 19 Ю 10 13 19.15 19.37 19.38 1940 1941 |9 4Л 1945 1945 19 46 19.47 19 48 1949
Э 4 1:11.1 7 71 9.55 6 94 9 28 6 59 9.12 6.39 901 6 26 8 94 6 16 R89 600 8 85 604 881 600 8 79 596 8 74 5.91 8 70 5 86 866 5 80 ЯМ 5.77 8 62 5 75 Я 59 5.72 8.57 5.69 Я 55 566
5 661 5 79 5 Я 5 |9 505 4 95 4 88 4 4 77 4 74 4 68 4.62 456 4.5? 4.50 4 46 4 4? 4 U)
6 5 99 5.14 4 7$ 453 4 19 4 78 4 21 4 15 4.10 4 06 4'1) U4 3.87 1 84 3.81 ? 77 к?4 1 ю
7 5 59 4.74 4.35 4 12 39/ 3 87 31» 373 3 68 364 3 57 351 1 44 141 39Я 3 34 3.30 ЗТ2
ч 5 12 1 46 407 з.м 3 69 1 58 1 50 3.44 3.39 3 35 3 28 1 VI 3 15 1.12 ? 08 304 3.01 297
<> 5 12 4 26 1 Ж> 3.63 3 48 3 37 3 29 3 23 1 18 3.14 3.0? 3.01 ? 04 7 70 2.86 2 Я? 2.79 275
10 4 96 4 10 1 1 ЗЛЯ 3.33 3 22 3.14 3 07 3 03 2 98 291 165 277 ?*»4 2 70 7 66 262 2 58
к 12 4 84 1 «И 1 59 3 36 я ?л 109 3.01 2 95 2 00 2 85 2 79 2 72 265 2.61 2Л7 2 53 2.49 7 45
4 75 3 89 349 3.26 111 1 оо 2 9! 2 85 2.80 275 2 69 2 62 2 54 251 247 2 43 238 2 34
п 4 67 ЗЯ 34| 3.18 3 03 2 92 2 83 277 2.71 2 67 260 2 53 2 46 242 2.3Я 234 1W 2 25
14 4 60 174 134 3.11 2 96 2 35 2 ?6 2 70 2 65 260 2 53 2.46 2.39 2 35 231 2.27 222 2 1Я
|5 4 54 168 1 29 3.06 2 90 2 79 271 764 2 50 2 54 2 48 2.40 2.33 229 2.25 220 2.16
16 4 40 3 63 3 24 301 2 R5 2 74 266 2 59 2 54 2 49 2 4? 2 35 2.28 2.19 2 |5 ZI1 ? ii6
17 3 59 1 20 2.96 2 81 2 70 261 2 55 2 49 2 45 7 ЗЯ 2 31 2.23 2.19 2.15 2 10 206 7 01
18 1 59 1 16 2.93 277 266 2 58 251 2 16 241 2 ^4 2.27 2 LI9 2»1 111 2"^6 2.02 1.97
19 4 38 1 52 3 13 2 чо 2.74 2 63 254 2 48 2 42 2 3R 131 Z23 И6 2.1! 2 07 2 03 1.98 1.91
20 4 15 1 40 3 ю 2 87 2.71 260 2.51 245 2 39 2 35 2.28 2 20 L12 2.08 204 1 99 1.95 1 90
21 4 32 3 47 1.07 2 84 2 68 2 57 249 2 4^ 237 232 225 2 18 2.10 205 2.01 1 96 1.92 1 87
4 W t И ЗС5 2.82 266 2 55 2 46 2 10 2 34 2 30 Z23 2.15 ..07 203 1 <>Я I 94 1.89 1 84
23 4 28 1 42 3 01 2.80 2М 253 244 2 37 2 32 2 27 2 20 2 13 205 201 1 96 1 91 1 86 1.87
4 26 7 40 101 2.78 2 62 2 51 2 42 236 230 2 25 2 18 2 11 2 »03 198 1.94 1 89 1.84 1 79
424 1.19 7J9 2 76 76П 7 49 2 Ю 2 34 2.28 224 2.16 2 09 2.01 1 96 1 9? 8^ 1.82
26 4 21 1 37 198 2-74 2 59 2 47 2 39 2 32 227 2.22 115 2 07 1 99 1.95 190 IIS 1.80 175
27 4.2! 2 25 296 2.73 257 2 46 3? 211 2 25 2 20 313 706 1 97 1.93 1 88 1 84 1 ’9 1.73
28 4 20 295 271 156 2 45 2 36 2 29 224 2.19 2.12 2.04 ! 96 1 01 1 87 1 82 1.77 1 71
29 4 18 3.33 2.93 2.70 2 55 2 43 2 35 228 222 2.18 2.10 201 1 Q4 190 1 85 1 81 1 75 1 ю
30 4.17 1 12 2.69 2 53 242 133 2 27 221 2 16 7 09 2 01 191 1.89 1 84 1 79 1 ?4 1 68
4- 4 ГН 123 2.W 261 2 45 734 2.25 2 18 212 208 2 00 1 02 1 Я4 1 1 74 169 1 М 158
60 4 00 1 15 176 2.53 2 37 225 117 2 10 ?<М 1 99 1.92 1 84 1 75 1 /П 1 65 159 1.53 1 47
120 ?92 307 268 2 45 720 2 17 ?Э9 2 02 1 96 191 1 83 1 75 1 .66 1 61 1 55 1 50 t .43 1 15
во 1 84 10П 260 237 221 2.0 2.01 194 1 88 1 83 175 1.67 1 37 1 52 1 46 1.39 1.32 1 п
Таблица П7. {продолжения}
'\у! 1 1 2 1 3 4 5 I 6 1л_ 8 1 9 1 »0 ’2 1 Г 15 2П 1 24 30 40 ]_ 60 | 120
v\ — • — />-0.075. а л-0,025
1 X 1 й?“8 Ж$' ~¥б4.2 ?пГ те:я toll 956.7 ЯП 968.6 961? 984 > оад.| 997.2 1001 КД* 1010 1014
2 38 51 39 (Ю 39 17 J9 25 39.30 19 33 <9 36 ТО 37 19 19 39 40 3941 19.43 3945 39 46 39 46 39 47 39 48 39 49
3 16 04 1544 15 10 14.88 4. ’ 14 62 454 14 47 14 42 14 34 1425 14.1? 14 12 14,08 14 04 1399 13.95
4 |2 7*^ 10 65 998 чч 9 ч .>0 9 07 898 490 844 8 75 8 66 8 56 8.51 846 8 4J 836 831
5 1001 8 41 7 76 7 39 7 15 6.98 6.85 6.76 668 6.62 6.52 6 43 М3 6.28 6.23 6.18 6 12 6 07
А 8*1 7 26 6 60 АЛ $ <Г4 Я»? 5.70 560 5.57 5 46 5 37 527 5.П $ 12 $07 501 496 4Л0
7 807 6 <4 5.89 552 S 5 12 4 99 4. ТО 4 82 4.76 4.67 4 57 А 4.42 4.36 4, Ч | 425 4.20
8 7 57 606 5.42 505 4 82 4 АЗ 4 53 4 4 4 436 4,30 4.20 4 10 А ПО 395 3 89 184 378 3.73
9 7.21 5 7! 5.08 4.72 448 432 4.20 4.10 403 3.96 3.87 3.77 3 67 3.61 3.56 351 3.45 3 39
10 6.М 5 46 4.83 4.47 4 24 4X17 3.95 3.85 3 78 3.72 3.62 3 52 3 42 3.37 3.31 3.26 это 3 14
II #172 5 26 463 4 ^8 4 04 3 88 3.76 366 3.59 1.53 341 3 33 3.23 3.17 3.12 3.06 3 00 2 94
12 6.55 5.10 4 4Т 4 12 3 89 3 73 3.61 351 1.44 3J7 3.28 3 18 3.07 102 246 19) 2.85 2 79
13 6.41 497 4.35 4 ЛГ 377 3 60 3.48 3.39 331 3.25 3.15 3.05 2.05 189 184 178 172 2.66
14 630 4 36 4 24 1.89 356 350 3.38 3.29 3.21 3 I5 3.05 2 95 284 2 79 173 26’ 2.61 2 55
15 6.2С д т 4 5 ?.8С 3 58 34! 3.29 320 3.12 3.06 2.96 186 2.76 170 2.64 159 2.52 2 46
'б 6.12 4.69 108 3.73 3 50 3 И 322 3.12 3.05 299 2.89 2 79 268 163 237 151 14$ 238
*-’И 4 «2 4.0! 1 Аб 344 3.28 3.16 3.06 2.98 2.92 282 172 162 156 230 244 138 2.32
II 5.9К 4 56 3 9$ 3 61 3 W 1-22 3.10 3.01 2.93 2.87 177 167 2.56 150 244 138 132 2 26
19 5.92 4 51 390 1.56 3 П 1.17 3 05 296 188 2.82 172 2.62 151 245 2.19 133 2 2 1 220
20 5.87 3.86 3.51 3.29 3.13 3 01 291 2М 277 268 157 246 241 2J5 229 122 2.16
21 5.83 4 42 3.82 3.48 3.25 3 09 2 97 2.87 2.80 271 7 64 2<з 242 2 37 f 1 2 25 2 18 11!
22 > 5.79 4 18 3.78 344 3.22 305 293 2М 2.76 2.70 2 60 2 50 139 2 33 127 121 2.14 2.08
23 5 75 4 35 3.75 141 3 18 302 2 90 2.81 273 2 67 257 2.47 2 36 2 30 7 ?4 2 18 7 П 704
24 4 12 3 3.38 3.15 209 2 87 178 2.70 264 254 244 2.33 127 121 2 15 10» 101
25 5 69 4 29 169 3.35 3.13 297 2 85 2.75 2.68 2.61 2.5) 141 2 30 124 118 2.12 2.05 1.98
26 566 д 27 3.67 1-33 3.10 294 2 82 173 2Л5 2 59 2.49 2.39 228 122 116 209 2Х)3 1.95
27 5 63 4 24 365 3.31 1.08 2 92 2 80 171 2.63 257 2.47 236 2 25 2 19 113 207 2.00 1.93
< 61 4 22 163 1 <06 2 90 2.78 2.69 261 2.55 2 45 134 2 23 117 2 11 2 05 1 98 191
29 5 59 4 ТО 3-М 327 1.04 2.KR 2 76 2.67 2.59 2.53 143 132 2.21 2.15 209 2 03 196 1 89
30 5 * 4.18 3.50 325 3.03 2.87 2 75 765 257 261 7 41 2.31 220 2.14 2 07 201 | 94 1.87
40 S 4П 405 346 ЗВ 2.90 2.74 262 153 245 2 39 2 29 118 2 <17 101 1.94 1 ЯЯ 1 80 1 72
^0 5 29 393 3 V4 301 2.79 263 151 241 2.33 7 77 2 17 7 06 1 94 1 ЯМ 1 87 1 74 1 67 1 58
120 5 15 3 80 3.23 2 87 за? 2.52 2 39 2 30 2-22 2.16 205 1 94 1 82 1 76 1 69 1 61 1.53 143
•<1 <02 1.69 3.12 2 ТО 2 57 24| 2 29 112 211 2 05 1 94 1 83 171 IM 1.57 1 4# » ТО 1 77
ТаблицаП7 (продолжения}
1~Т Тл < I 5 6 ! ’ 1 8 1 9 Г |’ 1 р 1 L1? L. ’V Г 40 Loo 1 120
v>\ Р = О.99; ао=ю.т
Г г 4О5Т 4W 5 $403 562^ 5 Ы 5»^ $928 S982 6022 6056 6106 6157 tint 6235 6261 6287 6313 6339
2 4Х 50 99 00 90 7 ' i 99 10 49 33 99 36 99.37 99 39 09 40 99 4? 99 43 09 4$ 99 46 99 47 99 47 99.4g 94 49
3 м 12 10 82 29 46 28 71 28 24 27.91 27 67 27 49 27.35 27 21 27 05 26.87 16 69 26 60 26.50 26 41 26’2 26.22
4 21 20 1800 16 69 15 98 1 5 S" 15 21 1498 14 80 14.66 14 55 14 37 1420 1402 1393 13.84 13 7$ 13.65 13 56
5 16 26 13 27 12 (W II J4 1097 1067 1046 10J9 10.16 1005 989 9.72 9.55 9 47 9.38 9.29 9 20 9.H
6 13 75 10 92 9.78 9 IS Я 75 8 47 8 26 «:о 7 98 7.87 7?2 7.56 7.40 7 31 7 14 706 6 94
7 1115 9.55 8 45 7R5 7 46 7.19 6 99 6 84 677 662 6 47 6 11 6.16 6(П $ 99 591 5 82 5 74
8) 11 26 8.65 7 $9 7 01 6 63 6 И 6 18 6 03 591 581 5 67 <52 5.36 ?я 5 ТО 5 1? 5 0? 4,95
9 10 56 ЯП? А 70 64? 606 580 $61 5 47 S .1S 526 5 11 4 9А 4 81 4 4 65 4.57 4 48 4 40
10 1 1004 7 56 6 55 <99 <м 5 <9 5 20 506 4 04 4В$ 4 71 4 56 4 41 4Р 4 25 4 17 4 OS 4/Ю
И 9 65 721 6 22 <Ai 5 32 507 4 80 4 74 4 63 4.54 440 4 25 4.10 402 394 3.86 4 78 369
12 9 33 6.93 5 95 541 506 4.82 464 4.50 4.39 4 SO 4.16 401 3.86 3.78 3.70 362 354 3 45
:з 907 670 5.74 5.21 4 86 4 62 4 44 4 W 4 19 3 10 38? 3 66 3 59 151 3 43 3.25
4 886 651 S 56 r. 04 4 69 4 46 4 28 4 14 4 01 194 3 мп < М’ 3 51 141 < IS 127 1 18 109
15 S 36 542 4 МО 4 $6 4 12 4 14 4 00 389 3 во 3 67 152 3 37 3 29 321 3 13 3 05 2%
6 853 623 4 7^ 444 4 20 4 03 1 89 178 169 1 55 1 41 3 26 1 18 1 Ш 3 02 2 91 284
|7 840 6 11 5.1Я 4 67 4 ^4 4 10 3.93 179 1.68 3 59 V46 3.31 1 16 ) 08 ЗЮ 2 2.83 2 75
18 8^9 6 509 4 $8 425 401 384 3.71 ЗАО 351 3.23 3.08 1.00 292 84 175 266
19) 8.18 < 93 501 4 50 4 17 3 94 3.77 ЗАЗ 352 343 3.30 3.15 3.00 292 2 84 2 76 16? 2 58
20 я Ю 5 85 4 'М 443 4 10 >87 370 3 56 1 46 337 из 3.09 2 94 2.86 2.7Я 2 60 261 2 52
21 Я 0? $78 4 87 4 404 181 364 151 140 3 31 1 17 1.П1 7 88 2 80 2 7? 264 2 5$ 2 46
22 7.95 <72 4R2 4 31 399 1 76 3 $9 1.45 3 15 326 3 12 2.98 2 83 275 267 2 58 2 50 240
23 788 566 476 4 25 394 171 354 141 1 ю 3 21 107 ?ОЗ 2 7R 2 ТО 26? 2 54 2 45 ?1$
24 7.82 $61 4.72 4 2 190 167 150 136 3.26 3 17 3 03 289 2 74 2.66 2 <8 2 4о 2.40 131
25 7 5 <7 4А8 4 18 3.85 ЗАЗ 146 132 322 3 13 299 185 2 7П 2 62 154 2 45 236 127
и 7.72 5 $3 4 64 4 14 1.82 3.59 3-42 3.29 3.18 3.09 2 06 2.81 2.66 2.5» 150 2.42 133 211
27! 7АЧ 5 49 4 60 4 11 К 3 56 3 39 1 26 3.15 »06 2 93 2.78 2 63 255 2.47 2 31 2 29 2 20
?я 764 5 4$ 4.57 107 175 3 53 3 36 1.23 3 1?. 301 2 90 175 ?60 2 52 241 2 3$ 226 2 17
29 7.60 5 42 4.54 4 CM 1.73 3.50 3.11 1.20 3.09 мю 287 2.73 2 57 249 2.41 2 33 123 114
37 7 56 $ 39 451 4 170 147 3 10 117 307 208 ? 84 2 7П 255 247 139 2 Ш 7 71 2 II
♦0 7.3| $ 18 431 зп 151 3.29 ЗЦ 299 289 2.80 266 252 237 2 29 2 20 111 202 192
VI »П8 498 4 В 3 65 ) U 3 12 2 0$ 7 8? 2 72 2.6J 2 <Г> 2 35 220 2 12 2 03 f <м 1 84 1
120 6 85 4,79 3 95 3 18 3 17 296 2 79 266 256 2Л7 234 2 Ю 2X13 |9< 1.86 1.76 166 133
СП 6 63 4 61 3 78 3 32 102 чл 2М 2$1 241 2.32 .' Я 2 04 1 МЯ 1 79 t ?t> 1’0 1 47 14
Таблица 117 (продолжения)
V' Г 1 2 3 * J L ’ I 6 » 1 >0 L12 J L «5 IT1 L24 j [ JWj 60 120
Vj\ p 0.995; а^л
1 .6211 :i»K uson 15056 234)7 2з?15 JW5 !дЛ51 МЙ4 74426 244^ W “B(M4 25i48 2313J 25)59
2 198.5 .990 1992 199 2 199.3 1993 199.4 109 4 190.4 1994 1904 199.4 194 4 :o9< 1495 199 5 199 5 |9Q<
3 55 55 49 10 47 47 19 4S 30 44 Я4 44 41 44 13 43 88 4169 4 <39 43 08 42 78 42 62 424i 42 11 42 15 41 99
4 ’1 И 26 ?Я 24 >6 23 15 22 46 21 07 2162 21.15 21.14 20 97 20.70 20 44 20.17 20.03 19.89 19.75 19.61 19 47
4^ 22 ~8 18 51 16 53 15.56 14 94 14 51 14.20 1396 13.77 1362 13.38 13 15 1290 1278 12.66 12 5i 12 X I? 27
6 18 61 ММ 1292 1103 11 46 11.07 10.79 10.57 10 39 1025 10.03 981 939 0 47 9.36 924 9.12 9 X
т 16.24 12 40 10 38 10.05 9 52 9.16 Я 89 8 68 8 51 8 ’8 81< 797 7 75 7 53 7 42 4 J1 7 19
к М.69 11.04 9.60 8 81 130 7.95 769 7 50 7. M 7.21 7.01 6.81 661 6 50 640 6 29 6 18 606
«э 1161 1011 8.72 796 т V 7.11 6 88 6.60 6.M 642 6J3 6 03 5.83 573 <62 5 52 5 41 5 X
10 12 П 9 45 8 0S 687 654 630 6.12 5.97 5.85 566 5 47 527 5 17 5.07 4 97 486 4 75
1! 12.23 8 91 7*1 648 6 4^ 6.10 5 86 5 h* 5 54 5.42 5.24 5.05 486 4 76 4.65 4.55 4 44 4 34
12 11.75 8.51 7.21 6 52 607 5.76 5.52 535 5.20 5.09 4 91 4 72 453 4 43 411 4 71 4 12 401
И Я |9 6.93 6 23 $ 5.48 5.25 5.08 4.04 4.82 464 446 427 4 17 4.07 3.97 3 8? 3 76
И 11 06 792 6 68 6X 556 5.26 <03 4 86 4 7? 4 60 4.43 4.75 4 06 1 KA 3.76 366 355
15 13*0 7-0 6 48 550 5 17 5.07 485 4 67 4.54 4.42 4 25 4.07 388 379 169 158 348 .1.37
16 10.58 7 51 6 10 5 21 49| 4 69 4 $2 4 38 4.27 4.10 3.92 3.71 164 J 3.44 3 33 3.22
1? ЮЛ* 7ЛЗ 6 16 5 SC 5.07 4.78 4.% 4 39 4.25 4.14 197 3.79 361 331 141 3.31 3 21 3.10
И 10.22 7.21 6 03 5 37 <96 4.66 4 4 2* 4 14 4.03 1.86 3.61 3 V» 340 3.X 320 1 10 299
19 10.07 7 09 <9? 5 27 4 85 J 56 4.34 4.18 404 3 93 376 1.59 140 311 1?1 111 300 2X9
23 9 44 690 5 92 4.76 447 426 400 3.96 1.85 3.68 3 SO 3 32 1.22 3.12 3.02 2 92 2.81
21 083 4.89 573 579 4.68 4.39 4 18 401 3 88 377 160 <43 i 24 3.15 3.05 295 ? w 171
22 9.73 Ml 563 5 72 4.61 412 4 11 3 94 3.MI 3.70 3.54 3.36 3.i8 1.08 298 288 2 77 2.66
25 063 6.75 < <8 495 4 54 4 26 4 05 3 88 375 363 Э 330 3 12 H)2 2.92 2.82 2.60
24 9 55 656 5 52 4 89 449 4.20 3 99 3 83 3.69 3.59 3.42 3.25 3 36 2-97 2.87 2.77 266 2<5
25 9 ла h.M l.M t д 4 15 3<M 3.78 2 64 334 337 3-20 3 01 2 92 2 82 272 2 61 2 50
26 941 &я 541 4 ^9 4.18 4.10 1.89 373 360 349 333 3.15 297 2Г7 j 7 J 2 67 2 <6 245
Z 9 М 649 5 56 474 4.34 406 3 85 369 356 145 3 28 111 293 2 83 2.73 263 232 241
28 9 2* 6.44 5 52 4 70 4.30 4.02 3.81 365 3 52 1 41 125 1.07 2K9 2 H 2 69 2.59 248 2.37
29 923 64-7 5 28 466 426 318 3-77 3 61 3.48 3.38 3.21 3 CM 286 2.76 2.66 2.56 245 233
50 9 18 6.35 5 24 462 4.21 1 95 174 3 58 345 3.18 3.01 2 82 273 2.63 232 2 *2 2J0
40 1*1 607 4 « 417 <99 3.71 351 335 3.22 3.12 2.95 2.П 250 250 240 2.30 2 :i 2.06 •
60 *49 5 79 4 73 4.14 JJ6 3 49 3.20 з :з 301 290 174 257 2.39 2Л9 2 19 2 08 l 96 1.83
120 8 18 554 4 50 1.92 3.55 1.28 3.09 2 93 2 81 2.71 254 2 37 2 19 ?oo 1 ОЯ 1 87 1 75 1.61
л88 550 172 135 3.09 2.90 и* 2 52 ? 16 2.19 700 1 90 1 79 1 67 1.53 1.36
Таблица П7 (прадолженил}
\v 1 1 2 3 n • [5 1 6 г 7 Я 1 5“ 1 «П 1 12 1 15 1 20 1 L24 1 и ♦0 1 60 120
p -o.WjarOf^s Н 'Ъ F
Ю0 + <404 < 57M + 58594- ‘909 SQXI < 60П f 6I(P< 61&+ 6535* «М1-Г AS7 + 643 €?4C*
1 4b Xg.5 W) 0 9^0 2 OX 2 990 1 999.3 999 4 9994 9994 9994 799 4 999 4 999 4 W5 999 5 9995 999 5 5
1 167 0 14* 5 4 i n IMS 132 8 111 6 1X6 1209 120.2 1283 127.4 126 4 125 Q 125 4 1250 124 5 ;?40
4 4 4 6 MS S6 ’« 44 SI 71 $0 53 4‘>66 49 00 48 4? 48 05 47 41 46 "’б 46.10 45.77 4? 4? 45.09 ^5 44 40
s 47 18 17.12 13 X 31 09 29 75 ?IX4 2X 16 27 64 27.24 26 92 26.4? 25 91 25 19 25 14 24 87 74 60 ?4 13 74 Of
6 35 51 27 00 З’О 11 ^2 20X1 20 <>3 1946 1903 I8 60 18 41 17 94 17 56 17 13 16X9 16 67 16.Ф» 1621 В 99
7 29?5 18 77 17.19 16 21 1552 15 02 14 63 14.33 14.08 13.71 13 32 1293 1273 12 53 12.33 12.12 11.91
8 25 42 IX 49 IS 83 14 39 1 49 1? KA 1? 43 К П4 11 77 11 54 II 19 1ПЯ4 10 4” 10 X in 11 9 92 9 73 9 53
9 22 86 16 X 13 9Q 17 56 11 71 Г 11 1070 Ю 37 ion 0 49 9 57 9,24 FX 8 7? F $5 8 17 X 19 ВС
10 21 04 14 9| II 28 10 48 992 9.52 9 2C 896 8 75 8.45 8.13 <80 7M 747 7.Ю 7 12 6 94
11 I960 ’ 81 11 46 !0 3S 9<X 90S X 66 8 35 к :z 7.92 7.63 7J2 7 01 6 85 Ь68 652 6 15 6 17
12 UM 12 97 10 W 0 6.1 8 89 818 800 7 7! *> 4ft 729 7 00 6.71 640 6.25 609 593 5 4 5 <9
1.3 17.81 12 31 1021 907 Я 35 7 86 749 721 6 0g 6 RD 6 5? 621 5 93 5 78 5 61 5 47 $ X M
)« 17 '4 11 ** 973 8 62 792 7 41 7.08 6Л0 6 <8 6 X 6 13 5 85 S 56 641 5 25 5.10 494 ft 77
15 16Л0 11.34 934 8.25 757 709 6 74 6.4? 6 26 6.OR 581 5-54 52S 5.10 495 4 RD 4.M 447
16 IM? 10 97 9 00 7 94 777 SRI 6 46 610 5*8 $.81 5.55 527 499 4,XS 470 4 4 4.19 4.2) I
17 15 72 It 66 8 73 7M 7.02 7 56 6 2? 5.06 575 558 5 5 05 4.78 4.63 448 4.13 4 18 402
8 15 18 10 39 849 7.46 £M 6 15 6 02 $.76 $ S6 TQ 5 11 4 Я7 4 59 4 45 4 10 4 IS 4 00 1.84
19 15 08 1016 8 28 7 26 6.62 6 18 5.85 5 59 4 19 522 497 4 443 4 29 4 14 1<w 184 3 68
20 14 82 995 810 710 646 602 5.69 5.44 524 5.08 4.83 I 56 4.29 4.15 4.00 386 170 3-54
21 14 59 ОТ? 794 60S 6 32 SV <56 $ 31 5 11 495 4.70 4 44 4.17 4.03 1.88 3.74 338 1 ftX
22 14 33 961 780 681 6 10 5 76 «*4 5 I1» 499 483 458 4 33 406 3.9? 17g 1.63 3 48 112
23 14 19 9.47 7 67 6j69 ft OR 5 65 53.3 $09 489 4 H 4.4H 4 ?1 396 382 1АЯ 141 1 18 in
24 .4 03 >34 7 55 M9 598 5 55 523 499 4M 4M 4 19 4 14 3717 374 3.59 345 3.79 3.M
25 13 M 9.22 74< 640 5 ВД < 16 S.1S 4 0! 4.7| 456 4J1 4Э6 3 79 3.66 ЗЛ2 337 3.22 3.06
26 13 74 9.12 7 36 6 41 xn 5 18 5П7 d 81 4 64 4 48 4 24 199 3-^2 3 5‘* 1.X IB ? MM
27 1161 9j02 7 J7 533 5 5 11 <00 4 76 457 441 4.17 392 166 3.52 1 18 3.23 308 ?
2B 13 50 8.93 7 19 fjs 566 5.24 493 4 69 450 4 3$ 4 11 ISA 360 3 46 1 U 3 18 302 286
^9 13 ’9 H85 7 12 619 589 5 18 4 87 4 M 4 4 s 4 2'^ 405 3 <M 141 3.27 3.12 297 281
<0 В 29 877 70S 6 12 512 412 4 <8 4 19 4 24 400 3 75 3 49 336 1J2 3 07 292 2.76
40 1261 8.25 660 5 70 sn 173 4 44 4 21 4 0? 187 1 64 1 10 1 И 101 2 87 273 2 $7 241
60 11‘>7 7.76 6 r 5 31 4 76 4 37 400 3 87 3 60 3.54 3 3! 304 2 81 269 2Л5 14! 225 2ПХ
820 1’JI 7.1? 5 79 4 95 4 4 9 4.04 3.77 3 55 3.38 324 J 02 178 2 $3 140 2 26 1 11 195 1.76
oo 10 n 6 0] 5 42 4 62 ♦10 3 74 147 1 10 2 74 Ml 2 27 H) 1 9M 1 M4 166 145
40<7 означает 40>3 VI
Таблица П8 Таблица значений ")
X z и X 0.95 0,99 \ г 0.999 Ч 1я X 0,95 0,99 0,999
137 2.67 5,64 20 €.37 0.58 0,88
6 1,09 2.01 3.88 25 0,32 0.49 0.73
7 0.92 1.62 2.98 30 028 0.43 0.63
8 С .80 1.38 2,42 35 0Д6 038 0.56
9 0.71 1.20 2.06 40 0,24 0.35 0,50
10 0.65 1,08 1.80 45 0,22 032 0.46
11 0.59 0,98 1,60 50 0Д1 030 0.43
12 0.55 0,90 1.45 55 0.188 0.269 0.38
13 0,52 0,83 1,33 0,174 0.245 ол
14 0,48 0.78 1.23 65 0,161 0,226 0.3
И 0.46 0.73 1.15 70 0.151 0.211 С.29
16 0 44 0.70 1X7 75 0,143 0,198 0.27 |
17 €.42 П.66 1.01 80 0.115 0.160 0.211
18 0.40 0,63 0.96 R5 0.099 0,136 0,185
19 С. 39 0.60 0.92 ми 0.089 0.120 0.162
(аблнца 119. Критические значения \
распределения Колмогорова:
> 4L)«e
Уроне НК значимости 0.20 0.10 0.05 > 0.01 0,001
4 _ 1.073 1,224 1.358 1,520 1.627 1,950
2 (Ж
ЛИТЕРАТУРА
I Булдык ГМ Теория вероятностен и ма1ема1ическая статисти-
ка - Мн . Выш. 1ИК ,1989. - 285 с
2. Булдык 1 М Статистическое моделирование и прогнозирова-
ние.- Мь ПО ООО ‘БИГ1-С ” 2003.-399 с
3. Сборник задач по математике дли вгузоч 4.3. 1еорня вероят-
ностей и магматическая статистика Под редакцией А. В
Ефимова. - М Наука. 1090 -432 с
4. Сборник задач по теории вероятностей, математической стати-
стике и теории случайных функций Под редакцией А А
Свешникова. М : Наука, 1970 656с.
20ч
ОТВЕТЫ, УКАЗАНИЯ И РЕШЕНИЯ
1. Теория вероятностей
1.1. Случайные события. Вероятность
12. £бо);
/1 - {(•*> J Х'' ~х Ю; х - j < 1.3. Исход эксперимента
«у, - {бракованная деталь появится при r-том испытании}.
О, = |гу|,<у|<у2,/у|<у2ту|,...,сд|гу от,о>4} 1,5. Л-*{появился шар с
четным номером или кратным 3} и т.д. 1.6. г> - {средн 2п собрав-
шихся ровно i человек знакомы вошедшему}.
О. Учесть, что А^В-В. 1.Я. а)у- {выпала
грань, содержащая i очков на первой игральной кости}, тг - {вы-
на ia грань, содержащая / очков на второй игральной кости .
& - Мла.-лл,,-)|1 </<6:1</<б}. Л = ^1гл.,(у, )i +/ = 7 '.
ПЛ)= — =— 1.9. Номера кубиков могут появиться в любом по-
36 6
рядке. Число таких способов появления равно числу перес>ановок
ит 6 элементов: Л’ -6!=72О, Л = {(ЛЯ.Л?2,№3,____________Л*б)}.
/ (Л)- -I 1.10. б) = {«побраны пять лампочек из сорока}, i = 1.н;
и = Все ржнопозможны. А • {среди 5 купленных лампочек 2
бракованные}, 4 = {ft>J. ; = Lw; m = Cj,-C’;
С’,. С?
Р(А’ ~ - = 0.09. 1.11. <у - {отобран телевитлр для пронерки}.
1-1,2...30. А ~ {юД, у-=|,2^, |ак как 5 .’слсвизоров имеют де-
фекты Г(А)~
25
30
1.12. со {десять предприжий отобранных
5
б
тля проверки}, / I,п. л С . А~ {среди лесяги проверенных одно
предприятие, которое ведет неправильные бухт ал герские отчетно-
сти. имеет скрытые доходы}. Л - уу, {. /-l.w; т - С,;
1.13. Q - \f> }. » = 1,л п « , где <у, = {отобрана
|(Х)
210
бригада Hi пои сгроитслей) Л-{бригада состоит из 3 маляров и 2
Г*J • С ’
штукатуров}. /j(^) =—? г12 • Ы4.
и
Лл)=^п 1.16. а) Г(Л) = ^;
С’
rU)=bi
*•»
=t 0.298
«
б) ля)=ёг
' и
1.15.
1.17.
гч i..1204*0- 200 1
10000 10000 50
1.18.
Л^)=
16
600
• 0.027.
1.19.
Л=; выигрыш в первом тираже 1966 юда). Всего выпущено обли-
гаций: 100000000:20 5000000. Р(Л)=- ~0.00188.
5000000
Д-;выигрыш в последнем тираже 19R6 года}. За 20 лег было 159
тиражей, без последнего, и было выпущено 20-9400= 188000 выиг-
рышных облигаций. Обшсе число облигаций в последнем тираже
равно: 5000000-{ 159-9400)- 3505400. Р(Я)= - « 0.00268.
1.20. Q = = 1.n{, о = набраны три цифры}, и = Д5( - число
всех наборов трех цифр равно числу трехзл смешных упорядочен-
ных подмножеств из 10 элементов. А-{набраны три нужные циф-
ры}. Множество 4 состоит из одного элемента
и
1.21. П - /z-l./z), гд - {выбор пяти фирм}, число элементов 1)
определяется как произведение выбора пяти ticmchtob из остав-
шихся элементов исходного множества п = с ' Cf, С,’ G* =
2(У
(5’У
Для определения числа элементов множества А представим все
множество 20 фирм в виде двух множеств А = .£’>{.гу«' н
А = . ,о;|], где со'фирмы имеющие товаро-
оборот свыше 10 млн леи ел а ч>'.. / ~ 5,20 другие фирмы. Число
элемешов множества Л равно т. - С‘„, С' С'„С',, число мемен-
равно m- См. • С4 ( ,7 • ( t (а • < , • < л ( ,
Р(Л) —, />{«)-—. 1.22. О Lj/ = l.n}.
fj - (выбор шести
фирм для пров^ки ). п Cl
г(.1)= -
28
где А {проверены г.ер
?П
rhc шссгь фирм}. 1.23. ,4-{замок открыт},
= ~ 5*0.00013 1.24. Q UJ/ = 1,mI, <ц-{на-
6 6 6 6 6 6 • *
ораны ।ри цифры}, п = И, ( = 720 Время 7} 720-20 - 14400
(сек). {вошедший открыл дверь на один час). -3600сек.
ы и Г 3600 I I । z—I
МЯ)- = -т 1-25. П Ьц k = I, и.. 6) - {пассажир вышел
1п 14400 4 '
на каком-то этажи} 1 исло способов выйти 5 пассажирам на 8-ми
этажах л-5*. Я {ни один из пассажиров не вышел на 2. 3 и 4 эта-
жах}, чис ю способов m, - 55, {трое пассажиров выйдут на девя-
том паже}, при этом каждый из оставшихся гвоих может выйти на
ikMJom паже, т2 - I 2h; O{rcc пассажиры выйдут на одном эта-
же). Г(4)-^--1-; Г(С) - ± 1.27.
'•J \ J »р
9
О~{точка разрыва телефонной линии удалена от точки А не менее
9
чем на 1 км}, P(D) 1.2Я. А {студенту придется ждать поезда
метро 10 сск.}, Р(А)~— 1.29. Л-{одном} из пос тавщиков придет -
I о
ся ждать освобождения рампы}. Р<Л)-0.121 130. 4~ {автомобиль
2
проехал перекрссток без остановки}. Р{А)~ - 1.31. Пусть х и у
мометтты времени приходя автобуса и троллейбуса. Областью воз-
можных значений х и у является множество точек прямоугольника:
0<х< 18 и 0< у < 6, г.к. если д прон<во.1ьныи момент времени:
()<х<18 и моменты прихода автобуса 0. 6; 12: го моменты при-
хода троллейбуса: ,i;y*7. где 0<у<6. Л={первым подошедшим
транспортом окажигея автобус}. Благоприятствующие значения г и
I появлению события А удовлетворяют неравенствам ()< у£3.
у<х, г<6. у>7^х<18; при у>3. у<хт х<12 или
о т 81,1 1
<• 6 «к 12*3э- -3
> + 7<*<1Х, (рис I). Р(И)= ----2---=1£±
6 IR 216
R {ав:об)с или троллейбус подойдет через три минуты). Благо-
приятен ву ни диг значения х и у появлении» событии Я удовлетвори
ют неравенствам О < у < Т. 0< х < г, а при г> 3 у 3 д < у; или
212
3<л<6, 9<л<12. 15<x£lh. у * 7<х< v + IO. (рис.2)
_3-3-6+3-3+2+3 73
П ’ 5...« >08 “108
I I“
Рис I
Рис 2
R
133.
ла в куб} П)пь К pa лнус шара, а ребро куба 7 or да И. - — яЯ1.
2R
U- 7
-Д-л1
Р(Л)= зуз
-rtf'
1.41
495
= 0.495
1000
1.40. И= —
1000
р-0.246. 1.43. р ® 0366. 1.44.
— = 0.03 1.39.
500
. IK» —-0.7‘
1000
р в 0,067 1.45. р - 0.0001 1.46. р - -. 1.47. р = -
Свойства вероятностен. Условная вероя1ностъ. Независи-
мое! I. событии. Тепремы сложения и умножения перо
ятностей
2.2. Прсктранпы! «1смснтврных собьпнй определяется еле
дуюшими парами (АЛАЛ. (Л,ЛЛ; Л~{в семге есть дс-
влчка^ Н {в семье две девочки}, Я.Л*!в семье две девочки, сс и
211
известно, что уже сеть девочки}, )- —т—у = = ~
Р = 0.6 2.8. р -8 0.64 . 2.9. р =
р = - 2.13. р=—. 2.14.
3 21
24
2.10
20 19
-* 4
р = 0.9785
18 _ 57
23 " 115
2.12.
2.15.
Л={ наудачу взятый кинескоп имеет диагональ 72 с.м): А - {наудачу
взятый кинескоп имеет диагональ 51 см|; R (кинескоп отправляет-
ся на экспорт}; Л/?-{наудачу взятый кинескоп имеет диагональ 72
см и отправляется га экспорт); .4# = { наудачу взятый кинескоп
имеет диагональ 51 см и отправляется на экспорт}. АВ+АВ = В‘,
P{AR)+ Р(йв)- Р(В), Р(4В)= Р(В)-Р(АВ) »
= Р|В|- Р(4) Р(Л)-0,5-0.7 0.4 = 0.5- 0,28 = 0,22.
5_А.А= Ж1 1 *
Р 10 20 К' 20 2*4 2 4 4 8 8
111 _ 11112
326 ' 3 3 339
р = 0,95 0.1 ♦ 0.05 0,9-0.14 2.19. р- —
10 9 8
р = 0.95 0.85- =0,8075. 2.21. р, = 0,20 + 0.15 = 0,35;
р, - 0.10 ь 0,30 - 0.40; Р) = 0.20 + 0,25 = 0.45;
р, - 0Д0 ♦ 0,10 + 0.15 = 0.45; р, = 0.25 I 0.30 = 0.55. 2.22. а)
р = 0,418; 6) р = ОД52. 2.23. р = 0.99. 2.24.
Р = > PiPi-P)* PiP'Py 2.25. Р-0,15. 2.26. а) р = 0,15; б)
2.16.
2.17. а)
2.18.
— 2.20.
24
I |9
Р -- 0.6.2.27. б) р = — ; в) р - „ . 2.28. а)р- 0.56; б) р = 0,15.
2.29. Могут существовать 0. 1, 2. 3, 4 фирмы соответственно с вс
11 4 9 4 4 у л
роя гное гями , . —.—.— И - (к концу второго промежутка
32 32 32 32 32
времени все фирмы ликвидированы) А - (фирма ликвидировалась
к концу первого промежутка времени}; А. = {фирма работает с
прибылью к концу первого промежутка времени). Л -{фирма
раздели шсь на две к концу первого промежутка времени};
/?, (фирма, работавшая в первом промеж утке времени, разори-
214
лась}, В - (фирма, отделившаяся в
разорилась }, / = 1.2 Тогда
Р = 1-(1-О.«Х 2.33. р = 1
первом промежутке времени.
А = Л| 4 Л • В + Л, В, В,.
2.31. p=l (I 0,03)' . 2.32.
т - п
Формула полной вероятности. Формулы Байеса (теорема
гипотез)
3.2. Л {случайно выбранный из парши транзистор будет
признан лефсктным|. = {транзистор является дефектным);
Hj - {гранзисюр является исправным).
Р(а}~ Р{Н.}Р(АН,)-> 1\Н,)Р(А',Нг)~ЩП 0,95 + 0,9 0,03-0,122
3.3. р-0.105 3.4. А = {вторая игра будет проводиться новыми мя-
чами}; //, = (в первой игре были использованы новые мячи),
/72 = (в первой игре были использованы старые мячи); Я, ={в
первой игре быт использовал один старый и один новый мяч).
Г\А 1-0.445. 3.5. А {студент сдает экзамен); Н, = {студент знает
билет); Н = {студент те знает бизет}: Я,-{вызван Иванов или
Петров), В, = {вызнан Сидоров); В - (вызван отличник);
Н = В, А + В. А + В, А; Н} - В А+В А,А = Н А^Н- А
ПН.^Р'М Р|^)( ^,).А
I' jv tv -М1 I’’ ***•
P(WJ=-2
1 10 30 10 30 «0
=—•0.85 4—0.1 = 0.763 3.6. f>(A)-- -4-• 0 + - О-2. 3.7.
60 60 3 3 3 3 9
4 - (100 микросхем исправны), Н =- (/ микросхем бракованные}.
Р(И)=Р(Я,) Р(Л|//,)- ЛЯ:)-ф|//,) =
|=О,1.2.3 Р\Н.}-Р[Н}-Р{Н,} Р(Ну}-~. АН - {микросхе
4
мы признаны исправными, при условии, что среди IПСК) имеются /
бракованных). /-0,1,2,3. Р(л|Н„)=!; Р[^\Н,]
f ’too x-«l<4>
Р(Н|Л)=0,29 3.8. .1={все 100
1 IOOG * 1ОЮ
215
шмпочек исправны}; Н {число лампочек содержащих брак рав-
но 1}. 1 0,1.2,3,4.5. г(л)»Г(«.) )♦/•(« ) )• г(Н2) Р{а\Н )»
4 tin,) p(A\Ht)+P(H,)- P\A.H,)t PiHj ^Н,)*о.78.
Л-4*.)-
Ц(Н>
3.9. Рр) = Р(Я,) р(л|й,)4 AWJ ГЦ//.)-0.96 0,98 ( 0,04 0,05-0,908
3.10. р[ I)-?(//,) Н<н, )t Г(Н.) Ни1/; | 0.75 0,005 > 0.25 О,OS 0.02375
3.12. W,)-r(f/J r< 4 ^,)-0.R 0.01 + 0.2 0,7 0,148.
3.14. F(4)^ 0.5236
3.15. А - [обнаружение самоиста): W, - [самолет находи ся в /-том
районе}, 1-1, 2; Р(Я,) 0,7; Р(// )-0,3 Допустим, что в первый
район поисков отправлено т Бертолетов, тогда во агорой будет от-
правлено (5-от) вертолетов. Х|Л7, = {самолет обнаружен, если он
находится р 7-том районе), 1-1.2: р(л|Н()-1 (1 0.3)",
р(ия)=1 (I 03/". р(л)=0,7(1 (I 03D+030 (1 0,3)^)-
Нужно определить т так, чтобы вероятность Р(Л) была наиболь-
Q dP(A)
шеи Вычислим производную:
dm
= -0.7(1 0,3)" In 0.7+03-0,7* " 1п0,7 т-|и0,7(0.3 0.71 ’-0.7-*). Пола-
гая ——о, приходим к равенству: 0,3 0,7-0,7" 1-О или
dm
0.7“"-0J0.74, т - J * г 4 В первый район нужно напра-
nirrs 4 вер' пле д Р(Л)»О,74 3.17. р* 0.337 3.18. р - 0,429 3.19.
0.47. 3.20. Я,. 3.21. р-0,92. 3.22. п -0.59. 3.23. р- 0.146
3.24. А {взятая наудачу пара обуви .доброкачественная}
Н - (выбрана партия с доброкачественной обувью}; h, - [выбра-
на партия с недоброкачесгненнон обувью) Р\Н )-Р(Н^)
) I, Тогда по формуле полной вероятности
тп 1 . 13 7 п
1 (Л) 11^ . Посте первого испытания вероятность гою
что партия содержит недоброкачественную обувь, равна
216
1 3
2 4 3 n
- — . Ркр< ятн«1ь того, что партия
8
содержит доброкачественную обувь, равна
, , 1 I
й 7 ‘ 4 _ _
Г(Н Л) ---------;----=т— - ~ Введем событие В = !при ВТО
' 1 ' Р1А) 7 7
р м испыт ании пара обуви окажется недобр «качественной . Но вс-
роятнссП! । ине с> //, и Я2 найдены ранее и они равны Р{И,}-
7
В(н )~ _ Кроме того M&jW, 1 = 0, г(я{Н|)=—. Тогда
4 fl / 1 3.25. р = 0.6 3.26. Г 0,4, 3.29. р~~.
7 7 4 28 Г 7
3.30. г-—.
II
Случайные величины
Дискретные случайные величины
4.2.
Л( 0 1 2 3
Г. 0,2 ‘ 3-0,8 0,2- 3-0,81 0,2 08'
0. если г < 0;
0,(ЮЯ если 0 < * <. I;
Г(г) + 1о.008+0_Жссли1-о<2.
0,104 • 0,384, если2<х53.
0,4X8 + 0,512-1 ст иЗ<х
V - 0)-0.7 0,? 0 ? 0,008;
/V -1)-0.И О,?4 ( 0,2 0.8 0,2 0,2 0,8- -3-0,032 0.096.
Г\Х' 2) 0.8 0,8 0.2т 0,8 0,2 0,8 + 0,2 0.8 0.8 3 0.128- -0.384.
р(Х--3)-0,8 0,8 0.8 = 0512 AflAfi o 0,08 + 1 0.096 + 2 0.384+
+ 3 0.512 -2.4 ;
217
Г)(х}-О’ 0.084 I1 0,096 + 2’ U384 +3’0.512 -2.4’ 0.48;
^4ХИ),69
4.3.
гг 1 3 4 5
р. 0.2 0.8 0.2 (),«- 0,2 0,8J 0.2 0,8* 0,8+ 0,8 0,2
4.4. Л/(Л)— I 0.1 i 2 0,90.1 3 O.9--0.J + . 0,9' '• 0.1 -10;
0,1
сСМ-л^х’)-
-(Л/(А)Г=Г CJ-»2’ 0,9 0.1 *3 •Ц‘>: O.t+.. -n O.9-’ 0J+ -(luf9 -TO-
O.I-
4.5. X c |0.1.2.3;4|,
>.| о 1 2 4
0.25 0.125 | 0.0625 0,0625
A = E(A =xj =
p(1 p] для i - 1,2,3,4,
(1 p) для i = 5,
iмр - вероятность светофора задержать автомашину./) - 0,5
0 1 2 3 4 5
Р. С^б’5 С । z’* Н ’-W CiC; С’.
с5 UI<X С*' С G-л 4. 100
4.7.
х. 100 30
Е 0.65 0.35
I ПО 0.65 ♦ 30 0,35 - 75.5 (дсн.ел.)
4.8
X, 0 । 2 3
G’ с; ед с;_ ед с С
218
О
при » < О,
_1_
285
1 24
при
0<л$1.
25
285 2S5 2Я5
25 120 145
285* 285 " 285
145 <40 ,
1285 285
при
при
при
4.9. Л, {отказ А,-блока}, г-1.2.3,4 А’ - случайное число испы-
таний.
1 । 2 3 • • • - п ы
г, 0.4С8 0.125 0.038 (о,6 0.8jr' 0,48Ч । ...|
Р(А =1)= /44 + Л .4,4)- Р(4)+Р(4Л-А,)=0,4 + 0.2' =0.408
Г(А -2)-Г^ Т 4 4)г(Л,4Л, 44)=0.6 С.8' D.40S гО.125
Р(А -3) = (0.6 0,8;7 0.408 «0.038 и г.д
4.10.
•*< 0 1 2
Р, Q Q. Р Q. "Л р, Pi
4 11.
л, 0 40 70 250
F, 1 - 93 4 *> 1 —
100 100 100 100 1
4.12.
Случайная величина А зримо значение ранное I, если с первой по-
лыней замок будет открыл. А' -2. если первым ключом емок не
откроется а вторым будет открыл и л.л 4.13. А - {средн 10(1 пропс
репных банков нет банков с государственной формой собс гвеино
епф /V)" £ {ере®*
Цо*
100 проверенных банков ко<я бы
один t негосударственной формой собственности}; И (среди 100
219
проверенных банков вес с государственной формой собственно-
С*
стн}, F(#) = l Ру?)=1 - —тгг Среднее число банков с госутарст-
ИЖ)
венной формол собственности равно математическому ожиданию
Z’1' <••••' /"1 у»» у« Z-IU0
м*1-
*" 1№ ''UX1I *- iooii »- i.joj
4.14. Л' возможные выигрыши в ден.ел
V(x) = ( 11 — -2 - = - (дсн.сл.). Если Иванов будет заключать
4 4 4
акое пари мною раз то его выигрыш составит r среднем 1,25
ден.ед. на одну jtrpv
4.15. 0 1 2
Р, <1 С1 и12 С: i-и _£1_
Закон распределения дискретных случайных величин
5.3. 0 1 2 3 4 С,0002
А 0,6561 0,2916 0.04Я6 0,0036
фг=о) -0.9\ р(А _1>- G |>,1-0,9\ Л X - *2)— С‘ 0,1г 0,9? и т д
5.4. а) КО)- ”; Л 243 б) Р(А'>2)= —; в) />(3)- —; 243 И ' 243
ОД(А’> И 1,2 << р “атрыв в цепи произойдет, если иерыирит
хотя бы одна лампочка. Вероятпостт. равна Р = | 1 |,9 ~ 0,6513
0 при г <. 0; 27 — при 0<л<1; 125 5.6. PfX > 2)-ь0,663 при 1<х <2,
117 при 2<xS3; 125 1 при 3< г
5.7. M-V) 0.3; £|(А)-0,2Я5. S.8. Л/(Л)-О25. 001-0.2375,
о(А' I = 0,487 5.9. а) Г{Х < 2)- 0,24. б» /V >8) = 0.05
220
510. Р(5)-0,147 5.11. P(5) = 0,10l 5.12. PJ6H 0,0038.
5.13. P:nf {100)^0,051 5.14. а) Д(2)т Д(з)+ЛИ)" Л(5) =
= 1 - (Р,(о) + ps(l)) - I -|0,9’ -г с; + 0,1 - 0,4’ j * 0,0Х 1, б)
/*(2|-С?-0.15’-0Л5*0,057. 5.16. л>59. 521. Р= (Лл- а)
1И'
Р(Л) = ^ с ’ *0.175; 6) P(fi)=P(m>5)= =1 p(wfi5) 5.22.
Р(Я)=О.С18; /*(д)= 0.092. (Р(Л) = ^-е’\ Л=—=2 (вызова в
от’ 60
сек.)). 5.23. 2 опечатки с вероятностью р ~ 0.251 5.24. п> 300
5.25. Р„(^<;3)-Гхв(О)|Рж,(1)^Ря>(2)+Р>кО); л-.100 0.01-3
PjJffl 5 3) - - 3 е ’ + -е ’ а —е-' + - с’’ =е’[ Ь 3+ -4-\ 0,М7.
О’ 11 2! 3' 12 1)
5.26. в=1000 0,004=4.
Рию(т 51 Р}'& (0)+ 0)^»(2)«^™(i)+Cx.W< Р1 ок (S)
р
5.27. а - 1000 0.001 = I. ^(3) = €* я 0,061 5.28.
а = 5000— -ю
500
I0"1
**0.Ч5.
±5 Л!’
5.30. а) X, 1 2 3 ... к . •• О) т{ -
Д 0,16 0 128 ..4 0.8' 1 0,2 ...
5Л.а) X, . 1 2 3 • • • к ... 6) /ис -
Fn 0J_ 0.09 0.081 .. « 0.9‘ ' 0,1 •"
5.33. 1>\ А) - С И- * t 0,1 Я1 534. р - 1 - 0.075 0.925, а в а
рж неси гон что дегапь не стандартная, р вероятность того.
что деталь стандартная 1-р’?0,05: р‘ ь 1-0.95-0.05;
0 025' < 0.05 ;
I г. 0,05
In 0,925
211
Непрерывные случайные величины
О при ж < 0;
63. р(х)--1ссвх при 0<льу;
О при л > —.
0 при ж < 0;
6-4. р(х)= 2со$2х при о< rs—: 4
0 К при п X > —. 4
6.5. Л£Г(0=1; П(А')~0,47. 6.6. £>(А')=-. 6.7. С - ;
3 2 2
_г •
М(*)=0; D(X)- —2 6.8. 2"ха. 6.9. М, <т; Л/С«1.18ег.
2
— j Ли.
6.10. .W, = r, I . 6.11. Закон реннобсдрс много треугольника
0. х<, 5;
1 .-N 5 5J Г(с)=. &12L. -5<xso. 50
0. Н>! 1-(5 0<<XS5, 50
I. х > 5
Законы распределения непрерывном случайной величины
7.2. Р(0 < X < 21 0.6.73. /'{0.02 < А < 0.1) - 0,6
1П
7.4. I) Л. »], ,<1СЮ - 1
к V37 . V3 V3
2) г! О < Д' < 3 V /•(1 ?° I - Г(о)- —.
к V3j (s'lJ 2
0 при кВ. 0 пр4 л < 0:
7.S. р(.,)- при 0<л<10; Г(л) = при 0<к1С. 10
0 при х >10 1 при х>10
VI A U5; Л(А- 12 3
/’(7 < Л < 10) = I 0.7 0 3 7.12. р - 0.0028. 7.13. а * 2,942.
7.14. /и = 15.39; <7 = 3,26. Воспользоваться формулами-
Р(А >12) 0.15
16,2 п; j
к <7 ।
и /<¥>16.2)= 0.40; Ф* -0.15 и
= 1 0.4 0.6 7.15. /И(А)= 1.84. Найти гг из равен-
ства Г(1.82 < А <1X61 — 0,999 Воспольюваться форм} юй
/’(|г-^<0.01) = 2Ф’ -1 = 0.898. 7.16. /•(» - „||<2)-0,95.
.. J fi\ 6 2 3 2
। с. 2Ф* - 1-0.95 Ф‘ - =0.975: ‘=1,96. сг J.01;
ко-, w 7
/’(КХ) < А'< 130)-Ф" 68% ак-
ций имеет iet> н пределах от 119 то 121$. 7.17. р-0,75:
д-=1 0.75-0.25;
141 200-0 75
ф t=—
(V3W O.75 0.25
/‘(1400 < 180) - Ф
-0.94R4
1X0-2(111 0,7<
<7200 0.75 0.25
J4P
1 L’’ пл.’М
1-1
7.18. Воспользоваться формулой' Р{ г т|<2>)-2Ф* —1-1.. Из
\<г)
равежтна 2Ф*[ —j-1 = 0,9973. находим 5 ~0.3 и интервал
|< -10|<0,3,т.е. 917<Л <103.
7.19. р = 0..8; <7-1-0,8-0.2.
Р(70<Г<86) =
Кб 100 0,8
7100 0.8 0.2
70 -100 0,8
7100-0.8-0,2
7.20.
Р(А <!00%) = /J(0< X < 100)-ф’--
-Ф*| J00 1-0,5; 05 100% = 50%
I 9 )
предприятий не выполняют
мм»,. р(|ц1<л<151.>=ф-|Г12-^;-ф-''-И191№]=
1 - 0,8685 = 0.1335. Следовательно, 13,35% предприятий выполняют
план < т 110% до 150% 7.21. Объемы рса тюамми заводов Г\ и F?
ЗА и 2JG F-3A’, ь2Л‘:; М(Г)«ЗМ(Л'.> + 2М<Л,)=
— 3 6000т 2 1 5000 - 48(мЮ; ст(к’) = 3-30-+2-90 = 270. Прибыль рав-
на; 1 -10000. Нужно найти
Y >38500 + 10000 - 48^00
.Y48500-480001 , Г 5001 ,
Фф ------------ «1 Ф* — *1
< 270 ) 1 2 ,,
вероггностъ того. что
F(r>l20000)-=-O*(-Hr)-
0,9676-0 0124.
7.22. ао-мо-о.«» ] ф/ П^п.0.03 )
t^OO 0,97 0,03 I к V50O 0.47 0.03 J
7.23. Л’ ошибка оирс;ктенмя прибыли. Af(A )-O; (7(Х)-10
15)-ф
b o
I. 10 )
Ф*(О) = О,О392 0.5-0.4392
7.24. Г(|Л'|<1)-2Ф* “j-1 0-9544. Следовательно. 95.44%
tодних легален «топ а», швастся станком автоматом
<
22<
7.25. М(*)=3 (Р(|Л|<3,45) = 2Ф* -1-0,7495
Л/(У) - л P(jA'|< 3,45)-4 0,7495*3). 7.30. Лф)= * , 10=!,
А л
Л = ^=0.1. Нл)=(|-е -(l-eJU5)=e’ei-e " *0.39.
Г(5)=!-(|-г0”’)=<’’* *0,135. 733. I) Р(4)-
= <* ’ е п’*0,0112.
- ‘ <1 • • । I 1 . ’ - 2г ; 1 = 01976
3) Л0- - l-(l -e-°w) (1 с ’♦’)*! -0,7912 -0.2088 .
7.34. a) Р(л) 1-е ,б)Ля)= I е** ; в) Р(С) Л(Л) р(в)
Присльныетеоремы и законы больших чисел
8.3. Р(Х > Ю0)< уЬ_ - 0,15. (Восполыоватиш форм)лой (8.2)).
8.4. Р(Л <!$)- =1 Р(А'> 15) *0,667. 8.5. Воспользоваться фор-
м)лами Р(Х >g)s М-^ ); Цх )- Л/(г')-(А/(*)Л
Л
м(хг)=в(х)+(м(ху?.
И X > 150)= 10400 *0.46.
225СН
Р[Х > 200)= * 0.26. 8.7. Лф'Ь ир ИО 0,25-200;
40000
D(X ) = npq = = 800 - 0.25 0.75 = 150 , 5 = 250 - 200 = 50.
Р(Л-2О0|<5С)>1-^'! = 0.94 83. Haimi М(Х)-пг;
/ЦК)“«/'«/. г -250 АДА) и восгол1.к'ватьсч формулой (8.1).
8.10, Найти M.Y) £ ‘7 (W))’’. Г-0.2 и
жкгольэовагтыв формулой (8 1) 8.14. р-о.8. и =10600;
7=1 0.8 =0.7: f 0.0J. В<к';ю:1ьчова1ься формулой:
г. — - f ' с > I 1 . 8.16. г -3 к 500; С = 6 BixnoiblaMn
1л . . пг1
ся формулой иэ теорем и Чебышева
225
j I 1 * J I (
и S-v —г Я1К Вос no. it. Viiia г ься фор-
\«T7 1 ' W
мулой it« ieopt.Mii Чебышева:
C-25. ix сг(Л')<5, тогда /2(Л')<5а =25; г = 2
1-^-S 0,95 ^>« = 125. К.21. Р«г>(1400)=-1 ^х), где
п/* у/п/х/
т—пр 1400-2400-0,6
д= - -, г-1.07
yjnptj /2400-0,6-0,4
Р.4,/1400)* (1,0041
8.22. 1) Рк(50)« - -L=-------у
/100 0,512 0,488
2)/ия;июЬФ-| .|(,"-|Р0'°5IJ I
I /|СК> 11,512 (1.4ЯХ I
4У- 1.67) c.^lX'7)-0.0989
*0.516.
8.23. а) р(И70^К<1500) = Ф
;о .oogsu ;
/100 0.512 0,488 у
51-100 0,512
I./00-0.512 0.488
1500 2100 0.7^ л .'’147O-2.OO 0,7'
, -Ф* I * *
/2100 0,7 0,3 I /21 НО-0.7 (1.3 f
«0,4236. б) Р, ,,.(147О. 2100)*0.5; в) Р2<х,(0; 1470)«0,5.
8.24 Рм,(31;60)«(1,9066; Рм(30;42)*0.8858 8.26. л-100.
8.27. п -177 8.29. Веспелыоиагъся формулой:
---р <« |»2Ф* г,
I. Наименьшим интернат равен:
482^т<498. 8.30. 49875-50125 8.31. £ * 4.16-1(1 '.
833. Вскпольтовагься формулой: Р р
< п
834. Л„Г1(87О,92О)- Ф
п находим из равенства с-.1- - 2.96, п неуда п - 1117]
I Р<1
| <>20 1000 0,9
I /ГОСЮ-0.9 0.1
8.35. В'ч ( 1ьм'ваться формулой:
’ 870 10061-0.9
^/Гооо о.ч 0.1 Г
' . С
м<г >1--------г, где
FJ Г
( “81, е 4 п находим из неравенства.
81
>0,95, их 102.
п 16
1
??Л
8.36. 459 мест, или посетители приходят па, иии и 450 мест, если
noct (Hieтн ирмходхт ио одному 837. /jjo(25:250)* 0.0314
1П I ।
8.38. Из неравенства <0.01 накопим т. 95<т<105
1500 5J
Рю (95.105)-ф* й 105 - 50П- 5 Ф* 95-5001 « 0.4246.
Jsoo 1 4 \ 5 5 J Jsoo 1 4 5 5}
а1-0.5 = 0.5:
8.39.
4<J-40A
& J
Г(Л)-Ф*| Ф*| ^-^ко.8858. 8.40. п-753.
I х/40 J V V40 J
227
Учебное издание
Булдык Гсор» н»1 Митрофанович
РУКОВОДС I ВО К РЕШЕНИЮ ЗАДАЧ ПО ТЕОРИИ
В Г РОЯ I HOC 11-1 И М А ТВ МА Г И 4FC КОЙ С IА ГИС ГИКЕ
Для практической и самостоятельной работы
студентов экономических специальностей
Редактор Д. К. Васильев
Компьютерная нередка А В. Липницким
Корректор Р А Кузнецова
Подписано в печать 24.08.2009.
Формат Ы)х90'16. Бумага «>]>cciHiiw Гзрннтура «Таймс».
Псчя ъ офсетная Уч. im л. 13.7. Уел печ. и. 8.0.
Тцраж 10U0 экз. Заказ Ks 557.
СХЮ «ФУАмнформ»
ЛИ N' 02330/0549451 or KOI 7009
У.| Кульман. 2 220. 220013, Минск
Озпечапшо и пшпгрзфии ПЧУН гЬизнссофсет»
ЛИ К 02330'0150481 от 25 02 ’009
Пр-т Нсзарнсимостн. 95 - 3, 220043. i Минск.
Пе вопросам гриобре ения книги обретаться по тел г Минске
1X 017) 292-7 Ь1
I mail: 11 lAinfbrmCarut by