'.V ?*¦?
-¦ ¦ •• "
С
V
к
* v
о
" ^К
Т Б.
3 AT- «9 •

Б. ДЕЛОНЕ и О. ЖИТОМИРСКИЙ
ЗАДАЧНИК
ПО ГЕОМЕТРИИ
ИЗДАНИЕ ЧЕТВЕРТОЕ
БИБЛИОТЕКА НМУ
МАТЕМАТИЧЕСКИЙ
КОЛЛЕДЖ
ГОСУДАРСТВЕННОЕ ИЗДАТЕЛЬСТВО
ТЕХНИКО-ТЕОРЕТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА 19 4 9 ЛЕНИНГРАД

11-3-1
Редактор В. А. Калакуцкий.	Техн. редактор Г. А. Негримоеская.
Подписано к печати 10.11 194S г. 1В печ. л. ?0,2' уч.-изд. л. 42 600 тип. зн. в печ. листе.
А-11457. Тираж 25 ССО вкз Цена книги 7 р. Переплет 1 р. Заказ J* 1365.
2-п типография Издательства Академии Наук СССР
Москва, Шубинсний пер., д. 10

Задачи на построение
Пропорциональные отрезки в кругах
Задачи на построение .
ОГЛАВЛЕНИЕ
Предисловие ко второму изданию	7
ЗАДДЧИ Номера	Стр.
Планиметрия задач
Отрезки и углы	 1—4	9
Соотношения между сторонами и углами треугольников . . . 5—11	9
Сравнительная длина объемлемых и объемлющих	12—17	10
Перпендикуляры и наклонные	18—22	10
Параллельные линии	23—25	11
Сумма углов треугольника	26—34	11
Параллелограммы и трапеции . •	35—44	12
Круг	45—66	12
Замечательные точки и линии в треугольнике	67—S3	14
Задачи на построение	89—141	16
Подобные фигуры		142—159	20
160—170	21
171—182	22
183—ISO	23
Площади . . ."	 . 191—203	24
Применение площадей для доказательств	201—210	25
Числовые соотношения в треугольниках и четырехугольниках 211—252	26
Правильные многоугольники	25J—266	28
Измерение круга	 .... 267—272	29
Начала геометрии кругов	273—605	29
Стереометрия
Задачи на доказательства и построения
Прямые и плоскости и многогранные углы	106—524	34
Куб	325—328	35
Параллелепипед	 	329—332	36
Правильный тетраэдр . . 	 . . 333—336	36
Произвольный тетраэдр . ..... 557—348	36
Правильный октаэдр	 	349—550	37
Правильные додекаэдр и икосаэдр	351—354	38
Задачи на сжатия (растяжения) и сдвиги пространства . . . ?55—363	38
Цилиндр и конус	364—373	39
Шар 	374—389	40
Задачи, в которых соображения стереометрии применяются
для решения вопросов планиметрии	 . ?90—395	42
Задачи на вычисления
Перпендикуляры и наклонные 	396—?99	42
Параллельные прямые и плоскости и перпендикуляры, опу-
опущенные на плоскости	400—411	43

Номера
задач
412—413
414—426
427—433
434—435
436—451
452—459
460—463
464—468
Стр.
44
44
45
46
47
47
48
48
ОГЛАВЛЕНИЕ
Трехгранные углы
Куб
Правильный тетраэдр
Призматоиды
Правильные многогранники
Цилиндр
Конус .
Шар
Более трудные задачи на доказательство
Некоторые задачи из общей теории выпуклых многогранников 469—478	49
Задачи из теории разбиения пространства на одинаковые
параллельно расположенные выпуклые многогранники
(параллелоэдры)	479—496	51
Задачи на прямолинейные преобразования плоскости и перспек-
перспективу ... 	 . 497—505	53
РЕШЕНИЯ
Планиметрия
Отрезки и углы	 1—4	55
Соотношения между сторонами и углами треугольников . 5—11	56
Сравнительная длина объемлемых и объемлющих . 12—17	58
Перпендикуляры и наклонные 18—22	61
Параллельные линии .... 23—25	62
Сумма углов треугольника . 26—34	63
Параллелограммы и трапеции J5—44	67
Круг	 45—56	71
Замечательные точки и линии в треугольнике 67—88	84
Задачи на построение . -.» 89—141	92
Подобные фигуры . . 142—159	112
Задачи на построение	 160—170	122
Пропорциональные отрезки в кругах 171—1S2	127
Задачи на построение . . . 183—190	133
Площади	 . 191—203	143
Применение площадей для доказательств	204—210	150
Числовые соотношения в треугольниках и четырехугольниках 211^-252	156
Правильные многоугольники . . 253—266	179
Измерение круга	 . 267—272	186
Начала геометрии кругов . . 273—305	188
Стереометрия
Задачи на доказательство и построения
Прямые и плоскости и многогранные углы . 306—324	209
Куб	 . . 325—328	214
Парачлелепипед . . . 329—332	215
Правильный тетраэдр 333—366	216
Произвольный тетраэдр 337—348	218
Правильный октаэдр . . . . 349—350	222
Правильные додекаэдр и икосаэдр	 351—354	223
Задачи на растяжение и сдвиги в пространстве . 355—363	226
Цилиндр и конус . 364—373	228
Шар 374—389	231

ОГЛАВЛЕНИЕ	5
Номера	Стр.
задач
Задачи, в которых соображения стереометрии применяются
для решения вопросов планиметрии	 . . 390—395	239
Задачи на вычисления
Перпендикуляры и наклонные	396—399	242
Параллельные прямые и плоскости и перпендикуляры, опущенные
на плоскости . . . . . . 400—411	243
Трехгранные углы . 412—413	248
Куб	 . 414—426	249
Правильный тетраэдр . 427—433	258
Призматоиды 	 434—435	263
Правильные многогранники . . . 436—451	265
Цилиндр .... - . 452—459	272
Конус ... . ... 460—463	275
Шар . . . .... 464—468	277
Более трудные задачи на доказательство
Некоторые задачи из общей теории выпуклых многогран-
многогранников .... 	 ... 469—478	281
Параллелоэдры	479—496	289
Задачи на прямолинейные преобразования плоскости и пер-
перспективу . . . 497—506	297

ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
Чрезвычайно важно поднять геометрическую культуру кон-
кончающих нашу среднюю школу. Для этой цели необходимо
иметь достаточно полный сборник геометрических задач, осо-
особенно на доказательство и построение, а также и на вычи-
вычисление.
В основу предлагаемого нами сборника положены два прин-
принципа: во-первых — давать по возможности только задачи, имею-
имеющие хоть какой-нибудь принципиальный геометрический интерес,
т. е. такие, которые выясняют существенные свойства плоских
или пространственных геометрических фигур, и, во-вторых —
не давать задач одинаковых типов, т. е. отличающихся лишь
численными или иными несущественными данными. Наиболее
распространенными подобными наборами задач были, пожалуй,
задачи мелким шрифтом, помещенные в учебниках геометрии
Давидова и Киселева, а также в учебниках Адамара и Руше
и Комберусса. Наш задачник несколько полнее, так как за-
заключает почти все задачи из указанных четырех источников и
сверх того многие другие. В планиметрию включен набор задач
по геометрии кругов, представляющий как бы монографию по
этому вопросу, а стереометрия кончается тремя такими же
наборами: по общей теории выпуклых многогранников, по тео-
теории параллелоэдров и по теории прямолинейных преобразований
плоскости и перспективы. Всех задач по планиметрии около
трехсот, а по стереометрии около двухсот.
Все задачи снабжены подробными решениями, но решения
выделены в отдельную часть. Предполагается, что изучающий
будет пытаться всегда сначала самостоятельно решить пред-
предлагаемую задачу, употребив, если это окажется нужным, на
более трудную задачу по крайней мере несколько часов на

о	ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
размышления, и только в случае неудачи обратится к предлага-
предлагаемому нами ее решению; оно, к слову сказать, может быть не
всегда наилучшее, которое можно для данной задачи при-
придумать.
Нам кажется, что всех геометрических задач не очень
большой трудности, существенно различных друг от друга и
имеющих принципиальный геометрический интерес, не так-то
много, так что наш сборник можно считать довольно полным.
Мы не говорим, конечно, о задачах, отличающихся друг от дру-
друга лишь численными данными или совершенно искусственных
(например, на тела вращения или на пересечение разных тел),
которых можно составить любое число (мы поместили та-
таких задач очень мало). Было бы весьма желательно собирать
дальнейшие принципиально интересные задачи, в духе на-
нашего сборника, но уже не давать их решения, чтобы можно
было их использовать в разных соревнованиях.
Планиметрическая часть этого задачника составлена О. К.Жи-
К.Житомирским, а стереометрическая — Б. Н. Делоне.
Б. Делоне
\О. ЖшпомирскиЩ
Настоящее, третье издание печатается без изменений. Ис-
Исправлены замеченные ошибки и опечатки.

ЗАДАЧИ
ПЛАНИМЕТРИЯ
Отрезки и углы
1.	На прямой даны два отрезка а, Ь и общая часть их с.
Определить отрезок, покрываемый обоими отрезками вместе.
2.	На прямой даны два отрезка ОА = а, ОВ = Ъ. Определить
расстояние АВ и расстояние между точкой О и серединой М
отрезка АВ.
3.	Углы MON = a, NOP = Р приложены друг к другу.
Определить угол между их биссектрисами. Применить резуль-
результат к случаю, когда эти углы смежные.
4.	Углы MON — a, NOP = p, POQ = у приложены друг
к другу. Определить угол между биссектрисами углов MON,
POQ. Применить результат к случаю, когда углы MON, POQ
вертикальные.
Соотношения между сторонами и углами треугольников
5.	Можно ли разрезать разносторонний треугольник на два
равных треугольника?
6.	Сколькими способами можно разрезать равносторонний
треугольник на два равных треугольника?
¦ 7. Точка М лежит внутри треугольника ABC. Который из
углов ВАС, ВМС больше?
8.	В треугольнике ABC проведена медиана AM. Если
АВ^>АС, то который из углов АМВ, АМС больше и кото-
который из углов ВАМ, САМ больше?
9.	В треугольнике ABC проведена биссектриса AD. Если
АВ>АС, то который из углов ADB, ADC больше и который
из отрезков BD, CD больше?
10.	В треугольнике ABC проведена высота АН. Как распо-
расположена точка Н по отношению к точкам В, С, когда углы
ABC, ACB оба острые, когда один из них тупой и когда один
из них прямой?
11.	В треугольнике ABC проведены медиана AM, биссек-
биссектриса AD и высота АИ. Доказать, что точка D лежит между
точками М и И, если стороны АВ, АС не равны.

20	задачи	12—22
Сравнительная длина объемлемых и объемлющих
12.	По известной теореме сумма боковых сторон треуголь-
треугольника больше основания. Доказать, что она превышает осно-
основание менее чем на удвоенный отрезок, соединяющий вершину
с какой угодно точкой основания.
13.	Если выпуклый многоугольник заключен внутри какого-
нибудь другого многоугольника, то по известной теореме
периметр наружного многоугольника больше периметра внут-
внутреннего. Доказать, что наружный периметр превышает внут-
внутренний менее чем на удвоенную сумму отрезков, соединяю-
соединяющих вершины наружного многоугольника с какими-нибудь
последовательно расположенными точками контура внутрен-
внутреннего.
14.	Доказать, что сумма расстояний всякой точки от вер-
вершины многоугольника больше полупериметра его.
15.	Доказать, что медиана треугольника меньше полу-
полусуммы сторон, между которыми она заключается, и больше
разности между этой полусуммой и половиной третьей сто-
стороны.
16.	Зная стороны треугольника, найти границы, между ко-
которыми заключается сумма его медиан.
17.	Найти точку, сумма расстояний которой от вершин дан-
данного четырехугольника наименьшая.
Перпендикуляры и наклонные
18.	Доказать, что отрезок, заключенный между вершиной
и противолежащей стороной треугольника, меньше наибольшей
из остальных сторон.
19.	Доказать, что отрезок, заключенный между двумя сто-
сторонами треугольника, меньше наибольшей из его сторон.
20.	Доказать, что отрезок, заключенный весь внутри тре-
треугольника, меньше наибольшей из его сторон.
21.	В прямоугольном или тупоугольном треугольнике один
из острых углов разделен на несколько равных частей. Дока-
Доказать, что делящие прямые разделят противоположную сторону
на части, возрастающие при удалении от вершины прямого
или тупого угла.
22.	В прямоугольном или тупоугольном треугольнике одна
из сторон прямого или тупого угла разделена на несколько
равных частей. Доказать, что прямые, соединяющие точки де-
деления с вершиной противолежащего угла, разделят этот угол
на части, убывающие при удалении от другой стороны тупого
или прямого угла.

23—33	ПЛАНИМЕТРИЯ	Ц
Параллельные линии
•	23. Доказать, что прямая, проведенная через вершину равно-
равнобедренного треугольника параллельно основанию, делит внеш-
внешний угол при вершине пополам.
24.	Через точку пересечения биссектрис внутренних углов
при основании треугольника проведена прямая параллельно
основанию. Доказать, что часть этой прямой, заключенная меж-
между боковыми сторонами, равна сумме отрезков боковых сторон,
заключенных между этой прямой и основанием.
25.	Как изменится предыдущая теорема, если одну из бис-
биссектрис внутренних углов или обе заменить биссектрисами
внешних углов?
Сумма углов треугольника
26.	Определить углы равностороннего треугольника.
27.	Определить углы прямоугольного треугольника, гипоте-
гипотенуза которого вдвое больше одного из катетов.
28.	По углу при вершине треугольника определить острый
угол между биссектрисами внутренних углов при основании,
острый угол между биссектрисами внешних углов при осно-
основании и острый угол между биссектрисой внутреннего угла
при одном из концов основания и биссектрисой внешнего угла
при другом конце.
29.	В треугольнике ABC проведена биссектриса угла при
вершине А до пересечения с основанием ВС в точке D,
на большей из боковых сторон АВ отложен отрезок АЕ,
равный меньшей боковой стороне АС, и точки D, Е сое-
соединены. По данным углам В, С треугольника определить
угол BDE.
30.	В треугольнике ABC проведена биссектриса внешнего
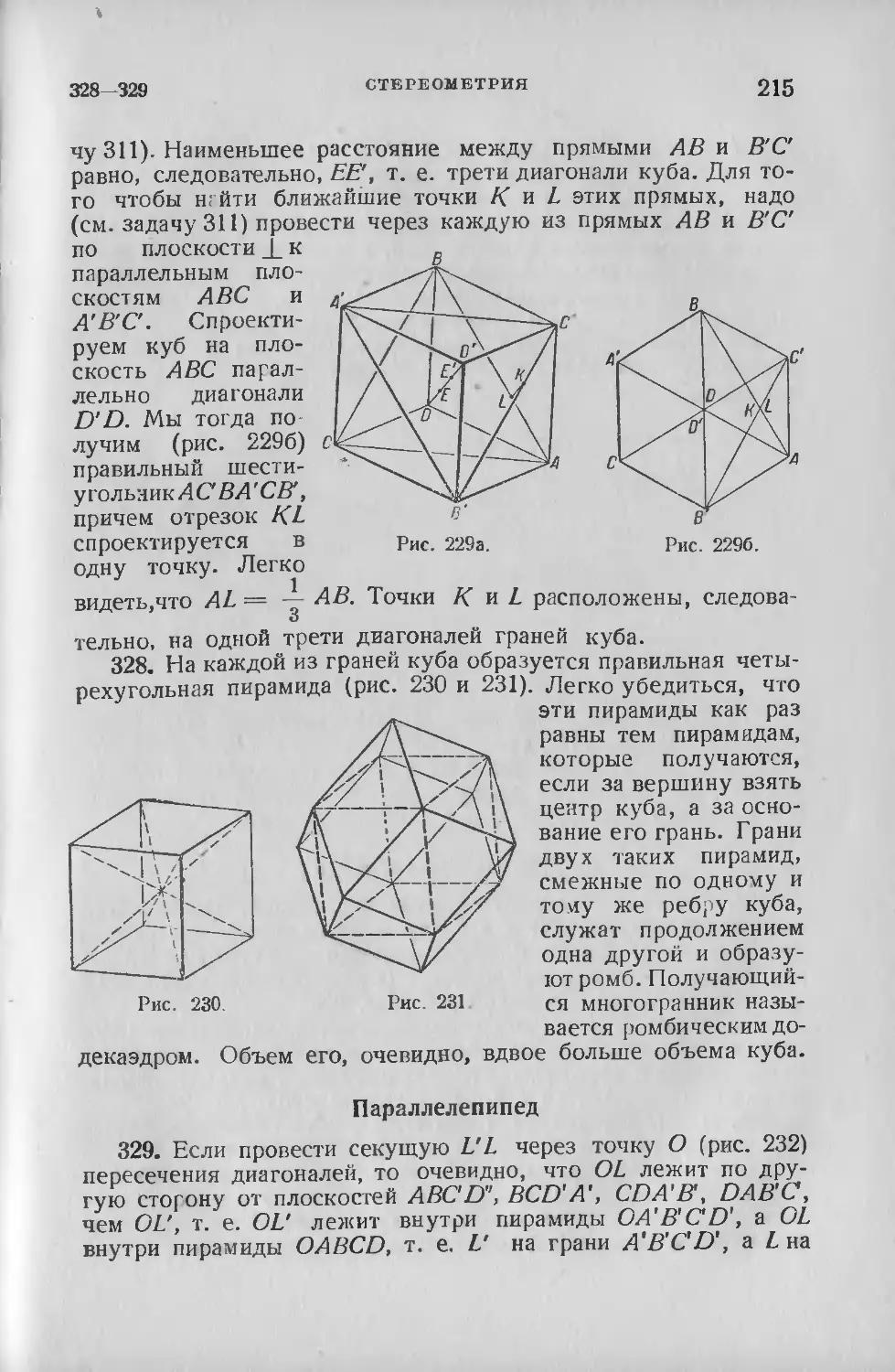
угла при вершине А до пересечения с продолженным основа-
основанием ВС. в точке D, на продолжении большей из боковых
сторон АВ отложен отрезок АЕ, равный меньшей боковой
стороне АС, я точки D, Е соединены. По данным углам В, С
треугольника определить угол BDE.
•	31. По углам при основании треугольника определить угол
между высотой и внутренней биссектрисой угла при вершине,
противолежащего основанию.
32.	По углам прямоугольного треугольника определить угол
между высотой и медианой, проведенными из вершины пря-
прямого угла.
33.	Доказать, что в прямоугольном треугольнике с нерав-
неравными катетами биссектриса прямого угла делит пополам угол
между высотой и медианой, проведенными из вершины пря-
прямого угла.

]2	задачи	34—47
34. По углам четырехугольника определить углы между
биссектрисами двух соседних углов, между биссектрисами двух
противоположных углов и между биссектрисами двух углов,
образуемых парами противоположных сторон, продолженных
до пересечения.
Параллелограммы и трапеции
• 35. Доказать, что в шестиугольнике, противоположные сто-
стороны которого равны и параллельны, три диагонали, соеди-
соединяющие противоположные вершины, пересекаются в одной
точке.
36.	Доказать, что во всяком четырехугольнике середины
сторон суть вершины некоторого параллелограмма.
37.	Доказать, что в четырехугольнике с непараллельными
противоположными сторонами середины диагоналей и середины
двух противоположных сторон суть вершины некоторого парал-
параллелограмма.
38.	Доказать, что в четырехугольнике с непараллельными
противоположными сторонами три прямые, соединяющие сере-
середины противоположных сторон и середины диагоналей, пере-
пересекаются в одной точке.
39.	Доказать, что в трапеции середины диагоналей и сере-
середины боковых сторон лежат на одной прямой.
40.	По данным основаниям трапеции определить отрезок,
соединяющий середины ее диагоналей.
41.	По данным расстояниям концов отрезка от прямой оп-
определить расстояние его середины от той же прямой.
42.	По данным расстояниям двух противоположных вершин
параллелограмма от прямой, проходящей через третью верши-
вершину, определить расстояние четвертой вершины от той же
прямой.
43.	Доказать, что сумма расстояний всякой точки основания
равнобедренного треугольника от его боковых сторон равна
высоте, проведенной из конца основания. Какой вид принимает
эта теорема для точек на продолжениях основания?
44.	Доказать, что сумма расстояний всякой точки внутри
равностороннего треугольника от его стороны равна его вы-
высоте. Как изменится эта теорема для точек вне треугольника ?
Круг
45.	Какому условию должен удовлетворять параллелограмм,
чтобы около него можно было описать окружность?
46.	Какова должна быть трапеция, чтобы около нее можно
было описать окружность?
47.	В какой параллелограмм можно вписать окружность?

48—62	планиметрия	13
48.	Которая из хорд, проходящих через точку внутри круга,
наименьшая?
49.	Которая из секущих, проходящих через точку вне круга,
имеет наибольшую внутреннюю часть?
50.	Найти наименьшее и наибольшее расстояние точки от
окружности.
51.	Найти наименьшее и наибольшее расстояние двух ок-
окружностей.
52.	Найти наименьшее и наибольшее расстояние прямой и
окружности.
53.	Каково относительное положение двух кругов радиусов
R и 3R, когда расстояние между их центрами равно 3R, R,
5Я, AR и 2/??
54.	Сколько кругов одинакового радиуса можно располо-
расположить вокруг одного круга того же радиуса так, чтобы каждый
из них касался этого круга и двух соседних?
55.	Расположить на плоскости бесконечное множество рав-
равных кругов так, чтобы каждый касался шести соседних.
56.	По углам между диагоналями и между противополож-
противоположными сторонами вписанного четырехугольника определить углы
этого четырехугольника.
57.	По углам при основании вписанного треугольника опре-
определить угол между касательной к кругу в его вершине и
основанием.
58.	По углам вписанного треугольника определить углы
треугольника, ограниченного касательными к кругу в его вер-
вершинах.
59.	Доказать, что хорды двух пересекающихся кругов,
соединяющие концы двух секущих, проходящих через точ-
точки пересечения, параллельны между собой. Как изменится
эта теорема, когда концы секущих на одном из кругов сов-
совпадут?
60.	Доказать, что хорды двух касательных кругов, соеди-
соединяющие концы двух секущих, проходящих через точку каса-
касания, параллельны между собой. Как изменится эта теорема,
когда секущие совпадут?
61.	Доказать, что отрезки общей секущей двух внутренне
касательных кругов, заключенные между обеими окружностями
и не налегающие друг на друга или, наоборот, налегающие
друг на друга, видны из точки касания под равными углами. Как
изменится эта теорема, когда секущая обратится в хорду
наружного круга, касательную к внутреннему?
62.	Доказать, что отрезки общей секущей двух внешне
касательных кругов, заключенные между обеими окружностями,
один'из которых составляет часть другого, видны из точки
касания под углами, в сумме составляющими два прямых. Как

14	ЗАДАЧИ	63—73
изменится эта теорема, когда секущая обратится в общую
касательную обоих кругов?
63. Доказать, что прямая, параллельная касательной в вер-
вершине вписанного треугольника и пересекающая боковые сто-
стороны, отсекает от него четырехугольник, который может быть
вписан в круг.
. 64. Противоположные стороны четырехугольника продолже-
продолжены до пересечения, и около четырех образовавшихся треуголь-
треугольников описаны круги. Доказать, что все они пересекаются в
одной точке.
65.	Стороны пятиугольника продолжены до образования
пятиугольной звезды и около пяти треугольных лучей
описаны круги. Доказать, что пять наружных точек пересече-
пересечения соседних кругов лежат на одной окружности (теорема
Микеля).
66.	Равносторонний треугольник вписан в круг. Доказать,
что расстояние всякой точки дуги, стягиваемой какой-нибудь
из его сторон, от противолежащей вершины равно сумме рас-
расстояний той же точки от остальных вершин.
Замечательные точки и линии в треугольнике
67.	Как известно, перпендикуляры в серединах сторон тре-
треугольника сходятся в точке, равноудаленной от вершин, — в
центре описанного круга. К которой из сторон эта точка ближе
всего ?
68.	При каких условиях центр описанного круга лежит
внутри, вне и на границе треугольника?
69.	Найти части плоскости, в которых лежат вершины
остроугольных и тупоугольных треугольников, опирающихся
на заданное основание.
70.	Доказать, что высота треугольника и радиус описанного
круга, проведенный к вершине, образуют равные углы с бо-
боковыми сторонами.
71.	Треугольник разбит на два других треугольника прямою,
проведенной из вершины. Доказать, что центры кругов, опи-
описанных около всех трех треугольников, лежат на одной окруж-
окружности с вершиной.
72.	Известно, что биссектрисы внутренних углов треуголь-
треугольника сходятся в точке, равноудаленной от сторон треугольника,
— в центре вписанного круга. К которой из вершин эта точка
ближе всего?
73.	Доказать, что биссектриса внутреннего угла при всякой
вершине треугольника сходится с биссектрисами внешних углов
при двух других вершинах в точке, равноудаленной от стороны,

74—SS	планиметрия	15
противолежащей этому внутреннему углу, и от продолжений
двух других сторон (центр вневписанного круга).
74.	Доказать, что прямые, проведенные через вершины тре-
треугольника параллельно противолежащимсторонам, ограничивают
треугольник, для которого высоты данного треугольника оказы-
оказываются перпендикулярами в серединах сторон. Вывести отсюда,
что высоты треугольника пересекаются в однойточке(ортоцентр).
75.	Доказать, что прямые, соединяющие основания высот
треугольника, ограничивают треугольник, для которого высоты
данного треугольника оказываются биссектрисами. Вывести
отсюда теорему о пересечении высот.
76.	К которой из вершин ортоцентр ближе всего?
77.	К которой из сторон ортоцентр ближе всего?
78.	Которая из высот наименьшая?
79.	Доказать, что из четырех точек, одна из которых есть
ортоцентр треугольника, образуемого тремя остальными, каж-
каждую можно рассматривать как ортоцентр треугольника, обра-
образуемого тремя остальными.
80.	Доказать, что из шести биссектрис треугольника каждые
три, сходящиеся в одной точке, суть высоты треугольника,
ограниченного тремя остальными.
81.	Доказать, что каждая медиана треугольника отсекает
от каждой другой одну треть, считая от основания. Вывести
отсюда, что медианы треугольника пересекаются в одной точке
(центр тяжести).
82.	К которой из вершин и к которой из сторон центр
тяжести ближе всего?
83.	Которая из медиан наименьшая?
84.	Доказать, что прямые, соединяющие вершину параллело-
параллелограмма с серединами сторон, сходящихся в противоположной
вершине, рассекают диагональ, соединяющую две другие вер-
вершины, на три равные части.
85.	Доказать, что расстояние центра описанного круга от
стороны треугольника вдвое меньше расстояния ортоцентра
от противолежащей вершины.
86.	Доказать, что центр описанного круга, ортоцентр и
центр тяжести лежат на одной прямой (прямая Эйлера).
87.	Доказать, что основания перпендикуляров, опущенных
из любой точки окружности на стороны вписанного треуголь-
треугольника, лежат на одной прямой (прямая Симеона).
88.	Доказать, что окружность с центром в середине отрез-
отрезка, соединяющего центр описанного круга и ортоцентр, и с
радиусом, равным половине радиуса описанного круга, про-
проходит через основания высот, середины сторон и середины
отрезков, соединяющих ортоцентр с вершинами (круг девяти
точек).

16	ЗАДАЧИ
Задачи на построение
Пояснение. При решении задач на построение чаще всего приме-
применяется метод геометрических мест. Возьмем простейший случай,
когда задача заключается в построении некоторой точки, удовлетворяющей
данным условиям. Если этим условиям удовлетворяет только одна или не-
несколько точек, то, отбросив одно из условий, мы обычно получаем уже це-
целую линию—геометрическое место точек, удовлетворяющих остальным
условиям.
Если это геометрическое место есть окружность или прямая, кото-
которую мы можем построить на основании данных условий, то дальнейшее ре-
решение облегчается, так как мы можем искать требуемые точки не среди
всех точек плоскости, а только среди точек найденного геометрическо-
геометрического места.
Если нам удастся, отбросив другое условие, построить другое геометриче-
геометрическое место, то искомые точки найдутся как общие точки обоих геометриче-
геометрических мест. Может случиться, что нужно построить не точку, а какую-нибудь
другую фигуру, но очень часто нетрудно свести задачу к построению точки.
Например для построения прямой, одна точка которой известна, достаточно
найти еще одну точку; для построения круга данного радиуса достаточ-
достаточно найти его центр и т. п. Но допустим, что геометрические места, полу-
получаемые поочередным отбрасыванием условий задачи, не удается построить,
или они не могут быть построены, потому что это не окружности и не
прямые.
Отсюда еще не следует, что мы должны отказаться от применения ме-
метода геометрических мест. Нужно поискать такие вспомогательные точки,
с помощью которых можно наверное построить искомую фигуру и которые
можно рассчитывать построить по методу геометрических мест. Все это,
конечно, относится к тому случаю, когда условия задачи не подсказывают
применения другого метода.
Полезно проверить, что и простейшие задачи, как деление отрезка
пополам, опускание перпендикуляра, построение треугольника по его эле-
элементам и т. д., решаются но существу с помощью метода геометриче-
геометрических мест.
Иногда нужно найти не точку, а прямую, удовлетворяющую некоторым
условиям. Отбросив одно из условий, мы часто получаем такую совокуп-
совокупность бесчисленного множества прямых, из которой уже нетрудно выбрать
требуемую, например, совокупность прямых, проходящих через данную точ-
точку, или касательных к данному кругу и т. п. Этот метод есть простейшее
обобщение метода геометрических мест.
Часто удается притти к решению задачи с помощью метода преобра-
преобразования фигур, и даже во многих случаях успех этого метода можно
предвидеть с первого взгляда. Этот метод состоит в замене данной, или ис-
искомой фигуры, или какой-нибудь части их, новой фигурой, связанной с
первоначальной определенным построением и позволяющей решить задачу
или приблизиться к ее решению. Мы рассмотрим пока только такие преоб-
преобразования, при которых новая фигура равна старой и отличается от нее
только положением. Такие преобразования называются перемещения-
м и. Сюда относятся:
a)	параллельный перенос, при котором все точки фигуры перемещаются
на равные параллельные и одинаково направленные отрезки; все прямые
фигуры остаются цри этом параллельными сами себе;
b)	поворот, при котором некоторая точка остается неподвижной, а все
полупрямые, исходящие из нее. поворачиваются вокруг нее на данный угол
в данном направлении;
c)	симметрия относительно точки, илн поворот на сто восемьдесят гра-
градусов;

39	90	ПЛАНИМЕТРИЯ	| J
d) симметрия относительно прямой, при которой эта прямая остается
неподвижной, а вся фигура поворачивается вокруг нее, как вокруг оси, и
¦нова падает на плоскость обратной стороной.
Первые три перемещения можно осуществить непрерывным движением,
не выходя из плоскости. При непрерывном параллельном перемещении точ-
точки фигуры описывают параллельные прямые, а при непрерывном врашении —
концентрические круги. Мы получаем как бы геометрическое место целой
фигуры.
Симметрии можно просто определить, не прибегая к движению:
я) в симметрии относительно точки отрезки, соединяющие
две симметричные точки с неподвижным центром симметрии, равны
и направлены в разные стороны от центра;
Ь) в симметрии относительно прямой перпендикуляры,
опущенные из двух симметричных точек на неподвижную ось сим-
симметрии, имеют обшее основание, равны и направлены в разные стороны
от оси.
Отметим, что указанными преобразованиями по существу исчерпывают-
исчерпываются все возможные перемещения, так как всякое перемещение или наложение
сводится к параллельному переносу, повороту и, если нужно, симметрии
относительно прямой.
В заключение упомянем еще о методе обратности. Он заключается
в том, что искомую фигуру строят в произвольном положении, пристраи-
пристраивают к ней данную фигуру с соблюдением указанных в условии взаимоот-
взаимоотношений между обеими и, пользуясь новыми соотношениями, полученными
в результате построения, строят искомую фигуру уже в надлежащем поло-
положении по отношению к данной.
Если связь между данными и искомыми неясна с самого начала, то сле-
следует попытаться установить между ними несколько посредствующих звень-
звеньев. Поскольку эта связь нам неясна, мы не можем, конечно, с уверенностью
вставлять эти звенья и вынуждены рассуждать до известной степени ощупью,
но при известном терпении и внимании удается установить требуемую связь.
Такое обдумывание задачи называется анализом.
После построения нужно прежде всего проверить, не было ли допу-
допущено какой-нибудь неполноты, последствием которой могло бы оказаться
получение лишь части решений. Это бывает, например, когда вычер-
вычерчиваются только отрезки геометрических мест, отчего пропадают некоторые
точки пересечения. Затем нужно подсчитать, сколько решений полу-
получится при тех или иных данных. Это называется исследованием
решения.
Хотя построению предшествует обсуждение задачи, тем не менее полез-
полезно в некоторых случаях проверить, действительно ли построенная фигура
удовлетворяет условиям. Источником ошибки мог послужить неправильный
предварительный чертеж, которым пользовались при анализе, поспешность
самого анализа и т. п.
Последующая проверка правильности построения называется дока-
доказательством.
Рекомендуем читателю решать задачи подробно и фактически применять
циркуль и линейку: мы в своих решениях часто ограничиваемся краткими
указаниями и, вообще, считаем задачу решенной, если она сведена к ос-
основным построениям или решенным ранее задачам; построения, излагаемые
в курсах элементарной геометрии, мы считаем известными.
89.	Построить окружность данного радиуса, проходящую
через данную точку и касательную к данной прямой.
90.	Построить окружность дчнного радиуса, касательную
к данной прямой и к данной окружности.
2 Б. Делопе н О. Житомирский

18	ЗАДАЧИ	91-111
91.	Построить окружность, касательную к двум данным
параллельным прямым и к данной окружности.
92.	Построить окружность, касательную к двум данным
концентрическим окружностям и к данной прямой.
93.	Построить окружность, проходящую через три данные
точки.
94.	Построить окружность, касательную к трем данным
прямым.
95.	Построить окружность, касательную к данной прямой
в данной точке и к другой данной прямой.
96.	Построить окружность, касательную к данной окружно-
окружности в данной точке и к данной прямой.
97.	Построить окружность, касательную к данной прямой
в данной точке и к данной окружности.
98.	Построить окружность, касательную к данной окруж
ности в данной точке и к другой данной окружности.
99.	Построить точку, из которой данный круг и данный
отрезок видны под данными углами,
100.	Построить прямую, равноудаленную от трех данных
точек.
101.	Провести касательную к данной окружности, одинаково
наклоненную к двум данным прямым.
102.	Через точку вне круга провести секущую, внешня»
часть которой была бы равна внутренней.
103.	Через точку пересечения двух окружностей провести
секущую, часть которой внутри окружностей была бы равна
данному отрезку.
104.	Около данного треугольника описать треугольник
равный другому данному треугольнику.
105.	В данный треугольник вписать треугольник, равный
другому данному треугольнику.
106.	Провести к данной окружности касательную, часть
которой между продолжениями двух данных радиусов была
бы равна данному отрезку.
107.	Построить отрезок, равный и параллельный данному,
концы которого лежали бы на данной прямой и данной окруж-
окружности.
108.	Построить отрезок, равный и параллельный данному.
концы которого лежали бы на двух данных окружностях.
109.	Построить хорду данного круга, равную и параллельную-
данному отрезку.
110.	Через данную точку внутри круга провести хорду,
равную данному отрезку.
111.	Построить равносторонний треугольник, одна вершинг.
которого лежала бы на данной окружности, другая на данно!'
прямой, а третья в данной точке.

Ц2—141	ПЛАНИМЕТРИЯ	19
112.	Построить равнобедренный прямоугольный треуголь-
треугольник, гипотенуза которого опиралась бы на две данные
окружности, а вершина прямого угла лежала бы в данной
точке.
113.	Через точку пересечения двух окружностей провести
секущую, часть которой внутри кругов делилась бы в этой
точке пополам.
114.	Через данную точку провести прямую, часть которой
между данной прямой и данным кругом делилась бы в этой
точке пополам.
115.	На данной прямой построить точку, сумма расстоя-
расстояний которой от двух данных точек наименьшая.
116.	На данной прямой построить точку, разность рассто-
расстояний которой от двух данных точек наибольшая.
117.	Построить треугольник наименьшего периметра, две
вершины которого лежали бы на сторонах данного угла, а
третья в данной точке внутри угла.
118.	Построить равнобедренный треугольник, основание кото-
которого лежало бы на одной стороне данного угла, вершина—на
другой стороне того же угла, а боковые стороны проходили
бы через данные точки внутри этого угла.
Замечание. В задачах 119—134 требуется построить треугольник, и
указаны только данные. Для сокращения углы его обозначены через А, В, С,
противолежащие стороны — через а, Ь, с, проведенные к этим сторонам
медианы, высоты и бессектрисы — соответственно через та, т^, тс, через
ha, hb, hc и через f)e, p^,, pf, периметр—через 2р.
119.	Ь, с, та.	127. а, Ь + с, А.
120.	а, та, ть.	128. В; С, 2р.
121.	та, mh, mc.	129. а, с — Ь, В.
122.	Ь, с, ha.	130. а, с — Ь, С.
123.	a, kb, hc.	131. а, с — Ь, А.
124.	а, та, ha.	132. b, с, С —В.
125.	a, ha, A.	133. а, с — Ь, С —В.
126.	ha, pe, А.	134. а, b + с, С —В.
135.	Построить параллелограмм по углу и диагоналям.
136.	Построить трапецию по четырем сторонам.
137.	Построить трапецию по основаниям и диагоналям.
138.	Построить четырехугольник по трем сторонам и углам,
прилежащим к четвертой.
139.	Построить четырехугольник по сторонам и углу между
двумя противоположными сторонами.
140.	Построить четырехугольник по диагоналям, углу между
ними и двум каким-нибудь сторонам.
141.	Построить четырехугольник по сторонам и расстоянию
между серединами двух противоположных сторон.

20	задачи	142—155
Подобные фигуры
142.	Стороны треугольника равны 5, 7 и 4. Наибольшая
сторона подобного треугольника равна 21. Найти остальные
его стороны.
143.	Доказать, что два квадрата всегда подобны.
144.	Доказать, что два прямоугольника подобны, если име-
имеют равные отношения соседних сторон.
145.	Стороны угла соединены двумя параллельными отрез-
отрезками, и в концах каждого отрезка проведены перпендикуляры
к сторонам угла до взаимного пересечения. Доказать, что
точки пересечения перпендикуляров лежат на одной прямой
с вершиной угла.
146.	По основанию а треугольника определить расстояние
между точками, делящими боковые стороны в отношении т,
считая от вершины.
147.	По основаниям а, Ь трапеции определить расстояние
между точками, делящими боковые стороны в отношении т,
считая от основания а.
148.	По расстояниям р, q, r вершин треугольника от пря-
прямой, не пересекающей его, определить расстояние его центра
тяжести от той же прямой.
149.	По основаниям a, b трапеции определить отношение,
в котором ее диагонали делят друг друга.
150.	По основаниям a, b трапеции определить отношение,
в котором ее боковые стороны, продолженные до пересече-
пересечения, делят друг друга внешним образом.
151.	По основаниям a, b трапеции определить отрезок
прямой, проведенной параллельно основаниям через точку
пересечения диагоналей, заключающийся между боковыми
сторонами.
• 152. По основаниям а, Ь трапеции определить отрезок
прямой, проведенной параллельно основаниям через точку
пересечения продолженных боковых сторон, заключающийся
между продолжениями диагоналей.
153.	По основанию а и боковым сторонам Ь, с треуголь-
треугольника определить отрезки, на которые биссектриса внутреннего
угла при вершине делит основание.
154.	По основанию а и боковым сторонам Ь, с треуголь-
треугольника определить расстояния от концов основания до точки
пересечения биссектрисы внешнего угла при вершине с осно-
основанием.
155.	Прямая пересекает стороны треугольника или их про-
продолжения. По отношелиям т, п, в которых она делит две
стороны, считая от третьей, определить отношение, в котором
она делит третью сторону.

156—159	ПЛАШШКТРИЯ	21
156.	Вершины треугольника соединены с некоторой точкой
По отношениям т, п, в которых прямые, исходящие из двух*
вершин, делят противолежащие стороны, считая от третьей
стороны, определить отношение, в котором прямая, исходящая
из третьей вершины, делит противолежащую сторону.
157.	Доказать, что прямая, соединяющая точки пересече-
пересечения биссектрис двух внутренних углов треугольника с проти-
противолежащими сторонами, пересекает третью сторону в той же
точке, что и биссектриса внешнего угла при противолежащей
вершине.
158.	Доказать, что прямая, соединяющая точку пересечения
диагоналей и точку пересечения продолженных боковых сторон
трапеции, делит основания пополам.
159.	Треугольники ABC, A1B1C1 расположены так, что
точки пересечения соответственных сторон лежат на одной
прямой. Доказать, что прямые, соединяющие соответственные
вершины, сходятся в одной точке или параллельны (теорема
Дезарга).
Задачи на построение
Пояснение. Решение многих задач на построение основано на свой-
свойствах подобных фигур. На этих свойствах основан, прежде всего, вывод
некоторых геометрических мест. Но чаще всего приходится применять ич
в качестве метода преобразования.
Обычный способ применения метода подобия состоит в том, что часть
требований, предъявляемых к искомой фигуре, отбрасывается, так что оста-
остающимся требованиям удовлетворяет бесчисленное множество фигур, по-
подобных искомой, каждую из которых мы можем построить. Построив одну
из них, мы должны затем перейти от нее к искомой. Последняя операция
требует изучения взаимного расположения подобных фигур.
Простейшее взаимное расположение есть подобное расположе-
расположение, или гомотетия. Две фигуры называются подобно располо-
расположенными, или гомотетичными, если они подобны и сходственные
прямые их параллельны. Прямые, соединяющие сходственные точки двух
подобно расположенных фигур, сходятся в одной точке, которая называется
центром подобия. Сходственные отрезки этих фигур направлены или все
одинаково или все противоположно. В первом случае сходственные точки
расположены по одну сторону от центра подобия, во втором — по разные
стороны. Сообразно этому различают прямое и обратное подобное
расположение. Отношение отрезков, соединяющих сходственные точки с
центром подобия, равно отношению сходственных отрезков фигур: это от-
отношение называется отношением подобия. Поэтому для построения
фигуры, подобно расположенной с данной фигурой относительно данного
центра подобия и имеющей к ней данное отношение подобия, нужно растя-
растянуть или сжать все отрезки, соединяющие точки данной фигуры с цент-
центром подобия в определенном отношении, и в случае обратного подобного
расположения еще повернуть полученную фигуру на 180° вокруг центра
подобия.
Два круга всегда подобно расположены и притом как прямо, так и об-
обратно. При прямом подобном расположении сходственными точками буду!
концы параллельных и одинаково направленных радиусов, а при обратном —
концы параллельных и нротивоположио направленных радиусов. Соответ-

22	ЗАДЛ.ЧИ	160—J 73
ствующие центры подобия делят линию центров внешним и внутренним
образом в отношении радиусов. В случае равных кругов центр прямого
подобия удаляется в бесконечность, а центр обратного подобия обращается
в центр симметрии. В случае концентрических кругов оба центра подобия
сливаются с центром кругов.
Переход от данной фигуры к прямо подобно расположенной можно осу-
осуществить непрерывным изменением фигуры, заставляя отношение подобия
изменяться от единицы до требуемой величины. При этом точки фигуры
перемещаются по прямым, исходящим из центра подобия.
Свойства подобно расположенных фигур доказываются в большинстве
курсов элементарной геометрии. Впрочем было бы хорошо, если бы чита-
читатель попытался сам найти требуемые доказательства.
160.	Через точку вне круга провести секущую, внешняя
часть которой была бы вдвое больше внутренней.
161.	Провести в данном направлении прямую так, чтобы
отрезки ее между данным кругом и двумя не пересекающи-
пересекающими его прямыми были равны между собой.
162.	Вписать квадрат в данный треугольник так, чтобы одна
из сторон квадрата лежала на основании треугольника.
163.	Вписать квадрат в данный сектор так, чтобы одна
сторона лежала на радиусе.
164.	Вписать квадрат в данный сектор так, чтобы одна
сторона стягивала часть дуги.
165.	Вписать квадрат в данный сегмент так, чтобы одна
сторона лежала на хорде.
166.	Вписать в четырехугольник параллелограмм с задан-
заданными направлениями сторон.
167.	Около данного четырехугольника описать четырех-
четырехугольник, подобный другому данному.
168.	В данный четырехугольник вписать четырехугольник,
подобный другому данному.
169.	Вписать в данный круг треугольник, подобный дан-
данному.
170.	Построить треугольник по двум углам и расстоянию
между центрами описанного и вписанного кругов.
Пропорциональные отрезки в кругах
171.	Через середину хорды круга длины а проведена дру-
другая хорда длины Ь. Определить длины отрезков, на которые
хорда b делится хордой а.
172.	Окружность пересекает одну из сторон угла на рас-
расстояниях а, b от вершины и касается другой стороны. Опре-
Определить расстояние точки касания от вершины.
173.	Расстояние точки внутри круга радиуса г от его
центра равно d. Определить длину хорды, проведенной че-
через эту точку перпендикулярно к диаметру, проходящему
через* нее.

174	183	планиметрия	23
174.	Расстояние точки вне круга радиуса г от его
центра равно d. Определить длину касательной к кругу из
этой точки.
175.	Вывести из свойств пропорциональных отрезков в
чруге известные числовые соотношения в треугольнике: вы-
выражение для квадрата стороны любого треугольника и выра-
выражения для квадрата катета и квадрата высоты из вершины
прямого угла в прямоугольном треугольнике.
176.	Доказать, что расстояние точки окружности от хорды
круга есть среднее пропорциональное между расстояниями кон-
концов хорды от касательной к окружности в этой точке.
177.	От точки пересечения М двух прямых отложены на
одной прямой отрезки МАХ, МВХ, на другой отрезки МА2,
МВг, связанные соотношением МАХ-МВХ = МА2-МВ2, и притом
на обеих прямых в одну сторону или на обеих в разные
стороны от точки М. Доказать, что точки Ах, Ви А2, В2 лежат
на одной окружности.
178.	Доказать, что общие хорды трех попарно пересе-
пересекающихся окружностей сходятся в одной точке или парал-
параллельны.
179.	Доказать, что общие хорды всех окружностей, прохо-
проходящих через две данные точки, с данным кругом сходятся
в одной точке или параллельны.
180.	Доказать, что касательные к двум пересекающимся
окружностям из всякой точки продолжения их общей хорды
равны между собой.
181.	Из точки на окружности проведены полупрямые, пере-
пересекающие прямую, перпендикулярную к диаметру, проходя-
проходящему через эту точку. Доказать, что произведение отрезков,
отсекаемых окружностью и прямою от всякой полупрямой,
есть величина постоянная.
182.	Из центра подобия двух окружностей проведены секу-
секущие к ним. Доказать, что произведение отрезков всякой секу-
секущей от центра подобия до двух несходственных точек окруж-
окружностей есть величина постоянная.
Задачи на построение
Пояснение. Здесь предложены задачи на построение окружности
по трем условиям, которые могут состоять в прохождении её через данную
точку и в касании к данной окружности или к данной прямой. Некоторые
задачи этого рода были предложены выше; здесь помещены более трудные
задачи, требующие применения метода подобия и свойств пропорциональных
отрезков в кругах.
183.	Построить окружность, проходящую через данную
точку и касательную к двум данным прямым.

24	ЗАДАЧИ	184—199
184.	Построить окружность, касательную к данной окруж-
окружности и к двум данным прямым.
185.	Построить окружность, проходящую через две данные
точки и касательную к данной прямой.
186.	Построить окружность, проходящую через две данные
точки и касательную к данной окружности.
187.	Построить окружность, проходящую через данную
точку и касательную к данной окружности и данной прямой.
188.	Построить окружность, касательную к двум данным
окружностям и данной прямой.
189.	Построить окружность, проходящую через данную
точку и касательную к двум данным окружностям.
190.	Построить окружность, касательную к трем данным
окружностям (задача Аполлония).
Площади
191.	Разрезать данный параллелограмм на две части, из
которых можно было бы сложить прямоугольник.
192.	Разрезать данный треугольник на три части, из кото-
которых можно было бы сложить прямоугольник.
193.	Из двух равных трапеций сложить параллелограмм.
Применить результат к выводу формулы площади трапеции.
194.	Трапеция разбита диагоналями на четыре части. Дока-
Доказать, что части, прилегающие к боковым сторонам, равнове-
равновелики.
195.	Параллелограмм разбит на четыре части прямыми,
проведенными через какую-нибудь точку диагонали параллель-
параллельно сторонам. Доказать, что части, расположенные по разные
стороны от диагонали, равновелики.
196.	Параллелограмм разбит на четыре части прямыми,
соединяющими какую-нибудь внутреннюю точку с верши-
вершинами. Доказать, что суммы площадей противолежащих частей
равны.
197.	Через середину каждой диагонали четырехугольника
проведена прямая параллельно другой диагонали. Доказать,
что прямые, соединяющие точку пересечения -этих прямых е
серединами сторон четырехугольника, разбивают его на равно-
равновеликие части.
198.	Прямая, параллельная основанию треугольника, делит
его площадь пополам. В каком отношении делит она боковые
стороны треугольника?
199.	В параллелограмме ABCD каждая сторона разделена
на равные отрезки, число которых т для противоположных
сторон АЁ, CD и п для противоположных сторон AD, ВС.
Начало первого, второго и т. д. отрезка стороны АВ,

200—210	ПЛАНИМЕТРИЯ	25
считая от точки А, соединено с концом первого второго и т. д.
отрезка стороны CD, считая от точки D. Точно так же ко-
конец первого, второго и т. д. отрезка стороны AD, считая
от точки А, соединен с началом первого, второго и т. д.
отрезка стороны ВС, считая от точки В. Эти\ш прямыми
параллелограмм разбивается на части, имеющие вид тре-
треугольников, трапеций и параллелограммов. Какую часть
площади всего параллелограмма составляет площадь одного
такого параллелограмма?
200.	Каждая вершина параллелограмма соединена с середи-
серединами противолежащих сторон. Какую часть площади парал-
параллелограмма составляет площадь фигуры, ограниченной прове-
проведенными прямыми?
201.	Трапеция разделена диагоналями на четыре части.
Определить площадь трапеции по площадям частей, прилегаю-
прилегающих к основаниям.
202.	Прямая, параллельная основанию треугольника площа-
площади S, отсекает от него треугольник площади s. Определить
площадь четырехугольника, три вершины которого совпадают
с вершинами меньшего треугольника, а четвертая лежит на
основании большего треугольника.
203.	Внутри многоугольника площади 5 лежит многоуголь-
многоугольник площади s, прямо подобно расположенный с ним. Опре-
Определить площадь 2 многоугольника, вписанного во внешний
многоугольник и одновременно описанного около внутреннего
многоугольника.
Применение площадей для доказательств
204.	Вывести из рассмотрения площадей теорему задачи 43.
205.	Вывести из рассмотрения площадей теорему задачи 44.
206.	В треугольнике ABC найти геометрическое место то-
точек М, для которых площади треугольников МАВ, MAC рав-
равны между собой.
207.	Вывести из рассмотрения площадей теорему задачи 81.
208.	Дано два непараллельных отрезка АВ, CD. Найти
геометрическое место точек М, для которых сумма или раз-
разность площадей треугольников МАВ, MCD равна данной вели-
величине.
209.	Доказать, что прямая, соединяющая середины ди-
диагоналей четырехугольника, проходит через середину от-
отрезка, соединяющего точки пересечения противоположных
сторон.
210.	Доказать, что прямая, соединяющая середины диаго-
диагоналей четырехугольника, описанного около круга, проходит
через центр этого круга.

26	задачи	211—227
Числовые соотношения в треугольниках и четырехугольниках
211.	Радиусы двух кругов равны R и г, а расстояние ме-
между их центрами равное?. Определить длину общей внешней
и общей внутренней касательной.
212.	Определить длину общей касательной двух внешне
касательных кругов радиусов R, г.
213.	Два круга радиусов R a r внешне касательны. Опре-
Определить радиус круга, касательного к ним и к их общей каса-
касательной.
214.	На отрезке и двух его половинах построены полу-
полукруги в одну сторону. По радиусу R меньших полукругов
определить радиус круга, касательного ко всем трем полу-
полукругам.
215.	Прямоугольный сектор радиуса R разделен на две
части дугой круга того же радиуса с центром в конце дуги
сектора. Определить радиус круга, вписанного в меньшую из
этих частей.
216.	На отрезке и двух его неравных частях построены по-
полукруги в одну сторону. По радиусам R, г меньших полукру-
полукругов определить радиус круга, касательного ко всем трем
полукругам.
217.	По катетам Ь, с прямоугольного треугольника опреде-
определить высоту h из вершины прямого угла.
218.	По сторонам Ь, с и высоте ha треугольника определить
сторону а.
219.	По сторонам а, Ь, с треугольника определить высоту
ha и площадь S.
220.	По высотам ha, hb, hc треугольника определить его
площадь S.
221.	По сторонам а, Ь, с треугольника определить его
медианы та, ть, тс.
222.	По медианам та, ть, тс треугольника определить его
стороны а, Ь, с и площадь 5".
223.	По сторонам а, Ь, с треугольника определить биссек-
биссектрису рв.
224.	Доказать, что квадрат биссектрисы равен произведе-
произведению боковых сторон без произведения отрезков основания.
225.	По сторонам а, Ь, с треугольника определить радиус
R описанного круга.
226.	Доказать, что площадь остроугольного треугольника
равна произведению радиуса описанного круга на полупери-
полупериметр треугольника, образуемого основаниями высот. Обобщить
на случай тупоугольного треугольника.
227.	По сторонам а, Ь. с треугольника определить радиус
г вписанного -круга и радиусы ра, рь. рс вневписанных кругов.

228	24в	планиметрия	27
228.	По сторонам а, Ь, с треугольника определить длины
<асательных из его вершины к вписанному и вневписанным
кругам.
229.	По сторонам прямоугольного треугольника определить
эадиусы вписанного и вневписанных кругов.
230.	Доказать геометрически соотношение:
rPa^iP — Ь)(р — С).
231. Вывести геометрически формулу
232.	Доказать," что высота треугольника есть геометриче-
;кое место точек, для которых сумма квадрата расстояния от
конца основания с квадратом противолежащей этому конц\
стороны имеет равные значения для обоих концов осно
вания. Вывести отсюда теорему о пересечении высот в одной
точке.
233.	Доказать, что сумма квадрата расстояния ортоцентра
эт вершины с квадратом противолежащей стороны равна квад
оату диаметра описанного круга.
234.	По высоте h и отрезкам основания т, п определить
прилегающий к основанию отрезок высоты, отсекаемый от нес
другой высотой. Вывести отсюда теорему о пересечении высот
в одной точке.
235.	Доказать, что сумма произведений высот остроугольного
треугольника на отрезки их от ортоцентра до вершин равна
полусумме квадратов сторон. Обобщить на случай тупоуголь
ного треугольника.
236.	Доказать, что сумма квадрата расстояния центра впи-
вписанного круга от центра одного из вневписанных с квадратом
расстояния между центрами двух других вневписанных не за-
зависит от выбора первого вневписанного круга.
237.	Доказать, что произведение расстояний вершины тре-
треугольника от центра вписанного круга и центра вневписанного
круга при противолежащей стороне равно произведению рас-
расстояний той же вершины от центров двух других вневписанных
кругов.
238.	По сторонам а, Ь, с треугольника определить расстоя-
расстояния ортоцентра от вершин.
239.	По сторонам а, Ь, с треугольника определить расстоя
ния центра описанного круга от сторон.
240.	По сторонам а, Ь, с треугольника определить расстоя-
расстояния центров вписанного и вневписанных кругов от вершин и
между собою.

28	задачи	241—258
241.	Выразить разность квадратов диагоналей р, д парал-
параллелограмма через расстояния а, Ь, с, d произвольной точки
от его вершин.
242.	Выразить разность квадратов диагоналей р, q парал-
параллелограмма через его стороны т, п и площадь 5.
243.	Выразить площадь 5 параллелограмма через стороны
т, п и расстояния а, Ь, с, d произвольной точки от вершин.
244.	По основаниям a, b и боковым сторонам с, d трапе-
трапеции определить ее диагонали т, п.
245.	Доказать, что сумма квадратов диагоналей трапеции
равна сумме квадратов боковых сторон с удвоенным произве-
произведением оснований.
246.	По сторонам а, Ь, с, d трапеции определить ее пло-
площадь.
247.	Выразить площадь четырехугольника через стороны
а, Ь, с, d и диагонали т, п.
248.	Выразить диагонали т, п вписанного четырехугольни-
четырехугольника через стороны а, Ь, с, d.
249.	Вывести из выражений диагоналей вписанного четырех-
четырехугольника через стороны теорему Птолемея.
250.	Выразить площадь вписанного четырехугольника через
стороны.
251.	По радиусу R и хордам a, b дьух дуг круга определить
хорду суммы и разности этих дуг.
252.	По хордам а, Ь, с трех дуг, в сумме составляющих
полуокружность, составить уравнение для определения диаме-
диаметра круга.
Правильные многоугольники
253.	Из каких правильных многоугольников одного вида
можно сложить паркет?
254.	Как сложить паркет из правильных 'восьмиугольников
и квадратов, или двенадцатиугольников и треугольников?
255.	Можно ли сложить паркет из правильных десятиуголь-
десятиугольников и пятиугольников?
256.	Может ли вписанный многоугольник иметь равные
углы, но неравные стороны, или равные стороны, но неравные
углы?
257.	Может ли описанный многоугольник иметь равные
стороны, но неравные углы, или равные углы, но неравные
сто юны?
258.	В круг радиуса R вписаны три равных круга, каса-
касательных между собой. Определить их радиус.
259.	Круг радиуса R обложен четырьмя равными кругами,
каждый из которых касателен к двум соседним. Определить
радиус этих кругов.

260—272	планиметрия	28
260.	Вычислить сторону правильного описанного треуголь-
треугольника, квадрата и шестиугольника.
261.	Вычислить сторону и все диагонали правильного
вписанного десятиугольника.
262.	Вычислить сторону и диагональ правильного вписан-
вписанного пятиугольника.
263.	По стороне правильного десятиугольника определить
его площадь.
264.	Вычислить сторону правильного вписанного двенад-
двенадцатиугольника.
265.	Вычислить сторону правильного вписанного пятнад-
чатиугольника.
266.	Вычислить сторону правильного вписанного шестиде-
сятиугольника.
Измерение круга
267.	Вывести из рассмотрения вписанного шестиугольни-
шестиугольника и описанного квадрата, что число тс заключается меж-
между 3 и 4.
268.	Какую верхнюю границу для числа тс дает рассмотре-
рассмотрение правильного описанного шестиугольника?
269.	Вычислить число тс с помощью правильного вписанного
шестидесятиугольника и оценить погрешность.
270.	Какова погрешность приближенного спрямления полу-
полуокружности как суммы сторон правильного вписанного тре-
треугольника и правильного вписанного квадрата?
271.	В круг радиуса R вписаны три равных круга, касатель-
касательных друг к другу. Вычислить площадь криволинейной фигу-
фигуры, ограниченной этими тремя кругами.
272.	На диаметре полукруга радиуса R построен правиль-
правильный треугольник. Вычислить площадь части его вне полу-
полукруга.
Начала геометрии кругов
Геометрия кругов есть сравнительно новая глава элементарной геоме-
геометрии. По характеру применяемых в ней методов ее можно рассматривать
как переходную ступень к высшей геометрии. Будучи основана на немногих,
но общих понятиях, она легко приводит к решению сравнительно сложных
вопросов.
Мы дадим сейчас только самые основные определения. Вывод вытекаю-
вытекающих из них теорем предлагается читателю в виде задач, в формулировке
которых попутно вводятся и дальнейшие определения.
I. Пусть будет К некоторый круг и Рнекоторая точка. Если М и М'—
точки пересечения с кругом К какой-нибудь прямой, проходящей через
точку Р, то произведение отрезков РМ-РМ' не зависит, как известно, от
выбора этой прямой. Условимся приписывать отрезкам РМ и РМ' одинако-
одинаковые знаки, когда направления движения от Р к М и М' совпадают, и об-
обратные знаки, когда эти направления противоположны. Тогда произведение

30	ЗАДАЧИ	273—?7t
РМ-РМ будет положительным или отрицательным, смотря по тому, лежит
ли точка Р вне или внутри круга К- В случае, когда точка Р лежит иг
окружности круга К, произведение РМ-РМ' равно нулю. Всегда можно
выбрать направление прямой РМ так, чтобы оба отрезка имели одинаковую
абсолютную величину к: если Р лежит вне круга К, то за РМ нужно при-
принять касательную из Р к кругу К; если Р лежит внутри круга К, то за PiV
нужно принять перпендикуляр к диаметру круга К, проходящему через Рш
в случае, когда Р лежит на окружности круга К. оба направления совпа
дают. После этого можем написать:
РМ-РМ' = ±&.
Число + к" называется степенью точки Р относительно круга К ИЛ1
круга К относительно точки Р.
II.	Пусть будет О — некоторая точка и + k2 — некоторое положительное
или отрицательное число. Две точки М. М' называются взаимно обрат
ными, если они расположены на одной прямой с точкой О, и притом так
что
ОМ-ОМ' = ±kK
Две фигуры F, F' называются взаимно обратными, если соответ-
соответственные точки их взаимно обратны. Определенное таким образом соответ-
соответствие между фигурами на плоскости называется инверсией. Точка О
иазываетсяцентром инверсии, а число + k"— степенью инверсии.
Различают инверсию эллиптическую (степень — k2) и гиперболиче-
гиперболическую (степень + k2). В случае гиперболической инверсии круг с центром
О и радиусом \rk2 = к, все точки которого сами себе обратны, называете»
кругом инверсии, и взаимно обратные точки М, М' называются от-
отражениями друг друга в этом круге. В случае эллиптической инверсиу
также иногда говорят о круге инверсии мнимого радиуса V — к2.
III.	Два круга называются взаимно ортогональными, если онь
пересекаются и касательные к ним в каждой из точек пересечения взаимно-
перпендикулярны.
273.	Показать, что степень точки относительно круга всегда
равна d2— г2, где d— расстояние точки от центра круга i
г — радиус круга.
274.	Показать, что геометрическое место точек, имеющих
равные степени относительно двух данных кругов, есть пря-
прямая, перпендикулярная к линии центров (радикальная ось)„
Исследовать положение радикальной оси относительно данных
кругов в зависимости от положения этих кругов.
275.	Показать, что радикальные оси трех данных кругоЕ
либо совпадают, либо пересекаются в одной точке (радикаль-
(радикальном центре). Вывести отсюда способ построения радикаль-
радикальной оси двух кругов, не имеющих общих точек.
276.	Совокупность кругов, радикальные оси которых, взятые
попарно, совпадают, называется пучком кругов. Показать.
1) что пучок вполне определяется, если заданы один из его кру-
кругов и радикальная ось, или два из его кругов; 2) что все
круги пучка либо пересекают радикальную ось в одних и
тех же точках (эллиптический пучок), либо касательны
к ней в одной и той же точке (параболический пучок)-

277	286	ПЛАНИМЕТРИЯ	31
либо не имеют с ней общих точек (гиперболический
пучок).
277.	Содержащиеся в пучке круги нулевого радиуса (точки)
называются его предельными точками. Показать, что
гиперболический пучок содержит две предельные точки, пара-
параболический — одну, эллиптический — ни одной.
278.	Пучок задан одним из своих кругов и радикальной
осью. Построить круг пучка: 1) проходящий через данную
точку; 2) касательный к данной прямой; 3) касательный к дан-
данному кругу.
279.	Показать, что круг, ортогональный к двум кругам
пучка, ортогонален ко всем кругам того же пучка.
280.	Показать, что совокупность всех кругов, ортогональ-
ортогональных ко всем кругам данного пучка, образует другой пучок
(ортогональный к первому), и что первый пучок в свою
очередь ортогонален ко второму. Показать, что общая точка
всех кругов одного из пучков всегда будет предельной точкой
другого, и наоборот.
281.	Совокупность кругов, радикальные центры которых,
взятые по три, совпадают, называется связкой кругов. По-
Показать: 1) что связка вполне определяется радикальным цен-
центром и одним из своих кругов; 2) что радикальный центр ле-
лежит либо внутри всех кругов связки (эллиптическая
связка), либо на окружности всех кругов связки (параболи-
(параболическая связка), либо вне всех кругов связки (гиперболи-
(гиперболическая связка).
282.	Показать, что круги нулевого радиуса (предельные
точки) гиперболической связки образуют окружность круга,
центром которого служит радикальный центр связки (предель-
(предельный к р у г), что в параболической связке предельный круг
обращается в точку, а в эллиптической совсем исчезает.
283.	Показать, что единственным кругом, ортогональным
ко всем кругам связки, является предельный круг, и наоборот,
совокупность всех кругов, ортогональных к данному кругу,
образует связку.
284.	Показать, что прямые, проходящие через радикальный
центр связки, пересекают круги связки в парах точек, обрат-
обратных в инверсии, центром которой служит радикальный центр
связки, а степенью — степень связки.
285.	Показать, что всякий круг, проходящий через пару
точек, обратных в данной инверсии, принадлежит связке,
радикальным центром которой служит центр инверсии и сте-
степенью — степень инверсии.
286.	Связка задана радикальным центром и одним из своих
кругов. Построить тот круг этой связки, который проходит
через две данные невзаимнообратные точки.

32	задачи	287—299
287. Две различные связки заданы, как в предыдущей за-
задаче. Построить общий обеим связкам круг, проходящий через
данную точку.
28д. Построить круг данной связки, имеющий данный центр.
289.	Показать, что пучок, два круга которого принадлежат
данной связке, весь принадлежит этой связке.
290.	Показать, что два пучка одной связки имеют один об-
общий круг, кроме случая гиперболической связки, когда об-
общего круга может и не быть.
291.	Показать, что две связки всегда имеют общий
пучок.
292.	Найти линию, обратную прямой линии в данной ин-
инверсии.
293.	Найти линию, обратную окружности в данной ин-
инверсии.
294.	Показать, что две точки, являющиеся отражениями
друг друга в данном круге, делят диаметр круга, на котором
и на продолжении которого они лежат, внутренним и внешним
образом в одном и том же отношении.
295.	Около середины основания треугольника, как центра,
описан круг, проходящий через точки касания к основанию
двух вневписанных кругов, прилежащих к боковым сторонам.
Показать, что отражение в этом круге той общей касательной
вневписаиных Kpyi ов, которая не является стороной треуголь-
треугольника, есть круг девяти точек, рассмотренный в задаче 88.
Показать, что этот результат сохраняет силу, если заменить
вневписанные круги, прилежащие к боковым стрронам, вписан-
вписанным кругом и вневписанным кругом, прилежащим к основанию.
296.	Показать, что круг девяти точек всегда касается впи-
вписанного и трех вневписанных кругов (теорема Фейербаха).
297.	Показать, что касательные к взаимнообратным кругам
во взаимнообратных точках образуют с прямой, соединяющей
эти точки, равные односторонние углы. Обобщить этот резуль-
результат на случай прямой и обратного ей круга.
298.	Углол между двумя дугами круга, исходящими из од-
одной точки, называется угол между касательными к ним, про-
проведенными по направлению сам ix дуг. Показ1ть, что угол
между двумя дугами круга равен углу между обратными ду-
дугами круга, но направления этих углов противоположны, т. е.
направления вращения, в которых две соответственные сторо-
стороны должны описывать эти углы, чтобы совпасть с двумя дру-
другими сторонами соответственными сторонами, противоположны
друг другу.
299.	Три дуги круга образуют треугочьник и при продол-
продолжении сходятся в одной точхе. Показать, что сумма внутрен-
внутренних углов такого треугольника равна двум прямым.

300-305	планиметрия	33
300.	Найти инверсию, в которой два данных круга взаимно
обратны.
301.	Показать, что всякий круг, касательный к двум дан-
данным кругам, сам себе обратен в одной из инверсий, отно-
относительно которых данные круги взаимно обратны.
302.	Показать, что шесть центров подобия трех кругов,
центры которых не лежат на одной прямой, суть точки пере-
пересечения четырех прямых (осей подобия).
303.	Применить результаты двух предыдущих задач к ре-
решению задачи Аполлония (построить круг, касательный к трем
данным кругам).
304.	Даны два круга. Показать, что всегда можно найти
инверсию, в которой эти два круга будут обратны двум пря-
прямым или двум концентрическим кругам.
305.	Свести задачу Аполлония к возможно простым частным
случаям с помощью изменения радиусов и инверсии.
3 б. Делоне ¦ О. Житомирски!

СТЕРЕОМЕТРИЯ
ЗАДАЧИ НА ДОКАЗАТЕЛЬСТВА И ПОСТРОЕНИЯ
Замечание. Во всех задачах на построение в стереометрии мы будем
предполагать, что мы имеем возможность: проводить плоскость через три
заданные точки (а следовательно, и через точку и прямую), получать пря-
прямую пересечением двух плоскостей, проводить прямую через две точки про-
пространства, а также производить в любой плоскости пространства все построения
циркулем и линейкой, которые изучаются в планиметрии.
Прямые и плоскости и многогранные углы
306.	Построить прямую, проходящую через данную точ-
точку А пространства и пересекающую две данные прямые про-
пространства.
307.	Построить прямую, которая была бы параллельна дан-
данной прямой а пространства и пересекала бы две другие за-
заданные прямые пространства Ъ и с, не лежащие в одной пло-
плоскости.
308.	Построить прямую, лежащую в данной плоскости Р,
проходящую через заданную точку А этой плоскости и перпен-
перпендикулярно к заданной прямой а пространства.
309.	Построить отрезок данной длины d, параллельный
данной плоскости Р и такой, что концы его опираются на
данные две прямые а и Ъ.
310.	Показать, что перпендикуляры, опущенные из одной
точки А на ряд плоскостей, пересекающихся по параллельным
прямым, лежат в одной плоскости.
311.	Построить отрезок, который является кратчайшим из
всех, концы которых лежат на двух заданных скрещивающих-
скрещивающихся (т. е. не лежащих в одной плоскости) прямых пространства
(кратчайшее расстояние между двумя прямыми пространства).
312.	Показать, что четырехугольник, соединяющий середи-
середины сторон любого четырехугольника (также и не плоского),
есть параллелограмм.
313.	В пространстве дана плоскость Р и две точки А и В,
не лежащие в плоскости Р. Найти, где надо взять на пло-
плоскости Р точку С, чтобы ломаная АСВ была кратчайшей.

314—327	СТЕРЕОМЕТРИЯ	35
314.	Показать, что если имеется конечное число прямых
таких, что каждые две из них пересекаются, то или все они
лежат в одной плоскости, или все проходят через одну точку.
315.	Каково геометрическое место точек пространства, рав-
равноудаленных от всех трех вершин заданного треугольника?
316.	Найти все прямые, проходящие через заданную точку
пространства и делающие одинаковые углы с двумя задан-
заданными прямыми, не лежащими в одной плоскости (скрещиваю-
(скрещивающимися).
317.	Найти геометрическое место точек, равноотстоящих от
обеих граней заданного двухгранного угла.
318.	Найти геометрическое место точек, равноудаленных от
двух заданных пересекающихся прямых.
319.	Показать, что биссекториальные плоскости всех трех
двухгранных углов трехгранного угла пересекаются по одной
прямой.
320.	Показать, что плоскости, проходящие через биссектри-
биссектрисы граней трехгранного угла и перпендикулярно к этим гра-
граням, все три пересекаются по одной прямой.
321.	Показать, что плоскости, проходящие через ребра трех-
трехгранного угла и через биссектрисы его противоположных гра-
граней, все три пересекаются по одной прямой.
322.	Показать, что плоскости, проходящие через ребра
трехгранного угла и перпендикулярные к противоположным
граням трехгранного угла, все три пересекаются по одной
прямой.
323.	Показать, что любой четырехгранный угол можно
пересечь так, чтобы в сечении получился параллелограмм.
324.	Две правильные треугольные пирамиды (равных или
разных высот— все равно) с одинаковыми основаниями сложе-
сложены вмгсте основаниями и вершины их соединены. Показать,
что отрезок, соединяющий вершины, перпендикулярен к ос
нованиям.
Куб
325.	Показать, что куб можно пересечь плоскостью так,
чтобы в сечении получился правильный шестиугольник.
326.	Показать, что две плоскости, проходящие через кон-
концы обеих троек ребер куба, сходящихся в концах диагонали
куба, рассекают эту диагональ на три равные части.
327.	Построить кратчайший отрезок, опирающийся конца-
концами на две диагонали граней куба, принадлежащие двум смеж-
смежным граням и не встречающиеся. В каком отношении делятся
эти диагонали теми точками, в которых этот отрезок на них
опирается?
3*

36	задачи	328—33
328.	Рассмотреть, какой многогранник ограничен плоско-
плоскостями, проходящими через все 12 ребер куба и делающими по
45° с гранями куба, сходящимися в этих ребрах. Найти, во
сколько раз объем этого многогранника больше объема куба.
Параллелепипед
329.	Показать, что всякая хорда параллелепипеда, прохо-
проходящая через точку пересечения его диагоналей, делится эгою
точкою пополам.
330.	Построить параллелепипед, три ребра которого лежат
на трех заданных прямых, попарно не лежащих в одной пло-
плоскости.
331.	Показать, что две плоскости, проходящие через кон-
концы обеих трогк ребер параллелелииеда, сходящихся в концах
диагонали параллелепипеда, рассекают эту диагональ на три
равные части.
332.	Через три вершины параллелепипеда, являющиеся вто-
вторыми концами ребер, исходящих из одной точки, прэведена
плоскость. Показать, что треугольник, получающийся в пере-
пересечении параллелепипеда этой плоскостью, пересекается диаго-
диагональю параллелепипеда, исходящего из той же точки, в центре
тяжести.
Правильный тетраэдр
333.	Найти угол между двумя противоположными ребрами
правильного тетраэдра.
334.	Показать, что правильный тетраэдр можно пересечь
плоскостью так, чтобы получился квадрат.
335.	Показать, что в правильном тетраэдре сумма расстоя-
расстояний от любой его внутренней точки до всех его четырех гра-
граней имеет постоянную величину, а именно, равна его высоте.
336.	Показать, чго, если три ребра параллелепипеда, схо-
сходящихся в одной вершине, образуют правильный тетраэдр, то
параллелепипед этот можно пересечь так, чтобы в сечении
получился правильный шесгиугольник.
Произвольный тетраэдр
Если принять три ребра некоторого тетраэдра, сходящихся в одной его
вершине, за три ребра параллелепипеда, то полученный параллелепипед мы
будем называть «достроением» тетраэдра до параллелепипеда «через такую-
то грань» или «исходя от такой-то вершины тетраэдра».
337.	Достроить некоторый заданный тетраэдр до паралле-
параллелепипеда четырьмя способами, исходя от каждой из четырех
вершин тетраэдра, и принять четыре вершины этих четырех

338	350	стереометрия	37
параллелепипедов, противолежащие в каждом параллелепи-
параллелепипеде вершине тетраэдра, за четыре вершины некоторого боль-
большего тетраэдра. Рассмотреть, как расположены параллелепи-
параллелепипеды и заданный тетраэдр по отношению к этому большему
тетраэдру и во сколько раз объем полученного тела больше,
чем объем данного тетраэдра.
338.	Рассмотреть, какими способами можно ррзрезать па-
параллелепипед на тетраэдры такие, чтобы вершины этих те-
тетраэдров были вершинами параллелепипеда.
339.	Показать, что объемы двух тетраэдров, или паралле-
параллелепипедов, с одинаковыми трехгранными углами относятся
как произведения их ребер, сходящихся в этих углах.
-34U. Показать, что объем тетраэдра, противоположные реб-
ребра которого суть два отрезка заданной длины, лежащие на
двух заданных прямых, не лежащих в одной плоскости, не
зависит от того, где эти отрезки на этих прямых расположены.
341.	Показать, что всякая плоскость, проходящая через
середины двух противоположных ребер тетраэдра, делит
этот тетраэдр на две равновеликие части.
342.	Пересечь тетраэдр плоскостью так, чтобы в сечении
получился параллелограмм.
343.	Показать, что все шесть плоскостей, проходящих
через середины ребер тетраэдра и перпендикулярно к ним,
пересекаются в одной точке.
344.	Показать, что все четыре прямые, проходящие через
центры кругов, описанных вокруг граней тетраэдра, и пер-
перпендикулярно к граням, пересекаются в одной точке.
345.	Показать, что все шесть биссекториальных плоскостей
всех двухгранных углов тетраэдра пересекаются в одной
точке.
346.	Показать, что все четыре прямые, соединяющие вер^
шины тетраэдра, с точками пересечения медиан противопо-
противоположных граней, пересекаются в одной точке.
347.	Найти условие, при котором центр шара, описанного
вокруг тетраэдра, лежит внутри тетраэдра.
348.	Показать, что если все шесть двухгранных углов те-
тетраэдра острые, то и все двенадцать его плоских углов острые
Правильный октаэдр
349.	Показать, что правильный октаэдр можно пересечь
плоскостью так, что в сечении получится правильный шести-
шестиугольник.
350.	Рассмотреть соотношение между кубом и правильным
октаэдром (связь между числом их вершин, ребер и граней
и возможное взаимное их расположение).

38	ЗАДАЧИ	351—359
Правильные додекаэдр и икосаэдр
351.	Показать, что можно так провести по одной плоскости
через каждое из двенадцати ребер куба, чтобы эти плоскости
замкнули правильный додекаэдр.
352.	Показать, что правильный додекаэдр можно пересечь
плоскостью так, чтобы в сечении получился правильный шести-
шестиугольник.
353.	Рассмотреть соотношение между правильными икоса-
икосаэдром и додекаэдром (ср. задачу 350).
354.	Получить срезанием частей из правильного икосаэдра
последовательно правильный додекаэдр, куб и правильный
тетраэдр.
Задачи на сжатия (растяжения) и сдвиги пространства
Пояснение I. Представим себе, что мы «сожмем» все пространство,
а вместе с ним и все фигуры, в нем находящиеся и состоящие из его то-
точек, к некоторой заданной плоскости Р так, чтобы точки самой плоскости
Р остались неподвижны, точки же, не лежащие в плоскости (как лежащие
по одну, так и лежащие по другую от нее сторону), приблизились бы к
плоскости Р, оставаясь на тех же перпендикулярах к плоскости Р, на ко-
которых они сначала находились, и притом так, что если расстояние от ка-
какой-либо точки до плоскости Р было h до сжатия, то оно станет h-k после
сжатия, где k — некоторый заданный положительный, постоянный для всех
точек коэффициент, характеризующий сжатие. Если k = 1, то никакого
сжатия, конечно, не произойдет, все точки останутся на месте; если k
меньше 1, произойдет сжатие, если же k больше 1, то произойдет, собствен-
собственно, растяжение пространства- от этой плоскости Р. Такое равномерное рас-
растяжение или сжатие всего пространства к плоскости Р называется также
афинитетом к плоскости Р.
355.	Показать, что при афинитете к плоскости прямые
остаются прямыми.
356.	Показать, что при афинитете к плоскости другие
плоскости пространства остаются плоскостями.
357.	Показать, что при афинитете к плоскости середина
отрезка остается серединой, и вообще точка, делящая отре-
отрезок в данном отношении, остается точкой, делящей его в
том же самом отношении.
358.	Показать, что при афинитете к плоскости параллель-
параллельные прямые и плоскости остаются параллельными.
359.	Показать, что при афинитете к плоскости объемы
всех тел, независимо от их формы, величины и положения,
изменяются в ? раз.
Пояснение И. Пусть заданы в пространстве некоторая плоскость
Р и некоторое направление, параллельное этой плоскости. Представим себе,
что мы «сдвинем» все пространство подобно колоде карт так, чтобы все
точки самой плоскости Р остались неподвижны: всякая точка, лежащая по

360—370	СТЕРЕОМЕТРИЯ	39
одну сторону от плоскости Р, сдвинулась бы в указанном направле-
направлении на некоторый отрезок а, пропорциональный ее расстоянию Л от пло-
плоскости Р, так что а = hk, всякая же точка, лежащая по другую сторону от
плоскости Р, сдвинулась бы в обратном направлении и опять пропорционально
ее расстоянию h от плоскости Р, с тем же коэффициентом пропорциональ-
пропорциональности k. Мы будем такое искажение пространства, а вместе с ним и всех
фигур в нем, называть сдвигом по отношению к плоскости Я—в данном
направлении и с данными коэффициентами k.
360.	Доказать, что при сдвиге прямые тоже остаются пря-
прямыми, плоскости остаются плоскостями, параллельные пря-
прямые и плоскости остаются параллельными, середина отрезка
остается серединой и т. д.
361.	Доказать, что объем любого тела при сдвиге не
меняется.
362.	Показать, что путем сжатий и сдвигов (сдвиг, сжатие,
сдвиг и сжатие) можно превратить любой тетраэдр в пра-
правильный.
363.	Показать, что при помощи сдвигов и сжатий можно
превратить любой параллелепипед в куб.
Применить принцип сжатий и сдвигов (т. е. принцип афин-
ности) к решению задач 331, 332, 346.
Цилиндр и конус
Замечание. В задачах 364—369, ради краткости, мы будем вместо
•>цилиндрическая поверхность вращения» и «коническая поверхность вра-
вращения», т. е. бесконечно продолженная боковая поверхность прямого кру-
кругового цилиндра и прямого кругового конуса, говорить просто: цилиндри-
цилиндрическая и коническая поверхность
364.	Показать, что если прямая имеет больше двух общих
точек с цилиндрической или конической поверхностью, то она
есть ее образующая.
365.	Исследовать, как могут пересекаться две цилиндри-
цилиндрические поверхности с параллельными образующими или две
конические поверхности с общей вершиной.
366.	Построить плоскость, проходящую через заданную
точку А и касающуюся заданной цилиндрической или задан-
заданной конической поверхности.
367.	Найти конические поверхности, для которых три за-
заданные прямые, проходящие через одну точку, являются
образующими (построить оси искомых конусов).
368.	Найти конические поверхности, касающиеся трех за-
заданных плоскостей (построить оси конусов).
369.	Исследовать, при каком условии вокруг четырехгран-
четырехгранного угла может быть описана коническая поверхность.
370.	Показать, что линия, получаемая в сечении прямого
кругового цилиндра плоскостью, есть равномерное сжатие

40	задачи	371—379
или растяжение окружности от прямой. Эта линия называется
эллипс ом.
371.	Показать, что эллипс есть геометрическое место то-
точек плоскости, сумма расстояний от которых до двух задан-
заданных точак этой плоскости, называемых фокусами эллипса,
постоянна.
372.	Показать, что сечение прямого кругового конуса
плоскостью, не параллельною его основанию, если оно есть
замкнутая линия, есть эллипс.
373.	Показать, что бесконечно продолженная боковая по-
поверхность косого кругового конуса, кроме плоскости симме-
симметрии, проходящей через его вершину и центр его основания
в том направлении, куда наклонен конус, имеет еще вторую
плоскость симметрии, перпендикулярную первой, проходящую
через его вершину и пересекающую его основание по ту
сторону от его центра, куда наклонен конус, и что она есть
не что иное, как боковая поверхность прямого эллиптического,
т. е. такого, основание которого эллипс, а вершина лежит на
перпендикуляре к основанию, восставленном в его центре.
Как следствие отсюда, вывести, что косой круговой конус,
кроме очевидных круговых сечений, параллельных его осно-
основанию, имеет еще вторую этой не параллельную систему
друг другу параллельных круговых сечений.
Шар
Замечание. Под словом «сфера» мы будем понимать поверхность
шара.
374.	Найти геометрическое место центров всех сфер, про-
проходящих через три заданные точки А, В и С.
375.	Предполагая заданными центры трех сфер и ради-
радиусы этих сфер, найти построением точки, общие одновремен-
одновременно всем этим трем сферам.
376.	Найти построением центр сферы заданного радиуса, ко-
которая бы: 1) проходила через две заданные точки и касалась
заданной плоскости, 2) проходила через две заданные точки
и касалась заданной сферы, 3) проходила через заданную точку
и касалась двух заданных плоскостей, 4) проходила через за-
заданную точку и касалась двух заданных сфер, 5) касалась
трех заданных плоскостей, 6) Касалась трех заданных сфер.
377.	Найти построением плоскость, касающуюся трех за-
заданных сфер.
378.	Какова та поверхность, которая получается при вра-
вращении окружности вокруг оси, проекция которой на пло-
плоскость этой окружности проходит через ее центр.
379.	Найти геометрическое место центров сечений заданной
сферы плоскостями, проходящими через заданную точку.

380—387	стереометрия	41
380.	Найти геометрическое место проекций заданной точ-
точки на все плоскости, проходящие через другую заданную
точку.
381.	Найти геометрическое место концов отрезка, равного
и параллельного данному (заданному по длине и направле-
направлению) отрезку, если концы этого подвижного отрезка находят-
находятся каждый на своей заданной сфере.
382.	Найти положения треугольника, равного и параллель-
параллельного заданному треугольнику, если каждая из вершин
искомого треугольника лежит на своей заданной сфере. Ис-
Исследовать число возможных решений задачи.
383.	На плоскость положены одинаковые шары в беско-
бесконечном числе так, что центры их находятся на одной прямой
и чго они касаются друг друга. Рядом с полученным рядом
шаров на эту же плоскость положен параллельно ему другой
ровно такой же ряд шьров так, что каждый из шаров второ-
второго ряда приходится в «выемку» между двумя соседними ша-
шарами первого ряда и касаегся их обоих и т. д. Так, вся пло-
плоскость окажется покрытой слоем одинаковых шаров, к каждому
из которых касается шесть шаров. Между каждыми тремя
взаимно касающимися шарами этого слоя образуется сверху
«ямка». Показать, что можно сверху так наложить на этот
первый слой второй, параллельный ему, и ровно такой же слой,
чтобы шары этого слоя не приходились в ямки первого слоя
(не во все ямки), и рассмотреть, сколькими различными спо-
способами это можно сделать.
384.	Предполагая, что на второй слой также наложен
третий слой и т. д. до бесконечности, найти, какую часть
всего бесконечного пространства занимают эти шары, и какая
часть приходится на промежутки между ними.
385.	Исследовать, сколькими способами при таком наложе-
наложении и как может быть обложен касающимися его шарами
шар этой системы.
386.	Найти, как надо располагать слои друг на друге для
того, чтобы все шары системы были одинаковым образом
окружены прилегающими к ним шарами системы.
Разобранные в задачах ?83—386 вопросы о двух замечательных распо-
расположениях шаров в пространстве имеют большое значение в физике — в тео-
теории расположения атомов в твердом веществе.
387.	Показать, что если поверхность такова, что окруж-
окружность, проходящая через любые три ее точки, всеми точками
своими лежит на ней, то эта поверхность—сфера.
Замечание. Проекция сферы прямолинейными лучами из «екоторой
точки сферы на плоскость, перпендикулярную к диаметру, проходящему через
эту точку, называется стереографической проекцией.

42	задачи	388—396
388.	Показать, что величины углов между линиями, про-
проведенными на сфере, при стереографической проекции сохра-
сохраняются.
389.	Показать, что при стереографической проекции окруж-
окружности, лежащие на сфере, будут проектироваться в виде окру-
окружностей же на плоскость проекций.
Задачи, в которых соображения стереометрии применяются
для решения вопросов планиметрии
390.	На плоскости заданы три полупрямые, исходящие из
одной точки и такие, что угол между каждыми двумя соседними
из них меньше 180°; внутри каждого из этих трех углов задано
по одной точке. Показать, что существует, и притом только
один, такой треугольник, стороны которого проходят через
заданные точки, а вершины лежат на заданных прямых.
391.	На плоскости заданы два треугольника ABC и А'В'О
такие, что прямые АА',ВВ' и СС пересекаются в одной точке.
Показать, что три точки пересечения прямых АВ и А'В', АС
и А'С, ВС и В'С лежат на одной прямой.
392.	На плоскости заданы три круга (как угодно располо-
расположенные и каких угодно разных радиусов); для каждой пары
этих кругов построены внешние касательные. Показать, что
точки К, L, М пересечения каждой из этих пар внешних ка-
касательных лежат на одной прямой.
393.	На плоскости заданы три круга (произвольной вэли-
чины и положения), имеющих общую внутреннюю часть. По-
Показать, что три хорды, каждая из которых общая двум кругам,
пересекаются в одной точке.
394.	Доказать, что диагонали, соединяющие противополож-
противоположные вершины любого, хотя бы и неправильного, шестиуголь-
шестиугольника, описанного около круга, пересекаются в одной точке
(теорема Брианшопа).
395.	Доказать, что три точки пересечения продолжений
трех пар противоположных сторон всякого шестиугольника,
вписанного в круг, находятся на одной прямой (теорема Па-
Паскаля).
ЗАДАЧИ НА ВЫЧИСЛЕНИЯ
Перпендикуляры и наклонные
396.	Из точки А пространства опущены на плоскость Р
перпендикуляр h и наклонная а. Из середины проекции на-
наклонной а на плоскость Р восставлен к ней в плоскости Р
перпендикуляр Ь. Найти расстояние от конца его В до сере-
середины Е перпендикуляра к.

397	407	стереометрия	43
397.	В одной из вершин прямоугольника восставлен пер-
перпендикуляр к плоскости прямоугольника. Конец его отстоит
на расстоянии а, Ь, с от трех других вершин прямоугольника.
Найти его длину h.
398.	Точка М равноудалена от всех трех вершин некото-
некоторого заданного прямоугольного треугольника на расстояние Ь.
Гипотенуза треугольника равна а. Найти расстояние h от точ-
точки М до плоскости треугольника.
399.	Из некоторой точки М опущен на плоскость Р пер-
перпендикуляр h и проведены две наклонные, углы которых с
перпендикуляром равны 30°, угол же между наклонными 60°.
Найти расстояние между основаниями наклонных.
Параллельные прямые и плоскости и перпендикуляры,
опущенные на плоскости
400.	Найти расстояние от середины отрезка, не пересекаю-
пересекающего плоскости Р, до этой плоскости, если расстояния от его
концов равны а и Ь.
401.	Найти расстояние от середины отрезка, пересекающе-
пересекающего плоскость Р', до эгой плоскости, если расстояния от его
концов равны а и Ь.
402.	Расстояния от концов отрезка до плоскости Р равны
а и Ь. Найти расстояние до плоскости Р от точки М отрезка,
которая делит его в отношении т: п.
403.	Расстояния от вершин некоторого треугольника до
плоскости Р суть а, Ь, с. Найти расстояние h от центра тя-
тяжести этого треугольника до плоскости Р.
404.	Расстояния трех вершин некоторого параллелограмма
от плоскости Р суть a, b, d. Найти расстояние от четвертой
вершины.
405.	Расстояния от четырех вершин некоторого параллеле-
параллелепипеда до плоскости Р суть а, Ь, с, d. Найти расстояния
от четырех других вершин. Предположить, что вершины
В, С, D находятся на концах трех ребер, сходящихся в вер-
вершине А.
406.	Расстояния от четырех вершин некоторого тетраэдра
до плоскости Р суть а, Ь, с, d. Найти расстояние h от центра
тяжести этого тетраэдра до плоскости Р.
407.	Расстояния от точки М до трех взаимно перпенди-
перпендикулярных плоскостей Pv P2, Р3 (взаимно перпендикулярны,
например, две стены и пол комнаты, образующие трехгранный
угол, или, например, три грани куба, сходящиеся в одной
вершине) суть ах, а2, а3. Найти расстояния от точки М до
точки О пересечения плоскостей Plr P2, Ps.

44	задачи	408—417
408.	Расстояния от двух точек пространства А и В до трех
взаимно перпендикулярных плоскостей Plt Р2, Ps суть соот-
соответственно аг, а2, а3 и blt b2, b3. Найти расстояние между
точками А и В.
409.	Проекции отрезка АВ на три взаимно перпендику-
перпендикулярные плоскости Рг, Рг, Рг суть bx, b2, bs. Найти длину
отрезка.
410.	Проекции отрезка на три взаимно перпендикулярных
прямых пространства рг, р2, р3 (взаимно перпендикулярны,
например, три ребра куба, сходящиеся в одной вершине) суть
аг, а2, as. Найти длину отрезка. (Проекцией отрезка на пря-
прямую в пространстве называется отрезок этой прямой, заклю-
заключенный между плоскостями, проходящими через концы
проектируемого отрезка перпендикулярно прямой, на которую
его проектируют.)
411.	Расстояния от четырех вершин некоторого тетраэдра
до трех взаимно перпендикулярных плоскостей пространства
Pi, Р* Ps суть соответственно ах, а2, а3; bv b2, b3; clt c2, cs;
dlt d2, d3. Найти объем тетраэдра.
Трехгранные углы
412.	Плоские углы трехгранного угла имеют 45°, 45° и 60°.
Найти величину двухгранного угла между плоскостями плоских
углов в 45°.
413.	Плоские углы трехгранного угла имеют 60°, 60° и 90°.
На ребрах, от вершины, отложены одинаковые отрезки ОА,
ОВ, ОС. Найти величину двухгранного угла между плоско-
плоскостью плоского угла в 90° и плоскостью ABC.
щ Куб
414.	Ребро куба а. Найти длину его диагонали, длину
диагоналей его граней и длину отрезка, соединяющего сере-
середины двух не параллельных и не сходящихся в вершине его
ребер.
415.	Ребро куба а. Найти площади его граней, его диа-
диагональных сечений, площади сечений, проходящих через центр
грани и ребро противоположной грани; площади сечений,
проходящих через концы трех ребер, сходящихся в одной
вершине.
416.	Ребро куба а. Найти площадь того сечения куба,
которое представляет собою правильный шестиугольник.
417.	Ребро куба а. Найти величину кратчайшего рассто-
расстояния от ребра куба до его диагонали, не встречающейся с
ребром. *

418	428	стереометрия	45
418.	Ребро куба а. Найти величину кратчайшего расстоя-
расстояния между не встречающимися диагоналями двух его смеж-
смежных граней.
419.	Два куба с ребром а имеют общий отрезок, соеди-
соединяющий середины двух противоположных граней, но один куб
повернут на 45° по отношению к другому. Найти объем об-
общей части этих обоих кубов, а также объем тела, представ-
представляющего собою совокупассть этих двух кубов.
420.	Два одинаковых куба с ребром а имеют диагонали
на одной и той же прямой, вершина второго куба лежит в
центре первого, и второй куб повернут вокруг ди. гонали на 60°
по отношению к первому. Найти объем общей их части.
421.	Два одинаковых куба с ребром а имеют общий отре-
отрезок АВ, соединяющий середины двух противоположных ре-
ребер, но один повернут вокруг этого отрезкя на 90° по отно-
отношению к другому. Найти объем обшей их части.
422.	Два одинаковых куба с ребром а имеют общую диа-
диагональ, но один повернут вокруг этой диагонали на 60° по
отношению к другому. Найти объем общей их ччсти.
423.	Через каждые три вершины куба с ребром а, лежа-
лежащие в концах каждых трех ребер, сходящихся в одной вер-
вершине, проведена плоскость. Найти объем тела, ограниченного
этими плоскостями.
424.	Взяты четыре вершины куба такие, что никакие две
из них не лежат на одном ребре. Через каждые три из этих
четырех вершин проведена секущая плоскость. Найти объем
тела, вырезанного из куба этими плоскостями. Ребро куба а.
425.	Произвольно выбранная секущая плоскость пересека-
пересекает куб с ребром а. Обозначив через г, s, t отрезки, которые
эта плоскость отсекает от трех параллельных ребер куба,
считая эти отрезки от одного из оснований куба (перпенди-
(перпендикулярного эгим ребрам) до точек пересечения секущей
плоскости с самими этими ребрами или с их продолжениями
под это основание или за противолежащее основание куба, рас-
рассмотреть все возможные случаи и вычислить объемы частей куба.
426.	Вычислить площади всех сечений куба, рассмотрен-
рассмотренные в задаче 425, выразив их через отрезки г, s, t.
Правильный тетраэдр
427.	Ребро правильного тетраэдра равно а. Вычислить
площадь того сечения тетраэдра, которое представляет собою
квадрат.
428.	Два одинаковых правильных тетраэдра с ребрами а
имеют общую высоту, но один из них повернут на 60° по
отношению к другому. Найти объем общей их части.

46	задачи	429—435
429.	Два одинаковых правильных тетраэдра с ребром а
имеют общую высоту, но вершина одного из них лежит в центре
основания другого, и наоборот. Стороны треугольников их
оснований расположены параллельно. Найти объем общей
части этих тетраэдров.
430.	Два одинаковых правильных тетраэдра с ребром а
имеют общую высоту, но вершина одного из них лежит в центре
основания другого, и наоборот. Основание второго тетраэдра
повернуто на 60° по отношению к основанию первого. Найти
объем общей их части.
431.	Два одинаковых правильных тетраэдра с ребром а
имеют общий отрезок, соединяющий середины двух противо-
противоположных ребер, но один тетраэдр повернут на 90° по отно-
отношению к другому. Найти объем общей их части.
432.	Правильный тетраэдр с ребром а рассечен произ-
произвольной секущей плоскостью. Обозначим через г, s, t от-
отрезки, которые отсекает эта плоскость от трех ребер
тетраэдра, сходящихся в одной вершине А, считая эти отрез-
отрезки от вершины А до точек пересечения секущей пло-
плоскости с самими этими ребрами тетраэдра или с их продол-
продолжениями за грань, противолежащую вершине А. Рассмот-
Рассмотреть все возможные случаи и вычислить объемы частей
тетраэдра.
433.	Вычислить площади всех сечений правильного тетра-
тетраэдра, рассмотренных в задаче 432, выразив их через отрезки
г, s, t.
Призматоиды
434.	Найти объем тела, ограниченного сверху и снизу
гранями, которые представляют собою прямоугольники, рас-
расположенные в параллельных плоскостях и так, что стороны
одного параллельны соответсгвенным сторонам другого, а
боковые грани суть четыре трапеции, если стороны одного
основания а и Ъ, а другого—а' и Ь'.
435.	Доказать, что объем любого выпуклого призматои-
призматоида (тела, ограниченного двумя параллельными основания-
основаниями, когорые суть любые выпуклые многоугольники, могу-
могущие быть и разных наименований, и представляющего наи-
наименьшее выпуклое тело, имеющее эти основания) равен
V = -{s -\-s' -j- 4Sj), где И — высота призматоида, т. е. рас-
расстояние между его основаниями, s — площадь нижнего,
s' — площадь верхнего основания и sx — площадь среднего
сечения, т. е. сечения плоскостью, параллельной основаниям
и проходящей посредине между ними.

436—455	СТЕРЕОМЕТРИЯ	47
Правильные многогранники
436.	Найти объем V правильного тетраэдра с ребром а.
437.	Найти радиус R шара, описанного вокруг правильного
тетраэдра с ребром а.
438.	Найти радиус г шара, вписанного в правильный те-
тетраэдр с ребром а.
439.	Найти величину кратчайшего расстояния между двумя
противоположными ребрами правильного тетраэдра с ребром а.
440.	Найти объем V и радиусы R и г описанного и впи-
вписанного шара для куба с ребром а.
441.	Найти объем V правильного октаэдра с ребром а.
442.	Найти радиус R описанного шара для правильного
октаэдра с ребром а.
443.	Найги радиус г вписанного шара для правильного
октаэдра с ребром а.
444.	Найти полную поверхность правильного додекаэдра с
ребром а.
445.	Найти радиус R описанного шара для правильного
додекаэдра с ребром а.
446.	Найти радиус г вписанного шара для правильного
додекаэдра с ребром а.
447.	Найти объем V правильного додекаэдра с ребром а.
448.	Найти полную поверхность правильного икосаэдра
с ребром а.
449.	Найти радиус R описанного шара для правильного
икосаэдра с ребром а.
450.	Найти радиус г вписанного шара дла правильного
икосаэдра с ребром а.
451.	Найти объем правильного икосаэдра с ребром а.
Цилиндр
452.	Из квадрата со стороною а свернута боковая поверх-
поверхность цилиндра. Найти его объем.
453.	Цилиндр пересечен двумя наклонными плоскостями
так, что плоскости эти пересекают боковую поверхность
цилиндра, но внутри цилиндра не пересекаются и не пересекают
оснований цилиндра. Зная, что радиус цилиндра г и расстояние
между точками с и с', где секущие плоскости пересекают
ось цилиндра, есть d, найти объем куска цилиндра, заключен-
заключенного между секущими плоскостями.
454.	Найти объем и полную поверхность коленчатой ци-
цилиндрической трубы.
455.	Найти объем цилиндра, так описанного вокруг пра-
правильного тетраэдра с ребром а, что два противоположных

48	задачд	456—466
ребра этого тетраэдра являются диаметрами оснований этого
цилиндра.
456.	Найти объем цилиндра, так описанного вокруг куба
с ребром с, что две противоположные грани куба являются
квадратами, вписанными в окружности его оснований.
457.	Найти объем цилиндра, так описанного вокруг пра-
правильного октаэдра с ребром а, что две противоположные
грани октаэдра являются треугольниками, вписанными в его
основания.
458.	Найти объем цилиндра, так описанного вокруг пра-
правильного додекаэдра с ребром а, что все вершины этого
додекаэдра лежат на поверхности цилиндра.
459.	Найги объем цилиндра, так описанного вокруг пра-
правильного икосаэдра с ребром а, что все вершины этого икоса-
икосаэдра лежат на поверхности цилиндра.
Замечание к задачам 455—459. Легко видеть, что эти цилиндры
суть цилиндры наименьшего объема, которые можно описать вокруг пра-
правильных многогранников.
Конус
460.	Из полукруга с радиусом R свернута боковая поверх-
поверхность конуса. Найти объем этого конуса.
461.	Квадрат вращается вокруг оси, проходящей через
вершину и середину стороны, не проходящей через эту
вершину. Найти объем и полную поверхность полученного
тела вращения.
462.	Показать, что объемы конусов, получаемых от враще-
вращения треугольника последовательно вокруг всех его сторон,
обратно пропорциональны этим сторонам.
463.	Вычислить объем конуса, описанного вокруг правильного
додекаэдра с ребром а так, что ребра, идущие- к вершинам
одной из его граней, лежат на образующих конуса, а проти-
противоположная грань — на основании конуса.
Шар
464.	В сферу радиуса R вписана правильная треугольная
призма. Радиус сферы, проведенный в вершину этой призмы,
делает с ее боковою гранью, проходящей через эту верши-
вершину, 22112°. Найти высоту призмы.
465.	Шар касается всех 12 ребер куба с ребром а. Найти
объем той части шара, которая заключается внутри этого куба.
466.	Сфера переменного радиуса R проходит через центр
некоторой заданной сферы радиуса г. Показать, что площадь
шапочки, вырезанной этой последней из поверхности перемен-
переменной сферы, имеет постоянную величину.

467—470	СТЕРЕОМЕТРИЯ	49
467- В сферу радиуса R вписан правильный тетраэдр, и три
грани его, исходящие из одной вершины, продолжены до
пересечения со сферой. Вычислить площадь той части поверх-
поверхности сферы, которая заключается внутри этого трехгранного
угла.
468.	Имеются два одинаковых шара большего радиуса R,
два одинаковых шара меньшего радиуса г, весьма длинный
цилиндр радиуса р и плоскость. Всего шесть предметов. Как
они расположены в пространстве — не сказано, но известно,
что каждый из этих шести предметов касается остальных
пяти, причем цилиндр касается плоскости по образующей,
а шаров — боковою поверхностью. Зная радиус г малых шаров,
найти радиусы /? и р больших шаров и цилиндра.
БОЛЕЕ ТРУДНЫЕ ЗАДАЧИ НА ДОКАЗАТЕЛЬСТВО
Некоторые задачи из общей теории выпуклых
многогранников
Не надо думать, что пирамидами, призмами, усеченными пирамидами,
призматоидами и правильными многогранниками исчерпываются все возмож-
возможные многогранники; разумеется, есть и многие другие. Наиболее важные
многогранники — так называемые выпуклые. Все рассмотренные нами в пре-
предыдущем многогранники выпуклые. Многогранник называется в ып у к л ы м,
если весь он лежит по одну сторону от плоскости любой его грани. В
настоящем отделе мы рассмотрим в качестве задач ряд теорем о выпуклых
многогранниках.
469.	Показать, что все точки отрезка, соединяющего две
точки выпуклого многогранника, суть тоже точки этого мно-
многогранника, и обратно, что если это имеет место для всякого
такого отрезка, то многогранник выпуклый.
470.	Показать, что сечение выпуклого многогранника пло-
плоскостью есть выпуклый многоугольник (многоугольник назы-
называется выпуклым, если он весь лежит по одну сторону от
прямой, являющейся продолжением любой из его сторон).
Замечание. Два выпуклых многогранника называются топологи-
топологически, тождественными, если: 1) они имеют одинаковое число граней,
2) одинаковое число граней одинаковых наименований (например, если первый
имеет пять четырехугольных граней, то и второй имеет пять четырехугольных
граней и т. д.), 3) схема смежности граней у обоих многогранников одна и та
же, т. е. если как-либо перенумеровать грани первого, то можно так пере-
перенумеровать грани второго (конечно, при этом грани с теми же номерами долж-
должны иметь одинаковые наименования), что если две грани первого смежны по
ребру, то грани с соотвчтственными номерами второго тоже, и обратно,
а если две грани первого смежны по вершине, то грани с соответственными
номерами второго тоже, и обратно. Два топологически тождест «енных
многогранника могут быть совершенно различной формы и величины.
4 Делоне и Житомирский

50	задачи	471—478
471.	Показать, что наименьшее число граней выпуклого
многогранника четыре и что все такие много! ранники топо-
топологически тождественны правильному тетраэдру.
472.	Показать, что топологически различных выпуклых
многогранников с пятью гранями два, один — топологически
тождествен правильной четырехугольной пирамиде, другой —
правильной треугольной приеме.
Замечание. Можно аналогично показать, что топологически различных
многогранников с 6-ю, 7-ю, 8-ю гранями—7, 34, 257 и т. д. Число это быстро
растет с возрастанием числа граней. Число топологически различных
12-гранников превосходит уже десятки тысяч. Число это точно определено
и все эти многогранники построены только для случаев 4, 5, 6, 7, 8 граней.
473.	Показать, что число N топологически различных
выпуклых многогранников с данным числом п граней огра-
ограничено.
474.	Показ 1ть, что существуют такие топологические типы
выпуклых многогранников, среди коюрых нет многогранников,
описуемых вокруг шара.
Замечание. Эта теорема была впервые доказана Штейнитцем в
1928 г. Общее решение вопроса о том, какие топологические типы суть те,
среди которых есть многогранники, описуемые вокруг шара, до сих пор не
найдено.
475.	Показать, что если выпуклый многоугольник разбит на
куски, каждый из которых есть выпуклый или невыпуклый
многоугольник с центром симметрии, то и сам рассматриваемый
мноюугольник имеет центр симметрии (центром симметрии
выпуклого или невыпуклого многоугольника называется точка,
делящая пополам любую хорду этого многоугольника, через
нее проходящую). (Теорема Минковского.)
476.	Показать, что если грани выпуклого многогранника
имеют центры симметрии, то и сам многогранник имеет центр
симметрии. (Центром симметрии многогранника называется
такая точка, которая делит пополам любую хорду многогран-
многогранника, через нее проходящую.) (Теорема А. Д. Александрова,
1932 г.)
477.	Показать, что для всякого выпуклого многогранника
с числом граней /, числом вершин 5 и числом ребер а имеет ме-
место соотношение:
(Теорема Эйлера.)
478. Показать, что йсякии выпуклый многогранник —жесткий,
т. е. что, если мыслить грани многогранника жесткими (т. е.
неизменяемыми, например сделанными из картона), но считать,
что по ребр™, по которым они друг с другом смежны, они
соединены шарнирно, то тем не менее мноюгранник неизме-
неизменяем. Каждый, клеивший многогранник из картона, по опыту

479—4*3	СТЕРЕОМЕТРИЯ
знает, что, как только наклеена последняя грань, многогранник
становится жесткие. Эту теорему предполагал верной еще
Эвклид, около 300 лет до н^шей эры, однако доказать ее
удалось только Коши в 1815 г.
Задачи из теории разбиения пространства на одинаковые
параллельно расположенные выпуклые многогранники
(параллелоэдры)
Замечание. Мы будем говорить, что некоторыми равными много-
многогранниками можно «заполнить» пространство в параллельном положении, если
можно неограниченное их число так складывать друг с другом, чтобы они:
1) не входили друг в друга, 2) не оставляли пустот между собою, 3) были
все между собою параллельно расположены. Очевидно, что кубами можно
заполнить пространство. Достаточно вспомнить детские кубики, которые,
укладываясь в ящике, ке оставляют пустот между собою и расположены
параллельно друг другу. То же очевидно и для параллелепипедов.
479.	Показать, что одинаковыми правильными шестигран-
шестигранными призмами можно заполнить пространство.
480.	Показать, что додекаэдрами подобными тому, который
был рассмотрен в злдаче 328, можно заполнить пространство.
481.	Разрежем додекаэдр задачи 480 плоскостью, проходя-
проходящей параллельно одной из пар параллельных граней того
куба, при помощи которого он построен, и вставим между
двумя его половинками правильную четырехугольную призму,
основание которой есть грань этою куба. Получится додекаэдр,
восемь граней которого—ромбы, а четыре — шестиугольники.
Показать, что такими одинаковыми между собою додекаэдрами
можно заполнить пространство.
482.	Куб мысленно разбит на восемь малых кубов тремя
плоскостями, параллельными трем парам параллельных граней
куба и проходящими посередине между ними. От каждого
из малых кубов отрезана половина той плоскостью, которая
в сечении дает правильный шестиугольник и перпендикулярна
той диагонали этого малого куба, которая идет в центр боль-
большого. Оставшаяся часть представляет некоторый 14-гранник.
Исследовать форму этого 14-гранника и показать, что такими
одинаковыми между собою 14-гранниками можно заполнить
пространство в параллельном положении.
Федоровым A880 г.) и Минковским A897 г.) было показано, что нет ни-
никаких других тел, которые существенно отличались бы от параллелепипеда,
шестиугольной призмы, двух додекаэдров и четырнадцатигранника, рассмот-
рассмотренных в задачах 479—482, и которые способны были бы в параллельном
положении заполнить пространство.
Перейдем теперь к рассмотрению этой более общей теории.
483.	Пусть трехмерная система бесконечного числа точек
в трехмерном пространстве такова, что: 1) если взять любые
три точки этой системы точек А, В, С и провести из точки С
4*

52	задачи	484—491
отрезок, равный и параллельный АВ, то конец его D будет
тоже точкой этой системы и 2) вокруг хоть одной точки этой
системы, как центра, можно описать такой шар некоторого
определенного не равного нулю радиуса г, что, кроме цен-
центральной, внутри этого шара не будет ни одной точки этой
системы. Показать, что эта система есть параллепипед-
ная система точек, т. е. такая, которая представляет со-
собою совокупность всех вершин равных параллелепипедов, смеж-
смежных по целым граням, которые получатся, если провести три
разно наклоненные бесконечные системы параллельных пло-
плоскостей, проходящих в каждой отдельной системе на одина-
одинаковых расстояниях друг от друга. (Эта теорема имеет очень
большое значение в теории чисел и кристаллографии.)
Замечание. Можно показать, что параллелоэдры, если требовать
только того, чтобы они были равны, параллельны, выпуклы и заполняли
все пространство, не входя друг в друга, непременно должны иметь центры
симметрии, но доказательство этой теоремы, впервые данное Минковским
(не элементарное), и недавно предложенное другое доказательство А. Д. Алек-
Александрова (элементарное) очень трудны, и поэтому мы их пропускаем,
принимая эту теорему без доказательства. Итак, мы будем, сверх всего
предыдущего, принимать, что параллелоэдры имеют центры симметрии
и, для простоты, еще, что они смежны целыми гранями, как например,
кубики в детской коробке, а не как кирпичи в кирпичной кладке.
484.	Показать, что центры параллелоэдров образуют парал-
лелепипедную систему.
485.	Показать, что грани параллелоэдров имеют центры
симметрии.
486.	Показать, что, исходя от всякого ребра е параллелоэдра,
можно образовать на нем замкнутую зону граней.
487.	Показать, что проекция параллелоэдра вдоль ребра е
на плоскость, ему перпендикулярную, есть выпуклый много-
многоугольник с центром.
488.	Показать, что проекции комплекса параллелоэдров,
имеющих общее ребро е, суть равные параллельно располо-
расположенные выпуклые многоугольники с центрами, облегающие
со всех сторон ту точку е, которая есть проекция ребра е,
и не налегающие друг на друга.
489.	Показать, чго сход в точке е этих многоугольников
либо такой, как у трех шестиугольников, облегающих точку,
либо как у четырех параллелограммов.
490.	Показать, что в первом случае предыдущей задачи
эти многоугольники суть шестиугольники с центрами симмет-
симметрии, а во втором случае—параллелограммы.
491.	Показать, что если пристроить к первому параллелоэдру
все те, которые смежны с ним по граням зоны, соответствую-
соответствующей данному его ребру е, затем пристроить к этим параллело-
эдрам те, которые с ними смежны по еще не занятым граням

492—498	стереометрия	53
этих же их зон и т. д., то получится бесконечный слой паралле-
параллелоэдров, все центры которых лежат в одной плоскости, и
который непроницаем, т. е. нельзя с одной стороны этого слоя
перейти на другую, не пересекая самого елок.
492.	Показать, что аналогичный слой, построенный от лю-
любого другого параллелоэдра разбиения, не входящего в первый
слой, не пересекает первого слоя.
493.	Показать, что если мыслить ребро s зоны вертикальным,
т. е. плоскость центров параллелоэдров зоны—горизонтальной,
и называть верхней «шапочкой» параллелоэдра комплекс всех
тех граней, которые расположены поверх от той зоны, кото-
которой он касается других параллелоэдров слоя, то всякая грань
верхней шапочки параллелоэдра исходного слоя (мы будем
называть его нулевым) есть одновременно грань нижней
шапочки некоторого параллелоэдра соседнего к нему сверху
слоя (мы будем называть его первым).
494.	Показать, что в силу результата предыдущей задачи
проекции шапочек параллелоэдров слоя получатся, если в
одной плоскости начертить разбиение ее на одинаковые шести-
шестиугольники с центрами и такое же параллельное этому, но
смещенное разбиение, или если начертить два одинаковых
и параллельных, но смещенных друг по отношению к другу
параллелограмматических разбиений.
495.	Показать, что топологически различных параллелоэдров
может существовать только пять.
496.	Показать, что если выпуклый многогранник, все грани
которого имеют центры симметрии, имеет один из найденных
пяти топологических типов, то он—параллелоэдр (принять во
внимание результат задачи 476).
Задачи на прямолинейные преобразования плоскости
и перспективу
Преобразованием плоскости Р в себя мы называем пере-
перемещение всех точек этой плоскости в ней самой. Примерами являются: пе-
передвижение всей плоскости как целого по себе самой, равномерное растя-
растяжение плоскости во все стороны от некоторой ее точки (так называемая
гомотетия), равномерное растяжение плоскости от прямой, при котором
все круги плоскости превращаются в эллипсы. Особенно важно (например,
при съемке плана самолетом, при которой вследствие качки самолета фо-
фотоаппарат в момент съемки, вообще говоря, стоит косо) так называемое
перспективное преобразование или коническая проек-
проекция, при которой параллельные прямые превращаются в сходящиеся.
497.	Показать, что преобразование плоскости, при котором
прямые остаются прямыми и сохраняются углы, есть преобра-
преобразование подобия.
498.	Показать, что две подобные фигуры всегда могут быть
повернуты так, чтобы быть гомотетичными, т. е. такими, что

54	ЗАДАЧИ	499—506
одна получается из другой путем равномерного ее растяжения
от некоторой точки плоскости, называемой центром гомо-
гомотетии или центром подобия этих фигур.
499.	Показать, что при гомотетии плоскости все фигуры,
на ней нарисованные, увеличиваются одинаково — как те,
которые расположены близко к центру гомотетии, так и те,
которые от негодллеко,—т.е. что преобразование самих фигур
не зависит от положения центра гомотетии, а только от
коэффициента гомотетии.
500.	Показать, что так называемое афинное преобразо-
преобразование плоскости, т. е. такое, при котором прямые остают-
остаются прямыми и параллельные параллельными, сводится к двум
равномерным сжатиям или растяжениям or двух взаимно пер-
перпендикулярных прямых, так называемых осей преобра-
преобразования, плюс, может быть, движение всей плоскости как
целого и плюс, может быть, отражение ее в прямой.
501.	Показать, что при равномерном растяжении или сжатии
плоскости к прямой все фигуры искажаются одинаково, неза-
независимо от того, лежат ли они далеко от оси сжатия или нет,
и что их искажение зависит только от направления оси сжатяя
и от коэффициента сжатия.
502.	Показать, что самое общее афинное преобразование
вполне определяется тем, куда при нем перешли заданные три
точки, не лежащие на одной прямой.
503.	Показать, что путем перспективной проекции любой
выпуклый четырехугольник может быть превращен в квадрат.
(Перспективной проекцией называется проекция из
точки лучами одной плоскости на другую, вообще говоря,
ей не параллельную.)
504.	Показать, что самая произвольная коллинеация,
т. е. такое преобразование плоскости, при котором только изве-
известно, что прямые переходят в прямые, вполне определяется
тем, куда перешли заданные четыре точки, по три не лежащие
на одной прямой.
505.	Показать, что самая общая коллинеация может быть
получена перспективой.
Замечание. Эти две последние задачи—504 и 505—имеют фундамен-
фундаментальное значение в теории аэрофотосъемки.
506.	Показать, что по трем точкам на местности и трем
углам между прямыми, проведенными к этим точкам с само-
самолета, можно определить положение самолета относительно
местности с точностью до одной из четырех возможностей.

РЕШЕНИЯ
ПЛАНИМЕТРИЯ
Отрезки и углы
1. Дано АВ—а, CD—b, CB=c (рис. 1). Требуется опреде-
определить AD. Из чертежа находим:
=AB + BD=AB + (CD — CB)=AB + CD — CB=
= a-\- b—с
2. Точки А, В могут лежать по одну сторону или по раз-
О А М В
Рис. 1.	Рис. 2.
ные стороны от точки О (рис. 2). Если а<?, то в первом
случае:
а во втором случае:
ОМ=ОВ — МВ=Ь — —{Ь + о)=4
2
Если с>&, то в полученных формулах нужно переставить
а и Ь. Если а=&, то полученные формулы остаются верными,
если считать отрезки с совпадающими концами равными нулю.
1 . 1 о
3. Из рис. 3 видно, что искомый угол равен — «¦+• —Р,
или — (а+ Р)- Если углы MON, А/ОР смежные, то а+ P=2d,

56
РЕШЕНИЯ
4—7
и, следовательно, — (а + Р) =d. Таким образом, биссектрисы
смежных углов взаимно перпендикулярны.
1	]
4. Из рис. 4 видно, что искомый угол равен —a-f-p-j	у,
2	2
если рассматривать и углы, большие 2с?. Если углы MON,
„ POQ вертикаль-
вертикальные, то у=а, и
искомый угол бу-
1 .
дет равен-^- a-г
1
или
м
Рис. 3.
Рис. 4.
=2d, так как
углы MON, NOP
в этом случае
смежные. Следовательно, биссектрисы вертикальных углов
составляют продолжение друг друга.
Соотношения между сторонами и углами треугольников
5. Допустим, что треугольник ABC разрезан на равные тре-
треугольники ABD, ADC (рис. 5). Тогда угол ADB треугольника
ABD должен быть ра-
равен одному из углов
треугольника ADC. Но
он не может быть ра-
равен углам DAC, ACD,
так как внешний угол
треугольника всегда
больше внутренних, _ и	т	__
с ним не смежных.	"	' с В \ ~Г~ с
Поэтому он должен	рис. 5.	Рис. 6.
быть равен смежному
углу ADC. Но тогда противолежащие стороны АВ, АС были
бы равны, что противоречит условию, в котором треуголь-
треугольник ABC предположен разносторонним. Отсюда следует, что
разносторонний треугольник нельзя разрезать на два равных
треугольника.
6.	Тремя способами, а именно высотами, проведенными из
каждой вершины.
7.	</.ВМС~>^_BDC, как внешний по отношению к тре-
треугольнику MDC, aZ-BDC>Z. ВАС, как внешний по отношению
к треугольнику BAD (рис. 6). Следовательно, ^ ВМ С > ^ВАС.

8-Ю
ПЛАНИМЕТРИЯ
57
Рис 7.
8.	В треугольниках АМВ, АМС (рис. 7) стороны AM, MB
соответственно равны сторонам AM, MC, но сторона АВ боль-
больше стороны АС. Следовательно, угол АМВ больше угла АМС.
Чтобы сравнить углы ВАМ, САМ, продолжим медиану AM
на отрезок MD, равный AM, и соединим
точки С, D, как это делается при дока-
доказательстве теоремы о внешнем угле тре-
треугольника. Треугольники АМВ, DMC
будут равны, причем AB=DC и
/_BAM=Z-CDM. Таким образом, усло-
условие АВ^>АС заменится условием DC^>
^>АС, и вместо углов ВАМ, САМ нужно
будет сравнить углы CDM, САМ. В тре-
треугольнике ACD против большей из сто-
сторон DC, AC лежит больший из углов
CDM САМ. Следовательно, угол САМ
больше угла CDM. Мы видим, таким обра-
образом, что из двух углов АМВ, АМС боль-
больше тот, который обращен к большей из
боковых сторон, а из двух углов ВАМ, САМ больше тот,
который прилежит к меньшей из боковых сторон треугольника.
9.	Отложим на стороне АВ отрезок АЕ, равный АС, и со-
соединим точки D, Е (рис. 8). Треугольник ADE будет равен
треугольнику ADC, причем Z. ADE=
=^ADC и ED=CD. Мы можем по-
поэтому сравнивать вместо углов ADB,
ADC углы ADB, ADE и вместо отрез-
отрезков BD, CD отрезки BD, ED. Так
как по условию АВУ-АС, то точка Е
лежит между точками А, В, и угол
ADE есть часть угла ADB; следова-
следовательно, </_ADB>2.ADE. Чтобы сра-
сравнить отрезки BD, ED, нужно сравнить
противолежащие углы BED, EBD тре-
треугольника BDE. Но угол BED равен
внешнему углу BCF треугольника
ABC, так как эти углы смежны с равными углами треуголь-
треугольников ADE, ADC, а угол BCF больше внутреннего не смеж-
смежного с ним угла EBD треугольника ABC. Следовательно,
угол BED больше угла EBD, и вместе с тем BD > ED.
Итак, и из двух углов ADB, ADC и из двух отрезков
BD, CD больше тот, который обращен к большей из боковых
сторон.
10.	Если углы при основании оба острые, то Н лежит на
основании; если один из углов при основании тупой, то И
лежит на продолжении основания за вершину этого угла;
Рис. 8.

58	решения	U_12
если один из углов при основании прямой, то Н совпадает с
вершиной этого угла. Докажем первое утверкдение (рис. 9).
Если бы Н лежало на продолжении основания, например за
вершину С, то по теореме о внешнем угле для треугольника
АСН острый угол АСВ был бы Солыне прямого угла АНС,
что невозможно. Если бы И совпадало с одним из концов
в	 с(н) н	в	мо и и
Рис. 9.	Рис. 10.
основания, например, с вершиной С, то острый угол АСВ был
бы равен прямому углу АНВ, что также невозможно. Остается
принять, что И лежит на самом основании. Доказательство
двух остальных утверждений предоставляем читателю.
П. Пусть АВу-АС (рис. 10). На основании решения 9 име-
имеем BD^>DC. Следовательно, BD больше половины ВС, и
точка D дальше от точки В, чем точка М. На основании
того же решения 9 имеем ^_ADB~^>/^_ADC. Следовательно,
угол ADB тупой, и, согл-сно решению 10, точка Н лежит на
продолжении основания BD треугольника ABD за точку D.
Таким образом точка D лежит между точками М и Н, что
и требовалось доказать. Полученную теорзму выра-
выражают иногда так: биссектриса лежит между медианой и
высотой.
Сравнительная длина объемлемых и объемлющих
12. Требуется доказать (рис. 11):
AB + BC-AC<2BD.
Имеем:
AB<AD-\-BD. BC<DC +
Складывая почленно, находим:
АВ + ВС<АС.
Вычитая по АС, получаем:
АВ + ВС — AC<2BD.

13-14
ПЛАНИМЕТРИЯ
59
13. Вершины Л, В, С, D наружного многоугольника
(рис. 12) соединены с точками Av Bv Cv D± контура внут-
Рис. 11.
реннего, так что этот контур разбит ими на ломаные части
Афг, B±Clt QOl ?>А- Если обозначим периметры наружного
и внутреннего многоугольника
соответственно через Р, Plt то
требуется доказать:
P-P1<&AAl+BBl+CCl+DD1).
Имеем:
+ ВВХ,
вс< ввг 4- вхсх 4- ccv
CD < CQ + CxDt + DDV	Рис. 12.
DA < DDx-\- DXAX 4 AAv
Складывая почленно, получаем следующее неравенство:
-f 2BBX 4- 2CQ 4- ^DDX 4-
или
CQ
Р< 2 (^х + ВВ1
Вычитая по Рг, получаем:
Р — Рг < 2 (ЛЛХ + ^^ + ССХ 4" i)
14. Пусть будет ABC ... KL данный многоугольник и М
данная точка. Имеем вообще:
МА + МВ>АВ, МВ + МС>ВС, .... MK + ML>KL,
ML-\-MA->LA.
Если точка М лежит на одной из сторон, то одно из этих
неравенств обратится в равенство. Если точка М совпадает с
одной из вершин, то-есть принадлежит двум сторонам, то два
неравенства обратятся в равенство. Но так как число всех
неравенств равно числу сторон многоугольника и, следова-
следовательно, не менее трех, то при всяком положении точки М
некоторые из них останутся неравенствами. Поэтому, сл0жив

60
РЕШЕНИЯ
15—16
их почленно, мы всегда получим неравенство, а именно:
2МА -f 2MB + 2МС + • • • + 2МК + 2ML >
Деля почленно пополам, получим:
MA + MB + .. - +
4... + kl
что и требовалось доказать.
15. Требуется доказать (рис. 13), что
¦у (АВ + ЛС) - -L BC< AM < -1- (Л5 + АС).
Первое неравенство вытекает из теоремы 12, согласно которой
АВ + АС — ВС<2АМ,
откуда делением пополам и получаем:
— (AB-+-AQ— — ВС<АМ.
Чтобы получить второе неравенство,
удваиваем медиану как в решении 8.
Имеем:
AD<DC+AC,
или
Рис. 13.
откуда делением пополам получаем АМ<С—(АВ-^-АС).
16. Обозначим стороны треугольника через а, Ъ, с, а со-
соответственные медианы через та, ть, тс. По теореме 15 имеем:
~Ф + с)—l-a<ma<±{b + c),
i-(c + fl)—j- b<mb<±(c + a),
{ + )
Складывая почленно, получаем:
4"(д+ b + с)<та -г Щ + тс<а + b -f с
Итак, сумма медиан треугольника заключается между полу-
полупериметром и периметром его.

J7—20	ПЛАНИМЕТРИЯ	gj
17.	Искомая точка есть точка пересечения диагоналей.
В самом деле: для точки, не лежащей ни на одной из диаго-
диагоналей, сумма расстояний от двух противоположных вершин
больше соединяющей их диагонали, и следовательно, сумма
расстояний от всех вершин больше суммы диагоналей; для
точки, лежащей на одной из диагоналей, сумма расстояний от
концов этой диагонали равна этой диагонали, но сумма рас-
расстояний от концов другой диагонали больше этой диагонали, и
следовательно, сумма расстояний от всех вершин все-таки
больше суммы диагоналей; только для точки, лежащей на
обеих диагоналях, то-есть для точки пересечения их,
сумма расстояний от всех вершин ргвна сумме диагоналей.
Таким образом, для этой точки сумма расстояний от всех
вершин действительно наименьшая, и притом только для нее
одной.
Перпендикуляры и наклонные
18.	Примем сторону треугольника, ограничивающую наш
отрезок, за основание и проведем соответствующую высоту.
Если углы при основании оба острые, то высота лежит внутри
треугольника; наш отрезок или совпадает с высотой и тогда
наверное меньше обеих боковых сторон, или лежит между
высотой и одной из боковых сторон и тогда наверное меньше
этой стороны; во всяком случае, он меньше наибольшей из
боковых сторон. Если один из углов при основании тупой, то
наибольшая из боковых сторон лежит в этом угле, а высота
в смежном угле; наш отрезок лежит между ними и, следова-
следовательно, меньше, чем наибольшая из боковых сторон. Случай пря-
прямого угла при основании предоставляем рассмотреть читателю.
19.	Пусть будет ABC данный треугольник (рис. 14) и DE
данный отрезок. Проведем отрезок AD и применим к тре-
треугольнику ABD теорему 18. Найдем, что
отрезок DE меньше наибольшего из отрезков
AD, BD. Но по той же теореме отрезок AD
меньше наибольшей из сторон АВ, АС, а от-
отрезок BD меньше стороны ВС, как часть ее.
Следовательно, отрезок DE меньше наибольшей
из сторон АВ, АС, ВС.
20.	Продолжив отрезок, заключенный весь
внутри треугольника, в обе стороны до пере-	^ИС- 14-
сечения с контуром, получим отрезок, заклю-
заключенный между вершиной и противолежащей стороной или
между двумя сторонами треугольника. По теоремгм 18 и 19
такой отрезок меньше наибольшей из сторон треугольника.
Тем более это справедливо относительно части такого отрезка.

62
РЕШЕНИЯ
21—24
21. Так как угол С треугольника ABC (рис. 15) тупой или
прямой, то весь треугольник лежит по одну сторону от вы-
высоты АН. Поэтому
HC<HD<HE<HF<... <НВ,
и, следовательно,
AC<AD<AE<AF<...<AB.
В	FTDC—н В треугольнике АСЕ линия AD
есть биссектриса; согласно решению
Рис. 15.	9 имеем CD<iDE. Точно так же
в треугольнике ADF линия АЕ
есть биссектриса, откуда заключаем DE<CEF.
Продолжая таким образом, получаем:
CD<DE<EF<...,
что и требовалось доказать.
22.	Доказательство этой теоремы предоставляем читателю.
Оно вполне сходно с предыдущим, с той только разницей,
что приходится применить решение 8.
Параллельные линии
23.	Угол DAE равен углу В как соответственный, а угол
DAC равен углу С как внутренне накрестлежащий (рис. 16).
Так как углы В, С равны
как углы при основании
равнобедренного тре-
треугольника, то и углы
DAE, DAC равны, что и
требовалось доказать.
24.	Угол EBD равен
углу DBC, так как BD
есть биссектриса угла В
треугольника ABC (рис.
17). Углы DBC, EDB рав- Рис 16	Рис. 17
ны как внутренне на-
крестлежащие при парал-
параллельных ВС, ЕР. Следовательно, углы EBD, EDB равны, и
треугольник BDE равнобедренный, с основанием BD. Так же
найдем, что треугольник CDF равнобедренный, с основанием
CD. Таким образом:
ED = BE, DF = CF.
Складывая почленно, найдем: EF = BE-\-CF, что и требо-
требовалось доказать.

25-28
ПЛАНИМЕТРИЯ
63
25. Пусть BD биссектриса внутреннего угла при вершине
В и CD биссектриса внешнего угла при вершине С (рис. 18).
Проведя DFE па; аллельно ВС и применив совершенно те же
рассуждения, что и в предыдущем решении, убедимся, как и
тогда, что треугольники BDE, CDF рав-
равнобедренные, с основаниями соответст-
соответственно BD, CD. Отсюда попредшему:
ED = BE, DF = CF.
Вычитая почленно, получим:
CF.
Таким образом получаем: часть нря-	Рис. 18.
мой, проведенной параллельно основанию
через точку пересечения биссектрис одного внутрзннего и
одного внешнего угла при концах основания треугольника,
заключенная между боковыми сторонами, равна разности от-
отрезков боковых сторон ме-кду этой прямой и основанием. Слу-
Случай двух внешних биссектрис предлагаем рассмотреть читателю.
Сумма углов треугольника
26. ±d.
27. В прямоугольном треугольнике ABC гипотенуза АВ
вдвое больше катета АС (рис. 19). Приложив к треугольнику
ABC равный треугольник
BDC, получим равносто-
равносторонний треугольник ABD.
Отсюда ясно, что в тре-
треугольнике ABC острые
углы А, В равны соогвет-
С -&Z	N^_	2.1.
ственноТ" и Тй-
О	О
28. В треугольнике
ABC прямые BDE, CD
суть биссектрисы внут-
внутренних углов при вер-
вершинах В, С, а прямые
Рис.19.	Рис.20.	BF, FCE—биссектрисы
внешних углов при тех
же вершинах. Условимся обозначать углы треугольника ABC
просто через А, В, Си обозначим углы между биссектрисами
через 1, 2, 3, как показано на рис. 20. Заметим предварительно,
что углы DCE, DBF прямые, так как биссектрисы смежных
углов взаимно перпендикулярны. В треугольнике BDC внешний

C4	РЕШЕНИЯ	29—30
угол при вершине D равен сумме внутренних при вершинах
В, С, которые в свою очередь равны половинам углов В, С
треугольника ABC:
Так как сумма всех углов треугольника равна 2с?, то сумма
их половин равна d, и мы можем написать:
Так как треугольник DCE прямоугольный, то сумма его острых
углов равна d; отсюда
Так как треугольник FBF также прямоугольный, то по той же
причине
Углы 1, 2, 3 острые, как и требует условие задачи. Действи-
Действительно, угол А меньше 2с? и, следовательно, — А = ^_ 2 мень-
меньше d, а потому и d	А =^/1 =^,3 меньше d. Итак, ис-
искомые выражения суть:
29Л.На рис. 21 Z.BDE = /_AED — /_DBE = /_ACD —
= С—В. Мы воспользовались тем, что в треуголь-
,F
D	С	ВС
Рис. 21.	Рис. 22.
нике BDE внешний угол при Е равен сумме внутренних при
В, D, и равенством треугольников AED, ACD.
30. На рис. 22 /_BDE = /_DEF-/_EBD = ^АСВ-
— ^_EBD = С—б. Мы применили теорему о внешнем угле к
треугольнику BDE и воспользовались равенством треугольни-

31-32
ПЛАНИМЕТРИЯ
ков AED, ACD для обнаружения равенства внешних углов
при вершинах Е, С.
31. Проведем в треугольнике ABC биссектрису AD и вы-
высоту АН (рис. 23). Пусть АВ^>АС. Тогда на основании реше-
решения 11 точка D лежит между точками В и И. Поэтому мы
можем написать:
?.DAH = ? ВАН -/_BAD.
Но из прямоугольного треугольника В АН находим: ^_ВАН =
= d — В, a Z. BAD = ^A = d~~B-^C. Таким образом
Предоставляем читателю проверить полученную формулу
при АВ = АС.
А.
Рис. 24.
32. В прямоугольном треугольнике ABC (рис. 24) проведем
из вершины прямого угла А медиану AM и высоту АН. Пусть
АВ^>АС. Тогда на основании решения 11 точка М лежит
между точками В и Н, и мы имеем:
?МАН = Z.BAH—^_ВАМ.
Из прямоугольного треугольника ВАН находим:
= d — В.
Чтобы определить угол ВАМ, удвоим медиану, продолжив ее
до точки D, и проведем BD. Вследствие равенства треуголь-
треугольников MAC, MBD прямые AC, BD образуют с секущей AD
равные внутренне накрестлежащие углы и, следовательно, па-
параллельны. Так как АСЛ-АВ, то и BD Л-АВ, и треугольник
ABD прямоугольный. Треугольники ABC, ABD имеют общий
катет А В и равные катеты AC, BD. Поэтому они равны, и
^ Делоые ¦ Житомирский

66
РЕШЕНИЯ
33—34
следовательно, равны и углы ABC,
катетам AC, BD. Таким образом:
ABM, противолежащие
Отсюда получим:
Z.MAH = (d — В) — В = d — 2B.
Для применения к следующий задаче удобнее заменить
d — B через С. Тогда получим:
/_МАН^С — В.
Если АВ=АС, то треугольник ABC равнобедренный и медиа-
медиана совпадает с биссектрисой, так что ^.МАН обращается в
нуль. Это подтверждает формулу, так как в этом случае
В = С.
33.	На основании решения 11 биссектриса лежит между
медианой и высотой. На основании решений 31 и 32 биссектри-
биссектриса образует с высотой вдвое меньший угол, чем медиана.
Следовательно, биссектриса делит пополам угол между медиа-
медианой и высотой.
34.	Каждые две биссектрисы образуют при пересечении
две пары вертикальных углов. Вертикальные углы между
биссектрисами двух соседних
углов четырехугольника, в ко-
которых не лежит сторона, соеди-
соединяющая вершины этих углов,
равны полусумме их. Вертикаль-
Вертикальные углы между биссектрисами
двух противоположных углов
четырехугольника, в которых не
лежит диагональ, соединяющая
вершины этих углов, равны
полуразности двух других углов. Вертикальные углы между
биссектрисами углов, образуемых парами противоположных
сторон четырехугольника, продолженными до пересечения,
равны полусуммам тех углов четырехугольника, вершины ко-
которых лежат внутри этих вертикальных углов.
Докажем для примера последнюю из трех теорем, как более
сложную. Обозначим углы четырехугольника через А, В: С, D,
углы между парами противоположных сторон, продолженных
до пересечения, через Е, F, углы между их биссектрисами
EH, FH, в которых лежат вершины А, С, через х, вспомо-
вспомогательный угол ECF через а. Из треугольника FGH (рис. 25)
находим:
х а F
О
Рис. 25.

35	ПЛАНИМЕТРИЯ
Из треугольника АЕС находим:
Подставляя, получаем:
а = А — — Е.
2
х = A — -E—-F.
2	2
Остается определить углы Е, F. Из треугольников CDE, BCF
находим соответственно:
E=2d — C—D, F = 2d — B — C.
Подставляя, получаем:
х = Л + С + -В+-/) — Id.
2
Так как сумма всех углов четырехугольника равна 4с?, то
сумма их половин равна 2с?. Поэтому:
- B + -D = 2d — -А — -С.
2	2	2	2
Подставляя, получаем:
2 * 2
ИЛИ
Полученная формула доказывает высказанное утверждение для
пары углов между биссектрисами, в которых лежат вершины
А, С. Углы оставшейся пары равны:
dx d(
что также согласно с этим утверждением. Тем самым оно
вполне доказано.
Параллелограммы и трапеции
35. Отрезки АВ, DE (рис. 26) можно рассматривать как
противоположные стороны параллелограмма. Так как диагона-
диагонали всякого параллелограмма взаимно делятся пополам, то BE
проходит через середину AD. Точно так же убедимся, что и
CF проходит через середину AD. Таким образом., AD, BE,
5*

РЕШЕНИЯ
36—39
CF проходят через одну и ту же точку, что и доказывает
теорему.
36. Пусть Р, Q, R, S середины сторон АВ, ВС, CD, DA
четырехугольника ABCD (рис. 27). Отрезки PQ, RS, как сред-
средние линии треугольников ABC, ADC, параллельны их общему
Рис. 27.
основанию АС и равны половине его. Следовательно, они рав-
равны и параллельны между собой. Таким образом, в четырех-
четырехугольнике PQRS противоположные стороны PQ, RS равны и
параллельны. Следовательно, четы-
четырехугольник PQRS есть параллело-
параллелограмм.
37. Пусть будут U, Т середины
дизгоналей AC, BD и S, Q середины
сторон AD, ВС четырехугольника
ABCD. Отрезки UQ, ST равны и
параллельны, как средние линии тре-
треугольников ABC, ABD с общим осно-
основанием АВ. Следовательно, точки S,
Т, Q, U суть вершины параллело-
параллелограмма, если только они не лежат все
нэ одной пряйой. Но отрезки ST,
SU, как средние линии треуголь-
треугольников ABD, ADC, параллельны их основаниям АВ, DC,
которые по условию непараллельны между собой. Сле-
Следовательно, прямые ST, SU не совпадают, и точки STQU
суть действительно вершины параллелограмма (рис. 28).
38.	Из теоремы 37 вытекает, что отрезки, соединяющие
середины противоположных сторон" четырехугольника, в ко-
котором противоположные стороны непараллельны, делят попо-
пополам отрезок, соединяющий середины диагоналей. Таким обра-
образом, все три отрезка пересекаются в середине послед-
последнего.
39.	По известной теореме, прямая, проведенная через сере-
середину боковой стороны треугольника параллельно основанию,
Рис. 28;

40—42	ПЛАНИМЕТРИЯ	gp
проходит через середину другой боковой стороны. Пусть
будут Е, Н середины боковых сторон и F, С середины диа-
диагоналей трапеции ABCD (рис. 29). Проведем через Е прямую
параллельно основаниям АВ, CD тра-
трапеции. Из треугольника ACD видим,
что она пройдет через F, затем из тре-
треугольника ABC видим, что она пройдет
через Н, а после этого из треугольника
BCD видим, что она пройдет через С.
Таким образом точки Е, F, С, Н все
лежат на этой прямой. Мы имеем здесь
случай, исключенный в задаче 37.	РиС- 29-
40. Пользуясь обозначениями пре-
предыдущего решения, имеем по теореме о средней линии для
треугольников ABD, ACD:
= -АВ, EF=~CD.
2	2
Вычитая почленно, получаем:
-{AB — CD).
2»
Таким образом, отрезок, соединяющий середины диагоналей
трапеции, равен полуразности ее оснований.
41. Обозначим расстояния концов А, В к середины М дан-
данного отрезка от данной прямой через a, b, m (рис. 30). Если
точки А, В лежат по одну сторону от данной прямой, то по
теореме о средней линии трапеции
найдем:
Если же точки А, В лежат по раз-
разные стороны от данной прямой, то
по теореме 40 найдем:
Рис.30.	« = !(<*-*) или т = \{Ь-а),
смотря по тому, какое расстояние больше, а или Ъ.
42. Обозначим расстояние вершин В, С, D и точки пере-
пересечения М диагоналей параллелограмма ABCD от прямой,
проходящей через вершину А, соответственно через Ь, с, d,
т. По теореме о средней линии треугольника имеем:
Но то же расстояние можно определить и по теореме 41 для

70
РЕШЕНИЯ
43
отрезка BD. Если данная прямая не пересекает отрезка BD,
то
Если же данная прямая пересекает отрезок BD, то, смотря по
тому, будет ли она ближе к В или к D, получим:
т=—(Ъ — d) или m=—(d—b).
Приравнивая выражения для т, полученные двумя спосо-
способами, получим в зависимости от случая:
с = b -f- d, или с = b — d, или с = d — b.
43. Из точки М на основании ВС равнобедренного треуголь-
треугольника ABC опущены перпендикуляры МР, MQ на боковые
м
Рис. 31.
Рис. 32.
стороны, и из вершины В проведена высота BR (рис. ЗП.
Требуется доказать:
MP-\-MQ = BR.
Проведя через точку М параллельную MSD к стороне АС,
отсечем от BR часть SR, равную MQ (рис. 32). Остается
доказать, что остальная часть BS равна МР. Но это ясно из
того, что BS и МР суть высоты равнобедренного треугольни-
треугольника DBM, проведенные из концов основания.
Если сделаем то же построение для точки М на продол-
продолжении основания, то получим (рис. 32):
МР = BS, MQ = SR,
и, вычитая почленно, найдем:
МР—MQ = BR.

41-45
ПЛАНИМЕТРИЯ
71
44. Из точки М внутри равностороннего треугольника ABC
опущены перпендикуляры МР, MQ, MR на стороны, и прове-
проведена высота AS (рис. 33). Требуется доказать:
МР -\- MQ + MR = AS.
Проведем через точку М прямую DTE, параллельную к сторо-
стороне ВС. В равностороннем треугольнике ADE сумма MP-\-MQ
равна высоте, проведенной из конца стороны DE. Но так как
в равностороннем треугольнике все высоты равны, то сумма
МР -j- MQ равна также высоте AT. С
другой стороны MR равно TS, как от-
отрезки параллельных между параллель-
параллельными. Итак,
= TS.
Складывая почленно, получаем:
s й
Если точка М лежит вне треуголь-	Рис- 33-
ника, то в первой части этого равенства
нужно заменить знак -|- знаком — перед расстояниями точки
М от тех сторон, относительно которых точка М и треуголь-
треугольник расположены по разные стороны. Доказательство предо-
предоставляем читателю.
Круг
45. Пусть будет ABCD параллелограмм, вписанный в круг
(рис. 34). Так как хорды АВ, CD параллельны, то заключен-
заключенные между ними дуги AD, ВС равны. Прибавив к этим дугам
по дуге АМВ, получим равные дуги BAD, ABC,
откуда следует равенство хорд BD, АС, т. е.
диагоналей параллелограмма. Но параллело-
параллелограмм с равными диагоналями есть прямоуголь-
прямоугольник. Наоборот, около всякого прямоугольника
можно описать круг, так как точка пересече-
пересечения его диагоналей находится, вследствие ра-
равенства диагоналей, на равных расстояниях от
вершин. Таким образом, чтобы около паралле-
параллелограмма можно было описать круг, необхо-
необходимо и достаточно, чтобы он был прямоугольником. Если
воспользоваться теоремой о сумме противоположных углов
вписуемого четырехугольника, то полученное условие важно
вывести еще проще. Действительно, чтобы параллелограмм
ABCD был вписуем, необходимо и достаточно, чтобы сумма
углов Л, С была равна 2d, то-есть, чтобы каждый из них
был равен d, так как они равны.
7В
Рис. 34.

72	Решения	46—48
46.	Пусть будет ABCD трапеция, вписанная в круг (рис. 35).
Вследствие параллельности хорд АВ, CD, заключенные между
ними дуги AD, ВС равны, а потому и хорды AD, ВС равны.
Следовательно, трапеция ABCD равнобочная. Наоборот, если
трапеция ABCD равнобочная, то около нее можно описать круг,
так как окружность, описанная около треугольника ABC,
пройдет и через точку D. Действительно,
эта окружность пересечет прямую CD в
точке, расстояние которой от точки А равно
ВС. Таких точек две, а именно D и Dv
но через точку Ьх наша окружность не
пройдет, так как четырехугольник ABCDX
есть параллелограмм, отличный от прямо-
прямоугольника, и около него нельзя поэтому
Рис. 35.	описать круг. Таким образом, чтобы около
трапеции можно было описать круг, не-
необходимо и достаточно, чтобы она была равнобочная. То же
самое можно вывести из теоремы о виисуемом четырехуголь-
четырехугольнике. Действительно, условие А -}- С = Id равносильно усло-
условию А = В, так как во всякой трапеции В -f- С = Id. Но А=В
только в равнобочной трапеции.
47.	Пусть будет ABCD параллелограмм (рис. 36), описанный
около круга. Соединим центр круга О с вершинами параллело-
параллелограмма. Углы DAB, СВА в сумме составляют
2d как внутренние односторонние. Полови-
Половины этих углов ОАВ, ОВА в сумме соста-
составляют d. Поэтому третий угол АОВ в тре-
треугольнике АОВ также равен d. Подобным
образом докажем, что все четыре угла
вокруг точки О равны d. Отсюда следует,
что АОС, BOD суть прямые линии и что
эти прямые перпендикулярны. Но паралле-
параллелограмм с перпендикулярными диагона-	рис зв.
лями есть ромб. Наоборот, во всякий ромб
можно вписать круг, так как точка пересечения его диагона-
диагоналей, как легко убедиться, равноудалена от его сторон. Таким
образом, чтобы в параллелограмм можно было вписать круг,
необходимо и достаточно, чтобы он был ромбом. То же
можно вывести и из теоремы: для того, чтобы в четырех-
четырехугольник можно было вписать круг, необходимо и достаточно,
чтобы суммы противоположных сторон были равны. Действи-
Действительно, в случае параллелограмма это условие равносильно
условию равенства всех сторон, так как противоположные
стороны равны.
48.	Хорды, проходящие через данную точку, можно сра-
сравнивать по их расстояниям от центра. Дальше всех от цен-

49—50
ПЛАНИМЕТРИЯ
73
тра та из них, которая перепендикулярна к прямой, соединя-
соединяющей данную точку с центром. Следовательно, эта хорда
меньше всех.
49.	Наибольшую внутреннюю часть имеет секущая, прохо-
проходящая через центр круга, потому что только у нее внутрен-
внутренняя часть есть диаметр, а диаметр больше всякой другой
хорды.
50.	Обозначим радиус данного круга через R и расстояние
его центра О от данной точки Р через d (рис. 37). Предполо-
Предположим сначала, что Р не
совпадает с О. Тогда чер-
чертеж показывает наглядно,
что ближайшая к Р точка
окружности есть конец А
диаметра ОР, располо-
расположенный с Р по одну сто-
сторону от О, а самая даль-
дальняя есть другой конец В
того же диаметра. Чтобы
проверить это, нам нужно
доказать, что для всякой точки М окружности, кроме А,
будем иметь
РМ>РА,
и что для всякой точки М окружности, кроме В, будем иметь:
РМ<РВ.
Если Р лежит внутри круга, то
Р"с
PM~>OM—OP=R — d,
и, следовательно.
РМ>РА.
Если Р лежит вне круга, то
и. следовательно, также
РМ>РА.
Если Р лежит на окружности, то она совпадает с А. В этом
случае
РА = 0, РЖ>0,
и, следовательно, попрежнему
РМ>РА.
Таким образом, неравенство РМ^>РЕ доказано во всех слу-

74	решения	51
чаях. Что касается неравенства РМ<СРВ, то его доказательство
не требует рассмотрения отдельных случаев. Имеем:
откуда находим:
РМ<РВ.
Если теперь предположим, что Р совпадает с О, то для всех
точек М имеем:
В этом случае расстояние Р от всех точек окружности одно
и то же и не существует ни наи-
меньшего, ни наибольшего расстоя-
ния.
51. Обозначим радиусы данных
кругов через R, R' и расстояние
между их центрами О, О' через d.
Предположим сначала, что О, О' не
Рис 38	совпадают. Если наши окружности
имеют две или одну общую точку,
то в каждой общей точке совпа-
совпадают две точки различных окружностей, расстояние между
которыми равно нулю и, следовательно, наименьшее. Если
круг О' лежит вне круга О, то, насколько можно судить из
рис. 38, наименьшим расстоянием будет
АА1 = 00' —ОА — О'А1 = d — R-R1.
Нужно поэтому попытаться доказать, что всякое другое рас-
расстояние
— R — R'.
При проверке этого неравенства удобнее заменить его равно-
равносильным неравенством:
не содержащим знака вычитания. В этой форме оно легко
проверяется. Действительно,
ОМ -|- ММ + МО' > 00',
то-есть
что и требовалось получить.

51
ПЛАНИМЕТРИЯ
75
Если круг О1 лежит внутри круга О (рис. 39), то наимень-
наименьшим расстоянием будет:
АА' = R — d — R,
так что всякое другое расстояние
MM'>R — d — R.
Действительно, утверждаемое неравенство равносильно нера-
неравенству:
которое только по форме отличается от очевидного неравенства:
ММ + М'О' + О'О>МО.
Таким образом, наименьшее расстояние найдено во всех
возможных случаях. Чтобы найти наибольшее расстояние,
достаточно заметить, что вообще
ММ' < МО + 00' + ОМ = R + d + R\
и только тогда, когда радиусы ОМ, О'М составляют продолже-
продолжения линии центров 00',
ММ' = МО + 00' +
Концы этих радиусов
и есть самые далекие
друг от друга точки кру-
кругов О, О'. На рис. 38 это
будут точки В, В', а на
рис. 39—точки В, А .
Предположим теперь, что
О, О' совпадают (рис. 40).
Для всякой точки М наружной окружности О найдем самую
близкую точку М и самую далекую точку М" внутренней
окружности О', проведя диаметр МММ". Наименьшее рас-
расстояние будет
ММ1 = ОМ — ОМ =R — R,
а наибольшее
ММ = ОМ + ОМ" =# + /?'.
Следовательно, наименьшее расстояние окружностей О, О'
будет R — R', а наибольшее R + R*. Но в отличие от преды-
предыдущих случаев один из концов наибольшего или наименьшего
расстояния можно выбрать как угодно на соответствующей
окружности.
Рис. 39.
Рис. 40.

76
РЕШЕНИЯ
52-54
52.	Если прямая и окружность имеют общие точки, то
наименьшее расстояние их есть расстояние между точками,
совпадающими в общих точках, и равно нулю. Если нее пря-
прямая лежит вне окружности, то опустим из центра круга пер-
перпендикуляр О А А' на прямую и возьмем на окружности и пря-
прямой какие-нибудь две точки М, М, не совпадающие обе сразу
с точками А, А' (рис. 41). Так как пер-
перпендикуляр есть кратчайшее расстояние
точки от прямой, то
ОМ + ММ >ОА + АА\
Отняв от частей неравенства равные от
резки ОМ, О А, получим неравенство
ММ'>АА',
Рис. 41.	которое показывает, что наименьшее рас
стояние есть АА'. Наибольшего же рас-
расстояния вовсе не существует, так как на окружности и пря-
прямой можно найти сколь угодно далекие друг от друга точки.
53.	В первом случае окружности пересекаются, во втором
первый круг лежит внутри второго, в третьем они лежат вне
друг друга, в четвертом внешне касаются, в пятом внутренне
касаются. Для решения такого рода вопросов нужно составить
сумму и разность радиусов данных кругов и сравнить с этой
суммой и разностью расстояние между центрами. В нашей
задаче сумма радиусов равна 4R, а раз-
разность 2R. В первом случае расстояние
между центрами 3R меньше суммы ради-
радиусов 4/? и больше их разности 2R. Следова-
Следовательно, окружности пересекаются. Во вто-
втором случае расстояние между центрами
R меньше разности радиусов 2R. Следова-
Следовательно, один круг лежит внутри другого
и т. д.
54.	Приложим к О кругу круги Ov Os,
О3 ,... того же радиуса так, чтобы каждый	Рис. 42-
следующий касался предыдущего (рис. 42).
Треугольник ОО]О2 равносторонний, так как все три его стороны
равны удвоенному радиусу наших кругов. Поэтому угол ОгОО2
равен — d. По той же причине и угол О2ОО3 равен —din. д.
3	3
Всего вокруг точки О можно расположить шесть таких углов,
6. Следовательно, и кругов Olt О2, О3, . . -
коснется круга Ог, как и тре-
так как 4d : — d
3
будет шесть, причем круг О6
бует условие задачи.

55
планиметрия
77
55. Отложим, or точки А на прямой в ту и другую сторону
бесконечный ряд равных отрезков ААХ, АгА2,. . . и АА\
А'А", . .. (рис. 43). Затем опишем около центров A, А1УА2, ... и
А', А", . .. круги вдвое меньшего радиуса, чем эти отрезки.
Получим бесконечный в обоих направлениях ряд равных кру-
кругов .... А", А', А, AVA*, . .., центры которых расположены
на одной прямой, и каждый из ко-
которых касается двух соседних.
Теперь расположим по одну сто-
сторону от этой прямой ряд кругов
.... В", В', В, Bv В2, . . . того" же
радиуса, каждый из которых ка-
касается двух соседних кругов ряда
... , A", A', A, Av Л2, ... Дока-
Докажем, что ряд кругов, . . . В", В',
В, В1г Bit . . . имеет те же свой-
свойства, что и ряд . . . , А", А', А,
Аг, Л2, . .., то-есть что центры
всех его кругов расположены на
одной прямой, и каждый круг ка-
касается двух соседних. Треугольники ААХВ, Л1Л2Б1 равносторон-
ние, и, следовательно, углы ААф, А2А1В1 равны — d. Так как
о
Рис_ 43.
углы ААгВ, ВА1В1, Д^Лз, расположенные по одну сторону от
прямой ААХА2, в сумме составляют 2d, то угол ВА1В1 также равен
~r d.B треугольнике ВА1В1 стороны AJ3. Л,^ равны удвоенному
радиусу наших кругов, а угол между ними
2
равен— d.
о
Следовательно, этот треугольник равносторонний, и третья его
сторона ВВ± также равна удвоенному радиусу наших кругов.
Отсюда следует, что круги В, Вх касаются. Так как наши рас-
рассуждения применимы к любой паре соседних кругов ря-
ряда. .., В", В', Bt, В2, . . . , то, очевидно, каждый круг этого
ряда касается двух соседних, как и требовалось. Что точ-
точки ... В', В', Вг, В2, . .. расположены на одной пгямой,
видно из того, что соседние отрезки ряда .... В"В', В'В, BBlt
ВуВ^ . . . составляют продолжение друг друга. Например, от-
отрезки В'В, ВВг составляют продолжение друг друга, потому что
углы В ВА, ABAV АгВВ1У равные — d, как углы равносторон-
о
них треугольников В'ВА, ABAlt Ajifi, в сумме равны 2d. Итак
ряд кругов ... , В", В', В, Blt В2, . . . имеет те же свойства,
что и ряд..., А", А', А, Аг, Аг, .... и можем поэтому при-
приложить к нему еще такой же ряд..., С", С, С, Сг, С2, . ..

78
РЕШЕНИЯ
56-57
и т. д. до бесконечности. Точно так же к ряду кругов ..., А",
А', А, Аг, Л2, .. . можно приложить такой же ряд . . ., ф\ C''
Р, Pi» Рг» • • • » к нему еще такой же ряд . . . , у", у', у, ух, у2, . - ,
т. д. до бесконечности. Каждый,
круг полученной системы касается
двух соседних с ним кругов того
же ряда и двух пар соседних с
ним рядов. Таким образом эта
система удовлетворяет всем требо-
требованиям задачи.
56. Обозначим углы четырех-
четырехугольника через А, В, С, D, углы
между диагоналями и между проти-
противоположными сторонами через а, C,
у, стягиваемые сторонами четырех-
Рис 44.	угольника дуги через х, у, z, и, как
показано на рис. 44. Теми же буквами, что и дуги, будем
обозначать соответствующие центральные углы. Имеем:
Решая уравнения, находим:
х = a + Р> У = <*¦— Р>
г = 2d— a -|- у, и = Ы — a — у.
После этого получим:
57. Обозначим (рис. 45) углы при основании треугольника
через В, С, стягиваемые боковыми сторонами АВ, АС дуги и
соответствующие центральные углы — через у, р, искомый угол
через х, как показано на рис. 45. Имеем:

58-60
ПЛАНИМЕТРИЯ
79
58. Обозначим (рис. 46) углы треугольника через А, В, С,
стягиваемые его сторонами дуги и соответствующие централь-
Рис. 45.
Рис. 46.
ные углы через а, р, у, искомые углы через х, у, г, как пока-
показано на рис. 46. Имеем:
=Bd — А)- А = 2d — 2A = 2(d — А).
Так же найдем у и г. Итак:
x = 2(.d — A), y = 2(d-B),
z = 2(d — C).
59.	Рассмотрим случай, когда секущие МАМ', NBN'^ne пе-
пересекаются внутри кругов О, О' (рис. 47). По свойству впи-
вписанных четырехугольников имеем:
Z.MNB = 2d— ZMAB = / М'АВ,
^M'N'B = 2d—/_M'AB = /_МАВ.
Складывая почленно, получаем:
/_MNB + /LM'N'B =
= /_МАВ + ?МАВ = 2d,
откуда следует, что хорды NM,
N'M' параллельны. Рассмотрение
случая, когда секущие пересекаются внутри одного из
кругов, предоставляем читателю. В случае, когда концы
секущих на одном из кругов совпадают, соответствующая
хорда обращается в касательную, которая остается параллель-
параллельной другой хорде.
60.	Рассмотрим случай, когда круги О, О' внешне каса-
тельны (рис- 48). Углы AMN, CAN измеряются полови-
половиной одной и той же дуги AN и, следовательно, равны. Точ-
Точно также углы AM'N', BAN' измеряются половиной одной и
Рис. 47.

80
РЕШЕНИЯ
61-62
той же дуги AN' и потому равны. Но углы CAN, BAN' рав-
равны как вертикальные. Следовательно, и углы AMN, AMN'
равны, откуда вытекает параллельность хорд MN, M'N'. Слу-
Случай внутреннего касания кругов предлагаем разобрать чита-
читателю. Когда секущие совпадают, обе хорды обращаются в
касательные, которые остаются параллельными.
61. Пусть будет PMNQ общая секущая кругов О, О', внут-
внутренне касательных в точке А (рис. 49). Требуется доказать
равенства
?МАР = Z.NAQ, /LNAP= /_MAQ.
Второе получается из первого .прибавлением к обеим частям
по /_MAN. Чтобы доказать первое, продолжим AM, AN до
Рис. 48.
Рис. 49.
Рис. 50.
пересечения с окружностью О' в точках М, N'. По теореме
60 хорды MN, MN' параллельны. Следовательно, заключенные
между ними дуги РМ, QN' круга О' равны, а потому равны
и опирающиеся на эти дуги вписанные углы MAP, NAQ того
же круга, что и требовалось. Если бы хорда PQ круга О'
была касательна к кругу О, то точки М, N совпадали бы с
точкой касания и мы "получили бы следующую теорему: если
два круга внутренне касательны и хорда наружного круга
касательна к внутреннему, то прямая, соединяющая точку
касания кругов с точкой касания хорды к внутреннему кругу,
делит пополам угол между прямыми, соединяющими точку
касания кругов с концами хорды. Предлагаем читателю до-
доказать эту теорему самостоятельно.
62. Требуется доказать (рис. 50):
/_MAQ ¦\-/_NAP = 2d.
Продолжим MA, NA до пересечения с окружностью О' в точ-
точках М, N'. По теореме 60 прямые MN, M'N' параллельны,
и, следовательно, дуги PAN', QBM' равны. Угол QAM' изме-
измеряется половиной дуги QBM',a угол PAN' измеряется поло-
половиной дуги PBN', которая вместе с дугой PAN', равной дуге

63—64
ПЛАНИМЕТРИЯ
81
Рис. 5].
QBM', составляет полную окружность. Отсюда видно, что углы
QAM; PAN' в сумме измеряются половиной окружности, и
следовательно, составляют 2d. Поэтому и смежные с ним
углы MAQ, NAP должны в сумме составлять 2d, что и тре-
требовалось доказать. Если бы общая секущая MNPQ обрати-
обратилась в общую касательную к кругам О, О', то точки М, N
слились бы с точкой касания к кругу О, а точки Р, Q с точ-
точкой касания к кругу О', и мы получили бы
теорему: общая касательная двух внешне
касательных кругов видна из точки касания
их под прямым углом. Предлагаем читателю
доказать эту теорему отдельно.
63.	Угол BED равен углу ВАТ как соот-
соответственный, а угол ВАТ измеряется полови-
половиной дуги АСВ (рис. 51). Угол DCB изме-
измеряется половиной дуги AFB. Так как дуги
АСВ, AFB вместе составляют полную окруж-
окружность, то измеряемые половинами этих дуг углы BED, DCB
в сумме равны 2d, и следовательно, около четырехугольника
BCDE можно описать круг, что и требовалось доказать.
64.	В четырехугольнике ABCD (рис. 52) стороны АВ, DC
продолжены до пересечения в точке F, а стороны AD, ВС
продолжены до пересечения в точке Е.
Окружности, описанные около треуголь-
треугольников BCF, CDE, имеют кроме точки С
еще одну общую точку G. В противном
случае эти окружности касались бы в
точке С, и по теореме 60 прямые BF,
DE были бы параллельны, тогда как в
действительности они пересекаются в
точке А. Нужно доказать, что точка G
лежит также и на окружностях, описан-
описанных около треугольников ABE, ADF.
Доказательство одно и то же для обоих
треугольников, и мы приведем его толь-
только для треугольника ADF. Чтобы доказать, что точки А,
D, F, G лежат на одной окружности, достаточно проверить,
что в четырехугольнике ADGF внутренний угол DGF при
вершине G равен внешнему углу FAH при противоположной
вершине А.
Имеем:
Z DGF = Z DGC + /CGF.
Далее имеем:
/_DGC= /DEC,
так как эти углы вписаны в один и тот же круг и опираются
6 Делоне и Шитомирскнп
Рис. 52.

82
РЕШЕНИЯ
на одну и ту же дугу, и
/.CGF '== /_СВА,
так как угол CGF внутренний при вершине G, а угол СЯД
внешний при вершине В вписанного четырехугольника. Отсюда
/_DGF = ^DEC + ZJOBA,
то-есть сумме двух внутренних углов треугольника ABE, не
смежных с внешним углом FAH. Так как эта сумма равна
углу FAH, то мы получаем
= Z.FAH,
что и доказывает теорему.
65. Стороны пятиугольника ABCDE (рис. 53) продолжены
до образования пятиугольной звезды KLMNP, и около тре-
треугольных лучей ABN, ВСР, CDK,
DEL, EAMописаны окружности. Как
и в задаче 64, убедимся, что окруж-
окружности, описанные около соседних
лучей, пересекаются кроме вер-
вершины пятиугольника еще в одной
точке. Обозначив новые точки пе-
пересечения через А', В', С, D', Е'.
Требуется доказать, что эти точки
лежат на одной окружности. Доста-
Достаточно доказать, что точки А', В',
С, D' лежат на одной окружно-
окружности и что точки В', С", D\ E ле-
лежат на одной окружности, так как
из этого будет следовать, что точки
А\ Е лежат на окружности, про-
проходящей через точки В', С, D', то-
есть, что все пять точек лежат на
этой окружности. Так как для любых четырех точек доказатель-
доказательство одинаково, то мы докажем только, что точки В', С, П\Е
лежат на одной окружности. Предварительно докажем,
что точки Р, В', А, Е', L лежат на одной окружности. Это
вытекает из теоремы 64. Применяя эту теорему к четырехуголь-
четырехугольнику ABCL, находим, что точка В' лежит на окружности,
описанной около треугольника PAL, а применяя ее к четырех-
четырехугольнику AEDP, убеждаемся, что и точка Е' лежит на ок-
окружности, описанной около треугольника PAL. Таким образом
точки Р, В' А, Е', L действительно лежчт на одной окруж-
окружности. Переходя к нашей теореме, заметим, что она будет
доказана, если мы проверим равенство:
/.С D'?¦' = ?С В' F,

gg	ПЛЛПИМЕТГИЯ	g3
так как это покажет, что четырехугольник B\C',D,E впи-
суемый. Представим это равенство в виде
/_С D' ?> + /DD'E' = /С В'Р+ /PEF
и докажем, что первые и вторые слагаемые равны в отдель-
отдельности.
Действительно:
/С D1 D = /ССР
по свойству вписанного четырехугольника С D' DC;
/ССР = /С В1 Р,
так как эти углы вписаны в один и тот же круг и опираются
на одну и ту же дугу; следовательно,
/С D' ?>= /.СВ Р,
как и требовалось. Далее:
/DD'Е1 = /DLE',
так как эти углы вписаны в один и тот же круг и опираются
на одну и ту же дугу;
ADLE = /_PB'F
по свойству вписанного четырехугольника РВ'Е'Ц следо-
следовательно,	¦
ADD' Е' = /_РВ' F,
что заканчивает доказательство.
66. Требуется доказать фис. 54), что
AM = BM + СМ.
Для доказательства нужно разбить отрезок AM на части,
равные в отдельности отрезкам ВМ и СМ. Если отложим на
отрезке AM отрезок АР, равный отрезку
ВМ, то останется доказать, что отрезок РМ
равен отрезку СМ. В треугольниках САР,
СВМ имеем С А = СВ, АР=ВМн /.САР =
= /СВМ, так как эти углы вписанные и
опираются на одну и ту же дугу СМ. Сле-
Следовательно, треугольники САР, СВМ равны
и СР = СМ. Таким образом треугольник СРМ
равнобедренный с основанием РМ. Но угол
при основании РМС вписанный и опирается
на дугу АС, равную трети полной окруж-	Рис 54.
ности. Следовательно, угол РМС равен
2
¦g" а, откуда легко вывести, что и остальные углы треуголь-
6*

84	РЕШЕНИЯ	67—70
2
ника PMC равны — d, так что он оказывается равносторонним.
Отсюда находим:
РМ = СМ,
что только и осталось доказать.
Замечательные точки и линии в треугольнике
67.	Центр описанного круга ближе всего к наибольшей сто-
стороне, потому что хорда круга тем ближе к центру, чем она
больше.
68.	Центр описанного круга может лежать или внутри тре-
треугольника, или внутри одного из трех сегментов, прилегаю-
прилегающих к сторонам треугольника, или на одной из трех сторон
треугольника. В первом случае сегменты не содержат центра
внутри себя. Поэтому дуги их меньше полуокружности, и
углы треугольника острые. Во втором случае дуга сегмента,
содержащего центр, больше полуокружности, и опирающийся
на нее угол треугольника тупой. В третьем случае дуга сег-
сегмента, прилегающего к стороне, содержащей центр, есть по-
полуокружность, и опирающийся на нее угол треугольника пря-
прямой. Эти три случая исчерпывают все возможности и исклю-
исключают друг друга. Поэтому необходимое и достаточное усло-
условие, чтобы центр описанного круга находился внутри, вне или
на границе треугольника, состоит в том, чтобы треугольник
был соответственно остроугольный, тупо
угольный или прямоугольный.
69. Пусть будет АВ (рис. 55) заданное
основание. Тогда вершины остроугольных
- треугольников лежат внутри полосы, огра-
ограниченной прямыми, перпендикулярными к
прямой АВ в точках А, В, но вне круга,
построенного на отрезке АВ как на диа-
диаметре. Вершины тупоугольных треуголь-
Рис. 55.	ников лежат по обе стороны от полосы
и внутри круга, но не на прямой АВ.
Вершины прямоугольных треугольников лежат на краях по-
полосы и на окружности круга, но не в точках А, В. На пря-
прямой АВ вообще не лежат вершины треугольников с основа-
основанием АВ.
70. Пусть будет АН высота и О центр описанного
круга треугольника ABC (рис. 56). Проведем радиус ОА, опу-
опустим из О перпендикуляр ОР на сторону АВ и продол-
продолжим его до пересечения М с окружностью. Требуется до-
доказать:
/_ОАВ= /.САН.

71
ПЛАНИМЕТРИЯ
85
Так как треугольники ОАР, САН прямоугольные, то вместо
этого можно доказать:
/_АОР = /_ACH.
Предположим сначала, что угол С треугольника ABC ост-
острый. Тогда угол АСН совпадает с углом С и измеряется по-
половиной дуги сегмента, прилегающего к стороне АВ. С дру-
другой стороны в этом случае центр О лежит вне того же сег-
сегмента. Поэтому продолже-
продолжение перпендикуляра ОР де-
делит пополам дугу именно
этого сегмента, и угол АОР
также измеряется полови-
половиной его дуги. Следователь-
Следовательно, углы АСН, АОР равны,
что и требовалось доказать.
Рис. 56.
Предположим теперь, что
угол С треугольника ABC
тупой. Тогда угол АСН
смежный с углом С и измеряется половиной дуги АСВ,
дополняющей дугу сегмента, прилегающего к стороне АВ,
до полной окружности. С другой стороны в этом
случае центр О лежит внутри того же сегмента. Поэтому про-
продолжение перпендикуляра ОР делит пополам дугу АСВ до-
дополнительного сегмента, и угол АОР измеряется половиной
этой дуги. Следовательно, в этом случае углы АСН, АОР
равны. Остается только случай, когда угол С прямой. Но в
этом случае высота АН совпадает
со стороной АС, а радиус АО
идет по стороне АВ, так что углы
АСН, ОАВ оба равны нулю, и
следовательно, равны между со-
собой, как и требует теорема.
71. Треугольник ABC разбит
прямой AD на треугольники ABD,
ACD (рис. 57). Центр описанно-
описанного круга О треугольника ABC
есть точка пересечения перпен-
перпендикуляров в срединах сторон АВ, АС; центр описанного
круга Oj треугольника ABD лежит на первом перпендикуляре,
центр описанного круга О2 треугольника ACD лежит на вто-
втором перпендикуляре. Нужно доказать, что четырехугольник
АОХ ОО2 вписуемый. Так как угол ОхООг, очевидно, дополняет
угол ВАС до 2d, то остается доказать, что противоположный
угол равен углу ВАС. Предположим, что прямая AD наклонна
к основанию АС и что через ADB обозначен тупой угол, а
Рис. 57.

86
РЕШЕНИЯ
72—75
через ADC острый. Тогда из рассуждений решения 70 видно,
что центр Ох лежит вне треугольника ABC, а центр О2 внутри
треугольника ABC. Поэтому:
/ОХАО2 = /.ВАС + /ВАОХ — /САО2.
Но по теореме 7U для треугольников ABD, ACD
/BAOr = /DAH, /САО2 = /DAH.
Следовательно, углы BAOt, CAO2 равны, и
/ ОХАО2= /ВАС,
что и оставалось доказать. Если теперь предположим, что прямая
AD перпендикулярна к основанию ВС, то доказательство толь-
только упрощается. В этом случае О1 ле-
лежит на АВ, и О2 лежит на АС, так что
мы сразу получаем:
/ OtAO2 = / ВАС.
72. Пусть АС<АН (рис. 58). Тогда
/АВС</АСВ. Так как / ОВС =
= 1/ЛВСи /ОСВ = - / АСВ, той
Рис. 58	2	2
/ОВС<^/ОСВ. Поэтому в треугольнике
ОВС имеем ОС <CQB. Таким образом из двух вершин треугольни-
треугольника центр вписанного круга ближе к той, которая лежит против
большей стороны. Следовательно, из всех вершин треугольника
центр описанного круга ближе всего к той, котор ;я лежит про-
против наибольшей стороны, то-есть к вершине наибольшего угла.
73.	Не приводим доказательства, так
как его мо/кно найти в курсах элемен-
элементарной геометрии.
74.	Это доказательство обычно приво-
приводится в курс 1х элементарной геометрии.
75.	Пусть будут АН, В К, CL высоты
треугольника АВС(рис59). Окружность,
описанная на АВ как " на диаметре,
пройдет через Н и К, так как углы
АНВ, АК.В прямые. Поэтому углы АНК>
АВК равны как вписанные углы, опи-
опирающиеся на одну и ту же дугу. Таким	Фиг. 59.
же образом из рассмотрения окруж-
окружности, описанной на АС как на диаметре, найдем, что равны
углы AHL, ACL. Итак:
/АНК= /АВК, /AHL = /ACL.
Но из прямоугольных треугольников АВК, ACL находим:
/ АВК = / ACL = d— /ВАС.

76—78	ПЛАНИМЕТРИЯ	g7
Следовательно,
/ АНК = / AHL,
и НА есть биссектриса угла KHL. Так же найдем, что KB,
LC суть биссектрисы углов HK.L, HLK- Таким образом высо-
высоты АН, ВК, CL суть биссектрисы внутренних углов треуголь-
треугольника HKL и, следовательно, пересекаются в одной точке D.
Мы воспользовались при доказательстве чертежом, на котором
треугольник ABC остроугольный. Если бы угол ABC был
прямой, то точки Н, К слились бы с точкой С, и треугольник
HKL перестал бы существовать, но высоты все-таки пересек-
пересеклись бы, а именно в точке С. Если бы угол АСВ был тупой,
то высоты НА, KB стали бы биссектрисами внешних углов,
а высота LC осталась бы биссектрисой внутреннего угла тре-
треугольника HKL, и высоты попрежнему пересеклись бы на
основании теоремы 73. Предлагаем читателю рассмотреть два
последних случая.
76.	На рис. 59 имеем АС<САВ. Поэтому НС<СНВ, так как
меньшая наклонная ближе к перпендикуляру. Отсюда находим
DC<C_DB, так как из двух наклонных меньше та, которая
ближе к перпендикуляру. Таким образом из двух вершин
ортоцентр D ближе к той, которая лежит против большей
стороны. Следовательно, из всех вершин ортоцентр ближе к
той, которая лежит против наибольшей стороны, то-есть, к
вершине наибольшего угла.
77.	На рис. 59 имеем АС<АВ; отсюда ?АВС</ АСВ;
отсюда в свою очередь /_ВАН<С/_САН, так как /_ВАН =
= d — / ABC, Z. САН = d — / АСВ. Окружность, описанная
на AD как на диаметре, пройдет через вершины К, L прямых
углов, опирающихся на AD. Из двух хорд DK, DL этой ок-
окружности меньше та, на которую опирается меньший из вписан-
вписанных углов KAD, LAD, т. е. хорда DK. Таким образом из
двух сторон треугольника ABC ортоцентр ближе к меньшей,
и следовательно, из всех сторон ближе к наименьшей. Однако
теорему эту еще нельзя считать доказанной для всякого тре-
треугольника, так как в нашем рассуждении имеет существенное
значение, что углы ABC, АСВ острые. Предлагаем читателю
проверить справедливость теоремы для случая прямоугольно-
прямоугольного и тупоугольного треугольника.
78.	На рис. 59 имеем АС<АВ, откуда / ЛВС< / АСВ.
Окружность, описанная на ВС как на диаметре, пройдет через
вершины К, L прямых углов, опирающихся на ВС. Из двух
хорд ВК, CL этой окружности меньше та, на которую опирает-
опирается меньший из вписанных углов ABC, АСВ, то-есть хорда CL.
Таким об^ азом из двух высот треугольника ABC меньше та,
которая опущена на большую сторону, и, следовательно, наи-

88	решения	79—82
меньшая та, которая опущена на наибольшую сторону. Это
доказательство неполно по той же причине, что и доказатель-
доказательство 77. Предлагаем читателю дополнить его.
79.	Из рассмотрения рис. 59 легко убедиться, что точки
А, В, С суть ортоцентры треугольников BCD, ACD, ABD. Но
можно высказать отношение между точками А, В, С, D в
такой форме, что точка D не будет играть особой роли по
сравнению с точками А, В, С: из четырех точек А, В, С, D
каждая есть ортоцентр треугольника, образуемого тремя ос-
остальными, когда прямые, соединяющие любые две различные
пары из эгих точек, взаимно перпендикулярны, то-есть, когда:
AB±CD, AC±BD, BC±AD.
80.	Биссектриса каждого внутреннего угла треугольника
перпендикулярна к биссектрисе смежного внешнего угла и
проходит через точку пересечения биссектрис двух других
внешних углов. Следовательно, внутренние биссектрисы суть
высоты треугольника, ограниченного внешними биссектрисами.
На основании теоремы 79 это отношение можно высказать и
в симметричной форме, которую требуется доказать. На
рис. 59 высоты и стороны треугольника ABC суть внутренние
и внешние биссектрисы треугольника HKL.
81.	Доказательство можно найти в курсах элементарной
геометрии.
82.	Пусть будет Q точка пересечения медиан AM, BN, СР
треугольника ABC (рис. 60). Если предположим АС<САВ, то
на основании решения 8 имеем:
Z.AMC<Z.AMB и Z.MAB<Z.MAC.
В треугольниках CMQ, BMQ имеем
СМ = ВМ, MQ = MQ, Z_CMQ</_BMQ.
Отсюда QC<^QB, то-есть из двух вер-
вершин центр тяжести Q ближе к той, ко-
которая противолежит большей стороне.
Следовательно, из всех вершин центр
тяжести ближе всего к той, которая про-
противолежит наибольшей стороне, то-есть
рис% 50.	к вершине наибольшего угла. При
сравнении расстояний QE. QF центра
тяжести от сторон АС, АВ можно пов-
повторить рассуждени я решения 77, пользуясь неравенством
Получим неравенство QF <C QE, которое показывает, что центр
тяжести ближе к большей из двух сторон, и, следователь-
следовательно, ближе всего к наибольшей стороне.

83—85
ПЛАНИМЕТРИЯ
89
83.	Всякая медиана в полтора раза больше расстояния
центра тяжести от вершины, из которой она проведена. Так
как на основании решения 82 центр тяжести наименее удален
от вершины, противолежащей
наибольшей стороне, то и наи-
наименьшая медиана та, которая
проведена к наибольшей стороне.
84.	Пусть будут М, N сере-
середины сторон ВС, CD параллело-
параллелограмма A BCD (рис 61). Требует-
Требуется доказать:
= -BD.
Рис. 61.
В треугольнике ABC прямые ВО, AM суть медианы. Отсюда
находим:
~ОВ= ~.~BD= -BD.
3	3 2	3
Точно так же из треугольника ACD найдем QD = -— BD.
О
Отсюда уже само собой следует:
PQ = BD — BP—DQ = BD — -BD	 BD = -BD,
3	о	О
что и требовалось доказать.
85. Проведем в треугольнике ABC (рис. 62) высоты к сто-
сторонам АВ, ВС до пересечения в ортоцентре D и перпендику-
перпендикуляры в серединах Р, М сторон АВ, ВС
до пересечения в центре описанного круга
О. Требуется доказать:
ОМ
-DA.
2
Рис. 62.
Средняя линия М'Р' треугольника ACD
равна и параллельна средней линии МР
треугольника АСВ, так как треугольники
ACD, АСВ имеют общее основание АС.
В треугольниках ОМР, DM'P1 стороны МР,
М'Р' равны по доказанному и, кроме того,
соответственные углы равны, так как со-
соответственные стороны параллельны. Сле-
Следовательно, треугольники ОМР, DM'P'
равны, и мы имеем:
= DM' =-DA,
2
что и требовалось доказать.

90
РЕШЕНИЯ
86—87
86.	В треугольнике ABC (рис. 63) проведем высоту АИ и
отметим на ней ортоцентр D, затем проведем перпендикуляр
в середине М стороны ВС и отметим на нем центр описанно-
описанного круга О, наконец, проведем медиану и отметим точку пере-
пересечения ее Q с прямой OD. Нужно доказать, что Q есть центр
тяжести. Отрезок МО параллелен отрезку AD и по теореме
85 равен его половине. Следовательно,
отрезок МО ргвен и параллелен средней
линии А'П треугольника ADQ. Поэтому
отрезки OD', MA' взаимно делятся попо-
пополам, и мы получаем:
MQ = QA' = - QA = - МА.
С Это показывает, что точка Q есть действи-
действительно центр тяжести, и мы видим, что
Рис. 63.	центр описанного круга О ортоцентр D
и центр тяжести Q лежат на одной пря-
прямой, как и требовалось доказать. Заметим, что нами рассмотрен
только общий случай, когда медиана не совпадает с высотой.
Но если медиана совпадает с высотой, то теорема становится
очевидной, так как в этом случае все три точки лежат на
высоте.
87.	Из точки М на окружности круга, описанного около
треугольника ABC, опущены перпендикуляры МР, MQ, MR
на стороне (рис. 64). Требуется до-
доказать, что точки Р, Q, R лежат на
одной прямой. Мы ограничимся рас-
рассмотрением случая, когда одна из
точек Р, Q, R лежит на самой сто-
стороне треугольника.
Пусть, например, точка Р лежит
на стороне ВС. Из двух противопо-
противоположных углов ABM, АСМ вписанного
четырехугольника АВМС или один
острый, а другой тупой, или оба пря-
прямые. Если они оба прямые, то R сов-
совпадает с В и Q совпадает с С. Сле-
Следовательно, точки Р, Q, R лежат на прямой ВС, и теорема
доказана. Предположим, напротив, что один из этих углов,
например угол АСМ, острый, и следовательно, другой угол
АВМ тупой. Тогда Q лежит на самой стороне AC, a R лежит
на продолжении стороны АВ за конец В. Из сказанного сле-
следует, что отрезки РВ, PC составляют продолжение друг дру-
друга, а отрезки PQ, PR во всяком случае расположены по раз-
разные стороны от прямой ВС. Нужно доказать, что и отрезки
Рис. 64.

88	ПЛШИМЕТРИЯ	gj
PQ, PR составляют продолжение друг друга, для чего доста-
достаточно проверить равенство
Z CPQ = Z BPR.
Заметив, что Р, Q лежат на окружности, описанной на МС как
на диаметре, и Р, R лежат на окружности, описанной на MB
как на диаметре, мы можем заменить углы CPQ, BPtt равны-
равными им углами CMQ, BMR и нам остается проверить равенство
Z CMQ = Z BMR.
Но из прямоугольных треугольников CMQ, BMR находим:
Z CMQ = d — /_ ACM, Z BMR = d — /_ RBM,
так что остается проверить только равенство
Z АСМ = Z RBM.
А это равенство следует из того, что во вписанном четырех-
четырехугольнике АВМС угол АСМ есть внутренний при вершине С,
а угол RBM есть внешний при противолежащей вершине В.
Таким образом в рассматриваемом случае теорема доказана.
88. Примем (рис. 65) точку А за вершину треугольника ABC,
проведем высоту АН и перпендикуляр в середине М основа-
основания ВС и отметим центр описанного круга О, ортоцентр D,
середину О' отрезка OD и середину А' отрезка AD. Достаточ-
Достаточно доказать, что окружность с центром О'
и радиусом - ОА проходит через точки
М, Н, А', потому что безразлично, кото-
которую из точек А, В, С принять за вершину
треугольника ABC. Отрезок ОМ паралле-
параллелен отрезкам АА', A D и по теореме 85
равен им. Поэтому ОАА'М есть паралле-
параллелограмм, откуда находим:
МА' =ОА.
Точно так же ОМ и A'D суть противопо-
противоположные стороны параллелограмма, диагонали которого суть
OD, MA'. Так как диагонали параллелограмма взаимно де-
делятся пополам, то мы видим, что МА' проходит через О', и
сверх того получаем:
ОМ = О'А' = J- МА' = -ОА.
2	2
Отсюда следует, что окружность с центром О' и радиусом
— ОА пройдет через М и А'. Так как МА' есть диаметр этой
окружносги и угол МИА' прямой, то она пройдет и через Н.
Итак, теорема доказана.

92	решения	89—90
Задачи на построение
89.	Искомый круг должен удовлетворять трем условиям:
его радиус должен быть равен данному отрезку R, он должен
проходить через данную точку Л, ион должен касаться данной
прямой а (рлс. 66). Отбросим третье условие и найдем гео-
геометрическое место центров кругов, удовлетворяющих первым
двум условиям. Центры таких кругов должны находиться на
расстоянии R от точки А, и наоборот,
всякая точка на расстоянии R от точки
А есть центр такого круга. Следователь-
Следовательно, искомое геометрическое место есть
окружность К с центром А и радиусом
R- Отбросим второе условие и найдем
геометрическое место центров кругов,
удовлетворяющих первому и третьему
Рис б6	условию. Центры таких кругов должны
находиться на расстоянии R от прямой
а, и наоборот, всякая точка на расстоя-
расстоянии R от прямой есть центр такого круга. Следователь-
Следовательно, искомое геометрическое место есть пара прямых Ь, Ъ\ па-
параллельных прямой а и находящихся от нее на расстоянии R.
Центры X искомых кругов должны удовлетворять всем трем
условиям и, следовательно, лежать на обоих найденных гео-
геометрических местах. Если эти геометрические места имеют
общие точки, то, описав около каждой из них круг радиуса
R, получим все круги, удовлетворяющие условиям задачи. На
рис. 66 окружность К пересекает прямую Ъ в точках Хи Х%,
и не имеет общих точек с прямыми Ь'. Следовательно, задача
имеет два решения. Но возможны и другие случаи. Если рас-
расстояние точки А от прямой а больше 2R, то окружность К
не имеет общих точек с прямыми Ь, Ъ'\ задача не имеет реше-
решений. Если расстояние точки А от прямой а равно 2R, то
окружность К касается одной из прямых b, b' и не имеет
общих точек с другой; задача имеет одно решение. Если рас-
расстояние точки А от прямой а меньше 2R, но больше нуля, то
окружность К пересекает одну из прямых b, b' и не имеет
общих точек с другой; задача имеет два решения. Если рас-
расстояние точки А от прямой а равно нулю, то окружность К
касается обеих прямых Ь, V; задача снова имеет два решения.
Таким образом задача может иметь 0, 1 и 2 решения, в зави-
зависимости от величины R и относительного положения А и а.
90.	Геометрическое место центров кругов данного радиуса
R, касательных к данной прямой, есть пара прямых, парал-
параллельных этой прямой, на расстоянии R от нее. Геометрическое
место центров кругов данного радиуса R, касательных к дан-

gj—92	ПЛАНИМЕТРИЯ	Q3
ному кругу радиуса R', есть пара окружностей, концентриче-
концентрических с этим кругом, радиусы которых равны сумме и разности
радиусов R, R'. Если радиусы R, R1 равны, то вторая окруж-
окружность имеет нулевой радиус, т. е. обращается в точку. Центры
искомых кругов суть общие точки обоих геометрических мест.
Число этих точек и тем самым число решений задачи может
достигать восьми.
91.	Геометрическое место кругов, касательных к двум дан-
данным параллельным прямым, есть параллельная им прямая,
делящая пополам расстояния между ними. Радиус R искомого
круга должен поэтому быть равен половине расстояния ме-
между этими прямыми. Геометрическое место центров круга ра-
радиуса R, касательных к данному кругу радиуса R', есть пара
окружностей, концентрических с этим кругом, радиусы которых
равны сумме и разности радиусов R, R'. Центры искомых
кругов суть общие точки обоих геометрических мест. Число
их, и тем самым число решений, может достигать четырех.
92.	Пусть будут Кг, К3 данные круги и Rlt R2 их радиусы
(рис. 67). Искомый круг не может касаться круга Кг внешним
образом, потому что он не мог бы тогда
касаться круга К%. Найдем круги, касатель-
касательные к кругу ATi внутренним образом в
какой-нибудь точке А и касательные также
к кругу К^. Центры этих кругов должны
лежать на прямой ОА и на той же прямой
должны лежать и точки касания их с
кругом К\. Отсюда видно, что точки каса-
касания их с кругом К2 суть В, С и, следо-
следовательно, центры их суть середины М,
N отрезков АВ, АС. Круг М касается	Рис- 67-
круга К% внешним образом; радиус
его равен — (Rx — /?2). Круг N касается круга К2 внутренним
образом, радиус его равен — (/?1+??г)- Мы нашли центры
М, N кругов, касательных к кругам Кг, К2, и притом к кру-
кругу Кг в точке А. Если заставим точку А описать окружность
К1г то точки М, N опишут концентрические окружности К',
К", которые и составляют в совокупности геометрическое
место центров кругов, касательных к кругам Кх, К2- При этом
окружность К' есть геометрическое место центров кругов
радиуса — (/?х — R^), а окружность К" есть геометрическое
место центров кругов радиуса — (/?х -\- R»). Второе условие за-

94
РЕШЕНИЯ
93—94
дачи, требующее касания искомых кругов к некоторой прямой
а, дает для центров кругов каждого из радиусов еще одчо
геометрическое место, а именно, пару прямых, параллельных
прямой а на расстоянии от нее, равном соответствующему
радиусу. Центры кругов каждого радиуса суть общие точки
обоих геометрических кругов.
93.	Обозначим данные точки А, В, С. Центр искомого
круга должен быть одинаково удален от всех трех точек А,
В, С Геометрическое место точек, равноудаленных от точек
А, В, есть перпендикуляр в середине отрезка АВ. Геометри-
Геометрическое место точек, равноудаленных от точек А, С, есть пер-
перпендикуляр в середине отрезка АС. Точка, равноудаленная от
всех трех точек А, В, С, может быть только точкой пересе-
пересечения этих двух перпендикуляров. Если точки А, В, С не
лежат на одной прямой, то перпендикуляры эти пересекаются
в некоторой точке. Эта точка есть центр круга, .описанного
около треугольника ABC. Если же точки А В,'С лежат на
одной прямой, то перпендикуляры' пара'ллельны' между собой
и не имеют общей точки. Итак, задача может иметь одно
или ни одного решения.
94.	Относительно взаимного расположения данных прямых
можно сделать только три предположения: или среди них нет
параллельных, или две из них парал-
параллельны, а третья пересекает их, или
все три параллельны. Если среди дан- -
ных прямых нет параллельных, то они
пересекаются или в трех различных
точках, или в одной точке. Таким
-° образом возможны четыре случая.
Рассмотрим их отдельно.
Пусть прямые Ь, с пересекают пря-
прямую а в различных точках С, В и
сами пересекаются в точке А (рис. 68).
Центры искомых кругов должны
быть равноудалены от всех трех
прямых а, Ь, с. Геометрическое место
точек, равноудаленных от прямых а,
с, есть пара биссектрис b', b" двух
пар вертикальных углов между пря-
прямыми а, с. Геометрическое место
точек, равноудаленных от прямых а, Ь, есть пара биссектрис
с', с" двух п?р вертикальных углов между прямыми а, Ь.
Точки, равноудаленные от всех трех прямых а, Ь, с, должны
прин?длежать обоим геометрическим местам. Так как прямые
а, Ь, с ограничивают в данном случае треугольник, то ка-
каждая из биссектрис b', b" пересекает каждую из биссектрис

95—96
ПЛАНИМЕТРИЯ
95
Рис. 69.
с', с". В решении 28 были даже вычислены углы между раз-
различными биссектрисами. Всего получим четыре точки nej ece-
чения О, Оа, Оь, Ос. Чтобы найти радиусы искомых кругов,
придется еще опустить из этих точек перпендкуляры г, ра, рь,
рс на одну из сторон. После этого остается описать около
точек О, Оа, Оь, Ос окружности радиусами г, ра, р„, рс. Это
будут вписанные и невписанные круги
треугольника ABC.
Пусть прямые Ь, с пересекают прямую
а в различных точках С, В, но параллельны
между собой (рис. 69). Как и раньше,
центры искомы* кругов должчы лежать в
точках пересечения биссектрис b', Ь" при
точке В с биссектрисами с', с" при точке
С. Но теперь биссектрисы b', Ь" парал-
параллельны биссектрисам с", с' и пересекают-
пересекаются только с биссектрисами с', с" в точках
О, О'. Таким образом в этом случае ре-
решений только два.
Если все три прямые пересекаются в одной точке, то ре-
решений не будет совсем, так как из одной точки нельзя про-
провести три касательных к окружности. Точно так же решений
совсем не будет, если все три прямые параллельны, так как
к окружности нельзя провести три параллельных касательных.
95. Требуется построить круг, касательный к прямой а в
точке Лик другой прямой b (рис. 70). Одно геометрическое
место для центра искомого круга есть пер-
перпендикуляр р к прямой а в точке А. Дру-
Другое геометрическое место есть геометри-
геометрическое место точек, равноудаленных от
прямых а, Ь. В случае, изображенном на
рис. 70, когда прямые a, b пе| есекаются в.
некоторой точке С, это геометрическое
место есть пара биссектрис с', с" углов
между а и Ь. Мы получим два пересече-
пересечения, если точка А не совпадает с точ-
точкой С, и одно пересечение, если точка А
совпадает с точкой С. В последнем слу-
случае искомые круги обращаются в точку С.
В случае, ко1да прямые a, b параллельны,
второе геометрическое место есть прямая, параллельная им
и делящая расстояния между ними пополам. Получим одно
решение. Впрочем, легко видеть, что для построения искомого
кру а вовсе нет надобности ст[ оить эту прямую.
96. Требуется построить круг, касательный к кругу О в
точке Лик прямой а (рис. 71). Проведем касательную b к

РЕШЕНИЯ
97
кругу О в точке А. Круги, касательные к кругу О в точке
А, те же самые, что и круги, касательные к прямой b в точ-
точке А. Таким образом задача сводится к задаче 95.
97. Пусть будет а данная прямая, А данная точка, К дан-
данный круг, О его центр (рис. 72). Одно геометрическое место
для центра искомого круга есть перпендикуляр р к прямой а
в точке А. Чтобы найти другое геометрическое место, построим
центры О', О" кругов К', К", касательных к прямой а в точке А
и равных кругу К. Каждый из искомых кругов должен быть
касателен и к кругам К', К", и притом к одному из них внутрен-
внутренним образом, а к другому внешним образом, потому что
круги К', К" расположены по разные стороны от а. Следова-
Следовательно, каждый из искомых кругов должен быть касателен
•одинаковым образом к кругу К и к одному из кругов К', К"¦
Но центр всякого круга, касательного одинаковым образом
к двум разным кругам, очевидно, находится от центров этих
кругов на равных расстояниях, и наоборот, всякая точка, равно-
равноудаленная от центров этих кругов, есть центр одного внешне
касательного и одного внутренне касательного круга к этим
кругам. Отсюда видно, что геометрическое место центров кру-
кругов, касательных одинаковым образом к кругам К, К", есть
перпендикуляр q в середине отрезка ОО', а геометрическое
место центров кругов, касательных одинаковым образом к кру-
кругам К, К", есть перпендикуляр г в середине отрезка ОО".
Центры искомых кругов суть точки пересечения р с q и г.
Заметим, что для построения нужны только центры О', О"
кругов К', К"; сами круги начерчены у нас только для при-
придания наглядности рассуждениям. С другой стороны, чтобы не
затемнять чертеж, у нас не начерчены отрезки ОО', ОО",
к которым нужно провести перпендикуляры в серединах;
действительно, для этого построения нужны только концы
отрезков.

98—102	планиметрия	97
98.	К этой задаче можно применить те же соображения, что
и к задаче 97.
99.	Геометрическое место точек, из которых данный отре-
отрезок виден под данным углом, состоит из двух дуг окружно-
окружностей, стягиваемых этим отрезком и вмещающих этот угол.
Геометрическое место точек, из которых данный круг виден
под данным углом, есть концентрическая с этим кругом окруж-
окружность, для построения которой достаточно найти одну ее точку,
что легко сделать. Искомые точки суть общие точки обоих геоме-
геометрических мест.
100.	Обозначим данные точки через А, В, С (рис. 73). Пря-
Прямая, равноудаленная от точек А, В, или проходит через сере-
середину Р отрезка АВ, или параллельна пря-
прямой АВ. Прямая, равноудаленная от точек
А, С, или проходит через середину N \
отрезка АС, или параллельна прямой АС. —^- „
Прямая, равноудаленная от всех трех точек / \ / \
А, В, С, или проходит через Р и N—это ^-—-^Цг~	с
будет прямая PN, или проходит через Р и	^^
параллельна АС—это будет прямая РМ,	рис 73
или проходит через N и параллельна АВ —
это будет прямая NM, или параллельна АВ
и АС — таких прямых не может быть, если точки А, В, С
не лежат на одной прямой. Таким образом, если точки А, В, С
не лежат на одной прямой, то искомые прямые суть средние
линии треугольника ABC. Но если точки А, В, С лежат
на одной прямой, то прямые PN, PM, NM сливаются с
этой прямой, и кроме того от точек А, В, С равноудалены все
прямые, параллельные этой прямой. Итак, в первом случае
имеем три решения, а во втором бесчисленное множество.
101.	Если данные прямые пересекаются, то к ним одинаково
наклонены биссектрисы двух пар вертикальных углов между
ними и все параллельные этим бис-
биссектрисам прямые. Каждой бис-
биссектрисе параллельны две касатель-
касательные данного круга. Таким образом
задача имеет четыре решения. Но
если данные прямые параллельны,
то все вообще прямые одинаково
наклонены к ним, и в частности
все касательные данного круга.
Ри „.	В этом случае, следовательно,
ис- '	задача имеет бесчисленное мно-
множество решений.
102.	Пусть будет А данная точка, К данный круг, О его
центр (рис. 74). Предположим, чтобы разобраться в задаче,
7 Делоне и Житомирский

98
решения
что она решена и что АМ'М есть одна из искомых секущих,
так чго М' есть середина AM. Пусть будет О' середина АО.
Прямая О' М' есть средняя линия треугольника АОМ, и следо-
следовательно, О' М' равна половине ОМ, то-есть половине радиуса
круга К- Таким образом для М имеем два геометрических
места — окружность К и окружность К' вдвое меньшею радиуса
с центром в середине О' отрезка АО; это позволяет найти М'.
Для экономии места мы сдглали анализ на том же рис. 74, на
котором находятся данные и должно быть выполнено построе-
построение. Но на практике следует, конечно, производить анализ на
отдельном наброске. Чтобы решить теперь нашу задачу, нужно'
разделить пополам отрезок АО и какой-нибудь радиус круга К
и [ адиусом, \ авным половине радиуса круга К, описать окруж- •
ность К' около середины О' отречка АО. Соединив затем
точку А с общими точками М окружностей К, К', получим
искомые секущие. Чтобы исследовать задачу, обозначим радиус
круга К через R и расстояние АО через d. Тогда радиус
круга К' будет — R и расстояние 00' будет — d. Сумма радиу-
3	1
сов кругов К, К' равна —R, а разность —R. Окружности К,
К' не имеют общих точек, и следовательно, задача не имеет
1	3
решений, если — d> — R, т. е. если d^>3R. Задача имеет
1	3
одно решение, если — d = — R, т. е. d = 3/?. Задача имеет
1	3
два решения, если —d < —R, т. е. d<^3R. Этим цсчерпы-
ваются возможные случаи, потому что — d не может быть
равно или меньше —R, так как тогда
d было бы равно или меньше R, и
точка А не лежала бы вне круга К,
вопреки условию задачи.
103. Пусть будут О, О' центры дан-
данных кругов, А — точка пересечения их,
через .которую требуется провести се-
Рис. 75.	кущую, и а —отрезок, которому эта се-
секущая должна быть равна Грис. 75). Пред-
Предположим, что задача решен?, и ВС есть
одна из искомых секущих. Опустим на нее перпендикуляры
ОМ, O'N и проведем О'Р перпендикулярно к ОМ.
Г

104
ПЛАНИМКТРИЯ
99
Имеем:
= ±ВА+±.АС = ±ВС
¦а.
Для точки Р имеем два геометрических места: екружност
с центром О' и радиусом — аи окружность, описанную на ОО'
как на диаметре, так как угол ОРО' прямой. Оба геометриче-
геометрических места можно построить по данным задачи. Найдя таким
образом точки Р, мы должны провести через точку А прямые,
параллельные прямым О Р. Это и будут искомые секущие.
Число решений задачи равно числу общих точек наших гео-
геометрических мест. Оно равно 2, когда — а<СОО'; равно 1,
когда — а = 00'; равно 0, когда —а>ОС.
Л	2
104. Пусть будут ЛВС, А'В'С данные треугольники (рис. 76).
Требуется описать около треугольника ABC треугольник
АгВгСх, равный треуголь-
треугольнику А'В'С.
Задача приобретет до-
достаточную определенность
только тогда, когда будет
указано, которая из сторон
треугольника A-^B-fi-^ дол-
должна проходить через каж-
каждую вершину треугольника
ABC. Пусть требуется, что-
чтоб	AB
Рис 7б
у ру
бы сторона A±Blt равная
А'В', проходила через С,
чтобы сторона АгСх, рав-
равная А'С, проходила через В и чтобы сторона ВхСг, рав-
равная В'С, проходила через А. Так как угол В1г равный углу В',
должен опираться на сторону АС, то точка Вг должна лежать
на дуге, опирающейся на АС и вмещающей угол, равный углу В'.
Точно так же точка Сх должна лежать на дуге, опирающейся
на АВ и вмещающей угол, равный углу С'. Сторона ВхСг
должна быть секущей этих двух дуг, проходящей через их
общую точку А и равной стороне В'С. Такие секущие мож-
можно построить по способу решения 103. Проведя затем прямые
СХВ, BtC до пересечения в точке Аг, получим треугольник
А1В1С1, равный треугольнику А'В'С вследствие равенства
сторон BXCV В'С и прилежащих углов Bv В' и С,, С". Число
решений равно числу секущих ВХСХ, равных В'С, и может
равняться 2, 1 и 0, как показано в решении 103. Так как в
условии не указано, в каком порядке сторон один треугольник
7*

100
РЕШЕНИЯ
105—106
Рис. 77.
должен быть описан очоло другого, то придется проделать
шесть построений рассмотренного вида, по числу возможных
комбинаций.
105.	Пусть требуется вписать в тоеугольник ABC тоеуголь-
тоеугольник, равный треугольнику А'Ч'С (рас. 77). Здесь мояно при-
применить метод обрат-
С	а д	С2	г ности. Сначала опи-
опишем около треуголь-
треугольника А'В'С треуголь-
треугольник Aj^BjC^ равный тре-
треугольнику ABC, как
показано в решении
104. Потом отложим на
сгоооне АВ отрезок
АС,, равный отрезку
АгС, на стороне ВС
отрезок ВА2, равный
отрезку ВгА', и на
стороне СА отрезок
СВ2, равный отрезку CtB'. Получим треугольник А,В„С^,
вписанный в треугольник ABC и равный треугольнику А'В'С,
что и требовалось. Мы видим, что каждому решению обратной
задачи соответствует определенное решение прямой задачи. Но
легко убедиться, что и наоборот, каждому решению прямой
задачи соответствует определенное решение обратной задачи.
Отсюда ясно, что метод обратное™ позволяет получить все
без исключения решения нашей задачи.
106.	Пусть будет О центр данного круга (рис. 78), О А,
ОВ данные радиусы и а данный отрезок. Требуется про-
провести к кругу О такую касательную, чтобы часть СО этой
касательной между продолжениями радиусов ОА, ОВ была
равна отрезку а. Обратим
задачу и попробуем восста-
восстановить данную фигуру ОАВ,
начиная с искомого отрезка CD.
Выражаясь точнее, мы должны
построить фигуру О'А'В', рав-
равную фигуре ОАВ и располо- °'
женную по отношению к от-
отрезку CD', равному отрезку а,
так же, как фигура ОАВ рас-
расположена по отношению к
отрезку CD. Отложим где-нибудь отрезок CD' и будем
искать точку О'. Точка О' должна удовлетворять двум условиям:
угол CO'D' должен быть равен углу АОВ, и расстояние О'Е
точки О' от прямой CD' должно равняться расстоянию ОЕ
о
С
Рис. 78.

107—110
ПЛАНИМЕТРИЯ
101
точки О' от искомой прямой CD, то-есть радиусу ОА. Это дает
для О' два геометрических места: дугу, вмещающую угол, рав-
равный углу АОВ, и опирйющуюся на CD', и прямую, параллель-
параллельную CD', расстояние которой от CD' равно ОА. СоСственно
говоря, первое геометрическое место состоит из пары дуг, а
второе из пары прямых, по обе стороны от CD'. Но так как
для нас существенно только относительное положение фигу-
фигуры О'А'В' и отрезка CD', то мы можем ограничиться рассмо-
рассмотрением дуги и прямой, расположенных по одну сторону от
прямой CD'. Эти*два геометрических места могут иметь не
более двух сбщих точек; пусть будет О' одна из них. Отло-
Отложим на продолженных радиус; х ОА, ОВ отрезки СС, OD,
равные отрезкам СС, CD'; прямая CD есть одна из искомых
касательных. Решений будет столько же, сколько общих точек
наших геометрических мест. Но для построения достаточно
найти одну из этих точек, в чем предлагаем убедиться читателю.
107.	Пусть будет АВ данный отрезок (рис. 79), а денная
прямая, К данная окружность, О ее центр. Искомый отрезок
должен быть равен и параллелен отрезку АВ и опираться сво-
своими концами на окружность К и прямую а.
Представим себе, что из всех точек окруж-
окружности К проведены в обоих направлениях
отрезки, равные и параллельные отрезку
АВ. Концы этих отрезков заполняют пару
окружностей К', К", получающихся из
окружности К смещением ее в обоих
направлениях на отрезок, равный и парал-
параллельный отрезку АВ. Условиям задачи
удовлетворяют те из этих отрезков, концы
которых одновременно лежат и на прямой а.
Отсюда ясно, как следует вести построение.
Проводим через точку О прямую параллельно прямой АВ,
откладывая на ней отрезки 00', СО", равные отрезку АВ, и
описываем около точек О', О" окружности К', К" радиусом,
равным радиусу окружности К- Затем из каждой общей
точки окружностей К', К" с прямой а проводим прямую,
параллельную прямой АВ, до такой точки пересечения с окруж-
окружностью К, чтобы получился отрезок, равный АВ. Число реше-
решений может достигать четырех. Можно было бы вместо окруж-
окружности К смещать параллельно прямую а, но такое построение
было бы несколько сложнее.
108.	Эта задача есть небольшое видоизменение задачи 107.
109.	Эта задача есть частный случай задачи 108, когда
данные окружности совпадают.
НО. Требуется через точку А (рис. 80) внутри круга К с
центром О провести хорду ВС, равную отрезку а. Построим
Рис. 79.

102
РЕШЕНИЯ
111
2
с
Рис. 80.
к?кую-нибудь хорду В'С, равную отрезку а, что легко сделать,
Если бы хорда ВС была дана, то мы могли бы совместить ее
с хордой В'С, вращая ее в каком-нибудь направлении
около точки О. При этом точка А хорды ВС
совпала бы с некоторой точкой А' хорды В'С,
которую мы можем построить и не зная
положения хорды ВС, прямо по данный за-
задачи. Действительно, при таком вращении
точка А описала бы окружность К' с цент-
центром О и радиусом О А. Следовательно, точка А'
должна быть общей точкой окружности /С
с хордой В'С. Если этих точек две, то за
точку А' можно принять любую. Из даль-
дальнейших рассуждений увидим, чго это без-
безразлично. Точка А должна делить хорду ВС на такие же
отрезки, на какие точка А' делит хорду В'С. Поэтому конец В
хорды ВС должен находиться от точки А на расстоянии,
равном А'В'. Описав около точки А окружность радиусом,
равным А'В', получим в пересечении с окружностью К искомые
концы В хорды ВС, после чего останется только соединить их
с точкой А и продолжить прямые ВА до пересечений С с
окружностью К- Для этого построения существенно только
то, на какие отрезки точка А' делит хорду В'С. Если окруж-
окружность К' имеет с хордой В'С две общие точки, то они-
делят хорду на одинаковые отрезки, только в различном
порядке. Поэтому и можно было за точку А' принять любую
из этих точек.
111. Пусть будет А (рис. 81) данная точка, а данная прямая
и К данная окружность. Обозначим вершину искомого тре-
треугольника, которая должна лежать на пря-
прямой а, через В, а ту, которая должна ле-
лежать на окружности К, через С. Вершину С
можно получить из вершины В посред-
посредством поворота около вершины А на угол „>
— d. Следовательно, для вершины С имеем
о
два геометрических места: пару прямых
а', а", которые получаются из прямой а
посредством поворота в том или другом
направлении около точки А на угол — d, ис-
о
и окружность К. Общие точки этих двух геометрических мгст
суть вершины С. Чтобы построить вершины В, нужно описать
около точки А окружности радиусами АС до пересечения с
прямой а. После этого останется соединить каждые три точки

1J2	115	ПЛАНИМЕТРИЯ	]Q3
о
А, В, С. Чтобы осуществить поворот прямой а на угол —d,
о
достаточно повернуть две ее точки и соединить их новые по-
положения. Проще всего поступить так: описываем около точки
А окружность, пересекающую прямую а в точках Р, Q; откла-
откладываем на этой окружности в определенном направлении дуги
РР, QQ', равные шестой части всей окружности, что можно
сделать, не меняя растворения циркуля; соединяем точки Р, Q'
прямой а'; меняя направление дуг на обратное, получим пря-
прямую а". На рис. 81 решений два, так как прямая а' пересе-
пересекает окружность К, а прямая а" не имеет с ней общих точек.
Но число решений может достигать и четырех. Можно было
бы вместо прямой а поворачивать окружность К-
112. Эта задача есть незначительное видоизменение задачи 111.
ИЗ. Пусть будут К, К' данные круги (рис. 82), 0,0' их
центры, А точка пересечения их, через которую требуется про-
провести секущую, делящуюся в этой точ-
точке пополам. Обозначим конец искомой
секущей на окружности К через В, а
конец на окружности К' через С. Точка С
должна быть симметрична с точкой В
относительно центра Л. Следовательно,
точка С должна лежать на окружности Klt
симметричной с окружностью К относи-
относительно центра А. Кроме того, она должна
лежать на окружности К'¦ Таким образом	Рис. 82.
точка С есть общая точка окружностей
K',Ki, отличная от точки А. Задача всегда -имеет одно реше-
решение. Действительно, окружность К имеет с окружностью Кг
общую точку А, но не может касаться ее в этой точке, потому
что тогда она касалась бы и симметричной окружности К>
между тем как она по условию пересекает окружность К.
Следовательно, окружности К',Кг имеют еще одну общую
точку С.
114.	Решение этой задачи сходно с решением задачи 113.
115.	Дана прямая а и точки А, В (рис. 83). Требуется найти
на прямой а такую точку М, чтобы сумма AM -\- MB была
наименьшая. Если точки А, В расположены по разные стороны
от прямой а, то отрезок АВ пересекает прямую а. Точка пе-
пересечения и есть искомая точка М. Действительно, если М' есть
какая-нибудь другая точка прямой а, то прямая АМВ короче
ломаной AM'В. Если точки А, б расположены по одну сторону от
прямой а, то можно заменить точку В точкой В', симметричной
с ней относительно оси а, так как расстояния всякой точки
М' прямой а от точек В, В' равны. Искомая точка М есть
точка пересечения прямой а с прямой АВ'.

104
РЕШЕНИЯ
116-118
Рис. 83.
116.	Если точки А,В расположены по одну сторону от
прямой а, то точка М прямой а, для которой разность рас-
расстояний от точек А, В наиболь-
наибольшая, есть точка пересечения
прямой а с прямой АВ. Если
точки А, В расположены по раз-
разные стороны от прямой а, то
точка М прямой а, для которой
разность расстояний от точек А, В
наибольшая, есть точка пересе-
пересечения прямой а с прямой, со-
соединяющей точку А с точкой В',
симметричной с точкой В отно-
относительно оси а.
117.	Пусть будет МгОМ2 (рис. 84) данный угол и А данная
точка. Построим точки Av Az, симметричные с точкой А,
относительно осей ОМг, ОМ«, проведем
прямую АгА2 и соединим с точкой А
точки пересечения ее В, С с прямыми OMV
ОМ2. Треугольник ABC и есть искомый.
Действительно, всякий другой треугольник
АВ'С, расположенный согласно требова-
требованиям задачи, имеет по сравнению с тре-
треугольником ABC больший периметр, так
как периметр треугольника ABC равен
отрезку прямой АХВ -\- ВС -{- СА2, а пери-
периметр треугольника АВ'С равен периметру
ломаной АХВ + В'С + С'А2.
118.	Пусть будет MON (рис. 85) данный угол и Р, Q
данные точки. Требуется построить равнобедренный треуголь-
м	ник, вершина которого А лежала бы
—*	на стороне ОМ, боковые стороны ко-
которого АВ, АС проходили бы через
точки Р, Q, а основание ВС лежало
бы на стороне ON. Пусть будет ABC
искомый треугольник, АН его высота
и Q' точка, симметричная с точкой Q
относительно оси ОМ. Имеем:
Рис. 84.
= 2НАО =
= 2d—2Z_MON.
Следовательно, точка А должна ле-
лежать, кроме стороны ОМ, на дуге PQ', вмещающей угол,
равный 2d—2/_M0N. Такую точку можно построить по
данным задачи, и тем самым задача будет решена.	'

119—121
ПЛАНИМЕТРИЯ
105
Рис. 86.
119.	Пусть будет ABC искомый треугольник и М середина
стороны ВС (рис, 86). Проведем удвоенную медиану AMD
и отрезок CD. В треугольнике ACD имеем АС = b, CD = с,
AD = 2та. Следовательно, этот треуголь-
треугольник можно построить по данным Ь, с, та.
Чтобы построить искомый треугольник
ABC, останется провести удвоенную
медиану СМВ треугольника ACD и
отрезок АВ.
Разумеется, для возможности построе-
построения треугольника ACD необходимо, чтобы
наибольший из отрезков Ь, с, 2та был
меньше суммы остальных.
120.	В искомом треугольнике ABC за-
заранее известны сторона ВС = а, медиана
AM = та и медиана BN = т„ (рис. 87).
Это дает возможность построить тре-
треугольник BMQ, в котором ВМ=" a, MQ =
1	-- 2	п
Для этого нужно, правда, уметь раз-
разделить данные отрезки та, ть на три
части, что не относится к основным
построениям.
Но это построение легко выполняется,
если пристроить к отрезкам та, ть какие-
нибудь треугольники, в которых они
были бы медианами, и провести еще по
одной медиане этих треугольников.
Когда треугольник BNQ будет построен,
останется продолжить ВМ на равный
отрезок МС и MQ на вдвое больший отрезок QA и провести
отрезки АВ, АС.
121.	Пусть будет ABC искомый треугольник, AM, BN, CP
его медианы, Q точка их пересечения
(рис. 88). Продолжим отрезок QM на
равный отрезок MR и проведем отре-
отрезок BR. В треугольнике BQR имеем
6	Рис. 88.
Следовательно, треугольник BQR
можно построить по данным отрезкам та, ть, тс, а после этого
легко построить и треугольник ABC.

106
РКШКНИЯ
122—123
122. Для возможности построения искомого треугольника
необходимо, чтобы обе боковые стороны Ь, с были больше
высоты ha, или только одна из них равна высоте ha. Поэтому мы
примем:
Рис. 89.
Рис. 90.
Проведем какую-нибудь прямую а и восставим к ней какой-
нибудь перпендикуляр р. Так как положение искомого тре-
треугольника ничем не ограничено, то мы можем мысленно нало-
наложить его на плоскость так, чтобы основание ВС пошло по пря-
прямой а, а высота ha по перпендикуляру р (рис. 89). Отложив
на перпендику-
перпендикуляре р отрезок,
равный отрезку
ha, найдем вер-
вершину А. Конец
основания В
должен лежать
на прямой а на
расстоянии от
вершины Л, рав-
равном отрезку с.
Иначе говоря,
точка В должна
'бытьобщей точ-
точкой прямой а и
окружности, описанной около точки А радиусом с. Таких
точек две, так как c^>ha, но мы можем считать за точку В
одну из них. Действительно, мы можем представить себе тре-
треугольник ABC наложенным на плоскость так, что конец осно-
основания В совпадает с любой из этих точек, так как он пере-
переходит из одной точки в другую при повороте треугольника
вокруг оси р на 180°. Теперь положение треугольника ABC
вполне определено, и различным возможным положениям
конца основания С соответствуют различные решения задачи.
Точка С должна быть общей точкой прямой а и окружности,
описанной около точки А радиусом Ь. Если b^>ha, то таких
точек будет две, и мы получим два треугольника ABC. Если
* = ^о> т0 такой точкой будет только основание высоты ha,
и мы получим один треугольник ABC.
123. Пусть будет К, L основания высот hb, hc (рис. 90).
Так как углы ВКС BLC прямые, то точки К, L должны на-
находиться на окружности у, описанной на отрезке ВС как на
диаметре. Точка К находится кроме того на окружности, опи-
описанной около точки В радиусом hb. Если эта окружность имеет
с окружностью у две общие точки, то за точку К можно при-
принять одну из них, потому что этим определится только

124—127
ПЛАНИМЕТРИЯ
107
Рис. 91.
положение треугольника ABC. За точки L следует уже принять
по-очереди все общие точки окружности, описанной около С
радиусом hc, с окружностью ?. После этого останется провести
секущие BL, С К окружности у до пересечения в точке А.
Число рашений может достигать двух.
124.	Пусть будет ВС = а основание искомого треугольника
и М его середина (рис. 91). Вершина А должна находиться
на расстоянии та от Ж и на расстоянии ha от ВС. Следо-
Следовательно, вершина А есть общая точка
окру лености, описанной около точки М
радиусом та, и прямой, проведенной
параллельно прямой ВС на расстоянии ha
от нее. Безразлично, с какой стороны
от прямой ВС проводить параллельную
и которую из общих точек ее с окруж-
окружностью принять за точку А, если этих
точек двэ, так как все полученные таким
образом треугольники отличаются только
положением на плоскости. Поэтому
решений не может быть более одного.
125.	Построив основание а, будем иметь для вершины А два
геометрических места: прямую, параллельную прямой а на
расстоянии ha от нее, и дугу, стягиваемую отрезком а и вме-
вмещающую угол А.
126.	Проведем две параллельные прямые на расстоянии ha
друг от друга (рис. 92), примем какую-нибудь точку одной
из них за вершину А, опишем около этой точки окружность
радиусом ро, примем
какую-нибудь общую
точку D этой окруж-
окружности со второй парал-
параллельной за другой ко-
конец биссектрисы ра и
отложим углы DAB.
DAC, равные — /?. Тре-
угольник ABC есть
искомый.
127. Пусть будет
ABC искомый треуголь-
треугольник (рис. 93). Чгобы
ввести в рассуждение b -f- с, продолжим сторону ВА=с на
отрезок AD = b. В треугольнике BCD имеем:
Рис. 92.
Рис. 93.
/_BDC= —A.

108
РЕШЕНИЯ
128-130
Рис- 94-
По этим данным треугольник BDC можно построить: проводим
отрезок BD, равный b -f- с, откладываем угол BDE, равный
-jj- А, и находим точку С, как общую точку стороны DE с
окружностью, описанной около точки В радиусом а. Число
таких точек, и вместе с тем и число треугольников BCD,
может достигать двух. Из каждо-
каждого треугольника BCD можно по-
получить один искомый треуголь-
треугольник ABC, проведя перпендикуляр
в середине CD до пересечения
с BD в точке А.
128. Пусть' будет ABC иско-
искомый треугольник (рис. 94). Чтобы
ввести в чертеж 2р— а -\- b -f- с,
отложим на продолжениях ВС отрезки BD = ct CB = b. В тре-
треугольнике ADE имеем:
DE=2p, Z.ADE = -! В, Z. AED = — С.
2	^
Следовательно, треугольник ADE можно построить по стороне
и двум прилежащим углам. От треугольника ADE перейдем
к треугольнику ABC, проведя перпендикуляры в серединах
сторон AD, AEro пересечения со стороной DE в точках В, С.
129.	Так как в условии упоминается отрезок, .равный с — Ь,
а не Ь — с, то подразумевается, что ?>?. Пусть будет ABC
искомый треугольник (рис. 95). Отложим на стороне АВ = с
отрезок AD = Ь. Треугольник BCD можно построить, так как
в нем известны стороны ВС = a, BD — с — Ь и угол между
ними CBD = В. От него можно перейти к треугольнику ABC,
проведя перпендику-
перпендикуляр в середине сто-
стороны CD до пересе-
пересечения с продолже-
продолжением стороны BD в
точке А.
130.	Пусть будет
ABC искомый тре-
треугольник. Отложим
на продолженной	рис- 95-	Рис- 96-
стороне АС = b от-
отрезок AD = с (рис. 96). Треугольник CBD можно построить,
так как в нем известны стороны СВ = a, CD = с—b и угол
между ними BCD = 2d — С. По треугольнику BCD можно
построить треугольник ABC, проведя перпендикуляр в сере-
середине стороны BD до пересечения с продолжением стороны
DC в точке А.

131—135	ПЛАНИМЕТРИЯ	109
131.	Решение этой задачи близко к решению 127.
132.	Пусть будет ABC искомый треугольник (рис. 97). Пе-
Перевернем его на другую сторону и наложим на плоскость в
положении А'ВС. Треугольник ВАА' можно построить по сто-
сторонам ВА = с, ВА' = Ь и углу между ними ABA' —С —В.
Чтобы построить затем искомый треугольник ABC, проведем
полупрямую BD, параллельную и одинаково направленную с
отрезком А'А, и найдем на ней точку С, находящуюся на рас-
расстоянии А'С = с от точки А'.
Рис. 97.
133.	Воспользуемся решением 29. В искомом треугольнике
ABC (рис. 98) проведем биссектрису AD, отложим АЕ=АС и
соединим D, Е. В треугольнике BDE известны сторона BE—
— c—b, противолежащий угол BDE=C — B и сумма двух
других сторон BD + DE-=BD -\- DC=
= ?С=а. По этим данным его можно
построить, как показано в решении 127.
Чтобы затем построить треугольник ABC,
нужно будет на продолжении BD отло-
отложить DC—DE и провести биссектрису
угла CDE до пересечения с продолже-
продолжением BE в точке А.
134.	Эта задача родственна задаче 133.	.	/
При решении ее придется использовать	 ^=—
решения 130 и 131.	рис gg
135.	Даны диагонали d, d' параллело-
параллелограмма и угол А, противолежащий диа-
диагонали d' (рис. 99). Чтобы построить параллелограмм, про-
проводим сначала отрезок BD, равный диагонали d', и нахо-
находим его середину М. Для вершины А имеем два геометри-
геометрических места: дугу BD, вмещающую угол А, и окружность,
описанную около М радиусом — d. Эти два геометрических
места имеют не более двух общих точек; если этих точек две,
то безразлично, которую из них принять за вершину А. Чтобы
найти четвартую вершину С, проще всего продолжить AM
на равное расстояние.

по
РЕШЕНИЯ
136—139
* f а-Ь
Рис. 100.
136. Даны большее основание а, меньшее основание b и
боковые стороны с, d трапеции; требуется построить ее по этим
данным. Пусть будет ABCD (рис. 100)
искомая тралеция. Проведем СЕ парал-
параллельно DA. Треугольник СЕВ можно
построить по трем сторонам СЕ = с,
СВ = d, ЕВ= а — Ъ. После этого оста-
останется отложить отрезок ЕА — b и по-
построить на EA.FC параллелограмм AECD.
137. Эта задача близка к задаче 135.
Нужно только произвести параллельный
перенос диагонали, а не боковой стороны-
138.	В искомом четырехугольнике даны .углы А, В и. сто-
стороны Ь, с, d, но которым можно последовательно перейти от
В к А (рис. 101). Пусть будет ABCD искомый четырехуголь-
четырехугольник. Непосредственному построению его
мешает то, что углы между известными
сторонами неизвестны, и сторона, при-
прилежащая к известным углам, неизвестна.
Чтобы сблизить известные части фи-
фигуры между собой, сделаем параллель-
параллельный перенос стороны AD в положение
BD'; при этом точка D опишет отрезок
DD'. Теперь построение можно вести
так: проводим произвольную прямую
ABE; откладываем углы ABF = В,
EBG = А; откладываем отрезки ВС = Ь,
BD' = d; проводим из точки D' полу-
полупрямую D' Н, параллельную и одинаково
направленную с полупрямой ВА; находим
на полупрямой D'H точку D на расстоя-
расстоянии с от точки С; проводим из точки D параллельную к
прямой D'B до пересечения с полупрямой ВА в точке А.
139.	Требуется построить четырехугольник по четырем
последовательным сторонам a, b,c,d\\ углу а между направле-
направлениями сторон b, d от стороны а к стороне с Пусть будет ABCD
(рис. 102) искомый четырехугольник; через А, В, С, D обозна-
обозначены начальные точки сторон а, Ь, с, d при последовательном
обходе их по контуру четырехугольника. Чтобы сблизить сто-
стороны b, d, между которыми известен угол, перенесем паргл
лельно сторону AD ь положение BD'. Мы можем построить
четырехугольник CBD'D, так как в нем известны стороны и
один из углов. При произвольной точке В строим угол, рав-
равный а; на сторонах ею откладываем отрезки BC—b, BD' = d;
строим точку D, находящуюся на расстоянии с от точки С и
на расстоянии а от точки ГУ. Чтобы получить искомый четырех-
/L Л
Рис. 101.

140—141
ПЛАНИМЕТРИЯ
111
угольник, остается провести из точек В, D параллельные к
прямым D'D, D'B до пересечения в точке А.
140. Предположим, что в четырехугольнике ABCD (рис. 103)
известны стороны АВ = a, CD = с, диагонали АС=т, BD=n
и угол между диагоналями а. Сделаем параллельный перенос
треугольника ABD, при котором вершина А описывает диаго-
=—'з
Рис. 102.
наль АС; при этом вершины В, D опишут отрезки ВВ\ DD',
равные и параллельные диагонали АС. Параллелограмм DBB'D'
можно построить по сторонам DD' = m, DB — п и углу
D'DB = а. После этого можно построить точку С по расстоя-
расстояниям а, с от вершин В', D этого параллелограмма. После
этого останется провести через точку D параллельную к D'C
и через точку В параллельную к ВС, до пересечения в точке А.
141. Пусть в четырехугольнике ABCD известны стороны
АВ = а, ВС = b, CD = с, DA = d и отрезок, соединяющий
середины сторон АВ и CD, MN = р (рис. 104). Перенесем
параллельно треугольник ABD в положение CB'D', как в ре-
решении 140, и докажем, что отрезок MN параллелен диагонали
BD' параллелограмма DBB'D' и равен
половине ее. Проведем MM', NN' в
направлении параллельного переноса.
ММ есть средняя линия треуголь-
треугольника ВАС, a NN' есть средняя линия
треугольника CDD'. Отсюда:
ММ'= — АС, NNf= — DD' =
2	2
Так как в четырехугольнике MM'N'N противоположные сто-
стороны MM', NN' оказались параллельны и равны, то этот че-
четырехугольник есть параллелограмм, и противоположные сто-
стороны MN, M'N' также параллельны и равны. Но отрезок

112	РЕШЕНИЯ	142—144
М'N' параллелен отрезку BD' и равен половине его как сред-
средняя линия треугольника CBD'. Следовательно, и отрезок MN
параллелен отрезку BD' и равен половине его, что и требо-
требовалось доказать. Треугольник CBD' можно построить по трем
сторонам СВ = Ь, CD' = DA = d, BD' = 2MN = 2p. После
этого проводим общую медиану СО треугольников CBD', CB'D,
продолжаем ее на равное расстояние до точки С и строим
точку D по ее расстояниям CD = с, CD = СВ' = АВ = а от
точек С, С. Наконец строим точку А по ее расстояниям В А =
=а, DA = d от точек В, D.
Подобные фигуры
142.	Наибольшая сторона 21 второго треугольника сходствен-
сходственна с наибольшей стороной 7 первого и больше ее втрое. Следо-
Следовательно, стороны второго треугольника, сходственные со сто-
сторонами 5 и 4 первого, также втрое больше их и равны 15 и 12.
143.	Пусть будут ABCD, A1BLC1D1 два квадрата. Имеем:
А = Аи В = Вг, С= С1% D = Dlt
так как все эти углы прямые, и
АВ	ВС	CD	DA
так как в каждом квадрате стороны равны. Согласно опреде-
определению подобия многоугольников, это доказывает подобие квад-
квадратов ABCD, AjBfiiDv
144. Пусть в прямоугольниках ABCD, A1B1ClD1
Переставив
средние
АВ
ВС
члены,
АВ
А1В1
ВгС,
найдем:
ВС
Эти отношения не изменятся, если заменить входящие в них
стороны прямоугольников противоположными сторонами. По-
Поэтому:
АВ _ ВС _ CD ^ DA
А& ~ BiCi ~~ CjDj ~ DlAl'
Кроме того, имеем:
A = AV B = BV C = Q, D = Dlf
так как все эти углы прямые.- Отсюда вытекает подобие пря-
прямоугольников ABCD, ABPD

145	146
ПЛАНИМЕТРИЯ
145. Пусть будет О вершина данного угла, АВ, А В' данные
отрезки, С, С точки пересечения перпендикуляров к сторонам
угла в концах отрезков АВ, А'В1
(рис. 105). Треугольники ОАВ, ОА'В'
подобны, так как они отсечены парал-
параллельными прямыми от одного и того	4,
же угла. Отсюда:
= Z_OA'ff
4.
ОА' А'В-
Треугольники ABC, A'B'C подобны, так
как их соответственные стороны параллельны. Отсюда имеем:
А В АС
Сопоставляя полученное, находим:
Отсюда следует, что треугольники ОАС, ОА'С подобны,
гак как они имеют по равному углу между пропорциональ-
пропорциональными сторонами. Вследствие этого углы АОС, А'ОС равны,
и потому стороны ОС, ОС' совпадают, что и доказывает теорему.
146. В треугольнике ABC (рис. 106) стороны АВ, АС раз-
разделены точками В'. С в отношени
АВ'
АС
=	= т.
С'С
В'В С'С
Кроме того, дано
ВС=а.
определить
Требуется
пропорции
В'С — х. Из
АВ_
В'В
С'С
следует, что прямые ВС, В'С параллельны. Поэтому треуголь-
треугольники ABC, AB'C подобны и мы имеем:
х
а
АВ'
АВ
Остается определить последнее отношение. Это можно сделать
с помощью производных пропорций:
АВ' 	 т	АВ' __ т	46	т_
В'В ~~ 1 ' АВ' + В'В ~т + ]	АВ ~~ т + 1
8 Делоне и Житомирский

j 14	решения	147—148
Можно сделать и так:
А В'
= т-В'В;
ВВ .
АВ =ABf-\- В'В = т-В'В+В'В = (т+\)В'В;
т
АВ . m -f- 1 "
Но проще всего вычисление ведется так: примем В'В= 1;
тогда АВ1 = т, и АВ — 1 -f- /га, так что
Т ~ 1+#и '
отсюда найдем:
	 та
1 -f- m'
147. В трапеции ABCD (рис. 107) дано:
АВ = a, DC= b,
АЕ _ BF _
ED~~ ЯС"
Из пропорции следует, что прямая EF параллельна основаниям
АВ, DC. Проведя DGH параллельно СВ, получим поэтому два
подобных треугольника DEGi, DAH. Положив ED = 1, и сле-
следовательно, АЕ — т и AD = 1 -f- m, найдем соотношения
EG	1 „„ я —*
		. i__,\J	 —
а-Ь \-\-m 1 +
Кроме того, очевидно:(
Отсюда
стояние:
GF = b.
находим искомое
1+1
т
рас-
Ь —
п-в И
Рис. 107.
V
\
ь
148. Чтобы построить центр тяжести Q треугольника ABC
(рис. 108), делим ВС пополам в точке М и затем делим AM
в отношении 2: 1, считая от А, в точке Q. Пусть будут
АА' = р, ВВ' = д, СС ?= г, ММ' = s, QQ' = х

149—150
115
расстояния точек А, В, С, М, Q от некоторой прямой. Из этих
расстояний р, д, г даны, а х требуется определить. Из трапе-
трапеции ВССВ' найдем по теореме о средней линии:
Из трапеции
АММ'А' найдем
на основании ре-
решения 147:
P±2s_
л.
«' <?' С g
Рис. 108
Рис. 109.
149. Из подобия треугольников ОАВ, OCD (рис. 109) нахо-
находим:
АО _ 1Ю _ а
6с~"оЪ~~~ъ '
то-есть, диагонали трапеции делят друг друга в отношении
оснований.
150. В трапеции ABCD (рис. ПО) боковые стороны AD, ВС
продолжены до пересечения в точке О. По данным основа-
основаниям АВ — a, DC = b требуется уз-
узнать отношения, в которых точка О
делит стороны AD, ВС, то-есть от-
отношения
АО ВО
OD ОС'
Рис. ПО
Из подобия треугольников ОАВ, ODC
находим:
АО _ ВО _ а
ob~ ос~~~ь~'
то-есть боковые стороны трапеции делят друг друга в отно-
отношении оснований. Сравнивая этот результат с результатом
решения 149, видим, что диагонали и боковые стороны тра-
трапеции делят друг друга в одинаковом отношении. Разница
только в том, что точка пересечения диагоналей лежит на
них самих, то-есть делит их внутренним образом в этом от-
отношении, а точка пересечения боковых сторон лежит на их про-
продолжениях, то-есть делит их внешним образом в том же от-
отношении.
8*

116	РЕШЕНИЯ	151-152
151. Согласно решению 149 отрезки АО, ОС диагонали АС
пропорциональны основаниям АВ, CD (рис. Ill) Отсюда на-
находим:
АО = ka, ОС = kb, AC=k(.a + b),
где ? —коэффициент пропорциональности. Из подобия тре-
треугольников АОЕ, ACD находим:
a
Рис.
У
1)\
\
111
1
\
ч
О/? Ла
b k(a + b)
откуда:
Таким же образом
OF — в*
а
а+ b
V
найдем:
Складывая оба равенства, получим искомый отрезок:
152. Согласно решению 150 расстояния АО, CD точки пере-
пересечения О боковых сторон от концов боковой стороны AD
пропорциональны основаниям АВ, DC (рис. 112). Отсюда
находим:
АО = ka, OD = kb, AD = k(a- b).
Из подобия треугольников АОЕ, ADC легко находим:
ОЕ	ka 	 a
b k (а — b) a — b
откуда
ab .
Таким же образом
найдем:	А
OF = -^—	Рис. 112.
а — Ь
Складывая оба равенства, сразу получим искомый отрезок:
EF = -^r.
a — b

\
153	154	планиметрия
153. Пусть AD—внутренняя биссектриса треугольника ABC
(рис. 113). Требуется по сторонам треугольника определить от-
отрезки BD, DC. По известной теореме отрезки BD, DC пропор-
пропорциональны сторонам АВ, АС:
=kc, DC = kb.
Складывая почленно, получаем:
Отсюда:
R c + b
и следовательно:
c+b
154. Пусть AD — внешняя биссектриса треугольника ABC
(рис. 114). Требуется по сторонам треугольника определить
отрезки BD, DC. По известной теореме отрезки BD, DC про-
пропорциональны сторонам АВ, АС:
Вычитая почленно, находим:
откуда:
с—
и следовательно:
с — Ъ
На рис. 114 Ь<^с. Если бы было
BD =	, DC =	.
Ъ — с	Ъ— с
При b = с выражения для BD, DC
теряют смысл, или, как говорят, обра- в'
щаются в бесконечность. И действи-
действительно, в этом случае биссектриса
внешнего угла при вершине А пере-
перестает пересекать основание ВС или. как говорят, пересекает
его в бесконечности.
то мы имели бы:

118
РЕШЕНИЯ
155-156
155. Прямая пересекает стороны АВ, АС, ВС треугольника
ABC или их продолжения в точках Ж, N, Р (рис. 115). По
данным отношениям:
ВМ	CN
— = tn, — = п
AM	' AN
требуется определить отношение:
ВР _
Проведем AQ, параллельную к прямой MNP. Имеем:
ВР ВМ	СР CN
— =	= т, — =	 = п.
PQ AM	PQ AN
с ^ч ° Итак:
m-PQ, CP = n-PQ, ^=^L
СР п '
Рис. 115.	п
Для доказательства безразлично, пересекает ли прямая MNP
самые стороны треугольника или их продолжения. Заметим
однако, что прямая может или пересекать две стороны и
продолжение третьей, как на нашем чертеже, или пересекать
продолжения всех трех сторон треугольника. Это нужно иметь
в виду, когда из соотношения:
т
желательно вывести, что точки М, М, Р лежат на одной пря-
прямой. Такое обращение нашей теоремы справедливо только
в том случае, когда две точки лежат, на самих сторонах, а
третья — на продолжении стороны, или
все три точки лежат на продолжениях
сторон треугольника. Ниже будут при-
приведены примеры такого пользования
теоремой. В несколько' -другой форме
эта важная теорема носит название тео-
теоремы Менелая.
156. Прямые, соединяющие вершины
треугольника ABC с точкой О, пересе-
пересекают его стороны АВ, АС, ВС или их
продолжения в точках М, N, Р (рис. 116). По данным отноше-
отношения
AN
Рис. 116
AM

157	планиметрия	U9
требуется определить отношение:
«	Zp~ Р'
Обозначим для простоты:
АО~
Применяя теорему Менелая к треугольнику АВР с пересекаю-
пересекающей МОС и к треугольнику АСР с пересекающей NOB, по-
получим:
PC к РВ k
ВС т ' СВ п
откуда
PC = kBC РВ = k'CB — = —
т	п ' PC n
Итак:
т
Р = —
п
Заметим, что точки М, N, Р или все лежат на сторонах,
или одна лежит на стороне, а две другие на продолжениях
сторон треугольника. Полученная теорема называется теоре-
теоремой Чевы.
157. В треугольнике ABC (рис. 117) проведены внутренние
биссектрисы BN, СМ и внешняя биссектриса АР. Требуется
доказать, что точки М, N, Р лежат на одной прямой. Обо-
Обозначим, как всегда
Точки М, IV делят стороны ВА,
СА внутренним образом в от-
отношениях:
BM__ja_ СЛ^__?_
AM ~ Ь ' AN~ с
п	дл	Рис- Ш
I ю теореме Менелая точка пе-
пересечения Р1 прямой MN с основанием ВС делит его внеш-
внешним образом в отношении:
Вр_	 а а _ с
СР' ~" Т ' с	Ь~
но в том же отношении:
СР~ ь

120	решения	158-159
делит его и точка Р, и тоже внешним образом. Отсюда за-
заключаем, что точки Р, Р совпадают, так что точка Р ле-
лежит на прямой MN, что и требовалось доказать. Мы восполь-
зовались тем, что две несовпадающие точ-
точки Р, Р' не могли бы делить отрезок АС
внешним образом в одном и том же отно-
отношении. Предоставляем доказательство это-
А/^ n.\	го положения читателю.
м
^	158. В трапеции ABCD (рис. 118)прове-
м в дена прямая через точку пересечения О,
Р us	диагоналей и боковых сторон- Тре-
"с"	буется доказать, что точки пересечения М,
N этой прямой с основаниями суть сере-
середины оснований. Применим теорему Чевы к треугольнику О'АВ
и точке О:
ЛМ AD ш ВС
ВМ O'D ' (УС '
Но из параллельности прямых АВ, DC следует:
AD ВС
o'd o:c
Отсюда находим:
AM
ВМ -*>АМ = вМ,
что и требовалось доказать относительно точки М. Точно так
же, применяя теорему Чевы к треугольнику O'DC, получим:
DN DA СВ , ^,г
что заканчивает требуемое доказательство. Можно, впрочем,
ограничиться применением теоремы Менелая и даже обойтись
без применения обеих теорем, что составляет полезное упраж-
упражнение.
159. Треугольники ABC, A'B'C расположены так, что
точки пересечения D, E, F соответственных сторон лежат на
одной прямой (рис. 119). Требуется доказать, что соедини-
соединительные прямые АА', ВВ', СО соответствующих" вершин
пересекаются в одной точке или параллельны. Выясним снача-
сначала расположение частей фигуры. Выберем обозначения так,
чтобы точка F лежала на продолжении отрезка DE, что всегда
возможно сделать. Рассматривая треугольники ADE, A'DE с
пересекающими FCB, FOB', убеждаемся на основании заме-
замечания, сделанного в конце решения 155, что точки В, С
доэжны одновременно лежать на отрезках AD, AE или на их

159
ПЛАНИМЕТРИЯ
121
продолжениях, и точно так же точки В', С должны одно-
одновременно лежать на отрезках A'D, A'E или на их продолже-
продолжениях. Переходя к треугольникам ADA', EAA', заключаем от-
отсюда, что точки В, В' расположены относительно отрезков
DA, DA' также, как точки С, С расположены относительно от-
отрезков ЕА, ЕА'. На основании того же
замечания из решения 155 мы вправе
сделать вывод, что прямые ВВ', СС
или обе пересекают отрезок АА' или
обе не пересекают его. Теперь перей-
перейдем к количественным соотношениям
частей фигуры, рассматривая те же
треугольники в том же порядке.
Обозначим для краткости:
DF
DB	EC
— = т, — = л,
АВ	АС
DB'
АВ'
EC_
AC
rGIH)
Рис. 119.
По теореме Менелая находим из треугольника ADE с пере-
пересекающей FCB и из треугольника A'DE с пересекающей FCB'.
т
откуда:
т = пр, т' = п'р.
Если прямая СС параллельна прямой АА', то она делит
отрезки ЕА, ЕА' одинаковым образом и в равных отноше-
отношениях и, и'. Тогда прямая ВВ' делит отрезки DA, DA' также
одинаковым образом и также в равных отношениях пр, п'р.
Поэтому прямая ВВ' также параллельна прямой АА'. Таким же
образом можно доказать, что из параллельности прямой ВВ'
к прямой А А' вытекает параллельность прямой СС к прямой
АА'. Следовательно, прямые ВВ', СС или обе параллельны
прямой АА', или обе пересекают ее. Остается доказать, что
в последнем случае точки пересечения совпадают. Обозначим
точки пересечения прямых ВВ', СС с прямой АА' через G, Н.
Применяя теорему Менелая к треугольнику DAA' с пересекаю-
пересекающей ВВ' и к треугольнику САА' с пересекающей СС, находим:
AG 	_l_ . _i	т' 	 п'
A'G
АН
mm'

122	решения	160—161
откуда:
У	AG АН
A'G АН
Таким образом, точки G, Н делят отрезок АА в одинако-
одинаковых отношениях, а по доказанному выше, и одинаковым об-
образом. Следовательно, точки G, Н совпадают, что и оставалось
доказать.
Задачи на построение
160. Пусть будет А данная точка, К—данный круг, О—его
центр (рис. 120). Требуется провести секущую АМ'М так,
чтобы было:
AM' = 2М'М.
Эта задача есть обобщение
задачи 102 и может быть ре-
решена сходным образом. Прове-
Проведем М'О' параллельно МО. Из
условия находим AM' — —¦ AM,
О
а затем из подобия треуголь-
треугольников АМ'О', АМО получаем
Рис. 120.	М'О' = — МО. Для точки М'
О
имеем два геометрических места: окружность К и окруж-
окружность К', описанную около точки О', находящейся на отрезке
АО на расстоянии двух третей его от точки А, радиусом, рав-
равным двум третям радиуса окружности К. Точки М' суть об-
общие точки этих геометрических мест. Но можно прийти к
тому же решению и более общим рассуждением. От точки М
требуется, чтобы она лежала на окружности К, а от точки М'
о
чтобы она лежала на отрезке AM на расстоянии — AM от его
О
начала А, и, кроме того, на окружности К. Если отбросим
последнее условие, то первые два условия дадут в качестве
геометрического места для точки М' окружность, прямопо-
добно расположенную с окружностью К относительно центра
2
подобия А с отношением подобия —, то-есть уже найден-
о	*
ную нами окружность К'. Этот метод применим, конечно, и
к задаче 102.
161. Пусть будет К данный круг, О —его центр, Ъ, с — дан-
данные прямые, а — прямая, показывающая направление искомой
прямой (рис. 121). Если ВС искомая прямая, так что BD—CE,

162
ПЛАНИМЕГГИН
123
Рис. 121
и Ж—середина DE, то М есть также середина ВС. Кроме того,
по известному свойству хорды, ОМ будет перпендикулярна
к ВС. Таким образом для М имеем два геометрических места:
диаметр круга /С. перпендикулярный к направлению а, и гео-
геометрическое место середин отрезков, заключенных между
прямыми Ъ, с и параллельных направлению а. Легко доказать,
1то последнее геометрическое
место есть прямая, которая про-
проходит через точку пересечения
прямых Ь, с, если они пересека-
пересекаются, и параллельна им, если они
параллельны между собой; пре-
предоставляем доказательство чита-
читателю. Чтобы построить это гео-
геометрическое место, достаточно
построить одну его точку — сере-
середину М какого-нибудь отрезка
В'С, заключенного между пря-
прямыми Ъ, с и параллельного на-
направлению а; после этого останется соединить эту точку с
точкой пересечения прямых Ъ, с или, в случае параллель-
параллельности этих прямых, провести через эту точку параллельную
к ним. Искомая точка М должна быть точкой пересечения
¦^вух найденных геометрических мест. Такой точки может
и не быть, но даже если она существует, она все же не
дает решения задачи, если она окажется вне круга К- Если
же точка М существует и лежит внутри или на окружности
круга К, то задача имеет определенное
решение. Предлагаем читателю подробно
провести исследование и доказательство.
162. Дан треугольник ABC (рис. 122).
Требуется построить квадрат DEFG со
сторолой DE на основании ВС, вершиной
G на стороне АВ и вершиной F на сто-
роне АС. Отбросив последнее требова-
требование, получим бесчисленное множество
квадратов вида D'E'F'G', к числу кото-
которых должен принадлежать и искомый
квадрат DEFG. Всякие два таких квад-
квадрата подобно расположены, потому что они подобны, как вся-
всякие вообще квадраты, и сходственные стороны их параллельны
в силу условий задачи. Так как сходственные вершины вида
D лежат на прямой ВС, а сходственные вершины вида G' ле-
лежат на прямой ВА, то центр подобия есть точка пересечения
В прямых ВС, ВА, и, следовательно, сходственные вершины
вида F' также лежат на прямой, проходящей через точку В.
о' со
Рис. 122

124
РЕШЕНИЯ
163—166
Рис. 123.
Отсюда вытекает следующее построение: строим какой-нибудь
квадрат вида D'E'F'G'; проводим прямую BF' до пересечения
со стороной АС в точке F; строим искомый квадрат DEFG.
Задача всегда имеет одно решение.
163.	Решение этой задачи почти в точности совпадает с
решением 162.
164.	Пусть будет ОАВ искомый сектор (рис. 123). Докажем,
что искомый квадрат CDEF должен быть симметричен отно-
относительно биссектрисы угла АОВ.
Перпендикуляр ОН к хорде DE де-
делит ее пополам. Поэтому он также
перпендикулярен к" стороне FC и
делит ее пополам. Следовательно,
ОН разбивает квадрат CDEF на
два симметричных прямоугольника ¦
GHDC, GHEF. Остается доказать,
что ОН есть биссектриса угла АОВ.
Но это видно из того, что в тре-
треугольнике OCF линия OG есть одно-
одновременно медиана и высота; следовательно, он равнобедренный,
и OG есть также и биссектриса. Теперь задача сводится к
тому, чтобы вписать в половину КОВ сектора АОВ пря-
прямоугольник GHEF с отношением сторон GH :GF=2 так,
чтобы сторона GH лежала на радиусе ОК, вершина F на ра-
радиусе ОВ и вершина Е на дуге КВ. Для этого строим какой-
нибудь прямоугольник G'H'E'F', удовлетворяющий всем этим
условиям, кроме послед-
последнего, проводим прямую
ОЕ' до пересечения с ду-
дугой KB в точке Е и строим
искомый прямоугольник
GHEF. Впрочем, найдя
точку Е, можно сразу
построить квадрат CDEF.
Решение всегда одно.
165.	Решение этой зада-
задачи родственно решению 164.
166.	Требуется вписать в четырехугольник ABCD (рис. 124)
параллелограмм, в котором стороны, отсекающие углы А, С,
были бы параллельны направлению а, а стороны, отсекающие
углы В, D, были бы параллельны направлению Ь. Указанным
требованиям наверное нельзя удовлетворить, если какая-либо
из прямых, проведенных через А, С параллельно а, или через
В, D параллельно Ь, не проходит вся снаружи четырехугольника
ABCD. Предположим поэтому, что направления а, Ъ выбраны
в согласии с последним требованием. Мы можем построить
Рис. 124.

167	планиметрия	125
сколько угодно параллелограммов с требуемыми направлениями
сторон и с тремя вершинами на требуемых сторонах четырех-
четырехугольника или их продолжениях. Для этого из произвольной точ-
точки К' прямой АВ проводим прямую в направлении Ъ до пересече-
пересечения с прямой ВС в точке L' и другую прямую в направлении а до
пересечения с прямой AD в точке N'; затем проводим из точек
V, N' прямые в направлениях а, Ъ до пересечения в точке Ж'.
Все параллелограммы K'L'M'N' имеют указанные свойства.
Если среди них имеются такие KLMN, у которых вершина М
лежит на стороне CD, то это и будут искомые. Иначе говоря,
искомые вершины М суть общие точки стороны CD и геоме-
геометрического места вершины М, когда вершина К' описывает
прямую АВ. Чтобы найти это геометрическое место, проведем
через вершину А прямую в направлении Ъ до пересечения с
прямой ВС в точке С и через точку В прямую в направлении
а до пересечения с прямой AD в точке D'. Мы докажем, что
прямая CD' есть искомое геометрическое место вершины М'.
Для этого достаточно доказать, чтр точки пересечения пря-
прямой CD' со сторонами L'M', N'M' совпадают. Обозначим эти
точки через М1г М2. Из рис. 124 легко найдем, следя за про-
произведенным выше построением параллелограмма K'L'M'N':
АК' __ CL _ С'Мг АК' _ AN' _ С М2
KB ~ L'B ~ MXD'' KB
Отсюда находим:
D'M2
то-есть точки Мх, М2 делят отрезок CD' в одинаковых от-
отношениях. Из того же хода рассуждений, который дает ра-
равенство всех этих отношений, видно, что точки Mv M2 делят
отрезок CD' не только в одинаковых отношениях, но и оди-
одинаковым образом. Следовательно, точки М1г М2 совпадают и
сливаются с точкой М'. Когда точка К' описывает прямую В А,
точка М описывает прямую D'C. Если прямая D'C пересе-
пересекает сторону DC в некоторой точке М, то от этой точки
можно построить параллелограмм KLMN, который удовлетво-
удовлетворит всем требованиям задачи, так что в этом случае получит-
получится одно решение. Если прямая D'C параллельна стороне ВС
или пересекает только ее продолжение, то задача не имеет
решения.
167. Требуется около четырехугольника ABCD (рис. 125)
описать четырехугольник E'F'G'H', подобный четырехуголь-

126
РЕШЕНИЯ
168—17С
нику EFGH, так чтобы углы Е', F', G', Н' опирались ка сто-
стороны АВ, ВС, CD, DA. Так как угол Е' должен быть равен углу
Е, то он должен лежать на дуге, опирающейся на сторону АВ
и вмещающей угол, равный Е. Так как угол F'E'G' должен быть
равен углу FEG, то он должен опираться на часть ВЕг остальной
дуги той же окружности, на которую опираются все вписанные
углы, равные FEG. Следовательно, диагональ E'G' должна про-
проходить через вполне определенную
точку Еи которую нетрудно построить
по данным задачи. Из такого же рас-
рассмотрения угла G' найдем вторую точ-
точку Gt диагонали G'E'. Построим точки
Ег, Glt проведем прямую E1G1 до пе-
пересечения с дугами, опирающимися т,
стороны АВ, CD и вмещающими углы
Е, G, в точках ?', G', проведем прямые
Е'В, G'C до пересечения в точке F' и
прямые Е'А, G'D до пересечения в
точке Н'. Четырехугольник E'F'G'H' и будет искомый
В том, что он подобен четырехугольнику EFGH, убе-
убедимся проще всего, замечая, что диагонали E'G', EG сход-
сходственным образом разбивают эти четырехугольники на тре-
треугольники с соответственно равными углами при сторо-
сторонах E'G', EG.
168.	Пусть требуется в четырехугольник Qx вписать четы-
четырехугольник Q", подобный четырехугольнику Q2. Применим
метод обратности. Опишем около четырехугольника Q2 четы-
четырехугольник Q', подобный четырехугольнику Qx, что мы можем
сделать на основании решения 167. После этого разделим
стороны четырехугольника QT в тех же отношениях, в каких
вершины четырехугольника Q2 делят стороны четырехуголь-
четырехугольника Q'. Точки деления и будут вершинами искомого четырех-"
угольника Q".
169.	Здесь можно применить метод обратности. Опишем
круг около данного треугольника и проведем радиусы к его
вершинам. Затем проведем в данном круге радиусы под те-
теми же углами и соединим их концы. Получим искомый тре-
треугольник.
170.	По двум углам можно построить треугольник, подоб-
подобный искомому, и в нем построить расстояние между центрами
описанного и вписанного кругов. После этого останется изменить
его линейные размеры в отношении данного расстояния между
центрами к построенному только что. Полученный треуголь-
треугольник будет искомый. Самое построение можно выполнить раз-
разными способами, и мы рекомендуем читателю поискать самый
удобный.

171-175
ПЛАНИМЕТРИЯ
127
Пропорциональные отрезки в кругах
171. Обозначив искомые отрезки через х, у, имеем:
Отсюда видно, что х, у суть корни квадратного уравнения
у
172.	Vab.
173.	Пусть будет А данная точка, О—центр данного круга
ВОАС—диаметр этого круга, проведенный через точку A, DAE—
хорда тога же круга, перпендикулярная к этому диаметру в
точке А (рис. 126). По свойству отрезков хорд будем иметь:
AD-AE=AB-AC=
=(ОВ+ ОА)(ОС—ОА),
или
0ТКУД&			Рис. ]26.	Рис. ]27.
DE=2 Vr2— dl .
174. Пусть будет А данная точка, О — центр данного кру-
круга, BOCA—диаметр, проходящий через точку A, AT—касатель-
AT—касательная из точки А (рис. 127). По свойству отрезков секущей
имеем:
AT2=-AB-AC=(OA-\-OB){OA — i
или
откуда
175. В треугольнике ABC (рис. 128) проведем высоту АИ
и обозначим ВС=а, AC=b, AB=c, CH=m. Опишем около Л
окружность радиусом АС=Ь и обозначим вторую точку пере-
пересечения ее с АС через D, а точки пересечения с АВ через Е»
F, как показано на чертеже. Имеем:
BE BF=BC-BD.

РИПЕНИЯ
175
Если угол С острый, то ато равенство можно переписать в виде:
(АВ + АЕ)(АВ — AF)=BC(BC- 2СН),
или
b)(c-b)=a(a-2m),
откуда найдем:
Если угол С тупой, то то же равенство можно переписать в виде:
{АВ~\- АЕ){АВ-~ AF)=BC(BC+ 2CH),
(с + Ъ) (с — Ь) = а{а + 2т),
или
откуда
Если угол С прямой, то, очевидно ВС из секущей превра-
С	О
Рис. 128.
Рис. 129	Рис. ISO.
щается в касательную, и мы таким же образом будем иметь:
с2=а2 + Ь2.
Доказательство соотношений в прямоугольном треугольнике
hz=mn, bz=an
ясно из рис. 129.

176-177
ПЛАНИМЕТРИЯ
129
176. Пусть будет А данная точка, ВС — данная хорда, AD —
перпендикуляр к ВС, BE и CF — перпендикуляры к касательной
EF в точке А (рис. 130). Требуется доказать:
~AD
CF
Прямоугольные треугольники ABD, ACF подобны, так как у
них острые углы ABD, CAF измеряются половиной одной и
той же дуги АС. Таким же образом докажем подобие треуголь-
треугольников ACD, ABE. Четырехугольники BEAD, ADCF подобны,
так как они сходственным образом составлены из подобных
треугольников. Приравнивая
отношения сходственных
сторон, получим:
BE
AD
AD
~CF'
Рис. 131.
что и требовалось доказать.
177. На рис. 131 изобра-
изображены два возможных случая
расположения точек М, Ал,
В1г А.2, В2. В первом случае
точки Av Bl и А2, В2 расположены по разные стороны от точ-
точки М, во втором случае по одну сторону. В обоих случаях
проведем окружность через точки А1г А2, В2 и обозначим
точку пересечения ее с прямой МА± через В'. По теореме
об отрезках хорд или секущих получим в обоих случаях:
Сравнивая это соотношение с предположенным в условии
МАХ ¦ МВХ=МА2 • МВ2,
заключаем, что
v
Теперь рассмотрим каждый случай отдельно. В первом случае
точка М лежит на самой хорде А2В2 и, следовательно, внутри
круга. Поэтому направление отрезка MB' обратно направле-
направлению отрезка МАХ. Таково же по условию и направление от-
отрезка МВХ. Так как отрезки MB', МВХ равны и отложены в
одну сторону от точки М, то их концы В', Вх совпадают, и,
следовательно, точки А1г Вг, А2, В2 лежат на одной окружно-
окружности. Рассмотрение второго случая предоставляем читателю.
Заметим только, что в этом случае точки Ах, Вх могут и сов-
совпадать. Тогда секущая МАХ обратится в касательную.
9 Делоне и Житомирский

130
РЕШЕНИЯ
178
178. Пусть общие хорды А^, А2В2 кругов Ох, О2 с кругом
О сходятся в точке М (рис. 132). Мы не предполагаем обяза-
обязательно, что точка М принадлежит
самим хордам, она может лежать и
на их продолжениях; частный случай,
когда она совпадает с их концами,
мы пока не будем рассматривать.
Если точка М лежит внутри круга О,
то она лежит на с: мих хордах Л^,
А2В2 и, следовательно, лежит и вну-
внутри кругов О1г О2. Если же точка М
лежит вне круга О, то она лежат на
продолжениях хорд АхВг, А2В2 и, сле-
следовательно, лежит и вне кругов О1г
О2. При леняя в первом случае тео-
теорему об отрезках хорд, а во втором случае теорему об отрез-
отрезках секущих, получим в обоих случаях:
Рис. 132.
МАХ -MB±=
Обозначив через А одну из точек пересечения окужностей
Ov О2, проведем прямую МА и отложим на ней отрезок MB,
равный k'MA, так что
МА-МВ=к,
причем в первом случае отложим его от точки М в направ-
направлении, обратном направлению отрезка МА, а во втором случае
в напр .влении отрезка МА. На основании равенства
МА-МВ=МА1-МВ1 и одинаковости расположения точек А, В
и Av Вг по отношению к точке М, заключаем по теореме 177,
что точка В лежит на окружности, проходящей через точки
Л, Лг, В1У то-есть, на окружности Ог Так же докажем, что
точка В лежит на окружности О2. Следовательно, точка В
есть общая точка окружностей Ох, О2, и, следовательно, АВ
общая хорда их. Мы видим, что общие хорды АВ, A±BV A,B2
окружностей О Ov O2 сходятся в одной точке М, что и тре-
требовалось доказать в рассматриваемом случае. Если теперь
хорды А±ВХ, А2В„ параллельны, то диаметр круга О, перпен-
перпендикулярный к ним, есть также диаметр круюв Ov О2, и, сле-
следовательно, перпендикулярен и к хорде АВ. Следовательно,
хорды АВ, AtBv A2B2 параллельны, что и нужно было дока-
доказать в этом случае. В случае, киторый мы вначале оставили
в стороне, когда точка М лежит на окружности круга О, она
ле кит также на окружностях кругов О1г О2, так что она будет
общим концом хорд АВ, A±BV А.гВг, которые таким образом и
в этом случае сходятся в одной точке.

j^g	181	ПЛАНИМЕТРИЯ	Jg|
179.	Пусть круги К, К', проходящие через точки А, В, пе-
пересекают круг L (рис. 133). Обозначим общую хорду кругов К, L
через CD и один из концов общей хорды кругов К', L через
С. Рассмотрев в решении 178 все
возможные случаи, мы ограничимся
теперь одним случаем, когда хорда CD
пересекает прямую АВ, и точка пере-
пересечения Р лежит вне круга К. По
теореме об отрезках секущих имеем:
PA-PB=PC-PD=k.
Отложим на прямой PC по направ-
направлению PC отрезок PD', равный
? :РС, так что
Рис. 133.
PD'-PC'=k.
Так как РА-РВ=РС-PD', и точки А, В и С, D' располо-
расположены по одну сторону от точки Р, то по теореме 177 точка
D' лежит на окружности, проходящей через точки А, В, С,
то-есть на окружности К'. Так же убедимся, что точка D'
лежит на окружности L. Таким образом точка D' есть общая
точка окружностей K',L, и, следовательно, CD' — общая хорда
их. Мы видим, что хорды CD, CD' пересекают прямую АВ
в одной и той же точке Р, что и требовалось доказать.
Заметим, что теорема остается верной и в том случае, когда
общая секущая CD' кругов К', L обращается в их общую
касательную.
180.	По известной теореме
= МА-МВ, МТ'2 = МА-МВ.
Отсюда:
МТ = МТ,
что и требовалось доказать (рис. 134).
181. Дана окружность К, точка А на ней и прямая CD,
перпендикулярная к диаметру АВ (рис. 135). Требуется дока-
доказать, что для всех прямых, проходящих через точку А и
пересекающих прямую CD, произведение отрезков АВ', АС,
отсекаелых на них окружностью и прямой, имеет одно и то
же значение. Пусть Сне совпадает с Л. В треугольнике ABB'
угол В' поямой, так как он вписанный и опирается на диа-
диаметр. Прямоугольные треугольники ABB', AC С подобны, так
как у них острый угол А общий. Следовательно:
АВ ~ АС
9*

132
РПШЕНИЛ
182
откуда:
АВ'-АС = АВ-АС,
что и доказывает теорему в рассматриваемом случае. Если же
D
Рис. 134.
Рис. 135.
С совпадает с А, то теорема вытекает из того, что АС, а сле-
следовательно, и АВ'-АС всегда нуль.
182. Из центра подобия S окружностей К, К' проведены
две секущие (рис. 136). Выберем на этих секущих две точки
А, В окружности К и найдем на
них же сходственные точки А', В'
и несходственные точки Аг, Вг
окружности К'. Требуется дока-
доказать:
SA-SAl = SB-SBt.
Так как точки А', В' сходственны
с точками А, В, то прямая А'В'
параллельна прямой АВ, и следо-
следовательно, угол А 'В' S равен углу ABS. С другой стороны, угол
A'B'S равен углу B^AXS, так как оба угла вписаны в круг К'
и опираются на одну и ту же дугу А'Вг. Следовательно, углы
ABS, B^S равны между собой. Эти углы принадлежат тре-
треугольникам ABS, 51Л15, которые сверх того имеют общий
угол S. По двум углам треугольники ABS, B^S подобны.
Отсюда находим:
SA SB!
Рис. 136.
SB
ИЛИ
что и требовалось доказать. На рис. 136 S есть центр прямого
подобия, но сходными рассуждениями теорема доказывается и
для центра обратного подобия.

183—184	ПЛА11ИЫЕТ1-ИИ	133
Задачи на построение
183.	Мы можем ограничиться случаем, когда данные прямые
пересекаются, и данная точка не лежит на них, потому что
случай, когда данные прямые параллельны, есть частный слу-
случай задачи 91, а случай, когда данная точка лежит на данной
прямой, был предметом задачи
95. Пусть будет PQR тот угол
между данными прямыми, внут-
внутри которо! о лежит данная точ-
точка А (рис. 137). Искомый круг
также должен лежать внутри
угла PQR. Построим какой-
нибудь круг К, касательный к
сторонам угла PQR. К числу
таких кругов принадлежит и	ис'
искомый. Докажем, что каж-
каждая пара таких кругов имеет центром прямого подобия
точку Q. Действительно, точки касания их к прямой PQ
сходственны при прямом подобии, потому что эти точки суть
концы параллельных и одинаково направленных радиусов.
Поэтому прямая PQ должна проходить через центр прямого
подобия. То же самое справедливо и относительно прямой
RQ. Следовательно, центр прямого подобия есть точка Q.
Сходственные точки всех этих кругов должны лежать на
полупрямых, исходящих из точки Q. Так, например, центры
их лежат на биссектрисе QS угла PQR. Точки круга К, сход-
сходственные с точкой А искомых кругов, должны лежать на по-
полупрямой QA. Вследствие этого их легко найти: это будут
точки пересечения А', А" окружности К с прямой QA. После
этого сейчас же находим центры искомых кругов, пользуясь
тем, что сходственные радиусы круга К и искомых кругов
должны быть параллельны: проводим радиусы ОА', ОА" кру-
круга К и параллельные им радиусы АО', АО" искомых кругов.
Остается описать около точек О', О" окружности радиусов
О'А, О"А; это и будут искомые окружности. Задача имеет
два решения. Если данные прямые пересекаются, то, согласно
решению 95, задача илгеет два решения также и в том слу-
случае, когда данная точка лежит на одной из данных прямых.
Исключение составляет только тот случай, когда данная точка
совпадает с точкой пересечения обеих данных прямых; в этом
случае искомые круги оба обращаются в эту точку пересечения.
184.	Случай, когда данные прямые параллельны, был пред-
предметом задачи 91. Мы предположим поэтому, что данные пря-
прямые пересекаются. В этом случае задачу можно свести к за-
задаче вида 183 при помощи особого преобразования, которое

134
РЕШЕНИЯ
184
Рис. 138.
мы будем называть увеличением или уменьшением радиуса
круга. Увеличить радиус круга К на отрезок d, значит отло-
отложить на каждом из его диаметров ОА по направлению от
центра наружу отрезок ААХ = d; точки Аг образуют окруж-
окружность Кг увеличенного радиуса. Уменьшить радиус круга К
на отрезок d, значит отложить на каждом из его диаметров
ОА по направлению к центру отрезок АА2 = d; точки Л2
образуют окружность /С2 уменьшенного радиуса. Уменьшение
радиуса на отрезок, равный самому
радиусу, приводит к окружности
нулевого радиуса, то-есть к точке.
, Уменьшение радиуса на еще боль-
больший отрезок приводит к окружно-
окружности отрицательного радиуса; это
значит, что радиусы ОА2 направ-
направлены противоположно радиусам
ОА, что и показано на рис. 138.
Если круг К касается некоторой
прямой t, то круги /Cj, К2 будут ка-
касаться прямых tlt t2, параллельных
прямой t и удаленных от нее на
расстояние d. Если два круга внешне
касаются, то касание не нарушится при одновременном увели-
увеличении радиуса одного из них и уменьшении радиуса другого
на один и тот же отрезок. Если два круга внутренне каса-
касаются, то касание не нарушится при одновременном увели-
увеличении или уменьшении радиусов обоих на один и тот же от-
отрезок. При этом мы считаем прямую
или окружность касательной к окруж-
окружности нулевого радиуса, то-есть к
точке, если она проходит через эту
точку. Пусть теперь будет К данный
круг и a, b данные прямые (рис. 139).
Требуется построить все круги, ка-
касательные к кругу К и к прямым а, Ь.
Обозначим радиус круга К через R.
Если какой-нибудь круг касается кру-
круга К внешним образом, то после уве-
увеличения его радиуса на R он прой-
пройдет через центр О круга К- Если этот круг, кроме того,
касался прямых а, Ь, то после увеличения радиуса он ко-
коснется одной из прямых av a2, параллельных прямой а на
расстоянии R от нее, и одной из прямых bl3 Ь.2, параллель-
параллельных прямой b на расстоянии R от нее. То же самое произой-
произойдет со всяким кругом, внутренне касательным к кругу К и
касательным к прямым a, b при уменьшении его радиуса на
Рис. 139.

jg4	ПЛАНИМЕТРИЯ	135
R. Таким образом, не изменяя положения центра круга, каса-
касательного к кругу К и к прямым а,Ь. можно одним увеличением
или уменьшением его радиуса на R превратить его в круг,
проходящий через точку О и касательный к одной из пар пря-
прямых а^, агЬй, афг, а.2Ь2. Среди центров этих кругов должны
поэтому находиться все центры искомых кругов. Но центрь
исковых кругов должны удовлетворять еще одному условию,
которому центры этих крутв не всегда удовлетворяют: они
должны находиться на биссектрисах пары пря 1ых а. Ь. Если
же мы найдем коуг, проходящий через точку О, касательный
к одной из пар прямых axbr, aib2, афх, аф2 и имеющий центр на
одной из биссектрис п ры прямых а, Ъ, то из этого круга
можно действительно получить один из искомых кругов про-
простым увеличением или уменьшением его радиуса на R. В са-
самом деле, центр такого круга находится на той из биссектрис
какой-нибудь пары прямых axbv агЬ2, a2bv аф2, которая в то
же время есть биссектриса пары прямых а, Ь, то-есть на ка-
какой-нибудь диагонали ромба, ограниченного прямыми аг, а2,
bv bo. Вследствие такого расположения касательные к этому
кругу стороны ромба нужно или обе приблизить к центру
круга или обе отдалить от него на расстояние R, чтобы они
совпали со средними линиями ромба а, Ь. Если при этом ра-
радиус круга соответственно уменьшить или увеличить на R, то
он коснется прямых a, b и круга К, то-есть превратится в
один из искомых кругов. Таким образом построение искомых
кругов сводится к построению всех кругов, проходящих через
точку О и к; сательных к парам прямых a-J}^ алЬ2, афх, афг,
ча исключением тех, центры которых не лежат на диагоналях
ромба, ограниченного прямыми av a2, bx, Ьг, с последующим
увеличением или уменьшением радиусов этих кругов на R. По
существу все сводится к решению нескольких задач вида 183,
числом не более четырех. Так как число решений задачи 183
не больше двух, то число решений нашей задачи не больше
восьми. Нетрудно сделать и более полное исследование. Если
точка О находится внутри ромба, ограниченного прямыми
а±, аг, bx, b2, то она лежит внутри всех четырех углов ромб!,
и, следовательно, проходящие через нее окружности, касатель-
касательные к парам соседних сторон ромба ахйд, axbo, аф1г а.2Ь2, имеют
центры на диагоналях ромба: мы получим четыре пары реше-
решений. Но эти решения не всегда различны: если точка О лежит
на окружности круга, вписанного в ромб, то этот круг будет
одним из решений каждой пары; вместе с остальными реше-
решениями каждой пары получим всего пять решений вместо вось-
восьми при общем положении точки О внутри ромба. Продолжпя
рассуждать таким образом, найдем число решений при всевоз-
всевозможных положениях точки О: внутри ромба 8 решений; вне

136	РЕШЕНИЯ	1.85—ISb
ромба 4 решения: на сторонах ромба 6 решений; в вершинах
ромба 3 решения; кроме того, на окружности вписанного
круга 4 решения сливаются в одно, так чго внутри ромба на
окружности вписанного круга различных решений только 5,
а в точках касания вписанного круга к сторонам ромба раз-
различных решений только 3. Можно провести исследование еще
дальше и выяснить зависимость числа решений и их характера
от положения круга К по отношению к прямым а, Ь, что
легко сделать после предыдущего исследования. Получим
следующие результаты: 8 решений, бели круг К пересекает
обе прямые а, Ь; 4 из них сливаются в одно, а именно обра-
обращаются в точку пересечения прямых а, Ь, если круг К пере-
пересекает прямые а, Ъ в точке пересечения их; 6 решений, если
круг К пересекает одну из прямых a, b и касается другой;
4 из них сливаются в одно, а именно, обращаются в точку
пересечения прямых а, Ь, если точка касания круга К к
одной из прямых a, b есть точка пересечения их; 4 решения,
если круг К не имеет общих точек хотя бы с одной из пря-
прямых а, Ь; 3 решения, если круг К касается обеих прямых а. Ь:
одно из этих решении есть сам круг К.
185.	Пусть будут А, В данные точки и а данная прямая.
Перпендикуляр р в середине отрезка АВ есть диаметр иско-
искомого круга (рис. 140). Прямая Ь.
симметричная с прямой а относитель-
относительно оси р, должна быть касательна к
искомому кругу, как и сама прямая
а. Прямая b будет отлична от прямой
а, если прямая А В не параллельна
прямой а и не совпадает с нею.
Если, кроме того, точки А, В лежат
"	" а по одну сторону от прямой а, то на-
Рис. 140	ша задача сводится к задаче 183, так
как искомые круги вполне определя-
определяются уже требованием проходить через одну только точку А
и касаться прямых а, Ъ. В остальных случаях задачу легко
решить непосредственно, и мы приведем только результаты:
если точки А, В лежат по разные стороны от прямой а, то
решений нет; если одна из точек А, В лежит на прямой А,
то есть одно решение; если точки А, В лежат по одну сто-
сторону от прямой, и прямая АВ не параллельна прямой а, то реше-
решений два; если точки А, В лежат на прямой а, то решений нет.
186.	Пусть будут А, В данные точки и К.—данный круг
(рис. 141). Проведем через точки А, В какой-нибудь круг,
пересекающий круг К в точках С, D, и общую хорду CD.
Ограничимся рассмотрением случая, когда прямая CD пере-
пересекает продолжение отрезка АВ в некоторой точке Р. По тео-

187
ПЛАНИМЕТРИЯ
137
Рис. 141.
реме 179 через ту же точку проходят и общие касательные
искомых кругов с кругом К. Для построения искомых кругов
нужно поэтому провести к кругу К касательные РТ, РТ из
точки Р и описать круги около треугольников АВТ. АВТ'.
Так как РТ2 = РТ'2 = PC-PD =
= РА-РВ, то по теореме 177 эти
круги коснутся РТ, РТ' в точках Т,
Т' и, следовательно, будут искомые.
В этом случае решений два. В том
случае, когда прямая CD параллельна
прямой АВ, решений будет также
два. Эти случаи имеют место, когда
точки А, В лежат обе внутри или обе
вне круга К- Если одна из точек А,
В лежит на окружности круга К, то
решение будет одно. Если обе точ-
точки Л, В лежат на окружности круга
К, то решение будет одно — сам круг К- Если одна из точек
Л. В лежит внутри, а другая вне круга К, то решений не
будет.
187. Пусть будет Л данная точка, о — данная прямая и/С —
данный круг (рис. 142). Предположим, что задача решена
и L есть искомый круг. Соединим точ-
точки касания В, В' круга L к прямой а
и кругу К и продолжим хорду ВВ'
до пересечения С с кругом К. По тео-
теореме 60 касательная к кругу К в
точке С параллельна прямой а. По-
Поэтому диаметр ССР круга К перпен-
дикулярен к прямой а. Пусть секущая
СА пересекает окружность L еще в
одной точке А'. По теореме об отрез-
Рис. 142.
ках хорд или секущих имеем:
СА-СА' = СВ-СВ'.
а по теореме 181:
СВСВ' =СР-СС.
откуда
СА-СА' = СР-СС.
Расположение точек А. А' и Р, С по отношению к точке С
одинаково, так как то и другое одинаково с расположением
точек В, В' по of ношению к точке С По теореме 177 точки
А, А' Р, С лежат на одной окружности. Отсюда ясно, что
все искомые круги могут быть построены следующим обра-
образом: проводим диаметр ССР круга К, перпендикулярный к

138	решения	187
прямой а; соединяем один из его концов С с точкой Л; про-
проводим окружность через другой конец С, точку А и точку Р;
строим все круги, проходящие через точку А, и вторую точку
пересечения А' этой окружности с прямой СА и касательные
к кругу К, как показано в решении 186. Докажем, что ка-
каждый круг, построенный таким образом, коснется и прямой а
и, следовательно, есть искомый. Пусть будет L такой круг, В'—
точка касания его с кругом К> В— точка пересечения прямой
СВ' с прямой а. Так как по построению точки А, А', С, Р
лежат на одной окружности, то по теореме об отрезках хорд
или секущих имеем:
СА-СА1 = СР-СС.
С другой стороны по теореме 181:
СР-СС = СВ-СВ'.
Отсюда:
СА-СА' = СВ-СВ'.
Расположения точек А, А' и В, В' по отношению к точке С
одинаковы с расположением точек Р, С по отношению к точке
С и потому одинаковы между собой. По теореме 177 точка В
лежит на окружности, проходящей через точки Л, А', В',то-есть
на окружности L. По теореме 60 касательная к кругу L в точке В
параллельна касательной к кругу К в точке С и, следовательно,
совпадает с прямой а. Это и нужно было доказать. Мы пред-
предполагали для простоты, что Р не совпадает с С, А с Л', и СА
с ССР, но наши рассуждения применимы с незначительными
изменениями и к этим случаям. При построении мы можем
использовать любой конец диаметра и приходим тогда к задаче
вида 186. Так как задача вида 186 имеет не более двух реше-
решений, то наша задача имеет не более четырех решений. Дока-
Докажем еще, что круги, построенные с помощью различных кон-
концов диаметра ССР, касаются круга К различным образом,
то-есть одни внешне, другие внутренне. Прямая а может пере-
пересекать окружность К, касаться ее и не иметь с нею общих то-
точек. Рассмотрим только последний случай, который и представ-
представлен на рис. 142. В этом случае вся окружность К лежит с
одной стороны от прямой а, и мы, очевидно, не получим ни
одного решения, если точка Л лежит с другой стороны. Пред-
Предположим поэтому, что и точка Л лежит с этой стороны. Если
мы используем для построения конец С диаметра ССР, кото-
который дальше от прямой а, как это сделано hi нашем чертеже,
то точки В, В' будут лежать по одну сторону от С, потому
что они расположены относительно С так же, как другой
конец С и Р. Но точки С, В' также лежат по одну сторону

188	ПЛАНИМЕТРИЯ	jog
от В, потому что вся окружность К, на которой лежат С, В',
лежит по одну сторону от прямой а, на которой лежит В.
Отсюда следует, что точки С, В лежат по разн-ле стороны от
В', а потому и окружности К, L, проходящие через С, В, лежат
по разные стороны от общей касательной, проходящей через
В', т. е. касаются внешним образом, как и получилось на нашем
чертеже. Но если мы используем для построения конец С", то
точки В, В' будут лежать по разные стороны от С, как дру-
другой конец С и Р. Следовательно, точки С", В будут лежать
по одну сторону от В', и окружности К, L будут касаться
внутренним об] азом. К тому же результату приводит рассмот-
рассмотрение остальных случаев. Итак, в числе решений нашей задачи,
которых всего не более четырех, может быть не более двух
кругов, внешне касательных к кругу К, и не более двух внут-
внутренне касательных.
188. Пусть будут К, L данные круги и а — данная прямая.
Предположим сначала, что круги К, L не равны и обозначим
радиус меньшего круга К через R. Если какой нибудь круг
касается кругов К, L и прямой а и притом круга К внешним
образом, то при увеличении его радиуса на R он пройдет через
центр круга К, коснется одной из прямых av o2, параллель-
параллельных прямой а на расстоянии R от нее, и коснется одного из
кругов Lv L2, концентрических с кругом L, но с радиусом на
R меньшим или большим. Если этот круг касается кругов К, L
и прямой а и притом круга К внутренним образом, то то же
самое произойдет с ним при уменьшении его радиуса на R.
Отсюда ясно, что все искомые круги могут быть получены из
кругов, проходящих через центр круга К, касательных к одной
из прямых а±, а2 и к одному из кругов Lv L2, путем увеличе-
увеличения или уменьшения их радиуса на R. Чтобы построить все
эти круги, мы должны решить четыре задачи вида 187, сооб-
сообразно четырем комбинациям данных аг1^, atL2, a2Lx, a2L2. Пред-
Предположим, например, что мы решили задачу axLu то-есть нашли
все круги, проходящие через центр круга К и касательные к
прямой aL и к кругу Lr Если центр круга К не лежит на
прямой alt то все найденные круги лежат с той же стороны
от прямой а1г что и центр круга К- Чтобы заставить найден-
найденные круги коснуться прямой а, параллельной прямой а± на
расстоянии R от нее, придется радиусы этих кругов все умень-
уменьшить или вое увеличить на R. После этого все они коснутся
круга К, но круга L коснутся только те, которые были каса-
тельны к кругу Ьг одним определенным образом, а именно:
в случае уменьшения всех радиусов только те, которые были
внешне касательны к кругу Lv а в случае увеличения всех
радиусов только те, которые были внутренне касательны к
кругу Lt. Так как число решений задачи вида 187, касательных

140	решения	189
к данному кругу каким-нибудь определенным образом, не
превышает двух, то число решений нашей задачи, соответст-
соответствующих комбинации axLv также не превышает двух. Если
теперь центр круга К лежит на прямой ах, то задача вида 187
сводится к задаче вида 97, число решений которой само не
превышает двух, так что и число выведенных из них решений
нашей задачи, соответствующих комбинации axLv не превы-
превышает двух. Все сказанное относится, очевидно, к любой из
четырех комбинаций a1L1, аг12, a2L±, a2L2. Следовательно, общее
число решений нашей задачи не превышает восьми, и мы видели,
что все они могут быть выведены из решений задач вида 187
В оставленном без рассмотрения случае, когда круги К, L
равны, круг L± обращается в точку, и наша задача сводится,
к задаче вида 185. Число решений и в этом случае не превы-
превышает восьми.
189. Требуется построить круги L, проходящие через дан-
данную точку А и касательные к двум данным кругам К, К'-
Обозначим точки касания круга Л
к кругам К, К' через В, В' и дока
жем, что прямая ВВ' проходит че-
через центр подобия 6".кругов К, К'
и что точки В, В' несходственны..
Рассмотрим случай, когда круг L
касается обоих кругов К, К'
внешним образом (рис. 143). Про-
Проведем радиусы РВ, РВ' круга Z.,
Рис- 143-	радиусы ОВ, ОС круга К и ра-
радиус О' В' круга К'. В равнобед-
равнобедренных треугольниках ОВС, РВВ' углы ОВС, РВВ' равны как вер-
вертикальные. Следовательно, и вторые углы при основаниях ОСВ,
РВ'В у них равны. Так как круги K.L касаются внешним
образом, то их центры О, Р расположены по разные стороны
от точки В, а следовательно, и от прямой СВВ'. Поэтому полу-
полупрямые СО, В'Р также расположены по разные стороны от пря-
прямой СВВ', откуда видно, что углы ОСВ, РВ'В накрестлежа-.
щие при прямых ОС, РВ' и пересекающей СВВ'. Из того же
внешнего касания кругов f(, L следует, что точка В лежит
между точками С, В', откуда видно, что углы ОСВ, РВ'В оба
внутренние при прямых ОС, РВ' и пересекающей СВВ'. Таким
образом углы ОСВ, РВ'В внутренние накрестлежащие при пря-
прямых ОС, РВ' и пересекающей СВВ'. Так как эти углы m
предыдущему равны, то мы заключаем, что прямые ОС, РВ'
параллельны. Так как радиусы ОС, О'В' параллельны, то концы
их С, В' суть сходственные точки кругов К, К' при некото-
некотором подобном расположении их. Отсюда ясно, что прямая СВВ'
проходит через некоторый центр подобия S этих кругов. Ясно

189	планиметрия	141
также, что точки В, В' несходственны при этом подобном рас-
расположении, так как точка В' сходственна с точкой С прямой
SB' и тем самым не сходственна ни с какой другой точкой
этой прямой. Все, что требовалось, доказано, но мы можем
добавить, что в данном случае, когда круг L касается обоих
кругов внешним образом, мы имеем прямое подобие. Дейст-
Действительно, в этом случае центры О, О' расположены относи-
относительно прямой СВВ' по другую сторону от точки Р. Поэтому
направления сходственных радиусов ОС, О'В' противоположны
направлению радиуса РВ' и, следовательно, одинаковы между
собой, что и доказывает прямое подобие. Рассуждая сходным
образом в трех остальных возможных случаях, убедимся, что
во всех случаях точки В, В' суть несходственные точки пере-
пересечения кругов К, К' с прямой, проходящей через один из их
центров подобия, причем это будет центр прямого подобия,
если круг L касается кругов К, К' одинаковым образом, т. е.
обоих внешне или обоих внутренне, и это будет центр обрат-
обратного подобия, если круг L касается кругов К, К' различным
образом, то-есть одного внешне, адруюго внутренне. Теперь
мы покажем, что по данным задачи можно найти вторую точку
пересечения А' всякого искомого круга L с прямой AS. Пусть
будут D, D' две несходственные точки пересечения окруж-
окружностей К, К' с какой-нибудь другой прямой, проходящей через 5.
По теореме об отрезках хорд или секущих имеем:
SA-SA' = SB-SB'.
С другой стороны, по теореме 182:
SB-SB' =SDSD'.
Отсюда:
SA-SA' = SDSD'.
Нетрудно проверить, как это не раз делалось выше, что и рас-
расположение точек А, А' и D, D' относительно точки 5 оди-
одинаково. По теореме 177 заключаем отсюда, что точка А' есть
вторая точка пересечения прямой SA с окружностью, прохо-
проходящей через точки D, D', А. Таким образом точку А' дейст-
действительно можно построить по данным задачи. После этого задача
сведется к построению круга, проходящего через точки А, А'
и касательного к одному из кругов К, К'¦ Можно доказать,
что круги, построенные таким образом, коснутся и BTopoi о из
кругов К, К'- но мы для краткости опускаем доказательство,
которое в общем состоит в повторении nj ежнего рассуждения
в обратном порядке, как это было и в решении 187. Так как
мы можем воспользоваться для построения точки А' любым из

142	решения	190
центров подобия, и так как после этого задача сведется к за-
задаче вида 186, имеющей не более двух решений, то наша задача
имеет не более четырех решений. При этом круги, построен-
построенные с помощью центра прямого подобия, касаются данных
кругов одинаковым образом, а круги, построенные с помощью
центра обратного подобия, касаются данных кругов различным
образом. Кругов каждого рода столько, сколько решений вспо-
вспомогательной задачи вида 186, т. е. не более двух.
190. Пусть будут К, L, М данные круги. Предположим,
что радиус круга К меньше двух других и обозначим его
через R. Если какой-нибудь круг касается кругов К, L, М и
притом круга К внешним образом, то, увеличив его радиус
на R, мы заставим его пройти через центр круга К и коснуться
одного из кругов Lx, L2 и одного из кругов Мх, М2, концентри-
концентрических соответственно с кругами L, М, из которых Lx, Мх
имеют радиусы на R меньшие, а ?г, М2 радиусы на к большие,
чем соответственные круги L, М. Если этот круг касается
круга К внутренним образом, то то же самое получится при
уменьшении его радиуса на R. Отсюда ясно, что все искомые
круги могут быть получены из кругов, проходящих через
центр круга К и касательных к одному из кругов Lx, L2 и к
одному из кругов Мх, М2 путем увеличения или уменьшения
их радиуса на R. Наша задача сводится таким образом к четы-
четырем задачам вида 189, сообразно четырем комбинациям LXMX,
LXM2, L2MX, L2M2. Предположим, что мы решили одну из этих
задач, например, Lx Mx. Иначе говоря, предположим, что мы
нашли все круги, проходящие через центр круга К и каса-
касательные к кругам Lv Mx. Допустим далее, что один из этих
кругов касается круга Lx внешним об|азол. Если мы умень-
уменьшим его радиус на R, то он коснется кругов К и L, но круга М
он коснется только в том случае, если он касался круга Мх
также внешним образом. Точно так же, если один из этих кру-
кругов касается Kpyi a Lx внутренним образом, то из него можно
получить круг, касательный к кругам К, L и М, только в том
случае, если он касается круга Мх также внут[ енним образом.
Таким обрлзом из решений задачи LXMX пригодны для даль-
дальнейшего построения только те круги, которые касаются кру-
кругов Lx, Mx одинаковым образом. То же самое относится и к
задаче L2M2. Наоборот, из решений LXM2 и L2MX пригодны для
дальнейшего построения только те Kpyi и, которые касаются
данных кругов различным об азом. На основании исследования
задачи 189 мы можем поэтому утверждать, чго каждая из
вспомогательных задач дает не более двух приюдных реше-
решений. А отсюда ясно, что число решений нашей задачи не пре-
превышает восьми. Мы исключили вначале случаи, когда радиус
одного из кругов L, М равен R, и когда радиусы обоих кру-

191—1S4
ПЛАНИМЕТРИЯ
143
Рис. ]44.
гов L, М равны R. В первом случае один из кругов Lx, Mlt
а во втором оба обращаются в точку. Соответствующие вспо-
вспомогательные задачи будут вида 186 или 93. Число решений
попрежнему не больше восьми.
Площади
191.	Пусть в параллелограмме ABCD угол А острый и
AD^-AB (рис. 144). Опустим перпендикуляр ВР из вершины В
на сторону AD и докажем, что его осно-
основание наверное попадет на самую сторону
AD, а не на ее продолжение. В треуголь-
треугольнике ABD угол А острый по условию,
а угол D также не может быть прямым
или тупым, так как тогда сторона АВ была
бы наибольшая, и мы имели бы AD<iAB,
воп1 еки условию. Поэтому точка Р лежит
внутри отрезка AD, и следовательно, от-
отрезок ВР разрезает параллелограмм ABCD
на треугольник АВР и трапецию PBCD.
Приложив к трапеции треугольник, в положении DCQ сложим
прямоугольник PBCQ. Если опустим перпендикуляр DP'из вер-
вершины D на сторону АВ, то построение не всегда удастся, как,
например, на рис. 144.
192.	Пусть в треугольнике ABC (рис. 145) сторона ВС больше
или, по крайней мере, не меньше сторон АВ, АС. Тогда углы
В,С острые, так как в противном случае
одна из сторон АВ, АС, была бы больше
стороны ВС. Опустим из середин М, N
сторон АВ, АС перпендикуляры МР, NQ
на сторону ВС. В треугольнике МВС углы
при стороне ВС острые, так как один из
них равен углу В, а другой есть часть
угла С. Следовательно, точка Р лежит на
самой стороне ВС. По тем же причинам
и точка Q лежит на стороне ВС. Таким образом отрезки
МР, NQ разрезают треугольник ABC на пятиугольник
AMPQN и треугольники MBP, NCQ. Повернув эти треу-
треугольники в надлежащих направлениях на сто восемьдесят
градусов вокруг вершин М, N, сложим из них и пятиуголь-
пятиугольника прямоугольник PQQ'P'.
193.	На рлс. 146 показано, как нужно сложить трапеции.
Площадь полученного параллелограмма равна (a-\-b)-h. Сле-
Следовательно, площадь каждой трапеции равна — (й -{-&)• h.
194.	Треугольники ADC, BDC (рис. 147) равновелики, так
как у них основание DC общее и вершины А, В лежат на
о-	А
Рис. 145.

144
РЕШКПИЯ
195—196
прямой, параллельной основанию. Если отрежем от треуголь-
треугольников ADC BDC по треугольнику ODC, то оставшиеся тре-
треугольники ОВС, ODA также должны быть равновелики, что и
требовалось дс казать.
195.	Имеем (рис. 148):
пл. MDBE = пл. ABC— пл. ADM — пл. МЕС.
пл. MD'B'E' = пл. Л?'С —пл. Л?>'/М — пл. MFC.
Правые части этих равенств равны почленно; следовательно, и
левые части равны:
пл. MDBE = пл. MD'B'E1,
что и требовалось доказать.
196.	Требуется доказать (рис. 149):
пл. МАВ + пл. MCD = пл. МВС -f пл. MAD,
то-есть, что эти суммы равны— пл. ABCD. Проведем PMQ
22=7
Рис. 147.
Рис. 14S.	Рис. 149.
параллельно АВ и CD. Имеем следующие соотношения:
пл. МАВ = — пл. ABPQ, пл. MCD = ~ пл. CDQP.
Складывая почленно, получим:
пл. МАВ + пл. MCD = — пл. ABCD,
что и доказывает теорему.

197-199
ПЛАНИМЕТРИЯ
145
Рис. 150.
197. Через середины М, N диагоналей AC, BD проведены
параллельные к диагоналям BD, АС до пересечения в точке О,
и точка О соединена с серединами Р, Q, R> 5 сторон АВ, ВС,
CD, DA (рис. 150). Требуется дока-
доказать, что площади OSAP, OPBQ,
OQCR и ORDS равны между собой,
то-есть каждая из них равна четверти
площади ABCD. Рассмотрим для при-
примера четырехугольник ORDS. Пло-
Площадь этого четырехугольника не из-
изменится от перенесения вершины О
в точку N. В самом деле, прямые
ON, SR параллельны между собой,
так как обе параллельны прямой АС,
первая согласно условию, а вторая
как средняя линия треугольника ACD. При перенесении вер-
вершины О в точку N треугольник SOR заменится поэтому рав-
равновеликим треугольником SNR, и тем самым четырехугольник
SORD заменится равновеликим четырехугольником SNRD.
Но четырехугольник SNRD подобен четырехугольнику ABCD
и имеет вдвое меньшие линэйные размеры,
так что площадь его вчетверо меньше.
Следовательно, и площадь четырех-
четырехугольника SORD составляет четверть пло-
площади четырехугольника ABCD, что и
нужно было проверить.
198. Если ВС делит площадь ABC
пополам (рис. 151), то
пд. ABC: пл. ABC=2.
Рис. 151.
Так как площади подобных треуголь-
треугольников относятся как квадраты сходственных сторон, то
АВ*:АВ'г=2,
откуда
' = У2—1.
Итак, искомое отношение есть
ВВ': АВ1 = СС: АС=/2: — 1.
199. На рис. 152
т—4, л=3.
10 Делоне ¦ ЖитоимрскЛ

148	решения	199
Чтобы узнать, во сколько раз площадь данного параллелограмма
ABCD больше параллелограмма HKLM, найдем сначала, во
сколько раз пл. ABCD больше пл. AEFG, а затем найдем, во
сколько раз пл. AEFG больше пл. HKLM. Примем в паралле-
параллелограммах ABCD, AEFG стороны АВ,
АЕ за основания. Тогда высоты их
будут равны, и площад% будут отно-
относиться как основания. Так как
АВ=т-АЕ,
то и
пл. ABCD=m-u.4. AEFG.
Рис. 152.	Примем в параллелограммах AEFG,
HKLM стороны AG, НМ за основания.
Высоты их будут равны и площади будут относиться как ос-
основания. Имеем:
AG=AM + MG.
Из рассмотрения треугольника AMD найдем:
АМ=п-НМ.
Из рассмотрения треугольника CDN найдем:
MG= — -CN.
т
Из рассмотрения треугольника CPQ и параллелограмма HMNP
найдем:
CN=NP=HM.
Сопоставляя все это, получим:
-f — НМ = (п~\-~) -НМ,
т	V	т/
откуда
пл. AEFG= fn + —) -пл. HKLM,
т
и затем
или
пл. ABCD=m (п + ±\ -пл. HKLM
пл. ABCD=(mn + 1) • пл. HKLM.
Следовательно,
пл. HKLM=	?	пл. ABCD,
тп -f- 1

200
ПЛАНИМЕТРИЯ
147
Рис. Ш
т. е. площадь маленького параллелограмма составляет
(/n«-|-l)-yio часть площади большого, например на нашем чер-
чертеже— тринадцатую часть.
200. Кроме прямых, соединяющих вершины параллелограмма
с середина «и противоположных сторон, проведем еще его
диагонали AC, BD и средние линии
EG, FH (рис. 153). Легко видеть,
что диагонали и средние линии АС,
BD, EG, FH взаимно делятся по-
пополам. Например, диагональ АС и
средняя линия EG взаимно делятся
пополам, как диагонали параллело-
параллелограмма AECG. Рассмотрим один из
отрезков, соединяющих точку О с
вершинами параллелограмма, напри-
например отрезок ОА. Прямые ВН, DE
отсекают от отрезка ОА одну
треть ОМ, так как АО, ВН, DE суть медианы треугольника
ABD. Точно так же и на отрезках ОБ, ОС, OD пересекается
по паре прямых, соединяющих вершины параллелограмма с се-
серединами противолежащих сторон, и отсекают от эгих отрезков
по одной треги. Рассмотрим теперь один из отрезков, соединяю-
соединяющих точку О с серединами сторон параллелограмма, например
отрезок ОЕ. Прямые AF, ВН отсекают от отрезка ОЕ полови-
половину ON, так как ОЕ есть средняя линия, a AF, ВН— диагонали
параллелограмма ABFH. Точно так же и на отрезках OF, OG,
ОН пересекается по паре прямых, соединяющих вершины па-
параллелограмма с серединами противолежащих сторон, и отсе-
отсекают от этих отрезков по половине. Таким образом на каждом из
отрезков, соединяющих точку О с вершинами и серединами
сторон параллелограмма, пересекается по две прямых, соединя-
соединяющих вершины с серединами противолежащих сторон. Точки пе-
пересечения образуют восьмиугольник, стороны которого лежат
на восьми прямых, соединяющих вершины параллелограмма с се-
серединами противолежащих сторон. Этот восьмиугольник и есть
фигура, ограниченная этими восьмью прямыми. Чтобы удосто-
удостовериться в этом, остается только доказать, что этот восьмиуголь-
восьмиугольник выпуклый, то-есть что ни одна из восьми прямых не входит
внутрь его. Рассмотрим для примера прямую ВН. Прямая ВН
разбивает параллелограмм на треугольник АВН и трапецию
BCDH. Точка О лежит внутри трапеции, как середина ее диаго-
диагонали BD. Поэтому шесть вершин восьмиугольника, лежащих
на отрезках OB, OF, ОС, OG, OD, ОН, соединяющих точку О
с точками В, F, С, G, D, Н на контуре трапеции, лежат внутри
трапеции. Остальные две вершины М, N лежат на стороне
трапеции ВН. Следовательно, весь восьмиугольник расположен
10*

J48
РЕШЕНИЯ
201
по одну сторону от прямой ВН, что мы и хотели доказать.
Вычислим площадь одного из восьми треугольников, на кото-
которые наш восьмиугольник разбивается отрезками, соединяющими
точку О с вершинами и серединами сторон параллелограмма,
например, площадь треугольника 0MN. Так как
ОМ=-ОА,
о
то по известной теореме
пл. OMN= — •— -пл.
3 2
= — пл. ОАЕ,
6	'
то-есть площадь части восьмиугольника между двумя соседними
отрезками, соединяющими точку О с вер-
вершинами и серединами сторон параллело-
параллелограмма, составляет одну шестую площади
части параллелограмма, заключенной меж-
между теми же отрезками. Отсюда ясно, что
площадь всего восьмиугольника составляет
также одну шестую площади параллело-
параллелограмма, что и требовалось узнать.
201. Обозначим площадь трапеции через
Рис. 154.	«S, а площади ее частей, прилегающих к
сторонам а, Ъ, с, d, соответственно через
Sa, Sb, Sc, Sd. Площади Sa, Sb даны; найдем площади Se, Sd.
Имеем (рис. 154):
Ss_—HL §с^КО_	LO _ КО
Se ~ NO ' St~ МО' NO МО '
Отсюда
sc
и, следовательно,
Также найдем
Складывая все части, получим
5- Sa + Sb + 2 VS^=
что и решает задачу. Полученное соотношение можно пере-
переписать в более изящной форме:

202	203	ПЛАНИМЕТРИЯ	149
202. Площадь четырехугольника АВ'DC (рис. 155) не зави-
зависит от положения точки D на прямой ВС, так как прямая ВС
параллельна основанию ВС треугольника DB'C Поэтому
можно заменить площадь четырехугольника АВ DC площадью
треугольника АВ'С. Имеем:
пл. ABC: ил. АВ'С=АВ:АВ\
пл. ABC: ил. АВ'С=АС:АС,
АВ:АВ'=АС:АС.
Отсюда
пл. ABC: пл. АВ'С=пл. АВ'С :пл. АВ'С,
или
5:пл. ABC = ил. AB'C:s,
откуда
пл.
и, следовательно, вообще
пл.
203. Пусть будет ABC . . . внешний многоугольник
А'В'С . . . внутренний многоугольник, О центр подобия их
DJD% . . . многоугольник, впи-
вписанный в ABC ... и описанный
около А'В'С . . . (рис. 156).
Обозначим:
пл. OAB^S^ пл. OBC=S2,. . . ;
пл. OA'B'=sv пл. OB'C=s2,. . ; в	Q
пл.
пл. 0В'О^С = а2, . . .	Рис. 155.
Пусть линейные размеры много-
многоугольника ABC. . . в k раз больше линейных размеров много-
многоугольника А'В'С . . . Тогда
На основании решения 202 имеем
Складывая, получим:
или

РЕШЕНИЯ
150
С другой стороны,
Следовательно,
Применение площадей для доказательств
204. Имеем:
пл. ЛБЖ + пл. АСМ=пл. ABC (рис. 157),
204—206
или
— АВ-МР + — AC-MQ = — AC-BR.
2	'2	^2
— АВ=-АС,
2	2
Сокращая на
получим:
что и требуется доказать. Аналогично доказывается и соотно-
соотношение
МР — MQ = BR
для случая, когда М лежит на продолжении ВС за конец С.
205.	Предоставляем вывод читателю.
206.	Искомое геометрическое место есть медиана AD. Дей-
Действительно, для всякой точки М медианы AD имеем (рис. 158):
пл. ABD = пл. ACD,
пл. MBD = пл. MCD.
Вычитая почленно, полу-
получим:
пл. МАВ = пл. MAC,
так что точки медианы
действительно имеют тре-
требуемое свойство. Остает-
Остается доказать, что точки
внутри треугольника, не
лежащие на медиане, этого свойства не имеют. Пусть будет N
такая точка и М точка пересечения CN с AD.
Имеем:
пл. ЛМБ>пл. МАВ = ил. МАС>пл. NAC, откуда:
пл. NAB>пл. NAC,
что и оставалось доказать.
Рис. 157.
Рис. 158.

207-208
ПЛАНИМЕТРИИ
151
207. В общей точке Q медиан AM, BN имеем на основа-
основании решения 206 (рис. 159):
пл. QAB = пл. QAC, пл. QAB = пл. QBC.
Отсюда следует:
пл. QAC = пл. QBC.
А это показывает на основании того же решенвя 206, что
точка Q лежит и на медиане СР. Далее имеем:
пл. BMQ = — пл. QBC = 1. 1 пл. ABC,
2	2 3
пл.
= - пл. ABC,
откуда
и следовательно,
пл. MQ=— пл. ВМА,
MQ = -МА,
О
что заканчивает требуемое доказательство.
208. Каково бы ни было положение точки М площади
МАВ, MCD не изменятся, если мы передвинем отрезки АВ, CD
вдоль прямых, на которых они лежат, например б положения
OP, OQ (рис. 160). Мы можем поэтому вместо площадей МАВ,
MCD рассматривать площади MOP, MOQ. Для всякой точки М
отрезка PQ имеем:
пл. МОР ~\- пл. MOQ = пл. OPQ,
для всякой точки N на продолжении отрезка PQ за точку Q
пл. NOP — пл. NOQ = пл. OPQ

152	РЕШЕНИЯ	208
и точно так же для всякой точки N на продолжении отрез-
отрезка PQ за точку Р
пл. NOQ — пл. NOP = пл. OPQ.
Таким образом для всех точек М прямой PQ сумма или раз-
разность площадей MOP, MOQ равна одной и той же площа-
площади OPQ. Проведем прямую P'Q', параллельную прямой PQ и
пересекающую продолжения отрезков OP, OQ за точки Р, Q.
Для точек отрезка P'Q' имеем:
пл. /И'ОР + пл. M'OQ = пл. OPM'Q =
= пл. OPQ + пл. QPM = пл. OPQ + пл. QPQ1 = пл. OPQ'.
Для точек продолжения отрезка P'Q' за точку Q' имеем:
пл. АГОР —пл. N'OQ^nn. OPN'Q =
= пл. OPQ + пл. QPN' =пл. OPQ + пл. QPQ1 = пл. OPQ',
и точно так же для точек продолжения отрезка P'Q' за
точку Р'
пл. N'OQ — пл. АГОР =пл. OPQ'.
Итак, для всех точек Ж прямой P'Q' сумма или разность пло-
площадей MOP, MOQ равна одной и той же площади OPQ'. Про-
Проведем прямую P"Q", параллельную прямой PQ и пересекаю-
пересекающую отрезки OP, OQ. Для отрезка P"Q" имеем:
пл. М"ОР +пл. .M'OQ = пл. OPM"Q ==
= пл. OPQ — пл. QPAT= пл. OPQ — пл. QPQ" = пл. OPQ".
Для продолжения отрезка P"Q* нужно рассмотреть разность
пл. N'OP — пл. N"OQ.
Отняв от уменьшаемого и вычитаемого по площади KON*
и прибавив затем по площади KPQ, превратим эту разность
в разность
пл. OPQ — пл. QPAT.
Таким образом
пл. N"OP— пл. jV"OQ =пл. OPQ - пл. QPN"=
= пл. OPQ — пл. QPQ" = пл. OPQ",
и точно так же для продолжения отрезка P"Q" за точку Р"
пл. N"OQ — пл. АГОР =пл. OPQ".
Итак, для всех точек Ж прямой P"Q" сумма или разность
площадей MOP, MOQ равна одной и той же площади OPQ'.
Объединяя полученные результаты, мы можем сказать, что
для точек М всякой прямой Р^ (рис. 161), параллельной

208	ПЛАНИМЕТРИЯ
прямой PQ и пересекающей стороны угла POQ, сумма или раз-
разность площадей MOP, MOQ, или равных им площадей МАВ,
MCD равна площади OPQ±. Но мы могли бы перенести от-
отрезки АВ, CD и в положения OR, OQ и тогда нашли бы,
что той же площади OPQ± равна сумма или разность площадей
МАВ, MCD для точек прямой QxRlt
параллельной прямой QR, и т. д.
Продолжая таким образом, най-
найдем, что площадь OPQt равна сумме
площадей МАВ, MCD для точек
М на сторонах параллелограмма
PiQiRiS! и разность площадей
МАВ, MCD для точек М на про-
должениях сторон того же парал-
лелограмма PjQ^S^ Для всякой
точки М внутри или вне параллело-
параллелограмма PiQlR^! сумма площадей	Рис- 161
МАВ, MCD будет, соответствен-
соответственно меньше или больше площади OPQ±. Следовательно, кон-
контур параллелограмма i^Qj/^Sj есть геометрическое место
точек N, для которых сумма площадей МАВ, MCD равна
площади OPQ±. Точно так же для всякой точки М внутри или
вне крестообразной области, ограниченной продолжениями
сторон параллелограмма PjQjRjS^ разность площадей МАВ,
MCD будет, соответственно, меньше или больше площади OPQt.
Следовательно, продолжения сторон параллелограмма P1Q1R1S1
образуют геометрическое место точек М, для которых раз-
разность площадей МАВ, MCD равна площади OPQ±. Площади
OPQ± можно дать любое неотрицательное значение, так как
при перемещении точки Q2 вдоль полупрямой OQ эта площадь
растет от нуля до бесконечности. Отдельные части найденных
геометрических мест можно рассматривать как геометрические
места внутри отдельных углов между прямыми АВ, CD. Так
например, отрезок /^Qj есть геометрическое место точек М
внутри угла POQ, для которых
пл. МАВ + пл. MCD = пл. OPQV
а продолжение Q^Q' этого отрезка есть геометрическое место
точек М внутри смежного угла QOR, для которых
пл. МАВ— пл. MCD = пл. OPQX.
Полупрямая RtR' в том же углу QOR есть геометрическое
место точек М внутри этого угла, для которых
пл. MCD — пл. МАВ =пл. OPQk.

154	решкния	209
209. Пусть будут Mlt M2, Л43 середины отрезков AC, BD,
EF (рис. 162). Имеем:
пл. МХАВ = - пл. CAB, пл. MXCD = - пл. ACD.
2	г	2
Складывая почленно, найдем:
пл. ЛГ^В + пл. MjCD= -^ пл. ABCD.
Точно так же найдем:
пл. М2АВ + пл. М?Ю = ^ пл. ABCD.
Далее имеем:
пл. М3АВ = - пл. FAB, пл. M3CD = - пл. FCD.
Действительно, треугольник MSAB имеет с треугольником
FAB общее основание АВ и вдвое меньшую высоту, и точно
также треугольник MbCD имеет с треугольником FCD общее
основание CD и вдвое меньшую высоту. Вычитая почленно,
найдем:
пл. М3АВ — пл. MZCD = — пл. ABCD.
К полученным соогношенияч
пл. МХАВ + пл. MjPD^tui. M2AB + пл. M2CD= ~ пл. ABCD,
пл. МаАВ — пл. M3CD=~ пл. ABCD
присоединим замечание, что точки Мх, М2 лежат внутри угла
AED, а точка М3 внутри смеж-
смежного угла DEG. На основании
решения 208 мы сможем заклю-
заключить отсюда, что точки Мг, М2
лежат на отрезке PQ, представ-
представляющем собой геометрическое
место точек М внутри угла AED,
для которых
пл. МАВ -f пл. MCD ==
=- пл. ABCD,
и что точка М3 лежит на продолжении QQ' отрезка PQ.

планиметрия
155
представляющем собой геометрическое место точек М внутри
угла DEG, для которых
пл. МАВ — ил.
= - пл. A BCD.
2
Итак, точки Mlt M2, M3 действительно лежат на одной пря-
прямой PQQ1.
210. Пусть будет ABCD четырехугольник, описанный около
круга, Мх, М2 середины его диагоналей AC, BD и О центр
круга (рис. 163). Если четырехугольник ABCD есть ромб, то
точки Мл, М2, О совпадают, так что точки Мг, М2 лежат на всякой
прямой, проходящей через точку О. Остается рассмотреть
случай, когда какие-нибудь две противоположные стороны
четырехугольника ABCD, например АВ, CD, непараллельны.
Относительно точек Мл, М2 уже было
доказано в решении 209:
пл. МХАВ + пл. MXCD =
= - пл. ABCD,
пл. М2АВ
пл. M2CD = — пл. ABCD.
Докажем, что и для точки О
пл. ОАВ -f нл. OCD
1
пл. ABCD.
пл. ABCD.
2	Рис. 1ЬЗ.
Обозначив радиус круга через R, найдем:
пл. ОЛВ + пл. OCD = -/?• АВ + -R-CD =-^ R-(AB -f- CD),
пл. ABCD = i R-{AB
DA).
Но по известной теореме:
АВ -f CD = AD + ВС,
откуда
AB-\-CD= ~ (АВ + ВС + CD + Ш).
Следовательно,
пл. ОЛЯ + пл. OCD = - пл. ЛВСО,
что и требовалось доказать. К доказанным соотношениям:
пл.
. M2CD =
2+	2
= пл. ОЛЯ -f пл. OCD = — пл.
1	г»

156	рвшвния	211—213
мы можем добавить, что точки Ми М2, О лежат внутри четы-
четырехугольника ABCD и, следовательно, внутри одного и того
же угла между прямыми АВ, CD. На основании решения 208
заключаем отсюда, что точки Mlt M2, О лежат на отрезке,
представляющем собой геометрическое место точек М внутри
упомянутого угла, для которых
пл. МАВ 4- пл. MCD = - пл. ABCD.
1	2
Теорема доказана для всех случаев.
Числовые соотношения в треугольниках
и четырехугольниках
211. Проведем O'Q параллельно Р"Р (рис. 164). В прямо-
прямоугольнике OO'Q имеем:
ОО = d,
= OP—QP= OP — O'P = R — r,
По теореме Пифагора находим:
x = yd2 — (/?— rf .
Для длины общей внутренней касательной таким же образом
найдем выражение:
212. Искомую длину найдем по формуле решения 211. по-
полагая в ней d=:R-\-r:
х = ViR + rf — (R-rJ = 2VRr.
213. Обозначим искомый радиус через х и точки касания
Р	Р'	Р ? f
Рис. 164.	Рис. 165.
общей внешней касательной к кругам радиусов R, г, х соот-
соответственно через Р, Р, Р" (рис. 165). Имеем:
РР" + Р"Р" = РР',

214—215
ПЛАНИМЕТРИЯ
157
или по формуле задачи 212
2 VRx + 2 У7х = 2 VRr ,
или
откуда
Rr
~ R + r+2VR? '
214. В прямоугольном треугольнике ABC (рис. 166) имеем,
если обозначим радиус искомого круга через л::
AB = R,
АС	 А Г) ГТ)	9/?	 г
По теореме Пифагора
ИЛИ
ИЛИ
откуда
_}_ 4R2 — ARx + х2 = R* + 2Rx -f jc2,
*-!«•
215. Соединим центр Л круга искомого радиуса jc с цен-
центрами В, С дуг, к которым он прикасается в точках F, О, и
i?^»?
Рис. 166.
Рис. 167.
с точкой Е, в которой он прикасается к отрезку CD (рис. 167).
В треугольнике ABC имеем:

158	решения	216
Кроме того, проведя высоту АН, найдем-
СИ = АЕ = х.
По известной теореме имеем:
АВ2 = АС2 + ВО — 2ВС-СН,
или
или
R2 + +
или
б/?х = /г8,
откуда
216. Соединим центр Л круга искомого радиуса х с цен-
центрами В, С, D кругов радиусов R, r, R -{- г, к которым он
прикасается в точках Е, F, G (рис. 168). Имеем:
AD = Z)G— ЛО = (/? + г) — х,
Между этими отрезками существует некоторое соотношение,
так как отрезок AD вполне определяется
заданием остальных отрезков. Чтобы найти
это соотношение, опустим перпендикуляр
АР на общий диаметр данных кругов и
		введем сначала вспомогательный отрезок:
Р С
Рис. 168.	По теореме о квадрате стороны для сторон
АВ, АС треугольников АВD, ACD, из ко-
которых один остроугольный, а другой тупоугольный, имеем:
(/? + Л'J = [(/? + г) — xf + г2 + 2гу,
(г + xf = [(R + г) - xf + R* - 2Ry.
Умножив первое уравнение на R, а второе на г и сложив по-
почленно, исключим у и получим искомое соотношение:

217—219
ПЛАНИМЕТРИЯ
159
или
R* + 2R*x + Rx2 + г3 + 2r2x + rx2 =
или
2 [Я2 + r2 + (tf-f rJJ jc= (/? + rf + /?r2 + R*r -R^ — r3,
или
откуда
2 [/? -f- r« + (/?+ гJ] л = 4/?r (/?+ r),
Rr(R+r)
217. Из рис. 169 имеем:
Отсюда найдем:
= ac\ b2
а а а
218. Обозначив (рис. 170) через Б острый угол при осно-
основании БС треугольника ABC, будем иметь два случая: угол С
Рис. 169.
также острый, и тогда: а= ВС = ВН + СН = \[ с2^?а +
— h°; угол С тупой, и тогда а = ВС = ВН
219. Требуемые выражения выводятся в курсах элемен-
элементарной геометрии. Заметим только, что их легко получить из
решения 218. Действительно, из уравнения
легко найдем:
-^'a ± V&IZK = a,

решения	220—221
Если разложить числитель на множители, то придем к
формуле
Если же просто развернуть числитель, то получим формулу:
ha = — VicPb2 + 2а2с2 -f 2b2c2 -а* — Ь*~с*у
также полезную во многих случаях. Отсюда найдем:
S = -aha= - V<2a2b2-\- 2а2с2-\- 2Ьгсг — а* — Ь* ^~с*~=
где
220. Вставим в формулу:
5
А
выражения
_ 2S __ 25 _ 25
После простых преобразований найдем:
hb hj \h, ht h
Отсюда получим искомое выражение:
221. Дополним треугольник ЛБС до параллелограмма ABDC
(рис. 171). По известной теореме найдем:
AD2 +	+ +
или
4/ив2 -f а2 = с* -f fea + с2 +- й2,

222
откуда
ПЛАНИМЕТРИЯ
161
2c«-a«f ma = l-V
Так же найдем аналогичные формулы:
,s = 2а* + 2с» - ft», да, = 1/2д«
^ "ус1ь будет Q центР тажести треугольника ЛЯС
(рис. 172). Продолжим медиану AQM на отрезок Л«?, равный
Рис. 171.
Рис. 172
QM. В треугольнике BQR отрезок ВМ= —а есть медиана, а
стороны суть:
~
По формуле решения 221 имеем:
или
откуда
9 с 9
' 1 Делоне и Житомирскил

РЕШЕНИЯ	222
и по аналогии:
Далее имеем:
пл. J5Q/? «= пл. fiQ/4 = i пл. ЛЯС = - 5.
Отсюда
5 = 3 пл. BQR =
или
1
3 . ч а + тЬ + те)- ¦ ¦ (та + Щ — те).
Можно также вывести выражение для а, Ь, с из формуя ре-
решения 221
4тя2 = 262 + 2с2 - а\ 4raft2 = 2а2 -j- 2с2 — Ь",
решая их относительно а2, б2, с2. Складывая все три формулы.
получим-
4me2 -f 4mft2 -f 4/и/ = За2 + 362 + 3<г2.
Умножая все три формулы на —, получим:
6тоо2 - 362 + Зс2 - Ъ- а2, бт„2 = За2 + Зс2 - i 62,
бот2 = За2 + 362- -с2.
с	2
Вычитая полученные формулы из предыдущей, получим:
4ть2 4 4т?2 — 2то2 = - а2, 4та2 -f- 4m,2 — 2тЛ2 = -| Z»2,
— 2mf2 = — с2.
Отсюда найдем, как и выше:
f

223—225	ПЛАНИМЕТРИЯ
После этого можно найти и S, но это требует по сравнению
с геометрическим выводом более сложных вычислений.
223. В треугольнике ABC (рис. 173) биссектриса AD — Р делит
основание ВС = а на отрезки CD = b', BD = с', пропорци-
пропорциональные боковым сторонам АС = Ь, АВ=с. Можно поло-
положить:
Ь' — kb, с' = кс,
и множитель к определится из условия:
kb 4 кс = а,
откуда
	 а
~~ Ь + с
По отрезкам а, Ь, с, b' = kb, с' = кс можно вычислить бис-
биссектрису р. Для этого проведем высоту АН и введем вспо-
вспомогательный отрезок DH = т. Имеем из треугольников ACD,
ABD:
№ = р2 4 k2b2 — 2«мя,
Чтобы исключить т, умножим первое уравнение на с, второе
на b и сложим почленно. Получим:
ЬЧ 4 c2b = р2с 4
или
Ьс(р 4 с) = Р2 (* + с) + ?2foF 4 с),
или, по сокращении,
6с = р2 4 ?2&с,
откуда
J	Рис. 173.
рг = ьс — №.
Подставляя сюда найденное выше значение к, получим:
224.	В решении 223 были получены формулы:
р = &с — ^2&с> ?& = &', ^с = с'.
Отсюда находим:
§* = Ьс— Ь'с',
что и требуется доказать.
225.	В треугольнике ABC проведена высота АН и центр
описанного круга О соединен с вершиной А и серединой Р
и*

164
РЕШЕНИЯ
226
стороны АВ (рис. 174). В решении 70 было доказано, что углы
ОАР, САН равны. Следовательно, прямоугольные треуголь-
треугольники ОАР, САН подобны, и мы можем написать:
откуда
Ьс
или. по умножении числителя и знамена-
знаменателя на а,
„	 аЬс
~ 45
Чтобы получить искомое выражение R через а, Ь, с, остается
подставить в эту формулу одно из выражений для 5.
226. В решении 219 выведены различные выражения 5
через а, Ь, с, а в решении 225 выведено выражение R через
а, Ь, с, S. Если мы выведем выражение полупериметра р'
треугольника, образуемого основаниями высот, через те же
величины, то нам останется
только проверить тождество:	•	4«
S = Rp'.
Пусть будет HKL этот тре-
треугольник (рис. 175), и введем
для краткости обозначения:
НК = С, KL = a', LH = V,
так что
Чтобы вычислить НК — С,
рассмотрим треугольник НКС.
Угол С общий у треугольни-	Рис. 175.
ков ИКС, ABC. Угол К тре-
треугольника НКС равен углу В треугольника ABC, вследствие
того, что четырехугольник АВНК вписуемый. Следовательно,
треугольники НКС, ABC подобны. Отсюда находим пропорцию.
НК:АВ = НС:АС,
или
С : с = НС: Ь,

226	ПЛАНИМЕТРИЯ	]55
откуда
Из уравнения
находим:
так что
ПЛАНИМЕТРИЯ
= а«-
ИС=
с'=-
с-НС
ъ
4-ft»-2а-
а2 4- Ь2 — с2
2а
аЧ 4- &с —
ИС
г
с3
ЧаЪ
По аналогии можем написать:
i — в3 ,,	 а?Ь-\-сгЬ~ i
2Ъс	1ас
Полусумма полученных уравнений дает для р' выражение:
- 2в2с2 + 2^с2 — в4 — Ь* — с4
Р	АаЬс
или, на основании формулы
S=— У%а2Ь2 + 2аЧг + 2b2c2 — а4 — б4 — с*,
4
более простое выражение:
Так как
то, перемножая, найдем:
p'R=S,
что и требовалось доказать. К тому же результату можно
прийти и геометрическим путем, более соответствующим его
простоте. Соединим центр описанного круга О с вершинами
треугольников HKL, ABC и вычислим S как сумму площадей
треугольников, на которые при этом разобьется треугольник
ABC. Заметим, что прямые ОС, ОА, ОВ соответственно перпен-
перпендикулярны к прямым НК, KL, LH. Действительно, по теоре-
теореме 70 полупрямая CL'O образует с полупрямой СИВ такой же
угол, как полупрямая CL с полупрямой СА. Так как СИ, СА
сходственные стороны подобных треугольников ИКС, ABC,
то CL', CL также сходственные линии этих треугольников, и

166	РЕШЕНИЯ	227
следовательно, CV есть высота треугольника НКС, то-есть
ОС перпендикулярна к НК. Так же убедимся, что О А, ОВ со-
соответственно перпендикулярны к KL, LH. Теперь имеем:
пл. OHC= — OC'HL\ пл. OKC=~OC-KL'
и, складывая почленно,
пл. OHCK=—OC-HK=—Rc\
2	2
Таким образом получим:
nn.OHCK=-Rc', пл. О КAL^-Ra1, пл. OLBH=-Rb'.
2i	Л	2,
Складывая почленно, получим, как и выше:
S=Rp'.
Изложенные рассуждения относятся к остроугольным тре-
треугольникам. Если бы угол С был тупой, то мы имели бы уже
,	 аЧ -f b*c — с3
С~	2^	'
и для р' получилось бы иное выражение. Чтобы получить
прежнее выражение, достаточно переменить знак с\ от чего р'
превратится в р'—с'. Получим:
И	2	*	' аЪс
Отсюда найдем:
{p'-c')R=S,
т. е. искомое обобщение. Геометрическое рассуждение также
можно обобщить, но при этом оно заметно усложняется.
227. Примем центр вписанного круга за вершину, а стороны
треугольника за основания трех других треугольников. Осно-
Основания этих треугольников равны а, Ь, с, а высоты их равны г.
Складывая их площади — аг, — Ьг, — сг, получим площадь
?	?i	?
данного треугольника 5. Таким образом:
или
или
pr=S,

228
ПЛАНИМЕТРИЯ
167
откуда
Для определения радиуса ра вневписанного круга, касатель-
касательного к стороне а и к продолжениям сторон Ь, с, найдем таким
же образом уравнение:
\ ЬРа + "у Сра — — ара= S,
откуда получим:
р — а
Таким путем придем к четырем формулам:
_S_	S	S	S
р
р — а
р-Ь
р — с
228. Обозначим длины касательных к вписанному кругу
из вершин А, В, С соответственно через х, у, z (глс. 176):
BDx=BDs=y,
CD1=CDt=z.
Эти величины связаны уравнениями:
y+z=a, jc + z=&, x-\-y=c.
Складывая почленно и деля пополам,
найдем:
Вычитая из полученного уравнения
каждое из предыдущих, найдем:
х=-р — а, y=p — b, z=p — c,	Рис. 176.
т. е. касательная из вершины треуголь-
треугольника к вписанному кругу равна полупериметру без противо-
противолежащей стороны. Теперь обозначим через х, у, z касатель-
касательные из вершин А, В, С к вневписанному кругу, противолежа-
противолежащему вершине А:
Для этих величин имеем уравнения:
y-\-z=a, x—z=b, к—у=с.
Складывая их почленно и деля пополам, найдем:

168	рбшвния	229—230
то-есть касательная из вершины треугольника к противолежа-
противолежащему вневписанному кругу равна полупериметру. Из второго
и третьего уравнений найдем теперь:
z=p — b,
у=р — с.
Сравнивая эти выражения с выве-
выведенными выше для случая вписанного
круга, убеждаемся, что сторона тре-
треугольника делится точками касания
вписанного и вневписанного кругов
на отрезки равные, но расположенные
в обратном порядке.
229. Радиусы вписанного или вневписанного круга, прове-
проведенные к точкам касания с катетами, образуют вместе с каса-
касательными к этому кругу из вершины прямого угла квадрат
и, следовательно, равны этим касательным. Это показано на
рис. 177 для вневписанного круга, противолежащего вершине
прямого угла. На основании формул решения 228 для длин
касательных найдем:
Те же формулы можно получить из общих формул реше-
решения 227. Например:
±-Ьс
51 .	2	be
р-а I	b + c-a
be_. be (b -l-c+Vbz+.c2
b-j-c — Vb* + c2 ~~ (b -f- cJ — (b2 -f с2) ~	2bc
230. В прямоугольных треугольниках OBDU OaBE3 (рис. 178)
углы OBDV OaBE3, как половины смежных углов, в сумме
равны d. Следовательно, углы OBDV Б00?3 равны и треуголь-
треугольники OBDV OaBE3 подобны. Отсюда следует:
OD1:BD1^BEs:OaE3,
или
г:(р — *)=(/' — с): Ря,
откуда
гра=(Р - Ь) (р ~ с),
что и требовалось доказать.

231—232
ПЛАНИМЕТРИЯ
231. В решении 230 получена формула:
С другой стороны, по общим формулам решения 227
Сравнивая, находим:
S3
	= (р — Ь) (р — с),
р(р — а)
откуда и получаем желаемое выражение:
S = ур(р—а)(р-Ь)(р-с).
Изложенный вывод имеет более геомет-
геометрический характер, чем обычный, так как он
ие основан на числовых соотношениях в
треугольнике и требует сравнительно простых	Рис. 178.
вычислений.
232. Требуется доказать, что для всех точек М высоты АИ
треугольника ABC (рис. 179) имеет место соотношение
МВ*+ АС2=МС2 + АВ2
и ч-ю это соотношение не имеет места ни для каких других
точек. Вместо этого соотношения
мы будем рассматривать следую-
следующее, равносильное ему:
Пусть будет М какая угодно
—у—ц	ь точка, и И основание перпендику-
"	ляра из этой точки на сторону ВС.
Рис. 179.	Имеем:
М& — МС?={ВН2 + Я'Ж2) - (СИ 2+ НАР)=ВН'* — СН2,
АВ* — АС2={ВН* 4- ЯЛ2) — {СИ2 + НА*)=ВНг — СИ2.
Отсюда видно, что соотношение
MB2 — МС2=А В2 — А С2
равносильно соотношению
ВИ'г — СН'2 = ВН2 — СИ2,
а последнее, как нетрудно убедиться, имеет место тогда и
только тогда, когда точка Я* совпадает с точкой Я, т. е. когда
точка М лежит на высоте АИ. Итак, мы доказали, что высоте
АИ есть геометрическое место точек М, для которых

170
РЕШЕНИЯ
233—234
Теорема о пересечении высот в одной точке выводится от-
отсюда по методу геометрических мест, совершенно так же, как
соответствующие теоремы для перпендикуляров в серединах
сторон и биссектрис, и как теорема о пе-
пересечении медиан в решении 207. Орто-
Ортоцентр D есть точка, для которой имеет
место соотношение
АГУ- 4- az=BD2 H
2=CD2 4" с2-
233. Пусть будет D ортоцентр тре-
треугольника ABC и СОЕ диаметр описан-
описанного круга (рис. 180). Четырехугольник
ADBE есть параллелограмм, так как
стороны AD, BE перпендикулярны к
прямой ВС и, следовательно, параллельны, а стороны BD, АЕ
перпендикулярны к прямой АС и, следовательно, также па-
параллельны. Отсюда заключаем:
AD=BE,
Рис. 180.
после чего находим:
AD1
или
что и требовалось доказать. То же самое можно получить из
георемы 85:
ВС2=ВЕ2 + ВС2=СЕ2,
AD2 + a2=
AD2~\- a2=
234. По данным AH—h, BH=m, СН—п требуется опре-
а.елить DH=x, где D — точка пересечения АН с ВК (рис. 181).
Треугольники BDH, АСН подобны вследствие перпендикуляр-
перпендикулярности сходственных сторон. Отсюда про-
пропорция:
DH:BH=CH:AH,
или
х :т—п :h,
откуда
х=
тп
Полученное выражение для х симметрично по отношению
к т, п и не изменилось бы, если бы мы искали вместо от-

235—238	планиметрия	\~j\
резка DH, отсекаемого высотой ВК, отрезок D'H, отсекаемый
высотой CL. Отсюда видно, что отрезки DH, D'H равны. Не-
Нетрудно также проверить, что они во всех случаях располо-
расположены по одну сторону от точки И. Следовательно, точки D,
U совпадают. Таким образом высоты ВК, CL пересекают вы-
высоту АН в одной и той же точке D(D'), то-есть все три
высоты пересекаются в одной точке.
235.	В обозначениях задачи 234 требуется доказать:
АН-AD + BK-BD + CLCD=— (АВ2 + ЛС2 + ВО).
Пользуясь тем, что четырехугольники ALDK, BLDH вписуе-
мые, найдем по теореме о произведении секущей на внешний
отрезок:
AH-AD=AB-AL, BK-BD=AB-BL.
Складывая почленно, получим:
AH-AD+BK-BD=AB-AL + AB-BL=AB(AL + ВЦ^
Таким путем найдем:
АН-AD +
АН-AD + CL ¦ CD=AC2,
BKBD + CL • CD=BO.
Складывая почленно и деля пополам, получим:
AH-AD + BK-BD+CL-CD = — (ЛБ2 + АО + ВС%
что и требовалось доказать. Если угол С тупой, то мы получим
сходным образом:
АН-AD + BK-BD—CL-CD = — (ЛБ2 + АС2 + ВС2).
236.	Центр вписанного круга есть ортоцентр треугольника
с вершинами в центрах вневписанных кругов. Предложенная
теорема непосредственно вытекает из свойства ортоцентра,
указанного в конце решения 232.
237.	Предложенная теорема непосредственно вытекает из
решения 234 в применении к треугольнику с вершинами
в центрах вневписанных кругов.
238.	Из подобия треугольников ADK, ВС К (рис. 182) следует
пропорция
или
Отрезок А К определим из соотношения

172
РВШВНИЯ
239—24?
которое дает
2Ъ
Подставляя это выражение в найденную пропорцию, получим-
Отсюда
и
Рис. 182.
2bhb
45
Таким путем получим три формулы:
а (Ь* + с2 — а2)
45
45
Знак -\- относится к расстояниям ортоцентра от вершин ост-
острых углов, а знак — к расстояниям от вершин тупых углов
239. В решении 238 выве-
выведены выражения для рас-
стояний ортоцентра от вер-
вершин. По теореме 85 расстоя-
расстояния центра описанного круга
от сторон вдвое меньше
расстояний ортоцентра от
противолежащих вершин.
Отсюда следует, что рас-
расстояния центра описанного
круга от сторон а, Ь, с со-
соответственно равны
_1_аF2 + са— а3)
±
Ъ (а3 4 с2 —
85
c(ali-f Ъ* — с
85
Рис. 183.
240. Пусть будут О, Оа, Оь, Ое центры вписанного и вневпи-
еанных кругов, OD, OaE, ObF, OCG радиусы этих кругов

240	ПЛАНИМЕТРИЯ
vpnc. 183). Имеем:
ОА* = OD- -f AD* = г* + (р - af = —2 -f- (P - аJ
а)] = р-=^- [(a+c-b)(a-\-b—с)+(а+Ь+с%Ь+с- -а)\ =
(р— аJ	р — а
_^_- [(р _ Л)(р _ С)
р—а
ООа = ОаА - О А =1 / -&-
__ -I / Р^с j	р—а I _ _я_| / pfcc
Г Р — я L	P J	р (/ р — а '
Присоединив к полученным формулам аналогичные, получим
следующую таблицу формул:
=1 A(
Р—а	р К р—а
р—ь
f ОО = Sj
р
e	f	\/
Р	У Р — с	рУ р — с
Далее имеем:
^
fe+«]-

174	решения	241—242
Присоединив аналогичные формулы, получим таблицу:
(Р-с)Ьс
/be
(р-а)(р-сУ
У
р-а
Р —
241. Требуется выразить разность квадратов диагоналей
АС—р, BD=q через расстояния ОА =а, OB=b, OC=c, OD—d
произвольной точки О от вершин (рис. 184). Треугольника
АОС, BOD имеют общую медиану ОМ. По формулам решения
221 имеем
4ОЛР = 2а2 + 2с2 —
Отсюда найдем:
= 2b2
— q2.
242. Требуется выразить разность квадратов диагоналей
= р, BD = q через стороны AB=CD = m, AD=CB=n
и площадь 5 (рис. 185). Проведем высоты СН, DK и обозна-
К
Рис. 184
Рис. 185.
чим еще CH=DK—h, BH=AK~k. Из треугольников ABC,
ABD найдем:
ръ = /и2 -f »2
Вычитая почленно, получим:
рг — q2 =
Из треугольника ВС/У или /4D/C найдем:

243—244	планиметрия	175
Следовательно.
/>г — д2 = 4/га j/n2 — Л2 =
Но
так что
Отсюда
р2 - д2 = 4 ]Лга2п2 — S*.
[ выражения для р
, найдем:
2 (а2 + с2 — ** — d2) = 4
243. Сравнивая выражения для р2 — д2, полученные в
шениях 241 и 242, найдем:
Vm*n* — (а2 + с2 — б2 —
или
5
1( + а2 + с2 —> - rf2) Bтп — а2 — с2
244. Даны (рис. 186) стороны .ЛБ = a, CD = b, AD = c
СВ = d. Нужно определить диагонали АС = т, BD = п. Диаго-
Диагональ т можно было бы определить из треугольника ABC
если бы был известен отрезок ВН = I? от вершины противо-
противолежащего угла до основания высоты:
Чтобы найти уравнение, связывающее от-
отрезок # с известными величинами, прове-
проведем СК параллельно DA. Из треуголь-
треугольника СКВ, в котором CK—DA=c,
KB=AB—AK=AB—CD=a—b, найдем
искомое уравнение:
с2 = (a — bf -f (? + 2(a-^.
Чтобы исключить k из двух полученных уравнений, умножаем
первое на a— b, второе на —а и складываем почленно. Получим
уравнение
m2{a — b) — c2a = ab(a—b) — <
откуда найдем:
„ _, , с2а — (РЬ
т аЬ\
1 а — Ь
По аналогии найдем: i
* = &+"—*
* а-Ъ

176
РЕШЕНИЯ
245-247
245. Складывая выражения для т2 и я2, выведенные в ре-
решении 244, найдем:
п* = 2аЬ+
= 2аЪ +
а — Ь
а — Ь
2ab,
что и требовалось доказать.
246. В обозначениях решения 244 имеем:
пл. СКВ =
= -L У (a—b-{-c-{-d)(a—?+с—d) {a—b-c+d) (c+d—a
пл. ABCD :пл. СКВ = ^~
лл. ABCD = ?-i-^ пл.
-CH : — KB-CH =
CD):KB = (a
: (a - ft);
247. Перенесем параллельно треугольник ЛШ) в положе-
положение Cfi'D' (рис. 187). Имеем:
пл. ABCD = пл. ЛВС 4- пл. CBD = пл. CB'D' + пл. CBD.
Но по теореме 196
пл. CBD4- пл. CB'D
Следовательно,
— пл. BB'D'D.
2
пл. ABCD = -|-пл. BB'D'D.
Задача сведена к определению площади параллелограмма
Рис. 187.
Рис. 188.
BB'D'D. Последнюю можно определить с помощью формулы
решения 243 по сторонам, равным диагоналям четырехуголь-

248—249	ПЛАНИМЕТРИЯ	yj-
ника, и расстояниям точки С от вершин, равным сторонам
четырехугольника. Получим:
пл. A BCD = — пл. BB'D'D =
= -~ V^mn + а2 + c2 — b2 — d2) Bтп — а2 — с2 4-
248. Проведем в треугольниках ЛЯС, /ШС высоты СЯ,
и определим из обоих треугольников диагональ АС (рис. 188):
т? = а2 + Ь2 + 2а-ВЯ, от2 = d* -f- с2 — Ы- DK.
Чтобы исключить из этих уравнений ВН и DK, достаточно
связать эти величины еще одним уравнением. Такое уравне-
уравнение получим из рассмотрения треугольников СИВ и CDK- По
свойству вписанного четырехугольника треугольники СВН и
CDK имеют равные острые углы СВН и CDK. Следовательно,
они подобны, и мы имеем пропорцию:
BH-.DK = Ь:с,
откуда
ВН-с = DK-b.
Полученное соотношение позволяет исключить из наших урав-
уравнений ВН и DK посредством умножения их соответственно
на ей и ab и сложения. Получим уравнение:
/л2 {ab + cd) = a4d + abd2 -f b2cd -f-
или
m2 (aft -f- erf) = (ac + bd) (ad + ftc
откуда
aft
В числителе имеем сумму произведений противоположных
сторон и сумму произведений сторон, сходящихся в концах
определяемой диагонали, а в знаменателе сумму произведений
сторон, сходящихся в концах другой диагонали. По аналогии
получим:
п
ad -j- be
249. Перемножая формулы решения 248, найдем:
т2п* = (ас + bdJ,
откуда
тп = ас -{- bd,
что и составляет теорему Птоломея.
12 Делоне а Житомирский

178	решения	250—252
250. Подставляя в формулу
S = — УBтп + а2 + с2 — Ь* — d2)B /ип — а2 —
4
решения 247выражение шп = ас -\- bd из решения 249, получим:
S = —
4
= — У(а+с+&-^Ха+с—b+d){b+d-\-a—c)(b-\-d—a+c),
или, полагая а -\- b -\- с -\- d = 2р,
S = V(p-a)(p-b)(p~c)(p-d).
251. Пусть будут РА = а, РВ = b данные хорды, АВ = х
искомая хорда, PQ=2R диаметр круга (рис. 189). Из треуголь-
треугольников PAQ, PBQ найдем:
AQ = J/4/?2—a2, BQ= УАКг — Ь2.
В случае, когда хорда АВ стягивает сумму дуг, стягиваемых
хордами РА. РВ, который представлен на рис. 189, найдем
по теореме Птоломея:
Рис.189.
Подобным же образом найдем для хорды разности данных
дуг выражение:
1	&1/ 1	.
4/г2 к 4/гг
Здесь а большая из данных хорд.
252. Пусть АВ = а, BC = b, CD = d, AD = 2R = х
(рис. 190). Тогда из треугольников ABD, ACD найдем:
BD = Ух2 — а2, АС = Ух* — с*.

253
ПЛМШМКТРИЯ
179
По теореме Птоломея:
— a2
— с2 = Ьх-\- ас.
Это и есть искомое уравнение. После возвышения в квадрат и
приведения подобных членов оно примет вид:
х4 — (а2 + Ь2 + с2) х2 — ЧаЬсх = 0.
Это уравнение можно еще сократить на х, так как иско-
искомый диаметр не может быть равен нулю. Окончательно
получим уравнение третьей степени:
х3 — (о2 + Ь2 + с2) х — 2abc = 0.
Правильные многоугольники
253. Так как между плитками паркета не должно быть про-
промежутков, то углы плиток, сходящихся в одной точке, должны
в сумме давать 360°. Следовательно, паркет можно сложить
только из таких правильных многоугольников, угол которых
содержится целое число раз в 360°. Углы правильных много-
многоугольников равны по порядку:
60°, 90°, 108°, 120°, ...
При увеличении числа сторон угол правильного многоуголь-
многоугольника возрастает, но остается все же меньше 180°. Углы 60°,
90°, 120° содержатся в 360° соответственно 6, 4, 3 раза,
го-есть целое число раз. Угол 108° содержится в 360° дробное
число раз, а именно 3— раза. Остальные углы, большие^ 20°
О
и меньшие 180°, содержатся в 360° менее 3 раз и более 2 раз,
Рис. 191.
то-есть также дробное число раз. Таким образом, ни из каких
правильных многоугольников, кроме многоугольников с углом
12»

180
РЕШЕНИЯ
254-255
60°, 90°, 120°, то-есть треугольников, квадратов и шестиуголь-
шестиугольников, нельзя сложить паркет. Остается выяснить, можно ли
сложить паркет из многоугольников этих трех видов.
Чтобы построить соответствующую фигуру для квадратов
(рис. 191 слева), достаточно провести две системы равноотсто-
равноотстоящих параллельных, перпендикулярных между собой. Чтобы
получить подобную же сеть из правильных треугольников
(рис. 191 справа), достаточно провести две системы равноотсто-
равноотстоящих параллельных, наклонен-
наклоненных друг к другу под углом
60°, что приведет к сети ром-
ромбов с острым углом 60°, и в
каждом ромбе провести мень-
меньшую диагональ. Сеть шести-
шестиугольников можно получить
из сети треугольников, объеди-
объединяя по шести треугольников
в один шестиугольник, как по-
показано на чертеже жирными
линиями.
Рис. 192.	254. Сеть восьмиугольников
и квадратов можно получить
из сети квадратов, если в каждый квадрат вписать восьми-
восьмиугольник, как показано на рис. 192 слева; промежутки между
восьмиугольниками окажутся квадратами. Точно так же сеть
двенадцатиугольников и треугольников можно получить из
сети шестиугольников (рис. 192 справа).
255. Угол десятиугольника равен —, а угол пятиуголь-
5
ника —. Если в одной точке сходится х десятиугольников и
5
у пятиугольников, то должно иметь место уравнение
-Г* + — у = Ы,
О	О
или
3_у= 10.
При этом нужно иметь в виду, что х, j/—числа целые и
положительные. Полагая х=1, 2, 3, ..., найдем из ур-ния
2	2
у = 2, —, ——, ... Из этих чисел первое целое и положитель-
3	3
ное, второе дробное и положительное, а все дальнейшие
отрицательные.- Таким образом единственно возможным ока-
оказывается предположение х=\, у = 2, то-есть что в каждой
точке сходятся один десятиугольник и два пятиугольника.

256—259	ПЛАНИМЕТРИЯ	jgj
Но легко убедиться, что паркет из десятиугольников и пяти-
пятиугольников все же невозможен. Из двух соседних сторон
пятиугольника к одной должен прилегать десятиугольник, а к
другой пятиугольник, потому что в вершине должны сходиться
один десятиугольник и два пятиугольника. При обходе пяти-
пятиугольника мы должны около одной стороны найти десяти-
десятиугольник, около следующей пятиугольник, около третьей
десятиугольник, около четвертой пятиугольник, около пятой
десятиугольник. Но тогда оказалось бы, что к двум соседним
сторонам, первой и пятой, прилегают десятиугольники, что
невозможно.
256.	Вписанный многоугольник может иметь равные углы,
но неравные стороны: например, вписанный прямоугольник
может и не быть квадратом. Но вписанный многоугольник не
может иметь равные стороны и неравные углы. Действитель-
Действительно, если стороны равны, то равны и стягиваемые ими дуги,
а следовательно, равны и вдвое большие дуги, вмещающие
углы многоугольника.
257.	Описанный многоугольник может иметь равные стороны,
но неравные углы: например, описанный ромб может и не быть
квадратом. Но описанный многоугольник не может иметь рав-
равные углы и неравные стороны. Действительно, из равенства
углов следует равенство дуг между точками касания соседних
сторон, а отсюда легко выводится равенство сторон.
258.	Пусть будет О центр данного круга, А, В, С центры
вписанных кругов, Р точка касания кругов А, В и Q точка
касания кругов А, О (рис. 193).
В правильном треугольнике ABC
имеем:
Соотношение
a=
дает уравнение
2x=(R
из которого находим:
х=/?B/3"-3).	Рис-193"
259. Центры внешних кругов (рис. 194) образуют квадрат,
в котором
а = 2х, r=R-\-x.
Соотношение

182
РЕШЕНИЯ
260—261
дает уравнение
2х =
из которого находим:
x=R(l +1/2).
260. Соединив точки касания сторон правильного описан-
описанного треугольника к кругу, получим правильный вписанный
треугольник, стороны которого
суть средние линии описанного
треугольника. Отсюда:
Соединив точки касания про-
противоположных сторон описанного
квадрата к кругу, получим диа-
диаметр круга, который равен сто-
стороне квадрата, как средняя линия
его. Отсюда
Ь4=2Я
Риг 1Q4
Сторону описанного шести-
шестиугольника вычислим по общей формуле:
_
6~
2а, R
2R-R
V 4Д2-
261. Обозначим для однородности сторону и диагонали
правильного вписанного десятиугольника через dt, ds, d3, dt,
db, по числу десятых полной окружности, содержащихся в
стягиваемых ими дугах. На
рис. 195
AB=dx, AC=ds; BD=dit
CD = d2, AD=db.
Для упрощения вычислений
примем радиус за единицу
длины и десятую часть пол-
полной окружности за единицу
дуги или угла. В курсах
элементарной геометрии
можно найти вычисление dx,
но мы повторим еще раз те же рассуждения, так как они
позволяют одновременно найти dt и ds и объясняют сходство
их выражений. Проведем радиусы ОВ, ОС и отметим точку
Рис. 195.

261	ПЛАНИМЕТРИЯ
пересечения Р прямых ОБ, АС. В выбранной единице угла най-
найдем непосредственно:
/_АОВ=1, /_ВОС=% /_АСС=3.
Так как в той же единице сумма углов треугольника равна 5,
то из равнобедренных треугольников АОВ, АОС найдем:
Z АВО=2, /_АСО= /_САО=1,
и по теореме о внешнем угле для треугольника АРО:
Z АРВ= /_ОРС=2.
Из равенства углов при соответствующих основаниях заклю-
заключаем, что треугольники АРВ, СРО, РАО равнобедренные.
Имеем:
OP=PA=AB=dlf PC=OC=l.
На основании первого из этих равенств и подобия треуголь-
треугольников ОАВ, АРВ обычно и вычисляют dx\
ОА:АВ=АВ:ВР; I :d1=d1:l — d1; d* + dx — 1=0;
2	2
Таким же образом можно на основании второго равенства
вычислить d3:
ОА:АС=АР:ОА; 1 :ds=ds— 1 :1; d32- ds— 1=0;
ds; dz
3	2	3	2
Но если считать d± известным, то dz можно вычислить так:
Проще же всего вычислять dlt ds одновременно:
АС-АР=РС; ds — d1 = l.
АС:АО=АО:АР;
Найденная система уравнений
показывает, что d3, —dx суть корни уравнения
л:2 — х— 1=0,
которое дает
1 + ^5
Л	•	в
2

184	ре ше н ия	262—263
За — dt нужно принять отрицательный корень, а за d3 поло-
положительный корень, откуда и получаем:
Й!= 	^ . "з— 	^	.
Из прямоугольных треугольников ABD, ACD найдем после
этого
\ + 2/5,
-AC* = /4=d? = -МЛо-2/5.
Наконец,
При произвольном выборе единицы длины те же формулы
дают отношения стороны и диагоналей к радиусу и при-
принимают вид:
d5=2R.
Изложенный способ вычисления самый простой, но не един-
единственный. Можно, например, исходить из известного выражения
dx = а10, найти d2 как хорду, стягивающую дугу вдвое
большую, чем dv затем определить ds, d^ из прямо-
прямоугольных треугольников ABD, ACD. Можно также воспользо-
воспользоваться тем, что высоты прямоугольных треугольников ABD,
ACD равны — d2, — с?4. Можно применять теорему Птоло-
мея к различным четырехугольникам, составленным из сторон
и диагоналей десятиугольника. Разыскание наивыгоднейших
способов вычисления представляет собой полезное упражне-
упражнение с точки зрения как геометрии, так и алгебры.
262.	Искомые величины уже вычислены в решении 261;
сторона пятиугольника равна d2, а диагональ его равна d4.
263.	Обозначим сторону правильного десятиугольника че-
через а, апофему через А, радиус описанного круга через /?,
площадь через S. Тогда:
Из соотношения

264—265	планиметрия	185
находим:
n =	+1)
Отсюда
5 = Ъа\/ R-	= I
У	4
264. Принимая радиус за единицу длины, найдем по фор-
формуле удвоения числа сторон:
Но можно получить более удобное выражение, замечая, что
сторона двенадцатиугольника стягивает дугу, равную разности
дуг, стягиваемых стороной треугольника и стороной квадрата
j_ _ J	i_
12 ~ 3	4
По формуле решения 251 найдем:
/а?	, / с?
2
Легко удостовериться в тожественности обоих выражений:
—2
1/2-/3 =
Второе выражение удобнее для вычисления, так как не содер-
содержит знака корня под другим знаком корня.
265. Дуга, стягиваемая а15, равна разности дуг, стягивае-
стягиваемых а6 и а10. По формуле решения 251 найдем, принимая для
простоты R = 1:
""> l/i аб , i/, 6-2^5
	4	ai°K 1—Т" = ЬК 2	16
V5-1 1 / .	1 /ю+2У5' VT-1 Уз _
= -L(l/lO+2/B + /3~- /15)

186	ркшвшгя	266—268
266. Дуга, стягиваемая ат. равна разности дуг, стягивае-
стягиваемых а10 и а12:
60 10 12 *
По формуле решения 251 имеем, полагая /?= 1:
Здесь
l/i a'2_i/"i 4-2УЗ" 1/^4+2 У" _|/Л3+2>гЗ"+1 _
\ 1 ~ 4 ~~ \ Х	8 ""К	8 — у	8	"~
/1 fl«o_l/\ 6-2 1/5 _ 1^
1 — Т~ ~ К '	16 —
Уъ +1
2\ ~2
Следовательно,
"	1Г3 —1
2	2V 2	\Г2	4
V1T—1 1г6~4-1'"" ^ 6—1- 2~ 1^10-;-1-20
= — (|/зо+Кш—/ - К"г—(У1Г— 17Т)
Измерение круга
267. Длина окружности заключается между периметрами
вписанного шестиугольника и описанного квадрата:
или по известным формулам
6/?<2тт/?<8/?,
что по сокращении на 2R дает:
3<7Г<4.
268. Имеем:
или, полагая /?= 1,

269—27J	планимктгия
откуда
269. Полагая R = 1, будем иметь приближенно с недо-
недостатком:
2тг = 60а60, тг = ЗОа^,,
или, согласно формуле решения 266:
* = il (|/зб +/Ю- /6 — \Г2 — (/6 — /2 ) /10 + J/20 ) -
С помощью таблицы квадратных корней, приложенной к таб-
таблице логарифмов Е. Пржевальского, найдем с точностью до
одной тысячной
30о60 = 3,140.
Иначе говоря,
3,139 <30aG0< 3,141.
Остается оценить погрешность нашего определения числа ir,
то-есть указать возможно узкие пределы, между которыми
это число заключается. Имеем:
3,139 < 30а60 < тг
3,141 • ——1-	<^ <3,1473.
/	°"8
1 4	К	302-4
Итак, число 7г заключается между границами 3,139 и 3,1473,
разность между которыми равна 0,0083. С ошибкой, не пре-
превышающей девяти тысячных, можно поэтому принять
к = 3.14.
270. Имеем, с одной стороны:
а3 + о4 = Я У + RV~2 = R- 3,1463,
с другой стороны:
Следовательно, сумма as -\- а4 больше полуокружности на
0,0044/?, что составляет около 0,0014 самой полуокружности.
271. Согласно решению 258 (рис. 193) радиус вписанных
кругов будет
Искомая площадь 5 есть разность площади треугольника,
образуемого центрами этих кругов, и площадей трех секторов

188
РЕШЕНИЯ
272—274
этих кругов с углом 60°: Отсюда найдем:
1 °=*2(V3—1-*)
5= х* /1—
тис
= R* B1-12 /з)(/3—!-*
272. Так как вписанный угол ЛВС равен 60°, то дуга /Ж?, на
которую он опирается, равна 120°, и следовательно, дуга BD
равна 60° (рис. 196). Так же най-
найдем, что и дуга СЕ равна 60°. От-
Отсюда видно, что треугольники OBD,
ОСЕ также правильные. Площадь
каждого из них составляет четверть
площади треугольника ABC, и сле-
следовательно, остающаяся площадь
A DOE составляет половину пло-
площади треугольника ABC. Вычтя
из площади A DOE площадь ODE,
составляющую шестую часть дан-
данного круга, получим искомую пло-
площадь:
Рис. 196
пл. ADE=nn. A DOE— пл.
Начала геометрии кругов
273.	Пусть будут М, М концы диаметра круга К, проходя-
проходящего через точку Р, причем через М обозначим тот конец,
который дальше от Р (если точка М совпадает с центром, то
выбор обозначений безразличен). Условимся при вычислении не
приписывать знаков отрезкам РМ, РМ. Тогда степень будет
равна — РМ-РМ' в том случае, когда она отрицательна. Если
точка Р лежит вне круга К, то РМ = d -f- г, РМ' = d — r,
и степень будет РМ-РМ' = d2 — г2. Если точка Р лежит внут-
внутри круга К, то РМ = d-\-r,- PM'=r — d и РМ-РМ' = r2—d2,
но степень равна —РМ-РМ' =d2 — r2. Если точка лежит на
окружности, то РМ! = 0, так что и степень РМ-РМ1 равна ну-
нулю. Это согласуется с выражением d2 — г2 для степени, так
как в этом случае d = г.
274.	Пусть будут Kv K2 данные круги, О1? О2 их центры,
М какая-нибудь точка искомого геометрического места. Обо-
Обозначим радиусы кругов Kv Ka через rv /2, расстояние их цен-

274	ПЛАНИМЕТРИЯ	239
тров от точки М через dx, d2 и предположим обозначения
выбранными так, что rx >- г2. Будем иметь]
d\ — r\= d\ — г\ или d\ — d% = г\ — г\,
откуда видно, что dx^-d2. Предположим, что центры Ох, О2
различны, и выясним сначала, существуют ли точки искомого
геометрического места на линии центров ОХО2. Такая точка
Р может лежать на отрезке ОХО% или вне его. Если
обозначим длину отрезка ОХО2 через d, то в первом слу-
случае имеем dx -J- d2 = d, а во втором dx — d2 = d. Чтобы вы-
выяснить возможность этих случаев, решим совместно уравне-
уравнение d\ — d\ = r\ — г\ с каждым из уравнений dx -f- d2 = d и
dx — d2 = d. Получим соответственно
и
1 ~ id
Если какое-либо из этих решений дает для dx и с?2 неотрица-
неотрицательные значения, то тем самым найдена точка, удовлетво-
удовлетворяющая поставленным условиям. В противном случае такой
точки не существует. Так как dx^>d2, то достаточно, чтобы
d2 не было отрицательным числом. Но полученные формулы
показывают, что в зависимости от двух сделанных предполо-
предположений относительно положения точки Р для d2 получаются
значения, равные по величине, но обратные по знаку, если
только оба они не равны нулю. В этом последнем случае
имеем dx = d, d2 = 0, т. е. точка Р совпадает с точкой О2.
Во всех других случаях пригодно либо только первое, либо толь-
только второе решение. Таким образом, если круги Кх, К2 не-
неконцентрические, то всегда сущест-
существует одна и только одна точка Р на
прямой ОХО2, для которой степени от-
относительно кругов КXI К2. равны ме-
между собой.
Пусть теперь будет М' какая угодно
точка, не лежащая на прямой ОХО2, и
Р' основание перпендикуляра, опущен-
опущенного из Р' на ОХО2 (рис. 197). Имеем	Рис. 197.
ОХМ'2 = О^'* + М'Р'*, О2М'2 =
=О2Р'2-\-М'Р2, откуда ОХМ12—О2М'* =О1Р'2-О2Р'2. Поэтому
ОХМ'2—О2М'2 равно г\ — г\ тогда и только тогда, когда ОХР'2 —
—О2Р'2 равно г\ —г\. Иными словами, точка М' имеет равные сте-
степени относительно кругов Кг, К2 тогда и только тогда, когда Р'

190	решения	274
совпадает с Р, т. е. когда точка М лежит на перпендикуляре
к OtO2 в Р. Таким образом, искомое геометрическое место
(радикальная ось) есть перпендикуляр к линии центров О1О2 в
точке Р, найденной выше.
Нам остается исследовать положение радикальной оси в
зависимости от относительного положения кругов Kv K2- Если
круг К2 лежит вне круга К1 или касается его внешне, то
и тем более d2 — rx2 -|- r22 >¦ 0. Отсюда следует, что из двух
предполагавшихся выше положений точки Р имеет место пер-
первое, т. е. на отрезке ОгО2. Далее, мы уже видели, что при
ri > Г2 всегда dx > d2, т. е. точка Р ближе к центру меньшего
круга. При гг = г2 точка Р, очевидно, делит отрезок Ofi^
пополам при любом относительном положении кругов Kv К2.
Если круг К2 лежит внутри круга Kt или касается его внутрен-
внутренним образом, то
и тем более rt2 — r22 — d2 > 0. Следовательно, для точки Р имеем
второе положение, т. е. вне отрезка ОгОг. Из dx^>d2 следует,
что точка Р лежит на продолжении ОгО2 за точку О2, т. е.
со стороны центра меньшего круга. Остается рассмотреть
случай, когда круги Кг, К2 пересекаются. В этом случае точ-
точки Olt О2 и одна из точек пересечения образуют треугольник
со сторонами d, rv r2. Из двух углов при стороне ОХО2 = d
большим будет угол при О2, так как он лежит против боль-
большей стороны. В зависимости от того, будет ли этот угол острым,
прямым или тупым, мы будем иметь d2 -j- r22 > rx2, = гг2 или
<г^2, т. е. d2 — rt2 -f- r22 >0, =0, или < 0, что соответствует
положению точки Р внутри отрезка ОгО2, в точке О2 или вне
отрезка ОгО2.
Предыдущий результат становится, впрочем, очевидным, если
заметим, что радикальная ось всегда проходит через общие
точки кругов Ki, K2- Последнее следует из того, что эти точ-
точки имеют степень нуль относительно обоих кругов. Ясно, что
радикальная ось двух пересекающихся кругов есть пря-
прямая, соединяющая точки пересечения, а радикальная ось двух
касательных кругов есть касательная к ним в их точке
касания.
Мы все время предполагали, что центры О^О2 кругов Кц К2
различны. Если круги Kv K2 имеют общий центр, то точек,
имеющих одинаковую степень относительно этих кругов, не

275	ПЛАНИМЕТРИЯ	|g]
существует, потому что d1=d2, rx=f=r2 и равенство d^ — г±2 =
= d.22 — г/ невозможно. Однако к этому случаю можно подойти
как к предельному, предположив, что О2 безгранично прибли-
приближается к Ov Для определения положения точки Р имеем
формулу
d1=— (г* - r? -f d2) = — (Г я - r2~) + - d,
l 2d	2rf	2
Эта формула показывает, что при безграничном уменьшении с?
безгранично растет dx, так что при безграничном приближении
О2 к О2 точка Р безгранично удаляется от О,. Поэтому иногда
говорят, что радикальной осью двух концентрических кругов
служит бесконечно удаленная прямая.
275. Пусть будут К1г К2, К3 три круга и р12, plZ, р23 — их
радикальные оси. Мы предполагаем круги К±, К2, К3 некон-
неконцентрическими, так как концентрические круги в прямом
смысле слова радикальной оси не имеют. Для доказательства
предложенной теоремы заметим, что всякая общая точка двух
из прямых р12, р13, р23 лежит и на третьей прямой. Например,
общая точка р12 и plS имеет одинаковые степени относительно
кругов Кг и К2 и относительно кругов Кг и К3- Поэтому она
имеет также одинаковые степени относительно кругов Кг и
/С и, следовательно, лежит также и на р2Я. Теперь, если р12 и
р13 совпадают, то все их точки — общие и, следовательно, будут
также точками р23, т. е. p2S совпадает с р12 и plS. Далее, если
°i2 и Pis пересекаются, то точка пересечения лежит и на />23,
и в этой точке р23 пересекает их, так как, если бы р23 совпа-
совпадала с одной из прямых р12, р13, то и вторая совпадала бы
с нею, вопреки сделанному предположению. Но может слу-
случиться, что р12 и pis не имеют общих точек. В этом случае и
р23 не будет иметь общих точек с />12 и pl3, т. е. все три
прямые будут параллельны. Чтобы теорема осталась в силе,
нужно условиться считать, что все прямые, параллельные
одному направлению, сходятся в одной бесконечно удаленной
точке.
Если круги Kv Кг концентрические, а круг К3 неконцен-
тричен с ними, то р12 есть бесконечно удаленная прямая, а
Pi3> Ргз параллельны. Если все три круга концентрические, то
все три радикальные оси бесконечно удаленные. Наша теорема
сохраняет силу и в этих случаях, если примем, что на плоско-
плоскости имеется только одна бесконечно удаленная прямая и что
она является геометрическим местом бесконечно удаленных
точек.
Пусть требуется построить радикальную ось р12 двух некон-
неконцентричных кругов К±, К2, не имеющих общих точек (рис. 198).
Строим два каких-нибудь круга /С3. Kit пересекающих оба

192	решения	27S-277
круга Кг, К2- Дальнейшее построение показано на рисунке:
Рш — радикальная ось кругов Kh и Kk\ Рнн — радикальный
центр кругов Kh> Кк и Ki- Читатель легко докажет правиль-
правильность этого построения на основании предыдущего.
276.	1. Пусть задан круг Ко и радикальная ось р пучка.
Круг К может принадлежать пучку лишь в том случае, если
он имеет с кругом Ко радикаль-
радикальную ось р. Но совокупность всех
таких кругов, вместе с кругом
Ко, действительно образует пу-
пучок с радикальной осью р. Дей-
Действительно, если Кг и К2 — два
каких-нибудь круга, имеющих с
кругом Ко радикальную ось р, то
они и между собой имеют ради-
радикальную ось р, как доказано в
предыдущей задаче. Таким образом, круг Ко и прямая р дей-
действительно определяют пучок: пучок состоит из круга Ко
и всех кругов, имеющих с кругом Ко радикальную ось р.
Если заданы два круга пучка, то можно определить
их радикальную ось, и задание сводится к предыдущему ре-
решению.
2. Это прямо следует из замечания в конце решения 274.
277.	Так как радикальная ось двух неконцентричных кругов
перпендикулярна к их линии центров, то центры всех кругов
пучка, определяемого двумя неконцентричными кругами, лежат
на одной прямой — линии центров пучка. Только на линии
центров такого пучка могут лежать его предельные точки,
так как круг нулевого г радиуса сводится к своему центру.
Степень всякой точки радикальной оси, например точки пере-
пересечения Р с линией центров, относительно предельной точки
та же, что и относительно любого круга пучка. Но степень
какой-либо точки относительно предельной точки, очевидно,
равна квадрату расстояния между этими точками. В эллипти-
эллиптическом пучке (рис. 199) степень точки Р относительно кругов
отрицательна и не может поэтому равняться квадрату какого-
либо расстояния. Следовательно, в эллиптическом пучке пре-
предельных точек нет. В параболическом пучке (рис. 200) сте-
степень точки Р равна нулю. Следовательно, предельная точка
должна совпадать с ней, и действительно, рассматриваемая как
круг нулевого радиуса точка Р принадлежит пучку, так как
этот круг касается в точке Р всех других кругов пучка.
В гиперболическом пучке (рис. 201) точка Р имеет положи-
положительную степень, равную квадрату касательной, проведенной
из нее к какому-нибудь кругу пучка. Предельными точками
пучка могут быть только точки Кг, К2 на линии центров на

278
ПЛАНИМЕТРИЯ
193
расстоянии от точки Р, равном этой касательной. И действи-
действительно, точки К1г Кг будут предельными точками, так как
степени всякой точки М радикальной оси относительно всех
кругов, центр которых лежит на линии центров пучка, отли-
отличаются от степеней точки Р относительно тех же кругов на
одно и то же слагаемое — квадрат расстояния между точками
М и Р; поэтому не только степень точки Р, но и степень
Рис. 199.
Рис. 200.
Рис. 201.
всякой точки М радикальной оси относительно кругов Кг, Кг
будет та же, что и относительно всех кругов пучка.
Особый случай гиперболического пучка представляет пучок
концентрических кругов; радикальной осью его служит бес-
бесконечно удаленная прямая, а единственной предельной точ-
точкой — центр всех кругов пучка.
278. 1. Предположим сначала, что заданная точка М не
лежит на радикальной оси р заданного пучка. Если пучок
эллиптический, то все его круги проходят через две заданные
точки А, В прямой р, и задача сводится к построению круга,
проходящего через три заданные точки А, В, М, не лежащие
на одной прямой.
Если пучок параболический, то все его круги касаются
прямой р в заданной точке Р, и задача сводится к построению
круга, касательного к заданной пря-
прямой р в заданной точке и проходя-
проходящего через заданную точку Р, не ле-
лежащую на этой прямой. Если пучок
гиперболический, то достаточно, кро-
кроме точки М, найти еще две точки
М', М" искомого круга. На рис. 202
показано построение одной точки М'.
Проводим через точку М какой-ни-
какой-нибудь круг К', пересекающий заданный
круг пучка Ко- Через точки пересечения А', В' проводим пря-
прямую до пересечения в Сер. Прямая СМ пересечет К' еще
в одной точке М, которая и есть искомая. Действительно,
если К — искомый круг, то р есть радикальная ось К9 и К,
13 Делоне и Житомирский
Рис. 202.

194
РЕШЕНИЯ
279
Рис. 203.
А'В' — радикальная ось Ко и К', С' — радикальный центр,
f@, К и К', СМ — радикальная ось К и К', и М' — вторая
точка пересечения К и К'• Найдя таким же образом еще
одну точку М" круга К, можем построить его по трем извест-
известным точкам М, М', М".
Мы предполагали, что М не лежит на р. Этот случай
можно рассматривать как предельный и считать, что при М,
лежащем на р, искомым кругом будет сама р. Таким образом
радикальную ось можно считать за один из кругов пучка. За-
Задача всегда имеет одно решение.
В случае пучка концентрических кругов решение очевидно.
2.	Если данный пучок эллиптический, то искомый круг
должен проходить через вполне определенные точки А, В, и
задача сводится к следующей: по-
построить круг, проходящий через
две данные точки А, В и касатель-
, ный к данной прямой. Это уже ре-
решенная выше задача 185. В случае
параболического пучка приходим
к еще более простой задаче: по-
построить круг, касательный к данной
прямой р в данной точке Р и к
другой данной прямой d. В случае
гиперболического пучка поступаем так: строим (рис. 203) линию
центров пучка о; из точки пересечения D прямых р и d про-
проводим касательную DP к кругу Ко\ откладываем на d отрезки
D/\, DP2, равные DP; восстайляем к d перпендикуляры в Pv
Р2 до пересечений О1г О2 с о; описываем около Ог, О2 круги
радиусов О^, О2Р2. Это и будут искомые круги Кг, К2.
Это построение применимо, впрочем, к какому угодно пучку,
но в частных случаях может терять силу. Предоставляя под-
подробное исследование читателю, заметим только, что задача
имеет не более двух решений.
3.	В случае эллиптического пучка- задача сводится к уже
решенной выше задаче 186. Тот же способ построения можно
применить и в общем случае. Задача имеет не более двух
решений.
4.	В случае пучка концентрических кругов задача имеет
одно очевидное решение.
279. Если два круга взаимно ортогональны, то радиус каж-
каждого из них, проведенный в одну из точек пересечения, ка-
касается в этой точке другого круга. Поэтому степень центра
круга радиуса г относительно всякого круга, ортогонального
к нему, есть г2. И наоборот, если степень круга радиуса г
относительно другого круга равна г2, то эти круги взаимно
ортогональны. Предположим теперь, что круг С радиуса г

280
ПЛАНИМЕТРИЯ
195
ортогонален к двум кругам пучка Кг, К2 и покажем, что он
будет ортогонален ко всякому кругу К того же пучка. Дей-
Действительно, степень центра круга С относительно обоих кру-
кругов Кг, К2 равна г2. Следовательно, центр круга С лежит на
радикальной оси пучка и степень его относительно круга К
также равна г2. Отсюда следует, что круг С ортогонален так-
также и к кругу К, что и требовалось доказать.
280. Пусть будут Кг и К2— два каких-нибудь круга дан-
данного пучка, Ог, О2 — их центры. Все круги С, ортогональные
ко всем кругам данного пучка, ортогональны в том числе и
к кругам Kv K2- Следовательно, точки Ov O2 имеют относи-
относительно всех кругов С одинаковые степени — первая степень
гг2, вторая степень г22. Отсюда видно, что любые два круга
С имеют радикальной осью прямую ОгО2, т. е. принадлежат
одному пучку с радикальной осью ОгОа. Но других кругов,
кроме кругов С, этот пучок не содержит, потому что всякий
круг этого пучка имеет относительно точек Ov O2 степени
rj2, r22 и, следовательно, ортогонален к кругам К1г К2, т. е.
является одним из кругов С. Таким образом круги С действи-
действительно образуют некоторый пучок, который мы и назвали
ортогональным к данному. Данный пучок совпадает с пучком
ортогональным к ортогональному пучку, потому что круги
Kv K2 принадлежат обоим [пучкам, а два круга определяют
Рис. 204.
Рис. 205.
один и только один пучок. Если общую точку всех кругов
пучка рассматривать как круг нулевою радиуса, то этот круг
будет ортогонален ко всем кругам пучка, т. е. будет предель-
предельной точкой ортогонального пучка. На рис. 204 и 205 показа-
показаны" возможные виды пар ортогональных лучков. На рис. 204
один пучок эллиптический, другой гиперболический, а на
рис. 205 оба пучка параболические. Отметим следующее
13*

195	решения	281—283
очевидное следствие предыдущих рассуждений: если два пучка
ортогональны, то радикальная ось одного есть линия центров
другого и наоборот.
Если задач пучок концентрических кругов, то кругов, орто-
ортогональных ко всем кругам пучка, не существует, но можно
принять за ортогональный круг любой диаметр кругов пучка.
Тогда пучком, ортогональным к данному, будет пучок прямых —
диаметров всех кругов данного пучка. Это — особый случай
эллиптического пучка.
281.	1. Пусть задан круг Ко и радикальный центр Р связки.
Круг К может иметь с кругом Ко и каким-нибудь третьим
кругом точку Р радикальным центром только в том случае,
если радикальная ось круга К с кругом Ко проходит через
точку Р. Но совокупность всех таких кругов, вместе с кру-
кругом Ко, действительно образует связку с радикальным центром
Р. Действительно, точка Р имеет относительно всех таких
кругов ту же степень, что и относительно круга Ко- Следо-
Следовательно, точка Р будет радикальным центром любых трех из
этих кругов.
2. Мы видели, что степень радикального центра относи-
относительно всех кругов связки одна и та же. Если она отрица-
отрицательна, то радикальный центр лежит внутри всех кругов
связки, если рг.вна нулю, то на всех кругах связки, если поло-
положительна, то вне всех кругов связки.
Предыдущие рассуждения предполагают, что радикальный
центр связки — конечная точка. Связка с бесконечно удален-
удаленным центром есть особый случай гиперболической связки;
она состоит из всех кругов, центры которых лежат на одной
прямой.
282.	Предельные точки связки — это те точки, квадрат рас-
расстояния которых от радикального центра равен степени связки.
Если связка гиперболическая, то степень положительна и
предельные точки образуют окружность круга, центр ко-
которого совпадает с радикальным центром связки, и радиус
которого равен квадратному корню из степени связки. В слу-
случае параболической связки степень равна нулю, и радиус
этого круга обращается в нуль. В случае эллиптической
связки предельных точек совсем нет, потому что степень от-
отрицательна и не может равняться квадрату какого-либо рас-
расстояния.
В особом случае гиперболической связки с бесконечно уда-
удаленным центром предельные точки образуют линию центров
кругов связки; эту прямую можно рассматривать как круг,
ортогональный ко всем кругам связки.
283.	Если некоторый круг ортогонален ко всем кругам
связки, то центр этого круга имеет относительно всех кругов

284—287	ПЛАНИМЕТРИЯ	197
связки одну и ту же степень, равную квадрату его радиуса.
Отсюда, прежде Есего, следует, что центр этого круга совпа-
совпадает с радикальным центром связки, а вслед затем, что сам
этот круг совпадгет с предельным кругом связки. Наоборот,
круги, ортогональные к данному кругу, имеют относительно
центра этого круга одну и ту же степень, равную квадрату
его ргдиуса, и, следовательно, образуют связку, для которой
данный круг служит предельным.
284.	Если Р— центр связки и М, Ж—точки пересечения
прямой, проходящей через Р, с каким-нибудь кругом связки,
то РМ-РМ' = ±?2, где -±zt>- — степень связки. Это показы-
показывает, что точки М, М' обратны относительно инверсии с цен-
центром Р и степенью + ?2.
285.	Если некоторый круг проходит через точки М, М',
обратные относительно инверсии с центром Р и степенью ±?2,
то РМ-РМ' = ±?'2. Следовательно, степень этого круга отно-
относительно точки Р равна =Н#2, т. е. он принадлежит связке с
центром Р и степенью±к2-
286.	Пусть будет Р центр связки, Ко — данный круг связ-
связки, и А, В — данные необратные точки, через которые тре-
требуется провести круг связки (рис. 206).
Построим точку А', обратную точке А
в данной связке. Для этого проводам
секущую РММ' к кругу Ко, затем круг
К' через точки М, М', А, наконец, секу-
секущую РАА' к кругу К'- Тогда А' и бу-
будет искомой обратной точкой. Так как
точка В по условию не обрагна точке А,
то точка А' не может совпасть с точ-
точкой В, т. е. точки А, В, А' различны.
Искомый круг есть круг, проходящий
через точки А, В, А'. Если точки А, В
не лежат на одной прямой с центром
связки Р, то это будет, действительно, некоторый круг К-
Если же точки А, В лежат на одной прямой с Р, то круг К
обращается в прямую РАВ.
287.	Предположим сначала, что центры Р1г Я2 данных свя-
связок не совпадают, и что данная точка А не лежит на прямой
Рг Р2 (рис. 207).
Находим, как и в предыдущей задаче, точку А', обратную-
А в первой связке, затем точку А", обратную А' во второй
связке. Эти точки не лежат на одной прямой, и круг Д\ про-
проходящий через них, и есть искомый круг. Если точка А ле-
лежит на прямой PjP2» т0 круг К обращается в прямую Plt P2-
Если связки имеют общий центр Р, то кругом К будет
прямая РА.

198
РЕШЕНИЯ
288-291
Рис. 207.
288.	Пусть связка задана центром Р и кругом Ко. Предпо-
Предположим сначала, что она эллиптическая (рис. 208). Проводим
диаметр О0Р и перпендикулярную к нему полухорду РА. Если
степень связки равна — ?2, то РА = ?. Через данный центр О
искомого круга проводим диаметр ОР, на перпендикуляре к ОР
в точке Р откладываем РВ = РА = t>, и описываем круг с
центром О и радиусом ОВ; это и бу-
будет искомый круг К. Задача имеет
единственное решение. В случае пара-
параболической связки также имеем един-
единственное решение: искомый круг име-
имеет данный центр О и проходит через
центр связки Р. В случае гиперболи-
гиперболической связки (рис. 209) проводим из
Р касательную РА к Ко и описываем
круг К' с центром Р и радиусом РА;
это будет предельный круг связки.
Затем проводим, если это возможно, касательную ОВ из
О к К' и описываем круг К с центром О и радиусом ОВ.
Это и будет искомый круг. Задача имеет одно решение, если
точка О не лежит внутри круга К', а в этом последнем слу-
случае—ни одного. Если О — бесконечно удаленная точка, то
круг К обращается в прямую, перпендикулярную к РО в Р.
289.	Если два кру-
круга пучка принадлежат
связке, то центр связ-
связки имеет относительно
этих кругов одну и ту
же степень (связки) и,
следовательно, лежит
на радикальной оси этих
кругов. Но тогда он
имеет ту же степень и
относительно всех кру-
кругов пучка, так что все
круги пучка принад-
принадлежат той же связке.	Рис 208.	Рис. 209.
290.	Линии центров
данных пучков не могут совпадать — в противном случае и
сами пучки совпадали бы. Следовательно, эти линии имеют
одну общую точку, конечную или бесконечно удаленную, ко-
которая только и может быть центром искомого общего круга.
Круг связки с этим центром, если таковой существует, и
будет искомым кругом.
291.	Предположим, что центры связок различны. Построим,
как показано в решении 287, два общих круга этих связок.

292—293
ПЛАНИМЕТРИЯ
199
По теореме задачи 289 пучок, определяемый этими кругами,
принадлежит обеим связкам. Кроме кругов этого пучка, связки
не могут иметь ни одного общего круга, потому что три
круга, не принадлежащие одному пучку, вполне определяют
связку, так что наши связки не могли бы в этом случае быть
различны между собой. Итак, в этом случае теорема доказана.
В случае же, если центры связок совпадают, общими кругами
будут прямые, проходящие через их общий центр. Это уже
указанный выше особый случай эллиптического пучка. Его
можно получить как предельный, когда одна из двух общих
точек кругов пучка удаляется в бесконечность.
292.	Если данная прямая d проходит через центр инверсии О,
то она, очевидно, обратна сама себе. Предположим теперь,
что d не проходит через О, и опу-
опустим из О перпендикуляр OF на d
(рис. 210). Пусть будет М произволь-
произвольная точка прямой d и Р', М—точ-
М—точки, обратные Р, М. Из ОМ-ОМ' =
= ОР-ОР' выводим пропорцию ОМ' :
: OP = OF : ОМ, откуда следует, что
треугольники ОМ'Р', ОРМ подобны.
Следовательно, угол ОМ'Р прямой и
точка М' лежит на окружности К,
описанной на ОР' как на диаметре.
Конечным точкам прямой d обратны все точки окружности К,
за исключением точки О, а точка О обратна бесконечно уда-
удаленной точке прямой d.
293.	Если данная окружность К проходит через центр ин-
инверсии О, то обратной линией будет некоторая прямая, парал-
параллельная касательной к К в О, как это ясно из предыдущего
решения. Предполо-
Предположим теперь, что К не
проходит через О.
Пусть будут P,Q— кон-
концы диаметра круга К,
проходящего через О,
и М — какая - нибудь
третья точка круга К
(рис. 211). Точки, об-
обратные точкам Р, Q, М,
обозначим через Р, Q',
Рис. 211.	М'. Как и в преды-
предыдущем решении, из
ОМ-ОМ' —ОР-ОР' выводим подобие треугольников ОМ'Р и
ОРМ, а из ОМ-ОМ' = OQ-OQ' — подобие треугольни-
треугольников OM'Q' и OQM. Отсюда найдем: / NM'P = Z MPQ,
Рис. 210.
к'

200	решения	294—295
Z OM'Q' = Z MQP, Z NMP+Z. OM'Q' = /i MPQ +Z MQP.
Ho Z -MPQ + Z -/WQP = d, так как угол PMQ есгь вписан-
вписанный угол в круге К, опирающийся на диаметр PQ. Значит, и
Z.NMP + /.OM'Q' = d, а потому и /_P'M'Q' = с?, как до-
дополняющий эту сумму до Id. Таким образом, точка М' лежит
на окружности К', описанной на PQ', как на диаметре, которая
и будет линией, обратной окружности К-
294. Пусть будет О — центр данного круга, М и М'—две
точки, обратные относительно него, Р и Q — концы диаметра
ОММ' (рис. 212). Выразим отношения, в которых точки М и
о м 0
Рис. 212.
М' делят отрезок PQ, через радиус круга г и один из отрез-
отрезков ОМ = х, ОМ' = х', принимая во внимание зависимость
хх'
Мы
= г2
РМ г
QM r
видим,
+ ¦*
— X
что
РМ'
QM'
г
X
+ х'
' — г
РМ
ОМ
ГХ +
хх' —
РМ'
~ QM'
хх'
гх
гх -f- г*
г*-гх
г
г
+ х
— X
что и требовалось доказать.
295. Пусть будут Мг, М2, М3 — середины сторон треуголь-
треугольника АУА2АЪ\ Кг, К2 — вневписанные круги при сторонах
АгАг, АгА3; О1гО2 — их центры; Рг, Р2 — точки касания их к
стороне Аг, А2\ t — четвертая общая касательная кругов Klf
К% (рис. 213). Прежде всего нужно убедиться, что около точ-
точки Ms действительно можно описать круг К', проходящий
через точки Р1г Р2, т. е. что М3Рг = MSP2. В самом деле,
если обозначим стороны треугольника АгА2Аъ через а-,, а2, а3
и его полупериметр через р, то будем иметь АгРг = А2Р2 = р,
АгМ3 = А2М3 = — а3 и вычитая из первого равенства второе,
MjPi = MSP2 = p	аг — — (а^ + аа). Круг девяти точек К
определяется тремя точками Mlt M2, Ms. Мы дадим два дока-
доказательства того, что круг К есть отражение прямой t в
круге К'-
1. Прямые t и АгА2 суть общие внешние касательные, а
прямые Л^з, А2А3 — общие внутренние касательные кругов
KVK2. Обе пары прямых поэтому симметричны относительно
линии центров ОгО2. Вследствие этого симметричны и тре-

295
ПЛАНИМЕТРИЯ
201
угольники АХА2А3, BXB2AS. Далее заметим, что прямые MZMX,
М3Мг параллельны сторонам А3АХ. А3А2 треугольника АхАгА3,
как средние линии его. Воспользуемся этими замечаниями,
чтобы вычислить произведения М3Мг-М3Мх, MZMZ-MSM2.
Если окажется, что эти произведения равны квадрату радиуса
Рис. 213.
— (ах + аа) круга К', то тем самым будет доказано, что точки
Ми Mz суть отражения точек Af/, M2' прямой t в круге К'.
Так как треугольники МгМхАг, BXMXMJ подобны равным тре-
треугольникам AxAzAi, ВхАгВъ то они подобны между собой.
Отсюда
Так же найдем М3М2-М3М'2= -
Итак, отраже-
отражения точек Мх', М% в круге /С' суть действительно точки Ми
Мг. Отражение прямой t в круге К' есть поэтому круг, про-
проходящий через точки Мх, Ж2. Кроме того, как отражение
всякой прямой в круге К', это отражение проходит через
центр Mz круга К'¦ Следовательно, оно совпадает с кругом
девяти точек К.

202	РЕШЕНИЯ	296—297
2. Покажем, что касательная М3Т к кругу К в точке М3
параллельна прямой t. Для этого достаточно доказать, что
внутренние накрест лежащие углы ТМ3МХ и ВХМ-1МХ равны.
Но /_В1М1'М1 равен /_А2 треугольника АгА2А3. Значит, нужно
доказать, что //77И3М1= /_Аг. Мы можем предположить, что
точка А2 лежит вне круга К, потому что из двух точек А1г
А2, по крайней мере, одна лежит вне хорды М3Н3; в против-
противном случае середина М3 стороны Л1Л2 лежала бы вне этой
стороны. Поэтому /_Аг измеряется половиной дуги uAVW2-f-
-f- uMJix — иЖД круга К- Но по теореме о цугах, заклю-
заключенных между параллельными хордами, имеем: иЖ3Ж2-[-
-f- иМ2Нг — <иМгН3 = <uMiH1 = уиМ3Мх. Половиной дуги
М3Мг измеряется /_ТМ3МХ. Параллельность М3Т и t таким
образом доказана. Отсюда следует, что отражение прямой t
в круге К' во всяком случае имеет с кругом К в точке М3
общую касательную. Достаточно теперь доказать, что какая-
нибудь точка круга К, отличная от точки М3, есть отражение
некоторой точки прямой t в круге К. С этой целью заметим,
что точки Н3 и S делят отрезок РгР2 в тех же отношениях,
в каких точки А3 и S делят отрезок Ofi2. Но точки А3 и S
суть центры подобия кругов Л\, Кг и> следовательно, делят
отрезок ОхОг внутренним и внешним образом в одинаковых
отношениях. То же самое верно поэтому и для точек S, Н3
и отрезка РгР2 — диаметра круга К'. Тгким образом, точка Ня
есть отражение точки 5 в круге К', что и заканчивает дока-
доказательство. По сравнению с предыдущим это доказательство
имеет тот недостаток, что оно теряет силу, когда АХА3 =
= А2А3. Напротив, первое доказательство в этом случае толь-
только упрощается.
Совершенно аналогичные рассуждения применимы и к рас-
рассмотрению вписанного и одного из вневписанных кругов. Пре-
Предоставляем это читателю, как очень полезное упражнение.
296.	В решении 295 доказано, что круг К есть отражение
прямой t в круге К'. Добавим к этому, что круги Кг, К2
являются своими собственными отражениями в круге К', так
как они ортогональны к этому кругу. Но прямая t касается
кругов Ki, K2-
Следовательно, и отражение К касается отражений /Сх, К2,
так как число общих точек двух линий и их отражений всегда
одно и то же. Из второй части теоремы задачи 295 следует
таким же образом, что третий вневписанный круг и вписан-
вписанный круг также касаются круга К- Относительное положе-
положение всех пяти кругов дано на рис. 214.
297.	При доказательстве следует, строго говоря, различать
случаи эллиптической и гиперболической инверсии и случаи,
когда центр инверсии лежит внутри или вне обратных кругов.

298
ПЛАНИМЕТРИЯ
203
Для краткости ограничимся случаем, когда инверсия гипербо-
гиперболическая, центр инверсии лежит вне обратных кругов
<рис. 215).
Рис. 214.
Имеем: Z.O'M'P' = 1_О'Р'М' = РММ', /_Р'М'М = /
= /_0МР; отсюда /_ОМРХ + АР'М'М = /_0МР-\-/_РММ\
или /_0'М'М = Z.OMM'. Таким образом, радиусы, проведен-
проведенные во взаимно обратные точки, образуют с секущей равные
односторонние углы, а потому то же самое верно и для ка-
касательных.
298. Для краткости ограничимся случаем гиперболической
инверсии и предположим, что дуги, образующие один из углов,
а потому и дуги, образующие другой угол, направлены в одну

204
РЕШЕНИЯ
299—300
сторону от прямой, соединяющей вершины углов с центром
инверсии (рис. 216). Имеем: /_UM№ = U'M'M, /_TMM! =
= Т'М'М. Вычитая, найдем: /_UMT = U'MT. Чертеж пока-
показывает, что направления углов UMT, U'M'T' противоположны.
Рис. 215.
299. Инверсия относительно точки, в которой сходятся
стороны криволинейного треугольника, превратит его в пря-
прямолинейный треугольник, не изменив его углов. В последнем
же сумма углов равна двум прямым.
Рис. 216.
Рис. 217.
300. Пусть будет Р центр инверсии, относительно которой
круги К, К' взаимно обратны, и М, М — какие-нибудь две
взаимно обратные точки (рис. 217). Радиусы ОМ, О'М' обра-
образуют с секущей РМ'-М равные односторонние углы. Отсюда
видно, что радиусы ОМ, O'N' образуют с той же секущей
равные соответственные углы, и следовательно, параллельны
между собой. Так как это относится к любой секущей, про-
проведенной из точки Р, то точка Р должна быть одним из цент-
центров подобия кругов К, К'. Теперь'докажем, что каждый центр
подобия есть действительно центр вполне определенной ин-
инверсии, относительно которой круги К, К' обратны. Имеем
—- = -~, PM-PN' =/>', где г, г1 —радиусы кругов К, К\п
Ж IS	Г	-щ
р'—степень центра подобия Р относительно круга К'. Пере

SOI—30/
ПЛАНИМЕТРИЯ
205
множая, найдем РМ-РМ'=Г-^-, откуда следует, что круги
К, К' обратны относительно инверсии с центром Р и сте-
степенью — .
г
301. Рассмотрим отдельно случаи, когда круг К касается
обоих данных кругов внешне, ,обоих внутренне, и одного
внешне, другого внутренне (рис. 218, 219, 220). На рис. 218
имеем:
—соот-
—соотЧертеж показывает, что равные углы ОаМлТ,
ветственные при пере-
пересечении прямых О1Л/2.
ОгМг прямой PN2M2.
Следовательно.радиусы
Ot_N2, O2M2 параллель-
параллельны и одинаково направ-
направлены. Отсюда видим,
что точка Р есть центр
прямого подобия кру-
кругов Кц К2 И ЧТО ТОЧКИ
Мг, М2 взаимно обрат-
обратны относительноинвер-
относительноинверсии е центром Р, по отношению к которой взаимно обратны
круги Klt K2- Так как круг К проходит через взаимнообратные
точки, то он обратен сам себе. На рис. 219 имеем внутреннее
Рис. 219.
Рис. 220.
касание К к KL и Kz, на рис. 220 внешнее касание к^и внут-
внутреннее к К2. Результат получается тот же, но в первом случае
Р есть, как и раньше, центр прямого подобия, а во втором
случае — центр обратного подобия.
302. На рис. 221 показаны только центры кругов Olt О2, О%,
центры прямого подобия Pl2, P13, P,, и центры обратного по-
подобия Q12, Q13, O23. Точка Phk делит отрезок OhOk внешним

206	решения	303
образом, а точка Qh Qk — внутренним образом в отношении
rh:rk> гДе О ~ РаДиУс круга с центром Ot. Применяя результат
задачи 155, позволяющей по отношениям, в которых прямая
делит две стороны треугольника, определить отношение, в
котором она делит третью, убедимся, что три центра прямого
подобия лежат на одной прямой и что каждый из них лежит
на одной прямой с двумя центрами
обратного подобия, относящимися
к двум другим парам кругов.
303. Требуется построить круг К,'
касательный к трем данным кругам
Кг, К2, К3- Все круги, касающиеся
кругов Л*1, К2 обоих внешне или
обоих внутренне, сами себе обратны
по отношению к инверсии с цент-
Рис 22]	ром Р12, по отношению к кото-
которой круги Кг, К2 обратны
друг другу. Следовательно, они
принадлежат определенной связке Rl2 с центром Р12. Точно
так же все круги, касающиеся круга Кг внешне, а круга К%
внутренне, или круга К\ внутренне, а круга К2 внешне, при-
принадлежат определенной связке S12 с центром Q12. Аналогич-
Аналогичным образом, круги, касающиеся кругов К1г К3> распреде-
распределяются между двумя связками R1S, Sl3. Следовательно, всякий
круг К, касательный ко всем трем кругам Ки К2, Kz, .одно-
.одновременно принадлежит одной из связок Rl2, Sl2 и одной из
связок R13, S13. Но общие круги двух связок образуют пучок,
радикальная ось которого проходит через центры связок. Сле-
Следовательно, искомые круги К распределяются между четырьмя
пучками, радикальными осями которых служат оси подобия
^12 ^1з> Рц Qi3» Q12 Pi3y Q12 Qi3- При этом в каждом пучке мо-
могут содержаться только круги К, касающиеся всех трех кругов
некоторым определенным образом (например, всех трех внешне)
или всех трех противоположным образом (в данном примере —
всех трех внутренне). Если в каком-либо из этих пучков
найдется круг К, касательный к кругу К1г то он будет ка-
касаться и кругов К2, К3- Действительно, принадлежа одной из
связок R12, S12, такой круг обратен сам себе относительно
инверсии с центром Р12 или Q12, по отношению к которой
круг Д'а обратен кругу Кх- Так как круги, обратные двум
касательным кругам, также, очевидно, касательны, то круг К
будет также касаться круга К2, и также докажем, что он ка-
касается круга К3- После эгого построение становится вполне
ясным. Пусть, например, желательно построить круги, касаю-
касающиеся всех трех кругов Кх, К2, К3 внешне или всех трех
внутренне. Проведя три параллельных и одинаково направлен-

303
ПЛАНИМЕТРИЯ
207
ных радиуса кругов Кх, К2, К$, строим центры подобия
Р\г> Рш и ось подобия P12P1S. Это будет радикальная ось пуч-
пучка, к которому должны принадлежать искомые круги. Чтобы
найти какой-нибудь круг этого пучка, берем какую-нибудь
точку Мх круга Kv проводим прямую Р^М-у до пересечения
\
Рис. 222.
с кругом К2 в точке М2, обратной точке Мх по отношению
к инверсии с центром Рг2, и далее проводим прямую Р1ЯМ2
до пересечения с кругом Kz в точке М3, обратной точке М2
по отношению к инверсии с центром Plz. Круг К', проходя-
проходящий через точки Мх, М2, Ms, будет одним из кругов рассмат-
рассматриваемого пучка. Теперь пучок задан радикальной осью P1ZP13
и кругом К'- По этим данным мы можем построить круги
пучка, касательные к кругу Кл, как показ .но в решении 278, 3.
Это и будут искомые круги К. Число их не превышает двух,
и мы видим отсюда, что общее число кругов К, касательных
к кругам Kv Къ, Kz, не превышает восьми. Задача Аполлония
уже была решена выше другим способом, но дшное решение
яснее с теоретической точки зрения. Построение представлено
на рис. 222.

208	решения	304—305
304.	Возможны три случая: 1) данные круги Kv К2 пере-
пересекаются в двух точках А, В; тогда любая инверсия с цент-
центром в А или В превратит их в две пересекающиеся прямые;
2) круги К1г К2 касаются в точке Р; тогда инверсия с центром
Р превратит их в параллельные прямые; 3) круги Кх> Кг не
имеют общих точек; тогда ортогональные к ним круги имеют
две общие точки, и инверсия, превращающая эти круги в пря-
прямые, пересекающиеся в одной точке, превратит круги Kv Кг
в круги, ортогонально пересекающие эти прямые, так что эти
прямые будут общими диаметрами этих кругов, а точка пере-
пересечения прямых — общим центром кругов.
305.	Укажем два способа.
1. Подвергаем данные круги такой инверсии, чтобы два из
них превратились в прямые или концентрические круги, и
строим круги, касательные к полученным обратным линиям,
что сравнительно просто. Затем полученные касательные кру-
круги подвергаем той же инверсии. Обратные круги будут ка-
касаться первоначально заданных. 2. Имея в виду построить
круги, касательные к данным определенным образом, изменяем
соответственно радиусы дпнных кругов так, чтобы один круг
превратился в точку. Производим какую-нибудь инверсию
двух остальных кругов, принимая эту точку за центр инверсии,
и проводим к ним соответствующие общие касательные. Кру-
Круги, обратные этим касательным, будут проходить через круг
нулевого радиуса и касаться двух остальных кругов. Соответ-
Соответствующим изменением радиусов превратим их в искомые круги

СТЕРЕОМЕТРИЯ
ЗАДАЧИ НА ДОКАЗАТЕЛЬСТВО И ПОСТРОЕНИЯ
Прямые и плоскости и многогранные углы
306.	Проведем через точку А и первую заданную прямую
плоскость и аналогично через точку А и вторую прямую. Пло-
Плоскости эти, имея общую точку (точку А), пересекаются по
прямой. Эта прямая, находясь с первой заданной прямой в од-
одной плоскости, пересекает ее (на конечном или бесконечном
расстоянии, если ей параллельна), аналогично пересекает
она и вторую заданную прямую, т. е. является искомой
прямой.
307.	Проведем через кгкую-нибудь точку прямой Ъ прямую
а', параллельную прямой а, и через прямые b и а' плоскость; эта
плоскость Ьа' II прямой а. Аналогично проведем через прямую
с плоскость || прямой а. Прямая пересечений этих двух пло-
плоскостей будет пересекать обе прямые а и Ь, так как лежит с
каждой из них в одной плоскости и будет || прямой а, т. е.
является искомой.
308.	Проведем через точку А плоскость Q _|_к прямой а;
плоскость эта пересечет плоскость Р по некоторой прямой Ь.
Прямая b плоскости Р_|_к прямой а, так как всякая вообще
прямая плоскости Q _|_ к прямой а.
309.	Проведем через прямую а плоскость В II прямой b, a
через прямую Ъ плоскость А II прямой а. Плоскость Р пере-
пересечет параллельные между собою плоскости А и В по парал-
параллельным прямым р и /?'. В плоскости Р построим отрезок,
концы которого находятся на прямых р и р' и длина которого
равна d, что делается одной засечкой циркуля. Очевидно, что
этот отрезок будет параллелен искомому, так как, наоборот,
искомый отрезок, будучи перенесен в пространстве параллельно
самому себе на плоскость Р, так чтобы его концы скользили
по плоскостям А и В, будгт отрезком длины d, имеющим
концы на прямых р и р'. Дальше остается пповести прямую,
параллельную полученному направлению и пересекающую за-
заданные прямые а и b (как это указано в предыдущей задаче),
14 Делоне и Житомирский

210	решения	310—3i2
отрезок ее между прямыми и будет искомый. Если расстояние
между параллельными прямымир и р' больше d, решений нет,
если оно р;.вно d, есть одно решение, если оно меньше d,
есть два решения, так как засечка циркулем дает два пересе-
пересечения.
310.	Перпендикуляры эти не изменятся, если мы передви-
передвинем плоскости, на которые они опущены, параллельно самим
себе, например так, чтобы все эти плоскости прошли через
точку А. Все эти плоскости будут тогда пересекаться по од-
одной прямой а, проходящей через точку А, а следовательно,
все перпендикуляры будут перлендикулярами к этой прямой,
восставленными в одной ее точке А, т. е., как известно, будут
лежать в одной плоскости.
311.	На плоскости две прямые или при продолжении пе-
пересекаются или параллельны, т. е. пересекаются на бесконеч-
бесконечности, т/ е. всегда пересекаются или на конечном расстоянии,
или на бесконечности. В пространстве, кроме этих двух слу-
случаев, возможен еще один третий случай, когда прямые не
лежат в одной плоскости, «скрещиваются»; в этом случае есгь
один отрезок KL, соединяющий обе эти прямые, который
самый короткий из всех та.<их отрезков. Точки К и L суть
те точки этих прямых, расстояние между которыми наимень-
наименьшее. Требуется найти эти точки. Проведем через прямую а
плоскость В || второй прямой Ъ, а через прямую Ъ плоскость
А || первой прямой а. Плоскости эти А и В (те же са лые,
которые рассматриваются в задаче 309) параллельны между со-
собой. Кратчайшее расстояние между точками двух параллель-
параллельных плоскостей дает перпендикуляр к этим плоскостям, но
прямые а и Ъ лежат в этих плоскостях, и следовательно, ника-
никакое расстояние между их точками не может быть меньше этого
перпендикуляра.-Проведем через пря-
прямую а плоскость Р_1_к плоскости Л,
а через прямую Ъ плоскость Q±_ к пло-
плоскости В. Плоскости Ри Q пересекутся
по некоторой прямой с, которая пере-
пересечет обе прямые а и Ъ и будэт пер-
перпендикулярна к обеим плоскостям А
и В. Отрезок этой прямой с, заключен-
заключенный между точками К и L ее пересече-
пересечения с прямыми а и Ь, и будет, таким
образом, кратчайшим отрезко л, соеди-
Фиг. 223.	няющим эти прямые, а точки К и L —
ближайшими их точками.
312. Из треугольника ABD (рис. 223) видно, что отрэзок
НЕ || BD и равен половине BD, а из треугольника BCD видно.

313-315
СТЕРЕОМЕТРИЯ
211
Рис. 224.
что отрезок FG || BD и равен его половине. Отрезки НЕ и FG
равны и параллельны, т. е. /yf/^G—параллелогр. мм.
313.	Докажем сначала, что плоскость АСВ должна быть _L к
плоскости Р (рис. 224). Предположим, что С не лежала бы
в плоскости Q, п| оходящей через точки А и В _|_к плоскости
Р. Опустим из точки С" по плоскости Р перпендикуляр С С
на п| ямую пе| есечения плоскостей Р и Q. Треугольники АС" С
и ВС" С прямоугольные с прямыми углами у вершины С",
так как С С" ± к плоскости Q и, следовательно, ± ко всякой
прямой плоскости Q. Мы имеем, следовательно, АС меньше
АС, ВС меньше ВС, и следова-
следовательно, ломаная АС"В короче АСВ,
т. е. у кратчайшей ломаной АСВ
плоскость АСВ J. к плоскости Р.
Дальше задача становится плани-
планиметрической: найти в плоскости Q
такую точку С на прямой DE,
чтобы ломаная АСВ была кратчай-
кратчайшей. Задача эта уже была решена
раньше, достаточно построить точ-
точку А' плоскости Q, симметричную
с точкой А по отношению к пря-
прямой DE, и соединить эту точку
с точкой В; искомая точка С будет точкой пересечения
прямых DE и А'В, углы (падения) ACD и (отражения)
ВСЕ равны.
314.	Пусть а и Ъ две из наших прямых, они пересекаются,
по условию, в некоторой точке А. Все остальные прямые
наши или 1) проходят через эту точку А, т. е. все прямые
пересекаются в одной точке, или 2) есть хоть одна такая прямая
с среди них, которая через точку А не проходит. Но с, по
условию, должна пересехагь а и Ь, следовательно, прямые а,
Ъ, с образуют треугольник и сами лежат в плоскости Р этого
треугольника. Если теперь d кзкая-либо из остальных прямых,
то она, как пересекающая все три прямые а, Ъ и с, имеет с
плоскостью Р по крайней мере две общие точки, т. е. ле кит
в Р. В этом втором случае все прямые наши лежат, следова-
следовательно, в одной плоскости.
315.	Пусть А одна из таких точек; тогда и расстояние
ее проекции С на плоскость Р треугольника от вершин тре-
треугольника должно быть тоже одинаково, т. е. С должно быть
центром круга, описанного вокруг треугольника, а А лежит,
следовательно, на перпендикуляре к плоскости Р треугольника,
восставленном из этого центра. Очевидно и обратное, что всякая
точка этого перпендикуляра равноудалена от вершин треуголь-
треугольника.
41*

212	решения	316—322
316.	Так как углы между прямыми не меняются при их
параллельном перенесении, то можно заменить заданные пря-
прямые а и Ъ параллельными им а! и Ъ', проходящими через
заданную точку А. Если провести в плоскости Р этих прямых
биссектрису угла между ними и через нее плоскость Q _]_
плоскости Р, то все искомые прямые будут прямыми плоско-
плоскости Q, проходящими через точку А. Действительно, пусть АВ
такая прямая; проведем через точку В плоскость Q _L к биссек-
биссектрисе, пусть С и D — точки ее пересечения с прямыми а' и Ъ'.
Треуг льник ACD равнобедренный; если Во проекция В на
плоскость Р, то, следовательно, В0С = B^D, но если проекции
равны, то и наклонные равны, т. е. BD = ВС. Треугольники
ABC и ABD равны по трем сторонам, т. е. /_ВАС = /_BAD.
Аналогично доказываем обратное. Очевидно, что условия за-
задачи будут удовлетворены тоже плоскостью Q, построенной
на второй биссектрисе прямых а' и Ь'.
317.	Геометрическим местом будет плоскость, проходящая
через ребро угла и через биссектрису линейного угла двух-
двухгранного угла, т. е. биссекториальная плоскость.
318.	Геометрическим местом будет плоскость _L к плоскости
прямых и проходящая через биссектрису угла между ними.
319.	Прямая пересечения двух из биссекториальных пло-
плоскостей есть геометрическое место точек, равноудлленных от
первой и второй и от первой и третьей граней трехгранного
угла, т. е. равноудаленных от всех трех граней трехгранного
угла, т. е. и от второй и третьей. Но все точки, равноудален-
равноудаленные от второй и третьей грани, суть все точки третьей биссгкто-
риальной плоскости, следовательно, она проходит через пря-
прямую пересечения первых двух.
320.	Прямая пересечения двух из указанных плоскостей
есть геометрическое место точек, равноудаленных от первого
и второго и от первого и третьего ребра трехгранного угла
и т. д., как в предыдущей задаче.
321.	Отложим на всех трех ребрах от вершины О трехгран-
трехгранного угла одинаковые отрезки О А, ОВ и ОС; получится тре-
треугольник ABC. Биссектрисы граней трехгранного угла делят
каждую из сторон АВ, АС, ВС пополам, тек как треугольники
ОАВ, ОАС, ОВС равнобедренные. Рассматриваемые в задаче
плоскости пересекают, следовательно, треугольник ABC по
медианам. Но медианы пересекаются в одной точке D, а
следовательно, все эти три плоскости имеют две общие им
всем точки О и D, т. е. пересекаются по одной прямой OD.
Эти плоскости можно назвать медианными плоскостями трех-
трехгранного угла.
322.	Пусть OK, OL прямые пересечения двух из рассматри-
рассматриваемых в задаче плоскостей с гранями трехгранного угла

323—324
СТЕРЕОМЕТРИЯ
213
Рис. 225.
(рис 225). Возьмем на одном из ребер произвольную точку А
и опустим из нее по граням перпендикуляры АХС и ALB на
ОК и OL. Тогда, так как плоскость ВОК J_k плоскости АОС,
то КО есть проекция наклонной ВК на плоскость АОС, пря-
прямая же АСА- к КО в плоскости АОС, и следовательно, ВК _1_
к АС, т. е. ВК высота треугольника ABC; аналогично пока-
покажем, что и CL высота э того треуголь-
треугольника. Плоскость ВОК, таким обра-
образом, _L к прямой А С, а следовательно,
и к плоскости треугольника ABC,
плоскость COL по такой же при-
причине _1_ к плоскости ABC, следо-
следовательно, прямая OD J. к этой пло-
плоскости. Проведем плоскость AOMD.
AM проходит через точку D пере-
пересечения двух высот треугольника,
следовательно, AM третья высота,
т. е. ВС±АМ. Но OD есть пер-
перпендикуляр к плоскости ABC, а ОМ
наклонная и MD ее проекция, причем MD _\_ВС, и следова-
следовательно, ОМ _L ВС. Таким образом ВС как перпендикуляр к AM
и МО _)_ к плоскости АОМ. Отсюда следует, что плоскость
АОМ _]_ к плоскости BGC, т. е. и есть тре-
третья из рассматриваемых в задаче плоско-
плоскостей. Все три плоскости пересекаются по
одной прямой OD. Эти три плоскости мож-
можно назвать высотными плоскостями .трех-
.трехгранного угла.
323. Пусть А, Л' В, В' грани четырех-
четырехгранного угла, причем А противоположна
А', а В противоположна В'. Пусть при про-
продолжении грани А а А' пересекаются по
прямой а, а грсни В и В' — по прямой Ъ
(прямые а и Ъ проходят через вершину
угла). Любая плоскость, параллельная обеим
прямым а и Ъ, т. е. параллельная плоскости
аЪ, пересекает че-ibipexri анный угол по па-
параллелограмму, так как она пересекает гра-
грани А и А' по пар-!ллельным прямым, а так-
также и грани В и В' по параллельным прямым.
324. Треугольники ОАО', ОБО', ОСО (рис. 226) равны (по
трем сторонам); следовательно, если опустить на сторону 00'
перпендикуляры из вершины А, В, С, то основания их будут
в одной и той же точке D. Прямая 00', таким образом, пер-
перпендикулярна к двум (даже трем) прялым плоскости ABC, a
следовательно, перпендикулярна и к самой этой плоскости.

214
РЕШЕНИЯ
i25—327
Куб
325.	Сечения ABC и А'В'С представляют равносторонние тре-
треугольники, плоскости их параллельны, так как АВ\\А'В' и
т. д. Если провести плоскость, параллельную этим сечениям
и по середине между ними, то в сечении получится шзсти-
угольник DEFGHK. Стороны его равны, так как каждая из
них равна половине диагонали хранл куба, нппример, D/: равна
половине СВ, так как D есть середина А'С и Е—сечедлна
А'В, а следовательно, DE — средняя линия в треугольнике
А'ВС. Но и углы этого шестиугольника все одинаковы, по
120°, так как стороны их || сторонам равностороннего треуголь-
треугольника ABC. Шестиугольник DEFGHX, таким образом, правиль-
правильный* (оис. 227).
326.	Продолжим мысленно плоскость ABC и провед°м через
точку С прямую || диагонали DD' до пересечения в F с этой
Рис. 227.
Рис. 228.
плоскостью (рис. 228). Так как ADBC—параллелограмм, а пло-
плоскость ABC проходит через его диагональ АВ, то очевидно»
что параллельные между собою отрезки СF и DE, проведен-
проведенные через две другие вершины параллелограммп до пересечения
в точках F и Е с плоскостью ABC, равны. Но СF = ЕЕ как
параллельные отрезки между параллельными плоскостями ABC
и А'В'С. Итак, DE = EE'. Аналогично покажем, что D'E =
= ЕЕ'. Итак, DE = ЕЕ' = E'D'.
327. Пусть рассматриваемые диагонали суть АВ и В'С
(рис. 2296). Диагональ DD' куба ± к плоскостям ABC и
А'В'С, что следует из рассмотрения двух правильных пира-
пирамид A BCD и A BCD', сложенных основаниями (см. задачу 324).
Плоскости ABC и А'В'С проходят через прямые АВ и В'С и
каждая II прямой, через которую проходит другая, т. е. это
как раз те плоскости, которые надо проводить, чтобы найти
величину наименьшего расстояния между прямыми (см. зада-

328—329
СТЕРЕОМЕТРИЯ
215
чу 311). Наименьшее расстояние между прямыми АВ и В'С
равно, следовательно, ЕЕ', т. е. трети диагонали куба. Для то-
того чтобы н; йти ближайшие точки К и L этих прямых, надо
(см. задачу 311) провести через каждую из прямых АВ и В'С
по плоскости _[_ к
параллельным пло-
плоскостям ABC и
А'В'С. Спроекти-
Спроектируем куб на пло-
плоскость ABC парал-
параллельно диагонали
D'D. Мы тогда по-
получим (рис. 2296) ck
правильный шести-
уголъ-лик АС В А'СВ',
причем отрезок KL
спроектируется в	Рис. 22да.	Рис 229б.
одну точку. Легко
видеть.что AL — — АВ. Точки К и L расположены, следова-
О
тельно, на одной трети диагоналей граней куба.
328. На каждой из граней куба образуется правильная четы-
четырехугольная пирамида (рис. 230 и 231). Легко убедиться, что
эти пирамиды как раз
равны тем пирамидам,
которые получаются,
если за вершину взять
центр куба, а за осно-
основание его грань. Грани
двух таких пирамид,
смежные по одному и
тому же ребру куба,
служат продолжением
одна другой и образу-
Рис. 230.
Рис. 231
ют ромб. Получающий-
Получающийся многогранник назы-
называется ромбическим до-
додекаэдром. Объем его, очевидно, вдвое больше объема куба.
Параллелепипед
329. Если провести секущую L'L через точку О (рис. 232)
пересечения диагоналей, то очевидно, что OL лежит по дру-
другую сторону от плоскостей ABCD", BCD'A', CDA'B', DAB'C,
чем OL', т. е. OL' лежит внутри пирамиды OA'B'C'D', a OL
внутри пирамиды OABCD, т. е. V на грани А'В'СП, a L на

216
РЕШЕНИЯ
330-335
грани ABCD. Треугольники OL'D' и OLB подобны, так как
L'D' и BL, как прямые пересечения параллельных плоскостей
одной и той же плоскостью BL'D'L, параллельны, но ОБ =
—OD' и, следовательно, треугольники эти равны, т. е. OL=OL'.
330.	Пусть заданы прямые, а, Ь, с. Проведем через каждую
из них по две плоскости, параллельные двум другим; получат-
получатся три пары параллельных плоскостей. Тело, замкнутое этими
шестью плоскостями, и будет искомый параллелепипед.
331.	Лего видеть, что доказательство этого же свойства,
данное для куба в задаче 326. дословно годится и для парал-
параллелепипеда.
Рис. 232
Рис. 233.
332.	Точка G есть середина ВС, следовательно. A G — меди-
медиана треугольника ABC (рис. 233). Диагональ DE пересекает,
следовательно, треугольник ABC в точке К. лежащей на меди-
медиане A G, но аналогично покажем, что К лежит и на двух дру-
других медианах, т. е. есть точка их пересечения.
Правильный тетраэдр
333.	Построим вспомогательный куб, такой, что вершины
нашего тетраэдра будут в его вершинах, для чего достаточно
построить куб, диагональ грани которого равна ребру тетраэд-
тетраэдра. Теперь очевидно, что ребро CD || диагонали грани CD'
и, следовательно, _L к ребру АВ (рис. 234).
334.	Пересечем тетраэдр плоскостью, параллельной двум
граням вспомогательного куба и проходящей посередине
между ними; в сечении, очевидно, получится квадрат, верши-
вершины которого находятся в центрах граней куба (рис. 235).
335.	Пусть внутренняя точ/а О, а длины перпендикуляров,
опущенных из нее на грани А, В, С, D тетраэдра Т, сугь
а, Ь, с, d. Надо доказать, что a-\-b-\~c-\-d = k, где h —
высота тетраэдра Т. Проведем через точку О вспомогатель-
вспомогательную плоскость || грани А. Точка О окажется на грани А'
оставшегося тетраэдра Т', и остается доказать, что Ь-\- с -\-

336
СТЕРЕОМЕТРИЯ
217
-f- d = h'', где h' — высота этого нового тетраэдра Т. Проведем,
далее, через точку О секущую плоскость || грани В' этого тет-
тетраэдра Т; тогда точка О окажется на ребре оставшегося тет-
тетраэдра Г", и остается доказать, что с -f- d = h", где ft" —
высота этого нового тетраэдра Т". Проведем, наконец, через
точку О секущую плоскость || грани С" этого тетраэдра Т";
с
Рис. 235.
тогда точка О окажется в вершине оставшегося тетраэдра Т'",
а отрезок d, единственный не отрезанный, его высотой (рис. 236).
336. Плоскости ABC и А'В'С (рис. 237) параллельны между
собою, так как АВ\\А'В', АС\\А'С, ВС\\В'С. Если, следова-
следовательно, пересечь параллелепи-
параллелепипед плоскостью, параллельной
этим плоскостям и проходящей
посередине между ними, то
ребра АС, АВ', ВС',ВА', СА',
СВ' пересекутся этой плоско-
Рис. 236.
стью в их серединах. Треугольники ABC, AB'C, АСВ',АВ'С,
А'ВС, ВА'С равносторонние я, следовательно, все стороны
шестиугольника EFGHKL равны половине ребра тетраэдра.
Все же углы его имеют по 120°, так как, например, стороны
угла EFG параллельны сторонам равностороннего треугольника
ABC. Шестиугольник этот, таким образом, правильный.

218
РЕШЕНИЯ
337—338
Произвольный тетраэдр
337.	Весьма советуем читателю испробовать «достроить»
тетраэдр через четыре его грани. Получается четырехрогое
тело, состоящее из четырех параллелепипедов, имеющих об-
общею частью достраиваемый тетраэдр ABCD. Грани DA', DB' и
DC параллелепипе-
параллелепипедов А А', ВВ1 и СС
параллельны грани
ABC тетраэдра и
имеют общую точ-
точку D, следователь-
следовательно, лежат в одной
плоскости, которая
есть грань А'В'С
большего тетраэдра
А'В'CD'. Легко ви-
видеть, что тетраэдр
CDKL равен (или,
вернее, симметри-
симметричен) заданному. Та-
Таким образом, полу-
полученное рогатое те-
тело получается из
большего тетраэд-
тетраэдра A'B'C'D' вырезанием шести (по числу ребер заданного тетра-
тетраэдра) тетраэдров, симметричных заданному. Объем большего
тетраэдра, как подобного
тетраэдру CDKL, но линейно
в три раза большего, равен
27 v, если объем заданного
есть v. Объем четырехро-
гого тела равен, следо-
следовательно, llv — 6v = 2\v
(рис. 236).
338.	Один из способов
разрезания на такие тетра-
тетраэдры указан на рис. 239. От-
Отрезается тетраэдр ABCD',
достройкой которого полу-
получается параллелепипед и	Рис. 239.
противолежащий ему тет-
тетраэдр A'B'C'D. Оставшееся тело BCB'C'DD' представляет
октаэдр, состоящий из двух сложенных друг с другом основа-
основаниями симметричных четырехугольных пирамид с параллело-
грамматическими основаниями ВСВ'С и вершинами D и D'. Раз-

339
СТЕРЕОМЕТРИЯ
219
резав обе эти пирамиды или диагональною плоскостью ВВ'СС,
как показано на рисунке, или диагональною плоскостью
DD'CC, мы получим еще четыре тетраэдра. Таким обра-
образом параллелепипед оказывается разрезанным на шесть те-
тетраэдров одинаковых объемов, но разных по форме. Среди
них три пары симметричных друг с другом тетраэдров. Тгк,
тетраэдгы ABCD' и A 'BCD друг другу симметричны, BCDB1
и В'CD'В симметричны и
BCDB' и B'C'D'B симмет-
симметричны. Существенно иной
способ разрезания паралле-
параллелепипеда на тетгаэдры ука-
указан ни рис. 240. Отреза-
Отрезают от параллелепипеда те-
тетраэдры ABCD', A'BCD,
AB'CD, ABCD и остается
еще тетраэдр ABCD. Объем s	Рис. 240.
каждого из четырех первых
равен - объема параллелепипеда, объем последнего равен, сле-
следовательно, — = — объема параллелепипеда.
6 3
Предлагается читателю самому разыскать все другие, суще-
существенно отличающиеся от двух этих, способы разбития парал-
параллелепипеда на тетраэдры, вер-
вершины которых лежат в верши-
вершинах параллелепипеда.
339. Отложим на ребрах
трехгранного угла от верши-
вершины его О отрезки О А, ОВ,
ОС, равные единице длины
(рис. 241). Получится некото-
некоторый специальный тетраэдр
ОАВС. Пусть высота его осно-
основания АОВ есть h, а высота
его самого, опущенная на это
основание, есть Н. Пусть
О А'В'С—какой-либо тетраэдр
Рис. 241.	с этим же трехгранным углом,
и пусть ребра его равны
О А' — а, ОВ'— Ь, ОС'=с, высота его основания К,
а его собственная высота Н'. Мы имеем h': h = b: I,
т. e. h' = hb. Кроме того, мы имеем Н' :Н = с:1; Н' = Не.
Объем тетраэдра ОА'В'С равен - •— ah'H' = I hHabc,

220
РЕШЕНИЯ
340-342
но —hH есть объем тетраэдра О ABC, и, следовательно, объем
б
тетраэдра ОА'В'С1 равен произведению аЪс его ребер на по-
постоянный объем v0 специального тетраэдра ОАВС, ребра ко-
которого ОА, ОВ и ОС равны 1. Совершенно аналогично объем
параллелепипеда с данным трехгранным углом равен произ-
произведению его ребер, сходящихся
в этом углу, на объем vQ такого
же специального п. раллелепипе-
да, у которого эти ребра равны 1.
340.	Действительно, при пере-
передвижении ребра АВ в новое по-
положение А'В', площадь основа-
основания ABC не меняется, а высота
тоже не изменяется, так как она
есть перпендикуляр, опущенный
из точки D на плоскость, прохо-
проходящую через точку С и прямую
а (рис. 242).
341.	Плоскость CDE, прохо-
проходящая через середины Е и G
двух прогивоположньтх ребер, де-
делит тетраэдр на две равновеликие части фис. 243). Если по-
повернуть эту плоскость вокруг прямой EG в положение EFGH,
то от одной из этих двух частей отрежется пирамида с ос-
основанием EFGH и вершиной D, а к другой прибавится пирамида
с тем же основанием и вершиной С. Но эти пирамиды равно-
равновелики, так как G — середина отрезка CD.
Рис. 242.
Рис. 243.
342. Пересечем тетраэдр любою плоскостью, параллельною
двум противоположным ребрам тетраэдра АВ и CD (puc. 244);
эта плоскость пересечет грани ABC и ABD по || прямым, грани
CDA и CDB она пересечет тоже по || прямым. В сечении по-
получится параллелограмм. Таких систем параллелограмматиче-

343—348
СТЕРЕОМЕТРИЯ
221
ских сечений у тетраэдра три, по числу пар противоположных
ребер.
343.	Рассмотрим три из этих плоскостей, например, соот-
соответствующие ребрам АВ, АС и AD; точка О их пересечения
равноудалена от всех четырех вершин тетраэдра (центр опи-
описанного шара), так как она так же удалена от В, С и D, как
и от А. Плоскость, соответствующая каждому из трех остав-
оставшихся ребер, например, плоскость, соответствующая ребру
ВС, есть геометрическое место точек, равноудаленных от В
и С, т. е. точка О должна на ней лежать. Таким образом все
шесть плоскостей проходят через точку О.
344.	Прямые эти представляют прямые, по которым пере-
пересекаются каждые три плоскости предыдущей задачи, соответ-
соответствующие ребрам, принадлежащим одной грани (см. задачу 343),
т. е. геометрические места точек, равноудаленных от трех
вершин тетраэдра. Ясно, что они должны проходить через
точку, равноудаленную от всех трех вершин тетраэдра.
345.	Три биссекториальные плоскости одного из трехгран-
трехгранных углов тетраэдра пересекаются по одной прямой (си. за-
задачу 319), которая есть геометрическое место точек, равно-
равноудаленных от граней этого трехгранного угла. Возьмем
какую-нибудь из трех других биссекториальных плоскостей;
пусть она пересечет эту прямую в точке О. Точка О равно
удалена от всех четырех граней тетраэдра (центр вписанного
шара). Две оставшиеся биссекто-
биссекториальные плоскости суть геометри-
геометрические места точек, равноудален-
равноудаленных от пары граней; они должны
проходить через точку О.
346.	Проведем через каждое
из ребер тетраэдра плоскость,
параллельную противоположному
ребру (рис. 245). Таким обра-
образом получится параллелепипед, для
которого прямые DE, соединяющее
вершины с центрами тяжести (точ-
(точками пересечения медиан) противо-
противоположных граней тетраэдра, явля-
являются диагоналями DD' (см. задачу
332). Но диагонали параллелепипеда пересекаются в одной
точке.
347.	Читателю самому предлагается найти красивую форму
этого условия.
348.	Для этого достаточно доказать, что если в трехгранном
угле имеется не острый плоский утл, и прилежащие к нему
двугранные углы острые, то противолежащий ему двугранный

222
РЕШЕНИЯ
349
угол тупой. Пусть АОВ прямой или тупой угол рассматриваемого
трехгранного угла ОАВС (рис. 246). Если прилежащие к нему
двугранные углы острые, то проекция ОК третьего ребра
трехгранного угла на плоскости АОВ будет лежать внутри
угла АОВ. Через любую точку С этого третьего ребра
проводим плоскость, перпендикулярную к этому ребру,
пересекающую трехгранный угол по треугольнику ABC,
в котором угол АСВ—плоский угол двугранного угла с реб-
ребром ОС. Повернем треугольник ABC вокруг АВ так, чтобы
он слился с плоскостью АОВ; тогда
точка С упадет на прямую ОК и бу-
будет лежать внутри треугольника АОВ,
например в точке С, так как DC<^
<OZ) (DC—катет, a OD—гипотенуза
в COD). Отсюда следует, что /_ ЛС?<
<^/_АОВ, следовательно, /_АСВ
тупой.
Когда /_ АОВ тупой, проекция тре-
третьего ребра ОК может составлять с
Фиг. 246.	одной из ei о сторон прямой или же
тупой угол. В первом случае (рис. 247)
плоскость, перпендикулярная к третьему ребру, будет парал-
параллельна О А, во втором случае (рис. 248) она пересечется с про-
продолжением ОА по другую сторону точки О в некоторой точке
Рис. 247.
Рис. 248.
А'. В первом случае /_ ВСА' равен острому углу CBD, а во
втором случае /_ ВСА' < /_CBD как внутренний угол треуголь-
треугольника СА'В. Следовательно, /_А'СВ острый, а дополнительный
ему /_А"СВ тупой.
Правильный октаэдр
349. Пересечем октаэдр плоскостью, параллельной грани и
проходящей посередине между эгой гранью и противополож-
противоположной параллельной ей грянью. Эта плоскость разделит пополам
все шесть ребер АВ, AF, DF, DC, EC, ЕВ, соединяющие эти
грани (рис. 24d). В сечении, следовательно, получится шести-

350—351
СТЕРЕОМЕТРИЯ
223
угольник, все стороны которого равны половине ребра окта-
октаэдра. Углы между ними также равны (по 120°), тлк как сто-
стороны их параллельны сторона л равностороннего треугольника
FBC. Таким образом, шестиугольник GHKLMN правильный.
350. Куб и правильный октаэдр об-
обладают некоторой взаимностью. Цент-
Центры граней куба (рис. 250) могут быть
взяты за вершины правильного окта-
октаэдра, и обратно. У октаэдра столько
же граней, ребер и вершин, сколько
у куба, наоборот, вершин, ребер и
граней, а именно: 8, 12 и 6. Наиме-
Наименования граней у октаэдра такие же,
как наименования многогранных углов
при вершинах куба, и наоборот. Те
же точки на шаре могут быть при-	Рис- 249-
няты за вершины вписанного октаэдра,
которые суть точки касания граней описанного куба и обратно
(рис. 251). [Можно доказать, что для всякого многогранника
Рис. 250
Рис. 251.
(и неправильного) существует ему взаимный, подобно тому
как куб взаимен октаэдру.]
Правильные додекаэдр и икосаэдр
351. Возьмем по произволу одну из граней куба ABCD
(рис. 252) и проведем через ребра АВ и CD плоскости Р и Q, ко-
которые делали бы с гранью ABCD одинаковые углы <р, а через реб-
ребра ВС и AD плоскости R hS, которые делали бы с гранью ABCD
одинаковые углы ф, дополнительные к <р до 90° (т. е. <р настолько
же больше 4о°, насколько ф меньше). Над гр.:нью ABCD по-
получится, очевидно, «крыша», pe6pi AE, BE, CF и DF кото-
которой все одинаковы, «конек» же EF, в зависимости от величи-
величины угла <р, может быть той или иной длины. Увеличивая угол

224
РВШЕНИЯ
351
<Р (а следовательно, уменьшая дополнительный к нему до 90°
угол ф), непрерывно начиная от 45°, когда «конек» EF = 0
(см. задачу 328), мы можем получить, наконец, такой угол <р,
что EF = АЕ. Действительно, при та-
таком вращении плоскостей Р и Q и пло-
плоскостей R к S высота крыши очевидно
уменьшается, конек ее, очевидно, уве-
увеличивается, а следовательно, ребро АЕ
уменьшается. Конек увеличивается отО
до Ь, если Ъ — ребро куба, а ребро АЕ
уменьшается до половины АВ, т. е. до
—, т. е. будет такой угол <р между 45°
и 90°, при котором АЕ = EF. Если на
всех гранях куба построить крыши,
у которых углы <р и ф дополнительные
до 90 , и повернуть их коньками соответственно, то треуголь-
треугольный скат одной будет продолжением трапецеидального ската
соседней, и получится до-
додекаэдр (двенадцатигранник),
ограниченный пятиугольника-
пятиугольниками, но, вообще говоря, непра-
Рис. 252.
Ь-а
Рис. 253.
Рис. 254.
вильными Если же за угол ф взять тот, при котором EF = АЕ,
то все эти пятиугольники будут равносторонними (рис. 252).
Теперь надо показать, что кроме того они будут одновре-
одновременно и равноугольными. Для этого опустим (рис. 253) из
одной из двух вершин крыши перпендикуляр h на ту грань
куба, на которой крыша стоит, и по скатам крыши перпенди-
перпендикуляры « и р на стороны этого квадрата. Тогда вследствие
того, что углы, которые делают эти два перпендикуляра с
плоскостью квадрата, дополнительные до 90°, выходит, что,
если «расправить» треугольники а/г и $h в одну плоскость,
то а и C будут катетами прямоугольного треугольника
(рис. 254), высота которого h делит гипотенузу на часты
b Ъ — а	, 2Ь — а Ъ ,„
— и 	. Мы имеем, следовательно, аг = —-— • —; Ла =
2	2	^

352
СТЕРЕОМЕТРИЯ
225
—-— • —. С другой стороны, из треугольника ka\ мы имеем
а2 = Л2 -J- >.2 или так как
Ъ-а
> — я\2
или, после сокращений,
Ь2 — ab — а1 = О,
а из треугольника ах мы имеем
v-2
0)
ИЛИ
Х =
а2 +
36' +
/ft + a\
V 2 /
яй -(- аг
Принимая во внимание A), мы имеем х2 —	= Ь2, т. е.
4
х = Ь. Приняв, далее, во внимание равнобедренносгь треуголь-
треугольников, составленных парами смежных сторон рассматриваемой
пятиугольной грани (рис. 255), и равнобедренность треуголь-
треугольника, составленного диагоналями Ь и х, мы получим равенство
всех его углов.
352. Рассмотрим две противолежащие вершины додекаэдра
А и В (рис. 256). В каждой из этих двух вершин сходится
н
Рис. 255.
Рис. 256.
по три пятиугольные грани; остается еще шесть граней, ко-
которые образуют «венчик» граней, соединяющий эти две «ша-
«шапочки». Ребра, по которым смежны эти грани венчика, суть
ОС", D'D", E'E", F'F", G'G", H'H"; эти ребра соединяют
между собою шапочки. Рассмотрим верхние концы этих ребер
С, D', Е', F', G', Н'. Все эти шесть точек лежат в одной
плоскости, так как ребра CD' и G'H', например, при продол-
продолжении пересекаются в силу того, что все пять граней, смеж-
15 Делоне и Житомирски»

226
РЕШЕНИЯ
353—355
Рис. 257.
ные с некоторой гранью, делают с ней одинаковые углы, и
следовательно, при продолжении образуют над ней правиль-
правильную пятиугольную пирамиду. Соединив середины рассмотрен-
рассмотренных ребер венчика, мы получаем шестиугольник CDEFGH,
все вершины которого лежат в одной плоскости, параллель-
параллельной плоскости C'D'EF'G'H', так как стороны его, как средние
линии трапеций, параллельны сторонам шестиугольника
C'D'E'F'G'H''. Стороны этого шестиугольника равны, так как
трапеции равны. Углы
тоже равны; так напри-
например, углы при С и. Н'
равны, как дополни-
дополнительные до 180° к углам
при основании в равно-
равнобедренном треуголь-
треугольнике С'Н'К- Углы при
С ъН равны углам при
С и Н' как углы с || сто-
сторонами. Шестиуголь-
Рис. 258.	ник CDEFGH, следо-
следовательно, правильный.
353.	Подобно тому как куб и правильный октаэдр много-
многогранники взаимные, правильный додекаэдр и правильный
икосаэдр также взаимные многогранники. Число граней, ребер
и вершин правильного додекаэдра равны 12, 30, 20; таковы
же числа вершин, ребер и граней правильного додекаэдра.
Наименование многогранных углов при вершинах правильного
икосаэдра таково же, как наименование граней правильного
додекаэдра, и обратно. Свойство описанного и вписанного
шара, указанное для куба и октаэдра, тут тоже имеет место
(рис. 257 и 258).
354.	Срежем пятигранные углы правильного икосаэдра пло-
плоскостями, проходящими через центры граней, сходящихся в
каждом из этих углов; получится правильный додекаэдр (см.
задачу 353); срежем «крыши» правильного додекаэдра (рассмот-
(рассмотренные в задаче 351); получится куб; срежем четыре трех-
трехгранные пирамиды,основания которых проходят через верши-
вершины, находящиеся на концах трех ребер, сходящихся в одной
вершине (см. задачу 333); получится правильный тетраэдр.
Задачи на растяжение и сдвиги в пространстве
355.	Пусть АВ—некоторая прямая, причем А— та точка,
где она пересекается с плоскостью Р. Рассмотрим произволь-
произвольную течку С прямой А В. Пусть Вх и Сх — проекции точек В
и С на плоскость Р, а В' и С — те точки, куда точки В я С

356—362
СТЕРЕОМЕТРИЯ
227
перейдут после сжатия пространства к плоскости Р с коэффи-
коэффициентом к (рис. 259). Очевидно, что точка С останется лежа-
лежащей на прямой АВ', так как
С'СХ : CQ = B'Bt: BBX = к.
356.	Следует из предыдущей.
357.	Следует из подобия треугольников.
358.	Так как, если бы они пересекались, то пересекались
бы и до аффинитета.
359.	Покажем, что это верно для треугольной прямой
призмы, основание которой лежит в плоскости Р. Объем V
такой призмы равен:
где S—площадь ее основания, a hx,h^,hs — длины ее ребер
(сумма объемов трех пирамид,
основанием которых является
основание призмы, а вершина-
вершинами — вершины верхнего осно-
основания призмы). Но после сжа-
сжатия основание не изменяется,
а высоты заменяются высота-
высотами 1цк, h2f>, h3k, т. е. объем
V заменяется объемом V-к.
Всякий многогранник можно
составить сложением и вычитанием из таких призм. Объем
всякого многогранника, после сжатия, помножится, следова-
следовательно, на к.
От многогранников можно перейти к любым телам, при-
применяя способ пределов.
360.	Из подобия треугольников.
361.	Формула
Рис. 259.
годится и для косой призмы, если через h обозначены высо-
высоты пирамид. Но если основание 5 лежит в плоскости Р, то
при сдвиге ни оно, ни высоты не меняются.
362. Сделаем сдвиг пространства параллельно одной из сто-
сторон основания, так чтобы плоскость Р, неподвижная при
сдвиге, проходила через эту сторону J. к основанию, такой,
чтобы основание сделалось равнобедренным треугольником.
Затем сделаем сжатие (или растяжение от этой плоскости Р)
такое, чтобы основание сделалось равносторонним треуголь-
треугольником. После этого сделаем сдвиг по отношению к плоскости
основания, как к неподвижной, такой, чтобы проекция вер-
15*

228	решения	363—368
шины оказалась в центре основания, и, наконец, сжатие (или
растяжение) по отношению к плоскости основания, такое, что-
чтобы боковые ребра сделались равны сторонам основания.
363.	Подобно тому, как в предыдущей задаче, можно сдви-
сдвигами и растяжениями тетраэдр, ребрами которого являются
три ребра параллелепипеда, исходящие из одной вершины,
превратить в такой, у которого эти ребра взаимно перпенди-
перпендикулярны и равны между собою. После этого параллелепипед
станет кубом.
Цилиндр и конус
364.	Пусть прямая имеет три точки А, В, С, общие с цилин-
цилиндрической поверхностью. Спроектируем на плоскость, перпенди-
перпендикулярную к образующим. Цилиндрическая поверхность спро-
ектируется в виде окружности, прямая, если она не параллель-
параллельна образующей, спроектируется в виде прямой, которая будет
иметь с этой окружностью три (разные) общие точки,- что
невозможно. Прямая эта должна быть, следовательно, || обра-
образующей (тогда она спроектируется в одну точку), но, имея
с поверхностью общую точку, т. е. с одной из ее образующих,
она должна совпадать с этой образующей.
Доказательство для конической поверхности совершенно
аналогично, но проектировать надо на секущую плоскость J_
к оси конуса лучами, исходящими из вершины конуса.
365.	Пусть А— общая точка двух цилиндрических поверх-
поверхностей с II образующими, через А, следовательно, проходят как
образующая первой, так и образующая второй, которые || и,
следовательно,- совпадают, т. е. поверхности пересекаются по
целым образующим. Чтобы узнать, по скольким, надо спро-
спроектировать || образующим на плоскость Р, перпендикулярную
к образующим. Все сведется на пересечение окружностей.
Для двух конусов с общими вершинами рассуждение ана-
аналогично.
366. Проведем через точку А плоскость Р, перпендикулярную
к образующим цилиндра. В плоскости Р получится окружность.
Проведем в плоскости Р две касательные из точки А к этой
окружности; пусть точки касания суть Вх и В.*. Плоскости
Q1 и Qo, проходящие через точку А и через те образующие
В1С1 и ~62С2 цилиндра, на которых лежат точки В± и В.2, и
будут искомыми касательными плоскостями. Для конуса плос-
плоскость Р надо проводить _]_ оси конуса.
367.	За ось конуса надо, очевидно, принять ту прямую,
о которой говорится в задаче 320.
368.	За ось конуса надо, очевидно, принять ту прямую,
о которой говорится в задаче 319.

369
СТЕРЕОМЕТРИЯ
229
369. Пусть задан четырехгранный угол OABCD, вокруг ко-
которого может быть описан конус вращения (т. е. такой, четыре
ребра которого суть четыре образующие некоторого конуса
вращения) (рис. 260, 261). Построим к этому конусу касатель-
касательные плоскости OA'D'OA'B', OB'C, OC'D', касающиеся его по
образующим О А, ОВ, ОС, OD. Двугранные углы, образованные
плоскостью ОАВ
с плоскостями ОАА'
и ОБА', равны, так
как пирамиды с ос-
новациями О'АА'
и О'ВА', и верши-
ной О равны (снимет-
ричны относительно
плоскости 00' А). Мы
предполагаем, что
ABCD — круговое
сечение конической
Рис. 260.
Рис. 261.
поверхности враще-
вращения, О' —его центр,
т. е. 00' — ось конуса, a OA=OB=OC=OD. Для того
чтобы проще было рассуждать, пересечем все плоскостью
ABCD и будем соответственные двугранные углы обозначать
•так же, как плоские углы, получающиеся в результате их се-
сечения плоскостью ABCD. Итак, мы имеем относительно дву-
двугранных углов / 1 = / Г, аналогично получим /2=/_2',
,/3 = </3', Z4 = Z4r. Двугранные углы Г, C, 2 имеют общее
ребро ОВ и представляют в сумме весь угол по одну сторону
от плоскости ОА'В', т. е. 180°. Мы имеем таким образом
все относительно двугранных углов; отсюда мы получаем
или, принимая во внимание, что
мы получаем
Суммы противоположных двугранных углов четырехгранного
угла, если этот четырехгранный угол может быть вписан в
конус вращения, должны быть, следовательно, одинаковы.
Можно показать, что это условие не только необходимо, но

230
РЕШЕНИЯ
370—371
Рис. 262.
и достаточно для вписуемости четырехгранного угла в конус
вращения.
У четырехугольника, вписанного в круг, сумма противопо-
противоположных углов равна Id; здесь этого нет. Действительно,
плоские углы а, {}, у, & не суть линейные
углы двугранных углов а, {}, у, 8, а мень-
меньше их, но сумма плоских углов oc-f-y че-
четырехугольника ABCD, вписанного в круг,
равна 2d, а следовательно, сумма двугран-
двугранных углов a -j- у четырехгранного угла,
вписанного в конус вращения, больше 2с?.
370. Из подобия прямоугольных тре-
треугольников ABC и А'В'С видно (рис. 262),
что все перпендикуляры к диаметру DE в
одно и то же число раз больше у линии,
получаемой в сечении, чем у окружности
с диаметром DE. Следовательно, эта линия
есть равномерное растяжение окружности
от прямой (в данном случае, например, от диаметра ее DE).
С другой стороны, если эту линию во столько же раз растянуть
от перпендикулярного этому диаметра, то получится большая
окружность с радиусом АС, так как, как легко видеть, два после-
последовательных одинаковых растяжения от двух взаимно перпен-
перпендикулярных прямых просто удаляют все точки плоскости
равномерно в это число раз во Все стороны от точки пересечения
этих прямых. Следовательно, обратно: можно рассматривать
нашу линию как равномерное сжатие к прямой этой большой
окружности. (Равномерное растяжение или
сжатие окружности к прямой называется
эллипсом.)
371. Впишем в цилиндр два одинако-
одинаковых шара (рис. 263), касающиеся цилиндра
по окружностям ab и а'Ь' и касающиеся
секущей плоскости Р один снизу в точке
F, а другой сверху в точке F'. Возьмем
любую точку М на линии, получаемой в
сечении, соединим ее по плоскости Р
отрезками с точками F и F' и проведем
через нее образующую цилиндра до пере-
пересечения в точках Л и Л' с окружностями
ab и а'Ь'. Ввиду того, что две касатель-
касательные, проведенные из одной и той же точки к одному и
тому же шару, одинаковы, мы имеем MF=MA и аналогич-
аналогично MF'=MA' и, следовательно, складывая эти равенства,
MF-\-MF' = MA -f- МА' — АА', т. е. образующей прямого
кругового цилиндра с нижним основанием ab и верхним
Рис. 263.

372—374
СТЕРЕОМЕТРИЯ
231
Рис. 264.
a'b', т. е. постоянной величине, независимо от выбора точки
М на линии, получаемой в сечении. (Точки F и F' называ-
называются фокусами эллипса.)
372.	Впишем в конус два шара (рис. 264), из которых один
касался бы поверхности конуса по окружности ab и секущей
плоскости Р снизу в точке F, а другой —
поверхности конуса по окружности a'b' и
секущей плоскости сверху в точке F'.
Возьмем любую точку М на линии, по-
получаемой в сечении, соединим ее по пло-
плоскости Р отрезками с точками F и F' и
проведем через нее образующую конуса
до пересечения в точках А я А' с окруж-
окружностями ab и a'b'. Как в предыдущей за-
задаче, получаем MF -\~ MF' = AA', где
АА'— образующая прямого кругового ко-
конуса с нижним основанием ab и верхним a'b', т. е. величина
постоянная. Таким образом сечение конуса есть эллипс, т. е.
равномерное растяжение круга от прямой.
373.	Можно рассматривать косой круговой конус (рис. 265)
как результат сдвига некоторого прямого кругового конуса
параллельно его основанию. Рассмотрим се-
сечение ab косого конуса плоскостью, на-
наклоненною в направлении сдвига и делаю-
делающею одинаковые углы с образующими, ле-
лежащими в плоскости 00'АВ. Оно получает-
получается при сдвиге, очевидно, из некоторого
сечения a'b' прямого конуса сжатием его
к его диаметру c'd', растяжением которого
сечение a'b' получается из окружности. Сле-
Следовательно, и сечение ab есть тоже эллипс.
Вершина О косого конуса лежит в силу вы-
выбора наклона сечения ab на перпендикуля-
перпендикуляре, восставленном в центре этого эллипса.
Так как диаметр cd является осью симмет-
симметрии этого эллипса, то плоскость Ocd является плоскостью
симметрии косого конуса. Но в таком случае, кроме системы
круговых сечений, параллельных основанию, он имеет еще
другую их систему, к этой плоскости симметричных.
Шар
374.	Пусть О центр круга, описанного вокруг треуголь-
треугольника ABC; искомое геометрическое место есть перпенди-
перпендикуляр к плоскости этого треугольника, восставленный в
точке О.
Рис. 265.

232	решения	375—376
375.	Точки, общие сферам / и //, лежат на окружности, по
которой эти сферы пересекаются. Эта окружность пересекает,
вообще говоря, третью сферу /// в двух точках, т. е. точзк,
общих всем трем сферам, две. Может, однако, быть, что эта
окружность только касается сферы ///, или сферы / и //, только
касаются в одной точке, но эта точка лежит как раз на сфере.
В этих двух случаях общая точка у сфер /, // и /// только
одна. Если же сферы / и // вовсе не имеют общих точек;
или же окружность, по которой они пересекаются, не имеет
общих точек со сферой///, или точка, по которой они касаются,
не лежит на сфере ///, то точек, общих всем трем сферам,
нет. Сферы же могут, тем не менее, каждая пересекаться
с двумя другими.
Чтобы найти построением точки, общие всем трем сферам,
проведем плоскость Р через центры сфер и опишем из этих
центров по плоскости Р три окружности радиусами этих сфер.
Проведем через хорды, общие этим кругам, плоскости,
перпендикулярные к плоскости Р, т. е. JL к линиям центров сфер.
Плоскости эти будут плоскостями окружностей пересечения
сфер. Искомые точки должны лежать на всех трех этих
плоскостях, т. е. если есть точки, общие этим трем сферам,
то плоскости эти пересекаются по одной прямой, перпендику-
перпендикулярной плоскости Р. Пусть а — эта прямая. Проведем через
центр одной из сфер, например /, и эту прямую пло-
плоскость Q. Искомые точки лежат на пересечении прямой а с
окружностью, центр которой лежит в центре сферы /, а радиус
равен радиусу этой сферы.
376.	1) Пусть R—заданный радиус, А и В — заданные точ-
точки, Р—заданная плоскость. Искомый центр есть точка, общая
двум сферам радиуса R, с центрами в точках А и В и той или
другой из плоскостей, параллельных плоскости Р, проходящих
по одну или другую сторону от нее на расстоянии R. Так
как две сферы пересекаются по окружности, а окружность
может пересекать и ту и другую из этих плоскостей, каждую
в двух точках, то может быть четыре решения, но может
быть и меньше — три, два, одно или ни одного. Чтобы
найти центр О построением, т. е. проведением прямых и
плоскостей в пространстве и построениями в этих плоско-
плоскостях циркулем и линейкой, надо провести прямую АВ
и через нее две плоскости, в каждой из которых восставить к
прямой АВ в середине С отрезка АВ перпендикуляр. Плоскость
Q, проходящая через оба эти перпендикуляра, будет геомет-
геометрическим местом точек, равноудаленных от А и В. Аналогично
построим плоскости Р' и Р" || Р, проходящие на расстоянии
R от нее. Пусть, например, Р' пересекается с Q по прямой а';
эта прямая есть геометрическое место точек, равноудаленных

377
СТЕРЕОМЕТРИЯ
233
от Л и Б и удаленных на R от плоскости Р (и лежащих по
ту сторону ее, где лежит Р'). О лежит на а'. Проведем через
А к а' плоскость и в этой плоскости окружность радиусом R
из центра А. Точка пересечения этой окружности с прямой
а' и аналогично полученные точки на прямой а" пересечения
плоскости Q с Р" и будут искомыми центрами.
Вопросы 2), 3), 4), 5), 6) этой задачи решаются аналогично.
377. Пусть имеются две сферы (рис. 266), и плоскость Р
касается их обоих. Радиусы OD и О'D' перпендикулярны к
плоскости Р, следовательно || меж-
между собою. Прямая DD' лежит, ~~
следовательно, с прямой 00' в од-
одной плоскости (перпендикулярной
к плоскости Р). Пусть С — точка
пересечения этих прямых. Если
провести через OD, O'D' и С пло-
плоскость, то она пересечет каждую из
сфер по большому кругу и пря-
прямая DD'C будет общей внешней касательной к этим двум кру-
кругам. Если эти два круга и прямую CD'D вращать вокруг линии
центров 00'С, то круги дадут наши сферы, а прямая CD'D опи-
опишет общий внешний касательный конус. Для того, чтобы по-
получить точку С, достаточно, следовательно, пересечь обе
Рис. 266.
Рис. 267.
сферы произвольной плоскостью, проходящей через их
центры О и С и построить внешние касательные. Точка их
пересечения одной из них с линией центров и будет точка С.
Для построения плоскости Р (рис. 267), касательной к трем
заданным сферам 0,0',О", достаточно, следовательно, провести
плоскость Q через их центры, найти в этой плоскости точки
С" и С, соответствующие парам сфер ОО' и ОО", и тогда

234	решения	378—381
плоскость Р должна проходить через точки С и С" (причем
точка С, соответствующая сферам О' и О", должна, следова-
следовательно лежать на прямой С'С", так как она лежит и в пло-
плоскости Р и в плоскости Q (см. задачу 392). Проведем затем
через точки С, О", О плоскость J_к плоскости Р, и в этой
плоскости внешнюю касательную C'D"D к кругам, описанным
на этой плоскости из центров О" и О радиусами, равными
радиусам сфер О" и О. Плоскость, проведенная через 'пря-
'прямые С'С" и CD, и есть плоскость Р. Другая общая касатель-
касательная плоскость Р' получится, если исходить от второй внешней
касательной к указанным кругам.
378.	Восставим в центре О' вращающейся окружности
перпендикуляр к плоскости этой окружности; он пересечет
ось вращения а в некоторой точке О, так как точка О' лежит
на проекции оси а на плоскости окружности. Опишем из
точки О сферу таким радиусом, чтобы она прошла хоть через
одну точку вращаемой окружности; тогда и вся вращаемая
окружность будет лежать на поверхности этой сферы, так как
плоскость ее перпендикулярна к радиусу сферы, проходящей
через ее центр. Шар есть тело вращения относительно любой
оси, проходящей через его центр, т. е. и относительно оси а.
Но если какую угодно линию, начерченную на поверхности
вращения, вращать вокруг оси этой поверхности, то она будет
оставаться в этой поверхности, что непосредственно следует
из определения поверхности вращения. Наша окружность
будет, следовательно, описывать часть поверхности нашего
шара, как легко видеть — шаровой пояс..
379.	Пусть центр заданной сферы—О, центр сечения—О',
заданная точка—А. Отрезок соединяющий центр сферы О с
центром сечения О', перпендикулярен к плоскости сечения,
угол ОО'А, следовательно, прямой. Точка О' описывает, сле-
следовательно, часть геометрического места вершин прямых углов,
опирающихся на отрезок ОА, т. е. часть сферической поверх-
поверхности, для которой ОА—диаметр, а именно, как легко видеть,
ту часть этой сферы, которая заключена внутри заданной сферы.
380.	Получается, очевидно, сфера, для которой отрезок, •
соединяющий обе заданные точки, есть диаметр.
381.	Заставим один конец А' отрезка А'В' (рис. 268), равного
и параллельного заданному отрезку АВ, описать всю поверх-
поверхность одной из заданных сфер, например сферы О; тогда дру-
другой его конец В' опишет такую же сферу О", получаемую из
сферы О передвижением ее параллельно АВ и на величину АВ.
Затем заставим отрезок А'В' скользить по сфере О концом В';
тогда его конец А опишет такую же сферу О"', лежащую по дру-
гуюсторонуот сферы О. Одна или обе эти сферы могут пересечься
со сферой О' по некоторой окружности каждая. Искомым местом

382
СТЕРЕОМЕТРИЯ
235
концов отрезка будут эти окружности, а геометрическим ме-
местом самого отрезка — боковая поверхность цилиндра, для
которою эти окружности являются окружностями основания.
Рис. 268.
382. Пусть ВИВ" — заданный в пространстве треугольник
(рис. 269). Пусть мы хотим, чтобы вершина равного ему и
параллельного треуголь-
треугольника, соответственная В,
лежала на сфере О, а со-
соответственные В' и В"—
на сферах О' и О". Пусть
С — окружность, лежа-
лежащая на сфере О, которая
(см. пред. задачу) есть
геометрическое место
концов А отрезка АА',
равного и и ВВ', а окруж-
окружность С" — соответствен-
соответственная окружность для от-
отрезка АА", равного и
И ВВ". Эти окружности
могут пересекаться в
двух точках, и тогда есть
два треугольника, удов-
удовлетворяющие требова-
требованиям задачи, как изображено на рис. 237; если они только
касаются — один треугольник. Если вовсе не имеют общих точек,
то нет решений. Кроме того, может быть, что сфера О" преды-
Рис. 269.

236
РЕШЕНИЯ
383-384
дущей задачи только коснется сферы О' или соответственно —
О", тогда окружности С или С" превратятся в точки, и может
быть не больше одного решения и т. д.
383. Легко видеть, что как раз те «ямки», которые не заняты
шарами верхнего слоя (заштрихованными) на первом рисунке,
заняты на втором, и наоборот (рис.270—271). Это и есть два
Рис. 270.
Рис. 271.
различных возможных наложения второго слоя на первый так,
чтобы шары второго пришлись над „ямками" первого. Оче-
Очевидно, что других таких наложений быть не может, так как
если положить один шар верхнего слоя, то тем самым уже
предопределено положение всех других шаров верхнего слоя,
а первый шар можно наложить либо над одной из ямок, заня-
занятых на первом, либо над одной из занятых на втором рисунке.
384. Рассмотрим плоскости Р и Р', в которых лежат центры
шаров двух соседних слоев. Если мы вырежем этими двумя
плоскостями из всех простран-
пространства «пластину», то ясно, что рас-
расположение полушаров в пластине,
вырезанной плоскостью Р' и со-
соседней еще кверху такой плос-
плоскостью Р", будет совершенно
такое же, как в пластине РР',
так что обе эти пластины можно,
параллельно перенеся и в случае
необходимости повернув на 180°,
совместить. Достаточно, следова-
следовательно, найти отношение части,
занятой шарами, к незанятой для
одной такой пластины. Рассмотрим (рис. 272) четыре такие шара,
что каждый касается трех остальных; центры их О ABC обра-
образуют, правильный тетраэдр. „Достроим" этот правильный тетра-
тетраэдр до параллелепипеда ОАВ'С, ВС'О'А' так, как указано в задаче
337. Легко видеть, что точка В' будет центром шара нижнего
Рис. 272.

385
СТЕРЕОМЕТРИЯ
237
слоя ОАС, а точки А', С, О' — центрами шаров сверху нало-
наложенного на него слоя, предопределенного способом наложения
шара В. Легко также видеть, что вся пластина, вырезанная
плоскостями ОАС и О'А'С, будет составлена из равно таких
же параллелепипедов и с равно так же входящими в них ша-
шарами. Достаточно, следовательно, подсчитать только, какую
часть этого одного параллелепипеда занимают шары. Для этого
заметим, что если бы окружить точку О восемью такими парал-
параллелепипедами, то оказалось бы, что куски шаров, входящих
в параллелепипед ОАВСО'А'В'С, как раз все вместе состав-
составляют один шар. Пусть радиус шара есть г; тогда ребро тетра-
тетраэдра ОАВС есть 2г и объем параллелепипеда ОАВСО'А'В'С
равен 6	— г3 (см. задачу 436), а объем одного шара — w3,
т. е. отношение объема, занятого шарами, к объему, не заня-
занятому, равно
7V~2	/ .
385. Пусть на слой Рг положен слой Р. Хотя слой Р и можно
класть на слой Рх или в одни, или в другие ямки (см. зада-
Рис. 273.
Рис. 274.
чу 383), т. е. двумя разными способами, однако пока слоя
только два, оба расположения совершенно подобны, так что
одну систему обоих слоев шариков Рх и Р можно совместить с
другой, повернув на 180° и параллельно перенеся в пространстве.
Итак, пусть как-нибудь наложен слой Р на слой Рх. Будем на
слой Р накладывать третий слой Р'; теперь уже не все равно, как
класть: можно класть двумя и только двумя способами (см.
задачу 383), и эти способы уже дадут существенно разные распо-
расположения:!) можно класть шарики слоя Р' в те ямки, которые
снизу не заняты шариками слоя Pv 2) можно класть шарики
слоя Р' в те «ямки», которые снизу заняты шариками слоя Рх.
Никаких других способов, очевидно, нет. И в том и в другом
случае каждого шарика слоя Р касается всего 12 шариков, а

238
РЕШЕНИЯ
386—367
именно 6 шариков самого слоя Р, 3 шарика слоя Рх и 3 шарика
слоя Р'. Обратимся к рисункам обоих случаев (рис. 273 и 274).
На каждом левом рисунке нарисован шарик и 12 шариков,
его облегающих, а на каждом правом — пространственная схема
из восьми заштрихованных треугольников, все вершины кото-
которых представляют центры 12 шариков, прилегающих к обле-
облегаемому среднему шарику. Все эти 12 шариков касаются
среднего, касания же их между собою происходят так, как
связывают их центры стороны нарисованных заштрихованных
треугольников.
386.	Если всякий раз следующий слой класть по отношению
к двум предыдущим первым способом, то все шарики системы
будут окружены 12-ю прилегающими первым способом. Если
всякий следующий слой класть по отношению к двум преды-
предыдущим вторым способом, то и все шарики будут окружены
вторым способом. Если же путать оба способа наложения после-
последующих слоев, то не все шарики, будут окружены одинаково.
387.	Всякое сечение исследуемой поверхности плоскостью
есть круг или прямая (круг с бесконечно большим радиусом),
или точка, или же по крайней мере состоит из кругов. Пере-
Пересечем поверхность плоскостью, и пусть—О одна из окружностей,
при этом получаемых. Пересечем ее
перпендикулярной плоскостью, пере-
пересекающей окружность в точках А
и В; если поверхность наша не есть,
та самая плоскость, в которой лежит
круг О, то в сечении получится опять
окружность Р с центром О'. Восста-
Восставим в центрах этих окружностей пер-
перпендикуляры к их плоскости; они пе-
пересекутся в некоторой точке С. Опи-
Опишем из этой точки С, как из центра,
шар радиусом С А. Обе окружности О
и О' будут его малыми (или может
Рис. 275.
быть большими) кругами. Плоскость ОСО' пересечет нашу по-
поверхность по кругу N, плоскость, ей перпендикулярная, про-
проходящая через диаметр ВСЕ, по кругу М. Если пересекать по-
поверхность плоскостями J_ к CD, будут получаться круги, на-
например KFG, геометрическое место которых будет поверх-
поверхность шара С. Никакая точка S, не принадлежащая этому
шару, не принадлежит нашей поверхности, так как иначе любая
прямая, пцрходящая через точку 5 и пересекающая поверх-
поверхность нашего шара в двух точках, как проходящая через три
точки нашей поверхности, должна была бы вся в ней лежать,
и если продолжить это рассуждение, то вышло бы, что всякая
точка пространства принадлежит нашей поверхности (рис. 275).

388—390
СТЕРЕОМЕТРИЯ
239
Рис. 276.
Рис. 277.
388.	Действительно, углы 8, у, которые делает луч SE с ка-
касательной плоскостью Р' и с плоскостью проекции Р, одинаковы,
так как каждый из них (левая половина рис. 276 и 277) изме-
измеряется соответственно — (SD + DE) и — (SC-\~DE) и сле-
следовательно, если провести через него две плоскости, то углы,
высекаемые ими на
плоскостях Р' и Р,
одинаковы.
389.	Возьмем пло-
плоскость проекции Р
проходящею через
центр сферы. Так
как от большего или
меньшего ее удале-
удаления от точки 5 будет
только зависеть величина проекций, но не их форма, они будут по-
подобны. Если ЛБ есть окружность на поверхности шара, а А'В'—ее
проекция из точки 5 на плоскость Р (правая половина рис. 276 и
277), то угол ос измеряется дугой — (SC -f- CB), a угол р—дугой
— (SD -f CB), но SC = SD = 90°, и следовательно, а = p.
Теперь можно применить доказанное в задаче 373 свойство
косого кругового конуса, которым здесь является конус с вер-
вершиной S и основанием АВ, и получается, что А'В' — тоже
круговое его сечение, но из другой системы круговых сечений.
Задачи, в которых соображения стереометрии применяются
для решения вопросов планиметрии
390.	Пусть точки К, L, М лежат в плоскости Р чертежа.
Представим себе, что точка О лежит над плоскостью Р так,
что проекция ее получается в О. Получается трехгранный
угол O'KLM. Проведем через точки А, В, С плоскости Р
(рис. 278) перпендикуляры до пересечения с гранями трехгран-
трехгранного угла в точках А', В', С; проекции этих точек на плос-
плоскость Р суть А, В, С. Пересечем трехгранный угол пло-
плоскостью Q, проходящей через точки Л', Б', С пространства.
Эта плоскость пересечет трехгранный угол по треугольнику D'
Е' F'. Проекция этого треугольника на плоскость Р рисунка
дает искомый треугольник DEF, вершины которого лежат
на полупрямых OK, OL, ОМ, а стороны которого проходят
через точки Л, Б, С. Очевидно, что другого такого треуголь-
треугольника быть не может, так как, если бы был другой DEF, то,

240
РЕШЕНИЯ
391—392
проведя через его стороны плоскости j. к Р, мы получили бы
пересечения с гранями трехгранного угла по прямым, прохо-
проходящим через те же три точки А'В'С и пересекающимся в не-
некоторых точках D',E', F' с ребрами,
т. е. плоскость Q, проходящая чераз
эти прямые, была бы второй секущей
плоскостью, проходящей через те же
три точки пространства А', В', С, что
невозможно.
391. Представим себе (подобно
тому, как это подробнее сказано в
решении предыдущей задачи), что ри-
рисунок представляет проекцию следую-
следующей пространственной фигуры :ОАВС—
тетраэдр, А'В'С — секущая плоскость
(рис. 279). Точки К, L, М суть тогда
проекции точек пересечения боковых
граней тетраэдра с прямой, по кото-
которой пересекается основание его (продолжение основания) с
секущей плоскостью А'В'С. Эти три точки, следовательно,
лежат на одной прямой, а именно на проекции на плоскость
чертежа этой пространственной прямой.
392. Построим на каждом круге, как на экваторе, сферу.
Вокруг каждой пары сфер опишем внешний касательный конус.
м
Рис. 278.
Рис. 279.
Рис. 280.
Точки К, L, М пересечения внешних касательных к кругам
будут вершинами этих конусов (рис. 280). Проведем две пло-
плоскости Р и Q, из которых первая сверху, вторая снизу
касается всех трех сфер; эти плоскости каждого из трех кону-
конусов касаются по образующей (см. задачу 377), т. е. проходят
через их вершины, т. е. точки К, L, М. Все три точки К, L, М

393-394
СТЕРЕОМЕТРИЯ
241
лежат, следовательно, на прямой пересечения этих двух каса-
касательных плоскостей.
393.	Построим на каждом круге, как на экваторе, сферу.
Проекция А обеих точек, общих всем этим трем сферам, на
плоскость центров сфер есть точка, через которую проходят
все три их общие хорды, которые являются проекциями на
плоскость, проходящую через центры сфер, плоскостей, про-
проходящих через общие окружности сфер. Эти плоскости, как
известно, х к линиям центров, а следовательно, и к плоскости
центров (рис. 280 и 281).
394.	Пусть задан любой неправильный шестиугольник, опи-
описанный вокруг круга. Обозначим точки касания номерами /, 2,
3, 4, 5, 6; этими же номерами будем
обозначать и соответственные его сто-
стороны (рис. 282 и 283).
Рассмотрим следующую вспомогатель-
вспомогательную пространственную фигуру. Выведем
из плоскости чертежа в пространство
каждую из сторон нашего шестиугольни-
шестиугольника, повернув его в пространстве вокруг
радиуса круга, проведенного в точку ее
касания, на одинаковые углы к плоско-
плоскости чертежа (например на 45°), но так,
чтобы у всех нечетных сторон передняя
часть (указанная на чертеже стрелкой)
была поднята кверху от плоскости чер-
чертежа, а задняя, следовательно, опущена под плоскость чер-
чертежа, а у всех четных наоборот. Обозначим прямые, получае-
получаемые при продолжении этих повернутых в пространство сторон,
Рис. 281.
Рис. 283.
через /, 2, 3, 4, 5, 6. Докажем сначала, что каждая такая
нечетная прямая пересекается с каждой четной в пространстве
(а не скрещивается). Это почти очевидно; действительно,
16 Делоне и Житомирский

242	решения	395—ЗЭ7
например / и 2 симметрично расположены в пространстве по
отношению к плоскости, проходящей через биссектрису угла
между радиусами, проведенными в точке / и 2, и перпенди-
перпендикулярной к плоскости круга, а следовательно, в какой точке
пересекает эту плоскость прямая /, в той же прямая 2, т. е.
прямые 1 и 2 пересекаются. .Аналогично пересекаются / и 4,
и т. д. Таким образом прямые 1, 2, 3, 4, 5, 6 образуют прост-
пространственный (т. е. стороны которого не лежат в одной пло-
плоскости) шестиугольник А' В' С D' E F'. Заданный плоский
шестиугольник ABCDEF есть, очевидно, проекция этого про-
пространственного шестиугольника. Диагонали, соединяющие про-
противоположные вершины шестиугольника А'В'СD'E'F', оче-
очевидно, в пространстве попарно пересекаются; например В'Е'
и A'D' потому пересекаются, что прямые / и 4 разной четно-
четности, и, следовательно, как было доказано, пересекаются, т. е.
лежат в одной плоскости; но тогда в этой же плоскости лежат
и прямые В'Е' и A'D'; но проекции их BE и AD пересекаются,
а следовательно, и сами они пересекаются. Итак, все три диа-
диагонали A'D', В'Е', СF' попарно пересекаются в пространстве.
Но в таком случае они или лежат в одной плоскости, или
пересекаются все три в одной точке (см. задачу 314). Однако
лежать в одной плоскости они не могут, так как тогда и все
шесть точек А', В', С, D', E', F' лежали бы в одной плоско-
плоскости (этой же). Но в той же плоскости тогда лежали бы и
точки /, 2, 3, 4, 5, 6, т. е. это была бы плоскость чертежа, что
противоречит тому, что прямые /, 2, 3, 4, 5, 6 делают некото-
некоторый угол с плоскостью чертежа. Диагонали A'D', В'Е', СF'
пересекаются в пространстве, следовательно, в одной точке;
значит и их проекции AD, BE, CF тоже пересекаются все три
в одной точке.
395.	Доказательство теоремы Паскаля предоставляем чита-
читателю.
ЗАДАЧИ НА ВЫЧИСЛЕНИЯ
Перпендикуляры и наклонные
396.	Мы имеем (рис. 284):
= 1 А
CD = Va? — /г2; BD = 1 А?2 + - (с2 — й2);
BE =
397. Мы имеем (рис. 285):
AD = Va?^?; CD = ]/сг —Л2; BD = V^^

398—400
СТЕРЕОМЕТРИЯ
243
AD2 + CD2= BD\
но
т. е.
откуда
h = yf c2 + c2 — b2.
398. Из того, что сама точка М равноудалена от вершин
треугольника, следует, что и ее проекция О тоже равноуда-
о
Рис. 284.
Рис. 285.
Рис. 286.
лена от вершин треугольника, так как основания равных на-
наклонных равноудалены от основания перпендикуляра (рис. 286),
О есть, следовательно, центр кру-
га, описанного вокруг заданного
прямоугольного треугольника,
т. е. середина гипотенузы. Сле-
Следовательно,
399. Треугольник, образован-
образованный наклонными и отрезком х,	Рис> 287-
соединяющим их основания, рав-
равнобедренный, так как наклонные равны. Но угол его при
вершине 60°, и, следовательно, треугольник равносторонний.
Наклонные, следовательно, тоже имеют величину х. Из прямо-
прямоугольного треугольника АВМ имеем, следовательно (рис. 287),
х =
2/г
Параллельные прямые и плоскости и перпендикуляры,
опущенные на плоскости
400. Опустив перпендикуляры из концов отрезка на пло-
плоскость Р (рис. 288) и соединив основания этих перпендикуля-
перпендикуляров, мы получаем трапецию, основания которой суть а и Ъ.
16*

244
РЕШЕНИЯ
401—402
Перпендикуляр, опущенный на плоскость Р из середины от-
отрезка, есть средняя линия этой трапеции; он равен, следо-
следовательно:
а + Ъ
401. Проведем (рис. 289) на расстоянии h, большем чем а,
вспомогательную плоскость Р || плоскости Р. Мы будем тогда
(как в предыдущей задаче) иметь:
к _|_ h =
откуда
X = ¦
Ь — а
(Если длины перпендикуляров, опущенных с разных сто-
сторон на плоскость, считать разных знаков, например опущен-
Рис. 288.
Рис. 289.
ные сверху положительными, а снизу — отрицательными, то во
в всех случаях мы получаем одну и ту же
V формулу:
а + Ь
2
причем, если
выйдет отрицательным, это значит, что
Рис. 290.	середина отрезка лежит снизу от пло-
плоскости Р.)
402. Пусть искомое расстояние есть А; тогда (рис. 290) из
подобия треугольников АММ' и МВБ' мы получаем:
ММ' :ВВ' = т:п,
но

403—405
СТЕРЕОМЕТРИЯ
245
следовательно,
откуда
и (А — а) = т(Ь — К),
и _ an -\-Ьт
т -(- п
(Можно сделать то же замечание относительно правила
знаков.)
403. На применение предыдущей задачи (рис. 291). Центр тя-
тяжести треугольника есть точка пересечения его медиан. Медиа-
Медианы отсекают трети друг от друга, т. е.
DM: MC= 1:2.
Мы имеем, следовательно (по формуле предыдущей задачи),
ММ' = h =
но
СС' = с, DD'-
откуда
ЛА' + ВВ' _ а + Ь ,
+с
Рис. 291.
404. Пусть a, b, d заданы, а с ищется (рис. 292). Очевидно,
что с настолько же больше d, насколько b больше с, т. е.
c — d = b—a, откуда c = d-\-b — а. Опустим из точки А
перпендикуляр АВ' на Ъ, а из точки D перпендикуляр DC
на с. Треугольники ABB' и DCC равны, так как DC = АВ, углы
Рис. 292.
Рис. 293.
при А и В равны, вследствие параллельности сторон, углам
при D и С, следовательно, СС=ВВ'.
405. Аналогично тому, как в предыдущей задаче, мы по-
получаем сначала расстояния е, /, g точек Е, Р, G (рис. 293):
e = d-\-b — a; f = b-\rc — a; g = d + c — а, а затем расстоя-

246
РЕШЕНИЯ
406—408
ние h точки Н при помощи, например, расстояний точек G,
А и В,
406. Центр тяжести однородного тетраэдра или, что все
равно, четырех одинаковых масс, сосредоточенных в верши-
вершинах тетраэдра, есть точка пересечения (рис. 294) медиональ-
ных прямых тетраэдра (см. задачу 346); эта точка М лежит
на медиональной прямой DE на % ее длины, считая от осно-
л
Ч
о, М/
о}—"""'
У °з
/
i
Рис. 294.
Рис. 295.
вания ее Е. Для нахождения высоты е точки Е пользуемся
формулой задачи 403 и получаем:
с_д+ь+с
Рг
А
Для нахождения высоты h точки М
пользуемся формулой задачи 402 и
получаем
h= l-d + з-е _
4
rf + 3
Рис. 296.
b ~\-c
407. Проведем через точку М три плоскости || плоскостям
Рг, Р2, Р3 (рис. 295); они замкнут вместе с плоскостями Pv
Р2, Р3 прямоугольный параллелепипед, ребра которого суть
а1г с2, а3, отрезок же ОМ есть диагональ этого параллелепи-
параллелепипеда, т. е.
408. Проведем через каждую из точек А и В по три пло-
плоскости || плоскостям Рг, Р2, Р3 (рис. 296). Эти три плоскости

409—411
СТЕРЕОМЕТРИЯ
247
замкнут прямоугольный параллелепипед, грани которого || плос-
плоскостям Рр Р2, Р3. Ребра этого параллелепипеда равны, очевидно,
bi — «г h — а2> ь-б — аз-
Мы имеем, следовательно,
409. Построим тот же параллелепипед, как в предыдущей
задаче. Проекции Ьг, Ъ%, Ь3 отрезка АВ на плоскости Рг, Рч, Р3
равны, очевидно, диагоналям граней параллелепипеда. Пусть
ребра параллелепипеда суть av a2, а3; тогда мы имеем:
но
и, следовательно,
= a\
a\
410. Пусть p1} pv p3 — три заданные взаимно перпендикуляр-
перпендикулярные прямые. Обозначим через Рг, Р2, Р3 плоскости, параллель-
параллельные pv P3;ps, Pi, рг, р2, и построим
тот же параллелепипед, как в пре-
предыдущей задаче. Проекции о1Т с2,
а3 равны ребрам этого параллеле-
параллелепипеда, т. е.
Р,
АВ =
а\
411. Пусть расстояния (коорди-
(координаты) точек А, В, С, D от плоско-
плоскостей Pv P2, Р3 суть (av a2, а3),
(Ьг, b2, bs), (clt cv c3), (rfj, d2, d3).
Опустим из всех четырех вершин
А, В, С, D тетраэдра (рис. 297)
перпендикуляры на плоскость Р3. Длины этих перпендикуляров
суть а3, b3, c3, d3. Основания их Л', В\ С, D'. Получились
четыре призмы с вертикальными ребрами с3, b3, c3, d3 и с верх-
верхними основаниями ABD, ACD, BCD и ABC и нижними A'B'D',
A'C'D', B'C'D' и А'В'С. Если сложить три первые и вычесть
четвертую, то останется тетраэдр ABCD. Для вычисления
объема тетраэдра достаточно, следовательно, уметь вычислять
объемы таких призм. Займемся призмой ABDA'B'D'. Объем
такой призмы равен, как известно, одной трети произведения
площади 5 ее нижнего основания на сумму высот вершин

248
РЕШЕНИЯ
412
верхнего основания над плоскостью нижнего, т. е. в данном
случае 1lsS{a3 -\- b3 -\- d3). Остается уметь вычислять S. Но
расстояния от вершин треугольника A'B'D' до прямых р1 и
р2, которые взаимно перпендикулярны, равны сх, а2; bl3 b2; dx
и d2 и, следовательно, его площадь по известной формуле равна
- {axb2 -f a2dx + bxd2 — b2dx — a2bx - Ojda)*).
Подставив это значение S, получаем объем призмы
ABDA'B'D'. Аналогично вычисляем объемы трех остальных и
затем складываем три первых и, вычитая четвертый, получаем
объем тетраэдра в виде следующей, весьма сложной формулы:
bxc 2d3
t — b3cxd2
— a2bsdx — аф^ + ajJdx + a2bxd3 + агЬ^2 + axb2c3 + a2b3cx +
-j- a3b1c2 — a3b2c1 — a2bxc3 — aj)^).
В так называемой «теории определителей» дается простой
способ запомнить эту формулу.
Трехгранные углы
412. Проведем секущую плоскость ABC, перпендикулярную
к ребру ОА интересующего нас двугранного угла, и пусть
О А = а. Треугольники ОАВ и ОАС суть равные равнобедрен-
равнобедренные (так как острые их углы равны 45°) прямоугольные
треугольники, следовательно,
= АС=а,	V"
Рис. 298.
Но так как Z ВОС = 60°, то,
ВС = ОВ = ОС,
т. е.
BC = aV~2.
Итак, в треугольнике ВАС
АВ = АС = с;
ВС = а V %
следовательно, треугольник этот равнобедренный прямоуголь-
прямоугольный, т. е. Z ВАС прямой, но это линейный угол интересую-
*) Эта формула для площади треугольника выводится в планиметрии
совершенно аналогичным способом путем представления площади треуголь-
треугольника, как суммы площадей двух трапеций за вычетом площади некоторой
третьей трапеции.

413—415
СТЕРЕОМЕТРИЯ
249
оНпоСч ДвУгРанного Угла, следовательно, последний прямой
(рнс. )
опал* РассмотРим половину правильного октаэдра (рис. 299
и 300) с ребром а. Очевидно, что пирамида ОАВС есть поло-
половина этой верхней пирамиды октаэдра. Но у правильного окта-
октаэдра плоскость ОАВ _]_ к плоскости ABC (рис. 299, 300).
Если не прибегать к октаэдру, то доказательство может
быть, например, следующее. Мы имеем:
АС = ВС^а; АВ= a
Пусть D середина АВ; тогда
2
откуда видим, что в треугольнике CDO Z.CDO прямой. Но
uuj_au, cu±AB (из равнобедренности треугольника АОВ
Рис. 300.
и АСВ) и, следовательно, плоскость CDO _]_ к АВ, т. е. угол
CDO линейный угол интересующего нас двугранного угла.
414. Диагональ куба равна
Куб
У а? + с2 + а2 = а У 3.
Диагонали граней суть
j/a2 + a2 = a ]/~2.
Отрезок АВ, соединяющий середины двух непараллельных и
не сходящихся в вершине ребер куба, равен
415. Площади граней равны а2. Площади диагональных се-
сечений

250
РЕШЕНИЯ
416-418
Площади сечений, проходящих через центры граней и ребра
противоположных граней, равны
Сечение, проходящее через концы трех ребер, сходящихся
в одной вершине, есть равносторонний
треугольник, сторона которого есть ди-
диагональ грани, т. е. равна а У 2; пло-
площадь этого сечения равна, следовательно,
Рис.301.
4	2
416. Сторона этого шестиугольного
сечения (рис. 301) равна (см. задачу 325)
половине диагонали грани куба, т.' е.
Площадь этого сечения, как площадь правильного шести-
aV~~2
угольника со стороною 	, равна
417. Если соединить середину диагонали куба О с середи-
серединой К ребра, скрещивающегося с ней (рис. 302), то отрезок
OK ± к ребру АВ,
так как О А = ОВ, и
„ 1 к диагонали CD,
Рис. 302.
Рис. 303.
так как К. С = KD.
Отрезок ОК пред-
представляет, следова-
следовательно, кратчайший
отрезок, соединяю-
соединяющий диагональ CD с
ребром АВ:
aV~2
418. Кратчайший отрезок, соединяющий две такие диа-
диагонали АВ и CD, имеет свои концы в точках К и L таких,
что (рис. 303)
= -АВ, CL = -
3	3

419—420
СТЕРЕОМЕТРИЯ
251
(см. задачу 326), причем KL равен — диагонали куба, т. е.
о
419. Получается, очевидно, правильная восьмиугольная приз-
призма, высота которой есть а. В основании этой призмы лежит
правильный восьмиугольник. Мы имеем (рис. 304):
ВС=ВЕ= АВУ^2; CD = АВ,
следовательно,
AD = а = АВ + АВ\Г2 + АВ = АВ{2 -f \Г2),
откуда
Треугольник ABE есть половина квадрата со стороною А В;
площадь его, следовательно,
1	я2
2	B + 1г1J
Площадь восьмиугольника, лежащего в основании призмы,
равна площади квадрата со стороной а за вычетом площадей
четырех таких треугольников, т. е.
B + ПJ
или
2а2 (/2-1).
Объем призмы равен; следовательно,
2-1).
Совокупность обоих кубов представляет
невыпуклую 16-гранную призму, получае-	Рис. 304.
мую из куба, если на каждую из его бо-
боковых граней положить узенькую треугольную призму. Объем
этого тела равен удвоенному объему куба минус ординарный
объем общей части (так как при удвоении объема куба эта
общая часть будет сосчитана дважды), т. е.
2#з	2ft3 Cl/ 2	1) = 2g3 B	1/"~2)
420. Легко видеть, что общая часть этих двух кубов пред-
представляет собою пару правильных треугольных пирамид, ело-

252
РЕШЕНИЯ
421
женных вместе основаниями, причем плоские углы при вер-
вершинах этих пирамид все прямые, так что каждая из них пред-
представляет собою — куба с ребром Ъ = АВ. Искомый объем
ь
V общей части кубов равен, следовательно,
6	3
Остается найти ребро Ъ. Для этого заметим, что высота каждой
из пирамид равна J_§ (рис 305), как треть диагонали куба
о
с ребром b (см. задачу 326). Но уд-
удвоенная высота пирамиды равна по-
половине ОВ диагонали заданного куба с
ребром а, т. е.
- bV~3 =
3
аУ 3
2
т. е.
Ъ = —а.
4
Рис. 305.
Объем V равен, следовательно, -^-,
64
421. Пересечем куб плоскостью, перпендикулярной к отрез-
отрезку АВ и проходящей на таком расстоянии от точки А, чтобы
получающийся в сечении прямоугольник CDEF был квадратом,
т. е. чтобы CF = FE = а. Очевидно, что повернутый куб
Н	_—	G
Н
Рис. 306.
будет пересекать заданный куб по этому квадрату и по тако-
такому же квадрату, лежащему по другую сторону от центра ку-
куба. Вся часть, общая обоим кубам, представляет правильную
четырехугольную призму, основаниями которой служат ука-
указанные два квадрата, а высота которой есть FM, на каждом
из оснований которой поставлено по правильной четырехуголь-

422—423
СТЕРЕОМЕТРИЯ
253
ной пирамиде с этими же основаниями и вершинами в точках
А и В (В противоположна точке А по отношению к центру
куба и на рисунке не видна) (рис. 306 и 307).
Мы имеем:
FM = 2HN=aV2 -a,
т. е. объем призмы равен
а2 (а У — а) = а3 (/ — 1).
Высота же каждой из пирамид равна (рис. 307)
Объем всей общей части равен, таким образом,
а3A/~2 — 1) + 2-а2- = а3//2— -
кг	' л 3 2	у	з
422. Легко видеть (рис. 308), что общая часть обоих кубов
представляет собою две правильные шестиугольные пирамиды,
сложенные вместе основаниями, вершины которых находятся
в концах А и В диагонали, а основаниями служит правильный
шестиугольник, рассмотренный в задаче 325, плоскость кото-
которого X к диагонали АВ. Высота каж-
каждой из этих пирамид есть, следова-
тельно,
Рис. 308.	Рис. 309.
, а площадь основания (см. задачу 416) равна
¦. Объем V всей общей части обоих кубов равен, следо-
вательно,
423. Получается, очевидно, правильный октаэдр, вершины
которого лежат в центрах граней куба (рис. 309). Ребро этого

254
РЕШЕНИЯ
424—425
октаэдра равно, очевидно, половине диагонали грани куба, т. е.
	Высота каждой из двух пирамид, половин октаэдра,
а
равна тр . Объем октаэдра равен, следовательно.
2-
а
2
6 '
т. е. одной шестой объема куба.
424. Получается правильный тетраэдр с ребром a\f 2 . Он
получается, если отрезать от куба
, четыре пирамиды такие, как EBCD
' (рис. 310).
Объем каждой из пирамид равен
Объем тетраэдра равен, следова-
следовательно,
4_ = _
б з '
D	a3
Рис. 310.
т. е. равен одной трети объема куба.
425. 1) Пусть плоскость пересекает: все четыре вертикаль-
вертикальных ребра куба (а не их продолжения) и пусть отрезки этих
ребер, прилежащие к нижнему основанию куба (рис. 311), рав-
равны г, s, t, и. Рассматривая трапе-
трапеции с основаниями г, t, s, и, мы
видим, что
т. е.
2	2 '
U = Г -\- t — S,
Рис. 311.
т. е. что если три из отрезков,
например г, s, t, даны, то четвер-
четвертый тем самым уже задан. Повернем
секущую плоскость вокруг одной
из диагоналей параллелограмма,
получившегося в сечении так, что-
чтобы отрезки, идущие к концам другой диагонали, например
и и s, сравнялись. К отсеченному телу (отсеченным телом
мы будем называть нижнюю часть куба) прибавится неко-
некоторый тетраэдр и равно такой же отрежется, так что объем

425
СТЕРЕОМЕТРИЯ
255
тела не изменится. Повернем теперь секущую плоскость
вокруг этой второй диагонали сечения, которая теперь гори-
горизонтальна, так, чтобы сравнялись и два других отрезка rat.
Совершенно аналогично отрежется и прибавится по одинако-
одинаковому тетраэдру, и следовательно, объем не изменится.
В результате обе диагонали сечения
окажутся горизонтальны, т. е. секущая
плоскость || основанию куба. При обоих
поворотах точка D секущей плоскости
(т. е. точка пересечения диагоналей па-
параллелограмма сечения) оставалась на
месте. Высота правильной четырехуголь-
четырехугольной призмы, получившейся в результате,
равна, следовательно,	, а объем ее,
т. е. и объем исходного тела, равен
Рис. 312.
2) Пусть отрезки г, s, t суть отрезки ребер куба, а отре-
отрезок и есть отрезок продолжения ребра вниз под плоскость
основания куба (рис. 312). Дополним куб книзу еще на высоту и.
Так же, как и в предыдущей задаче, вычисляем объем ниж-
нижней части этого «дополненного» куба, только теперь вместо
г, s, t, и мы имеем
г -\- и, s -\- и, t -\- и, 0.
Объем этот равен, таким образом,
Остается вычесть из этого объема объем аги, дополняю-
дополняющий куб книзу правильной четырехугольной призмы с высо-
высотою и, и прибавить затем объем маленькой пирамидки с реб-
ребрами и, w, v. Искомый объем получается в форме
,7	с, r-\-14- 2и о i 1
V = с —!—!	аг и -\	WVW.
Остается вычислить v и w. Из подобия треугольников мы
имеем:
v :«. = a:(s~t); w :u = a :(s — г),
откуда
v =
аи
s — t
W =
аи
s — г

256
РЕШЕНИЯ
425
Подставляя эти величины и упрощая, мы находим, если заме-
заменим и через s — г — t,
3) Пусть отрезки s и t суть отрезки ребер куба, а отрезки
г и и суть отрезки продолжений двух других ребер вниз под
Рис. 313.
Рис. 314.
плоскость основания куба (рис. 313). Отсеченное тело есть
треугольная усеченная пирамида. Из подобия треугольников
мы имеем:
v :s = (а — v) :r,
откуда
as
Линейные размеры верхнего и нижнего оснований нашей усе-
усеченной пирамиды относятся как t: s, площадь большего (на
рисунке) основания равна
vs	 as2
~2~ 2(r + s) '
следовательно, площадь меньшего
as2	t-
2(r+s) s3
а площадь среднепропорционального
2(r+s) s '
Искомый объем V равен, следовательно,
6 (r + s)

425
СТЕРЕОМЕТРИЯ
257
4) Пусть rut суть отрезки ребер куба, s — отрезок от
нижнего основания куба до точки на продолжении ребра квер-
кверху от верхнего основания, а и — отрезок продолжения четвер-
четвертого ребра под плоскость нижнего основания (рис. 314).
Искомый объем нижнего куска куба можно вычислять, как в 2),
только тогда будет еще захвачена лишняя пирамидка, стоя-
стоящая над верхним основанием куба. Ее надо вычесть. Объем
нижней пирамидки с ребрами и, v, та; оказался в 2) равным
а3 а3
G(s-t){s-r) '
верхняя пирамидка, как легко видеть, подобна нижней, при-
причем отношение их линейных размеров
равно s — а:и. Объем верхней пирамид-
пирамидки равен, следовательно,
а1 и3	(s — a) _ a*(,s—af
>—г3 - п — (S - аK}
-г)	и*	6(s-t)(s~r)-
Объем V всего искомого тела равен,
следовательно,
&(s-()(s-r)
5) Пусть только s отрезок ребра
куба, отрезки же г, t, и суть отрезки
продолжений ребер куба вниз. Из подобия треугольников
мы имеем (рис. 315)
as	,	as
r+s
1
Искомое тело есть пирамида с ребрами s, k, I, взаимно пер-
перпендикулярными, т. е. — прямоугольного параллелепипеда с
этими же ребрлми, т. е. искомый объем V равен
.	 1	a"s3
Легко убедиться, что этими пятью возможностями исчер-
исчерпаны все случаи, так как секущая плоскость может или пе-
пересекать четыре параллельных ребра куба (а не их продол-
продолжения) (случай 1), или только три (случай 2) или только два,
прилежащие по грани (случай 3), или только два, не приле-
прилежащие по грани (случай 4), или только одно (случай 5).
Всего существенно различных сечений куба плоскостью на
две части получилось пять.
17 Делоне и Житомирский

258	РЕШЕНИЯ	426—427
Соответственно этому и возможных существенных различ-
различных сечений тоже пять: параллелограмм, пятиугольник (по-
(получаемый из параллелограмма отрезанием уголка), шестиуголь-
шестиугольник (противоположные стороны которого параллельны) и
треугольник. Сами куски куба получаются восьми сортов.
426. 1) Стороны параллелограмма сечения равны (из прямо-
прямоугольных треугольников):
— rf и Va2 + (s — if.
Одна из диагоналей
следовательно, по формуле площади через стороны треугольника
можно вычислить площади треугольников половин паралле
лограмма, а следовательно, и самого параллелограмма.
2) Вычислив площадь всего параллелограмма сечении
«продолженного» куба, как в предыдущем случае, остается
вычесть площадь треугольника, стороны которого суть:
т. е. известны, и площадь которого опять вычисляем по
формуле
5 - VpiP-a)(p-b)ip-c).
3)	Сечение есть трапеция. Легко вычислить ее боковые
стороны и основания, а следовательно, и высоту, а затем
площадь.
4)	Разбиваем шестиугольник, получающийся в сечении, на
четыре треугольника диагоналями, проведенными из одной из
его вершин. Все стороны получившихся треугольников нетруд-
нетрудно вычислить из подобия треугольников и прямоугольных
треугольников. Применяем формулу площади по сторонам.
5)	Стороны треугольника, получившиеся в сечении, равны
Как вычислить k и /, было показано в задаче 120; применяя
формулу площади треугольника по сторонам, получаем ре-
результат.
Правильный тетраэдр
427. Пусть АВа CD — два прогивоположных ребра (рис. 316)
нравильного тетраэдра; если соединить середины Е, F, G, И
остальных четырех ребер, то получится квадрат, так как:
EF =— и GH = —
2	2

428- 429
СТЕРЕОМЕТРИЯ
259
и EF Ц CD, GH || CD; аналогично и FG равен и || ЕЙ. Пло-
Площадь этого квадрата равна, следовательно,
/ я_\а_ «^
12; ~ 4
428. Общая часть (рис. 317 и 318) есть правильная
шестигранная пирамида. Высота этой пирамиды равна высоте
тетраэдра, т. е. равна а	(см. задачу 436), сторона же
Рис. 318
а
основания равна — Площадь основания равна, следовательно,
6
а объем
v = —
3
aV~E
6	з	is
Апофема этой шестигранной пирамиды равна высоте грани
тетраэдра, т. е. 	, и следовательно,
полная боковая ее поверхность равна
с 1 а aVW a?V"b
2 3 Z * 2
и полная поверхность пирамиды равна
| й2]/~— д2
3
Рис. 319.
429. Общая часть есть шестигранник,
который представляет собою два одина-
одинаковых сложенных вместе основаниями правильных тетра-
тетраэдра (рис. 319), линейные размеры кбторых вдвое меньше,
17*

260
РЕШЕНИЯ
430—432
чем у заданных. Ребра их суть, следовательно, ^- , объем
каждого из них равен, следовательно (см. задачу 436),
—) —, т. е. объем всей общей части равен
= ал
48
430. Общая часть есть параллелепипед (рис. 320), все грани
которого суть одинаковые ромбы с углом в 60°. Рассмотрим
треугольник ЛВС. Так как АС—медиа-
АС—медиана основания тетраэдра, a D — точка пе-
пересечения медиан, то CD = — АС, а
о
2л, следовательно, и DE = — АВ, т. е. реб-
/	3
ро получающегося параллелепипеда рав-
равно -f-. Но объем такого параллелепи-
педа в 6 раз больше объема правильного
тетраэдра с ребром —, т. е. (см. задачу
о
436) равен
Рис. 320.
12
54
431. Представить себе непосредственно, какая получится
общая часть, довольно трудно. Однако это совсем просто,
если воспользоваться кубом (рис. 321). Вершины обоих тет-
тетраэдров будут вершинами одного куба. Каждому тетраэдру
будет принадлежать четверка вершин куба, попарно не свя-
связанных ребром. Общая часть тетраэдров — как раз тот октаэдр,
который рассмотрен в задаче 423. Если ребро тетраэдра а, то
, и следовательно (см. задачу 423), объем v
ребра куба ;
октаэдра равен
24
432. Рассмотрим три ребра, сходящиеся в одной вершине А.
Секущая плоскость должна пересекать хотя бы одно из этих ре-
ребер так как иначе (т. е. если бы она пересекала только их продол-
продолжения) она проходила бы мимо тетраэдр i (вовсеего не пересекая).
1) Пусть секущая плоскость пересекает все три ребра,
сходящееся в Л, и отсекает на них отрезки г, s, t (рис 322).

432
СТЕРЕОМЕТРИЯ
261
Известно (см. задачу 339), что объемы двух тетраэдров
с одинаковыми трехгранными углами относятся как произве-
произведения ребер этих трехгранных углов. Объем правильного
тетраэдра с ребром а равен
a3 V2
12
(см. задачу 436). Отсекае-
Отсекаемый тетраэдр с вершиной А имеет такой же трехгранный
Рис. 321.	Рис. 322»
угол, как у правильного, и ребра r,s, t, а слэдовательно, объем
rstV~2
его равен 	.
1	12
2) Пусть секущая ^плоскость пересекает только два из
ребер, сходящихся в вершине А, и дает на них от вершины А
отрезки г и s, третье же ребро не пересекает, но пересекает лишь
продолжение его в точке В, и отрезок AB = t (рис. .323).
Часть тетраэдра, отсеченная
этой плоскостью и приле-
прилегающая к вершине А, пред-
представляет собою пятигранник
ACDEFG; он получается,
если от тетраэдра ABCD
отрезать тетраэдр BEFG.
Объем тетраэдра ABCD, так
же как в предыдущей за-
задаче, получается равным
rst V~2 „
	. Для вычисления
1 о
объема тетраэдра BEFG заметим, что он, очевидно, равновелик
тетраэдру BEF'G, который из него получается, если точку Е
перенести || АВ в точку Е так, чтобы было GE II АС, а точку
F в точку F' так, чтобы было GF' \\ AD. Но GE = GE,
GF' — GF и, следовательно, объем тетраэдра BEFG = объему
Рис. 323

262	РЕШЕНИЯ	433
тетраэдра GE'P'B, у которого при вершине G такой же трех-
трехгранный угол, как у правильного. Итак, объем GE'P'B равен
GB - GE' -GF' — .
12
Но GB = t — a. Проведем (рис. 324) GH\\ AD. Из подобия
треугольников ADB и GHB имеем:
GH = s{t~a) .
t
Из подобия треугольников DKF и HGP имеем:
GF:GH={a — GF):(a — s),
откуда
^Р 	 a-GH 	 s(t — a)
а — s-\-GH	t — s
Аналогично получим:
GE= r{t-a)
t — r
Объем тетраэдра BEFG равен, следовательно,
r{t-d) sit-a)	y-2	V~
t — r	t-s	' 12
t — r	t-s	' 12 (t — ryt- s)-12
а объем исследуемого пятигранника ACDEFG равен, таким
образом,
V rst,
12	(t — r)(t — s) 12
Легко убедиться, что этими двумя
возможностями исчерпываются все слу-
случаи, так как остающийся еще случай,
Рис. 324.	когда секущая плоскость пересекает
только одно из ребер, сходящихся в
вершине А, дает то же сечение, как и в случае 1) только
по отношению к другой вершине.
433. 1) В треугольнике ABC (рис. 322) /_ВАС имеет 60°,
следовательно, сторона ВС = г2 — rs-f-s2. Аналогично
= s2 — st -|-*г2; CD = г2 - rt + t*.
Далее применяем формулу площади треугольника по его
сторонам.
2) Площадь треугольника BCD (рис. 323) вычисляем, как
в предыдущем случае. Затем, зная GB, GE, GF (см. задачу 432)
и то, что углы BGE и BGF имеют по 120°, а угол EGF — 60°,
находим стороны BE, BF и EF треугольника BEF и затем, все
по той же формуле, площадь этого треугольника. Вычитание
дает площадь четырехугольника CDEF, получаемого в сечении.

СТЕРЕОМЕТРИЯ
263
Призматоиды
434. Предположим, что и больше а' и b больше Ь'\ тело
ABCDA'B'C'D' (рис. 325) может тем не менее не быть
усеченной пирамидой, так как плоскость DCD'C может быть
гак наклонена, что она не проходит через ту точку плоскости
АВА'В1, в которой пересекаются прямые АА' и ВВ' (продол-
(продолжения ребер). Проведем плоскости А'В'А"В" || D'CDC и
В'СВ"С" 1| A'D'AD. Тело наше разрежется на параллелепипед/,
аве треугольные призмы // и /// и четырехугольную пира-
пирамиду IV. Так как призмы // и /// суть половины паралле-
параллелепипеда с основаниями // и /// и высотой h, то четыре
казанных тела будут иметь последовательно объемы:
v\,, = -
¦a')b'h;
.)бъем всего тела
V=Vi-\-V
'lv=l(a-a') {b-b')h.
равен, следовательно,
t,,+Viv = - Ba' • b' -fa • V +a' - b -f 2a. b).
6
Предположим теперь, что a больше a', но b мень-
меньше b' (рис. 326). Проведем плоскости В'С'В" E\A'D' AD и
D"EDC || A'B'AB.
Тело наше разрежет-	?	-с
ся на параллелепи-
параллелепипед /, две треуголь-
треугольные призмы // и /// и
треугольную пира-
пирамиду ЕСЁ'С. Пере-
Передвинем точку С па-
параллельно ЕЕ', так,
чтобы она оказалась
на плоскости осно-
основания ABCD в точке
F. Очевидно, что пи-
пирамида ЕСЕ' С рав-
равновелика пирамиде,
имеющей основанием треугольник СЕР и вершиною точку Е.
Объем Viv этой пирамиды равен (угол GEF прямой)
-CE-EF- ~h^^{a a')(b' — b)h.
Рис. 325.

264
РЕШЕНИЯ	435
Объемы параллелепипеда / и призм // и /// суть:
Vi = a'b-h;Vn = -| {а — a') b-h;
Vm = 1 a' {b' - b)-h.
Объем всего тела равен, следовательно,
V = Vi -\- Vn + Vm + Viv = — Ba'bf -f- аи' -f- a'b-f-2a&).
Получилась та же самзя формула, как в предыдущем слу-
случае. Очевидно, что предположения: а меньше a', b меньше b
и а меньше a'; b больше Ь' равносильны предыдущим, если
только повернуть наш призматоид. Выведенная формула есть,
следовательно, общая для такого рода тел.
435. Боковые грани такого выпуклого призматоида, если
основания уже даны, получаются так: через каждую из сто-
сторон нижнего основания проведем плоскость и будем ее вра-
вращать вокруг этой стороны до тех пор, пока она не прико-
прикоснется к верхнему основанию. Аналогично проведем плоскости
через все стороны верхнего основания и
будем их вращать вокруг этих сторон до
тех пор, пока каждая из них не прикос-
прикоснется, к нижнему основанию. Замкнутое
основаниями и этими плоскостями тело и
называется призматоидом с этими основа-
основаниями (это есть наименьшее выпуклое тело,
имеющее эти основания). Призма с парал-
параллельными основаниями и усеченная пира-
пирамида с/ть частные случаи призматоида
Если у оснований призматоида нет «прямо
параллельных» сторон (т. е. таких, кото-
Рис. 327	рые параллельны и имеют основания по
одну сторону от них), то все боковые гра
ни суть, очевидно, треугольники. Каждой же паре прямопарал-
прямопараллельных сторон оснований соответствуют трапецеидальные
грани (рис. 327). Проведем среднее сечение. Возьмем где-
нибудь на нем (все равно где) внутри призматоида точку О и
разобьем весь призматоид на пирамиды, имеющие вершину в
точке О и основаниями верхнее и нижнее основание призма-
призматоида и его боковые грани. Первые две пирамиды будут имет1
объемы
\ н 1 „ н
— s, — и —So— ¦
3 1 2	3-2

436
СТЕРЕОМЕТРИЯ
265
Рассмотрим какую-нибудь из пирамид (рис. 328), основа-
основанием которой является одна из боковых граней призматоида,
и предположим, что эта грань трапеция, так как, если бы она
была треугольником, то мы только считали бы, что одно из
оснований трапеции равно нулю. Опустим из точки О перпен-
перпендикуляр OD на эту боковую грань АВА'В' и через точку D
проведем по боковой грани СС _|_ АВ. Тогда АхВг — средняя
линия трапеции ABA'В1, СС—ее высота, т. е. площадь ^е
равна АХВХ-СС, а следовательно, объем пи-
пирамиды О ABA 'В' равен- AXBX-CC-OD. Ону-
О
стим из точки С перпендикуляр С'КХ на
плоскость ОАгВх среднего сечения; тогда он
будет высотой треугольника ОС'СХ. Вычисляя
площадь этого треугольника, мы имеем:
CC-OD = 2ОСХ- СКХ = ОСХ-Н,
так как
С'КХ = ?.	Рис 328.
Подставляя, мы получаем, что объем пирамиды ОАВА'В' —
х и, следовательно,~ АХВХ-ОСХ
2
д,	у
= - -АХВХ-ОСХ-Н. Но ОСХ _L
3	2
есть площадь треугольника ОАХВХ\ следовательно, объем пира-
пирамиды ОАВА'В' равен
- -(пл. А ОАхВх)-4-Н.
Складывая все эти пирамиды с двумя первыми, основаниями
которых служат основания призматоида, мы получаем для
объема всего призматоида:
так как сумма площадей всех треугольников, аналогичных
треугольнику OAXBV даст площадь sx среднего сечения.
Правильные многогранники
436. Из равенства прямоугольных треугольников AED,BED
и CED (по катету и гипотенузе) мы видим, что основание Е
высоты есть точка, равноудаленная от вершин основания
(рис. 329), но так как основание—равносторонний треугольник,
то Е — точка пересечения его медиан (они же и биссектрисы
и высоты). Ввиду того, что CF—высота и, следовательно.

266
РЕШННИН
J_ кАВв EF проекция DF (рис. 317), то DF j_ AB. Мы имеем,
таким образом,
DF_aV~3
2
(как высота равностороннего треугольника со стороною а),
FP —
(как — медианы CF, которая одновременно и высота равно-
О
стороннего треугольника со стороною а). Из прямоугольного
треугольника DFF получаем, следовательно,
h = DE=
-EF* = л /** - **. = aJU.
[/ 4	36	3
Площадь основания s как площадь равностороннего треуголь-
D	ника со стороною а равна
s =
4
Следовательно, объем V правильного
тетраэдра равен
3	12
Другой способ. Рассмотрим куб,
четыре из вершин которого суть вер-
Рис 329 э	шины данного правильного тетраэдра
' *	(см. задачу 333). Объем тетраэдра
нредставляет — объема куба, так как объем каждой из четы-
О
рех пирамид, отрезание которых от куба дает тетраэдр, равен
— объема куба, так как высота такой пирамиды равна высоте
6
куба, а площадь ее основания вдвое меньше площади основа-
основания куба. Если ребро тетраэдра а, то ребро куба, для которого
ребро тетраэдра — диагональ грани, равно	. Следователь-
Следовательно, объем куба равен
2 J

437-439
СТНРЕОМЕТРИЯ
267
i объем тертаэдра
V = ¦
12
437.	Шар, описанный вокруг правильного тетраэдра, оче-
очевидно, есть тот же самый, который описан вокруг вспомога-
вспомогательного куба, рассмотренного в предыдущей задаче, т. е.
радиус его равен половине диагонали этого куба, т. е.
, _ 1 a V2 nz _ a V&
1\ 	 ¦	у О 		.
2 2	4
438.	Шар, вписанный в параллельный теэраэдр, будет ка-
касаться его граней в точках пересечения их биссектрис. Соединяя
эти точки, мы получим меньший правильный тетраэдр
(рис. 330) с ребром а', для которого этот же шар будет описан-
описанным. Но В'С = ±ВС и А'С = — АС (так как точки В' и А' суть
точки пересечения медиан), и следовательно, А'В = —АВ, т. е.
о
г' — —а, т. е. малый тетраэдр в три раза меньше в отноше-
О
нии своих линейных размеров, чем заданный. Радиус г впи-
Рис. 3S0.
Рис. 331.
-энного шара, следовательно, в три раза мейьше радиуса R
вписанного, т. е.
— i
~ 3
12
439. Рассмотрим опять вспомогательный куб. Отрезок GH
(рис. 331), соединяющий середины двух противоположных ре-
ребер тетраэдра, соединяет центры противоположных граней куба
и, следовательно, J_ к этим граням, т. е. представляет собою
_L к обоим этим ребрам, а следовательно, кратчайший отрезок
между ними GH, очевидно, равен ребру куба, т. е.

268
РЕШЕНИЯ
440—443
440.	Объем куба равен 1/=а3, радиус описанного шара
п 1/Т	*	а
R=-—l—, радиус вписанного шара f—~г •
441.	Сечение AECF правильного октаэдра (рис. 332) есть
квадрат, следовательно, высота пирамиды ABCDF, половины
октаэдра, равна
и
ft—
Объем этой пирамиды равен, следова-
следовательно,
а
ъа	2 '
и, следовательно,	объем V всего окта-
октаэдра	_
Рис. 332.
3	2	3
442. Диаметр описанного шара равен диагонали EF, и сле-
следовательно, радиус
443. Вписанный шар будет касаться граней октаэдра в точ-
точках пересечения их биссектрис. Эти точки будут вершинами
куба, а сам вписанный в октаэдр
шар — шаром, описанным вокруг этого
куба. Для нахождения ребер куба рас-
рассмотрим проекцию (рис. 333) октаэдра
и этого вписанного куба на пло-
плоскость сечения ABCD. Вершина К
куба будет находиться на — медианы
О
MF грани октаэдра (в точке пересече-
пересечения ее медиан), т. е. KM—— MF, но
О
в таком случае и проекция КМ= —
О
проекции MF. Проекция же KL ребра KL куба, как парал
лельного плоскости, на которую проектируем, сохранит свою
длину, т. е. KL—KL. Мы имеем:
АВ=а,

444—445
СТЕРЕОМЕТРИЯ
269
т е. ребро вписанного куба равно
i следовательно, радиус шара, описанного вокруг этого куба,
равен	__	_
a V'6 a V(T
6
г. е.
г
444.	Площадь правильного пятиугольника со стороною а
равна
jl/25+10/57
следовательно, полная поверхность S правильного додекаэдра
* ребром а равна
5=3а21/25 + Ю/5".
445.	Разрезав додекаэдр по отрезкам, соединяющим середины
С, D, Е, F, G, Н 6 ребер, показанным на рис. 334, мы, по-
повернув «шапочку» А, сможем ее в
точности вложить в шапочку В так,
что они совместятся. При этом ока-
окажется, что АС=ВС, AD=BD, AE=
=В?, AF=BF, AG=BG, AH=BH,
т. е. все шесть точек С, D, E, F, G, N
лежат в одной плоскости (j_ к АВ
и проходящей через середину О от-
отрезка АВ, т. е. через центр додека-
додекаэдра) (см. задачу 324). Шестиуголь-
Шестиугольник CDEFGH, следовательно, плоский
и правильный. Из свойств правильного
пятиугольника находим, что сторона
а' этого шестиугольника, как полусумма стороны а и диаго-
Рис. 334.
нали о— а
правильного пятиугольника, равна
, 3 -i-VW
Изпрямоугольноготреугольника ODK получаем, следовательно,
~V 18

270	решения	44&-*tv
Замечание. Как в этой задаче, так и в задаче 323, доказательстве
того, что
АС=ВС, AD—BD, АЕ^ВЕ, AF=BF, AG=BG, АН-^ВИ
можно произвести и следующим образом. Повернем додекаэдр вокруг оси
проходящей через точку Е, так, чтобы грань ED совместилась с равной
ей гранью EF, и обратно — грань EF с равной ей гранью ED; тогда, вслед-
вследствие равенства всех граней и всех двугранных углов между ними, вег
грани додекаэдра совместятся с соответствующими гранями, т. е. весь
додекаэдр совместится сам с собою. Отрезок ЕА совместится при этом
с отрезком ЕВ, т. е. ЕА = ЕВ. Аналогично и для других пар отрезков
Ось, вокруг которой при этом приходится поворачивать додекаэдр, прохо-
проходит, как легко видеть, через середины двух противоположных ребер его.
446. Вписанный шар касается граней додекаэдра в центрах
кругов, описанных вокруг его граней. Если, следовательно, R —
радиус описанного шара, г — радиус вписанного и р — радиус
круга, описанного вокруг грани, то г и р — катеты прямоуголь-
прямоугольного треугольника, в котором R — гипотенуза, т. е.
Радиус р круга, описанного вокруг правильного пятиугол*
ника со стороной а, есть
„/!
Радиус R шара, описанного вокруг додекаэдра, равен
(см. предыдущую задачу). Мы имеем, следовательно,
/18+ ЪУ~5 5 + К5~_ а л /25+ llKf
16	10	2 К	10
447. Разобьем додекаэдр на 12 пирамид, основаниями кото-
которых служат его грани, а вершины которых — в центре додекаэд-
додекаэдра. Площадь основания каждой из этих пирамид, как площад!
правильного пятиугольника со стороною а, равна
jl/25+lO/f,
высоты же равны радиусу г вписанного шара, т. е.
25 + 111^5
10
(см. предыдущую задачу). Объем V додекаэдра равен, следо-
следовательно,
3 8 у	10

448-449
СТЕРЕОМЕТРИЯ
271
448. Площадь правильного треугольника со стороною а рзвла
Уз
	, следовательно, полная поверхность правильного икоса-
икосаэдра с ребром а равна
А
449. Очевидно, что отрезок, соединяющий любые дье
противоположные вершины (рис. 335) икосаэдра, например FG,
есть диаметр описанного шара, т. е. FG=2R. Рассмотрим тре-
треугольник FGA. Угол FAG, как имеющий вершину А на по.
верхности описанного шара и опирающийся на диаметр его
прямой; треугольник этот, следовательно, прямоугольный'
При поворачивании икосаэдра вокруг
360° о 360°
диаметра FG на -jt-» * -г- и т. д., тре-
треугольники FAG, FBG и т. д. совме-
совмещаются, следовательно, пятиугольник
ABCDE плоский и правильный, и плос-
плоскость его JL к отрезку FG. Если Н—
точка пересечения плоскости этого пяти-
пятиугольника с FG, то АН _\_FG, т. е.
АН—высота прямоугольного треуголь-
треугольника FAG. Мы имеем, следовательно,
a2=2R-FH.
или
е
Рис. 335.
Остается вычислить FH; АН как ра-
радиус круга, описанного вокруг правильного пятиугольника с
стороною а, равен
АН
= fl/J
10
Теперь из треугольника AFH получаем:
*== а у
5-V5
10
Мы получаем таким образом
откуда
10

272	РЕШЕНИЯ	450—453
450. Вписанный шар касается граней икосаэдра (рис. 335)
в центрах кругов, описанных вокруг граней:
(см. предыдущую задачу),
РС=~^-
греугольник ОРС — прямоугольный, следовательно,
ОР=VOC7-PC2 = ^ I /7Л^± .
Г	2 У	6
451. Объем V правильного икосаэдра, как сумма объ-
объемов 20 пирамид с площадями оснований	 и высотами
(см. предыдущую задачу), равен
у_20
~ '
. а 1/^7 + 31^5^5 д3 , /7 + ЗК5
2 |/	6	6 К	2
Цилиндр
452. Пусть г радиус основания, a h — высота цилиндра;
	 а
тогда h — a и 2w=a, т. е. г~2п> и, следовательно,
453. Пусть Р—наклонное сечение цилиндра (рис. 336).
Рассмотрим сечение Q плоскостью J_ к оси и проходящей
через ту точку С оси, где ось пересекается плоскостью Р. Пло-
Плоскость Р пересекает плоскость Q по диаметру АВ того круга,
который получается при пересечении цилиндра плоскостью Q.
Боковая поверхность цилиндра и плоскости Р и Q ограничи-
ограничивают два ломтеобразных тела р и д; объемы этих тел одина-
одинаковы. Действительно, если повернуть тело q вокруг диаметра
АВ, как вокруг оси, на 180°, то оно совместится с телом р.
Из этого замечания выходит, что рассматриваемый кусок ци-
цилиндра равновелик цилиндру с тем же радиусом г и высотою
СС = а, т. е.

454—455
СТЕРЕОМЕТРИЯ
273
454. Срежем косо (рис. 337) два параллельно расположенных
цилиндра одинаковых радиусов, так чтобы секущие плоско-
плоскости были параллельны. Очевидно, что линии, получаемые в
Рис. 336.
Рис. 337.
сечении, будут одинаковы (эллипсы). Очевидно также, что
э™ линии симметричны по отношению к прямым АВ и А'В',
Рис. 338.
Рис. 339.
получаемым в пересечении секущих плоскостей с плоскостя-
плоскостями, проходящими через оси цилиндров и им перпендикуляр-
перпендикулярными. Если, следовательно, повернув второй из срезанных
цилиндров вокруг А'В' как вокруг
оси на 180° и перенеся его затем па-
параллельно самому себе, так приста-
приставить к первому, чтобы отрезок А'В'
совпадал с отрезком АВ, то срезы
совместятся и образуется (рис. 338)
колено. Принимая во внимание пре-
предыдущую задачу, мы видим, что
объем и полная поверхность такой
коленчатой цилиндрической трубы
равновелики объему и боковой по-
поверхности такого прямого цилиндра,
радиус г которого равен радиусу трубы, а высота — длине
(ломаной) оси (рис. 339) трубы.
455. Цилиндр, описанный так вокруг тетраэдра, есть вме-
вместе с тем и цилиндр, описанный вокруг куба (рис 340) с реб-
18 Делоне и Житомирский
Рис. 340.

274
РЕШЕНИЯ
456—45S
ром 	 (см. задачу 333), и следовательно, радиус его/-=—.
А	2
, aV'2
а высота п=	, т. е.
456. г=-
2 ' "--'-	2 "
457. Радиус г основания цилиндра есть радиус круга, опи-
описанного вокруг правильного треугольника со стороною а,
т. е- г =Ш-— (рис. 341). Высота h
О
равна диаметру шара, вписанного в ок-
таэдр, т. е.А=
(см. задачу 443).
Мы получаем, следовательно.
458. Это возможно (см., например,
рис. 334); для этого достаточно взять
Рис. 341.	за ось цилиндра отрезок, соединяю-
соединяющий центры двух противоположных
граней додекаэдра, а радиус его такой, чтобы он был радиусом
круга, описанного вокруг правильного пятиугольника, сторона
которого равна диагонали
правильного пятиугольника со стороной а. Тогда вершины тех
двух граней, центры которых лежат в центрах оснований ци-
цилиндра, лежат на основаниях цилиндра, все же остальные 10
вершин распадаются на два правильных пятиугольника и
лежат на боковой поверхности цилиндра. Мы имеем, следо-
следовательно,
высота же h цилиндра, как диаметр шара, вписанного в иоде
каэдр (см. задачу 446),
\

459—461	стереометрия	275
откуда
3
=nr2h= ^-1/ 47+21/5.
459. Это возможно (см., например, рис. 335);для этого до-
достаточно взять за ось цилиндра отрезок, соединяющий центры
двух противоположных граней икосаэдра, а радиус его такой,
чтобы он был радиусом круга, описанного вокруг равносторон-
равностороннего треугольника, сторона которого есть диагональ Ь пра-
правильного пятиугольника со стороною а. Тогда вершины тех
двух граней; центры которых лежат в центрах оснований ци-
цилиндра, лежат на основаниях цилиндра, а остальные шесть
вершин разбиваются на два равносторонних треугольника и
лежат на боковой поверхности цилиндра. Мы имеем, следова-
следовательно,
г ьуъ _
г ¦—	 — а
3
а высота, как диаметр шара, вписанного в икосаэдр (см. за-
задачу 450),	_____
п-а\/	6
откуда
ТC+/б) G+3/5).
Конус
460. Пусть г — радиус основания полученного конуса,
ah — его высота, очевидно, I = R. Длина окружности осно-
основания
_1 __ 9тгг
2 "~ '
откуда			_
и, следовательно,
кг*Л
v=-
3	24
461. Получаются (рис. 342) сложенные основаниями конус
и усеченный конус и коническая выемка. Остается вычислить
радиус R=BE основания конуса, его высоту h=AB, радиус
r= CF малого основания усеченного конуса, его высоту //=
= ВС и высоту h' — CD конической выемки. Задача эта пла-
планиметрическая, как, впрочем, почти всегда бывает в столь
18*

276
РЕШЕНИЯ
462
многочисленных задачах на тела вращения, предлагаемых в
разных задачниках. Треугольники ABE, DGA, DCF, EKF
подобны:
следовательно,
ВЕ =
аУЪ
5
2aVb
АВ=а
5 '
10
2а V 5
и тогда
V=— nBEt-AB-^- — -к(BE2 -\-BE-CF -\- CFZ)ВС — —CF2• CD.
3	3	3
462. Пусть стороны треугольника а, Ь, с, пусть ha — высота,
опущенная на сторону а, я а± я az — отрезки от основания
высоты до концов основания а. При вращении вокруг стороны
Рис. 342.
Рис. 343.
а получаются два конуса, сложенных вместе основаниями, ес-
если углы при основании оба острые, один конус, если один
из углов прямой, или конус с конической выемкой, если
один из углов тупой. Объем тела получается соответственно
у	IZft CL-^ ¦
a== з ~*~
3 ' a 3
что дает во всех трех случаях
• r 	Ttft2fli
но это иначе можно переписать так:
3 а 4
3 a V

463—464
СТЕРЕОМЕТРИЯ
277
где Q — площадь треугольника. И мы получаем
V ¦ I/,. • V = —: — ¦ —.
а " с а Ь ' с
463. Из правильного пятиугольника ABCDE, ,; сторона
(рис. 343) которого b есть диагональ правильного прямоуголь-
прямоугольника, со стороною а, т. е.	_
мы получаем, что FA — радиус круга, описанного вокруг
этого пятиугольника, равен
FA = l
_/т1/ю + 4УХ
10
Отрезок z = FA — р, где р = а
10
далее, из подо-
подобия треугольников мы имеем у :р = У"а2 — т2 :t; откуда
далее опять из подобия х:2г=р:_у, т. е.
__ 2/-Т
г, как радиус вписанного шара, равен
Ю
(см. задачу 446 на стр. 270), и объем легко вычисляется.
Шар
464. Угол между радиусом О А и гра-
гранью АВ есть (рис. 344) угол между ОА
и диагональю грани АВ, так как перпен-
перпендикуляр, опущенный из центра сферы
О на грань АВ, очевидно, имеет осно-
основание в центре этой грани, т. е. в сере-
середине D ее диагонали. OD есть, следо-
вательно, половина стороны правиль-
правильного восьмиугольника, вписанного в круг радиуса R, так как
р
т.е. OD=—

278	решения	465—466
следовательно,
AD=YOA2—OD2 =—
т. е.
AB=R
ВС есть сторона восьмиугольника, вписанного в круг с ра-
радиусом АВ, т. е.
ВС=А В V-2 - ]/2"= R V2= AE.
Но
h=CE=VABz — AEz, т. е. RY'2.
465. Если шар касается двух пересекающихся прямых, то
центр его лежит на плоскости, перпендикулярной к плоскости
этих прямых и проходящей через их биссектрису. Отсюда ясно,
что центр шара лежит в центре куба (рис. 345 и 346). Шар
этот выступает из куба шестью сегментами, окружности осно-
оснований которых (сегментов) вписаны в квадраты граней куба.
Мы имеем, следовательно, радиус шара
высота сегмента
, a \f~2 а	\Г2 — 1
П~ 2	2 ~° 2 '
радиус окружности основания сегмента р = — следовательно,
объем сегмента
V ~ * h
Объем,
W=—¦
3
4-
общий
8
6
шару и
^ 4
кубу,
24
a VT-
2 2
8 24
равен, следовательно,
О о 1О 	 О г Л |-\о 1 О
12
5
6
466. Площадь шаровой поверхности сегмента равна 5=
= 2nR-h, но из прямоугольного треугольника 2Rh = r2 и, сле-
следовательно,
т. е. не зависит от величины радиуса R (рис. 347).

467-468
СТЕРЕОМЕТРИЯ
279
467. Продолжим все четыре грани тетраэдра до пересечения
с поверхностью сферы. Поверхность сферы разрежется этими
четырьмя плоскостями на следующие куски: четыре «треуголь-
«треугольных» куска, соответствующих граням тетраэдра, и шесть
Рнс. 345.
Рис. 846.
Рис. 347.
«двуугольных» кусков, соответствующих ребрам тетраэдра.
Обозначая через х и у площади этих кусков, мы имеем,
с одной стороны,
4х -\- 6_у = пов. сферы,
а с другой,
х -\- 3_у=пов. сегмента,
откуда
пов. сферы — 2-пов. сегмента
X—	-	.
Высота h сегмента равна разности между R и радиусом
г сферы, вписанной в тетраэдр, вписанный в сферу R;
(см. задачу 438), и следовательно,
Мы имеем, следовательно,
2_
3
468. Вот то единственное положение, которое могут при
этом иметь эти предметы (рис. 348). Это нетрудно доказать.
Пусть С (рис. 349)— центр одного из больших шаров, А —
точка их касания, В — точка касания малых шаров (эти обе
точки лежат, очевидно, на перпендикуляре к плоскости, вое-

280
РЕШЕНИЯ
466
ставленном в середине между точками прикосновения больших
шаров к плоскости, которая есть вместе с тем и середина
между точками прикосновения малых шаров к плоскости,
н	о
Рис. 348.
Рис. 349.
С — центр одного из малых шаров. Опустим из точки С пер-
перпендикуляр на OD и соединим В с D.
R + r, OD=R — r.
Из треугольников OBD и ОВС мы имеем
OB2=R2 -\-(R- r)*=(R + rf — г2,
откуда для определения R мы имеем квадратное уравнение
R2 — 4/?г+г2=0,
т. е.
только одно значение корня годится, так как при
•г
Рис. 350.
Рис. 351.
мы будем иметь /?О, что невозможно,
и, следовательно,

469	СТЕРЕОМЕТРИЯ	281
Пусть (рис. 350) теперь ST — проекция оси цилиндра, а М
и К — проекции центров шаров на плоскость. Мы имеем
(рис. 351)
/а2 = (Я + р)г - (R- рJ=4 /?р,
аналогично
MN2 = 4гР.
Из треугольников KLQ и QNM, которые подобны, получаем
KL:KQ = QN : QM
или
4/?p:#2 = (r2 —4rp):r2,
откуда
rR
Р
ИЛИ
р г	.
24
БОЛЕЕ ТРУДНЫЕ ЗАДАЧИ НА ДОКАЗАТЕЛЬСТВО
Некоторые задачи из общей теории выпуклых
многогранников
469. Рассмотрим бесконечную прямую АВ. Части ее, не
принадлежащие нашему мног ограннику, лежат по внешнюю
сторону по отношению к плоскости хоть одной из его граней.
Станем отрезать от бесконечной прямой АВ части последо-
последовательно всеми плоскостями его граней. Очевидно, что в ре-
результате останется некоторый один отрезок А В', состоящий
из точек, принадлежащих нашему многограннику. Точки А и
В принадлежат, следовательно, отрезку А'В', и, следовательно,
все точки отрезка АВ принадлежат многограннику. Предпо-
Предположим теперь, что многогранник не выпуклый, т. е. что он
имеет хоть одну грань, которая при продолжении пересекает
его. Пусть А — какая-нибудь внутренняя точка этой грани и
около нее многранник лежит по нижнюю сторону этой грани
(мы предполагаем, что он так повернут, что грань эта гори-
горизонтальна); тогда, так как плоскость этой грани его пересекает,
он имеет часть, лежащую по верхнюю сторону от плоскости
этой грани. Пусть В — какая-нибудь точка этой части. Очевид-
Очевидно, что отрезок АВ соединяет две точки нашего многогран-

282	РЕШЕНИЯ	470—474
ника, но не весь ему принадлежит; так например, наверно,
лежит вне его некоторая часть этого отрезка, прилежащая к
точке А.
470.	Станем последовательно отрезать от секущей плоско-
плоскости части всеми плоскостями граней нашего многогранника;
очевидно, что останется выпуклый многоугольник, который и
есть сечение нашего многогранника этой плоскостью.
471.	В вершине многогранника сходится по крайней мере
три грани, следовательно, число граней замкнутого многогран-
многогранника по крайней мере равно четырем. У многогранника, у ко-
которого четыре грани, все они не могут сходиться в одной
вершине; следовательно, все его углы трехгранные. Возьмем
один из этих трехгранных углов, плоскость четвертой грани
должна пересекать его ребра на конечных расстояниях от его
вершины. Получается тетраэдр.
472.	В многограннике с пятью гранями наивысшее наиме-
наименование многогранного его угла 4. Пусть имеется такой угол;
тогда, как в предыдущей задаче, убеждаемся, что наш много-
многогранник — четырехугольная пирамида. Если же все углы трой-
тройные, то возьмем один из них и рассмотрим четвертую и пятую
грани. Через каждый из концов ребер рассматриваемого трех-
трехгранного угла ОАВС проходит только одна из этих граней,
так как, по предположению, нет четырехгранного угла. Пусть,
например через два из этих концов А я В проходит четвертая
грань, а через третий С— пятая. Грань ОАВ тогда треуголь-
треугольная, а грани ОАС и ОВС — четырехугольные, причем четвертая
и пятая грани пересекаются по ребру, соединяющему четвер-
четвертые вершины граней ОАС и ОВС, и получается «треугольная
призма», «основания» которой суть грань
ОАВ и пятая грань.
473. Если число всех граней много-
многогранника п, то наивысшее возможное
наименование его граней п—1, что
будет только, если он п — 1-угольная
пирамида, а рассматриваемая грань — ее
основание. Итак, в зависимости от п
ограничены наименования всех граней
Рис. 352.	многогранника, а следовательно, и число
различных типов смежности его граней.
474. Возьмем любой многогранник, число вершин которого
не меньше чем число граней (например куб — такой много-
многогранник), и срежем все его вершины плоскостями (рис. 352)
так, чтобы образовались маленькие новые грани, такие, кото-
которые бы не касались друг друга даже вершинами. Представим
себе, что старые грани выкрашены белым, а новые черным.
Покажем, что многогранник такого топологического типа не

475	СТЕРЕОМЕТРИЯ	283
может быть описан вокруг шара. Действительно, предполо-
предположим противное и рассмотрим на всех гранях, как белых, так
и черных, точки их касания к шару. Построим на всех этих
гранях все треугольники, для которых вершинами будут эти
точки, а основаниями те стороны этих граней, которые суть
стороны черных граней. Тогда каждая черная грань вся разо-
разобьется на такие треугольники, а на всякой белой грани они
займут только часть, образуя как бы крест или звезду, так
как по предположению черные грани нигде не доходят друг
до друга, и, следовательно, на каждой белой грани те ее сто-
стороны, по которым она смежна с черными гранями, идут через
одну со сторонами, по которым она смежна с белыми гранями.
Каждый из таких треугольников имеет себе парный, а именно:
каждому такому треугольнику на белой грани соответствует
тот черный, который имеет с ним общее основание. Два тре-
треугольника такой пары равны, так как, если провести две каса-
касательные плоскости к одному и тому же шару, то треугольники,
основания которых представляют собою один и тот же отре-
отрезок прямой пересечения этих плоскостей, а вершины лежат
в точках касания, одинаковы. Рассмотрим суммы углов при
вершинах (лежащих в точках касания) во всех наших белых
треугольниках и во всех черных. Эти суммы должны быть
равны. А между тем сумма эта для черных равна 2тг раз число
черных граней, а эта же сумма для белых равна меньше чем
2тс раз число белых граней, так как углы эти при точке касания
белой грани, не налегая друг на друга, не покрывают всей
плоскости вокруг этой точки. Но число белых граней само
тоже меньше, чем число черных, и мы приходим к противоречию.
Замечание. Даже многогранников, получаемых таким срезанием,
как легко показать (среди многогранников с данным числом граней), весьма
много, но можно было провести все доказательство, предположив еще меньше,
а именно, что на многограннике нашем как-либо можно выделить комплекс
граней, друг до друга не доходящих, в котором не менее половины всех
граней многогранника.
475. Рассмотрим какую-нибудь сторону разбиваемого ''боль-
''большого» многоугольника; она состоит из одной или нескольких
сторон прилегающих к ней «малых» многоугольников, на
которые разбит «большой». Но каждый «малый» имеет центр
симметрии и, следовательно, имеет сторону, равную и парал-
параллельную противоположной стороне его, прилежащей к рассма-
рассматриваемой стороне «большого», она одновременно сторона
другого прилегающего к ней «малого» (предположим, для
простоты, что «малые» многоугольники смежны по целым
сторонам, а не по их частям) и т. д. Мы убедимся так, что
каждая из частей, на которые разбита рассматриваемая сторона

284	решения	476
«большого», будет иметь соответствующую себе часть на
противоположной стороне «большого». Рассматриваемый «боль-
«большой» многоугольник имеет таким образом для каждой своей
стороны противоположную ей равную (так как она составлена
из таких же частей) и параллельную; отсюда легко следует,
что он имеет центр симметрии, а именно в точке пересечения
прямых, соединяющих накрест концы таких двух параллель-
параллельных сторон.
476. Рассмотрим выпуклый многогранник, все грани кото-
которого имеют центры симметрии. Пусть ах — какое-нибудь его
ребро и Р± — одна из граней, сходящихся в этом ребре.
Ввиду того, что она имеет центр симметрии, она имеет ребро
а2, равное и параллельное и противоположное ребру аг. Пусть
по ребру а2 к грани Рх прилегает грань Р2. Ввиду того, что
и грань Р2 имеет центр симметрии, она имеет ребро а3, равное
и параллельное и противоположное ребру а2. Пусть по ребру
а3 к грани Р2 прилегает грань Р3 и т. д. Таким образом по-
получается замкнутая «зона» граней, окружающая поясом весь
многогранник. Замкнута эта зона потому, что если мы спроек-
спроектируем весь многогранник параллельно ребру ах на некоторую
плоскость, ему перпендикулярную, то грани Р19 Р2, Р3 и т. д.
спроектируются в виде отрезков, так как они все параллельны
направлению проекции, и отрезки эти, очевидно, будут после-
последовательными сторонами того многоугольника, в виде которого
на эту плоскость проектируется весь многогранник. Если же
принимать во внимание и проекции отдельных граней много-
многогранника, видимых с той стороны, например, с которой идет
проектирующий луч, т. е. граней той «шапочки», которая с
этой стороны покрывает зону, то получится „большой" мно-
многоугольник, разбитый на ряд «малых», которые будут проек-
проекциями отдельных граней этой «шапочки». Но очевидно, что
проекция многоугольника с центром симметрии есть опять
многоугольник с центром симметрии, и следовательно, так как
грани нашего многогранника, по предположению, все имеют
центры симметрии, то и все эти «малые» многоугольники будут
иметь центры симметрии. Применяя теперь результат, получен-
полученный в предыдущей задаче, мы видим, что рассматриваемый
«большой» многоугольник тоже имеет центр симметрии. Итак,
каждая проекция нашего многогранника вдоль его ребра имеет
центр симметрии, т. е. каждой проекции грани Pk параллельно
ее стороне соответствует параллельная ей проекция некоторой
грани Рг, т. е. каждой грани Рь соответствует на многогран-
многограннике некоторая грань Pv ей параллельная и противоположная
на многограннике. Следовательно, во всякой зоне граней, со-
содержащих Pk, будет содержаться и Р1г т. е. для каждой сто-
стороны грани Рк есть равная и параллельная ей сторона у грани

477	СТЕРЕОМЕТРИЯ	285
Pt. Отсюда ясно, что грани Р* и Рг равны и параллельны. Так
как, кроме того, грани Ph и Р1 имеют центры симметрии, то
они имеют общий центр симметрии О их совокупности, лежа-
лежащий в пространстве посредине между их центрами. Переходя
теперь от этих граней к соседним через симметричные по
отношению к О их ребра и т. д., мы убедимся, что и сам
многогранник имеет центр симметрии.
477. Теорема Эйлера. Если поверхность шара разбита на
N многоугольных областей с М сторонами и L вершинами,
то N — М -\- L ^- 2. Если при этом ни один многоугольник
не лежит внутри другого, то N — М -\- L = 2. Докажем
сначала это последнее утверждение. Выбросим одну область;
N уменьшится на единицу, а М и L останутся без изменения,
потому что все стороны и вершины выброшенной области
принадлежат в то же время и другим областям. Раз внутри
выброшенной области не было многоугольников, то оставшиеся
многоугольники образуют один сплошной кусок, ограниченный
многоугольником Р. Если у нас осталось больше одной обла-
области, то возьмем на Р вершину А многоугольника Т, имею-
имеющего на Р хоть одну сторону. А берем так, что от нее идет
сторона внутрь (такая вершина имеется, так как иначе все
многоугольники лежали бы внутри Р). Пойдем от А внутрь
нашего куска. Идя все время по сторонам многоугольника Т,
мы где-то впервые снова выйдем на границу Р, в какой-то
вершине Р. Если дальше от В к А можно перейти только по
сторонам многоугольника Т, идя только по границе Р, то зна-
значит линия АВ отрезает от всего куска только одну область,
ограниченную как раз многоугольником Т. В противном слу-
случае она отделяет от нашего куска вместе с нею еще и дру-
другие области. Возьмем вершину А', лежащую на Р и принад-
принадлежащую одной из этих областей. Берем А' так, что от нее
идет сторона внутрь. Чтобы выбранная область не лежала
внутри куска, берем, как и раньше, вершину области, имею-
имеющей на Р целую сторону. Исходя из А', отрежем от нашего
куска еще новую часть, и так дальше, до тех пор, пока не
отрежем одну область, имеющую на Р хоть одну сторону.
Выбросим эту область: число М уменьшится на единицу; число
N уменьшится на т, если выброшенная область имела на Р
т сторон; число L уменьшится на т — /, потому что мы вы-
выбросили только те вершины, которые разделяют выброшенные
стороны (крайние вершины остаются). Следовательно, число
N — М -J- L не изменится. Повторяя эту операцию, мы дойдем
наконец до того, что у нас останется один многоугольник; но
у него число сторон равно числу вершин, так что, когда мы
выбросим и этот многоугольник, число N — М -\- L уменьшит-
уменьшится на единицу и станет равным нулю, раз ничего больше не

286	решения	478
осталось. Но N— М ~\- L уменьшалось на единицу только при
выбрасывании самого первого и самого последнего многоуголь-
многоугольника. Следовательно, N — М -f- L = 2.
Пусть теперь поверхность шара разбита на произвольные
многоугольные области. Пусть внутри многоугольника Q лежит
многоугольник R. Возьмем точку А на Q и точку В на R и
соединим их новым ребром АВ. Если А, скажем, не было
вершиной Q, то число вершин увеличится на единицу, но зато
и число сторон у Q увеличилось на единицу (точка А разде-
разделит одну сторону на две), так что на число N — М-\- L ока-
окажет влияние только прибавление ребра АВ. Проводя одно или
два таких ребра (в зависимости от того, имели ли Q и R со-
соединяющее их ребро или общую вершину, или нет), мы полу-
получим, что многоугольник R не будет лежать внутри другого
многоугольника. При этом у нас появится одна новая область,
так что число N — М-\-L или не изменится, или уменьшится
на единицу, если нам пришлось добавить два ребра. Но таким
образом мы получим наконец, что ни один многоугольник
не будет лежать внутри другого, а для такого разбиения
N — М -j- L = 2, так что для нашего разбиения N — М -\- L ^> 2.
478= Теорема Коши. Два выпуклых многогранника, оди-
одинаково составленных из равных граней, равны. Возьмем мно-
многогранник и перенумеруем его грани /, //, ///,... и стороны
каждой грани 1г, /2, .. . , IIV //2, . . . Другой многогранник
называется составленным из тех же граней /, //, ///, . . ., если
всякие две грани, имевшие общие стороны на первом много-
многограннике (например, грани // и /// имели общие стороны /Л, и
II/j), имеют общие стороны на втором многограннике. Два
таких выпуклых многогранника могли бы отличаться друг от
друга двугранными углами между соседними гранями. Если
все эти углы у одного многогранника те же, что и у другого,
то многогранники равны, т. е. их можно совместить или
просто путем движения, или взяв сперва многогранник, сим-
симметричный одному из них. Действительно, приложим один
многогранник к другому так, чтобы грани / их совпали так,
чтобы совпали их соответственные стороны. Тогда могло бы
оказаться, что многогранники будут лежать по разные стороны
плоскости этой грани. В этом случае отразим один многогран-
многогранник в этой плоскости. Теперь оба многогранника лежат по
одну сторону от этой плоскости. Пусть, например, по стороне
/х к грани / прилегает грань //. Раз двугранные углы между
гранями / и II равны и грани / обоих многогранников совпали,
то совпадут и грани //. Переходя таким образом все к новым
граням, убедимся, что все они совпали, так что многогранники
равны. Таким образом для того, чтобы доказать нашу теорему,
достаточно доказать, что у двух выпуклых многогранников,.

478	СТЕРЕОМЕТРИЯ	287
одинаково составленных из равных граней, соответственные
двугранные углы между соседними гранями должны быть рав-
равны. Возьмем два таких многогранника. Если соответственный
двугранный угол на втором из них больше, чем на первом, то
будем писать на ребре этого угла плюс, если он меньше,
то — минус, а если они равны, то — нуль. Приняв это, дока-
докажем следующую лемму.
Число перемен знаков при обходе от ребра к ребру во-
вокруг вершины >- 4, или равно нулю, и тогда на всех ребрах
стоит нуль. (Нули при подсчете перемен знаков просто не
считаются.)
Опишем вокруг вершины А шар радиуса единицы. Пло-
Плоскости граней, сходящихся в А, вырежут на нем выпуклый
многоугольник. Стороны этого многоугольника измеряют углы
на гранях с вершиной в Л, а углы между сторонами равны
двугранным углам между гранями. Поэтому вместо того, чтобы
говорить о гранях и двугранных углах, мы можем говорить
о выпуклых сферических многоугольниках. Поэтому нашу
лемму можно формулировать так: если у двух выпуклых мно-
многоугольников стороны равны, а углы не равны, то число пере-
мен знаков разностей между углами при обходе вокруг мно-
многоугольника %>4, или оно равно нулю, и тогда все углы равны.
1.	Если в двух треугольниках стороны равны, а углы, заклю-
заключенные между ними, не равны, то против большего угла лежит
большая сторона. Эта теорема известна для плоских треуголь-
треугольников (она доказывается, например, в книге Киселева). Для
того чтобы доказать ее для сферических треугольников, доста-
достаточно повторить ее доказательство для плоских, заменяя слово
«прямая» словом «дуга большого круга».
2.	Если у двух выпуклых многоугольников все стороны,
кроме одной AG, равны, а углы, кроме прилегающих к сто-
стороне AG, во втором многоугольнике больше (или меньше),
чем в первом, то сторона а во втором многоугольнике больше
(или меньше), чем в первом. (Для краткости мы говорим, что
все «углы больше», когда хотя бы один из них больше, а
другие равны. То же относится к слову «меньше».)
Возьмем первый многоугольник и начнем увеличивать
(уменьшать) угол В так, чтобы он стал равным соответствую-
соответствующему углу во втором многоугольнике. Раз длины сторон и
прочие углы при этом не меняются, то ВО останется на ме-
месте, а АВ будет поворачиваться так, что угол C в треугольнике
ABG будет расти (убывать), а значит, в силу п. 1 будет расти
(убывать) и сторона AG. Повторяя те же рассуждения после-
последовательно для всех углов, докажем то, что нам нужно.
3.	Если у двух выпуклых многоугольников все стороны
равны, то углы в одном не могут быть все больше (или мень-

288	решения	478
ше), чем в другом. Если бы так было, то по п. 2 хоть одна
сторона в одном многоугольнике должна была бы быть боль-
больше (или меньше), чем в другом, а они равны.
4. Если у двух выпуклых многоугольников все стороны рав-
равны, а углы не равны (хотя бы не все), то число перемен
знаков разностей углов при обходе вокруг многоугольника
^> 4. По п. 3 разности всех углов не могут быть все одноги
знака (нули не считаются). Число перемен знаков, если они
есть, — четное число, потому что при обходе мы возвращаемся
к прежнему знаку. Число их больше двух. Допустим, что мы
имеем всего две перемены знаков. Соединим две вершины
многоугольника диагонально так, что по одну сторону от нее
все углы больше, а по другую меньше, чем в другом много-
многоугольнике. Тогда, применяя теорему п. 2 сперва к одной
части нашего многоугольника, а потом к другой, получим,
что диагональ должна быть одновременно больше и меньше
аналогичной диагонали в другом многоугольнике, а это абсурд.
Следовательно, число перемен знаков больше двух, а раз оно
четное, то оно;>4.
Теперь мы можем приступить к доказательству основной
теоремы. Возьмем выпуклый многогранник, на ребрах кото-
которого по указанному нами принципу написаны плюсы,' минусы
и нули. Выбросим из рассмотрения все ребра,' на которых
стоят нули. Ни одно из оставшихся ребер не будет иметь свобод-
свободного конца, так как к вершине, к которой подходит ненулевое
ребро, подходят в силу леммы и другие ненулевые ребра.
В результате получим разбиение поверхности многогранника
на некоторое число N областей с М ребрами и L вершинами.
При обходе от ребра к ребру вокруг вершины мы получаем
не меньше четырех перемен знаков (вершины, в которых
сходятся только ребра с нулями, у нас отброшены), так что
при обходе вокруг L вершин число перемен знаков будет
!>4 L. Но это число перемен знаков можно считать и иначе,
идя от ребра к ребру не вокруг вершин, а вокруг областей;
получится, конечно, тоже самое, потому что ребра, соседние
при обходе вокруг вершины, будут соседними и при обходе
вокруг области. При обходе треугольника число перемен зна-
знаков не больше 2 (оно, конечно, четное), при обходе четырех-
четырехугольника не больше 4, пятиугольника — тоже не больше 4
и т. д. Если у нас есть Ns треугольников, Nt четырехуголь-
четырехугольников и т. д., то число перемен знаков
+ ...,	A)
с другой стороны, v>4Z.. Но
Ы3 + ЛГ4 + N, + ... = N, ЗА', + 47V4 -f 5.VS + ... = 2Л1

479
СТЕРЕОМЕТРИЯ
289
BЛГ — потому что каждое ребро принадлежит двум областям
и поэтому при подсчете, произведенном в левой части равен-
равенства, оно учитывается дважды), и по теореме Эйлера
Отсюда
AL>4 (М ~ N + 2)
Но
N —
2 (ЗЛЛ, + 4Nt + 5N5 + ...) -
B)
Это неравенство противоречит неравенству A). Следова-
Следовательно, когда мы выбрасывали все ребра, на которых стояли
нули, мы должны были выбросить все ребра, так что никако-
никакого разбиения на области не получилось. Следовательно, на
всех ребрах должны стоять нули, т. е. все двугранные углы
у обоих многогранников равны и равны сами многогран-
многогранники.
Параллелоэдры
479. Пусть /, 2, 3, 4, 5 — ряд одинаковых (рис. 353) правиль-
правильных шестиугольников, сложенных параллельными сторонами.
Легко показать, что ровно такой же ряд /', 2\ 3', 4' можно
приложить к этому первому ряду так, чтобы между ними не
оставалось не покрытых ими частей плоскости. Прикладывая
так дальнейшие ряды Г, 2", 3", 4",... мы покроем такими
равными и параллельно распо-
расположенными шестиугольниками
всю плоскость (так расположены
ячейки в пчелиных сотах). По-
Построим теперь на каждом шести-
шестиугольнике, как на основании, пра-
правильные шестиугольные призмы
одинаковой высоты h. Легко ви-
видеть, что верхние основания этих
призм будут все лежать в одной
и той же плоскости, параллель-
параллельной плоскости, в которой нахо-
находятся их нижние основания, и находящейся от нее на расстоя-
расстоянии h, а боковые грани призл! будут прилегать друг к другу,
так что весь промежуток между указанными плоскостями
будет заполнен призмами.
Если построить ровно такой же второй слой таких же
призм и наложить на первый так, чтобы призмы верхнего слоя
19 Делоне и Житомирский
Рис. 353.

290
РЕШЕНИЯ
480—482
были параллельны призмам нижнего и т. д., то и получится
заполнение всего пространства такими призмами в параллель-
параллельном положении.
480.	Разрежем додекаэдр задачи 328 плоскостью, проходя-
проходящею через центр куба параллельно его основаниям; эта пло-
плоскость пройдет через верши-
вершины четырех ромбов и даст
в сечении квадрат. Верхняя
половина додекаэдра будет
представлять собою нечто
вроде пирамидальной крыши,
ограниченной четырьмя поло-
половинами ромбов и четырьмя
ромбами. Построим в некото-
	рой плоскости Р сетку квадра-
~7	7	7	тов> покрывающих всю эту
плоскость, и поставим на ка-
Рис. 354.	ждый такой квадрат (рис. 354)
такую крышу. (Четыре такие
крыши изображены на чертеже.) Так как вершины крыш А,
В, С, D и т. д. проектируются в центры квадратов и лежат все
на одной и той же высоте над плоскостью Р, то Они образуют
опять совершенно такую же параллельную первой сетку квад-
квадратов в некоторой плоскости Р', параллельной плоскости Р. (Один
из таких квадратов намечен на чертеже пунктиром.) Под каждым
из таких квадратов плоскости Р' расположена выемка, обра-
образованная четырьмя крышами, поставленными на плоскость Р,
вершины которых А, В, С, D суть вершины соответствующего
квадрата плоскости Р'. Выемка эта О, А, В, С, D представляет
собою как раз нижнюю половину нашего додекаэдра, в чем
легко убедиться наложением. Вставив во все эти выемки
додекаэдры, мы, очевидно, над плоскостью Р' получим ровно
такую же совокупность крыш, какая была построена над
плоскостью Р.
На этот слой додекаэдров можно наложить новый слой
и т. д. Если так продолжать до бесконечности кверху и кни-
книзу, то все пространство заполнится такими додекаэдрами.
481.	Если между верхней и нижней половиной додекаэдра
предыдущей задачи вдвинуть правильную четырехугольную
призму OKLM, OXKXLXMX, то получится додекаэдр, у которо-
которого четыре грани шестиугольные (рис. 355). Для доказательства
заполнения ими пространства достаточно в доказательстве
предыдущей задачи заменить плоскости Р, Р' и т. д. слоями
квадратных призм OKLM, O1/('1Z.1AJ1.
482.	Если мы заполним такими кубами (рис. 356) все про-
пространство так, чтобы кубы прилегали друг к другу плотно

482
СТЕРЕОМЕТРИЯ
291
целыми гранями, то четырнадцатигранники, каждый из кото-
которых находится внутри своего куба и занимает лишь часть его
объема, заполнят еще не все пространство — останутся пусто-
пустоты. Рассмотрим восемь больших кубов, сходящихся в одной
Рис. 356
вершине О', и затем те восемь малых кубов (восьмушек боль-
больших), которые сходятся в этой же вершине О'. Половины
этих восьми малых кубов (отрезанные по шестиугольным се-
сечениям), не прилежащие к вершине О', будут заняты восьмуш-
восьмушками тех восьми 14-гранников, которые вписаны в восемь
больших кубов. Половины же восьми малых кубов, приле-
прилежащие к вершине О', образуют пустоту, представляющую как
раз такой же 14-гранник, но вписанный в большой куб, состав-
составленный из этих восьми малых кубов. Точка О' будет центром
этого большого куба и вписанного в него 14-гранника. Если
все такие пустоты заполнить такими
14-гранниками, то все пространство
окажется ими заполнено.
Дело обстоит совершенно гак, как
было бы в следующем планиметри-
планиметрическом построении: вся плоскость
(рис. 357) разбита на большие квад-
квадраты ABCD; каждый из них разбит
(пунктиром) на четыре малых квад-
квадрата. Из четырех половинок каждого
из четырех малых квадратов, на кото-
которые разбит один большой квадраг, при-
прилежащих к центру О большого квад-
квадрата, составлен многоугольник (там 14-гранник, здесь квадрат,
заштрихованный). Квадраты эти (заштрихованные) не покрыва-
покрывают всей плоскости, между ними остаются пустоты. Если
рассмотреть четыре больших квадрата, сходящихся в одной
19*
Рис. 357.

292	решения	483
вершине О', и четыре малых—сходящихся в этой вершине, то
четыре половинки этих четырех малых составляют как раз
«пустоту» с центром в О'; она есть опять такой же квадрат (бе-
(белый). Совокупность всех таких черных и белых квадратов за-
заполняет всю плоскость.
Эту задачу можно решить способом, примененным в зада-
задаче 480, и наоборот, задачу 480 — способом, примененным в
этой задаче.
483. Так как система точек Е, нами рассматриваемая, пред-
предполагается трехмерной, то в ней есть по крайней мере четыре
точки О, А, В, С, не лежащие в одной плоскости. Рассмотрим
параллелепипед, получаемый «достроением» тетраэдра ОАВС
(см. задачу 337) до параллелепипеда, и ту параллелепипе-
дальную систему Т, которая получается в результате запол-
заполнения пространства этим параллелепипедом и равными этому
параллелепипедами, смежными с ним и друг с другом по
целым граням. Из свойства 1 следует, очевидно, что в нашу
систему точек, кроме точек О, А, В, С, входят во всяком
случае все точки (вершины параллелепипедов) этой парал-
лелепипедальной системы. Если ни внутри, ни на границе
параллелепипеда ОАВС, кроме точек в его вершинах, нет
других точек Е, то же самое имеет место и для других парал-
параллелепипедов системы Т, так как в силу свойства 1, если
была бы точка в каком-нибудь из этих параллелепипедов., то
была бы точка и в параллелепипеде ОАВС. В таком случае
система Т исчерпывает все точки системы Е, и, следовательно,
наша система Е— параллелепипедальная система. Предположим
теперь, что, кро^е точек Е, в вершинах параллелепипеда
ОАВС, внутри или на границе его, есть другие точки Е. За-
Заметим прежде всего следующее. Соединяя свойства 1 и 2,
мы получаем, что вокруг каждой точки рассматриваемой нами
системы точек можно описать шар радиуса г, такой, что в
нем не будет других точек нашей системы, т. е., другими сло-
словами, что если вокруг всех точек нашей системы Е описать
шарики радиусами —, то эти шарики не будут входить друг
в друга. Отсюда следует, что в параллелепипеде ОАВС есть
только ограниченное число точек системы Е, так как иначе,
если мы увеличим это г параллелепипед, отодвинув его грани
во вне параллельно самим себе на расстояние —, то в этом
увеличенном параллелепипеде было бы неограниченное число
шариков радиуса —, которые не входят друг в друга, что не-
невозможно. Нельзя в конечный ящик насыпать бесконечно
много шариков. Итак, если в параллелепипеде ОАВС внутри

484—485	СТЕРЕОМЕТРИЯ	293
или на границе, кроме точек в его вершинах, есть еще дру-
другие точки ?, то число их ограничено. Пусть А' есть сама
точка А, если на ребре О А нет других точек Е, кроме точек
в его концах, и ближайшая из его внутренних точек Е к точ-
точке О, если такие точки есть. Пусть В' — сама точка В, если
внутри или на границах параллелограмма О А'В нет точек Е,
кроме точек Е в его вершинах (на стороне его О А' и парал-
параллельной ей стороне точек Е нет в силу выбора точки А'), и
ближайшая к прямой О А' точка этого параллелограмма, если
такие точки есть. Пусть С — сама точка С, если внутри и на
границе параллелепипеда О А'В'С нет точек Е, кроме точек Е
в его вершинах (на основании его О А' В' и ему противополож-
противоположном основании таких точек нет в силу выбора точек А' и В'),
и ближайшая к плоскости О А'В' точка Е этого параллелепи-
параллелепипеда, если такие точки есть. В силу выбора точек А'В'С
очевидно, что внутри и на границе параллелепипеда ОА'В'С
нет точек Е, кроме точек Е, которые лежат во всех его вер-
вершинах, в силу того, что точки О, А', В', С принадлежат Е
и в силу свойства 1. Система Е, следовательно, совпадает с
параллелепипедальиой системой /', построенной на парал-
параллелепипеде О'А'В'С.
484.	Пусть А, В, С — центры трех параллелоэдров. От парал-
параллелоэдра А можно дойти до параллелоэдра В, переходя через
цепь параллелоэдров, попарно смежных по граням, так как парал-
лелоэдры заполняют все пространство. Построим от парал-
параллелоэдра С такую же цепь параллелоэдров, т. е. которые по-
последовательно касались бы друг друга по граням, соответствен-
соответственным тем, по которым касаются друг друга последовательные
параллелоэдры цепи АВ; тогда ввиду равенства, параллель-
параллельности всех параллелоэдров и того, что они касаются по целым
граням, следует, что отрезок CD, где D — центр последнего
параллелоэдра цепи, построенной от параллелоэдра С, равен
и параллелен отрезку АВ, и следовательно, для системы Е
центров параллелоэдров выполняется условие 1 предыдущей
задачи. С другой стороны, ни к одному центру параллелоэдра
не лежит центр никакого другого ближе, чем на некотором
расстоянии г, которое равно, например, удвоенной длине пер-
перпендикуляра, опущенного из центра параллелоэдра на ту из его
граней, которая ближе всего к его центру. Следовательно,
удовлетворяется и условие 2.
485.	Ввиду того, что сами параллелоэдры имеют центры
симметрии и равны и параллельны, то совокупность любых
двух параллелоэдров имеет центр симметрии, лежащей посре-
посредине между их центрами. Если эти параллелоэдры смежны по
грани, то этот центр их совокупности, как легко видеть, ле-
лежит на этой грани и является ее центром.

294	решения	486-491
486.	Рассуждаем совершенно аналогично тому, как в за-
задаче 476.
487.	Рассуждаем аналогично тому, как в задаче 476.
488.	Проведем от ребра е во все стороны те плоскости,
которые разделяют между собою все параллелоэдры разбиения
пространства, которые сходятся в этом ребре. Очевидно, что
проекции этих плоскостей будут сторонами многоугольников,
являющихся проекциями этих параллелоэдров, что они в пло-
плоскости проекции окружают точку е, являющуюся проекцией
этого ребра, и что эти прямые, следовательно, разделяют между
собою эти многоугольники, т. е. что многоугольники эти не
налегают друг на друга.
489.	Пусть А и В—два из этих многоугольников, смежных
по стороне т, исходящей из точки е. Толщина такого много-
многоугольника в направлении т нигде не меньше, чем длина т, так
как многоугольник этот выпуклый и имеет центр симме-
симметрии. Сторона 8, по которой смежные два других С и D из
этих многоугольников, облегающих точку е (если предполо-
предположить, что их всех больше трех), не может быть не параллель-
параллельна т (т. е. не быть продолжением т), так как иначе тот из
этих многоугольников С, D, для которого сторона 8 была бы
нижней (мы мыслим себе т вертикальной, и что е — ее ниж-
нижний конец), имел бы в соседстве с точкой е толщину нуль в
направлении т. В точке е могут, следовательно, сходиться
только три или четыре (рис. 358) таких многоугольника, и в
случае, когда сходятся четыре, стороны, по которым они
смежны, суть попарно продолжения одна другой.
490.	В случае тройного схода в точке е многоугольник А
имеет три угла, равных и параллельных последовательным
Ai	углам при точке е, так как все сходящиеся в
	 ней многоугольники (проекции параллело-
параллелоэдров) равны и параллельны. Но А имеет
центр симметрии, а следовательно, он имеет
Рис. 358.	и углы, симметричные этим трем углам.
Если мы еще заметим, что прямо-параллель-
прямо-параллельные стороны (т. е. такие, которые параллельны и имеют мно-
многоугольник по одну и ту же сторону от себя) выпуклого
многоугольника должны быть идентичны, мы убедимся, что
многоугольник А есть шестиугольник с центром симметрии.
В случае четверного схода мы аналогично убедимся, что много-
многоугольник этот параллелограмм.
491.	Будем образовывать этот слой таким образом. Будем
пристраивать к исходному параллелоэдру все следующие и

492—493	СТЕРЕОМЕТРИЯ	295
следующие параллелоэдры по граням, параллельным некоторой
грани зоны, и образуем так бесконечную в обе стороны «ко-
«колонну» параллелоэдров, центры которых, очевидно, будут ле-
лежать на одной прямой, образуя на ней ряд равноудаленных
точек. В проекции на плос-
плоскость Р параллельно ребру е
этой зоны получится полоска
(рис. 359) шестиугольников А
(предполагая, что А — шести-
шестиугольник). Затем будем при-
пристраивать по другим граням
этой зоны ту аналогичную ко-
колонну параллелоэдров, кото-	рис 359.
рая будет проектироваться в
виде смежной полоски шестиугольников. Вследствие сущест-
существования центров у шестиугольников А выступающие углы
этой полоски будут точно входить во входящие углы первой
полоски, так что полоски эти, не налегая друг на друга, будут
без зазоров прилегать друг к другу. Будем пристраивать так
следующие и следующие такие колонны; очевидно, что обра-
образуется бесконечный во все стороны слой параллелоэдров, все
центры которых лежат в одной плоскости и образуют в ней
параллелограмматическую систему точек. Очевидно также,
что слой этот непроницаем, т. е. не имеет дырок в том смы-
смысле, что нельзя даже сколь угодно малый шарик пронести
с одной его стороны на другую.
Если многоугольник А — параллелограмм, рассуждаем ана-
аналогично.
В обоих случаях все дело связано с тем, что эти много-
многоугольники А (шестиугольники с центрами симметрии и парал-
параллелограммы) суть параллелоэдры плоскости (так называемые
параллелотопы), заполняющие ее без налеганий в параллель-
параллельном положении и соприкасаясь целыми сторонами.
492.	Ввиду непроницаемости два слоя могли бы пересе-
пересекаться только, если бы они имели общие параллелоэдры, но
тогда эти слои можно было бы начать строить с параллело-
эдра, общего им обоим, и мы убедились бы, что слои эти
тождественны.
493.	Действительно, ввиду того, что слои непроницаемы
и не пересекаются, существует такой слой, первый, который
принадлежит к слоям, лежащим над нулевым, и не отделен от
него никаким другим слоем. По любой грани F верхней ша-
шапочки параллелоэдра нулевого слоя к этому параллелоэдру
смежен некоторый параллелоэдр первого слоя, так как все
параллелоэдры более высоких слоев отделены от нулевого
слоя непроницаемым первым слоем.

296
РЕШЕНИЯ
494-496
494.	Из предыдущей задачи очевидно, что проекция верх-
верхних шапочек параллелоэдров первого слоя на плоскость Р
параллельно ребру е получится, если на сетку многоугольни-
многоугольников А, являющихся проекциями парчллелоэдров нулевого слоя,
наложить сетку многоугольников А, являющихся проекциями
параллелоэдров первого слоя, т. е. сетку такую же и ей па-
параллельную, но, вообще говоря, смещенную.
495.	Легко видеть, что топологически разных проекций
шапочки (рис. 360 и 361) всего 7, а именно:
I	п ш tv м
IV
откуда получаются семь многогранников:
IV'
Из этих многограников только пять топологически раз-
различны.
496. Пусть П—такой многогранник. В силу результата
задачи 476 он будет тогда иметь центр симметрии. Ста-
Станем выстраивать, подобно тому как в задаче 491, такие
многогранники в колонны, а затем из таких колонн слой;
мы убедимся тогда, что в силу топологического типа парал-
лелоэдра и того, что он сам и его грани имеют центры сим-
симметрии, выпуклости последующей колонны будут в точности
приходиться в выемки предыдущей, и получится непрони-
непроницаемый слой, центры многогранников которого будут лежать
в одной плоскости и составлять в ней параллелограмматиче-
скую систему. Будем теперь сверху на этот слой накладывать
такие же слои друг на друга; тогда опять вследствие указан-
указанных свойств наших многогранников выпуклости последу-
последующего слоя будут в точности приходиться в выемки пре-
предыдущего, и пространство окажется все заполнено такими
равными и параллельно расположенными многогранниками,
смежными по целым граням.

497-500
СТЕРЕОМЕТРИЯ
297
Задачи на прямолинейные преобразования плоскости
и перспективу
497.	Пусть на плоскости Р начерчена квадратная сетка
(сетка равных квадратов). После преобразования, т. е. на пло-
плоскости Р' (через Р' мы обозначим новое распределение точек
на плоскости Р), она опять превратится в квадратную сетку,,
так как вследствие сохранения прямых прямыми и сохранения
углов, квадраты ее превратятся в прямоугольники, а вслед-
вследствие сохранения и углов между диагоналями ее квадратов
эти прямоугольники будут квадратами, так как если прямо-
прямоугольник не квадрат, то угол между его диагоналями не
прямой. Так как исходная квадратная сетка могла быть взята
сколь угодно густой, то очевидно, что всякая фигура пло-
плоскости Р преобразуется на Р' в фигуру, ей подобную, т. е.
все линейные размеры будут в одно и то же число раз k боль-
больше (или меньше), чем соответственные линейные размеры
фигуры на Р, и угловые величины такие же.
498.	Если квадратная сетка плоскости Р' не параллельна
сетке плоскости Р, то можно, повернув ее на известный угол,
сделать параллельной сетке на Р. Взяв теперь две пары со-
соответственных точек этих сеток А и А', В и В', мы получим
на пересечении прямых АА' и ВВ' точку О такую, что, как
это легко видеть из подобия треугольников, если С и С —
любые две соответственные точки сеток, то прямая СС тоже
проходит через точку О и мы имеем О А : О А' = ОВ : ОВ' —
= OC:OC'—k- О называется центром, a k — коэффициентом
гомотетии.
499.	Гомотетия просто увеличивает квадратную сетку на
Р в k раз, и следовательно, очевидно, где бы ни лежала на ней
фигура, она претерпевает, если она расположена параллельно
тому,как в первом по-
положении, то же самое
преобразование незави-
независимо от того, близко
или далеко от центра
гомотетии О она лежит.
500.	Раз прямые ос-
остаются прямыми и па-
параллельные параллель-
параллельными, то квадратная
сетка плоскости Р пре-
превращается на плоскости Р' в сетку параллелограммов. По-
Покажем, что все эти параллелограммы (рис. 362 и 363) будут
одинаковы. Действительно, пусть заштрихованный квадрат сет-
сетки Р преобразуется в заштрихованный параллелограмм на Р'\
р
с
0
ч
1
ч
ч
1
/
В
¦>
/
Рис. 362.
Рис. 363.

298	решения	501
тогда прямая ОВ превратится в прямую О'В'. Где на этой пря-
прямой будет лежать точка В'? Очевидно, что так, что А'В' — О'А',
так как, если бы, например, она лежала ближе в точке В'',
то диагональ CD преобразовалась бы на Р' в ломаную C'A'D"
(аналогично — если дальше); так как прямые переходят в пря-
прямые, то это невозможно. Таким образом получается, что все
четыре нарисованных параллелограмма одинаковы. Аналогично
покажем, что и все к ним прилежащие одинаковы, и т. д.
Будем теперь постепенно поворачивать квадратную сетку вР
вокруг точки О, ее изображение в Р' будет тоже постепенно
Рис. 364.	Рис. 365.
изменяться, оставаясь сеткой равных параллелограммов. Ког-
Когда заштрихованный квадрат в Р повернется в запунктиро-
ванный, заштрихованный параллелограмм в Р' превратится в
запунктированный; при этом угол его а из острого пре-
превратится в тупой Р; следовательно, в силу непрерывности
изменения угла а, будет такое положение сетки Р, при ко-
котором этот угол будет прямой. Если, значит, в плоскости Р
взять разумно повернутую (рис. 364 и 365) квадратную сетку,
то ее изображением в плоскости Р' будет сетка равных прямо-
прямоугольников. Таким образом рассматриваемое преобразование
равномерно растягивает всю плоскость Р перпендикулярно от
прямой ОХ (или сжимает) и равномерно растягивает плоскость
Р перпендикулярно от перпендикулярной к ней прямой OY
(или сжимает), причем коэффициенты растяжений kv #2, во-
вообще говоря, различны. ОХ и OY называются осями рассма-
рассматриваемого афинного преобразования. После указанных растя-
растяжений вся плоскость может быть еще передвинута как целое
и отражена в прямой.
501. Такое равномерное растяжение плоскости от прямой
превращает сетку равных квадратов в сетку равных прямо-
прямоугольников, и следовательно, это растяжение совершенно одина-
одинаково влияет на все размеры двух одинаковых и параллельных
между собою фигур, где бы они ни лежали на этой квадрат-
квадратной сетке.

502—503
СТЕРЕОМЕТРИЯ
299
502.	Действительно,пусть А, В, С—три точки в Р, не лежащие
на одной прямой, и пусть после афинного преобразования РвР1
эти точки получают положения А', В', С*. Построим на
А, В, С параллелограмм ABCD. Тогда точка D', соответст-
соответственная D на Р', будет в четвертой вершине параллелограмма,
построенного на А', В', С. Сетка равных параллелограммов
ABCD на Р превращается, что можно показать, как в задаче
500, на Р' в сетку равных параллелограммов A'B'C'D', и
следовательно, положением всякой точки М на Р будет опре-
определено и ее положение на Р'.
503.	Пусть имеется (рис. 366) на плоскости Р любой вы-
выпуклый четырехугольник. Проведем противоположные сто-
стороны этого четырехугольника до взаимного пересечения в
точках А я В (четырехугольник, нами рассматриваемый, пред-
предполагается произвольным, т. е. что его противоположные
стороны попарно не параллельны; если в одной или обеих
парах они были бы параллельны, мы бы это рассматривали
Рис. 366.
как предельный случай). Рассмотрим также точки С и D, в
которых продолжения диагоналей нашего четырехугольника
пересекают прямую АВ (то же замечание надо сделать о слу-
случае, когда одна из этих точек уходит на бесконечность).

300
РЕШЕНИЯ
504
Проведем через прямую АВ плоскость Q' под любым углом
<р к плоскости Р и какую-нибудь плоскость Q, параллельную
плоскости Q'. Начертим в плоскости Q' две полуокружности,
опирающиеся на АВ и на CD как на диаметры, и пусть они
пересекутся в точке S; тогда, проектируя из точки 5 наш
четырехугольник с плоскости Р на плоскость Q, мы получим
в плоскости Q квадрат. Действительно, стороны его GH и
KL проектируются плоскостями, проходящими через прямую
SA, лежащую в плоскости Q', параллельной плоскости Q,
и следовательно, о аи параллельны SA; стороны же GK и
HL аналогично параллельны SB, но угол ASB вписанный,
опирающийся на диаметр, т. е. прямой. Таким образом GHLK
прямоугольник. Аналогично убеждаемся, что диагонали его па-
параллельны SC и SD, следовательно, тоже взаимно-перпенди-
взаимно-перпендикулярны. Но если у прямоугольника диагонали взаимно-пер-
взаимно-перпендикулярны, то он — квадрат.
504. Пусть А, В, С, D — четыре точки на плоскости Р и
A'B'C'D' — те точки плоскости Р', куда перешли эти точки
в результате рассматриваемой коллинеации (рис. 367 и 368)
Рис. 367.
Рис. 368.
В таком случае точки Е, F, G, очевидно, перейдут в точки
Е', F', G', так как любая прямая, проходящая через две
точки плоскости Р, преобразуется в прямую плоскости Р1.
проходящую через те две точки плоскости Р', в которые
эти точки преобразовались, и точка пересечения двух прямых,
конечно, переходит в точку пересечения тех прямых, в которые
эти прямые преобразовались. Проводя прямые на Р через
так новополученные точки, мы будем получать все новые
точки пересечения, например точку Н и т. д., относительно
которых мы тоже будем знать, в какие они точки преобра-
преобразуются, если будем проводить соответственные прямые на
Р'. Получаемая так сетка прямых называется сеткой Мебиу-
Мебиуса (см. Mobius, Der barizentrische Kalkul, 1829). Если бы по-
показать, что получаемые так все новые точки пересечения
густо покроют всю плоскость Р и аналогично плоскость Р'г
то все и было бы доказано, так как тогда вследствие пред-

504
СТЕРЕОМЕТРИЯ
301
полагаемой непрерывности преобразования, т. е. что, вообще
говоря, бесконечно близкие точки переходят в бесконечно
близкие, окажется, что если мы знаем, куда перешли точки
к.
Плоскость Р
Плоскость О
Е
Рис. 369.
A BCD, то мы знаем и куда переходит любая точка М
плоскости Р. Дело в том, что если даже точка М не будет
сама одной из точек пересечения,
то во всяком случае будет сколь
угодно много точек пересечения
- сколь угодно к ней близких, а об
этих точках мы будем знать, куда
они переходят.
Рассмотрим перспективную про-
проекцию плоскости Р на плоскость Q,
подобную рассмотренной в предыду-
_ щей задаче, при которой четырех-
четырехугольник CEDF сетки Мебиуса (рис.
369) перейдет в квадрат C'E'D'F'
(рис. 370) на плоскости Q. При этом
точки В и Л и вообще вся прямая
АВ, а следовательно, и точки пере-
пересечения ее К с диагональю EF сетки
Мебиуса, уйдут на бесконечность.
Прямые, пересекающие прямую EF плоскости Р в точке К,
превратятся вследствие этого на плоскости Q в прямые, парал-
Г
0'
г'4 /Vs
Рис. S70.

302	решения	505-506
лельные прямой E'F', прямые исходящие на плоскости Р из точ-
точки В — в прямые, параллельные прямой СЕ', а исходящие иа
точки А,—в прямые, параллельные прямой СF'. На плоскости Q,
начиная с четырех прямых, являющихся сторонами квадрата
C'E'D'F', можно построить постепенно все прямые квадратной
сетки с квадратом C'E'D'F', как основным, если поступать так:
провести через точку D' диагональ, параллельную диагонали
E'F', и так получить точки Ег' и Z7/; затем через эти точки про-
провести прямые, параллельные CF' и СЕ'; через точку ?)/ провести
диагональ, параллельную E'F', и там получить точки Е2' и F2',
затем через эти точки провести прямые, параллельные CF' и СЕ',
и т. д. Параллельно с этим построением на плоскости Q произ-
производим аналогичное построение на плоскости Р, заменяя только,
конечно, проведение прямых, параллельных прямые E'F', C'F'
и СЕ', соответственно проведением прямых, проходящих через
точки К, Л я В.
Проделав затем на Q и соответственно на Р построение,
указанное пунктиром, можно получить на Q более мелкий
квадрат C'e'd'f и затем соответственно более густую квад-
квадратную сетку, и параллельно более густую сетку Р и т. д.
Итак, точки пересечения прямых сетки Мебиуса при неогра-
неограниченном продолжении ее построения густо покроют пло-
плоскость Р и соответственно плоскость Р'. Отсюда следует, как мы
это уже указали, что самая произвольная коллинеация вполне
определяется тем, куда перешли четыре точки по три, не
лежащие на одной прямой.
505.	Пусть имеется некоторая коллинеация, преобразующая
плоскость Р в плоскость Р'. Рассмотрим на плоскости Р' не-
некоторый квадрат; он будет получен при помощи рассматри-
рассматриваемой коллинеации из некоторого четырехугольника плоско-
плоскости Р. В задаче 503 было показано, что всякий четырехугольник
может быть спроектирован перспективой в квадрат (любой
величины, так как плоскость Q можно было взять на любом
расстоянии от точки S). Рассмотрим ту перспективу, при по-
помощи которой рассматриваемый четырехугольник плоскости Р
будет проектироваться в рассмотренный квадрат плоскости Р'.
При перспективной проекции прямые преобразуются в пря-
прямые, т. е. перспектива есть коллинеация. Итак, рассмотрен-
рассмотренная сейчас перспектива есть коллинеация, преобразующая
четыре вершины нашего четырехугольника плоскости Р в че-
четыре вершины нашего квадрата плоскости Р', но рассматри-
рассматриваемая нами коллинеация преобразует те же четыре точки
плоскости Р в эти же четыре точки плоскости Р', и следо-
следовательно, она и есть эта перспектива.
506.	Геометрическое место в плоскости точек, из которых
данный отрезок на этой плоскости виден под данным углом,

5С6	СТЕРЕОМЕТРИЯ	303
есть одна из двух дуг некоторой окружности, для которой
этот отрезок есть хорда; следовательно, геомгтрическое место
таких точек в пространстве есть поверхность вращения, по-
получаемая, если эту дугу вращать в пространстве вокруг этого
отрезка как оси. Оказывается, что три такие поверхности,
построенные для каждой из сторон основания пирамиды, со-
соответственно углу при вершине пирамиды той ее боковой
грани, которая из этой стороны основания исходит, если их
подробно рассмотреть, вообще говоря, пересекаются в четы-
четырех разных точках (этот результат очень важен для аэро-
аэросъемки).

огиз
ГОСУДАРСТВЕННОЕ ИЗДАТЕЛЬСТВО
ТЕХНИКО-ТЕОРЕТИЧЕСКОЙ ЛИТЕРАТУРЫ
«ГОСТЕХИЗДАТ»
Москва, Орликов пер., 3
ИМЕЮТСЯ В ПРОДАЖЕ КНИГИ ДЛЯ УЧАЩИХСЯ:
Бсрман Г. Н., Число и наука онём. 164 стр., цена 2 р. 50 к.
Берман Г. Н., Циклоида. 116 стр., цена 2 р.
Бронштейн И. Н. и Семеидяев К. А., Справочник по математике
для инженеров и учащихся втузов. 556 стр., цена 27 р.
Выгодский М. Я., Справочник по элементарной математи-
к е. 280 стр., цена 7 р. 50 к.
Выгодский М. Я-, Краткий учебник высшей математики.
Пособие для самообразования. 479 стр., цена 11 р. 50 к.
Зетель С. И., Задачи на максимум и минимум. 224 стр.,
цена 4 р.
Каган В. Ф., Великий русский учёный Н. И. Лобачевский
и его место в мировой науке. 84 стр., цена 1 р. 50 к.
Хохлов А. И., Карманные математические таблицы.
209 стр., цена 7 р. 85 к.
КНИГИ ДЛЯ ПРЕПОДАВАТЕЛЕЙ:
Моденов П. С. и Невяжский Г. Л., Курс высшей математики.
560 стр., цена 17 р.
Перепслкин Д. И., Курс элементарной геометрии, ч. I. Гео-
Геометрия на плоскости. 343 стр., цена 8 р. 20 к.
ГОТОВИТСЯ К ПЕЧАТИ:
Перепёлкин Д. И., Курс элементарной геометрии, ч. II.
Геометрия в пространстве.
У