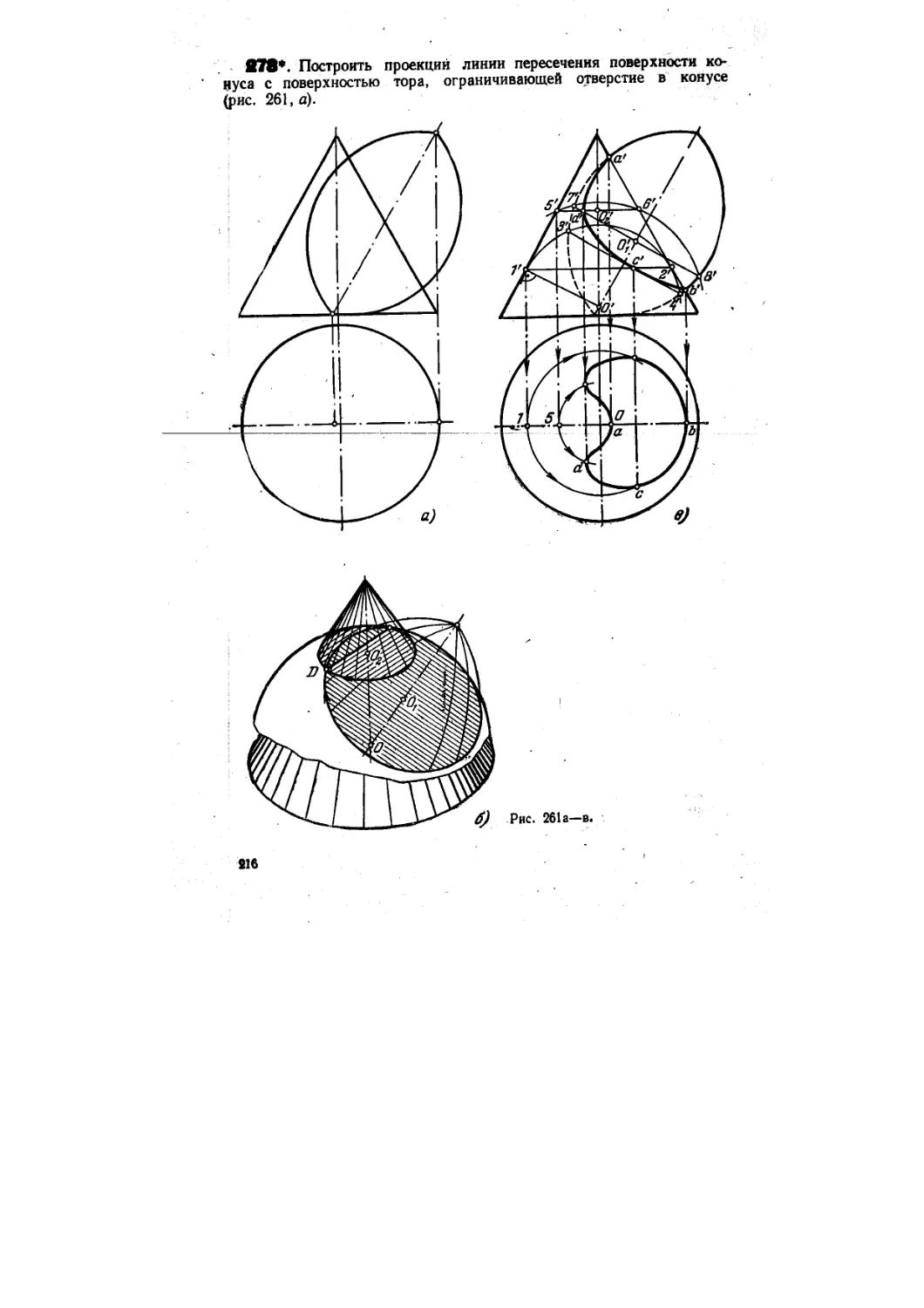
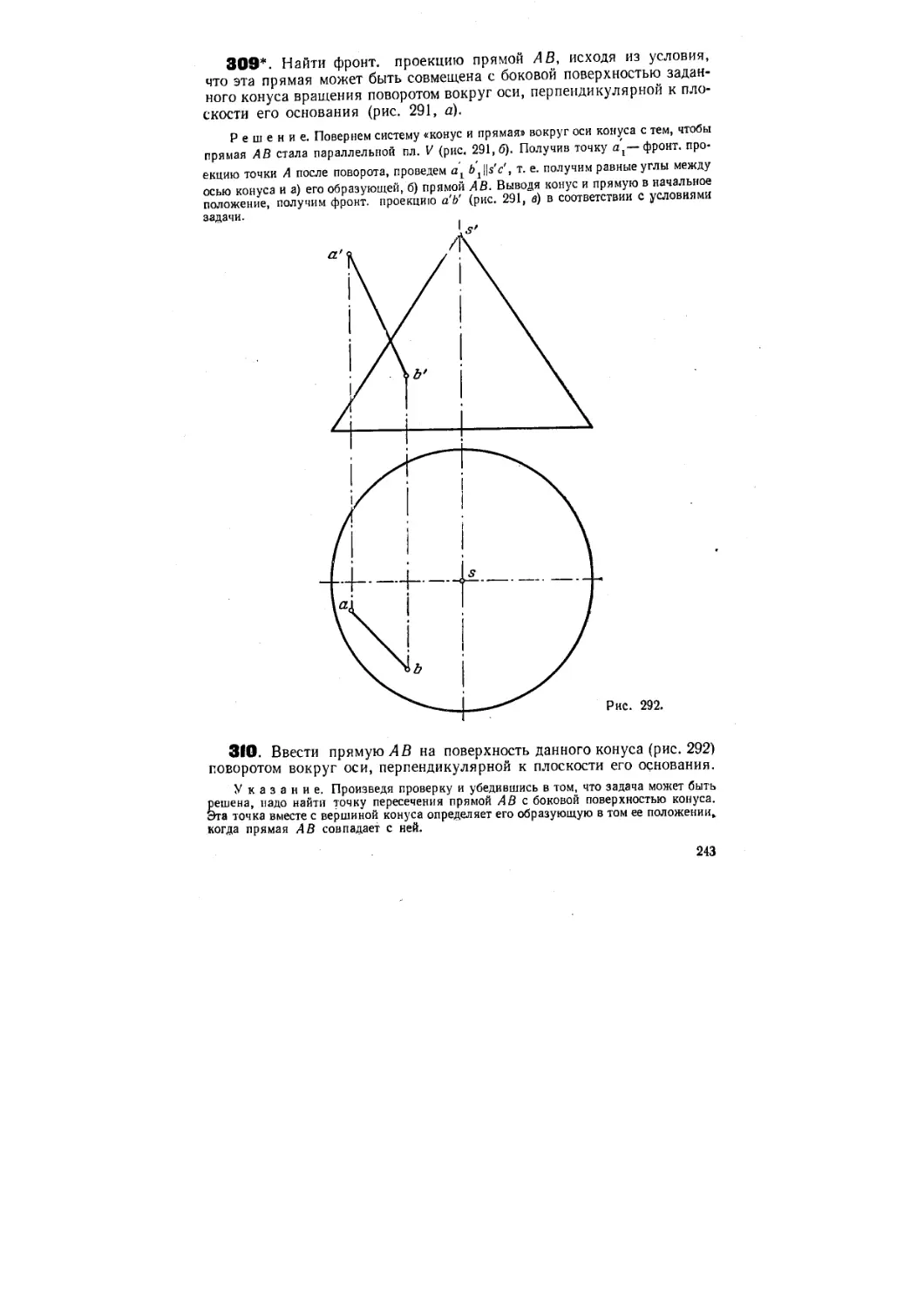
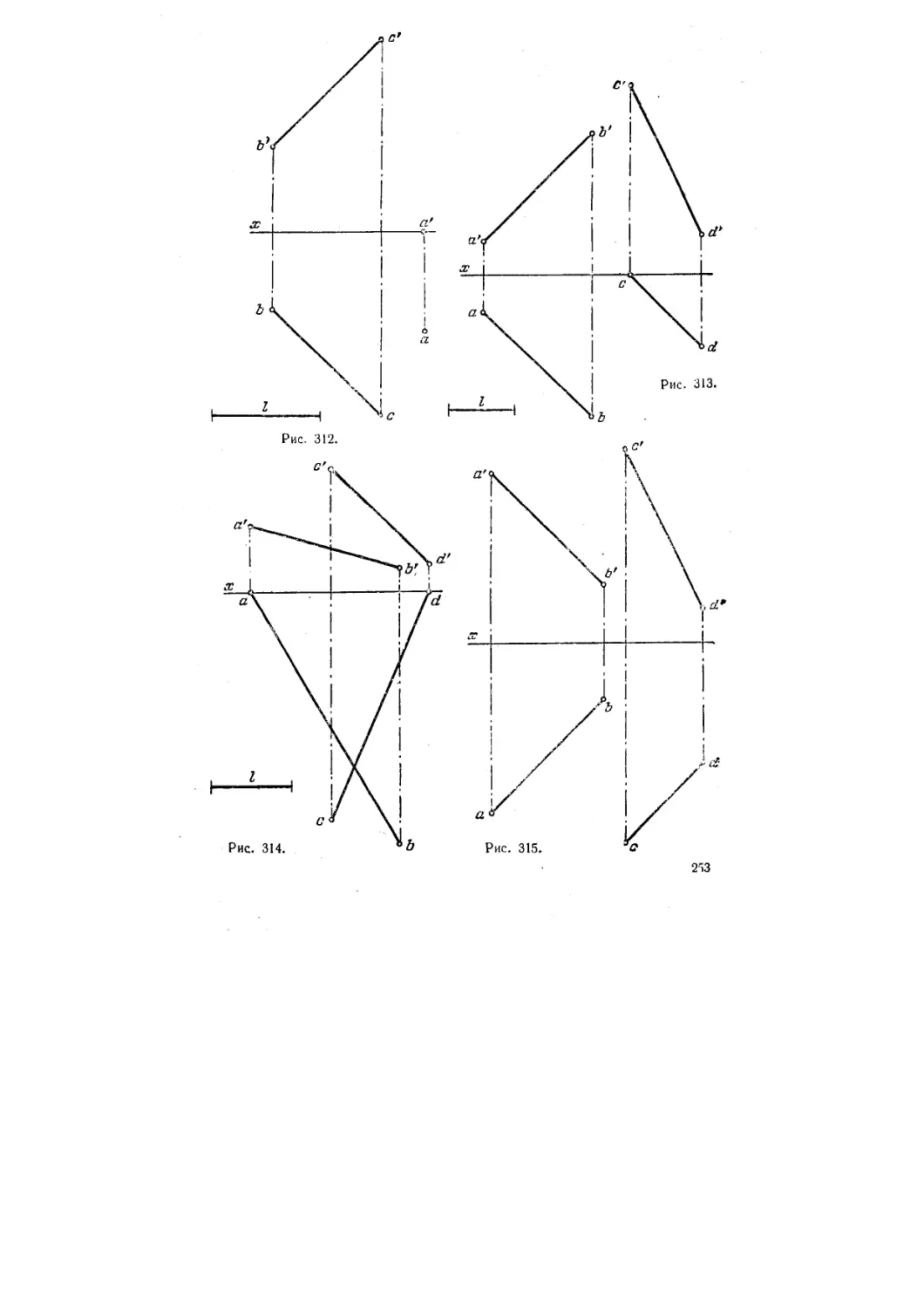
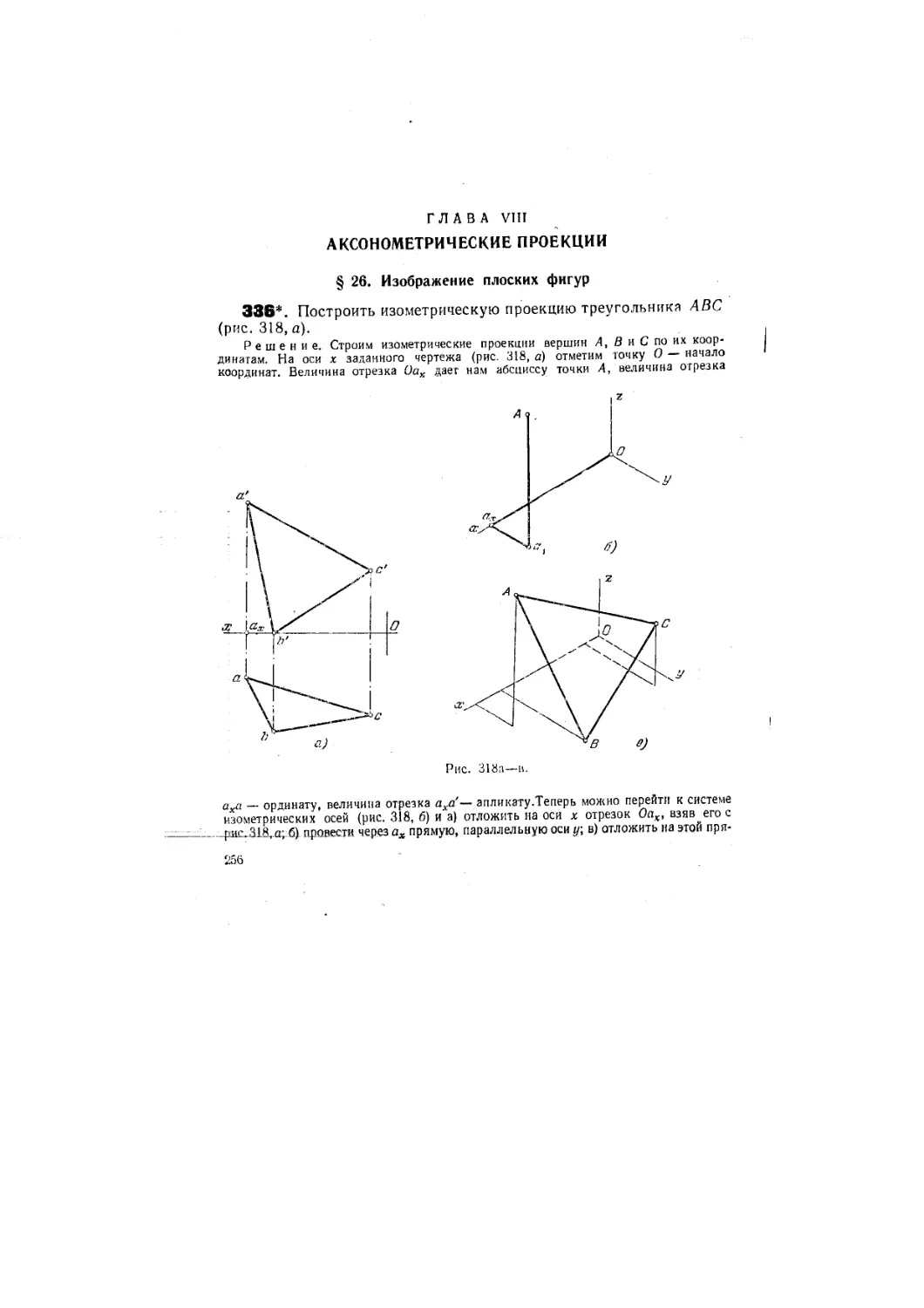
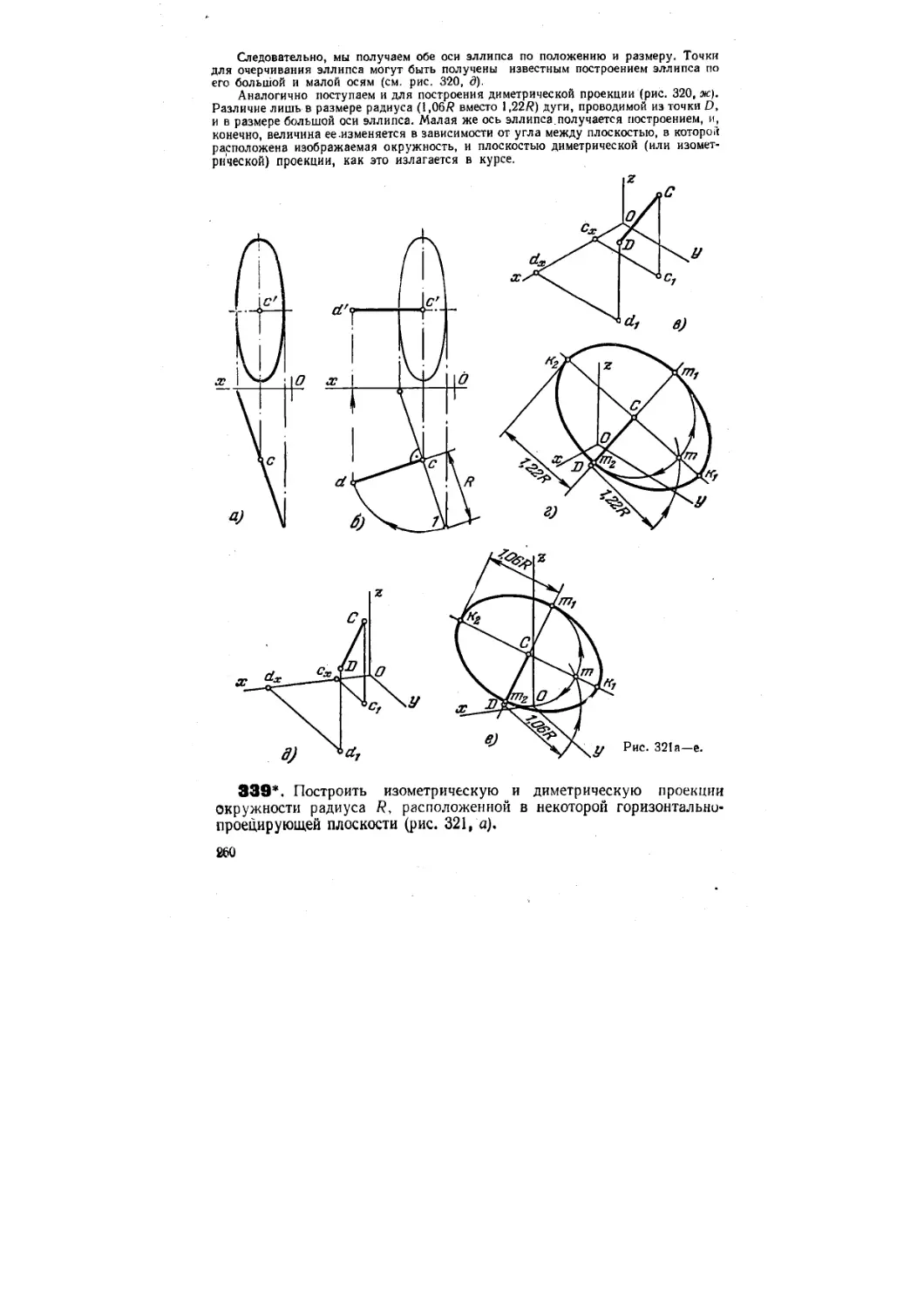
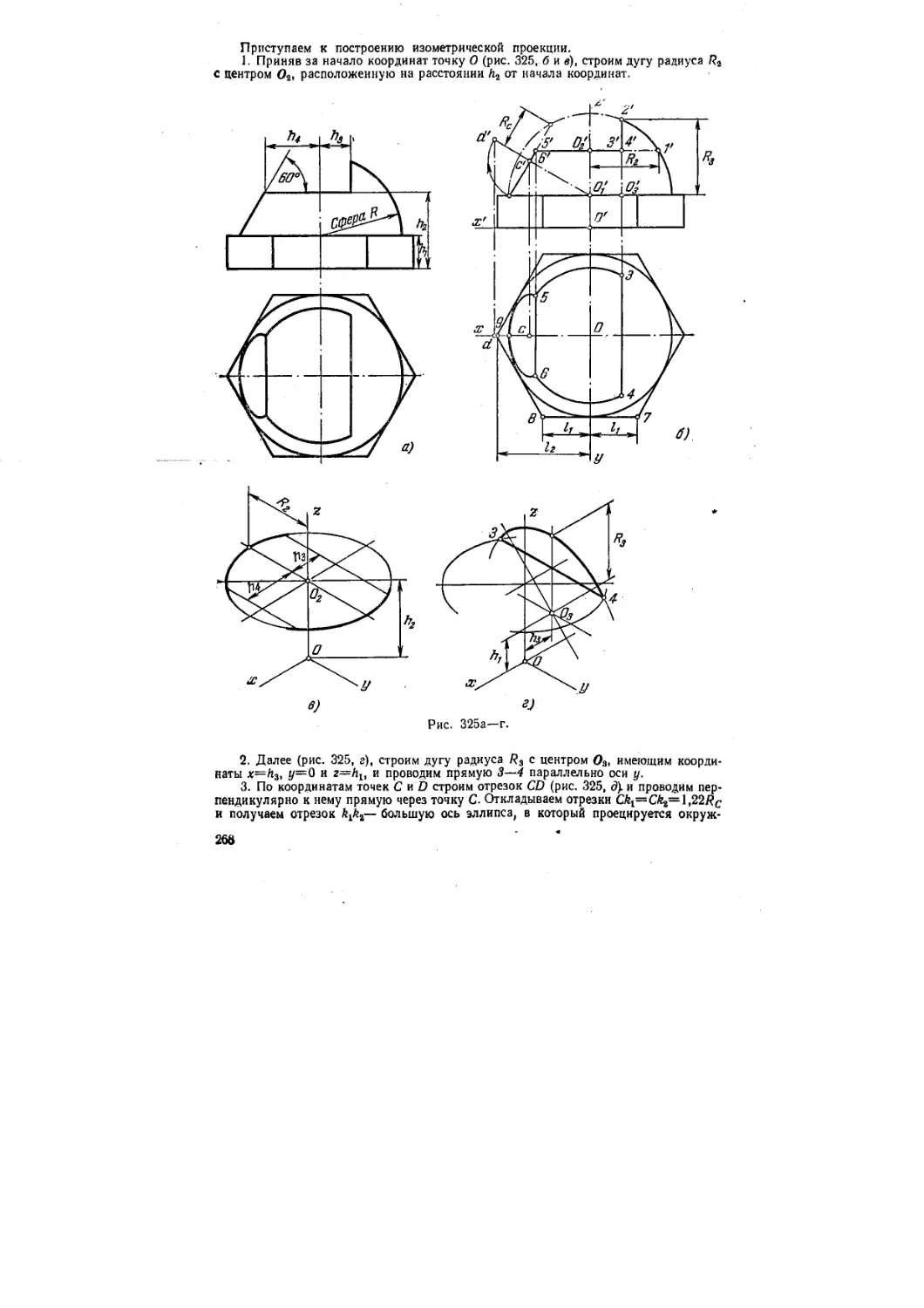
Текст
В. О. ГОРДОН, Ю. Б. ИВАНОВ, Т. Е. СОЛНЦЕВА
СБОРНИК ЗАДАЧ
ПО КУРСУ
НАЧЕРТАТЕЛЬНОЙ
ГЕОМЕТРИИ
ИЗДАНИЕ ПЯТОН,- СТЕРЕОТИПНОЕ
Допущено Министерством
высшего и среднего специального образования СССР
в качестве учебного пособия
для студентов машиностроительных
и приборостроительных специальностей вузов
ИЗДАТЕЛЬСТВО «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА 1977
6J5
Г 68
УДК 515.0@75.8)
Сборник задач по курсу начертательной геометрии. Гордон В. О.,
Иванов Ю. Б., Солнцева Т. Е., Главная редакция физико-ма-
физико-математической литературы изд-па «Наука», 1977 г.
В сборнике подобраны задачи но начертательной геометрии при-
применительно к программе для машиностроительных, приборострои-
приборостроительных и механико-технологических специальностей птузов. Сборник
может служить учебным пособием для студентов всех форм обуче-
обучения, особенно заочной, и будет очень полезен изучающим курс в их
самостоятельной работе. В задачнике показан процесс решения типо-
типовых задач, иллюстрирующих основные положения курса, даны по-
подробные решения ряда задач.
В конце книги приведены ответы к задачам, предлагаемым для
самостоятельного решения. Ответы даны в текстовой пли графической
форме в зависимости от характера условия задач.
Сборник составлен в соответствии и применительно к учебнику
«Курс начертательной геометрии» В. О. Гордона и М. А. Семенцова-
Огиевского. Однако такая согласованность не исключает возможности
пользоваться другими учебниками, так как для понимания задач
из данного пособия требуется лишь знание тех основных положении,
которые должны содержаться в любом учебнике.
053@2)-77
10-77
ОГЛАВЛЕНИЕ
Преднглсвие 4
Глава I. Точка и прямая 7
§ 1. Точка A—5) 7
§ 2. Прямая F—9) 11
§ 3. Взаимное положение прямой и точки A0—11) 12
§ 4. Следы прямой A2—16) 13
§ 5. Натуральная величина отрезка прямой и углы наклона прямой
к плоскостям проекций A7—23) IS
§ 6. Деление отрезка в данном отношении B4—25) 19
§ 7. Взаимное положение прямых B6—30) 20
§ 8. Построение проекций прямого угла C1—39) 23
Глава II. Плоскость 23
§ 9. Прямая и точка в плоскости D0—51) 23
§ 10. Следы плоскости E2—60) 34
Глава III. Пересечение прямой линии с плоскостью и двух плоскостей меж-
между собой 3:)
§ 11. Пересечение прямой с проецирующей плоскостью F1—66) ... 39
§ 12. Пересечение плоскостей между собой F7—76) 45
§ 13. Пересечение прямой с плоскостью общего положения G7—85) . . А'.)
§ 14. Общие случаи пересечения плоскостей (86—91) 56
Глава IV. Параллельность и перпендикулярность прямой и плоскости и двух
плоскостей 61
§ 15. Параллельность прямой и плоскости и двух плоскостей (92—101) 61
§ 16. Перпендикулярность прямой и плоскости и двух плоскостей A02—
110) 66
§ 17. Смешанные задачи без применения способов преобразования чер-
чертежа A11 — 154) 70
Глава V. Применение способов преобразования чертежа 103
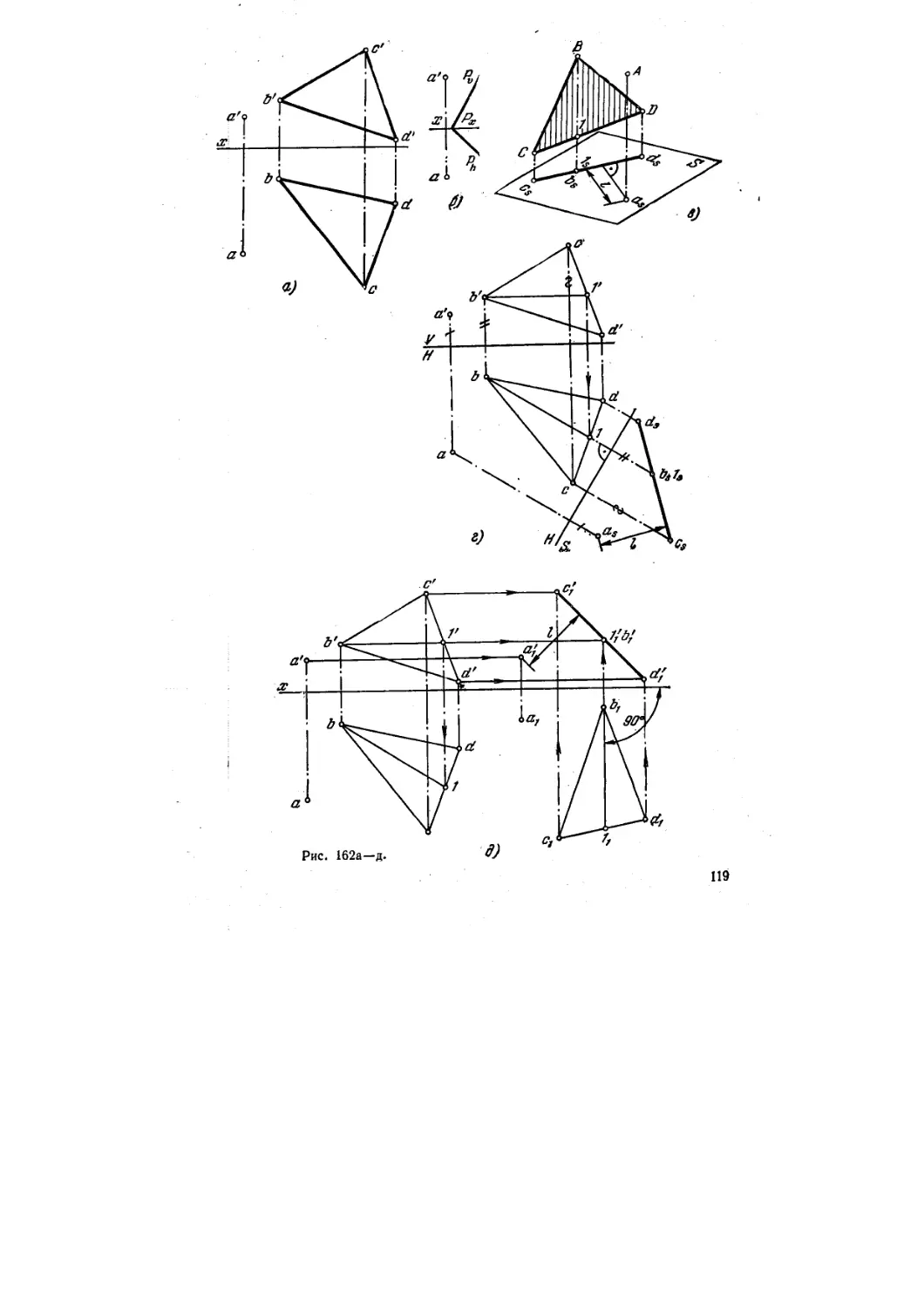
§ 13. Определение расстояний A55—170) 10J
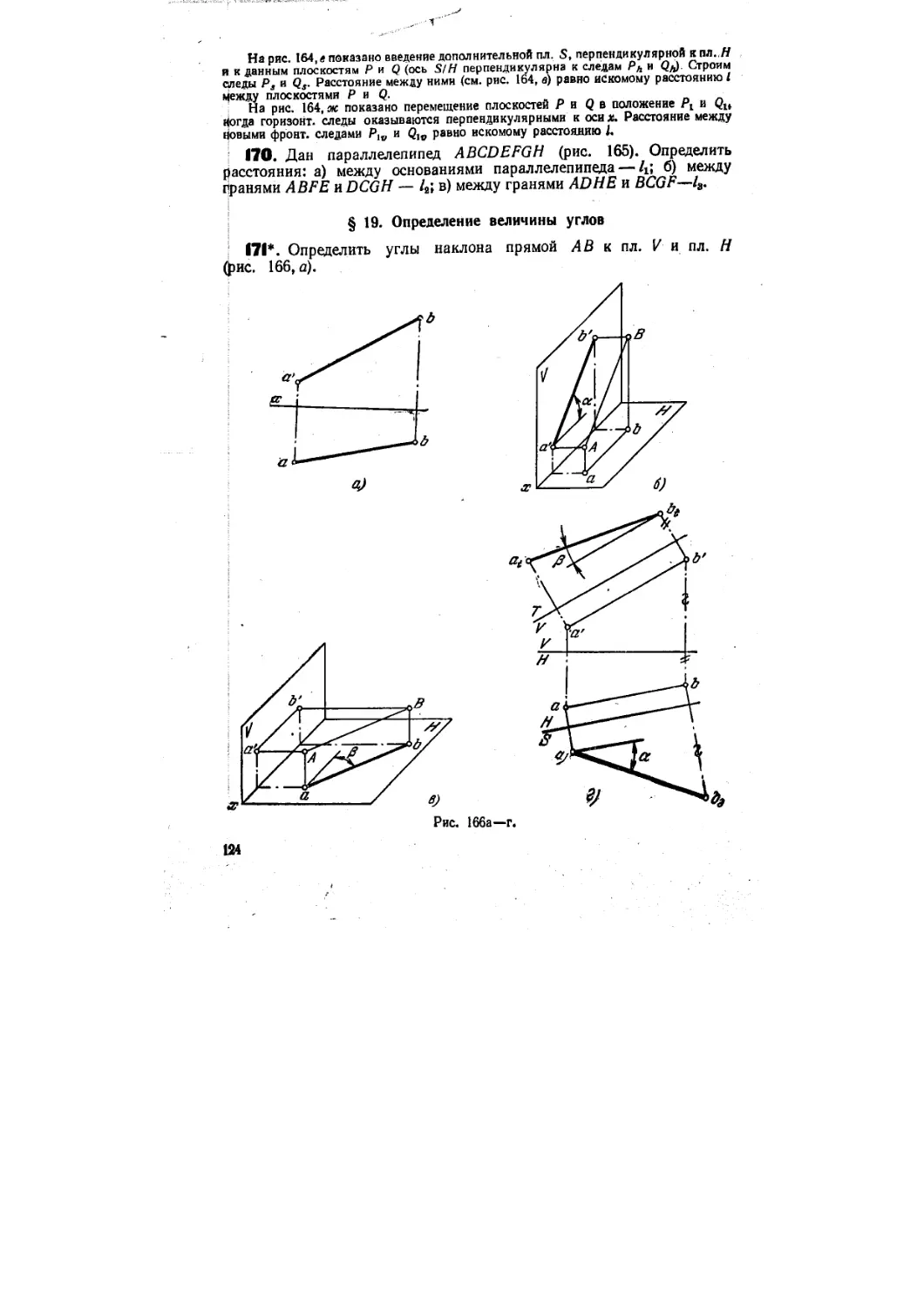
§ 19. Определение величины углов A71 —186) 121
§ 20. Смешанные задачи с применением способов преобразования чер-
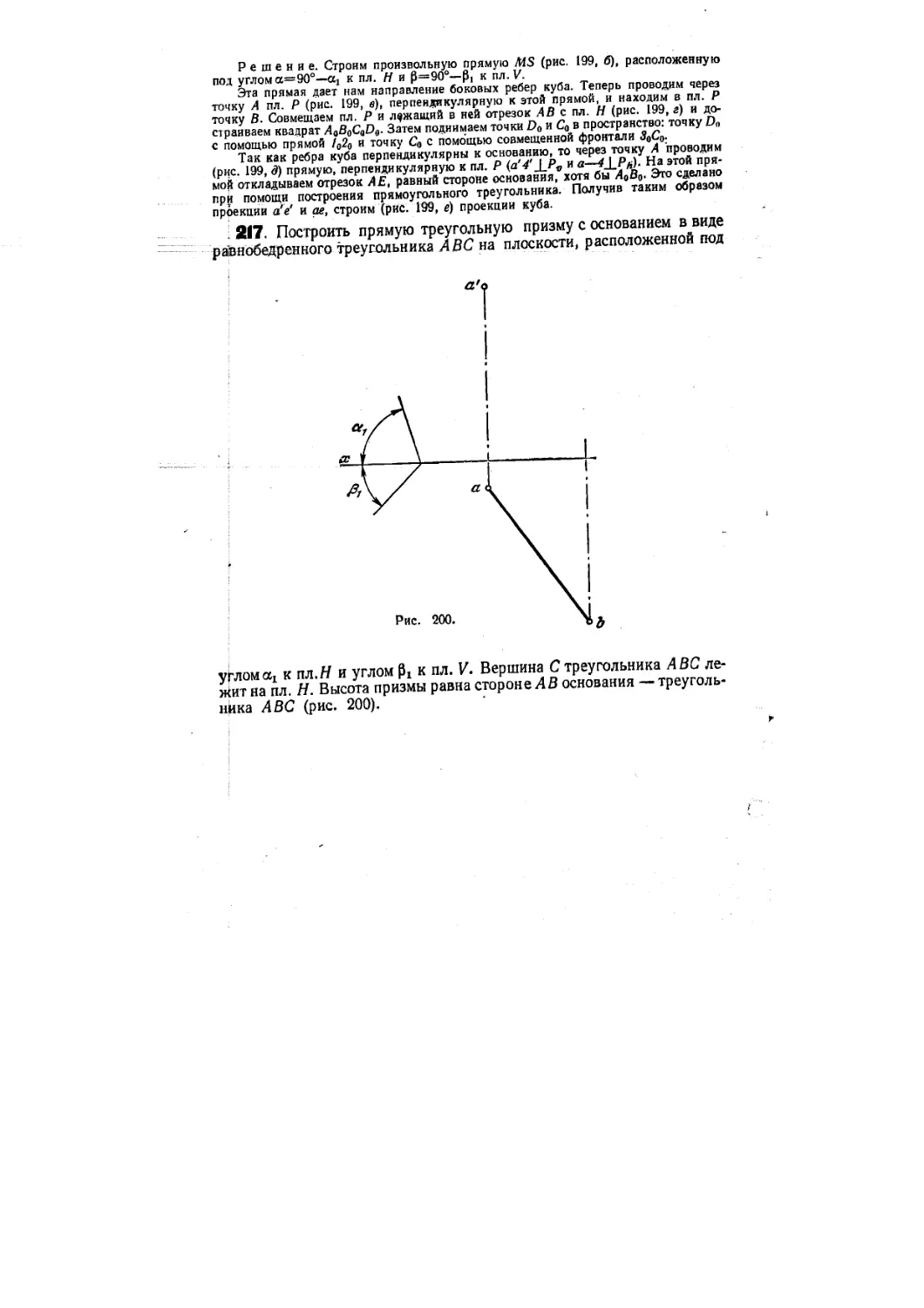
чертежа A87—217) 134
Глава VI. Кривые линии и поверхности . 155
§ 21. Кривые линии. Поверхности. Точки на поверхностях B18—246) 15")
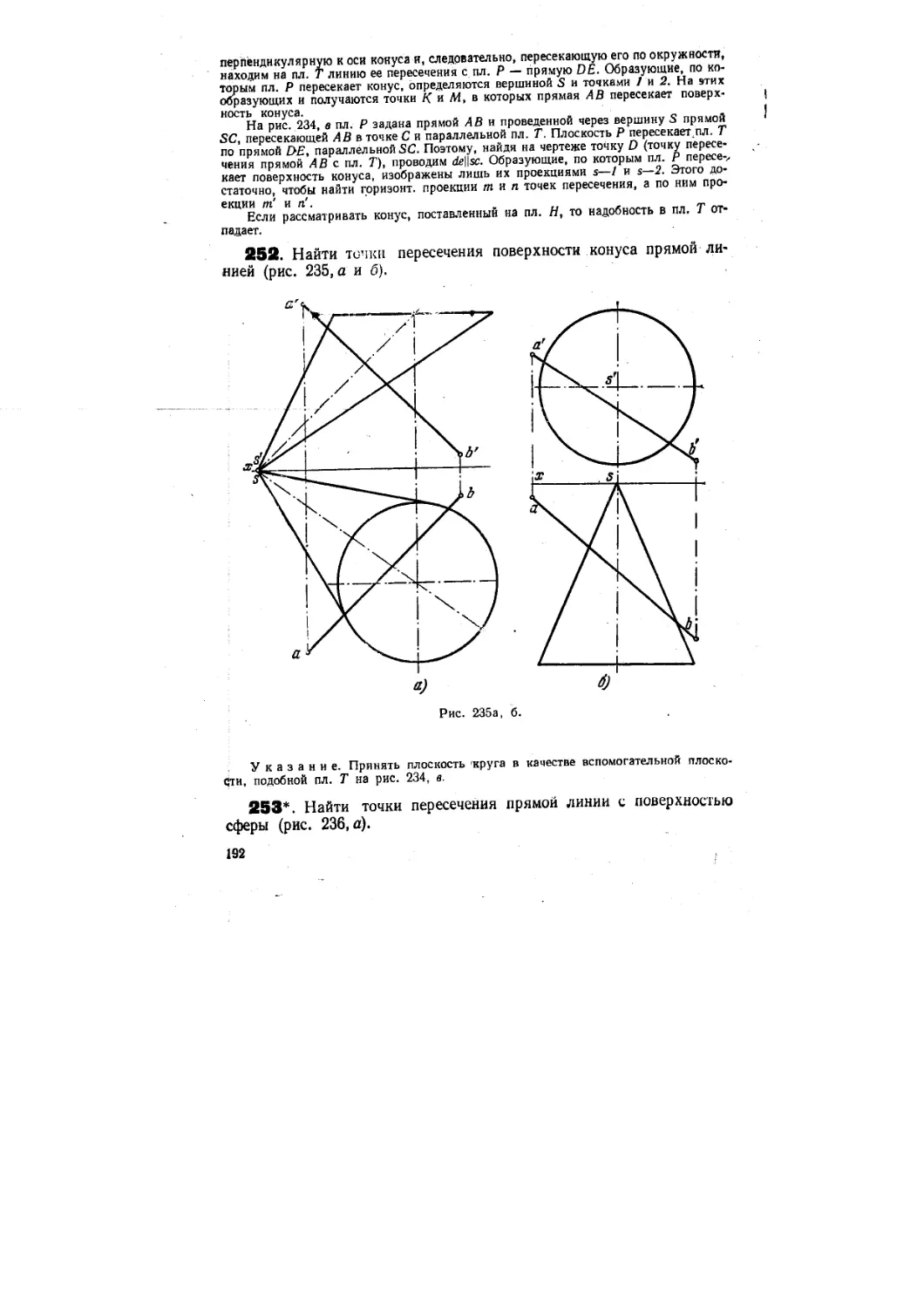
§ 22. Пересечение поверхности плоскостью и прямой линией B47—264) 185
§ 23. Взаимное пересечение поверхностей B65—281) 202
Глава VII. Смешанные задачи по всему курсу 221
§ 24. Задачи с решенными прототипами B;-2—315) 221
§ 25. Задачи для самостоятельного решения C16—335) 243
Глава VIII. Аксонометрические проекции 256
§ 26. Изображение плоских фигур C36 — 339) 256
§ 27. Изображение тел C40—344) 261
Ответы 272
1* 3
ПРЕДИСЛОВИЕ
Данный сборник задач и упражнении соответствует программе
курса начертательной геометрии для машиностроительных, приборо-
приборостроительных и механико-технологических специальностей высших
технических учебных заведений.
Сборник составлен в соответствии и применительно к учебнику
«Курс начертательной геометрии» В. О. Гордона и М. А. Семенцова-
Огиевского, из которого в данный сборник перенесен ряд примеров
и задач.
Авторы стремились помочь изучающим курс в их самостоятельной
работе. Этим определился характер пособия, а именно показ процесса
решения ряда типовых задач, относящихся к основным вопросам
курса. Вместе с тем даны и условия задач для самостоятельного их
решения. Условия большинства задач подобны условиям решенных
задач, но имеются также задачи и без решенных прототипов, что тре-
требует от учащегося проявления большей самостоятельности и творче-
творческой инициативы.
Ограничение курса начертательной геометрии в часах и его пре-
преимущественно односеместровое прохождение обусловливают и про-
программное ограничение круга рассматриваемых вопросов. Очевидно,
зто предельный минимум; авторы исходили из него при составлении
сборника
В основном задачи, решенныех) и предлагаемые для решения,
относятся к взаимному сочетанию геометрических элементов и их
расположению в пространстве и к применению способов преобразова-
преобразования чертежа вращением и введением дополнительных плоскостей про-
проекций. Объектами рассмотрения являются точки, прямые и кривые
линии, плоские и некоторые другие поверхности — отдельно и в их
взаимном расположении. Рассматриваются задачи на определение рас-
расстояний п углов, на построение аксонометрических проекций — пря-
прямоугольных — изо- и диметрических (с сокращением по оси у вдвое).
Чертежи в большинстве случаев даны в поэтапном их выполнении.
Это облегчит чтение чертежей и рассмотрение последовательности их
построений. Для лучшего понимания сущности вопроса и представле-
') Их номера отмечаются звездочкой кверху.
ния пространственной картины в некоторых из решенных задач ламы
наглядные изображения. Даны также примеры составления планов
решения задач и анализа полученных решений.
Такие сборники задач по начертательной геометрии с их решениями
уже издавались, например, в 1928 г. «Сборник задач по ортогональным
проекциям с подробными решениями» С. К. Руженцова и Б. А. Ива-
Иванова. Опыт показывает их полезность.
Особенностью данного сборника является наличие ответов к зада-
задачам, предложенным для самостоятельного решения. Правильно лп
решена задача? Этот вопрос при самостоятельном решении по большей
части является открытым, что затрудняет работу учащегося. Для
того чтобы он сам мог убедиться в правильности полученного им реше-
решения, в сборнике помещены ответы. Они даны в текстовой или графиче-
графической форме в зависимости от поставленных в задаче вопросов. Ответ
к задаче в форме чертежа содержит положение искомых элементов на
фоне задания.
В сборнике даны преимущественно чертежи с указанием оси х
как базы для отсчета размеров при построениях и для удобства при
перечерчивании заданий. Наличие оси х как направляющей линии
облегчает введение в чертеж любой информации и построение черте-
чертежей-ответов. Если же ось не показана (как это сделано в некоторых
задачах), то ее роль для отсчета размеров может быть присвоена ка-
какой-либо из прямых на данном чертеже. Все это находится в логиче-
логической связи с техническими чертежами, где всегда имеет место база
отсчета, хотя и не обозначаемая так, как на чертежах в начертательной
геометрии. Однако ось х сохраняет и присущее ей значение линии пере-
пересечения плоскостей проекций V и Н, что имеет значение для представ-
представления пространственной картины рассматриваемого положения. Но
и вне этого значения (определяемого названием «ось проекций») такая
прямая является неотъемлемой составляющей каждого чертежа для
построения его по заданным размерам. При этом выбор положения оси
не является ограниченным и определяется исходя из необходимости
и целесообразности.
Авторы придерживаются в основном обозначений, примененных
еще в XIX столетии отечественными учеными Н. И. Макаровым и
В. И. Курдюмовым и в настоящее время используемых в учебной
литературе и в практике кафедр без каких-либо осложнений. Эти
обозначения, в отличие от всех других, в достаточной степени просты,
выразительны, легко читаемы и не загромождают чертежи.
В сборнике применен термин проецировать (от латинск. projicere)
взамен проектировать, так как последнее имеет и другое значение,
а именно «разрабатывать, составлять проект» (например, сооружения,
механизма, перевозок и т. д.). Переход на слово проецировать вызвал
также такие названии, как проецирующая прямая, горизонтально-
проецирующая плоскость и т. п.
В том же смысле, в каком в некоторых курсах начертательной гео-
геометрии применено слово «эпюр» (а иногда «эпюра»), в данном сборнике
взято слово «чертеж» (что, вообще, не является новым).
Для лучшего понимания решенных в сборнике задач и усвоения
построений рекомендуется перечерчивать исходный чертеж и выпол-
выполнять на нем все описанные построения.
Следует обратить особое внимание на то, что для сравнимости полу-
полученного учащимся чертежа-oi пета предложенной для самостоятель-
самостоятельного решения задачи с приведенным в сборнике ответом необходимо
как можно точнее воспроизвести чертеж-задание, пользуясь осью к
как базой отсчета. При желании можно чертеж-задание увеличить, что
должно быть учтено при сравнении полученного ответа с ответом
в сборнике.
При решении задач, для которых нет решенных прототипов, можно
использовать помещенные в конце сборника краткие указания.
Выражение изобразить наглядно, дать наглядное изображение,
означает построить изображение в косоугольной фронтальной диметри-
ческой проекции (хотя бы в известной под названием «кабинетная»).
Рекомендуется при самостоятельном решении задач предвари-
предварительно дать рисунок требуемого построения и составить план решения,
как это сделано в сборнике для некоторых решенных задач, а лишь
затем выполнять построение.
Согласованность данного сборника задач с учебником «Курс начер-
начертательной геометрии» В. О. Гордона и М. А. Семенцова-Огиевгкого не
исключает возможности пользоваться другими учебниками, так как
для понимания и решения задач поданному сборнику требуется знаниа
тех основных положений, которые должны содгржаться в люэом учеб-
учебнике. При этом, если имеется различие в некоторых обозначениях,
можно сопоставить обозначения при помощи таблицы, которую можно
найти в учебнике.
Для линий связи применена штрих-пунктирная линия с одной точ-
точкой между смежными штрихами. Но если линия связи проведена лишь
для проверки правильности построения, то использована линия
с двумя точками.
Номера решенных задач отмечены звездочками. Ответы па нерешен-
нерешенные задачи помещены в конце сборника.
Некоторые сокращения слов и условные
обозначения в сборнике:
пл.— плоскость;
горизонт. — горизонтальный, -ая, -ое;
фронт. — фронтальный, -ая, -ое;
_L — перпендикулярно;
|| — параллельно;
= — совпадает;
— прямой уюл.
ГЛАВА I
ТОЧКА И ПРЯМАЯ
§ 1. Точка
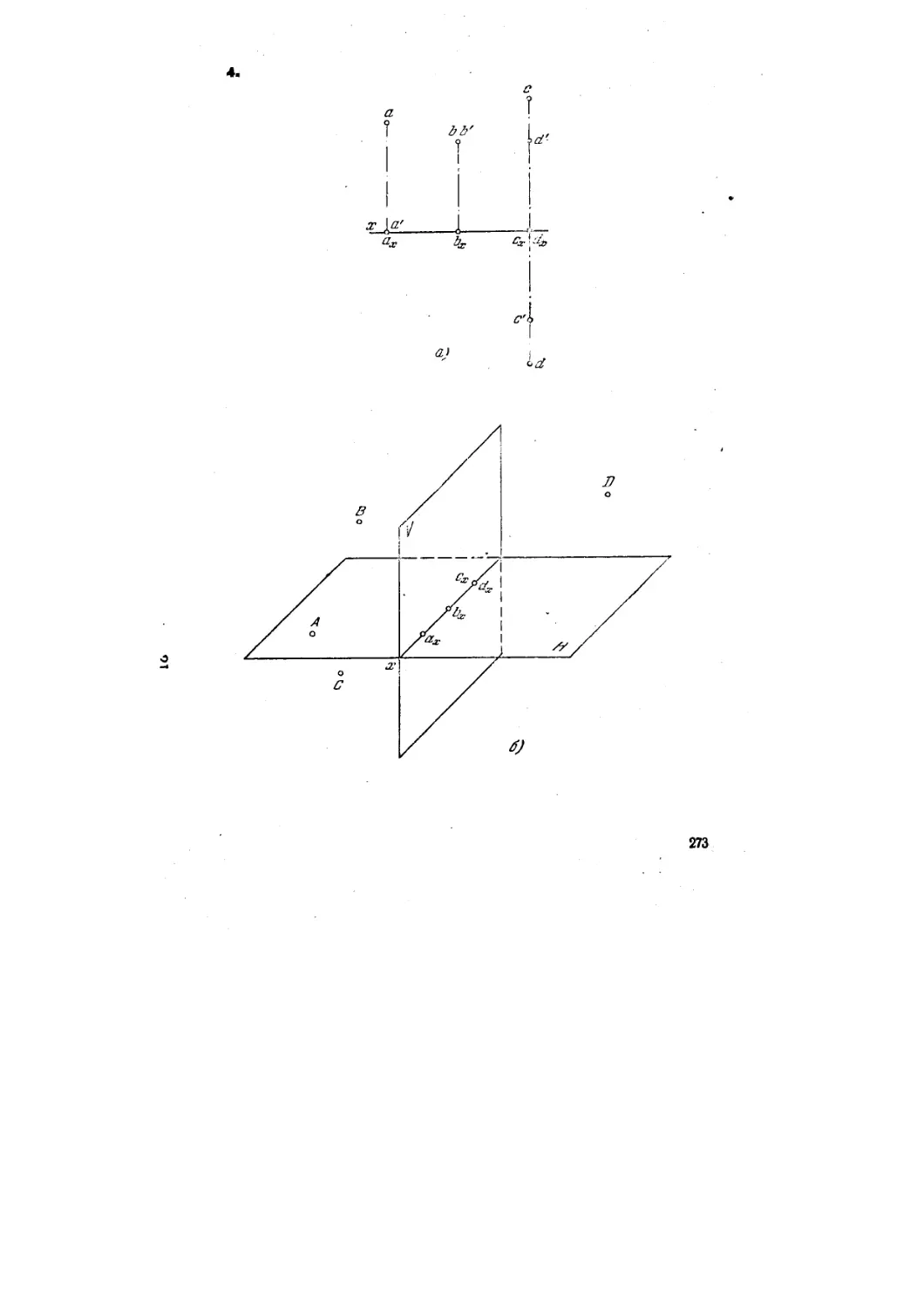
I*. Дать наглядные изображения точек А, В, С, D относительно
плоскостей V и И. Точки заданы своими проекциями (рис. 1. а).
,а'а
ax
ad'
?
А
Рис. 1а. б.
Решение. Точки ах, Ьх, схп dx (рис. 1,6) выбираем на оси г произвольно.
Так как точка А находится по второй четверти (апликата точки положительна, ор-
ордината отрицательна), то отрезок аха, соответствующий значению ординаты, откла-
откладываем влево от пл. V. Отрезок аха', соответствующий значению апликаты, отклады-
откладываем вверх от пл. Н.
При построении точки D, находящейся в первой четверги (апликага и ордината
положительны), отрезок dxd откладываем вправо от пл. V, а отрезок dxd' — вверх
от пл. Н.
Положения точек А и D получены на пересечении перпендикуляров, проведен-
проведенных через точки о и d (к пл. Я) и через точки а и d (к пл. V).
Точка В лежит в пл. V; это следует из того, что горизонт, проекция Ь точки лежис
(рис. I, а) на оси х (ордината равна нулю). Следовательно, на рис. 1,6 точка ч
1
совпадаете 6„, Отрезок^6', соответствующий отрицательному значению апликаты,
откладываем вниз от пл. Н, Положение самой точки В совпадает о положением -е
фронт, проекции Ь'.
Точка С располагается в пл Н\ это следует из того, что проекция е' лежит (рис.
1, о) на оси х (апликата точки С рагзна нулю) Поэтому и на рис.1, б с' совпадает с ••,..
Так как для точки С ордината положительна, то соответствующий этой ординате
отрезок сх с откладывается (рис. I, б) вправо от пл.1Л Положение самой точки С сов-
совпадает с положением ее горизонт, проекции с.
2. Изобразить наглядно положения точек А, В, С, D и ?, задан-
заданных своими проекциями (рис. 2).
С
а
«g j,
а'
"f
—-о—
Рис. 2.
3*. Построить проекции точек А и В по их координатам. Пост-
Построить проекцию точки С, расположенной симметрично точке А отно-
относительно фронт, пл. проекций. Изобразить наглядно положение этих
точек относительно плоскостей V и /У.
^^^^^ нут-
ТОЧКИ ^\^^
А
В
«
13,5
6,5
20
-20
Решение. Намечаем ось х (рио. 3, а) и на ней точку аг.Так как точка А рас-
расположена в первой четверти (апликата и ордината положительны), то проекция а
находится над осью х на расстоянии 20, а проекция а — под осью х на расстоянии 13,5.
Для построения проекций точки S сначала задаемся (на оси х) произвольно точ-
точкой Ьх и откладываем вниз от нее отрезок htb, равный значению ординаты F,5), и от-
отрезок ЬКЬ', соответствующий отрицательному значению апликаты (—20). Точка В
находится в четвертой четверти.
Точка С должна быть расположена симметрично точке А относительно пл. V.
Следовательно, ордината точки С раина —1И,5, а апликата равна '20. Точка сх сонпа-
даетс точкой ах, с—с а, а горизощ. проекция с находится над осью к на расстоя-
расстоянии 13,5.
!
i
la
6 b'
Рис. За, б.
На рис. 3,6 дано соотнетстсующее наглядное изображение положений точек
А, В и С. Расстояние axbx на рис. 3, б равно половине расстояния axbx на рис. 3, а.
4. Построить проекции точек Л, В, С по их координатам. Пост-
Построить проекцию точки D, расположенной симметрично точке С относи-
относительно оси х. Изобразить наглядно положения этих точек относительно
плоскостей V и И.
"""\ Коорди-
^s. И Л Т.!
1'пчк 1 \^
А
В
С
(у
-25
—20
—30
0
20
—20
5*. Построить три проекции каждой из точек Л и 6 по их коор-
координатам.
^ч Koop-
\.
ГОЧк,, ^ч
Л
в
*
33,
5
5
и
16
-26
,5
,5
>
20
-13
.5
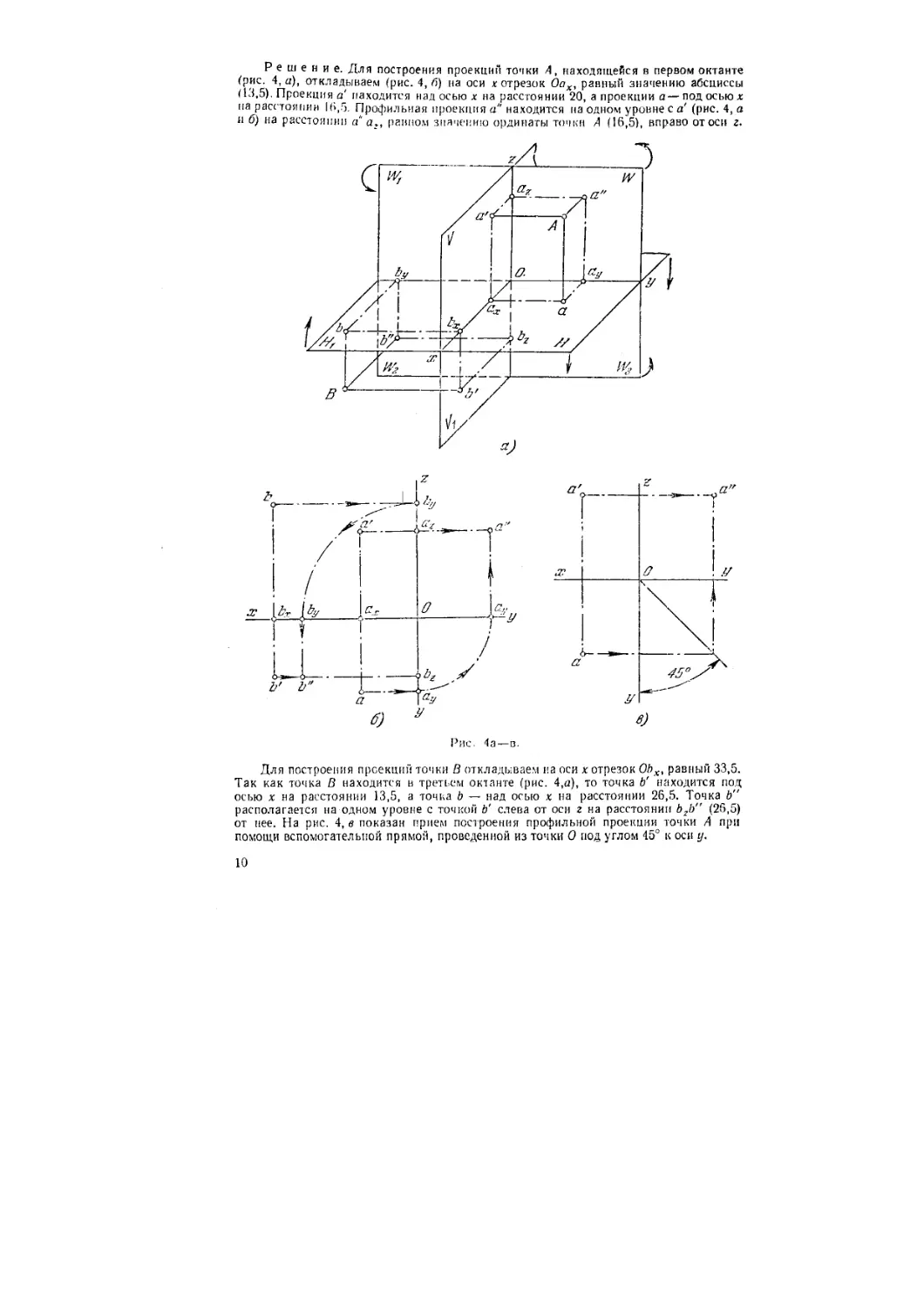
Решение. Для построения проекции точки А, находящейся в первом октанте
(рис. 4, а), откладьшаем (рис. 4, б) на оси к отрезок Оах, ранный значению абсциссы
A3,5). Проекция а' находится над осью х на расстоянии 20, а проекции а— под осью х
на расстоянии 1A,5. Профильная проекция а" находится на одном уровне с а' (рис. 4, а
и 6) на расстоянии а" аг, ранном значению ординаты точки А A6,5), вправо от оси г.
С
Рис. 4а—п.
Для построения проекции точки В откладываем на оси х отрезок ОЬХ, равный 33,5.
Так как точка В находится в третьем октанте (рис. 4,а), то точка Ь' находится под
осью х на расстоянии 13,5, а точна Ь — над осью х на расстоянии 26,5. Точка Ь"
располагаете!! на одном уровне с точкой Ь' слева от оси г на расстоянии Ь2Ь" B6,5)
от нее. На рис. 4, в показан прием построения профильной проекции точки А при
помощи вспомогательной прямой, проведенной из точки 0 под углом 45° к оси у.
10
§ 2. Прямая
6*. Изобразить наглядно положение отрезка А В относительно
плоскостей V и И. Отрезок задан своими проекциями (рис. 5, а).
а
Решение. Определяем положения концевых точек отрезка, как это было
показано в задаче 1*. Отрезок АВ определяется точками А и 8 (рис. 5, б)
С d
, ?
Т----.
т*
«г-
а'
а)
с
Рис. fia. б.
7. Изобразить наглядно положения отрезков А В и CD относи-
относительно плоскостей V и Н. Отрезки заданы своими проекциями
(рис. 6, а и б).
8. Построить чертеж отрезка АВ, если он:
а) находится в первой четверти пространства, расположен парал-
параллельно пл. V, концом В упирается в переднюю полу пл. Н;
11
б) расположен в биссекторной плоскости четвертой четверти про-
пространства, конном В упирается в ось проекций;
в) расположен во второй четверти пространства параллельно пл.
V, концом В упирается в заднюю иолу пл. //, конец А равноудален от
плоскостей V и Н;
г) расположен произвольно на нижней поле пл. V, концом В упи-
упирается в ось проекций;
д) расположен в четвертой четверти пространства параллельно
пл. Н, конец В равноудален от плоскостей проекций;
е) расположен в третьей четверги пространства перпендикулярно
к пл. V, концом А упирается в ее нижнюю полу;
ж) расположен в четвертой четверш пространства перпендикулярно
К пл. Н, конец А равноудален от плоскостей проекций.
9. Прочитать чертежи отрезков, изображенных на рис. 7, а—г.
d'~
г"'
,т
Ю
Рис. 7а — г.
§ 3. Взаимное положение прямой и точки
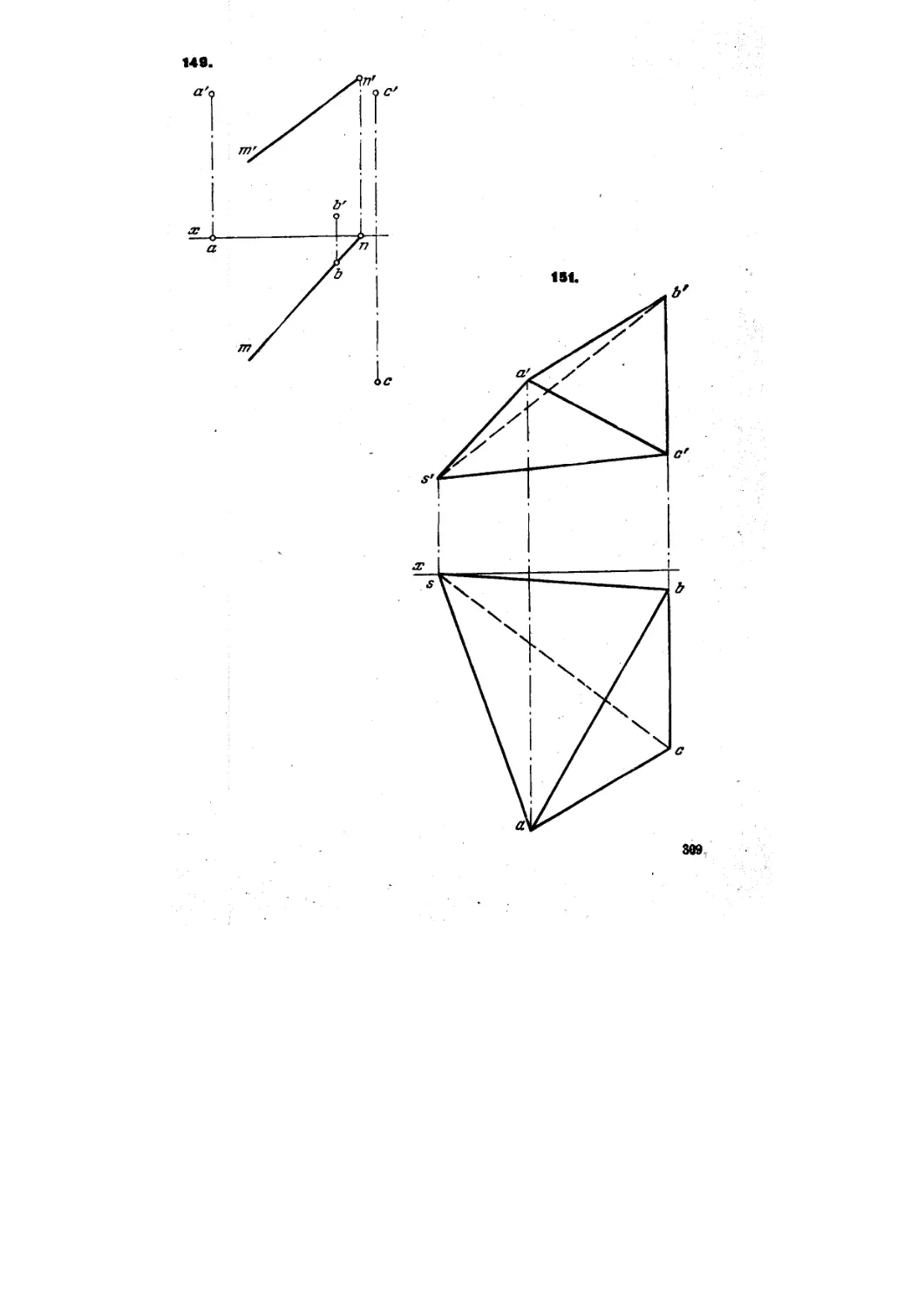
tO*. Определить, лежат ли точки В и С на прямой AD, а точка
Л' па прямой MN (рис. 8, а и б).
Решение. Так как проекции Ь и ft', с и с' (рис. 8, а) не находятся на одно-
одноименных с ними проекциях прямой AD, то точки В и С на этой прямой не лежат.
12
Для определения, лежит ли точка К на прямойMN(рис. 8, в), построим профиль.
ные проекции точки К и прямой М N (рис. 8, в). Точка К не принадлежит Прямой М N,
та« „„„рр пппАильная проекция к" не лежит на профильной проекции т"п".
так
профильная проекция i
а
b a)
777'
Л"
л'
<}777
К
п
б)
о а'
Рис. 8а--в.
Рис.
il. Построить горизонт, проекцию точки С, принадлежащей
прямой А В (рис. 9).
§ 4. Следы прямой
12*. Построить следы прямой, проходящей через точки А и
В (рис. 10, а), и указать, через какие четверти пространства она про-
проходит.
Решение. Проиодим проекции а'Ь' и ab прямой А В.
Для построения ее горизонт, следа продолжаем (рис. 10,6) фронт, проекцию
а'Ь' до пересечения с осью х в точке (/и'), которая является фронт, проекцией горизонт,
следа прямой. Затем ич точки т' проводим перпендикуляр к оси х. (линию связи)
до пересечения с продолженной горнчонт. проекцией прямой в точке (т), которая
является горизонт, проекцией горизонт, следа прямой Точка т совпадает с самим
горизонт, следом — точкой М.
Для построения фронт, следа прямой продолжаем ее горизонт, проекцию at)
до пересечения с осью х в точке («), которая является горизонт проекцией фронт,
следа прямой. Из точки п проводим перпендикуляр к оси х до пересечения с продол-
продолженной проекцией а'Ь' в точке (га'), которая является фронт, проекцией фронт, следа
прямой. Точка ft' совпадаете самим фронт, следом прямой — точкой N. Из расположе-
расположения проекций т' и т, п и я следует, что точка М (горизонт, след прямой) лежит
13
на передней поле пл. И, а точка N (фронт, след прямой)—на верхней поле пл. V. Сле-
Следовательно, прямая проходит через вторую, первую и четвертую четверти про-
С
d)
13. Построить следы прямой, определяемой точками А и В
(рис. 11, о и б), и указать, через какие четверти пространства она
проходит.
а
t'a
Рис 11а. б.
14*. Построить следы профильной прямой АВ (рис. 12, а) и ука-
указать, через какие четверти пространства она проходит.
Решение. Из построения (рис. 12, б) следует, что горизонт, проекция п фронт,
следа прямой и фронт, проекция т' горизонт, следа совпадают в точке пересечения
проекций прямой с осью х. Для построения точек т и п' находим сначала профильные
14
проекции т" и п". Для этого продолжаем профильную проекцию а"Ь" до пересече-
пересечения с осями г и у. Получив проекции т" и п", находим т и п .
а
о)
Из расположения проекций т и т', п и п' следует, что точка М (горизонт, след
прямой) лежит на передней поле пл. Я, а точка N (фронт, след прямой) — на верхней
поле пл. V. Прямая проходит через вторую, первую и четвертую четверти.
Б5. Построить следы прямой АВ (рис. 13) и изобразить наглядно
их положение.
а:
т?
л'
Рис. 13. Рис. 14.
16. Построить проекции прямой, зная положение проекций ее следов
(рис, 14), и указать, через какие четверти пространства она проходит.
15
§ 5. Натуральная величина отрезка прямой и углы наклона прямой
к плоскостям проекций
17*. Найти натуральную величину отрезка прямой АВ, задан-
заданного его проекциями, и определить углы наклона прямой к плоско-
плоскостям V и /) (рис. 15).
Р е ш е и и е. Как известно, натуральная величина отрезка может быть опреде-
определена как величина гипотенузы прямоугольного треугольника, одним катетом кото-
которого является проекция отрезка на какой-либо плоскости проекций, а другим — раз-
иость расстояний концов отрезка до этой же плоскости. Если одним из катетов яв-
является горизонт, проекция, то угол между гипотенузой и этим катетом равен углу
наклона (а) прямой к горизонт, плоскости проекций. Угол наклона (Р) этой же прямой
к фронт, ил. проекций определяется из треугольника, п котором в качестве первого
катета взята фронт, проекция отрезка, а второй катет определен по разности расстоя-
расстояний концов отрезка до фронт, пл. проекции.
Для определения натуральной величины отрезка АВ и углов а и р на рис. 15
построены прямоугольные треугольники ЬаА nb'a'A. В треугольнике ЬаА катет аА
равен разности расстояний точек А и В до горизонт, пл. проекций. В треугольнике
Ь'а'А катет а'Л равен разности расстояний точек А и Й до фронт, пл. проекций.
/I
15.
Рис !б.
Ш. Определить натуральную величину отрезка прямой АВ
(рис. 16) и углы наклона его к плоскостям проекций.
16
19. Определить натуральную величину отрезка заданно?! прямой
между ее фронт. (N) и горизонт. (/VI) следами и углы наклона этой
прямой к обеим плоскостям проекции (рис. 17).
а)
Рис. 17. Рис. 18а.
20*. Отложить на заданной прямой отрезок А В, равный /
(рис. 18, а).
Решение. На заданной прямой (рис. 18, б) берем произвольный отрезок А К
и определяем его натуральную величину. Строим прямоугольный треугольник с ка-
катетами ah и кК, равным разности расстояний точек А и К от пл. И. На гипотенузе по-
построенного треугольника откладываем отрезок аВ заданной длины /. Из точки В про-
проводим прямую параллельно 1гК- Получаем точку b и горизонт, проекцию ab искомого
отрезка А В, равного /. По точке 6 находим точку Ь'; а'Ь — фронт, проекция искомого
отрезка АВ.
а
Рис. 18Г> Рис. 19.
21. На прямой АВ (рис. 19) отложить отрезок АС, равный I.
17
г
tr
°а
а)
Рис. 20а—d.
Рис 21.
18
22*. Провести в первой четверти через точку А (рис. 20, а) пря-
прямую, составляющую с. пл. Н угол а=30° и с пл. V угол ^ =--45°.
Решение. Следует проверить условие: каждый из углов (а и р") должен быть
острым, а сумма этих углов должна быть или меньше 90° (для прямой общего положе-
положения), или равна 90° (для профильной прямой). В заданииа+р=30°+45°= 75°, т. е.
меньше 90°. Следовательно, построение может быть выполнено.
С углами а и р мы уже встречались и задаче 17*. Если задаться каким-либо от-
отрезком А В прямой и принять его за гипотенузу некоторого прямоугольного треуголь-
треугольника, то, зная углыа и [S, можно построить два таких треугольника (рис. 20, б). В од-
одном из них (с углом а) катет А—/ выражает горизонт, проекцию отрезка АВ, а ка-
катет В—/ — разность расстояний концов отрезка А В от пл. Н\ в другом треугольнике
(с углом C) катет А—2 выражает фронт, проекцию отрезка АВ, а катет В—2 — раз-
разность расстояний концов отрезка от пл. V.
Теперь можно построить чертеж (рис. 20, в).
Откладываем на линии связи а'а отточки а' иниз отрезок л'—3, равный найден-
найденному на рис. 20,6 катету В—I. Через точку 3 проводим прямую, перпендикулярную
к линии связи а а, а из точки а проводим дугу окружности, радиус которой должен
равняться кагету А—2 (рис. 20, б). В пересечении прямой и дуги получим точку ft'.
Для построения точки b откладываем на линии связи а а от точки а вниз отрезов
а—4, равный катету В—2 (рис.20, б), проводим через точку 4 прямую перпендикуляр-
перпендикулярно к линии связи а а и находим на ней точку Ь.
При точном построении проекция аЬ (рис. 20, в) должна получиться ранной кате-
катету A—I (рис. 20, б).
Конечно, можно получить при тех же данных еще три положения отрезка А В;
соответствующие чертежи показаны па рис. 20, г. Построение по существу не отлича-
отличалось бы от приведенного па рис. 20, в.
23. Через точку А (рис. 21) провести (вправо вниз, от себя)
прямую, составляющую с пл. Н угол а = 15° и с пл. V угол Р=ЗСГ,
до пересечения ее с пл. V.
§ 6. Деление отрезка в данном отношении
а
(рис. 22, а).
АС
2<4*. Разделить отрезок АВ точкой С в отношении "оц
Решение. Так как делению отрезка в каком-либо отношении соответствует
такое же деление его проекций, то делим (рис. 22, 6) проекцию аЬ (можно было бы на-
начать и с фронт, проекции) на 5 частей. Для этого через точку о проводим произволь-
произвольную прямую и откладываем на ней пять каких-либо рав.ных между собой отрезков.
19
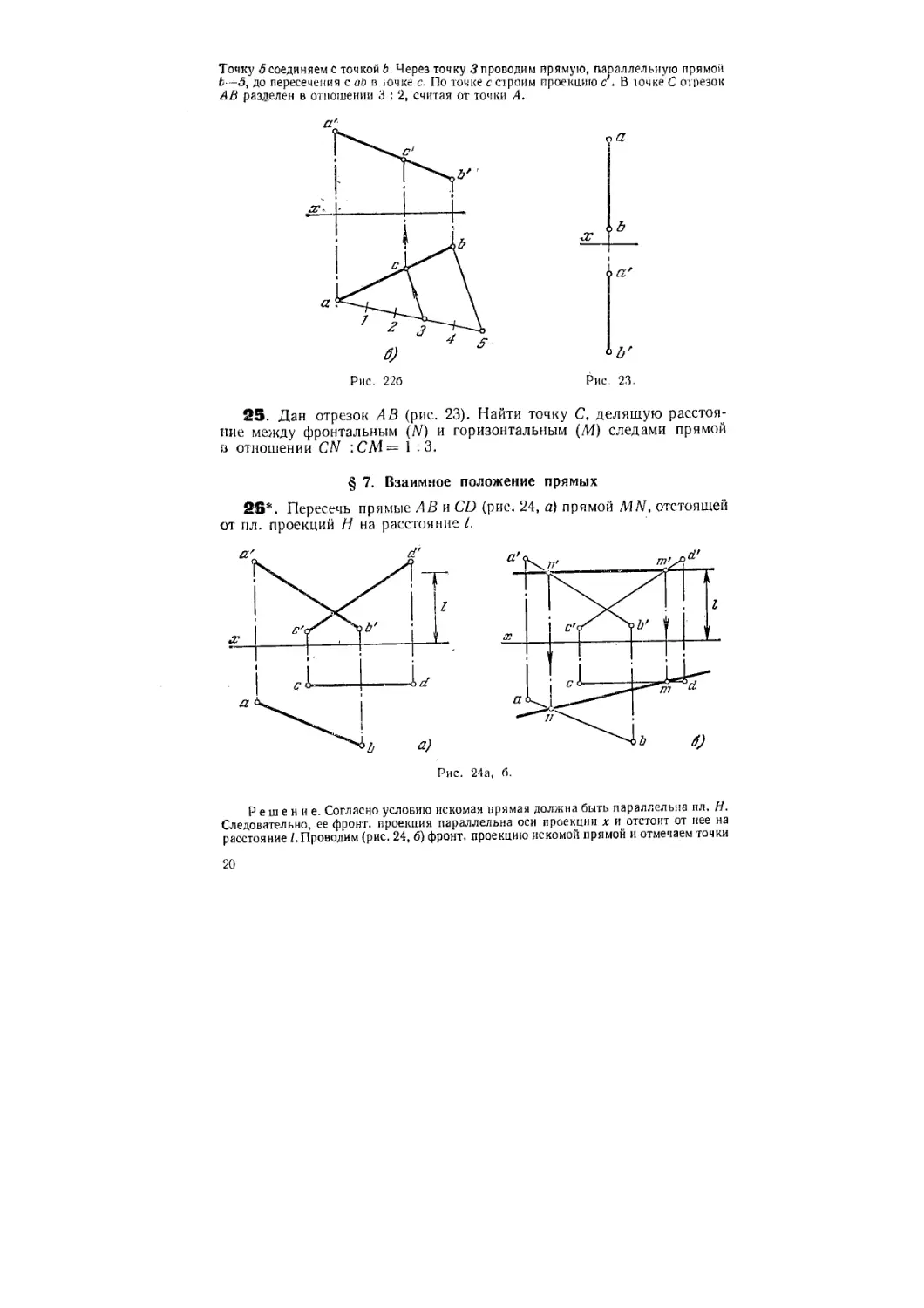
Точку б соединяем с точкой Ь. Через точку 3 проводим прямую, параллельную прямой
Ь—5, до пересечения с а* в ючке с. По точке с строим проекцию с . В точке С отрезок
-4? разделен в отношении 3 : 2, считая от точки А.
к а'
Ь'
Рис 23.
25. Дан отрезок А В (рис. 23). Найти точку С, делящую расстоя-
расстояние между фронтальным (N) и горизонтальным (М) следами прямой
а отношении CN :СМ= 1 3.
§ 7. Взаимное положение прямых
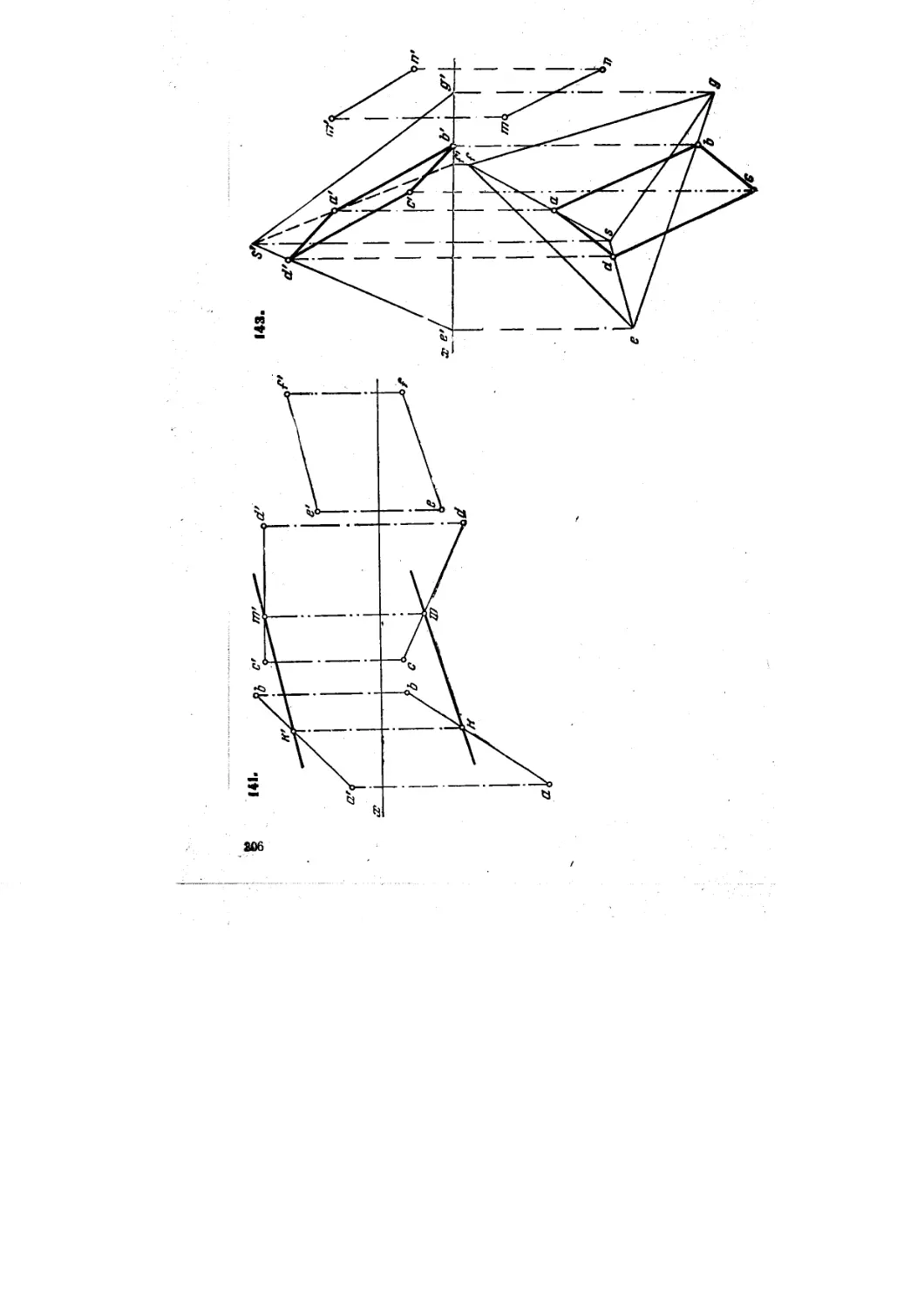
26*. Пересечь прямые АВ и CD (рис. 24, а) прямой MN, отстоящей
от пл. проекций Н на расстояние /.
а
Рис. 24а, б.
Решение. Согласно условию искомая прямая должна быть параллельна пл. Н.
Следовательно, ее фронт, проекция параллельна оси проекции х и отстоит от нее на
расстояние /.Проводим (рис. 24, б) фронт, проекцию искомой прямой и отмечаем точки
20
п' и in' пересечения ее с одноименными проекциями заданных прямых. Строим горн-
зонт, проекции п и т соответственно па ub и cd и проводим горизонт, проекцию п\л
искомой прямой.
Рис. 25.
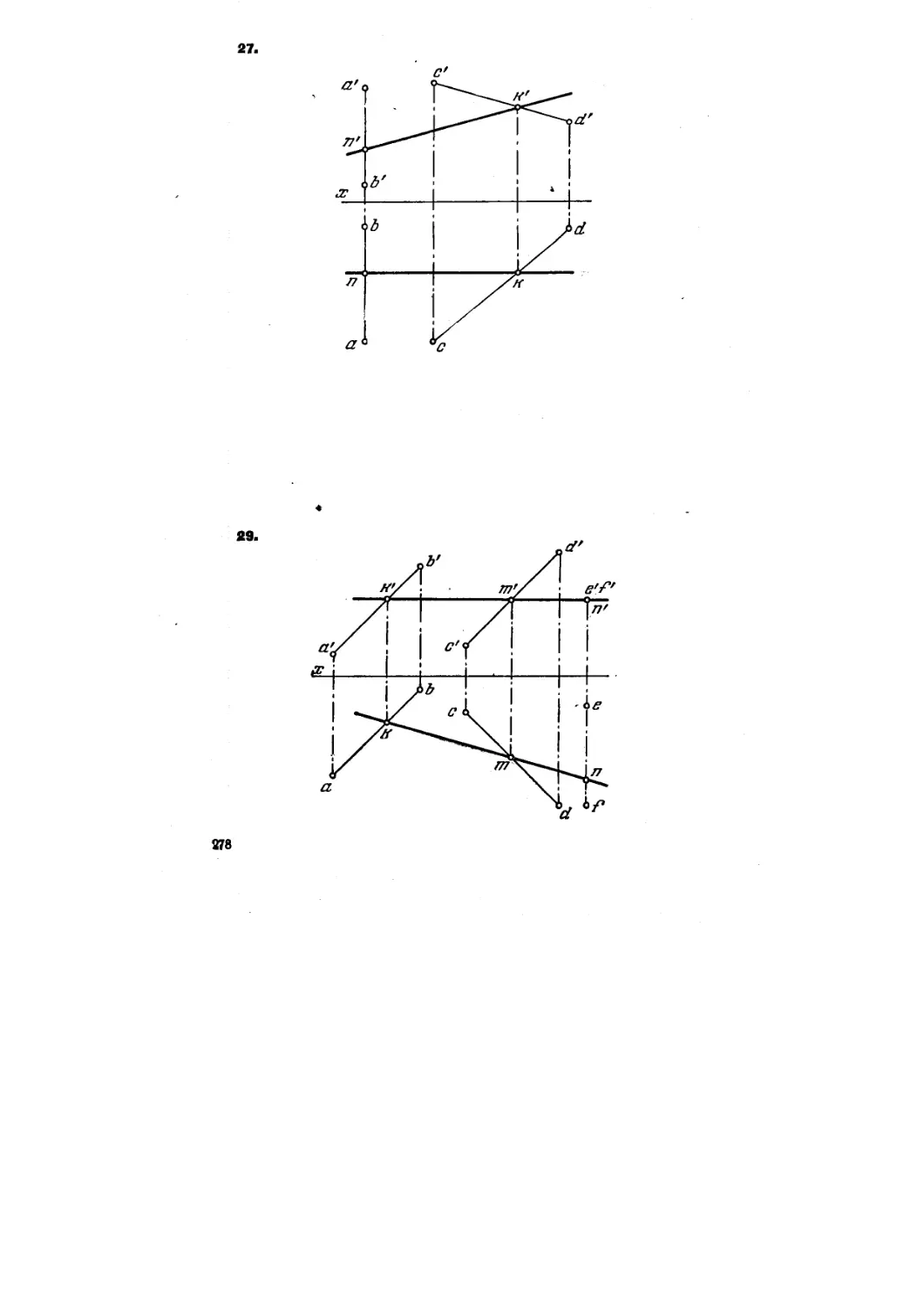
27. Прямые А В и CD (рис. 25) пересечь прямой, параллельной
пл. проекций V и отстоящей от нее на расстояние /.
28*. Через точку Е (рис. 26, а) прозести прямую, пересекающую
заданные прямые А В и CD.
C'9
с
I
Рис. 26а, 6.
Решен» е. Искомая прямая должна удовлетворять трем условиям:
1) проходить через точку ?, 2) пересекать прямую АВ, 3) пересекать прямую
CD. Поэтому на чертеже (рис. 26, б): 1) проекции прямой должны пройти через
соответствующие проекции точки Е;
21
e't
Рис. 27.
с а
а'
У
V
2) горизонт, проекция искомой прямой должна пройти через точку, являющуюся
горизонт, проекцией прямом А В;
3) точки пересечения проекций искомой прямой с одноименными проекциями
прямой CD должны лежать на одном перпендикуляре к оси проекций.
Построение искомой прямой начинаем с проведения ее горизонт, проекции через
точки е и a (ft).
Отмечаем точку пересечения с cd — точку g, находим g' на c'd' и через g' и г
проводим прямую — фронт, проекцию искомой прямой.
Точки k' и k являются проекциями точки пересечения искомой прямой с пря-
прямой А В.
29. Пересечь прямые А В, CD и EF (рис. 27) прямой, параллель-
параллельной пл. проекций И.
30. Провести через точку С прямую, пересекающую прямую А В
и ось проекций х (рис. 28, а и б).
Примечание. Следует помнить, что ось проекций х проецируется на про-
профильную плоскость проекций в точку, совпадающую с началом координат — точ-
точкой О.
§ 8. Построение проекций прямого угла
31*. Провести из точки С перпендикуляр на прямую А В
(рис. 29,я, где Л3||пл. V).
Р е ш е и и е. Известно, прямой угол проецируется на плоскость в виде прямого
угла в том случае, если одна из его сторон параллельна плоскости проекции, а другая
пересекает эту плоскость под острым углом.
Рис. 29а, С.
В данном случае (рис. 29, а) прямая А В параллельна пл. V. Поэтому можно из
точки с (рис. 29, б) провести прямую перпендикулярно к а'Ь' и найти проекции
точки К, в которой СК пересекает АВ. Получаем проекции c'k' и ck искомого
перпендикуляра.
23
32. Провести in точки С прямую перпендикулярно к прямой
ABi I) ЛЯ||пл. И (рис. .30, а), 2) АВ\\чл. W (рис. 30, б).
С'\
а'
Рис. 30а, б.
Рис. :ля Г).
33*. Пересечь прямые АВ и CD (рис. 31, а) третьей прямой, пер-
перпендикулярной к ним, т. е. найти кратчайшее расстояние межлу скре-
скрещивающимися прямыми А В и CD, из которых одна прямая (CD) пер-
перпендикулярна к пл. проекций И,
24
-"г1
1—J
1
1
Рис. 32а, б.
Рис. 33.
25
Решение. Так как прямая CD перпендикулярна к пл. Н, то любой перпенди-
перпендикуляр к нем располагается параллельно пл. И. Поэтому прямой угол между искомой
прямой и прямой А В изображается на пл. Н в виде прямого угла. Горизонт, проекция
точки пересечения искомой прямой с прямой CD — точка m — совпадает cc(d)
(рис. 31, б). Проводим через точку т горизонт, проекцию прямой перпендикулярно
к nb до пересечения с ней в точке k и находим k'. Фронт, проекция искомой прямой
(к'т') располагается параллельно оси х.
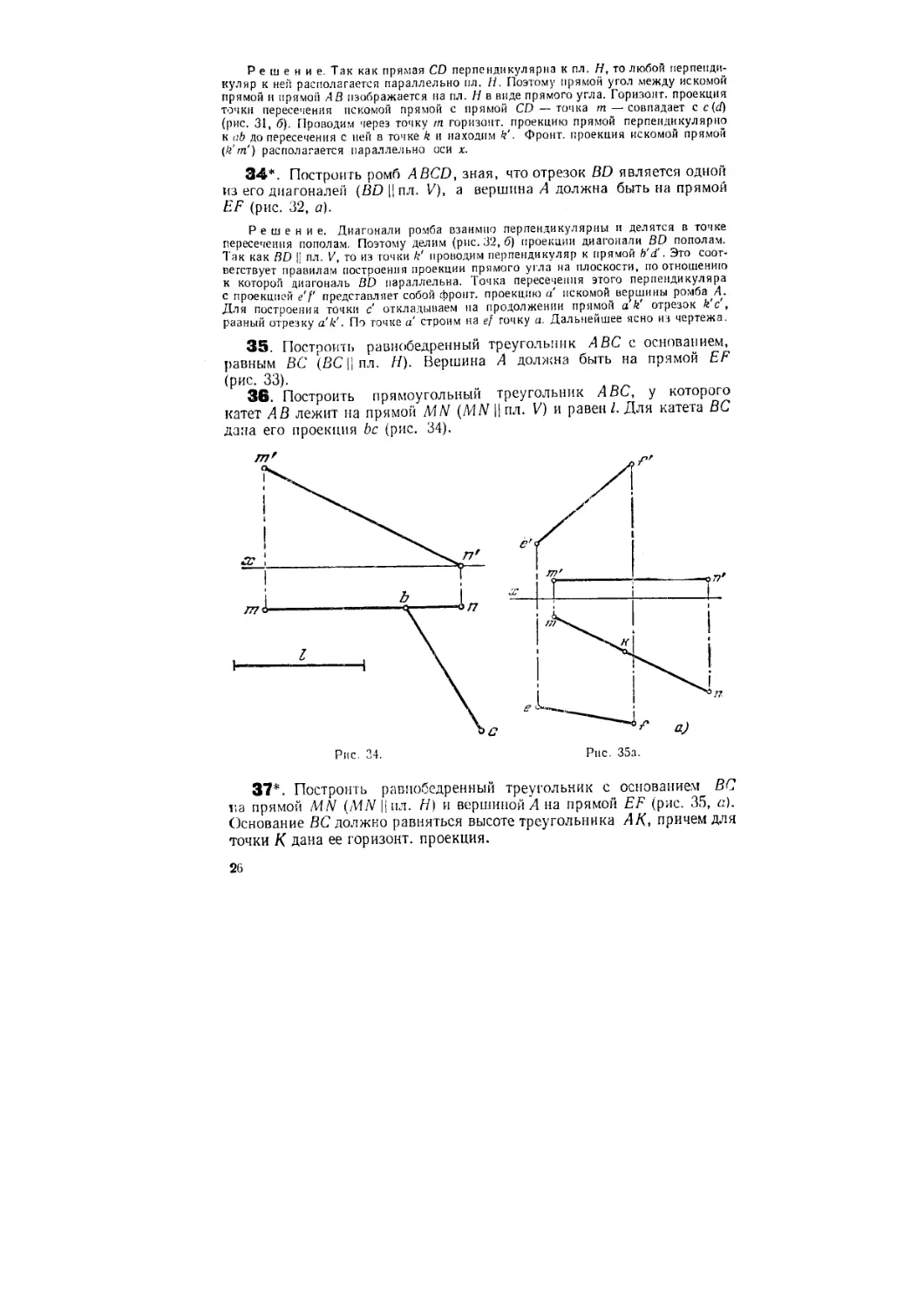
34*. Построить ромб ABCD, зная, что отрезок BD является одной
из его диагоналей (BD \\ пл. V), а вершина А должна быть на прямой
EF (рис. 32, а).
Решение. Диагонали ромба взаимно перпендикулярны и делятся в точке
пересечения пополам. Поэтому делим (рис. 3'2, б) проекции диагонали BD пополам.
Так как ДО || пл. V, то из точки к' проводим перпендикуляр к прямой b'd'. Это соот-
соответствует правилам построения проекции прямого угла на плоскости, по отношению
к которой диагональ BD параллельна. Точка пересечения этого перпендикуляра
с проекцией e'f представляет собой фронт, проекцию а искомой вершины ромба А.
Для построения точки с откладываем па продолжении прямой a k' отрезок k'c ,
разный отрезку a k'. По точие а строим на е/ точку а. Дальнейшее ясно из чертежа.
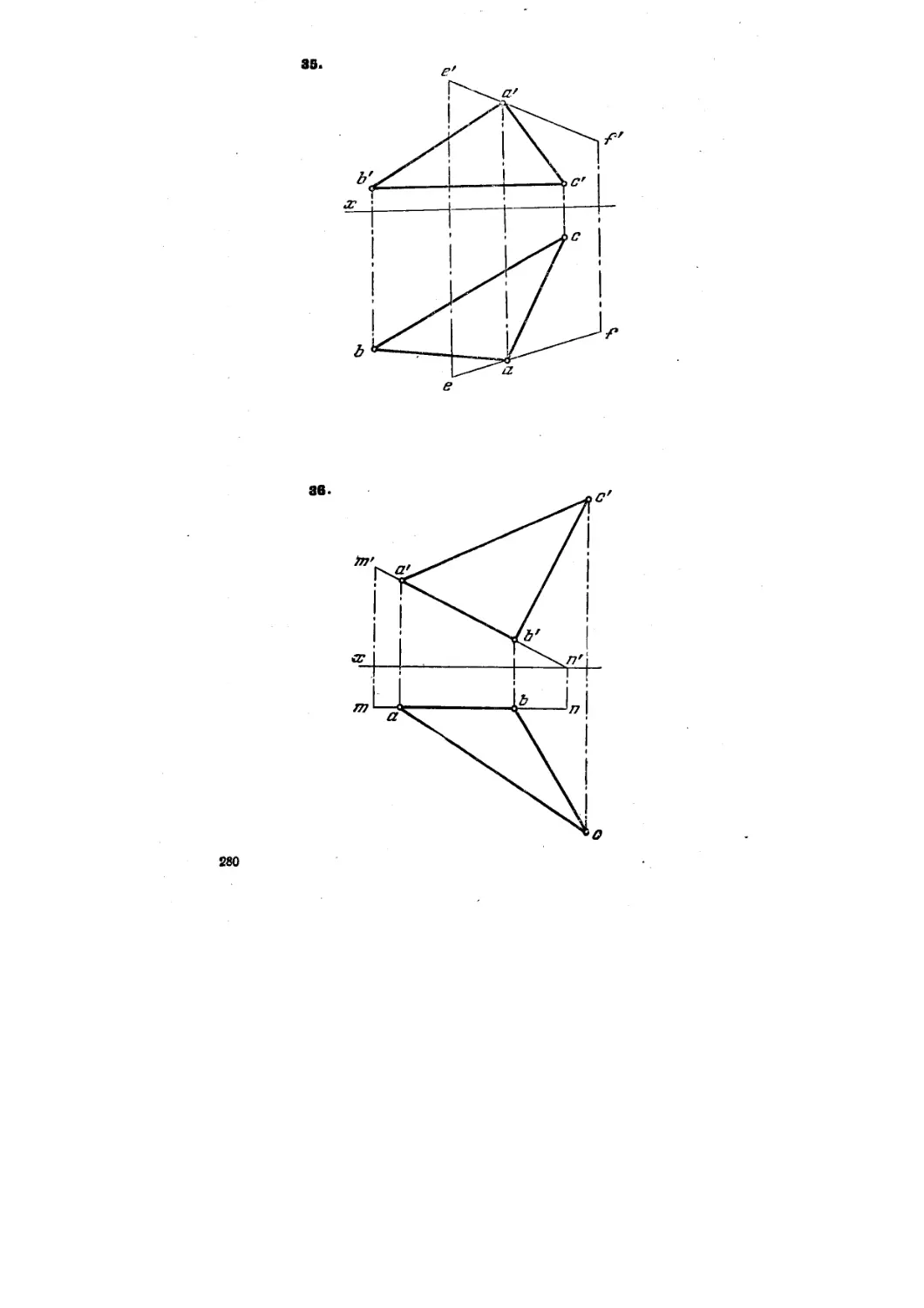
35. Построить равнобедренный треугольник ABC с основанием,
равным ВС (ВС || пл. Н). Вершина А должна быть на прямой ЕР
(рис. 33).
36. Построить прямоугольный треугольник ABC, у которого
катет АВ лежит на прямой MN (MN || пл. V) и равен /. Для катета ВС
дама его проекция be (рис. 34).
/77'
Рис. 34.
Рис. 35а.
37*. Построить равнобедренный треугольник с основанием ВС
г.а прямой MN (/МЛ/||пл. Н) и вершиной Л на прямой EF (рис. 35, а).
Основание ВС должно равняться высоте треугольника АК, причем для
точки К дана ее горизонт, проекция.
26
¦»f"
Решение. Для построения тре-
треугольника надо найти его высоту АК и
отложить половину ее величины на прямой
MN по обе стороны от точки К- На
рис. 35, б лоточке k строим точку k'. Из
точки k проводим перпендикуляр к прямой
тп (прямой угол между высотой АК и
основанием ВС, лежащим на MN, изоб-
изображается на пл. проекций Н в виде пря-
прямого же угла, так как прямая MN парал-
параллельна пл. Н). Продолжаем зтст перпен-
перпендикуляр до пересечения с ef. По точке а
строим а на е I'; получаем фронт, проек-
проекцию высоты АК-
Теперь можно найти натуральную ве-
величину высоты АК- Для этого строим пря-
прямоугольный треугольник ak К,, у которого
катет /г/С равен разности расстояний точек
А и К от пл. Н. Гипотенуза аК выражает
высоту Л К- Откладывая на прямой тп от-
ручки kb и kc, равные половине высоты
АК (т. е. половине отрезка аК), получаем
точки Ь и с, а по ним проекции Ь' и с'.
Дальнейшее ясно из чертежа.
38. Построить квадрат A BCD со стороной ВС на прямой ММ,
которая || пл. V (рис. 36).
Рис. 36.
Рис. 37.
39 Построить прямоугольный треугольник ABC с катетом ВС на
прямой МЫ (МЛП|пл. Н). Для катета АВ дана проекция а'Ь'. Катет
ВС должен быть в 1,5 раза больше катета АВ (рис. 37).
27
ГЛАВА II
плоскость
§ 9. Прямая и точка в плоскости
40*. В плоскости, заданной точками А, В и С, провести горизон-
горизонталь на расстоянии / от пл. проекций Н (рис. 38, а).
а)
б)
Рис. 38а, A.
Решение. Переходим от задания плоскости тремя точками к заданию ее дву-
двумя прямыми АС и ВС (рис. 38, б). Проводим фронт, проекцию искомой горизонтали на
расстоянии / от оси х. Отмечаем точки я' и /' на проекциях ас нЬ'ё и находим про-
проекции е и / на ас и be. Горизонт, проекция искомой прямой проходит через точки ей/.
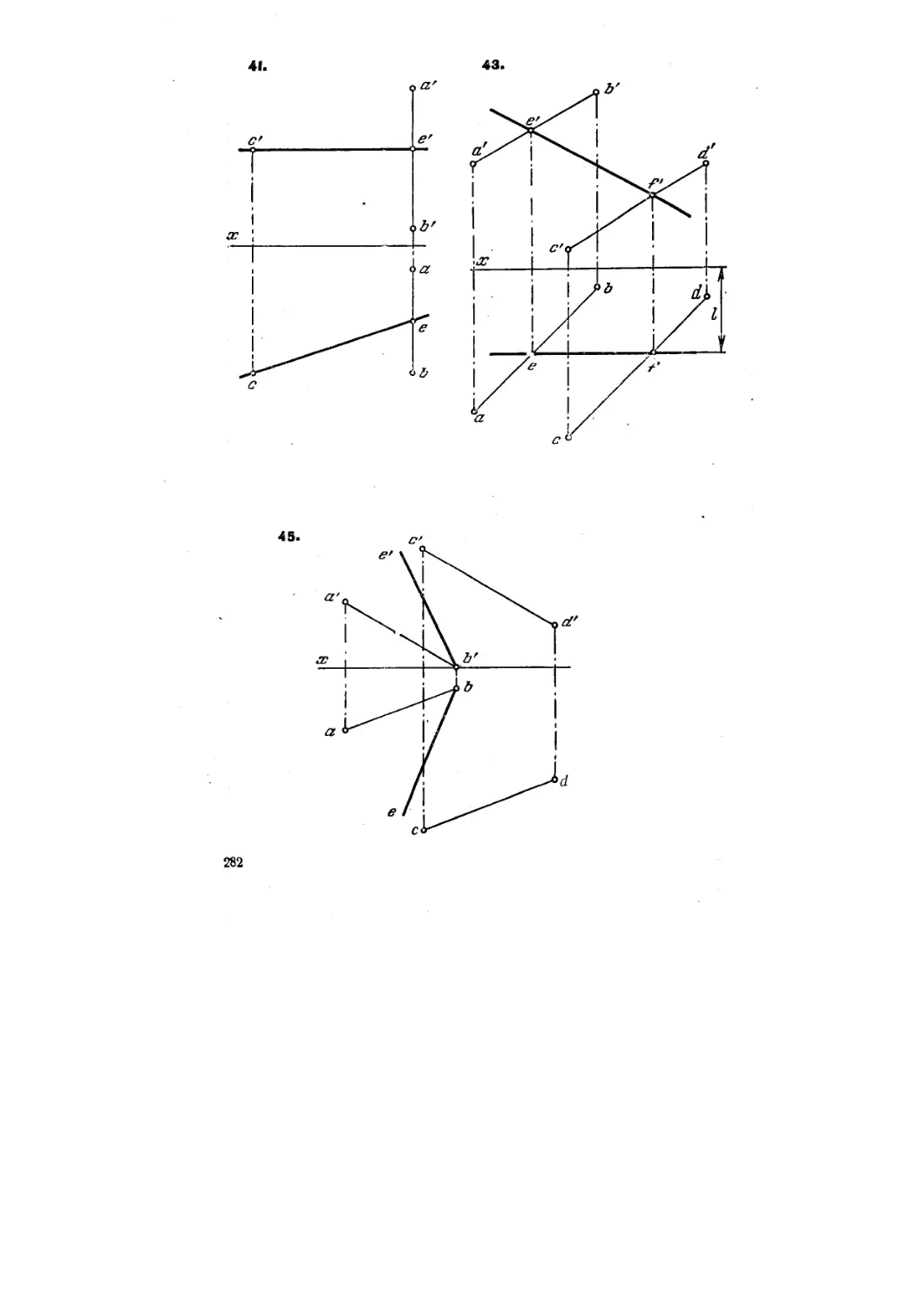
41. Провести через точку С горизонталь плоскости, заданной
прямой АВ п точкой С (рис. 39).
42*. В плоскости, заданной пересекающимися прямыми АВ и
CD, провести через точку К фропталь (рис. 40, а).
Решение. Так как направление горизонт, проекции фронтали известно, то
начинаем построение с проведения этой проекции через точку к: прямая km должна
быть параллельна оси х (рис. 40, б). Чтобы построить фронт, проекцию искомой фрон-
фронтали, надо построить фронт, проекцию какон-лиоо точки, принадлежащей фронтали.
Выбираем на проекции фронтали произвольную точку е, проводим через нее горизонт,
проекцию с] некоторой прямой, лежащей в заданной плоскости. Строим далее точку f
на прямой а'Ь', проводим c'f и находим на ней точку ё. Фронт, проекция искомой
фронтали проходит через точки k'i\ ё.
Рис. 406.
Рис. 41
43. В плоскости, заданной параллельными прямыми АВ и CD,
провести фронталь на расстоянии / от пл. проекций V (рис. 41).
44*. В плоскости, заданной прямой А В и точкой С, провести
через точку А линию ската плоскости (рис. 42, я).
с* а)
Рис. 42л, б.
Решение. Как известно, линия ската перпендикулярна к любой горизонтали
плоскости. Горизонт, проекции, линии ската и горизонтали взаимно перпендикуляр-
перпендикулярны. На рис. 42, б проведена горизонталь через точку С, сначала получена точка d',
а по ней точка d на продолженной проекции ab. Таким образом, получена проекция cd
горизонтали СП.Через точку а проводим горизонт, проекцию линии ската до пересе-
пересечения с прямой cd в точке е, находим е' нас'^' и проекцию а е' искомой линии ската.
а'
Рис. 43.
4S. В плоскости, заданной параллельными прямыми А В и CD,
провести через точку В линию ската (рис. 43).
30
Рис. 44а, б.
а
Рис. 45.
31
»*. Найти недостающую проекцию точки К, лежащей в плоско-
плоскости, заданной прямой АВ и точкой С (рис. 44, а).
Решение. Известно, что если точка принадлежит плоскости, то она принад-
принадлежит какой-либо прямой этой плоскости. Поэтому через точки с' и k' (рис. 44, б)
проводим фронт, проекцию вспомогательной прямой, лежащей в данной плоскости.
Получив точку d', находим точку d на проекции аЪ. Теперь проводим прямую из точки
с через точку d и на этой прямой находим горизонт, проекцию точки К.
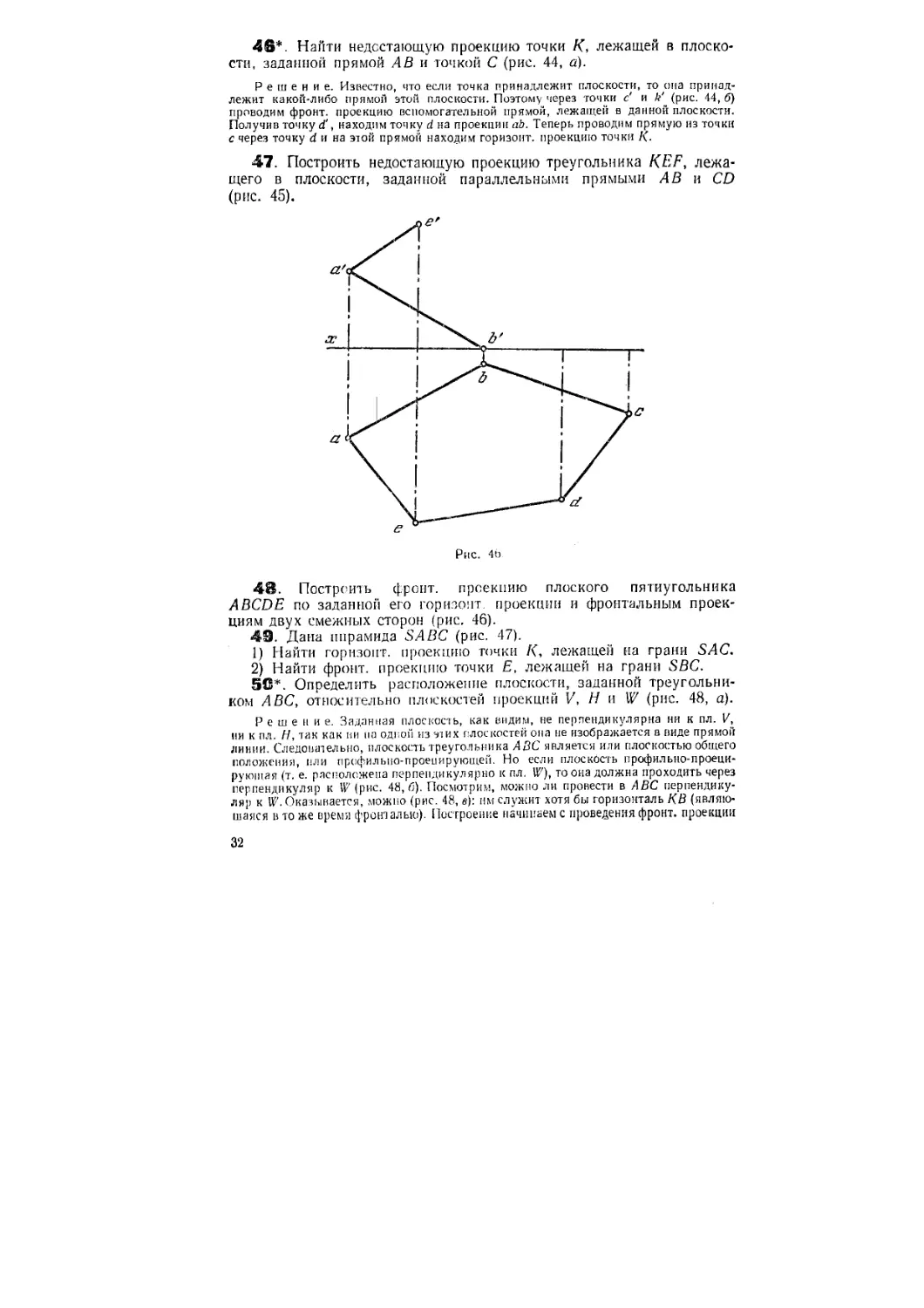
47. Построить недостающую проекцию треугольника KEF, лежа-
лежащего в плоскости, заданной параллельными прямыми АВ и CD
(рис. 45).
Рис. 4Ь
Построить фронт, проекцию плоского пятиугольника
ABCDE по заданной его горизонт, проекции и фронтальным проек-
проекциям двух смежных сторон (рис. 46).
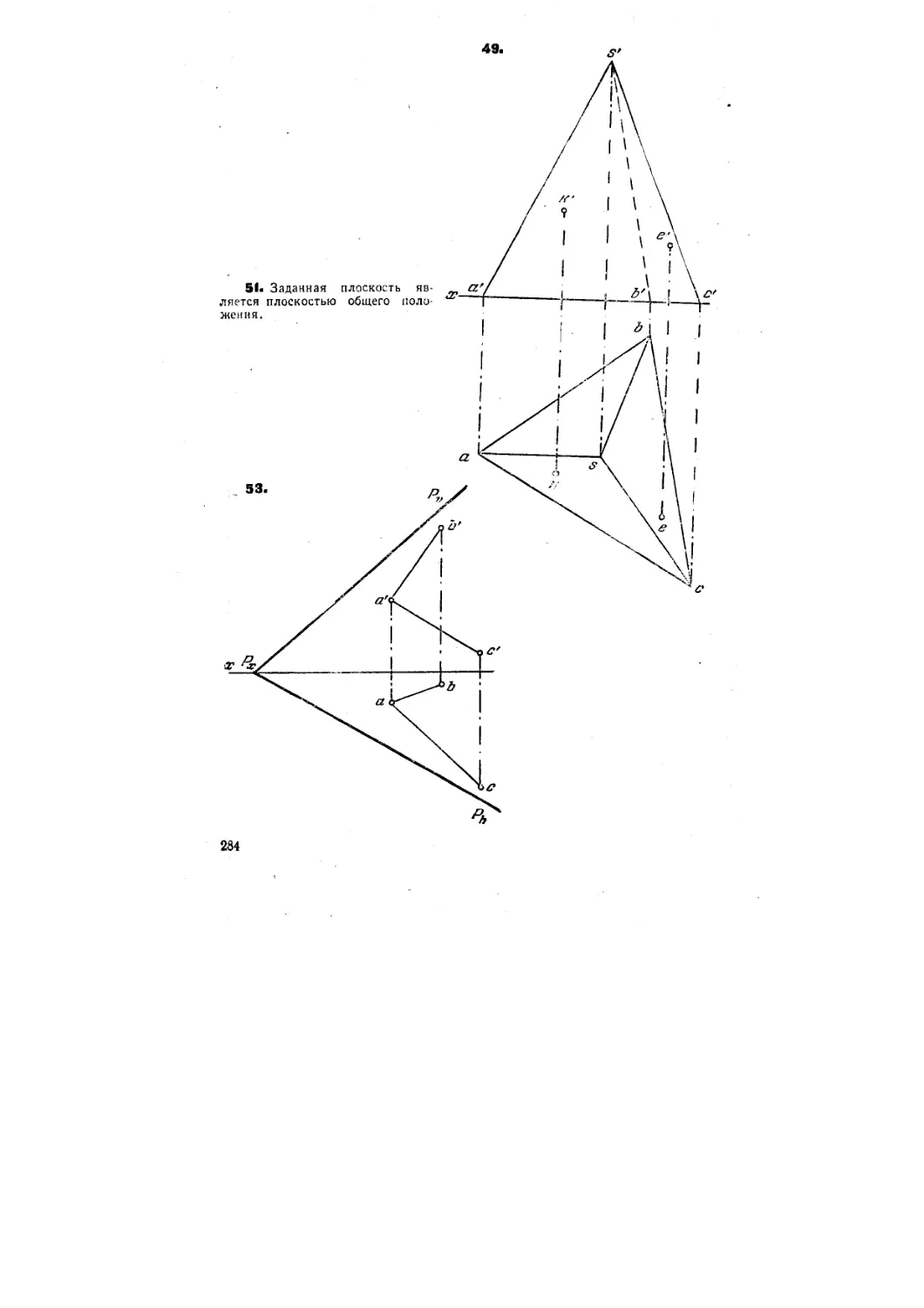
49. Дана пирамида SABC (рис. 47).
1) Найти горизонт, проекцию точки К, лежащей на грани SAC.
2) Найти фронт, проекцию точки Е, лежащей на грани SBC.
5СВ*. Определить расположение плоскости, заданной треугольни-
треугольником ABC, относительно плоскостей проекций V, Н и W (рис. 48, а).
Решение. Заданная плоскость, как видим, не перпендикулярна ни к пл. V,
ни к пл. Н, так как ни на одгон из чтих плоскостей она не изображается в ниде прямой
линии. Следовательно, плоскость треугольника ABC является или плоскостью общего
положения, пли профильно-проецирующей. Но если плоскость профильно-проеци-
профильно-проецирующая (т. е. рясполсжеиа перпендикулярно к пл. 117), то она должна проходить через
перпендикуляр к W (рис. 48,6). Посмотрим, можно ли провести в ABC перпендику-
перпендикуляр к ^.Оказывается, можно (рис. 48, в): им служит хотя бы горизонталь KB (являю-
(являющаяся в то же время фрошалыо). Построение начинаем с проведения фронт, проекции
32
2 В. О. Гордон и др.
33
b'k' горизонтали, затем находим горизонт, проекцию bk. Так как bk\\b'k' (конечно,
в пределах графической точности чертежа), то прямая ВК, а следовательно, и плос-
плоскость ABC перпендикулярны к пл. W.
Мы здесь обошлись без построения профильной проекции треугольника ABC.
Конечно, можно было начать с ее построения: если она оказалась бы отрезком прямой,
то этим устанавливалось бы, что плоскость ABC профильно-проецирующая.
51. Определить расположение плоскости, заданной двумя парал-
параллельными прямыми, относительно плоскостей проекций V, Н и W
(рис. 49).
§ 10. Следы плоскости
52*. Построить следы плоскости, заданной параллельными пря-
прямыми А В и CD (рис. 50, а).
а
Рис. 50а, 6>
Решение. Если прямая лежит в плоскости, то следы прямой лежат на одно-
одноименных с ними следах плоскости (рис. 50, б). Чтобы построить следы заданной пло-
плоскости, надо построить следы прямых АВ и CD. Фронт, след Ро пройдет через фронт,
следы прямых, т. е. через точки /V, и Л/2, а горизонтальный — через следы Mt и Мг.
Строим следы прямых АВ и CD, как это рассмотрено в § 4 (например, задача 12*).
Через точки тх и т2 проходит горизонт, след Р/,, а через точки я/ и пг' — след Pv
(рис. 50, в). Если построение выполнено точно, то оба следа пересекаются в точке Рх
на оси х.
53. Построить следы плоскости, заданной двумя пересекающи-
пересекающимися прямыми АВ и АС (рис. 51).
54*. Построить следы плоскости, заданной двумя пересекающи-
пересекающимися прямыми АВ (АВ || пл. Н) и CD (рис. 52, а).
34
в)
а
Рис. 50в.
Рис. 51.
Рис. 52а, 6i
35
Решение. Так как следы плоскости должны проходить через одноименные
с ними следы прямых, лежащих в этой плоскости (рис. 52, б), то надо построит ь фронт,
следы обеих прямых — точки М2 и Nlt и провести через них фронт, след плоскости
(Pv). Направление горизонт, следа плоскости известно: след Ph должен быть парал-
параллелен горизонтали АВ (рис. 52, б). Поэтому след Ph пройдет через точку пересечения
следов (Рх) параллельно горизонтали А В. На рис. 52, в показано, что проекции ab
и cd продолжены до пересечения их с осью х в точках п2 и «j и по ним построены точки
л./ ил/ на проекциях ab' uc'd'. Через п2' и п\ проведен след Pv до пересечения с осью
х в точке Рх. Через точку Рх проведен след Рл параллельно прямой ab.
I i Л1
Рис. 52в:
Рис. 53.
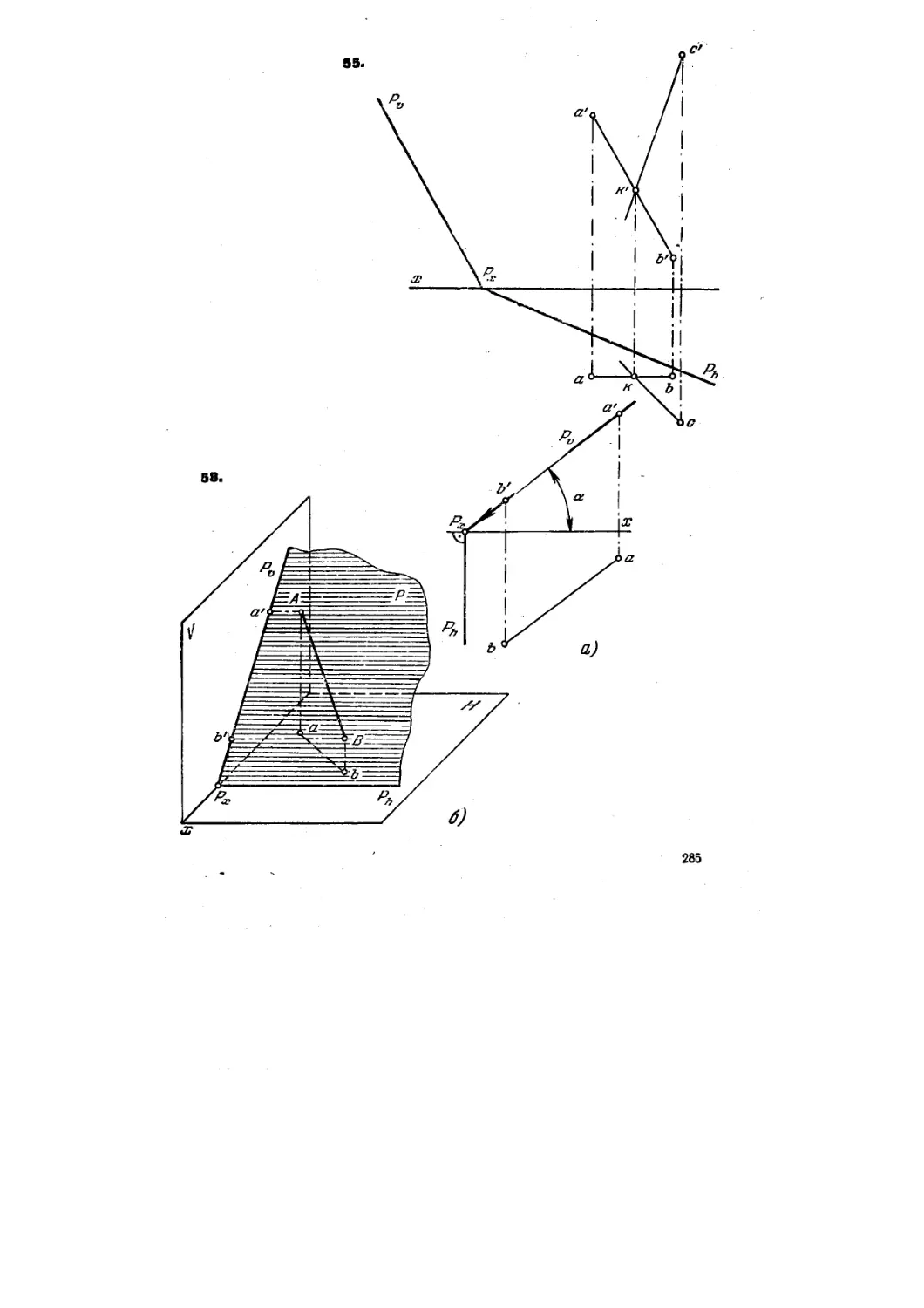
55. Построить следы плоскости, заданной пересекающимися пря-
прямыми АВ и КС (рис. 53).
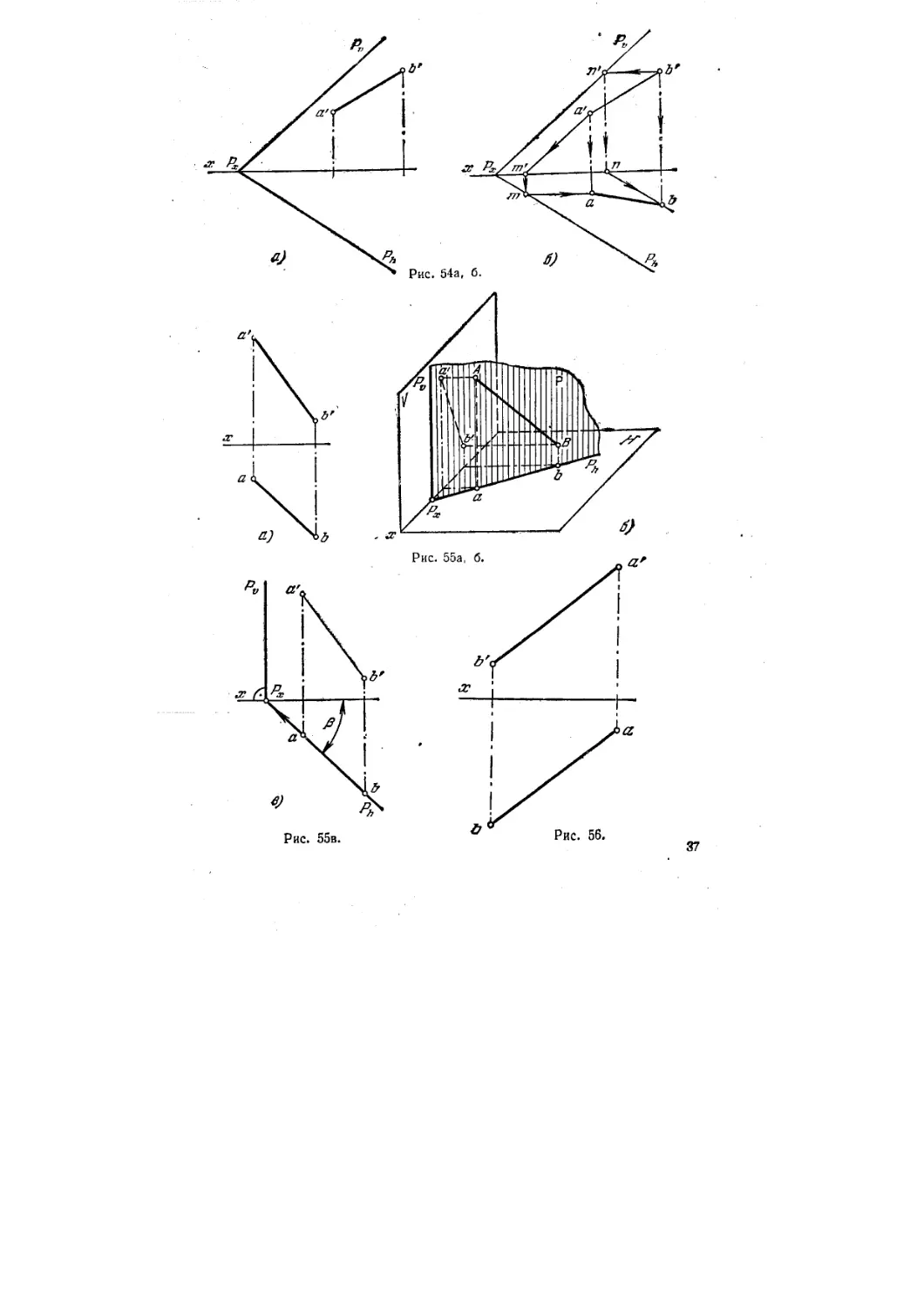
56*. Построить недостающую проекцию отрезка АВ прямой, ле-
лежащей в плоскости Р (рис. 54, а).
Решение. Чтобы построить горизонт, проекцию отрезка АВ, надо найти го-
горизонт, проекции точек А и В (рис. 54, б). Проекцию b находим с помощью горизон-
горизонтали, проведенной в плоскости. Сначала проводим проекцию Ь'п' параллельно оси х,
затем через точку п — горизонт, проекцию горизонтали параллельно Рh и на ней на-
находим проекцию Ъ. Горизонт, проекцию точки А находим при помощи фронтали, хо-
хотя, конечно, можно было бы и для этой точки применить горизонталь. Через а' про-
проводим фронт, проекцию фронтали (параллельно Pv), находим точки т! и т (проекции
горизонт, следа фронтали). Горизонт, проекция фронтали проходит через точку т
параллельно оси х; на этой проекции получаем точку а. Искомая проекция отрезка АВ
определяется точками а ч Ь,
36
а
Рис. 55в.
Рис. 56.
37
57*. Заключить прямую АВ (рис. 55, а) в горизонтально-проеци-
горизонтально-проецирующую плоскость, задав эту плоскость ее следами на пл. И и V
Решение. Горизонтальные проекции всех элементов, лежащих в горизонталь-
горизонтально-проецирующей плоскости, находятся на Ph. Поэтому (рис. 55, б) след Рн совпадает
с ab. Через точку Рх, получаемую при пересечении Pft с осью х, проводим перпенди-
перпендикулярно к оси х фронт, след искомой плоскости (Рю)
Угол между следом Ph и осью х равен углу р* между пл. Р и пл. проекций V (рис.
65, в).
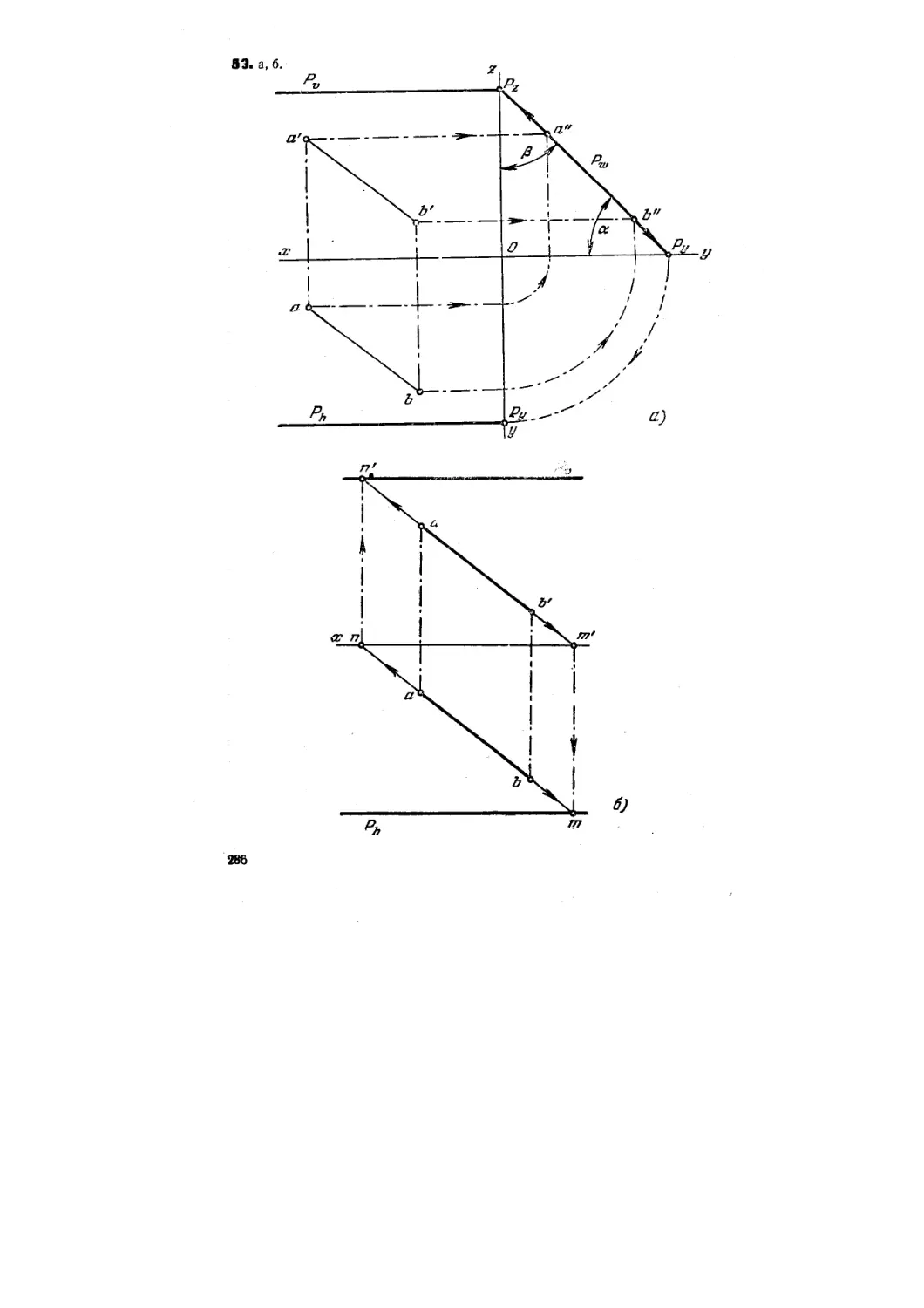
58. Заключить прямую АВ (рис. 56) во фронтально-проецирую-
фронтально-проецирующую плоскость, выразив эту плоскость следами на пл. V и Н. Пост-
Построить чертеж и наглядное изображение. Указать угол наклона пл. Р
к пл. Н.
59. Заключить прямую А В (рис. 57) в профильно-проецирующую
плоскость, выразив эту плоскость следами. Построить чертеж и дать
наглядное изображение. Указать углы наклона пл. Р к пл. V и Н. Пост-
Построение следов пл. Р выполнить с помощью профильной проекции пря-
прямой и без нее.
Г
а
Рис. 57.
Рис. 58.
60. Построить недостающую проекцию точки К (рис. 58), лежа-
лежащей в пл. Р (профильной плоскостью проекций не пользоваться).
ГЛАВА III
ПЕРЕСЕЧЕНИЕ ПРЯМОЙ ЛИНИИ С ПЛОСКОСТЬЮ
И ДВУХ ПЛОСКОСТЕЙ МЕЖДУ СОБОЙ
§11. Пересечение прямой с проецирующей плоскостью
81*. Найти точку пересечения прямой А В с пл. Т (рис. 59, а),
заданной ее фронт, следом Tv.
Решение. В данном случае пл. Т параллельна пл. Н и, следовательно, пер-
перпендикулярна к фронт, плоскости проекций; для пл.Г в системе V, Я дан только фронт.
а
Рис. 59;;—в.
след Tv, параллельный оси проекций х. Очевидно, фронт, проекция (k1) искомой точки
пересечения должна лежать как на следе Tv, так и на фронт, проекции прямой АВ,
т. е. на а'Ь' (рис. 59, б). Поэтому точку k' (рис. 59, в) находим в точке пересечения
следа Tv с проекцией а'Ь'. По точке k' находим точку k на ab.
Так как прямая АВ в направлении от К к А находится под пл. Т, то на чертеже
соответствующая часть горизонт, проекции изображена штриховой линией,
39
62. Найти точку пересечения прямой А В с пл. S (рис. 60).
63*. Найти точку пересечения прямой АВ с пл. R (рис. 61, а).
о а'
?>'
Рис. 60.
а
Решение. Пл. R является фронтально-проецирующей. Очевидно, фронт,
проекция (k') иско!иой точки пересечения должна находиться как на следе Rv, так и
на фронт, проекции прямой АВ, т. е. на а'Ь' (рис. 61, б).
На чертеже .(рис. 61, в) находим ?' в точке пересечения следа Rv с а'Ь', а проек-
проекцию k — на ati. Прямая А В в направлении от К к В находится подпл. R; поэтому на
чертеже соответствующая часть горизонт, проекции изображена штриховой линией.
84*. Найти точку пересечения прямой АВ о ил. R (рио. 62, а).
Решение. Пл. R является горизонтально-проецирующей.Очевидно, горизонт,
проекция искомой точки пересечения должна находиться как на следе Rht так и на
аЬ (рис. 62, б). Поэтому точку k (рис. 62, в) получаем как точку пересечения следа RH
с аи. По точке к находим проекцию k' на а'Ь'.
Прямая АВ в направлении от К к В находится за плоскостью /?; на чертеже со-
соответствующая часть фронт, проекции изображена штриховой линией
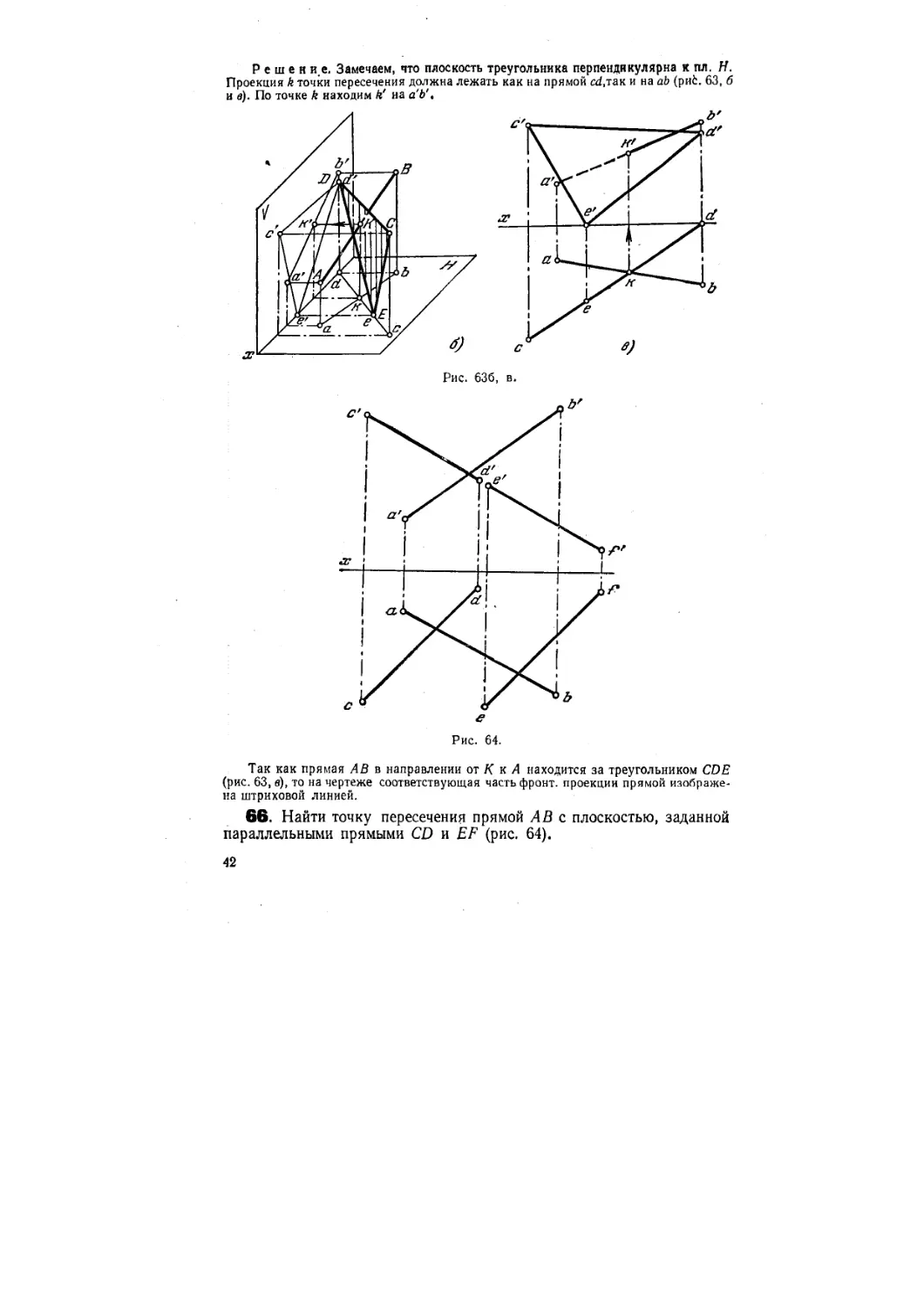
65*. Найти точку пересечения прямой АВ а плоскостью, заданной
треугольником CDE (рис. 63, а).
41
Решен и.е. Замечаем, что плоскость треугольника перпендикулярна к пл. И.
Проекция k точки пересечения должна лежать как на прямой cdjax. и на аЪ (рис. 63, б
и в). По точке k находим к' на а'Ь',
*)
Рис. 636, в.
Так как прямая АВ в направлении от К к А находится за треугольником CDE
(рис. 63, в), то на чертеже соответствующая часть фронт, проекции прямой изображе-
изображена штриховой линией.
66. Найти точку пересечения прямой А В с плоскостью, заданной
параллельными прямыми CD и EF (рис. 64).
42
§ 12. Пересечение плоскостей между собой
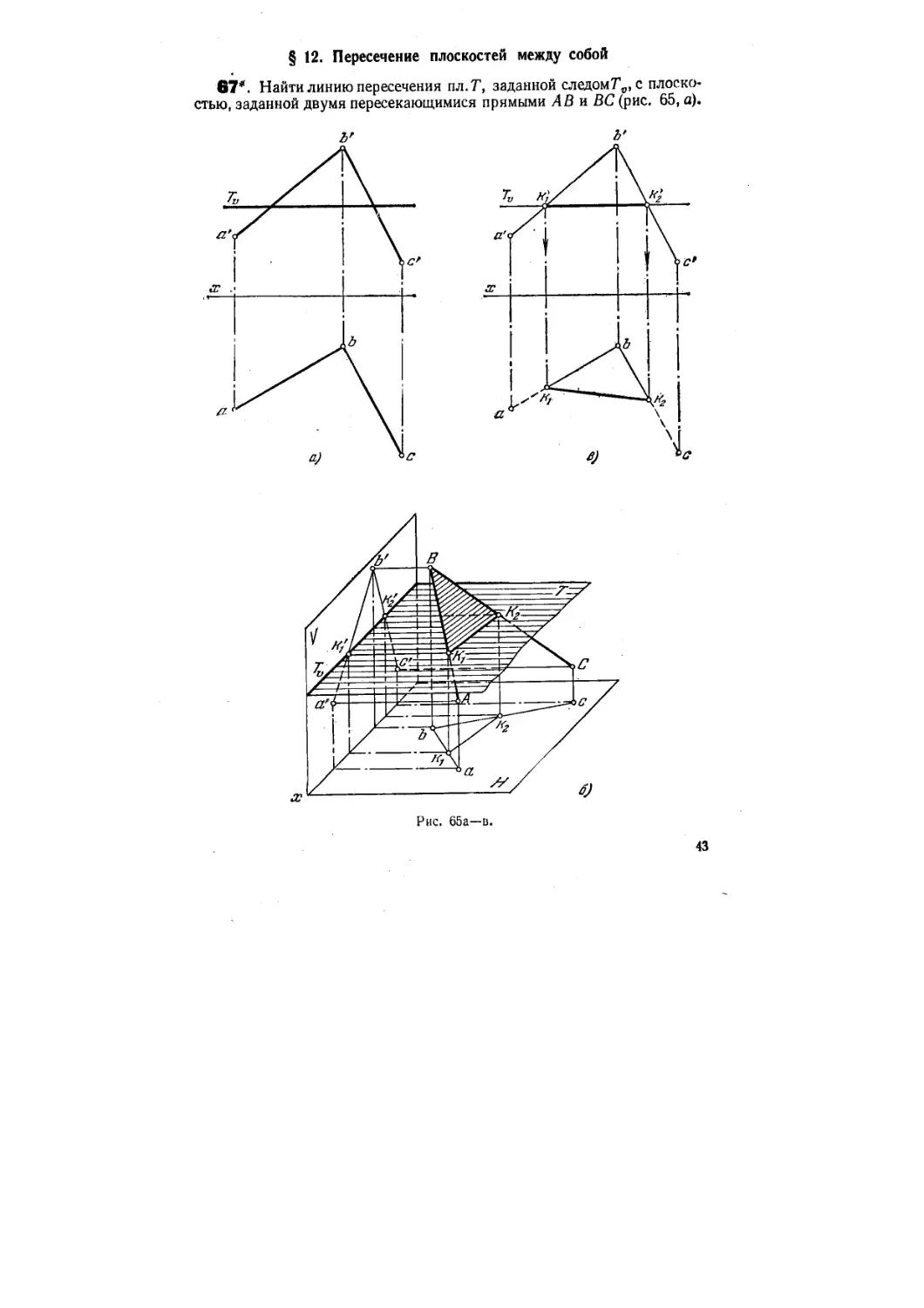
67*. Найти линию пересечения пл.Т, заданной следомТ0, с плоско-
плоскостью, заданной двумя пересекающимися прямыми АВ и ВС (рис. 65, а).
То
Рис. 65а—в.
43
Решение. Как известно, построение линии пересечения двух плоскостей сво-
сводится к нахождению двух точек, общих для обеих заданных плоскостек, или одной
такой точки при известном направлении искомой линии.
В данном случае искомая прямая может быть определена, если найти точки пе-
пересечения прямых АВ и ВС с пл. Т (рис. 65,6). Следовательно, построение точек Ki
и Кг сводится к показанному на рис. 59, бив.
Если считать плоскости непрозрачными, то горизонтальные проекции участков
прямых А В и ВС, находящихся под пл. Т, следует изображать штриховыми линиями.
Пл. Т не влияет на видимость прямых АВ и CD на пл. V, так как перпендикулярна
к ней (рис. 65, в).
Рис. 67.
Рис. 68а.
вв. Найти линию пересечения пл. S, заданной следом Sh, с пло-
плоскостью, заданной параллельными прямыми АВ a CD (рис. 66).
69. Найти линию пересечения фронтально-проецирующей пл. R,
заданной следом Ra, с плоскостью, заданной треугольником ABC
(рис. 67).
70*. Найти линию пересечения плоскостей Р и R (рис. 68, а).
Решение. Для построения линии пересечения плоскостей можно использо-
использовать точку N пересечения следов Pv и Ro и точку М пересечения следов Рн и RH
(рис.68,б). Прямая МN, проходящая через эти точки, является искомой линией пере-
пересечения. Ее проекция тп совпадает со следом Rh, так как пл. R является горизон-
горизонтально-проецирующей. Эти построения показаны на рис. 68, в.
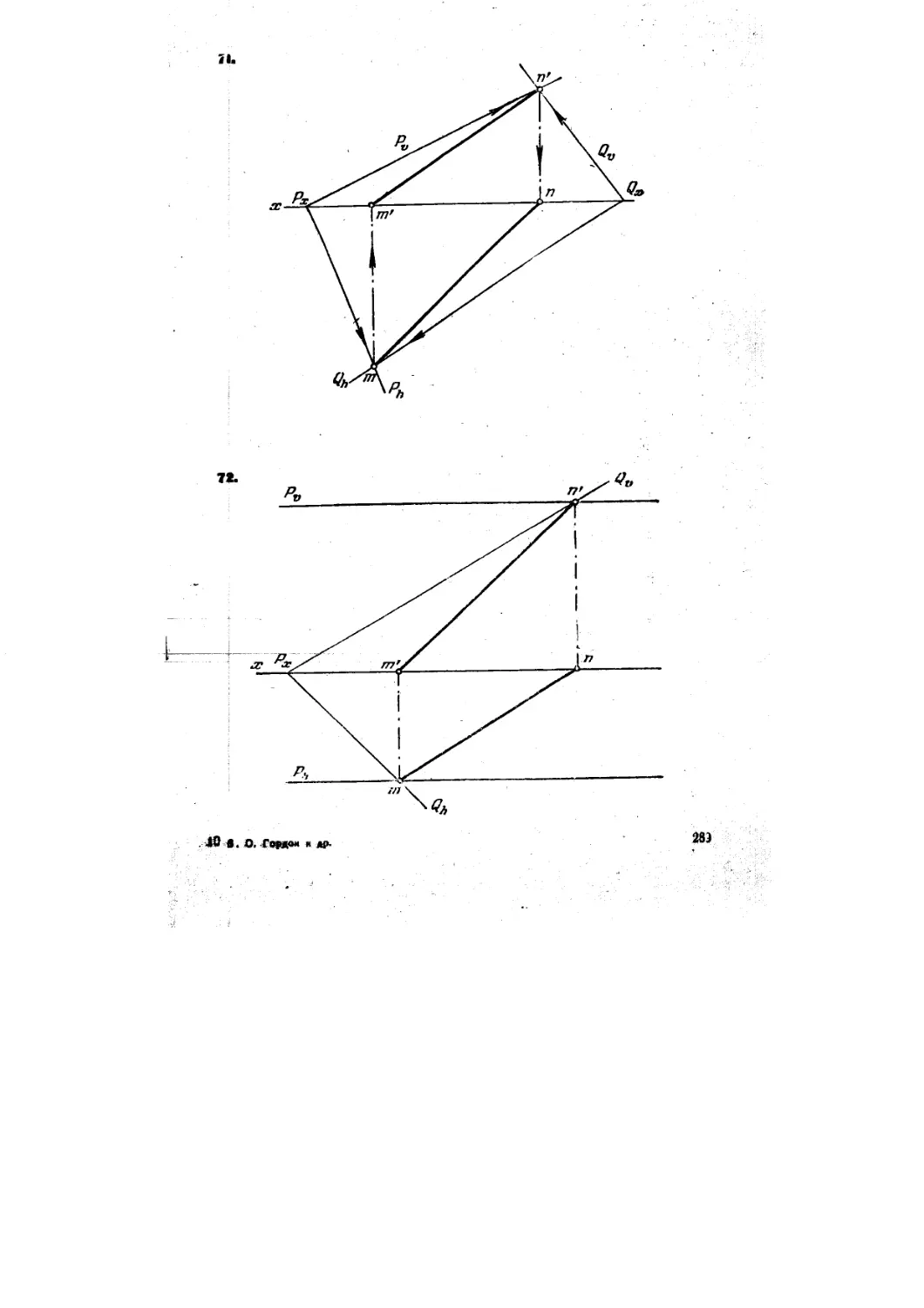
71. Построить линию пересечения плоскостей Р и Q (рис. 69).
45
72. Построить линию пересечения плоскостей Р и Q (рис. 70).
Профильной плоскостью проекций не пользоваться.
\
Рис. 70.
73*. Построить линию пересечения плоскостей Р и Q, у которых
О (рис. 71,а).
Ре
вначит,
46
Рис. 71а, б.
ш е н и е. В данном случае горизонт, следы плоскостей параллельны. Это
что искомая прямая параллельна пл. Н и для плоскостей Р и Q является го-
ризонталью (рис. 71, б). Чтобы провести эту горизонталь, достаточно построить одну
принаплежащую ей точку. Используем точку N пересечения следов Pv и Qv. Пост-
Построив проекции (рис. 71, в) я' и п, проводим па' параллельно оси х, а па — параллель-
но следам Ph и Qh.
.Р.,
Рис. 71в. Рис. 72.
74. Найти линию пересечения плоскостей Р и Q (рис. 72).
а)
Рис. 73а, б.
75*. Найти линию пересечения плоскостей Р и Q (рис. 73, а),
пользуясь профильной плоскостью проекций и не пользуясь ею.
47
Г L Щ/ »
Рис. 74.
48
Р е щ е н и е. Так как заданные плоскости являются профильно-проецирующими,
то линия их пересечения МЛ? (рис. 73, б) параллельна оси х. Чтобы найти эту прямую,
надо построить одну принадлежащую ей точку. Вводим (рис. 73, бив) вспомогатель-
вспомогательную плоскость S и строим линии пересечения ее с пл. Р A—2) и Q C—4). Эти линии,
пересекаясь, дают точку М (т', т), общуюдля пл. Р и Q. Через т' и т проводим
проекции искомой прямой т'п' и тп параллельно оси х. В качестве вспомогательной
плоскости можно использовать и профильную плоскость проекций (рис. 73, б и г):
линия MN проходит через точку пересечения следов Pw и Qw.
76. Построить линию пересечения плоскостей треугольника ABC
и четырехугольника DEFG (рис. 74), пользуясь профильной плоско-
плоскостью проекций и не пользуясь ею. Определить видимость плоскостей.
§ 13. Пересечение прямой с плоскостью общего положения
77*. Найти точку пересечения прямой А В с плоскостью, задан-
заданной треугольником CDE (рис. 75, а).
Решение. Как известно, для нахождения точки пересечения прямой с пло-
плоскостью общего положения следует через прямую провести вспомогательную пло-
(Д),-построить линию пересечения этой плоскости с заданной (/—2) и найти
Рис. 75а,
тонку пересечения (К) заданной и построенной прямых. Точка К является искомой
точкой пересечения прямой с плоскостью (рис. 75, б). В качестве вспомогательной
плоскости обычно используют горизонтально- или фронтально-проецирующую пло-
плоскость.
На рис. 75, в через прямую А В проведена фронтально-проецирующая плоскость
R, ее след Rv совпадает с а'в'. Горизонт, след плоскости в данной задаче не нужен
fa и поэтому не показан.
*™ Строим линию пересечения плоскости R и плоскости, заданной треугольником
CDE (пример такого построения см. в задаче 67). Построив линию 1—2 (рис. 75, в),
находим точку пересечения ее с прямой АВ — точку К (k, ft')-
Для определения участков прямой АВ, которые будут закрыты треугольником,
следует воспользоваться анализом положения точек на скрещивающихся прямых.
49
Например, точки / и 3 находятся на скрещивающихся прямых (соответственно) ED
и АВ. Фронтальные проекции этих точек совпадают, т. е. точки / и 3 одинаково уда-
удалены от пл. Н. Но расстояния их от пл. V различны: точка 3 находится дальше от
пл. V, чем точка /. Поэтому по отношению к пл. V точка 3 закрывает точку / (направ-
(направление взгляда указано стрелкой i). Следовательно, прямая АВ проходит перед тре-
треугольником CDE до точки К- Начиная же от точки К влево прямая АВ закрывается
треугольником, и поэтому этот участок прямой показан штриховой линией.
Для выявления невидимого участка на горизонт, проекции прямой А В рассмот-
рассмотрим точки 4 и 5, лежащие соответственно на прямых АВ и CD.
Если смотреть на эти точки по направлению sb мы видим сначала точку 5. Точка
4 закрывается точкой 5. Следовательно, прямая АВ в этом месте закрыта треуголь-
треугольником CDE, и участок ее проекции от точки k до точки 4 должен быть показан штрихо-
штриховой линией. В данном случае точка К оказалась внутри контура треугольника CDE.
При ином взаимном положении пересекающихся элементов возможен случай,
когда точка К окажется вне треугольника (рис. 75, г). Это означает, что прямая АВ
пересекает плоскость, заданную треугольником CDE, вне контура этого треугольника.
АВ становится невидимой за точкой К (влево).
78. Найти точки пересечения прямой АВ с гранями пирамиды
(рис. 76). Грани пирамиды следует рассматривать как плоскости,
заданные треугольниками.
79. Найти точки пересечения прямой АВ с гранями призмы
(рис. 77). Грани призмы следует рассматривать как плоскости, задан-
заданные параллельными прямыми.
80*. Найти точки пересечения прямой АВ с плоскостью Р
(рис. 78, а).
Решение. Проводим через прямую АВ (рис. 78, бив) фронтально-проецирую-
фронтально-проецирующую плоскость R (ее след RD совпадает с а'Ь') и строим линию MN пересечения обеих
плоскостей — заданной и проведенной через АВ (построение подобно выполненному
в задаче 70). Искомая точка K{k, к') пересечения прямой АВ с плоскостью Р находится
в точке пересечения MN с АВ.
В данной задаче видимость участка прямой от точки А до К очевидна; однако
в более сложных случаях следует видимый участок прямой определять на основании
50
a
О,
s
51
анализа положения точек. Например, взяв точку / (на прямой АВ) и точку N (на следе
Р„), видим, что точка / располагается дальше относительно пл. V, чем точка N. Сле-
Следовательно, прямая АВ до точки К видима. За точкой К прямая показана штриховой
линией — она невидима. Аналогично определяется видимость на горизонт, проекции.
Рис. 78а,
•77
Рис. 78в. Рис. 79.
81. Найти точку пересечения прямой АВ с плоскостью Р (рис. 79).
52
82*. Найти точку пересечения прямой АВ с плоскостью Р
(рис. 80, а).
Решение. Через прямую А В проводим горизонтально-проецирующую пло-
плоскость R (след R/, совпадает с ab) и строим линию пересечения плоскостей Р и Rt
Рис. 80а—г.
используя точки М и N пересечения их одноименных следов (рис. 80, 6 и в). Иско-
Искомая точка (ft', ft) находится в точке пересечения М N с А В. На рис, 80, г точка К
построена с помощью пл. W. Так как пл. Р профильно-проецирующая (рис. 80, б),
63
то профильная проекция k" лежит в точке пересечения следа Pw с а"Ь". Зная k",
строим К на а'Ь' и ft на ab. Видимые участки прямой АВ определяются так же, как в
задачах 77 и 80.
83. Найти точку пересечения прямой АВ с плоскостью Р (рис. 81).
84*. Найти точку пересечения прямой А В с плоскостью, заданной
треугольником CDE (рис. 82, а).
Решение. Через прямую АВ проводим (рис. 82, бив) пл. R, параллельную
пл. W. Она пересекает заданную плоскость по прямой MN (точки т', п', т и п лежат
на пересечении следов Rv и Rh с одноименными проекциями соответствующих сторон
а'у
Рис. 81.
Рис. 82а. б.
треугольника CDE). Так как прямые АВ и MN профильные, то для нахождения точки
(К) их пересечения строим профильные проекции а"Ь" и т"п". Проекция k" нахо-
находится на пересечении а"Ь" и т"п". По k" строим к' на а'Ь' и ft на ab.
?4
.—о а»
а
Рис. 83.
85. Найти точку пересечения прямой EF с плоскостью, заданной
четырехугольником A BCD (рис. 83).
55
§ 14. Общие случаи пересечения плоскостей
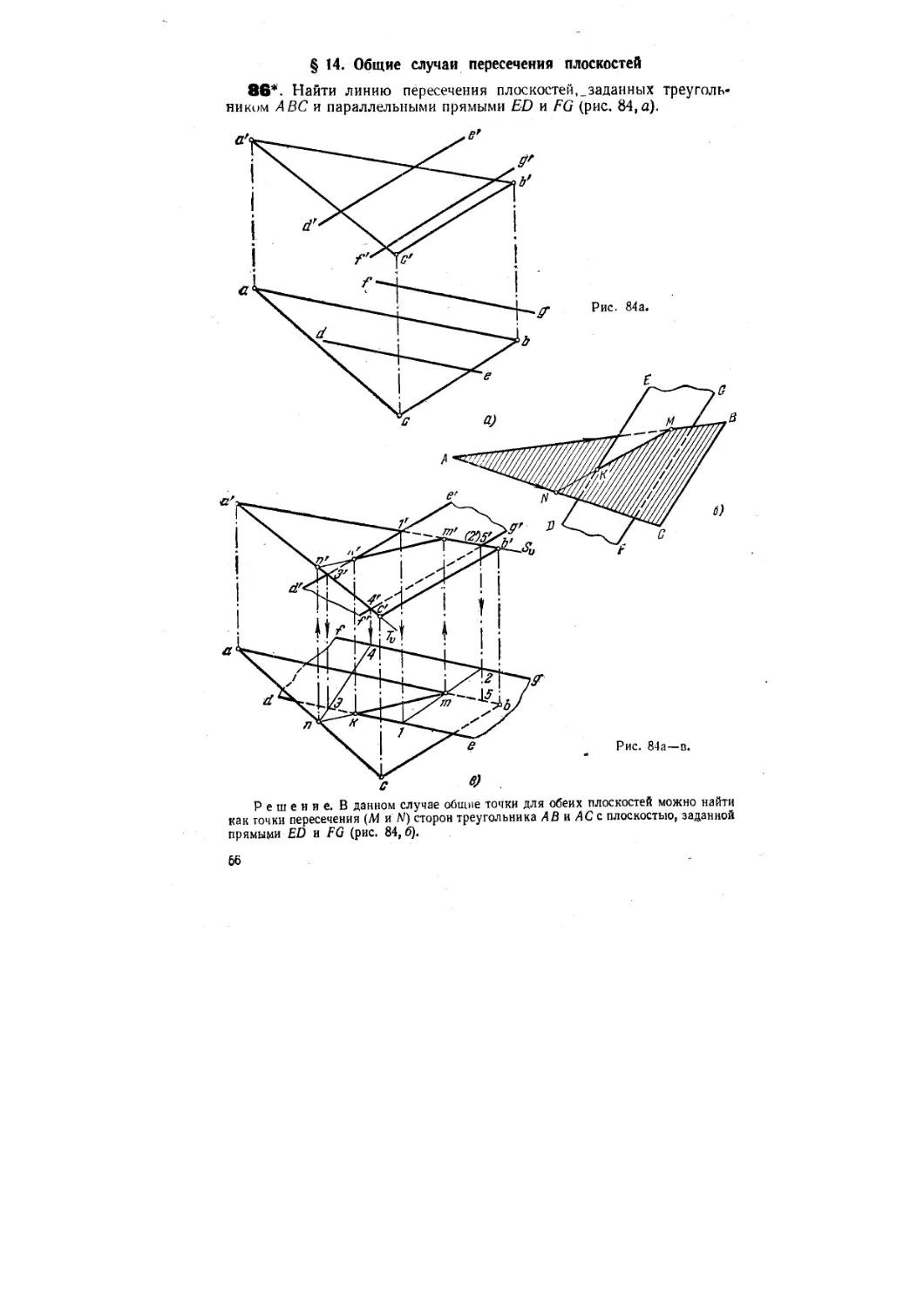
86*. Найти линию пересечения плоскостей,_заданных треуголь-
треугольником ABC и параллельными прямыми ED и FG (рис. 84,а).
6)
Рис. 84а—D.
Решение. В данном случае общие точки для обеих плоскостей можно найти
как точки пересечения (М и N) сторон треугольника АВ и АС с плоскостью, заданной
прямыми ED и FG (рис. 84, б).
56
a
.*'
a'
d
p^L IP
e/ 1
/
i
i
i
i
f'- i.
i -
Рис. 85.
d'
i-ис. 86.
67
a)
Рис. 87a—d.
68
a
Рис. 88.
Рис. 89.
59
Через прямую А В проводим фронтально-проецирующую плоскость S, задав ее
следом Sv (рис. 84, в). Она пересекает плоскость параллельных прямых по прямой
/—2A'2', 1—2), которая пересекается со стороной АВ в точке М (mm').Фронтально-
проецирующая плоскость Т, проведенная через прямую АС, задана следом Tvi
эта плоскость пересекает плоскость параллельных прямых по линии 3—4 C'4',
5—4), которая в пересечении со стороной АС дает точку N (п, п'). Искомая линия пе-
пересечения плоскостей проходит через точки М и N.
Для определения видимости плоскостей при взаимном их пересечении следует
вообще применять прием, указанный, например, при решении задачи 77. Рассмот-
Рассмотрим точки 2 (лежит на прямой FG) и 5 (лежит на прямой АВ). Анализ положения
этих точек показывает, что на пл. V точка ,5 закрывает точку 2, а это значит, что
прямая АВ в этом месте проходит перед FG, т. е. треугольник ABC виден до пря-
прямой КМ. Остальное ясно из чертежа.
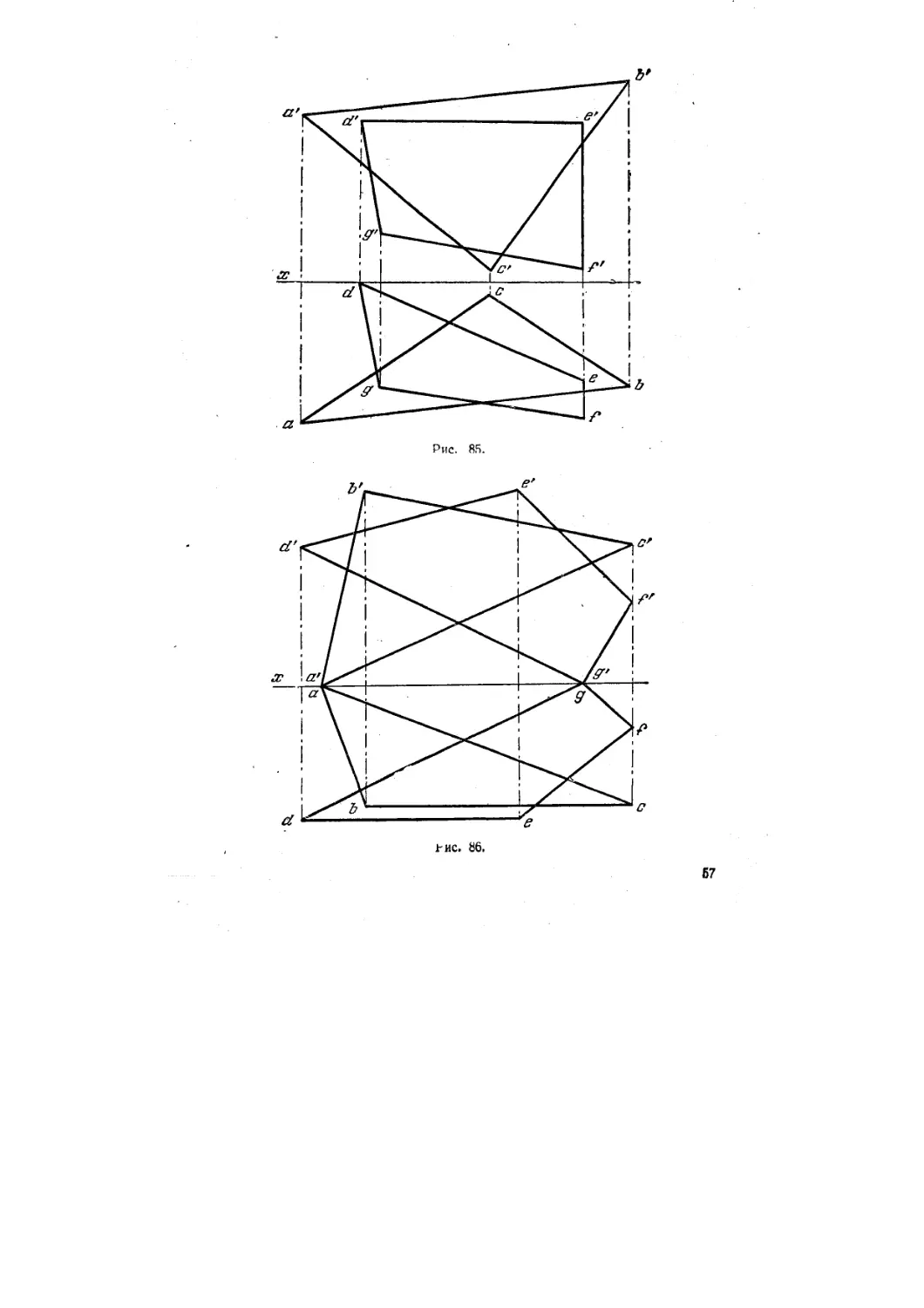
87. Найти линию пересечения плоскостей, заданных треуголь-
треугольником ABC и четырехугольником DEFG (рис. 85).
88. Найти линию пересечения плоскостей, заданных треугольни-
треугольником ЛВС и четырехугольником DEFG (рис. 86).
_ 89*. Найти линию пересечения плоскостей, из которых одна
задана параллельными прямыми АВ и CD, а другая — пересекающи-
пересекающимися FE и EG (рис. 87, а).
Решение. Для нахождения общих точек данных плоскостей введены две вспо-
вспомогательные плоскости S и Т (рис. 87, б) и построены линии пересечения этих пло-
плоскостей с заданными. Через точки М и N пересечения этих линий проходит искомая
прямая. На рис. 87, в плоскости S и Т параллельны пл. Н. Они пересекают заданные
плоскости по горизонталям 1—2, 3—4 и 5—6, 7—8 (см. задачу 67).
Прямые / — 2 и 3—4, пересекаясь, дают точку М (т, т'), а прямые 5—6
и 7 — 8 — точку N (п, п'). Прямая MN (mn, т'п') — искомая линия пересече-
пересечения плоскостей.
90. Найти линию пересечения плоскостей, из которых одна за-
задана треугольником ABC, а другая — параллельными прямыми ED
и FG (рис. 88).
91. Найти линию пересечения плоскостей, из которых одна
задана треугольником DEF. другая — прямой ВС и точкой А (рис. 89).
Г Л А В А IV
ПАРАЛЛЕЛЬНОСТЬ И ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМОЙ
и плоскости и двух плоскостей
§ 15. Параллельность прямой и плоскости и двух плоскостей
92*. Через точку А провести какую-либо прямую, параллельную
плоскости треугольника BCD (рис. 90, а).
Решение. Прямая параллельна плоскости, если она параллельна какой-либо
прямой, лежащей в этой плоскости. Поэтому через точку А можно провести неопреде-
неопределенное число прямых, параллельных данной плоскости. Например, проведя (рис. 90, б)
а)
Рис. 90а, б.
через точку а! прямую e'f параллельно b'd' и через а прямую ef параллельно bd, мы
получаем проекции прямой EF, параллельной стороне треугольника BD, а следо-
следовательно, и его плоскости. Выбор прямой BD был произволен.
93*. Через точку А провести какую-либо прямую, параллельную
пл. Р (рис. 91, а).
Решение. Строим (рис. 91,6) проекции т.п. и т'п' некоторой" прямой MN,
лежащей в пл. Р. Затем через а' проводим фронт, проекцию Ь'с' параллельно т'п',
61
а через а горизонт, проекциюбс параллельно тп. Прямая ВС параллельна прямой М N,
а следовательно, и плоскости Р.
а',
а
a)
Рис. 91а, б.
94*. Определить, параллельна ли прямая А В плоскости Р
(рис. 92, а).
Решение. Для определения, параллельна ли прямая А В пл. Р, надо попы-
попытаться провести в этой плоскости прямую, параллельную данной. На рис. 92, б про-
проведена фронт, проекция c'd' параллельно а'Ь'. Строим горизонт, проекцию ей
а)
Рис. 92а, б.
соблюдая условие, что прямая CD должна лежать в пл. Р. Так как построенная
проекция cd оказалась не параллельной ад, то прямые А В и CD не параллельны
а это значит, что прямая АВ и пл. Р также не параллельны.
62
Можно было начать с проведения горизонт, проекции некоторой прямой парал-
параллельно ab, построить ее фронт, проекцию, придерживаясь условия, что эта прямая
должна лежать в пл. Р, и сопоставить построенную фронт, проекцию с-а'Ь'.
95. Определить, параллельна ли прямая АВ
а) плоскости, заданной двумя параллельными прямыми CD и EF
(рис. 93, а),
а
а
Рис. 93а—в.
б) плоскости Р (рис. 93, б),
в) плоскости Q (рис. 93, в).
96*. Провести через точку А плоскость параллельно плоскости,
заданной точками В, С и D (рис. 94, а).
d'
Q a'
Н—f
I
а)
n
Рис. 94а, б.
Решение. Две плоскости параллельны, если две пересекающиеся прямые
одной из них соответственно параллельны двум пересекающимся прямым другой пло-
плоскости (рис. 94, б).
63
Для построения искомой плоскости проводим в заданной плоскости две пересекаю-
пересекающиеся прямые BD и CD (рис. 94, б и в). Затем через а' проводим a'f параллельно
b'd' и а'е параллельно c'd', а через а проводим af параллельно bd и ае параллельно
cd Прямые AF и АЕ параллельны прямым BD и CD\ следовательно, параллельны
между собой и определяемые ими плоскости.
Рис. 94в.
97*. Через точку А (рис. 95, а) провести плоскость параллельно
пл. Р.
Решение. Как известно, горизонтали параллельных плоскостей параллельны
между собой, параллельны между собой и фронтали. Также одноименные следы
параллельных плоскостей соответственно параллельны между собой (рис. 95, б).
64
На рис. 95, в задаем искомую плоскость двумя прямыми — горизонталью АС я
фронталью А В, для чего через а' проводим а'Ь' параллельно Ро и а'с' параллельно
оси х, а через точку а проводим ас параллельно Рд и ab параллельно оси х. Так как
след Р„ есть одна из фронталей пл. Р, а след Рй — одна из ее горизонталей, то полу-
получаем параллельность горизонталей и параллельность фронталей одной и другой пло-
плоскостей, т. е. параллельность этих плоскостей. На рис. 95, г показано построение для
искомой плоскости ее следов Qo и Qh. Для их построения проводим через точку А
горизонталь искомой плоскости параллель- . ,'
н о следу РА и находим фронт, след Л/(я, п') odf
этой горизонтали. Теперь через п' прово-
проводим Qv || Pv, находим точку Qx на оси я
и проводим след Q/, параллельно Рд.
Рис. 95г.
98» Через точку А (рис. 96) провести плоскость, параллельную
плоскости, заданной параллельными прямыми CD и EF; выразить
искомую плоскость двумя пересекающимися прямыми.
99. Через точку А (рис. 97) провести плоскость параллельно
пл. Р; выразить искомую плоскость ее следами.
А
\и,
Рис. 97.
Рис. 98.
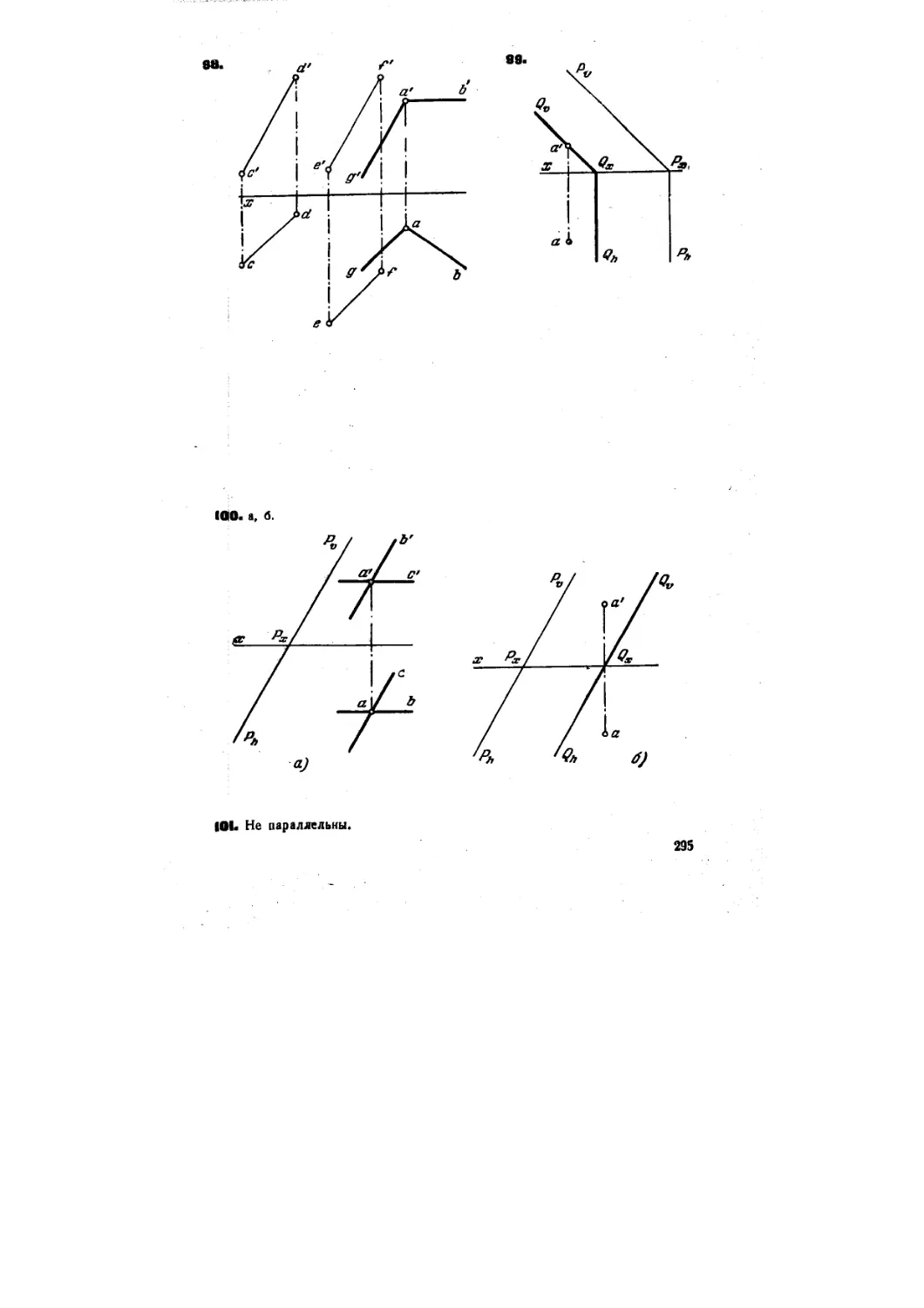
100. Через точку А (рис. 98) провести плоскость параллельно пл. Р.
Дать ответы: а) выразить пл. горизонталью и фронталью, б) следами.
3 Ь. О. Гордон а др.
65
Ю1. Определить, параллельны ли плоскости, из которых одна
задана параллельными прямыми АВ и CD, а другая — пересекающи-
пересекающимися прямыми EF и EG (рис. 99).
§ 16. Перпендикулярность прямой и плоскости и двух плоскостей
102*. Провести через точку А перпендикуляр к плоскости, задан-
заданной прямыми АВ и АС (рис. 100, а).
с'?
I.
Рис. 100а, б.
Решение. Известно, что фронт, проекция перпендикуляра к плоскости пер-
перпендикулярна к фронт, проекции фронтали плоскости, а горизонтальная — к го-
горизонт, проекции горизонтали плоскости. На чертеже (рис. 100, 6) проводим фронт,
проекцию перпендикуляра aV перпендикулярно к фронт, проекту фронтали а'Ь',
а горизонтальную его проекцию <к — перпенаикудярио к. проекции ас горизонтали.
66
ЮЛ. Через точку ? провести перпендикуляр к плоскости, задан-
заданной параллельными прямыми АВ и CD {рис. Ш).
104. Через точку А провести перпендикуляр к пл. Р (рис. 102).
-2?
Рис. 101.
Рис. 102.
Рис. 103.
а
105. Через точку А плоскости Р провести перпендикуляр к пло-
плоскости и отложить на нем отрезок, равный / (рис. 103).
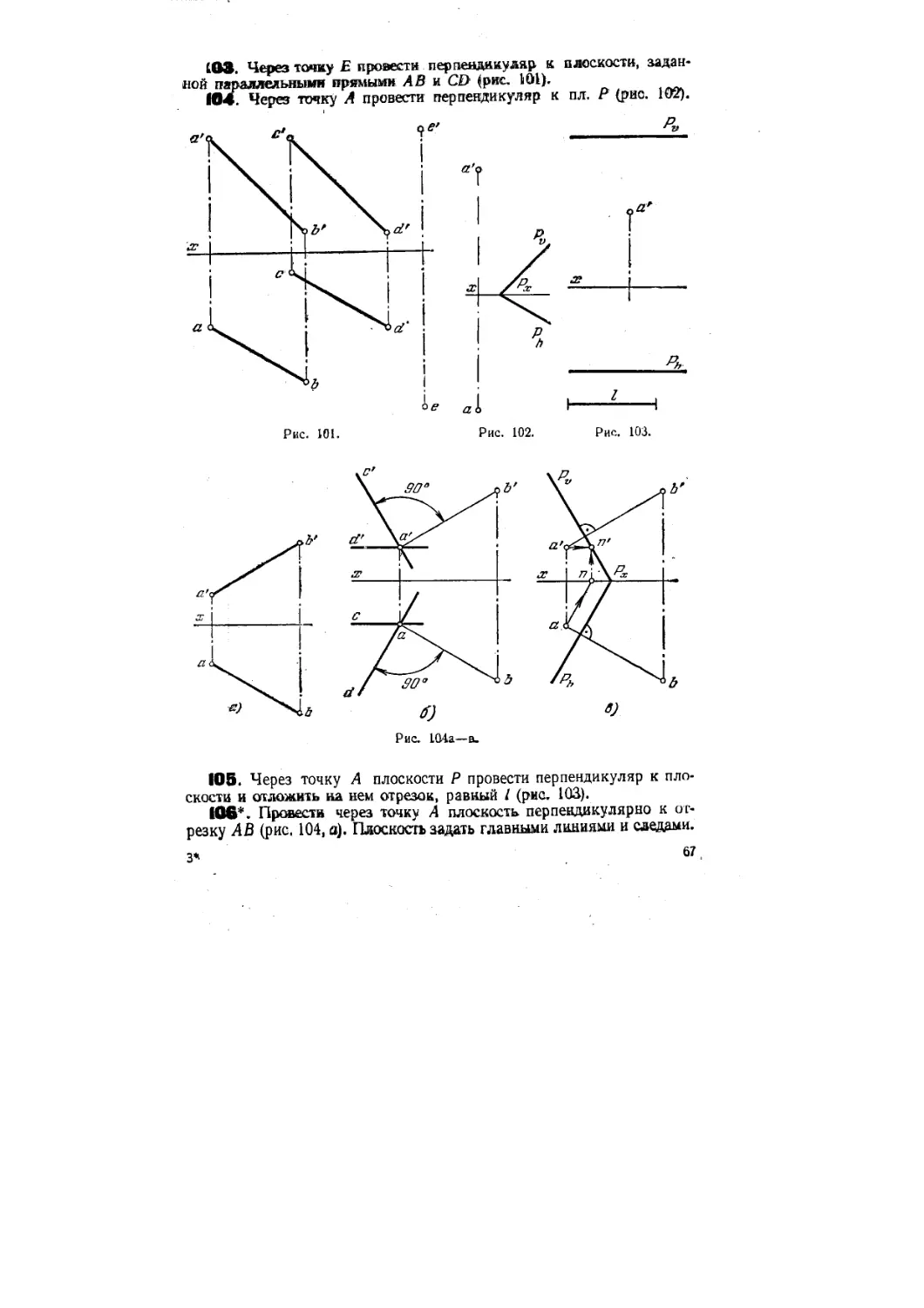
106*. Провести через точку А плоскость перпендикулярно к от-
отрезку АВ (рис. 104, а). Плоскость задать главными линиями и следами.
3* 67
Решение. Проводим через точку А (рис. 104, б) фронталь АС и горизонталь
AD искомой плоскости перпендикулярно к АВ. Фронт, проекция а'с' фронтали пер-
перпендикулярна к а'Ь', а горизонт, проекция ad горизонтали перпендикулярна к ab.
Прямые АС и AD задают искомую плоскость. Чтобы задать плоскость следами
(рис. 104, в), строим проекции п и п' фронт, следа ее горизонтали A D. Через п' про-
проводим след Р.о перпендикулярно к а'Ь , а через Рх—след Ph перпендикулярно к аЬ.
107. Провести через точку А
плоскость перпендикулярно к от-
отрезку ВС (рис. 105); следов пло-
плоскости не строить
108*. Провести через пря-
прямую А В плоскость перпендику-
перпендикулярно к плоскости треугольника
CDE (рис. 1'06, а).
а'
а
¦б)
Рис. 105.
Ри... 106а. о.
Решение. Если плоскость содержит в себе перпендикуляр к другой плоско-
плоскости, то эти плоскости взаимно перпендикулярны. Чтобы провести через АВ искомую
плоскость, надо из какой-либо точки прямой, например В провести перпендикуляр
К данной плоскости. Так как в треугольнике CDE сторона CD является фронталью, а
СЕ — горизонталью (рис. 106, а), то, проведя b'f'J_c'd', bf\_ce (рис. 106, б), полу-
получим перпендикуляр к плоскости треугольника CDi?T~Прямые АВ и BF определяют
109. Через точку К провести плоскость перпендикулярно к двум
данным плоскостям, из которых одна задана параллельными прямыми
АВ и CD, а другая — треугольником EFG (рис. 107),
68
a
Рис. 107.
Рис. 108а, б.
110. Определить, будут ли две плоскости взаимно перпендику-
перпендикулярны: а) плоскость, заданная прямой ВС и точкой А, и плоскость Р
(рис. 108, а); б) плоскость треугольника ABC и плоскость,, заданная
прямыми DE и FG (рис. 108, б).
69
§ 17. Смешанные задачи без применения способов
преобразования чертежа
III*." Провести перпендикуляр из точки А к плоскости, заданной!
а) треугольником BCD (рис. 109, а); б) следами (рис. 109, б); в) тре-
треугольником BCD (рис. 109, в). Во всех случаях построить основание
перпендикуляра на заданной плоскости.
Решение, а) Через точку В (рис. 109, г) проводим фронталь В—/ заданной
плоскости, а через точку D — горизонталь D—2. Фронт, проекция искомого перпен-
перпендикуляра проходит через а' перпендикулярно к b Г, а горизонтальная — через а
перпендикулярно к d— 2. Основание перпендикуляра (рис. 109,5) определяется как
точи пересечения этого перпендикуляра с плоскостью. Заключаем его в горизон-
горизонтально-проецирующую плоскость R (задаем ее следом Rh) u наюднм линию переее-
70 '
чения этой плоскости с плоскостью треугольника — прямую NM. Получаем точку
k' — фронт, проекцию основания перпендикуляра — и по k' находим k.
б) На рис. 109, е фронт, проекция перпендикуляра проведена под прямым углом
к следу Pv, а горизонтальная — под прямым углом к Р/,. Для построения основания
перпендикуляра заключаем его (рис. 109, ж) во фронтально-проецирующую плоскость
R, строим линию пересечения плоскостей R и Р — прямую MN. Получаем точку k—
горизонт, проекцию основания перпендикуляра; по ней находим k!.
Рис. Ю9ж, з.
в) Проведя горизонталь В—/ (рис. 109, а), видим, что эта прямая параллельна
оси х. Из этого заключаем, что плоскость треугольника является профильно-проеци-
профильно-проецирующей. Следовательно, перпендикуляр к ней — прямая профильная.
Строим профильные проекции треугольника и точки А. Из а" проводим пер-
перпендикуляр на с"d". Точка k" — профильвая проекция основания перпенди-
перпендикуляра. По k" находим k' и k на одноименных с ними проекциях искомого перпен-
перпендикуляра.
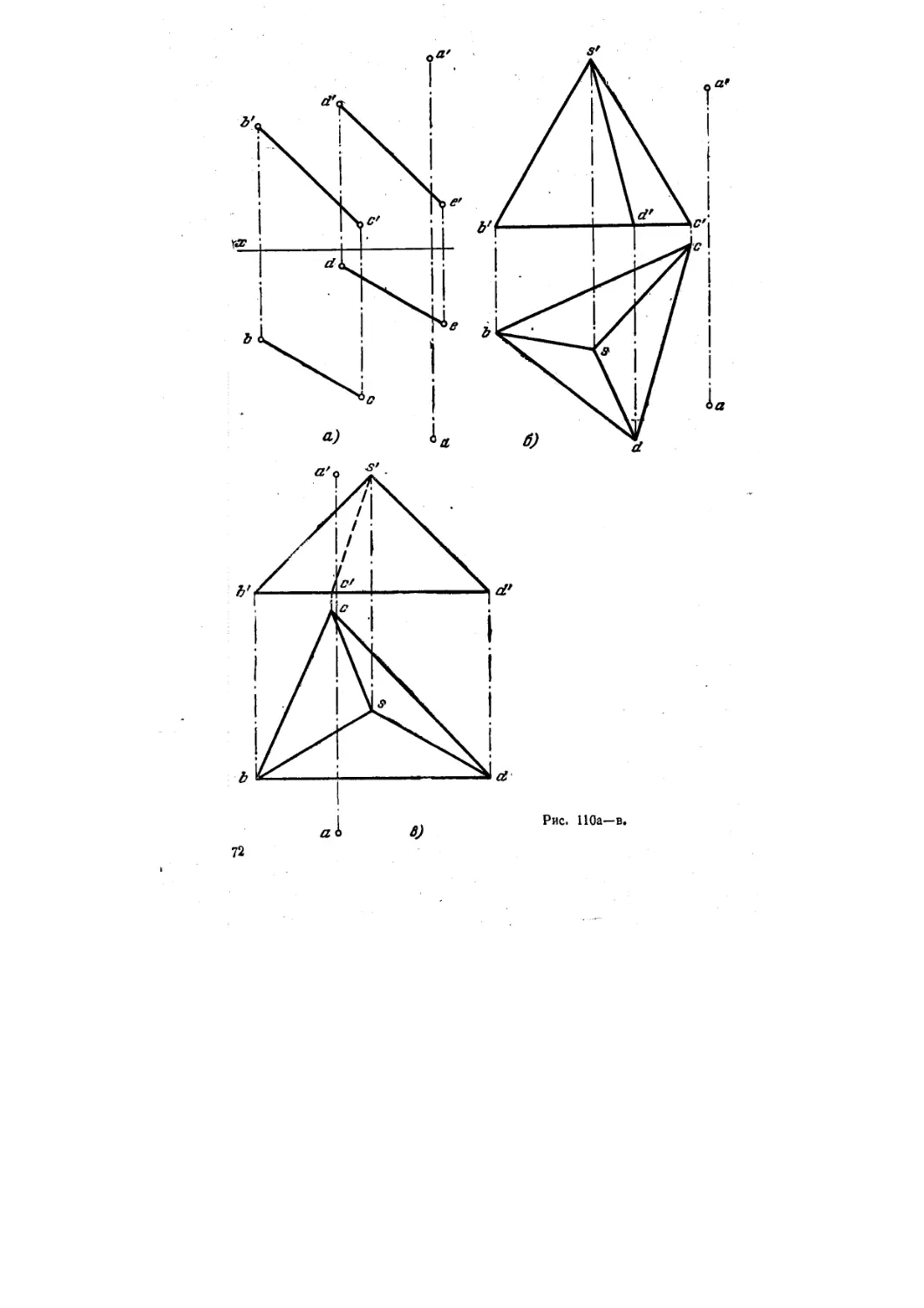
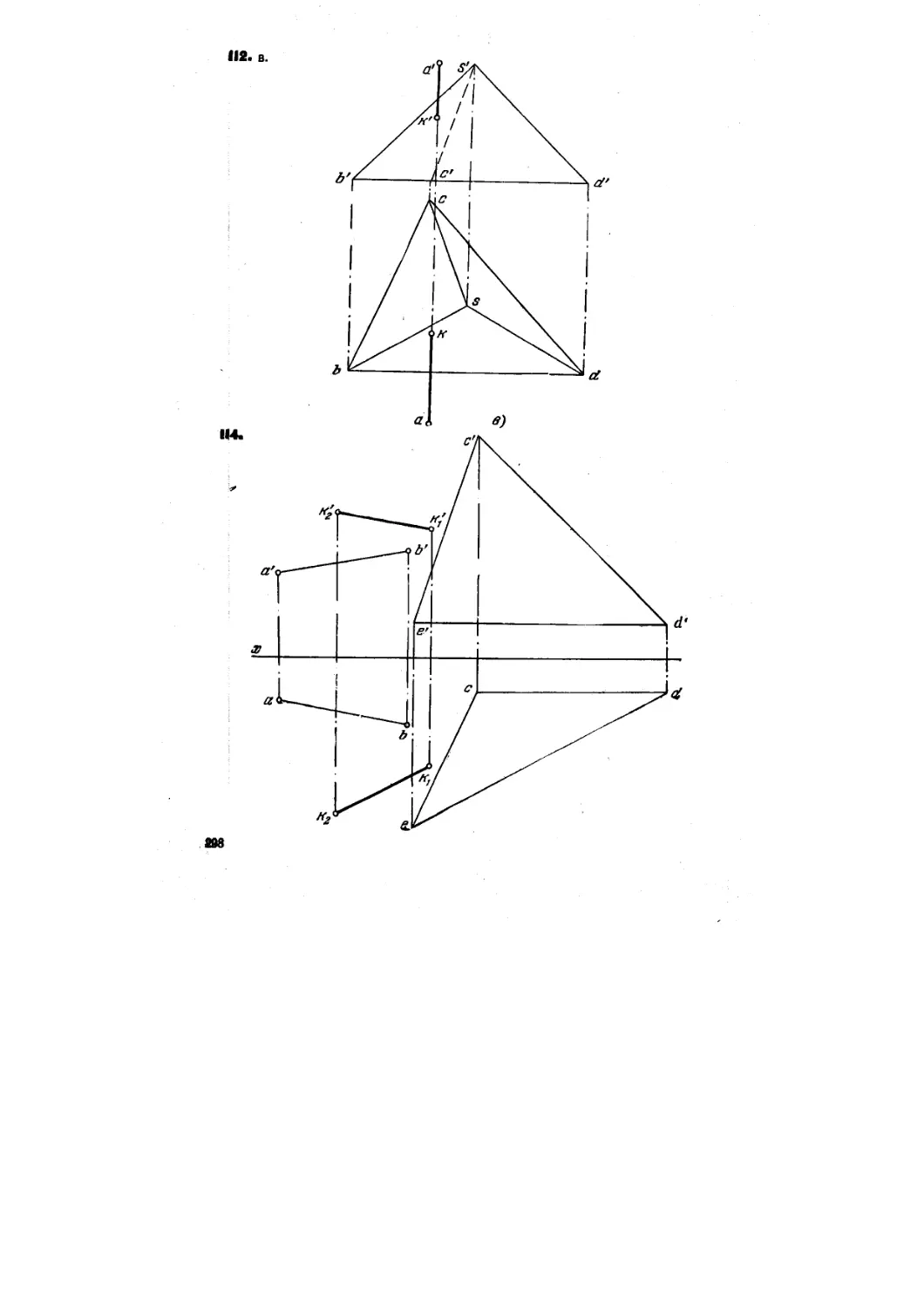
112. Найти основания перпендикуляров, проведенных из точки А:
а) к плоскости, заданной параллельными прямыми ВС и DE
(рис." ПО, а);
б) к плоскости грани SCD пирамиды SBCD (рис. НО, б);
в) к плоскости грани SBD пирамиды SBCD (рис, ПО, в). .
113*. Построить на плоскости, заданной параллельными пря-
прямыми CD и EF, геометрическое место оснований перпендикуляров,
проведенных из точек прямой А В к этой плоскости (рио. 111, а).
Решение. Искомым геометрическим местом точек является (рис. 111, 6) ли-
линия пересечения К\Кг плоскостей, 1) заданной и 2) перпендикулярной к ней, проне-
денной через прямую АВ.
Проводим (рис. 111, в) в заданной плоскости горизонталь С—/ и фронталь С—2.
Фронт, проекции перпендикуляров перпендикулярны к с'Т, а горизонтальные —
к с—/.
Для построения искомого геометрического места точек находим (рио. 111, г)
точки Ki и Кг пересечения проведенных перпендикуляров с заданной плоскостью.
Прямая KiKi и есть искомое геометрическое место.
71
Рис. 110а—в.
72
a'
73
114. Построить на плоскости, заданной треугольником CDE,
геометрическое место оснований перпендикуляров, проведенных из
точек прямой А В к этой плоскости (рис. 112).
а
Рис. 112.
115*. Из вершины А провести перпендикуляр к плоскости тре-
треугольника ABC (рис. ИЗ, а) и отложить на нем отрезок длиной /.
Решение. Для построения перпендикуляра проводим (рис. 113, б) горизон-
горизонталь Лт-/ и фраяталь А—2 плоскости треугольника; фронт, проекция перпенди-
перпендикуляра перпендикулярна к а', а горизонтальная — к а—1.
Дальнейшее ггостроеште (рис. 11Э, в) аналогично выполненному в задаче 20. Пря-
Прямые ad' и ad являются проекциями искомого отрезка.
Эта задача имеет два решения. Во втором случае надо продолжить перпендикуляр
в другую стороеу от заданной плоскости.
116. Из точки- D провести перпендикуляр к плоскости, заданной
параллельными прямыми А В к CD, и отложить на нем отрезок длиной /
(рис. 114).
117*. Построить геометрическое место точек, удаленных от некото-
некоторой плоскости на расстояние /. Дать решение для случаев, когда плос-
плоскость задана треугольником ABC (рис. 115, а) или следами (рис. 115, б).
Решение. Искомым геометрическим местом точек являются две плоскости,
параллельные данной и расположенные гго обе стороны от нее на расстоянии /.
На рис. 115, в показана одна из таких плоскостей. Для построения этой плоскости
(рис. 115, г) проводим из любой точки данной плоскости (например, С) перпендикуляр
74
a
Рис. 114.
75
X
/
/
\€'
N,
д)
е)
к плоскости (обратите внимание на то,
что в заданном треугольнике сторона
АС является горизонталью, а ВС —
фронталью) и откладываем на нем от-
отрезок КС длиной /. Затем через точку
К (рис. 115,3) проводим прямые KN и
КМ, параллельные хотя бы сторонам
ВС и АС треугольника ABC.
Если плоскость задана следами
(рис. 115, б), то удобно взять точку на
одном из следов. На рис. 115, е взята
точка N на следе Pv. Проведя из этой
точки перпендикуляр к пл. Р и отло-
отложив на нем отрезок, равный /, прово-
проводим через точку К (рис. 115, ж) гори-
горизонталь CD и -фронталь АВ искомой
плоскости.
Рис, 115а—ж.
76
118. Построить геометрическое место точек, удаленных от пл. Р
(рис. 116) на расстояние/. Дать два решения.
Рис. 116.
б)
Рис. 117а—в.
119*. Провести перпендикуляр к прямой ВС из ее точки А до
пересечения его с прямой EF (рис. 117, а).
Решение. Геометрическим местом перпендикуляров к прямой ВС, проведен-
проведенных из точки А, является пл. Р, проходящая через точку А перпендикулярно к пря-
прямой ВС (рис. 117, б). Точка К пересечения этой плоскости с прямой EF является точ-
точкой пересечения искомого перпендикуляра с прямой EF.
ТГ
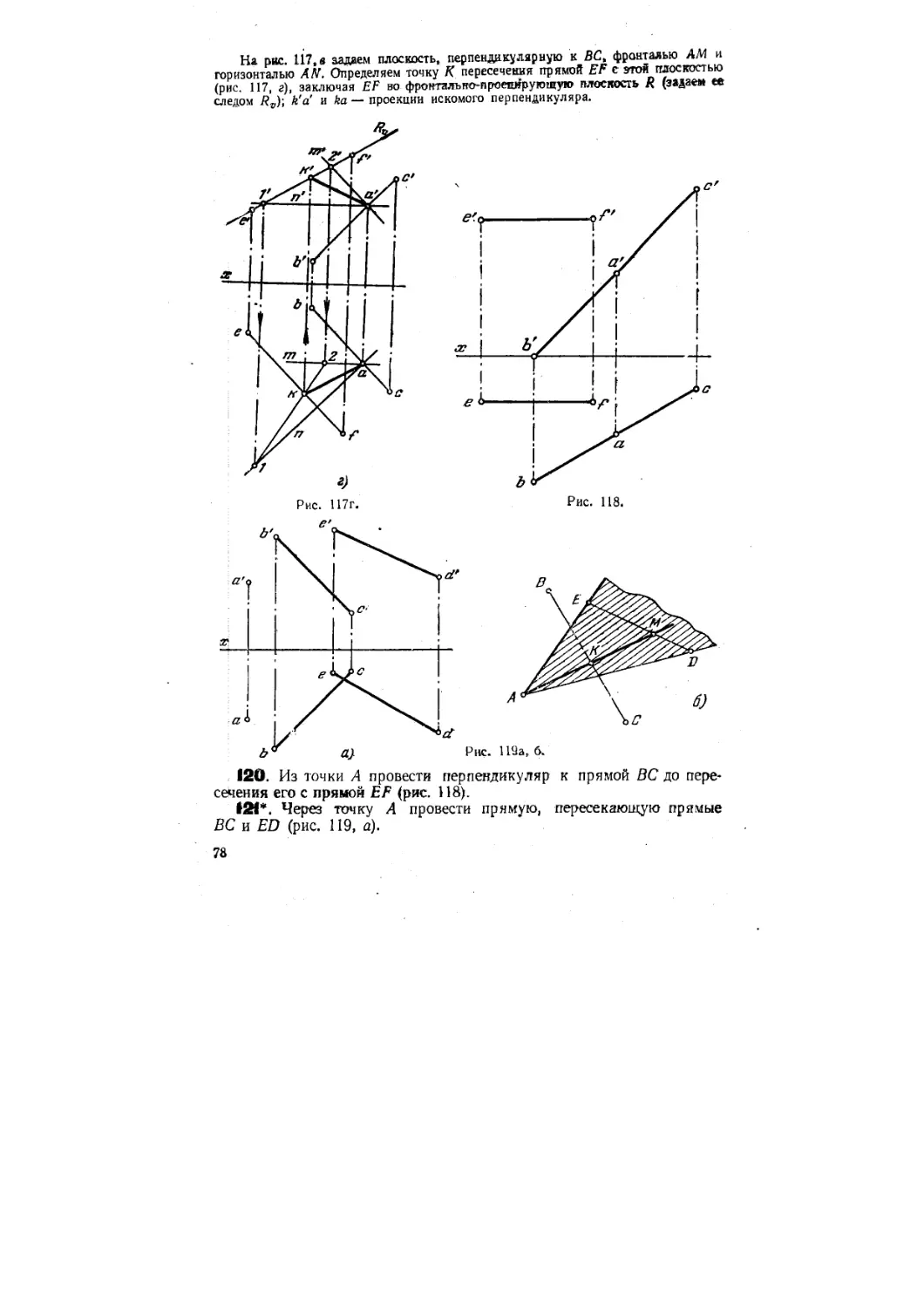
На рис. 117, в задаем плоскость, перпендикулярную к ВС, фронталью AM и
горизонталью AN. Определяем точку К пересечения прямой EF с этой плоскостью
(рис. 117, г), заключая EF во фронтальпо-проетдаругощую плоскость R (задаем ее
следом Rv)\ k'a! и ka—проекции искомого перпендикуляра.
Рис. 119а, 6.
120. Из точки А провести перпендикуляр к прямой ВС до пере-
пересечения его с пряной EF (рис. 118).
1Я*. Через точку А провести прямую, пересекающую прямые
ВС и ED (рис. 119, а).
Решение. Геометрическим местом прямых, проходящих через точку А и
пересекающих прямую ЕВ, является плоскость, задаваемая этими элементами (рис.
119, б). Если построить такую плоскость и найти точку К ее переоеченяя со второй
прямой {ВС), то искомая прямая пройдет через точки А 9 К. Такое построение выпол-
выполнено на рис. 119, ей 119, г, где сначала плоскость, определяемая точкой А и прямой
ED, выражена треугольником AED, а затем найдена точка К пересечения второй
прямой (ВС) с плоскостью этого треугольника.
а',
а
Искомая прямая проходит через точки Ли^я пересекает прямую ED в течке М
(ряс. 119, д). Конечно, при точном построении проекции тат' должны оказаться на
линии связи т'т, перпендикулярной к оси х.
Данную задачу можно решить и иначе: взять две плоскости — одну, определяе-
определяемую точкой А и прямой ED (как это сделано на рис. 119, в), а другую — точкой А я
прямой ВС. Линия пересечения этих двух плоскостей н Судет искомой прямой, про-
проходящей через точку А и пересекающей ВС в ED.
79
122. Через точку А провести прямую, пересекающую:
а) ребро SD и сторону ВС основания пирамиды SBCD (рис. 120, а),
б) ребро BG и сторону EF верхнего основания призмы (рис. 120,6).
а)
!23*. Построить геометрическое место точек, равноудаленных
от точек А и В (рис, 121, а).
Решение. Искомым геометрическим местом является плоскость, проходящая
через середину отрезка АВ перпендикулярно к нему.
Делим проекции отрезка АВ пополам (рис. 121,6). Через середину (точку С)
проводим горизонталь CD J_ А В и фронталь СЕ J_ А В (рис. 121, в) искомой плоскости.
Чтобы выразить эту плоскость следами, надо задаться осью проекций и построить
хотя бы фронт, след горизонтали (точка Л/, рис. 121,г) и через него провести соответ-
соответствующий след пл. Р. След Ро ]_а'Ь', аследРд J_ab (или || пс)..
124. Построить геометрическое место точек, равноудаленных от
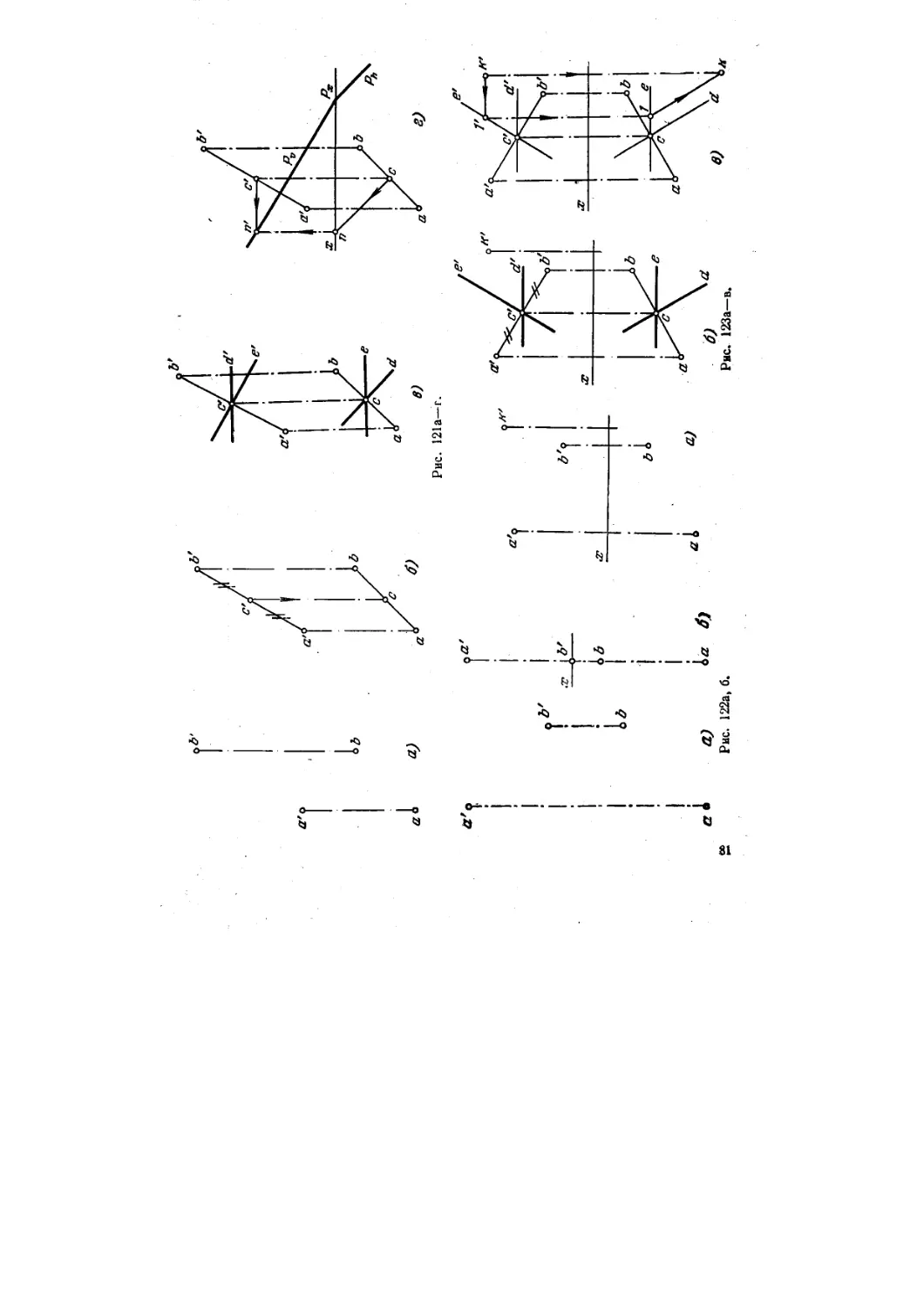
точек Л" и В (рис. 122, а и б). В первом случае ответ дать без следов,
а со втором — в следах.
I2S*. Построить недостающую проекцию точки К, равноуда-
равноудаленной от точек Л и В (рис. 123, а).
80
Решение. Так как геометрическим местом всех точек пространства, равно-
равноудаленных от точек А и В, является плоскость, проходящая через середину отрезка АВ
перпендикулярно к нему, то точка К должна принадлежать этой плоскости.
На рис. 123, б т^кая плоскость определена фронталью СЕ и горизонталью CD,
проходящими через середину отрезка АВ.
Проводим {рис. 123, в) через к' фронт, проекцию k' I' горизонтали плоскости и
строим ее горизонт, проекцию, на которой отметим точку k — искомую проекцию
точки К-
126. Построить недостающую проекцию отрезка
точка которого равноудалена от точек А и В (рис. 124).
CD, каждая
а
Рис. 124.
*)
Рис. 125а—в.
127*. Построить на плоскости геометрическое место точек, равно-
равноудалённых от двух данных точек А и В: а) плоскость задана параллель-
параллельными прямыми (рис. 125, а); б) плоскость задана следами (рис. 125, б).
82
ffj
Ж)
Рис. 125г—ж.
83
Решение. Так как геометрическим местом точек, равноудаленных от точек
А я В, является плоскость, проходящая через середину отрезка АВ перпендикулярно
к нему (рис. 125, в), то искомым геометрическим местом будет линия пересечения этой
плоскости с заданной (прямая МЛ').
На рис. 125, г плоскость, перпендикулярная к отрезку АВ в его середине, выра-
выражена фронталью КС и горизонталью ТС.
Теперь надо найти линию пересечения двух плоскостей, что сделано путем
нахождения точек пересечения прямых DE и FG (рис. 125, д), определяющих задан-
заданную плоскость, с плоскостью, выраженной горизонталью ТС и фронталью КС (см.
задачу 86).
На рис. 125, е плоскость Q, перпендикулярная к отрезку АВ в его середине, вы-
выражена следами. Находим точки М и N пересечения одноименных следов плоскостей
Р и Q и проводим через них искомую прямую MN (рис. 125, ж).
128. Построить геометрическое место точек, равноудаленных от
точек А и В:
а\
а о
а) на плоскости, заданной треугольником CDE (рис. 126, а);
б) на пл. Р (рис. 126,6).
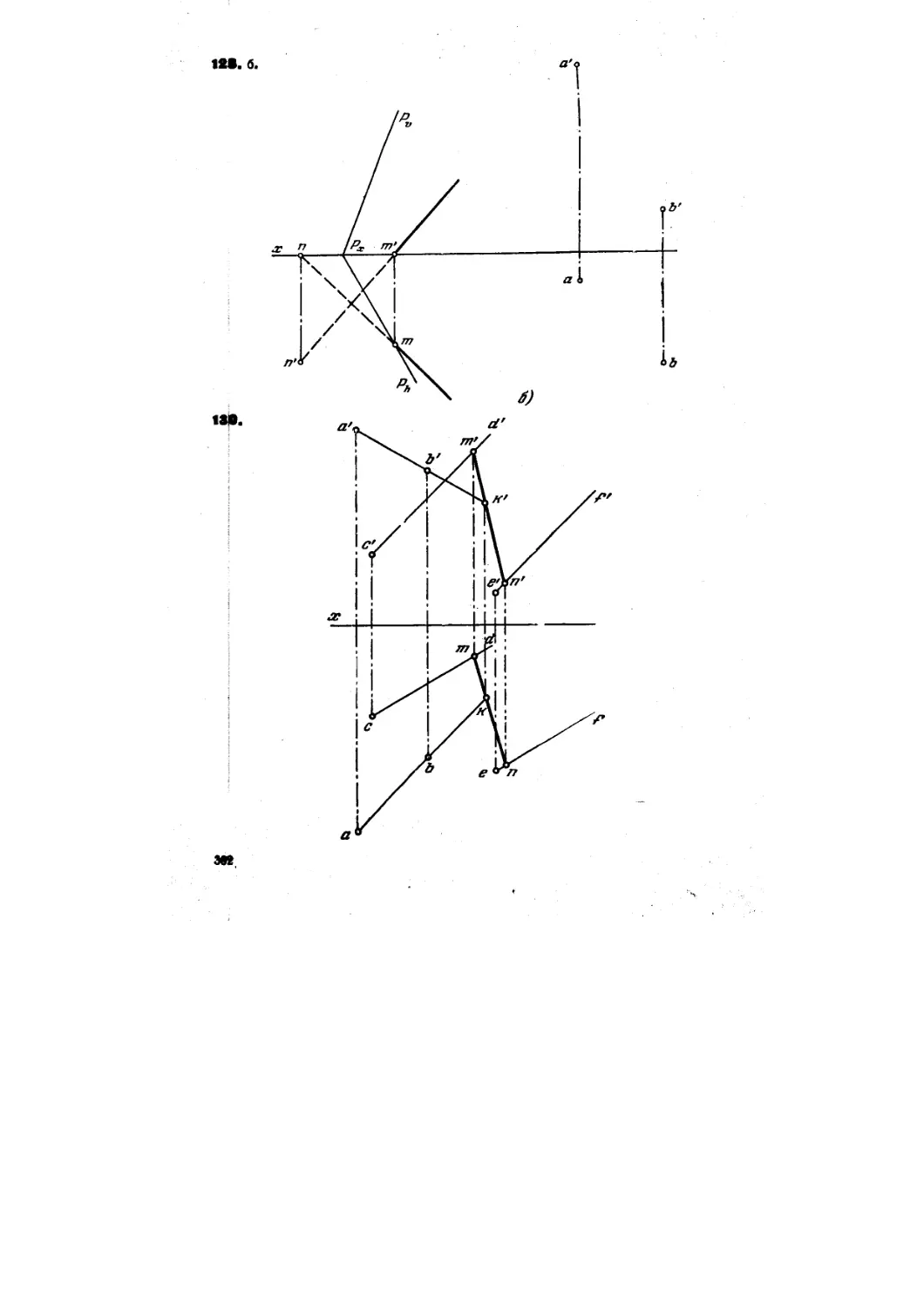
129*. Дана плоскость треугольника CDE и прямая А В
(рис. 127, а). Провести в этой плоскости прямую, пересекающую АВ
под прямым углом.
Решение. Искомая прямая получится (рис. 127, 6) как линия пересечения
плоскости треугольника (Р) с пл. Q, перпендикулярной к АВ и проходящей через
точку (К) пересечения АВ с заданной плоскостью.
84
а'с
Рис. 1266.
в
/
i
У
А]
л\
т (
IU
Рис. 127а, б.
d'
8) d
a'
a
Поэтому находим (рис. 127, в) точку К
пересечения прямой А В с плоскостью тре-
угольникаСОЕ. В качестве вспомогатель-
вспомогательной плоскости взята фронтально-проеци-
фронтально-проецирующая плоскость R, проведенная через
прямую АВ. Найдя проекции k и k', про-
проводим через них проекции горизонтали и
фронтали плоскости, перттендикулярной
к АВ (рис. 127, г). Для построения иско-
искомой линии пересечения плоскостей нахо-
находим (рис. 127, д) точку (т'\ т) пересечения
стороны треугольника ED с проведенной
через точку К плоскостью. Прямая МК
(tn'k'\ mk) является искомой прямой.
86
130. Дана прямая АВ и плоскость, заданная параллельными
прямыми CD к EF. Провести в этой плоскости прямую, пересекаю-
пересекающую прямую АВ под прямым углом (рис. 128).
Рис. 128.
131. Дана прямая АВ и пл. Р. Провести в этой плоскости пря-
прямую, пересекающую прямую А В под прямым углом (рис. 129).
132*. Даны плоскость треугольника LMN и прямые АЕ и FG.
Построить параллелограмм, у которого сторона AD лежит на прямой
А Е, сторона А В параллельна плоскости треугольника, вершина В
принадлежит прямой FG, диагональ BD перпендикулярна к стороне AD
(рис. 130, а).
Решение. Наметим план решения (рис. 130, б и в).
1. Через точку А провести плоскость (Р), параллельную плоскости треугольника
LMN.
2. Найти точку пересечения (В) прямой FG с пл. Р.
3. Череа точку В провести плоскость (Q), перпендикулярную к прямой АЕ.
4. Найти точку пересечения (D) прямой АЕ с пл. Q.
5. Провести отреэон АВ и параллельно ему прямую через точку D, а через В —
прямую, параллельную AD.
На рис. 130, виг показано построение пл. Р, параллельной плоскости треуголь-
треугольника LMN. Пл. Р, проведенная через точку А, задана двумя пересекающимися пря-
прямыми A—J и А— 2, из которых А—/ параллельна LM, а А—2 параллельнаLN.
87
Рис. 129.
88
На тех же рисунках показано нахождение точки В пересечения прямой FQ
с пл. Р, для чего через FG проведена фронтально-проецирующая плоскость S, задан-
заданная следом So. Горизонт, проекция /—2 линии пересечения плоскостей Р и S пересе-
пересекает горизонт, проекцию fg в точке Ь. По точке Ь находим проекцию Ь' на/'g'.
На рис. 130, д показано построение пл. Q, перпендикулярной к АЕ. Эта плоскость
проведена через точку В и выражена горизонталью В—4 и фронталью В—3, перпен-
перпендикулярными к АЕ. На том же чертеже показано построение точки D, в которой пря-
прямая АЕ пересекает пл. Q, выраженную горизонталью В—4 и фронталью В—3.
Через АЕ проведена горизонтально-проецирующая плоскость Т, выраженная ее сле-
следом Тд, построены проекции 3—4 и 3'4' линии пересечения плоскостей Т и Q и
проекции d'a d.
На рис. 130, е показано построение искомого параллелограмма, для чего прове-
проведены проекции а'Ь' и ab, a'd' и ad двух сторон параллелограмма, а затем b'c'\\a'd';
be [| ad; d'c'\\ a'b' adc || аи. Точки с' и с должны оказаться на линии связи ее', перпенди-
перпендикулярной К ОСИ X.
133. Даны треугольник LMN и прямые АЕ и FG. Построить
параллелограмм, у которого сторона AD лежит на прямой АЕ, сто-
сторона А В параллельна плоскости треугольника, вершина В при-
принадлежит прямой FG, диагональ BD перпендикулярна к стороне AD
(рис. 131).
134*. Через точку А провести прямую, параллельную ил. Р
и плоскости треугольника CDE (рис. 132, а).
90
Б'
m
Рис. 131.
Рис. 132а, б.
91
Решение. Если искомая прямая должна быть одновременно параллельна
двум плоскостям, то она должна быть параллельна линии пересечения этих плоскостей
Рис. 132в. г.
(рис, 132, б). Вводя две вспомогательные плоскости Т и S, находим линию пересече-
пересечения MN плоскостей (рис. 132, в). Проекции искомой прямой b'f и bf проходят через а'
ил параллельно одноименным с ними проекциям прямой MN (рис. 132,г).
Рис. 133.
135. Через точку А провести прямую, параллельную пл. Р и
плоскости, заданной пересекающимися прямыми DE и DF (рис, 133).
82
136. Через точку А провести прямую, параллельную пл. Р и
плоскости, заданной параллельными прямыми DE и FG (рис. 134).
Рис. 135а, б.
*)
137*. Провести прямые, каждая из которых отстоит от пл. Р
на расстояние 1Ъ а от плоскости, заданной прямой ВС и точкой А, на
расстояние/2 (рис. 135, а).
Решение. В основе решения лежит представление о геометрическом месте
прямых, отстоящих от данной плоскости на определенное расстояние, т. е. от плоско-
плоскости параллельной данной.
Искомыми прямыми являются линии MN пересечения двух плоскостей Q, па-
параллельных пл. Р и расположенных по обе стороны от нее.на расстоянии 1и с
93
5'.
плоскостями S, параллельными второй
из заданных плоскостей и отстоящими
от нее на расстояние /2. Всего таких
прямых может быть четыре. На рис.
135, б изображена одна из них.
На рис. 135, в показано: 1) прове-
проведение перпендикуляра к пл. Р из взя-
взятой в ней точки Мг и построение точ-
точки К] на этом перпендикуляре на рас-
расстоянии М jKj ¦= V> 2) проведение пер-
перпендикуляра к плоскости, заданной
точкой А и прямой ВС, из точки А (при
помощи горизонтали А •—2 и фронтали
А — 3) и построение точки л на атом
перпендикуляре на расстоянии ЛД2=
На рис. 135, г показано проведе-
проведение через точку Кг пл.Q параллельно
лл. Я и через точку К2 плоскости S,
выраженной горизонталью Кгб и фрон-
талью К^б, соответственно параллель-
параллельными горизонтали /!¦—2 и фронтали
А—3, принадлежащими плоскости, за-
заданной точкой А и прямой ВС.
На рие. 135, д построена линия
пересечения пл. Q и плоскости S, вы-
выраженной горизонталью /С2Л в фрон-
талью A'jjff. Полученная прямая MN
параллельна обеим заданным плос-
плоскостям.
94
188. Провести одну из прямых, отстоящих от ал. Р на расстояние
/х и от плоскости треугольника ABC на расстояние 4 (рис. 136).
Рис. 136.
139*. Провести прямую, пересекающую заданные прямые АВ
к CD и параллельную прямой EF (рис. 137, а).
Рис. 137а, б.
Решение. Наметим план решения задачи (рис. 137, б).
1. Через прямую 'CD провести плоскость (Q), параллельную прямой. ЕР.
2. Найти точку (К), в которой прямая АВ пересечет ал. Q.
3. Через точку К провести прямую (КМ), параллельную заданной прямой EF.
Н-а рис. 137, в показано построение пл. Q, проходящей через прямую CD и парал-
параллельной прямой EF Пл. Q выражена пряной CD и пересекающей ее прямой DG,
проведенной через точку D параллельно EF.
85
На рис. 137, в показано построение точки К, в которой прямая АВ пересекает
пл. Q. Прямая АВ заключена в фронтально-проецирующую'плоскость, Я. выражен-
выраженную ее следом Rv. Пл. R пересекает пл. Q по прямой 1-2. В пересечении 1-2 и
аЬ получается проекция ft; по точке k находим фронт, проекцию ft .
Наконец, на рис. 137, д показаны проекции km и k'm' искомой прямой: k'm' \\e'f
И km || ef. Конечно, проекции от' и т должны получиться на линии связи т'т, пер-
перпендикулярной к оси х.
140. Провести прямую, пересекающую заданные прямые А В
и CD и параллельную прямой EF (рис. 138).
141. Провести прямую, пересекающую заданные прямые АВ
и CD, параллельно прямой EF (рис. 139).
ее
Рис. 139.
142*. Даны прямые ?F, MN, KL и Я/. Построить прямоуголь-
прямоугольник ABCD, у которого сторона АВ параллельна прямой EF, вершина
А лежит на прямой KL, вершина В — на прямой MN и вершина С —
на прямой HI (рис. 140, а).
В. О. Гордон ¦ др.
s
a.
99
Решение. Сторона А В должна пересечь KL и MN и быть параллельной EF
(см. задачу 139).
Если (рис. 140, б) провести хотя бы через точку 0, лежащую на K.L, пря--
мую, параллельную EF, то получим пл. Q, параллельную EF. Далее надо найти точ-
|у В пересечения этой плоскости с прямой MN и через точку В провести в пл. Q.
Йрямую, параллельную ЕР. Эта прямая АВ пересекает прямые MN и KL и параллель-
параллельна EF.
Построение показано на рис. 140, в. Так как стороны ВС и Лв должны быть
взаимно перпендикулярны, то проводим (рис. 140, гид) через точку В пл. Р, пер-
перпендикулярную к стороне АВ, и строим точку С пересечения ее с прямой HI.
; Через точки А и С проводим прямые (рис. 140, г и ё), параллельные прямым ВС
k АВ, go пересечения их в точке D.
Рис. 141.
143. Даны пирамида SEFG и прямая MN (рис. 141). Построить
прямоугольник ABCD, у которого сторона А В параллельна прямой
MN, вершина А лежит на ребре SF, вершина В — на стороне основа-
основания EG, вершина D — на ребре SE. ,
100
144. Даны пирамида SEFG и прямая MN (рис. 142). Построить
прямоугольник A BCD, у которого сторона А В параллельна прямой
MN, вершина А лежит на ребре SQ, вершина В — на стороне основания
EF и вершина D — на ребре SF.
Рис. 142.
145*. Через точку А провести прямую/параллельную плоскости,
заданной параллельными прямыми EDm FG, и пересекающую прямую
ВС (рис. 143, а).
?' е ш е и и е. Можно составить следующий план решения задачи (рис. 143, о):
) через точку А провести плоскость (Я), параллельную заданной плоскости)
2) найти точку (К) пересечения ВС о пл. Р;
3) провести искомую прямую АК.
На рис. 143, в пл. Р, проведенная через точку Л, выражена прямой AM\\ED
(а'т! We'd', am. ||ed) и горизонталью AN,для проведения горизонт, проекции которой
101
взята горизонталь Е—1 в плоскости, заданной прямыми ED я FG (an || ef). На
рис. 143, г показано построение точки К, в которой заданная прямая ВС пересекает
пл. Р: через ВС проведена фронтально-проецирующая плоскость (она выражена
а)
следом Rv), построены проекции 2'3" и 2—3 прямой пересечения плоскостей Р и R,
получена точка k в пересечении прямой 2—3 и be. По проекции k найдена проек-
цЦя k'. Проекции искомой прямой a'k' к ak.
• 146. Через точку А (рис. 144) провести прямую, параллельную
пл. Р и пересекающую прямую ВС.
147. Через точку А (рис. 145) провести прямую, параллельную
плоскости, заданной пересекающимися прямыми DE и DF, и пересе-
пересекающую прямую ВС.
148*. Построить геометрическое место точек, равноудаленных от
заданных точек А, В и С (рис. 146, а),
102
a
Рис. 146а.
103
Решение. Искомым геометрическим местом является линия пересечения MN
(вис. 146, б) плоскостей Р и Q, соответственно перпендикулярных к отрезкам АВ и
ВС и проходящих через точки Kt и Кг в серединах этих отрезков. На рис. 146, «эти
а
а
Рис. 146 6, в.
плоскости выражены их следами. Используя (рис. 146, г) точки пересечения одноимен-
одноименных следов плоскостей, строим линию их пересечения MN.
г)
а'ъ
—o-
a
Рис. 146 г.
Рис. 147.
149. Построить геометрическое место точек, равноудаленных от
Заданных точек А, В и С (рис. 147).
150*. Дан треугольник ABC (рис. 148, а). Построить пирамиду
SABC, вершина S которой равноудалена от точек А, В и С. Расстоя-
Расстояние от точки S до пл. V ъ 1,7 раза больше расстояния ее до пл. Н*
104
P e пте н и е. Геометрическим местом точек, равноудаленных от точек А, В и С
(см. задачу 148*), является линия пересечения MN плоскостей Q и Р, проведенных
через середины (Ki и Кг) отрезков АВ и ВС перпендикулярно к ним (рис 148, б и в).
Вершина S должна лежать на этой прямой. Геометрическим местом точек, для кото-
которых ордината а 1,7 раза больше апликаты, является осевая плоскость Т< ее про-
профильный след Т„ проходит (рис. 148, в) через точку О и точку, расстояние которой до
а'
г)
Рис. 148а—г.
оси у равно 10 единицам, а до оси г — 17 единицам. Точка S принадлежит этой пло-
плоскости. Профильная проекция s" вершины пирамиды находится на пересечении т"п"
со следом Tw (на рисунке для упрощения чертежа построена профильная проекция
точки D, лежащей на прямой MN). По s" находим s' и s. На рис. 148, г показаны проек-
проекции искомой пирамиды.
105
151. Дан треугольник ABC (рис. 149). Построить проекции пира-
пирамиды SABC, вершина S которой равноудалена от вершин основания
ABC и лежит в пл. V.
п> а а'
ГП'а
Г I
Л7° '
I
б)
Рис. 149.
Рис. 150а, б.
152*. Даны точки A, L, М и N (рис. 150,а). Построить па-
параллелограмм ABCD, у которого вершина В лежит на пл. Н,
сторона CD — на прямой, равноудаленной от точек L, М и Л/,
вершина D равноудалена от плоскостей V и Н.
Решение. Так как сторона CD искомого параллелограмма должна лежать на
прямой, равноудаленной от трех точек, то начинаем с построения этой прямой. По-
Йобное построение уже встречалось: прямая EF получается как линия пересечен
ния двух плоскостей (рис. 150, 6 и в) Р и Q, проведенных перпендикулярно к отрез-
отрезкам LM и MN через их середины. Точку D на этой прямой находим из условия, что
106
она равноудалена от пл. V и пл. И (рис. 150, г): проведем через точку /' вспомогатель-
вспомогательную прямую f'5 подтем же углом к оси х, что и прямая f'e', получаем на проекции
ef точку d, а по ней d", причем d=d—6.
Итак, мы получили одну из вершин искомого параллелограмма (точку О) и нап-
направление стороны, проходящей через эту точку (прямая EF). Проведя через заданную
1
Рис. 150в—д.
точку А прямую, параллельную EF, получаем сторону А В, зная, что по условию
точка В должна быть в пл. Н.
Остается закончить построение проекций параллелограмма, проведя а'Ь' и аЬ
(рис. 150, д), Ь'с' И a'd' и be \\ ad. Точки с' и с должны оказаться на линии связи с'о,
перпендикулярной к оси х.
107
IS3. Даны точки A, L, М п N (рио. 151). Построить параллело-
граммМBCD, у которого вершина" В лежит на пл. Н, сторона CD лежит
на прямой, равноудаленной от точек L, М и N, вершина D равноуда-
равноудалена от пл. V и пл. Н. г,'
ТВ'с
/77 <
Рис. 151.
?*'
Рис. 152.
154. Дан треугольник ABC (рис. 152). Построить проекции пира-
!миды SABC, вершина S которой равноудалена от точек Л, В и С и
} находится на равных расстояниях от пл. V и пл. Я.
ГЛАВА V
ПРИМЕНЕНИЕ СПОСОБОВ ПРЕОБРАЗОВАНИЯ ЧЕРТЕЖА
§ 18. Определение расстояний
155*. Определить натуральную величину отрезка А В прямой
общего положения (рис. 153, а).
Решение. Как известно, проекция отрезка прямой на какой-либо плоскости
равна самому отрезку (с учетом масштаба чертежа), если он параллелен этой плоскости
(рис. 1J53, б). Из этого следует, что путем преобразования чертежа надо добиться па-
параллельности данного отрезка пл. V или пл. Н или же дополнить систему V, Н еще
одной Плоскостью, перпендикулярной к пл. V или к пл. Н и в то же время параллель-
параллельной данному отрезку. ' ,
На рис. 153, в показано введение дополнительной плоскости S, перпендикулярной
к пл. Я и параллельной заданному отрезку АВ.
Проекция aJ>s равна натуральной величине отрезка Л В.
На рис. 153, г показан другой прием: отрезок А В повернут вокруг прямой, про*
ходящей через точку В и перпендикулярной к пл. Я, до положения, параллельного
109
tui.V. При этом точка S остается на месте, а тачка А занимает новое положение Ах.
В новом положении горизонт, проекция аф || оси х. Проекция а\Ь' равна натуральной
величине отрезка А В.
Рис. 154.
• 136. Дана пирамида SABCD (рис. 154). Определить натураль-
натуральную величину ребер пирамиды AS и CS, используя способ перемены
плоскостей проекций, и ребер BS и DS, используя способ вращения,
причем взять ось вращения перпендикулярно к пл. Н.
157*. Определить расстояние от точки А до прямой ВС
(рис. 155, а).
но
Решение. Расстояние от точки до прямой измеряется отрезком перпендику-
перпендикуляра, проведенного из точки на прямую.
Если прямая перпендикулярна к какой-либо плоскости (рис. 155,6), то расстояние
от точки до прямой измеряется расстоянием между проекцией точки и точкой—
проекцией прямой на этой плоскости. Если прямая занимает в системе V, Я общее по-
положение, то, чтобы определить расстояние от точки до прямой способом перемены
плоскостей проекций, надо ввести в систему V, Я еще две дополнительные плоскости.
Сначала (рис. 155, в) вводим пл. S, параллельную отрезку ВС (новая ось SIH
параллельна проекции be), и строим проекции Ь^ и as. Затем (рис. 155, г) вводим еще
пл. Т, перпендикулярную к прямой ВС (новая ось TIS перпендикулярна к bgCs).
Строим проекции прямой и точки — ct(ftt) и щ. Расстояние между точками сц и ct (bt)
равно расстоянию I от точки А до прямой ВС.
На рис. 155, д эта же задача выполнена с помощью способа вращения в той его
форме, которую называют способом параллельного перемещения. Сначала прямую
ВС и точку А, сохраняя неизменным их взаимное положение, поворачиваем вокруг
некоторой (не обозначенной на чертеже) прямой, перпендикулярной к пл. Я, так,
чтобы прямая ВС расположилась параллельно пл. V. Это равносильно перемещению
точек А, В, С в плоскостях, параллельных пл. Я. При этом горизонт, проекция
заданной системы (ЯС+ А) не изменяется ни по величине, ни по конфигурации,
лишь изменяется ее положение относительно оси х. Располагаем горизонт,
проекцию прямой ВС параллельно оси х (положение Ь^) и определяем проек-
проекцию Oj, откладывая е^ = с—/ и alt1= а—/, причем a1l1 _|_Ci/,. ^Проведя пря-
прямые b'b\, а'а\, с'с\ параллельно оси х, находим на них фронт, проекции ft',,«',, сх.
Далее, перемещаем точки Вг, Суп А\Ъ плоскостях, параллельных пл. V (также не
изменяя их взаимного расположения), так, чтобы получить B.fii Д_ пл. Н. При этом
фронту проекция прямой расположится перпендикулярно к оси х, Ь2 с'2= b\ с\, а для
построения проекции а'2 надо взять b'2 2'2= ft'x 2\, провести 2'2 а'2 _[_&'„ с'2 и отложить
а 2 2>2=а1 2\. Теперь, проведя cxc2 и а^ || х, получим проекции 6ас2 и а„ и искомое
расстояние I от точки А до прямой ВС. Определить расстояние от А до ВС можно,
повернув плоскость, определяемую точкой А и прямой ВС, вокруг горизонтали этой
плоскости до положения ГЦ пл. Я (рис. 155, е).
В плоскости, задаваемой точкой А и прямой ВС, проводим горизонталь А—/
(рис. 155, ж) и поворачиваем вокруг нее точку В. Точка В перемещается в пл. R (за-
(заданной на чертеже следом ЯА), перпендикулярной к А—/; в точке О находится центр
вращения точки В. Определяем теперь натуральную величину радиуса вращения ВО
(рис1.155, в). В требуемом положении, т. е. когда пл. Т, определяемая точкой А и пря-
прямой ВС, станет || пл. Я, точка В получится на Rh на расстоянии ОЬХ от точки О (может
быть и другое положение на том же следе Rh, но по другую сторону от О). Точка Ьх —
это горизонт, проекция точки В после перемещения ее в положение В1 в пространстве,
когда плоскость, определяемая точкой А и прямой ВС, заняла положение Т.
Проведя (рис. 155, и) прямую ЬХ1, получаем горизонт, проекцию прямой ВС, уже
расположенной || пл. Я в одной плоскости с А. В этом положении расстояние от а до
6,/ равно искомому расстоянию /. Плоскость Р, в которой лежат заданные эле-
элементы, можно совместить с пл. Я (рис. 155, к), повернув пл. Р вокруг ее горизонт,
следа. Перейдя от задания плоскости точкой А и прямой ВС к заданию прямыми ВС и
А—1 (рис. 155, л), находим следы этих прямых и проводим через них следы Ро и Pfr
Строи^ (рис. 155, м) совмещенное с пл. Н положение фронт, следа — Pv0.
Через точку а проводим горизонт, проекцию фронтали; совмещенная фронталь
проходит через точку 2 на следе Рй параллельно Ро0. Точка Ао — совмещенное с пл. Я
положение точки А. Аналогично находим точку Во. Прямая ВС в совмещенном с пл. Я
положении проходит через точку Во и точку m (горизонт, след прямой).
Расстояние от точки Ао до прямой ВОСВ равно искомому расстоянию /.
Можно выполнить указанное построение, найдя только один след Ph (рис. 155, н
и о). Вре построение аналогично повороту вокруг горизонтали (см. рис. 155, ж, в, и):
след Рй— это одна из горизонталей пл. Р.
Из приведенных для решения данной задачи способов преобразования чертежа
предпочтительным является способ вращения вокруг горизонтали или фронтали.
111
8)
Рис. 1556-д.
112
Рис. 15бе—к.
113
JO
о)
Рис. 155л—о.
114
158. Дана пирамида SABC (рис. 156). Определить расстояния:
а) от вершины В основания до его стороны АС способом параллель-
П ПРПР1ЧР1ПРНИЯ?
^^ т ^^ ш ь>* ^^ ш^ - - - л ш ш ш м^Л Щщ^ ^^Ч^** ^^ *-^ *^ • • щ ш ш Я ^^«rf '^¦i "^ ^^ ^ *^ ш* ** ^^ ш^т ш w -ш^ ~^ т т »^ -^- »— — " ¦¦- ™™ ^"" ^ш ^™ ¦¦ ¦¦ — ™ г »-
ного перемещения;
б) от вершины S пирамиды до сторон ВС и А В основания способом
вращения вокруг горизонтали;
в) от вершины S до стороны Л С основания способом перемены
костей проекций.
плос-
а'
а
Рис. 156.
159. Дана призма (рис. 157). Определить расстояния:
а) между ребрами AD и CF способом перемены плоскостей про-
проекций;
б) между ребрами BE и CF вращением вокруг фронтали;
в) между ребрами AD и BE способом параллельного перемещения.
115
КЮ. Определить натуральную величину четырехугольника
ABCD (рис. 158) совмещением с пл. Н. Пользоваться только горизон-
горизонтальным следом плоскости.
161*. Определить расстоя-
расстояние между скрещивающимися
прямыми А В и CD (рис. 159, а)
и построить проекции общего
к ним перпендикуляра.
Решение. Расстояние между
акрещивающимися прямыми измеряет-
измеряется отрезком (М/V) перпендикуляра к
обеим прямым (рис. 159, б). Очевидно,
> dr если одну из прямых расположить пер-
перпендикулярно к какой-либо пл. Т, то
а а'
Рис. 158.
d
отрезок MN перпендикуляра к обеим прямым окажется параллельным пл. Т него
проекция на этой плоскости отобразит искомое расстояние. Проекция прямого угла
ме^сду MN н АВ на пл. Т оказывается также прямым углом между /Л(Я( и афх,
тац как одна из сторон прямого угла AMN, a именно<Л1Л\ параллельна пл. Т.
На рис. 159, виг искомое расстояние / определено способом перемены плоскостей
проекций. Сначала вводим дополнительную пл. проекций S, перпендикулярную к пл.
Я н параллельную прямой CD (рис. 159, в). Затем вводим еще одну дополнительную
пл.; Т, перпендикулярную к пл. S и перпендикулярную к той же прямой CD (рис.
159, г). Теперь можно построить проекцию общего перпендикуляра m^i, проведя
mtt\i из точки Cfldt) перпендикулярно к проекции а(й(. Точки ntf и щ— проекции
то*к пересечения этого перпендикуляра с прямыми АВ и CD. По точке mj (рис.
159, д) находим ms на asbs: проекция msits должна быть параллельна оси 77S. Далее,
по ms и ns находим m и п на ab и cd, а по ним т' и п' на а'Ь' и c'd'.
'На рис. 159, е показано решение этой задачи по способу параллельного перемеще-
перемещение. Сначала ставим прямую CD параллельно пл. V: проекция c.rfj || х. Далее переме-
перемещаем прямые CD и АВ из положений ClDl и ArBx в положения С2Ьа и АгВг так,чтобы
С24а расположилась перпендикулярно Н: проекция с, d'3 'j_x. Отрезок искомого пер-
перпендикуляра располагается || пл. Н, и, следовательно, тфг выражает искомое рас-
расстояние / между АВ и CD. Находим положение проекций т'а и'п'д на а, Ьг и c'tdtt
затем проекций т1 и mv nt и п% и, наконец, проекций т! и п', тип.
116
в
в)
Рис. 1596—е.
117
162. Дана пирамида SABC (рис. 160). Определить расстояние
между ребром SB и стороной АС основания пирамиды и построить
проекции общего перпендикуляра к SB и АС, применив способ пере-
перемены плоскостей проекций.
i 163. Дана пирамида SABC (рис. 161). Определить расстояние
между ребром SA и стороной ВС основания пирамиды и построить
проекции общего перпендикуляра к SA и ВС, применив способ парал-
параллельного перемещения.
164*. Определить расстояние от точки А до плоскости в случаях,
когда плоскость задана: а) треугольником BCD (рис. 162, а); б) следами
(ррс. 162, б).
Решение. Как известно, расстояние от точки до плоскости измеряется вели-
величиной перпендикуляра, проведенного из точки на плоскость. Это расстояние проеци-
проецируется на какую-либо пл. проекций в натуральную величину, если данная плоскость
перпендикулярна к пл. проекций (рис. 162, в). Добиться такого положения можно,
прообразуя чертеж, например, способом перемены пл. проекций. Введем пл. S (рис.
163, г), перпендикулярную к пл. треугольника BCD, Для этого проводим в пл. тре-
треугольника горизонталь В—/ и располагаем ось проекций S перпендикулярно к проек-
проекции Ь—1 горизонтали. Строим проекции точки и плоскости — а, и отрезок с^.
Расстояние от as до csds равно искомому расстоянию / точки до плоскости.
118
A
a
Рис. 162а—д.
119
На рио. 162, д применен способ параллельного перемещения. Перемешаем всю
систему до тех пор, пока горизонталь В—1 плоскости не станет перпендикулярна
к плоскости V: проекция bj^ должна быть перпендикулярна к оси, ж. В этом положе-
„ нии плоскость треугольника станет фрон-
тально-проецирующей, и расстояние / от
точки А до иее получится на пл. V без иска-
искажения.
е)
№
Рис. 162е, ж.
i На рис. 162, 6 плоскость задана следами. Вводим (рис. 162, е) дополнительную
пл. S, перпендикулярную к пл. Я; ось S/H перпендикулярна к Pfr Дальнейшее ясно
из чертежа. На рис. 162, ж задача решена при помощи одного перемещения: пл. Р
переходит в положение Р,, т. е. становится фронтально-проецирующей. След.Р1Д
перпендикулярен к оси х. Строим в этом положении плоскости фронт, след горизон-
горизонтали —точку я,,я,. След Pio пройдет через Р1х и п1. Расстояние от а\ до Я1р равно
искомому расстоянию /.
| ИНг, Дана пирамида SABC (см. рис. 160). Определить расстоя-
расстояние от точки А до грани SBC пирамиды, применив способ параллель-
параллельного перемещения.
1вв. Дана пирамида SABC (см. рис. 161). Определить высоту
пирамиды, применив способ параллельного перемещения^
167*. Определить расстоя-
расстояние между скрещивающимися
прямыми АВ и CD (см.рис. 159,а)
как расстояние между парал-
параллельными плоскостями, прове-
проведенными через эти прямые.
Решение. На рис. 163, а по-
показаны параллельные между собой
плоскости Р и Q, из которых пл. Q про-
проведена через CD параллельно А В, a
пл. Р — через АВ параллельно пл. Q.
Расстояние между такими плоскостями
и считается расстоянием между скре-
Рис. 163а. щивающимися прямыми АВ и CD.
Однако можно ограничиться построе-
построением только одной плоскости, например Q, параллельно АВ, а затем определить рас-
расстояние хотя бы от точки А до этой плоскости.
120
На рис. 163, в показана плоскость Q, проведенная через CD параллельно АВ;
в проекциях проведено с'е'\\а'Ь' и ce\\ab. Применяя способ перемены пл. проекций
(рис. 163, в), введем дополнительную пл. '5, перпендикулярную к пл. V и в то жевремя
б)
в)
Рис. 163 6, в.
перпендикулярную к пл. Q. Чтобы провести ось SJV, берем в этой плоскости фронталь
D — 1. Теперь проводим S/U перпендикулярно к d'V (рис. 163, в). Пл. Q изобразится
на пл. ? в виде прямой csds. Остальное ясно из чертежа.
168. Дана пирамида SABC (см. рис. 160). Определить расстоя-
расстояние между ребрами SC и АВ. Применить: 1) способ перемены пл. про-
проекций, 2) способ параллельного перемещения.
fee1". Определить расстояние между параллельными плоско-
плоскостями, из которых одна задана прямыми АВ к АС, а другая — прямыми
DE\» DF (рис. 164, а). Выполнить также построение для случая,
когда плоскости заданы следами (рис. 164, б).
Решение. Расстояние (рис. 164, в) между параллельными плоскостями можно
определить, проведя перпендикуляр из любой точки одной плоскости на другую пло-
плоскость. На рис. 164, г введена дополнительная пл. S перпендикулярно к пл. Н и
к обеим данным плоскостям. Ось S\tf перпендикулярна к горизонт, проекции гори-
горизонтали, проведенной в одной из<плоскостей. Строим проекцию этой плоскости и точ-
точки ^ другой плоскости на пл. 5. Расстояние точки ds до прямой lsas равно искомому
расстоянию между параллельными плоскостями.
На рис. 164, д дано другое построение (по способу параллельного перемещения).
Для того чтобы плоскость, выраженная пересекающимися прямыми АВ и АС,оказа-
АС,оказалась перпендикулярна к пл. V, горизонт, проекцию горизонтали этой плоскости ста-
ставим перпендикулярно к оси х: 1$± 1 х. Расстояние между фронт, проекцией d[ точки
D и прямой а[2[ (фронт, проекцией плоскости) равно искомому расстоянию между
плоскостями.
121
122
123
На ряс. 164, ё показано введение дополнительной пл. S, перпендикулярной к пл. Я
и к данным плоскостям Р и Q (ось S/H перпендикулярна к следам Яд и Q/J Строим
следы Р, и Qf. Расстояние между ними (см. рис. 164, в) равно искомому расстоянию I
между плоскостями Р и Q.
На рис. 164, ж показано перемещение плоскостей Р н Q в положение Pt и Qu
ногда горизонт, следы оказываются перпендикулярными к оси*. Расстояние между
Новыми фронт, следами Р,„ и Qlo равно искомому расстоянию /.
: 170. Дан параллелепипед ABCDEFGH (рис. 165). Определить
расстояния: а) между основаниями параллелепипеда — 1ц б) между
Гранями ABFE и DCGH — /2; в) между гранями ADHE и BCGF—la.
\ § 19. Определение величины углов
\ 171*. Определить углы наклона прямой А В к пл. V а пл. Я
фис. 166, а).
124
Решение. Если прямая параллельна пл. V (рис. 166, б), то угол между этой
прямой и пл. Я (угол а) изображается без искажения на фронт, проекции. Если же
прямая параллельна пл. Я (ряс. 166,в), то образуемый этой прямой угол с пл. V (угол р)
изображается без искажения на горизонт, проекции. Поэтому, поставив заданную пря-
прямую общего положения сначала параллельно пл. V, а затем параллельно пл. Я,
можно определить соответственно углы а и р.
На рис. 166, г показано применение способа перемены пл. проекций для опреде-
определения углов а и р. Так, для определения угла а введена дополнительная пл. S, пер-
перпендикулярная к пл. Я и параллельная АВ, а для определения угла Р — дополни-
дополнительная плоскость Т X V и в то же время \\АВ.
На рис. 166, д прямая как бы повернута: а) вокруг оси, проходящей через точку а
и перпендикулярной к пл. Я, до параллельности пл. V (положение oj о , йхО)
3)
Рис. 166д.
определен угол а; б) вокруг оси, проходящей через точку А перпендикулярно и
пл. У, до параллельности пл. Я (положение a'b'^ aft,) — определен угол [5.
Конечно, можно изобразить эти оси на чертеже; но, как видно, построение воз-
возможно и без этого.
172. Дана пирамида SABCD (см. рис. 154). Определить углы
наклона ребер пирамиды к пл. V и пл. Н.
IJ73*. Определить углы наклона плоскости, заданной треуголь-
никфм ABC (рис. 167, а), к пл. Я и пл. V.
Решение. Как известно, угол наклона (а) плоскости к пл. Я проецируется
без искажения на пл. V, если плоскость перпендикулярна к ил. V (рис. 167, б), а угол
наклона (р) плоскости к пл. V проецируется без искажения на пл. Я, если плоскость
перпендикулярна к пл. Я (рис. 167, в).
На рис. 167, г для определения углаа переходим к системе S, Я, где пл. S перпен-
перпендикулярна к пл. Я и к заданной плоскости (ось S/H перпендикулярна к горизонт,
проекции а—/ горизонтали).
Определение угла Р произведено путем перехода от системы V, Я к системе Т, V,
где nj. T перпендикулярна к пл. V и к данной • плоскости треугольника (ось T/V пер-
перпендикулярна к фронт, проекции с'2' фронтали).
На рис. 167,дтаже задача решена способом параллельного перемещения. Сначала
все вершины заданного треугольника ЛВС перемещены в плоскостях, параллельных
Я, так, чтобы плоскость треугольника оказалась перпендикулярной" к пл. V. Это
125
a
b'
Рис. 167а—д. /
126
достигнуто с помощью горизонтали А—/, перемещенной так, что она расположилась
перпендикулярно к пл. V (горизонт, проекция a-Jy перпендикулярна к оси х).
Получаем угол а наклона плоскости треугольника к пл. Я без искажения.
Для определения величины угла р* наклона плоскости треугольника ABC к пл. V
треугольник повернут так, чтобы он расположился перпендикулярно к пл. Я. Это
сделано при помощи фронтали С—2: она поставлена перпендикулярно к пл. Я (по-
(положение Сг2ъ фронт, проекция с'2 2'2 _|_*). и, следовательно, проходящая через эту
фронтвль плоскость также перпендикулярна к пл. Я.
174. Дана пирамида SABC (см. рис. 161). Определить углы нак-
наклона граней SAB, SAC и ABC к пл. Н и пл. V.
175. Дан параллелепипед (см. рис. 165). Определить углы нак-
лона;основания ABCD и грани CDHG к пл. V и грани ADEH к пл. Н.
176*. Определить величину угла ВАС (рис. 168, а).
В
6)
Рис. 168а, б.
Решение. Если плоскость угла параллельна какой-либо пл. проекций, то
данный угол проецируется на нее без искажения (рис. 168, б).
На рис. 168, а задача решена при помощи способа перемены пл. проекций. Так
как плоскость угла ВАС является плоскостью общего положения (ее горизонталь не
перпендикулярна ни к одной из плоскостей V, Я, W), то приходится сначала допол-
дополнить систему V, Я пл. S, взяв ее перпендикулярно к пл. Я и к плоскости угла ВАС.
В результате этого преобразования проекция угла на плоскости S получится в виде
отрезка as ls. Теперь можно ввести еще одну дополнительную пл. проекций (Г),
проведя ее перпендикулярно к пл. S и в то же время параллельно плоскости угла ВАС.
Угол If at 2f представит собою натуральную величину угла ВАС.
На рис. 168, г искомый угол <р определен способом параллельного перемещения.
Сначала плоскость угла перемещена так, чтобы она стала перпендикулярной к пл.
Qy этого располагаем горизонт, проекцию горизонтали перпендикулярно коси *).
Затем располагаем плоскость угла параллельно пл. Я, для чего перемещаем проекцию
/j а\ в положение /2'аг' (т. е. Цосих). Еще одно построение показано на рис. 168, д.
Здесь! для определения величины угла применен поворот вокруг горизонтали: плос-
плоскость угла расположится параллельно пл. Я (положение Т).
Построения выполнены в следующем порядке:
1L Проведена плоскость вращения точки А — горизонтально-проецирующая пл.
R, перпендикулярная к горизонтали (т. е. коси вращения).
2. Отмечен центр вращения точки А в пересечении горизонтали с пл. R (точка
О, О') и указаны проекции радиуса вращения (Оа и О'а').
_ 3. Определена натуральная величина радиуса вращения (ее выражает гипотенуза
ОА треугольника ОаА).
127
Рис. 168в—д.
128
4. Проведана дуга окружности радиуса Ol в на Яд найдена точка о, — горизонт,
проекция вершины угла после его поворота вокруг горизонтали до совмещения с пл.
Т — и построен угол 1ах2, равный искомому.
Для решения задач типа 176 наиболее рациональным является применение вра-
вращения вокруг горизонтали (или фронтали), как это показано на рис. 168, д.
177. Дана пирамида SABC (см. рис. 156). Вращением вокруг го-
горизонтали определить угол между ребрами SA и SB, SB и SC, SC и SA.
178. Дан параллелепипед (см. рис. 165). Определить углы между
ребрами DH и CD, CG и CD, АВ и ВС.
179*. Определить величину угла между скрещивающимися пря-
прямыми АВ и CD (рис. 169, а).
off
m
Рис. 169а—г.
Решение. Угол между двумя скрещивающимися прямыми определяется уг-
углом, (оставленным пересекающимися прямыми, соответственно параллельными дан-
данным скрещивающимся. Для определения величины угла надо начать с его изображе-
изображения на чертеже. Это сделано на рис. 169,6, причем использована одна из заданных пря-
прямых -+- CD, через точку С которой проведена прямая СМ, параллельная другой яа-
даннай прямой—АВ. Величина угла MCD (рнс.169, в) выражает угол между прямыми
АВ и CD. Это сделано при помощи поворота вокруг горизонтали 1—2 (рис. 169, г),
взятой в пл. угла MCD.
А, О- Гордон а др.
129
180. Дана пирамида SABC (см. рис. 160). Определить величину
угла между ее ребрами: a) SB и АС, б) SA и ВС.
181*. Определить величину угла ф наклона прямой АВ к пло-
плоскости, заданной треугольником CDE (рис. 170, а).
а'
i
.—
2
I
4—-
j
' i
yjf?
b
SO"
г)
Рис. 170а—г.
Решение. Как известно, углом между прямой (АВ) и плоскостью (Р) назы-
называется острый угол (ф) между прямой и ее проекцией (арК) на этой плоскости. Для
построения (рис. 170, б) этого угла надо найти точки пересечения с пл. Р прямой АВ
и перпендикуляра, проведенного из какой-либо точки прямой АВ на пл. Р. Но если,
как в данной задаче, требуется лишь определить величину угла наклона прямой к пло-
плоскости, то проще определить величину угла б, дополнительного к углу ф: найдя угол
б, можно определить величину угла ш из соотношения ф=90° — б. На рис. 170, в
показано построение проекций am и а т! перпендикуляра к плоскости треугольника
CDE, для чего взяты горизонталь цфронталь этой плоскости: amj_e—/, а'т'_[_е'2'.
что
Теперь можно определить (рис. 170,г) натуральную величину угла 6 с вершиной А,
сделано поворотом вокруг горизонтали Ь'З', Ь—3. Искомый угол <р=90 —о.
130
182. Дана пирамида SABC (см. рис. 161V Определить углы нак-
наклона ребер SA, SB и SC к грани ЛВС
183*. Определить угол между гранями ABC и ABD (рис. 171, а).
в)
Рис. 171а—в.
Решение. Двугранный угол измеряется линейным углом, полученным в пе-
пересечении граней двугранного угла плоскостью, перпендикулярной к обеим граням
двугранного.а следовательно, н к линии их пересечения, т. е. ребру двугранного угла.
Если это ребро АВ окажется перпендикулярным к какой-либо пл. Г (рис. 171,E),
то полученная на пл. Т проекция двугранного угла выражает его линейный угол.
5*-
131
Для решения задачи (рис. 171, в) применен способ перемены пл. проекций. От си»
стемы V, И совершен переход к системе S, V, где S I V и 5 || АВ, а затем от этой сис-
системы S. V переход к системе Г, S, где Т \S и Т±АВ.
Треугольники проеирю а Т
S. V переход к системе Г, S, где Т \S и Т±АВ.
Треугольники проецируются на пл.Т в виде отрезков a$i
ними-равен искомому углу ф.
. Угол между
1 U 1 Ul
На рис. 171, г показано решение той же задачи при помощи способа параллельного
перемещения: ребро АВ поставлено перпендикулярно к пл. Н.
\ 184*. Определить величину угла, образованного плоскостью Р
И плоскостью треугольника ABC (рис. 172, а).
а
а.)
=780-0
Рис. 172а, б.
Решение. Если, решая данную задачу, придерживаться схемы решения пре-
предыдущей, то необходимо построить прямую пересечения заданных плоскостей. Но
можно поступить и иначе, без построения этой прямой, т. е. не определяя ребра иског
мого двугранного угла. Можно поступить следующим образом: определить не непос-
редственно угол <р, а угол о (рис 172, б) между перпендикулярами КМ и KN, прове-
проведенными из какой-либо точки К на заданные плоскости. Найдя угол а, получаем <р =-
— 180° — а.
Такое решение отличается в своей сущности от решений по рис. 171, в и 171, г.
Взяв некоторую точку К (рис. 172, в), провезем из нее перпендикуляры KN и КМ соот-
соответственно к плоскости треугольника ABC н к пл. Р: из точки k' проводим k'ri _|_ a'tf
и k'm* J_ Р„, а из точки k — kn I ас и km J_ Ph. Таким образом получается угол с про-,
екциями mkn и m'k'n' (угол dJ7 Натуральная величина этого угла получена поворо-
поворотом вокруг фронтали /—2 (рис. 172, г). Так как получен острый угол, то можно
в,
Рис. 172в, г.
считать, что он определяет искомый угол между заданными плоскостями, так как из
смежяых углов, полученных при взаимном пересечении двух плоскостей, углом между
плоскостями считается острый.
185. Дана пирамида SABCD (см. рис. 154). Определить способом
перемены плоскостей проекций углы между гранями SAB и SBC,
SBC и SCD, SAD и SAB.
188. Дан параллелепипед (рис. 165). Определить углы между
гранями CDHG и EFGH, BCGF и CDHG-
§ 20. Смешанные задачи' с применением способов преобразования
чертежа
(рис|
Поворотом вокруг прямой MN ввести точку А в пл И
173,а).
решение. Ось вращения — прямая MN j- в данном случае параллельна пл. Н.
Поэтому плоскость вращения точки А является горизонтально-проецирующей. Ее
след $ь (рис.173, 6) проходит через проекцию а. Точка А при повороте ее вокруг MN
описывает в пл. S окружность, горизонт, проекция которой совпадает с SfA центр
этой окружности находится в точке О пересечения оси вращения MN с пл. S. Так как
пл. S составляет с пл. V острый угол, то проекция окружности, расположенной в пл. S,
получится на пл. V в виде эллипса. Чтобы избежать построения этого эллипса, сов-
совместим пл. S и лежащие в ней точки О и А с пл. И. Это даст возможность изобразить
дугу окружности, по которой перемещается точка А, без искажения. По условию
133'
аадачи точка А, находясь в пл. S, должна оказаться в пл. Н; следовательно, точка А
должна получиться после поворота на следе SA и совпасть со своей горизонт, проеюш-
; Рис. 173а, б.
ей. Поэтому, проведя дугу радиусом'О0Л0, получим точки ах и аг— горизонт, проекции
точки /1, приведенной в пл. Н. По точкам ах и (ц строим на оси д: проекции а/ и я./.
188. Поворотом вокруг прямой MN ввести точку А в тш. V
(рис. 174).
т
\ 189*. Построить проекции окружности, расположенной в пл. Р
(рис. 175, а). Известна величина радиуса этой окружности (/?) и поло-
положение фронт, проекции (с') ее центра.
.134
Решение. Прежде всего находим проекцию с центра окружности (при помощи
горизонтали CN). Точки с' и с будут центрами эллипсов — проекций окружности,
расположенной в плоскости общего положения Р.
На рис. 175, б показано построение
осей эллипса — горизонт, проекции ок-
окружности. Большая ось расположена на
горизонт, проекции горизонтали CN и
равна 2/?. Положение малой оси также из-
известно: она перпендикулярна к /—2. Для
определения величины этой оси (а также
малой оси фронт, проекции) применено со-
совмещение пл. Р с пл. Н, что дает возмож-
возможность изобразить окружность без искаже-
искажения. Ее диаметр /020 соответствует отрезку
1—2, т. е. большой оси эллипса — гори-
горизонт, проекции окружности, а диаметр
3040 f- малой оси этого эллипса. Проведя
через точку 3„ фронталь плоскости Я в ее
совмещенном положении (|| Ро0), а затем
горизонт, проекцию этой фронтали, нахо-
находим точку 3 и тем самым полуось с—3. От-
Откладывая с—4 = с—3, получаем малую
ось ёллипса 3—4.
Построение осей эллипса—фронт, про-
проекции окружности—показано на рис. 175,в.
Здес|> также известно положение боль- Рис. 1756—р.
шой реи — она лежит на фронт, проекции
фроЦтали, проходящей через с',— и величина этой оси G'в'=2Я). Малая ось перпен-
перпендикулярна к 7'8'. Величина же малой оси определяется при помощи диаметра 5фа
окружности в ее совмещенном с пл. Н положении: большой оси эллипса TS соответ-
соответствует диаметр 7Д окружности, а малой оси 5'6' — диаметр 5фа, перпендикулярный
к 708в. Проведя через о0 фронталь плоскости Р до пересечения о Рл, находим затем
133
г)
фронт, проекцию этой фронта ли и на вей точку б'—конец малой оси: эллипса. Откла-
Откладывая с'а'-ас'б', получаем малую ось б'б'. ч
На рис. 175, е показано построение проекций некоторых точек окружности.
Взяты точки $о в Юо на прямой АаВв. Построив горизонт, и фронт, проекции этой
прямой, находим сначала проекции 9' и 10, а затем 9' и 10'.
Найдя ряд точек, проводим через ни* и через концы осей эллипсы—проекции
окружности.
190*. Построить проекции окружности, расположенной в пло-
плоскости, заданной ее горизонталью ВС и фронталью СЕ (рис. 176, а).
Известны величина радиуса этой окружности и положение центра —
точка С.
Решение. Находим горизонт,
след фронталн (рис. 176, б) и проводим
через точку т. след Р/, параллельно cb.
Определяем величину радиуса СО как
величину гипотенузы прямоугольного
треугольника с катетами сО и сС и на-
находим совмещенное с пл. Я-положение
центра окружности Со. На рис. 176, в
точка 3 построена с помощью прямой
/Д,, продолженной до пересечения с
Яй в точке А0(а), а точки 5 и 6—с помо-
помощью прямой 50б0, проходящей через
центр Со н пересекающей при своем
продолжении след Яд в точке D0(d).
Дальнейшие построения аналогич-
аналогичны выполненным на рис. 175, бив.
Оии ясны из чертежа.
136
801. Построить проекции окружности, описанной вокруг тре-
треугольника ABC (рис. 177).
198*. Плоскость, заданную треугольником ABC, повернуть вокруг
оси ООг так, чтобы точка К оказалась в этой плоскости (рис. 178, а).
Решение. Если точка К войдет
в плоскость, то она окажется на одной
из горизонталей этой плоскости, а
именно на той, которая расположена
на одном уровне с точкой К (рис. 178,6).
Поэтому проводим через k' фронт, про-
проекцию горизонтали, находим точки /' и
2', а по ним точки / и 2 и проводим го-
горизонт, проекцию /—2 горизонтали.
Теперь надо повернуть горизон-
горизонталь так, чтобы она прошла через
точку К- Для этого опускаем из
точки О(О{) перпендикуляр на /—2
и радиусом О—3 проводим дугу
Рис. 177.
Рис. 178а, б.
окружности, по отношению к которой горизонт, проекция горизонтали является ка-
касательной в любом положении при повороте плоскости вокруг данной оси 00х. По-
Поэтому, проведя из k касательную к этой окружности, мы определяем положение го-
горизонт, проекции горизонтали, на которой должна находиться точка К после тре-
требуемого поворота. Наносим на нее точки lt и 2\ (Зг 11=1—3 и I12i=l^2), а затем
строим точки аъЬх и сх на основании известного вывода, устанавливающего неизме-
неизменяемость горизонтальной проекции фигуры по форме и по размерам при повороте
вокруг оси, перпендикулярной к пл. Н.
По проекции ojVi строим проекцию а\Ь\с\. В положении А^В^ треугольник
проходит через точку К.
137
Если из К провести вторую касательную к окружности, то получится второе ре-
решение. Предоставляем читателю найти это положение треугольника ABC.
193. Плоскость, заданную треугольником ABC, повернуть вок-
вокруг оси ООХ так, чтобы точка Показалась в этой плоскости (рис. 179).
Ъ'
Рис. 179.
194*. Найти предельное положение осей, при котором еще воз-
возможно получить решение в задаче 192.
i Решение. Положим, что плоскость, как и в задаче 192, задана треугольником
(Дне. 180, а), ось, вокруг которой надо повернуть плоскость, должна быть перпен-
перпендикулярна к пл. Н и точка К должна оказаться в плоскости треугольника.
[ Из рассмотрения рис. 180,6 следует, что горизонт, проекция"оси ОО1 должна
быть расположена так, чтобы проекция k не оказалась внутри окружности с радиусом
О-,—3, так как из точки к надо провести касательную к этой окружности. Следова-
Следовательно, расстояние точки О от А должно быть не меньше расстояния этой же точки до
прямой /—2.
Если провести к—3 перпендикулярно к прямой 1—2 и разделить отрезок к—3
прполам, то точка О может служить горизонт, проекцией оси, при повороте вокруг
которой горизонт, проекция горизонтали 1—2 пройдет через точку k и, следовательно,
точка К окажется в плоскости треугольника А ВС. Очевидно, если взять еще какую-
либо точку, расстояния которой до точки А и до прямой 1—2 равны, то и эта точка мо-
может быть принята в качестве горизонт, проекции оси, пригодной для решения постав-
поставленной задачи. Но все такие точки, расстояния которых до точки ft и до прямой /—2
138
равны между собой, принадлежат параболе с фокусом в точке k и директрисой в виде
прямой 1—2. Следовательно, предельное положение осей получается, если их го-
горизонт, проекции образуют параболу, а самые оси представляют собою образующие
параболического цилиндра. На рис. 180, б показано построение параболы с фокусом
в точке ft и с директрисой /—2. Если взять отрезок, например llt провести прямую
параллельно /—2 на расстоянии /х и дугу радиуса /, из точки ft, то получатся две
точки параболы. Вершина параболы — в точке О.
Рис. 180а, б
Очевидно, оси, горизонт, проекции которых оказались бы внутри параболы,
непригодны для соблюдения условия задачи 192. Если же взять оси вне параболиче-
параболического цилиндра, то за один оборот плоскости точка дважды окажется в ней.
Г
аг<
Рис. 181.
195. Найти предельное положение осей, перпендикулярных к
пл. V, при повороте вокруг которых точка К окажется в плоскости,
заданной треугольником ABC (рис. 181).
130
Найти точку К, находящуюся внутри пирамиды и отстоя-
отстоящую от грани SAB на расстояние /1( от грани SAC — на I,, от грани
ABC (основание пирамиды) — на /а (рис. 182, а).
Рис. 182а, б
__.__! Р е ш е н и е^ Искомая^точка нолучится как точка пересечения трех плоскостей,
из! которых каждая является геометрическим местом точек, отстоящих на определен-
определенное расстояние от граней пирамиды.
; Введя дополнительную пл. Г, перпендикулярную к грани SAB (рис. 182, б),
поручаем проекцию пирамиды, на которой грань 5.45 изображается прямой stat.
Плоскость, параллельная грани SAB и удаленная от нее на расстояние 1и изобра-
изображается прямой Jt2f, эта плоскость пересекает пирамиду по треугольнику /—2—3
(т рис. 182, б показана только горизонт, проекция).
Плоскость, удаленная от грани SAC на расстояние /2, изображается на дополни-
дополнительной пл. Q, перпендикулярной к этой грани (рис. 182, в), в виде прямой 4,fiq и
пересекает пирамиду по треугольнику 4—5—6 (дана лишь горизонт, проекция этого
треугольника).
| Искомая точка К должна принадлежать линии пересечения плоскостей, заданных
треугольниками /—2—3 и 4—5—б. Эта прямая проходит через точки М и N, полу-
получаемые при пересечении сторон 2—3 и 6—5, 1—3 и 4— 5 треугольников /—2—3 и
4-\5—б (рис. 182, г).
! Находим фронт, проекцию *' (рис. 182, д) на т'п' из условия, что точка К от-
отстоит от грани ABC на расстояние /3.
¦ Геометрическим местом таких точек является пл. Р, параллельная грани ABC.
Щ k' находим ? на тп.
\ 197. Найти точку К, находящуюся внутри призмы на расстояниях:
/х — от грани BCEF, /а — от грани ABDE, L — от основания ЛВС
(рис. 183).
КО
a
в)
a
Рис. 182в—д.
Рис. 183.
141
198. Найти точку К, находящуюся внутри пирамиды SABC на
расстояниях: /х — от грани SAC, /а — от грани SBC, /я — от грани
SAB (рис. 184).
а'
п
Рис. 185.
а—г.
199*. Построить геометрическое место точек, равноудаленных от
сторон угла ВАС (рис. 185, а).
142
Решение. Искомым геометрическим местом является плоскость, проходящая
через биссектрису данного угла перпендикулярно к его плоскости (рис. 185, 6). Сле-
Следовательно, искомая плоскость будет определяться этой биссектрисой и пересекаю-
пересекающим ее перпендикуляром к плоскости угла ВАС.
Для проведения биссектрисы угла ВАС приходится построить его натуральный
вид, так как непосредственное проведение биссектрисы в заданных проекциях угла
возможно лишь в особых случаях, например при одинаковом наклоне сторон угла к
плоскости проекций. На рис. 185, в показано совмещение плоскости угла ВАС с
пл. Ц, для чего построен горизонт, след (/—2) этой плоскости.Теперь может быть про-
проведена биссектриса угла 1А02 — прямая А0М0—и построены ее проекции атиа'т'.
Остается провести перпендикуляр к плоскости угла ВАС через какую-либо точку
его биссектрисы и этим определить искомую плоскость. На рис. 185, г перпендикуляр
проведен через вершину угла—точку А, для чего использован горизонт, след /—2 и
проведена фронталь 2—4; проекция перпендикуляра an _|_/—2 и проекция а' п! \2' 4'.
200. Построить геометрическое место точек, равноудаленных от
сторон угла ВАС (рис. 186). Искомую плоскость задать следами.
Рис. 186.
201*. На прямой EF (?/=Ч1пл. V)
найти точку, равноудаленную от сторон
угла1 ВАС (рис. 187, а).
Решение. Геометрическим местом точек,
равноудаленных от сторон угла ВАС, является
плоскость Р, проходящая через биссектрису это-
этого угла и перпендикулярная к его плоскости
(рис.:187, б). Очевидно, искомая точка (К) на
прямой EF получится при пересечении этой
прямой с пл. Р.
Щостроение пл. Р на рис. 187, в аналогично
построению на рис. 185, а, с той лишь разницей,
что н$ рис. 187, в уголЛЛС совмещен с пл. V вра-
вращением вокруг фронт, следа Г 2' плоскости этого
угла. Для построения проекций перпендикуляра
AM использован след 1'2' и горизонталь А—3:
а'т'\1'2' и ат±аЗ.
Рис. 187а, б.
Точка К на прямой EF найдена обычным способом построения точки пересечения
прямой с плоскостью (рис. 187, г);
1) через ?F проведена вспомогательная пл. Т (так как прямая EF\\nn. V, то ока-
млось возможный провести через нее фронтальную плоскость Г),
2) построена прямая пересечения пл. Р (заданной прямыми AM и AN) с пл. Т
(это фронталь плоскости Р — прямая с проекциями 5'6', 5—6),
3) найдена точка пересечения этой фронтали с прямой EF—точка К.
е'
Рис. 187в. г.
! 202. На стороне АВ основания пирамиды SABC (рис. 188) найти
трчку К, равноудаленную от ребер SA и SC.
\ 203. На ребре SC пирамиды SABC (см. рис. 188) найти точку М,
равноудаленную от ребра SA и стороны А В основания.
' 204*. Найти геометрическое место точек, равноудаленных, от пл.
Р\ и пл. Q (рис. 189, а).
\ Решение. Искомым геометрическим местом является (рис. 189, б) пл. R, де-
делящая пополам двугранный угол, образованный'данными плоскостями. Пл. R про-
проходит через ребро двугранного угла, т. е. через прямую MN. Если ребро MN рас-
пфюжить перпендикулярно к какой-либо пл. проекций Т, то каждая из плоскостей
Р и Q, а также и пл. R изобразятся на этой плоскости проекций в виде прямых, как
втр показано на рис. 189, б, причем Rf делит угол между Р( и Qt пополам.
I Построив (рис. 189, в) прямую MN пересечения плоскостей Р и Q, вводим (рис.
180, г) дополнительные плоскости S (SJ_H и S\\MN) и Т (T±_S и T±_MN). Угол
мфвду построенными прямыми nitPxt и mtQxt равен углу между плоскостями Р и Q,
а фиссектриса этого угла mtRxt представляет собою след искомой пл. R на дополни-
тельной пл. Т. Относя точку Rx к прямой Рх Qx, т. е.. к оси V/H, находим проекцию Rxs
?xs Qx
на
x
прямой Рх Qx, т. е.. к оси V/H, находим проекцию Rxs
М xs Qxs х хх' на оси VIН. В точке Rx следы искомой плоскости
пересекают ось VIH, а так как пл. R проходит через прямую MN, то след Rv проходит
через точку п', а след R^—через т.
| 205. Найти геометрическое место точек, равноудаленных от
nil. P и плоскости, заданной прямыми АВ и CD (рис. 190).
206'*. Найти на прямой АВ точку, равноудаленную от плоско-
плоскостей, заданных треугольниками MNC и MND (рис. 191, а).
И4
e)
ntf7?t
Рис. 189а—г.
145
146
Решение. Искомой точкой является точка пересечения прямой АВ с пло-
плоскостью (R), делящей угол между данными плоскостями пополам (рис. 191, 6).
Ход построения аналогичен примененному в задаче 204. Путем введения допол-
дополнительных пл. проекций S и Г получаем положение, при котором ребро MN про-
проецируется на пл. Т в точку (рис. 191, в).
В этом положении изображаем плоскость, делящую пополам угол между гранями
MNC и MND, в виде прямой Rt. В пересечении прямой atbt cRt получим проекцию
искомой точки К на пл. Т; по ней находим ks на asbs, а затем k на аЬ и к' на а'Ь'.
207. На ребре SB пирамиды SABC найти точку К, равноудален-
равноудаленную от грани SAC и основания ABC (см. рис. 188).
208. На стороне АВ основания ABC пирамиды SABC найти
точку М, равноудаленную от граней SAC и SBC (см. рис. 188).
209*. Через точку А провести прямую общего положения, рас-
расположенную под углом а к пл. Н и под углом {J к пл. V (рис. 192, а).
Решение. Известно (см. задачу 22), что для прямой общего положения
а + р<90°.
На ?ис. 192, 6 и в показано построение искомой прямой с применением способа
вращения. На этих рисунках изображены две прямые: одна (ABj) расположена
aj
Рис. 192а—в.
параллельно пл, V и другая (ЛВа)—параллельно пл. Я. На обеих прямых отло-
отложены равные отрезки ABi и АВ2: a'b\ = ab2.
Если теперь повернуть отрезок /IS, вокруг оси, перпендикулярной к пл. Н, а
отрезок ABt—вокруг оси, перпендикулярной к пл. V, причем обе оси вращения
проходят через точку А, то в некоторый момент оба этих отрезка совпадут (на рис.
192, б это показано в виде отрезка АВ), и, следовательно, искомая прямая ока-
жетая построенной.
Всего можно провести через точку А четыре прямые. На чертеже (рис. 192, в)
проводим дугу окружности радиуса abt до пересечения в точке b с прямой, про-
проходящей через точку Ьг иараллельно оси х. По точке Ь находим Ь'.
На рис. 192, в показано еще одно (из четырех возможных) положение прямой,
обозначенное АВа.
147
I. Через точку Л провести вправо от нее прямую общего поло-
положения ЛЯ, расположенную под углом а к пл. Н и под углом р* к пл. V
(рис. 193), при условии, что точка В расположена в пл. Н и ближе
к пл. V, чем точка А.
за'
Рис. 193.
Рис. 194.
211. Через точку А провести вправо от нее отрезки А В, AC, AD
и АЕ, расположенные под углом а к пл. Я и под углом р* к пл; V
Орис. 194).
! 212*. Провести через точку А плоскость, составляющую с пл. Н
у^ол «х и с пл. V угол р\ (рис. 195, а).
Рис. 195а, б.
Решение. Для построения искомой плоскости в ванном случае использована
зависимость между углами, составляемыми некоторой прямой с пл. Н (угола) и с пл. V
(угол Р), и углами, составляемыми плоскостью, перпендикулярной к этой прямой,
с теми же плоскостями проекций Н (угол aj и V (угол pj. Известно, чтоа1+а=90°
148 '
(рис. 195, б) и pVf Р=- 90°. Отсюда следует, что 180е>л1+^1> 90е. Это шиволяет
проверить правильность задания углов оц и ft (рис. 195, а).
Итак, определив утлыа=90°—otj и р==90 —рх, проводим через точку /4 прямую
под углами а и р соответственно к пл. Я и пл. У (рис. 195, в), как это имело место в за-
задаче 209. Теперь через точку А проводим плоскость, перпендикулярную к построен-
построенной прямой А В. Эта плоскость на рис. 195, ? выражена горизонталью н фронталью:
a'd'J_a'b't ac±ab.
Рис. 196.
Рис. 195в, г.
SI3. Провести через точку А две плоскости (выразив их следами)
! к пл. Я и рх к пл. V (рис. 196), построив вспомогательные
прямые под углами а=90°—ах к пл. Н и C=90°—рх к пл. V — одну
вправо, вглубь, вниз, от точки А, другую — вправо, вглубь, вверх.
$14*. Построить правильную треугольную пирамиду с вер-
шифй в точке S. Высота пирамиды наклонена к пл. Н под углом а
и Ц пл. V под углом р. Точка А — одна из вершин основания
(риф 197, а).
Решение. Проводим (рис.197, б) через точку S прямую SM под заданными уг-
углами а и р к пл. Н и пл. V (см. задачу 209). Плоскость основания пирамиды должна
пройти через точку А перпендикулярно к SM; задаем эту плоскость горизонталью
AN и фронталью АК (рис. 197, в). Находим точку О пересечения прямой SM с
плоскостью основания. Для этого заключаем SM в фронтально-проецирующую
149
\
150
I
СП
X
a.
151
пл. R, изображенную только фронт, следом Rv. Для построения вершин В и С
пирамиды поворачиваем плоскость основания вокруг горизоятали A—3gp совмеще-
совмещения ее с пл. Г (рис. 187, г).
В плоскости основания через точку О проводим произвольную прямую 3—4.
Строим совмещенное с пл. Г положение точки 4 \4Y\ и соединяем 4\ с точкой 3. На
прямой 8—4i находим точку Ои из которой радиусом Ог—а проводим окружность.
Разделив ее на три части, находим вершины Ьг и сх. Зная^ и ci, находим (рис. 197, д)
горизонт, проекции: с — на продолжении прямой а—б (найдя сначала точку 5 по 5,),
НН-—на прямой а—€ (найдя сначалаложку^по 6,Х, Затем строим прямые а'5' и а 6
и на них точки с'и b'\ ab'd' иаЬс — проекции основания пирамиды. На рис. 197, в
проекции—вершии-з'—й—д соедппспы—с одаои»кнными с ними проекциями вершин
основания. •
^вг-Пвс*рой№ правильную четырехугольную пирамиду с вер-
вершиной в точке S. Высота пирамиды наклонена к пл. Н под углом а и
к пл. V под углом р\ Точка А — одна из вершин основания (рис. 198).
Рис. 198.
Рис. 199а, б.
21в*. Построить куб с основанием на плоскости, расположенной
под углом<*! к пл. Н и углом р\ к пл. V. Отрезок а'Ь'— фронт, проекция
стороны основания куба (рис. 199, а).
152
в)
X
Рис. 199 в—е.
163
Решение. Строим произвольную прямую MS (рис. 199, б), расположенную
под углом <х=90°—ai к пл. И и (J=90°—р\ к пл.У.
Эта прямая дает нам направление боковых ребер куба. Теперь проводим через
точку А пл. Р (рис. 199, в), перпеидакулярную к этой прямой, и находим в пл. Р
точку В. Совмещаем пл. Р и лежащий в ней отрезок АВ с пл. Н (рис. 199, г) и до-
достраиваем квадрат /4080С0О0. Затем поднимаем точки ?>0 и Со в пространство: точку Do
с помощью прямой /020 и точку Со с помощью совмещенной фронт ал и 30С0.
Так как ребра куба перпендикулярны к основанию, то через точку А проводим
(рис. 199, д) прямую, перпендикулярную к пл. Р (а'4'_L_PV и а—4\.Рц). На этой пря-
прямой откладываем отрезок АЁ, равный стороне основания, хотя бы А0В0. Это сделано
при помощи построения прямоугольного треугольника. Получив таким образом
проекции а'е' и ае, строим (рис. 199, е) проекции куба.
: 217. Построить прямую треугольную призму с основанием в виде
равнобедренного треугольника ABC на плоскости, расположенной под
Рис. 200.
уГлом^ к пл.Н и углом Рх к пл. V. Вершина С треугольника ABC ле-
якт на пл. Н. Высота призмы равна стороне Л В основания — треуголь-
треугольника ABC (рис. 200).
ГЛАВА VI
КРИВЫЕ ЛИНИИ И ПОВЕРХНОСТИ
§21. Кривые линии. Поверхности. Точки на поверхностях
218*. Построить проекции правой цилиндрической винтовой
линии, проходящей через точку А, принадлежащую поверхности ци-
цилиндра. Точка задана своей фронт, проекцией (рис. 201). Провести
прямую, касательную к винтовой линии в точке А. Шаг винтовой ли-
линии взять равным высоте цилиндра.
ф
w
f/
1
t
1
фС 1
< s
7
H\
гг\н
\
H
Рис. 201а—в.
Решение. При заданном на рие. 201, а положении цилиндра горизонт, про-
проекция внитовой линии на нем представляет собою окружность. Делим (рис. 201, б)
окружность, начиная от точки а, на 12 равных частей. Вверх и вниз от точки а
откладываем отрезки, равные Н : 12. Строим фронт, проекции ряда точек, принад-
принадлежащих винтовой линии (построение ясно из чертежа}.
155
о
i
ем
S
и
S
Си
156
Исходя из того, что касательная к кривой проецируется в касательную к проек-
проекции этой кривой, проводим касательную к окружности в точке а (рис. 201, в). Это го-
горизонт, проекция касательной к винтовой в ее точке А.
Все касательные к цилиндрической винтовой линии пересекаются с плоскостью,
перпендикулярной к оси этой линии, в точках, которыми образуется эвольвента ок-
окружности. Находим точку Ь как точку эвольвенты, отложив на касательной от
точки а отрезок ab, равный по длине трем дугам (а—11)+A1—10)+A0—9). Фронт,
проекция V получается на уровне точки 9'. Фронт, проекция касательной проходит
через точки а' и Ь'.
219. Построить проекции левой цилиндрической винтовой ли-
линии, проходящей через точку А, заданную на поверхности цилиндра
(рис. 202). Провести прямую, касательную к винтовой линии в точке
А. Шаг винтовой линии взять равным удвоенной высоте цилиндра.
220*. Построить проекции участка цилиндрической винтовой
линии радиуса R (рис. 203, а), проходящей через данные точки А и В,
и определить длину этого участка (кратчайшее расстояние между точ-
точками А и В на цилиндрической поверхности).
решение. Горизонт, проекцией искомого участка винтовой линии является
дуга ab. Делим (рис. 203, 6) угол а и расстояние Н на п равных частей (в данном слу-
случае л=4) и строим проекции л—1 точек, принадлежащих винтовой линии, не считая
точек А и В.
Для определения кратчайшего расстояния между точками А и В строим раз-
развертку участка АВ винтовой линии. Она представляет собой гипотенузу прямо-
прямоугольного треугольника, один катет которого равен Я, а другой -т^г-.
221. Построить проекции участка цилиндрической винтовой
линии радиуса R (рис. 204), проходящей через данные точки А к В,
и О1феделитАДллнузтогд участка (кратчайшее расстояние между точ-
точками Л и В на цилиндрической поверхности).
222*. Найти линию пересечения цилиндрической поверхности,
заданной (рис. 205, а) образующей CD и направляющей АВ, с пл. Я.
Решение. Задаем на кривой АВ ряд точек и проводим (рис. 205, б) через
них Образующие. Геометрическим местом горизонтальных следов образующих будет
исковая кривая линия тутг, тутг-
223. Найти линию пересечения цилиндрической поверхности,
заданной (рис. 206) образующей СВ и направляющей АВ, с пл. V.
2124*. Построить проекции прямого кругового цилиндра, осью
которого является прямая MN (ЛШ||пл. V, рис. 207, а), окружность
нижнего основания проходит через точку А, а плоскость верхнего —
через точку В.
Решение. Пользуясь тем, что ось цилиндра по заданию параллельна пл. V,
проводим (рис. 207, б) перпендикуляры из точек В и А к оси цилиндра и находим
точки О\ и 0а (центры окружностей оснований) и высоту цилиндра (отрезок О'у О'2).
Теперь надо найти радиус основания цилиндра. Применяем способ перемены пл. пр.
Вводим дополнительную пл. S, перпендикулярную к пл. У и к оси цилиндра. Иско-
Искомый радиус определяется проекциями Ом и as (рис. 207, в).
Строим фронт, проекцию искомого цилиндра. Для построения горизонт, проек-
проекции цкпиндра находим (рис. 207, г) малые оси 1—2 и 3—4 эллипсов — проекций
оснований цилиндра. Большие оси эллипсов равны диаметру основания. Строим
эти эллипсы и, проведя проекции очерковых образующих, получаем горизонт,
проекцию цилиндра.
167
158
171'
т
п
а)
г)
Рис. 207а—г.
159
160
\
225. Построить проекции прямого кругового цилиндра, ось
которого лежит на прямой ОМ (ОМЦпл. Н, рис. 208), точка О является
центром одного из оснований, точка А принадлежит цилиндрической
поверхности; высота цилиндра равна диаметру основания.
226*. Построить проекции прямого кругового цилиндра с осью
ОМ (рис. 209, а), касательного к плоскости, заданной треугольником
ABC. Высоту цилиндра, считая от точки О, принять равной полуто-
полутора диаметрам основания. Прямые ОМ и ВС параллельны между
собою.
Решение. Если ось цилиндра окажется перпендикулярной к плоскости
проекций, то касательная к цилиндру плоскость изобразится на той же пл. пр. в
виде прямой, касательной к окружности — проекции цилиндра. Этим определится
радиус основания цилиндра. Осуществляем такое построение, применяя способ пере-
перемены пл. пр. (рис. 209, б). Вводим дополнительную пл. S, взяв ее перпендикулярно
к Н и параллельно оси цилиндра ОМ (ось SIH\\0m), а затем еще одну дополнитель-
дополнительную пл. Т, перпендикулярную к пл. S и к ОМ (ось T1S]_0sms).
На пл. Т цилиндрическая поверхность проецируется в окружность с центром
в точке О(, а плоскость треугольника ABC, касательная к цилиндру и, следовательно,
параллельная оси ОМ,— в отрезок afti прямой, касательной к этой окружности.
Отсюда получаем диаметр окружности основания цилиндра, равный 2^0
г)
Рис. 209г.
;На рис. 209, в показано построение горизонт, проекции цилиндра.
lHa рис. 209, г показано построение фронт, проекции цилиндра. Для определе-
определения величины малой оси эллипса на этой проекции введена еще одна дополнительная
ил. Q, перпендикулярная к пл. V и параллельная ОМ (ось Q/V||0'm'). Находим
проекцию цилиндра на пл. Q и с ее помощью фронт, проекцию цилиндра.
6 а. о. Гордон ¦ др.
161
227*. Найти линию пересечения конической поверхности, задан-
заданной вершиной S и направляющей АВ, с пл. Н (рис. 210, а).
а
а)
Рис. 210а, б.
Решение. Задаем на кривой А В ряд точек (рис. 210, б) и проводим через
них образующие конуса. Геометрическим местом горизонтальных следов образующих
будет искомая кривая МхМг.
¦- 228, Найти линию пересечения конической поверхности, задан-
нрй вершиной S и"направляющей АВ, с пл. V (рис. 211).
; 229"'. Построить проекции прямого кругового конуса, ось кото-
которого лежит на прямой SM(SM\\hr. V) (рис. 212, а). Высота конуса равна
Ц окружность основания касается пл. Я.
Решение. Так как в данном случае прямая SM параллельна пл. V, то
мржно отложить (рис. 212, б) на s'tn' отрезок s'O , равный /. Точка (О), О) является
центром окружности основания. Эта окружность проецируется на пл. V в отрезок
прямой. Поэтому, проводя через точку б' прямую, перпендикулярную к s'O , по-
получим точку /', радиус основания 04 и весь диаметр основания !'3 .
Точка (/', /) является точкой касания основания конуса с пл. Н. Фронт, про-
проекция конуса — треугольник l's'3'. На пл. Н окружность основания проецируется
в!эллипс, большая ось которого 2—4 равна отрезку 1'3', а малая ось — отрезку /—3.
Для построения очерка горизонт, проекции конуса надо найти те его образую-
образующие, горизонт, проекции которых касаются эллипса, т. е. те, которые являются
самыми крайними, если смотреть на конус сверху. На рис. 212, в показан вписанный
в конус шар; он касается конуса по окружности, фронт, проекция которой 5'6'.
Точки 7 и 7L этой окружности принадлежат также и экватору вписанного шара.
162
a
e)
3)
163
я
с*
О.
J64
.Д ¦ '
Искомые образующие проходят через точки 7 и 7, и пересекают окружность основа-
основания ы точках 8 и 8,.
Горизонт, проекции s—7 и s—?l этих образующих касаются эллипса, построен-
построенного (рис. 212, д) по осям 2—4 и /—3, в точках 8 и 8V
Очерк горизонт, проекции конуса составляется из прямых s—8 и s—8, и части
эллипса 8—2—3—4—8,.
Касательные к эллипсу из точки s можно провести и так, как это показано на
рис. 212, г: сначала провести касательную из точки s к окружности, построенной на
малой оси эллипса как на диаметре, получить точку k и по ней точку 81. Повернув
окружность основания конуса до параллельности пл. V (на рис. 212, г показана
только часть этой окружности, проведенная из точки (У радиусом 04'), получаем
точку 80 и полухорду в'8о. Откладывая от прямой sO вверх и вниз отрезок, равный
этой полухорде, получаем точки 8 и 8t—точки касания очерковых образующих о
эллипсом. Эллипс должен пройти через эти точки.
230. Построить проекции прямого кругового конуса, если точка
S — вершина конуса, а точка О — центр окружности основания; эта
окружность одной своей точкой касается пл. V (рис. 213).
231*. Построить проекции прямого кругового конуса, основание
которого должна быть в плоскости^.?...(дис^.2144_д)ж._вершина кону-
конуса— в точке S. Точка А принадлежит окружности основания конуса.
Решение. Из точки S проводим (рис. 214, б) перпендикуляр к пл. Р и нахо-
находим точку их пересечения (О1, О), являющуюся центром окружности основания ко-
конуса. Совмещаем (рис. 214, в) пл. Р с пл. Н и строим совмещенные положения точек О
и А (Ро и <4о)- Радиус окружности основания конуса равен расстоянию между этими
точками. ¦
Из точки 0о проводим окружность основания и строим с ее помощью (рис. 214, г)
эллипсы, в которые она проецируется на пл. Н и пл. V (см. задачу 189).
Проведя из точек s' и s касательные к соответствующим эллипсам, получаем
искомые проекции конуса (рис. 214, д).
232. Построить проекции прямого кругового конуса, ось кото-
которого лежит на прямой SM, а точка А принадлежит окружности есо
основания (рис. 215). Применить при решении способ совмещения.
233*. Построить проекции прямого кругового конуса, если его
ось проходит через точку / (рис. 216, а), основание расположено на
плоскости, заданной параллельными прямыми АВ и CD, а плоскость,
заданная треугольником EFG, касается этого конуса.
Решение. На рис. 216, б показано, что искомый конус оказывается в дву-
двугранном угле, образованном плоскостью основания (она задана параллельными
прямыми АВ и CD) и касательной плоскостью (заданной треугольником EFG). Ось
конуса, проведенная через точку / перпендикулярно к плоскости основания, опре-
определяет в пересечении с этой плоскостью центр основания — точку О, а в пересечении
с касательной плоскостью вершину конуса — точку S. Тут же определится и радиус
основания ОК. Очевидно, надо найти прямую, по которой взаимно пересекаются
плоскость основания конуса п касательная к нему плоскость. Это прямая MN.
Если ввести дополнительную плоскость проекций так, чтобы она расположилась пер-
перпендикулярно к MN, то на полученном чертеже сразу обнаружатся точки О и S
и радиус окружности основания конуса.
Итак, начинаем с построения линии пересечения плоскости основания конуса
с плоскостью, касательной к конусу (рис. 216, в). Это делаем путем нахождения
точек пересечения прямых АВ и CD с плоскостью треугольника EFG. Через АВ и
CD проведены вспомогательные горизонтально-проецирующие плоскости R и Q.
Теперь (рис. 216, г), последовательно вводя дополнительные плоскости проек-
проекций — пл. U, перпендикулярную к пл. V и параллельную MN, и пл. Т, перпенди-
перпендикулярную к пл. U и к прямой MN, можно получить чертеж, на котором обе пло-
плоскости — основания и касательная к конусу — изображены в виде прямых. Проводя .
Щ
166
Рис. 215.
Рис. 216а—в.
167
90°
168
на этом чертеже через точку it проекцию высоты конуса перпендикулярно к плоскости
его основания, получаем проекцию О( центра основания и Sf— проекцию вершины
конуса. Получаем также отрезок Otmt, равный радиусу основания.
Рис. 216д.
Получив на рис. 216, г проекции s'O' и sO, переходим к заключительной стадии
построения (рис. 216, д), т. е. к получению чертежа конуса.
234. Построить проекции прямого кругового конуса, если
(рис. 217) точка О является горизонт, проекцией центра основания,
расположенного в пл. Р, а плоскость, заданная прямыми АВ н CD,
касается поверхности искомого конуса.
1235*. Даны (рис. 218, а) точки: О — центр сферы, А — точка на
ее поверхности. Построить проекции сферы.
Решение. Радиус искомой сферы выражается отрезком с проекциями <Уа'
и Оа (рис. 218, б). Определяем натуральную величину R этого отрезка и проводим
нэ точек О' и О окружности радиусом R.
189
Рис. 219,
170
236. Построить проекции сферы с центром в точке О; точка А
принадлежит экватору сферы (рис. 219).
237*. Построить сферу радиуса R, касательную в точке D к пло-
плоскости, заданной треугольником ABC (рис. 220. а).
а'.
Решение. Центр сферы должен лежать
на перпендикуляре, проведенном в точке О к
пл. треугольника ABC. Найдя (рис. 220, б) про-
проекцию а, проводим в пл. треугольника горизон-
горизонталь А—2 ифронталь С—3 (рис. 220, в), исполь-
используя их для построения проекций de и d'e' пер-
перпендикуляра к этой плоскости.
Теперь надо отложить на прямой DE от
точки D отрезок, равный R. Взяв некоторый от-
отрезок DF (рис. 220, г), находим его ^атураль-
ную величину DF, откладываем на DF отрезок,
равный R, и получаем сначала проекцию О, а
по ней О'. Остается провести окружности из
точек О и О' радиусом R. Изображена лишь одна
сфера — по одну сторону плоскости. Если от то-
точек d и d! отложить на продолжении прямых de
и d'e' отрезки dO^=dO и d'O'^d'O1 (эти построе-
построения на чертеже не показаны), то точка О, будет
центром второй сферы с тем же радиусом R, ка-
касательной к плоскости треугольника ABC в
точке D.
6}
Рис. 220а—в.
238. Построить сферу, касательную к плоскости, заданной тре-
треугольником ABC (рис. 221), если центр тяжести площади треуголь-
треугольника является точкой касания, а радиус сферы равен половине сто-
стороны ВС.
171
т
Рис. 222а, б.
172
239*. Построить сферу с центром на прямой АВ (рис. 222, а),
касательную к плоскостям, заданным треугольниками MNC и MND.
Решение. Геометрическим местом центров сфер, касательных к задан-
заданным Плоскостям Р и Q (рис. 222, б), является плоскость (II), проходящая через
линию их пересечения MN и делящая двугранный угол между плоскостями
пополам.
Центр искомой сферы — точка О находится в точке пересечения плоскости U
с прямой А В. Радиус R сферы равен расстоянию от точки О до любой из заданных
плоскостей.
Все это легко получить, применяя способ перемены пл. пр. (рис. 222, в). Первую
дополнительную плоскость проекций (S) вводим так, чтобы она была перпендикуляр-
перпендикулярна к пл. Я и параллельна ребру MN двугранного угла, а затем вторую дополнитель-
Рис. 222в.
нуго пл. Т перпендикулярно к пл. S и к тому же ребру MN. Получив проекцию дву-
граиного угла в виде угла Cttntdf, проводим в нем биссектрису, изображающую пл. О,
находим точку 0( и отрезок Otkt=R. Остальное ясно из чертежа.
240. Построить сферу, касательную к граням ABC и SAB пира-
пирамиды SABC (рис. 223), взяв ее центр на ребре SC.
241*. Провести через прямую АВ плоскость, касательную к дан-
данной сфере (рис. 224, а).
173
Рис. 223.
б)
Рис. 224а, б.
174
S\T
t)
Рис. 224в, r.
17S
Решение. Представив себе пространственную картину (рис. 224, 6), можно
видеть, что сфера касательна к двум плоскостям, составляющим двугранный угол
с ребром АВ. Отсюда вытекает следующий План решения: а) применяя способ пере-
перемены пл. пр., расположить дополнительную пл. Т перпендикулярно к АВ, б) полу-
получить на этой же пл. Т проекцию сферы, в) провести из тачки — проекции АВ н& пл.
Т — две касательные к окружности, представляющей собою проекцию сферы на
пл. Т. Эти касательные можно рассматривать как проекции плоскостей, касательных
к сфере (они перпендикулярны к пл. Т), и в то же время как проекции двух прямых,
проведенных из некоторой точки на АВ касательно к сфере. Очевидно, прямая АВ
и каждая из этих касательных определяют плоскость, проходящую через АВ каса-
касательно к сфере. Если же выделить точки касания М и N (рис. 224, б), то каждая из
касательных плоскостей будет выражена прямой АВ и точкой касания (М или N).
На рис. 224, в показано построение проекций прямой АВ и сферы на пл. Т и
проекций /И| и tit точек касания, на прямцх, проведенных из точки щ (Ь{) касатель-
касательно к окружности с центром
ct\ Заключительная стадия
построения показана на рис.
224, г: проведя через точку
с5 прямую параллельно оси
77S, получаем на этой пря-
прямой проекции ms и ns, a
также ks— проекцию точки
К. на прямой АВ; из точки
К проведены касательные
КМ и KN к сфере.
Остальное ясно из чер-
чертежа.
"!
Рис. 225а, б.
242*. Построить проекции тела вращения, ограниченного по-
поверхностью тора и двумя кругами (основаниями), плоскости которых
перпендикулярны к оси этого тела; ось задана прямой МУУ(ЛШ||пл. V,
рис. 225, а). Точки А, В а С принадлежат поверхности тела, причем
176
точка А лежит на окружности одного из оснований тела, а С — на
окружности другого Основания.
Решение. Так как ось тела параллельна пл. V, то очерком фронт, проекции
будет главный меридиан тела. Проведя через а' и с' (рис. 225, б) прямые, перпенди-
перпендикулярные к т'п', мы получим фронт, проекции плоскостей оснований тела, а введя
П'
в)
Рис. 225в, г.
дополнительную пл. S, перпендикулярную к пл. V и к MJV, получим натуральный'
вид обоих оснований — круги радиусов mscs и msas. Пл. S взята совпадающей с
плоскостью меньшего основания. Построена также параллель, на которой распо-
расположена заданная точка В.
По точкам cls, als и bls находим точки cit a( и ft,. Через эти точки должна пройти
дуга окружности — фронт, проекция образующей тора в ее крайнем положении
(рис. 225, в). Проведя эту дугу и ей симметричную относительно оси т'п', получим
фронт, проекцию тела вращения. Для его горизонт, проекции строим эллипсы — про-
проекции оснований.
Чтобы получить горизонт, проекцию полностью, надо построить ее очерк
(рис 225, г). Для этого прибегаем к помощи ряда сфер, вписываемых в тело вращения.
' Эти сферы касаются поверхности тела по окружностям, фронт, проекции кото-
которых — отрезки прямых, перпендикулярных к т'п'. В пересечении окружностей ка-
касания с экваторами сфер находим точки 7, 6, 1,2 и др. для очерка горизонт, проекции.
Например, взяв центр сферы в точке F, проводим прямую f'O, определяем точку
касания очерка сферы с очерком тора, проводим проекцию окружности касания,
177
перпендикулярную к т'п', и находим точку б' пересечения ее с проекцией экватора
сферы. Проведя из точки f окружность — горизонт, проекцию экватора, находим
на ней точку 6.
Так же поступаем, взяв, например, центр сферы в точке О; находим точку B , 2).
Через найденные проекции точек проводим кривую ffffiUS и кривую
7—,6—/—2—k, являющуюся искомой очерковой линией горизонт, проекции поверх-
поверхности тора. Горизонт, проекции точек кривой, расположенных ниже точки К, не-
невидимы.
243. Построить проекции тела вращения, ограниченного поверх-
поверхностью тора и двумя кругами (основаниями), плоскости которых
перпендикулярны к оси тела вращения, ось задана прямой MN
Рис. 226.
(MN\\nn, И, рис. 226). Точки А, В а С принадлежат поверхности тела,
причем точка А лежит на окружности одного, а точка С — на окруж-
окружности другого основания.
244*. Построить проекции тела вращения, ограниченного по-
поверхностью тора и кругом (основанием), плоскость которого перпен-
перпендикулярна к оси этого тела. В точке 5 (рис. 227, а) находится вершина
178
Q\T
Рис. 227а, 6.
179
тела, основание лежит в плоскости, заданной треугольником AMN.
Радиус основания тела равен R. Плоскость, заданная треугольником
BMN, касательна-к поверхности тела.
Решение. Легко представить себе такое положение заданных элементов
относительно некоторой пл. проекций, при котором двугранный угол между пло-'
скостями с ребром MN изобразится в виде угла, стороны которого являются проек-
проекциями заданных треугольников; перпендикуляр, проведенный из проекции вершины
S на соответствующую сторону угла, определит высоту тела вращения и центр круга
основания. Действительно (рис. 227, 6), применяя способ перемены плоскостей про-
проекций, получаем соответствующую конфигурацию в проекции на дополнительной
пл. Т. Образующая тела вращения на этой плоскости должна изобразиться дугой
окружности, проходящей через точки ц и cj (точка cj должна лежать на прямой
О на расстоянии R от точки Oj) и касательной к прямой
Рис. 227в.
; ^Построение такой дуги показано на рис. 227, а. Через точки sj и ct проведена пря-
прямая до пересечения с прямой mtbt в точке /. Отрезок Sf! разделен пополам, и из
тонки 2 как из центра проведена окружность (показана ее половина) радиусом Sf2.
Из точки С( проведен перпендикуляр к stct до пересечения с окружностью в точке 3.
Проводя дугу радиусом /—3, получаем на прямой щЬ^ точку 4 Теперь, проведя пер-
перпендикуляр в точке 4 к прямой тф% и к отрезку s&i в его середине, находим точку 5—
центр дуги, проходящей через точки st и с< и касательной в точке 4 к прямой тф^
; Итак, из рис. 227, б и в мы получаем высоту тела вращения, натуральную вели-
величину радиуса дуги, дающей очерк его меридиана, и проекции О' и О центра основания.
Теперь переходим к построению проекций тела вращения на пл. V и пл. Н
(рис. 227, г). Используем способ перемены пл. пр. Сначала вводим дополнительную пл.
Р перпендикулярно к пл. Н и параллельно оси тела вращения: ось PIH проводим
параллельно sO. Построив sp0p, проводим через 0р прямую, перпендикулярную к
SpOp, и получаем на пл. Р проекцию основания в виде отрезка прямой, равного 2R,
а по ней — проекцию на пл. Н в виде эллипса. Проекция тела на пл. Р очерчивается
дугами радиуса, величина которого получена на рис. 227, в. Пользуясь изображением
186
на пл. Р, находим очерк горизонт, проекции при помощи вписанных сфер (подобно
рассмотренному в задаче 242 на рио. 225, г). Например, взяв проекции сферы о цент-
центрами в» и е, получаем точку / для очерка проекции тела вращения.
Аналогично поступаем и для построения фронт, проекции тела, вводя допол-
дополнительную пл. ?/..
245. Построить проекции тела вращения, ограниченного по-
поверхностью тора и двумя кругами в плоскостях, перпендикулярных
к оси тела вращения, если дано! а) точка Ог— горизонт, проекция
центра основания, расположенного в пл. Р и имеющего радиус /?х;
Рис. 228.
б| Rt ~- радиус другого основания; в) Л — расстояние между основа-
основаниями; г) пл. Q касательна к поверхности тора (рис. 228).
246*. По заданной проекции точки, принадлежащей изображен-
изображенной на чертеже поверхности, найти другую проекцию этой точки.
: Решение. При решении применен общий прием, заключающийся в отнесении
рассматриваемой точки к некоторой линии, заведомо принадлежащей поверхности.
\ На рис. 229, а по заданным проекциям а и Ъ точек, принадлежащих цилиндриче-
цилиндрической поверхности, надо было найти проекции а и Ь'. Построение выполнено при по-
мющи образующих А—1 и В—2. Также и на рис. 229, б применены образующие
конической поверхности S—/ для нахождения проекции точки а по заданной а' и
S—2 для нахождения проекции точки Ь' по заданной Ь.
На рис. 229 , в найдены проекции а и а" по заданной проекции а' точки, принад-
принадлежащей сфере. Проведена горизонт, проекция параллели, взятой на уровне точки
А,— окружность радиуса OJ'. Дальнейшее ясно из чертежа.
182
г)
Рис. 229а—г.
183
a' f
i bj/\ TST
1 111 Не
аа
Ж)
Рис. 229д—ж.
194
На тем же рис. 229, в показано, что можно, например, построить проекцию b
точки В, принадлежащей сфере, по заданной проекции Ь' иначе, чем это сделано для
точки А, а именно: представить себе сечение сферы плоскостью, параллельной пл. V,
по ркружности' радиуса О'Ь', найти положение горизонт, проекции этой Окружности
и н<а ней взять проекцию Ь. Проекцию Ь" можно найти, построив профильную про-
проекцию окружности радиуса О'Ь'.
Можно было бы представить себе плоскость, проходящую через заданную точку
параллельно пл. W. Это показано на рис. 229, в на примере нахождения проекций с
и с точки С по заданной ее проекции с'. Плоскость, параллельная пл. W, рассечет
сферу по окружности радиусаО24'=О24"¦ Находим на профильной проекции этой'
окружности проекцию с". Затем находим проекцию с.
Все построения на рис. 229, в выполнены в предположении, что точки А, В и С
даны на той части сферы, которая видима на пл. V.
На рис. 229, г найдена проекция а по заданной а' и проекция Ь' по заданной 6;
точки принадлежат поверхности тора. Применены параллели поверхности.
На рис. 229, д по заданным проекциям а' и 6 точек А и В, принадлежащих пря-
прямой винтовой поверхности, найдены проекции а и Ь'. Это сделано путем отнесения
точек к соответствующим положениям образующей — прямой линии. Горизонт,
проекции образующих направлены радиально, а фронт, проекции — перпендику-
перпендикулярно к фронт, проекции оси поверхности.
Для нахождения фронт, проекции точки В, принадлежащей косой винтовой
поверхности (рис. 229, е), по заданной ее горизонт, проекции Ь также использована
прямолинейная образующая поверхности. Ее горизонт, проекция определена точ-
точками / и 2, по ним взять; точки /' и 2' на фронт, проекции винтовых линий, и прове-
проведена проекция /' 2', на которой и найдена точка Ь'. Точность построения (так же, как
и на рис. 229, д) зависит от тщательности построения синусоид — фронт, проекций
винтовых линий. Чтобы повысить точность, можно применить расчет подъема точек
на фронт, проекции в зависимости от углового перемещения на горизонт, проекции.
Например, точка, образующая винтовую линию, в положении / переместилась вдоль
оси цилиндра на долю шага, соответствующую доле полного поворота вокруг оси:
шаг ~~ 360° '
Что же касается нахождения горизонт.проекции точки А по заданной проекции а'
(см. рис. 229, е), то здесь применено сечение косой винтовой поверхности плоскостью,
перпендикулярной к ее оси. Получающаяся при этом спираль Архимеда изобразится
без искажения на горизонт, проекции. Проведя фронт, проекцию спирали Архи-
Архимеда — Отрезок 3'4', находим проекции точек 3 и 4; затем делим угол а на п равных
частей и на такое же число равных частей делим отрезок 5—4, равный /. Точки спи-
спирали получаются в пересечении соответствующих прямых и дуг, как это показано
на чертеже. Искомая точка а находится на спирали.
На рис. 229, ж показано построение проекции а' точки А и проекции Ь' точки В,
принадлежащих косой плоскости (гиперболическому параболоиду). Плоскостью
параллелизма является пл. Н. Через заданную проекцию а проведена проекция 1'2'
образующей этой поверхности (/'2'[|оси х), построена проекция 1—2, на которой и
получена искомая горизонт, проекция точки А.
Для нахождения проекции 6' проведена через точку Ь прямая 3—4 — горизонт,
проекция некоторой линии, принадлежащей поверхности. По точкам пересечения
прямой 3—4 с образующими E—6, 4—8 и др.) найдены точки для проведения фронт,
проекции 3'4' полученной кривой, на которой определяется искомая проекция Ь'.
§ 22. Пересечение поверхности плоскостью и прямой линией
247*. Построить проекции части прямого кругового цилиндра,
остающейся после пересечения его фронтально-проецирующей пло-
плоскостью Р (рис. 230). Дать натуральный вид сечения и полную раз-
развертку поверхности.
186
186
Решение. Судя по положению секушей пл. Р относительно оси цилиндра,
линия на его боковой поверхности, получаемая в пл. Р, представляет собой эллипс
с центром в О (на оси цилиндра); большая ось эллипса равна отрезку 1'Т, а малая—
диаметру цилиндра. Учитывая, что пл. Р пересекает и одно из оснований цилиндра,
получаем сечение в виде фигуры, ограниченной дугой эллипса и отрезком прямо&АВ.
Для построения этой фигуры применен способ перемены плоскостей проекций, а
именно введена дополнительная пл. S, перпендикулярная к пл. V и параллельная
пл. Р. Построение можно было бы осуществить, не вводя пл. S и осей V/H и S/V,
а пользуясь большой осью эллипса для откладывания от нее отрезков, взятых на
горизонт, проекции, как, например, отрезка / для получения точек as и bs.
Примененное на рис. 230 деление ок-
окружности основания на некоторое число
равных между собою дуг (взято 12 дуг) пред-
представляет собою обычный прием для построе-
построения развертки в подобных случаях Полная
развертка составлена из. а) развертки боко-
боковой поверхности, ограниченной пятью отрез-
отрезками прямой линии и кривой А0СаВ0— си-
синусоидой, в которую развернулся эллипс,
б) круга основания цилиндра, в) натурального
вида сечения, г) сегмента, полученного на
верхнем основании.
248*. Найти точки пересечения
поверхности цилиндра прямой линией
(рис. 231, а).
Решение. Применяем для решения
задачи общий прием построения точек пере-
пересечения прямых линий с любыми поверхнос-
поверхностями, а именно: 1) заключение прямой в не-
некоторую плоскость, 2) построение линии пе-
пересечения поверхности этой плоскостью, 3)
нахождение точки пересечения заданной пря-
прямой и этой линии. В данной задаче возьмем
вспомогательную плоскость так, чтобы она
рассекла поверхность цилиндра по прямым
линиям — образующим. Это наиболее прос-
простой прием для заданного случая. На рис.
231, б показано, что вспомогательная пл. Р
определяется прямой АВ и пересекающей ее
прямой CMit параллельной образующим ци- рис 231 a
линдра. Такая плоскость рассечет цилиндр
по его образующим.
Построение показано на рис. 231, в. Чтобы определить образующие, по которым
плоскость, проведенная через АВ, пересечет цилиндр, построены горизонт, следы
прямой АВ (точка/п,/^) и прямой СМг (точка тгот2). Через следы прямых проведен
горизонт, след плоскости — прямая тхтг. Этот след пересекает в точках ./ и 2
окружность — след цилиндрической поверхности на той же пл. Н. Проведя/—k и
2—п параллельно стг, получаем точки k и п — горизонт, проекции искомых точек
пересечения АВ с поверхностью цилиндра, а затем k' и п'—фронт, проекции этих
точек.
249. Найти точки пересечения поверхности "Цилиндра прямой
линией (рис. 232, а и б).
250*. Построить проекции части прямого кругового конуса, ос-
оставшейся после пересечения его фронтально-проецирующей пло-
плоскостью (рис. 233, а и б). Дать натуральный вид сечения и полную раз-
развертку поверхности изображенного тела.
187
las
Решение. Судя по положению секущей плоскости относительно образую-
образующих конуса, линия на его боковой поверхности, получаемая в пл. Р, представляет
собою эллипс. Большая ось этого эллипса может быть представлена отрезком m'k'.
Деля m'k' пополам, получаем фронт, проекцию центра эллипса — точку О', а по
ней и проекцию О. Теперь можно найти малую полуось, проведя секущую плоскость
а)
Рис. 2.33а.
через точку О перпендикулярно к оси конуса и взяв в полученном круговом сечении
полухорду lt. Малая ось эллипса равна 21Х. Горизонт, проекция эллипса также пред-
представляет собою эллипс; его большая ось mk, а малая — cd, равная 21Х.
Последующие построения подобны выполненным на рис. 230. Натуральный вид
фигуры сечения построен при помощи способа перемены пл. пр., причем дополни-
дополнительная пл. S взята совпадающей с пл. Р. Замечание на стр. 187 о том, что построение
можно было бы осуществить, не вводя пл. S и осей VIH и S/V, справедливо и для дан-
данного случая.
Зная, что боковая поверхность конуса развертывается в круговой сектор с уг-
углом ф=-т-180° при вершине, где d — диаметр основания, а I — длина образующей
конуса, строим сектор с разбивкой его на равные части соответственно разметке
189
образующих па чертеже конуса. Зная, например, положение образующей S—3 на
чертеже и на развертке, находим положение точки No на развертке при помощи нату-
натуральной величины отрезка /э образующей от вершины S до точки N. i
б)
Рис. 2336.
В полную развертку оставшейся части поверхности входят: а) развертка боковой
поверхности, ограниченная дугой окружности радиуса / и построенной кривой
Ио^оМоВо; б) части круга основания, в) натурального вида сечения, причем круг
и сечение граничат по хорде А0Ва.
251*. Найти точки пересечения поверхности прямого кругового
конуса прямой линией (рис. 234, а).
Решение. Применяя вспомогательную плоскость, проведенную через дан-
данную прямую линию, задаемся целью обеспечить простейшее пересечение конуса
этой плоскостью. Секущую плоскость надо провести через вершину конуса. Она
будет пересекать конус по прямым линиям (образующим). На рис. 234, б показана
пл. Р, проведенная через данную прямую АВ и вершину конуса. Проведя пл, Т,
190
a
Рис. 234а—в.
191
перпендикулярную к оси конуса и, следовательно, пересекающую его по окружности,
находим на пл. Т линию ее пересечения с пл. Р — прямую DE. Образующие, по ко-
которым пл. Р пересекает конус, определяются вершиной S и точками / и 2. На этих
образующих и получаются точки К и М, в которых прямая АВ пересекает поверх-
поверхность конуса.
На рис. 234, в пл. Р задана прямой АВ и проведенной через вершину S прямой
SC, пересекающей АВ в точке С и параллельной пл. Т. Плоскость Р пересекаетjm. T
по прямой />?, параллельной SC. Поэтому, найдя на чертеже точку D (точку пересе-
пересечения прямой АВ с пл. Т), проводим de\\sc. Образующие, по которым пл. Р переев-,,
кает поверхность конуса, изображены лишь их проекциями s—/ и s—2. Этого до-
достаточно, чтобы найти горизонт, проекции шип точек пересечения, а по ним про-
проекции т' и /г'.
Если рассматривать конус, поставленный на пл. Н, то надобность в пл. Т от-
отпадает.
252. Найти точки пересечения поверхности конуса прямой ли-
линией (рис. 235, а и б).
а'
Рис. 235а, б.
Указание. Принять плоскость круга в качестве вспомогательной плоско-
Сги, подобной пл. Т на рис. 234, в.
253*. Найти точки пересечения прямой линии с поверхностью
сферы (рис. 236, а).
192
Решение. Используя вспомогательную секущую плоскость, проходящую
через данную прямую (рис. 236, б), получаем окружность. Искомые точки М и N
получаются при пересечении этой окружности с прямой линией.
а* а)
Рис. 236а—в.
4
На рис. 236, в показаны графические построения а помощью способа перемены
пл. dp. .
Дополнительная плоскость S перпендикулярна к пл. И и параллельна вспо-
вспомогательной горизонтально-проецирующей плоскости W, проведенной через пря-
прямую Л В.
На пл. S изображаем не данную поверхность сферы, а лишь получаемую
на ней окружность от пересечения плоскостью Т. Получив также проекцию ajba,
находим точки /и, в п„ а по ним т и п и далее м! и п'.
7 Ы. О. Гордон а др. №
214. Найти точки пересечения прямой линии с поверхностью
сферы (рис. 237, а и б).
V
Рис. 237а, б.
255*. Найти точки пересечения прямой линии с поверхностью
Вращения (рис. 238, а).
! Р е ше н и е. Проводим через прямую АВ (рис. 238-, б) горизонтально-проеци-
горизонтально-проецирующую плоскость R и строим линию пересечения ею данной поверхности. Точки
»той линии находим при помощи параллелей поверхности. Например, проведя дугу
(жружности радиуса s—3, получаем на фронт.проекции главного меридиана точку 3, ,
Определяющую уровень соответствующей параллели, и по точке 3 находим 3'. Точ-
¦|<и 4' и 5' получаем по точкам 4 и 5. Высшую точку кривой /' находим по ее горизонт,
рроекции /. /
¦ Построив фронт, проекцию кривой, находим точки ее пересечения с фронт", про-
проекцией а Ь', а именно точки т и п' — фронт, проекции искомых точек пересечения
прямой АВ с заданной поверхностью. По точкам т' и п' строим m и п.
Если через А В в качестве вспомогательной плоскости провести фронтально-
Проецирующую (рис. 238, в), то также придется построить кривую линию. Теперь
сначала найдем точки т и п, а по ним тип'.
Оба рассмотренных решения по существу друг от друга не отличаются. Но можно
представить себе другую схему построения, когда проведение плоскости через
194
a
a
Рис. 238а—г.
195
заданную прямую отпадает. Дело в том, что заданная прямая может играть роль
образующей однополостного гиперболоида вращения при той же оси, что и у задан-
заданной поверхности (рис. 238, г). Так как обе поверхности вращения соосны, то они
пересекутся по окружностям. Искомые точки пересечения прямой с поверхностью
вращения получаются на этих окружностях. Предоставляем выполнить такое по-
построение читателю.
Отрицательным моментом в построениях, показанных на рис. 238, б н в, явля-
является необходимость пользоваться кривой; это снижает точность определения поло-
положения точек М и N. Но и в случае использования гиперболоида вращения прихо-
приходится строить по крайней мере одну ветвь гиперболы, т. е. опять кривую. Это также
снижает качество такого приема решения разобранной задачи
256. Найти точки пересечения прямой линии с поверхностью
вращения (рис. 239, а и б).
Рис. 239а, б.
: 257*. Найти точку пересечения прямой А В с поверхностью ко-
коноида, заданного направляющими CD a EF и плоскостью параллелизма
Н (рис. 240, а).
,*
Р е ш е н и е. Через прямую АВ проводим (рис. 240, б) фронтально-проецирую--
п^ую плоскость R и строим кривую MN пересечения этой плоскости с коноидом.
Задавая на кривой CD ряд точек, проводим через них образующие параллельно пл.Я;
горизонт, проекции этих образующих проходят через точку e(f). Находим точки их
пересечения с плоскостью R. ,.
Точка k пересечения кривой тп и прямой ab является горизонт, проекцией иско-
искомой точки; по k находим к' на а'Ь'.
196
Рис. 240а, б.
e'f
Рис. 241.
Рис. 242.
197
258. Найти точку пересечения прямой А В с поверхностью ко-
коноида, заданного направляющими CD и EF и плоскостью параллелизма
V (рис. 241).
259. Найти точку пересечения прямой А В с поверхностью коно-
коноида, заданного направляющими CD и EF и плоскостью параллелиз-
параллелизма — фронтально-проецирующей плоскостью Р (рис. 242).
260"'. Найти точку пересечения прямой АВ (рис. 243, а) с косой
плоскостью, заданной направляющими CD и EF и плоскостью парал-
параллелизма — фронтально-проецирующей плоскостью Р.
а
а
Рис. 243а, б.
Решение. Через прямую А В (рис. 243, б) проводим фронтально-проецирую-
фронтально-проецирующую плоскость R и находим кривую пересечения ее с заданной поверхностью. Так же,
Как в задаче 257, берем на прямой CD ряд точек, проводим через них образующие
^параллельно плоскости параллелизма Р) и строим точки пересечения этих обра-
образующих с плоскостью R. Получаем кривую с проекциями 1'2', 1—2 и точку пересе.
Т1ения проекций /—2 и ab — точку к. Это горизонт, проекция искомой точки. По k
Заходим k' на а'Ь'.
\ 261. Найти точку пересечения прямой А В с косой плоскостью,
Заданной направляющими CD и EF и плоскостью параллелизма И
(рис. 244).
\ 262. Найти точки пересечения прямой А В с косой плоскостью,
заданной направляющими CD и EF и плоскостью параллелизма V
(рис. 245).
¦ 263*. а) Разбить поверхность заданного на рис. 246, а тела вра-
вращения на зоны различных по своему виду поверхностей; б) построить
фронтальную и профильную проекции данного тела вращения, усечен-
усеченного плоскостями Рх и Р2.
198
Рис. 244.
Рис. 245.
199
Решение. Заданное тело вращения состоит из конуса, цилиндра, кругового
кольца и сферического сегмента. Соответственно поверхность тела содержит зоны:
/ — коническую, // — цилиндрическую, /// — кругового кольца, IV — сфериче-
сферическую (рис. 246, б). "
-к
Рис. 246а, б.
! Коническая поверхность образована отрезком АВ, цилиндрическая — отрез-
Цм ВС, поверхность кругового кольца — дугой CD радиуса Ru сферическая —
дугой DE радиуса Яг.
: Каждая из этих зон граничит с соседней по окружности. Окружности проходят
соответственно через точки В, С и D.
Плоскость Р2 пересекает (рис. 246, в) коническую поверхность по гиперболе
S-^-J—4—9, цилиндрическую—по образующим, проходящим через точки 5 и 9,
поверхность кругового кольца — по кривой 5—7—8 и сферу — по окружности ра-
радиуса R=0'I . Линии, образуемые на поверхности тела секущей плоскостью Ри
такие же, как от плоскости Р2, и на рис. 246, в их проекции совпадают с построенными,
так как плоскости 7^, и Р, параллельны и отстоят на равные расстояния от плоскости
симметрии заданного тела, .
200
Взяв, например, секущую плоскость Su получаем окружность радиуса О".
Эта-окружность дает в пересечении с пл. Р% точку 4", по которой получаем на фронт,
проекции точку 4', принадлежащую гиперболе. Чтобы получить вершину гипер-
гиперболы, отмечаем точку /"— профильную проекцию этой вершины — и строим со-
соответствующую ей проекцию /' на поверхности конуса.
j На рис. 246, в показан также пример построения фронт.. проекции одной из го-
чек! G) кривой, по которой пл. Р2 срезает тело в зоне кругового кольца.
8"
Рис. 247.
264. Построить линию среза на поверхности тела вращения
(рис. 247). Секущую плоскость взять параллельной плоскости проек-
проекций V и отстоящей от оси тела вращения на расстояние, равное 1'0'.
Назвать полученные линии, входящие в состав линии среза.
201
§ 23. Взаимное пересечение поверхностей
265*. Построить: а) проекции линии взаимного пересечения по-
поверхностей призмы и сферы; б) натуральный вид сечения А — А
(рис. 248, а).
Рис. 248а—в.
Решение. В данном случае одна из проекций линии пересечения, а именно
горизонтальная, известна, так как сливается с горизонт, проекцией боковой поверх-
202
ности призмы. Это значительно упрощает построение: оно сводится к насаждению
фронт, проекций точек, принадлежащих поверхности сферы, по их горизонт, проекци-
проекциям. Так, проекция с' (рис. 248, б) найдена при помощи горизонтали на поверхности сфе-
сферы; эта горизонталь имеет радиус Ос. Точки d' и е' получены на фронт, проекции глав-
главного меридиана сферы по проекциям d и е, точка а' —на фронт, проекции экватора.
1 Другим обстоятельством, имеющим большое значение в построении, является
то, что получаемая линия пересечения известна: каждая боковая грань призмы пере-
пересекает поверхность сферы по дуге окружности. Из этих дуг одна, лежащая на задней
грани, проецируется на пл. V без искажения; ее радиус равен а—3. Две другие дуги
проецируются на пл. V в виде дуг эллипсов.
Проведя перпендикуляры 0—1 и 0—2, мы определяем горизонт, проекции вер-
вершин эллипсов—точки / и 2; по ним находим проекции /' и 2'. На рис. 248, б дуги
эллипсов показаны за точками с' и Ь' штрих-пунктирными линиями. Тело на
рис. 248, б представлено как монолит (например, отливка). Поэтому сечение на
рис. 248, в представлено в виде одной фигуры, что подчеркивается и штриховкой..:
266. Построить: а) проекции линии пересечения поверхностей
призмы и цилиндра; б) натуральный вид сечения А —А (рис. 249).
Указание. Горизонт, проекция линии пересечения в задачах 266 и 267
совпадает с частью соответствующей проекции тела.
Рис. 249.
Рис. 250.
267. Построить: а) проекции линии пересечения поверхностей
призмы и коруса; б) натуральный вид сечения А —А (рис, 250).
233:
288« Построить: а) проекции линии пересечения поверхностей
призмы и кругового кольца; б) натуральный вид сечения А — А
рис. 251).,
Указание. Фронт, проекция линии пересечения совпадает с частью соот-
соответствующей проекции призмы.
Рис. 251.
269*. Построить: а) проекции линии пересечения поверхностей
цилиндра и сферы; б) натуральный вид сечения А —А (рис. 252, а).
; Решение. Все точки фронт, проекции цилиндра (рис. 252, 6) могут Сыть
приняты за фронт, проекции точек, принадлежащих искомой линии пересечения.
А|отсюда легко найти, например, проекции d, m, n на горизонт, проекциях соответ-
соответствующих параллелей сферы, проекции a, b, k на горизонт, проекциях дуг окруж-
окружностей, проводимых на фронт, проекции сферы радиусами с'а', c'b', c'k'. Точки а и 6
представляют собою горизонт, проекции характерных точек линии пересечения,
наименее и наиболее удаленных от пл. V. Проекции т', т и п', и определяют
то:чки пересечения очерковых образующих цилиндра со сферой.
¦ Изображенное тело — сочетание . части сферы и цилиндра — рассматривается
как монолитное. При построении сечения А —А получено сечение части сферы, ог-
ограниченное дугой окружности радиуса 0„/„ и двумя отрезками прямых, по которым
плоскость А — А пересекает «четвертинки» кругов, ограничивающих справа и снизу
рассматриваемую часть сферы. Затем получена часть эллипса (на рис. 252, в он пока-
показан целиком) как сечение цилиндра. Отрезок 2а21п получен от пересечения плос-
плоскости, ограничивающей цилиндр.
204 *
Рис. 252б„в.
20S
270. Построить: а) проекции линии пересечения поверхностей
цилиндра и конуса; б) натуральный вид сечения А — А (рис. 253У.
Указание. Фронт, проекция линии пересечения совпадает с частью соот-
соответствующей проекции цилиндра.
Рис. 253.
Рис. 254.
; 271. Построить: а) проекции линии пересечения поверхностей
цилиндра и тела вращения (с осью //,, перпендикулярной к пл. Н)\
б) i натуральный вид сечения А — А (рис. 254).
5 Указание. Горизонт, проекция линии пересечения совпадает с соответ-
соответствующей проекцией цилиндра.
I 272*i Построить: а) проекции линии пересечения поверхностей
конуса и сферы; б) натуральный вид сечения А — А (рис. 255, а).
Решение. В этом случае ни одна из проекций ни одного из данных тел не
совпадает полностью или частично с проекциями искомой линии пересечения. Мы
не можем исходить из того, что положение проекций ее точек нам известно, как это
было в задачах 265 и 269. Поэтому мы используем здесь общий прием построения
206 •
Рис. 255а—в.
.«07
точек взаимного пересечения поверхностей, а именно введение вспомогательных се'
¦сущих плоскостей (рис. 255, б), пересекающих каждую из заданных поверхностей
по некоторым линиям, и определение точек, общих для этих поверхностей, в пере-
пересечении линий, полученных на них.
Учитывая свойство и положение заданных поверхноетей, применим в данном
случае серию секущих плоскостей, параллельных пл. Н. Каждая такая плоскость
пересекает поверхности конуса и сферы по окружностям (рис. 255, в). Например,
А-А
г)
Рис 255г.
пл| R на конусе дает окружность радиуса s—2, а на сфере окружность радиуса
с—*й. Эти окружности в своем пересечении определяют точки D и ?, общие для
поверхностей конуса и сферы.
I Но кроме точек, получаемых подобным образом, надо построить еще некоторые
карактерные точки, положение которых уточняет искомую линию. Это прежде всего
выршая и низшая точки на фронт, проекции. Для их нахождения мы также исполь-
ау*м некоторую пл. 5: она проходит через ось конуса и через центр сферы и явля-
является для этих тел общей плоскостью симметрии. Пл. S пересекает поверхность ко-
конура по образующим, а поверхность сферы по окружности; повернув пл. S вместе
с полученными в ней линиями вокруг оси конуса до положения, параллельного
пл. V, получим точки аг и b\, а по ним сначала а' и V, затем а и Ь.
Имеют значение точки /', f и I', i на главном меридиане конуса, так как в них
определяются точки пересечения крайней образующей s' l'lt s—li с поверхностью
сферы; для нахождения этих точек взята вспомогательная nn.il, соответствующая
208
"авному меридиану конуса и рассекающая поверхность сферы по окружности ра-
-я с'4'.
Также следует найти точки на экваторе сферы, для чего в серии горизонтальных
секущих плоскостей надо взять пл. Р: в точках тип горизонт, проекция экватора
смыкается с видимой частью проекции линии пересечения на пл. Н.
Сечение А — А (рис. 255, г) очерчено дугой окружности (от пересечения поверх-
поверхности сферы), частями гиперболы (от пересечения конической поверхности) и отрез-
отрезком H0Ga (от пересечения основания конуса). Надо обратить внимание на смещение
центра кругового сечения сферы относительно оси гиперболы.
273. Построить проекции линий пересечения: а) поверхностей
-тора и эллипсоида вращения (рис. 256, а); б) поверхностей тора а
сферы (рис. 256, б). В обоих случаях построить сечения А — А.
Рис. 256а, б.
274*. Построить проекции линии пересечения поверхностей ко-
конуса и цилиндра (рис. 257, а).
Решение. Здесь так же, как и в задаче 272, приходится прибегать к вспомо-
вспомогательным секущим плоскостям. Какие же плоскости наиболее удобны в данном
случае? Это плоскости, проходящие через вершину конуса и параллельные образую-
образующим цилиндра (рис. 257, б). Такие плоскости (например, пл. Р) пересекают обе по-
поверхности по прямым—образующим, положение которых определяется точками
?09
/У
1
1
1
\
а)
Рис. 257а. б.
210
s
Рис. 257в, г.
211
пересечения оснований данных тел ср следом секущей плоскости на плоскости осно-
оснований. Построение показано на рис. 257, в.
Через точку s' ,s проведена прямая параллельно образующей цилиндра; найдены
проекции т! и т горизонт, следа этой прямой.
Если горизонт, следы секущих плоскостей проводить через точку т так, чтобы
каждый из них пересекал или касался оснований конуса и цилиндра, то на поверх-
поверхностях цилиндра и конуса обнаруживаются образующие, в пересечении которых
получаются точки искомой линии. Сначала займемся точками на образующих, яв-
являющихся очерковыми на горизонт, проекции Проводим следы плоскостей по на-
направлениям т—6 и т—/ касательно к окружностям оснований, получаем на каждой
из поверхностей по три образующих: на конусе образующие s—/, s—5 и s—4, на
цилиндре образующие из точек 6, 2 и 3.
777'
д)
Остается взять точки пересечения образующих — на горизонт, проекции точки
в; Ь, с, d и на фронт, проекции а',Ь', с', d'.
; Теперь для нахождения точек, лежащих на очерковых образующих фронт, про-
проекций тел, проводим еледы секущих плоскостей через горизонт, проекции концов
соответствующих образующих — точки 7, 8, 9 ij 10 (рис. 257, г).
1 Таким образом, находим точки g, h, k, I, n, о, р, а по ним фронтальные проекции.
На рис. 257, д показан пример нахождения промежуточных точек (Е и F) и про-
проведены обе проекции искомой линии.
275. Построить проекции линий пересечения: а) двух цилиндри-
цилиндрических поверхностей (рис. 258, а); б) двух конических поверхностей
(рис. 258, б).
Й12
Рис. 258а, б.
б)
Рис. 259а, б.
21*
276*. Построить, проекции линии пересечения цилиндрической
поверхности с косой плоскостью. Косая плоскость задана направ-
направляющими АВ и CD при пл. Я как плоскости параллелизма (рис. 259, а).
Решение. Учитывая свойства и положение заданных поверхностей, а имен-
именно то, что цилиндр имеет ряд круговых сечений в плоскостях, параллельных пл. Н,
и что образующие косой плоскости параллельны той же пл. Н, берем серию вспомо-
вспомогательных плоскостей (Т, Рит. д.), параллельных пл. И (рис. 259, б).
Они пересекают цилиндрическую поверхность па окружностям с центрами О,
О, и т. д., а косу» плоскость — по прямым 1—2, 3—4 и т. д. Горизонт, проекции
искомых точек (е, f и др.) лежат на пересечении соответствующн*- проекций етнх
окружностей и прямых. По горизонт, првекциям находим фронт, проекции — е , Г
я др. Искома* линяя пе]икжчения проходит через найденные точки.
На рис. 269, б показаны результат пересечения косой плоскости с цилиндром
и самый цилиндр, а косая плоскость не изображена.
Рис. 260а, б.
277. Построить проекции линии пересечения: а) конической
поверхности с косой плоскостью, направляющими которой являются
прямые АВ и CD, а плоскостью параллелизма —пл. Я (рис. 260, а);
б) коноида, направляющими которого являются кривая АВ и прямая
CD, a плоскостью параллелизма — пл. Я, с цилиндрической поверх-
поверхностью (отверстие) (рис. 260, б).
215
I*. Построить проекций линии пересечения поверхности ко-
конуса с поверхностью тора, ограничивающей отверстие в конусе
(рис. 261, а).
б) Рис. 261а—в.
216
Решение. В данной задаче мы имеем случай взаимного пересечения двух
поверхностей вращения, оси которых пересекаются и расположены в плоскости,
параллельной пл. V. В подобных случаях наиболее простым является применение
вспомогательных сфер, проводимых из точки пересечения осей обеих поверхностей
(рис. 261, б). Эти сферы пересекают данные поверхности по окружностям, в пересе-
пересечении которых получаются точки, общие для
обеих поверхностей.
На рис. 261, в показано применение двух
сфер. Фронт, проекция одной из них прове-
проведена как окружность с центром О' радиусом
0'5'. Отрезок 5'6' является фронт, проекцией
окружности, по которой сфера пересекает
коническую поверхность, а отрезок 7'8'—
фронт, проекцией окружности, по которой
эта сфера пересекает поверхность тора. По-
Получается точка сГ—фронт, проекция одной
из точек, общей для поверхности тора и
конуса. По точке й' находим на параллели
конуса проекцию й и ей симметричную.
: Сфера радиуса О'/' лишь касается кони-
конической поверхности по окружности, но по-
поверхность тора пересекает. Поэтому точка с',
полученная с помощью этой сферы,-имеет осо-
особое значение: если брать сферы с радиусом
меньшим, чем О'V, то общих точек для дан-
данный поверхностей мы с помощью таких сфер
не получим. В точке с' фронт, проекция линии
пересечения лишь коснется прямой 3'4', но
ее не пересечет.
Положение точек а' и Ь' очевидно.
Радиусы вспомогательных сфер следует
брать в данном случае в пределах от 0'1'
ЯР О'а'.
И)
Рис. 262а, б.
279* Построить проекции линии пересечения: а) поверхности
вращения с поверхностью гиперболоида вращения (рис. 262, а); б) по-
поверхностей двух торов (рис. 262, б), и в обоих случаях сеч. А—А.
217
¦ ф
Рис. 263а, 6V
218
Рис. 264а, б
219
)*. Построить проекции линии пересечения цилиндрической
поверхности с поверхностью конуса вращения, ограничивающей
отверстие в цилиндре (рис. 263, а).
Р е ш е н и е. Из двух заданных поверхностей лишь одна поверхность вращения—
коническая. Другая же поверхность не является поверхностью вращения. Это ци-
цилиндр, называемый наклонным круговым,— круговым, так как он имеет ряд круго-
круговых параллельных между собою сечений. В данном случае такие сечения параллель-
параллельны пл. Н. Кроме того, имеется общая для конуса и цилиндра плоскость симметрии,
параллельная пл. V. '
Эти обстоятельства подсказывают использование вспомогательных сфер, но не
с постоянным центром, как в задаче 278.
Действительно, круговое сечение цилиндра можно принять за параллель неко-
некоторой сферы. Например, окружность радиуса c[l' (рис. 263, б) может быть парал-
параллелью многих сфер, центры которых располагаются на прямой, проведенной через
с перпендикулярно к плоскости параллели. Если же мы на этом перпендикуляре
возьмем точку в пересечении с осью конуса, то такую точку (с фронт, проекцией О',)
можно принять за центр сферы с радиусом ОгГ, пересекающей цилиндр по окруж-
c'j'^ а конус вращения — по окружности с диаметром 2'3'. Отсюда мы
получаем точки, фронт, проекции которых сливаются в одну точку е' (одна из
этих точек — на обращенной к нам части линии пересечения, другая — на ей сим-
симметричной,).
На рис. 263, б дан еще один пример подобного построения. Задавшись на цилинд-
цилиндре окружностью радиуса с24', находим фронт, проекцию центра сферы в точке О'г и
радиус сферы, равный 0^4'. При помощи этой сферы получены точки, общие для
поверхностей конуса и цилиндра, с фронт, проекциями в точке /'.
Положение точек а' и Ь' очевидно.
Горизонт, проекции точек по найденным их фронт, проекциям строим на окруж-
окружностях — горизонт, проекциях окружностей, взятых на поверхности цилиндра.
281. Построить проекции линии пересечения: а) конической
поверхности с поверхностью эллипсоида вращения (рис. 264, а); б) по-
поверхности тора с поверхностью параболоида вращения (рис. 264, б).
В обоих случаях построить сечения А—А.
. ГЛАВА VII
СМЕШАННЫЕ ЗАДАЧИ ПО ВСЕМУ КУРСУ
§ 24. Задачи с решенными прототипами
282*. Определить расстояние от точки А до ближайшей точки
на поверхностях: а) конуса (рис. 265, а); б) сферы (рис. 265, б); в) тора
(рис. 265, в).
Рис. 265а, б.
Решение, а) Искомое расстояние (рис 265, а) равно расстоянию от данной
точки до ближайшей к ней образующей. Эта образующая лежит в пл. Л', проходящей
через точку А и ось конуса.
221
резком at lx,
Поворачиваем эту плоскость вокруг оси конуса до положения, параллельного
пл. V. Точка А займет положение Av(au а'х), и искомое расстояние выразится от-
перпендикулярным к s'b\.
6) На рис. 265, б показано, что искомое
расстояние измеряется по прямой АО. Повер-
Повернув прямую АО вокруг оси, проходящей
через точку О перпендикулярно к пл. Н,
так, чтобы АО стала параллельна пл. V, по-
получим l=*AxO— R^a^O'—R.
, в) Расстояние от точки А до поверхности
тора (рис. 265, в) измеряется величиной отрез-
отрезка нормали к поверхности тора в плоскости,
проходящей через точку А и ось тора. Повер-
Повернув эту плоскость вокруг оси тора до поло-
положения, параллельного пл. V, и проведя пря-
прямую аг<У', получим точку 1Х и отрезок at ly.
Это и есть нормаль к поверхности тора, про-
проходящая через точку Аи а до поворота —
через точку А.
283*. Поворотом вокруг оси О^ точку А совместить с поверх-
поверхностью конуса вращения (рис. 266, а).
222
JP e ш е н и е. Поворот точки А вокруг оси О^ происходит в пл.Т (рис. 266, б),
перпендикулярной к Oi<?2. Центр дуги окружности, по которой перемещается точка
А, находится в точке пересечения оси О^Оъ с плоскостью'вращения Т. Горизонт,
проекция этого центра совпадает с точками Ох и О2. Итак, проведя из точки 0^0^)
дугу радиуса О^а, получим на этой дуге горизонт, проекцию точки А в любом ее
полфкении в пл. Т при повороте вокруг оси ОгОг. Но чтобы точка А оказалась при
этом! на поверхности данного конуса вращения, надо, очевидно, взять параллель ко-
конической поверхности на уровне пл. Т, т. е. окружность радиуса О'Г. На этой ок-
окружности и находим точку А, когда она при повороте вокруг оси OiOj оказывается
на поверхности заданного конуса. По горизонт, проекциям ах и я2 находим проек-
проекции a'j и а2. В положении Аг точка А окажется невидимой относительно пл. V, а в
положении Аг— видимой. Точка А в положениях Ах и Аг относительно пл. Н будет
видимой.
284. Поворотом вокруг оси 0i02 точку А совместить: а) с шаровой
поверхностью (рис. 267, а); б) с поверхностью тора (рис. 267, б).
Рис. 267а, б.
Поворотом вокруг оси 0!02 точку А совместить с винтовой
поверхностью (рис. 268, а).
Решение. Заданная косая винтовая поверхность имеет ось, параллельную
оси OiOt. В указанном на чертеже положении поворот точки А происходит в пл. У?
(рис. 268, б), параллельной пл. Н и пересекающей данную поверхность по дуге спи-
спирали ; Архимеда. Строим горизонт, проекцию этой дуги, проводя для нахождения
точек 3 и 6 плоскости Рг и Рг через ось поверхности. Они пересекают поверхность
по ее образующим 1—2 и 4—5. Находим точки 3' и 6' в пересечении следа Rv с /'21 •
223
Рис. 268а, б.
Рис. 269а.
и 4'5', по ним строим проекции 3 и 6. Проводим через точки т, б, 3 и я кривую п
находим точку пересечения (at) этой кривой с горизонт, проекцией окружности,
описываемой точкой А. По аг находим ах; Oj и at служат проекциями точки А в
искомом положении.
286. Поворотом вокруг оси OtO2 точку А совместить: а) с винто-
винтовой поверхностью (рис. 269, а); б) с косой плоскостью (рис. 269,6),
а";
заданной направляющими прямыми CD и EF и плоскостью паралле-
параллелизма Н.
287*. Указать положения осей, перпендикулярных к пл. //,
поворотом вокруг которых можно ввести точку А на заданную поверх-
поверхность вращения (рис. 270, а).
Решение. В отличие от задач 283 и 285 в данной задаче ось для поворота
точки не задается; оговаривается лишь то, что эта ось должна быть перпендикулярна
к пл. Н. Однако нельзя взять любую прямую, перпендикулярную к пл. Н, и
принять ее за ось, пригодную для решения этой задачи.
На рис. 270, 6 показано, что имеется такая область, в которой было бы бесцель-
бесцельным брать точки в качестве горизонт, проекций осей вращения. Например, приняв
точку О4 за горизонт проекцию оси, мы получим радиус вращения точки А равным
О^а, но 0ta меньше расстояния точки а до ближайшей точки на окружности радиуса
R, и, следовательно, дуга радиуса О^р. даже не коснется этой окружности. Или точка
Oft: совершенно очевидно, что дуга радиуса Оъа не может иметь общих точек с
окружностью радиуса R.
Но если взять точку О, так, чтобы 0,0—0^1, или точку Оя так, чтобы О^а—ОгЗ,
то в положениях I и 3 точка а окажется на окружности радиуса R. Взяв оси, прохот
дящие через точки О, и Оп перпендикулярно к пл. Н, мы можем решить задачу о
введении точки А на заданную поверхность вращения. Легко видеть, что решение
смодится к построению гиперболы, у которой фокусами служат точки а и с, а верши-
вершинами — точки О, и О3. Эта гипербола определяет область (на рис. 270, б она заштри-
заштрихована), в которой любая точка может быть принта за горизонт, проекцию оси,
при повороте вокруг которой точка А окажется в двух положениях на данной
8
В. О Гордон и др,
225
поверхности вращения. Если же точку взять на одной из ветвей гиперболы, то
такая точка определяет ось, при повороте вокруг которой точка А окажется на по-
поверхности вращения лишь в единственном положении. Например, точка 02: дуга
радиуса 0га лишь коснется в точке 2 окружности радиуса R.
а)
Рис. 270а, б.
288. Указать положение осей, перпендикулярных к пл. Я, по-
поворотом вокруг которых можно точку А совместить с заданной поверх-
поверхностью вращения (рис. 271).
289*. Указать положение осей, перпендикулярных к пл. Н,
поворотом вокруг которых можно точку А совместить с заданной по-
поверхностью вращения (рис. 272, а).
Решение. Отличие этой задачи от задачи 287* в том, что точка задана внутри
поверхности вращения. Здесь также вопрос выбора положения осей решается при
рассмотрении взаимного положения точки А и окружности радиуса R (параллели)
на поверхности вращения (рис. 272, 6) Очевидно, что горизонт, проекция оси
вращения (какая-либо точка О) должна быть расположена так, чтобы радиус Оа
был не меньше расстояния точки О до ближайшей точки на окружности радиуса R.
Предельные положения точки О (например, О,, Ог и др.) расположатся как точки
эллипса с фокусами в точках а и с, с большой осью 0г03 на прямой /—3. Точка Ot
делит пополам отрезок а—1, а точка Оя—отрезок а—3. Если взять точки внутри
этого эллипса и принять их за горизонт, проекции осей вращения, то вращением
вокруг таких осей нельзя данную точку совместить с поверхностью вращения.
Горизонт, проекции осей надо брать или на эллипсе, или вне его.
290. Указать положения осей, перпендикулярных к пл. Н, по-
поворотом вокруг которых можно точку А совместить с заданной поверх-
поверхностью вращения (рис. 273).
226
Рис. 271.
-ус" а/
Рис. 272а.
а)
Рис. 2726.
Рис. 273.
227
291*. На прямой CD найти точки, отстоящие от прямой А В на
расстояние / (рис. 274, а).
Решение. Геометрическим местом точек пространства, отстоящих от прямой
АВ на расстояние /, является цилиндрическая поверхность с осью АВ и радиусом I
С
Рис. 274а—в.
(рис. 274, б). Искомые точки М и К являются точками пересечения прямой CD с этой
поверхностью.
Очевидно, для упрощения построения надо сделать так, чтобы ось цилиндриче-
цилиндрической поверхности оказалась перпендикулярной к какой-либо плоскости, принятой
за плоскость проекций. Сначала (рис. 274, в) вводим пл. S_[_H а параллельно АВ,
затем пл. Т_Ц> и _[_АВ. В системе Т, S прямая АВ перпендикулярна к пл. Т. Проек-
Проекция цилиндрической поверхности на этой плоскости — окружность радиуса I с
центром в точке at(bt). Точки пересечения (mt н kt) окружности с проекцией ctdt яв-
являются проекциями искомых точек на пл. Т. По mt. и kt находим та и ks, затем га
и ft, а по ним — т' и к'.
228
292. На прямой А В найти точки, отстоящие от оси х на расстоя-
расстояние / (рис. 275).
293*. Построить недостающую проекцию прямой CD, параллель-
параллельной прямой АВ, если расстояние между ними равно / (рис. 276, а).
Р ел1 е н и е. Прямые линии, параллельные АВ и находящиеся от нее на рас-
расстоянии /, являются образующими цилиндра, осью которого служит прямая А В,
а радиусом нормального сечения — отрезок /. Исходя из этого, следует добиться того,
чтобы прямая АВ оказалась перпендикулярной к некоторой плоскости: цилиндр с
осью А В изобразится на этой плоскости п виде окружности, на которой окажется
соотнетствующая проекция прямой CD.
Построение показано на рис. 276, 6. Последовательно введены дополнительные
плоскости S_|_W и 7'J_S, причем S\\AB и Т\_АВ Найдя точку щ(Ь() — проекцию
А В на пл. Т, очерчиваем дугу радиуса I. Это проекция на пл. Т цилиндра, одной из
образующих которого должна быть прямая CD. Проекцией этой прямой на пл. Т
229
должна быть точка на проведенной дуге окружности на расстоянии от оси TIS,
равном расстоянию проекции cd от оси S/H. Получаем две точки: ct( (du) и c2j (d2(),
т. е. два ответа: обе прямые отвечают условиям задачи. Найдя проекции <?if(dii)
и cit(d2t), проводим clsdls\\asbs и cisd.is\\asbs, а затем с\ й\[]а'Ь'\\сл d\.
294. Построить горизонт, проекцию прямой CD, параллельной
прямой АВ и отстоящей от нее на расстояние / (рис. 277).
еЧ"
Рис. 278а—в.
295*. В треугольнике ABC найти точку, отстоящую от прямых
АВ и EF на расстояние / (рис. 278, а).
230
Решение. Геометрическим местом точек на плоскости треугольника, отстоя^
щих на расстояние / от прямой А В, является прямая, ей параллельная и проведен-
проведенная от нее на расстоянии I. Таких прямых может быть две; ограничимся той, которая
находится в пределах треугольника ABC. На рис. 278, б треугольник ABC повер-
повернут вокруг горизонтали до параллельности пл. И. Горизонталь проведена через точ-
точку С. Найдена натуральная величина радиуса вращения точки В — отрезок OS и
положение Л^С треугольника ABC, когда его плоскость параллельна пл. Н.
Проведя прямую 2^ параллельно о161 на расстоянии /, находим точки 2 и 3,
а по ним 2' и 3' на проекциях соответствующих сторон треугольника.
Переходим ко второму условию, связанному с прямой EF.
Геометрическим местом точек пространства, отстоящих от прямой EF на рас-
расстояние /, служит цилиндрическая поверхность с осью EF и радиусом /. Точка пере-
пересечения этой поверхности с прямой 2—3 является искомой точкой. Таких точек мо-
может быть две. Но в пределах данного треугольника, как это следует из рассмотрения
рис. 278, в, получится лишь одна точка — точка К.
Так как EFJ_V, то получаем непосредственно фронт, след цилиндрической по-
поверхности в виде дуги окружности с центром e'(f') и радиусом /. В пересечении этой
дуги с проекцией 2 3' получается точка k!— фронт, проекция искомой точки, отстоя-
отстоящей от АВ и от EF на расстояние /.
На рис. 278, в показана также точка УМ, отвечающая условиям задачи о равно-
удаленности от АВ и EF (на /). Точка М находится в плоскости, заданной треуголь-
треугольником ABC, но вне его пределов. В условии же задачи сказано: «В данном треуголь-
треугольнике...». Поэтому полностью отвечает условиям задачи только точка /(.
Рис. 2ГЭ.
296. В данном треугольнике ABC найти точку, отстоящую от
прямой АВ на расстояние 1Ъ а от прямой EF на расстояние /2 (рис. 279).
231
297*. Провести прямую MN, равноудаленную от прямых А В, CD
и EF и параллельную одной из них, а именно прямой CD (рис. 280, а).
Решение. Представим
себе, что прямая CD располо-
расположена перпендикулярно к неко-
некоторой плоскости проекций; тогда
каждая прямая, параллельная
CD, также будет перпендикуляр-
перпендикулярна к этой плоскости, в том числе
и искомая. В данном случае пря-
прямая CD параллельна пл. V;
поэтому можно сразу ввести
плоскость S, перпендикулярную
к прямой CD, взяв ось S/V]_c d'
(рис. 280, б). Построим проек-
проекции asbs, cs(ds) и esfs. Проекция
искомой прямой MN на пл. S
представляет собой точку ms(ns),
равноудаленную от прямых asb^
cs(ds), т. е. ин-
окружности,
а
проходящей через точку cs{ds) и касающейся прямых
Рис. 2ЙОа, б.
и ejs. Для ее по-
построения проводим биссектрису угла aslfs и через какую-либо точку о на ней прово-
проводим окружность, касающуюся этих прямых. Соединяем точки / и cs(ds) прямой ли-
линией и находим точку 2 пересечения ее с проведенной окружностью. Теперь проводим
прямую через точки О и 2. Искомая точка ms(ns) лежит на пересечении упомянутой
выше биссектрисы с прямой, параллельной прямой 2—О и проходящей через точку
cs(ds). По проекции ms(ns) находим m'n'(\\c'd') и mn\\cd.
232
298. Провести прямую MN, равноудаленную от прямых АВ, CD
и EF и параллельную прямой CD (рис. 281).
а
Рис. 281.
299*. Провести прямую MN, равноудаленную от прямых АВ,
CD и EF и параллельную прямой GK (рис. 282, а).
а)
а
Рис. .282а.
Решение. И в этой задаче, очевидно, надо сделать так, чтобы прямая CD,
а следовательно, и искомая параллельная ей прямая MN оказались перпендикуляр-
перпендикулярными к некоторой плоскости проекций. Так как гю заданию GK параллельно пл. Н,
то сразу можно ввести пл. S (рис. 282, б), перпендикулярную к пл. Я и к G/C.
Теперь строим проекции asbs, csds и esfs. Проекция искомой прямой на ил. 5
должна быть точкой. Очевидно, надо отыскать точки, равноудаленные от проекций
e.Ai Csdjt и ejs. Проведя биссектрисы углов asles и cs2bs, получим в их пересечении
233
точку ms(ns). Это и будет проекция на пл. S искомой прямой, находящейся на равных
расстояниях от АВ, CD и EF и параллельной прямой GK.
Здесь дано одно из четырех возможных решетш.
Рис. 283.
300. Провести прямую MN, равноудаленную от прямых АВ, CD
и EF и параллельную прямой GK (рис. 283).
234
Указание. В задаче 300, для того чтобы прямая GK оказалась перпенди-
кулярной к некоторой плоскости проекций, требуется введение двух дополнительных
плоскостей.
301*. Провести прямую, равноудаленную от четырех заданных
точек А, В, С и D (рис. 284, а).
Рис.
284а—я.
Решение. Представляя сеОе пространственную картину, можно заключить,
что искомая прямая является осью цилиндрической поверхности, образующие ко-
которой проходят через заданные точки (рис. 284, б).
235
Для построения этой поверхности проведем через любые две заданные точки,
например А и В, прямую и примем ее за образующую цилиндрической поверхности.
Теперь проведем пл. Г перпендикулярно к прямой АВ и найдем проекции at(bt),
ct, df. Проекция цилиндрической поверхности на пл. Т является окружностью, про-
проходящей через точки с,, dt и at(bt). Центр этой окружности — точка т((иг) — явля-
является проекцией искомой прямой.
Построение показано на рис. 284, в. Вводим пл. S\H и \\АВ, а затем пл. Т, пер-
перпендикулярную к пл. S и к А В. Построив проекцию afyt), ct и dt, находим щ— про-
проекцию одной из точек (М) искомой прямой MN.
Затем находим ms, m и rri. Проводим m'n'\\a'b' и mn\\ab.
Можно было бы соединить точки Ли С, А и D, б и С, Я и D, С и D и получить
еще пять решений.
302. Провести прямую MN, равноудаленную от четырех задан-
заданных точек А, В, С и D (см. рис. 284, а). Дать два варианта решения:
a) MN\\BD и б) MN\\AC.
303*. Построить фронт, проекцию треугольника ЛВС, если даны
его горизонт, проекция abc и горизонталь DC, а также известно рас-
расстояние / от точки К до плоскости этого треугольника (рис. 285, а).
Г
ее 1
i
d'
¦
Л
Л"
а
Рис. 285а, б.
Решение. Если представить себе сферу радиуса / как геометрическое место
точек, удаленных на расстояние / от точки К, то искомая плоскость будет одной из
плоскостей, касательных к этой сфере. При этом, если плоскость окажется фрон-
фронтально-проецирующей, то ее фронт, след будет касательной прямой к фронт, проек-
проекции сферы — окружности радиуса /, и фронт, проекция треугольника ABC совпа-
совпадет с этой касательной. .
Поэтому преобразуем заданный чертеж так, чтобы плоскость треугольника ABC
стала фронтально-проецирующей. Для этого применим поворот треугольника и
точки К вокруг оси, перпендикулярной к пл. И, но положение этой оси не покажем
(способ параллельного перемещения). При таком повороте (рис. 285, б) гори-
горизонт, проекция в целом лишь изменит положение относительно оси х. А чтобы
236
плоскость треугольника ABC стала фронтально-проецирующей, надо горизонталь
DC расположить перпендикулярно к пл. V, т. е. проекции) dc вывести в положение
^lCl_L ОСИ X.
Теперь, очертив из точки k{ окружность радиуса /, мы можем провести через
точку ct (dt) касательную к окружности. На рис. 285, б проведена одна касательная,
хотя можно провести еще одну, т. е. дать второе решение. Но так как методика по-
построения не изменяется, то ограничиваемся одним решением, принимая в качества
фронт, проекции треугольника отреяок аг Ьх. Точки а1 и Ь^ определяются по точкам
о, и ftj.
В заключение остается возвратиться к заданным проекциям abc, k и k', и получить
проекции а' и Ь', исходя из построенных проекций ал и b v т. е. получить фронт,
проекцию а'Ь'с'.
304. Построить горизонт, проекцию треугольника ABC, если
даны его фронт, проекция а'Ь'с' и фронталь AD, а также известно
расстояние / от точки К до плоскости этого треугольника (рис. 286).
Дать оба решения.
Рис. 286.
Рис. 287а.
305*. Через точку S провести прямую, равнонаклоненную к за-
заданным прямым А В, CD и EF (рис. 287, а).
Решение. Искомая прямая является осью конуса с вершиной S, три
образующих которого параллельны соответственно прямым АВ, CD и EF
(рис. 287, б).
Через s' и s (рис. 287, в) проводим проекции прямых, параллельных данным
прямым (например, s'l'\\a'b', s—l\\ab, s'2'\\c'd' и т. д.).
237
Рис. 2876—д.
238
Вяяв на прямой S— 1 некоторый отрезок SM (рис 287, г), откладываем на двух
других прямых отрезки SK=SN=SM.
Точки К, М и Л/ задают (рис. 287, б) сечение конуса плоскостью, перпендику-
перпендикулярной к его оси.
Получив точки k, k'; т, т'; п, п', строим треугольники ktnn и k'tn'n'— проекции
треугольника KMN, в плоскости которого надо найти точку, равноудаленную от
точек К, М и Л/, т. е. центр окружности, описанной вокруг этого треугольника. Про-
Проведя через эту точку и через точку S прямую, можно получить требуемый ответ. По
достаточно будет только провести перпендикуляр из точки S на плоскость, опреде-
определяемую треугольником KMN, что и сделано на рис. 287, д при помощи горизонтали
М—7 и фронтали М—8.
306*. Ввести прямую АВ в пл. Р вращением вокруг оси, перпен-
перпендикулярной к пл. И (рис. 288, а).
Рис. 288а, б.
Решение. Если найти точку пересечения прямой АВ с пл. Р, то останется
повернуть только одну точку прямой так, чтобы эта точка оказалась в пл. Р. Поэтому
начинаем.с того, что находим точку S пересечения прямой АВ с пл. Р (рис. 288, б),
а далее проводим ось вращения через S перпендикулярно к пл. Н. При вращении
вокруг этой оси точка S остается в пл. Р, а прямая А В описывает коническую
поверхность. Линии пересечения (S/1, и S/42) этой поверхности с пл. Р {Р про-
проходит через вершину конуса) представляют собой искомые положения прямой А В
в пл. Р.
Построение показано на рис. 288, в. Для нахождения точки S через прямую А В
проведена фронтально-проецирующая пл. R. Точка А при повороте вокруг оси OS
(рис. 288, г) описывает окружность радиуса Оа, лежащую в пл.Г, которая пересека-
пересекается с пл. Я по горизонтали. Эта горизонталь пересекает окружность в точках с про-
проекциями а, и а'р а2 и а2. Проведя прямые s'at и s'av sax и sa2, находим на этих пря-
прямых положение точек b'v b'2, ft, и Ь%. Л,б, и /12fi.2— искомые положения прямой АВ.
307. Вращением вокруг оси, перпендикулярной к пл. Н (рис. 289),
совместить данную прямую ЛВ с а) гранью SDE, б) гранью SCE.
Указание. Начать с нахождения точки пересечения АВ с соответствующей
гранью.
239
ш
00
00
СМ
s
О.
240
308*. Определить, можно ли прямую АВ совместить с поверх-
поверхностью конуса вращения поворотом ее вокруг оси, перпендикулярной
к плоскости основания конуса (рис. 290,а).
Р е ш е н и е. На рис. 290, б показано, что
прямая АВ совпадает с поверхностью конуса
вращения в том случае, если совпадет с его
образующей в одном из ее положений. Это
положение образующей получим, найдя точку
S, пересечения прямой АВ с поверхностью
конуса. Образующая S—/, определяемая точ-
точками S и St, и есть та, с которой должна
совпасть прямая АВ, если она может быть
совмещена с поверхностью конуса. Но чтобы
такое совмещение получилось, должны ока-
оказаться равными между собой углы, состав-
составляемые образующей конуса и данной пря-
прямой А В с осью конуса или с прямой, прове-
проведенной через точку Sx параллельно этой оси.
Так как в данном случае ось конуса пер-
перпендикулярна к пл. Н, проверку можно
а)
Рис. 290а—в.
свести к определению угла между АВ и пл. Н (рис. 290, в): приняв ось конуса за ось
вращения для всей системы «конус и прямая», поворачиваем прямую АВ до парал-
параллельности пл. V. Так как углы а и ф не равны между собой, то прямая Л В не может
быть введена на поверхность данного конуса поворотом вокруг оси, перпендикуляр-
перпендикулярной к плоскости его основания.
241
s'
\
ar
Рис. 291а—в.
242
309*. Найти фронт, проекцию прямой А В, исходя из условия,
что эта прямая может быть совмещена с боковой поверхностью задан-
заданного конуса вращения поворотом вокруг оси, перпендикулярной к пло-
плоскости его основания (рис. 291, а).
Решение. Повернем систему «конус и прямая» вокруг оси конуса с тем, чтобы
прямая АВ стала параллельной пл. V (рис. 291,6). Получив точку а1— фронт, про-
проекцию точки А после поворота, проведем al b^s'c', т. е. получим равные углы между
осью конуса и а) его образующей, б) прямой АВ. Выводя конус и прямую в начальное
положение, получим фронт, проекцию а'Ь' (рис. 291, в) в соответствии с условиями
задачи.
а'
А Ц__41
Рис. 292.
310. Ввести прямую АВ на поверхность данного конуса (рис. 292)
поворотом вокруг оси, перпендикулярной к плоскости его основания.
Указание. Произведя проверку и убедившись в том, что задача может быть
решена, надо найти точку пересечения прямой А В с боковой поверхностью конуса.
Эта точка вместе с вершиной конуса определяет его образующую в том ее положении»
когда прямая АВ совпадает с ней.
243
311*. Построить фронт, проекцию угла АКВ, натуральная вели-
величина которого равна его горизонт, проекции akb (рис. 293, а)
Решение. Известно, что проекция острого (или тупого) угла может равняться
проецируемому углу не только в случае параллельности плоскости угла и плоскости
проекций. На рис. 293, б показано, что, например, все углы, стороны которых со-
соответственно расположены в пл. Р и Q, перпендикулярных к пл. Н, имеют своей
os a
К
а)
Рис. 293а—в.
горизонт, проекцией угол, равный углу akb. Очевидно, среди различных углов име-
имеется угол, равный этой проекции.
Далее показано построение фронт, проекции угла, равного в натуре его заданной
горизонт, проекции. Сделано это тремя способами.
1. Через стороны ak и bk угла akb (рис. 293, в), лежащего в пл. Н, проводим две
плоскости — пл. V и горизонтально-проецирующую пл. S. У гола является линейным
углом двугранного, образованного этими плоскостями. Стороны угла, равного его
горизонт, проекции, должны лежать — одна в пл. V, другая в пл. S. Этот угол по-
построен при помощи треугольника АКВ, подобного некоторому треугольнику MkB,
взятому на пл. Н. Построение проводится так, чтобы стороны А В и ВМ были сход-
сходственными.
Задаемся некоторым коэффициентом подобия \. На ребре двугранного угла вы-
выбираем точку К так, чтобы BK=h-Bk. Если теперь построить точку А с тем, чтобы
AK=k-Mk и АВ^Х-ВМ, то треугольники АКВ и MkB окажутся подобными, и
угол АКВ будет равен а.
Для построения точки А используем два геометрических места точек: геометри-
геометрическое место точек в пл. V, удаленных от точки /< на расстояние AK=K-Mk (т. е.
окружность, проведенная из точки К радиусом X-Mk), и геометрическое место то-
точек, отстоящих от точки В на расстояние АВ=К-ВМ.(т. е. сфера радиуса АВ с цент-
центром в точке 6). Точка А должна лежать в пл. V, т. е. должна быть на окружности, по
которой пл. V пересекает указанную сферу и центром которой является фронт, про-
проекция точки В.
В пересечении обеих окружностей, расположенных в пл. V, получаем две точки,
из которых на рис. 293, я показана одна — точка А.
Соответствующий чертеж приведен на рис. 293, г. Принимаем А.= 2. Из точки Ьа
(построение ее ясно из чертежа) проводим дугу радиуса R,=2kb до пересечения в точ-
244
ке k' с линией связи, проходящей через точку k. Из точки k' проводим дугу радиуса
R2=2km. Если теперь из точки b радиусом R3=2bm провести окружность, то полу-
получим проекцию упомянутой выше сферы.
Окружность, по которой эта сфера пересекается плоскостью V, имеет центр в
точке ft и радиус, равный cb'. Точка а лежит на пересечении дуг радиуса /?2 и ра-
радиуса, равного ей', точка а — на оси х. Угол а'к'Ь'— искомая фронт, проекция угла,
равного своей горизонт, проекции.
Рис. 293г.
2. Возьмем точку k (рис. 293, д) на ребре двугранного угла, образованного пло-
плоскостями V и Я, проведенными через стороны ak и bk угла akb. Из этой точки про-
проведем в пл. V прямые АК и /4,К, образующие между собой угол, равный а, и повернем
прямую AtK вокруг прямой АК. При этом образуется коническая поверхность с об-
образующей АХК и осью АК. Линия KR пересечения конической поверхности плоско-
плоскостью Р будет стороной угла АКВ, в натуре равного а. Чтобы найти эту линию пере-
пересечения, надо построить прямую /—2 пересечения пл. Р с пл. Т основания конуса.
Тогда точки С и В пересечения окружности основания с прямой /—2 определят об-
образующие, по которым нл. Р пересекает коническую поверхность.
Чертеж показан на рис. 293, е, причем плоскости V и Р изображены прямоуголь-
прямоугольниками / и //. Через точку k' в прямоугольнике / проведены прямые ak' и a[k' так,
чтобы угол между ними был равена. Через точку а, перпендикулярно к a'k' прове-
проведен след Tv плоскости Т — основания конуса. Точка 0'0 — центр окружности
основания конуса. Прямая с проекциями 1'2' и /—2 — линия пересечения плос-
плоскостей Г и Р.
Введя дополнительную пл. S _[_ V и _[_ АК, построим проекции Osaals, а также
IS2S. Окружность, проведенная из точки os радиусом osals, пересекает прямую t;2s
в точках cs и bs— проекциях точек, принадлежащих образующим KB и КС.
На рис. 293, е показано построение фронт, проекции только точки В: по точке bs по-
построена точка Ь'. Угол a'k'b' является фронт, проекцией угла, в натуре равного
углу а.
3. В этом случае использовано совмещение плоскости искомого угла с пл. Я
(рис. 293, ж).
Проводим прямую ab — горизонт, след плоскости, в которой лежит рассматри-
рассматриваемый угол, и поворачиваем вокруг него точку К до совмещения ее с пл. Н- Чтобы
245
при этом угол аКф оказался равныма, надо вписать угол аКФ в окружность, прове-
проведенную через точки а, Ь и k. Тогда углы akb и аКф, как вписанные, опирающиеся на
3)
Рис. 293д—ж.
одну и ту же дугу, будут равны между собою. Остается найти точку Ко в пересечении
окружности, проведенной через точки а, Ь и ft, со следом плоскости вращения точки
К вокруг прямой ab. Зная натуральную величину сК радиуса вращения точки К
246
и его горизонт, проекцию ck, находим отрезок kK — превышение точки К над пл. Я,
а это дает нам возможность получить точку k'. Угол a'k'b' является искомой фронт,
проекцией угла АКВ, равного своей горизонт, проекции. Во всех примерах мы
ограничились показом построения лишь
одного угла, хотя углов, натуральная вели-
величина которых равна заданной горизонт, про-
проекции, множество.
Рис. 294.
312. Построить горизонт, проек-
проекцию угла АКВ, равного в натуре
своей фронт, проекции a'k'b' (рис.294).
Решить всеми тремя способами.
313*. Найти направление фронт,
следа фронтально-проецирующей плос-
плоскости, пересекающей заданный конус вращения так, чтобы профиль-
профильная проекция эллипса сечения оказалась окружностью (рис. 295, а).
Решение. В общем случае профильная проекция эллипса, получаемого
при пересечении конуса вращения, представленного на рис. 295, а, фронтально-
проецирующей плоскостью Р, является эллипсом (рис. 295, б), оси которого равны
величинам отрезков Ь'4' и cd.
Если окажется, что b'4'=cd, то эллипс сечения изобразится на пл. W окружно-
окружностью. Этого можно достичь, если след Ро искомой плоскости направить по диагонали
равнобочной трапеции а'е'Ь']' (рис. 295, б), в которую вписывается окружность с
центром в точке 2'. Для построения такой трапеции проводим биссектрису угла а' 1'Ь'
до пересечения с осью симметрии трапеции а точке 2'. Проводим из этой точки
перпендикуляр к биссектрисе и находим точку У (рис. 295, в).
247
.314. Дан след Ph фронтально-проецирующей пл. Р, пересекаю-
пересекающей конус вращения по эллипсу. Построить фронт, след этой пло-
плоскости из условия, что профильная проекция эллипса является ок-
окружностью (рис. 296).
S'
\ph
Рис. 296.
Рис. 297.
315. Будет ли (рис. 297) проецироваться на пл. W в виде окруж-
окружности эллипс, получаемый при пересечении данного конуса вращения
фронтально-проецирующей пл. Р?
§ 25. Задачи для самостоятельного решения
316. Построить проекции равнобедренного треугольника ABC
с основанием ВС, лежащего в плоскости (рис. 298), заданной линией
ската AM и точкой В (дана ее горизонт, проекция).
317. Пересечь две скрещивающиеся прямые А В и CD прямой
КМ, перпендикулярной к плоскости, заданной треугольником EFG
(рис. 299).
318. Косая плоскость задана направляющими АВ и CD и пло-
плоскостью параллелизма — горизонтально-проецирующей пл. Р (дан
горизонт, след Рн). Построить профильную проекцию линии пересече-
пересечения косой плоскости профильной плоскостью S (рис. 300).
319. Построить фронт, и горизонт, проекции точки К, принад-
принадлежащей поверхности сжатого эллипсоида вращения (дана проекция
k", точка видима), и натуральный вид сечения А—А (рис. 301).
320. Построить проекции сферы, касательной к данной сфере
в точке К, расположенной на ее передней стороне (дана фронт, проек-
проекция точки). Радиус искомой сферы Ri = 2/:t R (рис. 302).
321. Построить проекции прямого кругового конуса, касатель-
касательного к данному в заданной на его боковой поверхности видимой точке
К (дана горизонт, проекция этой точки). Вершина S искомого конуса
должна быть на пл. Н. Высота и диаметр основания обоих конусов
одинаковы (рис. 303).
248
249
Рис. 301.
s'
X
Рис. 302.
Рис. 303.
322. Через точку А (дана ее фронт, проекция), принадлежащую
поверхности вращения (рис. 304), провести нормаль к поверхности;
отложить на нормали отрезок А К длиной /.
323. Даны призма и отрезок Л В на ее грани. Пересечь призму
плоскостью, проходящей через прямую АВ, так, чтобы в сечении полу-
получился равнобедренный треугольник ABC с основанием АВ (рис. 305).
324. Вращением вокруг фронт, следа Pv ввести прямую А В
(ДВ||пл. V) в пл. Р (рис. 306).
325. Построить на пл. Р геометрическое место точек, равноуда-
равноудаленных от ближайших точек двух скрещивающихся прямых АВ и CD
(рис. 307).
250
a
Рис. 306.
Рис. 307.
251
n
252
Рис. 310.
Рис. 311.
d>
Рис. 314.
243
326. Даны два положения прямой А В, повернутой вокруг неко-
некоторой прямой CD. Определить положение этой прямой и величину угла
поворота а (рис. 368).
327. Даны два положения прямой АВ, повернутой вокруг неко-
некоторой прямой. Построить проекции этой прямой, задав ее горизонт,
следом М и произвольной точкой С (рис. 309).
328. Даны прямая АВ я точка С. Через точку А провести прямые,
пересекающие А В под углом а = 30° и отстоящие от точки С на рас-
расстояние /. Дать все решения (рис. 310).
329. Даны прямые EF и MM (MN || пл. И), пересекающиеся в точке
К. Построить точки, удаленные от точки К. на расстояние /3, от прямой
EF — на /3 и от прямой ММ — на 1Х (рис. 311). Построить в:е точки,
отвечающие условию.
а
Рис. 316.
Рис. 317.
254
330. Даны точка А и прямая ВС. Через точку А провести пря-
прямые, отстоящие от ВС на расстояние / и составляющие с ней угол
а = 45*. Из всех решений дать те, в которых прямые, проходящие че-
через точку А, приближаются к точке С, а не к В (рис. 312).
331. Даны две скрещивающиеся прямее А В и CD. Через точку А
провести прямые, пересекающие прямую А В под углом а = 30° и от-
отстоящие от прямой CD на расстояние /. Дать все решения (рис. 313).
332. Даны две скрещивающиеся прямые А В и CD. Провести пря-
прямые, пересекающие А В, параллельные CD и отстоящие от последней
на расстояние / (рис. 314).
333. Даны две скрещивающиеся прямые АВ и CD. Провести пря-
прямую EF, их пересекающую и образующую с прямой АВ угол а. = 46*
и с прямой CD угол Р = 53°. Дать решение, в котором прямая EF
пересекает заданные в пределах первой четверти (рис. 315).
334. Построить геометрическое место точек, удаленных отточки Л
на расстояние / и равноудаленных от сторон угла BCD (рис. 316).
335. Даны две точки Л и В и прямая CD. Через точку А провести
прямые, пересекающие прямую CD и отстоящие от точки В на расстоя-
расстояние /. Дать все решения (рис. 317).
ГЛАВА VIII
АКСОНОМЕТРИЧЕСКИЕ ПРОЕКЦИИ
§ 26. Изображение плоских фигур
336*. Построить изометрическую проекцию треугольникя ABC
(рис. 318, а).
Решение. Строим изометрические проекции вершин А, В и С по их коор-
координатам. На оси х заданного чертежа (рис. 318, а) отметим точку О — начало
координат. Величина отрезка Оах дает нам абсциссу точки А, величина отрезка
с'
Рис. 318а—и.
аха — ординату, величина отрезка аха'— апликату.Теперь можно перейти к системе
изометрических осей (рис. 318, 6) и а) отложить на оси х отрезок Оах, взяв его с
ЛШ^й^ провести через ах прямую, параллельную оси у; в) отложить на этой пря-
256
мой отрезок ахаи взяв его равным отрезку аха на рис. 318, а; г) провести прямую
а,/4 параллельно оси г и отложить на ней отрезок ахА, равный a^d на рис. 318, а.
Получаем изометрическую проекцию вершины А. Построив аналогично проекции
вершин В и С, получим (рис. 318, в) изометрическую проекцию треугольника ABC.
337*. Определить координаты точки К, лежащей в плоскости
треугольника ABC, заданного его диметрическои проекцией и вторич-
вторичными проекциями вершин на плоскости Юу (рис. 319, а).
Решение. Если точка К принадлежит плоскости треугольника ABC, то она
лежит на какой-то прямой (например, AD) в этой плоскости (рис. 319, б).
Рис. гд19а— в.
\^
Построив на пл. хОу вторичную проекцию йх точки D и вторичную проекцию
a^dt прямой AD, находим (рис. 319, в) вторичную проекцию ?, точки К- Теперь можно
найти координаты точки К, выраженные отрезками Okx (абсцисса), 2kykx (ордината),
k,K (апликата). Коэффициент 2 при отрезке kykx взят в связи с сокращением вдное
отрезков, параллельных оси Оу, при построении диметрическои проекции.
338*. Построить изометрическую и диметричхкую проекции ок-
окружности радиуса R, расположенной в плоскости, заданной треуголь-
треугольником ABE (рис. 320, а) Центр окружности — в точке С.
Решение. Окружность, которую надо изобразить в изо- и диметрическои
проекциях, расположена в плоскости общего положения. Поэтому мы не можем при-
применить здесь известные правила о том, что большая ось эллипса, изображающего
окружность в изо- или диметрнческой проекции, перпендикулярна к так называемой
9 и; О. I ордов в др.
267
свободной оси, что малая ось эллипса в изомегрической проекции равна 0,7d, где d —
диаметр изображаемой окружности, и т. д. Эти правила справедливы для случаев,
когда изображаются окружности, расположенные в фронтальных, горизонтальных
и профильных плоскостях. Для данного же случая справедливым остается лишь то,
что большая ось эллипса в изометрической проекции равна l,22d, а в диметрической
1,06d. Но положение этой оси надо найти, и оно. естественно, меняется в зависимости
01 положения плоскости, в которой расположена изображаемая окружность.
а)
п
Рис. 320а, б.
Помня об этом, мы воспользуемся известным из курса способом построения, при-
пригодным для любого положения окружности. По этому способу мы прежде всего долж-
должны построить на данном чертеже перпендикуляр к плоскости, в которой расположена
окружность. Построенный затем в изо- или диметрической проекции этот перпенди-
перпендикуляр даст направление малой оси эллипса. Построение такого перпендикуляра с
проведением его из центра окружности показано на рис. 320, б. Далее, на этом пер-
перпендикуляре надо отложить отрезок CD, равный радиусу R окружности. Это пока-
показано на рис. 320, в. Если теперь построить изометрическую (рис. 320, г) и диметри-
часкую (рис. 320, ё) проекции отрезка CD, то получим направление малой оси эл-
эллипса и центр изображаемой окружности.
Проведя (рис. 320, д) в точке С перпендикуляр к CD, мы получаем направление
большой оси эллипса, а отложив на нем по 1,22/? в обе стороны от С, получаем боль-
большую ось эллипса — отрезок kxk^.
Чтобы определить величину малой оси эллипса, поступаем так: из точки D про-
проводим дугу радиуса 1,22/?, засекая ею направление большой оси. Полученный при
втом отрезок Cm и выражает малую полуось,
2ЗД
д)
Рис. 320в — ж.
259
Следовательно, мы получаем обе оси эллипса по положению и размеру. Точки
для очерчивания эллипса могут быть получены известным построением эллипса по
его большой и малой осям (см. рис. 320, д).
Аналогично поступаем и для построения диметрической проекции (рис. 320, ж).
Различие лишь в размере радиуса A,06/? вместо 1,22/?) дуги, проводимой из точки D,
и в размере большой оси эллипса. Малая же ось эллипса.получается построением, и,
конечно, величина ее-изменяется в зависимости от угла между плоскостью, в которой
расположена изображаемая окружность, и плоскостью диметрической (или изомет-
изометрической) проекции, как это излагается в курсе.
Рис. 321а—е.
339*. Построить изометрическую и диметрическую проекции
окружности радиуса R, расположенной в некоторой горизонтально
проецирующей плоскости (рис. 321, а).
?60
Решение. В задаче 338 мы имели дело с окружностью, расположенной в пло-
плоскости общего положения. Очевидно, тот общий способ, который мы применили в той
задаче, пригоден и в данном случае. Но построение упрощается, так как упрощается
проведение перпендикуляра к плоскости, в которой расположена окружность, и от-
откладывание на нем размера R. Для изометрической проекции построения показаны
на рис. 321, б, в, г. На рис. 321, б проведен перпендикуляр c'd', ей (причем cd=R)
и взята точка 0 — начало координат. На рис. 321, в отрезок CD построен в изометри-
изометрической проекции по координатам, взятым с рис. 321, б. Полученный в изометрической
проекции отрезок CD, дает направление малой оси эллипса и положение его центра
(точка С).
На рис. 321, г через точку С перпендикулярно к CD проведена большая ось эл-
эллипса, равная l,22d, где d=2R — диаметр изображаемой окружности, и определена
величина малой полуоси эллипса, а также изображен сам эллипс.
Такие же построения выполнены и для диметрической проекции (рис. 321, д и е).
§ 27. Изображение гел
340*. Определить координаты точки А, лежащей на поверхности:
цилиндра (рис. 322, а), конуса при наличии вершины (рис. 322, б),
усеченного конуса (рис. 322, в), сферы (рйс. 322, з), заданных в изомет-
изометрической проекции.
Решение. Через заданную на поверхности цилиндра (рис. 322, о) точку А
проведена образующая (|| оси г), и найдена на плоскости кОу вторичная проекция aL
а)
Рис. 322а, б.
точки А. Изо, проведена прямая параллельно оси у до пересечения с осью х в точ-i
ке а,.
Апликата точки А определяется величиной отрезка Ааи а абсцисса и ордината —
соответственно величинами отрезков Оах и axat.
На рис. 322, б через точку А также проведена образующая (S—/) и построена
ее вторичная (на пл. хОу) проекция 0—1. Теперь на 0—1 может быть найдена точка
а,— вторичная проекция точки А. Величины отрезков Ааь Оах и а^ определяют
соответственно координаты г, * и у точки А.
261
3)
Рис. о22в-з.
262
Если точка задана на поверхности усеченного конуса и по условию нельзя по-
получить на чертеже его вершину, то поступаем следующим образом.
Рассмотрим сначала сечение конуса плоскостью, проходящей через точку А
и ось конуса (рис. 322, г). Проведя прямые АО и SC || /—2, получаем гг~. = -^—«. Это
соотношение сохранится и в изометрической проекции. Поэтому (рис. 322, д) прово-
проводим прямую О А и строим конус с вершиной S и образующей, параллельной образую-
1 Q ? QQ
щей усеченного конуса; получаем, сравнивая рис. 322, г с рис. 322, г, ^—~7=
Q О
Теперь делим О А в отношении ——^ •
• Через полученную точку К проводим образую-
образующую SC внутреннего конуса и полудиаметр О—2 эллипса, где точки С и 2 соот-
соответствуют точкам С и 2 на рис. 322, г. После этого мы имеем возможность спрое-
спроецировать точку А на плоскость хОу (рис. 322, ж) и получить координатные отрезки
Ааи алах, ак0.
Для определения координат точки А, лежащей на поверхности сферы (рис. 322,э),
следует построить (рнс. 322, и) дополнительные проекции сферы и координатных осей
У"
на плоскости, перпендикулярной к пл. изометрических проекций (картинной пл.)
и параллельной оси г. Это как бы профильная проекция, если считать, что изомет-
изометрическая проекция служит фронт, проекцией. Пл. Г, проходящая через точку А,
пересекает сферу по окружности диаметра 1—2. Строим проекцию этой окруж-
окружности и находим на ней проекцию данной точки — А". По А" находим точку а'[,
которая является профильной проекцией вторичной проекции aj точки Л.
Теперь можно изобразить отрезки Аа^, a-fi.x и Оах. Величина этих отрезков по-
позволяет определить координаты точки А относительно центра О.
241*. Построить диметрическую проекцию шайбы по чертежу
рис. 323, а.
Решение. Прежде всего, рассмотрев чертеж на рис. 323, а, устанавливаем,
что данная шайба представляет собою тело вращения, боковая поверхность которого
состоит из цилиндрической части с диаметром D и высотой Л и из поверхности тора,
образованной вращением дуги окружности радиуса R вокруг оси г, причем центр
263
этой дуги описывает окружность диаметра dx. В шайбе имеется цилиндрическое от-
отверстие диаметра d2. Сверху и снизу шайба ограничена плоскостями.
Обращаясь к построению диметрической проекции, прежде всего представим
себе, что в поверхность тора, ограничивающую частично шайбу, вписаны сферы ра-
радиуса R, центры которых располагаются на окружности диаметра dx.
0а,
о:
О'
н
а)
У В)
Рис. 323а—в.
Очерковая линия диметрической проекции построена с помощью сфер, вписан-
вписанных и ту часть поверхности шайбы, которая представляет собою поверхность тора,
образованную вращением дуги окружности радиуса R вокруг оси г (рис. 323, а).
Центры сфер, вписываемых в эту поверхность, располагаются на окружности диамет-
диаметра dx с центром в точке Ох на расстоянии h от опорной плоскости шайбы.На рис. 323, б
показан эллипс — диметрическая проекция этой окружности. Взяв на нем ряд точек
(рис. 323, в), проводим из них окружности радиуса 1,06/?, представляющие собой
очерки диметрических проекций шаров радиуса R. Очерковая линия проекции по-
поверхности тора является огибающей семейства окружностей.
264
Затем строим эллипс — проекцию верхней кромки отверстия диаметра dj с
центром в точке О2 (рис. 323, г) и часть эллипса (рис. 323, д) с центром в точке О,
представляющего собою проекцию окружности основания цилиндрической части
шайбы. Из концов большой оси этого эллипса проводим прямые линии (рис. 323, е)—
аг/2
д)
Рис. 323г—е.
очерковые линии проекции цилиндрической части шайбы. Эти прямые касаются по-
построенного ранее очерка поверхности тора. Если представить, что из данной шай-
шайбы «вырезана» часть плоскостями хОг и уОг, то получится более наглядное изобра-
изображение шайбы. Но при этом меняется порядок построения (см. далее задачу 344).
265
342*. Построить изометрическую проекцию тела вращения, изо-
изображенного на рис. 324, а.
Решение. Данное тело вращения ограничено комбинированной поверхно-
поверхностью, состоящей из плоскости, цилиндра вращения, поверхности тора и сферы.
а)
Рис. 324а, б.
Выполняем построение в следующем порядке:
1. Приняв точку О (рис. 324, б) в качестве начала координат, откладываем по
оси г отрезок, равный Н, и проводим из точки С как из центра окружность радиуса
1,22/?. Так изобразится в изометрической проекции сфера радиуса R.
2. Чтобы построить очерк поверхности тора в изометрической проекции, изобра-
изображаем верхнюю часть данного тела в наклонном положении (рис. 324, в), причем на-
клон оси тела определяется отношением тргу— I/ —, что соответствует значению
коэффициента искажения по осям х, у, г в изометрической проекции. Теперь выпол-
выполняем построение, как в задаче 242, что дает нам возможность к изображению сферы
в изометрической проекции добавить видимое очертание поверхности тора.
3. Далее строим (рис. 324, г) изометрическую проекцию цилиндра, находящегося
в основании данного тела. Здесь применимо правило, по которому большая ось эл-
эллипса, изображающего в изометрической проекции окружность, перпендикулярна
к «свободной» оси, каковой служит ось г. Большая ось эллипса принимается равной
1.22D, малая ось — 0.7D.
343*. Построить изометрическую проекцию тела, изображенного
на рис. 325, а.
Решение. Прежде всего устанавливаем, что данное тело состоит из шести-
шестиугольной правильной призмы и половины сферы, срезанной тремя плоскостями. Под-
Подготавливаем размеры элементов тела, необходимые для построения изометрической
проекции (рис. 325, б).
266
Рис. 324в, р.
267
Приступаем к построению изометрической проекции.
1. Приняв за начало координат точку О (рис. 325, б и в), строим дугу радиуса
с центром О2, расположенную на расстоянии Л2 от начала координат.
Рис. 325а—г.
2. Далее (рис. 325, г), строим дугу радиуса Ra с центром Оа, имеющим коорди-
координаты x=h3, y=Q и г=Ни и проводим прямую 3—4 параллельно оси у.
3. По координатам точек С и D строим отрезок CD (рис. 325, д). и проводим пер-
перпендикулярно к нему прямую через точку С. Откладываем отрезки СА1=Сй2=1,22У?с
и получаем отрезок kji^— большую ось эллипса, в который проецируется окруж-
26ё
ность радиуса Rc с центром С (см. рис. 325, б). Малую ось щт^ получаем, сделав из
точки D как из центра засечки на большой оси эллипса дугой радиуса 1.22/?с и от-
отложив отрезок Ст=Ст1=Сгщ на прямой CD. Проводим прямую 5—6 параллельно
оси у.
4. Из центра О,, расположенного на оси г на расстоянии Л, (рис. 325, е) от осно-
основания данного тела, проводим окружность радиуса 1,22/?, представляющую собой
Рис. 325л—ж.
очерк изометрической проекции сферы радиуса R. Эта окружность должня касаться
всех трех построенных ранее эллипсов.
По координатам точек 9, 8,7 и им симметричных строим проекции видимых сто-
сторон шестиугольника верхнего основания.
5. Достраиваем (рис. 325, ж) проекции видимых участков нижнего шестиуголь-
шестиугольного основания, зная его высоту Л,.
344*. Построить диметрическую проекцию детали, изображен-
изображенной на рис. 326, а.
Решение. Во избежание излишних построений при выполнении изображе-
изображения детали с отверстием наиболее целесообразно вести построение в следующем
порядке:
1. Начертить (рис. 326, б) сечения, входящие в состав фронтального и профиль-
профильного разрезов при секущих плоскостях, совпадающих с плоскостями симметрии
детали.
A-A
II
Рис. 326а—в.
270
e)
Рис. 326г— е.
2. Начертить грань / верхнего фланца детали (рис. 326, в).
3. Начертить (рис. 326, г) все остальные видимые элементы верхнего фланца я
цилиндрическую часть детали, а также эллипсы внутренних цилиндров.
4. Начертить грань // основания детали и окружности цилиндрических отвер-
отверстий в этом основании (рис. 326, д).
6. Достроить основание детали и нанести штриховку сечений (рис. 326, е).
271
ОТВЕТЫ
272
4.
a
x \a'
a,.
ЬУ
?
d'-
В
273
7.
аа'
х а
I
274
8. д—ж.
I
a'\—
\a'ab
a e) <ж)
9> a) CD—отрезок прямой общего положения, находится в первой четверти
пространства, концом D упирается в переднюю полу горизонт, пл. проекций.
Конец С равноудален от обеих пл. проекций.
б) Отрезок АВ расположен в третьей четверти пространства параллельно
фронт, пл. проекций. Концом В упирается в заднюю полу горизонт, пл. про-
проекций.
в) Отрезок EF расположен на верхней поле фронт, пл. проекций парал-
параллельно оси проекций.
г) Отрезок IK расположен во второй четверти пространства перпендику-
перпендикулярно к фронт, пл. проекций. Конец К равноудален от обеих пл. проекций.
П.
а а'
275
13.6.
//v. I//четверть
m
—f Г
IS.
> a
m'\n
a)
A
276
18.
/ v. IV четверть Шч.
18.
13.
Ham. вел. Л В
се =27° /2=4Ой
Ham. вел. /IB
л = 35° 0=23°
21.
23.
2S.
о а
q а'
277
27.
29.
a
A/»
278
a)
S2. a, 6.
279
38.
b'
зв.
in'
m
280
38.
a
зз. а'
281
41.
43.
а'
45.
а
282
47.
a
48.
a
c>
283
49.
51. Заданная плоскость яв- а',
ляется плоскостью общего поло-
жения.
53.
284
ss.
285
53. а, б.
a)
59. e.
в)
60.
S2.
9а'
¦л"
т
к
hd
287
21.
7*.
40 в. О. Гордо* к др.
28)
74.
76-
ttfiO
10*
2Ш
81.
83.
Я!
85.
87.
88.
293
во.
а
с о
Ъ\
в',
К
ТП'
98.1 а Параллельна, б) не параллельна, в) параллельна.
№
99.
100. я, 6.
Q» d)
101. He аараляельны.
295
103,
10S.
a
see
109.
110. а) Плоскости перпендикулярны, б) плоскости не перпендикулярны.
«' AS'
а)
т
112. в.
SOS
lie.
к
lip.
tso.
?fr
л"
a. 6.
¦г.
m*.
300
124.
12В.
¦>a'
Pv
x \Ъ'
«28.а.
а'
т'
301.
126. б.
<3t.
133.
/77'
303
Po
304
138.
UO.
805
806
144.
807
148.
147.
151.
IBS.
154.
I'
156.
н. в. AS
н. e. BS
h. в. CS
и. в. Z)S
158.
от В до AC
от S 3d ВС ,
от S до А В
от S do AC
159.
AD u CF
BE и CF
АЛ и BE
311
tea.
IBS.
1ВБ.
188.
170.
172.
17*.
Грань
SAB
SAC
ABC
Угол
a
57*
51*30'
24-30'
В
22'30'
72"
73*
177.
178. L
131'
180. a) 73°; 6) 82*.
182. Угол, который грань ABC об-
образует с ребром AS, равен 46°, с реб-
ребром BS — 46*, с ребром CS —70*
185. Угол между гранями SAB и
SBC равен 108°, между SBC и SCD равен
104*. между SAD и SAB равен 89*,
18В. Угол, между гранями CDHG
и ?fG// равен 28", между BCGF и
CDHG равен 24*.
312
188.
191.
a:
313
199.
Ш
217.
317
«21.
ааз.
i N
У
;¦
!
К
-ч
i
у
su
228.
319
'320 "
11 В. О. Гордон ii др.
321
24S.
322
249. a, 6.
a)
11*
323
254. а. б.
ее)
256. а, 6
324
2B9.
261.
A! ! M
325
262.
264.
826
see.
327
267.
270.
328
271.
A-A
273. б.
А-А
330
275. а, б.
a)
331
a)
332
со
ем
333
i
286. a.
333
290.
a
294.
азе
298.
е'ч
298.
а
837
800.
a
n Ф
338
?39
340
317.
318
841
319.
820
342
322.
323.
324.
a
a
343
825. a, 6.
Искомым геометрическим местом яв-
является прямая MN пересечения пл. Р
с пл. Q (рис. б) ответа). Пл. Q парал-
параллельна обеим заданным прямым и про-
хрдит через точку F — середину отрезка
ЁК общего перпендикуляра к прямым.
При решении задачи строить пря-
прямую ЕК не обязательно: пл. Q следует
провести посередине между параллель-
параллельными пл. S и R, проходящими соответ-
соответственно через прямые А В и CD
План решения. 1. Через АВ
провести пл. S О CD (или наоборот/.
2i Определить расстояние между пл. S
и R (пл R для этого не требуется).
3", Провести пл. Q, равноудаленную от
них и параллельную им. 4. Построить
Линию пересечения пл. Р и Q.
326.
]
х j
1
j
а К
Ъ
\
с
d>
cd
~&
i
а,
ь,
344
При повороте точки А и В враща-
вращаются в плоскостях Р и Q, перпен-
перпендикулярных искомой оси СМ 'рис. 6)
ответа). Прямая СМ равноудалена
как от точек А и Аи так и от В и
В,. Поэтому она определяется как
линия пересечения плоскостей S и /?,
проходящих соответственно через се-
середины отрезков /4/4, и BBt (рис. в)
ответа) перпендикулярно к ним.
845
в28. а, б
Искомые прямые АЕ и AF яв-
являются линиями пересечения дпух
конических поверхностей с вершиной
в точке А (рис. б) ответа): одмой —
с осью А В и углом а наклона обра-
образующих к оси; другой — описанной
вокруг сферы радиуса / с центром
в точке С.
329. а. Искомые точки А и В являются точками пересечения двух окруж-
окружностей (рис. б) ответа): окружности пересечения сферы радиуса /3 с центром
в точке К с цилиндром радиуса lt и осью MN и окружности пересечения той
же сферы с цилиндром, осью которого является прямая EF, а радиус равен /а.
346
329. 6
N
330. а. Искомые прямые, во-первых, находятся в плоскостях Р и Т, про-
проходящих через точку А и касательных к цилиндрической поверхности радиуса /
с осью ВС (рис. б) ответа); во-вторых, принадлежат конической поверхности,
вершина которой—точка А, ось —прямая, параллельная ВС, и угол наклона
образующих к оси —а. Искомые прямые —результат пересечения этой поверх-i
ности с плоскостями Р и Т.
а)
347
аао. б.
331. Искомые прямые, во-первых, принадлежат конической поверхности
(рис. б) ответа) с осью АВ и углом а между образующими и осью; во-вторых,
пл. Р, проходящей через Чочку А и касательной к цилиндру, ось которого —
прямая CD и радиус — /. Следовательно, эти прямые определяются как линии
пересечения пл. Р с конической поверхностью.
I* a)
348
332i Искомыми прямыми явля-
являются образующие цилиндра (рис. б)
ответа), имеющего ось CD и радиус
/, проходящие через точки пересече-
пересечения прямой АВ с поверхностью этого
цилиндра
с
383а Для определения направления
прямой EF следует (рис. б) ответа)
через произвольную точку (S) провести
прямые S — 1\\AB и S —2 || CD, опи-
описать вокруг них конические поверхности
с углами наклона образующих » оси
соответственно а и Р и найти линию их
пересечения SK (SN). Прямая EF парал-
лельма этой линии. В дальнейшем реше-
решение задачи аналогично решению зада-
задачи 140.
с'
334. Искомым геометрическим местом точек (рис. б) ответа) является окруж-
окружность пересечения сферы с центром в точке А и радиусом / с плоскостью,
проходящей через биссектрису угла BCD перпендикулярно к плоскости этого угла.
350
335> Искомыми прямыми являются образующие конической поверхности о
вершиной в точке А, описанной вокруг сферы с центром в точке В и радиу-
радиусом /, проходящие через точку пересечения этой поверхности с прямой CD
(рис. б) ответа).
D
351
Владимир Осипович Гордон,
Юрий Борисович Иванов.
Татьяна Евгеньевна Солнцева
СБОРНИК ЗАДАЧ ПО КУРСУ
НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ
М„ 1977 г. 352 стр. с илл.
Редакторы А. В. Бубенчиков. А. П. Баева
Техн. редактор С. Я. Шкляр
Корректоры Т. С. Плетнева, В. П. Сорокина
Печать с матриц. Подписано к печати
19/11 1977 г. Бумага 60X90'/.» тип. № 3.
Физ. печ. л. 22. Условн. печ, л. 22. Уч.-изд. л. 21,8.
Тираж 260 000 экз.
Цена книги 75 коп. .Заказ № 1176.
Издательство «Наука»
Главная редакция физико-математической
литературы
Москва, B-7I, Ленинский проспект, 15
Союзполиграфпром при Государственном комитете
Совета Министров СССР по делам полиграфии и
книжной торговли.
Отпечатано в Ордена Трудового Красного Знаме-
Знамени Ленинградском производственно-техническом
объединении «Печатный Двор» им. А. М. Горь-
Горького. 197136, Ленинград, П-13Й, Гатчинская, 26
с матриц Ордена Трудового Красного Знамени
Первой Образцовой типографии имени А. А. Жда-
Жданова. Москва, М-54, Валовая, 28,