Ю. С. Завьялов,
Б. И. Квасов,
В. Л. Мирошниченко
МЕТОДЫ
СПЛАЙН-ФУНКЦИЙ
Под редакцией
Н. Н. ЯНЕНКО
МОСКВА «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
1980

22.19
3-13
УДК 519.6
Методы сплайн-функции. Завьялов 10. С, К в а с о в Б. И., Ми-
р о ш и и ч е и к о В. Л.— М.: Наука. Главная редакция
физико-математической литературы, 1980.
В книге излагаются методы построения, исследования и применения
сплайн-функций в численном анализе. Наиболее подробно рассматриваются
приближение фупкций, численное дифференцирование и интегрирование,,
решение краевых задач для обыкновенных дифференциальных уравнении.
Изложение сравнительно простое и доступное широкому кругу читателей»
знакомых с основами численного анализа. Книга может служить учебным
пособием для студентов университетов и втузов.
Значительная часть результатов публикуется впервые, причем
большое впимапие уделя'ется построению алгоритмов, эффективно реализуемых
на ЭВМ. С этой точки зрения книга интересна для научных работников*
и инженеров, применяющих методы сплайнов на практике.
JOvtiii Семенович Завьялов,
Борис Ильич Квасов,
Валерий Леонидович Мирошниченко
МЕТОДЫ СПЛАЙН-ФУНКЦИЙ
М , 1980 г., 352 стр. с илл.
Редактор С М Цидилин
Техн. редактор И. Ш. Акселърод
Корректоры Г. В. Подвольспая, А. Л. Платова
ИБ М 11249
Сдано в набор 05 06 80. Подписано к печати 05.1180. Т-20603. Бумага бОхОО'Ав. Тип,
№ 3. Обыкновенная гарнитура. Высокая печать. Условп. печ. л 22 Уч.-изд. л. 22,9*
Тираж 11 000 экз Заказ № 192. Цена книги 1 р. 60 к.
Издательство «Наука»
Главная редакции чжзико-математическоп литературы
117071, Москва, В-71, Ленинский проспект, 15
4-я типография издательства «Наука». Новосибирск, 77, ул. Станиславского, 25.
(Q) Издательство «Наука»*
о 20204 —145 ,пяп 47П9П7ПППП Главная редакция
«Етго/ппч а А—40-60. 1702070000 физико-математической
053@2)-80 литературы, 1980

ОГЛАВЛЕНИЕ
Предисловие редактора • « 6
Предисловие авторов 7
Введение 9
Глава I. Пространство сплайн-функций 15
§ 1. Определение сплайнов. Пространство сплаппоп .... 15
§ 2. Базисные сплайны с конечными носителями 18
§ 3. Нормализованные базисные сплайны ц представление имп
многочленов 23
§ 4. Фундаментальные сплайны..Интерполяционная формула Лаг-
ранжа для сплайнов 26
§ 5. Вычисление сплайнов и их производных 29
§ 6. Сплайн-функции двух переменных на прямоугольной сетко 36
Глава II. Локальные сплайны » . * ¦ 41
§ 1. Сплайы первой степени 41
§ 2. Оценка остаточного члепа интерполяционного сплайна
первой степени 42
§ 3. Сходимость иптерполягшоипого процесса. Интерполяция с
заданной точностью . 49
§ 4. Сплайны первой степени двух переменных на прямоугольной
сетке 54
§ 5. Эрмитовы кубические сплайны 58
§ 6» Оценки погрешности интерполяции эрмитовыми кубпчеекпмп
сплайнами - ... 60
§ 7. Интерполяция с заданной точностью эрмитовыми
кубическими сплайнами 70
§ 8. Другой способ интерполяции эрмитовыми кубическими
сплайнами ... 72
§ 9. Эрмитовы кубические сплайиы двух переменных па
прямоугольной сетке 75
§ 10. Эрмитовы сплайиы произвольной печетпой степепи » 81
§11. Получение оценок погрешности интерполяции эрмитовыми
сплайнами с помощью ЭВМ 82
§ 12. Сплайиы двух переменных на перегулярпой сетке • . . 87
Глава III. Кубические сплайны класса С2 ..,,... 96
§ 1. Задача интерполяции. Существование и единственность ро-
шения 96
§ 2. Оценки погрешности иптериоляции. Сходимость в классе С 1 01
§ 3. Оценки погрешности интерполяции (продолжение) , . . 109
§ 4. Локальные свойства кубических сплайнов 123
§ 5. О выборе граничных условий и узлов интерполяции.
Интерполяция с заданной точностью 127
§ 6. Кубические сплайпы двух перемепных. Существование и
единственность. Алгоритм ',,,,,,,,,, 131

ОГЛАВЛЕНИЕ
§ 7. Оценки погрешности интерполяции кубическими сплайнами
двух переменных 136
§ 8. Кубические #-сплайны 139
§ 9. О применении /?-сплайпов для решения задачи интерполяции 141
§ 10. О применении Л-сплайттов для решения задачи
интерполяции. Случай двух переменных ¦ 145
Глава IV. Экстремальные свойства сплайнов 147
§ 1. Экстремальное свойство интерполяционных кубических
сплайнов 147
§ 2. Сглаживапие экспериментальных данных 1 49
§ 3. Экстремальное свойство интерполяционных кубических
сплайнов двух переменных 157
§ 4. Сглаживапие экспериментальных данпых. Случай двух
переменных 160
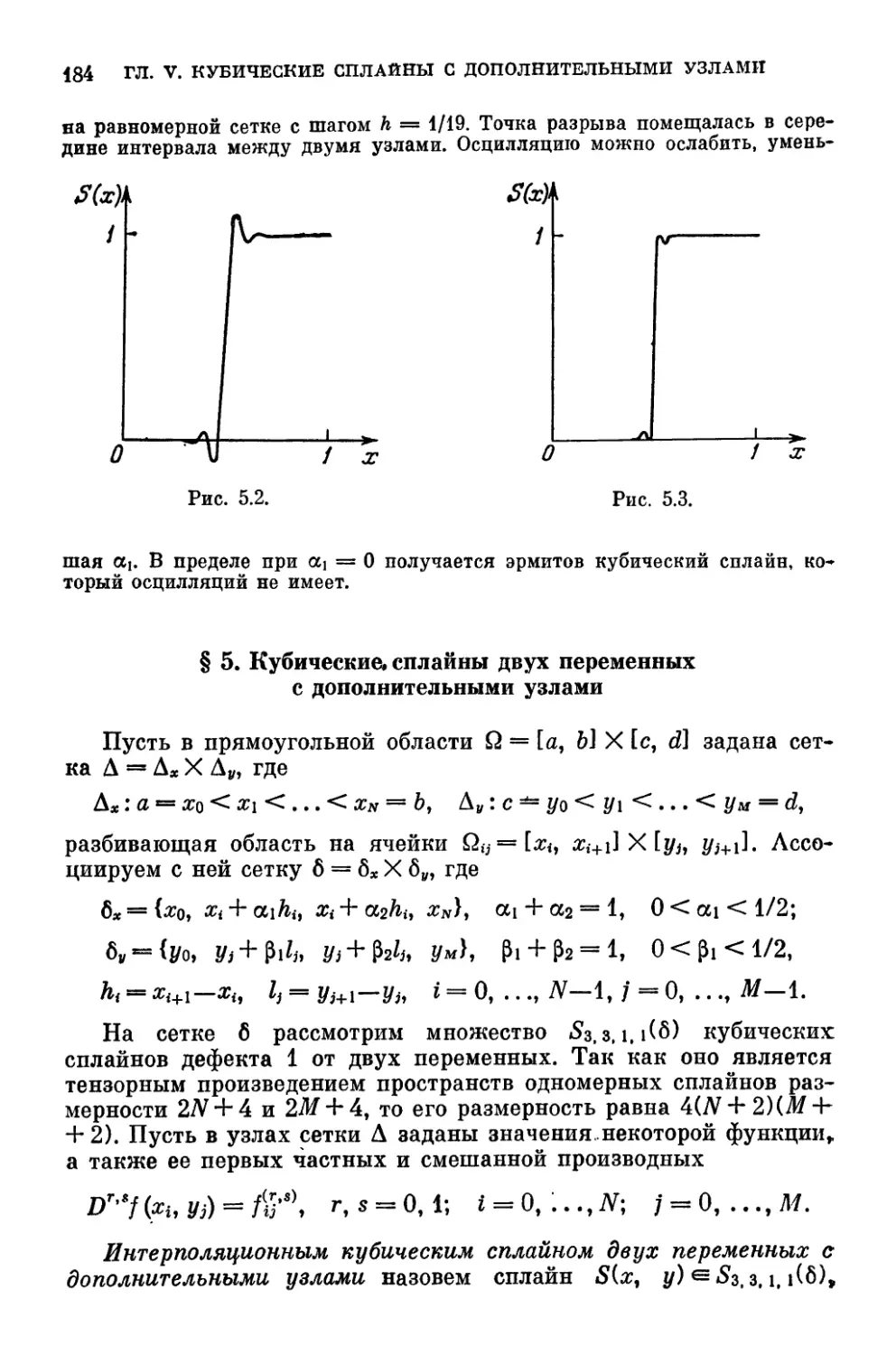
Глава V. Кубические сплайны с дополнительными узлами , . 165
§ 1. Локальная интерполяция 165
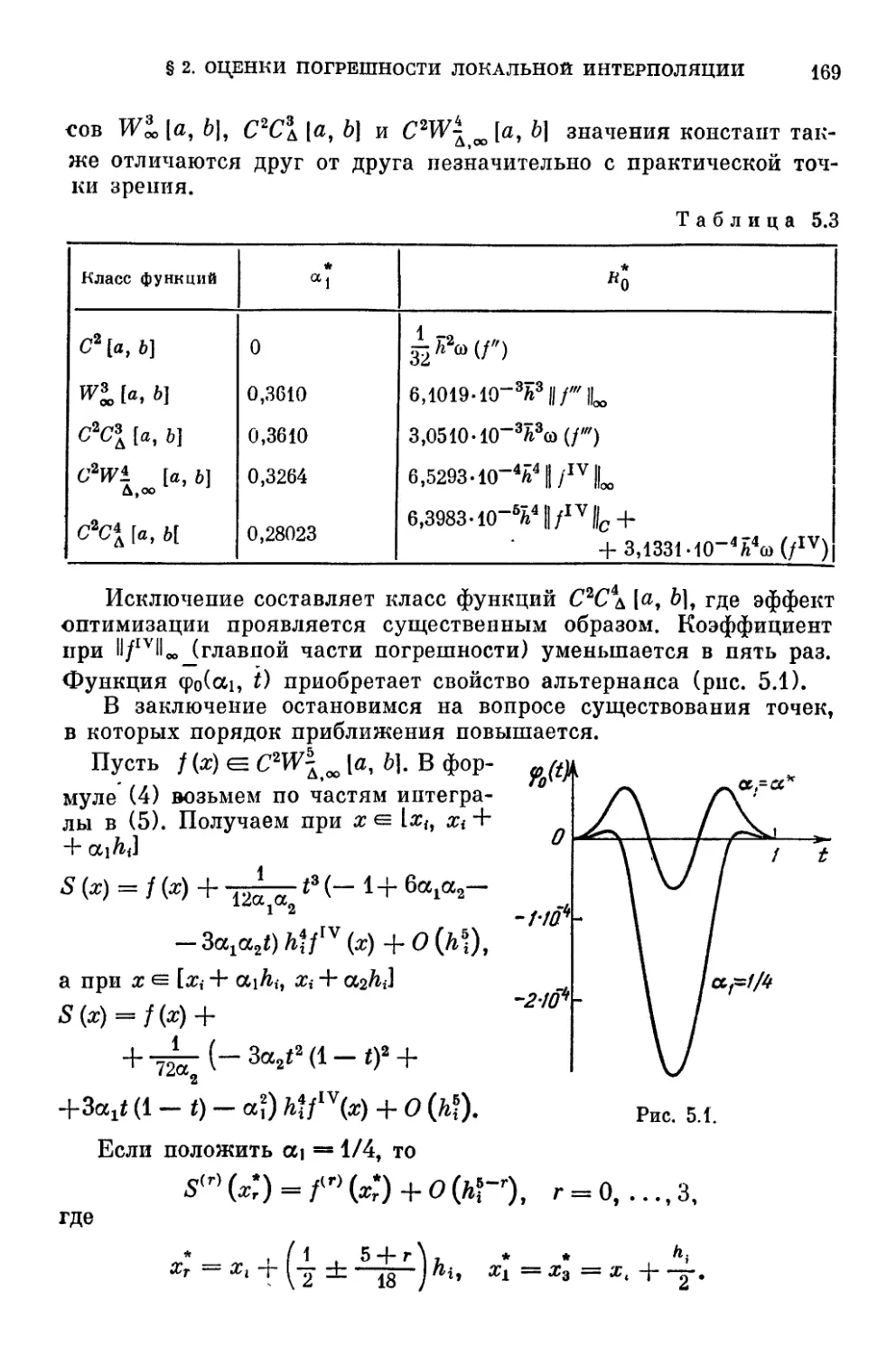
§ 2. Оценки погрешности локальней интерполяции 166
§ 3. Нелокальная интерполяция. Существование и единственность
решения 170
§ 4. Оценки погрешности нелокальной интерполяции .... 172
§ 5. Кубические сплайны двух переменных с дополнительными
узлами , 184
Глава VI. Обобщенные кубические сплайны 187
§ 1. Рациопальные сплайны * 187
§ 2. Кубические нелокальные сплайны класса С1 193
§ 3. Дискретные кубические сплайны 198
% "§ 4. Кубические сплайны с разрывными производными . . . 204
Глава VII. Приближение кривых и поверхностей ..... 207
§ 1. Параметрические сплайны 207
§ 2. Интерполяция кривых локальными сплайнами .... 209
§ 3. Интерполяция кривых параметрическими кубическими и
рациональными сплайнами 215
§ 4. Сглаживание кривых 220
§ 5. Приближение поверхностей 221
Глава VIII. Численное дифференцирование и интегрирование . . 225
§ 1. Численное дифференцирование 225
§ 2. Асимптотические формулы для кубических сплайнов класса С2 229
§ 3. Численное дифференцирование на равномерной сетке . . 232
§ 4. Численное интегрирование 233
§ 5. Оценки погрешности формул численного интегрирования.
Интегрирование с заданной точностью 236
§ 6. Интегрирование сильно осциллирующих функций , 238
Глава IX. Локальная аппроксимация сплайнами ..... 243
§ 1. Простейшая формула локальной аппроксимации. Сглаживав
ющие формулы 243
§ 2. Аппроксимация кубическими сплайнами; простейшая
формула 245
§ 3. Аппроксимация кубическими сплайнами; формула, точная па
кубических многочленах . . . ...«.., 250
§ 4. Общие формулы локальной аппроксимации • • » » ¦ 253
§ 5. Остаточный член аппроксимации ..•«..., 259

ОГЛАВЛЕНИЕ 5
§ б. О сплайнах, периодических на сетке ..•¦'... 263
§ 7. Моносплайны 267
§' 8. О задаче квазинаилучшего равномерного приближения
сплайнами. Асимптотически наилучшие приближения . . . 276
§ 9. Асимптотически наилучшие равномерные приближения
сплайнами первой степени 280
§ 10. Квазиинтерполяция и квазинаилучшие равномерные
приближения кубическими сплайнами 281
Глава X. Метод сплайн-коллокации ¦ . .,,.... 284
§ 1. Понятие о методе сплайн-коллокации 284
§ 2. Сведение схем метода сплайн-коллокации к разностным
схемам 286
§ 3. Использование ^-сплайнов в методе сплайн-коллокации . . 289
§ 4. Метод сплайн-коллокации для уравнений с разрывными
коэффициентами 294
§ 5. Схемы повышенной точности на равномерной сетке . . . 296
§ 6. Схема повышенной точности на неравномерной сетке . . 299
§ 7. Обсуждение результатов. Численные эксперименты . . « 304
Глава XI. Метод конечных элементов ¦ 309
§ 1. Понятие о методе конечных элемептов 309
§ 2. Примеры реализации метода на сплайнах 315
§ 3. Способы построения пространств аппроксимирующих функций 324
§ 4. Сходимость метода конечных элементов 328
Добавления 333
§ 1. Матрицы с диагопальным преобладанием 333
§ 2. Метод прогонки для решения систем уравнений с трехдиаго-
нальными матрицами 336
§ 3. Алгоритмы решепия систем уравнений с пятидиагольными
матрицами 342
Литература 346
Предметный указатель ¦¦••». 351

ПРЕДИСЛОВИЕ РЕДАКТОРА
Сплайн-функции — это новая быстро развивающаяся область
теории приближения функций и численного анализа. Получив
распространение в 60-х годах, главным образом как средство
интерполяции сложных кривых, сплайны в дальнейшем стали
важным методом для решения разнообразных задач вычислительной
математики и прикладной геометрии. Крупный вклад в развитке
теории сплайн-функций и ее приложений внесли сибирские
ученые.
По сравнению с классическим аппаратом приближения мпого-
членами сплайн-функции обладают по крайней мере двумя важ*
ными преимуществами. Во-первых, бесспорно, лучшими
аппроксимативными свойствами и, во-вторых, удобством реализации
построенных па их основе алгоритмов на ЭВМ. Хотя в мировой
литературе имеется уже около десятка монографий по теории
сплайнов, по среди них нет такой, где бы вычислительная
сторона дела для широкого круга задач была отражена с достаточной
полнотой.
Предлагаемая читателю книга восполняет этот пробел. Она
представляет собой, с одной стороны, введение в теорию сплайн-
функций, а с другой — подробное изложение онлайновых методов
в численном анализе с алгоритмами и рекомендациями по их
практической реализации на ЭВМ. При этом без ущерба для
математической строгости авторам удалось ограничиться такими
сведениями из математического анализа, которые входят в
вузовские программы инженерных специальностей с повышенной
математической подготовкой, что делает книгу доступной самому
широкому кругу читателей.
Н. Н. Янепко

ПРЕДИСЛОВИЕ АВТОРОВ
Методы сплайн-функций в настоящее время широко
применяются в вычислительной математике и инженерной практике.
Между тем, существующие по данной проблеме монографии
адресованы в первую очередь математикам, занимающимся теорией
сплайнов или обоснованием ее приложений в численном анализе,
и не содержат систематической информации о вычислительной
специфике сплайнов. При написании этой книги авторы
стремились, во-первых, создать пособие для изучающих основы
теории сплайн-функций и, во-вторых, дать практическое
руководство для широкого круга специалистов, использующих сплайны
при решении конкретных задач.
При отборе материала авторы учитывали накопленный ими
опыт по применению сплайновых методов в вычислительной
практике. Большое внимание уделено вопросам аппроксимации
функций одной и двух переменных, а также аппроксимации
кривых и поверхностей. Особенно детально исследуются сплайны
невысоких степеней (первой и третьей), хорошо
зарекомендовавшие себя при решении самых разнообразных задач. Чтобы в
оценках погрешности приближений получать достаточно
«хорошие» или даже точные константы, пригодные для практического
использования (чего нет в существующих руководствах),
разработан метод их .вычисления с применением ЭВМ. Достаточно
полно изложены задачи сглаживания экспериментальных данных,
непосредственно примыкающие к проблемам аппроксимации. На
основе изучения аппроксимаций рассмотрены методы численного
дифференцирования и интегрирования функций. Последние
главы книги посвящены численному решению дифференциальных
уравнений методом сплайн-коллокации и методом конечных
элементов. К сожалению, в силу ограниченности объема книги
оказалось возможным привести только самые простые задачи для
линейных обыкновенных уравнений и уравнений в частных про-
изводпых эллиптического типа с двумя независимыми
переменными. Все рассмотренные в книге задачи доведены до
алгоритмов, пригодных для практической реализации. Они
иллюстрируются большим количеством численных примеров. Исключение
составляет метод конечных элементов, для которого такие
примеры можно найти в специальных руководствах [24, 27]. Часть
результатов^ представленных в книге, публикуется впервые.

8 ПРЕДИСЛОВИЕ АВТОРОВ
Задавшись целью сделать книгу доступной возможно
большему кругу читателей без ущерба к требованиям математической
строгости доказательств, авторам пришлось в ряде вопросов
пойти на отказ от общности результатов в пользу конкретных
примеров. При изложении материала учтен опыт преподавания
методов сплайн-функций в Новосибирском государственном
университете. Для чтения книги достаточно математической
подготовки в пределах общих вузовских курсов по специальности
«прикладная математика» и инженерным специальностям с
расширенной программой по математике.
В список литературы включены источники, пепосредствеппо
использовавшиеся авторами при написании книги. Из других
работ приводятся те, которые близко примыкают к содержанию
книги, расширяя и углубляя рассмотренные в ней вопросы.
Подробные библиографические обзоры имеются в цитируемых
монографиях [1, 4, 10, 23, 27, 29]. Практически полная библиография
работ по 1972 г. включительно содержится в [28]. Для лемм,
теорем, следствий, таблиц и рисунков принята двойная
индексация по главам (теорема 1.3 — глава I, теорема 3). Нумерация
формул производится по параграфам. В случае ссылки на'
формулы из другого параграфа применяется двойной индекс, а на
формулы из другой главы — тройной индекс, например, B.9.3) —
глава II, параграф 9, формула 3). Если вместо первой цифры
стоит буква Д, то это означает ссылку на добавления в конце
книги.
Авторы считают своим долгом отметить, что исследования по
теории сплайн-функций и ее приложениям в вычислительной
математике и инженерном деле, начатые в середине 60-х годов
в Новосибирском научном центре АН СССР, пользовались
неизменной поддержкой академиков Г. И. Марчука, С. Л. Соболева,
Н. Н. Яненко. В процессе работы над книгой авторы имели
полезные обсуждения отдельных вопросов с профессором Г. Ш.
Рубинштейном, а также с В. В. Вершининым, А. И. Имамовым,
В. А. Леусом, В. А. Скороспеловым, С. И. Фадеевым, Б. М.
Шумиловым. Всем названным лицам авторы выражают искреннюю
благодарность.
Ю. С. Завьялов,
Б. И. Квасов,
В. Л. Мирошниченко

ВВЕДЕНИЕ
Большинство численных методов решения задач
математического анализа так или иначе связано с аппроксимацией функций*
Это и собственно задачи приближения функций (интерполяция,
сглаживание, наилучшие приближения) и задачи, в которых
аппроксимация присутствует как промежуточный этап
исследования (численное дифференцирование и интегрирование,
численное решение дифференциальных и интегральных уравнений).
Типичной задачей приближения является задача
интерполяции: по заданной таблице чисел ix{, /(#<)), i = 0, ..., N,
восстановить функцию fix) с той или иной точностью на отрезке [а, Ь]
действительной оси. Классический метод ее решения состоит в
построении интерполяционного многочлена Лагранжа,
определяемого равенством
N N
Хотя согласно теореме Вейерштрасса всякая непрерывная
функция fix) на отрезке [а, Ь] может быть как угодно хорошо
приближена многочленами, практические возможности
применения многочленов Лагранжа ограничены. Прежде всего,
используя подобный аппарат, хмы должны быть уверены, что, выбрав
достаточно большое число узлов интерполяции, получим хорошее
приближение интерполируемой функции. Однако, как показывает
ряд простых примеров, это часто нельзя гарантировать.
С. Н. Бернштейном A916 г.) было установлено, что
последовательность интерполяционных многочленов Лагранжа {LNix))y
построенных для непрерывной функции fix) = \х\ на отрезке
[—1, 1] по равноотстоящим узлам (#o — — I, xN = i), с
возрастанием N не стремится к fix). Еще более любопытен другой
пример, восходящий к Рунге A901 г.) и состоящий в том, что
указанный интерполяционный процесс не сходится на [—1, 1] даже
для гладкой сколь угодно раз дифференцируемой функции fix) =
= A + 25я2)-1 (рис. 0.1). В обоих случаях
Ню max \f(x) — LN(x)\ = оо.
Иногда эти трудности удается преодолеть путем специального

10
.ВВЕДЕНИЕ
выбора узлов интерполяции или за счет перехода к каким-либо
обобщенным многочленам. Однако такой путь, как правило,
весьма усложняет вычисления и к тому же не избавляет нас от
второй проблемы — быстрого накопления ошибок округления
с ростом степени многочлена. Поэтому иа практике для того,
чтобы достаточно хорошо приблизить функцию, вместо построения
интерполяционного м ногочле-
иа высокой степени
используют интерполяцию
кусочными многочленами.
Примером такого рода
является кусочно-линейная
интерполяция. В общем
случае отрезок [а, 61 точками
а = §о < Ъ < •. ¦ < §п = Ъ
разбивается на части и на
каждом промежутке \\и h+\h
i = 0, ..., га— 1, строится
свой интерполяционный
многочлен. Полученные таким
образом многочлены
(обычно одной и той же
степени) дают интерполяцию
функции f(x) на всем
отрезке [а, 6], которая, вообще
говоря, не обеспечивает
гладкого перехода от одного
звена к другому и может быть
даже разрывной, если точки
Рис< 01- ?г, i = l, ..., га—1, не
включаются в число узлов
интерполяции. Это допустимо, если не требуется восстанавливать
функцию с заданной степенью гладкости. В частности, различные
таблицы составляются с таким шагом, чтобы промежуточные
значения функции с принятой точностью можно было вычислить
с помощью линейной или квадратичной интерполяции. Для
гладкого восстановления таблично заданной функции нужно
увеличить степень составляющих многочленов, а остающиеся
свободными коэффициенты определять из условий гладкого сопряжения
многочленов иа соседних промежутках. Получающиеся при этом
гладкие кусочио-мттогочлепные функции с однородной
структурой (составленные из многочленов одной и той же степени)
называются сплайн-функциями или просто сплайнами. Простейший
и исторически самый старый пример сплайна — ломаная.
Термин сплайн произошел от английского spline, что в
переводе означает рейка, стержень — название приспособления, кото-
-58

ВВЕДЕНИЕ 11
рое применяли чертежники для проведения гладких кривых через
заданные точки. Возьмем гибкую стальную линейку, поставим
ее на ребро и, закрепив один конец в заданной точке (#о, /(#о)),
поместим между опорами, которые располагаются так, чтобы
линейка проходила через заданные точки (рис, 0.2). Согласно
30j 30*
Рыс. 0.2.
закону Берпулли — Эйлера линеаризованное дифференциальное
уравнение изогнутой оси линейки имеет вид
где S" ix) — вторая производная прогиба, М(х)—изгибающий
момент, изменяющийся линейно от одной точки опоры к другой,
EI — жесткость. Проинтегрировав это уравнение, получим, что
функция Six), описывающая профиль линейки, является
кубическим многочленом между двумя соседними точками опоры и
дважды непрерывно дифференцируемой функцией на всем
промежутке интегрирования. Для определенности задачи на концах
должны быть заданы краевые условия, в частности, при
отсутствии внешних нагрузок па линейку S"(xq) = S"(xN) = 0.
Функция Six) представляет собой другой пример (теперь уже
гладкого) сплайна. Она относится к интерполяционным
кубическим сплайнам, обладающим рядом замечательных свойств,
которые и обеспечили им успех в приложениях.
В отличие от интерполяционных многочленов Лагранжа,
последовательность интерполяционных кубических сплайпов на
равномерной сетке узлов всегда сходится к интерполируемой
непрерывной функции, причем сходимость повышается с
улучшением дифференциальных свойств функции fix). Так, для функции
fix) = A + 25#2)~1 из примера Рунге кубический сплайн на
сетке с числом узлов N = 6 дает погрешность того же порядка, что
и многочлен Lsix), но для N = 21 она настолько мала, что в
масштабах рис. 0.1 не может быть показана (ср. с многочленом
/Ы)
Алгоритмы построения кубических сплайнов являются весьма
простыми и эффективно реализуются на ЭВМ, причем влияние
ошибок округления при вычислениях оказывается незначительным.
Кроме того, кубические сплайны обладают интересными
экстремальными свойствами, связанными с тем фактом, что про**.

12 ВВЕДЕНИЕ
филь рейки, проходящей через заданные точки с краевыми
условиями S'W-f'(zo) и S'(xN) = f(xN) или S"(x0)=S"(xN) = 0,
принимает форму, при которой потенциальная энергия рейки
минимальна. В линейном приближении это выражается
соотношением
где равенство имеет место только для fix) = Six).
Исследование двух проблем — интерполяции функций
сплайнами и оптимальной аппроксимации линейных фупкционалов, где
точными решениями оказываются сплайн-функции,— привело в
настоящее время к образованию двух направлений в теории
сплайнов: алгебраического и вариационного.
В первом из них сплайны трактуются как некоторые гладкие
кусочно-мпогочленные (включая обобщенные многочлены)
функции с однородной структурой. Сюда относятся так называемые
L-сплайны, составляемые из решений линейного однородного
дифференциального уравнения LS(x) = 0. Случай кубических
сплайнов соответствует L = d4/dx4 [1, 4]. Решение задач
аппроксимации и изучение аппроксимативных свойств сплайнов при
этом сводятся к исследованию линейных алгебраических систем.
Вопрос об экстремальных свойствах является здесь производным
в том смысле, что отыскиваются постановки вариационных задач,
решепиями которых были бы сплайн-функции.
В вариационном направлении под сплайнами понимают
элементы гильбертовых (или банаховых) пространств,
минимизирующие определенные функционалы, а затем исследуются свойства
этих решений. В некоторых работах понятие сплайнов
распространяется и па такие объекты, которые не являются сплайнами
в первом смысле.
В предлагаемой читателю книге рассматривается
алгебраический подход в теории сплайнов, преимуществом которого
(перед вариационным) является простота изложения и большая
близость к практическим потребностям вычислительной математики.
Укажем на некоторые особенности в реализации этого подхода.
Бурное развитие теории сплайн-функций одной переменной
как аппарата численного анализа было обусловлено главным
образом двумя причинами: 1) хорошей сходимостью сплайнов к
аппроксимируемым объектам; 2) простотой в реализации
алгоритмов построения сплайнов на ЭВМ.
Обращаясь к сплайн-функциям многих переменных,
приходится признать, что если мы хотим сохранить для них эти два
свойства, установленные для одномерных сплайнов, то неизбежно
должны ограничиться функциями с клеточной структурой. Под

ВВЕДЕНИЕ 13
этим мы понимаем функции, область определения которых
разделена на ячейки (в плоском случае прямоугольники,
треугольники и т. п., в многомерном — параллелепипеды, пирамиды
и т. п.). В каждой ячейке функция определена в некотором
смысле однородным способом с условиями гладкости вдоль границ
ячеек. При интерполировании функций многих переменных для
сплайнов, в отличие от многочленов, не возникает особых
трудностей с проблемой существования и единственности решения.
Для областей, разделенных на прямоугольники
(параллелепипеды), тенденция в развитии многомерных сплайнов состоит в их
рассмотрении как тензорного произведения одномерных сплайнов,
что обеспечивает сохранение свойств сходимости и алгоритмич-
ыости, а во многих задачах — и экстремальных свойств. Кроме
того, вскрыта тесная связь этого направления с теорией конечно-
разностных схем. Идея триангуляции области реализована в
математической физике в методе конечных элементов, когда
решение вариационной задачи строится в виде сплайн-функции.
Опыт применения сплайн-функций как аппарата
приближения функций в численном анализе показывает, что во всех
известных случаях удавалось добиться ощутимых результатов по
сравнению с классическим аппаратом многочленов. В одних
задачах переход к сплайнам приводит к повышению точности
результатов, в других — к значительному сокращению
вычислительных затрат, в третьих — достигаются оба эффекта одновременно.
Наконец, с помощью сплайнов удалось решить и такие задачи,
которые другим путем решить было бы невозможно.
Среди них на первом месте стоит проблема представления и
хранения геометрической информации в самых" различных
областях знания, будь то естественные науки, техника, архитектура,
картография. Традиционно в более или менее сложных
ситуациях эта задача решается путем изображения объекта или
процесса на плоскости в виде графиков, чертежей и т. п. Вследствие
ограниченности масштабов изображений этот способ
принципиально не может обеспечить требуемую точность во всех случаях.
Применение для данных целей сплайнов (как одной, так и
многих переменных) позволяет хранить геометрическую информацию
в числовой форме и с любой точпостыо. При обработке
информации на ЭВМ использование сплайнов позволяет на единой
методологической основе разрабатывать математическое
обеспечение средств машинной графики (графопостроители и дисплеи).
Особенно широкое применение получили сплайны в технике
как аппарат для математического моделирования поверхностей
деталей и агрегатов сложной формы, таких, как
аэродинамические обводы летательных аппаратов, корпуса судов, лопасти
гидротурбин (рис. 0.3), кузова легковых автомобилей и т. п. Такие
математические модели стали необходимыми при создании систем

14 ВВЕДЕНИЕ
автоматизации проектирования изделий на основе ЭВМ,
технологической подготовки их производства, включая разработку
программ для оборудования с цифровым программным управлением,
В математической физике всегда были популярны метод кол-
локации и вариационный метод Ритца — Галеркина решения
краевых задач для дифференциальных уравнений. Но их
применение на базе многочленов было весьма ограниченным из-за
больших вычислительных трудностей. Перевод этих методов на
сплайповую основу буквально вдохнул в них новую жизнь.
Прогресс был столь значителен, что новые варианты методов
получили специальные названия: метод сплайн-коллокацпи и метод
конечных элемептов.
Область применения сплайнов непрерывно растет.
Литература к введению. [1—4, 10, 13, 14, 23, 97, 98].

Г л а в а I
ПРОСТРАНСТВО СПЛАЙН-ФУНКЦИЙ
В этой главе вводятся основные понятия теории сплайнов,
необходимые для изучения сплайиовых аппроксимаций. В
задачах приближения заданной функции, принадлежащей некоторому..
линейному множеству, аппроксимирующая функция обычно
отыскивается среди элементов конечномерного подпространства этого
множества. В линейном множестве вещественных функций таким
подпространством является, например, пространство многочленов
степени не выше заданной. Здесь мы покажем, что сплайны
заданной степени и гладкости с узлами па фиксированном
разбиении тоже образуют конечномерное пространство. Будут
рассмотрены некоторые наиболее употребительные базисы в этом
пространстве, а также вопросы организации вычислений с помощью
базисных сплайнов.
§ 1. Определение сплайнов. Пространство сплайнов
Пусть на отрезке [а, Ь] задано разбиение Д: а = Хо<Х\<...*
+ .. < xN=b. Для целого к > О через Ck = Ch[a, b] обозначим
множество к раз непрерывно дифференцируемых па [а, Ь] функций,
а через С [а, Ы — множество кусочно-непрерывных функций с
точками разрыва первого рода.
Определение. Функция Snv(x) пазывается сплайном
степени п дефекта v (v — целое число, O^v^ra+1) с узлами на
сетке Д, если
а) на каждом отрезке [я*, хщ] функция Sn>v(x) является
многочленом степени /г, т. е.
п
?niV(x)= 2 aaix—Xi)* для х^\хи Si+il, г=0, . •., iV—1; A)
а-о
б) Xn,vWGC""vK Ь].
Определение сплайна имеет смысл и па всей вещественной
оси, если положить а = — о°, Ъ = + оо. На каждом отрезке
[хг, хи]] для сплайна, помимо формулы A), возможно
представление
Sn.v(*)= fjbl(x-xi+1)«, i = 0,...,#-l. B)

16
ГЛ. I. ПРОСТРАНСТВО СПЛАЙН-ФУНКЦИЙ
При этом на полуоси (—°°, х\] берется только формула B), а на
полуоси [xN-U °°) только формула A).
Итак, сплайн SntV(x) имеет непрерывные производные до
порядка п — v. Производные сплайна порядка выше п - v, вообще
говоря, терпят разрывы в точках xiy
i = l, ..., N — 1. Для
определенности будем считать, что функция
*^n,v(я), r>n-r-v, непрерывна
справа, т. е.
з г
п — v+ 1, ..., щ
Множество сплайнов,
удовлетворяющих определению, обозначим
через ?П/ЛД). Ясно, что этому множе-
Рис. 1.1. ству принадлежат и сплайны
степени п дефекта vi < v и сплайны
степени п\<п дефекта vi<^v, если щ — vi ^ n — v, в том числе
многочлены степени не выше п. Так как обычные операции
сложения элементов из Sn,v(A) и их умножения на
действительные числа не выводят за пределы множества, то оно является
линейным множеством или линейным пространством.
Простейшим примером сплайна является единичная функция
Хевисайда
при
с которой естественным образом связана усеченная степенная
функция
п va/ \ Iх ПРИ #
х+ = xnQ (х) = n F
* [ 0 при #
при
Функции Q(x) и #+ являются сплайнами соответственно
нулевой степени и степени п дефекта 1 с единственным узлом в
нулевой точке (рис. 1.1). Мы будем рассматривать также
усеченные степенные функции (х — х\)% > связанные с точками сетки
А. При n — v + l^a'^n они принадлежат множеству »5П|У(А).
Теорема 1.1. Функции
ха, а = 0, ..., /г,
C)

§ I. ОДРЕДЕЛЕНИЕ СПЛАЙНОВ. ПРОСТРАНСТВО СПЛАЙНОВ 17
линейно независимы и образуют базис в пространстве Snv(A)
размерности (п + 1) 4- vl/V — 1).
Доказательство/ Предположим противное, т. е. что
существуют постоянные й.и сга>, не все равные нулю и такие*
что
S^+s' 2 <&(*-*,)+=о.
а=0 г=1 а'=п—v+l
Тогда для а: ^ Х\ имеем Cq + с\х + • • • + с%хп = 0 ив силу
линейной независимости функций ха находим с^ = 0, а = 0, ..., п.
Беря # е (#,, х2), получаем c\-v+l (x— x^-v+i +... + ^п (ж —
— ^iO1 = 0 и, по той же причине, с\> == 0, а' = гс — v + 1, • • •, п*
Продолжая этот процесс, убеждаемся, что все сха* = 0.
Следовательно, функции C) линейно независимы.
Пусть теперь задан сплайн Sn,y(x). На отрезке 1хи хн\]г
i = 0, ..., N—1 он является многочленом степени п, Рп{х), и
может быть записан в виде A) или B). При этом, так как
первые п — v производных сплайна непрерывны в точках х^ т. е»
[РГ1 (*0](г) = И (*0Г\ г = 0, ..., п - v, то «i = 6*Г\
а = 0,..., тг—v; i = 1, ..., iV—1.
Покажем, что сплайн 5П/Д#) на отрезке [а, 6] может быть
представлен в виде
Sn,v (X) - Р°п (X) + 2 2 4' (X - Xi)%% D)
г=1 a'=n—v+l
ГДе Са* = «а' — Ьа.
Действительно, преобразуя это выражение при х^1х{,
получаем
Sn,v («) = 2 ^ (ж - *0)a +2 2 * (« - ^)a' =
p=l a'=n—v+l
<Х=0
i
2
)=2 а'=
I
1
n
2 c,
=n-v+l
п
V V (
=n—v+l
а
¦ —
'=n—v+l
«,)«' = ...
n
^j aa\x x^j
n
a=o
Это доказывает, что всякий сплайн ?Ы е5ял(Д) может быть
представлен в виде линейной комбинации функций C), т. е. эти
2 ю. С, Завьялов и др.

1
-18 гл. т. пространство сплайн-функций
функции образуют базис в 5n,v(A), и представление D)
единственно. Эта формула называется представлением сплайна в виде
суммы усеченных степенных функций. Итак, множество Sn>v{&)
является конечномерным
пространством размерности " п +
+ l + v(tf —1).
Задачи, а) Показать, что
функции х, я+, \х\ обрадуют
линейную зависимую систему.
_ б) Записать функцию, изобра-
_* _ j п * j 2 X жеппУ10 на Рис- ^-2^ в виде линейной
комбинации усеченных степенных
функций первой степени.
Рис. 1.2. Ответ. 1(х) = (jc-H2)+— (x +
+ 1)+-(х-1)++(*-.2)+.
в) Показать, что произвольная непрерывная кусочно-линейная функция
дюжет быть записана в виде
S(x) =aa? + 6 + c1(a;-g)+, сг=:С-а.
г) Показать, что многочлен Рп (х) при х р> х0 может быть записан
з виде
<если ж_п < ... < я_1 <. хо, р = —щ ..., — 1.
§ 2. Базисные сплайны с конечными носителями
В математическом анализе встречаются конструкции, связан-»
вые с финитными функциями, т. е. гладкими функциями,
которые определяются на всей действительной оси, но отличны от
нуля лишь на некотором конечном интервале (носителе). Ниже
мы исследуем финитные сплайны из пространства Snt\(A) В
последующем изложении они играют исключительно важную роль.
Расширим сетку "А, добавив дополнительно точки
я-п < ... < s-i < а; Ъ < xN+1 < ... < xN+n
(можно положить, например, x-i = XQ — i(x\ — xq), xN+i = #iV+;
+ iixN — Zn-i), 1 = 1, ..., юХ.
Возьмем функцию ф„(ж, ^) = (—1)п+1(лг + 1)(о: — ^)^_ и
построим для нее разделенные разности (/г+1)-го порядка по
значениям аргумента t = xh ..., х^п+и В результате получаются
функции переменной х:
Вп(х) = ц>п[х\ хи ..., a;i+n+i|, i = — л, ..., iV — 1. A)

§ 2. БАЗИСНЫЕ СПЛАЙНЫ С КОНЕЧНЫМИ НОСИТЕЛЯМИ 1$>
Так как для разделенной разности (п+ 1)-го порядка от
функции git) по точкам xiy ..., хНп+\ справедливо равенство
g(xp)
g[xu ..., ^i1 ^
^d ©^ 1г(хУ +^) 1
[2, с. 38], то
Если использовать тождество
(х - t)n+ = (х- «)» + (-
то можно получить песколько иную форму записи этой функции::
_ п
^ ! 4t < = -nf...f^-l. C)
Из определения усеченных степенных функций следует, что
функция Вп(х) является сплайном степени п дефекта 1 на
сетке узлов хи .. .,.sHn+i.
Лемма 1.1. Справедливо тождество
я "Г
n-X (х) + г- Дп-iW. D)
Доказательство. Если git) = g\{t)g2U)y то разделенная
разность функции #Ш по точкам #*, а:г+1 может быть вычислена
по формуле Лейбница:
gixu Xi+\] =sgdxi)g2lx
Для разности (и-f l)-ro порядка путем рассуждений по
индукции нетрудно получить
г+п+1
g [XU . . ., ^i-f-n+ll = 2 gi I^f, • • •, ^г+р] g2 [*i+p, • • •, a?l+n+l].
i
Представим функцию фп(#, t) в виде фп(#, t) =
*= —77— Фп-i (я, 0 (* —• я?) п построим ее разделенную разность
(п+ 1)-го порядка по формуле Лейбница. Получим
у-. гуА\ ¦ ' \(д \Х* X' ?• 1
2*

20 ГЛ. I. ПРОСТРАНСТВО СПЛАЙН-ФУНКЦИЙ
Отсюда, если учесть определение сплайнов Вп{х) A), следует
тождество D). ^
Лемма 1.2. Сплайны Вгп (я), i = — /г, ..., ЛГ — 1, обладают
следующими свойствами:
•О ЯпИ^п Т ж;;*"*•+*«); E)
б) j BUx)dz = t. F)
—оо
Доказательство. Функция q>n(#, ?) равна пулю при
и является многочленом степени ц от х при #>?. Поэтому ее
разделенпые разности (/г+1)-го порядка по значениям
аргумента ? = Хъ, ..., ^t+n-ц тождественно равпы нулю при я < #< и
л: > #*+п4 ь т« ©• ^п (^) ^ 0, а: ^ (^7 Xi+n+1). Внутри интервала
fa, #i+n+i) 5A (л?) > 0. В самом деле, при п = 0 согласно B)
#о (#) = (^i+i — ^0">0 . Пусть, далее, утверждение а) верно
при /г = Z — 1. Тогда при и = 1 в силу D) на интервале (xh xi+i+\)
функция В] (х) является линейной комбинацией с
положительными весами функций #/-i (x) и B]t\ (x), причем по
предположению в произвольной точке указанного интервала хотя бы
одна из этих функций больше пуля. Следовательно, В] (х) > 0
для х е (хи х{+1+\1, и утверждение а) установлено.
Докажем утверждение б). Всякую п + 1 раз непрерывно
дифференцируемую функцию g(t) на промежутке a ^t ^ Ъ можно
представить формулой Тейлора с остаточным членом в
интегральной форме:
G)
Здесь под знаком интеграла вместо обычного сомножителя (t ¦— т)п
стоит усеченная степенная функция, что позволяет заменить
переменный верхний предел t постоянной величиной Ь. Из G)
следует разностное соотношение
где а < хи ..., a?i4.n41 < Ь- Так как

§ 2. БАЗИСНЫЕ СПЛАЙНЫ С КОНЕЧНЫМИ НОСИТЕЛЯМИ 21
{2, с. 40], то, полагая gix) « хп+\ поручаем
Поскольку Z??(;r)sO вне интервала (а, 6), то это равенство
совпадает с F) и лемма доказана.
Лемма 1.3. Функции Вгп{х) являются сплайнами
степени п дефекта 1 с конечными носителями минимальной длины.
Доказательство. Предположим, что существует сплайн
Six) ^ Snt i(A), отличный от нуля на интервале, меньшем, чем
(хь Xi+n+\). Такой интервал, очевидно, не может иметь границей
точку, не являющуюся узлом сетки А. Поэтому пусть это будет
интервал (хи xi+n).
Возьмем представление сплайна дефекта v = 1 через
усеченные степенные функции A.4). Вследствие того, что Six) = 0 при
х ^ Xi, в этом представлении аа = 0, а = 0, ..., п; с°п = 0, р =
= 0, ..., 1 — 1. Так как Six) = 0 при x>xi+ni то ее производные
до порядка п — 1 равны нулю в точке xi+n. Имеем
i+n-i
2
Последние равенства представляют собой однородную систему
линейных уравнений для определения коэффициентов с?, р =
= i, ..., i + д—1. Ее определитель пропорционален определителю
Вандермонда ?г-го порядка, который отличен от нуля, и система
имеет только нулевое решение. Наконец, из того же условия
Six) & 0 при х > Xi+n следует, что cvn = 0, р = J + л, ..., ЛГ —- 1.
Значит, iSn.iC^) ва 0 на [а, 6], и лемма доказана.
Теорема 1.2. Функции Вгп(х), i = — л, .*., iV— 1, ,/ш-
нейно независимы и образуют базис в пространстве сплайнов
Л(А)
Доказательство. Покажем сначала линейную
независимость функций Вп (х), i = — п, ..., N — 1, на всей
действительной оси. Предположим противное, т. е. что существуют такие
постоянные с_п, ..., cN-\, не все равные нулю, что
c-jBn п (х) + ... + cn^M'1 (x) = 0. (8)
Выбирая x€=ix-n, х-п+\], получаем, что C-nBZn (х) = 0 и,
значит, с-п = 0. Беря затем же (х~п+1, а;„п+2), находим, что c_n+i = 0
и^ т. д., т. е. с^ = 0, ? = — w, ..., ЛГ—1. Следовательно, функции
2??(я) линейно независимы на (-*•«>, +оо).

22 ГЛ. I. ПРОСТРАНСТВО СПЛАЙН-ФУНКЦИЙ
Предположим теперь, что соотношение (8) выполняется
только на [а, Ы. Это значит, что на отрезках [#*, xi+\] обращаются
в нули сплайны вида
Sl(x}= сг-пВг-п{х)+... + СгК{х), i = 0, ..., N - 1.
Каждый из них отличен от нуля самое большее на интервале
(xi-n, xi+n+\). Поэтому из предположения 54^)^0 при х е-
^ [xi, xi+\] согласно доказательству леммы 3 следует, что S{(x) ^
^0 на интервалах (х{-п, хд и (xi+i, хг+пЛ\), а значит, и на всей
действительной оси. В силу линейной независимости функций
Вп(х) на (—«>, +°°) должно быть ср = 0, р = i — п, ..., г, и это
для всех i =» 0, ..., N — 1. ^
Таким образом, функции Вп (#), i = — п, ..., N — 1, линей-
по независимы, и так как согласно теореме 1.1 размерность
пространства Snti(A) равна п + Л/, то они образуют базис в этом"
пространстве. Теорема доказана.
Функции Вгп(х), i = — п, ..., N — 1, называются базисными
сплайнами с конечными носителями минимальной длины {В-
сплайнами), В силу теоремы 1.2 всякий сплайн Six) е?п>1(Д>
может быть единственным образом записан в виде
% Жх), (9)
где Ь* — пекоторые постоянные коэффициенты. Эту запись
сплайна называют его представлением через В-сплайны.
Из теоремы 1.2 вытекает
Следствие 1.1. Всякий сплайн S(x)^k01 принадлежащий
5п1(Д), с конечным носителем минимальной длины с точностью
до постоянного множителя совпадает с В-сплайном.
Доказательство. Минимальным конечным носителем
сплайна являе^тся один из интервалов (#<, xi+n+i), i = 0, ...
..., N — л — 1. Согласно (9)
5 (X) = Ьг-п?ГП (*)+...+ Ь;+Ж+Г1 (X).
Так как 5(^) = 0 для хФ {хи xi+n+\), то, выбирая
последовательно х е (д;Р) ^р41)» p = i — п, ..., t — 1, получаем, что Ьр = 0.
Аналогично, Ьр = 0 для р = г + ?г, ..., i + 1. Следовательно,
Замечание. Представление сплайнов через /i-сплайпы в виде (9)
имеет смысл для конечного отрезка [а, Ь]. Чтобы получить его для всей
вещественней оси, нужно положить х~п = ...'= z-i = а = — оо и 6 = '
= xn+i'= ... = xn+п = + оо. Тогда точки ± оо оказываются узлами
кратности в + 1и при построении 5-сплайнов с номерами i= — тг, ..., —1 и
i = jV — гс, ..., TV—1 нужно учитывать правило для разделенных разностей-

§ 3. НОРМАЛИЗОВАННЫЕ БАЗИСНЫЕ СПЛАЙНЫ
23
с кратнымп узлами [2, с. 43 — 441 • Мы не описываем подробно эти
конструкции, ибо все практические задачи, где используются 2?-сплайны,
рассматриваются на конечном отрезке.
Задачи, а) Пусть S {х) = Ai (х — 2)+» где Ai/(z) = f(x + 1) — f(x).
Показать, что
S(x)
) для я е (—- 2,2),
) для х&(— 2/2).
б) Пусть S(x) g53)i (Л). Показать, что если
-*= f(x + h) —/(ж), то S(x) —кубический многочлен.
в) Показать, что
D
при
где
1 х{
D — определитель Вапдермонда, a D — определитель, получающийся из него
при замене элементов x7j последнего столбца на {х- — х^_, / = i, ...
i + n+1.
г) Пусть Bt) (х) = 0 I х + -j I — 8 (х — y J. Показать, что функции
-f-oo
^ (х) = \ Вп__л (х — г/) 5П (г/) йг/, и = 1,2, • • м
—оо
являются Л-сплайнами степепи п с узлами хр = р— —^—, p = Q, .,fc
«.., л + 1, и выражаются формулами
П+1
где C^+i — число сочетаний из п + 1 элементов по /.
§ 3. Нормализованные базисные сплайны
и представление ими многочленов
При практических вычислениях удобпее использовать не
сами ?-сплайны, а функции, получающиеся из них умножением
на постоянные множители:
(I)

24 ГЛ. I. ПРОСТРАНСТВО СПЛАЙН-ФУНКЦИЙ
Эти функции называются нормализованными В-сплайнами. Нор*
мирующий множитель равен среднему арифметическому шагов
hi — Xi+\ — Xi на отрезке, где В-сплайн отличен от нуля.
Тождество B.4) для нормализованных 5-сплайнов имеет вид
Вп-1
С его помощью легко можно построить последовательность
сплайнов В], В{(х), ... Приведем первые четыре функции этой
последовательности для случая равноудаленных узлов ht = h.
Будем обозначать oin = ~ /ж— ж. n+i V Точка х
это середина отрезка-носителя 5-сплайна. Тогда имеем
. ^ |1 для ze=[zi9
0 \0 для х#.\хи
В\ (с) == A + аи) В*о+A- ог1) Bl+1;
В\ (о) « 1 D + *i2J*S + (т - ^) 5о+1 + у
В\ (а) = 1 B
 °гЗ Н «Н ° + б" '
Эти Б-сплайны изображены на рис. 1.3, а, б, в, г
соответственно.
В § 1 было отмечено, что многочлены Рп(х) степени не.
выше п являются элементами пространства сплайнов ?П/ДД)#
Следовательно, они представимы через базисы этих пространств,
в частности через базис из В-сплайнов в пространстве Sn>i(&).
Для вывода формул воспользуемся тождеством B). После
умножения обеих его частей на число Ь \ и суммирования по индексу
i получаем
2 ь^в1п (х) = 2
г
где
2 bf3 (z) su (x), C)
г
i^ir i r^ № ()
Лемма 1.4. Справедливо тождество
(^-х)п = 2сОп,н1@5пИ, con>i+iW= П (*-*;) E)
предположении оо.ДО s 1.

§ 3. НОРМАЛИЗОВАННЫЕ БАЗИСНЫЕ СПЛАЙНЫ
25
Доказательство. В формуле D) положимb[oj = o)n,t+i(t).
Тогда получаем
1 ' 1{Х — Xt) C0n,i+1 (t) + {Xi+n — X) G)n,i (^)] =
Бодставля b\0] и б*11 в C), находим
(t) (t — a:).
CDn.i+1
гп (X) - (t - X
.+ ) ) 2 ,+ (О ()
i i
Повторяя это преобразование п раз, получим справа
(t - *)* 2 сом+1 (t) B\ (x) = (t- xf 2 В\ (х) - (t- x)n.
г i
Теперь разложим обе части тождества E) по степеням t.
При этом
».i+i W = 2 (- lf*n~a syma (ж,+Il •.., яч+n). G)
a=o

26 ГЛ. I. ПРОСТРАНСТВО СПЛАЙН-ФУНКЦИЙ
Здесь syma(#i+h ..., xi+n) суть символы элементарных сим*
метрических функций от п аргументов степени а. Это
многочлены, состоящие нз Сп слагаемых. Они имеют вид
symo(a4+i, ..., Xi+n) = 1,
y+, » + + .. xi+n.
Подставляя разложения F) и G) в E) и приравнивая
коэффициенты при одинаковых степенях ?, находим представления
мономов ха через нормализованные В-сплайны на отрезке [а, Ъ\:
х* = 7^ 2 sym« (**+ь • • •»-i+«) ^^ W, a = 0, ..., п. (8)
Сп г
В частности, при ее = 0 получаем соотношение
S *»(*) = !, (9)
г
которое для нормализованных ^-сплайнов играет ту же роль, что
свойство B.6) для самих /?-сплайнов.
Полученные формулы (8) решают вопрос о представлении
произвольного многочлена п-п степени через нормализованные
В-сплаины. Они будут использоваться при изучении локальной
аппроксимации сплайнами в гл. IX.
§ 4. Фундаментальные сплайны. Интерполяционная
формула Лагранжа для сплайнов
Интерполяционный многочлен Лаграпжа .явным образом
выражается через фундаментальные многочлены, такие, что
каждый из них принимает значение, равное единице, в одном из
узлов интерполяции и нулевые значения в остальных [2, с. 36].
В этом параграфе мы построим сплайновые аналоги таких
многочленов и установим соответствующую интерполяционную
формулу Лагранжа для сплайнов.
Будем рассматривать две сетки узлов, одна из которых — уже
использовавшаяся ранее сетка А: а'== xq < ..'. < Хг < ... < xN,
а другая б: — «> < gi < ... < |Р < ... < ?*-п < + °°.
Ставится задача: построить сплайн Six) e ?п> iF),
удовлетворяющий интерполяционным условиям
SiXi)=ft ДЛЯ Яг^Д, A)
где Д, i = 0,..., N, — заданные действительные числа. Такой
сплайн называется интерполяционным. Исчерпывающий ответ на
вопрос, когда эта задача разрешима, дает следующая

§ 4. ФУНДАМЕНТАЛЬНЫЕ СПЛАЙНЫ
27
Теорема 1.3. Для того чтобы существовал единственный
интерполяционный сплайн Six) e ?n>iF), удовлетворяющий уело*
виям A), необходимо и достаточно, чтобы
i-l < Ь < X
i+n,
1,
N - П.
B)
Доказательство. Обратимся к представлению сплайна
Six) через усеченные степенные функции A.4). Тогда условия
A) будут равносильны соотношениям
2 aaxt
2 cp
- \r)l = U, * = 0, ...,
C)
образующим систему Л^ + 1 линейных уравнений для определения
iV+1 неизвестных коэффициентов сплайна: яа, а = 0, ..., п, и
ср, р = 1, .,., N — n. Решение системы существует и единственно,
если ее определитель DN-n^Q (N — n — число узлов сплайна).
Таким образом, доказательство теоремы сводится к установлению
того факта, что
(=7^=0, если условия B) выполняются,
1=0 в противном случае.
D)
Если сетка б пе содержит узлов (Af — тг = О), то
сформулированная задача есть задача лаграижевой интерполяции
многочленом. Как известно [2, с. 35], эта задача разрешима, ибо Do "Ф 0
как определитель Ваидермонда (тг+ 1)-го порядка.
Пусть теорема верна для N — п = 1— 1. Покажем, что тогда
она справедлива и для N — п = 1. В последнем случае
E)
Если |, > xi+n, то все элементы последнего столбца
определителя будут равны пулю и Д = 0. Если g, < arz-i, то в правом
нижнем секторе определителя (х{ — gp)!|L = (х{ — |р)п, г = I — 1,
...; Z+n; р = 1, ..., Z. Из первых /г + 1 столбцов составим ли-
кейпые комбинации вида

28 ГЛ. I. ПРОСТРАНСТВО СПЛАЙН-ФУНКЦИЙ
и вычтем их из соответствующих столбцов правой части
определителя Dh В результате получаем
1 *о
\ Т*
1 *|+п
•••ж0 КТО Si,
• • • xl+n
)+-(^o-?i)n
0
0
0
0
В нижних я + 2 строках определителя отличны от нуля только
элементы первых п + 1 столбцов. Разлагая его по минорам этих
строк, убеждаемся, что А = 0.
Остается исследовать случай, когда Xi-\ < |/ < я*+п. Для это*
го разложим определитель Dt E) по элементам последнего
столбца, из которых первые I равны нулю. Получаем
1+п
где Ct — алгебраические дополнения (с соответствующими
знаками) элементов fa — ^)+» по предположению все отличные от
нуля. Очевидно, Д(^) как функция аргумента |* является
сплайном с конечным носителем минимальной длины te_i, xt+n).
Внутри этого интервала Д(^) ^ 0,# а впе его Д(|*) s 0. Но тогда
согласно* следствию 1.1 Д(^) может отличаться от сплайна
BjT1 (х) только постоянным множителем и, значит, не
обращается в нуль ни в одной точке интервала (#z-i, Xi+n). Так как
теорема справедлива при N — п = 0, то она верна при любом
значении N — п.
Пусть ограничения B) выполнены и система сплайнов
Fn (x) e Sntl (б), 2 = 0, ...', N, удовлетворяет условиям
интерполяции вида Fn (хр) = 6ip для '^еД, i = 0, ..., N. Здесь б1Р —
символ Кронекера, т. е.
J1
при * = р,
при гфр..
Сплайны Fln(x) называются фундаментальными сплайнами
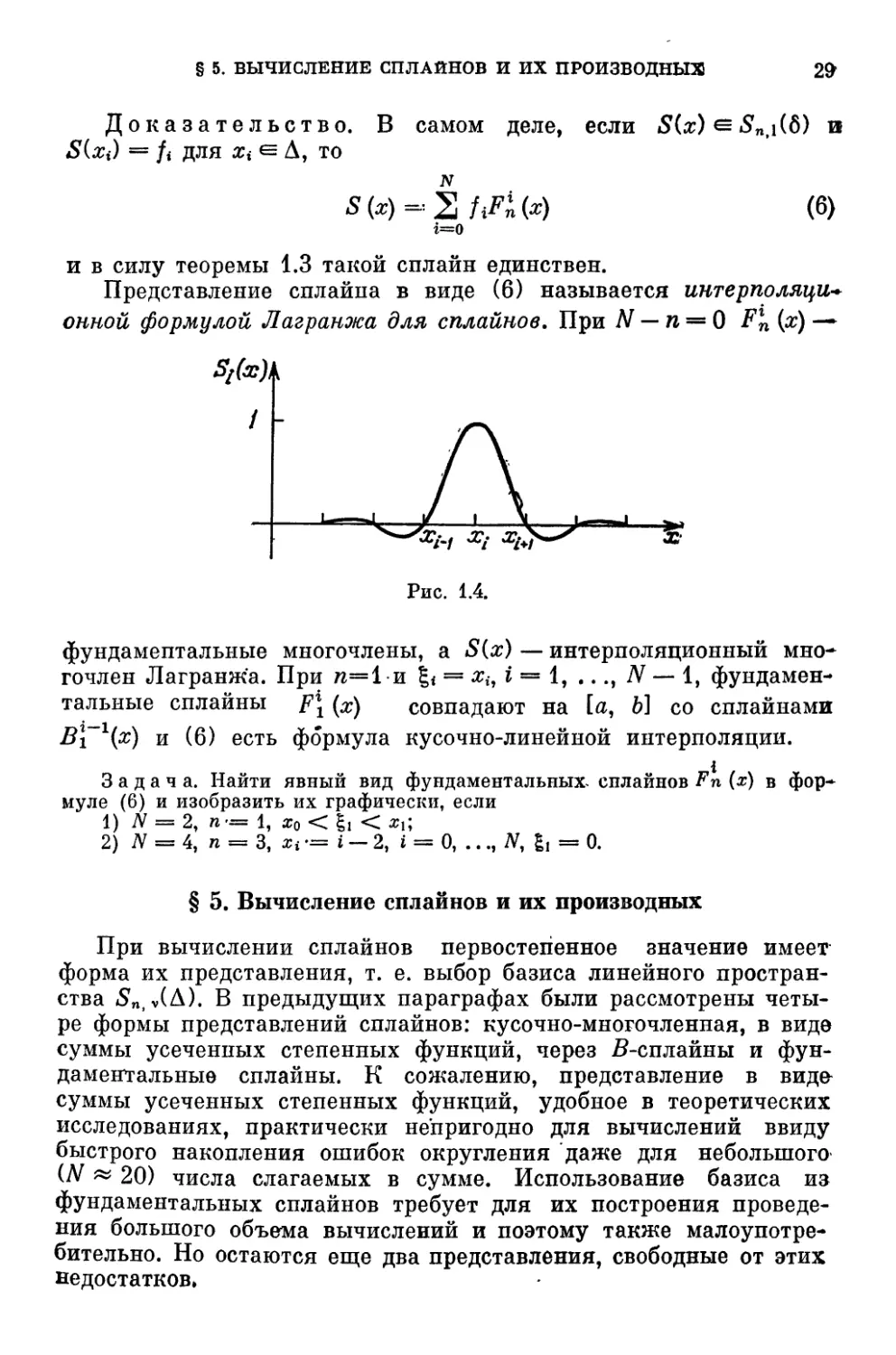
(рис. 1.4, где SM =*Fln (x)).
Теорема 1.4. Фундаментальные сплайны Fln (x), i = 0,...
...,iV, образуют базис в пространстве Sn>iF).

§ 5. ВЫЧИСЛЕНИЕ СПЛАЙНОВ И ИХ ПРОИЗВОДНЫХ
Доказательство. В самом деле, если Six) ^ ?n,i (б) и
J fi ДЛЯ Xi ^ Д, ТО
2J(*) F)
г=0
и в силу теоремы 1.3 такой сплайн единствен.
Представление сплайна в виде F) называется интерполяции
онной формулой Лагранжа для сплайнов. При N — п = 0 Fxn (x) —
фундаментальные многочлены, a Six) — интерполяционный
многочлен Лагранжа. При тг=1 и \i = хи i = 1, ..., N — 1,
фундаментальные сплайны F\ (х) совпадают на [а, Ь] со сплайнами
Вг{~1{х) и F) есть формула кусочно-линейной интерполяции.
Задача. Найти явный вид фундаментальных* сплайнов Fn (x) в фор*
муле F) и изобразить их графически, если
1) JV = 2, п= 1, хо< h <xu
2) iV = 4, /г = 3, хг-= i-2, i = 0, ..., N, Ei == 0.
§ 5. Вычисление сплайнов и их производных
При вычислении сплайнов первостепенное значение имеет
форма их представления, т. е. выбор базиса линейного
пространства Sntv(A). В предыдущих параграфах были рассмотрены
четыре формы представлений сплайнов: кусочно-многочленная, в виде
суммы усеченпых степенных функций, через В-сплайны и
фундаментальные сплайны. К сожалению, представление в вида
суммы усеченных степенных функций, удобное в теоретических
исследованиях, практически непригодно для вычислений ввиду
быстрого накопления ошибок округления даже для небольшого
(Af ~ 20) числа слагаемых в сумме. Использование базиса из
фундаментальных сплайнов требует для их построения
проведения большого объема вычислений и поэтому также
малоупотребительно. Но остаются еще два представления, свободные от этих
недостатков»

20 ГЛ. I. ПРОСТРАНСТВО СПЛАЙН-ФУНКЦИЙ
На практике в настоящее время наиболее распространенным
лвляется кусочно-многочленное представление сплайнов A.1).
В этом случае для запоминания сплайна требуется хранить N + 1~
абсцисс узлов и коэффициенты многочленов Pln (х), i = 0, ...
..., /V — 1, количество которых равно (ra+lW, т. е. всего
(п + 2W+1 чисел. Вычисление значения сплайна в точке
состоит в вычислении значения многочлена и при использовании, па-
пример, схемы Горнера требует выполнения 2п арифметических
операций. Коэффициенты составляющих сплайн многочленов
связаны (п — v + 1){N — 1) условиями гладкости в узлах сетки.
Поэтому запоминать можно не все Ы+DN коэффициентов (или
какие-то их линейные комбинации), а лишь часть их, но не
менее п+ I -\- v(N — 1) чисел, что равно размерности пространства
?n,v(A). Остальные коэффициенты находятся непосредственно в
процессе вычисления сплайна, что естественно приводит к
увеличению числа арифметических операций на этом этапе. Какие из
коэффициентов выгодно запоминать, а какие вычислять, зависит
от условий конкретной задачи и используе-мых вычислительных
средств.
Обратим внимание читателя па одну существенную
особенность. А именно, прежде чем вычислить значение сплайпа в
некоторой точке х е [а, ft], необходимо найти интервал [х{, xi+\]y
которому принадлежит точка х. Процедура поиска должна быть
достаточно экономичной, иначе можно оказаться в ситуации,
когда на это будет расходоваться большая часть машинного времени.
Очень важной характеристикой любого вычислительного
алгоритма является поведение его по отношению к ошибкам входные
данных. Неустойчивые алгоритмы, в которых конечный
результат сильно зависит от этих ошибок, практически непригодны для
использования. Вычисление сплайнов в этом смысле не является
исключением, и в каждом конкретном случае приходится делать
анализ устойчивости алгоритма.
В этом параграфе мы остановимся подробнее на вычисления
сплайнов дефекта 1, представленных через нормализованные
Л-сплайны. На отрезке [xiy х{+\]
?(*)= 2 ЪрВУЦх). A)
р=г—п
Для запоминания сплайна нужно храпить минимальный объем
информации BN + п + 1 чисел).
Согласно B.1) и C.1) нормализованные В-сплайны
выражаются через (?г+1)-е разделенные разности функции фп (ж, t) =я
= (--1)"+1(гг +1)(я-- t)l по.аргументу t:
Bl (x) = *7*

S 5. ВЫЧИСЛЕНИЕ СПЛАЙНОВ И ИХ ПРОИЗВОДНЫХ
или через ее п-е разности:
вп (х) = -j^piD>п'[х; хр+и ..., Яр+n+i] — Фп \х\ хр, .. .,х
Однако эти формулы мало пригодны для вычислений из-за
неустойчивости при сильно неравномерных сетках.
Функция фп(#, *), а вместе с нею и Вп(х) имеют по
аргументу х непрерывные производные до порядка «-1 и
разрывные производные порядка п. При этом -г; срп (я, I) = — (п + 1) X
X Фп-i (я, t). Нормализованные 5-сплайны суть линейные
комбинации значений функции фп(ж, t) при t = хр, ..., ^Р+п+ь и,
очевидно, операции составления разделенных разностей и
дифференцирования по аргументу х перестановочны. Имеем
[В1 (х)]' = Фп-i 1^; хр, .. .,#Р+Г1] — Фя-1 [х; хр+и .. .,xp+n+i\ =
Вп-х (X) —г Пп-1 \Х).
Тогда производная сплайна имеет вид
где
Производная сплайна порядка г выражается формулой
i
5(г) (ж) = п ... (п - г + 1) 2 Ь(рг)Я5-г И, B),
p=j_n+r
если обозначать
1,@) _ и j,@ _ P? °i-i /—I r П^
S1 {х) = п S Ъ^Врп-г (х),
p=i—?j 4-1
Формулы A), B) и рекуррентное соотношение C.2):
дают необходимые средства для построения алгоритмов
вычисления сплайнов и их производных.
Алгоритм 1. Учитывая тождество D), выразим сплайн
A) через 5-сплайны более низких степеней с коэффициентами^

32 ГЛ. I. ПРОСТРАНСТВО СПЛАЙН-ФУНКЦИЙ
являющимися многочленами от х:
причем
—;— fp — i -j — Up,
Продолжая эту процедуру, получаем
i
S (x) = У* bu^ (х) Вр (х)
где
I = 1, ..., П.
Так как
то S(x) = bi*(x) для же[агь a?1+i). Чтобы вычислить значение
сплайна в какой-либо точке х этого промежутка, по формулам E)
построим таблицу
G)
Число Ь| ^ (ж) и является искомым значением Six). Такая
организация вычислений требует выполнения 4я(га+1)
арифметических операций.
Вычисление значений производных S{r)(x) производится
следующим образом:
1) По формулам C) находятся коэффициенты bpr\ p = t —
Ч- г, ..., i, заполняющие таблицу
ь?2
п+т

§ 5. ВЫЧИСЛЕНИЕ СПЛАЙНОВ И ИХ ПРОИЗВОДНЫХ 33
2) По формулам E) с исходными данными Ьр = Ьр
аналогично таблице G) строится таблица
(9)
3) Искомое значение S{r) (х) = п ... (п - г + 1)Ъ\п~г} (х).
На весь процесс вычислений расходуется 4 (и—г)(»—r+l)-f-
-J-JLBn — г + -з")г арифметических операций.
Алгоритм 2. Пусть по-прежнему x<=lx(, ar«+il. По форму*
ле D) с учетом F) находим все числа Bn-i(x), которые не
равны нулю для заданного х, и образуем из них таблицу
B\(x)
В1гп(х) .... В1гГх(х) Вгп(х)
Значение сплайна находится по формуле A). Такая
организация вычислений требует выполнения [-^п + 1)(га + 1)
арифметических операций.
Вычисление производных S{r)(x) осуществляется следующим
образом:
1) Составляется таблица (8).
2) По элементам последней строки таблицы (8) и (п — г + 1)-й
строки таблицы A0) по формуле B) находится S{r)(x).
На весь процесс вычислений расходуется -тг (я — г) + 1 (п —
3/ 5\ L J
—r,+ 1) + yBя — г + -g-1 г арифметических операций.
Если значение S{r)(x) найдено, то для вычисления 5(r+r ) (х)
используется уже имеющаяся (л + 1 — г — г')-я строка таблицы
A0) и необходимо только продолжить таблицу (8) до (г + г')-й
строки, после чего Sir+rf){x) вычисляется по формуле B). На все
^ Ю. С. Завьялов и др.

34 гл. i. пространство сплайн-функций
это дополнительно затрачивается только Bга — 2r — rl -F
+ 1) (-j г' + 1) арифметических операций.
Сравнение эффективности приведенных алгоритмов по числу
выполняемых арифметических операций показывает, что
алгоритм 1 экономичнее, когда вычисляются только значения
сплайна. В этом случае он требует 4га(га+1) арифметических операций,
/С) \
тогда как алгоритм 2 — 1-^ п + 1 |(га + 1) операций. Из пих
«длинных» операций (умножений и делений.) 2га(га+1) к
Bга+1)(га + 1) соответственно. Если же нужно пайти
одновременно значепия функции Six) и некоторых из ее производных,,
то экономичнее при больших га. оказывается второй алгоритм..
В частности, если требуется, например, вычислить значения SixI
и S'ix), то необходимо выполнить соответственно 8га2 + Зга + 1 ir
9 21
Y га2 + -«г n ~^~ ^ арифметических операций. Из них «длинных^
операций 4га2 + га + 1 и 2га2 + 5га + 2 соответственно (второе
число меньше первого при га ^ 3).
Обратимся к исследованию устойчивости алгоритмов.
Вычисление элементов таблиц в алгоритме 1 осуществляется по
формулам E). Пусть на некотором шаге вместо точных величин:
bp~13 ix) мы нашли величины b^1 ix), причем \Ц}~1J (я) —
— frf/~~13 (#) I ^ е. Тогда на следующем шаге получится b^ ix}
и, очевидно,
hm ЫI <: S+n+i-/ — х , * — ху
—— С/т» \«*'/ I 5=5>. —————-^——^-^ С ^^ —~————— с О.
Значит, процесс составления таблицы G) в этом алгоритме, а тем-
самым и вычисление значения сплайна S ix) = 6-n] («г)
устойчивы. Результаты получаются с той же точностью, с какой заданы
исходные значения, т. е. коэффициенты Ър. Совершенно
аналогично, вычисление таблицы A0) в алгоритме 2 по формулам D)'
тоже устойчиво, а некоторое накопление ошибки при вычислении;
Six) A) может произойти только за счет операций сложения.
Гораздо хуже обстоит дело с вычислением производных S(r)ixY
B). Если значения bp~l) найдены с ошибкой 8, то погрешность
вычисления Ьр° по формулам C) уже будет
При густой сетке узлов знаменатель справа мал, что -приводит
к возрастанию ошибки в определении bvl). Так как эти
величины в обоих алгоритмах играют роль исходных данных, то все:
последующие, хотя и устойчивые, вычисления проводятся с той

§ 5. ВЫЧИСЛЕНИЕ СПЛАЙНОВ И ИХ ПРОИЗВОДНЫХ 35
точностью, с какой найдены Ьр1 . Следует также учесть
возрастание ошибки на последнем шаге вычисления S{r)(x) за счет
умножения на число п ... (п — г + 1).
Приведенные рассуждения показывают, что в случае
вычисления производной от сплайна следует особое внимание уделить
выбору сетки, шаг которой должен увязываться с величиной
погрешности исходных значений коэффициентов Ьр. В противном
-случае попытка получить более точный результат путем
использования густой сетки может дать прямо противоположный
ожидаемому эффект. Иногда с целью повышения точности
результата разумнее сделать сетку более «редкой», выбросив некоторые
шз узлов. Мы отметили здесь только погрешность метода, не
затрагивая вычислительной погрешности за счет округлений.
Оба рассмотренных выше алгоритма не связаны с конкретной
задачей нахождения сплайна, лишь бы в процессе ее решения
получались коэффициенты при нормализованных S-сплайнах в
представлении A). В качестве примера укажем на особенности
их нахождения при решении задачи интерполяции.
Пусть на отрезке [а, Ь] заданы сетки Д: а = хо <Х\ <...
.... < xN = b и б: а < gi < ... < iN-n < b и требуется построить
интерполяционный сплайн S(x) e?n>iF), удовлетворяющий
условиям S(xi) = ft для Xi е= А, где /*, i = 0, ..., /V,— заданные
действительные числа. Согласно теореме 1.3 такой сплайн
существует и единствен тогда и только тогда, когда Xi-\ < \г < #i+n, i =*
= 1, ..., N-n.
Расширим сетку б, введя дополнительно узлы |_п < ... < |о ^
<; a, b ^ f N_n > ... > gtf+ь Ha новой сетке построим
нормализованные Я-сплайны Вп (х), р =—л, ..., N —тг, и представим
через них сплайн S(x) на [а, Ы.
Условия интерполяции дают систему N + 1 линейных
алгебраических уравнений для определения N +1 коэффициентов
сплайна Ьр:
2bpB*(xi) = fu * = 0 ЛГ. (И)
Так как Вп {х\) Ф 0 тогда и только тогда, когда х{ е
е (?р, gp+n+i), то матрица системы 4 = [?n(#i)], р = — п, ...
..., N — щ ? = 0, ..., N, является неотрицательной ленточной
матрицей с шириной ленты 2п + 1, причем, если узлы сплайна %и
j = 1, ..., N — п, расположить специальным образом относительно
точек интерполяции xiy то число ненулевых диагоналей матрицы
А может быть уменьшено до п. В силу свойства C.9)
нормализованных 5-сплайнов сумма элементов матрицы А по строкам
равна 1, т. е. она масштабирована по строкам, что удобно при
вычислениях. Хотя в общем случае матрица А не обладает свойст-

36 ГЛ. I. ПРОСТРАНСТВО СПЛАЙН-ФУНКЦИЙ
вом преобладания диагональных элементов, тем не менее ее
специфика позволяет использовать для решения системы A1)
эффективные методы, по которым созданы стандартные программы*
B5, с. 71—90]. В частном случае кубических сплайнов дефекта
1 эти вопросы будут изучены подробно в гл. III.
§ 6. Сплайн-функции двух переменных
на прямоугольной сетке
Различные обобщения сплайн-функций на случай многих
переменных характеризуются двумя признаками, а именно: формой
заданной области и ее разбиением на подобласти и определением
пространства сплайнов. Эффективные в приложениях
конструкции получаются, когда оба этих фактора учитываются в
совокупности. В данной книге мы ограничиваемся рассмотрением
только функций двух переменных. В настоящем параграфе
изучается наиболее простая теория, когда заданная область есть
прямоугольник с прямоугольной сеткой на нем. Случай
триангуляции многоугольной области будет рассмотрен в гл. II и XL
Итак, пусть в прямоугольной области Q = [а, Ь] X [с, d]
введена сетка липий Д = Дж X Ду, где
Дх: а = хо < х\ < ... < xN = 6,
ДУ: с = у0 < у\ <... < ум « d,
делящая область Q на прямоугольные ячейки
У е l#
Для целых к > 0 и I > 0 через Ch> l[Q] обозначим множество
непрерывных на Q функций /(#, у)у имеющих непрерывные
частные и смешанные производные Dr> 'fix, у) {r^k4s^ I). Символом
C~lt~][Q] обозначается множество кусочно-непрерывных функций
с разрывами первого рода на некоторых замкнутых линиях,
содержащих, быть может, границы области.
Определение. Функция SHtто>v,»(х, у) называется сплайном
двух переменных степени п дефекта v @<v^w+l) по х и
степени m дефекта ц @<|A<tfi-fl) no у с линиями склейки* на
сетке Д, если
а) в каждой ячейке Й„ функция ?„, m, v, цЫ является
многочленом степени п по х и степени m по у, т. е.
S«,m,v,n (*, У) = 2 i <э (* - *if (У -
* = 0, ...,ЛГ-1; / = 0, ...,M-U
б) 5w#(*I»)sr1'''|-|l[ffl.

§ 6. СПЛАЙН-ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ 37
Множество сплайнов, удовлетворяющих определению,
обозначим через Sn, m, v, ц(Д). Очевидно, оно является линейным
пространством. Выясним, в каком отношении это пространство
находится с пространствами сплайнов одной переменной «Sn,v(A*) и
5т,ДДу).
Если Т\ и Гг — два конечномерных функциональных
пространства с базисами %J\ ix = 1, ..., plf и %l2, tt — U • • •* Ра»
то пространство Т размерности р = рдо с базисом, образованным
всевозможными произведениями вида %г Хг » называется
тензорным произведением двух npoctpaHCTB и обозначается
Т » Г, ® f 2.
Теорема 1.5. Пространство сплайнов двух переменных
совпадает с тензорным произведением двух пространств сплайнов
одной переменной:
Sn.m,v.|i (А) = 5n,v (А*) ® ^ц (А,). B)
Доказательство. Согласно § 1 пространства 5n,v(Ax) и
5т,м(Ду) имеют размерности г\ =л+ 1 + v(iV— 1) и Гг^т+И-
Ч-|ы(Л/ —1). В качестве базисов этих пространств возьмем
системы функций
#а, а=0, ...,тг, (дг—a?0+'t а' = w— v+1, .,.,/1; г=1, ...,ЛГ— 1;
Тогда элементами тензорного произведения будут функции вида
+ 21 2 2 Ьра' (Ж - *«)? (У - У0)Р +
+ 212 2 ь1»- {х - хо)а (у - У})% +
+ 2llf2 2 2- clU(*-Xi)X(y-yi)%. C)
Очевидно, что такие функции удовлетворяют определению и,
значит, Six, у) е5П(т( v, p(A). Обратно, всякий сплайн двух
переменных является сплайном по каждой из них, и имеют место
формулы: при фиксированном у
5»,«,v.u (х, у) = 2««(у) (« - *0)в + 21 2 4 (у) (* - »о+.
a=o i=l a'=n—v+1

38 ГЛ. I. ПРОСТРАНСТВО СПЛАЙН-ФУНКЦИЙ
а при фиксированном х
т М—1 т
s».».-v.!i (*, у) = 2 «з <*) (г/ - и>)э +2 2 4- (*) (у - vi)% •
0=0 ;-=! 0'=т-ц+1
Эти формулы говорят о том, что коэффициенты в первой из них,
йа(у) и сга> (у), при переменном у являются функциями,
даваемыми второй формулой. Но тогда сплайн 5П§ГО,У, м(#» у) имеет ту же
структуру, что и функции Six, у) C). Утверждение теоремы
доказано.
Установленный факт позволяет легко переносить свойства
пространств сплайнов одной переменной на случай двух
переменных. Проиллюстрируем ото примерами.
1. Если сетки Ах и Ду расширить, как указано в § 2, то для
пространств Sn, i(A*) и Smt i(Ay) можно построить базисы из
нормализованных 5-сплайнов: Вгп (х), i = — n, ..., N — 1, и Bjm (у),
у =з — т, ..., М — 1. Тогда всякий сплайн Six, у) е Snt m, \, i(A)
мол^ет быть представлен единственным образом в виде
S{x,y)= 2 ? Ъ1}В1П{Х)В1{У), D)
где bij — постоянные коэффициенты.
2. В области Q введем еще одну сетку б = 8Х X 8У, причем
6*: - оо < %{ < §2 < ... < gw_n < + оо,
бу: ~ оо < Til < Г]2 < . . . < Т)м-т < + оо
(см. § 4), и пусть выполняются условия
Xi-i <li< Zi+n, i = 1, ..., N — n\
Уз~\ < Чз < J/j+m, / = 1, . . ., ^ — W,
для ^^Дх и ^еДу, Согласно теореме 1.3 существуют две
системы фундаментальных сплайнов Fln(x) ^ Snti(8x) и GJm{y) e
^^пд^) таких, что
^n(*p) = 6ip, *fp = 0, ...,iV; Gjm(yq) = 8jq, 7,^=0,. ...Af,
которые образуют базисы в пространствах ?n>iFj и ?т, iFv)
(теорема 1.4).
Тогда всякий сплайн Six, у) е 5n> w> i, i может быть
единственным образом представлен в виде
N М
S{x,y)= 22 /«*¦»(*)<&(?) E)
i=0 j=0
с постоянными коэффициентами /у. Очевидно,
<, Уз) = /« для (д:<, у,) ^ А, F)

§ 6. СПЛАЙН-ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ 39
т. е. сплайн E) решает задачу интерполяции. Это представление
есть интерполяционная формула Лагранжа для сплайнов двух
переменных. При N = га и М = т она превращается в интерполя*
ционную формулу Лагранжа для двух переменных.
Ограничиваясь этими примерами, мы предоставляем
читателю самостоятельно распространить другие свойства сплайнов,
изложенные в §§ 1—4, на случай двух переменных. Здесь же
сделаем только несколько замечаний об их вычислении.
Самый простой способ состоит в расщеплении процесса на
последовательное вычисление сплайнов одной переменной. При
кусочно-многочленном представлении сплайна A) для (х, у) е
е Qij приходится вычислять многочлен п-& степени от х с
коэффициентами — многочленами т-й степени от у. Роли хну
можно поменять местами.
В случае представления сплайна Six, у) е Sntm,i,i(A) через
JS-сплайны D) для (х, у) е Qtj имеем
Ы*/)= 2 bvqBqm(y), p = i-n+l, ...,*;
S(x,y)= S bv{y)Bl{x).
Дифференцируя эти функции, получаем
cp(y) = D°'\(y)= S Ьи[г«,(у)]@, p = t-n,...,t;
q=3-m
Dr'sS(x,y)= 2 Cp(y)[5^(x)](r).
Если учесть выражения производных сплайна одной
переменной E.2), то эти формулы можно представить в виде
7
= m...(m-s + l) 2 Ь%Вят-.(]/), р = i-n + г, .. .,*;
(8)
где
(г-1) (9>

40 ГЛ. I. ПРОСТРАНСТВО СПЛАЙН-ФУНКЦИЙ
Таким образом, в этом случае вычисление сплайна двух
переменных (и его производных) сводится к последовательному
вычислению /г —г + 2 сплайнов (и их производных) одной
переменной. Соответствующие алгоритмы были изложены в § 5.
Задача. С помощью Я-сплайнов первой степени построить
непрерывную функцию такую, что
Г> 0 для #eQ\
1*»У)|_.0 для х<?п\
где Q'= @, 1)Х@, 1)\[1/2, 1)Х[1/2, 1). (Символ \ означает исключение
множества.)
Ответ. Примером такой функции является сплайн
S (х, у) = Aj
Литература к главе I. [1, 4, 5, 15, 23, 25, 48, 74—77, 84t 80, 101].

Глава II
ЛОКАЛЬНЫЕ СПЛАЙНЫ
Из материалов предыдущей главы видно, что для построения
интерполяционного сплайна необходимо решить систему
линейных алгебраических уравнений. Размерность ее определяется
количеством интерполяционных условий и может быть велика.
Однако для некоторых типов сплайнов эта система распадается
на совокупность подсистем небольшой размерности. В этом
случае для вычислепия каждого из параметров сплайна
используется лишь несколько интерполяционных условий, что существенно
упрощает задачу. Такие сплайны называются локальными.
§ 1.,Сплайны первой степени
Мы начнем изложение со всем знакомого примера, за
внешней простотой которого скрываются многие специфические
особенности сплайнов.
Сплайны первой степени S\(x) дефекта 1 на сетке Д: а~
= хо < х\ < ... < xN = Ь — это непре- q /и
рывыые кусочно-линейные функции. '
Пусть в узлах сетки Д заданы
значения /< = /(#<) некоторой
функции /(#), определенной на [а, Ы.
Интерполяционный сплайн
определяется условиями
Sx(Xi)=fu i = 0, ,.., N. A)
\
Геометрически он представляет со- я
бой ломаную, проходящую через Рис 2д.
точки (хи уд, где у< = /< (рис. 2.1).
Если обозначить hi = xi+\ — #<, то при х^[хи xi+\] уравнение
сплайна будет иметь вид
Si (х) = fi -^~ + /i+1 —j^, B)
или
-/О- C)

42 ГЛ. II. ЛОКАЛЬНЫЕ СПЛАЙНЫ
Иногда, чтобы выделить интерполируемую функцию, вместо
S\(x) будем писать S\(f; х).
Для запоминания сплайна нужно хранить 2{N +1) чисел.
Вычисление его удобнее всего проводить в таком порядке:
сначала находится щ = {fi+\ — fd/hi и затем S\(x) = f{ + (х — хг)ии
Тогда для вычисления сплайна в одной точке потребуется
выполнить шесть арифметических операций. Если же нужно
вычислять значения в других точках того же отрезка [хи xi+\], то
дополнительно понадобится производить только по три операции
па каждую точку.
Если величины /* заданы с погрешностью, не превосходящей
8, то значения S\(x) вычисляются с такой jKe точностью.
Значения производной Sl {ос) находятся с точностью 2&/1г{ (см. § 1.5).
§ 2. Оценка остаточного члена интерполяционного
сплайна первой степени
Качество приближения функций, в том числе и интерполяции,
характеризуется остаточным членом. В данном случае это
R(x) = S\{x) — fix). Оценка остаточного члена зависит от того,
какими дифференциальными • свойствами обладает
интерполируемая функция fix). Задача интерполирования будет
рассматриваться для функций из наиболее распространенных в
вычислительной математике нормированных пространств и классов.
Прежде всего, это пространство С [я, Ь] непрерывных на fa, b]
функций с нормой
На сетке Д: а-= х0 < хх < ... < xN — b эти фупкции будем
характеризовать их колебанием на отрезках [хи xi+l]
а также величиной
со (/) =- max со{ (/).
Характеристикой функции, пе зависящей от сетки А, является модуль
непрерывности
ю(/;Л)= max | / (*") - / (*') |,
Если обозначить h = max h^ то очевидны неравенства
*>(№)• A)
Для непрерывных функций в дальнейшем нам будет полезен следующий
вариант теоремы о среднем. Если /(i) g C[a, b] и величины а, & имеют

§ 2. ОЦЕНКА ОСТАТОЧНОГО ЧЛЕНА 43
одинаковые знаки, то
«/(«) + ?/(*) '= (а + Р)/F), « < Е < *•
При /(а) •= /F) это очевидно. Если f(a) Ф /F), то функция ty(x) = а/(а) +
+ Р/F) — (а + Р)/(#) принимает на концах отрезка [а, &1 значения
разных знаков и, следовательно, существует точка | е [а, &], в которой
¦ F) = 0.
Теорема о среднем для интегралов
ь ъ
*J / (х) g (х) dx = / (Е) J g (*) dx, a < g < &,
а а
имеет место, если /(я) и #(z) непрерывны на [а, 61 и ^(л:), кроме того,
знакопостоянна.
Будем рассматривать также класс Ck[a, b] функций, имеющих на [а, Ь]
непрерывную производную к-то порядка. Такие функции разложимы по
формуле Тейлора с остаточным членом в форме Лагранжа
,/х -> * • Г (*)(*-*) , , /^-"(яНа-д)*-1 , 1{k)(l)(x-a)h
f(x)=sf(a)+ + ...+ ^—fjj + й г
где | — некоторая точка из промежутка [а, х].
Далее, Lp[a, Ъ] — пространство измеримых па [а, Ь] функций /(я),
для которых функция \f(x)\p интегрируема по Лебегу на [а, 6]. Норма в
атом пространстве есть
ь \ 1/р
1]
Говорят, что измеримая функция /(я) ограничена в существенном на
[а, Ь], если существует такое число jli, что мера множества точек, для
которых \f(x)\ > И-, равна нулю. Минимальное из чисел jn, обладающее этим
свойством, обозначается символом ess sup \ f (x) |. Введем пространство
?.ов [а, Ь] измеримых и ограниченных в существенном функций с нормой
Обозначение L«, оправдано тем, что для f(x) e?«>[a, b] при конечных а
и Ь [17, с. 19]
lim|/(*)HL гв Ь| = ess sup | / (ж) |.
Заметим, что пространству ?«>[а, Ь] принадлежат, в частности,
кусочно-непрерывные на' [а, Ь] функции с разрывами первого рода. При этом,
если f(x) е= С [а, 6], то|| / (х) ||СЕа$ь] = || / (х) llLoo[a,br Иногда, если это не
приводит к путанице, вместо обозначений ||/ (х) ||с-а^и К/ (х) \\L ^аЬ. мы
будем использовать \\f(x)\\c и ||/(я)||оо соответственно.
Класс функций /(#), имеющих на [а, Ь] абсолютно непрерывную
производную порядка Z — 1 и /-ю производную из Lv[a, Ь], 1 ^ р ^ оо,
обозначается через Wlp[a, b]. Формулу Тейлора для функций из этого класса бу-

44 ГЛ. II. ЛОКАЛЬНЫЕ СПЛАЙНЫ
дем применять с остаточным членом в интегральной форме:
~ v)"lfU) {v) dv-
Если f(x) elpK Ь] и ?(*)€= ?„К b]t 7*+"?"=з1' 1<Р<°°» то
справедливо неравенство Гёльдера
б
J I / <*> I I * (*
Через С*С^ [а, Ь}у I > к, обозначим класс функций f(x) таких, что
/(*) е С*[а, 6] и /(*) s C[*,f *,+,], I— О, 1 ЛГ—1.
Обозначение СЛ^д,р [а, 6], Z > Аг, 1 < р < оо, будем использовать
для класса функций /(ж), удовлетворяющих условиям
/ (*) cs С* [«, Ч, / (*) s W? [*i>
Приступим теперь непосредственно к оценкам погрешности
интерполяции.
Теорема 2.1. 2?с/ш сплайн первой степени S\(x)
интерполирует функцию f(x) на сетке Д, го справедливы оценки
| Д(г) (ж) |» - || 5<г> (яг) - /о (х) ||м < Rr, г = 0, 1,
гЗе Лг даются в таблице 2.1.
Таблица 2.1
Класс функций
СС\[а,Ъ\
р
-g-II/ И Иов
(Прочерк в таблицах здесь и в дальнейшем означает, что
данная оценка не существует.) -
Доказательство. Используя для Six) представление A.2),
при х&[хи xi+\] имеем
R(x) - S(x) - fix) - A - t)U + tf{+l - fix), B)
где t = ix — Х{)/кг.

§ 2. ОЦЕНКА ОСТАТОЧНОГО ЧЛЕНА 45
Пусть f(x)^C[a, Ы. Применяя к выражению A— *)/«+*/«+i
теорему о среднем, получаем
R(x) - /(?) - fix), I e [ж
Следовательно, |i?(ar) I ^ ю,(/) < ©(/).
Если f{x)& Wlo[a, b], то по формуле Тейлора
fip)dv.
Подставив эти выражения в B), получаем
J \f'(v)\dv.
C)
[х *i+l "I
(l-*)J* + « j dv И/' (х) lU — 2*A -*) Ai || /'(a?) IU.
Применяя к каждому из интегралов неравенство Гёльдера,
находим
[х *i
J
Отсюда \R(x)\<\h\f(x)U.
Пусть / (x) e CC\ \ay b]. По формуле Тейлора с остаточным
членом в форме Лагранжа
/, = /(*)- ***/' (Б), /i+x =»/(*) + (!- *) fci/' (П).
g, Л е [a?i, xi+1]. D)
Подставив эти выражения в B), получаем
Я (*) = t(l-
Следовательно,
| R (х) )
Далее, из B) вытекает
Я'(*) = (/i+i-/i)/fci-/'(*). E)
Используя D), находим
Я'Ы = A - f)f(n) + tf(%) - fix).

46 . ГЛ. II. ЛОКАЛЬНЫЕ СПЛАЙНЫ
Отсюда по теореме о среднем
и, значит, Г#'Ы1 < со(/'). Оценки в классе СС\ [а, Ы получены.
Наконец, пусть f(x) e CWli<x> [a, b\. По формуле Тейлора
хг
П «/(*)- thd' (х) + j (Xi - v) Г (v) dvy
х
хг+1
J {xM-v)f'{v)dv.
х
Из формулы B) следует, что
хг хг + 1
R (х) = A - t) j (^i - v) Г (v) dv + t j (*<+1 - i;) f (i;) do.
Применяя неравенство Гёльдера, после несложных
преобразований получаем
I Д (*) I < у *?* A - *) IIГ ИIU < | Л21| Г (х) I».
Аналогичные рассуждения позволяют из E) вывести оценку
Д' (д) | < 1 A - 2* + 2*2) ft, ||Г (х)
\ h
Доказательство теоремы закончено.
Мы получили оценки погрешности интерполяции на различных
классах функций. Все они выражаются в виде некоторых неравенств.
Естественно, возникает вопрос, можно ли полученные оценки улучшить. В том?
случае, когда этого сделать^нельзя одновременно для всех функций из
данного класса и всех рассматриваемых сеток, оценку будем называть неулуч-
шаемой или точной в этом классе. Бесспорно, получение точных оценок
представляет значительный интерес как в теоретическом, так и в
практическом плане.
Покажем, что все оценки, установленные в данном параграфе, точные.
Очевидно, чтобы доказать неулучшаемость какой-либо из них, достаточна
указать некоторое разбиение промежутка fa, 61, а также функцию f(x) +
принадлежащую рассматриваемую классу, для которых оценка достигается*
и при этом правая часть ее не обращается в нуль. Такие функции будем
называть экстремальными.
Йусть разбиение промежутка [а, Ь] <— равномерное с шагом h. В силу
локальности сплайна Si(x) нам достаточно построить требуемую функцию»
только на одном промежутке, например [х{, s*+i], положив вне его функцию»
тождественно равной нулю.

§ 2. ОЦЕНКА ОСТАТОЧНОГО ЧЛЕНА
47
Экстремальная функция в классе С [а, Ь] может быть определена соот-
еошениями
х* — х. ' xe=[xvx*],
где х* — произвольная точка из (xi, xi+\). Действительно, с одной стороны,
\\S\ (/о; х) —/о (х) || с = И/о (я) II с = 1 и, с другой стороны, со (/о) = @i(/o) = 1,
т. е. для этой функции оценка достигается.
В классе W^ |a, Ь] экстремальной будет функция fi(x), производная
которой задается равенством
h\
- xi - YJ»
f -
Б самом деле, из C) для сплайна, интерполирующего fi(x), имеем R(xi+
+ А/2) = 1/2 А, что совпадает с величиной,
даваемой соответствующей оценкой/
В классе ОС\ [а, Ь] мы не можем построить
экстремальную функцию в указанном выше
-смысле. Однако очевидно, если для
произвольного малого е > 0 удастся указать такую
функцию, что
1
Рис. 2.2.
то неулучшаемость оцепки для |#(я)| будет до- -Qt5
казана. Такие функции будем называть квази-
якстремалъными. Легко проверить, что в
данном случае квазиэкстремальной функцией
€удет функция /2 (я), производная которой задается соотношениями
1
— •?•, если
( - --
[* xi 2
если
[А А 1
]*» 2 xi ^ 2 ° J»
¦«¦, если х <
Квазиэкстремальной функцией для оценки [R'(x)] в классе СС\ [а, Ь]
^будет функция U(x) такая, что
3
Л)» если
1, если
Графики функций /2 (х) и /3 (а:) изображены на рис. 2.2.
В классе CW\ ^ [а, Ь] в качестве экстремальной функции может быть
взят любой многочлен второй степени, например парабола /(#)•= х2.

48 ГЛ. II. ЛОКАЛЬНЫЕ СПЛАЙНЫ
Последовательное усиление требований к гладкости
интерполируемой функции в теореме 2.1 приводило к соответствующему
увеличению порядка аппроксимации. Так, для
1{x)^CW\^\a, b]
имеем |i?(r) (х)!«, = О (А2~"г)> г = О, 1. Однако дальнейшее
повышение гладкости функции fix) уже не дает повышения порядка
аппроксимации. Происходит, как это принято говорить,
насыщение интерполяционного процесса.
Теорема 2.2. Если f(x) e CC\ [a, b], fc>3, то для
l ]
a=2
- t)a]
а=з
Доказательство. Чтобы получить формулу F), нужна
величины /*, /<+i в A.2) разложить по формуле Тейлора в точке
х = Xi + Jft*. Соответствующие выкладки мы опускаем. Равенства
G) получается из F) дифференцированием по х.
Отметим один результат, непосредственно вытекающий из
теоремы 2.2.
Следствие 2.1. Если f (x) е= СС\ [а, Ь], то
[[f; хг + ^) = /' (*« + j) + O (А?), < = 0э
(8)
Формула (8) показывает, что порядок аппроксимации первой
производной функции fix) повышается на единицу в середине
каждого из промежутков [хи х{+\\. Во всех остальных точках
порядок аппроксимации 0{к{). Если учесть, что
то (8) представляет собой известную оценку приближения
производной с помощью центрально-разностной аппроксимации.

§ 3. СХОДИМОСТЬ ИНТЕРПОЛЯЦИОННОГО ПРОЦЕССА 49*
§ 3. Сходимость интерполяционного процесса.
Интерполяция с заданной точностью
1. Пусть на отрезке [я, Ь] задана последовательность
разбиений Av: а = #v, о <х*. i < ... < я». nv= Ь, v == 1, 2, ...,
удовлетворяющая условию Av -* 0 при v -> «>, где
ftv = max Ау,ь ^v,i == #v,i+i — #v,i«
Предположим, что /(#) ^ C[a, Ы и что эта функция может
быть вычислена в любой точке отрезка. Для каждого Av можно
построить интерполяционный сплайн 5i,av(#). Тем самым на
последовательности {Av) будет определен интерполяционный
процесс. Говорят, что указанный интерполяционный процесс
сходится в Cla, 6J, если
для любой функции f(x)^Cia, Ь]. Аналогичное понятие
сходимости вводится и для других классов функций. В случае, если
j{x) дифференцируема, естественно рассматривать также
сходимость производной ?1>Av (x) к /' (х). Если
то говорят, что имеет место сходимость с порядком *у.
Исследование сходимости интерполяционного процесса и
выяснение порядка сходимости необходимы при решении вопроса о
возможности интерполяции с любой наперед заданной точпостью.
Действительно, если сходимость имеет место, то, очевидно, для
любого е > 0 существует такое разбиение Av, что
A)
Большим преимуществом сплайнов по сравнению с мпогочле-
нами Лаграпжа является то, что для исследования сходимости
здесь обычно достаточно установить оценку погрешности
интерполяции.
Изучим сходимость интерполяции сплайнами первой степени.
Для сплайнов более высоких степеней характер рассуждений
остается тем же самым. Обратимся к оценкам, установленным в
теореме 2.1. Если f(x)^C[a, b], то в силу неравенства B.1)
H/?v(#)IL = ШЛх)\\с ^ to(/, hv). Но модуль непрерывности
о)(/, Av)-^ 0 при ftv-^О, и тем самым сходимость обеспечивается.
Если, кроме того, fix) удовлетворяет условию Липшица
порядка 7«
\j{x")-jU')\<L\x" -x'\\ L = const,
4 ю. С. Завьялов и др.

ГЛ. II. ЛОКАЛЬНЫЕ СПЛАЙНЫ
{р со (/; fev) ^ LhX и сходимость будет иметь порядок
^Аналогично, если fix) e Cl[a, ft], то || #Jr) (х) {«, -> 0 как /^~~гсо(/';
Av), г = 0,1.
Совершенно очевидна сходимость для функций fix) e
^ Wi [а, Ь]_и / (#) е W?> [а, Ь]. В первом случае она имеет
порядок 0(AV), а во втором |ДуГ) (з)|«> = О (hl~r), г = 0, 1.
До сих пор мы не налагали никаких^ ограничений на
последовательность сеток {Av}, кроме условия К -+¦ 0. В некоторых
случаях целесообразна ввести дополнительные условия. Пусть,
например, / (х) е CW2Zoo [а, Ы с: TFi [а, Ь], где Д: |0 < 6i < • • • < Ь.*
^j^ta, 6], / = 0, ..., Z. Это означает, что fix) и /"(.г) имеют
разрывы первого рода в узлах сетки Д. Для такой функции на
произвольной последовательности сеток, как было отмечено выше,
l\Rvix)\\c = Oihy). Однако, если дополнительно потребовать, чтобы
при каждом v узлы сетки Д включались в сетку Av, то по
теореме 2.1 \\Rvr) (x)loo = 0{hl"r), r = 0,1. Порядок сходимости
повысился на единицу. Полученный эффект есть следствие того,
что существенную роль в оценках погрешности интерполяции
играют свойства интерполируемой функции только внутри
интервалов [xh Xi+i].
2. На практике обычно требуется осуществить интерполяцию
с некоторой заданной точностью. Эта задача решается путем
выбора сетки на отрезке la, b] с учетом свойств интерполируемой
функции и соответствующих оценок погрешности интерполяции.
Ниже даются рекомендации по выбору узлов интерполяции.
Как было отмечено, точность интерполяции определяется в
основном гладкостью функции внутри промежутков [хи xi+i\.
Поэтому прежде всего следует позаботиться о том, чтобы точки,
в которых функция имеет особенности, например разрывы
производных, были включены в число узлов интерполяции.
Оценки погрешности интерполяции.дают возможность
определить величину максимального шага сетки для обеспечения
заданной точности. Пусть, например, fix) e С2[а, Ь\ и требуется
осуществить интерполяцию этой функции так, чтобы выполнялось
условие A). Согласно таблице 2.1 имеем
Поэтому, если h выбрать таким, чтобы h2 \\ f (x) \ciatb\ ^ 8s, или
то требуемая точность достигается, например, на равномерной
сетке с шагом h = /г*.

§ 3. СХОДИМОСТЬ ИНТЕРПОЛЯЦИОННОГО ПРОЦЕССА 51
Однако подобное решение вопроса не является оптимальным
в том смысле, что при этом мы, как правило, будем иметь дело о
очень завышенным числом узлов интерполяции. Это влечет за
собой необходимость хранения большого объема информации об
узлах и узловых значениях сплайна. Типичным примером
являются любые таблицы функций, которые обычно даются на
равномерной сетке с целью облегчения ручных вычислений.
При выводе формулы B) мы никак не учитывали локальных
свойств функций fix). Из доказательства теоремы 2.1 следует,
что на тех участках промежутка la, Ы, где величина f"(x) мала,,
можно взять более редкую сетку по сравнению с теми участками,
где она велика. Очевидно, если мы выберем узлы интерполяции
так, чтобы выполнились равенства
то поставленная задача интерполяции с заданной точностью
будет решена с числом узлов, вообще говоря, меньшим, чем при
равномерном разбиении. Опишем два алгоритма для построения
сетки, удовлетворяющей условиям C).
Алгоритм 1. Пусть функция 1/"Ы1 монотонна на [a, 6L
Предположим для определенности, что 1/"(#I монотонно
убывает на [а, Ъ\. Если узел хг найден, то в силу монотонности имеем
ll I/"(*«)!• Поэтому из C) вытекает
88
Если /"(#<) =5^ 0, то полагаем xi+\=x{+hu Если же /"(#*)= О, то
Хг+\ = b. Начиная эт'от рекуррентный процесс от левой границы
отрезка [а, 6], мы последовательно находим все узлы сетки.
Построение заканчивается, когда очередной узел выходит за
правую границу отрезка. Если !/"(#)! монотонно возрастает, то,
очевидпо, процесс построения сетки следует начинать с правой
границы интервала [а, Ь].
Алгоритм 1 можно, конечно, применять и в случае, когда
функция !/"(#) I кусочно-монотонная, если предварительно
разбить промежуток [а, Ы на промежутки ее монотонности. Затем
к каждому из них следует применить один из вариантов
алгоритма. Однако для выделения этих промежутков следует выполнить,
вообще говоря, очень большой объем вычислений, особенно,
когда их много. В таких ситуациях предпочтительнее выглядит
другой способ построения сетки, который не накладывает
ограничений на качественный характер функции !/"(#)!.
Алгоритм 2. Пусть нам известен узел сетки #<. Возьмем
достаточно большое положительное число т и построим последо-
4*

52 ГЛ. II. ЛОКАЛЬНЫЕ СПЛАЙНЫ
вательность точек х^ ~%1 + ] %т » /==0,1,... Для каждого /
будем вычислять величину
ej - i {хц - x{f max | /" (*is) | E)
5 0<s4j
и сравнивать ее с 8. Возможны две ситуации:
1) На отрезке [#<, Ь] найдется точка хц+ такая, что е^е
О'^О, 1, ..., /* —1) и 8j*>e. В этом случае полагаем
l цг
2) Для всех Хц^[хь Ь\ выполнено условие е^е. В таком
случае считаем xi+i — 6.
После нахождения точки xi+\ процесс повторяется. Начинать
выбор узлов сетки следует с точки хо = а. В качестве h-\ можно
взять величину й*, определяемую формулой B).
Нетрудно заметить, что алгоритм 2 представляет собой метод
приближенного решения системы C). В пределе при т ->• оо
получим точное решение этой системы. Однако при практической
реализации алгоритма достаточно взять т не очень большим.
Хорошие результаты получаются уже при т = 10. Дальнейшее
увеличение т не приводит к заметному уменьшению числа узлов,
а объем вычислений при этом возрастает (параметр т
определяет количество вычислений функции \f"(x)\).
Алгоритмы 1 и 2 легко программируются. Единственным
условием их реализации является наличие априорной информации
о функции |/"(#I. Точнее, достаточно иметь хорошую
мажоранту для нее. Не вдаваясь в описание способов получения подобной
информации, отметим, что на практике можно, например,
используя разделенные разности, приближенно вычислить значения
\f"(x)\ на некоторой сетке узлов и затем вместо !/"(#)I взять
сплайн, интерполирующий эти значения.
Рассмотрим несколько численных примеров, иллюстрирующих
полученные выводы. В таблице 2.2 приведены погрешности приближения
функций
и их производных на отрезке [0, 11 при равномерном расположении узлов
интерполяции с шагом h. Здесь обозначено
Rr = max | /(r> (*) - ^г) (/; *) I, г » 0,1,
где Д^— равномерная сетка на [0, 11 с шагом /г/10.
Результаты близки к теоретическим оценкам погрешности.
__ В_таблице 2.3 приведены данные, характеризующие количество точек
Лг и N{ (включая граничные точки) соответственно при равномерном в не-

$ 3. СХОДИМОСТЬ ИНТЕРПОЛЯЦИОННОГО ПРОЦЕССА 53
равномерном разбиении отрезка ГО, 1], необходимое для достижения
заданной точности интерполяции е. Для построения неравномерных разбиений
для функций М*), h(x) использовался алгоритм 1, а для /з(#), /ч(з)
—алгоритм 2.
Таблица 2.2
h
0,1
0,05
к*
0,0032
0,0008
0,077
0,024
0,011
0,003
Л(*>
0,07
0,04
Rt
0,130
0,067
2,7
0,5
0,3
5,0
4,0
е
10
ю-*2
10~3
10
10
3
7
20
60
186
3
6
16
48
147
i\T
13
37
ИЗ
355
1120
л. ,
5
10
26
74
226
Т аб л и
FT
5
13
37
ИЗ
353
5
11
30
88
276
ца 2.3
7?
17
52
160
502
1583
8
19
51
150
462
Данные таблицы 2.3 показывают значительное уменьшение числа уз*
лов неравномерной сетки по сравнению с равномерной для функций, у ко*
торых модуль второй производной сильно меняется на промежутке
интерполирования.
3. В заключение параграфа остановимся на выборе шагов
при интерполяции функции, заданной с погрешностью е > 0.
В этом случае, как мы видели в § 1, значения сплайна Six)
вычисляются с той же точностью, а значения его производной
сильно зависят от величины шагов сетки.
Важность правильного выбора шага показывает следующий
пример; Значения функции ех, округленные до первого знака
после запятой (точность 0,05), интерполируются на сетке с
постоянным шагом h = 0,05. Возьмем значения функции в трех точках:
е°00 = 1,0, е^-Ц е°'10 = 1,1. Построенный^ по ним сплайн
имеет значения производных St @) = 2,0, *SX @,05) =-- 0,0, „не
похожие на значения производной функции ех. В то же время
легко можно проверить, что вычисление производной при более
грубой сетке, например, с шагом 0,2 дает гораздо более точные
результаты.
В связи с этим покажем, что при заданной величине
погрешности исходных данных и наличии некоторой априорной
информации относительно интерполируемой функции существует оп-
тимальная величина шага сетки, при котором погрешность
аппроксимации производной минимальна. Действительно, пусть,
папример, /WeC%, Ъ] и интерполируются значения /с,, для ко-

54 ГЛ. II. ЛОКАЛЬНЫЕ СПЛАЙНЫ
торых \fi — /il<8, f = 0, 1, ..• Погрешность приближения
производной функции fix) на интервале [хи xi+\] производной сплайна
S\(f\ x) может быть оценена следующим образом:
I Si G; *) - /' (*) I < \s[ (/; х) - Г (х) | + | S[ (/; х) - S[ (/; *) |.
Первое слагаемое в правой части оценивается величиной
~о ^ II/" (х) h[xvxi+i] (теорема 2.1). Для второго слагаемого имеем
оценку 2г/Ы (см. § 1). Следовательно,
Функция ф(й<, е) при фиксированном е достигает мипимума при
Это и есть оптимальное значение шага при заданном уровыо
погрешности е. Совершенно ясно, что пользоваться
интерполяцией с меньшим шагом, вообще говоря, не имеет смысла. Для
рассмотренного выше примера оптимальный шаг сетки h « 0,45.
§ 4. Сплайны первой степени двух переменных
на прямоугольной сетке
Введем в области Q == [а, Ъ] X [с, d] сетку А = Дж X Дуг
Дх: а = х0 < ... < xN = 6, Ду: с == уо< ...<yM = d. Пусть в узлах
(хь 2/j)e Д заданы значения некоторой функции /« = /(#*, i/j).
Интерполяционным сплайном первой степени S\t\(x, у) будем на-
вывать функцию, которая в каждой ячейке Qi3 = 1^, х{+\] X
X [уи Уз+\\ представима в виде
S], 1U, у) = сц + ацх + Ъцу +
и удовлетворяет условиям
Si. iU«, й) = Ai, * = 0, 1, ..., N; 1 = 0, 1, ..., M. A)
Рассмотрим алгоритм построения S\%\{x, у). Так как при
фиксированном значении одной из переменных ху у S(xy у) является
сплайном первой степени относительно другой переменной, то,
используя формулу A.2), имеем
Si. ite, yq) = A - «Л. я + */*+i. „9е 7, 7 + 1, B)
где ? = (ж — Xi)/hu hi = a:i+i — #<. Интерполируя теперь найденные
значения S\t \(x, у>) и S\, i(x, yj+\), получаем
Si. i(*f ») = (!- иM1§ !U, »,) + uSlt г{х, yM\ C);

§ 4. СПЛАЙНЫ ПЕРВОЙ СТЕПЕНИ ДВУХ ПЕРЕМЕННЫХ 55
тде м = (у — yj)/ljy lj = Уз+\ — У). Окончательно из B) и C) имеем
Si. i(*, у) = A - и)[A - *)/« + */,+!.,] + и[A - t)/u+i + tfi+i. i+il.
D)
Нетрудно убедиться, что сплайн «Si.iCtf, #) единствен.
Вычисление сплайна в точке (#, у) организуется так: вначале
вычисляем hu lu t, и, затем А = /<,j + *(/<+i, j — /*, j), jB = /ftj+i +
-H(/<+i,,+i — /t,;+i) и Si.iU, у)«=Л + и(Д —Л). Всего требуется
15 арифметических операций.
При изучении погрешности интерполяции, как и в случае одной
переменной, будем рассматривать пространство непрерывных функций C\Q]
и пространства измеримых функций LpfQ], 1 ^ р ^ оо, нормы в которых
юпределены соответственно соотношениями
В/(*1 у) him = max 1/(ж»^)Ь
1 J
fl / f <V tt\ \\ —— QCO С111Л I / / **• T/\ I
I! / \xi У) \]r ГЙ1 — eS)b bllP I / \xi У) г
Производные функции f(x, у) будем обозначать символом
>s __ dr+s f(z, у)
дхгду*
Через Ck [Q] обозначим класс функций, производные которых Dr> *f(xt
у), г + s *^ к, непрерывны в Q.
Класс функций, имеющих на Q абсолютно непрерывные по каждой из
переменных производные Dr> sf(x, у), r-fs^Z — 1, и производные Dr* 8f(x, y)t
г + s = I, из Lp [Q], 1 < р < оо, обозначим через Wlp [Q]. Класс Wlp [Щ
содержит, в частности, функции с кусочно-непрерывными производными
порядка I.
Через Ck> m[Q] будем обозначать класс функций с непрерывными
производными Dr' *f(x, 1/), г ^ к, s ^ т.
Символом W*?m [Q] обозначим класс функций, у которых Dr**f(x, у),
г ^ I — 1, s ^ т — 1, абсолютно непрерывны по каждой из переменных и,
кроме того, Dl*m'lf(x, у), Dl~l. mf(x, у), Dl>mf(x, у) &LP\Q]. В частности,
в этом классе содержатся функции с кусочно-непрерывными производными
По аналогии со случаем одной переменной мы будем использовать
обозначения OhC1^ [Q], ChWl^p[Q], I > А:, и т. д. для классов функций, которые
имеют более высокую гладкость в ячейках пц по сравнению со всей
областью Q. В этих обозначениях первый Символ, Ck, характеризует свойства
функций в области &, а второй, СЛ, ^д,р» — в ячейках Q*j»
Колебанием функции в области Qij назовем величину
wi> (/) = _ _та* _ I / (*t У) — / (*» У) !•
Обозначим со (/) =¦ max юу (/).

56 ГЛ. II. ЛОКАЛЬНЫЕ СПЛАЙНЫ
Получим оценки погрешности интерполяции для сплайнов
^1,1^1 у)* Из формулы D) имеем
- *)/, ,+1 + tfi+lt м - /(я
[A - u)/(*f д) + a/(*f yJ+1) - /(*, y)]. E)
Выражения в квадратных скобках представляют собой
погрешности интерполяции сплайнами одной переменной. Это
обстоятельство позволяет получить оценки для сплайна 5jfi(#, у)
через соответствующие оценки для сплайнов одной
переменной (§ 2).
Например, если /U, у) eCtQ], то из E) по теореме 2.1 в
ячейке пц имеем
Отсюда, очевидно, следует оценка
HSi.i(*, »)-M »)Нс<2ю(/). F)
Далее мы рассмотрим лишь те классы функций, для которых
достигаются максимальные порядки приближения. Однако
техника доказательства без каких-либо изменений может быть
использована для получения результатов и в других классах.
Теорема 2.3. Если fix, у) е CW\t0O [Q], то
'0/ (*, у)U + ^12\\ D°'2f (*, У) Ik, G)
Ui (*, У) - / (** У)\ U < у (rT+ sh) || д
/ (^ у) |oof г + 5 = 1. (8)
Доказательство. Неравенство G) легко следует из E)
и теоремы 2.1. Для получения оценки (8) в случае г=1, 5 = 0
воспользуемся тождеством, непосредственно вытекающим из E):
- и) [1 (/i+lfi - /и) -
+ [A - u)Dlo/(*, W)
СноЪа привлекая оценки из таблицы 2.1, мы убеждаемся в
справедливости неравенства (8). Аналогичным образом оно
доказывается и в случае г = 0, s = 1.

§ 4. СПЛАЙНЫ ПЕРВОЙ СТЕПЕНИ ДВУХ ПЕРЕМЕННЫХ 57
При несколько более жестких требованиях к функции fix, у)
можно получить оценки приближения для Dx>xfix<, у).
Теорема 2.4. Если f (х, у) е= CWltOO [Q], то
II D" \SM (х, у)-f(x, у)] U < -1 А| Dm/(*, у)Цоо +
+ ^nD^f(x,y)U + ^lh\D^f{x4y)U. A0)
Доказательство* Дифференцируя (9) по у и вводя
функцию
Ф (У) = ? I/ («1+ь .V) - / (*ь УI - Dbo/ (*, у)%
получаем
D^-i lSltl (*, у) - / (*, у)\ = J1 (ф (yj+1) - Ф (у,-I - Ф^ (
"/ (*, у) - 1 ID"/ (xl+ll у) - Do.t/ (*lf у)] j.
Используя одномерные оценки, получаем
1 /,-1 <p" (y) |beelOwl +
ol. A1)
Так как |ф"(у)||ьв<([о{,)<-|'А<1^*'*^;г» y^°°' то из A1) слеДУет
A0). Теорема доказана.
Если f{x, у) е СС\ |Q|, то, используя теорему 2.2, легко
получить из D) для (х, у) е Qw
«Si.i (*, У) = / (*, У) + j«A - 0 uiOJ-°/ (*, J/) +
+ 1 и A - и) ^D».«/ (*, у) Ч- О (Af + if). A2)
Отсюда, в частности, имеем
XiM, У)+О (Л? + /|),
О (А? + $, A3)
О (А? + #),
где « = * + A y = У + J

58
ГЛ. II. ЛОКАЛЬНЫЕ СПЛАЙНЫ
Эти соотношения показывают, что в некоторых точках (на
линиях) возможно повышение порядка аппроксимации
производных.
В таблице 2.4 представлены числовые результаты интерполяции
сплайнами S1X (х, у) в области Q== [О, 1] X [0, 1] на сетке Д = Д* X Ду, где-
Ах: Xi « VlO, i-= 0, ..., 10; Ау: у, = 7710, / = 0, ..., 10. Здесь
х, &у— сетки по переменным х, у с шагом 0,01;
K IDhjl [Sli (*i+i/2! Vj+i/t) - f (
Для рассмотренных примеров /?од = /?10, /?од = Л2 0.
Таблица 2.4
Л0,0
Л1,0
Л1,1
0,017
0,36
0,70
0,011
0,005
sin(^+j/)
0,0025
0,05
0,10
0,0017
0,0008
Ьх*у*
0,023
0,50
1,95
0,024
0,000
Задачи, а) Оцепить количество операций, необходимое для
вычисления Sj г (х, у) в нескольких точках из Qij.
б) Показать, что при / (я, у) е= CW^ [Q]
\Dr*s р1Д (^, у) - / (х, „)] [^ = тО (А +72) + *0 G + Й2), г + s = 1.
в) Показать, что при / (х, у) е СС1^1 [Q]
§ 5. Эрмитовы кубические сплайны
Пусть в узлах сетки Д: а = х0 < хх < ... < xN = b заданы
значения некоторой функции fix) и ее производной fix):
Кубическим интерполяционным сплайном дефекта 2
(эрмитовым кубическим сплайном) будем называть функцию 53,2(/; х) в
?() удовлетворяющую условиям:

§ 5. ЭРМИТОВЫ КУБИЧЕСКИЕ СПЛАЙНЫ 69
1) на каждом из промежутков [хи хг+{\
2) 5з,2 fa) - fu S'3t2 fa) - /i, * - 0, .;., N.
Очевидно, 5зр2(^) s Cx[a, Ы. Вторая производная эрмитова
кубического сплайна, вообще говоря, разрывна в узлах сетки А.
В целях сокращения записи мы будем опускать индекс,
указывающий дефект сплайна.
Учитывая условия интерполяции, для вычисления
коэффициентов aia, а == 0, 1, 2, 3, при каждом i имеем систему уравнений
S3 (*i) = fu S3 fe+i) = /i+i, S'3{xi) =» fu S's (xi+l) = f[+x.
Решив эту систему, получаем на [хи xi+\]
S3 (*) = Фг (t) fi + Ф2 (t) /i+i + Фз (t) hii\ + ф4 (t) h/w, A)
причем
ф1(*) = A-^JA + 20, Ф2@ = ^C-2^), <p*{t) = t(i-t)\
Ф4 (t) = — t2 A — f), fei = a;i+1 — xu t = (x — Xi)/hi.
Формула A) удобна для теоретических исследований. Для
практического вычисления сплайна в точке х ^ [хи xi+\] более
выгодно с точки зрения количества выполняемых арифметических
операций использование следующей формулы:
?з (*) = fi + (x- Xi) [f\ + t(B + tA)l
где
в - - А + (fi+1 - иуъ - п.
Для вычисления сплайна в одной точке достаточно выполнить
16 арифметических операций, пз них 6 «длинных».
Нетрудно видеть, что алгоритм вычисления сплайна устойчив
по отношению к ошибкам входных данных. Но при вычислении
производных эрмитова сплайна Sp(x), r =1,2,3, нельзя при
наличии ошибок в исходных данных использовать слишком
густые сетки. Величина оптимального шага сетки для вычисления
какой-либо производной сплайна может быть установлена после
получения оценок погрешностил интерполяции таким же образом,
как и в случае сплайна первой степени.

60.
ГЛ. II. ЛОКАЛЬНЫЕ СПЛАЙНЫ
§ 6. Оценки погрешности интерполяции
эрмитовыми кубическими сплайнами
Исследуются оценки остаточного члена интерполяции Rix) =
e Szif; x) — fix) в зависимости от гладкости функции fix).
Теорема 2.5. Если Szix) интерполирует на сетке Д
функцию fix), то имеют место оценки
!^г)(*)-/(г)(*)|~<Яг, г = 0,1, 2,3, A)
где R, даны в таблице 2.5.
Класс фуннций
С1\а, Ь]
Wl la, Ь]
С*С| [а, 6]
Во
1 l
m%4flV{x)L
0y2A150h\\rn\L
0,12375йю (/")
0,016151Я2(й (Jm)
Та
—
4 со (Л
4 - m
блица 2.5
—
Доказательство. 1. Вначале рассмотрил! случай, когда
fix) е СЧа, Ь]. Согласно E.1) при х& [хи х{+\]
R (х) = /с
B)
Заменяя величины /*, fi+\ их разложениями в точке х = х{ + tht
по формуле Тейлора с остаточным членом в форме Лагранжа,
получаем
R(x) = M(l - 0 ф,@/' E) - *Ф1(*)/' (л) + ф. W /I + Ф4 W/i+iJ.
Здесь и в дальнейшем буквами 5» Л» li Л1 и т- Д«
обозначаются некоторые точки из промежутка [#*, Xi+\). Применяя теорему
о среднем к слагаемым одного знака, имеем
Отсюда
Rix)
\Rix)\
- f'(r\)].

§ 6. ОЦЕНКИ ПОГРЕШНОСТИ ИНТЕРПОЛЯЦИИ 61
Эта оценка является поточечной, так как ее правая часть
зависит от точки, в которой оценивается обтаточный член. Из нее
вытекает утверждение теоремы для Ш(х)\\с. Отметим, что в
поточечной оценке правая часть симметрична относительно точки
i = 1/2 (х = Xi + hi/2). Это свойство имеет место для всех
получаемых ниже оценок. Поэтому мы, как правило, будем
ограничиваться рассмотрением случая ?е Ю, 1/2J.
Далее, дифференцируя B), имеем
После примепепия формулы Тейлора получаем
R' (х) = 6* A - t) Г (I) + Фз W /I + ф! @ /I+i - Г (*)• (*>
Непосредственно в D) нельзя применить теорему о среднелг
из-за знакопеременности функций Ф3 (t) = 1 — 4^ + 3^ и ф4 (^) =»
с= — 2t + 3i2. Функция Фз (t) меняет знак в точке t —1/3,
а функция <pi (t) — в точке t = 2/3. Рассмотрим выражение D>
отдельно на промежутках [0, 1/3], [1/3, 1/2].
При *е@, 1/3] имеем Фз(*)^0, Ф4<0^0. Применяя
теорему о среднем к группам слагаемых одного знака в D), имеем
/?'Ы - A + It - 3*2)[/'(Т) - /'(
Отсюда
max A + 2«
При ieIl/3, 1/2] имем Фз@<0, ф!@<0. Поэтому
R' (х) = 6t A - ОI/' (I) - /' fo)J, | Д' (*) I < 4 «i (/). F)
Из E) и F) следует оценка для R'(x).
2. Пусть f(x) e С Сд [а, Ь|. Вначале получим интегральное
представление остаточного члена /?(ж). Для этого в формуле B)
величины /ь /ь /i+ь /i+i разложим по формуле Тейлора в
точке х = х{ + th{ с остаточным членом в иптегральном виде. После^
приведения подобных получаем при х^[хи х{+\]
х
R (х) = J A - О2 [- rti + A + 2t) (v - х{)\ f {v) dv +
*i
«i+i
j'

$2 ГЛ. II. ЛОКАЛЬНЫЕ СПЛАЙНЫ
В каждом из интегралов сделаем замену переменной днтегри-
рования v — Xi = xhi. Тогда
R (х) = hi IJ г|)х (*, т) /" (xt + thi) dx + J г|J (*, т)Г (Xi + xh{) dxV
0)
Это представление остаточного члена является исходным для
всех дальнейших рассуждений. Рассмотрим вначале первый
интеграл в G). Если бы функция ty\(t, т) была знакопостоянной при
т ^ [0, t], то можно было бы применить теорему о среднем для
интегралов. Однако это не так. Действительно, t|)i(?, т) = 0 при
т= т* = t/(l + 20, и т* е [0, t]. При фиксированном t функция
i|)iU, т) меняет знак в точке t = t*U). Разбивая промежуток [0, п
на два —[0, г*] и tx*,rf, на каждом из которых i|)iU, т)
знакопостоянна, мы имеем возможность применить теорему о среднем.
В итоге
t
т* t
= /" (I) J *{ («, т) dr + /" (n) J *i(t,' т)<гт= 2
*
Аналогичные рассуждения, проделанные для второго
интеграла в G), приводят к равенству
1
t
В результате G) преобразуется к виду
R (я) = 2 i, ~ {At2 C — 2t) f (ц) — C —
+ 4 A - tf A + 2t) Г (f) - A + 20 f (л)}. (8)
Применение теоремы о среднем для непрерывных функций
слагаемым одного знака в (8) позволяет получить оценку
91,2/2 /л f\1
UtH О)

§ 6. ОЦЕНКИ ПОГРЕШНОСТИ ИНТЕРПОЛЯЦИИ 6?
Максимальное значение правой части достигается при t = 1/2..
Следовательно,
Отсюда вытекает утверждение теоремы о WR(x)Wc для функций
из рассматриваемого класса.
Получим теперь оценку для 1/?'Ы1. Дифференцируя G) по гг
и учитывая, что dtldx = l/hu имеем
R< (x) = hj" (х) №г (*, t) - г|J (*, t)} +
/ t 1 ч
+ Ч№ '" (** + Thi) dx+ij\^r f (** + t7**) dT •
Так как ^(f, t) =г|J(^ ^), то отсюда
з («, т) f (xL + гЛ4) dt + J г|L (*, т) f (Xi + xA*) dxl
где
Выделим промежутки знакопостоянства функций -фз(?, т) при
т^[0, t] и г|L(^ т) при те^, 1]. Функция г|)з(^ х) обращается а
нуль при т = тГ= C^ — 1)/F*); х* е [0, ff, если 0 ^ C^ - 1)/F*) < ^,
т. е, при i ^ 1/3. Поэтому г|)з(^, х) знакопостоянна при t e [0, 1/31
и меняет знак в точке х == Тт, если t > 1/3. Аналогичные
рассуждения относительно if^J, x) приводят к выводу, что i|54(^, х)
знакопостоянна, если t ^ 2/3, и меняет знак при х = х2 = D —
— 3f)F — 6f)~l, если fe[0, 2/3]. В дальнейшем будем учитывать,,
что обе функции г|K(^ х) и г|L(^ х) знакопеременны при t e Ll/3,
2/31, а при ?^ [0, 1/31 знакопеременна только ^(^ х).
Пусть ?,^[0, 1/3]. Тогда из A0), применяя теорему о
среднем, находим
Г Ч
1' '
- Г AI

ГЛ. II. ЛОКАЛЬНЫЕ СПЛАЙНЫ
Отсюда
|Л'(х)|<hi[t(I - t)A -3*
Для is [1/3, 1/21
Г _ч _ , "I
Я' (X) = hi /" Ы J ^4 (*, Т) <*Т + /" Ы J ^4 («, Т) dX U
L J
+ hi Г (Ei) J П>з (t, r) dx + f (|4) J ip3 (f, т) dt .
Отсюда приходим к оценке
A2)
Для завершения доказательства нужно найти максимумы
правых частей неравенств (ll)t A2) в соответствующих границах
изменения параметра t и выбрать наибольший из них. Расчеты,
выполненные с помощью ЭВМ, дают величину 0,12375. Это значение
достигается при t => 0,23433.
Выведем оценку для Д"Ы. Дифференцирование A0) дает
t 1
R»(x) = J г|M (*, т) f (хг + xhi) dx + J % (t, т) Г (Xi + ih{) dx - /" (x),
о t
где
^5U, t)==4-6^~6tA-2«, t|>6(*. t) = -2 + 6^ + 6A-2^A-t).
Исследование показывает, что функция ito${t4 т) при fs
е [0, 2/31, т ^ [0, п не имеет корней, а при t s [2/3, 1J, т е [0, t]
имеет корень х\^B-ЫКЪ-Ы)'х\ tf6(*, ^) при t^[0t 1/31, те
•е [ty 1] имеет корень Тз = х\ и не имеет корней при t& [1/3, И,
те[*, 1].
Рассматривая промежутки felO, 1/31, ?е[1/3, 1/21,
приходим к неравенствам
| R" {х) | < [l + щЕл?] ю* (П. * е 1°.
, 1/2].

§ 6. ОЦЕНКИ ПОГРЕШНОСТИ ИНТЕРПОЛЯЦИИ 63
Так как максимум правой части в первом неравенстве
достигается при t = 0 и равен 4/3, то отсюда вытекает утверждение
теоремы для II/?" (ж)II».
3. Если f{x) e И^[а, Ь], то, применяя неравенство Гёльдера,
из G) получаем
Чтобы вычислить интеграл от модуля некоторой непрерывной
функции, нужно определить точки, в которых она меняет знак,
и затем вычислив интегралы по промежуткам знакопостоянства
данной функции, просуммировать полученные величины.
Свойства функций \|)i(?, т), я|J(?, т) исследовались в п. 2. Используя эти
результаты, легко показать справедливость оценки для Ш{х)\\с*
Аналогично получается и оценка для 11/?'ЫНс.
4. Прежде чем перейти к изучению погрешности интерполяции
для других классов функций, сделаем несколько замечаний
относительно техники доказательства. Анализируя ход рассуждений
в пп. 2, 3, легко выделить следующие этапы.
Первый этап. Получение интегрального представления
погрешности интерполяции. Особых трудностей здесь нет.
Достаточно применить формулу Тейлора с остаточным членом в
интегральном виде и привести лодобные.
Второй этап. Анализ подынтегральный функций с целью
выделения промежутков знакопостоянства той части
подынтегрального выражения, которая не зависит от интерполируемой
функции. Практически такой анализ сводится к нахождению
действительных корней многочленов. Трудности здесь в основном
связаны с тем, что и количество этих корней, и их значения
зависят, вообще говоря, от точки, в которой оценивается
погрешность.
Третий этап. Получение поточечной оценки погрешности.
Если интерполпруемая функция имеет непрерывную
производную, которая присутствует в интегральном представлении
остаточного члена, то для вывода оценки используются теоремы
о среднем для интеграла и непрерывной функции. Если эта
производная принадлежит пространству !/«,, то применяется
неравенство Гёльдера.
Четвертый этап. Вывод оценки погрешности по норме
пространств С или ?«,. Это требует вычисления максимумов
функций параметра t. На этом этапе может возникнуть необходимость
в применении численных методов и ЭВМ, как это было,
например, при нахождении оценки для \R'(x)\ в п. 2.
Заметим, что в некоторых случаях поточечные оценки,
получаемые в итоге выполнения третьего этапа, могут представлять
5 ю. С. Завьялов и др.

66 ГЛ. II. ЛОКАЛЬНЫЕ СПЛАЙНЫ
гораздо большую ценность, нежели оценки в нормах С и Д».
Например, они используются для вывода оценок погрешности
интерполяции кубическими сплайнами дефекта 1 в гл. III.
5. Описанная техника доказательства применяется для
анализа погрешности интерполяции и в других классах функций.
С целью сокращения записи мы не будем приводить подробных
доказательств, ограничиваясь лишь итоговыми результатами
первого, третьего и четвертого этапов. Промежуточные выкладки
рекомендуем читателю проделать в качестве упражнения.
Пусть / (х) <= С1 С\ [а, Ь]. При х е [Xt%
t'
(х, + xft.) dx + J-^-2/'" (x, + т*,) drj,
г =0,1.2, A3)
, т) =, t'(l -1)[- A - t)
t
1
Д'" (х) = б j т A - т) /'" (ж, 4- т/г;) йт - /'" (х). A4>
о
Из A3) при *е[0, 1/21
IЯ (х) 1 < f h\ ;'A ~ "' со; (/'"). A5>
Для f s [0, 1/31
I Я'(*I<*1 ''2'^,(/"), A6)
04 A i)
|Я'(*)| <Л,
Для I s [1/3, 1/21
| Д^ (ж) | < 2t2 A - OfAi®« (Л- A9)
Из A5) следует оценка для Ш(хЖ Максимум погрешности —
в точке хг + h{/2, t = i/2.
Максимумы правых частей^ в A6), A8) достигаются
соответственно в точках ^=E —У13/6), * = 1/3 и равны A3V13—
*- У46)/54, 1/72. Отсюда следует оценка для ИД'(

§ 6. ОЦЕНКИ ПОГРЕШНОСТИ ИНТЕРПОЛЯЦИИ 67
Для оценок A7), A9) максимумы правых частей равны
соответственно 4/27 (достигается при I = 0) и 1/8 (достигается при
? = 1/2). Отсюда вытекает оценка для H/?"U)IL.
Наконец, из A4) получаем неравенство
1/ГЫ1 «? ©,(/"), *е[0, И,
из которого следует оценка для Ш'"(.г)Исо.
Если f(x)^CLW'itOOla, fc|, то оценки для l!/?(r>(#HL, г = 0, 1,
2, вытекают из A3) после применения неравенства Гёльдера.
6. Если f(x) e C^i.oo К Ь|, то для х^ lxu xi+\]
j^ \, r = 0, 1,2,3, B0)
где
ф,(*, х) = A - tJt4-3t + A
ifctt, т) = f2d - тJ[-3A -1) + C - 20A - тI.
Отсюда
что приводит к оценке для Ш(л:I1с.
Далее, из B0) получаем
WlU «elO.ll, B1)
[0,1/3], B2)
*s|l/3f 1/2]. B3)
Максимумы правых частей в B2), B3) равны соответственно
1'3/216 (достигается при t = 1/2—ТЗ/6) и 1/162 (достигается при
t = 1/3). Отсюда имеем оценку для Ш'{х)\\с.
Далее, из B0) находим
r{X)U «в[0,1/3],
B4)
^! (- 1 + 6*- 6t*)f/IV (x)U, t€ [1/3,1/21.
B5)
5*

68 ГЛ. II. ЛОКАЛЬНЫЕ СПЛАЙНЫ
Так как максимумы правых частей в B4), B5) равны
соответственно 1/12 (достигается при t = 0) и 1/24 (достигается при
t =¦ 1/2), то отсюда приходим к оценке для Ш"(#)Иоо.
Наконец, из B0) получаем
\R'U*)\<^ll-2t(l-t)(l+t-t*)]\\fIY(z)U ts[0,l].
Здесь максимум правой части достигается при i=»0 и равен
1/2. Это дает оценку для 11Д"'(яI1<». Теорема доказана.
7. Порядки погрешности в классе С1 Wl,oo [#, Ь] являются
наивысшими для эрмитовых кубических сплайнов. Легко показать,
что дальнейшее увеличение гладкости функции fix) не приводит
к повышению порядка аппроксимации. Более того, при этом не
могут быть уменьшены и константы в оценках. Однако это
касается оценок по норме. Если же рассмотреть поточечные оценки,,
то в определенных точках интервала [х{, xi+\] некоторые из
них могут быть существенно улучшены при достаточной
гладкости f(x).
Теорема 2.6. Если }(х)<=СЧх{, xi+il, &>4, то
s3 (/; х) - / (*)+ 2 ! (а! * /(а) С») {(- 1) V A + 2« - а) +
а4
+ (l-0a~2C-2f-a)}+O(fe?). B6)
Доказательство этого равенства получается
непосредственным применением формулы Тейлора в соотношении E.1).
Дифференцируя B6), легко получить
S'3 (/; х) = /' (x)-±t(l-1) A - 20 Ь\Г (x) -
_ htf{x) + Q W)
Si (x) = /" (x) -J-(l-6t + 6t«) fe?/IV (*) -
- -i A - 2/) [1 - Ы A - *I /if/v (x) + О (Aj), B8)
S* (/; *) = /'" (x) + Ц^- fe;/IV (x) +
+ ^ [18 - 60* A - t)} h\f (x) + О (/if). B9)
Из этих равенств вытекает, что в точке #* = #< + fti/2
5; (/; х*) = /' (х*) - -^ Г (х*) + О (А?), C0)
5," (/; х*) = /'" (х*) + -^ A?/v (х*) + О (А?). C1)

§ 6. ОЦЕНКИ ПОГРЕШНОСТИ ИНТЕРПОЛЯЦИИ
69
В точках х
х{ + C ± У3)йг/6
S" (/; х) = /" (х) ±
540
(х) + О (hi).
C2)
Сравнение этих соотношений с оценками погрешности по норме
позволяет сделать вывод о том, что при достаточной гладкости
функции fix) порядок аппроксимации производных этой функции
соответствующими производными эрмитового сплайна в
некоторых точках интервала [х{, xi+\l увеличивается на единицу.
8. Все оценки, установленные в теореме 2.5, неулучшаемы. Это можно
доказать путем построения экстремальных и квазиэкстремальных функций.
Мы проведем построение только для оценок величины ||Д(яI1« в классах
^Ц^Ь] * Wl[a, Ъ].
Из формулы G) получаем
C3)
*? г1?
Пусть функция /i (x) такова, что
/i(;ri + T i)-|sgnC
По формуле C3) для /i(z) имеем
1/4
J
1/2
J
}
1/2
> если
если
3/4
J
1/4
1т — 1) dT + J C — 4x) ¦
1/2 3/4
= 1,то полученное зпачение совпадает с оцепкой
[а, Ь]. Следова-
Если учесть, что]/! (^
для ЦД (х) IIс в классе
гельно функция f{(x) является экстремаль-
ной в этом классе.
Квазиэкстремальной функцией в
классе ?х?д [а, Ъ] будет функция /г(#),
вторая производная которой изображена на
рис. 2.3 (знаком «•» помечены
соответственно слева направо точки ач+ A/4) А<,
*< + A/4) А, + е/гь *, + C/4) Л, - Bhu x% +
¦+¦ C/4)hг). В этом легко убедиться,
вычислив для f2(x) величину R(x{ + hi/2) no
формуле C3). Обратим внимание
читателя на то, что /а (х) получается
«сглаживанием» функции f (х).
Задачи, я) Объяснить, почему постоянные в оценках для класса
W» lai Ь] ровно в два раза больше постоянных в соответствующих
оценках для класса СХС\ [а, Ь].
Рис. 2.3.

70 ГЛ. II. ЛОКАЛЬНЫЕ СПЛАЙНЫ
б) Показать, что при f(x) e С4 [а, Ь]
§ 7. Интерполяция с заданной точностью
эрмитовыми кубическими сплайнами
Задача об интерполяции с заданной точностью эрмитовыми
кубическими сплайнами решается путем выбора узлов
интерполяции. Здесь снова могут быть использованы методы и
алгоритмы, описанные в § 3 для сплайнов первой степени. Мы укажем
лишь на те изменения, которые нужно внести в расчетные
формулы.
Пусть, например, f{x) e СЧа, Ъ] и требуется осуществить
интерполяцию так, чтобы выполнялось условие
где е — заданное число. Чтобы решить эту задачу на
равномерной сетке, достаточно выбрать шаг сетки из условия
384e
в соответствии с оценкой погрешности интерполяции для
функций из класса С4[а, 6].
Для построения неравномерных сеток могут быть
использованы алгоритмы 1 и 2 из § 3. При этом, очевидно, нужно всюду
заменить f"(x) на /IV(#) и, кроме того, вместо формулы D) в
алгоритме 1 использовать формулу
-VvH
В алгоритме 2 выражение E) следует заменить на
е. в * (хц — я?4L max | /I
384 o^s^j
Приведем численные результаты для интерполяции эрмитовыми
кубическими сплайнами. Обозначения и интерполируемые функции — такие же,
как в § 3. В таблице 2.6 даны значения величин
Rr - max | /(r> (x) - S{p (x) |, r = 0, 1, 2, 3.
Сопоставление таблиц 2.6 и 2.2 показывает существенное увеличение*
точности интерполяции кубическими сплайнами по сравнению со
сплайнами первой степени.
Следующая таблица 2.7 содержит данные о числе точек Лг и Nt
соответственно равномерной и неравномерной сеток, которое необходимо для
достижения заданной точности интерполяции 8.
Сравнение этих результатов с соответствующими результатами для
сплайнов первой степени говорит о значительном уменыиепии числа узлов
в случав интерполяции кубическими сплайнами.

§ 7. ИНТЕРПОЛЯЦИЯ С ЗАДАННОЙ ТОЧНОСТЬЮ
71
В таблице 2.8 приведены данные, иллюстрирующие соотношения F.30) —
F.32). Здесь обозначено
Яг = max | S? (*« + 4) - /<r> (*t + т) |. г = 1,3;
Ro = max
2 i
Расчеты выполнены для равномерной сетки с шагом h •= 0,1.
Таблица 2.G
ft
од
0,05
h
0,1
0,05
ft(x)
1-10-6
5.10"8
0,0016
0,0001
/.(X)
2,.
1/
5.10"»
M0"e
2,2-10
6,0-10-4
5,7
1,7
0,08
0,02
Ux)
50
24
0,013
0,0013
/.<*)
0,13
0,07
2,4-10'»
з,о.ю-6
380
216
0,051
0,008
8-10-4
1-10-4
4,8
2,5
3
4
U*)
0,45
0,09
f«(*)
-103
• to3
Таблица 2.7
8
ю-1
10*2
ю-3
Ю-4
ю-»
iV
2
2
3
4
7
N,
2
2
3
4
6
N
6
9
14
24
42
4
5
7
11
18
/i(X)
N
3
4
5
9
14
N,
3
4
5
8
13
/4ix>
N
10
17
30
52
90
6
9
14
22
36
я,
1,3-
8,1-
6,4-
ю-7
ю-6
10-4
««)
3-10-3
0,2
15
2
1
8
•ю-*
Таблица
««,
0,15
15
7-102
2.8
Задача. Сравните результаты, приведенные в таблицах 2.6 и 2.8, с
теоретическими оценками погрешности.

72 гл. ii. локальные сплайны
§ 8. Другой способ интерполяции эрмитовыми
кубическими сплайнами
Для построения эрмитова кубического сплайна необходимо задать в уз-*
л ах сетки А значения интерполируемой функции ft и ее производной /$.
Однако в практических задачах часто известны только узловые значения fu
Наиболее простым выходом из этой ситуации является использование
вместо точных значений производной некоторых величин /j,
аппроксимирующих Д. Мы построим такую аппроксимацию на основе разделенных
разностей. Положим
1-1,2,...,*-!, A)
B)
где jiiv= hi-i(hi + &<_i)-\ k{ = 1 — [if.
Интерполяционный эрмитов кубический^сплайн, построенный по
значениям /|, f{, будем обозначать S3 (/; х) = S3 (#).
Рассмотрим погрешность интерполяции для введенных сплайнов. Для
дифференцируемой функции f(x) имеем
| Цг) (*) - /(Г) (*) I < 1 S? (х) - 4Г) (*) | + | W (х) - /A"> (х) |, D)
г = 0, 1, 2.
Оценки второго слагаемого в D) были получены в § 6.
Для первого слагаемого согласно E.1)
138 (*) - 5, (*) | < * A - *) A, max | f\ -"}[ |,
|3i(*)-s;(*)|<[(l-t)| 1-3*| +«12-3*1 lmaxl/J-7'il,
I 5j (») - 5j (x) | < | 6* - 4 11?,' - /; I АГ1 + 12 - 6* | \J'l+1 - f'i+11Ь7».
Принимая во внимание соотношения A) —C), нетрудно оценить
величины max | /J —7'j|> |/i—?il/Ai» Pi+i —/i+i |Ai и затем, используя
результаты § 6, получить необходимые оценки. Не останавливаясь на
вычислениях, приведем окончательные результаты в виде таблицы 2.9, где
даны правые части оценок
р()М| г-0, 1,2,
в зависимости от гладкости /(ж). Эти результаты справедливы для
промежутка [xh tfjv-i]. Для отрезков [я0, #i], Ixn-u xn] оценки будут несколько
хуже из-за того, что аппроксимация производных в граничных точках а:0, xN
с помощью выражений B), C) грубее аппроксимации во внутренних точках
Х{, t «= 1, 2, ,.м # — 1. Однако большинство иэ приводимых оценок остаются
справедливыми и для промежутков [х0, xi], [xN-u ^л]> если hQ ц /гл--1 при-

§ 8 ДРУГОЙ СПОСОБ ИНТЕРПОЛЯЦИИ
73
мерно в два раза меньше h. Кроме того, очевидно, несоответствие оценок
полностью устраняется,ч если в точках #о, xn заданы точные значения
/о» /jv
Отметим некоторые особенности полученных оценок по сравнению с
аналогичными оцепками для эрмитовых сплайнов Бг(х) (таблица 2.5).
Прежде всего, оценки (одинаковые по порядку) для сплайна S$(x) получаются
при существенно более жестких требованиях к гладкости
интерполируемой функции 1(х). ^ __
Максимальный порядок приближения сплайнами S$(x) есть 0{к% Для
сплайна ?3(#) максимальный порядок О (/г4). Третья производная S3 (x)
в отличие от S3 (х), не аппроксимирует f"(x). Отметим также, что констап-
ты в оценках для ?3(я) значительно больше констант в соответствующих
оценках для ?3(#). Все эти особенности обусловлены свойствами
аппроксимации величин /| с помощью соотношений A) — C).
Таблица 2.0
Класс
функций
О1 [а, Ь]
С2 [а, Ь]
С3[а, 6]
в.
¦§*»</'>
3 -2 „
й**«<л
| _
1 ~31! '"Г
0,58577Й|Г (*)ILee
0,50626Лсо (/')
1 -2 w
».
7 у© (Л
0,14815/г о (/'") -|-
ОД
0,05
Ко
0,00016
0,00002
/,(х; | /,(х)
0,03
0,005
0,002
0,0003
/4<*>
0,02
0,01
Л(х) |/,(«)
0,009
0,002
0*6
0,1
0,03
1,0
1,4
Т
а б л ]
л ц a
2.10
я,
/.<*>
0,26
0,13
/¦(ж)
60
38
/,<*>
3,0
1,5
90
106
В качестве иллюстрации приведем для S^(x) некоторые численные
результаты (таблица 2.10). Обозначения и функции — такие же, как в
таблице 2.6. ^
Так как в формулу ?3(я), в отличие от S5(x), не входят значения
производной функции /(я), то такие сплайны могут быть использованы для
интерполяции функций из класса С [а, Ь]. Оценим погрешность
интерполяции в этом классе. Нетрудно получить следующее выражение для остаточ-»

ГЛ. II. ЛОКАЛЬНЫЕ СПЛАЙНЫ
ного члена при х е [xt, ж(+1], i = 1, ..., N — 2:
R (») - [1 _ ф («)] Д
(Л f) 1
+ М A - <) зг: (Л - ft-i)
где
ф(*) = *2C - 20+ МA - О2- W2(l - *).
Легко лроверить, что 0<фD) < 1. Применяя теорему о среднем для
непрерывных функций, имеем
Обозначив max fy/A; = Р, отсюда получаем
H-j|^=i
Можно показать, что эта оценка справедлива и для промежутков [х0,
(л;^~ь хц]. Следовательно,
IR (*) "сга.ы < I i + ТгПГТуГ r0 (')• F)
Наличие разрывов производных у интерполируемой функции
отрицательно сказывается на точности приближения сплайнами Ss(x). Однако,
если число точек разрыва невелико, то можно существенно ослабить их
влияние надлежащим выбором узлов сетки.
Пусть, например, f(x) трижды непрерывно дифференцируема всюду на
[а, 6], за исключением точки 6, в которой производные /(г), г = 1, 2, 3,
имеют разрывы первого рода. Во-первых, при выборе сетки следует
обязательно включить точку | в число узлов. Пусть Xk = €• Во-вторых,
расположим узлы хк-х и xk +1 так, чтобы hk-\ = hk = h, причем h <c &a-2,
h «с hb+\. Остальные узлы могут быть взяты произвольными. В
соответствии с таблицей 2.9 "имеем
Для промежутка [xk-\, xi,+i] из E) легко получить
Выбирая А достаточно малым, всегда можно добиться, чтобы
погрешность интерполяции на отрезке [xk-u #a+i] была меньше погрешности для
остальной части промежутка fa, b].
В качестве численного примера рассмотрим интерполяцию функции
j(x)=*\x\ на отрезке [—1, 1]. При выборе в качестве узлов интерполяции
точек —1; —0,5; 0; 0,5; 1 погрешность интерполяции равна 0,072. Если
добавить еще два узла в точках —0,01; 0,01, то погрешность снижается до 0,0015.
В принципе, используя более точные, чем A) — C), разностные
аппроксимации для производных iv можно повысить точность
приближения сплайнами §з(#). Одна из таких возможностей реализуется в § 3 гл. VI»
Задача. Получить формулы для аппроксимации /.. с точностью

§ 9. ЭРМИТОВЫ КУБИЧЕСКИЕ СПЛАЙНЫ
75
§ 9. Эрмитовы кубические сплайны
двух переменных на прямоугольной сетке
В области Q = [а, Ы X [с, d] введем сетку А •= Д*ХДУ, где Дх:
а *= зг0 < ... <xN = 6, Д„: с = i/0 < ... <Ум == d. Пусть в узлах
feu у) заданы значения
Интерполяционным эрмитовым кубическим сплайном двух
переменных назовем функцию ?з.з(#, y)aS%iz(f; x, у), которая
в каждом из прямоугольников О#=* [х{, xi+\] X [yiy y^\] имеет вид
и удовлетворяет условиям интерполяции
0 JV; / =
Рассмотрим алгоритм построения сплайна «5з,з(^, 2/). Заметим
что при фиксированном значении одной из переменных сплайн
5з,з(#, У) и его первая производная по этой переменной
превращаются в одномерные эрмитовы кубические сплайны
относительно другой переменной. Поэтому
Dr °53,8(*„ У) - Sz[Dr' *f(z» у); у], г - 0, 1; р - lt i + 1.
В правой части этих равенств стоят одномерные сплайны,
которые можно вычислить по формуле E.1):
S3 [Dr'°f (*„ у); у] = ф1 (и) f(prf + ф2 (и) /^°Л +
где /j «= yi+i - yh и = (i/ - р,
По той же формуле E.1)
Swix, y)-*<pi(t)S*[f(xu у); у] +<p2tt)S3[/Ul+if »);
где А»
у); у], B)
+1 ,
Определим векторы q>U), ф(и) и матрицу F соотношениями
/
A,0)
/(9,1)
/@,1)
7ij
/@,1)
/@,1)
'4+J
г)
M,j+1
/A.1)
/A,0)
'i+l.i
Л1.1)
/A,1)

76 ГЛ. II. ЛОКАЛЬНЫЕ СПЛАЙНЫ
С учетом A) формула B) может быть записана в виде
5з.з(я, у)=*ф) -У.ф(»), C)
или, если обозначить символом Т операцию транспонирования,
SZJtLz, у) = q>4u).FT .ФГШ. D)
Если производить вычисления в следующем порядке: hif lu
(х — х{), (у — у{), t; и, A — *), A — и), ф!Ш, ф2Ш, ф1(м), ф2Ы,
h{(pz(t), А<ф4(?), />фз(и), Iffliiu), S(x, у), то для нахождения ?з,з(#, у)
потребуется 56 арифметических операций, из них «длинных» 34.
Перейдем к анализу погрешности при интерполяции
сплайнами «5з,з(/; я, у). Существенным моментом здесь является
использование частичных сплайнов. Интерполяционный сплайн Ssif{xf
у); х] называется частичным, если он представляет собой
эрмитов кубический сплайн для функции fix, #.) на сетке Дх, а у пг-
рает роль параметра. Очевидно, этот сплайн можно записать
в виде
з
?8 [/ {х, У)\ х] = 2 аа (у) (х — Zi)a, х е= [хи хг+1]. E)
Аналогичным образом вводится частичный сплайн Szifix, у); у].
Лемма ,2.1. Справедливы тождества
D°><S3[f(x, у); х) = S3[D°>*f(x, у); *],
D'*Szlf(x, У)\ У} =Sz[D'>«f(x, у); у].
Доказательство. Докажем первое из равенств F).
Второе доказывается аналогично. В соответствии с определением
эрмитова сплайна коэффициенты аа(у) в E) находятся из системы
Dr>° 2 аа (у) (хр - хг)а = Z)r'°/ (хр, у), p = i, i + l; r = 0, 1.
а=о
Дифференцированием по у отсюда получаем равенства
Dr'° 2 а^ (у) (хр - Xif = Dr's/ (xp, у),
а=о
из которых следует, что функции #а (у) являются
коэффициентами интерполяционного сплайна
S3 [D°'ef (х, у); х\ = S <№ (у) (х - хг)а. G)
а=о
С другой стороны, из E)
D°''S, [f (х, у); х] = S а<,8) (у) (ж - *0а. (8)
а=о
Сравнивая G) и (8), приходим к F). Лемма доказана.

§ 9. ЭРМИТОВЫ КУБИЧЕСКИЕ СПЛАЙНЫ 77
Введем в рассмотрение функции
7i(*. у) = S3[f(x, у); у} -)(х, у), Т2(х, у) = S3lf(x, у); x]-f{x, у).
Используя формулу B), легко получить для погрешности
интерполяции следующие четыре представления:
S3fi(x, у) - fix, у) = cpiU^U,, у) + фа(*)Г1(в,+ь у) +
+ htftWD^Tiix,, у) + k^t)Dl'°Ti(x^.u У) + Та{х, у), (9)
¦5з,з(ж, у)~fix, у) = q>iiu)T2ix, у,) + <p2iu)T2ix, yi+\) +
+ lm{u)D°'lT2ix, ys) + lm{u)D°'lT2(x, yj+i) + Tiix, у), A0)
5з.8(«, »)-/(*, ff)={5r8[7I,U, i/); jfJ-TiU, у)) + Т^х, y) + T2ix,y),
A1)
^з.8(«, »)-/(*, у) = ^[^(x, у); г/J - T2ix, у)) +
+ Tl(x,y) + fa(x,y). A2)
Тождества (9)—A2) служат отправным пунктом для
получения всех оценок. Отличительной чертой этих соотношений
является то, что в их правые части входят лишь погрешности
интерполяции для одномерных эрмитовых сплайнов. Это обстоятельство
позволяет без особого труда получать нужные оценки. Мы
рассмотрим только два класса функций. Другие случаи исследуются
совершенно аналогично.
Теорема 2.7. Если f(x,y)^C1-1Wi,eo[Q], то
tD^o{S?,3(x, у)-fix, у)}||ао<Л(г1)Л4-г || ZL.o/ {Xi з,Iоо +
+ А{ГЧ3~Г~11| ZK.i/ (a?f у) |м + А\Ч*-Г | D^-'f (x, у) U A3)
\ o°-s {ss,s ix. у) - f ix, у)} i» < 44"' I o°'4/ (x, y) g. +
+ A't4V-' I D**f {x, y) |U + A{3rh*-" || D*-.-'f ix, y) I», A4)
r, s = 0, 1, 2;
»/(ж, y)U + h*\D'<4(x, y)U), A5)
tf = Л^2) = Л(п3) = 1/384,, ^i1' = /3/216, A™ = 0,0080377,
3> = i/98, 4" = 1/12, 42) = 2/27, 43) = 1/16, А1Л = 0,032303.
Доказательство. Используя тождество A0), имеем в
каждом из прямоугольников fiy
\DrHS3,zix, у)-fix, 0)}| «SfodOIUWjU, у,Hо +
+ <Ра(и)Ш'.«»7>а(аг, yi+l)Wc + 1^3Ы)\\Ю^Т^х, у,)\\с +
+ *,|ф4(»)IШг''Г2и, yi+1)l0 + №-°Т^х, y)Wc. A6)
Далее, учитывая результаты, относящиеся к одномерной интерпо-

78 ГЛ. II. ЛОКАЛЬНЫЕ СПЛАЙНЫ
ляции (таблица 2.5), получаем
\Dr*T%(x, yP)\\c<K4,rhl-r\\D^J(x, i/p)||oc, г = 0, 1-, 2;
P-/.J + 1; ^,0=1/384, #4J - /3/216, #4,2 = 1/12.
Согласно лемме 2.1
?'•%(*, y,)-D'-4SZtZlD*4(x, ур); х\-№Ц*, У,».
Поэтому ввиду того, что D°*1f(x, у) е Wi[Qijl, имеем
\\D^T^y^)\\c<K3trhrr\\D^f(x,yp)U ^ = 0, 1,2; A8)
р = /, j + 1; #з.о = 1/96, Кял == 0,032302, Кзл = 8/27.
Аналогично,
/WiU, у) = Sz,3[Dr0f(x, у); y]-Dr>*f(x, у).
Следовательно,
l^er1(if»)||c<^ri4.rzrrPM-7(*,»)U ^ = 0,1,2; A9)
^о,4 = 1/384, К1Л = 1/96, K2t2 = 1/16.
Подставляя A7)—A9) в A6) и принимая во внимание, что
<Pi(w) + ф2(и) = 1, 1ф3(и)| + 1ф4(ыI ^ 1/4,
приходим к A3). Аналогичным образом, исходя из тождества (9)г
выводятся оценки A4).
Докажем теперь неравенство A5). Из тождества A1) следует,
что
\D"{S3,3(x, у)-1(х, у))\ < |Я'.'7\(я, у)\ +
+ \D^T2{x, у)\ + \D]4S3[T,(x, у); х\-Тх(х, у))\. B0)
Учитывая, что ""
ID'-TiU, У)\ = Ю^'ШО'оДх, у); у\ -Z)'.o/(x, y))\ ^
I D''iГ2 (ж, у) |<0,032302/if |D».'/(ж, у) |„
S [71, (ж, у); а;| - Т1 (х, у)) | =
^(«, у); а:] - D^T1 (x, у)) | <
< | ш (О1.1ГХ (*, •))< 3||D^T, (x,y) ||те>
из B0) получаем A5). Заметим, что, используя вместо (И)
тождество A2), мы пришли бы к оценке

§ 9. ЭРМИТОВЫ КУБИЧЕСКИЕ СПЛАЙНЫ 79
Из A3), A4) мы имеем две оценки для И?3,з(#, у)— /(#, p)'L.
Еще одну оценку этой величины можно получить, исходя из
тождества A1) или A2). Действительно, учитывая, что
IS3 [Тг (х, у); х] - Тг (хч у) Цоо < ~ й21 D^TX (x, у) {„ =
(х y)\U<h4
= ±h*\Su(D*-*f(z, у); у)-ВЩ(х, y)\U2
и используя A7), A9), из A1) приходим к неравенству
Л ^з.з (*, У) -fix, У)\с<ш *№>-Ч(х, V)U +
Л
Теорема 2.8. Если f (х, у) е= Cl'xW%% [Q], то
Ч{х, УЖ, г, 8-0, 1, 2, 3, B2)
1/384, Kt = УЗ/216, К2 = 1/12, Я3 = 1/2.
Доказательство. Из A1) и леммы 2.1 имеем
WHS3,3{x, у)-fix, y))\*Z
^W-HSsUP-'Tilx, у); x]-D°''T1U, у)Ж +
+\\Dr'Tl(x, уЖ + Wr-'T2(x, уЖ. B3)
Используя одномерные оценки (теорема 2.5), получаем
W'.T,(i, уЖ = W°'{S3W'-°f(x, у); у] -Dr-°f(z, у)Ж<
< К.Т*-ЫУ-*Пх, уЖ,
Ш'-Т8(х, уЖ ^ КгЪ*-гЮ^(х, уЖ,
^x, у); х\ -D^'T^x, у)Пм <
х, уЖ.
Подставив эти неравенства в B3), приходим к оценкам B2).
Некоторое представление о точности интерполяции дают результаты для
функции f(x, у) = ехр (х + у) в области [0, 1] X [0,1]. Узлы интерполяции
по каждой из переменных взяты с шагом 0,5. В таблице 2.11 с двумя
входами приведены значения величин
Лг>,= max_ \Dr'*{S33(f;x,y)-f(z, у)}\, г, « = 0,1,2, 3,
*едж,г/еду
где Д*, А» — сетки по переменным х, у с шагом h = 0,05.

80
ГЛ. II. ЛОКАЛЬНЫЕ СПЛАЙНЫ
В каждом из прямоугольников [хи xi+\] X [yh ум] имеются
точки (линии), в которых порядок аппроксимации производных
интерполируемой функции на единицу выше, чем это
гарантировано оценками B2). Такие точки легко могут быть выделены на
>v Г
S -ч^
0
1
2
3
0
0,0015
0,0059
0,13
1,6
1
0,0059
0,011
0,13
1,6
Та
2
0,13
0,13
0,25
1,7
блица 2.11
3
1,6
1,6
1,7
2,9
основе формул F.29) — F.32). А именно, порядок аппроксимации
повышается: для производных Dl-°f(x,y), D*'sf{x,y), s = 0, 1, 2,—
вдоль прямой х = хг + hi/2, для производных Dr>3j(x, у), г = 0, 1, 2Г
D°>lf(x, у) — вдоль прямой У = Уз + lyiB, для производных
D2t*f(x, у), s = 0, 1,— вдоль прямых х =х{ + A/2 ± У3/6)/г«, для
производных Dr>2f(x, у), г = 0, 1, —вдоль прямых г/= г/,+A/2 ±.
=fc УЗ/6) lj. Наконец, для производных Dr>rf(x, г/), г = 1, 3,
порядок повышается в одной точке (х* + &У2, */; + IJ2) и для
производной D^>2J(x, у) —в четырех точках: {х{ + hJ2 ± А^УЗ/б, у}^г
rb //2 ±
0
1
2
3
0
0,0009
0,0023
0,027
1
0,0009
0,0003
0,0075
0,028
Таб
2
0,0023
0,0075
0,0041
. 0,075
л» ца 2.12
0,027
0,028
0,075
0,042
В таблице 2.12 приведены численные результаты, иллюстрирующие этпт
эффект. Исходные данные — такие же, как для таблицы 2.11. При этом для
производных Dr>2f(x, y)_1D2»rf(x, у), г ==j), 1, 2, погрешность вычислена в
точках (xi + hi/2 ± й*УЗ/6, yj + Zj/2± */УЗ/6), а для всех остальных
производных— в точках (xi + hi/2, yj 4- lj/2).
На практике значения производных f%}' , fif*\ /(г5д), как
правило, не заданы. Так же, как и в одномерном случае (§ 8)>
их можно заменить подходящими разностными аппроксимациями.

§ 10. ЭРМИТОВЫ СПЛАЙНЫ ПРОИЗВОЛЬНОЙ НЕЧЕТНОЙ СТЕПЕНИ 8f
§ 10. Эрмитовы сплайны произвольной нечетной степени
Пусть в узлах сетки А: а = #0 < х\ < ., ¦ < xN «=» Ь заданы
значения /(ir) = /(г) (х{), г - 0, 1, ..., го; i = 0, 1, ..., N.
Эрмитовым интерполяционным сплайном степени 2т+1
называется функиил S2m+\,m+\(f; x) =«S2m+i,m+iU), которая
удовлетворяет условиям:
1) на каждом промежутке [х{, xi+i\ 52m+i,m+i(^) — многочлен
гг'епени 2т + 1;
2) ^+1,m+1fe) = /ir), * = 0, 1 7V; г-0,1,..., го.
Выведем формулу для такого сплайна. Очевидно, если
построить многочлены ф«Ш, tyAt), ос = 0, ..., иг, степени 2иг + 1 та*
кие, что
Фа}@) = ва,Г| Ф^ A) = 0, г^г)@) = 0, <r)d)-Sa,r,
а = 0, 1, ..., т; г = 0, 1, ..., т,
где 8а, г — символ Кропекера, то при х^[хи xi+\], t =» {х — х{)/к*
(х) - 2 Л? {<р« @ /ia) + г|,а @ /&). A>
Заметим, мто \fa(?) = ( — l)acpa(l—t). Поэтому достаточно
получить выражение для <раШ. Так как ФаГ) A) = 0, г = 0, .-.., т, и
Фа'^^О, г = 0, ...,а-1, то
S Ма+Р. B)
Коэффицпепты а& определяются из условий
ФаГ)@) = ба,г, Г = а, ,.МН1.
По формуле Лейбница
?аг) (о =2с; [A - от+11(г^> *2*
V г! (те +D!(- l)r~j A
^ /!(Г_/)|AЛ+1^
Отсюда
Ф^г) @) = г!" 2 (- i)<-i ОД!^-. = г! 2* (~ l)r-«-j <%?Г} Ъ.
j
Следовательно, коэффициенты а0, ..., ат_а определяются из
системы с треугольной матрицей и ненулевыми диагональными эле-
в Ю. С. Завьялов и др.

452 ГЛ. II. ЛОКАЛЬНЫЕ СПЛАЙНЫ
ментами
2Г(-1У"С^?ГЧвдва.г, г = а,а + 1,...,то, C)
которая имеет единственное решение.
Положим Сп = О, если к < О или /с > гс; Сп = С? = 1.
Лемма 2.2. Длл любых целых р, т > О
Доказательство проводится методом индукции.
Сравнивая теперь D) с C), имеем
а} = 1 cL+h 1 = 0, ..., т- а.
Подставив эти значения в B), получаем
2
Б итоге при х е [хи
m m—а
а=о Э=о
E)
§ 11. Получение оценок погрешности интерполяции
эрмитовыми сплайнами с помощью ЭВМ
Рассмотрим вопрос об оценке остаточных членов
Д(г) (х) = 5Й+1§ж+1 (х) - /(г) (х), г = 0, 1, .. м 2т + 1,
при различных требованиях к гладкости функции fix). Отметим,
что случаи т = 0, /га = 1 с достаточной полнотой были изучены
.нами ⧧2и6. В § 6 при выводе оценок для кубического эрми-
тового сплайна (лг = 1) была описана техника получения этих
юценок. В принципе она может быть использована и для сплайнов
произвольной нечетной степени. Однако трудности, возникающие
на этом пути, вообще говоря, непреодолимы без привлечения ЭВМ.
Начнем исследования со случая, когда /(ж)еСтСд[а, 6],
I = т, ..., 2т + 2. В силу локальности эрмитового сплайна
достаточно оценить погрешность на одном из отрезков [#*, х{+\].
Используя явную формулу A0.5) для S2m+\tm+\(z) и формулу

§11. ПОЛУЧЕНИЕ ОЦЕНОК ПОГРЕШНОСТИ ИНТЕРПОЛЯЦИИ 8$
Тейлора для /i00, /i+i имеем
7?r.i(x,v)fv)dvt A)
r = 0, 1, ..., Z — 1; Z = w + 1, ..., 2m+ 2;
Z = m + 1, ..., 2тл + 1.
В случае Z = m
frWX (t) hT~T + /ftitfi? @, Af"r, r = 0, ..., w - 1; C),
= J
+ /,m V^ (t)
Дальнейшие рассуждения будем проводить для соотношения
A). Для формул B)—D) выкладки аналогичны. Сделаем в A)
замену v — xi — jhu В результате получаем
1
Rir) (Xi + thi) = tirr J Kr,t (t, т) /«> (х{ + xhi) dr. E>
0
На этом «ручная» работа заканчивается. В результате имеем
выражения для функций KrJ(t^ т) и, кроме того, уже получены
порядки приближения. Все дальнейшие вычисления выполняются'
с помощью ЭВМ. Они состоят в следующем.
Пусть f е Ю, 1] фиксировано. Определим точки тД$), в
которых KTtl(t, т) меняет знак. G этой целью вычислим для
уравнения КГ%МЛ т) = 0 все действительные корни нечетной кратности.
Решается эта задача следующим образом. Вначале, путем
составления достаточно густой таблицы значений функций ifr,i(?, т), т Q
е [0, 1], выделяются границы корней. Затем корни находятся
методом деления пополам. Используя теоремы о среднем, имеем
R(r) (*, + tht) = Н1Г 2 J Kra (t, t) /(O (Xi + ihi) dx
Г f
j
J f
9 Tj@ i xj(O J
F)
6*

ГЛ. II. ЛОКАЛЬНЫЕ СПЛАЙНЫ
где §, r\^lxh xt+\l, символами 2+, 2~ обозначены суммы
интегралов, имеющих соответственно положительные и отрицательные
лодынтегральные выражения.
Очередным этапом является вычисление интегралов
J Kr,i{t,T)dx.
Так как Kr,i(t, т) — многочлен стедени не выше 2т +1, то здесь
наиболее целесообразно использовать квадратурную формулу
Гаусса, точную для многочленов степени 2т + 1. После вычисления
интегралов имеем
Д(г) (хг + Щ = hlCT {A (t) /«> F) + В (t) /со (л)}.
Отсюда
| Д(г) (хг + Щ | < hlCr{V (t) |1 Я> ||с + W (t) со (/@)}, G)
где
Оценка G) является поточечной оценкой погрешности. Для
вычисления оценки в норме С необходимо найти максимальные
значения функций F(?), W(t) при t e [0, U. Для этого
составляется таблица поточечных оценок в узлах достаточно густой сетхш или
организуется вывод графиков функций V(t), W(t). Затем на
интервалах, «подозрительных» на максимум, строится таблица
(график) с более мелким шагом. Этот процесс продолжается до
достижения точности ЭВМ. В результате находим нужную оценку и,
кроме того, попутно определяются точки, в которых она
достигается. Отметим, что тем же способом можно.найти и точки, в
которых поточечная оценка погрешности минимальна.
Рассмотрим далее случай, когда / (х) е CmW\yOO [а, Ь], I = т +
Ч- 1, .,., 2т + 2. Здесь, используя неравенство Гёльдера, вместо
<6) имеем
^ т*(О
а вместо G)
| Rir) (Xi + tin) | < h\-r I /«(x) ||Loo V (t), (9)
где V(t) = \A(t)\ + \B(t)\. Таким образом, алгоритм, описанный
для функций /(ж)еСтСд[а, Ь], не требует здесь существенных
изменений. Отличие состоит лишь в том, что на заключительном
этапе отыскивается максимум другой функции.
Пусть / (х) е= CmWl^p [а, Ь], I = т + 1, ..., 2т + 2; р >1.
В этом случае применение неравенства Гёльдера к A)

§ 11. ПОЛУЧЕНИЕ ОЦЕНОК ПОГРЕШНОСТИ ИНТЕРПОЛЯЦИИ
<с последующей заменой v — х{«= тА< приводит к неравенству
ip |Я>(*)ЪР2 J |*м(*,т)|««И .A0)
\ j tj<«) /
Здесь подынтегральная функция, вообще говоря, не является
многочленом. Для вычисления этих интегралов можно
использовать ту же квадратурную формулу Гаусса, что и в предыдущих
случаях, но предварительно разбив каждый из промежутков
[tjU), tj+iU)] на более мелкие отрезки, чтобы обеспечить
требуемую точность.
Наконец, если / (х) <= CmWlAtl [а, Ь], I =« m + 1, ..., 2m + 2,
то вместо A0) имеем
I R(r) (Xi + Щ | < ИГ1"'I /<» (x) 1г max | iCr>I (*f т) |f
Здесь вместо процедуры вычисления интеграла должна
работать процедура вычисления максимума функции \КГ,№, т)| при
фиксированном t. Для получения оценки в норме С нужно
вычислить max max | KrJ (t, т) |.
Еслр1 бы все арифметические операции при реализации
данного алгоритма выполнялись точно, то полученные оценки были бы
неулучшаемыми. Однако в реальных условиях близость оценок
к неулучшаемым определяется разрядностью конкретной ЭВМ.
В практических задачах естественно считать эти оценки точными.
По предложенному алгоритму была написана программа «ERROR» на
языке Basic, с помощью которой можно вычислить оценки погрешности при
произвольных m; Z ^ m; г-= 0, ..., 2/л + 1; 1 ^ р ^ °о.
Здесь мы приводим только результаты для сплайнов пятой
степени. В таблице 2.13 даны значения величин Rr для оценок
E?3 (X) - /(Г> (X) (со < Дг, Г = 0, 1,
в зависимости от гладкости функции fix). Кстати, большинство из
них получено впервые. В литературе имеются лишь оценка
Hfl(r)U)ILf r = 0, 1, ..., 5, для функций из C2WltOO[a, Ъ] (послед-
няя строка таблицы) и оценка Ш(х)\\с для фупкций из С2С\[а, Ь].
Изложенная методика получения оценок путем использования
ЭВМ пригодна не только для эрмитовых, но и для любых других
локальных сплайнов. Можно использовать ее и при получении
оценок погрешности квадратурных формул.

86
ГЛ. II. ЛОКАЛЬНЫЕ СПЛАЙНЫ
со
csi
И"
И
ч
? '
СО t*"
eo « «ч!
1 I I
О О О
2 S
8 8
CM
Я S3
^ О О чм
fill
8 S
^ О
J *=*
-ч 'it
л
со ч<
СО ^1
3
17737)
о
ь
ю
см
о
о
О
см
о
2301-1
о
СО
СО
1
о
со
о
1^-
3 со со О
О О LO О
Ю СО ^ «^
^ о о о
и
я я
tr S ^^ ^ ^
3^3=^3=3 =
и Е8 Е^ 13е 3е 3е 2е 5й
I I I Т i I I I
оооооооо
ОООЭ**чН'*Н<000'*-«
N чС СМО1ЛЮСМО
00 00 О5 1> 00 СО 00 1^»
об^^0^1>^С0^1^00'*н
vH* ZQ СО (D* СО О vt CM
^ >
со
I
О5 -^н
СМ чн
8;
'о "о то "о
к
С4С4
«
о о
е-1
о

§ 12. СПЛАЙНЫ НА НЕРЕГУЛЯРНОЙ СЕТКЕ
87
§ 12. Сплайны двух переменных на нерегулярной сетке
До сих пор при построении сплайнов двух переменных мы
исходили из предположения, что значения интерполируемой
функции заданы в узлах регулярной (прямоугольной) сетки.
Нарушение этого условия существенно осложняет задачу. В данном
параграфе один из способов ее решения рассматривается на
примере сплайнов первой степени.
Пусть на плоскости хОу задано множество точек РЛхи у<),
i = 0, 1, ..., Лт, в которых известны значения некоторой функции
j(Pi) = U Построим в плоскости хОу многоугольник такой, чтобы,
во-первых, его вершины принадлежали множеству заданных
точек и, во-вторых, все точки, не попадающие в вершины, лежали
внутри него. Полученный многоугольник разобьем на
треугольники с вершинами в точках Pi таким образом, чтобы каждая точка
области, ограниченной многоугольником, принадлежала одному,
и только одному, из треугольников (рис. 2.4). Описанная
процедура называется триангуляцией. Заметим, что триангуляция
осуществляется не единственным способом. Вопрос о выборе «хорошей»
триангуляции будет рассмотрен ниже.
О х
Рис. 2.4.
Рис. 2.5.
Предположим, что на плоскости хОу построена некоторая
триангуляция. Интерполяционным сплайном первой степени назовем
функцию S{{x, у) = S\(P), которая в каждом из треугольников
имеет вид S\(P) = ах + by + с и удовлетворяет условиям
51(Pi)=/i, * = (), 1, ..., N. A)
Геометрически такой сплайн представляет собой поверхносгь,
составленную из кусков плоскостей (рис. 2.5).
В силу локальности сплайна S\(P) достаточно рассмотреть
один из треугольников, например треугольник Q с вершинами

Е8
ГЛ. II. ЛОКАЛЬНЫЕ СПЛАЙНЫ
в точках Pi, Рг, Рз« Очевидно, SX(P) удовлетворяет уравнению
ft
у i
Ух *
Уг 1
у. 1
= 0.
Введем обозначение
Х2
хз
у*
у*
1
1
1
A(PUP2,PS) =
Из аналитической геометрии известно, что величина -j M (Рц Р2,
Рз)! равна площади треугольника Q, причем, если нумерация
вершин соответствует обходу треугольника против часовой
стрелки, то А(Ри Р2, Рг) >0.
Разрешая уравнение B) относительно S\(P), имеем
йг(Р) - А(р р р. {hA(P, Р„ Р3) +
+ fzA(Pu Р, Р.) + f,A (Plf Р„ Р)}. D>
Условие <4СРЬ Рг» Рз)^0 является условием существования
единственного сплайна S\(P) и предполагается в дальнейшем
выполненным. Из геометрического смысла величины A (Pi, P2, Р3)
следует, что оно эквивалентно требованию невырожденности
треугольника Q. Таким образом, необходимо, чтобы точки Pi, P2, Ра
не лежали на одной прямой.
,Для того чтобы вычислить значение интерполяционного
сплайна в некоторой точке Р, очевидно, вначале следует выделить тот
треугольник, которому эта точка принадлежит. Если вершины
всех треугольников упорядочены в направлении против часовой
стрелки, то признаком принадлежности точки Р треугольнику Q
будет одновременное выполнение условий 4(Р, Р2, Р3) >0г
А(Ри Р, Рз)>0, А(Ри Р2, Р) >0. Пусть точка Р принадлежит
треугольнику Q. Вычисление S\{P) можно организовать
следующим образом:
п\ ¦¦ Х\ —
Ь\ — l/i -
А1 »
— #3» «3 = х\ —
X —
#5 = X —
В этом случае необходимо выполнить 27 арифметических
операций: 17 сложений, 9 умножений, 1 деление.
Перейдем к изучению вопроса о погрешности интерполяции*

§ 12. СПЛАЙНЫ НА НЕРЕГУЛЯРНОЙ СЕТКЕ 89
Лемма 2.3.
А(Р, Р2> Р3) +А(Ри Р, Р3)+А(Ри Р2, Р) - А(Ри Р2 Р3).
Доказательство очевидно.
Лемма 2.4. Для любых х, у справедливы равенства
, Р2, Ръ)+(х2-хШРи Р, Pz)+(xs-x)A(Pu Р2, Р)-0,
, р2, р8)+(»2-уМ(Л, Л Рз>+(»з-рШрь ft, «-о.
Доказательство. Докажем лишь первое равенство.
Второе доказывается совершенно аналогично. Имеем
{хх -х) А (Р, Рг, Р,) + (х2-х) Л (Plt Р, Р3) + (х3-х) А (Рг, Р2, Р) -
О х у 1
Этот определитель равен нулю, так как его первый столбец
является линейной комбинацией второго и четвертого.
Теорема 2.9. Если f(x, у) е C[Q], то
И5,(«, ») + /(*, yJUe <«>(/). E)
Доказательство. Из D), используя лемму 2.3, имеем
JS(х, у)- f(x, у) = А(р * {(Л-/(х, у)) А(Р, Pt, Pa) +
-f U, - f (*, У)) А (Ри Р, Р,) + (/,-/ (ж, у)) A (Plt Plf P)}. F)
Отсюда следует неравенство
15(г, у)-fix, у) | «?©(/),
из которого вытекает E). *
Теорема 2.10. Если / (ж, у) е= Wl [Q], то
II Si (*, У) - / («, J/) ||с < у || Л V (*, у) Цоо, G)
ID>".«{5i(*,»)-/(*.y)}K^I|O2/(*,»)l|»,r+*-l, (8)
г<9е А — длина наибольшей стороны треугольника, у —
наименьший из его углов,
IIД2/ (ж, У) ||» = max {|| Я'.»/ (*,
Доказательство. По формуле Тейлора с остаточным
членом в интегральном виде имеем

Ш ГЛ, II. ЛОКАЛЬНЫЕ СПЛАЙНЫ
В свою очередь
Уг
Уг
_ У
В итоге
/i = / (#, У) + (Xi — х) D1'0/ (а:, у) + A/{ — i/) D<u/ (х, г/)
где
Vi
0/i— y) D°'2/ (^ y)dv + & -
Применяя неравенство Гёльдера, получаем
J (*i - a:J1 D*-°f (x, У) |» +
J/
+ -j Cif* -1/J10°'2/ (*,У) IU + |х{ - ж11 y{ - у 11 Z)i.i/ (
Так как |ж{ — a;11yi — у|<у(ж{ — xJ + |-(у{ — уJ, то
y)L. A0)
Подставив разложения (9) в F) и учитывая леммы 2.3, 2.4,
получаем
Sl{x,y)-1(x,y)=%llRu A1)
где обозначено
А(Р,Р„Р3) _ A (Pv Р, Рэ) A (Pv Р%, Р) _
Mpvprp,) u A(pvprpJ 2' А(р1'ргр»)~**
Используя оценку A0), из A1) находим
\S1(x,y)-f(x,y)\<lD*f(x,y)\\<x>'2ihl(xl-x)* + (yi-yn A2)
Функции xi — х, yt — у являются сплайнами цервой степени и
поэтому согласно формуле D)
Vi-У = (yy)E + (»»)E + (»УN

§ 12. СПЛАЙНЫ НА НЕРЕГУЛЯРНОЙ СЕТКВ 91
Кроме того, очевидно, Е^Ег + Ез —1- Подставляя A3) в A2) т
полагая Ез — 1 — Si — Ь, имеем
-= Ei (l — Ei) a + E«(l — 5.) Ь + Eii. (c — a — b) =« ф Elf b)t
где a, Ь, с — квадраты длин сторон треугольника:
а = (Xi-zz)* + (г/i—г/3J, Ъ = U2-*3>2 + (»2-»зJэ
A4)
Найдем максимум функции <р(Еь Еа) в области gf
О < Еа ^ 1» Si + la < Di так как только при этих условиях точка
Р принадлежит треугольнику Q. Из необходимых условий
экстремума (О1>0ф(?ь Еа)вЯОр1<р(?ь EaJ—O) находим, что он может
достигаться в точке j(Ei> E2) где
6* Ь(а + с — Ь) >¦ __ а(Ь + с — а)
Имеем
_
>г6) > 0.
Это следует из того, что Уа, lib, Ус — длины сторон
невырожденного треугольника. Так как
D-°<? ill It) -Л«.«ф (ЕГ, Й)
то в точке (Ei, S2) функция ф(Еь Е2) имеет максимум. Нетрудно
вычислить
7
Нас интересует лишь тот случай, когда (%*, it) e Л.
Используя равенства A5), легко получить, что это будет иметь место
только при выполнении неравенств
a + c-b>Of b + c-a>0, a + b-c>0. A7)
Найдем максимум функции i|)(a, Ь, с) при выполнении условий
A7). Необходимые условия экстремума имеют вид
Aab - (с - а - ЬJ - 2Иа + с - Ь) » 0, A8),
4аЬ - (с - а - ЬJ + 2с(с - а - 6) - 0.

92 ГЛ. II. ЛОКАЛЬНЫЕ СПЛАЙНЫ
Среди решений системы A8) имеется единственное, которое
обладает тем свойством, что ни одно из неизвестных не равно
нулю. Мы имеем в виду решение а~Ь = с. Обозначим max {а, Ь, с) =
•= h2. Таким образом,
Ф (Й, It) < ¦ №2, h\ fe2) - /*2/3. A9)
Осталось вычислить максимум функции <p(gi, Ы на границах
области А. Имеем:
при Ь = 0 ф(|ь Ы - |!A - 6i)a ^
при Ь + Ь = 1 Ф(|ь Ы = Sid ~
Объединяя эти результаты с A9), приходим к оценке
из которой следует G). Заметим, что для треугольников, не
содержащих точку (Й, 1%), постоянную 1/3 в G) можно, очевидно,
заменить на 1/4.
Перейдем к доказательству оценки (8). Дифференцируя D)^
находим
D^S(х, у) = А(р * [/iB/2—Уз) +/з(Уз—У1)+/з(У1—2/2I. B0)
Подставив сюда разложения (9) для /<, получаем
D^[S1(xty)-f(x9y)]^
Учитывая A0), выводим
ID^ [Sx (х, у) - / {х, у)} | < А(р(ХрУ)р, IIЩ (х, у) U B1)
где
а(хг у) - [Ui - яJ + (yi - уJ] Iу2 - Уг\ +
Так как
D2>Qa(x, у)
, у) - 211й - Уз1 + 1уз - У\\ + \У\ - йП > 0,
то функция а(#, у) будет иметь в экстремальной точке минимум.
Поэтому для нахождения максимального значения этой функции
достаточно исследовать ее поведение на границе треугольника.
Используя соотношения A3), перейдем в выражении для а(х, у)

§ 12 СПЛАЙНЫ НА НЕРЕГУЛЯРНОЙ СЕТКЕ 93-
к переменным ?*. Из предположения о принадлежности точкхг
(#, у) границе треугольника вытекает, что одна из переменных ?f
равна нулю. Пусть для определенности ?з "= 0. Тогда |з в 1 — Ъ и
Отсюда легко установить, что а^ (ат, у) > 0 и, следовательно^
а(х, у) может достигать максимума только на концах отрезка
0 < li < 1, т. е.% вершинах треугольника Р\, Р%* Аналогично,
случаи gi = 0 и §2 ^ 0 дают еще одну точку возможного максимума
Р$. В итоге функция а(х, у) достигает максимума в одпой из вер-
Шин треугольника.
Пусть для определенности maxaGr, y)s=sa(x\1 у\). Тогда из.
B1) получаелх
Минимальный по величине угол треугольника заключен
между двумя большими его сторонами. Поэтому А{Ри Р2, Р$) &*
^ У ас sin "у, где ч — величина н-аименьшего угла. Следовательно,.
x, у)-f(x,
|Z)/(
Отсюда вытекает оценка (8) в случае г = 1, s =» 0. Совершенно
аналогично устанавливается оценка (8) при г«=»0, $ = 1. Теорема
доказана.
Существенным моментом в оценке (8) является то, что ее
правая часть зависит от минимального угла треугольника.
Можно показать, что в общем случае это ограничение убрать нельзя.
Однако для одного важного с практической точки зрения типа
треугольников можно получить оценки приближения
производных, не зависящие от величины его минимального угла.
Теорема 2.И. Пусть Q — прямоугольный треугольник,
катеты которого параллельны осям координат. Если fix, у) е
eWL[Ql, то
(x y)U +
B2>
\D^ [Sx(x, y)-f(x, y)]U<h{\D^f(x9 y)U + jlD«>*f(x, y)
еде h — длина наибольшего из катетов треугольника*

ГЛ. II. ЛОКАЛЬНЫЕ СПЛАЙНЫ
Доказательство. Пусть вершины треугольника Р&Рз
расположены так, что катет Р\Р2 параллелей оси Ох и катет
i*A — оси Оу (рис. 2.6). Тогда из B0) следует
Используя формулу Тейлора, находим
+ —Цг I Г (*2 - v) D*>«f (v, Vl) dv - f (x, - v) D*»f (v, У1) dv\
^a — ^i [ J J J
^f (x, y) + § D*.*f (x, w) dw
у
! \U $v- x,) D*.o/ (p. y,) dv]
Отсюда
Учитывая, что максимум правой части полученного неравенства
достигается в точке х=*хи у = #3, получаем первую из оценок
B2). Вторая получается аналогичным образом.
На основе установленных выше оценок
можно дать некоторые рекомендации по
выбору триангуляции. А именно, если узлы
интерполяции заданы произвольным
нерегулярным образом и необходимо приближать
Pf P2 производные интерполируемой функции, то
« ^ следует стремиться к тому, чтобы не возни-
и х кало треугольников с очень острыми углами,
р «я Однако, если речь идет только о
приближении функции, то существенны лишь
размеры треугольников, а величина нх углов не играет
никакой роли.
Очень важной областью применения интерполяции на
треугольниках является метод конечных элеАментов. При этом мы,
как правило, имеем возможность выбирать положение вершин
треугольников. Согласно теоремам 2.10 и 2.11 следует стремиться
к тому, чтобы триангуляция была образована прямоугольными
треугольниками с катетами, параллельными осям координат, или
треугольниками, близкими к равносторонним.

§ 12. СПЛАЙНЫ НА НЕРЕГУЛЯРНОЙ СЕТКВ
95*
В таблице 2.14 приведены численные данные, характеризующие
интерполяцию сплайнами ?i(#, у). Как и в § 4, исходные данные берутся в
узлах сетки Л '= А* X Лу- Результаты даны для двух триангуляции: величины*
Яг8 относятся к случаю, когда каждый из квадратов \xf, Х{+г] X [*/i, У}+\]
делится на два треугольника диагопально, проходящей через вершины.
Таблица 2.14
Vv4. л*, у)
г, s ^S.
Л0,0
^0,0
.«.
0,033
1,03
0,95
0,009
0,36
0,36
sin (х+у)
0,005
0,15
0,14
0,0013
0,05
0,05
.,.
0,068
2,3
2,1
0,023
1,31
1,31
), (%i+u Уj)> а величины Rr, а соответствуют случаю, когда диагональ,
связывает точки (х^ t/j), (xi+u yj+j). - ^
Обратите внимание на резкое отличие значений Rr8 и Йгs. Этот ре-
вультат не случаен. Как показывает более тонкий анализ, погрешность
интерполяции действительно зависит от направления диагонали. В этом
смысле билинейная интерполяция (§ 4) гораздо менее капризна.
В заключение отметим, что реализация алгоритмов
интерполяции сплайнами на нерегулярных сетках требует значительно
больших вычислительных затрат по сравнению со случаем
регулярной сетки. Поэтому в большинстве случаев такую интерполяцию
целесообразнее использовать в качестве аппарата для пересчета
исходных данных с нерегулярной сетки на регулярную
(прямоугольную) с последующим применением алгоритмов
интерполяции для регулярных сеток
Литература к главе П. [12—14, 23, 24, 29, 30, 33, 60, 67, 70„
71, 96].

Г л а в а III
КУБИЧЕСКИЕ СПЛАЙНЫ КЛАССА
Мы переходим к изучению кубических сплайнов дефекта 1,
являющихся дважды непрерывно дифференцируемыми
функциями. Именно они дали толчок развитию всей теории сплайнов.
Хорошие аппроксимативные свойства в сочетании с простотой
реализации на ЭВМ сделали их эффективным средством
решения самых разнообразных прикладных задач. В дальнейшем,
следуя общепринятой терминологии, мы будем называть такие
сплайны кубическими без указания дефекта.
В этой гл&ве рассматривается задача интерполяции
кубическими сплайнами одной и двух переменных. В процессе ее
исследования наряду с применением традиционного
кусочно-многочленного представления сплайнов мы покажем, как работает
аппарат fi-сплайнов.
§ 1. Задача интерполяции. Существование
и единственность решения
Пусть на отрезке [а, Ъ] в узлах сетки А: а = хо<х\<...
.. .< xN = Ъ заданы значения некоторой функции /f = /(#*), i =*
= 0, ..., N. Интерполяционным кубическим сплайном ?(/; x)
называется сплайн, удовлетворяющий условиям
Sihxd-U ; = 0, 1, ..., N. A)
Сплайн ?(/; х) на каждом из отрезков [xt, Xi+\] определяется
четырьмя коэффициентами, и поэтому для его построения на
всем промежутке [а, Ь] необходимо определить AN
коэффициентов. Условие ?(/; х) е СЧа, Ь] эквивалентно требованию
непрерывности сплайна и его производных Sir){x), r = 0, 1, 2, во всех
внутренних узлах #<, i«l, 2, ..., iV—1, сетки Д, что дает
3(iV—1) равенств. Таким образом, вместе с равенствами A)
получается AN —2 соотношений. Два дополнительных условия
обычно задаются в виде ограничений на значения сплайна и
его производных на концах промежутка [а, Ъ] (или вблизи
кондов) и называются краевыми условиями. Существует
несколько различных видов краевых условий, из которых наиболее

§ 1. ЗАДАЧА ИНТЕРПОЛЯЦИИ 97
употребительными являются следующие типы:
I. ?'(/; а)=/'(а), ?'(/; 6)~/'(Ь).
II. S"(f; a)=/"U), S"{f; b) = /"(&).
III. S(r)(/; a)=S(r)(/; 6), г =1,2.
IV. S'"(f; xp + 0) = ?'"(/; ягр - 0), p = 1, N-l.
Условия типа III носят название периодических. Естественно
требовать их выполнения в том случае, когда интерполируемая
функция j(x) — периодическая с периодом b — а. В дальнейшем,
как правило, мы будем рассматривать только перечисленные
краевые условия.
Перейдем к непосредственному описанию алгоритмов
построения интерполяционных кубических сплайнов. Введем
обозначение
?'(/; Xi)*=mh г-05 ..., N. B)
Очевидно, сплайн S{f; x) можно рассматривать как эрмитов
кубический сплайн (§ 5 гл. II), удовлетворяющий условиям A),
B). В соответствии с формулой B.5/1) для x^[xh xi+\]
получаем
S(f; x) =
- т -1L1 + 20+/«+1*43 - 20+ 7ПЛД1 - i? - тмНгН1 -1), C)
где, как обычно, h{ = xi+\ — хи t == (х — x{)/ht.
Кубический сплайн, представленный в таком виде на
каждом из промежутков [#*, Xi+\\, непрерывен вместе со своей
первой производной всюду на [а, Ь]. Выберем величины т{ так,
чтобы была непрерывна и вторая производная. Так как
S* (/; х) = (/i+1 - А) F - i2t)lh\ + т{ (- 4 + 6^)/^ +
+ mi+1 (- 2 + ЫIЫ D)
то условие непрерывности второй производной ?"'(/; ^ + 0)a
= S'r'{j; Xi — 0) в точках #<, i=»l, 2, ..., TV—1, принимает вид
2m, + iami+1 = 3 L ^~—^ + Xj Ц^М. E)
Здесь \ii = ht-iihi^ + к{)"\ Хг — 1 — jut*.
К уравнениям E) следует добавить уравнения,
вытекающие из краевых условий. Таким образом, получается система
7 Ю. С. Завьялов и др.

98 ГЛ. III. КУБИЧЕСКИЕ СПЛАЙНЫ КЛАССА С*
N +1 уравнений для определения N +1 неизвестных ти.
* — 0f ¦.., N.
В случае краевых условий типов I и II находим
2т0 + \х1т± = Со,
*ь г = 1, ...,#— 1, F)
причем
Н 1 г—1
Здесь для условий типа I
(х0 = A,jv = U, с0 = z/0? cN = 2/iv,
а для условий типа II согласно Dа),
CN — о
Чтобы вывести систему ^уравнений в случае краевых условий
типа IV, из формулы D) определим
Отсюда получаем условия непрерывности функции 5W(/; x}
в точках Яр, р = 1, N— 1:
из которых вытекают уравнения, отвечающие краевым условиям*
типа IV:
- v5) «1 - yX = 2 (^ - т; ^),
= 2
где 7о == ^о/^ь Чя ~ hsr-i/hx-fr Исключив неизвестные 7п0, ??глт иф
уравнений E) и G), приходим к системе
A + у0) mL + у0т2 = с*и
li+l = CU I == 2, . . ., N — 2, (8)

§ 1. ЗАДАЧА ИНТЕРПОЛЯЦИИ 99
где
Если fix) — периодическая функция, то, продолж'ая периоди*
ческим образом сетку Айв соответствии с этим полагая
/о = /*> /iv+i = /i, ^o = w,v, т\ = my+i, hN = ho,
можем записать условие E) в точке xN. «Система для определен
лия mi выглядит следующим образом:
2Ш\ + \li17l2 + %\inN = Си
+ 2т{ + iiiirii+i = си i = 2, ..., N — 1, (9)
Итак, построение интерполяционного кубического сплайна по
формуле C) сводится к вычислению величин т{. Для
граничных условий типов I и II они находятся из системы F), для
условий типа IV из уравнений G), (8), а в периодическом
случае из (9) в предположении то = mN,
Матрицы систем во всех четырех случаях суть матрицы с
диагональным преобладанием (§ ДЛ). Такие матрицы невырож-
депы, п потому системы имеют и притом единственные решения.
Таким образом, справедлива
Теорема 3.1. Интерполяционный кубический сплайн ?(#),
удовлетворяющий условиям типа I и одному из типов краевых
условий I—IV, существует и единствен.
Решения систем уравнений относительно тп{ находятся
методом прогонки (§ Д.2). При этом для вычисления
коэффициентов системы уравнений требуется выполнить 10iV
арифметических операций п для реализации алгоритма прогонки еще 8N
или IAN операций соответственно в непериодическом и
периодическом случаях. После определения mt вычисление сплайна
проводится, как указано в § 5 гл. II.
В некоторых случаях более удобным является другое
представление кубического сплайна, в котором вместо величин nti
присутствуют Мг = S" (х{), г =» 0, .• •., N. Используя то
обстоятельство, что на каждом промежутке [хи xi+\] Six) есть
кубический многочлен, а также условия
нетрудно получить для Six) следующую формулу:
? (х) = П A - *) + /i+i«- -^ t A - t) [B-0 Mi + A + t) Mi+1],
A0)
0 1 Y 1
7*

100 ГЛ. III. КУБИЧЕСКИЕ СПЛАЙНЫ КЛАССА С2
Отсюда
S' (х) = fM~ U - h-1B - 6* + З*2) М{ + A - З/2) Мш], A1)
i
Из A0) очевидно, что функция Six) непрерывна в точках
х{, ? = 1, ..., iV—1, а из A2) следует, что непрерывна и ее
вторая производная. Далее, согласно A1)
S' (Xi + 0)= 'i+\~f* - ^- BА/4 + А/Н1),
fi-fi-i hi-i (lla>
h%-\ 6
и, следовательно, для того, чтобы была непрерывна первая
производная сплайна, необходимо выполнение условий
Эти уравнения вместе с краевыми условиями одного из
типов I—IV образуют систему относительно неизвестных М{. Для
условий типов I и II она имеет вид
2А/0 + O'i = 4,
+ UMi+i = du i = 1, ..., N - 1, AГ>)
где
В случае граничных условий типа I согласно A1а)
* *
о / f /
Aq —= |XiV — 1» tt0 — /. /7 / 0 »
а для условий типа II
%*0 «= |л^ = 0, dl = 2/o, diY
/ d

§ 2. ОЦЕНКИ ПОГРЕШНОСТИ ИНТЕРПОЛЯЦИИ 101
Система уравнений при краевых условиях типа IV имеет вид
A + Хг) Мг + (К - |гх) М2 = Мъ A6)
|XiAf4_x + 2Л/г + М/г+i = di9 г = 2, •.., N - 2,
Наконец, в периодическом случае
= du i = 2f ...,ЛГ —2, A8)
= d
Ni
Матрицы систем во всех четырех случаях — снова матрицы
с диагональным преобладанием.
После вычисления всех Ми i = 0, ..., iV, зпачение
кубического сплайна в любой точке х е [а, Ь] может быть найдено по
формуле A0). С точки зрения экономии вычислений целесообразно,
во-первых, системы A5), A6) и A8) переписать относительно
неизвестных М, = М/6 и, во-вторых, вместо A0) использовать
формулу
- (Хг+1 - X) \{xi+1 -Х + hi) Mi + (hi + X - Xi) Mi+l]}. (Щ
В этом случае для построения сплайпа (нахождения М{)
требуется 16iV арифметических операций в непериодическом случае
и 22N в периодическом.. Для вычисления Six) необходимо 14
арифметических операций: 9 сложений, 4 умножения, 1
деление.
§ 2. Оценки погрешности интерполяции.
Сходимость в классе С
Получение оценок погрешности для кубических сплайнов
дефекта 1 представляет собой гораздо более сложную задачу, чем,
например, для эрмитовых кубических сплайнов. В основном
трудности связаны с неявным заданием сплайнов.
Пусть Six) — интерполяционный сплайн, удовлетворяющий
условиям A.1). Если )ix) — периодическая, то естественно
подчинить Six) периодическим краевым условиям (тип III). В
дальнейшем фраза «Six) удовлетворяет краевым условиям типа III»
будет означать одновременно, что интерполируемая функция

102 ГЛ. III. КУБИЧЕСКИЕ СПЛАЙНЫ КЛАССА С2
является периодической. При интерполяции непериодических
функций из С[а, Ъ\ будем использовать разностный аналог
краевых условий типа I:
S' (*0) = (/i - foVK S' (xN) - (fN - /*-i)/btf-i. A)
Обозначим
h
max h
mm i
i
Теорема 3.2. Если f(x)^C[a, b] и Six) удовлетворяет
краевым условиям A) или условиям типа III, то
4
Доказательство. Из A.3) для х е [xiy xi+\] имеем
\Six)-f(x)\^hitil~-t)[(l-t)\mi\+t\mi+1\] +
+ | /i A - tf A + 20 + fmt* C - 20 - / (я:) |. C)
По теореме о среднем
Таким образом,
В периодическом случае из системы A.9) согласно следствию
Д.1 получаем
о
| ш{ |< max | а |< у со (/).
Такие же неравенства вытекают при граничных условиях A)
из системы A.6). В обоих случаях из D) следует оценка B).
Особенностью полученной оценки является зависимость
коэффициента при со(/) от отношения максимального и
минимального шагов сетки. Сейчас мы установим другую оценку, в
которой этот коэффициент зависит от величины
h.
р= max -тЦ
характеризующей соотношение соседних шагов сетки.
Теорема 3.3. Если fix) e= С[а, Ь] и Six) удовлетворяет
краевым условиям A) или условиям типа III, то
U(/), E)
Р)Р-Р -

§ 2. ОЦЕНКИ ПОГРЕШНОСТИ ИНТЕРПОЛЯЦИИ ЮЗ
где п — положительное целое число, р<р*, р* — положительный
корень уравнения
2р A + Р) — Р3 — 1к^Р = 0. F)
Доказательство. Рассмотрим вначале периодический
случай. Переходя в системе A.9) к неизвестным Zi^*
nhi-n+i • • • Ai+n-ь получаем
* = l,...,tf, G)
где обозначено
3-/1 i | * t / f ./ \ I 1 11 X
h.
4-n
Установим неравенства
on—1 2n~-l
"" 2П
Р 2n <*i<P 2" , (8)
-i
П1 j^
7 /^1 T • • • —7 ^ P Si
Очевидно, система G) будет с диагональным преобладанием,
если ври выполнении условий (8) min ф(^, ^)>0. Так как вто-
Ci. Ч)
рэя производная функции cpU,-, 5f) по переменной U
отрицательна, то минимум ф(?{, Si) может достигаться только при U =»
гп К т. е.
?тг-1 \ / 2п-г
I
p^,5j) = mm mui(p\p , s^/, ттф\р
D.8i) I *% H

104 ГЛ III. КУБИЧЕСКИЕ СПЛАЙНЫ КЛАССА С* '
Выполнив элементарные вычисления, получаем
При р ™ 1 правая часть этого равенства положительна и
остается таковой для любого р < р*, где р* — положительный корень
уравнения F). Но в этом случае матрица системы G) есть
матрица с диагональным преобладанием. Тогда из (9), A0)
согласно следствию Д.1 находим
" "А1"_(/), « —1 iv. (И)
Учитывая связь между неизвестными z{ и miy получаем
|mi|<t-K|pn/3, K+iK^K-hIp^
Обращаясь к неравенству D), выводим искомую оценку. В
непериодическом случае все выкладки сохраняют силу, если
дополнить сетку .узлами zo — kho, xN + khN-u к «=» 1, 2, ,«,, п.
Доказательство закончено.
Полученная оценка (б) зависит от целочисленного
параметра п. При п «= 1 уравнение F) переходит в уравнение
откуда р*A) = 1 + У2. С ростом п величина р*(тг) монотонно
возрастает, и при п -*• <» из F) имеем
что дает предельное вначение р*(оо) =» C + У5)/2 « 2,6180. При
практическом использовании оценки E) простым перебором
находим такое тг, чтобы при выполнении условия р < р*(?г) дробь
в коэффициенте при (&(/). имела наименьшее значение.
Например, при р < 2 это будет п =» 1.
Мы получили две оценки B) и E) погрешности интерполяции
непрерывной функции. На практике следует предпочесть ту из
них, которая лучше отвечает условиям конкретной задачи.
Заметим, что ограничения, при который получены оценки,
довольно слабые и их наличие не вызывает каких-либо
затруднений при использовании кубических сплайнов.
Теорема 3.4, Если f {x) e Wl> [а, Ь) и S (#) удовлетворяет
краевым условиям A) или условиям типа III, то

§ 2. ОЦЕНКИ ПОГРЕШНОСТИ ИНТЕРПОЛЯЦИИ j 05
Доказательство. Будем исходить из неравенства C).
Разлагая /<, fi+\ по формуле Тейлора, получаем
А = П A - t? A + Щ + /1+1i2 C - 2*) - / (х) =
- A - tf A + 2«) j /' (v) dv + f C - 2f) f /' (v) dv.
Используя неравенство Гёльдера, находим
U! < Ш - tLl + 2t)
В периодическом случае для правых частей уравнений A.9)
имеем оценку IcJ ОИ/ЧаОН», г = 1, 2, ..., N. Поэтому, согласно
следствию Д.1,
Ы311
Легко видеть, что эта же оценка справедлива и в случае
краевых условий вида A). Теперь из C) находим
Далее, изучим вопрос, как влияет наличие в оценках B) и
E) отношений шагов сетки на сходимость интерполяции в
пространстве С[а, Ы. Зададим последовательность разбиений
Ду г а — xVt о < xVt i < ... <?viVv= &, v = 1, 2, ...
Положим
Vti ,+1 ,U vti» ^v == ПШХ /iv>i.
Обозначим через *SAv(/; #) интерполяционный кубический сплайн
для функции fix) е С[а, Ь] на сетке Av.
Для того чтобы интерполяционный процесс сходился на
последовательности сеток Av, т. е. при v ->¦ °°, Av ¦**¦ 0 S&v (/; #) —
— / ix) -> 0, достаточно, согласно теоремам 3.2 и 3.3, чтобы
выполнялось одно из ограничений
?o, A2)
-TV
A3)
причем р < C + У5)/2.
Ограничение A2) говорит о том, что для обеспечения
сходимости все шаги hVt < при v -> ©о должны стремиться к нулю
одинаково быстро. Условие A3) более сильно ограничивает только

106 ГЛ. III. КУБИЧЕСКИЕ СПЛАЙНЫ КЛАССА С»
отношение соседних шагов, но допускает, что отношение шагов
К, Jhv% j может быть даже как угодно большим при v ->¦ «> и
U — /1-*• °°. Условие A3) является в некотором смысле и
необходимым. А именно, ограничение р < C + У5)/2 не может быть
ослаблено. Мы покажем, что при р > C + У5)/2 существуют
непрерывная функция fix) и последовательность сеток Av (v -*¦ «>,
Av-*"'0) такие, что S&v (/, х) не сходится к fix) при v-*- °°.
Ради сокращения изложения при доказательстве этого утверждения
мы используем более сложные понятия из функционального анализа, чем
в предыдущих разделах книги.
Теорема Банаха — Штейнгауза. Пусть линейные ограничен-*
ные операторы Рч, v = 1, 2, „.., и Р отображают банахово пространство В
в нормированное пространство В\. Для того чтобы lim Pv (и) = Р {и) Олл
всех и&В, необходимо и достаточно, чтобы выполнялись условия:
а) limP (u)*=*P (и) для всех и из множества D, всюду плотного в В;
v-юо
б) существует такое число М, что ||PVII^ Л/, v = 1, 2, ...
Определим Pv как оператор, ставящий в соответствие функции f(x)
сплайн «Уд (/; я). В качестве Р возьмем тождественный оператор. Будем
предполагать, что эти операторы действуют из С[я, Ь] в С\а, Ь]. Каждый из
операторов Pv ограничен. Действительно, используя теорему 3.2, получаем
ml I 5av (/: x) \c < §& (I 5av (/; x) ~f
3
Так как со (/) ^ 2||/(я) ||Cr то отсюда || Pv Ii < 3 + -y
Легко видеть, что условие а) теоремы Банаха — Штейнгауза будет вы-
полпено для введенных операторов и пространств, если /гу->0 при v->oo,
В самом деле, в качестве множества D можно взять, например, множество
интерполяциоппых сплайнов первой степени, которое всюду плотно в
С [а, Ь] согласпо результатам § 3 гл. II. Сходимость интерполяционных
кубических сплайнов на этом множестве следует из теоремы 3.4.
Таким образом, вопрос о сходимости^ интерполяционных кубических
сплайнов к непрерывной функции эквивалентен вопросу об
ограниченности последовательности {IIPvll}. _
Покажем, что при любом р < C +• У5) /2 существует последовательность
сеток {Av}, для которой ||Pv|| -> оо при v-^oo. В целях упрощения выкладок
ограничимся рассмотрением периодического случая.
Зафиксируем число р ^ 2. Алгоритм построения последовательности
{Av}, v = 1, 2, ..., состоит в следующем. Обозпачим
Ъ — а
На отрезке [а, Ь] мон^ет быть уложено 2v + 1 промежутков длиной //v.
Зафиксируем концы среднего из них и введем разбиение отрезка \а, Ь] на
гри части: а < a+vHv < а + (v + l)#v < b. Па отрезке [а, а + v//v] откла-

§ 2. ОЦЕНКИ ПОГРЕШНОСТИ ИНТЕРПОЛЯЦИИ 107
дываются, начиная с правого конца, равные промежутки длиной Av в коли*
•честве 1-— [kv]. Здесь [кх] —целая часть числа kv = vHvlhv. Остаток дли*
ной ahv, a = kv—[kv]4 присоединяется к соседнему промежутку, если а<1/2,
и будет самостоятельным промежутком, если а ^ 1/2. В последнем случае
число отрезков будет равно /'= [Arv]+1. Таким образом, на [a, a + v#v]
введено разбиение
+ (l + a)uv, если a < 1/2,
+ auv, если a>l/2;
Аналогичным образом, начиная с левого конца, делится и отрезок
[а+ (v+l)H*, Ъ].
Отрезок [а + vHx, a+(v + l)//v] разбивается на 2v + 1 промежутков
а + v//v = *Vf, < a-VjZ+1 < ... < ^v,/+2v+i = « + (v + 1) Ял? так, что
*v,i в P2V"(J*v> / "= I + v + 1, ..., I + 2v.
Суммарная длина этих промежутков равна ЯУ.
Очевидно, построенная таким образом последовательность сеток удов*
летворяет условию A3), если только р ^ 2. Периодический кубический
сплайн, интерполирующий /(я), может быть записан в виде
42/iv
где F{A^ (x)«— фундаментальные периодические кубические сплайны. Те*
верь находим оценку
Функция Fl(x) -{-Fl+2v+l(x) (индекс сетки ДУ опущен) симметрична от-»
носительно точки (а + Ь)/2. Поэтому, если обозначить тг = [^;(#v {) -^
+ i?l+av+1K,i)]/,TO
i»! = — tojvv_4» *«0, li..-i' + v. A4)
Так как Fi(xi) •=» 6<j, то па отрезке [^V|z+v« ^v.i+v+ii согласно A.3)
находим
Таким образом, для того, чтобы оценить ||PV|I снизу, достаточно
вычислить величину /W/+V. Из условий периодичности имеем mQ = w^y щ
Сравнивая с A4), получаем mQ = mN^ » 0. Учитывая это обстоятельство, из A,9)'

108 ГЛ. III КУБИЧЕСКИЕ СПЛАЙНЫ КЛАССА С2
получаем следующую систему относительно неизвестных тг-, i = 1, ..., 1+vr
2тх + [1\т2 = 0, A5а)
/тгг-_, + 4тг- + mi+1 = 0, *•= 2, ..., J — 2, A56)
wz_2 + 4wz_i + /тг/ '= 3Mv, A5в)
m/-i + Ami + mi+i '= 0, A5r)
pmt + 2A + p)mi+l + mi+2-= — Зр//ч A5д)
p7»<-i + 2(l + р)те< +ro«+, = 0, i = Z + 2, ..., Z + v — 1, (loe)
v-i + A + 2p) Wi+v = 0. A5ж)
Используя уравнение A5r), исключим из уравнений A5в), A5д)
неизвестное mi, В итоге приходим к системе
2тх + [i\m2{
TTZf | -f- Ami -f* Wf^j
Ami—2 ~Ь 15wij-_i •— Wj.fl
-i — (8 + 7p) flfy-н — 4/W/+2
pmf«.i+2(l + р)'И{"т"'Юг+-
'=0,
= 0, 1 = 2,..., Г
= 12/Av,
= 12р/Лу,
,= 0, г = Z + 2, .
A + 2р)ттгн.у = 0.
~2,
..Л + v-l,
(!0a)
A66)
A6b)
A6r)
A6д)
A6e)
Общее решение уравнепий A66) имеет вид
т{ = схо\ + c2ol, i = 1, ..., I — 1#
где d •== — 2 + УЗ, а2 = — 2 — УЗ — корни характеристического уравнения
с2 + 4о + 1 = 0. Потребовав, чтобы это решение удовлетворяло уравнению
A0а), получаем
Слодолательно,
Общее решепие уравнений Aбд) можно записать в виде
JTI. зег СЛО)< -4- С-СОЛ « i = Z -4- 1, .1 ~j— V.
где Wl«— A + р) +У1 + р + р2, ю2 = —A + р) — У1 + Р + Р2 — корни
уравнения со2 + 2A + р)са + р = 0. Из A6с) следует
Таким образом,
A/ V), * = Z + 1, ..., Z + v. A8)
Потребуем, чтобы величипы m/_2, m^b ^+ь ^г+2, определяемые
формулами A7) 1 A8), удовлетворяли уравнениями A6в), A6г). Это приводит к
системе

§ 3. ОЦЕНКИ ПОГРЕШНОСТИ ИНТЕРПОЛЯЦИИ (ПРОДОЛЖЕНИЕ)
Ю9
где
Определив отсюда с3, из A8) находим
12 «г-
i"* D + 15ах) + о'Г2 D + 15а,), рг = -а», - р2 со2,
i-i , (-1 а 8+7р + 4м 8 + 7р +
В итоге
«А-«А
Учитывая, что ai/аг <С 1, @|/(о2 <С 1, легко получаем
Поэтому для всех достаточно больших v имеем ||Pvl|> c|pa)i|v, где
постоянная с отличпа от нуля. Значит, последовательность {||Pv||} будет
неограниченной, если | рсо11 > 1, что, как нетрудно видеть, эквивалентно
неравенству р2 — Зр + 1 > 0, которое имеет место при р > C + У5)/2.
Несколько видоизменив рассуждения, можно доказать^ что
последовательность {||Pvll} будет неограниченной и при р= C + У5)/2. Таким
образом, существуют некоторая непрерывная функция и последовательность
сеток прп р ^5 C + У5)/2, для которых интерполяционный процесс расходится.
Отметим интересную особенность сеток Av, использованных при
доказательстве утверждения. А именно, они становятся почти всюду
равномерными при v-*oo, так как длина участка, на котором нарушается
равномерность сетки, стремится к нулю при v->-oo. Тем не менее последовательность
сплайнов может расходиться. В то же время для сплайнов па
последовательности всюду равномерных сеток сходимость имеет место для любой
непрерывной функции.
Задача. Показать, что уравнение F) при любом п > 0 имеет в
области 1 ^ р < оо только один корень.
§ 3. Оценки погрешности интерполяции (продолжение)
В данном параграфе мы изучаем погрешность интерполяции
кубическим сплайном Six) дефекта 1 дифференцируемых
функций fix). В этом случае на той же сетке А можно построить
кубический интерполяционный сплайн дефекта 2: Sz^ix) (§ 5
гл. II). Запишем тождество
Six) - fix) = [S3>2ix) - fix)] + ISix) - S3t2ix)].
Используя для Six) и
B.5.1), получаем при х
соответственно формулы A.3) и
A)
- f\) - A - t)

НО ГЛ. III. КУБИЧЕСКИЕ СПЛАЙНЫ КЛАССА С*
Отсюда
mi-fi\. {2}
Дифференцируя A), находим
S'(*)-/'<*) = К, (ж)-/'(*I +
+ 1A - t) A - 3t) (m, - f\) -tB- Ы) (m,+1 - /i+1)}. C).
Следовательно,
4- {A — i) 11 — 3t | + f 12 — Зг I} max 1 /; — mi |. D)
i
Напомним, что оценки приближения сплайнами Sz^ix) были
установлены в § 6 гл. II.
Далее, на основании формулы A.12) можно записать
s" (х) - г (*> = A - *) (м4 - /I) +*(м<+1 - /;+1) +
+ A-*)/3 + 4-/"D E)
Выражение /| A — t) + i/i+i — Г (х) есть не что иное, как
погрешность интерполяции функции /"(#) сплайном первой
степени Sm\(f"; х) (§ 1 гл. I). Поэтому
Mi-/;!. F)
г
Из E) получаем
S" (х) - Г И = ц [{Mi+1 - /hi) - (Mi - /I)] +
+ s[{r\*)-r(x). o>
Отсюда
15- (x) - Г {x) I < 15'x (f; x) - Г <*) I + 4 mf I M* - /" !• (8>
Соотношения * B), D), F), (8) в дальнейшем используются-
при выводе оценок погрешности. По существу дело сводится к
получению оценок для величин \тг —¦ j{ |, | М\ — /* \ в
зависимости от того, к какому классу принадлежит функция fix).
Лемма 3.1. Если Six) интерполирует функцию fix) и
удовлетворяет краевым условиям типов Л, II, III, то для всех i »
«0, 1, ..., N справедливы оценки
ki-/'!<?, (9)
еде q даны в таблице 3.1.

g 3. ОЦЕНКИ ПОГРЕШНОСТИ ИНТЕРПОЛЯЦИИ (ПРОДОЛЖЕНИЕУ Ш
Доказательство. Пусть Six) удовлетворяет краевым
условиям типа I. В этом случае величины mt определяются из
системы A.6). Переходят ней к неизвестным дг=тг-- fu по-*
лучим
?i +
= 1 ЛГ —1,
(Ю)
где
Согласно следствию Д.1 1д*|^||с|| = max|ci|, и поэтому до-
статочно оценить |с*|. Это достигается путем применения
стандартной техники, изложеиной в гл. II (формула Тейлора с оста-
.точным членом в интегральном виде, теоремы о среднем для
Таблица 3.1
Класс функций
С1 [а, Ъ]
С2 [а, Ь]
С-С\ [а, Ъ]
я
Зо> (/')
-|/гсо(Л
|/Ао(Г)
Класс функций
W% [а,Ъ]
Wl [а, Ь]
Я
s*8l/IV(*)L
интегралов и непрерывных функций, неравенство Гёльдера
и т. д.). Рассмотрим два характерных примера.
Пусть f(x)eEO[a, b]. Тогда
gM+1) + 3W' (li-,,0 - >-/i-i - 2/'i - щ/',+1 =
*i [/' (Si.i+i) - /Hi] + 2(ii I/' FifHi) - /'i].
A1)
Отсюда
IcJ < За, + |л,)ю(/') = 3o)(f),
и требуемая оценка получена.
Пусть теперь / (х) е С2И^д,оо [я, Ь]. Обратим внимание на
то, что мы не требуем непрерывности f"(x) в узлах сетки Д.
Учитывая это обстоятельство, разложим в выражении для ct
величины /i-ь /г-ь /г+i, /i+i по формуле Тейлора в точке хи

112
Получим
1 III. КУБИЧЕСКИЕ СПЛАЙНЫ КЛАССА С*
/I+Tf/Г+в + вг f fa+i-")8/1^)
b Ыг{ J
i " h1-i '» 1 ?\ з
У г g /г—0 B/i^j j г— J
+ у/г+О + Y J
*'
4+1
1
/i - Ai_i/I + Hjy /Г-о
§ J
Интересно отметить, как удачно исключились односторонние
значения /i-o» /но- Сделаем в полученных интегралах
соответственно замены переменных v — #г= т/гг-, г; — хг-\ = тА,_ь В итоге
= —^ijx(l — тJ/1 v
^ф1 j г2 A -
^) dr. A2)
Применяя неравенство Гёльдера, находим
Ci I < 41| /Iv И loo |щЛ? J т A - тJ йт + Я^^х Jt2A — t)

§ 3. ОЦЕНКИ ПОГРЕШНОСТИ ИНТЕРПОЛЯЦИИ (ПРОДОЛЖЕНИЕ)
Замечая, что
окончательно получаем оценку
^IU, A3)
из которой вытекает оценка (9) в классе C2W\^ [а, Ъ]. Таким
же образом получаются оценки и для других классов.
Предлагаем читателю проделать это в качестве упражнения,
Для краевых условий типа II из A.6) следует
2?0 + Яг =^о,
hQi-i + 2дг + \цд{+1 =~си * = 1, ..., ДГ— 1, A4)
где
C,v = о 7 1 9~~ /^V — Z/iV — JN-
Все рассуждения здесь совершенно аналогичны проведенным
выше для условий типа I. Необходимо лишь проверить
справедливость уже найденных оценок для d также и для с0, с^.
Наконец, в периодическом случае (тип III) все оценки
выводятся из системы, получающейся из A.9):
hqi-\ + 2q{ + \1ф+\ = си 1 = 1,..., N, A5)
где величины с индексом N + j считаются равными
соответствующим величинам с индексом /.
Лемма 3.2. Если Six) интерполирует функцию fix) и
удовлетворяет краевым условиям .одного из типов I, II, III, то для
всех I = 0, ..., iV справедливы оценки
\Mi-f"i\<Q, A6)
где Q даны в таблице 3.2.
Доказательство. Техника доказательства здесь такая
же, как в лемме 3.1. Разница состоит лишь в том, что вместо
системы с неизвестными шг используются соответствующие
системы с неизвестными М{. Пусть, например, Six) удовлетворяет
краевым условиям типа II. Тогда из системы A.15) получаем
в 10. С. Завьялов и др.

114 ГЛ. III. КУБИЧЕСКИЕ СПЛАЙНЫ КЛАССА С»
следующую систему относительно неизвестных Qi = Mi — /":
m<?i-i + 2Qi + KiQi+1 «2,, t = 1, ..., N - 1,
где
?«¦
6 /7i+1 - fi U- /f_
Отсюда | ^i|
два примера.
|, и нужно оценить dt. Рассмотрим снова
Т а б л и ц а 3.2
Класс функций
С2 [а, Ь]
С2СЦа, Ь)
Q
За) (/»)
2^3Аа>(П
Класс функций
W», [а, 6]
4^3Л||/'"(х)||ж
i^i/ivwL
Пусть /ЫеЯа, Ь]. Тогда
2i = з [ц«г Ei-i,i) + hf" (hi+i)] - Hi/i'-i - 2/1 -
Отсюда
141 ^ За, + |Xi)o)(/v) = ЗсоС/"), A7)
и требуемая оценка получена.
Пусть теперь f (%) е C2W\tOO [a, b\. В этом случае с помощью
формулы Тейлора после несложных преобразований находим
di - %М j 1A - тK - 1 + т] /iv (X. + Thi) dx +
1
Отсюда получаем неравенство
из которого вытекает оценка A6) в классе C2W\iOO[a, Ь].
Аналогично находятся оценки A6) для граничных условий
типов I, III.

§ 3. ОЦЕНКИ ПОГРЕШНОСТИ ИНТЕРПОЛЯЦИИ (ПРОДОЛЖЕНИЕ) Ц5
Теорема 3.5. Если Six) интерполирует функцию fix) и
удовлетворяет'краевым условиям одного из типов I, II, III, то
имеют место оценки
1!5(г)Ы-/(г)ЫИоо^/?г, г = 0, 1,2,3, A9)
где /?г даются таблицей 3.3.
(В таблице обозначено E = А/А. Для граничных условий типа
II классы С1 [а, Ь|, Wl>[a, b] не рассматриваются.)
Доказательство. Техника доказательства одинакова для
всех классов функций, и мы ограничимся рассмотрением случая
\(х) е C2W\|O0 [a, b]. Из B), используя лемму 3.1 и оценку
B.6.21), получаем при х^ [хи xi+\]
<ША*1/1У(*I- B0>
Из D), используя лемму 3.1 и оценки B.6.22), B.6.23),
находим при t e [0, 1/3]
| S' (х) - Г (х) |< ij A - 20 A + 2* A - *)) & IZ1 v (*) IU,
а при fe[l/3, 1/2]
Вычисляя максимумы правых частей эдвух неравенств,
получаем при /е [О, 1/2J оценку
15' (х) - f (х) | < Jj Л» || /iv (Я) !„,
которая по соображениям симметрии имеет место и для
еЦ/2, 1].
Из формул (G), (8), леммы 3.2 и теоремы 2.1 получаем
Все требуемые оценки найдены.
Среди оценок, приведенных в таблице 3.3, две являются
^улучшаемыми. А именно, в классе C2W\fOO [а, Ь\ неулучшаемы оценки B0), B1).
Действительно, введем на [а, Ь] равномерную сетку с шагом h = (b^a)/BN)t.
8*

Класс функций
С1 [а, Ъ]
W%, [a, b]
С2[а,Ь]
Wi [a, b]
С-С\ [а, Ц
А ,оо ' ' J
9 -
8
13 -2
41 7
804
41
1728
До
Рсо (/'")
.'./"и.„
»,
4со (/')
0,8В229Й \\ j" (x) Ц^
2 -
4 /г2 II /"' С^^ I!
27
1 v
4со (у'
( ~ь
( "Ь
U
¦)
4 У
9
2V
9
*
—
-)*1Г(*I»
%со(Г)
(-
Таб л
я,
41/3 '
9 ,
и ц а 3.3
) © (/w)
|У1У(^I|ос

§ 3. ОЦЕНКИ ПОГРЕШНОСТИ ИНТЕРПОЛЯЦИИ (ПРОДОЛЖЕНИЕ? Ц7
'Определим функцию <р (х) = ^ (я4 — 2/г.г3 + ^ *1) и положим
/(*)«[ Ф (* - *2l)' еСЛП *.S l*2Z> *« + lb
i-<p(*-*2m), если *е[*2,+ 1, *2/+2],
г = о,..., iv — 1.
Легко проверить, что /(я*)=0, * = 0, ..., 2N, /'(х0) = /'(.r2V), /"(Vr—
= f'(x2N) = 0 (рис. 3.1). Кубический сплайн S(f; х), интерполирующий
функцию f(x) и удовлетворяющий краевым условиям типа II или III,
тождественно равен нулю. Это следует из единственности интерполяционного
сплайна и того, что функция, тождественно равпая пулю на [а, Ь],
является сплайном, интерполирующим /(#). Следовательно,
1 S^ (х) - /<') (х) ||с = | /<"> (х) ||с, г = 0, 1, 2, 3.
Легко вычислить
384 '
II/' (х) \\с « И Ф' ix) \\cl0M = Ф'@) = g h\
Если учесть, что 1 /IV (х) fl^ = || ф1у (х) !lLoo|0ffcj = 1, то отсюда вытекает
неулучшаемость оценок B0), B1).
Что касается других оценок, то вычислепие погрешпостп приближения
для различных конкретных функций показало, что большинство из них
довольно близки к неулучшаемым. Более
того, нам известен алгоритм,
позволяющий уточнить некоторые из них.
Однако в связи с тем, что при этом
приходится иметь дело с очень
громоздкими выкладками, а достигаемый эффект
незначителен, мы не будем
рассматривать данный вопрос.
Осталось исследовать случай
краевых условий типа IV, когда Рис. 3.1.
третья производная сплайна
непрерывна в точках х\ и xN-\. В связи с этим при интерполяции
функций fix), имеющих кусочно-непрерывные третьи
производные, будем предполагать, что последние непрерывны в
указанных точках. Сетку Д с исключенными точками х\ и xN-\
обозначаем через Д'.
Нетрудно показать, что в этом случае будут справедливы
оценки погрешности, совпадающие по порядку с
соответствующими оценками из теоремы 3.5. Чтобы обеспечить совпадение
их и по константам, приходится накладывать дополнительные
ограничения на сетку Д.
Лемма 3.3. Если Six) интерполирует функцию fix) и
удовлетворяет граничным условиям типа IV и если выполнены ог+
раничения

113
ГЛ. III. КУБИЧЕСКИЕ СПЛАЙНЫ КЛАССА С2
где 7* заданы таблицей 3.4, то для дг=т1 — /ь* = 1, ..., N—l,
имеют место оценки (9) со значениями q из таблицы 3.1.
Доказательство. Из системы A.8) следуют уравнения
= *ь г = 2, ..., N -2,
где
^T^ - A + To) fx - Y0/.2,
дт-1 , /л
V (Ajv-1
T
nN-2
При анализе этой системы мы по-прежнему находимся в
условиях следствия Д.1, и потому
|<7i|<max{ max \с{\, fill \cn-i\ К
2<i<iV2
Рассмотрим примеры. Пусть fix) ^СЧа, Ь]. Для ct, г = 2, ...
i.., iV — 2, верпа оценка (И). Утверждение леммы будет дока-
Таблица 3.4
Класс функций
СЧа, Ь)
СЦа, Ь]
С*С\. [а, Ъ]
У*
Класс функций
1,00000 W'i [at Ъ]
0,58732 ^[д, Ъ]
0,43497 |[ CHF^^le, 6]
V*
0,90478
0,53586
0,61803
вано, если такие же оценки справедливы для cXi c
тельно,
Ъ = Kf «e.i) + (И1 + 2?о) /' (Ei.t) - A + Ye) /i - Yo/1
_x.
Действи1 [ л) ]i][ ,) ]
Отсюда
I сГ ! < <*i + I*i + 2Yo) со (/') - A + 2Yo) со (/').
Аналогично, I'cw-i | ^ A + 2yjv) o)J/')^Следовательно, при уо < 1,
7jv^ 1 оценка (И) вериа и для с*и с^-г.
Пусть теперь /(a:)eCW4A')OO|a,J|. В'этом случае нужно
показать, что для Ci, cjv-i сохраняет силу оценка A3). В самом
деле, преобразуя выражения с] и cjv-i с помощью формулы Тей-

§ 3. ОЦЕНКИ ПОГРЕШНОСТИ ИНТЕРПОЛЯЦИИ (ПРОДОЛЖЕНИЕ)' Ц9
лора, получаем
*х
Объединяя интегралы с одинаковыми пределами интегрирования
и выполняя замену переменных, приходим к формуле
- ^ } A - т)г [Yo + т C + 2yoI /iv (xl + thj dx.
0
Применяя неравенство Гёльдера, находим, что
Эта оценка совпадает с оценкой A3), если Yo(l + Yo)^l или
^0 ^ ^* = (—1 + У5)/2 « 0,61803. Так как то же самое при tN^
^ -у* справедливо и для c^-i, то утверждение леммы для
рассматриваемого класса функций доказано.
Другие классы функций рассматриваются аналогичным
образом. Заметим лишь, что при этом для вычисления *у* приходится
иметь дело с довольно сложными неравенствами. Результаты
в таблице 3.4 получены с помощью ЭВМ.
Лемма 3.4. Если Six) интерполирует функцию fix) и
удовлетворяет граничным условиям типа IV и если выполнены
ограничения
h0 ^ hu Ajr-i < /г*-2,
го для Q; = Mi — /", i = 1, ..., N — 1, имеют место оценки A6)
со значениями Q us таблицы 3.2.
Доказательство. Из A.16) для неизвестных Qi% i =-
«= 1, ..., iV — 1, получаем систему
- 2, ..., N - 2t

120 ГЛ III КУБИЧЕСКИЕ СПЛАЙНЫ КЛАССА С2
где
г (^Р^ - г} -
nN-2 "Г ft.V-l ( flN-l llN-2 J »
— (i-lJV-1 — ?WV-l) /jV-2-
По условиям леммы ho^hu hN-\^hN-2. В этом случае ?ц ^
[ii, Ajv-i < Jbtjv—i п, следовательно,
Пусть /(ж) е С2[а, 61. Для f/f справедлива оценка A7).
Лемма для данного класса функций будет доказана, если
\Х | < 3 A + ^) со (Г), Г^-11 < 3 A + Ky-J со (Г).
Но это так. Действительно,
21 = зкг ixj" (Elt2) + [кг (?o,i)i - (l+^i) /;' - (*i -14) /;
Отсюда нетрудно получить
Аналогично доказывается неравенство для |d4v-i|.
Рассмотрим еще случай f(x) е С21Уд',оо [я, &1. Для d4 была
установлена оценка A8). Поэтому достаточно показать, что
|«С|<4-A + Ю^2 В/IV (*)!«., p*v-i|<|(l +^-i)fc*l/IV(a:)I,.
Используя формулу Тейлора и неравенство Гёльдера, для d*
в этом случае получаем оценку
где
¦ (К W. То) =
1 — 4f», -h 4li^ -f- p?
2>"i + 2*) = ' A < 1 + !'i.
Первое неравенство доказано. Второе доказывается аналогично.
Утверждения лемм 3.3 и 3.4, в отличие от лемм 3.1 и 3.2,
сформулированы не для всех точек сетки А, а именно: точки

§ 3. ОЦЕНКИ ПОГРЕШНОСТИ ИНТЕРПОЛЯЦИИ (ПРОДОЛЖЕНИЕ) 121
х§ и xN исключены. Поэтому здесь аналог теоремы 3.5
формулируется так:
Теорема 3.6. Пусть Six) интерполирует функцию fix) v
удовлетворяет краевым условиям типа IV. Для х^[х\, xN-\\
справедливы оценки
где Rr даются таблицей 3.3 со значением Р = М rnin h{)~1,
если выполняются ограничения: при г = 0, 1 Чо^7*> Т*5^*"» пРи
г = 2, 3 fo^l, -у*<1.
Для промежутков [#0, #il и [#*r-i, ^vl все оценки имеют тот
же порядок малости, но с увеличенными значениями констант.
Однако при несколько более жестких ограничениях на
величины 7о, yN большинство из них будут верны для всего
промежутка [а, Ь]. Не вдаваясь в подробности, в качестве справки
приведем таблицу 3.5 величин у*, обеспечивающих оценки A5) для
соответствующих г на отрезке [а, 6].
Таблица 3.5
Класс функций
СЦа, Ь]
Wlla, Ь]
СЧ«, Ь)
W^la, Ь]
C*Cl,[a, Ь]
0,76749
0,801С2
0,58732
0,53586
0,43497
0,61803
*
0,28078
0,46149
0,3\598
0,39658
0,24440
0,35321
*
—
0,34055
0,31207
0,42296
В заключение параграфа укажем некоторые результаты,
связанные с повышением класса гладкости интерполируемой
функции.
Теорема 3.7. Если fix) ^ СЧа, Ы и Six) удовлетворяет
краевым условиям типов I или III, то
I S<r) (х) - fw (х)Цс< К0,г7ь1-г\Г (х)||с + Kurh*-^{Г), B2;
г = 0,1,
где Ко.о = 2/384, К1Л = 1/96, Кол = 0,014731, К1Л = 1/24.
Если сетка А равномерная, то оценки B2) справедливы при
г =• 0, 1, 2, 3 со значениями коэффициентов:
= 1/384,
К, 2 = 1/
1/2,
¦1/2.

122 ГЛ. III. КУБИЧЕСКИЕ СПЛАЙНЫ КЛАССА С
Доказательство. Рассмотрим случай краевых условий
типа I. Применяя в A2) теорему о среднем для интегралов,
подучаем
с,
Отсюда
"in W_lt M) со (/lv). B3)
Правая часть неравенства симметрична относительно
Пусть, например, h{ > /г<_ь т. е. &f-i «= 7^? Tf ^ 1- Тогда
-mm{At_b hi) =
h _l fa ***"* ilv%—i» '*г J — A + v) l "^2
В результате из систем A0) и A5) следует, что
' '")• B4)
Теперь для получения оценок B2) достаточно повторить
рассуждения, использованные при доказательстве теоремы 3.5.
В случае равномерной сетки из B3) и систем A0) и A5)
находим
). B5)
Согласно формуле A)
- SZl (x) - /(r) (x) + k\-r [<r<rt (t) (m, - /',) ^ ФBг)@ {mi+l - f'i+1)},
B6)
где <piW = Kl -1J, у2М = <2d - 0.
Утверждение теоремы немедленно следует из неравенства
\S(r)(x)-fr)(*)\<
& (х) - fr) (х) I + tiCr [ I Ф(хг)
и соответствующих оценок для j ^3^2 (^) — /(г) (s)| (§ 6 гл. II).
Утверждение теоремы 3.7 в некоторой степени объясняет
причину широкого применения кубических сплайнов дефекта 1.

§ 4. ЛОКАЛЬНЫЕ СВОЙСТВА КУБИЧЕСКИХ СПЛАЙНОВ 123
Действительно, как мы видим, для достаточно гладких функций
оценки приближения такими сплайнами сравнимы с
соответствующими оценками для эрмитовых кубических сплайнов. При
эюм для построения кубических сплайнов дефекта 1 не
требуется задания производных в узлах сетки. Обстоятельство —
крайне важное при решении многих практических задач.
Теорема 3.8. Если Six) интерполирует функцию / (х) s
<= Wlo [a, b] на равномерной сетке и удовлетворяет краевым
условиям типа I или III, то при х^[хи xi+\]
5(г) (х) - № (х) - Ф(г) @ fc*-r/IV (х) + О (h*-'), г = 0, 1, 2, 3,
B7)
еде Ф @ = -^*2 (!-*)*.
Доказательство. Из B5), так как o(/IV) < uII/v(#MLf
имеем mi—/4=0(Л4). После этого для получения B7) доста*
точно учесть тождество B6) и теорему 2.fr.
Из теоремы 3.8 следуют результаты о повышении порядка
аппроксимации производных в некоторых точках промежутка
[л, Ь]. Действительно, так как
Ф" @ = -^ A — 6« -
= 4 A - 20,
ТО
S'{x) = fix) + О(й4), если x = Xi + h/2,
если х = xt + Л/2 ± Ш/8, B8)
если x^xt + h/2.
§ 4. Локальные свойства кубических сплайнов
Кубический сплайн Six) относится к нелокальным сплайнам
в том смысле, что его, значения в точках, не совпадающих с
у .злами сетки Д: а = х0 <.. ,<xN = 6, зависят от всей
совокупности величин fi=zf(xiI ? = 0, ..., Л7, а в случае краевых
условий типа I или II еще и от значений первых пли вторых
производных функции fix) в точках а и Ь. Тем не менее кубический
сплайн обладает достаточно четко выраженными локальными
свойствами. Они проявляются, в частности, в том, что
существенное влияние на величину Six) оказывают лишь те /<,
которые заданы в точках, близких к х. Локальные свойства
представляют большой практический иптерес.
Пусть /(s)e Wlo[a, b]. Формулу A.3) для Six) можно
разбить на две части: локальную, в которую входят /<, /i+lf и не-

124
ГЛ. III. КУБИЧЕСКИЕ СПЛАЙНЫ КЛАССА С2
локальную, содержащую величины тг, mt+i. Выясним, как
влияет информация, заданная в узлах, удаленных от
рассматриваемого интервала [#*, #ifi], на значения ти mi+\. Ограничимся
изучением случая, когда S(x) удовлетворяет краевым условиям
типа I (предполагается, что f'(a) и fib) существуют). При
других краевых условиях рассуждения аналогичны.
Обозначим матрицу системы A.6) при краевых условиях
типа I через А. А означает обратную матрицу с элементами ах).
Решение системы представляется в виде
N
Для
а по теореме Д.
3=0
справедлива оценка
N,
'С целью упрощения дальнейших рассуждений введем величины
а%з = 0, cj = 0, 7<0, ]>N. Тогда можно записать
1П[ = 2а aijcji
где для всех | а^ \ и \Cj\ будут выполнены указанные выше
неравенства.
Пусть к — целое число, 0 < к < N. Тогда получаем
V t
i+k
Каждая пз сумм в правой части меньше, чем A/2)\ Поэтому
i+h
mi —
j=i-h
A)
Будем называть точки #,-, ^ близкими или удаленными друг
от друга в зависимости от того, мало ли число U — /| или
велико. Оценка A) показывает, что если пренебрегать информацией
(коэффициентами с,) в точках, удаленных от хг на It —/'!>&,
то допускаемая при этом погрешность в определении mf будет
порядка (l/2)h~l, т. е. влияние точек с удалением от точки хг
убывает в геометрической прогрессии со знаменателем 1/2.
Если предположить, что / (х) е Wlo [a, fc], то из уравнений
AЛ5) для величин М{ можно получить такой же результат»

§ 4. ЛОКАЛЬНЫЕ СВОЙСТВА КУБИЧЕСКИХ СПЛАЙНОВ
125
Но тогда из формул для ?(Г)Ы, г = О, 1, 2, (§ 1), при х&
€= [хи xi+\] следует, что информация о функции fix) в точках,
удаленных от отрезка lxit xi+\], мало влияет на значения
сплайна *и его двух нервых производных. В этом смысле кубический
сплайн обладает локальными свойствами.
Таблица 3.6
а
1
2
3
4
5
S(-0,75)
1,000001
1,000002
1,000003
1,000004
1,000006
S(-0,55)
1,00001
1,00002
1,00004
1,00005
1,00006
S4-0.5)
—7,1-Ю-4
—1,5.10"»
—2,2-10~3
—3,1-10"»
—3,9-10
S"(-0,5)
—2,5-10~2
—5,М(Га
—7,8-10-2
—0,11
-0,14
В таблице 3.6 приведены результаты интерполяции функции
если х < О,
х, если х > О,
на отрезке [—1, 11с шагом h-= 0,1 при различных значениях параметра а.
Использовался кубический сплайн с краевыми условиями типа IV.
Как видим, довольно сильное изменение интерполируемой функции на
отрезке [0, 11 мало влияет на значения «S(r)(:r), даже если точка х не очень
удалена от этого промежутка.
Таблица 3.7
1
5
?'(-0,5)
-1,4.10
—6,9-КГ3
S'(Q)
1,9-10
9,5-Ю
77?О
10
100
S'<-0,5)
—1,4-КГ2
—0,14
S'@)
i,9-10
1,9-10"!
В таблице 3.7 приведены данные, характеризующие поведение сплайна»
интерполирующего функцию f(x) =0, хе [—1, 1], на равномерной сетке
с шагом h-= 0,1 и краевыми условиями ?'(—1) = mOi *S'A) = 0, в
зависимости от значений величины т0.
Хорошо видно, что даже задание совершенно вычурных краевых
условий на левом конце отрезка мало влияет на S'(x) в удаленных от него
точках.
Естественно ожидать, что качество приближения fix) сплатг-
пом Six), например, на отрезке [a", fe"]cz[a, b] будет
определяться в основном дифференциальными свойствами функции fix)
в некоторой его окрестности. Покажем, что это действительно
так. Пусть, например, fix) е Wl> [а, Ь] и fix) е Wi [a', 6'], а <
< a7 <a" <b" <b' <b, причем точки а" и Ъ" достаточно
удалены (в указанном выше смысле) от точек а' и Ь'. Точно так

126 ГЛ. III. КУБИЧЕСКИЕ СПЛАЙНЫ КЛАССА С3
же, как мы вывели оценку A), можно лолучить аналогичные
оценки для величин mi — /$ и Mi — fi. Тем самым оценки для
них будут определяться через свойства функции fix) на отрезке
[а\ &']. Следовательно, будут иметь место оценки
1 S(r) (х) - fr) DlU««,b''] < Krh 4"r I /IY (x) U«',ъ'ъ
где г = 0,1,2, h=a max hx и постоянные Кт близки н
соответствующим постоянным из таблицы 3.3. Степень близости
определяется тем, насколько удалены точки а\ Ь' от а"', Ъ"*
Рассмотрим теперь поведение кубических сплайнов на
специальных сетках. Пусть сетка А такова, что для некоторого к
выполняются условия Aft = 71^+1» /^ = 42/^-1, где ^1 и Т2
достаточно малы. Предположим, что кубический сплайн Six)
интерполирует функцию / (х) е-W%> [a, b] и удовлетворяет краевым
условиям типа I.
Дл^ решения системы A.15) легко получаем
\Mt\*Z3Wf"(x)\L\-i = 0, 1, ..., N. B)
Далее запишем эту систему в виде
^!= d0,
i+l = dt, f = lf ..., ft-lf C)
Г«+1=*, г-Л + 2, ..., iV-1, D)
Л/jv-i + 2M* = d*,
где
v-i \ лл-1
), dk+1= dk+1 + \ih+1 (Mh+2—Mk).
Представим
(f Ч^1) + f h±zIjL
Заменим в правой части dh = \ikMh^\ + 2Mk + %hMh^x и

§ 5. ВЫБОР ГРАНИЧНЫХ УСЛОВИЙ И УЗЛОВ ИНТЕРПОЛЯЦИИ 127
Тогда
т—
ЛЛ-1
где
Ч = 6V2 J A - т) Г (xh + thh) dx - у2 BMh + Мк+1).
О
Применяя неравенство Гёльдера и оценку B), находим
Отсюда вытекает, что при малом ^2 величины Л/о, ¦ «¦, Mkr
вычисленные из системы A.15), мало отличаются от
соответствующих величин, вычисленных из системы C), если в
выражении dk пренебречь величиной eft. Но измененная таким образом
система C) определяет коэффициенты сплайна Six), который
интерполирует fix) _на отрезке [а, хк] и удовлетворяет при этом*
краевым условиям Sf (xQ) = /о, S' {xk) *= f'h. Точно так же из D)
получаем, что при малом у\ коэффициенты Mh+\, ,.., MN близки
к коэффициентам сплайна Six), интерполирующего fix) на [xh+\r
Ъ] и удовлетворяющего условиям S' ixh+x) =¦ fh+u S' ixN) « /^.
В пределе при -yi = *уг = 0 поведение сплайна Six) на отрезке
[а, хк] не зависит от информации, заданпой на [xh, Ь], и
наоборот.
Из проделанных рассуждений, в частности, следует, что
эрмитов кубический сплайн Szjix) можно рассматривать как
предельный случай кубического сплайна дефекта 1, Sz,\ix). В
самом деле, пусть сетка Д: а~хо<. ..<x2i+\ — Ь такова, что
U2*+i = Ti. i ^2i+2, h>2i+\ e Tf2, i ^2<, i »= 0, ..., i, и 53> i(/; x)
интерполирует fix) на сетке Д и удовлетворяет краевым условиям типа I,
Если ?3,2(/; #) интерполирует /U) на сетке Д: а = хо<х2<. ...
<< Ь, ТО
lim 58д(/; «) = 58|2(/; *).
§ 5. О выборе граничных условий и узлов
интерполяции. Интерполяция с заданной точностью
1. При практическом использовании кубических сплайнов для
целей интерполяции неизбежно приходится иметь дело с
проблемой выбора краевых условий. Особую важность этот вопрос
приобретает в том случае, когда требуется обеспечить хорошее
качество приближения вблизи концов промежутка интерполяции

128 ГЛ. III. КУБИЧЕСКИЕ СПЛАЙНЫ КЛАССА С2
[а, Ъ] (вдали от пих, как это было показано в предыдущем
параграфе, влияние граничных условий незначительно). Выбор
краевых условий осуществляется в зависимости от того, какими
данными мы располагаем об интерполируемой функции fix).
В этой связи дадим некоторые рекомендации.
Если fix) периодическая, то следует использовать
периодические краевые условия (тип III).
Когда известны значения fix) или frrix) в точках а и Ь, то
естественно воспользоваться краевыми условиями типа I или II.
При этом, если существует возможность выбора между ними,
то предпочтительнее условия типа I.
Наибольшие трудности возникают, когда заданы только
узловые значения /*. Вначале рассмотрим некоторые из известных
рекомендаций. Часто предлагается использовать естественные
(смысл этого термина будет ясен из § 1 гл. IV) краевые
условия: S"ia) =S"ib) = 0. Однако такое решение весьма неудачно.
Дело в том, что тогда, как легко установить из формул A.10),
A.11), для точек х, близких к концам отрезка [a, 6J, в лучшем
случае можно получить \S{r)ix) — fr)ix)\ = Oih2~r), r = 0, 1.
To есть здесь точность приближения кубическим сплайном
снижается до точности приближения сплайном первой степени.
О приближении fix) говорить вообще ие приходится.
Другой подход состоит в том, что используются краевые
условия типа I или II, по необходимые значения производных
заменяются подходящими разностными аппроксимациями.
Недостаток этого способа состоит в том, что приходится использовать
односторонние аппроксимации, которые, как известно, имеют
невысокую точность.
На наш взгляд, в большинстве случаев кардипальным
решением вопроса является применение краевых условий типа IV.
Этот вывод подтверждает и практический опыт расчетов.
Иногда можно рекомендовать краевые, условия общего вида
i + MN = dNy
где свободные параметры Kr jn, d0, dN выбираются из каких-либо
соображений. Аналогичные краевые условия можно записать и
в терминах величин т{.
Многие специалисты склонны видеть в необходимости
задания краевых условий один из недостатков кубических сплайнов.
На самом же деле более правильной следует считать
противоположную точку зрения. Действительно, по существу через
краевые условия мы включаем- в конструкцию сплайна свободные
параметры, выбором которых можно в известной степени
управлять поведением сплайна.
Перейдем теперь к другому вопросу техники
интерполирования — выбору узлов интерполяции. Прежде всего следует об-

§ 5. ВЫБОР ГРАНИЧНЫХ УСЛОВИЙ И УЗЛОВ ИНТЕРПОЛЯЦИИ 129
ратить внимание на точки разрыва производных функций fix).
В § 3 мы уже установили, что для получения наибольших
порядков приближения функций с кусочно-непрерывными
третьими производными точки разрыва fix) должны быть включены
в число узлов сетки.
Рассмотрим случай, когда разрывна /"Ы. Такие фупкции
часто встречаются в инженерно-технических задачах, где
наличие точек разрыва второй производной обычно связано с
гладким сопряжением (непрерывная касательная) кривых разного
типа. Если при интерполяции
таких объектов сплайном не
принять специальных мер, то для
сплайна будет характерным
появление осцилляции (рис. 3.2)/
Пусть при выборе сетки точка
%, в которой разрывна fix),
попадает в промежуток [xk, xh+\].
Тогда следует позаботиться о том,
чтобы выполнялось условие hk — Рис- 3-2-
= *у min{/^ft_i, hh+i}, где *f мало
(на практике обычно достаточно положить 7 = 0,01). Из
результатов § 4 следует, что при таком выборе узлов наличие
разрыва в точке \ практически не влияет на поведение сплайна
вне промежутка [#А, xk+{]. Отметим, что для вычисления S" ix)
при x^[xh, xk+\] вместо A.12) нужно использовать формулы
В ситуации, изображенной на рис. 3.2, целесообразно построить
промежуток lxk, xk+\] так, чтобы ?A+i=§.
Рассмотрим, наконец, случай, когда в точке х = ц терпит
разрыв fix). При выборе узлов, во-первых, точку г\ включим
в число узлов. Пусть 4\=xk. Во-вторых, узлы хь-и xk+\ выберем так,
чтобы hk-\ = fi^fe-2, hh = 42hh+u где Yh 72 — малые числа.
В-третьих, в системе уравнений для определения величин М{ положим
dh = 0. Смысл условия dk = 0 состоит в том, чтобы обеспечить
выполнение неравенств D.2). Проделав примерно такие же
рассуждения, как и в § 4, нетрудно убедиться в том, что эти меры
действительно устраняют влияние разрыва. Наличие разрыва в
точке xk следует учесть в формулах для S'(x) и S"[x) на
отрезке [xh-\j xh+\]. А именно,
5'Ы =¦ (Д - Д-1)/Л*-1 - fck-i(l - 2t)Mh-i/2f х е [xh.u xh);
S'(x) = (fh4l - fk)/hh - hk(l - 2t)Mh+l/2, x s (xh, xh+l];
S"ix) = Mh-U x^[xk-u xh)\ S"(x)=Mk+u xez(xk
В качестве численного примера рассмотрим интерполяцию функции
(х) из § 4 при а=1 (граничные условия типа I). Если обозначить
10 С Завьялов и др.

130 ГЛ. III. КУБИЧЕСКИЕ СПЛАЙНЫ КЛАССА С2
Rr = max | &r^ (x) — /(r) (x) | (Aj — сетка с шагом 2/201), то для интерпо-
ляции на равномерной сетке с шагом 0,1 будем иметь /?0= 0,009, R{ = 0,5,
R2 в» 16. При добавлении узлов в точках — 0,001 и 0,001 получаем
Ло = 0,004, R\ = 0,2, /?2 = 8. Если же, кроме того, положить d^ = 0, то Ro =
=5-Ю-6, /?г= 3-Ю, Л2= Ю-2.
2. Рассмотрим задачу об интерполяции с заданной точностью.
Если ограничиться равномерными сетками, то она решается
довольно просто на основе оценок, полученных в § 3. Методика
здесь такая же, как и для локальных сплайнов. Конечно,
подобное решение не является оптимальным с точки зрения
количества узлов интерполяции. С целью сокращения числа узлов
необходимо прибегнуть к неравномерным сеткам.
Мы опишем один из способов построения неравномерной
сетки в случае, когда интерполируемая функция fix) достаточно
гладкая. Пусть, например, fix)^C4[a, b]. Теорема 3.7 лутвеРж*
дает, что на равномерной сетке кубические сплайны дают
практически ту же точность приближения, что и эрмитовы
кубические сплайны. Этот вывод сохраняет силу и в случае
неравномерной сетки, если только выполнены условия
A^u^ + Ofa?-,). A)
Действительно, при этом из C.23) следует, что с{ = о(кг) и
поэтому rtii — /i = o(/i3). Но тогда согласно C.2)
S(x) - fix) = S3,2ix) - fix) + оШ).
Следовательно, для построения неравномерной сетки можно
использовать алгоритмы, разработанные для эрмитовых
локальных сплайнов (§ 7 гл II), если в процессе их реализации
контролировать выполнение условия A). Если на очередном шаге
оно нарушается из-за того, что hi значительно превышает hi-[>
то следует просто уменьшить hi. Если же A) не выполняется
по причине малости ht, то нужно еще уменьшить его, положив
hi = 4hi-\, где y достаточно мало. Из результатов § 4 ^следует,
что в таком случае поведение сплайна на промежутке [xi+\, b\
практически не зависит от его поведения на [а, хг+\]. Таким
образом, процесс построения сетки на [a, xi+\] закончен. Для
отрезка [#i+i, b] сетка строится независимым образом.
Численные эксперименты по интерполяции кубическими сплайнами с
краевыми условиями типа I, выполненные для тех же функций и сеток
(в том числе неравномерных), что и в § 7 гл. II, дают результаты,
практически совпадающие с соответствующими результатами для эрмитовых
кубических сплайнов.

§ 6 КУБИЧЕСКИЕ СПЛАЙНЫ ДВУХ ПЕРЕМЕННЫХ 131
§ 6. Кубические сплайны двух переменных.
Существование и единственность. Алгоритм
Пусть в области Q = [а, Ь] X [с, d] введена сетка A = A*XAy,,
где Ах: а = х0 < #i <.. .< я* = 6, Ау: с = у0 < у\ <.. .< Ум = d.
На этой сетке рассматриваются кубические сплайны дефекта 1
от двух переменных (класса С22Ш]). В ячейке &« = [#*, #<+i] X
X [z/j, г/j+il они имеют вид
S (*, у) = 2 2 <4 (* - *0" (I/ - #/• A)
а=0 3=о
Множество таких сплайнов б'з.з.мСА) мы условились
рассматривать (гл. I) как тензорное произведение пространств
одномерных сплайнов ?3,i(Ax) и Яз.ДАу) размерностей N + 3 и М + 3
соответственно, и размерность пространства *S3 3ii(A) равна
Ш + ЗНМ + 3).
Пусть в узлах сетки Д заданы значения функции /#.
Интерполяционным кубическим сплайном двух переменных называется
сплайн, принимающий на сетке Л значения
Sizu ys) =f /«, i = 0, ..., N; j = 0, ..., M. B)
Это дает (TV + 1)(Л/ + 1) условий. Недостающие 2(N + М + 4)
ограничений задаются в виде краевых условий.
Как и в случае одной переменной, будем рассматривать
условия четырех типов.
Тип I. Граничные условия этого типа возникают, когда
сплайны одной переменной из пространств 5зд(Ах) и 5з,1(Ду)
удовлетворяют граничным условиям типа I (§ 1). Выясним
характер краевых условий, которые необходимо наложить в этом
случае на сплайн Six, у).
Введем фундаментальные сплайны Ft(#), i = 0, I, ..., N9
и Fh{x), k = 0, N, удовлетворяющие условиям
Они образуют базис в пространстве сплайнов 53,i(Ax).
Аналогичным образом ^определяются фундаментальные сплайны Gj(y),
7 = 0, ..., М, и d(у), I = 0, М, образующие базис в
пространстве S3,i(A»).
Так как 5з,з,и(А) есть тензорное произведение пространств
?з,1(А*) и 53,1(АУ), то базис в нем образуют функции
i = 0, ..., N; ] = 0, ..., М\ k = 0,N; I - 0, М.

132 ГЛ. III. КУБИЧЕСКИЕ СПЛАЙНЫ КЛАССА &
Любой сплайн Six, у) из пространства 5з,з,м(Д) представим в
виде
S (*, у) =
N М М ___ М ' __
= 22 с«Л (ж) G; (у) + 2 cJ'X (*) G; (J/) + 2 <Ж,У* (х) Gj (у) -f
i=0J=0 j=0 . ^=0
+ 2 c°i:10Fi(x)G0(y) + 2 cZhFiWGubi) +
i=0 i=0
+ cl:lF0(x)G0 (y) + difFo (x)Gu (y) + ctf0FN (x) Go(y) +
+ cWMFN(x)GM(y). C)
Из свойств базисных функций непосредственно-вытекают
соотношения
су = S (хи z/i), c\f = D^S (xh, y}),
cb1 = D^S (xu y,), c\'} = D"S (xh, Vl),
1^0, ...,N; j = 0,...,M; /e = 0, TV; 1 = 0, M.
Теперь становится ясно, что в дополнение к условиям B) для
однозначного определения интерполяционного сплайна
достаточно потребовать, чтобы
P1'°5(xi,i/j) = /«>0), i = 0, N; j = 0 Л/;
^(«tJ^/U111, i = 0,...,N; j = O,M;
D^SixuyD^ffr», i = 0,N; j = 0; M.
Это и есть граничные условия типа I.
Тип II. Краевые условия в этом случае выводятся таким
же образом, как и граничные условия типа I:
D2'°S(xuyj) = f%0\ J = 0,7V; 7 = 0, ...,М;
D°-2S (хи у-) = /(>2), i = 0 N; ; = 0,М;
D2'2S(xuy}) = f-l'2), i=0,N; j = O,M.
Тип III. Пусть 5з,з,1л(А) есть тензорное произведение
пространств ?3,i(A*) и 5з,1(Ау) одномерных сплайнов, периодических
соответственно по х или г/. Базис в пространстве ^.iCA*)
состоит из фундаментальных сплайнов Рг{х), удовлетворяющих
условиям
, г-0, 1,2; i,p = l,2, ...,
Таким же образом строится базис в пространстве ?3,1 (Ду).

§ 6. КУБИЧЕСКИЕ СПЛАЙНЫ ДВУХ ПЕРЕМЕННЫХ 133
Для интерполяционного сплайна Six, у) ^Здз.цСД)
получаем следующее представление:
5(^) = 2S fnFi{x)Gi{y). D)
Из этой формулы вытекает, что все производные сплайна
Dr>*S(x, */), г, s = 0, 1, 2, будут, периодическими функциями с
периодом Ъ — а по переменной х и периодом d — с по у.
Тип IV. Предположим, что пространства ?з,1(Ах) и S3,i(Av)
состоят из одномерных сплайпов, удовлетворяющих граничным
условиям типа IV. Фундаментальные сплайны Р{(х)
определяются условиями
f! (Xn_x _ 0) = F'l fev-i + 0), _ *, p = 0, 1, ..., N.
Аналогично определяя Gj(y), получаем
?(*,*/) = 22 /i/iWCid/). E)
i=0j=0
Следовательно, сплайн определяется только условиями B).
Из формулы E) и свойств введенных фундаментальных
сплайпов вытекает, что на линиях х = х{ и x = xN-\ непрерывны все
производные сплайна до порядка D3>2S(x, у), а на линиях у = у\
и У = г/м-i — до порядка D2>3S(x, у). Кроме того, в областях
ixh, xh+2i X [yh J/и-г], А = 0, iV —2; Z = 0, Л/ — 2, прилегающих к
вершинам прямоугольника Q, непрерывны все производные,
включая D3'zS(x, у).
По существу, в процессе анализа краевых,условий доказана
Теорема" 3.9. Интерполяционный кубический сплайн двух
переменных, удовлетворяющий условиям B) и одному из типов
краевых условий I — IV, существует и единствен.
Действительно, существование следует из формул C)—E),
а едиястэенность вытекает из однозначности разложения
элемента конечномерного пространства по базисным функциям.
Кроме перечисленных, возможны и смешанные краевые
условия, т. е. условия разных типов по разным переменным. При
этом, если по одной из них, например по х, заданы условия
типа I, а по другой — у типа II, то в вершинах прямоугольника,
точках (хи У)), i = 0, N; / = 0, А/, должны задаваться смешанные
производные D{l>2)S(xu у,).
Явные формулы C) —E) для интерполяционного сплайна
практически непригодны для использования по причинам,
изложенным в гл. I. Рассмотрим алгоритмы, основанные на кусочно-
мпогочлешюм представлении сплайна.

134
ГЛ. III. КУБИЧЕСКИЕ СПЛАЙНЫ КЛАССА С2
Исходную информацию удобно располагать в виде таблицы
3.8. Во внутренней части таблицы размещаются значения
функции. Окаймляющие строки и столбцы заполняются только в
случае краевых условий типов I и II. Если краевые условия смр-
шанные, например, по переменной х типа I или И, а по у типа
III или IV, то свободными остаются граничные строки.
Таблица 3.8
fir, s)
J0,M
/r,0)
/O,Af
^oVt
^or,'o
/or,o
A),M
/ t
^0,0
^o.o'
^1,M • • •
':•" :::
/1,1
/1,0
^1,6 # * *
^iV.A/
• *
Ay, m
is i
Av.o
Ay,'o
'iV.AI
• Алгоритм решения интерполяционной задачи строится с
учетом того, что при фиксированном значении одной из переменных,
например г/, сплайн и его частные производные по у являются
кубическими сплайнами от переменной х. Каждые строка и
столбец таблицы 3.8 содержат информацию, достаточную для
построения кубического сплайна вдоль одной из линий, х = Хг или
У - Vi*
Первый шаг алгоритма. Строятся кубические
сплайны от переменной х, Six, у,), / = 0, ..., Л/, по строкам таблицы
3.8, включая граничные, если они имеются, с краевыми
условиями из граничных столбцов. Дело сводится к решению систем
уравнений (§ 1), число которых зависит от вида краевых условий
и равно М + 3 (типы I, И), М+1 (тип IV) и М (тип III).
В результате находятся значения т\)'0) = D*'°S (хг, у-), (^,г/^)е
еД. Эти значения располагаем спова в виде таблицы,
аналогичной таблице 3.8, без граничных столбцов. В граничных
строках при условиях типов I и II помещаются значения
m$s) - D^'S (xu ft), s = 1 или 2; i = 0, ..., N; j = 0, M.
Второй шаг. Строятся кубические сплайны по переменной
у, S(xi, i/), ? = 0, ..., N, по столбцам второй таблицы. Это будут,
очевидно, частные производные по х, Dl'°S(xu у), искомого
сплайна на линиях х = хи На этом шаге решается N+1 одномерная
задача в непериодическом случае и N задач в периодическом.
Значения производных сплайнов Z>°'15r(^, у) в узлах сетки Д суть

§ 6. КУБИЧЕСКИЕ СПЛАЙНЫ ДВУХ ПЕРЕМЕННЫХ
135
смешанные производные искомого сплайна на сетке, т. е.
щ}Л) = DltlS (хи yj).
Третий шаг. По данным исходной таблицы 3.8 строятся
сплайны S(xu у), i = 0, ..., N, в результате чего находятся
значения иг?/1 = DOtlS (хи у}). Число решаемых задач — такое же,
как на втором шаге.
В итоге получены значения величин /и, яц} , т^'1 , тгУ
в узлах сетки Л. Как мы уже знаем (§ 9 гл. II), они полностью
определяют некоторый кубический сплайн двух переменных.
Этот сплайн по построению удовлетворяет интерполяционым
условиям B) и заданным краевым условиям. Его вычисление
проводится по формуле B.9.3), в которой fiY заменяются на wj's.
Построение двумерного сплайна свелось к решению 2N + M +
+ 5 (не менее 2N + М) одномерных задач. Можно пользоваться
и другим вариантом описанного алгоритма, поменяв ролями
переменные хну. В этом случае придется решить N + 2М + 5
(не менее N + 2M) одномерных задач.
Последние будем решать методом прогонки. В этом случае
при решении задач иптерполяции по одной из переменных
коэффициенты левых частей уравнений в системах будут
одинаковыми, что избавляет нас от повторения некоторой части
вычислений. Общее число арифметических операций при
непериодических краевых условиях будет 33NM (с точностью до линейных
членов относительно N и М) и 397VM в периодическом случае.
Если описанный алгоритм применить к нахождению величин
гз 6 13 > v g гз » гз 30 %з >
пропорциональных вторым частным и четвертым смешанным
производным сплайна, то потребуется выполнить 27NM и 3SNM
арифметических операций соответственно в непериодическом и
периодическом случае. Вычисление сплайна производится по
формуле, аналогичной B.9.3):
где
= [l>i (t),
(t), h2^ (I)],
F =
1O@,2).
= 1--*, г|JШ = *,
>-1)B-*),
!-1).

136 ГЛ. III. КУБИЧЕСКИЕ СПЛАЙНЫ КЛАССА С2
Замечание. Можно рассматривать различные «полуэрмтт-
товы» сплайны. Например, возможен случай, когда в узлах
сетки известны не только /tJ, но и производные /ij'0), fif1}. Чтобы
воспользоваться формулой B.9.3), необходимо определить лишь
каким-то образом значения /J'1 . Последние можно получить,
например, интерполируя либо значепия /ij'0) вдоль линий у = yh
ЛИбо fij'1 ВДОЛЬ ЛИНИЙ X = Хи
§ 7. Оценки погрешности интерполяции
кубическими сплайнами двух переменных
Методика получения оценок погрешности интерполяции
локальными кубическими сплайнами двух переменных через
оценки погрешности для сплайнов одной переменной была подробно
изложена в гл. II (§ 9). Без существенных изменений подобная
техника может быть использована и в данном случае.
Она основывается на понятии частичных сплайнов Slfix, у);
х] и S[f(x, у); у], для которых, как и для эрмитовых сплайнов,
верны тождества
D°>sSlfix, у); х\ =SW°'sf(x, у); х],
D^Slfix, у); y]=S[D'>Qf(x, у); yh A>
Sif; x, y)=S{Slf(x, у); d; у). B)
Введем далее функции
Тх(х, y) = S[f(x, у); у]-fix, у),
Т2(х, y) = S[f(x, у); x]-f(x, у).
Используя тождество B), получаем
S(f; х, у)-fix, y) = SiS[fix, у); х\\ у)-fix, у) =
= S{T2ix, y)+fix, у); у)-fix, ?/) =
= SlT2ix, у); y)+S[fix,y); у) -fix, у) =S[T2ix,y); у] + Т^х,у).
Отсюда
S(f;z,y)-f{x,y)-
- {SlT2(x, ~у)\ у] - T2ix, у)) + T{ix, у) + T2ix, у). C)
Аналогично,
Sif; х, у) —fix, у) =
-{SlTiix, у); x]-Ti(x, y)) + Txix, y) + T2ix, у). D)
Правые части равенств C), D) содержат только погрешности
интерполяции сплайнами одной переменной, оценки которых

§ 7. ОЦЕНКИ ПОГРЕШНОСТИ ИНТЕРПОЛЯЦИИ 137
установлены в § 2, 3. Обозначим
h{ = xi+1 — хи Ъ = max hu Ц = у}+1 — у}, 1 — max Ц.
г О
Теорема 3.10. Если /{х, у) е Wi> \п] и
интерполяционный кубический сплайн Six, у) удовлетворяет краевым условиям
одного из типов I, II, III, то
{S (х, у) - f (х,
4?№ф/) Цоо, E)
Лй = 5/384, 411 = 4/27,
А(о]1 = 1/24, Ли = 3/8, Л$ = 81/864, 4!i = 13/48,
А{оюо = 0,073349, Л'Д - 0,74354, 4?d = 4>д = 0,23353,
Ли = 4?о = 13/6.
Доказательство. Из C) получаем
|| Dr'° {S (х, у) - f (х, у)} |, < | Dr-'T, (х, у) I. +
+1|/?Г'8Г2 (*, у)U +1^r>S 15 \Тг(х, у); у) - Тг (х, у))\\х. F)
Учитывая A), оценим каждое слагаемое в правой части:
II Dr''Tx (х, у) U = | D°'s [S [Dr'°f (х, у); у] - Dr'°f (x, у)} |Ц.
Так как Dr'°f (х, у) е WtTr [Щ, то согласно теореме 3.5 находим
I D'-'T, (х, у) I < 4<»!4-г- II D^-r1 (x, у) I.
Аналогичным образом выводится оценка
r''T, (х, у) |Ц
Далее, снова используя результаты теоремы 3.5 для классов Wl,,
С2, при г, s < 1 имеем
'0Гг (х, j/); tf] - D^T, (x,
= Л,1а—|/>Г-° {5 [D0'2/(x, у); х] - D°'*f(x,
где Ло = 13/48, Л, = 0,80229.

138 ГЛ. III. КУБИЧЕСКИЕ СПЛАЙНЫ КЛАССА С2
При г = 0, s = 2
\D0'i{S[Ti(x1y);y]-Tt(x,y)}lo<
< 4@ (D°'*T2(х, у)) <8|| О0'2Г2(*, г/) |» =
= 81S [D°'2f (х, у);х}- Dn'2f (х, у) \\х < f /? | ZJ'2/ (ж, у) |Ц.
Следовательно, при г < 1, г + s = 2
1 Dr's {S [Г, (*,«/); у] - Г2 (х, у)} |» < 4'fli-ih'-r || Z??'2/ (*, у) \\х.
Подставив полученные оценки в F), убеждаемся в
справедливости утверждения теоремы для r^l, r + s = 2. При г = 2, s = 0
оценка E) выводится из тождества D).
Теорема 3.11. Если / (х, у) е С2'2^!'^ [Q] и
интерполяционный сплайн Six, у) удовлетворяет краевым условиям одного
из типов I, II, III, то
(х, у) I + К(Г1*-° IZ/-4/ (х, у) I +
.«л4-1!4-!^4/^ уI, г, 8 = о, 1, 2, з,
Я<« = 42) = 5/384, Мх) = 42) = 1/24, ЛС^1» = ЯB2) = 3/8,
^К^1' = A + Р,)/2, Я^г) = A + Р2)/2,
Рх = й/min Аи C2 = Z/min lj.
г 3
Теорема доказывается точно так же, как и теорема 2.8.
Чтобы получить оценки E), G) в случае, если сплайн
удовлетворяет граничным условиям типа IV, необходимо паложить
на сетки Д*, Ау такие же ограничения, как в теореме 3.6.
Естественно, полученные результаты сохраняют силу, если
сплайн удовлетворяет смешанным краевым условиям, например,
типа I по х и типа III по у и т. д.
Техника доказательств без существенных изменений может
быть использована для получения оценок и в других классах
функций.
Нетрудно сформулировать двумерный аналог теоремы 3.7,
а также получить результаты о повышении порядка
аппроксимации производных. Предоставим это сделать читателю.
Задача. В условиях теоремы 3.10 получить оценки для \\Dr>* (S — /)[!«>
при г + s = 3.

§ 8. КУБИЧЕСКИЕ В-СПЛАЙНЫ J39
§ 8. Кубические В-сплайны
В предыдущих параграфах мы рассмотрели задачу
интерполяции кубическими сплайнами при кусочно-многочленном их
представлении. Этот путь и во многих других случаях является
удобным средством как при решении теоретических вопросов,
так и в вычислительном отношении. Тем не менее в целом ряде
приложений более эффективным оказывается представление
кубических сплайнов через /?-сплайны. Например, использование
такого представления при решении задачи интерполяции требует
минимального объема памяти ЭВМ. В гл. I Я-сплайны были
определены аксиоматическим образом. Здесь мы изложим другой
способ их построения, применимый не только для
полиномиальных сплайнов, но и различных их обобщений.
Дополним сетку Д: а = хо< х\< ... <xN = b узлами
х-з < х-2 <х-\ < а, Ъ < xN+\ < Xn+2 <#лг+з. Эти узлы вполне
произвольны, . только в периодическом случае должно выполняться
ограничение hN+i= hu
Построим кубический Б-сплайн, отличный от нуля па
интервале (xi-2, Xi+2). В приложениях 5-сплайиы нечетных степеней
удобно нумеровать по среднему узлу их интервалов-носителей.
Искомый 5-сплайн будем обозначать через В Ах) вместо Вг3~2(х)
(гл. I). Положим еще уР = В{(хр). Мр —В\ (хр).
Как и для всякого кубического сплайна, для Вг{х) имеют
место уравнения A.14):
i
р = i — 1, i, i+ 1.
Так как ВАх)=0 при хФ (хг-2, Xi+t)% то В[г) (^_2) =
= В\г)(хг+2) = 0, г = 0, 1, 2. Эти условия вследствие A.10) —A.12)
можно представить так:
Z/i__2 = Уг+2 = 0, Mi-2 = Mi+2 = 0,
Л?Л/ Z/
Найденные параметры исключим из уравнений A).
Последние приводятся к виду
(hL_2 -|- A^O Mi-i + (hi-i + hi) Mi + (h + hi+1) Mi+i = 0, C)
K\Mi + (A* + Ai+l) BAt
Получилась система трех уравнений для определения четырех
параметров: z/t-, Мг-\, Ми Mi+\. Одним из параметров можно рас-

140
ГЛ. III. КУБИЧЕСКИЕ СПЛАЙНЫ КЛАССА С2
порядиться по своему усмотренщо. Положим
*ji (*|2 + *ii) УК + fei+i) + hi {hi + Чц
hi
Тогда из уравнений C) находим
E)
Формулы B), D), E) полиостью определяют сплайн В{(х) на
промежутке [xi~21 ^i+г]. В таблице 3.9 приведены его значения
в узлах хР, р = i — 2, ..., Н-2.
Таблица 3.9
, (х)
В. (х)
4-2
4-2
X (*i+i - Хг-2)
1 —
X
г-2
4+2 '
сЛ X
0
*(
(-
ЗА.
- ,з
X
3
*-2
:i-2) X
v
г
i+1 ^г—2
¦ г-'i) x V
X
X I -
4-
(
1
i-
6
xi
6
—
f-1
• Л'
г)
+ :
1
1-2
i)
X
t —
г-l
.
1
—
X
*i
X
-2
^.
-2)
\
-1/
НетруДно показать, что выбор параметра уг по формуле D)
соответствует тому, что построенный 5-сплайн оказывается
нормализованным. Действительно, так как два кубических 5-сплай-
на с одним и тем же носителем (xi-2, #1+2) могут отличаться
лишь постоянным множителем, то для и« совпадения достаточ-

§ 9. О ПРИМЕНЕНИИ В-СПЛАЙНОВ ДЛЯ ИНТЕРПОЛЯЦИИ 141
но, чтобы они принимали равные значения в одной точке
интервала (#г-2> #<+2). Сравнение табличных значений со
значениями нормализованного Б-сплайна. из § 3 гл. I показывает,
что это действительно так.
§ 9. О применении В-сплайнов для решения
задачи интерполяции
Интерполяционный кубический сплайн Six) можно паходить,
используя его представление через В-сплайны:
S(x) = 2 ЪгВ<(х). A)
г=—1
Рассмотрим конкретный пример сплайна, удовлетворяющего
условиям A.1)^и краевым условиям типа I. ,Для определения
коэффициентов Ъ{ -получаем систему уравнений
Ъ-гВ'-г (х0) + ЬОВ'О (х0) + ЬгВ[ (х0) = f'o, B)
b^Bi-г (xi) + ЬгВ{ (xi) + bi+1Bi+1 (хг) = fu I = 0, ..., N, C)
iiv-iBiv-i (xn) + bNB'N (xN) + feiv+i^iv+i (%n) = In- D).
Элементы матрицы системы вычисляются с помощью таблицы
3.9. То, что в каждой строке матрицы только три элемента
отличны от нуля, объясняется фииитностьдо 5-сплайнов.
Исключим из полученной системы неизвестные b-i и bN+\. Получим
К [Во {х0) - к0В-х (*„)] + Ьг [В, (х0) - к^-г (х0)] = /0 - к'пВ-х (а0),
ii-l^i-l (Xi) + ЬгВг (Xt) + bi+1Bi+1 (Х<) = fU * = 1, - • •, N - 1, E)
fyv-i [BN-i (xn) — fcjv-i#iv+i (xN)\ + bN [BN (xn) — кхВп+г (xN)] =
= In — 1znBn+i
где
BN + 1 (XN) BN + l (XN)
После нахождения из системы E) величин bh i = 0, ..., TV;
Ъ-\ и &jv+i вычисляются из равенств B), D). Разрешимость
системы B) —D) и подобных ей систем при других граничных
условиях следует из единственности интерполяционного сплайна
(теорема 3.1).
Когда коэффициенты Ъг в A) найдены, для вычислепий
значений сплайна и его производных можно воспользоваться алго-

142 ГЛ. III. КУБИЧЕСКИЕ СПЛАЙНЫ КЛАССА С2
ритмами, описанными в § 5 гл. I. Однако в некоторых случаях*,
например при вычислении сплайна в нескольких точках из
промежутка [xi, xi+i]j более эффективным является другой способ.
Из A) следует, что
/р = | (Ьр_, - Ьр) В'р-^х,,) h2p + bp+± (ftp+1 - Ьр) Втр+1 (х,) А* _ь
Мр = ~ (Ьр^ - ЬР) В^-х (*р) + | (Vn - Ьр) B"v+l (x,).
По этим формулам находим /,, /i+i, M{, Afi+i, что позволяет в
дальнейшем использовать формулу A.19).
Применение В-сплайнов для вычислений значений'
интерполяционных кубических сплайнов приводит к увеличению
необходимого числа операций по сравнению с алгоритмами из § L
Но зато количество хранимой информации здесь меньше, а
именно: требуется запомнить координаты узлов Хг и
коэффициенты 6г, т. е. всего 2GV4-5) чисел. При использовании
алгоритмов из § 1 нужно хранить 3(iV + 1) величин хи уи т( или Ми
Рассмотрим вопрос о решении системы E). При этом будем
сравнивать ее с системой A.6), описывающей ту же
интерполяционную задачу. Для формирования матриц и векторов правые
частей в обоих случаях приходится выполнить совершенно
одинаковый объем вычислений. Матрица системы A.6) есть
матрица с диагональным преобладанием, а матрица системы E) в
общем случае этим свойством не обладает. Чтобы оно имело место,
необходимо, прежде всего, чтобы
гг = ВгШ — ?t-iЫ—B(+iW>0, г=1, ..., N—1.
Используя данные таблицы 3.9, получаем
2 ( Щ H
U
_2 + *,_, + *, + AJ_1 + ht + Hi+
? = 1 IV—1.
Сетка А характеризуется числом р>1. Очевидно, г,
принимает минимальное значение, если Л1_2=р~|А,_1, hl+i = p~lh,,
которое равно
Полагая fe(-i =р,й(, где р «? р( < р, имеем
~ » о <1 + р) A + Р?) — р,

§ 9. О ПРИМЕНЕНИИ В-СПЛАЙНОВ ДЛЯ ИНТЕРПОЛЯЦИИ 143
Нетрудно вычислить
[A+Р)Рг + РПРРг+1 + РГ
Б точке рг- = 1 функция ф(рг) достигает максимума. Поэтому
Ф (Рг) = Ф (Р) = Ф (Р) = /о f / Р.~~Р, 2V
B + р) (l + р + р')
Так г» > ф(р), то гг будет больше пуля, если 3 + р—р2 > 0.
Отсюда следует ограничение р < A + У13)/2.
Неравенства го > 0 и rN > 0 для первого и последнего
уравнений системы выполняются, если, например, выбрать
дополнительные узлы сетки так, чтобы Л-з = ^-2 = fe-i = feo и hN-\ =
= hN = hN+\ = hN+2. Этого же достаточно и в случае граничных
условий типа II.
Мы не касаемся здесь краевых условий типа IV, для которых
использование аппарата В-сплайнов менее удобно из-за того, что
граничные уравнения B), D) содержат в этом случае по четыре
неизвестных.
Итак, при условии р<A + У13)/2 матрица системы E) есть
матрица с диагональным преобладанием и для решения системы
рекомендуется применять метод прогонки. Если же эти условия
не выполяются, то следует прибегнуть к методам' универсальной
или немонотонной прогонки, которые корректны для всякой
хорошо обусловленной матрицы.
К сожалению в общем случае хорошую обусловленность
матрицы нельзя гарантировать. Чтобы не загромождать изложение
несущественными подробностями, рассмотрим периодический
случай. Уравнения системы, описывающей задачу интерполяции,
имеют вид
В матричной форме это будет
Ab-f, F)
где Ъ = (&,,..., Ъя)т, / = (/,, ...,/«)г-
Оценим погрешность интерполяции. Из F) следует
A(b-f)=f-Af. G)
Выбирая норму векторов и согласованную с ними норму
матрицы, как указано в § Д.1, находим
1/ - А] \ = max | U - /i-iSi-x (*i) - UBx (*i) - /i+15i+1 fa) | <
< max {Bi-г (хг) \ U - /i-i I + Bi+1 fa) I /i - fi+i I } < со (/).

144
ГЛ. III. КУБИЧЕСКИЕ СПЛАЙНЫ КЛАССА С2
Здесь использовапо свойство нормализованных 5-сплайнов:
2#*(#) = 1. Теперь из G) находим
Далее,
\S(z)-f(x)\ =
iV+l
2
ИЬ_/|| < у
lbi-f(x)]Bi(x)
N+l
2 [bi-fi]BV
(8)
2V+1
S
lfi-f(x))Bi(x)
Учитывая (8), получаем
N+l
2
Кроме того, для всякого х
2V+1
Окончательно имеем
 !
i+2
2
р=г—1
(9)
Возьмем последовательность сеток (Av) такую, что hv -> 0 при
v -*¦ <*>. Ей соответствует последовательность (ЦЛ^1!). Тогда
согласно (9) для любой функции fix) ^ Cla, b]
последовательность интерполяционных сплайнов {S(AV; x)} сходилась бы к
fix), если только
|< К<С, оо. Но мы видели (§ 2), что
суф
ществуют непрерывные функции и последовательности сеток,
для которых процесс расходится, если р^C+У5)/2. Поэтому
остается допустить, что для таких р | А^11 может неограниченно
возрастать при v -*¦ °°.
Возвращаясь к системе F), напомним, что число
обусловленности матрицы системы есть jli = 11Л1П1Л!!. И так как НЛО = 1 по
свойству нормализованных 5-сплайнов, то fx = П^." II и, значит,
матрица А может быть плохо обусловленной, если р> C+ У5)/2.
Поэтому следует использовать сетки, для которых р < C + У5)/2.
В качестве примера приведем числовые данные, характеризующие
величину числа обусловленности системы F) для сетки:
Хг = 0,2ц i -= 0, ..., 5, Хб = 1 + a, xi = 1 + (i — 6) 0,2, i = 7, ..., 11„
в зависимости от параметра а. Для сравнения укажем, что на равномерной
сетке |л-= 3 (см. табл. 3.10).

§ 10 СЛУЧАЙ ДВУХ ПЕРЕМЕННЫХ 145
Задача. Пусть в представлении A) сплайны В{{х) нормированы так,,
что Bi(xi) •= 1. Показать, что система C) будет иметь диагональное
преобладание, если р < р* « 2,439, где р* — корень уравнения 6 + ?Р +-
-fr" Р2 — 2р3 = 0.
Таблица 3.10
а
М'
10
3,5
10* 2
14,5
10
135
ю-*
1,3-103
10
1,3-104
§ 10. О применении ^-сплайнов для решения задачи
интерполяции. Случай двух переменных
Кубический сплайн двух переменных представим в виде
iV-fl М+1 _
2 2
систему сплайн-функций
М+1
Тогда сплайн S(x, у) может быть выражен формулой
S (х, У) = 2 vi (У) Вi (х). C}
Рассмотрим задачу интерполяции с условиями F.2) и
краевыми условиями, например, типа I. Ее решение заключается в
нахождении коэффициентов Ьг;- в A). Дадим описание алгоритма,,
основанного на представлении сплайна в форме C).
Исходную информацию задачи будем представлять в виде
таблицы 3.8. Значения функций vt(y) и их производных в узлах
сетки А обозначим через v\f= i4s)(*/j)> s = 0, 1; i = — 1, ..., N +-
+ 1; /=-l,...f A/+1.
Первый шаг алгоритма. Используя формулу C),
построим иптерполяционпые кубические сплайны по всем строкам
таблицы 3.8, а именно: S{x, у>), / = 0, ..., М\ D°>lS(x, i/,), / =
= —1, М+1. В результате получаем значения vih i = —1, ...
..., iV + 1; / = 0, ..., Л/, и v'ij, i = — 1, ..., iV + 1; /,== — 1,
M +1, которые располагаем в виде новой таблицы такого же
рода.
Второй шаг. Используя формулу B), построим
интерполяционные кубические сплайны по столбцам второй таблицы: иг(у)ь
i = —1, ..., N + 1. Эта процедура дает значения bih i = —1, ..,
..., N + 1; / = —1, ..., М + 1, и задача решена.
iO 10 С. Заньчлон и др.

146 ГЛ. III. КУБИЧЕСКИЕ СПЛАЙНЫ КЛАССА С2
Таким образом, по сравнению с алгоритмом из § 6 здесь
потребовалось решить не три серии одномерных задач, а только две
общим числом N + М + 6. (В периодическом случае таких задач
1\1 + М.) Если используется обычный метод прогонки, то общее
количество арифметических операций приблизительно равно
10NM в непериодическом случае и 14/VM в периодическом.
Можно «применять и другой вариант алгоритма, поменяв ролями
переменные х и у. При этом ни число решаемых одномерных
задач, ни общее число арифметических операций не изменяется.
Вычисление сплайна S(x, у) и его производных можно
производить с помощью алгоритмов, описанных в § 6 гл. I. При этом
по сравнению с алгоритмами вычисления сплайнов из § 6 объем
вычислений возрастает, но зато практически в четыре раза
сокращается объем хранимой информации. Здесь, кроме узлов
сеток Ах, Ау, приходится запомнить только (N + 3){М + 3)
коэффициентов Ьц, а в § 6 4(N-f 1)Ш+1) величин/ij, ^}|0)>
jitf» т%» или Пи Ш0\ М\^\ Щм.
В целом использование представления A) дает существенные
преимущества по сравнению с кусочно-многочленным
представлением. Эти преимущества становятся решающими при переходе
к сплайнам трех и более переменных.
Литература к главе III. [1, 12—14, 15*, 26, 29, 30. 36—38, 44,
56,72,74,76,82,83, 87, 89, 951.

Г л а в а IV
ЭКСТРЕМАЛЬНЫЕ СВОЙСТВА СПЛАЙНОВ
Во введении уже отмечалась связь, существующая между
теорией сплайн-функций и теорией экстремальных задач. Хотя мы
и не намереваемся подробно обсуждать этот вопрос, но тем не
менее одну задачу обойти нельзя. Речь идет об экстремальных
свойствах интерполяционных сплайнов. Их анализ, с одной
стороны, позволяет глубже понять сущность сплайновой
интерполяции, а с другой — естественным образом приводит к практически
важной задаче приближения сплайнами со сглаживанием
исходных данных, если последние известны с некоторой погрешностью.
Исследование проведено на примере кубических сплайнов одной
и двух переменных, но методика применима и для сплайнов
любых нечетных степеней.
§ 1. Экстремальное свойство интерполяционных
кубических сплайнов
Рассмотрим задачу о минимизации функционала
ь
J(f) = jj\f'(x)\*dx. A)
а
В качестве множеств допустимых фупкций возьмем класс
W\\a, b\ и его подклассы W \а, Ь\ и W\[a,b], где W\ [а, Ъ]
состоит из фупкций, периодических с периодом Ъ — а, и
W) [а, Ь\ — из функций fix), удовлетворяющих условиям /' (а) =
= я», /' Ф) = z'n («о, 2/v — заданные числа).
Пусть в узлах сетки А: а = хо< ... < xN == Ъ заданы
значения z\ i = 0,...,N.,
Теорема 4.1. Среди всех функций f (x) e W\ [а, Ь],
интерполирующих значения z^, кубический сплайн Six) с краевыми
условиями
S" (а) = ?"(&)= 0 B)
минимизирует функционал J(f).
___ Если функции f(x) принадлежат одному из классов W\ [а, Ь]г
Wl[a, Ь\,то минимум функционалу доставляет кубический сплайн
из того о/се множества.
10*

«148 ГЛ. IV. ЭКСТРЕМАЛЬНЫЕ СВОЙСТВА СПЛАЙНОВ
Во всех случаях функция, дающая минимум, единственна.
Доказательство. Пусть fix) и Six) принимают
одинаковые значения %\. Запишем тождество
//2/, C)
где
/ = J [/" (Х) _ S" (х)] S" (х) dx = S J [Г (*) - S" (s)l S» (х) dx.
Интегрированием по частям получаем
J \r(x)-S№(x)\S"(x)dx =
= [/' (x) - S' (x)\ S" (x) g+1 - f [/' (x) - S' (x)] S'" (xt +) dx =
xi
= I/' (*) - S' (x)} S" (x) Q+1 - S'" (Xi +) [f (x) - S (x)] ?+1
При выводе этой формулы учтено, что S'"{x) постоянна для х^
<^[хи Xi+\]. Так как [fix)—S'ix)]S"(x) — непрерывная
функция, то
/ = - 2 S" (хг +) [/ (х) - S (х)] $+1 + [/' (х) - S' (х)] S" (х) \l
Пусть Six) удовлетворяет условиям B). Тогда второй член
ъ выражении / равен нулю. Если fix), Six)^W\ [a, b], то это
имеет место в силу_/'(а) - S'ia) =f'ib) - S'ib) и S"U) = S"ib).
Если / (#), *Ь"(^) е W\ [а, Ь], то равенство нулю достигается за
счет того, что f'ia)=S'ia) и /ЧЬ) —S'ib). Следовательно, можем
записать в непериодическом случае
I = (/о - So) S"' (Яо +) 21 if г - 50 [5- (Ж1 +) - S" fe_x +)] -
-(Ь-ЗД^(зд-1+), D)
-а «в периодическом
/ = 2 if г - 5,) [5W fe +) - Sw (xt-г +)]. E)
г=1
Так как fixi) = Sixi), i = 0, ..., iV, то / = 0 и из C) вытекает
соотношение
Л/-5). F)

§ 2. СГЛАЖИВАНИЕ ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ 149
Очевидно, Д/ — S)>0, и, следовательно, JiSXJif), т. е.
сплайн Six) сообщает минимум функционалу /(/). Функция Six)
единственна. В самом деле, если fix) — другая минимизирующая
функция, то /(/) = J(S) и, значит, /(/ — S) = 0. Последнее
означает, что почти всюду на [a, b] fix) =S"(x), откуда fix) =
= Six) + ах + [}. Но постоянные а, E равны нулю, так как
fixi) = Sixi), i = 0, ..., N.
Иногда установленное экстремальное свойство берут в
качестве определения кубического интерполяционного сплайна как
функции, интерполирующей заданные значения А и
минимизирующей функционал /(/). Однако при этом сужается множество
рассматриваемых сплайнов, в частности, исключаются сплайны
с граничными условиями типов II, IV.
§ 2. Сглаживание экспериментальных данных
"На практике часто приходится иметь дело со случаем, когда
значения z< в узлах сетки Д заданы с некоторой погрешностью.
Например, они могут быть результатами каких-либо измерений.
Если погрешность исходных данных отно- д
сительно велика, то это крайне
неблагоприятно влияет на поведение
интерполяционного сплайна и особенно его
производных. В частности, график сплайна
обычно имеет резко выраженные
осцилляции. Поэтому возникает вопрос, нельзя ли
построить сплайн, проходящий вблизи
заданных значений, но более «гладкий», чем
интерполяционный (рис. 4.1). Такие сплай- Рис* 41#
иы называются сглаживающими, а процедура их построения
сглаживанием..
Покажем, что сглаживающие сплайны возникают при
решении задачи о минимизации функционала
А (/) = j I /" (*) I2 dx + 2 рГ1 (U - 4J, A)
где Z| и pi > 0 — заданные величины. Очевидно, чем меньше
коэффициенты pt, тем ближе проходит функция, минимизирующая
функциоп^л /i(/), к заданным значениям z%. В качестве
множеств допустимых функций будем рассматривать те же классы
функций, что и в § 1.
Теорема 4.2. Среди функций / {х) е W\ [a, b] кубический
сплайн Six), удовлетворяющий условиям A.2), минимизирует
функционал J\if).

150 ГЛ. IV. ЭКСТРЕМАЛЬНЫЕ СВОЙСТВА СПЛАЙНОВ
Если функции fix) принадлежат одному из классов, W2 [я, Ь]
или Wl[a, Ь), то минимум функционалу доставляет кубическийв
сплайн из того же класса.
В каоюдом случае функция, дающая минимум, единственна.
Доказательство. Рассмотрим класс W\ [#, Ь]. Выясним:
вначале необходимые "условия минимума. Пусть функция ф (х) е
е W2 [a, b\ минимизирует J\if). Покажем, что <р(я) должна быть
кубическим сплайном с краевыми условиями A.2).
Действительно, предположим, что это не так. Возьмем интерполяционный
кубический сплайн S(cp; x) с граничными условиями A.2).
Второе слагаемое в выражении J\(J) одинаково для функций )
и ?(ф; х). Но в силу теоремы 4.1
Поэтому J\(S) < /Дф), а это противоречит предположению, что
() минимизирует J\(f).
Итак, пусть Six) — кубический сплайн, минимизирующий
/i(/). Возьмем сплайн Six) = Six) + aFhix), где Fhix), 0^k<
<:N,— фундаментальный кубический сплайн, удовлетворяющий,
условиям
Из A) следует
ь N
i (Sj = J 15Г (x) + aFl (x) |2 dx + 2 РГ1 (Si - z^2 +
a *—^
^ (Sk-zk)+а*рь\
Тогда
где
6
6 b
ak = j | F"h (x) |2 d^ + рГ, bft = J Fl (x) S" (x) dx
Здесь aft>0. Предположим, что Ьл ?= 0. Выберем а так, чтобы
\a\<i2\bk\ab\ sgn a = — sgn bk. Тогда ^E) - JiE) < 0, т. е.
JiiS) < J\if). Но это противоречит предположению, что сплайн
Six) минимизирует функционал J\(j). Следовательно, bfe = 0. Так
как к — любой индекс от 0 до N, то соотношения
йй = 0, /с = 0, ..., N, B>
суть необходимые условия минимума.

§ 2. СГЛАЖИВАНИЕ ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ 151
Преобразуем интеграл, входящий в bh, таким же образом, как
интеграл / в § 1. По аналогии с A.4) можно записать
ь
j F"h (х) S" (x)dx = Fh (х0) S'" (x0 +) +
а
N-l
+ 2 Fh (xi) [S" (*«+) — S'" (*i_i+)] - Fh (xN) S'" (xN-!+) = Dh.
По свойствам функции Fk(x) отсюда следуют формулы
S'"(xo+), к = 0,
Dh = S'" (xh+) - S'" (x,-), k=i,...,N-l, C)
- S'" («л-), k= N.
Окончательно необходимые условия минимума B) запишем в
виде
Si + PiDi = zl i = Q,...,N. D)
Покажем далее, что соотношения D) и краевые условия A.2)
являются достаточными условиями минимума. Действительно,
пусть существует удовлетворяющий им сплайн Six). Для любой
функции / (х) е W\ [а, Ь\ справедливо тождество
u-z4)\, E)
где
J, (f - 5)= I/" (x) - S" (x)Y2 dx+% рГ1 (fi - Stf,
а / определяется формулой A.4). Легко видеть, что при
выполнении условий D) выражение в квадратных скобках обращается
в нуль. Поэтому
;1(/)=у1E) + Л/-5). F)
Так как J\(f — S)>0, то сплайн Six) сообщает минимум
функционалу J\(f).
Нам осталось доказать, что удовлетворяющий условиям A.2)
и D) сплайн существует и единствен.

152
ГЛ. IV. ЭКСТРЕМАЛЬНЫЕ СВОЙСТВА СПЛАЙНОВ
Обозначим Zi? = S(xi), Мг~S"(х{) и введем векторы и
матрицы:
= (М0, ...,MNf;
1 О
О Bl Лх
u
N-2
где
ui=2(hi..l
# =
Величины z<, Д/f связаны уравнениями C.1.15). Запишем их
в матричной форме:
N = 0, пред*
(8)
Учитывая, что »S///(^+) = (Л/*+1 — ЛЛ)/й* и
ставим равенства D) в виде
Равенства G), (8) образуют систему 2(iV+l) уравнений
определения параметров сплайна zu Mu г = 0, ..., /V. Покажем
ее разрешимость.
Из G) и (8) следует, что
(А + bHRIDM = 6IIz°. (9)
Матрица А в системе G) симметричная с диагональным
преобладанием, причем диагональные элементы положительны.
Поэтому все ее собственные числа по теореме Гершгорина [7,.
с. 415] положительны, а сама она положительно определенная.
Матрица HRHT — тоже симметричная (она совпадает со своей
транспонированной). Кроме того, она положительно полуопре-

§ 2. СГЛАЖИВАНИЕ ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ 453
деленная. В самом деле, если обозначить т = HTt, то tT(HRHT)t =
= %tRt > О, так как матрица R — положительно
полуопределенная.
Матрица А + QHRHT системы (9) будет также положительно
определенной, так как соответствующая ей сумма квадратичных
форм положительна Следовательно, она невырождена. Тем
самым доказано существование и единственность кубического
сглаживающего сплайна в классе W\ ]a, Ь].
Доказательство утверждения теоремы для классов W\ [а, Ъ\,
W\ [а, Ъ\ проводится аналогично. При этом в классе W\ [а, Ъ\
необходимые условия минимума D) остаются без изменений, а в
периодическом случае следует учесть, что Do = DN = S'"(xq+) —
— S'"(xN—), и достаточно рассматривать условия D) при
Выпишем в развернутом виде системы уравнений, которые
необходимо решать при построении сглаживающего сплайна.
В непериодическом случае они имеют пятидиагональную струк-
а0М0 + b0Mi + c0M2 = go,
Ь0М0 + п\ М\ + 6i7l/2+ С\Мг = gu
Ct-tMt-t + bt-iMt-i + aJAi + biMi+l + dMi+2 = gu (Ю)
Cn-3^/n-3 + bN-2MN-2 + aN-\MN-i + bN-\MN = gs-u -
cN-2MN-.2 + bjr-iMN-i + aNMN = gN.
Коэффициенты этой системы определяются формулами
а, = 4 <*•<-. + '.) + -^ р.- + (-^ + 4;)' Pi + -jr р<«
A1)
Гй Pi+i» J = 1, ..., iV о,
глг+1
„О 70 _0 -О
Если сглаживающий сплайн Six) удовлетворяет условиям 5" (а) =
-=?"(&) = 0, то
а0 = aN = 1, feo = со = cN-2 = bN-\ = go = gw = 0. лA2)

154 ГЛ. IV. ЭКСТРЕМАЛЬНЫЕ СВОЙСТВА СПЛАЙНОВ
Если S(x) удовлетворяет условиям S' (а) = z0, Sr (b) = zN, то
6
Pjv),
b^1=^^^^^+^)pN-l^-^-PiV,
_ _ PiV-i
В периодическом случае система состоит из уравнений
I — 1, 4, . . ., iV,
где для всех i коэффициенты определяются формулами (И). При
этом величины с индексами N + к и к считаются равными: Мо =
= Д/л, ho = hNi ao = aN, ... Для решения систем A0), A4)
наиболее подходят методы, основанные на разложении матриц систем
в виде LWLTi где L — нижняя треугольная матрица с единичной
диагональю, a W — диагональная матрица с положительными
элементами (§ Д.З). Кроме того, для системы A0) можно
использовать метод немонотонной прогонки.
После вычисления Mi из системы A0) или A4) величины zt
определяются соотношениями D). Перепишем их в виде
Zi — z\ = — PiDi» $ = 0, ..., Af, A5)
причем
Do==-г-(Мх —Л/о), A6)
о
hi h' i \ /
DN= -j=^- (MN — Mn-i). A8)
В периодическом случае hN = feo, Mo = MN, M\ = MN+\ и все
величины Г){ определяются формулами A7), где г = 1, ..., /V.
Наиболее важным моментом при построении сглаживающего
сплайна является выбор весовых множителей р*. Заметим, что
если, все Pt = O, то z% = z\% i = 0, ...,N, и сглаживающий

§ 2. СГЛАЖИВАНИЕ ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ 155
сплайн превращается в интерполяционный. Отсюда следует, что
чем точнее заданы z\ в узлах сетки, тем меньше должны быть
весовые множители р*. В частности, если возникает
необходимость закрепить точку с номером Z, то нужно положить р*= 0.
В практических задачах обычно известны ошибки в
определении величин zf, т.е. р? — Zj|^6j, где ъг — точные значения.
В этой ситуации естественно потребовать, чтобы сглаживающий
сплайн Six) удовлетворял условиям
* = 0, ...,ДГ, A9)
или, что то же, условиям
p«lD<|<6,, * = 0, ..., N. B0)
Используем эти ограничения для вычисления весовых
множителей р^ Построим итерационный процесс, реализация которого
позволяет получить неизвестные Mt и множители р*, i = 0,..., N:
(А + QHRWHT)M™ = 6Hz°, B1)
М^/0|, еслиЯ^О,
о, если D<» = 0, B2)
где к — номер итерации.
В пользу выбора формул B2) для вычисления весовых
множителей говорят следующие соображения. Пусть на к-й
итерации в точке Xi нарушается условие A9), т. е. 8^ > б|. Так как
<:<"> =. 9\h) \D\k)\, то из B2) следует
п, значит, на (А + 1)-й итерации весовой мпожитель р*
уменьшается. Это способствует уменьшению ги С другой стороны, если
на к-й итерации &\ <С б| и Df =^0, то множитель р,- па
следующей итерации увеличивается, что способствует более
полному использованию «коридора» A9) в целях обеспечения большей
гладкости сплайна.
В качестве начального приближения естественно взять
Рг = 0, что соответствует интерполяциопному сплайпу со
значениями Di = D(i*). Итерационный процесс должен продолжаться
до тех пор, пока значения сплайна zt в узлах сетки не окажутся
и «коридоре».
При практической реализации описанного алгоритма на ЭВМ
необходимо учитывать следующие рекомендации. Во-первых,

156
ГЛ. IV. ЭКСТРЕМАЛЬНЫЕ СВОЙСТВА СПЛАЙНОВ
вместо B2) нужно использовать формулы
Q6i/\D\h\ если |z?{w|>xf
О, если \D\k)\<x.
Коэффициент В < 1 должен быть не очень близок к единице
(хорошие результаты получаются при 0 = 0,9). Величина к
выбирается с учетом величин бг-, а также в зависимости от
разрядности конкретной ЭВМ и точности решения системы для
неизвестных Ми Эти меры позволяют избежать зацикливания и
переполнения. Во-вторых, несколько первых итераций, например
пять-десять, следует сделать в принудительном порядке, не
обращая внимания на выполнение условий A9). В-третьих, при
сглаживании непериодических данных целесообразно на (к + 10-й
итерации строить сплайн ?<*+1)(#), удовлетворяющий краевым
условиям S{k+l)(a) = A(kh S(k+1)(b) = Вш, где A(k)y Bik)
представляют собой разностные аппроксимации первой производной
соответственно в точках а и 6, вычисленные по результатам fc-й
итерации. Рекомендуется использование трехточечной
аппроксимации.
Таблица 4.1
0
0,05
0,10
0,15
0,20
0,25
0,30
0,35
0,40
0,45
0,50
1,0
1,1
1,1
1,2
1,2
1,3
1,3
1,4
1,5
1,6
1,6
1,000
1,000
0,998
1,007
0,975
1,092
0,658
2,275
2,242
0,758
0,725
1,0078
1,0584
1,1104
1,1643 1
1,2206
1,27981
1,3426
1,4097
1,4810
1,5563
1,63531
1,0000
1,0257
1,0571
,0994
1529
2175
1,2977
1,3858
1,4666
1,5449
,6113
1,0000
1,0513
1,1052
1,1618
1,2214
1,2840
1,3499
1,4191
1,4918
1,5683
1,6487
0,55
0,60
0,65
0,70
0,75
0,80
0,85
0,90
0,95
1,00
1,7
1,8
1,9
2,0
2,1
2,2
2,3
2,5
2,6
2,7
2,342
1,907
2,031
1,969
2,092
1,663
3,256
3,313
1,492
2,718
1,7178
1,8055
1,8972
1,9952
2,1000
2,2121
2,3311
2,4557
2,5849
2,7186
1,7012
1,7922
i,8906
2,169k
2,3143
2,4391
2,5397
2,6294
2,7183 2
1,7332
I,8221
1,9155
2,013'
2,1170
2,2255
2,3396
2,4596
2,5857
,7183
По сравнению с интерполяционным сплайном построение
сглаживающего сплайна требует значительно большего объема
вычислений. При решении вопроса о том, каким сплайном
пользоваться, нужно учитывать в первую очередь погрешность
исходных данных, а также те требования, которые предъявляются к
сплайну. Практически бесполезно применение сглаживающих
сплайнов, когда исходная информация задана, например, с
точностью, сравнимой с точностью представления чисел в ЭВМ.
В то же время неизбежно приходится строить сглаживающие
сплайны, когда накладываются жесткие ограничения на каче-

§ 3. ЭКСТРЕМАЛЬНОЕ СВОЙСТВО ДВУМЕРНЫХ СПЛАЙНОВ 157
ственные характеристики сплайна или когда сплайн
используется для вычисления производных по экспериментальной
информации.
В таблице 4.1 приведены результаты сглаживания с помощью
описанного алгоритма значений я9 функций ех, округленных с точностью до 0,05г
на сетке с шагом 0,05 на отрезке \0, 1"|. Сплайн строился с краевыми
условиями S'@) = 1, S'(l) = е. Данные получены после выполнения 32
итераций при 6* = 6 = 0,05, 0 = 0,9, к = 0,0001. Эффект сглаживания особенна
хорошо виден при сравнении производных S' (z°; х) u S' (z; х)
интерполяционного и сглаживающего сплайна.
§ 3. Экстремальное свойство интерполяционных
кубических сплайнов двух переменных
В области Q = [a, Ъ\ X [с, d] с сеткой Д = ДЖХД1/, где Ах:
а — хо < ... < xN = Ъ и Ду: с = г/о < ... < ум = d, рассматриваем
задачу о минимизации функционала
ъ d
а с
+ S РГ1 j [D^f (xu y)\* dy + % oj1 \ [D*'°f {x, y-)Y dx, A>
i=0 с j=0 a
где pt и Gj — произвольные положительные числа.
Множества допустимых функций — это класс W\i<l [Q], а так*
же его подклассы: W\>2 [Q], состоящий из функций,
периодических по обеим переменным с периодами Ь — and — с, и W\'2 [a,
Ь], состоящий из функций, удовлетворяющих условиям
Dl'°1{xuy-) = z\y>\ i = 0,N; / = 0, ...,М;
Dulf (xu Vi) = 4Ь1), i = 0, N; j = 0, M,
где z([/s), r, s = 0, 1, — заданные числа.
Пусть в узлах сетки Д задапы значения zfj.
Теорема 4.3. Среди всех функций f (х, у) е Wf2 [Q]r
принимающих значения zy, кубический сплайн Six, у) с
краевыми условиями
D2'°S(xt, г/,) = 0, i = 0, N; j = 0,...,M;
D°-2S(x,, ys) = Q, i = 0, ..., N; ; = 0, M; B>
D2-2S(xh yj) = 0, i = 0, N; / = 0, M,
минимизирует функционал /(/).

158 ГЛ. IV. ЭКСТРЕМАЛЬНЫЕ СВОЙСТВА СПЛАЙНОВ
Если функции f(x, у) принадлежат одному из классов
W\'2 [Q] или Wl*2 [Я], то минимум функционалу доставляет
кубический сплайн из того же множества. ,
Во всех случаях функция, дающая минимум, единственна.
Доказательство. Пусть fix, у), и Six, у) интерполируют
значения z\$. Справедливо тождество
j)] C)
причем
Ь d
J J
d
1А - J J ZJ'2 [/ (х, y)-S (x, у)] D**S (x, у) dx dy,
а с
Ъ
7} = j ?>2'0 [/ (х, у}) - S (х, yi)\ D2-°S (x, у,) dx,
а
d
/4 = j Р0'2 [/ (xu y)-S (хи у)] D°>2S (xu у) dy.
Для упрощения последующих выкладок условимся считать,
что в непериодическом случае сплайны характеризуются
условиями
i/) = 0, s = 0, 1, 2, 3,
Dr<*S(x, у) = 0, г = 0, 1, 2, 3,
Эти соотношения не являются какими-то ограничениями, так как
касаются поведения функций вне рассматриваемой области.
Обратимся теперь к вычислению интегралов /<, Ij, /д.
Интегралы по одной переменной мы уже рассматривали в § 1
(формулы A.4) и A.5)). Имея в виду полученные там результаты,
можно записать, что
N
7; = 2 (/i;-Sii)?3'°?(*,i/i)
M
•^i = ^Ll (fij — $гз) & '
E)
F)
Здесь и в дальнейшем в периодическом случае суммирование
проводится по i от 1 до iV и по / от 1 до М.
Преобразуем кратный интеграл /д, выполняя интегрирование
по частям по каждой переменной и учитывая свойства производ-

§ 3. ЭКСТРЕМАЛЬНОЕ СВОЙСТВО ДВУМЕРНЫХ СПЛАЙНОВ
пых D3>sSixi+, у) и Dr**Six, у,+)9 г, 5 = 0, 1, 3. Получаем
1 ь— 2j Zj \ и \J\x,y)—o(x,i
159
i=o j=o
xi
М-\ (N-
(I/ («, У) - S (*, у)} D3'SS (*,
0
- D0'1 [f (x, y)-S (x, y)] DS'2S (Xl+, y) -
- Dl-° [/ (x, y)-S (x, y)] D™S (x,
1'1 [/ (x, y)-S (x, y)\ D2-2S (x, y)}
xi+i\\vj+i
Ik
Так как функции и их производные до порядка D2>2fix, у)
непрерывны в области Q, а производные Ds'2Sixi+, у) и
D2>zSix, Уз+) непрерывны вдоль линий х = const и у = const
соответственно, то формулу /д можно преобразовать к виду
M-l (-N-1
' ~ 5 (х, у)).
= 22
i=o и=о
fJV-i
j l
7=0
СЛ^—1
-2
I ;-0
(x, y)-S (x, y)] D'-
.if)
xi
Vj
+ D1'1 [/ (*, y)-S (x, y)] D^S (x, y) I \i
Если функция Six, у) удовлетворяет краевым условиям B),
ТО
/J. -5(а, г/) = D2. S5(b, г/) = 0, 5 = 0, 1, 2, 3;
Dr]?Six, с) = ^'25(д:, d) = 0, г = 0, 1, 2, 3.
Тогда в выражении /д все-члены, кроме двойной суммы, равны
нулю. Если fix, у), Six, у) е Wl'2 [Q], то то же самое имеет
место вследствие равенства функций и их производных в
противоположных точках границы области. Для класса Wl'2 [Q]
равенство нулю достигается за счет того, что функции fix, у)
и Six, у) удовлетворяют одним и тем же граничным условиям.
В результате получаем
N М
г=0 з=0
4+
«0*+
G)

460 ГЛ. IV. ЭКСТРЕМАЛЬНЫЕ СВОЙСТВА СЛЛАЙНОВ
^ По условиям теоремы /tj = Sih (хи у3) е= Д, поэтому интегралы
lh h и /д равны нулю и из C) следует соотношение
Л/)=Л5) + Л/-5). (8)
Так как Л/ — S)>0, то JiS)<>Jif). Покажем, что функция,
дающая минимум, единственна.
Действительно, пусть fix, у) — некоторая другая функция,
минимизирующая функционал, т. е. Л/) = JiS). Тогда из (8)
J4/ — S) = 0. Но это возможно только при условиях, что почти
всюду в области
Д2' °L/tef у3) - Six, у ft - 0, / — 0 М;
D0'4f(x{, у) - S(xu »)] « 0, г = 0, ..., N; (9)
D2>4f(x, у)-Six, г/I=0.
Обозначим
/U, I/) - 5(ж, I/) = g(x, у), D*> *g(x, у) = uix, у),
Из равенств (9) находим, что и(х, у) = ио(у) + щ{у)х и и(хиу) =
0, #<еДж. Отсюда гго(г/) = Ki(i/) =0 и 1г(д;, г/) = 0. Аналогично,
I/) = 0. Следовательно, g{x, у) = аху +$х + уу + 6. Но так
как g(xh Уз) = 0 на сетке Д, то постоянные а = $ = *{ = 6 = 0 и
?(х, у) ^ 0. Теорема доказана.
§ 4. Сглаживание экспериментальных данных. Случай
двух переменных
Задача сглаживания в случае двух перемеппых
рассматривается как задача минимизации функционала
N М
Ji (/) = /(/) + 2 2 рГЧ (/« - *?iJ, A)
г=0 7=0
где /(/) определяется формулой C.1) с заданными числами pi,o}.
Отметим, что в этой постановке весовые множители в двойной
оумме берутся в виде произведения коэффициентов,
соответствующих узлам сеток Дж и Ду. Очевидно, выбор таких
коэффициентов будет оказывать влияние на характер сглаживания не в
одной точке, а на целых линиях х = xt или у = Уз соответственно.
В качестве множеств допустимых функций будем
рассматривать те же классы функций, что и в § 3.
Теорема 4.4. Среди функций f (х, у) е IF22'2 [ЗД
кубический сплайн Six, у), удовлетворяющий условиям C.2),
минимизирует функционал J\if).

§ 2. СГЛАЖИВАНИЕ ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ 161
Если функции fix, у) принадлеоюат одному из классов,
W\9*\Q] или W\*2 [Q|, то минимум функционалу доставляет
кубический сплайн из того же класса.
В каждом случае функция, дающая минимум, единственна.
Доказательство проводится совершенно аналогично
доказательству теоремы 4.2. Поэтому мы приведем только его
схему без подробных рассуждений.
а) В силу теоремы 4.3 минимум функционалу /i(/) в классе
Wl'2 [Q] доставляет кубический сплайн Six, у) с краевыми
условиями C.2).
б) Рассматривая сплайн Six, y)=Six, у)+ aFhix)Gi(y), где
Fkix) i(Xk^N), Giiy) @ < I ^ M) — фундаментальные
кубические сплайны, и исследуя вариацию J\iS) — J\iS) функционала,
можно получить необходимые условия минимума в виде
Ь d d
bhl - j j F"h (x) G"t (y) D™S (z, y) dx dy +p^ J G\ (y) D°-2S (xh, y) dy+
а с с
b
+ oj1 J F'k (x) D2-0S (x, yt) dx + p^oT1 (SM - z°u) = 0, B)
a
k = 0,...,N; 1 = 0, ...,M.
Если преобразовать интегралы по формулам C.5)—C.7) и
обозначить
xh+
'+oT1D3-°S(x, у,)
'+Pb1D°'aS{xh, у)
У1+
- vi-
C)
то необходимые условия минимума B) можно представить в виде
Sij + piOjDij = z% i = 0, . •., Лг; / = в, ... f ilf. D)
в) Достаточность этих условий (вместе с условиями C.2))
вытекает из тождества
Г jv м
= Л(/)-Л(?)-2 /л + 2 Pr1/i + Sar1/j +
L i=0 ^=о
JV М -I
+ 2 2 рТ'оТ1 (/« - 5W) (/у - 4) . E)
i=0 j=0 J
Последнее при выполнении условий D), C.2) переходит в
соотношение
/i(/)-/i(S) + /i(/-S)f F)
*• *• Ю. С. Завьялов и др.

1G2 ГЛ. IV. ЭКСТРЕМАЛЬНЫЕ СВОЙСТВА СПЛАЙНОВ
из которого следует, что J\iS) </i(/), т. е. Six, у) сообщает
минимум функционалу /i(/).
г) Докажем, что сплайн, удовлетворяющий условиям C.2) и
D), существует и единствен. С этой целью вернемся к
кубическим сплайнам одной переменной на отрезке [а, Ы с сеткой Д*.
Множество таких сплайнов с краевыми условиями S"(a) =
= ?"'(&) = О образует линейное пространство S(AX) размерности
N+i. В этом пространстве рассмотрим сплайны ФpixI р = 0,...
..., N, являющиеся решениями задач сглаживания со
специальным выбором векторов исходных данных z°, а именно: z°p=if
z? = 0, гфр, при фиксированных весовых множителях рР>
/э = 0, ..., N. Функции ФР{х), /? = 0, *.., N, удовлетворяют
условиям B.4):
Фр (Xi) + Pi [Фр (*,+)] - Ф; (**-)] = брЬ t = 0, ..., N, G)
где положено Ф"® (х) = 0, если хФ [а, Ы.
По аналогии с фундаментальными сплайнами, через которые
выражаются решения задач интерполирования, назовем функции
Фр{х) фундаментальными сглаживающими сплайнами.
Покажем, что всякий сплайн Six), сглаживающий
произвольный вектор исходных данных z°, выражается через функции
Фpix) в виде
2 °*)- (8)
Чтобы убедиться в этом, подставим даваемые формулой (8)
значения сплайна и его третьих производных в условия B.4).
Получаем
S 4 (фр (*о + pi К fo+) - фр М] 1 = гь i = о,...,
0
Эти равенства тождественно выполняются в силу формул G).
Покажем, что система функций ФРЫ, р = 0, ..., N, линейна
независима и, следовательно, образует базис (N+ 1)-мерпого
пространства 5(ДЖ). Это значит, что Six) в 0 на [а, Ь] тогда и
только тогда, когда z? = 0, р = О, ...,7V. Условие 5(д:) ss 0
эквивалентно равенствам z{ = 5(a;i) = 0, M-S^W^O для всех t.
Поскольку сплайн в виде (8) есть решение задачи сглаживания,
то из ее условий B.8) получаем 4 = 0, i = 0, ...,iV.
Аналогично строится базис 4%(г/), <7 = 0, ..., М, пространства сплайпов
A4AV) на отрезке [с, d] с сеткой Ду.
Рассмотрим пространство сплайнов двух переменных Si А)
в области Q с сеткой Д как тензорное произведение двух про-

§ 2. СГЛАЖИВАНИЕ ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ
163
страпств 5(А) = 5(ДХ) ® iS(Ay). Его базис образуется функциями
«DpUWtf), р = 0, ..., /V; 5 = 0, ..., Л/.
Всякая функция из
представима в виде
N М
(9)
Покажем, что функции такого рода удовлетворяют
необходимым условиям минимума D) в задаче сглаживания исходных
данных {zpg}. Подставляя значения, даваемые формулой (9),
в D), получаем
N М
^^
Отсюда
JV М
2 2^
?=0 9=0
/%{
^р (Xi) X?q {Уэ) +PiO
г-0 Р
следует
Фр (^t) + Рг \Фр (х
+ )"<
х
*«f
X
Oj [<
^)]} « 4,
Эти равенства тождественно выполняются в силу условий G)
и аналогичных условий для функций *Ря(у).
По переменным хну на сглаживающие сплайны могут быть
наложены граничные условия разных типов. Во всех случаях
можно повторить необходимые рассуждения и получить
представления сплайна вида (9). Это доказывает существование
сглаживающих сплайнов двух переменных. Единственность вытекает
из однозначности разложения элемента конечномерного
пространства по базисным функциям.
Формула (9) для сглаживающих сплайнов двух переменных
показывает, что их построение можно свести к решению
одномерных задач сглаживания. В самом деле, представим эту
формулу в виде
S (х, y)=^Sq (x) 4q (у), Sq (x) - 2 4*Ф* (*)•
q=0 р=0
Функции Sq(x) суть сплайпы, сглаживающие исходные
данные z'pq на лпиях у = yq) q — 0, ..., М.
11*

164 ГЛ. IV. ЭКСТРЕМАЛЬНЫЕ СВОЙСТВА СПЛАЙНОВ
Функция Six, у) есть сплайн, сглаживающий значения Sq(x)r
зависящие от х как от параметра, в узлах сетки Ду. Построим
следы этого сплайна SPiy) = SixPt у), р = 0, ..., N, беря в
качестве исходных данных Sqixp), q = 09 ..., М. В результате
получим новую систему значений z°vq = Sv (yq) = S (xp, yq), p = 0,..»
,.yN. Для этих значений достаточно построить
интерполяционный сплайн, который и будет искомым сглаживающим
сплайном Six, у) для исходных данных z%, р=0, .. ,,N\ q=0, ..., М.
Все изложенные выше результаты относятся к случаю, когда
весовые множители в функционале /i(/) A) представляются
произведениями рГ^Г1» 1 = 0,...; / = 0, ..., М. Каждый из
наборов величин, pi или aJ? должен быть задан, ибо способ,
изложенный в § 2, здесь не помогает. Пользуясь им, например, для
определения весовых множителей pt, мы можем найти значения р* (j)r
i = 0, ..., N, зависящие от номера линии у = у5. Решение же
задачи сглаживания нами получено в предположении, что pt от /
не зависят, так же как значения о;, / = 0, ..., М, приписываются
всем сечениям х = х{.
На практике могут встретиться случаи, когда возникает
необходимость задавать весовые множители т«, i = 0, ..., N; / == 0,...
..., Л/, в каждой точке независимым образом, так что их нельзя
представить в виде произведения т« = рф, или же они не заданы
вовсе. Тем не менее и в этих ситуациях можно рекомендовать
для применения описанный алгоритм последовательного решения
двух серий одномерных задач с заключительным построением
интерполяционного сплайна двух переменных.
В первом^ случае можно представить т# = piij)Cj(i) при рД/) ==*
= Oj(i) = Уха. Затем сглаживание исходных данных {z?j} вдоль
линий у = Уз проводить с весовыми множителями рг(/), а
получаемые значения {z^} сглаживать вдоль линий х = х{ с
множителями Gjii). Во втором случае весовые множители р*(/) и Ojii)
определяются в процессе решения одномерных задач. При этом,
если допустимый «коридор» задан ограничениями \Z\j — я?л^
^6|j, то сглаживание по двум переменным можно проводить,
например, с условиями | z^ — z?j | ^ Ьц12 и | z^ — z^ \ ^ 6ij/2.
В обоих случаях можно получить удовлетворительные
результаты. Но, разумеется, предлагаемые процедуры не соответствуют
минимизации функционала J\(f) с весовыми множителями т«=»
()Д)
Литература к главе IV. [1, 5, 10, 12—15, 23, 30, 31, 39—43, 58»
69, 94,99].

Г л а в а V
КУБИЧЕСКИЕ СПЛАЙНЫ
С ДОПОЛНИТЕЛЬНЫМИ УЗЛАМИ
В гл. II мы уже сталкивались с проблемами эрмитовой
интерполяции сплайнами, когда по условиям задачи, помимо
значений функции, требуется интерполировать и ее производные до
некоторого порядка. Для решения подобных задач приходится
либо переходить к сплайнам с меньшей гладкостью (с большим
дефектом), либо повышать их степень. И то, и другое может
оказаться неудобным. Однако существует способ, позволяющий
избежать этих затруднений путем введения узлов сплайна, не
являющихся узлами интерполяции. Такие конструкции принято
называть сплайнами с дополнительными узлами. Их
использование пе приводит к увеличению размерности решаемых
алгебраических систем, а только к некоторому усложнению
элементов матриц и правых частей.
§ 1. Локальная интерполяция
Пусть на отрезке [а, Ъ] требуется интерполировать некоторую
функцию f(x) по известным значениям f\ = fr) (xi), r = 0, 1, 2,
па сетке Д: а = хо <х\ < ... <xN = Ъ. Обычный способ решения
этой задачи с помощью локальных сплайнов состоит в
использовании сплайнов пятой степени с узлами на сетке А. Мы
применим здесь кубические сплайны с дополнительными узлами.
С этой целью введем на [а, Ь\ еще одну сетку
б = Ьг + а^1/ = 1, 2; ; = 0, ..., iV-1},
где Ы = Хг+\ — хи ai + аг = 1, 0 < ai < 1/2. _
Кубический сплайн Six) дефекта 1 с узлами на сетке А «=
= A U б, удовлетворяющий условиям
5°>0 =/ir), г = 0,1, 2, для *,€=Д, A)
назовем локальным кубическим сплайном с дополнительными,
узлами.
Условия интерполяции A) на концах промежутков [хи xi+\],
i = 0, ..., /V — 1, дают N линейных систем, по 6 уравнений в
каждой, для определения коэффициентов сплайна, решая которые

166 ГЛ. V. КУБИЧЕСКИЕ СПЛАЙНЫ С ДОПОЛНИТЕЛЬНЫМИ УЗЛАМИ
получаем при х^ [xiy xi+\]
и \*л>1 — "тг л^ yju —— JL/\] ~~Х~ 7" / г х*-*' *^i/ ~\ ! i \ь*/ ** г) Т J i ~Т~
О <L
+ сц (x—Xi— axhi)% + c2i {x — Xi — а^ц)\ B)
с коэффициентами
/» in el I —— /¦ Iп а 1 а! . —— "
^2г V^l? а2/ — ^1г 4^2» ^1/1 *^i — J,
8адачи, а) Показать, что при а! = а2= 1/2, когда дополнительные
узлы сплайна совпадают, он превращается в сплайн дефекта 2, у которого
вторые производные, вообще говоря, разрывны в точках Х{-\-A/2Iг{, i =0, ...
...,N-1.
Указание. В формуле B) выполнить предельпый переход при
б) Показать, что при а\ = 0 (а2 = 1) сплайн S(x) превращается в
эрмитов кубический сплайн, интерполирующий значения /* и f v i = 0, ..., iV.
§ 2. Оценки погрешности локальной интерполяции
Оценим точность приближения функции fix) сплайном Six)
в зависимости от ее дифференциальных свойств. В данном
случае константы в оценках будут зависеть от параметра ссь В силу
сложности получаемых выражений мы приведем результаты
только для фиксированного оы = 1/4.
Теорема 5.1. Если Six) интерполирует на сетке Д функ*
цию fix), то имеют место оценки
№Чх)-рЧх)\\„^11Г9 г = 0, 1,2,3, . A)
где Rr при ai = 1/4 даны в таблице 5.1.
Доказательство. Представление сплайна Six) на
отрезке [х{, Xi+\l A.2) можно переписать в виде
2
S (х) =» 2 А« (фй («1, 0 /^ + ^и («х, t) /{ill, B)
где

§ 2. ОЦЕНКИ ПОГРЕШНОСТИ ЛОКАЛЬНОЙ ИНТЕРПОЛЯЦИИ
167
12
t =
Пусть, например,
нием значений /ift),
^la, Ь], Пользуясь
разложев B) по формуле Тейлора в точке
Таблица 5.1
Класс функций
С2[а, Ь]
Wl [а, Ь]
С2С\ [а, Ь]
C2Wt [a, b]
Д,оо
С2С% [а, Ы
Класс функций
С2 [а, Ь]
С2С| [а, Ь]
C2Wi [а, Ъ]
Д,оо
С2С\[а,Ъ]
Но
4,6682.10-2^а) (/")
6,3302.10-3Р||////||оо
3,1650- 10~3/г3 о (/'")
9216 У/ 11о°
2,8935.10"^4ll/Ivfc +
+ 2,3510 -Ю-4/"г40)(/1У)
я*
2,0278со (/'')
0.20833Л ||/^Ц^
0,10417to (D
25 т2 || ЛУ 11
П52А ljf 'lo°
1,7361-10-2P||/IV ||с +
+ 6,1729- 10^3Л2ш (/Iv)
0,17033/То)(///)
2,2367- lO-^fl/"'^
1,1184.1О-2Д2со(>///)
864 ll7 l!o°
1,5432.10-3Р||/1У||с +
+ 9,1450-10-4P(o(/IV)
из
1,2287со(//7/)
T^II/IYic +
-h7,2917-10-2to(/IV)
x = Xi + thi, имеем
при
R(x) = S (x) - f (x) = h\I (t)
Jg(i-I, 1^T)/IV,
D)
E)

168
ГЛ. V. КУБИЧЕСКИЕ СПЛАЙНЫ С ДОПОЛНИТЕЛЬНЫМИ УЗЛАМИ
g (*,
т3 т2
.ai, *)"«- — Ф1 К> t) -it + ф2 <
т.
Отсюда, применяя неравенство Гёльдера, находим
I Д(г) И I < Фг (alt t) Л?-г | /lv IU, г = О, 1, 2, 3,
где
F)
Дальнейшие вычисления для нахождения максимумов
функций фгA/4, t) проводятся по программе на ЭВМ, как описано в
§ И гл. II. Это дает оценки в рассматриваемом классе функций.
Таким же образом они устанавливаются и в других классах.
Ясно, что, придавая параметру ai различные конкретные
значения, нетрудно выяснить характер зависимости констапт в
получающихся оценках от аь В частности, в случае f(x) e
eCW^^t^, Ь] эта зависимость характеризуется таблицей 5.2,
где сг — постоянная в Rr из A).
Таблица 5.2
0,05
0,15
0,25
0,35
0,45
Со
2,0946-Ю-з
1,2502-Ю-з
7,5954-10
6,6168-10
8,1737-10'4
Ci
6,7986-10
4,4846-Ю-з
2,8351-Ю-з
2,4102-10-3
3,8058-10-3
6,8114.1-0-2
3,2374-Ю
2,1701-10-2
2,4886-10-2
4,5564-Ю
С3
2,2052
0,35482
0,28125
0,29291
0,96125
Естественно возникает вопрос об оптимальном выборе ai, при
котором константы принимают наименьшие значения. Оказалось,
что такие значения параметра а\ различны как для разных
классов интерполируемв1х функций, так и для оценок функции и ее
производных в одном и том же классе. Однако в большинстве
случаев оптимальные константы в оценках мало отличаются от
соответствующих констант при а\ = 1/4.
Оптимальные значения ax = aL и соответствующие им
константы в оценках A) приводятся только для величин Ro, которые
оказались наиболее чувствительны к изменению параметра ol\
(таблица 5.3).
Сравним таблицу.5.3 с соответствующей графой таблицы 5.1.
Видно, что для функций класса СЧа, Ь] наилучшая оценка
получается при а 1= 0, когда кубический сплайп с
дополнительными узлами переходит в сплайн дефекта 2, но значения констант
в /?о отличаются друг от друга всего в полтора раза. Для клас-

§ 2. ОЦЕНКИ ПОГРЕШНОСТИ ЛОКАЛЬНОЙ ИНТЕРПОЛЯЦИИ
169
сов Wlo (a, frj, C2C\ [а, Ь\ и C2W\ то [а, ft] значения констант
также отличаются друг от друга незначительно с практической
точки зрения.
Таблица 5.3
Класс функций
С2{а,Ь]
W*. [а, Ь]
С2С\ [а, Ъ]
0 W~ [я, Ъ\
Д,оо
СгС\ [а, Ь[
*
0
0,3610
0,3610
0,3264
0,28023
*
32 v/ '
6,1019-10-3P ||Г lloo
3,0510-10-3Л3о) (Г)
6,5293-10й4 ||/^L
6,3983- 10~6/i4 || fl v \\c +
Исключение составляет класс функций СЮ\ \ау Ь], где эффект
оптимизации проявляется существенным образом. Коэффициент
при ll/IYH<x> (главной части погрешности) уменьшается в пять раз.
Функция фо(аь i) приобретает свойство альтернаяса (рис. 5.1).
В заключение остановимся на вопросе существования точек,
в которых порядок приближения повышается.
Пусть / {х) е C2W\ ж [а, Ь]. В
формуле D) возьмем по частям
интегралы в E). Получаем при х е= [хи х{ +
S(x)
12
) hiflv
а при x e [х{ + a\hi, xx +
О
-Ип1*-
a^ A - t) - a?) hiflv(x) + О (hf).
Если положить ai = 1/4, то
рис. 5.1.
где
хг =
J ftit ^

170 ГЛ. V. КУБИЧЕСКИЕ СПЛАЙНЫ С ДОПОЛНИТЕЛЬНЫМИ УЗЛАМИ
§ 3. Нелокальная интерполяция. Существование
и единственность решения
Снова эадаются две сетки узлов: А: а = хо < х\ < * ¦, < xN = Ъ
и б = {хг + ajhilj = 1, 2; i = 0, ..., N — 1}, где h{ = xi+\ — хи oci +
+ a2el, 0<ai<l/2. Кубические сплайны рассматриваются на
сетке 6, а не Д = Д U б, как в предыдущих параграфах.
Интерполяционным кубическим сплайном с дополнительными узлами
назовем сплайн Six) дефекта 1 на сетке б, удовлетворяющий
условиям
S (Xi) = fh S' (Хг) = П ДЛЯ Хг Z= A A)
и одному из следующих краевых условий:
I. S"(a)=f"(a), S"{b)=f"(b).
II. 5w(a)-r(a), 5///(&)=Г(Ь).
III. S{r)(a) = S{r)(b), r = 2, 3 (условия периодичности).
IV. S'"{xq + aih0 + 0) = S'"{x0 + сыЛ0 - О),
1 + 0) = S'"{xN-x + a2^-i—0).
Опишем алгоритмы построения интерполяционных
кубических сплайнов. Введем обозначения Мг = S" (хд, i = 0, ..., TV.
Очевидпо, сплайн ?(#) можно рассматривать как локальный
кубический сплайн с дополнительными узлами, интерполирующий
значения /*, /ь Ми i — 0, ...,iV. Для него на отрезке [^, ^l+iJ
справедлива формула A.2), в которой fi и /i+i заменяются
соответственно на Ми Mi+\.
Кубический сплайн, представленный в таком виде, имеет две
непрерывные производные. Выберем величины Mi так, чтобы в
точках Xi e Д была непрерывна третья производная. Так как
S"(zt + 0) =Ait S"'(xi-0) = i4?-i + 6(ci.«-i + c2J-i), B)
то условие непрерывности третьей производной принимает вид
VLiMt+^dt, i = l, ..., N-lb C)
где
6

§ 3. НЕЛОКАЛЬНАЯ ИНТЕРПОЛЯЦИЯ 171
К уравнениям C) следует добавить соотношения, вытекающие
из краевых условий. В случае условий типов I и II находим
— аЛ/0 + jioA/i =-• dj,
+ |Х1АЛ+1 = йь * = 1 ^V — 1, E)
Здесь для условий типа I
l^o = Ajv = U, а0 = — а/0, им = — а/лг,
а для условий тина II
/ /х - /0 2/p +
—^ _
hN-l
Краевые условия типа IV эквивалентны условиям сю
с2, j>r_i = 0:
„ М с М G \1lZ1* A + а*)*о+У + а1)
а2М0 — ctiMi = у —^ g
л г I *г 6 I /iV — /iV—1
— ttiA/jy-i + а2л/дг = — т ^т——^ —
з = dx- \ь)
Исключив неизвестные Mq и Afw из уравнений C) и F),
приходим к системе
M^i+i = di, * =» 2 ЛГ — 2, G)
(а \
а— [iw-i ^ J Afjv-i = d^-tt
где
Если fix) — периодическая функция, то, продолжая
периодическим образом сетку А и полагая hN =» Ао, MN = MQi MN+i = MXf

172 ГЛ. V. КУБИЧЕСКИЕ СПЛАЙНЫ С ДОПОЛНИТЕЛЬНЫМИ УЗЛАМИ
из C) находим
+ X\MN = du
jfcT,-, — аМ{ + \л,Мм = du * — 2, , iV — 1, (8)
Итак, построение интерполяционного сплайна сводится к
определению величин Ми Для граничных условий типов I и II они
находятся из системы D), для условий типа IVе из уравнении
F), G), а в периодическом случае из (8) при MN = Л/о.
Матрицы систем суть матрицы с диагональным преобладали-
ем, что обеспечивает существование и единственность решения
этих систем, а следовательно, и существование и единственность
соответствующих им интерполяционных кубических сплайнов.
§ 4. Оценки погрешности нелокальной интерполяции
Для исследования вопроса о точности приближения,
даваемого нелокальной интерполяцией, используются те же идеи, что и
в гл. III. Снова как промежуточный шаг применяется локальная
интерполяция. Кроме результатов § 2 нам потребуется
Лемма 5.1. Пусть }(х)&СЧа, Ь] и SH{x) — локальный
кубический сплайн с дополнительными узлами, удовлетворяющий
условиям интерполяции
SH fa) = fu Sh {х\) = /i, S"H (xi) = 0 для хк *= A.
Тогда
II S$ (x) - /(r) (x) jo < crfr-'co (/'), г = 0, 1, A)
Доказательство. Возьмем формулу B.2) при fl= /i+i= 0.
Разлагая /< и fi+\ по формуле Тейлора в точке x = Xi + thiy
получаем
S(x) = f (х) + h [-1% к, *) /' (I) + (i-t) % К, t) Г (л) +
+ Ф1 («1, *) /г + Ч>1 (аЬ t) /i+l], Б, Л S [XU Xi+1\. B)
Отсюда, применяя теорему о среднем для непрерывных
функций, находим оценку A) для г = 0. Дифференцируя B.2),
аналогично устанавливаем оценку A) при г= 1.
Приступим к рассмотрению погрешности нелокальной
интерполяции. В следующей теореме при интерполяции
непериодических функций используется разностный аналог краевых условий

§ 4. ОЦЕНКИ ПОГРЕШНОСТИ НЕЛОКАЛЬНОЙ ИНТЕРПОЛЯЦИИ 173
типа I
Теорема 5.2. Ясли /ЫеС'Ь, Ь] и S(x) удовлетворяет
краевым условиям C) или условиям типа III, то
1S(r) (х) - /(г) (*) |с < (с, Ч; fc.) Йх-Г(о (/'), г = 0,1,
еде постоянные сг определены в лемме 5.1, а
сх = 6axa2, р == ^ (А = min й4).
Доказательство. Из B.2), где fl и fi+l заменены соот-
Бетствепно па Ми Mi+u при х^[хи xi+\i имеем
S (х) = SH (х) + Ф2 (alf t) h\Mi + фя (alt «) Л|Af 1+1.
Здесь б'я(ж)—локальный сплайн, удовлетворяющий условиям
леммы 5.1. Тогда
15'г> (х) - /(г) (х) | < | Stf (х) - /(г> (х) | +
+ Фг (olf t) Л?" max (| Mi |, | Mi+11), г = 0, 1, D)
тде
$r (alf t) = фг (о,, l-f) = l Ф?/0 («1, *) I + | № («1, *) |. E)
Элементарные вычисления показывают, что
(аь t) = % (аи ±) = 04 f 1 — -rj-l
max ф0
max $! (ах, i) = max [фг (ь ^),
L
= max f аь а2, -§-j < 2аха2.
Оценим величины Л/г, г = 0, ..., Ny входящие в D). В случае
периодических краевых условий для правых частей системы ли-
иейпых алгебраических уравнений C.8) получаем
А так как матрица системы C.8) с диагональным
преобразованием, то согласно следствию Д. 1
|Л/{|<|со(/'), г = 0 N.
Такие же неравенства вытекают при граничных условиях C)
из системы C.5). В обоих случаях из D) с учетом леммы 5.1
следует утверждение теоремы.

174 ГЛ. V. КУБИЧЕСКИЕ СПЛАЙНЫ С ДОПОЛНИТЕЛЬНЫМИ УЗЛАМИ
Пусть Six)—кубический сплайн дефекта 1 с
дополнительными узлами — интерполирует функцию fix) на сетке Д и
удовлетворяет краевым условиям одного из типов I—IV. Предполагая,
что fix) дважды непрерывно дифференцируема, можно построить
на сетке Д локальный сплайн SHix) с, дополнительными узлами,
удовлетворяющий условиям A.1).
Запишем тождество
Six) - fix) = lSB(x) - /(*)] + ISix) - SHix)l.
Сплайн SHix) представляется формулой A.2), а сплайн Six) —
той же формулой с заменой fi и /i+1 на Mt и Mi+i
соответственно. При х^[хи Xi+\] получаем
Rix) = S (x) -/(*) = [SH (x) - f ix)\ + ф2 К, t) h\ [M{ - f\\ +
где ф2(аь t) и ^(ai, t) даются формулами B.3).
Дифференцируя это равенство но х г раз, находим
| R(r) (х) | < | S%> (x) - Г (х) | + фг (alf t) hi~r max | Mг - f\ |f F)
i
где функции фг(ос1, t) определены формулой E), причем
max Ф2(аь t) = max [$2(alf 0), ф2(а1э a2)J= max 1, ^——— L
0<t<l/2 I U2 J
Оценки приближения сплайном SHix) при ai = 1/4 были
получены в § 2. Таким образом, для нахождения при данном
значении cti оценок погрешности Rir)ix) в F) по существу остается
оценить величины \Мг — /, |, i = 0, .., N.
Лемма 5.2. Если Six) удовлетворяет краевым условиям
типов I, II, III, то для всех 1 = 0, 1, ..., N справедливы оценки
|A/i-/"|<?, G)
где Q при <х\ = 1/4 даны в таблице 5.4.
Доказательство. Техника получения оценок — стандарт^
ная. Проиллюстрируем ее на одном примере.
Пусть /(^GCW^Ia, ft], а Six) удовлетворяет краевым
условиям типа I. Тогда величины М{ определяются из системы
C.5). Перейдя в ней к неизвестным Qi = М% — /*, получим
inQi+г = dlt i = 1, ..., N - 1,
Qs = 0,

§ 4. ОЦЕНКИ ПОГРЕШНОСТИ НЕЛОКАЛЬНОЙ ИНТЕРПОЛЯЦИИ 175
где
i^di — Ufi-i + a/i — Hi/i+i.
Так как матрица системы с диагональным преобладанием и а
— 1 + (оцаг), то согласно следствию Д.1 | Qi
Таблица 5.4
Класс функций
С2- [а, Ъ]
W*, [а, Ь]
С*С\ [а, Ь)
Q
/3,7 У7\ -. ,ю
\ 4'"* ' 94fi /
4
/3 _j_ 7 V 7 j т / ////v
V16 432 /
Класс функций
С4 [а, Ь)
Q
3V28/IVIL
96 ?
+»(/IV)}
и, значит, достаточно оценить |d<l. Пользуясь разложением по
формуле Тейлора в точке ^, имеем
1
! dx
и
л 1
^ ^ « 7lX Т (Т "" al) (T "" a2) /IV (^i-l + Ui-i
1
aia2 J
Отсюда, применяя неравенство Гёльдера, при ai = 1/4 находим
|5i|<4-fe2l/IV||oo, « = lf ...,N-1, (8)
ii, следовательно,
В случае краевых условий типа II систему C.5) перепишем
в виде
— a(?0 + Q± = Зо = do + а/о — /ь
Все рассуждения здесь совершенно аналогичны только что
рассмотренному случаю краевых условий типа I. Необходимо

176 ГЛ. V. КУБИЧЕСКИЕ СПЛАЙНЫ С ДОПОЛНИТЕЛЬНЫМИ УЗЛАМИ
лишь проверить справедливость уже найденных оценок (8) для
di также для do и d*N.
Для периодических краевых условий снова имеет место
оценка (9), причем в этом случае она выводится из системы,
эквивалентной системе C.8):
где величины с индексом N + j считаются равными
соответствующим величинам с индексом /.
Таким образом, оценки G) в классе C2Wj те [а, Ъ] найдены.
Получение их для других классов оставляем читателю в качестве
упражнения.
Таблица 5.5
Класс функций
Сг [а, 6]
Wl [а, Ь]
СгСЦа,Ь]
C2Wt[a, Ь]
С* [а, Ъ]
Класс функций
С2 [а, Ь]
wl [«, ъ]
С2С% [а, Ь)
CV?[a, Ъ]
С4 [а, Ъ]
Яо
8,8928- 10Д2со (/")
1,39201- 10~2h31| /"X
9,5642-10~3Pco(/IV)
3072 h "' "«>
5,7870- 10-47>i/IV||c +
4- 5,2445- iO-4h4(d(f1Y)
я2
3,29514со (f")
0,409832^ || /"ML
0,28304Шо (Г)
— h2 II /IVII
1152 h И' и«
2,6042 -10—2Ла || /IV |fc +
+ 1,0851-10-2fe2o(/IV)
я,
0,3066857ш (/")
4,46612- iO~2h21| /"X
3,0798- 10~2/i2cd (/'")
_L 13 И ЛУП
192 n «* "«>
2,1567-10^3 || /IV|IC +
+ 1,8990- 10-3/&d(/iv)
2,6113@ (fm)
0,47917/* || /IVL
0,32639fe||/IV||c +
+ 0Д313Ш) (/Tv)
Теорема 5.З. Если'Six) удовлетворяет краевым условиям
одного из типов I, II, III, то имеют место оценки
lSw(x)-fw(x)\\c<Rr, r = 0,1, 2,
еде Rr при а\ = 1/4 даются таблицей 5.5.

§ 4. ОЦЕНКИ ПОГРЕШНОСТИ НЕЛОКАЛЬНОЙ ИНТЕРПОЛЯЦИИ 177
Доказательство. Техника доказательства одинакова для
всех классов функций, и мы ограничимся случаем f(x) &
е CW| ^ [а, 6]. Из F) при cci = 1/4, используя теорему 5.1 и
лемму 5.2, находим для х ^ [я,, a:f+i]
| R(r) (х) | < [фг A/4, 0 + ^- Фг A/4,
где функции q>r(ai, t) из B.6), a $r(ai, ?) заданы формулой E).
Вычисление максимумов по ?^[0, 1] функций ФГШ в силу того,
что фгA/4, t) заданы в виде интегралов, производится опять па
алгоритму, описанному в § 11 гл. II. В результате имеем
требуемые оценки.
Отметим, что приведенные в таблице 5.5 оценки для R^(x) в класса
C2W\ [а, Ъ] при г = 0,1 в случае краевых условий типов I и III явля-
А, оо
ются неулучшаемыми. Они достигаются, например, для функции
^ 1, i =0f 1 ЛГ— 1,
где
Нам осталось получить оценки приближения третьих
производных. С этой целью понадобится другое представление
кубического сплайна с дополнительными узлами, в котором вместо
величин Mi присутствуют величины Л*»= ?"'(#<), 1 = 0, ..., N. На
промежутке [хи xi+\] в этих терминах получаем
S (х) = -^ А{ (х— x{f + -| Di (x—Xif + fl (х — хг) +fi +
+ Сц (x — X\ — (X^i)^. + C2| (x — X\ — О&2^0+» (Ю)
где
Г U - fi+i , /i + /i+i _
ia2)h2il hi 2
i+1) a\ A + 2a2) -i I, c2i(ab a2) = c1{ (a2, ax)y
-± + {A{ — A
Положим
R'"(x)=S'"(x)-f"(x).
10. С. Завьялов и др.

178 ГЛ. V. КУБИЧЕСКИЕ СПЛАЙНЫ С ДОПОЛНИТЕЛЬНЫМИ УЗЛАМИ
На промежутке [хи Xi + a\hi\ получаем
IR'" (*) | < I /Г - /'" (*) | + max М4 - /Г |. (И)
Для жеЬ{ + а\hu Xi + о^йЛ находим
где сн получаются из Си заменой Лг-, Л1+1 на /г, /i+i
соответственно.
На промежутке [xi + a,2hi, xi+\]
IR'" (x) |<| /Гц- Г (х) | + max| At - /¦'|. A3)
г
Для того чтобы воспользоваться неравенствами (И) —A3),
I л У" I
нужна оценка для max \А{ — f{ |.
г
Лемма 5.3. Если Six) удовлетворяет краевым условиям
одного из типов I, II, III, то для всех i == 0, 1, ..., N справедливы
оценки
М<-/Г|<?/, A4)
где U при а\ = 1/4 даны в таблице 5.6.
Таблица 5.6-
с3
с4
[а,
.[«
[а,
Класс
ы
..«
Ч
функций
8353
5184 е
3*1
{II/
')
L
1V ifo -Ь
и
со (/IV)}
Доказательство. Из A0) следует, что функция Six)
непрерывна в точках х^ г = 1, ..., N, и имеет в них непрерывные
первые и третьи производные (последние могут иметь разрывы
в узлах сетки б). Так как
S" ixi + 0) = A, S" ixi - 0) = Ai-iht-i + D,.i + 6(а2сн + ccic2i)Ai-b
tq отсюда можно получить условия непрерывности второй
производной сплайна
i-aAi + hAi+i^gi, i = l, ..., ЛГ-1, A5)

§ 4. ОЦЕНКИ ПОГРЕШНОСТИ НЕЛОКАЛЬНОЙ ИНТЕРПОЛЯЦИИ
где
,
fi-П-х
Af-Д V, 3
Граничные условия типа I пли II дают уравнения
- аЛ0 + XlAL « g*
В случае граничных условий типа I Хо = \i0 = 1,
A-агод/; + B + <у*2)/о
3
3 J iV-lJr
а для условий типа II X* = [X/v = 0, g* = — a/o', g^ = —. а/^
В периодическом случае веб уравнения имеют вид A5) с
циклической заменой индексов.
Из систем A5), A6) получаем систему относительно
неизвестных Ui — Ai—/i# В случае краевых условий типа II это будет
i-! - aUi + XiUi+1 = gu i = 1, ..., N - 1, A7)
да /// л т
где g, = gi— и-*/*—i + a/i —
Пользуясь разложением по формуле Тейлора, получаем
8i = Л1^ (t - ах) (т - «2)(т + alC
«is ^J
12*

180 ГЛ. V. КУБИЧЕСКИЕ СПЛАЙНЫ С ДОПОЛНИТЕЛЬНЫМИ УЗЛАМИ
откуда после применения к интегралам неравенства Гёльдера
"лри ai ¦=¦ 1/4 находим
Согласно следствию Д.1 из A7) получаем
Аналогичным образом устанавливается справедливость этой
оценки в случае краевых условий типов I и III.
Оценки A4) для других классов функций выводятся таким
же способом.
Теорема 5.4. Если Six) удовлетворяет краевым условиям
одного из типов I, II, III, то справедливы оценки
IIS'"U)rU)IL^/?3, A8)
еде i?3 при «i = 1/4 даются таблицей 5.7.
Таблица 5.7
Класс функций
Сг[а,Ь]
WI [а, Ь]
С*[а,Ъ]
2,6113<о (/"")
1*1/IVL
0,32639Й|| /Iv lc + 0,13131Лш (/IV)
Доказательство. Пусть /(х) е W%> (a, b]. Положим
1/4. В формуле A1) на отрезке [хи J]
|/Г-/'"(х)|<^||ПМ. A9)
Тогда из A1) и A4) получаем
В формуле A2) при х е [Xi + kJA, x{ + C/4)А;]
6с + /ГГ(*)
тде

§ 4. ОЦЕНКИ ПОГРЕШНОСТИ НЕЛОКАЛЬНОЙ ИНТЕРПОЛЯЦИИ
181
Отсюда
Тогда из A2) и A4) находим
B0)
На отрезке [хг+ C/A)hu х{+\] из A3) имеем оценку A9).
Объединяя A9) и B0), получаем оценку A8) в классе W%> 1^,6]. Оценки
в классах СЧа, Ь], к = 3, 4 устанавливаются таким же образом.
Теоремы 5.3 и 5.4 характеризуют погрешность аппроксимации
при значении параметра оц = 1/4. Таким же образом можно было
бы получить оценки и при других значениях ai и выяснить
характер зависимости констант в оценках от ai, а также найти
оптимальные значения aj, при которых эти константы
принимают наименьшие значения. Расчеты показали, что при а\ = 1/4
оценки близки к оптимальным, причем в двух случаях, г = 0, 1
б классе С 2W| ^ [а, Ь], константы в них* принимают
минимальные значения точно при ai = 1/4. Для сравнения приведем
таблицу 5.8 оптимальных значений ах и соответствующих оценок
погрешности приближения функции fix).
Таблица 5.8
Класс функций
С2 [а, Ь)
Wl [а, Ъ]
С2С\ [а, Ь]
CV± 1<я [а, Ъ]
С4 [а, Ь]
•к
0
0
0
1
4
0,2442
-о*
1 ,3
3072 *4'^ У"°°
0^ /оlO • i\) Л II у ||л"-]"" 0)^0^0 * 1.U Л СО \/ )
Мы не даем отдельно результаты для граничных условий
типа IV. Как и в задаче лагранжевой интерполяции (гл. III),
оценки в этом случае могут отличаться от оценок для других
граничных условий только в отношении коэффициентов и только вблизи
концов отрезка. Специальным выбором узлов можно добиться их
полного совпадения с приводимыми в таблицах 5.5 и 5.7.

182 ГЛ. V* КУБИЧЕСКИЕ СПЛАЙНЫ С ДОПОЛНИТЕЛЬНЫМИ УЗЛАМИ
Укажем некоторые результаты, связанные с повышением
гладкости интерполируемых функций при равномерной сетке узлов Д.
Теорема 5.5 Если f (х) е РР« [а, Ь] — периодически
продолжаемая за отрезок [а, Ь] функция и Six) удовлетворяет
периодическим краевым условиям, то при а\ = 1/4 и равномерной
сетке Д
«&'> (х) - /("> (г) |L < cr(ty 1Г \с + О (Л—), г = 0, 1, 2, 3,
B1)
где
с0 = 1/384, сх = /3/216, et = 1/12, сЛ = 1/2.
Доказательство. В предположениях теоремы решение
системы уравнений C.8) имеет вид
Мг = П + {^f1 - Т2)h2f\v + О (Л»), i = 1, ..., N. B2)
В самом деле, преобразуем C.8) в систему относительно
неизвестных F{ = Mi — fl - (^^ - -jjj A2/-v. Получаем
JLv^-aVi + ^Vi+^du < = 1 ЛГ,
с соответствующей заменой индексов 0 на N и TV + 1 па 1. Если
входящие в правые части значения функции и ее производных
разложить по формуле Тейлора в точке #<, то придем к выводу,
что t?i = O(fe3). Но так как норма обратной матрицы системы
ограничена, то Wi\ =0(fe3) для всех L
Выражение для Six) на отрезке [хи xi+\l получается из A.2)
ваменой /i, /i+i соответственно на Ми Mi+\. Подставляя в него
вместо Mi выражения B2) и пользуясь опять разложением
Тейлора, получаем: при х^ ixh хг + ai^J
S(x) = f (x) + ?- /IY (х) Fаха2 - 1 - t*)t* + О (й5); B3)
при х ^ [х{ + a\hi, xi + a2hi]
S(x) = f (x) - ^ /IV (x) [t* A - if - Gait il-t)+ 2а?] + О (А5);
B4)
при x&lxi + otoht, xi+\] снова получаем равенство B3), где t
заменено на A — t).
Отсюда при ai = 1/4 для х^ [xh xi+\] находим
II S(x)-f (х) ||с < -L (|j41 /Jv |c

§ 4. ОЦЕНКИ ПОГРЕШНОСТИ НЕЛОКАЛЬНОЙ ИНТЕРПОЛЯЦИИ 183
Отметим, что при оы = C — У2)/8 вместо 1/384 получаем
7DУ2—5)/2048 и это наименьшее значение коэффициента.
Дифференцируя соотношения B3) и B4), аналогично
получаем оценки для г= 1, 2, 3. Теорема доказана.
Из теоремы 5.5 следует, что если интерполируемая функция
У (х) е Wlo [я, Ь\ — периодическая, то при равномерной сетке Д
использование интерполяции кубическими сплайнами с
дополнительными узлами при специальном выборе значения параметра o&i =»
= 1/4 требует 4для достижения заданной точности приближения
функции и ее производных примерно вдвое меньше узлов
интерполяции по сравнению с эрмитовыми кубическими сплайнами,
рассмотренными в гл. II.
Использование представлений B3), B4) позволяет указать
точки повышения порядков приближения интерполяционными
кубическими сплайнами с дополнительными узлами,
удовлетворяющими периодическим краевым условиям. Если cti = 1/4, то
о \%г) == 1 \%г) Н~ О \гЬ J, Г = U, 1, Z, О,
где х*0 = хг + А/2, х\ = х\ + ftA/4, /с = 1, 2, 3, ^ = Xi + у ±
h, х\ = хг + (i- ± ^-) Й, 4 = ж, +Ш2, ft=0, 1, 2.
( ) ( )
Нетрудно показать также, что ?(#*+ ft/2) = /(#< + А/2) +
Предоставляем это сделать читателю в качестве упражнения.
Численные эксперименты по интерполированию функций /j(#), / = 1, 2,
3, 4, из § 7 гл. II кубическими сплайнами с дополнительными узлами
показали хорошее совпадение результатов с выводами теории. В частности,
погрешность интерполяции па сетке А с шагом h = 0,1 оказалось
практически одинаковой с погрешностью приближения, даваемой эрмитовыми
кубическими сплайнами на сетке с шагом h = 0,05.
В заключение этого параграфа отметим важное обстоятельство.
Если для интерполяции функций, имеющих скачки, использовать
кубические сплайны, рассмотренные в гл. III, то вблизи jO4eK
разрыва возникают осцилляции, амплитуда которых при h -*- 0,
вообще говоря, не затухает, а стремится к некоторому конечному
значению. Это явление известно как эффект Гиббса. Можно
показать, что для кубических сплайнов с дополнительными узлами
эффект Гиббса отсутствует и они хорошо приспособлены для
интерполяции такого рода функций.
На рис. 5.2, 5.3 изображены соответственно «обычный» кубический
сплайн и кубический сплайн с дополнительными узлами при oti = 1/4,
интерполирующие «ступеньку»
f0'
f0'
A,

184 ГЛ. V. КУБИЧЕСКИЕ СПЛАЙНЫ С ДОПОЛНИТЕЛЬНЫМИ УЗЛАМИ
на равномерной сетке с шагом h = 1/19. Точка разрыва помещалась в
середине интервала между двумя узлами. Осцилляцию можно ослабить, умень-
/ X
Рис. 5.2.
/ X
Рис. 5.3.
шая ось В пределе при ах = 0 получается эрмитов кубический сплайн, ко*
торый осцилляции не имеет.
§ 5. Кубические» сплайны двух переменных
с дополнительными узлами
Пусть в прямоугольной области Q = [а, Ъ\ X [с, d\ задана
сетка Д =* Д* X Ду, где
Ах: а = хо < х\ < ... < xN = Ь, &у: с =*= уо < у\ < ... < Ум = d,
разбивающая область на ячейки Qy = [^, xi+i\ X [у}, j/j+J.
Ассоциируем с ней сетку б = бх X бу, где
б* = {х0, Xi + a\hu x{ + агА», #*}, osi + аг = 1, 0 < ai < 1/2;
= yM—yh i = 0, ..., iV—1, /=
На сетке б рассмотрим множество ?3,3,1,1F) кубических
сплайнов дефекта 1 от двух переменных. Так как оно является
тензорным произведением пространств одномерных сплайнов
размерности 2N + A и 2Л/ + 4, то его размерность равна 4(# + 2)Ш4-
+ 2). Пусть в узлах сетки Д заданы значения.некоторой функции,
а также ее первых частных и смешанной производных
Dr'9f(xuyj) = №\ r,s = 0,l; i = 0, :..,N; / = 0, ...,М.
Интерполяционным кубическим сплайном двух переменных с
дополнительными узлами назовем сплайн Six, у) ^?з,з, i, 1F),

§ 5. КУБИЧЕСКИЕ СПЛАЙНЫ ДВУХ ПЕРЕМЕННЫХ 185
удовлетворяющий условиям эрмитовой интерполяции:
Dr'sS(xuyj) = №s\ r, s = 0,l, (хиуйеЬ, A)
и определенным краевым условиям, например, типа I:
Dr'2S(xuyj)rfr\ r-0,1, * —0 ЛГ; / = 0,М;
D^S (хи у3) = fr\ * = 0, ЛГ, /= О, М.
(Можно сформулировать также краевые условия типа II, III, IV).
Доказательство существования и единственности
интерполяционного сплайна проводится по аналогии с таким
доказательством в случае лагранжевой интерполяции (§ 6 гл. III) путем
введения базиса из фундаментальных сплайнов.
Алгоритм решения задачи тоже имеет сходство с алгоритмом
из § 6 гл. III. Обозначим
Первый шаг алгоритма. Строятся кубические сплайны
по переменной х. а) По исходным данным fff0 (г = 0, 1) в узлах
сетки Д и граничным данным f\]y0\ i = 0, N; j = 0, ..., M,
находятся сплайны Six, у5). Дело сводится к решению систем
уравнений C.5) в количестве Л/+1, в результате чего определяются
значения M\j*°\ б) По данным f\j*1} (r=0, 1) в узлах Д и
граничным данным /ifa), i = 0, N; j = 0, ..., М, строятся сплайны
D°'lS{x, i/j). Снова решается М+1 задач и определяются
значения М\]л)/
Второй лпаг алгоритма. Строятся кубические сплайны
по переменной у. а) По данным /J1^ (s = 0, 1) в узлах Д и
/$'2\ * = 0, ...,Nf*j = 0, М, находятся сплайны S(x{, у). Здесь
решаются системы уравнений типа C.5), а в результате
определяются величины M|j|2). б) По данным /i}'s) (s = 0, 1) на сетке
Д и fij'2\ i = 0, ..., N; / = 0, М, находятся значения M\jt2\
На этом шаге решается 2(N+1) одномерных задач.
Третий шаг состоит в определении величин МЦJ).Это
можно сделать двумя- путями. Первый из них заключается в
решении задач по построению сплайнов по переменной х по
вычисленным значениям М%л) (г = 0, 1). Для этого требуется знать
величины Afyf2)при i = 0, N; / = 0, ..., М. Последние находятся
из решения двух интерполяционных задач по переменной у по
граничным данным /(J's) (s = 0, 1), / = 0, ..., М; г=0, N, и
данным в угловых точках области /{2'2), i == 0, N\ j = 0, М. В этом

186 ГЛ. V. КУБИЧЕСКИЕ СПЛАЙНЫ С ДОПОЛНИТЕЛЬНЫМИ УЗЛАМИ
варианте приходится решить М + 3 одномерных задач. Другой
вариант отличается от описанного переменой ролей х и г/. При
его реализации решается N+3 одномерных задач.
Всего приходится решить 2N + ЪМ + 7 (или 3iV + 2М + 7)
одномерных задач, в результате чего находятся величины М^ч\
г = 0, 1, 2, 5 = 2; г = 2, 5 = 0, 1.
Формула кубического сплайпа двух переменных с
дополнительными узлами в ячейке Qy, t = 0, ..., iV — 1; j = Q, ...
..., М— 1, может быть представлена в виде
i / Фф, B)
где t = (х — Xi)
Ф (*) = [ф0 (Ъ
MB
фт(гг) —транспонированный вектор
Ф (и) = [ф0 И, *j<Pi И, Jj9a И, ^0 (и), Щ± {и), 1Ц2 (и)],
а функции фаШ, ^v(^), а = 0, 1, 2,— из B.3).
Использование формулы B) означает, что вначале находятся
значения сплайна и его производных по нормали на
противолежащих сторонах ячейки Qij, а затем уже производится
интерполяция в точку (х, у).
Литература к главе V. [12,14,48,51—53].

Г л а в а VI
ОБОБЩЕННЫЕ КУБИЧЕСКИЕ СПЛАЙНЫ
Отличительной чертой сплайнов, рассматриваемых в данной
главе, является присутствие в их формулах большого числа
свободных параметров. В одних случях эти параметры
используются для изменения уравнений, которыми описываются звенья
сплайна, в других — для изменения условий стыковки звеньев
между собой. Выбор термина «обобщенные кубические сплайны»
обуСловлеп тем, что при определенных значениях параметров
-«обобщенный» сплайн переходит в обычный кубический. Для
каждого пз обобщенных сплайнов существуют задачи, где их
применение приводит к лучшим результатам по сравнепию с
кубическими сплайнами. При этом сохраняется одно из важней-
шпх свойств кубического сплайна — простота и эффективность
реализации алгоритмов на ЭВМ.
В данной главе рассматриваются только обобщенные
сплайны одной переменной. Заметим, что в случае двух переменных
могут быть использованы идеи и алгоритмы, изложенные в гл.
III для кубических сплайнов,
§ 1. Рациональные сплайны
Изучаемые в данпом параграфе рациональные сплайны по
сравнению- с кубическими позволяют полнее учитывать
особенности интерполируемой функции. Например, с их помощью
можно приблизить функции с большими градиентами или точками
излома, сохраняя при этом свойства выпуклости и вогнутости,
т. е. устранить осцилляции.
Пусть на отрезке La, Ъ\ задана сетка Д: а = хо <х\ <. ,.<
< xN = Ъ.
Определение. Рациональным сплайном называется
функция SR(x), которая
1) на каждом промежутке [хи xi+\\ имеет вид
где t = (x — Xi)/hi, hi = xi+\ — xu p{, qt — заданные числа, — 1<
2) ШеЯа, Ы.
Таким образом, рациональный сплайн отличается от
кубического лишь более сложным аналитическим выражением.

188 ГЛ. VI. ОБОБЩЕННЫЕ КУБИЧЕСКИЕ СПЛАЙНЫ
Пусть в узлах сетки Д заданы значения /,-, i = О, ..., N.
Рациональный сплайн называется интерполяционным, если
SnM-U i = 0, ..., N. B)
Как и в случае кубических сплайнов, для построения
интерполяционного рационального сплайна необходимы краевые
условия. Мы будем рассматривать четыре типа краевых условий:
Н. S
III. Условия периодичности:
SV (x0) = S% (**), г =1,2.
IV. 5л (*0) + A - Yo) ^л fe) - ylS'R (x2) = ct,
) + S'R (xn) = зд
где
To =
x —r-
Первые три типа условий совпадают по форме и содержанию
с аналогичными условиями для кубических сплайнов. Смысл
условий типа IV будет выяснен в дальнейшем.
Рассмотрим алгоритм построения интерполяционного
рационального сплайна.
Из условий интерполяции следует
Подставляя отсюда выражения для Л,-, Вг в A), получаем
Sr (х) = /{A - t) + fi+1t +
Сплайн, записанный в #виде C), непрерывен в узлах сетки А
и удовлетворяет условиям* B). Определим коэффициенты Сц Dt
так, чтобы были непрерывны его первая и вторая производные.
Так как
ДЛ-3A-*JA + ?0 + 2A-гK?{ \

§ 1. РАЦИОНАЛЬНЫЕ СПЛАЙНЫ
ТО
r (xi
Обозначая mi = <Sfl (a:j), i = О,..., Л^, получаем уравнения
С{ + B + ft) Д{ = (/i+i - /0 - ТОЛ,
B + Pi) Cx + Di = - (/i+i - /0 + ml+1hi.
Из них вычисляем
- C + gj) (/i+1 - U) + fe{m{ +B + 9j) \т.+1
bi B + 9i) B + PO -1 '
л _ C + PQ (/<+1 - h) - hmi+1 - B + Pl) himt
Формулы E) являются сдествием непрерывности S'R(x).
Далее, из D)
Я \Щ =
[1 + Pi (I -
V
-4— LJ i n
(i + «г**)" *l
Отсюда
2Z)
2C
S"R (xt -) = _*=! C + 3PJ.J + pf-i),
и условие непрерывности 5д (х) в точке xt имеет вид
A?Ci-i C + Зр{_х + р?_х) = hUiDi C + 3ft +
Подставляя сюда Z)j и C,_i из E), получаем
+ [XjP,-! B + ft_!) + ц^4 B
= ^i/»i_1 C + ft.,) ^Ы + ^i^, C + Pi) fj±^-\ G)
i = l, 2, .... ЛГ-1,
где Я« = hAlii-i + ht)-\ ц( = 1 — Я4,
p - 3 + 3Pi-i + Pl-i n _ f

190 ГЛ. VI. ОБОБЩЕННЫЕ КУБИЧЕСКИЕ СПЛАЙНЫ
Для сокращения записи будем обозначать левую и правую
части G) соответственно через q>(mt-u mu ^i+i) и си
К уравнениям G) небходимо присоединить уравнения,
вытекающие из граничных условий. Опуская несложные выкладки,
выпишем системы уравнений относительно неизвестных гп\ для
каждого вида краевых условий.
Т и п ы I и II.
<?о B + Ро) Щ + }Jk0QQmi == cj,
Ф (тг_и mu mi+l) = си ъ = 1, 2, ..., N - 1, (8)
VnPn-i ™>n-i + Pn-i B + Qn-i) mN = cN,
где для типа I
Яо = |ijv = 0, со = (?0 B + Ро) /о, ^iv = ^y~i B + giv-i) //v;
для типа II
1 ГГ~ /iV
Тип III.
Ф (^i-ь rnu mi+1) = q, г = 1, 2, ..., /V, (9)
причем
T и п IV.
( 2 ) ?x B
Ф (?л,_ь mif m1+1) = й, i = 2, ..., N — 2, A0)
-2 + ^iV-lYN^JV-l) /^iV-2 + [kN-lPN-2 B + ^iV-2) +
V>n-iQn-i (l + У% + Pn-i)] ^iv-i = Civ-i — H-iv-i^JV-i^-i,
mN = (у?/ — l) галг-1
Матрицы всех полученных систем с диагональным
преобладанием. Это позволяет использовать для их решения метод
прогонки п обеспечивает существование и единственность
интерполяционного рационального сплайна SR{x) при любом типе
краевых условий. После вычисления значений т^ t==0, 1, ..., N,

§ 1. РАЦИОНАЛЬНЫЕ СПЛАЙНЫ
191
по формулам E) определяются коэффициенты С*, Du
Вычисление сплайна и его первой и второй производных производится
по формулам C), D), F). Для полноты картины дадим формулу
для вычисления третьей производной
При /?i = ^,==0, i = 0, ..., TV — 1, рациональный сплайн
превращается в кубический. Действительно, из A) видно, что в этом
случае на каждом промежутке [хи xi+\] SR(x) является
кубическим полиномом. Кроме того, приведенные выше системы
относительно величин Ш{ переходят в соответствующие системы для
кубического сплайна (§ 1 гл. III).
Можно считать, что сплайн первой степени также является
частным случаем рационального сплайна. Действительно,
исследуем поведение SR(x) на некотором промежутке [xh, xk+\] в
случае, если pft, gA -»¦ °°, р<, qi ^ 0, i Ф к. Сетку Д считаем
фиксированной. Ограничимся рассмотрением периодического случая, так
как для других типов граничных условий рассуждения
совершенно аналогичны. Используя следствие Д.1, из системы (9)
имеем
Vi
г
hi-X
3F.
Теперь из E) получаем
-т —> 0 при рь —> оо,
-т -> 0 при qk ->¦ оо.
Обращаясь к формуле C), находим при х^ [xh1 och+{l
lim SR(x) = fk(l-t)+tfk+1.
В частности, если для всех i одновременно р{ q{ -> oo, T0 SR(x) -*>
->?i(#), т. е. сплайн первой степени является предельным
случаем рационального сплайна.
Скажем несколько слов о граничных условиях типа IV для
рационального сплайна SR(x). Как нетрудно видеть, они
представляют собой не что иное, как требование непрерывности
$"я(х) в узлах хи %n-\ в случае, когда p< = g< = 0, 1 = 0, 1, ...
..., N — 1. Так как при этом SR{x) превращается в кубический

192
ГЛ. VI. ОБОБЩЕННЫЕ КУБИЧЕСКИЕ СПЛАЙНЫ
сплайн, то такой выбор естествен. В принципе можно было бы
потребовать непрерывность SR(x) в указанных узлах при всех
Ри Ъ ^ 0» Однако эти условия имеют довольно сложный вид и,
как показывает анализ, не дают каких-либо преимуществ в
смысле точности приближения.
Мы не будем заниматься получением оценок погрешности
интерполяции рациональными сплайнами. Заметим лишь, что из
рассмотренных выше частных случаев следует, что при /?*, q^
близких к нулю, оценки погрешности близки к
соответствующим оценкам для кубических сплайнов (гл. III), а при
достаточно больших piy qt — к оценкам для сплайнов первой
степени (гл. II).
Рациональные сплайны сочетают в себе свойства наиболее
распространенных на практике сплайнов — первой степени и
кубических. Кубические сплайны дают, как правило, высокую
точность приближения гладких функций. Однако при этом
трудно удовлетворить требованиям качественного характера.
Например, если интерполируемая функция выпукла, то в ряде случаев
необходимо, чтобы и сплайн был выпуклым. Кубический сплайн
удовлетворяет этому требованию далеко
не всегда. В то же время сплайн
первой степени в указанной ситуации будет
выпуклым, но зато здесь трудно
обеспечить необходимую точность
приближения. К тому же сплайн первой
степени не является гладкой функцией.
Особенно значительные трудности
возникают при приближении функций с
большими градиентами. Применение в
этом случае как кубических сплайнов,
так и сплайнов первой степени
обычно связано с большим числом узлов
интерполяции.
При использовании рациональных
сплайнов путем надлежащего выбора
свободных параметров ри q{, как
правило, всегда удается одновременно
удовлетворить требованиям и
количественного и качественного характера,
в том числе при интерполяций функций с большими
градиентами. Это обстоятельство делает рациональные сплайны
практически универсальным средством приближения функций.
Выбор параметров ри q{ обычно не вызывает особых
затруднений. Небольшой практический опыт работы с рациональными
сплайнами позволяет, как правило, с «первого взгляда»
достаточно точно задавать их значения. В большинстве случаев мож-
/ х
Рис. 6.1.

§ 2. КУБИЧЕСКИЕ НЕЛОКАЛЬНЫЕ СПЛАЙНЫ КЛАССА С» 193
но полагать pt — qu Конечно, представляет интерес разработка
алгоритмов автоматического выбора величин ph qit
Используя метод, изложенный в § 8 гл. III, можно получить
формулы для рациональных в-сплайновч Не останавливаясь на
этом вопросе подробно, отметим, что предельными случаями
рациональных fi-сплайнов являются /i-сплайны первой и третьей
(кубические) степеней.
В качестве численного примера, демонстрирующего возможности
рациональных сплайнов, рассмотрим интерполяцию функции
ехрA00.г)-ехр(-100.г)
'<*>в*- ехрA00)-ехР(-100; • ^t0'1''
на сетке с узлами xi = 2/10, i = 0, ..., 10. На рис. 6.1 изображены графики
интерполяционных сплайнов — кубического Sz(x) и рационального SR(x).
Оба сплайна удовлетворяют граничным условиям типа I: S3 @) =0, S3 A) =
« — 100; SR @) = 0, SR A) = — 100. Сплайн SR (x) строился с параметрами
р{ = q{ = о, i — 0, ..., 7; ре'— ?8 = 10; рд = ^э = 6. В масштабе рисунка
график функции f(x) не отличается'от графика сплайна SR(x).
§ 2. Кубические нелокальные сплайны класса С1
Пусть в узлах сетки Д: а = х0 <х{ <...<#* =¦ Ъ заданы
значения /i, i = 0, ..., ^V. Определим интерполяционный кубический
сплайн Sc(x) как функцию, удовлетворяющую условиям:
1) па каждом промежутке lxh xi+\] Sc(x) — кубический
многочлен;
2) Sc(x)e=Cl\a,b];
3) 5с fe +) - Sc (хг -) = a, [^ (x, +) - Sc (xx -)],
* —1 ЛГ —1, A)
где a< — заданные числа;
4) SclxJ-U * = 0 iV.
Отметим, что если ak = 0, то в точке xk сплайн Sc(x) имеет
две непрерывные производные. В частности, при a< = 0, i = l, ...
..., N — 1, Sc(x) переходит в кубический сплайн Six) класса
С2 (гл. III). Для однозначного определения сплайна Sc(x)
необходимы краевые условия. Будем использовать такие же типы
краевых условий, как в § 1 гл. III.
Рассмотрим алгоритм построения сплайна Sc(x). Обозначим
mx = S'c(Xi), i = 0, 1, ..., N. В соответствии с формулой C.1.3)
имеем при х^ [хи xi+i\
Sc (x) = П A - tf (I + 2f) + fi+1t* C - 20 +
+ m,fclt(l-t)»-m1+1M1(l-*), B)
13 10. с. Завь «лов и др.

194 ГЛ. VI. ОБОБЩЕННЫЕ КУБИЧЕСКИЕ СПЛАЙНЫ
где hi = xi+\ — хь t = (# — Xi)/hu Вычисляя отсюда величины
$с{хг+), S'c(xi—), Sc(zi+)y Sc(zi—) и подставляя их в A),
получаем
О)
1-1, ..., TV —1,
где |i< = hi-i/(hi-\ + /г»), X* == 1 — М-*-
К этим уравнениям нужно добавить соотношения,
вытекающие из граничных условий. Они записываются точно так же,
как и в случае кубических сплайнов класса С2. Например, для
краевых условий типов I и II соответственно имеем
то = /о» mN = /n, D)
Существование сплайна Sc(x) не гараитнровагто для
произвольных параметров аи Однако при выполнении неравенств
сплайн 5с(х) существует и единствен для всех типов граничных
условий. Это следует из того, что в этом случае матрицы нсе\
систем будут с диагональным преобладанием.
Отметим некоторые интересные с практической точки зрения
варианты выбора параметров а*. Для определенности будем
рассматривать сплайн с краевыми условиями типа f.
Пусть oti = — Af/3, i=l, ..., /V—1. В этом случае система
C), D) становится двухдиагопальной:
™>0 = /о,
т» = /л-,
что позволяет находить неизвестные mt робурреитным образом,.
ве прибегая к алгоритму прогонки. При этом наличие
диагонального преобладания обеспечивает устойчивость вычислитель-

§ 2. КУБИЧЕСКИЕ НЕЛОКАЛЬНЫЕ СПЛАЙНЫ КЛАССА С 195
ного процесса. Аналогичная ситуация получается, если
положить а< = /&i-i/3, i = 1, .. .,/V — 1.
Возьмем в i-u уравнении C) a, = /&*-i/3, а в (i+D-м
af+i в - hi+x/3. Тогда
+х) -+V""« - vB+ад ^+*¦ *icr-
С)
и, следовательно, величины ти mi+\ определяются независимо
от других уравнении. Таким образом, на отрезке [хг1 Xi+\] сплайн
Sc(x) становится локальным.
Еще один интересный случаи получается, если все параметры
а,- равны нулю, за исключением одного, например aft, равного
hh-\/3 или — hk/3. Нетрудно видеть, что при этом сплайн Sc(%)
-состоит из двух кубических сплайнов класса С2, состыкованных
в точке xh до непрерывности первой производной.
Коэффициенты одного из этих сплайнов, определяются независимо от
коэффициентов другого, что позволяет использовать такой выбор а„
например, для устранения осцилляции.
Получим оценки погрешности интерполяции для указанных
частных случаев выбора параметров а*.
Лемма 6.1. Пусть f (x) ^Wi\a, b]. Если Sc(x)
удовлетворяет граничным условиям одного из типов I—III и каждый из
параметров а, равен /г^/З или — АУЗ, то
ki-/'i<~il/IVW«oo, * = 0, ...,ЛГ. (8)
Доказательство. Рассмотрим случай граничных условий
типа I. Из C), D) для величии дг = тп{ — ft имеем систему
ft+ieCf, * = 1,2,...,ЛГ-1, (9)
= qs = 0,
где
12*

196 ГЛ VI. ОБОБЩЕННЫЕ КУБИЧЕСКИЕ СПЛАЙНЫ
Используя формулу Тейлора, получаем при а* = —
Сг = у ^ J ^ - Т)8 /IV fo + Tfei) dT ~
1
- \Ш-г J * [(l +-^) т - (l + A-)]
0
,_, + rh^) dr.
Применяя к интегралам неравенство Гёльдера, находим
\а\< V*' (*Г + Ч И /rv (*) «~ < § 11 /IV (x) Ik. (И)
Такая же оценка получается и при <Xi= fet--i/3.
Из (9) и A1) вытекает требуемая оценка (8).
Другие типы краевых условий исследуются подобным
образом.
Теорема 6.1. Пусть Sc(z) интерполирует функцию /(#)е
е Wto [а, Ь] и удовлетворяет граничным условиям одного из ти~
пов I, II, III. Если каждый из параметров а< равен hi~\/3 или
-hJ3, то
*-г | /iv од |epf r M о, 1, A2)
гй<? Ао-3/128, ^i - 1/12.
Доказательство. Техника доказательства — такая же,
как и в случае кубических сплайнов класса С2 (теория 3.5).
Для получения оценок используются неравенства
I S{cr) (х) - fr) (х) | < | Sft (z) - fT) (x) | + | SP (x) - Sir,\ (x) |, A3)
где ?з,2(#)—- кубический эрмитов сплайн. Имеем
I Sc (х) - 53,2 (*) | < t A - 0 max | mi ~ f\ \hu A4)
|;||т4—/;|. A5)
Используя теперь лемму 6.1, а также поточечные оценки для
погрешности приближения сплайном Sz${x) (§6 гл. VII), из
A3) — A5) приходим к A2). •
Сравним полученные результаты с аналогичными
результатами для кубических сплайнов класса С2 (таблица 3.3).
Во-первых, отметим, что постоянные в оценках A2) примерно в два
раза больше. Во-вторых, выше требования к гладкости
интерполируемой функции. Читатель может проверить, что. эти
требования по существу. Так, если допустить наличие разрывов у
функции /"'(#) в узлах сетки Д, то порядок приближения в

§ 2. КУБИЧЕСКИЕ НЕЛОКАЛЬНЫЕ СПЛАЙНЫ КЛАССА С1 197
оценках A2) снижается на единицу. Эти замечания следует
иметь в виду при использовании «удобных» значений
параметров аи
Можно показать, что при значениях параметров аг^ (— hi/3,
hi-\/3) оценки будут лучше, чем в доказанной теореме.
Естественно возникает воцрос о поиске оптимальных величин а*.
Лемма 6.2. Если f(x) e Wbx [a, 6], Sc (x) удовлетворяет
граничным условиям типа I или III и
°Ч == Г \'Ч—1 — 'Чь fr = 1, • • •, iV — 1, VAU/
о '
ГО
I mi—/i I ^ cq ^4|/v (^)IU, i = 0, ..,,N. A7)
Доказательство. Из A0) по формуле Тейлора
с% = 24 ^*-1^* K^i—1"~ ^0 — 6ai] Д +
о
Отсюда, в соответствии с A6),
1
+ g Х,Л?-, J [т4 B -f A-) - 2x*(l + ^-)] /v (г,-1 + xhi-J dr.
о
Применяя к интегралам неравенство Гёльдера, получаем оценку
Iс' I < ш hihi~i {hi + hi~iJ1/v (x) H- < iS>й4 II/v (x) II-' A8>
из которой вытекает A7).
Теорема 6.2. Если /(i)Gf'Jo(a, i], Sc(%) удовлетворяет
граничным условиям типа I или III u параметры а<
определяются формулами A6), го
1 S^ (*) - /(Г) («) I» < ^О,гЙ4~Г | Г (X) Цоо + КХ,гкЪ~Г II /V («) Hoc,
г-0, 1,
где ^0,0 = 1/384, ifOii = УЗ/216, Klfi = 1/240, Ки == 1/30.

198 ,ГЛ. VI. ОБОБЩЕННЫЕ КУБИЧЕСКИЕ СПЛАЙНЫ
Доказательство основано на использовании неравенств
A3) —A5), теоремы 2.5 и леммы 6.2 и не вызывает затруднений.
Таким образом, сплайн Sc(x) с «оптимальными» значениями
параметров а* A6) при интерполяции достаточно гладких
функций на произвольной неравномерной сетке обеспечивает
практически такую же точность приближения, как и кубический
эрмитов сплайн.
Задача. Указать набор параметров а* таких, что Sc (х) не существует.
§ 3. Дискретные кубические сплайны
При построении сплайнов для стыковки звеньев между собой
мы накладываем ограничения на производные сплайна (обычно
требовалась их непрерывность). Однако этот способ не является
единственным. В данном параграфе рассматривается другой
подход, состоящий в том, что стыковка звеньев осуществляется
путем приравнивания разделенных разностей от многочленов,
описывающих соседние звенья сплайна.
Пусть на отрезке [а, Ъ] задана сетка А: а = хо < ... < xN = 6,
в узлах которой известны значения /,-, i = О, ..., N. Дискретным
интерполяционным кубическим сплайном назовем функцию
SD(x), которая
1) на каждом из интервалов О,-, xi+\] является кубическим
многочленом
з
SD (х) е== Р* (х) = ^ аи {х - х{)\ х е= \хи xi+l];
3=0
2) при заданных г{ > 0, i = 1, ..., N — 1,
Р1 (х. + г,) - Р1 (*¦ - е,) Р*~* {х{ + е,) - Р1'1 {х. - г{)
? f
B)
3) SD{xi)~fu i = 0, ..., N.
Условия A), B) можно рассматривать как дискретный аналог
условий непрерывности первой и второй производных. Этим и
объясняется употребление термина «дискретный сплайн».
Очевидно, при е* -*• 0 дискретный кубический сплайн переходит в
кубический сплайн класса С2.
Для сплайна SD(x) необходимы граничные условия, в
качестве которых будем рассматривать условия типов I—IV,
сформулированные в § 1 гл. III.

§ 3. ДИСКРЕТНЫЕ КУБИЧЕСКИЕ СПЛАЙНЫ
199
Рассмотрим алгоритм построения дискретного сплайна.
Введем обозначение
ЛГ1 = ±(Рг(х1 + *г)-2Рг{*1)+Р1(х1-Ъ)), * = 0, ..мЛГ, C)
e
Нетрудно видеть, что в таком случае сплайн SD(x) при х^
^ [#г, xi+\] записывается в виде
SD(x)^fi(l^t)+tfi+l-t^^hUB^t)Mi + (l + t)Mi+lh D)
где hi = xi+\ — хи t = (x — хд/hu
Формула D) по виду совпадает с формулой C.1.10) для
кубического сплайна класса С2. Различный смысл имеют лишь
величины Ми
Отметим, что из D) следуют соотношения
SD{xi+)=-SD(xi-) = Mu * = 0 iV. E)
Сплайн SD(x), записанный в виде D), удовлетворяет
условиям интерполяции и условиям B).
Подставляя в A) вычисленные из D) значения сплайна,
получаем
i + 1
li-hzLb.±i) i = i
где, как обычно, jli,- = hi-\/(hi-\ + ht), ta = 1 — f.i<.
К этим соотношениям необходимо добавить уравнения,
вытекающие из граничных условий. В периодическом случае
добавляется уравнение F) с индексом ?= N и полагается Mq — Mn.
В непериодическом случае, как это следует из E), граничные
уравнения совпадают с аналогичными уравнениями из § 1 гл.
III. Например, для условий типа II имеем
Л/о = /о,
Обозначим
hUi
— hi
1 — —
Легко проверить, что
r{ > 1, если ег < max {/гг-1, Аг},
r< = 3, если е? >max{Ai-i, fej.
G)
(8)
(9)

200 ГЛ. VI. ОБОБЩЕННЫЕ КУБИЧЕСКИЕ СПЛАШТЫ
В силу этих соотношений матрицы систем относительно
неизвестных Mi будут с диагональным преобладанием при любых
Ei и для всех рассматриваемых типов краевых условий. Тем
самым обеспечивается существование и единственность
дискретного кубического силайна при произвольных е*.
Что касается различных частных случаев выбора "параметров
е*, то положение здесь аналогично рассмотренному в
предыдущем цараграфе. В частности, можно построить дискретные
сплайны, не требующие применения алгоритма прогонки,
локальные дискретные сплайны и т. д. Отметим один интересный
случай. А именно, если при равномерной сетке положить е< = &,
то из F) получаем
< ч
Перейдем теперь к исследованию погрешности интерполяции
кубическими дискретными сплайнами.
Лемма 6.3. Если SD(x) интерполирует функцию /(х) е
е Wi> Ja, Ь] и удовлетворяет краевым условиям одного из типов
I, II, III, то при е, < max {A<_i, A,}, i = 1, ..., N — 1,
1|1У A0)
а при 6i>max{A,-.b /г*}, i = 1, ..., N — 1,
\М. _ /'. |^ |max e; |/JV (x) JU, A2)
f^^|U A3)
Доказательство. Рассмотрим, например, случай
граничных условий типа II. Из уравнений F), G) для неизвестных
= Мi — f\ имеем систему

§ 3. ДИСКРЕТНЫЕ КУБИЧЕСКИЕ СПЛАЙНЫ
201
где
6 //,+,-/, W,- ef N
Используя формулу Тейлора в точке я(, получаем
*?-,
т* —т 1 —
'i-l
/ (л:;-.! +xAi_1)<
A _ т)» — A — Т) 1
-*>]¦
Применяя неравенство Гёльдера и рассматривая различные
варианты соотношения шагов A(_i, /it и параметра е^ находим:
\di\<jh*\\flw(x)U если в,
|d,Kf eil/ WiU, если e,s
Теперь из A4), учитывая (9) и следствие Д.1, получаем
оценки A0), A2).
Далее из формулы D) имеем
S* (х ^ = fi+*-fi _ ^L
Отсюда
t ! I,
A5)
где
Последовательно применяя формулу Тейлора и неравенство
Гёльдера, получаем
1
1
1а
Учитывая найденную оценку, а также принимая во внимание
A0) и A2), из A5) выводим неравенства A1),, A3) для 5^(я.-М.
Аналогичным образом они получаются и для »SW«. —).

202 ГЛ VI. ОБОБЩЕННЫЕ КУБИЧЕСКИЕ СПЛАЙНЫ
Теорема 6.3. Если SD(x) интерполирует функцию
^lWIo\u. b\ и удовлетворяет краевым условиям одного из типов
I, II, 111, то
1 S# (х) - /(г) (х) loo < lK0JiA-r + КХш&-т max e?J || /Iv (x) |U
г^О, 1, 2, 3,
где
#0i0 - 17/384, #0, = 1/6, #0i2 = 3/8, #0>3 - 1/2 + р/2,
#1|Г - 0, г - 0, 1.2, 3, р =¦ /
если ?г <max {Af-i, АД, ?= 1, ..., iV — 1;
ХО)о = 5/384, iCo.i = 1/24, Х0J = 1/8, Я0,з = 1/2,
JSTi,о = 9/384, Ки = 1/12, #1,2 = 1/6, #1,з = р/3,
€С^ггг ef > max {A<-i, АД, г = 1, ..., yY — 1.
Доказательство сформулированной теоремы
выполняется на основе леммы 6.3 и ничем не отличается от доказательства
теоремы 3.5.
Требования к гладкости интерполируемой функции здесь
выше, чем для кубических сплайнов класса С2. Очевидно, не
следует выбирать параметры е* чрезмерно большими.
Целесообразно ограничиться значениями е,-^ max {Аг_1, АД. Отметим, что
для конкретных значений е* постоянные в оценках A6) могут
быть уменьшены.
Большой практический интерес представляет следующая
Теорема 6.4. Если SD(x) интерполирует функцию f (x) e
G Woo [а, Ь], удовлетворяет краевым условиям типа II или III и
е? = 4-(Л?_1-Л1_1Л, + Л?). i = l,...,N-l, A7)
ТО
I Mi - п |< ^ fr | /V (т) I + | А« 1Г (х) U), A8)
г = 0, ...,Лг.
?с^1г сетка Д равномерная, то
|Mi-/;|<-T^^||/VIH|U * = 0 ЛГ. A9)
Доказательство. Используя формулу Тейлора, получаем
для правых частей системы A4) выражение
Ъ = Т (~ Л'-1 + ft'-l/li - й? + 2е|) /*V +
+ ж ^ - hi-i) [1Ое* -7 (fei-i + h')} /T +

§ 3. ДИСКРЕТНЫЕ КУБИЧЕСКИЕ СПЛАЙНЫ
203
3A-тM-10A-тK l--f
rlV
Коэффициент при /* обращается в нуль в силу A7).
Коэффициент при /7 равен нулю для равномерной сетки, а для
неравномерной сетки с учетом A7) принимает вид
~hi
i [2 (к-,. -
и, как нетрудно видеть, не превосходит /г3/30.
Оценим интегральные слагаемые в формуле B0). В случав
неравномерной сетки точные оценки получить довольно трудно.
Поэтому мы ограничимся здесь сравнительно грубой оценкой.,
Находим
(|3t5-iot3(i- Fr
Аналогично, второй интеграл оценивается величиной
Если учесть, что для равномерной сетки г\ — h2/2, то в этом
случае каждый из интегралов не превосходит C/4) Ii/VI(#)IL.
Объединяя полученные оценки, имеем при неравномерной
сетке

204 ГЛ. VI. ОБОБЩЕННЫЕ КУБИЧЕСКИЕ СПЛАЙНЫ
Так как
то отсюда
* К w (Кз
Для равномерной сетки
|<М<55-И/У1(*)|Ж. B2)
Из формулы (8) при выполнении условий A7) нетрудно
получить оценку r{ ^ 2. Утверждение теоремы вытекает из B1), B2)
и следствия Д.1.
§ 4# Кубические сплайны с разрывными производными
В математической физике часто приходится иметь дело с
непрерывными, кусочно-дифференцируемыми на [а, Ъ\
функциями fix) такими, что выражение p{x)f'(x) (поток), где р(х)
кусочно-непрерывна, является непрерывной функцией. Рассмотрим
сплайны, которые можно применять для интерполирования
подобных функций.
Пусть в узлах сетки Д: а = хо< .. .< xN = Ь заданы
значения ft, i = 0, ..., N. Введем кусочно-постоянную функцию р(х)
такую, что р(х) = р{ Ф 0, x^lxu xi+\]. Определим сплайн Sp(x)
как функцию, которая на каждом из промежутков [хи pi+\]
является кубическим многочленом и удовлетворяет условиям
Sp(xi) = fu i = 0,...,N, A)
Pi-1S%)(xi-) = piS?(zi+), r=\2; *=1, ...,tf-l. B)
Отметим, что цри p\i = p = const, i = l, ..., N — 1, сплайн
Sp(x) превращается в кубический сплайн класса С2. В качестве
граничных условий для введенных сплайнов будем
рассматривать условия тех же типов, что и в § 1 гл. III. При этом в
случае граничных условий типа III (периодических) считаем, что
B) выполняется при i = N и ро — ^л-. Для граничных условий
типа IV полагаем р0 = р\, pN-2 = Pn-i*
Обозначим

§ 4. КУБИЧЕСКИЕ СПЛАЙНЫ С РАЗРЫВНЫМИ ПРОИЗВОДНЫМИ 205
Очевидно, на каждом из промежутков [xiy xi+\] сплайн Sp(x)
можно рассматривать как эрмитов кубический сплайн,
интерполирующий значения /i,/i-i, ?р(^+), Зр(х1+г —)• Поэтому в
соответствии с формулой B.5.1) и условиями B) имеем
Sp (х) = /* A - tf (I + 2t) + /1+1t« C - 2t) +
^^t>, О)
где hi = xi+i — xu t = (x — x{)/ht.
В формуле (З) учтены условия интерполяции A) и условия
<2) при г=1. Дифференцируя C), получаем при же[х{) xi+\]
Отсюда
,A(,+)-^t-/,)-^-^, D)
Определяя из E) Рг-т^р С2^-") и Учитывая условия B) для
г = 2, приходим к соотношениям
Ktmt-i + 2mi+\Limi+\4*ci i = l, ..., iV — 1, F)
где
"i-i "i
К уравнениям F) следует присоединить уравнения,
вытекающие из граничных условий. Для краевых условий типа I они
имеют вид
Для условий типа II
2пъл -4- шл
*о -г "п — у о ° —тг~
1 о
-t \ 3 Nh ^ N-1 -h у f"N |.

206 ГЛ. VI. ОБОБЩЕННЫЕ КУБИЧЕСКИЕ СПЛАЙНЫ
Для краевых условий типа IV, с учетом сделанных выше
соглашений относительно величин р^ получаем
т0
- 7о) Щ - ylm2 = 2р0 l^ - То
= 2/77V-1 h ^Л? Тг '
Г * у nN-l /гЛг-2 /
где Чо=* h^/fiu Чя*=Ъ,я-\/1ък-2.
Наконец, в периодическом случае записываем уравнение (бI
при i = N и полагаем ш0 = тпу, ш\ = /nN+i.
Полученные таким образом системы уравнений для
неизвестных mi отличаются от соответствующих систем для кубических
сплайнов класса С2 только правыми частями. В связи с этим на
вызывает сомнении существование и единственность
рассматриваемых сплайнов.
Исследование погрешности приближения выполняется
совершенно аналогично тому, как это было сделано в гл. ПТ для
кубических сплайнов класса С2. Приведем без доказательства
следующий результат.
Теорема 6.5. Если /(х) е CW\iOO [#, &I и выполнены
условия
р^/(гЧ*«-) = р,/(г)(*,+), г=1, 2; i='l, ..., 7V — 1, G)
где величины рг — такие же, как в условиях B), то
В S{Pr) (х) - fr) (z) U = О (h*-r), г = 0, 1, 2. (8)
Отметим, что условие G) играет существенную роль при
выводе оценок (8). Нарушениеjero для г = 2 приводит к снижению
порядка приближения до Oih2). Однако и в этом случае порядок
О(Л4) будет достигаться, если в окрестности каждой из точек, где
не выполнено G), выбрать узлы сетки специальным образом.
Л именно, если Pi-if"(xi—) Ф /?</" (#<;+), то узел хн\ (xi~\)
должен быть таким, что ht-\ > /га < hi+x (Ы-2 > /г»-1 < А,-).
Выбор величин /?г-, которые необходимы для построения
сплайна Sp(x), не вызывает затруднений, если при
кусочно-постоянной функции р{х) непрерывен агрегат p(x)f'(x). Сложнее
обстоит дело, когда р(х) не является кусочно-постоянной. В этом
случае коэффициенты рг в условиях B) можно выбирать,
например, по формулам
Естественно предполагается, что точки разрыва производной
fix) включены в число узлов сетки Д.
Литература R главе VI. [1, 4, 30, 32, 40, 47—50, 64, 85, 911.

Г л а в а VII
ПРИБЛИЖЕНИЕ КРИВЫХ И ПОВЕРХНОСТЕЙ
В вычислительной практике при работе с геометрическими
объектами, кривыми и поверхностями, нужно иметь их
математическое описание. Традиционные методы аналитической
геометрии позволяют работать лишь с «хорошими» объектами, такими,
как прямые и плоскости, кривые и поверхности второго
порядка и т. п. Если же рассматриваются кривые и поверхности
сложной геометрической формы, например, обводы летательных
аппаратов, корпусов судов, лопасти турбин, для которых нужно
уметь строить гладкие приближения и притом с высокой
точностью, то эти средства оказываются не эффективными. И по
существу только методы, основанные на сплайнах, позволяют
решать подобные задачи.
§ 1. Параметрические сплайны
С помощью рассмотренных в предыдущих главах сплайнов
одной переменной можно приближать лишь такие плоские
кривые, которые в выбранной системе координат (не обязательно
декартовой) описываются функциональной зависимостью вида
у = j(x). Однако не все кривые могут быть представлены
подобным образом (рис. 7.1). Более универсальным способом
является параметрическое задание их координат в виде двух функций
х = х(и), у = у(и) некоторого параметра а.
При интерполяции кривой,
заданной параметрически,
естественно ввести разбиение на
промежутке изменения
параметра и: uo <u>i<.. .< uN, затем
вычислить соответствующие
значения координат точек на Рис. 7.1.
кривой, Xi = x(iii), г/< = г/Cwi), и
построить для функций хЫ), у(и) интерполяционные сплайны
S(x; и), S(y; и). Совокупность этих двух сплайнов называется
интерполяционным параметрическим сплайном. В зависимости
от вида функций Six; и), S(y; и) будем говорить о
параметрических сплайнах первой степени, эрмитовых параметрических
сплайнах и т. д.

208 ГЛ. VII. ПРИБЛИЖЕНИЕ КРИВЫХ И ПОВЕРХНОСТЕЙ
В качестве погрешности приближения кривой
параметрическим сплайном проще всего взять величину
; u)-x(u)\2+\S(y; и)-уШ2. A)
Очевидно, при выполнении определенных требований к
гладкости функций хЫ), у(и) можно оценить выражения \S(x; и) —
—•#(»)!, \S(y; u) — y(u)\ по какой-либо норме, например,
пространства С. Тогда
IIR (и) ||с < V\\ S (х; и) - х (и) |Гс + || S (у; и) - у (и) «?. B)
Главной особенностью практических задач о приближении
кривых является то, что заданы бывают только упорядоченные
массивы точек на них, а информация о способе параметризации,
которая необходима для построения сплайнов, отсутствует.
В дальнейшем мы рассмотрим способы построения
параметрических сплайнов в этой ситуации, уделив основное внимание
интерполяции плоских кривых. Построение интерполяционных
параметрических сплайнов для пространственных кривых
осуществляется аналогичным образом. Разница лишь в том, что
приходится оперировать с совокупностью трех сплайнов одной
переменной.
Гораздо сложнее обстоит дело с приближением поверхностей*
Рассмотренные раньше сплайны двух переменных позволяют
эффективно решать эту задачу только в случае, если поверхность
описывается функциональной зависимостью вида z = /Gr, у) в
прямоугольной области Q. При использовании локальных
сплайнов не возникает трудностей также и для области, составлея-
пой из прямоугольников со сторонами, параллельными осям
координат. В общем случае, когда Q произвольной форАмы, можно
рекомендовать два способа действий. В первом из них область
погружается в прямоугольник и функция fix, у)
доопределяется подходящим образом в точках, не принадлежащих Q (точнее,
в узлах сетки, не попадающих в Q). И затем уже строятся
сплайны па прямоугольнике. Другой подход состоит во введении
в области Q криволинейных координат и, v таким образом,
чтобы она отображалась па прямоугольник в плоскости (w, v).
В частности, если область Q представляет собой круг или
круговой сектор, то можно использовать полярные координаты. Оба
подхода связаны с большим объемом вычислительных, работ.
Таковы трудности, возникающие при приближении
поверхности, заданной в виде z = f(x, у). Однако не все поверхности
могут быть определены подобным образом. Наиболее
универсальным способом является параметрическое представление их
координат в виде трех функций:

§ 2. ИНТЕРПОЛЯЦИЯ КРИВЫХ ЛОКАЛЬНЫМИ СПЛАЙНАМИ 2091
параметров щ v. Естественно в качестве приближения в этом
случае, брать поверхность, координаты которой описываются
сплайнами
Six; и, v), Siy; и, и), Siz; и, v).
Основным препятствием на этом пути, как и в случае
кривых, является то, что поверхность обычно задается
совокупностью точек, лежащих на ней, а соответствующие значения
параметров и, v отсутствуют. Поэтому вначале необходимо
параметризовать поверхность и только потом строить
аппроксимирующие сплайны. Некоторые наиболее употребительные приемы
параметризации будут рассмотрены в § 5.
Для эффективного решения задач математического описания
поверхностей требуются ЭВМ как минимум средней
производительности (~105 операций в секунду) и большим объемом
оперативной памяти. Кроме того, необходимы средства машинной
графики, графопостроители или дисплеи, с высокой
разрешающей способностью.
§-2. Интерполяция кривых локальными сплайнамя
Пусть на некоторой кривой L задана последовательность
точек Pt(xu уд, * = 0, 1, ..., N (рис. 7.2). Введем на ней
естественную параметризацию x = xis), y = yis), взяв в качестве
параметра длину дуги s кривой, отсчитываемую от точки Ро. Узлу Р{
соответствует значение параметра,
равное Si.
1. Рассмотрим
интерполяционный параметрический сплайн
первой степени. Согласно формуле
B.1.2) на промежутке между
точками Р{ и Pt+i он задается
соотношениями
о\\х; s) = vl t)Xi "г txi+ij ,..
S\iy; s) === A — t)yi H~ tyi+\,
где t = is — Si)/li, U = Si+\ — St.
Геометрически параметрический сплайн первой степени
представляет собой ломаную, состоящую из отрезков прямых,
соединяющих точки Р{.
Из A) следует равенство
Sx(x;s)
B
V 7
которое используется для приближенного вычисления наклона
касательной к кривой L между точками Р^ Pi+\. Если Xi
Ю. С. Завьялов и др.

210 ГЛ. VII. ПРИБЛИЖЕНИЕ КРИВЫХ И ПОВЕРХНОСТЕЙ
то это означает, что данное звено сплайна расположено
параллельно оси у.
Отметим интересное свойство формул A), B), а именно:
координаты точек интерполяционного параметрического сплайна
первой степени и угол наклона касательной к нему можно
вычислять, не зная фактически ничего о длине дуги
интерполируемой кривой. В самом деле, по формулам A) эти точки
вычисляются путем задания величины t^lO, U, а в формуле B) правая
часть вообще не зависит от s.
Обозначим через R\(s) погрешность интерполяции
параметрическим сплайном первой степени. Оценить ее можно по
формуле A.2), учитывая оценки, установленные в § 2 гл. II.
Отметим два результата, вытекающие из факта
использования естественной параметризации кривой.
Теорема 7 Л. Ecaux(s), у (s) e Wlo (s0, S;v], то
<y2l/2, C)
где I = max li%
г
Доказательство. По теореме 2.1
Так как величины x'{s) и y'(s) представляют собой
направляющие косинусы вектора касательной к кривой в точке
, г/Ы), то Ня'ЫИоо<1, H/(s)IL^l и из A.2) следует C).
Теорема 7.2. Если x(s), у (s) e= CWii<x Но, sN], то
^k, D)
где K(s)— кривизна кривой L.
Доказательство. Согласно таблице 2.1 имеем
Кривизна кривой в точке (x(s), y(s)) определяется равенством
K(s) = Пх"Ш2+1у"Ш2, и, значит,
Wx" (e)IL < ИЯЫИоо, Ц"
Для завершения доказательства теперь достаточно обратиться к
формуле A.2).

§ 2. ИНТЕРПОЛЯЦИЯ КРИВЫХ ЛОКАЛЬНЫМИ СПЛАЙНАМИ 21 f
Так как построение параметрического сплайна сводится к
построению двух сплайнов одной переменной, то остаются в силе-
все рекомендации по выбору узлов интерполяции, сделанные
в § 3 гл. П. Практическое применение оценок C), D) затруднена
присутствием в них величины I. Если обозначить через dt длину
хорды, стягивающей концы дуги U, то при достаточно густом
расположении узлов интерполяции на кривой L имеем dt ~ h и:
вместо I можно использовать реально вычислимую величину d =
= max di.
i
2. Параметрическим эрмитовым кубическим сплайном будем
называть совокупность двух эрмитовых сплайнов 5з, 2^х; $\
Sz,2^y\ s). Погрешность интерполяции Rz(s) для такого сплайна
можно оценить обычным способом с помощью формулы A.2)г
используя результаты § 6 гл. И. В частности, имеет место
Теорема 7.3. Если x{s),> у (s) e Wl> [s0, sN], то
Если x{s), у (s) e ClC\ \sQ, sN], то
Доказательство очевидно.
Отметим, что максимальный порядок приближения
параметрическим эрмитовым сплайном есть ОA4). Этот порядок
достигается, если х (s), у (s) e ClW\jOO |s0, s.v|.
На практике применение параметрических эрмитовых
кубических сплайнов, построенных на основе естественной
параметризации кривой, обычно оказывается невозможным. Действительно,,
чтобы вычислять, например, значения сплайна
58.2 (*; s) = хг A - tf A - 20 + xi+lt* C - 20 + x\t A - 02А -
#i+1?2 A t)h G)
(здесь я* означает производную по параметру s в точке $*),
необходимо знание величии Z?-, х.;, Х|+1. Такая информация, как
правило, отсутствует. Поэтому вместо сплайна S3, г(#; s) будем
строить в некотором смысле близкий к нему сплайн ?3, г(#; ^).
Во-первых, точные значения производных х% заменим
значениями х\ по формулам, аналогичным B.8.1) —B.8.3):
^.. ;__ ц. Лр. —^. ^л ^Т j_ j^-. /^. ^. \ C^~2 i = 1 JV 1 (^9V
14*

212 ГЛ. VII. ПРИБЛИЖЕНИЕ КРИВЫХ И ПОВЕРХНОСТЕЙ
XN= A -f" ^iv-l) (#JV — ^ЛГ-l) djv-i — Я;у-1 (#JV— 1 — #2V-2) ^
)"
(Hi d|i (^-i + |) , i (ji
Если кривая замкнута, т. е. точки Ро и PN совпадают, то вместо
<8), A0) следует использовать формулу
dN-l
Во-вторых, для описания сплайна введем параметризацию по
суммарной длине хорд du Если обозначить новый параметр через
?, то сетка узлов будет А: 0 = so < s\ <.. - < sN, где
^ t-i
Параметр 5 при этом пробегает отрезок [0, sN].
Тогда эрмитов кубический сплайн принимает вид
Зз,2 (*Г*) = Щ A - tf A + 20 + *i+i*2 C - 20 +7{t A ~ Q44 -
-*;+1*2A-*Иь A2)
где ^ = (s — Si)/du Все величины, входящие в выражение для
^з, г(#; ^), реально вычислимы. Аналогичные формулы
получаются и для 5з. г(у; $)•
Нетрудно видеть, что параметрический эрмитов кубический
сплайн не меняется при переходе к новому параметру s =» 7^,
где y — произвольное положительное число. Действительно,
в этом случае значения s{ переходят в ^su величины <2t=s{+1—st —
в ^й{ и из (8) — A0) следует, что %i переходят в у~хХ{. Обра-
"щаясь к формуле A2), убеждаемся, что ^-координаты точек
параметрического сплайна не изменяются. То же самое
справедливо и для г/-координат. В некоторых случаях удобно полагать
7 = sn1- При этом s^ [0, 1]. Будем называть такую
параметризацию нормированной параметризацией по суммарной длине хорд.
Рассмотрим вопрос об оценке погрешности интерполяции
||Я@||с = тах||Д{@!с, A3)
где величина
V
>-x(s)\$ + \\S3ii(y,s)-y(s)lc
характеризует отклонение сплайна от кривой на промежутке
между точками Pt и Р{+\. Здесь s — St + lit, s*=*Si + dj, и
сравнение сплайнов и функций x(s)t y(s) делается при одинаковых
значениях промежуточного параметра t.

§ 2. ИНТЕРПОЛЯЦИЯ КРИВЫХ ЛОКАЛЬНЫМИ СПЛАЙНАМИ 213
Установим два вспомогательных результата.
Лемма 7.1. Если х (s), у (s) e Wl> [su si+1], то
di = h+O(lf). A4)
Доказательство. Используем тождество
1\ — d\ = 1\ — (xi+1 — x{f -у (yi+1 — уг)\
Jlo формуле Тейлора получаем
*Hi — х{= 1гх'г+1/2 + О (li)y yiJrl — ух-* hy'i+i/г + О (if),
где x'i+1/2 = x1 (Si + h/2), y'i+i/2 = у' ($i + h/2). Следовательно,
Так как кривая параметризована естественным образом, то
U'E)]2 + ly'(s)]2 = 1. Поэтому Z? ~d\ = O Of), откуда
Ь - Ъ = (Zf - d?) (k + d-)-1 = О (if).
Если сетка узлов достаточно густая, то l{»dt и из A4)
следует
ii- = l + O(Z?). A5)
Лемма 7.2. Если x(s), jf(s)eFL[so,sA-], го
*; = *;+О (]*), < = 0 ЛГ, A6)
где х\ определяются формулами (8) — A0).
Доказательство. Разлагая в (9) xi+\ и х{-\ по формуле
Тейлора в точке su находим при i = 1, ..., N — 1
Используя лемму 7.1, получаем соотношения
Но тогда для х{ верна формула A6). Точно так же, исходя из
(8) и A0), ее можно проверить при г«=0, N.

214 ГЛ. VII. ПРИБЛИЖЕНИЕ КРИВЫХ И ПОВЕРХНОСТЕЙ
Аналогичные результаты имеют место и для*/!.
Теорема 7.4. Если х (s), у (s) щ Wl> [s0, sN], то
Доказательство. Очевидно,
\&,2(х; $)-s(s)l < 15з.2(^; 5)-53,2(^; 5I + \S3t2(x; s)-x(s)\.
Для второго слагаемого правой части по теореме 2.5 имеем
\Sz,2(x; s) — x(s)\ =*O(P). Далее, учитывая G), A2), получаем
<* (l - tf [\х\-х[ | и +~x\ | и - di|} +
+ *2 A - *) {| xi+1 - 7i+11 h + 7i+1 \h-di\
Отсюда, принимая во внимание леммы 7.1 и 7.2, находим
15з.2(я; s)-S3>2(x; s)\
Следовательно,
Аналогично,
Г =O(J3).
Из полученных соотношений вытекает утверждение теоремы.
Порядок погрешности Oil3), гарантируемый теоремой 7.4, паи-
высший. Дальнейшее повышение гладкости функций х($), y{s)
не изменяет его. Вероятно, нелишне подчеркнуть, что если
оценки остаточного члена E) и F) имеют место при любых /, то-
^ ^ оценка A7) как оценка по порядку
справедлива только при достаточно малых I.
Приведем несколько примеров интерполяции
кривых параметрическими эрмитовыми кубическими
сплайнами с использованием описанной техники. На
рис. 7.2 представлены результаты интерполяции
последовательности заданных точек Ро, ..., Pn. На
рис. 7.3 показан характер интерполяции нерегулярной
кривой — единичного квадрата. Наличие особенностей
" в его вершинах приводит к потере точности. Однако
Рис. 7.3. здесь можно применить технику борьбы с
особенностями, описанную в § 8 гл. П. Если в соответствии с
этим ввести дополнительные узлы (отмечены знаком •), то отклонение
сплайна от кривой не превышает 0,002, в то время как без них оно
составляло 0,04. На рис. 7.1 приведен сложный пример интерполирования кривой,
содержащей различные по характеру звенья, а также нерегулярные точки.

§ 3. ИНТЕРПОЛЯЦИЯ КРИВЫХ КУБИЧЕСКИМИ СПЛАЙНАМИ 215
На практике широко используются различные варианты рас-
смотренных сплайнов, отличающиеся в основном способами
вычисления касательного вектора (значения #ь 2/0-
Задача. Построить алгоритмы для вычисления координаты у
интерполяционных параметрических сплайнов первой и третьей степеней по
заданной координате х.
§ 3. Интерполяция кривых параметрическими
кубическими и рациональными сплайнами
1. Интерполяционный параметрический кубический сплайн
есть совокупность двух кубических сплайнов Six; w), Siy; и)
класса С2, интерполирующих соответственно координаты х^ у\
точек Р„ i = 0, ..., iV, кривой L на сетке Д: щ< щ < ... < uN.
Для однозначного определения каждого из этих сплайнов должны
быть заданы краевые условия. Будем полагать, что для обоих
сплайнов они одинакового типа. Если кривая незамкнутая, то
удобЯо применять краевые условия типа IV, а для интерполяции
замкнутой кривой естественно использовать периодические
краевые условия (тип III).
В качестве параметра снова берем суммарную длину хорд s.
В этом случае, согласно формуле C.1.10), сплайн Six; s) может
быть записан в виде
S(х; 7) = х{ A- t) + *i+1t- ^Ц=^ d\ [B-0 Mi + (l+t)Mi+1l A)
где t = is — Si)/du di=: si+\ — Si. Величины М{ определяются из
систем уравнений C.1.15) — C.1.18), в которых /г< заменяется на
du Например, для периодических сплайнов система имеет форму
{Ж_, + 2Mt +\iMi+l = ЗЁи * = 1....,ЛГ, B)
где Hi — dj-iWj-i + dt)~\ kt — i — ц.-,
Аналогичные формулы имеют место и для сплайна Siy\ s).
Погрешность интерполяции параметрическим кубическим
сплайном определим формулой B.13), где положим
1 Я{ (t) [с - V\\ S (x; 7)-x (s) ||S +«S (у; 1)-у (,) $. C)
Как и в предыдущем параграфе, сравнение сплайнов и
интерполируемых функций делается при одинаковых значениях
параметра t. Получим оценки погрешности интерполяции. При этом,

216 ГЛ. VII. ПРИБЛИЖЕНИЕ КРИВЫХ И ПОВЕРХНОСТЕЙ
чтобы не загромождать изложение, рассмотрим только случаи,
когда кривая L замкнута.
Наряду со сплайном Six; s) введем сплайн Six; s), построен*
ный с использованием параметризации по длине дуги:
Six;s)^xiil^t) + txi+l^t^^lUi2-t)Mi + {l+t)Ali+1l D)
Здесь Mi вычисляются из системы
\LiMi-! + 2Мг + UMi+l = 3?|, * = 1, 2, . . ., А', (Г)>
где уц = li-\/(U-\ + h)-\ h «= 1 — fii,
Лемма 7.3. Если xis), у is) e C2W%iOO [50, s.v|, ™
Л?,-ЛГ,-О(Г), г=^0, ..., iV. F>
Если, кроме того,
Zi-i = Zi + O(/?). * = Of...,iV-lf G)
Доказательство. Вычитая из уравнений B) уравнения
E), получаем
- Л/г+i), « = 1, • • •, N. (9)
Имеем
h-\d\ —
Подставляя сюда d<_i, d< из B.14), находим
A0)
Дадее, используя формулу Тейлора, получаем ?» = #"(!)>
gef^-ь 5<+il. Воспользовавшись теперь следствием Д.1, из
системы E) выводим оценку

§ 3. ИНТЕРПОЛЯЦИЯ КРИВЫХ КУБИЧЕСКИМИ СПЛАЙНАМИ 217
Разлагая в формулах для 2?< и Е{ величины xi+\, #<-i как
фупкции параметра s по формуле Тейлора в точке su находим
«*»_!
+ о G2).
Применяя лемму 7.1, последовательно получаем
_ о ,73
Аналогично, коэффициент при х;_ —величина порядка
Таким образом, все слагаемые в выражении Ei — Eif кроме
первого, имеют порядок ОA2) и выше. Оценим
Так как d\ = to+1 — x{J + {yi+1 — ytf и
+ 7% x"i+1/j* + О
TO
Учитывая тождество [x'(s)]2+ [y'(s)]2^ 1 и вытекающее из
него после двукратного дифференцирования соотношение
х'ШтЬ) + y'(s)y'"(s) - -\х* Ы12 - [
получаем

218 ГЛ. VII. ПРИБЛИЖЕНИЕ КРИВЫХ И ПОВЕРХНОСТЕЙ
Представляя таким же образом di_i, имеем
l\d\ Jd? = 'i^i [^?/^i ^/^i + О 0?)
Так как K\+ll% = K\+O (Z4), #i-i/2 - Я? + О (Zw), то
Отсюда А{ = 0A). Если же выполнено условие G), то/? — it-i —
() и 4i«0("p). В итоге
Ei-Ei = l) A2)
10 (Z2), если выполнено условие G).
Учитывая теперь оценки A0), A1), A2) и следствие Д. 1, из
системы (9) приходим к оценкам F), (8).
Теорема 7.5. Если х (s), у (s) e C2W%tOO [s0, sN]y то
Если, кроме того, выполняется условие G), то
Доказательство. Очевидно,
\S(x\ 7)-x(s)\<lS(x; s)-Six; s)\ + \S(x; s)-x(s)\. A3)
Для второго слагаемого в правой части по теореме 3.5 имеем
\S(x; s)~x(s)\=O№. A4)
Что касается первого слагаемого, то из A) и D) следует
S (x; s) — S (х; 1) =
= 1 t(l - t) d\ |B - t) (J\U - Щ + (l + t) (Mi+l - Mi+1)] +
+ i * A - t) [B - t) (Z? - d\) Мг + A+ t) (Z?+l ~ d\+1) A/i+1].
Отсюда, учитывая оценку (И) и лемму 7.1, выводим
| S (х) 7) - S (x; s) |< max | Mi - М{ \ О (Z2) + 0A% A5)
Используя теперь лемму 7.3, из A3)—A5) получаем
rs)-x(s)\ = [0{iy
[О (Z4), если выполнено условие G).

§ 3. ИНТЕРПОЛЯЦИЯ КРИВЫХ КУБИЧЕСКИМИ СПЛАЙНАМИ
219
Точно такие же оценки справедливы и для \S{y; s) — y{s)\.
Теперь утверждение теоремы вытекает из формулы C).
Как видно, наивысший порядок погрешности ОA4)
обеспечивается при условии G),. т. е. когда соседние звенья кривой
отличаются на малые второго порядка. На практике более полезны
другие условия, равносильные G), а именно
i = l, ...,/V-l. A6)
В частности, при малых U можно выбрать d{ = d = const и тем
самым добиться наибольшей точности приближения.
На рис. 7.4 представлен пример интерполяции параметрическим
кубическим сплайном. Всего использовано 18 узлов, причем на границах
прямолинейного участка кривой были взяты по два близких
узла. Если этого по сделать, то возникают заметные
осцилляции (см. § 5 гл. III).
2. Среди всех сплайнов, используемых при
аппроксимации кривых, наиболее
универсальными свойствами обладают параметрические
рациональные сплайны. Они представляют собой
совокупности пар рациональных сплайнов SR{x; s),
SR{y; s). В качестве параметра будем брать по-
прежнему суммарную длину хорд. Согласно F.1.1)
каждый из сплайнов SR(x; s) и SR(y; s)
представляется на участке между точками Рг, Pi+\
в виде
Sя \х\ s) = A\t -\- В% A — t) -j-
i+P{{l-t)
A7)
Таблица 7.1
где pi, g<— заданные числа (—Kpf, qt <<*>). Величины ри q{
целесообразно выбирать одинаковыми для обоих сплайнов.
Параметрический
рациональный сплайн при Pi=qx=
= 0, i-0, ..., ЛГ-1,
превращается в
параметрический кубический сплайн.
В пределе при ри q{ -*- оо?
i = 0, ..., N — 1, имеем
параметрический сплайн первой
степени. Выбором величин р<,
qt обычно удается при относительно малом числе узлов
интерполяции обеспечить и высокую точность приближения, и хорошио
качественные характеристики. Например, выбирая их достаточно
большими, можно полностью устранить осцилляции.
N
4
6
20
0,12
0,03
0,00023
0,03
0,004
0,00026

220
ГЛ. VII. ПРИБЛИЖЕНИЕ КРИВЫХ И ПОВЕРХНОСТЕЙ
Возможности параметрических рациональных сплайнов демонстрирует
рис. 7.5 E3 узла интерполяции).
В таблице 7.1 приведены результаты интерполяции окружности
единичного радиуса при использовании N равномерно расположенных на ней
узлов интерполяции. Через еи е2, ег обозначены
отклонения по радиусу соответственно для
параметрического эрмитова (§2),
параметрического кубического и параметрического
рационального (pt = qi = —0,29) сплайнов. Все сплайны
строились периодическими.
Если использовать для интерполяции
единичного квадрата только четыре узла,
расположенные в его вершинах, то при pi = qi = 10*
отклонение параметрического рационального
сплайна от квадрата не превышает 5-Ю.
В заключение отметим, что
параметрические кубические и рациональные
сплайны не изменяются при переходе к
нормированной параметризации по суммарной
длине хорд.
§ 4. Сглаживание кривых
На практике кривые задаются
точками. Координаты точек получаются в
результате некоторых измерений и поэтому
содержат ошибки, абсолютная величина
которых обычно известно. В этой
ситуации естественно строить не интерполя-
Рис. 7.5. ционный параметрический сплайн, а
сглаживающий. В § 2 гл. IV описана
методика построения кубического рглаживания сплайна. С
небольшими изменениями, связанными с параметрическим заданием
кривой, эта методика применима и в данном случае.
Параметрический сглаживающий кубический сплайн будем
рассматривать как совокупность двух сглаживающих кубических
сплайнов Six; s), Siy; s). Для каждого из них зададим
допустимый «коридор» и будем использовать при вычислении весовых
множителей итерационный процесс, описанный в § 2 гл. IV.
Параметризацию возьмем по суммарной длине хорд. Отметим,
что в ходе сглаживания изменяется расстояние между точками
и поэтому на каждой итерации необходимо осуществлять
пересчет параметров s{. Сглаживающие сплайны Six; s), Siy; s) можно
строить либо последовательно: сначала, например, сгладить
величины Xi, а затем у<; либо одновременно, сглаживая на каждой
итерации и #,-, и у{. В любом случае после завершения процесса
сглаживания из-за изменения значений s< необходимо построить

§ 5. ПРИБЛИЖЕНИЕ ПОВЕРХНОСТЕЙ
221
по сглаженным значениям координат #, у параметрический
интерполяционный сплайн.
X
0,0
0,25
0,5
0,75
1,0
1,25
2,5
5,0
7,5
10
15
20
25
30
35
40
V
0,0
7,35
9,8
11,45
13,25
14,7
20,25
25,8
30,0
33,1
38,15
42,0
45,2
47,45
49,05
49,9
К(х% у)
—0,007
-0,013
—0,037
0,030
—0,039
0,023
-0,050
—0,078
—0,043
-0,012
—0,025
—0,007
-т0,032
-0,020
—0,013
-0,093
"х
0,0
0,27
0,50
0,70
0,96
1,20
2,54
4,96
7,54
9,96
15,00
19,96
25,05
29,96
35,00
40,00
Та
и
0,0
7,36
9,81
11,47
13,27
14,72
20,22
25,80
29,99
33,09
38,19
42,05
45,15
47,42
49,09
49,9
блица 7.2
-0,009
—0,013
—0,013
—0,013
—0,012
—0,018
—0,032
—0,025
-0,025
—0,022
-0,019
-0,018
—0,021
—0,021
-0,021
-0,084
Приведем численный пример. В таблице 7.2 даны значения координат
заданных точек Р(х, у) и кривизны К(х, у) параметрического
интерполяционного кубического сплайна, а также соответствующие значения ху г/,
К(х, у) для сглаживающего сплайна. Ширина «коридора» по каждой из
переменных 0,05. Крайние точки зафиксированы и в них задано
направление касательной (в точке @, 0) касательная вертикальна, а в точке D0;
49,9) горизонтальна).
§ 5. Приближение поверхностей
Пусть на некоторой поверхности 2 задано множество точек,
для которых известны их декартовы координаты х, i/, z.
^Требуется по этим точкам построить поверхность, в некотором смысле
близкую к 2.
Алгоритм решения поставленной задачи рассмотрим на
примере поверхности, изображенной на рис. 7.6. Для поверхностей
других типов, например гомеоморфных цилиндру или тору,
необходимы только незначительные изменения в рассуждениях.
В процессе построения алгоритма используются параметрические
сплайны. Однако их конкретный вид (первой степени, кубические
или рациональные) для самого алгоритма несуществен. Выбор
тех или иных сплайнов осуществляется в зависимости от
требований, предъявляемых к приближению: гладкость, точность,,
локальные свойства, время счета и т. д.

222
ГЛ. VII. ПРИБЛИЖЕНИЕ КРИВЫХ II ПОВЕРХНОСТЕЙ
Разобьем границу поверхности точками Pj, P2, Р$, Ра на
четыре части. На поверхности 2 рассмотрим семейство линий,
обладающих следующими свойствами:
1) никакие две линии не имеют между собой общих точек;
2) начало и конец каждой линии находятся в точках,
расположенных на противоположных участках границы; два других
участка границы включаются в
число рассматриваемых линий;
условимся в дальнейшвхМ называть линии,
удовлетворяющие перечисленным
условиям, координатными.
Введем на поверхности 2
семейство координатных линий Lk, к =*
= 0,..., iVo, таким образом, чтобы
Рис. 7.6. каждая из линий проходила через
некоторые из заданных точек
поверхности, причем начало и конец линии совпадали с заданными
точками (на рис. 7.6 эти линии выделены пунктиром).
Заметим, что вовсе не обязательно, чтобы каждая из заданных
точек принадлежала какой-либо линии. Практически построение
упомянутого семейства линий сводится к выделению из
множества заданных точек поверхности упорядоченных подмножеств. Эта
работа должна быть выполнена при вводе данных в ЭВМ.
Описание алгоритма удобно разделить на ряд шагов.
Первый шаг алгоритма. Для каждой линии Lk
построим интерполирующий е& параметрический сплайн
Sk(x; 5), Sk(y; s), Shiz; s)
с использованием нормированной параметризации по суммарной
длине хорд (§ 2). Для дальнейшего необходимо, чтобы
построенные сплайны обладали свойствами координатных линий.
Обеспечить выполнение этого требования можно выбором исходных
линий Lh. Во-первых, нужно стремиться к тому, чтобы они были
по возможности более плавными, во-вторых, на каждой из них
должно быть достаточно много заданных точек и, в-третьих,
линии не должны лежать^ слишком близко друг к другу. На отрезке
изменения параметра s [0, 1] введем сетку Av: O = vo<v\<...
*..<vM = l и вычислим координаты точек
P&iShfaVj), Sk(y;v,), SfcU;^)}, / = 0 М; А: = 0 ЛГ0.
Второй шаг. Для каждого ; = 0, ..., М построим
параметрические сплайны
S3{x; I), S,iy; s), $,(*; *),

§ 5. ПРИБЛИЖЕНИЕ ПОВЕРХНОСТЕЙ
223
интерполирующие точки Р[}\ Р^з * •••» Pn0J" Вновь используется
нормированная параметризация по суммарной длине хорд.
Необходимо, чтобы линии, соответствующие построенным сплайнам,
были координатными (рис. 7.7). Далее, введем сетку Au: 0вио<
< щ < ... < uN = 1 и определим
координаты точек Рц(х15, yi5, Zij):
i = 1, ..., N; / = 1, ..., M.
Третий шаг. В области [0,1] X
X [0, 1] образуем сетку А = Аи X
ХД,. В качестве декартовых коор- рис 77
динат поверхности в ее узлах (ии Vj)
принимаем значения xih yih zi$. Интерполируя их на сетке Аг
получаем для координат искомой поверхности следующие-
формулы:
x = S(x; и, v), y = S{y; и, v),
; щ v).
Рис. 7.8.
Описанный алгоритм дает хорошие результаты, если соседние-
линии семейства Lh не сильно отличаются по геометрической
форме и по количеству точек, заданных на них. Например, это
обычпо имеет место, когда поверхность
задается достаточно густым набором
плоских сечений. В общем случае
можно рекомендовать после
выполнения второго шага, отправляясь от
построенных точек P,j, повторить первый
и второй шаги алгоритма. Ввиду того,
что исходные данные для построения
поверхности обычно представляют собой результаты измерений,
целесообразно, по крайней мере на первом шаге алгоритма,
использовать вместо интерполяционных сглаживающие сплайны (§ 4).
Для приближения поверхностей, гомеоморфпых цилиндру,
все проделапные рассуждения сохраняют силу. Достаточно лишь
условиться, что два из четырех участков границы поверхности
совпадают между собой. Это означает, что на одном из шагов
алгоритма требуется строить периодические параметрические
сплайны.
Для поверхностей, гомеоморфных тору, считаем, что
противоположные участки границы попарно совпадают. Здесь
периодические сплайны строятся и па первом и па втором шаге. Кстати,

224 ГЛ. VII. ПРИБЛИЖЕНИЕ КРИВЫХ И ПОВЕРХНОСТЕЙ
периодические сплайны удобнее непериодических — не возникает
проблем с граничными условиями.
В некоторых случаях, например, при построении поверхностей
конической формы целесообразно изменить требования к
координатным линиям. А именно, удобно предположить, что
координатные линии одного из семейств пересекаются в одной точке
(рис. 7.8). Естественно, при реализации алгоритма
соответствующие сплайны должны иметь общее начало (конец).
При построении поверхности, гомеоморфной сфере, линии
одного из семейств пересекаются в двух точках-полюсах сферы.
Литература к главе VII. [13—15, 15*, 30, 54, 88].

Глава VIII
ЧИСЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ И ИНТЕГРИРОВАНИЕ
В данной главе изучаются методы численного
дифференцирования и интегрирования функций одной переменной, основанные
на сплайнах. Во многих случаях они эффективнее традиционных
методов, использующих приближение многочленами. Перенесение
результатов на функции двух переменных не вызывает
принципиальных затруднений. На практике в большинстве случаев
достаточно использовать кубические сплайны.
§ 1. Численное дифференцирование
Самый простой способ приближенного вычисления
производных функции fix) состоит в замене их производными
интерполяционного сплайна, построенного по значениям fi^fixi), ? = 0, ...
..., /V, заданным на сетке Д: а = хо < х\ < ... < xN = b. С этой
целью можно использовать различные кубические сплайны, что
позволяет вычислять производные до третьего порядка
включительно.
Обозначим через Six) кубический сплайн класса С2, Scix)—
кубический нелокальный сплайн класса С1, SDix)—дискретный
кубический сплайн, 53, г(#)—эрмитов кубический сплайн.
Кубический сплайн Six) на каждом промежутке [хи xi+[]
представляется одной из формул
S ix) - /i A - tf A + 2t) + /i+1t» C - 2t) +
+ mxt A - tf hi - mi+lt2 A - t) hu A)
S (x) = il-t)h + tfi+l - ^ t A -1) [B -1) Мг + A +1) Mi+1], B)
где, как обычно, ht^ xi+\— x{, t = ix — x{)/hu m{==5"(^i), M{ =
= iS//(^l). Из выражений A), B) вытекают следующие формулы
численного дифференцирования:
S' ix) = Ы A - t) h+l^fi + A - it + З*2) mt - B* - Щ mi+u C)
s" № = lTt [6 A - 2') fj±TT^ ~ <4 - 6') "I - B - Щ i»l+1]f D)
10. С. Завьялов и др.

226 ГЛ. VIII. ЧИСЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ И ИНТЕГРИРОВАНИЕ
'" (х) -1 (mi+1 + пц - 2 Ц=^), E)
5' («) - b&jlk _ ? [B _ 6* + 3*а) Mi -HI - З*2) Мi+1], F)
j
*) + Afi+1*f •
С практической точки зрения предпочтительнее формулы F) —
(8), так как они требуют меньшего количества арифметических
операций. Напомним, что алгоритмы вычисления величин тг и
Mi рассмотрены в гл. III. Там же приведены необходимые
результаты о погрешности приближения производных функции fix}
производными сплайна Six). В частности, при достаточной
гладкости функции fix) имеют место соотношения
15(г) (х) - /(г) (х) |U = О [h*-% г = 0,1, 2, 3, (9>
где h =f max /ц.
г
Если использовать представление сплайна Six) через
кубические В-сплайны (§ 8 гл. III):
JV+1
* 2 Ъ0г(х), A0)
i
то, очевидно,
+
S{r)(x)= 2 hBV{x\ г= 1,2,3, (И)
и дело сводится к вычислению производных от В-сплайнов.
Формулы численного дифференцирования для сплайнов Sc(x)
и Sd(x) совпадают соответственно с формулами C)—E) и F) —
(8). Различие состоит лишь в способе вычисления величин т*
и Mi (гл. VI). Формулы дифференцирования для эрмитова
сплайна 5з,2Ы получаются из C)—E) путем замены в них величии
nti на /{, которые, естественно, должны быть заданы. Во всех
случаях максимальные порядки приближения — такие же, как
в формуле (9).
С помощью сплайнов Sc(x) и Sd(x) можно вычислять первую
и вторую производные функции fix) в узлах сетки Д с более
высокой точностью, чем это гарантируется оценками (9). При
соответствующем выборе параметров, входящих в системы для
определения величин mi} Mi (теоремы 6.2, 6.4), на произвольной

§ 1. ЧИСЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ 227
неравномерной сетке имеем
A2)
A3)
Интерполируя с помощью кубического сплайна вычисленные
таким образом значения производных в узлах, можно повысить
точность приближения производных функции fix), теперь уже
всюду на [а, Ь], по крайней мере на порядок. Кроме того,
появляется возможность вычисления производных более высокого
порядка, чем в формулах C) —(8). Например, построив
интерполяционный кубический сплайн S (Sd (#); х), будем иметь
Можно показать, что в случае достаточно регулярной _сетки А и
f(x) e Wlo [я, Ъ] точность такого приближения будет O(h).
Еще одно применение формул A2), A3) связано с
построением сплайнов, дающих большую точность приближения в
сравнении с кубическими сплайнами. Рассмотрим интерполяционный
эрмитов сплайн пятой степени S$t $ix). По формуле B.10.5)
<?5,з (х) - Л A - t)* A + 3* + №) + fi+1t* A0 - 15i + 6*2) +
4- hi/it A - tf A + 3t) - А/|+1«» A -1) D - 3t) +
+4 ь*fit% (i - *K+i*w+i*8 (* - w- <14>
В § И гл. II для достаточно гладких функций получена оценка
l-STe.8 (ж) — / («)|с — О (Ав). A5)
Заменим в A4) величины /i, fi+u fu /t+i подформулам A2), A3),
Для построенного таким образом сплайна S$t $(x), очевидно,
выполняется соотношение
\S6t3(x)-S5lS(x)\ = O(P).
Учитывая A5), получаем
Следовательно, порядок приближения сплайном S^zix) на
единицу выше, чем у любого из кубических сплайнов, причем для
построения 5б. з(#) не требуется знания производных
функций fix).
В таблице 8.1 приведены результаты численного дифференцирования
функции /(я)= е~1Ох на равномерной сетке Ai с шагом h = ОД и
неравномерной сетке Д2 с узлами 0; 0,01; 0,03; 0,06; 0,1; 0,15; 0,21; 0,28; 0,36; 0,45;
0,55; 0,66; 0,8; 1,
15*

228 ГЛ. VIII. ЧИСЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ И ИНТЕГРИРОВАНИЕ
В первом, третьем и пятом столбцах таблицы приведены погрешности
приближения первой, .производной во внутренних узлах сетки
соответственно для сплайнов S(x), Sc(x) и трехточечной разностной аппроксимации.
Во втором, четвертом и шестом столбцах даны погрешности приближения
второй производной соответственно для сплайнов S(z), SD(x) и трехточечной
Таблица 8.1
А1
1
3,1-ИГ*
6,1-10-4
2
54
0,62
3
3,М(Га
1,2-10~3
4
0,19
0,03
5
0,64
0,12
6
3,2
2,8
разностной аппроксимации. При вычислении первой производной
использовались сплайны с граничными условиями типа I, при вычислении второй,
производной — с условиями типа II. Для сплайнов Sc(x) и SD(x) были
взяты оптимальные значения параметров.
До сих пор мы предполагали, что исходные значения /* He-
содержат ошибок. Однако на практике они всегда присутствуют.
В случае, если ошибки велики, целесообразно использовать
сглаживающий сплайн с выбором параметров сглаживания в
зависимости от величины ошибки (гл. IV). Если же ошибки в
исходных данных невелики, то можно применять интерполяционные*
сплайны. При этом нужно обратить особое внимание на выбор
шага сетки. Этот вопрос мы уже затрагивали при рассмотрении
сплайнов первой степени (гл. II). Здесь на конкретном примера
покажем способ решения этой задачи для нелокальных
кубических сплайнов.
Пусть на равномерной сетке с шагом h известны
приближенные значения /< функции /Ы^С4[а, Ь], причем)/* — /г|^е.
Предположим, что вторая производная функции fix) вычисляется
с помощью кубического сплайна Six), интерполирующего
значения /г, по формуле
)ii) i+l.
Тогда
| S*(х) - /" (х) |<max|Цк - М{| + | S" (х) - f"(x) |, A6}
где Six)—сплайн, интерполирующий точные значения ft.
Чтобы не загромождать изложение несущественными
подробностями, будем считать fix) периодической. В этом случае
(Mi-х - Мг-г)'+ 4 (Мг - Mi) + (fMi+1 - Mi+1) =
- g [(/i-i - /i-i) - 2 (U - fi) + (/hi - /hi)], * = 1, 2, ..., N.

§ 2. АСИМПТОТИКИ ДЛЯ КУБИЧЕСКИХ СПЛАЙНОВ КЛАССА С> 229
Иепользуя следствие Д. 1, отсюда получаем
Согласно теореме 3.7
| S" (х) - f (х) | < ± Ь? || /iv (Х) ||с + о (Л«).
В итоге из A6) следует
15" Ы -/" ЫI < Ф(е, h) + o(h2),
где
Пренебрегая величиной oih2), определим оптимальный шаг h*
из условия минимума функции ф(е, К). Это дает
1/^C-) [о1, <р (е, Л») = 2/е||/iv (*)[<,.
Очевидно, при заданном е пе имеет смысла использовать сетки
с шагом, меньшим ft*. Например, если fix)=$inx и 8 = 10~8, то
Л* « 0,035 и ф(е, Л») = 2 • 10.
Задача. Показать, что формулы G), (8) предпочтительнее формул
D), E) с точки зрения влияния на конечный результат ошибок в
исходных данных.
§ 2. Асимптотические формулы
для кубических сплайнов класса С2
Пусть кубический сплайн Six) интерполирует функцию fix)
на равномерной сетке Д: Xi = a + ih, г = 0, ..., /V; xN = b. В
дальнейшем мы не будем оговаривать требования к гладкости jf(#)t
считая, что она имеет столько непрерывных производных,
сколько нужно для выполнепия преобразований. Вначале рассмотри.^
случай, когда fix)—периодическая функция с периодом Ъ — а.
Для величин Д/< имеем систему
Mi-i + Шг + Л/1+1 = -J (А-1 - 2А + /i+1), * = 1, ..., N, A)
где полагается Mh = MN+k, Д == fN+h, к = 0, 1.
Будем искать решение системы A) в виде
Мг = /1 + аг/г2/Г. B)
Подставляя B) в A) и разлагая обе части 1-го уравнения по
формуле Тейлора в точке хи находим
= 6/1 + ^ /{v + О (А4),

230 ГЛ. VIII. ЧИСЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ И ИНТЕГРИРОВАНИЕ
Сравнивая коэффициенты при одинаковых по порядку
производных, получаем систему
1/2, * = 2, ..., ЛГ-1,
ai + a*-i + 4a* = —1/2,
которая имеет единственное решение а* = —1/12, i — 1, ..., iV.
При таких а* величины М,-, определяемые формулой B),
удовлетворяют системе A) с точностью O(h4). В силу теоремы
Д. 2 норма матрицы, обратной к матрице этой системы, не
превышает 1/2, и поэтому внесение в правую часть погрешности
порядка O(h4) приводит к изменению решения на величину того
же порядка. Следовательно,
Mi = fl-±h*j\v + O(h% t = O,...,N. C)
Точно так же можно получить выражения для Ми
содержащие производные функции fix) более высоких порядков.
Приведем одно из них:
м /' h2 ,iv , Л4 ,vi , 17/г6 .VIII , п /7}8v (/л
Mi = fi-j2fi +360" +'60480" +0(Л)« D>
Подставляя выражения для Mi и Mi+\ в соотношение
т. = Ь±11± _
и выполняя разложение по формуле Тейлора, получаем
Используя D), A.2) и разложение Тейлора в точке х
Хг + ^f, находим
*) - / (х) - '^ Г {х) - A~2*i8@1 + 3u) ^5/v (*) + О (Л«), F)
где обозначено w = i(l —^).
Дифференцируя F), имеем
5' (х) - /' (z) - ^-^ ^iv (х) _ Ц^.2 A«/
5" (*) - /" (х) - 1^ Л'/iv (Х) + »li=if) Л3/у (
(х) - Г (*) + i^ ft/iv (Ж) + Ц^" Й2/У И + О (П О)

§ 2. АСИМПТОТИКИ ДЛЯ КУБИЧЕСКИХ СПЛАЙНОВ КЛАССА С* 231
Формулы F)—(9) дают исчерпывающую характеристику
погрешности приближения кубическим периодическим сплайном.
В непериодическом случае все полученные выводы сохраняют
силу, если в качестве граничных условий задать величины Mq и
MN по формулам D) или величины то, mN по формулам E).
Нетрудно показать также, что C) имеет место, если в качестве
граничных условий взять соотношения
Мк = -JL (- /й_2 + 10/м - 18/, + 10/fc+1 - /,+2), к - 2, N - 2.
о/г
При этом в формулах F)—(9) сохраняются слагаемые,
содержащие flY(x).
Кроме того, формула D) и все полученные на ее основе
результаты верны при любых граничных условиях, если только
рассматривается интервал [х{, xi+\], расположенный достаточно
далеко от концов отрезка [а, 6].
Отметим, что асимптотические разложения для величин Miy
rrti можно получить и для неравномерных сеток. Но в этом
случае коэффициенты при производных, в отличие от формул D),
E), будут зависеть от сетки и их вычисление, за исключением
некоторых частных случаев, требует применения ЭВМ.
Получим теперь разложение для коэффициентов 6* в
интерполяционной формуле A.10). В частности, это позволит выяснить
их смысл. Учитывая выражения для узловых значений
нормализованных Б-сплайнов (таблица 3.9), в периодическом случае на
равномерной сетке приходим к следующей системе относительно
неизвестных 6,:
6,-1 + 46, + 6>+1 = 6/,, i = l, .,., N. A0)
Отыскивая ее решение в виде 6^=/| -J- yji^fi, получаем
— —l/6f i = l, ..., N, и
A1)
Следовательно, на равномерной сетке коэффициент 6< с точ
ностью O(h2) равен узловому значению /«.
Если в формуле A.10) заменить 6* на 6*, где 16*— 6*1 =0(/И)
то в силу свойств нормализованных 5-сплайнов сплайн
будет удовлетворять условию \§(х) — Six)\ =O(h4). Одно из
приложений формулы A1) состоит в том, что на ее основе можно
указать эффективный способ определения таких 6*, не требую-»

232 ГЛ. VIII. ЧИСЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ И ИНТЕГРИРОВАНИЕ
щий решения системы уравнений. Действительно,
Подставляя это выражение в A1), получаем
bi--j/i-i + T/«-T'*+i+0(ft«),
т. е. можно положить
В итоге получены явные формулы для Six). Естественно, этот
сплайн не интерполирует заданные значения fu но по порядку
обеспечивает такую же точность приближения, что и
интерполяционный. Такие сплайны называются локально аппроксимацион-
ными. Подробнее они рассматриваются в гл. IX.
В заключение параграфа отметим, что использованпый метод
построения асимптотических разложений пригоден и для других
сплайнов.
§ 3. Численное дифференцирование на равномерной сетке
Отметим некоторые формулы численного дифференцирования,
получающиеся, когда для построения кубического сплайна
используется равномерная с шагом h сетка. В частности, из A.10),
используя вначения производных нормализованных 5-сплайнов
(таблица 3.9), получаем
S' (хг) = t+1 г~\ A)
b (Xi) =¦ ^ . B)
Обратим внимание, что эти формулы по виду совпадают с
обычными разностными аппроксимациями первой и второй
производных. Различие лишь в том, что величины f{ заменены
коэффициентами Ь{ разложения кубического сплайна по базису из иорма-
лизовапных Б-сплайнов. При этом, согласно B.5), 6" {х) «•
- /i + О {h% в то время как (/m ~ /4-i)/2A = f\ + О {h%
Ряд интересных формул получается на основе полученных в
предыдущем параграфе асимптотических разложений. Возьмем
разностную аппроксимацию второй производной
-t = /i+r2/. +O(h).
Комбинируя ее со сплайновой аппроксимацией, в силу B.3) по-

§ 4. ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ 233
лучаем
¦I (л/, + /i~1~% + /i+1) « п + о (П C)
Таким образом, среднее арифметическое сплайновой и
разностной аппроксимацией второй производной дает точность O(hA),
хотя в отдельности каждая из них имеет точность O(h2).
Учитывая соотношения B.1), формулу C) можно записать в
другом виде:
1 (М 1-х + iOMi + Mi+1) = fl + О (h% D)
При использовании 5-сплайнов, принимая во внимание B.10)
и B), из C) получаем
Из B.9) имеем соотношения
S'" (Хг +) = Г (*,) + 4 Г (Xi) + О {h\
S" (ж, -) = /'" (*0 - 4/IV (хг) + О (h*),
И8 которых вытекает формула для аппроксимации /'"
Пожалуй, наиболее неожиданным является следующий результат:
который является следствием разложения B.4). Несмотря на то,
что 5IV(a:) = 0 почти всюду на [а, Ь] и, казалось бы, не имеет
смысла составлять вторую разделенную разность от величин Д/<,
мы получаем аппроксимацию четвертой производной функции
fix) с очень высокой точностью.
Задача. Получить оценки величин О(h4) в формулах C), F) через
производные функции f(x).
§ 4. Численное интегрирование
Наиболее простой способ получения формул численного ин-»
тегрирования для интеграла
ъ
J A)

234 ГЛ. VIII. ЧИСЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ И ИНТЕГРИРОВАНИЕ
основан на применении аппарата интерполирования. При этом
функция fix) заменяется некоторым интерполяционным сплайном
Six) и в качестве приближенного значения интеграла A) берется
величина
ь
\ B)
Погрешность вычисления интеграла A) можно оценить, например,
следующим образом:
ь
J |S (a?) —/,(s)| Ac<
а
-/(*)|с. C)
Следовательно, достаточно иметь оценку погрешности
приближения функции fix) сплайном Six). Несколько более сложные
рассуждения позволяют уточнить оценку C) (см. § 5).
Получим формулы вычисления интеграла B) для конкретных
сплайнов. Мы будем рассматривать сплайн первой степени Siix)
и различные виды кубических сплайнов (обозначения такие же,
как в § 1).
Пусть на [а, Ь] задана сетка А: а = хэ< ...<xN = b. Сплайн
S\ix) на промежутке [xif xi+\] записывается в виде
i
Поэтому
J $!(*)**- 2! j St(x)dx^ S *iJ [АA — *)
Отсюда
Формула D) есть не что иное, как всем известная составная
(обобщенная) формула трапеций. Особенно часто она
используется на равномерной сетке:
j Sx(x)dz-±fQ+h 2 /i+|/iv. E)
о i=l
Аналогичным образом выводятся формулы интегрирования
для кубических сплайнов. Если Six)—кубический сплайн класса

§ 4. ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ 235
С2, то при нспользовании представления A.1) получаем
2V-1 JV-1
12 (т« -
о
!¦
2 ^y '*» \! x \ J t+i/ i ^2
На равномерной сетке вторая сумма в правой части упрощается
и формула приобретает вид
!
S (х) dx = у /0 + Л 2 / + 4 ^ +
12
Фактически применение этой формулы не требует предваритель-»
ного построения сплайна. Например, если Six) удовлетворяет
краевым условиям типа I, то т0 = /0, tun = /#• В других случаях
можно заменить то и mjv разностными аппроксимациями.
Совсем просто выглядит формула G), когда
fix)—периодическая функция с периодом Ъ — а. В этом случае /о = /*, то = mN и
J S {x) dx = Л 2 /i.
a i=0
Эта формула совпадает с формулой трапеций E). Полученный
результат является частным случаем общего утверждения о том,
что использование сплайнов произвольной степени дефекта 1
для численного интегрирования периодических функций на равно*
мерной сетке приводит к формуле трапеций. Довольно просто
это утверждение доказывается, если использовать аппарат
Б-сплайнов. Читатель может проделать необходимые выкладки в
порядке упражнения.
Если для Six) используется представление A.2), то
\ S (х) dx = 1 2 hi </« + /i+i) - Я 2 h* Шг + Мг+г). (8)
Аналог формулы (8) для равномерной сетки проще всего
получить из G), используя соотношения
Находим

236 ГЛ. VIII. ЧИСЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ И ИНТЕГРИРОВАНИЕ
Пусть сплайн Six) записан в виде разложения по В-сплайнам
A.10). Тогда
§S(x)dx=s 2 bi§Biix)dx. A0)
а г=—1 а
Интегралы от Л-сплайыов легко вычислить, используя, например,
формулу (8) и таблицу 3.9. Опуская промежуточные вычисления,
запишем конечный результат
JV-1
- 1 b1h.1B1 (*„) + j
- j Ьх-^Вх-г (xN) + Ь^ {^р
г==1
- ^ [^n fav-i) + ^^ (^я)] + -J" ^iv+i^-i
Как видно, использование 5-сплайков при численном
интегрировании приводит к более громоздким формулам по сравнению о
F), (8). Исключение составляет случай, когда сетка А
равномерна у концов отрезка [а, Ь].
Для сплайнов Sc(x) и SD(x) формулы интегрирования
совпадают соответственно "с формулами F), G) и (8). При этом в
случае равномерной сетки целесообразно параметры сплайна Sc(x)
выбирать таким образом, чтобы обеспечить вычисление величин
mQi mN без решения системы уравнений. Если используется
эрмитов сплайн Sz, 2^x), то в F), G) нужно заменить величины т{
на /'ь * = 0, ...,7V.
§ 5. Оценки погрешности формул
численного интегрирования. Интегрирование
с заданной точностью
В предыдущем параграфе при выводе оценки D.3) мы
предполагали, что известна оценка по норме С погрешности
приближения сплайном Six) подынтегральной функции fix). Более
точные оценки можно получить, если привлечь поточечные оценки
для погрешности \Six) — }ix)\.

§ 5. ОЦЕНКИ ПОГРЕШНОСТИ 237
2
При доказательстве теоремы 2.1 для функций/(#) е Wl> [at b]
была установлена оценка
1 1 /" ( lk X GE [Zix
< 2}
Учитывая ее, получаем
ь ъ
' ( /уЛ Л ф _ V "ft v\ /s7 у
J I *^ l W
iV—1
A =
г=0
Полагая h = тахйь отсюда находим
i
ь ь
i=0
A)
Аналогично, используя поточечную оценку погрешности
интерполяции B.6.21) эрмитовым сплайном Sz, 2(х) для / (х) q
•е Wi [а, Ь], приходим к оценке
ь
е (r\rlr I i(r\flr *<h (b~~ah\ /ту /y\n /o\
°з,2 Vх;aJ- j у \x; «•*' ^ 720 il / v^; ||«>- \^)
a a
Если /(ж) е И^[а, Ь], то с точностью до малых порядка
ООьъ) оценка B) справедлива для кубических сплайнов класса С2
на равномерных и близких к ним сетках. На произвольной сетке
это справедливо при использовании сплайна Scix) с
оптимальными параметрами.
В вычислительной практике широко используется
квадратурная формула Симпсона на равномерной сетке узлов. В этой свя-
зи отметим, что постоянная в оценке B) ровно в ч-етыре раза
меньше постоянной в оценке погрешности формулы Симпсона.
Для формулы трапеций мы установили оценку A). Приведем
€ще одну оценку для этой формулы на равномерной сетке.
Из D:5) и D.7) имеем
ь ъ 2
j [S1 (х) - /(*)] dx = J [58|2 (х) - /(x)]jlx +^(fN- /о).

238 ГЛ. VIII. ЧИСЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ И ИНТЕГРИРОВАНИЕ
Отсюда, используя B), получаем
В большинстве случаев можно пренебречь вторым слагаемым в
правой части C) и мы получаем очень удобную для
практического использования оценку.
Пусть требуется вычислить интеграл D.1) с заданной
точностью е. На примере формулы трапеций рассмотрим способы
решения этой задачи. Учитывая оценку A), можно обеспечить
требуемую точность, если, например, использовать равномерную-
сетку с шагом
Однако, если /"Ы сильно меняется на промежутке
интегрирования, то такой подход приводит к использованию большого числа
узлов. Это нежелательно по следующим соображениям.
Вычисление интеграла связано с суммированием большого числа
слагаемых. Здесь неизбежно возникают погрешности округления, и их
суммарная величина растет пропорционально А~р, где р > 0. При
большом N (малом К) эта погрешность может испортить
результат. Поэтому следует стремиться к использованию сеток с
минимальным числом узлов.
Пусть сетка А такова, что погрешность интерполяции
сплайном S\(x) на каждом отрезке [#<, Xi+\] не превосходит ei. Тогда
Отсюда понятно, что обеспечить заданную точность вычисления
интеграла можно, выбрав сетку, удовлетворяющую условиям
1S1 (*) -1 (х) \\c[xilXi+l] = ex = ?-а% * = 0,
...
Алгоритмы построения таких сеток изложены в § 3 гл. II.
Количество узлов сетки при этом будет, как правило, существенно
меньше, чем в равномерной сетке с шагом А, определяемым из
условия D).
§ 6. Интегрирование сильно осциллирующих функций
Пусть требуется вычислять интегралы вида
ь ъ
J cos ax f(x) dxx j sin axf (x) dx. A)

§ 6. ИНТЕГРИРОВАНИЕ СИЛЬНО ОСЦИЛЛИРУЮЩИХ ФУНКЦИЙ 239
При больших значениях параметра а здесь невыгодно
использовать квадратурные формулы, основанные на замене сплайном
всей подынтегральной функции, так как это потребует большого
числа узлов. Более удобные формулы получаются, когда функции
cosa#, sinaa: рассматриваются как весовые, а сплайном
приближается только fix). Будем использовать с этой целью сплайн
первой степени S\(x) и кубический сплайн Six) класса С2*
Вначале вычислим интеграл
ь jv-i 1
J e^S1 (х) dx = 2 Л» f *'«<**+%) [fh A - *) + tfk+l]dtt
а Ь=0 о
где i = V~l.
Интегрируя по частям и выполняя несложные преобразования,
приходим к формуле
\ **Sl (х) dx=-L //-« _ JL
B)
Выделив здесь действительную и мнимую части, получаем
ь
С 11
J cos axSx {х) dx = —. — /0 sin ax0 + -^ /iv sin axN +
г Vh+l — ««
b
j sin axSx (x) dx = — /0 cos ax0 — ~ fN cos ал:^ +
•a
1 xiSina^^sina^
+ -2 ^ Г (/a+i — /ft)
Оценим погрешность вычисления интегралов A). Для
формулы C) имеем
ь ь
J cos axSx (x) dx — j cos алг/ (x) dx ^

240 ГЛ. VIII. ЧИСЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ И ИНТЕГРИРОВАНИЕ
Такая же оценка справедлива и для формулы D). Если,
например, / (х) е Wlo [а, Ь], то погрешность вычисления интегралов A)
при любом а не превосходит величины
Аналогичным способом получаются формулы при замене fix)
кубическим сплайном Six). Используя для Six) представление
A.2), получаем
1 B, + 22) - \ Z е- j-i— (Mk+l - М„),
где
iv-г
к
Так как
JV-1
iV-l
V ^+1 ~~ ^
то Si + 2г приводится к виду
2, + 2г = eiaxo (^ BМ0 + М,) - f-^
f* hk-l
V „ia«fc f*fc-l лf
Все выражения в фигурных скобках равны нулю в силу того, что

§ 6. ИНТЕГРИРОВАНИЕ СИЛЬНО ОСЦИЛЛИРУЮЩИХ ФУНКЦИЙ 24i
для Six) выполняются соотношения C.1.14). В итоге
e**S (x) dx = - 1 2 f ТГ1 (M*+i ~ M*) +
* a ft=o *
+ eto* (Л + 1С) + eiaXN (В + Ш), E>
где
[^^4 с
(M
D- i (? M» - '4
Выделяя в E) действительную и мнимые части, получаем
формулы
Ъ JV-1
с IV* cos axk+i"~ cos axk
\ cos axS (x) dx = 3 >. ^-r (Мк+1 — Мъ) +
2 a ft=o **
+ A cos ад:0 — С sin ax0 -\-Bcos<xxn—Dsinaor^f F)»
ь N-i .
I -^1 sin o-x.,1 — sin axh
sin a^*S (л:) Йл: = ^
+ -4 sin ax0 + С cos ax0 + Б sin ax^ + D cos a#iy G)
Отметим, что среди всех известных формул, точных для
полиномов третьей степени, формулы E)—G) самые простые.
В качестве численного примера рассмотрим задачу о вычислении
коэффициентов ряда Фурье для функции ех, х е [—я, я]:
«* =
C0S ПХ + Ьп sin
*dx - (-l)n(e"-g~")
Коэффициенты ап, Ьп определяются формулами
n
a — — I cos nxexdx
я J.
—л
л
я J
f sin „Л, =
В таблице 8.2 для некоторых значений п приведены значения ап, ЪПг
вычисленные по формулам (8), (9), и an, bn, вычисленные по формулам F),
^6 ю. с. Завьялов и др.

1242 ГЛ. VIII. ЧИСЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ И ИНТЕГРИРОВАНИЕ
G). Использовался кубический сплайн с граничными условиями типа I.
Отрезок [-—я, я] разбивался равномерным образом на 20 частей.
Заметим, что примерно такую же точность можно получить, если раз-
бить отрезок [—я, я] на 500 частей и использовать формулы C), D). При
этом общий объем вычислений в несколько десятков раз больше.
Таблица 8.2
п
1
10
20
50
100
200
а
п
—3,67608
0,0727936
0,0183346
2,93969-10'8
7,35142-10-*
1,83799-10-*
—3,67604
0,0728027
0,0183892
2,94676-10*3
7,42277.10"*
1,90866-10-*
ь
п
3,67608
—0,727936
—0,366691
—0,146984
—0,0735142
—0,0367599
3,67604
—0,727920
—0,366696
—0,146985
—0,0735143
—0,0367599
Задачи, а) Оценить погрешность вычисления интегралов A) по фор-»
;мулам F), G).
б) С помощью формулы E) вычислить преобразование Фурье от куби*
ческого ^-сплайна на равномерной сетке.
Литература к главе VIII. [2, 14, 18, 22, 23, 34, 35, 56, 58, 63,
79, 93],

Г л а в а IX
ЛОКАЛЬНАЯ АППРОКСИМАЦИЯ СПЛАЙНАМИ
В предыдущих главах мы уже исследовали методы локальной
сплайновой интерполяции. Их отличительная черта состоит в том,
что значение сплайна на промежутке между двумя узлами сетки
зависит от значений интерполируемой функции и, быть может,
ее производных только из некоторой окрестности этого
промежутка. В данной главе изучается еще один вид локальной
аппроксимации, включающей ряд разнообразных по характеру
приближений, в том числе в некотором смысле наилучших.
Эта аппроксимация основана на представлении сплайнов
степени п дефекта 1 на сетке — °° <хо<х\<. ..<хп< + <х> через,
нормализованные 5-сплайны (§ 3 гл. I)
?»(*)-2 Ъ (Л Д» И,
г
где bi(f) — последовательность линейных функционалов, выбор
которых и определяет вид приближения. Алгоритмическая сторона
дела состоит в вычислении функционалов W/), которые
выражаются обычно через значения функции, ее производных или
разделенных разностей, интегралов и определяются по данным
на отрезках [#*, xi+n+\], являющихся носителями сплайнов Вп(х).
В то же время нелокальные задачи, например интерполяционные,
требуют для определения величин Ь<(/) решения систем
уравнений. Это отличие особенно существенно при построении сплайнов,
высоких степеней, а также сплайнов двух и более переменных.
Мы изложим основы локальной аппроксимации функций одной
переменной. Распространение большей части результатов,
исключая § 8—10, на случай многих переменных можно провести,
опираясь на представление соответствующих пространств как
тензорных произведений пространств сплайнов одной переменной.
§ \. Простейшая формула локальной аппроксимации.
Сглаживающие формулы
Задачи аппроксимации будем рассматривать для ограниченных
функций fix), определенных на всей действительной оси или е&
отрезке [а\ Ь']. В последнем случае, чтобы не иметь дела с
граничными условиями, аппроксимацию будем строить на некотором.
16*

.244 ГЛ. IX. ЛОКАЛЬНАЯ АППРОКСИМАЦИЯ СПЛАЙНАМИ
отрезке [а, Ь] с= [а\ Ь']. При этом на отрезках [а\ а] и [6, Ь']
должно размещаться по п узлов сетки.
В гл. VIII мы видели, что для интерполяционных кубических
сплайнов на равномерной сетке коэффициент с точностью до
O(h2) равен значению функции в узле интерполяции. Поэтому
^начнем изучение локальной аппроксимации с простейшей
формулы
1*огда коэффициенты при 5-сплайнах суть значения функции в
.некоторых точках.
Выбор последовательности этих точек достаточно произволен,
но не рекомендуется выводить |< за пределы
интервала-носителя сплайна Вгп (х). Например, в ряде случаев, как увидим ниже,
выгодно принять
h = — (xi+l + ... + xi+n). B)
В других случаях предпочтение отдадим формулам
Здесь |i соответствует среднему узлу сплайна Вгп (х) при п
нечетном и середине промежутка \х , х 1 при п четном. При
L i+T i+T+1J
п = 0, 1, 2 формулы B) и C) совпадают при любой сетке узлов,
*а при п > 2 только на равномерной.
Аппроксимация типа A) может применяться для
сглаживания исходных данных. Посмотрим, как это происходит на
примерах п = 0, 1, 2, 3 в случае равномерной сетки узлов. Значения
сплайна A) в точках ?* = х п+1 суть
p=i-[n/2]
где [ ] — символ целой части числа.
Отсюда, используя результаты § 3 гл. I, получаем с точностью
до нумерации точек

§ 2. АППРОКСИМАЦИЯ КУБИЧЕСКИМИ СПЛАЙНАМИ 245
Две первые формулы соответствуют интерполяции сплайнами
нулевой и первой степеней. Две другие, как и все последующие
при п > 3, относятся к категории формул локального сглаживания.
Подобного рода формулы известны, например, в теории сгла-
яшвания многочленами по методу наименьших квадратов L3J.
Приведенные формулы представляют собой суммы здачений
функции и ее вторых разделенных разностей (с
соответствующими коэффициентами). Поэтому они точны для многочленов первой
степени, т. е. значения /(#,) таких многочленов ими не
сглаживаются. Этот факт имеет место и при неравномерной сетке узлов,
если только |» определяются формулой B).
Действительно, пусть fix) = а+ Ъх. Так как & «—
«= — sym1(^i+1, ..., xi+n) есть симметрическая функция первой
Сп
степени, то в силу известных формул A.3.8) Sn(x) = fix).
Чтобы не возвращаться более к этому вопросу, отметим, что
для целей сглаживания пригодны и общие формулы локальной
аппроксимации, рассматриваемые в последующих параграфах. Для
сплайнов степени п они могут быть сделаны точными для
многочленов вплоть до степени п.
При практическом использовании локального сглаживания
для обработки экспериментальных данных следует иметь в виду,
что хорошие результаты получаются только при сравнительно
плавном изменении данных и отсутствии грубых ошибок. При
этом сглаживание можно проводить несколько раз, беря на
каждом последующем шаге результаты предыдущего в качестве
исходных данных. Контроль естественно осуществлять путем
вычисления разделенных разностей, например, второго порядка
от сглаженных значений. При большом числе сглаживаний,
очевидно, любой набор данных будет приближаться к кривой,
изображающей многочлен, для которого сглаживающая формула
точна.
Численный эксперимент по локальному сглаживанию кубическими
сплайнами был проведен с округленными значениями функции f(x)=e*
на [0, 1] (таблица 4.1). Погрешность исходных данных 0ДM. После десяти
сглаживаний она уменьшилась до 0,01, а затем вновь стала увеличиваться.
Здесь проявился эффект стремления сглаженных данных к прямой линии
(формула сглаживания точна для многочленов первой степени),
проходящей через неслаживаемые концевые точки исходного множества.
§ 2. Аппроксимация кубическими сплайнами;
простейшая формула
Рассмотрим локальную аппроксимацию кубическими
сплайнами по формуле A.1). При условии A.2) она точна на
многочленах первой степени. Изучим погрешность этой аппроксимации
в случае равномерной сетки узлов, когда gf =¦ xi+2.

246
ГЛ. IX. ЛОКАЛЬНАЯ АППРОКСИМАЦИЯ СПЛАЙНАМИ
Будем обозначать S3 (х) = S (х), В\ (х) = БН2 (х). В этих
обозначениях формула A.1) на отрезке 1хи х{+х] принимает
вид
i+2
S(x)= 2 f(x9)Bp(z). A)
Из выражений кубических В-сплайнов при равномерной
сетке узлов (§ 3 гл. I) через переменную а получим их выражения
на отрезке [хи xi+\] через параметр t = (х — d/h
^г (х) = ± A - t)\ Вг (х) = 4- И + 3 A - *) + 3* (l-t)«l,
Тождества A.3.8) при гс = 3 на этом отрезке имеют вид
i+2
Т^г 2 syma(^P-b^^P+iMP(^) = ^a, a = 0,1,2,3. C)
Отсюда посредством несложных выкладок при hp =
i+2
S (хр - ^)а 5Р (*) = ^0)/га, а = 0,1, 2,3.
находим
Дифференцируя зти равенства по х и переходя к параметру tt
получаем
2 (p-t)aB#p(xi + th) = e%\ a = 0,1, 2,3. D)
Величины ^(a представлены в таблице 9.1.
Таблица 9.1
0
1
0
0
0
1
0
i/h
0
0
2
1/3
0
2/А»
0
8
0
0
6//18

§ 2. АППРОКСИМАЦИЯ КУБИЧЕСКИМИ СПЛАЙНАМИ
247
Покажем, что в оценках погрешностей аппроксимации
функций f(x) из классов Ск и И^+\ к = 0,1, по норме в Ь„\
E)
(*) U = II 5(г) (х) - /(г) (я;) Цоо < R,
правые части соответствуют таблице 9.2.
Таблица 9.2
Класс
функций
С
с1
П
в.
•g-«(/)
•J- to (/')
Hi
JAI/"ilco
1. Пусть fix) ^ С. Тогда, используя тождество D) при а]
г = 0, для х <= [#,-, a;i+i] получаем
R(x)
S
F)
Отсюда, учитывая расстояние между точками xi+p и #, находим
поточечную оценку погрешности
1(а:) + Bt(x) + Bi+X(x) + 2Bi+2(x)] -
где о)»(/) — максимум колебания функции на сетке узлов х{~и ...
-.., я\-+2, соД/) < соф. Максимум кубического многочлена справа
достигается при t = 0, 1 и равен 7/6.
2. Пусть / (ж) е W». Подставляя в F) разложения значений
) в точке х, получаем
2
G)
Применяя к интегралам неравенство Гёльдера и исключая Bt(x)
и Z?*+i(#) с помощью тождества D) при а = 0, 1, г = 0, находим
21 р - * I
- *) ^i-i (*)+tBl+t (x)\.

248 ГЛ. IX. ЛОКАЛЬНАЯ АППРОКСИМАЦИЯ СПЛАЙНАМИ
Максимальное значение функции справа достигается при t = 1/2*
и равно 13/24.
3. /(я)еС1. Снова имеем формулу G). Интегралы в ней
разбиваются на суммы интегралов по промежуткам [/?, p+U.
Используя теорему о среднем для интегралов, находим
R(x) - М- A-i(*)/'(r|<-i.«) - tlBi-i(x) + Bi(x)]f'{r\l) +
+ A - t)[Bi+l(x) + Bi+2(x))f'(rJ) + ft+at^J/'trii+i, <+2J>.
Здесь и далее r]p> р+\ е (д:р, #p+i), г]'^(о:<, xi+\). Применяя теорему
о среднем для непрерывных функций, получаем
ЯЫ = h{Bt-.i(x)lf'(xi) - f'(r)i-ut)] + [-A
- tBi(x)f'(r\l) + A - t)Bi+l(x)f (r|2) + B -
Используя тождество D) при а =» 1, г = 0, находим оценку
1ДЫI < ha>(f)lt(l -t) + B - t)Bi-i(x) + A +
Максимум функции' справа достигает при t ==» 1/2 и равен 1/3.
Дифференцируя G) по х и снова применяя теорему о среднем
и затем тождества D), находим
I Л' (*) I < со (/') [1 - КВ\-г (х) + hB[+2 (х)].
Максимум функции справа достигается при ? = 0, 1 и равен 3/2.
4. f{x)^Wl>. Из F), беря разложения значений /Ui+P),
находим
1 (8)
) 1
Применяя к интегралам неравенство Гёльдера, получаем
^\ги 2 (p-
Дифференцируя (8) по а: и снова используя неравенство
Гёльдера, получаем оценку
|Л'<*)|<1Г1П. 2 lP-W\B'm(x)\.
Сумма в правой части упрощается, если применить
тождество D) при а = 2, г = 1. Так как Bi_i(х)<0, В\ (х)<0
то нетрудно получить

§ 2. АППРОКСИМАЦИЯ КУБИЧЕСКИМИ СПЛАЙНАМИ 249
Максимум функции справа достигается при t = О, 1 и
равен 1/2.
Посмотрим, как изменится оценка (9), если fix) e С2. Из (8)
до теореме о среднем для интегралов получаем
2? (*) = ¦?{? (Р- W Г (Лр) Bi+V (*) +
+ [/" (rii-u) - Г (Т1)! Si-i (*) + If (тц+u+t) - Г (П*)] ^i+2 И}-
Отсюда, используя тождество D) при а = 2, г == 0, находим
Здесь существенно то, что норма функции f"(x) вычисляется на
отрезке lxu xi+\], а не [я<-1, Xi+\].
Наконец, пусть fix) допускает разложение
/ (*i+P) = 2 Чг- h°{р - ^
* а=о
Тогда из F) с помощью D) можно получить
S{r)ix) = fir)ix) + O{h*-r)y r =2,3.
Как видно, порядок приближения функции по сравнению с
функциями из класса Wlo не возрос, но порядок приближения
первой производной увеличился на единицу. Прозводные высших
порядков теперь также аппроксимируются.
Полученные выше оценки имеют место для равномерной
сетки. Но их можно использовать и при не очень неравномерной
сетке. Это замечание будет уточнено в § 5.
Задача. Показать, что для функции / (#) ^ W^ формула A) дает
приближение
r), r = 1,2.

250 ГЛ. IX. ЛОКАЛЬНАЯ АППРОКСИМАЦИЯ СПЛАЙНАМИ
§ 3. Аппроксимация кубическими сплайнами;
формула, точная на кубических многочленах
В втом параграфе рассмотрим более сложный пример
локальной аппроксимации кубическими сплайнами, а именно:
S (х) = S (bi.-i/i-i + Ью/i + bii/i+i) B{ (х) A)
(в обозначениях предыдущего параграфа). Если положить
b= Ьг* b 1 b
j7» цзн
B)
где jbii = Ai-i(Af_i + А*)", Я* = 1 — |х<, то формула A) будет точной
на кубических многочленах. Для этого достаточно убедиться, что
она точна на функциях 1, х, х2, хъ. Последнее проверяется
непосредственно подстановкой этих функций в формулу A) и
сравнением результатов с тождествами B.3). Очевидно, данную схему
целесообразно применять для аппроксимации в классах Ск и
И^+1при &=*2, 3 (или к>3). На этих классах она даст
приближения с порядком выше 0(й2), в_то время как для простейшей
схемы B.1) он не превосходит 0{h2).
Изучим погрешность аппроксимации в случае равномерной
сетки узлов, когда
«4,-1--1/6, feii == —1/6, Ью-4/3,
и аппроксимационная формула A) на отрезке [хи х{+{1 принимает
вид
У^ C)
1+2 /
P=i1 Ч
Нахождение оценок остаточных членов аппроксимации Шх) =°
¦»¦ Six) — j(x) представляет здесь несравненно более трудную
задачу, нежели в предыдущем параграфе. Однако дело облегчается
тем, что при локальной аппроксимации можно применить
методику с использованием ЭВМ, развитую в гл. II для локальной
интерполяции эрмитовыми сплайнами. Рассмотрим пример.
Пусть f(x) e W\o. Имеют место разложения
з ^
2 ^т

§ 3. ФОРМУЛА, ТОЧНАЯ НА КУБИЧЕСКИХ МНОГОЧЛЕНАХ 251
Подставляем значения fp, р = i—2, ..., i + 3, в формулу
остаточного члена R(x) = Six) — fix). Если использовать обозначения
h
4'° (*i, *,) = f (P - *)* /IV (*i +
то на [xi, Xi+\] он принимает вид
Р ~ 1) + 843) (t, p) -
Далее, разделяем интегралы Ipk) (tu t2) на суммы интегралов
по отрезкам [р, р + 1J, например:
43'«, - 2) = - If (- 2, - 1) - /^ (- 1,0) - If @, t)
и учитываем тождества
вытекающие из свойств разделенных разностей второго порядка.
После приведения сумм интегралов по отрезку [р, р + 1] к одному
интегралу получаем
4 Г °
R (*) = ЖI 7-2 (~ 2- - *) Б'~10 +1^1 (f'T) /IV & + rh)dx +
t 1
+ j Фо (t, т) /IV (^i + тЛ) dt + j ^o (*, т) /Iv («j + tA) dt +
0 t
+ j *i V, т) /lv («t + tu) dt - /C3) B,3) Bi+2 (t). D)
Здесь обозначено
<pi(f, т) = tA2 + 18t + ix^Bi-tU) - A + tKS(U),
Фо(*. т) = 6tA + x)B + tM,-i@ - A - т)A + 4т + 7т2M(Ш -
-т35<+1(«,
, т) = - A - тJЯ(Ш - xA2 - 18t + 7x2)Bi+1(t) +
+ 6A-т)B-т)C-т)В,+2Ш,
. t) - - B - TKBt+iit) + A - t)C7 - 32t + 7x2)B{+2U).
Все остальные вычисления выполняются по программе на
ЭВМ. Таким образом, находится оценка \\R(x)Wx. Для получения
оценок производных Ш(г)(ж)Но. в выражении D) достаточно заме-

252
ГЛ. IX. ЛОКАЛЬНАЯ АППРОКСИМАЦИЯ СПЛАЙНАМИ
нить 5-сплайны их производными r-го порядка. Результаты
расчетов для рассмотренного примера и других классов функцшг
сведены в таблицу 9.3.
Характеризуя формулы B.1) и A) кубической
сплайн-аппроксимации в целом, следует отметить, что при их применении
погрешность аппроксимации больше, чем при интерполяции
кубическими сплайнами. Это особенно относится к функциям из
классов С3, С4 и Wto и их первым производным. Кроме того, оценки
в таблице 9.3 получены при больших требованиях к гладкости
Таблица 9.3-
Класс

функций
С2
W3
vv оо
С3
R.
0,14222&2со(/")
0>53530Л»||////||вв
0,052495Л3со(/'")
0,030382u4||/IV[|oo
Rt
0,51191Лю(/")
0Д3294/г2||/'"||оо
0,097014/г2со(/'")
0,055556^11/^11^
R*
1,8519со(/")
0,50695fc||/'" Ц^
0,30904/icd(/"/)
0,14087^11/^1^
п.
—
1,3361 ©(/'")
0,50720*||/IVIL
Таблица 9.4
h
од
0,05
4
1
,5-
,1-
к)
Ю-3
Ю-3
0
0
н
,18
,043
и
1,6
4,1
(ос)
-Ю-2
.Ю-3
0,17
0,07
4
1
и
,5
,1
(*)
•Ю-3
•Ю-3
Uix)
1,8
0,42
/»(
5,1-
1,3.
х)
Ю-2
10
2,9
1,5
Таблица 9.5
h
од
0,05
/i(
7,6-
5,0-
.)
10
10~7
0,033
0,0018
/з
2,9-
1,8-
<*)
10
10
0,067
0г017
/г
2,7
3,1
(X)
• 10
/|
о,
о,
R
(X)
38
021
/з
1,2
1,2
(*)
Ш)
1,8
0,60
функций, чем в таблице 3.3. Поэтому на практике следует
предпочесть интерполяцию, прибегая к простым схемам локальной
аппроксимации, когда по каким-либо причинам нежелательно
решать системы уравнений. Но схемами вида B.1) и A), как
увидим ниже (§ 10), не исчерпываются возможности локальных
процедур, в частности, для функций из класса С4.

§ 4. ОБЩИЕ ФОРМУЛЫ ЛОКАЛЬНОЙ АППРОКСИМАЦИИ 253
В заключение параграфа приведем результаты численных
экспериментов по аппроксимации четырех функций foix), /=*1, 2t.
3, 4, на отрезке [О, 1L Обозначения — такие же, как в § 3,.
7 гл. П. Результаты для формулы D.1) приведены в таблице 9.4,.
а для формулы A) — в таблице 9.5. Погрешность
аппроксимации етарших производных в последнем случае близка к
погрешности, даваемой локальной интерполяцией (таблица 2.6).
§ 4. Общие формулы локальной аппроксимации
В этом и последующих параграфах мы изучим локальную-
аппроксимацию вида C.1) для сплайнов любых степеней. Пусть.
причем bi(j) — линейные комбинации разделенных разностей
/[&<ь ..., bqi ДО порядка q = no^n.
В связи с этим нам придется вспомнить некоторые свойства
разделенных разностей. Для функций Ха(х) = ха они являются
однородными функциями координат ?го, ..., %{9. В частности,
При равноудаленных точках %><*, 5 = 0, ..., q, и четных q эта
разделенная разность выражается через q-ю производную
функции xq+l:
. [bio? • • • i big] —
где ?< — символ «средней» точки множества {?<Л. Если же q
нечетное, то точка, в которой вычисляется производная, не
совпадает с точками множества {?*,}. Чтобы избежать возникающей
несимметричности, при нечетных q на практике часто берут
сумму с весами двух разностей, отличающихся сдвигом
аргументов на один шаг. Такие разности имеют по q аргументов
одинаковых и по одному разному. Поскольку порядок аргументов роли
не играет, то подобные конструкции будем обозначать через
где 0 < \iiq < 1, kiq + \iiq = 1. При четных q \iiq == 0, hq
q нечетных веса удобно определять из условий
—(^ + + 5i)

54 ГЛ. IX. ЛОКАЛЬНАЯ АППРОКСИМАЦИЯ СПЛАЙНАМИ
Например, если |*о, Ьи Ы соответствуют узлам сетки xi+2, xi+\f
^i+3, то [in «= hi+i(hi+i + hi+2)-\ hi — 1 — [in.
Итак, рассматриваем аппроксимацию, когда
ne
Ь\ (/) =* 2 biqf [|io, . . ., liq(q+l)], B)
где |fo» • • •» It*. 9+i e f^f> . •., xi+n+\]. В частности, разделенные
разности могут переходить в производные, если некоторые или все
точки ?го, ..., ?*, q+x совпадают. В зависимости от выбора
постоянных biq получаются аппроксимации с теми или иными свойствами.
В том числе, при Ь<о =» 1, biq*=*0, q>0, имеем простейшую схему
(§ 1).
Мы видели (§ 3 гл. I), что через нормализованные В-сплайны
гг-й степени могут быть представлены многочлены степени щ < п.
.Для этого служат соотношения
7• •»х*+*) B«W» ос == 0, ..., Аг, C)
°п г
сами относящиеся к формулам типа A).
Если функция fix) имеет щ непрерывных производных, то ее
разложение по формуле Тейлора представляет собой многочлен
степени щ плюс остаточный член. Поэтому можно поставить
задачу: определить коэффициенты biq так, чтобы формула A) была
точной для многочленов степени по. Это значит, что она должна
быть точной для всех мономов Ха(х) ~ха, а == 0, ..., щ, что
соответствует равенствам
Zj biqXa [?i0, . . ., hq(q+l)] #n (x) = Xa(z)t CX = 0, . . ., ГС0.
i g=o
Суммирование по g распространяется от 0 до а, ибо
разделенные разности более высокого порядка для функции ха равны
нулю. Учитывая C) и линейную независимость 5-сплайнов,
отсюда для каждого i получаем соотношения
ГУ.
q=0 n
а == 0, ..., щ.
Они представляют собой систему линейных уравнений для
определения коэффициентов biqi q=0, ..., щ. Матрица системы —
нижняя треугольная с единицами на главной диагонали, и, значит,
задача разрешима. Ее решение можно выписать в явном виде.
С этой целью приведем две леммы о симметрических
функциях.

§ 4. ОБЩИЕ ФОРМУЛЫ ЛОКАЛЬНОЙ АППРОКСИМАЦИИ
Лемма 9.1. Имеют место тождества
а=о
E).
Доказательство проводится методом математической
индукции по числу к.
Лемма 9.2. Пусть и = (щ, ..., ип) и v = (ии ..., vq)—dea
вещественнозначнъьх вектора и п&* q. Пусть определена функция
г|> (и, i;) = (п - j)! 2g {uh + vx)... (ulq + vqL F)
еде 2g — символ суммы по всем размещениям из п элементов щ.
по q элементов. Тогда
$ (и, v) «
¦= S (» — g + a)! (q — а)! symg..a (uu ...,un) syma (i;lt..., vq). G>
Доказательство. Прежде всего заметим, что
-ft- \Uh • • • И/д = (Я - ? + 1) 2g-iW^i • • • ^a-1- »'a+l ' • • И'в« (8>'
1а
где справа стоит сумма всех размещений из п элементов по
5 — 1. Процесс дифференцирования можно продолжить.
Так как симметрическая функция sym,(»i, ..., ип) есть сумма-
всех сочетаний из п элементов по д, то она связана с суммой
размещений соотношением
^quh ...ulq = q\ symg (uu ..., ип).
Из F), (8), (9) следует
-ф (м, 0) = (/г — ?)!#! symq (мь ..., wn),
-^j-— - (п - q + 1)! (q - 1)! sym,-! (иь ..., ип),
(u, 0)
Но тогда нетрудно видеть, что G) есть разложение по
формуле Тейлора многочлена г|)(н, v) по переменным v\9 ..., vq в
окрестности нуля. Лемма доказана.
Л#йдем теперь коэффициенты biq из системы D). Чтобы
определить коэффициент Ьгл, обе части уравнения с номером а ум-

-256
ГЛ. IX. ЛОКАЛЬНАЯ АППРОКСИМАЦИЯ СПЛАЙНАМИ
ножим на (—l)ft-asymft-a(?to, ..., &, *-i) и просуммируем
результаты по индексу а от 0 до &. Получаем
h a
2 2(- 1)*~а biqXa Ню, ..., Si
¦2
/
syma (*i+ll ..., *i+n) symft_a (?fOl ..., gifft-1I A0)
При фиксированном g < к коэффициент при biq в левой части
«равенства есть
Рй} =¦ 2 (- l)"""a^a lEio, • • •, Eigrg+i)l Symft_a (gl0l . . ., U,k-i)-
a=o
Разделенную разность функции Ха(х) можно представить в
•виде отношения определителей [3, с. 73]. Поэтому
)
.где Ag — транспонированный определитель Вапдермоида:
i 6i0 — ?'
«a Diq*— определитель получающийся из него заменой элемептов
последнего столбца на ??о» . ..Д?д. В определителях Di(q+i> и
вместо gig стоят gi,g+i. Имеем
(И)
Так как определители D$ получаются из Diq заменой элементов
последнего столбца на %>%, . ..,l?q, то Dfi =0 при a<q и
J)iq} =« Dig- Совершенно аналогично, Z?i(V+i) «= 0 при a < ^ и
2?i(e+i). Но тогда из (И) следует что
A2)

§ 4. ОБЩИЕ ФОРМУЛЫ ЛОКАЛЬНОЙ АППРОКСИМАЦИИ 257
Далее,
D{k) D{.h)
P(#-i = - sym1 (?iOl ... Д^) + Xitk^ ^*=L + |4lfc-1F^ -
O, • • -, Si,fc-2i Ei.fe-
ll
Разделенные разности q-то порядка от Xh(x) = xh являются
однородными многочленами относительно своих аргументов степени
к-q [3, с. 71] Тогда
i,fe—2
Покажем, что
p{» = 0f g = 0,...ffc-2. A4)
Для этого в формуле (И) величины (~l)ft~a symft_a(|i07 .!.,"&, ь-i)
внесем в определители D^ и D^+i) множителями элементов
последних столбцов. Суммируя определители, находим
где Dig — определитель, получающийся из Diq заменой вектора
последнего столбца на вектор с компонентами
a Z)i(9+i) отличается от Diq педстановкой на место %iq
значений §i,q+l- _
При q < к — 2 величины a2} в определителе Diq имеют индекс
s^k — 2 и равны нулю согласно лемме 9.1. Соответствующие
величины в определителе Di(q+\) имеют индекс s< к— 1 и тоже
равны нулю. Равенства A4) доказаны.
Обращаясь теперь к формулам A0) и учитывая A2) — A4),
видим, что они эквивалентны соотношениям
!4fc-i Sift ~" Si.b-l^bi.fe-l + bih =
ft
, • • •, zi+n).
a=0
Заменяя индекс к на q и а на ^ == g — а, окончательно получаем
17 ю. С. Завьялов и др.

258 ГЛ. IX. ЛОКАЛЬНАЯ АППРОКСИМАЦИЯ СПЛАЙНАМИ
(штрихи опущены)
(si+1, ..., xi+n) —
V=0
— fAi,g-i (lig — 5i,9-i) Ь{,9-1, q = 0, • . ., Щ. A5)
Здесь при q нечетном fXif9-i==O, а при q четном 0 < jj,*, q-\ < 1*
Исследуем свойства формул A5). По лемме 9.2 их можно
преобразовать к виду
— fXi^-x (gig — Sif9-i) bt.g-1, ? = 0, . . ., 7lOf
где сумма берется по всем размещениям из п элементов по q+
Отсюда вытекают следующие очевидные свойства
коэффициентов biq.
Свойство 1. Коэффициенты biqj q = 0, ..., nOj инвариантны
относительно переноса начала координат.
Свойство 2. Если ?<0 определяется формулой A.2), т. е_
sym (zi+1, ..., ari+Tl), /о fetl = 0.
В этом случае простейшая схема аппроксимации из § 1 будег
точной на многочленах первой степени, что и обнаружилось на
рассмотренных в § 1 примерах.
Далее, исследуем случай, когда
)ъгО = х. п+1 1 his = х. п—.«; <, fei,s+l === х*. "+± ,»
В формуле A6) при q нечетном слагаемые в сумме содержат
множитель вида (xi+i0 — х т)+1\ и пары множителей
n+s \, 8=1,3,...,д.
г-\ (-1 /
2 /
Для каждого слагаемого найдется сходственное слагаемое,
получающееся из первого заменой
Эта замена, произведенная в сходственном слагаемом, снова дает
исходное слагаемое. Таким образом, сумма разбивается на пары
слагаемых. Сходственные слагаемые имеют противоположные*

§ 5. ОСТАТОЧНЫЙ ЧЛЕН АППРОКСИМАЦИИ 259
знаки. Это следует из того, что
sgn хШз —
В случае равноотстоящих узлов сетки {xt} сравниваемые
множители (пары) равны по абсолютной величине и, значит,
сходственные слагаемые отличаются только знаками. Справедливо.
Свойство 3. Если ?го, • • •» 5<.д-\ определены формулами A7),
ро при равномерной сетке узлов {х{} коэффициенты biq = 0 для
нечетных номеров q.
Пусть формула A) точна для многочленов степени п. Тогда
при п нечетном, согласно A7), множества xi+\, ..., xi+n и ?г-о, ...
, |«, n-i совпадают. В формуле A6) при q = n сумма берется
по всем перестановкам из п элементов. Каждая из них имеет
сходственную, получающуюся заменой (xi+i, — ?i«) -*Eis — xi+is)
и отличающуюся от исходной только знаком. Отсюда следует
Свойство 4. Если ?го, ..., §*,n-i определены формулами A7),
го при нечетном п коэффициент bin = 0.
§ 5. Остаточный член аппроксимации
Погрешность локальной аппроксимации будем изучать, как
обычно, для непрерывных и дифференцируемых функций.
Пусть fix) определена на всей вещественной оси или отрезке
la', b']. Рассмотрим ее аппроксимацию D.1) на [а, Ь] <= [а\ &'],
где %i задается одной из формул, A.2) или A.3).
Пусть fix) такова, что допускает разложение по формуле
Тейлора в окрестности точки х\
1 и = г
Остаточный член р(#) есть функция из того же класса, что и
)• Очевидно,
p(')(x)-Ot г = 0, ..., к. B)
Приведем функцию р(х) для двух случаев.
a) fix) ^ Ск. Остаточный член можно представить в виде
х
ас'

260 ГЛ. IX. ЛОКАЛЬНАЯ АППРОКСИМАЦИЯ СПЛ\ЙНАМТТ
Отсюда дифференцированием по х с помощью теоремы о среднем
для интегралов получаем
р(г) (х) = ^(у-^иу) {х _ х,г^ г = Ot _ л D)
Т]9е/? / — минимальный интервал, содержащий точки х и х\
б) f {x) e Wk?l. Остаточный член возьмем в обычном виде:
Дифференцирование интеграла по параметру х для / (v) e 1
остается в силе. Получаем
X
L/ ^«Л/ I —— , . * I It*/ ^^ I/I J \ ) Ml/* I VJ, • • • , Iv» V*-'/
Аппроксимируем функцию fix) сплайном Snix) по формуле
D.1), полагая щ> к. Так как эта формула точна для многочленов
степени щ, то справедливо равенство
*^п (,"¦?/ / \*^) === ^J ^J ^igP ifeiO? • • • ? Ь29(<7+1)] ^?i V^/ — P \^)#
г q={)
Дифференцируя обе его части по х и учитывая C), получаем
для любого х ^ [хи xi+i]
г ' ^0
ip=i—n q=o
r = 0, ...,7s.
Это общие формулы остаточных членов аппроксимации
функции fix) и ее производных. Получим, далее, их оценки.
В формулах F) используются данные на отрезке [хг-и art-+n+iJ.
"Условимся считать
hi = max hp, z%^ m*n A» -p ^ Pi < oo.
Возьмем формулу нормализованного Б-сплайна степени ^:
где фп (от, ^) = (-— l)n+1 (п + 1) (х — t)\, а разделенные разности

§ 5. ОСТАТОЧНЫЙ ЧЛЕН АППРОКСИМАЦИИ 261
составляются по аргументу t. Дифференцируя ио х, получаем
[Вп \Х'\ = фх-1 [Х\ Хр, . . ., Хр+п] — фп-1 [Х\ Хр+и - • ., ?p+n-i] =
— п rv (г\ - #р+1 (т\
~  ИТ~ "-1 ^ ' ~~ 1- ~ n~1 * '"
Отсюда согласно D.3) при а = 0 следует оценка
I [В* (х)]' | < К1 (В*-! (х) -|- В*±\ (х)) < АГ1.
Продолжая подобным образом, находим, что
Производная 7?-го порядка 5-сплайпа разрывна и доопределяется
в точках хР как производная справа (§ 1 гл. I).
Для biq имеем формулы D.16). Обозначим
max I xp+i — Hps I ^ dpq.
При этом, очевидно, \lPq— |P, q-\\ < dPq. Тогда из D.16)
Величина iiip, g-i может быть отличной от нуля только для q
четных. В этом случае | bPfg-i | ^ ^p^-i- Так как dpq = ^Pqhu чР2 —
const, то __
\bpq\ ^cPq hi, cpg —const. (8)
Разделенные разности функции р(х) связаны с ее
производными формулами
Р Про, • - -Ul р{Ф &^ (9)
^q е /рд, /Р9 — минимальный отрезок, содержащий точки |р0, • •«
• ••» Sp9(9+i>- Рассмотрим два случая.
а) f(x)^Ck. Из D) и (9), учитывая, что \^,q — xf\ ^pqhu при
g ^ & находим
| Р Про, • • ч ZpQ(q+l)] KCpqhi~4®i(jm)% Cpq ~ COnsl, A0)
(Oi(f{k)) — максимум колебания функции на сетке точек |р>„ р =
= i—?г, ..., t; s = 0, ..., «о, или точек Хр, р = ?—^г, ..., i + /г + 1.
б) /(a;)elf«+1. Из E) и (9), используя неравенство Гёльдера,
при q^ к получаем
I Р Про, • • •, ?p**+i)l | < 4^"'+11 //А+1) I», с; - const, (И)
где норма H/(fe+1)JlTO берется на отрезке [#,--„, ?i+n+i].

262 ГЛ. IX. ЛОКАЛЬНАЯ АППРОКСИМАЦИЯ СПЛАЙНАМИ
При выводе оценок остаточных членов аппроксимации F)
ограничимся случаем щ = к, для которого верны оценки A0) и A1).
а) f(x)^Ck. Из соотношений F) и неравенств G), (8) и
A0) при х^ [хи xi+\] находим (штрихи у х опускаются)
IS? (х) - /(г) (*) \\c[Xi,Xi+l] < РА^ГЧ (/«), г = 0, ..., к. A2)
б) /(*)€= Whx+1. Из F) с учетом G), (8) и (И) следует
1S^ (х) - fr) (х, \\c[Xi,Xi+l] < BР,)Г e'M+1-r\ fh+l) U A3)
г = 0, ...,&.
Нами доказана
Теорема 9.1. Если аппроксимациоиная формула D.1) точна
для многочленов степени к < п, то
а) для функций f(x) e С*
IS? (х) - /(г) (х) \\с{ам < сй'г-со (/'«), г = 0, ..., к;
б) для функций / (х) <= W^1
\\S{nr) (x) - frr (х) |с[а,Ь] < chh+1-1 /(ft+1) \\LM, r = O,..,,k,
где постоянные с не зависят от fix).
Оценки A2) и A3) получены в предположении, что щ = к.
Применять для рассматриваемых классов функций аппроксимаци-
онные формулы, точные на t многочленах более высокой степени, пе
только бесполезно, но в общем случае и вредно. Дело в том, чт.ок
разделенным разностям функции р(х) порядка д = &+1, ..., щ
нельзя непосредственно применять формулу (9). Предварительно
их приходится привести к разностям порядка к. Поэтому
порядок аппроксимации функции относительно /г, определяемый
произведениями bpqpi^po, ..., ^Pq(q+\)], не может быть повышен,
коэффициент же с*, или С|, может увеличиться за счет дополнительных
членов при суммировании по q. Исключение составляют случаи,
когда при переходе от схемы с щ = к к схеме с щ = к-\г1
коэффициент bPt ь+1 = 0 (свойство 4, § 4) и усложнение схемы пе
увеличивает константу с. Этот факт будет использован в
последующих параграфах.
Достаточно «хорошие» значения констант с вычислить
трудно не только при произвольном щ но и для малых п, например
п == 2 или п «=» 3. Это сравнительно просто делается лишь в случае
равномерной сетки узлов (§ 3 гл. II).
Как уже отмечалось, при не слишком неравномерной сетке
следует ориентироваться на оценки для равномерных сеток.
Уточним это замечание. Пусть
hp == Ы + бР, р = i — п, ..., i + п.

§ 6. О СПЛАЙНАХ, ПЕРИОДИЧЕСКИХ НА СЕТКЕ 263
В формуле остаточного члена F) коэффициенты bpq суть
однородные многочлены шагов hp степени q, В разделенных разностях
р[?Ро, ..., |^9(g+i)] такими функциями, причем с положительными
коэффициентами, являются знаменатели. Что касается В-сплайнов
и их производных порядка г, то они, будучи разделенными
разностями от усеченных степенных функций, на промежутке [я*,.
xi+i\ представляются отношениями однородных многочленов,
а именно: знаменатели — многочлены степени п от шагов hPj
а числители — многочлены степени п—г от тех же шагов и
значений х — Xi, Xi+i — x. Но тогда остаточный член F) может быть
разложен по формуле Тейлора по степеням параметров 6Р, р =
== i — п, ..., i + п, в окрестности бР = 0:
R (х; к{-п, ..., hi+n) = R (х;
(max 6p
V
Предположим, что бр = О \hf). Тогда
R (x; hi-n, ..., hHn) = R (xy h{) [1 + 0 (hi)]. A4)
Величины Rix; A<_n, ..., hi+n) и R(x; h{) одного порядка малости,
а их разность малая более высокого порядка. В этом смысле при
неравномерной сетке можно пользоваться оценками погрешности,
полученными для равномерной сетки.
Указанное обстоятельство в ряде случаев позволяет
осуществлять аппроксимацию с заданной точностью е путем выбора
шагов Ы, Например, если fix) e С2, то, пренебрегая в оценке B.10)
величиной (ОгС/'7) по сравнению с ||/1с[зс4,х4+1], в соответствии с
A4) получаем условие
О решении подобных неравенств уже было сказано в § 3 гл. II.
§ 6. О сплайнах, периодических на сетке
Речь пойдет о некоторых вспомогательных сплайнах,
используемых для построения моносплайнов (§ 7). Они
рассматриваются на всей действительной оси. Сетка узлов предполагается
равномерной с шагом h.
На такой сетке, как мы знаем, В-сплайны степени п являются
четными функциями относительно точек, определяемых форму*
лами A.3):
Eft^+^A, A)
в которых они принимают максимальные значения.

264 ГЛ. IX. ЛОКАЛЬНАЯ АППРОКСИМАЦИЯ СПЛАЙНАМИ
Обозначим
х — 1^-п^
<*\п (Х) = т-1-
и рассмотрим функции вида
S (/г, у; х) = (_ 1)п 2 аТп (х) Вгп (х). B)
г
Эти функции, во-первых, являются сплайнами степени не
выше п + у с непрерывными производными до порядка /г — 1. Во-
вторых, ?(тг, -у; х) — периодические функции с периодом h. В
самом деле, в силу определения cin(x) и свойств 5-сплайнов
S (П, Y; ^ + Л) = 2 CUi (* + Л) В1п (X + h) = Ъъ1-1.п (X) В'п1 (X) =-
i
г
Приведем простейшие примеры такого рода сплайнов, когда
один из параметров, п или у, равен нулю. Если f = О» то
5Gг, 0; #) = (— 1)п. При п=0 В\{х) =1 на промежутке lxu xi+x\
и 5о(^) = О вне его. Поэтому на [хи xi+\] 5@, «у; х)=от(л:) при
Функция 5@, ч; д:) представляет собой сплайн степени у с
разрывами в точках ХхУ иначе говоря, сплайн дефекта ^. К сплайнам
рассматриваемого здесь вида относятся и левые части тождеств
B.4) (с точностью до знака).
Для изучения свойств введенных сплайнов в общем сдучае
установим рекуррентную формулу. В B) перейдем к ^-сплайнам
(п— 1)-й степени по формуле A.3.2):
Тогда
S (п, г, х) = (- 1)" 2 Тг [4L
Из определения oin(x) вытекают формулы
оm (х) = Oi,n-i (х) — т, <х w,n И = а|>п_! (а:) -|- —;
Подставляя их в выражение Sin, ^; #) и разлагая (о,-, n-i(x) ± 1/2)т

§ 6. О СПЛАЙНАХ, ПЕРИОДИЧЕСКИХ НА СЕТКЕ 26S
по формуле бинома, получаем соотношение
S(n,y; x) = (— 1)П^] 2
где
(О, если т четное,
6 (т) = {.
' 11, если т нечетное.
Меняя порядок суммирования и учитывая определение функций
Sin, у; х) B), получаем искомую рекуррентную формулу;
S (п, у: х) = — У, \ ) —тт- «5 Gг — 1,y — /71 + 8 (ту, х). C)
Для всех т разность т—8(т)—четное число. Поэтому, если
Ч четное, то параметр ^ — т + Ь(т) пробегает четные значения
от 0 до Y- Если 7 нечетное, то оп принимает нечетные злачения
от 1 до ч- Коэффициент при Sin—1, *y; х) равен i—n + y)/n.
Применяя формулу C) п раз, получим
S (п, у; х) = (- 1)п 2 аг (п, у) S (О, Z; х). D)
Здесь ai(n, 4) — постоянные коэффициенты, причем
av (п, у} - (-n + V)(~n ¦ ^ V)---(-l + Y) ^ E)
Формула D) позволяет установить несколько полезных свойств
рассматриваемых сплайнов.
Свойство 1. На каждом промеэюутке [xiy xi+\] S(n, f; x)
является многочленом от переменной а степени не выше у
nv l * ' }J
причем только по четным (Z = 0, 2, .«., 7) или только нечетным
(I = 1, 3, ¦.., if) степеням.
Переменная а принимает на концах промежутка [хи х{+\]
значения ± 1/2, а в середине его — нуль. Любая четная функция
этой переменной непрерывна. Нечетная функция обращается в
нуль при о = 0, и, кроме того, если она непрерывна, то и в
точках а = ±1/2. В частности, при «у четном (нечетном) сплайн
S(n, y; #) и все его производные четных (нечетных) порядков
непрерывны, а производные нечетных (четных) порядков г^гг—1
непрерывны и равны нулю в узлах сетки и /на серединах
расстояний между соседними узлами. Отсюда следует, что если у
сплайна S(n, if; x) параметры п и у одновременно четные или
нечетные, то он обладает непрерывными производными до порядка п%

266
ГЛ. IX. ЛОКАЛЬНАЯ АППРОКСИМАЦИЯ СПЛАЙНАМИ
а не только п — 1. Следовательно, при *f ^ n сплайн будет просто
многочленом степени не выше «у. По свойству периодичности он
должен принимать постоянные значения в точках хи Но такой
многочлен может быть только константой.
Свойство 2. а) При f ^ n S(n, ^; х) = const.
б) При 7 > n степень сплайна в точности равна у.
Последнее утверждение следует из того, что в формуле F)
коэффициент ат(гс, *у) E) отличен от нуля.
Установим еще одно свойство сплайнов S(n, n + l; х).
Функции S(n, n + 1; х) на промежутке [я<, xi+\] являются
многочленами Qn,n+\(o) со старшим коэффициентом ап+\(щ дг+1) = 1.
В частности, Qo\(g) =о и определено на [хг, xi+\). По
рекуррентной формуле C) находим Qwio) = о2—1/4. Этот многочлен имеет
минимум в точке а = 0, а наибольшие значения (равные нулю)
принимает при о = ± 1/2.
Пусть, далее, тг>1. Производные (тг+O-ro порядка много-
чденов Qn,n+i(o) суть Q{ntni\ (о) = (тг+1)! Интегрируя это
равенство по,о и учитывая нечетность Ql?l+i (tfj, имеем
Qnr!Ui(o) = (n + l)\G. G)
Эта функция меняет, знак только в точке а = 0. Она является
второй производной для функции Qw+\ (®)- Последняя поэтому,
обращаясь в нуль в точках о=—1/2, 0, +1/2, как непрерывная
нечетная функция па интервалах ( — 1/2, 0) и @, +1/2)
оказывается выпуклой вверх или вниз соответственно и имеет па
отрезке [—1/2, +1/2] два экстремума с равными по величине и
Таблица 9.6
0
1
2
3
0
*• 1
—1
—1
1
о
0
0
0
2
а2
-CF2i_1/4
1/4
-1/3
3
а3
2а(а2—1/4)
а(а2—1/4) .
0
4
а4
3(а2—1/4)(а2+1/12)
3(а2—1/4L-1/16
(а2_1/4J_1/3
противоположными по знаку значениями. Таким свойством об-
б () г*
•
Замыкап — б (л)
дадают все функции Qn,n+i (о), г=1, 2, ..., ^
ют этот ряд при п четном многочлен Qn,n+\(o), а при п нечетном
его производнал Qntn+i ip) • В последнем случае сам многочлен
есть четная функция с экстремумами в точках 0 = —1/2, 0, +1/2.
Дтак, доказано

§ 7. МОНОСПЛАЙНЫ 267
Свойство 3. Сплайны S{n, п+1; х) на отрезке [хи хг±\]
при п четном имеют две точки о = ±о*, в которых они принимав
ют наибольшее и наименьшее значения, а при п нечетном наи±
большие {или'наименьшие) значения достигаются при о = ±1/2
и наименьшее {или наибольшее) значение при о= 0.
В заключение приведем таблицу 9.6 многочленов Qn^o),
определяющих сплайны S{n^ у; х), для п = 0, 1, 2, 3 и ^ = 0, 1, 2, 3, ?
Задачи, а) Доказать, что сплайн S(n, п + 1; х), п = 0, 1, ..., является
производной сплайна S(n + 1, п + 2; х) с точностью до множителя и
аддитивной постоянной.
Указание. Интегрировать равенство G) последовательно по а,
учитывая четность или нечетность функций Q^n+i (а)» и положить п = г =
— 0,1,...
б) Показать, что с точностью до аддитивных постоянных многочлены
Qn,n+i{o) совпадают с многочленами Бернулли степени п + 1 [3].
§ 7. Моносплайны
Определение. Моносплайном степени п+1 называется
функция
определенная на всей действительной оси или отрезке [а, Ы,
являющаяся комбинацией монома xn+l и сплайна степени п дефекта 1.
Эта функция, будучи на каждом промежутке lxu xi+\]
многочленом степени п + 1 со старшим коэффициентом единицей и
имея п — 1 непрерывную производную, является сплайном
степени п + 1 дефекта 2.
В теории аппроксимации сплайнами моносплайны в
известном смысле играют ту же роль, что и многочлены Чебышева в
классической теории приближения функций. По аналогии мы
изучим Bonpoq о моносплайнах, наименее уклоняющихся от нуля
в какой-либо метрике, в частности, пространств С и Ь2.
Вначале рассмотрим моносплайны Z^+i (x)y являющиеся
остаточными членами приближения мономов Хп+\{х) = xn+l
какими-либо сплайнами Snix). Используем для этой цели локальную
аппроксимацию типа D.1), точную на многочленах степени п:
п
Sn И = 2 2 biqXn+i lliO, • • •, ?ig(g+l)] Bn (*). A)
г 9=0
Это обеспечивает порядок приближения O{hn+l).
Моном xn+i по формуле Тейлора в окрестности точки х
представляется многочленом:
xn+1 = (*У+1+ (» I

268 ГЛ. IX. ЛОКАЛЬНАЯ АППРОКСИМАЦИЯ СПЛАЙНАМИ
Функция tyn+iix, х) = ix -- x')n+l играет роль остаточпого члена
разложения. Мопосплайн Zn+i (x) как остаточный член
аппроксимации имеет вид
п
z°n+i (*0 = - 2 2 Mn+i i*'; S«o, • • м 5*«в+жI я» (*).
i 9=0
Здесь и далее в этой главе под остаточным членом
аппроксимации понимается разность fix) — Snix), а не Snix) —fix), как это
было ранее.
Функцию ipn+i(#, #') разложим по формуле бинома:
Ч>»+1 (*, *') = 2* С+Да И &о - *')п+1~а,
а=о
где ХаЫ — (ж — 1ю)а. Тогда получаем
zS+i (*') = - 2 "s cS+1fta (?i0 - ^')n+1"a^n и, B)
г a=0
причем
г?
^ia = 2 &г<^а [SiO, • • • , liq(q+l)], & = 0, . . . , П + 1. C)
Предположим, что сетка равномерная с шагом h и точки
аппроксимации выбраны по формулам D.17):
? , Я ~L 1 7 О , П .9 ,
Х ^ ^ Л
В этом случае коэффициенты fc^ = feg не зависят от индекса г и
согласно свойству 3, § G, bq = 0 для g нечетных.
Далее, разделенные разности Ха[|,-о, ..., ^(^-М)], будучи
однородными функциями координат 0, ± h, ..., ± qh, очевидно,
равны нулю, если а — q — нечетное число. По тогда из C) следует,
что, во-первых, gia = ^a не зависят от индекса i и, во-вторых,
ga = 0 для а нечетных.
Моносплайн в форме B) преобразуем, меняя порядок
суммирования и переходя к функциям Sin, 4; х) F.2):
а=0
a5 (в, » + 1 - о; х). D)
(Здесь штрихи у х опущены.)
Моносплайн является функцией, периодической на сетке, так
как этим свойством обладают функции Sin, п + 1 — ее; х).

§7. МОНОСПЛАЙНЫ 20%
Рассмотрим две возможности.
а) п четное. В этом случае при сс>0 четных по свойству 3,
§ 6, S(n, п+1 — а; #) = 0, а при а нечетных ga = 0. В D)
отличен от нуля только один член, соответствующий а = 0, и
моносплайн имеет особенно простой вид:
Zl+x(x) = hn+1S(n, n + 1; х). E)
б) Пусть теперь п нечетное. В этом случае при а нечетных
ga. = 0 и Sin, п + 1 — а; х) = 0, а при а > 0 четных эти величины
постоянны, но отличны от нуля. В результате из D) получаем
выражение
Z°n+i И = hn+1S (п, п + 1; х) + сп+1 F)
при
Примеры моносплайнов при п = 0, 1, 2, 3. Моносплайны
определяются формулами E), F) и таблицей 9.6.
1) гг = 0.
Ъ\ (х) = ha. (8а)
2) гг = 1. Из G) и C) следует, что сг = ?2 = 0. Тогда *
согласно F)
() (86)
3) л = 2.
ZS(*)=A»a(o2-!)- (8в)
4) ?г = 3. В этом случае по формуле C) находим ?2 — ~у^2
«I
и g4 = —у^4 и з^тем из G) получаем с4 = /г4. Тогда
согласно F)
j f(iJ|l (8г)
Эти моносплайны с точностью до сдвига по оси ординат
изображены на ppic. 9.1, а, б, в, г соответственно.
Ниже речь пойдет о моносплайнах, наименее уклоняющихся
от нуля. В аппроксимационную формулу A) добавим
(параметры fcf.n+l*
g=o

270
ГЛ. IX. ЛОКАЛЬНАЯ АППРОКСИМАЦИЯ СПЛАЙНАМИ
равномерной сетке узлов сплайна коэффициенты biq>
ч-^О, .... /г, не зависят от индекса г. Будем считать, что этим
свойством обладают и величины 6<§п+ь т. е. при всех i bt n+1 «
— Ьп+ь Но тогда моносплайны типов E) и F) тоже будут
определяться с точностью до этогр параметра:
Т _ I /VI \
Zn+1 (х) = Z°n+1
A0)
Для построения моносплайнов, наименее уклоняющихся от
нуля, в рассматриваемых ниже задачах оказывается
достаточным выбрать подходящим образом свободный параметр bn+l.
36
Рис. 9.1.
Вначале рассмотрим более "простую задачу.
1. Моносплайны, обращающиеся в нуль на множестве узлов
, d=l,
(И)
где о* — фиксированное число, —1/2 ^ о* ^ 1/2.
Этим свойством обладает моносплайн A0) при
fen+i = Zn+i (a*). A2)
а) При п четном в выражении моносплайна A0) функция
Zn+i{o) обращается в нуль на серединах промежутков ixu xi+x\
(о*=0), а при п>0 также на их концах (о*=±1/2). Графики на
рис. v 9.1, айв показывают с точностью до множителя hn+l пове^'
деыие таких моносилайнов при п = 0 и п = 2.

§ 7. МОНОСПЛАЙНЫ 271
б) При п нечетных функция Zn+i (<*) достигает наибольшего
и наименьшего значений в точках а = —1/2, 0, +1/2. Поэтому
можно добиться, чтобы моносплайн на каждом промежутке
[х{, xi+\] принимал нулевые значения либо в двух точках о* =
= ±Gi, либо в точке у{ (oi=0). Пусть О\ = ±1/2. При п=\
согласно (86) находим Ъ^ = 0; график на рис. 9.1, б следует
о
сдвинуть на —1/8. При п = 3 в силу (8г) получаем^ = -о"^4»
и график на рис. 9.1, г сдвигается на 1/32.
Таким образом, * моносплайн Zn+\(x) может иметь либо
простые нули уц, уг2, либо двукратные г/г-о, i = 0, ±1, ...
Теорема 9.2. Среди всех моносплайнов Мn41{х) степени
п+1 моносплайн Zn+\(x) при условии A2) единственный,
принимающий нулевые значения на заданном множестве узлов г/л,
Уг2 или г/г0, I = 0, ±1,
Доказательство. Предположим, что существует другой
моносплайн Mn+i(x) с таким же свойством. Тогда разность
Мп+\{х) — Zn+\(x) = Sn(x) есть сплайн степени п дефекта 1 с
условиями 1) SniytJ = 0, а = 1, 2, или 2) Sn(yi0) =^>п(Ую) = 0»
i = 0, ± 1, . •. Покажем, что ?„Ы = 0. При п = 0 п п = 1 это
очевидно, поэтому полагаем п ^ 2.
Для доказательства воспользуемся теоремой 1.3. Хотя она
сформулирована для всей числовой оси, но очевидна ее
справедливость и для конечного отрезка [go, gjv-n+i], заключающего
N — п узлов сплайна и все узлы интерполяции. В качестве
такового возьмем произвольный отрезок [хи х^р]{р ^ п). В случае 1)
сплайн Sn(x) имеет на нем не менее 2р нулей, из которых
можно выбрать р + п, удовлетворяющих условиям A.4.2). Тогда по
теореме 1.3 получаем Sn(x) = 0 на lxh xHv\. В случае 2) сплайн
Sn (х) степени п — 1 имеет на [хц xi+P] не менее 2р — 1 нулей,
из которых можно выбрать р + п — 1, удовлетворяющих
условиям A.4.2). Тогда 5^@:) = 0 и, значит, Sn(x) ^ 0 на [#*, Хцр].
Таким образом, теорема доказана для отрезка, а в силу его
произвольности и для всей числовой оси.
2. Моносплайны, наименее уклоняющиеся от нуля на всей
числовой оси в метрике.пространства С.
а) п четное. В выражении моносплайна Zn+1 (x) A0)
функция Zn+i(o) имеет на каждом промежутке по две точки, в
которых она принимает равные по величине и противоположные
по знаку значения ±Еп, не зависящие от номера L Если
положить в A0) &n+i=0, то таким же свойством будет обладать и
моносплайн Zn+ilx) (рис. 9.1, а и в).
б) п нечетное. В этом случае функции Zn+i (сг) имеют
наибольшие и наименьшие значения на концах промежутков

272 ГЛ. IX. ЛОКАЛЬНАЯ АППРОКСИМАЦИЯ СПЛАЙНАМИ
[х{,Х{+\] и на их серединах. Чтобы в этих точках моносплайп Zn+\(x)
имел равные по величине и противоположные по знаку значения
=fc/?n, следует положить в A0) Ьп+1= — Zn+1@) -f Zji+Л -^ )!•
Например, при тг = 1 должно быть Ь2 = — -g-&2, а при гс=3 &4=
й(рис. 9.1, б и г).
Итак, построены мокосплайны, принимающие последователь-»
ность экстремальных значений, равных по величине и
чередующихся по знаку, т. е. последовательность точек чебышевского
альтернанса. На отрезке [я,-, xi+\] имеем две (при п четном) или
три (при п нечетном) такие точки. Присоединение к нему
отрезков слева или справа добавляет по две точки па каждый отрезок.
Теорема 9.3. Среди всех моносплайнов Мп+ х (х) степени
п+ 1 для моносплайпа Zn+\{x) при
{О, если п четное,
-j [Zj+i @) + Zl+i A/2)], если п нечетное,
имеет место неравенство
Моносплайн Zn+\(x), обладающий этим свойством, единствен.
Доказательство. Предположим, что существует другой
моносплайп Мп+\(х), для которого \\Мп+\(х)\\с < HZn+1(#)llc. Сплайн
Sn(x) = Мп+\(х) — Zn+\{x) на последовательности точек {у{\, yi2y
i = 0, ±1, ...}т в которых Zn+\(x) достигает максимума или ми-
нимука, удовлетворяет ограничениям
eSniyn) < 0, eSn(yi2) > 0, i = 0, ± 1, ... A3)
(е =» + \ или 8 = — 1). В тех точках yiay где выполняются
равенства, имеют место соотношения Sn (г/ia) = Sn (yia) = 0.
Нетрудно видеть, что при п = 0 и п = 1 возможны только равенства и
S'n(^) s 0. Рассмотрим п > 2.
Несложный анализ показывает, что сплайн Sn (x) на
произвольном отрезке [х{, xi+p] (p> п+ 1) имеет не менее 2/? — 2
нулей. Из них можно выбрать *р + п — 1 нулей, удовлетворяющих
условиям A.4.2), и тогда по теореме 1.3 <Sn(.r)s==0 на [xiy xi+p].
Отсюда Sn(x) S3 0 на этом отрезке, а значит, и на всей
числовой оси. .
3. Моносплайны, наименее уклоняющиеся от нуля в метрике
пространства L2.
В выражении моносплайна Zn+\(x) A0) постоянную Ъп+\
определяем из условия минимизации среднеквадратичного

§ 7. МОНОСПЛАЙНЫ 273
уклонения Zn+\{x) на промежутке Ixi, xi+i\: найти
min j [Zn+i (x) — bn+tYdx.
x%
Условие экстремальности по параметру Ьп41 имеет вид
xi + l xi+l
Zn+1 (x) dx = Zn+i (^) — bn+1\ dx = 0. A4)
Отсюда, переходя к переменной а, получаем
1/2
bn+i= J Z°n+I(a)da. A5)
-1/2
Это условие обеспечивает минимизацию Zn+\(x) в среднем на
любом отрезке, кратном h.
а) п четное. Моносплайн Z?°1+1 (а) есть нечетная функция
о, и потому интеграл в A5) равен нулю, т. е. Ъп+\ = 0. В
рассматриваемых нами примерах па рис. 9.1, а и в картина не
меняется.
б) п нечетное. Здесь Zn+i {о) — четная функция, и в общем
случае bn+i ^ 0. В соответствии с (86) и (8г) находим Ь2 = — -ттй2,
Ь4 = -Т7Г hu. Графики на рис. 9.1, б и г сдвигаются на 1/24 и
на -1/480.
Рассмотрим, далее, моносплайиы Мп+\(х) на отрезке [а, Ы
с сеткой узлов х{ = а + ih, i = 0, ..., N, b = a + Nh.
Теорема 9.4. Среди всех моносплайнов Мп+Х(х) степени
тг+1, периодических с периодом Ъ — а, моносплайн Zn+i(x) при
условии A5) единственный, для которого среднеквадратичное
уклонение достигает минимального значения, т. е*
о о
J Zl+1 {x) dx < J Ml+1 (х) dx.
Доказательство. Пусть Мп+\(х) = Zn+X(x) + Sn(x). Нуя^-
но показать, что
ь ь
j Z2n+1 (x) dx < j [Zl+1(x)^2Zn+1(x) Sn(x) + *Sl (x)] dx.
a a
Так как значение интеграла от Sn {%) больше нуля, если
18 Ю. С. Завьялов и др. <*

274 ГЛ. IX. ЛОКАЛЬНАЯ АППРОКСИМАЦИЯ СПЛАЙНАМИ
?п(х) & 0, то достаточно убедиться, что
ъ
Zn+1(z)Sn(x)dx = 0, • A6)
каково бы ни было Sn(x).
Продолжим сетку за пределы отрезка [а, Ь] и представим
сплайн Sn(x) через 5-сплайны:
г=—п
Учитывая периодичность функций (с периодом Ъ — а), можно
представить A6) в виде
JV-1 хг+п+1
2 \ \ Zn+1 (х) В\ (x) dx «= 0.
*=° 4
Покажем, что в этом соотношении каждый из интегралов
равен нулю, т. е*
xi+n+i
Zn+1(x)Bin(x)dx = 0, i = 0f ...-, ЛГ — 1. A7)
Пределы интегрирования в A7) соответствуют отрезку, на
котором сплайн Вгп (х) отличен от нуля. Вгп (х) — четная
функция относительно середины отрезка ?io = xi Ч ъ— ^ и
обращается в нуль на его концах вместе с производными до порядка
п— 1 включительно.
Если п четное, то функция Zn+\(x), как мы знаем, нечетная
относительно точек ?,-о. Поэтому произведение Zn+i (x) Вгп (х) есть
нечетная функция и интегралы A7) равны нулю.
Пусть теперь п нечетное. В этом случае Zn+\(x)—четная
функция относительно точек |ш- При п = 1 на отрезке [xh xj+\]
сплайн первой степени можно представить линейной функцией
переменной о# (§ 6). В частности, В\ (х) = oi0 + 1/2 на [#*, xi+{]
и В\(х) = —o»+ifo+ 1/2 на [zi+x, xi+2l. Тогда из A7) получаем
xi+2
Z%(z)\oi0+±)dz-- j
Интегралы от произведений Z2(x)ojo равны нулю как интегралы
от нечетных функций на [zi9 xi+\] и lxi+u хч2\, а интегралы от
Z2(x) равны нулю согласно A4). Поэтому G\ = 0.

§ 7. МОНОСПЛАЙНЫ 275>
Остается рассмотреть случай нечетных п > 3. Будем
обозначать через Zn+1+rU), г = 1, ..., лг—1, последовательность
первообразных для функции Zn+\(x). Они определяются с точностью до
констант. На первом шаге получается функция Zn+2(x), которая
в силу A4) имеет в точках хр, р = i, ..., i + n + 1, одинаковые
значения, равные значению константы интегрирования.
Следовательно, функция Zn+2(#) является, как и Zn+i(#), периодической:
на сетке. Если положить константу интегрирования равной
нулю, то Zn+2(#) будет нечетной функцией относительно середин
промежутков [#р, хрл\]. Но тогда имеет место
Zn+1+P (x) dx = 0, р = г, ...,i
оср
Здесь г=1. На втором шаге получаем четную периодическую
функцию Zn+z(x) при любом значении константы
интегрирования. Выберем последнюю так, чтобы снова выполнялось A8) для
г = 2. Продолжая этот процесс, получим соотношения A8) для
г = я -1. т. е. для функции Z2n(?).
Будем интегрировать в A7) по частям. На первом шаге*
получим
х +Н
G« - Zn+2 {х) В*п (х) x\+n+1 - J Zn+2 (x) [В1п (x)Y dx.
*i
Согласно свойствам 5-сплайнов первый член снрава равен нулю..
Повторяя ийтегрировяние по частям п — 1 раз приходим к
формуле
J Z2n(x)[Bin(x)Yn'1)dx.
Но \Вп {х]\{п~г) есть сплайн первой степени, и, повторяя
рассуждения, сделанные для случая п = 1, приходим к выводу, что
Сгп s= 0. Это завершает доказательство теоремы.
Р заключение отметим, что хотя теоремы 9.2 и 9.3 доказаны
для всей числовой оси, а теорема 9 4 для отрезка [а, Ь] с
достаточно большим числом узлов сплайнов, но из доказательств
нетрудно видеть, что все теоремы справедливы для конечных
отрезков, если только на них размещается не менее п + 2 узлов-
сетки.
Полученные здесь результаты о моносплайнах, наименее
уклоняющихся от нуля, в заключительных параграфах данной
главы используются при решении задач приближений сплайнами,,
близких к наилучшим.
18*

276 ГЛ. IX. ЛОКАЛЬНАЯ АППРОКСИМАЦИЯ СПЛАЙНАМИ
. § 8. О задаче квазинаилучшего равномерного
приближения сплайнами. Асимптотически
наилучшие приближения
Задача о наилучшем равномерном приближении функции
fix) ^ С[а, Ъ] сплайнами Snix) степени п дефекта 1,
образующими конечномерное множество {Sn(x)} в Cia, b], формулируется
следующим образом. Найти сплайн Sn (x) такой, что
|/ (х) - Sn (х) ||с[а,ы = Еп = min || / (х) - Sn (х) \\с[аМ. A)
{Sn(x))
Здесь возможны два варианта. Первый, когда сетка узлов
сплайна
А: а = х0 < х\ < ... < xN = Ъ B)
фиксирована и размерность множества сплайнов п + М. Этот
вариант по методам решения наиболее близок к классическим
задачам наилучших приближений многочленами,
дробно-рациональными функциями и т. п. [23, гл. V]. Второй вариант: число
узлов сетки фиксировано, но дх координаты х\у ..., xN~\
произвольны. Размерность множества допустимых функций
увеличивается до п + 2N — 1, что не только уменьшает величину
уклонения Еп, но и приводит к новым качественным результатам [77, 80].
Мы предлагаем третий вариант. В задаче со свободными
узлами (ее решение не единственно) привлекаем дополнительные
условия. Разумеется, без ограничений задача A) смысла не
имеет, ибо непрерывную функцию fix) можно как угодно хорошо *
приблизить сплайном Sn(x) за счет выбора достаточно малого
шага сетки. В качестве новых ограничений введем равенства,
подсказанные теорией моносплайнов, наименее уклоняющихся
от нуля. Как было показано в § 7, уклонение мопосплайпа па
каждом промежутке [#*, х{+\] принимает одно и то же значение.
По аналогии с этим потребуем, чтобы
| / (X) - Sn (X) \c[xitxi+l] = Еп, * = 0, 1, . . ., C)
Когда структура решения задачи будет установлена,
попытаемся задавать величину Еп и по ней находить число узлов и
шаги сетки.
Таким образом, вместо задачи A) на безусловный экстремум
(в первом варианте) или с простыми ограничениями B) (во
втором варианте) возникает задача на условный экстремум с
ограничениями типа равенств C). Не вдаваясь в теорию подобных
задач, мы остановимся на практических методах построения их
приближенных решений в предположении, что Еп достаточно
мало.

§ 8. ЗАДАЧА КВАЗИНАИЛУЧШЕГО ПРИБЛИЖЕНИЯ СПЛАЙНАМИ 277
Пусть задана функция fix) e Cn+l[a, b]. Она допускает
разложение по формуле Тейлора
/ (*) = 2 ^Р-(х - х'У + о ((х - х'Г1). ¦ ¦ D)
г=0
Решение задачи приближения ищется в виде
Sn (х) = S 2 biqf [|i0, ..., 1Ыд+1)] Bln (x) + Sn (x). E)
г <J=O
При этом узлы сплайна не фиксированы; коэффициенты biq
выбираются так, чтобы двойная сумма была формулой локальной
аппроксимации, точной на многочленах степени п; Sn(x) —
произвольный сплайн. Согласно результатам § 5 остаточный член
приближения фуикции fix) представляется соотношением
^,
где Xn+i = (;г—a;')n , /i = maxfei. Замечая, что двойная сумма
справа есть моносплайн G.2) степени и+1 на произвольной
сетке, находим (штрихи у х опускаются)
Наряду с произвольной сеткой узлов рассмотрим
равномерную сетку с шагом ft,-. В § 5 мы отмечали, что если шаги
неравномерной сетки подчинить условиям hp = hi + О (/г?), р = i —
— п, ..., i+ n, то остаточные члены аппроксимации для двух сеток
на промежутке [хи хН\] будут отличаться на малые порядка па
единицу больше, чем они сами. Ограничения можно ослабить в
отношении порядка ht и продолжить на большее число шагов,
а именно:
hv = hi + oihi), p = i — 72, ..., i + 2n. G)
Тогда остаточные члены аппроксимации будут отличаться на
малые порядка oiRix)) на.отрезке [xiy xi+n+\]. В частности, так
как моносплайп Zn+i (z) (остаточный член аппроксимации
монома хп+{) имеет порядок Oihn+l), то на [хи xi+n+i] Zn+i(x) —

278 ГЛ. IX. ЛОКАЛЬНАЯ АППРОКСИМАЦИЯ СПЛАЙНАМИ
—Zn+i {х) = о (/&Г+1)« где Zn+i (х) — моносплайп на
равномерной сетке.
От сплайна Sn(x) естественно требовать, чтобы он не
увеличивал порядок остаточного члена O(hn+l) и уменьшал его
абсолютное значение. При переходе к равномерной сетке Sn(x)
заменяем на сплайн Sn(x).
Представим /(П+1)Ы = /(n+1)(ri) + б, где т] е [Х{, х{+х]. В силу
непрерывности функции /(п+1)(#) величина б = fin+l)(x) —
—/(п+1)(т]) = оA) при достаточно малых hu (При произвольном
hi это справедливо, если функция fix) мало отличается от
многочлена степени л+1).
На приведенных соображениях и основан прием решения
задачи A) с ограничениями C). Если все их учесть, то остаточный
член Rix) можно переписать в виде
Z°n+1 (х) - Sn (x) + о (ЛГ1). (8>
Итак, остаточный член на отрезке [хи xi+n+\] является некоторым
моноснлайном Мп+\(.х) на равномерной сетке с шагом hi с
точностью до малых более высокого порядка. " ч
Обращаясь к задаче наилучшего приближения A), заметим,,
что если найдена функция Sn (x) такая, что
| / (х) - Sn (х) h[xitxi+n+l] = mm | / (х) - Sn (x) |c[xll«i+n+l]
{Ьп\хЦ
для любого промежутка [хи xi+n+\li с [я, Ы, то эта функция
будет решением задачи A) на всем отрезке [а, Ы.
Но на промежутках [xh Xi+n+il главная часть уклонения
R(x) = / (х) — Sn (x) (8) является мрносплайном, и задача ми-
пимизации сводится к нахождению моносплайна^ наименее
уклоняющегося от нуля. Этот вопрос был решен в предыдущем
параграфе. Согласно теореме 9.3 сплайн Snix) =* cbn+i есть просто
постоянная на каждом промежутке [#«, Xi+n+\]. Если взять
д ру
с = . у j(n+v (^ то Ц{х) можно представить в виде
R (х) = cZn+1 (х) + о [hni+1) = с [ZX+1 (х) - Ьп+1] + о(Л?+1)я (9)
где постоянная Ъп+\ определяется теоремой 9.3.
Согласно результатам § 7 максимальные уклонения мопо-
/ сплайна Zn+\(x) от нуля на промежутках [хр, хр+\] <=[хи хг+п+\\
равны вп^?+1, где еп не зависит от hi. По условиям C) на
каждом промежутке [#,, х{+\] cr [a, b] уклонения должны быть
одинаковыми и равны Еп. Но это значит, что шаги ht должны опре-

§ 8. ЗАДАЧА КВАЗИНАИЛУЧШЕГО ПРИБЛИЖЕНИЯ СПЛАЙНАМИ 279
делиться соотношениями
1
где х\^1хг1 xi+\]. Значение сплайна Sn{x) через Еп выражается так:
(Н) ,
В формулах A0) и A1) постоянные bn+li еп— характеристики
моносплайна Zn+\(x), не зависящие от шага h{.
Таким образом, мы нашли приближенное решение Sn(x) E)
задачи A) с ограничениями C). Оно получено в предположениях
G), которые гарантируют нам, что даваемые им уклонения на
промежутках lxu xi+\] отличаются от заданного Еп на малые
более высокого порядка. Такую аппроксимацию называем
квазинаилучшим равномерным приближением. Она характеризуется,
наличием 2N (п четпое) и 2ЛН-1 (п нечетное) точек альтернанса
(§ 7). Достаточный признак обычного наилучшего приближения
для задачи .со свободными узлами требует 2/V + п таких точек.
Поэтому построенное решение при п = 0 и п = 1 можно назвать
асимптотически наилучшим равномерным приближением по hu
На практике точное решение задачи о наилучшем
приближении требуется лишь в исключительных случаях. В подавляющем
же большинстве примеров достаточно получить приближения,
близкие к наилучшим. Главное преимущество введенных здесь
нами квазинаилучших приближении в простоте их реализации.
Она сводится к нахождению шагов Нг по формулам A0) и
вычислению точек и коэффициентов аппроксимации ?<в и biq (§ 4),
а также постоянного значения сплайна Sn(x) A1). Все процедуры
описаны в предположении знакопостояыства функции fn~*~l)(x)
на отрезке [а, Ь]. Если /(п+1)(#) меняет знак в некоторых точках
отрезка, то приходится либо строить приближения по участкам
зиакопостоянства f{n+l)(x), независимые друг от друга, либо
как-то находить приближение в окрестности точек, где f{n+1)(x) =
= 0, и к нему добавлять звенья по общему правилу. Такие
примеры для сплайнов первой и третьей степеней будут приведены
в последующих параграфах.
В заключение отметим, что аналогично можно решать
задачу также о квазисреднеквадратичном приближении функции
/ЫеСп+1[а, b] сплайнами степени п дефекта 1, т. е. задачу
минимизации ||/ (х) — Sn (x) ||ь2[а,ы с заданными
среднеквадратичными уклонениями на каждом [хи xi+\]. Решение можно
искать в виде E) при Sn{x) «= const. Если для квазинаилучших
равномерных приближений последнее условие было доказано, то
здесь его приходится принять априори, ибо для установления
этого факта имеющихся средств (теорема 9.4) недостаточно.

280 ГЛ. IX. ЛОКАЛЬНАЯ АППРОКСИМАЦИЯ СПЛАЙНАМИ
§ 9. Асимптотически наилучшие равномерные
приближения сплайнами первой степени
Решение задачи об асимптотически наилучшем равномерном
приближении функции 1(х)^СЧа, Ь] согласно (8.5) и (8.11)
отыскивается в виде
) %f)(x) + b2f A)
г
где следует положить |г- = xi+\, чтобы получить формулу
локальной аппроксимации, точную на многочленах первой степени.
На отрезке [х{, xi+\] отличны от нуля только два 5-сплайпа:
ВГ1 (х) = 1 - t, B\ (х) = *, * = (я - Xi)/hi.
Остаточный член аппроксимации на этом отрезке имеет вид
R(x) = f(x) - /.(l - t) - fi+lt - b2.
По аналогии с доказательством теоремы 2.2.1 получаем
R (х) = -1 h\f" (ti) t A - t) - bit B)
где ц ^ {х{, Хг+\) зависит от t. Здесь ие потребовалось
предположения о близости шагов сетки h{, hi+\.
При &2 = 0 R(x) представляет собой остаточный член
интерполяции. Его оценки есть
li^Hllq^i+l]<4^l|/"llCK=Ci+l]. C)
Чтобы получить асимптотически наилучшее приближение,
следует с помощью параметра Ь2 осуществить сдвиг остаточного
члена интерполяции на половину его уклонения от нуля. Для
этого при заданном Е\ полагаем согласно (8.10), (8.11)
± Еи D)
тО^ , E)
где х\ теперь фиксировано.
Итак,
R (х) = - sgn /" (r\) [8t (l-t)- 11 Et + o (hr) F)
имеет три точки альтерпанса t = 0, 1/2, 1, в которых
IIR И Uq*i.*i+1] = ЖI /" (Л) I h\ + о (А?). G)
Особенность наилучшего приближения сплайнами первой
степени состоит в том, что на каждом промежутке lxit #l+1] оно

§ 10. КВАЗИИНТЕРПОЛЯЦИЯ
281
строится независимо от соседних. Поэтому число точек альтер-
канса определяется теоремой Чебышева [2, с. 226], согласно
которой, чтобы многочлен степени п был многочленом наилучшего
приближения функции на отрезке, необходимо и
достаточно существования не менее п + 2 точек альтериапса.
Изложенные результаты
относятся к случаю, когда функция
/"(#) в области аппроксимации не
меняет свой знак. При этом,
если существует точка хо, в
которой /"(.го) = О, то в формуле D)
при вычислении шага
промежутка, заключающего эту точку,
вместо 1/"(т]I следует взять
шах | /" (г|) |. Если в точке
Рис 9 2
xoj" Кх) меняет знак, то в
окрестности точки аппроксимация
должна строиться, исходя из каких-либо других соображений. Самый
простой способ состоит в следующем. Если
fix) = f(x0) + f'(xo)(x — xq) + р(я),
(8)
то звено сплайна задается в виде
Sxix) = /Uo) + f'ixoKx -
В точке хо р(#о) = 0, а границы заключающего ее промежутка
[#-i, х\] определяются условием IpC^i)! = Е\, причем берется
ближайшие к xQ корни данного уравнения. На этом промежутке
имеем не три, а только две точки альтернанса. Следовательно,
формула (8) не обеспечивает здесь наилучшее приближение.
Влево и вправо от отрезка [х-и х\] построение сплайна наилучше-,
го прнближения^лроизводится по общему правилу (рис. 9.2).
§ 10. Квазиинтерполяция и квазннаилучшие
равномерные приближения кубическими сплайнами
Будем применять формулу локальной кубической
аппроксимации, точную па многочленах третьей степени, с добавлением
свободного параметра
s3 И = 2 2 W &о. • • •, 5и(в+1I в\ (х) + ъм A)
i
где Si0=
bi2 = — j
bi3 = 0.

282 ГЛ. IX. ЛОКАЛЬНАЯ АППРОКСИМАЦИЯ СПЛАЙНАМИ
Относительно аппроксимируемой функции предполагаем, что
она имеет непрерывные четвертые производные fY(x) и, значит,
представима разложением
/ (*) = 2 ^р- С* - *'У + о{(х- х')% B>
г=0
Остаточный член аппроксимации в точке х будет
R (х') = / (*') - S3 (х') = -L /IV (x')Zl (*') - Ъ, + о (h<),
где ,Zl(xf) есть моносплайн G.2) на произвольной сетке. В
предположениях (8.7) с точностью до малых порядка o(h4) он
заменяется моносплайном G.$г) на равномерной сетке.
Замечая, что t(l — t) = 1/4 — о2, получаем
R (х) = ± hfflv (rO |> A - tf + §] - &4 + о (hi), C)
если г\ е [д;, +
1. Квазиинтерполяция. Пусть главная часть R(x) в точках
t'= 0 и ^ = 1 обращается в нуль, т. е. в этих точках R(x) есть
малая порядка о (hf). Такую аппроксимацию назовем квазииы-
терполяцией. Если задана допустимая погрешность приближения
е, то согласно п. 1 § 7 следует взять
IV(r1)-^-e. E)
Остаточный член квазиинтерполяции имеет вид
R (х) = sgn /IV (Tj) 1№ A - t)% + о (h\\ F)
2. Квазинаилучшее равномерное приближение. Оно
реализуется при заданном уклонении Еъ формулами
Остаточный член имеет вид
R (х) = sgn /IV (л) [32i2 (I - tf - 1] Е3 + о (hf). (9)
Точки альтернанса* суть t = 0, 1/2, 1.
Если в области аппроксимации имеется точка аг0, где
меняет знак, то в ее окрестности уравнение звена сплайна

§ 10. КВАЗИИНТЕРПОЛЯЦИЯ 283
и концы промежутка [я-ь х+\\, заключающего точку #э, можно
определить следующим образом. Пусть Р$(х) — первые четыре
члена разложения функции fix) B), и пусть /lv(#_i)<0- и
fY(x+\) > 0. Составим уравнения
= ± с%
= 0,
- Si (xTl) = =f d.
В случае квазиинтерполяции с = 0, d = 32е, а при
квазинаилучшем приближении с = Е3у d = 64^з. Система шести
алгебраических" уравнений определяет коэффициенты сплайна и
точки х-1, х+\. Она обеспечивает гладкое сопряжение остаточного
члена аппроксимации на отрезке [x_i, x+[] с общими формулами
F), или (9), в точках х-\, х+\ с точностью до малых порядка
о{(х+\ — a:_iL), В этом же смысле обеспечивается и гладкость
аппроксммационного сплайна.
Литература к главе IX. СЗ, 4, 15, 15*, 18, 19, 23, 24, 34, 35, 62, 73,
77, 80, 81, 92, 98, 100].

Г л а в а X
МЕТОД СПЛАЙН-КОЛЛОКАЦИИ
Традиционно метод коллокации строился на основе аппарата
приближения многочленами. Однако в силу сложности
реализации, а также не вполне удовлетворительных аппроксимационных
свойств многочленов этот метод представляет чисто теоретический
интерес. На практике он оказался полностью вытесненным
конечно-разностными методами.
Метод сплайн-коллокации, в отличие от классического
метода, основывается на аппроксимации сплайнами. Такой подход
позволяет построить алгоритмы, численная реализация которых
не сложнее реализации разностных схем. Принципиальное
отличие метода сплайы-коллокации от разностных методов
заключается в том, то приближенное решение находится в виде сплайна
во всей области определения решения задачи, в то время как
разностное решение определяется только на сетке. Это позволяет
получить гораздо более полную информацию о точном решении.
В данной главе метод сплайн-коллокации рассматривается на
примере краевой задачи для обыкновенного дифференциального
уравнения второго порядка.
§ 1. Понятие о методе сплайн-коллокации
Пусть требуется найти решение уравнения
L[y(x)] ^y"(x) + p(x)y'(x) + q(x)y(x)=r(x), x&la, Ы, A)
удовлетворяющее краевым условиям
В дальнейшем всюду предполагается, что двухточечная
краевая задача A), B) имеет единственное решение у(х). Требования
к гладкости у(х), а также ограничения на заданные
коэффициенты pix), q(x), r(x); а<, (J<, ft, i = 1, 2, будут оговариваться
особо в каждом конкретном случае.
Введем на [а, Ь] сетку А: а = х0 < х{ < ... < xN = b. Будем
искать приближенное решение задачи A), B) в виде
кубического сплайна S(x) класса С2 с узлами на сетке Д.

§ 1. ПОНЯТИЕ О МЕТОДЕ СПЛАЙН-КОЛЛОКАЦ1Ш 285
Потребуем, чтобы сплайн Six) удовлетворял уравпештю A)
в точках* |А е [а, Ы, к = О, ..., N {условия поллокации), и
краевым условиям B):
S" (V + p(tk)S'(lh) + qiVSiV = г(Ы, C)
k = 0, ..., N,
hS'{a) = 4U a2Sib) + faS'(b) = f2. D)
Соотношения C), D) представляют собой систему
алгебраических уравнений относительно параметров сплайна. Точки S&
называются узлами коллокации. Их количество определяется
размерностью пространства сплайнов класса С2, которая, как мы
знаем, равна N + 3. Так как Six) удовлетворяет двум граничным
условиям D), то количество узлов коллокации должно быть
равно N + 1. Их расположение на отрезке [а, Ъ] не может быть
произвольным. Так, например, на любом из промежутков [xh
xi+\] не должно быть более трех узлов коллокации. В противном
случае сплайн Six) на [хи xi+\] определялся бы независимо от
других промежутков и, в частности, независимо от граничных
условий. Ясно, что такой сплайн, вообще говоря, не имеет
никакого отношения к решению задачи A), B). Кроме того,
очевидна, в качестве узлов коллокации не могут быть взяты точки, -
в которых коэффициенты уравнения A) имеют особенности.
В дальнейшем мы предполагаем, что узлы коллокации
упорядочены: |о < Si < ... < ?*.
Конкретный вид системы C), D) зависит от выбранного
способа представления сплайна Six) и от расположения^ узлов
коллокации. В последующих параграфах мы изучим вопросы,
связанные с разрешимостью этой системы, и получим оценки
погрешности \Six) — yix)\. Будут рассмотрены и более сложные, по
сравнению с описанным, варианты методы сплайп-коллокацпи.
Метод сплайн-коллокацип может быть использован как
средство построения разностных схем (§ 2). Такие схемы обладают
рядом полезных свойств, например, они имеют одинаковый
порядок точности па равномерных и неравномерных сетках. Однако
этот подход пригоден для сравнительно простых задач и не
исчерпывает всех возможностей, заложенных в методе сплайн-кол-
локации. Наиболее полно они могут быть' реализованы только
при использовании аппарата 5-сплайпов. С этой точки зрения
ведется изложение в §§ 3—6.
Отметим, что в методе сплайи-коллокацип можно использовать
и другие типы сплайнов — более высокой степени, эрмитовы,
дискретные и т. д. Однако именно на основе кубических сплайнов
класса С2 удается построить алгорр1тмы, наиболее простые по
реализации и в то же время пригодные для решения широкого
круга задач.
\

•286 гл. х. метод сплайн-коллокации
§ 2. Сведение схем метода спл&йн-коллокации
к разностным схемам
Будем называть разностную схему для задачи A.1), A.2)
эквивалентной схеме метода сплайн-коллокации, если
получающиеся в процессе их реализации значения приближенного
решения в узлах сетки Д совпадают.
Простейшие схемы метода сплайн-коллокации получаются,
когда узлы коллокации выбираются совпадающими с узлами
сплайна: ?< = хи i = О, ..., N. В этом случае систему A.3), A.4)
можно преобразовать в эквивалентную разностную схему.
Пусть в уравнении A.1)
р(х)^0, A)
Обозначим S(xi) = ии S"(xi) = М{. Сплайн Six) при х^ [хи xi+\]
определяется формулой C.1.10), в которой величины Д, fi+\
следует заменить на щ, щ+\. Из A.3) имеем
ru j = 0, .., JV, B)
где q{ = q(xi), гг = г(ж<). Вычисляя отсюда величины Mi и
подставляя их в соотношения C.1.14), получаем
Я* (l + %ft-i) "i-i - (l - -^ ft) щ + i ( | )
* = 1 ЛГ—1. C)
Напомним обозначения
xu iii = hi-\/(fyi-i +hi),
Далее, используя вытекающие из формулы C.1.11) выражения
.для S'(xo), S'{xN) в уравнениях A.4) и учитывая B)г находим
щ [а А — Pifi— 4- ЯоК)] + ^iPi A + 4- ^о) =
L \ /J ' \ /
= УгК+±№1Bго + Г1), D)
-i — -g PaftN-i (rN-i + 2rN). E)
Уравнения C)—E) образуют разностную схему для.решения
задачи A.1), A.2). Пусть выполнены условия
Pi<0, p., aj>0, |а,| + |рЛ^О, / = 1, 2, q(x)^q<0, F)
* = 1,.'..,ЛГ. G)

§ 2. СВЕДЕНИЕ К РАЗНОСТНЫМ СХЕМАМ 287
Нетрудно видеть, что в этом случае система C) — E) при
произвольной сетке А имеет матрицу с диагональным преобладанием
и, следовательно, она однозначно разрешима.
Таким образом, реализация метода сплайн-коллокации фак-»,
тически сведена к реализации разностной схемы. Методом
прогонки из системы C) — E) вычисляются неизвестные uiy 2 = 0, ..^
..., N. Определяя затем из соотношений B) величины М{,
получаем приближенное, решение задачи A.1), A.2) в виде
кубического сплайна Six).
Оценим теперь погрешность приближенного решения.
Теорема ЮЛ. "Пусть в задаче A.1), A.2) выполнены
условия A), F), G). Если ее точное решение у(х) е C2W%tOO [а, Ь], та
WS(x) - у(х)\\с = O(h2),
где Ъ = max hi.
г
Доказательство. Пусть S(y; x) — кубический сплайн,
интерполирующий на сетке А решение yix). Нам удобно считать,
что S(y; x) удовлетворяет граничным условиям типа I. Имеем
\S(x) - у(х)\ ^ \S(x) - S(y; x)\ + \S(y; х)-у(х)\. (8>
Согласно теореме ,3.5
\S(y; x)-y(x)\=O(h*). (9>
Учитывая выражения для Six) и S(y; х), при х е [х{,
находим
Для сплайна S(y; x) в условиях теоремы вместо B)
справедливы соотношения
S" (г/; *i) + gi2/i = rt + 0U2), i = 0, ..., N.
Отсюда и из B)
\Mi-S4y; хд\^Ы\щ-у>\+ОС№.
Следовательно,
|^(^) — .5(г/;^) | ^(l + -|-^2il ^(^)lie)max| ^,_ yif + О (fe2). (И)
Таким образом, для доказательства теоремы достаточно
установить оценку величин \щ — уг\.
Запишем систему C)—E) в матричном виде:
Аи = d, A2)
где и — вектор-столбец с компонентами и0, • • •» и^. Если прв

288 гл. х. метод сплайн-коллоклшш
выводе системы A2) вместо соотношений B) использовать A0)
и учесть, что S'(y; xk) = y'ixk), /с = 0, iV, то получим
Ay = d + e, A3)
где компоненты вектора 8 имеют вид
e0 = hl.O(h*), eJV = ^1.O(Aa), е, = ^-Л-ОС*2),
* = 1, ...,ЛГ—1.
Из A2) и A3)
Л(М — у) = 8.
Как уже отмечалось выше, при выполнении условий (&), G)
матрица А с диагональным преобладанием. Тогда, используя
следствие Д.1, находим
Объединяя полученный результат с оценками A1), (8), (9),
получаем утверждение теоремы.
Замечания. 1. Ограничение на функцию q(x) в F) можно
ослабить до qix) <#0, если для получения оценки \щ — уг\
воспользоваться принципом максимума [20]. Во многих случаях
может быть опущено условие G). Например, если qix) = q < 0,
то диагональное преобладание имеет место на любой
неравномерной сетке.
2. Попутно мы доказали, что построенная с помощью
кубических сплайнов разностная схема C) — E) имеет точность Oih2)
на неравномерной сетке.
3. Условие у (х) е C2W% оо [а, Ъ\ будет выполнено, если qix);
i)l
Рассмотренный способ реализации метода сплайп-коллокацпн
путем построения эквивалентной разностной схемы
привлекателен своей идейной простотой. Однако попытка распространить
его на более сложные уравнения, когда pix) ^ 0, приводит к
громоздким разностным схемам, что затрудняет не только их
исследование, но и численную реализацию. К тому же практически
невозможно построение эквивалентных разностных схем в
случае, когда узлы ноллокации отличны от узлов сплайна. В
частности, это не позволяет реализовать одно из мощных средств
повышения качества схем — выбор узлов коллокация. • Все
упомянутые недостатки связаны с небходимостью исключения из
систем уравнений некоторых параметров сплайна (в наше'м
случае Mi). Отметим, что эти обстоятельства менее существенны для
нелинейных краевых задач в силу того, что для их решения
приходится прибегать к итерационным методам и поэтому вместо
исключения параметров их можно брать с предыдущей итерации.

§ 3. ИСПОЛЬЗОВАНИЕ Я-СПЛАЙНОВ 289
§ 3. Использование Я-сплайнов в методе
сплайн-коллокации
Представим кубический сплайн Six) в виде разложения по
базису из нормализованных кубических S-сплайнов (§ 3.8):
s(x)= 2 biBi(x). (i)
Чтобы все базисные функции в A) были определены, сетка Л
должна быть дополнена узлами х~$ < х-2 < х~\ < xOj xN+$ >
> Zx+2 > ^jv4 i > ^.v. Для дальнейшего нам удобно выбирать их
так, чтобы выполнялись условия
h.j = Л,-ь A*-i4J = hN_u j = 1, 2, 3. B)
Рассмотрим вначале случай, когда узлы коллокации ^ совпадают
с узлами сплайна xt. Подставляя A) в A.3), получаем
+ bMBAxt)] + bHiLlBi+l{xt)} = п,
i = 0, ..., N.
Если учесть выражение для узловых значений В-сплайна и
его производных (таблица 3.9), то эти уравнения можно записать
в виде
bt-iAt + bfii + Ь1+1Вг = Du i - 0, .. M N% C)
где
=%—4— fl+4
= - Л1 - Si + -g- qi (hi
Из уравнений A.4) с учетом условий B) получаем
Ъ-хА-х + ЬоС-1 + bifi-i == D-lt D)
где
Уравнения C), D) образуют систему jV + 3 уравнений
относительно N + 3 неизвестных 64. Исключив с помощью уравнений
49 ю. С. Завьялов и др.

290 гл. х. метод сплайн-коллоклции
D) неизвестные Ь-\ и Ьх+\ из C) (это всегда можно сделать прп
выполнении условии B.6)), приходим к системе с трехдиагопаль-
ной матрицей
ЬоСо + Ь\Въ = Do,
bi-xAt-x + blCi + bi+iBi = Db * = 1, ..., N-l, E)
bx-iAN + bKC* = DN,
где
С лАп ^ В лАп D ЛЛ
-1 0 оту —1 0 Г) г) —1
лАп ^ В лАп D ЛЛ
-1 0 о ту —1 0 Г) г) —1 О
л-1
CN+1B
N+1BN
При выполнении згсловий B.6) и достаточно малых А,- таких, что
1-fMi + ir^^0' i + yM^x + lg^i-i^o, F)
система E) с диагональным преобладанием. Для внутренних
уравнений это непосредственно следует из формул для
коэффициентов A i, Bu d. Для первого и последнего уравнений в этом
нетрудно убедиться, если принять во внимание B).
В итоге реализация метода сплайн-коллокации сводится к
вычислению коэффициентов bQi ..., bN из системы E) и
последующему определению 6-i, bN+x из уравнений D>.
Теорема 10.2. Если выполнены условия B.6), F) и
y{x)c=C*Wl4OO\a,b], то
G)
Доказательство аналогично доказательству теоремы
10.1. Отличие состоит в оценке величины Six) — S(y; x). Пусть
JV+1
S(y;x)= 2 ЪгВг(х).
i = -l
Тогда
JV+1
\S(x)^S(y;x)\<: Ц |Ь1-Ъ|Д,(*)<тах|Ь1-'Ь1|. (8)
г=-1 i
Погрешность аппроксимации 8, = LlS(y\ xt)] — г{ уравнений
A.1) в узлах сетки Д удовлетворяет условиям е, = O(h2).
Если записать систему E) в матричном виде: АЪ = d, то
АЪ = d + е, причем вектор е имеет компоненты г{ = е,-(Л,-—i +
+ Аг)/6. Отсюда, учитывая, что матрица А с диагональным пре-

§ 3. ИСПОЛЬЗОВАНИЕ В-СПЛАЙНОВ 291
обладанием, согласью следствию Д.1 нетрудно получить оценку
max | b{ -Ъг | = О (h2).
Учитывая этот результат, из D) легко находим, что
\ ), /=7-1, N + 1,
и теперь утверждение теоремы следует из (8), B.9), B.8).
Перейдем к изучению схем метода сплайы-коллокации в
случае, когда узлы коллокации не совпадают с узлами сплайна. Если
подставить выражение A) для Six) в A.3), A.4), то структура
полученной при этом системы для коэффициентов л будет
определяться выбором узлов коллокации. Например, если на каждом
отрезке [хи xi+\] расположено не более двух узлов коллокации,
то матрица системы будет, вообще говоря, пятидиагональной. Мы
наложим на выбор узлов коллокации некоторые ограничения,
которые, с одной стороны, позволят свести реализацию метода
к решению трехдиагоналыгых систем и, с другой стороны,
оставляют достаточную свободу действий при построении схем
повышенной точности и схем для уравнений с разрывными
коэффициентами.
Будем считать, что число узлов сетки Д четное (iV = 2n + l),
а узлы коллокации |ft, к = 0, ..., N, удовлетворяют условиям
\2i^[x2i, X2i+\), ^2i+l G t#2i, #2f+J, 1 = 0, . . ., П. (9)
Таким образом, на каждом промежутке lx2h x2i+\] имеются по
два узла коллокации, а на со- ^ ^
седних интервалах (^2г-ь x2i), . у ¦ ,;# у'+t ,
(x2i+u ^+г) их нет совсем х х& х^ Xff
(рис. 10.1). Заметим, что
совпадение узлов коллокации с узла- р .„,
ми сетки Д не исключается.
С учетом ограничений (9) уравнения A.3) принимают вид
b2iL[B2i(l2i)] +
] + b2i+2L[B2i+2(l2i)} « НЬ), (Ю)
b2iLlB2i(l2i+l)) +
+ b2i+lL[B2i+l(l2i+l)l + b2n2L[B2i+2(bi+\K - КЬ+i), (ID
i = 0, ..., n.
К шш добавляются уравнения D), учитывающие граничные
условия. Исключив с их помощью из уравнений A0), A1)
неизвестные Ь-ь 6y+i, приходим к системе уравнений относительно
коэффициентов fco, • •., bN, матрица которой схематически
19*

292 ГЛ. X. МЕТОД СПЛАЙН-КОЛЛОКАЦИИ
изображается в виде (знаком «+» отмечены ненулевые элементы)
A2)
Рассмотрим вопрос о разрешимости этой системы. Положение
узлов коллокации будем характеризовать величинами ^е[0, Ut
?2f — Х2х + t2ih2u hi+\ = #2* + t2i+\h2i, t2i < t2i+\. Чтобы матрица
A2) была с диагональным преобладанием, необходимо
выполнение следующих условий для уравнений A0), A1):
A3)
\LlB2t+2(l2ul)]l. A4)
Исследуем подробнее первое из них при ограничениях B.6),
Нетрудно видеть, что при выполнении соотношений
из тождества
2i+2
0,
j (ж) = 0,
A5)
[х2Ь ar2i+1],
вытекает соотношение
и, очевидно, A3) будет выполнено при всех достаточно малых h{.
Таким образом, задача сводится к нахождению таких ^Лй»),
при которых имеют место неравенства A5). Из них последние
два выполнены при любом ?г<е I#2<» #2*+il- Действительно, при
«^ [X2i, Z2i+\]
-г (х) — Bli-г {x2i) (l — t)+ 2?2«-

§ 3. ИСПОЛЬЗОВАНИЕ В-СПЛАЙНОВ 293
Согласно таблице 3.9 B2i-i (#21) > 0» #21-1 (#2*4-1) — 0- Поэтому
-fiji-i (?2i) > 0. Аналогично находим, что B2i+2 (?2|) > 0.
Далее,
Bli (х) - В\ (x2i) A - 0 + Bji (
Так как В"; (x2i) < 0, S^ (^21+1) >0f то в?* (я) обращается в
нуль в точке х* = #2» + t*h2i, где
V „ - —
Отсюда ясно, что неравенство B2iE2i)<0 будет выполнено,
если только
Функция t*(v) — возрастающая. Поэтому
min t* (v) > t* (I) = 1/2.
V
Итак, узел коллокации |г< должен быть таким, что
*2<^1/2. A6)
Обратимся теперь к исследованию неравенства B2'i+i (?2i)^0»
Функция B2i+i (^) равна нулю в точке хх = х2\ +
где
l
— l
Так как B2j+t (х2г) >0, то неравенство B2i+i(?2j)^0 будет
иметь место, если
t2i ^ min ti (w).
w
Введем в рассмотрение характеристику сетки А:
р = max hjhj. A7)
Тогда
2i
Следовательно, w < 1 + р и min ^ (ш) «= 1/B + р).. Поэтому узел
W
коллокации \<ц должен быть таким, что
р). A8)

294 гл. х. метод сплайн-коллокацип
Сравнивая A6) и A8), получаем, что неравенства A5), а
следовательно, и A3) выполняются, если имеет место A8). Точно так
же устанавливается, что A4) выполняется, если
*2<+i > 1 - 1/B + р). A9)
Мы показали, что при всех достаточно малых ht для всех
строк матрицы A2), которые содержат коэффициенты уравнений
вида A0), A1), при ограничениях A8), A9) будет выполняться
условно диагонального преобладания. Для остальных строк
(первой, второй, последней и предпоследней) этот вывод можпо
получить, если учесть условия B), B.6). В итоге коллокациоиная
задача разрешима.
Пусть выполнены условия B.6), A8), A9) и у{х) s
е C2W\fOO [я, Ц. По аналогии с теоремой 10.2 можно показать,
что при всех достаточно малых hi для сплайна Six),
коэффициенты bi которого удовлетворяют соотношениям D), A0), A1), будет
справедлива оценка G).
В принципе коэффициенты Ъ$, ..., bN могут быть вычислены
из системы с матрицей A2) путем применения метода прогонки
для пятидиагональпых матриц. Мы предлагаем более простой и
эффективный алгоритм численной реализации описанной схемы,
использующий специальную структуру уравнений A0), A1). Суть
его состоит в следующем. С помощью A0) исключим из
уравнения A1) неизвестное 621-1. Затем полученное уравнение
используем для исключения неизвестного 621+2 из A0). Проделав эту
процедуру для всех i = 0, ..., п, объединим полученные
уравнения и исключим из них с помощью D) неизвестные 6_i, 6w+i.
В результате придем к трехдиагональной системе относительно
неизвестных 60, • •., bN. Для ее решения рекомендуется
использовать либо алгоритм немонотонной прогонки, либо алгоритм
универсальной прогонки, так как в процессе преобразования
уравнений A0), A1) возможна потеря диагонального преобладания.
§ 4. Метод сплайн-коллокации для уравнений
с разрывными коэффициентами
До сих пор мы предполагали, что коэффициенты уравнения
A.1), как минимум, непрерывные функции на [а, 6]. При этом
решение задачи A.1), A.2) у(х) имеет две непрерывные
производные. На практике приходится сталкиваться с задачами,
когда р(х), q(x)y rix) имеют в некоторых точках отрезка [а, 6]
разрывы первого рода. В этом случае решение у(х) имеет, вообще
говоря, разрывы второй производной в тех точках, где разрывны
коэффициенты уравнения. Эти особенности должны быть
учтены при решении таких задач. Естественным выходом здесь
представляется использование в методе •сплайн-коллокации эрмнто-

§ 4. УРАВНЕНИЯ С РАЗРЫВНЫМИ КОЭФФИЦИЕНТАМИ ?^5
вых кубических сплайнов 5з,2(я). Однако при всей
привлекательности этого способа следует отметить, что размерность системы
алгебраических уравнений, с решением которой в конечном
итоге приходится иметь дело, будет равна 2GV+1), т. е. в два раза
больше по сравнению с алгоритмами решения задач с гладкими
коэффициентами, рассмотренными в §§ 2, 3. Кроме того,
система будет содержать неизвестные разной природы (узловые
значения сплайна и узловые значения его первой производной),
коэффициенты при которых сильно отличаются по абсолютной
величине. Не приходится говорить и о таком свойстве, как
диагональное преобладание у матрицы системы.
Мы предлагаем другой подход к решению задач для
уравнений с разрывными коэффициентами, основанный на
применении тех же кубических сплайнов класса С2, что и в §§ 2, 3,
по со специальным выбором узлов сетки А в окрестности точек
разрыва коэффициентов уравнения.
Пусть г| — точка разрыва по крайней мере одной из функций
р(х), qix), r(x). При построении сетки узлов сплайна Six)
выберем в окрестности ц узлы xk и хк+\ так, что
Таким образом, каждая точка разрыва «зажимается» между
двумя близко расположенными узлами сетки Л. На выбор
остальных узлов сетки не накладывается никаких ограничений. Что
касается выбора узлов коллокации, то они могут быть взяты
либо совпадающими с узлами сетки А, либо отличными от них.
В последнем случае на промежутках, содержащих точки
разрыва, не должно быть узлов коллокации. Отметим также, что с
учетом малости длин этих промежутков ограничения C.18),
C.19) могут быть существенно ослаблены.
Эффективность предложенного рецепта обусловлена тем, что
при указанном выборе сетки А сплайн Six) ведет себя в
окрестности точки разрыва коэффициентов так же, как эрмитов
кубический сплайн (см. § 4 гл. 3). В результате порядок точности
приближенного решения Oih2), установленный в §§2, 3 для
уравнений с достаточно гладкими коэффициентами, сохраняется
и для уравнений с разрывными коэффициентами, если,
например, потребовать, чтобы решение yix) принадлежало классу Wto
на промежутках между точками разрыва.
Довольно часто уравнение с разрывными коэффициентами
записывается в виде
[kix)y'ix)Y + pix)y'ix) + qix)yix) = rix), are [а, Ы, (I)
где kix) > 0.

296 гл. х. метод сплайн-коллокации
В связи с этим заметим, что путем замены независимой
переменной х по формуле
х
dv /оч
X~J
Ш
уравнение A) приводится к виду, уже изученном у:
у" [х) + р (х) у' (х) + Я (*) * (х) У&) = к (х) г (х), C)
ь
rcf0 Л т х dv
Если краевые условия для A) заданы равенствами A.2), то
после преобразования B) они заменяются соотношениями
aik(a)y@) + ^iy'(O) -
В результате применения метода сплайн-коллокации к зада-
че^C)^D) мы получим приближенное решение в виде сплайна
S(x), х s [0, 71. Чтобы вычислить приближенное решение
исходного уравнения A) в точке х^[а, &], необходимо вначале по
формуле B) определить соответствующее значение х.
Иногда более удобно вместо B) использовать замену
х
- , Ь — a f dv
В этом случае в уравнении C) х^ [а, 6].
§ 5. Схемы повышенной точности на равномерной сетке
Построенные в предыдущих параграфах схемы метода
сплайн-коллокации позволяют найти приближенное решение
задачи A.1), A.2) с точностью O(h2). Схемы более высокой
точности O(AV), v>2, называются схемами повышенной точности»
В этом параграфе строятся две такие схемы на равномерной
сетке.
Пусть сетка А образована узлами Xi; =» а + ih, i = 0, ..., N,
хп e fr, причем iV «= 2п + 1 — нечетное число. Рассмотрим на пен
схему сплайн-коллокации с выбором узлов коллокации,
удовлетворяющих условиям C.9). Точность метода сплайн-коллокации
зависит от величины погрешности аппроксимации уравнения

§ 5. СХЕМЫ ПОВЫШЕННОЙ ТОЧНОСТИ НА РАВНОМЕРНОЙ СЕТКЕ ?97
A.1) в узлах коллокации ?к:
Ц fc = 0, ..., N, A)
ii погрешности аппроксимации граничных условий A.2).
Последняя равна нулю, так как мы рассматриваем сплайн S(y\ к)
с граничными условиями типа 1.
Запишем A) в другом виде:
IJ - y(&)J, Л — 0 tf. B)
Согласно формулам (8.2.6), (8.2.7) при у(х) ^Wlola, Ъ] и любых
?* будем иметь
S(y; W-y(W = OW), S'(y; V - »'(?*) = О(Й3).
Далее, из (8.2.8) следует, что в двух точках на каждом проме-»
жутке [хи xi+\] S"{у; gfc) — г/"(?А) = 6Кй3). Эти точки суть
gil = ХХ + t[k, li2 = Xi + ^,
*i = 1/2 - У6/3, ^ = 1 - t\ « 1/2 + V6/3. C)
Естественно выбрать именно эти точки в качестве узлов кояло*
кации. В этом случае eh = O(hz). В дальнейшем такие узлы кол-
локации будем называть оптимальными.
Итак, в соответствии с условиями C.9) полагаем
hi^^t + tih, ht+\ = *21+ t2h, i = 0, ..., п. - D)
Отметим, что выбранные этим способом узлы коллокации
удовлетворяют условиям C.17), C.18). Вопросы, связанные о
реализацией схемы и оценкой погрешности, разобраны в § 3.
Эта схема имеет точность 0{h3) и для своей реализации требует
решения системы уравнений с трехдиагоыальпои матрицей.
Вторая рассматриваемая схема, строго говоря, уже не
относится к схемам метода сплайн-коллокации. . Однако при ее
построении мы существенно используем свойства кубических
сплайнов и, так же как в методе коллокации, приближенное
решение получается в виде сплайна.
Пусть А — равномерная сетка с узлами х{ = а + г/г, i = 0, .. •
,.., N (iV — произвольное), и у (х) е Wlo [a, 6]. Рассмотрим
выражение B) в предположении, что §* = #* и S(y; #)-сплайн,
удовлетворяющий краевым условиям следующего вида:
S"(у;*о) = у1 --J2 >*Уо\ S*(у,xN) = yN-±h2y™-
Из (8.2.7) вытекает, что S'(y; х{) - у'Ш = ОШ). Так как
по условиям интерполяции Siy; хд — у(хд = 0, то оказывается,
что погрешность аппроксимации B) определяется величиной

298
гл- Х-
СПЛАЙН-КОЛЛОКАЦИИ
S"(y; хд — у"(хд. Очевидно, еслн повысить точность
аппроксимации только величины у"{хд до О(й4), то е* будет иметь
порядок Oih4). Используем с этой целью аппроксимацию (8.3.3).
В результате во внутренних узлах сетки Д имеем
p.s,{Xi) + giUi =
1 = 1,2,....ЛГ-1.
После перехода в этих соотйошениях к представлению через
В-силайны C.1) получаем уравнения
Ь{.2
Ь,(—18
bi
+2
F)
Присоединим к ним уравнения C.4), соответствующие
краевым условиям задачи. С учетом равномерности сетки они
записываются в виде
b^iaji—3Pi) + iboaih + b{(a{h + 3^i) =» 6^^,
bN-\(a2h — 3^2) + ^bN0L2h + bN+l{a2h + 3p2) = 672^.
В совокупности мы имеем N + 1 уравнение. Но количество
неизвестных коэффициентов Ь{ уф нас равно iV + З. Поэтому для
вамыкания системы необходимы еще два уравнения, причем
такие, чтобы погрешность аппроксимации для них была O(hA).
Рассмотрим промежуток [хи хг+\\. Учитывая соотношения
(8.2.6)—(8.2.8), в точках ?u, |f2, определяемых формулами C),
имеем
LlSiy;
LlSiy;
где
Отсюда
ex
L[y(ltl)] + 2ch*y4ln) -
+ OW),
12
где
Очевидно,
x + e2)
е\ =» O(A), e2 == Oih) и, следовательно, величина
+ LlSiy; Ii2)] аппроксимирует агрегат L[y(ln)\ +.
с погрешностью 4

§ 6. ПОВЫШЕНИЕ ТОЧНОСТИ НА НЕРАВНОМЕРНОЙ СЕТКЕ 299
На основании этого результата возьмем недостающие
уравнения в виде
LlSixs + tih)\ + LlS{xs + t2h)] = r{x, + txh) + rix, + t2h)9
j = O,N-l,
или, с учетом выражений для 5-сплайнов,
Ь,- гА, + Ь& + ЪМС> + bj+2 Es = Dh j = 0, N - 1, (8)
где
,2 .2 » t
A} = 1 + -g- ^2*1 + X *??ji - — ^2Pjl - -J *?Pi2,
^ = - 1 + *. [4 + t\ (- 6 + ЗУ ]й1 + 4"I4 + ^ (
Cj - -1 + ^I4 + *«(-6 + 3f*)l »i + x ^4 + *i(
^; = 1 + T- ^»i + T
Dj = /i2 (ГЛ + rj2), /?;ft = p (ДГ; + tkh),
Qjh = ? (*j + *ftfe), ^jfe = г fe + W.
Уравнения F), G), (8) образуют пятидиагональпую систему
уравнений относительно неизвестных Ь-i, ..., bN+\. Если с
помощью уравнений G).исключить из нее неизвестные b-i и Ьд+i,
то при выполнении условий B.6) у полученной системы
матрица будет с диагональным преобладанием для всех достаточно
малых h. Отсюда, принимая во внимание установленные выше
оценки о погрешности аппроксимации, нетрудно показать, что
построенная схема имеет точность O(hA)t
§ 6. Схема повышенной точности на неравномерной сетке
Пусть на [а, Ь] задана, вообще говоря, неравномерная сетка
Л: а = хо < х2 < Х\ <.. .< х2п < х2п+\ = Ь. В окрестности каждого
из ее внутренних узлов x2j, / = 1, ..., п, возьмем точку #2j-i
таким образом, чтобы выполнялись условия
, x2i — x2j-i = a min {x2j — я2*-2, aty+2 — аъЛ A)
где а < 1 — достаточно малое положительное число и принято
аг2п+2вв*^2п+1." Обозначим через Д сетку, составленную из узлов
0 2 + 1

300 ГЛ. X. МЕТОД СПЛАЙН-КОЛЛОКАЩШ
Задачу A.1), A.2) будем решать методом сплайн-коллокации
с использованием кубических сплайнов класса С2, определенных
на сетке Д. Узлы коллокации ^ выберем по правилу
Ьз = Х2з + hh2h J-2j+i = x2i + t2h2j, у==1,..., п, B)
U = 1/2 - У3?6, h = 1 -1{ - 1/2 + Г376.
Таким образом, отличительной особенностью предлагаемой
схемы является специальный выбор узлов сплайна и узлов кол-
локации. Напомним, что такие схемы для произвольной сетки и
их численная реализация подробно рассмотрены'в § 3.
Предположим, что выполнены условия B.6). В § 3 исследование
существования приближенного решения и анализ его погрешности
опираются на наличие диагонального преобладания в матрице
системы для коэффициентов Ь{. Это свойство имеет место при
выборе узлов коллокации так, чтобы удовлетворялись
ограничения C.17), C.18). В нашем случае они заведомо нарушаются.
Однако, если учесть специальный вид сетки Д, то, повторяя
рассуждения § 3, нетрудно показать, что для узлов коллокации B)
и достаточно малых а матрица системы будет с диагональным
преобладанием при
р*= max ^</3. C)
Это ограничение на шаги сетки Д в дальнейшем предполагается
выполненным. Так как а мало, то его можно трактовать как
ограничение на соотношение соседних шагов исходпой сетки Д.
В предыдущих параграфах получение оценок погрешности
приближенного решения основывалось на введении
вспомогательного сплайна Six) и использовании неравенства
\S(x)-y(z)\<\S(x)-S(z)\ + \iS(x)-y(x)\. D)
В качестве Six) выбирался интерполяционный сплайн Siy; x).
Такой подход позволяет использовать для оценки второго
слагаемого в правой части D) известные результаты. Что* же
касается величины \Six) '—Six)\, то при наличии у матрицы
системы для неизвестных Ь{ диагонального преобладания вопрос
об ее оценке сводится к исследованию погрешностей
аппроксимации сплайном Six) краевых условий A.2) и уравнения A.1)
в узлах коллокации
е« = aiSia) + frS'ia) - >{и еь = f
ti - LCSb)] - г(Ы, i = 0, ..., 2n + 1. E)
Из результатов § 4 гл. 3 следует, что эрмитов сплайн S^^ix),
определенный на сетке Д, можно рассматривать как предельный

§ 6. ПОВЫШЕНИЕ ТОЧНОСТИ НА НЕРАВНОМЕРНОЙ СЕТКЕ 301
случай (при а ->¦ 0) кубического сплайна класса С2,
определенного на сетке Д. Принимая во- внимание это замечание, будем
использовать в формулах D), E) в качестве Six) кубический
эрмитов сплайн Н(х). Отметим, что сплайн Н{х) строится
специальным образом и не является интерполяционным для
функции у(х). Поскольку в дальнейшем изложении используется
только сетка Д, то в целях сокращения записи перенумеруем ее
узлы так, что Д: а = х0 < х\ <.. .< хп+\ = Ъ. Соответственно
формулы для узлов коллокации, принадлежащих отрезку lxti xi+\]f
запишем в виде
1г = Хг + tJlU ^{ = Хг + tjliu
Предположим, что решение задачи A.1), A.2) у (х) е W^ {а, 61.
Пусть #з,2(*/; %)•—эрмитов сплайн, интерполирующий функцию
у{х). Определим сплайн Н(х) соотношениями
Н (а) = 53,2 (у; а)=у (а), И (Ъ) - 53,2 (у; Ь) = у (Ъ),
Н" fa) = 5gf2 (у; li) + Y \l
H" (li) = S3t2 (у; li) — CxhiyY+i/2 + Pi+i/2^A?y 1+1/2.
где
( К \
J = У [*i + — J.
Покажем, что ff(x) существует и единствен. Из теории
дифференциальных уравнений известно, что решение задачи
U"(x)~j(x), же [а, Ы,
может быть получено по формуле
ь
U(z) = $G(x,v)f(v)dvt ' G)
а
где функция Грина Gix, v) определена соотношениями

302 ГЛ. X. МЕТОД СПЛАЙН-КОЛЛОКАЦНИ
Функция Н"(х) линейна на каждом промежутке [х(, Xi+\] и
в соответствии с F) записывается в виде
, (9)
2 1
где t = (x —
Разность U(x) = H(x) — Sz,2(yi х) можно, очевидно,
рассматривать как решение краевой задачи ,
Тогда, используя формулу G), получаем
h
Н (х) = S3,, (у; x) + $G (x, v) U" (у) dv. A0)
а
Тем самым доказано существование и единственность Н(х).
Выведем теперь оценки величин
\y,x), r = 0,1, 2.
Из (9) и аналогичного выражения для St2 (у; х):
2 1
имеем при д:^ [хи
I ^" W I < 1*-М + ^-'1 max {| V (U
Отсюда, учитывая F), находим
A2)
Из A0) для ж<= [<г(, xi+l]
#(*) = 2 j G (x, v) U" (v) dv =
L ОС
G (x, v) U" (v) dv + J G (x, u) U" (u) do +
j G(x,v)U"(v)dv + JZ J G(x,v)U"(v)dv. A3)

§ 6. ПОВЫШЕНИЕ ТОЧНОСТИ НА НЕРАВНОМЕРНОЙ СЕТКЕ
Принимая во внимание формулы (8), получаем
л.
J G (x, v) U" (у) do
< || U" (x)
Аналогично,
хг+1
G{x,v)U"{v)dv
303
). A4)
A5)
При *;<;# выражение G(x, v)U"iv) является многочленом вто-
poir степени относительно переменной v. Используя
квадратурную формулу Симпсона, получаем при / < i
G (x, v) U» (v) dv = fEfr {(*i ~
f 4 (^ + -^- - a) t77/ (^ + -^-
6F —a)
Из формул F), (9) нетрудно вычислить
h-
A6)
В результате из A6) при /< i имеем
A7)
Точно так же это соотношение получается при / > i. Теперь,
учитывая A4), A5), A7), из A3) находим
Далее, из A0)
IIU (х) ||с = 2 О (/if) -!- О (Л4) = О (А4).
3=0
A8)
A9)
Повторив рассуждения, проделанные при выводе соотношения
A8), отсюда находим
B0)

SOi ГЛ. X. МЕТОД СПЛАЙН-КОЛЛОКАЦИИ
Из A8) и теоремы 2.5 получаем
\Н(х)-у(х)\ < \S3t2ix)-yix)\ + \U(x)\=OUiA). B1)
Оценим величины ев, е&, е* E) при Six) = Щх):
га = аг\Н (а) - у (а)] + рх [#' (а) - .у' (а)] =
- рх [Я' (а) - ^з,2 (У\ a)] - № (а).
Отсюда, используя B0), выводим ea = O(h4). Аналогично, гь&
*=0(/г4). Далее, учитывая F), получим следующее выражение
для погрешности аппроксимации уравнения A.1) в узле колло-
кации |г:
«I = [Si.* (у; h) - yff (h)] + Ф*уУ+1/2 +
+ Р Иг) [5з,г iV, li) — У' (li)] — Pi+l/2C2hbAZl/2 +
+ qili)[Sst2iy;li)-yili)l
Так как -_
и, в соответствии с формулами B.6.27), B.6.28),
5з,2 (I/; Si) - У" ih) = - cAV (?i) + О (Л?) = - cxh1y?+m + О (hf)t
Р Ид [S'3t2 iy; li) - у' ih)} = р (It) c>Ji\yly Цг) + О [hi) =
то 8г = O(hA). Такой те порядок имеет погрешность
аппроксимации и в точке ?i- Отметим, что отсюда становятся понятными
причины выбора Hix) из условий F). Действительно, нетрудно
видеть, что при использовании обычного интерполяционного
сплайна Sz,iiy\ x) в роли вспомогательного сплайна Six)
справедливы соотношения е< = Oih3). Учитывая полученные
результаты и оценку B1), а также принимая во внимание
высказанные в начале параграфа соображения о диагональном
преобладании в системе для коэффициентов йг-, ^приходим к выводу, что
предложенная схема имеет точность Oih4).
Замечание. Схема сохраняет порядок точности Oih4),
если производные y{r)ix), r > 2, имеют разрывы первого рода, при
условии, что каждая из точек разрыва «зажата» между двумя
близкими узлами сетки.
§ 7. Обсуждение результатов. Численные эксперименты
В настоящем параграфе обсуждаются свойства построенных
схем метода сплайн-коллокации.
Рассмотрим вначале схемы точности Oih2) (§§ 2, 3). Их
характерной особенностью является то, что они сохраняют второй

* § 7. ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ. ЧИСЛЕННЫЕ ЭКСПЕРИМЕНТЫ 305
порядок точности на любой неравномерной сетке. Для
разностных схем это свойство далеко не всегда имеет место. Отметим
также, что второй порядок точности для сплайновых схем
достигается при сравнительно невысоких требованиях к гладкости
решения краевой задачи (допустимы, например,, разрывы
третьей производной в узлах сетки).
Общим моментом при построении сплайповых схем является
отсутствие каких-либо трудностей, связанных с аппроксимацией
краевых условий. Нет никакой необходимости в выделении, как
это делается в разностных схемах, краевых условий первого
рода, второго рода и т. д. Указанное свойство сплайновых схем
объясняется тем, что кубические сплайны обеспечивают
высокую точность аппроксимации первой производной решения. По
этим же соображениям можно утверждать, что сплайновая
схема точности O(h2) хорошо приспособлена для решения тех
задач, когда в уравнении A.1) коэффициент р{х)?*0, особенно
если он велик по абсолютной величине, так как при этом
погрешность аппроксимации схемы в основном будет
определяться точностью аппроксимации выражения р(х)у'(х).
Обращает на себя внимание простота построения сплайновых
схем для уравнений с разрывными коэффициентами (§ 4). По
существу, дело здесь сводится к изменению сетки путем
добавления к ней специально выбранных узлов, количество которых
равно числу точек разрыва коэффициентов уравнения. Сама же
схема остается такой же, как в случае гладких
коэффициентов.
В § 5, 6 построены сплайыовые схемы повышенной
точности. При этом в § 5 используется равномерная сетка и
предполагается высокая гладкость решения задачи A.1), A.2). В
отличие от этого, в схеме § 6 сетка может быть неравномерной и,
кроме того, требования к гладкости решения невысоки.
Например, уравнение может иметь разрывные коэффициенты. Поэтому
создается впечатление о нецелесообразности применения схем,
рассмотренных в § 5. Однако это не так. Дело в том, что
непоследнюю роль в выборе той или иной схемы играет объем
вычислительной работы, необходимый для ее реализации. А он
определяется сложностью коэффициентов схемы, а также
затратами, связанными с вычислением функций р(х), q(x), Ax). В этом
смысле обе схемы из § 5 экономичнее схемы из § 6. Например,
в каждой из них требуется TV раз вычислять функции р(х), q{x),
r(z), в то время как при реализации схемы из § 6 это придется
делать 2N раз.
Условия, при которых исследовалась точность построенных
схем, носят только достаточный характер. Отметим, что на
практике о точности приближенного решения (в нашем случае это
сщгайп) можно в некоторой мере судить по невязке в уравнении
20 ю. С. Завьялов и др.

soe
ГЛ. X, МЕТОД СПЛАЙН-КОЛЛОКАЦИИ
A.1), вычисленной в узлах достаточно густого разбиения
промежутка [а, Ы.
Одно из полезных свойств метода сплайя-коллокации
заключается в том, что построенный с его помощью сплайн, как
правило, хорошо приближает не только само решение краевой
задачи, но и его производные. К сожалению, мы не дюжем
остановиться на этом вопросе подробнее.
Перейдем теперь к описанию численных экспериментов по решению
краевых задач с помощью сплайновых схем. Для сравнения приводятся
также результаты, полученные при решении на сетке А: а = х0 < .. .< xN-= b
краевой задачи A.1), A.2) с помощью разностной схемы, которая при
?j 'ш р2 ±=х о имеет вид
~l, • A)
UN
При Pi, p2 ^ 0 вводятся фиктивные узлы *_,, xN+u уравнения A)
записываются при i = 0, ..., N, а для аппроксимации производных, входящих
в краевые условия, используются трехточечные разностные формулы.
В табдицах приведены максимальные значения погрешности
приближенного решения в узлах сетки.
Обозначения:
у (х) — точное решение краевой задачи,
h — шаг равномерной сетки,
а— параметр сетки в формуле F.1),
ER — погрешность разностной схемы,
ESi — погрешность сплайновой схемы с узлами коллокации в узлах
сетки,
ES2, ES3 —- погрешности соответственно первой и второй схем
повышенной точности из § 5,
ESi — погрешность схемы повышенной точности из § 6.
Таблица 10.1
А -
ER
ESi
0
1,2-1(Г*
1,2.10"*
1
5,8-10-*
9,0.10-3
10
3,2.10
3,3.10"*
100
9,3.10"*
lJ.UT5
В таблице 10.1 приведены численные результаты для задачи
У@)=0, 1/A) =0,5, y{x)=x/
при h = 0,05 и различных значениях параметра А.

§ 7. ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ. ЧИСЛЕННЫЕ ЭКСПЕРИМЕНТЫ 807
В таблице 10.2 приведены данные в случае, когда граничные условия
имеют вид
Наглядно видно преимущество сплайновой схемы, когда в уравнение л
в граничные условия входит у'(х).
Таблица 10.2
А
ER
ESi
0
8,4.10"*
5,8.10"*
д
л1
1
8,7-10"*
5,1.10"*
Taf
ESt
2,6-10
2,7-10
10
8,1.10"*
1,6-10'*
100
7,9.10"*
1,8-10-e
лица 10.3
ES10
0,18
8,6-10
В таблице 10.3 приведены результаты для задачи с разрывным
коэффициентом
у" (х) = 100 sgn (х) + ех,
г/ (— 1) =0, у\1) = Ь
1 - 99.r 2 (х + 1)е х — 1
у (х) = —2— + БОх s^n (х) +е — —2— + "гГ"*
Здесь Д| — сетка с шагом 2/25, сетка А2 отличается от А\ двумя
дополнительными узлами —0,0001, 0,0001. Через 22S1O обозначена погрешность в
случае, когда узлы коллокации определяются по условиям C.9), причем
В таблице 10.4 приведены результаты решения задачи при t = 1
**(х)-10*A-2*)/(*) —(*
10V@,5-«)
[10V@,
При ^> 1 с точностью до 10~12
1-1
2 Vn J
-«•л
20*

308
ГЛ. X. МЕТОД СПЛАЙН-КОЛЛОКАЦИИ
Решение последней задачи резко изменяется практически от
пуля до единицы в небольшой окрестности точки х = 0,5. Это
крайне затрудняет ее решение на равномерной сетке даже при
сравнительно небольших *у. Так, при *\ = 3 не удается получить
Таблица 10.4
h
0,1
0,05
ER
0,24
1,4-Ю-2
Е81
4-10
5-10-8
ES3
1,1-10
3,8-10-4
ES4
(а=0,01)
2,5-Ю-3
1,6-10-!
удовлетворительное приближение, взяв h = 0,002. Наиболее
простой выход состоит в использовании неравномерной сетки, cry-*
щающейся в окрестности точки х = 0,5. .*
Расчеты, выполненные на сетке с узлами на [0; 0,51:
xt = 0,05 • i, i = 0,..., 8; xt = 0,4 + 0,01 • i, i = 8, ..., 15;
*i6 = 0,475; Xi - 0,48 + 0,001 • *, i = 17 37,
и симметрично расположенными узлами на [0,5; 1] с общим их
числом, равным 75, дают следующие значения: ER === 0,08, ES1 =»
*» 0,004. Сравнение явно в пользу сплайиовой схемы.
Литература к главе X. [9, 11, 12, 14, 15, 15*, 20, 29, 45, 46, 55, 57
59, 61, 66, 68, 74, 76, 78, 901.

Г л а в а XI
МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ
Метод конечных элементов завоевал всеобщее признание как
эффективный метод решения самых разнообразных задач
математической физики и техники. Такая популярность метода,
несомненно, объясняется простотой его физической интерпретации,
математической формы и гибкостью численного алгоритма,
облегчающей программирование сложных задач. Являясь в своей
основе вариационным методом, восходящим к
основополагающим работам отечественных математиков Бубнова и Галеркина,
метод конечных элементов получил быстрое развитие и широкое
практическое применение благодаря идее использования
сплайнов. Хотя первоначально эти две теории развивались
параллельно, но в дальнейшем успехи в теории сплайнов в значительной
степени обеспечили и разработку математических основ метода
конечных элементов.
В этой главе мы дадим исходные понятия метода конечных
элементов и установим его связи с теорией сплайнов,
проиллюстрировав это примерами.
§ 1. Понятие о методе конечных элементов
1. Рассмотрим две задачи для одномерного и двумерного
уравнений Пуассона.
Задача 1.
и"Ы = -/Ы, A)
u(a) = u(b) = 0. B)
3 а д а ча 2.
«|г = 0, D)
где й = (я, b)X(c, d), Q = QUT. Уравнения A), C) являются
модельными для более общих уравнений
гИ^-г(х)«--/(х), E)

810 ГЛ. XI. МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ
описывающих различные физические процессы (например,
распределение температур в неоднородном теле и др.).
Известно [16], что вместо задач 1 и 2 можно рассматривать
эквивалентные им вариационные задачи о минимизации
некоторых функционалов.
Пусть U\ — множество функций, непрерывных вместе с
производными до второго порядка включительно и
удовлетворяющих условиям B). Тогда решение задачи: найти функцию
и(х) е Uи дающую минимум функционалу
G)
будет одновременно и решением задачи 1. Уравнение A)
является уравнением Эйлера указанной вариационной задачи.
Пусть теперь U^ — множество функций, непрерывных вместе
со своими производными до второго порядка включительно в
области Q и удовлетворяющих однородным краевым условиям D).
Тогда решением задачи 2 будет функция и(х, у) е [72, дающая
минимум функционалу
Решение сформулированных вариационных задач будет
осуществляться методом конечных элементов.
Прежде всего, нам потребуется использовать функции,
производные которых могут иметь конечные разрывы. В связи с
о
втим введем в рассмотрение пространство Соболева Wz [a, b]f
состоящее из функций, удовлетворяющих нулевым граничным
условиям B) и обладающих первыми производными, квадраты ко-
о
торых интегрируемы на [а, Ь]. Норма в W2 [a, b] определяется
формулой
\1/2
о
Множество U\ является подпространством в W2 [а, Ь]. Из фупк-
о
ционального анализа известно, что пространство W2 [я, Ь]
является полным. Это означает, чт{о предел всякой сходящейся
последовательности функций этого пространства будет опять
функцией из W\ [a, fc]# Более того, решение задачи минимизации:

§ i. ПОНЯТИЕ О МЕТОДЕ КОНЕЧНЫХ .ЭЛЕМЕНТОВ 811
найти такое и, что
u^Wlla.b] и Jx(u)=* inf Jx(v),
о
существует и единственно. Ясно, что функции из Wi[a,b\,
доставляющие экстремум функционалу J\(u), в силу того, что их
производные могут быть разрывны, не будут решениями задачи
1 в обычном смысле. Их называют обобщенными решениями.
Определим теперь пространство W2(Q), которое состоит из
функций, имеющих в области Q суммируемый с квадратом
производные и обращающихся в нуль на ее границе Г. Норма в
о
пространстве W2 (й) определяется формулой
Аналогично одномерному случаю, это пространство является
полным и задача минимизации: найти такое и, что
uefl(Q) и /2(u)« inf J2(v)f
имеет единственное решение. Это решение также будет
обобщенным решением краевой задачи 2.
о о
Пространства W2 [a, b] и W2 (Q) называют энергетическими
пространствами IIА соответственно оператора двукратного
дифференцирования d2/dx2 и оператора Лапласа L. Это название
отражает тот факт, что функции из этих пространств в смысле
введенных выше норм обладают конечной энергией, т. е.
интегралы от них вида (9) и A0) ограничены.
Запишем задачи 1 и 2 в операторном виде:
Ли-/. (И)
В силу сказанного выше задача построения обобщенного
решения этого уравнения равносильна задаче об отыскании элемента
энергетического пространства НА, реализующего минимум
функционала
Ли) «(Ли, в)-2(/, в) A2)
в этом пространстве.
2. Для отыскания минимума функционала Ли) обычно
строят так называемую минимизирующую последовательность.
В предположении ограниченности снизу значений функционала
существует точная нижняя граница [х его значений |л =» inf J(u).

812 А ГЛ. XI. МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ
Тогда последовательность функций ип, тг = 1, 2, ¦ ¦.,
принадлежащих области определения функционала, называется
минимизирующей для этого функционала, если Нт / (ип) = [г. Предел ми-
П-»оо
нимизирующей последовательности доставляет нам искомое
решение.
Одним из способов построения минимизирующей
последовательности является процесс Ритца. В классическом варианте
метод Ритца формулируется следующим образом.
Выберем последовательность элементов {фг}, f = l, 2, ,?., п,
удовлетворяющих трем условиям:
1) все элементы ф* принадлежат энергетическому
пространству НА;
2) при любом п элементы фь ф2, ..., фп линейно независимы;
3) последовательность {ф{} полна в HAi т. е. для всякого
элемента и^ На и любого е > 0 существуют такие натуральное
число N и элемент
п
Un = 2 агфг, «i = COnstjg A3)
что || и — ип |]н < 8 для всех п> N.
Тогда п-е приближение или п-й элемент минимизирующей
последовательности ищется в виде A3), где* числовые
коэффициенты щ выбираются из условия минимума J(un).
Нам потребуется, однако, несколько более общая
формулировка метода Рнтца. Введем последовательность конечномерных
подпространств Vu F2, ..., Vn энергетического пространства НА-
Будем говорить, что эта последовательность полна в НА, если
для любых и е НА и 8 > 0 существует такое натуральное число
N, что inf || и — v || < е для всех п> N. Другими словами, полнота
последовательности подпространств {F<} означает, что каждый
элемент и^НА с любой степенью точности может быть
приближен элементом iineFn, если п достаточно велико. Тогда п-и
приближением или тг-м элементом минимизирующей
последовательности назовем элемент ип е Fn, который минимизирует
функционал Ли) на этом подпространстве.
В данной формулировке метод Ритца реализуется следующим
образом. Пусть q>i , ...,Фп —базис подпространства Vn, т. е.
любой элемент ип е Vn может быть записан в виде
»»-Sfl(in). A4)
г=1
Подставим ип вместо и в функционал A2). Тогда мы получим

§ 1. ПОНЯТИЕ О МЕТОДЕ КОНЕЧНЫХ ЭЛЕМЕНТОВ 813
функцию п независимых переменных ахп , •.., а,п \
2j а\ Щг 9 2а ар Фр I — ^ \ 2j ар ФР д
=1 Р=1 / \р=1
- 2
г,р=1
Коэффициенты а(|П) выберем таким образом, чтобы эта функция
принимала минимальное значение по всем а", 1 = 1, ..., гг, для
чего приравняем нулю ее первые производные по этим
переменным:
Так как
то получаем систему Ритца
), фГг)) «Г = (/, <pin)), г = 1 п. A5)
Матрица этой системы симметрична, так как (Аи, v) = (и, Av).
Определитель системы линейных алгебраических уравнений A5)
есть определитель Грамма линейно независимых элементов и
поэтому отличен от пуля. Найдя коэффициенты a(xn), ...,a(nn) и
подставив их в A4), получим элемент unj являющийся
приближенным решением уравнения A1) по Ритцу.
Приближенное по Ритцу решение тем ближе к точному, чем
больше п [16, 24]. Как следствие, для достижения высокой
точности приходится решать систему линейных алгебраических
уравнений A5) с матрицей большой размерности.
Метод Ритца основан на вариационной формулировке
краевой задачи. Более общим вариационным методом, который
непосредственно применим к уравнению A1), является метод Га-
леркпна (называемый также проекционным методом Бубнова —
Галеркина). Теперь оператор А может быть любым линейным
оператором, определенным на множестве DA1 всюду плотном в
гильбертовом пространстве НА. Запишем уравнение A1) в так
называемой слабой форме или в виде уравнения Галеркина;
(Аи, v) = (/, v) для всех v&HA. AG)
Как и в методе Ритца, выбирается последовательность
конечномерных подпространств VnaHA с базисами [ф{П)К Прпбли-

S14 ГЛ. XI. МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ
жение по Галеркину по-прежнему ищется в виде A3). Но те*
перь коэффициенты а " определяются не из условия
минимизации функционала, а из условия ортогональности разности Au — f
при замене и на ип элементам базиса {фг }, т. е.(Аип—/, у\п))**
*=0, г = 1, , ..,тг. Это снова дает систему вида A5). Полученное
совпадение в общем случае носит формальный характер, а по
существу имеет место только в случае, когда оператор А
обладает свойством самосопряженности, т. е. (Аи, и) «=* (и, Av). В
задачах 1 и 2 это условие выполняется и для них приближение
по Галеркину совпадает с приближением по Ритцу. Из
сказанного ясно, что метод Галеркина применим к гораздо более
широкому классу задач, в частности к нестационарным
задачам.
3. Метод конечных элементов можно рассматривать как
специальный вариант метода Рнтца — Галеркина. Классический
подход имеет два существенных недостатка. Во-первых, на
практике построение базисных функций легко осуществимо только
для некоторых специальных областей и, во-вторых,
соответствующие матрицы Ритца — Галеркина являются полными
матрицами и очень часто, даже для простых задач, плохо
обусловлены. Принципиальное различие между методом конечных
элементов и классической техникой Ритца — Галеркина лежит в
построении базисных функций. В методе конечных элементов
базисные функции выбираются в виде локальных сплайнов и для
областей общего вида могут быть вычислены весьма просто.
Главная особенность этих базисных функций состоит в том, что
они финитны, т. е. обращаются в нуль всюду, кроме
фиксированного числа элементарных подобластей, на которые делится
данная область. Это свойство влечет за собой разреженность и
ленточную структуру матрицы Ритца — Галеркина и
устойчивость процесса численного решения системы.
Для того чтобы применить метод Ритца — Галеркина, по
определению мы должны построить последовательность конечно-
° 1 л
мерных подпространств Vn пространства НА типа W2 [#, b], W2 (Й)
и т. д. В методе конечных элементов это построение
характеризуется следующими тремя основными аспектами: __
1. Прежде всего нужно осуществить разбиение Тп области Q
на конечное число подобластей К (треугольников,
четырехугольников и т. д.), называемых конечными элементами, причем
таким образом, чтобы выполнялись следующие свойства:
a) Q= U К;
т
п
б) конечные элементы К^Тп не вырождаются (треугольники
не переходят в отрезки, четырехугольники в треугольники и т. д.);
в) соседние конечные элементы не перекрываются.

§ 2. ПРИМЕРЫ РЕАЛИЗАЦИИ МЕТОДА НА СПЛАЙНАХ 815
2. Строится конечномерное подпространство функций Vn та*
ких, что на каждой подобласти выбранного разбиния эти
функции являются многочленами степени не выше заданной. Вместо
многочленов могут быть использованы и другие легко
вычисляемые функции, например, рациональные. Это свойство весьма
важно в том отношении, что оно позволяет относительно легко
находить коэффициенты системы Ритца — Галеркииа.
3. В пространстве Vn должен существовать iio крайней мере
один базис из функций с минимальными носителями.
Предполагается, естественно, что такой базис может быть легко описан.
Приближение по Галеркину ищется по этому базису. Его
существование обеспечивает большое число нулей в матрице
системы A5), что облегчает нахождение ее решения. На практике
это одна из наиболее трудоемких задач.
Успех в использовании метода конечных элементов в
значительной степени зависит от того, насколько удачно осуществлено
указанное построение применительно к условиям конкретной
задачи.
§ 2. Примеры реализации метода на сплайнах
В этом параграфе на ряде простых примеров мы покажем,
как реализуется общая схема метода конечных элементов. В
частности, будет показано, что такой подход позволяет получать
известные разностные схемы, что дает основание называть эти
схемы вариационно-разностными.
1. Пусть решается краевая задача 1. Она эквивалентна
вариационной задаче: найти такое и, что
и е= W\ [а, Ь\ и / (и) = inf J (v)t
где
ь ъ
J (V) = J (р'}*dx-2$fv dx. A)
а а
Согласно общей схеме метода конечных элементов разобьем
отрезок [а, Ь] на N конечных элементов, для чего введем на [а, Ъ\
равномерную сетку A: Xi = a+ih, i = 0, ..., TV, с шагом А=*
- (b - a)/N.
а) В качестве конечномерного подпространства Vn возьмем
пространство сплайнов первой степени дефекта 1 на сетке Д,
удовлетворяющих однородным краевым условиям A.2). Размер-
о \
ность этого пространства п = N — 1, VN^1 с: W2 \a, b\. Базисом из
функций с минимальными носителями в VA-_i будет система

316 ГЛ. XI. МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ
/?-сплайнов первой степени
Ф(^~1} (я) = Ф (—~JTjt i = 1, 2, ..., ЛГ — 1, B) *
где
или
^^[0, 11, C)
Функция фШ изображена на рис. 1.3, б. Любая функция
uN~\{x) e VN-i единственным образом записывается в виде
iV-l
где коэффициенты у* являются неизвестными значениями
функции uN-\(x) в узлах сетки Д.
Вычислим коэффициенты матрицы системы Рптца A.15) для
функционала A) и базисных функций B):
b
V-1 A
J ~~ J **фг
ИЛИ
0, |i-p|>l.
Тогда система A.15) запишется в виде
-J- (— Vi-i + 2i;i — i;i+1) = A^i, t = l,2, ...,tf-l, D)
y0 = yiV = o,
где
ь
Если теперь предположить функцию fix) непрерывной, то,
заменяя в правых частях уравнений D) приближенно /(#) на
f(Zi) и умножая уравнения D) на А, получим обычную
разностную схему точности Oih2):
0.

§ 2 ПРИМЕРЫ РЕАЛИЗАЦИИ МЕТОДА НА СПЛАЙНАХ
317
б) В качестве конечномерного подпространства Vn возьмем
пространство сплайнов второй степени дефекта 2 на сетке Д,
удовлетворяющих однородным краевым условиям A.2). Размер-
ность этого пространства равна 2N — 1 и V2n—i с: W21#, Ь].
Если рассмотреть систему квадратических сплайнов с
конечными носителями
Фг
= Ф
•* N - Ъ
E)
где
2A + *) A/2 + t), t €=1—1,0],
2(l — *)(l/2--.t), *€=[0, Ц,
o, t^l—1, U;
o, t <=? io, li
(рис. 11.1, а и б), то нетрудно показать, что функция E)
линейно независимы и, следовательно, образуют базис в Ггл-ь Тогда
произвольная функция U2n-\(z) e 172лт~1 может быть
единственным образом записана в виде
iV-l N—1
, * v ( ) 4- У м;-\1)' fa) FV
г=1 г=0
причем коэффициенты у, суть значения ^2^-1@:) в узлах сетки А»
у ft)
О
а)
Рис. 11.1.
а н;< — ее значения в промежуточных точках {хг + хч\)/2, г =
-0, ...,iV-l.
Система Ритца A.15) в данном случае будет иметь вид
JV-1 Л'-1
2 2 р, фг) ^ = (/, фг),, I = 1, . . .х N - 1;
р=0
Лт-1
i = 0, ..., N - U

318 г ГЛ. XI. МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ
Пользуясь финитностью функций ф„ \рг и вычисляя скаляр-
лые произведения, получим систему линейных алгебраических
уравнений с блочной матрицей для определения неизвестных
коэффициентов в F):
f vi+1 — 8wt — 8wi+1) = gu i" = 1, 2, ..;, N—l;
где
Ъ ' b
3f,M , ч , 3 (\ ' , 7
a a
По-видимому, самый простой подход к решению систем G)
будет состоять в исключении неизвестных wt. В результате
приходим к разностной схеме точности 0{h2):
^о = yiv = 0.
в) В качестве конечномерного подпространства Vn возьмем
пространство кубических сплайнов дефекта 2 на сетке Д,
удовлетворяющих однородным краевым условиям A.2). Размерность
этого пространства равна 2N и V2y с: W\ |a, Ъ\. Базисом в
пространстве V2n будет система сплайнов с конечными носителями
* = 1 ЛГ—1,
t, (*) = max {о,
гдв
Z(t - IK - 3 (t - 1Д «€=10,11,
0, *еН-1, 1];
(t + IK - (t + IJ, te[-lt0U
0, te?\-l,i)
(рис. 11.2, а и б). Как следствие, всякая функция щк{х)
может быть единственным образом записана в виде
Л'-l JV
«2JV (^) = 2 fi<Pi (*) + 2 v'i ^i(X)x

§ 2. ПРИМЕРЫ РЕАЛИЗАЦИИ МЕТОДА НА СПЛАЙНАХ
819
причем коэффициенты и{ суть значения функции Щх(х) в узлах
сетки А, а ь\ — значения ее первой производной на А.
Система Ритца A.15) принимает вид
JV-1
?
1, 2, ..., N - 1;
0, l,..., 'N.
В силу фшштности функций ф/, \|)f нетрудно вычислить
соответствующие скалярные произведения. В результате получаем
-1
Q1'
В)
+1 t
Рис. 11.2.
следующую систему линейных алгебраических уравнений для
определения неизвестных коэффициентов v\y Vi в (8):
г T '
¦'git
1, 2, .. м ЛГ - 1>в
где
Если теперь исключить из этой системы неизвестные г/ц то при-

820 ' гл. xi. метод конечных элементов
дем к разностной схеме повышенной точности O(h4):
*
h
-g- (*,+1 - 8*4 + gi-j) +1 (el+1 - «»_,), г = 2, 3, .... iV - 2,
h »,-
5
v0 = vN = 0.
Аналогично можно рассмотреть подпространства У„,
составленные из кусочных многочленов более высоких степеней, беря,
например, в качестве дополнительных неизвестных параметров
значения производных высших порядков искомой функции в
узлах сетки Д. Это позволит повысить порядок аппроксимации, но,
естественно, усложнит систему уравнений. Характерной
особенностью этих уравнений является присутствие в них наряду со
•значениями в узлах сетки Д неизвестной функции значений ее
производных. Последние не обязательно исключать. Их можно
вычислять одновременно со значениями функции и тем самым
получать высокой точности аппроксимацию не только самой
функции, но и ее производных высших порядков, не
отказываясь от локального характера разностных уравнений.
2. Обратимся теперь к краевой задаче 2. Она эквивалентна
вариационной задаче:
найти такое и, что
u^W\(Q) и J(u)= inf J (v),
где
Чтобы построить приближенное решение задачи
минимизации, согласно общей схеме метода конечных элементов прежде
всего требуется осуществить разбиение области Q на конечное
число элементарных ячеек. Это может быть выполнено
различными способами, из которых наиболее употребительным
является разбиение области на прямоугольные и/или треугольные
элементы.
а) Рассмотрим вначале случай, когда область Q = (a, b) X
К (с, d), Q = QUr разбивается на одинаковые прямоугольники.

§ 2. ПРИМЕРЫ РЕАЛИЗАЦИИ МЕТОДА НА СПЛАЙНАХ
321
С этой целью введем в Q сетку Д = Дх X Ду, где
Ах: Xi = a + ih, i = 0, ..., N% при h = (Ь — a)/N,
Ду- Уз и с + А 7 = 0, ..., М, при Z = (d — c)/Af.
В качестве конечномерного подпространства Vn возьмем
пространство сплайнов первой степени двух переменных,
удовлетворяющих однородным краевым условиям A.4). Размерность
этого пространства равна п = (N — 1)(Д/ — 1) и Vn cz W\ (Q).
Базисом из функций с минимальными носителями в Vn будет
система сплайнов, являющихся произведениями fi-сплайпов первой
степени от переменных х и у:
(х — хЛ [У— У Л
%i te У) = Ф (—г2) Ф (—ГJ.
1=1, •.., iV—1; /=1, ..., Af—lj
причем фШ определена
формулами C). Функция г|)(?, 5) = фи)фE)
изображена на рис. 11.3.
Тогда любая функция ип(х, у) &
е Vn может быть единственным
образом записана в виде
ип (х, у) = S S "irtij (*, У),
i j
Рис. 11.3.
где коэффициенты 1?у — неизвестные значения функции ип{х, у)
в узлах сетки Д.
Подставляя функцию ип(х, у) в (9) и приравнивая нулю
производные от J{un) no vih получим систему линейных
алгебраических уравнений для определения v^:
JV-1 М-1
2 2
= 1 iV —1; / = 1 Af — 1.
(И)
В силу финитности функций г|^(#, у) элементы матрицы этой
системы (Atypq, г|5у) = 0, если выполняется хотя бы одно из двух
неравенств U —р|>1, I/ —д|>1. Следовательно, матрица
системы A1) будет блочной трехдиагональной матрицей.
Непосредственно вычисляя скалярные произведения в A1), являющиеся
интегралами
A2)
21 ю. С. Завьялов и др.

322 ГЛ. XI. МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ
приходим к 9-точечной разностной схеме
где
vi0 = viM = 0,
^ 0? = VNj = 0,
= 0,
Точность схемы O(h2+l2).
б) Рассмотрим теперь случай разбиения области Q па
прямоугольные треугольники. С этой целью, считая, что на Q введена
определенная выше сетка А, разобьем каждый элементарный
прямоугольник Qij = [хи xi+\] X [уи yj+i], i = О, ..., N — I; j ==»
= 0, ..., M— 1, на два треугольника диагональю, проходящейг
например, через вершины (я*, yi) и (xi+u Уз+О-
В качестве конечномерного подпространства Vn возьмем
пространство непрерывных кусочно-линейных функций двух
переменных, линейных над всяким треугольником указанного выше
разбиения и обращающихся в нуль на границе области Q (см.
§ 12 гл. II)/ Нетрудно подсчитать, что, как и в предыдущем
примере, размерность этого пространства равна (TV— l)(Af — 1)
(появление дополнительных параметров компенсируется
условием непрерывности при переходе через диагонали
прямоугольников разбиения). Базисом из функций с минимальными
носителями в Vn будет система функций
,„_,. ,._,.л ^
где
1-t,
1-S,
t + 1-s,
*,
i-t
о,
(?, s) e Dl,
(t, s) e Д.,
(t, s) e= Д5,
(t, s) s /L,
(*', *) e ^1!
(*, s) ^ Z);, / = !,.
,.,6.

§ 2. ПРИМЕРЫ РЕАЛИЗАЦИИ МЕТОДА НА СПЛАЙНАХ
323
Треугольники D5 показаны на рис. 11.4, а вид функции a|)U, s)
изображен на рис. 11.5.
Тогда произвольная функция ип{х, у) е Vn опять может быть
единственным образом записана в виде A0), где г^Дя, у) из A3),
и для определения коэффициентов v{j в этом представлении
имеем систему линейных алгебраических уравнений A1). Матрица
системы A1) снова будет блочной трехдиагональной, поскольку
Рис. 11.4.
в силу финитности функций A3) элементы матрицы этой
системы Ыг|)рд, tyn) = 0, если U — р\ > 1 и/или I/ — q\ > 1. Проводя
вычисление остальных элементов этой матрицы, являющихся
интегралами вида A2), приходим к 5-точечной разностной схеме
точности Oih2 + I2):
i — 1 N — 1- 7 — 1 M — i •
vOj = vNj = O, У = 0, ..., M,
Где
r r
= J J
Полученные в последних двух примерах схемы метода
конечных элементов с точностью до правых частей совпадают с
обычными разностными схемами. Это позволяет применять для
решения соответствующих систем эффективные итерационные
методы типа расщепления, продольно-поперечной прогонки и др.
Мы привели примеры вариационно-разностных схем для
уравнений A), C). Для более общих уравнений E), F)
вариационно-разностные схемы строятся таким же образом. Заметим,
что коэффициенты получающихся при этом схем будут
вычисляться с помощью интегралов от коэффициентов самого
уравнения. Эти интегралы в предположении соответствующей
гладкости коэффициентов без потери точности схемы могут быть
аппроксимированы соответствующей квадратурной формулой.
21*

324
ГЛ. XI. МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ
§ 3. Способы построения пространств
аппроксимирующих функций
Рассмотренные в предыдущем параграфе примеры
показывают, что схемы метода конечных элементов существенно зависят
от выбора разбиения области и способа построения
конечномерных пространств аппроксимирующих функций Fn. Для случая
прямоугольной области рассмотренные нами приемы разбиения
ее на элементарные прямоугольники и прямоугольные
треугольники являются наиболее естественными и приводят к
регулярным сеткам.
Если получаемая точность недостаточна, то можно
детализировать сетку, разбивая каждый прямоугольный треугольник
еще на четыре (рис. 11.6). В ряде случаев точность повышается при
смене диагоналей, разбивающих прямоугольник на два
треугольника. Сгущая сетку, следует руководствоваться правилом:
дальнейшее разбиение данного участка области производится только
в том случае, если предшествующее привело к заметному
повышению точности. В результате, начиная с некоторого момента,
уточняется триангуляция только некоторых участков области..
Мы теряем регулярность сетки, но зато существенно сокращаем
оощий объем вычислений.
Если область отличается от прямоугольника, то указанное
разоиение также может быть использовано, но при этом, как
правило, для предотвращения потери точности вблизи границы
требуется дополнительная триангуляция, учитывающая
особенности последней. Кроме того, при аппроксимации краевых задач.
а)
8)
Рис. 11.6.
в)
возникают трудности, связанные с необходимостью построение
пространств Fn, удовлетворяющих граничным условиям.
Употребителен и другой подход. Данная область с криволи-^
нейной границей (или отдельные ее части) с помощью
подходящего преобразования отображается в единичный квадрат,
который разбивается на элементарные прямоугольники или
прямоугольные треугольники. Производя обратное преобразование, мы
получим на исходной области криволинейную сетку, хорошо
учитывающую геометрию области. Например, если задана область

§ 3. ПОСТРОЕНИЕ ПРОСТРАНСТВ АППРОКСИМИРУЮЩИХ ФУНКЦИЙ 325
Д изображенная на рис. 11.7 а, то одно из возможных
преобразований, переводящих единичный квадрат в область Д может
быть записано следующим образом. Пусть вектор (pit) = (—1,
<PoU), <pi(?)), фтЫ — транспонированный вектор фЫ,фоШ =
= 1 — t, (p\(t) = t. Через r(t, s) обозначим радиус-вектор
произвольной точки в области D относительно прямоугольной системы
ro(s)
0.1
0,0
170
Рис. 11.7.
координат, и пусть точки rih i, j = 0, 1,— вершины
криволинейного четырехугольника Z), отвечающие соответственно
вершинам единичного квадрата U, /), i, ; = 0, 1. Нужное нам
преобразование будет иметь вид
где Fit, s) — матрица:
'00
ho
'01
Если требуется повысить порядок аппроксимации решения,
то следует рассмотреть пространства Fn, составленные из
кусочных многочленов более высоких степеней. Как правило,
пространства Vn выбирают совпадающими с пространствами
многочленов вида
,y)= S
на треугольных элементах и многочленов вида
т
на прямоугольных элементах.
21
а,р=о
(i)
B)

326 ГЛ. XI. МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ
Рассмотрим несколько способов построения таких
пространств- Vn, определенных на односвязной области D в плоскости
(х, у) с кусочно-линейной границей, когда D разбивается на
подобласти в соответствии с требованиями, сформулированными
в § 1.
Обратимся вначале к случаю разбиения D на треугольники.
Пусть пространство Vn состоит из функций ип(х, */),
совпадающих на каждом треугольнике нашей триангуляции с некоторым
квадратическим многочленом вида A) при т = 2. Нетрудно
показать, что коэффициенты этого многочлена для конкретного
треугольника с вершинами Pi, Pz, Р& и средними точками
сторон Р2, Ph Pq (рис. 11.8, а) однозначно определяются заданием
значений функции ип{х, у) в точках Р„ ?=1, .., 6.
Непрерывность функции ип{х, у) в D следует из того факта, что на
каждой из сторон любого треугольника эта функция определяется
однозначно.
Сходным образом строится пространство Vni состоящее из
функций ип(х, г/), совпадающих на каждом треугольнике
разбиения области D с некоторым кубическим многочленом вида A)
д)
Рис. 11.8.
при та = 3. Кубический многочлен двух переменных х и у имеет
10 коэффициентов и однозначно определяется заданием значений
функции ип(х, у) в 10 узлах: вершинах треугольников, точках,
получающихся делением всех его сторон на три равные части,
и центре тяжести (рис. 11.8, б). Непрерывность функции ип(х, у)
в D опять следует из того факта, что 4 узловых значения на

§ 3. ПОСТРОЕНИЕ ПРОСТРАНСТВ АППРОКСИМИРУЮЩИХ ФУНКЦИЙ 327
каждой из сторон треугольника однозначно определяют
заданный на этой стороне кубический многочлен.
Для пространства Vni составленного из кусочно-кубических
многочленов, возможна и другая конструкция, требующая
использования существенно меньшего числа узлов. С этой целью
уберем средние точки па сторонах и будем считать, что в
вершинах треугольников кроме значений функции и^х, у)
задаются ее производные первого порядка по х и у (рис. 11.8, в).
Таким образом, 10 коэффициентов кубического многочлена
определяются значениями ип,ип'°\ ипл'в каждой вершине и
значением ип{х, у) в центре тяжести треугольника. На сторонах
треугольника кубический многочлен однозначно определяется
заданием 4 значений (функции ип(х, у) и ее производной по
направлению стороны на обоих концах этой стороны), откуда
следует непрерывность ип(х, у) в D.
Обращаясь к разбиению области на элементарные
прямоугольники, следует сказать, что на плоскости очень многие важные
задачи решаются в прямоугольных областях или в областях,
состоящих из прямоугольников. В случае областей более сложной
формы чаще всего имеется возможность комбинировать
прямоугольные элементы внутри области- с треугольными
элементами вблизи границы. Отметим также, что прямоугольные
элементы особенно удобны в трехмерных задачах.
Пусть пространство Vn состоит из функций ип(х, у),
совпадающих на каждом элементарном прямоугольнике с некоторым
дважды квадратическим многочленом B) при т = 2. Тогда 9
коэффициентов этого многочлена будут однозначно
определяться заданием значений функции ип(х, у) в вершинах, серединах
сторон и центре тяжести прямоугольника. Непрерывность
ип(х, I/) на В будет следовать из однозначности определения
квадратического многочлена на каждой стороне прямоугольника.
Если рассмотреть пространство конечных элементов У„,
состоящее из функций ип(х, у), совпадающих на каждом
элементарном прямоугольнике с некоторым дважды кубическим
многочленом вида B) при т = 3, то всякий такой многочлен будет
полностью определяться заданием в вершинах прямоугольника
значений функции ип(х, у), а также значений ее частных и
смешанной производных по х и z/. Аппроксимирующая функция
ип{х, у) будет уже не только непрерывна, но и непрерывно
дифференцируема в Z), что также следует из однозначности
определения соответствующих кубических многочленов на сторонах
прямоугольника.
Указанные конструкции могут быть непосредственно
обобщены на случай построения на треугольных и прямоугольных
сетках пространств Vn кусочных многочленов более высоких
степеней.

328 ГЛ. XI. МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ
§ 4. Сходимость метода конечных элементов
Для изучения сходимости конечно-элементных
аппроксимаций к точному решению краевой задачи нам потребуется одно
экстремальное свойство таких аппроксимаций.
Для функционала Пи) из A.12) имеем
•Ни + ц) - Ни) + 2(Аи - /, т|) +. U^, ч).
Если теперь и — точное решение уравнения A.11), то, полагая
т) = v — и, находим ,
Hv) - Пи) = (A(v-u), v-u) = \\v- и\\2.
Отсюда, заменяя и конечно-элементной аппроксимацией решения
ипу получим
|| иа — и ||2 = / (ип) — J (и) = niin J (v) — J (и) = min || v — и ||2,
V V
т. е.
|| ып — и | = min | и — и (|. A)
1. Обратимся вначале к краевой задаче 1. Пусть и (х) е
^ Wlo [ay b] '— точное решение этой задачи, а ип(х) — его
конечно-элементная аппроксимация в пространстве Vn сплайнов
первой степени дефекта 1 на сетке Д, удовлетворяющих
однородным краевым условиям A.2). Нам нужно оценить величину
[ м — ип (с = max \u(x) — ип (х) |.
В данном случае, используя интегрирование по частям для
о -
всякой функции v {x) e W2 \ay Ь], имеем
Так как
ее
р* (ж) = 2 J i> @ у' («) Л,
а
то, применяя неравенство Буняковского, получаем
/ Ь \ 1/2 / Ъ \ 1/2
!>¦(*)< 2 И i;2 (t) А И (i;' (i)J^ < 2 (Ь - a)i/21| i;||с||иII

§ 4. СХОДИМОСТЬ МЕТОДА КОНЕЧНЫХ ЭЛЕМЕНТОВ 329
для любого х ^ [а, Ъ\. Отсюда
IMIc^2(&-aI/2IML ' B)
Пусть ип(х) — сплайн первой степени на сетке А,
интерполирующий в ее узлах решение и(х) краевой задачи. Тогда
согласно результатам гл. II справедлива оценка
и' — ип\\с<-2 К||оо \h = -jf-J.
В силу A), B) получаем
\и - ^п|с<2 (Ь - аI/2\\и - ил||<2(Ь - аI/2\\и -йп\\ =
/ Ь \1/2
= 2A- аI/21 | (и' - ипУйх I < (Ь - л) АЦ !*!«, = О (ft).
Более топкий анализ показывает, что в действительности
справедлива оценка с порядком O(h2).
Аналогичным образом могут быть получены оценки
погрешности и для других типов конечно-элементных аппроксимаций
задачи 1. Пусть, например, Vn — пространство кубических
сплайнов дефекта 2 на сетке Д, удовлетворяющих однородным
краевым условиям. Через ип(х) обозначим сплайн из Уп,
интерполирующий решение и(х) задачи 1 и его первую производную
на сетке А. Согласно результатам гл. II
Тогда, если ип(х) — конечно-элементная аппроксимация для
и(х) в пространстве Fn, то в силу A), B), как и выше, находим
Таким образом, мы видим, что для доказательства
сходимости конечно-элементной аппроксимации достаточно знать
соответствующую оценку погрешности сплайн-интерполяции.
2. Обратимся теперь к задаче 2. Пусть и(х, у) е C4Q] —
точное решение этой задачи, а ип(х, у) — его конечно-элементная
аппроксимация в конечномерном пространстве Fn. *
Здесь хотелось бы оценить величину
||и — ип\\с = max | и (х, у) — ип (х, у) |.
(*V)SQ
Однако значительно легче получить оценку для разности и — ип
в норме пространства L2(Q):
и-ипЦ =
[и (х, у) - ип {х, у)\ЧхdyY\

330 ГЛ. XI. МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ
Эта величина, как мы знаем, зависит от вида разбиения
области Q и способа построения пространства аппроксимирующих
функций.
Рассмотрим вначале случай, когда область Q = [а, Ъ\ X [с, d\
сеткой А = Дх X Ду разбивается на равные прямоугольники Q{j =»
=» Ixi, xi+i]X[yj, г/j+J, а пространство Fn, где ищется
приближенное решение, есть пространство сплайнов первой степени
двух переменных, линейных отдельно по каждой из переменных
х и у во всяком элементарном прямоугольнике Q^ и
удовлетворяющих однородным краевым условиям A.4).
Нужная нам оценка основывается на применении так
называемого неравенства Фридрихса. Пусть и{х, у) — непрерывно
дифференцируемая в области Q функция, обращающаяся в нуль
на ее границе, а (хи у\) — точка в Q. Тогда
~1
(**Уд ,
1i—d*«
Применяя к нему неравенство Бунякозского, имеем
Яд I2 Г Г д I2
— и (х, ух) \ dx ^ {Ь — а) \ — и (х, уд dx.
ОХ \ J \_ОХ J
а • а
Проинтегрировав эти соотношения в пределах а < х\ ^ Ь, с ^
*^y\^d, получим неравенство Фридрихса
J J  (*i, tfi) Ar^i < F - a) J j [1 и (х, у)\
В нашем случае
|| и Г = (- М и) - - J J Lu.udxdy = §j Щ + [Щ\ dx dy ¦
и, следовательно, в силу C)
1Ы12<(Ь-аIЫ1. D)
Пусть w(x, у) — сплайн из Уп, интерполирующий в узлах
сетки Д точное решение и(ху у) задачи 2. Тогда согласно

§ 4. СХОДИМОСТЬ МЕТОДА КОНЕЧНЫХ ЭЛЕМЕНТОВ 331
результатам гл. II
1ог'8[Ип(х,у)-и(х,у)]1я^±Що2и{х,у)\», г + * = 1, E)
где Л = max (A, Z), h=(b-a)/N, l = {d-c)/M,
||#2w(*,2/)||oo= max {\\Dr'su(x,y)\U.
В силу (З), D), E) получаем
|и — un\\2< (b — a)|| и ~ un
_ af2 (d - cI/2 X^
Предположим теперь дополнительно, что каждый элементар-
пый прямоугольник fiii, на которые разбивается область Q
диагональю, проходящей через вершины {хи у^) и (xi+u г/j+i),
делится на два прямоугольных треугольника и пусть
пространство Vn есть пространство сплайнов первой степени двух
переменных, линейных над всяким треугольником указанного
разбиения и обращающихся в нуль на границе области Q. Через
ип(х3 у) обозначим сплайн из Vn, интерполирующий точное
решение и(х, у) задачи 2 в вершинах прямоугольных
треугольников. Согласно результатам гл. II
|| Dr>s [un (х, у)-и (ху у)] |U < ft! D4 (х, у) |!10О. (G)
Тогда, если ип(х, у) — конечно-элементная аппроксимация
для и(х, у) в пространстве Vn, то в силу A), D), F), как и
выше, получаем
\\и - ип\\2 < /2 (Ь - аK/2 (d - cI/2h\\D2u (х, у) \„ = О (h).
Рассмотрим теперь случай, когда задача 2 решается на од-^
носвязной области D в плоскости (х, у) с кусочно-линейной
границей Г. Предположим, что нам задано некоторое разбиение D
на треугольники, углы которых ограничены снизу величиной
^ > 0, а пространство Vn есть пространство сплайнов первой
степени двух переменных, линейных над каждым из
треугольников, составляющих область D и обращающихся в нуль на ео
границе. Если ип(х, i/)e7n — сплайн, интерполирующий
решение и(х, у) задачи 2 в вершинах этих треугольников, то, как
было показано в гл. II,
\Dr's [un (х, у)-и (х, у)\ \U < -j^. || D*u (x, у) U G)

332 ГЛ. XI. МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ
где h — длина наибольшей из сторон треугольников, входящих
в разбиение области D.
Заключим D в прямоугольник Q\ = [аь 6J X lc\y dj. Пусть
и(х, у) — непрерывно дифференцируемая в D функция, равная
нулю на Г. Продолжим и(х, у) на весь прямоугольник Qi,
полагая ее равной нулю вне D. Тогда, поступая аналогично тому,
как это было сделано выше, и учитывая, что и(х, у) = 0 вне Z>,
получим неравенство
fJ[(gI(g)'J (8)
Если теперь ип(х, у) — конечно-элементная аппроксимация в
Vn решения и{х, у) задачи 2, то в силу A), G), (8) найдем
\\и-ип р, = (Ьг - atf1* (dt - схI/2 2-01D4 (х, у) \я = О (Л).
Аналогичным образом может быть доказана сходимость и
для других типов конечно-элементных аппроксимаций. Такое
доказательство основывается на использовании соответствующих
оценок сплайн-интерполяции.
Литература к главе XI., [4, И, 16, 24, 27, 84].

ДОБАВЛЕНИЯ
§ 1. Матрицы с диагональным преобладанием
Ряд важных результатов теории и практики сплайнов связан со
свойствами матриц с диагональным преобладанием. Любопытно, что многие из
этих свойств, несмотря на их простоту, были установлены сравнительно
недавно и своим открытием непосредственно обязаны теории сплайнов.
Квадратная матрица А = [ац] порядка п называется матрицей с
диагональным преобладанием, если выполняются условия
Ki|-2'K| = ^>°> *,/ = i,....#. A)
1. Критерий регулярности Ада мара.
Теорема Д.1. Матрица с диагональным преобладанием невырождена.
Доказательство. Действительно, если предположить, что матрица
вырождена, т. е. \А\ = 0, то однородная система уравнений Ау = О имеет
нетривиальное решение у = (уи ..., у<\)т (Г—операция транспонирования),
Пусть к таково, что | ук | ^ I г/» 1, i = 1, ..., N. Тогда из к-то уравнения
следует
Отсюда
1
что противоречит предположению A).
2. Оцепка нормы обратной матрицы. Если в пространстве
векторов у норма введена соотношением
|| у ||= max \y.L
то согласованной с ней нормой в пространстве матриц А = [<z</|, I, / = 1, ...
,,., N, является норма
Ц А || = su p .. '.. = max 2] \ ац \"
о
Пусть задана система уравнений Ay = d с невырожденной матрицей Л.
Ее решение можно представить в виде y=A~ld. Норма обратной матрицы
А~1 есть

334 добавления
Отсюда || у || ^ЦЛ1| ||d||. Следовательно, чтобы оценить норму решения
системы через норму ее правой части, достаточно вычислять или оценить
IW-'il.
Теорема Д.2. Если А — матрица с диагональным преобладанием^ то-
справедлива оценка
\А'г\< шах —. C)
iN ri
Доказательство. Пусть у — произвольный непулевой вектор.
Если к таково, что \\у\\-= \уь.\, то
\\d\\ = \\Ay\\ =
г з'Фк
Следовательно,
||с?|| max —-.
) Ki<N ri
Учитывая эту оценку в равенстве B), получаем C).
Следствие Д.1. Если матрица системы Az = d с диагональным пре*
обладанием, то
\di\
max l—\ D)
Д о к а з ат^е л ь с_т в о. ^Разделив каждую из строк системы на г,-, полу-
чим систему Ау*= d, где di = di/rt. Согласно теореме Д.2 ИЛ-^К li и
поэтому IMKIIdll, ч. т. д.
Оценка C) для широкого класса матриц является точной. В этой связи
обратимся к матрицам монотонного вида.
Матрица А •= [а*7-] называется матрицей монотонного вида, если из
А у ^ 0 следует г/^0 и из 4у^0 следует у ^ 0 (знакп ^, ^ означают,,
что неравенства имеют место для всех компонент). Все элементы
матрицы А~\ обратной к матрице монотонного вида, неотрицательны, и наоборот»
Лемма Д.1. Если А—матрица с диагональным преобладанием,
аи > 0, аи < О U Ф О* ' W = 1. • •.. #.
то она монотонного вида.
Доказательство. Покажем, что из Ау ^ 0 следует у ^ 0.
Предположим противное. Пусть среди координат вектора у имеются
отрицательные и yk та из них, которая максимальна по модулю. Возьмем вектор z
такой, что все его координаты равны \ук\* Так как
3 3
то Az > 0 и, стало быть, A(z + y)-= Az + Ay > 0. С другой стороны,
3 3'Фк
Полученное противоречие доказывает лемму.

§ 1. МАТРИЦЫ С ДИАГОНАЛЬНЫМ ПРЕОБЛАДАНИЕМ 335
Теорема Д.З. Если А—матрица с диагональным преобладанием и
(/^0. «,/ = 1, ...,#; E)
ан + 2 aij = r = const, i = 1, ..., N, F)
i
\\А-Ц\ = 1/г. G)
Доказательство. Матрица ^-1 = Га'.1 удовлетворяет матричному
уравнению А~1А-=Е, а элементы ее i-й строки удовлетворяют системе
aiiaih + ai2a2h + • • • + aiNaNk = 6ift' A = 1, ..., ЛГ,
где б,й — символ Кропекера. Суммируя эти уравнения по индексу А\
получаем
ft к k
Отсюда, учитывая F), находим
24 = 1/г.
j
Но так как по лемме Д.1 матрица А монотонная, то слева стоит норма
11-4"" 41 обратной матрицы.
Теорема Д.4. Пусть В= [Ьц] — матрица с диагональным преобла-
дапием,
и существуют диагональные матрицы С и D с элементами, равными либо
-fl. либо —1, такие, что матрица А = CBD удовлетворяет условиям E).
Тогда
\\В-Ч = 1/г. (9)
Доказательство. Так как B~l = DA~lC, то элементы матриц В
и А~1 могут отличаться лишь знаками и, значит, Hi^ll^lH"!!. Для
элементов матрицы А вследствие условий (8) выполняются соотношения F).
Поэтому Ц^4 — Ч1 = 1/г.
3. Оценка элементов обратной матрицы. Рассматриваются
матрицы вида А = Е — В, где Е — единичная матрица, а матрица В такова,
что
Ц?||=<7<1. A0)
Для матрицы А~\ обратной к матрице А, известно разложение [2, с. 346],
Л = (Е - В) -1 = 2 Ва. A1)
Среди таких матриц А выделим ленточные, т. е. матрицы с элементами
аи = 0, если \i— /|>wi>0. A2)
Теорема Д.5. Если А = Е — В — ленточная матрица с условия*
ми A0), A2), то элементы а^ обратной матрицы А~1 удовлетворяют

336 ДОБАВЛЕНИЯ
неравенствам
Доказательство. В силу ленточной структуры матрицы В из A1)
оо
следует, чтоа\. есть элемент матрицы 2j Ba, где 5^-— целое число,.
a=sH
удовлетворяющее условию \i — /| = s^m — l, О ^ I < т. Но тогда
Теорема Д.6. Если ленточная матрица А = [яг?1 с условиями A2)
есть матрица с диагональным преобладанием, то для элементов а[.
матрицы А~~х справедливы неравенства
| • •• • » | | I Л Л 1\, \ ШЙЧ0
max
Доказательство. Введем диагональную матрицу С с элементами
l/|a21|, i = 1, ..., /V. Тогда можно записать С А =Е — В, причем по
определению нормы и условиям A)
\\В\\= max l-r—-г =1- min г—=-j < 1.
Kh<N\ \akk\/ kN\akk\
Используя теорему Д.5, для элемеытбв матрицы (СА)~1= А~ХС~1 получаем,
оценку
min г-—, | I 1 —
Kh<N \ahh
из которой очевидным образом вытекает A4).
§ 2. Метод прогонки для решения систем уравнений
с трехдиагональными матрицами
Многие задачи теории сплайнов приводят к решению систем липейных
уравнений с ленточными матрицами А у = d.
Величина \х(А) = ЦЛ'МПИИ называется мерой (числом)
обусловленности системы или матрицы. Системы уравнений и матрицы с небольшими
значениями мер обусловленности принято называть хорошо
обусловленными. Известно [6, с. 53], что возможность эффективного решения системы
зависит от того, является она хорошо обусловленной или нет.
Если А — матрица с диагональным преобладанием, то из теоремы Д.2.
следует оценка
МЛ) < |! Л Ц max —,

§ 2. МЕТОД ПРОГОНКИ
337
где гг определяются формулами A.1). Очевидно, если величина /тах|а^ |\х
v (min гЛ—* невелика, то А — хорошо обусловленная матрица.
\ * /
1. Метод прогонки в случае матриц с диагональным
преобладанием. Пусть имеется система
С2
0
bN
Ь1
п2
0
0
0
0
0
... 0
... cN_t
... 0
0
0
CN
cl
0
1 bN-l
aN _
~yl
y*
yN-i
.Jn _
~d1
d2
dN-l
Jn _
Рассмотрим сначала случай, когда с\ = Ь^ = 0. Решение ищется в
виде
У%
1, ..., Л^ — 1.
B)
Используя выражение для iji-\ из B), исключим это неизвестное из i-то
уравнения системы. Получаем
Сравнивая это соотношение с B), выводим рекуррентные формулы для про-
гоночных коэффициентов у*, и{ (прямая прогонка):
^о = ^о = 0,
Очевидно, yN-=uN. Все остальные неизвестные находятся по
формулам B) (обратная прогонка). Для реализации алгоритма требуется
выполнить 8W арифметических операций: 3iV сложений, 3N умножений, 2N
делений.
На практике часто приходится иметь дело со случаем, когда
требуется решить несколько систем, отличающихся лишь правыми частями.
Нетрудно видеть, что в формулах C) величины v( и аг+ с{и{^ не зависят от
правой части системы. Поэтому, если вычислить их и запомнить, то для
решения каждой из систем потребуется 57V арифметических операций.
Пусть теперь с\ и bN отличны от нуля. Будем искать у г в виде
Уг = и{у{+1 + wtyN + uu i-= 1, ..., W— 1. D)
Подставив выражение для yi-\ из D) в i-e уравнение системы, получаем
(а,- -Ь CiVi-fiiji + b{yi+l + CiWiyN = dN —
Отсюда приходим к формулам C) для коэффициентов vu uu i = 1, ..., Л7 —1.
Величины Wi определяются соотношениями
= 1. w. = —
Теперь выразим все у% через улг в виде
У г = Sf у лт + *,', * '= 1, . . ., N —
Подставляя выражение для yi+i в D), получаем
22 ю. С. Завьялов и др.

338 ДОБАВЛЕНИЯ
Сравнивая это соотношение с F), находим рекуррентные формулы для
величин Sf, til
sN = 1, tN = 0, .
Si=ViSi+l+wu ti= Uiti+l+Ui, i-= N — 1, ..., 1. G)
Подставляя у\ и ijn-\ из F) в последнее уравнение системы A),
находим
U Ъ
( '
после чего решение вычисляется по формулам F). Всего необходимо
выполнить 1AN арифметических операций: 5N сложений, 6N умножений и 3N
делений.
При решении серии систем с одинаковой матрицей предварительно
следует вычислить и запомнить независящие от правой части величины: ии wiy
$i, dt + CiVi-i. Тогда для решения каждой из систем потребуется IN
арифметических операций.
Алгоритм называется корректным, если все действия, необходимые для
-его реализации, выполнимы. Исследование корректности алгоритма
прогонки сводится к выяснению условий, при которых знаменатели в формулах
C), E), (8) не равны нулю.
Будем называть алгоритм прогонки устойчивым, если выполняются
неравенства •
\»Л < 1, К'1^1, < = 1, 2 7V — 1. (9)
В этом случае при счете по формулам C), E) — G) ке происходит
прогрессивного накопления погрешностей округления за счет операций
умножения.
Покажем, что если система A) с диагональным преобладанием, то
алгоритм прогонки корректен и устойчив. Вначале установим неравенства
Ы + 1»<1<1, i = l, 2, ..., W-1, A0)
из которых вытекают неравенства (9). Имеем |г;0| + \wo\ -= 1.
Предположим, что A0) выполняется при i — 1. Тогда
Так как \а{\ — |с»||у*_г| > |л*| — \с,\ > 0 и \аг\ > |&г| +"|с«|, то отсюда
следует, что |ь>г-| + |дег| ^ !• Неравенства A0) доказаны. Попутно
установлено, что знаменатель в формулах C), E) отличен от нуля. Кроме
того, из G) вытекает, чго |s*| =^r |t>i||sf+i| -f \wt\. Учитывая A0) и то, что
sN = 1, отсюда по индукции легко получаем | s< | ^ 1, i = 1, ..., N — L
Теперь очевидно, что знаменатель в формуле (8) пе обращается в нуль,
так как
К + bNsi + CNSN-1 \> \aN\ - | bN | \*г | - | cN || SN_X | > 0.
Пусть система A) хорошо обусловлена, но без диагонального
преобладания. В этом случае изложенный выше способ, вообще говоря,
некорректен, ибо не исключена возможность обращения в нуль знаменателей
л< + CiVi-v в формулах C). Например, а\ + c\v0 = 0, если а\ = 0.
В случае с\ ¦-= Ьн =» 0 мы опишем другие алгоритмы, свободные от
этого недостатка. Единственное условие их корректности —
невырожденность матрицы системы A).

§ 2. МЕТОД ПРОГОНКИ 339
2. Метод немонотонной прогонки. Алгоритм прогонки,
описанный в п. 1, есть не что иное, как реализация алгоритма исключения
Гаусса для систем с трехдиагональными матрицами. При этом ,в случае
матриц с диагональным преобладанием автоматически используется
главный элемент, что обеспечивает устойчивость вычислений. Алгоритм,
который рассматривается ниже, основан на методе Гаусса с выбором главного
элемента по строке для матриц без диагонального преобладания.
Пусть в результате i-ro шага процесса исключения получена система
F, ' A1)
где hi; ^ i. В частности, при i = 1 полагаем
*,«=!, H = аи В = с2, F = du G = d2.
Оппшем (г + 1)-й шаг процесса исключения. Возможны два случая,
а) |Я| ^ \bi\. Уравнение A1) запишем в виде
Укг - viyi+i = UV
где vi = —bi/H, U{ = F/H, причем \ui\ ^ 1. С помощью этого соотношения
исключим из A2) неизвестное yk.». Находим
(и{В + ai+l) yi+l + bi+iiji+2 = G — щВ. A4)
Объединяя уравнение A4) с оставшимися уравнениями исходной
системы и обозначая // = v{B + Яг+ь F «= G — щВ, ki+l = i + 1, Л = сг+2,
G = di+2, снова приходим к системе вида (И) — A3), в которой i заменено
на i + 1.
б) |Я| < \bi\. Это озпачает, что 6г-— главный элемент в строке.
Преобразуем A1) к виду
где Vi = —Я/6г, Ui — F/bii причем опять |р*| ^ 1. Используя это
уравнение, исключаем yi+\ из A2) и A3). Находим
(В + *л+1) yfti + 6.+1^.+2 = (? - »л+1>
ViCiWJki + йг+2^г+2 + 6г+2^г+3 = di+2 ~ Мгсг+2-
Объединяя полученные уравнения с оставшимися уравнениями системы
и вводя обозначения к1+х = ки
Н = В -\- Uiui+u В = Vid+2, F = G — Uidi+i, G — di+2 — ci+2iii,
снова приходим к системе вида A1) — A3).
Итак, описан один шаг алгоритма исключения. Этот шаг выполним,
если Н и bi одновременно не обращаются в нуль. Но это действительно
так, потому что в противном случае система A) была бы вырожденной.
Следовательно, описанный алгоритм исключения корректен.
В результате исходная система A) заменяется уравнениями
Ущ = vil^i + uv * e 1, 2, ..., tf— 1,
A5)
V*N = UN-
При этом каждое неизвестное войдет хотя бы в одно уравнение.
22*

340 ДОБАВЛЕНИЯ
Суммируя проделанные рассуждения, приведем расчетные формулы
для вычисления коэффициентов viy иг и индексов at-, р*. Знак ( = )
используется как символ операции присвоения.
Полагаем Я = аи В = с2, F = du G = d2i (Jo = 1» «j = &,¦ = с* = dj =»
0/ЛГ+1Л + 2
Для i = 1, 2, ..., N выполняются описапные выше действия:
а) -если \Н\ ^ |Ь<|, то i>< = — 6,/Я, щ = F/Я,
Я = ViB + ai+u В = Cf+2, F^G — тВ,
G = di+2, at = h-u pi==i+l;
б) если |Я| < 16,|, то I?< = —H/bu щ == F/6<,
Я = # + У,а1 + Ь Я = УгСг+2, F = G— Ui
G = di+2 — w»Ci+2? a,- = t + 1, ^ = рг-_,.
На обратном ходе алгоритма из A5) вычисляются пеизвестпые у и
Порядок вычисления определяется индексами а*, рг- и может иметь
немонотонный характер. Отсюда название алгоритма. Однако всегда \vi\ ^ 1,
и поэтому обратный ход устойчив по отношению к накоплению
погрешностей округления.
Объем арифметических операций в методе немонотонной прогонки
не превышает \2N. При решении систем с одинаковой матрицей на
каждую из них тратится не более IN операций.
Отметим, что аштод иемопотоиной прогонки автоматически переходит
в метод прогонки, описанный в п. 1, если он применяется к системе с
диагональным преобладанием.
3. Метод универсальной прогонки. Первый этап
алгоритма состоит в преобразовании системы A) к двухдиагопальному виду.
Опишем одип шаг этого преобразования. Пусть (i — 1)-е уравнение
системы приведено к виду
Si-\yi-f+ Vi-\yi = Ui-\. A6)
Если St_i Ф 0, то, суммируя уравнение A6) и i-e уравнение
системы A), умноженные соответственно на —сг- и st_i, получаем
где
Si = aiSi-i — CiVi-u Vi = &iS-b wt- = diSi-\ — с,-и<_1. A7)
Тем самым неизвестное yt-i исключено из i-ro уравнения. Пожалуй,
самой существенной деталью алгоритма является последующая
нормировка величин Si, vu щ:
Если 5i_i' =: 0, то указанным преобразованием нельзя исключить yt-i
из i-ro уравнения. Формальное выполнение операций A7), A8) дает
st = —p*_i, Vi = 0, Ui == —Mf-i
и соответствует замене г-ro уравнения системы A) уравнением A6) (с
точностью до множителя —-1).
В целом первый этап алгоритма состоит в следующем: полагая sQ =
вя 1, v0 = щ = 0, по формулам A7), A8) вычисляем коэффициенты $,-, uiy

§ 2. МЕТОД ПРОГОНКИ 341
т, i = 1, ..., N. В результате имеем уравнения
= uu i = 1, ..., ЛГ — 1,
A9)
= uN.
Если система A) певырождена, то преобразование ее к виду A9)
осуществимо. Чтобы убедиться в этом, достаточно заметить, что в
формулах A8) 7i и щ не могут одновременно обратиться в нуль, ибо это означало
бы линейную зависимость первых г строк матрицы и как следствие
вырожденность системы A).
Второй этап алгоритма заключается в аналогичных преобразованиях,
по выполняемых, начиная с последнего уравнения системы A). В
результате получаем
**!/*_! + »*Уг = <> * = 2 ЛГ, B0)
где коэффициенты s*t v*t uf вычисляются по формулам
Третий этап алгоритма. В результате первых двух этапов получены
уравнения A9), B0). Составим из них пары
s*i+l'Ji
f = 1,3, ...,2|—2~ +1.
B2)
(Здесь [ ] — символ целой части числа.) При нечетном N последняя
группа состоит из одного уравнения sNyn = wjv.
Система B2) невырождена. Действительно, ее уравнения получены
в результате линейной комбинации соответственно первых i уравнении
и последних N — i уравнений системы A). Поэтому равенство нулю
определителя системы B2) означало бы линейную зависимость строк матрицы
системы A), что противоречит предположению об ее невырожденности.
Каждая из систем B2) определяет пару неизвестных у^ yi+{. Всего
необходимо решить —2— +1 таких систем.
Для реализации алгоритма универсальной прогонки необходимо
выполнить не более 267V арифметических операций, в том числе 6N сложений,
13W умножений, IN делений.
При решении систем, отличающихся лишь правыми частями,
целесообразно в формулах A8), B1) положить
Яг = max { | 7. |, |^ | }, q\ = max {\~s* |, p* |}.
В этом случае объем операций, необходимых для решения каждой
из систем, может быть снижен до 8iV.

342
ДОБАВЛЕНИЯ
Алгоритм устойчив по отношению к накоплению вычислительных
погрешностей. Это достигается за счет нормировки прогоночных
коэффициентов A8), B1) так, что все они оказываются не больше единицы.
§ 3. Алгоритмы решения систем уравнений
с пятидиагональными матрицами
1. Вначале рассмотрим алгоритм для решения систем с симметричными
положительно определенными матрицами
Лу = g, A>
или
Ьо с00 ... О
Ъ1 п2
... О
CN-1 bN
О cN
О О
сл_х 0 0 0 ... bN_2 aN^ bN_x
Jn
cN 0 0 ... cN_2
-1 aN ^JV _ _^iV _
el
Sn-i
B)
Известно [7, с. 55], что матрица А представима в виде
А = UWUT, C>
где U — нижняя треугольная матрица, a W — диагональная матрица с
диагональными элементами, отличными от нуля.
Пусть в системе B) bN =cN = cN~v = 0. Будем искать матрицы С/, W
в виде

ил 1 О
vo их i
О
W=~-
О
Сравнивая левую и правую части в C), получаем рекуррентные формулы
для коэффициентов щ, и и u>i-
Wi = di — Уг-2Сг~2 — Kf —l^i —1*»
Ui = Si/Wi, Vi = Ci/Wi,
i = 0, 1, ..., N,
u-l = w-l === сЛГ-1 =
где с
значая
C-2 = У-1 = ^-
гапишем A) в виде
WUTy = z,
Uz = g.
= bN = 0. Обо-
E)
Отсюда находим неизвестные Zii
.., N.
G)

§ 3. АЛГОРИТМЫ РЕШЕНИЯ
343
Здесь формально введены неизвестные z_b z_2. Теперь из E) вычисляем
(формально введены yN+u J/N+2)
yi
Uiyi+i —
, i = N9 ..., 0.
Общее количество арифметических операций, необходимое для реше-
лия исходной системы, равно 177V: из них IN сложений, IN умножений,
3N делений.
Перейдем к случаю, когда в системе B) хотя бы один из элементов
<?л-_1, bN, cN отличеп от нуля. Снова используем разложепие C), но на
этот раз матрицу U будем искать в виде
о
vQ
0
0
0
ро
1
ui
vi
0
0
1
U2
0
0
P2
1
0
0
рз
lN-b
~3 PN-2
По формулам D) вычисляем wu и», uit i = 0, ..., N — 2. Далее
находим
N-2
N-2
WN-1 = aiV-l -
WN = aN -
4
"^Г» i = 0, 1, ...,7V —2,
По формулам G) определяем z*, г = 0, ...,
JV-2
^ — 2. Кроме того,
JV-1
i=0

344
ДОБАВЛЕНИЯ
Наконец, из системы E) находим неизвестные у*:
yN = zN/wN, y^-i = zn-i/wn-i — 9n-iVn>
УХ-Т, = ziV-2 /wN-2 — PN^N^l — Vn-2Vn>
^JV-3 = zN-JWN-b ~ wiV-3^iV-2 — PN-3VN-1 — ?iV-
* = # — 4, ... f 0.
Общее число арифметических операций равно 39W: 17iV сложений,
умножений, 5N делений.
2. Рассмотрим систему
Л 60 С0
0
аз ьз с»
О
tN-2
*iV-l аЛГ-1 "iV-1 °1Ч
Уз
. (8)
Для ее решения можно использовать метод немонотонной прогонки.
Алгоритм строится аналогично случаю системы с трехдиагональной матрицей.
Приведем расчетные формулы алгоритма. Знак ( = ) в пих означает
операцию присвоения.
Положим Н = а0, В = &о, D = go, с = du Е = av, F = gu Q = е2, R =
= ^2, « =* g2, L = 0, T = e3, ^ = ?з, P-i == 0, 7_, = 1, bN = cjV = Cjv-i ==
= 0, at = д* = rfi = e<= gi = 0, i = iV -f 1, W + 2, iV + 3, iV +- 4.
Последовательно для i == 0, 1, ..., iV вычисляем прогоночные
коэффициенты Ui, Vi, u?i и индексы oti, Pi, ^ff. При этом в зависимости от
соотношений между расчетными величинами на (i + 1)-м шаге выполняется одна
из трех групп операций:
а) если |#| ^ \В\ и \Н\ > |cf|, то
щ = -В/Я,
r л Т -
¦L — U, i -
V = г + 2,
D = F— Wi
S = K—
К =

§ 3. АЛГОРИТМЫ РЕШЕНИЯ
б) если \В\ > |#| и \В\ ^ |с<|, то
345
<Xi = ft'-h Рг =
С = Q +mR, Е =
Q = L + тТ, R =
L = О, Г -
в) если |е<| > \Н\ и |сг| >
Bi = -H/cu vi =
ViT4
4i = i +
D = F —
|, то
-В/а,
Я = с +
С = ^ + Uidi + 2,
Е
R
Т
R + Угаг+2,
Теперь, полагая
мулам
Wi = Dlcu
Ъ = Чг-1,
D = F—\
F = S— i
К = gi+4 —
О, вычисляем неизвестные
lvi + wit i = N,...,0.
по
форОбъем арифметических операций, необходимых для решения системы
(8), не превышает 3(W: 1Ш умножепий, 137V сложений, ЗЛ^ делений.
Если система (8) имеет диагональное преобладание, то в описанном
алгоритме на каждом шаге выполняется только группа операций а).
В этом случае достаточно 19iV операций: SN сложений, 8N умножений,
ЗА7 делений.
Литература к добавлениям., [2, 6, 7, 9, 12, 15, 21, 25, 87].

ЛИТЕРАТУРА
Учебники, монографии и отдельные выпуски
1. АлбергДж., Нильсон Эм Уолш Дж. Теория сплайнов и ее
приложения.— М.: Мир, 1972.
2. Блхвалов II. С. Численные методы, т. I.— M.: Наука, 1973.
3. Б е р е з и и И. С, Жидков Н. П. Методы вычислений, т. L— М.:
Наука, 1966.
4. В а р г а Р. Функциональный анализ и теория аппроксимации в чис-
лепном анализе.— М.: Мир, 1974.
- 5. В а с и л е н к о В. А. Теория сплайн-функций.— Новосибирск: НГУ, 1978.
¦'6. Воеводин В. В. Вычислительные основы линейной алгебры.— М.:
Наука, 1977.
7. Г а н т м а х е р Ф. Р. Теория матриц.— М.: Наука, 1966.
8. Жидков Н. П. Линейные аппроксимации функционалов.—М.: Изд-во
МГУ, 1977.
9. К о л л а т ц Л. Функциональный анализ и вычислительная
математика.— М.: Мир, 1969.
10. Лоран П.-Ж. Аппроксимация и оптимизация.— М.: Мир, 1975.
11. М арчу к Г. И. Методы вычислительной математики.—М.: Наука, 1977.
12. Методы сплайн-функций (Вычислительные системы, 65)/Ред. 10. С.
Завьялов.— Новосибирск: Ин-т математики СО АН СССР, 1975.
13. Методы сплайн-функций (Вычислительные системы, 68)/Ред.
Ю. С. Завьялов.— Новосибирск: Ин-т математики СО АН СССР. 1976.
14. Методы сплайн-функций (Вычислительные системы, 72)/Ред.
Ю. С. Завьялов. В. Л. Мирошниченко.— Новосибирск: Ин-т математики
СО АН СССР, 1977.
15. Методы сплайн-функций (Вычислительны^ системы, 75)/Ред.
Ю. С. Завьялов, А. Имамов.— Новосибирск: Ин-т математики СО АН
СССР, 1978.
15*. Методы сплайн-функций (Вычислительные системы, 81)/Ред.
Ю. С. Завьялов.— Новосибирск: Ип-т математики СО АН СССР, 1979.
16. М и х л и н С. Г. Вариационные методы в математической физике.— М.:
Наука, 1970.
17. Никол ьс кий С. М. Курс математического анализа, т. I, т. II.—
М.: Наука, 1973.
18. Н и к о л ь с к и й СМ. Квадратурные формулы.— М.: Наука, 1974.
19. Р е м е з Е. Я. Основы численных методов чебышевского
приближения.— Киев, Наукова думка, 1969.
20. Самарский А. А. Теория разностных схем.—М.: Наука, 1977.
21. Самарский А. А., Николаев Е. С. Методы решения сеточных
уравнений.— М.: Наука, 1978.
22. Соболев С. Л. Введение в теорию кубатурных формул.— М.: Наукаг
1974.
23. С т е ч к и н С. Б., Субботин Ю. II. Сплайны в вычислительной
математике.— М.: Наука, 1976.
24. Стренг Г., Фикс Д ж. Теория метода конечных элементов.—М.:
Мир, 1977.
25. Уилкинсон Дж., Райнш К. Справочник алгоритмов па языке
АЛГОЛ. Линейная алгебра.— М.: Машиностроение, 1976.

ЛИТЕРАТУРА 347
26. В б h m е г К. Spline-Funktionen. Theorie und Anwendungen.— Stuttgart:
ТеиЪпег Studienbiicher. Mathematik, 1974.
27. P r e n t e r P. H. Splines and variational methods.— New York: Wiley, 1974.
28. V a n R о о j P. L. J., S с h и г е г F. A bibliography on spline
functions, II.—Natherlands, Technological University Eindhoven, Department
of Mathematics, Т. Н. Report, 73-WSK-01, 1973.
29. Schultz M. H. Spline analysis.—Englewood Cliffs, N. Y.: Prentice-
Hall, 1973.
30. S p a t h H. Spline-Algorithmen zur Konstruction glatter Kurven und Fla-
chen.— Munchen — Wien: R. Oldenburg Verl., 1973.
Статьи
31. Бело носов А. С, Цецохо В. А. Вычислительный алгоритм и
процедуры сглаживания функций, заданных приближенно в узлах
нерегулярной сетки па плоскости.— В кн.: Некорректные задачи
математической физики и проблемы интерпретации геофизических наблюдений,
Новосибирск, ВЦ СО АН СССР, 1977, с. 6—29.
32. Василенко В. А. Аппроксимация сплайн-фупкциями в весовом
пространстве Соболева.— В кн.: Дифференциальные и интегродифферен-
циальные уравнения. Труды семинара «Методы вычислительной и
прикладной математики» под рук. Г. И. Марчука, I, Новосибирск, ВЦ СО
АН СССР, 1977, с. 120-126.
33. Великий В. Л. Точные значения приближения эрмитовыми
сплайнами на классах дифференцируемых функций,— Изв. АН СССР, сер. ма-
тем., 1973, 37, № 1, с. 165—185.
34. Ж е и с ы к б а е в А. А. Наилучшая квадратурная формула для
некоторых классов периодических дифференцируемых функций.— ДАН
СССР, 1976, 227, № 2, с. 277—279.
35. Ж е н с ы к б а е в А. А. О наилучших квадратурных формулах для
некоторых классов непериодических функций.— Изв. АН СССР, сер. ма-
тем., 1977, 41, № 6, с. 1110—1125.
36. Завьялов 10. С. Интерполирование функций одной и двух
переменных кусочно-полиномиальными функциями.— В кн.:
Математические проблемы геофизики, I, Новосибирск, ВЦ СО АН СССР, 1969,
с. 125—141.
37. 3 а в ь я л о в 10. С. Интерполирование кубическими многозвепииками
(сплайнами).— В кн.: Вычислительные системы, 38, Новосибирск, Ин-т
математики СО АН СССР, 1977, с. 23—73.
38. 3 а в ь я л о в Ю. С. Интерполирование бикубическими
многозвепииками (сплайнами).— В кн.: Вычислительные системы, 38, Новосибирск,
Ин-т математики СО АН СССР, 1970, с. 74—101.
39. Завьялов Ю. С. Экстремальное свойство кубических мпогозвеыпиков
(сплайнов) и задача сглаживания.— В кн.: Вычислительные системы,
42, Новосибирск, Ии-т математики СО АИ СССР, 1970, с. 89—108.
40. 3 а в ь я л о в Ю. С. ?-сплайп-функции многих переменных.— ДАН
СССР, 1974, 214, № 6, с. 1247—1249.
41. Завьялов Ю. С. Экстремальные свойства сплайн-функций многих
переменных.— В кн.: Теория приближения функций. Труды
Международ, коиф. по теории приближения функций. Калуга, 24—28 июля 1975,
М., Наука, 1977, с. 182-187.
42. Завьялов Ю. С, Имамов А. Алгоритм с расщеплепием решения
задачи елгаживания сплайн-функциями многих переменных.— Числ.
методы механики сплошной среды, 1976, 7, № 6, с. 52—61.
43. Завьялов Ю. С, Имамов А. О вариационных задачах теории
сплайнов.— В кн.: Математический анализ и смежные вопросы математики,
Новосибирск, Наука, СО, 1978, с. 27—36.

348 ЛИТЕРАТУРА
44. 3 м а т р а к о в Н. Л. Сходимость интерполяционного процесса для
параболических и кубических сплайнов,— Труды МИ АН СССР, 1975, 138,
с. 71—93.
45. Ильин В. П. О онлайновых решения обыкновенных
дифференциальных уравнений.— ЖВМиМФ, 1978, 18, № 3, с 620—627.
46. Ильин И. А., Лукьянов А. Т. Применение кубических сплайнов
к решению второй краевой задачи для уравнения теплопроводности с
разрывным коэффициентом.— Числ. методы механики сплошной среды,
1976, 7, № 1, с. 62-71.
47. К в а с о в Б. И. О построении ^-сплайнов.— Числ. методы механики
сплошной среды, 1972, 3, № 3, с. 64—71. . -
48. Квасов Б. И. Получение сплайнов осреднепием кусочно-постоянных
функций. Сплайны с дополнительными узлами.— Числ. методы
механики сплошной среды, 1973, 4, № 1, с. 39—55.
49. Квасов Б. И. Об итерационном методе построения сплайнов.— В кн.:
Вариационно-разностные методы в математической физике,
Новосибирск, ВЦ СО АН СССР, 1974, с. 107—115.
50. Квасов Б. И. Сплайн-решения смешанной задачи Лагранжа — Эрми-
та.— Числ. методы механики сплошной среды, 1977, 8, № 1, с. 59—82.
51. Квасов Б. И., К о б к о в В. В. Некоторые свойства кубических
эрмитовых сплайнов с дополнительными узлами.— ДАН СССР, 1974, 217,
№ 5, с. 1007—1010.
52. Квасов Б. И., К о б к о в В. В. Сплайны с дополнительными узлахми,
II. Их пределы и некоторые свойства. —Числ. методы механики
сплошной среды, 1974, 5, № 4, с. 48—70.
53. К о б к о в В. В. О сходимости кубических сплайнов с
дополнительными узлами.— В кн.: Численный анализ, Новосибирск, Ии-т теор. и
приклад, механики СО АН СССР, 1978, с. 60—74.
54. Л е у с В. А. Гладкая окружностпая интерполяция кривых.— В кн.:
Вычислительные системы, 38, Новосибирск, Ин-т математики СО АН СССР,
с. 102-127.
55. М и р о ш н и ч е п к о В. Л. Решение краевой задачи для
дифференциального уравнепия второго порядка с запаздывающим аргументом
методом сплайн-функций.— Изв. АН Каз. ССР, сер. физ.-мат., 1972, № 5,
с. 46-50.
56. Мирошниченко В. Л. Об интерполировании кубическими
сплайнами.— В кн.: Вычислительные системы, 56, Новосибирск, Ин-т
математики СО АН СССР, 1973, с. 18-22.
57. Мирошниченко В. Л. Решепие краевой задачи для дифферепциаль-
ного уравнепия второго порядка с запаздывающим аргументом
методом сплайн-функций. Схема повышенной точное!и.— Изв. АН Каз. ССР,
сер. физ.-мат., 1973, № 3, с. 37—42.
58. Мороз о*в В. А. Теория сплайнов и задача устойчивого вычисления
значений неограниченного оператора.—ЖВМиМФ, 1971, 11, № 3,
с. 545-548.
59. П е т е р с е и И. О кусочно-полиномиальной аппроксимации.— Изв. АН
Эст. ССР, сер. физ.-мат., и техн., 1962, I.
60. Рябенький В. С. Локальные формулы гладкого восполнения и
гладкой интерполяции функций по их значениям в узлах неравномерной
прямоугольной сетки.— М.: Ин-т прикладной математики АН СССР,
Препринт № 21, 1974.
61. С л е п ц о в А. Г. Сходимость метода локальной коллокации для
обыкновенных дифференциальных уравнений.— ЖВМиМФ, 1975, 15, № 6,
с. 1447—1456.
62. Филатов В. В. О чебышевском приближении кубическими сплайпа-
ми.— в кн.: Вычислительные системы, 56, Новосибирск, Ин-т
математики СО АН СССР, 1973, с. 23—26.

ЛИТЕРАТУРА 349
63. Ш е п е л е п к о В. Н. Использование сплайнов для приближеппого
вычисления интегралов с особенностью и решения трансцендентных
уравнений,— Числ. методы механики сплошной среды, 1973, 4, № 5, с. 125.
64. Я и е н к о Н. Н., Квасов Б. И. Итерационный метод построения
поликубических сплайн-функций.—ДАН СССР, 1970, 195, с. 1D55—1057.
65. Я н е н к о Н. Н., К в а с о в Б. И. Итерационный метод построения
поликубических сплайн-функций.— Числ. методы механики сплошной
среды, 1970, 1, № 3, с. 84—89.
66. A h I b е г g J. H., Ito T. A collocation method for two-point boundary
value problems.— Math, of Comput., 1975, 29, № 131, p. 761—776.
67. Akima H. A. New method of interpolation and smooth curve fitting-
based on local procedure.— J. ACM, 1970, 19, № 4, p. 589—602.
68. A 1 b a s i n у E. L., H о s k i n s W. D. Cubic spline solutions to two-point
boundary value problems.— Computer J., 1969, 12, № 2, p. 151—153.
69. Arthur D. W. Multivariate spline functions.—J. Approxim. Theory,
1974, 12, № 3, p. 396-411.
70. Birkhoff G., Priver A. Hermite interpolation error for
derivatives — J. Math. Physics, 1967, 46, p. 440—447.
71. Birkhoff G., Schultz M. H., Varga R. S., Piecewise Hermite
interpolation in one and two variables with applications to partial
differential equations.— Numer. Math., 1968, 11, № 3, p. 232—256.
72. De Boor C. Bicubic spline interpolation.—J. Math. Phys., 1962, 41,
p. 212—218.
73. D e Boor C. On uniform approximation by splines.— J. Approxim. Tim
ory, 1968, 1, № 3, 219—235.
74. D e Boor C. On calculation with 5-splines.— J. Approxim. Theory, 1972,
6, № 1 p. 50—62.
75. D e Boor C. Splines as linear combinations of 5-spIines.— In:
Approximation Theory, II, ed. G. G. Lorentz. New Jork, Acad. Press, 1976, p. 1—47.
76. D e Boor C. Packade for calculating with Z?-splines.— SJAM J. on Nu-
nier. Anal., 1977, 14, № 3, p. 441—472.
77. D e Boor- C, Fix G. J. Spline approximation by quasiinterpolants.—
J. Approxim. Theory, 1973, 8, № 1, p. 19—45.
78. D e Boor C, S w a r t z В., Collocation at Gaussian points.— SIAM J.
. on Numer. Anal, 1973, 10, № 4, p. 582—606.
79. Boh m W. Cubic Z?-spline curves and surfaces in computer aidid
geometric design.— Computing, 1977, 19, № 1, p. 29—34.
80. В г а е s s D. Chebyshev approximation by spline functions with free
knots.— Numer. Math., 1971, 17, № 3, p. 357—366.
81. В u с k R. С Alternation theorems for functions of several variables.—
J. Approxim. Theory, 1968, 1, № 3. p. 325—334.
82. С a r 1 s о n R. E., Hall C. A. Bicubic spline interpolation in L-shaped
domains.— J. Approxim. Theory, 1973, 8, № 1, p. 62—68.
83. С ar 1 sо n R. E., Hall C. O., "Error bounds for bicubic spline
interpolation.—J. Approxim. Theory, 1973, 7, № 1, p. 41—47.
84. С i a r 1 e t P. G., R a v i a r t P. A. General Lagrange and Hermite
interpolation in Rn with application to finite element methods.— Arch. Rat.
Mech. Anal., 1972, 46, № 2, p. 177—199.
85. С 1 e n s h a w С W., Negus B. The cubic X-spline and its application
to interpolation.— J. Institute of Math. Applies, 1978, 22, № 1, p. 109—119.
86. С u г г у Н. В., Schoenberg I. J. On J^olya freguency functions, IV. The
fundamental splines functions and their limits.—J. Anal. Math., 1966, 17r
№ 1, p. 71—107.
87. D e m к о S., Inverses of hand matrices and local convergence of spline
projections.— SIAM J. on Numer. Anal, 1977, 14, № 4, p. 616—619.
88. Epstein M. P. On the influence of parametrization in parametric
interpolation.— SIAM J. on Numer. Anal., 1976, 13, № 2, p. 261—268.

350 ЛИТЕРАТУРА
89. Hall С. A., Meyer W. W. Optimal error bounds for cubic spline
interpolation.— J. Approxim. Theory, 1976, 16, № 2, p. 105—121.
90. H о u s t i s E. N. Collocation methods for linear elliptic problems.— BIT,
1978, 18, № 3, p. 301—310.
91. Lyche T. Discrete cubic spline interpolation.—BIT, 1976, 16, № 3,
p. 281—290.
U2. L у с h Т., S с h u m а к e r L. L. Local spline approximation methods.—
J. Approxim. Theory, 1975, 15, № 4, p. 294—325.
D3. L u с a s T. Error bounds for interpolating cubic splines under various
end conditions.—SIAM J. on Numer. Anal., 1974, 11, № 3, p. 569—584.
94. M a n s f i e 1 d L. On the variational approach to defining splines on
L-shaped regions.—J. Approxim. Theory, 1974, 12, p. 99—112.
95. M a r s d e n M. Cubic spline interpolation of continuous functions.— J.
Approxim. Theory, 1974, 10, № 2, p. 103—111.
96. M-cLain D. H. Two-dimensional interpolation from random
data.—Computer J., 1976, 19, № 2, p. 178—181.
97. Runge C. Uber empirische Funktionen und die Interpolation zwischen
aquidistanten Ordinaten.— Z. Math. Phys., 1901, 46, s. 224—243.
98. S с h о e n b e r g I. J. Contributions to the problem of approximation of
equidistant data by analytic functions.— Quart. Appl. Math., 1946, 4, p. 45—
99, 112-141. -
99. S с h e e n b e r g I. J. Spline functions and the problem of graduation.—
Pfoc. Natl. Acad. Sci. U. S., 1964, 52, № 4, p. 947—950.
400. Schoenberg I. J, On cardinal monosplines of least Loo-norm on the
real axis.— J. Anal. Math., 1970, 23, p. 409—436.
401. Schoenberg I. J., Whitney A. On Polya frequency functions, III.
The positivity of translation determinants with an application to the
interpolation problem by spline curves.—Trans. Amer. Math. Soc, 1953,
74, p. 246—259.
102. Schoenberg I. J., Ziegler Z. On cardinal monosplines of least
Лоо-norm on the real axis.—J. d'analyse Mathematique, 1970, 23, pp.409—
436.

Страница
23
52
56
57
57
73
94
99
118
119
148
109
173
174
176
185 ;
202
210
259
262
266
314
320
329
331
340
344
Строка
14 св.
1 св.
13 сн.
3 св.
И св.
6 св.
9 св.
18 сн.
1 сн.
1 сн.
7 сн.
18 сн.
12 сп.
17 сн.
Табл.
4 св.
7 св.
i6 св.
4 си.
13 п
15 св.
Табл.
1 св.
6 св.
1 сн.
5 св.
14 сн.
5 сн.
СПИСОК
ОПЕЧАТОК
Напечатано
= | . . . |
,*211...И
6W2A,oo [Q]
[Я'.2/( )
S*(x)
xi
j
X
типа I
-* -*
.A + ЦЛГ-2)
(*o+J
II/1 V II со
(ai> <V щ
Ф2(а,, а2)
Dr**S (хь у.)
A' = 1/6
0,
)
Следует читать
0=1... I
А*-,
/211 ... II -
Г^1 °/( )
х2
J
ТС
A)
A+ЦЛГ-1)
(л-о+)+2
II/1 v II с
\
1 г 2> 2а у
Ф2(а,, а0
Исключить колонку /?3
ЛГ0Д - 1/6
k ^ 1/27/2
11
В заголовке поменять местами ^ и га
A3)
(еЛ-_2 — eN)
C)
A4)
B<?лг-2--*л)
Ц...|12
A)

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Аппроксимация"локальная 243
Асимптотически наилучшее
приближение равномерное 279
Интерполяционная формула Лаг-
ранжа для сплайнов 29
двух переменных 39
Интерполяция с заданной
точностью 50
Квазкинтерполяция 281
Квазинаилучшее приближение
равномерное 279
среднеквадратичное 279
Классы функций 42
двух переменных 55
Колебание функции 42
двух переменных 55
Конечный элемепт 314
Краевые условия для кубических
сплайнов 96
Матрица ленточная 335
— монотонного вида 334
• — с диагональным преобладанием
333
— хорошо обусловленная 336
Мера (число) обусловленности
матрицы 336
Метод Галеркина 313
— конечных элементов 309
— прогонки 337
немонотонной 339
универсальной 340
— сплапн-коллокации 284
Модуль непрерывности 42
Моиосплайи 267
—, паимепее уклоняющийся от
нуля 269
Неравенство Гельдера 44
Остаточный член аппроксимации 42
Параметризация по суммарной
длине хорд 212
нормированная 212
Представление сплайна в виде
суммы усеченных степенных
функций 18, 37
через 5-сплайны 22, 38
Пространство Соболева 310
— сплайнов 16
двух переменных 37
— энергетическое 311
Процесс Ритца 312
Сплайп, сплайн-функция 10
— базисный с конечным носителем
минимальной длины 22
— двух переменных 36
— интерполяционный 26
— кубический 96
¦ дискретный 198
¦ интерполяционный 96
¦ двух переменных 131
нелокальный класса С1 193
параметрический 215
сглаживающий 149
¦ двух переменных 163
с дополнительными узламвг
170
двух переменных 184
¦ локальный 165
с разрывными производными*
204
эрмитов (дефекта 2) 58
двух переменных 75
параметрический 211
— локальный 41
— параметрический 207
— первой степени 41
двух переменных 54
на нерегулярной сетке 87
— периодический на сетке 264
— рациональный 187
параметрический 219
— с дополнительными узлами 16S

352
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Сплайн степени п дефекта v 15
— фундаментальный 28
сглаживающий 162
— частичный 76
— эрмитов нечетной степени 81
Сходимость интерполяционного
процесса 49
с порядком 7 49
Тензорное произведение
конечномерных пространств 37
Теорема о среднем для интегралов
43
непрерывной функции 42
Триангуляция 87
Формула локальной аппроксимации
253
—: точная на кубических
многочленах 250
МНогочленах первой
степени 245
— сглаживающая 245
— Тейлора 43 , 44
Функция квазиэкстремальная 46
— усеченная степенная 16
— финитная 18
— экстремальная 46
Экстремальное свойство кубических
сплайнов 147
двух переменных 157
Узлы коллокации 285
оптимальные 297
— сплайна 15
Я-сплайн 22
— кубический 141
— нормализованный 23
L-сплайн 11