Текст
Б.Н.ОКУНЕВ
ВРАЩАТЕЛЬНОЕ
ДВИЖЕНИЕ
АРТИЛЛЕРИЙСКОГО
СНАРЯДА
огиз
ГОСТЕХИЗДАТ
IQ-43
Проф. Б. Н. ОКУНЕВ
ВРАЩАТЕЛЬНОЕ
ДВИЖЕНИЕ
АРТИЛЛЕРИЙСКОГО
СНАРЯДА
О Г ИЗ
ГОСУДАРСТВЕННОЕ ИЗДАТЕЛЬСТВО
ТЕХНИКО-ТЕОРЕТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА 1943 ЛЕНИНГРАД
ПРЕДИСЛОВИЕ
При изучении движения современного артиллерийского снаряда
особого внимания заслуживает вопрос о правильности полета снаряда,
от которой в очень большой степени зависит дальность полета,
кучность, правильное функционирование трубок и взрывателей и це¬
лый ряд других явлений. В свою очередь, правильность полета тесно
связана с вращательным движением снаряда около его оси симметрии,
причем это вращательное движение сообщается снаряду именно для
того, чтобы обеспечить правильность полета.
Поэтому как при стрельбе артиллерийскими снарядами, так и при
их проектировании и производстве необходимо иметь ясное и отчет¬
ливое представление о физической картине явлений, происходящих
при вращательном движении артиллерийских снарядов. С другой
стороны, и строевой артиллерист, и конструктор, и производствен¬
ник должны твердо знать, как изменение тех или других^ характе¬
ристик снаряда или условий стрельбы может отразиться на правиль¬
ности полета снарядов, а следовательно, и на эффективности их
действия.
Настоящая книга имеет целью дать представление о главнейших
явлениях, связанных с вращательным движением снаряда под углом
зрения правильности его полета.
Предназначена книга для строевого и инженерно-технического
начальствующего состава Красной Армии и Военно-Морского Флота,
для инженерно-технических и научных работников оборонной про¬
мышленности, для профессорско-преподавательского состава и сту¬
дентов высших технических учебных заведений.
В настоящей книге, как и во всех книгах, написанных мною,
принята десятичная система рубрикации.
Борис Окунеа
Март 1942 г.
Ленинград
1*
3
ОГЛАВЛЕНИЕ
0. Силы, действующие на вращающийся снаряд, движущийся
в воздухе ^ . у
00. Положение оси снаряда относительно касательной к траектории
его центра инерции 7
01. Силы, зависящие от положения оси снаряда относительно
касательной к траектории 9
02. Силы, зависящие от движения оси снаряда и от вращательного
движения снаряда около оси 14
03. Зависимость опрокидыгающего момента сопротивления возду¬
ха от скорости снаряда 16
1. Вращательное движение снаряда около его центра инерции
под действием одного опрокидывающего момента при рав¬
номерном прямолинейном и горизонтальном движении
центра инерции • 22
10. Основные допущения и определения 22
11. Кинетическая энергия снаряда . 26
12. Уравнения вращательного движения снаряда около его центра
инерции 28
13. Исследование уравнения нутации 32
14. Условие гироскопической устойчивости снаряда 34
15. Коэффициент гироскопической устойчивости снаряда 37
2. Вращательное движение послушного снаряда под действием
одного опрокидывающего момента при равномерном пря¬
молинейном и горизонтальном движении центра инерции. 43
20. Основные допущения и определения 43
21. Кинетическая энергия снаряда 47
22. Уравнения вращательного движения снаряда около его центра
инерции 49
23. Интегрирование уравнений движения оси снаряда 51
24. Определение постоянных интегрирования 53
25. Исследование уравнений движения оси снаряда 55
26. Движение оси снаряда при отсутствии начального угла откло¬
нения и ударов в момент вылета . 62
27. Движение оси снаряда при отсутствии начального угла откло¬
нения, но при наличии ударов в момент вылета ....... 63
28. Движение оси снаряда при наличии начального угла отклоне¬
ния, но при отсутствии ударов в момент вылета бб
29. Наибольшая угловая скорость оси снаряда на начальном участке
траектории 69
3. Вращательное движение послушного снаряда под действием
одного опрокидывающего момента при прямолинейном го¬
ризонтальном, но неравномерном движении центра инерции 72
30. Основные допущения 72
31. Уравнения вращательного движения снаряда около его центра
масс и приближенный метод их интегрирования 72
32. Уравнения движения оси снаряда 75
33. Исследование уравнений движения оси снаряда 80
34. Движение оси снаряда при отсутствии начального угла откло¬
нения и ударов в момент вылета 84
35. Движение оси снаряда при отсутствии начального угла откло¬
нения, но при наличии ударов в момент вылета 85
36. Движение оси снаряда при наличии начального угла отклоне¬
ния, но при отсутствии ударов в момент вылета 89
37. Коэффициент гироскопической устойчивости 91
4 Вращательное движение послушного снаряда под действием
одного опрокидывающего момента при криволинейном дви¬
жении центра инерции в плоскости бросания 92
40 Основные допущения и определения 92
41 Уравнения вращательного движения снаряда около его центра
инерции 97
42. Общий интеграл уравнения без последнего члена ...... 99
43. Частный интеграл полного дифференциального уравнения . . 100
44. Общий интеграл полного дифференциального уравнения . . « 104
45. Исследование уравнений движения оси снаряда 107
46. Положение динамической оси 112
47. Движение оси снаряда при отсутствии начального угла отклоне¬
ния и ударов в момент вылета , . 115
48. Коэффициент гироскопической устойчивости 119
49. Понятие о положении динамической оси при не малых углах
отклонения * 120
5. Гироскопическая устойчивость и правильность полета
артиллерийских снарядов ► » * . ... 122
50. Гироскопическая устойчивость и правильность полета артил¬
лерийского снаряда .......... .... 122
51. Правильность полета артиллерийского снаряда на начальном
участке траектории 130
S
51. Определение наименьшего значения коэффициента гироскопи¬
ческой устойчивости артиллерийского снаряда при стрельбе
из данного орудия 132
52. Определение наибольшей допустимой длины хода нарезов,
обеспечивающей артиллерийскому снаряду правильность пол-
лета на начальном участке траектории 137
51. Правильность полета артиллерийского снаряда у вершины
траектории 139
51. Определение положения динамической оси в вершине траекто¬
рии 141
51. Определение наибольшего допустимого значения динамическо¬
го угла в вершине траектории 146
51. Обеспечение правильности полета артиллерийского снаряда на
всем протяжении траектории 147
51. Движение центра инерции послушного снаряда под дейст¬
вием нормальной составляющей силы сопротивления воздуха 153
51. Общая характеристика задачи 153
51. Деривация 154
Вычисление деривации 157
0. СИЛЫ, ДЕЙСТВУЮЩИЕ НА ВРАЩАЮЩИЙСЯ СНАРЯД,
ДВИЖУЩИЙСЯ В ВОЗДУХЕ,
00. Положение оси снаряда относительно касательной
к траектории его центра инерции.
В основной задаче внешней баллистики мы считали, что сила
сопротивления воздуха приложена к центру инерции снаряда и на¬
правлена по касательной к траектории в сторону, противоположную
скорости, т. е., иначе говоря, допускали, что ось симметрии снаряда
все время совпадает с касательной к траектории. В дальнейшем мы
будем называть ось симметрии снаряда главной осью или
просто осью снаряда.
В действительности, как указывают экспериментальные иссле¬
дования, ось снарядД составляет с касательной некоторый угол,
называемый углом отклонения Ь. Этот угол для всех суще¬
ствующих на вооружении снарядов, вообще говоря, может считаться
малым.
Что же касается силы сопротивления воздуха, то линия ее дей¬
ствия не только не совпадает с касательной, но даже не проходит
через центр инерции снаряда. Для существующих артиллерийских
снарядов, на основанцн экспериментальных данных, можно считать,
что точка пересечения силы сопротивления воздуха с осью снаряда
расположена между центром инерции и вершиной снаряда, причем
угол у» составляемый осью снаряда и силой сопротивления воздуха,
по абсолютной величине меньше, чем угол (тт—j $]):
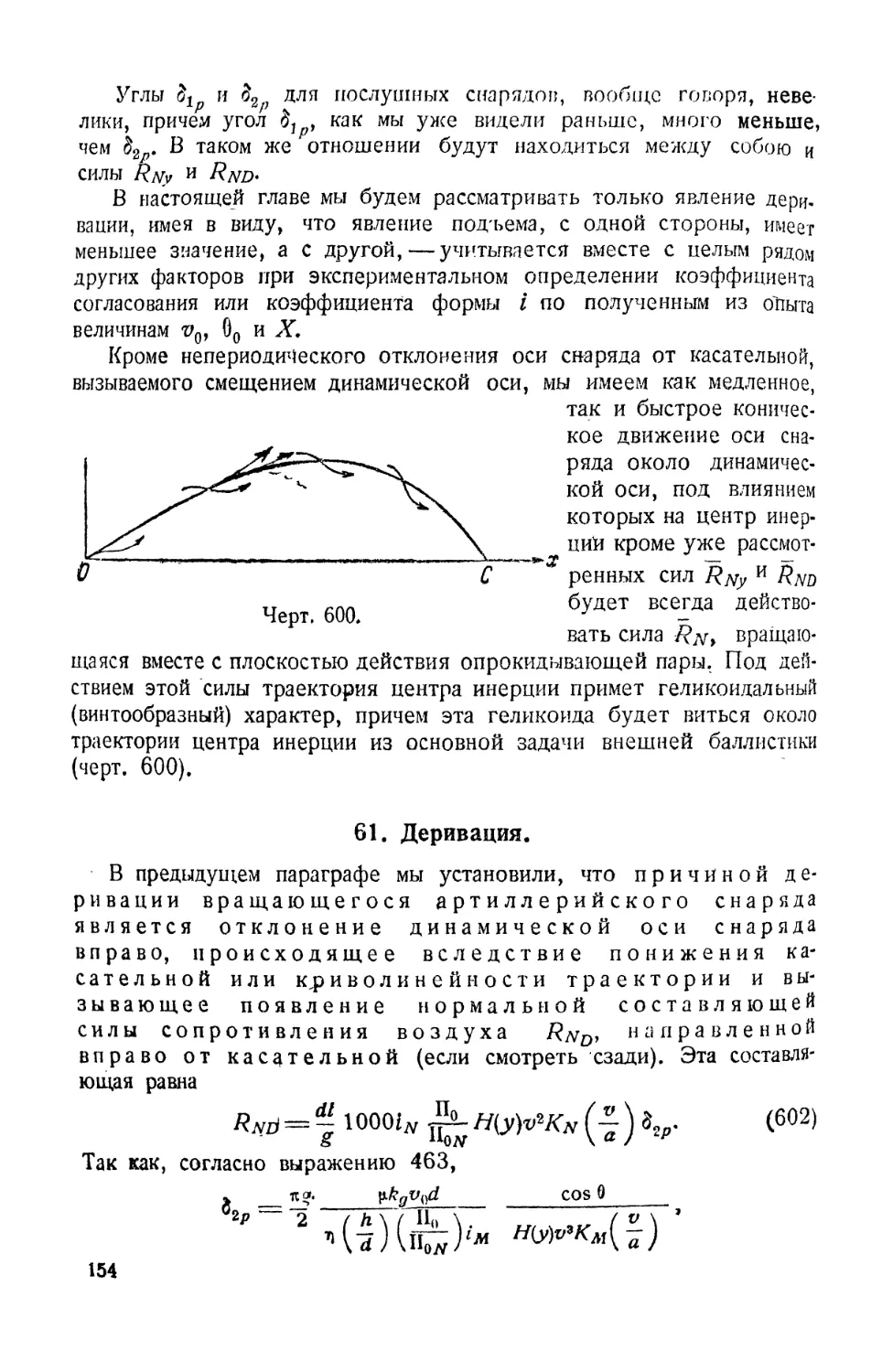
Взаимное расположение оси снаряда, силы сопротивления воз¬
духа R и касательной к траектории центра инерции изображено на
черт. ООО.
Результатом указанного расположения оси снаряда и силы сопро¬
тивления воздуха является стремление силы сопротивления воздуха
не только сообщить некоторое отрицательное ускорение центру
инерции снаряда, но и повернуть снаряд около экваториальной оси,
проходящей через центр инерции, в сторону увеличения угла отклоне¬
ния т. ем иначе говоря, опрокинуть снаряд.
7
Отсюда ясно, что стрельба продолговатыми невращающимися
снарядами совершенно невозможна, так как полет их будет непра¬
вильным, рассеивание очень большим и дальности малыми.
Вот почему для того, чтобы парализовать опрокидывающее дей¬
ствие силы сопротивления воздуха, снаряду сообщают быстрое вра¬
щательное движение около
его оси, так как уже издавна
известно, что тело, быстро
вращающееся около своей оси,
оказывает большое сопро¬
тивление всяким силам, стре¬
мящимся изменить положе¬
ние этой его оси, примером
чего может служить обыкно¬
венный волчок.
Таким образом стрельба
продолговатыми артиллерий¬
скими снарядами в воздухе
может производиться только
в том случае, если им будет
сообщено вращательное дви¬
жение с достаточной угловой
скоростью.
Основными допущения¬
ми, которые мы примем
при изучении вращательного движения снаряда, являются сле¬
дующие:
1) снаряд симметричен относительно своей оси как статически,
так и динамически, т. е. снаряд представляет собою тело вращения,
центральный эллипсоид инерции которого является эллипсоидом враще¬
ния, причем главная ось центрального эллипсоида инерции совпадает
с осью снаряда;
2) сила сопротивления воздуха пересекает ось снаряда, при¬
чем точка пересечения лежит между центром инерции и вершиной
снаряда;
3) сила сопротивления воздуха, ось снаряда и касатель¬
ная к траектории центра инерции расположены в одной плос¬
кости.
Остальные допущения мы будем вводить по мере надобности.
Заметим, что точка пересечения оси снаряда и силы сопротивле¬
ния воздуха называется центром сопротивления воздуха,
а плоскость, в которой расположена сила сопротивления воздуха,
ось снаряда и касательная,■— плоскостью действия силы
сопротивления воздуха или просто плоскостью дей¬
ствия.
Черт. ООО.
8
01. Силы, зависящие от положения оси снаряда относительно
касательной к траектории.
В баллистике материальной точки мы имеем дело с одной силой
лобового сопротивления воздуха R, направленной по касательной к
траектории в сторону, противоположную скорости, и зависящей толь¬
ко от скорости снаряда и плотности воздуха.
В баллистике твердого тела мы будем иметь дело с целой систе¬
мой сил, являющихся следствием сопротивления воздуха и зависящих
от различных факторов: от положения оси снаряда относительно
касательной, от вращательного движения снаряда около его оси, от
движения самой оси снаряда и т. д.
В настоящем параграфе мы остановимся только на главнейших
силах, зависящих от положения оси снаряда относительно касатель*
ной к траектории его цен¬
тра инерции.
Для более удобного
сравнения с баллистикой
материальной точки при¬
ведем при помощи обыч¬
ных механических методов
силу сопротивления возду¬
ха R к центру инерции
снаряда.
Для этой цели приложим к центру инерции снаряда С (черт. 010)
две силы Rt и /?2, равные по величине силе сопротивления воздуха Rt
параллельные ей и направленные противоположно одна другой:
Ri=R‘, R2=—R.
В таком случае сила Rj будет оказывать влияние только на:
движение центра инерции, а пара сил [R, R2) называемая опроки¬
дывающей парой, будет стремиться повернуть снаряд около
экваториальной оси, проходящей через центр инерции. Момент
опрокидывающей пары мы будем называть опрокидывающим
моментом и обозначать через М.
Далее, силу Rr разложим на касательную и нормальную со¬
ставляющие. Касательная составляющая RT в условиях на¬
шей задачи будет играть совершенно такую же роль, какую играла
сила лобового сопротивления воздуха в баллистике материальной
точки. Нормальная составляющая Rh будет стремиться
отклонить центр инерции снаряда от той траектории, которая была
наш определена в основной задаче внешней баллистики, и превра¬
тить таким образом плоскую траекторию центра инерции в кривую
двоякой кривизны.
9
Черт. 010.
Рассмотрим теперь зависимость Rt> Rn и М от величины угла
отклонения 8.
Прежде всего совершенно очевидно, что при 8 — О
В этом случае величина касательной составляющей RT равна
величине полной аэродинамической силы R, а величины нормальной
составляющей RN и опрокидывающего момента М обращаются
в нули.
Далее мы рассмотрим зависимость RT, RN и М от угла Ь для
специального случая, когда углы отклонения Ь в продолжение всего
полета снаряда остаются малыми. Такой полет снаряда называется
правильным полетом; снаряд, обладающий правильностью
полета, мы будем называть послушным снарядом.
Применим для этого случая разложение RT, RN и М в ряд
Маклорена по степеням отклонения Ь:
Отбрасывая в этих выражениях все члены, содержащие вторую
и более высокие степени 8, а также принимая во внимание равенст¬
ва 010, получим
Рассматривая первое из этих равенств с физической стороны, мы
должны обратить внимание на то, что величина касательной соста¬
вляющей RT по своей природе может зависеть только от величины
угла отклонения S, но не может зависеть от его знака, т. е., иначе
говоря, является функцией четной. Следовательно, все коэффициенты
при нечетных степенях 8 в выражении длй* RT равны нулю, И
поэтому
10
т. е. для послушных снарядов величина касательной
составляющей силы сопротивления воздуха не
зависит от угла отклонения 8 и равна величине пол¬
ной силы сопротивления воздуха.
Что же касается RN и Ai, то из полученных выражений следует,
что для послушных снарядов величины нормальной
составляющей RN и опрокидывающего момента М
пропорциональны углу отклонения §.
Исходя из этих основных положений, напишем выражения для
RN и М, построив их аналогично выражению для Rr, в котором
поставим у величин/ и Киндексы ...г для того, чтобы не
смешивать их в дальнейшем с соответственными величинами в вы¬
ражениях Rn и At. Получим
В выражение для RN длина снаряда I введена потому, что нор¬
мальная составляющая будет зависеть от площади продольного сече¬
ния, которую в первом приближении
можно считать пропорциональной про¬
изведению калибра снаряда d на его
длину I.
В выражение опрокидывающего
момента М введена величина h, пред¬
ставляющая собою расстояние между
центром инерции снаряда (С) и центром
сопротивления воздуха (Ц. С.), так
как совершенно естественно, что ве¬
личина М должна быть пропорциональной этому расстоянию.
Для определения величины h у нас чаще всего пользуются фор¬
мулами Морского Полигона:
для снарядов с оживальной головной частью
014
Черт. 011.
для снарядов с конической головной частью
Здесь Aj представляет собою расстояние центра инерции снаряда
от основания оживала, а Н—высоту головной части (черт. 011).
И
Кроме формулы Морского Полигона можно применять очень
простую формулу Бурцио, пользующуюся большим распространением
не только в Италии, но и в других западноевропейских странах.
015
Наконец, нз формул для h можно еще указать на формулы
Шарбонье
в ту сторону, откуда опрокидывающая пара будет казатсья стремя¬
щейся повернуть снаряд против часовой стрел ten.
12
где ф—угол, составленный осью
снаряда и касательной к обра¬
зующей оживальной части сна¬
ряда в вершине, а фА — угол,
составляемый осью снаряда и
ожнвальную часть (черт. 012).
образующей конуса, вписанного в
Направление вектора, изобра¬
жающего опрокидывающий момент,
определяется обычным для правой
координатной системы способом.
Этот вектор считается направлен¬
ным перпендикулярно к плоскости
действия опрокидывающей пары
Черт. 012.
Для общего представления о характере функций
можно привести результаты опытов, произведенных
и 1918 г. в Англии четырьмя английскими исследователями Фоуле¬
ром, Гэллопом, Локком и Ричмондом с 76-мм снарядом типа нашей
шрапнели старого образца (черт.
013 и 014). Эти опыты конста¬
тируют совершенно различный ха¬
рактер изменения исследуемых
функций. В особенности резко
отличается от других функция
KN ^ у Отсюда ясно, что прини¬
мать KN и Км пропорциональными
Кт, как это чаще всего делалось
ранее, ни в коем случае нельзя;
необходимо ставить специальные
опыты для определения всех ука¬
занных функций.
Что же касается выражений RT, RN и М при не малых углах Ь,
то для этого случая мы не обладаем достаточным количеством опыт¬
ного материала. Теми же английскими учеными были произведены опыты
по определению зависи¬
мости RT, Rn и Ж от
угла отклонения § при
малых скоростях (около
12 м/сек) при помощи
аэродинамической тру¬
бы. Результаты этих
опытов изображены на
графиках 015 и 016,
которые могут иметь
значение только для са¬
мого общего предста¬
вления об указанной
зависимости.
При аналитическом исследовании движения снаряда около его
центра инерции под действием одного опрокидывающего момента
во внешней баллистике принимают различные зависимости М от д.
Наиболее употребительной является следующая зависимость:
0
Черт. 015.
Черт. 016*
016
где
017
Этой зависимостью пользовались почти все исследователи враща¬
тельного движения, начиная с Н. В. Маиевского и кончая Муль-
тонОм. Нетрудно видеть, что, принимая эту зависимость, мы допу¬
скаем, что сила сопротивления воздуха параллельна касательной
к траектории.
Кроме этой зависимости можно указать на зависимость, применяе¬
мую Д. А. Вентцелем:
018
и зависимость, выведенную из опытов четырьмя английскими учеными
Для послушных снарядов углы 5 малы; следовательно, sin § = Ь
и cos 5=1. Тогда все три приведенные формулы принимают один
и тот же вид
019
т. е. превращаются в формулу 013,
02. Силы, зависящие от движения оси снаряда и от
вращательного движения снаряда около оси.
В настоящем параграфе мы вкратце рассмотрим второстепенные
силы и моменты, возникающие вследствие самого вращения снаряда
и колебательного движения его оси, ограничивая наше изучение
только случаем послушного снаряда.
При движении снаряда ось его будет совершать около центра
инерции сложное колебательное движение, угловую скорость кото¬
рого обозначим через ii. Сопротивление воздуха при этом будет
стремиться уменьшить угловую скорость оси снаряда и будет спо¬
собствовать так называемому затуханию колебательного движения.
Момент, который будет вызывать это затухание, мы назовем туша¬
щим моментом и обозначим через D.
Для тушащего момента D в баллистике принимается следующе
выражение:
020
причем направлен этот момент в сторону, противоположную угловой
скорости S2, на что указывает знак минус.
Вращательное движение снаряда около его оси прежде всего
имеет следствием появление момента трения воздуха о боковую
14
поверхность снаряда, который стремится уменьшить угловую ско¬
рость собственного вращения снаряда р.
Этот момент, называемый моментом трения и обозначаемый
через 1\ выражается следующим образом:
021
Направление его противоположно направлению угловой скорости
собственного вращения р, на что опять указывает знак минус.
Насколько момент трения оказывает влияние на уменьшение
угловой скорости снаряда, можно видеть из результатов опытов
Круппа со 110-миллиметровым снарядом весом <7=16 кг и длиной
/==:3,4 калибра.
Кроме этого, вращательное движение снаряда около его оси
при наличии угла отклонения § будет иметь следствием появ¬
ление ,так называемой силы Магнуса и момента силы
Магнуса I.
Величина силы Магнуса, зависящая от угловой скорости
собственного\ вращения р и от угла отклонения выражается сле¬
дующим образом:
022
Направлена сила Магнуса перпендикулярно к плоскости действия
опрокидывающей пары в сторому, противоположную опрокидываю¬
щему моменту М.
Таким образом, в случае если головная часть снаряда располо¬
жена выше касательной, сила Магнуса будет направлена влево от
плоскости стрельбы, если смотреть на снаряд сзади.
15
Так как точка приложения силы Магнуса, вообще говоря
не совпадает с центром инерции, то кроме силы Магнуса мы
будем иметь еще и момент этой силы /, расположенный в
плоскости действия опрокидывающей пары перпендикулярно к оси
снаряда. Величина момента силы Магнуса принимается равной
023
Направление момента силы Магнуса зависит от расположения
точки приложения силы Магнуса по отношению к центру инерции
эта точка может помещаться как ближе к голове снаряда, так и бли¬
же к его дну.
03. Зависимость опрокидывающего момента сопротивления
воздуха от скорости снаряда.
Из выражения опрокидывающего момента для послушного сна¬
ряда
030
мы видим, что величина опрокидывающего момента М принимается
пропорциональной квадрату скорости снаряда v2 и пропорциональной
некоторой функции от числа Бэрстоу, которая нами обозначается
через
Эта функция должна быть установлена экспериментально на
основании специальных тщательно поставленных полигонских стрельб
для снарядов, принятых нами за эталонные.
Результаты опытов по определению функции Км ^ j для каж¬
дого эталонного снаряда обычно сводятся в таблицу, отвечающую
нормальной артиллерийской скорости звука a0N— 340,8 м/сек, при¬
чём аргументом таблицы в таком случае будет являться уже не число
Бэрстоу а скорость снаряда v.
Применяя подобную таблицу к вычислению величины опрокиды¬
вающего момента М для эталонного снаряда, мы будем принимать
iM— 1. При определении же величины М для какого-либо другого
снаряда мы должны иметь значение коэффициента формы iM, опре¬
деленное на полигоне при помощи небольшого количества рядовых
опытных стрельб.
16
Особенное внимание необходимо обратить на то обстоятельство,
что величина представляющая собой расстояние между цент¬
ром инерции снаряда и центром сопротивления воздуха, обязательно
должна определяться по той же самой эмпирической формуле, ко¬
торая была принята при обработке опытных данных, вследствие чего
в каждой из таблиц функ¬
ции (v) необходимо
указывать, какой форму¬
лой следует пользоваться
при вычислении величи-
(I)-
В настоящее время мы
имеем весьма небольшое
количество надежных опыт¬
ных данных, характери¬
зующих зависимость вели¬
чины опрокидывающего
момента М от скорости
снаряда v для различных
типов снарядов. Наиболее
интересный и наиболее
надежный материал дают
нам экспериментальные
исследования, произведен¬
ные в Англин Фоулером,
Гэллопом, Локком и Рич¬
мондом (1919 г.), а также
работы Д. А. Вентцеля на
Артиллерийском Полигоне
(1927 г.).
В Англии опыты про¬
изводились с 76-миллимет¬
ровыми снарядами, имев¬
шими одинаковый по на¬
ружному очертанию кор¬
пус и различные . длину и
очертание головной части,
а также различное п<зло-
жение центра инерции.
В СССР опыты производились с 76-миллиметровой фугасной
гранатой старого образца.
Эти снаряды изображаются на чертеже 030, а их числовые
характеристики приводятся в следующей таблице:
2 Вращательное движение 17
Черт. 030,
Таблица числовых характеристик опытных снарядов
(в калибрах)
Результаты опытов в обработке автора изображаются на
черт. 031 и 032, причем на черт. 031 изображены кривые
при обработке опытных данных с помощью формулы
Бурцио
031
а на черт. 032 кривые Км (г>), вычисленные при употреблении фор¬
мулы Морского Полигона
Длина снаряда
Длина головной ча¬
сти
Длина корпуса
Расстояние центра
инерции от дна
Расстояние центра
инерции от осно¬
вания головной
части
Расстояние между
центром инерции
и центром сопро¬
тивления
Рассматривая эти графики, мы прежде всего обращаем внимание
на то, что при употреблении формулы Бурцио мы получаем
пучок кривых, довольно близко расположенных одна от другой.
Черт. 031.
Кривые же, вычисленные при помощи формулы Морского Поли¬
гона, значительно отличаются одна от другой при изменении формы
снаряда.
При малых скоростях, не превышающих 200 м\сек, функция
KM(v) остается постоянной.
19
Далее функция *м (v) быстро возрастает, достигая макси¬
мума вблизи скорости звука, после чего начинается довольно мед¬
ленное убывание с явно выраженным стремлением к постоян¬
ному значению функции при больших скоростях (выше 900-
1000 м/сек).
Черт. 032.
На основании английских и русских опытов автором составлены
таблицы функции Км {v), являющиеся синтезом всех указанных
опытов, причем таблицы эти даются в двух видах: 1) таблицы функ-
ЦИК KMi (v) при выражении величины — по формуле Бурцио; 2) таб-
20
лицы функции Кт (v) при выражении величины — по формуле
Морского Полигона.
Графически новые функции KM(v) изображаются на чер¬
теже 033.
Черт. 033.
Из двух приведенных законов, характеризующих зависимость
опрокидывающего момента М от скорости v, автор рекомендует
закон, основанный на применении формулы Бурцио, которая, как
мы можем видеть из графиков 031 и 032, дает лучшее согласование
опытных данных между собой.
21
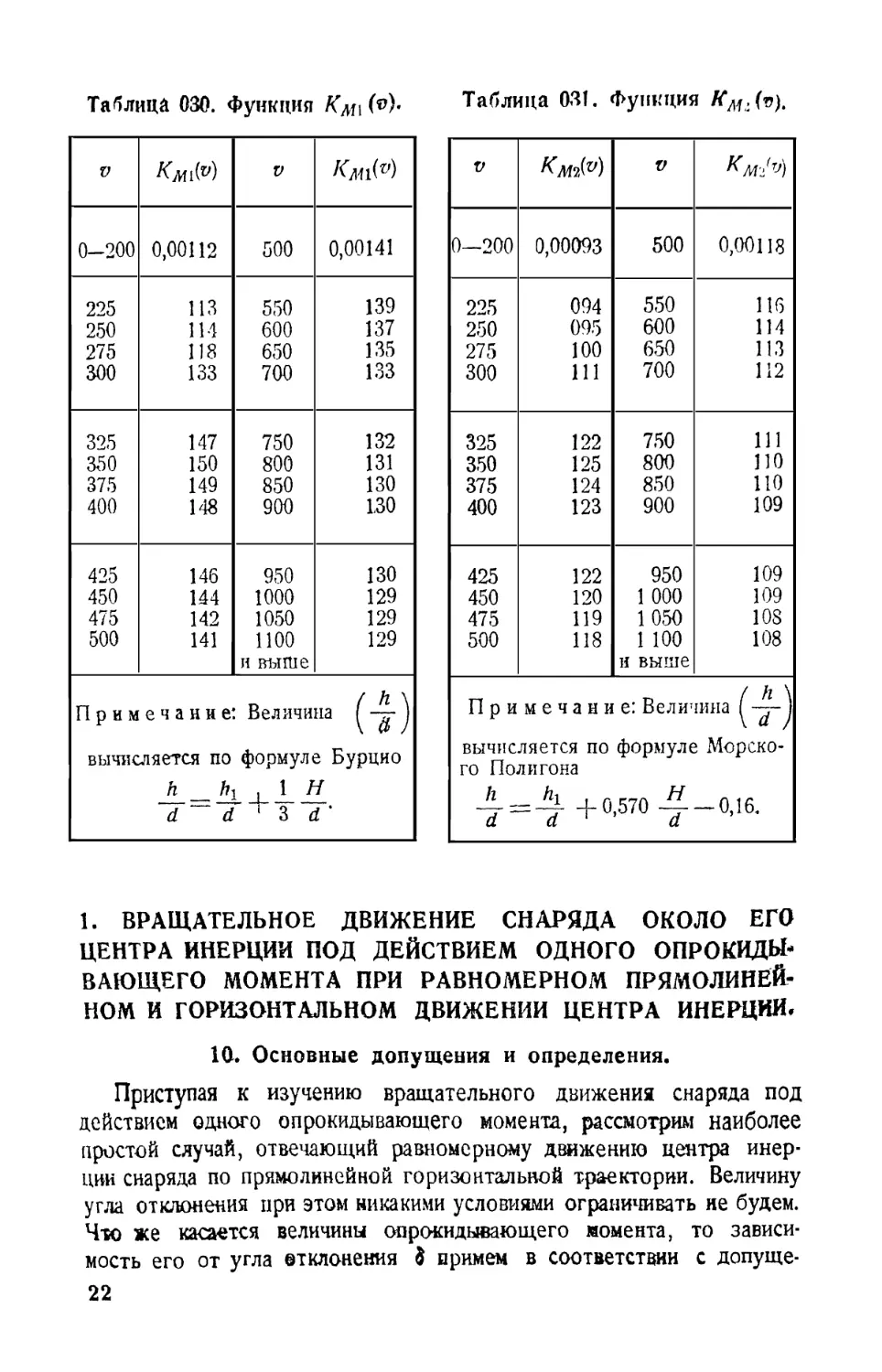
Таблица 030. Функция Км\ (**)'
Таблица 031. Функция fC^.(v).
1. ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ СНАРЯДА ОКОЛО ЕГО
ЦЕНТРА ИНЕРЦИИ ПОД ДЕЙСТВИЕМ ОДНОГО ОПРОКИДЫ¬
ВАЮЩЕГО МОМЕНТА ПРИ РАВНОМЕРНОМ ПРЯМОЛИНЕЙ¬
НОМ И ГОРИЗОНТАЛЬНОМ ДВИЖЕНИИ ЦЕНТРА ИНЕРЦИИ.
10. Основные допущения и определения.
Приступая к изучению вращательного движения снаряда под
действием одного опрокидывающего момента, рассмотрим наиболее
простой случай, отвечающий равномерному движению центра инер¬
ции снаряда по прямолинейной горизонтальной траектории. Величину
угла отклонения при этом никакими условиями ограничивать не будем.
Что же касается величины опрокидывающего момента, то зависи¬
мость его от угла ©тклонения $ примем в соответствии с допуще-
22
так как Н {у) = 1 и а — а0 вследствие горизонтальности прямоли¬
нейной траектории, a v — v0 вследствие равномерности движения.
Для нормальных артиллерийских условий ” ~
Тогда
102
Из формул 101 и 102 видно, что в условиях данной задачи р яв¬
ляется величиной постоянной:
Нетрудно заметить, что вращательное движение снаряда при
сделанных наш допущениях будет совершенно аналогично враща¬
тельному движению тяжелого симметрического волчка.
Что же касается соответствия сделанных нами допущений дейст¬
вительным услозиям стрельбы, то тут необходимо иметь в виду, что
наиболее близко эти допущения будут отображать действительность
в случае рассмотрения вра¬
щательного движения снаряда
на начальном участке траекто¬
рии при малых углах бро¬
сания.
Положение снаряда в про»
странстве определим следую¬
щим образом. В центре инер¬
ции С поместим начало двух
прямоугольных координатных
систем Cx1ylzl и
(черт. 100).
Система Cxlylzl будет
поступательно перемещаться
вместе с центром инерции,
причем оси ее Cxlt Cyv Сг, все время будут оставаться параллельными
координатным осям Ox, Оу, Oz основной задачи внешней баллистики.
При нашем допущении о прямолинейном горизонтальном движе¬
нии центра инерции ось Схх будет совпадать с направлением ско¬
рости центра инерции v или с самой траекторией центра инерции.
23
Черт. 100.
нисм Маневского (016) о пропорциональности опрокидывающего
момента М синусу угла отклонения 5.
Итак, для величины М мы будем иметь следующее выражение
100 yW=£psina,
где ^ для данного случая равно
Система С$т)? булст неизменно связана со снарядом, причем за
ось CS мы выберем ось симметрии снаряда; в таком случае оси Сг\
и а будут расположены и экваториальной плоскости, проходящей
через центр инерции.
Около центра инерции С проведем сферу единичного радиуса.
Черт. 101.
Положение снаряда или, что тоже самое, положение неизменно
связанной со снарядом системы С$Т)£ по отношению к постоянно
ориентированной в пространстве системе CxJy1z1 мы будем опреде¬
лять при помощи Эйлеровых углов v, § и <р (черт. 101).
Углом V мы будем называть двугранный угол, составленный вер¬
тикальной плоскостью, проходящей через касательную к траектории
центра инерции снаряда (Cxjjj), и плоскостью действия опрокиды¬
вающей пары, или плоскостью, проходящей через касательную Сх}
и ось снаряда CS.
24
Прощение по углу v мы будем называть прецессией, угол *
углом прецессии, a v'угловой скоростью премессии.
Вектор, изображающий угловую скорость прецессии v', направлен
по касательной к траектории центра инерции Схл.
Углом 3 мы будем называть угол, составленный вектором, изо¬
бражающим скорость сизряда v, или касательной к траектории
центра инерции Сх} и осью снаряда С£.
Вращение по углу д можно называть нутацией, угол £ —
углом нутации, а 5' — угловой скоростью нутации.
Обратим внимание на то, что угол отклонения или иутапии Ь
расположен в плоскости действия опрокидывающей пары, причем
этот угол может иметь как положительные, так и отрицательные
значения. Вектор, изображающий угловую скорость нутации Ь\ на¬
правлен перпендикулярно к плоскости действия опрокидывающей пары.
Углом ср будем называть угол, составленный пересечением эква¬
ториальной плоскости снаряда с плоскостью действия опро.чидываю-
щей пары и экваториальной осью снаряда О].
Вращение по углу <р называют ротацией или собственным
вращением снаряда около его оси, угол <р — углом ротации
(собственного вращения), а — угловой скоростью
ротации (собственного вращения).
Вектор, изображающий угловую скорость ротации направлен
по оси симметрии снаряда С£.
Итак, прецессией артиллерийского снаряда мы
будем называть вращение плоскости действия опро¬
кидывающей пары около касательной к траектории
центра инерции снаряда.
Нутацией артиллерий с кого снаряда мы будем
называть колебательное движение оси симметрии
снаряда в плоскости действия опрокидывающей
пары.
Наконец, ротацией или собственным вращением
артиллерийского снаряда мы будем называть вра¬
щение снаряда около его оси симметрии.
Переход от постоянно ориентированной в пространстве системы
Cxxyxzx к системе СЬнеизменно связанной со снарядом, осу¬
ществляется при помощи Эйлеровых углов следующим образом:
1) Вращение по углу v около
2) Вращение по углу Ь около
3) Вращение по углу <р около
25
Таким образом полное вращение снаряда складывается из трех
вращений: прецессии, нутации и собственного вращения.
Полная же угловая скорость снаряда о» будет равна геометри¬
ческой сумме, угловой скорости прецессии v', угловой скорости
нутации §' и угловой скорости собственного вращения у':
103
причем угловые скорости у' и $' характеризуют движение оси сим¬
метрии снаряда, а угловая скорость <р' — вращение снаряда около
этой оси. н
Указанные угловые скорости как было отмечено ранее, располо¬
жены: v' на оси Cxlt 8' на оси Cz2 и ср' на оси С$, причем на¬
правлены они по этим осям в ту сторону, откуда соответствующие
вращения кажутся происходящими против часовой стрелки.
Вектор, изображающий опрокидывающий момент М, должен
быть перпендикулярен к плоскости действия опрокидывающей пары,
т. е. к плоскости Cx-fcy^y^. Следовательно, он будет направлен по
оси Cz2 в ту сторону, откуда угол § будет казаться отложенным
против часовой стрелки.
11. Кинетическая энергия снаряда.
Для определения кинетической энергии снаряда Т воспользуемся
общей формулой из механики твердого тела:
110
где А, В и С представляют собой моменты инерции снаряда отно¬
сительно неизменно связанных со снарядам координатных осей
С$, Of] и СС, а р, q и г—проекции угловой скорости снаряда ю
на эти же оси:
Так как артиллерийский снаряд представляет собою тело вра¬
щения около оси С£, то моменты относительно двух других осей
Счj и С£ будут равны один другому:
С=£,
а потому для артиллерийского снаряда формула кинетической энер¬
гии примет более простой вид:
27
Момент инерции А мы будем называть главным аксиальным
моментом инерции снаряда- Момент инерции В—глав¬
ным экваториальным моментом инерции снаряда.
Найдем теперь проекции угловой скорости со на координатные
оси С£, Си} и СС, имея в виду, что
и что проекция геометрической суммы равна алгебраической сумме
проекций составляющих. Для проекции р получаем:
При нахождении проекции q нт придется проектировать на ось Ст\
, угловую скорость прецессии v\ Так как не¬
посредственное проектнровзние v' на ось Сг\
является довольно неудобной операцией, то
мы будем рассматривать v' как геометриче¬
скую сумму ее составляющих на взаимно¬
перпендикулярных осях С£ и Суь (черт. 110):
Ч' — v' cos (у', 5) У cos(v',^3).
Затем,, опять применив общеизвестную формулу о проекции гео¬
метрической суммы, получим:
Черт. 110.
Точно такой же метод мы применим и при определении г
И гак, окончательно мы имеем
113
114
115
Подставляя эти выражения для р, д и г в формулу для Т, по¬
лучим
12. Уравнения вращательного движения снаряда
около его центра инерции.
Для составления уравнений вращательного движёния снаряда
около его центра инерции воспользуемся уравнениями Лагранжа
второго рода
где qt представляют собою обобщенные координаты, a Q.— обоб¬
щенные силы.
В нашей задаче обобщенными координатами будут являться три
Эйлеровых угла V, 5 и ш, которые вполне определяют положение
артиллерийского снаряда, как твердого тела, около его центра
инерции. Обобщенными силами в нашей задаче, поскольку обоб¬
щенными координатами являются углы, будут проекции главного
момента всех внешних сил на направления отвечающих этим углам
угловых скоростей.
Составляем уравнения Лагранжа. Для параметра ср имеем:
Тогда первое уравнение напишется следующим образом:
23
пли окончательно
или, после интегрирования,
следовательно,
Замечая, что выражение (v' cos & <р') представляет собою не
что иное, как величину р, мы видим, что проекция угловой
скорости © на ось собственного вращения сна¬
ряда CS остается в продолжение всего движения
снаряда постоянной, равной ее начальному значе¬
нию р0:
Переходим теперь к параметру v'. Имеем
или, принимая во внимание уравнение 120,
Составляем второе уравнение:
или, после интегрирования,
Разделив полученное уравнение на В и обозначив постоянную ве¬
личину, получившуюся после этого деления в правой части уравне¬
ния, через а, мы будем иметь
Для удобства введем новое обозначение а, определяемое из условия
Тогда наше уравнение примет окончательный вид
Для определения а можно воспользоваться начальными усло¬
виями. Тогда
Для последнего параметра 5 получим
Третье уравнение будет иметь следующий вид:
или
Разделив это уравнение на Б и имея в виду, что, согласно вира-
/[
женшо 121 ъРо — 2а, получим
Последнее уравнение может быть упрощено при помощи не¬
сложных математических преобразований. Продифференцируем для
этой цели уравнение 122, умножим полученное выражение на V*
и сложим с уравнением 124, умноженным на Ь1:
Продолжаем преобразования, имея в виду интегрирование получен¬
ного выражения:
или
или
Теперь интегрируем полученное выражение, обозначая постоянную
интегрирования через Ь:
Величина постоянной b определяется из начальных условий:
Итак, окончательно мы имеем следующие дифференциальные урав¬
нения движения снаряда около его центра инерции, требующие
совместного решения;
откуда видно, что t выражается эллиптическим интегралом первого
рода в функции от и. Следовательно, и будет выражаться эллипти¬
ческой функцией времени t, которая в случае надобности может
быть определена при помощи теории эллиптических функций.
31
Дальнейшее упрощение этих уравнений может итти по ли¬
нии исключения из третьего уравнения величины у' при помощи
второго.
Из уравнения 122 имеем
Тогда уравнение 125 после подстановки вместо V его выражения
через § принимает вид
или, после умножения на sm28,
Обозначая теперь
получим
Таким образом могут быть переписаны и другие уравнения. Так
из уравнения 122, вводя это же обозначение и = cos 5, мы получим
Уравнение же 120, если принять во внимание только что получен¬
ное выражение для у', перепишется так:
Между прочим заметим, что уравнением 127 определяется ну¬
тация снаряда, уравнением 128 — прецессия и уравнением 129 —
собственное вращение.
Для решения полученных уравнений необходимо прежде всего
проинтегрировать уравнение 127, которое может быть приведено
к следующему виду:
Когда же будет известно а, то нахождение v и <р из уравнений
128 и 129 не представит особых затруднений.
Однако, вряд ли целесообразно применять довольно сложные
методы теории эллиптических функций в условиях настоящей за¬
дачи, основные допущения которой позволяют лишь ограниченное
использование результатов в артиллерийской практике. Поэтому
в настоящей книге мы ограничимся только исследованием уравнения
нутации без его интегрирования, имея в виду исключительно выяснение
вопроса о гироскопической устойчивости снаряда.
13. Исследование уравнения нутации.
Рассматривая уравнение 127 в виде
130
мы замечаем, что под знаком радикала у нас находится целая алге¬
браическая функция третьей степени, которую мы обозначим через/(и):
131
Тогда
132
Обратим внимание теперь на то, что в условиях нашей задачи
величина k = cos§ не может быть по абсолютной величине больше
единицы:
133
С другой стороны, в условиях нашей задачи величина и. может
иметь только такие значения, при которых
134
ибо в противном случае величина и'— — sin ЬЬ', характеризующая
угловую скорость нутации, была бы величиной мнимой.
Исходя из этих двух ограничительных условий, мы можем уста¬
новить тот интервал, который будет содержать все возможные для
нашей конкретной задачи значения и, т. е. установить крайние
пределы изменения угла д.
Так как /(и) является целой алгебраической функцией третьей
степени, то она будет иметь три корня. Обозначив эти корни через
«1, и2 и а8, мы сможем написать:
135
Построим теперь график функции /(и), откладывая по оси абс¬
цисс значения и, а по оси ординат — значения /(«). Естественно,
что кривая /(и) пересечет ось абсцисс не более чем в трех точках,
соответствующих ее корням их, и2 и и3. Для построения графика
прежде всего проследим за изменением знака функции /(а) по мере
перехода и через ряд вещественных значений от — оо до -|>- ос.
32
3 Вращательное движение
33
Получим:
Сведем все эти данные в таблицу:
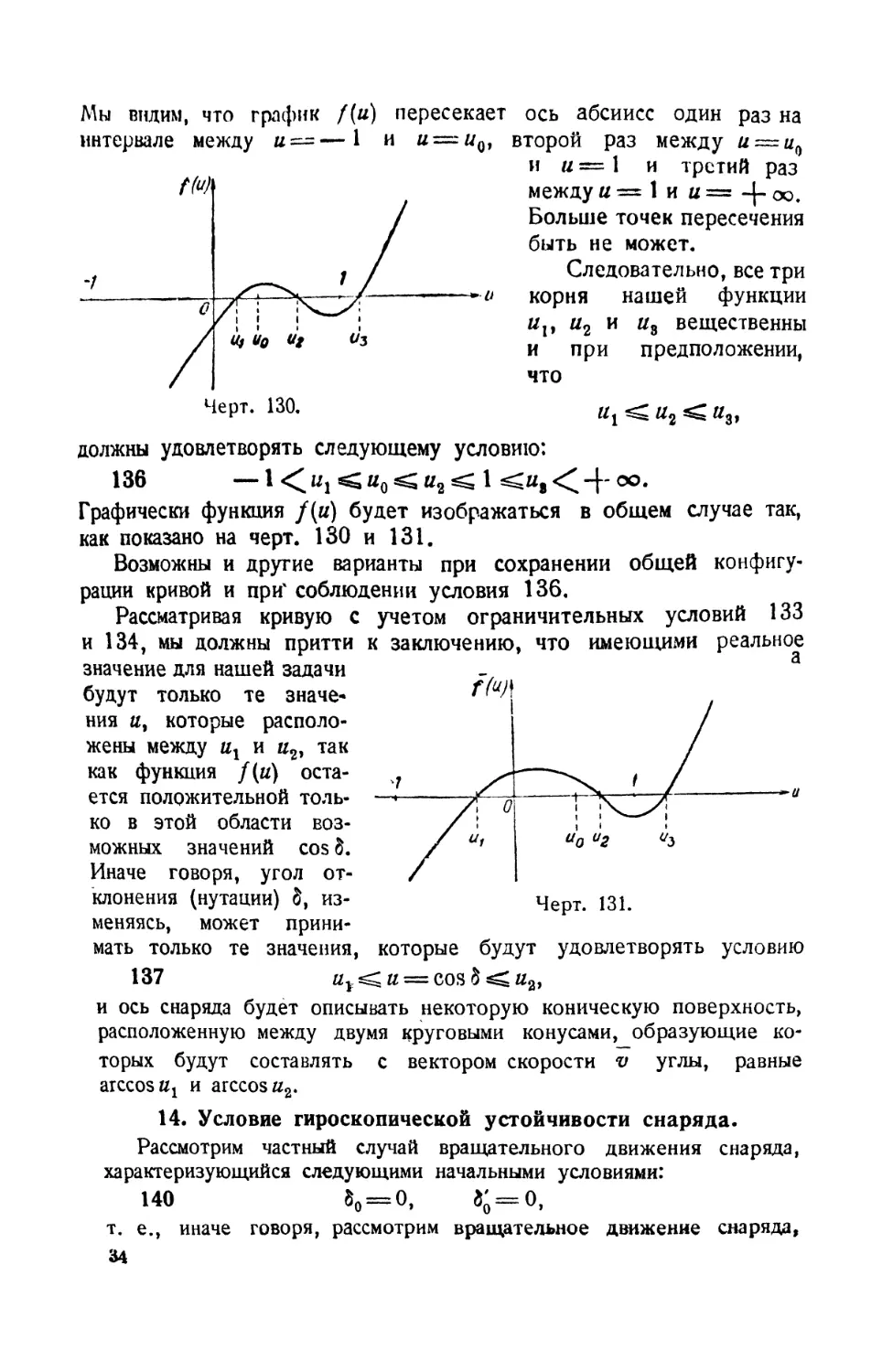
Мы видим, что график /(и) пересекает ось абсиисс один раз на
интервале между и = —1 и и — и0, второй раз между и = ц0
и и = 1 и третий раз
между и — 1 и и = -J- оо.
Больше точек пересечения
быть не может.
Следовательно, все три
о корня нашей функции
и,, и2 и и8 вещественны
и при предположении,
что
Kj Uj Ид,
должны удовлетворять следующему условию:
136 —1 < и, < и0 < н2 < 1 <и8 < оо.
Графически функция /(и) будет изображаться в общем случае так,
как показано на черт. 130 и 131.
Возможны и другие варианты при сохранении общей конфигу¬
рации кривой и при' соблюдении условия 136.
Рассматривая кривую с учетом ограничительных условий 133
и 134, мы должны притти к заключению, что имеющими реальное
значение для нашей задачи
будут только те значе*
ния и, которые располо¬
жены между «j и и2, так
как функция / (и) оста¬
ется положительной толь¬
ко в этой области воз¬
можных значений cos 8.
Иначе говоря, угол от¬
клонения (нутации) 8, из¬
меняясь, может прини¬
мать только те значения, которые будут удовлетворять условию
137 С и = cos 8 иа,
и ось снаряда будет описывать некоторую коническую поверхность,
расположенную между двумя круговыми конусами, образующие ко¬
торых будут составлять с вектором скорости v углы, равные
arccosttj и arccosK2.
14. Условие гироскопической устойчивости снаряда.
Рассмотрим частный случай вращательного движения снаряда,
характеризующийся следующими начальными условиями:
но s0=o, г;=о,
т. е., иначе говоря, рассмотрим вращательное движение снаряда,
34
Черт. 130.
Черт. 131.
В первом случае
я12=1,
1,
этому случаю соответствует
черт. 141. При этом необхо¬
димо иметь в виду, что двой¬
ному корню отвечает та точка
кривой, в которой ось абсцисс
является касательной.
Рассматривая эти графики, мы видим, что в первом случае при
уюл д может иметь одно и только одно значение, отве-
3* 35
ось которого в точке вылета совпадает с направлением начальной
скорости г>0 центра инерции и который не получает в момент вы¬
лета никаких ударов ни со стороны орудия, ни со стороны порохо¬
вых газов. Тогда
В этом случае функция f(u) имеет два одинаковых корня или
один двойной корень, опре- ^
деляемый из условия
и равный единице. Третий
корень определится из ус¬
ловия
и будет равен
Этот корень может быть как больше двойного корня, т. е.
единицы, так и меньше
Черт. 140.
и график функции будет иметь вид, изображенный на черт. 140;
во втором случае
чающее к
следовательно,
г. е. угол отклонения 8 остается равным нулю и ось снаряда сов¬
падает с направлением скорости прямолинейного движения в про¬
должение всего движения. Такой снаряд мы будем называть обла¬
дающим гироскопической устойчивостью. Этот термин отвечает тер¬
мину «сильный гироскоп» из
теории гироскопа.
Что же касается второго
случая, отвечающего условию
ttj игз, то здесь ясно, что
угол Ь мог бы иметь целый
и ряд значений от § = arccostt2g =
= arccos 1 = 0 до § = arccos
следовательно,
В этом случае мы будем называть снаряд гироскопически неустой¬
чивым (соответствует термину «слабый гироскоп» из теории гиро¬
скопа}.
Для предельного случая, когда
функция /(а) будет равна
т. е. мы будем иметь тройной корень, равный единице:
График функции f(u) для этого случая изображен на черт. 142.
Тройной корень, как известно, отвечает той точке кривой, где ось
абсцисс является одновременно и касательной, и секущей. Из рас¬
смотрения этого графика ясно, что и в этом случае снаряд может
быть назван гироскопически устойчивым, так как 8 = 0 является
для него единственно возможным значением угла отклонения.
Итак, условие гироскопической устойчивости сна¬
ряда будет состоять в том, чтобы
Черт. 142.
При а3< Р мы будем называть снаряд гироскопически не¬
устойчивым.
Рассмотрим теперь очень кратко случай, когда снаряд имея
в точке вылета совпадение оси с направлением движения центра
инерции, т. е. £ = 0, получает вследствие удара малую утловую
скорость &о = 8- Тогда среди корней функции /(я) одинаковых
уже не будет, и единице будет равен только один корень, а
именно «3=110=1. Из двух остальных корней один будет рас¬
положен весьма близко от
я2=.1, а другой на сравнитель¬
но большом расстоянии. При
а2^>р весьма близким к ut
будет корень аь а при
а8<^р — корень я,. Случаю
а3=^ будет отвечать весьма
близкое расположение от = 1
обоих корней их н а3. Графи¬
чески эти случаи изображены
на черт. 143, 144 и 145.
Из рассмотрения этих графиков видно, что для гироскопически
устойчивого снаряда, отвечающего условию а2 ^[5, легкие удары
будут вызывать незначительные колебания в угле 5, тогда как для
гироскопически неустойчивого снаряда (а2 р) даже небольших
ударов достаточно, чтобы заставить угол Ь изменяться в широких
пределах.
15. Коэффициент гиросконической устойчивости снаряда.
Формула 141 представляет собою неравенство, которое характе¬
ризует только качественную сторону явления гироскоянчеасой
устойчивости или неустойчивости снаряда, но не позволяет произ¬
водить количественное сравнение различных снарядов между собою,
37
Черт. 143.
Черт. 144.
Черт. 145.
т. е. давать ответ на вопрос, какой из двух снарядов является
более устойчивым.
С этой целью полезно ввести коэффициент гироскопи¬
ческой устойчивости а, равный
Для гироскопически неустойчивого снаряда о будет величиной мнимой.
Для гироскопически устойчивого снаряда а будет величиной веще¬
ственной, изменяющейся в пределах от нуля (при {J — а2) до еди¬
ницы (при а = оо или при £ = 0):
Очевидно, что увеличение коэффициента а будет соответство¬
вать увеличению гироскопической устойчивости снаряда, т. е. уве¬
личению способности снаряда выдерживать все более и более
сильные удары без нарушения правильности его полета в условиях
настоящей задачи.
Условие гироскопической устойчивости при вве¬
дении в рассмотрение коэффициента о может быть представлено
в следующем виде:
Напишем теперь выражение коэффициента гироскопической устой¬
чивости снаряда а в развернутом виде. С этой целью подставим
прежде всего в формулу для о (150) выражение а и (I. Согласно
выражению 121
где р0 является проекцией угловой скорости снаряда в момент вы¬
лета на ось симметрии сна рада С$. Что же касается величины £5,
то для нее в, условиях нашей задачи мы имели формулы 101 и 102.
В соответствии с формулой 101
150
Подставив эти выражения а и (J в формулу 150, получим
или
151
Заменим теперь аксиальный момент инерции А, не входящий
-А, его выражением через коэффициент веса
равный
и через аксиальный коэффициент инерции снаряда Д, характеризую¬
щий аксиальный радиус инерции р и равный
или
152
Тогда
или окончательно
163
Подставляя полученное выражение для А в знаменатель формулы
для ®, будем иметь
Дальнейшее упрощение выражения для а в условиях настоящей
задачи может быть произведено за счет замены /?0 его выражением
в соответствии с формулой 113:
Рассмотрим для простоты рассуждений случай, когда
т. е. когда ось снаряда в момент вылета не получает ударов.
Тогда
т. е. р0 равно угловой скорости собственного вращения снаряда
около его оси симметрии в момент вылета.
Величина же <f/ легко может быть определена, если известны,
с одной стороны, начальная скорость снаряда vo> а с другой, —
угол наклона нарезов или длина хода нарезов у дульного среза
орудийного ствола.
Напомним, что длиной хода нарезов постоянной крутизны на¬
зывается то расстояние, на котором нарезы, а следовательно, и сна¬
ряд, делают один оборот. Длиной хода нарезов переменной крутиз¬
ны в данном сечении называется длина хода нарезов такой постоян¬
ной крутизны, которая равна крутизне нарезов переменной крутизны
в данном сечении. Обычно длина хода нарезов выражается в калиб¬
рах и обозначается через V). В линей¬
ных единицах длина хода нарезов
будет равна yd. Угол наклона наре¬
зов к производящей канала орудия
обозначим через у.
Связь между длиной хода наре¬
зов 7] и углом наклона нарезов у
ясно видна из черт. 150, представляющего собой в развернутом
виде внутреннюю поверхность канала с одним нарезом постоянной
крутизны на протяжении одного оборота нарезов. Из чертежа
имеем
или
155
и
156
Для перехода от угла наклона нарезов у к длине хода нарезов
») и обратно приводятся две таблицы 150 и 151, вычисленные
Д. А. Вентцелем.
Таблица 150.
40
Черт. 150.
Таблица 151. rj = / (7).
Итак, выражаем <р' через vQ и tj:
Если выразить через угол наклона нарезов у, то, согласно
формуле 156, получим
Подставляем в выражение для а (154) в соответствии со сделан¬
ным нами допущением
Тогда
или после очевидных сокращений
Рассмотрим теперь выражение коэффициента гироскопической
устойчивости артиллерийского снаряда в случае прямолинейного н
равномерного движения его центра инерции при допущении /?0 = tp^
и при употреблении функции Км (?) вместо функции
и установим, какие факторы влияют на гироскопическую устойчи¬
вость снаряда.
Из формулы для а вытекает, что гироскопическая устой-’
чивость увеличивается
1) с увеличением коэффициента веса снаряда kq\
2) с увеличением аксиального коэффициента инерции снаряда д;
3) с уменьшением длины хода нарезов щ или с увеличением кру¬
тизны нарезки;
4) с уменьшением расстояния между центром инерции и центром
сопротивления, выраженного в калибрах ^j;
5) с уменьшением отношения экваториального момента инерции,
снаряда к аксиальному^^;
6) с уменьшением коэффициента формы iM;
7) с уменьшением плотности воздуха в точке вылета П0;
8) с уменьшением функции АГЛ(г»0).
При этом надо иметь в виду, что функция KM(v), как мы ви¬
дели из таблиц 030 и 031, меняется достаточно медленно, особенно
на участке от v=350 м\сек и выше, т. е. на наиболее важном
для нас участке. Во всяком случае из рассмотрения таблиц 030 и
031 можно вывести заключение, что при всех прочих равных^ усло¬
виях наименьшая гироскопическая устойчивость снаряда будет иметь
место на участке скоростей вблизи скорости звука.
Коэффициент гироскопической устойчивости а, как мы уже
установили ранее, для гироскопически устойчивых снарядов может,,
иметь значение в пределах от нуля до единицы, т. е.
0<о< 1.
При этом нцжнему значению (а = 0) будет отвечать снаряд,
находящийся на пределе гироскопической устойчивости, когда
а верхнему значению (о = 1) — снаряд, обладающий абсолютной
гироскопической устойчивостью, т. е. такой снаряд, ось которого
в продолжение всего движения будет оставаться параллельной
своему первоначальному направлению; в этом случае
Как пример абсолютной гироскопической устойчивости можно
привести движение вращающегося снаряда в безвоздушном прост¬
ранстве (П0 = О) или движение в воздухе такого вращающегося
снаряда, у которого центр инерции и центр сопротивления совпа¬
дают (Л=г0).
42
В заключение особое внимание обратим на то, что условие
гироскопической устойчивости снаряда, являясь
безусловно необходимым для правильности его
полета во всех случаях движения, является до¬
статочным только при прямолинейном движении
центра инерции снаряда.
При криволинейном движении центра инерции условие гироско*
пической устойчивости снаряда далеко не является достаточным для
того, чтобы снаряд был послушным.
2. ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ПОСЛУШНОГО СНАРЯДА
ПОД ДЕЙСТВИЕМ ОДНОГО ОПРОКИДЫВАЮЩЕГО МОМЕНТА
ПРИ РАВНОМЕРНОМ ПРЯМОЛИНЕЙНОМ И ГОРИЗОНТАЛЬ¬
НОМ ДВИЖЕНИИ ЦЕНТРА ИНЕРЦИИ.
20. Основные допущения и определения.
В предыдущей главе мы установили, что даже при тех допуще¬
ниях, которые были нами сделаны, уравнения движения снаряда ин¬
тегрируются только при помощи эллиптических функций.
Поэтому в настоящей главе мы, сохраняя все предыдущие
допущения, ограничим исследование только случаем малых углов от¬
клонения 8, т. е. таких углов, для которых, в пределах заданной
степени точности, мы можем считать, что
sm8 = tg$ = 8 и cosS=l.
Практически, последнее допущение является значительно менее
грубым, чем сделанные ранее, так как в громадном большинстве
случаев действительной артиллерийской практики мы имеем дело со
снарядами, обладающими правильным полетом, т. е. имеющими малые
углы отклонения.
В срответствии с выводами главы 1 снаряд будем считать гиро¬
скопически устойчивым, т. е. удовлетворяющим условию 141
или условию 151
где о — коэффициент гироскопической устойчивости, равный
Положение снаряда или неизменно связанной с ним системы С£т]С
относительно постоянно ориентированной в пространстве системы
Cxxy1z1 на этот раз мы будем определять не при помощи Эйлеро-
43
вых углов v, 8 и <р, а посредством трех других углов 8,, Ьг и Ьг,
которые будут более удобными как сейчас, так и, в особенности,
Черт. 200.
при дальнейшем исследовании. Углам $г, и мы дадим название
углов де-Спарра (черт. 200 и 201).
Углом мы будем называть угол, составленный проекцией оси
снаряда CS на вертикальную плоскость Схгуг, проходящую через
касательную к траектории центра инерции снаряда, с направлением
скорости центра инерции v, т. е. с осью Cxv
Углом мы назовем угол, составленный осью снаряда С£ с вер*
тикальной плоскостью Сххуъ проходящей через касательную к
траектории центра инерции снаряда.
Угол i8, аналогичный углу <р, будет представлять собой угол, со¬
ставленный экваториальной осью Сц с пересечением экваториальной
44
плоскости снаряда и вертикальной плоскости Cxtyt, проходящей
через касательную к траектории центра инерции снаряда.
Углы и связаны с углами » и } зависимостями, вытекаю¬
щими из сферического треугольника (черт. 202), стороны
которого равны
Из сферического треугольника
202
203
Черт. 202. Черт. 203
Так как мы приняли, что угол 8 является малым, то тем более ма¬
лыми будут углы $j и §2. Отсюда, полагая tg д1~д1, sin$2=s8a и
sin8 = tg$ = 8, получим
200 8j =ь 8 cos v,
201 $2== 8 sin v.
Этот же результат мы получили бы, если бы рассматривали
сферический треугольник х}х2£ как прямолинейный (черт. 203), на
что мы имеем право вследствие малости
углов 8, 8, и 82.
На основании уравнений 200 и 201 можно
написать выражения, определяющие 8 и v
в зависимости от 8j и 82, а именно:
г
tgv = jx.
Переход от постоянно ориентированной в пространстве системы
Cx1yizl к системе CSrjC, неизменно связанной со снарядом, при помощи
углов де-Спарра 8,, 82 и 83 осуществляется следующим образом:
,х „ > _ (ось Сх, переходит в Сх2,
1) Вращение по углу 8, около оси Сг\ < Л ^ t
' г 1 1 ( ось Cyj переходит в Су'.
„ ч ^ , ( ось Слг,, перфсодит в С$,
2) Вращение „о углу 8, около оси Су, | ^ в
3) Вращение по углу $е около оси С£ i ось пеРеходит 8 ^
' * 8 ^ ось Сг\ переходит в СС.
Угловые скорости 8'j, ^ и &з будут направлены: 8j — по оси
Cz 1, Ь\ — по оси Cy'v V, — по оси С£, — в ту сторону, откуда
соответствующие вращения будут казаться происходящими против
часовой стрелки.
Полная угловая скорость снаряда <о будет равна геометриче*
ской сумме трех указанных угловых скоростей dj, Ыг и 8J,:
204 ш = $j-j-^2 ”i~ ^з»
причем угловые скорости 8| и 8^ характеризуют движение оси
снаряда, а угловая скорость Ь'2 — вращение снаряда около этой оси.
Вектор, изображающий опрокидывающий момент М, будет на¬
правлен так же, как и раньше, ло перпендикуляру к плоскости
действия опрокидывающей пари Схх£, т. е, по оси Сгг в ту сто¬
рону, откуда угол 8 будет казаться отложенным против часовой
стрелки.
46
Величина опрокидывающего момента М, как нами было уже
установлено для движения снаряда при малых углах отклонения 3
(019), равняется
205
При этом величина р, равная в условиях нашей задачи
так же, как и в главе 1, является величиной постоянной. Функ¬
ция Н(у) в выражение для р не входит, потому что прямолинейная
траектория так же, как и в предыдущей главе, принимается горизон¬
тальной; следовательно, Н {у) — 1.
21. Кинетическая энергия снаряда.
Кинетическая энергия снаряда равна
210 Г=|[Л/?2-}- В(?2_|_Г2)] .
Для ее определения найдем прежде всего проекции р, q и г,
исходя из того, что полная угловая скорость снаряда равна
211
47
Для проекции р получаем выражения
При нахождении проекции q нам придется проектировать на ось Оj
угловую скорость 8{. Так как непосредственное проектирование
8' на ось Ci) довольно неудобно, то мы будем рассматривать век¬
тор как геометрическую сумму его составляющих на взаимно
перпендикулярных осях' С£ и Cz', располокенных в одной плоскости
с Ь'х (черт. 210); следовательно,
В этом случае
214
Теперь для проекции q получаем:
Точно так же находим проекцию г:
Итак, окончательно имеем
Подставляя выражения ру q н г в формулу для Г, после упроще¬
ний получим
Эта формула справедлива при любых значениях Ь, т. е. при любых
значениях Sj и S2.
Для малых углов § или, что то же самое, для малых углов Ь,
Ш
22. Уравнения вращательного движения снаряда около его
центра инерции.
Для составления уравнений движения снаряда около его центра
инерции мы будем пользоваться так же, как и в параграфе 12,
уравнениями Лагранжа
Принимаем за обобщенные координаты углы 5j, $2 и &8.
Для параметра §8 имеем
Тогда уравнение Лагранжа, отвечающее параметру §3, напишется
следующим образом:
или после интегрирования
следовательно,
Выражение -Ц— §з) представляет собою не что иное, как вели¬
чину р. Значит, проекция угловой скорости снаряда®
на ось симметрии снаряда остается в продолжение
всего движения постоянной, равной ее начальному
значению р0:
Для параметра 82 имеем
или, принимая во внимание уравнение 220,
Черт. 220.
50
Для того чтобы найти проекцию опрокидывающего момента М
на направление угловой скорости J 2, мы будем рассматривать век¬
тор М как геометрическую сумму его составляю¬
щих по взаимно перпендикулярным осям Су{ и Czu
расположенным в одной плоскости с вектором М
(черт. 220):
Тогда, имея в виду, что проекция геометриче¬
ской суммы равна алгебраической сумме проущий
составляющих, получим
- / V . ш t
или, так как.угол мал и, следовательно, можно принять coso1=?l,
Далее, подставляя вместо М его выражение (206)
а также имея в виду уравнение 201, получим
и окончательно
Составляем теперь уравнение Лагранжа:
Разделив полученное уравнение на В и заменив, согласно урав*
нению 121, через 2а, получим окончательно
Переходим теперь к параметру
или, в соответствии с уравнением 220,
или после подстановок
и окончательно
Составляем последнее уравнение Лагранжа
Разделив полученное уравнение на В и вводя величину
получим окончательно
Итак, движение снаряда около его центра инерции определяется
тремя дифференциальными уравнениями:
причем первое уравнение определяет вращение снаряда около его
оси симметрии, а два последних уравнения — движение самой оси
симметрии снаряду.
23. Интегрирование уравнений движения оси снаряда.
Для одновременного интегрирования двух последних дифферен¬
циальных уравнений введем комплексную переменную
производные которой будут равны
С этой целью умножим уравнение 221 на i и сложим с уравнением
222; получим
Введем теперь переменную Z, имея в виду, что
Тогда
231
или, после замены р через коэффициент гироскопической устойчи-
Это уравнение является .линейным дифференциальным уравнением
второго порядка с постоянными коэффициентами без последнего
члена (Р и сг, как мы уже говорили, постоянны вследствие равно¬
мерности движения центра инерции снаряда и горизонтальности пря¬
молинейной траектории). Составляем характеристическое уравнение
решая которое, получи»
Так как мы рассматриваем снаряд, обладающий гироскопической
устойчивостью, то
и корни характеристического уравнения будут мнимыми:
Обозначим теперь
233
234
Имея в виду, что (ог^>а)г и что
235 юг—<^=2аа,
после подстановки и юг в выражения для kx и Л2, получим:
Общий интеграл нашего дисЬАеоенниального уоавнения будет оавен
где С, и Сг являются постоянными интегрирования, определяемыми
из начальных условий.
Так как Z является комплексным числом, то постоянные С, и Сг
также должны быть комплексными числами. Представим их в виде
Тогда
Далее, имея в виду, что
мы можем привести уравнение для Z к виду
Теперь, когда интегрирование закончено, перейдем от комплекс¬
ной переменной Z к вещественным переменным и дг, исходя из
52
того, что
Z = », + /»,.
Сравнивая два последние выражения для Z и имея в виду, что
комплексные числа равны тогда и только тогда, когда по отдель¬
ности равны их вещественные и мнимые части, мы можем опреде¬
лить и $а: д
236
237
Зная же и мы легко можем написать выражения для 5 и v
на основании уравнений 203 и 204:
или, после простых преобразований,
Из уравнения 204 имеем
239
238
24. Определение постоянных интегрирования.
В систему уравнений
определяющих Sj и 83, у нас входят четыре постоянных величины
Рг Рг» Фг> значения которых будут определяться начальными ус¬
ловиями.
Предположим, что в начальный момент времени, т. е. при t = 0,
Подставим эти значения как в выражения, определяющие
(240), так и в выражения, определяющие их производные <
242
Тогда мы получим систему четырех уравнений с четырьмя неизвест*
ними р„ р,,
Решаем эту систему уравнений, определяя прежде всего cos и
соэф, из первого и четвертого уравнений системы:
и окончательно
Подставляя это выражение в формулу для cos получим
и окончательно
Далее, определяем sin и sin из второго и третьего уравнения
системы 242:
и окончательно
Подставляя это выражение в формулу для sin ф^, получим
и окончательно
Теперь мы легко можем найти p/f возведя выражения для sint|>, и
cos с{>, в квадрат и затем их суммируя:
Подобным же образом из выражений для sin фг и cos найдем рг:
Сводя все полученные выражения постоянных в систему, будем иметь
243
244
245
246
25. Исследование уравнений движения оси снаряда.
Исследуя уравнения 236 и 237, определяющие движения оси
снаряда, мы видим, что это движение можно рассматривать как со¬
стоящее из двух конических движений с круговыми основаниями,
наложенных одно на другое.
Одно из этих конических движений, медленное, с угловой
скоростью сог = а (1—а) и радиусом основания р, определяется
первыми членами уравнений 236 и 237:
Другое коническое движение, быстрое, с угловой скоростью
<ог —а(1-|-а) и радиусом основания рг определяется вторыми чле¬
нами этих же уравнений:
Таким образом, в условиях настоящей задачи
т. е. движение оси снаряда можно рассматривать как быстрое кони¬
ческое движение около некоторой оси, которая в свою очередь со¬
вершает медленное коническое движение около касательной к траек-
тории центра инерции. Ось быстрого конического движения мы
будем называть псевдоосью снаряда.
Спроектируем теперь движение конца оси снаряда *) на плоскость,
перпендикулярную к касательной к траектории, имея в виду, что
проекция дуги, отвечающей малому углу, может быть принята рав¬
ной самой дуге в том случае, когда касательная к этой дуге в одной
из точек параллельна или
почти параллельна данной
плоскости. При этом будем
рассматривать данную плос-
кость со стороны центра инер¬
ции снаряда, т. е. сзади
(черт. 250), так что положи¬
тельные углы должны будут
отсчитываться по часовой
стрелке. Плоскость эту, по
примеру В. М. Трофимова,
будем называть плоско*
стыо изображения.
В таком случае, для ме¬
дленного конического движе¬
ния мы получим картину, изо¬
браженную на черт. 251
и представляющую собою
траекторию проекции конца псевдоосн снаряда или оси быстрого
конического движения Lj в виде окружности радиуса pz с центром
*) Концом оси снаряда мы будем называть точку пересечения оси
снаряда со сферой единичного радиуса.
56
Черт. 250.
Черт. 251,
в точке пересечения плоскости изображения и касательной к траек¬
тории центра инерции снаряда Ct.
Для быстрого конического движения мы будем иметь картину,
изображенную на черт. 252 и представляющую собою траекторию
проекции конца оси снаряда
/v, в относительном движении
около псевдооси снаряда
опять в виде окружности ра¬
диуса рг с центром в точке Lv
В результате сложения
этих двух движений: отно¬
сительного около точки Z.J
по окружности радиуса рг
с угловой скоростью о)г и пе- ;
реносного вместе с точкой Lx
около точки Сх по окруж¬
ности радиуса pt с угловой
скоростью о)/# по схеме, ука¬
занной на черт. 253, мы будем
получать эпициклоиды различ¬
ного характера и формы в за¬
висимости от соотношения
между величинами р„рг, о>г.
Величины ф, и фг никакого
влияния на форму кривых,
описываемых проекцией конца
оси снаряда, иметь не будут.
Рассматривая величины р/?
рг, <о„ <ог, прежде всего обра¬
тим внимание на то, что
Черт. 252
и что, согласно уравнениям
233 и 234,
Что касается величин рг и рг,
то тут возможны три случая:
Рассмотрим каждый случай в отдельности, наблюдая за_измене-
инем скорости конца оси снаряда в абсолютном движении Va. Ско¬
рость V^ очевидно, будет равняться геометрической сумме скоро-
57
Черт. 253.
стей относительного Vr и переносного Ve движений:
к+ к-
Величина первой скорости или скорости конца оси снаряда в от¬
носительном движении около
псевдооси снаряда постоянна
и равна
Уг=Рг®г-
Величина второй скоро¬
сти, представляющей собой
скорость конца псевдооси сна¬
ряда в движении около ка¬
сательной к траекторий цен¬
тра инерции снаряда, также
постоянна и равна
Естественно, что наиболь¬
шая величина абсолютной
скорости Va будет соответ¬
ствовать моменту, когда век¬
торы, изображающие скоро¬
сти Vr и Vt будут парал¬
лельны один другому и на¬
правлены в одну и ту же
сторону, а наименьшая вели¬
чина Va будет соответство¬
вать моменту, когда эти век¬
торы будут параллельны, но
направлены в противополож¬
ные стороны (черт. 254).
Для простоты и наглядности
чертежа и фг приняты рав¬
ными нулю.
В дальнейшем нам будет
гораздо удобнее рассматри¬
вать не величину абсолютной
скорости Va, а величину ее
проекции на направление ско-
У рости переносного движения
е и наблюдать за изменением ее знака. Имеем
Черт. 254.
В первом случае, т. е. при р„>рг, нам могут представиться
три подслучая постольку, поскольку (0,<^<вг, а именно;
При рг(ог, т. е. при Ve^> Vrt мы видим, что проекция
абсолютной скорости V' на направление скорости переносного дви-
Черт. 255.
жения Ve всегда положительна, и, следовательно, конец оси сна¬
ряда всегда будет двигаться в одном направлении. Кривая, описы¬
ваемая концом вектора, будет укороченной эпициклоидой типа,
изображенного на черт. 255.
При p1wJ=pr®r, т. е. при Ve=z наименьшее значение абсо¬
лютной скорости V равно нулю, и кривая будет иметь характер
нормальной эпициклоиды (черт. 256).
При pjw(<^prwr, т. е. при проекция абсолютной
скоростьи на направление скорости переносного движения
59
60
Черт. 256.
Черт 257.
Черт. 258.
Черт. 259.
61
в некоторый момент времени будет менять знак, наименьшее значе¬
ние этой проекции будет отрицательным. Конец вектора в этом случае
будет двигаться попеременно то в одну, то в другую сторону,
описывая петли, и кривая будет удлиненной эпициклоидой (черт. 257),
Рассмотрим теперь второй случай, когда рг= рг. Так как сог, то
и следовательно, Ve<^ Vr Естественно, что кривая будет делать
петлн и эпициклоида будет удлиненной, причем характерной осо¬
бенностью данного случая будет то обстоятельство, что поскольку
радиусы медленного и быстрого конического движения равны между
собой, кривая обязательно будет проходить через точку С,
(черт. 258).
Наконец, в третьем случае при р*<Срг скорость Ve подавно
будет меньше Vr Следовательно,
поэтому кривая и здесь будет делать петли, но только эти петли
будут охватывать центр. Эпициклоида будет удлиненной, типа, изо¬
браженного на черт. 259.
26. Движение оси снаряда при отсутствии начального угла
отклонения и ударов в момент вылета.
В параграфе 24 постоянные величины plt рг, фг, зависящие
от начальных условий, были определены в общем виде. Найдем
теперь их значение в некоторых частных случаях.
Рассмотрим сначала наиболее простой случай, а именно, вылет
снаряда при строгом совпадении оси снаряда с вектором начальной
скорости и при отсутствии каких бы то ни было ударов или толч¬
ков при вылете как со стороны орудия, так и со стороны поро¬
ховых газов. Аналитическое выражение условий настоящей задачи
имеет следующий вид:
260
261
Подставляя эти значения в уравнения 243 и 244, мы получаем
262
Что же касается выражений для и фг (245, 246), то выраже¬
ния эти становятся неопределенными. Тем не менее, из уравнения
240 мы получим вполне определенные выражения для ij и $2
а именно:
263
62
Из равенств 263 следует, что нулю должен равняться и угол
отклонения §.
264
Кроме того, из уравнения 220 после подстановки в него 82 = 0
получим
265
Таким образом, если снаряд вылетает без начального угла от¬
клонения и без ударов, то в продолжение всего движения его
центра инерции по прямолинейной траектории ось снаряда будет1
совпадать с траекторией, а угловая скорость вращения около этой
оси будет оставаться постоянной.
27. Движение оси снаряда при отсутствии начального угла
отклонения, но при наличии ударов в момент вылета.
Предположим, что в момент вылета снаряду, ось которого сов¬
падает с касательной к траектории центра инерции (§0 = 0), нанесен
удар, т. е. сообщена угловая скорость §о в некоторой плоскости,
составляющей угол v0 с вертикальной плоскостью, проходящей че¬
рез касательную. Тогда
270
271
На практике рассматриваемый случай является наиболее, типич¬
ным, так как в момент вылета снаряд в громадном большинстве слу¬
чаев имеет весьма незначительный угол отклонения 80, но зато под¬
вергается значительным ударам как со стороны орудия, так и со
стороны пороховых газов.
Подставляем значения 810> 820, §ю, й» в уравнения 243 и 244;
а так как в данном случае, согласно уравнениям 271,
Находим теперь и пользуясь выражениями 245, 246:
Для установления характера движения обратим внимание на то, что
Р/=Рг*
Следовательно, движение конца оси снаряда происходит по удли¬
ненной эпициклоиде, проходящей через точку пересечения касатель¬
ной с плоскостью изображения (Сг) (черт. 258). При этом движе¬
ние начинается так, как показано на черт. 270, 271, 272.
Это движение можно выразить и в параметрах й и v на основании
формул 238 и 239. Из формулы 238
или при учете выражений 271
Черт. 270.
Из этих равенств следует, что
Подставляя найденные значения постоянных в, общие уравнения 240,
получаем
Черт. 271.
Черт. 272.
65
принимая во внимание, что
имеем
или, после извлечения корня и замены р; его выражением
Находим теперь выражение для угла прецессии v. имея в виду, что
и пользуясь непосредственно уравнениями 275:
Отсюда имеем
то
277
278
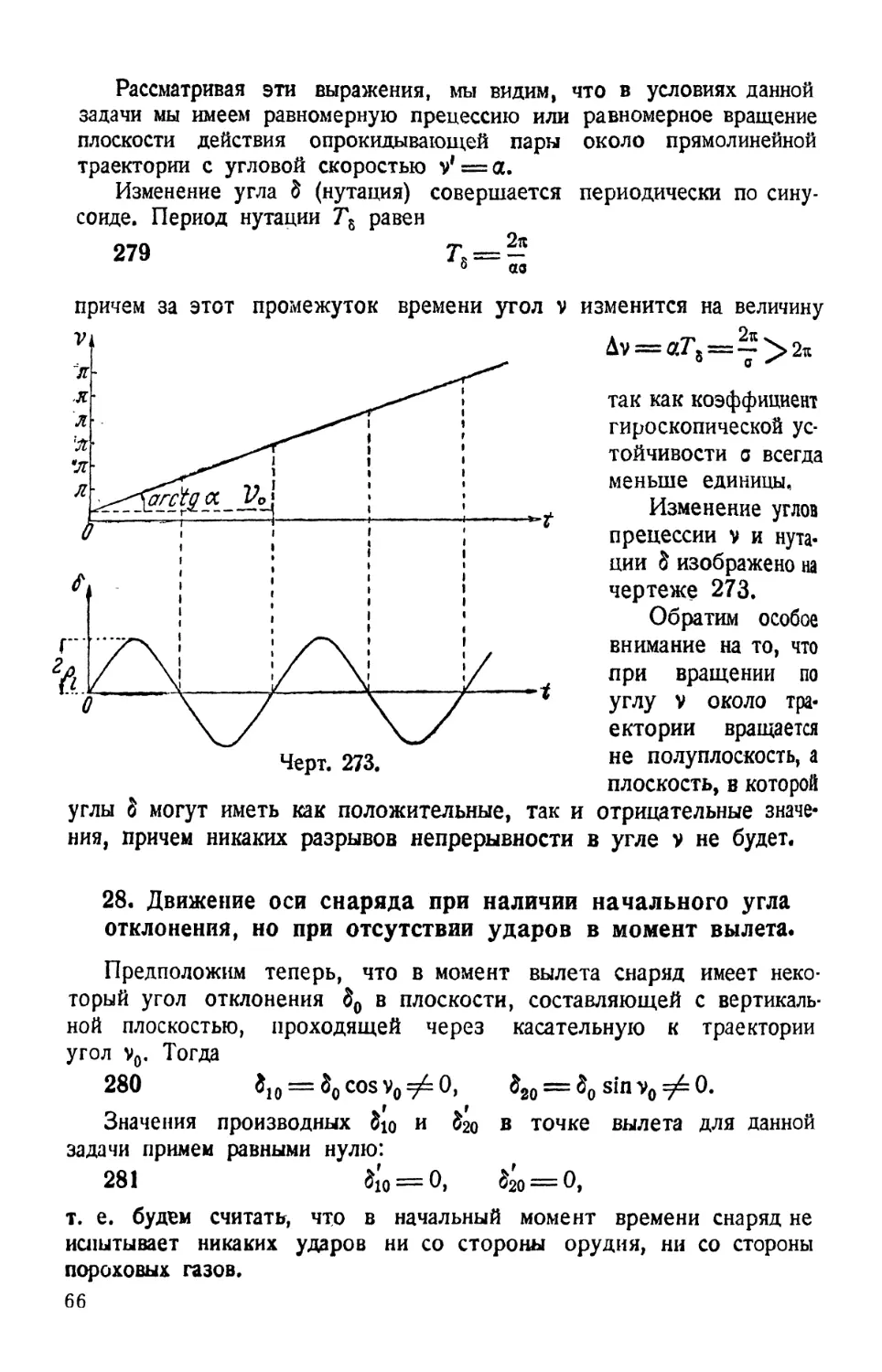
Рассматривая эти выражения, мы видим, что в условиях данной
задачи мы имеем равномерную прецессию или равномерное вращение
плоскости действия опрокидывающей пары около прямолинейной
траектории с угловой скоростью v' = a.
Изменение угла 8 (нутация) совершается периодически по сину¬
соиде. Период нутации Ть равен
причем за этот промежуток времени угол v изменится на величину
= 2,
так как коэффициент
гироскопической ус¬
тойчивости о всегда
меньше единицы,
Изменение углов
прецессии v и нута-
ции $ изображено на
чертеже 273.
Обратим особое
внимание на то, что
при вращении по
углу V около тра¬
ектории вращается
не полуплоскость, а
плоскость, в которой
углы 8 могут иметь как положительные, так и отрицательные значе¬
ния, причем никаких разрывов непрерывности в угле v не будет.
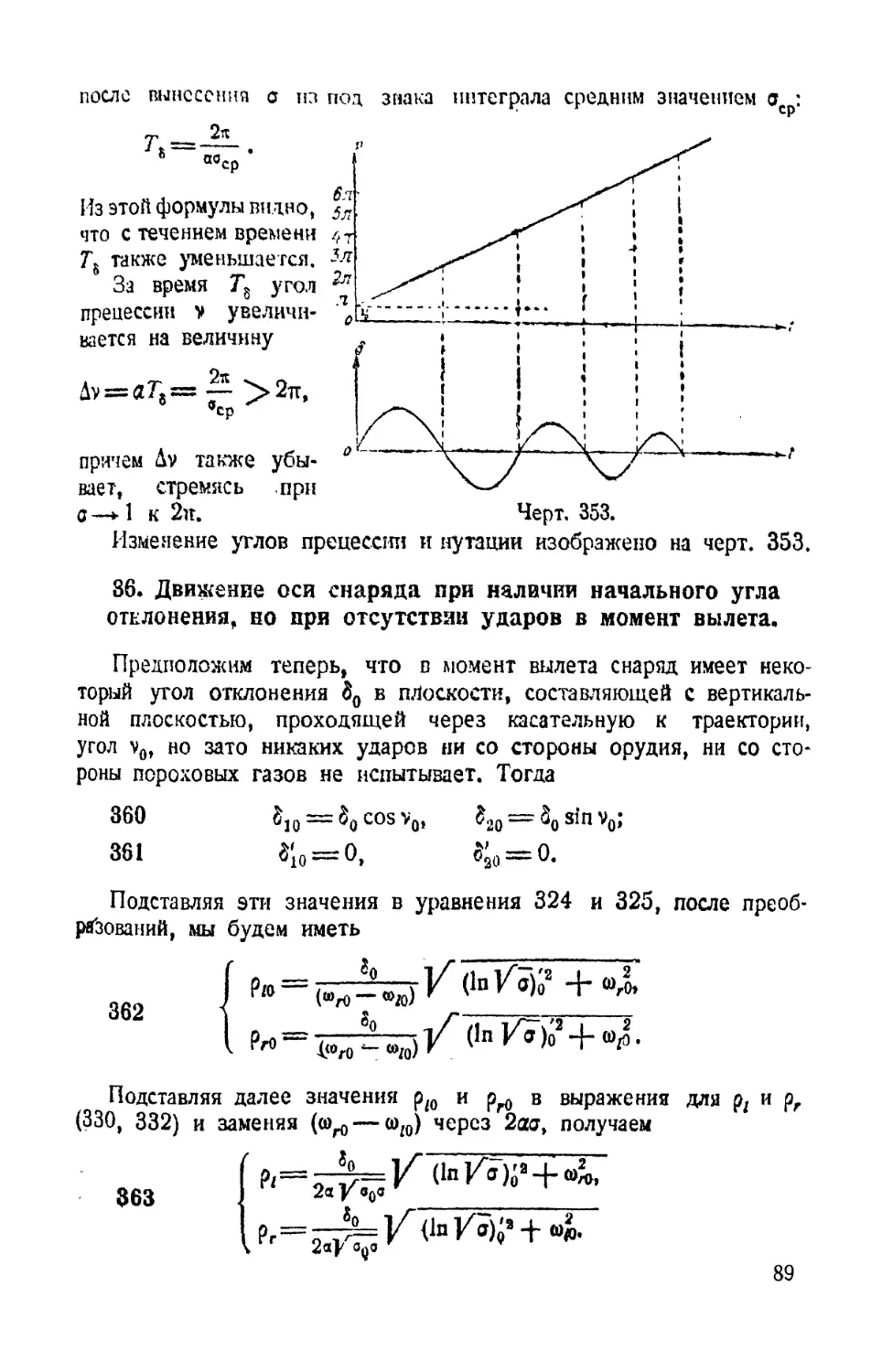
28. Движение оси снаряда при наличии начального угла
отклонения, но при отсутствии ударов в момент вылета.
Предположим теперь, что в момент вылета снаряд имеет неко¬
торый угол отклонения 80 в плоскости, составляющей с вертикаль¬
ной плоскостью, проходящей через касательную к траектории
угол v0. Тогда
280
Значения производных 8lo и 820 в точке вылета для данной
задачи примем равными нулю:
281
т. е. будем считать, что в начальный момент времени снаряд не
испытывает никаких ударов ни со стороны орудия, ни со стороны
пороховых газов.
66
Черт. 273.
На практике с начальным углом отклонения приходится особенно
считаться в случае стрельбы с движущегося корабля или самолета,
так как в этом случае ось снаряда в момент вылета даже при самых
благоприятных условиях будет составлять некоторый угол с направ¬
лением вектора, изображающего начальную скорость относительно
атмосферы. Особенно неблагоприятным для величины угла 80 будет
стрельба по направлению, перпендикулярному к движению корабля
или самолета.
Подставляем значения 810, £20, $ю, £20 в выражения 243 и 244:
Находим теперь при помощи выражений 245, 246 постоянные
или, так как
то
Из этих равенств следует, что
283
Подставляя значения постоянных в общие уравнения 240, по¬
лучаем:
Чтобы установить характер движения, заметим прежде всего, что
285
М/
^0*
Черт. 280.
различаются между собою на тг, то движение оси начинается как
раз сточки, где Кв = 0 (черт. 280, 281, 282).
Рассмотрим теперь специальный случай, когда снаряд обладает
очень большой гироскопической устойчивостью вследствие очень
большой скорости собственного вращения, т. е. иначе говоря, когда
1 А о р
а= ~2Q-Po очень велико по сравнению с р, а величина ^ , следо¬
вательно, может считаться малой.
В этом частном случае коэффициент гироскопической устойчи¬
вости снаряда
близок к Единице, и выражение его может быть представлено
в виде ряда, расположенного, по возрастающим степеням
с сохранением одной только первой степени этой величины
Действительно,
Делее, сравним величины
т. е.
286
Следовательно, мы имеем здесь случай, отвечающий движению по
нормальной эпициклоиде (черт. 256), причем, так как углы ^
Тогда
287
Таким образом снаряд, обладающий очень большой гироскопиче¬
ской устойчивостью, в случае прямолинейной траектории будет
иметь как бы одно прецессионное
движение, т. е. угол Ь будет как
бы оставаться постоянным. В действи¬
тельности он, конечно, будет менять¬
ся, но изменения его будут весьма
малыми, что показывает нам уравне¬
ние 287.
Далее, угловая скорость медлен¬
ного конического движения оси сна¬
ряда выражающаяся формулой 289,
может рассматриваться как скорость
псевдорегулярной прецессии. Из этой
формулы видно, что скорость медлен¬
ного конического движения для рас¬
сматриваемой задачи пропорциональна
опрокидывающему моменту М и обратно пропорциональна угловой
скорости собственного вращения />0, аксиальному моменту инерции
снаряда А и углу отклонения 8>
29. Наибольшая угловая скорость оси снаряда на
начальном участке траектории.
При проектировании снарядов, трубок и взрывателей иногда
необходимо бывает подсчитать те силы инерции, которые возникают
в отдельных деталях по отношению к снаряду вследствие колебаний
оси снаряда. Так как наибольшие колебания ось снаряда испыты¬
вает на начальном участке вследствие ударов как со стороны ору¬
дия, так и со стороны пороховых газов, то вполне рационально
будет воспользоваться теми формулами, которые мы вывели в пара¬
69
288
Последнее выражение, если принять во внимание, что
можно представить в следующем виде:
графе 27. Допущение относительно прямолинейности трлектории и
равномерности движения для начального участка являются вполне
допустимыми.
Для отыскания наибольших ускорений, которые могут иметь от.
дельные детали в относительном движении по оси снаряда, восполь¬
зуемся обычной формулой осестремительного ускорения
290
где через Qm обозначена наибольшая угловая скорость оси снаряда
, . С£, а через L — расстояние рас¬
сматриваемой детали, располо¬
женной на этой оси, от центра
инерции снаряда (черт. 290).
Угловая скорость оси сна¬
ряда Q определяется как гео¬
метрическая сумма проекций
угловой скорости ю на две дру¬
гие главные оси, неизменно евр-
Jfl и .1
(214)
70
Черт. 290.
заниые со снарядом. Эти проекции соответственно равны
Следовательно,
откуда
Но так как
Рассматривая уравнение 276
б
мы замечаем, что выражение —0 представляет собою не что иное
как наибольшую величину, которую может принять угол отклоне¬
ния 8 при atn (aot) = 1. Обозначим эту величину через дЛ1:
Тогда
Из уравнения 278 имеем
Подставляя полученные выражения для §, 5' и v' в уравнение 292,
получим:
Для определения наибольшего значения Q применим обычный
метод, т. е. найдем производную от Q2 по времени:
Приравняв эту производную нулю и решив полученное уравне*
ние относительно t, найдем:
Для того чтобы определить, который из этих корней отвечает
максимуму, найдем от Q2 вторую производную
и подставим в нее значения tml и tmV Вторая производная будет
отрицательна при tm2. Следовательно, максимуму отвечает значение
Подставляя это выражение в уравнение 294, получим после про¬
стого преобразования
Теперь подставам 0?т в первоначальное уравнение 290. Тогда вы¬
ражение для максимального осестремительного ускорения jm будет
иметь следующий вид:
или, поскольку
Из этой формулы видно, что особо важное значение для jn
имеет наибольшая величина угла отклонения Ьм, за уменьшение
которой надо всемерно бороться. Величина Ьм определяется из
опыта стрельбой по картонам
71
3. ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ПОСЛУШНОГО СНАРЯДА
ПОД ДЕЙСТВИЕМ ОДНОГО ОПРОКИДЫВАЮЩЕГО МОМЕНТА
ПРИ ПРЯМОЛИНЕЙНОМ ГОРИЗОНТАЛЬНОМ, НО НЕРАВНО¬
МЕРНОМ ДВИЖЕНИИ ЦЕНТРА ИНЕРЦИИ.
30. Основные допущения.
В настоящей главе мы будем рассматривать движение послуш¬
ного снаряда около его центра инерции под действием одного
опрокидывающего момента при прямолинейном, горизонтальном, но
неравномерном движении центра инерции.
Сравнивая условия настоящей задачи с условиями задачи, изло¬
женной в главе 2, мы видим, что единственное условие, которое
в настоящей задаче является новым, заключается в неравномерности
движения.
Итак, скорость центра инерции v теперь будет величиной пе¬
ременной; переменной, следовательно, будет и величина
Переменным будет и коэффициент гироскопической устойчивости з,
ранный попрежнему
При этом, поскольку скорость снаряда v по мере его движения по
прямолинейной горизонтальной траектории будет убывать, величина $
будет также убывать, а величина коэффициента гироскопической
устойчивости а — увеличиваться.
В остальном все условия остаются идентичными условиям пре¬
дыдущей главы.
31. Уравнения вращательного движения снаряда около его
центра масс и приближенный метод их интегрирования.
Так как настоящая задача отличается от предыдущей только
тем, что величина Р из постоянной превратилась в переменную, то
дифференциальные уравнения движения снаряда около его центра
инершш будут иметь тот же самый вид, как и в главе 2 (220—222),
а именно:
300
входящая в выражение олротдывающего момента
301
302
310
72
причем первое уравнение будет определять вращение снаряда около
его оси симметрии, а два других — движение самой оси симметрии
снаряда.
Для одновременного интегрирования обоих последних уравнений
введем, как и в параграфе 23, комплексную переменную
что позволяет оба эти уравнения заменить одним уравнением, им
эквивалентным:
или
311
На этом сходство рассуждений с предыдущей главой кончается.
Если раньше мы имели линейное дифференциальное уравнение вто¬
рого порядка с постоянными коэффициентами, которое могло быть
проинтегрировано, то теперь мы имеем такое же дифференциальное
уравнение, но с переменными коэффициентами, вследствие чего в
конечном виде это уравнение проинтегрировать нельзя.
Вследствие невозможности решить это уравнение точно, во внеш¬
ней баллистике решают его приближенно различными способами,
Из этих способов мы остановимся на классическом методе де-Сларра,
сущность которого состоит в разложении искомой функции в ряд,
расположенный по отрицательным степеням параметра а.
Для интегрирования уравнения 311 прежде всего, упростим его
при помощи введения переменной С» определяемой из-условия
312
Тогда
и уоавнение 311 поймет вид
или после сокращения на еш и приведения пфдобных членов
Для того чтобы найти интеграл этого уравнения, положим
313
где а и -се» являются функциями времени, причем одна из этих
функций, например w, может быть подчинена произвольному усло¬
вию. Тогда
или, после сокращения на elw,
314
Подчиним теперь функцию w условию, обращающему в нуль
последних члена этого уравнения.
t
Подставляя значения wf и w" в уравнение 314, получим
316
Для приближенного интегрирования этого линейного дифферен¬
циального уравнения с переменными коэффициентами представим
общий интеграл рассматриваемого уравнения в виде ряда, располо¬
женного по отрицательным степеням параметра а, который, как. мы
уже видели ранее, имеет достаточно большую величину при большой
скорости собственного вращения снаряда в момент вылета. Получим
где а0, uv я2,... являются также функциями времени. В соответ¬
ствии с последним уравнением
Подставляя а, и', а" в уравнение 316, получим
Так как полученное уравнение должно быть справедливым при
любых значениях параметра а, то суммы коэффициентов при одина¬
ковых степенях а должны равняться нулю, т. е.
Из первого уравнения определяем «0:
откуда после интегрирования получим
74
Произвольные постоянные мы введем при окончательном выражении
интеграла.
При достаточно большом а можно принять
318
Для Z, согласно выражению 312, получим
или
Введем теперь в это выражение величины
Тогда окончательно
* *
319
32. Уравнения движения оси снаряда.
В предыдущем параграфе нами был приближенно найден общий
интеграл уравнения 311, содержащий две постоянных интегриро¬
вания С, и Сг. Так как Z является комплексным числом, то и Ct и Сг
должны быть также комплексными. Поэтому мы можем, присоеди¬
нив к ним множитель —]= , изобразить их следующим образом:
Vo
При этом обратим внимание, что величины pz и рг в настоящей за*
даче будут уже не постоянными, а переменными, изменяющимися
73
Тогда в соответствии с выражениями 313, 315 и 317
Подставляя полученные значения kt и kr в выражения для pt и рг,
будем иметь окончательно:
320
321
76
обратно пропорционально
где kt и кг являются некоторыми постоянными коэффициентами
пропорциональности.
Обозначая значения в, pt и рг, отвечающие начальному моменту
(/=0), через <70, р10 и р,0, мы можем написать:
Теперь возвратимся к уравнению 319 и заменим в нем постоян¬
ные интегрирования Ct и Сг их выражениями через plt и рг, фг.
Тогда уравнение- 319 примет вид
или, так как eh = cos a -f- i sin а,
Сопоставляя полученное выражение с первоначальным—
мы можем написать окончательно:
322
77
Сравнивая эти выражения с выражениями 236 и 237, мы видим
что разница заключается только в том, что в настоящей задаче р,,
рг> со, и (Dr являются не постоянными, как раньше, а переменными
величинами.
Для определения величин pz, pr, «J>i и <|>г напишем выражение
для и $2* имея в виду, что рi и рг являются величинами пере¬
менными, равными, согласно уравнениям 320,
Тогда мы будем иметь:
323
78
или, замечая, что в фигурных скобках стоят выражения 5j и
Положим, что в момент вылета, т. е. при ^ = 0
Обозначим значения a, o', р/? pr, wlt <аг, соответствующие точке
вылета, через а0, о0, р/0, pr0, (0/0, <ог0. Подставляя эти значения в
уравнения 321 и 323, получим
Определяя из первого уравнения coscj^ и подставляя полученное
значение в четвертое уравнение, найдем cosc{>r^
Найденное выражение coscp^ подставим в уравнение для coscp,,
которое после всех необходимых преобразований будет иметь сле¬
дующий вид:
Далее таким же образом определяем sin ^ и sin <J>r из второго и
третьего уравнения нашей системы:
326
327
Таким образом все постоянные величины, входящие в систе¬
му 321, определены в зависимости от начальных условий.
Кроме углов де-Спарра, bt и д2, движение оси снаряда может
быть выражено в углах Эйлера i и v на основании уравнений 203
и 204. Из уравнения 203
«2 = 8? 4- af,
имеем
79
Теперь мы можем найти p/о» возводя выражения для sin и
cos Фг в квадрат и суммируя:
Подобным же образом из выражения для sin фг и cos находится
выражение для рг0
Сводя все полученные выражения в систему, будем иметь
и окончательно
328 3 =
Из уравнения 204 получаем
33. Исследование уравнений движения оси снаряда.
Исследуя уравнения 321, определяющие движение оси снаряда,
мы видим, что так же, как и в параграфе 25, движение оси снаряда
может быть разложено на два конических движения. Новым по
сравнению., с предыдущей главой является то, что в данном случае
как угловые скорости конических движений (о( и <ог, так и радиусы
оснований pj и рг будут не постоянными, а переменными.
Первое из этих конических движений, а именно, медленное,
с угловой скоростью G)j = a(l—а) и радиусом-вектором основания
Таким образом
80
определяется первыми членами уравнения 321:
Второе коническое движение, быстрое, с угловой скоростью
и радиусом-вектором основания [
ределяется вторыми членами этих же уравнений:
гг е. движение оси снаряда может рассматриваться как быстрое ко¬
ническое движение около псевдооси снаряда, которая в свою оче¬
редь совершает медленное коническое движение около касательной
к траектории центра инерции
снаряда.
Проектируя движение
конца оси снаряда и конца
псевдооси или оси быстрого
конического движения на
плоскость, перпендикулярную
к касательной к траектории*
таким же образом, как мы
это делали в параграфе 25,
мы будем иметь для ме¬
дленного коническо¬
го движения картину,
изображенную на черт, 330
и представляющую собою
траекторию проекции, конца
псевдооси снаряда (Ьг) в виде
спирали с радиусом-вектором
330
332
и угловой скоростью
81
Черт. 330.
и угловой скоростью
Так как о с течением времени
увеличивается, то и и
будут уменьшаться.
Для быстрого ко¬
нического движения
мы будем иметь картину, изо¬
браженную на черт. 331
и представляющую собою
траекторию проекции конца
оси сна ряда/Cj вотносительном
движении около псевдооси опять в виде спирали с радиусом- вектором
Черт. 331.
следовательно
показывающее, что отношение между переменными радиусами
медленного и быстрого конического движения остается постоянным
в продолжение всего движения. Следовательно, в случае, когда
Рм<СР/-э и pw — prt, характер эпициклоиды будет все время оста¬
ваться неизменным, т. е. эпициклоида все время будет удлиненной
как и была в начале движения.
Для случая необходимо проследить изменение отноше¬
ния между угловыми скоростями медленного и быстрого конических
движений, равного
335
Это отношение, как видно из формулы 335, с течением времени,
82
Так как о является возрастающей функцией, то рг будет умень¬
шаться, а (йг увеличиваться.
В результате сложения этих двух движений — относительного
©коло точки L^, по спирали с радиусом-вектором рг и угловой ско¬
ростью о)^ и переносного вместе с точкой Lv около точки Сх по
спирали с радиусом-вектором
р, н угловой скоростью Юр
по схеме, изображенной на
черт. 332, —мы получим кри¬
вую эпициклоидального типа,
причем характер этой эпи¬
циклоиды будет не постоян¬
ным, а будет изменяться в
связи с изменениями pz, рг,
ы(, (ог. Величины ф, и
никакого влияния на,форму
кривой иметь не будут.
Первое заключение, ко¬
торое мы можем вывести из
наблюдений за изменением р1
и рг в настоящей задаче,
состоит в том, что с тече¬
нием времени и медленное,
и быстрое конические дви¬
жения затухают, и снаряд делается все более и более послушным.
Далее, имея в виду, что pz=p,0 — и pr=pfe мы мо¬
жем написать следующее очень интересное выражение:
Черт. 332,
т. е. с увеличением а, будет уменьшаться вследствие уменьшения
числителя и увеличения знамена геля. Следовательно, уменьшаться
будет и отношение
Таким образом для случая р/0 р^ мы будем иметь определенное
стремление эпициклоиды, описываемой концом оси снаряда, перейти
в удлиненную, при общей тенденции угла отклонения 8 к уменьше¬
нию по абсолютной величине.
Итак, суммируя эти выводы, мы можем сказать, что во всех слу¬
чаях, когда в начале движения эпициклоида, описываемая проек¬
цией конца оси снаряда на плоскости изображения, является удли¬
ненной, она таковой и продолжает оставаться. Нормальная и укоро¬
ченная эпициклоиды с течением времени превращаются в удлиненную.
В заключение настоящего параграфа остановимся еще на вели¬
чине
же в целый ряд других формул, и характеризует изменение коэф¬
фициента гироскопической устойчивости о с течением времени.
Найдем производную от по времени
по аналогии с функциями, характеризующими зависимость лобового
сопротивления воздуха от скорости, получим:
836
которая входит в выражения для производных р/ и р, (332), а так-
или
Вводя обозначения
338
или, пользуясь обычной формулой основной задачи внешней балли-
83
стики для случай прямолинейной горизонтальной траекторий v'=—Jy
где
В данном случае Н{у)—\ и
E = cG(v).
Подставляя ft в формулу для (In V<з)\ будем иметь
или после подстановки р = а2(1—а2)
339
Из этой формулы видно: 1) что с течением времени коэффициент
гироскопической устойчивости увели-швается (о' 0), 2) что изме¬
нение коэффициента гироскопической устойчивости а происходит
тем быстрее, чем меньше при той же скорости- снаряда будет его
величина.
Начальное значение (1а]/а)о, входящее в выраяйния 324—327,
равно
34. Движение оси снаряда при отсутствии начального ума
отклонения и ударов в момент вылета*
Рассматривая вылет снаряда при строгое совпадения ос» снаряда
с вектором тачальной скорости, т. е. при
340 *м=0, «*.=#,
и при отсутствии каких бы то ни было ударов при вьпете, т. е. при
341 $jo = 0 ^20—
и, подставляя затем эти значения Ьи, dio, §20 в уравнения для
р/й (324) и для рГв (325), лолучим
342 Ь=°- Ргв — °
и далее, на основании выражений 330 и 332,
343
Тогда из уравнений 321; будем иметь
344
84
а из уравнения 203
345
Кроме того, из уравнения 220
подставляя в него §2 = 0, получим
Таким образом у нас получились те же самые результаты, как и
в параграфе 26. Следовательно, ось снаряда, вылетевшего без на¬
чального угла отклонения и без ударов в момент вылета, в про¬
должение всего движения его, центра инерции по прямолинейной
горизонтальной траектории будет совпадать с траекторией, а угло¬
вая скорость вращения снаряда около этой оси будет оставаться
постоянной.
35. Движение оси снаряда при отсутствии начального угла
отклонения, но при наличии ударов в момент вылета.
Предположим, что в момент вылета снаряду, ось которого со¬
впадает с касательной к траектории центра инерции (10 = 0), нане¬
сен удар, т. е. сообщена угловая скорость §о в некоторой плоскости,
составляющей угол v0 с вертикальной плоскостью, проходящей
через касательную. Тогда
Так как в данном случае, в соответствии с уравневдами 351,
ТО
Подставляя значение р<9 и выражения для р^ЗЗО) и р,.(332)
получим
Подставляем &10, 3^, $нь $20 в уравнения 324 и 325:
Находим теперь ф, и фг, пользуясь системами 326 и 327 и имея в
виду равенства 352 и 351:
или
355
или
356
86
Из этих равенств следует, что
Подставим значения для plt рг, <pJf с|>г в общие уравнения 321:
Для установления характера движения обратим внимание на то,
что р/—рг* Следовательно, движение проекции конца оси сна¬
ряда происходит по удлиненной эпициклоиде, проходящей че¬
рез центр С’| при постепенном уменьшении и и р, (черт. 350,
351, 352)
или окончательно
Черт. 350.
Черт. 351.
Выразим теперь аналитически это же движение при помощи
параметров § и v на основании уравнений 328 и 329, имея в виду,
что
s
Переходим к определению V, имея в виду, что tgv = =£,йполь-
зуясь непосредственно уравнением 356’
359 V' = a.
Рассматривая эти выражения, мы видим, что здесь, как и в слу¬
чае равномерного движения центра инер¬
ции снаряда (§27), мы имеем равномерное
вращение плоскости действия опрокиды¬
вающей пары около прямолинейной траек¬
тории с угловой скоростью
v' = a,
т. е., иначе говоря, мы имеем равномерную
прецессию.
Изменение угла Ь (нутация) также бу¬
дет происходитьпосинусоидальной кривой
с той только разницей, что амплитуда ко¬
лебания оси снаряда по углу Ь будет с
течением времени уменьшаться.
Период нутации Т. определится из условия
88
Черт. 352.
Счедовательно,
поело вынесения о из под знака интеграла средним значением оср:
причем Ду также убы- 0
вает, стремясь при
с—* 1 к 2п. Черт. 353.
Изменение углов прецессии и нутации изображено на черт. 353.
36. Движение оси снаряда при наличии начального угла
отклонения, но при отсутствии ударов в момент вылета.
Предположим теперь, что в момент вылета снаряд имеет неко¬
торый угол отклонения §0 в плоскости, составляющей с вертикаль¬
ной плоскостью, проходящей через касательную к траектории,
угол v0, но зато никаких ударов ии со стороны орудия, ни со сто¬
роны пороховых газов не испытывает. Тогда
Подставляя эти значения в уравнения 324 и 325, после преоб¬
разований, мы будем иметь
362
Подставляя далее значения р№ и в выражения для р, и рг
(330, 332) и заменяя (ш^ — <ог0) через 2аа, получаем
363
89
Из этой формулы видно,
что с течением времени
Ть также уменьшается.
За время Ть угол
прецессии v увеличи¬
вается на величину
Находим теперь ф; и фг, пользуясь системами 32G и 327 и
сокращая в числителе и знаменателе множитель (<i>r0 — <о/0):
причем определение того, в какой чет¬
верти расположены данные углы, целе¬
сообразно производить цо знаку числи¬
теля, который в формуле для tg ф,
одинаков со знаком sine}),, а в фор¬
муле для tg с|> противоположен знаку
sin фг.
Для .того, чтобы установить характер движения, заметим прежде
всего, что
366
Теперь нам надо установить взаимоотношение между величинами
(Pi^i) и (рг«>г). Так как в параграфе 33 нами было установлено, что
с течением времени отношение уменьшается, то, прежде
всего, нужно найти начальное значение этого отношения:
Итак, в начале движения
368
9Q
В данном случае более удобно выразить ф, и фг через тангенсы:
так как согласно формулам 363
и эпициклоида, описываемая проекцией конца оси снаряда, будет
удлиненной; следовательно, в соответствии с рассуждениями пара¬
графа 33, эпициклоида будет оставаться удлиненной и'в дальней¬
шем при общей тенденции к затуханию как медленного, так и
быстрого конических движений, т. е.
369 P/w/<Pr<V
Кривая, описываемая проекцией конца оси снаряда на плоскости
изображения, будет иметь вид, изображенный на черт. 360, 361,
362.
37. Коэффициент гироскопической устойчивости.
В параграфе 30 мы уже установили, что коэффициент гироско¬
пической устойчивости
370
в условиях настоящей задачи является переменной величиной, уве¬
личиваясь по мере движения снаряда по «прямолинейной траектории.
Напишем теперь его выражение в развернутом виде, заменяя
а и р их выражениями. Для Р мы имеем уравнение 300:
371
Что же касается а, то для нее мы воспользуемся обычным выра¬
жением 121:
372
при допущении о том, что
373
которое мы уже применяли в параграфе 15. Тогда, после простых
91
4. ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ПОСЛУШНОГО СНАРЯДА
ПОД ДЕЙСТВИЕМ ОДНОГО ОПРОКИДЫВАЮЩЕГО МОМЕНТА
ПРИ КРИВОЛИНЕЙНОМ ДВИЖЕНИИ ЦЕНТРА ИНЕРЦИИ
В ПЛОСКОСТИ БРбСАНИЯ.
40. Основные допущения и определения.
В предыдущих главах мы рассматривали вращательное движение
снаряда при прямолинейном движении его центра инерции. Сейчас
мы переходим к изучению вращдтельного движения снаряда для
случая криволинейной траектории его цеитра инерции, расположен¬
ной в одной плоскости, а именно, в плоскости бросания. При этом
все величины, относящиеся к траектории центра инерции, мы будем
92
преобразований под знаком корня, получим
Заменяем теперь аксиальный момент инерции А, находящийся
в знаменателе, его выражением через коэффициент веса k и
аксиальный коэффициент инерции ]х (153): 9
Тогда в окончательном виде мы будем иметь
Наименьшее значение коэффициента гироскопической устойчи¬
вости в условиях настоящей задачи будет - отвечать наибольшему
значению v, а именно v0, т. е. точке вылета.
Таким образом наиболее трудные условия в отношении гироско¬
пической устойчивости снаряд будет иметь в точке вылета, а сле¬
довательно, при расчете снаряда в условиях настоящей задачи
прежде всего необходимо определить начальное значение коэффи¬
циента гироскопической устойчивости а0, равное
Сравнивая это выражение с выражением 158, отвечающим равно¬
мерному движению центра инерции по прямолинейной горизонталь¬
ной траектории, мы видим, что они совершенно идентичны.
в случае надобности брать непосредственно из основной задачи
внешней баллистики.
Снаряд попрежнему будем считать послушным, т. е. имеющим
малые углы отклонения 8 на всем протяжении траектории, и гиро¬
скопически устойчивым, т. е. удовлетворяющим условию
о2> 0.
При определении положения снаряда или неизменно связанной
с ним системы C'StjC относительно постоянно ориентированной в прост--
Черт. 400.
ранстве системы Cx1y1z1, поступательно перемещающейся с центром
инерции С, новым явлением будет наличие в вертикальной плос¬
кости Сх0>л угла 0 между осью Схл и касательной к траекто¬
рии центра инерции, которую мы назовем осью Сх2 и по кото-
93
рой мы отложим вектор скорости центра инерции снаряда v
(черт. 400, 401, 402).
В задачах, рассмотренных в предыдущих главах, вследствие пря«
молинейности и горизонтальности траектории, касательная к траек¬
тории и сама траектория совпадали с осью Cxlt на которой и был
расположен вектор скорости v.
Положение снаряда относительно касательной к траектории мы,
как и в главе 2, будем определять при помощи углов де-Спарра
8,, Ьг и V
Переход от постоянно ориентированной в пространстве системы
Cxlylzl к системе С£г(С, неизменно связанной со снарядом, будет
происходить следующим образом:
94
Черт. 401.
1) Вращение по углу 0 около оси Czt / 0СЬ Сх* пеРех0ДНТ в Сх^
\ ось Су j переходит в Су,.
2) Вращение по углу § около осн qz / ось Сх% переходит в Cxtt
[ ось Су2 переходит в Су3.
3) Вращение по углу 8 около оси Суг ( 0СЬ Сх* пеРеходит в
( ось Czj переходит в Czj.
4) Вращение по углу к около оси ct / ось СУ* переходит в Су
[ ось Сг2 переходит в СС.
$
Черт. 402.
Соответствующие угловые скорости отложены: в' по оси Сг,; Si
тоже по осиСГ!; $2 по осиСуз; S3 по оси С$, причем направлены по
этим осям они должны быть в ту сторону, откуда соответствующие
вращение будет казаться происходящим против часовой стрелки.
95
Полная угловая скорость снаряда to будет равна геометрической
сумме четырех указанных угловых скоростей 81, 82 и §з-
При этом угловая скорость 6' характеризует движение касательной
к траектории, угловые скорости 81 и 02— движение оси сна¬
ряда относительно этой касательной, а угловая скорость 83— вра¬
щение снаряда около его оси.
Так как угловые скорости 9' и 81 расположены на одной
оси, то их геометрическая сумма равна алгебраической, а потому
полную угловую скорость со можно рассматривать как геометриче¬
скую сумму только трех угловых скоростей (O' —$1), 82 и S3,
т. е.
Последнее обстоятельство, между прочим, является весьма важным
преимуществом системы углов де-Спарра §2? й3 перед системой
Эйлеровых углов V, 8, ср, пользуясь которыми мы обязательно должны
были бы иметь для перехода от системы Cx1ylzl к. системе Clrt°
в случае криволинейной траектории четыре вращения около четы¬
рех различных осей.
Вектор, изображающий опрокидывающий момент М, будет
направлен так же, как и раньше, по перпендикуляру к плоскости
действия опрокидывающей пары Сх2$, т. е. по оси Cz2, в ту сто¬
рону, откуда угол 8 будет казаться отложенным против часовой
стрелки.
Величина опрокидывающего момента М так же, как и в гла¬
вах 2 и 3, будет равна
402 M =
поскольку углы отклонения § будут малыми.
Что же касается величины р, то в соответствии с общим выра¬
жением 017 она будет равна
403
Обратим внимание их на то, что поскольку траектория является не
горизонтальной, в выражении для р фигурирует Н ( v).
Величина р так же, как и в главе 2, является переменной, но
характер ее изменения будет уже иной. Если в главе 3 величина Р
все время убывала, то в условиях настоящей задачи р будет сна¬
96
чала убывать до некоторой точки на нисходящей ветви траектории
(эта точка расположена между вершиной и точкой, отвечающей
наименьшей скорости), а затем снова возрастать. Причина этого
лежит, в характере изменения функции Н (у), имеющей наименьшее
значение в вершине, и скорости v, имеющей минимум на., нисходя¬
щей ветви траектории.
Естественно, что переменным будет и коэффициент гироскопи¬
ческой устойчивости а = j/~ 1 — > который в соответствии с из¬
менением [5 будет увеличиваться до точки, отвечающей минимуму [5,
а затем уменьшаться.
41. Уравнения вращательного движения снаряда около его
центра инерции.
Так как настоящая задача отличается от предшествующей только
тем, что касательная составляет с осью Схх угол 0 и что вместо
угловой скорости Si мы имеем угловую скорость (Ь' —{— §i), то нам
нет надобности снова повторять все промежуточные рассуждения.
Напишем сразу окончательное выражение для проекций угловой ско¬
рости р, q и г и для кинетической энергии Г, заменяя в формулах
214 и 215 величину суммой (6' —|— §1):
Составляем теперь уравнения Лагранжа, принимая попрежнему за
обобщенные координаты углы §3, §2 и
Для параметра 83 имеем
410
412
97
причем первое уравнение определяет вращение снаряда око то его
оси симметрии а два других — движение оси снаряда относительно
касательной Движение касательной определяется обычным уравне¬
нием из основной задачи внешней баллистики
416
Для одновременного интегрирования двух последних уравнений
системы 415 введем, как и раньше комплексную переменную
и окончательно
и окончательно
Сводя все три выведенные уравнения в систему, получим
Это уравнение представляет собою линейное дифференциальное
уравнение второго порядка с переменным коэффициентом а2( 1—а2)
и с последним членом ( — 0"-|-2/а6'). Общий интеграл рассматри¬
ваемого уравнения будет поэтому равен сумме - общего интеграла
этого уравнения без последнего члена и частного интеграла полного
уравнения (с последним членом).
42. Общий интеграл уравнения без последнего члена.
Приступая к отысканию общего интеграла уравнения 419, но
без последнего члена, т. е. к интегрированию уравнения
420
мы видим, что это уравнение совершенно одинаково с уравне¬
нием 311, причем как в том, так и в нашем случае коэффициент a
является переменным. Разница имеется только в характере изменения а.
Поэтому, не повторяя рассуждений параграфов 31 и 32, мы
прямо напишем окончательные результаты, не упуская из виду, что
интегрирование уравнения 311 было произведено приближенно.
Итак, переписываем уравнения 319, 321 и 320:
421
422
где
423
Исследуя эти уравнения сравнительно с уравнениями главы 3,
“ч замечаем, что на восходящей ветви характер изменения pz, рг,
wj и остается таким же, как и в случае прямолинейной траекто-
7* 99
С этой целью к третьему уравнению этой системы прибавим второе,
умноженное на i:
или, после подстановки
рии. На нисходящей же ветви, от точки, где (5 имеет мини¬
мум, и далее, р начинает возрастать, а убывать, следовательно,
рг и рг будут возрастать, (о1 также будет возрастать, а <ог начнет
убывать.
43. Частный интеграл полного дифференциального уравнения.
При определении частного интеграла полного уравнения 419,
который мы обозначаем через Zp, будем искать его в виде ряда,
расположенного по отрицательным степеням параметра а:
430
Подставив это выражение для Z в уравнение 419, получим
Z
и.
Так как полученное равенство должно быть справедливо при лю¬
бых значениях а, то коэффициенты при одинаковых степенях а
в правой и левой части уравнения должны быть равны между собой.
Отсюда имеем уравнения
Решая эти уравнения, находим последовательно Z0, Zx, Z2, ... Из
первого уравнения имеем
из второго после подстановки Z„ = 0 получаем
. г р
В третье уравнение подставим Zo = 0 и выражение для Zi, которое
мы найдем, предварительно прологарифмировав последнее уравнение:
Так как Ър является комплексной величиной, равной
433
или, после подстановки вместо Ъх его выражения,
Тогда третье уравнение примет вид
Рассматривая выражения для Z0, Ъх и Z2, замечаем, что Z0 равно
нулю, Zj является мнимой величиной, a Z2 вещественной.
Подставляя эти значения в выражение для частного интеграла 430
и ограничиваясь в первом приближении только членами, содержа¬
щими от1 мы будем иметь
Подставим в полученную систему
то в первом приближении
432
431
Тогда уравнения 432 принимают другой вид:
Если же в выражении для частного интеграла взять на один
член болЬше, т. е. ограничиться членами, содержащими а-2, то мы
получим более точное решение, а именно:
или
1-а2=Д.
Тогда
Последние выражения удобнее представить в следующем виде:
Для преобразования полученных выражений найдем [1л (—
и [lnfl—о2)]', имея в виду, что
Второй член нами, был уже определен в параграфе 33 и согласно
уравнениям 337 и 338 равнялся
Что же касается первого члена, то, пользуясь для Н(у) показа¬
тельным законом
или окончательно
*) Окунев Б. Н« Внешняя и внутренняя баллистика, 1930, I, 5017,
§020.
|03
Теперь находим
мы получим
Итак,
Подставляя полученные величины в выражение для Я (437), будем иметь
Заменим в формуле для Р величины 0 , v и у' их выражениями
в соответствии с уравнениями основной задачи внешней бал¬
листики *):
Величина /г, представляющая собою ускорение лобового сопро¬
тивления воздуха, равна
Теперь мы будем иметь
Выражения 436 могут быть представлены окончательно в сле¬
дующем виде:
440
где Z можно выразить или формулой 431 или, более точно, фор*
мулой 434.
Переходя к определению величин и $2, мы мож&м, соответ¬
ственно у^вненшо 440 и на основании выражения 421, написать:
441
442
44. Общий интеграл полного дифференциального уравнения.
В соответствии с выводами параграфов 42 и 43, общий интеграл
полного дифференциального уравнения 419
где 6ip и 62р попрежнему могут быть определены и^и по форму¬
лам 4Ь2, 433, или более точно — по формулам 436, 439.
Для определения величин р,, рг, ф;, фг применим метод, анало¬
гичный использованному в параграфе 32. Для этой цели перенесем
в левую часть выражений ^ и 32 и их производных
непериодические члены bipt hp и члены, содержащие
104
Сравнивая эти выражения с выражениями 321 и 323, мы ви¬
дим, что разница между ними заключается только в замене
величии и §2 в левой части уравнений на величины (§j — Sj_) и
(S2 &2р)-
Следовательно, повторять всю цепь рассуждений и выкладок не¬
целесообразно, так как можно непосредственно написать оконча¬
тельные выражения, производя указанные замены в формулах 324—
327. Б результате получим
443
444
446
Выражения для р,0 и рг0 удобнее представить в следующем виде:
446
где
447 {
При 3^ = 0
В этом случае
!
448 {
Ч20 же касается величин рг и рг, то, как мы видели в пара¬
графе 42, они могут быть определены через рг0 и рг0 так же, как
и в предыдущей главе:
449
Общих выражений для S и v в данной задаче мы выводить не
будем вследствие нецелесообразности непосредственно пользовать¬
ся довольно громоздкими формулами. В случае надобности мы
всегда можем легко вычислить § и V, исходя из зависимостей 203
и 204;
103
45. Исследование уравнений движения осй снаряда.
Рассматривая уравнение 441, определяющее движение оси сна¬
ряда, мы видим, что по сравнению с предыдущей главой у нас
кроме периодических членов появились еще и непериодические ЬХр,
Ь2р> определяемые характером траектории центра инерции или, точ¬
нее, характером изменения угла наклона касательной 6 (см. уравие-
ния 432, 433, 436, 437).
Таким образом конические движения оси снаряда, которые в случае
прямолинейной траектории происходили около касательной к тра¬
ектории центра инерции снаряда, для криволинейной траектории будут
совершаться около некоторой другой оси, определяемой по отношению
к касательной углами Ь1р и Ь2р. Эта ось по предложению француз¬
ского ученого Эсклангона называется динамической осью.
Итак, общая схема явления может быть представлена следующим
образом. Ось снаряда совершает быстрое коническое движение
с угловой скоростью в>г и радиусом-вектором основания рг около
псевдооси снаряда. Псевдоось снаряда в свою очередь совершает
медленное коническое движение с угловой скоростью со, и радиусом*
вектором основания р, около динамической оси. Динамическая ось
составляет с касательной угол
который мы будем называть динамическим углом; при этом
плоскость, проходящая через касательную и динамическую ось, будет
составлять с вертикальной плоскостью, проходящей через касатель¬
ную, угол v„, определяемый из условия
45!
Итак, положение динамической оси определяется первыми непе¬
риодическими членами выражений 441: Ь1р и bip.
Медленное кон-ическое движение определяется вторыми членами:
Быстрое коническое движение определяется третьими членами:
450
452
453
107
Рассмотрим теперь движение проекций концов оси, псевдооси
и динамической оси снаряда на плоскость, перпендикулярную к ка¬
сательной к траектории, т. е. на плоскость изображения.
Начнем с непериодического движения. Проекция конца динами¬
ческой оси в каждый данный момент будет изображаться точкой
с координатами = $1р и да = §2„, определяемыми из уравне*
ний 433:
или более точно из уравнений 439:
где, в соответствии с выражением 438,
В обоих случаях Ьу, одинаково и, как мы в^дим из формул,
играет главную роль. Ввиду того, что все величины, входящие
в выражение для 8* , являются положительными на всем протяжении
траектории,
т. е. динамическая ось в продолжение всего движения снаряда
по траектории будет отклонена вправо, если смотреть на
движущийся снаряд сзади.
Что же касается Ь1р, то, рассматривая его выражение (439), мы
убеждаемся, что на восходящей ветви, где tg 9, а следовательно,
и Р больше нуля, эта величина будет, безусловно, положительной.
На нисходящей же ветви Ь1р может сделаться отрицательным тогда
и только тогда, когда tg 0, являясь отрицательным и увеличиваясь
по абсолютной величине по мере движения снаряда на нисходящей
ветви, начнет удовлетворять условию
/ ft \
ули sin 9 — усдовик)
108
Таким образом,
454
Следовательно, на восходящей ветви траектории динамическая ось
всегда будет расположена выше касательной, на нисходящей же
ветви в отдельных случаях (доволь¬
но редких) она может с некото¬
рого момента перейти под каса¬
тельную.
При этом необходимо отметить,
что абсолютная величина малого
угла Ь1р во всех случаях безусловно
будет меньше величины малого
угла Ь^р, являясь по отношению
к этой последней величиной вто¬
рого порядка малости, что не¬
посредственно видно из формулы
для Ь1р.
Обозначая конец динамической оси через D, а его проекцию
через Dv мы получим картину, изображенную на черт. 450.
Переходя к изображению проекций движения концов псевдооси
снаряда Lx и оси снаряда мы получим ту же самую картину,
как и в главе 33, с той только разницей, что спиральное движение
точки Lx будет происходить не около точки Сх, а около точки Dx
(черт. 451, 452).
Радиусы-векторы оснований и угловые скорости медленного
и быстрого конических движений попрежнему будут определяться
формулами
455
456
Обратим внимание, что в отличие от рассуждений параграфа 33,
где мы вследствие прямолинейности и горизонтальности траектории
имелй' постоянное возрастание а, в настоящей задаче, как мы уже
отмечали в параграфе 40, о будет сначала увеличиваться до той
точки, где величина fi будет иметь минимум, а затем снова умень¬
шаться.
Черт. 450.
шаться.
109
Итак, окончательно
Таким образом, до точки, отвечающей минимуму р, величина о
увеличивается, р„ <•>, и р, уменьшаются, а <ог увеличивается.
После этой точки о
уменьшается, рг, юг и рг
снова начинают увеличи¬
ваться, а юг уменьшаться.
В результате сложения
непериодического движе¬
ния и двух периодических
движений по схеме, изо¬
браженной на черт. 453,
мы получим на плоскости
изображения кривую эпи-
циклоидального типа с по¬
стоянно смещающимся
центром, причем характер
ее будет меняться в связи
с изменением рг, рг, ©г,
Величины и фг так же,;
как и раньше, никакого
влияния на форму кривой
оказывать не будут.
Наблюдая за измене¬
нием рг и рг в настоящей
задаче, мы видим, что зату¬
хание медленного и бы¬
строго конического дви¬
жения будет иметь место
только до той точки тра-'
ектории, где р имеет ми¬
нимум.
Соотношение между
переменным радиусом ме¬
дленного и быстрого кони*
ческих движений остается,
так же как и в предыду¬
щей главе, постоянньци:
457
Соотношение же между линейными скоростями точки в медленном
и точки Кх в быстром спиральном движении, которое выражается
так же, как и параграфе 33, формулой
Черт. 452.
будет сначала уменьшаться до точки, отвечающей минимуму р а за¬
тем увеличиваться.
Таким образом, если. р/0 < р^, то кривая, описываемая проекцией
конца оси снаряда Кj, будет все время иметь характер удлиненной
эпициклоиды.
В случае же, если рго Рго» 9Та кРивая в зависимости от изме¬
нения а может менять свой
характер, обнаруживая сна¬
чала тенденцию к переходу
укороченной и нормальной
эпициклоиды в удлинен¬
ную, ^ после точки, от¬
вечающей минимуму Р, в
обратном направлении.
Исследованию измене¬
ния Ь1р и в дальней¬
шем будет посвящен спе¬
циальный параграф 46.
Остановимся теперь на
изменении, величины р, о
которой мУ уже говорили,
что она имее*т минимум.
Для определения точки,
отвечающей этому мини¬
муму, приравняем нулю
производную Р или про¬
изводную In р, которая уже была найдена в параграфе 43:
Приравнивая это выражение нулю, мы падучим формулу для угла
tfpmin» отвечающего искомой точке:
Как было указано раньше, эта точка находится на нисходящей
ветви траектории.
Имея выражение для [In $]', мы легко можем определить и ве¬
личину [In У о]', которая нам необходима при определении рю, р^,
111
Черт. 453,-
ф, и фг (формулы 443—448) и которая в соответствии с рассужде¬
нием параграфа 33/равна
Подставляя сюда выражение для == р [In [5]', получим
На основании формулы 459 мы так же, как и в параграфе 33,
можем утверждать, что изменение коэффициента гироскопической
устойчивости о происходит тем быстрее, чем меньше его величина,
при прочих равных условиях.
В настоящем параграфе мы будем изучать изменение положения
динамической оси относительно касательной к траектории с целью
определения того участка траектории, на котором эта ось будет
дальше всего отстоять от касательной.
Положение динамической оси, как нами уже было выяснено ра¬
нее (параграф 43), определяется следующими двумя уравнениями:
причем главную роль из этих двух величин играет Ъ2р. Рассмотрим
сначала величину Ь2р, подставив в ее выражение значения {2 и а
или, после замены
Начальное значение этой величины равно
46. Положение динамической оси.
460
461
где
462
Для данного снаряда, выброшенного при определенных началь¬
ных условиях, величина \р будет меняться по мере движения цен
тра инерции по траектории и по мере изменения элементов этой
траекторий 0, у, v, фигурирующих в переменном множителе урав¬
нения 464
На восходящей ветви этот множитель будет все время увеличи¬
ваться, так как числитель будет увеличиваться, а знаменатель умень¬
шаться. /
На нисходящей ветви определенное уменьшение этого множи
теля произойдет после прохождения центром инерции снаряда точки,
отвечающей наименьшей скорости. Следовательно, на участке между
вершиной траектории и точкой, отвечающей наименьшей скорости,
величина Ь2р будет иметь наибольшее значение, и, значит, на этом
участке снаряд будет н ;имеыее послушным. Обычно для простоты и
удобства расчетов принимают, что наиболее трудные условия работы
8 Вр»щ»тольио» движение 113
при допущений о том, что р0*=•у':
Тогда мы будем иметь
Тогда, после простых преобразовании, получим
Произведем в полученном выражении необходимые преобразования
и заменим в нем А его значением из уравнения 153
463
или
464
снаряда будут как раз в вершине траектории. На самом деле, как
мы уже убедились, наиболее трудными будут условия в точке,
весьма близкой в точке, отвечающей наибольшей кривизне, которая
также расположена между вершиной 5 и точкой, отвечающей наи¬
меньшей скорости.
Найдем значения угла Ь2р в точке вылета О, в вершине траек¬
тории £ и в точке падения С:
465
466
467
Из этих формул видно, что угол $Sps в очеги» большой степени
зависит от К, весьма значительно увеличиваясь по мере увеличе¬
ния высоты траектории. Именно поэтому условия работы снаряда
у вершины при сверхдальних траекториях являются особенно
трудными.
Рассмотрим теперь зависимость величины 82р от конструктивных
\tkqd
данных снаряда и орудия, выражающуюся множителем ——*-
имея
При этом в виду, что наиболее желательными для нас будут воз¬
можно меньшие значения д2р.
Итак, с точки зрения выбора величины Ьгр для нас будет по¬
лезным:
1) уменьшение аксиального коэффициента инерции д;
2) уменьшение козффнциента веса 1гд;
8) уменьшение калибра снаряда d\
4) увеличение длины хода на резон1 г] или уменьшение крутизны
нарезки орудийного ствола у дульного среза;
б) увеличение расстояния между центром инерции снаряда и
центром сопротивления воздуха (выраженного в калибрах) .
Следует напомнить, что при исследовании настоящей задачи мы все
время стояли па точке зрения первоначальных допущений о малости
углов $ и об отсутствии других моментов, кроме момеита опроки¬
дывающей пары, в частности момента тренин, уменьшающего угло¬
вую скорость снаряда и улучшающего при известных условиях пра¬
вильность 1юлета снаряда,
114
Рассмотрим теперь величину и ее изменение по мере движе¬
ния снаряда по криволинейной траектории.
Из формулы 461 видно, что для послушных снарядов, где
и Ь2р являются малыми, 81р будет по отношению к Ьгр величиной
второго порядка малости. Следовательно, в основном величина
будет изменяться аналогично величине Ь2р, но только в еще более
резкой форме.
Что же касается функции Я, равной
то, не входя в подробный анализ ее изменения, мы должны обратить
внимание на общую тенденцию ее к уменьшению вследствие умень¬
шения tg 6 и перехода- его от положительных значений на восходя¬
щей ветзи к отрицательным значениям на нисходящей ветви.
47. Движение оси снаряда при отсутствии начального угла
отклонения и ударов в момент вылета.
Рассмотрим наиболее простой случай начальных условий, когда
При прямолинейном движении центра инерции снаряда эти на¬
чальные условия имели следствием абсолютную правильность полета
снаряда, т. е. ось снаряда в продолжение всего движения совпадала
с касательной к траектории центра инерции.
Таким образом, исследуя данный частный случай в условиях
криволинейного движения центра инерции снаряда в плоскости бро¬
сания, мы будем иметь возможность изучить движение оси сна¬
ряда, происходящее только под влиянием пониже¬
ния касательной к траектории центра инерции
снаряда.
Для определения ноложения .динамической оси мы будем иоль-
зоваться формулами 433:
из которых следует, что
113
Найдем прежде ficero величины р/0, р^,, ф, и фг, для чего под¬
ставим начальные условия в уравнения 443—448, прииимая во вни¬
мание, что Получим
470
причем
или
471
Для установления характера движения конца оси снаряда рассмо¬
трим отношения ^ и , имея в виду, что
Рг Рг*>г
472
Следовательно,
473
ИЛИ
Поскольку
Далее,
В начальный момент времени
т. е.
Следовательно, кривая, описываемая проекцией конца оси снаряда
на плоскости изображения, будет иметь характер удлиненной эпи¬
циклоиды.
В дальнейшем, но мере движения снаряда по восходящей ветви
траектории, коэффициент гироскопической устойчивости <з увеличи¬
вается. В зависимости от увеличения а уменьшается угловая скорость
медленного конического движения тг—а (I—а) и увеличивается
угловая скорость быстрого конического 'движения <er=a (1 -j- с).
траектории будет убывать, оставаясь, естественно, меньше единицы.
Кривая, описываемая проекцией конца оси снаряда на плоскости изо¬
бражения будет сохранять характер удлиненной эпициклоиды. Так
будет продолжаться до той точки на нисходящей ветви траектории,
где величина Р будет иметь минимум. После этой точки величины а,
о>„ (i>r, pi и рг начнут изменяться в противоположном направлении,
и характер движения оси снаряда может измениться.
В случае, когда коэффициент гироскопической устойчивости а0
имеет достаточно большую величину, радиус быстрого конического
движения рг, в условиях настоящей задачи, будет весьма невелик по
сравнению с радиусом медленного конического движения. Поэтому
при больших значениях а0 мы в первом приближении можем считать,
что конец оси снаряда, центр инерции которого движется по кри¬
волинейной траектории, описывает кривую, определяемую только мед¬
ленным коническим движением. Иначе говоря, в этом случае мы
можем рассматривать вместо движения оси снаряда движение его
псевдоосн.
Величины и фг мы можем найти, подставляя начальные усло¬
вия в уравнения 444 и 445 с учетом того, что 81р = 0 и Ь2р — Ьр:
Значит, отношение — при движении снаряда по восходящей ветви
Р/®г
117
причем, поскольку все множители, входящие в выражение для sin
и sin положительные,
Найдем теперь выражение величины [(1п о0)о -f- (!о кото¬
рая ({mrypfipyeT в целом ряде рассматриваемых уравнений. Из урав¬
нения
нмееы
В главе 45 нами было установлено, что
Следовательно,
или в соответствии с выражениями
полученным» нами в главе 43,
Подставив в последнее уравнение
после простых преобразований получим
48. Коэффициент гироскопической устойчивости,
В параграфе 40 мы уже установили, что коэффициент гироско¬
пической устойчивости
480
в условиях настоящей задачи является переменной величиной, кото¬
рая сначала увеличивается, по мере движения снаряда, а затем после
перехода через точку нисходящей ветви траектории, отвечающую
минимальному значению р, снова уменьшается;
Напишем теперь выражение коэффициента гироскопической
устойчивости в развернутом вйде. Для (3 мы имели формулу 403:
481
Что же касается величины а, то для нее чрл воспользуемся
обычным выражением 121:
482
при допущении о том, что
483
которое мы уже применяли в параграфах 15 и 37. Тогда
Заменяя теперь аксиальный момент инерции А, находящийся
в знаменателе перед величиной g, ^его выражением через коэффи*
циент веса kq коаксиальный коэффициент инерции ц (153)
>. 1000 <*6
484. A=~rr~-kaix,
Рассматривая полученное выражение, мы видим, что при движе¬
нии центра инерции снаряда по криволинейной траектории^ наимень¬
шее значение коэффициента гироскопической устойчивости будет
отвечать наибольшему знамению произведения | Н (у) v2Km( — ) |. На
протяжении траектории от точки вылета до точки падения функция
Н(у) будет иметь наибольшее значение при у — 0, т, е, в точке
U9
получим
вылета и в точке падения; наибольшее значение величины — J
будет отвечать наибольшему значению скорости на этом участке,
которое имеет место в точке вылета.
Таким образом наибольшее значение произведения
а следовательно, и наименьшее значение коэффициента гироскопиче¬
ской устойчивости а будет иметь место в точке вылета.
Это наименьшее значение коэффициента гироскопической устой¬
чивости <з0 равно
486
поскольку Н(у0) = 1, а = а0.
Сравнивая полученное выражение для наименьшего^ значения
коэффициента гироскопической устойчивости а0 при движении цен¬
тра инерции снаряда по криволинейной траектории с выражениями
376 и 158, отвечающими случаям неравномернЬго и равномерного
движения центра инерции снаряда по прямолинейной горизонтальной
траектории, мы видим, что все эти выражения совершенно идентичны.
Итак, наиболее трудные условия в отношении гироскопической
устойчивости артиллерийский снаряд всегда будет иметь в1 точке
вылета, а следовательно, при расчете снаряда прежде всего необхо¬
димо определить начальное значение коэффициента гироскопической
устойчивости а0, определяемре формулой 486.
49. Понятие о положении динамической оси при не малых
углах отклонения.
Рассматривая положение динамической оси при малых углах 8 и
ограничиваясь только- первым членом в разложении Zp, мы видели,
что динамическая ось отклонена вправо от касательной (если смо¬
треть на снаряд сзади) на угол, определяемый следующими усло¬
виями (435):
Обратим внимание на то, что в данном случае динамическая ось
является вто же самое время и мгновенным положением
равновесия для оси снаряда. Действительно, предположим, что
в некоторый момент времени угол отклонения 8, скорость пониже¬
ния касательной 6' и величина опрокидывающего момента М—В р8
120
сделались постоянными, т. е.
490
Движение octa снаряда попрежнему будет определяться уравне¬
нием 419
которое при сделанных нами предположениях поймет вид:
491
Отсюда получим
или
492
Таким образом, если ось снаряда будет отклонена вправо от каса¬
тельной на угол bk — ^ д2j |8'|, то при сохранении вели¬
чин 6' и а постоянными ось снаряда не будет перемещаться отно¬
сительно касательной. Так как в действительности и 0' и а меняются,
то величина Bk для каждого момента времени будет иметь свое зна¬
чение, и положение равновесия будет только мгновенным.
Сравнивая между собой выражения для и § при учете только
первого члена при разложении Ър в ряд, мы видим, что они равны
между собой. Этим обстоятельством и пользуются для определения
положения динамической оси при движении снаряда, когда углы 8
будут не малыш, допуская в первом приближении, что и в этом
случае мгновенное положение равновесия и динамическая ось будут
совпадать.
Д. А. Вентцель, принимая
493
получает для Ьк следующие выражения:
494
Последнши выражениями можно пользоваться в тех случаях, когда
угол 82р, определенный по формулам 432, 433, оказывается не
малым.
т
б. ГИРОСКОПИЧЕСКАЯ УСТОЙЧИВОСТЬ И ПРАВИЛЬНОСТЬ
ПОЛЕТА АРТИЛЛЕРИЙСКИХ СНАРЯДОВ.
60. Гироскопическая устойчивость и правильность полета
артиллерийского снаряда.
Рассматривая вращательное движение артиллерийского снаряда
и изучая влияние его на дальность полета и на кучность, мы по¬
стоянно должны иметь в виду необходимость строго разграничивать
два основных свойства вращающегося артиллерийского снаряда —
гироскопическую устойчивость артиллерийского
снаряда и правильность полета артиллерийского
снаряда.
Между тем эти два явления нередко смешивают, результатом
чего является ряд недоразумений, так как требования, предъявляе¬
мые к конструкции снаряда и орудия с точки зрения увеличения
гироскопической устойчивости снаряда и с точки зрения правиль¬
ности его полета, не только не совпадают, но сплошь и рядом
противоречат одни другим.
Напоминается, что гироскопической устойчивостью
(la stability gyroscopique) артиллерийского снаряда назы¬
вав тся способность вращающегося снаряда сопро¬
тивляться внешним силам, стремящимся изменить
положение его оси.
Вращающийся артиллерийский снаряд, обладающий гироскопи¬
ческий устойчивостью, называется гироскопически устой¬
чивым снарядом.
Условие гироскопической устойчивости артиллерийского снаряда,
как нами было установлено в главе 1, выражается формулой 141
Величиной, количественно характеризующей ги¬
роскопическую устойчивость данного артиллерий¬
ского снаряда, является коэффициент гироскопиче¬
ской устойчивости а, определяемый выражением 150:
500
При употреблении коэффициента гироскопической устойчивости а
условие гироскопической устойчивости (500) может быть переписано
следующим образом:
501
Таким образом коэффициент гироскопической устойчивости для
гироскопически устойчивых снарядов должен выражаться веществен¬
ным числом.
122
У гироскопически неустойчивых снарядов коэффициент гироско¬
пической устойчивости является мнимой величиной (а2<^0).
Так как величины а и 0 равные, согласно уравнениям 121, 157
и 017,
существенно положительны, то величина коэффициента гироскопи¬
ческой устойчивости а для гироскопически устойчивых снарядов
может иметь значения в пределах от нуля до единицы:
0<а<1.
При 0 снаряд находится на нижнем пределе гироскопической
устойчивости.
При а — 1 снаряд обладает абсолютной гироскопиче¬
ской устойчивостью, т. е. ось снаряда будет оставаться
параллельной своему первоначальному положению в течение всего
времени полета снаряда.
Положение оси снаряда, обладающего абсолютной гироскопи¬
ческой устойчивостью, по отношению к траектории его центра
инерции, в различные моменты его движения изображено на черт. 500.
Угол отклонения §, или угол нутации у снаряда, обладающего аб¬
солютной гироскопической устойчивостью, по мере движения сна¬
ряда все время увеличивается, и полет такого снаряда, очевидно,
является совершенно неудовлетворительным.
Анализируя формулу 500, мы видим, что коэффициент гироско¬
пической устойчивости о может равняться единице только при а — оо
или при р=.0. Следовательно, абсолютной гироскопической устой¬
чивостью артиллерийский снаряд мог бы обладать или при беско¬
нечно большой угловой скорости вращательного движения снаряда
около его оси (/?0=ос), или при движении в безвоздушном
пространстве (П0=О), или.*при совпадении центра сопротивления
123
Черт. 500.
воздуха движению артиллерийского снаряда с центром инерции снаряда
(* = 0).
Развернутое выражение коэффициента гироскопической устойчи¬
вости а, как мы установили в параграфе 48, имеет следующий
вид (485):
Правильностью полета (la bonne tenue) артиллерий¬
ского снаряда мы будем называть способность оси
снаряда следить за касательной к траектории его
центра инерции, т. е. иметь углы отклонения оси
снаряда от касательной к траектории его цент¬
ра инерции (8) малыми на всем лротяжении траек-
т о ри и.
Иначе говоря, правильность полета артиллерий¬
ского снаряда можно определить как способность
снаряда лететь головной частью вперед на всем
протяжении траектории.
Артиллерийский снаряд, обладающий правиль¬
ностью полета, мы будем называть послушным сна¬
рядом (le projectile sage).
Величиной, количественно характеризующей
правильность полета артиллерийского снаряда,
естественно, является угол отклонения 8 или угол
нутации.
Границей, отделяющей малые значения углов 8
от не малых, мы будем считать наибольшее допу¬
стимое значение 8, которое обозначим через 8доп.
Напомним, что все выводы, относящиеся к послушному снаряду,
были сделаны на основе допущения, что угол отклонения 8 является
малым и что sin8 = tg8 = 8, a cos8=1.
. При 8Д0П = 10°00' = 0,1745
sin гдоп = 0,1736, tg^on = 0,1763, cos адои = 0,9848.
124
Следовательно, при
Итак, условие правильности полета артиллерийского снаряда
будет иметь вид:
503 §<§доп.
Наилучшим случаем движения снаряда будет такое движение,
при котором ось снаряда все время совпадает с касательной к тра¬
ектории его центра инериии, т. е. при котором 5=0 в продолже¬
ние всего движения. Такой снаряд мы будем считать обладающим
Черт. 501.
абсолютной правильностью полета. Положение оси сна-
рада, обладающего абсолютной правильностью полета, в различные
моменты его движения изображается на черт. 501.
Величина угла отклонения оси снаряда от касательной к тра¬
ектории его центра инерции или угла нутации § определяется
125
уравнением 203:
Углы и £2 в самом общем из рассмотренных нами слу¬
чаев вращательного движения снаряда выражаются формулами 454:
При этом углы 81р и Ь2р определяют положение динамической
оси снаряда относительно касательной к траектории его центра
инерции; углы ЬииЬ2[—положение псевдоосн снаряда относительно
его динамической оси; углы Ь1г и §2г—положение оси симметрии
снаряда относительно его псевдооси.
Углы Sj и §2;; для послушного снаряда определяются форму¬
лами 433:
Углы 5И и Ь21 определяются формулами 452:
Углы и Ь2г определяются формулами 453:
Величина »f и аг представляют собой угловые скорости
медленного и быстрого комических движений и выражаются
12S
где
где
уравнениями
Постоянные величины р/0, рг0, cbz и фг зависят от начальных
условий и определяются для наиболее общего из рассмотренных
нами случаев формулами 442—446.
Анализируя формулы, определяющие угол отклонения оси сна¬
ряда от касательной к траектории его центра инерции, мы прежде
всего замечаем, что абсолютной правильностью полета артиллерий¬
ский снаряд может обладать только в случае движения его центра
инерции по прямолинейной траестории при отсутствии начального
угла отклонения и ударов в момент вылета, так как только в этом
единственном случае обращаются в нуль и угол отклонения динами¬
ческой оси снаряда от касательной к траектории его центра ипер-
цпи = и Угол отклонения псевдооси снаряда от его ди¬
намической оси (рг=0), и угол отклонения оси симметрии снаряда
от его псевдооси §г(рг = 0).
Во всех других случаях, т. е. во всех случаях действитель¬
ной артиллерийской практики, угол отклонения оси снаряда от
касательной к траектории его центра инерции не будет равен нулю.
Так как мй должны стремится к тому,, чтобы величина этого
угла была как можно меньше, то особенный интерес для нас будут
представлять наибольшие возможные для данного снаряда значения
угла 8.
Самое большое из всех возможных для каждого данного момента
времени значений угла отклонения 8- должно отвечать случаю,
когда в данный момент касательная к траектории центра инерции
снаряда динамическая ось, псевдоось и ось симметрии снаряда ока¬
зываются расположенными в одной и той же плоскости, причем
динамическая ось расположена между касательной к траектории
центра инерции снаряда и его псевдоосью, а псевдоось расположена
между динамической осью и осью симметрии снаряда.
В этом случае наибольший возможный для данного момента
угол отклонения 8, который мы обозначим через Ьм, равен
или, в соответствии с формулами 455,
504
Развернутое выражение угла отклонения динамической оси артил¬
лерийского снаряда от касательной к траектории его центра инерции
для послушного снаряда, поскольку &1р=0 и Ьр = Ьгр, имеет
127
в соответствии с формулой 464 следующий вид:
606
где
507
{
В том случае, когда начальный угол отклонения § равен нулю
и удары в момент вылета не имеют места, выражения для Pi и Рг
в соответствии с формулой 471 принимают вид:
Б08
Выражение [(1п§в)д-}-(1п Vo)<i\ определяется формулой 479.
Заменяя в выражении угла величины pjQ и р^ их выраже¬
ниями 506, мы будем иметь
509
При проектировании артиллерийского снаряда и артиллерий¬
ской системы в целом основной задачей конструктора должно
быть обеспечение возможно большей правильности полета артиллерий¬
ского снаряда на всем протяжении траектории его центра инерции.
Для этого прежде всего необходимо, чтобы в каждый момент
движения снаряда наибольший, возможный угол был как можно
меньше.
Анализируя выражение для угла (509), мы видщг, что вели¬
чина его, кроме начальных условий движения, определяемых посто¬
янными Р, и Рг, зависит от угла отклонения динамической оси
>28
Постоянные величины р!0 и рг0, зависящие от начальных условий,
в самом общем из рассмотренных нами случаев движения послушного
снаряда выражаются уравнениями 446:
снаряда от касательной к траектории его центра инерции Ьр и от
коэффициента гироскопической устойчивости о.
Угол Ьм уменьшается при уменьшении динамического угла Ьр
и при увеличении коэффициента гироскопической устойчивости о.
При анализе выражений для Ьр и а мы видим, что при движении
снаряда от точки вылета до точки падения наименьшее значение
угла Ьр отвечает точке вылета, а наибольшее значение этот угол
принимает на нисходящей ветви траектории около ее вершины,
точнее, — между вершиной и точкой, отвечающей наименьшей
скорости.
Что касается коэффициента гироскопической устойчивости а, то
и он наименьшее значение имеет в точке вычета, а наибольшее
около вершины траектории, — на участке нисходящей ветви траек¬
тории между вершиной и точкой, отвечающей наименьшей ско¬
рости vm.
Таким образом около вершины траектории 5 мы имеем самое
неблагоприятное для нас значение угла Ьр и самое выгодное значе¬
ние коэффициента з.
Наоборот, в точке вылета О величина динамического угла Ьр
валяется нзнлучшей, а величина коэффициента гироскопической
устойчивости а — наихудшей.
К этому надо добавить, что при дгашении снаряда на начальном
участке траектории большие значения коэффициента гироскопической
устойчивости необходимы не только потому, что они оказывают
влияние на величину угла определяемого формулой 509, но
н потому, что на начальном участке траектории снаряд находится
в особо трудных условиях, подвергаясь действию вырывающихся из
дудьниго среза пороховых газов, сообщающих ему дополнительные
угловые ускорения, помимо получаемых в момент вылета в учитывае¬
мых выражениями для Pj и
С другой стороны, надо иметь в виду, что затухание колеба¬
тельного движения оси снаряда относнтедьнр динамической осн.
в действ чтельноста происходит быстрее, чем это следует из рас¬
смотренных нами формул, готому что при выводе этих формуя мы
ее учитывали тушащего момента сопротивления воздуха, который
оказывзет весьма эффективное действие именно из начальном участке
траектории.
Подводя итоги всем нашим рассуждениям, мы видим, что при
баллистическом исследовании артиллерийского сна-
рядасточки зрения правильности его-полета наи¬
большее внимание должно быть уделено исследова¬
нию движения снаряда на начальном участке тра¬
ектории и на участке нисходящей ветви траектории
около ее вершины.
9 „ 129
Вращательное жвяжеяие
61. Правильность полета артиллерийского снаряда
на начальном участке траектории.
При движении вращающегося артиллерийского снаряда на на¬
чальном участке траектории мы имеем наиболее неблагоприятные
условия в отношении гироскопической устойчивости снаряда.
Наименьшее значение коэффициента гироскопической устойчиво¬
сти отвечает точке вылета О и равняется
Между тем гироскопическая устойчивость снаряда на начальном
участке траектории имеет особо важное значение как вследствие
того, что на этом участке в наибольшей степени сказываются на¬
чальные условия движения, зависящие от начального угла нутации
и от ударов, полученных снарядом в момент вылета, так и вслед¬
ствие того, что в продолжение периода последействия пороховых
газов снаряд подвергается действию этих пороховых газов и полу¬
чает дополнительные угловые ускорения, не учитываемые выведен¬
ными нами формулами.
Величина наибольшего возможного угла нутации ц точке вы-
лета §Л0 равняется
511
или
512
Величина динамического угла в точке вылета равняется
513
Это значение динамического угла, как мы уже установили, яв¬
ляется наименьшим на всем протяжении траектории от точки вылета
до точки падения.
Начальные условия вращательного движения снаряда в громадном t
большинстве случаев нам бывают неизвестны. Кроме того, враща¬
тельное движение снаряда на начальном участке траектории ослож¬
няется, как мы уже отмечали, последействием пороховых газов.
Таким образом сколько-нибудь точного значения величин р/0 и рг1
в каждом данном случае артиллерийской системы мы установить не
можем.
Единственно, что мы можем сделать — это экспериментально,
при помощи стрельбы по картонам, установить наибольшее
130
значение угле нутации на начальном участке тра¬
ектории, которое мы обозначим чорез Ъцк и принять это значение
за величину $Л0, т. е. считать
614
Очевидно, определенная таким образом величина, не должна
превышать наибольшего допустимого значения угла нутации iAOU:
81В
Теперь мы можем определить величину (р^-Ь Рго)* представляю¬
щую собой наибольшее значение угла отклонения оси снаряда от
динамической оси н равную
516
В случае, если величина Ьмк на опыте не определена, за вели¬
чину $м0 мы должны принять наибольшее допустимое значение угла
нутации $д0«:
Б17
Тогда из уравнений 511 определится наибольшее допустимое
значение суммы (рю”1*Pro)» е> наибольшее допустимое
значение угла отклонения оси снаряда от динами¬
ческой оси, которое мы обозначим через (р^-f* Рго)доч:
518
Далее экспериментально должно быть установлено наимень¬
шее допустимое значение коэффициента гироско¬
пической устойчивости Од™, обеспечивающее артиллерий¬
скому снаряду правильность полета на начальном участке траектории
и быстрое затухание колебательного движения оси снаряда. Для
этой цели рекомендуется производить стрельбу исследуемым,снаря¬
дом из орудий с различной крутизной нарезки по вертикальному
щиту при малых углах бросания и определять вертикальные и бо¬
ковые вероятные отклонения (Вщ и Вл). Критерием правильности
полета на начальном участке будет являться хорошая кучность сна¬
ряда, поскольку кривизна траектории в данных условиях стрельбы
будет весьма невелика, а, значит, положение и движение динами¬
ческой оси существенного влияния на кучность оказывать не будет.
В случае, если величина 0доп для данного снаряда на опыте не
установлена, за эту величину следует принять несколько увеличен¬
ное наименьшее допустимое значение коэффициента гироскопической
устойчивости для снарядов, конструктивно похожих на рассматрива¬
емый снаряд, или еще грубее, наименьшее допустимое значение
коэффициента о для всех снарядов того же типа, как и исследуемый
нами артиллернАсхий снаряд. Само собой разумеется, что » этом
в* 131
последнем случае запас гироскопической устойчивости должен быть
еще больше, чем в предыдущем.
В практике наших проектирующих организаций за величину наи¬
меньшего допустимого значения коэффициента гироскопической
устойчивости для современных снарядов чаще всего прини¬
мается 0,600.
Условие правильности полета артиллерийского
снаряда на начальном участке траектории имеет вид
519
т. е. для правильности полета артиллерийского сна¬
ряда на начальном участке траектории необходимо
и достаточно, чтобы значение коэффициента гиро¬
скопической устойчивости в точке вылета а0 было
не меньше наименьшего допустимого коэффициента
гироскопической устойчивости для данного сна¬
ряда.
52. Определение наименьшего значения коэффициента
гироскопической устойчивости артиллерийского снаряда
при стрельбе из данного орудия.
Наименьшее значение коэффициента гироскопической устойчи-'
вости при движении артиллерийского снаряда от точки вылета до
точки падения отвечает, как мы уже установили, точке вылета 0
и равняется
520 а0 =
Рассматривая это выражение, мы прежде всего видим, что на¬
чальное значение коэффициента гироскопической устойчивости и0
совершенно не зависит от угла бросания 0О. Из основных парамет¬
ров, которые могут изменяться при стрельбе данным снарядом из
данного орудия на величину а0 оказывает влияние только начальная
скорость и плотность воздуха в точке вылета Н0.
Следовательно, при стрельбе изучаемым артиллерийским снарядом
из данного орудия, имеющего постоянный заряд, наименьшее зна¬
чение коэффициента гироскопической устойчивости будет одинаковым
для всех траекторий, если одинаковой будет плотность воздуха
в точке вылета.
При изменении плотности воздуха в точке вылета начальное зна¬
чение коэффициента гироскопической устойчивости будет различным
в различных случаях стрельбы, причем наименьшее значение о0 будет
отвечать наибольшему возможному значению величины Н0 или отно¬
шения Наибольшее возможное значение (д^) имеет место
Ш
при наибольшем возможном давлении hQ, при наименьшей возможной
температуре Г0 и при абсолютном отсутствии влажности. Для
Л0 = 790 мм, Т0 248°К (— 25°С) и *0 = 0, отношение (^) =
= 1,227. °*
При наличии у орудия переменного заряда начальное значение
коэффициента гироскопической устойчивости должно бцть опреде¬
лено для каждого заряда в отдельности, поскольку функция KM{v)
не является монотонной. В этом случае особое внимание должно
быть обращено на тот заряд, при котором значение функции
является наибольшим,, а значение коэффициента о0 — наименьшим.
Рассмотрим теперь влияние на коэффициент гироскопической
устойчивости параметров, которые характеризуют конструктивные
особенности- снаряда и орудия и которые при стрельбе из данного
орудия данным снарядом остаются неизменными.
Из формул для а и для а0 следует, что коэффициент гироско¬
пической устойчивости увеличивается:
1) при увеличении коэффициента веса снаряда kq',
2) при увеличении аксиального коэффициента инерции снаряда р.;
3) при уменьшении выраженной в калибрах длины хода наре¬
зов 7) или при увеличении крутизны нарезки орудийного ствола;
4) при уменьшении выраженного в калибрах расстояния между
центром инерции снаряда и центром сопротивления воздуха
5) при уменьшении отношения экваториального момента инерции
снаряда к аксиальному
6) при уменьшении коэффициента формы в выражении опроки¬
дывающего момента iM.
Следовательно, улучшение правильности полета
артиллерийского снаряда на начальном участке тра¬
ектории конструктор может получить при помощи:
1) увеличения коэффициента веса снаряда kq\
2) увеличения аксиального коэффициента инерции снаряда ц;
3) уменьшения длины хода нарезов у дульного среза орудийного
ствола 7j;
4) уменьшения расстояния между центром инерции снаряда
и центром сопротивления воздуха
5) уменьшения отношения экваториального момента инерции сна¬
ряда к аксиальному
6) уменьшения коэффициента формы 1М.
Рассматривая все эти пути улучшения правильности полета сна¬
ряда на начальном участке траектории и сравнивая их между собою,
Ш
мы прежде всего должны констатировать, что величины kq,]i и
конструктор при проектировании снарядов основного назначения
может менять в очень небольших пределах, так что такими путями
значительного улучшения правильности полета на начальном участке
траектории добиться нельзя.
Величина iM и зависимость ее от формы и распределения массы артил¬
лерийского снаряда в настоящее время еще недостаточно изучена.
Наиболее эффективными методами улучшения
правильности полета артиллерийского снаряда на
начальном участке траекторий является увеличение
крутизны нарезки у дульного среза орудййного
ствола и уменьшение расстояния между центром
инерции снаряда и центром сопротивления.
Само собой разумеется, что внося конструктивные изменения
в проект снаряда с целью изменения какого-либо определенного
параметра, входящего в выражение а0, конструктор обязан смотреть
за тем, чтобы эти же самые конструктивные изменения не отразились
существенным образом на величине других параметров, от которых зави¬
сит значение коэффициента а0. В противном случае вместо улучшения
правильности полета снаряда может получиться отрицательный эффект.
Обратим внимание на то, что в громадном большинстве случаев
артиллерийской практики значения коэффициентов формы iM кон¬
структору бывают неизвестны. В таких случаях рекомендуется при¬
нимать iM~ 1 и несколько увеличивать запас гироскопической
устойчивости при установлении наименьшего допустимого значения
коэффициента гироскопической устойчивости адоп.
Точно так же можно принимать равным единице и отноше-
ние соответственно увеличивая величину адоп.
Принятое в практике наших проектирующих организаций наи¬
меньшее допустимое значение коэффициента гироскопической устой¬
чивости, равное 0,600, учитывает для современных снарядов два
указанных выше обстоятельства, а потому, задаваясь значением
Одод —0,600, конструктор может совершенно спокойно принимать
1М ■= 1 и щ5- = 1 в громадном большинстве случаев своей практи¬
ческой деятельности.
При вычислении коэффициента гироскопической устойчивости
постоянный множитель ^ ) удобнее всего присоединить к функ¬
ции Км{1>) и вместо таблиц 030 и 031 пользоваться таблицами
функций которые приводятся в настоящем параграфе
(таблицы 520 и 521).
Таблица 520. Функция Km{v). Таблица 521. Функция —
V
V
-^Кт{ь)
0—200
0,000454
500
0,000571
225
456
550
561
250
462
600
553
275
478
650
546
300
539
700
540
325
596
750
535
350
608
800
531
375
604
850
528
400
599
900
526
425
592
950
525
450
584
1 000
524
475
577
1 050
523
500
571
1 100
и
выше
523
Примечание: Величина
а
вычисляется по формуле Бур-
цио.
V
4
V
0—200
0,000377
500
0,000478
225
379
550
470
250
385
600
463
275
405
650
458
300
450
700
454
325
494
750
450
350
507
800
447
375
503
850
445
400
499
900
443
425
494
950
441
450
488
1000
440
475
483
1050
439
500
478
1 100
и
выше
438
Приметаете: Величина
вычисллется по
ского Полигона.
формуле Мор-
Пример. Стрельбе из 76-мил л име-тровой пушки ОС'
колочной гранатой.
Исходные данные:
Калибр d=0,0762 м;
Вес снаряда ^=6,23 кг;
Длина снаряда /=4,40 d;
Длина головной части . . Н =2,35 d;
Расстояние центра инерция снаряда от ос¬
нования головной части hi — 0,40 d",
Аксиальный момент инерции Л = 0,510*10~3 кг мсек?;
Экваториальный момент инерции 2? = 4,86-10“а кгмеляР;
Длина хода нарезов у дульного среза
(в калибрах) ч » 25,0;
Начальная скорость снаряда Щ — 630 м/сек;
Плотность воздуха в точке вылета . . . Но = Пвл^.
Определить наименьшее значение коэффициента
Гироскопической устойчивости, т. е. значение
135
коэффициента гироскопической устой ч и пости в точ¬
ке вылета О.
Вычисления производим по формуле 520, считая коэффициент фор¬
мы /до равным единице:
Прежде всего находим величины коэффициента веса снаряда kq, акси¬
ального коэффициента инерции ц и отношения экваториального момента
инерции к аксиальному.
h
Далее находим расстояние между центром инерции снаряда и цент-
h ( h \
ром сопротивления — и произведение величины f на соответствую¬
щие значения функции ^ Км как по формуле Бурцио, так и по
формуле Морского Полигона.
Формула Бурцио:
Формула Морского Полигона:
Теперь определяем коэффициент гироскопической устойчивости так¬
же двумя способами: при помощи функции Км\ (v) и функции Кдц (v).
Первый способ:
по второму слособу
или окончательно
631
137
В т о р о fi способ:
При длине хода ппрсзов — 30,0 мы имели бы по первому способу
БЗ. Определение наибольшей допустимой дляны хода нарезов,
обеспечивающей артиллерийскому снаряду правильность
полета на начальном участке траектории.
При определении наибольшей допустимой длины хода нарезов
ствола артиллерийского орудия у дульного среза *}дОП, которза
обеспечивала бы данному артиллерийскому снаряду правильность
полета на начальном участке траектории, мы должны задаться, tan-
меньшим допустимым значением коэффициента гироскопической устой¬
чивости а^,, и принять равным этому значению начальное значение
коэффициента гироскопической устойчивости а0> т, е. положить
Заменяя в этом уравнении коэффициент а0 его выраже!шем и пата-
гая 7] = ?]доп, ПОЛУЧИМ
откуда
Принимая П0 = Полг и 1Л,= 1 за счет увеличения запаса гиро-
скопической устойчивости, мы будем иметь следующее выражение
для наибольшей допустимой длины хода нарезов у дульного среза:
В практике наших проектирующих организаций, при условии,
что Н0 = П0ЛГ и iM— 1, наименьшее допустимое значение коэф¬
фициента гироскопической устойчивости чаще всего принимается
равным 0,600:
Особое внимание необходимо обратить на то, что пользоваться
значением адоп = 0,600 следует только тогда, когда у нас нет ни¬
каких других экспериментальных установочных данных как относи¬
тельно величины адоп так и относительно величины iM. Кроме того,
необходимо иметь в виду, что при выводе всех наших формул мы
не учитывали ударов по снаряду со стороны пороховых газов на
участке их последействия. В связи с этим при малых начальных
скоростях и при больших дульных давлениях мы будем иметь значи¬
тельно более трудные условия, чем в обычных случаях артиллерий¬
ской практики, а значит, запас гироскопической устойчивости
в указанных случаях должен быть увеличен.
Пример. Стрельба из 76- миллиметровой пушки оско¬
лочной гранатой.
Исходные данные: те же, что и в примере параграфа 52.
Найти наибольшее допустимое значение длины
хода нарезов у дульного среза.
Вычисление произведем по формуле 535, исходя нз наименьшего
допустимого значения коэффициента гироскопической устойчивости
о„пп = 0.600:
В примере параграфа 52 нами были определены следующие вели¬
чины:
634
И
При таком значении а имеем
Подставляя эти значения в формулу 535 и вычисляя т)д0п при помощи
функции К mi Ы» получим
Определяя т)ЦОп при помощи функции Кмч (у)> получим
т)доп = 0,800 /14,08*0,553*0,1049*1^76 = 26,8.
54. Правильность полета артиллерийского снаряда у
вершины траектории.
При движении вращающегося артиллерийского снаряда у вер¬
шины траектории, особенно на нисходящей ветви, мы имеем наибо¬
лее неблагоприятные условия в отношении динамического угла Ьр,
т. е. угла отклонения динамической оси от касательной к траекто¬
рии центра инерции снаряда.
Наибольшее значение динамического угла отвечает некоторой
неизвестной нам точке, расположенной на нисходящей ветви траекто¬
рии между вершиной траектории 5 и точкой, отвечающей наимень¬
шей скорости vm. В вершине траектории значение динамического
угла bpS не является наибольшим; однако это значение весьма не¬
много отличается от наибольшего значения, почему мы и можем
пользоваться им как характеристикой положения динамической оси
на всем рассматриваемом участке.
Значение динамического угла в вершине для послушного снаряда
в соответствии с формулой 505 равно
Величина наибольшего возможного угла нутации в вершине
траектории согласно уравнениям 504 и 509 равняется
Постоянные величины Р( и Рг зависят от начальных условий
н определяются формулами 507 и 508.
Так как в большинстве случаев начальные условия нам неизвестны
и мы не можем расчетом установить сколько-нибудь точное
значение величин Р, и Рг, то величину (р/0 -{- р^) целесообразнее
всего выражать через экспериментально определенное наибольшее
значение угла нутации на начальном участке траектории, которое мы
9 параграфе 51 обозначили через
Чдвп — 0,800 У14,08-0,553*0,1049*1543 = 28,4.
541
или
542
139
или
или
или
Следовательно, условие правильности полета артил¬
лерийского снаряда у вершины траектории может
бить выражено одним из следующих неравенств:
Последнему неравенству может быть придан вид
549
которым мы будем пользоваться при определении наибольшего
допустимого значения динамического угла в вершине траектории.
Итак, для правильности полета артиллерийского
снаряда у вершины траектории необходимо и доста-
140
Тогда согласно уравнению 516,
13 случае, если величина дм/( на опыте не установлена, величина
(pw-j~Pro) должна определяться при помощи формулы 51В. Тогда
Условие правильности полета артиллерийского снаряда у пер-
шикы траектории имеет вид
Заменяя в этом неравенстве угол одним из его выражений
541, 543 и 544, мы будем иметь
точно, чтобы значение динамического угла в вер¬
шине dps не превышало наибольшего допустимого
значения динамического угла.
55. Определение положения динамической оси в вершине
траектории.
Положение динамической оси в вершине траектории в общем
случае определяется углами vps и 5^. Принимая, в соответствии
с уравнением 433,
650 8,^ = 0,
Mi>i имеем
551
552
Развернутое выражение динамического угла в верщине траектории
определяется уравнением 540:
Из выражения для dps следует, что величина динамического уг¬
ла § у зависит, с одной стороны, от конструктивных характеристик
снаряда и орудия, а с другой, — от значения элементов траектории
в вершине.
Рассматривая влияние параметров, которые характеризуют конст¬
руктивные особенности снаряда и орудия и которые при стрельбе из
данного орудия данным снарядом остаются неизменными, мы видим,
что величина динамического угла 8ps увеличивается:
1) при увеличении коэффициента веса kq\
2) при увеличении аксиального коэффициента инерции fi;
3) при увеличении калибра d;
4) при увеличении выраженной в калибрах длины хода нарезов ij
или при увеличении крутизны нарезки орудийного ствола;
5) при уменьшении выраженного в калибрах расстояния между
центром инерции снаряда и центром сопротивления воздуха ;
6) при уменьшении коэффициента формы в выражении опроки¬
дывающего момента iM.
Следовательно, улучшение правильности по¬
лета артиллерийского снаряда у вершины траек¬
тории аа счет уменьшения динамического угла
ж и о получить при помощи:
141
1) уменьшения коэффициента веса снаряда kq\
2) уменьшения аксиального коэффициента инерции снаряда pi;
3) уменьшения калибра d;
4) увеличения длины хода нарезов у дульного среза орудийного
ствола 7];
5) увеличения расстояния между центром инерции и центром
сопротивления (^-j ;
6) увеличения коэффициента формы 1М.
Сравнивая эти выводы с выводами параграфа 52, мы видим, что
улучшение правильности полета снаряда у вершины траектории при
помощи изменения конструктивных характеристик снаряда и орудия
почти всегда связано с ухудшением правильности полета на началь¬
ном участке траектории.
Поскольку болыцинство из конструктивных параметров может
быть изменено в очень узких пределах, наиболее эффектив¬
ными методами улучшения правильности полета
артиллерийского снаряда у вершины траектории
является уменьшение крутизны нарезки у дульного
среза орудийного ствола и увеличение расстояния
между центром инерции снаряда и центром сопро¬
тивления во з духа.
Влияние плотности воздуха на правильность полета снаряда
у вершины весьма велико. Из формулУ видно, что динамический
угол Ьр5 увеличивается:
1) при уменьшении плотности воздуха в точке вылета П0;
2) при уменьшении значения функции H(Y), характеризующей
зависимость плотности воздуха в вершине от высо*гы траектории.
Величина П0 обычно меняется в довольно узких границах. Что
же касается функции H(Y), то она может иметь очень малые значе¬
ния при большой высоте траекторий из-за разреженности верхних
слоев атмосферы. Поэтому при стрельбе на дальние и сверхдальние
дистанции условия движения снаряда у вершины будут особенно
трудными в отношении правильности его полета.
Очень большое влияние на правильность полета снаряда у вер¬
шины оказывает величина скорости снаряда в вершине умень¬
шение которой, как мы видим из формулы 550, весьма значительно
увеличивает величину динамического угла bps.
При вычислении значения динамического угла в вершине Ьр5
постоянный множитель (^f) удобнее всего присоединить к функ¬
ции KM(v), причем вместо таблиц 030 и 031 целесообразно поль~
зоваться специально составленными таблицами, в которых непосред-
ственно дается функция и котоРые ПРИВ°ДЯТСЯ в настоя¬
142
щем параграфе (таблицы 550 и 551). Величину присоединять
к функции Км (v) нецелесообразно, так как в этом случае необходимо
будет уменьшить шаг таблиц и сделать их более громоздкими.
Таблица 550. Функция ,—^7—г. Таблица 551. Функция тг,у-~г\•
2Кмъ(‘0)
V
V
ng j
1Км\ <»)
2KMAv) j
f
0—200
1,38.10*
500
i
\
1,09-104
225
1,37
550
1,11
250
1,35
600
1,13
275
1,31
650
1,14
300
1,16
700
1,16
325
1,05
750
1,17
350
1,03
800
1,18
375
1,03
850
1,18
400
1,04
900
1Д9
425
1,05
950
1,19
450
1,07
1 000'
1,19
475
1,08
1050
1,19
500
1,09
1 100
и
выше
1,19
Примечание. Величина
вычисляется по
цио.
формуле Бур-
X)
V
к*
Ж mi (v)
2А0и2 (V)
0—200
1,66.10*
500
1,ЗЫ0*
225
1,65
550
1,33
250
1,62
600
1,35
275
1,54
650
1,36
300
1,39
700
1,38
325
1,26
750
1,39
350
1,23
800
1,40
375
1,24
850
1,40
400
1,25
900
1,41
425
1,26
950
1.42
450
1,28
1 000
1,42
475
1,29
1 050
1,42
500
1,31
1 100
и
выше
1,43
ft
Примечание: Величина -т-
вычисляется по
ского Полигона.
формуле Мор-
Значение скорости снаряда в вершине vs, если оно неизвестно,
удобнее всего определить при помощи вспомогательных функций
Сиаччи *). Точно так же при помощи вспомогательных формул Сиач-
чи находится и высота траектории Y. Для вычисления vg и У кроме
начальной скорости v0 и угла бросания 60 необходимо знать гори¬
зонтальную дальность X,
*) Вспомогательные функции Сиаччи имеются в книгах: О к у н е в,
Основная задача внешней баллистики и аналитические методы ее реше¬
ния, 1934; Веитцель, Окунев и Шапиро, Внешняя баллистика,
1933—1934; Вентцель я Шапиро, Внешняя баллистика, 1939. В ука¬
занных трудах имеется также и функция Н{у).
143
Система формул для определения У и v3 при помощи вспомога¬
тельных функций Сиаччи имеет следующий вид:
554
555
556
557-
Таблица 2,6 в книге Окуиев: Осиовиая задача внешней бал-
JSHCTUEH.
**) Таблицу JS 2,6 в кявге О к v и е в: Основная задача внешней бал¬
листики.
’**) Таблица й 11 в книге Вентце ль, О к v и е в н Шапиро:
Вньшш бшаствы, т. III. '
144
Из формулы 554 мы определяем приведенный баллистический
коэффициент с', а из формулы 556 — абсциссу вершины xs, необ¬
ходимую нам для1 вычисления vs по формуле 557.
Пример. Стрельба нз 76-миллиметровой пушки оско¬
лочной гранатой.
Исходные данные: те же, что и в примере параграфа 52.
Найти значение динамического угла в вершине
траектории при следующих значениях угла броса-
и'ия 5() в горазонтальной дальности А:
бе = 40°00\ Х= 12 000 м,
Вычисление производим по формуле 553;
считгч коэффициент формы равным единице.
Для определения vs и Y при помощи вспомогательных функций
Сначян мы прежде всего должны определить приведенный баллисти¬
ческий коэффициент с' по формуле 554*). _
После этого находим высоту траектории Y по формуле 555**) н функ¬
цию Н{¥)**% Имеем: ^
Далее находим xs и vs по формулам 556 и 557 *):
Теперь переходим к определению динамического угла tps при помощи
"функции Кmi(v)> пользуясь рядом величин, уже вычисленных в примере
параграфа 52:
г
или
*) Таблицы ■№№ 2; 5 й 2, 4 в книге О к у н е в: Основная задача
введшей баллистики.
145
10 Врашатедьчое жвяжение
Если для определения динамического угла Sps воспользоваться функ¬
цией Км2 {v)> *о мы будем иметь
3 (по формуле Морского Полигона)
56. Определение наибольшего допустимого значения
динамического угла в вершине траектории.
В соответствии с выражениями 546—548 наибольшее допусти¬
мое значение динамического угла в вершине траектории $ доп
равно
S
562
Первую формулу (560) мы будем употреблять тогда, когда нам
будут известны начальные условия вращательного движения сна¬
ряда. Второй формулой (561) можно пользоваться в том случае,
если стрельбой по картонам определено наибольшее значение угла
нутации на начальном участке траектории. Во всех остальных слу¬
чаях, т. е. чаще всего, необходимо применять последнюю формулу
(5G2), которая всегда будет давать несколько более жесткие требо¬
вания в отношении наибольшего допустимого значения динамического
угла $ , чем формулы 560 и 561.
Из формулы 562 следует
563
Величины ^р0> 30 И as' входящие в формулы 560—563, в соот¬
ветствии с уравнениями 513, 510 н 502 выражаются следующим
образом:
665 а0 -
Пример. Стрельба из 7 6-м илли метровой пушки оско¬
лочной гранатой.
Исходные данные: те же, что н в примерах параграфов 52 и 55.
Найти наибольшее допустимое значение динамиче¬
ского угла в вершине траектории.
Вычисление производим по формуле 563:
146
Расчеты начинаем с определения о0 и в, по формулам 564-566,
пользуясь величинами, уже найдсниыми в примерах параграфов 52 и 55
и применяя функцию Kmi(v) (таблицы 520 и 550):
571
147
) (пример параграфа 52)
Далее находим
Теперь можно перейти к определению bps 10п:
57. Обеспечение правильности полета артиллерийского
снаряда на всем протяжении траектории.
Для того чтобы обеспечить данному артиллерийскому снаряду
правильность полета на всем протяжении траектории от точки вылета
до точки падения, необходимо, чтобы были соблюдены два условия:
1) Условие правильности полета на начальном участке траектории (51)
2) условие правильности полета у вершимы траектории (54)
Система формул для определения з0, bps и bpt Л()П, в соответствии
с уравнениями 502, 505 и 563, имеет следующий вид:
572 а
е
573 а,
574
575
576 »
Ве тчины наименьшего допустимого значения коэффициента гиро¬
скопической устойчивости а доп и наибольшего допустимого значения
угла нутации 2Д0П должны быть установлены экспериментально или
заданы. Чаще всего в артиллерийской практике принимают
577
578
доп
Анализируя условия правильности полета артиллерийского снаряда
в связи с системой уравнений 572—576, мы видим, что одновременное
соблюдение обоих условий требует весьма большого' внимания кон¬
структора, так как эти условия противоречат одно другому. Почти
каждое изменение какого-либо одного из параметров, которое об¬
легчает соблюдение одного из условий правильности полета артилле¬
рийского снаряда, затрудняет соблюдение другого условия.
Особенно большое значение в этом отношении имеет изменение
величины начального значения коэффициента гироскопической устой¬
чивости з01 Если с точки зрения условия правильности полета сна¬
ряда на начальном участке траектории выгодно, чтобы величина а0
была возможно больше, то втдрое условие, гарантирующее правиль¬
ность полета снаряда у вершины, требует, чтобы величина а0 была
возможно меньше, так как увеличение а0 имеет следствием значитель¬
ное уменьшение наибольшего допустимого значения динамического
угла Ър ип. Излишняя гироскопическая устойчивость, или так называе¬
мая перестабилизация, снаряда безусловно нежелательна, и с нею
надо бороться.
Переходя к рассмотрению влияния отдельных конструктивных
параметров, ми можем притти к следующим заключениям:
148
1) увеличение коэффициента веса kq и аксиального коэффи¬
циента инерции ц улучшает правильность полета на началь¬
ном участке (вследствие увеличения <?0) и ухудшает правиль¬
ность полета у вершины (вследствие увеличения 8 и уменьше-
ния а/*аоп);
2) увеличение отношения экваториального момента инерции
к аксиал1ному ^ ухудшает правильность полёта на начальном
участке (вследствие уменьшения а0) и улучшает правильность
полета в вершине (вследствие увеличения доп);
3) увеличение выраженных в калибрах длины хода нарезов 7]
и расстояния между центром инерции и центром сопротивления воз¬
духа ухудшает правильность полета на начальном участке
(вследствие уменьшение а0) и улучшает правильность полета у
вершины (вследствие уменьшения bps и увеличения 8psjlon).
Из рассмотренных параметров величины kq, jx и для дан¬
ного тчпа снаряда могут меняться в очень небольших пределах.
Зьачнтсльно больше конструктор может изменить параметры tq и .
величиной которых и приходятся играть для того, чтобы одновре¬
менно удовлетворить обоим условиям правильности полета артилле¬
рийского снаряда.
Особенно легко и просто конструктор может увеличить -расстоя¬
ние между центром инерции снаряда и центром сопротивления j
при помощи завинчивания на головную часть снаряда пустотелого
баллистического наконечника. При этом все остальные конструктивные
параметры сохраняют свои прежние значения, не подвергаясь суще¬
стве ньы изменениям. Образцы снарядов с баллистическими наконеч¬
никами изображены на черт. 570.
В случае, если одно из условий правильности полета у нас не
соблюдено, а другое условие свидетельствует о наличии некоторого
запаса послушности артиллерийского снаряда, мы имеем возможность
за счет этого запаса послушности изменять конструктивные параметры,
главным образом и в желательном направлении.
Гораздо более трудным является положение, когда одно из условий
не соблюдено, а другое имеет предельный характер, не допуская
изменения фигурирующих в этом условии величин в сторону
ухудшения правильности полета снаряда на участке, отвечающем
данному условию.
Рассмотрим случай, когда на начальном участке траектория снаряд
находится на пределе послушности (о^ —5^,,), а у вершины траек-
149
тории условие правильности полета не соблюдено (bps Ь доп).
Необходимо уменьшить динамический угол в пертнипе не изме¬
няя начального значения коэффициента гироскопической устойчиво¬
сти а0.
Для этого мы должны увеличить параметр и уменьшить па¬
раметр Г/ таким образом, чтобы произведение оставалось по¬
стоянным:
В соответствии с выражением 572 величина коэффициента а0
остается в данном случае без1 изменения. В. выражение динамического
углао^ (уравнение 575) входит произведение Это произве¬
дение при указанном изменении параметров т} и увеличивается,
150
Черт. 570.
так как
В соответствии с выражением 575 величина динамического угла
^ в данном случае остается без изменения.
В выражение коэффициента гироскопической устойчивости (урав¬
нение 572) входит произведение [ri2'5"J* ^то произведение при
указанном изменении параметров ц и (~j) уменьшается, так как
151
Что же касается динамического угла bps, то он уменьшится, поскольку
произведение ^rJ j входит множителем в знаменатель выраже¬
ния 575.
Итак, для уменьшения динамического угла в вер¬
шине траектории bps без изменения начального зна¬
чения коэффициента гироскопической устойчи¬
вости с0 необходимо увеличить расстояние между
центром инерции снаряда и центром сопротивления
воздуха (jj'j и уменьшить длину хода нарезов у
дульного среза орудийного ствола г„ причем вели¬
чину параметра (Jj) следует изменять обратно
пропорционально квадрату величины параметра rj.
Величина Ь доп в этом случае почти не меняется, так как и ~0
и 3S остаются оез изменения, а имеет настолько малую величину,
что изменение его существенного влияния на значение угла
оказать не может.
Перейдем теперь к случаю, когда не соблюдено условие пра¬
вильности полета на начальном участке траектории (з0 зД0П), а у
вершины траектории снаряд находится на пределе послушности
(Zpt — ^ps лоп)- Необходимо увеличить начальное значение коэффици¬
ента гироскопической устойчивости с0, не изменяя значения дина¬
мического угла в вершине Ь^. Для этого мы должны увеличить па¬
раметр ^ j и уменьшить параметр 7J таким образом, чтобы произ¬
ведение -^-j оставалось постоянным:
Что* же касается начального значения коэффициента пфоскопи-
ческой устойчивости, то оно увеличивается, как это видно из урав¬
нения 572.
Итак, для увеличения начального значения-коэф¬
фициента гироскопической устойчивости а0 без
изменения величины динамического угла в вершине
траектории Ь s необходимо увеличить расстояние
между центром инерции снаряда и центром сопро¬
тивления воздуха и уменьшить длину хода
нарезов у дульного среза орудийного ствола ?],
причем величину параметра следует изме¬
нять обратно пропорционально величине пара¬
метра Г).
Величина 8 в этом случае может уменьшиться, что повле¬
чет за собой нарушение условия правильности полета снаряда у
вершины траектории. Если это нарушение будет существенным, то
необходимо будет одновременно с увеличением коэффициента а0 и
уменьшением угла Ьр5лт соответствующим образом уменьшить и
динамический угол bps. Для этой цели, увеличивая параметр
и уменьшая параметр jj, мы должны стремиться к тому, чтобы вели¬
чина изменялась обратно пропорционально величине цт, где
значение показателя т должно находиться в пределах от единицы
до двух:
1<><2-
Так же следует поступать и в тех случаях, когда не соблю¬
дено ни одно из двух условий правильности полета артиллерийского
снаряда.
Подводя итоги исследованию правильности полета артиллерийского '
снаряда на всем протяжении траектории от точки вылета до точки па¬
дения, мы видим, что наиболее эффективным мероприя¬
тием для улучшения правильности полета во всех
случаях артиллерийской практики является одно¬
временное увеличение расстояния между центром
инерции снаряда и центром сопротивления воз¬
духа и крутизны нарезки орудийного ствола
у дульного среза, причем характер этого увеличе¬
ния определяется в каждом отдельном случае
конкретными условиями задачи, стоящей перед
конструктором.
152
б. ДВИЖЕНИЕ ЦЕНТРА ИНЕРЦИИ ПОСЛУШНОГО СНАРЯДА
ПОД ДЕЙСТВИЕМ НОРМАЛЬНОЙ СОСТАВЛЯЮЩЕЙ СИЛЫ
СОПРОТИВЛЕНИЯ ВОЗДУХА.
60. Общая характеристика задачи.
Рассматривая влияние вращательного движения снаряда около его
центра инерции на движение самого центра инерции, мы видим, что
разница с основной задачей внешней баллистики будет состоять,
главным образом, в том, что в данном случае кроме касательной состав¬
ляющей силы сопротивления воздуха RT мы будем иметь еще и нор¬
мальную составляющую Rn, величина которой для послушного сна¬
ряда будет пропорциональна углу отклонения § (уравнение 012):
600
Направлена эта сила RN будет в плоскости действия ©прокиды¬
вающей пары в ту сторону, в которую отклонена головная часть
снаряда.
Имея в виду характер движения оси снаряда, изученный в пре¬
дыдущих главах, мы должны будем притти к заключению, что дви¬
жение центра инерции снаряда под действием нормальной составляю¬
щей силы сопротивления воздуха RN будет вызываться двумя факторами
различной природы.
Первым из этих факторов будет непериодическое смещение ди¬
намической оси снаряда вправо. и- немного вверх от касательной,
происходящее под влиянием понижения касательной и определяемое
выражениями 460, 461, 462:
Следствием этого систематического отклонения динамической оси
снаряда от касательной будут две силы, приложенные к центру инер¬
ции:
Первая из этих сил Rxy будет направлена противоположно силе
тяжести q и будет вызывать подъем снаряда, несколько увеличивая
его дальность. Вторая сила Rxo будет направлена вправо от каса¬
тельной, если смотреть на снаряд сзади, вызывая отклонение центра
инерции снаряда также вправо; это явление носит название деривации.
153
Углы ЬХр и %2р для послушных снарядов, вообще говоря, неве¬
лики, причем угол 81р, как мы уже видели раньше, много меньше,
чем §2 . В таком же отношении будут находиться между собою и
силы R/vy и Rnd-
В настоящей главе мы будем рассматривать только явление дерн,
ваши, имея в виду, что явление подъема, с одной стороны, имеет
меньшее значение, а с другой,—учитывается вместе с целым рядом
других факторов мри экспериментальном определении коэффициента
согласования или коэффициента формы i по полученным из опыта
величинам v0, 0о и X.
Кроме непериодического отклонения оси снаряда от касательной,
вызываемого смещением динамической оси, мы имеем как медленное,
так и быстрое коничес¬
кое движение оси сна¬
ряда около динамичес¬
кой оси, под влиянием
которых на центр инер¬
ций кроме уже рассмот¬
ренных сил RwyH Rnd
будет всегда действо¬
вать сила Rn> вращаю¬
щаяся вместе с плоскостью действия опрокидывающей пары. Под дей¬
ствием этой силы траектория центра инерции примет геликоидальный
(винтообразный) характер, причем эта геликоида будет виться около
траектории центра инерции из основной задачи внешней баллистики
(черт. 600).
В предыдущем параграфе мы установили, что причиной де¬
ривации вращающегося артиллерийского снаряда
является отклонение динамической оси снаряда
вправо, происходящее вследствие понижения ка¬
сательной или к,риволинейности траектории и вы¬
зывающее появление нормальной составляющей
силы сопротивления воздуха Rnq* направленной
вправо от касательной (если смотреть сзади). Эта составля¬
ющая равна
61. Деривация.
Так как, согласно выражению 463,
154
Черт. 600.
Составим теперь дифференциальное уравнение движения по оси Oz,
считая приложенными к центру инерции две силы: силу RT, направ-
' ленную по касательной
к траектории в сторону,
противоположную ско¬
рости, и силу Rnd-
Движение снаряда по
осям Ох и Оу будем
принимать таким, ка¬
ким оно было опреде¬
лено в основной задаче
внешней баллистики.
Проектируя траекторию снаряда на горизонтальную плоскость,
мы получим картину, изображенную на черт. 610.
Напишем уравнение движения центра инерции снаряда по оси
боковых отклонений
то выражение для R^D принимает вид:
Вводя по аналогии с основной задачей величину
Черт. 610.
611
получим
или
612
где
613
откуда
Следовательно,
Полученное дифференциальное уравнение второго порядка может
быть заменено двумя эквивалентными уравнениями первого порядка
В основной задаче мы обычно пользовались системой ур&внониЯ
при аргументе х,. Составим подобные же уравнения и для дерива¬
ции, имея в виду, что
Для определения
Но, с другой стороны, из уравнения 614, мы имеем
Учитывая, что
и подставляя dt -
Сравнивая уравнения 616 и 617, мы будем иметь
и окончательно, после замены Jm его выражением 612,
Итак, система уравнений, определяющих деривацию при аргументе х,
будет иметь следующий вид:
618
619
62. Вычисление деривации,
Наиболее точно деривация может быть определена по методу
численного интегрирования при условии, конечно, что функция
D(v) будет нам известна. Тогда, имея вычисленной обычным способом
интересующую нас траекторию, мы будем знать для любой точки
значения v и D{v). Далее численное интегрирование двух диффе¬
ренциальных уравнений
не будет представлять никаких затруднений *).
Так как величины ф и г, вообще говоря, незелики, то вполне
целесообразно во многих случаях практики вводить некоторые упро¬
щения. Во-первых, мы можем заменить единицей переменную вели¬
чину (1 -j-tg2 ф); во-вторых* функцию D(v) можно заменить постоянной
величиной D. Тогда система уравнений 620 принимает еще более
простой вид
Для интегрирования этой упрощенной системы дифференци¬
альных уравнений применим способ, идея которого была в
свое время предложена Н. В. Маиевскш!.
*) Для определения lg (1 —tg2 Ф) по величине tg £ ыожно пользоваться
таблицей 20 из книги Вентце ль, Оку нев и Шапиро: «Внешняя
баллистика», часть III.
620
621
и
Из первого уравнения системы 621 после подстановки г»=
имеем
157
Заменим теперь и и dx их выражениями через псевдоскорость
U в соответствии с обычными формулами Сиаччи:
Тогда
Для приближенного интегрирования полученного уравнения де¬
лается новое допущение о том, что
и вводится новая функция M(U), аналогичная функциям Сиаччи и
удовлетворяющая условию
Тогда мы будем иметь
или после интегрирования от точки вылета до произвольной точки
траектории в соответствующих пределах:
622
Подставляя найденное выражение для tg<]> во второе уравнение
системы 621, получим
или, после замены dx в первом члене правой части уравнения его
выражением через U,
Для интегрирования этого уравнения вводится еще одна функ¬
ция, обозначаемая через В (U) и удовлетворяющая условию
Тогда мы будем иметь
или после интегрирования от точки вылета до произвольной точки
траектории в соответствующих пределах:
или
625
Функции M(U) и В (U) впервые были введены Н. В. Маиев-
ским. Таблицы этих функций, вычисленные при одночленных зако¬
нах сопротивления воздуха Маиевского-Забудского для нормального
крупповского эталонного снаряда, имеются в труде Н. А. Забуд-
ского «Внешняя баллистика».
Величина D, равная
или входящая в выражение для D величина
быть определены опытным путем.
При экспериментальном определении величины D для какой-либо
определенной артиллерийской системы следует произвести несколько
стрельб с определением деривации в точке падения. На основании
этих стрельб устанавливается эмпирическая зависимость D—f(60)
в виде таблицы или графика, которыми уже можно пользоваться при
расчете z и Z для любых углов бросания.
В случае, когда нам необходимо определять значения деривации
только для точек падения (например при составлении наземных таб¬
лиц стрельбы), то в очень многих случаях артиллерийской прак¬
тики наиболее целесообразным путем будет непосредственное уста-
Z Z
новление эмпирической зависимости jf—/ (%) или =/(х) на
основании небольшого количества опытных стрельб из исследуемой
артиллерийской системы.
Далее, для. вычисления деривации в точке падения можно поль¬
зоваться очень простыми эмпирическими зависимостями:
159
откуда после подстановки сх = D(U) — D (w0) в соответствии
с обычными формулами Сиаччи, получим
Для точки падения формула 623 принимает вид
где Кх и К2 — коэффициенты постоянные для данной системы и опре¬
деляемые на основании двух-трех опытных стрельб.
Из этих эмпирических формул особенно можно рекомендовать
первую, устанавливающую пропорциональность деривации квадрату
времени полета.
Кроме этих формул автор в целом ряде случаев пользовался еще
более простой формулой
629
также дающей весьма неплохие результаты.
Из других способоз вычисления деривации можно указать на це¬
лый ряд самых разнообразных эмпирических формул, предлагаемых
различными авторами.
Формула Эли:
причем
где у—угол наклона нарезов в дульном срезе, а е — угол, состав¬
ляемый осью снаряда и касательной к производящей оживальной
части снаряда в вершине оживала.
Формула Браветты (Bravetta):
где A'j и К% — коэффициенты, определяемые из опыта.
Формула Хаупта и Шарбонье для больших начальных
скоростей:
и формула Щарбонье для малых начальных скоростей:
где Кг и — эмпирические коэффициенты.
Формула Кранца:
где К—эмпирический коэффициент, имеющий значения в пределах
от 0,005 до 0,010.
Как мы видим, все приведенные эмпирические формулы имеют
весьма разнообразный вид, отражая только те опыты, с которыми
имели дело их авторы. Поэтому совершенно очевидно, что универсаль¬
ного значения эти эмпирические формулы иметь не могут.
6 руб.