Автор: Кубо Р.
Теги: физика термодинамика
Текст
Р.Кубо
ТЕРМОДИНАМИКА
Настоящая книга представляет собой учебное пособие, которое должно
помочь студентам активно усвоить материал курса термодинамики. В каждой
главе кратко излагаются важнейшие необходимые теоретические сведения и
приводится большое количество задач и их решения.
Книга рассчитана на студентов и аспирантов, изучающих термодинамику; она
будет также полезна преподавателям вузов и лекторам, ведущим
соответствующие курсы.
Содержание
Предисловие редакторов перевода 5
Предисловие к английскому изданию 6
Предисловие к японскому изданию 7
Глава 1. Термодинамическое состояние и первый закон 11
термодинамики
Основные положения. 11
§ 1. Предмет термодинамики 11
§ 2. Понятие теплового равновесия (нулевой закон термодинамики) 12
§ 3. Термодинамический контакт 13
§ 4. Термодинамические величины 14
§ 5. Процесс изменения состояния 15
§ 6. Первый закон термодинамики 16
§ 7. Теплота и энтальпия 19
§ 8. Применение первого закона термодинамики к инфинитезимальным 20
процессам
§ 9. Температура 21
§ 10. Теплоемкость. Удельная теплоемкость 22
§11. Уравнение состояния 23
§ 12. Замена независимых переменных 29
Примеры 29
Задачи 42
Решения 48
Литература 71
Глава 2. Второй закон термодинамики 72
Основные положения. 72
§ 1. Обратимые и необратимые процессы 72
§ 2. Лемма (цикл Карно) 73
§ 3. Второй закон термодинамики 74
§ 4. Коэффициент полезного действия общего цикла Карно 75
§ 5. Абсолютная температура 77
§ 6. Неравенство Клаузиуса для произвольного цикла 81
§ 7. Энтропия 82
§ 8. Аддитивность энтропии 85
§ 9. Общая формулировка второго закона термодинамики 86
§10. Направление реальных процессов 87
§11. Максимальная и минимальная работа 89
Примеры 90
Задачи 97
Решения 106
Литература 141
Глава 3. Термодинамические функции и условия равновесия 142
Основные положения 142
§ 1. Термодинамические функции 142
§ 2. Преобразование Лежандра 146
§ 3. Уравнение Гиббса — Дюгема 146
§ 4. Определение термодинамических величин и термодинамические 147
соотношения
§ 5. Третий закон термодинамики (теорема Нернста —Планка) 149
§ 6. Равновесие двух систем 150
§ 7. Условия равновесия для заданного термостата 151
§ 8. Термодинамические неравенства 153
§ 9. Принцип Ле-Шателье — Брауна 156
Примеры 158
Задачи 170
Решения 176
Литература 198
Глава 4. Равновесие фаз и химическое равновесие 199
Основные положения. 199
§ 1. Фаза 199
§ 2. Равновесие между различными фазами чистого вещества 199
§ 3. Поверхностное натяжение 201
§ 4. Равновесие в многокомпонентной многофазной системе 202
§ 5. Правило фаз Гиббса 204
§ 6. Химический потенциал газа 206
§ 7. Химический потенциал и давление насыщенных паров 208
§ 8. Разбавленные растворы 209
§ 9. Идеальные растворы (идеальные твердые растворы) и регулярные 210
растворы
§10. Выражения для концентрации растворов 211
§11. Активность и коэффициент активности 211
§ 12*.Растворы сильных электролитов 212
§13 . Химическое равновесие 214
§14 . Термодинамика электрохимического элемента 216
§15 . Применение третьего закона термодинамики 219
Примеры 220
Задачи 237
Решения 251
Литература 297
Предметный указатель
299
Предметный указатель
Курсивом выделены номера тех страниц, на которых дается основное определение данного
термина.
Абсолютный нуль температуры 150,
170, 192
Адиабата 97, 108
Адиабатический температурный
коэффициент 171
Азеотропия 246
Активность 211
— коэффициент 235
Амфотерный электролит 285
Аналитическая формулировка
термодинамики 142
Аррениуса теория диссоциации 214
Атмосферное давление 44
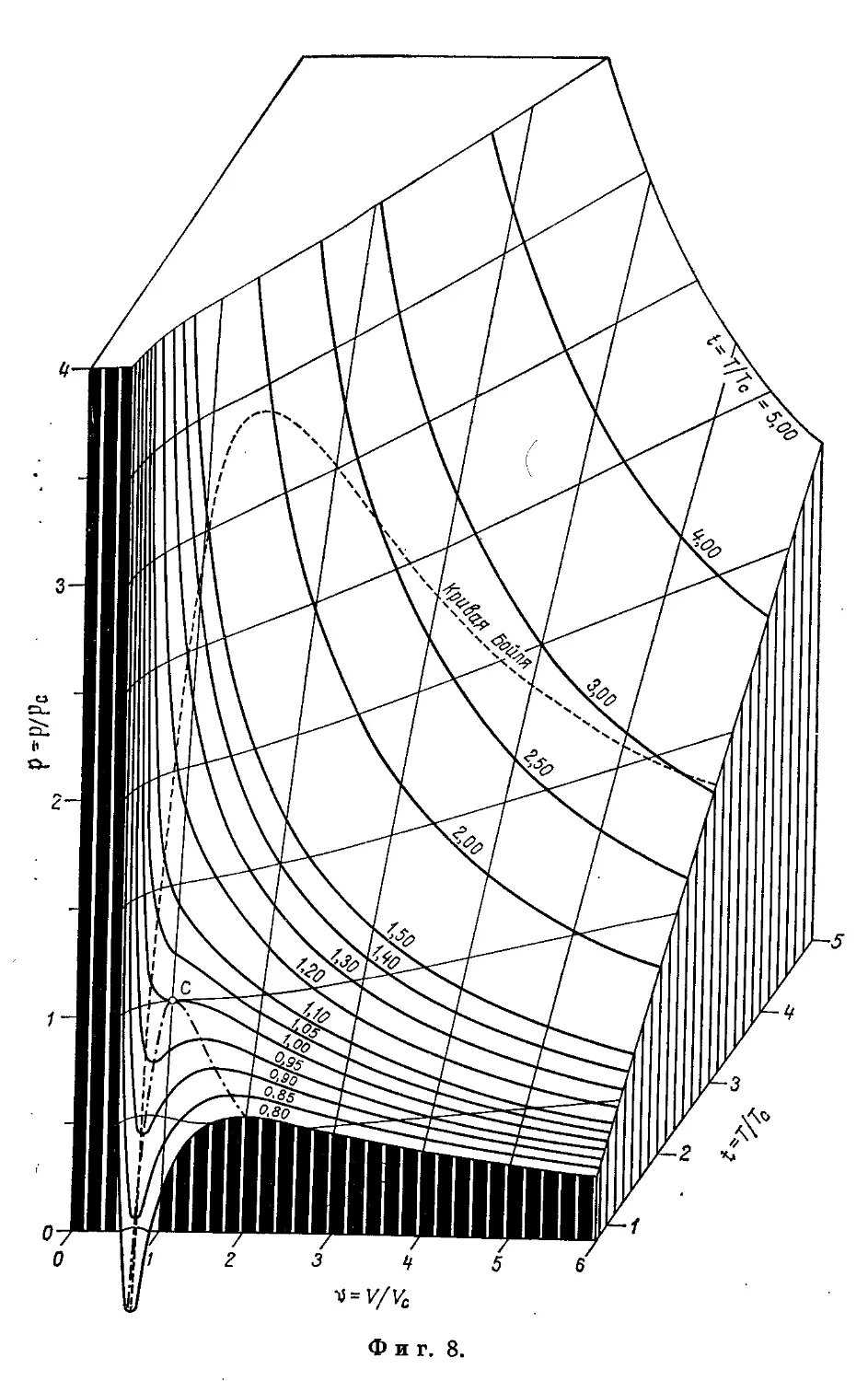
Бойля кривая 56, 40, 41
Больцмана постоянная 25, 269
Большой потенциал 143
Вагнера — Энгельгардта элемент 249
ван дер Ваальса газа внутренняя
энергия 129
-----критическое состояние 36
-----теплоемкость удельная при
постоянном объеме 103
-----термодинамический потенциал
244
-----уравнение состояния 26, 36, 38,
129, 135, 290
-----энтропия 129
-----эффект Джоуля — Томсона 135
Вант Гоффа закон 235, 284
Вечный двигатель второго рода 75
-----первого рода 17
Взаимодействие механическое 13
— тепловое 13
Вильсона камера 245, 251, 277
Вириальное разложение 28
Вириальный коэффициент 28, 119
Внутреннее трение 48
Внутренняя сила 21
— энергия 16, 143, 157
Водород 84, 85
Возгонка 246
Воздух 32, 45
— теплоемкость 163, 164
— энтальпия 160
Второй закон термодинамики 86
Высокополимерный раствор 247, 251
284, 296
Газовая постоянная 25
Гей-Люссака эксперимент 102
Генри закон 209, 240, 259
Г иббса — Г ельмгольца уравнение
105
Гиббса — Дю гема уравнение 146,
173, 190, 209, 222, 234, 240, 248.
258
Гиббса — Пойнтинга уравнение 201
Гиббса правило фаз 204
— уравнение 82
Давление атмосферное 52
— равновесное 253
Даниэля элемент 216, 217, 236
Двухкомпонентная система 222
Дебая — Хюккеля уравнение 213,
249
Джоулево тепло 70
Джоуля — Томсона коэффициент
101, 102, 105, 120, 135, 136
-----процесс 171, 180
-----эксперимент 41, 101
-----эффект 105, 135
Джоуля цикл 97
— эффект 176, 198
Дизеля цикл 97
Диссоциация 212, 243, 267
— давление 243
— степень 235, 242
— тепловая 23 5
Дитеричи уравнение состояния 44,
56, 105, 134
Диффузия 103, 248
Диэлектрик 175, 194—196
Доннана мембраны равновесие 248,
285
Дюгема — Маргулеса уравнение 259
Естественные независимые
переменные 142, 143
Жидкая фаза 219, 224
Жидкость 208
— переохлажденная 101, 118
Закон действующих масс 215
— сохранения энергии 16
Замерзание 226, 228, 230, 262, 263
Зонная очистка 281
— плавка 247
Идеальные газы, смесь 25, 56, 173,
183, 206
Идеальный газ, внутренняя энергия
46, 53, 167
----свободная энергия 116, 167
----теплоемкость 172
----термодинамический потенциал
116
----уравнение состояния 25
----энтальпия 46
----энтропия 97, 99, 111, 167
Изотерма 220
Интегрирующий множитель 83, 127
Интенсивная величина 14
Инфинитезимальный процесс 15
Ионизации энергии 236
Ионная сила 213
Источник частиц 13
Калория термодинамическая 19
Капля жидкости 276, 296
Каратеодори принцип 75, 103, 125,
126
Карно принцип 75
— цикл 44, 73, ИЗ, 122
Кельвина уравнение 105
Кипения точка 228, 229, 241, 262
Клаузиуса — Клапейрона уравнение
200, 252, 262, 274, 277
Клаузиуса неравенство 81
— принцип 74, 125, 126
— уравнение 44, 65
Конденсатор плоский 175
Конденсированная фаза 225
Константа равновесия 216, 219, 242,
296, 297
Контактная разность потенциалов
236
Контакт термодинамический 13, 15
Концентрация 211
Коэффициент полезного действия 75,
97
— продвижения реакции 215
Крамерса функция 143
Кривая газовой фазы 246, 279
Кривые жидкой и твердой фаз
(ликвидус и солидус) 241, 246,
265, 279
Критическое состояние 36, 56
Кюри — Вейсса закон 104, 187, 192,
250
Кюри закон 28, 95, 102, 174, 192
— константа 28
— температура 250, 293, 294
Лапласа формула 238
Лежандра преобразование 146
Ле-Шателье — Брауна принцип 156,
157, 172, 182, 190
Ле-Шателье принцип 156, 249
Магнитная восприимчивость
адиабатическая 46, 100, 114,
174, 191
-----изотермическая 46, 100, 104,
114, 173, 174
Магнитное поле 28, 45, 47, 57, 174,
175
-----критическое в
сверхпроводниках 245
Магнитный диполь 57
— момент 45, 46
— поток 30, 58
Магнитострикция 104
Майера соотношение 31, 32, 44, 130
— цикл 44
Максвелла правило 41, 222, 237, 250,
252, 293
— соотношения (теоремы
взаимности) 100, 116, 117, 119,
148, 166, 179, 189, 190, 197, 274,
291
— уравнения 48, 68, 69
Массье функция 143
Материальное взаимодействие 13, 21
Машина тепловая 73
Мейсснера эффект 245
Модуль упругости объемный 42
Мольная (молярная) доля 207, 211
Моляльность 211
Молярность (молярная
концентрация)211
Намагниченность 28, 45, 57, 70
— спонтанная 294
Намагничивания работа 29, 70
Насыщенный пар 208, 209
— — адиабатическое расширение
277
----давление 208—210, 212, 221,
238, 245, 275, 277
Натяжение 173, 176
Неголономная система 103
Независимые переменные 14, 29, 142,
149
Непрерывности уравнение 65
Нулевой закон термодинамики 12,
48, 68
Ожижение газа 138, 180
Окружающая среда И, 12
Ома закон 69
Осмотический коэффициент 234
Осмотическое давление 228, 285
Отто цикл 97
Парамагнетик, внутренняя энергия
132, 173
— идеальный 28
— свободная энергия 175
— термодинамический потенциал
173, 175
— энтропия 132, 173, 192
Пар перегретый 48
— пересыщенный 245, 277
Парциальное давление 26, 207
Первый закон термодинамики 16, 66
Переменные внешние 14
— внутренние 14, 204
Плавление 219, 262
Планка функция 143
Поверхностное натяжение 201, 223,
238
Полное давление 207
Полупроницаемая мембрана 248
Преобразование переменных 149
Принцип возрастания энтропии 88
— максимальной работы 89
Процесс адиабатический 16, 255
— квазистатический 15
-----изотермический 16
— необратимый 16, 72
— обратимый 15, 72
Пружина 169, 192, 193
Работа 13, 16, 17, 19, 21, 30, 47, 124
— источник 13
— максимальная 89
— минимальная 89, 96, 104, 124
Рабочее вещество 73
Равновесие локальное 12
— метастабильное 152, 253
— механическое 150
— тепловое 12, 88
-----в постоянном магнитном поле
293
-----условия 150—152
— устойчивость 152, 231
— химическое 214, 288
Равновесия константа 216, 219, 242,
296, 297
Размагничивание адиабатическое
102, 122, 174
Размагничивающее поле 30, 70
Раствор 209, 210, 212, 238, 259
— двухкомпонентный (бинарный)
209, 238
— идеальный 210, 240, 262
— многокомпонентный 209
— разбавленный 209, 262, 263
— регулярный 210
— сильных электролитов 212, 213,
238
— твердый 208, 257, 263
Растворенное вещество 209, 212, 240,
259
Растворитель 209, 228, 240, 259
Расширение адиабатическое 101, 110,
121, 174
— коэффициент 104
— свободное 44, 54, 99
Рауля закон 209
Реакция химическая 214, 288
-----внутренняя энергия
стандартная 267
-----равновесие 266
-----свободная энергия 214, 243
-----термодинамический потенциал
218
-----энтальпия 214, 243
— экзотермическая 289
— эндотермическая 289
Сакура — Тетрода формула 269
Сверхпроводящее состояние 245, 278
Свободная энергия (Гельмгольца) 87,
'143, 158, 170, 171, 175, 177, 187
-----диэлектрика 194, 196
-----поверхностная 224
— энтальпия 158
Сегрегации постоянная 246
Сжимаемость адиабатическая 35,
100, 114, 172
— изотермическая 35, 100, 104, 114,
172
Система замкнутая 12
— изолированная 11
— макроскопическая 11
— многокомпонентная 202
— открытая 12
— термодинамическая 11
Скорость звука 43, 46, 50
Соответственные состояния 36, 37,
45, 56
Состояние термодинамическое 13
Сосуществование двух фаз 199, 200,
221
Сплав Си — Ni 241
Степени свободы 204
Стефана — Больцмана закон 47
Твердая фаза 226
Температура 21
— абсолютная (Кельвина) 22, 77, 99,
104, 131
— критическая 36, 220, 244
— теорема существования 48, 68
— уменьшение при адиабатическом
расширении 110, 171, 180
----шкала 22, 77, 79, 80
Тепловое излучение 47, 63, 64, 92
Тепловой обмен (условия
равновесия)150
— резервуар 13, 74, 81, 88
Теплоемкость 22, 31, 147, 277
— молярная 22
— неотрицательная 167
— отрицательная 275, 277
— при постоянном давлении 22, 46,
105, 116, 147, 160, 161, 165
-------магнитном поле 46, 174
-------объеме 46, 116, 147, 160,
161, 165
-------химическом потенциале 174
-------электрическом поле 195
— удельная 22, 31, 147
----насыщенного пара 245, 274, 275
Теплопроводность 48
Теплота парообразования 219, 225
----скрытая 254
— перехода 200
— плавления 219, 263
— расширения скрытая 104, 131
Термодинамические неравенства 155
— переменные (переменные
состояния) 14
— потенциалы 142, 143
— функции 146, 147, 157
Термодинамический потенциал
Гибб-
са 96, 143, 147, 171, 183, 184
Термодинамическое состояние 13
Термометр газовый 22, 77, 105, 136
Томсона (Кельвина) принцип 74, 90,
97, 103, 125, 127
Томсона Дж. Дж. уравнение 296
Третий закон термодинамики
(теорема Нернста — Планка)
149, 170, 173, 186, 192, 219
Тройная точка 205, 226, 237, 252, 253
Удельные молярные величины 148
Уравнение состояния 23, 99
У стойчивость термодинамическая
185
Фаза 199, 200, 204
— внутреннее условие равновесия
204
Фазовая диаграмма 227, 233, 240,
247, 257, 263
Фазовое равновесие 199
Фазовый переход высших порядков
201
-----первого и второго рода 200
Фазы, разделение 222
Фарадея постоянная 218
Ферромагнетик 293
— теплоемкость 250, 294
Фугативность 207, 212, 215, 239
Функции состояния 14, 17
Химическая постоянная 183, 206 „
219, 269
-----условная 269
Химический потенциал 20, 148
-----газа 206
Цикл 15
— необратимый 73
— обратимый 73
Эвтектическая точка 226, 241, 264
Эйлера уравнение 147
Экстенсивная величина 14, 239
Электродвижущая сила 217, 218, 236,
243, 249
Электронейтральности условие 215
Электроны тепловые 243, 269
Электрохимический потенциал 218
Элемент электрохимический 216, 243
Энергия 14, 16, 17, 157
— переноса массы 16, 17, 202
— удельная молярная 148
Энтальпия 19, 41, 67, 143, 157, 171
— удельная молярная 148
Энтропия 82, 83, 143, 157, 171
— аддитивность 83
— зависимость от температуры 121
— плавления 264
— поверхности 255
— смешения 95, 207
— удельная молярная 148
Якобиан 149
Предисловие редакторов перевода
Настоящий учебник термодинамики, написанный профессором
Р. Кубо при участии X. Ичимура, Ц. Усуи и Н. Хасизуме, пред-
ставляет собой первую часть оригинального курса термодинамики
и статистической механики, в котором совмещается краткое изло-
жение основ теории с подробным решением большого количества
задач. Вторая часть курса, «Статистическая механика», была
издана на русском языке в 1967 г. издательством «Мир» и вызвала
большой интерес читателей, что свидетельствует о потребности
в учебных пособиях такого типа.
В учебнике рассмотрены обычные разделы термодинамики. Пер-
вая и вторая главы посвящены изложению первого и второго
законов термодинамики, где авторы, отступая от сложившихся
традиций, с самого начала формулируют законы таким образом,
что они пригодны и для открытых систем (с обменом вещества).
Это облегчает авторам изложение метода термодинамических
потенциалов и условий равновесия, которые рассмотрены в гл. 3.
Гл. 4 посвящена приложению термодинамики к теории равновесия
фаз и химическому равновесию. Как и в курсе «Статистической
механики», теоретические разделы в каждой главе изложены пре-
дельно кратко, но достаточно ясно и иллюстрируются подробно
разобранными примерами. Далее предлагаются задачи в порядке
возрастающей трудности с подробными решениями. Изложение
оживляют весьма интересные «Отступления», обычно содержащие
любопытные научные или исторические сведения.
Несомненно, что этот оригинальный учебник-задачник прине-
сет большую пользу студентам, приступающим к изучению курса
термодинамики, и аспирантам, как физикам, так и химикам;
он может быть широко использован также преподавателями уни-
верситетов и физико-технических вузов.
Перевод выполнили А. Г. Башкиров (гл. 1 и 2) и Е. Е. Тареева
(гл. 3 и 4).
Д. Н. Зубарев
Н. М. Плакида
Предисловие к английскому изданию
Предлагаемая книга представляет собой первые четыре главы
учебника «Задачи и примеры по термодинамике и статистической
механике», опубликованного в «Университетской серии» японским
издательством «Сокабо». Несмотря на то что английский перевод
второй части этого учебника под названием «Статистическая
механика. Современный курс с задачами и решениями» вышел
в издательстве «Норс' Холланд компани» раньше, предлагаемую
книгу следует рассматривать как первый том учебника.
Английское название несколько отличается от оригинального,
что, по-видимому, отражает некоторое недопонимание целей, пре-
следовавшихся авторами при наиисании книги. Это отнюдь не обыч-
ный учебник, а скорее пособие, призванное помочь студенту
активно изучить предмет путем самостоятельных размышлений
и решения задач. При этом приводимые в тексте решения задач
могут быть использованы самым различным образом. Поэтому
материал, помещенный в разделах «Основные положения», написан
по возможности сжато, с тем чтобы читателю было удобно про-
сматривать его повторно при решении задач. Значительная часть
вопросов, обычно рассматриваемых в учебниках, приводится
в замаскированной форме — в задачах и примерах. В зтом смысле
настоящая книга дает замкнутое изложение предмета. Тем не менее
следует порекомендовать студентам наряду с настоящей книгой
пользоваться также каким-либо стандартным учебником.
Перевод с японского на английский был сделан в основном док-
тором Хадзими Секи, некоторые разделы перевели авторы. Как
редактору японского и английского изданий мне хотелось бы выра-
зить глубокую благодарность доктору X. Секи, а также профес-
сорам Б. Спрингеру и Д. Уорсу, которые взяли на себя труд про-
читать рукопись и помогли нам преодолеть некоторые лингвисти-
ческие трудности. Я также благодарен миссис Н. Хасидзуме
и миссис М. Сузуки за помощь в подготовке рукописи.
Риого Кубе
Предисловие к японскому изданию
Термодинамика и статистическая механика совершенно необ-
ходимы при изучении физических свойств вещества. Статистиче-
ская механика наряду с квантовой механикой является основой
современной физики; ее цель состоит во всестороннем иссле-
довании физических явлений с микроскопической точки зрения
на основе атомной физики. Поэтому глубокие знания статистиче-
ской механики и умение применять ее на практике необходимы
не только студентам, изучающим физические свойства вещества,
но и тем, кто занимается ядерной физикой и даже астрофизикой.
Вне рамок физики статистическая механика теперь все больше
и больше проникает в такие науки, как химия, биология и те мно-
гочисленные области техники, развитие которых связапо ^успе-
хами современной физики.
Термодинамика всецело принадлежит классической физике,
и поэтому иногда студенты, увлеченные изучением современной
физики, считают ее малозначительной наукой. Даже для студен-
тов-химиков положение стало совершенно иным, чем несколько
десятилетий назад, когда физическая химия представляла собой
не что иное, как химическую термодинамику. Необходимо подчерк-
нуть, что и сейчас термодинамика, представляющая собой один
из основных разделов физики, играет столь же важную роль, как
и во второй половине прошлого века. Термодинамика демонстри-
рует ценность феноменологического подхода. В ней не исполь-
зуются в явном виде какие-либо физические образы или модели,
например представления об атомах или молекулах, а устанавли-
ваются соотношения между такими несколько абстрактными
величинами, как энергия, энтропия, свободная энергия и т. д. При
этом термодинамика не опирается на интуитивные представления,
как атомная теория; это является одной из причин того, что
студенты считают термодинамику трудной для усвоения и не умеют
применять ее для рассмотрения конкретных задач. Однако благо-
даря простоте логических построений термодинамика часто позво-
ляет с очень общих позиций разобраться в физической сути данной
задачи. В этом состоит огромное преимущество феноменологиче-
ского подхода.
8 Предисловие к японскому изданию
Очевидно, однако, что, ограничиваясь только термодинамиче-
ским рассмотрением, невозможно провести более глубокое иссле-
дование атомных процессов, происходящих при данном физиче-
ском явлении. Это возможно сделать лишь с помощью квантовой
механики и статистической механики. Статистическая механика
позволяет установить связь между физическими законами микро-
и макромира. Квантовая механика, взятая в отрыве от статистиче-
ской механики, не всегда могла бы описывать реальные физиче-
ские явления. В этом смысле статистическую механику необходимо
рассматривать как один из ключевых разделов современной
физики.
Как и во всякой другой науке, невозможно хорошо усвоить
статистическую механику, выучив только ее основные принципы.
Необходимо довольно долго тренироваться, чтобы овладеть мето-
дами статистики, т. е. научиться пользоваться статистической
механикой при решении конкретных физических задач. Некоторые
представления и методы статистической механики и термодина-
мики существенно отличаются от используемых в других разделах
физики. Нам часто приходилось встречать студентов, которые
знакомы с основными положениями термодинамики и статистиче-
ской механики, но с трудом овладевают их методами и не умеют
решать конкретные задачи. Это обычно связано с недостаточной
и неправильной подготовкой.
Цель настоящей книги — помочь студентам в изучении термо-
динамики и статистической механики и в овладении соответст-
вующими методами. Книга содержит основные положения теории,
примеры и большое число задач с полными решениями. Хотя
разделы «Основные положения» написаны довольно кратко, они
охватывают все наиболее важные вопросы теории. Предполагается,
что эту книгу можно читать, не пользуясь другими учебниками.
Изучив материал «Основных положений», читатель в достаточной
мере познакомится с основами термодинамики и статистической
механики. Примеры дополняют теоретические разделы, но в основ-
ном они должны показать читателю, как следует применять тео-
рию при решении физических задач.
Задачи разделены на три группы А, Б, В в порядке возрастания
трудности. Если читатель располагает достаточным количеством
времени, он может перерешать все задачи подряд в каждой главе.
В противном случае мы рекомендуем ему сначала решить задачи
группы А по всей книге, а при возможности вернуться к задачам
групп Б и В. Даже решив только задачи группы А, читатель почув-
ствует, что он стал лучше разбираться в физической стороне
явлений. Число задач в группе А достаточно велико, так что
сначала можно выбрать из них примерно половину и решить их,
вернувшись к оставшимся позже. Для удобства звездочкой (*)
Предисловие к японскому изданию
9
отмечены те параграфы и примеры, которые не нужны при реше-
нии задач группы А.
В приведенных в настоящей книге задачах по термодинамике
и статистической механике рассматриваются главным образом
равновесные состояния. Вероятно, было бы желательно охватить
и кинетические методы, а также приложения термодинамики и ста-
тистической механики к неравновесным проблемам. Нам пришлось,
однако, ограничиться лишь сжатым рассмотрением этих вопросов
в последней главе (гл. 6 «Статистической механики» 1). Это вызвано
тем, что объем книги и так оказался гораздо больше, чем пред-
полагалось ранее; кроме того, задачи на неравновесные процессы,
конечно, значительно более сложны.
Как упоминалось ранее, квантовая механика описывает дина-
мику микромира. В этом смысле статпстическая механика должна
быть квантовой. Поскольку, однако, целью настоящей книги
является обучение методам статистической механики, для решения
задач групп А и Б вполне достаточно элементарных сведений
по квантовой механике. Поэтому даже те студенты, которые не спе-
циализируются на изучении физики, но имеют простейшие пред-
ставления о квантовой механике, не встретят серьезных трудно-
стей, начав читать эту книгу.
При изучении физической проблемы очень важно понимать ее
как проблему именно физическую. Математические выкладки иног-
да скучны, а иногда требуют определенных технических навыков.
Не следует, конечно, пренебрегать изучением математических
методов, но было бы большой ошибкой увлечься математикой
и забыть про физику. Преподавателям часто приходится иметь
дело со студенческими работами, где студент получает правильные
значащие цифры, но при этом ошибается на два-три порядка по
величине или в размерности. Однажды проф. Нагаоко — пионер
японской физики — во время лекции проводил вычисления на
доске. В конце вычислений он поменял знак в ответе, заметив:
«Здесь скорее должен стоять плюс, чем минус. Не так ли?» Оши-
биться в математических выкладках очень легко. Поэтому физи-
ческие соображения особенно важны, ибо они позволяют опреде-
лить правильный знак, даже если вычисления подвели вас.
Во многих случаях результат, полученный при вычислениях, легко
понять, по крайней мере качественно. Его, может быть, трудно
угадать до вычисления, но, проведя все выкладки, не следует
лениться подумать над результатом еще раз и попытаться понять
его физический смысл. Подобные замечания не делаются в реше-
Напоминаем читателю, что в оригинальном японском издании термо-
динамика и статистическая механика содержались в одной книге.
10 Предисловие к японскому изданию
ниях задач, поэтому мы особенно подчеркиваем здесь важность
такого подхода.
Проводя семинары со студентами, мы иногда делаем перерывы,
чтобы поговорить о разных проблемах. Точно так же в разных
местах книги мы позволили себе так называемые «Отступления».
Изучая материал книги и решая задачи, читатель тоже, как мы
надеемся, найдет время немного отвлечься и за чашкой кофе или
сигаретой прочитать авторские отступления.
Разделы «Основные положения» почти целиком написаны
Р. Кубо. Примеры и задачи отбирались всеми авторами. Оконча-
тельная проверка решений была проведена Р. Кубо, а общая
компоиовка книги осуществлена Н. Хасизуме. Авторы будут бла-
годарны читателям за все замечания о тех ошибках, которые могли
ускользнуть от нашего внимания.
Риого Кубо
ГЛАВА 1
Термодинамическое состояние
и первый закон термодинамики
В этой главе обсуждается понятие термодинамического состоя-
ния, а также понятия, связанные с первым законом термодина-
мики. Приступающие к изучению термодинамики должны иметь
ясное представление о физическом смысле этих понятий. В част-
ности, нужно отметить, что работа и теплота не являются функ-
циями состояния, а зависят от пути перехода из одного состояния
системы в другое.
ОСНОВНЫЕ ПОЛОЖЕНИЯ
§ 1. Предмет термодинамики
Ниже перечисляются и поясняются некоторые основные поня-
тия и термины, используемые в термодинамике. Чтобы не загро-
мождать изложение, не всем понятиям дается строгое определе-
ние. В тех случаях, когда это необходимо по ходу рассуждений,
приводятся более строгие определения.
Термодинамические системы. Термодинамика занимается изуче-
нием макроскопических систем, пространственные размеры которых
и время существования достаточны для проведения нормальных
процессов измерения. Такого рода системы могут состоять из боль-
шого числа материальных частиц (например молекул, атомов,
электронов и т. д.), или полей, например электромагнитного по-
ля. В любом случае мы имеем дело с динамическими системами,
обладающими чрезвычайно большим числом степеней свободы.
Системы с малым числом степеней свободы термодинамикой не
рассматриваются.
Термостат. Если изучается часть полной системы, то осталь-
ную часть будем называть окружающей средой, или окружением.
Более абстрактно окружение можно рассматривать, как термо-
стат, который налагает некоторые условия на изучаемую систему
(например, условия постоянства температуры, давления, химиче-
ского потенциала и т. д.).
Изолированная система. Независимая система, которая совер-
шенно не взаимодействует с окружающей средой, называется изо-
лированной системой.
12 Гл. 1. Термодинамическое состояние и первый закон
Замкнутая система. Система, которая не обменивается веще-
ством с окружающей средой, называется замкнутой системой.
Открытая система. Система, которая обменивается веществом
с окружающей средой, называется открытой системой.
§ 2. Понятие теплового равновесия (нулевой закон термодина-
мики)
Состояние теплового равновесия изолированной системы. Изо-
лированная система (например, газ, заключенный в сосуде с не-
теплопроводящими стенками) независимо от своего начального
состояния в конечном итоге приходит в состояние, которое в даль-
нейшем уже не меняется. Это конечное состояние называется
состоянием термического, или теплового, равновесия. Если говорить
о микроскопической картине, то материальные частицы продол-
жают свое сложное движение, но с макроскопической точки зрения
термически равновесное состояние является простым состоянием,
которое определяется несколькими параметрами, как, напримерг
температурой и давлением *).
Тепловое равновесие двух систем. Если две изолированные систе-
мы А и В приведены в контакт друг с другом, то полная система
А + В в конечном итоге переходит в состояние теплового равно-
весия. В этом случае говорят, что системы А нВ находятся в состоя-
нии теплового равновесия друг с другом. Каждая из систем
А и В в отдельности также находится в состоянии теплового рав-
новесия. Это равновесие не нарушится, если устранить контакт
между системами, а затем через некоторое время восстановить его.
Следовательно, если установление контакта между двумя систе-
мами А и В, которые до этого были изолированными, не приводит
ни к каким изменениям, то можно считать, что эти системы нахо-
дятся в тепловом равновесии друг с другом (Л ~ В).
Нулевой закон термодинамики (закон транзитивности теплового
равновесия). Если системы'Л и В находятся в тепловом равновесии
и системы В и С находятся в тепловом равновесии, то системы
Л и С также находятся в тепловом равновесии между собой:
А~В, В~С-+А~С. (1.1)
Этот эмпирический закон называется нулевым законом термоди-
намики.
J) Термически равновесное состояние, определенное таким образом,
принято называть термодинамически равновесным.— Прим. ред.
Основные положения
13
Термодинамическое состояние, или просто состояние системы.
В буквальном смысле этот термин означает то же самое, что
и состояние теплового равновесия. Однако в общем случае можно
считать, что полная система находится в термодинамическом
состоянии, если различные ее части находятся в термически равно-
весных состояниях, тогда как для всей системы в целом это неспра-
ведливо. Например, если в системе из двух тел А л В каждое тело
имеет свою температуру ТА и Тв, то о полной системе можно ска-
зать, что она находится в термодинамическом состоянии, которое
определяется температурами (ТА, Тв). Термически равновесные
состояния, в которых находятся отдельные части системы, назы-
ваются локально равновесными.
§ 3. Термодинамический контакт
Термодинамическим контактом называется такая связь между
системами, при которой возможно хотя бы одно из следующих
типов взаимодействия между термодинамическими системами:
1. Механическое взаимодействие. Если одна система совершает
работу над другой системой с помощью механических или электро-
магнитных сил, то взаимодействие такого рода называется меха-
ническим.
2. Тепловое взаимодействие. Взаимодействие, которое приводит
к изменению энергии и совершается в форме передачи тепла посред-
ством теплопроводности или тепловой радиации, называется тепло-
вым взаимодействием. Стенка, через которую тепловое взаимо-
действие невозможно, называется адиабатической.
3. Материальное взаимодействие. Взаимодействие, которое
приводит к обмену веществом между двумя системами, назы-
вается материальным взаимодействием. Полупроницаемая мем-
брана обеспечивает взаимодействие такого рода.
Идеализацией взаимодействий 2 и 3 можно считать такое взаи-
модействие, которое является достаточно слабым, чтобы не влиять
на свойства системы, но вместе с тем достаточно сильным, чтобы
приводить к эффектам, которые могут быть обнаружены в процессе
наблюдения.
Если рассматривать термостат как источник, который дейст-
вует на исследуемую систему одним из вышеупомянутых способов,
то этот термостат можно называть соответственно источником
работы, тепловым резервуаром (тепловой баней ) или источником
(резервуаром) частиц. Обычно принимают, что источник, или
резервуар, намного больше системы и поэтому он остается в задан-
ном равновесном состоянии независимо от того, какое влияние
он оказывает на .систему, находящуюся с ним в контакте.
14 Гл. 1. Термодинамическое состояние и первый закон
§ 4. Термодинамические величины
Функции состояния. Физические величины, имеющие опреде-
ленное значение для каждого термически равновесного состояния
системы, называются термодинамическими величинами или функ-
циями состояния. К ним относятся, например, температура, давле-
ние, внутренняя энергия, энтальпия и энтропия.
Переменные состояния, или термодинамические переменные.
В узком смысле слова эти величины представляют собой упо-
мянутые выше термодинамические величины. В более широком
смысле термодинамического состояния они означают физические
величины, определяющие локально равновесное состояние. Если
соответствующим образом выбрать совокупность независимых
переменных так, чтобы она была необходимой и достаточной
для определения состояния, то остальные величины, характери-
зующие состояние, являются функциями этих переменных. Число
независимых переменных, описывающих термически равновесное
состояние, определяется эмпирически.
Интенсивные и экстенсивные величины. Если систему, находя-
щуюся в термически равновесном состоянии, разделить на части
с помощью непроницаемых перегородок, то каждая часть останется
в равновесном состоянии. Следовательно, равновесное состояние
однородной системы является ее внутренним свойством и опреде-
ляется термодинамическими переменными, не зависящими от раз-
меров системы. Такие величины называются интенсивными. К их
числу относятся, например, температура, давление, химический
потенциал. С другой стороны, переменные, значения которых изме-
няются пропорционально размерам или массе системы при ее
разбиении на части, не нарушающем равновесного состояния,
называются экстенсивными величинами. Пример: масса компонен-
тов, энергия, энтропия и др.
Внутренние и внешние переменные. В некоторых случаях тер-
модинамические переменные можно разбить на две категории:
внутренние и внешние. Внешние переменные определяют состоя-
ние окружающей среды. Например, внешними переменными
можно считать положение поршня в цилиндре, содержащем газ,
или напряженность электрического либо магнитного поля, дейст-
вующего на систему. Однако их можно рассматривать и как
внутренние переменные, если поршень или источники поля вклю-
чены в систему, а не в окружающую среду. Следовательно, разли-
чие между внутренними и внешними переменными зависит от того,
где мы проводим границу между системой и окружающей средой,
находящейся с ней в контакте. Во избежание недоразумений
необходимо всегда иметь в виду это обстоятельство, особенно
в случае механических контактов.
Основные положения
15
§ 5. Процесс изменения состояния
Термодинамика рассматривает только такие’измонония’состоя-
ния системы (происходящие или сами по себе, или под действием
контактов с другими системами), в которых начальное и_ конечное
состояния являются тер-
модинамическими (но не
обязательно термически
равновесными). Однако
промежуточные состояния,
через которые проходит
система, могут и не быть
термодинамическими. Вооб-
ще говоря, они могут быть
очень сложными состоя-
ниями. Промежуточные
состояния будут термоди-
намическими только в тех
случаях, когда процесс
совершается чрезвычайно
медленно. При таких усло-
виях процесс можно опи-
сать, рассматривая изме-
нение достаточного чис-
ла термодинамических ве-
личин.
Цикл. Циклом назы-
вается процесс, при кото-
ром начальное и конечное
Фиг. 1.
состояния системы совпа-
дают.
Инфинитезимальный процесс. Если разница между начальным
и конечным состояниями системы бесконечно мала, то такой про-
цесс называется инфинитезимальным.
Квазистатический процесс. Так принято называть идеальные
процессы, в течение которых система и окружающая среда остают-
ся в термически равновесном состоянии. Такой процесс прибли-
женно реализуется в тех случаях, когда изменения происходят
достаточно медленно. Например, для того чтобы сжать газ, внешнее
давление рбО должно быть незначительно больше давления газа р,
а чтобы расширить газ, внешнее давление должно быть незна-
чительно меньше р (фиг. 1). В предельном случае очень медленных
изменений оба процесса происходят по одной и той же траектории
в противоположных направлениях. Следовательно, квазистатиче-
ский процесс является обратимым (см. гл. 2, § 1). Перечислим
наиболее важные квазистатические процессы.
16
Гл. 1. Термодинамическое состояние и первый закон
а. Квазистатический изотермический процесс. В таком про-
цессе система находится в контакте с термостатом, имеющим
постоянную температуру (тепловым резервуаром), и процесс
происходит квазистатически при этой температуре.
б. Квазистатический адиабатический процесс. Так называется
квазистатический процесс, при котором система не имеет теплово-
го (и материального) контакта с окружающей средой, но при
воздействии системы на окружающую среду или, наоборот, окру-
жающей среды на систему может совершаться работа.
Квазистатические адиабатические процессы иногда называются
просто адиабатическими, но, так как может существовать адиаба-
тический необратимый процесс, нужно ясно различать оба эти
случая (см. гл. 2, § 1, где обсуждается различие между обрати-
мыми и необратимыми процессами).
§ 6. Первый закон термодинамики
Хотя первый закон термодинамики является частным случаем
общего закона сохранения энергии, он предполагает существова-
ние внутренней энергии, которая представляет собой термодина-
мическую величину.
Первый закон термодинамики. При переходе системы из началь-
ного состояния 1 в конечное состояние 2 получаемая системой от
окружающей среды сумма работы А, теплоты Q и энергии пере-
носа массы Z *) определяется только состояниями 1 и 2; эта
сумма не зависит от того, каким способом осуществляется переход
из 1 в 2. Это означает, что существует такая величина U,
характеризующая внутреннее состояние системы, что разность
.ее значений в состояниях 1 и 2 определяется соотношением
U2 - U, = А + Q + Z. (1.2)
Функция U представляет собой’ внутреннюю энергию системы.
Если система характеризуется механической энергией (кинети-
ческой или потенциальной), то соотношение (1.2) заменяется соот-
ношением
Е, - Е, = А + Q + Z, (1.2')
где Е — полная энергия системы, включая механическую энергию.
Первый закон термодинамики представляет собой закон сохра-
нения энергии. Его можно записать в форме
^полн = const,
где А’полн — полная энергия всей системы, включая все подсисте-
мы, участвующие в рассматриваемом процессе. Соотношение (1.2)'
*) Для величины Z автор пользуется термином «mass action», не име-
ющим однозначного эквивалента в литературе на русском языке. Мы будем
Пользоваться термином «энергия переноса массы».— Прим. ред.
Основные положения
17
или (1.2') записано для подсистемы, энергия которой изменяется
в результате того, что эта подсистема обменивается энергией
с другими частями системы (окружающей средой) с помощью раз-
личных механизмов взаимодействия. Работа А, теплота Q и энер-
гия переноса массы Z представляют собой количества энергии,
получаемой через соответствующие контакты.
Читатель должен быть знаком с понятиями работы и теплоты
хотя бы из курса элементарной физики. Об энергии переноса мас-
сы Z, возможно, известно меньше. Она представляет собой ко-
личество энергии, которая передается системе не в виде работы
или теплоты, а при переносе массы вещества из окружающей
среды. Эта величина обычно вводится в учебниках термодина-
мики значительно позже, а именно при рассмотрении неоднород-
ных систем. Здесь она введена для полноты формулировки пер-
вого закона термодинамики.
Вечный двигатель первого рода. Для циклического процесса
имеет место соотношение
А + Q + Z = 0. (1.3)
Следовательно, система производит работу — А над окружающей
средой, а получает от окружающей среды в свою очередь Q + Z.
Вечный двигатель первого рода должен был бы только совершать
работу над окружающей средой, ничего не получая от нее. Следо-
вательно, первый закон термодинамики можно назвать также
принципом невозможности вечного двигателя первого рода.
Внутренняя энергия. Внутренней энергией мы называем энер-
гию, заключенную в системе. При этом обычно не учитывается
кинетическая энергия системы в целом и потенциальная энергия
системы во внешнем поле (хотя в некоторых случаях потенциаль-
ную энергию можно рассматривать как часть внутренней энергии).
При микроскопическом рассмотрении это означает, что внутренняя
энергия равна сумме кинетической энергии отдельных молекул
и энергии взаимодействия между ними. Однако термодинамика
обычно не затрагивает вопроса о природе внутренней энергии.
Первый закон термодинамики утверждает, что внутренняя энергия
является функцией состояния. Аддитивную постоянную, входя-
щую во внутреннюю энергию, можно фиксировать, выбрав некото-
рое исходное состояние за нулевую точку отсчета внутренней
энергии. На фиг. 2 изображена внутренняя энергия воздуха как
функция температуры и давления. Точка С является критической
(см. пример 8).
Зависимость работы, теплоты и энергии переноса массы от про-
цесса. В отличие от U величины A, Q и Z в соотношениях (1.2)
и (1.2') зависят от того, каким способом осуществляется переход
из одного состояния в другое. Например, переход из состояния 1
2 р. Кубо
18
Гл. 1. Термодинамическое состояние и первый закон
в состояние 2 может осуществиться путем механического воздейст-
вия или путем передачи тепла, т. е.
Z72 — Ut = А (процесс I),
С72 — Ui = Q (процесс II). (1.4)
Отсюда следует, что A, Q н Z не являются функциями состояния
и что их невозможно выразить через разность функций состояния.
Ф и г. 2. Внутренняя энергия воздуха.
Тем не менее позитивная формулировка первого закона термоди-
намики состоит в утверждении, что сумма А + Q-j-Z является
функцией состояния.
ОТСТУПЛЕНИЕ 1
Основатели первого закона термодинамики. Если бы в 50-е годы
прошлого столетия был поставлен памятник неизвестному ученому, то
наиболее подходящей для него была бы следующая надпись: «В па-
мять горя и отчаяния тех, кто пытался создать вечный двигатель».
Но закон сохранения энергии, или первый закон термодинамики, дока-
завший тщетность этих попыток, связан преимущественно с тремя вели-
кими именами: Майер, Гельмгольц и Джоуль.
Юлиус Роберт Майер (1814—1878) действительно был гением,
пришедшим в наш мир с единственной целью; сделать это великое
открытие. Германн Людвиг Фердинанд Гельмгольц (1821—1894) назвал
этот закоп «Erhaltung der Kraft», т. е. законом сохранения энергии.
Основные положения
19
Подобно Майеру он начал свою деятельность как врач, но прожил
замечательную жизнь как величайший физиолог и физик того времени.
Джеймс Прескотт Джоуль (1818—1889) работал более сорока лет над
экспериментальным исследованием эквивалентности работы и теплоты.
Из этих трех гигантов Майер был первым, кому удалось прийти
к этому закону, и последним, чья деятельность была признана. Его
жизнь была наиболее драматичной. Ослепляющая вспышка гениаль-
ного предвидения озарила его, двадцатишестилетнего немецкого
корабельного врача, однажды вблизи Явы, когда он заметил, что веноз-
ная кровь у оперируемого больного оказалась необыкновенно ярко-
красной. Майер предположил, что это может быть связано с создан-
ной Лавуазье теорией окисления крови у животных. Из этой теории
следовало, что в тропических зонах процесс окисления крови может
происходить медленнее из-за уменьшения скорости теплообмена
организма животного с окружающей средой. Обобщение этого наблю-
дения привело Майера к идее об эквивалентности тепла и механиче-
ской работы. Следующие три года после этого путешествия Майер
работал дома как врач, отдавая все свободное время завершению своей
первой работы по сохранению энергии: «Bemerkungen uber die Krafte
der unbelebten Natur». Эта работа была послана в журнал «Poggendorf
Annalen», но никогда не была там опубликована. В 1842 г. Либиг
опубликовал ее в своем журнале <<Annalen der Chemie und Pharmacie»,
где в течение многих лет она оставалась незамеченной.
До 1851 г. Майер написал четыре статьи. В течение этих лет необык-
новенно напряженной работы он не занимался ничем, кроме своей
теории. В 1852 г. он заболел психическим расстройством и попал
в больницу. Через два года он вышел оттуда, но уже никогда более
не возвращался к научной деятельности.
§ 7. Теплота и энтальпия
Предположим, что переход из состояния 1 в 2, обусловленный
тепловым воздействием, может происходить также и под влиянием
механического воздействия [процесс I в соотношении (1.4)]. Тогда
количество тепла Q, которое вводится при тепловом воздействии
[процесс II в соотношении (1.4)], можно охарактеризовать экви-
валентной работой А. Этот способ определения количества тепла
показывает, что оно может измеряться в единицах работы. Приня-
тая единица определяется соотношением (для термодинамиче-
ской калории х))
1 кал = 4,1840 дж.
Эквивалентность теплоты и работы, чему соответствуют, в част-
ности, соотношения (1-4), по сути дела и представляет собой пер-
вый закон термодинамики. Экспериментальное определение тепло-
вого эквивалента работы было осуществлено Джоулем.
Если изменение состояния системы происходит при постоянном,
давлении (изобарический процесс), то механическая работа, свя-
занная с изменением объема AV, определяется просто как —pAV.
х) Существует несколько различных определений калории.
2*
20
Гл. 1. Термодинамическое состояние и первый закон
Если при этом не производится никакой другой работы, то, соглас-
но первому закону, должно выполняться соотношение
U2-Ui = p(Vi~V2) + Q.
Поэтому удобно ввести функцию
H = U+pV
и записать
я2-я1 = е. (1.4')
Введенная здесь величина Я называется энтальпией, или тепловой
функцией.
§ 8. Применение первого закона термодинамики
к инфинитезимальным процессам
Для инфинитезимального процесса соотношение (1.2) можно
записать в форме
dU = d'Q + d'A + d'Z. (1.5)
В частности, если окружающая среда представляет собой одну
простую систему, то
d'A = -p^dV+^X^dxt, (1.6а)
i
d'Z=i\^e)dNj (=j\G^dn}), (1.66)
i= i з= 1
где p(e) — давление окружающей среды, V — объем системы,
Xi6) — сила i-ro типа, действующая на систему со стороны окру-
жающей среды, xt — координата системы, соответствующая силе
Х[е\ Nj — число молекул или молей /-го компонента системы х),
— химический потенциал (отнесенный к одной молекуле или
одному молю) /-го компонента окружающей среды. При квазиста-
тическом инфинитезимальном процессе система находится почти
в равновесии с окружающей средой, в связи с чем имеют место
соотношения
d'A =—pdV + 2 Xtdxi, (1.7а)
d'Z = ^pjdNj. (1.76)
_________ i
x) Если Nj представляет собой число молей, то его обозначают через
nj', химический потенциал, отнесенный к одному молю, обозначается через
G) (см. гл. 3, § 3). Иногда вместо числа молекул или молей используется
масса /-го компонента Mj. В этом случае химический потенциал относится
к 1 г. В настоящей книге, если не оговорено иное, химический потенциал
обычно отнесен к одной молекуле или к одному молю.
Основные положения
21
В общем случае квазистатического процесса
2 2 2 2
U2-U^ \d'Q- JpdV+3 jx^i+2 JhA- (1-8)
1 1 i 1 j 1
где p и Hj — давление и химический потенциал системы, которые
равны соответствующим величинам для окружающей среды, ибо
система находится в равновесии с окружающей средой. Точно так
же внешние силы находятся в равновесии с силами действия си-
стемы на окружающую среду, поэтому верхний индекс е у Xi^
можно опустить. Интегрирование соотношений (1.8) производится
вдоль траектории процесса.
Обозначение d'. Так как передаваемое тепло, совершаемая
механическая работа и энергия переноса массы зависят от харак-
тера процесса, соответствующие бесконечно малые величины не
являются точными дифференциалами функций состояния. Обо-
значение d' введено, чтобы подчеркнуть этот момент.
Работа. В общем случае сила с которой окружающая
среда действует на систему, определяется таким образом, что бес-
конечно малая работа, производимая при изменении обобщенной
координаты х, равна X^dx. Соотношение (1.6а) лишний раз
подчеркивает это определение. В случае давления X —> —р.
В квазистатическом процессе система находится в равновесии
с окружающей средой, в связи с чем р(е~> = р, точно так же
X® = X (внутренняя сила).
Материальное взаимодействие. Аналогично соотношение (1.66)
можно рассматривать как определение химического потенциала
j-го компонента окружающей среды. Пока мы можем сказать
о химическом потенциале только то, что он является некоторой
характеристикой окружающей среды по отношению к у-му компо-
ненту системы, однако он будет широко использоваться начиная
с гл. 3. В квазистатическом процессе р,уе) = цу.
§ 9. Температура
Температура определяется как величина, позволяющая описы-
вать тепловое равновесие между телами, находящимися в тепловом
контакте. Если 0j и 02 — температуры двух тел, то соотношение
Gi = 02 является условием теплового равновесия. Если же
61 > 02? т0 ПРИ тепловом контакте между двумя телами темпера-
тура 0j будет уменьшаться, а 02 — увеличиваться. Очевидно,
если 0! = 02 и 02 = 03, то 0j = 03 в соответствии с условием (1.1).
В свою очередь понятие температуры основано на соотношении
(1.1) (см. задачу 23).
22
Гл. 1. Термодинамическое состояние и первый закон
Хотя выбор температурной шкалы на этом этапе рассуждений
совершенно произволен, можно ввести абсолютную шкалу, которая
будет обоснована при введении второго закона термодинамики.
Далее мы всюду будем пользоваться абсолютной или стоградусной
температурной шкалой.
Абсолютная температура будет обозначаться через Т. Для
построения эмпирической температурной шкалы можно восполь-
зоваться газовым термометром. Произвольную температурную
шкалу 0 можно преобразовать в абсолютную Т с помощью соот-
ношения
т . СрУ)е о
-уГ~ = lim ’ ^тройной точки воды = 273,16 К
(см. гл. 2, задача 37). Стоградусная температурная шкала (шкала
Цельсия) определяется соотношением
0°С= 273,15° К.
(1-9)
§ 10. Теплоемкость. Удельная теплоемкость
Пусть системе квазистатически сообщается количество тепла
d'Q. Предположим, что это осуществляется с помощью такого
процесса, который, сохраняя постоянной величину х, увеличивает
температуру системы на dT\ тогда величину
(1Л0>
будем называть теплоемкостью системы для такого процесса.
Теплоемкость, приходящаяся на единицу массы системы, назы-
вается удельной теплоемкостью. Теплоемкость одного моля веще-
ства называется молярной или молекулярной теплоемкостью.
Так как величина d'Q зависит от процесса, то она становится
функцией состояния, только когда процесс (или параметр х)
определен. Примеры: теплоемкость при постоянном давлении
(изобарическая теплоемкость) Ср, удельная теплоемкость при
постоянном давлении (изобарическая удельная теплоемкость)
ср, теплоемкость при постоянном объеме (изохорическая теплоем-
кость) Cv, удельная теплоемкость при постоянном объеме (изо-
хорическая удельная теплоемкость) cv. Можно формально
определить величину Сад(=0) для адиабатического процесса
и Сиз0т (=оо) для изотермического процесса.
ОТСТУПЛЕНИЕ 2
«Почему мы топим зимой?
Неспециалист ответит: чтобы сделать комнату теплее; изучающий
термодинамику выразится, возможно, таким образом: «Чтобы подвести
Основные положения
23
недостающую энергию». В таком случае правым окажется неспециа-
лист, а не физик.
В соответствии с фактическим положением вещей предположим,
что давление воздуха в комнате всегда равно атмосферному. В обыч-
ных обозначениях энергия единицы массы воздуха в комнате равна
(аддитивной константой пренебрегаем)
u = cvT
и, следовательно, энергия единицы объема равна
и1 = cvpT,
или, учитывая уравнение состояния p/p = RT,
Для воздуха при атмосферном давлении
«1 = 0,0604 кал/см^.
Следовательно, количество энергии в комнате не зависит от темпера-
туры и целиком определяется показанием барометра. Вся энергия,
которую мы вводим в комнату при отоплении, уходит через поры
в стенах наружу.
Я приношу бутылку красного вина из холодного погреба, и она
принимает температуру теплой комнаты. Она становится теплее,
однако внутренняя энергия ее увеличивается за счет наружного, а не
комнатного воздуха.
Почему же все-таки мы топим? По той же самой причине, по
которой жизнь на Земле была бы невозможна без солнечного излу-
чения. При этом дело заключается не в падающей энергии. Последняя
будет снова излучена вплоть до пренебрежимо малой доли, подобно
тому как человек не меняет своего веса, несмотря на принятие пищи.
Условия нашего существования требуют известной температуры,
и чтобы ее поддерживать, используется не увеличение энергии, а пони-
жение энтропии.
Будучи студентом, я с пользой прочел небольшую книгу Ф. Вальда
«Царица мира и ее тень». Имелась в виду энергия и энтропия. Достиг-
нув более глубокого понимания, я пришел к выводу, что их надо поме-
нять местами. В гигантской фабрике естественных процессов принцип
энтропии занимает место директора, который предписывает вид и тече-
ние всех сделок, в то время как закон сохранения энергии играет
лишь роль бухгалтера, который приводит в равновесие дебет и кредит».
Р. Эмден
Приведенная выше заметка была опубликована в английском
журнале «Природа» [1]. Она показалась А. Зоммерфельду настолько
интересной, что он счел нужным привести ее в своем учебнике [2].
Р. Эмден известен своими работами по астрофизике и метеорологии,
в частности своей статьей «Термодинамика небесных тел» в [3].
§ 11. Уравнение состояния
Существование уравнения состояния. Для однозначного опре-
деления термически равновесного состояния системы обычно
достаточно задать значения нескольких функций состояния.
Например, термически равновесное состояние простого газа или
жидкости определяется только двумя переменными: давлением р
24
Гл. 1. Термодинамическое состояние и первый закон
Фиг. 3. Давление идеального газа.
и удельным объемом и (иногда число переменных может быть боль-
ше; например если газ находится во внешнем электрическом или
магнитном поле, то значения напряженностей этих полей Е и Н
также являются переменными, от которых может зависеть состоя-
ние газа). Отсюда и иэ нулевого закона термодинамики (1.1) сле-
дует, что между температурой 0 (в произвольной шкале) и функ-
циями состояния должно существовать функциональное соотно-
шение (см. задачу 23). Если функциями состояния являются р и и,
такое соотношение можно записать в форме
0 = f (А г),
которая и является уравнением состояния. Подобным же образом
можно показать, что и для более общих систем существуют функ-
циональные соотношения между температурой и необходимым
и достаточным набором переменных (не включающих в себя тем-
пературу), т. е. существует уравнение состояния. Однако термо-
динамика ничего не говорит относительно функциональной формы
уравнения состояния, за исключением того, что уравнение состоя-
ния должно удовлетворять некоторым условиям устойчивости
(см. гл. 3, § 8). Для каждой конкретной системы уравнения
Основные положения
25
состояния определяются эмпирически или методами статистиче-
ской механики, так что в рамках термодинамики они считаются
заданными при определении системы.
Уравнение состояния идеального газа. Уравнение состояния
в общем виде записывается следующим образом: pV = g(Q). Одна-
ко если воспользоваться газовой температурной шкалой
(с помощью второго закона термодинамики можно показать, что
она совпадает с абсолютной температурной шкалой; см. гл. 2, § 5),
то это уравнение состояния принимает вид
pV = nRT = NkT, (1.11)
где п — число молей, N — число молекул, R — газовая постоян-
ная, к — постоянная Больцмана:
R = 8,314-107 эрг-моль'1 град'1 = 1,9872 кал-моль'1-град'1,
к — 1,3803-10-18 эрг-град'1 = 8,616-10"5 эв-град'1.
На фиг. 3 изображена поверхность, описываемая уравне-
нием (1.11). Любой реальный газ становится идеальным в пределе
высоких температур и низких плотностей. С помощью второго
закона термодинамики можно показать, что внутренняя энергия
идеального газа не зависит от объема V (см. гл. 2, задача 2):
(-g-)r = 0, и = ЩТ). (1.12а)
Вид функции U (71) определяется эмпирически или теоретически
методами статистической механики. При нормальных температу-
рах соотношение
U = пСуТ (1.126)
является хорошим приближением для большинства чистых газов,
поэтому теплоемкость будет постоянной. Для этих температур
молярная теплоемкость при постоянном объеме Су равна
3
у R (одноатомный газ),
C°v = 5 „ , „ (1.13)
v -?-R (двухатомный газ), ' >
31? (многоатомный газ).
Смесь идеальных газов. Смесь из г видов идеальных газов
подчиняется следующему уравнению состояния:
pV — nRT, п = ^П1, (1.14)
г
где nt — число молей i-го компонента (i = 1, 2, ..., г). Аналогом:
соотношения (1.12) является соотношение
U=^niC°viT, (1.15}
26
Гл. 1. Термодинамическое состояние и первый закон
Ф и г. 4. Поверхность, описываемая уравнением состояния для аргона.
которое обычно справедливо в области средних значений темпера-
туры.
Парциальное давление i-ro компонента pt определяется соотно-
шением
откуда следует
PiV = niRT,
P=^Pi-
г
(1.16)
Уравнение состояния идеального газа пригодно для описания
реальных газов в предельном случае достаточно низких давлений
и достаточно высоких температур. Для более высоких давлений
{более высоких плотностей) и более низких температур отклонения
от закона идеального газа становятся более существенными. Это
видно, например, из фиг. 4 и 5, на которых приведены данные
для аргона. Оказывается, что плотный газшри охлаждении может
Основные положения
27
перейти в жидкое состояние. Существует большое число уравне-
ний состояния, описывающих плотные газы. Мы упомянем только
два из них.
Уравнение состояния ван дер Ваалъса записывается в виде
(P + -^)(v~b) = RT, (1.17)
где v = Vln — молярный объем газа. Благодаря своей простой
аналитической форме это уравнение часто используется для при-
ближенного описания реальных газов. Постоянные а и Ъ для
28
Гл 1. Термодинамическое состояние и первый закон
различных газов приведены в табл. 1, взятой из книги Эпштей-
на [4].
Таблица 1
Газ а- 10-6, атм- см6/моль% Ь, смЗ/молъ
Не 0,03415 23,71
Ne 0,2120 17,10
н2 0,2446 26,61
Аг 1,301 30,22
n2 1,346 38,52
О2 1,361 32,58
со 1,486 39,87
со2 3,959 42,69
n20 3,788 44,18
н20 5,468 30,52
С12 6,501 56,26
so2 6,707 56,39
Вириалъное разложение (уравнение состояния Камерлинг
Оннеса). Для реальных газов часто применяется следующее раз-
ложение:
рр = яг(1 + А + А+...) , (1.18)
ИЛИ
pv = RT (1 + В2р + В3р2 +...), (1.19)
где А2, А3, . . ., В2, В3, . . являются функциями температуры
и называются еириалъными коэффициентами.
Идеальный парамагнетик и закон Кюри. Намагниченность М
магнитного тела является функцией внешнего поля Н и темпера-
туры Т. Вещество называют идеальным парамагнетиком, если его
уравнение состояния имеет вид
М = /(4") (f(0) = 0). (1.20)
В частности, если величина HIT мала, то уравнение (1.20) запи-
сывается в приближенной форме:
М = (1.21)
это соотношение называется законом Кюри, a С — константой
Кюри. Неметаллические кристаллы, содержащие ионы парамаг-
нитных металлов, часто подчиняются этому закону, однако он
несправедлив при температурах, близких к абсолютному нулю
(см. гл. 3, задача 26).
Примеры
29
§ 12. Замена независимых переменных
Иногда в термодинамике в качестве независимых переменных
рассматриваются р и V, а иногда Т и V. Поэтому запись частных
производных в виде dUldV не определяет однозначно выбора
независимых переменных, и у частных производных ставятся
индексы, указывающие, какие переменные сохраняются постоян-
ными, например (dU/dV)p, (dU/dV)T.
Некоторые термодинамические соотношения являются обыч-
ными соотношениями между частными производными с различным
выбором независимых переменных. Поэтому подобные соотноше-
ния получаются просто заменой независимых переменных.
Особенно удобно следующее тождество: если три переменные
х, у и z связаны функциональной зависимостью, то можно считать
z функцией от а: и у, или х функцией от у и z, или у функцией z и х.
В этом случае мы имеем
(JM (А) =_1, (1.22)
X дх )у\ ду )z \ dz /х
ИЛИ
( дх \ = (dz/dy)x ,.
\ ду Iz (dz/dx)y ’ \ )
что следует непосредственно из равенства
0.24)
Если z = const, то dz = 0 и отношение dxldy = (dxldy)z должно
иметь вид (1.23).
ПРИМЕРЫ
1. Магнитное тело помещено в катушку и намагничивается
магнитным полем, создаваемым током, протекающим через катуш-
ку. Для простоты предположим, что в намагничиваемом теле
поле Н и намагниченность М однородны. Показать, что отнесен-
ная к единице объема тела работа, совершаемая электрическим
источником в процессе намагничивания, равна
м
А = j Н dM.
о
Предполагается, что магнитное тело не деформируется в процессе
намагничивания.
30
Гл. 1. Тер модинамическое состояние и первый закон
РЕШЕНИЕ
Рассмотрим случай, когда катушка намотана вокруг достаточ-
но длинного цилиндрического магнитного тела (фиг. 6). Магнитное
поле в катушке, у которой на единицу длины приходится п витков,
равно Hj = 4лп//с, где J — ток, проходящий по катушке. Прле
Н внутри магнитного вещества равно сумме поля Hj и размагни-
чивающего поля Нм, которое, впрочем, мало, если образец имеет
форму длинной иглы. Следовательно, в этом случае можно считать,
Ф и г. 6.
что Н = Hj. Если катушка намотана по всей длине I цилиндра,
имеющего площадь поперечного сечения о, то магнитный поток
через катушку равен Ф = anlB = VnB, где V — al — объем
магнитного тела, а В = Н -р 4лЛ7 — плотность потока в магнит-
ном теле. Если ток J возрастает, то Н и М, а следовательно, и В
также изменяются таким образом, что, согласно закону индукции
Фарадея, возникает противо- э.д.с. — (1 /с) dQldt = —V (п/с) dB/dt.
Работа, совершаемая электрическим источником для компенсации
этой противо-э.д.с. за время dt при прохождении через сечение
проводника заряда
J dt~ lkcH-J- dt-,
лп
равна
±^Ljdt = ~VHdB =
с dt 4л
= ^-V (Н dH + 4лН dM) = d (-^-)+РЯ dM.
Первый член правой части этого выражения d (VH2/8n) предста-
вляет собой работу, необходимую для создания поля Н независимо
от наличия намагничиваемого тела. Следовательно, второй член
правой части HdM можно считать отнесенной к единице объема
работой, необходимой для увеличения намагниченности М на
величину dM. Отсюда следует, что отнесенная к единице объема
работа, необходимая для увеличения намагниченности от 0 до М-,
Примеры
3t
м
равна А = § HdM. (Если бы было возможно зафиксировать
о
окончательную величину намагниченности М, то работа СЯ'2/8л
могла бы быть возвращена электрическому источнику в процессе
уменьшения Н до 0, так как в этом случае мы имели бы dB = dH.)
2. Пусть d'q — теплота, необходимая для изменения темпера-
туры 1 г вещества на величину dT при сохранении величины х
постоянной. Для простоты предположим, что имеются только две
независимые переменные, а именно удельный объем v и темпера-
тура Т. Показать, что теплоемкость сх определяется уравнением
Сх~[ dT ( дТ L+ L( dv )т^~ PJ ( дТ )я’
где и — внутренняя энергия на единицу массы и р — давление.
РЕШЕНИЕ
Так как масса системы сохраняется постоянной, мы можем
ограничиться рассмотрением работы, совершаемой под действием
давления. Из соотношений (1.5) и (1.7а) следует, что первый закон
термодинамики для единицы массы можно записать в форме
d'q = du + pdv. Изменение du внутренней энергии и, вызванное
приращением dT температуры Т и приращением dv удель-
ного объема v, можно записать в форме du = (duldT)vdT +
+ (duldv}Tdv. Подставляя это выражение в соотношение для d'q,
получаем
й'’=Шл+[(4Я+'']Л’- <*>
Хотя параметр х определяется как функция от Т и v, для равно-
весных состояний можно считать v функцией от Т и х, если выбрать
Т и х в качестве независимых переменных. Тогда, если величина х
сохраняется постоянной, а Т меняется, то dv — (dvldT)xdT.
Подставляя этот результат в соотношение (1) и деля его на dT,
получаем искомое соотношение.
3. Доказать соотношение
Ср = Су+ 7? (соотношение Майера)
между изобарической теплоемкостью и теплоемкостью при постоян-
ном объеме для одного моля идеального газа.
РЕШЕНИЕ
Первый закон термодинамики для инфинитезимального квази-
статического процесса для одного моля газа имеет вид [см. (1.5)
и (1.7а)]
d'Q = dU + pdV.
32
Гл. 1. Термодинамическое состояние и первый закон
Так как внутренняя энергия U идеального газа не зависит от
объема V, мы можем считать dU = CV(T) dT и
d'Q = Cv (Г) dT + pcZE. (1)
Теплоемкость при постоянном объеме (d'Q!dT)v и есть Cv. Поэтому
перепишем соотношение (1) в виде
d'Q = CvdT + d(pV) - Vdp (2)
и, подставив туда уравнение состояния pV = RT, получим
d'Q = (CY + R)dT - Vdp, (3)
или
c»=(4rU«=cv+^.
4. Вычислить механический эквивалент тепла J, если известно,
что для воздуха при нормальных температуре и давлении (т. е. при
Т = 0° С, р = 1 атм) плотность р = 0,00129 г/см3, удельная
теплоемкость при постоянном давлении ср = 0,238 кал!г-град
и ее отношение к теплоемкости при постоянном объеме у = Cp!cv =
— 1,41. Предполагается, что воздух является идеальным газом,
объем которого при этих условиях равен 22,4 л!моль.
РЕШЕНИЕ
Газовую постоянную R, выраженную в дж!молъ-град, можно
получить из уравнения состояния идеального газа pV = RT.
Эту постоянную можно также выразить в кал/моль- град, восполь-
зовавшись соотношением Майера Ср — Cv = R (пример 3). Если
обозначить последнюю величину через R', то J = RIR'. Нормаль-
ное состояние является равновесным состоянием с температурой
Т = 0° С = 273° К и давлением р = 1 атм = 1,013-106 дин! см4-.
Объем 1 моль при нормальных условиях V = 22,4-103 см3. Отсюда
следует
pV _ 1,013-106.22,4-103_
Т ~~ 273 “
= 8,32-107 эрг!моль-град = 8,32 дж/моль-град.
Удельную теплоемкость при постоянном объеме можно предста-
вить как молярную теплоемкость при постоянном объеме, делен-
ную на массу моля воздуха (средний молекулярный вес), которая
равна
т = pF = 0,00129-22,4-Ю3 = 28,9 г!молъ',
отсюда следует
Ср = тСр = 28,9-0,238 = 6,88 кал!моль- град.
Теплоемкость на 1 моль при постоянном объеме Cv = mcv =
= тср!у = Ср!у — 6,88/1,41 = 4,88 кал!моль-град. Следователь-
Примеры
33
но, мы имеем
R' — Ср — Cv = 2,00 кал/моль- град,
откуда
J = =4,16 дж/кал.
fl z ,ии
5. а) Вычислить количество тепла, необходимое для нагревания
воздуха от 0 до 20° С при постоянном объеме, если первоначально
он находился при атмосферном давлении и занимал объем 27 м3.
б) Какое количество тепла потребуется для нагревания воздуха
от 0 до 20° С при постоянном давлении, если начальный объем
был равен 27 at3?
в) Пусть воздух находится в термически изолированной ком-
нате объемом 27 м3. В комнате имеется небольшое отверстие, через
которое воздух может просачиваться наружу, где давление равно
1 атм. Какое количество тепла необходимо подвести в комнату,
чтобы температура медленно увеличивалась от 0 до 20° С? Физи-
ческие характеристики воздуха следует взять из условия при-
мера 4. Теплоемкость воздуха можно считать постоянной.
РЕШЕНИЕ
а) Рассмотрим нагревание при постоянном объеме. Массу М
воздуха в объеме 27 м3 при температуре 0° С и давлении 1 атм
легко вычислить, зная его плотность при этих условиях р =
= 0,00129 г/см3,
М = 0,00129-27-106 = 3,48-104 г.
Теплоемкость при постоянном объеме Су можно вычислить, зная
удельную теплоемкость
Су = = 0,169 кал/г-град,
Су = Мсу= 10,169-3,48-104 = 5,88-103 кал/град.
Если теплоемкость постоянна, то количество тепла, необходимое
для увеличения температуры от Т± до Т2, равно
Тг
Qv^\ CvdT = {T2-Tl')Cy=
Ti
= 20-5,88-103 = 1,176-Ю5 кал.
б) В случае нагревания при постоянном давлении вместо Су
будем пользоваться теплоемкостью при постоянном давлении
Ср — Мер = уСу — 1,41-5,88-10® = 8,29-103 кал/град.
34
Гл. 1. Термодинамическое состояние и первый закон
Тогда требуемое количество тепла Qp равно
Qp = (т2 - Л) Ср = 20-8,29-103 = 1,658-10® кал.
в) Так как нагревание происходит медленно, можно считать,
что давление в комнате сохраняется равным 1 атм. В этом случае
нагревание воздуха происходит при постоянных давлении р
и объеме V, а изменение массы воздуха М (Г) можно определить
из уравнения состояния pV = RTM/m (т — средний молекуляр-
ный вес воздуха), откуда М (Т) Т = const. Если при температуре
Т\ масса воздуха в комнате равна то М (Г) = M\TJT. Так
как нагревание массы М (Г) воздуха происходит при постоянном
давлении, его теплоемкость будет равна М(Т)ср, откуда следует,
что количество тепла Q, требуемое для увеличения температуры
воздуха до Т2, равно
Т2 Т2
Q — М (Т) сpdT = CpMJ\ J = cpMJ\ In .
T1 Ti 1
Так как 7\ = 0° С = 273° К, Г2 = 20° С = 293° К и Ср = 8,29 <
X 103 кал/град, то
Q = 8,29 -103-273- In Щ-= 2,26-106- 0,0706 = 1,596 • 105 кал.
6. Доказать, что для квазистатического адиабатического про-
цесса, совершаемого идеальным газом, справедливо соотношение
рУт = const (уравнение Пуассона), и определить работу, совер-
шаемую газом при квазистатическом адиабатическом переходе
из состояния (pi, V\, Т^) в состояние (р2, V2, Т2). Удельную теп-
лоемкость можно считать постоянной.
РЕШЕНИЕ
Для идеального газа при квазистатическом процессе первый
закон термодинамики имеет вид d'Q = CvdT pdV [см. пример 3,
соотношение (1)]. Условие адиабатичности d'Q = 0 можно записать
в виде
CvdT-\-nRT (1)
где мы использовали уравнение состояния. Применяя соотноше-
ние Майера (пример 3) Ср = Cv nR (для п молей) и интегрируя
соотношение (1), получаем уравнение Cv in Т (Ср — Cv) In V =
= const, которое в силу соотношения CP!CV = у переходит в
ТУТ"1 = const. (2а)
Примеры
35
Если воспользоваться уравнением состояния, то найдем
pV? = const. (26)
[Мы можем также от уравнения состояния pV — nRT перейти
к соотношению dplp + dV/V = dTIT', исключая из него dTIT
с помощью (1), получаем dplp + ydV/V = 0, откуда следует (26).]
При адиабатическом изменении объема от Vi до V2 работа W,
совершаемая газом, определяется следующим образом:
V2 V’a
W = — А= § pdV = § piV]’ = (так как pVv = pj7^)
Vi Vi
= ^-?) = -- (PlVi-p2V2) = (3)
[так как Cy(V-l) =
= Cp — Cv = nR\. (4)
В случае адиабатического расширения (У2 > V4) 1\ > Т2. Газ
совершает работу за счет уменьшения внутренней энергии, поэтому
очевидно, что температура убывает (см. гл. Зг пример 5).
7. Показать, что между адиабатической хад — —(11и)(ди1др)ая
и изотермической сжимаемостью хт = —(llv)(dv/dp)T существует
соотношение
Су
%ад = ~
СР
где с„ и ср — удельные теплоемкости соответственно при постоян-
ном объеме и постоянном давлении.
РЕШЕНИЕ
Когда мы говорим об адиабатической или изотермической сжи-
маемости, мы, конечно, подразумеваем сжимаемость при квазиста-
тическом адиабатическом или квазистатическом изотермическом
сжатии. Если рассматривать внутреннюю энергию и как функцию
от р и и (мы имеем дело с единичной массой вещества), то условие
адиабатичности du pdv — 0 записывается в виде
Следовательно,
(4г)л+[Н&)Р+
( др \ _ Р + (ди/ду)р
I ди /ад (ди/др)в
(1)
3*
36
Гл. 1. Термодинамическое состояние и первый закон
Если считать, что и = и[Т(р, v), v], то
(».=(#). . <2>
а если считать, что и=и[Т (р, v), р], то
/ ди \ / ди \ / дТ \
к ди )р к дТ /р к dv )р'
откуда следует
где мы использовали соотношение ср = (ди/дТ)р 4- р (др/дТ)р. Под-
ставляя (2) и (3) в (1), получаем
/ др \______ср (дТ/ду)р
\ Зг /ад — cv(dT/dp)v W
Теперь с помощью соотношения (др1ди)т~ —(dTldv)pl(dTldp)v,
которое вытекает из равенства
находим
k ди /ад Cv к до )т ' >
откуда непосредственно вытекает соотношение, которое требова-
лось доказать. (Другой способ доказательства см. в гл. 2, задача 14.)
Замечание. Так как ср/с0 > 1, из соотношения (5) сле-
дует, что (5р/5п)'ад > (dpldv)T или, иначе говоря, в любой точке
р — ^-плоскости наклон адиабаты больше наклона изотермы.
8. Определить давление рс, объем Vc и температуру Тс в крити-
ческом состоянии газа, подчиняющегося уравнению состояния
ван дер Ваальса
(P + ^)(V~bn) = nRT,
где п — число молей, а > О, Ъ > 0. Записать уравнение состояния
в приведенных величинах р = р/рс, b = У/Ус и t = Т1Те. Исполь-
зуя такое приведенное уравнение состояния, изобразить на
р — b-плоскости изотермические линии, а также кривые (dp/c?b)t =
= 0 и (д (pb)/dp)t = 0 (последняя кривая носит название кривой
Бойля).
Замечание. Если на р — У-плоскости изобразить кривые,
соответствующие уравнению ван дер Ваальса при различных Т,
то при достаточно низких температурах кривые будут иметь мак-
J ---> b
Фиг. 7.
38
Гл. 1. Термодинамическое состояние и первый закон
симум и минимум, а при высоких
тонными, как это видно на фиг. 7.
ческая точка) соответствует точке
(dp!dv)T = 0.
температурах становятся моно-
Критическое состояние (крити-
на кривой Т = Тс, в которой
РЕШЕНИЕ
Запишем уравнение состояния в форме
пВТ ап2 ...
Р V — bn рз • '
Тогда условия (dp!dV)T = 0 и (d2p/5V2)T = 0 принимают вид
НТ 2ап
(V—bnp
и
ВТ Зап
(V —6п)з = ТГ •
Отсюда следует, что V — bn — 2V/3, или V = 3bn и RT = 8а/21Ь.
Подстановка этих значений в (1) дает р = а/27&2. Это и есть зна-
чения р, V и Т в критической точке, т. е.
Рс = ~27 ~b* ' Vc = %пЬ’ ~Rb~ •
Подставим теперь" в (1) р = рс$, V = Fcb и T = Tct и разделим обе
части на рс. Тогда
nBTct ап2
Р ~ Р<Усь — РсЬп pcT2i>2
Подставляя сюда значения рс, Vc и Тс из (4), получаем
8t 3
Зь —1 Ь2 ’
или
(р +-L) (3b-l) = 8t. (5)
В такой форме уравнение состояния не зависит явным образом
от констант а и Ь, характеризующих конкретное вещество. Поэтому
можно считать, что газы (подчиняющиеся уравнению ван дер
Ваальса) находятся в одном и том же состоянии, если они харак-
теризуются одинаковыми значениями р, Ь и t (которые для каждого
газа выражены через соответствующие значения рс, Vc и Тс). В этом
утверждении заключается закон соответственных состояний.
Отметим следующие особенности кривых t = const на р — Ь-
плоскости. Во-первых, можно не рассматривать области с отрица-
Примеры
39
тельным давлением, где Ь<1/3 и р <; — 3/Ь2. При b^>V3 и b >
9/8t уравнение (5) переходит в pb « 8/3t, т. е. при больших b
газ ведет себя как идеальный. Когда значение b оказывается
близким к 1/3, давление р становится бесконечным. Каждому зна-
чению b соответствует только одно значение р, но заданному зна-
чению р может соответствовать одно или три действительных
значения Ь. В случае когда имеется три значения Ь, будем обоз-
начать их как Рассмотрим производную
(=____________। 6 (5')
k дь (Зь —1)2 ьз ’ )
полученную дифференцированием уравнения (5). Первый член
в правой части соотношения (5') больше второго при b «1/3
и b —> оо, поэтому в этой области (dp/db)t < 0. Следовательно,
(5p/5b)t<0 при b = br>, b = bF и (dp/db)t > 0 при b = Ьв.
Так как правая часть соотношения (5') представляет собой раз-
ность двух монотонных функций, изотерма имеет минимум между
bD и Ь£ и максимум между Ь£ и bj?. Обозначим через bG и bJZ
абсциссы этих экстремумов, которые определяются равенством
(5p/9b)t = 0, т. е.
= (в)
Соответствующие значения pG и рн можно получить, подставив
в (5) значения bG и Ьн- При изменении t точки максимума
(bJZ, Рн) и минимума (bG, pG) описывают кривые на р—Ь-пло-
скости. Уравнения этих кривых можно получить, исключая пара-
метр t из (5) и (6), что дает
= (7)
Эта кривая проходит через точки р=—27 при Ь = х/3, р = 0
при b = 2/^ и р —* 3/Ь2 при b —> оо. Она имеет максимум в точке
Ь = 1, р = 1 (критическая точка) и точку перегиба’ при Ь = 4/3,
Р = 27/32- На фиг. 7 ей соответствует кривая JGCHK. Совместные
решения уравнений (5) и (7) определяют точки минимума G и мак-
симума Н кривой (5). Изотермическая кривая, описываемая урав-
нением (5) при 1 = 1, проходит через точку максимума С(р = 1,
b = 1) кривой, описываемой уравнением (7). На этой изотерми-
ческой кривой точки экстремумов G и Н сливаются в точке
перегиба С, которая является критической точкой. Если теперь
рассмотреть уравнение (5) при фиксированном Ь, то р будет
монотонно возрастающей функцией от 1, причем при t > 1 урав-
нения (5) и (7) не имеют общих решений. При 0 < t < 1 изотер-
Фиг. 8.
Примеры
41
мические кривые имеют максимумы и минимумы. Отсюда следует,
что они имеют форму ADGEHFB при 0 < t < 1 или LCM при
t = 1, или PQ при t>l, как показано на фиг. 7.
Наконец, определим кривую Бойля. Из уравнения (5) находим
/ 5(рь) \ _ 3 8t
t дь Ь2 (3b —1)2 ’
Отсюда для (д (рЬ)/5ЬД = О имеем
я 3(3b-l)2
81 - й2
Подставляя это равенство в (5) и исключая 1, получаем
» = (8)
Эта кривая проходит через точки (Ь = 1/3, р =—27), (Ь — 3/3,
р = 0) и (Ь = 1, р = 3). Она имеет максимум в точке (Ь = 4/3,
р = 2’/8), а при b —> оо, р —> 9/Ь. Точка перегиба имеет коорди-
наты b = 2, р — 3. На фиг. 8 изображена пространственная поверх-
ность, соответствующая уравнению ван дер Ваальса.
Замечание. На изотермической кривой при 0 < t < 1
имеются участки, где р < 0. Эти участки могут быть метастабиль-
ными [(dp/db)t < 0] или неустойчивыми [(dp/db)t > 0]. Равновесие
газовой (р > 0) и жидкой фаз определяется правилом Максвелла
(см. гл. 4), поэтому в устойчивом термически равновесном состоя-
нии давление р должно быть положительным.
/ 2
р, ГГорисгпая перегороди Рг итпи
р, 5 рг
Фиг. 9.
9. В эксперименте Джоуля — Томсона газ, имеющий давле-
ние pi, медленно продавливается сквозь пористую (ватную)
перегородку в область, где давление равно р2 (перегородка не
позволяет газу приобрести кинетическую энергию), как это изо-
бражено на фиг. 9. Показать, что в этом процессе перехода газа
из объема Vt в V2 энтальпия Н = U + pV сохраняется, а изме-
нение температуры Т7! — Т2 определяется из условия постоянства
энтальпии.
42
Гл. 1. Термодинамическое состояние и первый закон
РЕШЕНИЕ
В начальный момент поршень Р2 прижат к перегородке 5 и газ
находится между перегородкой и поршнем Pi в пространстве объе-
мом Vi, где он имеет давление рг и температуру Т^ Затем поршень
Pi начинает медленно двигаться к перегородке так, чтобы давле-
ние Pi сохранилось постоянным. Одновременно с этим поршень Р2
медленно отодвигается. Это движение продолжается до тех
пор, пока поршень Pj не придвинется вплотную к перегородке S.
Между Р2 и 5 к этому моменту образуется область объемом V2,
заполненная газом под давлением р2. Полная работа, совершенная
двумя поршнями, имеет вид
О У2
А = — j Pi dV — j p2 dV = piVi — p2V2.
У1 о
Из первого закона вытекает
. U(p2, V2)-U(Pi, Vi) = P1Vi-p2V2,
PiVi=^U2-\- p2V2, или H (pi,Vi) = H (p2,V2).
Следовательно, если энтальпию газа Н считать функцией от р и Т
при фиксированной массе газа, то соотношение (1) можно записать
в виде
Я (A, Ti) = H(p2, Т2). (2)
Из него определяется температура Т2 при заданных pi, Ti и р2.
ЗАДАЧИ
[А]
1. Показать, что если уравнение состояния имеет вид
р = р (Т, У), то справедливо соотношение
рар = kaVt
где ар = (dpldT)ylp — тепловой коэффициент давления при по-
стоянном объеме, ау = (dVldT)pIV — коэффициент теплового рас-
ширения при постоянном давлении, к = —V (dp/dV)T — изотер-
мический объемный модуль упругости.
2. Доказать соотношение
dp = к ( — Ц- av dT j ,
связывающее малые изменения dp, dV и dT давления р, объема V
и температуры Т при квазистатическом процессе.
Задачи
43
3. При нормальных температуре и давлении для кислорода
ср = 0,2203 кал/г^град, cv = 0,1578 кал!г-град. Считая кислород
идеальным газом, вычислить механический эквивалент тепла.
4. При постоянной температуре 20° С идеальный газ квазиста-
тически расширяется из состояния с давлением в 20 атм; конеч-
ное давление равно 1 атм. Какую работу совершает 1 моль газа
(в джоулях)? Какое количество тепла (в калориях) необходимо
передать газу?
5. Найти адиабатическую сжимаемость хад идеального газа
при квазистатическом адиабатическом сжатии. Скорость звука
определяется соотношением с = dp/dp (р — плотность). Считая,
что дифференцирование производится при адиабатическом изме-
нении, вычислить скорость звука в воздухе при 1 атм и 0° С
и найти ее зависимость от температуры.
6. Идеальный газ квазистатически и адиабатически переходит
из состояния (pt, Vi, h) в состояние (р2, Уг» ^г)- Показать, что
если в конечном состоянии сообщить газу (при постоянном объеме)
количество тепла, эквивалентное работе, совершенной газом при
этом переходе,’то температура его снова станет равной исходной.
7. Переход идеального газа из начального состояния (pt, Vi, Ti)
в конечное состояние (р2, Уг, Т’г) совершается с помощью трех
квазистатических процессов, изображенных на диаграмме фиг. 10:
а) 1Л2, б) 152 и в) 1DC2. Чем определяется возрастание внутрен-
ней энергии при переходе 1 -*• 2? Определить также для каждого
процесса работу, совершаемую системой, и передаваемое тепло.
Удельную теплоемкость считать постоянной.
44
Гл. 1. Термодинамическое состояние и первый закон
8. Принимая, что воздух, поднимаясь в атмосфере, расширяется
как идеальный газ, определить изменение его температуры с высо-
той. Насколько уменьшается температура на высоте 1 км?
9. Идеальный газ совершает квазистатический циклический
процесс (цикл Карно), изображенный на фиг. 11. Переход из 1
в 2 представляет собой изотермическое расширение, при котором
газ находится в контакте с тепловым резервуаром с температурой
Ti, переход из 2 в 3 — адиабатическое расширение, переход
из 3 в 4 — изотермическое сжатие, при котором имеет место кон-
такт с тепловым резервуаром с температурой Т2, и, наконец, пере-
ход из 4 в 1 является адиабатическим сжатием. Доказать соотно-
шение
211.22=0
Л т2
(уравнение Клаузиуса), где Qi — тепло, полученное от теплового
резервуара с температурой Ti, а ()2 — тепло от резервуара с темпе-
рн
ратурой Т2. Удельную тепло-
емкость считать постоянной.
10. Для процесса, при кото-
ром параметр х сохраняется
постоянным, доказать, что
рг/ = const, где / = (сх —
— Ср)1(сх — сг), р — давление,
v — удельный объем, сх, ср и ср
удельные теплоемкости соот-
ветственно при постоянном зна-
чении х, постоянном давлении
и постоянном объеме.
И. Один моль идеального
: : газа с начальными давлением pj
р1----и объемом Vi свободно (и адиаба-
' г v тически) расширяется до объема
Фиг. 12. V2. Затем он квазистатически
сжимается до объема при
постоянном давлении р2. Наконец, газ квазистатически нагре-
вается при постоянном объеме до тех пор, пока его давление
не станет равным pt. Такой цикл, изображенный на фиг. 12,
называется циклом Майера. Доказать с помощью этого цикла
соотношение Майера (см. пример 3). Молярную теплоемкость
считать постоянной.
12. Рассматривается газ, подчиняющийся уравнению состоя-
ния Дитеричи:
п = -гаД7, e-na/BTV
Г V — по
Задачи
45
где р — давление, V — объем, Т — абсолютная температура,
п — число молей, R — газовая постоянная, а и Ъ — константы,
характеризующие вещество. Показать, что в критической точке
давлению, объем и температура имеют вид
= V' = 2nb’ Тс = ^,
и записать уравнение состояния в универсальной форме закона
соответственных состояний.
13. Вычислить удельную теплоемкость воздуха при постоянном
объеме, считая его смесью кислорода О2 и азота N2 с отношением
масс компонентов 23 : 77. Удельная теплоемкость газообразного
кислорода при постоянном объеме равна 0,158 кал!г-град, а газо-
образного азота 0,176 кал!г-град.
[Б]
14. Первоначально ненамагниченная небольшая железная
иголка медленно вносится из бесконечности в магнитное поле
постоянного магнита прямоугольной формы. При этом ориентация
иголки все время сохраняется параллельной оси магнита, как
показано на фиг. 13. Пусть наличие иголки не меняет силы магнита
и объем иголки остается постоянным. Доказать в этих предположе-
ниях, что работа, совершаемая при намагничивании иголки до
значения ее магнитного момента mt, определяется соотношением
mi
А = j Н dm,
о
46
Гл. 1. Термодинамическое состояние и первый закон
где т — магнитный момент иголки в той точке, где магнитное
поле равно Н.
15. Рассмотреть вертикальный столб воздух^ бесконечной
высоты и постоянного сечения. Вычислить его теплоемкость, счи-
тая воздух идеальным газом, находящимся в постоянном грави-
тационном поле.
16. Пусть имеется замкнутая система, для описания термо-
динамически равновесного состояния которой в качестве незави-
симых переменных можно взять любую пару из трех величин:
давления р, объема V и температуры Т. Доказать, что:
а) теплоемкость при постоянном объеме Cv = (dUldT)v, а при
постоянном давлении Ср = {дШдТ)р,
+«)Д;
где U — внутренняя энергия, Н = U + pV — энтальпия.
Замечание. Так как в левой части соотношения «г» стоят
измеряемые величины, это соотношение можно использовать для
экспериментальной проверки первого закона термодинамики.
17. Доказать, что внутреннюю энергию и и энтальпию h едини-
цы массы идеального газа с постоянной удельной теплоемкостью
можно записать в форме
^2 7
и=—---— 4- const, П =---r4- const,
т(т —1) у —1
где с = Y(др1др)яп — скорость звука (р — давление, р — плот-
ность, производная вычисляется для адиабатического процесса),
у — отношение удельной теплоемкости при постоянном давлении
к удельной теплоемкости при постоянном объеме.
18. Доказать, что для однородного магнитного вещества тепло-
емкость при постоянном магнитном поле Н можно записать в виде
₽я=тн-я(#)н,
где U — внутренняя энергия, I — магнитный момент, Т —
абсолютная температура магнитного вещества. Изменением объема
при намагничивании можно пренебречь.
19. Доказать следующее соотношение между изотермической
и адиабатической магнитной восприимчивостью однородного
Задач.)
47
вещества:
Хад = ^Хт,
где См — теплоемкость при постоянной намагниченности, Ся —
теплоемкость при постоянном магнитном поле. Изменением объема
при намагничивании можно пренебречь.
20. Рассмотреть цикл Карно, в котором в качеств рабочего
вещества используется тепловое излучение. Плотность внутренней
энергии излучения и определяется законом Стефана — Больцмана
и = оТ4, где Т — абсолютная температура (постоянная о > 0),
а давление излучения р определяется уравнением состояния
р = и/3.
ОТСТУПЛЕНИЕ 3
Никола Леонард.Сади Карно. Первая половина девятнадцатого
столетия была периодом, когда паровая машина, усовершенствован-
ная Джемсом Уаттом (1765), добавившим к ней конденсор (низко-
температурный тепловой резервуар), совершала одно за другим заме-
чательные преобразования в промышленности и транспорте. Многие
выдающиеся физики, подобно Лапласу и Пуассону, занимались изу-
чением Движущей Силы Огня. Сади Карно (1796—1832) — сын Лазаря
Карно, которого называли «организатором победы» Французской
революции,— родился и умер в Париже. По-видимому, он был зна-
ком с калорической теорией тепла, согласно которой тепло представ-
ляет собой некую субстанцию, способную перетекать из одного тела
в другое (теплопроводность) и образовывать химическое соединение
с атомами вещества (скрытая теплота). Карно написал небольшую,
но очень важную книгу «Размышления о движущей силе огня» [5],
которая была издана его братом вместе с некоторыми другими посмерт-
ными записками ученого.
Основная идея Карно состояла в том, что тепловая машина произ-
водит работу не за счет, поглощения тепла, а благодаря передаче
тепла от горячего тела к холодному, поэтому невозможно использо-
вать тепло, не имея холодного тела, подобно тому как вода должна
падать из высокого резервуара в низкий. В своей книге Карно пред-
полагает справедливым закон сохранения тепла и считает, что коли-
чество тепла есть функция состояния. Правда, позже он отказался
от этого предположения и пришел к закону эквивалентности тепла
и работы, в частности, предложил различные способы оценки меха-
нического эквивалента тепла. Карно ввел цикл, известный теперь под
его именем, и установил принцип Карно.
Книга Карно оставалась незамеченной до 1834 г., когда Клапей-
рон представил теорию Карно в аналитической и графической
форме с помощью индикаторных диаграмм, введенных Уаттом. Осно-
вываясь на трудах Майера (1841) и Джоуля (1843—1849), Клау-
зиус (1850) изменил формулировку закона сохранения тепла, из
которой исходил Карно. Согласно формулировке Клаузиуса, для со-
вершения работы недостаточно только перераспределения тепла; необ-
ходимо также израсходовать некоторое количество тепла, пропорцио-
нальное работе, и наоборот. Это положение Клаузиус назвал первым
законом термодинамики. Гельмгольц (1847) и Клаузиус обобщили
48 Гл. 1. Термодинамическое состояние и первый закон
этот закон и пришли к принципу сохранения энергии. - В. Томсон
(лорд Кельвин), который, основываясь на работе Карно, предложил
(в 1848) шкалу температуры (шкала Кельвина), также пришел к за-
кону эквивалентности тепла и работы. Второй закон термодинамики
был сформулирован Томсоном (1851) и Клаузиусом (1867).
Обзор истории раннего периода развития термодинамики можно
найти в статье Мендозы [6], см. также книгу Маха [7].
[В]
21. Пренебрегая внутренним трением (вязкостью) и теплопро-
водностью, доказать, что сумма плотностей энтальпии и кинетиче-
ской энергии стационарного потока жидкости (или газа) сохра-
няется постоянной. Предполагается, что внешние силы типа грави-
тационного поля отсутствуют.
22. Найти конечную температуру и верхний предел скорости
стационарного потока перегретого пара, вытекающего через сопло
в атмосферу из камеры, где он имел температуру 300° С и нахо-
дился при давлении 5 атм; давление наружного воздуха равно
1 атм. Перегретый пар можно считать идеальным газом, у кото-
рого удельная теплоемкость при постоянном давлении ср =
= 0,49 кал/г-град и отношение теплоемкостей у = 1,33. Тепло-
проводностью и влиянием поля тяжести можно пренебречь.
23. Рассмотреть совокупность систем А, В, С, . . ., термически
равновесное состояние каждой иэ которых определяется давле-
нием р и удельным объемом и. Доказать, что в соответствии с нуле-
вым законом термодинамики для каждой системы существует
характеристическая функция 0А =/А (р, и), . . ., причем усло-
вием теплового равновесия между системами (например, А и В)
является равенство этих функций (например, 0А = 0В) (теорема
существования температуры). При этом следует воспользоваться
эмпирически установленным фактом существования функцио-
нального соотношения между независимыми параметрами двух
систем, находящихся в равновесии.
24. Обобщить задачу о намагничивании, рассмотренную в при-
мере 1, на случай, когда магнитное поле II, намагниченность М
и плотность магнитного потока В неоднородны. (Воспользоваться
уравнениями Максвелла.)
РЕШЕНИЯ
1. Из уравнения состояния получается следующее соотношение
между дифференциалами dp давления р, dT температуры Т и dV
объема V:
Решения
Согласно определению, имеем
dp= рар dT — к .
Отношение дифференциалов dV и dT при р = const (т. е. dp = O)
равно
/ dV\ Vp'Zp
следовательно, kav = рар.
2. Из предыдущего решения находим
dp — kavdT----к-^-=к (avdT-^ .
3. Как и в примере 4, ответ можно получить, сравнивая значе-
ния газовой постоянной, вычисленные с помощью уравнения
состояния и соотношения Майера. Молекулярный вес кислорода
равен 32, отсюда ш = 32 г!молъ. При стандартных условиях объем
1 моль газа равен 22,4-103 см3, поэтому объем 1 г кислорода при
стандартных условиях равен
v 22,4-Юз ,
V = —------= 7ии см3.
Так как 1 ашм= 1,013-10е дин/см2, то при р= 1 ашм тлТ = 273° К
— = = 2,60• 10е эрг/г град = 0,260 дж!г-град.
С другой стороны, из соотношения Майера имеем
-^- = ср — cv = 0,2203 — 0,1578 = 0,0625 кал/г град.
Следовательно, механический эквивалент тепла равен
/ = = 4,16 дж/кал.
0,0625 4
4. Если объем 1 моль идеального газа равен V, то совершаемая
им работа в соответствии с (1-7а) равна —d'A = pdV. Так как
процесс квазистатический, то давление р определяется уравнением
состояния pV = RT. Следовательно, работа, совершаемая газом
при абсолютной температуре Т при изменении объема от Vi до V2,
имеет вид
Vs Vs
— А = ( pdV = RT \= RT In ~ = RT Irt TL
J Jr Vi P2
Vi Vi
где мы использовали соотношения PtVt = RT и p2V 2 = RT. При
T = 20° C = 293° К имеем RT = 8,31-293 = 2,43-103 дж/молъ.
50 Гл. 1. Термодинамическое состояние и первый закон
Для pi = 20 атм, р2 = 1 атм ln(j>1//?2) = In 20 = 2,30-1,301 =
= 2,99. Следовательно, работа, совершаемая газом, равна
RT In (pi/p2) = 2,43-103-2,99 = 7,26-103 дж/молъ.
Поглощаемое при этом количество тепла получается из первого
закона термодинамики (1.2): U2 — Ui = Q + А. В термически
равновесном состоянии внутренняя энергия U одного моля газа
зависит только от Т и поэтому не меняется при изотермическом
процессе: U2 — Ui = 0. Отсюда следует, что количество тепла,
поглощенное газом, равно Q = —А = 7,26-103 дж/молъ. Разделив
эту величину на механический эквивалент тепла J, получаем ее
значение в калориях Q = 7,26-103/4,18 = 1,937 ккал/молъ.
5. Из уравнения Пуассона (см. пример 6) pV^ = const имеем
(dp/pj + Y (dV/V) = 0. Следовательно,
(#)ад = Т/’-
Если сжатие и расширение в звуковой волне можно рассматривать
как квазистатический адиабатический процесс (это справедливо
для звука с достаточно низкой частотой), то
/ 1 Р ( dp \ = Хад YP /94
I dp /ад р \ dV /ад р
так как dp/p = —dV/V. Если молекулярный
и в объеме V содержится п молей газа, то р
уравнение состояния можно записать в виде
р _ RT
р~ М '
Подставляя его в (2), получаем
При у = l^l, среднем молекулярном весе
и R = 8,31-10’ эрг/моль-град2 имеем
с = 3,32-104 см/сек = 332 м/сек.
Изменение скорости с температурой dc/dT = 1/2с/Т при Т = 273° К
равно 0,607 м/сек-град.
6. Для адиабатического процесса 1 —> 2 имеем U2 — UY =
= А = —W (W — работа, совершаемая газом). Для процесса
2 —> 3, при котором газ поглощает количество тепла Q, нагреваясь
при постоянном объеме и, следовательно^ не совершая работы,
получаем U3 = U2 + Q. Если Q — W, то Ua= U2 + И7 =
А так как внутренняя энергия идеального газа не зависит от объема,
а зависит только от температуры, то отсюда следует, что Т3 =
Р ' '
вес газа равен М
= nM/V. Поэтому
(3)
28,9, Т = 273° К
Решения
51
7. Внутреннюю энергию U можно выразить в виде U = СуТ 4~
-Ь const (Cv=const = пСу, где п — число молей, Су — молярная
Фиг. 14.
теплоемкость), откуда следует, что U2 — — Cv (Т2 —
Соответствующая поверхность приведена на фиг. 14.
Кг
а) А^а = 0, так что Л<а) = /1А_>2= — j p2dV = — р2(У2~У1),
К1
(1)
ТА Т?
J CydT=Cv(TA-TJ, Qa^ j CpdT=Cp(T2-TA).
Ti TA
С другой стороны, так как ТА определяется уравнением p2V{ =
= пВ.ТА, то с помощью соотношения Майера Cp — Cv-\-nR (см.
пример 3) находим
<2(а) = Q^a+Qa-,2=Срт2 - СуТ, - (Ср - Су) ТА =
— СрТ2 — СуТ, — р^\ — Су (Т2 — 1 () -|-р2 (V2 — V4). (2)
4*
52 Гл. 1. Термодинамическое состояние и первый закон
б) В процессе В —» 2 работа не совершается, поэтому
v2
Л(б) = J nR7\ = nRTt 1п£. (3)
А
Теплота, поглощения в процессе 1—>В, определяется из соотно-
шения d'Q~pdV (£7 = const, так как Т — const). Следовательно,
в
Qi->b = f pdV= -А^в = -nRT^n^,
J Г2
1
ИЛИ
Т2
Qb^2= j CydT^CytTz-Ti),
Т1
откуда
Q^Cv^-T^ + nRTtln^. (4)
в) В процессе С —> 2 работа тоже не совершается. Работу
в адиабатическом процессе 1—>С можно вычислить так же, как
в примере 6:
Л(в> = Л^с = Су(71с-7’1)= -СуЛ[1 -(Zl)7-1] . (5)
В процессе 1 —>С теплота не поглощается, поэтому
Та
<?(в) = <?с^2= J CvdT = Cr(T2-Tc) = Cv[T2-T1(^y~i']. (6)
тс
Во всех трех случаях сумма А + Q равна Cv (Т2 — Т^.
8. Прежде всего исследуем зависимость давления термически
равновесной атмосферы от высоты z. Эта зависимость определяется
из условия, состоящего в том, что при тепловом равновесии
силы уравновешивают друг друга. Рассмотрим цилиндрический
объем воздуха, находящийся на высоте от z до z -f- dz и имею-
щий сечение S. Силы давления, действующие на верхнюю и ниж-
нюю плоскости, соответственно равны —р (z-rdz) S в р (z) S. Сила
тяжести, действующая на этот объем воздуха, равна —p(z)Sgdz,
где р (z) — плотность воздуха, a g — ускорение свободного паде
ния. Из условия равенства нулю полной силы, действующей на
объем воздуха (фиг. 15),
—р (z + dz) S + р (z) S — p (z) S gdz — 0,
находим dp (z)/dz — —p (z) g. Если m — средний молекулярный
вес воздуха, то объем моля воздуха равен m/p (z). Следовательно,
уравнение состояния (1.11) можно представить в виде р (z) т/р (z) =
= RT (z). Выражая р (z) через р (z), находим dp (z)/dz =
= —mgp (z)/RT (z).
Решения
53
Условие адиабатического квазистатического расширения опре-
деляется соотношением (1) примера 6. Из уравнения состояния
pV = nRT имеем
dp dV dT
р V ~Т~ ’
Исключая dV/V, получаем
dT __ (у — 1) dp
Т ~~ ур ’
или
\ др /ад ур
Из этого условия можно определить зависимость температуры Т (г)
от z, используя соотношение, выражающее изменение давления р
с высотой z. Таким образом, находим
dT (z) _ / дТ \ dp (z) = (у — i)T(z) . — mgp (z) __ _ (у — 1) mg
dz \ др /ад dz yp (z) RT (z) yR
Значения констант для воздуха приведены в решении примера 4:
у = 1,41, т = 29 г!молъ, g = 980 см/сек2. Следовательно,
(V~= Р’^1 ~2')'989 = 1,00 • 10- град/см = 10,0 град/км,
yR 1,41 -8,3 -107 Г 1 г
т. е. при увеличении высоты на 1 км температура уменьшается
на 10° С.
Замечание. В тропосфере (атмосфере) имеются восходя-
щие и нисходящие потоки воздуха. Так как теплопроводность
воздуха пренебрежимо мала, то можно
считать, что при движении воздуха с ним p(z+dz)S
происходят адиабатические процессы.
Поэтому наличие таких потоков не должно
влиять на полученный результат. Однако
на самом деле уменьшение температур со-
ставляет 6° С на каждый километр высоты.
Расхождение связано с различными явле-
ниями, происходящими в атмосфере, типа
p(z)S
Фиг. 15.
конденсации водяного пара.
9. Так как в изотермическом про-
цессе внутренняя энергия идеального газа
не меняется, то поглощаемая в таком
процессе энергия равна производимой работе J pdV. Следователь-
но, в процессе 1 —> 2 для п молей газа
Кг
(?!= j nRT^-^nRTiln ^.
Л 1
(1)
54
Гл. 1. Термодинамическое состояние и первый аакон
Аналогичным образом в процессе 3—>4
Vt
Q2 = J nRT2 = nRT2 In . (2)
v3 3
Для процесса, изображенного на фиг. 11, (?t>0 и Q2 < 0, так как
V2Z>Vt и В3>У4. Для адиабатических участков 2—>3 и 4 —> 1
имеем
ТУГ1 = Т2УГ\ (3)
(из уравнения Пуассона pVv = const или TVv~1 = const; см. при-
мер 6). Из соотношения (3) следует, что = (Из/П4)?~1,
или = И3/И4- Следовательно, из (1) и (2) получаем
Qi _ __ 02_
Ti Т2 ’
10. Согласно определению, количество тепла d'Q, поглощенное
в процессе, равно CxdT, поэтому
CxdT^d'Q = Cv dT + pdV = CvdT + (Cp-Cv)^-,
где мы воспользовались соотношениями p = nRT/V и Ср— Cv — nR.
Отсюда следует равенство
(CX-CV)^ = (CP-CV)^-,
исключив из которого dT/T с помощью соотношения
dT _ dp dV
Т ~ р + V~’
получим
(CX-CV)^=(CP-CX)^.
Введя обозначение / = (Сх — СР)/(СХ — Cv), получаем,
In р + / In V — const,
или
pVf = const.
11. Свободное расширение не является квазистатическим про-
цессом. Следовательно, хотя начальное и конечное состояния 1 и 2
относятся к числу термически равновесных состояний, давление
р<-е> в выражении для работы d'A = — p<e>dV не определяется
из уравнения состояния газа, а представляет собой внешнее
давление. Последнее в случае свободного расширения равно нулю.
Решения
55
Следовательно, при свободном расширении газ не совершает рабо-
ты, т. е. Л1_>2 = 0- Так как тепло при этом также не поглощается,
то — 0 и внутренняя энергия U не меняется. Следовательно,
и температура остается постоянной: Т^ = Т2, так как газ пред-
полагается идеальным.
Если состояние 3 получается из состояния 2 в результате ква-
зистатического сжатия при постоянном давлении, то работа, произ-
водимая над газом при переходе 2 —> 3, имеет вид
П
Л2^3= - Jp2^ = p2(V2-V1). /
у2 у
При этом температура меняется от Т2 до Т3 и, следовательно, газ
охлаждается. Количество тепла, полученное газом, равно
Тз
^2->з — j CpdT = Cp(T3 — 712)<0,
т2
где Ср — молярная теплоемкость при постоянном давлении. В про-
цессе 3 -> 1, представляющем собой квазистатическое нагревание
при постоянном объеме, работа не совершается, т. е. = 0.
Если Су — молярная теплоемкость при постоянном объеме,
то поглощенное тепло можно записать в виде
Т1
<2з^1 = j Су dT — Cv (Тt — Т3).
Та
Из первого закона термодинамики следует, что для замкнутого
цикла сумма всего полученного тепла и произведенной работы
должна быть равна нулю. Следовательно,
<21->-2 + <?2-»-3 + 1 + 42 + 4 2-»3 + 4з_> t = 0.
Подставляя сюда найденные выше выражения для каждого из сла-
гаемых, находим
(Ср - CV)(T3 - Tt) + р2 (У2 - Vi) = 0. (1)
Из уравнения состояния для 1 моль идеального газа pV = RT
имеем
Pz^2 = КТ1!, р2Е\ = RT з
и
Рг (V2 - Vi) = R (Л - Т3).
Подставляя в (1) последнее из этих равенств, получаем требуемое
соотношение
(Ср - Су)(Т3 -TJ + R (71! - Т3) = 0
56
Гл. 1. Термодинамическое состояние и первый закон
ИЛИ
Ср - Су = R.
12. Критическим является такое состояние, в котором р, Т
и V одновременно удовлетворяют следующим соотношениям:
(Op/dV)T = 0, (d2p/dV2)T = 0 и уравнению состояния. Так как
то из условия (dp/dV)T = 0 следует
а из условия (d2p/dV2)T = 0 имеем
У3 _ 2па
(7 — nb)2 — RT ’ W
Поделив обе части Гуравнения (2) на соответствующие части урав-
нения (1), получаем
-т,-7с = 2, Ус = 2и&.
Vc — nb 1 с
Для определения критической температуры Те подставим найден-
ное значение Vc в (1). Тогда
гр na(Vc — пЬ)
lc= RVI •
Подставим в уравнение состояния выражения для Vc и Тс. Это даст
nRTc „___( па \ а
Рс = Vc — nb еХР I ~ RTCVC ) = 4ЬМ“ ‘
Введем теперь приведенные величины Р = р/р,:, t = T/Tc, b=F/Vc,
чтобы получить закон «соответственных состояний». Подставляя
nRTclр^Гс = 112е2, nblVc = 'il2 и na!RTcVc = 2 в выражение
nRTct / па \
Р - PcVc(b-nb/Vc) ехр I ~ ~RTcVcib J ’
получаем
te2/2 / 2 \
13. Согласно соотношению (1.15), внутренняя энергия смеси
химически нейтральных идеальных газов равна сумме внутренних
энергий отдельных компонентов. Если масса i-ro компонента газа
Решения
5Т
равна М,, а ее удельная теплоемкость при постоянном объеме cvir
то
М du = 2 Micvi dT,
где М = Mt — полная масса смеси, и — внутренняя энергия еди-
г
ницы массы смеси. Теплоемкость смеси при постоянном объеме-
определяется соотношением \
du __ Xi AQeyi
Cv ~ dT ~
Для воздуха она принимает следующее значение: cv = 0,23 X
X 0,158 + 0,77-0,176 = 0,036 + 0,136 = 0,172 кал/г-град.
14. Возьмем в качестве оси х прямую, проходящую через иголку
и через прямоугольный постоянный магнит, как показано на
фиг. 16. При этом направление магнитного поля Нs также будет
совпадать с осью х. Поле Н s (х) равно нулю при х = — оо и моно-
тонно возрастает при увеличении х. Игла медленно подносится
к магниту вдоль оси х от — оо до точки х, где приобретает*
магнитный момент тп, направленный, ко-
нечно, вдоль оси иголки. Размагничива-
ющее поле иголки, направленное навстре-
чу полю постоянного магнита Н s,
можно считать пренебрежимо малым. Так
как размеры иголки невелики, ее можно
рассматривать как магнитный диполь
с магнитным моментом ш (х), зависящим
от координаты х. Сила, действующая на
иголку, определяется выражением
К (х) = тп (х) . (1)
Чтобы иголка перемещалась от х = — оо
до точки х = Xt бесконечно медленно,
нужно ее удерживать с силой, незначительно меньшей —К {х).
Производимая этой силой работа (получаемая за счет механи-
ческого источника, например при перемещении груза в поле-
тяжести) над системой иголка — магнит имеет вид
£1 H(^i)
Ai = — К (х) dx = — j m(x) dx £ = — j m dH~^ . (2>
— co —co 0
Однако только часть этой работы идет на намагничивание иголки,
остальная работа расходуется на создание запаса потенциаль-
ной энергии. Если магнитный диполь с магнитным моментом*
-58 Гл. 1. Термодинамическое состояние и первый закон
•т (х) = mi поместить в поле Н (zj), то его потенциальная энер-
гия равна —пцН (xi) (энергия взаимодействия между диполем
и постоянным магнитом). Чтобы вычесть ее из (2), рассмотрим сле-
дующий процесс: пусть нам некоторым способом удалось зафикси-
ровать намагниченность иголки т^ = т (xi), после чего мы ее
перемещаем из точки Xf на — оо. При этом постоянный магнит
•будет притягивать иголку с силой
K(x) = mi^L-, (3)
таким образом, внешний механический источник должен совер-
шить работу
-Л2 = — j К' (х) dr -гщ ~
-го
*1
= т1Я(.г1)= j d^m^..^dx. (4)
— со
Следовательно, работа, необходимая только для намагничивания
иголки, будет иметь вид
Ai + A2= j Н (х) dx = J Hdm. (5)
— co 0
Замечание. Если рассматривать иголку и постоянный
магнит как единую термодинамическую систему, то их энергия
взаимодействия войдет во внутреннюю энергию системы V.
Если U — внутренняя энергия иголки, то
U' = U — Нт + const,
так что
dU' = dU — Hdm — mdH = —mdH.
Отметим зависимость величин U и Ur от определения термодина-
мических систем. Несмотря на свою очевидность, она часто приво-
дит к недоразумениям.
15. Так как плотность воздуха р зависит от высоты z, столб воз-
духа нельзя считать однородной системой. Тем не менее в состоя-
нии теплового равновесия температура Т должна быть однородной.
Если неоднородную систему можно разбить на такие части (под-
системы), что каждую из них допустимо считать однородной,
а взаимодействие между ними пренебрежимо малым, то энергия
полной системы будет равна сумме энергий ее частей. Цилин-
дрический объем, лежащий между z и z + dz, можно считать
однородной подсистемой такого рода с внутренней энергией
Решения
59
р (z) Su (Т) dz и потенциальной энергией р (z) Sgzdz, где S — пло-
щадь поперечного сечения цилиндра, и (Т) — внутренняя энергия
единицы массы воздуха, рассматриваемого как идеальный газ,
a g — ускорение силы тяжести. Так как суммарная энергия слоя,
лежащего между z и z 4~ dz, равна S [и (71) 4- g (z)] р (z) dz, то
полная энергия всего воздуха в цилиндрическом объеме от z = О
до z = оо имеет вид
ОО
Е(Т) = S j [u(T)4-gz] p(z)dz.
о
Зависимость р от высоты определяется уравнением dp(ti)ldz —
= —p(z)g (см. решение задачи 8). Чтобы исключить p(z), про-
дифференцируем уравнение состояния р (z) = RT<> (z)/m; тогда
dp(z) _ p(z) mg
dz ~ RT '
«откуда
, , „ mgz .
In p (z) =---- 4- const,
или
p (z) = p (0) e-msz!RT.
Вместо плотности воздуха p (0) вблизи поверхности Земли при z = 0
удобнее ввести полную массу воздуха в цилиндрическом объеме
М= f p(z)Sdz = p(O)S J e-msz/RTdz = ^~- ,
о о
что дает
_Mmg_ mgz/RT
RT
С помощью этого соотношения получаем энергию рассматри-
ваемого объема воздуха
Е (Т) = J [ и (Т) + gz] e~m^RT dz =
о
оо
= М J[u(Z) + ^-] e~ldl =
о
оо
=м [“ +4г J4«"sм [“ +4г] •
о
60
Гл. 1. Термодинамическое состояние и первый закон
Отсюда видно, что энергия является функцией только температуры.
Теплоемкость определяется выражением
с=^=‘«(-&+4)=«('.+4)-
Воспользовавшись соотношением Майера ср = с0 + R/т, получаем
С = Мср.
16. Количество тепла, полученное системой в квазистатическом
процессе, определяется первым законом термодинамики d'Q = dU —
+ р dV. Если считать внутреннюю энергию функцией от Т и У, то
dU=(-^) dT + (^-) dV.
\дТ Jv ‘ \ dv Jt
Тогда первый закон термодинамики принимает вид
(1>
Для энтальпии Н = U + pV имеем соотношение
dH = dU + р dV 4- У dp,
откуда
dU -j- pdV = dH — У dp.
Следовательно, можно записать
d'Q = dH — V dp.
Удобно рассматривать H как функцию от Т и р;
При этом выражение для количества теплоты запишется следующим
образом: .
<2>
а) Теплоемкость при постоянном объеме" равна производной
d'Q/dT при dV — 0, поэтому из (1) вытекает, что Cv = (dUldT^y.
При постоянном давлении dp = 0, тогда из (2) следует Ср =
= (дН/дТ)р.
б) Как было показано в решении примера 2, теплоемкость при
постоянном давлении можно получить из соотношения (1), если
считать У функций от р и Т, опрёделяемой уравнением состояния,
и подставить в (1) dV = {dVldT)pdT + (dV!dp')T dp, что дает
«^+[(^)r+p][(4L)/r + (-)/p].
Решения
61
Если положить здесь dp = O, то для производной d'Q/dT получим
Это первое из равенств «б». Чтобы, получить второе, выведем
из соотношения (2) выражение для Су. Так как dp = (др/дТ)у dT-\-
+ (dpldV)T dV, то
При dV = 0 производная d'Q/dT равна
Подставляя сюда соотношение «в», получаем второе из равенств «б»,
в) Так как Н = U -f- pV, то
( дН \ ( dU \ ( д (pV) \ ( dU \ / dV \ т/
г) Так как (dV/dT)p = i/(dT/dV)p, первое из равенств «б» можно
записать в виде
ir г \ \ _ ( dU \ г „
(Ьр-C-v) +
Считая обе части этого соотношения функциями от р и V, продиф-
ференцируем их по р; тогда
-(^)r(#)J=(SJ^)v + ‘- <3'
Рассмотрим теперь третий член в левой части и первый член
в правой части'этого уравнения. Хотя они являются частными про-
изводными по р при постоянном V, для удобства будем считать
Ср и {dU/dT)v функциями от переменных Т и V. Если в теплоем-
кости Cv (Т, V) переменную Т считать функцией от р и V, опреде-
ляемой уравнением состояния, то можно записать
/ дСу \ дСу(Т(р, V), V) / дСу \ / дТ \
X др /у др \ оТ )v\ др )у’
Аналогичным образом, если считать аргумент Т функции (dUldV)T =
— dU(T, V)!dV функцией от р и V, то для того, чтобы полу-
чить частную производную по р, нужно сначала продифференци-
ровать по Т, а затем умножить на частную производную от Т по р:
( д(дЦ/дУ)т \ d4J (Т, V) ( дТ \ _ / дСу \ / дТ \
V др )у дТ дУ I др )у \ дУ )т X др )у’
62
Гл. 1. Термодинамическое состояние и первый закон
откуда
7 дСу \ 7 дТ \ д (дЦ/дУ)т __
\ др )у\ дУ ) р др ~
<4>
С другой стороны, считая Т в функции Су (Г, У) функцией от />
и V, получаем выражение
f дСу\ _ дСу (Т (р, 7), 7) _ 7 дСу \ 7 дТ \ 7 дСу \
I дУ Jp дУ I дТ JyUpJp'T'k дУ )т’
с помощью которого соотношение (4) можно переписать в виде-
7 дСу \ 7 дТ \ d(dUldV\p 7 дСу \ 7 дТ \
I др ) у I дУ J р др ~ д V ) рк др J у ’
Подставляя это равенство в (3), получаем требуемое соотношение.
17. Используя решение задачи 5, а также следующие соотно-
шения: са = yjo/p,
м
р RT _(Ср-Су)Т W Т
~р~~М--------М----= (Ср-Су)7’=(у-1)су7’,
получаем, что с2 = у (у — 1) cvT, или cvT = с2/[у (у — 1)]. Кроме-
того, нам известно, что и = с„Т + const и
h = и + ри = и 4- (ср — с0) Т = и + (у — 1) cvT =
= ycvT + const.
Таким образом, мы пришли к искомому результату.
18. Выражение для работы в постоянном магнитном поле Н
имеет вид d'A = Hdl, поэтому из первого закона термодинамики
следует, что поглощаемое тепло определяется соотношением
d'Q = dU — d'A = dU — Hdl.
Если считать U и I функциями от температуры Т и магнитного
поля Н, то
Д7-(4)я‘'7'+(»,'и/’
И
dl= f-gr) + dH
\ дТ /н 1 \ дН }т
Искомая теплоемкость Сн равна d'QtdT при dH = 0. Таким обра-
зом, мы нашли решение задачи.
Решения
19. Для единичного объема магнитного вещества, участвующего-
в квазистатическом процессе, первый закон термодинамикщзапи-
сывается в виде
d'Q = dU — HdM
[согласно уравнению (1.5) и примеру 1]. Сравнивая это выражение-
с аналогичным соотношением для газа: d'Q = dU 4- pdV, находим-
соответствие р -> —Н, V -> М. Так ,
как величины
/ дМ \ I дМ \
^г \.~дТГ)г и
соответствуют величинам l/(dp/dV)T
и 1/(др/дУ)ад, то искомый результат
можно получить, обращаясь к ре-
шению примера 7 и действуя ана-
логичным образом.
20. Внутренняя энергия тепло-
вого излучения в замкнутой полости
с объемом V определяется выраже- о
нием U = Vu = sVTi. Так как дав-
ление р = и/3 = aTi/3 не зависит
от V, величины р и Т не являются
независимыми. Поэтому в качестве переменных естественно выб-
рать (7, Т) или (7, р). Для квазистатического процесса пер-
вый закон термодинамики записывается в виде
dU = d'Q — pdV.
Подставляя сюда выражения для U и р, получаем
d'Q^d (о7Л) + 4- пУ4 dV = оТ* dV + 4oT3V dT.
О О
Следовательно, условие адиабатичности принимает вид
|<тУ47 (-^- + 3-^)=0,
или после интегрирования
In 74-3 In Т = const, VT3 — const.
Используя уравнение состояния, находим
рУ*/з = const.
Теплоемкость при постоянном объеме равна
сН-зг),=4'’7”у‘
-64
Гл. 1. Термодинамическое состояние и первый закон
а теплоемкость при постоянном давлении можно считать беско-
нечной, так как при фиксированном давлении температура излу-
чения в полости не может меняться.
Как показано на фиг. 17, цикл Карно образуется квазистатиче-
•скими процессами, при которых система переходит из состояния 1
в состояние 2 путем изотермического расширения, из состояния 2
в состояние 3 путем адиабатического расширения, из состояния 3
в состояние 4 путем изотермического сжатия и возвращается
в состояние 1 путем адиабатического сжатия. Пусть в процессе
1 2 объем возрастает от Vi до У2 при постоянной температуре Ti.
Работа, получаемая тепловым излучением, записывается в виде
Л1^2= - J pdV = -LvTWz-Vi),
Vl
а полученное тепло
v2
<21-2 = 4 vT* \ dV = 4 oT* (У2- У0-
D J D
Vl
Следовательно, их сумма
Ai^ + Qi^aT^Vz-Vi)
-соответствует возрастанию внутренней энергии. Очевидно, что для про-
Уз
цесса 2—>3 (?2->з = 0, а чтобы вычислить Л-2^з= — pdV,
v2
воспользуемся соотношением
рУ4/з = АУ4/з=1аГ‘У‘/з.
Следовательно,
v3
А2_>з — -4-аГ^/з f V-i^dV = oTi1Vi^(V-1/3- У2-Уз) =
Уз
= oT^V-1^-gT{Vz.
Из равенства У27’1 = У371| находим температуру системы в состоя-
нии 3. Она равна Ts = Ti (Уг/Уз)^3, откуда
Л2^3 = аТ’‘Уз-а^У2.
При этом происходит также увеличение внутренней энергии.
(Действительно, ^2_>3 = 0, поэтому в силу первого закона термо-
динамики должна возрастать внутренняя энергия.) В процессе
Решения
65
3 —> 4 температура постоянна и
(23^4 = -g-a^(V4-V3),
Л3_4= —5-а^(Г4-У3).
Для процесса 4—>1 имеем = Q и = оТТ4— аТД7!-
Так как V2^>Vt, то (?1>2>0. Это означает, что происходит
поглощение тепла от теплового резервуара (с температурой Tj).
Из равенств — УзТ? и У47’| = У1Т? вытекает, что У3/У4 =
= У2/У1>1. Следовательно, (?з_>4<0- Это в свою очередь озна-
чает, что теплота передается более холодному тепловому резер-
вуару (с температурой 7':>), так как Т3 = Т\ (У2/У3) 13 < в силу
того, что V3 > V2. Полная энергия, полученная системой от тепло-
вого резервуара (Л->2— | С?з->41 = <21->2 + <?з->4, равна полной произ-
веденной работе —(И 1^2 -Лу-уз : Л3^4Л2 >i). Поэтому
= А оТ? (У4 - У3) = А оТ? (У. - У2) = - 4^,
откуда следует уравнение Клаузиуса <21->2/Л -г (?з-»4/Т3 = 0.
21 (См. пример 9). В стационарном потоке линии токов не изме-
няются со временем. В целом жидкость не находится в состоянии
термодинамического равновесия, так как из-за движения жидко-
сти скорость V, плотность р и давление р являются функциями
точки. Однако можно считать, что достаточно малые элементы
объема находятся в состоянии термодинамического равновесия
(локального равновесия), т. е. можно считать, что изменения
их состояния происходят квазистатически. В таком случае давле-
ние полностью определяется плотностью и температурой элемента
объема с помощью уравнения состояния.
Из уравнения неразрывности жидкости следует, что количество
жидкости, проходящей за единицу времени через поперечное
сечение St трубки тока, перпендикулярное направлению потока,
как показано на фиг. 18, равно количеству жидкости, проходящему
за то же время через другое сечение S2, т. е. = р252к2.
Обозначая через I расстояние вдоль трубки тока, можно записать
д (pSv)ldl = 0. Теперь применим первый закон термодинамики
к объему жидкости, заключенному между сечениями и S2,
расположенными на расстоянии dl друг от друга. Так как мы пре-
небрегаем теплопроводностью, можно не рассматривать теплооб-
мен этого объема жидкости с окружающей средой. Если пренебречь
еще вязкостью и гравитационной силой, то совершаемая работа
будет выражаться только через внешние давления р{ на поверх-
ность и р2 на S2. Работа, совершаемая над жидкостью за еди-
ницу времени, равна piSiVi — P2S2v2. Для бесконечно малого dl
5 кубо
66
Гл, I. Термодинамическое состояние и первый закон
она’равна —dld(pSv)/dl. Будем считать, что плотность внутренней
энергии и жидкости с помощью уравнения состояния можно
выразить через плотность р и температуру Т. Элемент объема
жидкости, находившийся в момент времени t между сечениями
Фиг. 18.
и S2, по истечении интервала времени dt будет расположен между
сечениями, смещенными относительно Sj и S2 на v^dt и v2dt соот-
ветственно. Поэтому его энергия возрастает на величину
— Pi («1 + 4yi) SiVidt + pz («г + у^) S2v2dt.
В первом порядке по dl возрастание энергии на единицу объема
будет равно
В силу первого закона термодинамики это приращение энергии
должно быть равно ранее полученному выражению для совершен-
ной работы, т. е.
(“+41’2)]_ д (pSv)
dl dl
Это равенство можно переписать в виде
(и+4р2+^/Р
_______
Решения
67
С помощью уравнения неразрывности д {pSv)/dl = 0 получаем
Отсюда следует, что сумма и + р/р + 1/аг;2 постоянна вдоль линии
тока. Так как величина 1/р представляет собой удельный объем,
то h = и + р/р есть плотность энтальпии, 1/2г2 — кинетическая
энергия единицы массы.
22. В предыдущей задаче мы нашли, что сумма плотности
энтальпии h и кинетической энергии V^2 постоянна вдоль линии
тока. Для идеального газа с постоянной удельной теплоемкостью
из уравнения для внутренней энергии и = cvT + const следует,
что h = и 4- р/р = с-рТ + const. Следовательно, для него вели-
чина срТ + 1/2п2 постоянна вдоль линий тока. При адиабати-
ческом изменении состояния идеального газа величина pA-v)/vT
постоянна, поэтому она должна быть постоянна также и вдоль
линий тока. Если теперь мы предположим, что в камере с перегре-
тым паром, где он находится при температуре Т = 200° С =
= 573° К и давлении р = 5 атм, скорость потока равна нулю, то
СрТ +1 цз = 0,19 573 = 281 кал/г = 1,174-1010 смЧсек*.
Когда /7=1 атм, температура становится равной
Т = 573- (I />)°’33/1'33 °к = 573.5-».248 °к.
Для вычисления х = 5-3.248 в03ьмем логарифм правой и левой
частей:
1g х = —0.248 1g 5 = -0,248-0,699 = —0,1734 =^,8266,
откуда следует, что х = 0,671. Таким образом,
Т = 573-0,671 = 384° К = 111° С.
Теперь нетрудно получить верхний предел скорости
р2 = 2(1,174-1010 — 0,49-384-4,18-Ю7) = 0,774-Ю10 слгУсек2,
т. е. и = 880 м/сек.
23. Пусть независимыми переменными системы А будут рА и vA,
а переменными систем В и С — соответственно рв, ив и рс, vc.
Если А и В находятся в равновесии, то между четырьмя перемен-
ными рА, vA, рв и vB существует некоторое соотношение. Запишем
его следующим образом:
Fs (Ра, va, Рв, »в) = 0. (1)
5*
68 Г.1. 1. Термодинамическое состояние и первый закон
Аналогично, если В и С находятся в равновесии, то будет иметь
место соотношение
Л (Рв, »в, Ре, ис) = 0. (2)
Согласно нулевому закону термодинамики, А и С также находятся
в равновесии, тогда из (1) и (2) следует, что должно иметь место
соотношение
Л (Ра, va, рс, vc) = 0. (3)
Если разрешить (1) и (2) относительно рв
Рв = <Р1 (Ра, »а, vb), рв = ф3 (рс, vc, vB),
то соотношение
Ti (Ра, va, vb) = ф3 (рс, vc, vB) (4)
должно быть эквивалентно уравнению (3). Следовательно, соотно-
шение (4) должно не зависеть от ив и должно быть эквивалентно
соотношению типа
/1 (рА, »А} = /з (Рс, vc). (5)
[Это означает, например, что ф! (рА, vA, vB) = /i (рА, vA) т] (ув) +
+ С (Ув), ф3 (рс, vc, vB) = /3 (рс, vc) ц (vB) + £ (vB).] Следова-
тельно, (3) и (5) должны быть эквивалентны. Таким же образом
можно показать, что (1) и (2) эквивалентны соответственно соот-
ношениям
fl (Ра> vA) = /2 (рв, VB), (6)
/2 (Рв, vB) = f3 (Рс, vc). (7)
[Идентичность функций в (5) и (6), /2 в (6) и (7) и /3 в (5) и (7)
следует из нулевого закона термодинамики.] Если теперь ввести
величину
9 = fi (Ра, va),
характеризующую тепловое равновесие, то она будет представлять
собой не что иное, как температуру в некоторой шкале. Условием
равновесия между системами А и В будет равенство между собой
величин 0Д и 0л.
24. При рассмотрении общего случая магнитного тела произ-
вольной формы приходится учитывать влияние размагничивающего
поля образца и неоднородности поля Н, намагниченности М
и плотности потока Б. Поэтому с самого начала будем исходить
из уравнений Максвелла. Эквивалентом закона Ампера является
первое уравнение Максвелла, в котором предполагается, что
намагничивание происходит достаточно медленно, чтобы можно
было пренебречь токами смещения
rot Н —J (первое уравнение Максвелла). (1)
Решения
69
Здесь j — плотность тока, протекающего по проводу катушки.
Если магнитное тело неподвижно, то закон индукции Фарадея
имеет вид
rotl?=------ (второе уравнение Максвелла), (2)
где JE — электрическое поле. Плотность магнитного потока удов-
летворяет уравнению
div В = 0 (четвертое уравнение Максвелла). (3)
Магнитное поле Н является суммой поля Нj тока в катушке
и поля Нм, связанного с намагниченностью:
И 11,11,.
Как известно, поля Hj и Нм удовлетворяют следующим урав-
нениям, которые вытекают из (1) и (3):
rot Hj = -^~j, divHj = Q,
rot Нм = 0, div Нм = — 4л div М.
Силовые линии поля Hj замкнуты и проходят вокруг катушки,
а поле Нм — безвихревое и его силовые линии соединяют поло-
жительный и отрицательный полюсы магнитного тела. Поле Нм
обладает (псевдо)скалярным потенциалом и определяется кулонов-
ским законом. Следовательно, интегрирование по всему простран-
ству дает
j Hj-HMdV = — j -grad q>dV = j cpdiv/fj dV = 0. (4)
Мы предположили, что на бесконечности поле обращается в нуль.
Умножим теперь скалярно уравнение (1) на cEl^n, уравнение (2)
на —сН1^я, затем сложим их и проинтегрируем полученную
сумму по всему пространству. Правая часть принимает вид
j (E-rotH — Н-rot E)dV — J div [Н X Е] dV = 0.
Поэтому для левой части можно записать
+ = (5)
Первый из этих двух интегралов нужно брать по области, где
ток j отличен от нуля, т. е. в проводах катушки и в батарее. Если
удельное сопротивление проводов или батареи равно р, то из
закона Ома Е + F = pj находим
J Е- j dV = j pj2 dV — J F j dV.
70
Гл. 1. Термодинамическое состояние и первый закон
Здесь F—э. д. с. батареи, a ^F-jdV— работа, производимая
батареей за единицу времени при прохождении тока J. Если тем-
пература полной системы сохраняется постоянной, то интеграл
J pj2 dV определяет долю работы, растрачиваемой на джоулево
тепло. Второй интеграл в (5) можно переписать следующим обра-
зом:
1 Г „ дВ лт/ 1 Г „ дН , Г т_ дМ
TST J —Л =7Т J -ff— »'+ J H- — dv-
<6>
Первый член суммы в правой части представляет работу, затрачи-
ваемую на создание поля. Так как, согласно (4), j Hj-HMdV =
= 0, то получаем
[ H2dv = [ H}dV+-А- [ Hltdv.
oJL j ojv J ojT J
Здесь нужно отметить, что в найденное выражение входит работа,
необходимая для создания поля катушки и размагничивающего
поля, возникающего при намагничивании магнитного образца.
Эту работу можно исключить из определения работы, необходимой
для намагничивания образца. Отнесенная к единице времени
работа намагничивания равна j H-(dMldt) dV. Умножая ее на dt,
получаем работу, производимую при увеличении намагниченности
образца от М до М + dM
d'A= j (H-dM)dV = J (Hj + HM)dM dV,
где интегрирование производится по всему объему образца. Сле-
довательно, полная работа намагничивания имеет вид
м
А= J dV J (Hj + HM)-dM.
о
Важно отметить, что размагничивающее поле Нм, связанное
с намагниченностью образца, в общем случае необходимо вклю-
чить в магнитное поле. Если магнитное поле Н и намагниченность
М однородны, то объемный интеграл соответствует просто умно-
жению на объем V.
Замечание. Магнитное поле внутри образца и его намаг-
ниченность однородны только в том случае, когда он имеет форму
эллипсоида. В этом случае размагничивающее поле вдоль осей
Литература
71
эллипсоида х, у и z определяется выражением
(Нм)а= (СС = Я?, у, Z),
где размагничивающие факторы Nx, Nv и Nz подчиняются правилу
Nx + ф- Nz = 4л.
Эти коэффициенты можно вычислить как функции отношений осей
эллипсоида.
литирл ТУ Р л
1. Emden R., Nature, 141, 908 (1938).
2. Sommerfeld A., Thermodynamik und Statistik (Vorlesungen liber
theoretische Physik, Bd. 5), Wiesbaden, 1952. (См. перевод: A. 3 оммер-
ф e л ь д, Термодинамика и статистическая физика, ИЛ, 1956.)
3. Enzyklopadie der mathematischen Wissenschaften, Leipzig-Berlin, 1926.
4. E p s t e i n P. S., Textbook of thermodynamics, New York, 1937. (Cm.
перевод: П. С. Эпштейн, Курс термодинамики, M.— Л., 1948.)
5. С а г п о t N. L. S., Reflexions sur la puissance motrice du feu et sur les
machines propres, Paris, 1878. (См. перевод в сб. «Второе начало термо-
динамики», М.— Л., 1934.)
6. Mendoza Е., Phys. Today, 14, No. 2, 32 (1961).
.7. М а с h Е., Principien der Warmelehre, Leipzig, 1923.
ГЛАВА 2
Второй закон термодинамики
В этой главе вводится второй закон термодинамики и рассмат-
риваются некоторые проблемы, непосредственно с ним связанные.
Главная цель состоит в том, чтобы уяснить сущность этого фун-
даментального закона и освоить понятие энтропии, которая пред-
ставляет собой наиболее важную физическую величину, но, к со-
жалению, часто кажется студентам чем-то весьма отвлеченным.
ОСНОВНЫЕ ПОЛОЖЕНИЯ
§ 1. Обратимые и необратимые процессы
Обратимый процесс. Предположим, что при переходе рассмат-
риваемой системы из состояния а в другое состояние а' термостат
переходит из состояния 0 в 0'. Если каким-либо образом возмож-
но возвратить одновременно систему в состояние а, а термостат —
в состояние 0, то процесс перехода (а, 0) (а', 0') называют обра-
тимым.
Такое определение обратимости является наиболее общим.
Часто приводится менее .общее определение: рассматриваемый
процесс является обратимым, если на каждой стадии его можно
обратить с помощью бесконечно малых изменений термостата.
В этом смысле обратимый процесс представляет собой не что иное,
как квазистатический процесс, рассмотренный в гл. 1, § 5. Любой
квазистатический процесс в этом смысле обратим. Обратимый
процесс в широком смысле необязательно обратим в узком смысле.
Например, чисто механические или электромагнитные явления
обратимы в широком смысле, но они могут и не быть обратимыми
при более узком определении обратимости 1). Обычно рассматри-
!) Примером такого рода может служить движение заряженной частицы
во внешнем магнитном поле. Чтобы обратить направление движения, необ-
ходимо из-за наличия силы Лоренца изменить направление магнитного поля.
Следовательно, без изменения магнитного поля такое движение в узком
смысле не является обратимым.
Основные положения
73
ваемые обратимые процессы являются комбинациями чисто меха-
нических или электромагнитных процессов и квазистатических
тепловых процессов.
Следовательно, мы можем воспользоваться более узким опре-
делением обратимости тепловых процессов; обратимым процессом
будем считать квазистатический процесс. На самом деле все
физические процессы протекают с конечной скоростью и, следо-
вательно, являются необратимыми, так как они всегда происходят
с некоторым трением. Обратимый процесс представляет собой иде-
ализацию.
Процессы, которые нельзя провести обратимым образом, назы-
ваются необратимыми.
Обратимые и необратимые циклы. Пусть изучаемая система
переходит из состояния а в это же состояние а, а термостат —
из состояния р в состояние р', причем процесс перехода (а, Р)—>-
—(а, Р') является обратимым. В этом случае переход а -> а
называют обратимым циклом. Если этот процесс необратим,
то цикл называют необратимым. В случае квазистатического
изменения процесс обратим на каждой стадии.
Обратимая и необратимая тепловая машина. Тепловой маши-
ной называется устройство, позволяющее производить работу
при циклическом процессе теплообмена между системой (рабочим
веществом) и термостатом. Такая машина может быть как обрати-
мой, так и необратимой в зависимости от того, обратимым или
необратимым является цикл.
§ 2. Лемма (цикл Карно)
Одним из наиболее мощных методов исследования проблем,
связанных со вторым законом термодинамики, является мыслен-
ный эксперимент, основанный на использовании цикла Карно.
Здесь мы дадим определение цикла Карно в узком смысле для
случая, когда рабочим веществом является идеальный газ (такой
цикл показан на фиг. 19 и схематически на фиг. 20). Пусть при
одном изотермическом процессе система получает от резервуара
У?! (7\) количество тепла Qlf а при втором — количество тепла Q2
от резервуара Н2 (Т2); тогда можно записать
Qi । С*2
Тг т Т2 “
0.
(2.1)
Так как для доказательства этого соотношения достаточно урав-
нения состояния идеального газа и первого закона термодинамики
74
Гл. 2. Второй закон термодинамики
(см. гл. 1, задача 9), то при изучении второго закона термодина-
мики его можно рассматривать как известную лемму.
Фиг. 19.
§ 3. Второй закон термодинамики
Второй закон термодинамики является эмпирическим, поэтому
его можно сформулировать различными способами, которые,
конечно, эквивалентны. Приведем эти формулировки.
а) Принцип Клаузиуса. Процесс, при котором не происходит
никаких изменений, кроме передачи тепла от горячего тела к хо-
лодному, является необратимым, иначе говоря, теплота не может
спонтанно перейти от более холодного тела к более горячему
без каких-либо других изменений в системе.
б) Принцип Томсона (Кельвина). Процесс, при котором работа
переходит в тепло без каких-либо других изменений состояния
системы,, является необратимым; иначе говоря, невозможно пре-
образовать в работу все количество тепла, взятое от тела с одно-
родной температурой, не производя никаких других изменений
состояния системы.
Основные положения
75
в) Принцип невозможности создания вечного двигателя второго
рода. Невозможно создать циклически работающую машину, кото-
рая производила бы работу за счет поглощения тепла от одного
теплового резервуара, не совершая при этом никаких других
изменений состояния системы (вечный двигатель второго рода).
г) Принцип Каратеодори. Вблизи любого термически равно-
весного состояния термически однородной системы существует
другое состояние, которое как угодно мало отличается от перво-
го, но никогда не может быть достигнуто из него путем адиабати-
ческого перехода.
Замечание. Под термином «другие изменения» подразуме-
ваются такие изменения системы, которые сохраняются после
завершения процесса. В формулировке «в» существенно условие
цикличности машины. Действительно, при изотермическом рас-
ширении идеального газа все тепло, взятое от теплового резерву-
ара, можно преобразовать в работу. Однако такой процесс не мо-
жет быть периодическим. Очевидно, что формулировки «б» и «в»
эквивалентны. В задаче 1 будет доказана эквивалентность форму-
лировок «а» и «б». Несколько сложнее (см. задачу 30) доказывается
эквивалентность формулировки «г» формулировкам «а» и «б».
§ 4. Коэффициент полезного действия общего цикла Карно
Общий цикл Карно. Хотя можно предложить ряд обобщений
несколько узкого определения цикла Карно, приведенного в § 2,
мы будем под обобщенным циклом Карно подразумевать цикл,
совершаемый тепловой машиной, которая поглощает тепло Qt
и Q2 от двух тепловых резервуаров Ri и R2 и совершает работу
А = Qi + 2 над окружающей средой (фиг. 20). Следовательно,
цикл Карно состоит из двух изотермических процессов и двух
адиабатических процессов. Если все эти процессы обратимые,
мы имеем обратимый цикл Карно.
Коэффициент полезного действия. Если Ri является горячим
резервуаром, а R2 — холодным резервуаром, то <2! >0, <2г < 0,
А = Qi + Q2 — <2i — | <22 I, а к. п. д. ц имеет вид
1 <?i <?i
(2-2)
следовательно,
= (2.3)
Принцип Карно. К. п. д. ц обратимого цикла Карно, дейст-
вующего между тепловыми резервуарами Ri и R2, однозначно
определяется температурами 01 и 02 тепловых резервуаров и не
76
Гл. 2. Второй закон термодинамики
Ф и г. 21.
зависит от рабочего вещества. Более того, к. и. д. ц' любого необ-
ратимого цикла Карно, действующего между теми же самыми
тепловыми резервуарами, мень-
ше ц, т. е.
П = П (91, 92), П > т|'- (2 *-4)
Доказательство. Рас-
смотрим два цикла Карно С и С'.
Первый из них является обра-
тимым. При этом от теплового
резервуара Rt берется количе-
ство тепла Qi, резервуару Rz
передается количество тепла
| Q2 | и совершается работа
А = Qt — | Q2 |. Цикл С мо-
жет быть обратимым или необ-
ратимым. В этом цикле от ре-
зервуара Ri берется количество
тепла Q[, резервуару R2 переда-
ется количество тепла | Q' | = | Qz |
и совершается работа А' = Qi— | Q2 |. Если цикл С производить
в обратном направлении (фиг. 21), то в результате выполнения
обоих циклов поглощается тепло Q' — Qi из резервуара R{ и
совершается работа
А' - А = Q{ —1 <2Д - (Qi-1 Q21) = Q[ —Qv
Согласно принципу Томсона, при этом должно выполняться нера-
венство
А' — А<0 или Qi <<2р
Следовательно,
11 Cl Qi л
Если цикл С является обратимым, то циклы С и С' можно заставить
действовать в противоположных направлениях *), откуда будет
следовать, что ц' ц, а поэтому ц = ц'.
!) Если циклы С и С' обратимы на каждой своей стадии, то они могут
осуществляться в обратном направлении. Если же эти циклы обратимы
в широком смысле слова, то возможно, что их нельзя производить в обрат-
ном направлении. Однако можно указать такие процессы С и С', которые при-
водят к противоположному эффекту для каждого цикла. Таким образом,
мы приходим к прежнему результату.
Основные положения
77
§ 5. Абсолютная температура
Отношение абсолютных температур Ti и Т2 тепловых резер-
вуаров Hi (0j) и R2 (02) определяется соотношением
^_==1М = 1_Т](01, 02), (2.5)
1 i V 1
где ц — к. п. д. обратимого цикла Карно, действующего между
двумя тепловыми резервуарами. Согласно соотношению (2.1),
температура, показываемая идеальным газовым термометром,
совпадает с абсолютной температурой. Чтобы однозначно опре-
делить абсолютную температурную шкалу, необходимо задать
значение температуры в некоторой опорной точке. Когда в каче-
стве такой точки выбрана тройная точка
^тройной точки воды = 27а, 16 К,
то шкала называется температурной шкалой Кельвина. В даль-
нейшем мы всюду, за исключением особо оговоренных случаев,
будем пользоваться абсолютной температурной шкалой.
ОТСТУПЛЕНИЕ 4
Абсолютная температура. Абсолютной температурной шкалой
называют температурную шкалу, которая определяется термодина-
мическим методом таким образом, что она не зависит от выбора термо-
метрического вещества. Нулевая точка этой шкалы определяется как
наинизшая термодинамически возможная температура. Абсолютная
шкала температуры, которая используется в теплофизике в настоящее
время, была введена лордом Кельвином (Вильямом Томсоном) в 1848 г.
и поэтому называется также шкалой Кельвина.
Для однозначного определения шкалы мы можем воспользо-
ваться любым из следующих двух способов. Первый из них основан
на использовании двух фиксированных точек, лежащих выше нуля,
причем разности температур, отвечающих этим точкам, приписы-
вается определенное значение. Другой способ заключается в исполь-
зовании одной фиксированной точки, которой приписывается опре-
деленное численное значение температуры. До недавнего времени
калибровка температурной шкалы Кельвина производилась по двум
фиксированным точкам: точке плавления льда То °К и точке кипения
То + 100° К чистой воды при давлении в одну стандартную атмо-
сферу (101 325 нъютон/м2'). Величину То можно измерить с помощью
газового термометра. При низких давлениях уравнение состояния
реального газа можно записать в виде
pV = a + x/i.
Измерим величины р, V, а и х в двух вышеназванных фиксирован-
ных точках. Полагая а равным nRT, находим
т Ю0«р
«юо — «о
78
Гл. 2. Второй закон термодинамики
Полагая То = 0, получаем термодинамическую температурную шкалу
Цельсия. Отсюда следует, что —То °C является абсолютным нулем при
измерении в этой температурной шкале.
Точные исследования в области газовой термометрии, проведенные
французским ученым Шаппюи (Р. Chappuis) между 1887 и 1917 гг.,
дали значение То, лежащее между 273,048 и 273,123. Под влиянием
этой работы к 1942 г. было проведено более 100 определений значения
То. Среди них отметим высокую точность результатов Хойзе (W. Heuse)
и Отто (J. Otto) в Германии, Кеезома (W. Н. Keesom) и др. в Нидер-
ландах, Битти (J. A. Beattie) и др. в США и Киносита (М. Kinoshita)
и Оиси (J. Oishi) в Японии. Найденные ими значения лежат между
273,149 и 273,174.
Учитывая эти результаты, а также то обстоятельство, что зна-
чение тройной точки чистой воды очень близко к 0,0100° С, Десятая
генеральная конференция мер и весов в 1954 г. постановила считать
тропную точку воды фиксированной точкой, которой соответствует
температура 273,16. Эта конференция также заново определила термо-
динамическую температурную шкалу Цельсия следующим образом:
t° С -= Т — 273,15, где Т — значение абсолютной температуры, уста-
новленное конференцией. Нуль новой термодинамической температуры
Цельсия отличается от точки плавления льда примерно на 0,0001°.
Для обычных целей различием между новым и старым определе-
нием шкалы можно полностью пренебречь. Однако в тех случаях, когда
абсолютная величина температуры должна быть определена с точ-
ностькГ 10"4 град, необходимо учитывать эту разницу.
Точна
плавления Тройная Пана
льда I точка кипения
о°к То То + юо°к
-ус Н i о°с Li : юо °с
0°К 273,16°К ‘К, 1954
273,15 ° К , :
ч-----------------------Ц _j____________________;_____
— 273,15°С 0°С 0,01 °C »С, 1954
Замечание. Из определения (2.5) следует, что соотно-
шение
ТТ+^ = ° (2-6)
справедливо для любого обратимого цикла Карно, так же как
и соотношение (2.1). Для того чтобы определение (2.5) было воз-
можно, необходимо доказать, что
1-71(01; 02) = /(04, 02), (2.7>
где
= (2.8>
Основные положения
79
Убедившись в справедливости соотношения (2.8), мы сможем
с помощью равенства Т (0) = Cg (0), где С — постоянная, связать
температуру 0 с абсолютной
температурной шкалой Т.
Доказательство со-
отношения (2.8). Рассмотрим
три цикла Карно С12, С23 и С13,
изображенных на фиг. 22. Каж-
дый из этих циклов действует
между двумя из трех резер-
вуаров и Н3. На фиг. 22
введены обозначения количеств
тепла, получаемых из каждого
теплового резервуара, и работы,
совершаемой над термостатом.
Из первого закона термо-
динамики следует, что
^12 = Qi — Qz, ^23 = Qz— Qs,
Л13 = Qi — <2з-
Согласно фиг. 22, цикл С13
является холодильным. Оче-
видно, что
<21 — Qi — ^412 + -^23 — ^41 з — Фиг. 22.
так как если Qi — Q[> 0, то
полная работа будет совершаться только за счет охлаждения
резервуара IQ, что противоречит принципу Томсона. Если же
Qi — < 0, то, обратив систему, мы получаем такое же про-
тиворечие принципу Томсона. Следовательно, должно иметь
место равенство Qi = Q'v Отсюда вытекает соотношение
f(0„ 03) = -g- = ^.-g-^f(01, 02)/(02, 03).
Решение этого уравнения имеет форму (2.8).
ОТСТУПЛЕНИЕ 5
Международная практическая температурная шкала. Теорети-
чески для калибровки леей температурной шкалы Кельвина доста-
точно располагать определением температуры тройной точки чистой
воды (273,16° К). Однако с практической точки зрения термодинами-
ческие способы, необходимые для точного измерения температуры,
слишком трудоемки, поэтому нужны практические стандарты, кото-
рые позволяли бы сравнительно легко производить достаточно точное
определение температуры. Такой стандарт был установлен Седьмой
80
Гл. 2. Второй закон термодинамики
генеральной конференцией мер и весов в 1927 г. и усовершенствован
в 1948 и 1960 гг. Определяемая им шкала температур известна под
названием Международной практической температурной шкалы.
Температура, измереннай’ с помощью этой шкалы, выражается в гра-
дусах Цельсия и обозначается ° С (Int. 1948). Иногда мы будем обо-
значать ее <меЖд- Международная практическая температура Кельвина
Тмея{д определяется соотношением 7межд = гмежд + 273,16 и обозна-
чается Т °К. (Int. 1948) х).
Международная практическая температурная шкала 1948 г.
основана на шести фиксированных значениях температуры; кроме того,
в ней используется метод интерполяции в четырех интервалах тем-
ператур. Ниже приводятся фиксированные- значения температур:
Точка кипения кислорода............—182,97° С (Int. 1948)
Тропная точка воды................... 0,01
Точка кипения воды................. 100
Точка кипения серы.................. 444,6
Точка затвердевания серебра .... 960,8
Точка затвердевания золота......... 1063
Вместо точки кипения серы можно использовать точку затвердевания
цинка (419,505° С). Все эти величины, за исключением тройной точки
воды, берутся при давлении в одну стандартную атмосферу.
Для определения всего диапазона температур используется сле-
дующий интерполяционный метод:
_ а) Интервал 0—630,5° С (точка затвердевания сурьмы). Темпе-
ратура t° С (Int. 1948) определяется соотношением
Rt = R0(i + At + Bt^,
где Rt— электрическое сопротивление платиновой проволоки, кото-
рая используется в качестве стандартного термометра сопротивления
при температуре t. Величины Ro, А и В должны определяться из зна-
чений Rt в тройной точке воды, точке кипения воды и точке кипе-
ния серы.
б) Интервал —182,97° С (точка кипения кислорода) — 0°. Тем-
пература t определяется соотношением
Rt = R0 [i-\-At-{-Btz-\-C (t —100) <3],
где Ro, А и В имеют то же значение, что и в интервале «а», а постоянная
С определяется из значения Rt в точке кипения кислорода.
в) Интервал 630,5°—1063° С (точка затвердевания золота).
Температура t определяется соотношением
Е =.а~-Ы^-ct2,
где Е — э. д. с. платино-платинородиевой термопары, у которой один
контакт поддерживается при 0° С, а другой — при температуре t. Кон-
станты а, Ь и с определяются из значений Е при 630,5° С,) в точке
затвердевания серебра и точке затвердевания золота.
г) Выше 1063° С (точка затвердевания золота). Температура t опре-
деляется соотношением
Jt _ ехР V'z/'k Цди ~Ь Уо)] 1
УAu 0ХР [С2/Х (t + То)]—1
!) В отечественной литературе иногда пользуются обозначениями
°C (МПТШ 1948) и Т °К (МПТШ 1948).— Прим, перев.
Основные положения
81
где Jt и 7Аи—спектральная интенсивность излучения на длине волны
X черного тела, имеющего соответственно температуру t и £ди (точка
затвердевания золота), Та = 273,16, С2 — 0,01438 м-град, а длина вол-
ны X выражена в метрах.
Детальное описание других экспериментальных условий приво-
дится в книге [1].
В качестве вспомогательных стандартов в добавление к шести
вышеназванным точкам рекомендуется еще около двадцати фиксиро-
ванных точек: точка затвердевания углекислого газа (—78,5° С),
точка затвердевания ртути (—38,87° С), точка плавления вольфрама
(3380° С) ит. д.— все при давлении в одну атмосферу.
Ниже точки кипения кислорода у нас еще нет международного
стандарта. Однако экспериментаторы, работающие при очень низких
температурах, пользуются температурной шкалой, основанной на
уравнении давления паров Не4 и Не3.
Определение практической шкалы было проделано очень тща-
тельно, поэтому она с очень высокой степенью точности дает прибли-
жение к абсолютной температурной шкале 1954 г. Однако в принципе
в любой точке эти шкалы могут отличаться друг от друга. Проведенное
в США их сравнение дало для точки кипения воды 99,994° С (термо-
динамическая шкала 1954 г.), в то время как в Международной практи-
ческой шкале она равна 100° С (Int. 1948).
§ 6. Неравенство Клаузиуса для произвольного цикла
Если система совершает циклический процесс, при котором
она находится в контакте с термостатом и поглощает теплоту Qt
(г = 1, 2, . . ., п) из теплового резервуара Rt с температурой
то справедливо неравенство
2
(2-9)
Суммирование можно заменить интегрированием, если изменение
состояния происходит непрерывно. Тогда (2.9) принимает вид
-^<0.
у<е)
(2.10)
Доказательство. Введем вспомогательные источники
тепла 2?о (с температурой То) и циклы Карно С4, С2, . . ., Сп.
Цикл С г действует между 7?0 и i-м тепловым резервуаром 2?;.
Пусть Qi — теплота, поглощенная циклом от 2?0, а А\ — рабо-
та, совершаемая окружающей средой, когда цикл Ct действует
таким образом, что передает резервуару 2?г теплоту Qt. С помощью
(2.5) получаем
6 Kvfio
82
Гл. 2. Второй закон термодинамики
Пусть теперь исходный цикл и вспомогательные циклы С4, . . .
. . Сп действуют вместе, тогда резервуары 7?4, . . Rn не будут
ни получать, ни отдавать тепло, поэтому окончательным резуль-
татом будет поглощение тепла ($+•••+ Q'n) из теплового
резервуара 7?0 и совершение работы
над термостатом.
Согласно принципу Томсона, эта величина должна быть равна
нулю или отрицательна. Таким образом, неравенство (2.9) дока-
зано. Равенство будет иметь место только для обратимого цикла,
так как тогда процесс может совершаться в обратном направлении.
§ 7. Энтропия
Определение. Пусть некоторое термически равновесное состоя-
ние а0 выбрано в качестве исходного состояния рассматриваемой
системы. Энтропия S (а) системы в другом равновесном состоянии а
определяется соотношением
а
5(a)=J-^-, (2.11)
ао
где'интегрирование проводится вдоль любого квазистатического
процесса/связывающего состояния а и а0, d'Q — количество тепла,
поглощенное системой при температуре Т за бесконечно малую
часть всего процесса. В дифференциальной форме это определение
принимает вид
dS=^-. (2.12)
Согласно первому закону термодинамики (1.5), это определение
можно переписать в следующей форме:
dS^~(dU-d'A-d"L}. (2.13)
Если воспользоваться соотношениями (1.7а) и (1.76), то (2.13)
переходит в соотношение Гиббса
= + (2.14)
i i
Это фундаментальное уравнение объединяет первый и второй
законы термодинамики. Уравнение (2.14) имеет вид пфаффовой
формы
dU=^ytdYt
(2.15)
s, кал/г-град
фиг. 23, Энтропия водорода.
Фиг. 24. Энтальпия водорода.
Л, кал/г
Основные положения
85
(где yi = Т, у2= — р, Уз = У1 = 8, Y2= V, У3 =
= Xi, . . .). Для замкнутой системы, у которой происходит толь-
ко изменение объема, уравнение (2.14) переходит в
dU = TdS — pdV. (2.16)
Энтропия. Функция состояния. Пусть L и L' представляют
собой два квазистатических процесса, связывающих состояния
а0 и а. Применяя к обратимому циклу а0 (L) а (Z7) а0 соотно-
шения (2.10), получаем
а ао
j 4Я-+ j 4^=о.
а0(Ь) а(Ь')
Как известно, это означает, что интеграл
а а
Г d'Q _ Г d'Q
J т — J Т
a0(.L) ao(L')
определяется состояниями а0 и а и не зависит от L и L'. Следо-
вательно, если состояние а0 фиксировано, то этот интеграл, или
S (а), является функцией состояния, определяемой однозначно
для заданного состояния а.
Замечание. Как указывалось в гл. 1, § 6, d'Q, d'A и d'Z
не являются полными дифференциалами, а зависят от процесса,
связывающего два состояния. В отличие от них величина d'QIT
является полным дифференциалом для квазистатического процесса
и равна бесконечно малому изменению функции состояния S.
Другими словами, Т~1 является интегрирующим множителем.
для d'Q.
На фиг. 23 изображена энтропия газообразного водорода как
функция температуры и давления, а на фиг. 24 — энтальпия
газообразного водорода как функция давления и энтропии. Отме-
тим, что во втором из этих случаев энтропия обычно рассматри-
вается как независимая переменная (см. гл. 3, § 1).
§ 8. Аддитивность энтропии
Почти очевидно, что энтропия представляет собой экстенсив-
ную величину. Для однородной термически равновесной системы
энтропия пропорциональна массе или объему, так как при пере-
ходе системы из исходного в рассматриваемое термодинамичес-
кое состояние количество тепла, поглощаемое на каждой стадии
процесса, пропорционально массе.
86
Гл. 2. Второй закон термодинамики
Термодинамическое состояние в общем смысле является локаль-
но равновесным состоянием. Пусть система состоит из термически
равновесных подсистем. В этом случае естественно обобщить
введенное выше определение энтропии и считать, что энтропия
системы равна сумме энтропий подсистем. Это значит, что полная
энтропия имеет вид
S = SA (а) + SB (Р) + . . . , (2.17)
где части системы А, В, ... находятся в состояниях а, р, . . .
с энтропиями, равными соответственно SA (a), SB (Р), . . . .
Выражение (2.17) и является обобщением понятия энтропии
на случай общего термодинамического состояния.
§ 9. Общая формулировка второго закона термодинамики
Для процесса перехода рассматриваемой системы из термоди-
намического состояния а' в другое состояние а" справедливы
следующие соотношения:
второй закон термодинамики
а’
J где /^ = 5(а')-5(а'); (2.18)
a'(L)
первый закон термодинамики
j d’Q —AU— А — Z, где AU = U (а") — U (а')- (2.19)
а'(Г)
Здесь d’Q — бесконечно малое количество тепла, полученное раз-
личными частями системы от термостата (с температурой ТЮ),
2 означает суммирование по различным частям системы, а интег-
рирование проводится вдоль траектории процесса L. Равенство
имеет место только в том случае, когда процесс L обратимый.
Для инфинитезимального процесса соотношение (2.18) прини-
мает вид
(2.20)
Если температура системы однородна, то можно считать, что тер-
мостат имеет температуру, очень близкую к температуре системы.
Тогда температуру ТЮ можно заменить температурой Т системы,
после чего соотношение (2.20) переходит в
d'Q < TdS, (2.21)
или
dU — TdS < d'A + d'Z. . (2.21а)
Основные положения
87
Доказательство. Рассмотрим квазистатический про-
цесс R перехода из состояния а' в а" и применим неравенство (2.9)
к циклу а'(Л) а"(7?) а' (фиг. 25). Тогда
а" а'
г d'Q । С d'Q <л
J у<е> ' J Т
а'(Ь) а"(Н)
откуда
а"
J <5 (а") -5 (а').
a'(L)
Соотношение (2.20) является дифференциальной формой соотно-
шения (2.18). Если температура системы однородна, то теплооб-
мен происходит при той же температуре, поэтому мы можем счи-
тать, что ТЮ = Т, т. е. перейти от (2.20) к (2.21). Неравенство
(2.21а) получается с помощью первого закона тер- „
модинамики (1.5). Укажем, что в неравенства (2.21) S
и (2.21а) входят только переменные рассматривав-
мой системы. / /
/
§ 10. Направление реальных процессов / /
/ Ув
Процесс L перехода между состояниями а' и а" I /
данной системы не может быть реализован, если / /
при этом будет нарушаться неравенство (2.18).
Это означает, что в том случае, когда на систему a
наложены некоторые ограничения, ее состояние Фиг. 25.
может меняться только таким образом, чтобы вы-
полнялось неравенство (2.18) при этих ограничениях. Если ни
одно из возможныхизмененийне удовлетворяет неравенству (2.18),
то никакие изменения не могут осуществиться и система оста-
нется в равновесии. Следовательно, неравенство (2.18) представ-
ляет собой условие возможности изменения состояния или усло-
вие равновесия при различных ограничениях. Эти условия указа-
ны в приводимой ниже (см. следующую стр.) таблице, в которой
А — работа, совершаемая над системой,
F = U — TS (2.22)
— свободная энергия Гельмгольца,
G = F + pV = Н — TS (2.23)
— свободная энергия Гиббса (термодинамический потенциал)
(см. гл. 3).
88
Гл. 2. Второй закон термодинамики
Ограничения Направление изменения Условие равновесия
а) Общая адиабатическая система:
<2=0 Д5>0 S =тах
at) Изолированная система: Q — 0, А=0, Z=0, ДМ=0* (Д£)и, у, м > 0 S = тах
б) Постоянная энтропия: Д£ = 0 дг/<л+/
6t) Замкнутая система, работа не производится: Д£ = ДМ=Л = 0 Д?7<0 U = min
в) Замкнутая система, температура постоянна: ДМ=0, ДГ=0 д/,<л
Bj) Замкнутая система, изотер- мический цикл: ДМ=0, ДТ=0 о<л
в2) Замкнутая система, темпера- тура и объем постоянны: ДМ=ДТ=Д7=0 ДГ<0 .F = min
в3) Замкнутая система, темпера- тура и давление постоянны: ДМ=ДГ=Др = 0 Д(?<0 G = min
* Условие ДМ = 0 означает, что не происходит обмена веществом.
Замечание. В случае «а» левая часть соотношения (2.18)
обращается в нуль, следовательно, неравенство AS 0 является
условием допустимости изменения. Конечно, его можно применять
и для замкнутой системы (принцип возрастания энтропии). Усло-
вие возможности процесса «б» с постоянной энтропией очевидно
из соотношения (2.21а). Отметим, однако, что, говоря о постоян-
стве энтропии, мы имеем в виду только энтропию рассматрива-
емой системы, в то время как в общем необратимом процессе может
также иметь место возрастание энтропии термостата. При изотер-
мическом процессе «в» изменение энтропии ASr теплового резер-
вуара имеет вид
д с _____ Q ________Q_
yt(e> у
(Т^ = Т). Так как принцип возрастания энтропии определяет пол-
ное изменение энтропии ASt = AS-| ASr системы и теплового
резервуара, то должно иметь место соотношение
ASt = AS — ~-~^-Q.
Основные положения
89
После подстановки Q = AZ7 — А это неравенство переходит в
AU — TAS < А.
В соответствии с определением свободной энергии F это неравен-
ство является условием для процесса «в». При постоянном давле-
нии А — — рАV, и это неравенство переходит в условие «в3».
§ И. Максимальная и минимальная работа
Принцип максимальной работы. Рассмотрим возможные про-
цессы, которые могут иметь место в системе тел, не находящихся
в термическом равновесии друг с другом. Работа, совершаемая
в каком-либо из этих процессов над окружающей средой, макси-
мальна, если процесс обратим.
Предположим, в частности, что термостат характеризуется
температурой 7,(е), давлением и химическим потенциалом у-го
компонента Пусть, далее, состояние системы меняется, чему
соответствуют приращения AS, AU, AV и AMПервый закон
термодинамики (1.5) для этого случая принимает вид
Q = AU 4- p<AAV - 2 p^AMj — W,
з
где W — дополнительная работа, совершаемая термостатом над
системой кроме работы —p^AV, связанной с изменением объема.
Из второго закона термодинамики (2.18) Q T^AS вытекают
следующие теоремы:
a) 1РМИП s AU-T^AS+p^AV-^ pWANf<W. (2.24)
Рассмотрим случай, когда Жци,, > 0. Тогда работа W, которую
должен совершить термостат для осуществления этого перехода
в системе, всегда будет не меньше минимальной работы И/мин-
Работа W равна ГУщин только в случае обратимого изменения,
б) WMaKC^-(AU-T(e)AS + p^AV-^p^ANj)>— W. (2.25)
Рассмотрим случай, когда И^акс > 0. Тогда работа, которую
можно получить от системы при таком изменении — W = | W | >
> 0, не будет превышать максимальную работу И^акс- Работа
| W | будет равна F7MaKc только для обратимого процесса.
ОТСТУПЛЕНИЕ 6
Аксиоматическое построение термодинамики. Современным физи-
кам аксиоматическое построение физики, возможно, уже не кажется
столь существенным. Действительно, сейчас физика в большей сте-
пени имеет дело с физическими фактами, чем с построениями формаль-
90
Гл. 2. Второй закон термодинамики
ной логики. В то же время не следует забывать, что систематическая
формулировка теории иногда может быть очень полезна, позволяя
ясно понять, какие факты являются наиболее существенными и какое
место занимают логические выводы при построении физической тео-
рии. В конце XIX столетия, когда физика стала царицей точных наук,
по крайней мере некоторые физики придерживались взгляда, что
конечной целью теоретической физики является строгое аксиомати-
ческое построение физических теорий. Такая точка зрения развивалась
под очень сильным влиянием аксиоматического подхода, которого
придерживались в то время почти все математики во главе с великим
Давидом Гильбертом.
Из всех физических теорий термодинамика, по-видимому, лучше
всех подходит для подобного аксиоматического построения, идеаль-
ным примером которого является евклидова геометрия. Действительно,
даже в классической физике термодинамика занимает особое положе-
ние, выделяясь своим строго логическим построением, опирающимся
на несколько фундаментальных законов. Эти законы являются абстрак-
цией нашего опыта и принимаются за аксиомы. По своей простой
структуре термодинамика напоминает геометрию.
Среди многочисленных попыток аксиоматического построения
термодинамики наиболее известной и наиболее успешной, по-види-
мому, является теория Каратеодори [2]. Он заменил традиционное вы-
ражение для второго закона очень простым утверждением, которое
приводилось в § 3. Это утверждение основывается на следующей
математической теореме: пфаффова форма
d'Q = Х dx-\-Y dy-{-Z dz
имеет интегрирующий множитель в том и только в том случае,
когда в любой окрестности точки Р существует хотя бы одна точка
Р', которая не может быть достигнута из точки Р вдоль какой-либо
кривой, лежащей на поверхности, определяемой условием d'Q = 0.
Критический обзор теории Каратеодори, написанный доступно для
студентов-физиков, содержится в старой статье Борна [3] (см.также[4]).
ПРИМЕРЫ
1. Вывести принцип Клаузиуса из принципа Томсона, а так-
же принцип Томсона из принципа Клаузиуса.
РЕШЕНИЕ
Чтобы*доказать, что принцип Клаузиуса можно вывести из
принципа Томсона, достаточно доказать, что если принцип Клау-
зиуса нарушается, то принцип Томсона также нарушается. Прин-
цип Клаузиуса будет нарушен, если от низкотемпературного теп-
лового резервуара 7?i будет взято количество тепла Qt > 0)
и передано более горячему тепловому резервуару Т?2 без каких-
либо других изменений системы. Предположим, что такой процесс
возможен. Объединим его с циклом Карно С, действующим меж-
ду двумя тепловыми резервуарами Т?2 и От резервуара Т?2
берется тепло С*г+ Q2 (величина Q2 также положительна), а ре-
зервуару Ri передается тепло Qt, при этом производится работа,
эквивалентная Q2 (фиг. 26, а). Тогда суммарным результатом дей-
Примеры
91
ствия двух процессов будет полное преобразование в работу
количества тепла Qz, взятого от резервуара Rz. Это является
нарушением принципа Томсона.
Докажем теперь, что в случае нарушения принципа Томсона
принцип Клаузиуса также нарушается. При нарушении принципа
Томсона возможно, как указывалось выше, получить положитель-
ное количество тепла Qz (Qz > 0) от теплового резервуара Rz
и полностью преобразовать это тепло в работу (без других измене-
ний системы). Объединим этот процесс с циклом Карно, при
котором от холодного резервуара 7?i берется количество тепла
Фиг. 26.
Qi (>0) и резервуару Лг передается тепло Qt + Qz (фиг. 26, б).
При этих двух процессах не происходит никаких других измене-
ний, кроме передачи тепла Qi от холодного резервуара к горя-
чему резервуару Rz. Это противоречит принципу Клаузиуса.
2. Показать, что внутренняя энергия вещества с уравнением
состояния в форме р = / (7) Т не зависит от объема. Здесь р —
давление, Т — абсолютная температура, / (V) — функция толь-
ко от V.
РЕШЕНИЕ
В соответствии с (2.16) внутренняя энергия U и энтропия S
удовлетворяют соотношениям
dS = (dUр dV), (1)
( \ =_1_ (2}
\ dV )т Т { dv )т г Т ,
\ дТ )v т \ дТ fv’ k 1
Из уравнения d2S!dTdV = d^S/dV дТ (условие того, что dS
92 Гл. 2. Второй закон термодинамики
является полным дифференциалом) имеем
3/1 9U \ . д / р \ 3/1 dU \
~дТ П Ж) '~дт' \Т)=~дУ \~Т~ ~дТ~ ) '
Так как d2U/dT dV = d2UldV дТ, то
) =Т2 — (X.) (4)
\ dV )т дТ \ Т )у ' V ’
ИЛИ
<5>
Подставим р = f (V) Т; тогда правая часть соотношения (4) обра-
щается в нуль, следовательно,
( —) =0,
I dV )т ’
т. е. U не зависит от V.
3. Внутренняя энергия и единицы объема газа является функ-
цией только от Т, а уравнение состояния газа имеет вид р =
= и (Т)/3. Определить функциональную форму и (Т).
РЕШЕНИЕ
Рассмотрим газ, имеющий температуру Т и заключенный
в объеме V. Внутреннюю энергию U можно записать в форме
U = Vu (Г). (1)
Подставляя в соотношение (5) примера 2 соотношение (1) и урав-
нение состояния р = и (Т)/3, получаем
u(T} = ^T^gl------±-и(Т), Т^Р—4и(Т) = 0. (2)
о dl О dl
Интегрируя, находим
In и (Т) — 41n Т = const, и (Т) = const- Г4,
т. е. внутренняя энергия и пропорциональна четвертой степени
температуры. (Таким газом является поле теплового излучения,
т. е. газ квантов света — фотонов.)
4. Пусть цикл Карно действует между тепловыми резервуара-
ми с температурами Т\ и Т2 = — dT, а рабочим веществом
служит газ. Используя этот цикл, доказать следующее уравнение:
где р — давление, V — объем и U — внутренняя энергия.
П римеры
93
РЕШЕНИЕ
Пусть V; — объем газа в состоянии i (i = 1, 2, 3, 4), и (>2—
количество тепла, поглощенного при изотермических процессах
1 -> 2 и 3 -> 4 (фиг. 27). Из первого закона термодинамики (2.19)
следует
2
* 1
(1)
2 3 4 1
& + &= j pdV+ jpdV + J pdV+ J pdV. (2)
12 3 4
Так как цикл Карно предполагается идеальным, справедливо
соотношение (2.6)
Поскольку разность температур
dT = Ti — Т2 бесконечно мала,
мы можем считать V2 ~ Уз и
[Л Vi и отбросить в уравне-
нии (2) второй и четвертый
члены. Кроме того, разность
давлений р в соответствующих
точках (т. е. точках, отвеча-
ющих одинаковым значениям |____________
объема) изотерм 1 -> 2 и 3-^4 v
бесконечно мала и ее можно Фиг. 27.
положить равной {др!дТ)у X
X (Гг— Л) = —(dpldT)ydT. При этом соотношение (2) принимает
вид
<?i + (?2= j pdV+ J PdV= j pdV — j pdV^dT j (^}vdV,
13 14 1
(4)
Теперь соотношение (3) можно переписать в виде
+ 1 (^1 + ^)—g-^1 = 0) (5)
1 1 i 2 1 2 1 2
ИЛИ
^ + С2 = -7Г^-
(6)
94
Гл. 2. Второй закон термодинамики
Из соотношений (4), (6) и (1) находим
2 2
1 1
(7)
Так как состоянием 2 может быть любая точка изотермы, прохо-
дящей через состояние 1, из соотношения (7) следует
(8)
5. Происходит диффузионное смешение идеальных газов двух
сортов, первоначально находившихся в двух сосудах и имевших
одинаковые давления и температуры. Показать, что при этом
энтропия возрастает на величину
Д5=_/?(„11п—, (1)
где Mj и п2 — число молей компонентов. Принять, что в процессе
диффузии не происходит изменения давления и температуры,
а парциальное давление каждого компонента смеси пропорцио-
нально молярной концентрации.
РЕШЕНИЕ
Вначале газы 1 и 2 занимали объемы Vi = n^RTIp и V2 =
= n^RTIp п были разделены перегородками. После устранения
а 5
Ф и г. 28.
перегородки они перемешиваются за счет диффузии. Вместо того
чтобы обсуждать диффузионный процесс, сначала рассмотрим
процесс, который обратимым образом разделяет смесь газов
Примеры
95
в состоянии (V — Vi + V2, Т, р) на чистые газы, находящиеся
в состояниях (V, Т, и(Т, Т, р2). Такой процесс может быть реа-
лизован с помощью устройства, изображенного на фиг. 28. Контей-
нер объемом V состоит из двух контейнеров, причем полупро-
ницаемая стенка В пропускает только частицы газа 2, в то время
как полупроницаемая стенка А пропускает только частицы газа 1.
Давление, которое оказывает на полупроницаемую перегородку
не пропускаемый ею газ, равно его парциальному давлению.
Отсюда следует, что при разделении двух контейнеров стенки
контейнера с газом 1 испытывают парциальное давление pi, так
что полная сила, действующая на контейнер, равна нулю.
Следовательно, при адиабатическом процессе работа не совершает-
ся, и внутренняя энергия и температуры остаются неизменными.
Соответственно не происходит и изменения энтропии. Чтобы вер-
нуть газы в исходные состояния, разделенные газы изотермиче-
ски сжимаются от объема V до объемов и V2 соответственно.
Интегрируя выражение dS = d'QIT = pdV/T = nRdV/V, полу-
чаем приращение энтропии для каждого компонента
, ДД2 = n2R In . (2)
Таким образом, сумма Д52 представляет собой изменение
энтропии при обратимом разделении смешанных газов. Следова-
тельно, увеличение энтропии при диффузии должно быть равно
Д5= -(Д54 + Д52)= — R (пДп-^ + пгЬ-^) =
— — R ( Yli In —---Ь п2 In ) .
\ 1 П1Ч-П2 ' rai + ra2 /
6. Показать, что для адиабатического изменения абсолютной
температуры Т магнетика, подчиняющегося закону Кюри Л/ = СШТ
(М — намагниченность, Я —магнитное поле, С —константа), спра-
ведливо соотношение
где Сн — теплоемкость на единицу объема при постоянном магнит-
ном поле.
РЕШЕНИЕ
Обозначим внутреннюю энергию, энтропию и намагничен-
ность на единицу объема соответственно' через и, $ и М (изменение
объема не учитываем). Энтропия s является функцией от Т и Н,
96
Гл. 2. Второй закон термодинамики
t
поэтому имеет место равенство
г'*=г'(^)а'/1’+г'(й-)г‘гя- о
Согласно определению, Сн — Т (ds/dT)H. Кроме того, имеет место
соотношение
<2>
которое доказывается следующим образом: из равенства du — T ds-'-
- Н dM вытекает
а=о.+<1ч
<3:
Продифференцируем первое из этих соотношений по Н, а второе
по Т; после этого, приравнивая их правые части, приходим
к соотношению (2). Подставляя (2) в (1), с учетом определения Сн
находим
Tds = CHdT + T (-W dH.
При адиабатических условиях (cZs = 0) отсюда получается требуемое
соотношение
dT= ~1г(^г}„аН=7ГтаН-
<н \ 91 ) н Сн1
7. Доказать, что если не происходит обмен веществом между
системой и термостатом, то минимальная работа с/И’ми,, равна:
а) приращению свободной энергии dF при постоянных тем-
пературе и объеме;
б) приращению термодинамического потенциала Гиббса dG
при постоянных температуре и давлении.
РЕШЕНИЕ
При изотермическом процессе температура системы равна
температуре термостата, поэтому (2.24) принимает вид
йРГмин, — dU — TdS + p^dV = dF + p^dv. (1)
Здесь мы воспользовались определением свободной энергии (2.22).
При постоянном объеме (dV = 0) соотношение (1) означает, что
«НГмин = dF. Если давление системы постоянно и равно внешнему
давлению р(е), то соотношение (1), согласно определению термо-
динамического потенциала Гиббса (2.23), дает = dG.
Задачи
97
ЗАДАЧИ
[А]
1. С помощью принципа Клаузиуса доказать неравенство
Клаузиуса
п
<2-9)
7-= 1 i
2. Если система путем обратимого изотермического изменения
возвращается в свое исходное состояние, то полное количество
поглощенного тепла равно нулю и совершенная работа также рав-
на нулю. Доказать это утверждение: а) с помощью неравенства
Клаузиуса и б) непосредственно с помощью принципа Томсона.
3. Доказать, что пересечение двух квазистатических адиабат
невозможно, так как это приводит к нарушению принципа Том-
сона.
4. Доказать, что к. п. д. тепловой машины ц не может превы-
шать 1 — (Тмин/^макс), где Тмакс — максимальная температура
тепловых резервуаров, от которых тепловая машина получает
тепло, а Тмин — минимальная температура тепловых резервуаров,
которым она передает тепло.
5. Доказать приводимые ниже выражения для к. и. д. следу-
ющих трех циклов (рабочим веществом является идеальный газ):
а) цикл Отто (фиг. 29, а)
1 \ V1 )
б) цикл Джоуля (фиг. 29, б)
Л
в) цикл Дизеля (фиг. 29, в)
п _ 1 1 (У2/И±)У —(Кз/И^У
Л У <V2/7i)-(73/7i) •
При этом считать, что Су, Ср и CPICV = у — константы.
6. Пусть для некоторого вещества адиабаты а, а' и изотермы
t, t' на р — Е-диаграмме пересекаются в точках А, В, С, D (фиг. 30).
Доказать, что при циклическом процессе АВ CD отношение коли-
чества тепла, поглощаемого при процессе АВ, к количеству тепла,
отдаваемого при процессе CD, определяется значениями t и t'
и не зависит от выбора адиабат.
7. Вывести выражение для энтропии идеального газа для слу-
чая, когда удельная теплоемкость при постоянном объеме Су =
= Су = const.
Фиг. 29.
Задачи
99
8. Идеальный газ адиабатически расширяется из объема Vi
в вакуум. Вычислить возрастание энтропии, если в конечном
состоянии газ имеет объем V2, и показать, что процесс расшире-
ния является необратимым.
р"
Фиг. 30.
Фиг. 31.
9. Рассмотреть возрастание энтропии при нагревании идеаль-
ного газа от до Т2: а) при постоянном давлении и б) при постоян-
ном объеме (фиг. 31). Доказать, что в первом случае возрастание
энтропии в у раз больше, чем во втором случае, где у — отноше-
ние теплоемкостей при постоянном давлении и постоянном объеме.
10. Для некоторого газа экспериментально установлено, что
произведение давления р и удельного объема v зависит только
от температуры и что внутренняя энергия также зависит только
от температуры. Что можно сказать относительно уравнения
состояния такого газа с точки зрения термодинамики?
И. Для газа заданы соотношения: a) pV = / (0) и б) (dU/dV)e —
= 0. Показать, что / (0) имеет смысл абсолютной температуры.
Здесь 0 — температура в некоторой произвольной температурной
шкале, р — давление, V — объем и U — внутренняя энергия.
12. Вычислить плотность энтропии s поля излучения, исполь-
зуя следующие соотношения между плотностью энергии и, радиа-
ционным давлением р и абсолютной температурой Т:
р = -^и, u = aTi (ст = const).
Изобразить также изотермы и адиабаты и рассмотреть цикл Кар-
но для такого газа.
7*
100
Гл. 2. Второй закон термодинамики
13. Известно, что внутренняя энергия парамагнетика не зави-
сит от его намагниченности М. Доказать, что температура, опре-
деляемая обратной величиной магнитной восприимчивости этого
материала 0 = 1/% (% = М/Н), пропорциональна абсолютной
температуре.
14. а) Доказать, что отношение адиабатической сжимаемости
к изотермической сжимаемости равно отношению теплоемкости
при постоянном объеме к теплоемкости при постоянном давлении.
(Указание. Эта задача уже была рассмотрена в гл. 1, пример 7,
по здесь мы используем понятие энтропии. Другой подход см.
в гл. 3, решение задачи 5.)
б) Доказать, что отношение адиабатической магнитной вос-
приимчивости к изотермической магнитной восприимчивости рав-
но отношению теплоемкости при постоянной намагниченности
к теплоемкости при постоянном магнитном поле.
15. Доказать следующие соотношения:
(Указание: dU—полный дифференциал.)
б) ® = “г(4г) +у-
' \ др J? \ dl Jp
(Указание: dS и dll— полные дифференциалы.)
16. Доказать следующие соотношения:
. (ср (—} =— •
a' \ дТ Т ' \дТ ) р— Т ’
« д2и ™ <>2s dVi __у, d-s
°) дТ dv — 7 дТ ди ’ дТ др дТ др ’
в) (-£)т=(М’ (соотношения Максвелла),
где и, h и s — соответственно энергия, энтальпия и энтропия
единицы массы, а с0 и ср — удельные теплоемкости при постоян-
ном объеме и постоянном давлении.
17. Доказать следующие соотношения:
„ч с _с =т(—\ =
а) ср с„ 1 дТ )р \ дТ )v р ’
где
а~Т \ дТ )р’ 0“ v I др )т;
(^L\ Т ( d2v } ( дс” 1 — Т (- д2р 1
' \ др )т \ <97’2 )р’ \ ди )т \ <97’2
Задачи
101
18. Вычислить изменение энтропии, свободной энергии и тер-
модинамического потенциала Гиббса при сжатии 1 моль идеаль-
ного газа от 1 до 100 атм при 20° С.
19. При 25° С объем воды V определяется выражением
V — 18,066 — 0,000715 р + 0,000000046 р2 см3/молъ
для давлений р от 0 до 1000 атм, а
(4f) = 0>0045 + 0,0000014 р см3/град-моль.
Определить работу, необходимую для сжатия 1 моль воды от 1 до
1000 атм при 25° С и найти возрастание ее внутренней энергии.
20. Теплота плавления льда при 1 атм и 0° С равна АН =
= 1436,3 кал/молъ, а теплота испарения при 1 атм и 100° С
АН = 9717,1 кал/молъ. Считая, что средняя теплоемкость воды
при 1 атм между 0 и 100° С равна 18,046 кал/град• моль, вычис-
лить разность между энтропией 1 моль льда при 1 атм и 0° С
и энтропией 1 моль пара при 1 атм и 100° С.
21. Теплоемкость некоторого вещества массой М в твердом
состоянии равна cs, а в жидком состоянии сг. При переходе из твер-
дого состояния в жидкое, происходящем при температуре То,
поглощается скрытая теплота Qo. Полагая, что все удельные
теплоемкости не зависят от температуры, вычислить приращение
энтропии этого вещества при температуре 1\ (< То) в переох-
лажденном жидком состоянии по сравнению с твердым состоянием
при той же температуре. (Считать, что удельная теплоемкость
переохлажденной жидкости также равна сг.)
22. Пусть для некоторого твердого тела экспериментально най-
дено, что при температуре Т в интервале давлений рА р рв
имеет место следующая зависимость:
(тг)Р = а+/7р+с;Л
Насколько возрастет энтропия при сжатии тела от давления рА
до рв при постоянной температуре Т?
23. Выразить коэффициент V (dT/dV)s, определяющий изме-
нение температуры при квазистатическом адиабатическом расши-
рении газа, через величины, которые могут быть найдены из урав-
нения состояния.
24. В эксперименте Джоуля — Томсона газ, заключенный
в трубку с адиабатическими стенками, протекает при стационар-
ных условиях через пористую перегородку из области с высоким
давлением в область низкого давления, причем давления по обе
стороны пористой перегородки поддерживаются постоянными
102
Гл. 2. Второй закон термодинамики
(фиг. 32). В результате этого температуры по обе стороны перего-
родки различны. Доказать, что в этом эксперименте энтальпия
остается постоянной, и выразить через Ср и (dV/dT)p величину
(дТ/др)н, определяющую изменение температуры (коэффициент
Джоуля — Томсона). Кроме того, для тех случаев, когда в доста-
точно хорошем) приближении уравнение состояния можно запи-
сать в виде pV — RT + В(Т)р, выразить коэффициент Джоу-
ля — Томсона через В.
(
• I
Ф и г. 32.
25. Гей-Люссак произвел измерения изменения температуры
газа, испытывающего свободное расширение в вакуум. Записать
уравнение, определяющее изменение температуры dT при свобод-
ном расширении газа от объема V до V + dV.
26. Магнитная'восприимчивость парамагнитного вещества под-
чиняется закону Кюри % = CIT (С — константа), а внутренняя
энергия определяется выражением U = aTi (а — положительная
константа).
а) Найти теплоту намагничивания, когда поле возрастает от 0
до Hi, а температура сохраняет постоянное значение
б) Как меняется температура при адиабатическом размагни-
чивании, т. е. при адиабатическом уменьшении поля от Hi до 0?
27. В результате измерений установлено, что в некоторой
области температур намагниченность М парамагнитного тела
зависит только от отношения HIT, т. е. М = / (HIT). Доказать,
что внутренняя энергия не зависит от М, и найти функцио-
нальную форму энтропии S.
28. Рассмотреть все возможные процессы, с помощью которых
тело с теплоемкостью С может охладиться путем отдачи тепла
от температуры Ti до температуры То (<ZTi) теплового резервуара.
Как добиться того,*чтобы работа, совершаемая при этом процессе,
была максимальной?. Какова эта максимальная величина? Для про-
стоты считать С константой.
29. При 0° С теплота плавления льда равна 1436,3 кал/моль.
Холодильник должен произвести тонну льда при комнатной тем-
пературе (25° С). Какое минимальное количество электроэнергии
(в квш-ч) необходимо для этого?
Задачи
103
[Б]
30. Вывести принцип Каратеодори из принципа Томсона.
31. Доказать, что процесс перемешивания двух различных
идеальных газов путем диффузии не может быть обратимым,
так как это несовместимо с принципом Томсона.
32. Два идеальных газа, по 1 моль каждого,.с теплоемкостями
Су и Су находятся в цилиндре, где они разделены адиабатическим
подвижным поршнем. Доказать, что эта термически неоднородная
система неголономна, т. е. для приращения d'Q не существует
интегрирующего множителя.
33. Доказать, что для вещества, внутренняя энергия которо-
го не зависит от объема, справедливы следующие утверждения:
а) Теплоемкость при постоянном объеме Су зависит только
от Т.
б) Объем V зависит только от отношения р/Т.
в) Разность теплоемкостей при постоянном давлении и постоян-
ном объеме зависит только от отношения р/Т.
34. Доказать, что у газа ван дер Ваальса теплоемкость при
постоянном объеме зависит только от температуры, и найти выра-
жение для внутренней энергии и энтропии.
35. Пусть газ подчиняется уравнению состояния ван дер Вааль-
са (р + а/У2) (V — b) = RT, а его молярная теплоемкость при
постоянном объеме Су постоянна и не зависит от температуры.
Показать, что внутренняя энергия (на 1 моль) такого газа U оп-
ределяется выражением
U = CyT--^ + const
и что при адиабатическом квазистатическом изменении выполняется
соотношение
Т (У — &)v-1 = const, или + — &)v = const,
где у = (Су + R)lCy. Кроме того, найти изменение температуры
этого газа при его свободном расширении в вакуум.
36. Вычислить коэффициент Джоуля — Томсона (дТ!др)н для
разреженного газа ван дер Ваальса с точностью до второго поряд-
ка по nb/V «1) и na/VRT (<^1). Кроме того, определить темпе-
ратуру Tj, при которой коэффициент Джоуля — Томсона обра-
щается в нуль, и выразить ее через критическую температуру
Тс = 8al21Rb.
37. Ни один из ре&льных газов на самом деле не является
идеальным. При малых значениях р уравнение состояния реаль-
ного газа можно записать в виде
pV = А + Вр + Ср* + . . . (1)
104
Гл. 2. Второй закон термодинамики
И
и = а + + ур2 + • • • , (2)
где А, В, С, ... и а, р, у, ... — известные функции от темпера-
туры. Показать, как с помощью этого газа можно измерить абсо-
лютную температуру.
38. Для заданного вещества коэффициент расширения а =
= У-1 (dV/dQ)p измеряется с помощью произвольной температур-
ной шкалы 0. Измеряется также количество тепла —d'Qldp = LP
(скрытая теплота расширения), поглощаемое при изотермическом
расширении вещества при изменении давления р. Рассмотреть
метод, позволяющий связать эмпирическую температуру 0 с абсо-
лютной температурой, и разобрать его принципиальные основы.
39. Показать, что внутреннюю энергию U и энтропию S еди-
ничного объема парамагнитного вещества, подчиняющегося зако-
ну Кюри — Вейсса х = СЦТ — 0) (где С и 0 — константы, Т —
абсолютная температура и х — восприимчивость), можно пред-
ставить в виде
т
U = f См dT — 4/г М2 + const,
с f r dT М*
S — j См ------const,
где См — теплоемкость при постоянной намагниченности М.
40. Доказать следующее соотношение между объемной магнито-
стрикцией и производной от магнитного момента по давлению:
\ЭН)р,т~ \др)н,т'
Далее показать, что при изотермическом увеличении поля от 0
до Н изменение объема (при | ДУ | < У) имеет вид
Здесь I — магнитный момент всего образца, р = — (1/У) х
X (dV/dp)HiT — изотермическая сжимаемость, х = HHV — изо-
термическая магнитная восприимчивость. Магнитное поле и намаг-
ниченность считать однородными во всем объеме образца.
41. Доказать, что количество тепла b'Q, полученное системой,
не обменивающейся веществом с окружающей средой, в случае
изотермического процесса при постоянном объеме связано с мини-
мальной работой бТУмин соотношением
\ b’Q ____Г д ( б^Умия \ 1
У Т2 ~ L эт ( т Лг’
Задачи
105
а в случае изотермического процесса при постоянном давлении —
соотношением
_ Г 3 ( \~|
' 7’2 L дТ \ Т Пр’
(Эти уравнения называются уравнениями Гиббса — Гельмгольца
или уравнениями Кельвина. Они используются для определения
бРКмии по измеряемой величине b'Q.)
[В]
6, °C м-
0 0,257
25 0,220
50 0,183
75 0,153
100 0,129
получить абсолютную
нужно прокалибровать
температуру 0, измерен-
42. Как можно вычислить молярную теплоемкость газа при
постоянном давлении в предельном случае р = 0, когда он ста-
новится идеальным газом, располагая реально измеренными зна-
чениями теплоемкости при конечном давлении р?
43. С помощью уравнения состояния Дитеричи р =
— nRT (У — пЬ)~г ехр (—naIRTV) определить зависимость тем-
пературы инверсии для эффекта Джоуля — Томсона от давления
и изобразить ее графически. Использо-
вать закон соответственных состояний
и выразить значения давления, темпе-
ратуры и объема через критические
величины; см. гл. 1, задача 12. Провести
такое же рассмотрение для газа ван
дер Ваальса.
44. Чтобы
температуру,
эмпирическую
ную с помощью газового. термометра
(при постоянном давлении). Для этого необходимо при фиксиро-
ванном давлении определить зависимость от 0 плотности р,
теплоемкости и коэффициента Джоуля — Томсона. Вывести основ-
ную формулу, необходимую для такой калибровки.
45. Значения коэффициента Джоуля — Томсона р. для воздуха
с давлением 1 кг! см? приведены в таблице. Плотность воздуха р
аппроксимируется формулой
_ 0,0012932 р _3
Р— 1 + 0,0036699 760 г'СМ ’
где р — давление в мм pm. cm. и 0 — температура в °C. В интер-
вале температур от 0 до 100° С удельная теплоемкость при постоян-
ном давлении почти не меняется и равна 0,240 кал-г^-град"1.
С помощью этих данных определить численное значение 0° С
в абсолютной температурной шкале.
106
Гл. 2. Второй закон термодинамики
РЕШЕНИЯ
1. Можно считать, что термостат состоит из тепловых резер-
вуаров /?!, /?2> • • •, Rn с температурами, равными соответствен-
но Т^\ Т2\ . . ., Г?. Рассмотрим п — 1 циклов Карно Ct,
С2, • • • , Cn-i> которые действуют следующим образом (см. § 6).
Цикл Ci совершается между резервуарами и Т?2 и получает
количество тепла Q'T от резервуара и Q[ — от резервуара
Т?2, цикл С2 — между резервуарами R2 и R3 и получает количе-
ство тепла Q2 от R2 и Q"3 от R3, . . ., цикл Cn_t — между резер-
вуарами Rn-i и Rn и получает количество тепла Qn-i от Rn-i
и Qn от Rn.
Пусть рассматриваемая система совершает цикл С. Если теперь
все циклы С, Ci, . . ., Cn_t действуют вместе, то количества
тепла, теряемого каждым резервуаром, будут иметь вид
Ri' <2i + <2i, R2'- <2г+<2а+<2а> • • •,
Rn-i' <2n-i + Qn—i + <2n—I, Rn- Qn + Qn-
Следовательно, согласно первому закону термодинамики, полную
работу, совершаемую над рассматриваемой системой, можно записать
в виде
= - [(<21+<2Э + (<22+<2; + <2"2)+ .. • +(<2п+<2п)]. (1)
Подберем циклы Карно Clt С2, ..., Сп таким образом, чтобы
2 (и — 1) величины Q[, ..., <2п-Г, <2а, • • •, Qn удовлетворяли следую-
щим соотношениям:
<22 + <2;+<2; = о,
<?3+<2;+<?;=о,
<2«-1 + Qn—i + Qn-i — 0,
Л = 0
(следовательно, <2i + <2i + <2n + <2n = O)- Кроме того, для циклов
Карно имеют место соотношения
<?;___п
т(е) “Г т(е) U-
п— 1 п
Уравнения (2) и .(3) образуют систему из 2 (и— 1) уравнений,
следовательно, ограничения (2), налагаемые на циклы Карно
Z71, . . ., Сп, всегда могут быть удовлетворены. Умножая каждое
Решения
107
уравнение системы (2), кроме последнего, на —l/Z1^, . . —1/Tn-i
соответственно и складывая все полученные уравнения и урав-
нения (3), находим
-£L_L J2" . = _ & . । Д23 . _L .
ут(с) ~ ут(е) ут(е) ~ ут(е) ~ ^(е) * \ /
1 тс 2 3 тс
Поскольку условия (2) выполняются, суммарный эффект всех
циклов заключается в потере тепла резервуарами Ri и Rn. Если
Tn) > ?ie), то из принципа Клаузиуса следует
Qn~\-Q'n^0, (5)
С другой стороны, из уравнений (2) имеем
Qn + Qn= -(Qi + Q't),
откуда
Qn+Q'n Qi + <2'i .
т(е) т(е) ’
п “ 1
ИЛИ
S1 + < — ( -21-L *2" \ . (6')
у(е) ‘ у(е) \ ^(е) ‘ у(е) ) ' >
Тогда из (4) и (6') следует
Зт+«о- <’)
г=1 *
Это неравенство является следствием неравенств (5) и переходит
в равенство в случае обратимого процесса.
2. а) Для изотермического обратимого процесса неравенство
Клаузиуса переходит в равенство
где d'Q — бесконечно малое приращение количества тепла, Т —
температура. Следовательно, полное количество тепла, поглощае-
мое из термостата Q — <^) d'Q, равно нулю. Кроме того, согласно
первому закону термодинамики [см. (1.2)], J72 — = Q + А
(где U2 — Ui — увеличение внутренней энергии, А — работа,
совершаемая термостатом). Так как U2 — U± = 0, то совершаемая
работа А = — Q = 0 также равна нулю.
б) Предположим, что для рассматриваемого процесса полный
приток тепла Q из термостата не равен нулю и положителен, т. е.
Q > 0. Так как система вернулась в свое исходное состояние,
то иэ первого закона следует, что Q + А = 0, а работа А, совер-
108
Гл. 2. Второй закон термодинамики
шаемая термостатом, равна А = — Q < 0. Это означает, что
в рассматриваемом обратимом процессе теплота берется от одного
теплового резервуара и превращается в работу, причем никаких
других изменений системы не происходит. Такой результат про-
тиворечит принципу Томсона, поэтому неравенство Q > 0 невоз-
можно. Таким же образом, рассматривая обратный процесс, можно
доказать, что неравенство
<2 < 0 также противоречит принципу
Томсона. Следовательно, должны
иметь место равенства Q ~ 0, А = 0.
3. Предположим, что на р — V-
диаграмме две адиабаты а и b пере-
секаются в точке С (фиг. 33). Рас-
смотрим изотерму, которая пересекает
адиабаты а и Ъ в точках А и В соот-
ветственно. (Такая изотерма всегда
существует, ибо наклон изотермы
всегда меньше наклона адиабаты;
см. гл. 1, пример 7.) Процесс
А —>- В -> С -> А можно считать обра-
----------------------у*- тимым циклом, при котором система
ф и г зз-------------получает тепло Q от термостата толь-
ко на изотермическом участке А-+В.
Работа А, совершаемая системой,
равна площади фигуры АВС и положительна. Из первого
закона термодинамики следует, что Q = А, поэтому величина
<2 также положительна. Это означает, что тепло, которое берется
от теплового резервуара, полностью преобразуется в работу.
Такой результат противоречит принципу Томсона. Следовательно,
адиабаты не могут пересекаться.
4. Согласно неравенству Клаузиуса, имеем
Г d Qi f d Qz а
I Т(е) I 7(e) 7
(а) (Ь)
ИЛИ
f d'Qi f d'Qb
j усе) J 7<e) ’
(a) (b)
(1)
где поглощение тепла тепловой машиной происходит в процессе
(a) (d'<2i > 0), а отдача тепла — в процессе (&) (</'<2г >0 — коли-
чество тепла, отдаваемое резервуару). Если Дикс — максималь-
ное значение в процессе (а), а ТМИн — минимальное значение
7’<е> в процессе (Ь), то из соотношения (1) следует
Qi
^макс
<?2
^мин
ИЛИ
Qz ^мин
Qi ^макс
Решения
109
(Равенство имеет место только в том случае, когда используются
всего два тепловых резервуара, а цикл обратим. В случае трех
и более резервуаров равенство не может иметь места даже для
обратимого цикла.) Работа W, совершаемая над термостатом,
равна W = Qi — Qz, откуда к. п. д.
п = = 1 — 1 — ^мпн
<21 <21 Т макс
5. а) Как показано в гл. 1, пример 6, полная работа, совер-
шаемая системой (газом), равна разности работы, совершаемой
газом в процессе с -> d, и работы, совершаемой термостатом над
газом в процессе а -> Ь, т. е. W = Cv [(Ге — Td) — (Ть — Та)].
С другой стороны, газ в процессе b -> с получает теплоту Q =
= Cv (Тс — Ть). Для адиабатического процесса [см. гл. 1, при-
мер 6, соотношение (2а)] ТУу-1 = const, откуда Т^У'^1 = ТгУ'у1
и ТУ^-1 = TaV'/-1. К. и. д. при этом принимает вид
.. -w __ Tc-Tb-Td + Ta _ . Td-Ta
1 <2 тс-ть тс-тъ
Так как
= Td-ra
Тс ТЪ \ Р1 / Тс — Ть ’
имеем
б) Работа совершается не только при адиабатических процессах
с—>d и а—>Ь, но также и в процессах b—>с, d—>a. Поэтому
W = Су [(Тс - Td) - (Ть - та)]+р2 (Ус - Vb) - Р1 (Vd - Va).
С помощью уравнения состояния pV=nRT=(Ср — Cv) T=Cv(y — 1) Т
получаем
W = CP (Tc-Tb-Td + Ta).
В процессе b—>c газ получает тепло Q = Cp(Tc— Тъ). Для адиаба-
тического процесса pVv = const и Tp(-1~v)/v = const, откуда вытекают
равенства
Уд __ ( Р1 ПУ-О/У Td = / Pi \(у-1)/у
Тъ \ Р2 ) Тс \ р2 )
Следовательно,
= 1 Td—Ta , _ \(v-d/v
1 Q Тс-Ть 1 {р2>
В) w = Су [Тс-Td-(Тъ -Та)] + р2 (Ус- Уь) =
= Су [Тс - Td - Тъ + Та + (у - 1) (Тс - П)] =
= Су [y(Tc-Tb)-(Td-Ta)].
110
Гл. 2. Второй закон термодинамики
Теплота, поглощаемая при процессе Ъ —>с, равна Q = Cp(Tc — Тъ)~
Следовательно,
Отсюда с учетом равенств
= т^УГ^ПУГ1 И Вд-^^УГ1
1Ъ И3
получаем соотношение, которое требовалось доказать.
Замечание. В соответствии с выводами задачи 4 к. и. д.
во всех трех случаях не должен превышать 1 — Та1Тс.
6. Приведенное утверждение очевидно, если абсолютная тем-
пература определяется с помощью неравенства Клаузиуса (2.9)
(равенство имеет место только в случае квазистатического процес-
са). Если абсолютная температура не определена, то следует
воспользоваться доказательством соотношения (2.8) в § 5.
7. При квазистатическом изменении состояния моля идеаль-
ного газа изменение энтропии dS определяется соотношением (2.16)
= -—У---- ,
где £7 — внутренняя энергия, р — давление и У —объем. С помощью
равенств dU = CydT и pV = RT получаем
dS=-^-dT + ^dV.
Следовательно,
5 = С?,1п7, + Д1пУ+5о, (1)
где 5'о — постоянная интегрирования.
Замечание. Если имеется п молей газа, то в силу экстен-
сивности энтропии S соотношение (1) принимает вид
S(T, У, n) = n (CHnT’ + .Rln-^+.S'o) • (2)
8. Так как газ адиабатически расширяется в вакуум, он не
совершает работы (d'A = 0) и не обменивается теплом с окружа-
ющей средой (d'Q = 0). Согласно первому закону термодинамики,
изменение его внутренней энергии U также равно нулю. Тогда
изменение его температуры также равно нулю, так как для идеаль-
ного газа в силу (1.12) dU = nCydT. Энтропия идеального газа
определяется выражением
S = n (CHnT’ + .Rln-^+So)
Решения
Hi
на фиг. 34, имеет место-
Фиг. 34.
(см. замечание к предыдущей задаче). Поэтому приращение энтро-
пии в этом процессе будет иметь вид
AS = S (Т, VZ)-S(T, VO = nR In ,
откуда вытекает, что AS > 0, так как V2 > Vp Следовательно,
при этом адиабатическом процессе происходит возрастание энтро-
пии. Согласно .второму закону термодинамики, такой процесс
является необратимым.
9. При квазистатическом изменении состояния идеального
газа, которому соответствуют кривые
следующее равенство [см. гл. 1, при-
мер 3, соотношения (1) и (3)]:
d'Q = CvdT + pdV = Cp dT— V dp.
(1)
Приращение энтропии (AS)P при
постоянном давлении имеет вид
/д5) _^pdT
Т1
а при постоянном объеме
(AS)y=
Ti
Следовательно, отношение приращений энтропии равно CP!CV
если Су и Ср постоянны.
10. Мы уже установили, что
pv = f(T) и и = и(Т).
термо динами ки
ds=du+^
Из основного уравнения
имеем (см. пример 2)
(1>
Умножая это уравнение на v, находим
-/(Т) = 0.
Интегрируя его, получаем
/ (Т) = const - Т.
(2>
(3>
112
Гл. 2. Второй закон термодинамики
Константа не зависит от температуры и объема, следовательно,
уравнение состояния имеет форму
pv = АТ (А — константа). (4)
11. Из равенства (dUldV)Q = 0 находим dU = g (0) dG. Разде-
лим на / (0) уравнение для квазистатического процесса
d'Q = dU + pdV = g (0) dG + pdV.
В результате получим
d'Q _ g (0) dQ pdV _ g (0) dQ dV
f ~ f + / - /(9) ' V ’
Это выражение, как нетрудно видеть, является полным дифферен-
циалом. Если теперь положить
^- = dS,
то S будет функцией состояния. Из рассмотрения цикла Карно
следует, что отношение количества тепла Qlt полученного от го-
рячего теплового резервуара с температурой 01т к количеству
тепла Qz, переданного холодному тепловому резервуару с темпе-
ратурой 02, определяется из соотношения
откуда
Qz _ f (9а)
Qi f (9i) '
Следовательно, согласно определению абсолютной температуры (2.5),
/ (0) = const-Г. (Другой способ см. в решении задачи 10.)
12. Пусть U — внутренняя энергия и S —энтропия излучения
в объеме V. Тогда
d(pTbV) + ±-oTidV
dS — db +pdV „ 3
= 4оГУ dT + А оТ3 dV = d (у <jTsV) , (1)
S = у oT3V const.
Следовательно, плотность энтропии s имеет вид
s = 4o7’3. (2)
Для изотермического процесса и = const и р = const, а для ади-
абатического T3V = const и, следовательно, pV4/3 — const. Рас-
Решения
113
смотрим цикл Карно, изображенный на фиг. 35. Количество
тепла, которым система обменивается с термостатами в процессах
А -> В и С -> D, равно соответственно Qi и Q2. Эти величины
определяются следующим образом:
в
(dU+p dV) = 4 (ув - VA),
A
<?2 = 4а^(Ус-Кп).
С помощью соотношений для адиабатических процессов V ВТ3В =
= VcT3c и VAT3A = VDT3D или VBTl^VcT32, VAT3^VDT32 получаем
Qi _ Qz_
Tt т2 •
Работа, совершаемая за весь цикл ABCD, имеет вид 4/зСТ^1(^2—Л)Х
X (VA — VB) и равна разности Qi~Q->-
13. Первый закон термодинамики d'Q = dU — d'A для ква-
зистатического процесса изменения состояния парамагнитного
тела имеет вид (см. гл. 1, пример 1)
d'Q = dU - HdM (1)
(мы рассматриваем единичный объем), где U зависит только от тем-
пературы и не зависит от М. Из соотношения М = уН следует,
что Н = М1% = Л/6. Здесь % и 0 = 1/% также не зависят от М,
а зависят только от температуры. Разделив (1) на 9, получаем
^- = ~-MdM = dS, (2)
п п ' '
8 кубо
114
Гл. 2. Второй закон термодинамики
где dS — полный дифференциал. Следовательно, величина 0 =
= 1/% является интегрирующим множителем для d'Q. Так как
величина 0 зависит только от температуры, она должна быть
пропорциональна абсолютной температуре. Действительно, если мы
рассмотрим цикл Карно для этого парамагнитного тела, то отно-
шение полученного от горячего резервуара количества тепла Qi
к количеству тепла Q2, отданного холодному резервуару, будет
равно 01/02, как это видно из соотношения
o=(£ds = (£^- = -jL—
У Of «2
14. (Другой способ решения см. в гл. 1, пример 7.)
а) Адиабатическая и изотермическая сжимаемости определяются
соответственно соотношениями
1 ( dV \
Fhds’
_ 1 ( dV \
Ху —
где S — энтропия. С помощью
1
V \ др )т
(1.23) xs можно записать в виде
(dS/dp)y
Если S считать функцией от Т и У, т. е. 5 (Т, V) = S (Т (р, У), У), то
) = \ др /V - (— \ ( дТ\ 1 дТ /у V др /V ~ Су / дТ \ Т ( др )v ' (3)
Аналогичным образом, считая S (Т, р) = S (Т (р, У), р), имеем
( dS 1 ( dS \ { дТ \ Ср / дТ \
1 dV )р \ЭТ Jp \ dV )р Т \dV )р'
Подставляя (3) и (4) в (2), находим
Су (дТ!др)у____________________
s vcp (дт/дУ^ cpv I др )т Ср т’ (°)
здесь мы снова воспользовались соотношением (1.23).
б) Если для вычисления адиабатической магнитной восприим-
чивости xs = (dMldH)s и изотермической магнитной восприимчи-
вости /г = (дМ1дН}т использовать такой же метод, что и при
вычислении сжимаемости (заменяя У -> М и — р -> Н), то полу-
чим xs = (См/Сн) 1т-
15. а) Один способ доказательства приведен в решении при-
мера 2. Здесь мы дадим другое доказательство. Из равенства
dU = TdS-pdV = T^vdT + \T(^T--p\dV (1)
Решения
115
следует
<2>
Подставляя это соотношение в выражение для dU/dV, полученное
из (1), находим
-/’==7’(-йИ -р-
\ dV )Т \ 9V )т г \ дТ /V 1
б) Подставляя в (2.16) выражение для энтальпии Н = U + pV,
имеем
dS = ^(dH--Vdp). (3)
Следовательно,
( dS \ _ 1 / \ ____i f дН x__V_
(sTJp-T (“srjp ’ \ dp )r~ t F’
С учетом равенства д23/дрдТ = д23/дТ др это дает
( дН } = —Тг — (— 1 = —Т (—) -L-У
\ др )т дт \ Т ) \ дТ )р '
При другом методе решения следует исходить из соотношения
dH = d (U + pV) — TdS + Vdp, а затем применить метод,
использованный в п. «а».
16. а) Согласно определению сс = (d’q'jJdT, откуда с помощью
второго закона термодинамики d’q — Tds [см. (2.12)], получаем
= .
Аналогичным образом находим
б) Из соотношения (2.16)
du = Tds — pdv (1)
следуют равенства {ди/дТ')к = Т (ds!dT)v, d2u/dv дТ = Т d2s/dv дТ.
Кроме того, из определения энтальпии h~u-\-pv имеем
dh = T ds-\-v dp, (2)
а также d2h!dT др = Т d2s/dT др.
в) Первое равенство доказано в решении задачи 15 [формула (2)].
Второе равенство доказывается следующим образом. Из (1) следует
\др)т \др)т Р\др)т' \ дт)р \ дТ )р Р\ дТ 1р •
8*
116 Гл. 2. Второй закон термодинамики
Так как д2и/дТдр = dhi/dpdT, то (ds/dp)T = — (dv/dT)p. Другой
способ решения аналогичен приведенному в примере 2. В каче-
стве независимых переменных следует взять р и Т и исходить
из соотношения (2).
17. а) Как найдено в решении задачи 16,
(1)
(2)
Считая s — s(T, v(T, р)) функцией от Т и р, имеем
I 'Js ) ( ) । ( \
[~дТ )р = \дТ )v+\~d^)r \дт)р '
Подставим теперь сюда соотношения Максвелла (ds/dv)T = (dp/dT)v
(см. задачу 16, п. «в»). Это дает
Теперь воспользуемся соотношением (др/дТ)„ = —(dv/дТ)р/(dv/др)т;
после подстановки значений аир получим ответ.
Другой способ решения состоит в следующем: подставим реше-
ние первой части задачи 15 из гл. 1 в решение задачи 16, п. «б»,
той же главы.
откуда
/ дсР ) т 92g д / dv \ „ / дЧ' \
\ др )т~ дрдт ~ 1 дТ \ дТ )р- \дТ2 )р’
где мы воспользовались соотношением Максвелла (dsldp}T =
— —(dv/dT)p (см. задачу 16, п. «в»). Аналогичным образом,
используя соотношение (ds/dv)T = (dp/dT)v, находим
( ,1С° 1 —т d2s —т(д2р 1
к ди ) т ~~ 1 дидТ \ дГ* )v '
18. Внутренняя энергия 1 моль идеального газа имеет вид
U = СVT + UQ (Су — молярная теплоемкость при постоянном
объеме), а энтропия S (Т, р) = Ср In Т — R In р + SQ (см. реше-
ние задачи 7). Здесь UQ и So — константы. Следовательно, сво-
бодная энергия будет иметь вид
F = U — TS = СуТ — СРТ InТ + RT In р + Uo — TS0,
а термодинамический потенциал Гиббса
G = U - TS + pV = СРТ—СРТ In Т + RT In р + Uo - TS0.
Решения
117
Изменение этих величин при сжатии газа от р = 1 атм до
р = 100 атм (при Т — const = 293° К) имеет вид
\S = S(T, 100) -S (Т, 1) =
= —R In 100= ——*00 « — 4,61? « —9,2 кал!град,
\F = \G = RT In 100 = 2931? In 100 «2,7 ккал.
Замечание. Здесь мы считаем Cv константой, но это допу-
щение необязательно.
19. Если объем V и его приращение определяются выраже-
ниями
V = а + bp + ср*, (1)
dV = (b + 2ср) dp, (2)
то необходимая работа А имеет вид
А = — ( pd,V = — (4- &р2 +-|- с/*3) Г ° • (3)
2 \2 3 |p=iooo v '
Подставляя сюда численные значения b = — 715-10-6 и с =
= 46- 1О-0, получаем А = 326,83 атм• см9/молъ = 33,116 дж/молъ.
Если при этом поглощается количество тепла Q, то приращение
внутренней энергии А17 равно
\U = А + Q- (4)
Для квазистатического процесса
<?= j7<i5 = rj45=7 J J ( + )//>. (5)
[Здесь мы использовали соотношение Максвелла (dS/dp)r =
= — (dV/dT)p', см. решение задачи 16, п. «в».] Следовательно,
Q=—.298* (4,5 + 4 • 1,4) атм’см31моль «— 157,0 дж/молъ, (6)
откуда ДС7 «— 123,9 дж/молъ.
20. Согласно определению, приращение энтропии имеет вид
р
A.S = S„ — St = j d’Q/T. Здесь интегрирование означает опре-
i~+v
деление полного количества поглощенного тепла d'Q, деленного
на значение температуры Т, на каждой стадии процесса квазиста-
тического перехода из состояния i (лед при 0° С и 1 атм) в состоя-
ние v (пар при 100° С и 1 атм). Процесс перехода i -> v мож-
но разбить на три стадии i -> w0 (где w0 — состояние воды
при 0° С и 1 атм) -> ш100 (ш100 — вода при 100° С и 1 атм) v.
118
Гл. 2. Второй закон термодинамики
В процессе i wQ
кал!град-мэлъхз 5,26 кал/град - моль. (1)
i-M»0
Предполагая, что при процессе ш0—>ш100 средняя теплоемкость
равна Ср, имеем
f d'Q _ с f dT _
j T — bp J ~f~~
WQ-^WlQQ W0->Wj00
(373\
273 J кал/г рад-моль 5,63 кал/г рад-моль, (2)
где мы использовали приближенное равенство In (373/273) =
= In 1,366 а 0,312. Для ю100—> п имеем
f d'Q 972-10 /а Of? < / a ZQ\
I -=- = —5=— кал/град-моль а; 26,1 кал/град-моль, (3)
J J- о /о
WlOO-^V
Складывая (1) —(3), получаем
Д5 = 37,0 кал/г рад-моль.
21. Рассмотрим квазистатический ^переход (фиг. 36) вещества
из твердого состояния при температуре 1\ в переохлажденную
жидкость при той же температуре Т,. Этот переход имеет вид:
твердое тело при 1\ твер-
m 2
дое тело при То —> жидкость
при То —> жидкость при Ti-
Возрастание энтропии ?[в про-
цессе 1 составляет
т°
Т1
Возрастание энтропии в про-
цессе 2 равно MQa/T0. Возра-
стание энтропии в процессе 3
имеет вид
тх ...
J ^-= -Mqln-^-.
то
Следовательно, у переохлажденной жидкости при температуре^
значение энтропии выше, чем у твердого тела при той же темпе-
ратуре Ti на величину \S = MQq/Tq — М (Ci — cs) In (То/Tj).
Решения
119
22. С помощью соотношения Максвелла {dS!dp)T——(dV/dT)p
искомое увеличение энтропии можно записать в виде
РБ РБ
f dS = f (4М dp = — f dp =
J i \ др )т r J \ dT )p 1
рл рл
= — [a (рв — Яа) + у^(Рв — Pa) + ^-c(p3b — p'\)J .
23. Из условия dS = (dSldT}Y dT-y{dSldV)TdV = Q находим
l dT \ _ (dS/dV)T
(dS/ODv
[cm. (1.23)]. Далее, с помощью выражения для теплоемкости при
постоянном объеме Cv = Т (dS/dT)v и соотношения Максвелла
(dS/dV)T = (dp/dT)v (см. задачу 16, п. «в») получаем
_ ( дТ \ УТ ( dp^X
\ д\ /s \ d In 7 /s CY \ дТ ) Y '
[Так как для газа (dpldT}Y > 0, при адиабатическом расширении
происходит уменьшение температуры Т. Это охлаждение проис-
ходит из-за того, что при расширении газ совершает работу над
термостатом.]
24. В гл. 1, пример 9, мы показали, что Н = const. Изменение
температуры при малом изменении давления получается из усло-
вия dH — 0, т. е.
! дТ \ (dH/dp}?
\~dp)H = ~ (дН/дТ)р •
С помощью равенства Ср = (дН!дТ'}р и формулы (дН1др)т =
= — Т (дУ/дТ)р + V (см. задачу 15, п. «б») находим
7^4 _у-| . (1)
\ dp /н Ср L \ dT )р J
Если в это соотношение подставить уравнение состояния pV =
= RT (1 4- Вр}, оно принимает вид
(£)„= <2)
Если 1 — точка, в которой касательная, проходящая через нача-
ло координат, касается кривой зависимости второго вириального
коэффициента В от Т, то при температуре Ti, соответствующей
этой точке, коэффициент Джоуля — Томсона меняет знак.
На фиг. 37 показана зависимость коэффициента Джоуля —
Томсона от р и Т, а на фиг. 38 — зависимость В от Т для угле-
кислого газа.
р, атм
Фиг. 37. Коэффициент Джоуля — Томсона для СО2.
Решения
121
25. При свободном расширении газа в вакуум (адиабатический
необратимый процесс) свободная энергия является константой.
Решение этой задачи аналогично решениям задач 23 и 24. [Исполь-
зуем при этом (1.23) и результат задачи 15, п. «б».] Находим
( дТ \ (дЦ/дУ)т 1 г т(др\ -|
I дУ )и~ (dU/dT)v Cv |Z I дТ fvj •
26. Для квазистатического процесса, в котором участвует еди-
Ф и г. 39.
ничный объем вещества, запишем соотношение
d'Q = dU — HdM. (1)
Как известно, при изотермическом намагничивании dU = 0 и М =
= СЫТ. Отсюда следует, что
III
ч--\нлШ = ^н'"
о
т. е. теплота изменяется на. —Q = CH\I21\. С помощью соотно-
шения
dS = ±(dU-HdM) = iaT2dT-C
получаем энтропию в виде
5 = Aar-|c(^-)2 + conSt. (2)
422
Гл. 2. Второй закон термодинамики
При адиабатическом размагничивании от Н = Н^ до Н = 0 энтро-
пия S не меняется (фиг. 39), откуда следует
^аТ1 = ±аТ1-±-С (^)2,
или
<3)
Так как С>0 и а>0, имеем Т2<^Т\. При малых значениях
поля Н{ изменение температуры также мало и можно воспользо-
ваться приближением
3 а м^е ч а н и е. Для получения температур, меньших 1° К,
используется адиабатическое размагничивание. На фиг. 40 изоб-
ражена трехмерная поверхность, представляющая энтропию (свя-
занную со спином электрона) железоаммониевых квасцов как
функцию магнитного поля и температуры. Цикл Карно (с диаграм-
мой типа изображенной на фиг. 40 жирной линией), в котором
в качестве рабочего вещества используется подобная парамагнит-
ная соль, может быть использован для создания охлаждающего
устройства. С помощью подобных холодильников была достигнута
-температура порядка 0,2° К.
Решения
123
Из соотношения (3) следует, что если при фиксированном зна-
чении Ti увеличить Hi до достаточно больших значений, то тем-
пература Т2 станет отрицательной. Однако выражение для энтро-
пии (2), полученное без учета третьего закона термодинамики,
неверно вблизи 0° К, поэтому его нельзя применять в тех случаях,
когда оно приводит к отрицательной температуре Т2. На самом деле
ни с помощью адиабатического размагничивания, ни каким-либо
иным способом невозможно достичь абсолютного нуля. Наиниз-
шее значение температуры, полученное к настоящему времени
путем адиабатического размагничивания, лежит вблизи 0,003° К.
27. Мы рассматриваем единичный объем. Из соотношения
dS =JU-HdM (1)
находим
/ dS х _ 1 / gC \ (ИЛ —/?\
I дТ )м~ т I дТ )м и \ дМ )т~ т { дм )т Т '
Подставляя сюда условие интегрируемости d2SldM дТ — d2S!dT дМ,
получаем
/ &U А _( д (-^/Т1) \ /о\
\дМ)т V дТ )м
(см. задачу 15, п. «а»). Так как М = f (Н/Т), правая часть равна
нулю (действительно, если намагниченность М постоянна, то отно-
шение HIT также постоянно). Следовательно,
Г—) =0
( ОМ )т
При этом соотношение (1) принимает вид
ds^dum-ir (4р (4)
или после интегрирования
н/т
£ = j dU^— t xf'(х) dx +const = g(T) — ^f (-^-1-
0
H/T
+ у / (ж) dx-\- const. (4)
0
28. Иэ принципа максимальности работы следует, что работа,
получаемая при обратимом процессе, максимальна. (Если тело
находится в непосредственном контакте с холодным резервуаром,
то никакая работа не совершается.) Чтобы обратимым путем взять
теплоту от тела и превратить ее в работу, можно воспользоваться
124
Гл. 2. Второй закон термодинамики
циклом Карно, при котором от теплового резервуара с темпе-
ратурой Т поглощается количество тепла d'Q = С | dT | =
= — CdT (dT <. 0), а резервуару с температурой То передается
количество тепла d'Qa = d'Q (То/Т) и совершается работа
d'W = d'Q-d'Q0 = (1 - A) d'Q.
В результате повторения этого цикла тело в конечном итоге
приходит в состояние с температурой То. При этом полная совер-
шенная работа имеет вид
то
W = j d'W = j j (i-^cdT =
Tl
= С[(Л-71 * * * *О)-Го1п A] .
29. Эта задача является обратной по отношению к предыду-
щей. Мы находимся в комнате с температурой 25° С (298° К),
которую можно считать тепловым резервуаром. Чтобы превратить
воду с температурой 298° К в лед при 273° К, необходимо охла-
дить ее, передав тепло резервуару с более высокой температурой,
чем вода. Это можно сделать только путем совершения работы,
которая будет минимальной в случае обратимого процесса. Исполь-
зуем цикл Карно, в котором количество тепла d'Q берется от воды
при температуре Т, а резервуару с температурой Т’ (> Т) пере-
дается количество тепла d’Q’ = d'Q + d'W. Так как d'Q/d'Q' =
= TIT', то d'W = d'Q (Г — T)/T, где d'Q = - CdT, С — пол-
ная теплоемкость воды. Работа, которая необходима для охлажде-
ния воды от 298 до 273° К, равна
298
273
298
1) (-CdT) = С [298In -(298-273)] . (1)
Минимальная работа, необходимая для передачи скрытой теплоты
замерзания L резервуару при 298° К, равна
ТЛ7 L- (298 -273)
----273-- '
Используя заданное значение скрытой теплоты замерзания во-
ды, теплоемкость Сн2о = 18,05 кал/град-моль и механический
эквивалент теплоты 4,18 дж/кал, находим W± = 4,64-106 дж и
Решения
125
W2 = 35,8-10® дж. Полная работа равна W = Wr + W2 =
= 40,4-10® дж, что соответствует 40,4-10®/3,6-10® = 11,2 квт-ч.
30. Достаточно доказать, что в случае нарушения принципа
Каратеодори принцип Томсона также нарушается. Предположим,
что переход термически однородной системы из состояния (1)
в состояние (2) происходит изотермически с поглощением поло-
жительного количества тепла Q. Из первого закона следует, что
Q = U2 - U, - А, (1)
где и U2 — внутренняя энергия в состояниях (1) и (2), Л —
работа, совершаемая над системой. Теперь адиабатически переве-
дем систему из состояния (2) обратно в состояние (1) (фиг. 41).
Если допустить, что принцип Каратеодори неверен, то такой пере-
ход будет возможен. Первый закон термодинамики утверждает,
что
0 = — U2 — А', (2)
где А’ — работа, совершаемая над системой в этом процессе.
Из (1) и (2) следует
Q = - (Л + А'). (3)
Следовательно, в цикле (1) -> (2) -> (1) система поглощает теплоту
<2 от термостата и совершает эквивалентное количество работы
— (А 4- А'), что является нарушением принципа Томсона.
Другой способ решения. Принцип Клаузиуса (или
Томсона) означает существование функции состояния S, причем
d'Q/T = dS, где Т — абсолютная температура. При адиабати-
ческом процессе d'Q = 0, dS = 0, а так как dS — полный диф-
ференциал, то S = а (= const). Это означает, что в пространстве
термодинамических переменных (например, х, у, z) существует
семейство поверхностей S (х, у, z) = а. Начальное состояние
(ж0, у0, z0) лежит на поверхности S (х0, у0, z0) = а. Следовательно,
все адиабатические обратимые процессы с исходным состоянием
(х0, у0, z0) должны лежать на этой поверхности, и ни одной точки
вне этой поверхности нельзя достигнуть путем адиабатического
126
Гл. 2. Второй закон термодинамики
адиа-
Кла-
нера-
адиа-
про-
Работа
Обратимое
смешение
IV
Смесь газов
Ф и г. 42.
обратимого процесса. Следовательно, в любой сколь угодно малой
окрестности исходного состояния (а;0, у0, z0) всегда существуют
такие состояния, которые не могут быть достигнуты адиабати-
чески. Это означает справедливость принципа Каратеодори.
Замечание. Принцип Каратеодори справедлив и для
батических необратимых процессов. Исходя из принципа
узиуса или принципа Томсона, можно доказать, что в силу
венства Клаузиуса при
батическом необратимом
цессе происходит возрастание
энтропии S. Следовательно, при
любом начальном состоянии
(х0, у0, z0) состояния с мень-
шими значениями энтропии,
лежащие по одну сторону от
поверхности S (х, у, z) =
= S (х0, у о, z0), не могут быть
достигнуты никаким обратимым
образом. Поэтому можно утвер-
ждать, что в сколь угодно близ-
кой окрестности любого состоя-
ния существует состояние,
в которое невозможно перейти
ни с помощью обратимого, ни
с помощью необратимого адиа-
батического процесса.
31. Рассмотрим смесь двух
газов: щ молей газа 1 и п2
молей газа 2. Каждый газ
имеет объем V, температуру Т
и давление р. Предположим,
что диффузионное перемешивание этих газов представляет собой
обратимый процесс. В таком случае можно разделить эту смесь
на газ 1 объемом 7} = Vn1/(n1 -(- п2) при температуре Т и дав-
лении р и газ 2 объемом V2 = Vn2/(ni + «2) при температуре
Т и давлении р без каких-либо иных изменений системы
(процесс I -> II на фиг. 42). Далее увеличим изотермически
объем каждого газа до V. Прц этом процессе (II -> III) теплота,
поглощаемая из резервуара, преобразуется в работу. После этого,
сделав в каждом контейнере одну стенку полупроницаемой
(см. пример 5), можно вложить один контейнер в другой и, обра-
тимым образом (без обмена теплом и совершения работы) смешав
оба газа, вернуться в исходное состояние (III -> IV -> V = 1).
При этом в суммарном процессе на этапе П -> III происходит1
поглощение теплоты, которая целиком преобразуется в работу
Решения
127
без каких-либо других изменений системы, что противоречит
принципу Томсона.
32. Количество тепла d’Q, поглощенное системой, равно сумме
d’Q’ и d’Q". Из первого закона термодинамики следует, что
d’Q’ = Су dT' + р' dV и d'Q" = CydT" + р" dV".
Давления p' и p" слева и справа от поршня всегда одинаковы
(р' = р" = р), так как части системы находятся в механическом
равновесии между соб.ой. С помощью уравнения состояния идеаль-
ного газа pV = RT выразим dV и dV" через dT', dp и dT", dp.
(Для этого умножим dV/V = dTIT — dptp на pV = RT, что дает
pdV = RdT — RTdp/p.) Тогда получим
d’Q = d'Q’ + d'Q" = (Cy + R) dT' + (C”v + R) dT" - (T' + T")dp. (1)
В этой системе d'Q является дифференциальной формой от трех
переменных Т', Т" и р. Воспользуемся теперь условием суще-
ствования интегрирующего множителя для формы
Х^х{-\- X2dx2-\-X3dx3; (2)
это условие имеет вид
у 7 дХ3 дХ2 \ । у 7 дХ^ дХ3 \ у 7 дХ2 дХ^ \ ~
(см. замечание 1). Полагая т1 = 7’', х2 = Т’", х3 = р, Xl = Cy4-R,
X2 = C'v-\-R и Х3= — (R/p) (Т'~\-Т"), представим левую часть
соотношения (3) в виде
- (Су + R) А + (Cv + 7?) А = А (Су - Су). (4)
Эта величина не может быть равна нулю, так как Су Су. Следо-
вательно, d’Q не имеет интегрирующего множителя.
Замечание 1. Если существует такой интегрирующий
множитель А (х^, х2,° х3), что A (XjdXi 4- X2dx2 -|- X3dx3) =
= СЙр (Xi, х2, х3), то
= -Jl = ax2, ^L = AX3.
дх1 11 дх2 дх3 °
Полагая 32(p/3x13x2 = д\(дх2дх^ и исключая из этих равенств А,
получаем в качестве условия интегрируемости соотношение (3).
Замечание 2. Этот пример свидетельствует о том, что
в системе, температура которой неоднородна, необязательна
существует интегрирующий множитель для d’Q. При доказатель-
стве существования интегрирующего множителя при помощи
второго закона термодинамики мы обязательно должны потребо-
вать термической однородности системы.
128
Гл. 2. Второй закон термодинамики
33. Введем внутреннюю энергию и и энтропию s на единицу
массы вещества. Если
du = [-^)vdT = g(T)dT, (1)
где g (Т) зависит только от Т, то из равенства
du = Tds — pdv (2)
получаем
Tds = g (T) dT + pdv,
a также, согласно определению,
<3>
Следовательно, с„ зависит только от Т, что доказывает утвержде-
ние «а».
Далее, с помощью (1) запишем (2) в виде
dv = -ds-1^-dT.
Р Р
Отсюда следует
(21) = (41
{ дТ /р р \дТ )р р
и
(21) = 2(21) . (5)
\ др J т р \ др /т ’
Продифференцируем (2) по Т и по р
[ ди \ т ( ds \ / dv \ f ди \ 7, / ds \ / до \
а затем приравняем вторые смешанные производные д-и/дрдТ
и д2и!дТ др. В результате получаем соотношения Максвелла
<«)
Из соотношений (5) и (6) следует равенство
(21) = _2(21) , (7)
\ др )т р \дТ )р'
которое фактически представляет собой доказательство утвержде-
ния «б». Чтобы убедиться в этом, будем считать и функцией
от х = р!Т и Т. Тогда
( dv \ (— } щ(21) £_/211 _|_(21) /я\
\дт)р \ дх )т\ дТ )р^ \ дТ )х Т* [ дх )т~ \ дТ )х ' ( )
( av ) = (21) (21) =2(21) (Q\
\ др ) т \ дх J т \ др ) т Т \ дх J т '
Решения
129
Следовательно, (7) означает, что
(-&) -о-
Таким образом, и зависит только от х = р!Т (что и требуется
доказать в и. «б»). По определению ср = Т (ds/dT)p; тогда из (3)
и (4) следует
ср-^ = р(-^)р
Так как и зависит только от х = р/Т, из (8) получаем
-___pL(JL.\ — Т2 dv
дТ )р~ Т- \ дх ]т '~ dx '
Следовательно, разность ср — cv также зависит только от х, что
доказывает утверждение «в».
34. Обозначим через Cv -(dU^dT)v молярную теплоемкость при
постоянном объеме, где U— внутренняя энергия на 1 моль, а У —
молярный объем. Тогда, учитывая решение задачи 15, п. «а»,
получаем
( dV )т dV дТ дТ L \ дТ )у ( дТ* )v ' 7
Так как уравнение ван дер Ваальса (1.17) можно записать в виде
то правая часть соотношения (1) равна нулю, т. е. Cv не зависит
от V, а зависит только от Т. С помощью соотношения (1) в реше-
нии задачи 15 получаем
"=(^)^7'+(4к)г^=
= Cv^ + [z(i)v-ppr = Cv<i7' + -i<ir. (3)
Интегрируя это выражение, находим
т
77 = J Су dT—-^--[-Uo (Uo— константа). (4)
С помощью (2) и (3) дифференциал энтропии записывается в виде
dS = ^dU + ^^^dT+-^dV, (5)
откуда
т
S = j dT -|-R In (И—b)-[-S0 (So — константа). (6)
9 кубо
130
Гл. 2. Второй закон термодинамики
35. Если считать, что Су = const, то для U будет справедливо’
соотношение (4) в решении предыдущей задачи. В случае адиаба-
тического квазистатического изменения соотношение (5) в решении
предыдущей задачи принимает вид
dS = dT + dV = dT + dV = о
(с учетом соотношения Майера), или
dT (Y —1W _л
Т V—Ъ —
откуда следует
Т (V — Ь)1 = const.
Подставляя это равенство в уравнение состояния ван дер Ваальса,
получаем
(р + дт) (V — b)y = const.
При адиабатическом расширении в вакуум (необратимом!) U =
= const, откуда следует
т2-Т1=^-(^—X).
Су k У1 /
36. В решении задачи 24 было получено следующее выраже-
ние для коэффициента Джоуля —Томсона:
Используя уравнение ван дер Ваальса, записанное в приближен-
ной (с точностью до 1/72) форме, p = nRT/V ~\-n2{RTb — d)/V‘2,
получаем
( dV \ ~ V i+nb/V ~ V Г п / 2а , \ Ч
\дТ)р~ Т l+(2n/V)(b-a/RT) ~ Т L ф V \ ВТ )] ( '
и
«-Ь-тС-О-М- <3>
где Ср — молярная теплоемкость при постоянном давлении. Для
температуры инверсии Ti, при которой коэффициент Джоуля —
Томсона (дТ1др)ц = 0, из (3) имеем
П = >. (4)
Критическая температура Те = 8al21Rb (см. гл. 1, пример 8),
откуда Tt = 27 Zg/4.
Решения
131
37. Простейший способ решения основан на использовании
соотношения (дН1др)т = V — Т (dV/dT)p (см. задачу 15, п. «б»).
Подставим в него Н = U -j- pV и приведенное в условиях задачи
разложение для V; тогда
(B + F) + 2(C + y)p+...=
= у(А-ТА,'! + (В-ТВ’) + (С-ТС') р+ • •
где А' = dA/dT, и т. д. В пределе р -> 0 это уравнение переходит
в уравнение А — ТА' = 0, решение которого имеет вид А =
= const X Т. Тогда абсолютную температуру можно определить
следующим образом. Измерим значения pV при различных давле-
ниях, но при фиксированной температуре Т, а затем экстрапо-
лируем эти значения: lim pV = А (фиг. 5). Проделаем такую
же процедуру при температуре какой-либо другой термометри-
ческой точки, например в тройной точке воды, температура кото-
рой То = 273,16° К точно фиксирована. Тогда искомое значе-
•ние абсолютной температуры будет определяться соотношением
AIAТр. точки = т/То-
38. Из равенства dQ = TbS вытекает следующее определение
скрытой теплоты расширения:
(1)
1 \ dp ) т \ dl ' >
(здесь использовано соотношение Максвелла из задачи 16, п. «в»).
Если вместо Т использовать 0, то
/ dV \ / dV \ dQ
\~dT'lp== \dQ)p~dT '
Подставляя это равенство в (1), получаем Lp=—(dV/dd)pT dQ/dT^
или
d In T _ 1 / dV \ _ Va (0)
dO ~ Lp \ dQ )p~~ Lp(Q) ‘
Интегрируя no 9, находим
e
м^)=-Чт5г=/(в'в«>- и
00
Правую часть можно определить путем численного интегрирова-
ния, используя экспериментально измеренные значения величин,
входящих в подынтегральное выражение. Тогда это соотношение
позволит установить связь между 9 и Т.
9*
132
Гл. 2. Второй закон термодинамики
39. Подставив в соотношение (3) решения задачи 27 соотно-
шение
g = y(^-Q), (1)
которое следует ji3 равенства
получаем
/ эи \ _ 0М
\ дМ )т~ С '
Умножая оба соотношения (2) решения задачи 27 на Т, а затем
дифференцируя их по М и Г, получаем соотношение Максвелла
(dS,'dM)T = —(дН/дТ)м. С его помощью находим
(дСм\ _ Td*S _ / дМГ \
\ дМ )т дТ дМ 1 \ дТ* )м и’
откуда следует, что См не зависит от М, а зависит только от Т.
Интегрируя полный дифференциал
JTT { dU \ . / dU \ Jrr &М dM
dU=(^)MdT+[^)rdM = C^dT-------------
получаем
т
ТТ f Jrr 0М2 , .
U = I CMdT--^-+const,
а интегрируя дифференциал
_ dU — HdM r dT MdM
—----у----— '-'M ~ji-q— ,
находим
M*
-^r + const.
40. Согласно первому и второму законам термодинамики,
dU = T dS- pdV + Hdl, (1)
где U — внутренняя энергия, S — энтропия и I — магнитный момент
системы. Из (1) следует, что
(") -И-F) •
\ др 1н X др )Н г \ др )н \ др )н
{ dU \ m I dS \ ( dV \ , тт ( д! \
Решения
133
Так как д2Х/дрдР = д2Х/дН др (X = U, S, V, I) , имеем
\ ОН )р \ Эр )н '
Подставляя в (3) I = yHV, получаем
(3)
или
Пренебрегая зависимостью % и (dytJdp)T от Н, проинтегрируем обе
части по Н от 0 до Н. Это дает
<5>
где AV — изменение объема. Обычно можно считать, что XV/V 1-
Разложим по этому параметру левую часть (5) и ограничимся
членом первого порядка. Тогда
41. а) Согласно примеру 5, при изотермическом процессе при
постоянном объеме дЙ^ин = б/'’, поэтому
Гд (Жмин/т &F 6S _ 8U
L дТ Jy Z2 Т 7'2 ’
При постоянном объеме (работа не производится) из этого соотно-
шения следует
б) При изотермическом процессе при постоянном давлении
бТРМин = бС!, откуда
Р (6ТГмин/7’)-| _ 60 65 _ №
L дТ Jp Z2 Т Z2 ’
В случае постоянного давления из этого соотношения следует
дЯ = б'(?.
42. Пусть уравнение состояния реального газа записано в виде
pV = f{p, Т) = А + Вр + Ср2+ ... .
С помощью соотношения (дСр!др')т= —Т (d2V/dT2)p (см. задачу 17,
п. «б») находим
134
Гл. 2. Второй закон термодинамики
где Ср” — молярная теплоемкость при нулевом давлении. Подставим
в это соотношение уравнение состояния и проведем интегрирование
с учетом того, что А — Т, А"(Т) = 0 (см. решение задачи 37).
При этом получаем
С^ = Ср + ТВ"р + ~ТС"р^+... . (1)
Следовательно, с помощью этого соотношения можно экстраполи-
ровать значения Ср, полученные при различных р и фиксирован-
i=7/7i
Фиг. 43.
ной температуре Т, и опреде-
лить Ср0>.
43. Обозначим критичес-
кую точку через (рс, Vc, Тс)
и введем b = p!pc, b = V/Vc,
t = T/Ta. Тогда уравнение Ди-
теричи запишется в виде
p(2b —l) = texp (2 — А)
(1)
(см. гл. 1, задача 12). Усло-
вие равенства нулю коэффи-
циента Джоуля — Томсона
(дТ/др)н = О означает, что
T(dV/dT)p — 7 = 0, или
( дЬ \ b
(2)
Дифференцируя (1) по t при
постоянном р и подставляя
туда (2) вместо db/dt, полу-
чаем
b = . (3)
Исключая с помощью этого
равенства b из (1) находим
р = (8 —t)exp А) . (4)
На фиг. 43 изображен график
этой зависимости. По одну
сторону от кривой темпера-
туры инверсии (дТ1др)н > Q, т. е. при расширении газа в про-
цессе Джоуля—Томсона происходит его охлаждение, а по дру-
гую (дТ!др)н <0, т. е. при расширении происходит нагрева-
Решения
135
ние газа. На фиг. 43 приведена также экспериментальная кри-
вая для водорода Н2. Аналогичное рассмотрение можно провести
и для газа ван дер Ваальса, уравнение состояния которого в при-
веденных величинах имеет вид
(см. гл. 1, пример 8). Дифференцируя его по 1, получаем
откуда
(4?)р = 3(р —3/ij2 + 2/ij3) • (
Подставляя сюда условие Т (dV/dT)p — 7 = 0, или
с учетом уравнения состояния (5) имеем
Ь2 ) (Ь з) — 3t b/ Ь2 + ьз ) >
откуда
» = КМ)- <8>
Подставляя уравнение (8) в (5), находим
18 ( h 1 V— 8 t
t>2 ( ь з ) з *’
ИЛИ
ь=------(9)
Исключая с помощью (9) b из (8), получаем
р = 24/31-121-27. (10)
Это уравнение и определяет кривую инверсии на р— 1-диаграмме.
Как показано на фиг. 43, эта кривая имеет максимум при 1 = 3,
где р = 9.
44. Коэффициент Джоуля — Томсона ц определяется (см. зада-
чу 24) следующим образом:
цср = Г (зу)р —у, (!)
136
Гл. 2. Второй закон термодинамики
где и ( = 1/р) — удельный объем, Т — абсолютная температура.
Обозначим через с'р и ц' значения коэффициентов и ц в эмпи-
рической температурной шкале 9. Они имеют вид
Ср = ср , (2а)
, / 39 \ и’Э ,оя
(2б>
Аналогично
( dv \ __ I dv \ d9
\~дТ )р~ \dQlp~df •
Если 9 — температура, определяемая с помощью газового термо-
метра, то 9 = const Хи, откуда ди/дЭ — vlQ. Следовательно, соотно-
шение (1) с учетом (3) будет иметь вид
, , Т d()
И cT>-~Q--df v~
ИЛИ
^ = i + p'c;ps/(9), (4)
откуда
Bi
, Л Г d9
Ь То - J О/ (9) ’ (5)
О о
где функция / (0) определяется соотношением (4) и может быть
вычислена по измеренным значениям плотности р, удельной теп-
лоемкости ср и коэффициента Джоуля — Томсона ц'. Если изве-
стно значение Т0, соответствующее какой-либо стандартной точ-
ке 0О, то калибровку 7’. и 9< можно осуществить, проводя числен-
ное интегрирование соотношения (5).
45. Согласно соотношению (1) решения предыдущей задачи,
имеем
Т ^Ср’
откуда следует, что
dT dv dv 1 dp 1
Т ~ vр.с р — v 1 + рцср~ р 1 + рцср ’
Подставим сюда
= — а(1 +а9)-х (а = 0,003669)
и проинтегрируем; в результате получим
* t
, Г __ Г czd3 1
Го J 1 4~а0 1Ц-р|лср
Решения
137
Пусть Т= 100 + Z’o (£=100), тогда
100
, , 100\ Г (xd0 1
In 14-— = \ =—5Г------------ . (1)
V TQ) J 1 + а9 1 + рцс„ х
0
В первом приближении (1 -1- рцсу)-1 ~ 1, тогда То 1/а. В следую-
щем приближении положим
(1 4- ррср) 1 = 1 + f (2)
и запишем (1) в виде
100
ln(l + ^)=ln(l + 100a) + a j ^d0. 3)
о
Далее можно записать То в виде То = а-1 -\-х, тогда (3) примет
вид
100
j ri+xg/jl + OT»,-, = Г df) 4
L 1-|-а:а J J 1 + а9 4 ’
о
Так как х и гга/(1 100а) малы по сравнению с а, левую часть
соотношения (4) можно разложить в ряд и ограничиться лишь
членом первого порядка по х. Тогда
100 100
ж ----------11= f С g(0)d0. (5)
\l-f-100a ) J 14-СХ0 J ° '
о о
Функцию g (0) = / (0)/(1 + а0) можно найти по численным дан-
ным, приведенным в таблице.
0, град f (0) g(9)
0 -0,00329 -0,00329
25 — 0,00258 — 0,00235
50 -0,00198 -0,00167
75 -0,00153 -0,00120
100 -0,00121 -0,00088
Укажем необходимые соотношения между различными физи-
ческими единицами: 1 кал = 4,18-107 эрг, 1 кГ/см2 =
= 0,98-10® ед. СГС, откуда рцср = рц'ср-4,18-107/0,98-10®
(где р/ и Ср — значения в использованных в условии задачи
единицах). Так как величина а задана лишь четырьмя знача-
щими цифрами, для х необходимо только две цифры. Поэтому
138
Гл. 2. Второй закон термодинамики
в рассматриваемой задаче можно ограничиться приближенным
интегрированием. При этом из (5) получаем
—0,269 х = — 0,183,
или
х = 0,68,
откуда
То = (0,00366g)-1 + 0,68 = 273,2.
ОТСТУПЛЕНИЕ 7
Ожижитель гелия Капицы. В 1908 г. Кэммерлинг Оннесу уда-
лось получить в жидком состоянии гелий, последний из так назы-
ваемых «вечных» газов. Трудность ожижения гелия объясняется тем,
что для него температура инверсии эффекта Джоуля — Томсона очень
низка. Поэтому для того, чтобы иметь возможность использовать
эффект Джоуля — Томсона, необходимо предварительно охладить
гелий до температуры жидкого водорода. В методе Кэммерлинг Оннеса
эффект Джоуля — Томсона использовался поэтапно; сначала он при-
менялся для охлаждения водорода, а затем гелия. В настоящее время
наиболее распространен метод, в котором на первом этапе охлажде-
ние производится не водородом, а путем адиабатического расширения.
Метод адиабатического расширения впервые был использован Кло-
дом и Хейландом при получении жидкого воздуха, а затем П. Л. Ка-
пица применил его для гелия. Примером ожижителя такого рода может
служить машина Коллинза.
Чтобы представить себе основные процессы, происходящие при
ожижении, рассмотрим фиг. 44—46, где схематически изображены
ожижитель, его S — 7-диаграмма и энтропия гелия. Для простоты
тепловую изоляцию системы будем считать идеальной, а падение
давления вдоль трубок — пренебрежимо малым. В процессе а -> Ъ
при температуре 7\ (-—300° К) производится сжатие газообразного
гелия от давления р, (~1 атм) до более высокого давления р2 (на-
пример, 15 атм). Это сжатие происходит адиабатически, поэтому оно
сопровождается увеличением температуры газа. Затем газ охлажда-
ется (Ъ -> с) водой до температуры Гр Далее газ охлаждается (с -> d)
до температуры Г3 (~77° К) с помощью жидкого азота, протекающего
через теплообменник I.
Затем поток газа разделяется на два потока 1 и 2, первый из них
попадает в детандер, где газ расширяется при адиабатических
условиях. При этом (энтропия постоянна, Д5 == 0) газ охлаждается
от Г3 до Г4 (d -> у) и проходит через теплообменник II, охлаждая дру-
гой поток (2) газообразного гелия. После этого он возвращается в ком-
прессор (у -> а). Поток 2 при прохождении теплообменника II охлаж-
дается до температуры Г4 (d -> е). Затем этот поток через клапан Джоу-
ля — Томсона поступает в контейнер для жидкого гелия. Темпера-
тура газа, проходящего через клапан, должна быть меньше темпера-
туры инверсии эффекта Джоуля — Томсона, чтобы могло происходить
охлаждение газа за счет этого эффекта. При этом часть газа сжижается
(/г). Остальной газ возвращается в теплообменник III (i -> у). Послед-
ний служит для охлаждения потока поступающего газа (е -> f) до
температуры Г6, при которой работает клапан Джоуля — Томсона.
Далее этот газ соединяется в точке у с потоком 1 и возвращается
В компрессор (у -> а).
6
Жидкий
азот
Фиг. 44.
Принципиальная [схема 'ожижителя
Капицы для гелия.
т
ф и г. 45, S — Г-диаграмма ожижителя,
Фиг. 46. Энтропия гелия.
Л итература
141
Значение к. п. д. всего процесса ожижения можно вычислить сле-
дующим образом. Процесс Джоуля — Томсона (/ -> g) характери-
зуется равенством
Hf^Hg (ЬН = О),
где Н — энтальпия на 1 моль газообразного гелия, а индексы соответ-
ствуют точкам диаграммы. С другой стороны,
Я^ = т]оЯ/г + (1— Ло) Hi,
где т]о— относительное количество газа, ожиженного в точке g, а индек-
сами h и i помечены значения энтальпии соответственно в жидком
и газообразном состояниях. При охлаждении газа на участке е -> /
потоку газа, идущему из контейнера для жидкости (г -> у), передается
тепло Не — Hf. Следовательно,
Яе—Я/ = (1 —т]0) (Hj-Н^.
Исключая из этих уравнений Hj и Н g, получаем
Н3^Не
^хч>=х1Ц=н^
где z—доля газа в потоке 2.
ЛИТЕРАТУГ1
1. Echelle Internationalle Pratique de Temperature de 1948, Edition amendee
de I960, Paris, 1960.
2. Caratheodory C., Math. Ann., 61, 355 (1909).
3. Born M., Phys. Zs., 22, 218, 249, 282 (1921).
4. Wilson A. H., Thermodynamics and Statistical Mechanics, Cambridge,
1957.
ГЛАВА 3
Термодинамические функции
и условия равновесия
В этой главе в качестве нового принципа вводится третий закон
термодинамики, однако основная задача заключается в том,
чтобы создать у читателя возможно более ясное представление
относительно общей структуры термодинамики. Применение раз-
личных термодинамических функций и составление уравнений
для них несколько напоминают математические упражнения.
Мы надеемся, что читатель не запутается в этих расчетах и сумеет
проследить физические идеи, которые в них заключены. Здесь
еще раз приводится формулировка условий теплового равновесия,
поскольку именно они лежат в основе применения термодинамики.
В связи с этим обсуждаются термодинамические неравенства
и принцип Ле-Шателье — Брауна и рассматривается их приме-
нение к простым системам.
ОСНОВНЫЕ ПОЛОЖЕНИЯ
§ 1. Термодинамические функции
Система в состоянии термодинамического равновесия характе-
ризуется термодинамическими функциями (или термодинами-
ческими потенциалами), которые представляют собой экстенсив-
ные величины — функции соответствующих независимых пере-
менных. Все термодинамические величины, характеризующие-
данную систему, могут быть получены как частные производные
термодинамических функций, а так называемые термодинамиче-
ские уравнения представляют собой связи между этими величи-
нами [аналитическая формулировка термодинамики). Термоди-
намика может дать только общие сведения относительно формы
термодинамических функций (см. § 8), но не может определить
их конкретный вид для каждой частной системы. Эта зависимость
должна устанавливаться эмпирически или с помощью статисти-
ческой механики.
Каждая термодинамическая функция зависит от своего набора
переменных. Эти переменные называются естественными незави-
симыми переменными. Если термодинамическая функция задана
Таблица 2
Термодинамические функции (определение) Естественные переменные Полный дифференциал
Внутренняя энергия U S, V, Ni d.U = TdS-pSVy'2ip.id.Ni (3.1)
Энтальпия H=--U-rpV S, Р, Ni dH = TdSyVdpy^p.icLNi (3.2)
Свободная энергия Гельмгольца (пли просто свободная энергия) F = U — TS Т, V, Ni dF = — SdT — pdV+^\.tdN i (3.3)
Свободная энергия Гиббса * (или термо- динамический потен- циал) G—F-^-pV—'ZNip.i Т, Р, Nt dG= — SdTyVdpy^indNi (3.4)
Большой потенциал ** 7= — pV—F — G Т, V, dJ =—SdT — pdV — ^Nidpi (3.5)
Энтропия S и, v, Ni dS = ^ + ^dV-^\^dNi (3.6)
Функция Массье —— Т у , V, Ni d4=-Ud + -^ydNi (3-7)
Функция Планка Ф=_^ Т у, Р, Ni / 1 \ V dtp——ffd j——dp— — ^~dNi (3.8)
Функция Крамерса J ч— т 1 V EL Т ’ ’ т + 2^(t) (3-9>
* В литературе на русском языке принято называть эту функцию термодинамиче-
ским потенциалом Гиббса, или просто потенциалом Гиббса.— Прим. ред.
** Эта функция нс имеет общепринятого названия. В современной литературе
по статистической термодинамике ее иногда называют большим потенциалом, так как она
свяаана со статистической суммой для большого канонического ансамбля.
Фиг. 47а. Внутренняя энергия натрия.
Фиг. 476. Энтропия натрия.
S, нал/моль град
500
- О
-—500
-—№00
-->500
- — 2000
V/Vt.
47в. Свободная энергия натрия.
— 2500
>- О
s
Фиг. 47г. Термодинамический потенциал натрия.
мл 1 моль
146
Гл. 3. Термодинамические функции и условия равновесия
как функция естественных независимых переменных, то термоди-
намические свойства системы определены полностью. Если же она
задана как функция другого набора независимых переменных,
то для определения всех термодинамических свойств этого недо-
статочно. [Для примера можно сравнить два случая, когда заданы
функции U (S, V) и U (Т, V).] В табл. 2 приведены основные
термодинамические функции для однородной системы, их есте-
ственные переменные и полные дифференциалы.
Поверхности, изображающие некоторые термодинамические
функции для твердого натрия, приведены на фиг. 47а — 47г.
§ 2. Преобразование Лежандра
В общем случае термодинамическая функция L естественных
независимых переменных х, у, z, . . . имеет следующий полный
дифференциал (пфаффова форма):
dL — Xdx -j- Ydy -j- Zdz -j- . . . . (3.10)
Здесь X, Y, Z, ... — функции переменных x, у, z, ... . Преоб-
разованием Лежандра называется следующее преобразование
функции L и независимых переменных:
L -> L — L — Хх,
х, у, z, . . . —> X, у, z, . . . , (3.11)
тогда
dL = — xdX + Ydy + Zdz +........
Различные термодинамические функции, приведенные в таблице,
получаются с помощью соответствующих преобразований Лежанд-
ра из функций U или S. Кроме функций, приведенных в табл. 2,
существует большое количество других разнообразных термодина-
мических функций, которые можно получить, например, из внут-
ренней энергии U (£, V, xlr х2, . . N\, N2, . ), осуществляя
последовательно преобразования Лежандра по переменным
хг, . . ., Xi, Х2, .... Эти переменные могут представлять собой
напряженность электрического поля, напряженность магнитного
поля, натяжение и т. д. Поэтому довольно трудно подобрать
подходящее название каждой такой термодинамической функции.
§ 3. Уравнение Гиббса — Дюгема
Уравнение Гиббса — Дюгема имеет вид
SdT-Vdp+^Njd^^O.. (3.12)
Основные положения
147
Здесь в явном виде рассматривается лишь работа, связанная с из-
менением давления. Поскольку числа частиц Л\, N2, . . ., от кото-
рых зависит потенциал Гиббса, являются экстенсивными пере-
менными, то, как легко видеть,
G (Т, р, aNit aN2, . . .) = aG (Т, р, N2, . . .).
Дифференцируя это соотношение по а и полагая а = 1, получа-
ем х)
V 7V; =0 (уравнение Эйлера).
. ' "^7 ' т, v, n'
з
Но так как в соответствии с (3.4)
/ dG \ _
V dNj) N’.
можно записать
(3.13)
3
Подставляя этот результат в выражение (3.4) для dG, полу-
чаем (3.12).
§ 4. Определение термодинамических величин
и термодинамические соотношения
7. Теплоемкость, удельная теплоемкость. С помощью соотно-
шений (1.10) и (2.12) имеем:
теплоемкость при постоянном объеме
; <ЗЛ4а)
\ dT /у \ дТ Jv \ дТ Jv '
теплоемкость при постоянном давлении
мачм+ОгО, <з.146>
2. Первые производные термодинамических функций. Из
(3.1) — (3.9) имеем
(^-1 =Т, (» = -р, (®) (3.15).)
\.dS/v,N \dF/s,N \dNi's, v, Nj V ’
( dS A = J_ (dS\ =P_ !dS\ _ zq ifiv
dU )v,N T , (5У )v,N T ' \dN i)u,V,N'. T ’ ' ‘ '
J 1
x) Через Nj обозначена совокупность чисел .Уг, i = 1, 2, . . ., при i Ф j.
а) Индекс N при производной обозначает дифференцирование, при
котором все JV2» • • • остаются постоянными.
10*
148 Гл. 3. Термодинамические функции и условия равновесия
(дт)у,п~ S’ ( dv )t,n~ ~Р' (ЗЛ7)
= —S, (“) _r, (-£.) =ll. (3.18)
\ ОТ / p, n \ dp ) t, N \ dNj ) t, p, N’. !j ' '
Производных от других термодинамических функций мы не при-
водим.
3. Удельные молярные величины. В многокомпонентной системе
с компонентами / = 1, 2, ... соотношение
(З-19)
определяет удельную молярную величину; здесь п,— число молей
j-ro компонента, а Ф —некоторая экстенсивная переменная.
Например,
77 ди /
Ui — ~дп~ \УДельная молярная энергия),
(УДельная молярная энтальпия),
d j = (удельная молярная энтропия),
V,-= (-^-1 (удельный молярный объем),
X. j / р
__ QQ
Q. = —- (удельный молярный термодинамический потенциал).
В частности, Gj есть не что иное, как химический потенциал
на 1 моль1).
4. Теоремы взаимности (соотношения Максвелла). Если выра-
жение (3.10) является полным дифференциалом, то
Эти соотношения являются условием того, что левая часть урав-
нения (3.10) представляет собой точный полный дифференциал
(условие интегрируемости, или условие существования функции L).
Легко написать уравнения, соответствующие условию (3.20), для
дифференциалов (3.1) — (3.9). Конечно, не все эти условия, назы-
ваемые соотношениями Максвелла, являются независимыми (см.
замечание к примеру 2). Из соотношений (3.17) и (3.18) имеем,
0 В связи с этим существуют различные наименования величины Gj
удельная молярная свободная энергия, свободная энергия Гиббса на 1 лоль,
(молярная свободная энергия и т. д.).
Основные положения
149
например,
IdTjy.A’’ \др)т, N~ \dT)p,N’ ^-Zla)
а из (3.7)—
(^-) = “б7Г/пШ v=7’(^f) -Р- (3‘216)
к б/ /T,N д(1/Т) V I /v,N к ОТ }v,N г '
Некоторые из этих соотношений мы уже получали в примерах и
задачах гл. 2, однако в этой главе мы исследуем их более систе-
матически.
5. Соотношения, получаемые преобразованием переменных. Тер-
модинамические функции и получаемые из них термодинамиче-
ские величины не всегда рассматриваются как функции своих
естественных переменных. В термодинамике часто бывает необ-
ходимо производить ту или иную замену независимых пере-
менных и выводить соотношения между различными производными.
При этом часто используется формула (1.23)
б.г \ (dz/dy)x
Oy/z (dz/dx)y ’
или в более удобном для запоминания виде
( \ =_1.
к ду )z к oz )х к дх /у
При преобразовании переменных удобно использовать
д{и, у, ) _ д(и, у, ...)/6(g, 1), ...)
d(z, у, ...) ~ д(х, у, ...)/6(g, Т], ...) ’
в частности,
/ ди \ __ д (и, у, z, .. .)
к Эх /у, Z, . . . ~ д (х, у, Z, ...)
(3.22а)
(3.226)
якобианы
(3.23)
(3.24)
§ 5. Третий закон термодинамики (теорема Нернста — Планка)
Энтропия химически однородного тела конечной плотности
при стремлении температуры к абсолютному нулю стремится
к предельному значению, не зависящему от давления, плотности
или фазы. Удобно поэтому принимать состояние при 0° К за некото-
рое начальное состояние [см. соотношение (2.11)1 и считать, что
limS = Sos0. (3.25)
Г->0
Тогда энтропия произвольного состояния определяется однознач-
ным образом. Найденную таким образом энтропию называют
иногда абсолютной энтропией.
150
Гл. 3. Термодинамические функции и условия равновесия
Из этой теоремы можно вывести несколько важных следствий.
mo-первых, никакими способами нельзя достичь абсолютного нуля
Вемпературы (недостижимость абсолютного нуля) и, во-вторых,
теплоемкость, коэффициент теплового расширения и некоторые
другие аналогичные величины должны стремиться к нулю при
температуре, стремящейся к нулю. Теорема Нернста — Планка
имеет большое значение для изучения химических реакций
(см. гл. 4, § 15).
Если говорить об истории вопроса, то эта теорема была выведе-
на из целого ряда экспериментальных фактов и поэтому представ-
ляет собой, как и другие законы термодинамики, эмпирически
установленный принцип. Вместе с нулевым, первым и вторым
законами он образует систему основных аксиом, на которых
покоится логическая схема термодинамики.
С точки зрения статистической механики, в которой исполь-
зуется атомистический подход, третий закон является следствием
квантовомеханической природы микроскопического движения
материи.
§ 6. Равновесие двух систем
Если две системы А и В находятся в термодинамическом кон-
такте, то в зависимости от природы контакта возможны следую-
щие условия равновесия:
1) механическое взаимодействие (механическое равновесие):
Ра = Рв и т. д. г); (3.26а)
2) тепловое взаимодействие (тепловой обмен): ТА — Тв; (3.266)
3) материальное взаимодействие (обмен частицами вещества):
pf = gf. (3.26в)
Доказательство. Если мы рассматриваем изолиро-
ванную систему, то условие равновесия для составной системы
имеет вид (см. гл. 2, § 10)
SA + SB = max. (3.27)
Поскольку система А + В является изолированной, имеем также
дополнительные условия
UA-\-UB = const, VaA~Vb = const, Nf + TVf = const,
7 = 1,2,....
0 В случае неплоской границы и отличного от нуля поверхностного
натяжения давление не будет одинаковым. Подобные случаи здесь не рас-
сматриваются (см. гл. 4, § 3).
Основные положения
151
Эти условия можно записать следующим образом:
&SA + dSB = O, (3.27')
dUA + dUB = 0, dVA + dVB = Q, dA^ + dA’f = O,
7 = 1, 2, ... . (3.27")
С помощью (3.6) перепишем соотношение (3.27') в виде
ЙУд _ 2 + 6FB - 2 V- = 0
1 А 1 А 1 А 1 В 1 В 1 в
или, учитывая (3.27"),
(т7“тг) 6/7а+(к~к) 6Уа~2 (гл~Гв} бл'*=°-
Условия (3.26а) — (3.26в) можно получить отсюда, рассматривая
различные возможные изменения состояния при заданных огра-
ничениях.
§ 7. Условия равновесия для заданного термостата
Условие теплового равновесия было сформулировано в гл, 2,
§ 10, и гл. 3, § 6. Подойдем теперь к нему с более общей точки
зрения.
Общее условие равновесия. Пусть рассматриваемая система
находится в контакте с термостатом, характеризующимся темпе-
ратурой Г<р), давлением химическим потенциалом /-го компо-
нента цУ (j = 1, 2, . . .), и пусть на нее действуют силы Xi^.
Если состояние системы претерпевает виртуальное смещение,
-определяемое величинами bU, &S, дУ, ёУj (j = 1, 2, . . .)
и dxt (j = 1, 2, . . .) при вышеупомянутых условиях, то в соот-
ветствии с первым законом [см. (1.5)1 имеем
t>'Q= 6U+ pw8V-2 Х[е)?1.щ - 2
i j
В силу второго закона такое смещение не может реализоваться,
если
W _ тшд8 + р?е,бУ- 2 X^dxt - 2 №Nj >0. (3.28)
2 j
Это и есть условие равновесия в его наиболее общей форме.
152
Гл. 3. Термодинамические функции и условия равновесия
Из неравенства (3.28) следует, что для функции U (S, V, х},
х%, ...) должны выполняться следующие условия:
дУ dS = Т dz? (в) dv~p~pm,
dU dxt = Xi = X(e\ 1 = 1, 2, ... , (3.29)
dU dNj = ГН = ^е), 7 = 1, 2, ... ,
которые представляют собой условия равновесия между системой
и термостатом. Эти условия являются следствием равенства нулю
вариации первого порядка левой части неравенства (3.28). Отно-
сительно величин второго порядка см. § 8.
Для различных частных случаев соотношение (3.28) можно
представить в следующем виде.
Условия равновесия для замкнутой системы в случае, когда
работа связана только с изменением объема, будут иметь вид:
6U > 0 в случае постоянного объема V и энтропии S системы;
(3.30а)
ЬН > 0 в случае постоянного давления р = рйд и энтропии
5 системы (3.306)
&S < 0 для адиабатического перехода; (З.ЗОв)
6F > 0 в случае постоянного объема V системы и Т = Т^; (3.30г)
6G > 0 для постоянного давления р — р^ и Т = Т^. (З.ЗОд)
Устойчивость теплового равновесия. В статике максимум потен-
циала соответствует неустойчивому равновесию; в термодинамике,
однако, неустойчивое равновесие не может существовать. Нера-
венства (3.28) или (3.30а) — (З.ЗОд) означают, что необходимым
условием равновесия является равенство нулю вариации первого
порядка. Выполнение этого условия не гарантирует, однако,
устойчивости равновесия. Необходимо, чтобы условие минимума
или максимума удовлетворялось и во втором (или более высоких)
порядке (см. § 8).
Метастабилъное равновесие. Рассмотрим случай, когда F имеет
более чем два минимума при постоянных, например, Т и V, как
показано на фиг. 48. При таких условиях наиболее устойчивым
является состояние, соответствующее наименьшему значению
свободной энергии. Наоборот, состояние, соответствующее самому
[Основные положения
153.
мелкому минимуму, является метастабильным равновесным
состоянием. Метастабильное состояние реализуется в действитель-
ности почти так же часто, как и стабильное состояние (примеры:
переохлажденное или перенасыщенное состояние), однако оно
Наиболее метастабиль- Переменная
устойчивое ное состояния
состояние состояние
Фиг. 48.
разрушается спонтанно или с помощью какого-либо «спускового»
механизма, причем система переходит в устойчивое состояние
с меньшим значением свободной энергии.
§ 8. Термодинамические неравенства
Чтобы состояние, определяемое уравнениями (3.29), было-
равновесным, левая часть неравенства (3.28) должна оставаться
положительной при любом изменении параметров состояния тер-
мостата. Запишем для простоты [см. (2.15)]:
(5, V, х2, Nz, ...) = (Yi, Yz, ...), (3.31a)
(Г, -p, Xi, X2, ..., И1,И2, = yz, ...) (2/i = ^) • (3-316)
Так как вариация второго порядка имеет вид
W7 =4 S 3 ^Гк erfiY, = 1-2 t,Sl6Y„
г k г
то вышеприведенное условие означает
ЕЕ
г k
(3.3 2а>
ИЛИ
2 byibYi = bTbS-8pf>V+ 2 + 2 (3.326)
154 Гл. 3. Термодинамические функции и условия равновесия
Условие (3.326) является более общим, чем (3.32а); например,
-если в качестве независимых переменных вместо (3.31а) выбрать
(2/1, У2, • • •, Уг, Yr+i, Yr+г, • ), то получим
'y’jYr+l ...
,6г/гбУл +
У, Yh
г=1
щУг+i-. •
tyi&Yk 4
,бУйбУг>0.
(3.32в)
Условие положительности вариации второго порядка. Чтобы
вариация второго порядка, т. е. квадратичная форма (3.32а)
или (3.32в), была положительна, должны быть положительными
главные миноры матрицы ее коэффициентов *). Например, для
•формы (3.32а) имеем
д'ЧЗ d2U дЧЗ
oYk! Vk, •• !jY^Yhn
дЧЗ дЧЗ d2U
эу12 ’ dYb dYk «2 КП >0 (» = 1, 2, ...). (3.33)
dW
дЧГ
dYkn
С Квадратичная форма
т ?п
Ф = 2 S aihxixk
г, fe=l
может быть приведена к диагональному виду
т
ф=2м
г=1
•с помощью ортогонального преобразования xt = S Т^у^. Положительная
определенность ф означает, что все собственные значения щ, . . ., ап матри-
цы А = (aik) положительны. Так как а! ... ап = де1Т~гАТ =
= detT-1 debl detT = det.4 (поскольку detT = detT-1 = 1), то det Л
должен быть положителен. Главным минором матрицы А называется опре-
делитель п X п матрицы, составленной из матрицы А путем выбора соответ-
ствующих п столбцов и строк (и, i2, • • ., in)- Квадратичная форма, соответ-
ствующая этой матрице, является частным случаем формы Ф, получающимся
при условии, что только определенные могут принимать конечные значе-
ния. Следовательно, эта квадратичная форма должна быть положительной.
С помощью аналогичных соображений приходим к выводу, что сам главный
минор должен быть положительным. Таким образом, получаем, что для
положительно определенной формы ф все главные миноры должны быть
иоложительны.
Основные положения
155
Здесь У^, . . ., Yhn представляют собой п произвольных пере-
менных из совокупности УУ2, ... . Аналогичные условия
можно написать и для (3.32в).
Термодинамические неравенства (1). а) Простейшее из условий
(3.33) заключается в том, что все диагональные элементы матрицы
коэффициентов (3.32а) или (3.32в) должны быть положительны:
( dyk X
I dYh )y
или
dPJ
IyI
>0,
k'
>0,
(3.34a)
(3.346)
V dyt )у.,уг+1.
dyk \
dYh )Vi. . ,yr, Yk.
Например,
(»«<«• o: / d^l \ dNi / s,V, N't 4 ' i ) =-^>0 (Cp>0), (3.35a) ' p '-'p )t<0, (3.356) 1 >0. (3.35b) ' T, p, N'i
б) Следующим простейшим условием является условие положи-
тельности определителя минора второго порядка. Например,
dW 94J
dS2 dp2
7 d2U
\ dS dV )
(3.36)
(см. пример 5).
Термодинамические неравенства (2). Если в качестве перемен-
ных в (3.31а) или (3.316) взять (Уь У2, ...) и (г/±, у2, ...), то
получим, что должны выполняться неравенства
( dyi X 7 dyt X
I dYi dYi )Yk'
\ dyt JYk^ \ dyt ) yh
например,
/ dT x 7 dT x 7 dS x / dS x г
I'dS'fv’ИЛИ1^Т )y<(’dT Jp’TaK 4T0
( dp \ 7 dp X I 7 dp X I I 7 dp X I
I dV )t^ I dV )s ’ I \ dV hr I I dV JT| '
(3.37a)
(3.376)
(3.38a)
(3.386)
156 Гл. 3. Гермодинамические функции и условия равновесия
Доказательство соотношений (3.37а):
( dyi \ _ d(yh yk) _ d(yhyk) d(Yh Yk) _
\dYi)yh d^Yi.yk) d(Yt,Yk} d(Yi, yk)
(dyi/dYi)yk (dyh/3Yfe)y; — {3yi/dYk)yt (dj/fc/dl" ^Yk
(dyk/dYk)r.
( dyt (dyt/dYkYYi dy.
I dYi )Yh (dyk/dYk)Yi '\dYt h’h'
(3.39)
Здесь мы использовали уравнение (3.34а) и соотношение Максвелла
/ dyi \ _ / дук \ _ d2U
I dYk /у. I dYi /Yk dYi dYk •
Аналогичным образом доказывается неравенство (3.376) (см. зада-
чу И).
§ 9. Принцип Ле-Шателье — Брауна
Принцип Ле-Шателъе. Если система в состоянии равновесия
подвергается воздействию А, то прямая реакция системы а будет
такова, чтобы уменьшить действие А. Этот принцип представляет
собой физическую интерпретацию неравенств (3.34а) и (3.346),
выражающих условие устойчивости равновесия.
Пример. Пусть два тела 1 и 2 находятся в равновесии при
температуре Т (фиг. 49). Предположим, что равновесие наруши-
лось, например увеличилась температура тела 1 (действие А);
1 2
Тепло Т+АТ 5= => Т
Фиг. 49.
тогда тепло будет переходить от тела 1 к телу 2 (реакция а). Это
приводит к уменьшению разности температур АТ. Наличие потока
тепла 6Q означает уменьшение энтропии 6S = — &Q/T тела 1:
так как (dT/dS)v = T/Cv > 0, то температура тела 1 уменьшается
на величину ЪТ = (T/Cv) 65 = — bQICv.
Замечание. Действие А и соответствующая прямая
реакция а определяются изменением сопряженных термодинами-
ческих величин (yt и У; или У; и у^).
Основные положения
157
Принцип Ле-Шателье — Брауна. Если система в состоянии
равновесия подвергается воздействию А, то обусловленная этим
воздействием косвенная реакция Ъ будет стремиться уменьшить
действие А. Этот принцип является физической интерпретацией
неравенств (3.37а) и (3.376).
Пример. Вещество заключено в теплопроводящий цилиндр
с поршнем (фиг. 50). Поршень уравновешивается внешним давле-
нием р. Затем веществу сообщается количество тепла AQ (дей-
ствие А) и равновесие нарушается. Прямая реакция состоит
Р
Т-*Т + ДТ
Смещение
Ф и г. 50.
в увеличении температуры вещества АТ (реакция а). Кроме того,
могут измениться давление и объем: при этом поршень сместится
(косвенная реакция Ь). Неравенство (3.38а) означает, что
(ДТ)у>(АТ-)р (А5 = ^).
Таким образом, изменение температуры будет больше в том слу-
чае, когда не может произойти изменения объема (фиксированное
положение поршня), чем в том случае, когда изменение объема
допускается (подвижный поршень). Полученное неравенство озна-
чает также, что во втором случае поршень будет двигаться таким
образом, чтобы уменьшить эффект действия А.
ОТСТУПЛЕНИЕ 8
О названиях термодинамических функций. Слово «энергия»
(svepyeia) можно найти уже в трудах Аристотеля, однако термин
«внутренняя энергия» был введен Томсоном (1852) и Клаузиусом (1876).
Приставка «эн» означает емкость, содержание (Inhalt = capacity),
а корень «эрг», аналогично единице с тем же названием, происходит
от слова e'pyov (работа). Термин «энтропия» также принадлежит Клау-
зиусу (1865); он образован от греческого sVTpeiteiv (изменение) и озна-
чает изменяющуюся величину (Verwandlungsinnalt). Каммерлинг
Оннес (1909) предложил термин «энтальпия», происходящий от слова
158
Гл. 3. Термодинамические функции и условия равновесия
evQaXneiv (нагреваться, sich erwarmen) и означающий теплосодержание
(Warmeinhalt). Гиббс называл эту величину тепловой функцией (при
постоянном давлении). Название «свободная энергия» обязано своим
происхождением Гельмгольцу (1882); оно используется для обозна-
чения той части внутренней энергии, которая может быть преобра-
зована в работу, как видно из уравнения dF = d'A для изотермиче-
ского квазистатического процесса. Остающуюся часть TS внутренней
энергии U = F + TS раньше часто называли связанной энергией
(gebundene Energie), однако теперь это не принято. Свободная энер-
гия Гиббса (для постоянного давления) была введена Гиббсом; немец-
кие ученые часто называют ее свободной энтальпией (die freie Enthal-
pie). Таким образом, термодинамические функции часто имеют раз-
личные названия на немецком и английском языках ]).
Что касается уравнения состояния, то Каммерлинг Оннес назвал
уравнение р = р (Т, V) термическим уравнением состояния (thermi-
sche Zustandsgleichung), а уравнение U = U (5, V) калорическим урав-
нением состояния (Kalorische Zustandsgleichung). Планк же (1908)
назвал последнее каноническим уравнением состояния (kanonische-
Zustandsgleichung).
ПРИМЕРЫ
1. Доказать справедливость следующих двух положений,
поясняющих физический смысл понятия энтальпии:
а) Энтальпия системы равна сумме внутренних энергий систе-
мы и источника работы, который оказывает на систему давлении
//'О, равное однородному давлению р внутри системы.
б) Если изменение состояния системы происходит при постоян-
ном давлении причем как до, так и после перехода она нахо-
дится в состоянии теплового равновесия, то поглощенное системой
количество тепла равно возрастанию энтальпии независимо от
того, является ли изменение обратимым или необратимым.
РЕШЕНИЕ
а) Рассмотрим цилиндр с площадью поперечного сечения ст,
показанный на фиг. 51. На невесомый поршень помещен груз, так
что внешнее давление обусловленное грузом, равно внутрен-
нему7 давлению газа. Это давление определяется соотношением
P = #e, = V’ (1>
где g — ускорение силы тяжести, а М — масса груза. Если пор-
шень находится на высоте -z, то занимаемый газом объем равен
V = az. Источником внешних сил будем считать груз, помещен-
ный на поршень, а также добавочный груз, находящийся на фикси-
рованном уровне вне цилиндра. Считая этот уровень нулевым,
мы можем записать потенциальную энергию груза, помещенного"
на поршень, в виде Ue = Mgz. (На самом деле эта энергия пред-
!) См. примечания на стр. 143.— Прим. ред.
Примеры
1 за-
ставляет собой энергию сложной системы, состоящей из грузов
и Земли, однако поскольку мы неявно признаем неизменность
состояния Земли, то имеем право называть величину Ue энергией
грузов.)
Рассмотрим далее изменение внутренней энергии U* полной
системы, состоящей из газа и грузов. Обозначая внутреннюю
энергию газа через U, запишем при учете соотношения (1)
dU* = dU + dUe = dU + d (Mgz) = dU + d (paz)—d (U+pV),
= dH. С точностью до произвольной постоянной мы
Перенесем некоторый добавочный вес
или dU*
можем положить U* = Н.
dM с нулевого уровня на
поршень; при этом произ-
водимая нашими руками
работа dMg (z -|- dz) = dMgz
(в пренебрежении члена-
ми второго[порядка мало-
сти вида dM dz) равна V dp.
В выражении
dU* = dU + pdV+V dp
первый член dU представ-
ляет собой изменение внут-
ренней энергии газа, а
член р dV (обусловленный
изменением высоты порш-
ня) вместе с членом V dp
составляет изменение энер-
dM
о о
гии источника внешних Фиг. 51.
сил. Заметим, что по пред-
положению давление газар 1
все время находится в равновесии с внешним давлением р(е),
а потому переменные (М и z), описывающие состояние внешнего"
источника чисто механической работы, однозначно определяются
переменными состояния термодинамической системы (газа).
б) В соответствии с первым законом для перехода из одного
равновесного состояния 1 в другое равновесное состояние 2 при
постоянном давлении р(е), имеем
u2-u1 = q + a = q- р™ (V2 - V1).
При этом предполагается, что не происходит никакого обмена
работой с окружением, за исключением обмена, связанного
с изменением объема. [Даже в том случае, когда давление в систе-
ме р не все время сохраняется равным р(е), выражение для работы
А = — р(е) (V2 — Vi) остается справедливым.] Поскольку р(е) —
160 Гл. 3. Термодинамические функции и условия равновесия
= р как в состоянии 1, так и в состоянии 2, то, очевидно,
(П2 + рУ2) - {Ul + pVi) = Нг-1Ц = Q.
Именно по этой причине Н называют тепловой функцией.
Хотя в качестве примера были рассмотрены газы, однако
доказательство носит весьма общий характер. Источник работы
может быть иным.
Замечание. На фиг. 52 представлен трехмерный график
энтальпии Щр, Т) для воздуха. Здесь С — критическая точка,
Фиг. 52. Энтальпия воздуха.
{дН1дТ)р = Ср — теплоемкость при постоянном давлении. Что
такое (дН/др)т?
2. Показать, что справедливо следующее соотношение между
внутренней энергией U, энтропией S, объемом V, температурой Т,
давлением р и теплоемкостью при постоянном объеме Су’.
Примеры
161
РЕШЕНИЕ
Первое равенство уже было доказано выше [см. соотношение
(3.216), а также гл. 2, примеры 2 и 4 и задача 15]. Для доказатель-
ства второго равенства преобраз>тем левую часть соотношения
Максвелла (3.21а), (dSldV)T,N = (dpldT)v,N. Используя (3.226),
получаем
/ dS \ / дУ \ / дТ \ = _
I дУ дТ Js.H dS )v,n Ъ
Но в соответствии с (3.14а) (dSldT)VtN = CvIT, так что
/ dS \ / дТ \ Су
\ дУ J Т, N \ дУ J S, N Т
Замечание. Первое равенство было выведено выше
с помощью соотношения (3.7). Его, однако, можно получить
и из других уравнений, причем в этом случае задача сводится
к замене переменных в соотношении Максвелла. Это означает,
что не все соотношения Максвелла являются независимыми. Так,
в гл. 2, пример 2, мы исходили из уравнения (3.6). Другое дока-
зательство приведено в решении задачи 5.
3. Показать, что уравнение состояния р = f (Т, V) определяет
зависимость теплоемкости при постоянном давлении Ср (Т, р)
от давления и зависимость теплоемкости при постоянном объеме
Cv (Т, V) от объема V. Для частного случая, когда уравнение
состояния задано в виде разложения pV = А (Г) + В (Г) р +
+ С* (Г) р2 + . . ., получить соответствующее разложение для
теплоемкости, используя температурную зависимость коэффи-
циентов А, В, С*. . . . .
Показать далее, что для газа, для которого справедливо урав-
нение состояния типа идеального газа, выполняется соотношение
(дСр!др)т = 0. Показать, что если известно уравнение состояния,
то температурную зависимость Ср можно получить из температур-
ной зависимости Су (или наоборот).
РЕШЕНИЕ
Как показано в решении задачи 17, справедливы соотношения
Максвелла
( 8S \ / дУ \ ( \ — ( др \
\др)т~ \дт)Р и I ду )т~ \дт )v ’
откуда
162
Гл. 3. Термодинамические функции и условия равновесия
так ЧТО
Р
СР(Т, р) = Ср(Т, Ро)-Т j (^)pdp. (1)
Ро
Второй член в этом выражении можно вычислить с помощью
уравнения состояния. В частности, если
рУ = А(Т) + В(Т)р + С*(Г)р*+... , (2)
то имеем
(S)P = А" Р~Х + В" + С*" р + • • •
и, следовательно,
СР(Т, р)=Ср(Т, р0)-
- Т [ А" (Г) In + В" (Г) (р - р0) +
+4-С*"(Л(Р2-^)+ ...], (3)
где Ср (Г, р0) представляет собой экспериментальное значение
теплоемкости при давлении р0. В случае идеального газа А ~ Т,
а В = С — ... = 0, так что (d2V/dT2)p = 0. Следовательно, получаем
(дСр/др)т = 0.
Аналогичным образом имеем для Су
/ dCv \ _у, / 52р \
k dV )т \ дТ* )у'
так что
v
Cv (Т, V) = Cv (Т, Vo) + Т J (^)У dV, (4)
VO
где Vo— произвольно выбранный фиксированный объем. В этом
случае удобно пользоваться следующим вириальным разложением
уравнения состояния:
pV = A^ + ^ + ^+... . (5)
Используя это выражение, читатель может написать разложение
для Су.
Чтобы получить Ср из Cv или наоборот, можно использовать
решение задачи 17, п. «а» из гл. 2. Можно также действовать
другим способом и провести вычисления, аналогичные выпол-
ненным в (3.39), а именно
Ср,шл]мт-гра9
200
фиг. 53а. Молярная удельная теплоемкость воздуха при постоянном давлении.
164
Гл. 3. Термодинамические функции и условия равновесия
т ( dS \ d(S, р) д(8, р)/д(Т, V)
р { дТ )р д(Т, р) д(Т, руд(Т, V) ~
_ т (dSfdT)v (dp/dV)T-(dp/dT)v (dS/dV)T _
(dP/dV)T
= _ (эР/йУ)У ~| f т (др/дТ)у
LUr/v (dp/dV)TJ (др/дУ)т
(6)
т, °к
Фиг, 536, Молярная удельная теплоемкость воздуха при постоянном
объеме.
Здесь мы использовали соотношение Максвелла (dpldT)v =
= (dS/dV)T.~Аналогичным образом
„ d(S, V) Тд(8, У)/д(Т, р) „П as \ , (дУ/дТ^Л
1 д(Т, V) _I д(Т, v)/d(T, р) Lk дТ (дУ/др)т J
= СР + Г
(ЭУ/ЭПр
(дУ/др)т •
(7)
Величину Ср — Cv можно получить в явном виде, если подста-
вить (2) в (о) и (5) в (7).
Примеры
165
Замечание 1. В приведенном выше методе используются
якобианы. Это часто применяемый метод преобразования пере-
менных, который очень важно хорошо усвоить. Эквивалентность
соотношений (6) и (7) легко показать с помощью равенств
(др/дТ^у _ / ЗУ \ / Эр \ (av/gr)^
(Op/dV)T \. дТ /р’ \. дТ )у (дУ/др)т
Замечание 2. Фиг. 53а и 536 иллюстрируют зависимость
молярной удельной темплоемкости при постоянном давлении Ср
и молярной удельной теплоемкости при постоянном объеме Cv
от р и Т в случае воздуха.
4. Показать, что если (dU/dV)T = 0, то и (dUldp}T = 0. Здесь
U — внутренняя энергия, Т — абсолютная температура, V —
объем и р — давление.
РЕШЕНИЕ
Задача сводится к преобразованию независимых переменных
от р, Т к V, Т. Используя (3.24) и (3.23), можно написать
/ dU \ d(U,T) д (U, Т)/д (V, Т) (dU/dV)T
\.др ) г д(р,Т) ~д(Р, Т)/д(у, Т'Г~ (dp/dV)T •
[Это равенство можно доказать также, если рассматривать
U {V, Т) как функцию U (V (р, Т), Т) и продифференцировать
ее по р.] Таким образом, (dU!dp)T = 0 при^(3£773И)т = 0, если
только (dp/dV)T У=0 .
5. Показать, что в случае однородной замкнутой системы
теплоемкости при постоянном давлении и при постоянном объеме
всегда положительны и что при изотермическом возрастании
давления объем уменьшается. Показать далее, что темплоемкость
при постоянном давлении никогда не бывает меньше теплоемкости
при постоянном объеме.
РЕШЕНИЕ
В § 8 аналогичная задача уже рассматривалась с более общей
точки зрения. Здесь мы дадим решение для данного конкретного
случая. В соответствии с (3.326) запишем условие устойчивости
в виде
dTdS — dpdV > 0. (1)
Если в качестве независимых переменных взять Т и V, то соотно-
шение (1) перепишется следующим образом:
WW- (»v «W- (»т«'=>0. (2)
166 Гл. 3. Термодинамические функции и условия равновесия
Далее, поскольку dF =—SdT — pdV, то (dS/dV)T = (dp/dT)v
(соотношение Максвелла), так что из (2) имеем
и, следовательно,
Cv>0, (»т<0. (3)
Если же взять в качестве независимых переменных Т и р, то соот-
ношение (1) переходит в
+ (4)
Используя соотношение Максвелла (dS!dp)T~—(dV/dT)p, пере-
пишем (4) в виде
^бЛ-2(-^) Шр-№] 8р*>0,
1 \ дТ ) р г \ др / р
так что
Проводя выкладки, аналогичные выполненным в (3.39), найдем
( dS \ __d(S, р) _ d(S, р) д(Т, V) _
I дт )р~ д{Т, р) ~ д(Т, V) д(Т, р) ~
__ (дЗ/дТ)у (dp/dV')T — (dS/dV)T (дР/дТ)у
(др/дУ)т ~
_ / dS \ (9S/дУ)т (др/дТ)у ( dS \ (др/дТ)у
\ дТ )у (dp/dV)T_V дТ /у (др/дУ)т
[Здесь мы использовали соотношение Максвелла (9S/dV)T =
— (др/дТ)у]. Учитывая, что (dp/dV)T <Z 0, имеем
(#')p>(4f)v’ или Ст>Су-
Замечание 1. Из (1) легко получить, что (dp!dV)s О,
так что CpICy = ит/и8 > 0, и, следовательно, при Cv = 0 имеем
Ср = 0.
Замечание 2. Неравенства, аналогичные неравенствам
(3) и (5), можно получить для теплоемкости, соответствующей
произвольному конкретному процессу. Следует заметить, однако,
что в случае неоднородной системы теплоемкость может быть
отрицательной. Например, это имеет место в том случае, когда
из-за гравитационных сил система обладает высокой плотностью
в центре, или в случае открытой системы, обменивающейся веще-
ством с окружением (см. гл. 4, задача 39).
Примеры
167
6. Показать, что в случае квазистатического расширения одно-
родного тела при постоянном давлении энтропия тела возрастает
или уменьшается в зависимости от того, положителен или отрица-
телен коэффициент теплового расширения при постоянном дав-
лении.
РЕШЕНИЕ
Для решения надо рассмотреть знак производной от энтропии
по объему при постоянном давлении (dS/dV)p. Для исследования
коэффициента теплового расширения при постоянном давлении
а = (1/V) (dVldT)p удобно в качестве независимых переменных
использовать Т и р. При этом задача сводится к замене независи-
мых переменных V, р на Т, р в производной (dS/dV)p. Это осуще-
ствляется следующим образом [применяем формулы (3.23) и (3.24)]:
/ dS \ _ g(5, р) _ d(S, р)/д(Т, р) _ (.dS/8T)p _ Ср/Т
\ 8V )р d(V,p) d(V, р)/д(Т, р) (dV/dT)p~~ Va
Как было показано в примере 5, для однородного тела Ср ^-0,
и, следовательно, так как Г 0 и V 0, то знак (dS/dV)p опре-
деляется знаком а.
7. Для идеального газа известна теплоемкость при постоянном
объеме Cv = Nf (Г) (N — число молекул). Найти свободную
энергию F, внутреннюю энергию U, энтропию S и химический
потенциал ц (см. задачу 12).
РЕШЕНИЕ
Интегрируя соотношение {dS!dT)v — CVIT, получаем
j + Д7)=Д7 j /^pdr + gl(V, TV). (1)
Здесь gi (У, TV) есть некоторая функция переменных У и N.
Поскольку (j)F!dT)v = — S, интегрируя (1), находим
F= - J 5(Г)ЙГ + ^(У, ЛГ) =
= - tV рГ j f {Г>Т" - Tgi (У, N) + g, (У, N), (2)
где g2 (У, N) — функция от У и N. Интегрирование по частям дает
j dr j f {T-^dT- = T j /(7p,dr- j / (Г) dr (3)
168
Гл. 3. Термодинамические функции и условия равновесия
И
т
U = F + TS = N^ f(T’)dT' + g2(V, N). (4)
Подставляя выражение (2) в уравнение (1.11) (dF!dV)T = —р =
= —NkT/V, имеем
dg±~=Nk_ dg2 =f)
dV V ’ dV
и, следовательно,
gl = MclnV4-*(Pim, g2 = q>2GV). (5)
Подставляя далее выражения для gt и g2 в соотношение (2) для F
и дифференцируя по N, находим
Н = -^ = - J dT' J ^dr-kT^V-kT ->+-^ • (6)
Так как химический потенциал р, представляет собой (функцию
от V/N, должно выполняться соотношение
= — In N + а, или ф! = — ЛЧп Лг + N + Na (а — постоянная), (7)
~ = 0, или <р2 = Wo (фо — постоянная). (8)
Получив таким образом gt и g2 и подставив их в (1), (2), (4) и (6),
находим
F= - J dT' j Cv(T")~-NkT^-^--NkT + N(f0-NkTa, (9)
т
J Cv(T')dr + Nq0, (10)
т
s = ^Cv(T')^ + Nkln-^ + Nk + Nka, (11)
- J dT' J /(Г)-^-*7’1п-^- + ф0-*7’а =
= -рГ (/(Г^ + ^Ы^ + Фо-ЛТ’а, (12)
G = Np. (13)
Замечание. Вид функции G, обычно используемый
в случае идеального газа, приведен в решении задачи 12, соотно-
шение (5).
Примеры
16»
8. Имеется упругая пружина, подчиняющаяся закону Гука:
при постоянной температуре удлинение х пропорционально натя-
жению X. Константа пропорциональности (упругая постоянная)
к является функцией температуры. Найти свободную энергию F,
внутреннюю энергию U и энтропию 5 как функции х. Тепловым
расширением пренебречь.
РЕШЕНИЕ
Если рассматривать F как функцию удлинения х и температу-
ры Т, то
dF = - Sd Т 4- X dx. (1)
Здесь X — натяжение пружины, уравновешивающееся внешней
силой Хе, как показано на фиг. 54, и равное ей в случае квази-
статического процесса. Поэтому мы и записали работу, совершае-
мую внешней силой, в виде d'A = Хе dx = X dx. Из соотноше-
ния (1) следует ________________.
(Эг-Х = ^- <2> I
После интегрирования получаем g
F(T, х) ~ F (Т, 0)-\--^кх2, (3) g „
откуда < g х
с (т г\________ dF ’ 0)_____L к'х2_ Л
д ’ х> дТ dT 2 К х
= 5(7’,0)-1*'^ = (4)
1
U(T, х) = F-\-TS = U (I, О)+±(к-Тк’)х2.
(5) Фиг. 54.
Замечание. Обычно в механике
потенциальная энергия пружины Um и упругая сила К записы-
ваются в виде
Um = К = - = - кх.
Знаки К и X различны, так как —К dx = X dx представляет-
собой работу, производимую внешней силой. В механике условия,
при которых происходит сжатие или растяжение пружины, не-
всегда конкретизируются явным образом; Um определяется лишь-
как механическая потенциальная энергия, безотносительно-
к термодинамике. Если удлинение происходит изотермически,
то Um совпадает со свободной энергией F. Если же процесс осуще-
170
Гл. 3. Термодинамические функции и условия равновесия
ствляется адиабатически, то Um совпадает с внутренней энерги-
ей U.
9. Исходя из третьего закона термодинамики, показать, что
теплоемкость стремится к нулю при стремлении температуры
к абсолютному нулю.
РЕШЕНИЕ
Теплоемкость для некоторого заданного процесса можно запи-
сать в виде Сх = Т (dS/dT)x. Здесь (dS/dT)x представляет собой
частную производную по абсолютной температуре, взятую при
постоянном значении величины х. В соответствии с третьим зако-
ном имеем при Т -> 0.
lira S = lim — = lim
Т-^0 Т-+0 1 Г->-0
[а (Т8)/дТ\х __
(ЭТ/дТ)х
йт»[5+г(Ш=
= lim 5 lim Сх
Т-,0 Т-+0
и lim 5 = 0. Таким образом, limC’x = 0.
Т-+0 Т-+0
ЗАДАЧИ
[А]
1. Доказать следующие свойства свободной энергии Гельм-
гольца:
а) Система А находится в тепловом контакте с тепловым резер-
вуаром R, имеющим температуру Т^, равную однородной тем-
пературе Т внутри системы. Изменение свободной энергии Гельм-
гольца F системы А равно изменению суммы внутренней энергии
системы А и теплового резервуара R при условии, что тепловой
резервуар R отдает тепло только системе А и над резервуаром
не производится никакой внешней работы.
б) При изотермическом процессе работа, производимая над
системой, равна увеличению ее свободной энергии.
2. Внутренняя энергия U и энтальпия Н системы определяются
давлением р и объемом V. Доказать, что в этом случае справедли-
вы следующие соотношения:
a)
Задачи
171
Здесь Ср и Cv соответственно темплоемкости при постоянном
давлении и при постоянном объеме, х — изотермическая сжи-
маемость, а а — коэффициент теплового расширения.
3. В случае адиабатического квазистатического сжатия выра-
зить %s = (dT/dp)s (адиабатический температурный коэффициент)
через коэффициент теплового расширения при постоянном
давлении а и теплоемкость при постоянном давлении Ср. В
случае квазистатического расширения системы при постоянном
давлении выразить через %s возрастание энтропии.
4. Найти формулу для вычисления термодинамического потен-
циала Гиббса G, энтальпии Н и энтропии S по экспериментальным
значениям коэффициентов А (Г), Б (Г), С (Т), . . . разложения
уравнения состояния
pV = А (Т) + В (Г) р + С (Г) р2 + . . . .
5. Используя свободную энергию F и термодинамический
потенциал G, доказать справедливость следующих соотношений:
\dV/T 1 \ дТ Jv \др)т \дТ/р
6. Показать, что
7. Показать, что в случае газа, давление которого при постоян-
ном объеме изменяется пропорционально абсолютной температуре,
энтропия S возрастает с увеличением объема V.
8. Доказать неравенства:
») (^) <0-
' \ др )н
б) >0.
' \dV ) и
Здесь U, Н, S, Р и V — соответственно внутренняя энергия,
энтальпия, энтропия, давление и объем.
9. Показать, что следующие процессы являются необрати-
мыми: а) свободное адиабатическое расширение газа от объема V
до V + dV (dV >0) и б) процесс Джоуля — Томсона, т. е.
адиабатическое расширение газа из состояния с давлением р
до р + dp (dp < 0).
10. Коэффициент объемного расширения при постоянном дав-
лении для газов положителен. Показать, что в случае квазистати-
ческого адиабатического расширения всегда происходит пониже-
ние температуры, которое имеет большую абсолютную величину,
172
Гл. 3. Термодинамические функции и условия равновесия
чем при соответствующем уменьшении давления в адиабатическом
процессе Джоуля — Томсона.
11. а) Показать, что отношение адиабатической сжимаемости
к изотермической равно отношению теплоемкости при постоянном
объеме к теплоемкости при постоянном давлении (использовать
преобразование переменных с помощью якобиана).
б) Доказать неравенство (3.376) и использовать его для срав-
нения величин сжимаемостей при постоянной энтропии и при
постоянной температуре.
в) Дать физическую интерпретацию этого сравнения на основе
принципа Ле-Шателье — Брауна.
12. Теплоемкость при постоянном давлении (для п молей)
идеального газа обычно записывается в виде
Ср = пСр пСКОЛ (Т).
Здесь Ср — удельная теплоемкость при постоянном давлении,
обусловленная поступательным и вращательным движением моле-
кул (Ср = 5/27? для газа одноатомных молекул, Ср = 7/27? для
газа двухатомных молекул, Ср = 47? для газа из многоатомных
молекул), а Скол (Т) — удельная молярная теплоемкость, обу-
словленная молекулярными колебаниями [lim Скол (Т) = 0].
т^о
Вывести формулы для термодинамического потенциала и энтропии.
ОТСТУПЛЕНИЕ 9
лярные одна другой:
направо от р к V,
Мнемонические термодинамические диаграммы. Уравнение Гиббса
(3.1) является следствием применения первого и второго законов термо-
динамики к инфинитезимальному квазистатическому процессу,
а уравнения (3.2) — (3.4) получаются далее путем повторного приме-
нения преобразования Лежандра (3.11).
Если вы овладели двумя основными зако-
нами и запомнили определения термодина-
мических потенциалов, то для вас не пред-
ставляет труда написать уравнения (3.1) —
(3.4) с помощью приема, описанного выше.
Однако еще лучше запомнить и следующий
метод, так сказать, про черный день.
Мнемонический способ написания уравне-
ний (3.1) — (3.4) основан на использовании
диаграммы, придуманной, кажется, Максом
Борном еще около 1929 г. Прежде [всего
надо нарисовать две стрелки, перпендику-
одну сверху вниз от S к Т, а другую слева
1к показано на фиг. 55. Рисуя стрелки, вы
должны сказать себе, что солнце (Sun)-посылает лучи вниз на деревья
(Trees), а ручей течет с вершины (peak) в долину (Valley). Далее вы
дополняете диаграмму названиями четвертей круга Е (=U), F, G
и Н в алфавитном порядке по часовой стрелке. Теперь вы можете
использовать диаграмму следующим образом. Напишем, например,
Задачи
173
уравнение (3.4). Естественными переменными для термодинамиче-
ского потенциала G являются р и Т, стоящие на краях квадранта G.
В выражении для dG вы пишете —S и -|-Т7 в качестве коэффициентов
при dT и dp соответственно. Знак минус у S связан с тем обстоятель-
ством, что для того, чтобы от Т дойти до S, нужно следовать в обрат-
ном направлении ио отношению к стрелке ST.
В описанной выше диаграмме член опущен по той при-
чине, что диаграмма двумерна, а этот член одинаков для всех урав-
нений (3.1) — (3.4). В случае необходимости можно нарисовать более
общую диаграмму, включив и члены, связанные с другими
видами работы. Некоторые примеры можно найти в учебнике Колена
(1], где показано также, как применять диаграммы для написания
соотношений взаимности Максвелла.
13. Получить термодинамический потенциал Гиббса для смеси
идеальных газов, состоящей из п± молей одного и п2 молей другого
компонента.
14. Путем измерения натяжения X резиновой ленты, растяну-
той до фиксированной длины I, найдено, что X = АТ, где
А (>0) — постоянная, зависящая только от длины I, а Т — абсо-
лютная температура. Показать, что внутренняя энергия U такой
резиновой ленты является функцией только температуры, а энтро-
пия ее S уменьшается с увеличением длины.
15. Показать, что при адиабатическом растяжении описанной
в предыдущей задаче резиновой ленты температура повышается.
Показать также, что лента будет сжиматься, если повышать тем-
пературу, оставляя натяжение постоянным.
16. Из рассмотрения свободной энергии вывести уравнение
Гиббса — Дюгема (3.12).
17. Показать, что в соответствии с третьим законом термоди-
намики коэффициент теплового расширения (1/У) (dVldT)p и коэф-
фициент (др!дТ)у стремятся к нулю при Т -> 0.
18. Пусть X и х обозначают соответственно натяжение прово-
локи и ее длину. Показать, что
>0 и >0.
\dx)s,p \ дх )т,р
19. Показать, что
>о.
\dN Jt.p^
20. Парамагнитное тело имеет изотермическую магнитную
восприимчивость Хт- Найти свободную энергию F как функцию
намагниченности М и температуры Т и получить из нее внутрен-
нюю энергию U и энтропию 5.
174
Гл. 3. Термодинамические функции и условия равновесия
[Б]
21. Система состоит из N частиц одного сорта; U, Т, V и р,
обозначают соответственно внутреннюю энергию, абсолютную
температуру, объем и химический потенциал на одну частицу.
Доказать следующие соотношения:
22. Вывести формулу для вычисления теплоемкости при
постоянном объеме Cv как функции абсолютной температуры Т,
объема V и химического потенциала р,.
23. Сравнить теплоемкость системы при постоянном объеме
и постоянном числе частиц CVtN с теплоемкостью той же системы
Су, и при постоянном объеме и постоянном химическом потенциа-
ле. Объяснить физический смысл полученного результата на осно-
ве принципа Ле-Шателье — Брауна.
24. Показать, что для парамагнетика имеет место следующее
соотношение между изотермической и адиабатической восприим-
чивостями:
Cjw
Ха = Хтё|;
здесь См — теплоемкость при постоянной намагниченности,
а Сн — теплоемкость при постоянном магнитном поле Н. Измене-
ние объема парамагнитного вещества предполагается пренебрежи-
мо малым. При условии, что зависимость намагниченности М
от Т и Н задана, получить также формулу для вычисления
См — Сн. (Использовать преобразование переменных с помощью
якобиана.)
25. Рассмотреть парамагнетик, восприимчивость которого под-
чиняется закону Кюри: = СИ\ а теплоемкость при нулевой
намагниченности имеет вид: Со = ЫТ2. Получить теплоемкость
при постоянном магнитном поле Ся, теплоемкость при постоянной
намагниченности См и адиабатическую магнитную восприимчи-
вость Xs(#o) = (дМ/дН)8 (Н = Но) при бесконечно малом изме-
нении магнитного поля вблизи заданного значения Но.
26. Показать, что изотермическая восприимчивость %г удовле-
творяет условию д%т1дТ —>- 0 при Т —>- 0.
27. Показать, что с помощью адиабатического размагничива-
ния нельзя достичь абсолютного нуля температуры.
Задачи
175
28. Задачу, рассмотренную в примере 8, можно решить так-
же, используя свободную энергию F* (Т, X) = F (Т, х) — Хх.
С помощью рассуждений, аналогичных проведенным в примере 1,
выяснить физический смысл этой свободной энергии и, в частности,
dF* (Т, X).
29. Свободную энергию парамагнетика с изотермической маг-
нитной восприимчивостью Хг, помещенного в магнитное поле Нг
часто записывают в виде
F*(T, H) = F*(T, 0)-у Fxr#2-
Аналогично в качестве свободной энергии диэлектрика с диэлек-
трической проницаемостью 8 в электрическом поле Е можно-
использовать функцию
F* (Т, E) = F* (Т, 0)--^(8-1)Е2,
где V — объем. Следуя предыдущей задаче, провести сравнение
этих свободных энергий со свободными энергиями F (Т, М)
и F (Т, Р), где М — намагниченность, а Р — поляризация.
Получить также выражение для энтропии в обоих случаях.
30. Диэлектрик с зависящей от температуры диэлектрической
проницаемостью 8 (?’) помещен между пластинами плоского кон-
денсатора, соединенного с батареей, являющейся источником
Фиг. 56.
Фиг. 57.
постоянной э. д. с. (фиг. 56). Исследовать теплоемкость в случае
замкнутой цепи и ее поведение при размыкании. Объем диэлектри-
ка предполагается неизменным.
31. Определить количество тепла, выделяющееся в конденсато-
ре, описанном в задаче 30, при квазистатическом возрастании
разности потенциалов от 0 до Ф.
32. Объяснить, почему диэлектрик втягивается в конден-
сатор, если ввести его между пластинами конденсатора, как пока-
зано на фиг. 57.
176
Гл. 3. Термодинамические функции и условия равновесия
[В]
АТ в
ние
33. Химический потенциал однокомпонентного идеального га-
за имеет вид ц = <р (Г) + kT In [р/р0 (Т)]. Получить выраже-
ние для (большого) термодинамического потенциала J (Т, V, ц)
и доказать справедливость соотношения (3.5).
34. На фиг. 58 приведены экспериментальные данные для
напряжения в случае опреде-
ленным образом вулканизирован-
ной резиновой ленты, длина
которой поддерживается постоян-
ной. Пусть 10 — естественная
нормальная длина ленты при тем-
пературе То, а I — ее действи-
тельная длина. Полное натяжение
(равное напряжению, умножен-
ному на поперечное сечение) свя-
зано с I соотношением
Х = АТ
I *0
-Ц + сЦТ-То)]^)2} .
Здесь а — коэффициент теплового,
расширения, равный примерно
7-10-4 град"1. Вычислить измене-
ie, когда резиновая лента, находя-
щаяся при температуре То, быстро адиабатически растягивается
от ее естественной длины 10, до длины, в L раз большей. (Этот
эффект называется эффектом Джоуля.) Представить графически
зависимость АТ от L.
РЕШЕНИЯ
1. Доказательство аналогично приведенному в примере 1.
В данном случае мы должны лишь рассмотреть кваэистатический
процесс, так как температура по определению однородна. Рас-
смотрим уравнения для инфинитезимального процесса.
а) Температура Т^ теплового резервуара не меняется, когда
он отдает системе А конечное количество тепла. Так как над
тепловым резервуаром не совершается никакой работы, можно
считать, что изменение его состояния связано только с отдаваемым
им количеством тепла d'Q. Изменение внутренней энергии t7(e)
и энтропии резервуара определяется первым и вторым зако-
нами термодинамики
dU(e)= -d'Q и dS^ =. (1)
Решения
177
Если внутреннюю энергию и энтропию системы А обозначить через
U и S, то внутренняя энергия и энтропия составной системы будут
U* —JU + U<e> и S* = S + Эти величины являются функ-
циями состояния составной системы. Так как составной системе
не сообщается тепла, то в соответствии со вторым законом имеем
dS* = Q, или dS^ =—dS. (2)
Учитывая (1), можем написать
dU(e} = 7,(е) dS^ = — Т™ dS.
Таким образом, изменение энергии составной системы
dU* = dU + dU(e)
может быть записано в виде
dU* = dU-T(e'> dS = dU — TdS, (3)
так’как = Т. Последнее выражение записано в переменных,
определяющих состояние системы А, и представляет собой в дей-
ствительности dF.
б) Применим к составной системе первый закон термодинамики.
Так как работа d'A, совершенная над заданной системой, пред-
ставляет собой единственную работу, произведенную окружением
над составной системой, то dU* = d'A. Учитывая (3), получаем
dF = d'A.
Это соотношение и определяет смысл термина «свободная энергия».
2. Если рассматривать S как функцию переменных р и V,
то уравнения (3.1) и (3.2) переходят в
(1)
йв=г®+к<гР=[г(£)г+фр+г(^)1>Л'. (2)
Если же ^считать S функцией Т и V, т. е. рассматривать
S (Г, V) = S (Т (р, V), V) (Т есть функция р и V в силу уравне-
ния состояния), то
Up/г т UpM
Аналогично, считая S(T, p) = S (Т (р, F), р), имеем
\dV)р~ \ЭТ)р\ dV)р Т UlJp TVa. ' ( '
Применяя (1.23) к соотношению (3), находим
/ дТ \ (dV/др)т х
(dV/dT)p ’
.178
Гл. 3. Термодинамические функции и условия равновесия
ИЛИ
( 98 ) _Сук
к др )у Та •
Искомые соотношения получаются при подстановке (4) и (5) в (1)
И (2).
Замечание. Преобразование переменных в соотношениях
(3) — (5) можно произвести следующим образом:
_ Э (5, F) __ [9 (5, У)/д (Т, F)] [3 (Т, У)/д (р, 71)]
к др )v~ д(р,У) 3 (р, V)/d (р, Т) ~~
_(dS/dT)y [—(дУ/др)т] Сук
(дУ/дТ)р аТ '
/ д8 \ __ д (S, р) _ д (8, р)/д (Т, р) _ (д8/дГ)р
\dV)p~~ д (V, р)~д (V, р)/д (Т, р) ~ (дУ/дТ)р •
Следует обратить внимание на запись частных производных в виде
якобианов путем добавления дополнительных переменных.
3. Так как а = (1/F) (dV/dT)p, a Cp — T(dSldT)p, то, поль-
зуясь методом якобианов, получаем
(дТ\ д (8, Т) _ д(8, Т)/д (р, Т) _
ls ~ к др )s ~ д (8, р) ~д (5, р)/д (р, Т) ~
(dSldp)T {9V!9T)p TV а
(dS/dT)p - (дЗ/дТ)р ~ cp
Здесь мы применили соотношение Максвелла (3.21а), являющееся
следствием уравнения (3.4). Зависимость энтропии от объема при
постоянном давлении определяется величиной (dS/dV)p. Исполь-
зуя соотношение (4) из предыдущей задачи, находим (dS/dV)p =
= 1/%S. Это можно получить также с помощью соотношения
Максвелла (3.21а) и первого равенства в (4) следующим образом:
/Э5\ (д^\ (др/дТ)3 ( дТ \ (,?Р\ =J_
UHp \дТ)р{дУ)р (др/д8)т\дУ )р \dTJs xs '
4. Подставим уравнение состояния в соотношение V = (dG/dp)Tt
(^)т = 7+В + Ср+ •••
и проинтегрируем полученное выражение
С(Г,р)==в(Г,ро) + Л1п-^ + В(р-ро)+4с(Рг-^)+... • (1)
Отсюда
-(1т)Р=5<2’’»>-4'1п-£-в'<'-«)-
-±С'(р‘-р‘) + ... (2)
Решения
179
И
H = G + TS = H(T, p0') + (A-TA')in-^ +
+ (B-TB')(p-p0) + ^(C-TC')(p^pl)+... (3)
Здесь A’ — dA/dT и т. д. Для определения величин G(T, р0),
S (Т, ро), Н (Т, р0) должна быть известна теплоемкость. Из при-
веденных выражений легко полупить U и F как функции р и Т.
5. Из уравнения (3.3) имеем F = U— TS, 5=—(dFldT)v,
так что
U=F-T(^)v
Дифференцируя найденное соотношение по V и подставляя
(dF/dV)=—р, получаем (dU/dV)T=—рА-'T (dp/dT)v. Аналогично
G = H—TS и 5=—(dGldT)-p, и, следовательно,
я=с-7'(1т)„-
Из соотношения (dGidp)T = V получаем {дН!др)т = V —
- Т (dV/9T)p.
Замечание. Эта задача уже рассматривалась в примерах
2 и 4 и в гл. 2, задача 15, однако с помощью свободной энергии
она решается проще.
6. Задача аналогична примеру .2. Первая часть уже решена
(см. задачу 5). Второе равенство можно доказать, подставляя
соотношение Максвелла (дУ1дТ)р = — (dSldp)T [которое получает-
ся при рассмотрении полного дифференциала (3.4)] в соотношение
IdSx д (S, Т) __д (S, Т) д (S, р) _
к ~др/Т ~ д(р, Т) ~ 9(3, р) д(р, Т)~
— ( ] / dS ] _ Ср ( дТ\
~ \ др )s \ дТ )р~ Т \ др )s’
7. , Уравнение состояния рассматриваемого газа имеет вид
р = f (V) Т. В соответствии с (3.21а)
Так как р > 0 и Т > 0, то здесь в правой части стоит положи-
тельная величина.
8. а) При dH = 0 получаем из уравнения (3.2) Т dS A-V dp = 0.
Таким образом,
» =_Z.<0.
\др)н Т
12*
180 Гл. 3. Термодинамические функции и условия равновесия
б) Из уравнения (3.1) имеем Т dS — pdV — Q при dU = 0,
так что
Замечание. Как было показано в гл. 2, пример 2, если
уравнение состояния имеет вид р — j (У) Т, то внутренняя энер-
гия’не зависит от объема. Мы можем написать поэтому (dS/dV)v —
— (dS/dV)T, так что задача 7 является частным случаем настоящей
задачи.
9. Вщервом случае мы имеем процесс, при котором постоянна
внутренняя энергия U; во втором случае постоянной остает-
ся энтальпия. Но в предыдущей задаче было показано, что
(dS/dV)v >0и (dS!dp)a < 0, так что энтропия возрастает в обоих
случаях. Это значит, что оба процесса необратимы.
10. При уменьшении внешнего давления происходит квази-
статическое адиабатическое расширение газа. Так как давление
газа равно внешнему давлению, изменение температуры можно
определить, вычисляя (дТ!др)3, где Т — абсолютная температура
и S — энтропия газа. Эту величину мы назвали адиабатическим
температурным коэффициентом. В задаче 3 было получено ее
выражение через коэффициент теплового расширения а и тепло-
емкость при постоянном давлении Ср. Оно имеет вид (ЭТ1др)3 =
= TValCp. Так как величины Т, V и Ср положительны, то при
а > 0 имеем и (дТ!др)3 > 0, т. е. температура понижается при
уменьшении давления.
Как было показано в гл. 2, задача 24, понижение температуры
в процессе Джоуля — Томсона описывается выражением
(дТ\ Vrr(dV\ TZ-| 1 _ (Ta-1) 7
l др )h L \dT )p J Cp Cp
Эта величина не всегда положительна, она может принимать
и отрицательные значения (см. гл. 2, задача 44). Температура падает
до тех пор, пока Та — 1 > 0. В случае адиабатического квази-
статического расширения в этом неравенстве отсутствует член —1.
Рассмотрим достаточно малое падение давления, —Ар > 0. Раз-
ница между понижением температуры —(&.T)S > 0 при адиабати-
ческом процессе и —(AT)H > 0 при процессе Джоуля — Томсона
равна
I - Wsi -1 - (ЛОЛ=[ () s - «)Д (-&р>=£ (- ад > о.
З'аТм е ч а н’и’е. Как видно из приведенного решения, для
охлаждения (например, ожижения) газа выгоднее применять
квазистатическое адиабатическое расширение, чем процесс Джоу-
ля — Томсона, по двум причинам: во-первых, так можно охлаж-
. Решения
184
дать любой газ; во-вторых, в первом случае падение температуры
больше *).
11.
zs _ (1/V) (&V/dp)3 _ д (V, S)/d (р, S)
> хт (1/У) (dV/dp)T д (V, Т)/д (р, Т)
___ 9 (7, S)/9 (V, Т) (9S/dT)v Cv
9 (р, s)/d (р, Т) (д8/дТ)р - Ср •
б) (^] = 9 Vi, yfe) = 9 Vi, Yk)/d(Ui, Ук)
\9у1 )Yh d(yt,Yk) д (pi, Yk)/9 (yt, yk)
(ЯУг/дгц) (dYk/9yk) ~(dYt/dyk) (dY^dyA
________yK_______° i____________& i________&k
(9Yh/dyh)yi
(1)
(2)
Так как dU = г/г- dYi + Уь dYk -J- ..., то, полагая Ф = £7—г/гУг—
— ykYk, получаем
d<I>= —Yidyl — Yhdyk+ или = . (3)
\ дуь /уг х дуг i yk
Подставляя (3) в (2), имеем
(р) _(р) или (Щ) <(Р) . (4)
\9У1 )Yk \dyi)yk (9Ук/дук) \dyt )Yk \9yi)yk v
В частности, если Уг- = У, =—р, Yk = S, ук = Т, находим:
из (4)
Т !9V\2 1 /Сч
zs = zr-v(^-)p^. (5)
[Соотношение (5) можно также получить из соотношения (1)
в настоящем решении и формулы (6) примера 3.] Таким образом,
xs<xr. (6)
в) Рассмотрим^, некоторое количество вещества, заключенное
в цилиндр с поршнем. При движении поршня объем V меняется
на величину ДУ < 0. В соответствии с (6) изменение давления
имеет большую величину в том случае, когда тепло не может
передаваться внутрь цилиндра, чем в случае, когда тепловой обмен
допускается:
(Др)8 > (Др)г.
Пусть сначала происходит адиабатическое сжатие вещества,
а затем становится возможным тепловой обмен (фиг. 59, а). Изме-
нение давления при этом уменьшится от значения (Др)я до (Др)г
(фиг. 59, б). Это означает, что косвенным следствием теплового
J) Обратимое адиабатическое расширение газа применяется в турбо-
детандере Капицы для ожижения воздуха,— Прим. ред.
182
Гл. 3. Термодинамические функции и условия равновесия
потока, вызванного сжатием А, является уменьшение непосред-
ственного действия А (т. е. уменьшение возрастания давления)
в соответствии с принципом Ле-Шателье — Брауна.
р
ZZZZZZZZZZZZZZZZZZZZZZZZZZZ --------
а
Фиг. 59.
12. Вычисления проводятся так же, как в примере 7. Инте-
грируя теплоемкость Ср (Г) и добавляя gi (р, ri) в качестве
постоянной интегрирования, получаем
т
5= jcp(r)^ + gl(p,«) =
т
= пС°р\ъТ + п j CKOn(T')^+gi(p,ri). (1)
о
Так как (dG/dT)p — — S, то, проведя еще одно интегрирование,
найдем
G(p, Т, п) = — пСр(Т1пТ — Т) —
Т Т’
-п J dr СК0Я(Т")^-Т81(р,п)+ёг(р,п). (2)
о о
Учитывая, что (dG/dp)T = V, имеем
rdgj .
- др др р ’
ИЛИ
dgt____nR dg2 _ л
др ~ P др
так что
gi (р, ri) = — nR In p + <pi (и), gz — Фг (и)- (3)
Решения
183
Здесь через cpi и <р2 обозначены постоянные интегрирования. Под-
ставляя (3) в (2) и учитывая, что Gin не зависит от п, получаем
(п) = п а (а = const) и ф2 («) == (U0 = const). (4)
Таким образом, полагая а — С°р = iR ( = const), имеем из
(2) - (4)
G(p, Т, n) = n^U0 — СрТ In Т + RT In р —
Т Т’
АТ" \
dT' \cKoa(T")^-iRT) (5)
о о
(величина i называется химической постоянной). Используя соот-
ношение (1) [или дифференцируя соотношение (5)], получаем
выражение для энтропии
г
5 = п [С°р In Т - R In р + j СКоЛ (Г) + iR + С»] . (6)
о
Замечание. В соответствии с выражением (5) термодинами-
ческий потенциал на 1 моль (химический потенциал) можно запи-
сать в виде
G(T, p) = G(T, Po) + RTlnj~. (7)
Здесь G (Т, р0) — значение G для некоторого начального давле-
ния р0.
13. Свободная энергия смеси идеальных газов в соответствии
с гл. 2, пример 5, записывается в виде
F (Т, V, щ, п2) = (Т, Vif nJ 4- F2 (Т, У2, п2)— T&S. (1)
Здесь V—полный объем смеси газов, a Vi = Уп^щ + п2)
и 72==Fn2/(n14-n2) —объемы, занимаемые соответственно газами 1 и 2
до смешения. Энтропия смешения Д5 дается выражением
Д5 = - R (щ In —-----1- п2 In —п1 ) . (2)
\ »l + n2 ni + nz ) v >
В соответствии с соотношением (9) примера 7, Fj (Т, nJ
и F2 (Т, V2, п2) имеют вид
Fi(T, nJ-njOJ^-n^Tln-^- ,
ni
Fz (T, V2, n2) = п2Ф2 (T) - n2RT In .
n2
184
Гл. 3. Термодинамические функции и условия равновесия
Таким образом,
Л (Т, V., щ) + n.RT In —%— = Щф,(Г) - niRT 1П^ = Л (Т, V, щ),
Р'г (Т, V2, п2) + n2RT In -5— = F2 (Т, V, п2).
»*1 -j- »«2
Следовательно, соотношение (1) переходит в
F(T, V, n^n^F^T, V, ni)+F2(T, V, п2). (3)
Из (3.13) имеем
G(Т, р, щ, n2) = ni^- + n2^- = nfii (Т, + n2G2(Т, р2). (4)
кс/«Ц
Здесь
_гц11Т_ pn-i _п2НТ рп2 Г (П1 + п2) RT ~\
Pl V ni + n2 ’ Р2 V П1 + п2 |/ V J
— парциальные давления, а 6^(7’, р±) и G2(T, р2) — термодинами-
ческие потенциалы на} 1 моль для веществ 1 и 2 при давлениях
Pi и р2. Эти величины соответствуют химическим потенциалам
веществ в смеси.
Замечание. Учитывая замечание к предыдущей задаче,
можно переписать соотношение (4) в виде
G = rii Gt (Т, ро) 4- n2G2 (Т, р0) + RT ( щ In-^- + n2 In , (5)
где Ро есть некоторое начальное давление. Химический потенциал
каждого компонента будет
G^GiiT, Pi) = Gi(T,Po) + RTln-^. (6)
14. Обозначим свободную энергию через F(T, Г). Тогда имеем
(О
f7 = F+TS = f-r(g.)i, (2)
<3)
(Бесконечно малая работа d'A при изменении длины есть d'A =
= Xdl.) Уравнение (2) дает
о»
а дифференцирование соотношения (1) приводит к равенству
/dS\ d^F _ tdX\
\д1)т~ dldT \дТ)Г ’'°-'
Решения 185
Подставляя X = АТ, находим
(^) =0 и (4И = -4<0.
\ д1 )т \ д1 )т
Таким образом, U не зависит от I, a S уменьшается с возраста-
нием I. (Следует отметить аналогию с идеальным газом.)
15. В случае адиабатического квазистатического удлинения
(S = const) имеем
(дГ\ _ (dS/dl)T_ Т fdS\ _ТА „ ,
\dl)s (dS/dT)i~ Сi \ dl )т
Здесь Ci есть теплоемкость при постоянной длине, а А— кон-
станта, фигурирующая в предыдущей задаче. Имеем также
(Л) == .... _ А
\дТ)х (дХ/дГ)т (дХ/&1)т ’ '
Согласно условию термодинамической устойчивости, (5X/5Z)r>0
[см. (3.34) и (3.356)]. Формулы (1) и (2) и дают решение задачи.
16. Являясь экстенсивной величиной, свободная энергия
F (Т, V, Ni, Nz, ...), как функция температуры Т, объема V
и числа частиц, должна иметь вид
F(T, aV, aNi, aN2, ...) = aF(T,V, Nlt Nz, - )•
Дифференцируя по а и полагая a = 1, находим
F==V ( эй)t,n+ 2 v,Nr’
что соответствует
F^-pV+^Njiij.
Уравнение (3.12) получается путем дифференцирования обеих
частей последнего уравнения при учете (3.3).
17. Соотношения Максвелла (3.21а) дают:
/ дУ \ _ / dS \ / др \ / dS \
\дТ)р~ \др)т И \дТ )V~ Up )т-
В соответствии с третьим законом энтропия однородного тела
при Т —» 0 стремится к постоянной величине, не зависящей от дав-
ления или плотности при условии, что плотность остается конеч-
ной. Это значит, что
lim
Г->0
lim 1^-} =0
г_>о /г
и, следовательно,
186
Гл. 3. Термодинамические функции и условия равновесия
Другое решение: на основе третьего закона можно записать
Г ст>
S=^—~dT,
О
т
— г / \ dT —
\ дТ )Р I др )т~ J \ др )т Т
о
__?(«) +11ш(»
J V дТ2 /р \ дТ )р \ дТ )р
и, следовательно,
=0.
\ dl Jp
Здесь использовано соотношение (дСр!др)т =—T(d2V/dT2)p (см.
пример 3). Аналогичную процедуру можно применить и для вычис-
ления (д p/dT)v.
18. Учитывая, что (&Uldx)s = X, можно переписать (3.326)
следующим образом:
2б2С7 = 6Х&с=(-?Ц &г2>0,
\ дх )s,p
положив 8S = 8р = 0. Следовательно,
(4И₽>0- (1)
Полагая далее 8Т = 8р = 0, приведем (3.326) к виду
28JU={^-\ 8x2>Q,
\ дх )т9р
ИЛИ
>0. (2)
\ дх ) т, р
Другой способ решения основан на использовании соотношения
I дХ \ д (X, S) д(Х, S)d(X, Т) д(х,Т) Сх / дХ \
{ дх )s~ д(х, S) ~ д(Х, Т) д(х, Т) д(х, S) ~ Сх \ дх )т
{р = const). Учитывая, что Cxz>Q, Сх^>0, легко видеть, что
производные (дХ!дх')5 и (дХ!дх)т имеют одинаковый знак.
19. Выбирая в качестве независимых переменных Т, р и N
и полагая затем 8Т = 8р = 0, получаем из (3.326)
ял“ (>)л„>°-
Решения
187
20. Эта задача аналогична задаче 39, гл. 2, однако носит более
общий характер. Рассмотрим единичный объем вещества, причем
изменением объема будем пренебрегать. Для производных от
свободной энергии F (Г, М) справедливы соотношения
-’WM <2>
По условию задачи связь между намагниченностью М и магнит-
ным полем Н дается соотношением
М = %ТН. (4)
Подставляя (4) в (3) и интегрируя, получаем
F(T, M) = F(T,0) + ±^-[=F(T, 0) + 4Ъ.Я2] • (5)
Таким образом,
^(7’,M) = -S(7’,0)-1(4xt1) М\ (6)
С7(7’,М) = С7(71,О) + 4-(хт1-71^гХт1)М2, ' (7)
где
S(T, 0)=—F'(T, 0), U(T, 0) = F(T, 0) — TF'(T, 0).
Замечание. В частном случае, когда справедлив закон
Кюри — Вейсса
решение задачи 39 в гл. 2 получается без использования соотноше-
ний (6) и (7).
21. а) В случае независимых переменных Т, V и N в качестве
термодинамической функции следует выбрать свободную энергию
Гельмгольца F ( = U — TS), так что имеем
/ dU \ _ _____у, / d2F 1 _ ______у, / дц \
\ dN )т, V к дТ 9N ) у ~~ к дТ )v, N '
б) Для перехода от независимых переменных Т, V, £ = V-/T
к Т, V, ц учтем, что
/211 =________Р_ /211 = 2_
к дТ Itx.v Т* ’ Up )t,v Т
188 Гл. 3. Термодинамические функции и условия равновесия
Тогда получим
( 3N \ _ d(N, g, У) _d (N, g, V)!d (Т, р, V)
I дТ )v,l~ d(T,^,V) ~ д (Т, g, V)/d (Т, р, У) -
/ dN \ / dN \
_ к дТ )p,V к (Эр )т, V 1 _
- (21 к (Wr,r“
\ дТ ) и, V \ др )t,V
_ / <7.У А ДОЛц, V / dN \ / Р ( dN \
~ к дТ )р., v (д£/др)т, v к (Эр ) т, V — к дТ V Т \ др )t,V '
Первое слагаемое легко переписать в виде
/ dN \ _д (N, р, V)_d(N, р, У) d(N, Т, У)_ / Эр \ / dN \
к дТ )ц, v~d (Т, р, У)- d(N, Т, У) д (Т, р, У)- к 97 М, у к ар )т, V ’
Таким образом,
( 9N \ =(JW\ I
к дТ ) V, ц/Т к др ) Т, V L Т к дТ ) V, -V J ‘
Подставляя в это выражение соотношение, полученное в п. «а»,
приходим к искомому результату.
в) Для решения задачи нужно знать разность теплоемкостей
при постоянном объеме в случае постоянного числа частиц и в слу-
чае В = const. Перейдя от независимых переменных Т, V и £
к Т, V и ТУ, получим
( dU \ _d(U, I, У) д (U, g, V)/d (Т, N, У)
k дТ )v, I ~ д (Т, I, У) ~ д (Т, §, У)/(Э (Т, N, У) ~
I dU ( dU
k dT )лг, V k dN )t,V
( dl
k dT )w, V k dN /т, V
V
k dT N, V (dc,!dN)Ti у
1
(^/Ж)т, Y
к dN )t,V
Первое из равенств «в» получается путем подстановки соотноше-
ния «б». Для доказательства неравенства используем тот
факт, что в нашем случае соотношение (3.35в) переходит
в (dp,/dN)Tt у 0. Тогда очевидно, что (dN/dp)T, v =
= il(dpldN)T, у > 0.
22. Теплоемкость при постоянном объеме обычно определяется
для постоянного числа частиц, т. е. CVt N — Т (dS!dT)Vt N.
Решения
189
Перейдем от переменных Т, V и N к Т, V и~ц:
/ dS \ д (S, N, V) _д (S, 1V, V)/d (Т, р, V) _
\ дТ )v,N~ д(Т, N, V) ~ д(1‘, N, V)/d^T, р, V) —
('dS \ / dS \
\ дТ /ц, у \ Зр /Г, v 1 _ / dS \
( 'J^ \ ( dN \ (5A,/5p)r, у \ дТ /и, у
\ дТ ) м, v К 5р / т, V
(dN/dT)^ у / dS \
(dN/dp)T< у \ бр / т, V '
Первый член в правой части связан с теплоемкостью при постоян-
ном объеме и постоянном химическом потенциале CVt }I. — T (OS/dTjy, м.
Для преобразования производной (dS/d[i)T, v во втором члене вос-
пользуемся одним из соотношений Максвелла. Из (3.5) имеем
0 _ / \ ___ _ ( \ дг _ _ ( д! \
° — klrjy, м ’ р~ \дУ)т,ц' Up )т, V
и, следовательно,
/ as \ _ a2J ( dN \
\ ар / т, V дцдТ ~ \ дТ )у, м ’
/ as \ (а^У/аг)^, м
\ дТ /у,№ \ дТ /у, ц (d;V/ap)Tl У
Умножая обе стороны на Т, получаем
T{dN/dTfv^
'V, N ^v, ц (dN/dy.)T, у ‘
23. Согласно соотношению (2) предыдущей ^задачи,
(аналогично неравенству СУ<.СР)
(1)
(2)
имеем
Су,Л’<Су,Ц- (1)
Для выяснения физического смысла этого неравенства будем
следовать примеру, рассмотренному в § 9. Пусть ДТ1 представляет
|«
'777'7/7///\///777////777~.
' J РезерВуар
частиц
Фиг. 60.
увеличение температуры в результате передачи тепла Q (действие
И) системе, окруженной стенками, проницаемыми для частиц
(фиг. 60). Кроме потока тепла, имеется также поток частиц JM
190
Гл. 3. Термодинамические функции и условия равновесия
(вторичная реакция Ъ). В соответствии с принципом Ле-Шателье —
Брауна увеличение температуры {\T)N в случае, когда поток JM
отсутствует, больше ее увеличения (&Т)ц при наличии такого
потока (т. е. при постоянном ц)
(ДПхХДПн- (2)
Так как = QICVi N, а (ДТ)И = Q!CV, ц, неравенства (2)
и (1) имеют один и тот же смысл.
Замечание. В случае постоянного давления нельзя
рассматривать теплоемкость Ср, и для однокомпонентной системы,
так как в этом случае переменные Т, р и ц не являются незави-
симыми, а связаны уравнением Гиббса — Дюгема.
24. Эта задача аналогична задаче 19 в гл. 1 и задаче 14 в гл. 2;
ее решение, однако, можно упростить, используя якобианы.
Имеем
/ дМ \ д(М, S) d(M,S) д(М, Т) д (Н, Т) _
~ \ ШТ )s~ д (И, S) ~ д (М, Т) д (Н, Г) д (И, S) ~
(дЗ/дТ)м(дМ/дН)т (9М/дН)т Т (dS/dT)M _ См
~ (9S/dT)H — Т (dS/дТ} н “Сн '
Проводя преобразования, аналогичные (3.39), находим
г т ( dS } __т d(S, М) _т d(S, М)/д(Т, Н) _
м \эт)м д(Т,М) д(Т, М)/д(Т, Н)
( dS \ / dS \
Т \ дТ )н \ дН )т
= (дМ/дН)т / дМ \ / дМ \ =
k"dF)н [~дН )т
Т Г / 35 \ t дМ \ / dS \ (ДХ 1
— (дМ/дН)т LV дТ /нк дН )т { дН дТ JnJ
T(dS' „(дМ/дТЪ (дМ/дТГн
~ \9Т)н (дМ!дН)т 1 (дМ/дН)? • ’
При ^переходе к последней строке мы применили соотношение
Максвелла
(-£).=(X- <2>
Это соотношение получается, если вместо dF ——SdT i-HdM
рассмотреть F* = F — НМ и
dF*=—S dT — M dH. (3)
(Здесь все величины S, М, См и Сн определены на единицу массы
магнетика.)
Решения
191
25. В соответствии с условием задачи
dS (Т, 0) Ь
— = ьм=о = уг • (V
Интегрируя, получаем
1 h
5(71,0) = -|^ + В (В = const). (2)
Проинтегрируем теперь соотношение dF(T,tyldT=- в итоге имеем -S(T, 0),
F(T, О')—А —ВТ —(H = const). (3)
Подставив выражение
M = (С = const) (4>
в соотношение (5) задачи 20, найдем
F(T, М) = А-ВТ-^ + ^. (5)
Таким образом, s (Т, М) В 2Т2 2С , :(б>
откуда (7)
Так как соотношение (6) можно переписать в виде S(T,ff) = B-^-^, (8)
то г — ъ+сн* Ьн~1\дт}11- Т* * (9)
Для получения адиабатической магнитной восприимчивости физическому смыслу этой величины следует исключить Учитывая (4), получаем по самому Т из (6). (Ю)
и, следовательно,
/ аМ \ (dS/dH)M
ZS \ дН )s,H=H0 (д8/дМ)н
_ 6М2/С2Я» _ С b
~ ЬМ/С*Н% + М/С~ Т Ь + СЩ'
192 Гл. 3. Термодинамические функции и условия равновесия
26. В соответствии с третьим законом при 71 -> 0 энтропия
стремится к, некоторому предельному значению, не зависящему
от Н. Это значит, что (08/дН)т 0 (Т —>0). Следовательно,
учитывая соотношение (2) из задачи 24, получаем Ит(дМ/дТ)н =
Г->0
= 0. Подставляя М = Хт#,
находим
lim
Т-+0 01
0.
Замечание. Отсюда
видно, что как закон Кюри
% = CIT, так и закон Кюри —
Вейсса х = С/(Т — 0) спра-
ведливы лишь до некоторой
конечной температуры. При
71 0 должны наблюдаться от-
клонения от этих законов.
27. Если построить энтропию
парамагнитного вещества как
функцию температуры при постоянном Н, то в соответствии
с третьим законом она будет стремиться при Т -> 0 к постоянному
значению (нулю) при любом Н. Кривые для Н 0 и Н = 0 стре-
мятся к одному и тому же пределу при 71 -► 0, как показано на
фиг. 61. Для не слишком больших Н можно использовать соотно-
шение (6) в решении задачи 20:
5 = 5 (Г, 0) - А ( х?1) = 5 (Г, °) +1 (хт ) Н\
При Т -> 0, как было показано в предыдущей задаче,
(d%T'dT) -► 0. Это значит, что если при некоторой конечной темпе-
ратуре уменьшать магнитное поле от заданной величины до нуля,
то температура^при этом будет уменьшаться лишь до определен-
ного конечного ^значения и никогда не достигнет 0° К.
28. К концу пружины привязана пластина, на которой уста-
новлен груз массой М. Вес этого груза уравновешивает натяжение
пружиныX- Пусть z0 — высота, на которой находится пластина
при X = 0 и М = 0, а х — растяжение при X = Mg (g — уско-
рение свободного падения). Полная потенциальная энергия W
груза, помещенного на пластину, и части груза (массой М'),
оставшейся на высоте z0 (фиг. 62), равна
W = Mg (zq — х) + M'gz0 =
= — Mgx + (М + М’) gz0 = — Хх + const.
Решения
193
Далее, если F (Т, х) обозначает свободную энергию пружины
при температуре Т и растяжении х, то
F* = F (Т, х) — Хх = F + W + const (1)
есть свободная энергия всей системы, включая грузы. (Так как
грузы представляют собой чисто механическую систему, то их сво-
Ф и г. 62.
бодная энергия совпадает с потенциальной.) Если обозначить
через к упругую постоянную пружины, то
X = кх (2)
и
F = F(T, 0) + y/cz2, (3)
так что
F* =±kx--Xx + F(T, 0)= —^- + F(T, 0), (4)
dF* = dF (Т, 0) + (кх — X)dx — х dX = dF (Т, 0) — х dX. (5)
Последний член в (5) можно переписать в виде
— xdX = d (у кх2 ) + dW = d (kx2 ) — d (Xx),
t. e. dF* представляет собой сумму возрастания свободной энергии
пружины и уменьшения потенциальной энергии грузов при растя-
жении пружины.
Замечание. Следует проверить, что (dF*ldT)x = — S,
а величина F* + TS = U действительно представляет сумму
внутренней энергии пружины и потенциальной энергии грузов.
29. Как было показано в задаче 20, при однородном намагни-
чивании парамагнитного тела объемом V его свободная энергия
возрастает на величину 1/2VM2/%T, где М — приобретенный телом
магнитный момент (на единицу объема; полный магнитный момент
194 Гл. 3. Термодинамические функции и условия равновесия
равен при этом VM). Таким образом,
F(T, М) = F(T, 0) + у V^-, (1)
где F (Т, 0) — свободная энергия при М = 0. Энергия взаимо-
действия между внешним полем Н и магнитным моментом имеет
вид
W = — HMV = — х-гЯ27.
(Эта величина аналогична энергии взаимодействия груза с грави-
тационным полем в предыдущей задаче.) При этом величину
F* = F-yW=F(T, 0)-^-ХтЯ2Т (2)
можно рассматривать как сумму свободной энергии системы
и энергии взаимодействия парамагнетика с магнитным полем.
Для диэлектрика с диэлектрической проницаемостью е элек-
трическая поляризация Р (величина, аналогичная магнитному
моменту М в рассмотренном выше примере) в электриче-
ском поле Е принимает значение Р = (е — 1) E/fat. [Величина
(е — 1)/4л соответствует величине %.] Таким образом, согласно
соотношениям (1) и (2),
9ттПР2
/’(T,jP) = Fl(T,0) + 4^-, (3)
F* (Т, Е) = F (Т, 0) — VE2. (4)
Энтропию S можно получить как из F, так и из F*. В случае
магнетика имеем
- s (Г, 0) + г,М= = 5 (7, 0) + | VxtB‘ (5)
^Хт 4
и
5 = - (^)н=5 0)+i (5'>
Аналогично, для диэлектрика
30. Из соотношения (6) предыдущей задачи имеем
S(T,E) = S(T,0)+^^E*. ' (1)
Решения
195
а) Когда цепь замкнута, между пластинами конденсатора удер-
живается постоянная разность потенциалов Ф и устанавливается
постоянное поле Е0 = Ф/а (фиг. 63). Из соотношения (1) находим
с*=г(#)1=с«<:г>+^-7'-да-е’- <2>
Здесь Со (Т) = TdS (Т, O)/dT.
б) Если цепь вообще не замыкалась, то Е = 0 и теплоемкость
равна Со (Т). Когда цепь замыкается при температуре То, на
пластинах конденсатора появляется поверхностный заряд о =
= D/kn = z0Ejfai [здесь D — электрическая индукция, е0 =
= е(7’о)]-При размыкании цепи поверхностный заряд остается
и индукция D в диэлектрике сохраняет постоянную величину.
Теплоемкость в этом случае будет
c°=r(4^L=c»<r>+^r <3>
Так как D = &E, имеем
I дЕ2 \ 2Е2 d&
~~dT*
Подставляя это выражение ' в (3) и учитывая, что &0Е0 = гЕ = D,
получаем
31. При изотермическом квазистатическом увеличении потен-
циала от 0 до Ф диэлектрик поглощает тепло d'Q — TdS. Зависи-
мость энтропии 5 от электрического поля дается соотношением (6)
в решении задачи 29:
5(T,5)-5(7’,O) = y^P-g-. (1)
13*
196 Гл. 3. Термодинамические функции и условия равновесия
Если расстояние между пластинами конденсатора равно а, а раз-
ность потенциалов Ф, то электрическое поле Е = Ф/а. Таким
образом, при увеличении потенциала от 0 до Ф в диэлектрике
выделяется тепло
ф
J TdS = T[s(0, Г) — (-J-, Г) J =
Ф=0
= yr dE (7) ф2
dT 8яа2 ‘
(2)
Эту формулу можно переписать в другом виде:
__о__сф2 •
2 din Г
(3)
здесь С — г А Апл — емкость плоского конденсатора, А — пло-
щадь пластин. Величина ^СФ2 представляет собой электростати-
ческую энергию, запасенную в конденсаторе.
32. Пусть а обозначает расстояние между пластинами,
b — ширину, I — длину пластин конденсатора, ах — расстояние,
на которое вдвинут в глубь конденсатора диэлектрик (фиг. 64).
Объем диэлектрика Vi в поле Е равен = abx. Оставшийся
объем конденсатора, не занятый диэлектриком, То = ab (I — х).
Так как электрическое поле Е = Ф/а постоянно, можно исполь-
зовать выражение для свободной энергии F*, полученное в реше-
нии задачи 29. Полная свободная энергия запишется в виде
Fno„ = F(r,0)-i-(«-l)E’+A£’ =
Решения
197
Здесь F(T, 0) — свободная энергия всего диэлектрика в отсут-
ствие электрического поля. Второе слагаемое представляет собой
сумму изменения свободной энергии диэлектрика при его поляри-
зации электрическим полем и энергию его взаимодействия сполем,
а третье слагаемое — энергию^электрического поля. При возра-
стании х свободная энергия уменьшается, так что диэлектрик
втягивается в конденсатор с силой
V _ _ ^ПОЛН _ Р2
дх — 8л
33.
J = -pV= — NkT, (1)
Ц = ф + йПп -^- . (2)
Из (2) следует
p=poe(u-<PW = JW , (3)
или
J (Т, V, р) = - p0Ve^-i>)/^. (4)
Дифференцируя (4) по ц и V, получаем, учитывая (3),
(_ PgL =—N (5)
\ др / t,V кТ ' '
И
(7г)г,ц=-^(,Л"Ф)/ЙГ==-^
Имеем также
г.„=
— _ /у (ьт э1п роэф н-ф
{ ЭТ дТ Т J •
Но в силу (2) это означает
(7)
34. Скорость изменения температуры резиновой ленты при ее
адиабатическом удлинении дается выражением
( дТ \ _ (dS/dl)T Т ( дХ X
\dl )s Сг к дТ Д’ V1'
Здесь Ci — теплоемкость при постоянной длине. Мы использовали
соотношение Максвелла (dS/dl)T = — (дХ/дГр, получающееся
198
Гл. 3. Термодинамические функции и условия равновесия
из соотношения dF = — S dT -\-Х dl. Для Т — То имеем
(^)=A(L-L-^-aAT0L~\
так что
(-зг)8 = ^л1£-(1 + “г'">-г'_‘|-
Изменение температуры, обусловленное адиабатическим увеличе-
нием длины в L раз (от L = 1 до Л), равно
Ll0 L
ДГ = ( (-^) dl = -^±- ( [L-(l + aT0)L-i]dL =
J \ Cfl / S Ь I J
1
= ^-Г0^-[Г2 + Г-2(1 + аГ0)]. (2)
ЫЧ-'l J-!
При То = 300° К имеем 6 = аГ0 = О,21. Выражение в скобках
в формуле (2) обращается в нуль при Л==1-'-е, где е опреде-
ляется из условия Зе + е2 = 2б, т. е.
е = -|-б-4е2 ~ 0,14 —у0,020 « 0,13.
На фиг. 65 представлена зависимость АТ от L, описываемая
формулой (2).
Замечание. Соотношение между напряжением и дефор-
мацией, использованное в этой задаче, может быть получено
для резины путем применения мето-
ЛТ / дов статистической механики в тео-
/ рии упругости. Его можно также
/ с успехом применять к не слишком
/ сильно вулканизированным резинам
/ и к некоторым другим видам резино-
/ подобных веществ. Рассмотренный
/ здесь тепловой эффект называется
,____,____, эффектом Джоуля. Как видно из
га w во во фиг. 65, при малых деформациях
М АТ < 0, что связано с тепловым
ф и г 65 расширением. Если же не говорить
об этой области, то такие резино-
подобные вещества нри адиабатиче-
ском удлинении нагреваются (АГ > 0). Это явление характерно
для упругости резинонодобных материалов. В правильности полу-
ченных результатов легко убедиться с помощью экспериментов
с резиновой лентой.
ЛИТЕРАТУРА
1. С а 11 е n Н. В., Thermodynamics, New York, 1960.
ГЛАВА 4
Равновесие фаз и химическое равновесие
В настоящей главе не вводится никаких новых принципов.
Здесь мы будем иметь дело лишь с наиболее важными примене-
ниями термодинамики в физике и в физической химии, а именно
с ее применениями к изучению равновесия между различными
фазами однокомпонентной системы и равновесия между фазами
системы, состоящей из двух или более компонентов. Мы обсудим
также использование термодинамики при решении общих проблем
химического равновесия, связанных с диссоциацией и рекомбина-
цией частиц, из которых состоят отдельные компоненты. В разде-
ле «Основные положения» рассматриваются некоторые теоремы
и представления, полезные при исследовании указанных задач.
ОСНОВНЫЕ ПОЛОЖЕНИЯ
§ 1. Фаза
Однородное в физическом и химическом отношении вещество
мы рассматриваем как одну фазу. Различные агрегатные состоя-
ния (газообразное, жидкое), а также различные кристаллические
состояния представляют собой разные фазы.
§ 2> Равновесие между различными фазами чистого вещества
Пусть между двумя фазами 1 и 2 (характеризующие их вели-
чины будем помечать соответственно одним или двумя штрихами),
находящимися в контакте друг с другом, существует равновесие.
В этом случае давление по обе стороны поверхности раздела может
быть или одинаковым, или разным в зависимости от природы
этой поверхности.
1) Плоская поверхность, передающая давление. Из соотношений
(3.26а) — (3.26в) дмеем
Р' = Р” = Р, (4.1)
Г = Т" = Т (4.2)
и
Н' (Р. Л = м" (Р, Л, или G' = G". (4.3)
200
Гл. 4. Равновесие фаз и химическое равновесие
Соотношение (4.3) представляет собой условие фазового равнове-
сия. В пространстве переменных р, р, Т линия пересечения
поверхностей р = р' и р = р" представляет собой линию сосущество-
вания двух фаз. При переходе через эту линию происходит
фазовое превращение. Всегда реализуется фаза с меньшим значением
химического потенциала, поскольку она более устойчива. Порядок
фазового перехода определяется порядком контакта между поверх-
ностями р = р' и р = р". На фиг. 66 представлен фазовый пере-
ход первого рода.
а) Фазовый переход первого
рода. Условия перехода пер-
вого рода имеют вид: Ар = р' —
-р' = 0, «ЭДр/дГ^О и
dkyJdp 0. Из условия (4.3)
имеем
Л<^ + Л^ЙГ = 0’
или
= =___(4 4)
dT др гдр
(уравнение Клапейрона — Клау-
зиуса). Здесь
q = TLS = T (S'-S")
— теплота перехода (на 1 моль),
Фиг. 66. а ДИ—изменение объема при
переходе (на 1 моль).
б) Фазовый переход второго рода. Условия перехода второго
рода имеют вид: Др = О, дкр/дТ = 0, 5Др/др = 0, в то время как
производные второго порядка, вообще говоря, не равны нулю.
Таким образом, вдоль линии сосуществования фаз
. дУ , . . дУ jrp л /SAG
д-^^+д1Г^=° (^Г=0)’
A dV , (dbG_n\
dT dP T dT 0 dT OJ .
(4.5)
Для того чтобы величина dpIdT была конечной, необходимо выпол-
нение условия
. дУ А дУ
др & дТ
. дУ .ср
Л дТ Л т
= 0, или b?LbCp + T (д4у)2 = °- <4-6)
Основные положения
201
При таком превращении скрытая теплота перехода отсутствует,
однако в точке фазового перехода теплоемкость может терпеть
разрыв или иметь сингулярности.
Фазовые переходы второго рода, возможно, менее знакомы
читателю. Однако нетрудно привести ряд примеров таких перехо-
дов в сплавах и в магнетиках. Особый интерес представляет
фазовый переход в газе в критической точке Т = Тс при постоян-
ной плотности, равной критической.
в) Фазовые переходы более высокого порядка. Если все частные
производные р. вплоть до п — 1-го порядка непрерывны, а терпит
разрыв лишь п-я производная, то говорят, что имеет место фазо-
вый переход и-го порядка.
2) Если поверхность раздела не является плоской, так что
существует, вообще говоря, некоторый эффект, обусловленный
поверхностным натяжением, а также если стенка между двумя
фазами проницаема для вещества, но не передает давления,
то в разных фазах давление будет различным, т. е.
р р •
С другой стороны, должны выполняться условия (4.2) и (4.3).
Это значит, что
G'(р', T) = G"(p", Т).
Таким образом, связь между р' и р" определяется условием
V dp' = V" dp" (уравнение Гиббса — Пойнтинга). (4.7)
§ 3. Поверхностное натяжение
Определение поверхностного натяжения. Работа, необходимая
для того, чтобы изменить площадь поверхности между двумя
фазами,— это работа против сил поверхностного натяжения. Если
учесть это, то уравнение (2.14) для изменения энергии при квази-
статическом процессе принимает вид
dU = TdS — p'dV — p"dV" + yda + yJdN' + p,"dN". (4.8)
Здесь p' и p" — внутреннее давление фаз 1 и 2, р' (Т, р')Т
р" (Т, р") — химические потенциалы фаз, а о — площадь поверх-
ности раздела. Поверхностное натяжение у определяется уравне-
нием
Т=(-^) - (4.8')
1 V да Is, V, V", N’, N" ' '
Разность давлений, ’ вызванная поверхностным натяжением.
В случае когда поверхность раздела между двумя фазами пред-
202
Гл. 4. Равновесие фаз и химическое равновесие
ставляет собой сферу радиусом г, разность давлений будет
= (4-9)
Это выражение получается из условия равновесия dU = 0 (3.30а)
при dS = dN' = dN" = 0, dV" = — dV' с учетом того обстоятель-
ства, что dV/do = r/2 в (4.8).
Условия равновесия для энергии переноса массы даются соот-
ношением
р' (Т, р') = ц" (Т, р"). (4.10)
Например, радиус г сферической капли жидкости и давление
ее паров связаны условием
Иг(Л Рг + ^)=МЛрг) (4.10')
(см. задачу 34).
§ 4. Равновесие в многокомпонентной многофазной системе
Предположим для простоты, что на поверхностях раздела
различных фаз существует механическое равновесие, так что дав-
ление однородно. Различные компоненты будем обозначать индек-
сами 1,2, . . ., с, а фазы — индексами 1, 2, . . ., г. Условия
равновесия имеют вид
р' = р"= • = p(r) = р, (4.11а)
Г£1 rpn = т(г) = т (4.116)
Их= Pi= • • = (4Г),
(4.12)
Цс — Цс = * •
или
&, = & = .. . = G<-r), 7 = 1, 2, . .с. (4.12')
Доказательство. Проведем обобщение доказательства, дан-
ного в § 6. Пусть каждая фаза обладает энтропией 5(/!), энер-
гией U(ll>, объемом а число молей каждого компонента обо-
значим через N^k\ Тогда условия равновесия запишутся в виде:
65 = 65' + 65" + ... + 65(Г> =
-=У + =0, (а)
I 9U^ dV<k> dJfW J
*=1 u з 3
Основные положения
203
Ы7= 2 &U^ = 0, (б)
' к—1
6У= 2 6V(/i’ = 0, (в)
k=i
6Nj= 2 57V<fe) = O, 7 = 1, 2, ..., с. (г)
k=i
Соотношения (а) — (г) получены при условии, что U, V и Nj
постоянны. Используя метод неопределенных множителей
Лагранжа, умножим соотношение (б) на — МТ, (в) на р/Т,
а (г) на —\ijlT и прибавим найденные выражения к (а). В итоге
получим
7=1
ft=l
3 J
Так как вариации можно считать независимыми, коэффициенты
при них, очевидно, равны нулю. Таким образом, мы получаем
условия (4.11а), (4.116) и (4.12).
ОТСТУПЛЕНИЕ 10
Равновесие гетерогенных систем
«Энергия Вселенной постоянна.
Энтропия Вселенной стремится к максимуму».
Этими простыми положениями Клаузиус (1822—1888) резюмировал
содержание своей работы «О различных удобных для приложений фор-
мах основных уравнений механической теории тепла». Эта работа уви-
дела свет в 1865 г., пятнадцать лет спустя после открытия второго зако-
на (сообщение о чем появилось в Poggendorf Annalen [1]). В этой
чрезвычайно важной работе Клаузиус дает те основные формулировки
первого и второго законов термодинамики, с которыми мы теперь уже
знакомы.
Спустя десять лет, в 1875 г., Гиббс (1839—1903) положил эти фор-
мулировки в основу своей знаменитой статьи «О равновесии гетеро-
генных веществ» [2]. Здесь Гиббс, исходя из первого и второго законов
термодинамики, дает наиболее общую формулировку условий равно-
весия для гетерогенных систем и впервые вводит понятие химического
потенциала.
Правило фаз — одно из наиболее красивых следствий условий
равновесия в формулировке Гиббса. Статья оставалась почти совсем
неизвестной европейским ученым в течение 15 лет, до 1891 г., когда
204
Гл. 4. Равновесие фаз и химическое равновесие
Оствальд перевел ее на немецкий язык (а позднее, в 1899 г., Ле-Ша-
телье — на французский). Одна из причин этого заключалась в]том,
что статья Гиббса была опубликована в очень мало распространенном
журнале Transactions of the Connecticut Academy [3]. Другая причина
была связана с трудностью статьи для понимания.
Оствальд писал: «Стремясь к наибольшей общности и строгости
исследования, автор выбрал столь абстрактную и трудно усваиваемую
форму изложения, что она требует от читателя незаурядной вниматель-
ности и самоотдачи».
Когда работа Гиббса спустя много лет после ее выхода в свет
стала известной в Европе, она совершенно не утратила своей новизны.
«Содержание работы и сегодня имеет непосредственную ценность,
и интерес к ней ни в коей мере не является чисто историческим. Дей-
ствительно, из того почти неисчерпаемого богатства результатов,
которые в ней содержатся или из нее вытекают, пока что может быть
использована лишь очень небольшая часть. Заключенные в главах
этой работы нетронутые сокровища во всем своем разнообразии и цен-
ности еще ждут исследователей — теоретиков и особенно экспери-
ментаторов. Научившись находить значения энтропии не только
для газов, но и для огромного класса разбавленных растворов, мы
имеем теперь возможность выразить общие функции, входящие в гиб-
бсовские уравнения, через экспериментально определяемые величины.
Частично это уже сделано, но еще больше предстоит сделать».
§ 5. Правило фаз Гиббса
Теорема. Число степеней свободы / равновесного состоя-
ния системы, состоящей из с различных компонентов в разных
фазах г, дается выражением
/ = с _ г + 2. (4.13)
Под числом степеней свободы подразумевается число внутренних
переменных, которые могут произвольно изменяться при заданных
условиях равновесия.
Доказательство. Внутренние условия равновесия для
одной фазы, состоящей из с компонентов, определяются относи-
тельными концентрациями компонентов. Это означает,, что мы име-
ем с — 1 внутреннюю переменную, описывающую состав фазы.
Кроме этих переменных, имеются еще переменные р и Т, оди-
наковые для всех фаз. Так что в случае г фаз мы должны
иметь всего (с — 1) г + 2 переменных. Химические потенциалы
(к = 1, . . ., г; j = 1, . . ., с), как интенсивные величины,
определяются только этими внутренними переменными. Так как
условия равновесия (4.12) состоят из (г — 1) с уравнений, число
свободных параметров, которые могут меняться в равновесном
состоянии, будет равно
/ = (с — 1)г + 2 — (г — 1)с = с — г + 2.
Основные положения
205
Пример. Равновесие двухфазной однокомпонентной систе-
мы: с = 1, г = 2, / = 1. Равновесие трехфазной однокомпонент-
ной системы: с = 1, г = 3, / = 0 (тройная точка). Равновесие
двухфазной двухкомпонентной системы: с = 2, г = 2, f = 2.
ОТСТУПЛЕНИЕ 11
Классификация фазовых переходов, рассмотренная в § 1, впервые
была предложена Эренфестом [12]. Его идея о порядке фазового пере-
хода основывается на разложении величины Дц (Т + dT, р + dp)
в ряд Тейлора по степеням dT и dp. Если отличны от нуля члены пер-
вого порядка, то мы имеем переход первого рода. Если же члены пер-
вого порядка обращаются в нуль вдоль кривой равновесия и отличны
от нуля члены второго порядка, то мы имеем переход второго рода,
который, вообще говоря, сопровождается конечным скачком тепло-
емкости.
Известно много фазовых переходов первого рода, например пере-
ход жидкость — пар в чистом веществе, за исключением критической
точки, когда теплоемкость Ср становится бесконечной (см. фиг. 53а).
Что касается фазовых переходов второго рода, то известно лишь неболь-
шое число примеров, причем имеются определенные отклонения от схе-
мы Эренфеста. Рассмотрим, например, случай перехода из сверхпрово-
дящего в нормальное состояние; этот переход описывается кривой
равновесия в плоскости переменных Н — Т {Н — магнитное поле).
Скрытая теплота перехода равна нулю только в точке Н = 0 кривой
равновесия, когда теплоемкость Сц (= Су) испытывает скачок. Как
показал Онсагер [4], для двумерного изинговского ферромагнетика
при Н = 0 теплоемкость Сн (=Су) логарифмически расходится
в точке перехода и непрерывна везде вне ее. Тисса [5, 6] указал, что
разложение в ряд Тейлора невозможно, поскольку коэффициенты при
производных от р, второго и более высоких порядков для одной или
обеих фаз могут обращаться в бесконечность. Таким образом, перво-
начальная классификация Эренфеста является в значительной мере
неполной.
Янг и Ли [7] доказали математическую эквивалентность теории
перехода жидкость — пар и теории перехода для простых моделей
ферромагнетика. Обе теории имеют одинаковую структуру; кривую
намагниченности можно получить из изотермы в плоскости р — V
и наоборот: магнитное поле соответствует химическому потенциалу,
а намагниченность — плотности. Это означает, что переход жид-
кость — пар становится переходом второго рода, когда испарение
вещества происходит в атмосфере его паров.
Теплоемкость Ср следует считать менее фундаментальной вели-
чиной, чем Су, в том смысле, что аномалии в поведении Су связаны
с механизмом упорядочения: дальнодействующие молекулярные
взаимодействия вызывают, по-видимому, скачок Су, в то время как
короткодействующие силы приводят к бесконечному значению Су
в точке перехода. Райс [8] показал, что если короткодействующее
взаимодействие не зависит от объема, переход остается переходом
второго рода, однако в противном случае система, у которой Су —
= оо, будет неустойчивой по отношению к изменению объема и переход
становится переходом первого рода. Он установил, что бесконечная
теплоемкость может наблюдаться только при переходах первого рода.
206
Гл. 4. Равновесие фаз и химическое равновесие
§ 6. Химический потенциал газа
Химический потенциал на 1 моль (термодинамический потен-
циал Гиббса) G (Т, р) однокомпонентного идеального газа имеет
вид
G(T, p) = G(T, р0) + ЯГ1п-^ (4.14)
= G (Г) + RT In р.
Здесь
(4.14')
G{T) = UO — CPT In Г-Г
С'
(Т2) dTz-RTi +RT\npo
(4.15а)
— химический потенциал при температуре Т и нормальном давле-
нии х) р0 (если принять его равным единице, то последний член
обратится в нуль), i — химическая постоянная.
Для внутренней энергии на 1 моль имеем также
т
U(T) = UO+(C°P-R)T + J С'(Л)^1- (4.156}
о
Здесь Uo — удельная молярная внутренняя энергия при Т = 0,
а Ср — удельная молярная теплоемкость при постоянном давле-
нии, обусловленная поступательным и вращательным движением
молекулы (для одноатомного газа Ср = 5/2R, для двухатомного-
Ср = 7/г-К, Для многоатомного Ср = 47?); С'(Т) — удельная теп-
лоемкость, обусловленная внутренними колебаниями молекул,
которые при комнатной температуре обычно малы.
Замечание. При обычных условиях, т. е. для не очень
низких температур и не слишком легких газов, соотношение
(4.15а) является хорошим приближением. Однако у легких газов,
например у водорода, вращательная теплоемкость не является
постоянной ниже 100° К, так что соотношение (4.15а) требует
некоторых поправок (см. книгу Кубо «Статистическая механика»,
[9], гл.' 3, пример 1 и задача 6).
Молярный химический потенциал j-го компонента в смеси
идеальных газов имеет вид
СДГ,р) = СИГ,Ро) + ЛПп^-^ (4.16)
= G) (Г) + RT In Pj = (Г) + RTlnp+RT In у7-. (4.16')
Далее двойной чертой над символом (например, G) будут отмечаться
величины, отнесенные к единице объема при нормальном давлении.
Основные положения
207
Здесь G} (Т, р0) представляет собой химический потенциалх) чистого
/-го компонента при давлении р0, — этот же химический
потенциал при нормальном давлении р0 = 1, р — полное давление и
Pj — HiP (парциальное давление),
И; /4 |7\
t/; = —— (молярная доля /-го компонента). v ‘ >
2jra>
Термодинамический потенциал смеси идеальных газов запишется
в виде
G (Т, р, п1г пс) = t п jGj (T,p)=j\ nfi] (Г, р) - TAS. (4.18)
1=1 j=l
Здесь
AS =——Rn^yjlxiyj (4.19)
— энтропия смешения (см. гл. 2, пример 5; гл. 3, задача 13).
Реальные газы. Чтобы учесть отклонение от идеальности, моди-
фицируем соотношения (4.14) и (4.16) следующим образом:
однокомпонентный газ
G(T, />) = ^(Г) + ЯГ1п/щ, (4.20)
смесь
G^T, р) = (?’) Ч- RT In pjV}.=
= Gaj(T) + RTlnp+RTlnyjVj. (4.21)
Здесь G или G°j обозначает химический потенциал чистого газа при
температуре Т и нормальном давлении р0. Величина v (или vj)
называется фугативностъю и обладает следующим свойством:
limv=l, limvy=l. (4.22)
р->0
Замечание. В случае реальных газов выражение (4.15)
для G и Gj не является точным. Кроме того, парциальное давле-
ние р}- = ру) в (4.21) представляет собой теперь лишь некую фор-
мально определенную величину и не имеет прямого физического
смысла, как в случае идеального газа. Так как при давлении р,
стремящемся к нулю, всякий реальный газ переходит в идеальный,
фугативность v должна стремиться к единице при р -> 0.
Ч В дальнейшем индекс 0 будет обозначать чистое однокомпонентное
вещество.
208
Гл. 4. Равновесие фаз и химическое равновесие
§ 7. Химический потенциал и давление насыщенных паров
жидкостей и твердых тел
В соответствии с (4.3) молярный химический потенциал чистой
жидкости (твердого тела) G№„jm (Т, р) [GTBep (Т, р)] должен быть
равен химическому потенциалу насыщенного пара (при давле-
нии р):
бДидк {Т, р) — Gras (Т, p) = Gra3 (T) + RT In р. (4.23)
Здесь Gras — химический потенциал насыщенного пара. [Мы
использовали уравнение для идеального газа (4.14), что воз-
можно, так как давление насыщенного пара жидкостей и твер-
дых тел сравнительно мало.]
Молярный химический потенциал j-го компонента раствора
(или твердого раствора) Gj,^^ (Т,р) определяется соотношением
G3, жидк (Т, р) = Gj, газ (Л Р) = < газ (Г) + RT In Pj. (4.24)
Здесь Gj, газ — химический потенциал у-го компонента в газовой
фазе (которая рассматривается как смесь идеальных газов),
газ — химический потенциал у-го компонента при нормальном
давлении р0 и температуре Т, a pj — давление насыщенного пара
у-го компонента в растворе (твердом растворе) [см. (4.16)]. Сравни-
вая соотношение (4.24) с аналогичным соотношением для чистого
жидкого у-го компонента, можно переписать его следующим обра-
зом:
G3t жидк (71, р) = Gj, жидк (71, p'j) + 7?Пп ——. (4.25)
ej
Здесь G°, жидк — химический потенциал у-го чистого жидкого ком-
понента. Для него имеем
_ — pQ
G°j, жидк = СЬаз + ЛПп-^-, (4.26)
где p'j — давление насыщенных паров чистого у-го жидкого ком-
понента при температуре Т. Исключая Gj, газ из (4.26) и (4.24),
получаем (4.25).
При давлениях, близких к нормальному (например, 1 атм),
химический потенциал жидкости (твердого тела) слабо зависит
от давления, так что р" в Gj, ’^Ида (Т, р')) в соотношении (4.25)
можно заменить на р. В’результате соотношение (4.25) упрощается
и принимает вид
Gj, жидк (71, р) = жидк (Т, p)+RTln^-. (4.27)
Основные положения
209
Таким образом, мы получили выражение для химического потен-
циала компонента раствора через химический потенциал чистой
жидкости и давление насыщенных паров для каждого компонента.
Если учесть изменение давления, которым мы пренебрегли при
выводе соотношения (4.27), то вместо него получим
р? _
Gjt жидк (Т, р) = G°t жидк (Г, р) -р RT In f V'j dp. (4.27х)
Pj i
Последний член здесь обычно мал.
§ 8. Разбавленные растворы
Двухкомпонентный раствор. Будем обозначать растворитель
индексом 1, а растворенное вещество — индексом 2. Молярная
концентрация равна : х2 (xj + х2 = 1). При достаточно малых
концентрациях давление насыщенных паров растворителя pj удо-
влетворяет уравнению
Pt. — ^iPi (Д’ — const, Xi -> 1, х2 -> 0). (4.28)
Это эмпирически установленное предельное соотношение называют
законом Рауля (величина р\ есть давление насыщенных паров
чистого растворителя). Давление насыщенного пара растворенного
вещества р2 удовлетворяет закону Генри-.
р2 = k2x2 (Т = const, х2 ~ 0). (4.29)
Здесь к2 — постоянная, характеризующая раствор. Химический
потенциал каждого компонента будет
ОДТ, p) = G°i(T, р) +ПТ In Xi (Zi~l), (4.30а)
G2(T, p) = G%(T, p) + 7?74n^- =
= <p“ (T) + ПТ In х2. (ж2~0) (4.306)
Соотношения (4.29) и (4.306) выводятся из уравнения Гиббса —
Дюгема (см. задачу 13).
Многокомпонентный раствор. Будем обозначать растворитель
индексом 1, а растворенные вещества — индексами 2, 3, . . . .
Молярные концентрации равны xf. х2-. х3: . . . . По аналогии
с (4.28) имеем в пределе Zj ~ 1, х2 -> 0, х3 0, ... (закон Рауля
для разбавленных растворов)
Pi = XtPi, или Р|^Р1 =х2 + х3+ ... . (4.31)
Hi
В этом случае не представляется возможным определить G2,
G3, . . ., р2, Рз> • • • из одного лишь уравнения Гиббса — Дюгема.
14 Кубо
210
Гл. 4. Равновесие фаз и химическое равновесие
Однако если допустить, что в пределе сильно разбавленного рас-
твора взаимодействие между растворенными веществами пренебре-
жимо мало, то можно положить
Pj = kjXj (у = 2, 3, ...; ^ — 0), (4.32)
Gj = G°j-}rRT\p.^- = ^-^ RTXnXj. (4.33)
pi
Таким образом, мы имеем полную аналогию с двухкомпонентным
случаем.
§ 9. Идеальные растворы (идеальные твердые растворы)
и регулярные растворы
Идеальным раствором (идеальным твердым раствором в случае
твердых веществ) называется система, для которой во всей области
температур, давлений и концентраций справедливы следующие
соотношения:
G^G^T^+RTXnx^
GZ = G°(T, p)+RTlnx2.
Хотя такое вещество и представляет собой идеализацию, однако
существуют реальные системы, мало отличающиеся от него.
Если идеальный раствор составляется из чистых веществ,
то изменение термодинамического потенциала при этом равно
ДС = x^G[ -j- x2G2 — = RT (^*i 1ч Xi -J- x2 In Х2),
или _
\H = Q, Д5 = -R(x1lnx1+x2lnx2). (4.35)
Последнее равенство определяет энтропию смешения для идеаль-
ного раствора Д*!> идеал-
Давление насыщенного пара равно:
Р1=Ж1Р;, р2=ж2р". (4.36)
Регулярный раствор. Гильдебранд рассматривал растворы, которые
он называл регулярными; для них
ДЯ=/=0 и Д5=Д5идеал. (4.37)
Существует целый ряд реальных систем, для которых справедливо
это приближение. Пусть Д77 является функцией от х2. Тогда
= + + = Х2) + РТ\ъХ1,
* иХо . _
яьГг (4-38)
G2 = G2° + MI + х2 Т— 4- RT In х2 = ф° (Т, р, х2) + RT In х2.
Основные положения
211
§ 10. Выражения для концентрации растворов
Существуют различные способы выражения концентрации
раствора. Обычно употребляются следующие:
1) мольная (молярная) доля,
Число молей растворенного вещества_____________________ __
''2 Число молей растворителя + Число молей растворенного вещества
_ п2 .
«l + re2 ’
2) моляльность т2 — число молей растворенного вещества
в 1 кг растворителя;
3) молярность, или молярная концентрация, С2— число молей
растворенного вещества в 1 л растворителя.
Обозначим через Mi и М2 соответственно молекулярный вес
растворителя и растворенного вещества, а через р и Pi — плотность
раствора и растворителя. Перечисленные величины связаны между
собой определенными соотношениями:
(4.39)
(4.40)
1000 х^ т2
п2 = —-------- , х2 =----------—— ,
Mi xi (1000/Afi)
С2 =---------------1000, т2 =------------------- .
1000 + М2т2 р - (С2М2/1000)
При х2 - образом: - 0 их можно приближенно представить следующим 1000 г т2 -=р~Х2, C2~pim2. (4.41) Az ।
§ 11*. Активность и коэффициент активности
Химический потенциал /-го компонента раствора можно по ана-
логии с (4.34) записать в виде
Gj (Т, р) = G? (Т, р) + RT In aj (Т, р) « (4.42)
~$(T) + RTinaj(T). (4.42')
Величины G°j и G" были определены ранее (см. § 7). Соотноше-
ние (4.42) или (4.42') является определением активности a,j (Т, р)
/-го компонента раствора. Обычно зависимостью величин G® (Т, р)
и aj(T,p) от давления можно пренебречь, так что соотношение
(4.42') является хорошим приближением. Положив в уравнении
(4.42')
aj = yjxj, или Ъ' = ^7> (4-43)
212
Гл. 4. Равновесие фаз и химическое равновесие
определим коэффициент активности yj. Пусть р— давление насы-
щенного пара, tjj — концентрация /-го компонента и v7- — фугатив-
ность, и пусть для чистого жидкого /-го компонента v® и p°j обо-
значают Тогда соответственно фугативность и давление насыщенного пара. УзР ,, ,, . Pj тч (насыщ. пар -+ идеальный газ) Pj = м.446) 'J xjPUj (насыщ. nap -+ идеальный газ) xjP°j Z
В случае идеального разбавленного раствора (xt ~ 1, ж2 0) имеем
с учетом (4.33)
У1~ 1, а2~^, у2~^|. (4.45)
Г2 Г2
Другое определение активности растворенного вещества в общем
случае разбавленных растворов. В зависимости от того, какое
выражение для концентрации использовать, химический потен-
циал растворенных веществ в идеальных разбавленных растворах
может быть записан несколькими различными способами:
ё2 = <р“ + 7?ПпЖ2= (4.46а)
= фз lnm2= (4.466)
= <р"4-7?711пС2. (4.46в)
Здесь
«ь = <р°—rt in и <p; = <p;-7?TinP1.
Чтобы в общем случае записать химический потенциал разбавлен-
ного раствора в виде, аналогичном (4.46а) — (4.46в), следует ввести
активности а', а" и коэффициенты активности у®, у', у" с по-
мощью следующих соотношений:
ёа = Ф« + Я7’1па“^ф» + ЯГ1п(у«Ж2) (а“ = у^2), (4.47а)
£г = ф2 + Я7’1па;==ф:;4-7?7,1п(у;т2) (а; = у;т2), (4.476)
G2 = ^+RT\na^^RT\n^Cz} « = у^2). (4.47в)
В предельном случае идеального разбавленного раствора все вели-
чины у®, уз и Уз равны 1.
§ 12*. Растворы сильных электролитов
Растворы, в которых молекулы растворенного вещества пол-
ностью диссоциированы на положительные и отрицательные ионы,
Основные положения
213
называются сильными электролитами. Рассмотрим молекулу
растворенного вещества Av+Bv-, которая диссоциирует в растворе
на v+ положительных ионов Az+ с валентностью z+ и v_ отрицатель-
ных ионов Bz~ с валентностью |z_| :
Av+Bv- —»v+Az+ + v_Bz_ (z+>0, z_<0). (4.48)
Из условия электронейтральности имеем
v+z+ 4- v_z_ — 0. (4.49)
Если x2 — концентрация растворенного вещества, х+ — концен-
трация положительных, а х- — отрицательных ионов (в молярных
долях), то
х+ = v+x2, х- - v„ar2. (4.50)
Пусть у+ — коэффициент активности положительных ионов,
а у_ — отрицательных. Тогда средний коэффициент активности
у определится из соотношения
yv = yV+yV-, v+ + V- = V. (4-51)
Молярный химический потенциал растворенного вещества в растворе
G2 = Gav+bv- записывается следующим образом:
G2 = Gav+bv_ = Tav+bv- (Д р) + In (y+z+) + In (y_z_) =
= <Pav+bv_ + In x2 + RT In (v^v^.-) + vRT In y. (4.52)
Для коэффициента активности у имеет место уравнение Дебая —
Хюккеля
, — z. [ z I е2 х
In у = 20^7 1+ ха ’
где
2 __ 4ne27Vo (v+z2 + v_zl) С2
Z ~ lOQQDkT
(4.53а)
(4.536)
Здесь D — диэлектрическая проницаемость, Хо — число Авогадро
(6,024-1023 моль'1), е — элементарный электрический заряд (заряд
электрона), а — средний диаметр ионов, а С2 — молярность
растворенного вещества.
Ионная сила определяется соотношением
/ = 1 У zlCt = 1 (v+z: + v_z2.) С2,
так что (4.53а) можно переписать следующим образом:
1пу=-г+.1г-'Л}4Г,
Г 1 + ВаУ/
(4.54)
(4.55а)
214
Гл. 4. Равновесие фаз и химическое равновесие
где
Л _ g3jVo ( 2л У/2 р ( \1/2
(М7)3/2 \1000j ’ Ь - \ IQQQDRT ) ‘ (4-ЭЭО)
В случае разбавленных растворов в знаменателе выражения (4.53а)
можно пренебречь величиной ха по сравнению с единицей. В этом
случае (4.55а) можно заменить приближенным соотношением]
In у= — z+1 z_ | А VI. (4.56)
Аддитивность энергий для ионов. Величина <Pav+bv- зависит
от выбора начального состояния. В качестве такового можно взять,
например, состояния чистых веществ А и В, положив
<Pav+bv_ = v+cpA2+ + v_cpB2_. (4.57)
Через <рАг+ и <рВ2 обозначены известные свободные энергии обра-
зования 1 моль ионов Аг+ и Bz- в растворе из чистых веществ.
Эти величины определяются экспериментально. Предположение
об аддитивности лежит в основе теории электролитической диссо-
циации Аррениуса. Однако поскольку ионы всегда появляются
в виде пар, каждая из .которых состоит из положительного и отри-
цательного ионов, общую аддитивную постоянную можно выбирать
произвольным образом. Для удобства обычно полагают
Фн+ (вод.) = 0. (4.58)
§ 13. Химическое равновесие
Рассмотрим теперь равновесие в случае химической реакции
aA + 6B+...^*ZL + mM4-..., (4.59)
или
vaA + vbB + . . . 4- vlL -l vmM + • • • — 0
/ i. 7 \ (4.59 )
(vA=—a, vB = — b, . .., vL = Z, vM = m, ...).
В дальнейшем будем предполагать, что р и Т постоянны, как это
часто имеет место при химических реакциях.
Термодинамический потенциал, энтальпия и энтропия реакции.
Обозначим термодинамический потенциал Гиббса через G (пА,
п%, . . р, Т). Будем рассматривать изменения числа молей
каждого компонента
6nA = vA6^, 6ив —vB5/., ..., = vL6Z, .... (4.60)
Соответствующее изменение 6G запишется в виде
6G=S^6nA = 6^2vAGA)
А А
Основные положения
215
так что dGId't. = AG,
AG = 2 vAGA =—aGA— 6GB 4 ... 4 ZGL 4mGM4 • • • . (4.61)
A
Здесь AG — термодинамический потенциал реакции, а К— коэффи-
циент продвижения реакции1). Энтальпию реакции А/Z и энтропию
реакции ДА можно получить из AG с помощью соотношений
&G = \H-TkS, (4.62а)
&Н=-Т*-^-^- , AS=--^\G. (4.626)
При AG<0 реакция (4.59) идет спонтанно слева направо (пока
не наступает подавления реакции).
Условие равновесия имеет вид 6G = 0, или
AG=2vaGa = 0. (4.63)
Стандартный термодинамический потенциал реакции. Пусть
GA, GB, ... —соответственно химические потенциалы чистых веществ
А, В, . . . при температуре Т и нормальном давлении (обычно 1 атм).
Тогда можно ввести следующие величины:
стандартный термодинамический потенциал реакции
AG=Sva^a; (4.64а)
стандартная энтальпия реакции
ДЯ = 2 vJh = д(^Т} ; (4.646)
стандартная энтропия реакции
aJ=2^1=-^-- (4.64в)
Закон действующих масс. Если реакция (4.59) протекает
в газах, то
АС = 2^а[^а + 7?Т1п(Ыа)]
(/а — фугативность2).
1) Иногда эту величину называют также химической переменной или
числом пробегов реакции.—Прим. ред.
2) Фугативность /А — безразмерная величина [вводится аналогично
величине vA в (4.21)]. Давление рд выражено через нормальное давление р0.
Точнее
Дб=2 VA (^а + Л71и£^А) .
216
Гл. 4. Равновесие фаз и химическое равновесие
Теперь (4.63) можно переписать в виде
I т fl ftn _
К П Ыа)1 - (4.65)
Величина К называется константой равновесия. Если газ можно
рассматривать как идеальный, имеем просто /а = /в = • • • = !•
Аналогично в случае реакции в растворе условие (4.63) можно
переписать в виде
а1 ат -
к П 4А=44^=e~^/RT- (4-66)
аАаВ ’ ’ •
Пример. 1/2N2 (газ) + 3/2Н2 (газ) = NH3 (газ).
Если считать газы идеальными, то в соответствии с (4.65) имеем
= pi/2p|/2 = еХ^ [ — ЛТ7 2"^h2)J •
§ 14. Термодинамика электрохимического элемента
Электрохимический элемент. Если поместить в электролит
(представляющий обычно жидкую, но иногда и твердую фазу)
два металлических электрода, то между ними возникает электро-
статическая разность потенциалов.
Примеры
Си | CuSO4 (вод.) | ZnSO4 (вод.) | Zn (элемент Даниэля).
(4.67а)
Ag (тверд.), AgCl2 (тверд.) | М+С1- (вод.) | Hg2Cl2 (тверд.), Hg(жидк.).
(4.676)
Если замкнуть внешнюю цепь элемента, то по проволоке от анода
к катоду потекут электроны (е), причем, вообще говоря, будут
происходить восстановление катода и окисление анода. Например,
Си++ 4- 2е —> Си (восстановление),
(4.68)
Zn Zn++ + 2е (окисление).
В результате таких реакций на электродах в элементе происходит
определенная суммарная реакция, которая сопровождается пере-
дачей во внешнюю цепь заряда q. В элементе Данизля (фиг. 67)
в соответствии с (4.68) происходит следующая реакция:
Zn + Cu++ -> Си + Zn++, или Zn + CuSO4 -> Си + ZnSO4.
(4 69)
Основные положения
217
Вообще говоря, из (2.25) следует, что должно выполняться условно
(4.70>
Здесь (—W) — работа, совершенная внешней средой, а (—6G) —
уменьшение термодинамического потенциала.
Полупроницаемая стенка,
через- которую проходят только ионы S0^~
Фиг. 67. Элемент Даниэля.
Обратимый элемент. Рассмотрим цепь, показанную на фиг/68.
Если к выводам элемента g приложить разность потенциалов Ее
с потенциометра, то ток через элемент перестанет течь и реакция
в элементе будет сбалансирована
Ее = Е (з. д. с. элемента g).
Если, однако, разность потенциалов Ее несколько меньше ЕТ
(Ее < Е), то реакция будет продолжаться, а если Ее несколько
больше Е, то реакция будет проходить в обратном направлении.
Если все физические и химические явления, происходящие в эле-
менте, обратимы, то, поддерживая разность потенциалов Ее рав-
ной Е, можно вызвать в элементе квазистатические изменения.
218
Гл. 4. Равновесие фаз и химическое равновесие
s
Потенциометр
Нормальный элемент
Ф и г. 68.
мы
Элемент такого рода называется обратимым, элементы же, в кото-
рых имеются контакты между растворами электролитов, обычно
необратимы, однако в некоторых случаях их можно рассматривать
приближенно 4как обратимые (при-
мер — элемент Даниэля).
Электродвижущая сила обрати-
мого элемента. Запишем реакцию,
которая протекает внутри элемента,
в виде (4.59). Если число молей
компонентов изменяется в 6% раз,
то при этом переносится электриче-
ский заряд
6q = zg dZ,
где % — постоянная Фарадея
fy = 96485,3 кул/г-экв,
a z = 2 для реакции (4.69). Работа
при этом равна —W = E6q. Так
имеем обратимый элемент, то в (4.70)
следует взять знак равенства, и для э. д. с. Е получаем
(4-7D
где AG— термодинамический потенциал реакции.
Электрохимический потенциал. Если в рассматриваемой
системе, находящейся в электростатическом поле с потенциалом
Ф (отсчитываемым от нулевого потенциала среды, которую мы
считаем заземленной), частица j имеет заряд г7-е, то выражение
(1.76) следует заменить на
= + (4.72)
i
Величина т]у = pj + г^еФ называется электрохимическим потенциа-
лом /-го компонента системы (если все величины отнесены к 1 моль
вещества, то е следует заменить на g).
Если имеются две фазы, находящиеся соответственно при потен-
циалах Ф' и Ф", то условия равновесия уже не будут определяться
соотношением (4.3), а запишутся в виде условия равновесия для
энергии переноса массы для /-го компонента по отношению
к фазам 1 и 2:
(4-73)
Замечание. Выражение (4.71) дляэ. д. с. можно получить,
рассматривая равновесие между различными фазами, находящи-
мися в контакте внутри элемента (см. задачу 10).
Основные положения
219
§ 15. Применение третьего закона термо дина мики
В соответствии с третьим законом термодинамики термодина-
мический потенциал, или стандартный термодинамический потен-
циал реакции, определяемый соотношением
Дё = ДЯ-7’Д5,
можно получить из калориметрических данных. Величина А77
определяется теплотой реакции, величину Д5 можно вычислить,
зная теплоемкость, теплоту плавления и теплоту парообразования
в интервале температур от 0° К до температуры, при которой
происходит реакция, для всех участвующих в реакции веществ.
Например, можно использовать формулу
Tf
Ть т
। f г ЛТ I Lv । f г &L. • С4 74)
"Г ] '-'Р, жидкий Г Tb - J LzP> газ у >
ть
здесь Тf — точка плавления при давлении р; Lf — теплота плав-
ления; Тъ — точка кипения при давлении р; Lv— скрытая теплота
парообразования; CPi твер, СР1 жидк, Ср, газ— теплоемкости при
постоянном давлении соответствующих фаз, указанных индексами.
Полученные таким образом значения Л 5', или Д5°, совпадают
со значениями, найденными по температурной зависимости кон-
станты равновесия или по э. д. с. элемента. На основании большого
числа экспериментальных данных такого рода Нернст и сформули-
ровал третий закон термодинамики. Таким образом, мы можем
вычислить постоянные химического равновесия, э. д. с. элемента
и т. д. по калориметрическим данным.
Химическая постоянная. Постоянная i в соотношении (4.15а)
дает абсолютное значение энтропии идеального газа. Ее называют
иногда постоянной давления пара, так как она дает также абсолют-
ное значение давления пара жидкой или твердой фазы. С помощью
статистической механики можно получить ее значение, исходя
из молекулярной структуры газа. В рамках термодинамики,
однако, эта величина представляет собой просто характеризующую
данное вещество постоянную, которую следует находить экспе-
риментально. Так как эта постоянная определяет константы рав-
новесия для газовых реакций, ее называют также химической
постоянной.
220
Гл. 4. Равновесие фаз и химическое равновесие
ПРИМЕРЫ
1. При температуре, лежащей ниже некоторой критической,
изотермы ван дер Ваальса имеют в р — V-плоскости минимум и
максимум. В интервале между минимумом и максимумом давление
падает при уменьшении объема, так что соответствующие состояния
являются неустойчивыми и не могут реализоваться. В этой области
система разделяется на две фазы: жидкую и газообразную. Каково
равновесное давление сосуществования двух этих фаз для задан-
ной изотермы ван дер Ваальса? Как распределяется вся масса
системы между этими фазами? Выполнить соответствующее построе-
ние.
РЕШЕНИЕ
На фиг. 69 представлена изотерма ABCDEFG для 1 моль газа
ван дер Ваальса. На участке АВ вещество находится в жидком
состоянии, а на участке FG — в газообразном. В том случае,
когда две фазы находятся в равновесии, должны быть равны
их давления [условие (4.1)] и химические потенциалы (4.3). Так,
для того чтобы состояния В и F находились в равновесии, они
должны лежать на одной горизонтальной линии. Что касается
Примеры
221
химических потенциалов (термодинамических потенциалов на
1 моль) состояний В, D и F, то их можно сравнить, рассмотрев
изменение химического потенциала вдоль изотермы. Из уравнения
dG = Vdp
находим
G (D) — G (F) = j 7 dp = площ. (FEDF)
FED
И
ё(Я)-ё(В) = площ. (DCBD).
Таким образом, состояние D обладает более высоким значением
термодинамического потенциала, чем В или F, и, следовательно,
является неустойчивым. В соответствии с написанными выше
уравнениями имеем
G (В) — G (F) = площ. (FEDF) — площ. (DCBD).
Если горизонтальная линия проходит таким образом, что обе
площади равны, то G (В) = G (F), т. е. мы получаем условие рав-
новесия двух фаз. Если горизонтальная линия проходит выше
или ниже, то G (В) < G (F) или G (В) > G (F) и становится устой-
чивой либо жидкая, либо газообразная фаза. Иначе говоря,
когда горизонтальная линия BDF разделяет площадь на две
равные части, то кривые А В (жидкая фаза) и GF (газообразная
фаза) становятся устойчивыми изотермами. Для заданной темпе-
ратуры сосуществование двух фаз имеет место при давлении
Рт?( = рв) (давление насыщенного пара).
При сосуществовании двух фаз часть системы находится в жид-
ком, а часть в газообразном состоянии. При этом состояние систе-
мы изображается какой-либо точкой на кривой BF. Таким обра-
зом, вдоль кривой GFDBA происходит квазистатическое изотер-
мическое сжатие. Отношение количества двух фаз в некоторой
промежуточной точке М определяется следующим образом. Пусть
из общего числа п молей вещества пх молей находятся в жидкой
фазе. Полный объем nVм представляет собой сумму nxVв
и п (1 — х) VF, или
4- (1 — х) Vp = VM.
Таким образом,
х ___ Ур—Ум
1—х Ум — Ув ’
т. е. отношение MF : МВ дает отношение числа молей в жидкой
и газообразной фазах.
222
Гл. 4. Равновесие фаз и химическое равновесие
Замечание. Определение равновесной кривой по условию
равных площадей называется правилом Максвелла.
Строго говоря, состояния, соответствующие кривой CDE,
не могут реализоваться как термодинамические состояния,
поскольку условие равновесия не удовлетворяется. Поэтому ква-
зистатические процессы, включающие эти состояния, фактически
являются лишь гипотетическими. В приведенном выше решении
мы применяли уравнение dG = V dp к таким неравновесным состоя-
ниям. Поэтому доказательство нельзя считать вполне строгим.
В случае газа ван дер Ваальса можно, однако, устранить этот
дефект, используя другое доказательство (см. задачу 47).
2. Термодинамический потенциал на 1 моль в двухкомпонент-
ной системе определяется соотношением G (х} = xfit^ x2G2. Здесь
Фиг. 70.
и х2— относительные молярные концентрации компонентов в 1 и 2,
a Gt и G2 — химические потенциалы на 1 моль. Показать, что если
кривая зависимости G (х) (х = хЛ или х2) от х имеет в двух точках
Q' и Q" общую касательную Q'Q" (фиг. 70), то состояния, лежа-
щие между Q' и Q", распадаются на две фазы.
РЕШЕНИЕ
Положим x = xt. Из уравнения Гиббса — Дюгема Xt dGJdXf}-
х2 dGJdxi = 0 имеем
Условие существования общей касательной Q'Q" запишем в виде
(2>
Примеры
223
Здесь мы ввели обозначения Glt 2 (эу) = б?), 2 и G\t 2 (4) = G"it 2-
Учитывая, что G = XiGt4- X2G2, получаем из (2)
ТЬ 7^' 77» fin •2'1^1Ч-*2-2^2 ^1Gj X2Gg
^2 ^2 х» х- »
откуда
x{G{—x{G2 _ —хф^х^ x'jGi-|-х'гб'з — x{G{— x'2G2 G2— G2
xj —x“ x)— x{ 0
И
— XgGJ-j- x2G2 x2G'i — x2G2 x'\G'{ + x2G2 •—x)G)—x2G2 G'{ — Gj
— x' x2 x)'— xj O’
Таким образом,
G; = G“‘ и G2 = G2, (3)
что эквивалентно соотношению (2). Если справедливо соотноше-
ние (3), то, очевидно, справедливо и (2). Соотношение (3) представ-
ляет собой условие сосуществования двух фаз с разными моляр-
ными концентрациями (обозначенными одним и двумя штрихами).
Таким образом, система, имевшая плотность г!, в интервале между
Q' и Q" распадается на две фазы, относительное количество
которых равно
gf = Х1 xi Q*______. Х1 (4.)
—~~ зс а? । — а? ।
причем термодинамический потенциал системы (точка Q на фиг. 70)
меньше G(x) (точка R на фиг. 70). Иначе говоря,
C'G'^CnG"<G(x). (5)
3. Основываясь на определении (4.8), показать, что свободная
энергия на единицу площади поверхности раздела равна поверх-
ностному натяжению у. Показать также, что внутренняя энергия
на единицу площади поверхности раздела равна у — Т dyldT.
РЕШЕНИЕ
Заметим прежде всего, что понятие поверхностного натяжения
имеет ясный смысл лишь в том случае, когда между двумя фазами
в состоянии теплового равновесия имеется четкая поверхность
раздела. Чтобы определить эту поверхность, надо разделить весь
объем на части, занимаемые первой и второй фазами. Тогда будем
иметь V = V + V" и N = n'V + n"V" г), где N — полное число
1) Точнее говоря, поверхность раздела выбирается перпендикулярной
градиенту п'.
224
Гл. 4. Равновесие фаз и химическое равновесие
частиц в объеме V, а п' и п" — плотности частиц в каждой фазе,
измеренные достаточно далеко от поверхности раздела. При
этом для сложной системы величина F (Т, V', V", a, N',
N") = U — TS отличается от величины F’ (Т, V, N') 4~
+ F" (Т, V", N"), т. е. от суммы свободных энергий объемов
V и V", на которые мы разделили систему. Так как это различие
связано с наличием поверхности, то свободная энергия поверх-
ности Fa определяется следующим образом:
Fa = F - (S' + F"). (1)
Из (4.8) можно получить следующие уравнения:
dF = d (U - TS) = - S dT - p' dV - p" dV" +
4- у do 4- p,' dN* 4- p" dN",
dF' = — S'dT — p’ dV + p,' dN'
и аналогичное уравнение для dF". Из них находим
dFa = — SQdT 4- у do. ’ (2)
Здесь Sa S — (S' 4* S") — энтропия поверхности. Из соот-
ношения (2) видно, что Fa является функцией Tso. Если при
постоянной температуре линейные размеры системы возрастают
в а1/2 раз, то площадь поверхности увеличится в а раз, так что
Fa (Т, асг) = aFa (Г, о). Дифференцируя полученное соотноше-
ние по а и полагая а = 1, находим
n dFa
Отсюда видно, что величина у представляет собой поверхностную
свободную энергию на единицу площади. Кроме того, так как
у является функцией только интенсивной переменной Т, то для
поверхностной энтропии имеем
<7 — dF° ~
° дТ ° dT •
Таким образом, внутренняя энергия определяется следующим
образом:
Ua = Fa + TSa=(v-T^O, ИЛИ ^ = у-Т^.
4. Показать, что давление пара ps (Т) в случае конденсирован-
ной фазы (жидкой или твердой) определяется формулой
ь0 Г dH
1ft Ps т” 1ft 1 T | ^2 | // T”
о о
Примеры,
225
Здесь — скрытая теплота парообразования при 0° К, а Ср —
удельная молярная теплоемкость при постоянном давле-
нии для конденсированной фазы [смысл величин Ср, С (Г) и дясен
из соотношений (4.15) и следующих за ними рассуждений].
РЕШЕНИЕ
Энтропию для 1 моль газа получим из (4.14) и (4.15):
_ т т
S(T, р) = -^^ = С”1п7'+ J ~ [ C'(T)dT +
о о
т
+ 4- J C(T)dT + Ri + C°p-Rlnp. (1)
о
В соответствии с третьим законом термодинамики эта величина
представляет собой возрастание энтропии при квазистатическом
нагревании 1 моль вещества в конденсированной фазе при давле-
нии р от 0 до Та КТи дальнейшем квазистатическом преобразо-
вании его в газ при Т° К путем передачи ему скрытой теплоты L,
т. е. равна
TeC^T)dT L
I 71 I 71 •
Далее, как мы знаем, L — II’—Н" и (дН/дТ)р = Ср, так что
т т
c=z0+J (с;-с;)й7’ = с0+с”7’ +J (С'-с;)^. <з>
о • о
[Здесь Со = Н' (0, р) — Н" (0, р) есть скрытая теплота перехода
при 0°К.] Приравнивая величины (1) и (2) и используя (3),
получаем
J -g-J С' (7)^ + 4- J С' (T)dTС°р InТ-
0 0 о
т т
* С" (Т} dT т 4 (*
+ е°+^-Д1пр= j-р4 -+^+с°+4- J (C'-Cp)dT.
о о
Интегрируя полученное выражение по частям, находим
С /iZ f 1 Г Г CvdT /
^4L^c’p(T)dT=-± Jcnn+J^-. (4)
оо оо
4 R
226
Гл. 4. Равновесие фаз и химическое равновесие
Отсюда и приходим к искомой формуле. Для вывода соотношения
(4) существенную роль играет использование того обстоятельства,
что lim Ср (Г) = 0 (третий закон).
т-»о
Замечание. Если удельная молярная теплоемкость, свя-
занная с вращением и колебанием молекул в газовой фазе, есть
Ci, то величины Ср и С' (Т) можно заменить соответственно
на &/2R и Ct (Г). Это справедливо для легких газов типа
водорода и гелия.
5. На фиг. 71 представ-
лена фазовая диаграмма си-
стемы Си — Ag. Жидкой фазе
соответствует область выше
кривой АЕВ, справа от ACF
находится область а-фазы
твердого раствора, а слева
от BDG — область (3-фазы
твердого раствора. Тройная
точка Е называется эвтекти-
ческой.
а) Как будет вести себя
раствор при охлаждении,
если первоначально он нахо-
дился в жидком состоянии,
соответствующем точке К на
фиг. 71?
б) Что будет происходить при нагревании твердого раствора,
если первоначально он находился в состоянии, отвечающем
точке Н (а-фаза)?
РЕШЕНИЕ
а) Изменение температуры жидкой фазы происходит практи-
чески по вертикали до тех пор, пока система не придет в состояние
К' на кривой BE (фиг. 72). При температуре, соответствующей
точке К', начинает образовываться (3-фаза твердого раствора,
причем концентрация ее определяется точкой К". Так как кон-
центрация серебра в образующемся твердом растворе меньше
исходной, то в остающейся жидкости его концентрация возра-
стает. Таким образом, при дальнейшем понижении температуры
происходит выпадение (3-фазы твердого раствора с возрастающей
концентрацией Ag. При этом изменение состояния жидкого
раствора описывается кривой К'Е, а (3-фазы твердого раствора —
кривой K"D. После того как жидкая фаза придет в состояние,
которому соответствует точка Е, начинается выпадение а-фазы
Примеры
227
твердого раствора, причем концентрация в жидкой фазе остается
постоянной; затвердевание a-фазы (С) и p-фазы (D) будет продол-
жаться до тех пор, пока весь раствор не затвердеет. [Если продол-
жать понижать температуру до значения, соответствующего,
например, точке Kt, то по истечении достаточно длительного вре-
мени твердые растворы, соответствующие точкам Ка и К$, будут
существовать в виде устойчивых твердых состояний. При этом
отношение числа атомов N (Ka)/N (К$) равно K$Ki : КхКа. Для
установления равновесия требуется, однако, очень большой про-
межуток времени, так как речь идет о реакции между твердыми
фазами.]
б) Аналогично при нагревании от точки Н (фиг. 73) а-фаза
остается неизменной до точки Н', когда начнет появляться жидкая
фаза с концентрацией Ag, соответствующей точке Н". Концентра-
ция Ag будет меньше, чем в твердой фазе. По истечении достаточно
большого периода времени концентрация Ag в a-фазе станет воз-
растать, а соответствующая точка на фиг. 73 перемещаться
вправо. Соответственно концентрация Ag в жидкой фазе также
будет увеличиваться, так что точки Н' нН" будут двигаться вправо.
Наконец точка Н' попадет в Я', а Н" в Н'[ и все вещество перей-
дет в жидкое состояние. В точке Н"х концентрация Ag должна
быть той же, какой она была в точке Н, ибо все вещество стало
жидким. Это условие и определяет положение точки Н'г Дальней-
шее нагревание^будет только повышать температуру расплава.
Если, однако, все время удалять расплавившуюся часть раствора,
то твердая Jфаза будет существовать и за точкой Я', причем
в точке А.'в ней останется лишь одно твердое серебро, которое
затем перейдет в жидкое состояние.
15*
228
Гл. 4. Равновесие фаз и химическое равновесие
6. Показать, что для произвольного раствора справедливы
следующие соотношения:
— кт —
nV°1 = ~-Ll — -RT^lnai.
Здесь аЛ обозначает активность растворителя, р{ — давление пара,
л — осмотическое давление, АГ — понижение точки плавления
(или повышение точки кипения), а р[, V°, Т° и Li — соответ-
ственно давление насыщенных паров, молярный объем, точку
плавления (или кипения) и молярную скрытую теплоту плавления
(парообразования) для чистого растворителя. При рассмотрении
повышения точки кипения или понижения точки плавления счи-
тать, что испаряющийся газ или выпадающая твердая фаза состоит
из чистого растворителя.
РЕШЕНИЕ
а) В соответствии с (4.42) химический потенциал растворителя
в растворе равен
G^G^T, р) + НТЫа1. (1)
Здесь — химический потенциал чистого растворителя. Хими-
ческий потенциал газовой фазы (в предположении, что она пред-
ставляет идеальный газ) есть
G1. газ = Glt газ (Т, р) = Gjt газ + RT In Pi,
где pi — давление пара растворителя. Условия равновесия Gl = Gl> газ
перепишем в виде
G\(T, р) + RT In а1 = ё1,газ(Т)+RT In Pl. (2)
Далее, давление насыщенного пара р° чистого растворителя опре-
деляется из соотношения
G°t (Т, p°t) = G°i, газ (Т, Р?) = ^1, газ + ЯГ Ы р?. (3)
Вычитая (3) из (2) и используя (4.14), получаем
„ G^T, p)-G°(T, р»)
А = Р1Я1 ехр рТ
Так как G? (Г, р) - (Г, p°t) « (р - р?) V°lt жидк < RT = р?7?; газ,
экспоненту в правой части равенства можно заменить единицей.
Тогда имеем
Pi = pjai. (4)
Примеры
229
б) Если чистый растворитель (давление р0) и раствор (давле-
ние р) разделены полупроницаемой мембраной (фиг. 74), то усло-
вия равновесия при температуре Т в соот-
ветствии с (1) можно записать в виде
G\(T, p0) = G°(T, p) + RTinai.
Так как изменение объема, вызванное
осмотическим давлением, очень мало,
можно использовать следующее приближе-
ние:
GJ(T, р)-^(Г,ро) = У?(р-ро).
Учитывая определение осмотического давле-
ния л = р — р0, получаем
Лшупроницаемая мемйрана
Фиг. 74.
лУ? = -ИТкиц.
в) Так как мы рассматриваем испарившийся газ как чистый
растворитель, температуру кипения следует считать равной той
температуре, при которой давление пара чистого растворителя
равно внутреннему давлению р0. Если точка кипения чистого
растворителя есть Т°, а точка кипения раствора Tj, то уравнения
(3) и (2) перепишутся следующим образом:
G° (Г®, р0) = Git газ(Г1, Ро) (чистый растворитель), (6)
G°i (Л, Ро) + KTl In aj = Gi, газ (Гр ро) (раствор). (7)
Вычитая (7) из (6) и учитывая, что dG/dT = —S, получаем разло-
жение по Тх— Т° с точностью до членов первого порядка малости
- RT{ In = Gi (Г, p0) - Gi (Ti, p0) -
-[б?.газ(Л, PoJ-^.raa^I, Po)] =
= (7\ - Г?) [ - 5°i (Tl, Po) + Si ra3 (Tl po)] = (Л - Ti)
и, следовательно,
— Ina! — -д- (уу — y^) • (8)
Если Ti — T^^T <^T°, to
In a( 7>! ’ (9)
где
Л = ri [Si газ Ot Po) - Si (Tl Po)]
230
Гл. 4. Равновесие фаз и химическое равновесие
— теплота парообразования растворителя при давлении р0 и тем-
пературе Т{.
Задача о понижении температуры плавления аналогична рас-
смотренной. Если мы обозначим через Т° точку замерзания чистого
растворителя при давлении р0, а через Ti температуру, при кото-
рой чистое твердое растворенное вещество начинает выпадать
из раствора, то для решения задачи нам достаточно лишь заме-
нить правые части соотношений (6) и (7) на бщ твер (Т®, Ро)
и (т1,твер (Л> Ро)- Тогда из (8) или (9) получим
Li = T°i (St, твер — S?) =—Теплота плавления <0. (10)
Таким образом, точка плавления понижается в противополож-
ность повышению точки кипения.
Замечание. Заметим, что знак изменения температуры
кипения и точки плавления может измениться на обратный в слу-
чае, когда Л1 больше единицы.
7*. Рассмотрим регулярный двухкомпонентный раствор, для
которого теплота смешения [см. (4.37)] АН = Ах{х2. Исследовать
соотношение между давлением пара и составом. Рассмотреть,
в частности, случай, когда обе фазы разделяются. Нарисовать
фазовую диаграмму.
(1)
(2)
РЕШЕНИЕ
Обозначим числа молей компонентов через щ и п2. Энтальпия
смешения АН запишется в виде
АН = А-1”* .
ni “Ь п2
Так как раствор регулярный, термодинамический потенциал
и энтропия смешения имеют вид
G (ni, п2) = + п2&2 + АН —TAS,
AS = — R (п{ In Xi + n2 In x2).
Здесь Xi = ni/(ni + n2), x2 = n2/(nt -}-n2). Получим парциальные
термодинамические потенциалы компонентов с помощью соотноше-
ний Gi = dG!dni и G2 = dG!dn2:
Gi^Gl+A^-x^ + RTXnxt, i = l, 2 (3)
[см. (4.38)]. Давление пара определим из условия Gf = Giiras.
Считая пар идеальным газом и используя (4.16), находим
G°i (Т, р) + А(1-х^+ RT In Xi = Gi, Газ (Л + RT In Pi. (4)
Примеры
231
Фиг. 75.
(5)
Здесь Pi и р2— соответственно парциальные давления компонен-
тов 1 и 2, а р = Pi + р2— полное давление. Что касается раствора,
то он также находится под давлением р, а его термодинамический
потенциал можно считать практически не зависящим от давле-
ния, так как рассматриваемые жидкости почти несжимаемы.
Поэтому, пренебрегая зависимостью
Gi (Т, р) от р в (4), получаем
А(1-х.)2/ДГ
Pi = Pi<sXie'- ' ,
где рго (Л = exp {[(?“ (Т)-£{, газ]/ЯГ}
— давление насыщенных паров чи-
стой г-ой жидкости при температуре Т.
При А = 0 зависимость pt от xt
линейна (закон Рауля), однако в общем
случае, когда А =^=0, она нелинейна.
а) А < 0. Энтальпия при смеше-
нии уменьшается. Компоненты сме-
шиваются легко, так что давление pt
должно быть ниже значения, опреде-
ляемого законом Рауля (фиг. 75).
Wis б) А > 0. Энтальпия при сме-
шении возрастает. Смешение проис-
ходит с трудом, так что давление pt
должно быть больше, чем следут из
закона Рауля (растворенное вещество
легко испаряется). Если отношение
А/RT велико, то начальный наклон
кривой pi в точке
xt — 0 ’будет большим. С другой стороны, при х, —> 1 значение
Pi приближается к линии pt = Pi0Xi в соответствии с соотноше-
нием (5). Это значит, что давление pt должно иметь максимум
и минимум, как показано на фиг. 75.
Из (4) имеем
ррр д Pi dGi
dxi dxi
тогда из условия dpJdXi < 0 вытекает, что dGJdxi < 0; зто нера-
венство соответствует термодинамически неустойчивым состояниям.
(Такая ситуация напоминает неустойчивые состояния газа ван
дер Ваальса.) Эти неустойчивые состояния могут появляться,
если кривая pt (xt) имеет максимумы и минимумы. Из соотноше-
ния (5) имеем
<6>
так что при А/RT > 2 (0 < 2RTIA < 1) экстремумы pt лежат
в области 0 <. х, < 1. С другой стороны, при А <0 или 0 < A/RT < 2
232
Гл. 4. Равновесие фаз и химическое равновесие
мы всегда имеем dppdx,i~p>G Следовательно, условие разделения
фаз записывается в виде
—-..> 1
2RT ’
(7)
Этот же результат можно получить, исследуя выражение
G{x^ ж2) = + ж26“ + Ах^-у- RT (xt lnzi + ж2 In x2), (8)
подобно тому как это было сделано в примере 2. Используя урав-
нение (2) в решении примера 1 и соотношение (4) настоящего
вой зависимости G от
примера, находим
=(4-4)+
+ Л[(1-Ж1)2-^] + й7’1п1^-. (9)
Отсюда следует
ЭЮ
дх?
RT
— + ^RT — 2А,
(Ю)
так как [Xi (1 —«1)]-1^-4; равенство
имеет место при Xi = 1/2. Таким
образом, если неравенство (7) выпол-
няется, то при «1 = х/2 имеем
d2G/dx2 < 0. Это значит, что у кри-
имеется общая касательная в двух
точках, соответствующих двум значениям переменной х, и, сле-
довательно, система разделяется на две фазы. Чтобы найти моляр-
ную долю двух фаз ж' и ж" в зависимости от температуры, надо
лишь найти точки касания с помощью уравнения (9). Так как
последнее симметрично по отношению к точке xt =. 1/2 (фиг. 76),
то точки касания ж' и х" определяются уравнением
A (l-2Xi) + RT In = 0,
которое можно записать в виде
1 ln 1+у Ay
2 1 1 —г/ ~ 2RT
(0<у<1),
ИЛИ
у — 2RT •
(И)
(12)
Примеры
233-
Здесь мы положили
*;=4(1-Z/), ^ = y(l + Z/)- (13)
На фиг. 77 показано графическое решение уравнения (12). Неравен-
ство (7) представляет собой условие того, что уравнение имеет
нетривиальные решения. [Наклон кривой, задаваемой левой
частью уравнения (И), при у = 0 составляет 45°. Поэтому при
A/2RT > 1 кривые пересекаются еще в одной точке, кроме точки
у = 0, тогда как при A/2RT < 1 они пересекаются только в точке
Фиг. 78.
у = 0.] Зависимость х\ и хг от Т, представленную на фиг. 78,
можно получить, подставив решение у (Т) уравнения (12) в (13).
Это и есть фазовая диаграмма раствора. Заштрихованная часть
соответствует двухфазной области, где система не может пред-
ставлять собой одну фазу. При более высоких температурах
Т>
’ А
с 27?
(14)
когда условие (7) уже не выполняется, однофазное решение имеет
место для всех концентраций. Температура Та, определяемая
соотношением (14), называется критической температурой
раствора.
8*. В случае разбавленного раствора сильного электролита,
диссоциирующего по уравнению
A^lV^v+A^ + v-B2'
осмотическое давление выражается формулой
vCzKT
л~~Тбоо~^’
234
Гл. 4. Равновесие фаз и химическое равное есие
Показать, что осмотический коэффициент gх) определяется
мулой
фор-
ГП2
1 Г
— I dm2,
'2 )Т,Р 4
(1)
g = H- m .
rrvO J
0
где обозначения ясны из (4.40) и (4.51). [Указание. Учесть соотно-
шение (4.52).]
РЕШЕНИЕ
Будем следовать решению примера 6, а затем вычислим актив-
ность растворителя Подставляя химический потенциал раство-
ренного вещества G [см. (4.52)] в уравнение Гиббса — Дюгема
<3.12)
п{ dGi -J- п2 dG2 = 0 (Т, р постоянны),
получаем уравнение для определения ар
dlnai-j-Vy-^—(din #2 + ^ In у) = 0. (2)
Так как = 1 при х2 = 0, то уравнение можно проинтегрировать;
при этом получаем
*2
lna{ = —V f (-у—---F т~2 - ) dx2 =
1 J \ 1—*2 1—*2 дх2 )
о
*2
= -v[-ln(l-z2)+ (2')
о
Подставив этот результат в выражение nV = — RT In 04, получим
(для х2 < 1)
Х2
_ vRT_ Г _ |п С * х2 . dlny
уо L 4 J 1 — ^2 ^2 J
1 О
*2
(1 + J ) (3)
F? \ *2 J ^2 /
1 О
х) Осмотический коэффициент g определяется обычно следующим обра-
зом. Пусть Xi есть молярная доля растворенного вещества в растворе, а хими-
ческий потенциал его имеет вид
G.^G^+gRT In
Тогда осмотический коэффициент g связан с активностью [см. (4.43)] соотно-
шением
In Yi = (g—1) Inxj.
Примеры
235
Используя (4.40) и (4.41), находим
^2______________________mzMj _ mzp _ Cz
po — lOOOVf Ю00 ~ 1000 ’
так что (3) можно переписать в виде
Ш2 _
vCzRT / . , 1 f a In у, \
л ~ л пап 14------\ "»2-5—-dmz .
1000 \ ™2 J дт2 '
о
Замечание. Осмотический коэффициент g характеризует
отклонение осмотического давления от значения, определяемого
формулой Вант Гоффа
vCzRT
тт —__i___
1000
Решая уравнение (1) относительно у при условии, что у—>1 при
т2—»0, получаем
_ln- С d «I-g) m21
‘J m2 •
0
Это выражение может быть использовано для нахождения коэф-
фициента активности, когда осмотический коэффициент g (mz)
известен.
9. В атмосфере некоторых звезд интенсивно протекает процесс
тепловой диссоциации металлических паров:
А А+ 4- е.
С помощью закона действующих масс найти зависимость степени
диссоциации а от температуры и давления. Энергия диссоциации
на 1 моль газа равна W.
РЕШЕНИЕ
Если степень диссоциации равна а, то молярное отношение
А, А+ и е есть (1 — а) : а : а, так что парциальные давления
компонентов определяются следующим образом:
1 — а а а
Ра = т~,— Р, Р.+ = т-,— Р, Ре = -г~,— Р-
14-а i-\-a
Тогда закон действующих масс (4.65) дает
££^L = ^l^p==e-AG0/HT. (!)
/>д 1 —<х2 7 v '
Если пренебречь внутренними степенями свободы компонентов,
то стандартный термодинамический потенциал реакции определяет-
236
Гл. 4. Равновесие фаз и химическое равновесие
ся с помощью (4.15):
AG° = G° + + G°-G1 =
= Uод+ -J- UOe — Uод —RTYnT — RT (гд+ -f- ie — i&).
Подставляя это в выражение (1), находим
а2 „ Т5/2P-W,!RT
i—a?p
где
lF = Z7OA+ + C7oe-t/oA
— энергия диссоциации.
Замечание. Энергия ионизации в результате процесса
А ->• А+ 4-е обычно значительно меньше, чем для процесса
А+ -> А++ 4- е- Поэтому часто можно пренебречь процессами иони-
зации более высокого порядка.
10. С помощью условия равновесия (4.73) для фаз в элементе
Даниэля получить формулу (4.71) для э. д. с. (разности потенциа-
лов) между двумя выводными контактами х) (сделанными из меди).
Считать, что на границе растворов CuSO4 и ZnSO4 разность потен-
циалов не возникает.
РЕШЕНИЕ
Пронумеруем различные фазы и выводные контакты элемента:
Си | CuSO4 (раств.) | ZnSO4 (раств.) | Zn | Си
I II III IV V
и обозначим соответственно потенциалы фаз через Фх, Фц и т. д.
Условия равновесия двух соседних фаз запишутся в виде
I — II (по отношению к Си++):
I и
Рси++ 4- 2бФх — цси"Н* 4- 2бФц; (1)
II — III (по отношению к SO4“):
ii ш
F* lsoj~ 2еФц = psoj- 2еФщ; (2)
III — IV (по отношению к Zn++):
ш IV
pzn++ 4- 2еФш = pzn++ 4- 2еФхУ; (3)
i) Если выводные контакты сделаны из разных металлов, то между
ними существует контактная разность потенциалов. Э. д. с. элемента опре-
деляется как разность потенциалов между двумя разомкнутыми выводными
контактами, сделанными из одинакового материала, чтобы избежать влия-
ния контактной разности потенциалов.
Задачи
237
IV — V (по отношению к электронам):
IV V
Ре — бФ1У = ре — еФу (4)
Далее, так как Си = Си++ + 2е на медном и Zn = Zn++ -р 2е на цинко-
вом электродах, можно положить
II I IV IV IV
PCu РСи++ Ч” 2ре, pzn PZn++ -р 2ре. (5)
По предположению Фц = Фш, так что уравнение (2) переходит
II ш
в Ksoj~= 9soj_ и им можно пренебречь. Сложив соотношения (1)
и (3) и вычтя из полученной суммы удвоенное соотношение (4), найдем
I III IV II IV v
Pcu++ Ч" pzn++ 2ре -|- 2еФх = pcu++ Ч" pzn++ 2ре • 2еФу
С помощью (5) последнее соотношение перепишем в виде
II I IV ш
2е (Фх — Фу) = рси++ — Pcu + Pzn — pzn++,
что эквивалентно соотношению
2%Е =—\G (Cu++ + Zn Си + Zn++).
ЗАДАЧИ
[А]
1. а) Пусть для а- и &-фаз однородного вещества известны сво-
бодные энергии Fa и Fb как функции Т и V. Показать, что точку
перехода между этими фазами можно определить, проведя общую
касательную к кривым Fa (V) и Fb (V) при заданной температуре Т
(фиг. 79).
б) Основываясь на решении п. «а», получить правило Максвелла
(см. замечание к примеру 1).,
2. Теплота плавления льда при 0° С и давлении 1 атм состав-
ляет 80 кал/г. Отношение удельных объемов льда и воды равно
1,091 : 1,000. Оценить изменение точки плавления при изменении
давления.
3. Известен коэффициент изменения температуры кипения воды
с давлением (при 100° С и давлении 1 атм):
dT 1 д,
~dp = 27 12 гРа°'мм Рт' ст'
Оценить теплоту парообразования воды при 100° С.
4. Вблизи тройной точки кривая равновесия (кривая р — Т)
между твердой и газообразной фазами имеет обычно больший
238
Гл. 4. Равновесие фаз и химическое равновесие
наклон к температурной оси, чем кривая равновесия между жид-
кой и газообразной фазами. Дать термодинамическое объяснение
этого явления.
5. Теплота плавления льда при 0° С и давлении 1 атм равна
80 кал/г, а отношение удельного объема воды к удельному объему
льда равно 1,000 :1,091. Давление
f насыщенного пара и теплота па-
рообразования для воды при 0° С
•а составляют соответственно 4,58 мм
I рт. ст. и 600 кал/г. По приведен-
\ ным данным приближенно оценить
температуру тройной точки. (Ука-
F зание. Тройная точка должна быть
ix. I6 очень ^близка к 0° С, так как тем-
\ пература равновесия между водой
i z и льдом очень мало изменяется
j в с давлением.)
; i 6. Предположим, что в системе'
__________;________i________ выполняются следующие условия:
va vg V а) температура не очень близка
к критической, так что давление ps
ф и г> 7 ’ достаточно мало; б) скрытую теп-
лоту парообразования L можно
считать постоянной во всей рассматриваемой области. Пока-
зать, что в этом случае справедлива следующая формула для
давления насыщенных паров жидкости:
ps ~ e~L/RT.
7. Пусть у — поверхностное натяжение кривой поверхности
с главными радиусами кривизны pi и р2. Показать, что разность,
давлений по обе стороны поверхности описывается формулой
(1 1 \
——J (формула Лапласа).
8. Поверхностное натяжение у(Г) задано как функция темпе-
ратуры. Найти количество тепла, поглощаемого при изотермиче-
ском расширении такой поверхностной пленки (см. пример 3).
Показать далее, что изменение температуры при адиабатическом
расширении определяется условием
dv ,
<т = const.
aJ
9. Бинарный раствор находится в равновесии со своим паром.
На фиг. 80 показана температурная зависимость (при постоянном
давлении) молярных долей жидкой и газовой фаз. Газообразной:
Задачи
23»
фазе соответствует область выше сплошной кривой, а жидкой —
область ниже пунктирной. Смесь газов постепенно охлаждается
от точки Р. При этом в точке А начинает появляться жидкая
фаза, а в точке С газообразная фаза исчезает полностью.
а) Найти молярные доли растворенных веществ в точке А.
б) Найти молярные доли в газовой фазе в точке С.
в) Найти молярные доли жидкости и газа в промежуточном
состоянии, представленном на фиг. 80 точкой В. Показать, что-
в этой точке отношение масс газа и жидкости определяется
величиной ВВ' : ВВ".
---* хг
Фиг. 80.
10. Бинарный раствор содержит tzj молей одного и п2 молейг
другого вещества. Пусть J есть некоторая экстенсивная величина,
характеризующая раствор. Зависимость величины РЦщ Д- ^2)
от молярной доли х2 изображается сплошной кривой на фиг. 81.
Пунктирная линия QPR касается этой кривой в точке Р. Доказать
справедливость следующих соотношений:
НЯ,,.."'1'
RO'=(~\ = J2.
11. Обозначим фугативности [см. (4.22)] компонентов газовой:
смеси через vt (i = 1, . . ., с). Показать, что при постоянных
240
Гл. 4. Равновесие фаз и химическое равновесие
давлении и температуре выполняется следующее соотношение:
с
2 ntd In Vj = 0.
i=i
Здесь пг (i = 1, . . с) — молярная доля i-ro компонента.
12. Пусть молярные доли двух компонентов в бинарном раство-
ре равны и х2. Химический потенциал одного компонента опре-
деляется соотношением
Gi = G*(T, р) + ЛТ1пх1.
Показать, что при этом химический
потенциал второго компонента имеет
вид
G2 = G*(T, ц) + 7?7’1пЖ2.
13. В разбавленном идеальном
двухкомпонентном растворе (при по-
стоянной температуре) давление пара
растворителя подчиняется закону
Рауля
Pi = XiP°i
(здесь р{[ — давление пара для чисто-
го растворителя). Это соотношение
справедливо при 1. Используя
этот закон и уравнение Гиббса —
Дюгема, получить закон Генри (4.29) для давления пара раство-
ренного вещества р2 и формулу (4.306) для химического потенци-
ала растворенного вещества.
14. Доказать справедливость следующих утверждений относи-
тельно кривых зависимости давления пара pi или р2 от молярной
доли хх (или х2) в случае бинарного раствора (фиг. 82).
а) Пусть aj и а2 — наклоны касательных к этим кривым
в точках Af и А2 соответственно, a pt и р2 — наклоны линий,
связывающих точки и А2 с началами координат (?i и О2. Тогда
«1 «2
₽1 ₽2
б) Если касательная в точке Ai проходит через начало коорди-
нат 01, то касательная в точке А2 проходит через О2.
15. В случае идеального бинарного раствора химический
потенциал i-ro компонента выражается формулой (4.34)
Gi = G?(T, p) + HTinxi.
Задачи
241
примерно пропорционально его
Фиг. 83.
фазовая диаграмма спла-
ва Си — Ni.
Здесь — молярная доля i-го компонента, a Gi — его химический
потенциал в чистом состоянии.
Пусть такой идеальный раствор получают путем смешения
чистых жидких компонентов. Доказать, что в этом случае спра-
ведливы следующие положения:
а) Не происходит изменения объема.
б) Не происходит поглощения и выделения тепла.
в) Изменение энтропии/равно энтропии смешения (4.19).
Найти также изменение внутренней энергии.
16. Имеется идеальный раствор, пары которого можно рас-
сматривать как идеальный газ. Показать, что давление пара
приближенно пропорционально молярной доле [см. (4.36)]. Пока-
зать далее, что это приближение справедливо в большинстве случаев.
17. Вывести формулу для осмотического давления в случае
идеального бинарного раствора.
18. В случае идеального разбавленного раствора давление pi
насыщенных паров растворителя
молярной доле Xi (~1). Исходя
из этого, показать, что измене-
ние точки кипения такого раст-
вора пропорционально моляр-
ной доле х2 (<К 1) растворенного
вещества. (Следует иметь в виду,
что растворенное вещество тоже
может испаряться.)
19. Концентрация раство-
ренного вещества х2 в твердой
фазе, выпадающей в осадок из
разбавленного раствора, про-
порциональна концентрации
(молярной доле х2) растворен-
ного вещества в растворе
(в жидкой фазе): х'2 = кх2. Здесь
к есть некоторая функция тем-
пературы. В предположении,
что жидкая фаза представляет
собой идеальный разбавленный раствор, а
. разбавленный твердый раствор, получить
щую изменение точки замерзания с молярной долей х2.
20. Два металла 1 и 2 (с точками плавления Т\ и Т2 и теплота-
ми плавления Li и £2) хорошо смешиваются в жидкой фазе и сов-
сем не смешиваются в твердой. Получить фазовую диаграмму
и уравнение для определения эвтектической точки, предполагая
для простоты, что теплота плавления не зависит существенно
от температуры.
16 Кубо
твердая — идеальный
формулу, связываю-
242
Гл. 4. Равновесие фаз и химическое равновесие
21. Два металла А и В хорошо смешиваются как в жидкой,
так и в твердой фазах. Пусть смеси ведут себя как идеальные
растворы, а температуры плавления и теплоты плавления (на
1 моль) для металлов А и В равны соответственно Ti, Т2 и Lt, L2.
а) Получить уравнения для кривых солидуса (твердой фазы)
и ликвидуса (жидкой фазы) на фазовой диаграмме в общем случае.
б) Упростить полученные уравнения и показать, что фазовая
диаграмма имеет сигарообразную форму (фиг. 83), если справедли-
вы следующие предположения: 1) энтропии плавления для метал-
лов А и В (на 1 моль) равны и имеют порядок величины газовой
постоянной R-, 2) температурной зависимостью величин Li и L2
можно пренебречь; 3) | Тх — Т2 | Ti, Т2.
22. Газовая реакция
аА -)- &В 4- . . . ^ ZL 4- игМ 4- • • •
происходит при постоянной температуре и постоянном объеме.
Показать, что величина
[L]4Mp... _v ,т.
[А]а [В]Ь ... '
зависит только от температуры (Гулдберг и Вааге, 1867). Квадрат-
ные скобки обозначают число молекул в единице объема. Считать,
что каждый компонент подчиняется формулам для идеального газа.
23. В случае химической реакции в смеси идеальных газов
получить уравнения
d In К„ &.U , .
—= (изохора реакции)
и
d in К „
ат (Вант Г°ФФ’ 188°^
Здесь i\U и А Я обозначают стандартную внутреннюю энергию
и стандартную энтальпию реакции (на 1 моль).
24. Константа равновесия реакции А2 2А, протекающей
в идеальном газе при 18° С, определяется соотношением
Кс (18° С) = = 1,70 • 10'4 моль!см3,
L а2 J
где квадратные скобки обозначают число молей в единице объема.
Определить степень диссоциации при давлении газовой смеси,
равном 1 атм. Какую величину должна иметь степень диссоциации
при 19° С и 1 атм,, если теплота реакции равна 5,0-104 кал!молъ1
25. Рассмотреть поглощение газа А2 твердым телом Т. Предпо-
лагая, что в Т молекулы А2 диссоциируют на атомы А, найти
соотношение между давлением газа рд2 и концентрацией А в Т.
Задачи
243
26. При нагревании твердый карбонат кальция (СаСО3) диссо-
циирует на твердую окись кальция (СаО) и углекислый газ.
Наблюдаемое значение (в атмосферах) давления диссоциации
(т. е. давление рсо2 газообразного СО2) между 1100 и 1500° К
может быть выражено следующей формулой:
1g Рсо2 = - 5,3881g Т + 26,238.
Найти изменение &Н°Т стандартной энтальпии этой реакции дис-
социации.
27. Внутри электрохимического элемента протекает реакция
(4.676)
Ag (тверд.) 4-у Hg2Cl2 (тверд.) —» AgCl (тверд.) + Hg (жидк.).
При 25° С и давлении 1 атм получены следующие эксперимен-
тальные значения для э. д. с. и ее температурной зависимости:
Е = 0,0455 в и {дЕ/дТ)р = 0,000338 в/град. Определить термоди-
намический потенциал, энтальпию и энтропию этой реакции.
28. Для ртути имеются следующие экспериментальные данные:
точка плавления Тт = 234,2° К; значение энтропии твердой
ртути при температуре Тт, полученное численным интегрировани-
ем теплоемкости при нормальном давлении
234,2
5S (234,2°)= j Ср~т = 59,9-10’ эрг/молъ-град',
о
теплота плавления 2330-107 эрг/молъ', точка кипения Тъ = 630° К;
возрастание энтропии жидкой ртути, определяемое по экспери-
ментальным значениям теплоемкости при постоянном нормальном
давлении
630
51 (630°)-51 (234,2°)= j Ср-^ = 26,2-107 арг/молъ-град',
234,2
теплота парообразования 59 300-Ю7 эрг/молъ. Исходя из этих
данных и предполагая, что пары ртути можно рассматривать как
одноатомный идеальный газ, получить значение для ее химической
постоянной г.
29. Металл, нагретый до достаточно высокой температуры,
начинает испускать электроны. Показать, что химическую постоян-
ную тепловых электронов можно определить по температурной
зависимости давления электронного газа, находящегося в равно-
весии с металлом, если предположить, что химический потенциал
электронов в металле постоянен.
244
Гл. 4. Равновесие фаз и химическое равновесие
30. Имеется электрохимический элемент с водородным элек-
тродом
(Pt)H2 (газ) | HG1 (вод.), х | AgGl (твзрд.) Ag (твзрд.),
на электродах которого происходят следующие реакции:
у Н2(газ) —>Н+ (HG1, вод., ж) 4-е,
AgGl (твзрд.) 4-s—>Ag (тверд.) 4-G1-(HG1, вод., ж).
Какова результирующая реакция? Показать, что э. д. с. Е этого
элемента можно представить в виде
Здесь х — концентрация HG1, у — средняя активность ионов,
a — давление газообразного водорода.
[Б]
31. Ниже критической точки рассматриваемая система под-
чиняется уравнению ван дер Ваальса. Показать, что при увеличе-
нии давления’при постоянной
температуре изменение термо-
динамического потенциала
происходит в’соответствии с
фиг. 84.
Объяснить, какие измене-
ния происходят с такой си-
стемой при этом процессе,
если температура меньше
критической.
32. Две фазы 1 и 2 на-
ходятся в равновесии друг
с другом. Показать, чтоАем-
пературная зависимость теп-
лоты перехода из фазы 1 в 2
определяется уравнением
dL г г , L r V2p2 — Vi^i
т -L ___ .
Здесь СР1 и Ср2 — удельные молярные теплоемкости при постоян-
ном давлении, a Pi и р2 — коэффициенты теплового расширения
фаз 1 и 2. Показать, в частности, что в случае, когда первая фаза
является жидкой или твердой, а вторая представляет идеальный
Задачи
245
газ, приведенное выше уравнение можно заменить приближенным:
dL ~ „
1F~ gP2—GPi-
33. Показать, что удельная теплоемкость насыщенного пара
при температуре Т, т. е. удельная теплоемкость, соответствующая
процессу нагревания, при котором пар все время остается насы-
щенным, дается выражением
с = с1~Т = ср~^1т ~+
Здесь г обозначает теплоту парообразования на единицу массы,
а Ср — удельную теплоемкость жидкости при постоянном давле-
нии.
Вычислить с для воды при 100° С, если для нее
dr
Ср = 1,01 кал!г-град, —0,64 кал!г • град, г = 539 кал! г.
Каков физический смысл отрицательных значений с?
34. Из-за поверхностного натяжения давление насыщенного
пара рг над жидкой каплей радиусом г (фиг. 85) больше, чем
давление р<х> (обычное значение давления
насыщенного пара) над плоской границей рг
жидкой фазы. v//7/7//////f>'fyl>,
а) Вывести соотношение между рт и г. /%//%//%
б) При каком критическом значении ра-
диуса гс такой капли она может расти в пе-
ренасыщенном паре, для которого р > p^t
35. Исходя из того, что теплоемкость
с насыщенного пара отрицательна (см. за- ^Щууууууу^г
дачу 33), объяснить, почему при внезапном
расширении в камере Вильсона возникает Фиг. 85.
пересыщенный пар.
(Указание. Рассмотреть адиабаты и кривую давления насы-
щенного пара в плоскости р — Т.)
36. При низких температурах некоторые металлы становятся
сверхпроводящими. В этом состоянии они обладают замечательным
свойством (эффект Мейсснера), заключающимся в том, что внеш-
нее магнитное поле не проникает внутрь металла (5=0 даже
при Н 0). Однако, когда внешнее магнитное поле становится
больше определенного критического значения Не (Т), сверхпро-
водящее состояние разрушается и переходит в нормальное, так что
В становится равным Н (при | Н | > Н„ имеем В = Н). На фиг. 86
приведена кривая зависимости критического магнитного поля
Нс (Г) от Т. Она делит плоскость Н— Т на две части, соответ-
246
Гл. 4. Равновесие фаз и химическое равновесие
ствующие сверхпроводящему состоянию s и нормальному состоя-
нию п.
а) Определить скрытую теплоту s -> re-перехода при Н =/= О
и Т < То.
б) Вывести формулу Рутгерса
/ АНс \ 2 __ 4л /С3—Сп \
\ dT / т=Т<ь ~~ V \ т / Т=т(! '
Здесь Cs и Сп — удельные молярные теплоемкости соответственно
состояний, а V — удельный
молярный объем.
в) Найти соотношение
между Cs и Сп при произ-
вольной температуре, считая,
что Нс = Но [1 - (Г/Г0)2]-
37. При возгонке смеси
двух разных сортов жидко-
стей может возникнуть такая
ситуация, что для некото-
рой температуры и концент-
рации состав раствора будет
совпадать с составом пара.
Это явление называется азео-
тропией. Показать, что ука-
занная температура соответ-
ствует максимуму или мини-
муму на кривых газообразной
и жидкой фаз на фазовых
диаграммах типа изображен-
ных на фиг. 87.
38. Рассмотрим вещество
А, содержащее примесь В.
сверхпроводящего и нормального
Фиг. 86.
В области фазовой диаграммы, соответствующей малым концентра-
циям В, кривые жидкой и твердой фаз можно приближенно
считать прямыми. Обозначим через С концентрацию примеси В
в твердой фазе, выпадающей в осадок из жидкой фазы, где концен-
трация примеси равна Ст. Отношение С1Ст = к называется кон-
стантой сегрегации. Изображенный на фиг. 88 расплавленный
стержень длиной L, концентрация вещества В в котором равна Ст,
охлаждается с левого конца и затвердевает. Показать, что кон-
центрация примеси В на расстоянии х от левого конца описыва-
ется формулой
С(х) = кС°т(1--£У
Задачи
247
Предполагается, что в твердой фазе диффузии атомов не происхо-
дит, а в жидкой фазе диффузия происходит так быстро, что кон-
центрация все время остается однородной (принцип метода зонной
плавки).
Фиг. 88.
39. Для некоторых типов высокополимерных растворов хими-
ческие потенциалы растворителя и растворенного вещества при-
ближенно выражаются следующим образом:
= GJ (Т, р) + RT [in Ф1 + (1 -1) (1 - Ti)] + W (1 - Ф1)2,
G2 = G° (T, p) + RT [In <p2 — (r — 1) (1 - ф2)] + rw (1 - ф2)2.
Здесь г обозначает степень полимеризации, а ф; — объемные доли:
Nl + rN2' f2- N^ + rNz '
где Nt и Nz — соответственно число молекул растворителя и высо-
кополимерных молекул растворенного вещества. Предполагается,
что каждая молекула полимера состоит из г мономеров, а объем,
занимаемый мономером, примерно равен объему молекулы раство-
рителя. В этом случае:
248
Гл. 4. Равновесие фаз и химическое равновесие
а) показать, что приведенные выше химические потенциалы
удовлетворяют уравнению Гиббса — Дюгема;
б) сравнить энтропию смешения данного раствора с энтропией
смешения идеального раствора;
в) вывести соотношение, связывающее теплоту смешения
с концентрацией раствора;
г) исследовать зависимость осмотического давления и давления
пара растворенного вещества от концентрации его в растворе.
40. Водный раствор с концентрацией х\ молекул .Vl X' налит
в резервуар I, а другой раствор с концентрацией молекул
M+R" — в другой резервуар II, отделенный от первого полупро-
ницаемой мембраной, через которую проходят ионы М+ и Х~,
но не проходят ионы R- (фиг. 89). В результате диффузии ионов
М+ и X- через мембрану в системе устанавливается равновесие
(равновесие мембраны Доннана). Найти равновесные концентра-
ции х'х и х"х вещества М+Х~ в резервуарах I и II. Растворы для
простоты считать очень сильно разбавленными и удовлетворяющи-
ми всем соотношениям для разбавленных идеальных растворов.
(Указание. Растворы все время должны оставаться электрически
нейтральными.)
Ф и г. 89.
41. В случае, рассмотренном в предыдущей задаче, на противо-
положных стенках полупроницаемой мембраны возникает разность
потенциалов. Рассмотрев электрохимические потенциалы, полу-
чить формулу для этой разности потенциалов.
42. Полупроницаемая мембрана (непроницаемая для ионов R-)
помещена в U-образную трубку, одна половина которой заполнена
раствором M' JU (фиг. 90). Измеряется осмотическое давление.
При добавлении раствора электролита М+Х_, который может
проходить через мембрану, наблюдается уменьшение осмотическо-
го давления. Объяснить это явление, считая для простоты раство-
ры разбавленными и идеальными.
43. В таблице приведены экспериментальные значения пони-
жения 9 температуры замерзания в зависимости от моляльности
Задачи
249
водного раствора НС1. Определить по этим данным осмотический
коэффициент g и сравнить его с предельным значением (4.56),
получаемым из закона Дебая — Хюккеля (см. примеры 6 и“8).
103 т2, моль/кг 102 0, град 103 тп2, моль/кг 102 0, град
0,627 0,228 3,526 1,286
1,179 0,434 4,520 1,644
1,245 0,455 6,879 2,494
1,474 0,542 10,633 3,843
2,228 0,815
44. В примесном полупроводнике гс-типа атом примеси (донор)
D ионизуется в ходе реакции D D+ + е, причем освобождается
электрон проводимости е. Считая кристалл с примесью атомов
D и ионов D+ идеальным разбавленным твердым раствором,
а электроны проводимости — идеальным газом, вывести на основе
термодинамического рассмотрения формулу для равновесной плот-
ности электронов проводимости.
Замечание. Так как электроны проводимости могут
свободно двигаться в кристалле, их можно рассматривать как
своего рода газ. При низкой концентрации электронов применимо
приближение идеального газа.
45. Расплавленное серебро хорошо растворяется в расплавлен-
ном золоте
Ag (жидк.) Ag (в Ап (жидк.)).
Чтобы этот процесс протекал обратимо, Вагнер и Энгельгардт
составили электрохимический элемент
Ag (жидк.) | AgCl, КС1 (смесь) | Agx Au^
и измерили его э. д. с. Экспериментальные данные относительна
зависимости э. д. с. от концентрации х приведены в таблице.
Предполагая, что жидкий раствор
Aga-Auj-x является идеальным, найти
э. д. с. при х = 0,5 и 1360° К. В таблице
приведены данные для э. д. с. при од-
ной и той;.же температуре. Определить
из этих данных коэффициент актив-
ности у, даваемый формулой (4.43).
46. В применении к случаю хими-
ческого равновесия принцип Ле-Шателье
означает следующее: а) Если при по-
X Е, в
0,846 0,021
0,716 0,045
0,602 0,074
0,471 0,114
0,263 0,198
стоянном давлении повышать температуру, то химическое равно-
весие смещается таким образом, чтобы происходило поглощение
250
Гл. 4. Равновесие фаз и химическое равновесие
тепла, б) Если при постоянной температуре увеличивать давле-
ние, то химическое равновесие сдвигается таким образом, чтобы
объем рассматриваемой системы уменьшался. Доказать справед-
ливость этих положений.
[Б]
47. Доказать правило Максвелла, рассмотренное в примере 1
для газа ван дер Ваальса. Заметим, что состояния, для которых
на р — У-диаграмме (др/dV)? > 0, являются не физическими,
так как в них нарушаются условия термодинамической устойчиво-
сти. Поэтому для доказательства равенства термодинамических
потенциалов для точек А и Е (фиг. 91) следует рассматривать
квазистатический процесс, при котором система проходит только
через физические состояния, не затрагивая упомянутые выше
нефизические состояния. Использовать тот факт, что Cv является
функцией только Т (см. задачу 34).
48. В парамагнитной области выше температуры Кюри Тс
магнитная восприимчивость ферромагнетика подчиняется закону
Кюри — Вейсса
А . . .
Хт = у—у (А — положительная постоянная).
* с
С помощью термодинамического рассмотрения исследовать скачок
теплоемкости такого вещества в точке Кюри и спонтанную намаг-
ниченность ниже температуры Кюри. (Указание. Если свободную
энергию F (М, Т) представить в виде разложения F (М, Т) =
= F (0, Т) + V2a (Л М2 + р (Г) М4/4! + . . ., то а (Л) = 0
Решения
251
и р (Ге) > 0. В качестве приближения рассмотреть разложение
лишь до членов порядка Л/4.)
49. Объяснить с помощью термодинамического рассмотрения,
почему в водяном паре капли воды конденсируются вокруг ионов
и при быстром расширении камеры Вильсона в ней видны следы
ионов. (Указание. Свободная энергия воды понижается при поля-
ризации ее электрическим зарядом иона.)
50. Определить условия, при которых высокополимерный
раствор, описанный в задаче 39, распадается на две фазы
РЕШЕНИЯ
1. а) Условия теплового равновесия для двух фаз заключаются
в том, что для этих фаз должны быть равны температуры, давления
и термодинамические потенциа-
лы G = F + pV (на 1 моль)
[см. (4.1) — (4.3)]. Давление
р = — (dF/dV)T определяется
взятым с обратным знаком на-
клоном кривой F (7) для задан-
ного значения Т. Таким образом,
в равновесном”состоянии имеем
dFa dFb
Р dVa ~ 9Vb <
Далее, так как Ga = Gb, т. е.
Fa + pVa = Fb + pVb, находим
Р Va-Vb'
Соотношения (1) и (2) показы-
вают, что равновесие устанав-
ливается между такими двумя
состояниями, которые соответ-
ствуют точкам на кривых Fa
и Fb, имеющим общую каса-
тельную (см. фиг. 79)
б) Пусть зависимости F — V
соответствует непрерывная кри-
вая, изображенная на фиг. 92
вверху. Полученное выше условие (2) можно записать в виде
ь
-\^dV = p(yb-Va),
а
252
Гл. 4. Равновесие фаз и химическое равновесие
так что
ъ
J pdV = p(Vb-VaY
а
(3>
Соотношение (3) означает (см. нижнюю часть фиг. 92), что пло-
щадь ADCEBba равна площади АВЬа, т. е. что площадь ADCA
равна площади СВЕС. Это и есть правило Максвелла.
2. Используя формулу Клапейрона — Клаузиуса (4.4), получаем
dTm
dp
_Tm(Vl-vs) 273 (-0,091) 1 ___
qm 80 3,13-Ю3
0,99-10-4 град/см pm. cm.,
где использовано то обстоятельство, что
1 кал!см3 = 4,18-107 0Qn = 3,13• 103 см pm. cm.
Io jо * У oU
3. С помощью формулы Клапейрона — Клаузиуса (4.4) находим
d p q
dT T(vg-Vl)‘
Удельный объем водяных паров vg значительно больше удельного
объема воды z?z. Поэтому мы можем положить vg — vt ~vg
и найти vg, воспользовавшись уравнением состояния идеального
газа
RT 1,987-373 с .. ,п_2 .
vs~~m-----~ 7fio is о? ~ 5,41 • Ю кал/мм pm. cm.-г = 1699 смЛ/г.
Имеем, таким образом,
q = 27,12-373-5,41-Ю’2 = 547 кал/г.
Замечание. Экспериментальное значение q составляет
539,032 кал/г. В приведенном выше расчете это соответствует
значению vg, равному 1672 см?/г.
4. Из формулы Клапейрона — Клаузиуса (4.4) имеем
I dP \
k dT )s-g
Sg — Ss
-vg-vs
(газ —твердое тело),
( dp \ Sg — ^i
[Чт Ji-g-Vg-Vt
(газ — жидкость).
Мы знаем, кроме того, что Vg^Vi, Vs и Sg/> Ss. Находим,
таким образом,
( dp \ ~ ~ ( dp \
Vg > Vg ^{dTJi-g-
5. Тройная точка определяется пересечением трех кривых
равновесия в р — ^-плоскости, а именно кривых температурной
Решения
253
зависимости равновесных давлений р01, р12 и р02; здесь индексы
О, 1 и 2 означают соответственно лед, воду и пар. Наклон кривой
равновесного давления определяется формулой Клапейрона —
Клаузиуса (4.4). Кривая р01 — Т равновесия фаз лед — вода
проходит через точку, соответствующую 760 мм pm. cm. и 0° С;
ее наклон в этой точке равен
dpoi __ got
dT То (vo— vl)
273(1,091-1)
(1)
Кривая равновесия pl2 — T между водой и паром проходит
через точку 4,58 мм pm. cm., 0° С; ее наклон в этой точке гораздо
меньше значения (1). [Хотя величина qi2 = 600 кал почти в 8 раз
объем v2 пара при давлении
больше, чем £01 в (1), удельный
4,58 мм pm. cm. и темпера-
туре 0° С в 105 раз больше,
чем v0 или i?i.J Кривую р12
можно приближенно заменить
прямой горизонтальной ли-
нией, а значение температуры, щ
при котором эта кривая 5
пересекается с кривой р01, f
можно вычислить по вели- 4
чине \Т, соответствующей
—Ар01 = (760—4,58) мм pm.cm.
Из (1) получаем
-= —0,0075 град'атм.
dpoi
Температура
Приближенно можно считать Фиг. 93.
АГ = 0,0075 для —Ар01 =
= 1 атм. Следовательно, температура тройной точки лежит около
0,0075° С (давление около 4,58 мм рт. ст.).
Замечание. Экспериментальные значения для давления
и температуры в тройной точке равны 4,579 мм рт. ст.
и 0,0098° С. В 1954 г. температуру тройной точки приняли равной
0,01° С, определив тем самым стоградусную шкалу температуры т).
На фиг. 93 изображены кривые р01, р12 и р02. Состояния, пред-
ставленные пунктирными линиями, не являются равновесными
устойчивыми состояниями; они лишь метастабильны. Так, равно-
весие между водой и паром при 4,58 мм рт. ст. и 0° С является
метастабильным.
0 См. стр. 78.— Прим. ред.
254
Гл. 4. Равновесие фаз и химическое равновесие
6. В данном случае формулу Клапейрона — Клаузиуса (4.4)
можно записать в виде
dp __ L
dT Т (vg — vi) '
где L — скрытая теплота парообразования. Условие «а» означает,
что vg Vi. Пренебрегая величиной и используя приближение
для идеального газа vg = RT!р, получаем
р RT2 0,1
Интегрирование этого соотношения с учетом условия «б» и дает
ps ~ e-VRT.
7. Используем соотношение (4.8). В настоящем случае условие
(3.30а) устойчивого равновесия примет вид
д/7>0.
При этом наложены следующие ограничения: общий объем остает-
ся постоянным (др' + дп" = 0), полная энтропия постоянна
____________г—(д/> = 0), число частиц в каждой фазе
постоянно (дЛ" = дЛ'" = 0). Учитывая
/ вариации первого порядка, получаем
Г—ъи = (-Р’ + р") дУ + удо = о,
\ РГ< Т Рг“2 /
' I / так что
\ I /
' / i . . п da
\ , / Ар = р-р=у^.
\ / *
\ I / Рассмотрим бесконечно малый прямо-
\ j / угольник, построенный на геодезичес-
\$, / / ких, как показано на фиг. 94. Здесь
\"7 / 61 и 02 — бесконечно малые углы, кото-
v'j / рые опираются на стороны этого прямо-
I, угольника и имеют вершины в соот-
I/ ветствующих центрах кривизны. Пло-
" щадь такого прямоугольника равна
Фиг. 94. Р1Р20102- Если поверхность раздела
смещается на величину др в направле-
нии радиуса, то объем изменяется на бесконечно малую величину
dV = Р1р2010гдр, а площадь прямоугольника возрастает на
da = (р! + др) (р2 4- др) 0102 — Р1Р20102 = (pl + Рг) др0102.
Имеем, таким образом,
da_________________________1 . 1
’dVr~ Pi + Р2 ’
Решения
255
так что разность давлений определяется формулой
л ( 1 , 1 А 2?
где 1/р —средняя кривизна поверхности. Соотношение (4.9) пред-
ставляет собой частный случай этой формулы.
8. Как показано в примере 3, энтропия поверхности
<?_____д dy
° dT '
Количество тепла Q, поглощаемое поверхностной пленкой при квази-
статическом изотермическом процессе, когда площадь ее увеличи-
вается от величины ст± до ст2, определяется выражением
С = 7,[5О (Т, ст2)-50 (Т, ctJ],
Следовательно,
(?=-Т-^-(ст2-ст1).
При квазистатическом адиабатическом процессе имеем
dSa = Q.
Таким образом,
или
da .d (dy/dT)__г.
dy/dT
Окончательно имеем
dv
CT -£ = const.
dl
Это и есть искомое условие в случае адиабатического процесса,
а величина Tz находится из уравнения
по известным сть Тх и ст2.
ОТСТУПЛЕНИЕ 12
Термодинамика и жизнь. Термодинамика и наука о жизни
являются старыми друзьями, что, впрочем, и не удивительно. Их
дружба началась давно, еще на заре термодинамики, когда молодого
немецкого доктора Майера осенила гениальная идея об эквивалентно-
сти работы и теплоты. Другой основоположник термодинамики Гельм-
гольц был, кроме того, великим физиологом (см. отступление 1).
256
Гл. 4. Равновесие фаз и химическое равновесие
Ученые пока еще не разгадали тайну жизни. Но разве вы не верите,
что когда-нибудь биологические явления будут объяснены с помощью
тех же самых физических законов, которым, как мы знаем, подчи-
няются все явления неодушевленной природы? Конечно, никто не
может отрицать возможность некоторого революционизирующего
открытия совершенно нового принципа, управляющего жизненными
процессами. Однако очень маловероятно, что такой принцип, даже
если он будет найден, окажется противоречащим законам физики
и химии. Биологи и биофизики, во всяком случае, сходятся во мне-
нии, что единственный плодотворный подход к раскрытию тайны жизни
основан на применении рабочей гипотезы об общей справедливости
физических законов в биологических процессах.
Пока не получено никаких данных, которые говорили бы о том,
что в биологических процессах может нарушаться первый закон
термодинамики — сохранение энергии. Мы не сможем работать, если
не будем питаться. Биологические наблюдения играли важную роль
при открытии первого закона. Насколько мы сейчас знаем, не суще-
ствует такой формы энергии, которая была бы характерна исключи-
тельно для живых организмов: любой вид энергии, с которым мы стал-
киваемся при рассмотрении биологических процессов, можно полно-
стью объяснить, обращаясь к физике пли химии. Каким бы сложным
ни казался биологический процесс, всегда оказывается, что баланс
энергии выполняется в нем строжайшим образом.
Более деликатным является вопрос о справедливости второго
закона термодинамики. Энтропия есть мера беспорядка. Именно
такую атомистическую интерпретацию второго закона дает стати-
стическая механика. Возрастание энтропии, вообще говоря, выра-
жает непреодолимую тенденцию природы к переходу в менее упорядо-
ченное состояние — тенденцию, которой можно противостоять, лишь
затратив некоторое усилие, т. е. некоторую работу.
«Представление о том, что Вселенная стремится к таким условиям,
при которых энтропия и степень беспорядка имеют самую большую
величину, глубоко повлияло на точку зрения многих биологов на при-
роду биологических явлений. Бросается в глаза то обстоятельство,
что живые организмы обнаруживают тенденцию к упорядочению их
окружения, т. е. к созданию «порядка» там, где раньше был беспоря-
док. Жизнь как бы противостоит всеобщему стремлению к беспорядку.
Каков смысл этого? Означает ли это, что живые организмы нарушают
или могут нарушать второй закон термодинамики?» (Бриджмен
[Ю]).
Максвелл однажды представил себе исключительно умное суще-
ство — демона, который управляет задвижкой в стенке, разделяющей
два сосуда, наполненных молекулами газа, и впускает только быстрые
молекулы (см. отступление 1 в «Статистической механике» [9]). Если
этот демон действует соответствующим образом, то газ по одну сторону
стенки будет нагреваться, а по другую — охлаждаться. Казалось бы,
это противоречит второму закону термодинамики.
Чтобы решить, действительно ли деятельность демона Максвелла
направлена наперекор природе, необходимо разобраться в том, как
устроен этот демон. Когда в живом организме совершается некоторый
переход от беспорядка к порядку, вполне возможно, что уменьшение
энтропии компенсируется чем-то скрывающимся в безнадежно сложном
механизме жизни.
В настоящее время все еще чрезвычайно сложно доказать или
опровергнуть существование демона Максвелла в живом организме.
По-видимому, точную экспериментальную проверку удастся осуще-
Решения
257
ствить лишь после, того, как будет решена проблема искусственного
создания жизни ’).
Читателям, интересующимся термодинамическими аспектами
биологических процессов, мы можем порекомендовать небольшую
книжку Лейнингера [11].
9. а) Молярную долю х2 растворенного вещества в жидкой
фазе, которая появляется в точке А, можно определить, находя
точку пересечения А' горизонтальной линии, проходящей через
точку А, и пунктирной линии (линии ликвидуса).
б) Аналогично молярная доля х2 в газовой фазе в точке С
дается точкой С.
в) В общем случае некоторой промежуточной температуры,
соответствующей точке В, молярные доли х2 растворенного веще-
ства в жидкой и газообразной фазах даются координатами точек
В' и В" соответственно. Обозначим
число молей в газовой фазе через Ng,
а в жидкой — через Ni (Ng + Ni =
= + N2),
Ngxl + Nix\ = N2,
где x% и xl2 представляют собой моляр-
ные доли второго вещества в газообраз-
ной и жидкой фазах и вместе с тем
абсциссы точек В" и В'. Поделив напи-
санное соотношение на полное число
молей N, получим
ZgZf + XiXl2 = Х = Х2 (xg + Xi)
и, следовательно,
xg xg xl2 — x2 _ НВ
Х1 ~ 1— xg~ х2 — Х1 ~~ В"В
Это и дает искомый результат.
Замечание. В рассматривае-
мом случае возникающая жидкая фаза
всегда однородна (в противоположность твердой фазе, выпада-
ющей из жидкого раствора). На фиг. 95 в качестве примера при-
ведена фазовая диаграмма для смеси N2 — О2.
10. По предположению J является экстенсивной функцией
переменных щ и п2, т. е.
J Хп2) = XJ (nt, п2),
(1)
*) Обсуждение демона Максвелла с точки зрения теории информации
приведено в книге: Л. Бриллюэн, Наука и теория информации, М.,
1960.— Прим. ред. •
17 кубо
258
Гл. 4. Равновесие фаз и химическое равновесие
Дифференцируя обе стороны по 1 и полагая 1 = 1, имеем
n2) = ni-^—+n2-^-= «i/i + raaA (2)
и
„ ! „ — (1 — х2) А + X2J2 (х2 = 1 ,
"Г п2 \ п1 "Г ^2 /
так что
—^=л-л+(1-^)-“+^4^-=/2-а- (3)
ах2 ' “/ дх2 дх2 1 ' '
(Мы использовали здесь уравнение Гиббса — Дюгема, которое полу-
чается в данном случае следующим образом:
dJ ~dni4!- + dn2-¥-
дщ 1 дп2
J । dn^ -J- J 2 dn2.
Из соотношения (2) имеем: dJ = Jidni-\-J2dn2JrnidJiJrn2dJ2.
Следовательно, nt d-|- n2 dJ2 — (n4 n2) [(1—£2) ^A + ^2 ^A1 = 0-)
Уравнение для касательной QPR можно записать теперь в виде
у = (1 — х[) Ji + x‘J2 + (А — А) (х2 — хг) = А + (А — А) х2.
Здесь ж'— координата точки Р.
В точке Q'. х2 = 0, OQ — Ji.
В точке R’. £2=1, RO' = J2.
11. В случае постоянного давления и температуры уравнение
Гиббса — Дюгема принимает вид
2М<А = 0. (1)
Из соотношения Pj — pnjl^ni имеем
и
П} ЙПу —
• • . 7 I ^7
3 3 3 i J г
У п} d In Pj = 2
у bitt = 0.
Искомый результат получается, если подставить в (1) определение
функции Gj (4.21) и. использовать приведенные соотношения.
12. Воспользуемся уравнением Гиббса — Дюгема (3.12) для слу-
чая постоянного давления и температуры
Xi dGi —[- х2 dG2 = 0 (£j —Г х2 = 1 )*
Решения
259
Если функция Gt известна, имеем
dGt = RT = - RT
и, следовательно,
dG2 = RT-^- .
х2
После интегрирования получаем
G2 = G*(T, р) 4~ RT In х2.
13. Обозначим химический потенциал (на 1 моль) растворителя
через Gb а растворенного вещества — через G2. Уравнение Гиббса —
Дюгема при постоянных р и Т имеет вид
dGi + х2 dG2 = 0. (1}
Используя определение (4.25) химических потенциалов G^ и G2,
получаем
xt din Pi+ x2dIn p2 = X! + x2= 0. (2}
Pl P2
(Это уравнение для давления пара называется уравнением Дюге-
ма—Маргулеса.) В соответствии с законом Рауля
dpi dx^
Pl ~ ’
а так как ^1 + ж2=1, то dx^=—dx2. Поэтому для а?2~0 имеем
dp2 dx2 ,
Интегрируя, получаем
р2 = к2х2 (закон Генри), (4)
где к2— постоянная. Подставляя этот результат в определение (4.25),
находим
G2 = G’(7\ р% +RT 1п^ = <&(?) +RT In х2-, (5)
Pi
здесь <р“ (Т) = G° -\-RT In (к2/р%) есть функция температуры.
Замечание. Если общее давление р поддерживается постоян-
ным, то уравнения (1) и (2) выполняются точно. Если же считать
полное давление р равным сумме парциальных давлений pt и р2,
то условие постоянства давления не будет выполняться точно, так
что (2) следует заменить на
‘ Xidlnpi + xz d 1пр2 = Ё-^г . (6)
17*
260
Гл. 4. Равновесие фаз и химическое равновесие
Здесь V — молярный объем раствора. Обычно правая часть уравне-
ния (6) значительно меньше каждого из членов, стоящих в левой
части. Пусть, например, изменение Др давления равно 1 атм,
Г = 0,1-103 см3 и Т = 300°К. Тогда УД р/RT ж 100-1/82-300 «
«0,004; последняя величина составляет менее 1/100 от членов
в левой части.
14. Полагая правую часть соотношения (6) в решении преды-
дущей задачи равной нулю, имеем
xi dpi __ х2 дРг /|\
Р1 Р2 9х2 ’ k '
При заданной концентрации (молярной доле) xt (a?t > х2) наклон
касательной к кривой давления пара равен = dpjdxi, а наклон
линии, соединяющей эту точку с началом координат, Р, = Рг/^г-
Следовательно, из,(1) имеем
«1 _ «2
₽1 ~
и
б) а2 = р2 (если ai = ₽i).
Замечание. Соотношение (1) может быть использовано для
проверки точности эксперимента.
15. В соответствии с (4.34) запишем термодинамический потен-
циал системы в виде
G = 2 nfit = nfiax (Т, р) + n2G°2 (Т, р) + RT (rii in Xf + п2 In х2).
а) Вычислим объем
Объем не должен изменяться.
в) Энтропию 5 =—(дС1дТ)р'П запишем в виде
5 = rifS^ + п25® — R In Xi + п2 In х2).
Таким образом, доказано положение «в».
б) Энтальпию Н — G -|- TS можно представить следующим
образом:
Н = П1Н° + п2Н° (Hl^Gl + TSl).
Это значит, что теплота смешения отсутствует. Как и в случае
внутренней энергии, энтальпия не должна изменяться, так как
не совершается никакой работы. Действительно, имеем
U = H-pV = niUa1 + n2Ua2 (Ul = Hl-pVt).
Решения
261
16. Из (4.27), (4.34) и (4.36) получим сразу Pj = XjP°j. Дадим,
однако, еще и подробный вывод с использованием химических
потенциалов (4.16) и (4.34). Условие равновесия С3-1ЖИДК = Gj, газ
можно записать в виде
Gj/жидк (Г, р) + In Xi = G°jt газ (Т) + RT Inpj,
а давление пара чистого вещества можно определить из соотно-
шения
Gjt жидк (Т, р°) = G°jt газ (Т) + RT In р°.
Таким образом,
PJ _______ жидк жидк
рО xi ехР Ду •
Оценим экспоненту в правой части, разлагая ее аргумент вблизи р°р.
~ ЖИДК Р Р? _______ Y70 Р Р) ^5, ЖИДК P—Pj
RT ~ др RT — жидк ду — уо Р?
Следовательно, соотношение Pj = XjP°j справедливой большинстве
случаев.
17. Если в растворе, разделенном полупроницаемой мембраной,
пропускающей только растворитель, установилось осмотическое
равновесие, то условие равновесия имеет вид
Gjp', Ж2) = ё;(д");
здесь р' — давление раствора, р" — давление чистого растворителя,
а х2— молярная доля растворенного вещества. Используя (4.34),
получаем
G°(T, р')+RT In (l-x^G* (Г, р").
Полагая р' = р"-{-л и считая л достаточно малым, имеем
g*(t;p')-g*(t, p")^n^-=nVi,
так что
RT . .. . ...
Л=-----=г-1п(1-Х2). (1)
Г1
Здесь Vi — молярный объем чистого растворителя.
Замечание. Если х2 1, то соотношение (1) переходит в
лУ1 = RTx2,
т. е. становится аналогичным по форме уравнению состояния иде-
ального газа.
262
Гл. 4. Равновесие фаз и химическое равновесие
18. В данном случае для давления пара растворителя сира
ведлив закон Рауля:
а для растворенного вещества — закон Генри:
р2 (Г) = k (Т) хг.
Точка кипения Тъ определяется условием
Р=Р1+Рг = Ро, или р'>1(Ть)х1 + к(Ть)х2 = р0. (1)
Точка кипения чистого растворителя Тъ дается соотношением
раЛП) = Р0. (2)
Полагая xi==i~-х2, Тъ = Тъ-\- АТ и считая х2 и АТ малыми, мы
можем разложить по ним соотношение (1). С точностью до членов
первого порядка малости получим
Р°1 (П) - р°! (П) х2 + АТ + к (П) х2 = р0.
Учитывая (2) и используя формулу Клапейрона — Клаузиуса
dpi = L ~ Т _ рЦ
дТ ~ Tl(Vg-Vi) ~ T^g ~ Я(7ь)2 ’
находим
[Попробуйте найти другой способ решения, используя соотноше-
ния (4.30а) и (4.306) и следуя решению примера 6.]
Замечание. Если к = 0 (растворенное вещество не лету-
чее), то величина АТ/ТъХ2 определяется только свойствами раство-
рителя. Как известно, это обстоятельство можно использовать
для определения молекулярного веса растворенного вещества.
19. В случае идеальной разбавленной смеси химический потен-
циал растворителя записывается в виде (4.30а). Учитывая, что
xt=l—Х2, Xf= 1 — х2, х2<^1, х2<^1, InXi^ti — х2, 1пж(« — х2,
имеем из условия равновесия Glt (Т, х2) = Gls (Т, х2)
G°il(T)-RTx2 = G°is(T)-RTx2, _ (1)
/т0 _ f __ ______
где Ьц — химический потенциал чистого растворенного вещества
в жидкой фазе, a G°ls — в твердой. Используя предположение
х2 = кх2, можно вычислить температуру Тj, при которой начи-
нается выпадение твердой фазы (точка замерзания), из соотношения
G^Tf) - G?, (Tf) = RTf (1 - к) х2 (2)
Решения
263
Точка замерзания Tf чистого растворителя определяется соот-
ношением
G°ll(T°f)-Gois(T^ = O. (3)
Считая, что величина АТ1} = Tf — Tf достаточно мала, находим
G (Tf) = G (T°f) - (Т}- Т°}) S (T°f).
Таким образом, из (2) и (3) с точностью до членов первого порядка
по АТ1/ и х2 получаем
ATf [ - 5°1г (71/) +5°ls (Т1/)] = RT°f (1 - к) х2,
или
^-^(1-^2. (4)
Ч Ч
Здесь — Sis) — теплота плавления для растворителя.
Замечание. При к < 1 происходит понижение точки
замерзания, а при к > 1 (это означает, что растворенное вещество
Фиг. 96. Изменение точки замерзания разбавленного
раствора.
охотнее проникает в твердую фазу, чем в жидкую) — повышение
точки замерзания. На фиг. 96 представлены фазовые диаграм-
мы, иллюстрирующие два эти случая.
20. В данном случае химический потенциал каждого компо-
нента определяется выражением (4.34). Условия равновесия между
чистой твердой фазой 1 и соответствующей жидкой фазой и между
чистой твердой фазой 2 и жидкой фазой 2 имеют вид
Gh + RTinxu^G^ G°2l + RT ln^ = GL (1)
Здесь хц и x2i — молярные доли в жидкой фазе, a G°i и — хими-
ческие потенциалы чистого i-го компонента-в жидкой и твердой
264
Гл. 4. Равновесие фаз и химическое равновесие
фазах соответственно. Соотношения (1) можно переписать в виде
х1г = еЛ1, x2t = e\ (2)
где т т
(ns — Gil f His — Hil jrp Г Li „
— RT ~ J RT% al ~ J RT* al ~ P)
<*>
Здесь мы использовали соотношение d (GIT)ldT = — Н. Следует
иметь в виду, что Хг = 0 при Т = ТВеличина = Hh — HiS
представляет собой теплоту плавления твердой фазы при темпе-
ратуре Т и предполагается постоянной, а аг = LJRTг есть не что
иное, как энтропия плавления А5г = LitTi, измеренная в едини-
цах R. Тогда имеем
х1г = exp (1 — , (5а)
z2z = exp [а2(1 —-у)] • (56)
Эти уравнения дают кривую жидкой фазы (линию ликвидуса),
а пересечение (5а) и (56)—эвтектическую точку ТЕ.
exp[oi(l — ^-)] + ехр[а2(1 — = (6)
Подставляя ТЕ в (5а) или (56), получаем значение концентрации
в эвтектической точке. Легко видеть, что (5а) определяет линию
ликвидуса от хц = 1 до точки Е, а (56) — от Е до x2t = 1 (Фиг. 97).
Фиг. '97. Фиг. 98.
Решения
265
21. а) Используя (4.34), запишем условия равновесия в виде
Gn + RT In хи = G°ls + RT In xls,
G2i-\- RT In x2i = G^RT In x2s, (1>
где индексы l и s относятся соответственно к жидкой и твердой
фазам. Вводя величины и Х2 (см. решение задачи 20), пере-
пишем (1) в виде
= ^L = eb. (2)
x2s
Учитывая, что
Хц “1“ = 1, ^is + ^2s = 1) (3)
имеем из (2)
j______________________________________________e—
xae-^^x-ae-^= 1, или ж2г = e-X2__e-V > (4>
e^i__j
+ aw112 = 1, или z2s = e%1_ex2~ • (5^
б) Второе предположение означает, что Zj определяется соот-
ношением (4) в решении задачи 20. В соответствии с первым пред-
положением
Хг = а(1-^.), (6)
а в соответствии с третьим предположением Хг 1. Из (4) и (5)
получаем
ж2г= Х1\2 [1+4^2 +^^2(М + А,2)+- • •] ’ (7>
Ж2з = -хД\2 [1—4Х2 + 4А'2(^1 + ^)+---] * (8>
Используя (6), находим окончательно
_ r-Ti _ £ (72-П (7-Л) , /ау
2г T2-Ti 2 Т(Т2—Тг) "Г---’
Т— Ti 1 (T2-T)(T-Ti) (10Y
m гр 12—^1 1 2 T(T2 — Ti) 1 ” \iv/’
При Ti<iT2 эти уравнения дают
Tt<T ^Т2, X2i<.x2s.
На фиг. 98 представлена фазовая диаграмма, построенная по фор-
мулам (9) и (10) для 7’1 = 1200°К, 7’2 = 1600°К и а = 1. Эта
фазовая диаграмма аналогична фазовой диаграмме сплава Си — Ni,
приведенной в задаче 21 (см. фиг. 83).
'266
Гл. 4. Равновесие фаз и химическое равновесие
22. Обозначим свободную энергию смеси идеальных газов
.А, В, ... (пА, пв, ... молей) в объеме V при температуре Т через
F (у, Т, пА, пв, • • •),
а изменения величин пА, пв, ... в ходе реакции — через
бПд = ¥д6Х, 6nB = vB6X, ... .
Тогда условия равновесия можно записать в виде
=0,
\ dk Jv,T
ИЛИ
;=А, В,. . . ;=А, В,. . .
и, следовательно,
2vA=o. (1)
Мы получили условие (4.63). Химический потенциал как функция
концентрации rijlV имеет вид
G} = Ga^T) + RT\n-^ .
Таким образом,
„ / п< \vj _yv. Г
П (4) L 7ехр|_-^ -]^АС(Т). (2)
i=A, в,...
Левая часть как раз и представляет собой искомое выражение,
если положить va= —a, vB = l и т. д.
Замечание. Определим величину КР(Т):
Кр = ЦР^ = Кр(Т). (3)
Связь между Кр (Т) и Кс (Т) дается соотношением
KP(T) = ^RT)^1 КС(Т). (4)
Соотношение (2) или (3) определяет изотерму реакции.
23. С помощью (4.65) получаем
1пАр= -4г 2 (Г)
и, следовательно,
dT
dT RT RT2 •
Решения
267
Здесь ЛЯ = 2 vjH°j — стандартная энтальпия реакции (4.646).
Используя соотношение (2) в решении задачи 22, имеем
In Кс = - + RT ln Rr>
и, таким образом,
In Кс 1 770 2^-7 1 XI .. /Г70 DT\
<jy Ду2 / I У дуг (“! “/).
При температуре Т и нормальном давлении р? мы можем считать
p^Vj — RT (для 1 моль). Тогда
S°j — RT = U°
и, следовательно,
где ЛЯ — стандартная внутренняя энергия реакции.
24. В соответствии с (1.14)
[А] + [А2] = = 8 31.107.(273+18) 4,19 • 10 5 молъ/см3.
Исключая [А2] из этого соотношения и из соотношения для вели-
чины К, приведенного в условии задачи, получаем [А]2 =
= (4,19-10"5 — [А])-1,70-IO’4, или
[А] = 3,5 • 10~5 молъ/см3.
Для степени диссоциации имеем теперь
____Н]__=______—_____= 071
[А] + 2[А2] 2-4,2 —3,5 ’
Чтобы ответить на второй вопрос, воспользуемся полученным
в предыдущей задаче уравнением изохоры реакции dAnK/dT =
= &U/RT3', тогда
dlnA_ 5,0-104-4,2-10’ _
dT ~ 8,3-107 (273 +18)2 ~ U’dU-
Таким образом,
In =0,30, так что К (19°С) = 1,35# (18°С).
Далее, проводя вычисления, аналогичные выполненным выше, полу-
чаем [А]2 = (4,18-10-5 — [А])-1,35-1,70-10-4, так что
[А] = 3,6-10-5 молъ/см3 и г ^,= = 0,75.
|AJ + Z IА2]
268
Гл. 4. Равновесие фаз и химическое равновесие
25. Для решения задачи необходимо определить условие равно-
весия для реакции А2 (газ)ч*2А (в Т). Таковым условием является,
очевидно, условие <?А2(газ) = 2<?а(Т), которое в соответствии с (4.14')
и (4.34) можно переписать в виде
In ра2 = 21пжа + /(7’),
где / (Т) — некоторая^функция температуры. Получаем, таким
образом,
*а~Л/2-
26. Условие равновесия для химической реакции СаСО3 (тверд.)
ч* СаО (тверд.) + СО2 (газ) имеет вид
^СаСОд (тверд.) — ^СаО (тверд.) + ^СО2 (газ)-
Если пренебречь зависимостью от давления химических потенциалов
СаСО8 и СаО, то условие равновесия можно переписать следующим
образом:
RT In Рсо2 = ^СаСОз — ^СаО — ^СОг(газ) = —
так что
dlnPco2 d / Дб \ ДЯТ
dT ~ dT I RT Л /77’2 '
Здесь мы использовали уравнение (4.14'); через \НТ обозначена
стандартная энтальпия перехода, которую можно вычислить с по-
мощью приведенной в задаче формулы
\НТ = 51,957— 10,7077 кал.
27. Так как в рассматриваемой реакции участвуют только
чистые вещества, то термодинамические потенциалы реакции совпа-
дают со стандартными термодинамическими потенциалами реакции
и, следовательно,
AG = GAgCl (тверд.) ”1“ ^Tig (жидк.) ^Ag (тверд.) ^Hg2Cl2 (тверд.) =
= AG = -SE.
Используя наблюдаемые значения Е и (дЕ/дТ)р, находим AG =
= -23068-0,0455= -1050 кал и
= =23068-0,000338 = 7,80 кал!град,
\ 01 fp
так что
\H = \G+T\S= -1050 + 298,16-7,80 = 1276 кал.
Решения
269
28. По данным, приведенным в задаче, определим энтропию
газообразной ртути:
£газ(630°, 1 атм)=( 59,9 ++ 26,2 + ^).107 =
= 190,1-107 эрг/молъ-град.
С другой стороны, используя (4.14') и (4.15), имеем (для энтро-
пии на 1 моль
&(Т, р) = R (4 In Т - In р + А + г)
(мы положили здесь Ср — 5/2й). Согласно третьему закону термо-
динамики, вычисленное по этой формуле значение энтропии при
Т = 630° К и р = 1 атм должно совпадать с полученным
выше значением. Имеем, таким образом, 190,1 • 107/8,32-107 =
= 16,1 — 0 + 2,5 + i, или
i = 4,2 (атм).
Для расчетов с помощью логарифмических таблиц удобна величи-
на / = i/ln 10, носящая название условной химической постоян-
ной:
7 = 1,83 (атм).
Замечание. Тетрод и Сакур получили с помощью моле-
кулярного рассмотрения теоретическое выражение:
i = In [(2лт)3''2/с5/2(о7г.-3],
где h -=- постоянная Планка, т — масса атома, к — постоянная
Больцмана, со — статистический вес основного состояния атома.
Полученное нами в задаче значение хорошо согласуется с вычис-
ленным по этой формуле, если положить в ней со = 1. Отметим,
что давление выражается в атмосферах.
29. В соответствии с (4.14') и (4.15) химический потенциал
электронного газа вне металла записывается в виде
Ge(T, p) = UeQ-^-RT\nT-RTi + RT\np.
Химический потенциал Gi внутри металла по предположению
постоянен. Из условия равновесия Ge = Gt получим
р = е*р/2е-^/вг.
здесь W = UeQ — Gi — постоянная величина. Так как In (р/7’6''2) =
= i— W/RT, значение i можно определить, строя в плоскости
(1/Т, In (р/7’6/2)) прямую, проходящую через экспериментально
найденные значения, и находя точку ее пересечения с осью
270
Гл. 4. Равновесие фаз и химическое равновесие
ординат:
i = lim In —.
г-wo Т!2
30. Результирующая реакция, протекающая в данном элементе,
имеет вид
1
у н2 (газ) + AgCl (тверд.) —> Ag (тверд.) + HG1 (вод., х),
так что термодинамический потенциал реакции определяется выра-
жением
= G Ай(тверд.) 4“ ^НСЦвод.) G Н2<газ) — G AgCl(TBepfl.)-
Здесь для Ag (тверд.) и AgCl (тверд.) можно использовать химиче-
ские потенциалы при нормальном давлении 6'ай(Твсрд.) и б^сцтверд.)-
Находя С?н2(газ) с помощью (4.14'), а Снсцвод.) с помощью (4.52),
получаем
AG= £^(тверд.) + фНС1 + 2RT In (ху)—
1 = —
2 (^Н2(газ) Ч' RT 1п Рн2) GА"С1(тверд.) ==
= AGo _|_ 2RT In (ху) - RT In
Учитывая (4.71) и вводя
Е1® _ AG0 Г। 1 7»о 7<о „о . "1 1
&------g —L^AgCl(тверд.) -f-~2 ^-гН2(газ) ^Ад(тверд.) ’ фНС1 J g ч
найдем искомое выражение для э. д. с.
31. Для термодинамического потенциала справедливо уравнение
dG=—S dT-rV dp, где р, V >и Т обозначают давление, объем
и температуру системы. Зависимость G от давления определяется
из соотношения
(^-)г = 7, или G(p, 7)= JV(P, 7’)dp + ?(7’); (1)
о
функция ф (71) зависит только от температуры. Объем V находим
из уравнения состояния ван дер Ваальса:
nRT п2а
(2>
Для температур ниже критической Тс = 8a/2"lbR это уравнение
трудно решить алгебраически относительно V. Чтобы получить
некоторое представление относительно зависимости G от давления,
следует использовать тот факт, что выражение в правой части (1)
Фиг. 99. Фиг. 100,
272
Гл. 4. Равновесие фаз и химическое равновесие
с точностью до последнего члена <р (Т) представляет собой площадь,
заключенную между изотермой и осью р в плоскости р — V,
как показано на фиг. 99 и 100.
На фиг. 99 представлены изотермы, описываемые уравнением
(2). Как видно из соотношения (1), значение термодинамического
потенциала в точке Р равно площади, лежащей под изотермой
IP, т. е. площади IPAOI (начиная с точки I изотерма асимптоти-
чески приближается к оси V) плюс добавочная функция ср (Г).
На фиг. 100 это значение представлено отрезком РА. Когда точка
Р движется вдоль изотермы и достигает точки К, значение функ-
ции G возрастает и становится равным площади IKXOI плюс
ср (Г) на фиг. 99, или отрезку КХ на фиг. 100. Затем изотерма
делает поворот, после которого точка Р движется уже в отрица-
тельном направлении оси р. Это значит, что dp < 0 и соответ-
ствующей площади в соотношении (1) следует приписать отрица-
тельный знак. В точке L значение термодинамического потенциала
уменьшается по сравнению со значением в точке К на величину
площади KXYLK, а в точке М — на величину площади KXZMLK
(фиг. 99). Так как далее от точки М изотерма опять поворачивает
в положительном направлении оси р, то термодинамический
потенциал снова возрастает и в точке Q определяется площадью
QBZMNQ плюс значение в точке М, что соответствует отрезку
QB на фиг. 100. Таким образом, используя уравнение ван дер
Ваальса, мы получаем кривую зависимости G от р, содержащую
отрезок KLM, соответствующий неустойчивым состояниям. В рав-
новесном состоянии, однако, изотерма изображается не кривой
JKLMN, а прямой линией JLN, параллельной оси V и проходя-
щей таким образом, чтобы в соответствии с правилом Максвелла
площади JKLJ и LNML были равны. Газ, которому соответствует
точка J, находится в равновесии с жидкостью, которой соответ-
ствует точка N. Так как правило Максвелла выводится из условия
равенства термодинамических потенциалов в точках J и N,
на фиг. 100 зти точки совпадают. Если применить соотношение
(1) к новой изотерме IPJLNQ, то получим кривую IPNQ на
фиг. 100. При движении точки Р от J к N скорость возрастания
площади претерпевает скачок, так что кривая G имеет излом
в точке J. Легко видеть, что части JK и MN кривой G, полученной
на основе уравнения ван дер Ваальса, относятся соответственно
к метастабильным газу и жидкости. При Т > Те термодинамиче-
ский потенциал G становится плавной монотонно возрастающей
функцией р. Что касается точки Т = Тс, то кривая для G плавно
подходит к ней со стороны высоких температур, но имеет излом
при подходе со стороны низких температур.
При квазистатическом сжатии газа при Т < Тс плотность
быстро возрастает* с уменьшением объема, так как количество
Решения
273
Фиг. 101. Свободная энергия как функция р и Т.
Все величины выражены в приведенных единицах. (При вычислении
химической постоянной использована атомная масса аргона.)
вещества остается постоянным, а жидкая фаза начинает образовы-
ваться уже в.точке J. Когда часть газа превращается в жидкость,
система становится двухфазной однокомпонентной. Полученная
выше функция G представляет собой термодинамический потен-
циал всей системы, состоящей из газообразной и жидкой фаз,
и остается постоянной до окончания процесса ожижения. Именно
по этой причине точка, описывающая состояние системы, не дви-
жется на р — G-диаграмме, но движется из J в Nна р — К-диа-
грамме. Когда все вещество системы переходит в жидкость,
18 ктбо
274
Гл. 4. Равновесие фаз и химическое равновесие
состоянию системы отвечает точка N. При дальнейшем повышении
давления происходит сжатие жидкой фазы. Возрастание термо-
динамического потенциала при этом происходит за счет того, что
при сжатии система получает работу и тепло от окружения.
Термодинамический потенциал как функция Тир представлен
на фиг. 101.
32. Теплота перехода определяется разностью энтальпий
на 1 моль: L = Ht — Н2. Вспоминая, что Gj = G2, имеем L = Ty.
X («51 — S2). В выражении
dL __ 7 dL \ / dL \ dp
~dT — (1F 1 p+ [~d/T ) т If ’
производная dpIdT определяется уравнением Клапейрона — Клау-
зиуса: dp/dT = L/T (Vi — V2). Остальные производные получим сле-
дующим образом:
( dL \ d (Н i—Н2)
(FF дТ -gpi~gP2’
( dL \ d (77 j H2) _f7 i t d(Si — S2)
\dp)T~ dp + 7 dp
Используя соотношение Максвелла dS/др — —dV/dT, находим
-V1P1+ Ш
и, следовательно,
dL f’ L L (V .(Pi — V'232)
FF~Cpl ^р2+ Т •
В частном случае, когда фаза 2 представляет собой идеальный газ,
имеем р2 = 1/Т и < У2, так что
L (У 1Р1 — У2Р2) ~ _L_
V1 — V2 ?
Отсюда'dL/dT « G₽1 — Ср2-
33. Будем вычислять с = Tds/dT вдоль кривой равновесия
(кривой давления насыщенного пара) р = р (Т), т. е. с =
= Т (ds/dT)p + Т (dsldp)T dp/dT. Подставляя сюда соотношение
Максвелла ds/dp — — dv/дТ = — vf} (В — коэффициент тепло-
вого расширения) и уравнение Клапейрона — Клаузиуса dp/dT =
= r/Т (у8 — vl), получаем с = с® — v^rKy8 — vl). Поскольку
Vя Э> и для идеального газа справедливо приближение р = Т~г,
т0 с = Ср — r/Т, или с = сгр + dr/dT — r/T = clp + Td (r/T)/dT.
Здесь мы учли приближенное уравнение из решения задачи 32.
Решения
215
Подставляя приведенные, в задаче величины, получаем для
воды при 100° С отрицательную теплоемкость с=—1,07 кал/г-град.
Это значит, что при отводе некоторого количества тепла темпе-
ратура водяных паров возрастает так, чтобы не нарушилось теп-
ловое равновесие их с водой.
Если не использовать приближение идеального газа, то оста-
нется добавочный член —гр1 — vl) и мы получим cf =
= cls + Td (r/T)/dT. Здесь cs обозначает теплоемкость вдоль кри-
вой равновесия. Для воды, однако, разница составляет лишь
5-10“5 кал/г- град, так что ею можно пренебречь.
34. а) Обозначим давление внутри капли жидкости через р'.
Тогда условия механического равновесия (4.9) запишутся в виде
Р'"Р = ~- (1)
Условия равновесия при обмене веществом между каплей и ее
паром определяются соотношением (4.10'):
здесь рг обозначает давление пара, находящегося в равновесии
с каплей радиусом г, т. е. давление насыщенного пара жидкой
капли. В этих обозначениях обычное давление насыщенного пара
ps запишется как ps = рОно определяется условием
Ц/ {Т, р оо) = p.g (Т, р<х>)- (3)
Из (2), (3) и (4.14) получаем
Р-i (ргН—— Pi (Р°°') = kT . (4)
Учитывая тот факт, что жидкость трудно сжимаема, т. е. хими-
ческий потенциал мало меняется при изменении давления, мы
можем разложить левую часть соотношения (4)
Pl (рг + v ) = Pi ( Роо + Рг-
по переменной Рт~Р » 1 г 1
тогда получаем (рг-роо+4- ) Vi = kT 1п-^, Роо (5)
или Рг | _ Роо (6)
18»
276 Гл. 4. Равновесие фаз и химическое равновесие
где мы использовали, что Vi — dpildp. Обозначим удельный объем
пара при давлении Доо и температуре Т через v„. Тогда VipxlkT =
— v^Vg^i. Положив Pr/p<» = l + y, перепишем (6) в виде
1п(1 + у) = ^_(г/+^). (б')
Так как vjvg — обычно малая величина порядка 10~3—10-4, то при
•определении точки пересечения функций, стоящих в обеих частях
написанного равенства (6'), можно пренебречь величиной у в скоб-
ках в правой части (правая часть представляет почти горизон-
тальную прямую линию, как показано на фиг. 102). Это экви-
валентно использованию вместо (6) приближенного соотношения
Из (7) получаем
pT = pxe^lrhT. (8)
В качестве примера на фиг. 103 приведена зависимость давления
пара от радиуса капли воды при 20° С.
б) Критический радиус гс для заданного давления р > р^
определяется условием р = рт = р^ exp (2vtf/rkT). Так как над
каплей, радиус которой меньше гс, давление пара больше р,
то такая капля, если она возникла, будет испаряться. Это значит,
что гс есть наименьший радиус, при котором может существовать
устойчивая капля.
Замечание. По указанным причинам капле жидкости
трудно образоваться в паре, в котором нет ядер конденсации,
и пар становится пересыщенным. Если же в паре имеются мель-
чайшие частицы, например частицы пыли, то вокруг них обра-
Решения
277
зуются капли жидкости при условии, что давление пара выше
величины рг, соответствующей радиусу частиц г.
35. На фиг. 104 АВ представляет собой кривую давления насы-
щенного пара. Отрицательная теплоемкость насыщенного пара
означает, что энтропия его в точке А больше, чем в точке В,.
С другой стороны, при понижении давления вдоль изотермы
от точки В энтропия, как легко видеть, возрастает [(ds/dp)T —
= — {dvldT)j, < 0] и значение ее в точке С на изотерме совпадает
со значением в точке А. Таким образом, изэнтропическая линия
АС имеет меньший наклон, чем кривая давления пересыщенного
пара АВ. К этому же результату можно прийти, сравнивая урав-
нение Клапейрона — Клаузиуса dp/dT = LIT (vg — 0) с урав-
нением (dpldT)s = Ср/Т (ди/дТ)р. Вспоминая решение задачи 33,
нетрудно видеть, что последний метод эквивалентен определению
знака теплоемкости пересыщенного пара. Мы видим теперь, что
при внезапном расширении камеры Вильсона, при котором про-
исходит адиабатическое расширение насыщенного пара, состоя-
ние пара изменяется вдоль СА и уходит влево от АВ в область
пересыщенного пара.
Замечание. Как указывалось в предыдущей задаче, кап-
лям жидкости трудно образоваться даже в пересыщенном паре,
если в нем нет ядер конденсации. Когда через камеру проходит
какое-либо излучение, вдоль его пути образуются ионы. Если
сразу же после этого происходит адиабатическое расширение
278
Гл. 4. Равновесие фаз и химическое равновесие
Камеры, то в ней возникает пересыщенный пар. При этом возник-
шие под действием излучения ионы служат ядрами конденсации,
на которых образуются капли тумана. Таким образом наблюдают
следы частиц в камере Вильсона. (См. задачу 49, где объясняется,
почему ионы являются ядрами конденсации.)
36. а) Следуя решениям задачи 24 в гл. 1 и задачи 29 в гл. 3,
запишем свободную энергию единицы объема с учетом энергии
магнитного поля в виде
1 \HdB.
V V 1 4л J
Здесь Fo (Т) — значение свободной энергии при Н = 0 и 5 = 0.
В нашем случае удобно вместо F рассматривать функцию
G(H,T)=F-V^~ (1)
и взять Н в качестве одной из независимых переменных. Эффект
Мейсснера означает, что
5(Я) = 0 при |Я|<ЯС
и
В (Н) = Я при | Я | > Яс.
Иными словами,
Gs = 50(7’)-^ ^BdH = F0(T) при |Я|<ЯС, (2)
о
Gn = F0(T)-^- (5ЙЯ = 5о(Л--^(Я2-Яс2) при |Я|>ЯС,
L J О« Ь
о '
(3)
так что
лл— дт + дТ 8я dT , или
Q = T(Sn-S.)=-±;-^. (4)
б) Для • теплоемкости всей системы, занимающей объем V, напи-
шем
г г _т d(Sn-Ss) _ ТУ <РН*С
— — l gj; — dT2 —
-даГ^]- <*>
Решения
279
Полагая Т = То и Нс = 0 и переходя к величинам, отнесенным
к 1 моль, получаем
,г-7> <»>
в) Положив — — (Т/Т0)2], найдем из (5)
й-й=-^[1-з(£Г]- <7>
Кривая Cs—Сп изображена на фиг. 105 пунктирной линией (сплош-
ная линия представляет экспериментальные значения).
Замечание. Типичный ход кривых Сп и Св приведен
на фиг. 106.
37. Обозначим какую-нибудь из концентраций или х2 через
х, а газообразную и жидкую фазы будем отмечать соответственно
индексами g и I. Кривые газовой фазы xg (Т) и жидкой X; (Т)
определяются условиями
Gig(T, хв) = (тц(Т, xt),
G2g(T, xg) = G2i(T, xt).
Их поведение вблизи азеотропической точки (Т°, x'g — xT) можно
определить, полагая в уравнениях (1) xg = Xg-\-8xg,
xi — x°i-[-8xi и находя соотношение между 8Т, &xg и бж/. Разлагая
280 Гл. 4. Равновесие фаз и химическое равновесие
в ряд по 67, 8xg, 8xi, получаем из уравнений (1) с точностью
до членов первого порядка малости
-5lg67+ -^67 + ^6^, (2а)
- S2g8T + 8xg = - ^67 + 8xh (26)
8 *
Здесь мы учли, что dGidT =—S, и обозначили через Slg, . .
. . ., dGlgldxg, ... значения этих величин в азеотропической точке.
Используя уравнения Гиббса — Дюгема — StdT + ж1гй61г-|-
+ x2idG2i = 0 и — SgdT + xigdGlg 4- x2gdG2g = 0, мы можем опреде-
лить 8Т следующим образом. Умножая (2а) на хЪ, а (26) на хи
и складывая их вместе, мы можем исключить бж2/. При этом
получаем —(х°цЗц^- xuS2i) 8Т = —8ц8Т в правой части и — Slg8T
в левой, где мы учли, что %u = xig и X2i = X2g- 1ак как —
— 51Z=0=O, то 8Т = 0. Это значит, что 8Т — величина по крайней
мере второго порядка малости вдоль кривой газообразной фазы
и кривой жидкой фазы.
38. Примем поперечное сечение стержня равным единице и обо-
значим через Ст (х) концентрацию примесей в жидкой части стерж-
ня, когда длина затвердевшей части, отсчитываемая от левого
конца, равна х. Пусть процесс затвердевания продолжается
и длина затвердевшей части увеличивается на dx. При этом коли-
чество примесей, перешедшее из жидкой фазы в твердую, равно
kCm (х) dx. Эта величина равна изменению d [Ст (ж) (L — ж)]
количества примесей в жидкой фазе Ст (ж) (L — ж), так что
d [Ст (ж) (Л — ж)] = — кСт (ж) dx,
dC W
^(£-ж)=-(А-1)Ст.
Интегрируя это уравнение, получаем
Ст (х) = А • (L — ж)*’1 (А — постоянная). (2)
Так как концентрация примесей в исходной жидкой фазе была
равна Ст, то ALk~1 = Cm и, следовательно,
Ст (ж) = Сй (1- -£-р. (3)
Концентрация примесей в твердой фазе, выпадающей в точке ж,
определяется следующим образом:
С (ж) = кСт (ж) = кС°т (1 - -^) ft-1. (4)
Решения
281
Эта функция изображена на фиг. 107
ченной формулы следует, что С (х)
точно. Ошибка обусловлена исполь-
зованием предположения о постоян-
стве величины к, что справедливо
лишь для малых С.] Мы видим, что
примеси* собираются в правом конце
стержня, а его левый конец очища-
ется от них.
Замечание. Зонная очистка.
При очистке полупроводниковых
материалов, например кремния и
германия, стержень из этого мате-
риала пропускают через катушку ин-
дукционного нагревателя (фиг. 108).
При этом часть стержня, находя-
щаяся вблизи катушки, плавится
для случая к < 1. [Из полу-
оо при х —Z,; зто не вполне
и перекристаллизуется, а примеси
собираются в правом его конце (расплавленная часть сохраняет
форму благодаря силам поверхностного натяжения). Причины
этого ясны из приведенных выше расчетов. Метод получения очень
Катушка
нагревателя
и г. 108.
чистых веществ, основанный на повторении такой зонной плавки,
называется зонной очисткой. Наоборот, добавляя примесь к чисто-
му веществу, можно с помощью зонной плавки получить вещество
однородной концентрации (зонное выравнивание концентрации).
39. а) Соотношения между <рг и молярными долями xt = Nt/^j Nt
имеют вид
r<Pi _ фг /р
1 ГФ1 + Ф2 ’ гф^фг ' k
Разрешая их относительно <р$, получаем
/ОХ
ф =------£--- ф —---------. (2)
Т ^1 + га:2 Y ^1 + ^2
282
Гл. 4. Равновесие фаз и химическое равновесие
Используя приведенное выражение для Gt, находим далее, что
при постоянных р и Т
У ZidGi^npj + cpz)-1 {А_(1-А)}_
— 2u? (1 — ф,)^ с/ф! Ц-<р2 [ЯТ {A- + (r—1)} — 2га>(1 —<р2) ] d<p2) =
= (r<Pi + фг)-1 ([RT {<pi + Гф2} — 2rw^^2\ dtp, +
+ [RT {qh + rq>2} — 2m\p{(p2] <йр2) = О
(так как dcpf + tZq>2) = 0).
б) Так как Si = —dGt/dT, имеем
51 = ^-Я[1пФ1+(1—1) ф2] ,
^2 = ^2 — Я [In ф2— (г— 1) фП
и, следовательно,
— Я [1Пф!+ (1—А) ф/| +ж2 [1Пф2 —(г—1)ф!]| =
= 2 XiSi ~ R (^11п Ф1 + Ж2 1П ф2). (3)
Здесь в противоположность случаю идеального раствора в выра-
жении для энтропии смешения вместо ж, в качестве независимых
переменных под знаками логарифмов стоят объемные доли ф;.
Произведя преобразование
— Я (xi In ф, + х2 In ф2) =
= — Я (Xt In а?! -\-х2 In х2) -|- Я {In [1 + (г— 1) х2] — х2 In г},
видим, что в данном случае энтропия, вообще говоря, больше, чем
в случае идеального раствора, если г>1.
в) Используя соотношение Ht = Gi-\-TSi, получаем выражения
для удельной молярной энтальпии:
+ Я2 = Я° + гшф*;
следовательно, теплота смешения определится следующим образом:
ДЯ = 2 жгЯг — 2 XiH°i = w (x^l + rxztpf) = ГХ^Х w- (4)
Она обращается в нуль при ж2 = 0 и х2 = 1 и достигает максималь-
ного значения ru>/(]/"r +1)2 при хч = 1/(1 + УУ)- На фиг. 109
в качестве примеров приведены кривые для г =10 и г =100.
Решения
283
г) Вычислим теперь давление пара и осмотическое давление.
Для -этого воспользуемся результатами примера 6. При заданном
химическом потенциале активность растворителя описывается выра-
жением
ai = (l-<p2)exp[(l-y) <рг + ^<р1] •
Таким образом, мы имеем
^- = ^ = (1 —<р2)ехр [(1 — у) <р2 + т§г <й] .
= -Ina^ -1п(1-<р2)-[1-у] ф2 —-Л_ ф|==
1 , I 1 W \ п ,
— у Фг+ [у —ду] <р2+ • • • —
—Л—
1 + (г —1)ж2
W
Нт
) [ц-(г — i) J + • • •
44
ж2+ (
2 RT ) г2ж2+ ‘ ‘ (г ^ !)•
(5)
(6)
284
Гл. 4. Равновесие фаз и химическое равновесие
При очень низких концентрациях, как и в случае идеальных
разбавленных растворов, выполняется закон Вант-Гоффа. Однако
при высокой степени полимеризации г отклонения от этого закона
возникают уже при относительно
циях. В качестве примеров на
малых молярных концентра-
фиг. 110 приведены кривые
зависимости
давления пара
Фиг. 110.
pjpi от <р2 при г -> оо.
40. Хотя между резервуа-
рами I и II и происходит об-
мен ионами М+ и X-, однако
в силу условия электрической
нейтральности
Хм+ = ^Х-! (1а)
Жми—*Гх—_1" ^2* (^-б)
Кроме того, из законов сохра-
нения для М+ и X- вытекает
жм+ + жм+==^4-ж®,
^- + ^х- = ^. (2)
С другой стороны, имеем
условие равновесия
£м+х-(1) = £м+х-(П)» (3)
откуда в предположении идеального разбавленного раствора имеем
RT In (жм+^х-) = RT In (ж'м+ж'х-) или х^х'х- = «м+^х— (4)
Мы использовали здесь соотношения (4.33); объемные доли <рм+ и
<Рх~ имеют одинаковые значения в резервуарах I и II. Из (1а),
(16) и (2) получим теперь (жх-)г = (ж? — х"х-)2 = (хх- + я^) х'х-
и, следовательно,
Хх~ 2х« + х« •
Аналогично
2х« + 4 ’
Это значит, что вещество М+Х“ распределяется между резервуа-
рами I и II в отношении («J + ж“) : х*.
41. Обозначим через Фг и Фц электростатические потенциалы
фаз I и II. Тогда электрохимические потенциалы будут
Цм+ = Км+Н-еФь 1'1х- = М'Х-— еФг,
'Лм+ = Нм+ + еФц, Цх- = Цх- — еФц.
Решения
285
Из условий равновесия т]м+ = 'Пм+ и т]х- = 'П,х- имеем
(1)
где мы использовали для Цм+, • • • соотношение (4.33). Подставляя
в (1) результаты, полученные при решении предыдущей задачи,
находим
Замечание. Из соотношений (1) можно получить соотно-
шение (4) решения предыдущей задачи.
42. Здесь мы опять имеем дело с равновесием мембраны
Доннана. Обозначим концентрацию ионов по одну и другую сто-
роны мембраны I и II через жм+, zx-> жм+, жх- и zr-. При добав-
лении М+Х~ осмотическое давление становится равным
_ RT
л — у (жм+ + х'х- + z"r- — ЖМ+ — Жх-)
(V — молярный объем воды). Используя решение задачи 40
(при ж° = ащ-), запишем
У 2И- + ^.)-21к. = 2^|^) .
Таким образом, осмотическое давление, имевшее начальное зна-
чение (RT/V) 2^r-, при добавлении М+Х- постепенно уменьша-
ется, стремясь в пределе больших количеств М+Х- к половине
своего начального значения. Этого и следовало ожидать. В фазе II
ионы R" все время сохраняют свою концентрацию zr— До добав-
ления раствора М+Х- ионы М+ не проходят через полупроницае-
мую мембрану из-за электрического притяжения ионов R-
и остаются в фазе II, так что осмотическое давление имеет значе-
ние, соответствующее раствору с концентрацией ионов R-, равной
2жи-. При добавлении М+Х" разность концентраций ионов М+
и X- в фазах I и II постепенно уменьшается (влияние наличия
ионов R- соответственно ослабляется), и наконец они становятся
равными: различие между двумя фазами теперь заключается
лишь в наличии ионов R-.
Замечание. В биологических явлениях большую роль
играет тот факт, что небольшие добавки электролитов чрезвычайно
сильно влияют на осмотическое давление коллоидных растворов,
например белка или крахмала. (Очень многие из таких коллоидов
представляют собой так называемые амфотерные электролиты, в
которых те или иные ионы могут быть либо положительными, либо
отрицательными в зависимости от значения />Н.)
286
Гл. 4. Равновесие фаз и химическое равновесие
43. Выведем прежде всего необходимые соотношения. Для
малых значений х2 имеем (см. пример 8)
-- «2
lna1=-vT2g=-^^g, g = l+^- J ^~^dx2. (1)
Используя решение примера 6, запишем
лт RTi21 RT^Mim.2 .
AZ = —Г? ln = v "ТГ WOO s - vKm^'
Подставляя сюда v = 2 (так как НС1 —> H+-J-СГ), 7’^ = 273,16°,
Li——1436 кал/молъ, R = 1,9870 кал!моль-град и Mi —
— 18,016 г/молъ, находим
пуог —
к =---юоол/ = 1 ’860 град кг!моль,
9= —АТ7 = 3,72m2g град (т2 в моль/кг).
Используя [уравнение (4.56) в качестве теоретического уравнения
Дебая — Хюккеля и считая Z? = 88,23, е = 4,802-10-10 эл. стат, ед.,
No = 6,025-1023 и к = 1,38- 10-1в эрг!град, находим 4 = 1,12. Так
как можно положить С2 = Pizn2 « т2, имеем
1пу =—a]Lm2, а=1,12. (3)
Заменяя в (1) х2 на т2, получаем
ТП2 _ ТП2
g = 1+iim2^£Zm2=1~2^5 =
О о
= 1—а УТп2 = 1 — 0,375 ]/т2. (4)
По данным, приведенным в условии задачи, можно вычислить
1 — g, используя выражения (2) и (4). Результаты сведены в таб-
лицу.
та, 10-3 моль/кг 1 -g
эксперимент уравнение Дебая Хюк- келя
0,627 0,021 0,009
1,179 0,011 0,012
1,245 0,017 0,013
1,474 0,011 0,014
2,228 0,017 0,017
3,526 0,020 0,022
4,520 0,022 0,025
6,879 0,025 0,031
10,633 0,027 * 0,039
Решения
287
44. Концентрацию доноров и электронов обозначим соответ-
ственно через Nd и пе. Тогда концентрации D и D+ будут равны
Nd — пе и пе. Используя для электронов проводимости приближение
идеального газа (ре = пекТ), получаем из (4.14') и (4.15а) химиче-
ский потенциал для электрона
це = — -5- кТ In Т — kTie + кТ In пе.
ы
Предполагая твердый раствор идеальным, найдем для D и D+
из (4.34):
Нп = нЬ(Л p) + kTln^^s,
pD+ = p»D+(r,p) + *nn-^.
В соответствии с (4.63) при равновесии Цп = Но+А Не и> следова-
тельно,
~Т /2ехр[~-£7-(М'? + 1ко+~Hd)] •
В правой части величина H* + Hd+ — Ни равна энергии ионизации
кристалла Ed~ Таким образом, при пе Nd ответ можно записать
в виде
ne^-Nd/2T3/ie-E4/zhT.
45. Результирующая реакция, записанная в условии задачи»
происходит в два этапа: Ag (жидк.) —> Ag+ (AgCl — КС1) + е
и Ag+(AgCl — КС1)4-е-^> Ag (Ag^Aut-x). В соответствии с (4.42)
э. д. с. определяется выражением
= ^Ag(AgxAu1_x) ^Ай(жидк.) =
= ^А§(жидк.) “Ь ЛТ In (.Ту) £?А§(жидк.) — RT In (.ту),
где у обозначает активность. Если считать раствор идеальным,
то у=1 и искомая величина при ж = 0,5 и Т = 1360° К будет
1,987-1360, 1 л лоо
—Шбо-1ПТ = 0’082 в-
Действительные значения у можно определить по приведенным в
условиях значениям х и Е, пользуясь нижеследующей таблицей.
288
Гл. 4. Равновесие фаз и химическое равновесие
X Е 8е/2,зознт 1g х 1g? V
0,846 0,021 0,078 -0,072 -0,006 0,986
0,716 0,045 0,167 -0,145 -0,022 0,950
0,602 0,074 0,274 -0,220 -0,054 0,884
0,471 0,114 0,422 -0,327 -0,095 0,804
0,263 0,198 0,734 -0,580 -0,154 0,701
46. Следуя (4.59'), запишем химическую реакцию
аА + 6В + ... ZL + тМ + ... (1)
в виде
3?дХд = 0 (vo=-a,Xo = A, ...). (2)
Коэффициент реакции X вводится с помощью соотношения (4.60),
причем в начальном состоянии Х = 0. Термодинамический потенциал
всей системы является функцией переменной X:
G (пА, пъ, ..., «ь, • • •) = S nkGk = G(k).
k
Химическое равновесие определяется соотношением (dG!dK)Pi т = 0,
т. е. в соответствии с (4.63):
(Х-46=2*=»- (3)
Чтобы равновесие было устойчивым, функция G (X) при значении X,
определяемом уравнением (3), должна иметь минимум, т. е.
<4>
а) Изменение X в зависимости от Т при постоянном давлении
определяется величиной (дк/дТ)? д^. При этом величина AG должна
оставаться равной нулю. Заметим, что
I ЭХ \ _ д (X, AG) _ д (X, AG) Э(Х, Т) = (дАС/ЭГ)р, х
V дТ /р,дё— д(Т, AG) 5(Х, Л д(Т, AG) ~ (ЭД£/ЭХ)р, т
И
(-Адё) = А-2тдсд=-ЗтдУд=-дУ=-^- (6)
(так как ДС? = АН—TAS = 0). Здесь ДЯ = 2 есть изменение
энтальпии в ходе реакции, равное в соответствии с (3) дН!д%.
Решения
289
Теперь соотношение (5) запишется в виде
/ дЬ \ 1 (дЯ/дЛ)р, г
v дТ /Р, лв ~~ т (дьё/дХ)р,т ’
Так как знаменатель в правой части положителен в силу условия
(4), то величины (дк/дТ) д § и (дН1д1к)р,т имеют одинаковый
знак. Если АН > 0, то реакция будет эндотермической и будет
идти в прямом направлении (X возрастает) при повышении тем-
пературы. При АН 0 имеем экзотермическую реакцию, и при
повышении температуры равновесие сдвигается в обратном
направлении.
б) Если давление р меняется при постоянной температуре Т,
то имеем аналогичным образом
/ 5М = (дЛС/аР)г, х = J17 8
\dP'T,bG (d\G/dX)p<T (dbG/dK)p,T ' {
Здесь
лу=2^=2„(4)^(^)лг
есть изменение объема в ходе реакции. Так как знаменатель
в правой части соотношения (8) положителен, то величины
(дк/др)т дд и ДУ имеют разные знаки. При ДУ >0, т. е. при
возрастании объема в ходе реакции, химическое равновесие при
реакции (1) смещается влево, если же ДУ < 0, то вправо. Таким
образом, реакция идет в таком направлении, чтобы общий объем
уменьшался.
47. Необходимыми условиями равновесия между газообраз-
ной фазой, которой соответствует точка Е, и жидкой фазой, кото-
рой соответствует точка А (фиг. 111), является равенство давлений
р, температур Т и химических потенциалов р, обеих фаз. Первые
два условия уже удовлетворены автоматически самим способом
выбора точек А и Е. Правило Максвелла можно получить из треть-
его условия
На (р, Т) = (р, Т). (1)
Для массы М, заключенной в объеме У, термодинамический
потенциал, соответствующий состоянию А, равен
Ga (р, Т) = МрА (р, Т) — UA — TSA + pVA.
Для состояния Е имеем МрЕ (р, Т) = UE — TSE + pVE, так
что соотношение (1) можно представить в виде
(£7Е _ £7А) _ р _ 5А) + р (Уе - УА) = 0. (2)
19 Кубо
290
Гл. 4. Равновесие фаз и химическое равновесие
Таким образом, задача сводится к нахождению разности внутрен-
них энергий UE — UA и энтропий SE — SA.
Уравнение ван дер Ваальса для п молей газа в объеме У имеет
вид
nRT п2а
P = v^b~-W
Здесь а и b — константы, характеризующие вещество, a R —
газовая постоянная. Следует заметить, что в случае равновесия
Фиг. 111.
уравнение (3) применимо лишь к частям КА и EN изотермы, т. е.
область АСЕ исключена. Если же уравнение (3) применимо,
то теплоемкость при постоянном объеме cv становится функцией
только Т (см. гл. 2, решение задачи 34). Чтобы вычислить раз-
ность энтропий SE — SA, достаточно рассмотреть произвольный
квазистатический процесс AJE, с помощью которого можно
осуществить переход из точки А в точку Е, не выходя из области
применимости уравнения (3), например процесс, изображенный
Решения
291
пунктиром на фиг. 111. При фиксированном значении М величина
<S является функцией V и Т и -
j dS — j =
A A
= J (^vdV+ \^dT. (4)
A A
При последнем преобразовании мы использовали соотношение
Максвелла (0S/dV)T = (dp!dT)v. Так как точки А и Е относятся
к состояниям с одинаковой температурой, то последний интеграл
в (4) должен обращаться в нуль. Учитывая уравнение (3), полу-
чаем
VE
SE-SA = [ ^^-г-dV^nRln „Е~пЬ--.
а j V~nb Vд — nb
(5)
Аналогичным образом, используя (3.216), найдем разность внутрен-
них энергий
UE-UA= J du= j [(f-)T<Jr+ (»v^] =
A A
E E
= И7, (M - ₽]+ W <r> =
A A
Из (5) и (6) имеем далее
(UE - UA) - Т (SE - 5А) = - ( nRT In ~ ) • (7)
Но эта разность как раз равна интегралу от pdV вдоль изотермы
ABLDE, если считать, что уравнение (3) справедливо для всех
состояний, включая мета стабильные и нестабильные,
ABLDE Vл
А
= [пяпО(Г-»Ь)+41]^.
(8)
19*
Фж». 112,
Решения
293
Таким образом, учитывая (2), получаем
j pdV = р (VB—VA). (9)
ABLDE
Так как р есть давление в точках А и Е, то правая часть (9) соот-
ветствует площади прямоугольника AEWQA на фиг. 111. Левая
часть соответствует площади фигуры ABLDEWQA между изотер-
мой ABLDE и осью V. Таким образом, соотношение (9) означает,
что площадь DELD равна площади ALBA. Это и есть правило
Максвелла. Чтобы перейти к удельному объему v = VIM, поде-
лим обе части уравнения (9) на полную массу М. Удельные объемы
в точках А и Е, т. е. vi и vg, становятся функциями только пере-
менной Т (или только р). [Давление р для заданной температуры
Т можно определить, решая уравнение (1). Обратное положение
также справедливо; например, при р = 1 атм для воды получим
Т = 100° С.]
Замечание. Для удобства на фиг. 112 изображена поверх-
ность, описываемая уравнением состояния ван дер Ваальса, где
показаны также горизонтальные линии типа АЕ на фиг. 111,
определяемые с помощью правила Максвелла и соответствующие
состояниям, в которых сосуществуют газообразная и жидкая
фазы.
48. Рассмотрим свободную энергию единицы объема F (М, Т),
причем будем считать, что изменением объема можно пренебречь.
Так как мы рассматриваем ферромагнетик вблизи точки Кюри,
величину М можно считать малой. Будем предполагать, что
F (М, Т) как функцию М можно разложить в ряд
F(M,T) = F(p, 7’) + а(Г)^- + р(7’)^-+... . (1)
(Здесь нечетные степени М отсутствуют, так как оба направления
намагниченности эквивалентны.) Намагниченность М (Н) опре-
деляется из условия равновесия при наличии магнитного поля
F (М, Т) — НМ = min. (2)
Прежде всего, при Т> Тс для Н =£ 0 намагниченность М = ^ТН
пропорциональна Н (для не слишком больших значений | Н | ).
Поэтому, сохраняя в разложении (1) только члены до второго
порядка по М, получаем из условия (2)
~(~аМ^-Нм}=0, или М = — , (3)
ЭМ \ 2 / . а ’ '
так что
а =---, или а = —-г—-. (4)
Хт A v '
294
Гл. 4. Равновесие фаз и химическое равновесие
При Т < Тс коэффициент а в разложении (1) становится отрица-
тельным, и кривая зависимости F (М, Т) от М имеет максимум
при М = 0. Если р > 0, то F (М, Т) имеет при М 0 два мини-
мума за счет членов Mi (фиг. 113). При Н = 0 эти минимумы обу-
Ф и г. ИЗ.
Фиг. 114.
словливают спонтанную намагниченность Ms. Для исследования
поведения вблизи точки Кюри мы можем положить р (Г) »
та р (Гс), при этом получаем
aMs + 4pMs3 = 0
и Г следовательно,
Ме
6“ ~ Г6(Гс-Т)-]‘/2
₽ ~ L (тс) J
(5)
Это выражение и описывает поведение спонтанной намагниченности
ниже'Т’с (фиг. 114).
_ Таким образом, при Л = 0 имеем
М = 0, Г(Г) = Г(0, Г) при Т>ТС, (6а)
M = MS, F (Т) = F (0, Т)при Т <ТС. (66)
Из этих соотношений можно вычислить 5 — — dFtdT и С =
— Т OS/dT = —Т d^F/dT1. Второй член в (66) определяет разрыв
теплоемкости. Имеем
ДС Стс_о Стс+о Л2р
(7)
На фиг. 115 качественно представлен ход кривой теплоемкости.
49. Представим себе каплю воды радиусом г, в центре которой
находится частица (ион) радиусом а с электрическим зарядом е.
На расстоянии р от центра капли имеется электрическое поле
Решения
295
Е = е/е.р2, где е — диэлектрическая проницаемость воды. Как
было показано в гл. 3, задача 29, вследствие поляризации, обу-
словленной электрическим полем, свободная энергия на единицу
Фиг. 115.
объема уменьшается на величину — (е — 1) Z?2/8n. Полное изме-
нение свободной энергии капли получаем, интегрируя это выра-
жение по объему капли:
AF-- (‘ (j(1—4 ± =
J 8л е2р4 ! i 2 К е ) К а г } е
= е2 4-const. (1)
9г<? 1 4 '
Если достаточно большой объем водяных паров вместе с каплей
рассматривать как заданную систему, а оставшуюся часть водя-
ных паров — как термостат (фиг. 116), то мы придем к условиям
равновесия (3.28):
6U — TbS + рб (V + V") - рб (N' + N") > 0.
Одним штрихом отмечены величины, относящиеся к жидкой
фазе. Подставляя для 6U выражение (4.8), в котором учтена
поверхностная энергия, получаем
(р — P')bV' +убо'4- [р/ (Т, р') —|х"(7\ p)]8N' +
Если пренебречь зависимостью е от плотности и положить do —
— (2/r)dVr, a dr = (1/4лг2) dV', то полученное неравенство можно
296
Гл. 4. Равновесие фаз и химическое равновесие
переписать следующим образом:
[-Р' + р + ^-~(!-67' + [!х'(7\ Х)-Н"(Л р)]6Я'>0.
При равновесии
р' = р + f1 — “) <УРавнеНие Дж- Дж- Томсона) (2)
и условие
И' (Т, р') = р" (Г, р)
выполняется. Из этих двух уравнений и определяется критиче-
ский радиус г.
Следует заметить, что в случае плоской границы для насыщен-
ного пара выполняется условие р/ (ps) = р" (ps), в то время как
в настоящем случае неравенство р' (р') <
<р" (р) может иметь место не только для пе-
ресыщенного пара [р' (р)<р" (р)], но и для
ненасыщенного пара [р' (р) >• р" (р)1, так
^^^zzzzzz^z/zzzA как при достаточно малых г уравнению (2)
^^wzzz^l^zzzzzz^ удовлетворяют р' < р {др!др = v > 0). Иными
^zzzz0z^zzzz^^ словами, жидкая фаза более устойчива
vzzzzzzzzzz^%^f (см. § 2, п. 1) и капля воды может расти.
X^zzzzz^^^^' Таким образом, электрические заряды играют
^<zzzzz^>^ важную роль при конденсации водяных
Фиг 116 паров и образовании облаков и тумана в
атмосфере. Относительно камеры Вильсона
см. замечание к решению задачи 35.
50. Общие условия разделения фаз приведены в примере 2.
Действуя аналогично примеру 7 и используя результат задачи 39,
запишем
/ (ф) = =
г_(г1_1)ф-[г(1 ~ф) 1д(1-<Р) + <р1в<р+^-ф(1-ф)] • (1)
Здесь мы заменили <р2 на <р. Будем дальше также заменять xz
на х. Разделение на две фазы происходит в том случае, когда
кривая зависимости \GIRT от х имеет два минимума. Сумма пер-
вых двух членов в квадратных скобках в соотношении (1) дает
кривую, имеющую вертикальные касательные при ~ 0 и <р ~ 1
и обращенную выпуклостью вниз при 0 < ф < 1, в то время как
третий член дает выпуклость вверх при w > 0. Таким образом,
если значение w/RT достаточно велико, на кривой имеются два
минимума и максимум между ними. Исследуем это условие.
Литература
297
Прежде всего имеем
dtp d гх ср2 d AG f (cp) m2
dx dx l + (r — i)x rx2 dx RT rx'i '
Для f (<p) = g(q>)/[r—(г—l)q>], где
g (cp) = r (1 — cp) In (1 — cp) + cp In cp 4 rw /л \ ]>p ф(1 ф)> (3)
находим
f’ / fr\ _ g' (Ф) ' r-(r—l)cp (r —l)g(cp) [r —(r— 1) cp]2 ’ (4)
/ (ф) г_(г_1)(р 1 2(r —l)g' , 2 (г — I)2 g
[Г —(Г —l)cp]2 [r —(r —1) cp]2 ~
_ g" r — (r— 1) cp H2(r-1)/'. (5)
Чтобы три корня уравнения /' (ср) = 0 совпадали, должны выпол-
няться условия /" (<р) = 0 и (ср) = 0, что эквивалентно услови-
ям g" (ср) = 0 и gm (ср) = 0. Действительно, при /' = 0 из (5)
имеем, что g" = 0, а получив из (5) значение (ср) и положив
его равным нулю, найдем g"' (ср) = 0. В соответствии с (3) эти
условия могут быть записаны в виде
г ,1 9 rw _ „
1 —ср + ср НТ ’
___________~ = о.
(1-Ср)2 Ср2
(6)
Обозначим корень
и 0< 1 — ср< 1,
и, следовательно,
нение, находим
зтих уравнений через сре. Так как 0<ср<;1
из второго уравнения имеем 1 — срс = — j/r фс
срс = 1/(1]/7). Подставляя зто в первое урав-
(?)
Как указывалось выше, разделение на две фазы имеет место при
w > 0 и Т < Тс (wIRT > w/RT^. Концентрации в разделенных
фазах ср' и ф" определяются условием /' (ср) = 0.
ЛИТЕРА ТУРА
1. Poggendorf Annalen (Annalen der Physik und Chemie), Bd. CXXV,
S. 351—400 (1850).
2. G i b b s J. W., The Scientific Papers, vol. 1, New York, 1906. (Имеется
перевод: Дж. Гиббс, Термодинамические работы, М., 1950.)
3. Gibbs J. W., Trans. Connecticut Academy, vol. Ш, p. 108—248
(1875).
.298
Гл. 4 Равновесие фаз и .тимическое равновесие
4. Onsager L., Phys. Rev., 65, 117 (1944).
5. Т i s z a L., M.I.T. Laboratory of Electronics Technical Report, № 127,
1949.
6. T i s z a L., Phase Transitions in Solids, New York, 1951.
7. Y a n g C. N., L e e T. D., Phys. Rev., 87, 404, 410 (1952).
8. Rice О. K., Journ. Chem. Phys., 22, 1535 (1954).
9. К u b о R., Statistical Mechanics, Amsterdam, 1965. (Имеется перевод:
P. К у б о, Статистическая механика, изд-во «Мир», 1967.)
10. Bridgeman Р. W., The Nature of Thermodynamics, London, 1943.
11. L e h n i n g e r A. L., Bioenergetics, New York, 1965.
12. Ehrenfest P., Leiden Commen., S. 75 (1933).
Предметный указатель1)
Абсолютный нуль температуры 150,
170, 192
Адиабата 97, 108
Адиабатический температурный
коэффициент 171
Азеотропия 246
Активность 211
— коэффициент 235
Амфотерный электролит 285
Аналитическая формулировка тер-
модинамики 142
Аррениуса теория диссоциации 214
Атмосферное давление 44
Бойля кривая 36, 40, 41
Больцмана постоянная 25, 269
Большой потенциал 143
Вагнера — Энгельгардта элемент 249
ван дер Ваальса газа внутренняя
энергия 129
— — критическое состояние 36
— — теплоемкость удельная при
постоянном объеме 103
— — термодинамический потенциал
244
— — уравнение состояния 26, 36,
38, 129, 135, 290
— — энтропия 129
— — эффект Джоуля — Томсона
135
Вант Гоффа закон 235, 284
Вечный двигатель второго рода 75
— — первого рода 17
Взаимодействие механическое 13
— тепловое 13
Вильсона камера 245, 251, 277
Вириальное разложение 28
Вириальный коэффициент 28, 119
Внутреннее трение 48
Внутренняя сила 21
— энергия 16, 143, 157
Водород 84, 85
Возгонка 246
Воздух 32, 45
— теплоемкость 163, 164
— энтальпия 160
Второй закон термодинамики 86
Высокополнмерный раствор 247,
251, 284, 296
Газовая постоянная 25
Гей-Люссака эксперимент 102
Генри закон 209, 240, 259
Гиббса — Гельмгольца уравнение
105
Гиббса — Дюгема уравнение 146,
173, 190, 209, 222', 234, 240, 248,
258
Гиббса — Пойнтинга уравнение
201
Гиббса правило фаз 204
— уравнение 82
Давление атмосферное 52
— равновесное 253
Даниэля элемент 216, 217, 236
Двухкомпонентная система 222
Дебая — Хюккеля уравнение 213,
249
Джоулево тепло 70
Джоуля — Томсона коэффициент
101, 102, 105, 120, 135, 136
— — процесс 171, 180
— — эксперимент 41, 101
— — эффект 105, 135
Джоуля цикл 97
— эффект 176, 198
Дизеля цикл 97
Диссоциация 212, 243, 267
— давление 243
— степень 235, 242
— тепловая 235
Дитеричп уравнение состояния 44,
56, 105, 134
Диффузия 103, 248
Диэлектрик 175, 194—196
Доннана мембраны равновесие 248,
285
Дюгема — Маргулеса уравнение 259
Естественные независимые перемен-
ные 142, 143
Жидкая фаза 219, 224
Жидкость 208
— переохлажденная 101, 118
!) Курсивом выделены номера тех страниц, на которых дается основное
определение данного термина.
300
Предметный указатель
Закон действующих масс 215
— сохранения энергии 16
Замерзание 226, 228, 230, 262, 263
Зонная очистка 281
— плавка 247
Идеальные газы, смесь 25, 56, 173,
183, 206
Идеальный газ, внутренняя энергия
46, 53, 167
— — свободная энергия 116, 167
— — теплоемкость 172
— — термодинамический потенциал
116
— — уравнение состояния 25
— — энтальпия 46
— — энтропия 97, 99, 111, 167
Изотерма 220
Интегрирующий множитель 83, 127
Интенсивная величина 14
Инфинитезимальный процесс 15
Ионизации энергии 236
Ионная сила 213
Источник частиц 13
Калория термодинамическая 19
Капля жидкости 276, 296 ,
Каратеодори принцип 75, 103, 125,
126
Карно принцип 75
— цикл 44, 73, 113, 122
Кельвина уравнение 105
Кипения точка 228, 229, 241, 262
Клаузиуса — Клапейрона уравнение
200, 252, 262, 274, 277
Клаузиуса неравенство 81
— принцип 74, 125, 126
— уравнение 44, 65
Конденсатор плоский 175
Конденсированная фаза 225
Константа равновесия 216, 219, 242,
296, 297
Контактная разность потенциалов
236
Контакт термодинамический 13, 15
Концентрация 211
Коэффициент полезного действия 75,
97
— продвижения реакции 215
Крамерса функция 143
Кривая газовой фазы 246, 279
Кривые жидкой и твердой фаз
(ликвидус и солидус) 241, 246,
265, 279
Критическое состояние 36, 56
Кюри — Вейсса закон 104, 187, 192,
250
Кюри закон 28, 95, 102, 174, 192
— константа 28
— температура 250, 293, 294
Лапласа формула 238
Лежандра преобразование 146
Ле-Шателье — Брауна принцип 156,
157, 172, 182, 190
Ле-Шателье принцип 156, 249
Магнитная восприимчивость адиа-
батическая 46, 100, 114, 174, 191
— — изотермическая 46, 100, 104,
114, 173, 174
Магнитное поле 28, 45, 47, 57, 174,
175
— — критическое в сверхпроводни-
ках 245
Магнитный диполь 57
— момент 45, 46
— поток 30, 58
Магнитострикция 104
Майера соотношение 31, 32, 44, 130
— цикл 44
Максвелла правило 41, 222, 237, 250,
252, 293
— соотношения (теоремы взаимно-
сти) 100, 116, 117, 119, 148, 166,
179, 189, 190, 197, 274, 291
— уравнения 48, 68, 69
Массье функция 143
Материальное взаимодействие 13, 21
Машина тепловая 73
Мейсснера эффект 245
Модуль упругости объемный 42
Мольная (молярная) доля 207, 211
Моляльность 211
Молярность (молярная концентра-
ция) 211
Намагниченность 28, 45, 57, 70
— спонтанная 294
Намагничивания работа 29, 70
Насыщенный пар 208, 209
— — адиабатическое расширение
277
— — давление 208—210, 212, 221,
238, 245, 275, 277
Натяжение 173, 176
Неголономная система 103
Независимые переменные 14, 29,
142, 149
Предметный указатель
301
Непрерывности уравнение 65
Нулевой закон термодинамики 12,
Ожижение газа 138, 180
Окружающая среда 11, 12
Ома закон 69
Осмотический коэффициент 234
Осмотическое давление 228, 285
Отто цикл 97
Парамагнетик, внутренняя энергия
132, 173
— идеальный 28
— свободная энергия 175
— термодинамический потенциал
173, 175
— энтропия 132, 173, 192
Пар перегретый 48
— пересыщенный 245, 277
Парциальное давление 26, 207
Первый закон термодинамики 16, 66
Переменные внешние 14
— внутренние 14, 204
Плавление 219, 262
Планка функция 143
Поверхностное натяжение 201, 223,
238
Полное давление 207
Полупроницаемая мембрана 248
Преобразование переменных 149
Принцип возрастания энтропии 88
— максимальной работы 89
Процесс адиабатический 16, 255
— квазистатический 15
— — изотермический 16
— необратимый 16, 72
— обратимый 15, 72
Пружина 169, 192, 193
Работа 13, 16, 17, 19, 21, 30, 47, 124
— источник 13
— максимальная 89
— минимальная 89, 96, 104, 124
Рабочее вещество 73
Равновесие локальное 12
— метастабильное 152, 253
— механическое 150
— тепловое 12, 88
— — в постоянном магнитном поле
293
— — условия 150—152
— устойчивость 152, 231
— химическое 214, 288
Равновесия константа 216, 219, 242
296, 297
Размагничивание адиабатическое
102, 122, 174
Размагничивающее поле 30, 70
Раствор 209, 210, 212, 238, 259
— двухкомпонентный (бинарный)
209, 238
— идеальный 210, 240, 262
— многокомпонентный 209
— разбавленный 209, 262, 263
— регулярный 210
— сильных электролитов 212, 213,
238
— твердый 208, 257, 263
Растворенное вещество 209, 212, 240, .
259
Растворитель 209, 228, 240, 259
Расширение адиабатическое 101, 110,
121, 174
— коэффициент 104
— свободное 44, 54, 99
Рауля закон 209
Реакция химическая 214, 288
— — внутренняя энергия стандарт-
ная 267
— — равновесие 266
— — свободная энергия 214, 243
— — термодинамический потенци-
ал 218
— — энтальпия 214, 243
— экзотермическая 289
— эндотермическая 289
Сакура — Тетрода формула 269
Сверхпроводящее состояние 245, 278
Свободная энергия (Гельмгольца) 87,
‘143, 158, 170, 171, 175, 177, 187
— — диэлектрика 194, 196
— — поверхностная 224
— энтальпия 158
Сегрегации постоянная 246
Сжимаемость адиабатическая 35, 100,
114, 172
— изотермическая 35, 100, 104, 114,
172
Система замкнутая 12
— изолированная 11
— макроскопическая 11
— многокомпонентная 202
— открытая 12
— термодинамическая И
Скорость звука 43, 46 , 50
Соответственные состояния 36, 37,
45, 56
Состояние термодинамическое 13
302
Предметный указатель
Сосуществование двух фаз 199, 200,
221
Сплав Си — Ni 241
Степени свободы 204
Стефана — Больцмана закон 47
Твердая фаза 226
Температура 21
— абсолютная (Кельвина) 22, 77,
99, 104, 131
— критическая 36, 220, 244
— теорема существования 48, 68
— уменьшение при адиабатическом
расширении 110, 171, 180
— шкала 22, 77, 79, 80
Тепловое излучение 47, 63, 64, 92
Тепловой обмен (условия равновесия)
150
— резервуар 13, 15, 81, 88
Теплоемкость 22, 31, 147, 277
— молярная 22
— неотрицательная 167
— отрицательная 275, 277
— при постоянном давлении 22, 46,
105, 116, 147, 160, 161, 165
— — — магнитном поле 46, 174
— — — объеме 46, 116, 147, 160,
161, 165
— — — химическом потенциале 174
— — — электрическом поле 195
— удельная 22, 31, 147
— — насыщенного пара 245, 274,
275
Теплопроводность 48
Теплота парообразования 219, 225
— — скрытая 254
— перехода 200
— плавления 219, 263
— расширения скрытая 104, 131
Термодинамические неравенства 155
— переменные (переменные состоя-
ния) 14
— потенциалы 142, 143
— функции 146, 147, 157
Термодинамический потенциал Гибб-
са 96, 143, 147, 171, 183, 184
Термодинамическое состояние 13
Термометр газовый 22, 77, 105, 136
Томсона (Кельвина) принцип 74, 90,
97, 103, 125, 127
Томсона Дж, Дж. уравнение 296
Третий закон термодинамики (тео-
рема Нернста — Планка) 149, 170,
173, 186, 192, 219
Тройная точка 205, 226, 237, 252, 253
Удельные молярные величины 148
Уравнение состояния 23, 99
Устойчивость термодинамическая 185
Фаза 199, 200, 204
— внутреннее условие равновесия
204
Фазовая диаграмма 227, 233, 240,
247, 257, 263
Фазовое равновесие 199
Фазовый переход высших порядков
201
— — первого и второго рода 200
Фазы, разделение 222
Фарадея постоянная 218
Ферромагнетик 293
— теплоемкость 250, 294
Фугативность 207, 212, 215, 239
Функции состояния 14, 17
Химическая постоянная 183, 206,,
219, 269
— — условная 269
Химический потенциал 20, 148
— — газа 206
Цикл 15
— необратимый 73
— обратимый 73
Эвтектическая точка 226, 241, 264
Эйлера уравнение 147
Экстенсивная величина 14, 239
Электродвижущая сила 217, 218,
236, 243, 249
Электронейтральности условие 213
Электроны тепловые 243, 269
Электрохимический потенциал 218
Элемент электрохимический 216, 243
Энергия 14, 16, 17, 157
— переноса массы 16, 17, 202
— удельная молярная 148
Энтальпия 19, 41, 67, 143, 157, 171
— удельная молярная 148
Энтропия 82, 83, 143, 157, 171
— аддитивность 83
— зависимость от температуры 121
— плавления 264
— поверхности 255
— смешения 95, 207
— удельная молярная 148
Якобиан 149
Оглавление
Предисловие редакторов перевода............................... 5
Предисловие к английскому изданию............................. &
Предисловие к японскому изданию............................... 7
Глава 1. Термодинамическое состояние и первый закон термодина-
мики ............................................ 11
Основные положения...................................... 11
§ 1. Предмет термодинамики......................... 11
§ 2. Понятие теплового равновесия (нулевой закон термо-
динамики) .......................................... 12
§ 3. Термодинамический контакт..................... 13
§ 4. Термодинамические величины.................... 14
§ 5. Процесс изменения состояния................... 15
§ 6. Первый закон термодинамики.................... 16
§ 7. Теплота и энтальпия........................... 19
§ 8. Применение первого закона термодинамики к инфи-
нитезимальным процессам............................. 20
§ 9. Температура................................... 21
§ 10. Теплоемкость. Удельная теплоемкость........... 22
§ 11. Уравнение состояния........................... 23
j 12. Замена независимых переменных................. 29
Приме ры............................................ 29
Задач и ............................................. 42
Решен ия ........................................... 48
Литература..................................... 71
Глава 2. Второй закон термодинамики........................ 72
Основные положения...................................... 72
§ 1. Обратимые и необратимые процессы............. 72
§ 2. Лемма (цикл Карно)........................... 73
§ 3. Второй закон термодинамики................... 74
§ 4. Коэффициент полезного действия общего цикла Карно 75
§ 5. Абсолютная температура....................... 77
§ 6. Неравенство Клаузиуса для произвольного цикла 81
§ 7. Энтропия..................................... 82
§ 8. Аддитивность энтропии........................ 83
§ 9. Общая формулировка второго закона термодинамики 86
§ 10. Направление реальных процессов............... 87
§ И. Максимальная н минимальная работа............ 89
Примеры................................................. 90
304
Оглавление
Задачи.................................................... 97
Решения.................................................... 106
Литература ........................................ 141
Глава 3. Термодинамические функции и условия равновесия . . . 142
Основные положения......................................... 142
§ 1. Термодинамические функции......................... 142
§ 2, Преобразование Лежандра........................... 146
§ 3. Уравнение Гиббса — Дюгема......................... 146
| 4. Определение термодинамических величин и термодина-
мические соотношения.............................. 147
§ 5. Третий закон термодинамики (теорема Нернста —
Планка) .......................................... 149
§ 6. Равновесие двух систем.......................... 150
§ 7. Условия равновесия для заданного термостата..... 151
§ 8. Термодинамические неравенства................... 153
§ 9. Принцип Ле-Шателье — Брауна..................... 156
Примеры.................................................. 158
Задачи .................................................. 170
Решения ................................................. 176
Литература ...................................... 198
Глава 4. Равновесие фаз и химическое равновесие............. 199
Основные положения....................................... 199
§ 1. Фаза......................................... 199
§ 2. Равновесие между различными фазами чистого веще-
ства ................................................ 199
§ 3. Поверхностное натяжение...................... 201
§ 4. Равновесие в многокомпонентной многофазной системе 202
§ 5. Правило фаз Гиббса........................... 204
§ 6. Химический потенциал газа.................... 206
| 7. Химический потенциал и давление насыщенных паров
жидкостей и твердых тел.......................... 208
§ 8. Разбавленные растворы........................ 209
§ 9. Идеальные растворы (идеальные твердые растворы) и
регулярные растворы......................... 210
§ 10. Выражения для концентрации растворов...... 211
§ 11. Активность и коэффициент активности....... 211
§ 12* . Растворы сильных электролитов........... 212
§ 13. Химическое равновесие..................... 214
§ 14. Термодинамика электрохимического элемента .... 216
I 15. Применение третьего закона термодинамики .... 219
Примеры.................................................. 220
Задачи .................................................. 237
Решения.................................................. 251
Литература............................................... 297
Предметный указатель........................................ 299