Рынок ценных бумаг. Количественные методы анализа - Малюгин В.И.

Глава 1. Общая характеристика рынка ценных бумаг
1.2.2.Понятие ценной бумаги и фондового рынка
1.3. Структура и принципы функционирования рынка ценных бумаг
1.3.2. Принципы функционирования биржевого и внебиржевого рынков
1.4. Виды ценных бумаг и цели их выпуска
1.5.2. Профессиональные участники рынка ценных бумаг
Глава 2. Методы анализа ценных бумаг без учета фактора неопределенности
2.1.2. Формулы простых и сложных процентов
2.1.5. Дискретное и непрерывное дисконтирование
2.2. Анализ краткосрочных финансовых активов
2.3. Анализ государственных краткосрочных ценных бумаг
2.4. Анализ ценных бумаг с помощью метода дисконтирования платежей
2.4.2. Анализ ценных бумаг на основе чистой текущей стоимости и внутренней доходности
2.5.4. Анализ облигаций при наличии временной структуры процентных ставок
2.5.5. Форвардные ставки и цены облигаций
2.6.2. Анализ стоимости и доходности акций
Глава 3. Модели и методы анализа ценных бумаг в условиях неопределенности
3.1.2. Многопериодная доходность ценных бумаг
3.2. Вероятностное описание финансовых активов в условиях неопределенности
3.2.2. Функциональные и числовые характеристики
3.2.3. Распределение вероятностей доходностей
3.3. Классификация эконометрических моделей финансовых переменных
$3.4.2. Модель \$
3.5. Регрессионные модели доходностей ценных бумаг
3.5.2. Оценки параметров регрессионных моделей и их свойства
3.5.3. Анализ адекватности регрессионных моделей
3.5.4. Проблемы, связанные с нарушением традиционных предположений регрессионного анализа
3.6.2. Стационарный временной ряд и его характеристики
3.7. Общая характеристика задач финансового анализа
Глава 4. Теория эффективного финансового рынка
4.1.2. Модели случайного блуждания для доходностей активов
4.1.3. Статистическая проверка гипотезы о случайном блуждании
4.2. Информация и основанные на ней ожидания участников рынка
4.2.2. Свойства прогнозов в виде условного математического ожидания
4.3. Информационная эффективность финансового рынка
4.3.2. Эффективность рынка и модель случайного блуждания
4.3.3. Проверка гипотезы эффективности рынка
4.4. Анализ ценных бумаг в предположении рациональных ожиданий
$4.4.3. Проблема \$
Глава 5. Методы оптимального портфельного инвестирования
5.1.2. Портфель ценных бумаг и его характеристики
5.1.3. Эффекты портфельного инвестирования
5.2. Оптимизация структуры портфеля рисковых ценных бумаг
5.2.2. Решение задачи оптимизации структуры портфеля
5.3. Формирование портфелей активов при возможности безрискового кредитования и заимствования
5.3.2. Характеристики и свойства комбинированного портфеля
5.3.3. Оптимизация структуры портфеля при возможности безрискового кредитования и заимствования
5.3.4. Свойства оптимальных комбинированных портфелей
5.4. Проблема оценивания характеристик ценных бумаг
5.4.2. Вычисление характеристик ценных бумаг на основе однофакторной модели
5.4.3. Бета-коэффициенты рисковых ценных бумаг
5.4.4. Анализ риска портфеля ценных бумаг
Глава 6. Анализ рынка ценных бумаг на основе моделей равновесия
6.2.2. Модель САРМ по версии Блэка при отсутствии безрискового актива
6.2.3. Учет различия безрисковых ставок кредитования и заимствования
6.4. Статистическая проверка адекватности моделей
6.4.2. Двухэтапная процедура тестирования адекватности САРМ
6.4.3. Построение и тестирование модели APT
Глава 7. Эконометрическое моделирование финансовых временных рядов
7.1.3. Модель авторегрессии и скользящего среднего
7.1.4. Построение модели авторегрессии и скользящего среднего
7.2. Модели нестационарных временных рядов
7.2.2. Модели интегрированных временных рядов
$7.2.3. Использование тестов единичного корня для проверки \$
7.3. Модели финансовых временных рядов с условной гетероскедастичностью
7.3.2. Модификации модели ARCH: модели GARCH и EGARCH
7.3.3. Построение моделей с условной гетероскедастичностью
$3.4.2. Модель \$
$4.4.3. Проблема \$
$7.2.3. Использование тестов единичного корня для проверки \$
Автор: Малюгин В.И.
Теги: денежное обращение банковское дело биржи экономика экономические науки математика математический анализ финансы
ISBN: 5-7749-0303-6
Год: 2003
Похожие
Количественные методы в финансах
Основы стохастической финансовой математики. Том 1. Факты. Модели
Эконометрика. Начальный курс
(Не)послушные рынки. Фрактальная революция в финансах
Текст
                    В.И. Малюгин
/ I
РЫНОК
ЦЕННЫХ
БУМАГ
Количественные
методы анализа
Рекомендовано в качестве учебного пособия
Учебно-методическим объединением вузов по специальности
"Математические методы в экономике"
С И В Л И О Т Е К А
Академия народного хозяйства
при Правительстве Российской Федерации
Москва
Издательство "ДЕЛО"
2003

УДК 336.761(075.8)
ББК 65.262.2я73
М18
Рецензенты:
кафедра прикладной математики и экономической кибер-
нетики Белорусского государственного экономического уни-
верситета (зав. кафедрой доктор экономических наук, профес-
сор Н.И. Холод);
кандидат физико-математических наук Л.Л. Пересецкый,
кандидат экономических наук C.J1.Кисель.
Малюгин В. И,
Ml8 Рынок ценных бумаг: Количественные методы ана-
лиза: Учеб. пособие. -М.: Дело, 2003. - 320 с.
ISBN 5-7749-0303-6
В учебном пособии последовательно и математически строго изла-
гаются количественные методы анализа рынка ценных бумаг в усло-
виях неопределенности. Описываются вероятностные модели курсов и
доходностей ценных бумаг, методы оптимизации структуры портфе-
лей ценных бумаг на основе подхода "доходность-риск" и моделей
равновесия фондового рынка САРМ и APT, методы статистической
проверки гипотез случайного блуждания, эффективности рынка и
адекватности моделей равновесия. Предназначено для студентов, ма-
гистрантов и аспирантов экономико-математических специальностей,
а также специалистов и профессиональных участников рынка ценных
бумаг, использующих количественные методы финансового анализа.
УДК 336.761(075.8)
ББК 65.262.2я73
ISBN 5-7749-0303-6 © Издательство "Дело", 2003

Оглавление
Основные обозначения и сокращения 8
Введение 10
Глава 1. ОБЩАЯ ХАРАКТЕРИСТИКА РЫНКА
ЦЕННЫХ БУМАГ 19
1.1. Источники, поставщики и потребители
инвестиционного капитала 19
1.2. Финансовый рынок и его части 22
1.2.1. Рынок банковских кредитов 23
1.2.2. Понятие ценной бумаги и фондового рынка 25
1.2.3. Валютные рынки 29
1.3. Структура и принципы функционирования рынка
ценных бумаг 31
1.3.1. Первичное размещение ценных бумаг 32
1.3.2. Принципы функционирования биржевого и
внебиржевого рынков 34
1.4. Виды ценных бумаг и цели их выпуска 38
1.4.1. Классификация ценных бумаг 38
1.4.2. Акции и облигации 42
1.4.3. Производные ценные бумаги 48
1.5. Участники рынка ценных бумаг 54
1.5.1. Инвесторы и эмитенты 54
1.5.2. Профессиональные участники рынка ценных
бумаг 55
Глава 2. МЕТОДЫ АНАЛИЗА ЦЕННЫХ БУМАГ БЕЗ
УЧЕТА ФАКТОРА НЕОПРЕДЕЛЕННОСТИ 64
2.1. Начисление процентов и дисконтирование 67
2.1.1. Принципы расчета процентов. Виды
процентных ставок 67
2.1.2. Формулы простых и сложных процентов 69
2.1.3. Номинальная и эффективная ставки 70
2.1.4. Непрерывно начисляемые проценты 72
2.1.5. Дискретное и непрерывное дисконтирование 73
2.2. Анализ краткосрочных финансовых активов 74
2.2.1. Анализ процентных активов 75
2.2.2. Анализ дисконтных активов 76
2.3. Анализ государственных краткосрочных ценных бумаг 77
3

2.3.1. Анализ ГКО при первичном размещении 77
2.3.2. Анализ ГКО на вторичном рынке 79
2.4. Анализ ценных бумаг с помощью метода
дисконтирования платежей 81
2.4.1. Общая характеристика метода
дисконтирования платежей 82
2.4.2. Анализ ценных бумаг на основе чистой
текущей стоимости и внутренней доходности 84
2.5. Анализ облигаций 87
2.5.1. Анализ купонных облигаций 88
2.5.2. Анализ бессрочных облигаций 90
2.5.3. Анализ бескупонных облигаций 91
2.5.4. Анализ облигаций при наличии временной
структуры процентных ставок 92
2.5.5. Форвардные ставки и цены облигаций 96
2.6. Анализ акций 101
2.6.1. Модели изменения дивидендов 102
2.6.2. Анализ стоимости и доходности акций 104
Глава 3. МОДЕЛИ И МЕТОДЫ АНАЛИЗА ЦЕННЫХ
БУМАГ В УСЛОВИЯХ НЕОПРЕДЕЛЕННОСТИ 107
3.1. Взаимосвязь цен, промежуточных платежей и
доходностей ценных бумаг 110
3.1.1. Доходность ценных бумаг за один период ПО
3.1.2. Многопериодная доходность ценных бумаг ИЗ
3.2. Вероятностное описание финансовых активов в
условиях неопределенности 116
3.2.1. Определение вероятностного пространства в
контексте задач финансового анализа 116
3.2.2. Функциональные и числовые характеристики
финансовых активов 118
3.2.3. Распределение вероятностей доходностей
активов 125
3.3. Классификация эконометрических моделей
финансовых переменных 128
3.4. Модели пространственных данных 131
3.4.1. Совместное распределение вероятностей 132
3.4.2. Модель "случайная выборка" и ее свойства 132
3.5. Регрессионные модели доходностей ценных бумаг 135
3.5.1. Определение моделей и модельные
предположения 135
3.5.2. Оценки параметров регрессионных моделей
и их свойства 139
4

3.5.3. Анализ адекватности регрессионных моделей 142
3.5.4. Проблемы, связанные с нарушением
традиционных предположений
регрессионного анализа 148
3.6. Модели финансовых временных рядов 149
3.6.1. Определение и основные свойства
временных рядов 150
3.6.2. Стационарный временной ряд и его
характеристики 152
3.6.3. Автокорреляционная функция 154
3.7. Общая характеристика задач финансового анализа 155
Глава 4. ТЕОРИЯ ЭФФЕКТИВНОГО
ФИНАНСОВОГО РЫНКА 160
4.1. Проблема предсказуемости цен и доходностей
финансовых активов 163
4.1.1. Модели случайного блуждания для цен
активов 164
4.1.2. Модели случайного блуждания для
доходностей активов 167
4.1.3. Статистическая проверка гипотезы о
случайном блуждании 170
4.2. Информация и основанные на ней ожидания
участников рынка 174
4.2.1. Прогноз в виде условного математического
ожидания 174
4.2.2. Свойства прогнозов в виде условного
математического ожидания 176
4.3. Информационная эффективность финансового рынка 178
4.3.1. Гипотезы и свойства эффективного рынка 179
4.3.2. Эффективность рынка и модель случайного
блуждания 182
4.3.3. Проверка гипотезы эффективности рынка 183
4.4. Анализ ценных бумаг в предположении рациональных
ожиданий 190
4.4.1. Случай постоянной ожидаемой доходности 190
4.4.2. Мартингальная модель цен акций 197
4.4.3. Проблема "спекулятивных пузырей" 199
Глава 5. МЕТОДЫ ОПТИМАЛЬНОГО
ПОРТФЕЛЬНОГО ИНВЕСТИРОВАНИЯ 203
5.1. Проблема выбора портфеля ценных бумаг на основе
подхода "доходность - риск" 205
5.1.1. Использование кривых безразличия 205
5

5.1.2. Портфель ценных бумаг и его
характеристики 209
5.1.3. Эффекты портфельного инвестирования 211
5.2. Оптимизация структуры портфеля рисковых ценных
бумаг 215
5.2.1. Модельные предположения и постановка
задачи 215
5.2.2. Решение задачи оптимизации структуры
портфеля 218
5.2.3. Свойства эффективных портфелей 219
5.3. Формирование портфелей активов при возможности
безрискового кредитования и заимствования 223
5.3.1. Понятие безрискового актива 223
5.3.2. Характеристики и свойства
комбинированного портфеля 225
5.3.3. Оптимизация структуры портфеля при
возможности безрискового кредитования и
заимствования 228
5.3.4. Свойства оптимальных комбинированных
портфелей , 230
5.4. Проблема оценивания характеристик ценных бумаг 232
5.4.1. Построение однофакторной рыночной
модели 234
5.4.2. Вычисление характеристик ценных бумаг на
основе однофакторной модели 236
5.4.3. Бета-коэффициенты рисковых ценных бумаг 237
5.4.4. Анализ риска портфеля ценных бумаг 239
Глава 6. АНАЛИЗ РЫНКА ЦЕННЫХ БУМАГ НА
ОСНОВЕ МОДЕЛЕЙ РАВНОВЕСИЯ 242
6.1. Модель оценки финансовых активов САРМ 244
6.1.1. Модельные предположения и свойства
САРМ 244
6.1.2. САРМ для отдельных ценных бумаг 248
6.2. Модификации САРМ 253
6.2.1. Предположение о невозможности операции
"короткая продажа" 253
6.2.2. Модель САРМ по версии Блэка при
отсутствии безрискового актива 254
6.2.3. Учет различия безрисковых ставок
кредитования и заимствования 257
6.3. Теория арбитражного оценивания 260
6.3.1. Модельные предположения и исходные
предпосылки для построения модели APT 260
6.3.2. Арбитражный портфель 263
6

6.3.3. Модель APT и ее интерпретация 265
6.3.4. Связь между моделями APT и САРМ 267
6.4. Статистическая проверка адекватности моделей 269
6.4.1. Тестирование САРМ на основе модели
многомерной линейной регрессии 269
6.4.2. Двухэтапная процедура тестирования
адекватности САРМ 276
6.4.3. Построение и тестирование модели APT 279
Глава 7. ЭКОНОМЕТРИЧЕСКОЕ МОДЕЛИРОВАНИЕ
ФИНАНСОВЫХ ВРЕМЕННЫХ РЯДОВ 281
7.1. Модели стационарных временных рядов 283
7.1.1. Модель авторегрессии 284
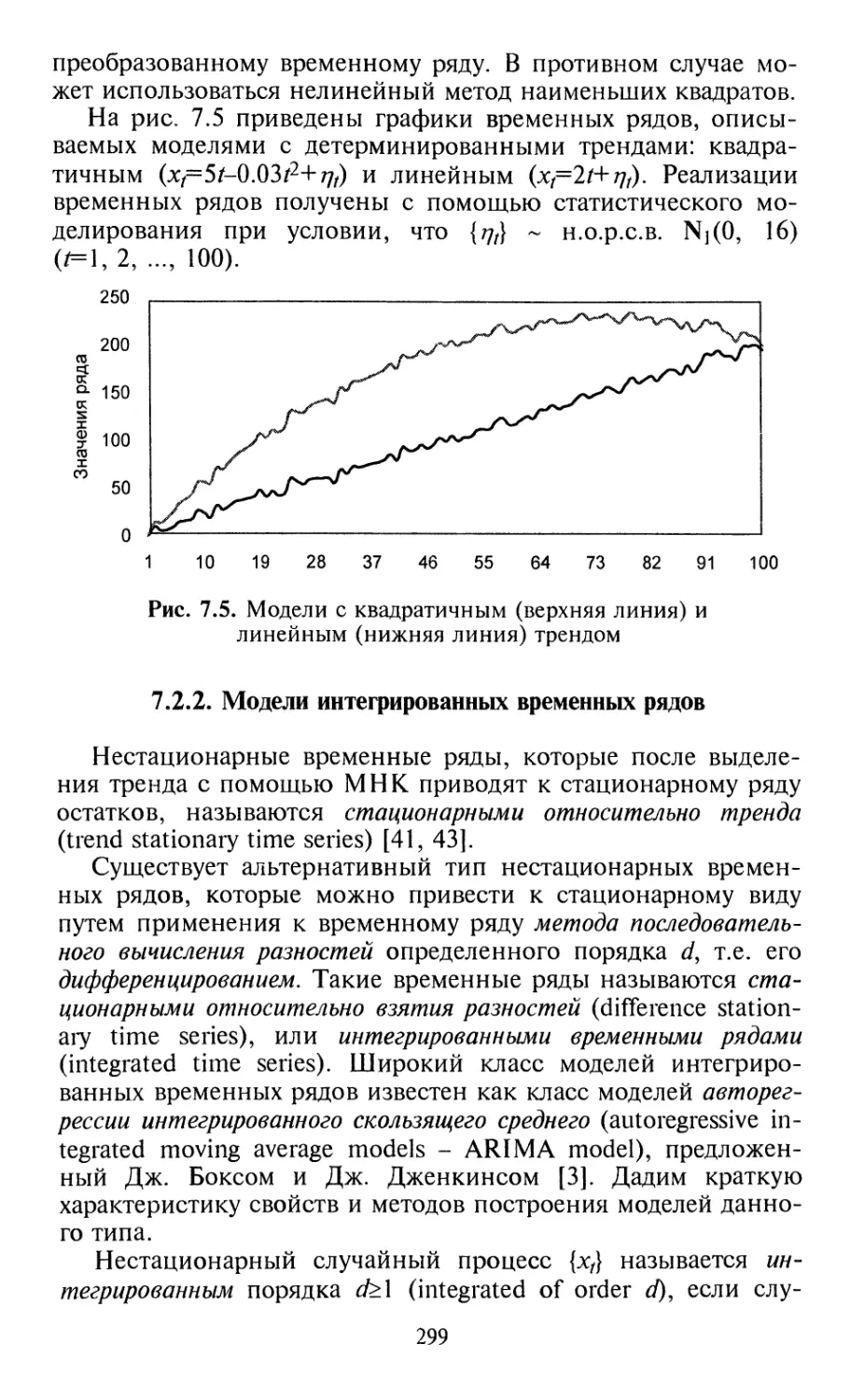
7.1.2. Модель скользящего среднего 289
7.1.3. Модель авторегрессии и скользящего
среднего 292
7.1.4. Построение модели авторегрессии и
скользящего среднего 294
7.2. Модели нестационарных временных рядов 296
7.2.1. Модели временных рядов с
детерминированным трендом 297
7.2.2. Модели интегрированных временных рядов 299
7.2.3. Использование тестов единичного корня для
проверки "гипотезы случайного блуждания" 306
7.3. Модели финансовых временных рядов с условной
гетероскедастичностью 309
7.3.1. Модель ARCH и ее применение для
описания финансовых временных рядов 310
7.3.2. Модификации модели ARCH: модели
GARCH и EGARCH 313
7.3.3. Построение моделей с условной
гетероскедастичностью 315
Литература 317

Основные обозначения и сокращения
№ — УУ-мерное евклидово пространство (/V>1);
Q = {со} — пространство состояний рынка;
3 — вся доступная информация о рынке;
Р=Р() — вероятностная мера (вероятность);
F={3/} (/>0) — поток информации, 3, -информация,
доступная к моменту времени t
включительно;
Е(А) — математическое ожидание случайной
величины X;
D(A) — дисперсия случайной величины Х\
Cov(Jf, Y) — ковариация случайных величин Хи Y;
ЩХ) — математическое ожидание случайного
вектора Х\
Соу(Д Y) — ковариационная матрица случайных
векторов 1иУ;
Е,(Л)=Е(Л1 3/) — условное математическое ожидание
случайной величины ЛГпри условии, что в
момент времени / имеется информация
— натуральный логарифм числа
е^ — экспонента числа z<^R\
|| — абсолютная величина числа, норма вектора,
определитель матрицы, мощность мно-
жества;
= — равенство по определению;
Pt — курс актива в момент времени /, PfAog(Pt);
Rt — простая ставка доходности за один период;
r^log(l + R() — ставка непрерывно начисляемых процентов;
RtK ~ ставка доходности актива за А>1 периодов
при использовании формулы сложных
процентов;
rtK — ставка непрерывных процентов за К>\
периодов;
h(X) — закон распределения случайной величины Х\
Nj(//,cr2) — одномерный нормальный закон
распределения с математическим ожиданием
/j и дисперсией а2;
NN(//,£) — /V-мерный нормальный закон распределения
с вектором математического ожидания ^ie^\N
и ковариационной матрицей I размерности

{ак}(к=\, 2, ..., А) - множество величин (значений) аи а2, ...,
тах{ак}
{£/}~н.о.р.с.в.
L
Л
<Pq = D(xf)
срк
— максимальное (min{aj -минимальное)
значение из множества значений {ак}'9
— независимые и одинаково распределенные
случайные величины;
— оператор сдвига "назад": Lxf=xt_b
Ldxt=xt_d, d>\\
— оператор вычисления разностей первого
порядка: Axt=xrxh\.
— дисперсия стационарного временного ряда
— автоковариационная функция
стационарного временного ряда хь
где к>\ -величина лага;
Рк = Фк /<Ро ~~ автокорреляционная функция (АКФ)
стационарного временного ряда xt (k>\)\
/ и I — единичный вектор и единичная матрица;
ОиО — нулевой вектор и нулевая матрица;
diag(y//) — диагональная матрица с элементами {щ} на
главной диагонали;
//т и Ет — транспонированный вектор ju и
транспонированная матрица Z;
Z"1 — матрица, обратная к невырожденной
(| ZI *0) квадратной матрице S;
о — статистическая оценка Д
САРМ — модель оценивания финансовых активов
(Capital Asset Pricing Model):
APT — арбитражная теория оценивания (Arbitrage
Pricing Theory);
ARMA — модель авторегрессии -скользящего сред-
него (autoregressive moving average model);
ARIMA — модель авторегрессии интегрированного
скользящего среднего (autoregressive
integrated moving average model);
ARCH — модель авторегрессионной условной
гетероскедастичности (autoregressive.
conditional heteroskedastic model).
Матрицы и множества обозначаются жирными пропис-
ными буквами, векторы - жирным курсивом, скалярные вели-
чины - нежирными прописными или малыми буквами, пара-
метры моделей - греческими буквами а, Д у, S, а случайные
компоненты моделей -буквами £ £ ?].

Введение
Важнейшими характеристиками финансовых активов, дос-
тупными для анализа всем участникам рынка, являются их
рыночные цены. Для различных типов финансовых активов
цены могут выражаться различным образом, например в виде
цен покупки и продажи акций и облигаций, обменных курсов
валют, процентных ставок по привлекаемым и размещаемым
депозитам. Совокупность значений этих характеристик для
всех активов в каждый момент времени определяет конъюнк-
туру финансового рынка и является объектом анализа со сто-
роны его участников.
Курсы ценных бумаг на конкурентном фондовом рынке
складываются на основе спроса и предложения ценных бумаг,
формируемых в соответствии с представлениями участников
рынка относительно их "истинной" стоимости. Истинная (true
value), или собственная, стоимость (intrinsic value) ценной бу-
маги К, как правило, неизвестна и является объектом оценки
со стороны участников рынка. Для этой цели используются
методы финансового анализа рынка ценных бумаг.
•Первоочередная задача финансового анализа при покупке
или продаже ценных бумаг состоит в том, чтобы выявить не-
верно оцененные рынком активы, т.е. активы, для которых их
рыночная цена Р не совпадает с предполагаемой истинной
стоимостью, т.е. PtV. Далее используется золотое правило
инвестирования: "покупай дешево и продавай дорого", т.е. по-
купаются "недооцененные" (при P<V) и продаются "переоце-
ненные" (при P>V) рынком ценные бумаги.
Участники рынка при этом рассчитывают на корректиров-
ку рынком цен активов в благоприятном для них направле-
нии, предполагая, что растущий спрос на недооцененные бу-
маги приведет к росту их курса, а увеличение предложения
переоцененных бумаг будет способствовать снижению их ры-
ночной цены. Такое ожидаемое в соответствии с экономиче-
ской теорией движение цен позволяет инвесторам надеяться
на получение дохода за счет обратных операций с ценными
бумагами, например в результате продажи по более высокой
цене ранее купленных "дешево" ценных бумаг.
В условиях "эффективного рынка" подобная деятельность
его участников приводит к достижению равновесия между
спросом и предложением ценных бумаг, а следовательно, к
установлению "равновесных" курсов ценных бумаг на уровне
их "истинной" стоимости.
10

Показателем эффективности подобных операций служит
относительное изменение капитала инвестора за период инве-
стирования денежных средств в ценные бумаги. Эта характе-
ристика называется ставкой доходности (rate of return) финан-
совых инвестиций или просто доходностью и определяется
выражением:
где Wq, W\ - соответственно капитал (wealth) инвестора в на-
чале и конце периода инвестирования.
При операциях с ценными бумагами, однако, приходится
не только ориентироваться на их доходность, но и учитывать
риск того, что фактическая доходность, как правило, отлича-
ется от ожидаемой доходности. Это обусловлено неопределен-
ностью относительно будущих цен активов и дохода по ним.
Различные категории инвесторов могут преследовать раз-
личные цели. Например, инвестор-спекулянт (трейдер) стре-
мится получить прибыль за счет разницы цен покупки и про-
дажи активов. Покупая некоторый актив сегодня, он надеется
на повышение цены актива в будущем. Поэтому для него
важно купить "недооцененный" рынком актив. Трейдер, со-
вершающий операцию "короткая продажа" (short sale), наде-
ется, что продает "переоцененные" рынком активы, и, следо-
вательно, в будущем, когда необоснованный спрос на них
упадет, сможет выкупить их на рынке по более низкой цене.
Портфельные менеджеры (portfolio managers), занятые управ-
лением портфелями активов, стремятся за счет оптимальной
диверсификации (разнообразия) вложений получить прием-
лемый доход с минимальным риском. Наряду с доходностью
и риском активов они учитывают взаимную зависимость, т.е.
корреляцию доходностей активов. Их также волнует проблема
страхования {хеджирования) риска обесценивания принадле-
жащих им активов за счет подходящего выбора стратегии
хеджирования портфеля или отдельных активов, например, с
помощью опционных или фьючерсных контрактов.
Во всех случаях применяются методы финансового анализа
рынка ценных бумаг. Большую прибыль получает тот, кто бы-
стрее распознает "неверно оцененные" активы, использует
более точные прогнозы цен, ожидаемой доходности и риска
финансовых активов, применяет наиболее эффективные стра-
тегии инвестирования и хеджирования.
11

Существует три основных вида финансового анализа фон-
дового рынка: технический, фундаментальный и количествен-
ный. Исторически первыми были технический и фундамен-
тальный анализ.
Технический анализ (Technical analysis) основан на выявле-
нии и изучении исторически сложившихся закономерностей
функционирования фондового рынка на основе анализа ста-
тистики рынка в виде курсов и объемов продаж активов. Ос-
нованием для использования лишь этой информации являет-
ся предположение о том, что вся доступная и относящаяся к
делу информация, включая так называемые фундаментальные
факторы, отражается в ценах активов.
В рамках технического анализа также предполагается, что
определенные закономерности функционирования рынка
имеют устойчивый характер, т.е. с достаточно большой веро-
ятностью повторяются, и их можно обнаружить с помощью
специальных графиков, индикаторов, осцилляторов и других
"технических" методов. Возникновение тех или иных зако-
номерностей служит "техническим" аналитикам сигналом для
покупки или продажи активов. Недостатком данного подхода
является отсутствие строгого и систематизированного обосно-
вания большинства составляющих его эмпирических методов.
Техническому анализу финансового рынка посвящено значи-
тельное число изданий, в том числе на русском языке, на-
пример [17, 18].
Фундаментальный анализ (Fundamental analysis) является
альтернативным подходом к анализу фондового рынка. Он
предполагает анализ макроэкономических и микроэкономи-
ческих "фундаментальных" факторов, влияющих на будущие
доходы компаний и курсы их активов.
Основной целью традиционного фундаментального анали-
за является [33] оценка состояния эмитента ценных бумаг,
т.е. его доходов, положения на рынке и т.д., на основе ин-
формации, содержащейся в балансовых отчетах, отчетах о
прибылях и убытках, других материалах, публикуемых эми-
тентом. Учитываются также макроэкономические факторы,
характеризующие состояние и перспективы соответствующей
отрасли экономики региона и экономики страны в целом,
например, такие макроэкономические показатели, как индекс
потребительских цен, процентные ставки, уровень безработи-
цы, динамика денежной массы и валового внутреннего про-
дукта (ВВП). Для анализа и прогнозирования макроэкономи-
ческих процессов используются эконометрические модели и
методы анализа [1, 10, 12, 33, 41, 43], а также соответствую-
щее программное обеспечение [13, 40, 44, 48].
12

Результатом анализа является прогноз ожидаемого дохода
и его распределения между кредиторами и собственниками
компании-эмитента (акционерами), на основе которого в со-
ответствии с методами оценивания активов (evaluation meth-
ods) рассчитывается текущая стоимость (present value) цен-
ных бумаг данного эмитента и даются рекомендации о целе-
сообразности их покупки или продажи в текущий момент
времени. Для определения текущей стоимости ценных бумаг
при заданном ожидаемом по ним потоке платежей традици-
онно используется метод дисконтирования платежей.
В настоящее время в практической деятельности на фи-
нансовом рынке участники рынка (трейдеры) применяют ме-
тоды технического анализа и активно используют при приня-
тии решений анализ фундаментальных экономических, а так-
же политических и форсмажорных факторов. Этому способ-
ствуют принципы организации современных информацион-
ных и торговых компьютерных систем типа Reuters, Dow
Jones Telerate и др., предоставляющих пользователю все воз-
можности технического анализа и обеспечивающих его необ-
ходимой "фундаментальной" информацией в виде экономи-
ческих, финансовых, политических и других новостей.
Количественный анализ (Quantitative analysis) финансового
(фондового) рынка основывается на построении по эмпири-
ческим данным статистических моделей финансовых времен-
ных рядов и использовании этих моделей для прогнозирова-
ния курсов и доходностей активов, оценивания риска финан-
совых инвестиций, оптимального управления портфелями ак-
тивов, хеджирования риска операций с финансовыми актива-
ми и др.
Применительно к экономическим и финансовым процес-
сам статистические модели и методы принято называть эконо-
метржескими. Количественный подход к анализу финансово-
го рынка на основе эконометрических моделей и методов
можно рассматривать как развитие традиционной финансо-
вой экономики и фундаментального анализа применительно
к исследованию финансовых процессов в условиях неопреде-
ленности.
Финансовые аналитики, применяющие количественные
методы анализа, как и "технические аналитики", активно ис-
пользуют статистику рынка, пытаясь построить прогнозы цен
и доходностей финансовых активов. Однако "количественные
аналитики" в отличие от "техников" используют статистиче-
ские модели и методы, имеющие строгое математическое
обоснование. Одним из предубеждений против технического
анализа со стороны академических аналитиков, использую-
13

щих количественные методы анализа, является своеобразная
ненаучная терминология, применяемая его сторонниками.
Однако, как отмечается в [37], в кругу академических финан-
совых аналитиков в последнее время растет интерес к техни-
ческому анализу, поэтому в ближайшее время это направле-
ние может стать областью более активных научных исследо-
ваний.
Ключевым в рамках количественного анализа является по-
нятие эффективного финансового рынка (Efficient Market Hy-
pothesis). При этом имеется в виду информационная эффектив-
ность относительно доступной и относящейся к делу инфор-
мации (available and relevant information).
В условиях эффективного рынка цены активов мгновенно,
полностью и корректно ассимилируют всю доступную и от-
носящуюся к делу информацию, достигая состояния равнове-
сия. При этом наилучшим прогнозом цены актива "на завтра"
по информации, доступной сегодня, оказывается значение
цены "на сегодня", а изменения цен носят характер "случай-
ного блуждания". Покупка-продажа ценных бумаг на таком
рынке напоминает "честную игру" (fair game) с равными воз-
можностями для всех участников, располагающих одной и
той же информацией, что исключает возможность регулярно-
го получения "сверхнормальной" доходности (abnormal re-
turn), т.е. доходности больше той, что соответствует равно-
весным ценам активов.
При нарушении гипотезы эффективности рынка перед
участниками рынка открываются возможности для построе-
ния нетривиальных прогнозов цен и доходностей активов на
основе эконометрических моделей финансовых временных рядов.
В то же время в условиях эффективного рынка разумной яв-
ляется стратегия "купил и владей" ("buy and hold"), в связи с
чем основной задачей финансового анализа становится задача
оптимального портфельного инвестирования. В рамках подхода
"доходность -риск" (mean -variance) данная задача сводится
к формированию портфеля активов, обеспечивающего полу-
чение приемлемой ожидаемой доходности с минимальным
риском.
При решении задач оптимального портфельного инвести-
рования возникает необходимость в статистическом оценива-
нии (прогнозировании) характеристик финансовых активов:
ожидаемых доходностей, рисков, ковариаций доходностей ак-
тивов и т.д. по статистическим данным. Один из традицион-
ных подходов к решению данной проблемы основан на при-
менении эконометрических моделей доходностей активов. В
качестве таких моделей могут использоваться как "рыночные
14

модели", не имеющие строгого экономического обоснования,
так и экономические модели равновесия фондового рынка, на-
пример модель САРМ (Capital Asset Pricing Model) и модель
APT (Arbitrage Pricing Theory model), разработанные на основе
подхода "доходность - риск". Указанные модели для равно-
весного состояния рынка устанавливают связи между доход-
ностью и риском активов, доходностью активов (или портфе-
ля активов) и доходностью рыночного портфеля (модель
САРМ), доходностью активов и экзогенными (внешними)
факторами (модель APT).
Таким образом, с принятием или отклонением "гипотезы
эффективности рынка" связан выбор участниками рынка той
или иной стратегии поведения. В связи с этим актуальной яв-
ляется задача тестирования эффективности рынка. Решение
данной задачи основано на применении методов статистиче-
ской проверки гипотез, лежащих в основе понятия "эффектив-
ный рынок" по реальным статистическим данным. Проверка
гипотезы эффективности рынка предполагает наличие адек-
ватной модели, на основании которой определяется ожидае-
мая доходность активов в состоянии равновесия рынка. Для
этой цели могут использоваться модели САРМ и APT и их
модификации. Использование данных моделей при проверке
гипотезы эффективности фондового рынка приводит к необ-
ходимости совместного тестирования как гипотезы эффектив-
ности рынка, так и адекватности моделей равновесия рынка.
Описанная выше схема поведения инвесторов заведомо
упрощает реальную ситуацию. Однако она позволяет показать
взаимосвязи между различными задачами и методами количе-
ственного анализа фондового рынка, которые составляют ос-
новное содержание предлагаемого учебного пособия.
Пособие состоит из семи глав. В гл. 1 содержится общая
характеристика принципов организации и функционирования
рынка ценных бумаг, его участников и основных видов цен-
ных бумаг. Данная глава является вводной и служит для
обеспечения систематизированного и замкнутого изложения
основного материала.
Глава 2 представляет собой краткое описание традиционных
детерминированных методов финансовой математики, исполь-
зуемых для оценки стоимости и доходности активов в предпо-
ложении полной определенности. Основное внимание уделяет-
ся анализу краткосрочных ценных бумаг, а также акций и об-
лигаций на основе метода дисконтирования платежей.
Целью гл. 3 является ознакомление с количественными
методами анализа финансовых активов в условиях неопреде-
ленности. В главе содержатся определения основных понятий
15

теории вероятностей, используемых в рамках вероятностного
подхода для описания финансовых переменных; дается харак-
теристика основных классов эконометрических моделей финан-
совых переменных ("случайная выборка", "регрессионные мо-
дели", "временные ряды"), а также методов их построения.
Приводится обзор методов решения традиционных задач ана-
лиза фондового рынка на основе эконометрических моделей.
В гл. 4 описываются вероятностные модели курсов и до-
ходностей финансовых активов, основанные на гипотезах
случайного блуждания и информационной эффективности рын-
ка. Рассматриваются задачи проверки гипотезы эффективно-
сти рынка и анализа акций и облигаций в предположении
рациональных ожиданий. Описываются мартингальная мо-
дель цен акций, а также модели спекулятивных "мыльных пу-
зырей".
Глава 5 содержит изложение методов оптимального порт-
фельного инвестирования на основе подхода "доходность -
риск". Описываются возможности выбора портфеля с помо-
щью кривых безразличия инвестора, а также эффекты дивер-
сификации и учета корреляции доходностей ценных бумаг.
Рассматриваются задачи оптимизации структуры портфеля
ценных бумаг, в том числе при возможности безрискового
кредитования и заимствования (risk free lending and borrow-
ing), а также проблемы статистического оценивания характе-
ристик ценных бумаг и анализа риска портфеля на основе
однофакторной эконометрической модели.
Глава 6 посвящена вопросам эконометрического модели-
рования и анализа рынка ценных бумаг на основе моделей
равновесия фондового рынка: модели оценки финансовых акти-
вов САРМ и модели APT на основе теории арбитражного
оценивания. Описываются модификации модели САРМ для
случаев, когда невозможна операция "короткая продажа", от-
сутствует безрисковый актив, безрисковые ставки кредитова-
ния и заимствования считаются различными. Приводится
экономическое обоснование и интерпретация модели APT, a
также обсуждается проблема ее практической реализации. Ус-
танавливается связь между моделью САРМ и APT. Рассмат-
ривается проблема тестирования этих моделей с помощью
методов статистической проверки гипотез относительно па-
раметров соответствующих эконометрических представлений.
Глава 7 содержит описание эконометрических моделей ста-
ционарных и нестационарных случайных процессов типа
ARMA и ARIMA, моделей с условной гетероскедастичностью
ARCH, GARCH и EG ARCH, используемых для анализа и
прогнозирования финансовых временных рядов, а также про-
16

верки гипотез случайного блуждания и информационной эф-
фективности рынка.
Центральной идеей, объединяющей основные разделы по-
собия, является использование эконометрических представ-
лений для традиционных моделей финансовой экономики,
позволяющих осуществлять их построение и проверку адек-
ватности по реальным статистическим данным. Автор старал-
ся придерживаться математически строгого описания рас-
сматриваемых задач и методов. Для удобства работы с посо-
бием необходимые сведения из теории вероятностей, теории
случайных процессов, математической статистики и эконо-
метрики приводятся во вводных разделах книги.
В пособие не включены численные примеры. Основная
причина - ограничение на объем издания. Кроме того, доста-
точное количество примеров по рассматриваемым в пособии
разделам финансовой теории содержится в рекомендуемой
дополнительной литературе. Примеры и задачи, связанные с
практическим применением методов эконометрического ана-
лиза, моделирования и прогнозирования финансовых вре-
менных рядов, требуют специального рассмотрения. Поэтому
данные проблемы предполагается рассмотреть в рамках от-
i дельного учебного пособия в виде компьютерного практику-
' ма.
Рукопись данного учебного пособия подготовлена при фи-
1 нансовой поддержке фонда Department for International Devel-
! opment (DFID, United Kingdom) в рамках проекта REAP
1 BEL/395/41/00071. Автор благодарен координатору REAP-
проекта с белорусской стороны заведующему кафедрой мате-
матического моделирования и анализа данных Белорусского
государственного университета доктору физико-математичес-
ких наук, профессору Ю.С. Харину за внимание и поддержку,
а также за полезные замечания и пожелания. Глубокую при-
знательность автор выражает координатору REAP-проекта с
британской стороны декану Школы бизнеса Манчестерского
университета (The Business School of the Manchester Metropoli-
tan University) профессору Найджелу Хили за всестороннюю
помощь в период работы по проекту в г. Манчестере.
Автор искренне благодарен заведующему кафедрой при-
кладной математики и экономической кибернетики Белорус-
ского государственного экономического университета доктору
1 This document is an output from the Regional Academic Partnerships Scheme
(REAP) funded by the UK Department for International Development (DFID).
Any views expressed are not necessarily those of DFID.
2 3ак.7О84 17 f~* £ Й 6 ^ ^ *•• "* ^ ^

экономических наук, профессору Н.И. Холоду, ведущему
научному сотруднику ЦЭМИ РАН кандидату физико-
математических наук А.А. Пересецкому и начальнику Управ-
ления ценных бумаг банков Национального банка Респуб-
лики Беларусь кандидату экономических наук, доценту
С.Л. Киселю за интерес к учебному пособию, а также конст-
руктивные замечания и пожелания, высказанные в процессе
его рецензирования. Автор признателен кандидату физико-
математических наук, доценту В.П. Кирлице за прочтение ру-
кописи и сделанные замечания.
Пожелания и предложения, связанные с данным учебным
пособием, просим направлять по адресу:
220050, Республика Беларусь, г. Минск, пр-т Ф. Скорины, 4.
Белорусский государственный университет,
кафедра математического моделирования и анализа данных,
факультет прикладной математики и информатики,
ГбУ7./(+375 17) 2265704, (+375 17) 2265548 (факс)
e-mail: Malugin@bsu.by

Глава 1
ОБЩАЯ ХАРАКТЕРИСТИКА
РЫНКА ЦЕННЫХ БУМАГ
Инвесторам следует относиться
скептически к тем, кто говорит им,
как использовать финансовый анализ
для "победы рынка", однако с помо-
щью финансового анализа они могут
попытаться понять рынок.
УФ. Шарп, Г.Дж. Александер, Дж.В. Бейли
В главе дается общая характеристика принципов организации и
функционирования рынка ценных бумаг, его участников и основных ви-
дов ценных бумаг. В рамках обсуждаемых тем определяются основные
понятия и термины, используемые в основных разделах учебного посо-
бия.
Более подробное изложение рассматриваемых в главе вопросов, а
также особенностей функционирования конкретных фондовых рынков
можно найти в следующей дополнительной литературе: [8, 22, 27, 33,
42] (американский и другие зарубежные фондовые рынки); [24, 25, 30]
(российский фондовый рынок); [23] (белорусский фондовый рынок).
1.1. ИСТОЧНИКИ, ПОСТАВЩИКИ
И ПОТРЕБИТЕЛИ ИНВЕСТИЦИОННОГО КАПИТАЛА
В любой экономике имеет место неравномерное распреде-
ление денежных ресурсов между участниками экономических
отношений: одни имеют временно свободные денежные сред-
ства, т.е. сбережения, другие нуждаются в дополнительном
финансировании. Это характерно для всех основных катего-
рий участников экономических отношений, включая:
• государство (в лице правительства страны) и местные
органы управления',
• хозяйства (субъекты хозяйствования);
• население (отдельные граждане);
• внешнеэкономический сектор (правительства, субъекты хо-
зяйствования и граждане иностранных государств).
Сбережения (savings) представляют собой разность между
суммой текущих доходов и суммой текущих расходов некото-
19

рого субъекта. Субъект может использовать свои сбережения
или их часть для инвестиций, т.е. выступать в качестве инве-
стора.
Под инвестициями (investments) понимаются вложения де-
нежных средств в некоторые активы в текущий момент вре-
мени с целью получения еще большей их суммы в будущем.
Различают реальные и финансовые инвестиции. Реальные
инвестиции (real investments) - это инвестиции в "реальные",
т.е. материальные, активы (землю, здания, оборудование).
Финансовые инвестиции (financial investments) - это инвести-
ции в финансовые активы, например акции, облигации и
другие ценные бумаги.
В развивающихся экономиках преобладают реальные, а в
развитых экономиках - финансовые инвестиции. Высокое
развитие институтов финансового инвестирования способст-
вует росту реальных инвестиций, т.е. различные формы инве-
стирования не конкурируют, а дополняют друг друга. Так,
вложенные в ценные бумаги средства могут использоваться
эмитентами (заемщиками), выпустившими данные ценные
бумаги, как инвестиционный капитал для реальных инвести-
ций, связанных с осуществлением инвестиционных проектов,
например, на строительство новых и реконструкцию, расши-
. рение и техническое перевооружение действующих предпри-
ятий (производственные инвестиции), на жилищное, комму-
нальное и культурно-бытовое строительство (непроизводствен-
ные инвестиции).
Таким образом, инвесторы (кредиторы) выступают на фи-
нансовом рынке в качестве поставщиков инвестиционного
капитала, а эмитенты (заемщики) - в качестве его потребите-
лей. Инвесторы предоставляют свои сбережения нуждающим-
ся в дополнительном финансировании заемщикам. Они рас-
стаются со своими сбережениями сегодня в надежде получить
еще большую их сумму в будущем. Сбережения при этом яв-
ляются источником инвестиций. Каковы же источники сбере-
жений?
Сбережения населения, или личные сбережения, составляют
ту часть дохода граждан, которая не идет на уплату налогов и
на текущее потребление товаров и услуг. Население в целом
имеет совокупный излишек денежных средств и, следователь-
но, выступает как чистый инвестор (net investor).
Сбережения хозяйств принимают форму нераспределенной
прибыли и амортизационных отчислений. Однако финансо-
вые потребности хозяйств, как правило, превышают их сбе-
режения. Поэтому на рынке хозяйства обычно выступают как
конечные заемщики, использующие привлеченные средства
20

для реальных инвестиций. В то же время хозяйства часто осу-
ществляют краткосрочные вложения временно свободных
денежных средств в надежные финансовые активы (напри-
мер, государственные краткосрочные ценные бумаги) с целью
сохранения капитала и получения дохода в течение короткого
периода времени.
Сбережения государства и местных органов управления оп-
ределяются разностью между величиной денежных поступле-
ний в соответствующий бюджет (доходами бюджета) и расхо-
дами бюджета за определенный срок. Если расходы государ-
ственного бюджета превышают его доходы, то говорят, что
имеет место дефицит государственного бюджета. В мировой
практике такие государства составляют большинство, и по-
этому, как правило, государство выступает на финансовом
рынке как чистый заемщик (net borrower), т.е. как потребитель
капитала, хотя отдельные отрасли, государственные предпри-
ятия и внебюджетные государственные фонды могут иметь
сбережения. Местные органы управления, так же как и госу-
дарство, для финансирования текущего дефицита своих бюд-
жетов вынуждены прибегать к внешним источникам, высту-
пая при этом в роли заемщиков.
Внешнеэкономический сектор обладает значительными за-
пасами денежных ресурсов, а значит, значительными инве-
стиционными возможностями. Применительно к каждой
конкретной стране внешнеэкономический сектор может вы-
ступать и как инвестор, и как заемщик. Интернационализа-
ция хозяйственной деятельности и развитие международного
предпринимательства способствовали установлению тесных
взаимосвязей между национальными, в том числе и финансо-
выми, рынками. Образовался международный финансовый
рынок, основными элементами которого являются крупней-
шие валютные и фондовые биржи. Возможность заключения
сделок с различными финансовыми активами на различных
финансовых рынках с помощью электронных торговых сис-
тем способствует высокому динамизму и избирательности ин-
вестиционного капитала, что порождает острую конкурент-
ную борьбу за его привлечение.
Инвестиционный капитал от внешнеэкономического сек-
тора может поступать в ту или иную страну в форме либо
ссудного (заемного) капитала за счет выпуска на международ-
ные рынки государственных ценных бумаг (облигаций) от
имени правительства страны (например, еврооблигаций), ли-
бо прямых инвестиций, например за счет продажи на между-
народных рынках ценных бумаг (акций или облигаций) на-
циональных компаний.
21

Определяя направления вложений своих сбережений на
международном финансовом рынке, инвесторы ориентируют-
ся на вложения с более высокой ожидаемой доходностью.
При этом они стремятся минимизировать возможные риски
вложений и поэтому большое значение придают такому поня-
тию, как инвестиционный климат внутри данной страны. По-
следний, в свою очередь, находится под влиянием экономи-
ческой и политической ситуации, особенностей фондового и
налогового законодательства, уровня развития институтов на-
ционального финансового рынка и его инфраструктуры. От
состояния инвестиционного климата в стране зависит не
только объем привлекаемых иностранных инвестиций, но и
их стоимость для заемщиков внутри страны. Высокие риски
вложений, сопутствующие неблагоприятному инвестицион-
ному климату, могут потребовать слишком больших компен-
саций {премий за риск) в виде увеличения процентных ставок
по привлекаемым денежным ресурсам, что делает их недос-
тупными для потенциальных заемщиков.
1.2. ФИНАНСОВЫЙ РЫНОК И ЕГО ЧАСТИ
В странах с централизованно планируемыми экономиками
отсутствует необходимость в развитых финансовых рынках,
поскольку денежные ресурсы распределяются, как правило,
между участниками экономических отношений в соответст-
вии с централизованными кредитными планами либо посту-
пают к ним в виде безвозмездного бюджетного финансирова-
ния.
В странах с рыночной экономикой возможности государ-
ственного вмешательства в распределение материальных и
финансовых ресурсов между участниками экономических от-
ношений ограниченны. Большинство предприятий основано
на частной или коллективной (акционерной) формах собст-
венности, поэтому они изыскивают самостоятельно необхо-
димые им ресурсы на рынках реальных и финансовых акти-
вов.
Рынок, на котором продаются и покупаются финансовые
активы, называется финансовым рынком (financial market). Фи-
нансовый рынок посредством своих институтов, выступаю-
щих как финансовые посредники (financial intermediates), на-
правляет потоки денежных средств от их собственников (ин-
весторов, кредиторов) к тем, кто в них нуждается (эмитентам,
заемщикам), а также способствует обмену финансовыми ак-
тивами по их рыночной цене.
22

Финансовый рынок по виду отношений, возникающих
между его участниками, и типу объектов сделок можно разде-
лить на рынок банковских кредитов (ссуд) и рынок ценных бу-
маг. Осуществление внешнеэкономической деятельности уча-
стниками экономических отношений невозможно без такой
части финансового рынка, как валютный рынок. Все части
финансового рынка неразрывно связаны, взаимодействуют и
дополняют друг друга. Их единство обусловлено общностью
участников, посредников и конъюнктуры. Приведем краткую
характеристику указанных рынков.
1.2.1. Рынок банковских кредитов
Рынок банковских кредитов (РБК) охватывает отношения,
возникающие по поводу предоставления кредитно-финан-
совыми учреждениями платных и возвратных кредитов (ссуд).
Отношения между кредитором и заемщиком по поводу
предоставления ссуды оформляются гражданско-правовым
договором (долговым обязательством), не предполагающим
его переуступку какому-либо третьему лицу. Таким образом,
исключается возможность самостоятельного обращения по-
добных обязательств на рынке.
РБК состоит из двух основных сегментов: рынка коммерче-
ских кредитов и рынка межбанковских кредитов. Заемщиками
на рынке коммерческих кредитов выступают физические ли-
ца, а также юридические лица с любой формой собственно-
сти. Роль главных финансовых посредников играют коммерче-
ские банки. Для них этот сегмент финансового рынка являет-
ся наиболее емким и значимым.
В качестве примера рассмотрим складывающиеся взаимо-
отношения на рынке коммерческих кредитов. Коммерческие
банки привлекают сбережения вкладчиков и предоставляют
ссуды тем, кто в них нуждается. Банки осуществляют целена-
правленный выбор будущих заемщиков, оценивая их надеж-
ность и степень кредитного риска, т.е. риска того, что заем-
щик не вернет в срок взятую ссуду либо проценты по ней.
Ставки процентов по ссудам на финансовом рынке форми-
руются в зависимости от спроса и предложения денежных ре-
сурсов и включают соответствующие поправки на риск. Так
формируется кредитный портфель коммерческого банка, со-
ставляющий значительную часть его активов. Очевидно, каж-
дый из участников данных отношений рассчитывает на дос-
тижение определенной цели. Банки ожидают получить доход
за счет положительной (с учетом инфляции) разницы между
23

ставками процентов по выдаваемым кредитам и ставками
процентов по принимаемым вкладам. Вкладчики рассчиты-
вают увеличить свой капитал в случае положительной разни-
цы между ставкой процентов по вкладам и темпом прироста
потребительских цен за срок вклада, а заемщики получают
доступ к необходимым им денежным ресурсам. Для каждой
стороны существует риск неполучения ожидаемой прибыли,
поскольку в момент совершения операций по вкладу денеж-
ных средств, а также в момент предоставления кредита имеет
место неопределенность относительно фактических уровней
инфляции и процентных ставок на дату истечения срока
вклада или займа. Нет полной уверенности и в том, что за-
емщику удастся эффективно распорядиться кредитом и вы-
полнить условия кредитного договора. В первую очередь рис-
кует сам банк, поскольку он может пострадать как от измене-
ния процентных ставок на финансовом рынке, так и от не-
выполнения обязательств со стороны заемщиков, т.е. для
банка имеют место и процентный, и кредитный риски. Осо-
бенно велики эти риски в условиях экономической неста-
бильности и высоких темпов инфляции. В странах с переход-
ной экономикой сложное финансовое положение многих
субъектов хозяйствования делает этот рынок наиболее риско-
ванным с точки зрения возврата выданных денежных средств.
Для компенсации возможных потерь банки устанавливают
достаточно высокие по сравнению с другими сегментами фи-
нансового рынка процентные ставки по ссудам и выдают их
под залог ликвидных активов.
Рынок межбанковских кредитов (МБК) традиционно ис-
пользуется коммерческими банками для осуществления крат-
косрочных кредитно-депозитных операций с целью привле-
чения необходимых денежных ресурсов (например, в процес-
се регулирования ликвидности банка) и размещения свобод-
ных средств в других кредитных учреждениях. Банк, нуждаю-
щийся в повышении степени ликвидности, покупает необхо-
димые ему ресурсы по согласованной ставке процентов у дру-
гого банка, располагающего временно свободными средства-
ми. По сравнению с коммерческим кредитованием и покуп-
кой ценных бумаг помещение средств в другие банки более
надежно, хотя и менее доходно.
Состояние рынков МБК характеризуется финансовыми
индексами типа ставок процентов по привлечению кредитов
(Interbank BID rate - IBID) и размещению кредитов (InterBank
Offered Rate - IBOR). Наиболее известными среди подобных
индексов являются ставки LIB1D и LIBOR международного
рынка межбанковских кредитов в Лондоне, которые являются
24

основой для установления процентных ставок на рынке ев-
рокредитов.
Коммерческие банки, как правило, редко выдают кредиты
на срок более одного года. Поэтому возникает необходимость
в специальном механизме привлечения денежных ресурсов на
более длительные сроки, требуемые для реализации крупных
инвестиционных проектов. Такой механизм предоставляет
участникам экономических отношений рынок ценных бумаг.
1.2.2. Понятие ценной бумаги и фондового рынка
Рынок ценных бумаг (РЦБ), или фондовый рынок (security
market), охватывает как отношения займа, так и отношения
совладения, возникающие через выпуск (эмиссию) специаль-
ных документов - ценных бумаг (securities). Посредством рын-
ка ценных бумаг заемщики (эмитенты,) привлекают необхо-
димые им средства, выпуская и продавая инвесторам свои
ценные бумаги.
Имеется большое разнообразие ценных бумаг, обладающих
различными свойствами и назначением, что затрудняет фор-
мулировку достаточно общего определения этого понятия.
Поэтому существует несколько определений ценной бумаги, в
которых, как правило, делается акцент на каких-то их качест-
вах или функциях. Такие определения не являются исчерпы-
вающими. Например, приводимое ниже определение характе-
ризует ценную бумагу с правовой точки зрения.
Ценная бумага (security) - это документ, удостоверяющий с со-
блюдением установленной формы и обязательных реквизитов имущест-
венные права, осуществление и передача которых возможны только при
его предъявлении. С передачей ценной бумаги новому владельцу пере-
ходят все удостоверяемые данной бумагой права.
Имущественные права, удостоверяемые ценными бумага-
ми, могут принимать форму отношений займа или отноше-
ний совладения (титула собственности), возникающих между
владельцами ценных бумаг (инвесторами) и лицами, выпус-
кающими ценные бумаги (эмитентами). Отношения займа
имеют место, если привлекаемый капитал является заемным,
т.е. подлежит возврату, а отношения совладения, - если капи-
тал привлекается в бессрочное пользование, а инвесторы при
этом становятся совладельцами компании, выпустившей дан-
ные ценные бумаги.
25

С позиций финансового анализа ценную бумагу удобнее
рассматривать как "законодательно признанное право на по-
лучение ожидаемых в будущем доходов при конкретных усло-
виях"[33].
Так называемые фондовые (рыночные) ценные бумаги могут
самостоятельно обращаться на рынке, т.е. свободно перехо-
дить от одного владельца к другому после их продажи первым
владельцам. Таким образом, рынок фондовых ценных бумаг
можно разделить на две части: первичный рынок и вторичный
рынок. На первичном рынке осуществляется первичное раз-
мещение ценных бумаг, т.е. продажа ценных бумаг их первым
владельцам. На вторичном рынке осуществляется обращение
фондовых ценных бумаг. Способность ценных бумаг свобод-
но обращаться на рынке существенно отличает их от долго-
вых обязательств, удостоверяющих отношения займа на РБК,
и позволяет каждому участнику фондового рынка в зависимо-
сти от стоящих перед ним целей проводить различные опера-
ции с ценными бумагами [25].
Операция с ценными бумагами - это законченное действие или по-
следовательность действий с ценными бумагами и (или) денежными
средствами на фондовом рынке для достижения поставленных целей.
Основными операциями с ценными бумагами являются их
покупка и продажа. Возможны и другие операции: наследова-
ние, дарение, уступка прав и т. д. Юридически каждая опера-
ция оформляется путем заключения одной или нескольких
сделок с ценными бумагами.
Сделка с ценными бумагами - это взаимное соглашение, связанное с
возникновением, прекращением или изменением имущественных прав,
заложенных в ценных бумагах.
Самостоятельное обращение ценных бумаг предполагает
наличие у них определенной стоимости (цены). Существуют
различные виды стоимостей ценных бумаг, например: номи-
нальная, эмиссионная и рыночная стоимость (или курс).
Эмиссионная цена (issue value) - это цена продажи эмисси-
онных ценных бумаг при их первичном размещении. Номи-
нальная стоимость (face value, par value или principal) отража-
ется в документах финансовой отчетности лица, выпустивше-
26

го ценную бумагу, и служит базой для начисления процент-
ного дохода по ценной бумаге, а также определения величи-
ны налоговых платежей эмитентом ценных бумаг. При раз-
мещении первых выпусков акций их эмиссионная цена не
может быть меньше номинальной стоимости. Повторные вы-
пуски акций размещаются по рыночным ценам акций того же
эмитента, находящихся в обращении. Облигации могут про-
даваться при первичном размещении с "дисконтом", т.е. ни-
же номинальной стоимости.
Рыночные цены (market price), или курсы (price), ценных
бумаг - это цены, по которым они продаются и покупаются
на вторичном рынке. Торговля ценными бумагами на рынках
осуществляется обычно по системе двойного аукциона, т.е. по-
средством установления цен покупки (bid price) и цен продажи
(ask price) на основе механизма спроса и предложения цен-
ных бумаг.
Фондовый рынок по сравнению с рынком банковских
кредитов предоставляет своим участникам качественно новые
возможности. Так, заемщики (эмитенты), выпуская ценные
бумаги, могут получить необходимые средства на сроки, соот-
ветствующие срокам реализации их инвестиционных проек-
тов. Инвесторы при покупке ценных бумаг могут преследо-
вать различные цели, например:
• вложение капитала на определенный срок с целью уве-
личения капитала и получения дохода (большая часть
инвесторов);
• получение прибыли за счет спекулятивных операций, т.е.
за счет разницы между ценой покупки и ценой продажи
ценных бумаг (инвесторы-спекулянты).
Операции покупки и продажи ценных бумаг совершаются
в условиях неопределенности относительно будущих курсов
ценных бумаг, уровня процентных ставок на финансовом
рынке, темпов роста инфляции и т.д. Неопределенность по-
рождает риск (вероятность) того, что фактическая доходность
операций с ценными бумагами может отличаться от ожидае-
мой доходности в момент осуществления операций. Однако
фондовый рынок предоставляет своим участникам возмож-
ность страхования от риска, или хеджирования риска1, инве-
стиций в финансовые активы за счет покупки так называе-
1 Глагол "/о hedge", от которого происходит термин "хеджирование", в
контексте рассматриваемой проблемы может быть переведен как "ограждать"
или "страховать" от возможных потерь.
27

мых производных ценных бумаг на рынках срочных (опционных
или фьючерсных) контрактов. Инвесторов, занимающихся
хеджированием своих активов, принято называть хеджерами
(hedgers). Хеджерами на фондовом рынке выступают, как
правило, крупные (институциональные) инвесторы, а также
производители, экспортеры и импортеры продукции. При
этом риски неблагоприятных для инвесторов-хеджеров изме-
нений курсов финансовых активов принимают на себя инве-
сторы-спекулянты.
Таким образом, благодаря наличию фондового рынка про-
исходит своеобразное раздвоение капитала. С одной стороны,
существует денежный капитал, привлекаемый посредством
выпуска ценных бумаг, а с другой стороны - "фиктивный ка-
питал" в виде ценных бумаг. Денежный капитал использует-
ся, например, как инвестиционный капитал при реализации
определенных инвестиционных проектов, а ценные бумаги
осуществляют самостоятельное обращение на фондовом рын-
ке. Прибыль от денежного капитала возможна только при ус-
ловии завершения полного цикла его использования (напри-
мер, после завершения инвестиционного проекта); доход от
операций с ценными бумагами может быть получен с момен-
та их появления на фондовом рынке, причем эти операции не
приносят дохода самому эмитенту ценных бумаг. Тем не ме-
нее между указанными формами капитала существует взаимо-
связь. Например, неэффективное использование некоторой
компанией привлеченного за счет выпуска ценных бумаг де-
нежного капитала (и, как следствие, невыплата дивидендов
или процентов владельцам ценных бумаг) может стать причи-
ной обесценивания соответствующего "фиктивного" капита-
ла, т.е. привести к падению курсов ценных бумаг данной
компании и создать трудности при размещении новых выпус-
ков. И тем не менее сам факт существования вторичного
рынка делает новые выпуски ценных бумаг более привле-
кательными и способствует росту реальных инвестиций за
счет их размещения по более высоким ценам.
Деятельность всех категорий участников фондового рынка
важна для поддержания его активности и стабильности. В ус-
ловиях динамично функционирующего фондового рынка
ценные бумаги обладают высокой ликвидностью. Под ликвид-
ностью ценных бумаг понимается возможность их обращения
в наличные деньги. Возможность продажи ценных бумаг по
их текущей рыночной стоимости, в свою очередь, компенси-
рует отчасти риск инвестирования на более длительные сро-
ки, чем сроки предоставления банковских ссуд.
28

1.2.3. Валютные рынки
В настоящее время участники экономических отношений,
являясь субъектами международной экономики, могут зани-
мать или кредитовать денежные средства, а также совершать
операции по обмену валют как на национальном рынке, так и
на мировых финансовых рынках. Для этих целей служат ва-
лютные рынки [18].
Валютным рынком принято называть всю совокупность конверси-
онных и депозитно-кредитных операций в иностранных валютах, осуще-
ствляемых между контрагентами (участниками валютного рынка) по
рыночному курсу или процентной ставке.
Конверсионные операции - это операции по обмену одной нацио-
нальной валюты на другую по согласованному двумя сторонами курсу на
определенную дату.
В зависимости от даты исполнения условий сделки разли-
чают: текущие конверсионные операции (операции спот), да-
та исполнения которых (дата поставки валют) приходится на
следующий день после заключения сделки; форвардные кон-
версионные операции с отложенной фиксированной датой
исполнения (срок поставки валют - от нескольких дней до
одного года). Операциям спот и форвардным операциям со-
ответствуют различные курсы обмена валют: курсы спот и
форвардные курсы.
I
Депозитно-кредитные операции ~ это совокупность краткосрочных
операций по размещению свободных денежных остатков - депозитов
(deposits) и привлечению недостающих средств - кредитов (loans) в ино-
странной валюте на определенный срок под фиксированный процент.
В международной практике различают два типа валютных
рынков:
• валютные рынки, на которых осуществляется торговля
национальными валютами в странах происхождения дан-
ных валют (например, на таком рынке немецкий банк
берет кредит в долларах у банка США);
• рынок евровалют (еврорынок), на котором ведется тор-
говля валютами независимо от стран их происхождения
(например, тот же немецкий банк оказывается на рынке
29

евровалют, если берет кредит в долларах США у банка в
Лондоне, Цюрихе, Париже и т.д.).
Под торговлей валютой в обоих случаях понимается сово-
купность всех конверсионных и депозитно-кредитных опера-
ций в иностранных валютах. Во втором случае возникает по-
нятие "евровалюта" (например, евродоллар) как одноименной
валюты на счетах банков, которые располагаются не в странах
происхождения данных валют.
Участниками валютного рынка являются:
• центральные банки, осуществляющие международную ди-
версификацию своих ресурсов, а также управление ва-
лютными резервами и регулирование обменного курса
национальной денежной единицы;
• коммерческие банки, выполняющие основной объем ва-
лютных операций (на счетах банков держат валютные
средства другие участники рынка и осуществляют с ними
необходимые конверсионные и депозитно-кредитные
операции, кроме того, банки проводят операции
самостоятельно за счет собственных средств);
• субъекты хозяйствования (экспортеры и импортеры, про-
дукции), осуществляющие внешнеторговые операции,
покупая (импортеры) или продавая (экспортеры) валюту
на валютном рынке;
• валютные биржи, в функции которых входит осуществ-
ление обмена валют и формирование рыночного (бирже-
вого) валютного курса;
• валютные брокерские фирмы, выступающие как профес-
сиональные посредники между продавцами и покупате-
лями валют, аккумулирующие и предоставляющие дру-
гим участникам рынка информацию о запрашиваемых
курсах и ставках и формирующие тем самым реальные
валютные курсы и процентные ставки по уже заключен-
ным сделкам;
• частные (физические) лица, совершающие покупку или про-
дажу наличной валюты, а также осуществляющие широкий
спектр операций, связанных с зарубежным туризмом, пере-
водом заработной платы, пенсий, гонораров и т.д.
Однако основными участниками валютных рынков явля-
ются банки. Поэтому валютные рынки представляют собой
рынки межбанковских сделок. И когда говорят о курсах ва-
лют и процентных ставках, то имеют в виду значения курсов
и ставок межбанковских валютных рынков.
Крупнейшими международными центрами торговли валю-
той в Европе, Северной Америке и Азии являются биржевые
30

рынки в Лондоне, Нью-Йорке и Токио. Крупный Междуна-
родный валютный рынок IMM (International Money Market)
функционирует на Чикагской товарной бирже. Внебиржевой
международный рынок валютных обменов известен как ры-
нок FOREX (FOReign EXchange).
В мировой практике операции на валютном рынке связаны
главным образом с осуществлением внешнеторговой деятель-
ности участников экономических отношений. Значительно
меньшую долю составляют спекулятивные и арбитражные
операции, основанные на получении прибыли за счет спеку-
лятивной игры на разнице валютных курсов в различные мо-
менты времени на одном и том же рынке, а также в один и
тот же момент времени на различных рынках. Для страхова-
ния риска операций, а также для спекулятивной игры актив-
но используются валютные фьючерсы и опционы (см. п. 1.4.3).
1.3. СТРУКТУРА И ПРИНЦИПЫ
ФУНКЦИОНИРОВАНИЯ РЫНКА ЦЕННЫХ БУМАГ
Как отмечалось, рынок ценных бумаг можно разделить на
две основные части: первичный и вторичный рынок.
Первичный рынок обслуживает подготовку и размещение
(эмиссию) новых выпусков ценных бумаг, т.е. продажу новых
выпусков ценных бумаг их первым владельцам - первичным
инвесторам.
На вторичном рынке обращаются ранее размещенные на
первичном рынке фондовые ценные бумаги. Вторичный ры-
нок, который реализуется посредством деятельности специ-
альных институтов рынка - фондовых бирж (security exchange),
называется биржевым рынком. Вторичный рынок, функцио-
нирующий вне фондовых бирж, принято называть внебирже-
вым рынком (out of corner market) (рис. 1.1).
РКЦ
Первичный рынок
1
Вторичный рынок
I I
Биржевой рынок
Внебиржевой рынок
Рис. 1.1. Структура рынка ценных бумаг
31

1.3.1. Первичное размещение ценных бумаг
1) Способы размещения.
Обычно выделяют два способа первичного размещения
ценных бумаг: прямое размещение и размещение через по-
средников.
При прямом размещении ценных бумаг эмиссионные опе-
рации совершаются с помощью сделок, заключаемых непо-
средственно между эмитентом и инвестором. При этом эми-
тент сам организует первичное размещение ценных бумаг и
продает ценные бумаги нового выпуска инвесторам. Приме-
ром могут служить размещения государственных ценных бу-
маг, а также ценных бумаг центральных банков, которые
осуществляются на регулярной основе.
Однако для большинства эмитентов размещение ценных
бумаг на фондовом рынке является эпизодическим мероприя-
тием, не связанным с основным видом их деятельности. По-
этому они прибегают, как правило, к размещению через по-
средников, являющихся профессиональными участниками
фондового рынка (см. п. 1.5.2).
2) Формы размещения.
В зависимости от статуса эмитента, вида ценных бумаг и
целей выпуска возможны различные формы первичного раз-
мещения ценных бумаг.
Основными формами первичного размещения являются
аукционная продажа, открытая продажа и индивидуальное
(частное) размещение.
Аукционная продажа проходит в форме открытых или за-
крытых аукционов для относительно узкого круга так назы-
ваемых первичных инвесторов (например, профессиональных
участников фондового рынка). Для участия в закрытых аук-
ционах допускаются только те первичные инвесторы, которые
удовлетворяют установленным эмитентом требованиям. Дата
проведения аукциона, его условия и характеристики выпуска
ценных бумаг публикуются в средствах массовой информа-
ции. Участники подают в адрес организаторов аукциона заяв-
ки, в которых обычно указывается предполагаемая цена и
объем покупки, а также перечисляют денежные средства в
объеме предполагаемой покупки. Торги проводятся в уста-
новленное время в форме сопоставления заявок. Заявки удов-
летворяются в порядке убывания указанных в них цен до
привлечения необходимого объема денежных средств либо до
достижения минимальной цены продажи Pmin ценных бумаг, ус-
танавливаемой эмитентом.
32

Возможны различные системы проведения аукционов в за-
висимости от формы удовлетворения заявок, например:
• американский аукцион, когда каждая заявка удовлетворя-
ется на тех условиях, которые в ней указаны, если эти
условия приемлемы для эмитента;
• голландский аукцион, когда все заявки удовлетворяются на
единых условиях, сложившихся в ходе торгов, например
по минимальной цене продажи, установленной эмитен-
том;
• комбинированная система, когда одна часть заявок, в ко-
торых указываются предполагаемые цены покупки (так
называемые конкурентные предложения) удовлетворяет-
ся на индивидуальных условиях, а другая часть, содер-
жащая лишь указания на объем покупки (неконкурент-
ные предложения), - на единых условиях, например по
средневзвешенной цене, сложившейся по завершении
конкурентных торгов.
Пусть в ходе конкурентных торгов были удовлетворены за-
явки с К (К>\) различными ценами Р\>Р2>...>Рк ^ Ртт- Если
ль - количество ценных бумаг, проданных в ходе конкурент-
ных торгов по цене Р^ (&=1, 2, ..., А), то средневзвешенная це-
на продажи Р определяется по формуле
/ к к
П k=l k=l
где /!=й1+Л2+~.+л* -общее число проданных ценных бумаг в
ходе конкурентных торгов; щ=пь/п -"вес", или доля, це-
ны Р/с в значении Р .
Аукционная продажа часто используется при размещении
государственных ценных бумаг, например, государственных
краткосрочных облигаций (ГКО) Российской Федерации
(см. п. 2.3.1).
Открытая продажа предполагает продажу ценных бумаг,
например акций открытого акционерного общества, широко-
му кругу инвесторов, включая юридических и физических
лиц. Открытая продажа может проводиться в течение доста-
точно длительного времени (от нескольких недель до не-
скольких-месяцев) всем желающим на единых условиях, пуб-
ликуемых в средствах массовой информации. Фактическому
размещению ценных бумаг в ходе открытой продажи обычно
предшествует подписка на них, порядок проведения которой
определяется законодательством. Продажа ценных бумаг осу-
ществляется на условиях и по итогам подписки. Таким обра-
3 Зак. 7084 33

зом, персональный состав инвесторов до завершения кампа-
нии подписки неизвестен. Размещение ценных бумаг в форме
открытой продажи обычно проводится при участии посред-
ников - дилеров или брокеров, которые являются профес-
сиональными участниками рынка ценных бумаг (см.
разд. 1.5).
Индивидуальное размещение имеет место тогда, когда весь
выпуск приобретается одним или заранее известной группой
инвесторов (как правило, крупными институциональными
инвесторами) на предварительно оговоренных с эмитентом
условиях, включающих объем выпуска, цену продажи, ставку
процентного дохода, сроки и условия погашения и др.
1.3.2. Принципы функционирования
биржевого и внебиржевого рынков
Первичный и вторичный рынки ценных бумаг тесно свя-
заны между собой. Бесперебойная, активная работа вторично-
го рынка обеспечивает ликвидность ценных бумаг и тем са-
мым способствует успешному размещению новых выпусков
ценных бумаг на первичном рынке. В свою очередь, разме-
щение новых выпусков ценных бумаг приводит к появлению
•на вторичном фондовом рынке новых "инструментов", что
способствует повышению его активности.
1) Биржевой рынок.
Биржевой рынок реализуется посредством деятельности
особого института фондового рынка -фондовой биржи.
Фондовая биржа представляет собой организацию с правом юриди-
ческого лица, создаваемую для обеспечения профессиональным участ-
никам рынка ценных бумаг необходимых условий для торговли ценными
бумагами и регулирования их деятельности.
Фондовая биржа может быть учреждена юридическими
или физическими лицами (членами фондовой биржи) в фор-
ме открытого акционерного общества (ОАО). Данное ОАО
должно быть зарегистрировано согласно действующему зако-
нодательству и иметь лицензию на право выполнения своих
функций. Требования, предъявляемые к членам фондовой
биржи, определяются действующим законодательством стра-
ны, а также правилами конкретной фондовой биржи. В раз-
личных странах фондовые биржи существенно различаются
34

по своему составу. Например, в США и Великобритании чле-
нами фондовой биржи являются физические лица, в Япо-
нии - только юридические лица, в Германии и Италии - фи-
зические и юридические лица, в России - юридические лица
и государственные исполнительные органы, осуществляющие
операции с ценными бумагами.
Фондовая биржа (биржевой рынок) представляет собой на-
учно, информационно и технически организованный рынок
ценных бумаг, работающий на основе следующих основных
принципов:
1) регистрации {листинга) ценных бумаг, принимаемых к
котировке на фондовой бирже после проверки качества и на-
дежности ценных бумаг, проводящейся на принципах аудита;
2) котировки ценных бумаг, т.е. установления единых ры-
ночных цен (курсов) покупки и продажи ценных бумаг на
одинаковые ценные бумаги одного эмитента и их публикация
для ознакомления всех заинтересованных лиц;
3) гласности совершаемых на бирже сделок. Этому способ-
ствует единое место (торговый зал) и время (торговая сессия)
совершения сделок, а также открытая публикация информа-
ции по совершаемым сделкам в информационных средствах;
4) соблюдения принципа справедливой конкуренции между
участниками рынка, что предполагает запрет на использова-
ние и передачу так называемой инсайдерной информации (in-
sider information), т.е. информации, доступной ограниченному
кругу лиц (инсайдеров) в силу их служебного положения, ис-
пользование которой ставит их в более выгодное положение
по сравнению с остальными участниками рынка;
5) доступа к торгам на бирже только членов биржи, яв-
ляющихся профессиональными участниками фондового рын-
ка и имеющих "место", т.е. право торговать на бирже.
Крупнейшей фондовой биржей в мире является Нью-
Йоркская фондовая биржа (New York Stock Exchange
NYSE)1, образованная в 1792 г. В настоящее время на NYSE,
имеющей 1366 "мест", осуществляется торговля акциями
примерно 3 тыс. компаний общей стоимостью около 6 трлн.
долл. Владельцами данных акций являются более 50 млн. че-
ловек.
Второй по величине является Лондонская фондовая биржа
(London Stock Exchange - LSE). LSE была образована в конце
XVII в. и является одной из старейших бирж в мире. Далее по
величине идут Токийская и Франкфуртская (Франкфурт-на-
Майне) биржи.
1 Современное название биржи существует с 1817 г.
35

В Российской Федерации наиболее крупные биржевые
рынки ценных бумаг функционируют на Московской меж-
банковской валютной бирже (ММВБ) и Московской фондо-
вой бирже (МФБ).
Биржевой рынок оказывает значительное влияние на раз-
витие фондового рынка и формирование его конъюнктуры,
поскольку именно на нем обращаются наиболее "качествен-
ные" ценные бумаги, эмитентами которых являются самые
крупные и известные компании. В настоящее время объемы
биржевой торговли для разных стран превышают объемы
внебиржевого оборота от 3 до 30 раз, хотя и имеет место тен-
денция к сокращению данного разрыва [18].
2) Внебиржевой рынок.
Внебиржевой рынок характеризуется следующими особен-
ностями:
1) большим числом и разнообразием участников рынка;
2) отсутствием единого курса у одинаковых ценных бумаг;
3) различным местом и временем заключения сделок;
4) отсутствием единого центра, организующего торговлю и
вырабатывающего ее методологию;
5) более низким качеством обращающихся на нем ценных
бумаг.
Внебиржевой и биржевой рынки тесно связаны между со-
бой. Эта связь обусловлена:
во-первых, единым контингентом инвесторов;
во-вторых, в основном совпадающим составом профессио-
нальных участников рынка;
в-третьих, единством конъюнктуры.
Появление и развитие новых информационных техноло-
гий, компьютерных аналитических и торговых систем типа
Reuters и Dow Jones Telerate, а также Internet способствуют
усилению роли внебиржевых фондовых рынков. Крупнейшей
в мире и наиболее развитой информационной системой, об-
служивающей внебиржевой рынок США, является Система
автоматической котировки Национальной ассоциации инве-
стиционных дилеров NASDAQ (National Association of Securi-
ties Dealers Automatic Quotations). Акции, по которым уста-
навливаются котировки в системе NASDAQ, подобно бирже-
вым рынкам, проходят процедуру регистрации. В настоящее
время в системе NASDAQ зарегистрировано около 5 тыс. ак-
ций из порядка 40 тыс. ценных бумаг, обращающихся на вне-
биржевом рынке США.
36

3) Фондовые индексы.
Для отражения тенденций в изменении цен на фондовом
рынке используются различные фондовые (рыночные или
биржевые) индексы. Они рассчитываются на основе опреде-
ленного списка ценных бумаг как специальным образом
взвешенные значения отношений текущих значений курсов
ценных бумаг к некоторым базисным значениям1.
Старейшим фондовым индексом является промышленный
индекс Доу-Джонса2 DJIA (Dow Jones Industrial Average),
предложенный в 1884 г. и рассчитываемый на основе курсов
акций 30 ведущих промышленных компаний США. Наряду с
промышленным индексом DJIA используются и другие от-
раслевые индексы Доу-Джонса: транспортный индекс DJTA
(Dow Jones Transportation Average), рассчитываемый на основе
акций 20 транспортных компаний; коммунальный индекс
DJUA (Dow Jones Utilities Average), рассчитываемый на осно-
ве акций 15 преимущественно энергетических компаний, а
также комплексный, или составной, индекс DJCA (Dow Jones
Composite Average), рассчитываемый по объединенному спи-
ску из 65 акций.
Существуют и другие фондовые индексы, отражающие со-
стояние рынка акций в США. К их числу относятся: индексы
Standard and Poor's (например, S&P 500 Index, рассчитывае-
мый на основе курсов акций 500 компаний); индексы NYSE
(промышленный, транспортный, коммунальный, финансовый
и комплексный), рассчитываемые на основе курсов акций,
зарегистрированных на NYSE; индексы NASDAQ (промыш-
ленный, страховых компаний, банков и комплексный); Wil-
shire 5000 Index, рассчитываемый по курсам акций самой ре-
презентативной выборки из 5 тыс. компаний.
В других странах наиболее известными индексами рынков
акций являются индекс FTSE 100 (Великобритания, LSE),
индекс DAX 30 (Германия, фондовая биржа во Франкфурте-
на-Майне), индекс Nikkei 225 (Япония, Токийская фондовая
биржа), индекс Hang Seng (фондовая биржа в Гонконге), ин-
декс САС 40 (Франция, Парижская фондовая биржа), индекс
Credit Suisse (Швейцария, Цюрихская фондовая биржа), ин-
декс РТС (Российская торговая система).
Примерами индексов рынков других ценных бумаг могут
служить индекс SCB (Salomon Corporate Bond Index), характе-
1 Описание основных видов ценных бумаг приводится в разд. 1.4.
2 Данный индекс был введен Чарльзом Доу и Эдвардом Джонсом, осно-
вавшими в 1889 г. наиболее известную финансовую газету "The Wall Street
Journal", впервые начавшую публикацию "цен закрытия" акций ведущих
американских компаний.
37

ризующий средний уровень стоимости корпоративных обли-
гаций США; индексы рынков облигаций в других странах,
публикуемые информационным агентством Lombard Odier &
Cie (Женева), например, Swiss Bonds, German Bonds, Japanese
Bonds и др.; индекс MAR (Managed Account Report Index), ха-
рактеризующий доходность инвестиций в производные цен-
ные бумаги (см. п. 1.4.3).
Начиная с 70-х годов фондовые индексы помимо традици-
онного использования в качестве "барометров" фондовых
рынков получили новое применение: они стали объектом за-
ключения срочных контрактов - фьючерсов и опционов
(п. 1.4.3).
Центром мировой торговли фьючерсами и опционами на
фондовые индексы является Лондонская биржа L1FFE (Lon-
don International Financial Futures and Options Exchange). Ак-
тивная торговля опционами на индексы акций S&P 100 и
S&P 500 ведется на Чикагской бирже СВОТ (Chicago Board of
Trade).
1.4. ВИДЫ ЦЕННЫХ БУМАГ И ЦЕЛИ ИХ ВЫПУСКА
1.4.1. Классификация ценных бумаг
На развитых фондовых рынках существует большое разно-
образие фондовых ценных бумаг. Их можно классифициро-
вать по следующим основным признакам:
• тип выраженных в ценной бумаге прав и отношений;
• срок обращения;
• статус лица, выпустившего ценную бумагу;
• форма существования;
• способ реализации имущественных прав;
• процедура выпуска.
С точки зрения финансового анализа наиболее важными
являются такие признаки, от которых существенно зависят
доходность, риск, а также особенности налогообложения
ценных бумаг. К ним относятся в первую очередь: тип выра-
женных в ценной бумаге имущественных прав, срок обраще-
ния, а также статус лица, выпустившего ценную бумагу. Да-
дим краткую характеристику основных видов ценных бумаг в
соответствии с перечисленными признаками.
1. По типу выраженных прав и отношений ценные бумаги
делятся на долговые и долевые.
38

Долговые ценные бумаги выражают отношение займа и
представляют собой долговые обязательства, гарантирующие
их владельцам возврат денежных средств в установленный
срок с оговоренной ставкой процентов.
Из определения следует, что долговые ценные бумаги яв-
ляются активами с фиксированными доходом и сроком об-
ращения, которые устанавливаются условиями выпуска цен-
ных бумаг. По окончании срока обращения долговые ценные
бумаги погашаются заемщиком, т.е. в дату погашения (date of
maturity) лицо, выпустившее ценные бумаги, выкупает их,
возвращая заемные средства владельцам. В течение срока об-
ращения заемщик обязан выплачивать по ним проценты, ес-
ли это оговорено условиями выпуска ценных бумаг. Невы-
плата процентов может быть основанием для признания его
банкротом. Долговые ценные бумаги могут выпускаться субъ-
ектами с любой формой собственности. Основным видом
долговых ценных бумаг являются облигации.
Другие виды долговых ценных бумаг - векселя, депозит-
ные и сберегательные сертификаты. Коммерческие банки для
привлечения заемных средств с целью их использования в ак-
тивных операциях банка прибегают обычно к эмиссии депо-
зитных и сберегательных сертификатов, а также к выпуску
векселей. Векселя и депозитные сертификаты выпускаются
для привлечения крупных денежных средств у юридических
лиц. Для физических лиц предназначены сберегательные
сертификаты.
Вексель - это ценная бумага, являющаяся письменным долговым
обязательством, составленная по установленной законом форме и даю-
щая бесспорное право его владельцу требовать уплаты указанной суммы
по истечении срока обязательства. Банковский вексель выдается банком
под размещаемые в нем денежные средства. На этот вексель банк обязу-
ется начислить определенный процент и погасить его по предъявлении к
оплате в указанный в нем срок.
Депозитные и сберегательные сертификаты представляют собой
письменные свидетельства банка-эмитента о вкладе денежных средств,
удостоверяющие права вкладчиков или их правопреемников на получение
по истечении установленного срока суммы вклада и процентов по нему.
Долевые ценные бумаги выражают отношения совладения и
предоставляют их владельцу право долевого участия как в
собственности, так и в прибыли эмитента. Долевыми ценны-
ми бумагами являются акции. Акции выпускаются только ак-
ционерными обществами.
39

В отличие от владельцев долговых ценных бумаг, высту-
пающих в качестве кредиторов, акционеры являются совла-
дельцами компании-эмитента и поэтому предоставляют свой
капитал данной компании в бессрочное пользование. Следо-
вательно, акции можно считать "бессрочными" ценными бу-
магами, не предусматривающими возврата вложенных средств
владельцам ценных бумаг.
2. По сроку обращения ценные бумаги делятся на кратко-
срочные, среднесрочные, долгосрочные долговые ценные бумаги
и бессрочные долевые ценные бумаги.
Финансовый рынок по сроку обращения активов, в свою
очередь, разделяют на денежный рынок и рынок капиталов.
Краткосрочные ценные бумаги являются инструментами де-
нежного рынка. Финансовые активы с более длительными
сроками обращения относятся к рынку капиталов. Кратко-
срочные ценные бумаги обычно выпускаются государством
(краткосрочные облигации и казначейские векселя) и ком-
мерческими банками (банковские векселя, депозитные и сбе-
регательные сертификаты и др.).
Денежный рынок обеспечивает оперативное поступление
денежных ресурсов в государственный бюджет, позволяет
коммерческим банкам привлечь денежные средства для ак-
тивных операций. Субъектам хозяйствования и частным ли-
цам он дает возможность получить доход по их временно сво-
бодным денежным средствам в течение короткого периода
времени.
Рынок капиталов, на котором обращаются акции, а также
среднесрочные и долгосрочные облигации, позволяет привле-
кать денежные ресурсы на длительные сроки. Без рынка ка-
питалов невозможно осуществление крупных инвестицион-
ных проектов, а следовательно, развитие как отдельных субъ-
ектов хозяйствования, так и экономики страны в целом.
3. По статусу лица, выпустившего ценную бумагу, различают
государственные, муниципальные и частные (корпоративные)
ценные бумаги.
Государственные ценные бумаги выпускаются от имени
правительства, несущего по ним ответственность всем иму-
ществом государства. Муниципальные ценные бумаги выпуска-
ются от имени местных органов управления и имеют кон-
кретное залоговое обеспечение в виде объектов муниципаль-
ной собственности. Государственные и муниципальные цен-
ные бумаги являются долговыми обязательствами. С целью
повышения привлекательности для инвесторов по этим цен-
ным бумагам могут устанавливаться льготы в налоговом об-
ложении доходов.
40

Ценные бумаги, выпускаемые всеми прочими субъектами
хозяйствования (предприятиями, организациями, акционер-
ными обществами), относятся к частным (или корпоратив-
ным) ценным бумагам. Акционерные общества могут выпус-
кать как акции, так и облигации. Частные бумаги иных эми-
тентов представляют собой долговые обязательства с различ-
ными сроками погашения и схемами получения дохода.
При финансовом анализе учитываются также такие при-
знаки, как форма существования ценных бумаг, способ реа-
лизации имущественных прав владельцев ценных бумаг и
процедура выпуска ценных бумаг.
4. По форме существования различают ценные бумаги в ви-
де отпечатанных на бумаге бланков и в виде записей на сче-
тах. Преимущественной формой на современных фондовых
рынках является вторая.
В виде отпечатанных на бумаге бланков выпускаются, как
правило, ценные бумаги, требующие указания на бланках
специальных реквизитов, например векселя и депозитные
сертификаты. Ценные бумаги в виде записей на счетах обыч-
но "хранятся" на специальных счетах депо компьютерных
систем, открытых на имя владельцев в так называемых депо-
зитариях (централизованных хранилищах) ценных бумаг, ли-
бо учитываются в специальных реестрах держателей ценных
бумаг. Существование ценных бумаг в виде записей на счетах
является более надежной формой, исключающей возможность
утраты и подделки ценной бумаги. Кроме того, такая форма
при развитой инфраструктуре фондового рынка позволяет по-
вышать скорость совершения сделок с ценными бумагами, а
также осуществлять контроль над ними. Независимо от фор-
мы существования ценных бумаг их владельцы получают на
руки, как правило, не сами бумаги, а документы (сертифика-
ты, свидетельства и т.п.), подтверждающие право на владение
ценными бумагами. Следует иметь в виду, что подобные сер-
тификаты не дают имущественных прав, вытекающих из вла-
дения ценной бумагой, т.е. не являются ценной бумагой.
5. По способу реализации имущественных прав владельцев
различают ценные бумаги на предъявителя, именные и ор-
дерные. Для реализации имущественных прав, связанных с
владением ценной бумагой на предъявителя, достаточно ее
предъявления. В случае именной ценной бумаги необходима
регистрация имени владельца в реестре держателей ценных
бумаг и на бланке сертификата ценной бумаги. Передача
именной ценной бумаги другому владельцу отражается измене-
нием соответствующей записи в реестре. Ордерные ценные бу-
41

маги (например, векселя, депозитные и сберегательные сер-
тификаты коммерческих банков) - это долговые ценные бу-
маги, которые выпускаются в виде отпечатанных на бумаге
бланков и предполагают возможность их передачи новому
владельцу в соответствии с распоряжением (order) прежнего
владельца. Передача ордерной ценной бумаги сопровождается
указанием специальных реквизитов на бланке ценной бумаги
(передаточной надписи - для векселей и двустороннего со-
глашения об уступке прав - для депозитных и сберегательных
сертификатов).
6. По процедуре выпуска ценные бумаги делятся на эмис-
сионные и неэмиссионные. Эмиссионные ценные бумаги (ак-
ции, облигации, депозитные и сберегательные сертификаты)
выпускаются единовременно в большом количестве и имеют
в рамках одного выпуска одинаковые свойства. Неэмиссионные
ценные бумаги выпускаются отдельными экземплярами. По
отношению к ним употребляется более общий термин "вы-
пуск" или "выписка" (для векселей).
1.4.2. Акции и облигации
Дадим более подробную характеристику облигациям и ак-
циям, которые относятся к основным ценным бумагам.
1) Облигации.
Основным видом долговых ценных бумаг являются обли-
гации.
"Облигация - эмиссионная ценная бумага, закрепляющая право дер-
жателя на получение от эмитента облигации в предусмотренный ею срок
ее номинальной стоимости и зафиксированного в ней процента от этой
стоимости или иного имущественного эквивалента"1.
Облигации имеют фиксированный срок обращения и мо-
гут быть краткосрочными (до 1 года), среднесрочными (от 1 до
10 лет) и долгосрочными (от 10 до 30 лет). Указанные сроки
являются типичными для развитых фондовых рынков, кото-
рые характеризуются относительной стабильностью и невы-
сокими уровнями инфляции (например, рынков в США, Ве-
ликобритании, Германии, Японии).
1 См.: Закон РФ "О рынке ценных бумаг" от 22 апреля 1996 г. № 39-ФЗ.
42

Примерами ценных бумаг с указанными сроками обраще-
ния являются государственные ценные бумаги США: казна-
чейские векселя (Treasure bills -T-bills), среднесрочные казна-
чейские обязательства (Treasure notes - T-notes) и казначей-
ские облигации (Treasure bonds - T-bonds) соответственно.
В условиях российского фондового рынка долгосрочными
ценными бумагами являются активы со сроком обращения
пять лет [30], в то время как на белорусском фондовом рын-
ке -активы со сроком обращения свыше одного года [23].
Среднесрочные и долгосрочные облигации, как правило,
предусматривают выплату процентного купонного дохода (cou-
pon yield) с установленной периодичностью (обычно один
или два раза в год) в течение срока обращения и называются
купонными облигациями (coupon bonds).
Купонный (процентный) доход определяется в соответствии
с заданной купонной ставкой процентов (coupon rate) от но-
минальной стоимости (principal) облигации. Купонная ставка
может быть фиксированной либо корректируемой (перемен-
ной), что оговаривается условиями выпуска облигаций. В по-
следнем случае она, как правило, "привязывается" к некото-
рым финансовым индексам, отражающим уровень процент-
ных ставок на финансовом рынке и учитывающим изменение
уровня инфляции, например, к индексу потребительских цен,
ставке рефинансирования центрального банка, доходности
краткосрочных государственных ценных бумаг и др. Облига-
ции с корректируемой купонной ставкой предпочтительнее в
условиях нестабильного финансового рынка и относительно
высоких темпов инфляции. Если процентный доход за весь
срок обращения выплачивается при погашении облигации, то
такие облигации считаются сберегательными.
Облигации, по которым не выплачивается процентный до-
ход, имеют обычно короткий срок обращения (до года) и на-
зываются бескупонными (zero coupon bond). Бескупонные об-
лигации при первичном размещении продаются по цене,
меньшей номинальной стоимости (с дисконтом), а погашают-
ся по номинальной стоимости. Разница в ценах покупки и
погашения (продажи) является источником дохода владельцев
бескупонных облигаций.
Таким образом, назовем основные характеристики облига-
ций, определяющие их ожидаемую доходность:
• номинальная стоимость;
• ставка купонного дохода (для купонных облигаций);
• цена покупки;
• срок обращения.
43

Как и любые финансовые инвестиции, покупка облигаций
связана с различными рисками, являющимися причиной не-
получения инвестором ожидаемой доходности. Основные
риски:
• риск невыполнения условий выпуска со стороны эмитен-
та (default risk);
• процентный риск (interest rate risk), т.е. риск, возникаю-
щий при долгосрочных вложениях вследствие изменения
процентных ставок на финансовом рынке;
• риск реинвестирования (reinvestment risk), имеющий ме-
сто при краткосрочных вложениях.
Все виды рисков требуют дополнительной компенсации в
виде надбавок (премий за риск) к ожидаемой доходности.
Наиболее надежными считаются государственные облигации.
Краткосрочные государственные облигации в задачах финан-
сового анализа часто рассматриваются как безрисковые акти-
вы, т.е. активы, для которых риск неполучения инвестором
ожидаемой доходности пренебрежительно мал. Премия за
риск для подобных активов полагается равной нулю.
В Российской Федерации на рынке облигаций доминиру-
ют государственные и муниципальные облигации [24, 25, 30].
Государственными облигациями являются: бескупонные госу-
дарственные краткосрочные облигации (ГКО РФ), купонные
облигации федерального займа (ОФЗ) и облигации государст-
венного сберегательного займа (ОГСЗ). Купонная ставка по
ОФЗ корректируется и определяется через доходность выпус-
ков ГКО РФ с близкими сроками погашения. Муниципаль-
ные ценные бумаги отличаются большим разнообразием. Их
выпуск преследует традиционные цели - финансирование
дефицита и текущих расходов местных бюджетов либо фи-
нансирование конкретных инвестиционных проектов, напри-
мер жилищного строительства. Рынок корпоративных обли-
гаций находится в стадии становления.
На развитых фондовых рынках корпоративные облигации
составляют широкий спектр долговых активов, различающих-
ся степенью надежности, что отражается в различных рейтин-
гах ценных бумаг [23, 33, 42]. Типичные корпоративные об-
лигации являются средне- и долгосрочными долговыми цен-
ными бумагами. Процентный доход по облигациям обычно
выплачивается один или два раза в год из валовой прибыли
корпорации до выплат дивидендов по акциям. Владельцы об-
лигаций пользуются приоритетом перед акционерами и при
удовлетворении имущественных прав в случае ликвидации
корпорации.
44

В зависимости от обеспечения материальными активами
облигации корпораций делятся на обеспеченные и необеспечен-
ные, но, как правило, корпоративные облигации являются
обеспеченными, т.е. имеют конкретное залоговое обеспечение. В
качестве залогового обеспечения могут выступать принадле-
жащие эмитенту недвижимость, оборудование или фондовые
ценные бумаги дочерних компаний (филиалов). В качестве
гарантов облигационных займов выступают коммерческие
или инвестиционные банки, которые в случае банкротства
или неплатежеспособности корпорации-эмитента вступают во
владение залоговым обеспечением от имени владельцев обли-
гаций, продают его по рыночной стоимости и распределяют
выручку между владельцами облигаций.
Меньшая надежность необеспеченных корпоративных об-
лигаций компенсируется более высокими ставками процент-
ного дохода или возможностью обмена при оговоренных ус-
ловиях на обыкновенные акции того же эмитента. Подобные
облигации называются конвертируемыми (convertible bonds).
Облигации могут быть отзывными (callable bonds), т.е. воз-
можен их выкуп эмитентом у владельцев до даты погашения с
некоторой надбавкой (премией) к их текущей рыночной
стоимости, если эта операция оговорена условиями выпуска.
Риск досрочного "отзыва" облигаций для инвесторов компен-
сируется повышенной доходностью подобных облигаций.
2) Акции.
"Акция - эмиссионная ценная бумага, закрепляющая права ее вла-
дельца (акционера) на получение части прибыли акционерного общества
в виде дивидендов, на участие в управлении акционерным обществом и
на часть имущества, остающегося после его ликвидации"1.
Дивиденды - часть чистой прибыли акционерного общества, распре-
деляемой между акционерами пропорционально числу акций, находя-
щихся в их собственности.
Различают простые (или обыкновенные) акции (common
stocks) и привилегированные акции (preference stocks). Владель-
цы обыкновенных акций обладают всеми перечисленными
выше правами. Кроме того, в зависимости от устава акцио-
нерного общества (корпорации) они могут иметь и некоторые
дополнительные права, например право на первоочередное
1 См.: Закон РФ "О рынке ценных бумаг".
45

приобретение акций нового выпуска. Таким образом, воз-
можно существование различных классов обыкновенных ак-
ций у одной и той же корпорации, различающихся набором
прав для их владельцев.
В отличие от обыкновенной акции привилегированная ак-
ция дает ее владельцу ряд "привилегий": преимущество при
распределении чистой прибыли, т.е. при получении диви-
дендного дохода, а также первоочередность удовлетворения
права на долю собственности акционерного общества при его
ликвидации. В обмен на подобные "привилегии" держатель
привилегированной акции обычно лишается права голоса, т.е.
права на участие в управлении акционерным обществом, а
также преимущественного права на первоочередное приобре-
тение акций нового выпуска.
Заметим, что акционер, т.е. владелец обыкновенной или
привилегированной акции, имеет право на получение диви-
дендов, однако эмитент не гарантирует ему их обязательную и
регулярную выплату. Дивиденды обычно не выплачиваются,
если не выполнены обязательства перед кредиторами, имеют-
ся убытки либо если выплата дивидендов может привести к
убыткам. Таким образом, невыплата дивидендов (в отличие от
невыплаты процентов по долговым ценным бумагам) не явля-
ется основанием для заявления о банкротстве корпорации.
По привилегированной акции, как правило, выплачивают-
ся фиксированные дивиденды в соответствии с установлен-
ной ставкой процентов (которая, как и в случае облигаций,
может быть корректируемой) от номинальной стоимости ак-
ции до выплаты дивидендов по обыкновенным акциям.
С целью повышения привлекательности привилегирован-
ных акций могут устанавливаться различные дополнительные
"привилегии", что приводит к появлению разновидностей
привилегированных акций. Например, не выплаченные в
срок дивиденды по так называемым кумулятивным привилеги-
рованным акциям (cumulative preference stocks) накапливаются
и полностью выплачиваются до того, как производятся вы-
платы дивидендов по обыкновенным акциям. Участвующие
привилегированные акции (participating preference sjg^fks) дают
право владельцам на получение дополнительшЯхдивидендов
при наличии у корпорации излишков нераспределенной при-
были.
Отсутствие у владельцев привилегированных акций права
голоса позволяет использовать эти акции для формирования
собственного (уставного) капитала акционерного общества
без угрозы потери управления над корпорацией со стороны
акционеров. Однако доля привилегированных акций в собст-
46

венном капитале эмитента, как правило, ограничивается за-
конодательно. Как и облигации, привилегированные акции
могут быть конвертируемыми (convertible preference stocks).
3) Цели выпуска облигаций и акций.
Для привлечения необходимого капитала эмитенты могут
прибегать к выпускам различных ценных бумаг и устанавли-
вать различные условия выпусков в зависимости от стоящих
перед ними задач. Укажем на наиболее важные цели выпуска
облигаций и акций, а также проведем их сравнительный ана-
лиз.
Облигации с различными сроками обращения являются
основным видом государственных ценных бумаг. Главными
целями выпуска этих бумаг являются финансирование дефи-
цита государственного бюджета, сглаживание неравномерно-
сти поступления в бюджет налоговых платежей, обеспечение
коммерческих банков текущими ликвидными активами, фи-
нансирование социально значимых программ, учреждений и
организаций. В условиях высокой степени риска и неопреде-
ленности, характерных для развивающихся рынков, государ-
ственные ценные бумаги обладают рядом привлекательных
для инвесторов качеств: невысоким риском, приемлемой до-
ходностью (в частности, за счет льготного налогообложения
дохода инвестора) и практически абсолютной ликвидностью в
силу отлаженной технологии торговли. Все это обусловливает
доминирующее положение сегмента государственных ценных
бумаг на развивающихся фондовых рынках.
Центральный банк может выпускать свои облигации с це-
лью регулирования объема денежной массы в обращении, а
также корректировки уровня процентных ставок на финансо-
вом рынке.
Вновь создаваемые акционерные общества осуществляют
первые выпуски акций с целью формирования собственного
(акционерного) капитала, например, при переходе от государ-
ственной или частной форм собственности к корпоративной
(акционерной). К повторным выпускам акций корпорации
прибегают при решении "специальных" задач, например:
• при увеличении уставного капитала;
• осуществлении операций слияния и поглощения (merger
and take-over) корпораций;
• формировании оптимального соотношения между собст-
венным капиталом и заемными средствами корпорации
[29].
Выпуск акций для привлечения средств в производствен-
ную деятельность обычно используется лишь в тех случаях,
47

когда исчерпаны все другие возможности. Непривлекатель-
ность акций для этих целей объясняется возможностью со-
кращения "доли" существующих акционеров (как правило,
учредителей акционерного общества) в управлении корпора-
цией вследствие расширения числа акционеров. Для сохране-
ния своих позиций они могут воспользоваться правом на пер-
воочередное приобретение акций нового выпуска, если это
право дают им принадлежащие им акции. Кроме того,
поскольку в отличие от процентов по облигациям дивиденды
по акциям выплачиваются не из валовой, а из чмстой прибы-
ли корпорации, то привлеченный за счет выпуска акций ка-
питал может иметь более высокую стоимость для эмитента,
чем заемные средства, полученные посредством! выпуска об-
лигаций. Поэтому для привлечения инвестиций в производст-
венную деятельность на длительные сроки акционерные об-
щества предпочитают прибегать к выпуску корпоративных
облигаций.
Очевидно, корпоративные облигации имеют более высо-
кий риск вложений, чем государственные ценные бумаги, по-
этому требуют соответствующей компенсации за счет более
высокой доходности (премии за риск) и залоговюго обеспече-
ния. |
В условиях экономической нестабильности вложения в
корпоративные облигации сопряжены с повышенным рис-
ком, что затрудняет их размещение на фондовом рынке. По
этой причине выпуск акций может оказаться для акционер-
ных обществ единственно возможным способом привлечения
инвестиционного капитала.
Открытые акционерные общества, выступающие на фи-
нансовом рынке в качестве институциональньих инвесторов
или профессиональных посредников, могут преследовать и
другие цели выпуска акций, связанные с осуществлением их
уставной деятельности. Например!, инвестиционные (или вза-
имные) фонды (mutual fund) формируют свои портфели цен-
ных бумаг за счет средств, вырученных от продажи собствен-
ных акций. Фондовые биржи, основанные в форме открытых
акционерных обществ, продают собственные акции для фор-
мирования состава членов биржи, к числу кото|хьвИЗтносятся
их акционеры.
1.4.3. Производные ценные бумаги
Как отмечалось, ценные бумаги могут рассматриваться как
фиктивный капитал, который может быть 1-го, 2-го, 3-го по-
рядков и т.д. (рис. 1.2).
48

Фиктивный
капитал
3-го порядка
2-го порядка
Производные
ценные бумаги
1 -го порядка
Основные
ценные бумаги
Денежный капитал у эмитента
Рис. 1.2. Основные и производные ценные бумаги
Акции, облигации и другие основные ценные бумаги отно-
сятся к фиктивному капиталу 1-го порядка. В их основе ле-
жит денежный капитал, которым распоряжается эмитент, вы-
пустивший эти ценные бумаги.
Ценные бумаги, в основе которых лежит не денежный, а
фиктивный капитал, например другие ценные бумаги или
финансовые инструменты (валюта, фондовые индексы), обра-
зуют фиктивный капитал более высоких порядков и называ-
ются производными ценными бумагами.
Актив, лежащий в основе производных ценных бумаг, на-
зывается базисным активом.
Производная ценная бумага дает право ее владельцу (или
обязывает его) совершить операцию покупки или продажи
базисного актива в установленный срок и по фиксированной
цене.
Примерами производных ценных бумаг, которые можно
рассматривать как фиктивный капитал 2-го порядка, являют-
ся опционы на акции (Stock Options), опционы на валюту,
или валютные опционы (Financial Options), опционы на обли-
гации (Interest Rate Options), опционы на фондовые индексы
(Index Options), фьючерсы на долговые обязательства, или
процентные фьючерсы (Interest Rate Futures), фьючерсы на
валюту, или валютные фьючерсы (Financial Futures).
Примером фиктивного капитала 3-го порядка могут слу-
жить опционы на фьючерсы или фьючерсные опционы (Fu-
tures Options). Использование финансовых инструментов, от-
носящихся к фиктивному капиталу более высоких порядков,
связано со сложностью их количественного анализа.
Производные ценные бумаги часто называют срочными
контрактами, поскольку исполнение обусловленных ими
сделок с базисными активами откладывается на оговоренный
срок. Подобные сделки принято называть срочными в отли-
4 Зак.7084
49

чие от сделок спот (spot) на рынке базисного актива, по ко-
торым заключение и расчеты осуществляются практически в
одно и то же время1.
Сделки с производными ценными бумагами оказываются
особенно эффективными в условиях значительных колебаний
рыночной конъюнктуры на рынках базисных активов. Произ-
водные ценные бумаги в периоды нестабильной рыночной
конъюнктуры выступают как факторы повышения активности
и надежности финансового рынка. Инвестиции в базисные
активы (акции, облигации, валюту) в подобные периоды со-
пряжены с высоким риском, что является причиной сниже-
ния активности соответствующих сегментов финансового
рынка, а следовательно, и доходов работающих на них инве-
сторов. Использование же производных ценных бумаг не
только позволяет активизировать спекулятивную игру (а сле-
довательно, увеличить биржевой оборот), но и преследует
другие цели, например страхование базисных активов от рис-
ка неблагоприятного для инвесторов изменения их курсов.
Финансовый рынок предоставляет инвесторам такие меры в
виде производных финансовых инструментов - форвардных,
фьючерсных и опционных контрактов.
Страхование базисных активов, а также операций с ними
.средствами самого финансового (фондового) рынка принято
называть хеджированием риска инвестиций в базисные активы,
а тех, кто занимается подобной деятельностью, - хеджерами.
Заметим, что в условиях повышенной нестабильности фи-
нансового рынка возрастает активность инвесторов в поисках
эффективных средств защиты имеющихся у них активов. Это
стремление к хеджированию риска финансовых инвестиций
характерно в первую очередь для крупных инвесторов (стра-
ховых компаний, инвестиционных и пенсионных фондов,
коммерческих банков), а также производителей, экспортеров
и импортеров товаров и услуг. Инвесторы-хеджеры распола-
гают значительными объемами финансовых активов и выну-
ждены сохранять их в течение длительного времени для ис-
полнения своей уставной деятельности.
Таким образом, на рынках срочных контрактов хеджеры
заключают срочные контракты главным образом для защиты
принадлежащих им активов, а не для торговли ими. ЛоэгЬку
практически все срочные контракты аннулируются до истече-
ния сроков поставки лежащих в их основе активов. Заметим,
что затраты, понесенные хеджерами-инвесторами на рынке
срочных контрактов, могут быть компенсированы увеличени-
1 С точностью до времени, необходимого для технического оформления
сделки.
50

ем цен на производимые ими товары и услуги. В результате
их фактические потери могут оказаться незначительными.
Средства, потраченные хеджерами на рынке срочных кон-
трактов, являются основным источником его финанси-
рования. Поэтому, чем больше хеджеров и чем выше их ак-
тивность, тем активнее функционирует данный рынок, при-
влекая все больше спекулянтов - профессиональных трейде-
ров. Спекулянты, получая соответствующее вознаграждение,
занимают противоположные хеджерам позиции и тем самым
берут риск неблагоприятного для хеджеров изменения курсов
активов на себя. Однако их привлекает "эффект рычага",
краткосрочность контрактов и, конечно, возможность полу-
чения прибыли, источником которой являются потери хедже-
ров в виде упущенной выгоды в случае благоприятных для
них изменений курсов базисных активов.
Рассмотрим основные типы срочных контрактов, к числу
которых относятся форвардные, фьючерсные и опционные.
Более подробное изложение вопросов, связанных с функцио-
нированием и анализом подобных рынков, можно найти в [4,
16, 33].
Форвардный контракт (forward contract) - это соглашение
между двумя сторонами о будущей поставке определенного
базисного актива, которое заключается вне фондовой биржи.
Все условия сделки (количество, цена поставки и дата по-
ставки базисного актива) оговариваются контрагентами в мо-
мент заключения контракта. Форвардный контракт является
обязательным для исполнения обеими сторонами. Заключе-
ние форвардного контракта не требует от контрагентов каких-
либо денежных расходов (за исключением возможных транс-
акционных издержек).
Форвардный контракт заключается, как правило, в целях
страхования операций, связанных с реальной продажей или
покупкой соответствующего актива от возможного неблаго-
приятного изменения курса актива. Поскольку форвардный
контракт преследует реальную поставку актива, то его усло-
вия отражают предпочтения конкретных участников сделки,
т.е. не являются стандартными. В связи с этим вторичный
рынок для форвардных контрактов ограничен или вовсе от-
сутствует, что порождает риск их "неликвидности". Сущест-
вует также риск невыполнения обязательств по контракту од-
ной из сторон. Указанными недостатками не страдают фью-
черсные контракты.
Фьючерсный контракт (futures contract) {фьючерс) - это
стандартизованное соглашение между двумя сторонами о бу-
дущей поставке определенного базисного актива, которое за-
ключается на фондовой бирже.
51

Как и в случае с форвардным контрактом, фьючерсный
контракт является обязательным для исполнения обеими сто-
ронами, а его заключение связано лишь с трансакционными
издержками, а также с определенными финансовыми гаран-
тиями исполнения контрактов в виде залогового обеспечения
в размере, устанавливаемом расчетной палатой фондовой
биржи.
В отличие от форвардных контрактов условия фьючерс-
ных контрактов устанавливаются самой фондовой биржей,
поэтому являются стандартными для всех контрактов на ак-
тив определенного вида. В связи с тем что условия контрак-
тов определенного вида одинаковы для всех инвесторов,
фьючерсные контракты являются высоколиквидными. У ин-
вестора всегда существует возможность ликвидировать свою
позицию с помощью обратной сделки (т.е. инвестор, заклю-
чивший контракт на продажу актива, может ликвидировать
свою позицию, заключив также контракт на поставку того
же актива, и наоборот). В то же время стандартный характер
условий фьючерсных контрактов, очевидно, может оказаться
неудобным для контрагентов, предполагающих реальную по-
ставку определенного актива. По этой причине заключение
фьючерсных контрактов имеет целью, как правило, не по-
ставку активов, а хеджирование риска неблагоприятного из-
менения курсов базисных активов и спекулятивную игру на
разнице цен. В мировой практике лишь 2-5% фьючерсных
контрактов заканчиваются реальной поставкой лежащих в их
основе активов.
Исполнение фьючерсных контрактов гарантируется рас-
четной палатой фондовой биржи, что выгодно отличает их от
форвардных контрактов. В то же время обязательность ис-
полнения фьючерсного контракта может быть причиной зна-
чительных убытков для инвестора при неблагоприятном для
него изменении курса базисного актива. Поэтому привлека-
тельным для инвестора мог бы быть такой срочный контракт,
который давал бы ему право выбора исполнить контракт или
отказаться от его исполнения в неблагоприятной ситуации в
обмен на некоторую премию, выплачиваемую инвестором его
контрагенту. А
Таким контрактом является опционный контракт, огранИ-11""
чивающий потери инвестора заранее зафиксированной сум-
мой, называемой премией за опцион (option premium).
Опционный контракт (option1 contract) (опцион) - это со-
глашение между двумя контрагентами, один из которых (про-
давец опциона) предоставляет другому (покупателю опциона)
1 От англ. "option" - выбор.
52

право купить или продать определенное количество некото-
рого базисного актива в обусловленное время по оговоренной
цене исполнения (цене поставки базисного актива).
В отличие от фьючерсов опционы покупаются и продают-
ся, а значит, имеют определенную цену - премию за опцион.
Покупатель опциона уплачивает продавцу опциона премию за
опцион и получает право выбора: исполнить или не испол-
нить контракт по указанной в нем цене исполнения. Решение
об исполнении опциона его владелец принимает на основе
сравнения цены исполнения и текущей рыночной стоимости
базисного актива с учетом личной выгоды, в то время как
продавец опциона обязан исполнить предъявленный к испол-
нению опционный контракт, даже если это для него невы-
годно. Этим объясняется более высокий риск у продавцов
опционов. Заметим, однако, что при благоприятной конъ-
юнктуре рынка продавцы опционов получают прибыль в виде
стоимости проданных опционов без каких-либо затрат собст-
венного капитала, а покупатели опционов за каждый кон-
тракт уплачивают определенную премию за опцион.
Различают опционы на покупку базисного актива - опцио-
ны коля (call options) и опционы на продажу - опционы пут
(put options). В зависимости от возможного момента исполне-
ния опционов различают европейские и американские опцио-
ны. Европейские опционы могут быть исполнены только в
оговоренную дату истечения контракта, а американские - в
любой день до даты истечения контракта включительно и, та-
ким образом, предоставляют большие возможности для инве-
сторов.
Расчет премии за опцион является при этом ключевой зада-
чей количественного анализа опционов [16, 33]. Основопола-
гающими работами в этом направлении являются статьи Фи-
шера Блэка и Майрона Шоулса1, а также Роберта Мертона2 .
Крупнейшими мировыми рынками срочных контрактов
являются:
Лондонская биржа LIFFE (London International Financial
Futures and Options Exchenge);
Чикагская биржа опционов СВОЕ (Chicago Board Options
Exchange);
Чикагская биржа фьючерсной торговли валютой СМЕ
(Chicago Mercantile Exchange).
1 См.: Black F., Scholes M. The pricing of options and corporate liabilities //
Journal of Political Economy. 1973. V. 81. P. 637-654.
2 См.: Meiion P.C. Theory of rational option pricing // Bell Journal of Eco-
nomics and Management Science. 1973. V. 19. P. 557-562.
53

1.5. УЧАСТНИКИ РЫНКА ЦЕННЫХ БУМАГ
Участников фондового рынка можно разделить на три ос-
новные категории: инвесторы, эмитенты и профессиональные
участники.
1.5.1. Инвесторы и эмитенты
Инвесторы на рынке ценных бумаг - это юридические или
физические лица, приобретающие ценные бумаги от своего
имени и за свой счет. Существуют различные категории инве-
сторов, но основными среди них являются индивидуальные и
институциональные.
Часто определения "индивидуальные" и "институциональ-
ные" ассоциируются соответственно с инвесторами - физиче-
скими и юридическими лицами [25].
В зарубежной практике эти понятия означают [33]: индиви-
дуальные инвесторы - это инвесторы, доходы которых от вла-
дения ценными бумагами принадлежат только им самим; ин-
ституциональные инвесторы - это финансовые посредники,
которые выпускают и продают собственные финансовые обя-
зательства, а на полученные таким образом средства приобре-
тают финансовые активы других компаний.
Как видно, в последнем случае предполагается, что в роли
индивидуальных инвесторов наряду с физическими лицами,
т.е. отдельными гражданами, могут выступать и юридические
лица, например компании и предприятия, использующие для
покупки ценных бумаг собственные средства. Термин "инсти-
туциональные инвесторы" часто ассоциируется с такими
крупнейшими финансовыми посредниками, как пенсионные
фонды, взаимные (инвестиционные) фонды, страховые ком-
пании и коммерческие банки. Иллюстрацией роли институ-
циональных инвесторов на современном фондовом рынке
служит тот факт, что в совокупности они владеют более чем
половиной акционерного капитала, выпущенного в обраще-
ние американскими корпорациями [33].
Инвесторы могут классифицироваться и по другим при-
знакам, например в соответствии с приемлемыми для них
уровнями доходности и риска вложений, сроками инвестиро-
вания и т.д.
Эмитентами ценных бумаг могут быть государственные ор-
ганы, органы местного управления, а также юридические ли-
ца с любой формой собственности, которые от своего имени
выпускают ценные бумаги и обязуются выполнять обязатель-
ства, вытекающие из условий их выпуска (см. также п. 1.4.1).
54

1.5.2. Профессиональные участники
рынка ценных бумаг
Профессиональные участники рынка ценных бумаг занимают-
ся коммерческой, посреднической деятельностью, а также
другими видами профессиональной деятельности по ценным
бумагам.
Профессиональными участниками рынка считаются юри-
дические лица любой формы собственности, получившие ли-
цензию на осуществление одного или нескольких видов про-
фессиональной деятельности по ценным бумагам.
Профессиональные участники выступают посредниками
между эмитентами и инвесторами, покупателями и продавца-
ми ценных бумаг, а также обслуживают процесс выпуска и
обращения ценных бумаг. Юридическое лицо, претендующее
на право заниматься профессиональной деятельностью на
рынке ценных бумаг, должно удовлетворять определенным
требованиям. В частности, в штате данного юридического ли-
ца должны быть сотрудники, имеющие соответствующие ква-
лификационные аттестаты профессиональных участников
рынка ценных бумаг. Виды профессиональной деятельности
по ценным бумагам, требования к профессиональным участ-
никам, а также порядок их лицензирования и аттестации оп-
ределяется законодательством страны. Лицензированием
юридических лиц и аттестацией их сотрудников занимаются
государственные органы, осуществляющие контроль и надзор
за рынком ценных бумаг. В Российской Федерации таким ор-
ганом является Федеральная комиссия по рынку ценных бу-
маг (ФКЦБ). Активную роль в регулировании рынка ценных
бумаг любой страны играют министерства финансов, цен-
тральные банки и некоторые другие государственные органы.
Значительное место в организации работы фондовых рынков
отводится саморегулирующимся организациям профессио-
нальных участников рынка, действующим в соответствии с
законодательством страны на принципах некоммерческой ор-
ганизации. Саморегулирующаяся организация [30] учреждает-
ся профессиональными участниками для обеспечения усло-
вий их деятельности, соблюдения стандартов профессиональ-
ной этики, защиты интересов владельцев ценных бумаг, уста-
новления правил и стандартов проведения операций с цен-
ными бумагами. Примерами подобных организаций являются
фондовые биржи, ассоциации инвестиционных фондов, уча-
стников фондового рынка и др.
К основным видам профессиональной деятельности по
ценным бумагам относятся:
55

• посредническая деятельность по ценным бумагам,
• коммерческая деятельность по ценным бумагам,
• деятельность инвестиционного фонда,
• доверительная (трастовая) деятельность,
• деятельность депозитария.
Более подробно остановимся на первых трех видах дея-
тельности, соответствующих основным профессиональным
участникам фондового рынка. Относительно двух последних
видов ограничимся лишь краткими характеристиками.
Доверительная (трастовая) (от англ. trust — доверие) дея-
тельность с ценными бумагами - это деятельность по управ-
лению ценными бумагами, принадлежащими конкретному
лицу на правах собственности, осуществляемая другим лицом
путем передачи ему на определенный срок этих бумаг во вла-
дение и доверительное управление.
Деятельность депозитария заключается в предоставлении
услуг по хранению ценных бумаг, учету принадлежности прав
по ценным бумагам и обеспечению расчетов по сделкам с
ценными бумагами, хранящимися в депозитарии.
1) Посредническая деятельность по ценным бумагам.
Сделки с ценными бумагами могут заключаться как непо-
средственно между продавцом и покупателем, так и через по-
средников. Сделки заключаются без посредников (рис. 1.3),
когда эмитент сам организует первичное размещение своих
ценных бумаг, а также между профессиональными участни-
ками (дилерами) на внебиржевом рынке. Обычно индивиду-
альные и институциональные инвесторы прибегают к услугам
профессиональных участников фондового рынка, занимаю-
щихся посреднической деятельностью.
Продавец
Деньги
Покупатель
Ценные бумаги
Рис. 1.3. Сделки без посредников
Посреднической деятельностью по ценным бумагам считается
покупка или продажа ценных бумаг за счет и по поручению
клиента. Посреднической деятельностью на фондовом рынке
занимаются брокеры.
Брокер (broker) - это профессиональный посредник при
заключении сделок с ценными бумагами, действующий от
имени и по поручению клиента (инвестора) и получающий за
это вознаграждение в форме комиссионных процентов.
56

Заметим, что брокер не использует в сделках собственный
капитал, что существенно отличает его от дилера. Сфера дея-
тельности брокера включает консультирование клиентов, со-
вершение сделок с ценными бумагами, участие в размещении
новых выпусков ценных бумаг на условиях "максимальных
усилий", создание и управление инвестиционными фондами.
Существуют различные схемы заключения сделок через бро-
керов. Простейшая схема представлена на рис. 1.4. В рамках
данной схемы брокер лишь находит продавца для покупателя
или наоборот, а исполнение сделки осуществляется продав-
цом и покупателем.
Деньги
Продавец
Заявка
на продажу
ч
\
Брокер
ч /
\
ША
Заявка
на покупку
Покупатель
Ценные бумаги
Рис. 1.4. Схема заключения сделки через одного брокера
Такие сделки могут иметь место при первичном размеще-
нии ценных бумаг (в этом случае продавцом выступает эми-
тент), а также при операциях, нерегулярно совершаемых ин-
весторами вне фондовой биржи. В последнем случае эффект
от применения схемы, приведенной на рис. 1.3, несомненно,
выше, так как инвесторы не несут расходов, связанных с вы-
платой комиссионного вознаграждения брокеру.
Более типичная схема сделки приведена на рис. 1.5. В дан-
ном случае в заключении сделки принимают участие два бро-
кера. Один представляет интересы продавца ценных бумаг,
другой - покупателя. Такая схема имеет место на фондовой
бирже, а также на "внебиржевом" рынке между непрофес-
сиональными участниками фондового рынка.
Заявка брокеру1 содержит указание на покупку или прода-
жу определенного вида ценных бумаг, а также ряд специфи-
каций:
1 Определение и примеры заявок брокеру соответствуют практике разви-
тых фондовых рынков и основываются на материале, излагаемом в [33].
57

• размер заявки (количество покупаемых или продаваемых
ценных бумаг);
• срок исполнения (срок, в течение которого заявка долж-
на быть исполнена);
• тип заявки (указание относительно цены исполнения).
Деньги
Заявка
на продажу ^—^ ^—^
Продавец
7 Л1 \
( Брокер I Брокер 1
V Vv V*
Покупатель
Ч^^^ ^ _?* Заявка
на покупку
Ценные бумаги
Рис. 1.5. Схема заключения сделки с двумя брокерами
При определении размера заявки обычно используется по-
нятие стандартного объема покупки, называемого лотом. По-
купая или продавая ценные бумаги, инвестор размещает за-
явки на полный лот, неполный лот или комбинацию из пол-
ного и неполного лотов.
Например, при сделках с обыкновенными акциями 1 лот
обычно равен 100 акциям. Полный лот означает количество
акций, кратное 100, неполный лот - количество акций от 1 до
99. Количество акций большее, но не кратное 100, рассматри-
вается как комбинация полного и неполного лотов.
По сроку исполнения заявки могут быть:
• однодневными (подлежат исполнению в течение дня по-
ступления);
• открытыми (действительны до исполнения брокером ли-
бо отмены инвестором);
• подлежащими немедленному исполнению (аннулируются
брокером при невозможности их немедленного исполне-
ния);
• заявками по усмотрению, позволяющими брокеру само-
му устанавливать все ее спецификации (полная свобода
действий) или некоторые из них (ограниченная свобода
действий). Если не указан срок исполнения, заявки счи-
таются однодневными.
Существуют следующие основные типы заявок:
58

• рыночные заявки, подлежащие исполнению в течение
дня по наилучшему рыночному курсу;
• заявки с ограничением цены предполагают указание ин-
вестором предельной цены исполнения, т.е. минимальной
цены продажи и максимальной цены покупки ценных
бумаг.
Приведем такой пример. Текущий рыночный курс акции
корпорации ABC равен 25 долл. Инвестор А подает заявку на
продажу 100 акций с ограничением цены до 30 долл. за шту-
ку. Заявка будет выполнена только тогда, когда курс акции
возрастет не менее чем на 5 долл.
Рыночная заявка является самым распространенным ти-
пом заявок. Выбирая между рыночной заявкой и заявкой с
ограничением цены, инвестор вынужден выбирать либо обя-
зательность исполнения заявки по неопределенной цене, ли-
бо неопределенность исполнения заявки при ограниченной
цене.
Два особых типа заявок - это стоп-заявки и стоп-заявки с
ограничением цены. При подаче стоп-заявки инвестор должен
указать стоп-цену, которая должна быть ниже рыночной в за-
явке на продажу и выше рыночной в заявке на покупку в мо-
мент подачи заявки. Стоп-заявка может рассматриваться как
условная рыночная заявка, сигналом к исполнению которой
является появление сделок, заключаемых по стоп-ценам.
Стоп-заявки могут использоваться для обеспечения потен-
циальной прибыли, однако существует риск того, что факти-
ческая цена исполнения может существенно отличаться от
стоп-цены.
На примере той же корпорации ABC видно, что стоп-
заявка на продажу акций за 20 долл. не будет выполнена до
совершения кем-либо сделки по цене 20 долл. и ниже. И на-
оборот, стоп-заявка на покупку акций за 30 долл. не будет
выполнена, пока кто-то не заключит сделку по цене 30 долл.
и выше.
Предположим далее, что в рассматриваемом примере ин-
вестор приобрел акции корпорации ABC ранее по 10 долл. за
штуку. Таким образом, в рассматриваемый момент времени
его потенциальная прибыль равна 25-10 долл. за штуку. По-
дача стоп-заявки на продажу акций по 20 долл. за штуку
обеспечит инвестору получение 10 долл. прибыли на каждую
акцию, если курс акции снизится до 20 долл. Если же курс
акций возрастет, то заявка инвестора на продажу останется
без внимания, и его потенциальная прибыль возрастет. Таким
образом, стоп-заявка в какой-то степени защищает потенци-
альную прибыль инвестора. Однако если падение курса акции
59

будет более стремительным - до 12 долл. за штуку, то в этой
ситуации можно не успеть выполнить стоп-заявку по цене,
близкой к 20 долл., и тогда реальная прибыль может оказать-
ся значительно ниже. Например, при продаже акций по 16
долл. за штуку прибыль составит всего 6 долл. на акцию вме-
сто ожидавшихся 10 долл.
При подаче стоп-заявки с ограничением цены инвестор
указывает две цены: стоп-цену и предельную цену исполне-
ния. При появлении на рынке сделок по цене, которая дости-
гает или переходит стоп-цену, это поручение превращается в
заявку с ограничением цены.
Гарантии исполнения заявок. Брокерская фирма, принимая
поручения от своих клиентов заявки на покупку или продажу
ценных бумаг, нуждается в определенных гарантиях, особен-
но если клиент выступает в качестве покупателя. В качестве
таких гарантий могут выступать вексель на всю сумму сделки;
залог в размере 25-100% объема сделки, внесенный на счет
брокера; текущий счет инвестора, открытый в брокерской
фирме и доступный для брокера; счет с использованием мар-
жи, т.е. текущий счет с правом производить овердрафт. При
открытии инвестором счета с использованием маржи он обыч-
но разрешает брокерской фирме отдавать свои ценные бумаги
другим клиентам данной фирмы, совершающим операции
продажи ценных бумаг "без покрытия " или так называемые ко-
роткие продажи (short sales).
Операция "короткая продажа " состоит в продаже ценных
бумаг, взятых в долг у брокера. Операцию проводит инве-
стор-спекулянт, рассчитывающий на падение курса ценных
бумаг до истечения срока возврата ценных бумаг брокеру. В
этом случае он получает прибыль за счет разницы цен прода-
жи и покупки в соответствии с золотым правилом инвестиро-
вания: "покупай дешево и продавай дорого". Однако данная
операция сопряжена с высоким риском понести значитель-
ные убытки при повышении курса ценных бумаг, поскольку в
этом случае для исполнения обязательств перед брокером ин-
вестор покупает на рынке ценные бумаги по более высокой
цене, чем была цена их продажи.
2) Коммерческая деятельность по ценным бумагам.
Коммерческая деятельность по ценным бумагам состоит в
выполнении профессиональным участником рынка ценных
бумаг сделок по купле-продаже ценных бумаг от своего име-
ни и за свой счет по объявленным им ценам покупки и про-
дажи. Коммерческая деятельность осуществляется дилерами
60

(dealer), которые получают прибыль за счет торговли ценны-
ми бумагами.
Дилеры обычно специализируются на работе с определен-
ными группами ценных бумаг. Объявляя свои котировки (це-
ны покупки и продажи) этих ценных бумаг, они тем самым
берут на себя обязательство заключать сделки именно по
этим ценам.
Дилеры следят за состоянием рынка, на котором работа-
ют. Своей деятельностью они поддерживают активность и
ликвидность рынка и оказывают стабилизирующее воздейст-
вие на курсы ценных бумаг. При этом они следуют золотому
правилу инвестирования: покупают дешево в условиях пре-
вышения предложения ценных бумаг и продают дорого при
возрастании спроса на них, компенсируя тем самым времен-
ные дисбалансы между спросом и предложением. Продавцы и
покупатели ценных бумаг на фондовой бирже и внебиржевом
рынке могут быть связаны через дилера (рис. 1.6). Таким об-
разом, коммерческую деятельность дилер может совмещать с
посреднической, выполняя функции брокера. Для многих
фондовых бирж более типичной является система двойного
посредничества, представленная на рис. 1.7.
Продавец
Деньги
Деньги
Покупатель
Ценные бумаги N^ ^~ Ценные бумаги
Рис. 1.6. Схема совершения сделки через дилера
Деньги
Деньги
Продавец
/БрокерЧ /
Заявка
Заявка
4 (Брокер м
Покупатель
i
Дилер
Ценные бумаги Ценные бумаги
Рис. 1.7. Схема двойного посредничества
Подобная система торговли ценными бумагами применя-
ется на российском рынке ГКО. В качестве дилеров при этом
выступают так называемые первичные инвесторы.
Первичными инвесторами считаются дилеры (как правило,
коммерческие банки), удовлетворяющие установленным эми-
61

тентом ценных бумаг требованиям, имеющие право на по-
купку ценных бумаг при их первичном размещении. Отдель-
ные дилеры или дилерские синдикаты могут участвовать в
размещении новых выпусков ценных бумаг на условиях га-
рантированного размещения.
Таким образом, основными функциями дилеров являются:
установление котировок ценных бумаг; поддержание актив-
ности и ликвидности рынка, а также стабилизация рыночных
курсов ценных бумаг посредством их покупки и продажи; по-
среднические услуги на рынке ценных бумаг; участие в раз-
мещении новых выпусков ценных бумаг.
На фондовом рынке брокеры и дилеры представлены спе-
циализированными брокерско-дилерскими фирмами, осно-
ванными на частной или акционерной формах собственности.
В условиях развитых фондовых рынков существует большое
разнообразие брокерских фирм в зависимости от категории
обслуживаемых клиентов, географического региона, специа-
лизации и полноты предоставляемых услуг.
Различают брокерские фирмы, ориентированные на об-
служивание индивидуальных или институциональных инве-
сторов. К первым относятся, как правило, крупные брокер-
ские фирмы, имеющие свою систему электронной связи с
многочисленными филиалами, отделениями и крупнейшими
фондовыми биржами, оказывающие своим клиентам полный
комплекс брокерских услуг. Институциональные инвесторы
обычно обслуживаются либо в специальных отделениях круп-
ных брокерских фирм, либо в более мелких брокерских фир-
мах, специализирующихся на работе с подобными клиентами.
Выделяются также региональные брокерские фирмы, рабо-
тающие с ценными бумагами, имеющими отношение к неко-
торому географическому региону, и так называемые брокер-
ские фирмы с пониженной комиссией, предлагающие ограни-
ченный спектр услуг за пониженную цену.
На российском фондовом рынке брокерские фирмы суще-
ствуют в форме товариществ (обществ) с ограниченной от-
ветственностью. В условиях переходной экономики они при-
нимают участие в процессе акционирования государственных
предприятий, в размещении государственных ценных бумаг,
содействуют предприятиям и местным органам управления в
выпуске облигаций.
3) Деятельность инвестиционного фонда.
Деятельность инвестиционного фонда состоит в выпуске
акций с целью привлечения денежных средств инвесторов и
их последующего вложения от имени фонда в другие финан-
совые активы.
62

Наибольшее распространение получили "открытые" паевые
(или взаимные) инвестиционные фонды, образованные в
форме открытого акционерного общества. Открытые инве-
стиционные фонды эмитируют ценные бумаги и продают их
всем желающим с обязательством выкупа ценных бумаг в те-
чение достаточно короткого срока (например, 15 дней со дня
подачи заявки инвестора [30]). Объем акций, выпускаемых
подобными инвестиционными фондами, не ограничен и по-
стоянно меняется. По этой причине их часто называют ком-
паниями с переменным капиталом. Доходы инвестиционного
фонда образуются за счет эффективного управления принад-
лежащим ему портфелем финансовых активов. Таким обра-
зом, для портфельных менеджеров инвестиционных фондов
особую актуальность имеют задачи оптимального портфельного
инвестирования, рассматриваемые далее, в гл. 5.
Законодательно, как правило, устанавливаются ограниче-
ния на вложения инвестиционных фондов, направленные на
уменьшение риска за счет диверсификации инвестируемого
капитала, т.е. распределения капитала между различными ак-
тивами.
В мировой практике известны инвестиционные взаимные
фонды (mutual funds), различающиеся целями, стратегиями и
методами работы. Инвестиционные фонды могут ориентиро-
ваться на достижение таких целей, как:
• высокие доходы при повышенном риске вложений (вло-
жения в акции быстро развивающихся "технологических
компаний");
• сравнительно невысокие доходы с минимальным риском
(вложения в государственные и муниципальные ценные
бумаги);
• получение приемлемой доходности с минимальным рис-
ком за счет диверсификации вложений и активного
управления портфелем активов.
Для обеспечения чековой приватизации государственных
предприятий в Российской Федерации [23, 30] были образо-
ваны специализированные чековые инвестиционные фонды.
Приобретение акций этих фондов было возможно как за де-
нежные средства, так и за приватизационные чеки. Привле-
ченные денежные средства и чеки использовались фондами
для покупки акций приватизируемых предприятий и форми-
рования собственных портфелей активов.

Глава 2
МЕТОДЫ АНАЛИЗА
ЦЕННЫХ БУМАГ БЕЗ УЧЕТА
ФАКТОРА НЕОПРЕДЕЛЕННОСТИ
Модели должны быть настолько
простыми, насколько возможно, но
не проще.
А. Эйнштейн
Глава содержит краткое описание традиционных детерминирован-
ных методов финансовой математики, используемых для оценки стои-
мости и доходности активов в предположении полной определенности.
Основное внимание уделяется анализу краткосрочных ценных бумаг, а
также анализу акций и облигаций на основе метода дисконтирования
платежей. Обсуждается проблема наличия временной структуры про-
центных ставок при анализе облигаций.
По рассматриваемым в главе вопросам рекомендуется дополни-
тельная литература: [8, 11, 19, 28, 33] (анализ основных видов ценных
бумаг); [15, 32] (методы детерминированной финансовой математики).
Целью финансового инвестирования является вложение
временно свободных денежных средств (сбережений) в фи-
нансовые активы (ценные бумаги) в текущий момент времени
для получения еще большей их суммы в будущем. Инвестор
оказывается перед выбором: больше потреблять сейчас или
инвестировать сейчас, чтобы больше иметь в будущем. Выбор
инвестора осложняется рядом проблем.
Первая проблема состоит в наличии риска потери потен-
циальной полезности при инвестировании средств. Действи-
тельно, инвестор отказывает себе в возможности получить
пользу от имеющихся у него денег немедленно (обратив их в
товары и услуги), довольствуясь более низким уровнем их по-
лезности в виде вложений в ценные бумаги. Эта потеря по-
тенциальной полезности должна быть каким-то образом ком-
пенсирована.
Другая проблема заключается в неопределенности относи-
тельно будущей стоимости и покупательной способности де-
нег в момент, когда они возвращаются к инвестору. Неопре-
деленность порождает риск, причем финансовые инвестиции
связаны с различными рисками, например риском невыпол-
64

нения обязательств по отношению к инвестору (default risk),
риском потери покупательной способности (purchasing power
risk) или инфляционным риском. Указанные риски делают
обладание деньгами сейчас предпочтительнее обещаний по-
лучить то же их количество в будущем, т.е. деньги имеют
свойство положительного временного предпочтения (positive
time preference).
Для того чтобы сделать инвестиции более привле-
кательными, связанные с ними риски должны быть компен-
сированы соответствующими премиями за риск (risk premiums).
Очевидно, чем больше срок инвестирования, тем больше не-
определенность (следовательно, и риски), а значит, тем
большая премия должна быть предложена для их компенса-
ции. Это дает основание говорить о "неравноценности" денег,
относящихся к различным моментам времени (time-value of
money), и необходимости учета фактора времени при приня-
тии инвестиционных решений. По этой причине выбор инве-
стора должен основываться на оценке и сравнении текущей и
будущей стоимости имеющихся в его распоряжении денеж-
ных средств и, конечно, их покупательной способности в раз-
личные моменты времени.
Традиционно учет фактора времени и связанных с ним
рисков при определении стоимости активов осуществляется с
помощью процентов. Проценты компенсируют риски, сопут-
ствующие вложениям денежных средств. Заемщики выплачи-
вают проценты инвесторам и кредиторам, пользуясь дополни-
тельной выгодой раннего потребления привлеченного капита-
ла. Для определения эффективности вложений и сравнения
альтернативных вариантов инвестирования служат ставки
процентов (interest rates), которые характеризуют доходности
активов (rates of return), соответствующие определенным пе-
риодам владения активами (holding periods). Для удобства
сравнительного анализа различных активов обычно исполь-
зуется один и тот же условный период владения, равный од-
ному году.
В данной главе будем предполагать, что все риски учиты-
ваются при назначении ставок процентов и все параметры
финансовых операций известны в момент их совершения. В
этом случае при анализе финансовых активов важны лишь их
стоимости и доходности, которые являются детерминирован-
ными (неслучайными) величинами. Оптимальная стратегия
при торговле ценными бумагами, как мы уже отмечали, за-
ключается в золотом правиле инвестирования: "покупай де-
шево и продавай дорого". Заметим, что именно такой "детер-
минированный подход" применялся для анализа финансовых
5 Зак. 7084 65

активов на начальном этапе развития теории инвестирования
(investment theory) в 1920-1940 гг.
На данном этапе основополагающими были работы
И. Фишера1, Дж. Вильямса2, а также более поздняя работа
Ф. Модильяни и М. Миллера3. Работа И. Фишера заложила
основы теории процентных ставок. Дж. Вильяме предложил
подход к оцениванию основных финансовых активов, а
Ф. Модильяни и М. Миллер - методы оценки стоимости кор-
поративного капитала. Основные принципы и методы этих
теорий легли в основу детерминированной финансовой мате-
матики и являются одним из элементов фундаментального
анализа рынка ценных бумаг.
Центральной идеей при оценке "фундаментальной" стои-
мости финансовых активов является предположение о том,
что "истинная" стоимость любого финансового актива в те-
кущий момент времени равна "текущей стоимости" всех
ожидаемых в будущем по данному активу платежей, т.е. на-
личных денежных потоков.
При этом основная задача фундаментального анализа со-
стоит в определении величины и моментов поступления пла-
тежей, а также нахождении их "приведенных" к текущему мо-
менту стоимостей. Операция "приведения" осуществляется с
помощью соответствующих процентных ставок, известных
как ставки дисконтирования (discount rates).
В рамках "классического" фундаментального анализа по-
токи платежей и ставки дисконтирования, определяемые
"экспертным" образом, полагаются фиксированными (неслу-
чайными), что приводит к использованию методов детерми-
нированной финансовой математики. Данный раздел финан-
сового анализа хорошо "обеспечен" учебной литературой
(см., например, [15, 32]). Поэтому в настоящей главе учебно-
го пособия ограничимся лишь кратким изложением указан-
ных методов применительно к задачам анализа основных ви-
дов ценных бумаг.
Принципы определения "фундаментальной" стоимости
ценных бумаг будут использоваться также в рамках вероятно-
стного подхода при описании количественных методов анали-
за ценных бумаг в условиях неопределенности (см. разд. 4.4).
1 См.: Fisher I. The Theory of Interest. New York; Macmillan, 1930.
2 См.: Williams J. B. The Theory of Investment Value. Amsterdam, North Hol-
land, 1921.
3 См.: Modigliani F., Miller M. The cost of capital, corporation finance and the
theory of investment // American Economic Review. 1958. V. 48 (June).
P. 261-297.
66

2.1. НАЧИСЛЕНИЕ ПРОЦЕНТОВ
И ДИСКОНТИРОВАНИЕ
Рассмотрим вначале задачу определения стоимости и до-
ходности финансовых активов с фиксированным доходом в
виде процентов, начисляемых в соответствии с установленной
ставкой от оговоренной суммы в течение установленного
срока (горизонта) инвестирования.
Будем предполагать, что срок инвестирования включает Т
(7>1) периодов владения активов, а частота начисления про-
центов за один период владения равна m (m > 1).
2.1.1. Принципы расчета процентов.
Виды процентных ставок
Рассмотрим простой случай, когда денежные средства
вкладываются на срок, равный одному периоду владения, т.е.
7М и при этом /и=1. Обозначим:
Pq — начальная стоимость вклада, т.е. сумма вклада в нача-
ле периода;
/ - величина процентного дохода по вкладу;
Р\ — конечная стоимость вклада (terminal value), т.е. сумма
вклада в конце периода (очевидно, данная операция имеет
смысл, если Р\ > Pq).
В зависимости от того, как учитываются проценты, разли-
чают два способа расчета процентов: наращение на началь-
ную сумму вклада и скидка с конечной суммы вклада. Этим
способам соответствуют два вида ставок.
1) Наращение на начальную сумму вклада.
При данном способе проценты учитываются при опреде-
лении величины суммы вклада Р[ в конце периода по извест-
ной начальной сумме вклада Pq. Проценты определяются от
суммы Pq в соответствии с заданной ставкой процентов (inte-
rest base rate) R (R>0) по формуле I=RPq. Тогда стоимость
вклада в конце периода будет равна:
Ставка R называется простой (декурсивной) ставкой. При
заданных значениях Pq и Р\ она может быть рассчитана по
формуле
* = ^ = ///&. (2-2)
67

Таким образом, если рассматриваются однопериодные
вложения, то наращение осуществляется в соответствии с
простой ставкой R.
Ставка R обычно задается для условного периода, равного
одному году. Если при этом продолжительность года равна N
(7V=360, 365 либо 366 дней [32]), а срок вложений равен п
(n<N) дням, то ставка наращения, соответствующая сроку
вложений п, равна Rn = nR/N.
Конечная стоимость актива согласно (2.1) определяется по
формуле
Л = РоО+Я„) = />0(1+ nR/N) , (2.3)
а сумма начисленных за п дней процентов будет равна
I=P$nR/N. Очевидно, доход инвестора в виде начисленных
процентов тем больше, чем больше ставка У?, и, таким обра-
зом, ставка R вида (2.2) характеризует доходность вложений
на заданный период.
2) Скидка с конечной суммы вклада.
При данном способе расчета проценты учитываются при
определении начальной суммы вклада /fo, необходимой для
получения по истечении срока вклада заданной суммы вкла-
да Л-
Проценты определяются на основании конечной стоимо-
сти вклада в соответствии с установленной учетной ставкой Q
(Q>0): / =QP\. Начальная сумма вклада Рц определяется пу-
тем учета процентов, т.е. вычитанием из конечной стоимости
вклада Pj суммы процентов:
Po = Pi~ 1= Л " QP\ = P\ (l-G). (2-4)
Если оговариваются обе суммы Pq и Р\ , то может быть
определена ставка Q по формуле
е = /Ц/Ь =///>,. (2.40
Р
Ставка Q называется простой учетной (антисипативной)
ставкой. Таким образом, если рассматриваются однопериод-
ные вложения, то текущая стоимость определяется с помо-
щью операции учета процентов в соответствии с простой
учетной ставкой. Ставка Q, так же как и ставка /?, характери-
зует доходность вложений: чем больше Q, тем больше вели-
чина процентного дохода и тем меньше начальных средств
требуется для получения заданной суммы в конце периода
вложений.
68

Ставка Q обычно задается для условного периода, равного
одному году. Если продолжительность года и срок вложений
равны соответственно N и п дням (n<N), то учетная ставка,
соответствующая сроку вложений л, будет равна Qn=nQ/N.
Текущая стоимость актива согласно (2.4) определяется по
формуле
Ро = Р\ (1-0,) = P\ (I" nQ/N)9 (2.5)
а сумма процентов (дисконта) равна / = P\nQ/N.
3) Соотношение между ставками.
Если в формулах (2.1) и (2.4) используются одни и те же
значения Pq и Р\, то Q<R. Действительно, на основании оче-
видного соотношения (1 —Q)(l+i?)=l получаем:
0 Л
откуда следует, что ставки Q и R связаны соотношением:
1-0 = -!-. (2.6)
Подставляя (2.6) в (2.4), находим, что стоимость вклада в
начале периода Р$ равна дисконтированной стоимости (dis-
counted value) суммы вклада в конце периода:
По этой причине ставку Q часто называют дисконтной
ставкой (discount base rate) за период владения активом, а ве-
личину 1/(1+7?) - дисконтным множителем или коэффициен-
том дисконтирования. Формула (2.7) далее будет обобщена на
случай финансовых активов, владение которыми связано с
более сложными потоками платежей.
2.1.2. Формулы простых и сложных процентов
Если денежные средства вкладываются на Т>\ периодов
инвестирования, то на практике для определения конечной
стоимости вклада Pj через Т периодов могут использоваться
два альтернативных способа начисления процентов, извест-
ных как формулы простых и сложных процентов. Эти спосо-
бы различаются базой, используемой для их начисления.
Если предполагается, что начисление процентов (compound-
69

ing) осуществляется в конце каждого периода владения, то
говорят, что процентный доход капитализируется, а ставка
наращения процентов называется ставкой капитализации
дохода.
Формула простых процентов используется в случае посто-
янной базы начисления, когда проценты начисляются только
на инвестируемую сумму денежных средств Pq, и имеет вид
Рт= Ро + RP0 + RPo +...+ RPo = I
Г раз
где величина \ + TR называется множителем наращения по
формуле простых процентов.
Формула сложных процентов используется при последова-
тельно изменяющейся базе начисления, т.е. в том случае, ко-
гда проценты начисляются на инвестируемую сумму Pq с уче-
том ранее начисленных процентов. Конечная стоимость вкла-
да Рт, рассчитанная по формуле сложных процентов, равна
РТ= Ро (1 + Л)Ц+ R) ... (1+Я) = Ро О + К)т>
Г раз
где (1 4- R)T- множитель наращения по формуле сложных про-
центов.
2.1.3. Номинальная и эффективная ставки
Предположим, что начальная сумма вклада равна Ро, а
срок инвестирования включает Т периодов владения. Пусть
проценты начисляются m (m>l) раз в течение периода владе-
ния через равные промежутки времени. Предположим также
для определенности, что период владения равен одному году.
Годовая ставка при условии m-кратного начисления процен-
тов называется номинальной годовой ставкой (nominal annual
rate) и обозначается R(m).
Конечная стоимость вклада Pj в рассматриваемом случае
будет равна
где R(m)/m - ставка процентов за один период начисления
(periodic interest rate).
70

Если срок инвестирования равен неполному числу лет, на-
пример Т+к/т, где 0< к< т, то справедлива формула
Номинальная годовая ставка R(m) при т>\ не отражает
точно действительную доходность вложений (как будет пока-
зано далее, дает заниженную оценку доходности). Для срав-
нения с альтернативными вариантами вложений требуются
точные характеристики доходности. Такими характеристика-
ми являются так называемые эффективные, или действитель-
ные, годовые ставки сложных процентов, приводящие к тому
же результату, что и ставки R(m)/m при начислении процен-
тов т раз в течение одного периода владения.
Найдем эффективную ставку для варианта вложений на Г
лет по номинальной ставке R(m) с m-кратным начислением
процентов.
Для нахождения эффективной годовой ставки рассмотрим
два альтернативных варианта вложений на Глет с начислени-
ем "сложных" процентов. Первый вариант - вложения с на-
числением процентов по некоторой годовой ставке Re, второй
вариант - вложения с начислением процентов m раз в году
при номинальной ставке R(m). Для того чтобы варианты были
эквивалентными, т.е. приводили по истечении Глет к полу-
чению одинаковой суммы Pj при вложении одной и той же
начальной суммы вклада Pq, необходимо, чтобы ставки удов-
летворяли соотношению:
V m
откуда следует:
Г1 + вдГ_ь (2в8)
I )
Таким образом, ставка Re является искомой эффективной
годовой ставкой (effective annul rate). Согласно (2.8) эффек-
тивная ставка при т>\ больше номинальной, а при т=1 сов-
падает с ней.
Далее, говоря о ставках сложных процентов, будем иметь в
виду, что если т>\, то используются эффективные ставки
сложных процентов, т.е. R =У?е.
71

При определении условий кредитных соглашений пред-
ставляет интерес и обратная задача, т.е. определение номи-
нальной ставки R(m) по заданным значениям Re и т. Из (2.8)
следует:
R{m) = т (ф + R, -1). (2.9)
2.1.4. Непрерывно начисляемые проценты
В аналитических исследованиях (при анализе акций, обли-
гаций, опционных и фьючерсных контрактов) удобно предпо-
лагать, что проценты начисляются непрерывно. Это эквива-
лентно предположению о том, что частота начисления про-
центов т->оо, а величина одного периода начисления при
этом становится сколь угодно малой.
Если через Rc>0 обозначить предельное значение номи-
нальной ставки R{m) при т-»оо, то в пределе должно выпол-
няться:
' где величина e^RcT> — множитель наращения по ставке непре-
рывных процентов Re.
Для того чтобы варианты вложений, соответствующие
двум способам начисления процентов, были эквивалентны,
необходимо, чтобы множители наращения, соответствующие
формулам сложных и непрерывных процентов, совпадали.
Тогда связь между ставками R(m) и Rc будет определяться то-
ждеством:
( Ш}Т7 (2.10)
j '
из которого следует, что при заданных R(m) и m эквивалентная
ставка непрерывных процентов удовлетворяет соотношению1:
(2.11)
При использовании формулы сложных процентов в случае
известных Rc и т соответствующая годовая номинальная
ставка равна:
1 В силу принятых обозначений log означает натуральный логарифм.
72

^- 1). (2.12)
Из (2.10) следует, что если начальная стоимость актива
равна Pq и проценты начисляются непрерывно в соответствии
со ставкой Rc в течение времени Т, то конечная стоимость
актива будет определяться по формуле
Рт=Рое(*ст). (2.13)
Важным для анализа является частный случай, когда пери-
од выплат процентов совпадает с периодом инвестирования,
т.е. /и=1.
Пусть в данном случае R=R(l) - простая ставка доходности
за один период инвестирования, а г - эквивалентная ставка
непрерывно начисляемых процентов. Тогда на основании
формул (2.11) и (2.12) получаем следующие соотношения ме-
жду этими ставками:
R=er-\, r=log(l + R). (2.14)
2.1.5. Дискретное и непрерывное дисконтирование
Если вложения осуществляются на Т>\ периодов владе-
ния, актуальной является задача определения в текущий мо-
мент стоимости денежных потоков, относящихся к различ-
ным будущим периодам. Для этой цели используется про-
цедура дисконтирования, которую можно рассматривать как
обратную операцию по отношению к операции начисления
процентов. В зависимости от того, как исчисляются процен-
ты - по формуле сложных процентов или непрерывно, раз-
личают соответственно дискретное и непрерывное дисконти-
рование.
1) Дискретное дисконтирование.
Пусть срок инвестирования равен Т периодам (7>1), в
конце каждого периода начисляются "сложные" проценты.
Допустим, через Т периодов должен поступить платеж Cj, a
простая ставка наращения процентов за один период по вкла-
дам на Т периодов постоянна в течение всего срока инвести-
рования и равна R.
Тогда стоимость платежа Cj в текущий момент времени,
т.е. текущая стоимость платежа Ко (индекс "0" указывает на
принадлежность к текущему периоду), будет равна его дис-
73

каптированной стоимости (discounted value) со ставкой дис-
контирования R:
<215>
или
означающей, что текущая стоимость актива Ко - это сумма,
вложив которую до срока платежа под заданную ставку R,
можно при начислении "сложных" процентов получить ожи-
даемую в будущем сумму платежа.
Если проценты начисляются т раз за один период (напри-
мер, т раз в году), то с учетом (2.15) текущая стоимость акти-
ва равна
0 (\ + {R/m))mT'
Откуда следует очевидное свойство: чем больше частота
начисления процентов, тем меньшая начальная сумма необ-
ходима для достижения заданной суммы в будущем.
2) Непрерывное дисконтирование.
По аналогии с начислением процентов при т-*оо можно
полагать, что дисконтирование осуществляется непрерывно. В
этом случае с учетом (2.13) имеем:
Vo = Сте~Тг, (2.16)
где простая и "непрерывная" ставки R и г связаны соотноше-
нием (2.14), т.е. г = log(l+ R).
2.2. АНАЛИЗ КРАТКОСРОЧНЫХ
ФИНАНСОВЫХ АКТИВОВ
К краткосрочным активам относятся, как известно, фи-
нансовые активы, имеющие срок обращения, не превосходя-
щий одного года. Примерами таких активов являются кратко-
срочные долговые ценные бумаги (казначейские и банковские
векселя, депозитные и сберегательные сертификаты, ГКО и
др.). При анализе краткосрочные активы удобно рассматри-
вать как "однопериодные" ценные бумаги (Т=\). При этом
срок их обращения обычно выражается в днях, а в качестве
74

характеристик доходности используются простые ставки на-
ращения и дисконтирования. Продолжительность года пола-
гается равной 360, 365 либо 366 дням в зависимости от кон-
кретного рынка, типа актива и статуса участников сделки
(см., например, [21, 32]).
Основная цель вложений в краткосрочные финансовые ак-
тивы - это получение дохода от вложений временно свобод-
ных денежных средств на короткие периоды. По форме (спо-
собу) получения дохода краткосрочные финансовые активы
можно разделить на процентные и дисконтные активы.
Процентные активы покупаются по номинальной стоимо-
сти, а доход по ним принимает форму начисленных процен-
тов, выплачиваемых при их погашении. Для определения
суммы процентов используется установленная ставка нараще-
ния. Примером процентных активов являются депозитные и
сберегательные сертификаты коммерческих банков.
Дисконтные активы продаются ниже номинальной стоимо-
сти, а погашаются по номинальной стоимости. Для определе-
ния суммы дисконта (учтенной суммы) используется установ-
ленная учетная ставка. Примером дисконтных ценных бумаг
являются казначейские и банковские векселя и "бескупон-
ные" облигации (ГКО, T-bills и др.).
Формулы для определения текущей стоимости и доходно-
сти краткосрочных финансовых активов могут быть получены
в соответствии с методами, описанными в разд. 2.1.
2.2.1. Анализ процентных активов
При анализе процентных активов обычно считаются за-
данными следующие характеристики:
Pq - номинальная стоимость актива (или начальная сумма
вклада);
R - годовая ставка наращения процентов;
п - количество дней, оставшихся до погашения актива
(срок вклада);
N - продолжительность года в днях (например, для депо-
зитных и сберегательных сертификатов 7V=365).
Искомыми являются:
Р\ - стоимость актива при погашении (конечная сумма
вклада);
/ - сумма начисленных процентов;
Rn - ставка доходности за фактический период владения
активом.
75

Предполагается, что проценты начисляются за каждый
день владения активом. Ставка доходности за один период
владения определяется на основании заданной годовой ставки
процентов по формуле
/? nR
R
Поэтому в соответствии с формулой наращения процентов
(2.3) по простой ставке (см. разд. 2.1) получаем:
(2.17)
При этом сумма начисленных процентов будет равна:
/= PonR/N.
2.2.2. Анализ дисконтных активов
Основная задача анализа дисконтных активов состоит в
определении текущей стоимости актива в момент его оценки
(например, при учете векселя) до истечения срока погашения.
При этом известными характеристиками считаются:
. Pi - стоимость актива в момент его погашения, как прави-
ло, это номинальная стоимость актива;
Q - годовая учетная ставка;
п - количество дней, оставшихся до погашения актива;
N - продолжительность года в днях (обычно при использо-
вании учетных ставок полагают N=360, участниками сделок
при этом являются, как правило, банковские учреждения).
Искомыми считаются:
Pq - текущая стоимость актива;
/ - сумма дисконта (например, учтенная сумма по вексе-
лю);
Qn - простая учетная ставка за фактический период владе-
ния.
В соответствии с результатами (2.4) текущая стоимость ак-
тива определяется по формуле
^^] (2.18)
а сумма дисконта, таким образом, будет равна / = P\nQ/N .
Заметим, что доходность одной и той же операции с дис-
контными активами может быть выражена как учетной став-
кой Q, так и некоторой ставкой наращения R.
76

Обычно ставкам R и Q соответствуют различные определе-
ния продолжительности года Nr и Nq9 причем Nr = 365, а
NQ = 360.
В соответствии с определениями (2.2) и (2.4') ставки R и Q
устанавливаются выражениями:
R= Л -Ро N_r_ = Л -Л) 365
Ро п Ро п
П ту \[ D D 1£.Г\
Нетрудно показать, что ставки Ли б связаны соотношени-
ем:
NrQ 3650
R = Iy R^ = ^—.
Ow 360-Q/i
Ставка 7?, определяемая по формулам (2.19), (2.21), назы-
вается доходностью к сроку погашения актива или просто до-
ходностью к погашению (Yield To Maturity - YTM).
2.3. АНАЛИЗ ГОСУДАРСТВЕННЫХ
КРАТКОСРОЧНЫХ ЦЕННЫХ БУМАГ
Применим описанные выше формулы для анализа госу-
дарственных краткосрочных ценных бумаг типа казначейских
векселей США, государственных краткосрочных облигаций
(ГКО) Российской Федерации. Для определенности будем
иметь в виду ГКО.
2.3.1. Анализ ГКО при первичном размещении
Рассмотрим отдельно задачи анализа ГКО на первичном и
вторичном рынках. Как известно, первичное размещение
ГКО осуществляется в форме закрытого аукциона для так на-
зываемых первичных инвесторов, выступающих в роли диле-
ров на рынке ГКО (см. п. 1.3.1).
Пусть Pmin - минимальная цена продажи облигаций, или
"цена отсечения", в ходе конкурентных торгов; Р - средне-
взвешенная цена продажи облигаций, по которой удовлетво-
ряются "неконкурентные" предложения участников аукциона.
Предполагается, что цена облигаций задается в процентах от
77

номинальной стоимости, т.е. номинальная стоимость облига-
ции равна 100%.
Основной характеристикой эффективности операции по-
купки облигаций при их первичном размещении является до-
ходность к погашению. Для облигаций со сроком обращения,
равным п дням, купленных инвестором на аукционе по цене
Р9 годовая ставка доходности к погашению определяется по
формуле (2.19), в которой следует принять Р\=100, Pq=P, т.е.
Основными характеристиками доходности выпуска обли-
гаций в целом являются:
• годовая ставка доходности к погашению для облигаций,
купленных по минимальной цене продажи:
_ m-Pmin 365
Л )
• годовая ставка доходности к погашению для облигаций,
купленных по средневзвешенной цене:
^100-^365
Р п
Соответствующие ставки в процентах равны: /?%=/М00%,
Из приведенных формул следует, что доходность облига-
ций, приобретаемых инвесторами на аукционе, определяется
ценой их покупки. В связи с этим ключевой проблемой,
стоящей перед участниками аукциона, является проблема
"предсказания" устанавливаемой эмитентом и априорно не-
известной "цены отсечения". На "цену отсечения" могут
влиять различные факторы, например уровень процентных
ставок и объем свободных денежных средств на финансовом
рынке, ставка рефинансирования, устанавливаемая централь-
ным банком страны, и другие "экзогенные" факторы.
Доходность покупаемых в ходе конкурентных торгов обли-
гаций, очевидно, тем больше, чем ближе цена покупки, ука-
занная в заявке инвестора, к минимальной цене продажи об-
лигаций на аукционе. Однако желание получить максимально
возможную доходность связано с риском не купить облига-
ции вовсе в том случае, если указанные в заявках цены ока-
жутся ниже "цены отсечения".
78

2.3.2. Анализ ГКО на вторичном рынке
На вторичном рынке ГКО основными являются операции
двух типов:
• "покупка облигаций до погашения";
• операция "репо", или RepoK
1) Анализ операции "покупка до погашения".
Операция "покупка до погашения" осуществляется с целью
получения дохода от вложений денежных средств на срок, ос-
тавшийся до погашения ценных бумаг. Именно такую цель
преследуют покупатели облигаций (например, субъекты хо-
зяйствования). Продавцы (обычно дилеры) также рассчиты-
вают на получение дохода, однако их доход образуется за счет
разницы цен первоначальной покупки и продажи облигаций.
Обозначим:
Р'ь и Рп - соответственно цена первоначальной покупки
(bid price) и цена продажи (ask price) облигаций инвестором-
продавцом на вторичном рынке;
па - количество дней, в течение которых продавец владеет
облигациями с момента покупки;
Рь - цена покупки облигаций инвестором-покупателем на
вторичном рынке;
пь - количество дней, оставшихся до погашения облига-
ций, купленных на вторичном рынке.
Тогда доходность операции для покупателя R^ и продавца
Ra определяется по формулам:
= Ра-Гь 365
Ка —w ~- (22Ь)
^Ь Па
Если облигации первоначально были куплены на аукционе
при первичном размещении, а ставки Rb и Ra определяются
для одной и той же сделки, то в формулах (2.25) и (2.26)
следует положить Ра = Р^ па+пь = п.
На основании (2.25), (2.26) могут быть получены формулы
для определения цен, по которым следует покупать Рь* или
продавать Ра* облигации для достижения приемлемой для по-
купателя или продавца доходности операций, обозначаемых
соответственно R^ и Ro*:
Repo - сокращенное от repurchase - "обратный выкуп".
79

Ш <100, (2.27)
(2.28)
2) Текущая стоимость ГКО.
Приведем формулы для определения текущей стоимости
(present value) ГКО спустя t дней после покупки облигации на
аукционе, т.е. за п - t дней до ее погашения. Пусть Рьл
()ук100%) - цена покупки облигации на аукционе в процен-
тах от номинальной стоимости, a RA - соответствующая до-
ходность к погашению для данной облигации. Очевидно,
ГКО относится к дисконтным активам, поэтому для опреде-
ления текущей стоимости V(t) облигации можно воспользо-
ваться формулой (2.18). С учетом принятых обозначений по-
лучаем:
V(t) = Ш . (2.29)
Заметим, что формула (2.29) эквивалентна следующей
формуле, основанной на соотношении (2.17):
Это следует из очевидного соотношения:
II I r
Из приведенных формул следует, что PbA<V(t)<]00 (0</<«),
причем минимальное значение текущей стоимости облигации
V(t) соответствует цене покупки облигации на аукционе, а
максимальное - ее номинальной стоимости при погашении,
т.е. К(0)=/у*, К(и)=100. Таким образом, по мере приближения
даты погашения "теоретическая" текущая стоимость облига-
ции растет: К(/)->100 при t-*n.
Сравнивая значение V{t) с реальной рыночной ценой Р
покупки облигации на вторичном рынке в момент времени /,
можно оценить "выгодность" покупки или продажи облига-
ции как спекулятивной операции (см. разд. 2.4).
80

3) Анализ операции "репо".
Операция "репо" - это продажа ценных бумаг с обязатель-
ством их обратного выкупа через установленный срок по ого-
воренной цене.
Данная операция, совершаемая на вторичном рынке ГКО,
может рассматриваться как операция кредитования под залог
государственных ценных бумаг. Заемщиком при этом высту-
пает продавец ценных бумаг, а кредитором - их покупатель.
Доход кредитора образуется за счет разницы между ценой по-
купки облигации Рь и ценой продажи Ра ценных бумаг их
владельцу, называемой также ценой обратного выкупа. Оче-
видно, при этом должно выполняться условие: Ра >Р^
Доходность операции "репо", т.е. ставка Rrepo по выдавае-
мому кредиту со сроком кредита, равным /, определяется го-
довой ставкой
Если цена покупки облигаций кредитором равна Р^ а
приемлемая годовая ставка по кредиту на срок, равный t
дням (1 <t<n), равна R*repo> TO соответствующая цена
обратного выкупа R*a определяется по формуле
Pb- (2.31)
К подобной операции на вторичном рынке ГКО обычно
прибегают коммерческие банки. При этом данный сегмент
рынка ГКО превращается в разновидность рынка межбанков-
ских кредитов (МБК). Однако кредиты под залог государст-
венных ценных бумаг являются более надежными. Кроме то-
го, доход инвесторов на вторичном рынке ГКО имеет льгот-
ное налогообложение, что позволяет устанавливать более
низкие ставки по кредитам с сопоставимыми сроками. Все
это делает операции "репо" более привлекательными как для
кредиторов, так и для заемщиков, владеющих облигациями.
2,4. АНАЛИЗ ЦЕННЫХ БУМАГ С ПОМОЩЬЮ
МЕТОДА ДИСКОНТИРОВАНИЯ ПЛАТЕЖЕЙ
Перейдем к задачам анализа "многопериодных" ценных
бумаг, срок обращения которых включает несколько перио-
дов владения. С подобными финансовыми активами связан
некоторый ожидаемый в будущем поток платежей, от которо-
6 Зак. 7084 81

го зависит текущая стоимость и доходность активов. При
этом текущая стоимость актива может рассматриваться как
сумма текущих стоимостей ожидаемых по активу платежей.
Таким образом, для определения текущей стоимости активов
может использоваться метод, который обобщает процедуру
дисконтирования, описанную в разд. 2.1, и известен как ме-
тод дисконтирования платежей, или метод капитализации до-
ходов [33].
2.4.1. Общая характеристика
метода дисконтирования платежей
Как отмечалось, первоочередная задача финансового ана-
лиза рынка ценных бумаг состоит в определении истинной
стоимости активов с целью выявления неверно оцененных
рынком ценных бумаг. Традиционно для решения этой зада-
чи используются методы фундаментального анализа, которые
позволяют построить прогноз ожидаемого потока платежей (в
виде процентов по облигациям или дивидендов по акциям),
связанного с владением ценной бумагой. На основе прогноз-
ных значений ожидаемых платежей находится оценка теку-
. щей стоимости (present value) ценной бумаги. Данная оценка
(так называемая фундаментальная стоимость ценной бумаги
V) сравнивается с ее рыночной ценой Р. Для этой цели, как и
в случае оценки инвестиционных проектов [11, 29, 32], может
использоваться характеристика, известная как чистая теку-
щая стоимость (net present value - NPV) ценной бумаги, оп-
ределяемая как разность "фундаментальной" и рыночной
стоимости ценной бумаги: NPV=F-P. Анализ NPV позволяет
дать рекомендации относительно инвестиционной привлека-
тельности ценных бумаг, т.е. о целесообразности их покупки
или продажи в текущий момент времени. Рекомендации для
ценных бумаг с сопоставимым риском опять-таки основыва-
ются на золотом правиле инвестирования "покупай дешево и
продавай дорого", т.е. рекомендуется покупать "недооценен-
ные" (при NPV>0) и продавать "переоцененные" (при NPV<0)
рынком ценные бумаги. Условие NPV=0 соответствует "рав-
новесным" рыночным ценам активов (P=V) и поэтому может
служить для определения "нормальной" или "внутренней" до-
ходности ценных бумаг (Internal Rate of Return - IRR), т.е. до-
ходности, на которую можно рассчитывать при покупке цен-
ной бумаги по ее "истинной" стоимости.
Для определения текущей стоимости ценной бумаги при
заданном ожидаемом по ним потоке платежей традиционно
82

используется метод дисконтирования платежей. Приведем
вначале общее описание данного метода, а затем применим
его для анализа некоторых основных видов ценных бумаг в
предположении полной определенности относительно харак-
теристик потоков платежей, а также ставок дисконтирования.
Используем следующие обозначения:
Т - количество периодов владения ценной бумагой, ос-
тавшихся до ее погашения;
Ct - сумма платежа по ценной бумаге, ожидаемая в перио-
де U P=h 2, ..., Т;
V=VO - текущая стоимость (present value) ценной бумаги в
текущем периоде t=0.
Схема потока платежей по ценной бумаге представлена на
рис. 2.1. При этом относительно потока платежей (cash flow)
{Q} предполагается:
1) платежи поступают в конце каждого периода владения и
подлежат капитализации с начислением процентов по форму-
ле сложных процентов;
2) ставка дисконтирования1 платежей остается постоянной
в течение всего срока обращения ценной бумаги и равна R.
С\ С2 C/_i С( С74 Ст
, + i V i 1 j
0 1 2 ... tA t ... ТА Т
Текущий * * Дата
момент t-й период погашения
Рис. 2.1. Схема потока платежей по ценной бумаге
Тогда в соответствии с методом дисконтирования платежей
текущая стоимость ценной бумаги определяется по формуле
откуда следует:
V{\+R)T= CX(\+R)T~X + C2(l+R)T-2+...+ СтцО+Л) + Ст. (2.33)
На основании (2.33) можно дать следующее обоснование
метода дисконтирования платежей. Левую и правую части
формулы (2.33) можно рассматривать как конечные стоимо-
сти вложений спустя Т периодов, соответствующие двум стра-
тегиям инвестирования, которые состоят в следующем:
1 По умолчанию всюду будем предполагать, что ставки задаются в долях.
83

1) вложение суммы V на Т периодов с начислением слож-
ных процентов по ставке R за один период;
2) покупка ценной бумаги, с которой связан поток плате-
жей {Q} (/=1, 2, ..., 7) при аналогичной схеме начисления
процентов.
Одним из принципов определения стоимости финансовых
активов является принцип отсутствия арбитражных возмож-
ностей (arbitrage opportunities) на рынке, находящемся в со-
стоянии равновесия. Такие возможности возникают, когда
можно получить гарантированный (безрисковый) доход без
каких-либо инвестиций (см. разд. 6.3). В соответствии с дан-
ным принципом описанные выше стратегии должны быть
одинаково выгодны для инвесторов в смысле конечного до-
хода, что приводит к необходимости выполнения соотноше-
ния (2.33).
Таким образом, текущая стоимость ценной бумаги может
интерпретироваться как сумма, вложив которую на срок, рав-
ный сроку обращения ценной бумаги, под некоторую ставку
R, можно в итоге получить сумму, равную стоимости всех
ожидаемых по ценной бумаге платежей. При этом ставку R
удобно интерпретировать как ставку ожидаемой доходности
вложений с сопоставимой степенью риска, например вложений
в соответствующие инвестиционные проекты (см. п. 4.4.3).
Очевидно, воспользоваться формулой (2.32) можно, если
известны характеристики R и {Q}. Однако на практике ис-
тинные значения R и {Q} неизвестны, поэтому используются
их ожидаемые (прогнозные) значения. В данном разделе пред-
полагается, что используются некоторые фиксированные зна-
чения этих характеристик. Задачи анализа стоимости и до-
ходности ценных бумаг в условиях неопределенности рас-
сматриваются в разд. 4.4.
2.4.2. Анализ ценных бумаг на основе
чистой текущей стоимости и внутренней доходности
Различные инвесторы на практике могут по-разному оце-
нивать ожидаемые значения R и {Q, а следовательно, полу-
чать различные оценки величины V. Найденные значения V
затем используются для оценки инвестиционной привлека-
тельности ценных бумаг на основе анализа NPV и IRR.
Чистая текущая стоимость NPV ценной бумаги определя-
ется как разность между ее текущей (дисконтированной)
стоимостью (discounted present value) V и рыночной стоимо-
84

стью (ценой покупки) Р ценной бумаги в текущий момент
времени:
NPV= V- P. (2.34)
Известное золотое правило инвестирования при покупке и
продаже ценных бумаг основывается на анализе NPV и в
формальной записи имеет вид:
• покупать (и не продавать), если NPV>0, т.е. ценная бума-
га недооценена рынком: V>P\
• продавать, в том числе совершать короткую продажу (и
не покупать), если NPV<0, т.е. ценная бумага переоценена
рынком: V<P.
Доходность Л* ценной бумаги, купленной по цене Р9 при
условии, что ее истинная стоимость равна V, определяется из
условия
NPV= V-P=0. (2.35)
Ставка R* при этом называется внутренней доходностью
(IRR) ценной бумаги. Для ее определения запишем (2.35) в яв-
ном виде относительно R, используя (2.32):
■ - Р = 0. (2.36)
Искомое значение R* находится как решение уравнения
(2.36) относительно Л. В общем случае уравнение (2.36) ана-
литического решения не имеет, поэтому используются при-
ближенные численные методы. Для этой цели удобно уравне-
ние (2.36) представить в виде:
с,х'=0, (2.37)
/=0
где Q)=-P, х£-1/(1+/?). Для нахождения решения х уравнения
(2.37) могут использоваться различные численные методы,
например метод Ньютона - Рафсона [6]. Искомое значе-
ние R* связано с х соотношением R*=(l-x*)/x*. Графиче-
ская интерпретация взаимосвязи между NPV, ЛиЛ* пока-
зана на рис. 2.2.
В простейшем случае "однопериодной" ценной бумаги,
когда 7М, Р - цена покупки актива в начале периода, а С\ -
стоимость актива в конце рассматриваемого периода, уравне-
ние (2.36) принимает вид:
85

а искомое значение внутренней доходности ценной бумаги
равно:
#=<±=^, (2.38)
что согласуется с ранее обсуждавшейся формулой (2.2) для
доходности вложений на один период.
Рис. 2.2. Связь NPVw IRR ценной бумаги
Неверно оцененные рынком ценные бумаги являются при-
влекательными для инвесторов с точки зрения покупки или
продажи, стимулируя соответственно увеличение спроса или
предложения. В условиях эффективного рынка активная дея-
тельность инвесторов по отношению к таким ценным бума-
гам приводит в результате к установлению на них равновес-
ных рыночных курсов на уровне их "истинной" стоимости,
т.е. к выполнению тождества Р= V. В этом случае внутренняя
доходность ценной бумаги Ft совпадает с "нормальной доход-
ностью" (normal return), т.е. с доходностью, которую в усло-
виях равновесного эффективного рынка должны обеспечивать
все активы с сопоставимым риском.
Ставка внутренней доходности /?*, так же как и NPV, ис-
пользуется для оценки инвестиционной привлекательности
конкретной ценной бумаги среди вложений с сопоставимой
степенью риска, ожидаемая (требуемая) доходность которых
определяется ставкой R. Решение относительно инвестици-
онной привлекательности ценной бумаги выносится на осно-
вании следующих правил:
86

1) если K*>R, то данная ценная бумага является привлека-
тельной для покупки, поскольку имеет более высокую доход-
ность (abnormal return), чем вложения с сопоставимой степе-
нью риска;
2) если /?*</?, то данная ценная бумага является непривле-
кательной для покупки, поскольку имеет более низкую до-
ходность, чем вложения с сопоставимой степенью риска;
3) если /?*=/?, то доходность данной ценной бумаги нахо-
дится на уровне доходности вложений с сопоставимой степе-
нью риска, т.е. может считаться "нормальной".
Между характеристиками NPV и IRR ценной бумаги, та-
ким образом, существует следующая зависимость: если
NPV>0, то Л*>Л; если NPV<0, то #<R; если NPV=0, то Л*=Л
(см. рис. 2.2).
Описанный выше подход может использоваться для оцен-
ки текущей стоимости и анализа инвестиционной привлека-
тельности различных активов. Проиллюстрируем его исполь-
зование для некоторых основных видов ценных бумаг.
2.5. АНАЛИЗ ОБЛИГАЦИЙ
Как известно (разд. 1.3), облигации представляют широкий
класс долговых ценных бумаг с ограниченным сроком обра-
щения и фиксированным доходом. По сроку обращения раз-
личают краткосрочные, среднесрочные и долгосрочные обли-
гации.
Краткосрочные облигации обычно являются бескупонны-
ми. При анализе их удобно рассматривать как однопериодные
активы, доход по которым образуется за счет разницы цен
покупки и продажи (погашения) (см. разд. 2.2, 2.3).
Облигации с более длительными сроками обращения
обычно являются купонными, т.е. предусматривают периоди-
ческие выплаты процентов (купонного дохода) в течение сро-
ка обращения и возврат номинальной стоимости облигации
при погашении.
Менее типичным видом облигаций являются так называе-
мые бессрочные облигации, т.е. облигации, погашение которых
не ожидается в обозримом будущем. Примерами бессрочных
облигаций (undated, irredeemable gilts) являются несколько
типов государственных облигаций, обращающихся на фондо-
вом рынке Великобритании. Наиболее известными среди них
являются "2,5-процентные консоли" 1888 г. выпуска [22].
Однако анализ подобных ценных бумаг представляет скорее
теоретической интерес.
87

В настоящем разделе приводится краткое изложение мето-
дов анализа основных типов "многопериодных" облигаций в
предположении полной определенности относительно пото-
ков платежей по ним и ставок дисконтирования.
2.5.1. Анализ купонных облигаций
Для определения текущей стоимости купонной облигации
воспользуемся общей формулой (2.32) при некоторых пред-
положениях, учитывающих особенности потока платежей по
купонным облигациям.
Обозначим:
7<оо - количество периодов владения, оставшихся до по-
гашения облигации;
F - финальная выплата по облигации (principal), совпа-
дающая с ее номинальной стоимостью;
(7>0 - ставка купонного дохода (купонная доходность) за
один период владения в долях;
т>\ - частота выплат купонного дохода за один период
владения;
R>0 - ставка дисконтирования купонного дохода, соответ-
ствующая одному периоду владения.
Ставка R интерпретируется как ожидаемая доходность
вложений.
Относительно потока платежей {Q} предполагается:
\ qF- купонный доход в периоде 7=1, 2, ..., 7-1;
Cf= -s qF+F - купонный доход плюс финальная выплата в
I периоде t=T.
Предполагается также, что платежи в виде купонного до-
хода поступают в конце каждого периода и подлежат капита-
лизации с начислением сложных процентов.
Рассмотрим вначале случай, когда 7<оо, q>0 и /и=1, т.е. ко-
гда период выплат купонного дохода совпадает с периодом
владения облигацией. С учетом сделанных предположений из
(2.32) следует, что текущая стоимость купонной облигации
определяется соотношением:
!^4V^ <239)
= qFaTtR +F0, (2.40)

где
^=S(iW (241)
- текущая стоимость ренты [32] с Г единичными выплатами и
постоянной ставкой наращения R;
<142>
- текущая стоимость финальной выплаты по облигации, Fq<F.
Обозначим аЦЦ-/?)"1 - дисконтный множитель. По фор-
муле для суммы Т первых членов геометрической прогрессии
имеем:
^=1-^. (2.43)
На основании (2.41)—(2.43) из (2.40) следует:
V=qF р-уЧ + ^0 = Fo + j(F-Fo). (2.44)
Если известна текущая рыночная стоимость облигации
(цена покупки) Р, то можно оценить инвестиционную при-
влекательность облигации на основе чистой текущей стоимо-
сти NPV и внутренней доходности /?*, которая, как известно,
является решением уравнения NPV=Q, т.е. удовлетворяет тож-
деству:
P=Fo + -%t(F-Fq). (2.45)
К
Ставка внутренней доходности облигации R* определяет
так называемую полную доходность облигации {доходность к
погашению), поскольку учитывает все виды платежей по обли-
гации до момента ее погашения.
Получить явное выражение для ставки Ft в общем случае
затруднительно, поскольку от нее зависит и величина Fq9 по-
этому выполним качественный анализ формулы (2.45).
На основании (2.45) можно сделать следующие выводы:
• рыночная цена купонной облигации прямо пропорцио-
нальна ставке купонного дохода q, причем P>FO для #>0;
• существует обратная зависимость между рыночной ценой
облигации (ценой покупки) и ее доходностью /?*.
89

Для купонных облигаций с несколькими выплатами ку-
понного дохода в течение одного периода владения (т.е. при
т>\) может быть проведен аналогичный анализ, если предва-
рительно принять:
R=R(m) - номинальная ставка начисления процентов за
один период владения в предположении, что т>\\
R/m - ставка начисления процентов за один период выплат
купонного дохода;
q/m - ставка купонного дохода за один период выплат.
По аналогии с предыдущим случаем можно получить сле-
дующую формулу для текущей стоимости облигации:
„т? тТ 1 it
v= SL. у 1 +
m ^(l + Л/т/ (\ + R/mfT'
Данная формула аналогичным образом может быть приве-
дена к виду (2.44).
2.5.2. Анализ бессрочных облигаций
Применим описанный метод для анализа бессрочных об-
лигаций.
Предположим, что т=1 и Г=оо, т.е. период выплат купон-
ного дохода совпадает с периодом владения облигацией, а ее
погашение не ожидается в обозримом будущем. При Г=оо те-
кущей стоимостью финальной выплаты в формуле (2.40)
можно пренебречь, поскольку по свойству предела
lim (1+Л)71=оо V ,
Т—>со
что влечет Fq-^О при Г->оо. Таким образом, для бессрочной
облигации
00 Л JJ 00
Так как d=(l+R)"*<\9 то по свойству суммы бесконечной
геометрической прогрессии имеем
На основании (2.47) из (2.46) следует:
V=^-. (2.48)
R
90

Из (2.48) следует, что текущая стоимость облигации прямо
пропорциональна величине выплачиваемого по ней купонно-
го дохода и обратно пропорциональна ожидаемой доходности
вложений.
Если Р - рыночная цена покупки облигации, то с учетом
(2.48) ставка Ft внутренней доходности облигации, опреде-
ляемая из условия NPV— У-Р=0, равна:
Ft=^L. (2.49)
Обычно ставка доходности, определяемая как отношение
купонного дохода к рыночной цене (цене покупки) облига-
ции, называется текущей доходностью (current yield) облига-
ции. Таким образом, в случае бессрочных облигаций полная
доходность, определяемая ставкой Ft, совпадает с текущей
доходностью облигации.
Соотношение (2.49) очевидным образом подтверждает сде-
ланные в п. 2.5.1 выводы относительно взаимосвязи рыноч-
ной цены Р, купонной ставки q и внутренней доходности об-
лигации Ft.
2.5.3. Анализ бескупонных облигаций
В предположении #=0 и 1<Г<оо из формулы (2.39) следует,
что текущая стоимость бескупонной Г-периодной облигации
совпадает с текущей ценой финальной выплаты, т.е.
V=^W = F°- <2-50)
Из (2.50) и условия NPV=zV-P=b следует, что внутренняя
доходность облигации Ft удовлетворяет тождеству
фу
и определяется по формуле
Ставка /Г определяет полную доходность, или доходность к
погашению, бескупонной Г-периодной облигации, так как
разность между ценой покупки облигации и ее номинальной
91

стоимостью, выплачиваемой при погашении облигации, явля-
ется единственным источником дохода владельца данной об-
лигации.
2.5.4. Анализ облигаций при наличии
временной структуры процентных ставок
Для оценки текущей стоимости облигаций с помощью ме-
тода дисконтирования платежей требуется знание ставок дис-
контирования для всех будущих периодов владения облигаци-
ей. В связи с этим возникает два вопроса:
• можно ли использовать одну и ту же ставку дисконтиро-
вания платежей, ожидаемых в различные периоды владе-
ния?
• какие ставки используются в качестве ставок дисконти-
рования ожидаемых платежей при оценке купонных об-
лигаций?
Из практики известно, что ставки доходностей для активов
с различными сроками до погашения различаются по величи-
не и находятся в постоянном движении. В каждый момент
времени на финансовом рынке имеет место некоторая сово-
купность процентных ставок (даже для активов с сопостави-
мой степенью риска), относящихся к активам с различными
сроками до погашения. Эта совокупность называется времен-
ной структурой процентных ставок. Поэтому ответ на первый
вопрос очевиден: каждому будущему периоду должна соответ-
ствовать своя ставка дисконтирования, что противоречит ра-
нее сделанному упрощающему предположению о постоянстве
ставок дисконтирования.
Ответ на второй вопрос требует более подробных поясне-
ний. Очевидно, ставки дисконтирования платежей, необхо-
димые для оценки стоимости облигаций в текущий момент
времени, должны зависеть от временной структуры процент-
ных ставок, сложившейся на финансовом рынке в анализи-
руемый момент времени. Дадим формальное определение по-
нятия "временная структура процентных ставок" и укажем
способ определения искомых ставок дисконтирования.
1) Спот-ставки и временная структура процентных ставок.
Для описания временной структуры процентных ставок
используются так называемые спот-ставки.
Спот-ставками (spot rates) будем называть соответствую-
щие текущему моменту времени ставки доходности к погаше-
92

нию бескупонных облигаций с различными сроками погаше-
ния.
Обозначим:
oRf(t=l, 2, ..., 7) - ставка доходности к погашению беску-
понной облигации с погашением в конце периода / (t-
периодной облигации), при этом индекс "О" указывает на то,
что ставка относится к текущему периоду, для которого /=0.
Спот-ставки {oRt} определяют внутреннюю доходность со-
ответствующих бескупонных облигаций и поэтому удовлетво-
ряют тождествам типа (2.51). Таким образом, в соответствии с
формулами дискретного и непрерывного дисконтирования
(2.15), (2.16), а также на основании свойства (2.51) спот-став-
ки {оЛ,} удовлетворяют тождествам (2.52), (2.53), т.е.
а) в случае дискретного дисконтирования
б) в случае непрерывного дисконтирования
0/>,= Qe(-'<4 (2.53)
где Q - номинальная стоимость f-периодной бескупонной об-
лигации; оЛ - текущая рыночная стоимость /-периодной
бескупонной облигации (цена покупки); Qrt = log(l+oRt) -
спот-ставка в случае непрерывно начисляемых процентов.
На практике бескупонные облигации, как правило, крат-
косрочные ценные бумаги, т.е. "реальные" бескупонные об-
лигации со сроком обращения свыше одного года, могут от-
сутствовать на финансовом рынке. Однако активы, подобные
бескупонным облигациям с различными сроками обращения,
могут быть получены на основе купонных облигаций. Дейст-
вительно, купонную Г-периодную облигацию можно рассмат-
ривать как портфель, состоящий из Г-Н бескупонной облига-
ции, если предположить, что каждый из Т купонов и финаль-
ная выплата являются самостоятельными облигациями.
В качестве спот-ставок {oRt} на практике используют до-
ходности к погашению бескупонных государственных облигаций
или соответствующих им активов в виде платежей по купон-
ным государственным облигациям1.
Данные активы имеют фиксированные сроки обращения и
цены погашения. Они не предусматривают промежуточных
1 Далее термин "бескупонные многопериодные облигации" будем пони-
мать в указанном смысле.
93

выплат и, как правило, свободны от риска невыполнения
обязательств со стороны эмитента. Поэтому можно считать,
что они имеют фиксированную доходность, не подверженную
риску невыполнения обязательств (default risk), а также риску
изменения процентных ставок (interest rate risk) при совпаде-
нии срока инвестирования и срока обращения облигации. В
этом смысле бескупонные облигации можно считать безрис-
ковыми активами, что делает их привлекательными для инве-
сторов1. В США рынок подобных активов функционирует в
рамках программы STRIPS (Separate Trading of Registered In-
terest and Principal Securities), разработанной Казначейством
США [33].
Практика показывает, что ставки доходности к погашению
(Yield To Maturity - YTM) зависят от срока, оставшегося до
погашения облигаций. Подобную зависимость принято назы-
вать временной структурой процентных ставок (term structure
of interest rate).
Для описания временной структуры процентных ставок на
финансовом рынке используется последовательность спот-
ставок о^ь о^2> •••> о^г> гДе Т - некоторый фиксированный
максимальный срок обращения долговых ценных бумаг.
Наличие временной структуры процентных ставок приво-
.дит к тому, что краткосрочные, среднесрочные и долгосроч-
ные спот-ставки различаются по величине, т.е. имеет место
условие:
o^i *0Л2* оД3 *...*o^r. (2.54)
Величина и характер различия спот-ставок меняются с те-
чением времени. Представление о временной структуре про-
центных ставок может быть получено посредством построе-
ния кривой доходности.
2) Кривая доходности.
Кривая доходности (yield curve) - это график зависимости
доходности ценных бумаг (YTM) от срока, оставшегося до их
погашения.
Кривая доходности может иметь различную форму, на-
пример возрастать или убывать (рис. 2.3). Заметим, что если
бы процентные ставки не зависели от времени, то кривая до-
ходности представляла бы собой прямую горизонтальную ли-
нию, проходящую через некоторую точку R на оси ординат.
Кривая доходности меняется ежедневно и на практике, оче-
1 Однако они не свободны от риска изменения покупательной способно-
сти денег, т.е. от инфляционного риска.
94

видно, не является такой гладкой, как это изображено на ри-
сунке.
Причиной "размытости" кривой доходности являются раз-
личные специфические особенности ценных бумаг, оказы-
вающие влияние на их доходность. Анализ и интерпретация
кривой доходности важны при оценки долговых ценных бу-
маг.
Рис. 2.3. Примеры кривых доходностей
Попыткам объяснить форму кривой доходности посвяще-
ны теории временной структуры процентных ставок, основан-
ные на различных гипотезах относительно поведения участ-
ников рынка. Наиболее известными из этих теорий являются:
• теория ожиданий (Expectations Hypothesis);
• теория чистых ожиданий (Pure Expectations Hypothesis);
• теория предпочтения ликвидности (Liquidity Preference
Hypothesis);
• теория сегментации рынка (Market Segmentation Hypothe-
sis).
Пример анализа формы кривой доходности на основе тео-
рии чистых ожиданий приводится далее, в п. 2.5.5. Более
подробное изучение различных теорий временной структуры
процентных ставок, а также соответствующих моделей и ме-
тодов анализа облигаций находится вне рамок данного учеб-
ного пособия. Поэтому ограничимся лишь ссылками на неко-
торые литературные источники. Математически строгое об-
суждение проблем в рамках указанного направления можно
найти в [14, 37, 39], более популярные трактовки этих теорий
приведены в [4, 19, 33].
95

3) Текущая стоимость облигаций.
Финансовая информация в виде значений спот-ставок
{о/У (/=1, 2, .., 7) обычно доступна участникам рынка, при-
чем последовательность {oRt} на развитых рынках охватывает
все типовые сроки обращения долговых обязательств, имею-
щихся на данном рынке. Например, подобная информация на
основе казначейских ценных бумаг США регулярно публику-
ется в выпусках Бюллетеня Казначейства (Treasury Bulletin).
Это позволяет финансовым аналитикам оценивать текущую
стоимость произвольного долгового обязательства на основе
метода дисконтирования платежей. В качестве ставок дискон-
тирования при этом используются соответствующие спот-
ставки. Проиллюстрируем это на примере купонной облига-
ции.
Пусть имеется Г-периодная купонная облигация, описан-
ная в п. 2.5.1, и для всех периодов выплат купонного дохода
известны спот-ставки {q/У (/=1, 2, ..., 7). Тогда текущая
стоимость купонной облигации определяется по формуле
V =
СТ
или
K = i>/> (2.56)
где QVt - текущая стоимость платежа за период t (/=1, 2, ..., 7),
которую можно рассматривать как текущую стоимость t-
периодной бескупонной облигации.
Таким образом, купонную Г-периодную облигацию можно
рассматривать как "портфель" из Т бескупонных облигаций с
последовательными сроками погашения / = 1, 2, ..., ТК
2.5.5. Форвардные ставки и цены облигаций
Во многих практических задачах, например при покупке
или продаже облигаций на фьючерсных рынках, появляется
необходимость в определении стоимости и ожидаемой доход-
ности облигаций в будущие периоды.
В связи с этим возникает еще один тип процентных ста-
вок, известных как форвардные ставки.
1 Платеж за последний период также можно рассматривать как "порт-
фель" из двух бескупонных облигаций, соответствующих купонному доходу и
финальной выплате.
96

1) Форвардные ставки.
Форвардными ставками (forward rates) в широком смысле
принято называть ставки, которые фиксируются в текущий
момент относительно займов или кредитов, которые должны
быть получены или предоставлены в некоторый будущий пе-
риод.
Применительно к долговым ценным бумагам под фор-
вардной ставкой будем иметь в виду ставку, которая устанав-
ливается в текущий момент и характеризует доходность к по-
гашению ценной бумаги, соответствующую некоторому буду-
щему периоду владения.
Обозначим: tRj - ставка доходности к погашению в перио-
де t бескупонной облигации со сроком обращения, равным Т-
периодам.
Пусть известна временная структура процентных ставок в
виде последовательности спот-ставок {oRt}, *=1, 2, ..., Т. Тогда
ставки {tRr)-> удовлетворяющие условию
(l+oJ?7)7'=U+o*/)'(l+/*7)7'-/, *=1, 2, .-, 7-1, Т>\, (2.57)
называются форвардными.
Заметим, что условие (2.57) - это условие эквивалентности
двух альтернативных стратегий инвестирования, исключаю-
щее возможность получения гарантированного дохода без ка-
ких-либо инвестиций, т.е. исключающее арбитражные воз-
можнЪсти (см. разд. 6.3).
Первая стратегия (ей соответствует правая часть соотно-
шения (2.59)) заключается в инвестировании средств сначала
на t периоды, а затем реинвестировании полученной суммы
на оставшийся до погашения срок, равный T-t периодам вла-
дения. На первом и втором этапах инвестирования использу-
ются соответственно спот-ставка $Rt для /-периодных вложе-
ний и форвардная ставка rRf, соответствующая периоду t.
Вторая стратегия (левая часть соотношения (2.59)) состоит в
инвестировании средств сразу на весь срок, оставшийся до
погашения облигации под ставку qRt (более подробный ком-
ментарий можно найти в [19]).
Из соотношения (2.57) может быть найдено представление
для форвардных ставок в случае капитализации дохода с ис-
пользованием формулы сложных процентов. Это представле-
ние определяется формулой (2.58), которая позволяет вычис-
лить по заданным значениям спот-ставок {о^}, а также ком-
бинациям значений t w T все необходимые для анализа фор-
вардные ставки:
7 Зак. 7084 97

(2.58)
В случае непрерывно начисляемых процентов с учетом
обозначения trj= log(l+,^7) получаем:
TfT-tort
fT T-t "
С учетом (2.55), (2.57) текущая стоимость купонной обли-
гации может быть представлена в виде
(2.59)
Воспользуемся формулами (2.58) и (2.59) для нахождения
форвардных цен облигаций, т.е. ожидаемых в текущий мо-
мент цен облигаций в будущие периоды.
2) Форвардные цены облигаций.
Пусть Vt (/=1, 2, ..., 7) - цена облигации в конце /-го пе-
риода владения после выплат по ней всех предусмотренных
платежей. Поскольку данные цены соответствуют будущим
периодам времени, их принято называть форвардными цена-
ми облигации.
Форвардные цены Vj-u ••, V\ для Г-периодной купонной
облигации при известных форвардных ставках {^+i}
(*=1, 2, ..., Т-\) могут быть определены с помощью следую-
щей рекуррентной формулы:
Vt= V^+Cm t = T_XT_2A (260)
Рекуррентная формула (2.60) основывается на интерпрета-
ции текущей стоимости ценной бумаги как некоторой суммы,
которая может быть вложена на определенный срок под соот-
ветствующую данному сроку и риску вложений ставку. Пред-
полагается, что полученная по окончании срока вложений
сумма будет равна стоимости потока платежей по ценной бу-
маге, представленного на рис. 2.4.
98

С] С2 С( С/+1 C^-i Ст
h
/4-1
< *
М-й период
ТА Т
Дата
погашения
О 1
Текущий
момент
Рис. 2.4. Схема потока платежей по облигации
В соответствии с указанным принципом стоимость обли-
гации после ее погашения в момент времени Т равна нулю,
поскольку после погашения по облигации не ожидается ни-
каких платежей. Таким образом, можно положить Vf=0.
В начале последнего периода по облигации ожидается пла-
теж, равный Cj, поэтому в момент времени Т-\ стоимость
облигации должна удовлетворять соотношению:
откуда следует:
Для цены облигации в момент времени Т-2 (т.е. в начале
Г-1-го периода) имеем:
Кг_2 (1+г_2Л7ч) = Ктч+Стч.
Аналогично для момента времени t, являющегося началом
произвольного Н- 1-го периода (t = T-l, Т-2, ..., 1), получаем:
что влечет (2.60).
При t=0 формула (2.60) эквивалентна формуле (2.59) и
приводит к вычислению текущей стоимости облигации.
Приведем некоторые частные случаи формулы (2.60):
• для купонных облигаций с потоком платежей вида
Ct=qF, *=1, 2, ..., Т-\\ Cf=qF+Fполучаем выражение ви-
да:
v = '+1 + ^ t = т \ т 1 \-v - f
yt 9 i J - L, J - Z, ..., 1, VT = Г ,
где с целью сохранения общности формально положено
VT=F;
• для бескупонных облигаций, полагая в предыдущем вы-
ражении 9=0, получаем:
99

V,= -^-,t = T-l,T-2,...,l;\
3) Интерпретация кривой доходности.
Форвардные ставки существенно используются в рамках
различных теорий временной структуры процентных ставок.
Например, в соответствии с теорией чистых ожиданий при
отсутствии на рынке арбитражных возможностей устанавли-
ваемые в текущий момент форвардные ставки для будущих
периодов должны быть равны ожидаемым в соответствующих
будущих периодах спот-ставкам с аналогичными сроками ин-
вестирования. Другими словами (используя терминологию
вероятностного подхода (гл. 3)), форвардные ставки должны
равняться математическому ожиданию соответствующих
спот-ставок.
На данном предположении основана интерпретация фор-
мы кривой доходности в рамках теории чистых ожиданий. В
качестве примера рассмотрим две стратегии инвестирования
на два периода. Первая заключается в покупке двухпериодной
бескупонной облигации, доходность к погашению которой
определяется спот-ставкой о^?2- Вторая стратегия представляет
. собой так называемую стратегию возобновления (rollover strat-
egy) и состоит в последовательной», покупке однопериодных
бескупонных облигаций. Доходность к погашению первой
однопериодной облигации определяется однопериодной спот-
ставкой о^ь а доходность второй облигации - форвардной
однопериодной ставкой {1R2}.
Предположение об отсутствии арбитражных возможностей
приводит по аналогии с (2.57) к тождеству
(l+0*i)(l+i(£4)2) = О+0Л2)2,
в котором в соответствии с теорией чистых ожиданий учтено,
что форвардная ставка ]/?2 равна ожидаемой в будущем пе-
риоде спот-ставке \(ER)2. Представим данное соотношение в
более удобном для интерпретации виде:
»■«>
На основании (2.61) можно сделать следующие выводы о
форме кривой доходности (см. рис. 2.3):
1) если кривая доходности имеет наклон вверх, т.е.
2> TO \(ER)2>oR\' Это означает, что инвесторы ожидают
100

в будущем периоде роста краткосрочных (однопериодных)
ставок;
2) если кривая доходности имеет наклон вниз, т.е. o^i>o^2>
то i(jEri?>2<o^b a значит, инвесторы ожидают в будущем пе-
риоде падения краткосрочных ставок;
3) если кривая доходности параллельна оси абсцисс, т.е.
o/?i=o#>, то i(£7?)2=o^b и, следовательно, в будущем инвесто-
ры ожидают, что краткосрочные ставки не изменятся.
Очевидно, аналогичные рассуждения могут быть проведе-
ны и для произвольного срока инвестирования.
2.6, АНАЛИЗ АКЦИЙ
Применим метод дисконтирования платежей для анализа
стоимости и доходности обыкновенных и привилегированных
акций (common and preference stocks).
Пусть Dt - величина дивидендов, выплачиваемых по акци-
ям в периоде владения t Предполагается, что дивиденды по-
ступают в конце каждого периода и подлежат капитализации
с начислением сложных процентов. При использовании ме-
тода дисконтирования платежей в рассматриваемом случае
необходимо учитывать две особенности потока платежей {Dt}
по акциям1:
1) поток платежей {Dt} (/=1, 2, ..., 7) по акциям представ-
ляет собой поток дивидендов, выплата которых ожидается в
течение всего периода обращения акций, откуда следует, что
Г=сю;
2) доход в виде дивидендов по обыкновенным акциям в
отличие от дохода по облигациям не является фиксирован-
ным, т.е. оговоренным условиями выпуска, и, следовательно,
при оценке текущей стоимости таких акций могут использо-
ваться лишь прогнозные значения будущих дивидендов.
Предположим, что ставка дисконтирования дивидендов,
интерпретируемая как ожидаемая доходность вложений с со-
поставимой степенью риска, в течение всего срока обращения
акций остается постоянной и равной R. Тогда в соответствии
с методом дисконтирования платежей текущая стоимость ак-
ции определяется как сумма текущих стоимостей всех ожи-
даемых по акции дивидендов:
1 Для обозначения платежей по акциям в виде дивидендов традиционно
используется символ Dt вместо С,.
101

Таким образом, для практического использования форму-
лы (2.62) инвестор должен знать прогнозные значения всех
будущих дивидендов {Dt} (/=1, 2, ...). В силу "неограниченно-
сти жизни" акций задача предсказания бесконечного потока
дивидендов оказывается неразрешимой без дополнительных
предположений в виде определенных моделей изменения диви-
дендов. Рассмотрим традиционные модели изменения диви-
дендов, а также используем их для нахождения текущей
стоимости, NPV и IRR акций. Методы анализа инвестицион-
ной привлекательности активов на основе NPV и IRR были
описаны в разд. 2.3.
2.6.1. Модели изменения дивидендов
Будем предполагать, что поток дивидендов по акциям по-
рождается следующей рекуррентной формулой:
А= A-id+&), *=1, 2, ..., (2.63)
. где Dt — некоторое известное значение, например величина
последних дивидендов, выплаченных по данным акциям.
Величина gt определяется соотношением:
g,= D'-Dl-l,t=l,2,..., (2.64)
Ut-\
т.е. является темпом прироста дивидендов за период владения /.
Различные предположения относительно темпов прироста
дивидендов {gt} приводят к различным моделям изменения
дивидендов. Наиболее известными являются модели нулево-
го, постоянного и переменного роста дивидендов.
Модель нулевого роста дивидендов (Zero Growth Model) опи-
сывается соотношением (2.63) при условии:
& = (U=1, 2, .... (2.65)
Условие (2.65) означает, что в будущем в течение всего
срока обращения акций по ним ожидаются фиксированные
дивиденды, т.е. D\s=D2=.^=zDq9 где Dq - некоторая заданная
величина дивидендов.
На практике данная модель оказывается полезной при
анализе привилегированных неучаствующих акций (поп раг-
102

ticipating preference stocks), по которым не предусмотрено ни-
каких выплат, кроме фиксированных дивидендов.
Модель постоянного роста дивидендов (Constant Growth
Model) предполагает, что ожидается рост дивидендов с посто-
янным темпом, т.е. в (2.63) следует положить:
gt=g= const, t=l, 2, ... ,
где g - постоянный ожидаемый темп прироста дивидендов.
Поскольку на выплату дивидендов может направляться
лишь некоторая доля чистой прибыли корпорации, то следует
положить, что g<R.
Таким образом, в данном случае поток дивидендов {Dt}
удовлетворяет следующему соотношению (Д> - известная ве-
личина):
А = A-lO+2)= А>(1+*)', М, 2, ... . (2.66)
Предположение о постоянстве дивидендов в течение всего
срока обращения акций, очевидно, трудноосуществимо на
практике. Однако в раде случаев подобная модель может быть
использована для оценки обыкновенных акций тех корпора-
ций, которые придерживаются определенной дивидендной
политики, направленной на поддержание курса акций за счет
постоянного (хотя, возможно, и невысокого) темпа прироста
дивидендов.
Модели переменного роста дивидендов (Multiple-Growth
Models) предполагают наличие двух и более этапов в жизни
корпорации, различающихся схемами выплаты дивидендов.
Опишем пример подобной модели [33]. Пусть срок обра-
щения акций разбит на два этапа. Первый этап состоит из
фиксированного числа Г<оо периодов владения, начиная с те-
кущего момента, второй этап - весь остальной срок обраще-
ния акций. Предполагается, что D\, />2, ..., Dt- заданные про-
гнозные значения дивидендов для первых Т периодов владе-
ния. На втором этапе ожидается изменение дивидендов в со-
ответствии с моделью постоянного роста дивидендов и тем-
пом прироста g.
DTH= DT+,-\(l+g)= Dj(l+gy9 t=l, 2, ... .
Возможны модификации данной модели, предполагающие
использование на обоих этапах моделей постоянного роста
дивидендов с различными темпами прироста дивидендов, а
также наличие большего числа этапов.
103

2.6.2. Анализ стоимости и доходности акций
Приведем формулы для вычисления текущей стоимости,
NPV и IRR акций в соответствии с описанными выше моде-
лями изменения дивидендов.
1) Модель нулевого роста дивидендов.
Формально применение метода дисконтирования платежей
(дивидендов) для модели нулевого роста аналогично рассмот-
ренному выше случаю анализа бессрочных облигаций.
Обозначим, как и ранее, d={\+R)A - дисконтный множи-
тель. Тогда на основании (2.62), (2.65) текущая стоимость ак-
ции в случае модели нулевого роста дивидендов допускает
представление
00 ГЛ П °°
Так как rf<l, то по свойству суммы бесконечной геометри-
ческой прогрессии имеем
что с учетом (2.67) влечет
К= ^L. (2.69)
R
Из (2.69) следует, что текущая стоимость акции прямо
пропорциональна величине выплачиваемых по ней дивиден-
дов и обратно пропорциональна ожидаемой доходности вло-
жений с сопоставимой степенью риска.
Для анализа инвестиционной привлекательности акций,
как и в случае облигаций, используются чистая текущая
стоимость NPV и внутренняя доходность IRR. Пусть Р - те-
кущая рыночная цена (цена покупки) акции. Для рассматри-
ваемой модели из условия NPV— V-P=0 получаем формулу для
определения внутренней доходности акции:
Л*=^-. (2.70)
Ставка вида (2.70) обычно называется ставкой дивидендной
доходности (dividend yield) акции. Соотношение (2.70) под-
тверждает известный факт: доходность актива тем больше,
104

чем больше ожидаемые по нему выплаты и чем меньше цена
покупки данного актива.
2) Модель постоянного роста дивидендов
На основании (2.62), (2.66) текущая стоимость акции в
случае модели постоянного роста дивидендов определяется по
формуле
v=f d, _ A(i + g)ffi + gY_A(i+g)f , (2m
где использовано обозначение:
Т7*
С учетом свойства суммы бесконечной геометрической
профессии из (2.71) следует:
^ D\
к
R-g R-g *
Из условия NPV= V-P=0 (где Р - рыночная цена покупки
акции) получаем соотношение для внутренней доходности
акции:
^ = Mn)+ir (273)
Формулы (2.72), (2.73) согласуются с ранее отмеченными
закономерностями. В частном случае при g=0 из них следуют
формулы (2.69), (2.70) для модели нулевого роста дивидендов.
Если на различных этапах функционирования компании-
эмитента имеют место различные схемы выплат дивидендов,
то для анализа акций может использоваться модель перемен-
ного роста дивидендов.
3) Модель переменного роста дивидендов.
Для определения текущей стоимости акции V на основе
модели переменного роста дивидендов (п. 2.6.1) применим
метод дисконтирования платежей.
Обозначим: V - текущая стоимость платежей по акции за
первые Т периоды; К+ - текущая стоимость платежей по ак-
ции за оставшийся спустя Т периодов срок обращения. Тогда
текущая стоимость акции будет равна К= V~+ V+. Величина V~
определяется как текущая стоимость актива с фиксирован-
105

ным потоком платежей, примером которого является купон-
ная облигация. Поэтому согласно (2.32) имеем:
К~=!^у> (2-74)
где R - ожидаемая доходность активов с сопоставимым рис-
ком.
Для нахождения V+ вычислим вначале текущую стоимость
акции VT в предположении, что текущим моментом является
момент Т и имеет место модель постоянного роста дивиден-
дов. Согласно (2.72):
VT- Ъ^Щ-£^- (2-75)
Величину Vj можно интерпретировать как единовременное
поступление, равноценное потоку платежей после периода Т
(например, как финальную выплату по Г-периодной облига-
ции). Поэтому для нахождения ее текущей стоимости к най-
денному значению Vj вида (2.75) следует применить процеду-
ру дисконтирования:
На основании (2.74), (2.76) и соотношения К=К + К+ полу-
чаем выражение для текущей стоимости акции в соответствии
с моделью переменного роста дивидендов:
Т п тл
v= У < + —
*—J (л . п V / г>
В разд. 4.4 данные модели получат строгое математическое
обоснование в рамках вероятностного подхода.

Глава 3
МОДЕЛИ И МЕТОДЫ
АНАЛИЗА ЦЕННЫХ БУМАГ
В УСЛОВИЯХ НЕОПРЕДЕЛЕННОСТИ
Отправной точкой для каждой фи-
нансовой модели является неопреде-
ленность, стоящая перед инвестора-
ми... В самом деле, при отсутствии
неопределенности проблемы финан-
совой экономики сводятся к упраж-
нениям по основам макроэкономики.
J.Y. Campbell, AW. Lo, AC. MacKinlay
Глава содержит определение основных понятий теории вероятно-
стей, используемых в рамках вероятностного подхода для описания фи-
нансовых переменных. Дается характеристика основных классов эконо-
метрических моделей финансовых переменных (случайная выборка,
регрессионные модели, временные ряды), а также методов их построе-
ния. Приводится обзор методов решения традиционных задач анализа
фондового рынка на основе эконометрических моделей.
По рассматриваемым в главе вопросам рекомендуется дополни-
тельная литература: [1, 3, 12, 31, 38, 41, 43] (методы прикладной стати-
стики, эконометрического анализа и статистического моделирования);
[14, 16, 34] (вероятностные модели и методы стохастической финансо-
вой математики); [5, 10, 28, 37, 39, 42, 45, 46, 47, 49, 50] (эконометриче-
ское моделирование, анализ и прогнозирование финансовых рынков).
Количественные методы анализа финансовых активов ос-
нованы на использовании наблюдаемых значений характери-
стик активов (цен, доходностей, дивидендов, фондовых ин-
дексов и т.д.), т.е. эмпирических данных для оценки и прогно-
зирования ожидаемой доходности и риска активов, а также
принятия обоснованных инвестиционных решений.
Анализ эмпирических значений характеристик активов
свидетельствует о том, что они подвержены нерегулярным и
на первый взгляд непредсказуемым, случайным изменениям.
По этой причине инвестор может делать лишь некоторые
предположения относительно будущих значений анализируе-
мых характеристик, но никогда не знает их точно. Традици-
онных "детерминированных" методов финансовой математи-
ки оказывается недостаточно для решения задач анализа фи-
нансовых активов в условиях неопределенности. В частности,
107

они не учитывают существующего в условиях неопределенно-
сти риска того, что фактическая доходность операции покуп-
ки или продажи ценной бумаги может отличаться от той, что
ожидается в момент совершения операции.
Для исследования процессов, которые имеют стохастиче-
скую (случайную) природу и в то же время обладают свойст-
вом устойчивости частот наступления тех или иных событий,
целесообразно использовать вероятностный подход.
В рамках вероятностного подхода предположения инвесто-
ра основываются на вычислениях (оценке) вероятностей тех
или иных значений характеристик финансовых активов в со-
ответствии с определенными вероятностными моделями. При
этом сами характеристики рассматриваются как случайные
величины, подчиняющиеся определенным законам распреде-
ления вероятностей. Таким образом, понятие "неопределен-
ность" в рамках данного подхода заменяется понятием "слу-
чайность", или "стохастичность". Вероятностный подход по-
зволяет использовать для описания характеристик активов
(например, ожидаемых доходностей и риска) характеристики
случайных величин (математическое ожидание, дисперсию
или среднеквадратическое отклонение), а для их анализа -
хорошо развитый аппарат теории вероятностей и математиче-
ской статистики.
Подход к анализу финансового рынка, основанный на
применении вероятностно-статистических моделей и методов,
принято называть количественным анализом финансового рын-
ка (quantitative analysis of financial market).
Первыми наиболее значительными работами в данном на-
правлении, послужившими началом современной теории оп-
тимального портфельного инвестирования и стохастической
финансовой математики, являются работы Г. Марковица1 и
М. Кендал л а2.
Работа Г. Марковица заложила основы теории портфеля
ценных бумаг (portfolio theory). В ней была впервые предложе-
на вероятностная формализация понятий "ожидаемая доход-
ность" и "риск" ценной бумаги как математического ожида-
ния (mean) и дисперсии (variance) ее доходности за некоторый
период владения (holding period), рассматриваемой как слу-
чайная величина. Такая формализация позволила сформули-
ровать подход "доходность — риск" (mean - variance analysis) к
1 См.: Markovitz Я. М. Portfolio Selection // Journal of Finance. 1952. V. 7.
№ 1. P. 77-91.
2 См.: Kendall M. G. The analysis of economic time series. Part 1. Prices //
Journal of the Royal Statistical Society. 1953. V. 96. P. 11-25.
108

анализу ценных бумаг, предполагающий учет как ожидаемой
доходности, так и риска ценной бумаги. В рамках данного
подхода была математически строго сформулирована и реше-
на проблема оптимального распределения (диверсификации)
инвестируемого в условиях неопределенности капитала между
различными активами с целью достижения приемлемой до-
ходности вложений с минимальным риском.
На основе подхода "доходность - риск" были разработаны
экономические модели для доходностеи ценных бумаг в усло-
виях равновесия финансового рынка. Наиболее известными
среди них являются две модели:
модель оценки финансовых активов САРМ (Capital Asset
Pricing Model)1;
модель APT (Arbitrage Pricing Theory) на основе "арбит-
ражной теории оценивания"2.
Указанные модели позволили для равновесного состояния
рынка установить связи между доходностью и риском акти-
вов, доходностью активов (или портфеля активов) и доходно-
стью рыночного портфеля (модель САРМ), доходностью ак-
тивов и экзогенными (внешними) факторами (модель APT).
Работа М. Кендалла, посвященная исследованию и моде-
лированию динамики поведения цен финансовых активов,
положила начало развитию теории эффективного финансового
рынка (Efficient Capital Market Theory). С данной теорией свя-
заны определенные модельные предположения о рынке (ги-
потеза "эффективности рынка", или "рациональных ожида-
ний", основанная на мартингальном свойстве цен финансо-
вых активов), которые являются отправной точкой для по-
строения динамических моделей цен и доходностеи активов в
условиях неопределенности.
Перечисленные выше различные аспекты количественного
финансового анализа требуют более детального обсуждения.
Количественные методы анализа финансового рынка исполь-
зуются в рамках определенной вероятностной модели эмпи-
рических данных. Поэтому в данной главе приводится крат-
кое описание основных средств вероятностного описания
1 Развита в работах: Sharpe W. F. Capital Asset Price: A Theory of Market
Equilibrium under Conditions of Risk // Journal of Finance. 1964. 29 (3). P.
425-442; Lintner J. The Valuation of Risk Assets and the Selection of Risky In-
vestments in Stock Portfolios and Capital Budgets // Review of Economics and
Statistics. 1965. № 2. P. 13-27; Mossln J. Equilibrium in a Capital Asset Market //
Econometrica. 1966. 34 (4). P. 768-783.
2 Предложена в работе: Ross S. A. The Arbitrage Theory of Capital Asset Pric-
ing // Journal of Economic Theory. 1976. V. 13. № 3. P. 341-360.
109

финансовых активов и основных типов вероятностных моде-
лей эмпирических данных, возникающих при различных мо-
дельных предположениях. Последующие разделы учебного
пособия посвящаются более детальному обсуждению класси-
ческих задач количественного анализа финансовых рынков.
3.1. ВЗАИМОСВЯЗЬ ЦЕН, ПРОМЕЖУТОЧНЫХ
ПЛАТЕЖЕЙ И ДОХОДНОСТЕЙ ЦЕННЫХ БУМАГ
Непременным элементом финансового анализа является
вычисление и сравнительный анализ доходности, риска и
других характеристик активов по их рыночным ценам. До-
ходности активов могут рассчитываться как за один, так и за
несколько периодов владения. Если котировки активов уста-
навливаются часто (например, ежедневно или еще чаще), то в
силу меньшей вариации предпочтительно использовать "мно-
гопериодную" доходность. Для сравнительного анализа акти-
вов целесообразно рассчитывать их доходность относительно
одного и того же условного периода владения. Установим
формулы, связывающие основные характеристики активов с
их рыночными ценами. Для определенности в качестве акти-
вов будем рассматривать, как правило, ценные бумаги.
3.1.1. Доходность ценных бумаг за один период
Пусть Pt.\ и Pt- рыночные цены (курс) актива в моменты
времени /-1 и /, соответствующие началу и окончанию ^-го
периода владения активом; Dt - периодические платежи по
активу за этот же период владения (дивиденды по акциям ли-
бо проценты по облигациям).
Доход инвестора Yt (net earning) за t-й период владения ак-
тивом равен:
Yt=P,-PtA+Dt. (3.1)
Доходность актива (return), или ставка доходности актива
(rate of return)1, за период владения / определяется выражени-
ем:
PP+D P + Dt , , 2 Т
I , /=1, 2, ..., /. (3.2)
"t-\ ч-\
1 Более точное название характеристики R, - ставка доходности (rate of
return), однако в финансовой литературе используется, как правило, сокра-
щенный вариант - доходность (return).
ПО

При практическом использовании формулы (3.1), (3.2) ну-
ждаются в дополнительных уточнениях. В частности, по-
скольку торговля финансовыми активами обычно осуществ-
ляется по системе "двойного аукциона", то в каждый момент
времени для каждого актива устанавливаются две цены (две
котировки): цена покупки Pbt (bid price) и цена продажи Pat
(ask price). Возможны два способа учета этого факта в (3.1)
при проведении финансового анализа.
При первом способе предполагается, что Pt.\ = P bt (цена
покупки актива в начале периода /), а Р,= Pat (цена продажи
актива в конце периода t). Относительно периодических пла-
тежей Dt (например, дивидендов по акциям) обычно предпо-
лагается, что они поступают непосредственно перед момен-
том установления котировки Pt и еще в ней не отражаются,
т.е. цена Pt рассматривается как цена актива без дивидендов к
моменту времени t (ex-dividend price at date /).
Если значения цен фиксируются через короткие времен-
ные интервалы, например ежедневно или еще чаще, то в ка-
честве Pt можно использовать среднее геометрическое значе-
ние двух котировок:
. (3.3)
В этом случае есть основание не учитывать периодические
платежи, так как они поступают значительно реже, чем уста-
навливаются котировки активов. Например, обычная частота
выплат дивидендов по акциям - один раз в квартал, а про-
центов по облигациям - один или два раза в год. Если перио-
дические платежи по активу не учитываются, то доходность
актива за период владения t определяется по формуле:
R~-^ = ^=Ц/=1, 2, .... Т. (3.4)
ч-
t-\
Ставки Rh определяемые по формулам (3.2) или (3.4), яв-
ляются простыми ставками, характеризующими доходность
актива за один период. Они используются при практических
расчетах для определения стоимости активов по формуле
сложных процентов.
Наряду с простой ставкой (simple rate) Rh характеризую-
щей чистую доходность актива, представляет интерес валовая
доходность актива (gross return), определяемая ставкой l+Rt. С
точки зрения экономической статистики ставки \+Rt и Rt
представляют собой цепные индексы, соответствующие темпу
111

роста и темпу прироста цены актива по отношению к преды-
дущему периоду. Интерес к характеристике \+Rt обусловлен
тем, что, как было показано в п. 2Л .4, с этой характеристи-
кой связана эквивалентная ставка непрерывно начисляемых
процентов (continuously compounded rate), кратко - ставка не-
прерывных процентов, или "логарифмическая доходность" акти-
ва гь которая более удобна в аналитических исследованиях:
/7EElog(l + Rt) = log -£- = Pt -Pt-u (3.5)
ч-\
где р{ = logPt. Заметим, что в формуле (3.5) неявно предпола-
гается 1+/?/ >0 (или —1 < /?,), что имеет определенную эко-
номическую интерпретацию (см. п. 3.1.2).
Преимущество принципа непрерывных процентов прояв-
ляется при анализе доходностей активов за несколько перио-
дов, что будет обсуждаться в следующем разделе.
Согласно выражению (3.2), однопериодную доходность Rt
можно представить в виде:
Я, = Az^L +A.= RP,+ RDht=it 2, ..., Т.
Ч-\ 4-Х
Из этого соотношения следует, что доходность актива в
периоде t складывается из двух компонентов: компонента Rpt9
обусловленного изменением рыночной стоимости (price gain
return), и компонента RDh обусловленного поступлением пла-
тежа Dt (current or dividend yield). Компонент Rpt является до-
минирующим для акций, а компонент RDt - основной состав-
ляющей доходности облигаций. Таким образом, доходность
актива в периоде t зависит от трех факторов: цены покупки,
цены продажи, промежуточных платежей.
Цена покупки является детерминированным фактором.
Она всегда известна в момент совершения сделки. Относи-
тельно двух других факторов существует неопределенность.
Для долговых ценных бумаг (например, облигаций) эта неоп-
ределенность обусловлена:
во-первых, возможностью невыполнения обязательств
эмитентом, связанных с выплатой процентного дохода или
погашением ценной бумаги в установленный срок, что озна-
чает наличие риска невыполнения условий кредитного со-
глашения (default risk);
во-вторых, изменением уровня процентных ставок на фи-
нансовом рынке, приводящим к изменению стоимости цен-
112

ных бумаг: с увеличением процентных ставок курсовая стои-
мость долговых ценных бумаг падает и наоборот, при этом
возможны (см. п. 5.3.1) как процентный риск (interest rate
risk), так и риск рефинансирования (reinvestment risk).
В меньшей степени этими недостатками страдают кратко-
срочные государственные ценные бумаги. Еще большая неоп-
ределенность характерна для обыкновенных акций, поскольку
они не связывают эмитента обязательством регулярной вы-
платы дивидендов.
На курсовую стоимость ценных бумаг оказывают влияние
и многие другие факторы: экономические, политические,
психологические, форсмажорные, приводящие к "случайно-
му", т.е. непредсказуемому, изменению их значений. Это
служит основанием для применения количественных методов
анализа рынка ценных бумаг на основе вероятностных моде-
лей цен и доходностей активов, рассматриваемых в после-
дующих параграфах данной главы.
3.1.2. Многопериодная доходность ценных бумаг
Актуальной для практики является задача сравнительного
анализа доходности различных вариантов вложений денежных
средств в различные финансовые активы (например, в цен-
ные бумаги или на банковский счет) и различные сроки.
Общий метод решения данной задачи состоит в вычисле-
нии и сравнении эквивалентных ставок доходности вложе-
ний, рассчитанных относительно одного и того же (как пра-
вило, условного) периода владения (holding period). Рассмот-
рим способы вычисления эквивалентной ставки доходности
вложений за один период владения, соответствующей различ-
ным вариантам вложений. Для определенности в качестве
вложений будем рассматривать покупку ценных бумаг.
Пусть в начальный момент времени t-K (f>K) инвестор
приобрел некоторый актив по цене Pt_K и владел им в течение
К периодов до момента времени / включительно. Фактиче-
ские значения ставок доходности Rh Rt.\, ..., Rt-K+\ данного
актива за К рассматриваемых периодов могут быть вычислены
по формуле (3.2).
Пусть R{ % - многопериодная доходность (multiperiod return),
т.е. доходность актива за К периодов между моментами вре-
мени t-K и /. В предположении, что стоимость активов опре-
деляется по формуле сложных процентов, ставка Rt к удовле-
творяет условию:
8 Зак.7084 1 13

1 + RuK = (1 + Rt)(\ + Дм)-... (1 + Rt.K+l). (3.6)
На основании (3.4), (3.6) имеем:
Ф- (3-7)
1 + *^ П% /
k=\ Ч-к Ч-К
или
т.е. ставка Rt % может интерпретироваться как ставка доходно-
сти вложений с сопоставимым риском, вложив под которую
сумму Pt_K на срок, равный К периодам владения, можно по-
лучить (при условии, что проценты начисляются один раз в
конце указанного срока) сумму, равную Pt.
С точки зрения экономической статистики ставка 1+Л/д
соответствует темпу роста цены актива по отношению к на-
чальному моменту времени t-K, т.е. является базисным ин-
дексом. Ставка Rtx (или \+Rtx) может использоваться при
сравнительном анализе доходности активов с одинаковым
сроком инвестирования и сопоставимой степенью риска.
Для сравнения альтернативных вариантов с различными
. сроками инвестирования используется эквивалентная ставка
доходности за один условный период владения, который в прак-
тической деятельности обычно равняется одному году. Если в
приведенных выше рассуждениях предположить, что период
владения равен одному году, то доходность за К лет может
быть выражена через годовую ставку доходности (annual rate of
return), обозначаемую At #. Ставка At к может рассматриваться
как эквивалентная постоянная ставка доходности при вложе-
ниях на К периодов владения, вложив под которую сумму
Pt_K, можно по истечении срока инвестирования получить
сумму
^_,). (3.8)
Выражение (3.8) можно рассматривать как обобщение
формулы сложных процентов на случай переменных ставок,
т.е. на случай, когда имеет место временная структура про-
центных ставок. Из (3.8) следует:
114

В тех случаях, когда доходности активов {Rt-k} принимают
малые значения и обладают незначительной изменчивостью
(волатильностью), для приближенных вычислений Atx может
использоваться формула, основанная на линейной аппрокси-
мации Atfx с помощью формулы Тейлора:
4,**t£V*- (зло)
Соотношения (3.9), (3.10) - это устроенные по "принципу
сложных процентов" формулы типа геометрического среднего
для l+At>K и типа арифметического среднего для Atfx соответ-
ственно. В аналитических исследованиях, однако, для описа-
ния стоимости и доходности активов часто более удобными
оказываются формулы, получаемые по принципу непрерывно
начисляемых процентов (continuous compounding), описанно-
му в п. 2.1.4. Приведем данные формулы.
Пусть Rf - простая ставка доходности за период / вида
(3.4), a rt - эквивалентная ставка непрерывных процентов ви-
да (3.5). Определим ставку непрерывных процентов riyx для
срока инвестирования, равного К периодам (А>1), эквива-
лентную "простой" ставке Rtx доходности актива за период
между моментами времени t-K и t.
На основании (3.5), (3.6) имеем:
*,_*H) = (3.11)
Таким образом, ставка непрерывных процентов rtfK за К
периодов равна сумме ставок доходностей за отдельные пе-
риоды. Вычислительная простота не единственное достоинст-
во ставки rttx. Гораздо более важным является то, что свойст-
во аддитивности (3.11) упрощает решение задач исследования
динамических свойств доходностей активов (см. гл. 4). В ча-
стности, в рассматриваемом случае конечная стоимость акти-
ва будет равна
Pt = РиК (1 + RUK) = Pt_K еГ/'К . (3.12)
В то же время ставка непрерывных процентов имеет один
недостаток по сравнению с простой ставкой доходности, ко-
торый проявляется при решении задач оптимального порт-
фельного инвестирования. Как будет показано в гл. 5, доход-
115

ность портфеля активов, определяемая простой ставкой, рав-
на средневзвешенной доходности отдельных активов. Ставка
непрерывных процентов этим полезным свойством не облада-
ет. Однако если значения доходностей активов малы (близки
к нулю), то доходность портфеля активов, определяемая став-
кой непрерывных процентов, близка к средневзвешенной до-
ходности отдельных активов.
Поскольку многопериодные доходности зависят от доход-
ностей за отдельные периоды владения активами, имеющих
стохастическую природу, то их также следует рассматривать
как некоторые "случайные" величины. Остановимся подроб-
нее на изложении основных принципов описания и анализа
финансовых переменных в рамках вероятностного подхода,
придерживаясь содержательных интерпретаций вероятност-
ных характеристик из [34].
3.2. ВЕРОЯТНОСТНОЕ ОПИСАНИЕ ФИНАНСОВЫХ
АКТИВОВ В УСЛОВИЯХ НЕОПРЕДЕЛЕННОСТИ
Вероятностной моделью принято называть [31] математиче-
скую модель реальных явлений стохастической (случайной)
• природы, построенную при некоторых упрощающих (модель-
ных) предположениях относительно объекта моделирования.
Модельные предположения позволяют абстрагироваться от
деталей, не существенных для цели построения модели.
Целью построения моделей финансовых активов, а точ-
нее, их характеристик является решение с помощью этих мо-
делей задач анализа активов, например задачи прогнозирова-
ния их цен, доходностей или риска. Основой для построения
различных вероятностных моделей служит определенное со-
ответствующим образом вероятностное пространство. Опре-
делим данное пространство в контексте рассматриваемых за-
дач финансового анализа и опишем основные характеристики
финансовых активов.
3.2.1. Определение вероятностного пространства
в контексте задач финансового анализа
Наступление событий на финансовом рынке можно рас-
сматривать как случайный эксперимент с бесконечным чис-
лом исходов. Каждый из возможных исходов такого экспери-
мента будем называть элементарным исходом или элементар-
ным {неразложимым) событием со, а совокупность всех таких
116

возможных событий - пространством элементарных событий
{состояний рынка) Q={o)}. Таким образом, в результате анали-
зируемого случайного эксперимента обязательно происходит
одно (и только одно) из элементарных событий.
Наряду с элементарными событиями будем рассматривать
случайные события А, представляющие собой подмножества
элементарных событий из Q. Будем говорить, что наступило
событие А, если сое А. Среди всех возможных событий будем
выделять так называемые наблюдаемые события — такие собы-
тия А, относительно которых по результатам эксперимента
можно определенно сказать, наступило данное событие или
нет. Другими словами, множество А элементарных событий
из Q, для которого возможен ответ одного из двух типов:
"соеЛ" (событие А наступило) или "со^Л" (событие А не на-
ступило) соответствует наблюдаемому на рынке событию.
Поясним эти понятия на примере1. Пусть результатом
эксперимента, связанного с наблюдением курса актива, явля-
ется регистрация факта "подъема" (со=+1) или "снижения"
(ео=-1) курса актива. Пространством всех элементарных со-
бытий, (исходов) для однократного эксперимента (наблюде-
ния) является П={+1,-1}. Предположим теперь, что состояние
курса анализируется в три последовательных момента време-
ни, т.е. эксперимент состоит в трехкратной последовательной
регистрации курса. В этом случае пространство всех исходов
состоит из восьми элементарных событий:
О={ю=(©1, со2, 0)3)}=
={(-1, -1,-1), (-1 -1,+1), ... , (+1,+ 1,+ 1)}.
Если имеется возможность регистрации курса во все ана-
лизируемые моменты, т.е. все значения a>i, а>2, соз могут быть
измерены, то, например, событие Л={(-1,+1,+1),
(+1,+1,+1)}еО, состоящее в том, что в моменты двух послед-
них измерений курс актива возрастает, является наблюдаемым.
В этом случае для любого о)=(а)1,со2,соз)еО можно определен-
но сказать "шеЛ" или "шеЛ". Однако если, например, значе-
ние о)2 не измеряется, то событие А уже не является наблю-
даемым (множество А не является измеримым), поскольку в
этом случае нельзя определенно ответить на поставленный
вопрос.
Обозначим 3 совокупность всех наблюдаемых случайных
событий на финансовом рынке (множество всех измеримых
подмножеств элементарных событий из Q).
1 Модификация примера из [34].
117

Таким образом, произвольное наблюдаемое на рынке со-
бытие А представляет собой некоторое подмножество элемен-
тарных событий из 3, т.е. Л={со}еЗ, coeQ. Множество 3 можно
интерпретировать также как всю доступную информацию о
рынке1.
Будем предполагать, что на множестве 3 определена веро-
ятность (распределение вероятностей) Р, т.е. для любого со-
бытия ЛсЗ может быть поставлена в соответствие вероятность
наступления этого события Р(Л), 0< Р(Л)<1, причем Р(у4)=0,
если А=0 - невозможное событие и Р(у4)=1, если A—Q - дос-
товерное событие.
Совокупность (Q, 3) называется измеримым пространством.
Тройку объектов (Q, 3, Р) можно рассматривать как вероят-
ностное пространство в контексте рассматриваемой задачи.
Вероятностное пространство является самой общей мате-
матической моделью случайного эксперимента, связанного с
наблюдением случайных событий. События на финансовом
рынке ассоциируются с теми или иными значениями количе-
ственных характеристик финансовых активов или некоторых
их совокупностей, например ценами и доходностями активов.
Как отмечалось выше, данные характеристики, называемые в
•дальнейшем также финансовыми переменными, целесообразно
рассматривать как случайные величины, а для их анализа ис-
пользовать числовые и функциональные характеристики слу-
чайных величин.
3.2.2. Функциональные и числовые характеристики
финансовых активов
1) Вероятностные модели финансовых переменных.
В качестве вероятностной модели некоторой финансовой
переменной X в фиксированный момент (период) времени
будем использовать модель ''случайная величина". Определим
данное понятие.
Пусть (Q, 3, Р) - описанное выше вероятностное про-
странство. Случайной величиной Х=Дсо) будем называть веще-
ственнозначную функцию, определенную на пространстве
1 В теории вероятностей множество 3 принято называть "ст-алгеброй под-
множеств Q", однако здесь и далее отдается предпочтение содержательной
интерпретации терминов теории вероятностей в контексте рассматриваемой
задачи, включая интерпретацию пространства элементарных событий Q и ст-
ал гебрыЗ [34, 35].
118

элементарных событий Q такую, что для каждого действи-
тельного числа хеК (KrfR1) можно поставить в соответствие
наблюдаемое событие Ах, определяемое как Ax={®eQ,:
Дсо)<х}сЗ.
Из ДхсЗ следует, что вероятность наступления события Ах
определяется вероятностной мерой Р, поскольку, как отмеча-
лось выше, для любого события А^аЗ может быть поставлена
в соответствие вероятность наступления этого события Т*(АХ),
0<Р(у4х)<1. При этом говорят, что случайная величина X явля-
ется ^-измеримой функцией.
Таким образом, будем полагать, что значения jcgX финан-
совой переменной, описываемой случайной величиной X,
складываются в зависимости от событий Л^еЗ, наблюдаемых
на рынке, где К - множество всех возможных значений слу-
чайной величины X, а 3 - совокупность всех наблюдаемых
событий на финансовом рынке.
Для вычисления вероятностей значений случайной вели-
чины X (т.е. вероятностей наступления событий Ах) будем ис-
пользовать функцию распределения вероятностей.
Функция Fx: К->[0,1] (т.е. функция, задающая отображе-
ние множества К в интервал [0,1]), определяемая как
7^(x)=P(^x)=P(coeQ| Дсо)<х), называется функцией распределе-
ния вероятностей случайной величины X. В дальнейшем бу-
дем использовать более лаконичную запись: Рх(х)=Р(Х<х),
хеХ.
Если для некоторой случайной величины X заданы множе-
ства всех возможных значений К и закон распределения веро-
ятностей в виде функции распределения вероятностей F%(x),
то случайная величина считается полностью описанной и нет
необходимости в конкретизации вида вероятностного про-
странства (Q, 3, Р).
Если группа из 7V>1 финансовых переменных анализирует-
ся совместно, то их целесообразно рассматривать как случай-
ный вектор, т.е. как N-мерный вектор, компонентами которо-
го являются случайные величины Х\9 Х2, ..., Хц.
Закон распределения вероятностей для случайного вектора
Х=(Х\, Х2, ..., Ад?)т определяется N-мерной функцией распреде-
ления, имеющей вид:
Fx(x) = F(AX) = Р(ш
<xu X2 <х2
119

где х=(х\, Х2, ..., jc^)tgK^c91^ - произвольный фиксирован-
ный вектор; ^={(oeQ|Ar1((o)<JC1, X2(®)<X2i -, X^{(i))<xN}e^ -
соответствующее наблюдаемое событие.
Для вероятностного описания значений финансовых пере-
менных, наблюдаемых в течение некоторого интервала вре-
мени, используется модель "случайный процесс".
Случайным (стохастическим) процессом будем называть се-
мейство вещественнозначных случайных величин {Х{}\
Xf=Xt{o), определенных на вероятностном пространстве (Q, 3,
Р), где параметр /<еТ интерпретируется как непрерывное
(Т=[0,оо)) или дискретное (Т={0, 1, 2, ...}) время.
Таким образом, случайная величина Хь описывающая зна-
чение некоторой финансовой переменной в фиксированный
момент времени /еТ, является примером случайного процесса
{Xt}, описывающего поведение данной переменной в последо-
вательные моменты времени. В дальнейшем, как правило, бу-
дем рассматривать случайные процессы с дискретным временем
t=\,2,..., Т.
Каждому фиксированному элементарному событию co*eQ
соответствует некоторая реализация {х{} (лу=Л/(со*), ^^2, ..., 7)
случайного процесса, которая представляет собой совокупность
' значений анализируемой переменной в последовательные
моменты и называется временным рядом.
В задачах количественного финансового анализа могут ис-
пользоваться два типа случайных величин: дискретные и не-
прерывные (абсолютно-непрерывные) случайные величины. В
многомерном случае им соответствуют дискретные и непре-
рывные случайные векторы.
Дискретные случайные величины (ДСВ) принимают конеч-
ное (К<оо) либо счетное (К—оо) множество значений
K={;ti, *2, •••> хк) (гДе К= 1 N |-мощность множества К, т.е. ко-
личество различных значений случайной величины).
Вероятности значений ДСВ X, так называемые элементар-
ные вероятности, определяются выражением:
pk ее Р(Х = хк) >0, хк еК, Л=1, 2, ..., А;
и удовлетворяют условию нормировки:
Функция распределения ДСВ JfeN={xi, x^ ..., х^} может
быть выражена через элементарные вероятности с помощью
соотношения:
120

Непрерывные случайные величины (НСВ) имеют континуаль-
ное (бесконечное и несчетное) множество значений К, на-
пример: Х=(-оо, +оо) - множество всех точек числовой пря-
мой; К=(а, />)е(-оо, +оо) - интервал, определенный на число-
вой прямой.
Случайная величина Хе^~(а, Ь) называется непрерывной,
если существует функция fx(x), называемая плотностью рас-
пределения случайной величины, такая, что
Функция плотности распределения неотрицательна f%(x)>0
и удовлетворяет условию нормировки:
Функции Fx(x) и/^(х) относятся к функциональным харак-
теристикам случайных величин. Наряду с функциональными
характеристиками для описания случайных величин исполь-
зуются числовые характеристики, важнейшими из которых
применительно к задачам количественного финансового ана-
лиза являются моменты распределения вероятностей: матема-
тическое ожидание (первый начальный момент) и дисперсия
(второй центральный момент).
Математическое ожидание /их случайной величины X
вычисляется по формуле:
к
УxkPk, если X ~ ДСВ
*=1
ъ (3.13)
\xfx(x)dx, если X - НСВ
о
и соответствует ожидаемому (в среднем) значению случайной
величины X для заданного закона распределения вероятно-
стей.
Говорят, что математическое ожидание случайной величи-
ны X существует, если выполняется условие:
E(U|)<co.
121

Е(Х2)
Математическое ожидание цх случайного N-мерного вектора
Х=(Х\, Х2, ..., Л#)т определяется выражением:
= Е(Х) =
Дисперсия а2х случайной величины X определяется по
формуле
ах = D(A) - Щ(Х - ЩХ))2 >0.
С учетом (3.13) для различных типов случайных величин
имеем:
(3.14)
<- дев
с, если Х- НСВ
Среднеквадратическое отклонение (СКО), или стандартное
отклонение, случайной величины X определяется как арифме-
тический корень из дисперсии:
Дисперсия g2x и СКО ах являются характеристиками рас-
сеяния значений случайной величины X относительно ожи-
даемого среднего значения /лх и используются как количест-
венные меры степени неопределенности или изменчивости
(волатильности) значений данной случайной величины.
Наглядной иллюстрацией такой возможности может слу-
жить неравенство Чебышева [35]:
V(\X-
(3.15)
Из (3.15) следует, что вероятность отклонения значений
случайной величины X от ожидаемого среднего значения //^
(т.е. неопределенность относительно значения случайной ве-
личины X) тем меньше, чем меньше величина <з2х.
Для случайного вектора Х=(Х\, Аг, ..., Х^)Т может быть оп-
ределена ковариационная матрица:
122

(2
а, а12
где ст/2=(т,7 - дисперсия случайной величины ^; о^- - ковариа-
ция случайных величин А/и А)(/,у-1, 2, ..., TV).
Ковариационная матрица Ъх является симметричной, т.е.
Ъх =21 (или Gij=Oji). В общем случае матрица Е^ неотрица-
тельно определена, однако обычно рассматривают невырож-
денные распределения вероятностей и поэтому предполагают,
что матрица Ъх является невырожденной, т.е. IZ^l^O.
2) Свойства математического ожидания и дисперсии.
Приведем некоторые свойства математического ожидания
и дисперсии, которые будут использоваться в дальнейшем без
специальных ссылок.
Свойства математического ожидания
Е.1. Пусть с - произвольная константа и Е(Х) существует,
тогда
ЩсХ) = сЩХ).
Е.2. Если X, Y - случайные величины и существуют Е{Х},
E(X+Y) = E(A) + Е(У).
Е.З. Если в условиях свойства Е.2 случайные величины X,
Y взаимно независимы, то
Свойства дисперсии
D.I. ЩХ)= EiX1) - (Е(Л))2.
D.2. Если а, Ъ - константы, то
Ща + ЬХ)= ЬЩХ).
D.3. Если X, Y- случайные величины, то
Б(Х+У)= D(X) + D(Y) + 2Cov(J, Y),
где
; Y) = E((X - Е(Л))( Y - E( Y)))
123

- ковариация случайных величин X и Y, служащая харак-
теристикой степени линейной зависимости (коррелиро-
ванное™) случайных величин. В частности, если Cov
(X,Y)=0, то X, Y- некоррелированные случайные величины.
D.4. Если X, Y - некоррелированные случайные величины,
т.е. Coy{X,Y)=$, to
D(X+Y)=D(X) + B(Y).
3) Коэффициенты корреляции и вариации случайных вели-
чин.
Если ах >0, cry >0 и аху^Со\(Х, Y) - ковариация случайных
величин X и У, то определен коэффициент корреляции случай-
ных величин X и У, вычисляемый по формуле
Рху= -^-- (3.16)
GXGY
Коэффициент корреляции является безразмерной норми-
рованной (что более удобно для практического применения)
характеристикой степени линейной зависимости случайных
величиной Y: \рху\<1.
Если pxy=±h то величины связаны функциональной ли-
нейной зависимостью, т.е. Y=a+bX. Имеет место прямая ли-
нейная зависимость (6Х)), если рху = 1, и обратная линейная
зависимость (6<0), если рху~-\.
Случайные величины X и Y являются некоррелированными,
если /^/=0; отрицательно коррелированными, если /?yk<0; по-
ложительно коррелированными, если /?ду>0.
Из независимости случайных величин, т.е. из свойства Е.З,
следует их некоррелированность, обратное, вообще говоря,
неверно. Однако для случайных величин, имеющих нормаль-
ное распределение (п. 3.2.3), некоррелированность случайных
величин влечет их независимость.
Коэффициент вариации случайной величины X с математи-
ческим ожиданием /их^О определяется по формуле
Ух=ТП- (3-17)
Коэффициент вариации является безразмерной нормиро-
ванной характеристикой степени рассеяния значений случай-
ной величины. Данную характеристику целесообразно ис-
пользовать для сравнения степени относительного по отно-
шению к ожидаемому среднему значению рассеяния значе-
124

ний случайных величин X и У, для которых jux^My- Очевидно,
если Vx< Vy, то относительное рассеяние значений случайной
величины ^меньше.
4) Коэффициенты асимметрии и эксцесса.
Коэффициенты асимметрии kj и эксцесса К2 для случайной
величины X с математическим ожиданием цх и дисперсией
сг^х определяются по формулам
(3.18)
1- (3.19)
Данные безразмерные (нормированные) числовые характе-
ристики случайной величины используются для сравнения
распределения вероятностей случайной величины X с нор-
мальным распределением.
Функция плотности нормального распределения, опреде-
ляемая по формуле (3.21) (см. далее п. 3.2.3), является сим-
метричной и имеет "нормальный эксцесс", так что для нее
к\=К2:=0. При /q*0 функция плотности распределения слу-
чайной величины X асимметрична с отрицательной (/q<0) или
положительной (/q>0) асимметрией. При лг2<0 кривая плотно-
сти распределения является более пологой, а при л:2>0 имеет
более острую вершину, чем плотность нормального распреде-
ления.
3.2.3. Распределение вероятностей
доходностей активов
1) Доходность и риск финансовых активов.
Описанные выше характеристики случайных величин ис-
пользуются в количественном финансовом анализе в качестве
характеристик финансовых активов. Пусть в приведенных
выше соотношениях вместо произвольной случайной величи-
ны X используется случайная величина Rh описывающая до-
ходность актива за период владения t (t=\, 2, ..., 7), тогда ос-
новные характеристики актива, соответствующие некоторому
периоду владения /, определяются следующим образом:
juf ^ E{Rt} - ожидаемая доходность актива;
о>2 = D{Rt} - дисперсия доходности актива;
a t - риск финансового актива.
Для 7V>1 активов, анализируемых совместно в некотором
периоде /, можно определить:
125

случайный вектор доходностей Rt=(Ru, R2h ...
вектор ожидаемых доходностей //Г=Е(1?Г),
ковариационную матрицу доходностей активов
It =(Gijt)=E((J?, -jut)(Rt -Mt)T) (o^gI ).
2) Использование нормального закона распределения.
Относительно доходности актива Rt за период t (/=1, 2, ...)
часто предполагается, что она описывается случайной вели-
чиной, имеющей нормальный закон распределения вероятно-
стей с математическим ожиданием jut и дисперсией о>2, т.е.
значения доходности актива {Rt} (/=1, 2, ...) являются гауссов-
скими случайными величинами. В данном случае будем исполь-
зовать обозначение L(/?/)=Ni(///,cr/2).
Предположение о нормальном законе распределения мо-
жет использоваться наряду с предположением о том, что {Rt}
(*=1, 2, ...) - независимые и одинаково распределенные случайные
величины (н.о.р.с.в.), для которых jut=ju, a &}=(?• (/=1, 2, ...).
Для сокращенной записи этого свойства будем использовать
обозначение: {/?г}~ н.о.р.с.в. NiC/^o2).
Функция распределения F(x) и плотность распределения
Дх) одномерного нормального закона распределения
имеют вид:
(3.21)
Это одна из наиболее простых и удобных в аналитических
исследованиях моделей доходностей активов. Однако она
имеет, по крайней мере, два серьезных недостатка. Во-
первых, это неограниченный интервал значений доходности
Л/€^Я1=(-оо, +оо). Это противоречит тому факту, что финансо-
вые активы предполагают, как правило, "ограниченную от-
ветственность" (limited liability) инвестора в пределах инве-
стированного капитала. Это означает, что инвестор не может
потерять больше той суммы, которую он инвестировал в дан-
ные активы и которая всегда ограниченна, т.е. -\<Rt. Конеч-
но, вероятность выхода значений {Rt} за эту границу может
быть сколь угодно мала, однако в рамках гауссовской модели
126

никогда не равна нулю, как того требует предположение об
"ограниченной ответственности".
Во-вторых, в то время как однопериодные доходности {Rt}
для каждого периода t подчиняются нормальному закону,
многопериодная доходность Rtx за К периодов, определяемая
по формуле (3.6), не является нормальной случайной величи-
ной. Нормальное распределение имеет величина, равная сум-
ме однопериодных доходностей, однако она не имеет какой-
либо значимой экономической интерпретации.
3) Использование логарифмически-нормального закона рас-
пределения.
В качестве альтернативы предположению о нормальности
однопериодных доходностей может использоваться предпо-
ложение о том, что однопериодные доходности, выражаемые
ставками непрерывных процентов {rt} (/*plog(l+ /?,), /?/>-1), яв-
ляются независимыми и одинаково распределенными случай-
ными величинами с нормальным законом распределения и
параметрами Е(гг)=// и D(r/)=a2, т.е.
{rt} ~ н.о.р.с.в. Niiju^o2). (3.22)
С учетом (3.5) и обозначения pt= logPt имеем:
r^log(l + Rt) = log и-*- =Л- PtA. (3.23)
Если {/у-н.о.р.с.в., то из (3.22), (3.23) следует, что случай-
ные величины 1 + Rt = еп е[0,+оо] (/=1, 2, ...) являются неотри-
цательными н.о.р.с.в. и имеют логарифмически-нормальное
распределение. Это означает, что Rt>-1 и выполняется предпо-
ложение об "ограниченной ответственности" инвесторов.
Функция распределения случайной величины 1+7?/, имею-
щей логарифмически-нормальное распределение, имеет вид [1]
F(x) = Р(1+Л,<х)= P(rr <log x)=
log х i (У-М)2
Л f e"2 -2 dy.
{
Из этого выражения путем дифференцирования по х полу-
чим функцию плотности логарифмически-нормального рас-
пределения:
127

I (logх-л)2
Согласно логарифмически-нормальной модели для математи-
ческого ожидания и дисперсии однопериодных доходностей
имеем:
■1).
Если заданы значения E(Rt)=juR и D(Rt)=a2R, то математи-
ческое ожидание и дисперсия случайной величины rt имеют
вид:
Е(г,) - log- ^"А , Щг{) =log| 1 ' "~
4) Использование устойчивых законов распределений.
Многие эмпирические исследования доходностей акций
[37, 47, 50] свидетельствуют о наличии в их распределении
таких отклонений от нормального распределения, как более
"острая вершина" и более "тяжелые хвосты" кривой плотно-
сти распределения. Для описания таких особенностей моде-
лей данных может использоваться широкий класс устойчивых
распределений (stable distributions), специальным случаем из
которого является нормальный закон (см., например, обзор
[7]). Альтернативный подход, основанный на моделях вре-
менных рядов с условной гетероскедастичностью, описывает-
ся далее, в разд. 7.3.
3.3. КЛАССИФИКАЦИЯ ЭКОНОМЕТРИЧЕСКИХ
МОДЕЛЕЙ ФИНАНСОВЫХ ПЕРЕМЕННЫХ
В задачах количественного финансового анализа объектом
исследования часто выступает не один актив, а группа акти-
вов, при этом значения анализируемых характеристик регист-
рируются в последовательные моменты времени. Таким обра-
зом, в общем случае используемые для анализа эмпирические
(статистические) данные можно рассматривать как простран-
на

ственно-временную выборку [1]. Кроме того, при построении
моделей финансовых переменных может возникнуть необхо-
димость в учете влияния на анализируемые характеристики
факторов, отражающих состояние внешнего экономического
окружения. Для описания подобных данных используются
эконометрические модели, т.е. статистические модели эконо-
мических и финансовых процессов, построенные на основе
реальных статистических данных.
Рассмотрим краткую характеристику некоторых основных
классов эконометрических моделей, применяемых в задачах
финансового анализа для описания динамики курсов и до-
ходностей активов, а также при практической реализации и
тестировании классических моделей финансовой экономики.
Для адекватного описания процессов на финансовом рын-
ке требуются модели, которые обладают тремя основными
свойствами:
• учитывают зависимость между совместно анализируемы-
ми финансовыми переменными;
• описывают динамику изменения финансовых перемен-
ных;
• учитывают влияние внешних (экзогенных) факторов на
анализируемые "внутренние" (эндогенные) характери-
стики финансовых активов.
Решение задач анализа, направленных на достижение пер-
вой и второй целей в отдельности, приводит к двум альтерна-
тивным типам моделей данных.
Так, если учитывают взаимосвязи между характеристиками
различных активов и пренебрегают зависимостью значений
анализируемых показателей от времени, т.е. рассматриваются
"пространственные связи" между различными активами, то
приходят к модели данных, известной как пространственные
или перекрестные, данные (cross-sectional data). Статистиче-
ские данные, описываемые такой моделью, можно рассмат-
ривать как выборку из некоторого многомерного распределе-
ния вероятностей (например, многомерного нормального
распределения), относящуюся к одному моменту (периоду)
времени. Таким образом, пространственные данные - это дан-
ные, соответствующие различным объектам в один и тот же
момент времени.
Если же данные рассматриваются как значения некоторого
показателя или группы показателей, полученные в последова-
тельные моменты времени, то для их описания используются
модели временных рядов (time series models). Причем если каж-
дый из показателей анализируется независимо от других, то
9 Зак. 7084 129

для их описания используются одномерные временные ряды
(univariate time series), например модели временных рядов с
трендом, модели авторегрессии, модели скользящего среднего
и т.д.
Достижение третьей цели требует использования моделей с
экзогенными переменными регрессионного типа (regression
models). Регрессионные модели по пространственным данным
являются статичными. Модели временных рядов с экзоген-
ными переменными известны как модели динамической рег-
рессии.
Дальнейшие обобщения данных моделей, применяемые
для достижения одновременно всех трех целей, приводят к
многомерным моделям финансовых временных рядов (multi-
variate financial time series). Наиболее известными моделями
данного типа являются [1, 41, 43]: модель векторной авторег-
рессии (vector autoregressive model - VAR), модель векторной
авторегрессии и скользящего среднего (vector autoregressive mov-
ing average model - VARMA), векторная модель коррекции оши-
бок (vector error correction model - VECM), модели в виде
систем одновременных уравнений (system of simultaneous equa-
tions model - SSE).
Каждая конкретная задача анализа предполагает введение
определенных дополнительных модельных предположений,
ограничивающих класс моделей. Выбор того или иного класса
моделей определяет функциональный вид модели с точно-
стью до набора неизвестных параметров. Подобные модели
принято называть параметрическими вероятностно-статисти-
ческими моделями. При этом имеется в виду, что априорная
неопределенность в описании моделей восполняется посред-
ством статистического оценивания неизвестных параметров
по эмпирическим данным.
Вероятностно-статистические модели, описывающие меха-
низм функционирования экономических (финансовых) сис-
тем или процессов, называются эконометрическими моделями.
Эконометрические модели финансовых процессов должны
основываться на моделях и закономерностях финансовой
экономики, придавая им количественную форму выражения.
Представление экономических моделей в количественной
форме делает их не только доступными для практического
применения, но и позволяет проверять их адекватность.
Приведем общее описание некоторых основных типов
эконометрических моделей, используемых в последующих
разделах учебного пособия при решении классических задач
финансового анализа.
130

3.4. МОДЕЛИ ПРОСТРАНСТВЕННЫХ ДАННЫХ
Предположим, что активы описываются одной характери-
стикой - доходностью за определенный период владения ак-
тивом. Использование именно этой характеристики в данном
разделе преследует две цели: первая - избежать излишней
сложности в описании моделей, вторая - сделать изложение
материала более конкретным.
Выбор в пользу доходности, а не рыночной цены актива
обусловлен также тем, что во многих аналитических и эмпи-
рических исследованиях в качестве анализируемых, модели-
руемых и прогнозируемых характеристик активов использу-
ются их доходности. Примером могут служить задачи опти-
мального портфельного инвестирования, задачи построения
экономических и эконометрических моделей равновесия
фондовых рынков, а также динамических моделей характери-
стик активов. Это объясняется двумя причинами: первая: до-
ходности - это безразмерные характеристики, которые удобно
использовать при сравнительном анализе альтернативных ва-
риантов инвестирования, соотнося их к одним и тем же пе-
риодам владения активами; вторая - более привлекательные
статистические свойства, чем у цен активов. Например, слу-
чайный процесс, описывающий доходности акции, может
быть стационарным при нестационарных "коинтегрирован-
ных" случайных процессах, соответствующих ценам акций и
дивидендам по ним [37].
Пусть объектом анализа являются N (N>1) финансовых ак-
тивов. На основании рыночных курсов активов, регистрируе-
мых в последовательные моменты времени /=0, 1, 2, ..., Т
(7>1), для каждого актива вычисляются доходности за соот-
ветствующие периоды (разд. 3.1), которые при необходимости
могут быть приведены к определенному одинаковому для всех
активов периоду владения.
Доходность актива / в периоде t будем описывать случай-
ной величиной Rit. Совокупность значений доходностей {Rit}
(/=1, 2, ..., /V, t=\, 2, ..., 7) образуют "пространственно-вре-
менную выборку", т.е. выборку значений доходностей в "про-
странстве активов", анализируемых в последовательные пе-
риоды.
Можно предложить различные варианты вероятностно-
статистических моделей выборки {/?,,}. Наиболее общей явля-
ется модель совместного распределения вероятностей.
131

3.4.1. Совместное распределение вероятностей
Если рассматривать доходности {Rit} (где /foeSR1) как сово-
купность случайных величин (например, как компоненты
случайного вектора доходностей активов), то в качестве моде-
ли этих случайных величин может служить их совместное
распределение вероятностей, определяемое функцией распре-
деления:
G(R]h /?12, ..., Кхъ ..., Rm, Rm, ..., RNT\Z,6), (3.24)
где GO - известная функция1; Ze%K (K>\) - заданный вектор
значений факторов (экзогенных переменных);
(т>\) - фиксированный вектор неизвестных параметров.
Функция (?(•), заданная с точностью до параметров 0, опи-
сывает стохастическое поведение и взаимосвязь доходностей
{/?7у}, а также учитывает влиянье на доходности активов,
включенных в модель факторов Z.
Процесс построения эконометрической модели предпола-
гает решение двух основных задач:
• задачу идентификации модели, т.е. статистического оце-
нивания параметров в;
• задачу проверки адекватности модели на основе стати-
стических тестов.
Модель (3.24) является слишком общей, чтобы ее можно
было использовать без каких-либо дополнительных предпо-
ложений. Поэтому приведем некоторые важные частные слу-
чаи данной модели, возникающие при некоторых дополни-
тельных модельных предположениях.
3.4.2. Модель "случайная выборка" и ее свойства
Из доходностей N активов за один и тот же период / обра-
зуем случайный вектор-столбец Rt—(R\t, /?2/, ..., /?м)те$Н^. Ис-
пользуя общую модель (3.24) и различные варианты модель-
ных предположений относительно {Rt}, опишем основные ти-
пы моделей пространственных данных.
Перечислим вначапе упрощающие модель (3.24) предпо-
ложения, которые используются в некоторых классических
задачах финансового анализа. К числу таких модельных пред-
положений относятся следующие условия:
1 Для упрощения записи обозначение неслучайных аргументов функции
(7(. \ZjG) совпадает с обозначениями соответствующих случайных величин.
132

P.I. Случайные векторы {Rt}(t=\, 2, ..., 7) являются незави-
симыми в совокупности.
Р.2. Случайные векторы {Rt}(t=l9 2, ..., 7) одинаково рас-
пределены.
Р.З. Компоненты {Rlt} (/=1, 2, ..., N) вектора Rt являются
гауссовскими случайными величинами, т.е. подчиняются
нормальному закону распределения вероятностей.
Р.4. Для любого t компоненты R\t, R2t, •••> R-м вектора Rt
являются независимыми в совокупности случайными величи-
нами.
Обозначим:
Fr{) - совместная функция распределения случайных век-
торов Rh R2, ..., RT;
Ft(xu хъ ..., xN)=F(Ru<xb R2t<x2, .», Rn&n) - Функция N-
мерного распределения случайного вектора Rb которая пред-
ставляет собой совместную функцию распределения компо-
нент Ru, R2i9 ..., Rm, вектора Rt (*=1, 2, ..., 7).
Функция распределения вероятностей /^(), таким образом,
служит математической моделью некоторой генеральной сово-
купности случайных векторов. Если предполагается Р.1, то
т
Х(х19х2,...9х„). (3.25)
Подобная модель данных позволяет исследовать "перекре-
стные" связи между характеристиками объектов при отсутст-
вии между ними временной зависимости.
Если наряду с Р.1 выполняется предположение Р.2, т.е.
случайные векторы {Rt} одинаково распределены и
Ft{x\, X2, ..., xn)=F(x\, X2, ..., xpj) для любого /, то совокупность
случайных векторов {Rt} можно рассматривать как случайную
выборку из генеральной совокупности, которая описывается
многомерной функцией распределения F(x\, x2, ..., х$-
При выполнении Р.З случайные векторы {Rt} являются га-
уссовскими и образуют случайную выборку объема Т из TV-
мерного нормального распределения, обозначаемого Nn(//,£).
Плотность распределения вероятностей случайного вектора
доходностей Rt при этом имеет вид:
f(x) =(2я)-^/21X | -1/2 ехр | -1 (*-//)T s-i (х-м) |, xeKN, (3.26)
где //, Z - параметры распределения.
133

Параметры //, I имеют следующий смысл: jLf=(jUi)=E(Rt)e
4lN - вектор ожидаемых доходностей активов за период вла-
дения; I=(cr^)=E((i?r-/i)(ifr-//)T) - (7Ух7У)-ковариационная мат-
рица случайного вектора Rt доходностей активов; /// =Е(Л,у) -
ожидаемая доходность актива /; ау = Е((/?/Г-///)(У?уГ-//у)) (%*) -
ковариация доходностей активов / и у; <т//=Е((/?/г-///)2)=сг?-
дисперсия доходности актива (i,j =1,2, ..., TV).
Если наряду с предположением Р.З имеет место предполо-
жение Р.4, то <j/y=E((/?/r-///)(/?y/-/iy))=O (fey) и, следовательно,
ковариационная матрица доходностей активов является диа-
гональной: £=diag( о2!).
Вместо неизвестных истинных значений параметров мо-
дели {///}, {а/у}, {o2j}(i9J=l9 2, ..., TV) используются их стати-
стические оценки по выборкам {Rjt}(t=\, 2, ..., 7). Для вы-
числения оценок неизвестных параметров могут использо-
ваться различные статистические методы [1, 12, 41, 43]. Если
справедливы предположения Р.1 - Р.З, то обычно использу-
ется метод максимального правдоподобия. При сделанных
предположениях в качестве оценок р =(j3/)? Z=(S/-/) пара-
метров //, Z рассматриваемой модели обычно используются
статистики:
(Л/7-Д)2, /,y = l,2,...,7V. (3.28)
А t=\
Оценки вектора // и матрицы Е определяются по форму-
лам:
(3.29)
Известно [1], что данные оценки при указанных предпо-
ложениях являются несмещенными, строго состоятельными и
эффективными.
134

3.5. РЕГРЕССИОННЫЕ МОДЕЛИ
ДОХОДНОСТЕЙ ЦЕННЫХ БУМАГ
К регрессионным моделям приходят, если учитывают
влияние внешних (экзогенных) факторов на анализируемые
"внутренние" (эндогенные) характеристики финансовых ак-
тивов. В данном случае делается предположение:
Р.5. Случайные величины {Rit\ (векторы {Rt}) зависят от
экзогенных факторов Zt (t=l, 2, ..., 7).
Если при этом пренебрегают временной зависимостью ме-
жду значениями характеристик финансовых активов (предпо-
ложение Р.1), то регрессионные модели являются статиче-
скими. Рассмотрим примеры таких моделей.
3.5.1. Определение моделей
и модельные предположения
Пусть на {/?,,} оказывают влияние К>\ факторов, которые
являются общими для всех анализируемых характеристик. В
момент (период) t их значения равны Zt\, Za> •••> ZtK
(/=1, 2, ..., 7), при этом зависимость между характеристиками
финансовых активов и факторами является линейной относи-
тельно параметров модели. Для описания подобных зависи-
мостей часто используется следующая модель множественной
линейной регрессии.
1) Модель множественной линейной регрессии.
Данная модель описывает зависимость доходности актива /
от К>\ факторов zu —> £* и имеет вид:
/=1,2,..., Г,
где для периода t Zt=(zt\, ...., 1гк)Т^^к ~ вектор-столбец зна-
чений факторов; %it = Rit -jult - случайная величина, интер-
претируемая как "неожиданная доходность" (unexpected
return), равная отклонению фактической доходности акти-
ва Rit от ожидаемой в соответствии с моделью доходности
актива //#. Параметр а7 называется свободным членом, а
вектор-столбец Д=(Дь ..., Ax)tg9?k - вектором коэффици-
ентов регрессии для уравнения, описывающего доходность
актива /.
Ожидаемая доходность juit определяется функцией регрессии
доходности актива / на факторы itu •••> Ьк- Функция регрес-
135

сии рассматривается как условное математическое ожидание
доходности актива при условии, что вектор факторов Zt при-
нимает некоторое фиксированное значение, т.е. /Utt=E(Rit\Zt).
В векторном представлении модель (3.30) имеет вид:
Ato=Z*,+$0,f=l,2,...,tff (3.31)
где i?(/)=(/?/i, Л/2, ..., Rjt)t£Wt - вектор-столбец доходностей
актива / за Т периодов; Af=(a/, Дь ..., 0ц()теЩт - вектор
параметров модели (т=К+\); £(/)=(£//) е 9?т - случайный
вектор отклонений фактических доходностей активов от
ожидаемых; Z=(^/) - (Tx^+l)) - матрица значений фак-
торов (*=1, 2, ..., Г, /=0, 1, ..., К).
Для регрессионной модели вида (3.30) со свободным чле-
ном £/о=! для всех f=l, 2, ..., Т, поэтому матрица Z имеет вид:
Z =
zu
Ztk
. Дополнительные модельные предположения относительно
модели (3.30)—(3.31) связаны со случайным вектором откло-
нений ф) и матрицей значений факторов Z.
Относительно матрицы Z предполагается, что она является
фиксированной матрицей полного ранга, т.е. ее ранг равен
числу столбцов, а число наблюдений (строк матрицы Z)
больше числа m=K+l оцениваемых параметров, т.е.
rank(Z)=m<7\ (3.32)
Предположение (3.32) означает, что столбцы матрицы Z
являются линейно независимыми векторами. В этом случае
матрица Z является невырожденной. Матрица ZTZ имеет тот
же ранг, что матрица Z, и является также невырожденной, а
следовательно, для нее существует обратная в обычном смыс-
ле матрица (ZTZ)~!.
Данное предположение относительно матрицы Z обуслов-
лено требованием идентифицируемости модели, т.е. требова-
нием существования единственной оценки вектора парамет-
ров модели bi по методу наименьших квадратов (МНК-
оценки).
Традиционными относительно {£,,} являются предположе-
ния:
136

£.1. Случайные отклонения доходностей активов имеют
нулевое математическое ожидание (среднее значение), т.е. от-
клонения являются симметричными относительно нуля:
Е(£//)=0 или в векторном виде Е(ф))=0е9?г (/=1, 2, ..., N9
/=1,2, ..., 7).
£.2. Отклонения доходностей {£,>} актива / (/=1, 2, ..., N) для
различных периодов времени являются некоррелированными
случайными величинами: Сог(£//, £г)=0 для /;*г(/,г=1, 2, ..., 7).
£.3. Дисперсия случайных величин {£,,} (/=1, 2, ..., N) по-
стоянна во времени: Щ^()=щ2=const для всех /=1, 2, ..., Г.
Данное свойство известно как свойство "гомоскедастжности"
(однородности) дисперсий отклонений. Отклонения {£#}, для
которых D(%jf)=y/it2itconst, называются гетероскедастичными.
£.4. Случайные отклонения {&} имеют нормальное распре-
деление: L(£,)=N,(0, w?) (/=1, 2, ..., TV).
£.5. Отклонения доходностей различных активов ^\h...,^t
являются взаимно некоррелированными: Сог(^^})=у/у—0 для
щ (1У у=1, ..., ЛО и любых ^=1, 2, ..., 71.
В моделях со случайными факторами дополнительно пред-
полагается:
£.6. Отклонения £# и факторы {zti\ являются взаимно не-
коррелированными: Сог(£/г Zr/)^ (/=1, 2, ..., TV, /=1, 2, ..., К,
/=1,2,..., 7).
Ожидаемая доходность актива / для периода / определяется
как функция регрессии Rit на Ztw с учетом предположения £.1
равна:
(/=1,2, ..., TV, /=1,2, ..., 7). V ^;
Функция регрессии вектора R^ доходностей актива / на
значения факторов Z имеет вид:
E(J?(0|Z)=ZA#-, (/=1,2, ..., N). (3.34)
Из свойств ^.1-^.3 следует, что ковариационная матрица
случайного вектора ^еЩТявляется диагональной:
) (3.35)
где 1т - единичная (7х7)-матрица.
Если дополнительно предполагается £.4, то случайный век-
тор £(/) имеет Г-мерный нормальный закон распределения
Ny(О^щЧ). Предположение ^.5 дает основание не учитывать
корреляции случайных величин %\ь ..., ^ при совместном
137

анализе доходностей активов, т.е. строить модели вида (3.30)
для каждого из активов в отдельности.
Модель множественной линейной регрессии (3.30) являет-
ся базовой эконометрической моделью доходностей активов в
теории арбитражного оценивания, изложению которой посвя-
щена гл. 6.
2) Модель простой линейной регрессии.
В частном случае, когда в модели (3.30) используется лишь
один фактор (например, доходность рыночного портфеля),
А=1 и соотношение (3.30) определяет модель простой (пар-
ной) линейной регрессии вида:
*=l, ..., Т. (3.36)
К данному виду сводится известная "рыночная" модель
Шарпа, рассматриваемая в п. 5.4.1, а также эконометрическое
представление модели равновесия САРМ, описываемой в
гл. 6.
3) Модель многомерной линейной регрессии.
Если имеют место предположения £.1-£.3, а условие £.5 не
выполняется, т.е. Сог( £,,<§•,)= у^ для щ (i,j=h 2, ..., N,
. /=1, 2, ..., 7), то целесообразно осуществлять совместный ана-
лиз доходностей активов.
В этом случае вектор Rt=(R\t, R^t, .., /?м)те9?^, образован-
ный из доходностей N активов за произвольный период t,
описывается моделью многомерной линейной регрессии вида:
&t=l, ..., Т, (3.37)
где ar=(aj)eWN - вектор, компонентами которого являются
свободные члены отдельных регрессионных уравнений
или "альфа-коэффициенты" активов (см. гл. 6); В=(/%*) -
(NxK) - матрица, строками которой являются векторы ко-
эффициентов регрессии Р?=(Рп> ..., Рид^^к 0~1> •••? ^0>
т.е. векторы, образованные из бета-коэффициентов акти-
вов; Zt-(ztb —v ZtidT^K - вектор значений факторов;
%t (Zit> ~> iWre^N ~ случайный вектор отклонений до-
ходностей N активов в момент времени t, имеющий нуле-
вое среднее значение E(^)=Oe9l7V и ковариационную мат-
рицу:
U=l, 2, ..., TV), ^=^т, №1*0.
Для диагональных элементов матрицы Ч? здесь и далее бу-
дем использовать обозначение щ^Щ^ы^Щ2- В СИЛУ условия
138

ковариационная матрица случайных векторов & и £ для
= 1, 2, ..., 7) является нулевой: Е(££ГТ)=О.
Если дополнительно предполагается справедливость усло-
вия £.4, то для фиксированных значений факторов {Z,} слу-
чайные векторы {£/} являются взаимно независимыми гаус-
совскими векторами, т.е. имеют JV-мерный нормальный закон
распределения:
L(£)=NN(0,4>)(/=1,2, ..., 7). (3.38)
С учетом (3.38) из (3.37) следует, что функция регрессии Rt
на Zt определяется соотношением:
E(Rt\Zt)=a+BZh
а случайные векторы {Rt} (f=l, 2, ..., 7) взаимно независимы,
распределены по нормальному закону, однако имеют различ-
ные математические ожидания, т.е. L(jR/)=:Nx(BZf,Z). Таким
образом, совместное распределение векторов {Rt} является ча-
стным случаем распределения (3.25).
Тест проверки адекватности экономической модели равно-
весия САРМ, основанный на многомерной модели линейной
регрессии, описан в разд. 6.4.
3.5.2. Оценки параметров
регрессионных моделей и их свойства
Регрессионные модели определены с точностью до неиз-
вестных параметров. Для моделей множественной линейной
регрессии это вектор параметров Ь^У1т и дисперсии щ2>0
(/=1, 2, ..., /V,), а для модели многомерной линейной регрес-
сии - это вектор ae$\N, матрица размерности NxK коэффи-
циентов регрессии В и ковариационная матрица ¥ размерно-
сти NxN.
Для нахождения статистических оценок параметров при
выполнении описанных выше модельных предположений
£.1.-£.3 традиционно используется метод наименьших квадра-
тов (МНК). Если дополнительно предполагается £.4, то при-
меним метод максимального правдоподобия (ММП). Заметим,
что оценки свободного члена и коэффициентов регрессии,
вычисленные с помощью обоих методов, т.е. МНК-оценки и
ММП-оценки указанных параметров, совпадают. Предполо-
жение £.4 о "гауссовости" случайных отклонений {£#} оказы-
вается существенным для построения статистических тестов
проверки гипотез относительно значений этих параметров,
включая гипотезы адекватности построенных моделей.
139

Дадим общую характеристику методов оценивания пара-
метров и анализа адекватности регрессионных моделей на
примере модели множественной линейной регрессии. Для
моделей простой и многомерной линейной регрессии эти ме-
тоды будут рассмотрены при решении конкретных задач ко-
личественного анализа ценных бумаг соответственно в
разд. 5.4 и п. 6.4.1.
Если выполняются предположения £.1.-£.4, а также усло-
вие (3.32), т.е. матрица Z является невырожденной фиксиро-
ванной матрицей, то МНК-оценка bj вектора коэффициентов
регрессии А; модели (3.30) является решением задачи миними-
зации суммы квадратов отклонений £(£,):
(3.39)
определена единственным образом и имеет вид:
/=1, 2, ..., N. (3.40)
При этом, как известно [1, 12], случайный вектор AJ имеет
нормальный закон распределения, т.е.
Ubi)=l*M{bb ^(ZTZ)-i) (*=1, 2, ..., 7). (3.41)
Из (3.41) следует, что Е(А/)=Л/, т.е. оценка bt является не-
смещенной. Ковариационная матрица случайного вектора Ь{
равна:
;;. (3.42)
Диагональные элементы данной матрицы являются дис-
персиями оценок До=5/9 {Д/} (^=Ь 2, ..., К) и вычисляются
по формуле:
1, ...,*, (3.43)
где v/p((ZTZ)"1)// - /-й диагональный элемент матрицы {7?Ъ)~Х.
Оценка bt является эффективной в классе линейных по
J?(0 несмещенных оценок вектора параметров bv Это означает,
что среди всех возможных оценок из указанного класса
МНК-оценки {/?,} компонент вектора Ь\ имеют минимальные
дисперсии, определяемые соотношением (3.43).
Если дополнительно выполняется условие Эйкера.
140

где ЯW/>7(ZTZ) - минимальное собственное значение матрицы
ZTZ, то оценка bt является состоятельной в среднеквадра-
тическом смысле, т.е. при увеличении числа наблюдений
Г дисперсии оценок {Д } стремятся к нулю:
Б(Д7)->0 при Г->оо (/=0, 1, ..., К).
Подстановкой в (3.33), (3.34) вместо неизвестных истин-
ных значений параметров их статистических оценок, вычис-
ленных по формуле (3.40), находятся значения эндогенных
переменных, соответствующие заданным значениям факто-
ров:
(/ = 1, 2, ..., TV).
При этом если /=1, 2, ..., Г, то {Rit} представляют собой
ретроспективные "прогнозы" эндогенных переменных, соот-
ветствующие прошлым периодам, а если t=T+l, ..., Т+т, то
{Rjt} - прогнозные значения ожидаемых доходностей активов
для будущих периодов с глубиной прогноза г>1.
Для построения прогнозных значений эндогенных пере-
менных необходимо дополнительно задать ожидаемые значе-
ния экзогенных переменных (факторов) {zti\ для будущих пе-
риодов /=74-1, .о., Г+г.
Ошибка прогноза в лериоде /, называемая остатком, рав-
на:
d,,= RirRir /=Ь 2, ..., TV, /=1, 2, ..., Т. (3.45)
Несмещенная оценка ц/} дисперсии у/} определяется как
нормированная сумма квадратов остатков:
у? = T-T-rtd»1>*l!s1'2'"''"'■ (3-46)
Известно [1, 12], что оценки bt и у/} являются статистиче-
ски независимыми, а случайная величина {T-K-\)y/J/у/}
подчиняется распределению хи-квадрат с Т-К-Х степенями
свободы.
141

ЩТ-K-l) tfly})^ хт-к-х. (3.47)
Подставляя оценку у/} вида (3.46) вместо неизвестного
значения дисперсии в формулу (3.42), находим оценку кова-
риационной матрицы случайного вектора bt. В частности, со-
гласно (3.43), оценки дисперсий D( Д7) принимают вид:
У и =^2v//, М), 1, ...,#,
откуда следует, что оценка среднеквадратического отклоне-
ния, известная как стандартная ошибка оценки (standard er-
ror) Д7, равна:
(3.48)
3.5.3. Анализ адекватности регрессионных моделей
Построение эконометрической модели не заканчивается
оцениванием неизвестных параметров и получением формулы
(3.44). Прежде чем использовать построенную модель в виде
(3.44) для вычисления прогнозов, необходимо удостовериться
в ее адекватности. Требуется убедиться в том, что найденные
количественные соотношения между эндогенными и экзоген-
ными переменными описывают статистически значимые свя-
зи между ними, а не являются результатом формального при-
менения метода оценивания параметров. Кроме того, качест-
во оценок параметров, а следовательно, модели в целом су-
щественно зависит от того, насколько реальные данные соот-
ветствуют постулируемым модельным предположениям. Раз-
личные нарушения этих предположений могут приводить к
построению ложных моделей, т.е. к отрицанию действительно
существующих и установлению мнимых связей между анали-
зируемыми переменными. Приведем краткое описание неко-
торых традиционных методов анализа адекватности регресси-
онных моделей.
1) Дисперсионный анализ регрессионных моделей.
Один из методов анализа адекватности регрессионной мо-
дели, не требующий предположения £.4 о нормальности оши-
бок, состоит в оценке доли дисперсии эндогенной перемен-
ной, объясняемой включенными в модель факторами z\9—9Zk
142

Рассмотрим модель множественной линейной регрессии
вида:
Rit = а, + finZti +...+PiKZ,K +&Р=1,2, ..., Т,
i =1, 2, ..., N,
описывающую зависимость доходности актива / от факторов
Zu ••> zk-
Для /-го регрессионного уравнения несмещенная оценка
дисперсии доходности актива aj2—D(Rjt) определяется по
формуле
где
— 1 т
1 /=1 t=\
- так называемая полная сумма квадратов (total sum of
squares - TSS) отклонений Rit от выборочного среднего
значения Rf, t=l, 2, ..., Т.
Полная сумма квадратов TSS допускает представление в
виде:
TSS= ESS+RSS,
т
що ESS ее ^(/?// - /?/) - сумма квадратов, объясняемая включен-
ными в модель факторами (explained sum of squares - ESS);
T
RSS = (T - К - l) \j/} = ^ djt2 - сумма квадратов остатков
t=\
или остаточная сумма квадратов (residual sum of squares -
RSS).
Каждая сумма квадратов связана с характеристикой, назы-
ваемой степенью свободы и равной числу независимых эле-
ментов информации, используемых для вычисления данной
суммы. Числа степеней свободы для сумм квадратов TSS,
ESS, RSS соответственно равны: vf=T-l, ve=K, vr=T-K-1 и
удовлетворяют условию: vt-ve + vr.
Оценкой доли дисперсии эндогенной переменной, объяс-
няемой включенными в модель факторами, служит величина
143

ESS /vE. Сумма квадратов ESS может быть представлена в
виде:
откуда следует, что вклад каждого отдельного фактора в ESS
определяется величиной | Д, |: чем больше | Д7 |, тем больше
вклад /-го фактора и, следовательно, тем большее влияние
оказывает данный фактор на эндогенную переменную. Малые
значения | Д7 | могут быть следствием линейной независимо-
сти этих двух переменных. Для проверки значимости отличия
Ри от нуля используются описываемые ниже методы стати-
стической проверки гипотез.
С описанными суммами квадратов связана важная харак-
теристика адекватности модели, известная как коэффициент
детерминации модели (coefficient of determination) или квадрат
множественного коэффициента корреляции (Л-squared) между
эндогенной переменной /?# и факторами z\, •.., Z& определяе-
мый выражением:
£Ж RSS
l U
TSS TSS'
Величина R2 указывает на долю полной суммы квадратов,
объясняемую включенными в модель факторами. Очевидно,
0</?2<1, причем значения Л2, близкие к единице, могут свиде-
тельствовать о наличии статистически значимой линейной за-
висимости между доходностью актива Rit и факторами
Z\9 •-., Zk-
При сравнении альтернативных регрессионных моделей,
отличающихся объемом выборки Т и числом факторов К,
предпочтительнее использование скорректированного коэффи-
циента детерминации (adjusted R squared):
- (352)
В качестве характеристики точности прогнозов на основе
построенной модели вида (3.44) часто используется средне-
квадратическая ошибка прогноза, совпадающая с оценкой
среднеквадратического отклонения у/{.

Особенности и недостатки характеристик R2 и R^dJ как
мер адекватности регрессионных моделей обсуждаются в
[1,12,38,41].
2) Проверка гипотез о значениях коэффициентов регрессии и
интервальные оценки.
Пусть для модели множественной линейной регрессии ви-
да (3.49) требуется проверить предположение о том, что ис-
тинное значение коэффициента регрессии Д/ равно некото-
рому заданному значению /3$, /е{1, 2, ..., К).
В терминах теории статистической проверки гипотез дан-
ная задача формулируется следующим образом: по эмпириче-
ским данным {/?#}, {Zti\ (^h 2, ..., 7) на заданном уровне зна-
чимости е (0<гК0.5) проверить гипотезу
2, ..., К) (3.53)
при альтернативе
#,:/%*/#• (3.54)
Для проверки гипотез (3.53)—(3.54) используется двусто-
ронний статистический критерий отношения правдоподобия
вида:
[не отклоняется, если \уТ\ < А
гипотеза Но \ ,' (3.55)
[отклоняется, если \ут\ > А,
где
л/ — Рн ~~ Pa a z£\
* и
- статистика критерия, известная как "t-статистика" или
"t-отношение" (Matio); Уц - стандартная ошибка оценки
Д7, определяемая по формуле (3.48); А - критическое зна-
чение статистики Y71, или порог статистического критерия1.
При истинной гипотезе Щ статистика у/1 имеет t-
распределение Стьюдента с Т-К-1 степенями свободы и
функцией распределения tr к \(и) (меЗ?1). Порог А критерия
(3.55) зависит от заданного уровня значимости s и определя-
1 Гипотеза Щ не отклоняется или, другими словами, принимается как од-
но из возможных решений, не противоречащих опыту.
ЮЗак. 7084 145

ется как квантиль уровня \-s/2 соответствующего t-
распределения:
^[f] (3.57)
Если верна гипотеза Щ, т.е. /5°// - истинное значение 1-го
коэффициента регрессии, то на основании (3.55)-(3.57) может
быть найдена интервальная оценка для /5°// в виде доверитель-
ного интервала [fi.j-S, Д +S] с доверительной вероятностью
\-£, определяемая соотношениями:
3) Проверка гипотез о значимости коэффициентов регрессии.
В частном случае, когда /3°/г=0, гипотезы (3.53)-(3.54) при-
нимают вид:
Яо: #/=0, Я,: /?/7*0, /е{1, 2, ..., К] (3.58)
и известны как гипотезы о значимости коэффициентов регрес-
сии.
Для их проверки используется критерий (3.55)—(3.57) с уче-
том того, что /3°//=0. Принятие гипотезы Яо означает, что зна-
чение оценки Д/ на уровне е незначимо отличается от нуля
и, следовательно, 1-Й фактор не оказывает существенного
влияния на эндогенную переменную. Это является основани-
ем для исключения этого фактора из модели. Отклонение ги-
потезы Яо в пользу Н\ наоборот, означает наличие статисти-
чески значимой линейной зависимости между анализируемы-
ми переменными.
4) Проверка гипотезы об адекватности модели в целом.
Для модели (3.49) рассмотрим задачу проверки гипотез ви-
да:
% Ai=A2=...=Ar=0, Я,: Яо (3.59)
по эмпирическим данным {/?„}, {ztj} (/=1, 2, ..., 7) на заданном
уровне значимости е. Здесь и далее Яо — альтернативное ут-
верждение по отношению к Яо (отрицание Яо).
Принятие Яо означает, что ни один из факторов, включен-
ных в модель, не оказывает значимого влияния на эндоген-
ную переменную, т.е. модель в целом является неадекватной.
146

В этом случае модель (3.49) принимает вид:
^=«/ + ^/=1,2,..., 7. (3.60)
В модели (3.60) свободный член щ выступает как параметр
сдвига'. Е(/?,>)=а,-. Оценкой аг по МНК для параметра а,- слу-
жит выборочное среднее значение /?,, рассчитанное по вы-
борке {Rit} (/=1, 2, ..., 7).
Выборочное среднее значение Ц является лучшим про-
гнозом для значений эндогенной переменной на основании
модели (3.60) для всех /=1, 2, ..., Т, т.е.
Отклонение гипотезы Щ означает, что среди факторов,
включенных в модель, есть по меньшей мере один фактор,
оказывающий значимое влияние на эндогенную переменную.
Незначимые факторы при этом могут быть исключены из мо-
дели.
Статистический критерий для проверки гипотез (3.59) в
отличие от критерия (3.55)—(3.57) является односторонним:
, \ не отклоняется, если ут < Л
гипотеза Но\ ' (3.62)
[отклоняется, если ут > Л,
где статистика критерия ут определяется по формуле
R Т - К -1 /- ^«ч
lT=l-R> К (363)
и при истинной гипотезе #о имеет F-распределение Фи-
шера с m и Т-К-1 степенями свободы.
Порог критерия определяется как квантиль данного рас-
пределения уровня 1-£
Д=Д(*)= Г]с\т-к-1{1-е). (3.64)
В формуле (3.63) статистика R2 представляет собой коэф-
фициент детерминации модели, вычисляемый по формуле
(3.51).
Описанные тесты используются при проверке адекватно-
сти экономических моделей САРМ и APT на основе соответ-
ствующих эконометрических представлений (разд. 6.4).
147

3.5.4. Проблемы, связанные с нарушением
традиционных предположений регрессионного анализа
Часто реальные статистические данные не удовлетворяют
модельным предположениям. Это приводит к тому, что стати-
стические оценки параметров модели, а следовательно, и ос-
нованные на них прогнозы теряют свои оптимальные свойст-
ва, например становятся смещенными и неэффективными.
Рассмотрим наиболее часто встречающиеся нарушения мо-
дельных предположений.
1) Мультиколлинеарность факторов.
Говорят, что имеет место мультиколлинеарность факторов,
если факторы, включаемые в модель, связаны линейной
(строгая мультиколлинеарность) либо близкой к линейной за-
висимостью.
В случае строгой мультиколлинеарности факторов матрица
Z является вырожденной (|z|=0), поэтому матрица (ZTZ)-1
необратима в обычном смысле, что порождает проблему
идентифицируемости модели. В данном случае оценки вектора
параметров модели Ь\ по методу наименьших квадратов
(МНК-оценки) определяются не единственным образом.
На практике ошибки, связанные с вычислением экономи-
ческих или финансовых переменных, а также ошибки округ-
ления вычислительных процедур приводят к "смягчению"
эффектов строгой мультиколлинеарности, в результате чего
определитель матрицы Z отличается от нуля, но принимает
близкие к нулю значения: | Z\ «0. В этом случае говорят, что
матрица Z является плохо обусловленной.
Плохая обусловленность матрицы Z является причиной
больших вычислительных погрешностей при нахождении
МНК-оценок bj и часто приводит к построению моделей, не
пригодных для практического использования. Эффекты муль-
тиколлинеарности можно смягчить за счет увеличения объема
данных. Однако это не всегда возможно на практике.
Данная проблема может иметь место при построении мно-
гофакторных моделей доходностей ценных бумаг, например
при практической реализации модели равновесия APT, рас-
сматриваемой в гл. 6.
2) Нарушение предположений относительно случайных от-
клонений.
На практике может нарушаться любое из традиционно
предполагаемых свойств £.1-£.6 относительно {£#}. Наиболее
частыми являются следующие нарушения:
148

• нарушение предположения £.2, приводящее к автокорре-
ляции случайных отклонений: Сог(^,^/г)^0 для ter
(/, z=l, 2, ..., 7);
• нарушение предположения £.3, т.е. гетероскедастичностъ
случайных отклонений: D(^if)=y/ft2^const (t = 1, 2, ..., Г);
• нарушение предположения £.4 о нормальном распреде-
лении случайных отклонений.
Эти и другие нарушения могут быть выявлены с помощью
анализа остатков. Основанием для использования подобного
подхода служит то, что остатки dit=RirRjt (/=1, 2, ..., N,
t=\, 2, ..., 7) можно рассматривать как оценки ненаблюдае-
мых значений %it. Поэтому если построенная модель регрес-
сии адекватна, то остатки {dit} должны обладать свойствами,
близкими к свойствам {£#}. Отсюда следует, что основные за-
дачи, решаемые при анализе остатков, состоят в проверке не-
коррелированности, гомоскедастичности, нормальности и т.п.
остатков {d,f}.
В тех случаях, когда нарушения традиционных предполо-
жений невозможно устранить, например, за счет корректи-
ровки (спецификации) модели или преобразования данных,
необходимо использовать специальные методы оценивания
параметров модели.
В случае мультиколлинеарности факторов это методы, ос-
нованные на использовании процедур псевдообращения мат-
риц; методы построения смещенных оценок параметров (на-
пример, ридж-оценок), минимизирующих суммарную диспер-
сию оценок коэффициентов регрессии; метод главных ком-
понент и др.
В случае автокоррелированных либо гетероскедастичных
отклонений {£#} для оценивания параметров используется
обобщенный метод наименьших квадратов.
Более подробное изложение методов анализа остатков, а
также методов оценивания параметров при нарушении тради-
ционных предположений можно найти в [1, 12].
3.6. МОДЕЛИ ФИНАНСОВЫХ ВРЕМЕННЫХ РЯДОВ
Описанные выше статические регрессионные модели и
модели данных типа ''случайная выборка" характерны для так
называемых пространственных данных (cross-sectional data).
Для многих практических задач финансового анализа стати-
стические данные представляют собой последовательно изме-
ряемые во времени значения характеристик финансовых ак-
149

тивов. Для описания таких данных используются модели вре-
менных рядов. Эти модели могут применяться как для самих
экономических или финансовых переменных, так и для опи-
сания остатков при построении моделей регрессионного типа
при нарушении предположения £.2. В последнем случае ис-
пользуемая для вычисления прогнозов модель должна вклю-
чать как регрессионную составляющую, так и модель времен-
ного ряда остатков.
Рассмотрим общую характеристику моделей временных
рядов, а также их основных характеристик. Приводимые да-
лее сведения необходимы для описания моделей финансовых
временных рядов, используемых в рамках теории эффектив-
ного финансового рынка (см. гл. 4). Более подробное изло-
жение моделей и методов анализа временных рядов можно
найти в[1, 3, 12,43,47, 49, 50].
3.6.1. Определение и основные свойства
временных рядов
Временным рядом обычно называют ряд значений
jq, X2, ..., xj анализируемой случайной величины, полученных
в последовательные моменты времени *=1, 2, ..., Т.
Будем рассматривать временные ряды с равноотстоящими
моментами наблюдения. Именно такими являются временные
ряды цен и доходностей активов, а также других экономиче-
ских и финансовых переменных.
Временной ряд можно интерпретировать как реализацию
некоторого случайного процесса, рассматриваемого как семей-
ство вещественнозначных случайных величин {Xt}, где пара-
метр / интерпретируется как дискретное время: /=1, 2, ..., Т
(см. п. 3.2.2).
Для удобства далее будем использовать одни и те же обо-
значения для временного ряда и соответствующего "порож-
дающего" его случайного процесса.
Случайный процесс {xf} (/=1, 2, ..., 7) может быть описан с
помощью Г-мерного распределения вероятностей, и, таким
образом, отношение между временным рядом и случайным
процессом можно рассматривать как отношение между слу-
чайной выборкой и "генеральной совокупностью". Однако
существуют два принципиальных различия между моделью
"случайная выборка" и моделью "временной ряд". Эти раз-
личия связаны с нарушением для моделей временных рядов
предположений типа Р.1 и Р.2 (см. п. 3.4.2) и состоят в сле-
дующем:
150

• значения х\, х2, ..., *г временного ряда не являются ста-
тистически независимыми;
• значения jq, х2, ..., xj временного ряда не являются оди-
наково распределенными.
С одной стороны, это означает, что методы статистическо-
го анализа пространственных данных, описываемых моделью
"случайная выборка", неприменимы для анализа временных
рядов. С другой стороны, зависимость между х\, х^, ..., xj от-
крывает новые возможности для исследования динамики и
прогнозирования временных рядов. При этом, исследуя вре-
менные ряды значений отдельных финансовых переменных,
часто абстрагируются от "перекрестных" связей между ними,
вводя предположения типа Р.4, что приводит к одномерным
моделям временных рядов. Для простоты изложения будем
рассматривать одномерные случайные процессы и временные
ряды.
Самой общей моделью временного ряда х\9 х2, .., х? явля-
ется совместная функция распределения F() случайных величин
х\, Х2, ..., х-р, определяемая соотношением1:
F(xu х2, ..., хТ) = F\(x\) F2(x2\xly
i , (3.65)
'F3(x3\xux2) -Fj(xT\xi, x2, ...,xt),
где F\(x\) - частная {маргинальная) функция распределения
случайной величины х\\ Ft{xt\x\, JC2, ..., xt.\) - условная
функция распределения случайной величины xt при усло-
вии, что значения х\, х2, ..., xt_\ являются фиксированны-
ми (/=2, 3, ..., 7).
Представление (3.65) учитывает оба свойства временного
ряда, т.е. взаимную зависимость и неодинаковую распреде-
ленность случайных величин хи х^ ..., xj. Однако модель
временного ряда х\, х2, ..., х?, определяемая функцией совме-
стного распределения F(x\, X2, ..., xj), как правило, не при-
годна для практического применения, поскольку функция
F{x\, X2, ..., xj) обычно неизвестна. Поэтому при описании
временных рядов обычно принимаются во внимание лишь
первые начальные и вторые центральные моменты совместного
распределения F(x\, Х2, ..., xj), т.е. математические ожидания
Е(х/), а также дисперсии B(xt) и ковариации Соу(х,, хТ)
, 2, ..., 7).
1 Для упрощения записи здесь и далее обозначение неслучайных аргумен-
тов функций распределения совпадает с обозначениями соответствующих
случайных величин.
151

Заметим, что если совместное распределение любых под-
множеств случайных величин из х\,Х2,...,хт является нормаль-
ным, то указанное множество параметров полностью характе-
ризует свойства временного ряда. Соответствующий случай-
ный процесс принято называть гауссовским.
Заметим, что даже при таком упрощенном описании моде-
ли временного ряда с помощью набора числовых характери-
стик (параметров) {E(x,)MD(x,)},{Cov(*/> *r)}(Kr, U *=1, 2, ..., 7)
задача идентификации модели, т.е. оценивания указанных
параметров по одной реализации х\, х^ •••> хт временного ря-
да, оказывается неразрешимой. Это связано с тем, что число
оцениваемых параметров равно Т+Т+Т(Т-\)/2=Т(Т+Ъ)/2, что
на порядок больше числа наблюдений Т. К тому же предпо-
ложение "гауссовости" не выполняется для многих экономи-
ческих и финансовых временных рядов.
Возникает необходимость введения дополнительных упро-
щающих предположений с целью уменьшения числа неиз-
вестных параметров модели. По этой причине обычно ис-
пользуется предположение о том, что исследуемый случайный
процесс является линейным в том смысле, что текущее значе-
ние случайного процесса генерируется посредством линейной
комбинации предшествующих значений самого процесса, а
также текущих и прошлых значений других процессов, соот-
ветствующих экзогенным (внешним) факторам. Оказывается,
что в данном случае указанный выше набор числовых харак-
теристик также отражает основные свойства случайного про-
цесса. В этом смысле важным является предположение о
стационарности случайного процесса (временного ряда).
3.6.2. Стационарный временной ряд и его характеристики
Временной ряд x^x(t) (/=1, 2, ..., 7) называется строго
стационарным или стационарным в узком смысле (strictly sta-
tionary), если совместное распределение вероятностей его
значений для любого подмножества моментов времени
*ь h> -"•> *т остается неизменным.
Другими словами, распределение вероятностей т значений
x{t\), x(/2), ..., x(tm) временного ряда является таким же, как и
распределение вероятностей т других его значений x(t\+k)9
xfa+k), ..., x(tm+k)9 сдвинутых во времени на величину (лаг) к
для любых m, t\, t2, ..., tm и к, т.е. свойства строго стационар-
ного временного ряда не зависят от начала отсчета времени.
В частности, при /и=1 из предположения о строгой ста-
ционарности временного ряда следует, что частное (марги-
152

нальное) распределение случайной величины xt не зависит от
времени /, а значит, не зависят от t и все его основные число-
вые характеристики. Так, если математические ожидания xt
существуют, т.е. Е(|х/|)<а>, то математические ожидания и
дисперсии xt постоянны:
Е(*,) =Мх, Щх<) =а2х, /=1, 2, ..., Т. (3.66)
Значение jux определяет некоторый постоянный уровень,
относительно которого совершают случайные колебания зна-
чения анализируемого временного ряда {xt}, а постоянная ве-
личина ах характеризует амплитуду этих колебаний. При ана-
лизе финансовых временных рядов величина <ух обычно слу-
жит мерой риска, связанного с неопределенностью относи-
тельно значений ряда, и называется волатильностъю.
Если /71 =2, то строгая стационарность случайного процесса
означает, что совместные двухмерные распределения для пар
случайных величин {x(t\), xfa)), (*(0), xfa-t])), (х(к),
x(ti-t\+k)) совпадают при любых t\, ti, к и зависят только от
разности t2~t\.
Соответственно ковариация Cov(xr, xt__k) (или Cov(xr, xt+k))
между значениями xt и xhk (ху**) зависит только от "сдвига по
времени", т.е. лага к, и не зависит от времени /:
Cov(x,, xt.k) = Е((хгМх)(хг_к-;их))^<рь / = 1, 2, ..., Т. (3.67)
Поскольку речь идет о ковариации значений одного и того
же временного ряда, то вместо термина "ковариация" исполь-
зуется термин "автоковариация". Автоковариация срк, рас-
сматриваемая как функция от значений лага к, называется
автоковариационной функцией.
Очевидно, значение автоковариационной функции для ла-
га, равного нулю (к=0), представляет собой дисперсию времен-
ного ряда:
щ = Е((хгМх)2) = D(*,) = а\ ,/=1,2, ..., Т. (3.68)
Временной ряд {xt} (/=1, 2, ..., 7), обладающий свойствами
(3.66), (3.67), называется слабостационарным (weak stationary)
или стационарным в широком смысле (stationary in the wide
sense).
Говоря далее о стационарных случайных процессах, будем
по умолчании иметь в виду стационарные в широком смысле
случайные процессы. Если хотя бы для одной из перечислен-
ных характеристик условия стационарности (3.66), (3.67) не
153

выполняются, то случайный процесс будем называть неста-
ционарным.
Очевидно, строгая стационарность влечет слабую стацио-
нарность. Обратное, вообще говоря, неверно. Однако если
случайный процесс является гауссовским, то слабая стацио-
нарность влечет строгую стационарность, поскольку первые и
вторые моменты однозначно определяют нормальное распре-
деление.
3.6.3. Автокорреляционная функция
Как известно, взаимная статистическая зависимость зна-
чений временного ряда хь Х2, ..., xj является одним из важ-
нейших его свойств, отличающим последовательность
х\, Х2, ..., xj от случайной выборки. По аналогии с парным
коэффициентом корреляции двух случайных величин для из-
мерения степени тесноты статистической связи между значе-
ниями стационарного временного рада xt и х^9 отстоящими
друг от друга на лаг к, используется коэффициент автокорре-
ляции pit
Co\{xt,xt_k) _ <рк
где учтено (3.68), т.е.
При анализе изменений характеристики р/с в зависимости
от лага к ее называют автокорреляционной функцией (АКФ).
Использование автокорреляционной функции р/с вместо авто-
ковариационной функции <pk на практике предпочтительнее,
поскольку АКФ рк является безразмерной (—1</%<1), т.е. не
зависит от масштаба измерения анализируемого временного
ряда. Из стационарности временного рада следует, что функ-
ции р/с и (р/с являются четными, т.е. р/с"Р-ь и Фк^Р-к- Это
свойство АКФ дает возможность рассматривать лишь поло-
жительные значения лага к.
Статистическая оценка АКФ по реализации х\, х2, ..., х?
временного ряда называется выборочной автокорреляционной
функцией и вычисляется по формуле
й=^-,*=1,2,..., 74, (3.70)
154

где <рк (к =1, 2, ..., Т-\), % - статистические оценки кова-
риационной функции и дисперсии временного ряда, оп-
ределяемые по формулам [40]':
г
9k = Z(x' ~ *) (*/-* ~ х,-к W - к),
"k+i T (3.71)
t=k+\
,-xf/T, x= fix = Y,xt/T. (3.72)
t=\ t=]
Наряду с АКФ при установлении свойств модели времен-
ного ряда используется так называемая частная автокорреля-
ционная функция (ЧАКФ) и ее статистическая оценка. В отли-
чие от автокорреляционной функции ЧАКФ применяется для
измерения степени тесноты статистической связи между зна-
чениями xt и Xf-k временного ряда {xt} (t=l9 2, ..., 7), отстоя-
щими друг от друга на лаг к, в предположении, что соответст-
вующие промежуточные значения ряда Х/.^+ь •••> xt-\
(/=1, 2, ..., Т-к) являются фиксированными. Таким образом,
ЧАКФ характеризует степень статистической взаимосвязи
между xt и Xf-к при устранении опосредованного влияния на
эту взаимосвязь со стороны всех промежуточных значений
ряда. Формулы для вычисления ЧАКФ и ее оценки можно
найти в [1, 12, 40].
Более подробное описание наиболее важных классов мо-
делей финансовых временных рядов приводится в гл. 7, после
определения вероятностных моделей цен и доходностей фи-
нансовых активов в рамках теории эффективного финансово-
го рынка (гл. 4).
3.7. ОБЩАЯ ХАРАКТЕРИСТИКА ЗАДАЧ
ФИНАНСОВОГО АНАЛИЗА
Прежде чем переходить к более подробному изучению
эконометрических моделей в последующих разделах, устано-
вим взаимосвязь между классическими задачами финансового
анализа и соответствующими классами моделей.
1 Соотношения (3.71), (3.72) несколько отличаются от теоретических
представлений оценок, однако более удобны с вычислительной точки зре-
ния.
155

1) Задачи оптимального портфельного инвестирования.
В оригинальных постановках задач оптимального порт-
фельного инвестирования Марковица1 и Тобина2 для описа-
ния доходностей активов Rx=(Ru,R2t,..., Я^)теЩм (t=l, 2, ..., 7)
неявно используются статические модели на основе про-
странственных данных в предположениях P.I, P.2 и Р.З (см.
п, 3.4.2).
Предположения о взаимной независимости, "гауссовости"
и неизменности распределения случайных векторов {Rt} в те-
чение анализируемого исторического периода дают возмож-
ность рассматривать {Rt} как случайную выборку из много-
мерного нормального распределения, параметрами которого
являются вектор математического ожидания доходностей (т.е.
вектор ожидаемых доходностей) активов ju и ковариационная
матрица случайного вектора доходностей активов I. С учетом
этого для построения статистических оценок /J, Е этих па-
раметров предполагается применение выборочного среднего и
выборочной ковариационной матрицы вида (3.29).
Оценки //, £ необходимы для решения задач оптимально-
го формирования портфелей ценных бумаг. Однако даже при
столь жестких предположениях относительно модели доход-
ностей активов возникают проблемы с применением формул
(3.29), обусловленные недостатком данных. Эти проблемы
приводят к необходимости использования факторных моде-
лей доходностей.
Простейшим примером такой модели является однофак-
торная рыночная модель Шарпа3. Однако более адекватными
моделями цен и доходностей активов, рассматриваемыми в
рамках современной теории портфельного инвестирования,
являются модели многомерных временных рядов, которые
учитывают не только "пространственные" связи между харак-
теристиками активов, но и временную корреляцию их значе-
ний. Примером таких моделей являются модели многомерных
временных рядов с переменными компонентами (multivariate time
1 См.: Morkowitz H. M. Portfolio Selection // Journal of Finance. 1952. 7. № 1
(March). P. 77-91; Jdem. Portfolio Selection: Efficient Diversification of Invest-
ments. N.Y.: John Wiley, 1959.
2 См.: Tobin J. Liquidity Preference as Behavior Towards Risk // Review of
Economic Studies. 1958. 26. № 1 (February). P. 65-88; Jdem. The Theory of
Portfolio Selection / The Theory of Interest Rates, ed. F.H. Hahn and F.P.
Brechling. L: Macmillan and Co, 1965.
3 См.: Sharp W. F. A Simplified Model for Portfolio Selection // Management
Science. 1963. 9. № 2 (January). P. 277-293.
156

series variance component - MTV models), предложенные в [45j.
Решению задач оптимизации портфелей ценных бумаг в тра-
диционной постановке посвящена гл. 5.
2) Моделирование доходностей активов на основе экономи-
ческих моделей равновесия фондовых рынков.
В финансовой экономике известны две экономические
модели, описывающие поведение доходностей активов в со-
стоянии равновесия так называемого совершенного финансо-
вого рынка: это модель оценки финансовых активов САРМ
(Capital Asset Pricing Model), а также модель APT на основе
"арбитражной теории оценивания" (Arbitrage Pricing Theory).
Стандартные версии моделей САРМ и APT (т.е. модели в
оригинальных формулировках) предполагают использование
статических регрессионных моделей при выполнении тради-
ционных модельных предположений регрессионного анализа.
Стандартная модель САРМ1 представляет собой модель
простой линейной регрессии, в которой используется единст-
венный фактор - доходность рыночного портфеля, относитель-
но которой рассчитываются доходности отдельных активов в
соответствии со значениями так называемых бета-коэффи-
циентов этих активов.
Бета-коэффициент актива - это коэффициент регрессии
доходности данного актива по отношению к доходности ры-
ночного дортфеля.
К этом^же классу моделей относится и более ранняя по
времени появления рыночная модель Шарпа. В отличие от
САРМ эта модель не имеет строгого экономического обосно-
вания. В качестве экзогенного фактора в ней возможно
использование любого макроэкономического или
финансового показателя, оказывающего значимое влияние на
доходность активов.
Обычно используется доходность так называемого индекс-
ного портфеля, т.е. портфеля, образованного на основе списка
ценных бумаг, соответствующих тому или иному фондовому
индексу, например индексу S&P 500. Обобщением этой моде-
ли являются многофакторные модели — модели множествен-
ной линейной регрессии.
1 См.: Shar W. F. Capital Asset Price: A Theory of Market Equilibrium under
Conditions of Risk // Journal of Finance. 1964. 29 (3). P. 425-442; Lintner J.
The Valuation of Risk Assets and the Selection of Risky Investments in Stock Port-
folios and Capital Budgets // Review of Economics and Statistics. 1965. 2. P.
13-27; Mossin J. Equilibrium in a Capital Asset Market // Econometrica. 1966. 34
(4). P. 768-783.
157

Стандартная модель APT1 - это модель множественной
линейной регрессии, в которой используется набор факторов
для построения так называемого арбитражного портфеля ак-
тивов. В обоих случаях традиционные предположения отно-
сительно случайных отклонений фактических доходностей от
ожидаемых включают весь набор условий £.1.-£.6.
Более подробно вопросы, связанные с экономическим
обоснованием и эконометрическим анализом этих моделей,
рассматриваются в гл. 6.
3) Модели цен и доходностей активов в предположении эф-
фективности финансового рынка.
Ключевым в определении эффективного рынка является
предположение о том, что рациональное поведение участни-
ков рынка, имеющих равные возможности, идентичные целе-
вые установки и однородные ожидания, приводит к такому
механизму формирования цен активов на рынке, при котором
цены мгновенно, полностью и корректно ассимилируют всю дос-
тупную информацию, достигая при этом состояния равновесия.
Математическое описание эффективного рынка основано
на понятии "мартингал". В соответствии с мартингальной мо-
делью эффективного рынка, как и в случае модели случайного
' блуждания, наилучшим прогнозом цены актива для будущего
момента времени по доступной в текущий момент информа-
ции является значение цены актива в текущий момент. Одна-
ко мартингальная модель цен активов, являясь обобщением
модели случайного блуждания, допускает возможность по-
строения нетривиальных прогнозов.
При моделировании цен и доходностей активов на основе
моделей равновесия рынка возникает проблема совместного
тестирования как гипотезы эффективности рынка, так и аде-
кватности используемых моделей равновесия рынка, или мо-
делей оценивания активов. Поэтому если гипотеза эффектив-
ности рынка отвергается, то это может означать как то, что
рынок на самом деле не является эффективным, так и то, что
используемая модель равновесия рынка или оценивания ак-
тивов является неадекватной. Наиболее известными моделями
равновесия рынка ценных бумаг, как отмечалось, являются
модели САРМ и APT, для проверки адекватности которых
используются методы статистической проверки гипотез, опи-
санные в разд. 3.5, 6.4.
1 См.: Ross S. A. The Arbitrage Theory of Capital Asset Pricing // Journal of
Economic Theory. 1976. 13. № 3. P. 341-360.
158

В качестве моделей оценивания активов обычно использу-
ются модели определения "фундаментальной" стоимости ак-
тивов в виде дисконтированной текущей стоимости связанно-
го с их владением потока платежей. В предположении рацио-
нальных ожиданий инвесторов данные модели рассматрива-
ются в разд. 4.4.
Для описания рыночных курсов финансовых активов ис-
пользуются модели, учитывающие различные проявления не-
стационарности финансовых временных рядов как по сред-
нему значению, так и по дисперсии. К их числу относятся
модель авторегрессии интегрированного скользящего среднего
(autoregressive integrated moving average model - ARIMA model)
и модели условной гетероскедастичности, например модель
авторегрессионной условной гетероскедастичности (autoregres-
sive conditional heteroskedastic model - ARCH model). В гл. 7
приводится описание указанных классов эконометрических
моделей применительно к решению задач прогнозирования
финансовых переменных, а также статистической проверки
гипотезы случайного блуждания цен активов и гипотезы мар-
тингальной эффективности рынка.

Глава 4
ТЕОРИЯ ЭФФЕКТИВНОГО
ФИНАНСОВОГО РЫНКА
Из всех принципов азартной игры
самый главный - это просто равные
условия... Все зависит от характера на-
рушения вами этого равенства: если
оно выгодно вашему противнику, вы
поступаете глупо, если выгодно вам -
нечестно.
Ж. Жардано
Рынок - это специально отведен-
ное место, где люди могут обманы-
вать друг друга.
Греческая пословица
В главе описываются вероятностные модели курсов и доходностей
финансовых активов, основанные на гипотезах случайного блуждания и
информационной эффективности рынка. Рассматриваются задачи про-
верки гипотезы эффективности рынка и анализа акций и облигаций в
предположении рациональных ожиданий. Описываются мартингальная
модель цен акций, а также модели спекулятивных "мыльных пузырей".
По рассматриваемым в главе вопросам рекомендуется дополни-
тельная литература: [34, 37, 39] (теория эффективного финансового
рынка и основанные на ней вероятностные модели финансовых пере-
менных); [35 44, 46, 48, 49] (эконометрическое моделирование финан-
совых временных рядов).
Исторически первой из известных работ, посвященных
применению вероятностных моделей для описания цен фи-
нансовых активов акций на Парижской фондовой бирже, бы-
ла работа Л. Башелье1, в которой была выдвинута "гипотеза
о случайном блуждании" цен акций. Так как результаты ис-
следований Л. Башелье были опубликованы на французском
языке, то они не получили достаточно широкой известности
в момент их появления2.
1 См.: Bachelier L. Theorie de le speculation // Annales de'lEcole Normale
Superiuer. 1900. V. 17. P.21-86.
2 В полном объеме результаты исследований Л. Башелье были переведены
на английский язык лишь в 1964 г.
160

Большую известность приобрели появившиеся спустя 30
лет работы Г. Воркинга1 и А. Каулеса2. Они были также по-
священы исследованию проблемы предсказуемости цен на
основе вероятностного подхода. Многие последующие иссле-
дования в данном направлении, например работа А. Каулеса
и Г. Джонса3, были связаны с эмпирической проверкой дан-
ной гипотезы.
Однако идеи количественного анализа (quantitative analysis)
финансового рынка на основе вероятностно-статистических
моделей и методов в течение длительного периода не имели
большого числа сторонников. Доминирующими подходами
среди финансовых аналитиков в 20-40-е годы были техниче-
ский и фундаментальный анализ. Предположения "количест-
венных аналитиков" о "случайном блуждании" цен финансо-
вых активов противоречили традиционным представлениям
"техников" и "фундаменталистов" о наличии в динамике цен
трендов, циклов и т.п., на выявлении которых и основана, по
их мнению, возможность предсказания цен.
Требовались более глубокое теоретическое обоснование
вероятностных моделей и практические доказательства их
адекватности. Большое значение для сторонников количест-
венных методов анализа финансовых рынков в этом смысле
имела упоминавшаяся ранее работа М. Кендалла (1957 г.), ко-
торая стимулировала дальнейшие интенсивные исследования
динамики цен активов с помощью вероятностно-статистиче-
ских методов. Результатом этих исследований явилось фор-
мирование теории эффективного финансового рынка (Efficient
Capital Market Theory)4.
Ключевыми в определении эффективного рынка являются
понятия "информация" и "рациональная реакция" рынка на
ее обновление, а также предположения о равных возможно-
стях, идентичных целевых установках и однородных ожида-
ниях участников рынка.
Рациональное поведение участников рынка, имеющих
равные возможности, идентичные целевые установки и одно-
родные ожидания, приводит к такому механизму формирова-
ния цен активов на рынке, при котором цены мгновенно,
полностью и корректно ассимилируют всю доступную ин-
1 См.: Working И. A random-difference series for use in the analysis of time se-
ries// Journal of American Statistical Association. 1934. V. 29. P. 11-24.
^ См.: Cowles A. Can stock market forecasters forecast // Econometrica. 1933.
V.I. P. 309-324.
3 См.: Cowles A., Jones H. Some a posteriori probabilities in stock market ac-
tion // Econometrica. 1937. V. 5. P. 280-294.
4 Более полный обзор литературных источников и соответствующие
ссылки по данному вопросу можно найти в [34].
ПЗак. 7084 j^j

формацию, достигая при этом состояния равновесия. Условие
равновесия цен означает отсутствие на рынке "неправильно"
оцененных рынком активов: рыночные цены активов равны
их "истинным" стоимостям, а спрос на активы равен их
предложению. Это исключает возможность регулярного полу-
чения безрисковой (спекулятивной) прибыли за счет реализа-
ции арбитражных возможностей, т.е. различий в ценах на
один и тот же актив в один и тот же момент времени.
Более высокая доходность на таком рынке возможна толь-
ко в виде премии за риск (risk premium) понести соответст-
вующие убытки. Получить "сверхприбыль" без дополнитель-
ного риска, т.е. "победить рынок", в условиях эффективного
рынка невозможно, ибо такая возможность для некоторого
участника существует только при нарушении в его пользу ус-
ловия равных возможностей, например, за счет использова-
ния информации, неизвестной другим участникам рынка.
Однако такое возможно только на "неэффективном" рынке.
Таким образом, эффективный рынок напоминает азартную
игру с равными условиями (возможностями) для всех участ-
ников.
Математическое описание эффективного рынка основано
на математическом понятии "мартингал". Исходное значение
этого термина связано с азартными играми и соответствует
азартной игре, в которой в конце концов не оказывается ни
победителей, ни побежденных1. Такую игру можно назвать
справедливой или честной (fair game). Поэтому утверждение
"рынок является эффективным" означает то, что в смысле по-
лучения дохода он эквивалентен честной игре. При этом
стремление участников "победить" рынок, основанное на "не-
честных" попытках нарушить правила справедливой игры, мо-
жет быть реализовано только в условиях, когда рынок не явля-
ется эффективным. Таким образом, именно "неэффективный"
рынок, следуя греческой пословице, это то "специально отве-
денное место, где люди могут обманывать друг друга".
В теории вероятностей понятие "мартингал" возникает
при исследовании зависимостей между случайными величи-
нами с помощью свойств условных математических ожиданий.
Применительно к эффективному финансовому рынку мар-
тингальным свойством обладают цены активов, а точнее, их
логарифмы.
Целью настоящей главы является математическое описа-
ние и содержательная интерпретация названных и других ос-
1 Например, игра с двумя участниками, в которой при каждом проигры-
ше первого участника происходит удвоение ставок, а при первом же его вы-
игрыше игра прекращается.
162

новных понятий теории эффективного рынка, используемых
при построении и проверке адекватности вероятностно-ста-
тистических моделей цен и доходностей финансовых активов.
4.1. ПРОБЛЕМА ПРЕДСКАЗУЕМОСТИ ЦЕН
И ДОХОДНОСТЕЙ ФИНАНСОВЫХ АКТИВОВ
Объекты исследования в настоящей главе — вероятностные
модели цен и доходностей финансовых активов с неог-
раниченным сроком обращения (например, акций, валют),
предназначенные для предсказания значений этих характери-
стик в будущие моменты (периоды) времени. Для описания
цен и доходностей будем использовать одномерные модели,
т.е. пренебрегать "перекрестными" связями между характери-
стиками, соответствующими различным активам. Для опреде-
ленности предположим, что речь идет об акциях.
Для анализируемого актива обозначим: {Pt} - цены актива
в последовательные моменты времени /=0, 1, 2, ..., {/?,} - со-
ответствующие значения доходностей актива за периоды
*=1,2, ...
Предположим вначале, что периодические платежи по ак-
тиву не учитываются (например, в силу малости интервала
регистрации цен), тогда доходности активов определяются по
формуле (см. разд. 3.1)
5 (4.1)
Я, 1.
Ч-\
Ставки Rt вида (4.1), как известно, характеризуют доход-
ность актива за один период и используются при определе-
нии стоимости активов по формуле сложных процентов.
Проблема предсказуемости цен активов в данной ситуации
состоит в ответе на вопрос: возможно ли по имеющимся к
моменту времени t значениям цен Р$, Рь Р^ ..., Pt предска-
зать цену актива Pt+{ в момент времени Н-1 и другие будущие
моменты времени? С данным вопросом непосредственно свя-
зан другой: возможно ли ожидать в среднем положительной
доходности от операций покупки и продажи активов, прини-
мая рациональные инвестиционные решения, основанные на
информации, заключенной в ценах активов за текущий и
прошедшие моменты времени? Положительный ответ на пер-
вый вопрос позволяет утвердительно ответить на второй. В
противном случае прошлые цены активов не несут полезной
для предсказания информации и поэтому не могут способст-
вовать получению относительно регулярной прибыли от опе-
163

раций с активами. Исследуем проблему предсказуемости цен
финансовых активов на основе традиционных вероятностных
моделей.
4.1.1. Модели случайного блуждания для цен активов
Как отмечалось, первым, кто предпринял попытку матема-
тического описания эволюции цен акций, был Л. Башелье1.
Он обнаружил, что регистрируемые с постоянным интерва-
лом времени А цены PtA (/=0, Л9 2Д ...) таковы, что прираще-
ния цен PA-PtAA за один интервал наблюдения имеют нуле-
вое среднее значение, а их абсолютные значения | PA-PtAA I
являются величинами порядка у[л . В связи с этим им было
предложено рассматривать процесс изменения цен акций как
случайный процесс, описываемый моделью случайного блужда-
ния (random walk), для которого справедливо представление:
ЛА=Л>+ Z^> (4.2)
к = \
где Pq - известная цена акции в начальный момент времени;
{^) - независимые одинаково распределенные случайные
величины, принимающие с вероятностями Ц значения
Из (4.2) следует:
Осуществляя в формуле (4.2) предельный переход при zl—>0
(в определенном вероятностном смысле), можно показать,
что предельный случайный процесс {Pt} с непрерывным вре-
менем t имеет вид:
Pf=P0+ cr\Vhf>0, (4.3)
где Wt - случайный процесс с независимыми гауссовскими
(т.е. имеющими нормальный закон распределения) при-
ращениями AJVf=Wf -Wt_Ah называемый стандартным
броуновским движением или стандартным винеровским
процессом, для которого И^О, Е(ЛИ^)=0, D(AWt)=At,
0<At<t[35].
1 Описание результатов J1. Башелье приводится в интерпретации из [34].
164

В практических исследованиях, например при проверке
"гипотезы о случайном блуждании" по эмпирическим дан-
ным, используется аналог модели (4.3) для дискретного вре-
мени /=1, 2, ...:
Л=Л-1 + & (4.4)
где {£} - независимые случайные величины, распределенные
по нормальному закону с нулевым математическим ожи-
данием и дисперсией а2, кратко: {Q ~ н.о.р.с.в. N^OjO2);
Pt_\ - известное в периоде / значение цены акции.
Модель (4.4) допускает очевидное представление в виде1:
Л=Яо+ Z&, (4-5)
к=\
где Pq - некоторое фиксированное начальное значение цены
акции.
Из соотношений (4.4), (4.5) следует, что при "случайном
блуждании" цен активов ожидаемые значения однопериодной
и многопериодной доходности равны нулю. Действительно,
так как E(PrPt.\)=E(^t)=0, то, согласно (4.4), ожидаемая в
произвольном периоде / доходность равна:
Е(/у = E{PrPt.x)/ Л-i = 0. (4.6)
Аналогично для многопериодной доходности (см. разд. 3.1)
Rtt за t>\ периодов, определяемой в момент времени t с уче-
том того, что.Е(&)=0 (Л=1, 2, ..., f), а также (4.5), получаем:
E(RfJ = Е(РГРО)/ Ро = 0. (4.7)
Заметим, что случайный процесс {Pt}, удовлетворяющий
(4.4), имеет условные (при условии, что Pq - некоторое фик-
сированное начальное значение цены акции) математическое
ожидание и дисперсию, определяемые по формулам2
Е(Л1 Ро) = Ро, О(Л1 Ро) = о2/, (4.8)
где параметр а, характеризующий степень неопределенности
цены актива за один период, известен как волатильностъ,
или изменчивость цены актива. Поскольку дисперсия
D(Pt\Po) линейно зависит от времени, процесс случайно-
го блуждания является нестационарным, причем с увели-
1 Представление (4.5) является решением разностного уравнения (4.4).
2 Более подробно понятие "условное математическое ожидание" обсужда-
ется в разд. 4.2.
165

чением срока наблюдения, т.е. при /-х», неопределен-
ность относительно цен активов становится сколь угодно
большой.
Таким образом, если цены активов описываются моделью
случайного блуждания, то информация, заключенная в ценах
за прошедшие и текущий моменты времени, не обладает про-
гностической способностью, т.е. не может быть полезной для
предсказания будущих значений цен активов. Это означает
также, что использование данной информации не может спо-
собствовать получению относительно регулярной прибыли от
операций с активами, т.е. ожидаемая доходность подобных
операций равна нулю. При этом рынок приобретает характер
"честной игры".
Обобщением модели (4.3) является модель случайного блуж-
дания со "сносом", или "дрейфом" {drift). В случае непрерыв-
ного времени / данная модель имеет вид:
Pt=PQ + tit+crlVt9 (4.9)
где ju, a - параметры модели, известные как параметр сноса
(drift) и волатшъность цены актива. Соответствующая мо-
дель для дискретного времени /=1, 2, ... является обобще-
нием модели (4.4) и имеет вид:
Л =/*+Л-1 + & (4.10)
(4Л1)
где {&} ~ н.о.р.с.в.
Аналогично предыдущему случаю можно показать:
Из (4.10) и (4.11) следует:
M)=/i, Е(РГР0)=
т.е. "снос" /и и jut - это ожидаемое изменение цены актива со-
ответственно за один и t>\ периодов времени.
Как и в предыдущем случае, если Pq - некоторое фиксиро-
ванное начальное значение цены акции, то:
| />о)= Л) + М В(Л I Ро)= #U
т.е. процесс случайного блуждания со "сносом" является не-
стационарным, причем для него не только условная диспер-
сия, но и условное математическое ожидание линейно зави-
сит от времени.
166

250
55 64
Момент времени
Рис. 4.1. Модели случайного блуждания
со "сносом" (/) и без "сноса" (2)
Графики реализаций процессов случайного блуждания со
"сносом" (Ро=О, ju=2) и без "сноса" (/)0=10, ju=0) приведены на
рис. 4.1. Реализации получены с помощью статистического мо-
делирования при условии: {<^}~н.о.р.с.в. Ni(0, 9) (/=1,2,..., 100).
4.1.2. Модели случайного блуждания
для доходностей активов
Недостатком описанных выше моделей случайного блуж-
дания для цен акций является то, что в рамках этих моделей
допускаются отрицательные значения цен акций. Действи-
тельно, предположение о том, что случайные величины {£} в
моделях (4.3), (4.9) распределены по нормальному закону
N1(0,0^, влечет положительную вероятность того, что Pt<0.
Оказывается, отмеченного недостатка удается избежать,
если предположить, что не сами цены акций, а их логариф-
мические значения подчиняются модели случайного блужда-
ния. Такая модель была предложена П. Самуэльсоном1 в
1965 г. и получила название модель логарифмического (геомет-
рического или экономического) броуновского движения.
Модель логарифмического броуновского движения активов
в случае непрерывного времени t описывается соотношением:
P,= PoeaiVi-tcx2, t>0, (4.12)
где {Wf) - стандартное броуновское движение.
Модель логарифмического броуновского движения с дис-
кретным временем /=1, 2, ... имеет вид:
Pt = Pt-\ + & (4.13)
1 См.: Samuelson P.A. Proof that properly anticipated prices fluctuated ran-
domly // Industrial Management Review. 1965. V. 6. P. 13-31.
167

где pt= \о%Рь pq = logPo - заданное начальное значение;
Ш ~ н.о.р.с.в. N1(0,0^).
Модель (4.13) может быть представлена в виде:
т.е. является моделью случайного блуждания для логарифмов
цен активов. Заметим, что величина ги определяемая как
П = Р,- Pt-\ = 1о
описывает доходность актива за один период, выраженную
ставкой непрерывно начисляемых процентов.
Из (4.13), (4.14) следует, что в рассматриваемом случае
ожидаемые значения однопериодной и многопериодной до-
ходности равны нулю, поскольку, согласно (4.13):
E(PrPt-\) = Е(6) = О,
а из (4.14) следует:
Е(ргРо) = Е(6) = 0.
Условное математическое ожидание и дисперсия случайно-
го процесса {pt} определяются по формулам:
E(ft I Ро) = A), D(A I А)) = ^ (4.16)
т.е. дисперсия {pt} зависит от времени /, а значит, случайный
процесс {/?/} является нестационарным. Таким образом, если
логарифмы цен активов {pt} удовлетворяют модели случайного
блуждания (4.13), то рынок может рассматриваться как "чест-
ная игра", ожидаемый доход в которой всегда равен нулю.
Основной формой представления модели логарифмическо-
го броуновского движения активов с непрерывным временем
f является модель со "сносом", или "дрейфом" /#Ю вида:
Pt = P0eafV'<M-a2/2)',t>0, (4-17)
где {Wt) - стандартное броуновское движение.
Соответствующая модель случайного блуждания для лога-
рифмов цен активов с дискретным временем /=1, 2, ... имеет
вид:
Л=/* + Л-1 + & (4.18)
Отметим, что "логарифмическая доходность" актива, или
ставка непрерывных процентов, для модели (4.18) равна
168

rt=n+<!;t и поэтому распределена по нормальному закону
Nj^o2), причем случайные величины {г,} являются незави-
симыми. Параметр "сноса" ju в данном случае имеет смысл
ожидаемой доходности актива за один период.
Как и {/*,}, случайные величины 1+/?,е[0,+оо] (/=1, 2, ...)
являдугся также н.о.р.с.в., но имеют логарифмически-
нормальное распределение (см. п. 3.2.3). При малых изменениях
цен между последовательными моментами их регистрации
(например, в случае частых котировок) возможна аппрокси-
мация:
rt = log(l + Rt) = logfl + f/:/>/-1l - Pf I Pf] » ^ (4.19)
Многие эмпирические исследования подтверждают пред-
положения о том, что логарифмические доходности (лога-
рифмические темпы роста цен) {rt} можно рассматривать как
независимые случайные величины с симметричным относи-
тельно ju распределением, например нормальным или некото-
рым другим устойчивым распределением (п. 3.2.3). Это дает
основание говорить о том, что последовательность {/>^} (К>\)
значений многопериодной доходности акции для К>\ перио-
дов (см. п. 3.1.2) вида
П,к=г,+ г,А + ... + /-,_*+! (4.20)
может рассматриваться как процесс "случайного блуждания".
В силу (3.12) и (4.20) логарифм цены актива в момент вре-
мени / равен:
pt= log Pt = log (Pt-Ket9K ) = Pt-K+rt,K =
где Pt_K - известное значение цены в начальный момент вре-
мени t-K, откуда следует, что если {rt_k} (k=K-\, ..., 1,0)--
н.о.р.с.в., то логарифмы цен {р{} так же ведут себя, как
"случайное блуждание".
Заметим также, что если доходности {rt_j^ статистически
независимы и распределены по нормальному закону Nj^o2),
то по свойству нормального распределения случайная вели-
чина rtfx, описывающая доходность актива за К периодов,
также имеет нормальный закон распределения, поскольку
равна сумме К независимых гауссовских случайных величин.
При этом ожидаемая доходность актива за К периодов равна
169

Е(а7,к)=7*АГ, а дисперсия многопериодной доходности актива
равна D(/> ^=cP-K.
Соотношение (4.21) является математической записью об-
разного выражения М. Кендалла из его упоминавшейся выше
работы, посвященной анализу динамики цен на финансовом
рынке: "Демон Случая извлекал случайным образом число...
и добавлял его к текущему значению для определения... цены
в следующий момент"1.
4.1.3. Статистическая проверка
гипотезы о случайном блуждании
Значительное число исследований (начиная с 30-х гг.) по-
священо эмпирическому доказательству или опровержению
гипотезы о случайном блуждании цен финансовых активов.
Одним из первых тестов для проверки данной гипотезы явля-
ется тест Каулеса - Джонса, опубликованный в 1937 г.2 С
момента его появления разработано большое число новых,
более "мощных" тестов, а также статистических моделей цен
и доходностей активов, позволяющих добиться более адек-
ватного их описания (см. гл. 7). И в то же время данный тест
представляет интерес как пример метода статистического ана-
лиза динамики цен и доходностей финансовых активов. В
связи с этим рассмотрим проблему тестирования гипотезы
случайного блуждания с помощью теста Каулеса - Джонса,
основываясь на описании данного теста из [37].
Рассмотрим модель случайного блуждания для логарифмов
цен активов вида (п. 4.1.2):
Pt = Pt-\ + &*= Ь2, ..., Г, (4.22)
где pfdogPh po=logPo - заданное начальное значение;
^t=Pt~Pt-\- изменение логарифма цены актива в периоде /,
{^-н.о.р.с.в. N^a2). Доходность актива за один период
владения, определяемая ставкой непрерывных процентов,
при этом будет равна r^pt-pt_\—^t
Введем случайные величины:
Г1, если г, >0
<0 (4'23)
1 Цит. по: Ширяев А.В. Основы стохастической финансовой математики.
Т. 1: Факты и модели. М.: Фазис, 1998.
2 См.: Cowles A.f Jones И. Some a posteriori probabilities in stock market ac-
tion // Econometrica. 1937. V. 5. P. 280-294.
170

которые при условии, что модель (4.22) верна, являются неза-
висимыми случайными величинами Бернулли [35] с вероят-
ностями значений:
7^?(vt=\)=P(rt>0) и 1-л=Р(у,=0)=Р(г,<0), t=U 2, ..., Т.
Последовательности, образованные из "разностей" {г,},
имеющих одинаковый знак, в математической статистике
принято называть серией (runs). Если модель случайного блу-
ждания (4.22) верна, то я=0,5, и последовательность {rt} будет
образована из большого числа коротких серий. Если модель
(4.22) неверна, например случайные величины {£,} коррелиро-
ваны, то я*0,5 и в последовательности {rt} следует ожидать
появления длинных серий значений rh имеющих одинаковый
знак, при этом общее количество серий соответственно будет
меньше ожидаемого.
На анализе числа и продолжительности серий в случайных
последовательностях при исследовании статистической зави-
симости между наблюдаемыми значениями основаны так на-
зываемые тесты серий (см., например, [1]), которые также
могут использоваться в рамках данной проблемы.
Перейдем к описанию самого теста. Пусть имеется после-
довательность значений доходности актива r\, r-i, ..., rj за Т
прошедших периодов. Исследуем последовательные пары
значений доходности актива (rh гж) (*=1, 2, ..., ТА). Опреде-
лим число N\ пар последовательных значений доходности ак-
тива, имеющих одинаковые знаки, и число N2 пар последова-
тельных значений доходности, имеющих различные знаки.
Воспользуемся формулой
7-1
N{ ^ ]►>, , w,e= v,v,+1 + (l-v,)(l-v,+1), N2 = Т- tf, -1. (4.24)
t=\
С учетом (4.24) случайные величины и7е{0,1} также явля-
ются случайными величинами Бернулли и имеют распределе-
ние:
с вероятностью щ = п1 + (l - к)2
О, с вероятностью 1 - к{ = 2я\\ - к).
Согласно (4.25), если л-=0,5 (т.е. модель (4.22) верна), то
Определим отношение Jj вероятностей щ и щ=\-щ и уч-
тем (4.25):
Т
= [
1-я-, 2л{\-я) [>1,если п ^0,5.
171
6

Таким образом, когда модель (4.22) верна, отношение Jj
равно 1, а при нарушении данной модели Jf>\. По эмпириче-
ским данным найдем оценку JT, используя в качестве оце-
нок вероятностей относительные частоты соответствующих
событий. На основании (4.24), (4.26) получаем:
(4.27)
т \-щ N2/T N2
Так как относительные частоты являются строго состоя-
тельными оценками вероятностей, то с вероятностью единица
JT-^JT при Т->оо. Таким образом, близость значения стати-
стики JT к единице может свидетельствовать о справедливо-
сти модели случайного блуждания (4.22) для логарифмов цен
активов.
В терминах теории статистической проверки гипотез дан-
ная проблема может быть сформулирована следующим обра-
зом. Определим гипотезы:
Щ\ Jt=\, т.е. модель (4.22) случайного блуждания адекват-
на;
Н\\ /т>1, т.е. модель случайного блуждания неадекватна.
Пусть с (0<£<1) - некоторое заданное значение вероятно-
сти ошибочного отклонения "гипотезы о случайном блужда-
нии" #о, называемое уровнем значимости статистического
критерия.
Для принятия на основе эмпирических данных {/>}
(/=1, 2, ..., 7) относительно гипотезы Щ решения, справедли-
вого с вероятностью 1-я, используется статистический крите-
рий, основанный на статистике JT . Распределение данной
статистики при условии, что гипотеза Щ верна, при доста-
точно больших значениях Т (Т-><х>) может быть аппроксими-
ровано нормальным распределением с параметрами [37]:
+ (1 - яг)3 -
1 - щ Т{\ - щ)
Эмпирические исследования, проведенные авторами дан-
ного теста, показали, что для многих акций значения стати-
стики JT оказались существенно больше единицы, что дало
основание сделать предположение о наличии некоторой за-
кономерности в изменении цен данных активов.
172

Заметим, однако, что подобные значения статистики JT
могут принимать и для активов, логарифмы цен которых под-
чиняются модели случайного блуждания со "сносом". Проил-
люстрируем этот факт. Предположим, что логарифмы цен ак-
тивов подчиняются модели случайного блуждания со "сно-
сом" вида:
Л=/* + Л-1 + 4 (4-28)
где /л - параметр "сноса", имеющий в данном случае смысл
ожидаемой доходности актива за один период; {£,} ~
н.о.р.с.в. N^Qjcr2).
Доходность актива за один период, определяемая ставкой
непрерывных процентов, будет равна:
,/=1,2, ..., Г,
поэтому доходности {rt} ~ н.о.р.с.в N^/ao2), и при //*0 полу-
чаем:
7r=P(vt=\)= (r)(/)
(4.29)
Ж5
где Ф() - функция распределения стандартного нормального
закона Nj(0,l).
Согласно (4.29) аналитическое значение отношения Jj, как
и при нарушении гипотезы случайного блуждания, больше
единицы независимо от знака //.
Иллюстрацией того, как существенно влияет "эффект не-
нулевого сноса" на значение отношения /^, служит пример
поведения индекса годовой доходности акций американских
корпораций на протяжении второй половины XX в. Исполь-
зуя оценки параметров [37] /7=0.08, а =0.21, построенные по
значениям {rt} за анализируемый период, а также табличное
значение функции Ф() [1], на основании (4.25), (4.26), (4.29)
получаем: ^=0.5444, п =Ф(0.08/0.21)=0.6484, 7Г=1.19.
Таким образом, с помощью теста Каулеса - Джонса можно
установить неадекватность модели случайного блуждания ви-
да (4.22), но невозможно отличить случаи, когда имеет место
модель случайного блуждания со "сносом", от случаев, когда
имеется сериальная корреляция цен и доходностей активов,
т.е. когда модель случайного блуждания действительно не-
верна.
Как отмечалось, теоретические и эмпирические исследо-
вания предсказуемости цен финансовых активов на основе
173

вероятностного подхода привели в итоге к формированию
теории эффективного финансового рынка, знакомству с ко-
торой посвящены последующие разделы данной главы.
4.2. ИНФОРМАЦИЯ И ОСНОВАННЫЕ НА НЕЙ
ОЖИДАНИЯ УЧАСТНИКОВ РЫНКА
Говоря об эффективности рынка, следует иметь в виду ин-
формационную эффективность рынка, т.е. эффективность
рынка по отношению и в зависимости от определенной ин-
формации, а точнее, информационного потока, если учесть
динамический характер поведения рынка. Приведем матема-
тическое определение данных понятий.
4.2.1. Прогноз в виде условного
математического ожидания
В соответствии с вероятностным подходом (см. п. 3.2.1)
для описания финансовых показателей будем использовать
случайные величины, определенные на вероятностном про-
странстве (Q, 3, Р)1, где Q - пространство состояний рынка;
3 - совокупность всех наблюдаемых случайных событий на
финансовом рынке, т.е. вся доступная информация о рынке;
Р - вероятностная мера (вероятность).
Поскольку анализ состояний рынка осуществляется в по-
следовательные моменты времени на основании имеющейся
информации о рынке, то для целей анализа в 3 удобно выде-
лить временной поток доступной участникам рынка и отно-
сящейся к делу информации (available and relevant infor-
mation), т.е. поток информации F={3,}, />0, такой, что:
3oc3ic...c3/c...c3, (4.30)
где 3/ - совокупность событий на рынке до момента времени
t включительно, т.е. информация, доступная участникам
рынка.
Будем предполагать, что значение Xt (/^O, 1, 2, ...) анали-
зируемой финансовой переменной (например, цены или до-
ходности актива) складывается в зависимости от событий, на-
блюдаемых на рынке до момента времени t включительно, т.е.
1 Здесь и далее отдается предпочтение содержательной интерпретации
терминов теории вероятностей в контексте рассматриваемой задачи, включая
интерпретацию пространства элементарных событий Q, а-алгебры 3 и потока
а-алгебр F={3 ,}[34, 35].
174

случайные величины Xt являются измеримыми относительно
информации 3, (3, -измеримыми).
В момент времени / будем строить прогноз будущего зна-
чения Xf+\ некоторой финансовой переменной при условии,
что имеется информация 3,. Соотношение (4.30) говорит о
том, что с течением времени информация не убывает, однако
в каждый фиксированный момент времени / участник рынка,
как правило, не обладает всей информацией о рынке, а рас-
полагает ограниченной информацией З/сЗ. Используя ин-
формацию 3/, он может строить прогнозы относительно зна-
чений анализируемых финансовых показателей в будущий
момент времени Н~1, а также вычислять их числовые и функ-
циональные характеристики.
Прогнозное значение анализируемого показателя X для
момента времени /+1 по доступной в момент времени t ин-
формации 3/ определяется как условное математическое ожи-
дание:
EXAi+i) - Е(Х,+113,), /= 0, 1, 2, ... , (4.31)
которое конечно, т.е. существует, если
Е(|Агж||з,)<оо. (4.32)
Заметим, что в отличие от безусловного математического
ожидания ECY/+i) условное математическое ожидание
E(Xt+\ |зг) является случайной величиной.
Использование условного математического ожидания для
вычисления прогнозных значений обусловлено оптималь-
ностью данных прогнозов в смысле квадратичной функции
потерь, известной как "среднеквадратическая ошибка прогно-
за". Пусть Х*+[у - некоторый прогноз Xt+\, основанный на
информации 3/, доступной к моменту времени /.
Среднеквадратическая ошибка прогноза (mean squared error -
MSE) X*+]i( определяется выражением
Можно показать [43], что наименьшая среднеквадратиче-
ская ошибка прогноза достигается, если X*+lif— E(Xt+\\3t),
т.е. если используется прогноз в виде условного математиче-
ского ожидания.
175

4.2.2, Свойства прогнозов в виде
условного математического ожидания
Укажем на некоторые необходимые в дальнейшем свойства
прогнозов в виде условного математического ожидания (4.31).
Прежде всего отметим, что для условного математического
ожидания справедливы свойства типа Е.1-Е.З безусловного
математического ожидания (см. п. 3.2.2). Будем предполагать,
что для всех рассматриваемых ниже случайных величин мате-
матические ожидания существуют, т.е. выполняются условия
типа (4.32).
Имеют место следующие свойства условного математиче-
ского ожидания (conditional expectation - СЕ).
СЕЛ. Если Зо = {0,Q} - "тривиальная информация", вклю-
чающая только два события - невозможное и достоверное, то
с вероятностью 1 (или "почти наверное" - п.н.):
т.е. тривиальная информация типа "курс акции не может
быть отрицательным" (отрицательный курс - невозможное
событие 0) и "курс акции неотрицателен" (достоверное со-
бытие Q) не отражается на ожиданиях участников рынка.
СЕ.2.
\t) = Xt(n.H.)9 (4.33)
т.е. информация 3, в момент времени / включает всю инфор-
мацию, доступную к этому моменту, включая и фактическое
значение Xt анализируемого показателя, поэтому его ожидае-
мое значение совпадает с фактическим.
СЕ.З. Если имеются потоки информации двух видов
FH3/1} и F2={3 ,2}, причем
3/сЗ/(/=0, 1,2,...), (4.34)
т.е. информация 3 } является более полной, чем 3 ,], то:
Е(Е(ХЖ | 3 }) | 3 }) = Е(Лж I 3 ,*) (п.н.). (4.35)
Данное свойство говорит о том, что ожидаемое в соответ-
ствии с ограниченной информацией З,1 значение прогноза
E(Xt+\ I З,2), построенного по более полной информации З,2,
совпадает с прогнозом по ограниченной информации
I 3,1)- Соотношение (4.35) можно представить в виде:
1 3 г2) | 3 ,!) = 0, (4.36)
где величина Xt+\-E(Xt+\ \ 3,2) может интерпретироваться как
ошибка прогноза на основе информации З/2. Из (4.36)
176

следует, что, основываясь на ограниченной информации,
нельзя улучшить прогноз, построенный по более полной
информации, или предсказать его ошибку.
СЕ.4. В условиях свойства СЕ.З
Е(Е(*/+11 3 ,0 13 } ) = E(Xt+l 13 ,*) (п.н.),
откуда следует:
ВД+1 - E(Xt+l 13 f1) 13 2) = E(Xt+l 13 t2) - E(Xt+] | 3 Д (4-37)
где Xt+\-E(Xt+i |з^) - ошибка прогноза на основе информа-
ции З/1.
Правую часть выражения (4.37) можно интерпретировать
как поправку к прогнозу, построенному по ограниченной (по
отношению к 3/?) информации З,1 за счет учета дополнитель-
ной информации, содержащейся в З,2. Таким образом, за счет
использования более полной информации можно корректи-
ровать прогнозы, построенные на основе ограниченной
информации.
Различия в полноте информации могут быть обусловлены
различием в источниках (видах) информации и времени по-
ступления информации. Например, возможны следующие ви-
ды информации:
F1 - только значения цен и доходностей активов;
F2 - вся доступная участникам рынка и относящаяся к де-
лу информация (all available and relevant information), напри-
мер дополнительно к F1 значения экзогенных переменных
(F* idFI);
F3 - вся информация, которая только может быть известна,
включая частную информацию (private information), доступ-
ную лишь ограниченному кругу лиц (F3z>F2z>F]).
Влияние временного фактора на полноту информации от-
ражено в соотношении (4.30): с течением времени информа-
ция не убывает. При этом относительно одного и того же по-
тока информации F={3,}, />0, удовлетворяющего условию
(4.30), можно сформулировать так называемые телескопиче-
ские свойства условного математического ожидания (law of it-
erated expectations) типа СЕ.З, СЕ.4, учитывающие различия в
полноте информации, обусловленные различием моментов
времени ее поступления:
СЕ.5. Е(Е(Х,+213 ж) 13 ,) = Е(Х,+213 ,) (п.н.).
СЕ.6. Е(Е(Х/+213 ,) 13 ж) = Е(Х/+213 ,) (п.н.).
123ак.7О84 177

Свойства условных математических ожиданий используют-
ся для описания и исследования временной зависимости цен
финансовых активов в условиях эффективного рынка. Мо-
дель зависимости последовательности случайных величин
(цен активов) при этом называется мартингалом.
4.3. ИНФОРМАЦИОННАЯ ЭФФЕКТИВНОСТЬ
ФИНАНСОВОГО РЫНКА
На понятии "мартингал" основывается гипотеза эффек-
тивности финансового рынка. Эффективный финансовый
рынок обычно определяется как рынок, на котором:
• информация в одинаковой степени доступна всем участ-
никам рынка, которые идентично ее интерпретируют и
мгновенно используют для принятия или корректировки
решений;
• участники рынка в совокупности поступают рациональ-
но, придерживаясь однородных целевых установок и
стратегий поведения.
Указанные особенности поведения участников рынка обу-
словливают выполнение основного свойства эффективного
рынка:
• цены активов мгновенно, полностью и корректно асси-
милируют всю доступную и относящуюся к делу инфор-
мацию (available and relevant information), достигая при
этом состояния равновесия, что исключает возможность
регулярного получения "сверхнормальной" (abnormal) до-
ходности, т.е. доходности более высокой, чем ожидаемая
на основе доступной всем информации.
Считается, что ожидаемая доходность актива включает
компенсации (премии) для всех систематических рисков, обу-
словленных рыночными факторами, и обеспечивает инвесто-
рам "нормальную" доходность, соответствующую активам с
сопоставимым риском.
Таким образом, говоря об эффективном рынке, имеют в
виду его эффективность относительно имеющейся у участни-
ков рынка и относящейся к делу информации, т.е. информа-
ционную эффективность рынка. Данная трактовка гипотезы
эффективности рынка (efficient market hypothesis - ЕМН) при-
надлежит Е. Фама1.
1 См.: Fama E. Foundations of Finance. Basic Books, 1976. P. 133.
178

Одним из формальных математических подходов к описа-
нию эффективного рынка является подход, основанный на
мартингальных моделях цен и доходностей финансовых акти-
вов [34, 37]. Приведем краткое описание данного подхода.
4.3.1. Гипотезы и свойства эффективного рынка
Пусть {Pt} - случайная последовательность цен финансово-
го актива в последовательные моменты времени /=0, 1, 2, ...,
определенная на вероятностном пространстве (Q, 3, Р) с вы-
деленным потоком информации F={3/}(*>0), где 3, - совокуп-
ность событий на рынке, наблюдаемых до момента времени /
включительно, т.е. информация, доступная участникам рынка
к этому моменту времени. Поток информации F={3/} удовле-
творяет условию (4.30), т.е. с течением времени информация
не убывает: 3qc 3jc...c З/c...c: 3.
Будем предполагать, что цена актива Pt складывается в за-
висимости от событий 3,, наблюдаемых на рынке до момента
времени t включительно (т.е. Pt - это 3-измеримая случайная
величина).
1) Гипотеза эффективности рынка.
Случайная последовательность цен активов {Pt} является
мартингалом (обладает мартингальным свойством), если
,)=Л, />0. (4.38)
Будем говорить, что если последовательность цен активов
{Pt} на финансовом рынке представляет собой случайный
процесс, который является мартингалом относительно потока
информации F={3/}, т.е. удовлетворяет условию (4.38), то фи-
нансовый рынок называется эффективным относительно по-
тока информации F={3r}, />0, т.е. имеет место информационная
эффективность рынка.
Предположительное утверждение о том, что имеет место
условие эффективности финансового рынка (4.38), интерпре-
тируется как гипотеза эффективности рынка (ЕМН).
Сформулируем свойства модели цен активов вида (4.38):
• модель (4.38) основывается на условных распределениях
вероятностей цен активов {Pf}, полученных при условии,
что используется определенный поток информации
179

• в соответствии с моделью (4.38) на эффективном рынке
наилучшим прогнозом цены актива для будущего момен-
та времени t+1 по доступной в момент времени t инфор-
мации 3/ является значение цены в текущий момент
времени t.
2) Гипотеза рациональных ожиданий.
Из (4.38) следует:
1feO, (4.39)
где £+] - случайная величина, имеющая нулевое условное ма-
тематическое ожидание:
E,(6+i) = E(£+1|3,) = 0. (4.40)
Предполагается, что вся информация Зг, доступная в мо-
мент / при построении прогноза, мгновенно отражается в це-
не актива Pt. Поэтому единственной причиной изменения це-
ны актива в момент времени Н-1 по сравнению с ожидаемым
значением является поступление в интервале времени между
моментами / и Н-1 новой по отношению к 3, информации
("новостей").
Таким образом, случайная величина &ц = Pt+] - E(/Vm 13/)
может интерпретироваться как случайная ошибка прогноза (или
смещение прогноза), обусловленная поступлением новой ин-
формации.
Согласно (4.40) ожидаемая в соответствии с информацией
3/ величина ошибки прогноза должна равняться нулю, т.е.
прогноз E(/Vh |3/) в виде условного математического ожида-
ния является несмещенным.
"Симметричность" случайных ошибок {£} относительно
нуля в соответствии с (4.40) объясняется тем, что могут быть
как "плохие", так и "хорошие новости", вызывающие движе-
ние курсов в различных направлениях. В зависимости от зна-
ка случайная ошибка прогноза £/+1 характеризует либо "не-
ожиданный" рост, либо "неожиданное" падение курса актива.
Свойство (4.39), (4.40) часто интерпретируется как гипоте-
за рациональных ожиданий (rational expectation hypothesis -
REH). Таким образом, данная гипотеза является одним из
элементов ЕМН.
3) Свойство ортогональности ошибок прогноза.
Из условия эффективности рынка следует еще одно важ-
ное свойство ошибок прогноза {&}, известное как свойство
ортогональности (orthogonality property), которое формулиру-
180

ется следующим образом: ошибка прогноза £+i не зависит от
информации 3/, доступной в момент времени t
Конкретные формулировки данного свойства зависят от
вида используемой информации и будут приведены в п. 4.3.3.
В любом случае необходимым условием ортогональности
ошибок прогноза является отсутствие автокорреляции слу-
чайных величин {£,}, т.е. условие:
Сог(6+1,6) =0, />0. (4.41)
Проиллюстрируем это на примере из [39].
Пусть доступной информацией на рынке являются цены
активов в текущий период и прошедшие периоды времени
(т.е. имеет место информация вида F1, см. п. 4.2.2). Таким
образом, в момент времени / имеется информация 3,, вклю-
чающая значения цен активов {Рь Pt.\, ...} до момента t вклю-
чительно. На основании этой информации могут быть рас-
считаны значения ошибок прогнозов^, £м, ...}.
Предположим, что имеет место корреляция между ошиб-
кой прогноза £+1 в будущий момент времени и ошибками
прогнозов в текущий ^ и прошедшие £,_i, <^_2, ... моменты
времени. Другими словами, ошибка прогноза £/+i зависит от
информации 3/, доступной в момент времени /. Пусть данная
зависимость описывается моделью авторегрессии первого по-
рядка AR (1) (детальное описание моделей авторегрессионно-
го типа см. в гл. 7):
' = 0, 1, ..., (4.42)
где р - коэффициент авторегрессии такой, что \р\ <1; £о - за-
данное начальное значение процесса; {r/t} - не зависящие
от Рь Pt.\, ... случайные величины с нулевым математиче-
ским ожиданием.
Запишем (4.39) с лагом на один период и умножим обе
части соотношения на р, в результате получим:
Вычитая полученное выражение из (4.39) и учитывая, что
=£н-1-/>£/> приходим к соотношению:
Л+1 = pPt + (Wm) ~ pE,-i(Pt)) + fh+i. (4-43)
Выражение (4.43) описывает модель авторегрессионного
типа для цены актива (величина Et(Pt+i)-pEt_i(Pt) в момент /
является фиксированной). Таким образом, автокорреляция
ошибок прогноза порождает автокорреляцию цен активов.
181

Другими словами, если имеет место автокорреляция ошибок
прогноза (т.е. свойство ортогональности ошибок нарушается),
то будущая цена зависит от текущей цены и поэтому в какой-
то степени предсказуема по текущей информации.
Если участники рынка располагают информацией вида
F2={3/} (F2z)FJ), включающей дополнительно к F1 значения
других (например, экзогенных) стохастических переменных,
то свойство ортогональности ошибок {£} дополнительно
предполагает некоррелированность &+\ со значениями этих
переменных в текущий и прошлые моменты времени.
Замечание. Описанная выше мартингальная модель эффек-
тивности финансового рынка сформулирована относительно
цен активов, а не их логарифмов, для того чтобы обеспечить
в большей степени согласование результатов данной главы с
результатами гл. 5 и 6, посвященных методам оптимального
портфельного инвестирования на основе моделей равновесия
фондового рынка. Использование самих значений цен приво-
дит (см. разд. 3.1) при определении доходности активов за
один период владения к "простым" ставкам, на применении
которых основаны методы решения задач портфельного инве-
стирования в традиционной постановке.
4.3.2. Эффективность рынка
и модель случайного блуждания
Как отмечалось в п. 4.3.1, если последовательность цен ак-
тивов {Pt} относительно потока информации F={3/} (/>0) на
финансовом рынке удовлетворяет условию (4.38), то финан-
совый рынок называется эффективным относительно данного
потока информации. Мартингальное свойство цен активов
(4.38) допускает эквивалентное представление в виде:
или
к=\
где {£,} - последовательность некоррелированных случайных
величин (ошибок прогнозов), для которых имеет место
свойство:
Е(£Ж|3,) = О. (4.46)
Представление (4.45) формально аналогично представле-
нию (4.5) для цен активов, описываемых моделью случайного
182

блуждания. Однако между двумя этими моделями существует
принципиальная разница, которая обусловлена различием
предположений относительно свойств ошибок прогнозов. Эти
различия состоят в следующем:
• модель (4.45) накладывает ограничение только на первый
момент условного распределения вероятностей ошибок
прогнозов, т.е. на условное математическое ожидание
E(£/+il3/), и не предполагает каких-либо ограничений на
второй момент данного распределения, т.е. на условную
дисперсию случайной величины £+1, равную о>2=
Е(£2/+1 |3f). В то же время модель (4.5) ограничивает свой-
ства и вторых моментов распределения £/+i требованием
постоянства дисперсии во времени: D(§+i)=o2= = const,
• модель (4.45) предполагает лишь некоррелированность
случайных величин {^}, в то время как модель (4.5) уста-
навливает более жесткое требование независимости. Как
известно, эти свойства эквивалентны лишь в случае
предположения о нормальном распределении случайных
величин {£,}. Некоррелированность {&} допускает поло-
жительную корреляцию {£?} (или {1&I}), при этом не
противоречит гипотезе мартингальной эффективности
рынка. Как будет показано в разд. 7.3, коррелирован-
ность отклонений {§?} может быть следствием условной
гетероскедастичности случайных величин {£/} и создает
возможности для построения нетривиальных прогнозов
цен активов.
Таким образом, мартингальная модель эффективного рын-
ка является обобщением модели случайного блуждания. Мо-
дель случайного блуждания получается из нее, если дополни-
тельно ввести указанные выше ограничения.
4.3.3. Проверка гипотезы эффективности рынка
Из формулировки гипотезы эффективности рынка (ЕМН)
следует, что если рынок является эффективным по отноше-
нию к информации F={3/}, то инвесторы не могут рассчиты-
вать на регулярное получение "сверхнормальной" доходности
(abnormal return), используя лишь информацию F={3r}. Ра-
зумной инвестиционной стратегией для инвесторов, избе-
гающих риска, в условиях эффективного рынка является
стратегия "купил и владей" ("buy and hold"). При этом основ-
ной задачей инвестиционных аналитиков и портфельных ме-
неджеров крупных институциональных инвесторов является
эффективная диверсификация капитала, т.е. формирование
183

"портфеля" активов, обеспечивающего получение приемле-
мой ожидаемой доходности с минимальным риском. Индиви-
дуальные инвесторы с целью снижения трансакционных из-
держек, связанных с заключением сделок (например, комис-
сионных процентов, выплачиваемых брокеру), могут приоб-
рести акции инвестиционных фондов, владеющих хорошо
диверсифицированными портфелями активов. Практика раз-
витых рынков показывает, что в данном случае трансакцион-
ные издержки составляют менее 2% стоимости портфеля ин-
вестора. Методы оптимального портфельного инвестирования
достаточно подробно рассматриваются в гл. 5. Таким обра-
зом, с принятием или отклонением ЕМН связан выбор уча-
стниками рынка той или иной стратегии поведения. В связи с
этим проблема проверки гипотезы эффективности рынка
представляет не только теоретический, но и практический
интерес.
1) Формы и условия эффективности рынка.
Тестирование эффективности рынка основывается на ста-
тистической проверке гипотез и свойств, лежащих в основе
понятия "эффективный рынок", по реальным статистическим
данным. В зависимости от вида используемой информации
(см. разд. 4.2) можно говорить о проверке трех форм
эффективности рынка:
• слабая форма (weak form) - при использовании информа-
ции вида F1, включающей только значения цен (доход-
ностей) активов;
• "полусилъная " форма (semi-strong form) - при использова-
нии информации вида F2 (F^dF1), включающей всю дос-
тупную всем участникам рынка и относящуюся к делу
информацию, например дополнительно к F1: значения
процентных ставок, обменных курсов, показателей ин-
фляции, фондовых индексов, отношений типа "дивиден-
ды - цена" и других экзогенных переменных. Как прави-
ло, эмпирической проверке подвергается именно эта
форма эффективности рынка;
• сильная форма (strong form) - при использовании инфор-
мации вида F3 (F3idF2z)F1), под которой понимается вся
относящаяся к делу информация, которая только может
быть известна, включая частную информацию, доступ-
ную лишь ограниченному кругу лиц.
Предположим, что в произвольный момент t вся полезная
для предсказания цен и доходностей активов информация
(relevant information) образует информационное множество 3,,
в то время как участникам рынка доступна лишь информация
184

(available information) 3/t3,. На основании информации З/7
участники рынка строят прогнозы ожидаемых доходностей
активов, используя при этом либо модели формирования до-
ходностей активов в состоянии равновесия рынка (equilibrium
model), либо модели оценивания их "фундаментальной стои-
мости" (evaluation model).
Пусть Е(/?,+1 |з/0 - ожидаемая на основе информации З/7 в
будущем периоде Н-1 доходность актива в соответствии с мо-
делью равновесия рынка либо моделью оценивания активов.
Ожидаемая доходность, как известно, включает компенсации
для всех систематических рисков, обусловленных рыночными
факторами, и обеспечивает инвесторам "нормальную" доход-
ность. При этом имеется в виду, что все участники рынка
одинаковым образом обрабатывают доступную информацию
и поступают так, как будто используют одну и ту же модель
равновесия или оценивания активов.
В соответствии с гипотезой рациональных ожиданий отно-
сительно доходностей активов по аналогии с (4.38), (4.39)
имеем:
Случайная величина
|з/0 (4.48)
в рамках рассматриваемой модели интерпретируется как "не-
ожиданная" или "сверхнормальная" доходность (в случае от-
рицательного знака <f ,+1 имеют место соответствующие убыт-
ки), обусловленная поступлением новой информации {''ново-
стей") в интервале времени между моментами t и /+1.
Если рынок является эффективным, то 3^=3^, т.е. участ-
ники рынка располагают всей относящейся к делу информа-
цией, которая находит мгновенное отражение в ценах акти-
вов. При этом "сверхнормальная" доходность инвесторов в
среднем должна равняться нулю
E(4Vil3/0 = 0,/;>0 (4.49)
и быть непредсказуемой, т.е. должно выполняться свойство
ортогональности ошибок прогнозов, состоящее в независимо-
сти случайной величины <fVn от информации 3/*=3,.
Рассмотрим некоторые подходы, используемые для про-
верки этих условий.
2) Тесты информационной эффективности.
Если ЗДгЗ,, то не вся относящаяся к делу информация от-
ражается в ценах, т.е. рынок не является эффективным, по-
185

этому возникают предпосылки для нарушения сформулиро-
ванных выше условий. Задачу проверки данных условий про-
иллюстрируем с помощью следующей модели.
Предположим, что ЗДгЗ,, причем не используемую в мо-
мент времени t информацию, оказывающую влияние на цены
(доходности) активов, можно выразить с помощью некоторого
вектора Zf=(z\u Zlt> —, £m/)T(E^m- Для проверки свойства неза-
висимости ошибок прогноза {<^t} от данной информации мо-
жет использоваться следующая модель регрессионного типа:
/?ж = Е(ЛЖ13/0 + 0{TZt + &н, />0, (4.50)
где E(Rt+113/0 - ожидаемая в соответствии с используемой
информацией З/7 доходность актива; 0 {=(в\, <%, ...,
вт)те^т - вектор параметров модели (коэффициентов
регрессии).
Ошибка прогноза на основе всей возможной информации
3/ в соответствии с моделью (4.50) равна:
£ж = Дж- Е(ЛЖ I 3/0 - 0tTZ,, />0. (4.51)
Если рынок является эффективным относительно всей
информации 3/, то случайная величина £ж не зависит от ин-
формации Зг и удовлетворяет условию типа (4.49):
,) = 0, />0. (4.52)
Задача тестирования гипотезы эффективности рынка отно-
сительно информации З/7 на основе модели (4.50) может быть
сформулирована как задача проверки статистических гипотез
о значимости коэффициентов регрессии {#/} вида:
Яо: б/=0,/= 1,2, ..., т
Н{: 0,*О, /е{1,2, ..., /я}.
Если гипотеза Яо принимается для всех /=1, 2, ..., /я, то,
согласно (4.51), (4.48), £Ж=ЛЖ-Е(/?Ж |з^)=^г+1. Это озна-
чает, что 3^=3/, т.е. рынок является эффективным относи-
тельно З/7 и "сверхнормальная" доходность ^\=^t+\ непред-
сказуема на основе информации З/7.
Если гипотеза Яо отклоняется, то не вся относящаяся к де-
лу информация используется при оценке ожидаемой доходно-
сти, т.е. ЗДгЗ,. В данном случае при использовании всей
возможной информации 3/ доходность актива поддается про-
гнозированию с помощью модели (4.50). Из (4.50) следует
модель для прогнозирования "сверхнормальной" доходности
в виДе:
186

3/0 =
т.е. относительно £Vi не выполняется свойство ортогональ-
ности: 4°/+i зависит от информации 3/. Это означает, что в
данном случае рынок нельзя считать эффективным.
От вида используемой информации 3/, т.е. от того, что
подразумевается под вектором Zb зависит конкретный вид
модели (4.50), а следовательно, и конкретный вид тестов, ис-
пользуемых для проверки гипотез Щ, Н\.
Проиллюстрируем это на примерах. Пусть при проверке
слабой формы эффективности рынка полагается:
1) Zf=(Rt9 /?м, ..., Rt-P-\)T - вектор значений доходности не-
которого актива за р прошедших периодов р>\, т=р;
2) Zt=(gh £>_i, ..., <^t-q-\)T - вектор значений ошибок прогно-
зов доходности некоторого актива за q прошедших периодов
<?>1, m=q;
3) Zf=(Rt9 Лм, ..., Rt-p-u 4 6-ь .»» %t-q-\)T ~ соответствую-
щий составной вектор размерности m=p+q.
Если предположить, что ожидаемая в соответствии с ин-
формацией доходность является постоянной, т.е.
E(/?/+i |з/0=/?, то спецификациям 1-3 вектора Zt соответству-
ют модели доходности типа ARMA (подробно данные модели
рассматриваются в гл. 7):
1) модель авторегрессии (autoregressive model) порядка р
%/?/, /=1, 2, ..., р), сокращенно AR(p):
2) модель скользящего среднего (moving average model) по-
рядка q (0^-ai, /=l, 2, ..., q), сокращенно
3) модель авторегрессии - скользящего среднего (autore-
gressive moving average model) порядков р и q соответственно
/, /=1, 2, ..., p, Ofz-cLj_pJ= /H-l, /?+2, ..., /?+^), сокращенно
A0)
Описанный подход к тестированию информационной эф-
фективности рынка предполагает наличие адекватной модели
187

равновесия рынка (либо модели оценивания активов), на ос-
новании которой определяется ожидаемая доходность активов
E(/?j+i |3/*). Наиболее известными моделями равновесия рын-
ка ценных бумаг являются модели САРМ и APT. Экономет-
рические модели формирования доходностей активов на ос-
нове данных моделей равновесия рынка принимают вид ли-
нейных регрессионных моделей, поэтому для проверки
адекватности данных моделей используются методы статисти-
ческой проверки гипотез относительно значений параметров
регрессионных моделей, описанные в разд. 3.5. Модели
САРМ и APT описываются в гл. 6. Там же рассматриваются
задачи тестирования адекватности этих моделей.
В качестве моделей оценивания активов используются мо-
дели определения "фундаментальной стоимости" активов в
виде дисконтированной текущей стоимости связанного с их
владением потока платежей, ранее рассматривавшиеся в гл. 2.
В предположении рациональных ожиданий инвесторов дан-
ные модели рассматриваются в разд. 4.4.
Таким образом, при моделировании доходностей активов
на основе моделей равновесия рынка возникает проблема со-
вместного тестирования как гипотезы эффективности рынка,
так и адекватности моделей равновесия рынка, или оценива-
ния активов. Поэтому если гипотеза эффективности рынка
отвергается, то это может означать, что рынок на самом деле
не является эффективным, а также, что используемая модель
равновесия рынка (или оценивания активов) является неаде-
кватной.
Общая схема решения задачи проверки ЕМН в рамках
данного подхода, таким образом, включает следующие основ-
ные этапы.
Этап 1. Определение экономической модели равновесия рын-
ка ценных бумаг (или модели оценивания активов),
описывающей образование "нормальной" доходности
(normal return) активов, т.е. доходности активов в со-
стоянии равновесия рынка.
Этап 2. Представление моделей образования доходностей ак-
тивов в виде эконометрических (статистических) моде-
лей и формулировка гипотезы равновесия рынка и ги-
потезы эффективности рынка в виде статистических ги-
потез относительно параметров и свойств полученных
эконометрических моделей.
Этап 3. Проверка статистических гипотез по эмпирическим
данным и интерпретация полученных статистических
выводов.
188

3) Анализ эффективности рынка на основе оценки деятельно-
сти портфельных менеджеров.
Как показано выше, регулярное получение "сверхнормаль-
ной" доходности в условиях эффективного рынка невозмож-
но. Если рынок не является эффективным, то не вся доступ-
ная информация отражается в ценах активов, поэтому за счет
эффективного использования "неучтенной" информации воз-
можно построение более точных по сравнению с моделями
равновесия прогнозов доходности активов, а следовательно, и
получение дополнительной положительной доходности, т.е.
"свернормальной" доходности.
На установлении такой возможности основан один из под-
ходов к проверке эффективности рынка, состоящий в оценке
деятельности "профессионалов рынка", например портфель-
ных менеджеров инвестиционных (взаимных) фондов (mutual
funds). Если портфельные менеджеры достигают более высо-
кой доходности (скорректированной с учетом риска), чем до-
ходность E(/?f+il3/0, ожидаемая в соответствии с имеющейся
информацией, либо более высокой, чем средняя доходность
по рынку, то считается, что рынок не является эффективным
по отношению к этой информации. Для оценки деятельности
"профессионалов рынка" могут использоваться различные
показатели, например индексы Шарпа (см. разд. 5.3), Йенсе-
на, Трейнера [37, 39].
Сделаем некоторые практические замечания, связанные с
проблемой тестирования эффективности рынка.
1. Очевидно, относительно реальных финансовых рынков
не следует ожидать "теоретической" эффективности (т.е. эф-
фективности, точно соответствующей теоретическим моде-
лям). Это означает, что обычно имеются возможности для
предсказания цен и доходностей активов. Однако наличие
возможности предсказания и достижения "сверхнормальной"
доходности еще не гарантирует получения экономической
прибыли (economic profits), т.е. скорректированной с учетом
риска прибыли после учета всех расходов, связанных с ее
получением (расходов, связанных с заключением сделок,
получением и обработкой информации). В связи с этим по-
нятие "рынок, эффективный относительно информации F"
целесообразно трактовать как рынок, на котором невозможно
получение экономической прибыли на основе информации F.
2. С практической точки зрения полезным является поня-
тие относительной эффективности рынка, т.е. более высокой
эффективности одного рынка по отношению к другому рын-
ку, например рынка NYSE (New York Stock Exchange) no
189

сравнению с рынком LSE (London Stock Exchange) или рынка
спот некоторого базисного актива по сравнению с фьючерс-
ным рынком и т.д.
3. Несмотря на то что "теоретическая" эффективность яв-
ляется достаточно абстрактной и нереальной моделью, мето-
ды ее анализа и тестирования предоставляют полезную мето-
дологию оценивания относительной эффективности рынка.
4.4. АНАЛИЗ ЦЕННЫХ БУМАГ В ПРЕДПОЛОЖЕНИИ
РАЦИОНАЛЬНЫХ ОЖИДАНИЙ
Описанная в соответствии с вероятностным подходом мо-
дель эффективного финансового рынка предполагает выпол-
нение ряда гипотез относительно поведения курсов и доход-
ностей активов в состоянии равновесия рынка (см. разд. 4.3).
К числу таких гипотез относится гипотеза о рациональных
ожиданиях инвесторов, в соответствии с которой фактическое
значение курса Pt+\ или доходности /?ж актива в периоде t+l
отличается от ожидаемого значения в соответствии с доступ-
ной в периоде t информацией 3, на случайную ошибку £/+ь
имеющую нулевое условное математическое ожидание. Нали-
чие ошибки прогноза при этом обусловлено поступлением
новой информации, не учтенной в периоде t, но важной с
точки зрения образования курсов активов.
Подобные модели цен и доходностей финансовых акти-
вов, таким образом, позволяют учитывать фактор неопреде-
ленности, который всегда имеет место на финансовом рынке.
На основании данных моделей можно дать математически
строгое обоснование представлений для характеристик акти-
вов, полученных в гл. 2 с помощью метода дисконтирования
платежей. Кроме того, они дают возможность осуществлять
анализ активов при более реальных для практики модельных
предположениях. Проиллюстрируем эти возможности на не-
которых примерах анализа акций и облигаций.
4.4.1. Случай постоянной ожидаемой доходности
Пусть {Pt} и {Rt} (t=l, 2, ...) - временные ряды цен (ры-
ночных курсов) и доходностей акций или облигаций в после-
довательные моменты (периоды) времени. Имеется информа-
ция вида F2={3r}, где 3/ - значения цен (доходностей) ценных
бумаг, а также платежей по ним до момента / включительно.
Рассмотрим задачу анализа активов, когда их ожидаемая до-
190

ходность постоянна в течение срока обращения, а рынок яв-
ляется эффективным.
Итак, будем считать, что цены активов {Pt} удовлетворяют
следующим предположениям:
• справедлива гипотеза о рациональных ожиданиях, т.е.
Л+1 = ехл+i) + £+1; (4.53)
• относительно ошибок прогноза {£} выполняются условие
ортогональности, т.е. ^t+\ не зависит от 3,, и условие ра-
венства нулю условного математического ожидания:
Е(£Ж|3,) = О. (4.54)
Пусть также ожидаемая доходность ценной бумаги Е,(/?ж)
на основе информации F2={3,} постоянна во времени:
Е,(ЛЖ) = ВД+11 Яь Rt-ъ .-.) - R >0, V/. (4.55)
Ставку R можно также интерпретировать как ставку до-
ходности вложений с сопоставимой степенью риска. Целью
данного пункта является получение в предположениях
(4.53) - (4.55) представлений для текущих цен акций и обли-
гаций, а также анализ чувствительности цен к изменениям
ожидаемой доходности.
1) Анализ цены акции.
Известно (см. разд. 3.1), что доходность акции за период
владения Н-1 (т.е. период между моментами времени t и Н-1)
определяется ставками Rt+\ или l+/?/+i вида:
(4.56)
Простые ставки Rt+\ и 1+Л/+1 определяют так называемую
чистую (net return) и валовую (gross return) доходность актива.
Заметим, что значение текущей рыночной цены акции Pt со-
держится в информации 3/, т.е. не является случайной вели-
чиной. Значения цены Pt+\ и дивидендов Dt+\ в будущий пе-
риод точно неизвестны и рассматриваются как случайные ве-
личины.
Вычислим условное математическое ожидание ЕХ-)=
=Е(-13,) от обеих частей (4.56) и запишем найденное соотно-
шение как уравнение относительно текущей рыночной цены
191

акции Pt. В итоге получим, что в предположении рациональ-
ных ожиданий инвесторов, определяемых условиями (4.53) -
(4.54), с учетом (4.55) цена акции в момент времени t опреде-
ляется выражением:
Согласно (4.57), текущая стоимость акции должна равнять-
ся ожидаемому на основании информации, доступной в мо-
мент /, значению платежа по акции в будущем периоде, дис-
контированному по ставке R.
Учитывая в (4.57) представления для цен акции в будущие
моменты t+k
pf+k = E/+*(ff+*+i+A+*+i) ,£=1,2, ..., К, (4.58)
получим:
Pt = Е,
\
,+1Е,+2
. (4.59)
Для преобразования формулы (4.59) используем "телеско-
пическое" свойство СЕ.5 условного математического ожида-
ния из п. 4.2.2:
Et(Em(Et+K(X))) = ЕАХ). (4.60)
С учетом (4.60) из (4.59) следует:
Л = е1-А*)+ е/у Аи-* 1= р/цю + рв(ю, (4.61)
где PtA(K), PtB(K) — ожидаемые в периоде / стоимость акции в
конце периода владения К и дивидендов за К будущих пе-
риодов соответственно.
Если учесть, что акция имеет неограниченный срок обра-
щения, т.е. А-^оо, то в (4.61) можно положить, что Д
при А^оо и, следовательно:
п *\ °° 17 (Л ^
т.е. при условии рациональных ожиданий инвесторов рыноч-
ная цена акции Pt совпадает с ее текущей "фундаментальной"
192

стоимостью (fundamental value) Vh определяемой как сумма
всех ожидаемых по акции дивидендов, дисконтированных по
ставке, равной ставке ожидаемой доходности акции.
Таким образом, в условиях эффективного рынка рыночные
курсы акций Pt достигают равновесных значений на уровне
их "фундаментальной" стоимости Vt, а внутренняя доходность
акций (IRR) при этом соответствует ожидаемой инвесторами
доходности R для активов с сопоставимым риском.
Делая различные предположения относительно модели из-
менения дивидендов в будущем, можно получить различные
частные случаи общей формулы (4.62).
Рассмотрим описанные в разд. 2.6 модели изменения ди-
видендов:
1) модель нулевого роста дивидендов
Е,(А+/) = Dh /=1,2, ...; (4.63)
2) модель постоянного роста дивидендов с темпом прирос-
та 0<g<R
E,(/W = (l+^E/ZWO = (l+g)*Z),, к = 1, 2, ... (4.64)
Аналогично разд. 2.6 на основании (4.62) в случае (4.63)
получаем:
„ fE,(Aj А у( 1 У.. А
а в случае (4.64) имеем:
(465)
(R-g)
Таким образом, описанные ранее, в разд. 2.6, модели нуле-
вого и постоянного роста дивидендов получили строгое обос-
нование в рамках теории эффективного рынка.
Исследуем чувствительность рыночной цены акции Рь оп-
ределяемой (4.65), к изменениям ожидаемой доходности ак-
ции (или доходности альтернативных вложений с сопостави-
мой степенью риска) R. Для этой цели определим соответст-
вующий коэффициент эластичности Л:
d(log(Pt)) dPt R = R
** d(tog(R))=iR'Tt ~1ГГ8-
Из (4.66) следует, что поскольку коэффициент эластично-
сти X имеет отрицательный знак, то цена акции (имеется в ви-
13 3ак.7О84 J93

ду цена покупки) и ожидаемая доходность акции связаны об-
ратной зависимостью. Кроме того, чувствительность цены ак-
ции к изменениям ожидаемой доходности акции R усиливает-
ся по мере того, как ожидаемая доходность R уменьшается и
приближается к темпу прироста дивидендов g. Л->оо при R-^g.
Для практических расчетов при оценке относительного
изменения цены акции (по отношению к начальной равно-
весной стоимости Pq) в случае малых ожидаемых абсолютных
изменений доходности акции AR (до 1%) за анализируемый
период с учетом (4.66) можно использовать следующую при-
ближенную формулу:
АР AR R AR AR
тгА"-1гт~-]Г7- (467)
С учетом предыдущего замечания из (4.67) следует, что ес-
ли /?->#, то даже незначительные колебания ожидаемой до-
ходности акции (доходности альтернативных вложений) могут
вызывать высокую изменчивость (волатильность) цен акций.
2) Анализ облигаций.
Исследуем, чему должна равняться рыночная стоимость
купонной облигации в предположении рациональных ожида-
ний в некотором периоде /за Т (Т >1) периодов до погаше-
ния облигации.
Для простоты предположим, что ставка ожидаемой доход-
ности облигации за один период владения (или ставка доход-
ности альтернативных вложений с сопоставимой степенью
риска) остается постоянной и равна R.
Ожидаемый в момент времени t поток платежей {Q+r}
(г=1, 2, ..., 7) включает купонный доход {Qt+T} для всех ос-
тавшихся периодов владения и финальную выплату F в по-
следнем периоде Н-Гв виде номинальной стоимости облига-
ции, т.е. определяется соотношениями:
+T9 т = \,2,...,Т-\
Доходность облигации в периоде Ж, определяемая став-
кой 1+/?/+ь будет равна:
1 + Л /k±£±L. (4.68)
В предположениях (4.53) - (4.56) на основании (4.68) ана-
логично предыдущему случаю получаем представление для Pt\
194

pt = e,
и, учитывая, что ЕХЛ+г)=Л+7^^ в итоге получаем:
= у М(?н-г) + F у (4 69)
т.е. при сделанных предположениях рыночная цена облига-
ции должна совпадать с ее текущей "фундаментальной"
стоимостью. Это говорит о том, что соответствующие форму-
лы из разд. 2.6 справедливы в условиях эффективного финан-
сового рынка (в предположении, что текущий период являет-
ся нулевым, т.е. /=0).
Исследуем чувствительность цены Pt купонной облигации
за Т периодов до погашения к изменению ожидаемой "вало-
вой" доходности 1+/?. Для этого найдем соответствующий ко-
эффициент эластичности, используя представление для Pt ви-
да (4.68):
_dPt ! + /?_
Pt
(4.70)
где принято обозначение:
w'--£fri£>O'i>V=l- (4.71)
Коэффициент эластичности Я имеет отрицательный знак,
поэтому цена облигации (имеется в виду цена покупки) и
ожидаемая доходность облигации связаны обратной зависи-
мостью.
Характеристика /)д/, определяемая по формуле
^ dPt 1 + R уг-*i /. _ЛЧ
известна как дюрация {дюрация Маколи) облигации (Macaulay's
duration), до погашения которой осталось Г периодов.
Дюрация облигации, согласно (4.72), может интерпретиро-
ваться как средневзвешенный срок платежей по облигации. Ве-
195

совой коэффициент wn соответствующий сроку платежа т
(z=l, 2, ..., 7), представляет собой долю, которую составляет
текущая стоимость платежа в периоде г от текущей стоимости
облигации Pt при условии, что дисконтирование производит-
ся по ставке R. Дюрация Dm характеризует величину относи-
тельного изменения цены облигации, приходящуюся на еди-
ницу относительного изменения ожидаемой "валовой"
доходности 1+/? облигации.
Дюрация бескупонной облигации, очевидно, равняется
сроку до погашения облигации. Действительно, если
Е/(С,+Г)=О (г=1, 2, ..., 74) и E,(C,+7)=F, то w=0 (r=l, 2, ...,
74) и wj — 1, а значит, Dm = T. Для купонной облигации дю-
рация меньше величины срока до погашения (Dm<T) и тем
меньше, чем больше ожидаемый купонный доход {Et(Ct+T)} и
ожидаемая доходность облигации R.
В практических расчетах при малых абсолютных измене-
ниях ожидаемой доходности облигации AR (до 1%) за анали-
зируемый период времени для оценки соответствующего от-
носительного изменения цены облигации AP/Pt может ис-
пользоваться приближенная формула, основанная на
соотношении (4.72):
Т * ~Dy rh=~DmodAR' (473)
где Dmoc] - модифицированная дюрация (modified duration), оп-
ределяемая по формуле
Зависимость цены облигации от ожидаемой доходности
имеет нелинейный вид, поэтому более точная аппроксимация
относительного изменения цены облигации может быть полу-
чена на основе формулы Тейлора, включающей члены более
высоких порядков относительно изменения ожидаемой до-
ходности облигации AR, например член второго порядка:
(4.75)
где CONV - характеристика нелинейности (выпуклости) кри-
вой зависимости цены облигации от ожидаемой доходно-
сти, обычно называемая "выпуклостью" облигации (convex-
196

ity of a bond). С учетом (4.71), (4.72), (4.74), (4.75) CONV
вычисляется по формуле
Выпуклость CONV может служить оценкой точности про-
гноза вида (4.73) относительного изменения цены облигации
на основе модифицированной дюрации Dmo(j.
4.4.2. Мартингальная модель цен акций
При анализе акций часто делается предположение о посто-
янстве ожидаемой доходности акции во времени:
Е, (Лн-i) = E(/?,+i 13,) = R = const W, (4.76)
где 3, - доступная к моменту t и относящаяся к делу инфор-
мация о рынке. Текущая стоимость акции при этом удов-
летворяет соотношению (4.57).
Часто предположение (4.76) ассоциируется с мартингаль-
ной моделью цены акции. Однако одного этого предположе-
ния недостаточно для того, чтобы случайный процесс {Pt},
описывающий цены акции, был мартингалом.
Действительно [37], мартингальное свойство для цен акций
определяется соотношением (п. 4.3.1)
= Pt,
в то время как из (4.57) следует другое представление:
i), (4.77)
свидетельствующее о том, что если при определении доходно-
сти акций не учитываются дивидендные платежи, то случай-
ный процесс, описывающий цены акций, не может быть мар-
тингалом.
На самом деле, можно показать, что в данном случае мар-
тингалом является случайный процесс, описывающий цены
портфеля акций, все дивидендные платежи по которым реин-
вестируются в покупку таких же акций на рынке, т.е. идут на
увеличение портфеля. Таким образом, если дивидендные пла-
тежи не учитываются, то можно говорить о мартингальной
модели для цены указанного портфеля акций. Установим этот
факт.
Предположим, что есть некоторый инвестиционный (вза-
имный) фонд (mutual fund), который владеет акциями, для
197

которых имеет место (4.76), и реинвестирует дивиденды по
ним в покупку этих же акций на вторичном рынке. Пусть в
момент времени t портфель акций данного фонда включает Nt
акций. Стоимость такого портфеля в период / будет равна
SfzNtPt. Поскольку весь дивидендный доход фонд вкладывает
в покупку акций, то должно выполняться соотношение:
St+]=Nt+lPt+l = NtPM+Dt). (4.78)
Согласно (4.77), (4.78) ожидаемая в периоде /+1 стоимость
портфеля будет определяться по формуле
Л+1)= Nt Et(Pt+l+Df)=
= (1+Л) NtPt=(l+R)St.
Таким образом, если ожидаемая доходность акций посто-
янна (R=const), то, согласно (4.78), случайный процесс, опи-
сывающий цены портфеля акций {St}, является: мартингалом,
если 7?=0; субмартингалом, если Л>0; супермартингалом, если
/КО (см. также гл. 7).
Заметим, что сами курсы акций {Pt} в предположении, что
ожидаемая доходность акций R постоянна, без учета прибав-
ляемых к ним дивидендов не являются мартингалом. Дейст-
вительно, преобразовав (4.77), имеем:
Отношение Dt/Pt известно в финансовом анализе как от-
ношение " дивиденды - цена" (dividend -price ratio), или "диви-
дендная доходность" (dividend yield). Предположим, что ожи-
даемая дивидендная доходность остается постоянной в тече-
ние всего срока обращения акций, т.е.
Е, (Dt)/Pt = d= const V t.
Тогда с учетом того, что R>d, получаем:
Et(Pf+i)=(l+R-d)Pt, V/,
т.е. случайный процесс {Pt} является: мартингалом, если R=d
(т.е. рынок является эффективным и компонент доходности,
обусловленный изменением курсовой стоимости акции, равен
нулю); субмартингалом, если R>d.
Таким образом, только в том случае, если при определе-
нии R учитываются дивидендные платежи, причем ожидаемая
дивидендная доходность остается постоянной в течение всего
срока обращения, можно говорить о мартингальной модели
цен акций.
198

4.4.3. Проблема "спекулятивных пузырей"
Как было показано в п. 4.4.1, в условиях равновесия рынка
и рациональных ожиданий инвесторов рыночная цена акции
Pt совпадает с ее текущей "фундаментальной" стоимостью Vb
определяемой как сумма всех ожидаемых по акции дивиден-
дов, дисконтированных по ставке R, равной ставке ожидаемой
доходности акции. В то же время появление "новостей", ка-
сающихся будущей деятельности корпораций, вызывает высо-
кую изменчивость цен даже в условиях эффективного рынка.
Практика динамично функционирующих рынков акций,
как правило, подтверждает наличие устойчивой связи между
рыночной и "фундаментальной" стоимостью акций. Если та-
кая связь существует, то ставки доходности котируемых акций
могут использоваться как скорректированные с учетом риска
ставки дисконтирования ожидаемого в будущем дохода от ин-
вестиционных проектов (реальных инвестиций) корпораций
при определении текущей стоимости проектов. Таким обра-
зом, с одной стороны, большей ожидаемой доходности акций
соответствует меньшая текущая стоимость инвестиционных
проектов, с другой стороны, чем больше ожидаемая прибыль
от новых инвестиционных проектов корпорации, тем выше
рыночная стоимость акций данной корпорации, а следова-
тельно, корпорация может привлечь необходимый ей капитал
за счет меньшего количества выпускаемых акций. На основа-
нии изложенного можно сделать вывод: несмотря на то что за
счет выпуска акций финансируется лишь незначительная доля
реальных инвестиционных проектов (например, в Великобри-
тании - около 4%), состояние рынка акций позволяет инве-
сторам принимать обоснованные инвестиционные решения
при размещении капитала в реальные инвестиционные проек-
ты. Это способствует притоку инвестиционного капитала.
Если цены акций не отражают действия "фундаменталь-
ных" причин, а находятся под влиянием некоторых "ирра-
циональных" факторов, несущих ложную информацию, то в
данном случае взаимосвязь между рыночной и "фундамен-
тальной" стоимостью акций нарушается. Ненормально низ-
кие цены на акции некоторой корпорации в данном случае
будут для нее препятствием при реализации возможно жизне-
способных инвестиционных проектов.
На практике также часто имеют место случаи, когда ры-
ночные курсы акций (или обменные курсы валют) растут на-
много быстрее, чем их "фундаментальные" стоимости. Пове-
дение курсов таких активов подобно росту мыльных пузырей:
курсы активов растут темпом, не объяснимым "фундамен-
199

тальными" факторами, однако в любой момент "пузырь" мо-
жет лопнуть. Активы типа мыльных пузырей или "дутых ак-
ций" привлекают многих участников рынка, рассчитывающих
на получение спекулятивной прибыли. Это способствует
увеличению спроса на данные активы и ведет к дальнейшему
росту их курсов. Однако в силу непредсказуемости поведения
"пузырей" инвестиции в подобные активы сопряжены с по-
вышенным риском. По этой причине представляют интерес
модели цен и доходностей подобных активов.
Познакомимся с одной из таких моделей "дутых акций", а
также отметим некоторые аспекты данной проблемы. При
получении соотношения (4.62) для цены акции предполага-
лось, что ожидаемая в произвольном периоде t дисконтиро-
ванная стоимость акции, продажа которой не предполагается
в обозримом будущем, равна нулю, т.е.
>0 (4.80)
где Pt>x — ожидаемая в соответствии с доступной в периоде /
информацией цена акции через К периодов владения.
С математической точки зрения условие (4.80) существен-
но для получения единственного решения уравнения (4.57).
Если снять это предположение, то существует бесконечное
множество решений данного уравнения относительно Pt.
Произвольное решение уравнения (4.57) при выполнении ги-
потезы рациональных ожиданий может быть записано в виде:
(4.81)
где Vt - фундаментальная стоимость акции; Bt - спекулятив-
ный, или рациональный, "пузырь"J (speculative or rational
bubble), который можно рассматривать как прибавку к
стоимости акции, не объясняемую "фундаментальными"
факторами:
' Bt= Pt- Vt>0. (4.82)
При выполнении условий (4.53)-(4.55) для Bt справедливо
представление:
1 Определение "рациональный" обусловлено построением модели рацио-
нальных "пузырей" в предположении выполнения гипотезы рациональных
ожиданий.
200

что эквивалентно:
,. (4.83)
На основании (4.83) статистическая модель для рацио-
нальных "пузырей" формально может быть записана в виде
модели авторегрессии первого порядка AR(1):
Яж=рЯ,+ £+ь (4.84)
где/?=1+/?- коэффициент авторегрессии, а случайные вели-
чины {Q} удовлетворяют условию
Поскольку /?>0, то р>\ и, следовательно, случайный про-
цесс {Bt} является нестационарным. Известно (см. гл. 7), что
для подобных процессов значения {Bt} имеют экспоненциаль-
ный тренд. Их рост носит "взрывной" характер (explosive be-
havior). В эконометрике такие процессы называются процес-
сами со стохастическим трендом (stochastic trend process).
Если предположить, что 7?=0, то (4.84) описывает так на-
зываемый процесс единичного корня (unit root process), кото-
рый является примером интегрированного нестационарного
процесса (integrated process). Подробно эти и другие экономет-
рические модели финансовых временных рядов рассматрива-
ются в гл. 7.
Таким образом, модель для цены "дутой акции" в услови-
ях рациональных ожиданий, согласно (4.81), (4.84), имеет вид:
Л= Vt+ Вь Bt=pBtA+ Q.
Примером модели спекулятивных "пузырей", учитываю-
щей возможность того, что "пузырь" может лопнуть, является
модель, предложенная О. Бланчардом и М. Ватсоном1. В со-
ответствии с данной моделью "необъяснимая" добавка к
"фундаментальной" стоимости акции определяется соотно-
шениями:
Ч, + Ct+\ c вероятностью к
с вероятностью 1 - п,
где величина \-к может интерпретироваться как вероятность
того, что "пузырь" лопнет в произвольный момент време-
1 Blanchard О., Watson M. Bubbles, Rational Expectation and Financial Mar-
kets / Crises in Economic and Financial Structure: Bubbles, Bursts and Shocks.
Lexington: Lexington, MA, 1982.
201

ни. С вероятностью п в каждый момент времени "пузырь"
продолжает расти со средним темпом прироста, равным:
'" '1±*1. (4.85)
) 1.
В, ) Bt
Так как 0<я<1, то из (4.85) следует, что l+gB>l+R, или
- Чтобы выяснить смысл данного условия, обратимся к
модели с постоянным темпом прироста дивидендов. Очевид-
но, в данном случае имеют место следующие соотношения
между величинами: #£>/?>#, т.е. темп прироста "пузырей"
выше темпа прироста дивидендов для "дутой акции". Это
может рассматриваться как компенсация за риск того, что
"пузырь" может лопнуть до того, как инвестор сможет реали-
зовать возможность получения "сверхприбыли" за счет про-
дажи акции по высокому курсу.
Необходимо учитывать следующие теоретические аспекты,
связанные с использованием подобных моделей рациональ-
ных "пузырей", ограничивающие возможность их примене-
ния [37]:
1) "пузыри" не могут быть отрицательными, т.е. 5/>0, по-
скольку отрицательные значения могли бы привести к отри-
цательным ожидаемым значениям курсов акций в некоторый
момент времени, что несовместимо с предположением об ог-
раниченной ответственности (см. разд. 3.1). Таким образом,
подобный подход не может быть использован для объяснения
"неправдоподобно" низких по сравнению с "фундаменталь-
ной" стоимостью цен акций;
2) "пузыри" не могут возникать внутри модели оценива-
ния. Если они имеют место сегодня, то они должны были
существовать с момента начала обращения данных акций. Это
основано на свойстве неотрицательных случайных величин
Bi>0: если для некоторого момента времени t "пузырь" не су-
ществует, т.е. Bt=0, то из (4.83) следует, что и его ожидаемое
в будущем значение также равно нулю, т.е. E/(jB/+i)=0;
3) "пузыри" не могут существовать, если имеются ограни-
чения сверху на цены активов. Так, "пузыри" не могут иметь
место для цен тех товаров, для которых существует замени-
тель с бесконечной эластичностью предложения. Наконец,
"пузыри" не могут существовать для таких активов, как обли-
гации, имеющие фиксированную стоимость на дату погаше-
ния.

Глава 5
МЕТОДЫ ОПТИМАЛЬНОГО
ПОРТФЕЛЬНОГО ИНВЕСТИРОВАНИЯ
Никогда не клади все яйца в одну
корзину.
Пословица
Глава содержит изложение методов оптимального портфельного
инвестирования на основе подхода "доходность - риск". Описываются
возможности выбора портфеля с помощью кривых безразличия инве-
стора, а также эффекты диверсификации и учета корреляции доходно-
стей ценных бумаг. Рассматриваются задачи оптимизации структуры
портфеля ценных бумаг, в том числе при возможности безрискового
кредитования и заимствования, а также проблемы статистического оце-
нивания характеристик ценных бумаг и анализа риска портфеля на ос-
нове однофакторной эконометрической модели.
По рассматриваемым в главе вопросам рекомендуется дополнитель-
ная литература: [19, 20, 33, 46] (традиционное теоретическое описание
задач и методов портфельного инвестирования); [37, 39, 45] (проблемы
разработки и практической реализации современных методов порт-
фельного инвестирования на основе эконометрических моделей).
Как известно [33, 45], инвестиционный процесс, связан-
ный с формированием портфеля ценных бумаг, состоит из
следующих основных этапов.
1. Выбор инвестиционной политики (investment policy). На
этом этапе инвестор определяется с целями инвестирования,
потенциальными объектами инвестирования (видами активов),
объемом инвестируемого капитала и сроками инвестирования.
Выбор инвестора определяется его статусом, а также целевыми
значениями ожидаемой доходности и риска вложений.
2. Анализ рынка ценных бумаг (security analysis). Целью ана-
лиза является оценка "истинной" стоимости и тенденций из-
менения курсов активов, относящихся к тем видам активов,
которые были выделены на предыдущем этапе. На этом этапе
могут использоваться различные подходы, модели и методы
анализа, например фундаментальный, технический или коли-
чественный анализ ценных бумаг. Результатом этапа является
целевое множество (target population) финансовых активов для
формирования портфеля.
203

3. Описание или моделирование и предсказание изменений
курсов активов (description or modelling and prediction of price
variations). Для решения этих задач в рамках количественного
подхода используются эконометрические модели цен и до-
ходностей активов. Некоторые из них основываются на эко-
номических моделях равновесия рынка ценных бумаг САРМ
и APT (см. гл. 6). Традиционные модельные предположения,
связанные с их практической реализацией на основе эконо-
метрических представлений, обсуждались в разд. 3.7. Данные
предположения приводят обычно к однопериодным моделям
(типа множественной или многомерной регрессии с некорре-
лированными ошибками), учитывающим лишь перекрестные
связи между характеристиками различных активов. При этом
временная автокорреляция значений анализируемых характе-
ристик не учитывается. Однако при моделировании цен и до-
ходностей активов, очевидно, следует принимать во внимание
не только перекрестные связи, но и временную корреляцию
их значений. Это приводит к необходимости использования
моделей многомерных временных рядов (разд. 3.3).
4. Определение структуры портфеля (portfolio construction).
На данном этапе осуществляется корректировка состава акти-
вов для вложения средств, а также устанавливаются пропор-
ции распределения инвестируемого капитала между активами,
т.е. определяется структура портфеля активов в соответствии
с выбранной инвестиционной политикой.
5. Оценка эффективности и корректировка портфеля (port-
folio performance evaluation and portfolio revision). Портфели
активов нуждаются в периодической оценке доходности и
риска. Для этой цели могут использоваться различные пока-
затели (performance measures) и соответствующие эталонные
значения. С течением времени портфель активов по разным
причинам (изменение целей инвестирования, представлений
инвестора относительно привлекательности активов и т.д.)
теряет свои оптимальные свойства и поэтому нуждается в пе-
ресмотре и корректировке посредством продажи одних и по-
купки других активов. Поэтому возникает проблема выбора
определенной стратегии покупки-продажи активов (trading or
rebalance role) для формирования портфеля с заданными
свойствами с учетом издержек, связанных с покупкой и про-
дажей активов.
Проблемы первого этапа требуют специального рассмотре-
ния в зависимости от статуса инвестора. Например, примени-
тельно к задачам формирования банковского инвестиционно-
го портфеля эти проблемы обсуждаются в [21].
204

Методы решения задач, возникающие на последующих
этапах инвестиционного процесса, в той или иной степени
рассматриваются в настоящем пособии. Методы анализа
фондового рынка, применяемые на втором этапе инвестици-
онного процесса, обсуждаются в гл. 2 и 4, а проблемы моде-
лирования и прогнозирования цен и доходностей активов - в
гл. 3, 6 и 7 настоящего пособия.
В данной главе главное внимание уделяется описанию ме-
тодов решения задач оптимизации портфелей ценных бумаг,
составляющих основное содержание четвертого этапа инве-
стиционного процесса. Акцент делается на традиционных по-
становках задач оптимального портфельного инвестирования
в рамках подхода "доходность - риск", предполагающих фор-
мирование портфеля активов на один период владения.
5.1. ПРОБЛЕМА ВЫБОРА ПОРТФЕЛЯ ЦЕННЫХ БУМАГ
НА ОСНОВЕ ПОДХОДА "ДОХОДНОСТЬ - РИСК"
5.1.1. Использование кривых безразличия
Как отмечалось в гл. 3, инвестиции в ценные бумаги в ус-
ловиях неопределенности сопряжены с риском того, что фак-
тическая доходность вложений может отличаться от ожидае-
мой доходности. Это дает основание рассматривать доход-
ность R ценной бумаги, соответствующую некоторому
периоду владения, как случайную величину, а выбор инве-
стиционной стратегии осуществлять на основе анализа ее
числовых характеристик: математического ожидания, диспер-
сии, среднеквадратического отклонения и т.д. При этом
математическое ожидание /i=E(7?) доходности актива соответ-
ствует ожидаемой доходности, а дисперсия o2=D(7?) или сред-
неквадратическое отклонение а доходности могут использо-
ваться как меры риска вложений в данный актив.
Идеальной для инвестора стратегией инвестирования в
рамках данного подхода была бы стратегия, обеспечивающая
достижение максимальной ожидаемой доходности при мини-
мальном риске вложений. Однако одновременное достижение
этих целей невозможно. Практика работы на финансовых
рынках свидетельствует о том, что большему значению ожи-
даемой доходности обычно сопутствует и большее значение
риска вложений.
Инвестируя в активы с более высоким риском, инвесторы,
как правило, рассчитывают на достижение более высокой до-
ходности в виде премии за риск (risk premium). Иллюстрацией
205

этой закономерности могут служить данные, приведенные в
табл. 5.1. Таблица содержит статистические оценки в виде
выборочного среднего для ожидаемой годовой доходности щ
и в виде выборочного среднеквадратического отклонения для
риска <т/, а также соответствующие значения коэффициента
вариации для трех видов ценных бумаг фондового рынка
США: казначейских векселей (T-bills), долгосрочных корпо-
ративных облигаций (Long Term Corporate Bonds - LTCB's) и
обыкновенных акций (Common Stocks - CS's). Для нахож-
дения оценок используются временные ряды годовых доход-
ностей ценных бумаг {/?,,} (/=1, 2, 3, /=1, 2, ..., 68) за
1926-1994 гг. (данные взяты из [33]).
Таблица 5.1
Соотношение между риском и ожидаемой доходностью
Оценки характери-
стик ценных бумаг
/
Mi
°i
Vi=cn/\Mi
T-bills
1
3.74
3.32
0.89
LTCB's
2
5.90
8.46
1.43
CS's
3
12.34
20.44
1.66
Из приведенных данных следует, что большему значению
ожидаемой доходности соответствует большее значение риска.
Кроме того, анализ значений коэффициента вариации доход-
ности ценных бумаг {Vj\ показывает, что с ростом доходности
растет и доля риска, приходящаяся на единицу доходности.
Существование двух противоположных целей инвестирования
позволяет сделать два важных вывода.
1. При осуществлении финансовых инвестиций в условиях
неопределенности необходимо учитывать не только ожидае-
мую доходность, но и риск финансовых активов. При этом
притязания инвесторов относительно доходности и риска
должны быть сбалансированы.
2. Не следует вкладывать весь капитал в один актив.
Действительно, вкладывая весь свой капитал лишь в один
актив, инвестор обрекает себя либо на заведомо низкую до-
ходность, либо на заведомо высокий риск. Следствием второ-
го вывода является необходимость распределения {диверсифи-
кации) капитала между разными активами.
Распределение инвестируемого капитала среди различных
ценных бумаг приводит к формированию портфеля ценных
бумаг инвестора. За счет использования "эффектов портфеля"
инвестор может достичь приемлемых для себя значений ожи-
206

даемой доходности и риска вложений. В этом состоит главное
преимущество портфельного инвестирования по сравнению с
инвестициями в отдельные ценные бумаги.
Выбор портфеля ценных бумаг на основе учета его ожи-
даемой доходности (mean) и риска (variance) известен как под-
ход "доходность - риск" (mean-variance)1, который был впер-
вые сформулирован Г. Марковичем2. Дальнейшее развитие
этот подход получил благодаря ранее упоминавшимся рабо-
там Дж. Тобина, У. Шарпа, С. Росса и др.
В рамках данного подхода предполагается, что инвестор
стремится максимизировать ожидаемую доходность портфеля
при заданном уровне риска либо минимизировать риск при
заданном уровне ожидаемой доходности посредством дивер-
сификации вложений. Для иллюстрации проблемы выбора
портфеля ценных бумаг с помощью подхода "доходность —
риск" удобно использовать кривые безразличия.
Кривые безразличия (indifference curves) - это линии, опи-
сывающие различные комбинации значений ожидаемой до-
ходности /лр и риска dp портфелей ценных бумаг, которые яв-
ляются равноценными в смысле определенных предпочтений
инвестора (рис. 5.1).
Рис. 5.1. Кривые безразличия инвестора
при подходе "доходность - риск"
1 В русскоязычной литературе термин "mean-variance" часто переводится
формально как "среднее-дисперсия". Использование термина "доходность -
риск", как мы считаем, точнее отражает суть данного подхода, основанного
на учете "ожидаемой доходности" и "риска" активов, при этом для количест-
венного выражения этих характеристик активов могут использоваться раз-
личные числовые характеристики случайных величин.
2 Основные результаты, полученные Г. Марковицем в данном направле-
нии, представлены в монографии [45].
207

В рамках подхода "доходность - риск" используются сле-
дующие предположения относительно предпочтений инвесто-
ра [33]:
1) предположение о "ненасыщаемости" (nonsaturation) ин-
вестора, которое может быть сформулировано следующим об-
разом: при выборе из двух идентичных во всем, кроме ожи-
даемой доходности, портфелей инвестор отдает предпочтение
портфелю с большей ожидаемой доходностью;
2) предположение о том, что инвестор избегает риска (risk
aversion), т.е. при выборе из двух идентичных во всем, кроме
риска, портфелей он отдает предпочтение портфелю с мень-
шим риском.
Избегать риска - значит идти на риск только при соответ-
ствующей компенсации за риск, т.е. "премии за риск": боль-
шему риску должен соответствовать больший доход. Напри-
мер, инвестор, избегающий риска, не станет участвовать в
"честной" азартной игре (fair game) типа подбрасывания мо-
неты, ожидаемый доход от которой равен нулю.
Пусть jup - ожидаемая доходность, ар - риск портфеля. В
силу сделанных предположений относительно предпочтений
инвестора в рамках рассматриваемого подхода соответствую-
щие кривые безразличия в системе координат "доходность —
риск" должны быть вогнутыми и иметь положительный на-
клон, как это имеет место на рис. 5.1.
Кривые безразличия инвестора обладают рядом свойств.
1. Каждая кривая линия описывает множество равноцен-
ных портфелей с характеристиками juPf ар, соответствующими
заданному уровню притязаний инвестора, и следовательно,
кривые безразличия одного инвестора не могут пересекаться.
2. Портфели, лежащие выше и левее, являются более при-
влекательными, чем портфели, располагающиеся ниже и пра-
вее. Так, изображенные на рис. 5.1 портфели А и В являются
равноценными, портфель С является более привлекательным,
чем портфели А и Д а те, в свою очередь, привлекательнее
портфеля D.
3. Каждый инвестор имеет бесконечно много кривых без-
различия, т.е. ему соответствуют так называемые карты кри-
вых безразличия.
4. Кривые безразличия для инвесторов, избегающих риска
в различной степени, т.е. различающихся склонностью к рис-
ку, имеют различный угол наклона (рис. 5.2).
Рассмотрим задачу вычисления характеристик /^, ар порт-
феля ценных бумаг, а также исследуем эффекты портфельно-
го инвестирования.
208

Рис. 5.2. Кривые безразличия инвесторов,
различающихся склонностью к риску:
а - невысокая склонность; b - средняя склонность; с - высокая склонность
5.1.2. Портфель ценных бумаг и его характеристики
Портфелем ценных бумаг (portfolio of securities) инвестора
будем называть совокупность ценных бумаг, принадлежащих
данному инвестору.
Пусть инвестор формирует свой портфель на множестве из
TV (N>\) различных ценных бумаг. Капитал инвестора распре-
деляется между различными активами в некоторых пропор-
циях х\, Х2, ..., хм, удовлетворяющих условию:
хх + х2+... + ** = 1. (5.1)
Совокупность величин {х,} (/=1, 2, ..., N) определяет струк-
туру портфеля ценных бумаг. Имеет место следующая интер-
претация значений {*/}:
а) х/>0 означает, что доля х,- капитала инвестора вложена в
ценную бумагу /;
б) Xf=0 означает, что ценная бумага / отсутствует в портфе-
ле инвестора;
в) Х/<0 означает, что относительно ценной бумаги / совер-
шена операция короткая продажа (short sale); средства, полу-
ченные за счет данной операции, составляют долю U/I от
первоначального капитала инвестора и использованы им для
покупки других ценных бумаг.
Определим векторы1: X=(xj) (/=1, 2, ..., TV) - вектор, опре-
деляющий структуру портфеля; 7=(1, 1, ..., 1)т - единичный
TV-вектор. Тогда условие (5.1) может быть представлено в ви-
де:
1. (5.2)
1 Всюду по умолчанию векторы рассматриваются как векторы-столбцы.
143ак.7О84 209

Для характеристик ценных бумаг, соответствующих одно-
му и тому же периоду владения, введем следующие обозна-
чения:
R=(Rj) - вектор доходностей ценных бумаг, образующих
портфель, причем компонента R/ (/=1, 2, ..., TV) данного век-
тора представляет собой "простую" ставку доходности ценной
бумаги за один период владения (см. разд. 3.1);
//= (///)=E(i?) - вектор ожидаемых доходностей ценных бумаг,
т.е. ///=Е(Л/)>0 (/=1, 2, ..., TV) - ожидаемая доходность ценной
бумаги / за один период владения;
£={<^//}=Е((Я~/')(Я~/')т) fa j=\9 2, ..., TV) - ковариационная
матрица доходностей ценных бумаг размерности (NxN). Мат-
рица Е является симметричной, т.е. Ет=£. Будем также пред-
полагать, что она является невырожденной: |е|*0. Диаго-
нальные элементы матрицы Е представляют собой дисперсии
доходностей активов:
aii^D(Ri)=E((RrMi)2) (/=1, 2, ..., TV).
Для удобства будем также использовать обозначение аг2=ац.
Среднеквадратическое отклонение <т/= ^(RJ > О доходности
ценной бумаги / будем интерпретировать как риск ценной бу-
маги.
Замечание. В п. 5.3.1 будет введено понятие безрискового
актива, доходность которого Rq считается фиксированной, а
риск равен нулю: <то=О. Ставка Rq при этом называется без-
рисковой ставкой. В связи с этим будем использовать также
при необходимости термин "рисковые активы" для активов с
ненулевым риском.
Недиагональные элементы матрицы Е являются ковариция-
ми доходностей ценных бумаг и определяются по формуле
и связаны с коэффициентами корреляции доходностей ру соот-
ношением:
Oij^pijOiOj, \ру |<1 (/,/=1, 2, ..., TV). (5.3)
С учетом принятых обозначений и соглашений характери-
стики портфеля ценных бумаг для одного периода владения
будут определяться следующими выражениями:
• доходность портфеля:
Rp^xiRil (5.4)
210

• ожидаемая доходность портфеля:
Мр = ЩЯр) = j^xi^Ri) =itxiMn (5.5)
• дисперсия доходности портфеля:
а\ = D(RP) = EKRp-Mp)2) =
= Z I xi xj E((RrMi)(Rj -Mj)) = Z Z ^ Jcy ^ •
Откуда на основании (5.3) получаем:
N N
ар = Z Z *' xv Ау ^ °"У ; (5.6)
• риск портфеля:
<гР = рЮ>0- (5.7)
В аналитических исследованиях более удобной является
векторно-матричная форма представления характеристик
портфеля:
, а] = XTLX, vp= (J^A)1/2. (5.8)
5.1.3. Эффекты портфельного инвестирования
Проиллюстрируем на примерах "эффекты портфеля", ко-
торые можно получить за счет диверсификации или учета
корреляции доходностей ценных бумаг.
Пусть портфель ценных бумаг инвестора включает N (N>1)
различных ценных бумаг с характеристиками {///}, {о-/}
(0<<т/<оо), {pij} (ij=l,2,...9N). Предположим для простоты, что
капитал распределяется между активами в одинаковых про-
порциях, т.е.
xrl/N(i=l,2,...9N).
Исследуем поведение ожидаемой доходности ^jUpiN) и
риска портфеля a^o-piN) при условии неограниченной дивер-
сификации портфеля, определяемой как N-#x>9 и различных
предположениях относительно корреляции доходностей цен-
ных бумаг.
211

1) Эффект диверсификации портфеля ценных бумаг.
Пусть доходности ценных бумаг являются взаимно некор-
релируемыми случайными величинами, т.е.
^•=0, />у,/,у=1,2, ..., N. (5.9)
Ожидаемая доходность портфеля, согласно (5.5), равна
среднему арифметическому значению доходностей ценных
бумаг:
/^=^(Л0=-^2>/ (5Л0)
и при 7V-»oo стремится к некоторой константе с>0.
С учетом (5.9) из (5.6) получаем представление для диспер-
сии доходности портфеля:
N N N
2
Откуда в условиях примера получаем оценку сверху для
риска портфеля:
где атах— тах{<т/}>0.
Из (5.11) следует, что риск портфеля при возможности не-
ограниченной диверсификации портфеля может быть сделан
сколь угодно малым:
сгр=<Тр(№)->0, 7V->oo . (5.12)
Свойство (5.12) портфеля ценных бумаг известно как эф-
фект диверсификации портфеля. На нем основано важное
практическое правило работы на финансовом рынке: если не
принимать во внимание трансакционные расходы (т.е. расхо-
ды, связанные с заключением сделок), то для уменьшения
риска вложений целесообразно распределять капитал среди
как можно большего числа активов, доходности которых рас-
сматриваются как некоррелированные случайные величины.
Предположение о существовании на финансовом рынке
сколь угодно большого числа активов с взаимно некоррели-
руемыми доходностями, очевидно, не является бесспорным.
На практике, как правило, имеет место обратная ситуация. С
одной стороны, курсы различных активов, а следовательно, и
их доходности часто зависят от одних и тех же макроэконо-
212

мических и политических факторов, форсмажорных событий
и т.д. Это может быть причиной их взаимной положительной
или отрицательной корреляции.
С другой стороны, у различных эмитентов существуют
собственные "микроэкономические" факторы, оказывающие
случайные воздействия на курсы и доходность их ценных бу-
маг. Часто именно эти воздействия могут рассматриваться как
некоррелированные случайные величины, и, следовательно,
диверсификация портфеля ценных бумаг может позволить
уменьшить ту составляющую риска портфеля, которая обу-
словлена действием данных факторов. Более полный анализ
риска портфеля приводится в п. 5.4.4.
2) Эффект положительной корреляции доходностей ценных
бумаг.
Рассмотрим теперь случаи, когда доходности активов яв-
ляются зависимыми случайными величинами.
Предположим вначале, что доходности различных ценных
бумаг, включаемых в портфель, связаны прямой линейной за-
висимостью, т.е.
Pij=\, %', i,y=l, 2, ..., N
Тогда при тех же предположениях относительно структуры
портфеля его ожидаемая доходность определяется соотноше-
нием (5.10), дисперсия доходности портфеля равна
* Ш •
а риск портфеля при 7V-»oo стремится к некоторой константе
d, равной среднеарифметическому значению рисков ценных
бумаг:
<Ъ = oAN)= —Yai->d>0.
Следовательно, в случае положительной корреляции до-
ходностей ценных бумаг эффекта диверсификации портфеля
не наблюдается, а происходит лишь усреднение рисков вло-
жений в отдельные активы.
3) Эффект отрицательной корреляции доходностей ценных
бумаг.
В отличие от положительной корреляции отрицательная
корреляция доходностей ценных бумаг приводит к уменьше-
нию риска портфеля. Проиллюстрируем возможность сниже-
213

ния риска портфеля за счет учета отрицательной корреляции
доходностей ценных бумаг.
Для простоты рассмотрим портфель из двух ценных бумаг,
доходности которых связаны обратной линейной зависимо-
стью. Следуя ранее установленной связи между ожидаемой
доходностью и риском финансовых инвестиций, для опреде-
ленности ПОЛОЖИМ, ЧТО //1>//2>0 И СГ\> <J2>0.
В рассматриваемом случае р\2=Р2\= -1, Р\\=Р22=1 и со~
гласно (5.6):
а/ = х\а\ - 2ххх2аха2 + x\g\ = (х{а{ - х2а2)2,
откуда следует, что в рассматриваемом случае существует
возможность построения портфеля с нулевым риском (безрис-
кового портфеля), для которого <Jp=0.
Для определения структуры безрискового портфеля необ-
ходимо решить систему из двух уравнений:
ap^=\xi(Ti-x2a2\= О, Х\+х2=\ (5.13)
относительно двух неизвестных - х\ и х2.
Искомые значения определяются по формулам
<71 + СГ2 СП + <Т2
При этом ожидаемая доходность портфеля равна
МР= Х\И\ -
<J\ + <Т2
Заметим, однако, что за снижение риска приходится "пла-
тить" и некоторым уменьшением ожидаемой доходности.
Для сравнения рассмотрим альтернативный портфель из
тех же активов, среди которых капитал инвестора распределен
в равных пропорциях, т.е. х\ = х2 = 1/2. Из (5.13) следует, что
риск и ожидаемая доходность данного портфеля будут соот-
ветственно равны:
°р = —(сгх -ст2)> 0, ц* =-{jul+ju2)>0.
Таким образом, ар<ар, однако jll^>jllp. Действительно,
выигрыш в доходности альтернативного портфеля по сравне-
нию с безрисковым портфелем при сделанных предположе-
ниях будет равен:
сп + о-2
214

Величина jl^p-hp тем больше, чем больше разности щ-с
и /*1-/^>0, т.е. чем сильнее различаются по ожидаемой доход-
ности и риску используемые активы.
От примеров, иллюстрирующих возможности управления
ожидаемой доходностью и риском портфеля ценных бумаг за
счет диверсификации и учета корреляции доходностей акти-
вов, перейдем к строгим математическим формулировкам за-
дач оптимизации структуры портфелей и методам их решения.
5.2. ОПТИМИЗАЦИЯ СТРУКТУРЫ
ПОРТФЕЛЯ РИСКОВЫХ ЦЕННЫХ БУМАГ
5.2.1. Модельные предположения и постановка задачи
Пусть инвестор распределяет свой капитал среди N {N>\)
рисковых активов в некоторых пропорциях xj, %2, ..., х& Как
известно, в рамках подхода "доходность - риск", предполага-
ется, что цены {Pit}, а следовательно, и доходности активов
{/?,,} (/=.1, 2, ..., N, /=1, 2, ..., 7) являются случайными вели-
чинами. Из доходностей N активов за один и тот же период t
образуем вектор доходностей Rt= (R\h Rib ..., Rm)t, а из ве-
личин {х/} - вектор, определяющий структуру портфеля
X=(xh х2, ...,хлг)т.
Решение задачи формирования оптимального в смысле
подхода "доходность — риск" портфеля основано на опреде-
ленных модельных предположениях относительно:
• вероятностной модели доходностей (курсов) активов
• рынка и поведения его участников.
1) Предположения относительно вероятностной модели до-
ходностей.
В разд. 3.7 обсуждались традиционные предположения от-
носительно вероятностной модели доходностей в задаче оп-
тимального портфельного инвестирования. Там же отмеча-
лись недостатки этих предположений с точки зрения адекват-
ности соответствующей им модели.
В соответствии с этими предположениями значения векто-
ров доходностей {!?,}, полученные за анализируемый истори-
ческий период, можно рассматривать как случайную выборку
из многомерного нормального распределения, параметрами
которого являются математическое ожидание вектора доход-
ностей активов (т.е. вектор ожидаемых доходностей) ju и ко-
215

вариационная матрица вектора доходностей активов 2. Это
позволяет не учитывать автокорреляцию значений доходно-
стей и считать ожидаемые доходности активов, дисперсии и
ковариации (ковариационную матрицу) доходностей активов
постоянными во времени, т.е. полагать, что V /=1, 2, ...:
(/,7=1,2, ..., N).
В качестве статистических оценок параметров //иЕ при
этом теоретически могут использоваться выборочное среднее
значение // и выборочная ковариационная матрица Е вида
(3.29). На практике, однако, как это будет показано в
разд. 5.4, для оценивания неизвестных параметров приходит-
ся использовать различные "факторные" модели.
Найденные оценки ju, S рассматриваются как прогноз-
ные значения соответствующих характеристик в будущем пе-
риоде владения и используются вместо неизвестных истин-
ных значений параметров в алгоритмах оптимизации структу-
ры портфеля ценных бумаг для одного будущего периода
владения, т.е. решаются однопериодные задачи оптимизации
структуры портфеля активов для каждого периода владения
независимо от других периодов1.
2) Предположения относительно рынка и поведения его уча-
стников.
Данные предположения состоят в следующем:
МЛ. Инвесторы осуществляют оценку портфелей, основы-
ваясь на ожидаемой доходности и риске активов.
М.2. При выборе из двух идентичных во всем, кроме ожи-
даемой доходности, портфелей инвестор отдает предпочтение
портфелю с большей ожидаемой доходностью.
М.З. При выборе из двух идентичных во всем, кроме рис-
ка, портфелей инвестор отдает предпочтение портфелю с
меньшим риском.
М.4. Характеристики активов и портфелей относятся к од-
ному заданному периоду владения.
М.5. Активы являются бесконечно делимыми, т.е. в каждый
актив может быть вложена любая доля капитала инвестора.
М.6. Отсутствуют какие-либо технические препятствия в
реализации оптимальных инвестиционных стратегий; относи-
1 Вопросы практической реализации подобных схем подробнее рассмат-
риваются в разд. 6.4 при обсуждении проблемы тестирования моделей равно-
весия фондового рынка.
216

тельно любого актива возможна операция "короткая прода-
жа"; налоги и издержки, связанные с покупкой и продажей
активов, не принимаются во внимание.
При выполнении свойства М.6 рынок часто называется
полным рынком (complete market) [45].
Предположения М.1-М.З выражают предпочтения инве-
сторов в рамках подхода "доходность - риск". Предположе-
ние М.4 говорит о том, что рассматривается однопериодная
задача оптимизации. Предположения М.5-М.6 носят техни-
ческий характер и вводятся для упрощения аналитического
решения задачи.
3) Постановка задачи оптимизации структуры портфеля.
Пусть инвестор формирует свой портфель сроком на один
период владения из N (N>\) различных рисковых ценных бу-
маг. Прогнозные значения вектора ожидаемых доходностей
активов и ковариационной матрицы доходностей активов для
рассматриваемого периода равны м=(мд и £=£т=:{сг(/}
(<j/=cr^>0). Будем полагать, что |l|*0, т.е. ковариационная
матрица £ является невырожденной (положительно опреде-
ленной как ковариационная матрица). Приемлемая для инве-
стора доходность портфеля ценных бумаг равна /лр.
Задача заключается в определении такой структуры порт-
феля Х=(х,*) (/=1, 2, ..., TV), которая обеспечила бы достиже-
ние заданной доходности портфеля jup с минимальным рис-
ком. Математическая формулировка данной задачи с учетом
(5.2), (5.8) имеет вид:
а] = *TZ.Y-> min, (5Л4)
^ = ///,, (5.15)
ХТ1 = 1. (5.16)
Соотношения (5.14)—(5.16) представляют собой формали-
зованное описание задачи определения оптимального в смыс-
ле подхода "доходность — риск" портфеля рисковых ценных
бумаг, которая известна как задача МарковицаК
Вектор X*, являющийся решением задачи Марковица, оп-
ределяет структуру оптимального в смысле подхода 'доход-
ность — риск" портфеля среди всех возможных портфелей с
ожидаемой доходностью /лр. Заметим, что в рассматриваемом
1 Приведенная математическая формализация задачи принадлежит Дж.
Тоби ну.
217

случае компоненты вектора Л*=(х/*) могут принимать отрица-
тельные значения, что означает рекомендацию инвестору со-
вершить относительно соответствующих активов операцию
"короткая продажа" (п. 1.5.2).
Множество возможных или достижимых портфелей (feasi-
ble set) в данном случае - это множество всех портфелей, ко-
торые можно образовать из N рассматриваемых ценных бумаг
при возможности использования операции "короткая продажа ".
5.2.2. Решение задачи оптимизации структуры портфеля
В математическом плане задача (5.14)—(5Л6) - это задача
минимизации непрерывной функции с двумя ограничениями
в виде равенств и поэтому может быть решена аналитически с
помощью метода неопределенных множителей Лагранжа.
Опишем кратко схему решения задачи. Функционал Ла-
гранжа с учетом (5.14)—(5.16) имеет вид:
Р (5.17)
где Aq, X\ - неопределенные множители Лагранжа.
Дифференцируя А по X и приравнивая к нулю вектор про-
изводных, получаем:
2LX- Aqju- Я{1= О,
откуда с учетом невырожденности матрицы Е следует:
х= 4^l-V/+ y*Ai' (5Л8)
Подставляя (5.18) в (5.15), (5.16), получаем представления
для До, Х\% Используя эти представления в (5.18), находим ре-
шение задачи в виде:
Х = Ь + сМр, (5.19)
где Ь, с - векторы размерности N9 имеющие вид:
* =
(^() п&м)), (5.20)
а
с =±(дп(1-^) - ап(Ъ-Ч))9 (5.21)
а
и использованы обозначения:
218

ап = Z1!"1//, ап = Z1!"1/ , я22 = /лтЪ'х/л, d = ana22 - л?2.
При невозможности операции "короткая продажа" необхо-
димо наложить дополнительное ограничение на структуру
портфеля вида:
х£0, /=1, 2, ...,N. (5.22)
Получаемая при этом задача оптимизации структуры
портфеля (5.14)—(5.16), (5.22) относится к задачам квадратич-
ного программирования, для решения которой используются
приближенные численные методы [6].
Портфель ценных бумаг со структурой, определяемой по
формуле (5.19), будем называть оптимальным по Марковицу.
Оптимальному по Марковицу портфелю ценных бумаг со-
ответствует минимальная дисперсия доходности портфеля,
определяемая по формуле
J (5.23)
5.2.3. Свойства эффективных портфелей
Портфели, оптимальные в смысле задачи Марковича, на-
зываются эффективными портфелями (efficient portfolios) рис-
ковых ценных бумаг или оптимальными по Марковицу порт-
фелями.
Осуществим качественный анализ решения задачи Марко-
вица и сформулируем некоторые свойства оптимальных
портфелей.
1. Согласно (5.19) с увеличением ожидаемой доходности
портфеля вклады {*/*} в ценные бумаги при возможности опе-
рации "короткая продажа" изменяются линейно: увеличива-
ются для более доходных и уменьшаются для менее доходных
активов. Известно (см., например, [20]), что при невозможно-
сти операции "короткая продажа" имеет место кусочно-
линейное изменение {*/*}.
2. Из (5.23) следует, что риск оптимального портфеля воз-
растает вместе с ростом ожидаемой доходности. При возмож-
ности операции "короткая продажа" достижима сколь угодно
высокая доходность при соответственно растущем риске. При
невозможности данной операции максимальной доходностью
обладает портфель, образованный из актива (активов) с мак-
симальной ожидаемой доходностью (на рис. 5.3 такому порт-
фелю соответствует точка А и доходность jumox).
219

Таким образом, из (5.23) следует, что функция сгр=ЛМр)>
описывающая зависимость между риском и доходностью оп-
тимальных портфелей, является вогнутой и имеет положи-
тельный наклон (см. рис. 5.3). Причем если fi(jip)9 А(Мр) ~
функции, соответствующие предположениям о возможности
и невозможности операции "короткая продажа", то имеет ме-
сто соотношение f\(jup)>f2(jup) \//ир. Это означает, что при ис-
пользовании операции "короткая продажа" всегда можно по-
строить более эффективный портфель за счет решения задачи
оптимизации на более широком множестве портфелей. Ил-
люстрацией данному свойству служит рис. 5.3.
Рис. 5.3. Графики зависимости риска эффективного портфеля
от его ожидаемой доходности при возможности (2) и
невозможности (1) операции "короткая продажа"
В теории портфельного инвестирования зависимость меж-
ду риском и доходностью оптимальных портфелей обычно
анализируется в системе координат "доходность - риск",
причем по оси абсцисс откладываются значения риска, а по
оси ординат - значения ожидаемой доходности портфеля.
Поэтому далее будем использовать именно такое расположе-
ние координат.
3. Эффективный портфель рисковых ценных бумаг с ха-
рактеристиками:
an
,, = Я12
аи
г2 =
1
(5.24)
(5.25)
(5.26)
220

будем называть "глобальным" эффективным портфелем (global
mean-variance portfolio [37] ), на рис. 5.4 ему соответствует
точка G.
Рис. 5.4. Фронт эффективных портфелей:
А, С - эффективные портфели; G - "глобальный" эффективный портфель;
В - неэффективный портфель
4. Эффективные портфели обладают двумя свойствами оп-
тимальности:
1) имеют максимальную доходность среди всех достижи-
мых портфелей с одинаковым риском (например, если А -
эффективный портфель с характеристиками //Л,<тЛ, то для лю-
бого достижимого портфеля с характеристиками /лр, ар. ца>/лр
ПрИ СТр^СТа);
2) имеют минимальный риск среди всех достижимых
портфелей с одинаковой доходностью (если С - эффективный
портфель с характеристиками //с,<тс, то для любого достижи-
мого портфеля с характеристиками /ир, ар: ар>ас при ^ip=juc).
Справедливы также следующие два свойства ковариаций
доходностей портфелей активов [37]:
5. Ковариация доходностей Ro, Rc двух эффективных порт-
фелей Аи С с ожидаемыми доходностями jua и /лс равна:
Rc) =^(ма~ Щис - 42-1 + —
d а К а) а
а\\
а\\)
(5.27)
6. Ковариация доходности глобального эффективного
портфеля Rg с доходностью любого другого портфеля или ак-
тива Ra равна:
Co\(Ro,Rg)= —.
221

Множество всех эффективных портфелей с характеристи-
ками jup,<jp в системе координат "доходность - риск" описы-
вается кривой, известной как фронт эффективных портфелей
(efficient frontier), ограничивающей множество всех портфе-
лей, достижимых на множестве из N ценных бумаг с характе-
ристиками ju, E (feasible set).
На рис 5.4 фронту эффективных портфелей соответствует
отрезок кривой от точки G (включая "глобальный" портфель
G) до точки А и выше. Портфели, лежащие на отрезке кривой
от точки G до точки В и ниже, не являются эффективными.
Портфели, лежащие в заштрихованной области, ограничен-
ной кривой (включая саму кривую), образуют множество
достижимых портфелей (feasible set).
Таким образом, в результате решения задачи Марковича
инвестор получает не один, а бесконечное множество эффек-
тивных портфелей. Индивидуальные предпочтения инвестора
при выборе единственного оптимального в смысле подхода
"доходность — риск" портфеля могут быть учтены с исполь-
зованием кривых безразличия данного инвестора. Проиллю-
стрируем этот выбор на примере.
Пусть приемлемые для инвестора портфели, соответст-
вующие различным уровням его притязаний, описываются
кривыми безразличия /j, /2, /3 (рис. 5.5)
Рис. 5.5. Выбор оптимального портфеля с учетом
предпочтений инвестора, задаваемых кривыми безразличия
Фронту эффективных портфелей соответствует кривая
G-A. Очевидно, портфели, принадлежащие кривой безразли-
чия 1\9 недостижимы. Среди достижимых и приемлемых для
инвестора портфелей эффективными являются портфели А, С
и D. Но более эффективным среди них является портфель С,
поскольку он лежит на кривой безразличия /2, что выше и
левее кривой /3.
222

Таким образом, оптимальным для конкретного инвестора
является портфель С, соответствующий точке касания фронта
эффективных портфелей и кривой безразличия данного инве-
стора.
Подход Г. Марковица, ядром которого является идея ди-
версификации вложений, можно рассматривать как теорию
портфельного инвестирования в ее микроэкономическом ас-
пекте, поскольку основным объектом исследования в рамках
данной теории является портфель инвестора, формируемый
им на основе индивидуальных представлений относительно
ожидаемой доходности и риска ценных бумаг.
5.3, ФОРМИРОВАНИЕ ПОРТФЕЛЕЙ АКТИВОВ
ПРИ ВОЗМОЖНОСТИ БЕЗРИСКОВОГО
КРЕДИТОВАНИЯ И ЗАИМСТВОВАНИЯ
Значимость идеи диверсификации еще больше усилилась
после появления работ Дж. Тобина, исследовавшего проблему
диверсификации с позиций макроэкономического анализа.
Его интересовали вопросы, связанные с распределением со-
вокупного капитала в экономике между двумя типами акти-
вов: ценными бумагами и наличными деньгами в виде бан-
ковских вкладов и кредитов. В частности, исследовались
факторы, побуждающие инвесторов формировать портфели,
включающие оба типа активов, а не вкладывать весь капитал
в активы одного типа. Основное качественное отличие этих
двух типов активов состояло в предположении того, что акти-
вы типа банковских вкладов и кредитов являются безриско-
выми (riskfree assets).
Определим вначале понятие "безрисковый актив", а затем
рассмотрим варианты его использования при формировании
портфелей ценных бумаг с заданными свойствами.
5.3.1. Понятие безрискового актива
Так как в рамках подхода Марковица рассматриваются ин-
вестиции на один период владения, то безрисковым может
считаться актив, доход по которому за данный период являет-
ся фиксированным. Это означает, что в момент покупки дан-
ного актива в начале рассматриваемого периода владения ин-
вестору точно известна его стоимость в конце этого периода.
Поскольку доходность такого актива за период владения,
определяемая простой ставкой /?о, является фиксированной,
223

то риск актива сто, определяемый как среднеквадратическое
отклонение доходности, будет равен нулю.
Для выполнения этих условий необходимо, чтобы вложе-
ния в безрисковый актив были свободны от таких рисков,
как:
• риск невыполнения обязательств (default risk);
• процентный риск (interest rate risk);
• риск реинвестирования (reinvestment-rate risk).
Среди множества активов, имеющихся на фондовом рын-
ке, первым из указанных свойств заведомо не обладают част-
ные (корпоративные) ценные бумаги, для которых риск не-
выполнения обязательств со стороны эмитента всегда имеет-
ся.
Таким образом, потенциальным множеством активов, на
котором следует искать безрисковый актив, является множест-
во государственных ценных бумаг, риск невыполнения обяза-
тельств по которым считается равным нулю.
Однако вложения в государственные ценные бумаги не
всегда свободны от двух других типов риска. Так, если срок
вложений денежных средств в некоторую государственную
ценную бумагу, т.е. период владения, оказывается меньше
срока, оставшегося до ее погашения, то имеет место процент-
ный риск. Если же период владения больше срока до погаше-
ния ценной бумаги, то возникает риск реинвестирования.
И тот и другой риск обусловлен неопределенностью отно-
сительно процентных ставок на финансовом рынке. В первом
случае непредсказуемое изменение процентных ставок, кото-
рое может произойти за период владения ценной бумагой,
порождает неопределенность ее рыночной стоимости в конце
периода владения (см. п. 4.4.1). Во втором случае точно неиз-
вестны ставки, по которым инвестор сможет реинвестировать
свой доход по ценной бумаге по окончании срока ее обраще-
ния (см. п. 2.5.4, 2.5.5).
Безрисковым активом, таким образом, может считаться го-
сударственная ценная бумага, срок до погашения которой
совпадает с периодом владения. Ставка процентов, опреде-
ляющая доходность безрискового актива, называется безрис-
ковой ставкой процентов (riskfree interest rate).
Заметим, что данное определение не учитывает риска из-
менения покупательной способности денег, т.е. инфляционного
риска. Этот тип риска при невысоких темпах роста инфляции
может быть ограничен выбором коротких периодов владения
либо использованием соответствующим образом индексируе-
мых государственных ценных бумаг.
224

Инвестирование в безрисковый актив называют безриско-
вым кредитованием (riskfree lending), поскольку покупку госу-
дарственных ценных бумаг можно рассматривать как предос-
тавление кредита правительству.
Если инвестор не ограничивается собственным капиталом
для покупки рисковых ценных бумаг, а имеет возможность
взять кредит под безрисковую ставку, то это называют безрис-
ковым заимствованием (riskfree borrowing). При этом часто
предполагается, что процентная ставка по займу равна ставке
доходности вложений в безрисковые активы.
На практике, однако, может не существовать актива, кото-
рый можно было бы рассматривать как безрисковый. В этих
случаях актуальным является использование в качестве такого
актива специальным образом построенного безрискового
портфеля. Подробно эта проблема обсуждается в разд. 6.2.
В рамках подхода Дж. Тобина задача оптимизации струк-
туры портфеля активов рассматривается при дополнительном
предположении о возможности совершения операций креди-
тования (lending) и заимствования (borrowing) по единой без-
рисковой ставке (riskfree rate). В связи с решением задачи оп-
тимизации портфеля в новых условиях представляют интерес
ответы на следующие вопросы:
• как новые возможности диверсификации портфеля отра-
жаются на его характеристиках, например на ожидаемой
доходности и риске?
• какой должна быть структура рисковой части портфеля,
включающего рисковые и безрисковый активы?
• в каких пропорциях следует распределять капитал между
рисковой и безрисковой частями портфеля?
Этим вопросам посвящены следующие пункты данного
раздела.
5.3.2. Характеристики и свойства
комбинированного портфеля
Пусть инвестор формирует свой портфель как комбинацию
из безрискового актива и заданного портфеля активов, вклю-
чающего только рисковые ценные бумаги. Для краткости бу-
дем называть подобные портфели комбинированными портфе-
лями. Получим представления для характеристик комбиниро-
ванного портфеля и отметим его свойства.
Обозначим:
Rq - ставка доходности безрискового актива за один пери-
од владения, или безрисковая ставка;
15 3ак.7О84 225

До - доля безрисковых вложений (xq<\) и соответственно
1-xq - доля рисковых вложений инвестора;
Rr, jur, ar2 и ay. - характеристики рисковой части портфеля
инвестора, относящиеся к одному периоду владения, соответ-
ственно: доходность, ожидаемая доходность, дисперсия до-
ходности и риск, удовлетворяющие в рамках подхода "доход-
ность - риск" условиям:
//г>Ло, о>>0. (5.28)
Величина 1—xq характеризует отношение инвестора к рис-
ку: чем больше значение 1— xq, тем больше доля рисковых
вложений, а значит, больше склонность инвестора к риску.
Из ограничения xq<\ следует возможность для инвестора
двух противоположных операций с нулевым риском:
• операции кредитования под безрисковую ставку Rq (напри-
мер, вложения на банковский счет, покупка государст-
венных краткосрочных ценных бумаг), при этом О<хо<1;
• операции заимствования по безрисковой ставке Ro, в
этом случае xq<0.
Вопросы о существовании безрисковой ставки, а также
возможности кредитования и заимствования по одной и той
же ставке Rq обсуждаются в разд. 6.2. Там же описываются
способы преодоления этих жестких ограничений.
1) Характеристики комбинированного портфеля.
Приведем характеристики комбинированного портфеля,
относящиеся к одному периоду владения, и формулы их оп-
ределения:
• доходность портфеля
Rp=xoRo + (l-XQ)Rr; (5.29)
• ожидаемая доходность портфеля
• дисперсия доходности портфеля
cr/=n(Rp) = (\-x0)W; (5.31)
• риск портфеля
ар = (1-хь)<тг . (5.32)
Вначале выполним качественный анализ характеристик
портфеля и установим некоторые его свойства. Из (5.30) сле-
дует:
226

Mp-Ro=(l-x0)(Mr-Ro), (5.33)
где /лр-RQ, Mr~Ro - дополнительная доходность (excess or ab-
normal return), т.е. превышение доходности рисковых
вложений над доходностью безрискового актива, извест-
ная также как премия за риск (risk premium).
Имеют место следующие свойства портфеля.
1. Согласно (5.33) премия за риск портфеля активов прямо
пропорциональна премии за риск рисковой части портфеля и
тем больше, чем больше доля рисковых вложений. Другими
словами, инвестируя определенную часть своего капитала в
рисковые активы, инвестор надеется получить компенсацию
за риск в виде дополнительной доходности.
2. Из (5.33) следует, что если инвестор владеет портфелем
рисковых активов {рисковым портфелем) с характеристиками
jun <jr и желает уменьшить риск вложений до некоторой
величины ар<ап то он должен вложить в безрисковый актив
долю своего капитала, равную
*Ь= 1 - ^. (5.34)
С учетом (5.34) из (5.33) получаем:
М,= *0+!*^*,. (5.35)
Or
3. Из (5.35) следует, что ожидаемая доходность jup и риск
портфеля <jp, полученного путем распределения капитала ме-
жду безрисковым активом и заданным рисковым портфелем,
связаны прямой линейной зависимостью: чем больше риск
вложений, тем большую компенсацию в доходности надеется
получить инвестор.
Инвестор, распределяющий свой капитал между заданным
портфелем рисковых активов и безрисковым активом, может
выбрать одну из следующих стратегий инвестирования (на
рис. 5.6 отмечены портфели активов, соответствующие раз-
личным стратегиям):
1) инвестировать весь свой капитал в рисковый портфель,
не прибегая ни к кредитованию, ни к заимствованию по без-
рисковой ставке, при этом xq~0 (портфель С с характеристи-
ками juc=jur, (Jc=ar);
2) инвестировать часть капитала в рисковый портфель, а
остаток вложить под безрисковую ставку, в этом случае
0<xq<1 (портфель В с характеристиками Ro<jub<jun 0<о^< ог);
227

3) вложить весь свой капитал в безрисковый актив, при
этом xq-1 (безрисковый портфель А с доходностью Rq);
4) инвестировать весь свой капитал плюс дополнительные
средства, заимствованные под безрисковую ставку, в риско-
вый портфель, при этом jcq<0, а заемные средства составляют
долю \xq\ от первоначального капитала инвестора (портфель
D с характеристиками //</>//г,
Ир
Иг
(
" /
Cl
ar Gpr
Рис. 5.6. Множество всех возможных комбинированных портфелей
Всем перечисленным выше портфелям соответствуют точ-
ки, лежащие на одной прямой линии, соответствующей мно-
жеству всех возможных при данных условиях портфелей.
Уравнение этой прямой имеет вид (5.35).
5.33. Оптимизация структуры портфеля при возможности
безрискового кредитования и заимствования
Пусть наряду с модельными предположениями М.1-М.6
из п. 5.2.1 выполняется следующее условие:
М.7. Существует безрисковая ставка Rq, по которой инве-
сторы могут кредитовать и заимствовать произвольную сумму
денег.
Будем полагать, что инвесторы формируют свои портфели
сроком на один период владения на множестве активов,
включающем TV рисковых ценных бумаг и один безрисковый
актив, одновременно решая задачу оптимального распределе-
ния капитала между рисковыми ценными бумагами.
Прогнозные значения вектора ожидаемых доходностей ак-
тивов и ковариационной матрицы доходностей активов для
рассматриваемого периода равны: м=(мд и s==2T={cr//'}
(оу/ест^Х)), причем матрица I является положительно опреде-
ленной.
228

Структура комбинированного портфеля инвестора задается
величинами xq, х\, х^ ..., *м которые удовлетворяют условию:
Xq -r X{ + X2 -Г...+ Xjy = JCq "
где Лг=(хь Х2, ..., x//)T - вектор, определяющий структуру рис-
ковой части портфеля, а ^=1-^/ и X-xq=zXt1 - соответст-
венно доли безрисковых и рисковых вложений инвестора.
Поскольку доходность безрискового актива — величина
фиксированная (неслучайная), то ее дисперсия, а также кова-
риация с доходностями других активов равна нулю. Поэтому
дисперсия доходности комбинированного портфеля активов
обусловлена только присутствием в портфеле рисковых акти-
вов и определяется, как и ранее, по формуле
а/ = Х^ЪХ (5.36)
Если заданы значения безрисковой ставки Rq и ожидаемой
(приемлемой для инвестора) доходности портфеля jup, то
структура оптимального в смысле подхода "доходность —
риск" портфеля будет являться решением следующей задачи,
известной как задача Тобина:
а] = ХТ1Х -► min, (5.37)
■■ftp- (5-38)
Данная задача, как и задача Марковица, допускает анали-
тическое решение с помощью метода неопределенных мно-
жителей Лагранжа. Функционал Лагранжа при этом имеет
вид:
Л(Х,Л) = Х^Х + Я(Мр - Хтм -(1 - ХТ1) Rq), (5.39)
где Я - неопределенный множитель Лагранжа.
Дифференцируя Л по X и приравнивая к нулю вектор про-
изводных, получаем:
2ЪХ- Mji-RqI) = 0,
откуда с учетом (5.38) следует:
(5.40)
где
229

Оптимальному портфелю со структурой (5.40) соответству-
ет минимальный риск, который с учетом (5.36) равен:
откуда следует, что характеристика gp допускает представле-
ние:
gp={Mp-Ro)/<r*p>0, (5.42)
т.е. равна величине ожидаемой дополнительной доходности
(премии за риск), приходящейся на единицу риска, и может
интерпретироваться как цена единицы риска на рассматривае-
мом множестве (рынке) рисковых ценных бумаг.
Представим (5.42) в виде:
JUp-Ro = gp€T*p.
Отсюда следует, что, чем выше цена риска gp, тем больше
ожидаемая премия за риск, т.е. тем выгоднее вложения в
данный портфель.
Характеристика gj = (ju^ - /?о)/а</>О известна как отношение
Шарпа (Sharpe ratio), или индекс Шарпа, и используется для
оценки привлекательности произвольного рискового актива
или портфеля D с характеристиками //</,а</. Очевидно, данная
характеристика принимает максимальное значение для эф-
фективных портфелей, т.е. gd<gp, где gp определяется соотно-
шением (5.42).
5.3.4. Свойства оптимальных комбинированных портфелей
Выражение (5.40) допускает представление:
Г=с(Мр)¥, (5.43)
где
с{/лр)=—£-5 , (5.44)
У=Е"1(//-ад, (5.45)
где c(jup) - скалярный множитель, зависящий от ожидаемой
доходности портфеля jup; Y - TV-вектор, определяющий с
точностью до множителя с(/лр) структуру оптимального
рискового портфеля, не зависящий ни от ожидаемой до-
230

ходности портфеля jup, ни от склонности инвестора к рис-
ку, определяемой величиной xq.
Таким образом, пропорции распределения рисковых вло-
жений, составляющих долю Х^1 капитала инвестора, опреде-
ляются вектором У вида (5.45) и не зависят от ожидаемой до-
ходности портфеля и склонности инвестора к риску.
Отсюда получаем следующие свойства оптимальных ком-
бинированных портфелей. (Геометрическая интерпретация
решения задачи Тобина приведена на рис. 5.7.)
Рис. 5.7. Множество оптимальных комбинированных портфелей
1. Все оптимальные портфели, включающие безрисковый
и рисковые активы, независимо от склонности инвестора к
риску и ожидаемой доходности портфеля имеют с точностью
до постоянного множителя одинаковую структуру рисковой
части. Они получаются в результате распределения капитала в
пропорциях xq и \-xq между безрисковым активом и одним и
тем же рисковым портфелем, структура которого пропорцио-
нальна вектору Y.
2. Данный рисковый портфель можно рассматривать как
частный случай оптимального комбинированного портфеля
при хо=:О, т.е. при отсутствии безрисковых вложений. В этом
случае весь капитал распределяется между рисковыми цен-
ными бумагами в пропорциях, определяемых вектором:
(546)
3. Ожидаемая доходность и риск оптимального комбини-
рованного портфеля при яо=О определяются соотношениями:
__i__
(54у)
231

4. С учетом (5.35) множеству всех оптимальных (эффек-
тивных) портфелей, включающих безрисковый и рисковые
активы, в системе координат "доходность — риск" соответст-
вует прямая линия.
Уравнение данной прямой имеет вид:
Mp=Ro+ t±zJka (549)
где jun or определяются по формулам (5.47), (5.48).
5. Оптимальный портфель с характеристиками junar вида
(5.47), (5.48) включает только рисковые активы и поэтому
принадлежит множеству оптимальных по Марковицу портфе-
лей, т.е. точка с координатами (junar) должна быть общей как
для множества оптимальных комбинированных портфелей,
так и для фронта эффективных рисковых портфелей (efficient
frontier). Поскольку структура данного портфеля определяется
единственным образом, то данному портфелю соответствует
точка касания этих двух линий.
Портфель в точке касания линий (Tangency portfolio)
обычно называется Т-портфелем (T-portfolio). Его характери-
стики {jut.cjt) определяются соотношениями: juf=/un crf=(Tr.
Перечисленные свойства оптимальных портфелей в усло-
виях задачи Тобина позволяют сделать следующий основной
вывод.
Если инвестор формирует свой портфель как комбинацию
вложений в безрисковый актив с заданной доходностью Rq и
портфель, включающий рисковые ценные бумаги, и при этом
стремится оптимизировать структуру рискового портфеля, то
существует единственная оптимальная структура рисковой
части портфеля. Эта структура определяется вектором X вида
(5.46) и не зависит ни от ожидаемой доходности портфеля jup,
ни от склонности инвестора к риску, определяемой xq.
5.4. ПРОБЛЕМА ОЦЕНИВАНИЯ
ХАРАКТЕРИСТИК ЦЕННЫХ БУМАГ
В рамках рассмотренных выше классических постановок
задач Марковица — Тобина предполагается, что инвесторы
формируют оптимальные в смысле подхода "доходность -
риск" портфели ценных бумаг сроком на один период владе-
ния, исходя из прогнозных значений ожидаемых доходностей
232

//=(///)eWN и ковариационной матрицы доходностей Е={сг^-}
(or/pa}-2) на рассматриваемый период инвестирования. Про-
гнозные значения данных характеристик строятся на основе
имеющихся "исторических" значений доходностей активов
{Rit} (/=1, 2, ..., N9 /=1, 2, ..., 7) за предшествующие периоды
времени. При этом предполагается, что параметры //, I оста-
ются постоянными в течение всего анализируемого периода.
В качестве искомых прогнозных значений параметров /у, S
естественным предполагается использование их выборочных
оценок вида (3.29). Однако на практике такой подход, как
правило, неприменим вследствие недостаточного объема дан-
ных для оценивания всех неизвестных параметров. Проиллю-
стрируем эту проблему на примере.
Число оцениваемых параметров т с учетом симметрично-
сти матрицы £ равно 7V(7V+3)/2 и включает N компонентов
вектора // плюс (№-N)/2+N=N(N+l)/2 независимых элемен-
тов матрицы I. Объем выборки М равен NT. Для корректно-
сти задачи статистического оценивания параметров необхо-
димо, чтобы объем выборки был больше числа оцениваемых
параметров, т.е. М>т. Поэтому даже при столь жестких пред-
положениях относительно модели поведения доходностей
формулы (3.29) неприменимы, если число N совместно ана-
лизируемых активов велико, а объем данных, определяемый
величиной Т, относительно мал (т.е. когда Г<(ЛН-3)/2).
Пусть, например, портфель формируется на множестве ак-
ций, котируемых на NYSE (New York Stock Exchange), а для
оценивания параметров используются квартальные данные за
25 лет наблюдений. Тогда следует положить: N«3000 (что
примерно соответствует числу акций, зарегистрированных на
NYSE) и Г=100. Это означает, что т*Ъ • 106, а М=Ъ • 105 и, та-
ким образом, число неизвестных параметров на порядок
больше количества имеющихся наблюдений, т.е. задача стати-
стического оценивания параметров является неразрешимой.
При более реалистичных предположениях относительно мо-
дели доходностей, учитывающих временную корреляцию и
нестационарность временных рядов {/?,,}, данная проблема
становится вовсе неразрешимой в рамках рассматриваемого
подхода.
Для преодоления указанных трудностей используются эко-
нометрические факторные модели (factor models) регрессион-
ного типа, описывающие зависимости цен и доходностей ак-
тивов от экзогенных переменных (факторов). В качестве фак-
торов в подобных моделях используются макроэкономические
показатели и финансовые индексы, оказывающие значимое
влияние на курсы (доходности) всех ценных бумаг. Использо-
233

вание эконометрических моделей зависимостей позволяет
существенно сократить число оцениваемых параметров. Ис-
торический интерес представляет первая попытка использо-
вания подобных моделей, предпринятая У. Шарпом в
1963 г.1, приведшая к разработке так называемой однофак-
торной рыночной модели Шарпа.
Приведем описание данной модели и проиллюстрируем на
ее примере возможность вычисления необходимых характери-
стик активов.
5.4.1. Построение однофакторной рыночной модели
Предположим, что для актива / его доходность Rit за пери-
од t (например, месяц, квартал и т.д.) связана с доходностью
так называемого индексного, или эталонного, портфеля (index
portfolio) Rjt за тот же период моделью простой линейной
регрессии вида (см. разд. 3.5):
Rit = a/+ ptRlt+ &ь 0'=1, 2, ..., TV, t=l, 2, ..., 7), (5.50)
где {а/, Д} - параметры модели: щ - свободный член, /% - ко-
эффициент регрессии.
Относительно случайных отклонений {£#} доходностей ак-
тивов от ожидаемых в соответствии с моделью значений вы-
полняются традиционные предположения:
1. Симметричность: Е(&)=0.
2. Взаимная некоррелируемость для различных активов и
различных моментов времени: Соу(£//,ф>)=Е(£//ф>)=^-=0 для
fet/, tez(t,r=l, 2, ..., Г, /, у'=1, 2, ..., N), что означает отсутствие
перекрестных связей и временной корреляции случайных от-
клонений.
3. Постоянство дисперсий: D(^,y)=^=coaw/ для всех
Г=1,2, ..., Т.
4. Взаимная некоррелируемость £# и Rjt: Со\(& Rjt)=0
(/=1, 2, ..., N, /=1, 2, ..., 7).
Данная модель, названная У. Шарпом рыночной моделью
(market model), не имеет строгого экономического обоснова-
ния и поэтому не требует каких-либо дополнительных пред-
положений относительно рынка и поведения его участников.
В качестве доходности индексного портфеля, называемой
также доходностью на рыночный индекс Rjh может использо-
ваться темп прироста некоторого рыночного (фондового) ин-
декса.
1 См.: Sharpe W. F. A Simplified Model for Portfolio Analysis // Management
Science. 1963. V. 9. № 2 (January). P. 277-293.
234

Известно, что многие инвестиционные фонды (mutual
funds) формируют свои портфели из списка ценных бумаг, на
основе которого рассчитываются некоторые известные фон-
довые индексы. Например, портфель образованного в 1976 г.
фонда "The Vanguard Index Trust-500 Portfolio" включает ак-
ции, курсы которых учитываются при расчете индекса S&P
500. Другие примеры подобных фондов можно найти в [34]. В
таких случаях в качестве доходности индексного портфеля в
рамках рыночной модели может использоваться доходность
реально существующего индексного портфеля конкретного
инвестиционного фонда.
Следует также отметить, что в рассматриваемой модели
могут использоваться и другие экономические и финансовые
индексы, например темпы прироста макроэкономических по-
казателей. Необходимым условием при этом является адек-
ватность регрессионной модели (см. разд. 3.5) и возможность
корректной экономической интерпретации результатов, полу-
чаемых на основе построенной модели.
Опишем метод вычисления искомых характеристик акти-
вов, основанный на использовании рыночной модели (5.50).
Обозначим:
juj, - ожидаемая доходность индексного портфеля;
о2!- дисперсия доходности индексного портфеля.
Предположим, что данные характеристики остаются неиз-
менными в течение анализируемого периода. Тогда с учетом
(5.50), свойств 1-4 случайных величин {£,}, а также свойств
математического ожидания и дисперсии (см. п. 3.2.2) получа-
ем:
S Cov(/?,,, RJt) = E((RU -
Откуда следует представление для коэффициентов регрес-
сии Р(.
Coy{Rit,Rrt)_ ал
й D(RIt) ~ aj2 x'2'•"'"• <5-51>
При сделанных предположениях относительно {£#} оценки
параметров {ah /?/} модели (5.50) по методу наименьших квад-
ратов имеют вид:
fij = Д -Д-Ду, (5.52)
235

т
^{Ru - MiX^n - mi) ~
Д. = id__ = ££. t (5 53)
. т;Л2 ai
где
а оценки параметров a/2, a//, ^2/ вычисляются по формулам:
(5.54)
r4
Анализ адекватности построенной регрессионной модели
осуществляется с помощью описанных в разд. 3.5 методов
статистической проверки гипотез о значимости параметров
{щу Д), а также на основе анализа свойств остатков.
Найденные статистические оценки параметров (при усло-
вии адекватности соответствующей регрессионной модели)
используются далее для вычисления искомых характеристик
ценных бумаг.
5.4.2. Вычисление характеристик ценных бумаг
на основе однофакторной модели
Пусть для модели (5.50) выполняются предположения 1-4
относительно случайных отклонений {&}. Тогда могут быть
получены следующие представления для ожидаемых доходно-
стей {///}, дисперсий доходностей {ay2} и ковариаций доходно-
стей {ay} (ij*j) (i,j=l9 25 ..., N) активов:
//,-= at+fiifi/, (5.56)
а? = fifa) + ¥?, (5.57)
Щ- = PiPja] , H. (5.58)
236

Подставляя в формулы (5.56)—(5.58) вместо неизвестных ис-
тинных значений параметров их оценки вида (5.52)—(5.55),
можно вычислить оценки соответствующих характеристик ак-
тивов //=(///) и £={<т#} (ojpoy2), которые необходимы для реше-
ния задачи оптимизации структуры портфеля ценных бумаг.
Заметим, что при использовании модели (5.50) число ста-
тистически оцениваемых параметров равно n=3N+2 (27V па-
раметров {ah ft} плюс N параметров {щ) плюс juj и &J) при
условии, что объем выборки равен 77V. Напомним, что при
непосредственном оценивании /i, E число оцениваемых пара-
метров равно m=N(N+3)/2, т.е. на порядок больше.
Таким образом, при наличии адекватной факторной эко-
нометрической модели задача статистического оценивания
характеристик активов //, £ становится вполне разрешимой.
На практике, однако, для адекватного описания исследуемых
зависимостей могут понадобиться более сложные экономет-
рические модели, например модели, учитывающие влияние
нескольких факторов (многофакторные модели); модели,
предполагающие совместный анализ доходностей некоторого
множества активов (многомерные модели); модели, учиты-
вающие динамику изменения курсов активов (динамические
модели). Обзор некоторых важных классов таких моделей
приводится в гл. 3 и 7.
Важным представляется класс эконометрических моделей,
имеющих строгое экономическое обоснование и справедли-
вых при некоторых дополнительных ограничениях на условия
функционирования фондового рынка. К числу таких моделей
относятся эконометрические модели на основе моделей рав-
новесия фондового рынка САРМ и APT, рассмотрению кото-
рых посвящена следующая глава.
5.4.3. Бета-коэффициенты рисковых ценных бумаг
Коэффициенты регрессии {/?,-} (/=1, 2, ..., 7V), определяемые
по формуле (5.51), характеризуют чувствительность доходно-
стей активов (акций) к изменению доходности индексного
портфеля. В финансовой литературе их обычно называют бе-
та-коэффициентами активов.
От знака и величины Д- зависят направление и скорость
изменения доходности актива при изменении доходности ин-
дексного портфеля. Если, например, предположить, что слу-
чайные величины Rjt и Rjt положительно коррелируют друг с
другом, то на основании анализа Д можно сделать следующие
выводы:
237

1) если /?/=1, то доходность акции / изменяется (растет или
убывает) с такой же скоростью, с какой изменяется доход-
ность индексного портфеля;
2) если Д>1, то доходность акции изменяется быстрее, а
если Д-<1— медленнее доходности индексного портфеля.
Важную содержательную интерпретацию приобретают ко-
эффициенты {/?,•}, если предположить, что индексный порт-
фель является эффективным портфелем рисковых ценных
бумаг при возможности операций кредитования и заимство-
вания по безрисковой ставке Rq (см. разд. 5.3), т.е. имеет оп-
тимальную структуру, определяемую вектором:
(5.59)
В этом случае доходность и ожидаемая доходность комби-
нированного портфеля вычисляется по формулам
Rp = xoRo + RTr, mp=xoRo+ /ЛГ, (5.60)
где xq - доля безрисковых вложений; RT=(Rj, R2, ..., Rn) ~
вектор доходностей активов; //т=(///, м, ..., mn) ~ вектор
ожидаемых доходностей активов.
Риск портфеля при этом определяется соотношениями (см.
п. 5.3.2):
где
а ковариации доходностей активов с доходностью портфеля
активов равны:
а^ = Соу(Л, , Rp) =Е((Д/ - щ )(R - //)Т)^Г. (5.61)
С учетом приведенных соотношений из (5.61) следует
представление для вектора бета-коэффициентов N рисковых
активов:
/?= (Д) = Д-
G
Р ~ Ro
238

Откуда следует, что бета-коэффициент актива / определя-
ется по формуле
Д= ^<^,/=1,2, ..., Ж (5.62)
MR
Согласно (5.62) для безрискового актива Д=0, для риско-
вого актива /?/ >0, а "бета" портфеля активов равна единице.
Выражение (5.62) эквивалентно выражению:
/4-Ло = #<///> "До), (5.63)
т.е. "бета" актива служит коэффициентом пропорционально-
сти в соотношении, связывающем премию за риск портфеля
рисковых активов и премию за риск отдельного актива из
данного портфеля.
5.4.4. Анализ риска портфеля ценных бумаг
В соответствии с (5.57) дисперсию доходности ценной бу-
маги можно рассматривать как меру общего риска (total risk)
ценной бумаги, состоящего из двух компонентов:
a}=pfa]+¥},Sx+S2, (5-64)
где S\ - систематический, или рыночный, риск (systematic or
market risk), связанный с неопределенностью относитель-
но состояния рынка, определяемого доходностью индекс-
ного портфеля;
^2 - несистематический, или собственный, риск (unsys-
tematic or unique risk), обусловленный действием случай-
ных неконтролируемых факторов, уникальных для каждо-
го актива.
Из (5.64) следует, что чем больше "бета" ценной бумаги,
тем больше ее рыночный риск. Однако, согласно (5.63),
большим значениям "бета" соответствует и большая премия
за риск, т.е. рыночный риск имеет соответствующую компен-
сацию, в то время как собственный риск не имеет подобной
компенсации.
Найдем представление для общего риска портфеля из TV
ценных бумаг, доходности которых описываются рыночной
моделью (5.50), а структура определяется долями {х/}.
Доходность портфеля за рассматриваемый период владения
будет равна:
N
Rpt= ]►>//?/, (5.65)
/=]
239

или с учетом (5.50)
Rpt = ap+fipRIt
(5.66)
где ар9 рр, %р — средневзвешенные значения соответствующих
величин:
N
N
(5.67)
(5.68)
(5.69)
Вычисляя дисперсию случайных величин в обеих частях
соотношения (5.66), находим:
9 Л1 9 9 /С тл\
а2р = fijaj + у/2р , (5.70)
где у/р2==Щ^р), т.е. общий риск портфеля также состоит из
двух компонентов — систематического риска /Зр2ар- и не-
систематического риска у/р2 портфеля ценных бумаг.
Если отклонения фактических доходностей активов от
ожидаемых в соответствии с рыночной моделью объясняются
для каждого актива уникальным набором собственных факто-
ров, то случайные величины {£//} можно считать взаимно не-
коррелированными, т.е. Соу(^у,фу)=0 для гф]. В этом случае
компонент ц/р2 риска портфеля может быть сделан сколь угод-
но малым за счет диверсификации портфеля (см. рис. 5.8).
PPW
V г-
А
Собственный риск
—.
— Рыночный риск
►
Рис. 5.8. Эффект диверсификации портфеля ценных бумаг
240

Действительно, полагая для простоты Xj=l/N, получаем
при N->co
где ч?-тах
На этом основании компонент у/р2 риска портфеля называ-
ется несистематическим риском. Как видно из рис. 5.8, дивер-
сификация портфеля не позволяет исключить систематиче-
ский риск портфеля, равный J3p2o\2. Однако его можно умень-
шить за счет целенаправленного включения в портфель
ценных бумаг с малыми значениями "бета" при соответству-
ющей потере в ожидаемой доходности портфеля.
163ак.7О84

Глава 6
АНАЛИЗ РЫНКА ЦЕННЫХ БУМАГ
НА ОСНОВЕ МОДЕЛЕЙ РАВНОВЕСИЯ
Все модели ложные, но
некоторые из них полезные.
Дж. Бокс
Глава посвящена вопросам моделирования и анализа рынка ценных
бумаг с помощью моделей равновесия фондового рынка. Рассматрива-
ется модель оценки финансовых активов САРМ и модель APT на основе
теории арбитражного оценивания. Описываются модификации модели
САРМ для случаев, когда: невозможна операция "короткая продажа",
отсутствует безрисковый актив, безрисковые ставки кредитования и за-
имствования считаются различными. Приводятся экономическое обос-
нование и интерпретация модели APT, а также обсуждается проблема
практической реализации данной модели. Устанавливается связь между
моделями САРМ и APT. Рассматривается проблема тестирования моде-
лей САРМ и APT с помощью методов статистической проверки гипотез
относительно параметров соответствующих эконометрических пред-
ставлений.
По рассматриваемым в главе вопросам рекомендуется дополни-
тельная литература: [8, 32] (общая характеристика моделей САРМ и APT
с позиций финансовой экономики); [37, 39, 45] (эконометрическое мо-
делирование и анализ фондового рынка на основе моделей равнове-
сия); [1, 2, 9, 12, 36, 41, 43] (методы регрессионного и факторного ана-
лиза) [13, 40, 44, 48] (эконометрическое программное обеспечение).
Из предыдущей главы следует, что одной из ключевых
проблем оптимального портфельного инвестирования являет-
ся построение адекватных эконометрических моделей цен и
доходностей активов. Для этих целей оказываются полезными
модели регрессионного типа, описывающие зависимости ана-
лизируемых показателей от определенных внешних (экзоген-
ных) факторов. Простейшим примером подобных моделей
является описанная выше однофакторная "рыночная" мо-
дель, известная в математической статистике как модель про-
стой линейной регрессии.
Естественным обобщением модели простой линейной рег-
рессии являются модели множественной линейной регрессии,
позволяющие учитывать влияние на цены и доходности акти-
вов одновременно нескольких факторов. Учет перекрестных
242

связей между ценами и доходностями активов, а также вре-
менной корреляции их значений приводит к более сложным,
но и более адекватным реальным процессам моделям много-
мерных временных рядов (см. разд. 3.3).
При построении регрессионных {факторных) моделей1 воз-
никает проблема выбора факторов, оказывающих значимое
влияние на анализируемые показатели. Одним из существен-
ных недостатков многих подобных моделей является то, что
они часто не имеют строгого экономического обоснования. В
то же время пример содержательной экономической интер-
претации бета-коэффициента ценной бумаги на основе тео-
рии оптимального портфельного инвестирования (п. 5.4.3)
свидетельствует о том, что если статистическая модель по-
строена на основе экономической теории, то это позволяет
получить более содержательные качественные выводы и ко-
личественные соотношения. Именно такие модели с полным
правом могут называться эконометрическими.
В теории и практике финансового анализа рынка ценных
бумаг большое распространение получили регрессионные мо-
дели доходностей активов, предполагающие, что рынок того
или иного актива или группы активов находится в состоянии
равновесия. При этом цены активов достигают своих "истин-
ных" значений, уравновешивающих спрос и предложение со-
ответствующих активов. В основе этих моделей лежат эконо-
мические модели равновесия (equilibrium models): модель
оценивания финансовых активов САРМ (Capital Asset Pricing
Model) и АРТ-модель, разработанная в рамках теории арбит-
ражного оценивания (Arbitrage Pricing Theory).
Поскольку модели равновесия справедливы только для
равновесного состояния рынка, то их использованию должна
предшествовать проверка соответствующих условий равнове-
сия рынка.
Таким образом, проверка гипотезы "равновесия рынка",
или, что то же самое, проверка адекватности моделей САРМ
или APT, является необходимым этапом построения соответ-
ствующих регрессионных моделей наряду с оцениванием па-
раметров и проверкой их статистической адекватности.
Настоящая глава посвящена описанию и анализу свойств
моделей равновесия САРМ и APT и их модификаций, а также
проблемам построения и тестирования соответствующих эко-
нометрических представлений.
1 Под "факторными моделями" в финансовой экономике обычно подразу-
меваются "регрессионные модели". Однако не следует отождествлять "факторные
модели" и "модели факторного анализа", являющиеся объектом изучения самос-
тоятельного раздела статистического анализа данных - факторного анализа [9].
243

6.1. МОДЕЛЬ ОЦЕНКИ ФИНАНСОВЫХ АКТИВОВ САРМ
Модель оценки финансовых активов САРМ является наи-
более популярной в финансовой теории моделью равновесия
фондового рынка. Ее можно рассматривать как дальнейшее
развитие основанной на подходе "доходность — риск" теории
оптимального портфельного инвестирования Марковица -
Тобина (Modern Portfolio Theory) в ее макроэкономическом ас-
пекте. Как отмечалось ранее, заслуга в разработке стандарт-
ной версии САРМ принадлежит трем авторам: У. Шарпу,
Дж. Линтнеру и Дж. Моссину.
Несмотря на то что стандартная модель САРМ основыва-
ется на очень строгих модельных предположениях, соответст-
вующая ей регрессионная модель играет важную роль как ос-
новополагающая модель, используемая при разработке мно-
гочисленных модификаций и альтернативных подходов,
применяемых на практике. Всюду далее по умолчанию будет
предполагаться, что речь идет о стандартной модели САРМ.
6.1.1 Модельные предположения и свойства САРМ
1) Модельные предположения.
Поскольку САРМ основывается на теории Марковица —
Тобина, то модельные предположения для этой модели долж-
ны включать предположения М.1-М.7 (см. п. 5.2.1).
Кроме того, вводятся дополнительные предположения от-
носительно использования участниками рынка доступной и
относящейся к делу информации (available and relevant infor-
mation).
M.8. Информация в одинаковой степени доступна всем
участникам рынка, которые идентично ее интерпретируют и
мгновенно используют для принятия или корректировки ре-
шений.
М.9. Инвесторы имеют однородные ожидания: поступают
рационально, придерживаясь однородных целевых установок
и стратегий поведения, а следовательно, имеют одинаковые
прогнозы относительно ожидаемой доходности и риска цен-
ных бумаг.
При выполнении предположений М.8, М.9 в рамках тео-
рии оптимального портфельного инвестирования рынок при-
нято называть совершенным рынком (perfect market).
Отсюда следует, что, как и при определении эффективного
рынка в рамках соответствующей теории (гл. 4), ключевыми в
определении совершенного рынка являются понятия "инфор-
244

мация" и "рациональная реакция" рынка на ее обновление, а
также предположения о равных возможностях, идентичных це-
левых установках и однородных ожиданиях участников рынка.
В обоих случаях имеется в виду, что рациональное поведе-
ние участников рынка, имеющих равные возможности, иден-
тичные целевые установки и однородные ожидания, приводит
к такому механизму формирования цен активов на рынке,
при котором цены мгновенно, полностью и корректно ассими-
лируют всю доступную информацию, достигая при этом со-
стояния равновесия.
Таким образом, в рассматриваемом случае различие в по-
нятиях "совершенный рынок" и "эффективный рынок" но-
сит не принципиальный характер, а объясняется тем, что обе
теории, т.е. теория оптимального портфельного инвестирова-
ния и теория эффективного финансового рынка, обязанные
своим появлением работам Г. Марковича1 и М. Кендалла2, в
течение достаточно длительного времени развивались относи-
тельно самостоятельно.
2) Свойства модели САРМ.
На совершенном (эффективном) рынке все инвесторы, по-
ступая рационально, стремятся сформировать свои портфели
активов оптимальным в смысле подхода "доходность — риск"
образом, используя одни и те же прогнозные значения харак-
теристик активов //, £.
В результате множество эффективных по Марковичу порт-
фелей для всех инвесторов в равновесном состоянии рынка
будет одним и тем же, т.е. все инвесторы получат одну и ту
же кривую фронта эффективных по Марковичу портфелей.
Распределение капитала между эффективным рисковым
портфелем и безрисковым активом с фиксированной ставкой
Rq приведет к однозначному определению оптимальной
структуры рискового портфеля (т.е. выбору Т-портфеля).
Свои индивидуальные предпочтения относительно риска и
ожидаемой доходности портфеля, выраженные, например,
кривыми безразличия, инвесторы смогут учесть за счет выбо-
ра доли xq безрисковых вложений. При этом множество оп-
тимальных комбинированных портфелей будет общим для
всех инвесторов. В системе координат ({ip,<yp) этому множест-
ву будет соответствовать прямая, касательная к фронту эф-
фективных рисковых портфелей, проходящая через точки
1 См.: Markovitz ИМ Portfolio Selection // Journal of Finance. 1952. V. 7.
№ 1. P. 77-91.
2 См.: Kendall M.G. The analysis of economic time series. Part 1. Prices // Jour-
nal of the Royal Statistical Society. 1953. V. 96. P. 11-25.
245

(7?о,О) и (jUT,crT), соответствующие безрисковому активу и Т-
портфелю.
Установившееся в результате соотношение между ожидае-
мой доходностью некоторого портфеля активов и ожидаемой
доходностью оптимального рискового портфеля (Г-портфеля)
с учетом (5.49) будет иметь вид:
^^р. (6.1)
рр
от
Выражение (6.1) связывает ожидаемую доходность jup про-
извольного портфеля и ожидаемую доходность jut оптималь-
ного рискового портфеля. Эта связь имеет место в состоянии
равновесия рынка ценных бумаг и позволяет сформулировать
первое свойство САРМ, известное как теорема о разделении
(separation theorem) [33].
Свойство 1. Оптимальный портфель рисковых ценных бу-
маг для всех инвесторов имеет одинаковую структуру (соот-
ветствующую Г-портфелю и определяемую вектором Xj), ко-
торая не зависит от предпочтений инвесторов относительно
риска и ожидаемой доходности портфеля. Откуда следует, что
определение оптимальной структуры портфеля рисковых
ценных бумаг и учет индивидуальных предпочтений инвесто-
ра относительно риска и ожидаемой доходности портфеля
могут осуществляться раздельно (последовательно).
Ключевым в САРМ является понятие рыночного портфеля
(market portfolio), под которым понимается совокупность всех
рисковых ценных бумаг, обращающихся на рынке.
Рыночный портфель будем называть М-портфелем, его
структуру обозначать вектором Хм=(хми хМ2, ..., xMn)t, гДе
N- количество ценных бумаг на рынке. Для ожидаемой до-
ходности и риска Л/-портфеля будем использовать обозначе-
ния (juM, <jm)'
Поскольку в состоянии равновесия все инвесторы имеют
одинаковый по структуре портфель рисковых ценных бумаг,
совпадающий с оптимальным Г-портфелем, то, очевидно, та-
ким же образом будет устроен и рыночный М-портфель, т.е.
Хм =Хт, мм>=Мт> &м ==<771- Таким образом, множество всех
эффективных портфелей инвесторов будет включать портфе-
ли, получающиеся в результате распределения капитала меж-
ду безрисковым активом и М-портфелем (см. рис. 6.1, а).
Прямая линия, соответствующая множеству эффективных
портфелей, представляющих собой комбинацию из М-порт-
феля и безрискового актива, определяется основным уравнени-
ем САРМ:
246

ом
-ар
(6.2)
и называется рыночной линией (Capital Market Line - CML).
Множество всех возможных, но неэффективных портфе-
лей, включая отдельные активы, располагается ниже рыноч-
ной линии, как это показано на рис. 6.1, Ь. Таким образом, в
соответствии с САРМ состояние равновесия рынка может ха-
рактеризоваться двумя величинами: безрисковой ставкой Rq и
величиной (mm-Ro)/^) равной тангенсу угла наклона прямой
CML.
а
Рис. 6.1. Геометрическая интерпретация САРМ:
а - множество эффективных портфелей (прямая Rq- Ми далее);
b - множество неэффективных портфелей (область ниже прямой Rq- M)
Ставка Rq интерпретируется в данном случае как плата за
ожидание (воздержание от риска). Величина (им-Ко)/ам из~
вестна как премия за единицу риска, или рыночная цена риска
(market price of risk).
Второе свойство САРМ касается рыночного портфеля.
Свойство 2. В состоянии равновесия рынка каждый риско-
вый актив имеет ненулевую долю в рыночном портфеле, т.е.
xMi>0 (/=1, 2, ..., N), хМ] + хМ2 +... + xMN= 1. (6.3)
Справедливость данного свойства основана на предполо-
жении о равновесии рынка и вытекающем из него первом
свойстве САРМ.
Действительно, если предположить, что для некоторого
актива х^г^О, т.е. все инвесторы начнут продавать данный
актив, то это приведет к росту предложения актива на рынке,
а следовательно, к снижению его цены и повышению ожи-
даемой доходности. Это сделает актив вновь привлекатель-
247

ным для покупки. Инвесторы опять начнут приобретать дан-
ный актив, что сделает невозможным достижение условия
хмгО. Невозможна также ситуация, когда xMi<0 V/, т.е.
"равновесный" рыночный портфель формируется без исполь-
зования операции "короткая продажа". Это следует из того,
что в состоянии равновесия на рынке устанавливаются
"истинные" цены и, следовательно, отсутствуют как
недооцененные, так и переоцененные активы. Отсутствие
переоцененных активов делает нецелесообразным совершение
операции "короткая продажа".
6.1.2. САРМ для отдельных ценных бумаг
1) Рыночная линия ценной бумаги.
Получим формулы, определяющие САРМ для отдельной
ценной бумаги, используя найденные ранее, в п. 5.4.3, пред-
ставления для бета-коэффициентов активов по отношению к
оптимальному портфелю рисковых ценных бумаг.
Предположим, что на рынке имеется N рисковых ценных
бумаг с доходностями {/?/}, ожидаемыми доходностями {//,},
среднеквадратическими отклонениями доходностей {ау} и ко-
вариациями доходностей {o^Kfcy), определяемыми по форму-
лам (п. 5.1.2):
Также обозначим: Л=(Л/) - вектор доходностей имеющихся
на рынке ценных бумаг; //=(///)=Е(Л) - соответствующий век-
тор ожидаемых доходностей ценных бумаг; I={cr#}=E((J?-//)(l?-
-//)т) - ковариационная матрица доходностей ценных бумаг
(/,/=1,2, ...,7V).
Если рынок находится в равновесии, то в соответствии с
САРМ рыночный портфель является оптимальным рисковым
Л/-портфелем с характеристиками Хм, /им, &м- Причем на ос-
новании формул (5.58) доходность и ожидаемая доходность
рыночного портфеля соответственно имеют вид:
RM =
а отклонение фактической доходности от ожидаемой опреде-
ляется выражением:
У=1
248

С учетом этого ковариация доходности произвольного ак-
тива i (/—1, 2, ..., N) с доходностью рыночного портфеля будет
равна:
*м= Cov(RhRM)= E((RrMi )(Rm-Mm)t) =
N N (6.4)
7=1 У=1
Бета-коэффициенты рисковых ценных бумаг {/?/} по отно-
шению к Af-портфелю имеют вид:
й=с.^) = ^и2 N (65)
Так как ^/-портфель является оптимальным портфелем
рисковых ценных бумаг, то коэффициенты {Д} удовлетворяют
соотношению типа (5.61), т.е.:
А--£^.,/=1,2, ...,*,
откуда следует представление вида:
(6.6)
Формула (6.6) устанавливает связь между ожидаемой до-
ходностью ценной бумаги и ее бета-коэффициентом.
Бета-коэффициент рыночного портфеля, очевидно, равен
единице, т.е. /?д/=1, "бета" произвольного рискового актива
принимает неотрицательные значения, поскольку считается,
что juj>Ro V/и мм>Ко-
На основании (6.5), (6.6) можно получить эквивалентное
соотношение, определяющее связь между ожидаемой доход-
ностью ценной бумаги и ковариацией ее доходности с доход-
ностью рыночного портфеля:
M (6.7)
Соотношения (6.6), (6.7) можно рассматривать как две
формы записи уравнения прямой, известной как рыночная ли-
ния ценной бумаги (Security Market Line - SML). Графики SML
для этих соотношений приведены на рис. 6.2, а и 6.2, b соот-
ветственно.
249

a b
Рис. 6.2. Рыночная линия ценной бумаги (SML)
Заметим, что в обоих случаях отсутствует непосредствен-
ная связь между ожидаемой доходностью ценной бумаги щ и
ее риском в виде среднеквадратического отклонения а/. Аль-
тернативными характеристиками риска активов в данных со-
отношениях выступают характеристики од// и Д. Причем бета-
коэффициент Д, согласно (6.5), может рассматриваться как
нормированная ковариация од//. Появление ковариаций до-
ходностей активов с доходностью рыночного портфеля {о^//}
вместо рисков активов {о/} не случайно и связано со свойст-
вом дисперсии доходности М-портфеля, которая с учетом
(6.4) равна:
=
N
N
XMiXMj<Jij = X XMiGMi
(6.8)
Согласно (6.8) дисперсия доходности оптимального порт-
феля (т2м не зависит от дисперсий доходностей, входящих в
него активов, а прямо пропорционально зависит от ковариа-
ций доходностей активов с доходностью рыночного портфеля
Коэффициентами пропорциональности при этом выступа-
ют доли вложений капитала {х^}. Соотношения (6.5), (6.6)
допускают следующую интерпретацию: вкладывая капитал в
активы с большими значениями ад// (или Д), инвесторы ожи-
дают получить соответствующую компенсацию в доходности
(премию за риск). На рис. 6.2 видно, что прямые линии, оп-
ределяемые выражениями (6.5), (6.6), пересекают ось ординат
в одной и той же точке Rq, но имеют в общем случае различ-
ный угол наклона, т.е. различным характеристикам риска со-
ответствуют различные премии за риск.
250

2) Анализ ценных бумаг на основе коэффициентов "альфа" и
"бета".
Соотношения (6.6), (6.7) позволяют осуществлять сравни-
тельный анализ ожидаемой доходности ценных бумаг, как
правило акций, при известных значениях {/?,-} и {од//}. В каче-
стве альтернативы при этом выступает рыночный портфель.
Возможны следующие случаи:
1) /?/ = 1, о-мг= °м > тогДа Mi =Мм;
2) 0</% <1, 0<о-м< а2м , тогда //,• <//м;
3) pi > 1, сгм> о-^, тогда /// >juM;
4) Д- = 0, сгм/= О, тогда //, =Rq.
В первом случае ожидаемая доходность соответствующей
ценной бумаги (акции) находится на уровне доходности ры-
ночного портфеля, т.е. на уровне средней рыночной доходно-
сти. Во втором случае акции считаются менее доходными, но
при этом обладают меньшим риском. Подобные акции при-
нято называть оборонительными (defensive stocks). В третьем
случае имеет место обратная ситуация: по акциям ожидается
более высокая доходность при соответственно большем рис-
ке, что дает основание называть их агрессивными (aggressive
stocks). Четвертый случай соответствует безрисковому активу.
Для актива /, имеющего неравновесную цену в начале не-
которого периода владения /, фактическая доходность //'# за
этот период будет отличаться от доходности щь ожидаемой в
соответствии с моделью САРМ в начале периода, на вели-
чину:
а/ = м',; - /in = М'и
При этом возможны следующие случаи:
1) ot/>0 (фактическая доходность больше ожидаемой), т.е.
ценная бумага в начале периода недооценена рынком, поэто-
му представляет привлекательный объект для покупки (актив
Сна рис. 6.3);
2) сс/<0 (фактическая доходность меньше ожидаемой), т.е.
ценная бумага в начале периода переоценена рынком, поэто-
му ее не следует покупать, а целесообразно продать либо со-
вершить операцию "короткая продажа" (актив А на рис. 6.3);
3) ос/=0, т.е. ценная бумага в начале периода имела равно-
весную ("истинную") цену, поэтому в данном периоде отсут-
ствует возможность получить дополнительный доход за счет
ее покупки или продажи (актив В на рис. 6.3).
251

Таким образам, для неравновесного рынка следует исполь-
зовать модификацию САРМ вида:
щ =Rq +(х/
(6.10)
На практике используются представления САРМ в виде
эконометрических моделей (см. разд. 6.4). В рассматриваемом
случае такой моделью может служить, как и в случае одно-
факторной рыночной модели Шарпа, модель простой линей-
ной регрессии.
Рис. 6.3. Геометрическая интерпретация
коэффициентов "альфа" и "бета"
Более удобным является вариант модели, описывающий
зависимость премии за риск актива от премии за риск ры-
ночного портфеля. Данная модель имеет вид:
Л=а/ + fiZt+ £/, *'=1, 2, ..., N, /=1, 2, ..., Г, (6.11)
где y^Rlf-R(), Zf^RMrRo ~ премии за риск актива и рыночного
портфеля соответственно; Rit и R^t - фактические доход-
ности актива и рыночного портфеля за период владения /;
%it - случайное отклонение фактической премии за риск
актива от ожидаемой при заданном значении доходности
рыночного портфеля.
Следует отметить, что в отличие от рыночной модели
Шарпа в регрессионной модели (6.11), описывающей САРМ,
не только параметры {/?,-}, но и параметры {at) имеют содер-
жательную интерпретацию и называются альфа-коэффициен-
тами ценных бумаг. Оценки коэффициентов "альфа" и "бе-
та" для различных активов обычно известны из источников
финансовой информации и используются участниками рынка
для оценки инвестиционной привлекательности ценных бу-
маг.
252

6.2. МОДИФИКАЦИИ САРМ
Описанная выше стандартная версия САРМ основана на
определенных достаточно жестких предположениях М.1-М.6
(п. 5.2.1), МЛ (п. 5.3.3), а также М.8-М.9 (п. 6.1.1). В связи с
этим возникает вопрос: насколько САРМ соответствует реаль-
ным процессам, происходящим на финансовом рынке? Ответ
на этот вопрос может быть получен с помощью проверки аде-
кватности САРМ по реальным статистическим данным.
Для практического применения и тестирования САРМ ис-
пользуются ее эконометрические представления в виде рег-
рессионных моделей. При этом проблема проверки адекват-
ности САРМ, т.е. выполнения условия равновесия рынка,
сводится к статистической проверке гипотез о значениях па-
раметров регрессионной модели и будет рассматриваться в
разд. 6.4.
Однако прежде чем переходить к проблемам тестирования
САРМ, целесообразно познакомиться с некоторыми ее моди-
фикациями, соответствующими более реалистичным предпо-
ложениям относительно поведения участников рынка ценных
бумаг. Различные модификации САРМ возникают при сня-
тии или ослаблении ранее принятых предположений. Подоб-
ные корректировки модельных предположений могут, напри-
мер, касаться возможности совершения операции "короткая
продажа", условий безрискового кредитования и заимствова-
ния, учета инфляции и налоговых платежей, однородности
ожиданий инвесторов, оптимизации портфелей на один пе-
риод владения и др. Ниже приводится описание некоторых
модификаций САРМ, получаемых на основе стандартной вер-
сии модели при ослаблении традиционных модельных пред-
положений.
6.2.1. Предположение о невозможности
операции "короткая продажа9'
Предположения о возможности либо невозможности опе-
рации "короткая продажа" (см. разд. 5.2) относятся к тем
предположениям, которые в рамках САРМ в итоге не влияют
на конечный результат. Действительно, как отмечалось в
разд. 6.1, "равновесный" рыночный портфель формируется
без использования операции "короткая продажа", поскольку
в состоянии равновесия на рынке устанавливаются равновес-
ные, т.е. "истинные", цены на активы. По этой причине у
инвесторов отсутствуют мотивы для совершения операции
253

"короткая продажа" относительно какого-либо актива. Таким
образом, одно и то же представление САРМ будет получено
как при возможности, так и при невозможности операции
"короткая продажа".
6.2.2. Модель САРМ по версии Блэка
при отсутствии безрискового актива
Одним из традиционных является предположение МЛ о
том, что инвесторы могут кредитовать или брать в долг про-
извольную сумму денег по безрисковой ставке Rq.
Очевидно, данное предположение противоречит реальной
ситуации. Можно допустить, что инвесторы способны вкла-
дывать любую часть своего капитала под безрисковую ставку
(например, покупая государственные краткосрочные облига-
ции со сроком обращения, совпадающим с периодом владе-
ния портфелем), однако они не могут заимствовать произ-
вольную сумму денег. Кроме того, если учитывать неопреде-
ленность, связанную с будущим уровнем инфляции, то
безрискового заимствования вовсе не существует. Хотя без-
рисковое кредитование в принципе возможно, если государ-
ственные облигации являются индексируемыми. В связи с
этим актуальным является обобщение САРМ на случай, когда
безрискового актива не существует. Такое обобщение модели
САРМ было предложено Ф. Блэком1 и основано на понятии
портфеля (актива) с нулевым "бета".
В соответствии с САРМ по версии Блэка рыночная линия
ценной бумаги (SML) описывается соотношением:
Mi=MZ+fi (MM-MZ), i=h 2, ..., N, (6.12)
где /// и Pi - ожидаемая доходность и "бета" актива / по отно-
шению к А/-портфелю; juz=^{R^ - ожидаемая доходность,
a Rz - доходность так называемого Z-портфеля, т.е. порт-
феля с нулевым "бета" (zero-beta portfolio), соответствую-
щего "рыночному" М-портфелю с ожидаемой доходно-
стью jum-
Так как Z-портфель, как и безрисковый актив, имеет нуле-
вое "бета" (/?^=0), то это дает основание использовать его в
САРМ вместо несуществующего безрискового актива. Оче-
видно, ключевая проблема при построении САРМ в виде
(6.12) состоит в выборе Z- и М-портфелей. Оказывается, в ка-
1 См.: Black F. Capital Market Equilibrium with Restricted Borrowing // Journal
of Business. 1972. № 45 (July). P. 444-454.
254

честве А/-портфеля может использоваться любой эффектив-
ный по Марковицу рисковый портфель (кроме "глобального"
портфеля). При этом для заданного М-портфеля можно одно-
значно определить соответствующий ему Z-портфель.
Дадим геометрическую интерпретацию задачи выбора Z- и
Л/-портфелей в системе координат "доходность - риск", ис-
пользовавшейся для иллюстрации решений задач Марковица
и Тобина. Зададимся некоторым произвольным эффективным
рисковым портфелем (кроме "глобального"). На рис. 6.4 ему
соответствует точка М кривой фронта эффективных портфе-
лей с координатами (//^, <тд/). Проведем прямую, касательную
к данной кривой в точке М, до пересечения с осью ординат в
точке А с координатами (д^, 0). Точка А соответствует некото-
рому гипотетическому безрисковому активу с ожидаемой до-
ходностью
Рис. 6.4. САРМ при отсутствии безрискового актива
Обозначим через & подмножество достижимых портфелей,
располагающихся на отрезке Z-C прямой (включая точку 2),
проходящей через точку А горизонтально оси абсцисс.
Очевидно, любой портфель из в, включая портфель в точ-
ке Z, имеет ожидаемую доходность, равную ju^, поэтому
При сделанных предположениях для произвольного риско-
вого актива / (включая портфель в точке Z) на основании
САРМ справедливо уравнение, описывающее рыночную ли-
нию ценной бумаги (SML):
255

Если в качестве актива / рассматривается портфель в точке
Z, то из (6.13) и (6.14) следует, что m-Mz^Ma и firftz*2®* по-
скольку jum-Ma*® по построению.
Портфель в точке Zco структурой X2r(xzi)e<RN, соответст-
вующий заданному эффективному рисковому М-портфелю,
будем называть Z-портфелем.
По построению Z-портфель обладает следующими свойст-
вами.
1. Коэффициент бета Z-портфеля равен нулю:
-0, (6.15)
т.е. доходность Z-портфеля не коррелирует с доходностью М-
портфеля.
2. На подмножестве $ достижимых портфелей Z-портфель
обладает минимальным риском (дисперсией доходности) а\,
3. Ожидаемая доходность Z-портфеля равна:
N
(6.16)
4. Z-портфель является неэффективным, поскольку ему
соответствует точка, принадлежащая нижнему отрезку кривой
фронта эффективных по Марковицу рисковых портфелей.
Очевидно, Z-портфель, обладающий свойствами 1-4, и яв-
ляется искомым портфелем с нулевым "бета". Причем первые
два свойства Z-портфеля используются для его построения.
Произвол в выборе М-портфеля приводит к бесконечному
числу вариантов пар М- и Z-портфелей. Для определения ва-
рианта, приемлемого для конкретного инвестора, обычно ис-
пользуется следующий подход.
Выбор М-портфеля осуществляется на множестве эффек-
тивных рисковых портфелей с учетом предпочтений (кривых
безразличия) инвестора относительно риска и доходностей
портфеля. Далее для заданного М-портфеля находится соответ-
ствующий ему Z-портфель, удовлетворяющий условиям 1, 2.
Определение М-портфеля с учетом индивидуальных пред-
почтений инвестора позволяет снять еще одно ограничение
стандартной модели САРМ относительно того, что все инве-
сторы имеют одинаково устроенные рисковые портфели, и
таким образом получить более реалистичную модель.
Описанная версия модели САРМ обладает еще одним дос-
тоинством. Как известно, стандартная модель САРМ не учи-
тывает инфляционных изменений цен и доходностей активов,
256

в то время как данная версия САРМ может рассматриваться
как модель равновесия, скорректированная с учетом инфля-
ции. При этом предполагается, что в модели используются
реальные ставки доходностей активов.
Модель САРМ, по версии Блека (6.12), допускает пред-
ставление в виде однофакторной рыночной модели типа
(6.11), в которой параметр щ имеет вид:
6.2.3. Учет различия безрисковых
ставок кредитования и заимствования
Стандартная модель САРМ предполагает, что инвесторы
могут вкладывать и занимать деньги по одной и той же ставке
Rq. Как отмечалось, данное предположение по ряду причин
является далеким от реальной ситуации. Проблема существо-
вания безрискового актива обсуждалась в п. 6.2.2. Там же бы-
ла предложена альтернативная версия модели САРМ в случае,
когда подобного актива не существует. Целью данного разде-
ла является снятие предположения М.7 (п. 5.3.3) о том, что
безрисковое кредитование и заимствование осуществляется
по одной и той же ставке Rq. Более правдоподобным для
многих индивидуальных инвесторов является следующее
предположение.
М.7.1. Инвесторы могут совершать операции кредитования
(lending) под безрисковую ставку R$i и заимствования
(borrowing) по более высокой безрисковой ставке Rqb, т.е.
ставки кредитования и заимствования различны, причем:
Яов> Rol- (6.17)
Условие (6.17) вытекает из предположения об отсутствии
на рынке арбитражных возможностей, т.е. возможностей по-
лучения безрискового дохода без затрат собственного капита-
ла (см. разд. 6.3). Очевидно, в силу (6.17) ситуация, когда
один и тот же инвестор занимает средства под ставку Rqb, а
дает в долг по более низкой ставке Rqi, не имеет смысла. По-
этому инвесторов в зависимости от стратегии инвестирования
можно разделить на три группы:
первая группа - инвесторы, не занимающиеся безриско-
вым кредитованием и заимствованием;
вторая группа - инвесторы, осуществляющие безрисковое
кредитование;
третья группа - инвесторы, осуществляющие безрисковое
заимствование.
17 3ак.7О84 257

Предположение М.7.1, как и предположение об отсутствии
безрисковой ставки, приводит к ситуации, когда портфель
рисковых ценных бумаг в состоянии равновесия уже не явля-
ется одинаковым для всех инвесторов. Так, инвесторы второй
и третьей групп имеют различные по структуре портфели рис-
ковых ценных бумаг. В соответствии с первым свойством
САРМ это так называемые касательные портфели (tangency
portfolios), которые однозначно определяются на множестве
эффективных по Марковицу портфелей при задании безрис-
ковой ставки. Поэтому различным ставкам Rqb и Rqi соответ-
ствуют различные эффективные рисковые портфели в точках
В и L соответственно (рис. 6.5). Однако эти портфели в со-
стоянии равновесия рынка идентичны по структуре для всех
инвесторов одной и той же группы. Множество всех эффек-
тивных (комбинированных) портфелей для инвесторов второй
группы включает портфели в виде комбинации из безриско-
вого актива с доходностью Rqi и рискового портфеля, иден-
тичного по структуре портфелю в точке L. Данному множест-
ву на рис. 6.5 соответствует отрезок Rql~L прямой Rqi~L'.
Mi
Rqb
MZ
Rol.
Рис. 6.5. Различные безрисковые ставки
кредитования и заимствования
Эффективные портфели для инвесторов третьей группы
формируются при использовании средств, заимствованных по
безрисковой ставке Rq^, и имеют структуру рискового порт-
феля в точке В. Им на рис. 6.5 соответствует отрезок В-В'
прямой Rob-B'. Множества портфелей, которым соответству-
ют отрезки L-L' и Rqb~B, являются недостижимыми. Нако-
нец, инвесторам первой группы соответствуют различные
эффективные рисковые портфели (в зависимости от их инди-
видуальных предпочтений относительно ожидаемой доходно-
258

сти и риска портфелей), сосредоточенные на отрезке L-B
кривой фронта эффективных портфелей. Этому же отрезку
должна принадлежать и точка, соответствующая рыночному
М-портфелю в состоянии равновесия рынка как средневзве-
шенному рисковому портфелю на множестве портфелей всех
инвесторов. Инвесторы первой группы по заданному М-
портфелю могут построить соответствующий Z-портфель (т.е.
портфель с нулевым "бета") для получения необходимого
представления САРМ в виде рыночной линии ценной бумаги.
Уравнение рыночной линии (SML) ценной бумаги / для
инвесторов первой группы имеет вид:
), i=h 2, ..., N, (6.18)
где щ - ожидаемая доходность актива /; Д- - "бета" актива / по
отношению к М-портфелю; //^ - ожидаемая доходность Z-
портфеля, соответствующего заданному М-портфелю с
ожидаемой доходностью juj^.
Инвесторам второй группы соответствует уравнение:
Mi= Rql + P,l (ml-Xql), '-Ь 2, ..., N, (6.19)
где fii - ожидаемая доходность портфеля в точке L; рц - ко-
эффициент "бета" актива / по отношению к портфелю в
точке L, определяемый по формуле
Cw(R,,RL)
PiL 2 *
Для инвесторов третьей группы имеем следующее соотно-
шение:
Mi= Rob + fiiB (мв- Ъв), i=h 2, ..., N, (6.20)
где /лв - ожидаемая доходность портфеля в точке В; р& - "бе-
та" актива / по отношению к портфелю в точке В, опреде-
ляемая по формуле:
Заметим, что для крупных институциональных инвесторов
различие в ставках может быть незначительным на фоне по-
грешностей в оценивании "бета" активов и ожидаемых до-
ходностей портфелей, участвующих в уравнениях (6.18),
(6.19). Поэтому в таких случаях на практике вместо описан-
ных модификаций САРМ может использоваться ее стандарт-
ная версия.
259

6.3. ТЕОРИЯ АРБИТРАЖНОГО ОЦЕНИВАНИЯ
Каждый инвестор при формировании своего портфеля
стремится использовать возможности увеличения ожидаемой
доходности портфеля без увеличения риска. Такие возможно-
сти принято называть арбитражными. Удобным "инструмен-
том" реализации арбитражных возможностей является арбит-
ражный портфель (arbitrage portfolio). Теория построения по-
добных портфелей известна как "арбитражная теория
оценивания" (Arbitrage Pricing Theory).
В рамках арбитражной теории оценивания, разработанной
С. Россом1, была предложена модель доходности активов (мо-
дель APT), которая, так же как и модель САРМ, справедлива в
условиях равновесия фондового рынка. Данная модель позво-
ляет инвестору исследовать возможности построения арбит-
ражных портфелей ценных бумаг. Эконометрическое пред-
ставление модели APT основано на модели множественной
линейной регрессии, т.е. в статистическом смысле модель
APT является более сложной, чем стандартная модель САРМ.
Более тонким является и экономическое обоснование данной
модели.
На практике при реализации модели APT возникает ряд су-
щественных проблем: отбор факторов, оказывающих значимое
влияние на доходности активов и обладающих некоторыми
специальными свойствами; тестирование адекватности модели
APT; определение структуры арбитражного портфеля; учет из-
держек, связанных с покупкой и продажей активов, и др.
Сформулируем более строго модельные предположения, в
рамках которых определяется модель APT и арбитражный
портфель. Установим также связь между моделями APT и
САРМ. В следующем разделе опишем методы построения и
тестирования обеих моделей.
6.3.1. Модельные предположения и исходные
предпосылки для построения модели APT
Предположим, что доходности N активов {Rlt} (i=l 2, ..., N,
f=l, 2, ..., 7) находятся под воздействием двух типов факто-
ров: систематических контролируемых (измеряемых) факто-
ров z\u Z2h —> Zmt> оказывающих влияние одновременно на все
активы, и случайных неконтролируемых факторов {£#}, собст-
венных для каждого актива.
1 См.: Ross S. Л. The Arbitrage Theory of Capital Asset Pricing // Journal of
Economic Theory. 1976. 13. № 3. P. 341-360.
260

Доходность актива / за один период владения t при этом
описывается многофакторной моделью типа множественной
линейной регрессии (разд. 3.5):
Rit = Я, + bnzu + .-.+ bimZmt + %it =
= at + 5
ы
где af=E(Rjt) - ожидаемая доходность актива при отсутствии
влияния систематических факторов; Ь?=(Ьц, Лд, ...,
i/JeJR"1 - вектор коэффициентов регрессии, характери-
зующих влияние соответствующих факторов на доход-
ность актива; Z?=(zu, Ziu —> Zmt)eMm - вектор значений
т>\ систематических факторов.
Относительно систематических факторов {z/t} и случайных,
неконтролируемых факторов {£#} (/=1, 2, ..., N, /=1, 2, ..., т,
t=\, 2, ..., 7) будем предполагать следующее:
1) случайные, неконтролируемые факторы {&} имеют ну-
левое среднее значение, постоянную дисперсию и являются
взаимно некоррелированными, т.е. удовлетворяют соотноше-
ниям:
= О, D(&) = «2 <оо, E(fi^) = 0 (%); (6.21)
2) систематические факторы {zu) обладают свойствами:
E(v/Y) = 0, D(v/r) = ^>0, E(vitvjt) = О (И) и E(v,,£,) = 0, (6.22)
где vit=Zir^(Zit) - разность между фактическим и ожидаемым
значениями фактора / в момент времени t, т.е. отклонения
{V/} имеют постоянную дисперсию, являются взаимно не-
коррелированными и некоррелированными с {£,}.
Относительно рынка будем предполагать, что он является
полным, т.е. имеет место предположение М.6 (п. 5.2.1), и со-
вершенным, т.е. выполняются условия М.8, М.9 (разд. 6.1).
Будем рассматривать однопериодную задачу формирования
портфеля ценных бумаг, т.е. задачу формирования портфеля
на один произвольный период владения. Поэтому для упро-
щения записи далее в этом разделе будем опускать индекс t,
указывающий на номер рассматриваемого периода времени.
Пусть на множестве ценных бумаг, удовлетворяющих мо-
дели (6.20) при сделанных предположениях, формируется
портфель ценных бумаг, структура которого в анализируемом
периоде определяется вектором Х=(х1)е^м. Исследуем харак-
теристики данного портфеля.
261

Введем векторы: Br=(Rj)e9lN; //=(///) e^N; a=(ai)e^RN;
br(bu)eKN(i=\, 2, ..., N, /=1, 2, ..., m).
Доходность портфеля за произвольный период владения с
учетом (6.20) будет определяться соотношениями:
N м
где n
ар = X Xi a*= ^Tfl' (6.24)
/=1
V= Z^^v =^T*/5 (6.25)
TV
Zp= TLxiSr (6.26)
Ожидаемая доходность портфеля с учетом (6,21) равна:
т
Мр - Е(^) = ар + ^ ft^ E(z/). (6.27)
Отклонение фактической доходности от ожидаемой опре-
деляется выражением:
Полный риск портфеля, определяемый дисперсией его до-
ходности, при условиях (6.16)—(6.17) допускает представление:
т
а2р = B(Rp) = E(Rp-Mp)2 = Y,bPicp] + ¥Р2 = ^l + *%, (6.28)
где
т.е., как и в случае однофакторной рыночной модели (разд.
5.4), полный риск портфеля включает систематическую S\ и
собственную *$2 компоненты риска, обусловленные неопреде-
ленностью относительно систематических и собственных
факторов для каждого актива.
Введем понятие хорошо диверсифицированного портфеля как
портфеля активов, удовлетворяющего условиям:
о? X/-1//V, (6.29)
262

где предполагается, что xt - величина порядка 1/7V, т.е. капи-
тал распределяется между активами достаточно равномер-
но.
Как было показано в п. 5.4.4, в условиях типа (6.21) собст-
венный риск портфеля, определяемый соотношением (6.28),
для хорошо диверсифицированного портфеля может быть
сделан сколь угодно малым, т.е. справедливо условие:
i52=^->0. Систематический риск S\, как известно, не подда-
ется диверсификации, но может быть устранен, если исполь-
зовать специально организованные портфели активов, ней-
тральные к изменению систематических факторов, т.е. обла-
дающие нулевым по отношению к этим факторам риском.
Такими портфелями и являются арбитражные портфели, рас-
сматриваемые ниже.
6.3.2. Арбитражный портфель
Арбитражным портфелем будем называть портфель акти-
вов, который обладает тремя свойствами:
• является безрисковым портфелем: о2р =0 (т.е. хорошо ди-
версифицированным (S2*0) и нейтральным по отноше-
нию к определенным систематическим факторам (^=0));
• не требует для формирования затрат капитала инвестора,
т.е.
jq +х2+...+ *# = 0; (6.30)
• имеет положительную ожидаемую доходность jup>0.
Если задача выбора активов и факторов в модели (6.20)
решена, то остается проблема определения структуры арбит-
ражного портфеля, описываемой вектором Х=(х\, х2, ..., х^)Т.
Определим ограничения, которым должен удовлетворять век-
тор X, для того чтобы соответствующий ему портфель был ар-
битражным, а также обсудим возможности практического
достижения данных ограничений.
Ограничение 1. Первое ограничение на вектор X определя-
ется формулой (6.30) или в векторной записи выражением:
^/=0. (6.31)
Данное ограничение, как отмечалось, означает, что для
формирования арбитражного портфеля не требуется затрат
капитала инвестора. Очевидно, такое возможно только при
использовании операции "короткая продажа", т.е. относи-
263

тельно идентичных активов, имеющих различные цены на
различных рынках, в один и тот же момент времени совер-
шаются две операции. Первая операция - это "короткая про-
дажа" активов, имеющих относительно высокие цены (соот-
ветствующие им компоненты вектора X принимают отрица-
тельные значения). Вторая операция — покупка активов,
имеющих относительно низкие цены (соответствующие дан-
ным активам компоненты вектора X положительны). На по-
купку активов расходуются средства, вырученные в результате
операции "короткая продажа".
Ограничение 2. Вектор X, определяющий структуру арбит-
ражного портфеля, ортогонален векторам bf=(bn)e^lN9 т.е.:
ЛГТ*/=О, /=1, 2, ..., т. (6.32)
Данное офаничение на вектор X имеет следующую интер-
претацию. Поскольку арбитражный портфель по определению
является безрисковым, т.е. <Jp2=S\ +52«0, то его фактическая
доходность близка к ожидаемой:
Rp*Hp=X*p. (6.33)
Заметим, что условие Sy^O достигается для хорошо дивер-
сифицированного портфеля с учетом (6.30). Для такого порт-
феля по свойству среднего арифметического значения неза-
висимых случайных величин с нулевым математическим
ожиданием на основании (6.26) имеем:
Из определения арбитражного портфеля также следует:
откуда с учетом ф^>0 получаем bpi=bp2=...=bpm=Q9 что, соглас-
но (6.25), влечет (6.32).
Ограничение 3. В состоянии равновесия рынка вектор X,
определяющий структуру арбитражного портфеля, ортогона-
лен вектору ожидаемых доходностеи составляющих его акти-
вов //=(//|)е$iN, т.е.
//,= ^=0. (6.34)
Приведем обоснование данного офаничения.
Согласно третьему свойству арбитражного портфеля вектор
X, определяющий его структуру, удовлетворяет ограничению:
264

что достижимо лишь в том случае, если на рынке возникают
арбитражные возможности, т.е. имеют место различные цены
на идентичные активы. Арбитражные возможности при этом
могут быть реализованы участниками рынка с помощью по-
строения хорошо диверсифицированного портфеля, который
бы удовлетворял ограничениям (6.31), (6.32) и имел положи-
тельную ожидаемую доходность, т.е. являлся арбитражным
портфелем.
В состоянии равновесия рынка все идентичные активы
имеют одну и ту же цену, а значит, отсутствуют арбитражные
возможности, т.е. возможности получить положительный
ожидаемый доход за счет одновременной покупки и "корот-
кой продажи" идентичных активов. Поэтому в состоянии
равновесия рынка ожидаемая доходность безрисковых порт-
фелей, обладающих свойствами (6.29), (6.31), (6.32), равна
нулю, откуда следует третье свойство вектора X
6.3.3. Модель APT и ее интерпретация
1) Основное уравнение модели APT.
Согласно (6.32), (6.34) в состоянии равновесия фондового
рынка вектор X должен быть одновременно ортогонален и
вектору //, и т векторам {bj\ (/=1, 2, ..., т). Тогда по извест-
ному из линейной алгебры свойству ортогональных векторов
[26] вектор ju представим в виде линейной комбинации векто-
ров {Ь/}:
+ЛтЬт, (6.35)
где {Я/} (/-0,1,..., т) - некоторые постоянные коэффициенты.
Пусть доходности активов для произвольного периода
времени описываются регрессионной моделью вида:
Ri = Щ + 6/iZi + ...+ bimzm + 4 (i=l, 2, ..., N) (6.36)
и сформирован арбитражный портфель, для которого выпол-
няются условия (6.29), (6.32), (6.33). Тогда, согласно (6.35),
ожидаемые доходности активов удовлетворяют условию, из-
вестному как основное уравнение модели APT.
+-.-+4A« (*=1, 2, ..., N). (6.37)
Основное уравнение модели APT устанавливает зависи-
мость между ожидаемой доходностью актива щ (/=1, 2, ..., N)
и коэффициентами {Ьц} (/=1, 2, ..., т), определяющими чувст-
265

вительность доходности данного актива к заданным система-
тическим факторам при условии, что рынок находится в со-
стоянии равновесия. В качестве актива / при этом может вы-
ступать как отдельная ценная бумага, так и некоторый порт-
фель ценных бумаг.
По аналогии с бета-коэффициентами активов по отноше-
нию к доходности рыночного портфеля в САРМ коэффици-
ент Ьц в модели APT можно рассматривать как "бета" /-го ак-
тива по отношению к /-му фактору. Из основного уравнения
модели APT следует, что ожидаемая доходность актива про-
порциональна соответствующим "бета" с коэффициентами
пропорциональности {Д/}.
Заметим, что бета-коэффициенты факторов принимают
различные значения для различных активов, т.е. являются ат-
рибутами отдельных активов. Коэффициенты {Я/} одинаковы
для всех активов. Это дает основание рассматривать Щ как
параметры модели APT в целом. Дадим им содержательную
интерпретацию.
2) Интерпретация параметров модели.
Пусть в качестве актива в (6.37) рассматривается Z-
портфель, т.е. портфель с нулевыми "бета": 6//=0 (/=1,2,..., т).
Тогда ожидаемая доходность данного портфеля juz совпадает с
параметром Яо- Таким образом, получаем первое соотношение
относительно {Я/}:
h = № (6.38)
Если выполняется предположение М.7 (разд. 5.3), т.е. на
рынке существует безрисковый актив, доходность которого
определяется безрисковой ставкой Rq, to
%=Яо. (6.39)
Для интерпретации параметров {Я/} (/=1, 2, ..., т) исполь-
зуется понятие чистого факторного портфеля.
Чистым факторным портфелем (pure factor portfolio) для 1-
го фактора называется портфель, который имеет единичный
коэффициент чувствительности по отношению к /-му фактору
и нейтрален ко всем остальным факторам, т.е.:
*,-/= 1, bik= 0, к*1,к=1, 2, ..., т. (6.40)
Ожидаемая доходность //,/ такого портфеля с учетом (6.37),
(6.38), (6.40) равна ////=//z+^/> откуда следует, что
Лу= MU-MZ, /=1,2, ..., /и, (6.41)
266

т.е. Я/ может интерпретироваться как премия за единицу фак-
торного риска (factor risk premium), т.е. риска, обусловленного
неопределенностью относительно 1-го фактора.
С учетом (6.38), (6.41) основное уравнение APT (6.37) мо-
жет быть представлено в виде:
Mi = MZ+ Ьц (///1 - juz) + Ьа(ма ~ MZ) +•••+ bim (jUim ~ Mz)- (6-42)
Таким образом, модель APT в виде (6.42) допускает сле-
дующую интерпретацию: в состоянии равновесия рынка ожи-
даемая доходность некоторого актива / зависит от коэффици-
ентов {Ьц} (/=1, 2, ..., т), определяющих чувствительность
фактической доходности актива к систематическим факторам.
Кроме того, каждый из коэффициентов {Ьц} входит в (6.42) со
своим "весом", равным соответствующей премии за фактор-
ный риск.
6.3.4. Связь между моделями APT и САРМ
Модели равновесия рынка ценных бумаг САРМ и APT по-
лучены, как известно, при существенно различающихся мо-
дельных предположениях. Однако это не является обязатель-
ной причиной взаимного противоречия между моделями.
Другими словами, адекватность одной из моделей не исклю-
чает адекватности другой.
В простейшем случае, если адекватной является однофак-
торная модель APT, причем в качестве единственного факто-
ра выступает доходность рыночного портфеля, то обе модели
описываются уравнением одного и того же вида. Действи-
тельно, в данном случае основное уравнение модели APT
имеет вид:
/i/=^)+MiO-l,2, ..., ЛО, (6.43)
где Ao=Rfi здесь Rf - либо безрисковая ставка Rq, либо, если
таковой не существует, ожидаемая доходность портфеля с
нулевым "бета", т.е. Z-портфеля Rg, A]=jUM~-Rf- премия
за единицу риска рыночного портфеля, ожидаемая доход-
ность которого равна jum! bu=j3j - "бета" актива / по отно-
шению к рыночному портфелю.
Таким образом, уравнение (6.43) может быть записано в
виде:
щ =% + Ммм-Rf) (/=1, 2, ..., TV), (6.44)
267

что соответствует уравнению САРМ, поэтому из адекватности
однофакторной модели APT следует адекватность САРМ и
наоборот.
Рассмотрим случай произвольного числа факторов и пока-
жем, что адекватной многофакторной модели APT может со-
ответствовать некоторая адекватная модель САРМ. Основное
уравнение модели APT с т факторами имеет вид:
bah + ... + bimXm (i=l, 2, ..., N), (6.45)
где, как известно, Яо=/?/, а Я/ - премия за риск, обусловлен-
ный неопределенностью относительно /-го фактора
(/=1, 2, ..., т).
Предположим, что в качестве факторов в модели APT ис-
пользуются некоторые портфели активов и, таким образом, в
данном случае Я/ может интерпретироваться как премия за
риск некоторого портфеля активов, используемого в качестве
/-го фактора в модели APT.
Поскольку модель САРМ в условиях равновесия рынка
справедлива для всех активов и портфелей активов, то в соот-
ветствии с моделью САРМ премии за риск портфелей-
факторов будут связаны с премией за риск рыночного порт-
феля соотношением:
Я/= йХмм-Rf), /=1, 2, ..., т, (6.46)
где {Д} - бета-коэффициенты портфелей-факторов по отно-
шению к рыночному портфелю.
Подставляя (6.46) в (6.45), получаем уравнение, соответст-
вующее САРМ:
Mi = Rf + fifaiM-fy) 0=h 2, ..., N), (6.47)
где "бета" актива / определяется соотношением:
Установленные взаимосвязи между моделью АРТ(т) (моде-
лью APT с т>\ факторами) и моделью САРМ позволяют сде-
лать важные при анализе адекватности этих моделей выводы.
1. Между моделями АРТ(1) и САРМ в условиях равновесия
рынка существует взаимно однозначное соответствие, если в
качестве фактора в модели APT используется доходность ры-
ночного портфеля.
2. Из адекватности АРТ(т) (т>1) нельзя сделать опреде-
ленных выводов относительно адекватности САРМ без до-
полнительных предположений.
268

3. Если APT(/w) (m>\) адекватна и, кроме того, выполняет-
ся условие (6.46), то соответствующая ей модель САРМ также
адекватна.
6.4. СТАТИСТИЧЕСКАЯ ПРОВЕРКА
АДЕКВАТНОСТИ МОДЕЛЕЙ
При практической реализации моделей САРМ и APT по-
мимо чисто статистических проблем, связанных с решением
задач статистического оценивания параметров и тестирования
соответствующих им линейных регрессионных моделей, воз-
никает дополнительная проблема эмпирической проверки
адекватности САРМ и APT как моделей равновесия рынка
ценных бумаг. В связи с этим регрессионные модели опреде-
ляются таким образом, чтобы учитывать возможность нерав-
новесного состояния рынка. Задача эмпирической проверки
адекватности САРМ и APT (т.е. проверки равновесия рынка
по реальным статистическим данным), как и первые две зада-
чи, решается с помощью методов статистической проверки
гипотез о значениях параметров регрессионных моделей.
Краткое описание методов статистического оценивания
параметров, а также методов тестирования статистической
адекватности регрессионных моделей было дано в гл. 3. Более
полное изложение методов решения данных проблем пред-
ставлено в учебной литературе, например в [1, 9, 12, 41]. Во-
просы статистического моделирования и анализа данных на
основе регрессионных и других статистических моделей под-
робно рассматриваются в [31]. Указанные методы реализова-
ны в различных статистических пакетах прикладных про-
грамм (ППП), например PC-GIVE [44], EViews [40], Microfit
[48], СЭМП [13]. Поэтому далее при анализе моделей САРМ
и APT основное внимание уделяется задачам проверки их
адекватности как экономических моделей равновесия фондо-
вого рынка. Дадим краткую характеристику методов решения
указанных задач, а также отметим проблемы, возникающие
при их применении.
6.4.1. Тестирование САРМ на основе модели
многомерной линейной регрессии
Поскольку речь идет о проблеме эмпирической проверки
адекватности САРМ по реальным статистическим данным, то
необходимо конкретизировать ряд понятий: интервал наблю-
дения данных г/>; доходность рыночного портфеля R^t\ без-
269

рисковая ставка Rq, если используется стандартная САРМ;
период времени тсотЬ в течение которого структура САРМ
полагается неизменной, т.е. параметры "альфа" и "бета" мо-
дели можно считать постоянными.
Обычно при проведении эмпирических исследований аде-
кватности модели САРМ [37, 39, 45] делают следующие пред-
положения.
1. Интервал наблюдения данных тр равен одному месяцу.
2. В качестве характеристики доходности рыночного порт-
феля Кмг используется некоторый фондовый индекс, характе-
ризующий состояние анализируемого рынка (п. 1.3.2).
3. В качестве безрисковой ставки используются изменяю-
щиеся во времени фондовые индексы /?о/ рынков краткосроч-
ных долговых обязательств, например Nikkei Short-term Bond
Index на японском фондовом рынке [45].
4. Период rconsh в течение которого структура модели
САРМ полагается неизменной, равен пяти годам; при этом
объем выборки в пределах одного предполагаемого периода
постоянства параметров равен T=\2-Tconst=60 (выбор данной
характеристики определяется компромиссом между получени-
ем объема выборки Г, необходимого для оценивания неиз-
вестных параметров, и требованием постоянства параметров
модели).
Заметим, что САРМ с постоянными параметрами традици-
онно используется в приложениях, хотя, как показывают не-
которые исследования [37, 39, 45], предположение о постоян-
стве параметров является слишком строгим и не всегда под-
тверждается на практике. Альтернативой в данном случае
являются версии САРМ со случайными параметрами (random
coefficient САРМ), т.е. модели САРМ с параметрами, изме-
няющимися во времени в соответствии с определенными ве-
роятностными моделями [45].
Перейдем к описанию методов тестирования САРМ.
Предположим для определенности, что объектом исследова-
ния является стандартная модель САРМ (разд. 6.1) с посто-
янными параметрами.
1) Эконометрическое представление САРМ и оценивание па-
раметров.
Согласно (6.11) модель САРМ для актива / (/=1, 2, ..., N)
допускает эконометрическое представление в виде модели
простой линейной регрессии:
R,t- Rot = а, + pt(RMt - Rot) + fa t=l, 2, ..., Г. (6.48)
270

Будем предполагать, что параметры {«,,$•} модели (6.48)
остаются постоянными на анализируемом интервале времени
Tconst и Для каждого момента (периода) времени / известно
значение безрисковой ставки Лцг. Чтобы упростить запись мо-
дели (6.48), сделаем замену переменных. Для периода /
(/=1, 2, ..., 7) обозначим:
yit= Rlf-RQt- премия за риск актива /;
ZMt- ^Mf-Rot- премия за риск рыночного портфеля;
щ =E(yit) — ожидаемая премия за риск актива /;
jUM =E(iMt) ~~ ожидаемая премия за риск рыночного порт-
феля;
ср2м =Е(хмгМм)2>® ~ дисперсия премии за риск рыночного
портфеля.
Тогда модель (6.48) может быть представлена в виде:
i=h 2, ...,/V, t=l 2, ..., Г, (6.49)
где £// - случайное отклонение фактической премии за риск
актива от ожидаемой при заданном значении доходности
рыночного портфеля.
Будем использовать векторы:
тогда система из N регрессионных уравнений (6.49) может
быть записана в виде модели многомерной линейной регрес-
сии с одним фактором:
Л=а+/?*А0+6,*=1,2, ..., Z (6.50)
где а и р - это векторы, образованные из коэффициентов
"альфа" и "бета" активов, а £ - случайный вектор откло-
нений.
В п. 3.3.3 приводится описание общего случая модели
многомерной линейной регрессии с произвольным числом
К>\ факторов, в которой вместо вектора 0 используется
(7УхА)-матрица коэффициентов регрессии В. При К=\ матри-
ца В имеет размерность Nxl, т.е. является вектором, и для
удобства записи в формуле (6.50) обозначается Д
Будем предполагать, что относительно векторов {£}
(/=1,2, ..., 7) выполняются традиционные предположения
типа £Л-£.3 из п.3.5.1, т.е.
)=0еИ", (6.51)
*0, (/,г=1, 2, ..., 7), (6.52)
271

где 5,r - символ Кронекера, *F=Cov(£/, £) - положительно оп-
ределенная ковариационная матрица случайного вектора
&
,£)=0e<H* (6.53)
NN(0, ¥), (6.54)
т-е- Ш - это гауссовские случайные векторы, которые имеют
нулевое среднее значение, являются взаимно некоррели-
рованными и не коррелируют с используемым в модели
фактором.
Поскольку случайные векторы {£} имеют нормальное рас-
пределение, то из взаимной некоррелированности следует их
взаимная независимость, т.е. {£} ~ н.о.р.с.в. Nn(0, ¥), что
влечет условную гауссовость и независимость случайных век-
торов {уг}:
{yt}~ н.о:р.с.в. NN(a +pLMb У) (t =1, 2, ..., 7). (6.55)
Для нахождения статистических оценок параметров а, Д ¥
модели (6.50) могут использоваться различные методы, на-
пример метод наименьших квадратов (МНК) и метод макси-
мального правдоподобия (ММП). При нахождении оценок
параметров по методу наименьших квадратов предположение
(6.54) не требуется, однако существенно используется при по-
строении статистических тестов адекватности модели.
В данном разделе для нахождения оценок параметров мо-
дели (6.48) используется метод максимального правдоподо-
бия, поэтому предположение (6.54) существенно используется
при вычислении функции правдоподобия для параметров a, J3,
¥ по выборке значений {ytZMt) (^h 2, ..., 7).
Функция правдоподобия для параметров а, Д ¥ имеет вид
условной плотности совместного распределения случайных
векторов {yt} при условии, что {z^} - некоторые известные
значения фактора. На основании (6.55) условная плотность
распределения случайного вектора yt является плотностью TV-
мерного нормального распределения и имеет вид (п. 3.2.3):
flyt\zMt)= (2^)k|exp{0ra^M,)
l (o.jo)
)}
В силу взаимной независимости {yt} их совместная услов-
ная плотность распределения определяется как произведение
условных плотностейXvJ z^) (/=1, 2, ..., 7). Поэтому с учетом
(6.56) получаем, что соответствующая логарифмическая функ-
272

функция правдоподобия относительно параметров а, Д
имеет вид:
Решая задачу максимизации
Ца,Д^)=> max,
находим оценки максимального правдоподобия (МП-оценки)
для параметров а, Д *F [36]:
a=ju-fi мм, (6.57)
т
Р = -^Ч 5 (6.58)
^Z^}^J(6.59)
где
? = -^Е^ ' ^ = ip^ZMt • (6.60)
Оценка параметра ^ имеет вид:
)2>0- (6.61)
Известно [36], что математическое ожвдание и ковариаци-
онная матрица случайного вектора а соответственно имеют
вид:
Е(а) = а, (6.62)
1 \ <Рм J
где Дд/И ^вычисляются по формулам (6.60), (6.61).
18 3ак.7О84 273

Соотношения (6.62), (6.63) означают, что статистика а ,
определяемая по формуле (6.57), является несмещенной и со-
стоятельной в среднеквадратическом смысле оценкой вектора
альфа-коэффициентов в модели САРМ. Кроме того, случай-
ный вектор а имеет условное нормальное распределение, т.е.
US) = Nyv(a, Ъа).
Оценка вектора бета-коэффициентов Д, определяемая по
формуле (6.58), также имеет условное нормальное распреде-
ление вида:
а случайная матрица Т1? вида (6.59) - условное распределение
Уишарпга [2, 36] с ковариационной матрицей Ч* и числом сте-
пеней свободы, равным Г-2, т.е.
2) Тесты адекватности САРМ.
Гипотеза об адекватности САРМ эквивалентна предполо-
жению о том, что рынок находится в состоянии равновесия,
т.е. коэффициенты "альфа" активов равны нулю, и, следова-
тельно, в терминах теории статистической проверки гипотез
(гл. 3) данное предположение может быть сформулировано в
виде:
#о : а = О (САРМ адекватна),
(6.64)
Н\' а ф О (САРМ неадекватна).
Предположим, что коэффициенты регрессии {Д}
(/=1, 2, ..., N) являются статистически значимыми и регрес-
сионная модель (6.50) адекватна в статистическом смысле.
Эти свойства модели устанавливаются с помощью статисти-
ческих тестов значимости {Д} и анализа остатков {dit}
(/=1, 2, ..., TV, /=1, 2, ..., 7) (см. п. 3.5.3, а также [1, 12]). Век-
тор остатков df=(djt)eyiN при этом определяется по формуле
dt=(dit)= yt-yt=yt-(p+fizMt),t=l92, ..., Г,
где {yt, iMt) ~ наблюдаемые, у,- прогнозные значения пере-
менных.
Для принятия решения относительно гипотез Щ, Н\ вида
(6.64) может быть сформулирован следующий тест:
274

гипотеза
[не отклоняется, если JT\ < a(s)
[отклоняется, если \JT\ > Ays),
(6.65)
где Jf — статистика критерия с условной функцией распределе-
ния Fj\Hq(u), (иеШ1) при условии, что гипотеза Щ верна;
(6.66)
- критическое значение статистики (порог критерия),
равное квантили распределения статистики Jj уровня
1-6-/2, где 8 - заданный уровень значимости критерия
Укажем на некоторые возможные способы определения
статистики Jj и соответствующие тесты проверки гипотез
(6.64).
Тест Вальда [37]. Статистика критерия в тесте Вальда име-
ет вид:
или с учетом (6.63):
( ~2 V1
^ (6.67)
Известно, что статистика критерия Jj вида (6.67) при усло-
вии, что гипотеза Щ верна, имеет распределение хи-квадрат с
N степенями свободы, и, таким образом, в рассматриваемом
случае порог критерия A(s) вида (6.66) - это квантиль уровня
1—с/2 распределения хи-квадрат с TV степенями свободы.
Однако непосредственно воспользоваться критерием
(6.65)—(6.67) не представляется возможным, поскольку неиз-
вестна матрица *Р. Поэтому используется модификация кри-
терия Вальда, в которой вместо неизвестного истинного зна-
чения данной матрицы используется ее состоятельная оценка,
например МП-оценка Ф вида (6.59). В данном случае рас-
пределение статистики Jj при условии, что гипотеза Щ верна,
асимптотически приближается к хи-квадрат распределению с
N степенями свободы при !Г-»оо.
Тест, использующий конечную выборку. Недостатком опи-
санного выше теста является требование асимптотически
большого объема выборки, что, как известно, сопряжено с
275

нарушением предположения о постоянстве параметров моде-
ли. В связи с этим одновременно несколькими авторами1 бы-
ла предложена модификация теста Вальда, применимого в
случае выборки ограниченного объема Г<оо.
Данный тест основан на статистике вида [37]:
(6.68)
Показано, что если верна гипотеза #0, то статистика J'j
имеет F'-распределение Фишера с N и T-N-X степенями свобо-
ды.
6.4.2. Двухэтапная процедура
тестирования адекватности САРМ
Опишем подход к тестированию адекватности САРМ, ко-
торый активно используется на практике [37, 39, 45]. В осно-
ве данного подхода лежит двухэтапная процедура: на первом
этапе используется исходная модель вида (6.49), на втором
этапе - соответствующая ей регрессионная модель по "про-
странственным данным". Приведем описание задач, решае-
мых на каждом этапе.
Этап!. Вычисляются статистические оценки параметров
{5/}? {/?/} 0"=1> 2, ..,, TV) и проводится проверка адекватности
регрессионной модели на основе тестов значимости коэффи-
циентов регрессии {/?/} и анализа остатков {dit}.
Этап 2. Вместо непосредственной проверки гипотез вида
(6.64) осуществляется проверка адекватности САРМ на осно-
ве модели регрессии вида:
Й = Го+ЯЙ+?/>*=!> 2, ..., N, (6.69)
где{Д} — статистические несмещенные оценки бета-
коэффициентов, вычисленные на первом этапе и исполь-
зуемые в данной модели как "эмпирические данные".
Значения {Д} (/=1, 2, ..., N) относятся к разным активам
и соответствуют одному и тому же периоду тсотЬ что дает
основания считать их пространственными данными (cross-
section data).
1 См.: Gibbons M., Ross S., Shanken J. A Test of Efficiency of a Given Portfolio
// Econometrica. 1989. 57. P. 1121-1152; MacKinlay A. C. On Multivariate Test of
CAPM // Journal of Financial Economics. 1987.18. P. 341-372.
276

Зависимая переменная yf (/—1, 2, ..., N) в регрессионной
модели (6.69) представляет собой среднее по выборке {yit}
значение премии за риск актива / по выборке {yit} за период
Tconst постоянства параметров САРМ и определяется соотно-
шениями:
^ ^т7^-^- (6-70)
1 t=\ L ы\ J ы 1 t=\
Значение переменной у,- может рассматриваться как оцен-
ка ожидаемой в периоде rcomt премии за риск актива /, а зна-
чения R/ и Rq в (6.70) - как оценки ожидаемой доходности
актива и безрисковой ставки за тот же период соответственно.
Если в течение данного периода САРМ верна, т.е. рынок
находится в состоянии равновесия, то параметры /о > У\ моде-
ли (6.69) должны быть, очевидно, равны:
т =0, п = rm - Яо >
где
r ХЛ
- оценка ожидаемой доходности рыночного портфеля для
периода постоянства параметров модели rcomt. В этом слу-
чае согласно (6.48) получаем:
Ri-RovftiRM-Ro), /=1,2, ...,7V,
что соответствует основному уравнению САРМ для неко-
торого актива / и имеет известную интерпретацию: ожи-
даемая премия за риск актива / прямо пропорциональна
премии за риск рыночного портфеля, причем коэффици-
ентом пропорциональности является "бета" данного ак-
тива. Заметим, что значения Rj,Rq и Rm (/-1, 2, ..., TV)
можно считать фиксированными для анализируемого пе-
риода Tconst.
На этом основании задача проверки адекватности САРМ,
т.е. предположения о равновесном состоянии рынка, сводит-
ся к статистической проверке гипотез относительно значений
параметров Д) и у\ модели (6.67). Эти гипотезы имеют вид:
А. #о: Л)=0,
277

В. Щ: y\-RM -
Гипотезы А и В - это гипотезы относительно значений
свободного члена и коэффициента регрессии модели простой
линейной регрессии, для проверки которых используются
тесты, описанные в разд. 3.5.
Если гипотезы Щ в случаях А и В принимаются, то САРМ
считается адекватной. Если хотя бы одна из гипотез Щ откло-*
няется, то САРМ не может быть признана адекватной. Так,
отклонение нулевой гипотезы в случае А свидетельствует о
том, что на рынке имеются неверно оцененные активы, а от-
клонение нулевой гипотезы в случае В означает, что премия
за риск на рынке в целом отличается от ожидаемой в соответ-
ствии с моделью САРМ в равновесном состоянии рынка.
При эмпирическом анализе САРМ типичными наруше-
ниями модельных предположений являются следующие: не-
линейность модели; отсутствие "полной диверсификации"
собственного риска активов в портфеле активов; автокорре-
ляция и гетероскедастичность ошибок наблюдений (см.
п. 3.5.4).
Это приводит к необходимости использования на втором
этапе тестирования адекватности САРМ более сложных моде-
лей. Примером такой модели является модель вида [39]:
Ц^Го+У^+Ъ^+Гз^+Ъ '-1,2, ..., N, (6.71)
где р2, у/? - несмещенные оценки соответствующих пара-
метров.
Нулевые гипотезы относительно параметров модели (6.71)
при проверке адекватности САРМ формулируются следую-
щим образом:
A. Но: уо= Rq,
B. Н$\ у\= RM - Rq,
C. Я0:г2 = 0,
D. Я0:гз = 0.
Во всех случаях в качестве альтернативы Н\ используется
противоположное утверждение Но.
Модель (6.71) позволяет выявить дополнительные типы
нарушений САРМ:
1) нелинейность рыночной линии ценной бумаги (SML),
если отвергается нулевая гипотеза в случае С, т.е.
278

2) отсутствие полной диверсификации собственного ком-
понента риска, если отвергается нулевая гипотеза в случае D,
т.е. yjtO.
Описание некоторых других тестов, а также обсуждение
результатов практического применения тестов адекватности
САРМ можно найти в [37, 39].
6.4.3. Построение и тестирование модели APT
Как следует из предыдущего изложения, модель APT тре-
бует более тонкого, чем САРМ, обоснования и не имеет та-
кой же прозрачной интерпретации. Практическое использо-
вание данной модели сопряжено с рядом существенных про-
блем, некоторые из них упоминались ранее. Дадим краткое
описание схемы построения и тестирования модели APT на
основе реальных статистических данных.
Как следует из п. 6.3.3, модель APT для т>\ факторов {щ}
может быть сведена к двум уравнениям (/=1,2, ...,т, /=1, 2, ...,
N, /=1,2, ..., 7):
= «/+
т
£*//*//+6/. (6-72)
Уравнение (6.72) представляет собой модель множествен-
ной линейной регрессии, а (6.73) описывает функцию регрес-
сии также для некоторой модели множественной линейной
регрессии. Однако между регрессионными моделями, опреде-
ляемыми соотношениями (6.72), (6.73), существует принци-
пиальное различие.
Регрессионная модель (6.72) строится по эмпирическим
данным {/?,/}, {zit}, которые можно рассматривать как временные
ряды, в то время как регрессионная модель, соответствующая
(6.73), основана на так называемых пространственных данных
(разд. 3.3), в качестве которых используются статистические
оценки {Ьц } коэффициентов регрессии {£,/} модели (6.72).
Относительно случайных отклонений {£,,} обычно делаются
предположения типа (6.51)-(6.54), что позволяет применять
традиционные методы статистического оценивания парамет-
ров: метод наименьших квадратов или метод максимального
правдоподобия.
279

Таким образом, процедура построения модели APT вклю-
чает следующие основные этапы.
Этап I. Оценивание параметров {д/},{6//}(/=1,2,..., N, /=1,2,
..., т) и тестирование адекватности модели (6.72) по эмпири-
ческим данным {Rit},{zit}Xt=l, 2, ..., 7).
Этап 2. Оценивание параметров Ц} (/=0, 1, ..., т) и тести-
рование адекватности модели, соответствующей функции рег-
рессии (6.43), по эмпирическим данным |б/7|(/=1, 2, ..., N).
Следовательно, как и в случае с моделью САРМ, для по-
строения и тестирования модели APT может использоваться
двухэтапная процедура. Однако при реализации данного под-
хода для модели APT возникают существенные проблемы,
связанные прежде всего с выбором факторов, обеспечиваю-
щих построение адекватной модели (6.72). Эти факторы
должны быть общими для всех активов, т.е. оказывать влия-
ние на доходности (курсы) всех анализируемых активов и
полностью объяснять корреляцию между доходностями раз-
личных активов. В этом случае компонент %it модели (6.72)
действительно можно интерпретировать как случайное откло-
нение, обусловленное действием собственных для актива /
факторов (/=1, 2, ..., N).
Один из традиционных подходов [37, 39] к определению
факторов {zit} (/=1, 2, ..., т) и соответствующих им коэффи-
циентов {факторных нагрузок) {Ьц} основан на применении
методов факторного анализа, описание которых применитель-
но к экономическим приложениям можно найти в [9].

Глава 7
ЭКОНОМ ЕТРИЧЕСКОЕ
МОДЕЛИРОВАНИЕ ФИНАНСОВЫХ
ВРЕМЕННЫХ РЯДОВ
Важнейший метод принятия ре-
шений для финансового экономиста -
это основанные на моделях статисти-
ческие выводы, т.е. финансовая эко-
нометрика.
Дж. Кэмпбелл, А. Ли, А. Маккинли
Глава содержит описание эконометрических моделей стационарных
и нестационарных случайных процессов типа ARMA и ARIMA, моделей с
условной гетероскедастичностью ARCH, GARCH и EGARCH, используе-
мых для анализа и прогнозирования финансовых временных рядов, а
также проверки гипотез случайного блуждания и информационной эф-
фективности рынка.
По рассматриваемым в главе вопросам рекомендуется дополни-
тельная литература: [1,3, 12, 41, 43] (общие вопросы эконометрическо-
го моделирования, анализа и прогнозирования); [37, 39, 45, 47, 49, 50]
(эконометрическое моделирование финансовых временных рядов); [13,
40,44,48] (эконометрическое программное обеспечение).
Описанные выше модели случайного блуждания и мартин-
гальной эффективности рынка являются лишь некоторыми
гипотезами относительно цен и доходностей финансовых ак-
тивов. Причем описываемый ими рынок можно рассматри-
вать как "рационально устроенный и честно функционирую-
щий". Предсказание цен на данном рынке либо невозможно
в силу случайности и независимости их изменений в случае
модели случайного блуждания, либо в случае мартингальной
модели приводит к тривиальным прогнозам типа: наилучший
прогноз "цены на завтра" - это значение "цены на сегодня".
Обе гипотезы требуют проверки адекватности реальным дан-
ным с помощью соответствующих статистических тестов.
Проблемы тестирования гипотезы случайного блуждания цен
активов и гипотезы мартингальной эффективности финансо-
вого рынка на основе моделей равновесия фондового рынка
обсуждались в гл. 4 и 6.
В данной главе приведем описание двух классов эконо-
метрических моделей, обобщающих описанные выше модели
281

цен и доходностей активов. Такими классами моделей явля-
ются:
• модель авторегрессии интегрированного скользящего сред-
него (autoregressive integrated moving average model -
ARIMA model), предложенная Дж. Боксом и Дж. Джен-
кинсом [3];
• модель авторегрессионной условной гетероскедастичности
(autoregressive conditional heteroskedastic model - ARCH
model), предложенная Р. Энглем1 и получившая даль-
нейшее развитие в многочисленных модификациях.
Указанные модели позволяют решать задачи проверки ги-
потез случайного блуждания цен активов и мартингальной
эффективности рынка; строить нетривиальные прогнозы в
рамках гипотезы мартингальной эффективности рынка
(ARCH-модель); прогнозировать цены и доходности активов
при нарушении гипотез случайного блуждания цен активов и
мартингальной эффективности рынка.
Основной акцент сделан на обсуждении свойств моделей,
что важно при установлении типа модели по эксперимен-
тальным данным с помощью пакетов прикладных программ
(например, EViews (Econometric Views) [40], PC-GIVE [44],
Microfit [46] и др.), в которых реализованы данные модели.
Алгоритмы статистического оценивания параметров и про-
гнозирования на основе рассматриваемых моделей подробно
не обсуждаются, поскольку для большинства пользователей
готового программного обеспечения проблемы, связанные с
практической реализацией данных алгоритмов, представляют
меньший интерес. Кроме того, достаточно полное изложение
данных алгоритмов можно найти в [1, 3, 12, 34, 40, 41, 43].
При описании моделей в качестве "источника случайно-
сти", обусловленного появлением новой информации {инно-
ваций), используется последовательность некоррелированных
в совокупности случайных величин {rjt} (/=0, 1, 2, ...) с нуле-
вым средним значением и ограниченной постоянной диспер-
сией:
Е(7,)=0, D(^)=E(/7/2)=o-7?2<cx), Cov(%7r)=0, &t. (7.1)
Случайную последовательность {r/t}, обладающую свойст-
вами (7.1), обычно называют "белым шумом".
Для компактной записи моделей временных рядов {xt} бу-
дем пользоваться оператором сдвига "назад" L:
1 См.: Engle R. Autoregressive Conditional Heteroscedasticity with Estimates of
the Variance of United Kingdom Inflation // Econometrica. 1982. № 50.
P. 987-1008.
282

Lxt=xt.u Ldxt=xt.d, d>\.
Приведем некоторые свойства данного оператора, которые
будут использоваться далее без дополнительных ссылок:
Lc=c; L(cxt)=cLxt; L(xt+yf)=Lxt+Lyt;
(c\L+c2L)xf=c\Lxt+ c2Lxt;
(l-cL)-l=\+cL+c2L2+..., \c\<\.
Определим также оператор вычисления (взятия) разностей
первого порядка А:
Разности порядка d>\ определяются рекуррентным образом
с помощью метода последовательного вычисления разностей'.
A2xt=A(AXf)=1A(xrXt.\):=AxrAxt_\=xr2xt_\+xt_2 и т.д.
Очевидно, между операторами L и А имеет место связь:
Axt=(\-L)xb Adxt=(\~L)dxt.
Будем использовать также обозначение для полинома от-
носительно оператора L:
-a\L -a2L2 -...-aplf. (7.2)
Познакомимся вначале с широким классом моделей
стационарных временных рядов ARM А, который служит от-
правной точкой при разработке моделей временных рядов
экономических и финансовых переменных. Далее приведем
описание моделей нестационарных временных рядов с детер-
минированным трендом, а также временных рядов, описы-
ваемых моделями ARIMA и ARCH. Проиллюстрируем воз-
можности использования этих моделей в задачах анализа цен
и доходностей финансовых активов.
7.1. МОДЕЛИ СТАЦИОНАРНЫХ ВРЕМЕННЫХ РЯДОВ
Для описания стационарных финансовых временных рядов
используется модель авторегрессии - скользящего среднего
ARM A (autoregressive moving average model). Обобщением
ARM А-моделей на случай нестационарных случайных про-
цессов являются ARIMA-модели. Модель ARMA - это ком-
бинация двух моделей временных рядов: модели авторегрес-
сии AR и модели скользящего среднего МА. Познакомимся с
каждой из них в отдельности.
283

7.1.1. Модель авторегрессии
Говорят, что временной ряд {xt} описывается моделью ав-
торегрессии порядка р>\ (обозначается - AR(p)), если ряд {xt}
подчиняется разностному уравнению порядка /?, т„е.
xt=ao + a\XtA + а2хи2 +...+ а^р+ r\t,t=\, 2, ..., (7.3)
или
xraxxtA -a2xt_2 -...-
что с учетом свойств оператора L и обозначения (7.2) эквива-
лентно представлениям:
(1 -щЬ -a2L2 -...-apLP)xt =«о + т (7.4)
или
a(L)xf=ao + rjt.
Параметры модели {а/} (/=1, 2, ..., р) называются коэффи-
циентами авторегрессии, параметр oq - свободным членом (час-
то полагается равным нулю). Параметр р определяет порядок
зависимости от прошлого, а случайные величины {rjt} являют-
ся "белым шумом".
Для полного описания модели AR(/?) необходимо задание
начальных значений временного ряда х\_р, х2-р, ..., xq. Проблема
задания начальных значений особенно актуальна при исполь-
зовании "коротких" временных рядов. Обычно их считают
случайными величинами, не зависящими от последовательно-
сти значений {77,} (/=1, 2, ...). В "эргодических" случаях, когда
поведение {xt} при Г->оо не зависит от начальных значений,
конкретный вид начальных значений не играет существенной
роли, поэтому часто полагают: xi.p=x2-p=...=:ixq=0. В дальней-
шем для упрощения анализа будем предполагать, что началь-
ные значения временного ряда принимают некоторые фикси-
рованные значения.
Разностному уравнению (7.3) можно поставить в соответ-
ствие так называемое характеристическое уравнение вида:
АР-а1АР-1-...-ар_]А-ар=О. (7.5)
Модель AR(/?) описывает стационарный случайный процесс,
если корни {Л/} (/=1, 2, ..., р) уравнения (7.5) удовлетворяют
условию:
Ц/| <1, /=1,2,..., р. (7.6)
284

Можно показать, что Л(=% К где {zi} (/=1, 2, ..., р) - корни
характеристического уравнения в виде:
\-a\Z-ct2#-...-ajg> =0. (7.7)
Поэтому условие стационарности модели AR(/?) вида (7.6)
эквивалентно следующему: U/I>1 (/=1, 2, ..., р), означающе-
му, что все корни характеристического уравнения (7.7) лежат
вне единичного круга1.
В предположении стационарности временного ряда {xt} ви-
да (7.3) его вероятностные характеристики имеют вид
(\<p<k<t):
• математическое ожидание: E(xt)=jux,
где Их =
\-(ах +... + ар)
• ковариационная функция для лага к:
<рк = Co\(xt,xt_k) =a{<pk-i + a2<pk-2+...+ap<pk-p9 (7.8)
• дисперсия:
ах2 ее T)(xt) = щ =a{<p\+a2<p2+-~+ap<Pp+°'i12- (7-9)
Достаточно полное описание модели AR(/?) можно найти в
[1, 34]. Поэтому из-за ограниченности объема настоящего
учебного пособия приведем более детальное исследование
свойств частного случая модели AR(p), когда р=1.
1) Модель авторегрессии первого порядка и ее характеристи-
ки.
Модель AR(1) упоминается в различных разделах данного
пособия и является (наряду с моделью AR(2)) наиболее часто
используемым на практике вариантом авторегрессионной мо-
дели. Из (7.3) следует, что модель AR(1) временного ряда {xt}
имеет вид:
xt=ao+ axxtA + Tjt (7.10)
или
(1-щЬ)х,=ао+ т- (7-11)
Характеристическое уравнение (7.5) в рассматриваемом
случае принимает вид Я-«1=0. Поэтому условие стационарно-
1 Поскольку в общем случае корни характеристического уравнения (7.7)
могут быть комплексными, то при формулировке условия стационарности
модели требование к абсолютным величинам корней характеристического
уравнения обычно заменяется на требование: "все корни характеристическо-
го уравнения лежат вне единичного комплексного круга".
285

сти (7.6) для модели AR(1) состоит в следующем: |ail<l,
или, что то же, корень z\ уравнения l-a\Z\=0 no модулю
больше единицы.
Модель AR(1) допускает представление в виде модели
скользящего среднего бесконечного порядка МА(оо). Действи-
тельно, на основании свойств оператора L из (7.10) следует:
х,= (1 -a,L)-1(ou+ m) = (l+alL+al2L2+...)(aQ+ rjt) =
откуда в предположении, что модель AR(1) соответствует ста-
ционарному временному ряду (т.е. | а\ | <1), с учетом свойства
суммы бесконечной геометрической профессии получаем
представление в виде модели МА(оо):
~ а\
(7.12)
Определим вероятностные характеристики временного ря-
да {xt}. Используя свойства "белого шума" {rjt}9 а также свой-
ства математического ожидания и дисперсии, на основании
(7.10), (7.12) получаем следующие соотношения:
• математическое ожидание и дисперсия xt имеют вид:
\-а{
• автоковариационная функция временного ряда {xt} для
к>\\
1 к
\-а{
• автокорреляционная функция (АКФ) временного ряда
{xt} с учетом (7.13), (7.14) принимает вид:
/>*s—=*i*- (7.15)
Щ
Из (7.15) следует вероятностная интерпретация параметра
а\ как коэффициента парной корреляции между двумя сосед-
ними наблюдениями временного ряда: а\—р\. Согласно
(7.13) если значение | «11 близко к единице, то ах2 значи-
тельно больше а2, т.е. даже относительно слабые "возмуще-
ния" {;//} являются причиной большой дисперсии временно-
го ряда {*,}.
286

В качестве примеров на рис. 7.1, 7.2 приведены графики
стационарных временных рядов, описываемых моделью
AR(1). Реализации временного ряда получены с помощью
статистического моделирования при следующих значениях
характеристик модели: ао=0, *о=О, {^} - н.о.р.с.в. Ni(0, 25)
(/=1, 2, ..., 100). Модели отличаются знаком параметра щ, ко-
торый имеет смысл коэффициента парной корреляции между
соседними наблюдениями временного ряда. Рассматриваются
два случая: случай положительной автокорреляции при cq=0.6
(рис. 7.1) и случай отрицательной автокорреляции при а\=
-0.6 (рис. 7.2).
20
19 28 37 46 55 64 73 82
91 100
Рис 7.1. Модель AR(1): положительная автокорреляция
15
10
5
о
-5
-10
-15
1 10 19 28 37 46 55 64 73 82 91 100
Рис. 7.2. Модель AR(1): отрицательная автокорреляция
2) Свойства АКФ и ЧАКФ случайного процесса AR(1).
Отметим свойства АКФ р^ вида (7.15) стационарного вре-
менного ряда {*/}, описываемого моделью AR(1):
1) если «1>0, то pic-^О при к->оо, причем автокорреляцион-
ная функция убывает монотонно (говорят, что имеет место
"экспоненциальное затухание" автокорреляционной функ-
ции);
287

2) если ai<0, то р^ также убывает до нуля при &-w, однако
при этом значения АКФ "осциллируют", совершая колебания
относительно нулевого значения.
В обоих случаях АКФ "затухает" тем быстрее, чем меньше
по модулю значение коэффициента авторегрессии щ. Таким
образом, зависимость между значениями xt и xt.k стационар-
ного временного ряда, описываемого моделью AR(1), убывает
по мере увеличения временного периода (&-»оо), разделяюще-
го моменты наблюдения этих значений. Характер убывания
зависит от знака коэффициента авторегрессии а\
Известно [1, 12, 34], что если модель AR(/?) (p>\) является
адекватной моделью стационарного временного ряда {xt}, то
частная автокорреляционная функция (ЧАКФ) принимает
нулевые значения для лагов, больших порядка авторегрессии,
т.е. для к>р. В случае модели AR(1) ЧАКФ должна принимать
равные нулю значения для всех к>\. Это свойство использу-
ется на практике для оценки порядка авторегрессии стацио-
нарного временного ряда. При этом вместо неизвестной ис-
тинной ЧАКФ используется ее статистическая оценка - вы-
борочная частная автокорреляционная функция.
Как и следовало ожидать, характеристики }лх и <тх2 стацио-
нарного случайного процесса {xt} типа AR(1), определяемые
по формулам (7.13), не зависят от времени /. Их статистиче-
ские оценки в виде выборочного среднего значения х и вы-
борочной дисперсии а\ по реализации временного ряда {xt}
(/=1, 2, ..., 7) определяются соотношениями:
т
Ч'^^1>-*)2. (7Л6)
1 f=l J t=\
Определим статистические оценки параметров а\ и <т,72 мо-
дели AR(1), предполагая для простоты, что «о=О. Для иден-
тификации AR-моделей, т.е. для построения статистических
оценок параметров моделей, могут использоваться различные
методы: метод наименьших квадратов или метод моментов и
метод максимального правдоподобия в случае гауссовского
"белого шума" {rjt} [1, 12, 41, 43].
Статистическая оценка коэффициента авторегрессии а\ с
учетом (7.16) может быть записана в виде:
т
288

Оценка дисперсии сг;/2, согласно (7.11), может быть вычис-
лена по формуле
7.1.2. Модели скользящего среднего
Временной ряд {xt} описывается моделью скользящего сред-
него порядка q>\ (обозначается - МА(#)), если его значения
формируются на основе "белого шума" {rjt}, по формуле:
*t=v + т-птл -nm-2 ---Yqm-q> *=Ь 2> - О7-17)
Учитывая, что y(L)=\ -y\L -y2L2 -...-yqL4, получаем:
xt =ju + (1 -nL -rJ? -...-п1Я)т (7.18)
или
где /и, {%} (k=l, 2, ..., q) - параметры модели (коэффициенты
скользящего среднего); rj\_q, r\i_q, ..., щ- начальные условия.
1) Модель МА(1) и ее свойства.
В частном случае, когда q=l9 имеет место модель скользя-
щего среднего первого порядка МА(1) вида:
1=192, ... (7.19)
Заметим, что в отличие от АЯ(/?)-моделей для обеспечения
стационарности МА(#)-моделей не требуется налагать каких-
либо ограничений на параметры. Ряды вида (7.18) стационар-
ны для любых вещественных значений параметров {%}
(&=1, 2, ..., q). Однако если, например, в модели (7.19) будет
иметь место | у\ |>1, то текущее значение xt анализируемого
ряда, согласно (7.20), будет зависеть от своих прошлых значе-
ний x,_i, Х/_2, ..., которые берутся с весами, бесконечно расту-
щими по мере удаления в прошлое. Чтобы избежать подоб-
ной ситуации, неестественной с практической точки зрения,
для МА(д)-моделей вводятся так называемые условия обрати-
мости. Определим данные условия.
Любая модель кЩр) (1</Коо) может быть представлена в
виде модели скользящего среднего бесконечного порядка
МА(оо). В частности, для модели AR(1) такое представление
имеет вид (7.12). Оказывается, что при определенных услови-
193ак.7О84 289

ях возможно и обратное представление, т.е. представление
модели MA(q) (\<q<co) в виде модели авторегрессии беско-
нечного порядка AR(oo).
Получим данное представление для МА(1). Согласно (7.19)
имеем:
xt +Y\ rjt.\=-ju + xt +y\(-ju + xtA
xt +n(-ju + xtA +n(-/u + xt
= -// (1 + /\ + П2 +...) + ^ + л *м + Л2 *t-2 + лЧ-3+ .»,
откуда может быть получено так называемое обращенное раз-
ложение:
х,=м (1 + П + Л2 +.-) -f>i V* + 7/ ■ (7.20)
Модель МА(1) называется обратимой, если в обращенном
разложении (7.18) бесконечный ряд весов при xt_ky (k=\, 2, ...)
сходится.
Условие обратимости для модели МА(1), очевидно, состоит в
следующем: \у\ |<1. В этом случае (7.20) принимает вид AR(oo):
Л-л+7/. (7.21)
В общем случае для модели МА(#) (1<#<оо) условие обра-
тимости формулируется в терминах характеристического
уравнения модели (7.21): все корни {Zk) характеристического
уравнения
1-Л^-^2-...-^ = 0 (7.22)
лежат вне единичного круга, т.е. \zi\ >1 для всех /с=1,2,...,#.
2) Вероятностные характеристики модели скользящего сред-
него.
Вероятностные характеристики случайного процесса, опи-
сываемого моделью MA(q) (q>\) вида (7.17), определяются со-
отношениями:
• математическое ожидание и дисперсия:
ковариационная функция для к>\ (в предположении, что
Y0-1):
290

П = \an Z У]Гк+], если * < Ч п 24)
1 У=о v ' '
[0, если к > q.
На основании (7.23), (7.24) вероятностные характеристики
для случайного процесса МА(1) вида (7.19) определяются со-
отношениями:
• математическое ожидание и дисперсия xt соответственно
равны:
ковариационная функция временного ряда {xt} для лага
к>\:
nJ-rK если к-Х (726)
[0, если к > 1;
автокорреляционная функция (АКФ) временного ряда
{xt} с учетом (7.25), (7.26) принимает вид:
- <Рк _ -ТтЧ
Рк \ 1 + Г\
щ [О, если к>\.
Таким образом, АКФ процесса MA(q) (q>\) принимает ну-
левые значения для лагов, больших порядка скользящего
среднего, т.е. для k>q. Поэтому значения процесса {xt}, разде-
ленные на более чем q периодов, являются независимыми. В
случае модели МА(1) АКФ вида (7.13) равна нулю для всех
к>\. Это свойство используется для определения порядка
скользящего среднего q в модели МА(#). При этом вместо не-
известной истинной АКФ используется ее статистическая
оценка - выборочная автокорреляционная функция:
т
£(*,-*)(*,-*-х)
где х,<т1 имеют вид (7.16).
Графическая иллюстрация модели МА(1) дана на рис. 7.3,
7.4. Реализации временных рядов получены с помощью ста-
тистического моделирования при следующих значениях ха-
рактеристик модели: ао=О, xq=0, {^Ьн.о.р.с.в. Nj(O, 25)
(/=1, 2, ..., 100). Модели различаются знаком параметра р\\
/?,=0.7 (рис. 7.3), А= -0-7 (рис. 7.4).
291

Рис. 7.3. Модель МА(1):
положительный коэффициент скользящего среднего
20
15
10
5
0
-5
-10
-15
-20
10
19 28 37 46 55 64 73 82
91 100
Рис. 7.4. Модель МА(1):
отрицательный коэффициент скользящего среднего
7.1,3. Модель авторегрессии и скользящего среднего
Временной ряд {xt} описывается моделью авторегрессии и
скользящего среднего порядков р и q (р, q>\) соответственно
(обозначается - ARMA (/?,#)), если
(7.28)
(7.29)
/=1,2,...
или
a(L)xt=ao+){L)T]t.
В соотношении (7.29) полагается
l -axL -a2L2 -...-apl
(7.30)
292

где {«/}(/=!, 2, ..., /О, Ш (*=1, 2, ..., ^) - параметры модели;
х\-р, х2-р, ..., xot m.q, т]2.д, ..., т/о- начальные условия.
Формальным обращением из (7.29) в предположении1, что
a\+...+aptl и л+...+^l, получаем:
Х,=/'+^^" »= ^
a(L) l-(flj +... + ap)
либо
(7.32)
В частном случае, когда p=q=l9 из (7.28) получаем пред-
ставление для модели ARMA(1,1):
^/-ад-i =«о + rjt-nit-h ^=Ь 2, ... (7.33)
Условиями стационарности и обратимости модели
ARMA(p, ^) являются соответствующие условия для ассоции-
рованных с ней моделей AR{p) и МА(^): все корни характери-
стического уравнения (7.7) лежат вне единичного круга {усло-
вие стационарности); все корни характеристического уравне-
ния (7.22) лежат вне единичного круга {условие обратимости).
Проиллюстрируем это на примере ARMA( 1,1).
Получим представления ARMA(1,1) в виде МА(оо) и AR(oo)
моделей. Учитывая в (7.31), что a{L)=\-a\L, y{L)=\-y\L, a
также свойства оператора L, получаем МА(оо)-представление:
* \-ах l-a^' \-ax [ /
Аналогично на основании (7.32) можно получить AR(oo)-
представление:
t\-k -Н7/. (7.35)
v~7\ k=\
Для сходимости рядов в (7.34), (7.35) необходимо, чтобы
выполнялись соответственно условия: | а\ \ < 1 - условие ста-
ционарности модели AR (1) и \/\\<\ - условие обратимости
модели МА (1).
1 Данные предположения выполняются для стационарной и обратимой
модели ARMA(p, q).
293

Из (7.34) непосредственно следуют выражения для матема-
тического ожидания и дисперсии случайного процесса ARMA
(1,1):
SllZ^Z 2. (7.36)
1 - ос\ \~а{
Получим представление для автокорреляционной функции
случайного процесса ARMA (1,1)- Согласно (7.34) значения
xt_\ не зависят от значений rjt+i (^0), соответствующих буду-
щим моментам времени, т.е. E(xt_\?]t+j)=0. С учетом этого и
независимости {rjt} из (7.33) следует, что E(xt?]t)=an2, а автоко-
вариационная функция допускает представление:
<Рк =
откуда следует:
<Р\ = «1^0-У1^;Л если к=1,
к-х, если к>2
и, следовательно, автокорреляционная функция определяется
соотношениями:
если fe2. (7.37)
Таким образом, согласно (7.37) АКФ процесса ARMA (1,1)
экспоненциально убывает при &-»оо от некоторого начального
значения р\ до нуля (рк->0 при /с-»оо): монотонно при щ>0,
либо знакопеременно совершая колебания относительно ну-
левого значения при а\<0. Известно [1], что ЧАКФ процесса
ARMA (1,1) ведет себя аналогичным образом, однако харак-
тер убывания определяется знаком параметра у\. ЧАКФ убы-
вает от некоторого начального значения монотонно при /i>0
и знакопеременно при
7.1.4. Построение модели авторегрессии
и скользящего среднего
В соответствии с методологией Бокса - Дженкинса [3]
процесс построения модели ARMA(/?,<7) по реализации вре-
менного ряда {xt} (/=1, 2, ..., 7) состоит из трех этапов: иден-
тификации модели, оценивании параметров, тестировании
адекватности.
Идентификация модели включает:
294

1) визуальный анализ графика временного ряда {xt} с це-
лью выявления "выбросов", "пропусков", структурных изме-
нений, а также признаков нестационарности типа временных
трендов и гетероскедастичности;
2) анализ ВАКФ и ВЧАКФ (выборочных оценок АКФ и
ЧАКФ) с целью исследования стационарности анализируе-
мого временного ряда {xt} и определения возможных значе-
ний параметров р и q;
3) проверка гипотез об отсутствии автокорреляции значений
временного ряда {xt} для отдельных лагов с помощью асимпто-
тического теста значимости значений АКФ, основанного на
нормальном приближении тестовой статистики [1, 43];
4) проверка гипотез об отсутствии автокорреляции значе-
ний временного ряда {xt} на заданном лаговом диапазоне,
включающем К>\ лагов, с помощью Q-статистики Лъюнга -
Бокса1, рассчитываемой на основании значений ВАКФ {рк}
по формуле
к=\
Распределение Q-статистики при условии, что верна нуле-
вая гипотеза об отсутствии автокорреляции значений времен-
ного ряда на заданном лаговом диапазоне, близко к хи-
квадрат распределению с К степенями свободы. Таким обра-
зом, если Q>A(s) (где А(^) - критическое значение статистики,
равное квантили уровня \-s хи-квадрат распределения с К
степенями свободы), то нулевая гипотеза об отсутствии авто-
корреляции отклоняется.
Для статистического оценивания параметров модели
ARMA(/?,g) с заданными значениями р и q могут использо-
ваться различные методы [1, 12, 41, 43]: линейный и нели-
нейный метод наименьших квадратов (МНК), полный и ус-
ловный метод максимального правдоподобия (ММП), а также
метод моментов (ММ).
Тестирование адекватности основано на анализе тестовых
статистик и статистической проверке гипотез относительно
параметров тестируемой модели (п. 3.5.3). Для адекватной
модели оценки параметров модели (коэффициентов авторег-
рессии и скользящего среднего) должны быть статистически
значимыми, а остатки построенной модели должны описы-
ваться процессом "белого шума", т.е. быть некоррелирован-
ными. Для установления некоррелированности остатков ис-
1 Liung G., Box G. On a measure of lack of fit in time series models // Biomet-
rica. 1978. №65. P. 297-303.
295

пользуется описанный выше анализ ВАКФ, ВЧАКФ и Q-
статистики. Кроме того, модель "должна быть наиболее эко-
номичной (parsimony) из возможных альтернативных моде-
лей", т.е. из нескольких моделей, признанных по результатам
тестирования на одном и том же наборе данных адекватными,
лучшей считается модель с меньшим числом параметров, т.е.
с меньшими значениями р и q. Для выбора наиболее "эконо-
мичной" модели могут использоваться Л/С-статистика Акаике
(Akaike information criterion) и ^УС-статистика Шварца
(Schwartz criterion), определяемые по формулам [41]:
где RSS - сумма квадратов остатков (sum of squared residuals);
m - число оцениваемых параметров, т.е. m=p+q+S (£=1,
если используется модель со свободным членом, £=0 в
противном случае). В соответствии с данными критерия-
ми следует выбирать модели с меньшими значениями ста-
тистик AIC и SC.
Наличие автокорреляции остатков может быть следствием
сезонных изменений временного ряда, что влечет необходи-
мость построения сезонной ARMA-модели [43]. При относи-
тельно монотонном увеличении дисперсии остатков (призна-
ке "безусловной" гетероскедастичности) целесообразно осу-
ществить логарифмическое преобразование временного ряда.
Если временной ряд остатков включает периоды с относи-
тельно высокой и относительно малой дисперсией, то целе-
сообразно рассмотреть возможность построения модели
ARMA с остатками в виде ARCH или GARCH (см. разд. 7.3).
7.2. МОДЕЛИ НЕСТАЦИОНАРНЫХ ВРЕМЕННЫХ РЯДОВ
Описанный выше класс ARMA-моделей применим для
описания стационарных (в широком смысле) временных ря-
дов {xt}. Однако большая часть финансовых и экономических
временных рядов являются нестационарными, поскольку их
вероятностные характеристики, такие, как математическое
ожидание, дисперсия, а также автоковариационная и авто-
корреляционная функции, изменяются с течением времени,
296

т.е. являются функциями времени /. По этой причине будем
использовать для них следующие обозначения:
)=crxf9 Co\(xhxt.k)=(pkfh Cor(xhxhk)=pkft.
При эконометрическом моделировании нестационарных
временных рядов различают временные ряды, нестационар-
ные по среднему значению и по дисперсии.
Временной ряд является нестационарным по среднему значе-
нию, если его математическое ожидание изменяется во времени
в соответствии с некоторым детерминированным или вероят-
ностным законом. В данном случае говорят, что временной
ряд содержит детерминированный или стохастический тренд.
Для описания временных рядов, нестационарных по сред-
нему значению, используются два основных класса моделей:
• модели временных рядов с детерминированным трендом, т.е.
модели с трендом в виде детерминированной функции
времени;
• модели интегрированных временных рядов, которые в об-
щем случае представляются в виде модели авторегрессии
интегрированного скользящего среднего (autoregressive inte-
grated moving average model - ARIMA model).
Дисперсия значений экономических и финансовых пере-
менных может также зависеть от времени, при этом говорят,
что соответствующий временной ряд является нестацио-
нарным по дисперсии. Эти временные ряды описываются двумя
классами моделей: с условной и безусловной неоднородностью
(гетероскедастичностью). Эффекты "безусловной" гетероске-
дастичности часто могут быть смягчены или устранены за
счет подходящих функциональных преобразований временно-
го ряда [43]. В задачах финансового анализа особой популяр-
ностью пользуются модели типа ARCH с условной гетероске-
дастичностью [34, 47, 50]. Рассмотрим данные модели.
7.2.1. Модели временных рядов
с детерминированным трендом
Модель временного ряда {xt} с детерминированным трендом
может быть представлена в виде:
xt = AtS+ 4*1=1,2, ..., (7.38)
где {77/} - "инновации" (innovation process), или случайные
ошибки наблюдения, описываемые стационарным слу-
чайным процессом с нулевым средним значением,
297

7/)=O; jLif=E(xt)=f{tf0) - детерминированная функция
времени t или так называемая функция тренда, заданная с
точностью до параметров /?.
Таким образом, под детерминированным трендом понима-
ется изменение во времени среднего значения временного
ряда в соответствии с некоторым детерминированным зако-
ном, определяемым функцией j{t,p). Применительно к эконо-
мическим и финансовым процессам детерминированные
тренды выражают основную тенденцию, или закономерность
функционирования данных процессов.
Построение прогноза на основе модели с детерминирован-
ным трендом предусматривает процедуру выделения тренда и
проверку модельных предположений относительно "иннова-
ций" на основе анализа остатков.
Часто предполагается, что имеет место полиномиальный
тренд, т.е. функция /(/,/?) {р=(р1)еУ\с1) является полиномом
степени d>\ вида:
Таким образом, модель временного ряда {xf} с детермини-
рованным полиномиальным трендом имеет вид:
+т7/,*=1,2, ... (7.39)
/=о
Представление (7.39) может рассматриваться как модель
множественной линейной регрессии относительно факторов
^■(/=1,2, ..., d, d>\):
d
*,=А)+2>*,/ + ?,,/*=1,2, ... (7.40)
7 = 1
Поэтому для выделения полиномиального тренда к регрес-
сионной модели (7.40) применяется линейный метод наи-
меньших квадратов (МНК). Анализ адекватности модели ос-
нован на использовании стандартного набора тестовых стати-
стик (п. 3.5.3) с целью решения таких задач, как анализ
значимости коэффициентов регрессии и адекватности модели
в целом; проверка предположения о том, что остатки являют-
ся "белым шумом"; выбор наиболее "экономичной" модели.
В случае нелинейных функций тренда, допускающих ли-
неаризацию за счет специальных функциональных преобразо-
ваний, также применяется линейный МНК по отношению к
298

преобразованному временному ряду. В противном случае мо-
жет использоваться нелинейный метод наименьших квадратов.
На рис. 7.5 приведены графики временных рядов, описы-
ваемых моделями с детерминированными трендами: квадра-
тичным (xt=5t-0.03fi+r/f) и линейным (xt=2t+r]t). Реализации
временных рядов получены с помощью статистического мо-
делирования при условии, что J7/} ~ н.о.р.с.в. Nj(O, 16)
(t=\929 ..., 100).
250
Рис. 7.5. Модели с квадратичным (верхняя линия) и
линейным (нижняя линия) трендом
7.2.2. Модели интегрированных временных рядов
Нестационарные временные ряды, которые после выделе-
ния тренда с помощью МНК приводят к стационарному ряду
остатков, называются стационарными относительно тренда
(trend stationary time series) [41, 43].
Существует альтернативный тип нестационарных времен-
ных рядов, которые можно привести к стационарному виду
путем применения к временному ряду метода последователь-
ного вычисления разностей определенного порядка d, т.е. его
дифференцированием. Такие временные ряды называются ста-
ционарными относительно взятия разностей (difference station-
ary time series), или интегрированными временными рядами
(integrated time series). Широкий класс моделей интегриро-
ванных временных рядов известен как класс моделей авторег-
рессии интегрированного скользящего среднего (autoregressive in-
tegrated moving average models - ARIMA model), предложен-
ный Дж. Боксом и Дж. Дженкинсом [3]. Дадим краткую
характеристику свойств и методов построения моделей данно-
го типа.
Нестационарный случайный процесс {xt} называется ин-
тегрированным порядка d>\ (integrated of order d), если слу-
299

чайный процесс разностей Adxt является стационарным, т.е.
если операция вычисления разностей порядка d приводит не-
стационарный случайный процесс xt к стационарному виду
впервые при данном значении порядка разностей. Для интег-
рированного порядка d случайного процесса будем использо-
вать обозначение \{d).
На использовании понятия "интегрированный случайный
процесс" основывается определение модели ARIMA.
Говорят, что нестационарный временной ряд {xt} описыва-
ется моделью ARIMA(/?, d, q), если временной ряд {xt} являет-
ся интегрированным порядка d>l, а случайный процесс Adxt
является стационарным и описывается моделью ARMA(p, q).
Таким образом, с учетом обозначений (7.30) модель
ARIMA(p, d, q) может быть описана соотношением:
(7.41)
где {r/f} - процесс "белого шума". Вводя обозначение
из (7.41), получаем более удобное для вычисления прогно-
зов представление модели ARlMA(p,d,q):
- (7 42)
qq *=1, 2, ...
Понятие "интегрированный процесс" становится очевид-
ным, если ввести обратный к оператору А оператор интегри-
рования (или суммирования) S*.
S= (1+L+L2+...) = (l-L)'1 = zf1.
Тогда с учетом (7.42) для d>\ имеем:
(7.43)
т.е. интегрированный процесс {xt} получается суммированием
(интегрированием) стационарного процесса {wt} d раз.
В практических задачах построения моделей финансовых
временных рядов типичными значениями параметров р, d, q
являются значения от 0 до 2. При этом через 1(0) обозначает-
ся стационарный случайный процесс, который в результате
однократного "суммирования" превращается в нестационар-
ный процесс типа 1(1).
Построение модели ARIMA включает два этапа:
1) определение порядка d интегрированное™ нестацио-
нарного временного ряда {xt} и получение временного ряда
разностей wt-Adxt\
300

2) выбор наилучшей модели для стационарного временно-
го ряда разностей {wt} в классе моделей ARMA.
На первом этапе для проверки стационарности временного
ряда и определения порядка интегрированное™ d для неста-
ционарного временного ряда используются тесты "единичного
корня" (см. п. 7.2.3). На втором этапе для построения и выбо-
ра модели ARM А используется методология Бокса-Джен -
кинса, описанная в п. 7.1.3.
В качестве иллюстрации модели ARIMA и возможностей
подхода Бокса-Дженкинса рассмотрим некоторые примеры
моделей нестационарных временных рядов.
1) Модель с детерминированным линейным трендом.
Исследуем вначале возможность исключения детермини-
рованного тренда с помощью метода взятия разностей. Рас-
смотрим модель временного ряда {xt} с детерминированным
линейным трендом (рис. 7.5), которая получается из (7.39),
если d—\, а инновации описываются процессом "белого шу-
ма" {/;,}:
х,=Д} + А>+^ *=1,2, ... (7.44)
Применяя оператор вычисления разностей первого поряд-
ка к обеим частям соотношения (7.44), получаем:
*t ~ *м =А +7/ - 7м (7-45)
или
= {\-L)xt =/
Разностное уравнение (7.45) описывает модель ARMA (1,1)
вида (7.36), у которой а\=у\=1, а аъ=р\. Характеристические
уравнения для AR- и МА-компонент ARMA-модели имеют
единичные корни (unit roots), и, следовательно, модель (7.45)
является нестационарной и необратимой. Случайный процесс
первых разностей wt описывается стационарной, но необра-
тимой моделью МА(1). Это говорит о неприемлемости метода
взятия разностей для исключения детерминированных трен-
дов.
Известно [43], что применение МНК к временным рядам
"стационарным относительно взятия разностей" также не
приводит к желаемым результатам, т.е. не позволяет получить
стационарные ряды остатков. Таким образом, первоочередной
задачей анализа нестационарных временных рядов является
задача определения типа нестационарности. Ее решению по-
священы многочисленные исследования, инициированные
301

работами Нельсона - Плоссера1 и Перрона2, которые позво-
ляют заключить, что временные ряды макроэкономических и
финансовых переменных содержат, как правило, стохастиче-
ские тренды.
2) Модель "интегрированного скользящего среднего".
Рассмотрим процесс ARMА( 1,1) вида:
xt~ ct\xtA =ao+?]t- y\r\t-\, t=\, 2, ... (7.46)
Если в (7.46) положить, что а\->\, то в пределе имеет ме-
сто процесс вида:
WfzAxt —ccQ+?]t -y\ rjt_\. (7.47)
Согласно (7.47) случайный процесс {wt} описывается моде-
лью МА(1), поэтому является стационарным. Если l/jl<l, то
процесс {wt} обладает свойством обратимости. С учетом (7.43)
предельный процесс {xt} типа ARIMA(O,1,1) является резуль-
татом "интегрирования" (суммирования) процесса скользя-
щего среднего {w,}, что дает основание говорить о нем как о
процессе "интегрированного скользящего среднего".
В [3] данная модель используется для описания курса ак-
ций IBM (см. рис. 7.6).
10 19 28 37 46 55 64 73 82 91
100
Рис. 7.6. Динамика курса акций корпорации IBM
3) Нарушение условия стационарности модели ARMA.
К альтернативному способу описания нестационарных
временных рядов по сравнению с моделями, содержащими
1 См.: Nelson Ch., Plosser Ch. Trend and Random Walks in Macroeconomic
Time Series. // Juornal of Monetary Economics. 1982. № 10. P. 130-162.
2 См.: Perron P. Testing for a Random Walk: A Simulation Experiment When
the Sampling Interval Is Varied. / Advances in Econometrics and Modeling (Ed. B.
Ray), Kluwer Academic Publishers, 1989.
302

детерминированный тренд, приводят ARMA-модели при на-
рушении условия стационарности. В качестве примера рас-
смотрим временной ряд {xt}, описываемый моделью типа ав-
торегрессии первого порядка AR(1) (которую можно рассмат-
ривать как модель ARMA(1,O)):
xt=a\xt_{ +?]h /=1,2, ... (7.48)
при условии, что а\>\, a {t]t} - процесс "белого шума".
Если /ft, xq - заданные начальные значения, то разностное
уравнение (7.48) имеет следующее решение:
xt =хоа{ +]£а177/-/ • (7.49)
/=о
Модель (7.48) при а\>\ интерпретируется как модель вре-
менного ряда, содержащая стохастический тренд. Интерпрета-
ция основывается на представлении (7.49).
Тренд в (7.49) содержит детерминированный и стохастиче-
ский компоненты. Детерминированный компонент в виде
экспоненциально возрастающей функции времени х$а\* мож-
но рассматривать как условное математическое ожидание xt в
начальный момент времени: Е{х^х^)=х^а\К
Стохастический компонент тренда представляет собой ус-
ловное математическое ожидание xf для моментов времени
1,2, ..., М.
Условные математические ожидания xt являются случай-
ными величинами, так как зависят от случайных инноваций
7о> т> •••> 7Ь-\ (*7ГХГа jxh\ ):
, Е(дс,|хь, xhx2) =
t-\
X\, ..., хм) / +^
Дисперсия xt с учетом (7.49) и формулы для суммы геомет-
рической прогрессии определяется выражением:
ax -1
из которого следует, что при /-»со дисперсия xt неограниченно
возрастает: D(*/)->oo.
Таким образом, временной ряд {xt} является нестационар-
ным как по среднему значению, так и по дисперсии, причем
рост xt имеет "взрывной" характер (explosive behavior).
303

Временной ряд, график которого приведен на рис. 7.7,
описывается моделью со стохастическим трендом вида:
jx>=1.04x/_i+/ft, *ь=0. Реализация временного ряда получена с
помощью статистического моделирования при условии, что
{77,}~н.о.р.с.в. N^O, 9) (/=1, 2, ..., 100).
900
800
то 700
| 600
к 500
I 400
| 300
W 200
100
о
10 19 28 37 46 55 64 73 82 91 100
Рис. 7.7. Модель со стохастическим "взрывным" трендом
4) Случайные процессы единичного корня и модель случайно-
го блуждания.
Рассмотрим, как и в предыдущем случае, модель типа
AR(1) со свободным членом и "белым шумом" в качестве ин-
новаций {77,}:
х,=оо+а1хм + Пь 1=1,2,... (7.50)
Как отмечалось ранее, временной ряд {xt} является стацио-
нарным при 0<а\<\1 и нестационарным (имеет "взрывной"
характер роста) при а\>1. Рассмотрим промежуточный слу-
чай, когда а\-\. В данном случае модель (7.50) принимает
вид:
/7/, f=l, 2, ...
(7.51)
и известна как модель случайного блуждания с дискретным вре-
менем, которая рассматривалась в разд. 4.1. Соотношение
(7.51) описывает модель случайного блуждания со "сносом",
если од?Ю, и без "сноса", если «о=О.
Если xq - заданное начальное значение, то решение раз-
ностного уравнения (7.51) имеет вид:
>, (7*52)
1 При моделировании финансовых временных рядов уместно полагать,
что oci>0.
304

откуда следует:
juXft =E(xt)=
t-k
Таким образом, если t значительно больше к, то значения
АКФ рь>t принимают значения, близкие к единице (р^г-»1 ПРИ
k/t->0), вследствие чего временной ряд представляется сильно
сглаженным, хотя и является нестационарным как по средне-
му значению, так и по дисперсии.
Процесс случайного блуждания является примером интег-
рированного процесса 1(1). Действительно модель (7.51) мо-
жет быть представлена в виде:
Ах,=аь+ г\ь /=1, 2, ...
Поскольку "белый шум" является стационарным процес-
сом, то и процесс Axt является также стационарным, т.е. вы-
числение разностей первого порядка для временного ряда {xf}
приводит к стационарному процессу.
Условие а\ = 1 для модели (7.50) означает, что корень z\ со-
ответствующего характеристического уравнения l-a\Z\—0 ра-
вен 1. По этой причине процессы 1(1) типа (7.51) часто назы-
вают процессами единичного корня (unit root process). График
реализации такого процесса в виде модели случайного блуж-
дания без "сноса" (ccq=0) приведен на рис. 7.7. Реализация
получена с помощью статистического моделирования при
следующих условиях: л<>=10, {rjt} - н.о.р.с.в. - Ni(0, 9)
(/=1, 2, ..., 100).
' 60
10 19 28 37 46 55 64 73 82 91 100
Рис. 7.8. Процесс единичного корня
20 Зак. 7084
305

7.2.3. Использование тестов единичного корня
для проверки "гипотезы случайного блуждания"
Как следует из приведенных выше примеров, значение па-
раметра а\ в модели (7.50) критическим образом влияет на
тип модели временного ряда. На практике в задачах анализа
временных рядов цен либо доходностей активов актуальной
является проблема выбора между двумя альтернативами:
• «i=l, т.е. временной ряд {xt} является нестационарным и
описывается моделью случайного блуждания;
• щ<\, т.е. временной ряд {xt} является стационарным и
описывается моделью AR(1).
В первом случае, когда подтверждается "гипотеза о слу-
чайном блуждании", будущие значения анализируемых харак-
теристик непредсказуемы, во втором случае возникает воз-
можность их предсказания.
Используемый в рамках методологии Бокса - Дженкинса
анализ ВАКФ позволяет сделать лишь предварительные вы-
воды относительно нестационарности временного ряда. Од-
нако анализ не дает возможности установить тип нестацио-
нарности, т.е. отличить стохастический тренд от детермини-
рованного. Действительно, медленное убывание ВАКФ при
увеличении значения лага может быть обусловлено как нали-
чием единичных корней, так и присутствием детерминиро-
ванного тренда. При анализе ВАКФ возникает также опас-
ность принять стационарный процесс "почти единичного кор-
ня" (near unit root process) за нестационарный процесс.
По этой причине для установления типа нестационарности
и определения порядка интегрированное™ для интегриро-
ванных нестационарных временных рядов были разработаны
статистические тесты, получившие название "тесты единич-
ного корня" (unit root tests) [38, 43]. Тесты разнообразны, что
обусловлено необходимостью учета различных особенностей
тестируемых временных рядов: сезонных эффектов и струк-
турных изменений, сериальной корреляции и гетероскеда-
стичности остатков и т.д. Наиболее известным тестом еди-
ничного корня является расширенный тест Дики - Фуллера
(augmented Dickey - Fuller test - ADF test)1. Данный тест целе-
сообразно использовать при отсутствии сезонных и структур-
ных изменений в тестируемом временном ряде. Приведем его
краткое описание.
1 См.: Dickey D. A., Fuller W. A. Distribution of the Estimators for Autoregres-
sive Time Series with a Unit Root // Journal of the American Statistical Associa-
tion. 1979. № 74. P. 427-431.
306

В терминах теории статистической проверки гипотез зада-
ча выбора из описанных выше альтернатив относительно па-
раметра а\ (а\>0) в модели (7.50) может рассматриваться как
задача проверки гипотез:
Яо: а,=1, Нх: а{<1 (7.53)
по реализации временного ряда {xt} (t=l, 2, ..., 7) на некото-
ром заданном уровне значимости б.
Формальная проверка1 гипотезы Яо вида (7.53) о значении
параметра а\ на основе стандартной /-статистики некоррект-
на, поскольку временные ряды xt и xt_\ в обеих частях соот-
ношения (7.50) являются нестационарными. Это является
причиной того, что "/-статистика", имеет распределение, от-
личное от стандартного t-распределения Стьюдента. Поэтому
при построении теста осуществляется переход от модели
(7.50) к модели со стационарным временным рядом в левой
части. Данная модель в предположении ао=0 принимает вид:
Act=nxt-i + % *=1,2, ... , (7.501)
где у\ =(«1-1).
Очевидно, исходная задача проверки гипотезы Яо вида
(7.53) эквивалентна задаче проверки гипотезы о значимости
коэффициента регрессии у\ в модели (7.50'):
Яо: л=0, Яь л<0. (7.53')
Пороговые значения для тестовой статистики в данном
случае хотя и отличаются от квантилей стандартного t-
распределения, однако могут быть получены с помощью ста-
тистического моделирования, т.е. методом Монте-Карло [31].
Предполагается, что в качестве "истинной" модели (data-
generating process) временного ряда может выступать модель
случайного блуждания со "сносом" или без "сноса", а в каче-
стве альтернатив - стационарный либо стационарный относи-
тельно линейного детерминированного тренда (trend
stationary) процессы. Поэтому тестируемая модель допускает
следующие расширения:
• дополнительное включение константы (свободного чле-
на) ю;
• дополнительное включение константы уо и линейного де-
терминированного тренда ¥it.
1 Статистические тесты относительно значений параметров регрессион-
ных моделей описываются в п. 3.5.3.
307

Кроме того, для учета возможной автокорреляции остатков
в тестируемую модель вводятся лаговые переменные по Axt.
Таким образом, ADF-тест предусматривает следующие вари-
анты тестируемой модели (/=1, 2, ..., 7):
/=2
/=2
/=2
Процедура тестирования включает два этапа: 1) оценива-
ние параметров тестируемых моделей с помощью МНК и
2) проверку гипотез о значимости коэффициентов регрессии
и свободного члена. Различным вариантам моделей соответ-
ствуют различные пороговые значения "/-статистики" Дики -
Фуллера относительно коэффициента у\, которые вычислены
и представлены в виде таблиц для трех различных уровней
значимости: #е{0.01, 0.05, 0.1} и различных значений длины
ряда Г [38, 43].
Задача выбора значения порядка авторегрессии р обычно
решается путем последовательного тестирования моделей, со-
ответствующих различным значениям данного параметра
(/?=/? *-1, />*-2,), начиная с некоторого достаточно большого
значения/?*. Руководствуясь "принципом экономности", сре-
ди адекватных моделей предпочтение отдается модели с
меньшим значением р. При этом используются статистики
Акаике и Шварца, описанные в п. 7.3.1.
При использовании ADF-теста возникает еще одна про-
блема - проблема кратных корней (multiple roots problem). По-
скольку процессу AR(p) соответствует р корней, то соответст-
вующий процесс единичного корня может иметь d*<p еди-
ничных корней. Это означает, что данный процесс является
интегрированным порядка d*, т.е. 1(*/*)-процессом, и, следо-
вательно, для приведения его к стационарному виду требуется
д?*-кратное взятие разностей. Для определения порядка ин-
тегрированности ADF-тест применяется последовательно для
различных предполагаемых значений d (начиная с d—l) до
получения в первый раз стационарного ряда разностей при
d=d*. На практике обычно d*<2.
308

Использование тестов единичного корня, очевидно, рас-
ширяет возможности решения задачи проверки "гипотезы
случайного блуждания цен финансовых активов", обсуждав-
шейся в разд. 4.1.
7.3. МОДЕЛИ ФИНАНСОВЫХ ВРЕМЕННЫХ РЯДОВ
С УСЛОВНОЙ ГЕТЕРОСКЕДАСТИЧНОСТЬЮ
Пусть случайный процесс {xt}, описывающий поведение
цен активов на финансовом рынке, является мартингалом от-
носительно некоторого потока информации {3/}, т.е. допуска-
ет представление в виде 3:
*ж = х/+ 6н, £0, (7-54)
где {^} - последовательность некоррелированных случайных
величин (ошибок прогнозов), для которых имеет место
свойство:
,)=О. (7.55)
Как отмечалось в п. 4.3.2, требование некоррелированно-
сти {£,} допускает положительную корреляцию j^2} (или
{1^/1}) и не противоречит гипотезе мартингальной эффектив-
ности рынка. Коррелированность отклонений j^2} может
быть следствием их условной гетероскедастичности (или не-
однородности), т.е. непостоянства условной дисперсии:
D(£,| 3 М)=Е(Й| 3 tA)=Gfficonst, />1. (7.56)
Учет подобной корреляции в модели случайных величин
{&} позволяет объяснить особенности поведения цен финан-
совых активов, которые не поддаются описанию в рамках
ARlMA-модели. Примерами таких "особенностей" могут
служить "эффект кластерности"', который состоит в том, что
большие и малые значения {£} образуют серии или кластеры
(скопления) больших либо малых значений; "островершин-
ность" и "тяжелые хвосты" функции плотности распределе-
ния {&}.
Исторически первой из моделей указанного типа является
нелинейная стохастическая модель авторегрессионной услов-
ной гетероскедастичности ARCH (Auto Regressive Conditional
Hetero-skedastic), предложенная Р. Энглем1. Приведем описа-
1 Engle R. Autoregressive Conditional Heteroscedasticity with Estimates of the
Variance of United Kingdom Inflation // Econometrica. 1982. № 50. P. 987-1008.
309

ние данной модели и таких ее модификаций, как модель
GARCH (Generalized ARCH model) и модель EGARCH (Ex-
ponential GARCH).
7.3.1. Модель ARCH и ее применение
для описания финансовых временных рядов
Говорят, что случайный процесс {%t} описывается моделью
ARCH порядка q>\, обозначается ARCH(<7), если:
• распределение вероятностей случайных величин £
(/=1, 2, ...) является условно-гауссовским, т.е.
(7.57)
где 3o={0,Q} - тривиальная информация; 3,_i - доступ-
ная к моменту времени и относящаяся к делу ин-
формация, включающая все прошлые значения от-
клонений £], й, •.., ^-1 для />2;
• условное математическое ожидание %t при условии, что
имеется информация 3/_i, равно нулю:
//,= Е(£,|3М)=О; (7.58)
• имеет место условная гетероскедастичность (непостоян-
ство дисперсии) {£} вида:
£,.£2/-/ , *=1, 2, ..., (7.59)
где ^i_^, ..., 4 ~ начальные значения, которые обычно
полагаются константами; {aj>0} (/=0, 1, ..., q) - пара-
метры модели, удовлетворяющие условиям:
а/>0, /=1, 2, ..., 9, (7.60)
которые обеспечивают неотрицательность значений {o-f2}.
Случайную последовательность {^} можно рассматривать
как последовательность, порождаемую стандартным гауссов-
ским "белым шумом" {77/} по формуле: ^<Jtrjt, где {rjt}
(t=l, 2, ...) - последовательность независимых случайных ве-
личин, распределенных по стандартному нормальному закону
Из (7.59) следует, что дисперсии (волатшьности) at2 могут
быть предсказаны по прошлым значениям £2,_ь •••> Z2t-q- При
этом большие (малые) значения £2М- приводят к большим
(малым) значениям о>2. Появление больших значений ^
310

вслед за некоторой серией малых значений обусловлено по-
явлением малого значения rjh и наоборот. Таким образом,
ARCH-модели позволяют объяснить "эффект кластерное™".
Полагая, что w^^t2~at2=at2(rjt-l), получаем представление
модели (7.59) в виде:
1,-£2>-/ + и7, (7.61)
где
E0v,|3M) = Е(#|зм) - а? = 0. (7.62)
В силу (7.61), (7.62) модель ARCH(#) может рассматри-
ваться как "негауссовская" авторегрессионая модель AR(g)
для квадратов инноваций {£,2}. Поэтому условием стационар-
ности (в широком смысле) случайного процесса {%t2} является
условие стационарности АЯ(^)-модели: корни характеристи-
ческого уравнения вида (7.7) лежат вне единичного круга.
Однако в отличие от "обычной" авторегрессионной модели
"инновации" {wt} для модели (7.61) являются гетероскеда-
стичными.
Используя оператор сдвига L и обозначение
a(L)=(l -axL -a2L2 -...-aplf), (7.63)
представим (7.61) в виде:
(1 -axl -a2L2 -...-ар1Я)& =oq + wt. (7.64)
Если процесс {^2} является стационарным, т.е.
#1+#2+...+а<7<1, то' согласно (7.58) и (7.62)-(7.64), безуслов-
ные математическое ожидание и дисперсия ^ определяются
по формулам:
0, (7-65)
а° -, f>0. (7.66)
\-(ax+... + aq)
Свойство (7.66) означает безусловную гомоскедастичность
случайных величин {£}. Таким образом, свойства (7.65),
(7.66), традиционно предполагаемые при определении модели
случайного блуждания, сохраняются в рамках мартингальной
модели цен активов.
В качестве иллюстрации основных свойств ARCH-модели
перечислим основные характеристики случайного процесса
311

{&}, описываемого моделью ARCH(l), в предположении, что
выполняется условие ее стационарности 0<aj<l и 3cq2<l.
Имеют место следующие соотношения для характеристик
случайного процесса {£2}:
• математическое ожидание
- ах
• дисперсия1
автокорреляционная функция для лага \<k<t
Рк =<*\к\ (7.67)
коэффициент эксцесса
6#i2 .л
Ч>0- (7.68)
1 -3^!
Согласно (7.67) случайные процессы ARCH(l) и AR(1)
имеют, как и следовало ожидать, одинаковую автокорреляци-
онную функцию. Из (7.68) и условия За\2<\ следует положи-
тельность коэффициента эксцесса tcj, причем его величина
тем больше, чем больше а\, т.е. чем сильнее корреляция меж-
ДУ & и £м- Учитывая, что для нормального распределения
аг2=О, положительные значения дг2>0 означают, что кривая
плотности распределения {£/} имеет более "острую" и "высо-
кую" вершину, а также более "тяжелые хвосты", чем кривая
плотности нормального распределения. Это свойство ARCH-
модели является еще одним ее достоинством, поскольку для
большинства финансовых активов коэффициент эксцесса яв-
ляется положительным [50].
Модель ARCH(#) вида (7.59), (7.60) позволяет предсказы-
вать величины $+1 или 1^74-/1 на t>\ шагов вперед, т.е. стро-
ить прогнозы U?+/ B виДе условного математического ожида-
ния |^+/=Е(^+/ \e3j) (где З71 включает значения £,2 для про-
шлых моментов времени (=1, 2, ..., 7). В частности, для
ARCH(l) имеет место следующая прогнозная функция:
1 Вывод этой и последующих характеристик приведен в [34].
312

1а
где предполагается, что «о, а\ - статистические оценки соот-
ветствующих параметров по реализации анализируемого вре-
менного ряда длиной Т. Однако модель ARCH не дает ответа
на вопрос, в каком направлении будет изменяться модели-
руемый показатель, поскольку знак величины &+/ остается
неизвестным. Укажем на некоторые модификации модели
ARCH(/?).
7.3.2. Модификации модели ARCH:
модели GARCH и EGARCH
Одним из недостатков моделей ARCH(#) является то, что
при их практической реализации приходится прибегать к
большим значениям порядка модели q, что часто приводит к
нарушению условия (7.60) положительности <jt2 некоторыми
из оценок параметров {«,-}(/= 1, 2, ..., q). Этой проблемы ино-
гда удается избежать при использовании обобщенной (General-
ized) ARCH-модели или модели GARCH (p,q) порядка р>\ и
<7>1, предложенной в 1986 г. Т. Боллерслевом1.
Модель условной гетероскедастичности {£,} в рамках
GARCH (p,q) определяется соотношением:
а} =
где gi_q9 ..., §), <*i-p, •••» ^o - начальные значения; а0, {«/} (/=1,
2, ..., ^), {/^} (/=1, 2, ..., /?) - параметры модели, удовлетво-
ряющие условиям положительности at2>0:
/=1, 2, ..., д,у=1, 2, ..., р).
Таким образом, условные дисперсии а} в соответствии с
(7.69) зависят от предыдущих значений {£2М-}, (/=1, 2, ..., q) и
у
Полагая в (7.69), что w^}—ot2 и делая замену at2=^f2—wh
получаем представление модели GARCH (p,q) в виде модели
ARMA(m,/?):
1 См.: Bollerslev T. Generalized autoregressive conditional heteroskedasticity //
Journal of Econometrics. 1986. V. 31. P. 518-537.
313

tf = ao+(a(L) + Д/,))£2,_,+ wt -p(L) wM, (7.70)
где m=max{/?, q).
Случайный ARMA-процесс {^2} является стационарным,
если все корни характеристического уравнения, соответст-
вующего a(L) + Д1), лежат вне единичного круга.
Популярным на практике частным случаем данной модели
является модель GARCH (1,1) вида:
b *=1, 2, ... (7.71)
Модель GARCH (1,1) зависит от трех параметров: оо>0,
а\>0 и /?i>0. Представление типа (7.70) для данной модели
имеет вид:
откуда следует, что условие стационарности модели
GARCH (1,1) имеет вид: щ + /?,<1.
В [50] была предложена модификация GARCH, которая
состоит в моделировании не условной дисперсии, а условного
среднеквадратического отклонения. В модифицированной
модели GARCH (1,1) вместо (7.71) при этом используется со-
отношение:
at= ао+ап£м|+/?10/_1, *=1, 2, ... (7.72)
В соответствии с (7.72) большие значения £м оказывают
меньшее влияние на условную вариацию, чем в стандартной
GARCH-модели.
Показатели волатильности, или изменчивости, цен активов
(дисперсия, среднеквадратическое отклонение цен активов и
их логарифмы) являются характеристиками риска для данных
активов. Одним из недостатков этих характеристик риска яв-
ляется их "нечувствительность" к знаку изменений цен акти-
вов. Популярной в задачах анализа финансовых временных
рядов является модель экспоненциальной GARCH (exponential
GARCH - EGARCH), которая была предложена Д. Нельсо-
ном1 в 1991 г. Модель EGARCH (p,q) позволяет моделировать
асимметричные отклики на повышение и понижение курсов
активов. Опишем частный случай данной модели при p=q=\.
Для модели EGARCH (1,1) имеет место соотношение:
), *=h 2, ... , (7.73)
1 См.: Nelson D. В. Conditional Heteroscedasticity in Asset Pricing // Econo-
metrica. 1991. № 59. P. 347-370.
314

где
- "функция влияния новостей", которая осуществляет
корректировку волатильности, определяемой log(a2/), в
соответствии с изменением цены актива gt_\.
Можно показать, что случайная последовательность
/o>_i)} является "белым шумом" с нулевым средним зна-
чением и постоянной дисперсией, так что случайный процесс
{log^,)} описывается моделью ARMA(1,1) и является стацио-
нарным при а\<\. Значение функции влияния Д) зависит от
величины и знака ее аргумента, причем
df J0, + в2, если £,_! >0
d£,_i [0j -02у если ^_|<0,
откуда следует, что модель EGARCH несимметрично реагиру-
ет на повышение и понижение курсов активов. При этом ми-
нимум волатильности достигается, когда "новости" отсутст-
вуют, т.е. £м=0.
Таким образом, использование "функции влияния ново-
стей" (7.74) позволяет моделировать несимметричные откли-
ки риска в виде log^,) на "хорошие" и "плохие" новости.
Благодаря такой асимметрии показатель волатильности в
большей степени реагирует на падения курса актива, чем на
его подъем, что является характерным свойством многих фи-
нансовых активов [47, 50].
7.3.3. Построение моделей с условной
гетероскедастичностью
Процесс построения моделей ARCH и GARCH состоит из
двух основных этапов.
Этап 1. Обнаружение признаков условной гетероскеда-
стичности в анализируемом временном ряде {xt}9 /=1, 2, ..., Г.
Данный этап включает следующие шаги.
1. Построение наилучшей модели для временного ряда {xt}
(/=1, 2, ...) в классе моделей ARIMA или в классе регресси-
онных моделей и получение временного ряда остатков |<^|
для построенной модели.
2. Анализ ВАКФ, ВЧАКФ и Q-статистик Льюнга - Бокса
(см. п. 7.1.3) для остатков {£,} и квадратов остатков \|,2}.
315

Свидетельством в пользу модели ARCH или GARCH является
ситуация, когда временной ряд остатков \%tf оказывается
"белым шумом", а временной ряд квадратов остатков \|,2j,
отличным от "белого шума" - стационарным процессом.
3. Использование теста множителей Лагранжа для ARCH-
моделей (Lagrange multiplier test for ARCH - ARCH LM test),
который реализуется следующим образом.
Для временного ряда квадратов остатков \%}\ строится
модель в виде
11 = «о + а$А + я2|Д2 +... + aq%_q + С, ■ (7.75)
Признаками условной гетероскедастичности являются:
• статистическая адекватность построенной модели (см.
п. 3.5.3), т.е. наличие статистически значимых коэффи-
циентов регрессии {я/} (/=1, 2, ..., q) в модели (7.75);
• выполнение условия: 77?2>А(^), где R2 - коэффициент де-
терминации построенной модели (7.75), A(s) - квантиль
уровня \-s распределение хи-квадрат с q степенями сво-
боды (в данном случае Т - длина временного ряда остат-
ков). Предполагается, что статистика ARCH LM теста
77?2 имеет асимптотическое при Г-^оо распределение хи-
квадрат с q степенями свободы.
Если признаки условной гетероскедастичности обнаруже-
ны, то выполняется второй этап.
Этап 2. Построение модели в форме ARCH или GARCH, т.е.
оценивание параметров и тестирование адекватности постро-
енной модели. Для оценивания параметров ARCH и GARCH
используется метод максимального правдоподобия для моде-
лей с условной гетероскедастичностью1 (см. также [43]).
Другие модели финансовых временных рядов с условной и
стохастической волатильностью, а также примеры их исполь-
зования описываются в [34, 47, 50], а также обзорной статье
Н. Шепарда2.
1 См.: Engle R. Autoregressive Conditional Heteroscedasticity with Estimates of
the Variance of United Kingdom Inflation // Econometrica. 1982. № 50. P.
987-1008.
2 См.: Шепард Н. Статистические аспекты моделей типа ARCH и стохас-
тическая волатильность // Обозрение прикладной и промышленной матема-
тики. 1996. Т. 3. Вып. 6. С. 764-826.

Литература
1. Айвазян С. А., Мхитарян В. С. Прикладная статистика и осно-
вы эконометрики. М.: ЮНИТИ, 1998.
2. Андерсон Т. Введение в многомерный статистический анализ.
М.: Физ.-мат. лит-ра, 1963.
3. Бокс Дж., Дженкинс Г. Анализ временных рядов. Прогноз и
управление. Вып. 1, 2. М.: Мир, 1974.
4. Буренин А. Н. Рынок ценных бумаг и производных финансо-
вых инструментов. М.: Первая федеративная книготорговая палата,
1998.
5. Бэстенс Д., Ван Ден Берг В., Вуд Д. Нейронные сети и финан-
совые рынки. ML: ТВП, 1997.
6. Васильев Ф. П. Численные методы решения экстремальных за-
дач. М.: Наука, 1980.
7. Гамровски Б., Ранее С. Финансовые модели, использующие ус-
тойчивые законы // Обозрение прикладной и промышленной
математики. 1995. Т. 2. № 4. С. 556 - 604.
8. Гитман Л. Дж., Джонк М. Дж. Основы инвестирования. М.:
Дело, 1999.
9. Дубров А. М., Мхитарян В. С, Трошин Л. И. Многомерные ста-
тистические методы для экономистов и менеджеров. М.: Финансы и
статистика, 1998.
10. Количественные методы финансового анализа / Под ред. С.
Брауна, М. Крицмена. М.: ИНФРА-М, 1996.
11. Коссов В. В., Лившиц В. В., Шахназаров А. Т. Методические
рекомендации по оценке эффективности инвестиционных проектов
(вторая редакция). М.: Экономика, 2000.
12. Магнус Я. Р., Катышев П. К., Пересецкий А. А. Эконометрика.
Начальный курс. М.: Дело, 2000.
13. Малюгин В. И., Харин Ю. С, Мурин Д. Л. и др. Система эко-
нометрического моделирования и прогнозирования СЭМП 1.1: Ру-
ководство пользователя. Минск: БГУ, 2000.
14. Медведев Г. А. Математические модели финансовых рисков.
Ч. 1. Риски из-за неопределенности процентных ставок. Минск:
БГУ, 1999.
15. Мелкумов Я. С. Теоретическое и практическое пособие по
финансовой математике. М.: ИНФРА-М, 1996.
16. Мельников А. В. Финансовые рынки: стохастический анализ и
расчет производных ценных бумаг. М.: ТВП, 1999.
17. Мерфи Дж. Дж. Технический анализ фьючерсных рынков:
Теория и практика. М.: ТВП, 1999.
317

18. Найман Э.-Л. Малая энциклопедия трейдера. Киев: Альфа-
Капитал Логос, 1997.
19. О'Брайен Дж., Шривастава С. Финансовый анализ и торговля
ценными бумагами (FAST). M.: Дело, 1995.
20. Первозванский А. А., Первозванская Т. Н. Финансовый рынок:
расчет и риск. М.: ИНФРА-М, 1994.
21. Роуз П. С. Банковский менеджмент. М.: Дело, 1996.
22. Рубцов Б. Б. Зарубежные фондовые рынки. М.: ИНФРА-М,
1996.
23. Рынок ценных бумаг Республики Беларусь и тенденции его
развития / Под ред. В. М. Шухно, А. Ю. Семенова, В. А. Котовой.
Минск: РИВШ БГУ, 2001.
24. Рынок ценных бумаг / Под ред. В. А. Галанова, А. И. Басова.
М.: Финансы и статистика, 1999.
25. Семенкова Е. В. Операции с ценными бумагами. М.: ИНФРА-
М, 1996.
26. Стренг Г. Линейная алгебра и ее применения, М.: Мир, 1980.
27. Тъюлз Р. Дж., Брэдли Э. С, Тъюлз Т. М. Фондовый рынок. М.:
ИНФРА-М, 1999.
28. Уотшоу Т. У., Паррамоу К. Количественные методы в финан-
сах. М.: ЮНИТИ, 1999.
29. Финансовый менеджмент: Теория и практика / Под ред. Е.
С. Стояновой. М.: Перспектива, 1996.
30. Харин Ю. С, Малюгин В. И., Кырлица В. П. и др. Основы ими-
тационного и статистического моделирования: Учеб. пособие.
Минск: Дизайн ПРО, 1997.
31. Ценные бумаги / Под. ред. В. И. Колесникова, В. С. Торка-
новского. М.: Финансы и статистика, 1998.
32. Четыркин Е. М. Финансовая математика. М.: Дело, 2002.
33. Шарп У. Ф.у Александер Г. Дж.} Бейли Дж. В. Инвестиции. М.:
ИНФРА-М, 1997.
34. Ширяев А. Н. Вероятность. М.: Наука, 1980.
35. Ширяев А. Н. Основы стохастической финансовой математи-
ки. Т.1: Факты и модели. М.: ФАЗИС, 1998.
36. Anderson T. An Introduction in Multivariate Statistical Analysis
(2nd ed.). New York, John Wiley and Sons, 1984.
37. Campbell J. Y., Lo A. W., MacKinlay A. C. The Econometrics of
Financial Markets. Princeton: Princeton University Press, 1997.
38. Charemza W. W., Deadman D. F. New Directions in Econometric
Practice. Cheltenham: Edward Elgar, 1997.
39. Curthbertson K. Quantitative Financial Economics. New York,
John Wiley and Sons, 1996.
318

40. EViews User Guide. Version 3.1. Irvine. California: Quantitative
Micro Software, 1998.
41. Jonston J., DiNardo J. Econometric methods (4th ed.). London,
McGraw-Hill, 1997.
42. Jorion P., Khoury S. J. Financial risk management. Oxford, Black-
well, 1996.
43. Hamilton J. D. Time series analysis. Princeton University Press,
1994.
44. Hendry D. F. PC-GIVE: An Interactive Econometric Modelling
System. Institute of Economics and Statistics. University of Oxford, 1993.
45. Kariya T. Quantitative methods for portfolio analysis: MTV model
approach. Dordrecht, Kluwer Acad. Publ., 1993.
46. Markowitz H. M, Mean Variance Analysis in Portfolio Choice and
Capital Markets. Oxford, Blackwell, 1990.
47. Mills Т. С The econometric modelling of financial time series.
Cambridge, Cambridge University Press, 1999.
48. Pesaran M. H., Pesaran B. Working with Microfit 4.0. Interactive
Econometric Analysis. Oxford, Oxford University Press, 1997.
49. Peters E. E. Fractal Market Analysis: Applying Chaos Theory to
Investment and Economics. New York, John Wiley and Sons, 1994.
50. Taylor S. Modelling of financial time series. Oxford, Blackwell,
1989.

Учебное пособие
Владимир Ильич МАЛЮГИН
РЫНОК ЦЕННЫХ БУМАГ
Количественные методы анализа
Главный редактор Ю.В. Луизо
Зав. редакцией Г.Г. Кобякова
Редактор И. В. Преловская
Художник Н.В. Пьяных
Компьютерная подготовка оригинал-макета С.К.-Р. Бибаева-Клебанова
Технический редактор JI.A. Зотова
Корректоры Ф.Н. Морозова, М.А. Миловидова
Санитарно-эпидемиологическое заключение № 77.99.02.953.Д.008700.12.02
от 24.12.2002 г.
Подписано в печать 31.01.2003. Формат бумаги 60х90'/16. Бумага офсетная.
Гарнитура Тайме. Печать офсетная. Усл. печ. л. 20,0.
Тираж 3000 экз. Заказ 7084. Изд. №371.
Издательство "Дело"
119571, Москва, пр-т Вернадского, 82
Коммерческий отдел - тел.: 433-2510, 433-2502
E-mail: delo@ane.ru
Internet: http://www.delo.ane.ru
ФГУИПП «Янтарный сказ»
236000, г. Калининград, ул. К. Маркса, 18