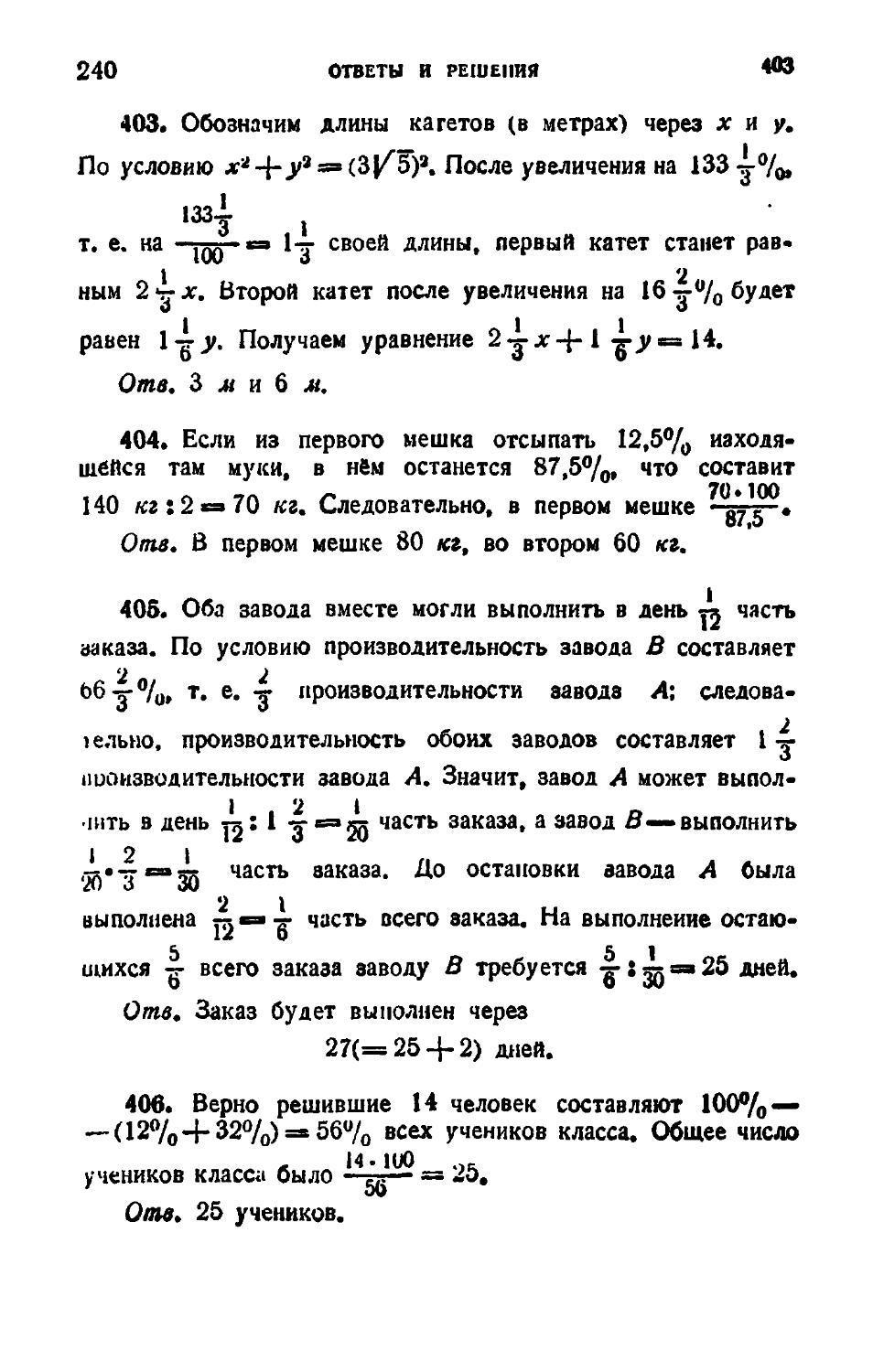Автор: Антонов Н.П. Выгодский М.Я. Никитин В.В. Санкин А.И.
Теги: математика задачи по математике
Год: 1960
Текст
Н. П. АНТОНОВ, М. Я. ВЫГОДСКИЙ, В. В. НИКИТИН.
А. И. САНКИН
СБОРНИК ЗАДАЧ
ПО ЭЛЕМЕНТАРНОЙ
МАТЕМАТИКЕ
ПОСОБИЕ
ДЛЯ САМООБРАЗОВАНИЯ
ИЗДАНИЕ ШЕСТОЕ
Ш
ГОСУДАРСТВЕННОЕ ИЗДАТЕЛЬСТВО
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА 1960
И-3-2
Антонов Николай Петрович» Выгодский Марк Яковлевич,
Никитин Владимир Васильевич» Санкин Александр Иосифович*
Сборник задач по элементарной математике.
Редактор С. М. Половинкин,
Техн. редактор К, Ф. Врудно. Корректор Л. Е. Андрианова
Печать с матриц. Подписано к печати 18/1 i960 г. Бумага 84х№8А&
Фиэ. печ. д. 16,63. У слови, печ. л. 27,26. Уч.-изд. л. 28,0.
Тираж 250000 экз. Цена книги 9 р. 40 к. Заказ 949.
Государственное издательство физико-математической литературы.
Москва, В-71, Ленинский проспект, 15.
Типография № 2 им. Бвг. Соколовой УПП Ленсовнархоза.
Ленинград, Измайловский пр., 29.
ОГЛАВЛЕНИЕ
Предисловие к третьему изданию 4
Предисловие к четвертому изданию 5
Предисловие к шестому изданию 5
Формулы для справок 6
ЧАСТЬ ПЕРВАЯ s д|
АРИФМЕТИКА И АЛГЕБРА В Е§
ГО Ос,
Глава 1. Арифметические вычисления (1—45) .... 13 121
Глава 2. Алгебраические преобразования (46—134), . 18 122
Глава 3. Алгебраические уравнения (135—253) .... 28 152
Глава 4. Логарифмические и показательные уравнения
(254—319) 38 192
Глава 5. Прогрессии (320—357} 43 214
Глава 6. Соединения и бином Ньютона (358—389) . . 48 228
Глава 7. Алгебраические и арифметические задачи
(390-50Э) 52 237
ЧАСТЬ ВТОРАЯ
ГЕОМЕТРИЯ И ТРИГОНОМЕТРИЯ
Глава 8. Планиметрия (510—596) 73 277
Глава 9. Многогранники (597—718) 82 327
Глава 10. Круглые тела (71£—789) 100 431
Глава 11. Тригонометрические преобразования (781—829) 108 479
Глава 12. Тригонометрические уравнения (830—904) . . 111 491
Глава 13. Обратные тригонометрические функции
(905-928) 116 519
ПРЕДИСЛОВИЕ К ТРЕТЬЕМУ ИЗДАНИЮ
Настоящее пособие для самообразования предназначается
для лиц с незаконченным средним образованием или окон-
чивших школу давно и готовящихся к поступлению в вузы.
Отклики читателей на первые два издания (вышедших под
несколько иным названием) показали, что множество учащихся,
занимающихся математикой без помощи преподавателя, дей-
ствительно, нуждаются в таком пособии. Составители хотели
помочь этим лицам научиться решать математические задачи.
и с этой целью дали решения для большинства задач.
Задачи, родственные по идее решения, мы сгруппировали
вмеае. Для первых задач каждой группы дается более
подробное решение, чем для последующих. Второстепенные
моменты рассуждений и вычислений, как правило, опускаются,
чтобы не стеснить самодеятельности учащегося. Напротив,
принципиальным вопросам, существенным для решения задач,
уделяется много места. Особенно это относится к вопросам,
мало освещенным в учебной литературе; таковы, например,
попросы об утрате корней уравнения н появлении посторон-
них корней, об арифметических корнях, о способах изображе-
ния пространственных фигур. Мы полагаем, что соответствую-
щие пояснения принесут некоторую пользу н учителю.
Однажды сделанное разъяснение, как правило, не по-
вторяется в последующих задачах. Однако всюду, где эго
требуется, дана ссылка на номер той задачи, в которой
помешено соответствующее разъяснение. Это сделано в инте-
ресах тех учащихся, которые будут пробовать свои сшы
на отдельных задачах. Все же авторы настоятельно реко-
мендуют решать задачи каждой главы в порядке номеров.
Порядок изучения глав безразличен.
Решение вадачи следует прочесть после того, как
задача решена самостоятельно, или после того, как выяснилось,
чго задача оказалась для .учащегося непосильной. Если после
ПРЕДИСЛОВИЕ
5
решения нескольких последовательных задач учащийся видит,
что они его не затрудняют» то он может пропустить не-
сколько задач; сколько именно — можно сообразить, бегло
просмотрев условия и решения.
ПРЕДИСЛОВИЕ К ЧЕТВЕРТОМУ ИЗДАНИЮ
В четвертом издании, хотя оно издается стереотипно,
оказалось иозможным учесть ряд замечаний, сделанных чита-
телями относительно рационализации решений, а также
исправить погрешности, обнаруженные в предыдущих изда-
ниях. Исполнение пожеланий, требующих более значительной
переделки текста, пришлось отложить до следующего издания.
Составители выражают глубокую признательность всем
лицам, приславшим свои отзывы о книге. Помимо лиц, упо-
мянутых в предисловии ко второму изданию, мы должны
особо поблагодарить тт. Бабушкина Э. (Москва), Бровак
(Москва), Добровольского Б. А. (Лабинск), Коба А. (Ленин-
град), Кравченко В. (Сталинград), Кубичного Г. (Вильнюс),
Лысова В. И. (Сталино), Нахумович Р. М. (Баку), Панова Э.
(Куйбышев), Старчевского Ч. А., Теплову (Кемерово),
Филайовича А. Г. (София, Болгария), Фоминкова В. Ф.
(Запорожье), Хованова Г. М., Шилышкову А. (Киров) и
Шмелькнна С. (Ленинград).
ПРЕДИСЛОВИЕ К ШЕСТОМУ ИЗДАНИЮ
В настоящем издании уточнены формулировки некоторых
задач и внесены некоторые дополнения в объяснения.
Составители выражают глубокую признательность всем
лицам, приславшим отзывы о книге. Помимо лиц, упомяну-
тых в предисловиях ко второму и четвертому изданиям, мы
должны особо поблагодарить тт. Архарову М. (Таганрог),
Заколоднипа Ю. (Горький), Клопкова В. Ф. (Москва), Кузь-
мина В. С. (Львов), Лежнева А., Турчанинова В. В, (Харь-
ков) и Шевченко А. (Одесса).
Заранее выражаем признательность тем читателям, кото-
рые захотят высказать свои пожелания и замечания.
Отзывы и пожелания адресовать: Москва В-7Ц Ленин-
ский проспект 15, «Фнзматгиз».
А/. Антонов, М. Выгодский, В. Никитин.
ФОРМУЛЫ ДЛЯ СПРАВОК
I. Арифметика и алгебра
Пропорции
л с
1. В пропорции -г- «■ -т; а и d — крайние члены, Ь и с — сред-
ние. Основное свойство пропорции а • d = & • с.
2. Перестановка членов пропорции:
v а с -v d с . а Ь v d b
а>7 = 7; 6>T",e; B>7 = J; Г)Т—а-
3. Производные пропорции: дана пропорция T*a-Ti справед-
ливы следующие пропорции:
\ a±b e±d rt4 а ± с а с
Действия со степенями
1. (а • Ь • с)п » ап • £п. сп, то есть ап • *п. сп «(а - Ъ • с)п.
(Д \Л л** д** / д \Я
J) - рт. w есть рг = (у) . 3. *».*•-*■+».
4. а«»; ап __ ат-п, 5. 1: а» = а0: ал = а~п.
6. (a*»)n = a»»»
Действия с корнями*)
т т m __ от __ т т __ m от
1. 1Л*.&.с=а>га.У&-уГс. то есть Y&*Yb-Y^= Y*■*•&
m я*
Yb Yb
*) Корни предполагаются арифметическими, ср. стр. 122—125.
ФОРМУЛЫ ЛЛЯ СПРАВОК
7
2L т т JL /т \Р »
3. ат =}ГаР, то есть Yan^am. 4.\УЗ*) =Vanp.
wb mp __^ mP я*
5. Van= Vanp. то есть V&* = Vi?.
Квадратные уравнения
1. Уравнение вида х* + рх + q = 0 решается по формуле
х _ Р + ЛГ Р% п
jflf2=B— -g- ± К ~4 ^*
2. Уравнение вида длс2 + Ьх + с = 0 решается по формуле
— Ь ± Y Ь* — 4ас
*ы- 25 *
3. Уравнение вида ая2 + 2йлс + с = 0 решается по формуле
— ft ± У^з—ас
*ьз - .
4. Если хх и л"2—корни уравнения я2 + /?лс + Я — ft то
5. jc2 + jwr -I- g = (х — JCi)(jc —лс2), где хх и *2— корни урав-
нения x* + px + q = Q.
6. ах2-{- Ьх + с = а{х — хг)(х — #2). где хг и лс2 — корни урав-
нения ах2 -{-бх + с — О.
Прогрессии (см. стр. 43).
Логарифмы*)
1. Запись \ogaN = лс равнозначна записи а» = W, так что имеем
тождество а ' = W.
2. logo а = 1. 3. loga 1=0. 4. !oga <tf ■ М) = !oga AT + loga M.
5. loga jg = loga * - loga M. 6. !oga (ЛГ) - m loga iV.
7.loSaYN = ±loSaN.
8. О модуле перехода от системы логарифмов с основанием «Ь»
к системе с основанием «а» см. стр. 192—193.
Соединения
1. Л£ = т(т — l)(m — 2). ..(т-л+1). 2. Рт= Ь2.3...т=т!
_ Л" m(m — l)(m — 2)...(m— п+\) _
т~ Рп Ь2.3...я ' С"»~С"» •
*) Числа а (основание логарифма) н N предполагаются поло-
жительными, причем а отлично от 1.
8
ФОРМУЛЫ ДЛЯ СПРАВОК
Бином Ньютона
1. (х + а)т = хт + С^ах™'1 + (?та2хт~г + ...
... + CS-^-V+C^-1^-1* +а™.
2. Общий член разложения: Тк^г = С^гакхт~к.
з. 1 + С1+С1+ ... + с*-%+с£-1+1 = я*.
4. 1-<4 + С-<4+ ...±1=0.
II* Геометрия и тригонометрия
Длина окружности и ее дуги
С = 2nR; I = тс • а /?я (# — градусная мера дуги, я — радиаи-
ная мера).
Площади
Треугольник: S = -^- (л—основание, h — высота);
S~Yp(p — л)(/> — *)(/> — О (р — полупериметр, at b н с —сто-
ч „ а£ sin С
роиы); S = 2 • -
a3VT
Для равностороннего треугольника S — —-г— (а — сторона
треугольника).
Параллелограмм: S = bh (b — основание, h — высота).
Ромб: S « —~- (di и rf3 —диагонали).
Трапеция: S — —i— Л (а и А — основания, Л — высота).
S~mh (т — средняя лииия).
Правильный многоугольник: 5=——(Р—периметр,а—апо-
фема).
Круг: S = к№.
Круговой сектор: S = -д— = -д— = -о~гг (а —градусная мера
дуги сектора, а — радианиая мера, I — длина дуги сектора).
Поверхности
Призма: 5б0В = Р/ {Р — периметр перпендикулярного сечения,
/ — боковое ребро).
ФОРМУЛЫ ДЛЯ СПРАВОК 9
Правильная пирамида: S6oB=-^—(Р—периметр основания,
а — апофема),
Р -4- Ро
Правильная усеченная пирамида: S6oK = 1Т 2а (Рг иР2-
пернметры оснований, а—апофема).
Цилиндр: S60B = 2nRH.
Конус: S6w = kRI (/ — образующая).
Усеченный конус: S6oK = те {R% + /?а) *•
Объемы
Призма: V = SH(S — площадь основания, И—высота).
Пирамида: V в —^-.
Усеченная пирамида: V я -я- (Sx + S2 + V SiSa) .
Цилиндр: V=kR?H.
Конус; К--=$2.
Усеченный конус: V=^o-(til + Ri + Л4Ла).
Перевод градусной меры угла в радианную
и обратно
яа° 0 180° ,
az==~iW'9 (а —радиаиная мера угла» а —градусная).
Формулы сложения
Ь sin (а ± Р) = sin а cos (f ± cos а sin p.
2. cos (а ± P) = cos a cos p x s"* * sin ft.
Двойные и половинные углы
1. Sin 2а = 2 sin а cos а. 2. cos 2а = cos' a — sin3 ct.
о * л 2tga . , a . _/"l—COSa
3-<22а=Т=%Г7- 4.sinT=±]/ —g—
e a , ,/*! + COS a ,„ , a _/~I —COSa
7 a Sin a ft * JL _ 1 — COS«
# g 2" "*"! + cos a ' ***"2~ Sina '
COS a
10
ФОРМУЛЫ ДЛЯ СПРАВОК
Приведение тригонометрических выражений
к виду, удобному для логарифмирования
аЧ-Р а —8
1. sin а + sin р в 2 sin —S-1- cos —тр2- •
аД-8 а — 8
2. sin а — sin р = 2 cos ~Р- sin ■ ^ " .
аД-В а — А
3. cos а + cos р = 2 cos —~- cos —^-.
д4-3 "а —В
4. cos а — cos р = — 2 sin —~- sin —^-.
6. 1 + cos а в 2 cos2 |-„ 7. 1 — cos а = 2 sin2 ^-.
Некоторые важные соотношения
1. sin.sinp^08*8-^0^4^..
2. COS» cosp= СО.С-|»)+совС + р)^
_ 0 , Q Sln(a=+P)-f shl(a — P)
3. Sin a COS P ■■ v T v Г1.
Соотношения между элементами прямоугольного
треугольника
(a, ft —катеты; с — гипотенуза; А, В— острые углы; С —прямой)
1. а = с sin А = с cos В. 2. Ь = с sin Я = с cos Л.
3, a = * tg А = * ctg Я. 4. 6 = a tg В = a ctg A
Соотношения между элементами произвольного
треугольника (a, 6, с —стороны; Л В, С — углы)
1. -—г = ——— = . ~ <теорема синусов),
sin A sin В sin С Л r J '
2. о2 = № + с2 — 2bc cos Л (теорема косинусов).
А + В
tg
tg
3. т" = —. р (теорема тангенсов).
Связь между значениями обратных
тригонометрических функций
(arcsin я; arc cos х\ arctgx — главные значения
соответствующих обратных тригонометрических функций)
1. Arcsin х = kn + (—1)* arcsin х. 2. Arccos х = 2nk ± arccos лс.
3. Arctg x = nk + arctg jc; fc — любое целое число (положитель-
ное или отрицательное).
ЗАДАЧИ
ЧАСТЬ ПЕРВАЯ
АРИФМЕТИКА И АЛГЕБРА
ГЛАВА 1
АРИФМЕТИЧЕСКИЕ ВЫЧИСЛЕНИЯ
3 -3Vo.3
(152 | - 148 {). О,;
1* " 0,2 '
*• 0,8-0,25 '
2J4-204+J
3* 0,0001:0,005
fc(^ + ^).4660--42J
л (85з^-83Г8):2
0,04
(1403l0-138f2):l8l
" ооб2 ■
(мя-юя)-ат+цнз
0,2
й (4927-4621о)-21 + 0'6
7.
14 ЗАДАЧИ
(l2l —6^ —5-i)-13,5 + 0,lll
1П (1Г2 + 21 + 214)-94 + 2ЛЗ
1U. p
(4-4)4
II.
(21 — 1,25): 2,5
2^—2.21
12. « 3 14
1Э.
(3f2+4'375):19i'
0,134 + 0,05
„1 11 2 „6
1A (581-5б1):0,8 + 2^0,225
14.
я 3 3
84* 5
IS. __ .
tA (2.1 —1,965): (1,2 ■ 0,045) 1:0,25
IO' 0,00325:0,013 1,6 • 0,625 *
0,008
[ (2,4+ly)-4,375 (2,75 — 1 A) • 21 "1
F4 4-0,45 J'
18.
19 Г (°-4h°3 (°-з-2р-4
[(з^-2,65).4+2 (l.88 + 2|).^0
30 ГЛ. 1. АРИФМЕТИЧЕСКИЕ ВЫЧИСЛЕНИЯ 15
20 »« . Г 3:<0,2-0,1) , (34,06-33,81).4 1.2.4
*"* *° ' 12,5.(0.4+12)"*"6,84:(28,57 — 25,15)J^ 3 ' 21"
3: |—0.09:(о,15:2^)
2!* 0,32.6 + 0,03—(5,3—3.88)4-0,67'
22. 1 ^: 2.7 4-2,7:1.35 +-(о.4: 2 ^) • (4.2 — 11).
23. (l0:2|+7.e:10).(J-J.0.25+g).
9
26. i4+-0.228:[(l.5291-^^.0.305):0.12].
07 J Ш17 L.4 91.1
"' 120—[28Д.-(13,333-0,3 + 0^)001 )]• 2,004"r** | 32'
[(б,2: 0^1 —g-. o,g\ • 0,2 + 0,15]: 0,02
28. 7— ^—j .
(2+l±.022:0.1).gg
29.6:4—0.8- » ' l ' l + rm
3 u""3 „, 50 ТГ . 46
Т°'4,ГТ 6"1+2,2.ю
'•2
(l.75: |—1.75.1 |):i
30. v—^ «Lii: (6t79: o,7+-0,3).
g-0,0325j:400
16 ЗАДАЧИ 31
4,5: [47,375 — ^26-1—18- 0,75^ • 2,4:0,88]
Зь — я с •
17,81:1,37 — 23 -±: 1 i
32. Найти число, 3,6% которого составляют
3 + 4,2:0,1
(l: 0,3 — 21\. 0,3125
33. Вычислить
(&!. 12 I II23- 260 5 I 800 • 12 28^ О'8-7'2-4^^
Г°25" w + 4la5" ^ои]4-Г8ии- и31) 6,5-2,7.1;92 '
34. Вычислить
Г1б :fflfl±ft^WliWlj(0,64e: 0.3-1 jg)(4S6.2e-
-t + T"1'96)-
35. Вычислить
K'4-«i-a=(»fT-'i)+i-a(i-Hx
v 20,4 • 4,8 - 6,5
X 22,Ы,2 '
36. Вычислить
2,045 - 0,033 + 10,518395 — 0,464774:0,0562
0,003092:0,0001—5,188
37. Вычислить
38. Вычислить
(«3-«S№-4(*4-'iM-
45 ГЛ. 1. АРИФМЕТИЧЕСКИЕ ВЫЧИСЛЕНИЯ
39. Вычислить
17
45^-44^
^63 ^84
31.
4(h Вычислить
X
0,8:(i--l,25) (l,08-|A:y .
0,64
К-К-4)К-4)]^я-
25
41, Вычислить
[
42. Вычислить
(б~4):о'°03 {°>*-%>У
2 ■ • 62 — -4-
[(•£-**)«]=; (-+'4)-tJ'""
-1-1731 : 0,0137.
43. Вычислить х, если
0 7 'Г' bd-h»^. 7 .|0 8-0,0125+6,9 J/ 44*
44. Вычислить х, если
13 9'
[(4,625 - || • ^): л: + (2,5:1,25): 6,75] :
53
68
(* _0,37б): 0,125 + (j — Q:(0,358 — 1,4796:13,7)
45. Найти х, если
17
27"
(2,7 — 0,8)2 -|
(5,2 -1,4):-|
+ х + 8 £ - (^6 + 154.66:70,3): 1,9 = ^
11 /2-g- —l,3j:4.3
18
ЗАДАЧИ
46
ГЛАВА 2
АЛГЕБРАИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ
Упростить выражения:
результат вычислить при а = 8,6; £ = |/1}; с = 3-^,
й-)
до __£ 2 Л ■ Зх + х*\
*°9 ах — 2Ф лгз + лг —2адг —2а*\ ^ 3 + лгГ
2д . 1 / - 3£-6\
а2 —4а:2+2л:2 + 6л: — ад: — За '\х^~ х — 2 /'
-л /2а+10 . 130— а . 30 Q\ За» + 8а»—За
4
- а* —&з а« —6«
6Ь а — * аз —63'
ко х - yU —У)3
ол# д:2 + у2 л:* —у* '
КЛ Г Д-' I 2(Д-П 4(д+1) | Д 1у
°*' La2-2a+l ~*~ «2 —4 д2 + Д — 2 ~Г" д^ — Зд + 2 J А
. 36д8 — 144д — 36д2 Ч-144
Х д» + 27
65 ГЛ. 2. АЛГЕБРАИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ 19
ЯК Г 3(лг + 2) , 2*»—«г-10 |.Г 5 ■
3 3 1
+ 2(лг + 1) ~2(ж—1)J*
ей Iх — У х*+у*-1гу — 2\.4х*+1хЪ+у'* — 4
5t>* ^у-лг лг« —лу —2у» У" *а + У + *У + * '
_ cfl + a — 2 Г(д + 2У —а» ._ 3 1
б7> ап+1_зд»»Ч 4я3 —4 сР—ау
б°* ап«— а8_2вз — а ' а2с — а(лс — с)"
Б9, а(а — Ь)(а — с)"+" 6(6 —а)(6 —с) "+" с(с —а)(с —6) *
60. !+<« + *>-;,. Г1-*-<', + *'П;
1 —(а + Jt)"1 L 2д* J
1
результат вычислить прих=^—р
га-
ек [2J^* — 6Й(4У—о2Гд] ; (гд^ + ЗдРЧ
„, Нт)>
6 ,VrtS X_t i ичу_, i-ч / - i i, a8—68
63. -*г1?г(* — 2в& +A») (* — *»)(«+*).
e __з __.
64. К8х(7Н-41/з)К2/бл; — 4/2*.
66. | V(«+!)•(*-1И1 +2»+.^ • (a9+g + 2)"
О Прежде чем приступать к решению дальнейших задач,
познакомьтесь с замечаниями на стр. 122—125.
20 ЗАДАЧИ
W* |/ За К 9+18«-» + Ув-а*
67. ab Val~nb-n - a~nbx-n V(a~bfl.
68. (»_+ * VM^ + H).
69. [уа-У^'Ь + Уа +Ув+*): (l +У ~^~Ь
1 1 ~V\ а~4"1
7°* (а_У^ + i + VaJ'a^-a-1*-8'
К l-g+У 1+Д »
Г 1 -в F 1 4-в
72. Определить значение выражения
при лг = 1(а+]-), jf = 4(*+t) («> J'*•>!)•
73. Определить значение выражения
Yb + bx+Ya — bx
Ya + bx—Ya — bx
яР"х-»(1+т«)' |W!<L
Упростить выражения:
,- (т+-У)а+(>и— *)*
(т + л:)а—(т —*)*
если
2тп
*=-^ЗГу-» причем т>0, 0<п<1.
82 ГЛ. 2. АЛГЕБРАИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ 21
7б. [<'-**>4+'] Vf0-^-1] \
если х = 2к'г (1 +Л)"1, причем &> 1.
<*+i)¥ 1
/(a'-DCa-l) J*
77. fo1/J—уз 2а» ч (дг*а-3-4 + 4«»дг-»)~»
2<w:(*a —а*) *
а
78.
79. (V^ + T^ _ Уа+х у*
гх)
\ Уа + х У* + Ул
-i
[Уа-Ух-__ Уа+xY
\ Уа + х yi-Yx J
1+ *
2\r ^ ^Улс*+*У^2 х+Ух*+а
х
Ух*+»
82. Вычислить
81. 2х+Ух^=\(\+-*-\ !^
ь
[— A i"l3
a~2*(«*'T,,(«-1faJ
22 задачи
83. Определить значение выражения
(e+ir'+p+t)-1
при в = (2 -f-l/з)"1 и ft = (2 — VW1-
Упростить выражения:
х + У"** — 4л: х — Ух* — Ах
' х— У"** — Ах х +Ух* — Ах '
gg n + 2 + Yri^A ■ n + 2-/?^=4
' я + 2 — Vn2 — 4 п+2 + У"п2— 4-'
ее лГ~~*~ • (У^-У^я _Ух,+УТ=&\
87.
88. (2« + 27^):[(т) '-мД-
89. Доказать тождество
1 9
а2-Л"2
90. Вычисдить
3 3
а*+Ь*
1"
i а = 1,2 и * = -§".
1 — л-2
1 1
а2 + <Г 2
2
а *УГ-
аУ~а—Ь
--1.-1 =
^ 8
а*
=Ь
Yb
97 ГЛ. 2. АЛГЕБРАИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ 23
Упростить -выражения:
91. [(аМ-НДв'-г-М*)—
— UT4- 2b*)\a2 _ 2£s)J . (2e-|-3flT6T);
результат вычислить при а = 54 и £ = 6.
г(а+Л)"г + <а-*ГУ1 + [(«+»)""'-(«-»)"*]
L(a+*)"T + (a—S)"TJ -Ця + й)~7-(л-*)Т1
92.
93. a2(l — a2)"2 —
~2
,(1 — я*)2 + д2(1—a2)
l + L(l-a2f 2J
l ia i _ aa
94.
95. {Я2— jc2)2— *2(R2 — *V2 +
ji _i_
96. (p¥+«T) (p-i+ ,-i)+
WW
97.
|~U+fP7):U+f^)-l i I6
L n-n nv
24 задачи 98
09 Г 4д— 9Д"1 ■ а —4 + За-П»
L2a*-За"7 а*-л"» J
,03. Г-r—^ г-Ч- ^^,-1"-^ + 8х + 16.
L*-4,c" '»^-4^J
toe <д—»3>Уз"—*Уз^—в*5, УД—У%_
107.
■.{/. + [(.»-^)*х-*]'}_-
— -у W — **Р+4л»дс« •
108. [(Vx-VeY%+ {Vx+fc)~*] :
ЛГ A
tVx+AVa*
117
ГЛ. 2. ЛЛГЕВРАИЧЕСКИБ ПРЕОБРАЗОВАНИЯ
25
111. Vy a [VcP + aV<P—&— V& — aVcP—pf.
_j- У (a* _|_ г&х + Зол? -f xY : a.
из. Г(Уг+/*у-е/уу
L л—6
_(.^)(.*+»*П:-{4-
,14. / a~f ±=»
a2+b
l
2 •
+ !
i. ± "
ЗсР + ЗьУаЬ аУа — Ь\~а
ЗАДАЧИ
118
118.
Г 1~* ,-Т
L *+V* J
120.
121.
123.
[Ф^ -Va*+x+2aVx].
I аУх+Yax J
x~]Tx X
y-\а + УШ*+ЬУЙ*+Ь> J _j___J__
a+je
■^длгз — }fa*x
124. Yb-¥*^Vb-fifa~+V* fa
Уд — y^
125.
1
2a4—2
126.
! J. ' Л _i J. £
a* + aB + 1 д* — д8 + 1 л* — д* + 1
VY~2~^T ^3 + 2/2 +V(x+12)/^ —блг — 8
^:^„vr72TTvr3-2>^
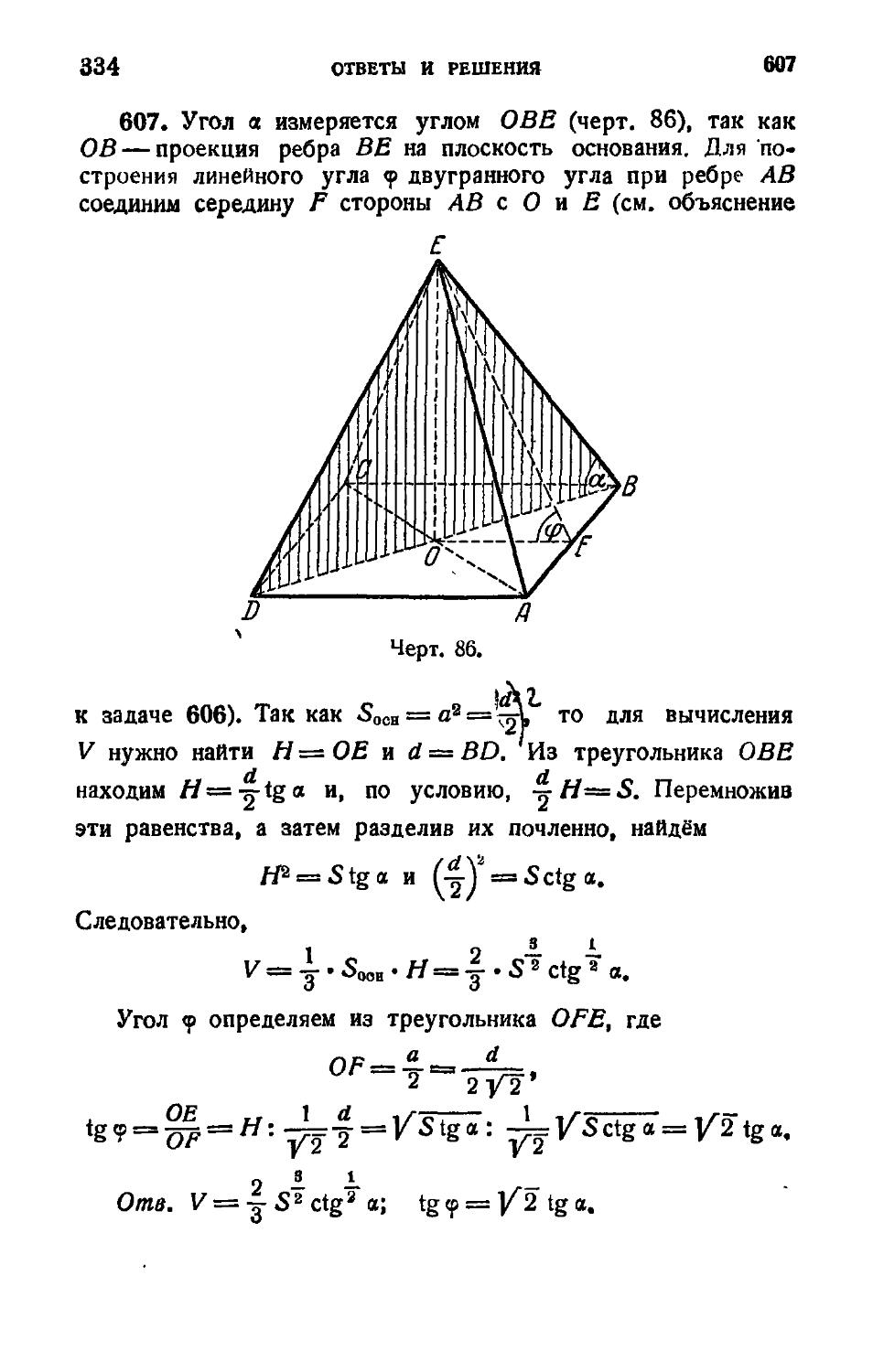
у *—1
132 ГЛ. 2. АЛГЕБРАИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ 27
3 6 _
127 У^У^ + У^^:Уа
-у/ Зл* a + b ab \
а \36 —6л + 2л6 —69 • зд — ab a + b)'
19ft ГЮ^ + Зях ■ ёх — # — ах + аЬ ... , <Л ,
L (4** — ла)"+1 J
|29- L2A:a-24:-4 + 2(jca + 3x + 2)J^X~"
130 О—?)"2+t . уг^т
lew. y ]Г- х — 2 ^
(1 + Х)~*+(1-х)2
■+(*■+ 1>(^+Т+ Х* — 4х ~ х*-Зх — 4У
(л« —аб —2ft2)f^6ft
. b_ /2fl + 26 . д + 36 лЗ + 21а6__\
"Т"а*\а — 46 ~+~2д + 26 2д* — бдб — 862 ) •
28 ЗАДАЧИ 133
133. \*У<**Уь-УаьУ*? , Л. *У*
L abYrt J *а
abYab
6* —4д^ / 1 3 \
* \ б2 + ЫЬ + 2да 2д2 + л* — 62 j#
4а
134.
4(2д6)* (а + 2Ь)-1 . У2бУ"2я6 + У"2д8&
■/д— У2Ь ' Y2ab
fi/ д 2* 86« \
DUa— 48* Зд —66 д2_юдб + 1662^
ГЛАВА 3
АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ
Решить уравнения;
ау
1ЧК 66 + 7д Зду _ 1
|00' 66 262 ~" 62 — аЬ '
1ЧА fl*~" * 1 bx + a — Д2 + ^2
lo°* ~л+Т" "*" л —6 ~~ да—62 '
10- х —д —6 , jf —6 —с , х — с — а о
Ы7. - 1 - 1 ъ —6.
|Чо c + 3z c — 2z _ 2c + z
1 °°* 4с2 + бсо" М* — 6cd ~~ 4с2 — 9л"2 •
1ЧО *-1 i 2яЕ(1 —*) _2аг—1 1-х
|да* "Й^ПГ"1" л*—1 — 1 —л* 1+я •
lAft 3fl* + ] „_ Здб , (2Д;Ц)* | &
1W. - X— a+l -t- а(д+1)3 "h (Л+1)3-
,4Ь ¥+6 + <Д + 6)3 + <*(а + Ь)* ~ дСх + ~Г'
АО х + т _ ах аШ *j£
14 * Д + 6 (Л + 6)2 " д2 —6* Д3 — д£2 + аЩ — 68
1АЧ w _) * t т(* — гп) _ z(z + m) __ мг „
IW| * ~*"m "f"1 *(* + «) m(z—m)~~~'n# — z*
158 ГЛ. 3. АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ 29
144в 6* — х ЬЪ + х ~ ** —х*
11R дд . (а + я) (дпх + пх* + х») ах . nx*
l45# д — x~T~ x*+nx* — a?x — a*n ~ n + x ~т~хЗ — дЗ *
146 /*+i , * + l v.г a + l
*(* + !) | il_ -*
ax+i tlJ"2'
--- д + * fl —jc Za
1 7e a? + ax + x* ал - л* — д* ~ x (Д4 + л*** + **) *
148. л(У"лГ— «) — *(V*" — 6) + «+* = V^
160. 2* * - *2
151. 1
152.
153.
x-\-b b — x 4(x* — *V
2д Й2 —д-'
x — д д- -f x* — 2дх *
x3 a—6 , x
аЬ — 2Ь* ~ ac^ — lbc* ^ be
x . 2x 5дз
x + a ' x — д 4 (x* — a?)
Ia*# ri>-x — 2n 2 — nx "~ я •
155. — * ' *-'
156. 1
(a — x)* a a* — дх (2a — x) *
2£ дЗ_ 6*
X — Д Д* -f- X3 — 2flX
lo'e 2/г + лх 2л: — x* — x» —4x '
i eo л + x — 2я д — 2л ,
,W- 2д-л х—=L
30 ЗАДАЧИ 159
1йо а Д—1 _ 1
10 лдг — х х* — 2пх**\-Фх*
/ а—х\2 ___ / а \а
1АА \ * J U+W _ 5
1А1 Х + х* ■ ]--fl2 — "*
IW1' 1— л:* ' (1 + Лд:)2 — (д + лг)2 — (ft — д)2 '
162. Разложить на линейные множители выражение
Пх — 3*« + 70.
163. Разложить ~ на два множителя, сумма которых
была бы равна ~-j—.
164. Разложить на множители 15х*-{-х2— 2jc.
166. Разложить на множители д:3-(- 2х*-]-4л:2-{-2-{-л\
165а. Решить уравнение
(1-{-х2)2 = 4х(1 — л:2).
« 166. Написать квадратное уравнение, корнями которого
были бы числа -т- и —.
Ь а
167. Составить квадратное уравнение, корнями которого
являются числа ==■ и —,
Ю — ЛрП 10+ 61^2
168. Написать квадратное уравнение, корни которого
а
Ya±Ya — b
ч 169. Корни хх и х% квадратного уравнения
х*-{-рх-\-12 = 0
обладают свойством хг— х2=1. Найти коэффициент р.
177 ГЛ. 3. АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ 31
170. В уравнении
5л*—£л;+1=0
определить к таким образом, чтобы разность корней уравне-
ния равнялась единице.
171. Корни xt и хг уравнения
х2—Зал;-{-я2 = 0
таковы, что л;2-{-л;2= 1,75. Определить величину а.
172. Определить коэффициенты квадратного уравнения
так, чтобы его корни были равны р и q.
173. Корни квадратного уравнения
flx2-f-*jc-f-c = 0
равны jct и х2. Составить новое квадратное уравнение, корни
которого были бы — и —.
Х2 Xi
174. Дано квадратное уравнение
ах2 -{- *дг -1- с = 0.
Составить новое квадратное уравнение, корни которого:
1) вдвое больше корней данного;
2) обратны корням данного.
175. Составить квадратное уравнение, корни которого
равны кубам корней уравнения
ax*-\-bx-{-c = 0.
176. Составить биквадратное уравнение, сумма квадратов
корней которого равна 50, а произведение корней равно 144.
177. Найти все корни уравнения
4л;* — 24л:3-Ь 57л:2 + 18я — 45 = 0,
если один из корней равен З-^/^б.
32 задачи 178
178. Определить свободный член уравнения
6л;*_7х2—16* -Ь«== О,
если известно, что один иэ его корней равен 2. Найти
остальные два корня.
179. Зная, что 2 и 3 являются корнями уравнения
2х* + тх* — 13лг + « = 0,
определить т и п и найти третий корень уравнения.
180. При каких численных значениях буквы а уравнение
х2 + 2ах УвГ^З + 4 = О
имеет равные между собой корни?
180а* В каком промежутке должно изменяться число т%
чтобы оба корня уравнения
хг— 2яи? + т2— 1 = О
были заключены между —2 и 4?
Решить уравнения:
204 гл- 3- АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ 33
»"• У лг + 2^Г jt + 3 * + 2Г х + 3'
e,.*^+yir+5 = ^Ц-
VJt-3 ух —3
92 4 13
93.
x + Yxi + x x — Yx^fx х
2 1 1
2 4-/4 — ха 2 — /4 — *« х'
94. )Л> /7 +У^ — К 2 /? - /* = ^28-
9S. Y7+7k-Y*-r*=\ }/Чттх'
' 1^27 + * —1^27—лг лг '
97. * = й — j/"a2 — л: У-*2 Ч- «2 ■
98 yi + a-**2-**-1 ^ '
* тЛ + я-**з + -га--1 4 '
99 Vl+ "***— а* = *
V"l + a3*2+aJC с3 '
200 х + с+>Л^:=Гр = 9<* + с>
je-fc—У*»—с» 8с
201. j/*jc-{-3 — 4/^=^-4-)/"*+ 8 — 6/^=7 = 1.
202. 2 Уд-f* 4-У* — х = У~а — х -\-Ух(а-\- *)'.
203. ^дя —ж-4-Уй« —jfs=fl + ft.
204. yjT^x + /*-4-л: = УОГ+Ь.
34 ЗАДАЧИ
206. Ух + а^а — У 1с.
206. -^=-2 Ь-*—г— = Vx.
а х
207. Yx-hVx=12.
208. (jc— 1)2+6(JC— 1)4 = 16.
209. 1/^24-/104- 2х= — у /15 — 2л: — 9.
210. ^4-1^2lT^3 = 1^12(jc—1).
211. ~^a^rx + f'b — x = ^ra-\-b — 2x.
212. -^i+2f3? = 3.
213. 2^Р — 31^J=20.
214. 1/оЯ-Зё— fe + x = 0.
-в"»' У x + 2 V 2дг + 2 ~~ 12
216. *ЧгН + /*«+11 = 42.
in?-i Vx + i
x — 4_
218. -^-Лг = а: —8
219. jgZIx)T^=* + (*-Zjoyr*-* =fl._^.
233
ГЛ. 3. АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ 35
221. -*=» 4-i=V*.
1+У^ 2
222. Vx2—3x + 5H-x2 = 3jc + 7.
223. 1/"3jc2 + 5x—8—УЗл2 + 5дг+1 = 1.
224. У>.+ 4j + 8 + У> + 4> + 4 = У2 (У+4j>+6).
Решить системы уравнений:
/ аг2 + ^ = 2(а:^ + 2),
■{
f * + *У + .У=11.
х + ? = 7.
226. ,
дг2^ + дг^2 = 30.
227,1 *jft=12.
228, ' -2--V = 23.
* ( дг^ = 50.
229.1 ^-Л^-180.
I хг—ху—у> = —П.
230. ( 3*2—2^ + 5^—35 = 0.
*' + У = Т*Л
231. ; .
5л:2—My* — 5 = 0.
5_
2
232J *■ + *>+>--18.
дг + ^ = 4.
233. < *'-^ + ^-71
X — J/=l.
36
ЗАДАЧИ
234
234.
235.
х a-L — £L
у "*■ х ~ VI9
х2 — у2 = 7.
(ограничиться положительными решениями, считая, что а > О,
Ь > 0. г > 0, 4 > 0 и тФп).
236.
г
*» —*,у + У = 7.
х»-}-у = 35.
х» + У = 7.
ху(х + у) = —2
(ограничиться действительными решениями).
ху(х-\-у) = Ъ0,
■«J-f-y}=--35.
237.
238.
239. { *~У
{
х+у
ху = Ь.
»i-
240.
241.
242.
•к-г-.У-г-*— 1.
aje-V-&y-r-c2 = d,
л:-|-2^-|-ЗгЧ-4и==30.
2* — З.у -I- Ъг — 2и = 3,
3x-T-4jr — 2г— и=^1,
4х — ^-|-б2 — Зи = 8.
*+■ .У-Ь 2 = 4,
JC И-2^ + 32 = 5,
х' + .У8 -1-22 = 14.
251
ГЛ. 3. АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ
37
243.
244.
245.
246.
247.
248.
249.
250.
251.
УАх + у — 32 + 7=2.
1^2.у +5л:+ 2 + 25,5=3,
j/7+2— V"6a? = 0.
х-\-у~{-г—\Ъ,
аг2 + У + 22 = 61,
лг_у + дг2 = 2 у г.
х2-\-у*=г2,
ху-\-уг-\-гх = 47,
(2 — ДГ)(2 — J/)=2.
а3 + а2д: + ау-\- г = О,
с3+с2а: + с^ + 2 = 0.
12 , 5
fx—l
8
V>+i
5,
-t-
10
= 6.
J аг + j; —2V^y = 4,
1 х + у=10.
xy — 54 = x-\-y.
??* + ?—yfl7=0.
1^^+7+/ЗГ=7 = б.
| V7=F7+V7=7=4i/'^
J l/F+3^—1/^^Г2=:(1/-41-_з)а#
38 задачи 252
I V^+? - V*=7 - j'.
262, j x* — у*=1Ш*.
253a* Найти все значения m, при которых система урав-
нений
х — у = т(1-\-ху),
2 + АГ + ^ + АГ^ = 0
имеет действительные решения.
ГЛАВА 4
ЛОГАРИФМИЧЕСКИЕ И ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ
Определить х без помощи таблиц:
— 1е9—1еЗ
254. Аг=10-100а
1 I,4/—
256. х*= 100
266.. * =тЛ&*".
257. л: = 491-:ог'а+5-,ое'4.
Решить уравнения:
268. log4logjlog2Jf = 0.
259, loge {1 + log611 + log, (1 + k>gp *)]} = 0.
260» log4 {2 log311 + toft О + 3 log2 x)\) = I.
26J. log2(A:+14) + log2(j: + 2)=S6.
262. loga.y-f-loga(.y-|-5)-f-loga 0,02 = 0.
276 ГЛ. 4. ЛОГАРИФМИЧЕСКИЕ И ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ 39
2ЯЧ 'St35-*3) _ о
264. l+lgx =
265. lg[* —а(1— a)"]^-Ilg(l+l)-
_lg/SfZ7^0.
266. log^5 + log* (5*) — 2,25 = (log,, /Г)2.
267. log16 at + \ogtx 4- log2jf= 7.
268. log0 л; — bga»x-\-logaAX = j.
269- (4) -(t) •
270. 7 ■ З^1 — 5ш+а = 3"+* — 5я+а.
271. 0.125. 4аа'-8 = (^)Л
272. 0,5a;a.2aaH-a=64-1.
a?+5 дя-17
273. 32^-7= 0,25 . 128^-3 •
275. [2(2^+3)а"7Г]/а'~1==4.
276. 2(2^+3)a"1<c4-^ = 0.
40 задачи 277
аЯ-1 2Я-2 _ 4
277. V*a3 VaVa-l=\t
278.. 3 logxtfX + y log_£_ x = 2.
279. к>£4(л;+12). 10^2=1.
280. 1о&а,(5х2).1о&^-1.
281. l + a+u2+fl3+ ... -\-а®-1-\-ая =
= (l+a)(l+a2)(l+a4)(l+a8).
282. 52 • 5* • 56 ... 52* = 0,04-28.
283. 4*-2— 17 • 2^-4+ 1=0.
284. 2 • 42*— 17 • 4Ж+ 8 = 0.
286. ЗУ81 —101/9 + 3 = 0.
lgg + 7
286. a: * =10lga!+1-
287. Ig(4-1 • 2^ — l) — 1 = Ig (/V®-2 + 2) —2 lg 2.
288. 2(lg2 — i) + ig(5/s"+ l) = lg(61_/" + 5).
289. б1*"—3,ea,-1=3lfe+1—5,ge_1.
'290. a:2 ieto-i.5 ig о» = ууо".
a*
291. Ig(64Vr2fl;,-40a!) = 0.
292. log2 (9 — 2*) = 3 — x.
293. lg2 + lg(4*'-2 + 9)=l+lg(2^-2-)-l).
294. 2Ig2+(l 4-^)^3 — !g(Vr3 + 27) = 0.
305 ГЛ. 4. ЛОГАРИФМИЧЕСКИЕ И ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ 41
296. Ig (3Kto+1 — 2*-^to+1)— 2 =
=4",gl6— lA* + 0,251g 4.
21g2 + lg(* —3) _1
2Вв' lg<7jr+l) + lg(Jr-6) + lg3 2*
297. log5 120 +- (jc — 3) — 2 log5 (1 — 5*-з) =
= —log5(0,2 —5*-*).
298- e *
Решить систему уравнений:
= 32 • 2*у~К
299.
300.
301.
302.
303.
304.
305.
АГ + ^ = 3,(3).
(
f logax + logay = '.
[ logbx — logby = '
{
!£(*• + >■)— I=lgl3,
\g(x-\-y) — lg(x — y) = blg2.
10ёху(Х — У)=1,
logcoy(x-\-y) = 0.
j log0(l+f) = 2-log0j/,
I loge,*H-log6J/ = 4.
f logo x + log0 .y + loge 4 = 2 + loge 9,
I lg*x
x-\-y— 5a = 0.
xy = a*,
H-tg2^ = 2,51g8(a2).
42
ЗАДАЧИ
306.
307.
308.
809.
310.
311.
312.
313.
314.
315.
3<* ■ 2» = 576,
f lgx-\-lgy=\ga
\2Qgx— lgy) = l
lgx-\-lgy=\ga,
Igb.
t
iogax-\-loga^y = j,
logb>x-\-logby = -2 .
l0gaX-\-l0ga*y=-2,
{ \ogb>x—logvy=l.
\ logva-\-loguv = 2,
[ u2-\-v=l2.
х2-{-ху-\-у* = сР,
Vl[
Vb
log^x—log2y = 0,
АГ2_53,2 + 4=:0>
iogzX+logiy + logt 2 = 2,
logzy-t-\ogQZ-\-\ogQ x = 2t
log* z -f logl6 x -f log1G у = 2.
co-y
Vx + y=2Vb,
lg(x + y) = lg40 — lg(x-
■y)-
319
ГЛ. 5. ПРОГРЕССИИ
43
316.
У>=32 У 8у ,
3J
7 | Q^V9^—27^27^ = 0,
' ( Ig(*— 1) — igd— у) = о.
318.
319.
■jlg' + Y'SJ' — lg(4—V^^O.
(25*" У"
loga,fl3'=p.
logff бд: = ?.
125-5^ =0.
ГЛАВА 5
ПРОГРЕССИИ
Обозначения и формулы
а^ —первый член, а„ — л-й член, d — разность арифм. прогрессии,
% — » i ,un — » », Я — знаменатель геом. » ,
Sn — сумма п членов прогрессии, S — сумма бесконечно убывающей
геометрической прогрессии.
Формулы арифметической прогрессии
an = a1-{-d(n — 1),
_ («1 + Дп) п
°" — 2 '
с [2д1 + ^(я—1)1 п
Формулы геометрической прогрессии
и» = fie"»-1,
s»=iffErL <*>!> или s»=ii^r (?<1)-
5й=М^-1) (?>1) иди 5я==М1^|!) (9<1)(
(1)
(2)
(3)
(4)
(5)
(6)
(7)
44
ЗАДАЧИ
320
Арифметическая прогрессия
320. Сколько надо взять членов арифметической прогрессии
5; 9; 13; 17; ....
чтобы получить сумму, равную 10 877?
321. Найти арифметическую прогрессию, зная, что сумма
первых четырех членов ее равна 26, а произведение тех же
членов равно 880.
322. В арифметической прогрессии ap = q; aq^=p. Найти
выражение ап через я, р и q.
323. Найти сумму всех двузначных натуральных чисел-
324. Найти четыре последовательных нечетных числа,
зная, что сумма их квадратов больше суммы квадратов за-
ключенных между ними четных чисел на 48.
326. В арифметической прогрессии 20 членов. Сумма чле-
нов, стоящих на четных местах, равна 250, а сумма членов,
стоящих на нечетных местах, равна 220. Найти два средних
члена прогрессии.
326. Дан ряд выражений: (a-\-xf\ (а2 + л:2); (а— л:)2; ...
Доказать, что они составляют арифметическую прогрессию, и
найти сумму п членов ее.
327. Обозначая через Sit S2 и S3 суммы я1 первых чле-
нов, п2 первых членов и я3 первых членов некоторой ариф-
метической прогрессии» показать, что
ф- (и, - "з) + |г («.—«!) + ~ 04 - и2) = 0.
«1 "2 "3
328. Написать арифметическую прогрессию, первый член
которой равен 1, причем сумма первых пяти членов равна
1
■j суммы следующих пяти членов.
329. Найти' арифметическую прогрессию, в которой, сколько
бы ни взять членов, всегда сумма их равна утроенному квад-
рату числа этих членов.
330. Найти сумму всех двузначных чисел, которые при
делении на 4 дают в остатке единицу.
339 гл- 5. прогрессии 45
Геометрическая прогрессия
331. Между числами 1 и 256 вставить три средних гео-
метрических.
332. Найти три числа, составляющих геометрическую
прогрессию, если известно, что сумма первого и третьего
членов равна 52, а квадрат второго равен 100.
333. Написать несколько первых членов геометрической
прогрессии, у которой разность между третьим и первым
членами равна 9, а разность между пятым и третьим членами
равна 36.
334. Найти четыре числа, составляющих геометрическую
ирогрехсию, в которой сумма крайних членов равна 27, а
произведение средних равно 72.
336. Найти четыре числа, составляющих геометрическую
прогрессию, зная, что сумма крайних чисел равна 35, а сумма
средних равна 30.
336. Определить геометрическую прогрессию, у которой
И
«2+%+«4+^5+И6 = 62.
337. В геометрической прогрессии пять членов; сумма их
без первого равна 19 у, а без последнего равна 13. Вычис-
лить крайние члены прогрессии.
338. Найти первый член и знаменатель такой геометри-
ческой прогрессии, состоящей из девяти членов, в которой
произведение двух крайних членов равно 2304, а сумма чет-
вертого и шестого членов равна 120.
339. Три числа составляют геометрическую прогрессию.
Сумма этих чисел равна 126, а их произведение равно 13 824.
Найти эти числа.
46
ЗАДАЧИ
340
340. Число членов геометрической прогрессии четно. Сумма
всех ее членов в три раза больше суммы членов, стоящих
на нечетных местах. Определить знаменатель прогрессии.
Бесконечно убывающая геометрическая прогрессия
341. Доказать, что числа
/Т + 1 1 _1_
Y2-19 2-/2 ' 2' '"
образуют бесконечно убывающую геометрическую прогрессию,
и найти предел суммы ее членов.
342. Вычислить выражение
(4/3 + 8) [уъ(УЪ-2) + ^=0± + Ц=1+ ...],
предварительно доказав, что слагаемые, стоящие в квадрат-
ных скобках, являются членами геометрической убывающей
прогрессии.
343. Найти сумму членов бесконечно убывающей геоме-
трической прогрессии, у которой все члены положительны,
первый член равен 4, а разность между третьим и пятым
32
членами равна -^г.
344. г Определить сумму бесконечно убывающей геометри-
ческой прогрессии, если известно, что сумма ее первого и
четвертого членов равна 54, а сумма второго и третьего
равна 36.
345. В бесконечно убывающей геометрической прогрессии
сумма всех ее членов, стоящих на нечетных местах, равна 36,
а сумма всех членов, стоящих на четных местах, равна 12.
Найти эту прогрессию.
346. Сумма членов бесконечно убывающей геометриче-
ской прогрессии равна 56, а сумма квадратов членов той же
прогрессии равна 448. Найти первый член и знаменатель.
353
ГЛ. 5. ПРОГРЕССИИ
47
347. Сумма членов бесконечно убывающе^ геометрической
108
прогрессии равна 3, а сумма кубов всех ее членов равна-j^-.
Написать прогрессию.
348. Определить бесконечно убывающую геометрическую
прогрессию, в которой второй член равен 6, а сумма членов
равна -н- суммы квадратов ее членов.
Задачи на арифметическую и геометрическую прогресса
349. В некоторой арифметической прогрессии второй член
равен 14, а третий равен 16. Требуется составить геоме-
трическую прогрессию, знаменатель которой был бы равен
разности арифметической прогрессии, а сумма первых трех
членов была бы одна и та же в обеих прогрессиях.
350. Арифметическая и геометрическая прогрессии имеют
первые члены, равные каждый 3, и равные третьи члены.
Написать эти прогрессии, если второй член арифметической
прогрессии на 6 больше второго члена геометрической про-
грессии.
351. В геометрической прогрессии можно ее первый, тре-
тий и пятый члены считать за первый, четвертый и шестнадца-
тый члены некоторой арифметической прогрессии. Определить
четвертый член этой арифметической прогрессии, зная, что
первый член равен 5.
352. Три числа, сумма которых равна 93, составляют
геометрическую прогрессию. Их можно рассматривать так же,
как первый, второй и седьмой члены арифметической про-
грессии. Найти эти числа.
353. В арифметической прогрессии первый член равен 1,
а сумма первых семи членов равна 2555. Найти средний член
геометрической прогрессии из семи членов, если первый и
последний члены совпадают с соответствующими членами
указанной арифметической прогрессии.
48
ЗАДАЧИ
354
364. Три числа, составляющих арифметическую прогрес-
сию, дают в сумме 15. Если к ним прибавить соответственно 1.
4 и 19, то получатся три числа, составляющих геометриче-
скую прогрессию. Найти эти числа.
Збб. Найти три числа, составляющих геометрическую
прогрессию, если известно, что сумма этих чисел равна 26
и что от прибавления к ним соответственно 1, 6 и 3 получатся
новые три числа, составляющих арифметическую прогрессию.
366. Три числа составляют геометрическую прогрессию.
Если из них третий член уменьшить на 64, то полученные
три числа составят арифметическую прогрессию. Если затем
второй член этой арифметической прогрессии уменьшить на 8.
то получится геометрическая прогрессия. Определить эти
числа.
367. Могут ли три числа одновременно составлять ариф-
метическую и геометрическую прогрессии?
ГЛАВА б
СОЕДИНЕНИЯ И БИНОМ НЬЮТОНА
368. Число перестановок из п букв относится к числу
перестановок из «—J- 2 букв, как 0,1 к 3. Найти я.
369. Число сочетаний из п элементов по 3 в 5 раз меньше
числа сочетаний из п-\-2 элементов по 4. Найти п.
360. Найти средний член разложения бинома l-j — х* 1 .
361. Определить номер того члена разложения бинома
(т^^ + Т^0) • К0Т0РЫЙ содержит а7.
362. Найти номер того члена разложения бинома
21
, который содержит а и Ь в одина-
ковых степенях.
<fii+V#)
371 гл. б. СОЕДИНЕНИЯ И БИНОМ НЬЮТОНА 49
i\0
363. Упростить выражение
\аа-а3+1 а-а'Ч
и определить член разложения, который не содержит а.
364. Показатель степени одного бинома на 3 более по-
казателя другого. Определить эти показатели, если сумма
биномиальных коэффициентов в обоих разложениях вместе
равна 144.
365. Найти тринадцатый член разложения (9х— ^т^) •
если биномиальный коэффициент третьего члена разложения
равен 105.
366. В разложении (х2-{- — j коэффициенты у четвер-
того и тринадцатого членов равны между собой. Найти член,
не содержащий х.
367. Найти средний член разложения la у а — у -тг= I,
если известно, что коэффициент пятого члена относится
к коэффициенту третьего члена, как 14:3.
368. Сумма коэффициентов первого, второго н третьего
(1 \т
jc2 -\—1 равна 46. Найти член, не со-
держащий х.
(_ -з _\т
xY*-\- Vх) •
который содержит х\ если сумма всех биномиальных коэф-
фициентов равна 128.
370. Найти шестой член геометрической прогрессии,
у которой первый член равен у, а знаменателем служит
комплексное число (1+/).
371. Найти седьмой член геометрической прогрессии,
знаменатель которой равен П -Ь-у)' а пеРвый член равен/.
50 задачи 372
372. При каком значении п коэффициенты второго,
третьего и четвертого членов разложения бинома (l + jc)n
составляют арифметическую прогрессию?
373.-Коэффициенты пятого, шестого и седьмого членов
разложения бинома (1 -f- х)п составляют арифметическую
прогрессию. Найти п.
(5 .8
~ \-а уах~1
YaP^1 I
так, чтобы четвертый член разложения бинома равнялся 56д5'6.
376. Определить х в выражении f 2 V2~*-h 4 а? | так»
чтобы третий член разложения бинома равнялся 240.
376. Определить л; в выражении /]/"2-|- -—\в, в котором
\ YS]
отношение седьмого члена от начала в разложении бинома
1
к седьмому члену от конца равно -g-.
377. Найти значение х в выражении (jc + «^lga,)5> третий
член разложения которого равен 1 000 000.
378. Найти значение х в выражении L(V'*)IgaH"1+ V"*J t
четвертый член разложения которого равен 200.
379. Определить х в выражении (- \~х1*У&\ так,
W* )
чтобы третий член разложения бинома был равен 36 000.
380. Шестой член разложения бинома (—3 [-jc21»^8
равен 5600* Найти х.
387 ГЛ. 6. СОЕДИНЕНИЯ И БИНОМ НЬЮТОНА 51
381. Девятый член разложения бинома
11
L(^)51ga?
равен 450. Найти *.
382. Определить xt если четвертый член разложения
бинома Л°1д1^+!£¥—V Равен 3 500 000.
383. Определить, при каком значении х в разложении
/6/— 1 \12
бинома ( у лг—|—-=\ член, содержащий х в степени вдвое
большей, чем в следующем за ним члене, будет на 30 меньше
егр.
384. Определить, при каком значении х четвертый
член разложения бинома \v 2x~x-\--z—\ в 20 раз больше
\ V*)
показателя бинома, если биномиальный коэффициент 4-го члена
в пять раз больше биномиального коэффициента 2-го члена.
386. Найти, при каких значениях х разность между четвер-
, г— 16 т
тым и шестым членами разложения бинома 1-^ f-^-^j
равна 56, если известно, что показатель бинома т на 20
меньше, чем биномиальный коэффициент третьего члена раз-
ложения.
386. Найти, при каких значениях х в разложении бинома
(У 2х -|— , .-■:, ) сумма третьего и пятого членов равна 135,
если сумма биномиальных коэффициентов трех последних чле-
нов равна 22.
387. Определить, при каком значении х шестой член раз-
г 5 ~\т
ложеиия бинома [Кг^-^ + Кг^"4"1*8] равен 21,
если известно, что биномиальные коэффициенты второго,
52
ЗАДАЧИ
388
третьего и четвертого членов разложения представляют соот-
ветственно первый, третий и пятый члены арифметической
прогрессии.
388. Определить, при каком значении х четвертый член
разложения бинома \\у 5) * + г ~o^ig3"
14
равен 16,8, если известно, что -^ биномиального коэффи-
циента третьего члена разложения и биномиальные коэффи-
циенты четвертого и пятого членов его составляют геометри-
ческую прогрессию.
389. Определить, при каком значении х разность между
увеличенным в 9 раз третьим членом разложения бинома
(т/^аГЛ ждя»
~5 (-1/4-22 ] и пятым членом того же разложения
У2 /
равна 240, если известно, что разность между логарифмом
утроенного биномиального коэффициента четвертого члена
разложения и логарифмом биномиального коэффициента вто-
рого члена равна 1.
ГЛАВА 7
АЛГЕБРАИЧЕСКИЕ И АРИФМЕТИЧЕСКИЕ ЗАДАЧИ1)
^390. Найти вес орудийного патрона, зная, что заряд ве-
2
сит 0,8 кг, вес отряда составляет -j веса всего патрона н
1
вес гильзы составляет -г- веса патрона.
391. На заводе 35°/0 всех рабочих — женщины, а осталь-
ные— мужчины, которых на заводе на 252 человека больше,
чем женщин. Определить общее число рабочих.
') Мы не подразделяем задачи на алгебраические и арифмети-
ческие, так как задачи, решаемые арифметически, всегда можно
решить и алгебраически. Наоборот, задачи, решаемые с помощью
уравнений, нередко допускают более простое арифметическое реше-
ние. В отделе решении мы даем иногда арифметическое, иногда
алгебраическое решение, но это не должно ни в какой мерс сте-
снять инициативу учащегося в выборе способа решения.
401 ГЛ. 7. АЛГЕБРАИЧЕСКИЕ И АРИФМЕТИЧЕСКИЕ ЗАДАЧИ 53
392. При продаже товара за 1386 руб. получено 10%
прибыли. Определить себестоимость товара.
393. Производственная артель, продав продукции на
3348 руб., понесла 4% убытку. Какова себестоимость этой
продукции?
394. Если из 225 кг руды получается 34,2 кг меди, то
каково процентное содержание меди в руде?
395. Пачка папирос стоила до снижения цен 2 р. 90 к„,
а после снижения 2 р. 60 к. На сколько процентов снижена
цена?
396. Килограмм товара стоил 6 р. 40 к. После сниже-
ния цен он стоил 5 р. 70 к. На сколько процентов была
снижена цена на товар?
397. Получаемый при сушке винограда изюм составляет
32% всего веса винограда. Из какого количества винограда
получится 2 кг изюма?
398. Для экскурсии нужно собрать денег. Если каждый
экскурсант внесет по 75 коп., то на расходы не хватит
4,4 руб.; если каждый внесет по 80 коп., то останется 4,4 руб.
Сколько человек принимает участие в экскурсии?
399. Несколько человек должны были заплатить по-
ровну 72 руб. Если бы их было на 3 меньше, то каждому
пришлось бы заплатить на 4 руб. больше. Сколько их
было?
400. Цена 60 экземпляров первого тома и 75 экземпля-
ров второго тома составляет 405 руб. Однако при 15% скидке
на первый том и 10% скидке на второй том приходится пла-
тить всего 355 р. 50 к. Определить цену первого и второго
томов.
401. Антикварный магазин, купив два предмета за 225 руб.,
продал их, получив 40% прибыли. Что стоит магазину каж-
дый предмет, если на первом прибыли было получено 25%,
а на другом 50%?
54 ЗАДАЧИ 402
402. Морская вода содержит 5% (по весу) соли. Сколько
килограммов пресной воды нужно прибавить к 40 кг морской
воды, чтобы содержание соли в последней составляло 2%?
403. Гипотенуза прямоугольного треугольника равна
3^5 м. Определить катеты, если известно, что после того,
как один из них увеличить на 133 -^-%, а ДРУ™Й — на
2
16-g-%» сумма их длин сделается равной 14 м.
404. В двух мешках находится 140 кг муки. Если из пер-
вого мешка переложить во второй 12,5% муки, находящейся
в первом^ мешке, то в обоих мешках будет поровну. Сколько
килограммов муки в каждом мешке?
405. Два завода Л и В взялись выполнить заказ в 12
дней. Через два дня завод Л был закрыт на ремонт, и в даль-
нейшем над выполнением заказа работал только завод В.
2
Зная, что производительность завода $ составляет 66-^%
от производительности завода Л, определить, через сколько
дней будет выполнен заказ.
406. При выполнении работы по математике 12% уче-
ников класса вовсе не решили задачи, 32% решили с ошиб-
ками, остальные 14 человек решили верно. Сколько учени-
ков было в классе?
407. От рельса отрезали часть, составляющую 72% его
длины. Вес оставшегося куска равен 45,2 кг. Определить
вес отрезанной части.
408. Сплав весит 2 кг и состоит из серебра и меди, при-
чем вес серебра составляет 14-=-% веса меди. Сколько сере-
бра в данном сплаве?
409. Трое рабочих получили вместе 4080 руб. Суммы,
* 13
полученные первым и вторым, относятся, как 7 у: 1 -т-;
сумма, полученная третьим, составляет 43-^-% того, что по^
лучил первый. Сколько получил каждый?
416 ГЛ. 7. АЛГЕБРАИЧЕСКИЕ И АРИФМЕТИЧЕСКИЕ ЗАДАЧИ 55
410. В трех ящиках имеется всего 64,2 кг сахара. Во
4
втором ящике находится -^ того, что есть в первом ящике,
в третьем — 42-2% того» чт0 есть во ВТ0Р0М' Сколько са-
хара в каждом ящике?
411. Имеется лом стали двух сортов с содержанием ни-
келя в 5% и 40%- Сколько нужно взять каждого из этих
сортов, чтобы получить 140 т стали с содержанием никеля
в 30%?
412. Кусок сплава меди с оловом весом 12 кг содержит
45% меди. Сколько чистого олова надо прибавить к этому
куску, чтобы получившийся новый сплав имел 40% меди?
413. Сколько чистого спирта надо прибавить к 735 г
шестнадцатипроцентного раствора иода в спирте, чтобы по-
лучить десятипроцентный раствор?
414. Сплав из меди и цинка весом в 24 кг при погру-
жении в воду потерял в своем весе 2 ^- кг. Определить ко-
личество меди и цинка в этом сплаве, если известно, что
1 2
медь теряет в воде П-д-% своего веса, а цинк 14-у%
своего веса.
416. На участке одноколейного железнодорожного пути
длиною в 20 км надо уложить рельсы. Для укладки имеются
рельсы длиной в 25 м и 12,5 м. Если уложить все рельсы
длиною в 25 л, то рельсов длиной в 12,5 м надо будет до-
бавить 50% от всего их количества. Если же уложить все,
рельсы длиною по 12,5 м, то рельсов длиною в 25 м надо
2
добавить 66-5-% от всего количества их. Определить коли-
чество рельсов того и другого рода.
416. После выпуска из школы ученики обменялись фото-
графическими карточками. Сколько было учеников, если они
обменялись 870 карточками?
56
ЗАДАЧИ
417
417. Среднее пропорциональное двух чисел на 12 больше
меньшего из этих чисел, а среднее арифметическое тех же
чисел на 24 меньше большего из чисел. Найти эти числа.
418. Найти три числа, из которых второе больше первого
настолько, насколько третье больше второго, если известно,
что произведение двух меньших чисел равно 85, а произве-
дение двух ббльших равно 115.
419. Число а есть среднее арифметическое некоторых
трех чисел, b есть среднее арифметическое их квадратов.
Выразить через а и b среднее арифметическое их попарных
произведений.
420. Из прямоугольного жестяного листа с периметром
в 96 см приготовлена открытая сверху коробка таким обра-
зом, что по углам его вырезано по квадрату со стороной
в 4 см и края спаяны. Каких размеров был лист, если
объем полученной коробки равен 768 смг?
421. Найти двузначное число, частное от деления кото-
рого на произведение его цифр равно 2-н-, а, кроме того,
разность между искомым числом и числом, написанным теми
же цифрами, но расположенными в обратном порядке, равна 18.
422. Найти двузначное число, зная, что число его еди-
ниц двумя больше числа десятков и что произведение иско-
мого числа на сумму его цифр равно 144.
423. Определить целое положительное число по следую-
щим данным: если приписать к нему справа цифру 5, то
.получим число, делящееся без остатка на число, большее
искомого на 3, и в частном получается число, на 16 мень-
шее делителя.
424. Найти два двузначных числа, обладающих следую-
щим свойством: если к большему искомому числу приписать
справа 0 и за ним меньшее число, а к меньшему приписать
справа большее число и затем 0, то из образовавшихся таким
образом двух пятизначных чисел первое, будучи разделено
430 гЛ- 7* АЛГЕБРАИЧЕСКИЕ И АРИФМЕТИЧЕСКИЕ ЗАДАЧИ 57
на второе, дает в частном 2 и в остатке 590. Кроме того
известно, что сумма, составленная из удвоенного большего
искомого числа и утроенного меньшего, равна 72.
425. Ученику надо было умножить 78 на двузначное число,
в котором цифра десятков втрое больше цифры единиц; по
ошибке он переставил цифры во втором сомножителе, отчего
и получил произведение на 2808 меньше истинного. Чему
равно истинное произведение?
426. Расстояние между двумя станциями железной дороги
96 км. Первый поезд проходит это расстояние на 40 мин.
скорее, чем второй. Скорость первого поезда больше ско-
рости второго на 12 км[час. Определить скорости обоих
поездов.
427. Два лица выезжают одновременно из городов А и В
навстречу друг другу. Первый проезжает в час на 2 км больше
второго и приезжает в В часом раньше, чем второй в А
Расстояние между А и В равно 24 км. Сколько километров
проезжает каждый в час?
428. Расстояние между А и В по железной дороге 66 км,
а по водному пути — 80,5 км. Из А поезд выходит на 4 часа
позже парохода и прибывает в В на 15 мин. раньше паро-
хода. Определить среднюю скорость поезда и парохода, если
первая больше второй на 30 км[час.
429. Одна мастерская должна была сшить 810 костюмов,
другая за тот же срок должна была сшить 900 костюмов; пер-
вая закончила выполнение заказа за 3 дня до срока, а вто-
рая— за 6 дней до срока. По скольку костюмов в день шила
каждая мастерская, если вторая мастерская шила в день на
4 костюма больше первой?
430. После встречи двух пароходов один из них пошел
на юг, а другой на запад. Через два часа после встречи рас-
стояние между ними было 60 км. Найти скорость каждого
парохода, если известно, что скорость одного из них была
на 6 км[час больше скорости второго.
58
ЗАДАЧИ
431
431. Собака, находясь в точке At погналась за лисицей,
которая была на расстоянии 30 м от собаки. Скачок собаки
равен 2 м, скачок лисицы—1 м. Собака делает два скачка
в то время, когда лисица делает три скачка. На каком рас-
стоянии от точки Л собака догонит лисицу?
432. Допуская, что стрелки часов движутся без скачков,
узнать, через какое время после того, как часы показывали
4 часа, минутная стрелка догонит часовую стрелку.
433. Поезд вышел со станции Л на станцию С через Б.
Участок от Л до Б он шел с установленной скоростью,
а участок от Б до С—с уменьшенной на 25%- На обрат-
ном пути участок от С до Б он шел с установленной ско-
ростью, а участок от Б до Л — со скоростью, уменьшенной
на 25%. Сколько времени шел поезд от Л до С, если из-
вестно, что на участок от Л до Б он затратил столько же
времени, сколько на участок от Б до С, и что на путь по
5
направлению от Л к С он употребил на — часа меньше, чем
на обратный путь (т. е. от С до Л)?
434. Велосипедисту надо было проехать расстояние
в 30 км. Выехав на 3 мин. позже назначенного срока, вело-
сипедист ехал со скоростью, большею на 1 км/час, и при-
был вбвремя на место. Определить скорость, с которой
ехал велосипедист.
435. Скорый поезд был задержан у семафора на 16 мин.
и нагнал опоздание на перегоне в 80 км, идя со скоростью,
на 10 км/час большей, чем полагалось по расписанию. Какова
скорость поезда по расписанию?
436. Поезд должен был пройти 840 км в определенное
время. На половине пути поезд был задержан у семафора на
-^- часа и, для того чтобы прибыть к месту назначения в срок,
увеличил скорость на 2 км/час. Сколько времени поезд на-
ходился в пути?
442 ГЛ. 7. АЛГЕБРАИЧЕСКИЕ И АРИФМЕТИЧЕСКИЕ ЗАДАЧИ 59
437. Из двух мест, расстояние между которыми 650 км,
отправляются два поезда друг другу навстречу. Если оба
поезда тронутся с места одновременно, то они встретятся
через 10 часов. Если же второй поезд отправится на 4 часа и
20 минут раньше первого, то встреча произойдет через 8 часов
после отправления первого. Определить среднюю скорость
каждого поезда.
438. Два поезда отправляются одновременно навстречу
друг другу со станций Л и Б, расстояние между которыми
600 км. Первый из них приходит на станцию В на 3 часа
раньше, чем второй на станцию А. В то время, как первый
делает 250 км, второй проходит 200 км. Найти скорость
каждого поезда.
439. Дачник, идущий к поезду, пройдя ва первый час
3,5 км, рассчитал, что, двигаясь с такой скоростью, он опо-
здает на 1 час. Поэтому он остальной путь проходит со ско-
ростью 5 км/час и приходит за 30 мин. до отхода поезда.
Определить, какой путь должен был пройти дачник.
440. Расстояние от Москвы "до Мытищ по шоссе 19 км.
Из Москвы в Мытищи выехал велосипедист с некоторой по-
стоянной скоростью; через 15 мин. псТсле него в том же на-
правлении вышел автомобиль; он через 10 мин. после выхода
нагнал велосипедиста и продолжал путь до Мытищ, где, ни
останавливаясь, повернул обратно и через 50 мин. после
своего выхода из Москвы встретил велосипедиста вторично.
Определить скорости автомобиля и велосипедиста.
441. Со станции А вышел в 5 час. утра почтовый поезд
по направлению к станции В, отстоящей от А на 1080 км.
В 8 час. утра вышел со станции В по направлению к А ско-
рый поезд, который проходил в час на 15 км больше, чем
почтовый поезд. Когда встретились поезда, если их встреча
произошла в середине пути АВ7
442. Расстояние между А и В равно 78 км. Из А выез-
жает велосипедист по направлению к В. Через 1 час ему
навстречу отправляется из В другой велосипедист, делающий
в час на 4 км больше первого. Встреча произошла на рас-
стоянии 36 км от В. Сколько времени до встречи ехал
каждый ив них и с какой скоростью?
60
ЗАДАЧ»
443
443. Два пешехода вышли одновременно друг другу на-
встречу и встретились через 3 часа 20 мин. Во сколько вре-
мени пройдет все расстояние каждый из них, если первый
пришел в то место, из которого вышел второй, на 5 час.
позже, чем второй пришел в то место, откуда вышел первый?
444. Два туриста идут друг другу навстречу— один из
пункта Л а другой из пункта £. Первый выходит из А на
6 час. позже, чем второй из пункта В, и при встрече оказы-
вается, чго он прошел на \2 км меньше второго. Продолжая
после встречи путь с той же скоростью, первый приходит
в В через 8 час, а второй в А— через 9 час. Определить
расстояние АВ и скорости обоих туристов.
445. Вылетев одновременно, дирижабль и самолет летяг
навстречу друг другу. К моменту встречи дирижабль прошел
на 100 км меньше самолета и на место отлета самолета при-
ходит через 3 часа после встречи. Самолет прибывает на
аэродром дирижабля через 1 час 20 мни. после встречи.
Найти расстояние между аэродромами и скорости самолета и
дирижабля.
446. Из двух мест А и В вышли одновременно два пеше-
хода навстречу друг другу. При встрече оказалось, что
первый прошел на а км больше, чем второй. Если они будут
продолжать путь, то, идя с прежней скоростью, первый
придет в В через т часов, а второй придет в А через п часон
после встречи. Найти скорость каждого пешехода.
447. По окружности движутся два тела; первое пробегает
окружность на 5 сек. скорее второго. Если они движутся
но одному направлению, то сходятся через каждые 100 сек.
Какую часть окружности (в градусах) пробегает каждое тело
ь 1 сек.?
443* Два тела, двигаясь по окружности в одном и том же
направлении, сходятся через каждые 56 мин. Если бы они
двигались с теми же скоростями в противоположных направ-
лениях, они встречались бы через каждые 8 мин. Далее
известно, что при движении в противоположных направлениях
ГЛ. 7. АЛГЕБРАИЧЕСКИЕ И АРИФМЕТИЧЕСКИЕ ЗАДАЧИ 61
расстояние (по окружности) между сближающимися телами
уменьшилось бы с 40 м до 26 м за 24 сек.
Сколько метров в минуту проходит каждое тело и какова
длина окружности?
449. По окружности длиной с равномерно и в одном на-
правлении движутся две точки, которые сходятся через ка-
ждые t сек. Найти скорость каждой точки, зная, что одна из
них пробегает всю окружность на п сек. быстрее другой.
450. Расстояние между двумя городами по реке 80 км.
Пароход совершает этот путь в два конца в 8 час. 20 мин.
Определить скорость парохода в стоячей воде, считая ско-
рость течения реки 4 км/час.
451. Моторная лодка спустилась по течению на 28 км и
тотчас же вернулась назад; на путь туда и обратно ей по-
требовалось 7 час. Найти скорость движения лодки в стоячей
воде, если известно, что вода в реке движется со скоростью
3 км\час.
452. Некто проехал в лодке но реке из города А в го-
род В и обратно, употребив на это 10 час. Расстояние между
городами 20 км. Найтн скорость течения реки, зная, что он
проплывал 2 км против течения в такое же время, как 3 км
по течению реки.
453. Пароход идет из Киева в Днепропетровск в течение
двух суток, обратно — в течение трех суток. Определить,
сколько времени будет плыть плот из Киева в Днепро-
петровск.
454. Расстояние между точками А и В равно 301 м;
из Л в В равномерно движется некоторое тело; достигнув
точки В, оно тотчас же возвращается назад. Второе тело,
выходящее из точки В по направлению к А через 11 сек.
после выхода первого, движется тоже равномерно, но мед-
леннее. На пути от В к А оно встречается с первым те-
лом дважды: через 10 сек. и через 45 сек. после своего
выхода из В.
Найти скорость движения каждого тела.
62
ЗАДАЧИ
455
455. Дорога из города А в город В сначала подымается
в гору на протяжении 3 км, потом идет по ровному месту
на протяжении 5 км, после спускается под гору на протяже-
нии 6 км. Посыльный, уйдя из А в В и пройдя полпути,
обнаружил, что взял не все пакеты. Он вернулся обратно
и через 3 часа 36 мин. после своего выхода из А вернулся в А,
Выйдя из А вторично, он прошел весь путь до Б за 3 часа
27 мин. и обратный путь в А — за 3 часа 51 мин. С какой
скоростью шел посыльный в гору, по ровному месту и под
гору, если считать эти скорости постоянными?
456. Машинистка рассчитала, что если она будет печатать
ежедневно на 2 листа более установленной для нее нормы,
то окончит работу ранее намеченного срока на 3 дня; если же
будет печатать по 4 листа сверх нормы, то окончит работу
на 5 дней ранее срока. Сколько листов она должна была
перепечатать и в какой срок?
457. Рабочий изготовил в назначенный ему срок некото-
рое число одинаковых деталей. Если бы он ежедневно изго-
товлял их на 10 штук более, то выполнил бы эту работу
на 4 у дня раньше срока, а если бы он делал в день на
5 деталей меньше, то опоздал бы на 3 дня против назначен-
ного срока. Сколько деталей и в какой срок он выполнил?
458. Машинистка должна была выполнить работу в опре-
деленный срок, ежедневно печатая определенное количество
листов. Она рассчитала, что если будет печатать ежедневно
на 2 листа больше установленной нормы, то окончит работу
раньше намеченного срока на 2 дня, если же будет печатать
на 60% больше нормы, то, закончив работу на 4 дня раньше
срока, напечатает на 8 листов больше намеченной работы.
Сколько листов она должна была печатать в день и в какой
срок окончить работу?
459. Двое рабочих, работая вместе, выполняют некоторую
работу в 8 час. Первый из них, работая отдельно, может вы-
полнить всю работу на 12 час. скорее, чем второй рабочий, если
этот последний будет работать отдельно. Во сколько часов
каждый из них, работая отдельно, может выполнить работу?
ГЛ. 7. АЛГЕБРАИЧЕСКИЕ И АРИФМЕТИЧЕСКИЕ ЗАДАЧИ 63
460. Бассейн наполняется двумя трубами за 6 час. Одна
первая труба заполняет его на 5 час. скорее, чем одна вто-
рая. Во сколько времени каждая труба, действуя отдельно,
может наполнить бассейн?
461. Двум рабочим было поручено изготовить партию
одинаковых деталей. После того как первый проработал
5
7 час, а второй 4 часа, оказалось, что они выполнили -д-всей
работы. Проработав совместно еще 4 часа, они установили
что им остается выполнить т« всей работы. Во сколько часов
каждый из них, работая отдельно, мог бы выполнить всю работу?
462. Пароход грузится подъемными кранами. Сначала на-
чали грузить 4 крана одинаковой мощности. После того как
они проработали 2 часа, к ним присоединили еще 2 крана
меньшей мощности, и после этого погрузка была окончена
через 3 часа. Если бы все краны начали работать одновре-
менно, то погрузка была бы окончена в 4,5 часа. Определить,
во сколько часов мог бы окончить погрузку один кран боль-
шей и один кран меньшей мощности.
463. Для строительства требовалось в течение 8 час.
перевезти со станции строительный материал. Для перевозки
было направлено сначала 30 трехтонных машин. После двух-
часовой работы этих машин было послано в помощь им еще
9 пятитонных машин, совместно с которыми перевозка и была
закончена в срок. Если бы сначала были направлены пятитон-
ные машины, а спустя 2 часа — трехтонные, то за указан-
13
ный срок было бы вывезено только -г^- всего груза. Опре-
делить, во сколько часов могла бы перевезти весь этот груз
одна трехтонная машина, одна пятитонная и в какой срок
перевезли бы весь груз 30 пятитонных машин.
464. Двум машинисткам было поручено выполнить некото-
рую работу.' Вторая из них приступила к работе на 1 час
позднее первой. Через 3 часа после того, как первая начала
работу, им оставалось выполнить еще -^ всей работы. По
окончании работы оказалось, что каждая машинистка выпол-
нила половину всей работы. Во сколько часов каждая из них
в отдельности могла бы выполнить всю работу?
64
ЗАДАЧИ
465
465. Со станций А и В вышли два поезда навстречу
друг другу, причем второй из них вышел на полчаса позже
первого. Через 2 часа после выхода первого поезда расстоя-
19
ние между поездами составляло ^ всего пути между Л и В.
Продолжая движение, они встретились на середине пути
между А и В. Сколько времени потребуется каждому поезду,
чтобы пройти весь путь между конечными станциями?
466. Для промывания фотографических негативов служит
ванна, имеющая форму прямоугольного параллелепипеда, раз-
мерами 20 см X 90 см X 25 см. Для постоянного смешения
коды о ванне в нее поступает вода через один кран и одно-
временно вытекает через другой. Для того чтобы опорожнить
посредством второго крана полную ванну, требуется на 5 мин.
меньше времени, чем для того, чтобы наполнить ее первым
краном, если закрыть второй. Если же открыть оба крана,
то полная ванна опорожнится в 1 час. Найти количество
коды, пропускаемое каждым краном в 1 мин.
467. При постройке здания требовалось вынуть 8000 мг
земли в определенный срок. Работа была закончена раньше
срока на 8 дней вследствие того, что бригада землекопов
ежедневно перевыполняла план на 50 м*. Определить, в какой
срок должна была быть окончена работа, и найти ежедневный
процент перевыполнения.
468. Ремонт пути производили две бригады. Каждая из
них отремонтировала по 10 км, несмотря на то, что вторая
бригада работала па один день меньше первой. Сколько кило-
метров пути ремонтировала каждая бригада в день, если обе
вместе ремонтировали в день 4,5 км?
469. Двое рабочих выполнили вместе некоторую работу
в 12 час. Если бы сначала первый сделал половину этой ра-
боты, а затем другой остальную часть, то вся работа была бы
выполнена за 25 час. За какое время мог выполнить эту
работу каждый в отдельности?
470. Два трактора различной мощности, работая совместно,
вспахали поле за t дней. Если бы сначала работал только
один трактор и вспахал бы половину поля, а затем один вто-
рой закончил бы работу, то при таких условиях поле было
*Я> ГЛ. 7„ АЛГЕБРАИЧЕСКИЕ И АРИФМЕТИЧЕСКИЕ ЗАДАЧИ 65
бы вспахано за k дней. Во сколько дней каждый трактор,
работая отдельно, может вспахать всё поле?
471. Для углубления фарватера при входе в гавань рабо-
тали 3 разных землечерпалки. Если бы действовала только
первая из них, то на работу потребовалось бы на 10 дней
больше времени; если бы работала только .вторая, то работа
затянулась бы на 20 лишних дней. При работе одной лишь
третьей землечерпалки углубление фарватера заняло бы в шесть
раз больше времени, чем при одновременном действии всех
трёх машин. Сколько времени потребуется для выполнения
всей работы каждой землечерпалкой в отдельности?
472. Двое рабочих, из которых второй начинает работать
1 у днями позже первого, могут выполнить работу в 7 дней.
Если бы эту работу выполнял каждый отдельно, то первому
потребовалось бы на 3 дня больше, чем второму. Во сколько
дней каждый из них отдельно выполнит эту работу?
473. При совместной работе двух тракторов различной
мощности колхозное поле было вспахано в 8 дней. Если бы
половину поля вспахать сначала одним трактором, то при
дальнейшей работе двух тракторов вся работа была бы закон-
чена в 10 дней. Во сколько дней можно было бы вспахать
всё поле каждым трактором отдельно?
474. Несколько человек взялись вырыть канаву и могли
бы окончить работу за 6 час, если бы начали ее одновре-
менно, но они приступали к работе один за другим через
одинаковые промежутки времени. Через такой же промежу-
ток времени, после выхода на работу последнего участника,
канава была вырыта, причём каждый из участников оставался
на работе до конца.
Сколько времени они рыли канаву, если приступивший
к работе первым проработал в 5 раз больше времени, чем
приступивший последним?
475. Трое рабочих могут совместно выполнить некоторую
работу за / час. Первый из них, работая один, может выпол-
нить эту работу вдвое скорее третьего и на один час скорее
второго. Во сколько времени каждый из них, работая отдельно,
может выполнить эту работу?
66
ЗАДАЧИ
476
476. Бассейн наполняется водой из двух кранов. Сначала
первый кран был открыт одну треть того времени, какое
нужно было бы, чтобы наполнить бассейн, открыв только
второй кран. Затем, наоборот, второй кран был открыт одну
треть того времени, которое требуется для наполнения бас-
сейна одним первым краном. После этого оказалось напол-
неиным -rg бассейна. Вычислить, сколько времени нужно для
наполнения бассейна каждым краном в отдельности, если оба
крана, открытые вместе, наполняют бассейн за 3 часа 36 мин.
477. При постройке электростанции бригада каменщиков
должна была в определенный срок уложить 120 тысяч кирпи-
чей. Бригада выполнила работу на 4 дня раньше срока. Опре-
делить, какова была норма ежедневной кладки кирпича и
сколько укладывали кирпичей ежедневно в действительности,
если известно, что бригада за 3 дня укладывала на 50Э0 кир-
пичей больше, чем полагалось укладывать за 4 дня по норме.
478. В трех сосудах налита вода. Если -*■ воды из пер-
вого сосуда перелить во второй, затем -j- воды, оказавшейся
во втором, перелить в третий и, наконец, уд воды, оказав-
шейся в третьем, перелить в первый, то в каждом сосуде
окажется по 9 л. Сколько воды было в каждом сосуде?
479. Из бака, наполненного чистым спиртом, вылили
часть спирта и долили тем же количеством воды; потоп из
бака вылили столько же литров смеси; тогда в баке оста-
лось 49 л чистого спирта. Вместимость бака 64 л. Сколько
спирта вылили в первый раз и сколько во второй раз')?
480. Сосуд в 20 л наполнен спиртом. Из него выливают
некоторое количество спирта в другой, равный ему, и, допол-
нив остальную часть второго сосуда водой, дополняют этой
1) Задача составлена в предположении, что объем смеси ра-
вен сумме объемов спирта и воды. На самом деле он несколько
меньше.
433 ГЛ. 7. АЛГЕБРАИЧЕСКИЕ И АРИФМЕТИЧЕСКИЕ ЗАДАЧИ 67
. 2
смесью первый сосуд. Затем из первого отливают о-д- л во
второй, после чего в обоих сосудах содержится одинаковое
количество спирта. Сколько отлито первоначально спирта из
первого сосуда во второй?
481. Сосуд ёмкостью в 8 л наполнен воздухом, содержа-
щим 16°/0 кислорода. Из этого сосуда выпускают некоторое
количество воздуха и впускают такое же количество азота,
после чего опять выпускают такое же, как и в первый раз,
количество смеси и опять дополняют таким же количеством
азота. В новой смеси оказалось кислорода Э°/0. Определить,
по скольку литров выпускалось каждый раз из сосуда.
482. Две колхозницы принесли на рынок вместе 100 яиц.
Продав яйца по разной цене, обе выручили одинаковые суммы.
Если бы первая продала столько яиц, сколько вторая, то она
выручила бы 72 руб., если бы вторая продала столько яиц,
сколько первая, то она выручила бы 32 руб. Сколько яиц
было у каждой?
483. Две колхозницы, имея вместе а л молока, получили
при продаже его одинаковые суммы, продавая молоко по раз-
ной цене. Если бы первая продала столько, сколько вторая,
то получила бы т руб., а если бы вторая продала столько,
сколько первая, то получила бы п руб. (т > п). Сколько
литров молока было у каждой колхозницы?
484. При испытании на экономичность двух двигателей
внутреннего сгорания одинаковой мощности было установлено,
что один из них израсходовал 600 г бензина, а второй, рабо-
тавший на 2 часа меньше, 384 г. Если бы первый двигатель
расходовал в час столько бензина, сколько второй, а второй,
наоборот, столько, сколько первый, то за то же время работы
расход бензина в обоих двигателях был бы одинаковым.
Сколько бензина в час расходует каждый двигатель?
485. Имеются два сплава золота и серебра; в одном коли-
чество этих металлов находится в отношении 2 : 3, в другом —
в отношении 3 : 7. Сколько нужно взять от каждого сплава,
чтобы получить 8 кг нового сплава, в котором золото и
серебро были бы в отношении 5:11?
68
ЗАДАЧИ
48й
486. Одна бочка содержит смесь спирта с водой в отно-
шении 2 ; 3, а другая — в отношении 3:7. По скольку вёдер
нужно взять из каждой бочки, чтобы составить 12 вёдер
смеси, в которой спирт и вода были бы в отношении 3:5?
487. Некоторый сплав состоит из двух металлов, входя-
щих в отношении 1 : 2, а другой содержит те же металлы
в отношении 2:3. Из скольких частей обоих сплавов можно
получить третий сплав, содержащий те же металлы в отноше-
нии 17 :27?
488. При вращении двух колёс, соединённых бесконечным
ремнём, меньшее из них делает в минуту на 400 оборотов
больше второго. Большее колесо делает 5 оборотов в про-
межуток времени на 1 сек. больше, чем время 5 оборотов
меньшего. Сколько оборотов делает каждое колесо в минуту?
489. На протяжении 18 м переднее колесо экипажа делает
на 10 оборотов больше заднего. Если окружность переднего
колеса увеличить на 6 дм, а окружность заднего уменьшить
на 6 дм> то на том же протяжении переднее колесо сделает на
4 оборота больше заднего. Найти окружности обоих колёс.
490. Баржа с грузом в 600 т была разгружена в три дня,
2
причём в первый и третий дни было выгружено -д- всего
груза. Во второй день было выгружено меньше, чем в первый,
а в третий меньше, чем во второй; при этом разность между
процентом уменьшения выгрузки в третий день по отноше-
нию к выгрузке второго дня и процентом уменьшения выгрузки
второго дня по отношению к выгрузке первого дня была
равна 5. Определить, сколько было выгружено каждый день
и процент уменьшения выгрузки во второй и в третий дни.
491. Два раствора, из которых первый содержал 800 г
безводной серной кислоты, а второй 600 г безводной серной
кислоты, соединили вместе и получили 10 кг нового раствора
серной кислоты. Определить вес первого и второго растворов,
вошедших в смесь, если известно, что процент содержания
безводной серной кислоты в первом растворе на 10 больше,
чем процент содержания безводной серной кислоты во втором.
493 ГЛ. 7. АЛГЕБРАИЧЕСКИЕ И АРИФМЕТИЧЕСКИЕ ЗАДАЧИ 69
492. Имелось два разных сплава меди. Процент содержа-
ния меди в первом сплаве был на 40 меньше, чем процент
содержания меди во втором сплаве. После того как их спла-
вили вместе, получили сплав, содержащий 36°/0 меди. Опреде-
лить процентное содержание меди в первом и во втором
сплавах, если известно, что меди в первом сплаве было 6 кг%
а во втором 12 «г.
493. Два поезда—товарный длиной в 490 м и пассажирский
длиной в 210 м — двигались навстречу друг другу по двум
параллельным путям. Машинист пассажирского поезда заметил
товарный поезд, когда он находился от него на расстоянии
700 м\ через 28 сек. после этого они встретились. Опреде-
лить скорость каждого поезда, если известно, что товарный
поезд употребляет времени на прохождение мимо светофора
на 35 сек. больше пассажирского.
494. Товарный поезд состоит из двухосных и четырёхос-
ных цистерн, гружённых нефтью. Вес поезда 940 т. Требуется
определить число четырёхосных и двухосных цистерн, а также
их вес, если известно, что число двухосных на 5 больше
числа четырёхосных; каждая четырёхосная цистерна весит
в три раза больше, чем одна двухосная, и чистый вес нефти
(без веса цистерн) во всех четырёхосных цистернах больше
веса всех гружёных двухосных цистерн на 100 т. Вес нефти
в четырёхосной цистерне равен 40 т, а в двухосной соста-
вляет 0,3 веса нефти в четырёхосной.
495. Две машины, работающие с двух сторон тоннеля,
должны закончить проходку в 60 дней. Если первая машина
выполнит 30% всей работы, которую за это время она
2
должна была сделать, а вторая 26 у % св°ей работы, то обе
они пройдут 60 м тоннеля. Если бы первая машина выпол-
2
пила у всей работы второй машины по проходке этого тон-
неля, а вторая — 0,3 всей работы первой машины, то первой
понадобилось бы для этого времени на 6 дней больше, чем
второй. Определить, сколько метров в день проходит каждая
машина.
70
ЗАДАЧИ
496
496, Две бригады, работая вместе, закончили ремонт
участка пути в 6 дней. Одной первой бригаде для выполне-
ния 40% всей работы потребовалось бы времени на 2 дня
больше, чем одной второй бригаде для выполнения 13-^°/о
всей работы. Определить, во сколько дней могла бы отре-
монтировать каждая бригада отдельно весь участок.
497. С пристани на станцию должно быть перевезено
690 т груза пятью трехтонными и десятью полуторатонными
грузовиками. После нескольких часов работы все грузовики
25
перевезли *—т- всего груза. Чтобы выполнить перевозку в срок,
оставалось времени для перевозки остального груза на 2 часа
меньше, чем было затрачено. Перевозка была закончена
в срок потому, что шоферы стали за час делать на одну
поездку больше, чем раньше. Определить, за сколько часов
был перевезен весь груз, а также сколько поездок в час
делали машины первоначально, если полуторатонка делала на
одну поездку в час больше трехтонки.
Примечание. Считается, что на одну трехтонную машину
грузилось полностью 3 т, а на полуторатонку 1 -^ т.
498. Спортивная площадка имеет форму прямоугольника
со сторонами ам и Ьм. Площадка окаймлена дорожкой,
внешний край которой имеет тоже форму прямоугольника,
стороны которого параллельны сторонам площадки и одина-
ково отстоят от нее. Площадь дорожки равна площади спор-
тивной площадки. Найти ширину дорожки.
499. В зрительном зале имеется а стульев, расположен-
ных рядами по одинаковому числу стульев в каждом ряду.
Если в каждом ряду добавить по Ь стульев, а число рядов
уменьшить на с рядов, то общее число мест в зрительном
зале увеличится на одну десятую прежнего количества
стульев. Сколько было стульев в каждом ряду?
600. Два тела, находящиеся на расстоянии им друг от
друга, движутся навстречу и встречаются через а сек. Если
они будут двигаться в одну сторону с теми же скоростями,
то встретятся через Ь сек. Определить скорость движения
каждого тела.
506 ГА 7. АЛГЕБРАИЧЕСКИЕ И АРИФМЕТИЧЕСКИЕ ЗАДАЧИ 71
501. Из пунктов А и В, расстояние между которыми d км,
навстречу друг другу выехали одновременно мотоциклист и
велосипедист. Через 2 часа они встретились и, не останавли-
ваясь, продолжали путь. Мотоциклист прибыл в В на / часов
раньше, чем велосипедист в Л. Найти скорости мотоциклиста
и велосипедиста.
502. Из пункта А по направлению в В вышел пешеход.
Через а часов из В навстречу пешеходу выехал велосипе-
дист; через b часов после своего выезда он встретил пеше-
хода. Сколько времени надо велосипедисту и сколько пеше-
ходу, чтобы пройти весь путь между А и В, если велосипе-
дисту на это требуется на с часов меньше, чем пешеходу?
603. Поевд Л, скорость которого v км/час, выходит после
поезда В, скорость которого т>, км/час. Задержка выхода
поезда А рассчитана так, чтобы оба поезда одновременно при-
2
были к месту назначения. Поезд В, пройдя -д- пути, вынужден
был наполовину уменьшить свою скорость. Вследствие этого
поезда встретились за а км до места назначения. Определить
длину пути до станции назначения.
504. Вкладчик на свои сбережения через год получил
15 руб. начисления процентных денег. Добавив еще 85 руб.,
он оставил деньги ещё на год. По истечении года вклад
вместе с процентами составил 420 руб. Какая сумма была
положена первоначально и какой процент даёт сберкасса?
505. Производительность станка А составляет т % от
суммы производителъностей станков В и С, а производитель-
ность станка В составляет п % от суммы производительно-
сти станков Л и С. Какой процент составляет производи-
тельность станка С по отношению к суммарной производи-
тельности станков А и В?
506. Прирост продукции на заводе по сравнению с пре-
дыдущим годом ва 1-й год составлял р %, за 2-й год q %.
Какой должен быть процент прироста продукции за 3-й год,
чтобы средний годовой прирост продукции за три года был
равен г %?
72
ВАДАЧИ
507
507. Из общего количества товара а % продано с прибылью
в Р %» а из оставшейся части b % продано с прибылью
в q %. С какой прибылью продана вся остальная часть то-
вара, если общий процент прибыли составлял г °/0?
508. От двух кусков сплава с различным процентным со-
держанием меди, весящих т кг и п кг, отрезано по куску
равного веса. Каждый из отрезанных кусков сплавлен с остат-
ком другого куска, после чего процентное содержание меди
в обоих сплавах стало одинаковым. Сколько весил каждый
из отрезанных кусков?
509. Некоторое количество денег было разложено на п
кучек. После этого из первой кучки переложили во вторую
—ю часть бывших в первой кучке денег. Затем из второй
кучки —ю часть оказавшихся в ней после перекладывания
денег переложили в третью кучку. Далее —ю часть денег,
получившихся после этого в третьей кучке, переложили в чет-
вёртую и т. д. Наконец, из /t-й кучки —ю часть оказав-
шихся в ней после предшествующего перекладывания денег
переложили в первую кучку. После этого в каждой кучке
стало по А руб. Сколько денег в каждой кучке было до
перекладывания (можно ограничиться случаем л = 5)?
ЧАСТЬ ВТОРАЯ
ГЕОМЕТРИЯ И ТРИГОНОМЕТРИЯ
ГЛАВА 8
ПЛАНИМЕТРИЯ
510. Периметр прямоугольного треугольника равен 132,
а сумма квадратов сторон треугольника—6050. Найти стороны.
511. В параллелограмме даны острый угол а и расстояния т
и р от точки пересечения диагоналей до неравных сторон.
Определить диагонали и площадь параллелограмма.
612. В равнобедренном треугольнике основание равно
30 см, а высота 20 см. Определить высоту, опушенную на
боковую сторону.
513. В треугольнике основание равно 60 см, высота 12 см
и медиана, проведённая к основанию, 13 см. Определить
боковые стороны.
514« На сторонах равнобедренного прямоугольного тре-
угольника с катетом b построены квадраты во внешние сто-
роны. Центры этих квадратов соединены между собою прямыми
линиями. Найти площадь получившегося треугольника.
516. Стороны квадрата разделены в отношении т к п,
причём к каждой вершине прилежит один большой и один
малый отрезок. Последовательные точки деления соединены
прямыми. Найти площадь полученного четырёхугольника, если
сторона данного квадрата раина а.
516. В квадрат вписан другой квадрат, вершины которого
лежат на сторонах первого, а стороны составляют со сторо-
нами первого квадрата углы по 30°. Какую часть площади
данного квадрата составляет площадь вписанного?
74
ЗАДАЧИ
517
617. В квадрат со стороной а вписан другой квадрат,
вершины которого лежат на сторонах первого квадрата. Опре-
делить отрезки, на которые стороны первого квадрата рас-
секаются вершинами второго квадрата, если площадь второго
квадрата равна 2blAQ площади первого квадрата.
618. В прямоугольник со сторонами 3 м и 4 м вписан
другой прямоугольник, стороны которого относятся, как 1 : 3.
Найти стороны этого прямоугольника.
619. В равносторонний треугольник ЛВС, сторона кото-
рого а, вписан другой равносторонний треугольник LMN,
вершины которого лежат на сторонах первого треугольника
и делят каждую из них в отношении 1 : 2. Определить пло-
щадь треугольника LMN,
620. Найти стороны прямоугольного треугольника по дан-
ным: периметру 2р и высоте h.
621. В равнобедренном треугольнике с основанием 2а и
периметром 2Р провести прямую, параллельную основанию,
так, чтобы она отсекла трапецию периметра 2р (2а < р <Р).
522. Дана прямоугольная трапеция с основаниями а, Ь и
меньшей боковой стороной с. Определить расстояния точки
пересечения диагоналей трапеции от основания а и от мень-
шей боковой стороны.
523. Найти площадь равнобедренного треугольника, если
основание его 12 см, а высота, опущенная на основание, равна
прямой, соединяющей середины основания и боковой стороны.
624. Периметр ромба содержит 2р см, сумма диагоналей
его т см. Найти площадь ромба.
626. Большее основание трапеции а, меньшее Ь\ углы
при большем основании 30° и 45°. Найти площадь трапеции.
526. Вычислить площадь трапеции, параллельные стороны
которой содержат 16 см и 44 см, а непараллельные—17 см
и 25 см.
535
гл. 8. ПЛАНИМЕТРИЯ
75
527. Найти площадь квадрата, вписанного в правильный
треугольник со стороной а.
628. Основание треугольника делится высотою на части
в 36 см и 14 см. Перпендикулярно к основанию проведена
прямая, делящая площадь данного треугольника пополам." На
какие части эта прямая разбила основание треугольника?
629. Высота треугольника равна 4; она делит основание
на две части, относящиеся, как 1 : 8. Найти длину прямой,
параллельной высоте и делящей треугольник на равновеликие
части.
630. Треугольник ABC разбит на три равновеликие фи-
гуры прямыми, параллельными стороне АС. Вычислить, на
какие части разбили эти прямые сторону ABt равную а.
631. Прямая, параллельная основанию треугольника, пло-
щадь которого равна 5, отсекает от него треугольник с пло-
щадью, равной д. Определить площадь четырёхугольника,
три вершины которого совпадают с вершинами меньшего тре-
угольника, а четвёртая лежит на оснований большего тре-
угольника.
532. Параллельные стороны трапеции равны а и Ь. Опре-
делить длину отрезка, параллельного им и делящего площадь
трапеции пополам.
533. Из вершины тупого угла ромба опущены перпенди-
куляры на его стороны. Длина каждого перпендикуляра равна а,
расстояние между их основаниями равно Ь. Определить пло-
щадь ромба.
534. Определить площадь треугольника, если две стороны
соответственно равны 27 см и 29 см, а медиана третьей
стороны равна 26 см.
Б35. Даны две стороны b к с треугольника и его пло-
щадь S=s-zrbc. Найти третью сторону а треугольника.
76
ЗАДАЧИ
536
536. По основаниям а и ft и боковым сторонам с и d
трапеции определить её диагонали тип.
637. Дан параллелограмм, в котором острый угол 60°.
Определить отношение длин сторон, если отношение квадра-
19
тов длин диагоналей параллелограмма равно у.
638. Внутри равностороннего треугольника взята произ-
вольная точка, из которой опущены перпендикуляры на все
его стороны. Доказать, что сумма этих трёх перпендикуля-
ров равна высоте треугольника.
539. Из точки вне круга проведены две секущие. Вну-
тренний отрезок первой равен 47 м, а внешний 9 м; внутрен-
ний отрезок второй секущей на 72 м больше внешнего её
отрезка. Определить длину второй секущей.
540. Из точки, отстоящей от центра круга на т см, про-
ведены касательные к кругу. Расстояние между точками ка-
сания равно а см. Определить радиус круга.
541. Внутри круга, радиус которого равен 13 см, дана
точка М, отстоящая от центра круга на 5 см. Через точку М
проведена хорда АВ = 25 см. Определить длину отрезков,
на которые хорда АВ делится точкой М.
542. В равнобедренном треугольнике угол при вершине
равен а. Определить отношение радиусов кругов вписанного
и описанного.
543. Стороны треугольника: а= 13, Ь= 14, £== 15. Две
из них (а и Ь) служат касательными к кругу, центр которого
лежит на третьей стороне. Определить радиус круга.
544. Около круга радиуса R описан равнобедренный тре-
угольник с углом 120°. Определить его стороны.
545. На большем катете, как на диаметре, описана полу-
окружность. Определить длину этой полуокружности, если
меньший катет равен 30 см> а хорда» соединяющая вершину
прямого угла с точкой пересечения гипотенузы с полуокруж-
ностью, равна 24 см.
552
ГЛ. 8. ПЛАНИМЕТРИЯ
77
546. В прямоугольный треугольник вписан полукруг так,
что диаметр его лежит на гипотенузе и центр его делит
гипотенузу на отрезки, равные 15 см и 20 см. Определить
длину дуги полукруга, заключённой между точками касания
его с катетами.
647. В равнобедренном треугольнике с основанием, рав-
ным 4 см, и высотой, равной 6 см, на боковой стороне, как
на диаметре, построена полуокружность. Точки пересечения
её с основанием и боковой стороной соединены прямой*
Определить площадь получившегося четырёхугольника, впи-
санного в полукруг.
548. Дан равнобедренный треугольник с основанием 2а
и высотой А. В него вписана окружность и к ней проведена
касательная, параллельная основанию. Найти радиус окруж-
ности и длину отрезка касательной, заключённого между
сторонами треугольника.
549. Из точки, лежащей вне круга, проведены две секу-
щие, внешние части которых содержат по 2 м. Определить
площадь четырёхугольника, вершинами которого служат точки
пересечения секущих с окружностью, зная, что длина двух
его противоположных сторон разна б м и 2,4 м.
550* Стороны треугольника равны 6 см, 7 см, 9 см. Из
трёх вершин, как из центров, проведены взаимно касающиеся
окружности, причём окружность, центр которой лежит в вер-
шине наименьшего угла треугольника, имеет с остальными
двумя окружностями внутреннее касание, а остальные две
между собой имеют внешнее касание. Определить радиусы
трёх окружностей.
551. Внешняя касательная двух окружностей радиусов 5 см
и 2 см в 1 у раза больше их внутренней касательной. Опре-
делить расстояние между центрами этих окружностей.
552. Расстояние между центрами двух окружностей, ра-
диусы которых равны 17 см и 10 см, равно 21 см. Опре-
делить расстояние центров от точки, в которой прямая центров
пересекается с общей касательной окружностей.
78
ЗАДАЧИ
553
ББЗ. К двум окружностям радиусов R и г, находящимся
в положении внешнего касания, проведены их общие каса-
тельные — внутренняя и две внешние. Определить длину
отрезка внутренней касательной, заключенного между внеш-
ними касательными.
654. К двум окружностям радиусов R п г, находящимся
в положении внешнего касания, проведены их общие внешние
касательные. Определить площадь трапеции, ограниченной
этими касательными и хордами, соединяющими точки касания.
ББб. Две окружности радиусов R и г находятся в положе-
нии внешнего касания. К этим окружностям проведена общая
внешняя касательная, и в образовавшийся при этом криволи-
нейный треугольник вписана окружность. Найти ее радиус.
5Б6. Через одну и ту же точку окружности проведены две
хорды, равные а и д. Если соединить их концы, то получится
треугольник площади 5. Определить радиус окружности.
5Б7. В круге радиуса R по одну сторону от центра про-
ведены три параллельные между собой хорды, соответственно
равные сторонам правильных вписанных в круг шестиуголь-
ника, четырехугольника и треугольника. Определить отноше-
ние площади той части круга, которая заключена между
второй и третьей хордами, к площади той части круга, кото-
рая заключена между первой и второй хордами.
ББ8. Определить площадь круга, вписанного в прямоуголь-
ный треугольник, если высота, опущенная на гипотенузу,
делит ее на отрезки, равные 25, 6 см и 14,4 см.
ББ9. В ромб со стороной а и острым углом 60° вписана
окружность. Определить площадь прямоугольника, вершины
которого лежат в точках касания окружности со сторонами
ромба.
660. К окружности радиуса R проведены 4 касательные,
образующие ромб, ббльшая диагональ которого равна 4/?.
Определить площадь каждой из фигур, ограниченных двумя
касательными, проведенными из общей точки, и меньшей
дугой окружности, лежащей между точками касания.
568
ГЛ. 8. ПЛАНИМЕТРИЯ
79
661. Площадь равнобедренной трапеции, описанной около
круга, равна S. Определить боковую сторону этой трапеции,
если известно, что острый угол при основании трапеции
равен -g-.
662. Около круга радиуса 2 см описана равнобочная
тр&пеция с площадью 20 см\ Найти стороны трапеции.
563. Около круга описана трапеция, боковые стороны
которой образуют с большей из параллельных сторон острые
углы аир. Определить радиус круга, если площадь трапе-
ции Q#
664. Около круга радиуса г описана прямоугольная тра-
3 ^
пеция, наименьшая из сторон которой равна -о-. Определить
площадь трапеции.
565. Центр круга, вписанного в прямоугольную трапецию,
отстоит от концов боковой стороны на 2 а и 4 см. Найти
площадь трапеции.
566. В равносторонний треугольник со стороной а вписан
круг, Затем в этот треугольник вписаны ещё три круга,'
касающиеся первого круга и сторон треугольника, и ещё три
круга, касающиеся только что вписанных кругов и сторон
треугольника, и т. д. Найти сумму площадей всех вписанных
КРУГОВ *).
567. Треугольник ЛВС вписан в окружность; через вер-
шину Л проведена касательная до пересечения с продолжен-
ной стороной ВС в точке D. Из вершин В и С опущены
перпендикуляры на касательную, меньший из которых ра-
вен 6 см. Определить площадь трапеции, образованной этими
перпендикулярами, стороной ВС и. отрезком касательной, если
ВС = 5 см, AD = 5V§ см.
568. В правильный треугольник, сторона которого равна а,
вписаны три равных круга, касательных друг другу. Каждый
из них касается двух сторон данного треугольника. Определить
радиусы этих кругов,
*) То-есть предел суммы площадей вписанных кругов.
80
ЗАДАЧИ
669* Внутри равностороннего треугольника со стороной а
расположены три равных круга, касающиеся сторон тре-
угольника и взаимно касающиеся друг друга. Найти площадь
криволинейного треугольника, образованного дугами взаимно
касающихся кругов (вершинами служат точки взаимного
касания).
670. Внутри квадрата со стороной а расположены четыре
равных круга; каждый из них касается двух смежных сторон
квадрата и двух кругов (из числа остальных трёх). Найти
площадь криволинейного четырёхугольника, образованного
дугами касающихся кругов (вершинами служат точки каса-
ния кругов).
671. Найти площадь сегмента, если периметр его равен р,
а дуга содержит 120°.
672. В треугольник вписан круг радиусом 4 см. Одна
из сторон треугольника разделена точкой касания на части,
равные б см и 8 см. Найти длины двух других сторон,
673. Перпендикуляр, опущенный из вершины угла при
основании равнобедренного треугольника на противоположную
сторону, делит последнюю в отношении т: /г. Найти углы
треугольника.
*• 574. Хорда, перпендикулярная к диаметру, делит его
в отношении т : п. Определить каждую из дуг 1)| на которые
разделится окружность хордой и диаметром.
675. Определить угол параллелограмма, если даны две
его высоты Нг и h4 и периметр 2р.
576. В прямоугольном треугольнике найти отношение
катетов, если высота и медиана, выходящие из вершины
прямого угла, относятся как 40:41.
577. В прямоугольном треугольнике гипотенуза с, а один
из острых углов равен а. Определить радиус вписанного
круга.
*) В дуговых единицах.
588
ГЛ. 8. ПЛАНИМЕТРИЯ
81
578. Стороны треугольника равны 25 см, 24 см и 7 см.
Определить радиусы вписанного-и описанного кругов.
579. Определить радиусы двух внешне касающихся кру-
гов, если расстояние между их центрами равно d, а угол
между общими внешними касательными равен <р.
580. Определить угол ромба, зная его площадь Q и пло-
щадь вписанного в него крута S.
581. В круг вписан правильный 2/г-угольник; вокруг этого
же круга описан правильный я-угольник. Площади этих
многоугольников отличаются друг от друга на Я. Определить
радиус круга.
682. Середины сторон правильного л-угольника соединены
прямыми, образующими новый правильный /i-угольник, впи-
санный в данный. Найти отношение их площадей.
583. Около правильного л-угольника со стороной а опи-
сана окружность и в него вписана окружность. Определить
площадь кольца между этими окружностями и ширину его.
584. В сектор радиуса R с центральным углом а вписан
круг. Определить его радиус,
585. К кругу радиуса R прозедены из одной точки две
касательные, составляющие между собой угол 2а. Определить
площадь между этими касательными и дугой круга.
586. Ромб с острым углом а и стороной а разделён
прямыми, исходящими из вершины storo острого угла, на
три равновеликие части. Определить длины отрезков этих
прямых.
587. Внутри угла 60° расположена точка на расстояниях а
и Ь от его сторон. Найти расстояние этой точки до вер-
шины данного угла.
588. В равнобедренном треугольнике длины боковых
сторон равны а каждая, а длина отрезка прямой, проведён-
ного из вершины треугольника к его основанию и делящего
угол между равными сторонами в отношении 1: 2, равна U
Опрелелить площадь этого треугольника.
82
ЗАДАЧИ
539
589. Определить площадь треугольника, если даны а и
Ъ — длины его сторон и t—длина биссектрисы угла между
этими сторонами.
Б90. Зная углы треугольника, определить угол между
медианой и высотой, проведёнными из вершины какого-ни-
будь угла.
691. Сторона правильного треугольника равна а. Из
центра его радиусом -% описана окружность. Определить
площадь части треугольника, лежащей вне этой окружности,
Б92. В прямоугольной трапеции, высота которой равна hf
на стороне, не перпендикулярной к основанию, как на диа-
метре, описана окружность, и оказалось, что она касается
противоположной стороны трапеции. Найти площадь прямо-
угольного треугольника, у которого катеты — основания тра-
пеций.
693. Доказать, что в прямоугольном треугольнике бис-
сектриса прямого угла делит пополам угол между медианой
и высотой, опущенными на гипотенузу.
694. Доказать, что в прямоугольном треугольнике сумма
катетов равна сумме диаметров вписанной и описанной
окружности.
595. Определить угол прямоугольного треугольника, зная,
что радиус описанного около него круга относится к радиусу
вписанного круга, как 5:2.
696. Доказать, что прямые, соединяющие последовательно
центры квадратов, построенных на сторонах параллелограмма
и примыкающих к нему извне, образуют также квадрат,
ГЛАВА 9
МНОГОГРАННИКИ
597. Стороны основания прямоугольного параллелепипеда
а и 6. Диагональ параллелепипеда составляет с плоскостью
основания угол а. Определить боковую поверхность парал-
лелепипеда.
606 гл. 9. МНОГОГРАННИКИ 83
598. Самая большая диагональ правильной шестиугольной
призмы, имеющая длину df составляет с боковым ребром
призмы угол а. Определить объём призмы,
699. Боковое ребро правильной четырёхугольной пира-
миды, длиной т, наклонено к плоскости основания под уг- *
лом а. Найти объём пирамиды.
600. Объём правильной четырёхугольной пирамиды ра-
вен V. Угол наклона её бокового ребра к плоскости ос-
нования равен а. Найти боковое ребро пирамиды.
601. Боковая поверхность правильной четырёхугольной пи-
рамиды содержит S см*, высота пирамиды Н ели Найти
сторону основания пирамиды.
602. Найти объём и боковую поверхность правильной
шестиугольной пирамиды, если даны боковое ребро / и диа-
метр d круга, вписанного в основание пирамиды.
603. Найти высоту тетраэдра1), объём которого ра-
вен I/,
604. В прямом параллелепипеде стороны основания равны а
и £ и острый угол — а. Ббльшая диагональ основания равна
меньшей диагонали параллелепипеда. Найти объём паралле-
лепипеда.
605. Диагонали прямого параллелепипеда равны 9 см и
"|/"33 см. Периметр его основания равен 18 см. Боковое реб-
ро равно 4 см. Определить полную поверхность и объём
параллелепипеда.
606. Боковое ребро правильной треугольной пирамиды /,
а высота пирамиды А. Определить двугранный угол при
основании.
J) Под тетраэдром здесь понимается правильный четырёхгран-
ник (иногда тетраэдром называется произвольная треугольная пира-
мида).
84
ЗАДАЧИ
607
607. Определить объём правильной четырёхугольной пи-
рамиды, зная угол а её бокового ребра с плоскостью осно-
вания и площадь 5 её диагонального сечения. Найти также
угол, образуемый боковой гранью с плоскостью основания.
608. Основанием правильной пирамиды служит много-
угольник, сумма внутренних углов которого 540°. Опреде-
лить объём этой пирамиды, зная, что боковое ребро её,
равное /, наклонено к плоскости основания под углом <х.
609. Определить углы, составляемые с основанием бо-
ковым ребром и боковой гранью правильной пятиугольной
пирамиды, у которой боковые грани — равносторонние тре-
угольники.
610. По объёму V правильной я-угольной пирамиды, у ко-
торой сторона основания равна а, определить угол наклона
бокового ребра пирамиды к плоскости основания.
• 611. Основание четырёхугольной пирамиды — прямоуголь-
ник с диагональю, равной Ь, и углом а между диагоналями.
Каждое из боковых рёбер образует с основанием угол р.
Найти объём пирамиды.
612. Основанием пирамиды служит равнобедренный тре-
угольник с боковыми сторонами, равными а, и углом между
ними, равным а. Все боковые рёбра наклонены к основанию
под углом {}. Определить объём пирамиды.
613. Основанием прямоугольного параллелепипеда служит
прямоугольник, вписанный в круг радиуса /?, причём мень-
шая сторона этого прямоугольника стягивает дугу окруж-
ности, содержащую (2<х)°. Найти объём этого параллелепи-
педа, зная его боковую поверхность S.
614. Основанием прямой призмы служит равнобедренный
треугольник, основание которого равно а и угол при осно-
вании равен а. Определить объём призмы, если её боковая
поверхность равна сумме площадей её оснований.
616. Апофема правильной шестиугольной пирамиды
равна т. Двугранный угол при основании равен а. Найти
полную поверхность пирамиды.
623
ГЛ. 9, МНОГОГРАННИКИ
85
616. Через гипотенузу прямоугольного равнобедренного
треугольника проведена плоскость Р под углом а к пло-
скости треугольника. Определить периметр и площадь фи-
гуры, которая получится, если спроектировать треугольник на
плоскость Р. Гипотенуза треугольника равна с.
617. В правильной л-угольной пирамиде площадь основа-
ния равна Qt а высота составляет с каждой из боковых гра-
ней угол ср. Определить боковую и полную поверхность
пирамиды.
618. Сторона основания правильной треугольной пирамиды
равна а, боковая грань наклонена к плоскости основания под
углом ср. Найти объем и полную поверхность пирамиды.
619. Полная поверхность правильной треугольной пира-
миды равна S. Зная, что угол между боковой гранью и ос-
нованием пирамиды равен а, найти сторону основания пира-
миды,
620. Основанием пирамиды служит ромб с острым углом а.
Боковые грани наклонены к плоскости основания под углом §.
Определить объем и полную поверхность пирамиды, если
радиус вписанного в ромб круга равен г.
621. Определить угол наклона боковой грани правилыо'1
пятиугольной пирамиды к плоскости основания, если площадь
основания пирамиды равна S, а боковой поверхности равна а.
622. Основанием прямого параллелепипеда служит ромб.
Плоскость, проведенная через одну из сторон нижнего
основания и противоположную сторону верхнего основания,
образует с плоскостью основания угол р. Полученное сече-
ние имеет площадь, равную Q. Определить боковую поверх-
ность параллелепипеда.
623. Основанием пирамиды служит равнобедренный тре-
угольник с углом а при основании. Каждый из двугранных:
углов при основании равен ср. Расстояние от центра круга, впи-
санного в основание пирамиды, до середины высоты боковой
грани равно d* Определить полную поверхность пирамиды.
86
ЗАДАЧИ
624
624. Основанием пирамиды служит многоугольник, опи-
санный около круга радиуса г\ периметр многоугольника
равен 2р, боковые грани пирамиды наклонены к плоскости
основания под углом у- Найти объём пирамиды.
625. Боковые рёбра правильной усечённой треугольной
пирамиды наклонены к плоскости основания под углом а.
Сторона нижнего основания равна af а верхнего — b (а>£).
' Найти объём усечённой пирамиды.
626. Основаниями правильной усечённой пирамиды слу-
жат квадраты со сторонами а и b (а > Ь). Боковые рёбра
наклонены к плоскости основания под углом а. Определить
объём усечённой пирамиды и величину двугранных углов
при сторонах оснований. —
627. Основанием пирамиды служит прямоугольный тре-
угольник с гипотенузой, равной с, и острым углом а. Все
боковые рёбра наклонены к основанию под углом р. Найти
объём пирамиды и плоские углы при вершине её.
628. В основании наклонной призмы лежит прямоугольный
треугольник ABC, сумма катетов которого равна т и угод,
при вершине А равен а. Боковая грань призмы, проходящая
через катет АС, наклонена к основанию под углом (3. Через
гипотенузу АВ и через вершину Ct противоположного трёх-
гранного угла проведена плоскость Определить объём
отсечённой треугольной пирамиды, если известно, что боко-
вые рёбра её равны между собой.
629. В основании пирамиды лежит равнобедренный тре-
угольник с углом <х при основании. Все боковые рГёбра на-
клонены к плоскости основания под равными углами
9 = 90°—а. Площадь сечения, проведённого через высоту
пирамиды и через вершину равнобедренного треугольника,
лежащего в основании, равна Q. Определить объём пирамиды.
630. Основанием пирамиды служит прямоугольник. Из
боковых граней две перпендикулярны к плоскости основания,
а две другие образуют с ней углы а и р. Высота пирамиды
равна Я. Определить объём пирамиды.
636
ГЛ. 9. МНОГОГРАННИКИ
87
631. Пирамида имеет в основании квадрат. Из двух про-
тиволежащих друг другу рёбер одно перпендикулярно
к плоскости основания, другое наклонено к ней под углом (3 и
имеет длину L Определить длины остальных боковых рёбер
и углы наклона их к плоскости основания пирамиды.
632. Основание пирамиды — правильный треугольник со
стороной а. Одно из боковых рёбер перпендикулярно к осно-
ванию, а остальные два наклонены к плоскости основания
под равными углами {3. Найти площадь наибольшей боко-
вой грани пирамиды и угол наклона её к плоскости осно-
вания.
633. Пирамида имеет в основании равнобедренный тре-
угольник; боковые стороны этого основания равны а и обра-
зуют угол в 120°. Боковое ребро пирамиды, проходящее
через вершину тупого угла, перпендикулярно к плоскости
основания, а остальные два наклонены к ней под углом а.
Определить площадь сечения пирамиды плоскостью, кото-
рая проходит через наибольшую сторону основания пира-
миды и делит пополам ребро, перпендикулярное к осно-
ванию.
634. Правильная треугольная пирамида рассечена плоско-
стью, перпендикулярной к основанию и делящей две стороны
основания пополам. Определить объём отсечённой пирамиды,
если даны сторона а основания первоначальной пирамиды
и двугранный угол а при основании.
635. Через вершину правильной четырёхугольной пира-
миды под углом <р к основанию пирамиды проведена пло-
скость параллельно стороне основания. Сторона основания
пирамиды равна а, а плоский угол при вершине пирамиды
равен а. Найти площадь сечения пирамиды.
636. Через вершину правильной" треугольной пирамиды и
середины двух сторон основания проведена плоскость. Опре-
делить площадь сечения и объёмы частей данной пирамиды,
на которые она разделена сечением, зная сторону а её осно-
вания, и угол а, образованный сечением с основанием.
88
ЗАДАЧИ
637
637. Тетраэдр г), ребро которого равно а, пересечен
плоскостью, содержащей одно из ребер тетраэдра и делящей
противоположное ребро в отношении 2:1. Определить
п ющадь сечения и углы этого сечения.
638. Определить объем правильной усеченной четырех-
угольной пирамиды, если сторона ббльшего основания равна а,
сторона меньшего основания равна Ь, а острый угол боковой
грани равен а.
639. Определить объем правильной четырехугольной
призмы, если ее диагональ образует с боковой гранью угол а,
а сторона основания равна Ь.
640. Основанием прямой призмы служит прямоугольный
треугольник с гипотенузой с и острым углом а. Через гипо-
тенузу нижнего основания и вершину прямого угла верхнего
основания проведена плоскость, образующая с плоскостью
основания угол (3. Определить объем треугольной пирамиды,
отсеченной о г призмы плоскостью.
641. В основании прямой призмы лежит прямоугольный
треугольник, у которого сумма катета и гипотенузы равна т
и угол между ними равен а. Через другой катет и вершину
противоположного трехгранного угла призмы проведена пло-
скость, образующая с основанием угол р. Определить объемы
частей, на которые призма делится плоскостью сечения.
642. В основании пирамиды лежит равнобедренный тре-
угольник с углом а при основании. Каждый двугранный угол
при основании равен ср — 90° — а. Боковая поверхность пира-
миды равна S. Определить объем пирамиды и полную по-
верхность ее.
643. Основанием пирамиды является равнобедренный тре-
угольник с боковой стороной а и углом а при основании
(а > 45°). Боковые ребра наклонены к плоскости основания
под углом р. В этой пирамиде проведена плоскость через ее
высоту и вершину одного из углов а. Найти площадь сечения.
1) Сч. подстрочное примечание на стр. 83.
650
ГЛ. 9. МНОГОГРАННИКИ
89
644» В оснований прямой призмы лежит четырёхугольник,
в котором два противолежащих угла прямые. Диагональ осно-
вания, соединяющая вершины непрямых углов, имеет длину /
и делит один из этих углов на части аир. Площадь сече-
ния, проведённого через другую диагональ основания пер-
пендикулярно к нему, равна S. Найти объём призмы.
645. Основанием пирамиды служит квадрат. Две противо-
положные грани — равнобедренные треугольники, одна из них
образует с основанием внутренний угол (3, а другая — внеш-
ний острый угол <х. Высота пирамиды равна Н. Найти объём
пирамвды и углы, образованные двумя другими боковыми
гранями с плоскостью основания.
646. В основании пирамиды лежит прямоугольник. Одна из
боковых граней наклонена к основанию под углом р = 90° — а,
а противоположная ей грань перпендикулярна к основанию и
имеет вид прямоугольного треугольника с прямым углом при
вершине пирамиды и острым углом, равным а. Сумма высот
этих двух граней равна т. Определить объём пирамиды и
сумму площадей двух других боковых граней.
647. В основании пирамиды лежит прямоугольник. Одна
из боковых граней имеет вид равнобедренного треугольника
и перпендикулярна к основанию; в другой грани, противопо-
ложной первой, боковые рёбра, равные bt образуют между
собой угол 2а и наклонены к первой грани под углом <х.
Определить объём пирамиды и угол между указанными двумя
гранями.
648. В правильной треугольной пирамиде со стороной
основания, равной а, углы между рёбрами при её вершине
равны между собой и каждый равен а (а ^90°). Определить
углы между боковыми гранями пирамиды и площадь сече-
ния, проведённого через сторону основания перпендикулярно
к противолежащему боковому ребру.
649. Определить объём правильного восьмигранника (ок-
таэдра) с ребром а и двугранные углы при его рёбрах.
650. Двугранный угол при боковом ребре правильной
шестиугольной пирамиды равен q>« Определить плоский угол
при вершине пирамиды.
90 ЗАДАЧИ 651
651. Пирамида имеет в основании правильный шести-
угольник ABCDEF. Боковое ребро МЛ перпендикулярно
к плоскости основания, а противоположное ему ребро MD
наклонено к плоскости основания под углом а. Определить
углы наклона боковых граней к плоскости основания.
652. Основанием пирамиды служит равнобедренный тре-
угольник ABCt где АВ = АС. Высота пирамиды SO прохо-
дит через середину высоты AD основания. Через сторону ВС
проведена плоскость перпендикулярно к боковому ребру AS,
образующая с основанием угол а. Определить объем пира-
миды, отсеченной от данной и имеющей с ней общую вер-
шину S, если объем другой отсеченной части ее равен V.
653. Сторона основания правильной треугольной пирамиды
равна а. Сечение, делящее угол между боковыми гранями
пополам, есть прямоугольный треугольник. Определить объем
пирамиды и угол между боковой гранью ее и плоскостью
основания.
654. Через сторону основания правильной треугольной
пирамиды проведена плоскость перпендикулярно к противо-
лежащему боковому ребру. Определить полную поверхность
пирамиды, если указанная плоскость делит боковое ребро
в отношении т : п и сторона основания равна д.
655. Диагональ прямоугольного параллелепипеда равна d
и образует с двумя смежными боковыми гранями равные
углы а. Определить объем параллелепипеда и угол, который
образует с плоскостью основания плоскость, проведенная
через концы трех ребер, выходящих из одной вершины.
656. В прямоугольном параллелепипеде точка пересечения
диагоналей нижнего основания соединена с серединой одного
из боковых ребер прямой, длина которой равна т. Она
образует с основанием угол а и с одной из боковых граней
угол р — 2а. Приняв другую смежную боковую грань за осно-
вание параллелепипеда, найти его боковую поверхность и
объем, (Доказать, что а < 30°.)
664
ГЛ. 9. МНОГОГРАННИКИ
91
657. В основании прямой призмы лежит трапеция, впи-
санная в полукруг радиуса R так, что ббльшее основание
её совпадает с диаметром, а меньшее стягивает дугу, рав-
ную 2а. Определить объём призмы, если диагональ грани,
проходящей через боковую сторону основания, наклонена
к основанию под углом а.
658. Диагональ прямоугольного параллелепипеда, равная
d, образует с боковой гранью угол (3 = 90°—а. Плоскость,
проведённая через эту диагональ и боковое ребро, пересе-
кающееся с ней, образует с той же боковой гранью угол <х
(доказать, что ос > 45°). Определить объём параллелепипеда.
659. В правильной треугольной призме две вершины верх-
него основания соединены с серединами противоположных им
сторон нижнего основания. Угол между полученными линиями,
обращенный отверстием к плоскости основания, равен а. Сто-
рона основания равна Ь. Определить объём призмы.
660. В правильной треугольной призме1 угол между диаго-
налью боковой грани и другой боковой гранью равен а.
Определить боковую поверхность призмы, зная, что ребро
основания равно д.
661. В основании прямой призмы лежит прямоугольный
треугольник ABC, у которого /_ С = 90°, /,Л = а и катет
АС = Ь. Диагональ боковой грани призмы, проходящей через
гипотенузу АВ, образует с боковой гранью, проходящей че-
рез катет АС, угол |3, Найти объём призмы.
662. Полная поверхность правильной четырёхугольной
пирамиды равна 5, а плоский угол боковой грани при вер-
шине равен ос. Найти высоту пирамиды.
663. В правильной я-угольной пирамиде плоский угол
при вершине равен а, а сторона основания а. Определить
Объём.
664. От правильной четырёхугольной призмы плоскостью,
проходящей через диагональ нижнего основания и одну из
вершин верхнего основания, отсечена пирамида с полной по-
верхностью 5. Найти полную поверхность призмы, если угол
при вершине треугольника, получившегося в сечении, равен а#
92
ЗАДАЧИ
685
665. Боковые рёбра треугольной пирамиды имеют одина-
ковую длину /. Из трёх плоских углов, образованных при
вершине пирамиды этими рёбрами, два равны а, а третий
равен (3. Найти объём пирамиды.
666. В основании пирамиды лежит прямоугольный тре-
угольник, являющийся проекцией боковой грани, проходящей
через катет. Угол, лежащий против этого катета в основа-
нии пирамиды, равен ос, а лежащий в боковой грани равен Э-
Площадь этой боковой грани больше площади основания
на S. Определить разность между площадями двух других
граней и углы, образованные боковыми гранями с плоскостью
основания.
667. В треугольной пирамиде две боковые грани суть
равнобедренные прямоугольные треугольники, гипотенузы ко-
торых равны b и образуют между собой угол а. Определить
объём пирамиды.
668. В пирамиде с прямоугольным основанием каждое из
боковых рёбер равно /, один из плоских углов при вершине
равен а, другой равен (3, Определить площадь сечения, про-
ходящего через биссектрисы углов, равных (3.
669. В параллелепипеде длины трёх рёбер, выходящих нз
общей вершины, равны соответственно а, Ь и с. Рёбра а и Ь
взаимно перпендикулярны, а ребро с образует с каждым из
них угол а. Определить объём параллелепипеда, боковую по-
верхность его и угол между ребром с и плоскостью основа-
ния. (При каких значениях угла а задача возможна?)
670. В параллелепипеде все его грани—равные ромбы
со сторонами а и острыми углами а. Определить объём этого
параллелепипеда.
671. Основанием наклонного параллелепипеда служит ромб
ABCD со стороной а и острым углом а. Ребро ААХ равно Ь
и образует с рёбрами АВ и AD угол <р. Определить объём
параллелепипеда.
676
ГЛ. 9. МНОГОГРАННИКИ
93
672. В прямоугольном параллелепипеде проведена пло-
скость через диагональ основания и диагональ большей бо-
ковой грани, выходящих из одной вершины. Угол между
этими диагоналями равен р. Определить боковую поверхность
параллелепипеда, площадь сечения и угол наклона сечения
к плоскости основания, если известно, что радиус окружно-
сти, описанной около основания параллелепипеда, равен R и
меньший угол между диагоналями основания равен 2а.
673. В основании прямой призмы лежит прямоугольный
треугольник ЛВС. Радиус окружности, описанной около него,
равен /?, катет АС стягивает дугу, равную 2(5. Через диа-
гональ боковой грани, проходящей через другой катет ВС,
проведена плоскость перпендикулярно к этой грани, обра-
зующая с плоскостью основания угол р. Определить боковую
поверхность призмы и объём отсечённой четырёхугольной
пирамиды,
674. Основанием пирамиды служит трапеция, в которой
боковые стороны и меньшее основание равны между собой,
большее основание равно а и тупой угол трапеции равен а.
Все боковые рёбра пирамиды образуют с плоскостью основа-
ния угол (3. Определить объём пирамиды.
675. В основании пирамиды лежит трапеция, у которой
диагональ перпендикулярна к боковой стороне и образует
с основанием угол а. Все боковые рёбра равны между собой.
Боковая грань, проходящая через большее основание трапе-
ции, имеет угол при вершине пирамиды <р = 2а и площадь,
равную 5. Определить объём пирамиды и углы, под кото-
рыми наклонены боковые грани к плоскости основания.
676. В основании пирамиды лежит правильный треуголь-
ник, сторона которого равна а. Высота, опущенная из вер-
шины пирамиды, проходит через одну из вершин основания.
Боковая грань, проходящая через сторону основания, противо-
лежащую этой вершине, наклонена к плоскости основания под
углом ср. Определить боковую поверхность этой пирамиды,
если за основание её принять одну из равных боковых
граней.
94
ЗАДАЧИ
677
677. В основании прямой призмы лежит равнобедренный
треугольник с боковой стороной, равной а, и углом при осно-
вании, равным а. Через основание треугольника, являющегося
верхней гранью, и противоположную вершину нижнего
основания проведена плоскость, образующая с плоскостью
основания угол р. Определить боковую поверхность призмы
и объем отсеченной четырехугольной пирамиды.
678. В основании пирамиды — квадрат. Две боковые грани
ее перпендикулярны к плоскости основания, а две другие
наклонены к нему под углом а. Радиус круга, описанного
около боковой грани, перпендикулярной к основанию, равен/?.
Определить полную поверхность пирамиды.
679. В основании прямой призмы лежит прямоугольный
треугольник с катетом а и противолежащим ему углом а.
Через вершину прямого угла нижнего основания проведена
плоскость, параллельная гипотенузе, под углом (3 = 90° — а
к противолежащей боковой грани и пересекающая ее. Опре-
делить объем части призмы между ее основанием и сечением
и боковую поверхность призмы, если известно, что боковая
грань, проходящая через катет а, равновелика сечению призмы.
Определить, при каком значении угла а плоскость сечения
пересекает боковую грань, проходящую через гипотенузу
основания.
680. Основанием пирамиды служит прямоугольник. Одно
боковое ребро перпендикулярно к плоскости основания, а две
боковые грани наклонены к ней под углами а и р. Опреде-
лить боковую поверхность пирамиды, если высота ее равна #.
681. В основании пирамиды лежит прямоугольный тре-
угольник, у которого один острый угол равен а и радиус
вписанного круга равен г. Каждая из боковых граней обра-
зует с основанием угол а. Определить объем, боковую и
полную поверхность пирамиды.
682. В основании призмы ABCAxBfix лежит равнобед-
ренный треугольник ABC (АВ==АС и ^АВС = а). Вер-
шина Bt верхнего основания призмы проектируется в центр
окружности радиуса г, вписанной в нижнее основание. Через
637
гл. 9. многогранники
95
сторону АС основания и вершину Bt проведена плоскость,
наклонённая к плоскости основания под углом а. Найти пол-
ную поверхность отсечённой треугольной пирамиды АВСВХ
и объём призмы.
683. Основанием пирамиды служит прямоугольный тре-
угольник, а высота её проходит через точку пересечения
гипотенузы с биссектрисой прямого угла основания. Боковое
ребро, проходящее через вершину прямого угла, наклонено
к плоскости основания под углом а. Определить объём пира-
миды и углы наклона боковых граней к плоскости основания,
если биссектриса прямого угла основания равна т и обра-
зует с гипотенузой угол 45° 4- а.
684. В основании пирамиды ромб со стороной а. Две со-
седние грани составляют с плоскостью основания угол а,
третья боковая грань составляет с плоскостью основания
угол () (доказать, что и четвёртая боковая грань наклонена
к основанию под тем же углом). Высота пирамиды Н. Найти
объём пирамиды и полную поверхность её.
685. В основании четырёхугольной пирамиды лежит ромб,
сторона которого равна а и острый угол равен а. Плоскости,
проходящие через вершину пирамиды и диагонали основания,
наклонены к плоскости основания под углами <р и ф. Опре-
делить объём пирамиды, если её высота пересекает сторону
основания.
686. В основании наклонной призмы лежит прямоуголь-
ный треугольник ABC с катетом ВС = а. Вершина Вг верх-
него основания проектируется на середину катета ВС. Дву-
гранный угол, образованный боковыми гранями, проходящими
через катет ВС и гипотенузу ABt равен а. Боковые рёбра
наклонены к плоскости основания под углом {3. Определить
боковую поверхность призмы.
687. В основании призмы ABCA1BiC1 лежит равнобед-
ренный треугольник ABC (АВ = АС и /JBАС = 2<х). Вер.
шина At верхнего основания проектируется в центр окруж-
ности радиуса /?, описанной около нижнего основания. Бо-
ковое ребро ААХ образует со стороной основания АВ угол,
равный 2<х. Определить объём и боковую поверхность призмы.
96
ЗАДАЧИ
683
688. Определить объём правильной четырёхугольной пи-
рамиды, боковое ребро которой равно /, а двугранный угол
между двумя смежными боковыми гранями равен fJ.
689. В правильной усечённой четырёхугольной пирамиде
даны: диагональ d, двугранный угол а при нижнем основа*
нии и высота //. Найти объём усечённой пирамиды.
690. Боковое ребро правильной четырёхугольной усечён-
ной пирамиды равно 2, оно наклонено к плоскости основания
под углом р. Диагональ пирамиды перпендикулярна к боко-
вому ребру её. Определить объём пирамиды.
691. Высота правильной четырёхугольной усечённой пи-
рамиды равна Ht боковое ребро и диагональ пирамиды на-
клонены к плоскости её основания под углами аир. Найти
её боковую поверхность.
692. Стороны оснований правильной четырёхугольной
усечённой пирамиды равны ana Уд, боковая грань накло-
нена к плоскости основания под углом 7- Определить объём
и полную поверхность пирамиды.
693. В правильную четырёхугольную пирамиду вписан
куб так, что его четыре вершины находятся на боковых
рёбрах * пирамиды, а остальные четыре—в плоскости её
основания. Определить ребро куба, если высота пирамиды
равна Я, а боковое ребро равно /.
694. В правильную четырёхугольную пирамиду вписан
куб так, что вершины его лежат на апофемах пирамиды.
Найти отношение объёма пирамиды к объёму куба, зная,
что угол между высотой пирамиды и её боковой гранью
равен а.
695. Основанием пирамиды является прямоугольный тре-
угольник с катетами 6 и 8. Вершина пирамиды удалена от
плоскости её основания на расстояние, равное 24, и проек-
тируется на эту плоскость в точку, лежащую внутри осно-
вания. Найти ребро куба, четыре вершины которого лежат
701
ГЛ. 9. МНОГОГРАННИКИ
97
в плоскости основания данной пирамиды, а рёбра, соединяю-
щие эти вершины, параллельны соответствующим катетам
треугольника, лежащего в основании пирамиды. Четыре дру-
гие вершины куба лежат на боковых гранях данной пира-
миды.
696. В правильной четырёхугольной пирамиде двугран-
ный угол при основании равен а. Через его ребро проведена
плоскость, составляющая с основанием угол р. Сторона ос-
нования равна а. Определить площадь сечения.
697. В правильной четырёхугольной пирамиде сторона
основания равна а, а двугранный угол при основании равен
а. Через две противоположные стороны основания пирамиды
проведены две плоскости, пересекающиеся взаимно под пря-
мым углом. Определить длину линии их пересечения, заклю-
чённую внутри пирамиды, если известно, что она пересекает
ось пирамиды.
698. В правильной четырёхугольной пирамиде через вер-
шину основания проведена плоскость, перпендикулярная
к противоположному боковому ребру. Определить площадь
сечения, если сторона основания пирамиды равна а, а боко-
вое ребро наклонено к плоскости основания под углом
9(9 > 45°; доказать это),
699. Правильную четырёхугольную призму требуется пе-
ресечь плоскостью так, чтобы в сечеции получился ромб
с острым углом а. Найти угол наклона секущей плоскости
к основанию.
700. Основанием прямого параллелепипеда служит ромб
с острым углом а. Под каким углом к основанию нужно пе-
ресечь этот параллелепипед плоскостью, чтобы в сечении
получился квадрат с вершинами на боковых рёбрах.
701. Прямой параллелепипед, имеющий в основании ромб
со стороной а и острым углом а, пересечён плоскостью, про-
ходящей через вершину угла а и дающей в сечении ромб
с острым углом -^*. Определить площадь этого сечения.
98
8АДАЧИ
702
702. Ребро тетраэдра равно Ь. Через середину одного
из рёбер проведена плоскость параллельно двум непересекаю-
щимся рёбрам. Определить площадь полученного сечения.
703* Пирамида имеет в основании прямоугольный тре-
угольник с катетом а. Одно из боковых рёбер пирамиды пер-
пендикулярно к плоскости основания, а другие два наклонены
к ней под одним и тем же углом а. Плоскость, перпенди-
кулярная к основанию, даёт в сечении с пирамидой квадрат*
Определить площадь этого квадрата.
704* В правильной четырёхугольной усечённой пирамиде
стороны верхнего и нижнего оснований равны соответствен-
но а и За и боковые грани наклонены к плоскости нижнего
основания под углом а. Через сторону верхнего основания
проведена плоскость параллельно противоположной боковой
грани. Определить объём четырёхугольной призмы, отсечён-
ной от данной усечённой пирамиды, и полную поверхность
остальной части её.
705» Из точки, взятой на ребре правильной треугольной
призмы со стороной основания л, проведены две плоскости.
Одна проходит через сторону нижнего основания призмы под
углом а к последнему, а другая — через параллельную ей
сторону верхнего основания под углом {Э к нему. Определить
объём призмы и сумму площадей полученных сечений.
t 706* В правильной четырёхугольной призме через сере-
дины двух смежных сторон основания проведена плоскость,
пересекающая три боковых ребра и наклонённая к плоскости
основания под углом а. Определить площадь полученного
сечения и острый угол его, если сторона основания призмы
равна Ь.
707* В основании прямой призмы лежит равнобочная
трапеция с острым углом а, описанная около круга радиуса л
Через боковую сторону нижнего основания и противополож-
ную вершину острого угла верхнего основания проведена
плоскость, образующая с плоскостью основания угол а.
Определить боковую поверхность призмы и площадь се-
чения.
714
гл. 9, МНОГОГРАННИКИ
99
708. В основании прямой призмы АВСАХВХСХ лежит рав-
нобедренный треугольник ABC с углом а при основании ВС.
Боковая поверхность призмы равна S. Найти площадь сечения
призмы плоскостью, проходящей через диагональ боковой
грани ВССХВХ параллельно высоте АО основания призмы и
образующей с плоскостью основания угол р.
709. В основании прямой призмы АВСА1ВХСХ лежит пря-
моугольный треугольник ABC с углом Р при вершине В
({3 < 45°). Разность между площадями её боковых граней,
проходящих через катеты ВС и АС, равна S. Найти площадь
сечения призмы плоскостью, образующей с плоскостью
основания угол ср и проходящей через три точки: вершину Вх
угла р верхнего основания, середину бокового ребра ААХ и
точку D, расположенную на плоскости основания симметрично
с вершиной В относительно катета АС.
710. Непересекающиеся диагонали двух смежных боковых
граней прямоугольного параллелепипеда наклонены к пло-
скости его основания под углами а к р. Найти угол между
этими диагоналями.
711. Даны три плоских угла трёхгранного угла SABC:
£Я5С = а; £CSA = §\ ^ASB — i. Найти двугранные углы
этого трёхгранного угла.
712. Один из двугранных углов трёхгранного угла равен А;
прилежащие к данному двугранному углу плоские углы соот-
ветственно равны а и fJ. Найти третий плоский угол.
713. В трёхгранном угле даны три плоских угла в 45°,
60° и 45°. Определить двугранный угол, заключённый между
теми двумя гранями, которые содержат плоские углы по 45°.
714. На ребре двугранного угла дан отрезок АВЯ В одной
из граней дана точка М, в которой прямая, проведённая из
точки А под углом а к АВ, пересекает прямую, проведённую
из В перпендикулярно к АВ. Определить величину двугран-
ного угла, если прямая AM наклонена ко второй грани дву-
гранного угла под углом р.
100
ЗАДАЧИ
715
715. Даны две скрещивающиеся прямые, наклонённые
дру! к другу под углом ср и имеющие общий пересекающий
их перпендикуляр PQs=k. На этих прямых даны две точки
А и В, из которых отрезок PQ виден под углами а и р.
Определить длину отрезка АВ.
716. На двух Взаимно перпендикулярных скрещивающихся
прямых, кратчайшее расстояние между которыми PQ = h,
даны две точки А и В, из которых отрезок PQ виден под
углами а н р. Определить угол наклона отрезка АВ к от-
резку PQ.
717. Секущая плоскость делит боковые рёбра треуголь-
ной пирамиды в отношениях (считая от вершины) ^, ^, ^.
nt я3 «з
В каком отношении эта плоскость разделит объём пирамиды?
718. Из середины высоты правильной четырёхугольной
пирамиды опущен перпендикуляр на боковое ребро, равный h,
и перпендикуляр на боковую грань, равный Ь. Найти объём
пирамиды.
ГЛАВА 10
КРУГЛЫЕ ТЕЛА
719. Образующая конуса равна / и составляет с плоско-
стью основания угол в 60°. Определить объём конуса.
720. Длина образующей конуса равна /, а длина окруж-
ности основания — с. Определить объём.
721. Боковая посерхность цилиндра развёртывается в квад-
рат со стороной а. Найти объём цилиндра.
722. Боковая поверхность цилиндра, будучи развёрнута,
представляет собою прямоугольник, в котором диагональ
равна d и составляет угол а с основанием. Определить объём
цилиндра.
723. Угол при вершине осевого сечения конуса равен 2а,
а сумма длин его высоты и образующей равна т. Найти
объём и полную поверхность конуса.
731
ГЛ. 10. КРУГЛЫЕ ТЕЛА
101
724. Объём конуса V\ Высота его разделена на три рав-
ные части и через точки деления проведены плоскости парал-
лельно основанию. Найти объём средней части.
725. Определить объём конуса, если в его основании
хорда, равная а% стягивает дугу а, а высота конуса соста-
вляет с образующей угол {3.
726. На одном и том же основании построены два конуса
(один внутри другого); угол между высотой и образующей
меньшего конуса равен а, а угол между высотой и образую-
щей ббльшего конуса равен [3. Разность высот конусов равна h.
Найти объём, заключённый между боковыми поверхностями
этих конусов.
727. Боковая поверхность конуса равна 5, а полная по-
верхность — Р. Определить угол между высотой и обра-
зующей.
728. Боковая поверхность конуса, будучи развёрнута на
плоскость, представляет круговой сектор с углом а и хор-
дой а. Определить объём конуса.
729. Через вершину конуса под углом <р к основанию
приведена плоскость, отсекающая от окружности основания
дугу а; расстояние плоскости от центра основания равно а.
Найти объём конуса.
730. В основание конуса вписан квадрат, сторона кото-
рого равна а. Плоскость, проходящая через вершину конуса
и сторону квадрата, даёт в сечении с поверхностью конуса
треугольник, угол при вершине которого а. Определить
объём и полную поверхность конуса.
731. Образующая усечённого конуса / составляет с пло-
скостью нижнего основания угол а и перпендикулярна к пря-
мой, соединяющей верхний конец её с нижним концом про-
тивоположной образующей. Найти боковую поверхность усе-
чённого конуса.
102
8АДАЧИ
732
732. Дан конус объёма Vt образующая которого накло-
нена к плоскости основания под углом а. На какой высоте
надо провести плоскость, перпендикулярную к оси конуса,
чтобы сечение конуса разделило пополам его боковую по-
верхность? Тот же вопрос для полной поверхности.
733. Определить объём и полную поверхность шарового
сектора, вырезанного из шара радиуса R и имеющего в осе-
вом сечении угол а.
734. Шаровой сегмент шара радиуса R имеет полную
поверхность 5, Найти его высоту.
735. Площадь треугольника ABC равна S, сторона ЛС== Ь
и £тСАВ = а. Найти объём тела, полученного при враще-
нии треугольника ABC около стороны АВ»
736. В треугольнике даны сторона а, угол В и угол С,
Определить объём тела, полученного от вращения треуголь-
ника около данной стороны*
737» Ромб с ббльшей диагональю d и острым углом f
вращается вокруг оси, проходящей вне его через вершину
ромба и перпендикулярной к ббльшей диагонали его. Опре-
делить объём тела вращения.
738. В треугольнике даны стороны йси угол между
ними а. Этот треугольник вращается около оси, которая
проходит вне его через вершину угла а и равно наклонена
к сторонам b и с. Определить объём тела вращения.
739. В равнобедренной трапеции диагональ перпендику-
лярна к боковой стороне. Боковая сторона равна b и соста-
вляет с ббльшим основанием угол а. Определить поверхность
тела, образованного вращением трапеции вокруг большего
основания.
740. Через вершину конуса проведены две плоскости.
Одна из них наклонена к плоскости основания конуса под
углом <х и пересекает это основание по хорде,. длина кото-
рой равна а, а другая наклонена к плоскости основания под
углом % и пересекает основание по хорде, длина которой
равна Ь. Определить объём конуса.
746
ГЛ. 10. КРУГЛЫЕ ТЕЛА
103
741. В конус вписан шар. Найти объем шара» если обра-
зующая конуса равна / и наклонена к плоскости основания
под углом а.
742. Прямая линия — касательная к боковой поверхности
конуса — составляет с образующей, проходящей через точку
касания, угол 8. Какой угол ср составляет эта прямая с пло-
скостью основания Р конуса, если образующие его накло-
нены к плоскости Р под углом а?
743. Тупоугольный треугольник, острые углы которого
а и р и меньшая высота равна Л, вращается около стороны,
противолежащей углу р. Найти поверхность тела вращения.
744. В конус, поставленный основанием вверх и пред-
ставляющий в осевом сечении равносторонний треугольник,
налита вода и положен шар радиуса /\ Тогда оказалось,
что уровень воды касается шара. Определить высоту воды
в конусе после того, как шар будет из него вынут.
746. В конус, радиус основания которого равен R и об-
разующие наклонены к основанию под углом -а-, вписана
прямая треугольная призма так, что ее нижнее основание
лежит на основании конуса, а вершины верхнего — на боко-
вой поверхности конуса. Определить боковую поверхность
призмы, если в основании призмы лежит прямоугольный
треугольник с острым углом а, а высота призмы равна ра-
диусу сечения конуса плоскостью, проходящей через верх-
нее основание призмы.
746. В треугольную пирамиду, в основании которой —
правильный треугольник со стороной at вписан цилиндр так,
что нижнее его основание находится на основании пирамиды,
а верхнее касается всех боковых граней. Определить объем
цилиндра" и объем пирамиды, отсеченной плоскостью, про-
ходящей через верхнее основание цилиндра, если известно,
что высота цилиндра равна 4. одно из боковых ребер пи-
рамиды перпендикулярно к плоскости основания, а боковая
грань наклонена к основанию под углом а (определить, при
каких значениях а задача возможна).
104
8АДАЧИ
747
747. В шар радиуса-/? вписана прямая треугольная призма.
Основанием призмы служит прямоугольный треугольник с
острым углом а, а наибольшая её боковая грань есть квад-
рат. Найти объём призмы.
748. Основанием пирамиды служит прямоугольник с острым
углом а между диагоналями, а боковые рёбра образуют с пло-
скостью основания угол <р. Определить объём этой пирамиды,
если радиус шара, описанного около неё, равен /?.
749. Радиус основания конуса равен Rt а угол при вершине
осевого сечения равен а. Найти объём правильной треуголь-
ной пирамиды, описанной вокруг конуса.
750. В усечённый конус вписан шар радиуса г. Образую-
щая конуса наклонена к основанию под углом а. Найти
боковую поверхность усечённого конуса.
751. Около шара описан усечённый конус, у которого
образующие наклонены к основанию под углом а. Определить
полную поверхность этого усечённого конуса, если радиус
шара равен г.
752. В усечённый конус вписан шар радиуса г. Образую-
щая конуса наклонена к плоскости основания под углом а.
Найти объём конуса.
753. В шаре радиуса R из точки его поверхности про-
ведены три равные хорды под углом а друг к другу. Опре-
делить их длину.
754. В шар радиуса R вписан усечённый конус. Основа-
ния усечённого конуса отсекают от шара два сегмента с ду-
гами в осевом сечении, соответственно равными аир. Найти
боковую поверхность усечённого конуса.
755. Боковые рёбра правильной четырёхугольной пирамиды
наклонены к основанию под углом а. Боковые грани накло-
нены к основанию под углом ср. Апофема пирамиды равна /п.
Найти полную поверхность конуса, описанного около пира*
МИДЫ.
763 ГЛ. 10. КРУГЛЫЕ ТЕЛА 105
756. Около правильной шестиугольной пирамиды описан
конус. Найти его объём, если ребро пирамиды равно / и
плоский угол между двумя соседними боковыми рёбрами ра-
вен «.
757. В правильную треугольную пирамиду вписан конус.
Найти объём конуса, если ребро пирамиды равно / и пло-
ский угол между двумя соседними боковыми рёбрами равен а.
758. В шар вписан конус, объём которого равен -j- объёма
шара. Найти объём шара, если высота конуса равна Н.
759. В правильную треугольную призму вписан шар,
касающийся трёх граней и обоих оснований призмы. Найти
отношение поверхности шара к полной поверхности призмы.
760. Шар радиуса R вписан в пирамиду, в основании
которой лежит ромб с острым углом а. Боковые грани пи-
рамиды наклонены к плоскости основания под углом <р-
Найти объём пирамиды.
761. В правильную четырёхугольную пирамиду вписан
лолушар так, что его плоская грань параллельна основанию
пирамиды, а шаровая поверхность касается его. Определить
полную поверхность пирамиды, если боковые её грани обра-
вуют с основанием угол а и радиус шара равен г.
762. В правильную четырёхугольную пирамиду вписан
полушар так, что плоская грань его лежит на основании
пирамиды, а шаровая поверхность касается боковых граней
пирамиды. Найти отношение полной поверхности полушара
к полной поверхности пирамиды и объём полушара, если
боковые грани наклонены к плоскости основания под углом а
и разность между стороной основания и диаметром шара
равна т.
763. В конус с радиусом основания R и углом а между
высотой и образующей вписан шар, касающийся основания
и боковой поверхности конуса. Определить объём части ко-
нуса, расположенной над шаром.
106
ЗАДАЧИ
764
764. Полная поверхность прямого кругового конуса в п
раз больше поверхности вписанного в него шара. Под каким
углом образующие этого конуса наклонены к плоскости его
основания?
765. В конус вписан шар. Отношение их объёмов равно я.
Найти угол наклона образующей к основанию (вычислить
при п = 4).
766. Определить угол между осью и образующей такого
конуса, у которого полная поверхность в п раз больше пло-
щади осевого сечения.
767. В конус вписана полусфера, большой круг которой
лежит на основании конуса. Определить угол при вершине
конуса, если полная поверхность конуса относится к боковой
поверхности полусферы, как 18:5,
768. Определить угол между высотой и образующей ко-
нуса, если известно, что объём конуса в 1 -д- раза больше
объёма полушара, вписанного в конус так, что плоская грань
полушара лежит в основании конуса, а полушаровая поверх-
ность касается боковой поверхности конуса.
769. Определить угол между высотой и образующей ко-
нуса, боковая поверхность которого делится на две равно-
великие части линией пересечения её со сферической поверх-
ностью, имеющей центр в вершине конуса и радиусом высоту
конуса.
770. Конус с высотой Н и углом между образующей и
высотой, равным а, надо рассечь сферической поверх-
ностью с центром в вершине конуса так, чтобы объём ко-
нуса оказался разделённым пополам. Найти радиус этой
сферы,
771. На высоте конуса, равной Ht как на диаметре,
описан шар. Определить объём части шара, лежащей вне
конуса, если угол между образующей и высотой равен а.
779
ГЛ. 10. КРУГЛЫЕ ТЕЛА
107
772. Даны два шара О и 019 касающиеся извне, и опи-
санный около них конус. Вычислить боковую поверхность
усечённого конуса, основаниями которого служат окружности
прикосновения шаров к поверхности конуса, если радиусы
шаров равны R и Rv
773. На столе, касаясь друг друга, лежат четыре шара
одинакового радиуса г. Сверху в ямку, образованную ими,
положен пятый шар того же радиуса. Найти расстояние от
верхней точки пятого шара до плоскости стола.
774. Определить угол при вершине в осевом сечении
конуса, описанного около четырёх равных шаров, располо-
женных так, что каждый касается трёх других.
775. Грани правильной усечённой треугольной пирамиды
касаются шара. Определить отношение поверхности шара
к полной поверхности пирамиды, если боковые грани пира-
миды наклонены к плоскости её основания под углом а.
» 776. В конус вписан цилиндр, высота которого равна
радиусу основания конуса. Найти угол между осью конуса
и его образующей, если полная поверхность цилиндра от»
носится к площади основания конуса, как 3:2.
777. Радиус шара, вписанного в четырёхугольную пра-
вильную пирамиду, равен г. Двугранный угол, образованный
двумя соседними боковыми гранями этой пирамиды, равен а.
Определить объём пирамиды, имеющей вершину в центре
шара, а вершины основания — в четырёх точках касания
шара с боковыми гранями данной пирамиды.
778. В конус вписан шар радиуса г. Найти объём конуса,
если известно, что плоскость, касающаяся шара и перпенди-
кулярная к одной из образующих конуса, отстоит от вер-
шины конуса на расстоянии d.
779. Ребро куба равно а\ АВ — его диагональ. Найти
радиус сферы, касающейся трёх граней, сходящихся в вер-
шине А и касающейся трёх рёбер, выходящих из вершины £.
Найти также часть поверхности этой сферы, которая лежит
вне куба.
108 ЗАДАЧИ 7В0
780. В тетраэдр*), у которого ребро равно а, вписан
шар так, что он касается всех рёбер тетраэдра. Определить
радиус этого шара и объём части шара, расположенной вие
тетраэдра.
ГЛАВА 11
ТРИГОНОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ
Доказать тождества:
781. secf-y + a)secf-£—aj = 2sec2a.
Sln(2«+T»^_ +р ginp
sin a ^x J r/ sin a
783. 2(cosec2a+ctg2a) = ctg~ — tg-|-.
COSa + Slna^
cos a— sin a & ч J '
_0- COS a + sin a . 0 , n
785. !—:— = tg 2a 4-sec 2a.
cos a — sin a & J
786.sin*(j + a)_sin*(|_a) = ^.
787. , асой—1
2«В(Т—)-,,и,(т + ")
т x q / TC N 1 — sin 2a
-nn cos 2a 1 , Qn
789. -r-o rT-=-r.sin22a.
ctg2 a — tg2 a 4 .
790 sin a + cos (2^-a) /£_ Л
/yu* cos a — sin (2P — a) "g \ 4 РГ
79b cos2a = T=tgiB^\4+V'
*) См. подстрочное примечание на стр. 83.
ГЛ. 11. ТРИГОНОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ 109
sinx + cos(2y--x) _= 1 + sin 2у
792* cos х — sin (2у — *)в* cos2y *
793. tga а — tga р = sin (а + Р) sin (а — Р) sec2 а sec2 %
«(т~т)в(| + в1пв)
™*« sin а '-<*«•
.«vf. А /л I я\ 1 — sin а -
706 2 (stn 2а+ 2 cos» а-1)
796* cos « — Sin а - cos За + sin За ~ C0SeC а*
797. slna-slnaa+slnSa^ з«.
cos а — cos За + cos 5а 6
798. sin(a — *)-f sin(a — t) + sin(& — c)=*
a — b . а — t fe—ь
= 4 cos —*-- sin —g— cos —j-.
799. 2(sinex + cos6д:) — 3(sln4x +cos*x)+1 =0.
800. slna4-sIn(e + ^)+sin(a4-^) = 0.
80b sina(45o4-a)-sin2(30o-a)-sinl5ocPs(15o + 2a)=3
=* sin 2a.
802. Показать, что
1--2cos*t
Sin <f> cos f * ' c S ?•
803. Показать, что
tg1
2Л — :
2 2 sin a -f- sin 2a*
804. Доказать тождество
cos2 <p + cos2 (a -f- <p) — 2 cos a cos <p cos (a -f- <f>) = sin2 a.
805. Упростить выражение
sin2 a + sin2 £ 4- 2 sin a sin p cos (a 4" P)«
110 ЗАДАЧИ
806. Упростить выражение
sin2 а + sin2 р +sin2?— 2 cos а cos р cos f,
если а + р + т =*•
807. Доказать, что
ctgi4ctgS-fctgi4ctgC + cfgSctgC=ll
если Л + В + С = 1с.
808. Доказать, что
к 2тс 1
COS -=- COS -г- =~гщ
О 5 4
809. Доказать, что
п , Зтс 1
COS-£- + COS-g-=-g-.
Привести к виду, удобному
для логарифмирования:
1 + cos а + cos у.
1 — У 2 cos а+cos 2а.
1 — sin2(a+p) — sin2(a— р).
1 +sina + cosa+tga.
1 + sin а — cos а
sln^
1 — tga+seca.
cos a + sin 2a—cos 3a.
810.
811.
812.
813.
814.
815.
816.
817.
ГЛ. 12. ТРИГОНОМЕТРИЧЕСКИЕ УРАВН^™* Ш
8 sin р— sin 23
e,°* 2sinp + sln2pe
У 2 — cos а — since
819 . sin а —cos а
820. ctg а + ctg 2а -f cosec 2а.
821. cos 2а -f- sin 2а tg а.
822. 2 sin2 а 4-/3*sin 2а — 1.
823.
l+tg2atga
ctga + tga *
824. 2 + tg 2a + ctg 2a.
825. tgx —l + sinx(l—tgx)+j-^>j.
826.
1 + cos a 4 cos 2a -f- cos 3a
cos a-f-2cosaa—1
827. 1—j sin2 2a —sin2 p —cos* a.
828. tgx + igy + tgz-~sixl(x+y + z\
u*^. S i 6 s 1 & COS JT COS jf COS 2
829. sin a + sin p-f-sin y, если a4*P + T = 18^°
ГЛАВА 12
ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ
Решить уравнения;
830. 1 — sin5* = (cos^ — day)1.
88Ь sin д: + sin 2лг -f- sin 3ftr -J- sin 4л; ^= 0.
832. sin (x 4-30^ 4. cos (x 4-60е) =1 4* cos 2#.
833. sin x -|- sin 2x 4- sin ox — cos x 4- cos 2x -}- cos 3#.
2 ЗАДАЧИ
834. cos 2л;—cos 8л;-f- cos 6л; = 1.
835. cos л:—cos 2x = sin Зл\
836. sin (л:— 60°)=* cos (л;+ 30°). •
837. sindx+sinx + ^sta**8"!-
838. slna.*(tgx-|- 1) = 3 япл;(созл:—sinjr) + 3.
839. cos 4л: = —2 cos9 x.
840. sin x 4- cos x = -—.
' sin x
841. в!пЗл; = cos 2x>
842. sin*^ + cos*|=-|.
843. 3tg3JC —sec2*^ L
844. (1 ■+- cos 4jc) sin 4л: = cos2 2xm
845* sin4*—cos4JC=s cos 4л.
846. Зсовал; — sin2 л;—sin 2л; —0»
847, соз3л: + 3 81п2л; + 21/"3 51пл:С08ЛГ= 1.
648. Gstoax-V*$staxcosx — 5cos2x = 2.
3 5
849. 51пал; + -^со89л: = у sin jccosjf.
850. sin x 4-/3 cos *= 1.
851. sin x+ соэл:= 1.
b52. sin x + cos x =* 1 + sin 2л\
853. sin Зл; + cos Зл; = y^.
854. sin X sin Ix « sin Ъх sin 5лг.
ГЛ. 12. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ ИЗ
855. cos х sin 7х — cos Зл: sin 5#.
856. "Sin jt-sin 2x sin Ъх = -? sin \x*
857. 2 cos* л; + 4 cos jct=3sin^.
858. 5 cos 2x = 4 sin x.
859. tg(j + *) + tg*—2 = 0.
860. etgaiz^i + seCA:.
861
008 й-*) *
• l-t-cos* SeC 2 1#
862. 1 —cos (it — *)+slni±£ = 0.
863. 2[l_sin(^_*)] = /3 tg^.
864. sin*—cosjc—4cosaAr sin л;»« 4 sintf л;.
865. ctgx-f-*1"* = 2.
** ' 1 -f- cos X
866. 2ctg(x—it)— (cosAr + sInx)(cosecxr— secjt) — 4.
867. sin (те—x) + ctg(-^ — *\,
sec jc — cos x
2 sin л:
868. ±- =*2 sin 4-..
1-ctgi
B69. sin (it — x) + ctg (^ -}- x) = sec (— дг)- cos (2*~лг).
114 задачи 870
870. sec2 *—tg2 x+ctg (j + *) = cos 2л: sec2 *.
871. sinsAr(l+ctgA:)+cossA:(l+igA:) = cos2Ar.
872. sin3 * cos Ъх -j- sin 3x coss x = 0,375.
873. tg*4-tg2x==tg3*.
874. l + sinx + cosx = 2cos^~45°V
875. 1— cos2 2* = sin Зл;—cos(y-f A
876. l-bcosx + cos2x = -^p^^Ll
' ctg2# — ctg*
877. [cos * _ sin (x—ir)]2 + 1 2 sin2 *
sec**—1 4
878. (dn* + cog^ = 2slng- + jc)aIn^J—A
879. 2 — Sin#cos2x~sin2xcos#=*
-Кт-*)-*MT-
880. (1 — tgл:)(1 + sin 2x) = 1 + tg*.
B82. (1 + sin 2jc)(cos x— sin л:) = 1 — 2 sin9x.
883. 2S^=g!2£e-n(x + 8<0*,(x-8n
884. »!дД$Р + *) + з111(В0Р—jQ tgjg . ctg a:
2 (1 -f tg» лг)а "Г (1 -f ctg* v)» *
> ГЛ. 12. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ 115
885. sec9 л — (cosjt-r-sinxtgije
sin (х—30°) 4- cos (60°—х)
cos* *
886. 8ta(5 + *)-sta(J-*) ^2ут '.
887. 2 V" 2 sin (45э + ж) = \1^ff.
888. 1_2(sio^-co22£tg£)ta=cos4jc_sin4jc>
889. sin Зх = 4 sin д: cos 2л;.
890. Sec д: + 1 = sin (я — #)— cos д:tg 2*»
891. J||iiS£_.—2sin(450 + *)sin<45°—x) = 0.
892. tg(*—45^ig*tg(*+45°)e_i£22LL_.
tgT-ctgT
893. tg(* + 45°) -ftg (ж--45°)_ ^,450)^ +45°)tg*.
894. tg(*+a)-Mg(* —a) = 2ctgx.
895. (sin f — COS £Y am —-—-——-.
sin x
u sin (30° + x) + sin (30° — *);
-Д+*(7 + 45°)-*(*В°-т)\
116 ЗАДАЧИ 897
897. sin4x + sin*(jt + ^) = j.
897а. sin4х-\- sin4 (х + х) + sin4(л; — ^ = ~.
Решить системы уравнений:
лло лс 4- у лс— yl 1
898. cos —p- cos —j^- — ~2> cosxcosy = —.
899. х + _У — a, sin л: sin з^ = w.
900. л; + .У —ot. tgAr-j-tgjy — m.
901. д: + ^=|, tgjp + tgj;=l.
902 2sinaJ4cos?<= 1 i5sIn3aI+C092^ _ 4
903. sinA:sin^==—г=-, tgxtgjy = y.
904. sin x = 2 sin jy, cos x = 15- cos .y.
ГЛАВА 13
ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
905. Вычислить
2 arc sin ^ ~ j 4- arc ctg (— 1)4- arc cos r^=" 4-
4-9-arc cos (— 1).
906. Доказать, что
tg (arc cos x) ■
917 ГЛ. 13. ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ 117
907. Доказать, что
tg(arc sin #)==
Вычислить:
908. sin Г— arcctg(— -^J.
909. sin I ~ arc sin ( |—)J •
910. ctg (д arc cos (— yYJ.
911. tg(5arctg^ larcsin^).
912. sin(3arctg/3+2arccos-^.
913. cos I 3 arc sin-^--j-arc cos ^—§"yj•
Доказать тождества:
9H. arctg(3 + 2/2) — arctg^^.
01Б. arc cosj/ тг — arc cos ^ it =*-^«
916. arc sin -g- -fare sin — -fare sin gg —|-.
91
7. arc cos -j -f arc cos (— ~) e a'c cos (— j|\
118 задачи 918—928
1 1 32
918. 2arctg-g- + arctg— = arctg^,
919. arctgj + arctg^ + arctgy + arctg-g =-£.
Решить уравнения:
920. 4arctg(*2—За: — 3) — я = 0.
921. 6 arc sin (л:2 —6л:+ 8,5) = тт.
922. arctg(# + 2) —arctg(#4-l)==^-.
1 те
923. 2arctg-2—arctgA:=-j.
924. arc sin —= — arc sinl^l — x = arc sin -*•.
3Y* r 3
925. arctg-|-— arctgj^ = arctgx.
926. arcsin3.x; = arccos4A\
10*
927. 2 arc sin x = arc sin-rj*
928. Решить систему уравнений
jc + ^ = arctgr^-2, tgx\gy = #{\a\<\).
ОТВЕТЫ И РЕШЕНИЯ
ЧАСТЬ ПЕРВАЯ
АРИФМЕТИКА И АЛГЕБРА
ГЛАВА 1
АРИФМЕТИЧЕСКИЕ ВЫЧИСЛЕНИЯ
1. 6,5625.
7
2. 29 j2«
3. 3651.
4. 3i.
Б. 181.
6. 50.
7. 23, 865.
8. 36 =5.
9. 599,3
10. 84,075.
И. 2,5.
12. 2gj.
13. 0,0115.
14 J2
1*. 280"
15. 38 g.
16. 6.
17. 700.
18. 100.
19. 10.
20. 7-L.
21. 5.
22. 3.
23. 2^.'
24. 5.
25. lg.
26. 10.
27. 1.
28. 1320.
29. 11.
80. 250.
31. 4.
32. 4000.
33. 66.
34. 2.
ЗБ. 9.5.
122
36. 0,09.
87.
38.
39.
40.
35
2.
1
""IS*
2!
ОТВЕТЫ И
РЕШЕНИЯ
41.
42.
43.
44.
45.
1
8"*
1301.
— 20,384.
2,25.
•f
ГЛАВА 2
АЛГЕБРАИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ
Предварительные замечания
При решении задач настоящей главы (начиная с задачи 62)
необходимо учесть следующее.
1. Напомним, что корень у а называется арифметиче-
ским, если число а, из которого он извлекается, положи*
тельно (или равно нулю) и если» кроме того» сам корень
берется положительным.
Примеры. Выражение 1^—27 не может представлять ариф-
метического корня, так как подкоренное число отрицательно. Выра-
жение |АГб представляет арифметический корень, если рассматри-
вать только положительное значение этого корня (т. е. 2). Выраже-
ние У"27 представляет арифметический корень (т. е. 3), если рас-
сматривать только действительное его значение (оно имеет еще два
з з V5" з 3 V1T \
мнимых значения — -«Н ^—/ и -*тт——\—*)• Выражение
У—16 не может представлять арифметического корня, так как под
ьорнем число отрицательное,
2. Излагаемые в алгебре правила преобразования радика-
лов безоговорочно верны только для арифметических корней.
г в
Например, равенство у х = у х9 не верно при отрица-
тельных значениях х. Так, при х =— 8 левая часть равен-
ства имеет только одно действительное значение V—8 = — 2»
а правая часть—два действительных значения |/64 = :±:2
ГЛ. 2. АЛГЕБРАИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ 123
(если рассматривать мнимые значения корней, то У—8 имеет
в-_
три значения, а |/64 — шесть).
Ввиду этого в настоящем разделе, где выполняются
тождественные преобразования иррациональных выражений,
мы принимаем, что все подкоренные выражения могут иметь
только положительные (и нулевые) значения1). Тем самым
на буквенные величины, входящие в упрощаемые выражения,
накладываются некоторые добавочные условия. В ряде случаев
(см., например, замечания к задачам 65—71) мы указываем
эти условия. Иногда условия, которым должны удовлетворять
буквенные величины, указываются в тексте задачи. Тогда
при решении надо доказать, что при этих условиях все под-
коренные выражения положительны,
3. Особо следует заметить, что равенство *Ух* = х (где
Ylfi есть арифметический корень) зерно только при х^О.
При отрицательном же значении х оно не верно; вместо него
имеет место равенство Ух* = — х. Оба случая можно объ-
единить равенством Ух* = | х |. Так, если х = — 3, то
У(_ З)3 =» У9 ~ — (— 3) (при этом У(— З)2 является ариф-
метическим корнем, так как подкоренное число (—З)2 поло-
жительно и значение корня взято положительным). Можно
также написать У(—З^^З]. Это замечание необходимо
сделать потому, что его нет в большинстве учебников (в том
числе и в «Алгебре» А. П. Киселёва во всех многочисленных
её изданиях). Важность замечания видна из следующих при-
меров.
Пример 1. Упростить выражение Ута—2тп+гА
Решение
Ута—.2тя+я*»У(т—л)*—т — л
правильно только при т > я. При т < я вместо него нужно написать
У/и* — 2отл + ла« — (т — л), т. е. У"т2—2тп + ла« п —. пи
*) В одном случае мы вынуждены были отступить от принятого
соглашения о положительности подкоренных выражений. Мы имеем
в виду задачу 64, где выражение, стоящее под знаком кубического
корня, ни при каких обстоятельствах не может быть положитель-
ным (см, на стр. 131 решение этой задачи).
124
ОТВЕТЫ И РЕШЕНИЯ
Так, если /«=й2ия=3, той? —л = — 1, тогда как
Ут* — 2тп + п2=* 1/4 — 12 + 9 = УТ = 1.
Общая формула имеет вид
Уда* —21ИЯ + Я*
да—л| или уда2
Пример 2. Упростить выражение
Y4 + 4p + p*— У 4 — 4р+^а
У4+4/7+р2+ У4 —4р+рЗ*
2/ил + л2 = | л —да(,
Обозначив для краткости данное выражение через И, имеем (при
РФ-2*
|2+р|-|2-/>| 1-1^=^1
.4=
1 —
|2 + />|+|2 —/>| 1 +
2+р
2-^
2 + />
Если дробь 947^ положительна,
2-2
'2 + Р
1 +
2—/> 2'
если же она отрицательна, то
W
2+Р
2-р
А = -
2 + р
2-р ~ ра
4 2 + Р
Исследуем, при каких значениях р имеет место тот и другой случаи.
Дробь 0~Р положительна, когда 2 — р и 2-\-р имеют одинаковые
л —р* р
знаки. Потребуем сначала, чтобы величины 2—р й 2+р были обе
положительны. Величина 2 — р положительна, когда jp<2; вели-
чина 2 + р положительна, когда />> — 2. Следовательно, обе вели-
чины 2 — /> и 2-\-р положительны при —2<р<2. Потребовав же,
чтобы величины 2 — р и 2+р были обе отрицательны, мы найдём,
что это требование невыполнимо, так как 2 — р отрицательна при
р > 2, а 2 + р отрицательна при р < — 2, а эти условия ие совместны.
Значит, дробь 0Т положительна только при — 2</><2, При
*~тР
2 я
значениях р>2, а также при значениях /><— 2, дробь 9 , отри-
цагельпа.
46 ГЛ. 2. АЛГЕБРАИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ 125
Таким образом, А = -^ прн |/М<2 и Л = — прн |р|>2. При
|/7l = 2 годятся оба выражения.
Пример 3. Равенство "|/"дб = д3 верно только при д!>0. При
отрицательных значениях д вместо него имеет место равенство
Уд8 = — дз. Так, при д = —1 имеем W- 1)6 = — (— 1) = + 1.
Здесь У(—1)в есть арифметический корень, так как подкоренное
число (— 1)в = 1 положительно, и значение кЪрня взято положи-
тельным.
Пример 4. Вынести множители за знак радикала в выраже-
нии У (а — 5)в(я — 3)3
Данный корень может быть арифметическим только при д>3,
так как лпри д<3 множитель {а—З)3, а вместе с ним и всё
подкоренное выражение отрицательны. Равенство
V(a — 5)в (д — З)3 = (д — 5)3(л — 3) /д^З
верно только при д>5. При д<5 вместо него нужно написагь
У> — 5)в (Д — ЗУ*= — (д — 5У* (а —3) Уа^З.
Общая формула будет
У(д — 5)в(д — ЗУ*=|д — 5|з(д — 3) Уд^З (при д>3).
4. Вообще равенство ухп=х (где левая часть обозна-
чает арифметический корень) верно только для положитель-
ных значений х (и при # = 0). Если п — чётное число, то
при отрицательном значении х вместо ухп=х имеем ра-
венство ухп = — х. Если же п — нечётное число, то при
отрицательном значении х вовсе нет арифметического корня.
46. Группируя последние три члена выражения в скобках,
разложим его на множители
& — № — са4-2&? = д9 — (b — с)* = (а + Ь — с) (а — Ь + с).
Заданное выражение примет вид
(а + с + £)(а + с — b) = (a + cf — Ь\
Отв. (а + 02 — Pi 139^.!
126 ОТВЕТЫ и РЕШЕНИЯ 47
47. Выражение в скобках равно —^т. В числителей зна-
менателе последней дроби удобно переменить все знаки на
обратные, после чего числитель разложим на множители;
дробь примет вид
(д + д)(я-1)(яНдН-1)
От*. £±JL±1.
48. Знаменатель второй дроби равен (1~)-х)(х — 2а).
Выражение в скобках равно 1 +х. Заданное выражение равно
х 2 I
а(* — 2а) х — 2а а*
Отв. -„
49. Отв.
60. Представим второе слагаемое в виде ^^—г. При*
Ой ■— 1
ведём дроби в скобках к общему знаменателю; получим
~ 3 (дТзо"—Д1 ^Г 10) ; пРиРавняв НУЛЮ трёхчлен 2аа+9а+ 10
и найдя корни ^ = — 2; а.2 = — -?-% разложим его на мно-
жители
2a3 + 9a + 10 = 2(a + 2)(a+f).
Теперь выражение в скобках примет вид
— 3(д+2)(2а+5)
д(3а — 1)
Умножим его иа
Зд»4-8Да — За а4а(д+3)(3д — 1)
!-■}* (2 + а){2-а)
12(2а + 5)(Д+3)^
54 ГЛ. 2* АЛГЕБРАИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ 127
5L Сокращаем каждую дробь, разложив числитель и зна-
менатель на множители.
62. Разложим на множители знаменатель второй дроби, и
эту дробь сократим. Данное выражение примет вид
X У(Х—У) 1__
Х*+У* (Х*+у*)(х+у) Х+Уш
Отв. j^y.
53. Знаменатели дробей после упрощения принимают вид
3 и 3 •
данное выражение преобразуется так:
2 3/ I _±_ _ l \ х^+1
Ъ*Т\Х*+Х+1~Х* — Х+1) (*2+1)2_ дгЗ
х*+У
л ** + *
Отв. v+* + l'
ДГ4 + ДГ2 + 1#
64. Разложим внаменатели первых четырёх дробей на
множители и сократим первую дробь на а—*1. Выражение
в скобках примет вдд
Л , 2(а— 1) 4(д+1) i а
а —1"*~ (д + 2)(а—2) (а— 1)(д + 2) "+" (л— 1)(л —2) в
2(« + 3)
(л-1)(а+2)(л-2)'
Это нужно помножить на дробь ЗбД3 — iy—«tf +144 4jfe
слитель последней дроби разлбжим на множители группиров-
кой членов, знаменатель —как сумму кубов да-4-33; тогда
эта дробь примет вид
36(д-^1)(д4-2)(д — 2)
(д + 3)(да —Зд + 9) #
128 Ответы и решения 55
55. Сумму дробей, составляющих делимое, обозначим че-
рез А, делитель — через В. Разложив на множители много-
члены, входящие в Л, найдём
3<*+2) . (л- + 2)(2лг-5) <
л~~ 2(jr+l)(*a+l) -1" 2(jr —1)(jc*+1) *
х 4- 2
В полученном выражении вынесем за скобку 9, 7, 1ч; имеем
и--*±^
_ ( Э I 2* —5~\ — (д- + 2)(^ —4)
'2(*» +
Далее находим
jc 4- 2
Разделив Л на S, получим- ^-.
Отв. *-±^9
56. Делимое обозначим через А\ делитель —через 5.
Приравняв нулю трёхчлен х%—ху—2у*9 входящий в выра-
жение А, решаем полученное уравнение относительно одного
из неизвестных, например неизвестного х; найдя хх = —у и
хэ = 2у, получим разложение трёхчлена на множители
д-э — Ху—2у2*=(х-гу)(х—2у). Теперь имеем
х~ у х* + у*+у — 2
л~ 2у — х (х + у)(х—2уУ
В вычитаемом напишем 2у — х вместо х — 2у, одновре-
менно изменив знаки в числителе этой дроби; затем дроби
приведём к общему знаменателю, получим
2х2+у-2
~(2у-х)(х+уу
В выражении В разлагаем на множители числитель [предста-
вив его в виде (2х*-{-уУ* — 22] и знаменатель (группируя
х* + ху и у-\-х). Тогда
о„С2*2+Г + 2)(2*2 + .У-2)
(х + у)(х+\)
X +1
Разделив Л на S, получим {2у — х){2х*+у+ 2)"
Птя х + 1
ит*' &у~х)&х*+у+2)и
59 ГЛ. 2. АЛГЕБРАИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ 129
67. Разложив на множители многочлены, входящие в за-
данное выражение, получим
(а + 2)(а-
ап(а — 3)
])_ Г 4(«+1) 3__1
14(а+1)(а—1) а{а-\)У
68. Делимое обозначим через А, делитель — через В.
Числитель дроби Л есть
^[Аа*(Ь + с?ъ— \] = ~[2а<р + сТ+\][2а(Ь + с)*— 1],
а знаменатель
a(n*—a? — 2a—\) = a[rP — (a+\f\ =
= ai tz —|— 1)(л — а—1).
В дроби В числитель оставим без изменения, а знаменатель
представим в виде — ас (п — а — 1).
пт* [2а(Ь + с)п + 1]с
ит$- 2{п + а + \) '
59. Первый способ. Приведём все дроби к общему
знаменателю:
be (Ь — с) — ас (д — с) -f- дЬ (а — fr) ( .
д*с (д — Ь) {а — с) (* — с) • W
Выполнив умножение двучленов, входящих в .знаменатель,
получим аЧ — а№-\-ЬЧ — аЧ-^-ас* — bd*% т. е. то же выра-
жение, что и в числителе. После сокращения получаем —г-.
Второй способ. Полагая в числителе дроби (а) а = Ь,
убедимся в том, что числитель обращается при этом в нуль.
Следовательно, по теореме Безу он делится на (а — Ь)*
Выполнив деление, найдём частное
а(Ь — с) — с(Ь — с) = (Ь — с)(а — с).
Таким образом, числитель равен (а — Ь)(р — с) (а — с).
Третий способ. Приведём к общему знаменателю
только первые две дроби заданного выражения. Получим
#3 — fa Д2 _|, ас
аЬ (а — Ь) (д — с) (Ь — с) *
130
ОТВЕТЫ И РЕШЕНИЯ
60
Группируя члены числителя (первый с третьим и второй
с четвертым), мы придем к выражению
(6-Ьа)(6 — а) — с{Ъ — я) = (а — b){c — а — Ь).
Теперь сокращаем дробь на {а — Ь) и прибавляем третью
дробь заданного выражения.
Отв. —г-.
abc
60. Первый множитель равен a_T*Zli ■ Выражение в ква-
дратных скобках равно ^д~г^ ~ — lgj±—Т J1 "*" 2,
Перемножая заданные выражения, находим -—L-s—i—— ■ При
1 д4
подстановке х = ——т числитель принимает вид, _.;а, а зна-
2я
менатель становится равным .
Отв.
2(в—1)"
61» Обозначим выражение в квадратных скобках через Л,
выражение в круглых скобках—через В. Имеем А : В~1 = АВ,
Выражение А освободим от степеней с отрицательными по-
казателями. Получим
л_ 2№ — ЪаЬ — 2сР _ (Ь —• 2а) (2Ь + а) _ 6 —2д
Л""д(а+2^(2<!У— а)-д (д + 2£) (2£ — л) ~~я (2£ —д)'
Преобразовав Б, получим
Наконец, находим АВ = ап"1Ь (в одной из перемножаемых
дробей переменим знаки членов в числителе и знаменателе).
Отв. ап~хЬ.
62. Числитель преобразуется к виду а2 — Ь2, знамена-
тель— к виду а-\-Ь.
Отв. а—Ь.
Замечание. Чтобы корни были арифметическими, числа
а и Ь не должны быть отрицательными.
64 ГЛ. 2. АЛГЕБРАИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ 131
63. Первый радикал равен
f(a — bf(a + b)* = (a — b)f(a + b)*.
Отв. b(a? — b%
Замечание. Предполагается, что а ;> Ь (иначе первый корень
не будет арифметическим).
64. В этом примере мы вынуждены отказаться от при-
нятого нами (см. стр. 123) соглашения о том, что подкорен-
ные выражения могут иметь только положительные значения.
Дело в том, что величина, стоящая под знаком кубического
радикала, всегда отрицательна. Действительно, выраже-
ния Убх и У2х (они имеют действительные значения лишь
при х^О) мы должны считать положительными (иначе вы-
ражение 2 Y§x— 4 Y%x теряет однозначность). Но тогда
разность отрицательна.
Итак, мы допускаем, чтобы под знаком кубического
корня стояло отрицательное число. Тогда и сам кубический
корень будет иметь отрицательное значение. Чтобы применять
правила преобразования радикалов, нам надо выполнить такое
преобразование:
f2]/6x— 4]/2* = —1^4|/*2^ — 2^дх.
Теперь радикал, стоящий в правой части, является арифме-
тическим корнем. После приведения к одному показателю
с первым из данных сомножителей получаем
— /4|/*2^ —2|/*6jc=: — К(4|/* 2* —21/"бл;)2 =
V =■
= _K8jc(7 — 4 J/3).
Перемножая корни, получаем: — V 64л:2 [49 — (41/*3)21 =
= 2fl.
Отвш —2 У я.
Замечание. Если ие обратить внимания на отрицательность
выражения под знаком кубического корня, то получится неверный
ответ 2Y'xv).
1) При подготовке первого издания настоящего сборника со-
ставители, исходя из вышеуказанного соглашения, не обратили
внимания на его невыполнимость в данном примере и получили
упомянутый неверный ответ.
132 ОТВЕТЫ и РЕШЕНИЯ 6S
65. Первый радикал равен у(а-\-1)*(а—1). Вынося
множитель (a -f-1) за знак радикала, получаем | а + 11У а — U
Заданное выражение равно
«|Д+111^.(а+^2)>
Приведём радикалы к одному показателю:
* (a + l){a + 2) *
Если число л-f-l положительно, то |a-f-1 |«sa-f- lt и по
a fria-W
сокращении получаем -^'—ц-н—.
Замечание. Число я + 1 и будет положительным. Действи-
тельно, так как подкоренное выражение (д + 1)< (л — 1) предпола-
гается положительным (или равным нулю), а множитель (а+ I)4 ни
" е не может бы:
гом условии
4,
в каком случае не может быть отрицательным, то а—1>0, т. е.
а > 1, а при этом условии а + 1 > £.
От$.
а + 2
66. Считая все корни арифметическими, приведём сомно-
жители
i/il±fl>frTT« л/ V'6 I3/ Т^5^
к одинаковому показателю 6. Первый и второй сомножители
примут соответственно вид
1У(1+Д)3П+а) '/" 3*
К 27д5 »F 81(1+д)<*
1 IV
Перемножив их, получим ^уа»
Замечание. Первый сомножитель является арифметическим
корнем только при условии я>0 (при д<0 подкоренное выражение
отрицательно, при а »0 оио теряет смысл). Второй же сомножитель
70 ГЛ. 2. АЛГЕБРАИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ 133
является арифметическим корнем при любом значении а (кроме
д = _ i)# Следовательно, величине а можно давать любые положи-
тельные значения.
1 в._
Отв. -у у д.
67. Введём аЬ под знак первого радикала. Данное выра-
жение примет вид
ya — b
Замечание. Чтобы данные радикалы были арифметическими
корнями, должно быть а > Ь. Случай а — Ь исключается, так как
второй сомножитель теряет смысл.
Отв. 1.
68. Освобождаемся от иррациональности в знаменателях;
получим
(/в—и)(уг"б+")-—Иб.
Отв. —115.
лл тт Уд — b + Va + b
69. Делимое равно - -у-* 1-—; делитель равен
Ya — b 4- гЛд-4- & V д —^
-* =£-!!■—2^; частное равно -^ .
Уд —£
Замечание. Чтобы все данные корни были арифметическими,
должны одновременно удовлетворяться три условия: а > 0, а — b > 0t
а + b > 0 (их можно заменить двумя условиями: д > О, I 6 |<! д |).
Отв. -^—г
70. Делимое равно ts ■• делитель т« . Частное -я-.
г оа —- а о* — д о
Величина а может иметь любое положительное значение; Ь
может иметь любое значение, кроме~±.Уа.
Отв. 1т
134 ОТВЕТЫ И РЕШЕНИЯ 71
71. Числитель первой дроби приводится к виду
(YT+a)* + (VT=~a)*_ [1+я| + 11-я|
/l — Ф ~~ /1—я*
Если выражения \-\-a и 1 — а оба положительны, то (см.
стр. 123, предварительные замечания, п. 3) числитель рапен
г . При том же условии знаменатель равен ' +g'~' "Z£l==a
2я Л 1
= -==-; дробь равна —, а данное выражение равно 0.
Замечание. Чтобы радикалы, входящие в данное выражение,
были арифметическими корнями, нужно, чтобы величины 1+я и 1—а
имели одинаковые знаки. Но невозможно, чтобы обе они были отри-
цательны, так как 1 + я<0 при условии я<—1, и 1 — я<0 при
условии я>1, а эти условия несовместны. Для того же, чтобы ве-
личины 1 + а и 1 — а были обе положительны, нужно, чтобы выпол-
нялось условие — 1<я<1, т. е. чтобы было |я|<1 (значения
а = rt 1 исключаются, так как при каждом из них одно из данных
«1+я 1 —а
выражении - J_ , у-ц— теряет смысл; значение а = 0 тоже исклю-
чается, так как дробь — теряет смысл).
Отв. 0.
72. Подставив лг = -^-^а + —J в выражение У л:2 — 1,
получим
в!| а_1|
2 | я |
Так как по условию а]> 1, то а ;>0. Поэтому
гг=1-4(.-А).
Точно так же найдём
Подставляем найденные значения радикалов в данное вы-
ражение.
Отв. ^^pj.
74 ГЛ. 2. АЛГЕБРАИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ 135
73. Подставляя ха^ ,, в выражения Ya-\-bxn
У а — Ьх, находим
^ps-/i.+TSi-|i+«ii/^
Так как величина 1-J-m2 всегда положительна, то и вели-
чина а должна быть положительной (при а < О оба корня
мнимы, при а =з 0 они равны нулю, и данное выражение не-
определённо). Так как, согласно дополнительному условию,
|wl<l, то обе величины \-\-m и 1 — т положительны.
Данное выражение" принимает вид
<1+'")/"тт^-(1-'и)1/'тт^
Отв. — (при а > 0).
74. Задача сходна с предыдущей. Имеем
Так как по условию я< 1, то
Аналогично
Отвш —
п
1Ж } —7^+Г
13t6 . ОТВЕТЫ И РЕШЕНИЯ 75
76. Подставляем х = утл, в выражение 1—л:2. Получаем
t ^ <1 Ч" ^)2—4^ (1 — Лг>
Теперь находим
(1—л;2) « = 1 :у 1— X*-.
|1+*1
и —*Г
Так как, согласно дополнительному условию, fc > 1, то вели-
чина 1-f-fc положительна, а 1—Л отрицательна. Поэтому
-- 14-*
(1 —л;2) г =5-~т. Внутри первых квадратных скобок
k 1 п
получается . , внутри вторых . , . Данное выражение
равно
Отв. У~к=л(\ + ^=).
76. Выражение в первых скобках равно -к — -г — т (п0"
казатель степени —2 относится только к числителю третьего
(а па
слагаемого!). После упрощений это выражение даёт ■— -
или
■0-д)2
4а
Выражения
будут арифметическими корнями только при условии а> — 1.
При этом условии и радикал
]/(а2—1)(а—1) = /(а—1)2(а+1)
будет арифметическим корнем (ибо множитель (а—I)2 не
может быть отрицательным). Равенство
77 ГЛ. 2. АЛГЕБРАИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ 137
верно только при а> 1. Если же а < 1, то
У (а — 1)2(а + 1) = -(а — 1) V^+l
(см. предварительные замечания, п. 3, стр. 123).
Данное выражение равно
(д — 1>яг Гд— 1 д + 1 1
4а # [а + 1 | я — 1 | J *
Замечание. При a = ztl выражение теряет смысл.
0^___При fl>l, Z{a+l) пРИ-*<<*<*.
т. е. при \а\ < 1.
77. Данное выражение можно представить в виде
2 [/*•(*»-а«) — «2 V^^i^-J •
У лг-i — a^
*./£-.#
Предполагается, что л:2 — аа > 0, т.е. |*|>|я| (в против-
ном случае корень \^х2—а2 не будет арифметическим; слу-
чай [л;| = |а| исключается, так как второе подкоренное вы-
ражение теряет смысл).
Первый сомножитель преобразуется к виду
2 \х -1— ' = 2 дг -—:
(так как л:2— а2 > О, то |л:2 — д2| = л:2 — а2).
Выражение у ( ——2 — j преобразуется к виду
К V аж / — |я|]лг| •
Здесь числитель можно записать в виде х2 — 2а2 только
в случае, если х2—2а2>-0, т. е. если | * | ;> | а | "|/1Г.
, Теперь данное выражение запишется в виде
138 ОТВЕТЫ И РЕШЕНИЯ 78
Принимая во внимание, что | х | • | х \ = 1 х I2 = х2 и производя
.Г2_2д2 ]а\
сокращение, получим • . 2_Д а-г х или, что то же,
д:2 —2д2| а I
От*. При условии | х I > а | данное выражение равно гЬ д:;
верхний знак берётся, когда > 0, нижний — когда
■ <0. Если = 0, т. е. если | х \ = [ а | у 2, дан-
ное выражение теряет смысл.
78. Освободимся от отрицательных показателей. Числи-
тель примет вид
2аЬ Va , 2ab Y~b 0 и
YH+Vb ' Va+Vb
а знаменатель будет
\я+Т^ b + Vab/
Заметив, что a-|-yraZ> = V^aQ/^a-f" У~#) и 6 + }^^ =
"= V^CV^ + V" л), представим знаменатель в виде
2ab(-=-L _ + _—U-—)^^L = 2V^l
теперь заданное выражение равно
2ab л г—г
—- =я у ab.
2Vab
Отв. Y~abu
79. Выражение в первой скобке преобразуется к виду
2Y~ax
Возведя его в степень —2, получим
(a + x)(Ya+YHf
box
83 ГЛ. % АЛГЕБРАИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ 139
Аналогично выражение во второй скобке преобразуется
к виду
Ьах
а ' I * х
При вычитании выносим за скобку ^ ■ (внутри скобок после
упрощений получим 4 У ах).
а-\-х
Уах
Отв. ' .
80. Последнее слагаемое после упрощения принимает вид
. Приведя все дроби к общему знаменателю, в сумме
2Yx* + a
получим
Отв. У**-\-а-
81. Отв. 2(x + V**— 1).
82. Внутри квадратных скобок имеем а *Ьа %Ьаг =а
= а 3£2. Заданное выражение равно а~4£6. Сюда подста-
вляем
2 "J^2
Отв. 1.
83. Заданное выражение представим в виде "тгт + ГдЛ'
сюда нужно подставить
Д=- , * — =2-/3 и£ = 1 =2 + ^3.
2+1^3 2—1^3
Находим а+1=3 — ^3, _i_ = i±_0. и т. д.
О/я*. 1,
140 ОТВЕТЫ И РЕШЕНИЯ ^84
«4. Orhe. ух*—Ах.
86. Отв. п.
86. Чтобы все корни были арифметическими, должно
быть х — а2 > 0. Выражение в скобках приводится к виду
4 У* УТ^Гдз
Ф— * Данное выражение равно
Ух_/ Д2 \_ а2
У^Г^а Д 4 У* УТ^РУ 4(* — д2)*
0Wtf. а2
4(лг —Я*)'
87. Знаменатель второй дроби равен
хТ— !=.(**) — 1 =(**"— 0U + *'+0'
О/яя. д:—^ 1.
88. Делимое равно
2* + 27y5=(^) + VW =
e(27 + ^T)\2 — 3 • 2*у*+9у*р
1 1
делитель рав^н 22 + Зу5'
Ож*. 2 — ЗК 32^ + 9 Ку>.
89. Освободимся во втором члене от отрицательных по-
казателей. Д^я этого можно числитель и знаменатель помно-
жить на а2, в числителе получим а3—1, а в знаменателе
а*\а*--а~^)^а?[а*\а*— a"*)\ = d*(a— 1).
По сокращенци получим % • Аналогично третий член
а
я—1
равен —5JT-.
92 ГЛ. 2. АЛГЕБРАИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ 141
90. Делимое и делитель преобразуются соответственно
к виду
11 JL
а2 +Ь* {а — Ь)ъ
1 1* If 1 1\ *
а\а-Ь)* aaW-b2)
Учитываем, что W +*V («* — Ь~Ч = а*—&■ в частном
О ч
получаем Ф -j- ab + №. При а = 1,2 и £ = —получаем 2,52.
Отв. а24-д* + *2; 2,52.
91. Раскрывая скобки и приведя подобные члены, пред-
ставим делимое в виде
11 If L Л\
U 1 1\
делитель представим в виде а2 \2а2 -\-ЪЬ*)т Частное есть
3|/ —; при данных значениях а = 54 и Ь*=6 оно равно 1.
Отв. 3|/ j; 1.
92. Умножая числитель и знаменатель данной дроби на
[(а + *)"Т + (в — b)"\[(a + b)~*— (а_£) Ч'
получим в числителе
= 2(а + £)'2;
в знаменателе получим
[(а + *Г7—(a —ft)~J —[(а + *Г7 + (* — &)~Ч==
= _-2(а — *)"2
О/вв,
142 01Ш&ТЫ И РЕШЕНИЯ 93
93* В вычитаемом первый сомножитель приводится к виду
1— а\ а второй—к виду (1 — я3)*7» Имеем
1 8
а*(1—a*f7—(1 — л*)(1 — л*)~?«
1 I 1
= аа(1 —а^«~(1—La»)"ii==Ci —а«)"аГ^—1)=»
i
От*. —I^l — Л
94. Данное выражение равно
ОМ. -^.
9б# Числитель третьего члена приводится к виду
/^(Z?3—**) V Знаменатель равен R\ Данное выражение
принимает вид
11 X
Отв. 2//?*—**.
96. Первое и второе слагаемые приведём соответственно
к виду
Р+4 2
03 ГЛ. 2. АЛГЕБРАИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ 143
Приведя эти слагаемые к общему знаменателю, получим
1 L
Числитель этого выражения равен \р2 -}-?а/
Отв. —.
РЯ
97. Вводим дробные степени. В выражении а-\-авх6
L -Li
выносим за скобку д3, а в выражении л:-|-д3д:3 выносим
эа скобку л;3. Тогда числитель первой дроби будет
£l_1 а3-л-3 W+xVW-x3)
X — у
л8 4-л-8
так что первая дробь преобразуется к виду—-~ • Выра-
хТ
жение в квадратных скобках теперь принимает вид
-L JL i.
я3 + лг3 1_ _£^_
*3 JC3 Л3
От*. j5,
98. Двучлена — У ах представим в виде Va{YH—Ух),
Числитель дроби будет
(|/"^4-1)а~Уг^ = « + /"л+Ь
Знаменатель равен Ъ (a-j-У~а-]-1).
Отв. 27.
144 ОТВЕТЫ И РЕШЕНИЯ 9$-
99. Освободимся от степеней с отрицательными показа-
телями; первое слагаемое (после сокращения на 2л—3) при-
2я4-3 , > «ч
мет вид—тг—» второе (после сокращения на а—1) даст
а—3
Отв. 9а.
100. В первом сомножителе вынесем за скобку а—Ь.
Величина а_ь не может быть отрицательной (иначе корни
не арифметические). Данное выражение примет вид
Отв. 2Ь(а—&).
101. Делимое и делитель представим соответственно
в виде
Частное можно сократить на {Ya-{- V Ь)(к а — V * )> если
учесть, что
Отв. а\П>(Уа + )Гь).
102. Данное выражение представим в виде
L У* ' 1/~5<1^-y5)J *
Числитель делимого разложим на множители, как сумму ку-
бов. После сокращения будем иметь в квадратных скобках
(У*+УЖУ* — V~b) = a — о.
Отв. f(a — bf.
105 ГЛ. % АЛГЕБРАИЧЕСКИЕ ПРЕОБРАЗОВАНИИ 145
103. Дробь —г—-^—в— сокращаем на Ух. Выражение
xYx—aYH
~\Гх -4-2
в квадратных скобках преобразуется к виду ■ _^ . Эту
дробь сокращаем на |/лг-}-2. Заданное выражение равно
(-^^)"8~K(T+4J?==(Kx-2)2-|x + 4|.
Предполагается, что jc>0 (при отрицательном х корень
Ух не будет арифметическим, при д: = 0 данное выражение
теряет смысл). Поэтому лг+4>0.
Отв. —4 Ух.
104. Дробь в квадратных скобках равна
ЫУх + Уу) _ 2
УИ(УИ+Уу) V~i*
Заданное выражение равно
& (-М*\/ хУ~х = х& • 32лг"X* = 32*.
Отв. 32*.
105. В числителе первой дроби выносим за скобку у ах.
Учитывая, что У~х*—Уа2=Ух—УЪ, сокращаем дробь.
Первый сомножитель принимает вид
Второй сомножитель есть Л/ (l+|/ ~ч • Так как
|/ — есть арифметический корень, то выражение 1-(- \■ ~
всегда положительно.
Отв. Va(yx + V~$.
146 ОТВЕТЫ И РЕШЕНИЯ 106
1 Об. Величины а и с должны быть положительными.
Поэтому знаменатель первой дроби, который приводится
к виду
]/"2(а— №f + 8ab* = К2(а + &2)2,
равен У*2(а-|-&2). Числитель этой дроби равен Y$(a-\-№).
Вторая дробь равна — —^-•уаСш
Отв. —Yac*
107» Уменьшаемое равно
{/l + Lalr-T-!]}"'-■£.
Подкоренное выражение вычитаемого равно (a2-f-jt2)2 (вели-
чина a2-j-jt2 положительна).
Отв. —1.
2Лрс 1
108, Выражение в квадратных скобках равно ._ —=;
ух— у а
возведя в степень —2, получим -11 — , Делитель
4у х
после сокращения на УХЛ~У а равен ——"7 " а «
О/и*. ■ у *~—•
V*
109. В числителе дроби выносим за скобку У х; сокра-
щаем дробь; заданное выражение принимает вид
(2>^^)8 + 4л:+4 + (1/^+1)2==5л:+10Кл+5.
Отв. 5 (Vx+1)*.
J10. В первой дроби переведём лг 8 в знаменатель (с
"о
положительным показателем); дробь окажется равной ^.
113 ГЛ. 2. АЛГЕБРАИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ 147
Вторую дробь сокращаем на д;8 , Заданное выражение при-
нимает вид
/ 3 1 \"г /1— 2х\'* _ (jc —2)(jc —1) 3jc —2
V7^2—дт —1У — \3х — 2J ~ 2лг —1 1—2лг *
х2
Отв*
2* —1 *
111. Первый сомножитель равен —. Возведя в квадрат
выражение в квадратных скобках, получим 2а2 — 2аЬщ
ОтвЛ(а — Ь).
1 1
112. Разность ух— ]7а = л:8— а3 возводим в куб;
числитель дроби равен
Зл:—3*3а3+3*3а3 =Ъх*\х* — хга* Ч-я3)'
знаменатель дроби равен
jL JL LI. L( — Л _L 1\
— За — Зд:3а3-|-Зд:8а3 = — Ъа* \a* -|-Jt3 — jt3a3)e
Сократив дробь, получим —. Заданное выражение равно
5.
a-|-jc)3P : а= 1.
Oms. 1.
113. Числитель первой дроби равен
a + 2Vab — 36 = (/"S)2 + 2V^V^~ 3(V7)?
Оли. ^р.
148 ОТВЕТЫ И РЕШЕНИ5Г 1М
114. Знаменатель первой дроби в круглых скобках
( - -Y
Знаменатель второй дробя равен \а%-\-ЪЬг) . Аналогично
разлагаем на множители числители.
Отв. -^IW.
116. Дробь в скобках сокращаем на Ya-\-YЬ. Первая
из дробей, в сумме составляющих данное выражение, равна
ЗУ~а(а—-Yab + b) 1
Вторая дробь равна
y-aiYj-VlL)^ 1
У" в (в — b) yi*+Yb '
Отв. 0.
116. Отв. 3.
117. Освобождаемся от отрицательных показателей. Вы-
ражение
a1 —ft2—U1/ -1*7
разлагаем на множители.
Отв. 1.
118. Преобразовав первое слагаемое в квадратных скоб-
ках, получим
Числитель этой дроби равен
(1-.)0+«)-[1-(?ЭД[1+(РЭ1.
Сумму и разность кубов разлагаем на множители.
Отв. а.
119. В числителе дроби выносим за скобку Y~a. Мно-
жимое равно У а—frx, а множитель 4 tycP-^Y ax-\-Y^*)*
Отв. 4 {а — х)щ
123 ГЛ. 2. АЛГЕБРАИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ 149
120. Дробь представим в виде
Ya—Vb
Выражение в первых скобках (делимое) равно
Делитель равен ]/а(Уа-\~УТ>)*
Отв. а.
121. Знаменатель уменьшаемого равен У а у х(Уа-±-У~х),
а числитель У~а ух [(Y~af + ( V^-*)3]* После сокраще-
ния приведем уменьшаемое к виду а—у а у х -\-Yx** Вы-
читаемое равно V (а-\-УхУ = \а-\-Ух\. Вместо послед-
него выражения можно написать а-]~Ух, так как а-\~У!с
есть положительная величина (величина а не может быть
отрицательной, ибо в данное выражение входит Ко).
Отв. а*х.
*_ */—
122. Сомножители знаменателя равны \-\-y х и 1 — ух.
Числитель можно представить в виде —х{\—У~х).
Отв. —jc8.
123. Числитель дроби в квадратных скобках равен
Заданное выражение равно
уцуъ-^шуТ)-1* ^ -
Yb — Y~a
Уд У~а
4-_
а
= 0.
уГаф'а — уь) fy а — у b
Отв. 0.
150 ОТВЕТЫ и РЕШЕНИЯ 124
124. Числитель уменьшаемого равен
(Г;У-(ПУ~ (П-П)3 =Уа~Ух-
V-
Oms. у а<
125. Сначала складываем первые две дроби; общий зна-
менатель равен
а*
[{а* + l)+ a«]|V + 0- *'] -У + О"
i. i.
= e» + a* + l.
f1 "I
2\й4 4-17
Получим —^—~—-—. Теперь вычитаем третью дробь; об-
щий знаменатель a-)-a2-[-l,
4
Отв.
а + а£ +1
126. j/V2—lp/"3 + 2/2 =
= ^(К2-1)2(3 + 2К2)=1.
Аналогичное преобразование выполняем в знаменателе.
Подкоренное буквенное выражение в числителе равно
(Ух — 2)3. Дробь *~ " х сокращается на Yх— 1.
Отв. 1.
127. Числитель первой дроби равен
в
Знаменатель преобразуется к виду (Ь + я) (Р— 2а)У аьЬь.
3/—
Таким образом, первая дробь равна -^Ар . Делимое в круг-
134
ГЛ. 2. АЛГЕБРАИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ
151
Лых скобках равно {Ь_™{Ъ_ьу Разделив его на £±^t
получаем (Ь_2а)(а-4-Ь)л Вычитая из этого ' д+Т* найдём
~(а + Ь)(Ь — 2а) '
Заданное выражение равно
а VI
а ъд(Ъа — Ъ)
Ь — 2а
Ь — 2а
П.
Отв. У^а.
128. Множимое равно 2 _ ,
ках равно Y%x— <*•
Отв. 2х-\-а.
129. Отв. V&.
1
Выражение во вторых скоб-
130. Отв.
131. Уменьшаемое равно ■ . , , а вычитаемое равно
(а + Ь){а + 2Ь)9
1
Отв.
а + 2Ь '
равно
132. Первое слагаемое равно , ; второе слагаемое
Ь 2а + Ь
Отв.
а + b *
а — Ь
133. Первое слагаемое равно —£—; второе равно —
Отв. -=-.
о
134. Отв.
2Ь—а
2Ь + а '
152
ОТВЕТЫ И РЕШЕНИЯ
135
ГЛАВА 3
АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ г)
135. Дробь —g-2 представим в виде 1+g--f-. Тогда
данное уравнение примет вид
а(Ь — Ъа) __ _7__£_
2b*(b — a) У~" 6 Ь ■
7b(b — a)
Откуда ^=з(^-3ДГ
л 7b(b—a)
0т*'У=г(Ь-За)'
136. Освобождаемся от знаменателя (общий знаменатель
О/из. лг — 0.
137. Решая данное уравнение по общему способу, по-
лучим —
Sabc + ab (a + b) + be {b + с) + са (с + а) \
х аЬ-\-Ьс-\-са А
Эту дробь можно сократить, разложив числитель на множи-
тели (выражение ЪаЬс представим в виде трёхчлена abc -f-
-\-abc-\-abc и каждый из последующих членов сгруппируем
с abc). Получим х = а-\-Ь-^-сч
Решение упрощается с помощью следующего искус-
ственного приёма. Слагаемое представим в виде
1) При решении задач этой главы не рассматриваются исключи-
тельные значения известных величин, при которых данное уравнение
теряет смысл или лишается решений, илн приобретает больше ре-
шений. Так, в задаче 135 данное уравнение теряет смысл при b = О
и при b — а = 0, ибо при Ь = 0 знаменатели первого и второго чле-
нов обращаются в нуль, а при b — а — 0 то же происходит с по-
следним членом.
Далее, при а = 0 данное уравнение имеет бесчисленное множе-
ство решений, так как уравнение принимает вид 1 = 1 и становится
тождеством. Наконец, при Ь = Заданное уравнение совсем не имеет
7
решений, так как оно приводится к виду 0»,у = -гтг.
140 ГЛ. 3. АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ 153
£—(fl-f- -t-c) _j_ i и аналогично два других слагаемых левой
части. Уравнение примет вид:
Отв. х = а^-Ь-\-с.
138. Общий знаменатель Ш {2с-±-3d) (2с— 3d).
_ с(4с'£ — М*)
Ums. z— 8^ + 27(Р *
139. Представим дробь ^ __ . ■ в виде —._д4 ■ (что-
бы получить тот же знаменатель, что у следующей дроби).
Дробь _.- полезно преобразовать к виду •=——. Перено-
сим все члены влево и группируем их (первый с четвёртым,
второй с третьим). Получаем
(1 -*)(rb + TT7r)+liil2ft2(jf- D-(2*- Dl = о.
Преобразовав — -^ щ1п" к ВИДУ 1 —Д2' освободимся от
знаменателя.
О/Ив. Jfscs—.
140. Переносим члены с х в левую часть уравнения,
а известные в правую, и каждую часть отдельно приводим
к общему знаменателю; получим
(ЗаЬ + 1) (а + 1)* — (2а + 1) _ dab (а + 1)* + аг
a(a + \f Х~~ (я+1)3 '
или
Sab (а + \у + Ф + 2а + 1 — 2а — 1 __а[36(а+ 1)2 + <*1
я(л+1)» *~ (а+1)«
Отсюда
вГ36(в+1)* + «]
e(e + lJP"
эащения находим
'—г+Т'
Д[36(Й+1)8 + д|
— (в + Ц«
Д
7+7*
154
ОТВЕТЫ И РЕШЕНИЯ
141
141. Производим группировку членов, как в задаче 140;
после преобразований получим
аЬ \Ъс (а + bf + Щ _ а \3с (а + &)2 +" ab\
Отв. д; = —r-7-ш
142. Общий знаменатель (а-\-Ь)*(а — Ь)ш
Отв. х = т^а~^ 2Ш
а
143. Дробь - а^^ представим в виде (—J^m%\* Об-
щий знаменатель будет mz(z%— т%\ Освободившись от него,
получаем после приведения подобных членов m2z9— 4m3^r= 0.
Это уравнение имеет два корня: z = 0 и г = 4т. Но при
отбрасывании знаменателя, содержащего неизвестную вели-
чину, могут появиться лишние корни; а именно, лишними
будут те, которые обращают общий знаменатель в нуль.
В данном случае лишним является корень z = 0. Он не удо-
влетворяет данному уравнению потому, что первый и третий
члены теряют смысл при г = 0. Корень z = 4m не обращает
в нуль общий знаменатель; поэтому он не является лишним.
Отв. z = 4/га,
144. Общий знаменатель будет Ь* — х2. Освобождаясь
от него, получим 2х (я2 -f- № — 2аЬ) = 2 (а2 — b\ откуда
х = —^Цг. Лишних корней нет, потому что знаменатель
№—х2 не обращается в нуль при х = Д_\ •
Отв. х = —L-r.
а — о
145. Общий знаменатель (х2—а2){х-\-п). Освобождаясь
от знаменателя, найдём х = —. При этом значении х зна-
менатель не обращается в нуль. Значит, х = — есть корень
данного уравнения.
Отв. х = —*
а
148 ГЛ. 3. АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ 155
146. Представим х-\-а-г в виде х-\- — . После преобра-
зований получим
2а 2 х
ах+\ * ах+\ ~~ 2'
Сокращая на ах-\-\9 найдём д; = 2а.
Замечание. Сокращение на ах +1 возможно при условии,
что ах + 1 не равно нулю. Но при х = 2а имеем ах -\-1 = 2а2 + 1 > 0.
Поэтому полученный корень — не лишний. Но если бы мы имели,
2а 2 х п
например, уравнение д2": __2 = -£, то сокращение на х — 2а
дало бы тоже х = 2а. Однако этот корень не годится, ибо дроби
'—~Т" и о теряют смысл при х = 2а. Таким образом, уравне-
2а 2 х
ние • х-: гГ- = -7г не имеет решении.
х — 2а х — 2а 2 г
Отв. х — 2а.
147. Перепишем уравнение в виде
а -\-х . а — х За
cP + x* + axi а? + х* — ах~ х (а* + а*х*+ jc4) '
Общий знаменатель левой части (а2 + л2 + я#) (л2 + я2 — ах)
можно преобразовать так:
Получаем
2дз За
Я4 _|_ фХЛ _|_ д;4 д- (д4 _|_ ф& _|_ д-4) •
3
2* *
148. Переносим члены с неизвестным в левую часть урав-
нения, а члены, не содержащие неизвестного, в правую:
(a—b—l)Vx = (a* — b*) — (a-)-b).
После разложения правой части на множители получим
(a — b—\)Vx = (a + b)(a — b—\\
Отсюда имеем Yх — а-\-Ъ.
Так как выражение У х означает положительное значение
квадратного корня, то при а-A-b < 0 задача не имеет решения.
Отв. х = (а-\-Ь)* (при условии, если а + £>0).
156 ОТВЕТЫ И РЕШЕНИЯ *4§
' 149. После освобождения от знаменателя и приведения
подобных членов получим 2*3+6а*-{-Зл3 = 0.
0Ш. Хх = «-Щ=*1; ,9=в_^£|±«.
150. Общий знаменатель будет 4 (лс+ £)(■*; — *)• После
упрощения получим
12^ — АЬх — £2 = 0.
Отв. хх^^\ *2 = — -g«
151. Общий знаменатель будет (лс — я)а. После освобо-
ждения от знаменателя получим
(дг—л)2—2д(* — Л)+(дЗ — £2) = 0.
Из этого квадратного уравнения находим
л: — а = а±Ь.
Отв. хг = 2а-\-Ь\ х2 = 2а— Ь.
152. Общий знаменатель будет be2 {а — 2Ь\ После осво-
бождения от знаменателя получим
{exf — (a — 2b).(cx)—Ь(а — £) = 0.
Из этого уравнения находим
сх-
2
Owe. хг*=—£—; д:2 = —у.
153. Освобождаясь от знаменателя, получим уравнение
4л;(л; — а)-\-Ъх(х-\-а)*=Ьа* или, после упрощения,
12лг2 + 4ол — 5л2 = 0.
О/гся. *i=2-; ^а^ g-*
154. Общий знаменатель п (пх — 2). После упрощений
уравнение принимает вид
(й — 1) х2 — 2х — (я + 1) = 0.
я + 1 .
Отв. хл = п __ 1 ; д;2 = —1.
158 ГЛ. 3. АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ 157
155. Общий знаменатель будет л (а-— х)2. После упро-
щений получим уравнение
(а + 1)х* — 2ах + (а — 1) = 0.
Отв. *,=■!; x^^^j.
156. Общий знаменатель будет (л; —а)2. После освобо-
ждения от внаменателя получаем уравнение
(x — af — 2b(x — а) — (а*—^)==0,
решая которое, находим
х—a = b3za.
Отв. х'х = 2а + £; #2 = £.
157. Общий знаменатель пх(х — 2)(х-\~2\ После упро-
щений получим уравнение
л;2 — (2 — л) х — (2л2 + 4л) = 0.
О/ля. лг, = л -J- 2; jc9 ^ — 2л.
158. Первый способ. После обычных преобразований
получаем уравнение
х*-\-(а — 2л — 2а + п)х — (а — 2л)(2а-^л) = 0.
Решение последнего уравнения можно найти сразу, если
обратить внимание на то, что свободный член есть произве-
дение величин —(а—2л) и (2а — л), а коэффициент при х
есть сумма тех же величин, взятая с обратным знаком.
Второй способ. Переносим единицу из правой части
в левую, получим:
а + х — 2п а — 2п + х ~
2а— п х •
или
(fl_2„ + ^)(^i_— ±)-о;
отсюда: 1) а — 2л + лг==0 или д;1=2л — а.
Отв. хг «а 2я — а\ х% = 2а — л.
158 ответы и решения 159
1Б9* Получаем уравнение
(л— I)2**—а(п — 1)х + (а —1) = 0;
чтобы избежать действий с дробями, можно положить
(л—1)лс = г или непосредственно найти (л— 1)* из урав»
нения
[(л — I)*!2—а [(л — \)х\ + а—1=0.
Получим
(л— I)*, a= а — 1; (л —1)*2= !•
160» Знаменатель левой части равен (а — л;)2. Помножив
на него обе части уравнения» найдём
/Д — лг\а / д \г 5 /д —дг\а 4 Ад_—£\а / <. у»
Извлекая корень, получаем одно нз двух уравнений:
2 д—лг а • 2 д— jc а
Ошв х ^2*(*+*> - v ^ 2д(а + 6)
161* Преобразуем сначала выражение
(1 +ax¥~(a + xf= 1 -J-a2*2—& — х\
Группируя в правой части первый член с последним, а вто-
рой с третьим, получаем (1— х*)(1—л2). Теперь заданное
уравнение приводится к виду
162. Трехчлен ах*-{-Ьх-\-с разлагается на множители
первой степени следующим образом: ах*+Ьх + с =
в*а(* — jCj)(a: — jcj); здесь jct и лс2 — корни уравнения
дх*+Ьх -{- с = 0. В данном случае а *= — 3, хг = 7;
xse ^-, так что получаем — 3(х— 7)(лг + Др).
Ош. (7 —jc)(3jc-J-10).
164
ГЛ. 3. АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ 159
163. Так как
£ b __ д* — V* _ (a + b)(a — b)
Ъ а аЪ аЬ '
то можно по догадке разложить у на множители 2-^t-
и ^у- (их сумма равна у-| ). Но надо еще выяснить,
будет ли это решение единственным. Пусть а и v—иско-
мые множители. По условию
а Ь . а . Ь
uv = -r и u-\-v — -r -\ .
Ь а ' Ъ ' а
Следовательно, и и v — корни квадратного уравнения
*Чт+1)*+(т-4Н'
В выражения для и и v войдет радикал
/(*+#-« (*Ч)-
Зная заранее, что задача допускает рациональное решение,
постараемся освободиться от радикала. Для этого напишем
(а . Ь\ъ (а &\г
вместо 1у-| j выражение (у ) и для компенсации
прибавим 4 • -г • — , т. е. 4; тогда под радикалом получим
полный квадрат |Yy — у\ — 2?.
Отв. ±±±.±=1.
a b
164. 15#3-f-x2— 2х = х(15х2-\-х—2). Корнями урав-
1 2
нения 15д;2 + д; — 2 = 0 будут ^ = -0-; лг2 = — у. Следо-
вательно,
15*2 + * —2 = 15 (х — 4)(А;+'§)==(3л:~ 0(5*+ 2).
Отв. дг(3лг— 1)(5* + 2).
160
ОТВЕТЫ И РЕШЕНИЯ
165
165* Первый способ. Сумму 2х*-\-4х2~\~2 предста-
вляем в виде 2(-я24-1)2-
Второй способ. Располагаем многочлен по убываю-
щим степеням х и член 4л;2 разлагаем на два слагаемых
2x2-{-2x2f после этого группируем первые три члена и по-
следние три и разлагаем на множители.
Отв. (х*~\-1)(2х* + х + 2).
165а. Левую часть уравнения напишем так:
(1— л;2)2 + 4л;2.
Уравнение примет вид
(1 — х*? — 4х (1 — л;2) + 4л;2 = О,
или
[(1 — л;2) — 2л;]2 = 0.
Отв. хх = — 1 -f /2; л;2 = —1 —/2.
166. Искомое уравнение есть [х— jj(x — т)~0'
Отв. abx* — (a*-{-b*)x-\-ab = Q.
167. Согласно теореме Виета корни х19 х% уравнения
x2-{-px-{-q = 0 в сумме дают —р, а в произведении q.
Значит,
/ 1 | 1 \ __ —2-10 20
Р V Ю— УП ~*~ 10+У72У 100 — 72 28V
1 1 _ 1
4 Ю— |^72 * 10+1/72 28#
Искомое уравнение: х*—-^г х -{- -§<г = 0»
О/гс*. 28л:2 — 20* -{- 1 = 0.
168. Решается аналогично предыдущей задаче.
Отв. bx* — 2аУах + а* = 0.
169. По теореме Виета хгх% = 12; по условию хг — х2 = 1.
Из этих уравнений можно найти хг и х2 (4 и 3 или —3
и —4) и затем р =—(л^-}--*^) — —7.
Но для разыскания хг^-х2 нет необходимости опреде-
лять хг и х$ по отдельности. Можно вычислить
(*, + лг2)2 = (хг — xjp+ 4*Л = 12+ 4 . 12 = 49,
откуда р = — (*!+ л:2)==±:7.
G/m?. p = zL7.
173 ГЛ. 3. АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ .161
170. Имеем
— 1 . — 1
х\хъ 5 * ^ ~~" ^2 — '
3
Далее, как в предыдущей задаче, находим хг -+- лс2 == ± —г==.
и учитываем, что jCj-J-j;a=-g-.
Owe. * —гЬЗ/б.
171. Имеем
jcJ + jcS= 1,76; jctjca = ^2; xx -f- *2 = Зд.
Здесь три неизвестных дгг, лс9, а. Нам нужно найти а. Воз-
водя третье уравнение в квадрат и вычитая удвоенное второе,
находим х\-\-х\ — 7а , Сопоставляя это с первым уравне-
нием, находим 7а2 =1,75.
Отв. а = ±2". '
172. По теореме Виета
P + Q = — Р и pq = q.
Эта система имеет два решения: 1) /? = 0, ^ = 0; 2) р=1,
^ = —2. В первом случае имеем уравнение д:2 ===== 0, во вто-
ром х*+х—2 = 0.
Отв. 1) р = 0, £ = 0,
2) р=1; ? = —2.
173. Корни искомого уравнения будут 34 = — и^2 = ~ •
Выразим ^1+^2 чеРе3 коэффициенты а, Ь, с. Для этого
, х\ + х\ {xi+x$ — 2x{xt
преобразуем ух+у2 = r г к виду — и за-
меним (л^! Ц- -^а) через — —, a xtx% через ~. Получим
■ ~а€-. Кроме того, имеем у^ = ^ • £* == 1. Следовательно,
искомое уравнение есть
« 6а —2ас
■jr+l=0.
Отв. асу** — (£2 — 2ас) 3; -j- ^ = 0.
162 ОТВЕТЫ И РЕШЕНИЯ 174
174. Эту задачу можно решить как и предыдущую, ио
лучше итти более коротким путем.
В первом случае оба корня искомого уравнения должны
быть вдвое больше соответствующих корней данного урав-
нения. Значит, нужно найти неизвестную величину у, кото-
рая вдвое больше неизвестной величины х, удовлетворяющей
уравнению ах^-^Ьх-^-с^О. Из условия у = 2х находим
х =а 4 и» подставляя в данное уравнение, получаем
Во втором случае делаем подстановку jt==--# Получаем
Отв. 1) ay2-f 2by~\-4c = Q;
2) cy* + by + a = Q.
]7б. Первый способ (см. решение задачи 173). Имеем
У\ +У* — ** + 4 = (*i 4- **/ — 3*t*g (хг + хй).
Подставляя сюда хх-{-х^ = — — и ххх% = —, находим
Л +Л — &— • Далее> УгУ% — (ЪхъГ = jj-. и по тео-
реме Виета составляем искомое уравнение.
Второй способ (см. решение задачи 174). По усло-
вию у = х*9 т. е. лс — Yy. Подставляя в данное уравнение,
получаем _
afp + bfy^ — с.
Чтобы избавиться от иррациональности» возведём обе
части уравнения^ куб и преобразуем сумму b(aYy*fbY~y +
+ Ъа]/y*{bfy)* к виду Zaby Utfyp + bfy]. Выраже-
ние в скобках в силу найденного уравнения равно —с.
Отв. aV4-(£3 — ЪаЬс)у-\- с» = 0.
176. Всякое уравнение д-й степени, имеющее корнн
xv дга, .... хп% можно представить в виде
(* — х^{х — Jfj)... {х—^ = 0.
177 ГЛ. 3. АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ 163
Биквадратное же уравнение имеет всегда две пары корней,
равных по абсолютной величине и противоположных по
знаку. Полагая аг3 = — хх и лс4 = — лс2, можно записать би-
квадратное уравнение в виде
(х—хг) (х—х^) (x+xt) (jr+jc^O, т. е. (**— х\) (х2 —х% = О
или
Но по условию
xi + 4 + (—xt)* + (—x2y*~b0
и
ххх% (— xj (— *a) = 144.
Следовательно,
д?4-*! = 25 и xtxl=U4.
Отв. *4 — 25**-+-144 = 0.
177. Если алгебраическое уравнение (с действительными
коэффициентами) имеет комплексный корень а-\-Ы, то кор-
нем его является также и комплексное число а — Ы (сопря-
жённое с числом a-\-bt). Таким образом, нам^известны два
сопряжённых корня заданного уравнения 3+*V6 и 3 — /|/Ts.
Оба эти корня можно проверить непосредственно, но проще
предварительно выполнить следующее преобразование.
По теореме Безу левая часть уравнения должна делиться
(без остатка) на выражения х — (З + ЛЛ)) и х—(3 — г^б),
а следовательно, и на произведение этих выражений, т. е.
на [(*— 3) — iY1\[(x — 3) + /1/'б]=л:2 — 6лг+ 15. Вы-
полнив деление, мы разложим левую часть на два множителя:
4х4 — 24*3 + 57*2-1-18л: —45=(*2 — 6*+1б)(4*« — 3), и
данное уравнение распадается на два:
1) *2_6:г+15 = 0 и 2) 4*» —3 = 0.
Первое имеет корни хх = 3 + 'Уб и х2 = 3 — / j/Т; кор-
У~з У~з
нями второго являются хь = ~- и х4 =— 9^*
Отв. xt - 3 + / j/"6; *2 = 3-/^6; *„- ^; *4«—^-
164
ОТВЕТЫ И РЕШТНИЯ
178
178- По условию х = 2 должно удовлетворять заданному
уравнению. Поэтому мы имеем 6 • 23—7 • 22—16 • 2 + ^ = 0,
откуда т= 12. Получаем уравнение 6х3—1х%—16х-(-12=0,
один иа корней которого равен 2. По теореме Безу его
левая часть должна делиться на (х — 2). Разделив, найдём
6х2-\-5х— 6. Следовательно, уравнение можно представить
в виде (х — 2) (6л:2 + 5л: — 6) = 0. Корнями его, кроме корня
xi = 2t являются корни л:2, х3 уравнения 6х*-\-5х — 6 = 0,
2 3
Отв. w=12; л:9 =-g-; л:3 = — -к.
179. Подставляя в данное уравнение х = 2 и х = 3
(см, решение предыдущей задачи), получаем
Ат-\-п = 10 и 9т-\-п = — 15.
Из этой системы находим т = —5, п = 30 и получаем
уравнение 2л? — 5х2— 13х-\-Ъ0 = 0. Левая часть должна
делиться на х — 2 и на л: — 3 и, следовательно, на произ-
ведение (л: — 2) (л: — 3). Уравнение перепишется в виде
(х — 2) (л; — 3)(2л: + 5) = 0. Корни его хх = 2> л:2 = 3,
___ 5
хь 2.
5
Отв. т = — 5; п = 30; л:3 = — -j.
180. Квадратное уравнение x2-]-px-\-q = Q имеет равные
корни, когда подкоренное выражение (^Л —q равно нулю.
В данном случае должно быть (aj/^a2 — З)2 — 4 = 0, т. е.
а* — За2 — 4 = 0. Это биквадратное уравнение имеет два
действительных корня (а = 2 и а = — 2) и два мнимых
(^?=/ио = —/). Ограничиваясь действительными корнямиl)f
получаем уравнение л:2 -j- Ах -\- 4 = 0 и х2 — 4л: + 4 = 0;
первое имеет корни х1 = х2 = — 2, * второе имеет корни
Ху = х% = 29
Отв. При а = 2 и при а = —2.
J) Мы предполагаем, что коаффициенты заданного уравнения
являются действительными числами.
183
ГЛ. 3. АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ
165
180а. Корни уравнения будут
хи 9 = т ± |Ляа—/»а+1= /и ±: 1.
По условию имеем
— 2<w + l<4, j _3< w<3,
— 2<m—1<4 ИЛИ \—l<w<5.
Owtf. — 1 < w < 3.
181. Уединим один из радикалов, например первый. По-
лучим 1/^ + 2 = 2 + }/^ — 6.
Возведём обе части в квадрат. После приведения подоб-
ных членов и сокращения на 4 будем иметь Yy— 6 = 1,
откуда у = 7. Проверка показывает, что этот корень годен.
Отв. у = 7.
Замечание 1. Здесь и в дальнейшем мы считаем корни квад-
ратные и вообще корни чётных степеней арифметическими. См. пред-
варительные замечания в начале решений главы 2 (стр. 122—125).
Относительно корней нечётных степеней см. ниже подстрочное
примечание к задаче 209.
Замечание 2. Проверка делается для того, чтобы обнару-
жить лишние корнн (они могут получиться при возведении обеих
частей уравнения в квадрат). В данной задаче лишних корней нет.
Но возьмём уравнение Yy+2 + Yy— б = 2, отличающееся от
данного только знаком. Решая его тем же способом, получим
У у — 6 = — 1. Возведя в квадрат, найдём тот же корень у = 7.
Он не годится; взятое уравнение вовсе не имеет решения. Здесь
можно было бы обойтись и без проверки, так как и без того видно,
что Yy— 6 не может равняться —1 (см. замечание 1). Но в дру-
гих случаях (см. задачу 184 и 190) без проверки обойтись нельзя.
182. Решается, как предыдущая задача.
Отв. х = 6.
183. Уединив первый радикал, возведя в квадрат и упро-
стив, получим х—1 *=2Ух— 1. Снова возведя в квадратг
находим (х— 1)2 — 4(л:— 1) = 0. Это уравнение можно
разделить на х—1, предварительно учтя, что д:=:1 есть
один из корней. Тогда найдём другой корень х = 5. Можно
также раскрыть скобки и решить квадратное уравнение.
Проверка показывает, что оба корня годятся.
Отв. xt= 1, xQ = 5.
166 ОТВЕТЫ И РЕШЕНИЯ t84
184. Поступая как в предыдущей задаче, найдём A;-f-22=*
= 7|/3jc—2, а отсюда л;а—103л;+ 582 = 0. Это урав-
нение имеет два корня: ^ = 6н jra = 97. Данному уравне-
нию удовлетворяет только первый корень, второй — лишний
(он удовлетворяет уравнению У^Ъх—2 — "[Лхг + З = 7, отли-
чающемуся от данного знаком при радикале).
Отв. х = 6.
185. Решается, как предыдущая задача. Из двух корней
хг = — 1; л;2 = 3 второй лишний.
Замечание, х = 3 есть корень уравнения
— Yx+i + УЯГ+Ъ = i.
Отв. х = — 1.
186. Отв. ^ = 34; x2—2.
187. Отв. х = 4.
188. Возводим в квадрат. Получаем уравнение
лг|/*л:а+24 — х* — 2л; = 0.
Оно распадается на два уравнения:
л; = 0 и У x2-f-24—л;—2 = 0,
Второе даёт х = 5. Выполняем проверку.
Отв. л;1 = 0; д:2 = 5.
189. Данное уравнение приводим к виду
Т^ 3 У 9 + л: К 9^х**
Возводим в квадрат и помножаем на л:2 (при умножении
на х* есть опасность ввести лишний корень # = 0). Полу-
чаем уравнение
1+!* = *]/ 4+1*-
Снова возводим в квадрат.
Отв, # = -т.
194 ГЛ. 3. АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ 167
190*. Помножив обе части уравнения на |/{#+2)(.х;-|-3),
получим
/(* — 5)(* + 3) + /(* — 4)(х + 2) = 7.
Поступая как в задаче 181, найдём
V(x — 4)(jc + 2) = 4.
Отсюда получим два корня ^ = 6, д:2 = — 4. Проверка
показывает, что л:а не годится, получается неверное равен-
ство IY2-—J/2.
Owa. а; = 6»
191. Освобождаемся от знаменателя. Получаем
Это уравнение имеет два корня х = 5 и д: = — 5. Однако
при дг = —5 выражение Ух—3 не имеет арифметического
значения (см. замечание 1 к вадаче 181).
Отв. х = 5.
192. Приведём левую часть уравнения к общему знаме»
нателю:
Зх — дУх* + х 3
— х х9
Отсюда
3(*+1)-5У*<*+1).
После возведения в квадрат получаем
9(д:+1)2 — 25(д: + 1)д:=:0
или
(л:+1)[9(дг+1) —25д:]==0.
Отв. хх = — 1; л:2 = ^.
193. Решается, как предыдущая задача.
Отв. jct=s2; #2 =— 1,6.
194. Возводим обе части данного уравнения в квадрат.
После тождественных преобразований получим |/28—х —1/7 .-
При возведении в квадрат есть опасность ввести посторон*
ний корень, удовлетворяющий уравнению, отличающемуся от
1б8 ОТВЕТЫ И РЕШЕНИЯ *95
данного знаком правой части. Уравнение у 28 — х = У 7
имеет единственный корень х = 21. Он не является посто-
ронним, так как
Отв. х = 21.
195. Перепишем уравнение так:
Г ^¥ Г V 2Vx+ Y*
Освободимся от знаменателя; при этом есть опасность ввести
лишний корень х = 0 (так как знаменатель обращается
в нуль при х«0). Других лишних корней быть не может,
так как х = 0 есть единственный корень уравнения
у х -|- Ух=*0 (см. решение задачи 143).
После упрощений получаем уравнение
2х — 2Ух^—х— \Пс = 0,
одним' из корней которого является л; = 0. Однако этот
корень лишний, так как при х = 0 правая часть исходного
уравнения теряет смысл. Выносим за скобку Ух:
Y~x(2 Ylc — 2 У^—i _ i) = о.
Решая уравнение 2 Ух — 2 Ух — 1 — 1=0 (см. решение
25
задачи 181), находим д: = у^. Выполняем проверку.
о 25
итв, •* = Tg»
196. Сначала освобождаемся от иррациональности в зна-
менателе. Умножаем для этого числитель и знаменатель на
— х\ получим
(Т^27 + х+ У 27 — л:)а_27
2х * х
или, после упрощений,
Z7+Y27* — л* _27
X X *
Отсюда находим # = :±;27. Оба корня годятся.
Отв. х = ±27.
|97 ГЛ. 3. АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ 169
197. Уединив радикал, возведём обе части уравнения
в квадрат. Будем иметь
х* — 2ах = — xV *2 + Д2.
Это уравнение имеет корень х = 0. Для отыскания дру-
гих корней разделим обе части уравнения на х (это можно
сделать, так как теперь х Ф 0). После этого снова возве-
гт 3
дём обе части в квадрат. Получим х = —а.
При проверке можно придти к ошибочному заключению,
3
что значения х = 0 и х = -т-а всегда удовлетворяют дан-
ному уравнению. Чтобы лучше уяснить суть ошибки, рас-
смотрим числовой пример. Когда а== — 1, данное уравнение
имеет вид
х = — 1 - У\— *}/**+?.
3 3
Ни х = 0, ни * —-j а — — Т не удовлетворяют этому урав-
нению (оно не имеет решений). Так же будет при любом
другом отрицательном значении а.
Источник ошибки в том, что величина у о2 считается рав-
ной а, тогда как это верно лишь при #1>0. При о<0
мы имеем Ya<2 = — а\ например, Y (—3)2 = —(—3).
Правильная общая формула (см. предварительное замеча-
ние, п. 3 на стр. 123) такова:
yifl = \a\.
Пользуясь этой формулой, мы найдём, что при л; = 0 (когда
левая часть уравнения обращается в нуль) правая часть равна
а — }/а2 = а — |а|. При а^О это выражение тоже paBHj
нулю, но при а < 0 оно равно 2а. Следовательно, если
о;>0, то значение лг=0 есть корень уравнения; если же
я < 0, то х = 0 не является корнем. То же относится и
о
к значению х = — а.
4
о
Отв. Если а ^ 0, то xt = 0, х% = — а; если а < 0, урав-
нение не имеет решений.
170 ОТВЕТЫ И РЕШЕНИЯ 198
198. Записанное без степеней с отрицательным показате-
лем данное уравнение имеет вид1)
/'+©■--=-
(А)
4*
Первый способ. Освобождаемся от знаменателя:
31/ 1 +(—) =5« —. Левая часть положительна; значит,
(х\% 9
— J гаг — #
Отсюда — =-г-(значение — — исключается, ибо — >0].
а 4 \ 4 а ^ J
Второй способ. Уничтожаем иррациональность в зна-
менателе:
l/'+GJ'-fM-
Выражение, стоящее в скобках, не может быть отрицатель-
ным
; поэтому jfi+(±)*-£~± или / 1 +(£)
-т+т• в08»0"1 в квадРат: ^(^W+f+S)*-
* з
откуда - = -4.
Owe. Х = 7Й'
4
!) В первом издании авторы по досадному недосмотру совер-
шили ошибку, против которой предупреждали в предыдущей за-
даче. Именно, уравнение (А) было ошибочно записано в следующем
виде; ■ . z =-г. Ошибка возникла так: в уравнении »А)
Y* + x* + x 4 J
числитель и знаменатель левой части были помножены на а,
затем а было подведено под корень. Но равенство а у 1-Н — 1 =*
= V a2 + *2 неверно прн я <0. В этом случае имеем а у 1+(-) =
= —Y~cCly 1+(—) =—Y а* + х\ Вследствие указанной
ошибки ответ, приведённый для случая д<0, был неверен.
200 ГЛ. 3. АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ 171
199. Решается, как предыдущая задача, Применяя вто-
рой способ, найдём
Выражение У^+а2.*;2— ах всегда положительно. Поэтому
y1+aW-ax = ±, т. е. ]Л + а*х* = ах-{-±].
I с 12 1
Возводим в квадрат. Получаем д:= ' , или, что то же,
_с«—1
*~~ 2л|сГ
Проверка. Подставляя л; — о~ТТ' находим
Учитывая, что величина £2 -}-1 всегда положительна, на-
ходим
Дальнейшие вычисления показывают, что данное уравнение
всегда удовлетворяется.
Отв. х= с|, т. е. при с>0 имеем х = —*—, при
1—с2
с<0 имеем * = 2дс '
200. Вынесем за скобки в числителе и знаменателе левой
части выражение Y х~\~с и сократим на него дробь1).
После сокращения получим
УТ+с +Ух — с _9(х + с)
Уничтожим иррациональность в энаменателе. После упро-
щений найдём 8|/"д:2 — с2 = д; + 9с. Отсюда х = — или
29 6
4 Сокращая на тЛс + с, мы предполагаем, что хф—с. Если
оы, решив полученное уравнение, мы нашли х = — с, то это значе-
ние не было бы корнем данного уравнегшя. Однако из дальнейшего
видно, что такого корня мы не получаем.
172
ОТВЕТЫ И РЕШЕНИЯ
201
Проверка показывает, что оба эти значения удовлетво-
ряют уравнению при с > 0 и не удовлетворяют при с<0.
Отв. При с>0 имеем xt = -^c и л:3 = —9тс;прис<Х)
уравнение не имеет решений,
201 *• Перное подкоренное выражение преобразуем так:
лг-f 3—4Vx=l=(x— 1)— 4j/"^4+4 = (|/"J^T—2)К
Аналогично второе подкоренное выражение равно (Yx—1—З)2,
Данное уравнение принимает вид
Ij/TZH —2| + |У£=1_з] = 1 (А)
(см. предварительное замечание ^к гл. 2, п. 3). Возможны
три случая: 1) ]/* — 1 > 3;2)|/*^=1<2; 3) 2<|/*jc^1<3.
В первом случае уравнение (А) принимает вид:
УЗГ^Т — 2+Ylc^i — 3=1, или |/*^*=Г1 = 3.
Этот результат не согласуется с условием Yx—1 >3.
Во втором случае уравнение (А) принимает вид:
_(|/*^ZT"i_2) — (/£1Г1—3)=1, или |/*^=Г1=2.
Этот результат также не согласуется с условием Y*—1<2.
Остаётся третий случай, когда уравнение (А) принимает вид:
(\Пс^Л— 2) — (\П^Г\ — 3)=1. (В)
Это равенство является тождеством, следовательно, уравне-
ние (А) удовлетворяется при всех х, для которых
Так как величина Yx—1 > 0, то все три части нера-
венства можно возвести в квадрат, после чего находим
5<*<Ю,
т. е. решения данного уравнения содержатся в границе между
5 и 10 (включая и значения 5 и 10). Все они являются ре-
шениями данного уравнения, так как они подходят под слу-
чай 3, когда данное уравнение (А) обращается в тожде-
ство (В).
Отв. 5<л:<10.
203 ГЛ. 3. АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ 173
202- Возведём обе части уравнения в квадрат, перенесём
все члены в одну сторону и вынесем за скобки Уа-\-х:
УаАгХ (4 ]/~а-\-х + 4 У а — х — Ух) = 0.
Это уравнение распадается на два. Из первого Уа-\-х = 0
находим х = — а. Проверка показывает, что при а ;> 0 это
значение удовлетворяет данному уравнению. При а<0 урав-
нение теряет смысл (так как У й — х становится мнимым).
Второе уравнение есть Ь{Уа-\-х-\-Уа— л;)—j/л;. Если
его решать, как в задачах 183—187, то получим (кроме
64д
заведомо лишнего корня х = 0) * —щн» Проверка пока-
жет, что и это — лишний корень, так что второе уравнение вовсе
не имеет решений. В этом проще убедиться, если применить
следующий способ решения. Переведём иррациональность
в знаменатель (помножив и разделив Уа-\-х-\-Уа — х на
сопряжённое выражение Уа-\-х — У а — х). Получим
8дг
:-1^.
Ya + x — Ya-
Разделив на Уд: (что возможно без потери корней, так как
д: = 0 не есть корень), получим Уа-\-х—У а — x = 8J/"jc.
Вычитая это уравнение из полученного выше Ya~\~x -f-
-уУа — х^-т-Ух, находим
2У^~=Пс=—^Ух.
Но это равенство невозможно, так как левая часть есть по-
ложительное число, а правая — отрицательное. Если бы, не
обратив на это внимания, мы возвели обе части в квадрат,
64
ТО ПОЛуЧИЛИ бы ЛИШНИЙ КОреНЬ х=иу2ьа-
Отв* Если а положительно, тод: = — а\ если а — отри-
цательно, то уравнение не имеет решения.
203. Здесь с успехом можно применить перевод иррацио-
нальности в знаменатель (см, предыдущую задачу).
Отв. х = 0*
174 ОТВЕТЫ И РЕШЕНИЯ 2М
204. Отв. ху = а; jcs =» — £.
206. Отв. л=»(?~1)8(при tf> О.
При а < 1 уравнение не имеет решений.
206. Данное уравнение можно представить в виде
или
ах *
1 8
(а + хУ=*ах~.
2 -
Возводим в степень «^. Получаем fl-|-x*=attJc. Отсюда
*=*—^—• Проверка:
а+дг^-^ , {а-\-ху ——| —. __=_ _#
а»-1
От*. *=» -у-2—; если значение а лежит между —1 и
о5*-!
+ 1, то уравнение не имеет решений.
207. Полагаем кх»г. Тогда
Уравнение примет вид
** + *_12 = 0.
4
Отсюда *t=*3, ^=3 — 4. Так как ух должен быть по-
ложительным числом, то второй корень лишний.
Отв. х = 81.
208. Полагаем (х— 1)*" = -?. Дальше решается, как пре-
дыдущая задача.
Отв. *= 17.
212 ГЛ. 3. АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ 175
209*). Возводим оба части уравнения в куб. Получим
|Л0 + 2х + \Л5 — 2х = 7.
Здесь можно уединить один из радикалов, а можно и не
уединять.
Отв. ^=3; лг2 = ——.
210. Возведём обе части уравнения в куб, применив фор-
мулу (а-\-Ь)* = сР-[-ЪаЬ(а-\-Ь)-]-1>ъ. Получим
х + 3^х(2х — 3)[1^х + 1^2дг—3|-f 2* — 3 = 12(лг — 1).
Выражение в квадратных скобках в силу заданного урав-
нения можно заменить выражением У 12(лг—ПГ). Получаем
1/лг(2лг— 3) • 12(л:— 1) = 3 (х— 1).
Возводим в куб. Перенося члены в одну сторону, найдём
(аг—1)[12аг(2лг —3)—27(аг—1Я = 0.
Это уравнение распадается на два:
дг—1 = 0 и 12л:(2л; — 3)—27 (лг— 1)9 = 0.
Найденные корни проверяем.
Отв. х^ = \г *3=3,
211. Задача решается, как предыдущая.
Отв. хх = а\ лг2 = Ь\ д:3 = —^—.
212. Полагаем ]/х"=г; тогда }/lc* = z*. Подставив ь
исходное уравнение, получаем 2z2 -\-z— 3 = 0, откуда
— 1. — 1
z1 — i; z% —- g •
27
Отв. *j=l; лг2 = — -g-.
]) Здесь и в дальнейшем корни кубические и вообще корни
нечётных степеней мы не считаем арифметическими,
допуская, что подкоренное число может быть и отрицательным
(но обязательно действительным). Значение корня мы 'также счи-
таем действительным числом.
176 ОТВЕТЫ И РЕШЕНИЯ 213
213. Решается, как предыдущая задача.
Отв. ^ = 64; £в = ^-.
214. Полагаем ]fa-^-x = z; тогда Уa-^-x^z* и
От», jfj =s — a; a:q=:1—a.
215. Полагаем у x*2 = г; тогда j/ ^"JT ,
■ 2 J_
■2 — -г
уравнение после ряда преобразований примет вид
12^—7^—12 = 0;
отсюда
■_ 4 — 3 '
Второе решение отбрасываем, как отрицательное (см. заме-
чание 1 к задаче 181 на стр. 165), Для определения х полу-
1/"2r + 2__j4_
JC = J
чим уравнение т/ —ЗГ'Г'^ТГ*
Omff. л = 7.
216. Отв. х = ±5.
217. Положим ]/Т=#; тогда |/jt2 = 2a
Получаем:
яг4—1 g« — 1 _А
2г»— 1 * + 1 ;
Сокращаем первую дробь на г*— 1, вторую на jsr —)— I.
Получаем г2—г—2 = 0. Но сокращение первой дроби за-
конно только при условии, что г2— 1 Ф О, а второй — только
при условии, что г+1=£0. Между тем из двух корней
21==2 и г2 = — 1 второй даёт г-}-1===0. Он не годится,
так кай при г = — 1 имеем л: = — 1, и левая часть данного
уравнения теряет смысл/
Отв. х = 8.
218. Полагая Yх =г* преобразуем уравнение к виду
222 ГЛ. 3. АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ 177
Сокращаем дробь на z-f-2 (см. объяснение к предыдущей
задаче). Получаем «*—г«— 6 = 0, откуда гг = Ь\ #Q = — 2.
Второй корень не годится, потому что, во-первых, выраже-
ние , су теряет смысл и, во-вторых, z не может быть от-
рицательным числом.
Отв. х = 9.
219« Здесь введение вспомогательного неизвестного, ко-
торым мы пользовались в предыдущих задачах, не приводит
к цели. Представляем уравнение в виде
a—x+Yx—b
Сокращаем дробь на У а— xJrVx—* (сокращение за-
конно, так как это число не может равняться нулю). После
упрощений получаем У (а— х)(х—£) = 0.
Отв. хх = а\ Хъ в Ь.
220. Заданное уравнение представим в виде
Это уравнение распадается на два: первое J/2 — д: = 0; его
корень ^«2; второе после освобождения от внаменателя-
будет У2(2—л:) = 2 — Yxl Его корни лга = 0; л;в=_.
Ome» хл = 2, Лд = 0, х3 = -д *
221. Отв. х = 81.
222. Если, уединив радикал, возведём обе части полу-
ченного уравнения в кзадрат, то получим уравнение 4-й сте-
пени. Но в данном случае можно применить искусственный
приём. Перепишем уравнение в виде
/л:2—Злг + 5-f *9— Злг-f 5=12.
Полагая Ух* — Ъх-\-Ь = г, получаем * г2 + z — 12 = 0. Бе-
рём только положительный корень г = 3.
Отв. хл = 4; д:9 = — 1.
178
ОТВЕТЫ И РЕШЕНИЯ
223
223. Можно применить тот же приём, что в предыдущей
вадачс Однако заранее можно сказать, что уравнение не
имеет решений. Действительно, величина 3*а + &х 4" * ПРИ
всяком х больше, чем Злг9+5л:—8. Поэтому
/3*3 + 5*+1 > /Зх«+5х—8,
значит, левая часть данного уравнения при всяком х отри-
цательна и, следовательно, не может равняться единице.
Огне. Уравнение не имеет решений.
224. Обозначим через z одно из подкоренных выраже-
ний— удобнее всего положить -у2 + 4у+6 = г. Уравнение
примет вид
Y7+2 + /F^2 = VTz.
Освобождаясь от радикалов, находим га = 4. Годится только
корень z = 2 (при z — — 2 два подкоренных выражения
отрицательны). Решаем уравнение у2 + Ау + 6 = 2. Про-
веряем.
Отв. у= — 2.
225 г). Можно решить по способу подстановки (из вто-
рого уравнения найти у = 6 — х или лг= 6—у и подставить
в первое). Несколько быстрее ведёт к цели следующий
искусственный приём. Первое уравнение преобразуется к виду
(л: — yf = 4, откуда х—у = 2 или х—у = — 2. Получаем
дзе системы:
1) ( х — у=2, 2) ( х—у = -2,
\ х + у = Ь\ \ х+.у = 6.
Отв. 1) хл = 4, уг =2;
2) дг2 = 2, з>2 = 4.
1) В задаче 225 и в большинстве следующих задач этой главы
применение искусственных приёмов совершенно необходимо для нх
успешного решения. Основная трудность этих задач в том, чтобы
подметить особенности данной системы и подыскать соответствую-
щий искусственный приём.
228
ГЛ. 3. АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ
179
226. Предстзвим данную систему в виде
I ху{хЦ-у)—ЪО.
Положим для краткости ху = гг; x-\-y = z^ Тогда имеем
систему
По теореме Виета гг и г2—корни квадратного уравне-
ния г2— 11*-|- 30 = 0. Находим: г, = 6, г2 = 5 или гг = 5,
^2==6. Получаем две системы;
J х+у = 69 и J * + з/ = 5,
\ ху = Ь \ лгу —6.
К «ждой можно снова применить теорему Виета (или решить
по способу подстановки).
Отв. 1) х = 5, у= 1; 2) д:= 1, у = 5;
3) х = 2, у = Ъ\ А) х = Ъ9 у = 2.
227'• Положим з'3 — ^; тогда имеем систему
Отв. 1) х=4, у = УЪ.
2) * = 4, з/ = — 1^3.
3) ^ = 3, jy = 2.
4) * = 3, з/ = —2.
228, Положим Xs = гг и —y = z%* Получим систему
1 *i*2 в —50«
Ome, 1) jc = 5, ^ = 2;
2) аг = — 5, у = 2;
3) аг = ;1/"2; ^ = — 25;
4) x = — iV% у = — 2Ь.
180 ОТВЕТЫ и РЕШЕНИЯ 229
229. Полагаем —ху=*гг; л:2—у = га. Получим систему
^2 = — 180;
Находим #j = 9; г3 = — 20 или гг = — 20; г2 = 9. Теперь
имеем две системы:
1) Г xy = —9f 2) ( ху=20>
\ х*—у = _20 И ( at9 — jf»=9.
Решим первую систему. Из первого её* уравнения находим
3* = . Подставляем во второе. Находим биквадратное
уразнение x*-\-2Qx2 — 81=0. Его корни
хм = dt |/"— 10 4-КТ8Г«±/3^5«± 1,86,
х8,4 = ±К— 10— /tff«± V^— 23,45 да :±4,Ю
Теперь находим
Уи = *9 ^_«^«й= 4,84,
1/ — 10+ 1^181 1,8е
Тем же способом решаем вторую систему.
Отв. 1) ж«1,86, з/да—4,84;
2) ж»—1,86, jy«4,84;
3) *«4,84i, j/«1,86i;
4) лг« —4,84/, у«—1,86/;
5) лг = 5, у = 4;
6) х = — 5, 3/ = — 4;
7) лг = 4/, з* = —5/;
8) л: = — 4i, > = 5/.
230. Исключим свободные члены, для чего помножим вто-
рое уравнение на 7 и вычтем из первого. Получим
— 32х3—2ху+75у2 «= 0.
Это —однородное уравнение второй степени (т, е.
уразнение, содержащее только члены второй степени;
"{
232 ГЛ. 3. АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ 181
членов первой степени и свободного члена в нём нет). Рав-
делив обе части уравнения на х2 (это можно сделать, так
как лг = 0 не есть корень), мы преобразуем его к виду
— 32 — 2 ^ —f- 75 Г—J =0, и, решив квадратное уравнение,
v 2 v 16 гч
найдём ^ = — или — = — ^. Этим способом из всякого
X о X £о
однородного уравнения второй степени можно найти отно-
шение —.
X
Теперь решаем две системы:
5ха—10^- -5 = 0, 2) | 5л:2—10^2 —5 = 0,
х~ 3 I х~ 25
(по способу подстановки).
Отв. 1) дг = 3, v = 2; 3) лг = -^=, у = £L=;
2) х = — 3, у = — 2; 4) х» ~9у = -^=.
} у Yw 1^пз
231. 1-е уравнение вапишем так: х2—2ху-\-у2 = -<?ху.
Тогда имеем (л:—у)2 = -^хУ* 2-е уравнение запишем в виде
2(х—у) — ^ху. Значит, (л:—у)2 — 2{х—у) = 0.
Отсюда находим х—у = 0 и х—у = 2. Получаем две
системы:
х—у = 09 и 2) (х—у = 2,
ху = 0 И \ ху=8.
Отв. 1)д:=^=:0;2)аг = 4, у = 2\ 3) х = — 2, jv = —4.
°{
232. Первое уравнение перепишем так:
(х*-\-2ху+у*)= 1Ъ + ху или {x+yf — 13 = ху.
Из второго уравнения х -f- ,у = 4; подставив, получим
15 — 13 = лу/. Решаем теперь систему
| лгу = 3,
1 *+У = *.
Отв. 1)лг = 3,^=1; 2) jc = 1а-у = 3.
182 ОТВЕТЫ И РЕШЕНИЯ 233
233. Решается, как предыдущая задача. Получим новую
систему
\х—у=1л
Oms. 1) л: = 3, 2) *=* — 2,
.у = 2; j; = — 3.
234. Полагаем ■£- = *; тогда ^в-, и первое уравне-
1 25
ние примет вид ^Ч'Т^3^ или *^#2—25^+12 = 0.
4 3 ~
Его кории ^1=з* и 02===f Теперь имеем две системы:
1) ( £ = 1 2) ( £с=з3
| У 3» ( у~4»
\х*—у* = 7; U*—>» —7.
Системы решаются подстановкой значения д; из первого урав-
нения во второе.
Отв. 1) л: = 4, > = 3;
2) * = -4, ,у=* — 3;
3) л: = 3/, ^ — 4/;
4) лг = — 3/, j/ = — 4/.
235. Систему можно записать в виде
{jfmyn —s cambn,
jc«y» = dambn.
Перемножаем эти уравнения и делим одно на другое.
Получаем {xy)m+H — cdcfimb*n и ^Гп»1; отсюда
ху.
1 g"> а» х /Л—
Перемножая эти уравнения, находим
гт an am 2n
jp2 -з ^m«-nfjn1»-wi0trt+rt^m+n» *
239
ГЛ. 3. АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ
183
Выражение для у% можно найти аналогично, взяв уравнение
У- у" s=3 — • Оно отличается от соответствующего уравне-
ния для х только перестановкой букв с и й%
т п т и
Отв. х = cm*-n*d^-7n*am+nbm+n *
у ._ £Па-та^т3-п9дт+п£т+м*
236. Во втором уравнении разлагаем хг-\-)р на множи-
тели (х~\-у)(х2— ху-\~У2) и Делим второе уравнение па
первое. Получим Jt-f-J>=5. В первом уравнении Прибавляем
к правой и левой частям уравнения по Ъху\ получим (jt-f-j/)2 =
*=7 -\-Ъху. Подставив 5 вместо (х-\-у) согласно получен-
ному уравнению, найдём jcy = 6. Теперь решаем систему
(х+у = 5,
\ ху = 6.
Отв. 1) л: = 3, у = 2\
2) х = 2, ^ = 3.
237. Помножим второе уравнение на 3 и сложим с первым.
Получим (at—f-^y)3 = 1* Если ограничиться действительными
решениями, то отсюда х-\-у=1. Заменяя во зтором урав-
нении х-\-у через 1, имеем ху=- — 2. Решаем систему
(х-\-у=\9
\ ху = —2.
Отв. 1) x=2f у = — 1;
2) х = — 1, у=2.
238. Решается, как предыдущая задача.
Отв. 1) х = 3, у = 2;
2) х = 29 у = 3.
239. Полагаем Х_^У- = %. Первое уравнение принимает
вид г -j- — == 5у. Отсюда z = 5 и z = ^-, т. е.
184 ОТВЕТЫ И РЕШЕНИЯ 240
х -f- v 2
Из уравнения J_-^ = 5 находим _у = -^ лг. Решаем это
уравнение совместно с заданным уравнением ху = 6. Таким
же образом используем уравнение J_ =-г«
О/ив. 1) jc = 3, ^ = 2;
2) л: = — 3, ^ = — 2;
3) лг=3/. у = — 2/;
4) аг= — 3ft ,у = 2*.
240. Исключаем из системы неизвестное г: второе урав-
нение вычитаем из первого, умноженного на с, третье урав-
нение вычитаем из второго, умноженного на с. Получим си-
стему
| (с — а)х-\-(с — b)y = (c — d)t
\а(с — а) х -\- b (с — b)y = d(c — d).
Отсюда находим хну. Аналогично находим г.
или. •* —(с_д)(£_д) . -V—(а__^)(с__^) .
<b-rf)(fl-rf)
(* —с)(а-<?)
241. Исключим сначала а; для этого: 1) второе уравнение
умножим на 2 и прибавим к первому; 2) третье уравнение
умножим на (— 2) и прибавим ко второму; 3) третье урав-
нение умножим на (—3) и прибавим к четвёртому. Получим
систему
5л:—4у —J— 13г = 36,
-4*—И.у+ 9г=1,
^ — 5л:— 13у+12г = 5.
Из этой системы исключим л:, предварительно вычитая из
второго уравнения третье. Получим
а) 5л: — 4у+13г = 36;
б) х + 2у — Зг = — 4;
В) _5л;—13.у+12г = 5.
244" гл. 3. АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ 185
Складываем уравнения а) и в), а уравнение б) умножаем на
5 и складываем с в). Получим
— 17з/ + 25г=41, i— 17у+25г = 4\,
\— 17j/ + 252=41, (
\ _3.у-3*=_15 ИЛИ \
j, + * = 5.
Отсюда находим г = 3 и у = 2. Из уравнения б) находим л:
и из третьего заданного уравнения находим и.
Отв. jc = 1; у = 2; 2 — 3; я = 4.
242. Вычитаем из второго уравнения первое. Получим
^-|-2г = 1. Отсюда у= 1 —2г. Подставляем это значение у
в первое уравнение, находим х = г-\-Ъ. Подставляем най-
денные значения х и у в третье уравнение, получим Зг3 -f-
2
-|- г — 2 = 0, Корни его гх = -^ и г2 = — 1. Подставляя
значения г в уравнения х = г + 3 и ,)/= 1—2г, найдём по
два значения для х и у.
п 11 12
Отв. 1)* = у, у = — "з", г=="з;
2) * = 2, j/ = 3, г = —1,
243. Первое уравнение возводим в квадрат, второе — в
куб и третье — в квадрат после переноса второго члена
в правую часть уравнения. Получим систему
\4x-\-y — Зг= — 3,
5* + 2j> + *= !Д
[6л:— у— 2 = 0.
9 6 33
Отв. х = ш, 3> = -29' * = 7М\
244. Возводим первое уравнение в квадрат и вычитаем
второе. Получаем ху-\-хг-\-уг = 54. В силу третьего урав-
нения можно заменить первые два слагаемых через 2yz%
Получаем 3^ = 54, т. е.
Яг =18. (а)
Теперь третье уравнение можно записать в виде ху -f-
-|-л;г = 2« 18, т. е.
*(у + *) —36. (б)
186 ОТВЕТЫ и решения 245
А так как первое уравнение имеет вид
* + СУ + *)=13, (в)
то из уравнений (б) и (в) можно найти х и^у+г. Получаем:
I * = 9, f * = 4,
\ i 4 или { ,
Чтобы найти у и г по отдельности, присоединим уравне-
ние (а). Получим две системы:
у + г = 4, 2) (у+г = 9,
1) ly + z = 4, 2) (
.у*—18.
Замечание. Прв возведении в квадрат первого уравнения
возникает опасность появления лишних решений. Но если бы они
появились, то удовлетворяли бы уравнению x+y + z = —13, что
противоречило бы уравнению (в).
Отв. 1) * = 9, ^ = 2 + i/l4f г = 2 — //14;
2) ха-99 ^ = 2 —/J/R *—2-ИИП;
3) * = 4, ^ = 6, г = 3;
4} л: = 4, ^ = 3, г = 6.
245. Третье уравнение представим в виде
г%—хг—уг-\-ху*=2щ
Сложив его со вторым, получим
*a^2jry = 49. (а)
Отсюда га = 49 — 2ху. Подставляем это выражение з пер-
вое уравнение. Получим (х-\~у)р = 49, т. е. JP+jf =szt7.
Положим сначала х-\-у = 7.
Представим второе уравнение в виде
ху + г{х+у)*=47
49—а»
и сюда подставим выражение ху = —~—, получаемое из
(а), и значение * + v = 7. Получаем г2—14г + 45 = 0. От-
сюда л=6 и г9 = 9. Если г = 5, то ху=-—*—=12;
49 &
если же г = 9, то ху — —=— === — 16. Имеем две системы:
1,{
* + .у = 7, 2) 1х+у = 7,
ху=12 И \ *y = -16,
246 ГЛ. 3. АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ 187
каждая из которых имеет по два решения. Всего получаем
четыре решения:
1) Х = Ъ, у = 4, г = 5;
2) * = 4, у = Ъ, г = 5;
4)Х=1=Ш, у=1±рШ,г=9.
Теперь положим х-\-у =— 7 и тем же способом найдём
ешё четыре решения.
Отв.
1) л: = 3, у = 4, г = 5;
2) л: = 4, ^==3, г = 5;
5) * =— 3, у= — 4, «=s — 5;
6) х = — 4, ,у = —3, * = — 5;
8),-z±^t>.=i^irai,..e.
246. Вычитаем сначала второе, а затем третье уравнение
из первого. Получаем:
(cP — b*)-±(a*—~b*)x + (a — b)y = Q> (а)
(& — <*) + (а* —<*)* + (<* —с)у = 0. (б)
Сокращаем уравнение (а) на (а — Ь) и уравнение (б) на
(а—с). Имеем:
(a* + ab + b*) + (a + b)x+y = Ot (в)
(а2 + ас + с2) + (а + с) х+у=*0. (г)
188 ОТВЕТЫ и решения
Вычитаем (г) из (в). Получаем
(ab — ac + № — с^ + ф — с)х = 0
Отсюда
х =
247
«»-« + *-* д_(д + д + 0.
Ъ — с
Неизвестное у находим из (в) или из (г). Теперь по любому
из данных уравнений найдём г.
Отв. * = — (а + & + с),;
y = ab-\-bc-\-caf
2 =—abc.
247. Положим . = и; г = v. Получаем
У л*— 1
систему
= 5,
8M+10x; = 6.
Её корни
1 2 11. 1 2
,_7; „ = т,т.е.7=т=7 -^_т.
/' + 4
Отсюда находим jc = 17; у = 6.
О/яв. jc= 17, ^ = 6.
248. В силу второго уравнения первое можно записать
так: 10 — 2 Уху = 4. Отсюда лгу = 9. Получаем систему
Отв. 1) л: = 9, ^= 1; 2) * = 1, ^==9.
249. Полагаем у =0, Первое уравнение примет
' •* *т" У
1 У—Зх~~
вид z — 2 + 7==0' Отсюда г=*1, т. е. |/ —цт"™1' Из
последующего уравнения находим у = 2х и подставляем во
второе уравнение.
Owe. 1) * = 6, ,у=12; 2) *= — 4,5,^ = — 9.
251 гл. 3. алгебраические Уравнения 189
250. Первое уравнение приводится к виду У х2-\-у2 =
к
еа2 у 17, откуда
*»+j"=»136. (а)
Второе уравнение возводим в квадрат; получим Yх<*—У*=»
= 18 — х9 откуда
У = 36* —324. ' (б)
Это выражение подставляем в (а). Получаем *2 + 36* —
— 460 = 0. Отсюда находим х = 10 и дг== — 46. Подстав-
ляя в (б), находим у. Получаем четыре пары решений:
1) *=10, у = 6; 3) * = —46, ^==6|/"55/;
2) х= 10, у^ — 6; 4) л:== — 46, ,у = —6/55*.
Третья и четвёртая пары решений не годятся, так ка^ выра-
жения Ух-\-у и Yx—.У» гДе радикалы должны означать
арифметические значения корня (в противном случае они не-
определённы ввиду двузначности корня), не имеют смысла
при комплексных значениях х-\-у и х—у. Первую и вто-
рую пару решений следует проверить.
Отв. 1) х= 10, j/ = 6; 2Хлг=10, ^= —6.
251. Система имеет смысл только при а>0 (см. преды-
дущее объяснение). Первое уравнение возводим в квадрат:
Ух*—уЧ = Ъа — х. (а)
Это выражение подставляем во второе уравнение; получаем
У&Л-У1 = (У 41 + 5) а — хт (б)
Возводим в квадрат уравнения (а) и (б):
у* = — 64а2+1 бал:, . (а')
у* = (|/*41 -f 5)3flS — 2 (К*Г + 5) ах. (б')
Исключая у из (а') и (б*), получаем
(130 + 10 / 41) аа «(26 4-2/41) оа;,
откуда #== 5а. Из (а') находим j/=:±:4a и затем произво-
дим проверку.
Qma. 1) х = 5a, .у = 4a; 2) * = 5a, у = — 4a.
190
ОТВЕТЫ И РЕШЕНИЯ
Ш
252* Возводим первое уравнение з квадрат; 2л;2 —
— 2]/х*—у* = у2. Подставляем сюда значение лс4—у*!=я
с=144а4 из второго уравнения. Получаем
У> = 2л;а—24аа. (а)
Отсюда находим у* и подставляем во второе заданное урав-
нение. Получаем
л;4_32аЗл:«+240а4 = 0.
Отсюда х = ±1^20 а и х = ±У\2а* Из уравнения (а) на-
ходим у. Для каждого из значений х = ± j/20 а имеем
^ = =t:4fl, а для каждого из значений ^ = ±1^12 а имеем
у = 0. Проверка показывает, что из полученных шести пар
решений одни являются лишними при а > 0, другие же
являются лишними при а < 0. Возьмём, например, пару решений
х = У 20 а, у = 4а. Подставляя в первое уравнение, мы нахо-
дим УЪба?— У 4а* = 4а, т. е. 6 [а| — 2\а\ = 4а. Это ра-
венство является тождеством при а>-0, но оно не верно
при а < 0.
Отв. При а^-0 решения будут:
1) д: = /2ба, ^ = 4а; 2) х = — У20а, у = 4а;
3) * = 1/*12а, ^==0; 4) х= — УТйа, у = 0.
При а < 0 решения будут:
5) * = /2ба, J== — 4а; 6) * = —/20а, j== — 4а.
253. Перзый способ. Из второго уравнения находим
х-{-у=14— У ху. Возводим в квадрат; получаем
*2_^уа_|. 2Ху = 196 + ху — 28 Уху»
откуда
& + & + ху= 196 — 28 l^jcy.
В силу первого уравнения имеем 84 =196 — 28 Уху. Отсюда
находим |/^лгу= 4, т. е. ху = 16. Подставляя во второе
уравнение значение Уху = 4, находим х~^-у = 10. Решаем
систему
* + ;V=10,
ху= 16.
253 ГЛ. 3 АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ 191
Второй способ. Левую часть первого уравнения раз-
лагаем на множители:
x* + xy+y* = (x + yf — (VwY =
= (x + y + Vw)(x+y— /*у) = 84.
Отсюда в силу второго уравнения получаем
U(x + y—Yw) = 84t
т. е. х-\-у—Wy==6. Из системы
f х+у — У*У = Ъ
\ x+y+Yxy= 14
можно найти х-\~у иУ^.
Отв. I) х = 2, ^ = 8;
2) x = S9 у = 2.
253а* Из первого уравнения находим у = ^г » из
2 + х
второго у = -—-7-J-—; приравняв эти два выражения, полу-
1 ~\~ X
х — m 2 + х
чаем i—i = —тп—* отсюда имеем уравнение
1 -|- ТПХ I "Т" х
(l+m)x* + (2 + m)x + (2 — да) = 0.
Это уравнение имеет действительные корни при условии
(2 + /я)а— 4(1+да)(2 — та)>0.
После упрощения левой части получим 5/я3— 4]>0, откуда
2
|otO"7=- ^ри этом условии х имеет действительные зна-
V 5
чения, значит, действительные значения имеет и у = « ' .
192
ОТВЕТЫ И РЕШЕНИЯ
ГЛАВА 4
ЛОГАРИФМИЧЕСКИЕ И ПОКАЗАТЕЛЬНЫЕ
УРАВНЕНИЯ
Предварительные замечания
На вступительных экзаменах нередко предлагается решить
уравнение, содержащее логарифмы по различным основаниям
(см., например, задачи 267, 268, 309—313), Для их реше-
ния может оказаться удобным привести все логарифмы
к одному основанию. Но соответствующие формулы не даются
в средней школе. Поэтому мы приведём их с необходимыми
пояснениями.
1. Формула
,0^в = Т5^Т (а).
позволяет поменять ролями основание логарифма и число.
Пример.
Пояснение. По определению логарифма log28 есть
показатель степени, в которую надо возвести 2, чтобы по-
лучить 8. Таким образом, запись loga8 = 3 есть лишь иная
форма записи 23 = 8. Но последнее равенство можно запи-
— 1.
сать ещё так: 1/8 = 2, т. е. 83=2. Стало быть,
Io£8£i^i--
Вообще равенство ах = Ь можно ваписать еще* так:
#*==а. Первое равенство означает, что log^^jc, а вто-
рое,— 4TOlogfta = —, откуда и следует формула (а).
2. Формула (а) есть частный случай более хзбщей формулы
выражающей следующий важный факт: зная логарифмы раз-
личных чисел по основанию Ь, можно найти логарифмы тех же
чисел по основанию а; для этого достаточно выполнить де-
ление на logba (т. е. на логарифм нового основания по ста-
•254 ГЛ. 4. ЛОГАРИФМИЧЕСКИЕ И ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ 193
рому). Вместо деления на logba можно [в силу (а)] выпол-
нить умножение на logfl£:
logflN=logfl£.logbW. (в)
Множитель logfl£ называется модулем перехода (от си-
стемы логарифмов с основанием Ъ к системе с основанием а).
Пример. Имея таблицу десятичных логарифмов, можно
составить таблицу логарифмов по основанию 2. Для этого
достаточно выполнить деление на lg 2 = 0,3010 или умноже-
ние Halog210 = 6-giT^ = 3,322. Так,
lg3 0,4771 1 со-
102*3^ = ОТ =1,585.
Пояснение. По определению логарифма имеем 21о^я3 = 3.
Прологарифмируем это равенство по основанию 10. Получаем
logs 3 • lg 2 = lg 3, откуда log2 3 = ^ • Таким же образом
из тождества al08aN=Nt логарифмируя по основанию Ь, по-
лучим формулу (б).
Чтобы не спутаться в обозначениях, полезно для проверки
применить следующий приём: вместо выражения log0# напи-
шем дробь -^- (разумеется, эти выражения не равны между
собой); аналогично поступим с выражениями logba, \ogaN и
т. д. Тогда вместо формул (а), (б), (в) получим другие, но
тоже верные, формулы. Так, вместо (в) получим
а а " Ь*\
254. Первый способ.
х =10. 102^,g9~Iff2'=10. \®е*-*Ъ*=\Ъ* ю,? *.
ig — д
Согласно определению, логарифма 10 4= —,х поэтому
*=10. 4=22,5.
4
Отв. х =22,5.
13 Зав. 949 Сборник задач
194 ОТВЕТЫ И РЕШЕНИЯ 255
Второй способ. Логарифмируя, будем иметь
Ig* = lgl04-(llg9 — Ig2)lgl00(
или
10. Q
Jgx = 1gl0 + lg9 — 2lg2 = lgiy.
Отв. х = 22,5.
255. Как в вадаче 254, будем иметь
lgAr = (I-i-)g4)igl0p:
lg*=l__]g4 = ]g —; я-^-.
256. Поступая, как в предыдущих задачах, будем иметь
]g^==l(2 4-^lgl6)iglO==l+llgl6==Jg(l0^l6);
* =10^16.
Отв. * = 20.
257. Обозначим у = 491-*l0ff'2f а ^ = 5-'°^; тогда
х = у + г.
Как прежде, находим, 4TOlog7-y = (l— log7 2)k>g749, или
log,y = (log7 7 — log7 2) 2 = 2 log7|« log, £,
49 I
откуда j>= j; аналогично найдём, что £ = —. Следова-
25
тельно, * = -£.
25
Отв. х = -^ш
258.Имеем log^ogB]og^x = \og4lt откуда log3log2х = 1;
l0g9AT = 3.
Owe. jc = 8.
262 ГЛ. 4. ЛОГАРИФМИЧЕСКИЕ И ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ 195
259# Аналогично решению предыдущей задачи имеем
1+ log6[l+iog^l-Hog,*)] - 1;
logb[l+logo(i + logpA;)l==0;
далее
1 + logc (1 + Iogp x) = 1; !og0 (1 + Jogp x) = 0;
1+^*=1, log^A^O; лг=1.
Отв. jc = 1.
260. Выражение в фигурных скобках должно быть поло-
жительным числом, так как отрицательное число не имеет
(действительного) логарифма при основании 4. Поэтому, пе-
реписав данное уравнение в виде
2Iog3[l +Jog2(l +3 log,*)] = 4^ = J/4,
мы должны взять только положительное значение |^4, т. е. 2.
Применяя аналогичные преобразования повторно, получим
далее
Jog3[l + iog2(l+3log2*)] = l, l+Iog2(l+3log2A;) = 3f
k>g2(l+3log2*) = 2;
следовательно, 1 + 3 log2 х = 4, log2* = 1.
Отв. x = 2.
26Ь Данное уравнение представим в виде
log2(A:+14)(A:4-2) = 6) или (дг+ 14)(д;-г-2) = 29 = 64,
откуда имеем х2-\-\6х— 36 = 0, ^==2, л;2 =—18. Вто-
рой корень не годится, так как в левую часть входят выраже-
ния log2(Jc-j- 14) и log2(jt-j-2), которые при отрицательном х
не имеют действительного значения.
Отв. х = 2.
262. Представим данное уравнение в виде
1oga[.y(.y + 5)-0,02]=0;
отсюда
у(у-\-5). 0,02=1 или у*-\-5у — 50 = 0;
получим два корня у{ = 5, у%~ — 10. Второй корень не го-
дится (см. предыдущее решение).
Отв. ^ = 5.
196 ОТВЕТЫ И РЕШЕНИЯ 263
263. Имеем
1g(35 — jts) = 31g(5 — х) или 1g(35 — A*) = lg(5 — xf\
следовательно,
35—л;» = (5 —#)3 или х3—5jc + 6 = 0.
Ота. хл в 2, х9 = 3.
264. Преобразуя выражение в квадратных скобках, получим
, (За—Ь){еР + аЬ)-1 b(a — b)*
Тогда заданное уравнение примет вид
Применяя в правой части теорему о логарифме произведения
(и дроби), получим
1 + lg* —!*(*—»)—lg*.
Заменяя единицу через \g 10, перепишем уравнение в виде
lgl0 + lg* —lg(e — *) — Ig*t или Ig(10^ = Jg^-;
отсюда IОх = *■"? •
0/м-*-ТЯГ-
гвб. Данное уравнение можно представить в виде
потенцируя, находим
или
откуда
у 1—я
27** ГЛ. 4. ЛОГАРИФМИЧЕСКИЕ И ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ 197
266. Данное уравнение можно иначе записать так:
1 Jog,, 5 + \ogx 5 + logx х — 2,25 = (-1 log, б)3;
так как \ogxx^=:\% то после упрощений получим
iog|5 — 6iog^5 + 5 = 0.
Решая квадратное уравнение (с неизвестным log^S), находим
два корня: loga)5 = 5 и log^S^ 1.
5
Отв. л:, = 1/ 5; / *8 = 5.
267. Первый способ. Положив ioglGх = гу имеем
х = 1 бг, отсюда
log4Jt = #l0g4 16 = 22 и log2Jt = 2log2 16 = 4я.
Данное уравнение примет вид 2-]~2z-\-42 = 7t т. е. г=1.
Второй способ. Приведём все логарифмы к основа-
нию 2. По формуле (б) (стр. 192) находим: fog4Jt = p§^ =
= о2*, аналогично logl6л = ■ */ ■. Получаем уравнение
7 ioSa х + -J1о&> * -f log3 * = 7, откуда iog2 х = 4.
Owie. jc == 16.
268. Решается, как предыдущая.
Отв. х = а.
269. Перепишем данное уравнение в виде
/&\За>-7 /3\3-1»
откуда Ъх — 7 = 3 — 7х.
Отв. х = 1.
270. Представим заданное уравнение в виде
7 « 3*+1 — За+4 = 5а+2 — 5Ж+^
Вынося за скобку Зда и 5°°9 будем иметь
3^(7.3 — 34) = 5*45* — 53), или (|y=L|f
откуда х = — 1.
О/ив. л; = — 1.
198 ОТВЕТЫ И РЕШЕНИЯ Щ
271. Перепишем заданное уравнение в виде
X
2-в. 2**-в = |ri» или 2**-9 = 2й ш ■
Отсюда имеем
О/яя. * = 6.
4*— 9 = -g- дг.
272. Заданное уравнение можно записать такт
2-tf . 2*»+ъ = 2-6, или г-^+^+^вя 2-в.
Следовательно, — Xй -f- 2л: + 2 = — 6.
Owe. л:, = 4; ягв = — 2.
273.
отсюда !
Отв{
Представим заданное
имеем
, х =
2 *"' =
Ъ{х + Ь) _
х — 7
10.
уравнение в виде
2-».
-2-
Кх+11)
.2 х~* ;
1 7(лг+17)
1—J=3~-
274. Так как j|g = g^U в з" • то заданное уравнение
можно переписать так:
/2\2а; /24(1-0)8 £
Следовательно,
2* + з;(1—jc)—1.
275. Представим заданное уравнение в виде
2\ *Ка> /Kaj-i ^2^;
приравнивая показатели, находим
-*^4±i_ = 2, или 2л; —5/* —3 = 0.
287 ГЛ. 4. ЛОГАРИФМИЧЕСКИЕ И ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ 199
Введём обозначение \^х = z; тогда будем иметь
2^2 — Ьг — 3 = 0, откуда ^ = 3, г2 =— у.
Но второй корень не годится, так как величина г (она пред-
ставляет арифметическое значение корня У^х) должна быть
положительной-. Итак, имеем г = |/д\ Отсюда х ==9,
Отв. х = 9.
276. Заданное уравнение можно представить в виде
, Т^ж+З 4
1+ ■==• —
2 ьУя _.2 ^#-1
Следовательно,
1 i V^+3_ 4
2|Л* Уд: —Г
откуда имеем 3* — 8V^#— 3 = 0. Обозначив Yx=z% будем
иметь Зя2— 8^ — 3 = 0; ^ = 3; ^2 = — -^; второй корень
zq = - не годится (см, решение задачи 275). Следовательно,
о
# = 9.
Отв. х = 9.
277, Данное уравнение можно записать так:
3 г+й 1 *
Следовательно,
3 • ] !=о.
л;2_1 I 2л: —2 4
После упрощений получаем *2 — 2х — 15 = 0.
Отв. хг = 5; *в =— 3,
278*. Пользуясь формулой (а) (стр, 192), получим
3 , 1
= 2.
= 2,
или
3 , I
1+21оелд ~ 2 — log^a
200 ОТВЕТЫ И РЬШЬНИЯ этэ
Решаем относительно log^a и получаем
7+)/"49 — 48 7±1
О/я*. ** =а; л;д = а9.
279, По формуле (б) (стр. 192) найдём
1и&я* |0g4^ 21og4*
Тогда данное уравнение примет вид log4(x-f-12) =з 2 log4 дг,
откуда 4К+12 = *3. Берём только положительный корень
jc=4; при отрицательном х выражение log£D2 не имеет дей-
ствительного значения.
Отв. X = 4.
280*. Данное уравнение запишем так:
(loga6 + 2)lQBjjc-l.
Так как ^^5 = 7 , то получаем уравнение
(i3ib+2)10^eU
Решив его относительно bgbxt найдём
0Чьх\ в 7 и CtoBi*)»^8 -1'
Ome. jc, — 1^5; х% =» -g-.'
281. Левая часть уравнения есть сумма jp+1 членов
геометрической прогрессии, а потому (в случае а Ф 1) имеем
Ц^-(1+«)(1+^(1+**)(1+^
или
1_^+1 = (1_а)(1+л)(14-а9)(1+а4)(1+л8)#
или
1 —a^ — l —в*
откуда дя,+1 = а1в; # + 1 — 16; лг=15. При а=»1 общая
формула суммы членов геометрической прогрессии неприме-
285 ГЛ. 4. ЛОГАРИФМИЧЕСКИЕ И ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ 201
нима. В этом случае .левая часть данного уравнения есть
сумма *+1 слагаемых, каждое из которых равно 1, так что
уравнение принимает вид jc —J— 1 == 16» и мы снова имеем
х = 15.
Отв. д: = 15.
282. Данное уравнение перепишем в виде
52+4+6 + ..,+205—. 556
откуда
2 + 4 + 6 + ...+2л;=:56, или 1 +2 + 3+ ,.. +д: = 28.
Левая часть уравнения есть сумма членов арифметической
прогрессии. Поэтому получаем уравнение
откуда ^ = 7, л;2=: — 8. Второй корень не годится, так как
по смыслу задачи число х должно быть целым положи-
тельным.
Отв. х = 7.
283. Заданное уравнение перепишем в виде
2^2"'— 17.2ш2"4+1=0.
Обозначая 2я, = г, получим
г2— 17*+16 = 0; ^=16; z% = 1,
откуда Jft=4; jt2=:0.
Отв. хх~ 4; д:2 = 0.
284. Аналогично предыдущей задаче, полагая 4Ш = г,
будем иметь 2г2—172 + 8 = 0.
п 3 . _ 1
итв. х^ = -к- J х% — — "2*.
285. Полагая 9^=2, получим уравнение
Зг8—10-г + 3=?'О.
Отв. *1 = 2; *2 =— 2.
202 ОТВЕТЫ И РЕШЕНИЯ 288
286. Логарифмируя данное уравнение (по основанию 10),
получаем
lg*4+71g*==1g.y+l, или ]g*x + 3\gx — 4 = 0,
откуда \gxt=\; \gx^ =— 4.
Отв. хг = 10, л;2 = 0,0001.
287. Преобразуем данное уравнение так, чтобы каждая
его часть представляла логарифм некоторого выражения. Для
этого вместо 1 в левой части уравнения напишем lg 10.
Теперь данное уравнение можно записать в виде
4-l2^-l f VV^-2 + 2
lg lo = !£ w^-'
Из равенства логарифмов следует равенство чисел, т. е.
IU ~ 4 #
После упрощений получаем уравнение
Ух
2>^ —5.2 * —24 = 0.
Так как 2Ух = \2 2 /, то, введя обозначение 2 й = г,
мы будем иметь г2 — Ъг — 24 = 0.
Корни этого уравнения гу = 8 и га = — 3. Взяв гх = 8,
— у--
получаем уравнение 2 а = 8, из которого находим 2^~ = 3,
т. е. * = 36. Второй корень г =—3 приведёт к уравнению
УЪ
22 = — 3, которое не имеет решений (никакая степень
положительного числа 2 не может быть отрицательным числом).
Отв. х = 36.
288. Последовательно находим (см. решение предыдущей
задачи):
2 lg £ + lg фу* +1) = lg (5i-^ + 5),
»g [(y)V° + 1)] = \g (5^ + 5);
23* ГЛ. 4. ЛОГАРИФМИЧЕСКИЕ И ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ 203
После упрощения получим
52^_ 124 . 5^ — 125 =0,
откуда 5*^ _- 125, или Ъ^ = — 1, Второе уравнение не
имеет решений; первое даёт J/х = 3; х = 9.
Отв. х = 9.
289. Представим данное уравнение в виде
5'е а -J- 5lg а!-1 = 3F*£D+1 + 3'* ^-Ч
Вынося за скобку 5*** и З1*35, будем иметь
5,в®(1+5-1) = 3|вв(3 + 3-1),
или
5^_25. /5_\lga,__ f5\2
3iff^— 9 * \3) —\з) '
откуда lg je = 2.
О/яя. * = 100.
290. Логарифмируя при основании 10, получим
Это биквадратное уравнение (относительно \g х) имеет два
действительных корня: lg х = 1 и lg jc = — 1; следова- *
тельно, ^=10, jcq == 0,1.
Отаь *г = 10; *а=:0,1.
291. Потенцируя, получим
64J/r2=i=5eBii или 2м* = (!)*,
т. е. 2*a-*°* = 2-e,S4; отсюда *2_40x+144 = 0.
Отд. л?! = 36, jc3 = 4.
292. Согласно определению логарифма данное уравнение
равносильно уравнению 9 — 2х = 23~а\ или 9 — 2х =s —,
откуда 2^ — 9 • 2я'+ 8 = 0. Решая это уравнение (квадрат-
ное относительно 2*), находим
Jbi —— Of Ла — U«
Отв. jq — 3; *а = 0.
204 ОТВЕТЫ И РЕШЕНИЯ 293
293. Как в задаче 288, получим
2(4*-a-f 9)= 10(2*-* 4-1).
Заметив, что
Г-г ^ 2х 2-2 ^ | в 2^ а 4*-2 ^ 4^4.2 ^ ^ ^
получим уравнение
г2*—20.2^ + 64 = 0,
откуда, как в предыдущей задаче, найдём xta4; лг, = 2.
Owe. jc, = 4; Xq =з 2.
294. Последний член удобно перенести в правую часть.
Затем, как в задаче 288, получим 4 • 31+s = 3^ + 27. За-
метив, что 3 ** =» 3 • З2^, получим уравнение
JL i.
12. 3^ = 3* + 27.
•i- - f -Y
Полагая З^вг, будем иметь 3я —уЗ^у, так что полу-
чим уравнение г2—12г + 27 = 0; корни его г, —9; г^ — З.
Х)да*. *t = f • #9 = -у •
295. Потенцируя (ср. решение задачи 288), будем иметь
100 ^V^+o.i»
это уравнение можно представить в виде
100 \ 2к^п>/ 2vs+ie
Освобождаясь ох знаменателя, получаем
6^S+T—16 = 200, т. е. б^^+^б3,
откуда х = 2.
Ome. * я 2.
299 ГЛ. 4. ЛОГАРИФМИЧЕСКИЕ И ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ 205
296. Представим данное уравнение в виде
41g2 + 2Ig(* — 3) = Ig(7*+l) + Igr(* — 6) + lg3;
потенцируя, находим:
24 (х — 3)2 = 3 (7х + I) (х — 6).
Корни этого квадратного уравнения суть #г = 9; л;2 = —3,6.
Второй корень не годится, так какой даёт х — 3=^— 6,6,
значит, выражение \g(x— 3) не имеет действительного зна-
чения [то же можно сказать и о выражениях lg(7jc*4-l) и
\g(x — 6)].
Отв. х = 9.
297. Правую часть представим в виде
-log6(0,2 — 0,2.5ж-3)=-1о&60,2 — log6(l — Ъх"\
Слагаемое (х — 3) представим в виде loggS*7"3. После пере-
носа членов получим уравнение
logb12O + l0g55*-8 + tog5O,2 =
= 21ogB(l—5"-^ —log5(i-5a-B)f
или
120 • 0,2 . 5Х"3= 1 —5^"3.
Отв. х =а 1.
298. Заданные уравнения можно представить в виде
/ 26л?+3 = 24г'+4
\ ' ±У+2
Приравнивая показатели степени, получаем систему
( 6л; —4у=1,
\ х — 3^ = 0.
3 1
Отв. х = ъ'> У = ц-
299. Потенцируя первое уравнение, получим систему урав-
нений
' , 10
Отв. дгг = 3, J/t= з*; ^9= з*. ^2 = 3.
206
ОТВЕТЫ И РЕШЕНИЯ
300
800, В алгебре обычно рассматриваются только логарифмы
положительных чисел при положительных основаниях; иначе
число может не иметь (действительного) логарифма. Поэтому
будем считать, что известные величины а и Ь (основания лога-
рифмов) положительны; неизвестные величины х, у («числа»)
также должны быть положительными.
Потенцируя, находим
ху = а\ £ = ft*.
Эта система имеет два решения:
1) x = ab\ У = $,
2) *--**», J —р.
Но второе решение не годится, так как при положительных
значениях a, b оно даёт отрицательные значения х и у.
Отв. х = ад*; У = щ*
301. Потенцируя, получим систему
10 * х—у
7
из второго уравнения у = -§ х; подставляя в первое уравне-
ние, будем иметь два решения:
1)*1 —9. ЗЧ=~7; 2) ** = — 9, Уъ = — 7.
Второе решение не годится, так как тогда лг-}-.У<0 и
х — ,у<0 (см. решение задачи 300).
Отв. * = 9; у = 7.
302. Потенцируя, будем иметь
( х—у = ху,
Эта система имеет два решения:
*i — 2 * У\ 2 *
ла— 2 » Уъ — 2 •
304 ГЛ. 4. ЛОГАРИФМИЧЕСКИЕ И ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ 207
При первом решении имеем
л: —у=*ху = — 2 + j/T>0.
При втором получаем
х — у = ху = — 2 — У~5"<0.
Второе решение не годится, так как основание логарифмов ху
должно быть положительным (см. задачу 300).
303. Потенцируя, получим систему
i + 7-js "-*•
ИЛИ
Эта система имеет два решения;
_fli»+Vfli —4М _^--угц4-4М.
6) ла 2 » .Уд— 2 *
Считая данные величины а и £ положительными (как основа-
ния логарифмов), мы должны различать два случая:
1) л4 < 4Ь\ т. е. л < YWb и 2) л4 > 4*\
т. е. а ^-1^2 А. В первом случае система не имеет решения,
так как х и j> — мнимые числа. Во втором случае х и у не
только действительны, но и положительны, так как и сумма
д-Ц-у = аэ, и произведение ху = ЬА положительны.
Отв. х = —х—*~2 ; у= !-g .
304. Потенцируя первое уравнение, получим систему
( 4ху = 9aaf
( х-\-у = 5ащ
Оба еб решения годны.
Отв. 1) xt = Y* Л —7 а> 2> *в —"2 а* У* = 1?'
208 ОТВЕТЫ и решения ^)5
305. Так как во втором уравнении неизвестные хну
входят под внаком логарифма» то оба они положительны (если
решение существует). Что касается величины аш то она может
быть и отрицательной (ибо под знаком логарифма стоит поло-
жительное число а*). Однако в этом случае вместо равенства
\g(дЭ) = 2 \g а надо написать \g(a-) = 2\g\a\. Для краткости
обозначим \g х = X; \gy = Y; \g\ a j ™ А. Логарифмируя пер-
вое уравнение заданной системы, получим систему
Х+У = 2А, Л*+У*«=1(Ь4^
Возвышая первое уравнение в квадрат и вычитая второе»
получим ^У« —ЗЛа, так что имеем равносильную систему
Х-*-У = 2А; *У« — ЗЛ*.
Следовательно, Хк К—корни уравнения г2~ 2Аг — ЗЛ* = 0.
Значит, одно решение есть X =* ЪАЬ У =* — А, т. е. х = \ a |ttt
У=^г Другое решение: л: — JL, у*=\а\\
Проверка показывает, что оба решения годятся.
Отв. хх = \а\\ ух = ±\ *t—[^л —1*1*.
806*. Из второго уравнения имеем .у —х = ()^2)< = 4.
Слеповательно, у =» х 4- 4. Подставив в первое уравнение,
получим З^.г^^бГб, или 6*. 2* = 576.
Отв. л: = 2; у = 6.
307, Данную систему можно ваписать так:
j xy = at
Так как оба числа хну должны быть положительными, го
получаем систему
1ху=*а
\f-yi
Отв. x—V*\Th y=*fi.
311 ГЛ. 4. ЛОГАРИФМИЧЕСКИЕ И ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ 209
308. Данную систему можно записать в виде
откуда
э э
я я з а
Перемножая эти уравнения, будем иметь х2у2 = л^£*\
или ху = а£. Последнее уравнение делим на каждое из пре-
дыдущих.
гл & &
Отв. x=j9 >^=д.
309. Решение аналогично предыдущему.
Отв. x = aVlfi; у*=—£=,
ьуь
310. Пользуясь формулой (а) (стр. 192), запишем первое
уравнение так:
!ogv я "^ togT^ *" 2' откуда l0gtf я в 1'
т. е. и =* v. Подставляя во второе уравнение, будем иветь
ц* 4- я — 12 = 0. Годится только положительное решение
(см. решение вадачи 300)*
Отв. а = v = 3,
хг—
31К Обозначим у а = и\ тогда
а)
JT
У
аналогично
•og?,^Vra = log„«a — т
"V^-S-
Следовательно, второе уравнение можно записать так:
210 ОТВЕТЫ И РЕШЕНИЯ 311
Получаем систему
<х*+ху+у* = а\ (1)
равносильную данной. Возведём уравнение (2) в квадрат»
Получим
*« + 2*>+У = -^-. (2а)
Вычитая (1) из (2а), найдём
Мы приходим к системе
1
, 2а
Она имеет единственное решение
а
(2)
(3)
Замечание. При возведении какого-либо уравнения в квадрат
мы можем получить лишние решения. Так и есть в данном случае:
уравнение (2а) имеет лишние решения по сравнению с (2). Например,
значения х *=у = —-^= удовлетворяют уравнению (2а), но не удовле-
V 3
4аа
творяют уравнению (2). Иными словами, уравнение х*+2ху+у* = —тг*
2а
не равносильно уравнению х+у=* ■; оно равносильно двум
уравнениям: х+у,= -р= и *+>>=* —. Тем не менее данная
система и система уравнений х+у^ -, ху=*— равносиль-
2а
ны, потому что в последнюю систему входит уравнение х + У ■"-=,
уз
2а
и тем самым исключается возможность равенства х+у = ^=
313 ГЛ« 4. ЛОГАРИФМИЧЕСКИЕ И ПОКАЗАТЕЛЬНЫЕ УРАВНЬНИЯ 211
прид^ьО (при а = 0 уравнения х +уш*-у=. и х+у=*--■ -
совпадают).
Но если бы мы взяли не систему (2)—(3), а систему (1)—(3),
т. е. систему
[х* + ху+у*=*Ф, (1)
да
(3)
то она не была бы равносильна данной. Действительно, кроме ре-
шения дг=у = —= она имела бы еще* решение де=у = —,
Поэтому в случаях, когда мы возводим одно илн несколько
уравнении в квадрат, всегда необходимо либо исследовать вопрос
о равносильности, либо с помощью подстановки проверить, какие
решения годятся, а какие нет.
312» Принимая во внимание формулу (б) на стр. 192,
будем иметь log4 х = -$ Iog2 х; вследствие этого первое урав-
нение приводится к виду х=у2ш Решаем систему
Отв. хх = 4, ух = 2; *2 =* 1, у2 = 1.
313. С помощью формулы (б) на стр. 192, данную си-
стему можно ваписать в виде
*Og4 * + у log4* + 2" J°g* ^ ^ 2-
Потенцируя, находим
х Ууг в 4,
( г/лгу = 16.
(а)
212 ОТВЕТЫ И РЕШЬНИЯ 314
Перемножая все уравнения (а), получим
(;еуг)9 = 4.9. 16,
откуда
xyz = 24 (б)
(берём арифметическое значение корня, так как по смыслу
данных уравнений л:, yt г должны быть положительны). Воз-
водим каждое из уравнений (а) в квадрат и делим на (б).
ъ 2 27 *. 32
Отв. * = у. У = -8~> г===~з"*
314. Из первого уравнения находим х-\-у = 2°°~уЪ 2 *
з из второго х-\-у = Ъ • 2x-vt следовательно,
3~ = 3 или £^L=\.
Значит, jc-f-_y = 3 . 2S= 12.
Отв. je = 7; ^ = 5.
£±Z = 1 *■-/-«.
315. Заданная система приводится к следующей:
±2
10
Ах
Разделив второе уравнение на первое, получим х—у = -у •
Решив систему
. 70 4л-
Х + У = — и * — ^ = -у-»
будем иметь xt = 7, ^ = 3; д:2 = — 7, у% = — 3. Корни
д:2, j/9 не удовлетворяют второму уравнению заданной
системы, так как числа ^2+^9 и *2—у2 отрицательны.
Отв. * = 7; у = Ъ.
816. Представим данную систему в виде
2v =2 * 3^ =3 * .
Отсюда ползаем
2л _^а-3-У * 1 ■ 2-2-У
м* ГЛ. 4. ЛОГАРИФМИЧЕСКИЕ И ЛОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ 213
Введём обозначение —==£ тогда из первого уравнения
будем иметь 2/3—5*—3 = 0; ^ = 3,^ = — -g-, т. е. ^ = 3
х I
или — = — -я-. Отсюда находим выражения х — Ъу и
* =— -^у; подставляя их во второе уравнение, найдём
*, = —2,^ = 4; х2=-^9у^ = ^.
3 1
Отв. *,=» —2, y, = 4f xQ=jty^ = j.
817. Данная система приводится к следующей:
i
у х '
I х+у = 2.
Из первого уравнения (см. решение вадачи 316) находим
х х \ 3
— = 3 или — = — тг. Второе уравнение дает хх = -у-.
Л = -5*! ^9=—2. Ь^4- Значения *fl, jy9
не подходят.
^ 3 I
Отв. * = -j» ^ = -2*
318. Данная система приводится к следующей:
\ 2\Гху = Ъ 4- Vy.
Введя обозначения У^ = я; Yy=av, получим яг* = 4— #;
Отв. xs = 4, jrt = 1; х2 =1, у2 — 9.
319. Перепишем данную систему в виде
ау=вх*% bxe=yv.
Так как х к у должны быть положительными (как основания
логарифмов), то исходная система может иметь решения лишь
при положительных вначениях а и (, Из первого уравнения
х&
найдём jiss ; подставляя во второе уравнение, получаем
214
ОТВЕТЫ И РЕШЕНИЯ
320
хт = aqbx% Отбрасывая корень х = 0 (л: должно быть по-
ложительным), получаем уравнение хт~1 == aqb. Если рд — 1,
то это уравнение либо вовсе не имеет решений (при aqb Ф I),
либо является тождеством (при айЬ= 1). В последнем случае
исходная система имеет бесчисленное количество решений
хр
(х — произвольное число, а у=.——\ или у— произвольное
число, a x=i~\ Если рдф\% то получаем решение:
*= Vaqb, у = Vtfa.
Отв. лг== Vaqb, у= V Ьра {рдф\).
ГЛАВА 5
ПРОГРЕССИИ
Арифметическая прогрессия
320. По условию аг = 5, rf==4. Подставляя эти значения
в (3), получим после некоторых преобразований уравнение
2Лз + Зл—10 877 = 0.
Корни его: л, =73 и Лд — — 74,5; из них годится только
первый.
Отв. 73 члена.
321. По условию
al+(a1 + d) + (al + 20) + (a] + 3d) = 26,
ах (a, +d)(al + 2d)(al -f 3d) = 880.
Первое уравнение даёт 4^ + 6^ = 26, откуда ах =—^—•
Подставляя во второе уравнение и упрощая выражения
в скобках, получаем
13 — 3^ 13 — d 13 + tf 13+ 3* QQ„
~2 2 2 ~=880.
323 гл. 5. прогрессии 215
Освобождаясь от знаменателя и перемножая числители (удоб-
нее всего перемножить первый числитель на четвёртый и
второй на третий), находим:
9tf* — 1690йР+ И 481 =ш 0.
Обозначим через d\ dr\ d"\ d,m корни этого биквадратного
уравнения, находим d! = 3; d" = — 3; dm as —Я- и
,„„ УТ609 13 — ЗдГ
а '=а —^—; из уравнения с^ ==»—«— находим соот-
ветствующие значения первого члена:
«j — а, а^ —■ 11, ttj —■ о » i ~" о •
От*. Задача имеет четыре решения:
1) -г-2; 5; 8; 11; 14; ...,
2) -е-11; 8; 5; 2; —1; ...,
13—У1Ш.39—УТббЭ .39+/1609. 13+УШЮ .
3) — 2 , 6 i 6 , 2 » ••• •
, 13+У1609 .39+УТ609 .39— У~1609. 13—УТбОЭ .
4) "*" 2 » 6 ■ 6 * 2 ; "•
322. Выражаем лр и aq через «j и d\ по условию полу-
чим систему уравнений
Г ^+<*(/> — 1) = ?.
Отсюда находим £ =— 1 и ax=p-\-q—1. По формуле (1)
находим:
яя = (/> + ? — 1) — («— 1)=SJP + ?—Л-
О/юз. д„ = /? + ?— Л-
323* Натуральные двузначные числа составляют арифме-
тическую прогрессию с разностью d=l; при этом первый
член аг = 10, а последний яЛ = 99. По формуле (1) находим
число членов « = 90. Формула (2) даёт:
5я==(10 + 99).90=4905>
Отв. 4905.
216 ОТВЕТЫ И РЕШЕНИЯ 324
324. Обозначим нечётные числа через п, (п -f- 2), (п -(- 4),
(л -(- 6). Тогда заключённые между ними чётные числа будут
(п-\~1), (я-J-3)» (л-J-5)" Согласно условию
Л2 + (л + 2)2 + (пЧ-4)2Ч-(йЧ-6)2-
= (л+1)2 + (/г + 3)2 + (л + 5)2 + 48,
или
/г* + [(лЧ-2)2 — (я + 1)«1 + [(я + 4)« — (й + 3)2] +
+ [(л + 6)2 —(й + 5)2] —48 = 0,
откуда
д24-(2л + 3) + (2л + 7) + (2л+11) —48 = 0.
или
n2-f 6л — 27 = 0.
Отсюда я = 3 или п = — 9.
Отв. 1) 3; 5; 7; 9 или 2) —9; —7; —5; —3.
325. Члены я2; а4; а6; ...; я20 составляют арифмети-
ческую прогрессию с разностью 2rf и числом членов 10.
Применяя формулу (3) (где нужно взять а2 вместо аг и 2d
вместо d), найдём
(2а2 + 2</.9)Ю = 250>
т, е.
Дэ + 9^ = 25.
Подставляя сюда а2 = Oj + **> имеем
at+ 10d== 25. (а)
Таким же образом, исходя из прогрессии -s-0t; а3; а&; ...; alQ
найдём
а, + 9^ = 22. (б)
Из (а) и (б) можно найти ах и d, а затем все члены про-
грессии. Но так как требуется найти только средние члены,
т. е. alQ = a1-^~9d и ап ==«,-(- lQd, то (а) и (б) сразу дают
а^о = 22 и аи я 25.
Отв. Средние члены равны 22 и 25.
327 ГЛ. 5. ПРОГРЕОГИИ 217
326. Введём обозначения Ьх = [а -\- х)\ &й = (а2 + х*),
Ьь =з (а—#)2. Находим fta — ftt = А, — д2 = — 2ад;. Следо-
вательно, члены ft,, ft2, ft3 образуют арифметическую про-
грессию с разностью d=* — 2ах. По формуле (3) имеем
g|,H(« + i).-2U(»-l)l,||||dl + g,|)g + ^
О/ма. S„=»[e8-J-(3 — л)о*-}-л:а]я.
827, По формуле (3) имеем
_2ai+d(nl-\) . .
о( = _ _ . nlf
"2 2 flI
„ 2at + rf(w3-l)
йл = 2 8'
или
|—в1+4-(я1-1)|
д=^+4^-1),
A-«,+4.04-1).
Умножаем полученные равенства соответственно на (я2— л^),
(/ц — »t) и (лг—л2) и складываем произведения, после чего
найдём
|-(*8-Л3)+|Чп8-«,)+|Ч"1-Я2> =
— «I ((«в —* «в) + (Л8 — nj + («t — Я9)] +
+ 4 K«t — 1)(»4—«в) + (п%— 1)(«з—»t) + (Яд—1)(я,—«а)].
Выражения в квадратных скобках тождественно равны нулю,
следовательно,
что и требовалось доказать.
218
OTBLTbl И РЕШ1НИЯ
323
328. Из условия следует, что S10 = 5S6. Выразив S6 и Sl0
по формуле (3) и учитывая, что по условию al= I, наПдЯм
(2 + 9rf) 10 - (2 + 4tf)5
2 ==5 2 '
откуда rf = — 3.
Отв. н—[-1; —2; —5; —8; ...
329» По условию
Sw = 3«» или Pg* + rffa-1>lB,3iA
Так как п Ф 0, то, сократив это уравнение иа я, получим
2at + rf/2 — rf = 6/i или
2at —*f=*(6 —йГ)л. (а)
По условию равенство (а) должно удовлетворяться при любом
значении я, но левая часть (а) не содержит и, тогда как
правая часть будет менять значение с изменением я, если
только множитель б — d не равен нулю. Лишь в случае
б — </ = 0 правая часть не зависит от п (равна нулю), поэтому
мы должны иметь d = 6. Тогда из (а) находим 2av — rf—О,
d л
т. е. ах = -к- и о.
От*. -+-3; 9; 15; 21; ..."
330*. Числа, которые при делении на 4 дают в остатке 1,
имеют вид 46 + 1 (к— любое натуральное число). Они обра-
зуют арифметическую прогрессию с разностью 4. Первое
из двузначных чисел этого вида есть 13 (оно получается при
к = Ъ); последнее есть 97. По формуле (1), где ^ = 13,
ап *= 97, d « 4 находим п = 22. По формуле (3) найдём иско-
мую сумму.
Для определения, при каких значениях к числа вида
46-J-1 будут двузначными, можно было бы воспользоваться
системой неравенств
4fe + l>10,
46+1< 100.
1 3
Из этой системы иаходим 2-j<[ft < 24-j ; следовательно,
к может иметь значения, равные 3, 4, 5, ..., 24, число ко-
торых л =-(24 — 3)-И=22.
Отв. 1210.
334 гл# 5. прогрессии 219
Геометрическая прогрессия
331. Среднее геометрическое двух (положитель-
ных; чисел а и Ь есть положительное число л:, определяемое
из пропорции а : х а х : Ь% Вставить три средних геометриче-
ских между числами 1 и 256 — значит найти три числа а2,
иь% #4t удовлетворяющих условиям:
1 :а9«й2:й8 = й8:й4«й4:256.
Значит, числа ил|» 1, я2, я3, и4 и аъ =» 256 образуют геометриче-
скую прогрессию- По формуле л-го члена прогрессии 256= 1 • ql.
Это уравнение имеет один положительный корень q =» ]/"256=4
(—4; +4''; —4/ не годятся). Теперь по той же формуле на-
ходим: а9=4; д8«г16; я4 = 64.
Отв. 4; 16; 64.
332. По условию я," -J- а3 = 52 и а? = 100, или аа = dt 10.
По свойству геометрической прогрессии а^ — ^» 100; сле-
довательно, ах и я»— корни уравнения я2—52я-|--100 = 0-
Отсюда найдём: ^«50 и ^«2 или и[ = 2 и яз=50*
Отв. Числа будут: 1) 50; 10; 2 или 2) 50; — 10; 2,
или те же числа в обратном порядке.
333. По условию: 1) а3 — aj=»9 и 2) ай—я3 = 36.
Применяя формулу ип = а1уп-1, запишем эти уравнения в виде:
1) «^9—д1 = 9; 2) я,#4— д,<72 = 36. Деля уравнение 2) на
1), получим ?а=»4; отсюда q=*±:2\ из 1) находим: я^З.
О/яа, 1) -ь*-3; 6; 12; 24; 48; ...»
2) -н-3; —6; 12; —24; 48; ...
334. По условию ят-{-а4=*27 и а^аа=*72; но так как
2?s=— или вдеав^ то имебм систему двух уравнений:
1) а,4-я4 —27 и 2) ягя4=*72,
откуда я^ = 3 и я4 = 24 или я, == 24 и я4 = 3. Из формулы
в4=а1<73 находим соответственна q =* 2 или tf^-g".
О/ив. 3; 6; 12; 24 или в обратном порядке: 24; 12; 6; 3.
220 ОТВЕТЫ И РЕШЕНИЯ 335
335* По условию 1) иг + «4 ™ 35 и 2) аз + а8 = 30* Так
же, как в задаче 333, для определения q получаем уравнение
или по сокращении
1+9"
40+Я) '
l-q + q*
Я
35
" 30'
7
~ 6*
Находим:
1) ? = |; Д]===8; 2) f —£; в, = 27.
Получаем две прогрессии:
1) +1-8; 12; 18; 27; 40,5; ...,
2) +f-27; 18; 12; 8; 5±; ....
у которых первые четыре члена одинаковы, но идут в об-
ратном порядке.
Отв. 8; 12; 18; 27.
336. Во второй данной сумме заменяем каждый член через
предыдущий, умноженный на q (согласно определению гео-
метрической прогрессии); получим
ЧЯ + ЧЧ + ЧЯ + ЧЯ + ЧЯ = 62
или
ч(ч+ч+ч+ч+аь) = 62-
По условию выражение в скобках равно 31; следовательно,
?=2. Пользуясь формулой Sn = Ul^^l) имеем 31 == Ы12(^~Д)
откуда ил = 1.
Отв. +5-1; 2; 4; 8; ...
337. По условию имеем:
1) Ч + Ч + Ч-^Ч=*19*5' 2) 4+4 + 4 + *** = J3«
Задача аналогична предыдущей.
Отв. а, = 1,6 и дБ=:8,1.
340
ГЛ. 5. ПРОГРЕССИИ
221
338. Члены ai и «q—равноотстоящие от начала и конца:
поэтому tt4«6=sata9. Так как по условию «i«9 = 2304, то
а4дв=:2304; кроме того, по условию и4-}-ив= 120. Из
этих двух уравнений находим д4 —24; йв = 96 и я4 = 96;
яв==24. Возьмём первое решение. По формуле un — uyqn-1
имеем:
1) 24 = 0^; 2) 96 = а, т6.
Разделив 2) на 1), находим q2 = 4, откуда q = 2 или q =* — 2.
В первом случае уравнение 1) даёт ^ = 3, во втором случае
«! = — 3. Девять членов прогрессии будут в первом случае:
3; 6; 12; 24; 48; 96; 192; 384; 768;
во втором:
— 3; 6; —12; 24; —48; 96; —192; 384; —768.
Взяв решение «1 = 96; ав =* 24, найдём те же два ряда чле-
нов, но в обратном порядке.
Отв* 1) иг =3; # = 2;
2) д1==:—3; ?=* — 2;
3)Д1~768; <7-1;
4) ах=* — 768; $ = — .1.
339. По условию 1) а, +«2+а3 = 126 и 2) ^«^=13 824.
Так как «9 есть средняя пропорциональная между ах и «а,
то uiu^ — iili поэтому вместо 2) можно написать i4 = 13 824t
откуда «2=3^13824. В данном случае, разлагая 13824 на
множители, легко найти, что д2=*24. Подставляя в 1) и 2),
получаем систему уравнений: «г-{-«3 = 102; аг«3 = 576. Ре-
шения её: о,=а6; я3=:96 и at ■=■ 96; «а = 6. Получаем две
прогрессии: ч-5-6; 24; 96 и -к-96; 24; 6, отличающиеся
только порядком членов.
Отв. 6; 24; 96.
340. из условия следует, что сумма членов, стоящих на
чётных местах, в два раза больше суммы членов, стоящих
на нечётных местах, т. е.
Дг+Д4 + «в+ .-- + «271 „до
"1 + «8 + «Б+.«.+Иап-1
222 ОТВЕТЫ И РЕШЕНИЯ 341
Заменяя члены а2; «4; я6; • ..; а2п выражениями Дд^а^;
u4 в "8*7'» • • *» аэп в й2п-1?» находим g == 2.
Отв. Знаменатель прогрессии равен 2,
Бесконечно убывающая геометрическая прогрессия
341* Для доказательства того, что данные числа образуют
геометрическую убывающую прогрессию, надо проверить, бу-
дут ли равны отношения — и — и будут ли они меньше 1.
Имеем:
\\ ** = _* _.t^+i= _ *„ -УР?+^= i_
Bt 2— 1^2 ' 1^2— 1 УЪО/Ъ—1)*УТ—1 2+^2 '
2) и*=1- Д ^^2-У2" = (2-1^2)(2+1^2)^ 1
к2 2 ' 2— 1^2 2 2(2 + У2) 2+^2 '
Так как -2=1^ = 0 = т=< 1» то данные числа обра-
т щ ч 2+УТ и
зуют геометрическую убывающую прогрессию. По формуле
её суммы находим
У2" + 1 _ (V2+l)(2+V2)_A , Q ^у
'2+vtJ
От*. 5 = 4 + 3^2,
■(/2"-1)Л 1-—\ (VS-iHVr+iV
\ 2+V2J
342. Как в предыдущей задаче, находим, что выражение
3(УУ—2) D „
в квадратных скобках равно ' -. Все выражение тогда
примет вид
(4V^+8).^^e-7^--6(/3+l).
Отв. _6(]/T+l).
343. По услозию
32
По формуле un^=£alqn"1 из второго равенства получаем
32
345 гл. 5. прогрессии 223
Учитывая, что иг = 4, получаем биквадратное уравнение
2 лГ2 1
81g*—81^ + 8=0;его корни; gb2t=z+:—^— и ^3?4 = ±-j.
Отрицательные корни не годятся, так как по условию все
члены положительны, положительные корни годятся оба, так
как они меньше единицы. Получим две бесконечно убывающие
прогрессии.
Отв. 5' = 12(3 + 2/2) и S" = 6.
344. По условию
дг-|-а4й=54 и ад + Яй^Зб.
С помощью формулы ип = uxqn~l получим систему двух урав-
нений:
I их+ихф=М, (ux(l + q)(l— <? + <р) = 54, (1)
1 «1<7 + «1<79 = 36, иИЛИ \ ма+?) = 36. (2)
Разделив (1) на (2), получим уравнение
Я ~"2'
из которого найдём дл =2 и //2=з-д.. Годится ?9 =-о"< 1.
Находим из (2) ах = 48.
Отв. 5 = 96.
345. Первый способ. По условию
1) «1 + «з + «б+...=36,
2) «9+«4 + «6+«ч ™ 12-
Члены первой и второй сумм составляют также бесконечно
убывающие прогрессии, знаменатель которых одинаков и равен
<72, первый член в первой прогрессии равен ах> а во второй
«й, т.. е. uxq. Выражая суммы первой и второй прогрессий
по формуле суммы бесконечно убывающей прогрессии
(где вместо д берём q2, а вместо иг во втором случае бе-
рём илц\ получим: 1) ^zr^ = 36 и 2) —^ =* 12. Деля 2) на
1), получим j=5j, а из первого уравнения находим а} — 32.
224 ОТВЕТЫ И РЕШЕНИЯ 346
Второй способ. Так как а2 = а1^) а4 = u%q и т. д.,
то вместо яэ + я4 + я0 + ... s=s ^ получим ахд + а3д + '
+ w5<7 + • •• = *2, или
?(ai+% + a6+..«) = 12. (1)
Разделив на (1) условие at + я3 + аБ + ... =36, най-
дём 0=-s-. С другой стороны, сумма всех членов прогрес-
сии есть 12-}-36 = 48. По формуле суммы бесконечно убы-
вающей прогрессии имеем 48 = - Ux« , откуда ах = 32.
1-т
п „0. 32. 32.
Отв. -*ч-32; -j; -<р
» •
346. По условию
«i + ^2 + % + • • • = 5б: а? + а2 + а1 + • • • == 448.
Слагаемые второй суммы образуют также геометрическую
бесконечно убывающую прогрессию с первым членом а\ и
знаменателем q2. Выражая суммы этих прогрессий, получим
^ = 56, -^- = 448
1 — q • 1 —^
или
^=56(1—0, (1)
я? = 448(1— д% (2)
Деля (2) на (1), находим
а, = 8(1+<7>. (3)
Исключая их из уравнений (1) и (3), получаем
8(1+0-56(1—0.
откуда <7 = -j-. Из (1) находим ах = 14.
Отв. их= 14, <7 = j.
349 гл. 5, прогрессии 225
347, Задача решается аналогично предыдущей. Для опре-
деления иг и q получим систему уравнений;
их --3. (1)
(2)
1-я:
и? 108
1 — q* ~~ 13 '
После исключения из этих уравнений и\ получим уравне-
ние 3<72—10?-[-3 = 0. Из двух корней его годится только
^ =-~ (другой 0 = 3 больше единицы). Из уравнения (1) на-
ходим at = 2.
2 2
Отв. -5-5-2; •£•; -д-; ...
348. Задача решается аналогично задачам 346, 347.
Для определения их и q получим систему уразкений:
| *1? = б. (I)
Уравнение (2) равносильно уравнению «2 = 8(1+7). Исклю-
чая и, из системы и20 = 6, «,==8(1 -j— ^), получаем уравне-
3
кие 4g2 + 4g— 3=0, Из двух его .корней ^ = — -j9
^9 = -я- годится только второй, так как абсолютная величина
первого больше единицы. Из (1) находим их = 12.
Отв. /-*-т-12; 6; 3; ...
Задачи на арифметическую и геометрическую прогрессии
349. Из условия находим:
<f= 16—14 = 2; дх= 14 — ^=12;
Л14-д2 + ав=12 + И+16 = 42.
Следовательно, в искомой геометрической прогрессии 1) # = 2
и 2) Hj -\-uxq-\-axq* = A2% откуда ^ = 6.
Отв. -*-*-6; 12; 24; ...
226 ответы и РЕШЕНИЯ 350
350. Первые три члена геометрической прогрессии суть
3; bq\ З^2. По условию at = 3; д^ — З^^б; так как
Яз — а<ъ = а%—аи то Да = 2а% — ал е=б7 + 9. По условию
этот третий член равен третьему члену геометрической про-
грессии, т. е. 3*72. Получаем уравкение 6q -|- 9 «= З^9;
корки его # = 3 и q = — 1. В первом случае геометрическая
прогрессия будет -*-*- 3; 9; 27; ..., а арифметическая
'-г-3; 15; 27; ... Во втором случае получаем два ряда чисел:
3; —3; 3; —3; ... и 3; 3; 3; ..., которые можно рас-
сматривать соответственно как геометрическую прогрессию со
знаменателем q = — 1 и как арифметическую прогрессию
с разностью d = Q.
Отв. 1) -*-3; 15; 27; ...; -к-3; 9; 27; ...,
2) -*-3; 3; 3; ...; ч-ьЗ; —3; 3; —3; ...
351. Задача сходка с предыдущей. По условию ах = ах = 5;
следовательно, иъ =■= bq*\ иь = 5#4. Далее по условию
а4 = иь = 5#а; й16 = а6к 5#4. Значит: 1) bq* = 5-f-3d,
2) 5^4 = 5-4-15^. Исключая tf, получаем уравнение
ф —- 5<72 -J- 4 == 0, откуда 72 = 4 или qs = 1. Так как я4 «= 5<72,
то четвёртый член арифметической прогрессии в первом слу-
чае равен 20, а во втором 5.
Замечание. В каждом из этих двух случаев получаем две
различные геометрические прогрессии; арифметические же прогрес-
сии—одинаковые. Имензо, в первом случае имеем геометрическую
прогрессию тг5; 10; 2Q; ... и -тг5; —10; 20; ...» арифметическая
же прогрессия (разность rf»"^"" =5) будет-ь 5; 10; 15; 20; ...
Во втором случае получаем геометрическую прогрессию -fr 5; 5; 5;...
и тг 5; —5; о; —5; ,..; арифметическая прогрессия состоит из рав-
ных членов -*-5; 5; 5; ...
Ошв, 20 или 5.
352. По условию ах = ах] а2 = u^q\ ал = a{q*. Отсюда
находим:
1) fif = a2—О} «в 0,(f— 1) и 2) 6^ = ^ — Oj =iUl(q2 — 1),
Исключив d, получим ах(92—l)==6«j (^ —1). Так как
ut Ф 0, то <7а— 1 = 6(9—1), откуда ? = 5 или q= 1. Из
условия ах -J- uxq + Wj?9 = 93 находим соответственно at = 3
и я, =31.
От$, 1) 3; 15; 75. 2) 31; 31; 31.
358 гл. 5. прогрессии 227
353. По формуле (2) на стр. 43 находим д7 = 729; следо-
вательно, в геометрической прогрессии имеем: ил —Oj = 1;
ц7 = а7 = 729. По условию требуется найти средний член, ко-
торый будет четвёртым с начала и с конца и, следовательно,
первый член uv искомый средний а4 и последний я7 образуют
непрерывную пропорцию ах: и4 = и4 : я7. Отсюда ul = axu7
и «4 = 729.
Ome. a4 = d=27.
354. По условию аг + я2 + л3== 15. Так как а2 — аг*=
=> я3—яа, то 2а% = flj -j- а3 и из условия имеем 2og -{- ^2 === 15.
Отсюда я2 = 5. Тогда ах = Ь — d\ а2=5; а3 = 5-|-^ и по
условию й1 = а1-т-1 = 6 — d; й2 = а24-4 = 9; я3 = а3-|-
-|— 19 = 24 —|— cf. Так как ul = uxu$, то имеем:
9* = (6 — d)(24 + d)9
откуда находим tf? = 3, aj = 2 или fi? = — 21, ах = 26.
Отз, 1) 2; 5; 8. 2) 26; 5; — 16.
355. По условию ах = ах -j- 1; я2 = и2 + 6; л3 — йз "т" 3;
отсюда ях + ^ + я3 = (ai 4~ as + аз) 4~ О ~j~ ^ -f- 3) или на ос-
новании условия, что al^a%^aB=z2Qf получим
ах 4-а2-}-а3 = 26 + 10 = 36.
Дальше задача решается аналогично предыдущей.
Отв. 2; 6; 18 или 18; 6; 2.
356. Положим, что искомые числа будут ах\ axq\ axq4\
тогда по условию числа а1$ игд и {uxq^ — 64) составляют
арифметическую прогрессию, и следовательно,
uxq — иг = (игд* — 64) — elflr. (1)
Кроме того, по условию числа й1; (йх<7— 8); (йх<79 — 64)
составляют геометрическую прогрессию, и следовательно,
(ихд — 8): их = (а^а — 64): (в^ — 8). (2)
После упрощений система уравнений (1) и (2) примет вид
*i(?2 — 2?+1) = 64, Й1(^_4) = 4,
откуда находим <7 = 13 и и1 = -д- или # = 5 и ых = 4,
Отв. 1)|; f; ^. 2) 4; 20; 100.
228 ответы и pfihfhwi 357
357. Положим, что искомые числа будут ии иц и а3. Если
эти числа суть члены геометрической прогрессии, то
4 = а,а^ (1)
а если эти числа суть члены арифметической прогрессии, то
2о*=*еЩ-ав. (2)
Исключив из (1) и (2) и9, найдём (^ + «а)* = 4а1ая или
(а, — а9)9 = 0( откуда а, =я иЧш а из (2) находим a<, = «i.
Следовательно, и, = ив = и3.
Отв, Возможно, если три числа равны между собой.
ГЛАВА 6
СОЕДИНЕНИЯ И БИНОМ НЬЮТОНА
Обозначения:
Л^ — число размещений чз т элементов ао %
Яп —число перестановок из п элементов,
С* — число сочетаний из т элементов по п,
7л+1 (— Сктанха*~к) есть (Л +■ I) й член разложения бннома
358. По условию
Р„ ОД Ь2.3...я I
^—= 3 • 11ЛИ 1-2.3 .^Гл4-Гм^4-5>""50'
откуда (я-f-l)(/t + 2) —30. Корни этого уравнения /^ = 4;
/igsss — 7» Второй корень не годится»
Ошв. д«4.
359. По условию
5CJ» = Сп^гэ
или
5я(я—1)(я —2) 1я+2)(я-Ц)я(я —1)
Ь2-3 ~ 1-2-3-4 '
откуда
Ода*. яй =* 14; /ц —3.
364 ГЛ. б. СОЕДИНЕНИЯ И БИНОМ НЬЮТОНА 220
360. Искомый член
16-15.14.13.12- 11.10* 9 л*
1-2-3-4«5»6-7»8 х4*
».-<-'**(*У(*Т
Отв. 12 870 g.
361. Имеем:
Тп„ = сЩУа)П$П>)*-П.
Буква а здесь содержится в степени -оЧ-—*—■;—. По ус-
ловию -j-f- Г~п =7, откуда л = 6, т. е. л+1 = 7.
Отв. Седьмой член.
362. Имеем:
21 -п п « 21-п
,, л 21 — я 21 —п п Л
По условию -д- g— = —2 ~н» 0ТКУда Л = 9-
Отя. Десятый член. -
/ i -±V°
363. После упрощения получаем: \л*—д 2/ . Имеем:
10-n »
По условию —з— — -g- = 0, откуда л = 4.
Offte. 7B = 2I0.
364. Пусть x есть показатель степени первого бинома.
Тогда сумма биномиальных коэффициентов есть 2х. Сумма
биномиальных коэффициентов у второго бинома есть 2х*г%
Получаем уравнение
2*4-2*+®= 144; 2*(1+8)=144; 2* = 2*; х=4.
Отв. 4 и 7.
230 ОТВЕТЫ И РЕШЕНИЯ ЗвЗ
865. Имеем т{™^Х> — ЮБ, откуда /я=* 15; тогда
л 455
Отв. «jy.
866. По условию С^» = СЦ, следовательно, «=»15. Тогда
инеем
По условию 30 —За « 0; л « 10.
Ода*. 7и«3003я1*.
867. По условию -j-я»г,т, е. /ю*—5т—50 =* 0, от*
^ т
куда m в 10 (корень m » —б не годится). Средний член
7в« tfo(-l)*(j/^J(* ^« -252.
Отв. Средний (шестой) член равен—252.
868. По условию 1 + m Н т1т£ " в 46. Дальше ре-
шается, как задача 367.
Отв. Искомый член (седьмой) Т7=»84.
869. По условию 2* «■ 128, откуда т=»7. Имеем
г^-с?*-*,*—,
По условию —-у + «у(7 —л)в5, откуда л=*3.
Отв. Искомый член (четвёртый) 74«35jc*.
870. Имеем: л^шяа^ш* у(1 +06. Множимое ^ равно
jjее —у «=-(, Множитель(I Ч-О6согласно формуле бинома
Ньютона равен 1+5/+ 10i*+ Ю^Ц-5/* +А Следовательно,
«в«— i — 5i*—ДО—1№ — 5/»—А
373 гл. 6. СОЕДИНЕНИЯ И БИНОМ НЬЮТОНА 231
Теперь заменяем степени мнимой единицы их выражениями:
^^ — 1; fimmpimm — i; /« = &•=_ // = -И;
/»»№_/; Р = — 1.
- Замечание. В данном примере, где основанием степени яв-
ляется 1 +/ (или, вообще, когда основанием является двучлеи вида
с±#0> возведение в степень можно выполнить проще. Именно,
возводим 14-/ в квадрат. Получим (1+*)* = 2«, отсюда (l+i)ee
-О+')М1+О-(20Ч1+О--\4(1+*
Отв. ив =— 4 4-4/.
371. Имеем и7 = *(1 +~)• Так как Т"—'■ Т0 а? =
=*/(!—0е* Дальше можно решать, как предыдущую задачу.
Можно также найти модуль и аргумент произведения шести
сомножителей, равных 1 —* каждый. Модуль величины 1 —/
есть ^2; аргумент равен —45°. Значит, модуль * произве-
дения равен (1/"2)* = 8. а аргумент 6(—45°) = —270°. Сле-
довательно,
(1 — if = 8 [cos (— 270°) + / sin (— 270°)] = 8i.
Отв. «7 = — 8.
372. По условию числа С\\ С\\ Съп составляют арифмети-
ческую прогрессию. Значит, Ci 4-С*1 = 2С£, т. е.
= 2 ^ •
Так как п Ф 0, то обе части равенства можно разделить
на я. Получим уравнение п2 — 9п -|» 14 = 0. Из его корней
nt = 7 и я9 = 2 второй не годится, так как при п = 2 раз-
ложение бинома имеет только три члена, а по условию имеется
четвёртый член.
Отв. п = 7.
373. Решается, как предыдущая задача. После сокраще-
на— 1)(п —2)(л —3) -
ния па —2 i-^-jj—— - (это число не равно нулю, так
как по условию л>6) получим tfi — 21л + 98 = 0.
Отв. п = 14 или п = 7.
232 OTBFTW и решкния 874
374. Первое слагаемое в скобках запишем в виде
a6' v »л^т; второе слагаемое в виде а • ах+х saax+l*
Ь -я их
Четвертый член разложения равен 56а л л+1 • Но условию
oba * **+■ ss оба-*"*. Следовательно,
0/«в, х а 2 или х = — 5.
375. Представим данное выражение в виде
2 Л + 2 «-* j . По условию
1о«2 ' 2 «-* «240,
т. е.
Следовательно,
4(д —1) , 4(3—у) 4
- * "*" 4 —д ■" *•
Отв. л « 2.
376. Седьмой член 77 разложения бинома \23Ч~3 */
равен
а седьмой член от конца
Следовательно,
7,:7; —V2V U V =2 * 3 * —6 ' .
По условию 6 * в17» т* е* 6 * «■б*1. Следова гел ыю,
Отв* х*=*9*
383 ГЛ. 6. СОЕДИНЕНИЯ И БИНОМ НЬЮТОНА 233
377. По условию Cj** (*'*")' = 10е, т. е. Ш*3+21** = 10*
или x3+21ga7 = 10б. Логарифмируя это равенство, найдем
(3 4- 2 \g х) \g х = 5. Решив последнее уравнение, получим
-*■ l
1 * 100/10
378. По условию
,l^-v
Iff л+ 7
СвОЛс)***1 (|/лг)3=200, т. е. 20jc*«ff'+-!t = 200.
Деля обе части этого уравнения на 20 и затем логарифми-
руя, получим после упрощений
0g*)fl + 31gjc — 4 = 0.
Отсюда Og *i) = 1. Off *а) = — 4.
Отв. хх= 10; д:2== 0,0001.
379. Решается как предыдущая. Получим уравнение
х\%х-2, _-. ЮОО. Логарифмируя полученное равенство, найдём
(lg*i) = 3 и (ig*2) = —L
Отв. хг= 1000; *Q = 0,1.
380. Решается как две предыдущие.
Отв. jq—10; х2 = — •
381. Отв. хх= 100; ха*———
у 100
382. Отв. ^=1000; х% = -^=г.
1 2 /10
где
383*.
^ft+i:
По условию
ft 12—ft
= 30,
I—2ft
3 и
7ft + 9
4
— 2k
(a)
234 ОТВЕТЫ И РЕШЕНИЯ «я
5 — 2ft 4 — 2ft
По условию показатель—^— вдвое больше показателя —^—,
т. е. —g— = 2* ^—, откуда А=1, Тогда равенство (а)
после упрощений примет вид:
L 2.
2*9 — 11jc9+5 = 0.
2
Применяем подстановку х*=у.
Отв. ^ = 51^5*; jcs = ij-.
384*, По условию 5Cm = C^f следовательно, имеем урав-
нение
к «(« — \){т — 2)
Так как тФ 0, то обе части уравнения можно разделить
на т. Получим т1 = 7 и т2 = — 4. Годится только m1 = 7f
так как m должно быть целым положительным*
По условию Т4 == 7 • 20; значит,
C?(2-^)S(2Ti)4==140-
Отз. х = 4.
385. Из условия имеем С2т — т = 20; *("^!? — т = 20.
Из двух корней тх = 8 и /и8 =—5 годится только пер-
вый, так как предполагается, что показатель бинома — це-
лое положительное число. Перепишем бином в виде
<2J "^_21в *). По условию
74_7в = 56
или
сЗг'^""^^"»)—c525^"%*^"s) = 56.
387 ГЛ, б. СОЕДИНЕНИЯ И ВИНОМ НЬЮТОНА 235
После упрощений получаем 56*2* — 56 • 2^ = 56. Положив
2х = у, получим уравнение у*—у — 2 = 0, откуда у1 = 2
и у% = — 1. Так как 2х =у не может быть отрицательным
числом, то годится только ух=2 и, следовательно, 2я* = 2,
т. е. х™ I.
Отв. *== 1.
386. Так как биномиальные коэффициенты членов, равно-
отстоящих от начала и конца, равны, то вместо коэффици-
ентов трёх последних членов можно взять коэффициенты трёх
первых членов, т. е. \-\-m-\—^ 2 ; = 22, откуда т = 6
(см. предыдущую задачу). Следовательно, бином будет
(2а + 2 » J . По условию
Гв+Г§-135
или
2 2 )\2*) +Ct\2 * )\2*) =135.
После упрощений получим
2*+14-2а-»=9 или 2.2*4-^ = 9-
Как в предыдущей задаче, найдем: 1) 2х = 4 и 2) 2х = ~.
O/zw. jct = 2; лс2 = —].
387. Числа at, *%, дб, являющиеся соответственно первым,
третьим и пятым членами арифметической прогрессии, сами
образуют арифметическую прогрессию, так что 2ць = ах -[- <V
Так как по условию яг — С^; а3 — с£»; д6 = Cj», то
2т{т—\)__ , т(т — 1)(т — 2)
Ь2 —m"i 1Т2Т3 *
Сократив на т (т Ф 0), найдем уравнение та— 9/» -f- И — 0,
корни которого mt = 7, /7ta = 2. Так как по условию в раз-
ложении бинома имеется не меньше шести членов, то /»>5,
эначит, годится только /7^ = 7. Бином будет
^•-л+,4*"]'.
236 ОТВЕТЫ И РЕШЕНИЯ
Но условию
1в = 21
или
Отсюда имеем
следовательно,
£,52^—2} ig »2Js(1°—**> __ 21
л
2^—2j ig в-t-ig iu—a j f_ . 20*
(x— 2)ig3 + lg(10 — 3*) = 0.
Потенцируя, получим
3*-2(Ю — 3*)=1
или
Дальше решается, как задача 385.
Отвт хх = 2; jcs « 0.
888. По условию числа -g-Cm, С« и Си образуют гео-
метрическую прогрессию; следовательно,
^ СтСт « (Сот) .
Обе части равенства можно разделить на т*(т — \f{m — 2),
так как ни т, ни т — 1, ни /и—--2 не равняются нулю (ибо
из условия следует, что /и > 3); получим т = 9. По Условию
74«16,8 или
Отсюда получим уравнение
^Ig(jc—1)—lg5—Ig(6 —KS5)--1.
После потенцирования имеем
Отсюда jct ак 50 и jca «а 2„_Первый корень не годится, так как
при х =» 50 число 6 — Уйх отрицательно и, эначит, не имеет
логарифма.
Отв. х=*2.
39* ГЛ. 7 АЛГЕБРАИЧЕСКИЕ И АРИФМЕТИЧЕСКИЕ ЗАДАЧИ 237
389. По условию
ig(3-ci>—igc;n=it
или
отсюда —— = 10. После упрощений найдём уравнение
га2— 3m—18 = 0, корни которого т1 = 6и/п.2 = —3. Сле-
довательно, показатель бинома т = 6.
Из условия 97^—7б = 240 получим уравнение
9Ce22^+^24("2 t)_q*24(*+?'2"^~") =240,
откуда найдём
9 . 23^-а —23а;+1= 16
или
Следовательно,
Отв. jc = 2.
9. 2*с
2^== 2е и л = 2.
ГЛАВА 7
АЛГЕБРАИЧЕСКИЕ И АРИФМЕТИЧЕСКИЕ ЗАДАЧИ
390, Вес патрона составляется из веса снаряда, заряда
и гильзы. Снаряд и гильза, взятые вместе, составляют по
2 111
весУ з"~г~Т = Т2 всег0 патРона- На долю заряда остаётся
1—то^То веса патРона» чт0 составляет 0,8 кг. Следова-.
тельно, вес патрона равен 0,8 кг:^ = 9$Ь кг.
Отв. 9,6 кг.
391. Мужчины составляют 100% — 35% = 65% от
общего числа рабочих. Мужчин больше, чем женщин, на
65% — 35% = 30%, что составляет 252 человека. Следова-
* * 252-100 олл
тельно, общее число рабочих равно —™— = 840.
Отв. 840 рабочих.
238 ОТВЕТЫ И РЕШЕНИЯ 392
392. Процент прибыли берётся по отношению к себе-
стоимости (принимаемой за 100%)- Значит, продажная цена
(1386 руб.) составляет 100% + Ю% = 110% себестои-
мости. Себестоимость равна
1386-100 10АЛ , пЛ.
—ns—= 1260 (руб.).
Отв. 1260 руб.
393. Убыток исчисляется в процентах по отношению
к себестоимости (принимаемой за 100%). Значит, 3348 руб.
составляют 100% — 4% = 96% себестоимости. Следова-
тельно, продукция обошлась артели в
i*^ = 3487,5 (руб.).
Отв. 3487 р. 50 к.
Ял О > 1 по
394. Содержание меди в руде составляет —т^5—%•
Отв. 15,2%.
395*. Цена снижена на 290 коп. — 260 коп. = 30 коп.
30 • 10Q
Эта сумма составляет —oqo % от старой цены. Число
30-100 1Л10 л л
■ 29Q ■■ = 10 щ заменяем приближённо десятичной дробью.
Отв. 10,34%.
396. Задача решается как предыдущая.
Отв. 10,94%.
397. По условию 2 кг составляют 32% от веса винограда.
Вес винограда равен ' 2 = 6,25.
Отв. 6,25 кг.
398. Обозначим число экскурсантов через х. В первом
случае взносы составят 75л: коп.; значит, на расходы нужна
сумма (75л: -j- 440) коп. Во втором случае взносы составят
80л; коп.; значит, на расходы нужно (80* — 440) коп. Следо-
вательно, 75* -j- 440 = 80л:—440.
Отв. 176 человек.
402 ГЛ. 7. АЛГЕБРАИЧЕСКИЕ И АРИФМЕТИЧЕСКИЕ ЗАДАЧИ 239
399. Пусть было х человек; каждый должен был запла-
72 п
тить --, По условию
<*-3>g+4)»72.
Отв. 9 человек.
400. Пусть цена одного экземпляра первого тома соста-
вляет х руб., а второго тома у руб. Первое условие даёт
уравнение 60л;+ 75^ = 405. При скидке в 15% цена экзем-
пляра первого тома составит 0,85лг руб.; при скидке в 10%
цена экземпляра второго тома составит 0,9^ руб. Из второго
условия получаем уравнение
60 • 0,85*+ 75 • 0,9^ = 355 i.
Решая систему двух уравнений, найдём дг = 3; ^ = 3.
Отв. Цена первого тома 3 руб.; цена второго тома тоже
3 руб.
401. Пусть первый предмет куплен за х руб. Тогда вто-
рой куплен да (225 — х) руб. При продаже первого предмета
получено 25% прибыли. Значит, он продан за 1,25* руб.
Второй предмет, на котором получено 50% прибыли, продан
за 1,5(225 — х) руб. По условию общий^процент прибыли
(по отношению к покупной цене 225 руб.) составляв 40%.
Значит, общая сумма выручки была 1,40 • 225 = 315, руб.
Получаем уравнение
1^*+1~-<225--jc) = 315.
Отв. Первый предмет куплен 8а 90 руб., второй — за
135 руб.
402. В 40 кг морской воды содержится 40 • 0,05 ==2«г
соли. Чтобы 2 кг составляли 2% общего веса, последний
должен равняться 2 : 0,02 = 100 /сг.
Отв, Нужно добавить 60 кг.
240 ОТВЕТЫ И РЕШЕНИЯ 4вЗ
403* Обозначим длины катетов (в метрах) через х и у.
По условию jf2+>'3 = (3^5)3. После увеличения на 133 у%э
т. е. на 1QQ «a 1-j своей длины, первый катет станет рав-
ным 2*г-лс. Второй катет после увеличения на 16-тг°/о бУдет
равен l-g-,y. Получаем уравнение 2-я-*-{-1-g-^« 14.
Отв. 3 л и 6 л.
404» Если из первого мешка отсыпать 12,5% находя-
щейся там муки, в нём останется 87,5%, что составит
140 #г:2»70 кг. Следовательно, в первом мешке ■ gl5 ♦
О/я*. В первом мешке 80 /сг, во втором 60 кг.
405* Оба завода вместе могли выполнить в день п часть
заказа. По условию производительность завода В составляет
Ьбтг°/0, т. е. -я- производительности завода А; следова-
гельно, производительность обоих заводов составляет I -я-
шхшзводительности завода Л. Значит, завод А может выпол-
1 2 1
•шть в день То* * Т^35) часть заказа» а завод А—выполнить
^•те>1 часть заказа. До остановки завода Л была
2 \
выполнена тс0-? часть всего заказа. На выполнение остаю-
щихся тг всего заказа заводу А требуется 7S^gsa>25 дней.
О/я*. Заказ будет выполнен через
27(=25 +2) дней.
406. Верно решившие 14 человек составляют 100% —
— (12% + 32%)=*56и/0 всех учеников класса. Общее число
учеников класса было ^ - = 2ош
Отз* 25 учеников.
409 ГЛ. 7. АЛГЕБРАИЧЕСКИЕ И АРИФМЕТИЧЕСКИЕ ЗАДАЧИ 241
407. Вес отрезанной части составляет 72°/0 от веса всего
рельса; значит, вес оставшегося куска (45,2 кг) составляет
100% — 72% = 28% веса рельса; 1% этого веса состав-
ляет ^2, а 72% составляют ^. 72 = 116 J кг «116,23 **.
Вместо того чтобы определять 1% веса рельса, можно
составить пропорцию х : 45,2 = 72 :28.
Отв. Вес отрезанной части (округлённо) 116,2 кг.
408. Вес всего сплава (2 кг) составляет 100%+ 14 у % =
2
»114у°/о веса меди. Значит, 1% веса меди составляет
4 2
-—'тркг. Следовательно, вес серебра, составляющий 14 у %
П4у '
веса меди, равен
2 1А 2 1
. 9 "147 = т*г-
114 у *
Вместо того чтобы определять 1% веса меди, можно
составить пропорцию
^:2 = 14у:114у#
Отвш Вес серебра -т«#.
3 17
409. Заработок второго составляет 1 — : 7 у « — заработ-
ка первого или, в процентах, gg* 100% = 23_-°/о- Общий
заработок трёх рабочих (4080 руб.) составляет
100% + 2з1% + 4з!%~16б|-%
от заработка первого. Один процент заработка первого соста-
вляет л- руб., значит, первый заработал
1бб|
-2£д- . ЮО — 2448 руб.
242 ответы и РЕцштя 4Ю
Второй заработал 23 -^% 9Т0Й СУММ". т. е.
2448- 2з4-
-_2-=*571,2 руб.;
третий заработал
2448-43i
j^^» 1060,8 руб.
Отв. 2448 руб.; 571 р. 20 к.; 1060 р. 80 к.
410. Если вес сахара в первом ящике х кг% то вес сахара
42 —
4 4 2 17
во втором ящике у х кг, а в третьем t^'-Tqq- =$\х кг*
По условию # + т* + 50*~64,2' откУда л — ЗО (кг). От
4 17
этого числа берём сначала -г, потому.
Отв. 30 кг, 24 кг, 10,2 кг.
411. Возьмём х т первого сорта; в нём будет 0,05* т
никеля. Второго сорта нужно взять (140 — х) т с содержа-
нием никеля в 0,40 • (140 — х) т. В общем количестве 140 т
стали по условию содержится 0,30* 140 т никеля. Следова-
тельно, 0,05дг+0,40 • (140 — х) =* 0,30 • 140. Отсюда х = 40.
Owe. 40 т первого сорта и 100 т второго сорта.
412. Сплав содержит 12 кг • 0,45 = 5,4 кг меди. Так как
в новом сплаве эти 5,4 кг меди составляют по весу 40%,
то вес нового сплава будет 5,4 :0,40 =* 13,5 кг. Значит, нужно
добавить 13,5 кг —12 *г=*1,5 кг.
Отв. 1,5 кг.
413. Решается как предыдущая задача: 1) 735 г «0,16=8
«117,6г;2) 117,6 г;0,10 =1176г;3)1176г — 735г = 441 г.
Отв. 441 г.
414» Пусть х — вес меди (в кг). Тогда 24 — х есть вес
цинка. Потеря веса составляет -g-jc (д7я меди) и у (24 — х)
I I 8
(для цинка). Следовательно, ^jc + j(24 — jc) = 2-g-. Or-
сюда х=* 17.
Отв. 17 кг меди, 7 кг цинка.
419 ГЛ. 7. АЛГЕБРАИЧЕСКИЕ И АРИФМЕТИЧЕСКИЕ ЗАДАЧИ 243
415. Количество рельсов длиной 25 м обозначим через х,
а рельсов длиной 12,5 м — через у. На участке 20 км =
= 20 000 м нужно уложить 40 000 м рельсов (две линии).
По условию
25*-1-0,50. 12,5^ = 40000 и 12,5^ + -^ • 25* = 40000.
Отв. 1200 рельсов по 25 м и 1600 рельсов по 12,5 м.
416. Пусть число учеников есть х. При обмене карточ-
ками каждый получит х—1 карточек, а все х учеников
получат х(х — 1) карточек; по условию имеем уравнение
х(х — 1) = 870.
Отв. 30 учеников.
417. Пусть х — меньшее, а у— большее число (х<у).
Первое условие даёт ^jcy = jc -f- 12. а второе условие —
* "J * = у — 24, т. е. у — х « 48. Решая систему, находим
jc = 6, ^ = 54. Так как 6<54, то это решение годится.
Отв. 6 и 54,
418. Пусть наименьшее число есть х, следующее у и
наибольшее г. Имеем три уравнения:
у — х = 2—у\ xy = Sb\ ^2=115.
Иэ первого уравнения находим г =±= 2у — л:; подставляя
в третье уравнение, находим 2у3 — jty=115 или в силу
второго уравнения 2у2 = 200. Из двух решений (хг = 8,5,
у1= 10» ^ = 11,5; л:2 = —8,5,^2 = —10, г3 = —11,5) пер-
вое гоаится (ибо хх < уг < гг)> а второе нет (ибо х2 > у% > г^).
Отв. 8,5; 10; 11,5.
419. Дано
Z±ftl=a n^±f±^ = b.
Требуется найти хУ~ттУ* + *х9 и3 первого уравнения имеем
*e+>a + *a + 2(jfj;4-^ + **)=9a9. В силу второго урав-
нения имеем х2-\-у2-\-г2 = ЪЬ. Следовательно, ЗЬ-\-2(ху-\-}
4- у г -f- zx) = 9a3.
244 ответы и решрния 420
420. Если длина листа х см, а ширина у сму то коробка
будет иметь длину [х— 8) см, ширину (у— 8) см и высоту
4 см. По условию 4(х — 8)Q/ — 8) =768 и 2х + 2у= 96.
Отв. Размеры листа 32 ^Х 16 ел*.
421. Пусть цифра десятков х, а цифра единиц у (х и
у — целые положительные числа, меньшие чем 10). Имеем
систему:
^±^ = 2-|; (10* + j»-(10y + *)=18.
Из двух решений (х = 6, у = 4 и х — -гг, ^ ^ — тт) го-
дится только первое.
Отв. 64.
422. Если число десятков равно л:, то число единиц равно
л:+ 2. Получаем уравнение
[10х + (* + 2)Н* + (* + 2)1=144,
2
откуда jc = 2 и х = — ^тт» по Условию второе решение не
годится.
Отв. Искомое число есть 24.
423. Пусть искомое число будет х. Если справа к нему
приписать 5, то получим число 10jc-f- 5* По условию имеем
Юдг + 5 = (лг + 3)(* — 13).
Отв. 22.
424. Пусть большее число есть л:, а меньшее у. рели
к большему числу приписать три цифры (нуль и две цифры
меньшего числа), то цифры большего числа будут выражать
число тысяч, так что в итоге получим 1000 лг-j-j/. Из мень-
шего же числа получим число lOOO^y-j-10 х. По условию
1000* + з/==:2(1000.у+10*) + 590, 2лг + Зд/ = 72.
Решая систему, находим л: = 21, у= 10. Эти числа, будучи
двузначными, удовлетворяют условию задачи.
Отв. 21 и 10.
429 ГЛ. 7. АЛГЕБРАИЧЕСКИЕ И АРИФМЕТИЧЕСКИЕ ЗАДАЧИ 245
425. Нсли цифра единиц множителя есть х(х— целое
число, меньшее 10), то цифра десятков 3jc. Множитель равен
3- 10х-^~х — Ъ\ х. Ошибочно записанный множитель был
10х -}-За: = 13 х. Истинное произведение равно 78 • 31 ху оши-
бочно йолученное произведение есть 78» 13 л:. По условию
78.31^ — 78.13x^=2808, Отсюда находим х = 2.
Отв. Истинное произведение равно 4836.
426. Скорость первого поезда х км/час, скорость второго
(х — 12) км/часл Имеем уравнение
Отв. Скорость первого поезда 48 км/час^ второго —
36 км!час.
427. Пусть скорость первого равна v км/час; тогда ско-
рость второго равна fa—2) км!час. Первый затрачивает
24 24
— час., второй -^п час. Получаем уравнение
24 24 t
к— — м 1.
v —2 v
Огт^ 8 км/час, 6 км/час*
428» Пусть скорость поезда х км/час; тогда скорость
66
парохода (#—• 30) км/час. Поезд затрачивает — час, а па-
80,5 п
роход - ^oq час. Получаем уравнение
80.5 66 д 15
*—30
Отв. Скорость поезда 44 км/час9 скорость парохода
14 гем/час.
429. Пусть первая мастерская шила в день по х костю-
мов; тогда вторая шила по jc-j-4 костюма, Перзая мастер-
810
екая зыполнила заказ в—дней; значит, срок заказа был
(~р + з) дней. Срок заказа второ/1 мастерской был тот же.
246 ОТВЕТЫ И РЕШЕНИЯ 430
Следовательно,
-Г + 3 =7+1 + 6.
Отв. Первая мастерская шила в день по 20 костюмов,
вторая —по 24 костюма,
430. Пусть скорость парохода, идущего иа юг# х км}час%
а парохода, идущего на запад, (х + 6) км/час. Так как на-
правления движения перпендикулярны, то по теореме Пнфа*
гора
(2х)а + [2 <* + 6)j» =*60*.
Отв. Скорость первого парохода 18 км/час, второго —
24 км/час.
431. Два скачка собаки составляют 4 м\ 3 скачка лисицы
составляют 3 л. Следовательно, когда собака пробегает 4 м,
расстояние между собакой и лисицей сокращается па
4 л— 3 м = 1 м. Первоначальное же расстояние между
ними в 30 раз больше. Значит, собака догонит лисицу, когда
пробежит 4 м • 30 = 120 м.
Отв. На расстоянии 120 м.
432* За 1 мнн. минутная стрелка поворачивается на 6\
I °
а часовая—-на •*-* Когда часы показывают 4 часа, угол
между часовой и минутной стрелками равен 120°. За х ми-
нут стрелки поворачиваются соответственно на &х н ^х гра-
дуса. По условию 6аг —-^ лгвз 120,
9
Отв. Через 21 гт минуты.
433. Обозначим через t время следования поезда от А
до С (в часах) и через г>—установленную скорость (в км/час).
По условию путь АВ пройден за я- час. при скорости
vkm/чос, а путь ВС — за -я-час, при скорости 0,75. vkm}4uc.
Значит, АВ = v -* км и ВС = 0,75 « v -j кмщ По условию на
обратном пути участок СВ был пройден со скоростью v,
а участок В А — со скоростью 0,75 v. Значит, участок СВ был
496 ГЛ. 7. АЛГЕБРАИЧЕСКИЕ И АРИФМЕТИЧЕСКИЕ ЗАДАЧИ 247
пройд€и за время ■' <Уг: v% т. е. за -Др час, а участок ВА —
8а ^-; 0,75 vf т. е. за 2 0- час. По условию
_1 . 0,75/_ 5 , ,
2-0,75 "1 2~~I2~t"'#
От*. 10 час,
434. Положим, что велосипедист ехал со скоростью
v км/нас; тогда скорость, которая предусматривалась, равня-
лась (v—1) км/нас. Фактически велосипедист был в пути
3.' 30 г,
— час, а полагался срок . час. По условию
30 30 3
V — 1 1>~~60'
Отрицательное решение г> = — 24 не годится.
Отв. 25 км/час.
435. Пусть скорость поезда по расписанию составляет
лг км/час. Тогда фактическая скорость была (дг+ 10) км'час.
30
Продолжительность пути по расписанию —час,, а фактиче*
80 „
екая г ючас' условию
80 80 16
х дг + Ю^бО*
Отв. 50 *л/*ас
436. Первую половину пути поезд шел х час. Тогда,
чтобы придти бев опоздания, он должен был пройти вторую
половину за х — -j часа. В первую половину пути скорость
420 420
поезда — км/час, а во вторую г- км/час. По условию
*-■5
420 420=2
1
Уравнение имеет один положительный корень.
От*. 21 час.
248 ОТВЕТЫ И РЕШГНИЯ 437
437. Пусть скорость первого поезда л? км/час, скорость
второго у км/нас. 3 первом случае первый поезд пройдёт
до встречи 10* км, второй 10 укмт Следовательно,
IOjc-Ь 10у = 650.
Во втором случае первый поезд пройдёт до встречи Ьх км%
а второй (который шёл 8 час,+ 4 часа 20 мин. = 12-^ часа)
пройдёт 12-j у. Следовательно,
8х-|-12уу = 650.
Отв. Средняя скорость первого поезда 35 км/час, вто-
рого—30 км\час*
438. Пусть скорость первого поезда х км/час, а вто-
рого у км/час. Расстояние и 600 км первый поезд проходит
600 600 п
за — час, а второй — за — час. По условию
600. з —— ?^а —
г ■ у ' л: ет у '
Отв. Скорость первого поезда 50 к -/час, второго —
40 км/час»
439. Если длина пути х кмь то при скорости 3,5 км/час
дачник пройдёт это расстояние за %-? часа. А так как >и
опоздает к поезду на час, то в момент его выхода до отхгма
поезда оставалось (т^— 1) час. Через час после вых<,и
дачника оставалось до отхода поезда hp- — 2)часа, апроши
нужно было ещё 'кх — 3,5) км. При скорости 5 км/час
y 35
дачник пройдёт это расстояние за ~ час. Так как он
о
нрид€т за -я- часа от отхода поезда, то
х_ 9 а- — 3,5 I
3.5 * 5~ "~2#.
Отв. 21 км.
443 ГЛ. 7. АЛГЕБРАИЧЕСКИЕ И АРИФМЕТИЧЕСКИЕ ЗАДАЧИ 249
440. Пусть скорость велосипеда л: /см/мин, а автомобиля
у км/мин. Автомобиль пробыл в пути 10 мин., а велосипе-
дист 10-}-15 = 25 мин,, когда его догнал автомобиль.
В этот момент расстояния, пройденные ими, были одинаковы.
Следовательно, 25х=10ру. Когда на обратном пути автомо-
биль встретил велосипедиста, автомобиль прошёл 50у км,
а велосипедист 65х км. Эти расстояния в сумме дают двой-
ное расстояние от Москвы до Мытищ. Поэтому 65jc -f- 50j/ = 38.
Решая систему уравнений, находим л: = 0,2; у = 0,5.
Отв* Скорость велосипедиста 0,2 км!мин=\2 км1час\
скорость автомобиля - 0,5 км/мин = 30 км/час.
441. Пусть поезда встретились через х час* после вы-
хода скорого поезда. Тогда почтовый поезд в момент встречи
находился в пути (лг + З) часа. До места встречи каждый
поезд прошёл 1080:2 = 540 (км). Значит, скорость первого
540 540
поезда — км/час, а второго - , » км/час. По условию
640 540
"з г-а^3!^. Годится только один корень # = 9.
* X -р о
Отв. Через 9 час. после выхода скорого поезда.
442» Пусть первый велосипедист ехал х час. Рассуждая,
36 42
= 4.
квк в предыдущей задаче, составим уравнение -_.— —
Отв. Скорость первого велосипедиста 14 км/час, а вто-
рого 18 км/час; первый ехал до встречи 3 часа, а второй
2 часа.
443. Пусть расстояние АВ между пунктами отправления
есть х кму и пусть первый пешеход пройдёт его за у час.
По условию второй проходит путь ВА за (у — 5) час.
Значит, за час первый проходит — км, а второй ■ км.
За час расстояние между пешеходами сокращается на
(у+у^)км*™гТ чает—на3т(7+7^* Так как
через Зтг часа они встретились, то 3-я-Г— -f- -—75)«^ *•
250 ОТВЕТЫ И РЕШЕНИЯ *44
Так как х Ф О, то обе части можно разделить на х. Получаем:
ч(}+^)-..
Отсюда находим ут Значение х остаётся неопределённым.
Отв. Первый пройдёт всё расстояние за 10 час, второй —
за 5 час.
444. Обозначим пункт встречи через С. Пусть АС = х км;
тогда по условию СВ — (х-{- 12) км. Далее, по условию пер-
вый турист прошёл путь СВ за 8 час. Значит, его скорость
Л "JT ■ км/час. Так же найдём, что скорость второго туриста
^г км/час. Следовательно, путь АС первый турист проделал
х 4- 12 8л:
за л: : -~— = - , 12 час, второй же турист прошёл путь ВС
9 (JC+12) * « - а
ва _л_1—i чаСв а так как второй был в пути на 6 час.
больше, чем первый, то
9(jt+12) 8х _fi
х лг-И2 '
При решении этого уравнения можно ввести вспомогательное
х -4- 12 8
неизвестное ^" =г. Получим 9z = 6. Из двух кор-
(4 2\
2t = -g- и 2g = — -g-j второй не годится, так как обе
величины х = АС и х-^-12 = СВ должны быть положитель-
ными. Из уравнения —-*-— = -j найдём х = 36. Значит, ЛС=:
= 36 км, СВ = 48 км.
Oma. АВ = 84 км. Скорость первого туриста 6 км\час\
скорость второго туриста 4 км/час,
445.3адача сходна с предыдущей. Пусть дирижабль пролетел
до встречи л: км\ тогда самолёт до встречи пролетел (л:4-100) км.
х -4- 100
Скорость дирижабля —-21— км/час; скорость самолёта
—г- км/час. От своего аэродрома до места встречи дири-
х -1- 100 3je
жабль летел х:~^—= QQ час; самолёт же летел от
446 ГЛ. 7. АЛГЕБРАИЧЕСКИЕ И АРИФМЕТИЧЕСКИЕ ЗАДАЧИ 251
I j (х + 100)
своего аэродрома до места встречи — час. Полу-
чаем уравнение
х + loo e * » т. е. ^+l00; — 9.
Следовательно, - , 10^=д± -*-, откуда #=:200; второй ко-
рень не годится.
Отв. Расстояние между аэродромами 500 км; скорость
дирижабля 100 км/час; скорость самолёта 150 /см/час.
446* Первый способ* Можно решать, как предыду-
щую задачу. Получим уравнение
/ х \« £ х yit
Отсюда
Затем найдём скорости
1 ^ т %1ев* п *
Второй способ. Обозначим через С точку встречи.
Так как первый пройдёт расстояние СВ за т часов, го
СВ*»югт км. Аналогично CA^v^t км> По условию
С А— СВ = а. Получаем уравнение «г>9—mvx*=a> На про-
хождение участка АС первый пешеход затратил время— час;
значит, с момента его выхода до встречи прошло %£ час.
Аналогично с момента выхода второго пешехода до встречи
прошло 2*2 час. Так как оба вышли одновременно, то
дйждй, Из последнего уравнения находим vt:щ«
*=УИ\Ут.% Это уравнение решаем совместное первым.
252
ОТВЕТЫ И РЕШЕНИЯ
447
Для симметрии полезно ввести вспомогательное неизвестное
/t=ira-p:, Подставляя в первое уравнение выражения
vx = Vnt\ v4 = Vm '# получим (л ^Ля—mYn)t = а, откуда
*==—7=^- т=г; теперь находим:
я ут — туп
i [ *П f—f f
Замечание. Задача имеет решевие только в том случае,
когда я !Ля> тУТ; деля обе частн^того неравенства на положи-
тельное число УтУщ получаем Уп > Ут, т. е. п>т. Эго >с-
ловне можно получить и иепосредствеиио из условия задачи: так
как до встречи первый пешеход прошёл большее расстояние, чем
н горой, то его скорость больше, чем скорость второго. С другой
с то ров ы, персому пешеходу до конца пути остаётся пройти меньше»
чем второму. Следовательно, первый при нет в В скорее, чем второй
придёт в А
Отв. Скорость первого пешехода —.„" п—т=- км/час,
_ п ут — туп
скорость второго — *у т .-+ км/час.
v r nYm — тУп
447, Пусть в 1 сек. первое тело пробежит х градусов,
ЗЬО 3G0
а второе у градусов. Из первого условия находим ——— — 5.
у ■*
Каждую секунду расстояние между телами (по дуге) увели*
чивается на (х—у) градусов. За время, протекающее от
одного схождения до следующего (т. е. за 100 сек.) рас-
стояние должно увеличиться на 360°. Поэтому 100(х—^)=э
= 360. Полученная система имеет два решения (jct = 18,
ylSal4(4; Л'а = —14,4, у2 — —\$). Оба они годятся, но
физический смысл их один и тот же (меняются только но-
мера тел и направление движения).
Отв. 18е; 14°24'.
448» Обозначим скорость одного тела (выраженную в
м{мин) через х% а скорость другого—-через у* Положим,
что х>у. Пусть тела движутся в одном направлении и
сходятся о некоторой точке Д. Пусть ближайшая следующая
449 ГЛ. 7. АЛГЕБРАИЧЕСКИЕ И АРИФМЕТИЧЕСКИЕ ЗАДАЧИ 253
встреча происходит в точке В (заранее не исключается,
что точка В совпадает с точкой Л; это будет, например,
в случае, если скорость первого тела вдвое больше скорости
второго; в этом случае до ближайшей встречи первое сде-
лает два полных оборота, а второе — один).
На пути от А к В (этот путь может для одного тела
или для обоих перекрывать сам себя) второе тело отстаёт
от первого, и в момент ближайшего совпадения отставание
составит длину полной окружности. Так как между двумя
ближайшими соединениями тел протекает 56 мин., за кото-
рые первое тело проходит 56л: м, а второе 56у и, то длина
окружности равна 56а; — 56у.
Пусть теперь тела движутся в противоположных напра-
влениях. Тогда пути, пройденные ими за время, протекающее
между двумя ближайшими встречами, т. е. за 8 мин., в сумме
составят длину окружности. Следовательно, длина окруж-
ности равна 8х + 8j/, Имеем уравнение 56л: — 56^ = 8х -j- 8j/.
В условии задачи сказано далее, что за 24 сек. расстоя-
ние между ними уменьшилось на 40 —26 ==14 (м). За ти
24 сек, тела не встречались; поэтому уменьшение расстоя-
ния равно сумме путей, пройденных телами за 24 сек. =
= -г мин. Получаем второе уравнение
Oms, 20 м/ман; 15 м/мин\ 280 м.
449. Пусть х и ^у—положительные числа, выражающие
скорости точек в соответствующих единицах Гесли с—дли-
на окружности з метрах» то единица скорости 1 м/сен и
т. п.; в задаче не указано, в каких единицах измеряется
длина). Положим/что х > у. Тогда имеем систему уравнений;
** — (у = с; у — ^ = п
(вывод первого уравнения см. в предыдущей задаче). Под-
становкой находим уравнение
«гу* + лсу — с*=*0.
254 ОТВЕТЫ И РЕШЕНИЯ 450
с (у л2 4-4л/ я)
Его положительный корень j/ = -AJ.—^- -(второй ко-
рень отрицательный).
с (V5P"-I- 4л/ 4- fi)
Отв. Ббльшая скорость численно равна ———^-—-*—-,
меньшая скорость *г ' -.
450. Пусть скорость парохода в стоячей воде х км/час*
Имеем уравнение j-p + jz^^S-g-f
Отв. 20 4см/час.
451. Отв. 9 км\час.
452. Пусть скорость течения х км/час, а скорость лодки
в стоячей воде у /см/час. Первое условие даёт уравнение
90 90 9
—ц f-—— = 10, второе условие—уравнение J_ =»
= —;—, Для решения этой системы удобно положить
У ~гх
1 1
7+7 = * y^F = v-
Решая систему
20« +20^=10; 2v = Zu,
находим
5
откуда * = ■£-,
От*. -^ /см/час.
453. Пусть плот проплывает расстояние а км от Киева
до Днепропетровска за х суток. Тогда его скорость, равная
скорости течения Днепра, есть -~ км/сутки. По условию
скорость парохода, идущего по течению, равна ~ км/сутки*
455 ГЛ. 7. АЛГЕБРАИЧЕСКИЕ И АРИФМЕТИЧЕСКИЕ 8АДАЧИ 255
Следовательно, скорость парохода в стоячей воде будет
(^——) /см/сутки, А так как скорость движения паро-
хода против течения составляет -*- км/сутка, то скорость
его в стоячей воде равна (^ + —) км/сутка. Имеем урав-
нение
а а а . а
3+7'
Отв. 12 суток.
454. Пусть скорость первого тела х м/сек, а второго —
у м/сек. Первая встреча происходит при движении первого
тела ох А к В (черев 10 сек. после выхода второго тела,
т. е. через 10 4*11 = 21 сек. после выхода первого тела).
Получаем уравнение 21л: -|— 10_у = 301. Вторая встреча про-
исходит при обратном движении первого тела (через 45 сек.
после выхода второго тела, т. е. через 56 сек. после выхода
первого тела). Если С есть пункт второй встречи, то пер-
вое тело проходит расстояние АВ-\-ВС, а второе —расстоя-
ние ВС. Разность этих расстояний есть ^45 = 301 м. Имеем
второе уравнение 56jc — 45^ = 301.
Отв. Скорость первого тела 11 м/сек, второго-—7 м/сек*
455. Пусть скорость при движении в гору х км/час, по
ровному месту—у /см/час и под гору — г км\час. Вернув-
шись обратно с полпути, посыльный прошёл 14:2 = 7 км;
3 км он шёл в гору, 4 км — по ровному месту, потом (на
обратном пути) ещё 4 км по ровному месту и, наконец,
3 км под гору. По условию
3,4,4,3 03 3.8,3 03
— — = 3-=-, т. е. — — = 3-=-.
х ' у ' у ' z 5 ' х * у* z 5 ,
Два других условия дают:
Т^У"1""^ §б' Г^Т"1"^"" 20*
Находим -—, -~, —, а затем х, у, г,
х у я
Отв. В гору 3 км/час; по ровному месту 4 км/час; под
гору 5 км/час*
256 ОТВЕТЫ И РЕШЕНИЯ 45в
456. Пусть норма х листов в день и срок у дней. Тогда
по условию
(х + 2)(у — Ъ)*тху и <jc + 4)0, — 5) = ху.
Отв. 120 листов, 15 дней.
457. Пусть рабочий сделал х деталей в у дней. Тогда
ежедневно он изготовлял — деталей. По условию, если бы
он ежедневно изготовлял — —|— 10 деталей, он выполнил бы
работу за у — 4-^ дня. Значит, \Т~^^)(у — ^f)—*-
Другое условие даёт уравнение (——» 5 j(_y -f- 3> == jc. Полу-
чаем систему уравнений:
-5j/ + 3i=*15.
Помножаем второе уравнение на 2 и складываем с первым;
получаем — = 50. Подставляя это значение во второе урав-
нение, находим _у = 27. Следовательно, лг = 50у = 1350.
Замечание. Эту задачу можно решить как предыдущую»
если вместо неизвестного х ввести величину г — число деталей, изго-
товляемых в день. Получилась бы та же система ураввеннй, где ве-
личина -— была бы заменена через г.
У
Отв. Рабочий сделал 1350 деталей ва 27 дней.
458. Пусть ежедневная норма машинистки jc листов,
а срок окончания работы у дней; тогда работа содержит ху
листов. По условию, вырабатывая в день jc-J-2 листа, ма-
шинистка затратит у — 2 дня. Значит, работа содержит
(х-{-2) (у — 2) листов. Следовательно,
(х + 2)(у — 2) = ху.
Таким же образом получаем другое уравнение
(jc + 0,60*) (у — 4) = ху -+- 8.
Ошв* Норма 10 листов в день; срок исполнения 12 дней.
462 ГЛ. 7. АЛГЕБРАИЧЕСКИЕ И АРИФМЕТИЧЕСКИЕ ЗАДАЧИ 257
459. Пусть первый рабочий выполняет работу в х час.
Тогда имеем уравнение 1—х*То = 1Г'
Отв. Первый рабочий может выполнить всю работу в 12 час,
второй — в 24 часа.
460. Если первая труба наполняет бассейн в х час, то
вторая наполняет его в (л; -J- 5) час. Условие задачи даёт
уравнение
I-L-1--1
х^х + 5 б#
Ошв, Первая труба наполняет бассейн за 10 час, вто-
рая— за 15 час.
461. Пусть, работая отдельно, первый может выполнить
работу за х час, а второй — за у час Тогда в один
час первый выполняет — часть всей работы, а второй —
1 15
часть. По условию 7 • —f- 4 • — = -g. После совместной
четырёхчасовой работы первый отработал 7 -f- 4 = 11 час,
а второй 4-f-4 = 8 qac. По условию оба вместе выполнили
1 — 75 ^ IS всей Раб°ты' Следовательно, 11 • —j- 8 • — = т^.
Помножая первое уравнение на 2 и вычитая из второго, на-
13 11
ходим 3»— = тё, откуда #=18. Затем находим — = 04»
откуда у = 24.
Owe. Первый мог бы выполнить работу за 18, второй — за
24 часа.
462. Обозначим искомые числа через х и у. Четыре
крана большей мощности работали 2 -{-3 = 5 час; два крана
меньшей мощности работали 3 часа. Поэтому (см. решение
предыдущей задачи)
4.5-- + 2-3.1 = 1.
х ' у
Второе условие даёт
4-4
Отвь В 24 часа; в 36 часов.
4.4,5-1+2'4,5.1=1.
' х ' У
258 ОТВЕТЫ И РЕШЕНИЯ 463
463. Пусть трехтонная машина может перевезти груз за
л; час, а пятитонная — за у час. По условию (см. решение
задач 461—462)
30 .8 . — + 9 • 6 • — = 1 и 9.8.-4-30.6.1 = ^'
х ' у у ' х 15
Отв. jc = 300; _у = 270; 30 пятитонных машин перевезут
груз за 270:30 = 9 час.
464. Пусть первой машинистке для выполнения всей ра-
боты требуется х час> а второй—у час. Когда первая про-
работала 3 часа, вторая проработала 2 часа. Обе они вы-
9 11
полнили 1 — 5о = 9о всей работы. Получаем уравнение
х^у 20 е
По окончании работы машинистки сделали поровну, т. е.
каждая сделала половину работы,- Значит, первая потратила
i- час, а вторая =£- час. А так как первая работала на час
дольше, чем вторая, то
2 2 1р
Система имеет два решения, но одно не годится, так как
даёт для" у отрицательное значение.
Отв. Первая машинистка в 10 час, вторая в 8 час.
465. Задача сходна с предыдущей. Получаем уравнения
2_ , 1£— П. ±_У_ 1
х~Т~ у ~~30' 2 2 = 2»
где х и у — продолжительность пробега поездов (в часах).
Из двух решений системы годится одно.
Отв. 10 час; 9 час
466. Пусть в одну минуту через первый кран поступает
х л, а из второго вытекает у л. По условию полная ванна,
вмещающая 2X9X2,5 = 45 л, при действии обоих кранов
опорожняется в 1 час Значит, в 1 мин. количество воды
45 3 3
уменьшается на сб = тЛв Следовательно, у — я = -рСдру-
468 ГЛ. 7. АЛГЕБРАИЧЕСКИЕ И АРИФМЕТИЧЕСКИЕ ЗАДАЧИ 259
гой стороны, через один первый кран ванна наполняется
за -- мин., а через один второй она опорожняется за — мин.
По условию
Система уравнений
45_45 ==5
х у
3
х у
имеет два решениям^ = 2-^-;^ = 3ил:2 = — 3;_уа = — 2 -Л.
Второе решение не годится (jc и у должны быть положитель-
ными числами).
Отв. 2-^л/ман\ 3 л/мин.
467. Пусть срок окончания есть х дней; тогда суточный
8000
план кубометров. Бригада работала х — 8 дней; зна-
■*" 8000
чит, ежедневно вынималось ^ кубометров. По условию
8000 8000 м т, * „ /
___ = 50. Из двух корней этого уравнения (хг = 40
и л:2 =— 32) годится только положительный л: = 40. Зна-
чит, суточный план составлял ==200 кубометров; пере-
выполнение плана на 50 м* составляло
50-100 5
200 /о-
Отв. Срок окончания 40 дней; процент перевыполнения 25.
468. Пусть первая бригада ремонтировала х км в день;
тогда вторая ремонтировала (4,5 — х) а в день. Первая
бригада работала — дней; вторая ±с__х дней. По условию
__—= 1. Уравнение имеет корни хг = 2 и х2 = 22,5.
Второй не годится, так как по смыслу задачи число 4,5 — х
должно быть положительным.
Отв. Первая бригада ремонтировала 2 км, а вторая 2,5 км
пути в день.
260 ОТВЕТЫ И РЕШЕНИЯ 469
469. Пусть первый рабочий может выполнить всю ра-
боту за х час., а второй — за у час. Значит, половину ра-
боты первый сделал за -^ час; остальную часть (т. е. тоже
половину) второй сделает за ^час» ^° условию уЬ? вя ^*
Другое условие (см. решение задачи 461) даёт —Ь"7в12'
Отв. Один из рабочих (либо 1-й, либо 2-й) может выпол-
нить работу в 20 час.» другой — в 30 час.
470. Пусть один трактор может вспахать поле да х дней,
а другой — за у дней. Имеем (ср. предыдущую задачу) си-
стему уравнений:
х + у t ч 2^2~ *■
Её можно заменить системой je-j-j> = 2&; xy = 2kU
Отв. Один из тракторов за (k-\-Y№ — 26/) дней; дру-
t k
гой — за (k—у б2— 2й/) дней. Задача возможна при -* >/.
471. Пусть все три землечерпалки, работая вместе, могут
выполнить работу в х дней. Тогда одна первая может выполнить
работу в (je-f-10) Дней. одна вторая — в (je-{-20) дней и
одна третья —в блг /шей. В один день первая машина вы-
полнит —х"Тп часть Работы, одна вторая - 2л часть,
третья g— часть, а все вместе — часть работы. Имеем урав-
нение
jc+I0~x + 20t6jc х*
Отв. Работа может быть выполнена первой землечерпал-
кой в 20 дней, второй — в 30 дней и третьей — в 60 дней,
472. Если второй рабочий может выполнить работу за х
дней, то первый — за (х-\~Ъ) дня. Первый рабочий, про-
7
работав 7 дней, выполнит . а всей работы; второй, про-
работав 7-—1-g- =5-^ дней, выполнит — всей работы.
474 ГЛ. 7. АЛГЕБРАИЧЕСКИЕ И АРИФМЕТИЧЕСКИЕ ЗАДАЧИ 261
Получаем уравнение
* ■ 4
Отв. Первый рабочий выполнит всю работу за 14 дней»
второй — за 11 дней.
473. Пусть первым трактором можно вспахать всё поле
да х дней, вторым — за у дней. Первое условие даёт
1+1 = 1
х^ у 8*
Первый трактор может вспахать половину поля за ^я-хдней.
По условию другая половина может быть вспахана двумя
тракторами за ПО — тг*) дней. Отсюда получаем второе
уравнение
1 _±_ 1
1
1
у ie-4*
Сравнивая два найденных уравнения, получаем #
I
1 1
Ю — jx
Отсюда jc=12; подставляя в первое уравнение, находим
j>«24.
Отв. Первым трактором можно вспахать поле за 12 дней,
вторым — за 24 дня.
474. Так как рабочие приступали к работе через равные
промежутки, и вследствие этого первый проработал в 5 раз
больше времени, чем последний, то число рабочих было
равно 5. Если последний работал х час, то общее число
человеко-часов было х -J- 2х -|- 3jc -J- 4jc -J- 5jc & 15jc. По
условию, работая впятером, оии могли бы выполнить ту же
работу в 6 час. Следовательно, 15дг» 5 • 6, откуда х *=» 2.
Работа по прорытию канавы продолжалась столько времени,
сколько работал первый рабочий, т. е. 5х час.
Отв. Работа продолжалась 10 час.
262 ОТВЕТЫ И РЕШЕНИЯ d7S
475. Пусть первый рабочий может выполнить работу за х
час; получаем уравнение
J_+_L_-+± = 1
Отв. x = j (5/ — 2 + /2б/в + 4/ + 4).
476. Пусть первый кран наполняет бассейн за # час,
8 второй — за у час. За 1 час первый кран наполнит —часть
бассейна, а по условию он был открыт (-*гу) час., значит,
1
вода из первого крана заполнила часть бассейна. Анало-
1
3"*
гично найдём, что вода из второго крана заполнила часть
—i 13
бассейна. Так как после этого заполнилось тб бассейна, то
М у -L-L £ —I?
3 * х~т~ з у — 18\
Второе условие даёт уравнение
J-J.JL — Л
л- "+" у ~ 18е
Эту систему можно решить следующим образом. Если
у
положить — = г, то первое уравнение примет вид
I 1 ] _ 13
3 г+3 ' г ~ 18"
3 2
Отсюда ^ == -п; га == -^. Второе уравнение представим
в виде
Подставляя сюда — == у» найдём д> = 9; значит, х =
2 у 2
= —_у=6. Подставляя ^- = -я-. найдём ^ = 6 и jc = 9.
Отв. Один из кранов наполняет бассейн за 6 час, дру-
гой— за 9 час.
Ill
480 ГЛ. 7. АЛГЕБРАИЧЕСКИЕ И АГИФМЕТИЧЕСКИЕ ЗАДАЧИ 263
477. Если норма ежедневной кладки была х тысяч штук,
а в действительности укладывали у тысяч шгук в день, то
будем иметь систему уравнений
/120 120 4
I Зу — 4д; = 5.
Отв. Норма в день 10 тысяч кирпичей; в действитель-
ности укладывали 15 тысяч кирпичей.
478. В следующей таблице даны последовательные коли-
чества воды (в литрач) в трёх сооу4ах 0» "» Ш):
j х; 2 х. 2.*. и[х(7*+^) + *]+7*;
" У 7*+* Щ*+у)%> Щ*+у}
« « Ki*+y)+« га[т(т*+>)+4
Каждое из выражений последнего столбца по условию равно 9.
Отв. 12 л% 8 л, 7 л.
479. Если первый раз вылили л: л спирта, то осталось
64— к
(64 — х) а спирта; второй раз было отлито —гг—л:л чистого
спирта. Осталось
чистого спирта. Получаем уравнение
1(64-*)* =49.
Отв. Первый раз вылили 8 л спирта, второй раз 7 л.
480. Перелив х л спирта и дополнив второй сосуд во-
дой, будем иметь во втором сосуде ^ л спирта на каждый
литр смеси. Обратно переливается х л смеси; в них содер-
жится gfi^ — oo^ спирта. После обратного переливания ко-
личество спирта в первом сосуде составляет (20—•* + -]?}) л*
Теперь из первого сосуда отливается 69/а л смеси, т. е.
264 ОТВЕТЫ И РЕШЕНИЯ 481
-яЗ составляет -я- всего количества этой смеси. Вместе с тем
на -х- уменьшается и количество спирта, т. е. в первом
сосуде остаётся з"(20— ЛГ4~2о) л спирта. Так как коли-
чество спирта в обоих сосудах неизменно равняется 20 л9
а по условию в обоих сосудах теперь содержится одинаковое
количество спирта (т. е. по 10 л), то
т(м-*+а5)-10-
Отв. 10 л.
481. Пусть из сосуда выпущено х л воздуха и введено
такое же количество азота. В оставшемся количестве (8 — х) л
воздуха содержится (8 — л:) ОД 6 л кислорода. Это количество
о 1 (8 — д:)0,16
приходится на 8 л смеси, так что на 1 л приходится -ф л
кислорода. Следовательно, когда вторично х л смеси заме-
няется х л азота, остающееся количество (8 — х) л смеси со»
держит * "g1 ' «(8 — дг) = (8 — xf • 0,02 л кислорода. Зна-
чит, по отношению к общему количеству смеси (8 л) содер-
жание кислорода составляет * """р—•—. 100 = ^ ~х* . По
/о „\2 о *
условию v 4 } = 9. Из двух корней (хх = 2, дг2 = 14)
годится только первый, так как больше 8 л выпустить нельзя.
Отв. 2 л.
482. Пусть у первой колхозницы было х яиц, а у второй
у яиц. Если бы первая продала у яиц, то, по условию, вы-
ручила бы 72 руб. Следовательно, она продавала яйца по
72 72
— руб. за штуку и выручила — х руб. Таким же образом
32
найдём, что вторая выручила —у руб. Имеем два уравнения:
м (У V 72 у 3 ,
Из первого находим (^ 1 я^, откуда ^я^ (отрица-
тельное значение — » — -к- не годится).
X £
Отв. У первой было 40 яиц, у второй 60 яиц.
486 ГЛ. 7. АЛГЕБРАИЧЕСКИЕ И АРИФМЕТИЧЕСКИЕ ЗАДАЧИ 265
483. При обозначениях предыдущей задачи получаем си-
стему
х у .
mJ = nx' Х+У = а-
Из первого уравнения находим х :у == У~п - Vm- Делим за-
тем а на части, пропорциональные ]/~п и V т*
Отв. У первой -==4—— л9 у второй ,_ •—= л.
Ym + УЧ Ym+Yn
484. Пусть первый двигатель расходует в 1 час л: г бен-
зина, а второй —у г; тогда 600 г бензина первый израсхо-
600
довал за — час, а 384 г бензина второй израсходовал за
384 „ 600 384 0 „ -
■— час. По условию = 2. Если бы первый расхо-
довал в 1 час у г бензина, то за —час. расход бензина был
- 600 - -
бы — • у г, а если бы второй расходовал в 1 час х г,
384 - 384
то за — час. он израсходовал бы х г; по условию
бООу 384л:
х = у •
Отв. Первый расходует 60 г\час, второй — 48 г[час.
2
485. В х кг первого сплава содержится -?■ х кг золота и
■£- х кг серебра. В (8 — л:) кг второго сплава содержится
3 7
Уд (8 — х) кг золота и т^(8 — х) кг серебра. Получаем урав-
нение
[т*+й(8-*)]:[т*+и<8-*)]-б!П-
Отв. 1 кг первого сплава и 7 кг второго.
486. См. решение предыдущей задачи.
Отв. 9 вёдер из первой бочки и 3 ведра из второй.
266 ОТВЕТЫ И РЕШЕНИЯ 437
487. Пусть третий сплав содержит х частей первого и
у частей второго сплава, т. е. на х кг первого сплава при-
ходится у кг второго сплава. Тогда в (х-\-у) кг третьего
сплава содержится nr * 4" ТУ) кг пеРвог0 металла и
(о я \
-s-jc + -г>) кг второго металла. По условию
Приведя делимое и делитель к общему знаменателю (15) и
деля их на yt получим
(5| + б):(10.|+9)=17:27,
х 9
откуда 7=-з5*
Отв. На 9 частей первого сплава нужно взять 35 частей
второго сплава.
488. Пусть в 1 мин. большее колесо делает х оборотов,
а меньшее—у оборотов, у>х. Имеем уравнения
у — jc = 400; ---«1.
* х у 60
Второе уравнение можно представить в виде ху = 300 (у — х)у
т. е. ху= 120000.
Отв. Большее колесо делает 200 оборотов в минуту,
меньшее — 600 оборотов.
489. Пусть окружность переднего колеса равна х дм,
а окружность заднего — у дм. Имеем два уравнения:
180 180 1Л 180 180 л
х у х + Ь у —6
Первое преобразуется к виду 18 (у — х) — ху; второе —
к виду 39 (у — л:) = ху + 504. Из этих двух уравнений
найдём у — jc = 24; jry=432.
От$т Окружность переднего колеса 12 дм, заднего —
36 cj*.
4&* ГЛ. 7. АЛГЕБРАИЧЕСКИ): И АРМФМЕГНЧкСКИЕ ЗАДАЧИ 267
2
490. В первый и третий дни било выгружено 600 * -*- =
«= 400 от; во второй лень выгружено 600 от — 400 от — 200 т.
Пусть в первый день выгружено х от; тогда в третий день
погружено (400 — х) от. Уменьшение выгрузки по второй
день по сравнению с первым днём было (х — 200) т, что
(.V — 200) 100 0/ .,
составляло % 0т выгрузки первого дня. Умень-
шение выгрузки в третий день по сравнению со вторым
днем было 200 — (400 — jc) == (jc—200)/к, что составляло
(г —200) 100 0/ х — 200 п/ ,-,
ЙдГ '° или —v-^ /о выгрузки второго дня. По ус-
ловию
х — 200 (* — 200)100
2 х ==0'
Найдём два корня л;, =250; *2=160. Второй корень не
годится, так как по условию выгрузка с каждый днём
уменьшалась, между тем как при х=160 выгрузка соста-
вляла бы: в первый день 1GJ от. во второй 200 от и в тре-
тий 240 от.
Отв. В первый день было ныгружено 250 от, во второй
200 от, в третий 150 от.
491. Пусть первый раствор весит х кг, тогда второй
песиг (10 — х) кг. Процентное содержание безводной серной
0.8.100 80 O.iMOO
кислоты в первом растворе ==3 F* а в0 ВТ0Р0М mZZ— ~
<>0
= тл , По условию
SO 60 _ ,л
х ~~ 10-л- ~~ lU'
Уравнение имеет два положительных корпя х1 = 20 и а:2 = 4.
Так как по условию лг< 10, то первое решение не годится.
Отв. 4 кг и 6 кг.
492. Если в первом сплаве было х°/0 меаи, то во второч
было (л: + 40)%. Первый сплав весил — кг, а второй —
12-100 - то , 1200 -л
утро *г* Пол>'чаем Уравнение — + 7 + 40"в 50"
Отв. 20% и 60%.
268 ОТВЕТЫ И РЕШЕНИЯ 493
493. Пусть скорость товарного поезда х м\сек^ а пасса-
жирского у м/сек. За 28 сек. товарный поезд прошёл 28 х(м\
а пассажирский 28 у(м)\ получаем уравнение
28л:+ 28^ = 700.
490
Товарный поезд идёт мимо светофора сек., а пассажир-
« 210 п
ский сек. Получаем второе уравнение
490 210 _ 35
х у
Отв. Скорость товарного поезда 10 м/сек, т. е. 36 км!час,
пассажирского—15 м/сек, т. е. '54 км/час.
494. Если число четырёхосных цистерн равно х, то число
двухосных равно (х -f- 5). Если одна двухосная цистерна весит
у т, то одна четырёхосная весит 3 у т. Вес нефти в двухосной
цистерне равен (40 • 0,3) т=\2 т. Четырёхосная цистерна
с нефтью весит (3^ + 40)/п, а двухосная (у-{-\2)т. Имеем
первое уравнение
*(33>+40) + (* + 5)(jy+12) = 940.
Вес нефти во всех четырёхосных цистернах (40 х)т, а вес
всех гружёных двухосных (х-1г5)(у-\-12)т. Имеем второе
уравнение
40х —(* + 5)(>+12)=100.
Отв. Четырёхосных цистерн было 10, весом каждая по
24 т, двухосных цистерн было 15, весом каждая по 8 т.
495. Пусть первая машина проходит в день х м, а вто-
рая у м. В первом случае первая машина выполнила бы 30°/0
„ - - 60л: -30 , п i ч
всей работы, т. е. прошла бы —щ-= \8х(м), а вторая
60-.у.80 1Д , х
300 = 16-У <*>■
Имеем уравнение
18л;+16^ = 60.
2
Во втором случае первая машина прошла бы -^ • 60^ (м),
затратив на это -% • 60 • ^ дней. Вторая машина затратила бы
497 ГЛ. 7. АЛГЕБРАИЧЕСКИЕ И АРИФМЕТИЧЕСКИЕ ЗАДАЧИ 269
3 х
_ . бо . — дней. Имеем второе уравнение
40у _ 18л: = g
х у
Полученная система легко решается, если положить ¥. = z.
К задаче подходит положительное значение £ = -г.
4
Отв. Первая машина проходит в день 2 м тоннеля;
вторая » » » » 1у л ».
496. Пусть первая бригада может отремонтировать участок
пути в х дней, а вторая — в у дней. По условию задачи имеем
систему уравнений
I + 1-I
х^ у 6'
40£__40у _о
100 300 '
О/п*. Первая бригада может отремонтировать участок
в 10 дней, вторая — в 15 дней.
25
497. Пусть первая часть груза (составляющая -^--690 =
е=375 т) была перевезена за х час, и каждая трёхтонная ма-
шина делала у поездок в час. Тогда каждая полуторатонная
машина делала (у-\-1) поездку в час. По условию вторая
часть груза (т. е. 690 — 375 = 315 т) была перевезена за
(л: — 2) часа, причём трехтонные машины делали по 0>+1)
поездок в час, а полуторатонные — по {у-\-1)+ 1 = (у-\-2)
поездок. Получаем систему уравнений
5 • Ъху + 10 • 1 у х(у +1) = 375,
5.3 (л; — 2)(jy+l) + 10.li-(* — 2)Су + 2) = 315.
После упрощений эти уравнения примут вид
\ 2ху-\-Ъх — 4у = 27.
Вычитая первое уравнение из второго, получим 2х — 4у = 2.
Отсюда 2у = х — 1. Подставляя в первое уравнение,
270 ОТВЕТЫ И РЕШЕНИЯ 498
получим х* = 25, т. е. х = 5. Первая часть груза была переве-
зена за 5 час,, вторая — за 5 — 2 = 3 часа.
Отв. Груз перевезён за 8 час; трёхтонные машины вна-
чале делали по 2 поездки в час; полуторатонные—по 3
поездки в час.
498. Если х — ширина дорожки, то площадка вместе
с дорожкой содержит (а -f- 2л:) (Ь + 2х) м*. Имеем уравнение
(a-\-2x)(Z>-\-2x) = 2at>.
Отв. i[/(a + 6)a-j-4a£ — (a + 6)].
499. Число стульев в каждом ряду обозначим через х\
тогда число рядов равно —. Получаем уравнение
(х + Ь)(±—с)*=1ш\а.
После упрощений имеем:
10сх*^(а-\-№с)х — Юа6 = 0.
Отсюда
— (а + Ше) ± У (a + 106с)а + Ш^с
Х~ 20с
Если радикал взять со знаком минус, то х < 0; если взять
со знаком плюс, то х > 0.
Отв. Число стульев в каждом ряду
У(д+ Щ6с)2+ 400д£с — (д+ ЮН
20с
500. Обозначим скорости тел (в м/сек) через #3 и #а;
пусть ^ > v%. Первое условие даёт уравнение аюл -\-av% = d\
второе даёт уравнение bvx — bv^ = d.
Отв. ^=~|(^ + |); ^ = 1(1 — |). Задача имеет
решение только при д < д.
БОЬ Обозначим скорость мотоциклиста (в км/час) через
х, а велосипедиста — через у. Получаем систему уравнений
2x + 2y = d; -—*- = t.
J * у х
Отв. Скорость мотоциклиста d "" 1*— — км/час,
, t + 4 — Yld+J^
скорость велосипедиста d—! ^ •—км/час.
503 ГЛ. 7. АЛГЕБРАИЧЕСКИЕ И АРИФМЕТИЧЕСКИЕ ЗАДАЧИ 271
Б02. Если велосипедисту требуется х час, то пешеходу'
требуется (# + с) час. Обозначим через у расстояние АВ
(скажем, в километрах). До места встречи пешеход прошёл
х ±с км* а велосипедист проехал ~км. Имеем уравнение
i^flZ + i_„ так «ак ,Ф0, то £±| + |= !. „лк
x* — (a-{-2b — с)х — Ьс=*0.
Это уравнение имеет один положительный и один отри-
цательный корень (так как произведение корней равно отри-
цательному числу —be). Годится только положительное ре-
шение
__ д + 26 — с+ V(a + 2b — c)*'+We
X 2 •
Расстояние у остаётся неопределённым. Величину х-\- с
можно найти либо из вышеприведённого выражения, либо
из уравнения —£-—|— = 1, положив х-\-с^=-г. Получим
X —J— С X
уравнение -^-t—|—:zr~~** Верём только положительное
решение.
Отв. Велосипедисту требуется
а + 2Ь — с + У" (д + 2Ь — с)а + Wc
2 чаС"
а пешеходу
a + 2b + c + }/(a + 2b—c)*+4bc _
2 —
(a + 2b + c) + Y{a + 2b + cy — 4(а + Ь)с
час.
БОЗ. Обозначим длину пути (в километрах) через х.
Согласно условию поезд А должен по расписанию нагнать
х
поезд В через — час. после выхода. Фактически он нагнал
лоезд В, пройдя (х — а) км, т. е. через х~~а- час. Следо*
вательно, оба поезда шли до встречи на — час. меньше полб*'
женного времени. Но поезд В должен был итти до встречи
272 ОТВЕТЫ и РЕШЕНИЯ 504
х 2
— час., фактически же он прошёл расстояние rJf со ско-
ростью vx и расстояние -кх— а со скоростью -xV\* затра-
__ _|_ — j час. Следовательно,
Отв. Длина пути равна —-—""" км. Задача имеет ре-
шение только при vx < 2v.
Б04. Пусть сберкасса даёт х°/0. Тогда первоначально было
1500 л Q
положено руб. В начале второго года на счету вкладчика
было -~+ 15 + 85, т. е. (^+ 100)руб. В конце второго
года эта сумма обратится в ( 1- 100JM -^—шо"У Р^*
Получаем уравнение
/1500
Отв. 300 руб.; 5%.
00+ж)
100 HI +-т^г) = 420.
505. Обозначим производительность станков А, В, С соот-
ветственно через х, у, г. По условию
Найдём из этих уравнений выражения х и у через z\ сложив
их, получим
Ю0(т + я) + 2/ия
*i~> — 10 000 — m« г#
Искомое число процентов равно , ■ 100.
Л 1ЛЛ 10000 —ти
О/я*. 100
ИХ) (т + и) + 2тл •
507 ГЛ. 7. АЛГЕБРАИЧЕСКИЕ И АРИФМЕТИЧЕСКИЕ ВАДАЧИ 273
БОб. Примем за единицу измерения продукцию года, пред-
шествующего первому. Тогда продукция 1-го года составит
1 -f- -7Щ-. По сравнению с ней продукция 2-го года возра-
стает на д°/0, т. е. на П -f- -тт^-тятт и составит
Если продукция 3-го года возрастает на х°/0, то она увели-
чивается на (1+^(1 + -jjrj-jjj-."
По условию
"Hloo^K1 + Too) loo "К1 ^"loojv + loojlooj
г
"loo"
о- РЧ
0т- Т^ЕЖ^ЦЧ'
507. Пусть себестоимость всего товара составляет m руб.
Тогда себестоимость первой проданной партии составляет
а°/0 от т9 т. е. -щ- руб* По условию полученная от про-
дажи прибыль составляет р°/0 этой суммы, т. е. -rgg- • -щг руб.
Себестоимость товара, оставшегося после продажи первой
партии, равна т —S^- =wfl Л^j руб. Себестоимость
второй проданной партии составляет Ь°/0 от этой суммы, т. е.
т(* ГОб")Too Р^*' ^Ри пРодаже второй партии было по-
лучено д°/0 прибыли; следовательно, эта прибыль составляет
/в(1-Т5о)-[Цо,1ЖРУб-
Себестоимость товара, оставшегося после второй продажи,
составляет
Пусть эта остальная часть продана с прибылью ;е°/0. Тогда
прибыль от её продажи составит т\\ — щ) (* — щ) Щ РУб#
274
ОТВЕТЫ И РЕШЕНИЯ
508
Общая прибыль будет
m[lW'Ioo"K1 Too^Tooe foo+V1 ТооЛ1 ~ш)ш\'
' По условию общая прибыль должна составить г% от т руб.,
т. е. -щ руб. Следовательно,
[а р . А а\ Ь д ,
100 " 100 ~*Л Ж) 100 " 100 "*"
^Л 100 Д* lOOyiOOJ 100'
Величина m сокращается.
- _££_ ^/, o\
Л*,, 100 100 У* 100 У о/
^ 100 Д 100/
608. Первый способ. Положим, что каждый из отре-
занных кусков весил х кг. Для краткости назовём первый
сплав (весом от кг) «сплавом Л», а второй — «сплавом В».
Из двух вновь полученных слитков первый содержит (от—х)кг
сплава А и х кг сплава В, а второй — х кг сплава А и
(п — л;) кг сплава В. По условию процентное содержание
меди в обоих слитках одинаково. А это возможно лишь в том
случае, когда в двух слитках количества сплава А и сплава В
пропорциональны. Получаем уравнение
откуда
т-\- п*
Второй способ. Пусть и кг есть вес меди в 1 кг
сплава A, a v — вес меди в 1 кг сплава В. Тогда в первом
слитке (от — x)u-\-xv кг меди, т. е. на 1 кг первого слитка
приходится Vя ~~ *) ц "г *р кг Меди. Аналогично выразится вес
меди, приходящийся на 1 кг второго слитка. Приравнивая
два найденных выражения, получим уравнение
п[{т — х)а-\- xv\ = т \{п — x)v-\-xu\y
&$ ГЛ. 7. АЛГЕБРАИЧРХКИЕ И АРИФМЕТИЧЕСКИЕ ЗАДАЧИ 275
содержащее три неизвестных х, и, v. Его можно представить
в виде
(и — v)(mx + пх — тп) = 0.
По условию сплавы А и В имеют различные процентные со-
держания меди, т. е. величина и — г> не может равняться нулю.
Следовательно»
тх -f- пх — тп « 0.
Отв. Каждый кусок весил —^ц— кг*
509. Пусть в первой кучке первоначально было хх руб.,
во второй было хг руб. и т. д.; в последней (л-й) кучке перво-
начально было хп руб. Первая кучка явно находится в осо-
бом положении, так как из неё сначала изымается — часть и
п
лишь в конце процесса она пополняется из л-й кучки, тогда
как по отношению к каждой из остальных сначала произво-
дится пополнение из предыдущей кучки, а затем изъятие
~ части. Поэтому рассмотрим какую-либо кучку, кроме пер-
вой. Обозначим её номер через k. Первоначально в ней было
хи РУб-f к ней прибавилось некоторое количество у руб. из
(k— 1)-й кучки, а затем из обшей суммы у-\-хк руб. была
изъята — часть. Осталось (у-Ь**) руб. По условию
имеем уравнение
В предыдущей же (6 — 1)-й кучке, если она ие была
первой (т. е. если к Ф 2), должно было остаться А руб.
(в первой кучке А руб. образуется лишь после пополнении
её из л-й кучки). Значит, до изъятия у руб. в ией было
Л-j-y руб. По условию изымаемая сумма у руб. составляет
— часть от Л + у, т. е.
Отсюда находим у =—^-т-Л. Подставляя в (1), получаем
лл = Л. Таким образом, во всех кучках, кроме, может быть,
275 ОТВЕТЫ И РЕШЕНИЯ 509
второй и первой (прежде исключённых из рассмотрения),
первоначально было по А руб.;
Х§ = Х^ = • • • = Хп = А, (о)
Неизвестное xt можно найти так. По условию сначала
из суммы хА руб. изымается — часть. Остаётся хг руб.
В конце процесса в первую кучку добавляется некоторая
сумма у руб. из последней кучки. Получаем уравнение
У + ^г^^А: (4)
Рассуждая (применительно к я-й кучке) так же, как выше,
найдём, что у= Л. Подставив в (4), найдём;
Для разыскания х2 имеем уравнение
где jtt определяется формулой (5). Решая это уравнение, на-
ходим:
г я(я-1)-(я-2) ,
ХЪ~ (Я —1)2 Л*
я2 — 2п - п* — 2п+2 Лл _ _ А
Х\ — /п 1)2 Л» *2 — tn 1)2 А» *8 — Xi — • ■ • — ХП — А*
ЧАСТЬ ВТОРАЯ
ГЕОМЕТРИЯ И ТРИГОНОМЕТРИЯ
ГЛАВА 8
ПЛАНИМЕТРИЯ
510. Пусть а и b — катеты прямоугольного треугольника,
а с — его гипотенуза. По условию а-\-Ь-\-с=\Ъ2 и
Ф 4- *а 4- с2 = 6050. Так как Ф + *3 = с2, то 2с2 = 6050, от-
куда с = 1^3025 = 55. Поэтому а -|- А = 77. Возводя это ра-
венство в квадрат и учитывая соотношение а3-}-£3 = 3025,
получим аЬ=Ы52% Следо-
вательно, а: и b суть корни
уравнения
*3— 77*+ 1452 = 0.
Отв. Катеты треуголь-
ника равны 44 и 33,гипоте-
нуза 55.
511. Высота ВАГ (черт. 1)
параллелограмма ABCD рав- Черт. 1.
на 20N*=2p. Так как
1_ ВАК = а, то AS = J^-. Аналогично AD
S = AD-BK=^.
sin а
Диагонали находим по теореме косинусов.
sin а '
#р _ 2 У> + ma — 2тр cosT
sin а *
j^q __ %Ур% + m* + 2m/? cos а
sin а
2m
sin а
. Находим:
27а
ОТВЕТЫ И РЕШЕНИЯ
512
512. По условию АС=30 см и BD = 20 ел (черт. 2).
Высоту АЕ можно найти из подобия прямоугольных тре-
)гольников BDC и ЛЕС (у них угол С—общий), но проще
Я J? С
Черт. 2.
сравнить два выражения площади 5 треугольника ABC,
Именно, 5 = -^ AC* BD и S = ~BC* АЕ. Следовательно,
АС:ВО_ 30-20 _2
Отв. 24 см.
513. Из треугольника BDE, где ££> == 12 ел и ЯЕ* = 13 ел,
находим D£"= |Лз2 — 122 = 5 (ел) (черт. 3). Следовательно,
В
Д D Е С
Черт. 3.
АО = АЕ— DE= -g- AC— DE = — 60 — 5 = 25 (ел) и
DC = ЕС -f- D£ = 35 (ел). Боковые стороны находим из
треугольников ADB и DC5.
Отв. ЛЯ =/7б9;^27,7 ел, ^ = /1369 = 37 ел.
515
гл. 8. ПЛАНИМЕТРИЯ
279
514. Пусть ЛВС есть данный треугольник (АС=СВ = Ь).
Требуется определить площадь 5 треугольника Ох0^0^
(черт. 4).
Имеем S^^O^-Ofi, где 0<fib= АВ н01С=АВ.
Следовательно, 5 = -^ АВ2 = b2t
в
/ X
С
X / /
X / /
\J/
/ и3 \
/ \
V N
Oi
й
Черт. 4.
Другое решение. Треугольник Ot02C равновелик
треугольнику OtBC (у них общее основание ОхС и равные
высоты). Треугольник ОхО^С равновелик треугольнику ОхАО
(по той же причине). Значит, треугольник ОхО^Ог равнове-
лик квадрату 0ЛВСАш
Ошв. S = £2.
515. По условию задачи отрезок АВ = а делится точ-
кой М в отношении m :я (черт. 5). Поэтому АМ = —j— и
MB
. Таким же образом
m +я
BN=CK=DL =
-^- и NC=KD = LA=-^-.
m + n m+n
280
Следовательно,
LM = MN*=NK = KL =
ОТВЕТЫ И РЕШЕНИЯ
516
=/:
т-\-п
Y т* + п?.
Кроме того, все углы четырёхугольника LMNK прямые
„ (ибо из равенства треуголь-
ников ALM и BMN имеем
J^LMA = j^MNB = 90° —
—1_ NMB\ следовательно,
. £LMA + £NMB*= 90°; no-
rf этому j^LMN= 90°). Значит,
четырёхугольник LMNK есть
квадрат и площадь 5 его
равна
аи» *<*+*>.
(w + л)^
Отв. S-
Д2 (СТ2 + П*)
516. По условию £ШЛ = 30° (черт. 5). Следовательно,
AL = ^ML и AM = ¥j-ML.
Значит,
Следовательно,
пл. ABCD :пл. LMNK = АВ* :ML* = (1 + К~3)2 :4,
т. е.
4
пл. ШЛИГ-
(14-/3)2
пл. ляса
Owe. Отношение равно-——^ = 2(2-/3)^0,54.
513
ГЛ. 8. ПЛАНИМЕТРИЯ
281
517. Обозначим AM (черт. 5) через х. Тогда Л1=»
= MB *= а— х. Следовательно,
пл. KLMN = LM* = AL* + AM* = (а — д:)2 + Л
25
По условию (а — х)* -|- х2 = tq а3. Решаем это уравнение.
Owe. Искомые отрезки равны -у и -^-.
518. Предварительное замечание. Из решения
выяснится, как отыскать положение вершин вписанного пря-
моугольника KLMN (черт. 6). Пока нужно выполнить по-
строение схематически, начав с построения прямоуголь-
ника KLMN.
Черт. 6.
Решение. Найдём отрезки МВ = х wBN = y. Так как
АВ = 4, то AM = 4— х. Треугольники DLK и BNM равны
(доказать!); следовательно, DL = ВМ = у и £Л = 3 —^ Тре-
угольники /,ЛЖ и ЖМ? подобны, ибо острые их углы ALM
и NMB равны (как углы с взаимно перпендикулярными сто-
ронами). А так как по условию ML втрое больше, чем MN9
то и LA = 3MB9 а также AM = 3BNf т. е. 3— у = 3х и
5 9
4 — х = 3у. Отсюда находим jc = -rt у = —. Теперь имеем
[^«1,29 м и
о
3,87 л.
Отв. Стороны прямоугольника равны
з уТоб
282
ответы и решения
519
519. Площадь равностороннего треугольника ЛбС(черт, 7)
равна -к й • -2-х- л = ~- я2. Треугольник ANLf у которого
1 2
по условию AL = -та и AN=-*at имеет общий угол А
с треугольником ABC. Значит, их тощади относятся, как
1 2
О/— ° ^
произведения сторон: -^-
5 ABC
Д-Д
Поэтому
1 2 2
5д#£ = -J • з"5лво = -g- Sabc*
Следовательно,
5л'лдг = Здсс — SSanl =
1 о ягУ~3 '
==з"^вс= 12 .
Замечание. Треугольник LMN, равно как и треугольник
АВС% рзносторонний (доказать). Но тем же способом можно опре-
делить площадь треугольника LMN в общем случае, когда треуголь-
ник ЛВС произвольный и стороны его разделены в произвольных
отношения*.
Отв.
а* УЗ
520, При обозначениях черт. 8 имеем а + * + с = 2/>.
Отсюда а + Ь = 2р — с и cfi-\-2ab-\-b* = (2p—cf. По
а2-(-6г = с2 и ab = ch (см. решение задачи 512). Поэтому
c2-f2d* = 4p3-
■4рс-|-с2, откуаа
2^
с =
h + 2p-
521
ГЛ. 8. ПЛАНИМЕТРИЯ
Теперь имеем а + Ь = Щ'-^1 и ab = -j^p^
тельно, а и b суть кори» уравнения
, 2p(h+p) , 2/flh _Q
х йТ1р~Х^Т+Чр •
283
Следова-
Отв. с
:+2р
__J.fi
h + ip'
а =w^7p[h^P + V^-^-2'1^
ъ = г!1-р['г+/> - V(p-w-w\-
случае, если
Задача имеет решение
р>*(/2+1).
лишь
том
621. Каждая из боковых сторон АС и ВС (черт. 9) тре-
угольника ABC раина —'-^ — Р— а. Пусть х есть длина
отрезка СМ (х = СМ = CN). Периметр 2р трапеции AMNB
получится из периметра 2Р треугольника ABC, если из 2Р
вычесть сначала CM + CN = 2х и к
разности прибавить MN. Из подобия С
треугольников ABC и MNC находим
„., АВ-А1С Чах
ЛС
Р-а
Следовательно,
откуда
2Р — 2х + -£?- = 2рш
(Р-а){Р -Р)
Р- 2а
Черт. 9.
'Гак как по условию />< Р и 2я < Р (а значит, тем более,
«</•>), то величина # положительна, н задача имеет ре-
шение.
Отв. На боковых сторонах нужно отложить от вершины
н {Р- а){Р -/?)
отрезки длиной -—jy___]~>£~~^*
284
ОТВЕТЫ И РЕШЕНИЯ
522
522. Требуется определить расстояние ЛГР = х точки N
(черт. 10) до основания АО = аг) и расстояние NM = y до
боковой стороны АВ=*с. Из подобия треугольников AMN
MN AM v х
и ABC (где ВС=Ь) находим "дс =уОГ ' т' е> I» 7f а из
подобия треугольников
— = —=^-. Решаем эти два уравнения,
MPD и BAD имеем "»1~ AD* т* е*
523, Пусть ЛВС (черт. 11)—данный треугольник. Так как
DE—средняя линия треугольника и DE = CD, то CD = тг-ДС.
Следовательно, /_CAD=2>Q°. Поэтому CD=^f^-=2Yd см.
Отв. S= 12 УЗ см2.
1) Решение останется тем же, будет ли а большим или мень-
шим основанием.
525
ГЛ. 8, ПЛАНИМЕТРИЯ
285
524» Положим лг = 50, у = АО (черт. 12). Тогда пло-
щадь 5 ромба ABCD равна 2ху. По условию je-j-J^-?-;
кроме того, из прямоугольного треугольника АОВ, где
АВ = j 2р « £ 9 находим дг2 + У — (£\ . Возводя в квад-
рат обе части первого уравнения и вычтя второе, найдём
Отв. 5-2L=£l^».
625. Обозначим высоту BE (черт. 13) через х. Тогда
в ъ с
Черт. 13.
АЕ — х uFD = xV~3. Так как AD = AE + EF+ FD, то
a-x + b + xV*. Отсюда *= -р^- » <—»></ J-'>.
Т^З + 1 2
О/ив. Si
(а1 — 6»)(тЛЗ— 1)
286
ОТВЕТЫ И РЕШЕНИЯ
526
526. По условию Л£> = 44 ел и БС= 16 см (черт. 14).
Следовательно, АЕ-\- FD = 28 см. Обозначив длину АЕ
(в сантиметрах) через х, имеем FD = 28— х. По условию
АВ = 17 см и CD = 25 см. Значит, Z?£2 = 172 —дг2 и СЯ2^
= 25а — (28 — х)2. Получаем уравнение
17а — jc3 = 25a — (28 — xf,
откуда х = 8 (глг). Следовательно,
h = В£ = 1Л72 — *а = 15 (ел).
Теперь находим S = -—2
Owe. 5 = 450 ел2.
627. Обозначим сторону вписанного квадрата (черт. 15)
через х. Из подобия треугольников AKL (где АК= ^ ==
= ^=^f a LK = x) и Л£Я(где АЕ=*\ и В£ = ±|3)
получаем уравнение
из
которого
Отв. S =
а — х л а
2 ' 2 =
находим
2+^"3
= 3^(2 —/3)2 =
дУ~3
* • 2 '
= aV/"3(2 —/3).
= 3(7 —4/3) да.
529
ГЛ. 8. ПЛАНИМЕТРИЯ
287
528. По условию >ID = 36 см и DC = 14 см (черт, 16).
Площади Sx и 5а треугольников ADB и CBD% имеющих
общую высоту, относятся как
основания, т. е.
Sx:S2 = bb:U = j.
18
Следовательно, 5Х = ^g 5, где
S = Sx + S2 есть площадь тре-
угольника ABC. По условию
прямая EG делит пополам пло-
щадь S; значит, эта прямая пересечёт основание АС между
точками А и D (а не между D и С). Получим треугольник
AGE; его площадь 53 равна jS. Так как площади подоб-
ных треугольников AGE и ADB относятся как квадраты
сторон Л О и AD, то
]^S:±S = №:AG'\
Отсюда найдём
уШ = 30 (см).
Значит,
GC = AC — AG =
= (36 + 14) —30 =
= 20 см.
Отв. 30 см и 20 см.
Черт. 17.
529. См. решение предыдущей задачи. Из условия
AD:DC= 1:8 находим, что площадь треугольника BDC
о
(черт. 17) составляет -*• площади 5 треугольника ABC. Так
как по условию ££> = 4, то имеем
EF*: 16 =
"2 6'?°-
Ome. Б/7:
288
ОТВЕТЫ И РЕШЕНИЯ
530
530. Так как Sebf^Sdefq^Sadoo (черт. 18), то пло-
щадь треугольника EBF вдвое меньше площади треуголь-
ника DBG и втрое меньше площади треугольника ABC.
Черт 18.
Так как эти треугольники подобны, то EB2:DB*;AB*= 1:2:3.
По условию АВ « а; следовательно, ЕВ = -~= и £>В=—^=-.
уз V 3
Отв. Сторона АВ разбита на части —=, -=(1/2—1)
у 3 V3
531. По условию плошадь треугольника ABC (черт. 19)
равна S, а плошадь треугольника КВМ равна qm Три верши-
ны четырёхугольника сов-
пала ют с точкам и К» В
и М; четвертую же вер-
шину L можно взять на
стороне АС произвольно.
Действительно, площадь Sx
четырёхугольника 1КВМ
есть сумма площади q
треугольника КВМ и пло-
щади треугольника KLM,
а последняя не меняется
при движении вершины L
по прямой АС, параллель-
Черт. 19.
ной основанию КМ. Пусть высота BE треугольника ABC прохо-
дит через точку Е основания АС. Поместив точку L в точку Еу
получим четырехугольник КВМЕ, диагонали которого взаимно
ГЛ. 8, ПЛАНИМЕТРИЯ
289
перпендикулярны; следовательно, St = у KM • BE. А так как
q = y /СЖ ♦ БД то 5t: q = BE : 5D. Но из подобия треуголь-
ников ЛВС и /СВЖ имеем 5 : q *= ЛЯ2 : ЯО3. Следовательно,
5г = ?
= <?/f = /S?.
Замечание. Если точка L не совпадает с точкой £, то ре-
шение видоизменяется так: находим
Sx~j KM-BD + ~KM'NL = ±KM{BD + NL) = у /CM. ££,
и дальше попрежнему.
Отв. У&д.
532. Пусть отрезок EF = x (черт. 20) делит площадь
трапеции ABCD(AD=a,
ВС = д) пополам. Тогда
(a + x)FL __(x + b)FM
2 ~ 2 '
т. е.
(a + x)FL = (x + d)FM.
Высоты FL и FM по от-
дельности найти нельзя
(длина одной из них мо- Л f
жет быть взята произ-
вольно), но отношение
FL : FM имеет опреде-
лённую величину. Именно, из подобия треугольников HFD
и CFK (где HD = a — х и СК = х — Ь) находим
а — х х — Ь
PL ~ FM •
Помножив почленно это равенство на предыдущее, получим
ла —*» = *»—fta,
откуда
Черт. 20.
2$0
ОТВЕТЫ И РЕШЕНИЯ
Другой способ. Продолжив боковые стороны, полу-
чим подобные друг другу треугольники BGC, EGF и AGD*
Их площади Sv S^ S3 пропорциональны квадратам сход-
ственных сторон Ь, х% а, так что 6\ = q№% 5S в qx\ S8 = qa%
где q—'некоторый коэффициент пропорциональности (вели-
чина его зависит от высоты трапеции). По условию 52—6\=
с= Og — Oft, Х> fc.
q&—&)=**{* —#h
а так как д Ф О, то
х* — № = а*—х\
Owe. * = J/ - ^ .
533. По условию BE = BF = a (черт. 21) и EF = b.
Значит, fG^^n 50== у а2—/-^-J . По теореме о про-
порциональных линиях в прямоугольном треугольнике (BDE)
находим BD =
BE*,
. Теперь найдем сторону
ромба (AD). Равнобедренные треугольники ABD и BEF по-
добны, так как их углы (все они острые) соответственно
равны (как углы с взаимно перпендикулярными сторонами).
Следовательно,
AD:BD = BE:EF$
535 гл. 8. планиметрия 291
т. е.
AD: а =*а\Ъ.
Отсюда находим AD, а затем площадь ромба 5 *= AD • д.
2л*
Отв.
ьу^—ь* *
534. Пусть АВ = 27 сми АС = 29 ел
(черт. 22); тогда медиана AD = 26 см.
Требуется найти ВС. Продолжим AD
на расстояние DE = AD. Четырёхуголь-
ник АВЕС будет параллелограммом (до-
казать!) со сторонами 27 см и 29 см;
а диагонали его АЕ = 2AD = 52 ел
и ВС = х см. Имеем
xa + 522 = 2(272 + 292),
откуда
л; = 1/436 (ел).
Теперь площадь треугольника можно
вычислить по формуле Герона. Имеем
р = 1 (27 + 29 + УЖ) = 28 + /Т09 Черт. 22.
и
5 = ^(28+|/Тб9) (28 — /109) (/109 + 1) (У 109 — 1) =*
= / (28а— 109) (109 — 1) = 270.
Отв. 270 см*.
535. По теореме косинусов д2 = #2 + е2 — 2fo? cos Л,
I 2$ 4
а так как S = 7T^s*n>*» т* е- sin^ = r—= -^» то
cos А =» ± У"1— sin2 Л = ± »-.
Получаем два решения; оба они годятся (в одном случае
угол А острый, в другом — тупой).
Отв. а = у £а + са—j be или а = у й» + с« + -|^.
292 ОТВЕТЫ и решения 536
636* При обозначениях черт. 23 имеем из треуголь-
ника ABC:
m*tmtP + c* — 2bccosB9
а так как cos В в» cos (180е—Л)е* — cos Л, то
Из треугольника ADC находим
т%=*а* + <Р—2adco%D.
Приравнивая это выражение предыдущему, получаем
2ftccos4 + 2odcosD~fl* — ft*-J-</»_с\ (1)
Таким же образом» рассматривая треугольники AMD и CBD%
получим
2ас cos А + 2М cos D — я*—fta—(<**—*2). (2)
Из уравнений (I) и (2) можно найти cos А и cos£>, а после
этого найдём т3 и а9. Вычисление удобно вести так:
У
/
/
Li
с
Г^
/
f
S
s*
Ъ
^
В
** 1 X
-*•* / N
/
_£/..._. _
\г
Черт. 23.
помножим (1) на ft, а (2) на а, после чего вычтем первое урав-
нение из второго. Получим
2(а« — b*)c cos А**(а* — b*)(a — ft)—(rf2 — c*)(a + b).
Разделив обе части равенства на (я*— Ь*)1Ф01, получим
4- — с*
2с cos А «* л — £———г-.
я—-о
Теперь находим
да* a fta + *e + (2c COS -А)* —
= *J-nh <*-*)» fl(C»-ft2)+ft(fl*-tf»)
537
ГЛ. 8. ПЛАНИМЕТРИЯ
293
Аналогично найдём
2d cos D = а — д + ^—£-
и затем
„a== t,* + d* + (2d cos Р)Ь g «1*-^+»<*-*>.
Замечание. Отрезок AD=*a меньше ломаной ABC О. По-
этому задача может иметь решение лишь при условии а < Ь + с -f- d.
Однако одного этого условия мало, что видно из следующего. Пусть
а > Ь и c^d (если эти неравенства не выполняются, то всегда можно
изменить обозначения и после этого неравенства будут иметь место).
Проведём прямую BL параллельно стороне CD. Получим параллело-
грамм DCBL, так что BL=*CD=*d и DL = CB=^b. В треуголь-
нике ALB сторона LA=xDA — DL = a — Ъ больше^ чем разность
сторон АВ = с и BL = rf. Поэтому должно соблюдаться ещё второе
условие я — 6>с—d. Если хотя бы одно из двух условий не вы-
полнено, то по крайней мере одно из выражений, полученных для
т* и п\ окажется отрицательным.
Двух условий а<^Ь -)-c-{-d и а — Ь^>с — й уже достаточлоу
чтобы задача имела решение. Действительно, первое условие можно
записать в виде а — о < с + rf. Следовательно, можно построить тре-
угольник ABL со сторонами AL =*а — Ь, АВ — с и BL — d. Про-
должив сторону AL на расстояние LD = Ь и построив параллело-
грамм DLBQ получим четырёх-
угольник ABCD] он будет трапе- В ь
цией с основаниями AD = а,
ВС = Ь и боковыми сторонами
АВ=с и DC=d.
0твт,= а^-Щ±Ь^-3_
я_ а(<Р — ^) + ^(ди — са) Д а Л
а — Ь * Черт. 24.
537. При обозначениях черт, 24, где ^Л = 60°,
имеем
£L>* = AD* + ЛВа — 2 • В А - >Ш. cos 60° = а2 + ^ — а/)
и
2у^х/
Так как ЛС больше £D, то данное отношение у равно д-т^
294
ОТВЕТЫ И РЕШЕНИЯ
538
(а не 2с2]т ^3 УРавнения
gt + b* + ab _19
аъ + Ь* — аЬ 7
или
(тУ+'+Т L9
(!)'+'~Г7
а 3 я 2 ~Л
находим -г- = -2" и Т ^З"* 9ТИ значения Дак)т один и
тот же параллелограмм (на черт. 24 можно изменить обозна-
чения— обозначить A3 через а и ,AD через. Ь).
Отвт Стороны относятся, как 3 :2,
Б38. Пусть О — произвольная точка внутри равносторон-
него треугольника АЗС (черт, 25). Соединим точку О с вер-
шинами. Площади треугольников АОВ> ВОС и СОА в сумме
дадут площадь треугольника ABC. Обозначая сторону этого
треугольника через а, а высоту через А, получим
(OK+OL + QM)-%=^.
Отсюда находим
k = OK + OL + OM.
Черт, 26,
539. По условию £С = 47 л и СЛ«9 л (черт. 26; на
этом чертеже истинные размеры не соблюдены); значит,
ВА = 56 м. Следовательно, AD • АЕ = 9 • 56 = 504. Пусть
AD = x\ тогда DE = x + 72 и, значит, АЕ = 2*+ 72. Из
уравнения х (2лг -f- 72) = 504 находим * = 6.
Отв. Л£ = 84 л.
541
ГЛ. 3. ПЛАНИМЕТРИЯ
295
540. Задача сводится к разысканию одного из катетов
треугольника ОЛВ (черт. 27) но данной гипотенузе ОА=т
и высоте BD = -2, Обозначим больший катет через х, мень-
ший— через у. Двоякое выражение площади треугольника
ОАЭ (см. решение задачи 512) даёт уравнение ху = а^, т. е.
2ху = ат\ кроме того, лг2-|-_у2 = /я2* Складывая и вычитая
эти уравнения почленно, получим
х -\-у = Ym% -{- am
и
х —у = ]/т2 — am.
Как xt так и у может служить искомым радиусом.
Отв. -~ <Ym* + am + Ym* — am)
или ^ Qfm? -\-am — Ym? — am).
Черт. 27.
Черт. 28.
541. Так как радиус круга равен 13 см и МО = 5 см,
то MD = 8 см, МС = 18 см (черт. 28). Обозначим MB че-
рез х. Тогда AM =± 25 — дг. Так как ЛМ ■ Л1В = AID • МС, то
(25 — *)*=18.8.
Отсюда хг = 16, лг3 = 9.
Отв, Отрезки равны 16 см и 9 см.
296
ОТВЕТЫ И РЕШЕНИЯ
542
542» Из треугольника ЕВ02 (черт. 29), тде В£=«Л5,
находим
R = 02B =
АВ
о а
2cosT
Из треугольника ADOlt где 1_ОАОХ = ^^АВ^Шо0--•-),
В находим
r~QxD=*AD* te(45° — -J).
Так как AD = АВ • sin -^- (из
треугольника ABD), то
ctg(45--|)
Черт. 29.
/?:г:
Оотв. £.
sin о *
с,8(45°-|)
Sin а
Б43. По условию л = ВС=13 ел, £ = СА=*14 см%
г = АВ=15 ел (черт, 30). Обозначим OE=OF через /?.
Площадь треугольника ABC равна
сумме площадей треугольников ВОС
и ДОС Так как площади этих
1 реугольников равны соответственно
13# 14/?
-тр и -у, то
С другой стороны, по формуле Герона &
/21(21 —15) (21 —14)(21 —13)«=
«= 84 ел2.
Черт, за
Приравниваем друг другу эти выражения площади.
2
Отз. /? = 6 •§■ см.
545
ГЛ. 8. ПЛАНИМЕТРИЯ
297
544. В прямоугольном треугольнике О ЕВ (черт. 31;
угол ЕВО равен 60°. Поэтому
1^3 1^3
Следовательно,
2 \ /?(^3 + 2)
Из треугольника ABD находим
следовательно,
4C = 2/?(j/3 + 2).
Отв. АВ = ВС = 2*(^+2), ЛС = 2Д(/3 + 2).
545. Из треугольника ABD (черт. 32) имеем
ВО =. УВА*—АП* = 18 ел.
Так как
BC-BD= BA*t
то
5С= |^-=50 ел.
Следовательно,
ЛС=*1/ВС2— ВЛ2 = 40 ел.
О/и*. Длина полуокружности равна 20ir.
298
ОТВЕТЫ И РЕШЕНИЯ
546
546. Так как углы В, D и Е четырёхугольника ODBE
прямые и DO = OE (черт. 33), то этот четырёхугольник
есть квадрат. Искомая дуга DE
В равна четверти длины всей окруж-
ности. Обозначим её радиус через R.
£ Из подобия треугольников ADO и
DjT /V ОЕС имеем
AD
АО
ОЕ 1
ОС\
Так как
ad = Vao*—od*=/159—/?3,
то
V 152— R*_R
15 ~"2G*
Отсюда /?=12.
Ота. 6и.
547. Площадь S четырёхуголь-
ника ADEB (черт. 34) равна
S=S
}двс
JV£09
Имеем
Черт. 34.
Завс = <ТВО<
12 {см%
Для разыскания SDm заметим, что треугольники DEC и DBC
имеют общую вершину D и одну и ту же высоту (на чер-
теже не обозначенную), причём SDBQ = -g SABQ =3 б (см*)т
Следовательно, SnMQ :Q==CE: СВ. Неизвестный отревок СЕ
найдём из свойства секущих, проведённых из одной точки (С).
лл f* А
Имеем СЕ «CB=CD-C,AfоткудаС£= —^—. Следовательно,
Отв. S=:10f8 см\
ев
ЙСЕ_ЙСР-СА_Й 2.4
°св ~ ° еда — ° г+е»'
1,2 (<м^
ГЛ. 8. ПЛАНИМЕТРИЯ
299
548. Площадь 5 треугольника ABC (черт. 35) равна
произведению его периметра 2а + 2|Л*9 + Л* на -2 (г — ра-
диус вписанной окружности):
S = (a + V& + №)r.
С другой стороны,
S = ^AC*BG = ah.
Приравнивая эти два выражения,
находим
__ ah
Отрезок DE находим из пропорции
DE:AC = BF:BG,
где
АС=2а, BF = h — 2r и BG = h.
Замечание. Величину г можно найти ещ& так: прямая АО
есть биссектриса угла А Значит, отрезки GO = г и OS = ft — г про-
порциональны сторонам ЛО и /Ш,
т. е»
О/и*. г =
ha
Ya* + h* + a '
Р£ = 2а T^g+*-« д
/аа + Л2 + д
Л2 •
549. Так как ОБ • ОЛ =
=ОС-0£(черт. 36) и ОВ=ОС,
то О А = OD. Противополож-
ные стороны ЛЯ и CD четырёх-
угольника ABCD равны; значит, данные длины 6 м и 2,4 м
относятся к сторонам AD и ВС (AD = 6 м% ВС = 2,4 л).
Прямые ЯС и AD, отсекающие на сторонах угла AOD равные
Черт. 36.,
300
ОТВЕТЫ И РЕШЕНИЯ
550
отрезки, параллельны, так что четырёхугольник ABCD —
трапеция (равнобочная). Из подобия треугольников ВОС
и AOD находим
BO:AO = BC:AD,
откуда
лп BO-AD 2-6 к/ ч
А0 = -вс- = у[ = 5(мУ'
значит, АВ = 3 л, Теперь на-
ходим высоту трапеции
h = BK = VA&—AK* =
Черт. 37.
;/з*_(6-^)!=2'4*-
Отв. S= 10,08 м*.
550. По условию АВ = 6 л, АС = 7 м, ВС = 9 м (черт. 37).
Пусть RA, RB и Rc—искомые радиусы окружностей с цен-
трами в Л, В и С. Тогда RA + RB = 6, Rc — Ra = 1*
Rc—RB = 9. Отсюда находим радиусы RA, RB и Rc.
Отв. RA = 4 м, RB = 2 Mt RG=ll м.
Черт. 38.
551. Проведём 02£ параллельно АВ и <Э2Я параллельно
DC (черт. 38). По условию AB=~CD. Обозначим <1D
582 ил. 8# ПЛАНИМЕТРИЯ 301
через х. Тогда 0%Р = л\ Оа£ = 4 л:. Из треугольников Ог£02
и ОхРО% имеем
O^'-O^ + J*1 и О&^О^ + А
Приравниваем эти два выражения и учитываем, что
ОхВ=ОхА — EA = OtA — 09Д = 5 — 2 = 3 (см)
и аналогично
0^ = 0^+090 = 7 (<гл).
Тогда получаем
9+!*9 = 49-|-*a,
откуда л;2 = 32. Поэтому
OiO/ = 49 + 32 = 8l.
Отв. 0^2 = 9 см.
552. Так как расстояние между центрами окружностей
меньше суммы, но больше разности их радиусов, то окруж-
Черт. 39.
ности пересекаются; значит, они имеют общую внешнюю
касательную и не имеют общей внутренней касательной.
Положим ОхС = х и 0QC=j; (черт. 39), Имеем *
Л — У = 0109 = 21 (см) и х:у = 01А:02В=17:10.
Отв. OtC = 51 см, О2С = 30 см.
302
ОТВЕТЫ И РЕШЕНИЯ
553* Через точку М (черт. 40) проходят две касательные
(MD и МА) к окружности Ov Значит, MD — МА9 Так же
докажем, что MD = MB. Следовательно,
= АМ + МВ = АВ.
Чтобы найти АВ, проведём
прямую ОаС, параллельную
АВт Из треугольника ОхО^0,
где Ofi = ABt Ot02 =
«#+г и OiC = R — r9
получаем-
ая =*/(tf+r)a— (/?—г)а
или
AB = 2V~&.
Ото. MN=2Yr?.
654. Пусть MN—общая касательная к двум окружно-
стям (черт. 41). Так как АМ = МР = МВ9 то MN— средняя
линия трапеции ABCD. Имеем AW= АВ = 2 j/tfr (см. реше-
ние предыдущей задачи). Найдём теперь высоту BG трапеции.
По теореме о пропор-
циональных линиях в пря-
моугольном треугольнике
(ЕАВ) имеем
АВ*
Черт. 40.
BG =
Но
BE*
BE = Ox02 = R + r.
Следовательно,
4/?г
/? + г#
8 (Яг)*
ЖЬ
Ome. S = -
* + '
555. Обозначим радиус искомой окружности через х+
Проведём через её центр 08 (черт. 42) прямую МЩАВ.
Так как прямая АВ перпендикулярна к радиусам OxAt 02В
и ObDt то AM = BN=x и, значит, OxM = R — x и 03М=з
= г — хл Кроме того, имеем Ог03 = /? + лг и ОаОа = г + д^
556 ГЛ. 8. ПЛАНИМЕТРИЯ 303
Следовательно,
точно так же
Черт. 42.
А так как MN=2Y^r (см. задачу 553), то
2 VRx + 2 У7# = 2 /£7,
откуда
YR+Y'
От$* Радиус окружности равен ■ _ 2.
556. Так как S = ^au sin С, где С — угол между хордами,
то задача не имеет решения при S^-^ab. Если S<2-a£,
2S
то находим sinC = —т и существует два треугольника, имею-
щих стороны а и b и площадь 5; у одного угол С — острый,
у другого — тупой, В первом случае cos С = у 1—~^t
1 щ% Следовательно,
С2 = а2 + *2—2a*cosC = a2 + *2q=2]/a262 — 4S3
(верхний знак, если угол С острый, нижний — если тупой).
304
ОТВЕТЫ И РЕШЕНИЯ
557
При S=-£ab получаем прямоугольный треугольник, так что
Радиус окружности, в которую вписан треугольник,
находится по формуле /?= 2Sin/**
^ о аЬ Vа* + b* zjz 2 у ФР — 45» „ с^ I .
Отв. /? = — ! т$ • При о>-кад ре-
шений нет, при S<~^ab — два решения (верхний знак, если
угол между хордами острый, нижний — если тупой). При
S =» -£■ аЬ — одно решение (хорды взаимно перпендикулярны).
667. По условию (черт. 43) АХВХ =^=8:Я, А^2=яа^^=^
=* tf |^2 и Л3Я3 = а3 = /? /З. Высоты треугольников ОЛ^,
0Ла52 и ОА&В& соответственно
равны ос-**1.
ос,=
2
2
Черт. 43.
1
ОС — —
Отсюда определим площади этих
треугольников. Затем найдём пло*
щадь сектора OAxDBx\ он соста-
вляет -тг площади круга; поэтому
1
Аналогично Soaj>Bi~ т1^2 и Зол^в^-п я/?2. Вычитая из
площади каждого сектора площадь соответствующего тре-
угольника, находим площади сегментов:
5.=*а(£-¥). V-«-(t-t). V-^ft-*?).
Площадь части круга, заключённой между хордами А1В1 и
i4252, разна
59 —^-^(«+3^3 —б);
559
ГЛ. 8. ПЛАНИМЕТРИЯ
305
площадь круга, заключённая между А2В9 и А$В% равна
S«-Ss = -g(«— 8/5 + 6).
О/ия. Отношение площадей равно —— -?=:•
я — о\2■—• УЗ)
568, Для определения радиуса ОК = г (черт, 44) впи-
санного круга воспользуемся формулой площади треуголь-
ника S = рг (р — полу периметр треугольника). По усло-
вию ЛО=14,4 см, DC = 25,6 смш поэтому ЛС = 40 см.
Значит,
ab^Vad. ЛС = *
= 24 (ел),
ВС = /DC^4C =
= 32 (ел).
Следовательно,
р= 48 ел* и 5=384^2.
Отв. Площадь круга
равна 64я ел2.
559. Прямая LN, соединяющая точки касания двух парал-
лельных прямых АВ и CD (черт. 45) есть диаметр окруж-
В
А
L^
м
\ к
V
—-^г
JE
N
D
Черт. 45.
ности. Поэтому вписанные углы LEN и LMN (и аналогично
углы MLE и MNE) — прямые» Следовательно, четырехугольник
306
ОТВЕТЫ И РЕШЕНИЯ
LENM действительно явится прямоугольником. Треуголь-
ник ABD — равносторонний (ибо AB = AD и^Л = 60°);
отрезок LN (высота ромба) равен высоте треугольника ABD,
a V"3~
т. е. LN=—у-. Площадь S прямоугольника равна
У LA/2. sin ^ LOE = ~ LA/2. sin ^ BAD
(стороны углов LOE и BAD взаимно перпендикулярны).
Следовательно, S = -■ (^тр-) sin 60\
ЗдзУУ
Отв. 5 = -
16
660. Требуется определить площадь St фигуры MCNF
(черт. 46) и площадь Sz фигуры KDNE (площади фигуры
KALG и LBMH соответственно равны Sx и S^. Так как
по условию задачи АС = 4/?, то ОС = 2 • ОМ; следовательно*;
£ОСМ = 30°. Значит, /_MON= 180° — 2 . 30°=» 120° и
^ KON= 60д. Площадь четырёхугольника CMQN равна
/?э j/^ tа площадь сектора MONF равна-*- я/?2. Следовательно,
Гя_**>
; так же найдём S2t^~-R} ~
,-±г«>-
0т. StSS**(3VT--.), s^^^2^/-").
те/?а
562
ГЛ. 8. ПЛАНИМЕТРИЯ
307
561. Так как £А = Ж (черт. 47), то высота BE=*h
трапеции равна -^ АВ. По свойству описанного четырёх*
В С
угольника ВС -)- AD = АВ + CD = 2ЛЯ. Поэтому
s = AB+£Dh = ^AB^
Отв. AB = V2S.
562. По площади S = 20 сла и высоте BE = 2г = 4 ел
(черт. 48) найдём полусумму оснований ~ = 5 (см),
ВМС
Ю
Следовательно, АВ = 5 см (см. предыдущую задачу). Теперь
находим AE — Vab*—ВЕ? = Ъ (см). Но АЕ есть полураз-
ность оснований трапеции. По полусумме и полуразности на-
ходим сами основания.
Отв. AD = 8 см% ВС = 2 см, A8~CD = 5 см.
308 ответы и решения 563
6вЗ. Площадь Q трапеции ABCD (черт. 49) равна
BC + AD BM = (BC + AD)R
(R— радиус вписанного круга). Так как эта трапеция опи-
сана около круга, то BC + AD = AB-{-CD. Но AB=*~.t
op
acDeib-ncmo,,v
sin q + sin ft
sin з sin £
4R* sin --?p- COS —^
0/И8,
„ 1 / <? sin a sin ?
у sin —-£-*- COS —tj-1-
sln з sin p
564. Так как боковая сторона АВ (черт. 50), перпенди-
кулярная к основаниям, равна 2г, то наклонная боковая сто-
рона CD больше, чем 2г. Значит, наименьшая сторона тра-
пении, равная ттг, есть (меньшее) основание ВС. Чтобы найги
большее основание AD, проведём прямые ОС и OD. Они
являются биссектрисами углов MCD и NDC, в сумме соста-
вляющих 180°. Следовательно, ^ МСО + ^ ODA/ = 90°.
Из прямоугольного треугольника ODN находим ^ NOD 4*
-f £ 0D/V = 90\ Следовательно, ^ /VOD = 2.мс0* так что
треугольники 0DW и ОСМ подобны. Получаем пропорцию
566 ГЛ. 8. ПЛАНИМЕТРИЯ 309
ND : CW= ОМ : МС, где ON= ОМ в г и ЖС f= у (по усло-
вию задачи). Отсюда WD = 2r, так что /Ш = ЛЛ^+М-^
= г + 2г = 3л
От». 5 = ~2-.
665. Треугольники ОМ? и OND (черт. 50) подобны
(см. предыдущую задачу). Так как -^ = j=»2, тобЛ1в2
и ^ = 2, т. е. ND = 20M = 2r и Ж«^={л Из
прямоугольного треугольника OND находим г2 + (2'02 = 4*.
откуда
12
Теперь находим i4D = AN-}-ND = r-\-2r = 3r — -f=* (?м)
и ВС = —=(см). Высота -/W/V трапеции равна
От». 5= 14,4 см*ш
566. Центр О первого круга (черт. 51) делит вы-
соту BN=h в отношении Z?0:0/V=2: 1. Следовательно,
2 1
диаметр -MV составляет у/г и, значит, /Ш = уЛ. Второй
круг вписан в треугольник D££, высота которого втрое
меньше высоты h треугольника ABC. Значит, радиус гг = 0}М
втрое меньше радиуса г = ОЛЛ Поэтому, если S есть пло-
щадь круга О S = icf^-~—J =="т|" ' т0 площаДь круга Ot
будет 5{ =-p-S. А так как таких кругов три, то общая их
площадь Q1 будет
Рассуждая так же, найдём, что общая площадь трёх еле-
310 ОТВЕТЫ И РЕШЕНИЯ 566
дующих кругов будет
Получим бесконечный ряд слагаемых
S + Qi+Q. + ee + S+1S + 1-S + 1-S4-...
Члены этого ряда, начиная с члена -g-S (слагаемое S выде-
В
ляется особо), образуют бесконечную убывающую геометри-
ческую прогрессию (ax=i^S; q^=s~\ Сумма этой прогрес-
сии равна
is
^ 3 ° 3
_«■>_£_ = _
9
1-Я
s.
Сюда нужно ещё прибавить слагаемое S.
Ошв, Искомая площадь равна -g- S«=ggita*.
569
ГЛ. 8. ПЛАНИМЕТРИЯ
311
667. Чтобы найти площадь трапеции BMNC (черт. 52),
нужно найти основание ВМ и высоту MN, так как CN из-
вестно. Определим сначала
Имеем
или
дг(5С + лг)=ЛОа
л;(5-[-х)=150.
Отсюда
CD = лг= 10 (ем).
Из подобия треугольников
~я„гл ^аго ВМ CN ВМ 6
BMD и СМ) следует -£27 = "СО или НПГ^То * 0ТКУДа
ВМ = 9 (ел). Высоту MN трапеции найдём из пропорции
^■b-S-, где M) = /CDa—СЛ/а.Получим MN=Acm.
ВС — CD
: 30 СЛ2.
668. Пусть Од, О^и 0^— центры равных вписанных кру-
гов и пусть г—их радиус (черт. 63). Так как АОг и С02 —
биссектрисы углов Л
и С, равных 60°, то
^OxAD = 30°; следо-
вательно, ЛО==£С=х
= rV"3. Далее DE =
= Ох02~2г.^ Поэто-
му 2г(1 + КЗ) = а.
Отв.
г =
2(У"3 + 1)
g(V"5-l)
£* 669. Искомая пло-
щадь LMW (заштри-
хована на черт. 53)
получается, если из площади треугольника OxO^Oz вычесть
общую площадь трёх секторов 0](/И1, O^LN и 08ЛШ (их
общая площадь равна площади полукруга радиуса г). Сторона
ai2
треугольника Ог020$ равна 2г
задачу); поэтому
ответы и РЕШЕНИЯ
Л(ТЛ5-1)
570
(см. предыдущую
00,0,0, = ^м — [g
Общая площадь трёх секторов равна
2 — 32 ™
ТСД2(2— тГз)
16
Отв. 5 = ra(/3 — -£) =
да (2— /3)(2У"3 — тс)
~ 16
670. Решается подобно пре-
дыдущей (черт. 54).
Ф (4— к)
Черт. 54.
Отв. S:
16
671. Определим радиус R дуги окружности сегмента.
Периметр его равен сумме длин дуги АСВ и хорды ЛВ
В
откуда
R
2 /—
(черт. 55). Получаем -^ тс/? + /? V 3 = Р.
Площадь 5 сегмента равна площади сек-
тора без площади треугольника ОАВ,
так что
s=hR*'
R2Y3
4
4(2я +З/З)2
672. Для того чтобы найти стороны АВ и ВС треуголь-
ника ABC (черт. 56), достаточно определить EB = BG = x,
573
ГЛ. 8. ПЛАНИМЕТРИЯ
313
так как АЕ = AD =^6 аи CG = CD = 8 см. Для этого
сравним два выражения для площади треугольника:
S = rp и S=*Yp(p — a)(p — b)(p — c),
где р есть полупериметр треугольника» т. е.
j(EA + AD + DC + СО + 05 + ВЕ)=± (28+2.*)=*14+дг.
Получим уравнение
4(14 + дг) = /(М + дОх-б-в.
Отсюда л; = 7 (ел).
Отв. АВ=\3 см: ВС =15 еж
Черт. 57.
Отсюда
1Я + Л
Б73- Пусть CDxDB^mxn (черт. 57). Тогда BD: ЯС
= л : (;&-4-я). Следовательно, cos 5 = -г^- == т—г в= -4~. 1
как Я=180° —2С, то cos2C = cos(180° — В) =
п ,/~l + cos2C _/ m
Отв. В = arc cos —-.— ;
С = агссоз|/"2(Дя) [=»|.arccos(-^)].
314
ОТВЕТЫ И РЕШЕНИЯ
574
574. Окружность разделится на четыре попарно равные
дуги ЛВ = ВС и CD = DA (черт. 58). Пусть дуга ВС со-
держит меньше чем 90° (мы оставляем в стороне простейший
случай т:л==а 1, когда все дуги содержат по 90°), Найдём
центральный угол a a £_ ВОС, измеряющийся дугой ВС.
По условию DE : ЕВ = т : л. Приняв за единицу измере-
DE
ния длин величину —, будем иметь DE = m и ЕВ*=*п.
Значит,
DB т + п
т
и
DE—DO.
= /»■
/72 + Л
т —я
Следовательно,
cos а ;
0£ m — я
ОС~~ т + п
Черт. 58.
Дуга CD содержит 180°—
те— arc cos
а = arc cos
т— п
arc cos _ , _ (градусов), т. е.
т—п
т + п
т + п
(радианов).
т—п
Отв. Дуга, меньшая чем -^ 9 равна arc cos , (tn > п);
Jt Tit ""J— n
дуга, большая чем -у, равна
m —-n n —m
те—arc cos --, =arc cos—5—.
676. Пусть а (черт. 59) есть
угол параллелограмма. Тогда
hi^BM^AB^nct
и Черт. 59.
hb^BN^BC'Slnct.
Значит, Н[ + йа = (ЛВ + ВС) sin а = р sin а,
откуда sin«t=a 1"ГЧ Если а —острый (или прямой) угол,
577
ГЛ. 8. ПЛАНИМЕТРИЯ
315
то а !
iarcsin ty + h. Тогда тупой (или прямой) угол парал-
лелограмма будет it — arc sin
Замечание. Задача не имеет решения, если ht-^ft2>Р<
Если же Й1 + ^<Я» т0 задача имеет решение (при hx + h% = р
имеем прямоугольник).
^1 + ^2
Отв.
и — arc sin
Один из
углов равен arc sin
другой
: 40 ; 41 (черт, 60)» Примем
В
576. По условию BD : ВЕ-
аа единицу длины ^ часть BD.
Тогда £D = 40, ЯБ=41, Так
как треугольник ЛДС прямо-
угольный и BE—медиана пря-
мого угла, то АЕ = £/: = 41.
Треугольник BDE прямоуголь-
ный, поэтому
DE=*Vb& — BD*=*9.
Следовательно, AD = AE—DE = d2. Из подобия треуголь-
лпп АпГЧ АВ АО 32 4
ликов ABD и ABC находим -^ =-g-jj = qjj =-g-.
Олю. -gc = 5-
Черт. 61.
577. Так как АО (черт. 61) есть биссектриса угла
а== LCAD> т0 LBA0™7[% ТакиМ Же обРазом П0ЛУчаем
31б ОТВЕТЫ И РЕШЕНИЯ 578
^ЛВО=г-5-(90° — а) «45° — -|. Из треугольников AOD
и BOD имеем
^4D«»ODctg-j
и
Dfl«OD.ctg (45е—-i).
Следовательно,
<;вЛВ«Л0 + £>В = О0 [ctgj + ctg(45°—J)].
Отсюда находим
Clgf+ Ctg(V- I) #
Знаменатель можно преобразовать к виду» удобному для
логарифмирования:
cos-J cos (45°—-я-J
;2
,g £+dg(4B--j) —4-+—)—if-
* ч " einj sm(45°—£)
cos j sHx (45° — j) + «»n J cos (45° — |Л
sin j sin (45° — ~\
sin 45°
sin | sin (45е-1)
Oma. r« с/2 sin-J sin (45° — ^).
578. Обозначим стороны треугольника через а, Ь и с и
пусть л =з 7 ел, & вя 24 <\к, а с я 25 см. Так как д* -|- № «я са,
то данный треугольник прямоугольный. Следовательно, радиус
R описанного круга равен -я-. Радиус вписанного круга най-
дём по формуле r=s — t где 5 — площадь треугольника,
а р — полупериметр.
Отв. /?«= 12,5 см, /■ = ;* см.
579 ГЛ. 8. ПЛАНИМЕТРИЯ 317
679. По условию £/М£ = <р (черт. 62). Следовательно,
Черт. 62.
^ВА01=^т Требуется определить R^O^B и г = 02С.
Имеем
fl + r — O^+^Ot —ОА —</
и
R — r = OxB — ObC=*OxD%
Из прямоугольного треугольника ОлЭО^ где
Z.o/VD-Z.AW.—f.
находим
О,/)—0,0,• sin«J-, т. е. /? — r = dTsln-|-.
Из двух полученных уравнений находим
^(l + sinf)
И
Т"
г =
'('-а"т)
Заменяя sin 4 через cos f 90°— ij, можно преобразовать
si и выражения.
Отв. R = dcos*(45° — ±), г« d sln*(45° —|).
318 ОТВЕТЫ И РЕШЕНИЯ 580
680. Из черт. 63 имеем
По условию MN*DC=Q> т. e. 2ra = Q и, кроме того,
яг2 я S. Из этих уравнений
можно определить отдельно г
и а, но так как нам нужно
знать лишь отношение —, то
лучше разделить почленно
второе уравнение на первое.
иг S
-, откуда
Получим •&- 0
г _2S
а ~* *Q9
45
Отв. [_ BAD — arc sin ~.
581. Площадь правильного вписанного 2д-угольника равна'
180°
я/?2 sin . Площадь правильного описанного д-угольника
180°
равна /t/?2tg——. По условию
180°
«*■(*"
Отсюда
/? = ■
■ sin if-),
Yp
где a=s-
так:
180°
V«(tga —sina) •
Выражение tga — sin a можно преобразовать
tga— sin a = tga(l — cos a) =*2tga sin2-^»
ГЛ. 8. ПЛАНИМЕТРИЯ
319
582. Правильные одноимённые многоугольники подобны;
поэтому (черт. 64) площади их (S1— площадь вписанного
многоугольника, 5а — площадь описанного) относятся, как
квадраты радиусов
S^.S^OD*: ОА\
Но нз треугольника ОАО имеем
OD
180°
^-cosZ.D<M~cos-=
Отв. S^Si —cos»-^.
Черт. 64.
Черт. 65,
683, Пусть АВ = а (черт. 65) есть сторона правильного
й-угольника» Тогда
£«W—-НЕ.,
*-» п [
LNAM = ±-*L
(как вписанный, опирающийся на дугу а). Площадь Q кольца
равна
<Э=»я(ОЛ2 —ОЩ^п. AM*aK(jJ>
Ширину d кольца можно найти из треугольника NAM,
Отв. Q = -j-; rf-^tg-j-^
320
ОТВЕТЫ И РЕШЕНИЯ
584
584. Обозначим искомый радиус через лг, так что
(черт. 66) 02Л = 025 = х. Из прямоугольного треугольника
О,09А где £РъО\А = %[ и 0x04 = 0xB — 02B = R — xt
имеем ОаЛ = 0,02sin-g-, т. е. # = (/? — J^sin-g-.
Отв. х =
/?sln
/?sin-J
l+sin-y 2cos^45° — j\ *
Черт. 66.
Черт. 67.
685. Площадь Sx четырёхугольника ЛВОС (черт. 67)
разна 2 • -я- 05 • ЛЯ = /?3ctg а. Из неё нужно отнять пло-
щадь 5а сектора COBD, центральный угол которого равен
(180 — 2<х)°. Имеем
:ictfs
180 —2а
>7с/га
90 —а
360 ч 180
(а — градусная мера).
Отв. S = St — S2 = /?2Tctgа — ^ + -щН. гДе а —гра-
дусная мера угла или
S = /?2[ctg<x'_ $ + *'].
где а' — радианная мера угла.
587
ГЛ. 8. ПЛАНИМЕТРИЯ
321
586. По условию площадь треугольника ABF (черт. 68)
1 2
составляет -g- площади ромба ABCD, т. е. у площади гре-
угольника ABC. Так как треугольники ABC и ABF имеют
общую высоту AG, то
Поэтому
AF* = /IS3 + S/72 — 2АВ . В/7 cos (180° — а) =
^«a + -i«2-b|«acosa.
Ome. ^/7=>l£ = -Jl^l3 + 12cosa.
£ В F С
Г / • / ^7 д
Черт. 68.
Черт. $9.
587. Продолжим £Ш (черт. 69) до пересечения со сто-
роной ОА угла ЛОБ в точке R. Из треугольника AMRt
где £_AMR = 1_АОВ = 60° (как углы с взаимно перпенди-
кулярными сторонами), находим MR = 2АМ = 2л. Следова-
тельно, /?£ = /?Л14~ М23 = 2л 4- Ь. Теперь из треуголь-
ника ROB, где OR = 205, находим (20В)*—ОВ* = (2а -f b)\
Следовательно,
2я + &
05:
^3
Искомое расстояние ОМ определяется из треугольника ОВМ.
322
ОТВЕТЫ И РЕШЕНИЯ
583
688. Положим £„BCD = а (черт. 70). По условию
/.ДС£> = 2а, так что /_ACB = 3a и £BAC= ^АВС^
^90°—-у-. Из треугольника ВСД где /mBDC= 90°+у ,
находим
За \ За , а . а 1)
sin
Л™ За \ За , а . а 3
(90° y) cos-к- 4cos3y*-3 cosy
(90° +1)
Отсюда cos-|- = l/ "V д. Далее вычисляем sin-к-,
sin
а
cos у
а
COSy
sin а = 2 sin у cos 4- и находим
5 = ya2sln3a;
1
a9 sin а (3 — 4 sin2 а).
О/ия. S = JL(2a + 0V"(3<* + ')(« — /).
затем
589. При обозначениях чертежа 71 имеем
ADa = ^a + ^ — 2^ cos а и D£2 = aa-f-/a — 2^cos а,
а по теореме о биссектрисе внутреннего угла треугольника
-^gj =* —- . Получаем уравнение
&2-f.;2_2ft/cosa __ b*_
*) По формуле косинуса тройного угла cos За = 4 cos3 a — 3cosa;
если она неизвестна читателю, то её легко вывести из формул для
cos(2a-f-a)> sin 2a и cos 2a.
59^ ГЛ. 8. ПЛАНИМЕТРИЯ <523
(a + b)t
из которого находим cos а = ■ ^ f ; затем находим sin а и
S = -j аЬ sin 2а = ab sin а cos а.
0/и*- 5 - **Ц)г V^b* -(а + д)*Р.
4аЬ
690. Обозначим искомый угол через <р (черт, 72). Пусть
угол В— больший из двух углов А и В. Тогда
1ВСО = ЦВСЕ+9 = 90° — В + 9,
а
£ЛСО = ^ЛС£—<р = 90° — Л — 9.
Применив теорему синусов к треугольнику АОС, получим
~АВ:ОС = sin ^АСО : sin А.
Аналогично из треугольника ВОС получим
-i- АВ : ОС = sin /.ЯСО : sin В.
Приравняв правые части и подставив найденные выражения
углов АСО и ЯСО, получаем уравнение
cos (А + у) cos (В — у)
sin Л ~~ sin В »
которое приводится к уравнению
2 sin <р = cos 9 (ctg Л — ctg Я),
Олю. tg<p=*y(ctg/l — ctg Б).
324
ОТВЕТЫ И РЕШЕНИЯ
591
591. Искомая площадь S (заштрихованная на черт. 73)
равна утроенной площади фигуры EMFB. По условию ОЕ =»
= -g-AB==-^- В прямоугольном треугольнике OED катет OD
(радиус вписанного круга) равен —~-; следовательно,
OD = ОЕ Jy^. Значит, Ц)ЕО = 60°. Точно так же
lmKFO = m°. Так как угол EBF тоже равен 60°, то EO\\BF
и OF\\BE, и четырёхугольник OEBF есть ромб со стороной
4 и с углом 60° при вершине О. Вычитаем площадь сек-
тора EOF, равную j я (~Y, из площади ромба (£\ ~— f
и разность утраиваем.
Отв. S = -J(3j/"3 — я).
Черт. 7а
Черт. 74.
592. Требуется найти S = jAB*DC (черт. 74). Угол
СРВ — прямой (как вписанный, опирающийся на диаметр).
Следовательно, DC = AFt так что 5 = -g- ЛЯ • Л/7. Но по
свойству секущей имеем
AB*AF=A& = (j)\
Oms. S = —.
595
ГЛ. 8. ПЛАНИМЕТРИЯ
325
593. Так как ЦУСА = £ОВС (черт. 75) и ЦВСО «
= JJOBC (ибо медиана ОС равна половине гипотенузы),
то £DCA = /_ВСО. Но по условию £АСЕ=: /_ВСЕ.
Д В Е О В
Черт. 75.
Вычитая из этого равенства предыдущее, получаем £JDCE-=^
= £jOCE% т. е. СЕ делит пополам угол DCO,
594. Диаметр 2/? окружности, описанной около прямо-
угольного треугольника ABC (черт. 76), равен гипотенузе АВ.
Д L В
Черт. 76.
Диаметр 2г вписанной окружности равен МС-\-СК (так как
МОКС есть квадрат). Следовательно,
АС + ВС = (АМ + ВК) + (МС + СК) =
= (AL + LB) + (МС + СК) = 2/? + 2г.
595. Как в задаче 594, докажем, что a-\-b — 2{r-\-R)t
т. е. д-f *==2(-|/? + /?) = у^ Кроме того, а2 + *2 = Л
326
ОТВЕТЫ И РЕШЬНИЯ
ОУО
Отсюда
д = -|л * = 4г (или а==4^ b — Jc)m
Отв. sin А = у, sin £ = -=■.
596. Построим (черт. 77) треугольники ОЕОх и О^Од
(точки Е и Z7 — середины сторон параллелограмма). Эти тре-
угольники равны. Действительно, ОЕ = FCt а из условия
следует, что FC=*02F. Следовательно, OE = 0%F. Так же
докажем, что OxE = OF. Углы ОЕОх и OFO% (оба они ту-
Черт. 77.
пые) равны, так как их стороны взаимно перпендикуляр-
ны. Из равенства треугольников ОЕОх и OFOq следует,
что ООх = ООъ и что £_QOxE = L02OF. А так как ОхЕ
и OF образуют прямой угол, то и прямые ООх и 00%
образуют прямой угол. Значит, треугольник ОхО^О— равно-
бедренный и прямоугольный. Таковы же и треугольники
02ОнО, 0А040 и OfixQ. Отсюда следует, что Ofi^Ofi^
есть квадрат.
597
ГЛ. 9. МНОГОГРАННИКИ
327
ГЛАВА 9
МНОГОГРАННИКИ
В этой и следующей главах приняты такие обозначения:
V — объем,
S или Soch — площадь основания,
5бок — боковая поверхность,
Sa — полная поверхность,
а — сторона основания,
г — радиус окружности, вписанной в основание,
R — радиус окружности, описанной около основания,
И—высота тела,
h — высота основания.
Если указанные величины обозначаются иначе, это каж-
дый раз оговаривается.
На изображениях пространственных фигур мелким пунк-
тиром обозначены невидимые линии; крупным пунктиром
изображены вспомогательные линии.
597. Проекция диагонали АХС параллелепипеда (черт. 78)
на плоскость основания ABCD есть АС (диагональ основа-
Черт. 78.
ния). Поэтому угол а между АХС и плоскостью ABCD из-
меряется углом AfiA. Из треугольника AAfi находим
ААх = АС • tgа = 1/а2 + £2tgа.
Подставляем в формулу S^* = (2а -f- 2b) • AAV
Отв. S6oK = 2 (а + *) У аг + Ьг tg а.
328
ОТВЕТЫ И РЕШЕНИЯ
594
598. Из каждой вершины призмы, например из вершины Ах
(черт. 79), можно провести три диагонали (AxEt AXD, АХС).
Они проектируются на плоскость ABCDEF диагоналями
основания (АЕ9 AD, АС), Из наклонных AxEf AXD, АХС — наи-
большая та, у которой проекция—самая большая. Следова-
тельно, наибольшая из трёх взятых диагоналей есть AXD
(в призме есть ещё диагонали, равные AXD% но ббльших нет).
Из треугольника AXAD9
где £_ DAXA = а и AXD =
= dt находим Н = ААХ =
«ai^cosa, AD=dsina. Пло-
щадь равностороннего тре-
угольника АОВ равна
-j • АО2 • У^Ъ. Следовательно,
=6
Черт. 79.
Отв.
з-^з
8
rf3 sin2 a cos а.
Замечание1). Для изображения правильного шестиугольника
(основания призмы) можно построить произвольный параллелограмм
BCDO. Откладывая на продолжениях прямых DO, СО, ВО отрезки
О А «в OD, OF=*OCnOE = OBt получаем шестиугольник ABCDEF.
Точка О изображает центр.
*) Наглядность чертежа часто облегчает решение задачи. Поэтому
в ряде задач указаны способы изображения пространственных фигур
на плоскости. Они могут дать хороший чертёж даже при построе-
нии от руки.
Изображения даются в параллельной проекции: направление
проектирования — произвольное. При таком проектировании изобра-
жениями параллельных прямых служат параллельные прямые (но
изображения перпендикулярных прямых, как правило, не перпенди-
кулярны). Равные отрезки, отложенные на одной прямой или на
параллельных прямых, остаются равными и на изображении (но
длина их, как правило, меняется). Равные отрезки, отложенные
на непараллельных прямых, могут изображаться неравными от-
резками.
601
ГЛ. 9. МНОГОГРАННИКИ
329
599. а) Способ изображения
в основании, изображается произ-
вольным параллелограммом ABCD
(черт. 80). Точка О пересечения диа-
гоналей изображает центр квадрата.
Соединяя середину F стороны A3
с вершиной пирамиды Е% получаем
изображение EF апофемы.
б) Решение, Имеем
* Квадрат, лежащий
Е
1
х*Н,
где х — сторона основания (АВ на
черт. 80) и Н—высота пирамиды "
(ОЕ). Угол а есть /_ ЕВО (см. ре- Черт. 80.
шение задачи 597). Из треуголь-
ника ЕВО находим tf=/wsina; из треугольника ОАВ
x = OB-V% = rnV^ • cos a.
Отв. V — -g- тъ cos2 a sin a =
гф sin 2a cos a
600. Обозначив через m искомое боковое ребро, найдём,
как в предыдущей задаче,
.. m3 sin 2д cos д
V — о •
Отсюда определяем т.
У ЪУ—
Отв. т = 1/ , 0 „„—.
г sin 2д cos a
601. Введём обозначения АВ = х; EF = y (черт. 80).
Тогда имеем S = 2ху. Из прямоугольного треугольника OEF,
где 0£ = #, находим ^ — ГтП+Я2. По исключении д;
из найденных уравнений получаем лг4 + ^//2л:2 — 52 = 0. Это
уравнение имеет два действительных решения, но лишь одно
из них положительно.
330 ОТВЕТЫ И РЕШЕНИЯ 602
602 *). Соединив середины М и N (черт. 81) сторон ВС
и FE, получаем изображение MN диаметра вписанного круга,
так что MN=d и ОМ = ^. Так как ОМ есть высота рав-
ностороннего треугольника со стороной а (== ВС = ОС=*
= ОВ\ то |- =а ^4^-, откуда а = -^, Высоту H=OS
находим из треугольника SCO:
Н = VCS*—0C*= Ур — а* = j/"/2 — ^ .
Апофему /и = SM пирамиды находим из треугольника SCM;
Отв. V = J/3/» —<Р. 5бов=~1/'12/2 — Л
5
603. а) Способ ивображения. Основание можно
изобразить любым треугольником ABC (черт. 82). Центр
основания изображается точкой О пересечения медиан а).
4) Об изображении правильного шестиугольника см. на стр. 328
замечание к задаче 598.
2) Затем две из этих медиан, как не имеющие значения для ре-
шения задачи, можно стереть, оставив только точку О на медиане АЕ»
как это сделано на черт. 85 на стр. 333.
6U4
ГЛ. 9. МНОГОГРАННИКИ
331
1
1 1
б) Решение. Имеем V = ~ • 500Н • Н = j • -j a? Y% Н.
Связь между а и Н найдём из треугольника AOD, где
AD = a, а АО есть радиус R круга, описанного около ос-
нования, так что а = /?|/Г3. Имеем H* = AD2 — АО* —
= аа — з* = -з^2- Подставляя cfi^-^H? в выражение У,
получаем
V=&-№.
Отв. Н = 2-\/~^=..
604. а) Способ изображения. В отличие от пря-
моугольного параллелепипеда, все грани которого —
прямоугольники, в прямом параллелепипеде в основании
находится параллелограмм,
а прямоугольниками явля- 4 %
ются только четыре боко-
вые грани. Но при изображе-
нии прямоугольного парал-
лелепипеда (см. черт. 78 на
стр. 327) мы вынуждены изо-
бражать основание также в
виде параллелограмма. По-
этому чертёж прямого па-
раллелепипеда по существу
ничем не отличается от чер-
тежа прямоугольного парал-
лелепипеда, и это создаёт
дополнительные трудности
при пользовании чертежом: необходимо помнить, что острый
угол параллелограмма на чертеже является острым и в самом
деле у изображённой фигуры. Для ббльшей ясности реко-
мендуется на чертеже делать этот угол очень острым,
как на черт. 83, и обязательно отмечать его буквой
(в данном случае — буквой а).
б) Решение. В прямом параллелепипеде диагонали
(всего их четыре) попарно равны: АХС — АСХ и BDX = BXD
(на черт. 83 ACV и DBX не проведены). Пусть острый угол
основания ABCD есть 2. DAB = а; тогда £ ABC = 180°— а
тупой, и ЛС> ВО. Значит, меньшая диагональ параллеле-
332
ОТВЕТЫ И РЕШЕНИЯ
605
пипеда есть BDX (ибо BD*=*H*-\-BD2> тогда как Afi*=*
= #*+ АС2; следовательно, ВО* < ^С2). Из условия#D, «
= ЛС можно найти Н. Именно, из треугольника BDDt имеем
Я2 = BD* — BD* = ЛС2 — SD2.
Из треугольника ABD находим
BD2 = а2 + *2 — 2а* cos а,
а из треугольника ABC находим
АС2 == а2 + Ь2 — 2а* cos (180°— а).
Следовательно, Я2 = 4а& cos а.
Owe. V = 2 sin а ]/\а*)3 cos а.
605. Обозначим большую сторону основания (АВ на
черт. 84) через а, меньшую (#С) — через *. По условию
а -\-Ь = 9 (ел). Чтобы найти а, 6, а также острый угол а,
вычислим диагонали основания. Как доказано в решении
предыдущей задачи, меньшая диагональ \BDX = ]^33 (см)\
параллелепипеда проектируется на плоскость основания диа-
гональю BD. Поэтому
BD* = BD? — DD? = (УЩ* — 42=17 (cjP).
Точно так же найдём АС2 = 65 (гл*2). Получаем два урав-
нения
аа + *2 — 2a£cosa= 17; a2 + *a + 2a£cos a = 65.
696 ГЛ. 9. МНОГОГРАННИКИ 333
Складывая их, находим rfs-j-fta = 41, что вместе с а-|-£ = 9
даёт а = 5, Ь = 4 (мы обозначили через а ббльшую сто-
рону). Вычитая, находим 4ab cos а = 48, т. е. cos а =
48
= j7g72 = 0,6. Следовательно,
Soch = ab sin а = 4 ■ 5 • 0,8 = 16 {см%).
Отв. 1/== 64 слР, Яд =104 см\
606. а) Способ изображения. О построении точ-
ки О см. в задаче 603 (черт. 82 на стр. 330). Чтобы по-
строить линейный угол двугранного угла при ребре ВС
Черт. 85.
(черт. 85), соединим середину Е отрезка ВС с точками D
и А. Точка Е является изображением середины ребра; так
как треугольники CDB и CAB — равнобедренные (в натуре),
то DE и АЕ перпендикулярны к ВС, т. е. ^ DEA =
= ср — искомый линейный угол. Высота пирамиды DO = h
лежит в плоскости DEA.
б) Решение. Имеем tgT — TjTf» гДе OD = h4 а ОЕ=»
1 ЛО (медианы делятся в отношении Г: 2). АО находим
из треугольника AOD, где ЛО = /.
2ft
I
0/wff. ^"^tg
У/2 — ft*'
334
ОТВЕТЫ И РЕШЕНИЯ
607
607. Угол а измеряется углом ОВЕ (черт. 86), так как
ОВ— проекция ребра BE на плоскость основания. Для по-
строения линейного угла <р двугранного угла при ребре АВ
соединим середину F стороны АВ с О и Е (см. объяснение
Черт. 86.
* \ т
к задаче 606). Так как 50СН == я2 == ^я, т0 для вычисления
V нужно найти Н=ОЕ и d = BD. Из треугольника ОВЕ
находим //=ytga и, по условию, -£■//=$. Перемножив
эти равенства, а затем разделив их почленно, найдём
№ = Stga и (J)* —Sctga.
Следовательно,
^ = j-SOOH.tf = j.S8ctg2a.
Угол <р определяем из треугольника OFE, где
OF = £ =
2 У?'
tg<P = §J = ": y=4 = VStga: ^VSctg.^V^tg»,
Отв. V = jS2ctg2 a; tg <p =/2 tg a.
60S
ГЛ. 9. МНОГОГРАННИКИ
335
608, а) Способ изображения. Основание пирамиды
есть правильный пяти-
угольник (из уравнения
180° (л — 2) = 540°
находим п = 5). А в пра-
вильном пятиугольни-
ке ABCDE (черт. 87, а)
каждая диагональ (напри-
мер AD) делится каждой
другой (например BE) в
крайнем и среднем отно-
шении, так что DM ■=
= Щ—[-А£>жО,6 AD.
Кроме того, каждая диа-
гональ параллельна од-
ной из сторон (например
AD\\BC). Центр О ле-
жит на пересечении СМ
и ЕМ. Поэтому изображе-
ние правильного пяти-
угольника можно постро-
ить следующим образом.
Строим произвольный
треугольник ABD (черт.
87, б). Делим стороны AD
и BD точками М и N в
крайнем и среднем отно-
шении — приблизительное
в отношении
>Ш:ЛШ = 2:3;
достаточно разделить од-
ну сторону и провести
МЩАВ. Проводим AE\\BD до пересечения с продолже-
нием прямой ВМ в точке Е. Аналогично строится точка С.
Изображение центра О лежит в пересечении СМ и EN.
б) Р е ш е н и е. Из треугольника COF, в котором /_ OCF=a
и С/7 = /, находим Н = OF = / sin а; ОС ==/ cos а. Площадь
336
основания
ОТВЕТЫ И РЕШЕНИЯ
5 = 5 . i . ОС • OD • sin i_COD = у - ОС* . sin 72° =
в|. /2 cos2 a sin 72°.
Отв. V = -i SH = -| /3 sin 72° cos* a sin а.
609 *). Для определения угла а рассмотрим треугольник
СО/7 (черт. 88), где FC = CB = a (по условию треугольник
CBF равносторонний).
Сторона же ОС (ра-
диус описанного кру-
га) выражается через а
из треугольника COU,
где угол COU равен 36°
и Ш=у. Имеем
i£ ОС =
2 sin 36'
ОС
^, так что
cos a — Cf — 2sin36o.
Угол ср определяется из треугольника OUF, где /*£/=—^—
(как высота равностороннего треугольника со стороной а), а
OJ7=gct|36°(H3 треугольника COU). Имеем
cos 9 '•
Отв. а = arc cos,
Q£/_flCtg36° а УЗ _ctg36°
ctg36°
"W
1
2 sin 36°
f <p = arc cos
Уз
610. При обозначениях чертежа 88 имеем ВС = а,
Of/ = -7rCtg . Площадь основания
с яй я . 180° ид2 |80°
S = ^-oCtg— —- ctg—.
2 2
i) Об изображении правильного пятиугольника см. в предыдущей
задаче.
611
ГЛ. 9. МНОГОГРАННИКИ
337
Из формулы V = -g- SH находим
и SV 12И, 180°
Обозначив искомый угол OCF через а, имеем
И
ОС
4 "
где
ОС
2 sin
180° *
п
180°
О/яя. a = arctg
10ЛО
ЛИ3
Предварительное замечание
и следующим
к задаче 611
Если все боковые рёбра пирамиды образуют равные углы
с основанием, то 1) все боковые рёбра равны; 2) около осно-
вания можно описать окруж- $
ность; 3) высота пирамиды
проходит через центр этой
окружности.
Доказательство. Пусть
рёбра SAt SB, SC н т. д. (черт. 89)
образуют с плоскостью ABCDE
равные углы. Рассмотрим прямо-
угольные треугольники AOS и
BOS (OS — высота пирамиды). У
них общая высота, а острые углы
OAS и OBS равны (так как онн
измеряют углы наклона рёбер SA,
SB к основанию). Следовательно,
AS = BS. Так же докажем, что
BS = CS и т. д. Из тех же тре-
угольников AOS и BOS находим
АО = ОВ. Так же докажем, что
ОВ = ОС н т. д. Значит, окружность
ОА пройдёт через точки В, С и т. д.
Черт,
с центром в О и радиусом
611. По доказанному, высота ЕО проходит через центр опи-
санной окружности, т. е. через точку О пересечения диагоналей
338
ОТВЕТЫ И РЕШЕНИЯ
612
(черт. 90). Площадь всякого параллелограмма равна половик/:
произведения диагоналей на синус угла между ними. Поэтому
£ Soon = -к &* s*n а- И3 треуголь-
ника АОЕ находим:
я-жыер—|tgp.
Отв. V = -г? ** ^п а !& Р*
612. а) Способ изо-
бражения. Высота пирами-
дм, согласно предварительному
замечанию (стр. 337), должна
проходить через центр окруж-
ности, описанной около равно-
бедренного треугольника ABC
(черт. 91). Поскольку угол
а = ^ CAB при вершине ос-
таётся произвольным, изобра-
жение центра О можно взять
в любой точке отрезка АВ
(Е—середина ВС) и даже на
продолжении его за точку Е
(в последнем случае угол а в
натуре тупой).
б) Решение. Высоту DO
определим из треугольника
AOD, где £ Oi4D=p, а АО ■=
s= R есть радиус описанной
окружности. Согласно теореме
синусов сторона ВС равна
произведению диаметра 2R
описанной окружности на синус
так что R =
Черт. 91.
противоположного угла а,
ВС
-j- s=s BE находится
Следовательно,
2 Sin а
Величина
из треугольника
(вс Л
ABE <-g- saa sin 2
■)•
H = /?tgp =
*sln -g-lgp
sin a
613
ГЛ. 9. МНОГОГРАННИКИ
339
Площадь основания
S = -g- a2 sin а.
дгз sin -j tg р
Отв. К = -г «
о
613. а) Способ изображения. Окружность изобра-
жается в параллельной проекции эллипсом»
Эллипс можно построить следующим образом. Прове-
дём какой-либо диаметр MN окружности (черт, 92) и из
произвольной точки Р окружности проведбм прямую PPf9
перпендикулярную к MN. Пусть R — точка пересече-
ния РР* с MN. Укоротим отрезок RP в каком-либо от-
ношении (например вдвое) и отложим укороченный отре-
вок RQ на той же прямой РР* по обе стороны от R
(RQ^RQ*). Поступая так с рядом точек окружности, по-
лучим ряд точек эллипса.
Эллипс симметричен относительно MN {большая ось эл-
липса) и относительно прямой UU\ проведенной через
центр О перпендикулярно к MN (отрезок W — малая ось
эллипса). Точка О называется центром эллипса.
Чтобы изобразить окружность, описанную около прямо-
угольника, удобнее сначала начертить эллипс ABCD, изобра-
340
ОТВЕТЫ И РЕШЕНИЯ
613
жающий описанную окружность (черт. 93). При этом боль-
шую ось эллипса лучше расположить наклонно1). Одну
сторону прямоугольника можно изобразить произвольной хор-
дой АВ эллипса; эту хорду целесообразно провести гори-
зонтально. Через центр О эллипса проводим прямые BD и
АС. Четырёхугольник ABCD есть изображение прямоугольника.
Черт. 93.
б) Решение. Вписанный угол CAB содержит <Л так как
опирается на дугу ВС в (2а)°. Из треугольника ВАС имеем
АВ = 2R cos а; ВС =» 2R sin а, так что
5 = 2(^5 + BC)H=4/?(cosa + sina)H.
Отсюда
Н =
4/? (cos a -f- sin a)
Теперь находим V =* АВ • ВС • Н. Условие, что дуга (2а.у
стягивается меньшей стороной прямоугольника; является
излишним.
SR cos a sin a SR sin 2a
Отв. V--
' cos a + sin a y~S cos (45° — a)'
i) На черт. 93 большая ось эллипса принята за диагональ АС
прямоугольника. Это упрощает чертёж, но не является обязательным.
615
гл. 9. МНОГОГРАННИКИ
341
614. Площадь основания 5 = -г- a2 tg а (черт. 94). По
условию 1
эбок :
С другой стороны,
'бок
\ ' cos а /
2а cos8 -н-
cos я
Я.
Приравнивая-два выражения S6oB» на-
ходим
a- sin a а , а
tgy.
н=
i cos«|
О/я*. V = Jlgatga
Черт. 94.
2'
6151)* Соединим середину М стороны АВ с О и 5
(черт. 95). Угол ОЛ15— линейный для двугранного угла а
(см. объяснение к задаче 606). Следовательно, ОМ =
■ == SM • cos a = m cos a. Из треугольника ЛОМ, где £ ЛОЖ =
>30°, находим
^i-f
VI
ОЛГ
УЗ"
3 -"*'■— з
Далее находим
SeoB = 6-^ • m.
/я cos a.
„ Подставив найденное выраже-
Черт. 95. ние Т» поучим
5П = 50он + 5б0В = 2]/r3m2 cos a (1 + cos a).
Отв. Sn = 4 1^3 /я2 cos a cos2 -£.
') об изображении правильного шестиугольвика см. на стр. 328
замечание к задаче 593.
342
ОТВЕТЫ И РЕШЕНИЯ
616
616. По условию наклонные АС и С В (черт, 96) равны.
Значит, равны их проекции: AD = DB. Угол DEC (Е— се-
редина АВ) есть линейный угол двугранного угла а.
Черт. 96.
Так как треугольник АСВ прямоугольный при вершине С, то
С£" = ЛЯ = у. Следовательно, ED = ~^ cos а. Наконец,
AD = BD = УДЕ* + ED2 = | V1 + cos2a.
С3 COS a
Owe. Sabd =
i4B + BD + i4D = c(l + Vrl+cos2a).
Предварительное замечание к задаче 617
и следующим
Если все боковые грани пирамиды наклонены к основа-
нию под одним и тем же углом а, а высота проходит через
некоторую точку О основания пирамиды, то
1) высоты всех граней равны;
2) в основание пирамиды можно вписать окружность,
центром последней будет точка О;
3) 50сн = 5бов cos а.
Доказательство. 1) Проведем (черт. 97) высоту FM бо-
ковой грани BFC и соединим М с точкой О. Отрезок ОМ есть
проекция FM на плоскость ABCDE, Следовательно, он перпенди-
кулярен к ВС («теорема о трех перпендикулярах»). Значит, угол
OMF— линейный для двугранного угла а. Из треугольника OMF
OF
имеем FM = ~. ; ОМ = OF ■ ctg а. Если из вершины F провести
высоты FL, FN и других боковых граней, то таким же образом
OF
найдем, что все они равны-—.
sin a
617 гл. 9. многогранники 343
2) Отрезки OL, ОМ и т. д. будут перпендикулярны соответственно
к сторонам АВ, ВС и т. д. и равны OF* ctg а. Поэтому если провести
из центра О окружность радиуса ОМ, то она будет вписана в осно-
вание ABCDE.
3) Точка О — основание высоты пирамиды, по доказанному есть
центр вписанной окружности.
4) S0BG = ± BC-OM = ±BC(FM.cos*) =
= (-q ВС» FMj cos a = S$BG cos a.
Точно так же найдём, что Sq^b = Sjp^H cos а, и т, д. Складывая эти
равенства, получим 500Я = S6oa cos a.
Черт. 97.
617. Высота FO всякой пирамиды (черт. 97) проектируется
на боковую грань BFC отрезком, лежащим на прямой FM.
Поэтому ^_OFM = y. Значит, a = 90° — <р, т. е. все грани
наклонены к основанию под одним и тем же углом. По до-
казанному
^бов cbsT-sln7#
Л « Q * П/IJL M 2QC°Sa(45°-'?)
°лл 5^=8тп7'5п==(3(1+ж?;^ isr?—•
«Н4 ОТВЕТЫ И РЕШЕНИЯ
618. Из треугольника DOE (черт. 98)!) находим
613
Имеем
W = 0£.tg?^i.C£.tg?===l.^l.tgcp.
(см. предварительное замечание к предыдущей задаче).
D
Черт. 98.
От* У-£*1. 5ц ■^yy(l+co»f)_flPyTco"T
Um*. к g—, Лл-4^5Г^ 2COS9 *
Замечание. Общее выражение для полной поверхности пи-
рамиды, у которой все грани наклонены к основанию под одинако-
вым углом <р, можно записать так:
5п = 5оон + 5во« = 5оои(1 + S5sT) =
<Р
COS<p
619. Пользуемся формулой Sa-
в предыдущей задаче.
_ 1 f2S cos а
cos-lK V3"
дзуз cos2-|-
2 cos? '
найденной
Отв.
*) Способ изображения — см. черт. 82 на стр.330.
ГЛ. 9. МНОГОГРАННИКИ
345
620. а) Способ изображения. Прямая LN, соеди-
няющая точки касания L и N противоположных сторон ромба
(черт. 99, а), проходит через центр окружности. Поэтому,
начертив сначала эллипс (черт. 99, 0), изображающий окруж-
ность1), проведём через центр О две прямые М, и КМ.
Через концы их N, Ц Kf М проведём прямые, касающиеся
ьллипса. Получим параллелограмм ABCD, изображающий ромб.
£
Черт. 99.
б) Решение. Чтобы определить S0CH, найдём высоту DF
ромба и его сторону АВ. Из черт. 99, а находим DF = 2 (Ж=»
в 2г; из треугольника AFD, где 2. А = а, имеем
DF 2г
Далее находим
Sin a
Sin a*
SQGB = AB.DF=a-2r = ^
Из треугольника ONE (черт. 99,6)t где ON — г,^^ ONE=pf
находим W. Для определения Sa используем замечание к пре-
дыдущей задаче.
3 sin a v
8r« cos21
sn =
sine cosg •
621. Использовать замечание к задаче 618.
Oms. 9 = arc cos —.
*) О вычерчивании эллипса см. стр. 339—340 (задача 613).
346
ОТВЕТЫ И РЕШЕНИЯ
622
622. а) Способ изображения1). Сечение есть па-
раллелограмм AXDXCB (черт. 100). Чтобы изобразить линейный
угол двугранного угла, образуемого сечением A^D^CB с пло-
скостью основания,
пронедём прямую DM,
изображающую высоту
ромба ABCD. Так как
в натуре DM н DDX
перпендикулярны к ре-
бру AD, то плоскость
£>D, NM перпендику-
лярна к AD, а значит,
и к ВС. Эта плоскость
пересекает плоскость
сечения по прямой
MDX, так что
£_DXMD=$
б) Решение. Боковая поверхность состоит из четырёх
равных прямоугольников (так как основание—ромб). Площадь
боковой грани AXDXDA равна
Sj = i4jDj • DDlf а площадь
сечения равна Q = Afix • D^M.
Из треугольника DMDX имеем
DD1=^D1M* sin Р; поэтому S^
= Q sin p.
Отв. 5в0В = 4Q sin p.
623. Учесть предваритель-
ное замечание к задаче 617. По
условию EO=*d (черт. 101).
Черт,
Точка Е (середина гипотенузы
ND треугольника NOD) есть
центр окружности, описанной
около треугольника NOD. По-
этому ND=2-ED=2-EQ=2d.
Из треугольника DON, где
l^OND — y, находим радиус
ON = r круга, вписанного в основание: r = 2tfcos<p,
-~^Д
Черт,
Чтобы
*) Об изображении прямого параллелепипеда см. стр. 331 (за-
дача 604).
624
гл. 9. МНОГОГРАННИКИ
347
найтв Soch, определим BN (половину основания равнобедрен-
ного треугольника ABC) и AN (его высоту). Центр О
вписанного круга лежит на биссектрисе угла ABC, равного о
т* ^ L, OBN= у. Из треугольника BON находим
BN= г ctg ~. Из треугольника ABN находим A/V=a SAMg а.
Следовательно,
Soob — у BC-AN= BN.AN= BTVMg a = ractg2-|.tg а =
= 4rfacos29Ctg2ytga.
Отсюда (см. замечание к задаче 618) найдём:
5д»
2SOOI,cos^
COS?
^Cfcr2-^
От*. Sn = 8rf2 cos ф cos2 ^ ctg2 ^ tg a.
624, Учесть предварительное замечание к задаче 617 *):
Высоту пирамиды найдём из треугольника ONP (черт. 102).
Н = г tg <р. Если лх> р
«а
И Т. Д.'
• стороны
основания, то
«Soch в $АОВ "Ь ^БОС +
+•■
c-i-AS>OAf +
> I 1 I
-JV+2V +
+ ... = 2•r(a,4-
^-л24-...)=
0me. K = ^iil.
/г/
Черт. 102.
i) О вычерчивании эллипса (изображения круга, вписанного
в основание) см. стр. 339—340 (задача 613).
348
ОТВЕТЫ И РЕШЕНИЯ
625
625, а) Способ изображения. Сделав изображение
правильной треугольной пирамиды DABC (черт. ЮЗ)1), по*
строим треугольник АхВхСи стороны которого соответственно
параллельны сторонам треуголь-
ника ABC. Треугольник АХВХСХ
изображает верхнее основание
усечённой пирамиды. Изобра-
жение центра Ох верхнего осно-
вания получается в пересечении
DO с одной из медиан А^Ег тре-
угольника АхВхСг. Отрезок АХМ,
параллельный ООг и оканчиваю-
щийся в точке Mt лежащей на
медиане АЕ, изображает высоту
усечённой пирамиды, опущенную
из точки Ах (отрезки DA1$ DB]t
DCX и DOx можно стереть).
б) Решение. Объём усе-
чённой пирамиды
где Q и_?—площади треугольников ABC и АХВХС1% так что
VI
/3
Q = ^ a2; q = -^ **• Высоту Н = АХМ найдём из треуголь-
ника ААХМ, где £МААХ = а и AM = АО — АхОх. Но
АО и АхОх—это радиусы окружностей, описанных около
ABC и АхВхСг. Поэтому ЛО==-^г и AxOx^yf Значит,
АМ =
а—1
W
следовательно.
а — Ь
Отв.
V=^ — lfi)iga.'
») Об изображении правильной треугольной пирамиды см,
стр. 330 (черт. 82).
ГЛ. 9. МНОГОГРАННИКИ
349
626» а) Способ изображения* Усечённая пирамида
изображается как в предыдущей задаче. Для изображения
линейного угла искомого двугранного угла проводим АХЕ и
ByF (черт. 104) параллельно ООг до пересечения с диагона-
лями АС и BD. Проводим прямую EF\ она будет параллельна
АВ и пересечёт рёбра AD н ВС в точках ЖиМ Плоскость
MA^Bfl перпендикулярна к ребру AD, так как она проходит
Черт. 104.
через прямые АгЕ и МЛ/, перпендикулярные к ребру. Сле-
довательно, ЦЕМАХ =ч= ср есть линейный угол двугранного
угла при ребре AD.
б) Решение. Из трапеции MAXBXN получаем ME =
л — Ь г*
= —g— - высоту усечённой пирамиды находим из треуголь-
ника АЕА*, где АЕ = "Т- . Имеем
jj
Объём находим по формуле V = -^-(d2 + °Ь + **)• Иско-
мый угол <р = /тЕМА{ находим из треугольника АХМЕ, где
ME = ~ - (из трапеции MNBXA^. Имеем
0»Л ^-(a37^-tga; ? = arctg(/2tg«).
350
ответы И РЕШЕНИЯ
027
627. См. предварительное замечание к задаче 611 на
стр. 337. Высота пирамиды должна проходить через центр
окружности, описанной около основания. Но в прямоугольном
треугольнике Л#С(черт. 105) центр лежит на середине гипоте-
нузы АВ в точке Е. Следовательно, АЕ9 BE и СЕ будут
проекциями боковых рёбер AD, BD и CD на плоскость осно-
вания, так что Ц)АЕ== £DBE= ЦУСЕ==$. Объём пи-
рамиды найдём по формуле У = -т • —%— • &Е. Из ДАВС
Черт. 105.
имеем АС = с cos at ВС = с sin а; из /\ADE находим DF=
"■у*£?• Обозначим плоские углы при вершине: ^i4DZJ = Glf
2lBDC = 02 и ^i4DC = 08. Так как эти треугольники равно-
бедренные, то высоты их D£, £>Ж и DN пройдут через се-
редины соответствующих сторон основания. Из Д ABD имеем
/А=180°—20; из Д£>ЯС имеем sin ^«до ииз ДЛОС
имеем sin -J-
л*
2cosfr и
из ДЛЯС находим МВ = Щ- = %-Sin а и i4/V = ^elcosa.
s ^. Из ДЛОЕ находим AD = DS:
От*. Г-**"**»; О(=180°-2р,
24
0а = 2 arc sin (sin a cos Р), 08 = 2 arc sin (cos a cos P).
628 гл. 9. МНОГОГРАННИКИ 351
628. Требуется найти объём пирамиды СгАВС (черт. 106).
Так как боковые рёбра её равны между собой, то они на-
клонены к основанию под одним и тем же углом (эта
теорема обратна доказанной в предварительном замечании
к задаче 611 на стр. 337), и высота СгО проходит через
центр О окружности, описанной около треугольника ЛВС.
Так как этот треугольник прямоугольный, то О лежит на
середине гипотенузы ЛВ (см. объяснение к предыдущей за-
даче). Угол ODCx (D — середина катета АС) измеряет наклон
боковой грани АССгАА к основанию. Катеты ВС и АС нахо-
дим из двух уравнений:
ВС-\-АС = т и BC = i4C-tga;
получаем
Ар т mcosa -jr> m sin at
1 + tg a Sin а + COS а ' sin a -j- cos а '
Затем находим S0CH =* -^ ВС • АС. Высоту Н находим из тре-
угольника DOCu где OD = ~2 ВС (как средняя линия тре-
угольника).
п т/ 1 тФ sin2 д cos а . о m3 sin2 a cos а . R
uma. ^-i2(sina + cosa)BtgP"24y2-cos3(flt_45^tffp-
352
ОТВЕТЫ И РЕШЕНИЯ
629
629. Точка О есть центр окружности, описанной около
основания ЛВС (черт. 107) (см. предварительное замечание
к задаче 611 на стр. 337).
О Л = R есть радиус этой
окружности. Объём пирамиды
=^M^™.BC=XrQ.BC
С { AE-DO
так как «
;(ДСторо-
Черт. 107.
ну ВС находим по теореме си-
нусов:
BC=2#sin(180° — 2а) =
= 2R sin 2а.
Д ADO оо Д ABE (так как £ ADO = £ ЛВ£ = а); имеем
пропорцию:
ЛО _ OP п
откуда
Подставив сюда
АЕ~ BE
AO-BE = AE-OD.
ВС
AO = R9 BE^~-t AE'OD = 2Qt
пэлучим
R-BC
= 2Q.
Исключив R из найденных формул, получим
ВС = V8Qsin2<x.
1 - -
Ome. K==4-"(2(2>2shl2 2a-
!) Черт. 107 (где АО<АЕ) явно не соответствует этому соотно-
шению. Но чертёж, точнее изображающий условие задачи
9 = 90° — а, был бы очень не нагляден.
гл. 9^ МНОГОГРАННИКИ
353
630. Если грани ADE и СОЯ (черт. 108) перпендикулярны
к плоскости основания, то ребро DE есть высота пирамиды,
Утол DAE есть линейный для двугранного угла ЕАВС, fak
как плоскость DAE перпендикулярна к ребру АВ (доказать!).
Следовательно, ^Di4£=a; аналогично £_DCE = $. Из тре-
угольников ADE и CDEr где DE = Ht находим AD и DCn
подставляем в формулу
Y = j AD-DC-H.
Отв. У = у tf&ctgactgp.
Е
Черт. 108.
631. Из треугольника BDE (черт. 109), где ^EBD = ^
(доказать!), находим
Значит,
DE = lsin$ и £D = /cosp.
лп~ВО £cos£
Из треугольника ADE находим AE = Y AD*-\-DE*. Угол 9
наклона ребра АЕ к плоскости основания есть ЦЭАЕ (до-
казать!). Из треугольника ADE имеем tg <р = -гту*
От*, Z>£ = /sinP; Л£ = СЯ —/j/*i±J££f
? —arctg(l/2tgp).
354
ОТВЕТЫ И РЕШЕНИЯ
632. Наибольшую площадь имеет грань ADB (черт. ПО),
так как её высота DE больше высоты DC двух других бо-
ковых граней, а основания у всех граней одинаковы. Из
треугольника ACD имеем
AD =
cosp
и Н=*а
Затем находим
de=Vad*-ae*=^J?z
ф
Р 4'
Угол <р наклона грани ADB к плоскости основания есть
£CED (доказать!). Имеем
и
где ЕС = -
0ш&- 5~ет^4-соз2Р' »-агс*^
Черт. 111.
633. Площадь 5 сечения равна -^ • АВ • NM (чер?* 111).
Из прямоугольного треугольника ACN, где £CAN = 30°,
находим
AN=>j.AB:
^■а и CiV=-g.o.
634
ГЛ. 9. МНОГОГРАННИКИ
355
Из треугольника NCM имеем
где H — atga (из треугольника ACD).
Отв. S = . * .
4 cos а
634. а) Способ изображения1). Чтобы изобразить
сечение, перпендикулярное к основанию ЛВС (черт. 112) и
делящее пополам стороны основания АВ и АСЛ проведём
среднюю линию MN. Из точки
F, где MN пересекает медиану
АЕ, проведём FK параллельно
высоте OD. Искомое сечение есть
NMK* Действительно, плоскость
NMK проходит через прямую
FK* перпендикулярную к плоско-
сти ABC (значит, плоскость
NMK перпендикулярна к плоско-
сти ABC). Двугранный угол а
измеряется углом AED (доказать!).
Плоскость AED проходит
через прямую KF, так как точки
/Си/7 лежат в плоскости AED.
б) Решение. Примем за основание пирамид'л KANM
треугольник AMN. Его площадь 5 составляет -j плсщади
треугольника ABC, т. е. 5 = т^а2уг3, Высоту KF выразим
через ОД пользуясь подобием треугольников AFK и AOD. Так
как AF составляет ~^АО (ибо AF = -jAEt а ЛО = -|л£),
то KF = -j OD. Отрезок OD находим из треугольника DOE,
где ОЕ = &$- и LDEO = е.
Ош. V-^t.
1) Об изображении правильной треугольной прфзмнды см, задачу
603 на стр. 330.
356
ОТВЕТЫ И РЕШЕНИЯ
635
635. Прямая ММ (черт. 113), по которой плоскость ос-
нования пересекается с плоскостью сечения, параллельна ВС.
Чтобы построить угол <р» проведём OF\\AB и соединим
точку К, где OF встречает MN, с Е. Тогда ^0/С£ = <р
(доказать всё это). Площадь сечения S =-j • AW •/("£, где
Черт. 114.
MN^a и КЕ =
И
sinv* высота Н определяется из треуголь-
ника EOFf где OF = -g- и FE = -jctg~ (из треугольника
EBF). Получаем
Отв.
636 *). В сечении получаем треугольник DKN (черт. 114).
Как в задаче 634, докажем, что плоскость AED перпенди-
кулярна к стороне ВС. Значит, она перпендикулярна и к сред-
я=
5 =
■К(т«*
а2У cos а
4 sin-л- sin 9
а \2
2 ) "
•
-(f)"-
Я У COS а
2 sin J
*) Об изображении правильной треугольной пирамиды см.
черт. 82 на стр. 330.
ГЛ. 9. МНОГОГРАННИКИ
357
ней линии /C/V. Следовательно, ^DAf£ — линейный угол
данного двугранного угла or. Из треугольника OMD, где
ОМ = ^- АЕ ss — g ^ находим
£Л1 =
дУ"3
Площадь сечения
1
S = ±.KN-DM*
12 cos а*
1 ± аУ<* — Уз"**2
2 * 2 ' 12 cos а 48 cos а*
Площадь основания пирамиды DAKN вчетверо меньше
площади основания пирамиды DABC, а высота у них об-
щая. Поэтому объём Vx пирамиды DAKN равен — К, где
V — объём пирамиды DABC. Следовательно, объём пирамиды
DKNBC V* = j V.
равен
Объём V
V =
1 9
1 ут
.#«
-т--^*'-^*'
дУЗ
Owe. 5==
12
48 cos а ■
17 Л3 х
17 ^а
Черт. 115.
637. По условию BE : ЕА =
е=2 : 1 (черт. 115). Сечение есть
l\DEC. Найдём его площадь S. Треугольник DEC—равно-
бедренный, так как ЕС = ED как соответственные стороны
равных треугольников АЕС и AED {АС = AD; сторона
ЛЯ—общая и £САЕ= / DAE=Q0°). Проведём высоту
его £iV; тогда $ = ■
Для определения £W найдём
сначала £С из /\АСЕ (по теореме косинусов):
ЯС^ЛС^ + ЛЯ2 — 2-Л£. ^Ccos60° = -g-aa.
358 ОТВЕТЫ И РЕШЕНИЯ 638
Теперь из Д ENC находим
Обозначим углы сечения ^ ECD = ^ £DC через а. Тогда
£_CED = it—2а. Из треугольника C£Af имеем
cos а = — =
> == -1 г; а == arc cos —•==
12 2/7
pssw—2 arc cos
2YT*
6381). Боковая грань ВССХВХ (черт. 116) — равнобочная
трапеция с основаниями ВС = а и ВгСг = b (а>Ь) и
углом а при основании а. Отрезок £,Л/—её высота. Находим
B^N^^—Ltga. Из треугольника ^ЛТ7. где FN=?^-f
находим
Я= 5^ = VNB? — /W2 = ^=^/tga а— 1.
Объём
У^^^ + ^ + а^^ g87^^tg2a~b
Замечание I. Если острый угол а меньше чем 45°, подко
§еииое выражение отрицательно. Но угол а не может быть меньше 45°.
действительно, сумма плоских углов BCCt = а и DCCi «= а трёхгран-
ного угла С всегда больше третьего плоского угла BCD; ио 2. BCD**
=90°, поэтому 2a>90°f т. е. а>45°.
Замечание 2. Выражение Уlg2a — 1 можно преобразовать
к виду
"sin2 a—cos2 a Y— cos 2а
COS2 a COS a
/5
') Об изображении усечённой пирамиды см. задачу 625» См.
также задачу 626.
ГЛ. 9. МНОГОГРАННИКИ
359
Так как 2а больше чем 90° (но меньше чем 180°, ибо а—острый
угол), то cos 2а всегда отрицателен. Значит, подкоренное выражение
(— cos 2а) всегда положительно.
Отв. V =
а*— #»
6 cos а
■cos 2а
' 6 COS а
Kcos(180°—2а).
Черт. 116.
Д
%
$
Ру
?
% I
В
Черт. 117.
639. Проекция диагонали BD^ (черт. 117) на боковую
грань ВССгВг есть BCV Поэтому /eClBD1 = a. Из тре-
угольника ВС^ОХл где D1C1 = b, находим ВС^ = bctgau Из
треугольника В£гВ имеем
н = Vbc?-ВА2=V^ctg»« —4» = ^,соз2а.
Sin а
Объём
у = &Н=Ь*
^6з У cos 2а а
Sin а
Замечание. Подкоренное выражение cos2a здесь (ср. замеча-
ние 2 к задаче 638) всегда положительно, нбо а<45°. Действительно,
lga =
fid — ВС2 •
Но ВгСл есть катет, а ВС\ — гипотенуза треугольника ВВ\Р\. Поэтому
iga<l, т е. а<45°.
Отв. V = tfi
дЗ У COS 2а
sin а
360
ОТВЕТЫ И РЕШЕНИЯ
•640"
640. Если CD (черт. 118) есть высота треугольника ЛВС,
опушенная на гипотенузу АВ = с (на изображении можно
провести CD произвольно внутри
угла АСВ), то ^CDCt = ^ (до-
казать!). Имеем
CD = АВ • since cos а =-?rC sin2а
и
Эти выражения подставляем в
формулу
V = \SH = ±.±cCD-H.
Отв. V=^sm*2a\g$.
641. Одна из частей призмы есть треугольная пира-
мида ВХАВС (черт. 119). Её объём К, =у V, где V—объём
призмы» Значит, объём V% дру-
гой части (четырёхугольной пира-
миды BxAfifiA) равен -~- V. Най-
дём V.
По условию £С + Л£==/я, а
из треугольника ЛБС находим
ВС = Л£ • cos а. Следовательно,
£С =
/Я COS a
т cos a
I + cos a
2 cos2 -
Площадь основания призмы 5
равна
S = \ • AC • ВС = -i . ВС* • tg a.
Высоту // = BZ?! определяем из треугольника ВСВ}, где
£ ЛСВ, = р (доказать!). Получаем Я = £С. tg р.
О/ИЗ. К _g»8CQS»gtgqtgp . ^ _w»cosJatgatgp
48 cose■
24 cose-
643
ГЛ. 9. МНОГОГРАННИКИ
361
642. Согласно предварительному замечанию к задаче 617,
S»o„ = S cos <р = S sin а. С другой стэроны, Soan = а' ^а .
Приравнивая эти два выражения, получим а = 2 J/^S cos а.
Точка О (центр окружности, вписанной в треугольник АБС\
черт. 120) лежит на пересечении биссектрис углов треуголь-
ника, следовательно,
LOCE = \ и 0£ = £Ctg| = f tg|;
из Д DOE находим И = ОБ • tg ср.
Owe. V = -g-(Scosa)Mg-|;
5n==5(l + coscp)==25cos2(45° — -J),
i? 2?
Черт. 120. Черт. 121.
643. На черт. 121 OA = OC=>R— радиусы окружности,
описанной около равнобедренного треугольника ЛВС (АВ =
= АС = а). В силу условия а > 45° центр О лежит внутри
треугольника ABC (при а <45° угол А =180° — 2а был
бы тупым, центр описанной окружности лежал бы вне тре-
угольника ABC, и тогда плоскость, проведённая через высоту
пирамиды и вершину С, не дала бы никакого сечения пира-
миды). Высота пирамиды проходит через центр О (см. на стр. 337
предварительное замечание к задаче 611).
362
ОТВЕТЫ И РЕШЕНИЯ
644
Из треугольника AOD имеем // = /?tgp. Так как по тео-
реме синусов АС а» а = 2/? sin а, то /У = 2 !* д- tg {}.
Найдём теперь основание СЕ сечения из треугольника АСЕ.
В иём £яСАЕ= 180°—2а, a J^ACE, лежащий в основании
равнобедренного треугольника АОС (AO = OC = R)f равен
^CAO^j £САЕ= 90°— а. Значит, ^_ ЛЕС = За — 90°.
СЕ а
По теореме синусов „и,|Ядо_0„, acin ^,^ » откУда
sin (180° —2з)
C£^flts1n(180°—2а)
sin (За — 90°) »
а sin 2а
sin (За — 90°) sin (За — 90°) *
Замечание. В знаменателе можно написать (— cos За); но
угол За заключен между 135° и 270°. так как 45°<а<90°; таким
образом. (—cos За) есть положительное числа Поэтому при вычи-
слениях с таблицами удобнее иметь дело с углом За — 90°, заключен-
ным между 45° и 1806.
Пт* с_ a2cosatgp
итв* °~~2sin(3a — УОУ
644. I) Найдём площадь Q основания призмы (черт, 122)»
Имеем: Q = Sx + 52( где
5( — площадь прямоуголь-
ного треугольника ABC, а
S2—площадь прямоуголь-
ного треугольника ADC,
с ЛВ-ВС /sin a-/COS a
/^ sin 2a M c _ /*smff
— — и*>« 5—
Следовательно,
Q = £ (sin 2a 4- sin 2?) =
/^SifKa + p) COS (a —fa)
2 •
2) Найдём высоту H призмы из условия S = BD • Я. Так
как в четырёхугольнике ABCD сумма углов при вершинах В
и D равна 180°, то около него можно описать окружность,
диаметром которой будет диагональ АС, потому что на неё
опираются прямые вписанные углы. Из треугольника BCD,
645 гл. 9. многогранники 363
вписанного в эту окружность, находим (по теореме синусов)
BD^AC- sin ^ DC£ = /sin (а+ {3).
Следовательно,
н_ s S
Отв. V = -J $ ' Icos (а — Р)-
645. Грани ADE и ВСЕ (черт. 123) — равнобедренные
треугольники. Плоскость EMN (М и N—середины рёбер
Черт. 123.
AD и ВС) перпендикулярна к ВС и AD и проходит через
высоту EF пирамиды (доказать!). По условию внешний угол
о = l_ EML треугольника EMN— острый. Поэтому высота EF
пересекает продолжение MN.
Чтобы определить V, найдём сторону АВ квадрата ABCD.
Имеем
АВ = MN = NF— MF = H(ctg Р — ctg а).
Следовательно,
V = jAB*.H = jFP(ctg$ — ctga)a.
Построим линейный угол <р двугранного угла, под кото-
рым грань ABE наклонена к основанию. Для этого пересечём дву-
гранный угол плоскостью EFK, перпендикулярной к ребру АВ.
Чтобы изобразить её, надо провести FK\\AD до пересечения
с продолжением ребра АВ (доказать!). Из треугольника EFK
364
находим
ОТВЕТЫ И РЕШЕНИЯ
_Н _ 2Н _ 2
Xg4 — FK~ АВ ctg Р — ctga-
646
Отв. ^«•(ctoP-ctetf-.^SSS?.
ср = arc tg
Ctgg — Ctga
. 2 sin a sin В
garctgsin(,-pr
646. Высота EF пирамиды (черт. 124) лежит в грани CED%
перпендикулярной к плоскости основания. Плоскость, прове-
дённая через EF перпендикулярно к ребру АВ, пересекает
основание пирамиды по прямой MF\\ ВС, а боковую грань
АЕВ — по прямой ME, перпендикулярной к АВ (^ EMF = р).
Прямые AD и ВС перпендикулярны к плоскости DEC, так
что /_ВСЕ = 90° и lmADE=Q0° (всё это надо доказать).
Найдём высоту H^EF. По условию EF-\-EM = m\
кроме того, ^^ — п—£• Поэтому EF\A Ч~^щ)===т» откуда
«-BF-« :(l +^) = » <1 +5jh)-T
mcos а
2 cos*-у
Далее из прямоугольного треугольника DEC находим
а = Dc в ^£ = __£_
cos о sin a cos а*
Наконец, находим
£ = ВС = Ж/7 = Я ctg {3 = Я tg а.
647
гл. 9. многогранники
365
Следовательно,
*->-»-T^TmSsT
W
3 COS* а '
Сумма 5j + ^2 площадей боковых граней ВЕС и AED
равна
24 cose к
с I с mS (s!n а + cos а) т% с03 (4^°~~ а)
Oj -j- о2 ^ " — ~ •
8 cos4у 4^2 cos4-|
647. а) Способ изображения. ВысотуEF(4tpr. 125)
проводим в середину F стороны DC. Соединяем вершину Е
с серединой М стороны АВ. Тогда <р = /^ FEM есть изобра-
жение угла между гранями
ABE и DCE (доказать!).
б) Решение. Треуголь-
ник ВСЕ—прямоугольный, и
в нём ^ ВЕС = а (доказать!).
Значит, ВС =а 6 sin а. Из тре-
угольника Л££ имеем >Ш в
e=2&sina и yW£=£cosa. Из
треугольника AIFE, где MF =
е= J3C = £sin а, находим
= Ъ j^cos2 а — sina а =
= ^Vrcos2a.
Замечание. Подкоренное выражение cos2a здесь всегда
положительно, так как 2а<90°. Действительно, сумма двух плоских
1 QflO Q-,
углов трёхгранного угла при вершине В (£ ABE — и
LCBI
180° —
2а
-а) больше третьего (£ ABC — 9Q0), т. е.
f (90° — а)>90°, так что 2а<90°.
Угол ср лучше всего найти по его синусу.
Отв. V = т Ьъ sin2 а у cos 2a; <р = arc sin (tg a).
366
ОТВЕТЫ И РЕШЕНИЯ
643
648. Плоскость ВСЕ (черт. 126) проведена через сторону
ВС перпендикулярно к ребру AS. Двугранные углы между
боковыми гранями (все они равны) измеряются углом ВЕС — <?•
Треугольник ВЕС — равнобедренный.
Чтобы определить площадь 5 сечения и угол <?, доста-
точно найти DE (D — середина ВС). Для этого последова-
тельно находим BS f из треугольника BSD, где BD = -^- и
^BSD = -|-), затем BE (из треугольника BSEt где /_BSE=a)
и, наконец, DE = YbE* — BD*. Получаем
D£ = ^|/rcos2|—».
Теперь находим
с а глтз а2~ш/ Г~й Г ■ ? BD 1
S^^.DE^^y cos2T-T И 501! = ^=- -.
2cos-^-
Замечание 1. Сумма плоских углов при вершине S всегда
меньше 360°. Поэтому 0<а<120°. При этом условии 2cos-|>l,
1 ф 1
т. е. г-<1> так что уравнение sin -тг== всегда имеет
2cos| 2 2cos|
решение.
649
гл. 9. МНОГОГРАННИКИ
367
Замечание 2. Если а > 90°, т. е. угол ASB при вершине бо-
ковой грани тупой, то высота BE треугольника ASB пересечёт про-
должение основания, и плоскость ВЕС не даст никакого сечения пи-
рамиды. Между тем формула
-4/
COS*
и при тупом угле а (меньшем 120°, см. замечание 1) даст определён-
ное значение S.
Отв. ср = 2 arc sin (-^ sec ~J;
5=т/^¥Ч=4/"-(60°+й8Ш(б0О-й-
649. Все восемь граней октаэдра — равносторонние тре-
угольники, так что NE = —|— (черт. 127). Четырёхугольник
ABCD — квадрат. Его плоскость разбивает октаэдр на две
равные правильные пирамиды, так что V = 2 • ^-а2 • 0£, где
oe = Ven*—ON* =
-v
Все двугранные углы октаэд-
ра равны. Угол а = /^BMD
(М—середина СЕ) изме-
ряет двугранный угол при
ребре СЕ (доказать!). Из
треугольника О МБ нахо-
дим
. а ОВ
—а У^ - а^ _ ,/"][
~ 2 • 2 ~ V 3*
Отв. V-.
V2 Ф
а = 2 arc sin
VI
363
ОТВЕТЫ И РЕШЕНИЯ
65а
650 *). Равнобедренные треугольники ВМА и FMA
(черт. 128) равны. Поэтому их высоты, опущенные из вер-
шин В и F, пройдут через
одну и ту жеточку Л^их общей
стороны и будут равны:
BN=FN. Угол BNF ра-
вен ср (доказать!). Угол
Р = IJ&AM выражается че-
рез искомый угол а =
^s/^BMA формулой
р = 90° — ~.
Найдём сначала тригономе-
трическую функцию угла £.
Из прямоугольного треуголь-
ника ABN имеем sin 8 = —
г а
(а — сторона основания).
RK
Из равнобедренного треугольника BNF находим BN= .
slnT
Но BK — 2-iF^ (ка*с высота
ника АВО). Следовательно,
равностороннего треуголь-
-nfl—*L.
т. е.
sin
(«•-*).
W
2 sin
Я»
Замечание, Двугранный угол при ребре правильной шести-
угольной пирамиды всегда больше, чем £ FAB (сравнить треуголь-
ники BNF и BAF), т. е. больше 120°. Поэтому величина —2-—
2sin|
всегда меньше единицы*
Отв. а = 2 arc cos ■
Уз
2 sin-2-
i) Об изображении правильного шестиугольника см. на стр. 328
замечание к задаче 598.
652
гл. 9. МНОГОГРАННИКИ
369
651. Грани AMF и АМВ (черт. 129, а), проходящие через
ребро AM (перпендикулярное к плоскости ABCDEF), обра-
зуют с плоскостью основания прямые углы. Найдём общую
величину (3 углов, образуемых гранями EMF и СМВ с пло-
скостью основания. Опустим из А перпендикуляр AG на пря-
Черт. 129.
мую СВ (изображение этой прямой должно быть параллельно CEt
черт. 129,6). Тогда $ = ^AGM (доказать!). Имеем tg (3=з
И _„. я^ „„ аУъ
АО
г, где AG = CK'-
(черт. 129, б). Но из треуголь-
И
ника AMD имеем \ga = ~\ следовательно,
2Н
«Bl
л 1^3
_4tga
Так как АС _L £*? (доказать!), то ] = ^АСМ есть ли-
нейный угол для двугранного угла, под которым грань DCM
(и DEM) наклонена к плоскости основания. Из треуголь-
Н /—
ника АСМ имеем tg^e—^#где АС = ауЗ (черт. 129,6).
О/и*. P^arctg--^;T = arctg—£=-.
652« Через прямую линию можно провести плоскость,
перпендикулярную к другой прямой, только в том случае,
370
ОТВЕТЫ И РЕШЕНИЯ
если эти прямые перпендикулярны. Докажем, что BCj_AS
(черт. 130). Проведём плоскость ASO через ребро AS и вы-
соту 50. Так как Л и О принадлежат плоскости ASO и
одновременно плоскости основания ABC, то эти плоскости
пересекутся по прямой АО, т. е. по высоте AD равнобед-
ренного треугольника ABC, Треугольники OCD и OBD равны
(доказать!), поэтому ОВ = ОС; следовательно, наклонные SC
и SB тоже равны, а значит, прямая SDt являющаяся медиа-
ной равнобедренного треугольника BSC, служит и его высо-
той. Так как прямые AD и
SD, по доказанному, пер-
пендикулярны к ребру ВС,
то ребро ВС перпендику-
лярно к плоскости ADS, а
значит, и к прямой AS, ле-
жащей в этой плоскости,
что и требовалось доказать.
Чтобы провести через
^д ВС плоскость, перпендику-
лярную к AS, достаточно
опустить перпендикуляр DE
на прямую AS. Плоскость
ВЕС перпендикулярна к ре-
бру AS, так как две пря-
мые, лежащие на ней (DE
и ВС), перпендикулярны к
AS. Плоскость ADS, пер-
пендикулярная к ребру ВС, в пересечении с двугранным
углом а даёт угол ADE (линейный угол этого двугранного
угла).
Треугольник ASD — равнобедренный (так как высота SO
проходит через середину основания AD). Следовательно,
/_ASD = 2 /_ASQ = 2а
(J^ASO = i^ADE =s а как углы с перпендикулярными сто-
ронами). Отношение объёма Vt пирамиды SBCE к объёму V
пирамиды АВСЕ (эти пирамиды имеют общее основание ВСЕ)
равно отношению высот, т. е. Vl: V = SE:AE. Из треуголь-
ника DSE имеем
SE = DE* ctg /_ESD = DE ' ctg 2ot»
Черт. 130.
633
гл. 9. МНОГОГРАННИКИ
371
из треугольника AED находим
АЕ = DE • tg а.
Следовательно,
Vt :V = ctg2a :tga.
Отв. Vx = V ctg a ctg 2a.
653 l). Чтобы провести сечение, делящее пополам двугран-
ный угол при ребре AD (черт. 131), нужно иметь линейный
угол этого двугранного угла. Таковым является угол BDC,
так как плоскость BDC пер-
пендикулярна к ребру AD. Дей-
ствительно, во всякой правиль-
ной пирамиде боковое ребро АО
перпендикулярно* к противопо-
ложной стороне ВС основания
(доказывается так же, как в
предыдущей задаче); кроме то-
го, в данном случае ребро АО
перпендикулярно также и к
прямой FD. Действительно, по
условию треугольник AFD —
прямоугольный, а так как его углы при вершинах Ли/7
непременно острые, то прямой угол есть ^ADF.
Так как OF = ±-OA = ~Rt то
Черт. 131.
2 ~"~ 2
OD — VOF'OA:
о
R
V2
где R == -р=) * Угол ф= ^ AFD измеряет угол наклона
грани BCD к плоскости основания. Имеем
tg<p:
0D — _*_..* — т/Т
OF
V2
Замечание. Боковое ребро AD образует с ребром BD
(и с ребром CD) прямой угол; так как наша пирамида — правильная,
то и рёбра BD и DC образуют прямой угол.
Отв. K = -^pl;<? = arctgj/"2.
J) Об изображения правильной треугольной пирамиды см. за-
дачу 603 на стр. 330.
372
ОТВЕТЫ И РЕШЕНИЯ
634
654*). Для вычисления полной поверхности неизвестна
только апофема ND. Для определения её найдём сначала
отрезки AM и МО (черт. 132), на которые делится ребро
AD перпендикулярной к нему прямой NM (N—середина ВС).
Затем из треугольника ANM, где AN =
дУЪ
, найдём MN
и, наконец, из треугольника NMD найдём ND.
В условии не сказано, какое из двух отношений—AM:MD
или MD: AM— равно т :п,
поэтому можно положить
МО = mxt MA = пх, так что
AD = (т-\-п) х. Из подобия
треугольников AMN и ADO
имеем
где
AM
АО''
AN--
AN
''АО'
' 2
АО:
,ldAN.
.?Уз
Получаем уравнение
пх • (т 4~ п) х «я "д— • *-т||—.
Отсюда находим
так что
У2п(т + п) '
V2n{m + n)
AM-.
Щ
У In (m + я)
*) Об изображении правильной треугольной пирамиды см. задачу
603 на стр. 330.
655
Далее,
гл. §. многогранники
MN* = AN*-AM* = £%±™>
373
ND* = MD* + MN* » qH" + 2m> .
Теперь найдём
с gaVT , 3q-ND
Од =—^ 1 g .
655. Имеем (черт. 133) /^BD^A^a и /_BDfi = a
(доказать!). Треугольники БО,Л и BDtC равны (доказать!).
Черт. 133.
Следовательно, основание ABCD — квадрат со стороной
а = d sin а. Далее находим
ADX = rf cos а
и
Я = УЛО^ — >Ш2 = j/> cos2 а —* d2 sin2 а = d VcosTa.
Плоскость ACDX образует с плоскостью основания угол
Отв. ^ = d»slnSal/'^i2?; у = arctg(^^-).
374
ОТВЕТЫ И РЕШЕНИЯ
656
656. Угол £ОС = а (черт. 134). Для построения угла р
отрезка ОЕ с боковой гранью BBfifi проведём OF _[_ВС.
Проекцией ОЕ на эту грань будет FE, так что ^OEF = $.
Если обозначим АВ — а\ ВС = Ь и СС^ = с, то К = аЬс
и S60]i = 2(a + c)b. Из ДОЯ/7
имеем
£ = О/7 = т sin {3 = w sin 2а;
FE=zmcos$ = m cos 2а;
из Д 0£С имеем
y = £C = wsina;
из /\FEC имеем
2
b = fc=Vfe2—ec*=
= т У cos2 2a — sin2 a.
Приведём подкоренное выражение к виду, удобному для ло-
гарифмирования:
. « 14* cos
— sin2 a = ~ п ■
cos2 2a— sin2 a
4a
1 — cos 2a cos 4a + cos 2a
= cos 3a cos a.
Следовательно,
д = 2т l^cos 3a cos a.
Замечание. Угол P — Z OEF меньше, чем ^ OEC =s 90° — a
(сравнить их синусы!). А так как по условию 0 = 2а, то 2а<90°—а.
Следовательно, должно быть а<30.
Отв. V = 8w3 sin 2а sin a j/^cos За cos а;
5бок = 16/га2 sin -^- cos у J^c°s За cos а.
657. а) Способ изображения. Полуокружность
изображается полуэллипсом (АВ — какой-либо диаметр эл-
липса; черт. 1351)), DC проводится параллельно АВ. Прямые,
*) О вычерчивании эллипса см. стр. 339 (задача 613).
657
гл. 9. МНОГОГРАННИКИ
375
перпендикулярные к АВ9 изображаются прямыми, параллель-
ными касательным AM и BL.
б) Решение. Обозначим АВ = a; DC = £; DF = CE = h\
тогда У== fl<J НИ.
По условию а = 2/?; сторону £ находим по теореме си-
нусов из треугольника
BCD, в котором /_DBC д
измеряется половиной ду- —
ги DC = 2а; имеем Ь =
= 2/? sin а. Из треуголь-
ника ODF, где OD = Я,
а ^ ЛОО измеряется
и л4^ 180° — 2а Л'
дугой AD — п = и
== 90°— а, находим
h = FD =
= /?sin(90° —а) =
= R cos а.
Черт. 135.
Высоту И находим из треугольника AtAD9 где ^AJDA^v.
(доказать!) и AD можно определить из прямоугольного тре-
угольника ADB9 где ^ABD — опирающийся на дугу AD,
равен ( 45° — -£-) • Получим
H=2Rsin(45°— y)tga.
Следовательно,
К= 2Я3(1 + sin a) sin (45°— -JW a cos a,
где можно произвести ряд упрощений:
1 -J-sin a = 2 cos2(45° — |Л
и т. д.
Отв. K = /?3sin2acos(45a—J)*
376
ОТВЕТЫ И РЕШЕНИЯ
653
658. Проекцией диагонали DXB на боковую грань AAlD1D
(черт. 136) будет ADX\ поэтому ^mADlB = ^. Угол а между
плоскостью сечения DBB^ и плоскостью грани ADDXAX из-
меряется углом ADB (доказать!).
Из треугольника ADXB находим
АВ и ADX\ из треугольника ABD
находим AD и из треугольника
ADXD находим DDX = И\
h^Vad^—ad2^
сР cos2 a ctg2 а =
sin a г
•cos*a =
Черт. 136.
= rr— V— cos 2a.
Sin a w ч
Замечание. Угол p всегда
меньше угла а (сравнить их танген-
сы!). Так как по условию (3 = 90°— а,
то 90—а<а, следовательно, <х>45°. Из неравенства
45°<<х<90°
следует, что угол 2а принадлежит второй четверти, так что
cos2a<0, а —cos 2а >0. Для вычислений удобнее заменить — cos2a
выражением cos (180° — 2a), так как угол 180° — 2а принадлежит
первой четверти.
Отв. V = db cos a ctg* a j/"cos (180° — 2a).
659. Проведённые линии суть AXN и BXM (черт. 137).
Четырёхугольник Ах BXNM — равнобочная трапеция (доказать!).
Из равнобедренного треугольника MKN, где ^mMKN = a и
MN = -£> имеем
4
/CD = TCtg£.
Из треугольника АХКВХ находим
Складывая эти равенства, получаем
DDi = — ^g Y
660 гл. 9. многогранники 377
Из треугольника DEDV где DE = у С£ =-^ £ J/1T, находим
H = EDl^yrctg^-l^yrctg^-ctg^O^
e tV (cts 1 + с«в 60°)(ct£i - cte 60°) =
3& ^sln (бО* + J) sin (60° --|)
4 sin—sin 60°
Отв. K^-^/sin(60o + j)sin(60°-y.
Черт. 137. Черт. 138.
660. Для построения угла, образованного диагональю
АВХ с боковой гранью BBtCxCf надо найти проекцию ЛВ,
на эту грань (черт. 138). Точка А проектируется в точку Д
середину ВС (доказать!). Проекция будет BVD, так что
/_ ABXD = а. Из Д BtBD находим
Я = ВВХ = Vbxd*—bd*\
Bfi найдём из прямоугольного треугольника ABXD. Пре-
378
ОТВЕТЫ И РЕШЕНИЯ
eei
образование выражения, полученного для //, такое же, как
в предыдущей задаче.
Л с 3«2 -J^sin (60° + a) Sin (60° — а)
Отв. Лбок = гп— •
sin а
661. Проекцией диагонали АВг на грань ААЛС^С будет
АСг (черт. 139), так что ^В1ЛС1 = {3, Высота призмы
ccx = Vac?—АС\
где АСг определяется из ДВ^С,; имеем
ССг = j/"£2tg2actgap — £2=&ctgPl/tg2a — tgsP =
cos a sin p
Vsin(a + p)sin(a —P).
0ял ^ = 2^sTs^^sin(a + P)sin(a_p).
662. По условию a2 + 2a-Af£ = S (черт. 140). Но из
треугольника ВМВ имеем ME = -=- ctg ^;
5 = a9(l + ctg-g-)J отсюда a=y
l + ctgT
следовательно,
-. Теперь из
663 ГЛ. 9. МНОГОГРАННИКИ
треугольника ОМЕ находим
S79
Выражение ctgy—^1 можно преобразовать;
cig -J— 1 = ctg f — ctg 45° =
sin (45° — y) VTsIn (45° — -J)
sin 45° sin -n-
sln2
Отв.
_/
Ssln
(»-т)
2 V2"sln ■
663. Имеем из треугольника
AOM (черт. 141), где
8начит,
с пФ , 180°
Из треугольника ЕОМ находим
Черт. 141.
Подкоренное выражение преобразуется, как в задаче 659.
Отв.
-л3л+„ 180°,/" Г / 180° а\ . / 180° . а\
24 sin -J sin.180
380 ОТВЕТЫ И РЕШЕНИЯ 664
664. Обозначив (черт. 142) OD = OA через х, получим
ODl = AO.ctg^ = xctg~
и
H=DDt = VOD^ — OD2 = х ]/*ctg2| — 1.
Полная поверхность S пирамиды йлАОС равна
S = DO • АО + AD • Н+АО • OD, ==
= л2 + ^К2л:]/с^|.~1+л.^с1§|.
^fsInY+^COSa^
Черт. 142. Sn = ^ - }—.
sin -n- + cos -^ 4" У"2 cos a
665. Высота DO проходит через центр О (черт. 143, а)
круга, описанного около треугольника ABC, где АВ = АС^=
= 2/sin-*- и ВС = 2i sin-g-1). Точка О лежит на перпенди-
куляре КО к стороне i4J5, проведённом через середину АВ.
Поэтому из подобия треугольников АОК и ABL имеем про-
L) См. на стр. 337 предварительное замечание к задаче 611.
ГЛ. 9. МНОГОГРАННИКИ
381
порцию АО : ~2 ЛВ = АВ : AL, откуда
2/а sin8-
AL
/
4/2 sin» j — /*sln*-|
Далее из треугольника ЛОО находим
н=ур—Л02 = /
/
sin* а — sin* -£■
4sin3^ — sin^i.
l/ = ^J5C^I.«=i./3sin|-]/"sin2a— sin»-J.
Подкоренное выражение можно преобразовать, как указано
в задаче 656.
Другой способ. Примем за основание пирамиды
грань BDC (черт. 143, б)\ площадь её 50СН = -n Р sin р. Грань
.5ZX7 перпендикулярна к плоскости Л£>1 (доказать!), и сле-
довательно, высота пирамиды АОх будет лежать в этой
плоскости. Проводим О^Е перпендикулярно к BD. Из
382
ОТВЕТЫ И РЕШЕНИЯ
подобия треугольников OxDE и BDL имеем -^ = -jrj-, где из
ED = lcosa, BD = l и DL = /cos
1.
отсюда
0^ =
/cosct
cos-|
Из треугольника ADOx находим
Н=АОх = V At? — DO? = —
cos
"J/ COS2
■COS2».
666. Так как треугольник ABC (черт. 144) есть проек-
ция треугольника DBC, то DA есть перпендикуляр к пло-
jj скости основания. Площадь 5,
треугольника ABC равна
Б1 = -^аЬ = -^Ф ctg а.
Площадь S2 треугольника BCD
равна
S2 = Ia2ctgp.
По условию
1
-^(ctgp— ctga) = Sf
откуда а = у -
2S
ctgP — Ctga '
Площадь 5S грани ОЛС равна S8 = yW, а площадь 54
грани DAB равна S4c = ^cH. Следовательно,
S4—S8 = itf(c— 6) = -i-a//^coseca~ct^a)-
Высоту Я определим из треугольника ACD; получим
Я = VdC* — AC* = Va2ctgap —a2ctg2a.
5П —
667 гл. 9. многогранники 383
Следовательно,
54 — 5ft = -~ Ф ]/ctg2?—ctg2« (cosec а—ctg а) =*
=т * "ctg p- ctg a ^Cts2 ?—cts2 а <cosec а—cte a> —
(1 — COS а) Г Ctg* ft — ctg» a __ p. Д - /"ctg 9 + ctg a
sin a V (ctg £ — ctg ay ° lg 2 К ctg p — cig a •
Боковые грани ADC и /Ш£ образуют с основанием пря-
мые углы. Грань BDC' образует с основанием угол, измеряе-
мый линейным углом DCA = <?;
AC ctg a
cos*-^-—.
667. Все боковые рёбра пирамиды равны как стороны
равнобедренных прямоугольных треугольников (черт. 145),
поэтому высота DO пирамиды ~
будет проходить через центр О Jt*>^
окружности, описанной около ^Slp^qw***^
основания; ^г *Н| ^^^^/j
50он = -я-*2 sin а. л^— tfX'-''''/
Из треугольника DOC на- ^^Чч>ч^ ч У^
ходим ^^Чч<Эу^
h=Vdc*—oc*, В
и Черт. 145.
где ZX: = ^pt а OC*=R
есть радиус окружности, описанной около треугольника
ABC. Так как треугольник ЛВС—равнобедренный, то
^ ЯЛС = 90°—-g- и, следовательно, по теореме синусов
ВС = 2/?sin (90° — у),
откуда
ОС = /? = -
Ow*. Ve I*» sin -J
2 cos y
384 ОТВЕТЫ И РЕШЕНИЯ 663
668. Высота пройдёт через центр окружности, описанной
около основания1) (черт. 146). Биссектрисы углов AED и
ВЕС будут также медианами равнобедренных треугольников
MN
AED и ВЕС. Площадь сечения MEN равна -у-»0£, причём
-— = /l/C = /sin -^-. Из треугольника ЕОК находим
OE=VEK* — О/С3,
где EK = lcos -^ и OK = BN = I sin -JL так что
0£ = /]/~cos*|- — sin*!-.
Отв. 50еч = Z2 sin -| у cos *Цр cos %р.
5
669, Проведём через вершину Ах (черт. 147) плоскости
АхЕО перпендикулярно к АВ и AxFO — перпендикулярно
к AD. Эти плоскости будут перпендикулярны к плоскости
основания (доказать!) и линия их пересечения АгО будет вы-
сотой параллелепипеда. Образовавшиеся прямоугольные тре-
угольники АХАЕ и АгАЕ равны между собой (по общей ги-
потенузе ААх=с и равным углам ^тА1АЕ^= ^mA1AF=a).
Следовательно, АХЕ^= AtF и поэтому будут равны треуголь-
J) См. на стр. 337 предварительное замечание к задаче 611.
670
гл. 9. МНОГОГРАННИКИ
385
ники АхОЕ и A^OFy а значит, OE = OF и прямая АО — бис-
сектриса угла BAD. Имеем H=YА^Е*— ОЕ*. Так как ABOF —
квадрат, то ОЕ = АЕ. Находим АЕ и АгЕ из треугольника
ААгЕ\ получаем ^ = c]/sin9a—cos9a = c~)f — cos 2a.
Замечание. В трёхгранном угле при вершине А два плоских
угла равны каждый а и третий угол прямой; следовательно, сумма
двух плоских углов 2а должна быть больше третьего (90°), т. е.
2а>90° или а>45°. При этом условии —cos2a>0 и, следова-
тельно, И имеет действительное значение. Боковое ребро AAi об-
разует с плоскостью основания /_ АхАО = у, так как АО — проекция
ребра на основание
cos <р = -j-j- = У2 cos a.
Отв. V = abcY cos (ISO0 — 2a); S6o^ = 2c(a-{-b) sin a;
<p = arc cos (j/lFcos a).
670. Построение в этой задаче то же, что в предыду-
щей, Биссектриса угла BAD будет диагональю ромба АС
(черт. 148).
S0OH = a2sina.
Из треугольника AAYE
находим
И = УАА^— АЕ*9
где АА.
•а;
для
определения АЕ на-
ходим сначала AF из
Д AA^F* а потом АЕ
из прямоугольного
Д AEFm Получим
АЕ =
a cos а
COS-
откуда
Я=.
а
COS-g-
V"
COS*
cos2 а.
Отв. V = 2a*sm
\V
. За . а
Sin у Sin -дч
386
ОТВЕТЫ И РЕШЕНИЯ
671
671. Задача решается аналогично предыдущей. Можно
использовать тот же чертёж 148, сняв в нём обозначение угла
а = [_ AtAB и введя обозначения £.ВАО*=ъ и Z.AXAD = <р.
Отв. V = 2аЧ sin ~ ^f sin (? — ~) sin (у -f -J.).
672. Основание ABCD—прямоугольник (черт. 149). Для
построения линейного угла двугранного угла D^ACD прово-
дим через ребро DDX плоскость,
перпендикулярную к АС\ в пере-
сечении с гранями двугранного
угла получим линейный угол
^ОхЕО = <?. Имеем
DE h<
Обозначим
AB = DC = а,
BC=*AD = b (а > b), DDX = Н,
DtE = kf DE = hv
В равнобедренном треугольнике
АОВ сумма внутренних углов при основании АВ равна
внешнему углу 2а, следовательно, /_ВАС-=а. Из /\АВС
находим
a = 2R cos а\ b = 2R sin а.
Из &DEC, где ^АСО = а, находим
ht = a sin а = 2/? cos а sin а и ЕС = a cos а = 2/? cos2 а.
Из Д Z^C находим
A==£C.tg|3 = 2/?cos2<xtgp.
Из /\,DtDE находим
Н^Ур.Е2 — РЕ2 = У k2 — h\ =
=У 4/?2 cos4 a tg2 р —4/?2sin2<x cosa<x=2/?cos2a jAg2 р—tg2oc.'
Выражение tgsp— tg2a преобразуем, как в задаче 659.
Отв. _____^_^__
S6oa = 8/?2 cos a cos (45° — a) sec p У 2 sin (p +a) sin(p—a);
S<m = 2/?2 cos2 a tg p; <p = arc cos (^.
673
ГЛ. 9, МНОГОГРАННИКИ
387
673. Если катет Ж? (черт. 150) стягивает дугу, равную 2р,
то /. ABC) как вписанный, опирающийся на эту дугу, будет ра-
вен р. Плоскость, проходящая через диагональ ВХС перпендику-
лярно к грани ВВХСХС, должна пройти через АС, так как АС
перпендикулярна к этой грани; линейный угол двугранного
угла ВгАСВ будет 1тВхСВ = §. Гидотенуза АВ есть диа-
метр описанной окружности и,
Обозначим ВС = а, АС = Ь и
АВ=с. Плоскость АСВХ отсекает
от призмы четырёхугольную пира-
миду BxAAxCfi. Так как объём
пирамиды BLABC равен -? объёма
призмы, то объём оставшейся че-
2
тырёхугольнай пирамиды равен -^
о
следовательно,
объёма призмы. Если через Vx обо-
значим объём пирамиды ВгААхСхС9
а через V—объём призмы, то
К=— V =
аЬН
Черт. 150.
Из Д ABC находим а и Ь, а из Д ВХВС находим Н. Для
боковой поверхности получим следующее выражение:
S6os = (2R cos Р + 2/? sin р + 2/?) ■ 2R cos ptgp =
= 4/?2 sin р (cos р -f sin р + О-
Выражение в скобках можно привести к виду, удобному
для логарифмирования: cos p-J-sin р+ l=»(l+cos P)-f-sin р=
==2cos2|. + 2sin|.cos|- = 2cos|(cos| + sin|-) =
- 2 cos { [sin (90° — 4) + sin I] =
= 2 cos I . 2 sin 45° cos (45° — 4) =
= 2 У2 cos 4 cos (45° — 4).
Ome. S60R = 8 V~2 /?2 sin p cos 4 cos ^45° — 4) 5
Vt= j/?3sinpsin2p.
388
ОТВЕТЫ И РЕШЕНИЯ
674
674. Высота ЕО (черт. 151, а) проходит через центр О
окружности, описанной около трапеции ABCD1). Дуги ADf
DC и СВ (черт. 151» ^f) равны (так как по условию стороны
AD, DC и СВ равны), причём ££=180° — а измеряется
половиной дуги ADC. Значит, дуги AD, DC и СВ содержат
£
Черт. 151.
по 180°—а; следовательно, дуга АтВ содержит 360° —
—3(180° — а) = За — 180°. Из треугольника АОВ, где АВ=а,
находим
а а
AO = R=*.
2 sin
За— 180°*
2 cos
За
За
2 2
(величина cos^отрицательна, ибо а — тупой угол, так что
,3а
2
135°<^<270°V Из треугольника ODC находим
DC =b = 2R sin
180° —а
а
a cos -^■
За #
cosT
Из треугольника ADFt где AD = b и £Л=180° — а, на-
ходим высоту трапеции
DF = k = bs\na = —
a sin a cos -*•
За" '
cos^
!) См. на стр.337 предварительное замечание к задаче 611*
675
ГЛ. 9. МНОГОГРАННИКИ
389
Из треугольника ВОЕ (см. черт. 151, а), где OB = R и
/жОБ£ = р, находим H = Rig$. Площадь основания
- Д2 I COS -s* — COS -7Г- J cos -g- sin а
S~J (« + *)*- ^ q 223a — =
2 cos 2
Отв. V= *rin8«tgp = d»si^atgp
12 cos3 (180°— ^V
Д2 Sin3 а
2cos2^#
12 cos3 Ц
675. Высота £0 проходит через центр О окружности,
описанной около трапеции ABCD1) (черт. 152). Угол ЛС£=90°,
как вписанный в эту окруж-
£ ность, должен опираться на диа-
метр. Иначе говоря, центр О
лежит на стороне АВ. Трапе-
2) L С
D—Г^С
Черт. 152.
ция ABCD, как вписанная в окружность, — равнобочная, так
что lmDAB= /^СВА.
Введём обозначения АВ = а; DC = b\ £_ АЕВ = о =* 2а.
По условию -jaH=S, а из равнобедренного треугольника
АЕВ имеем a = 2tftg -i = 2//tg a.
Из этих двух уравнений находим
H=VSctga и a = 2V~S{ga.
1) См. на стр. 337 предварительное замечание к задаче 611*
390 ОТВЕТЫ И РЕШЕНИЯ 675
Сторону * = DC найдём из треугольника ADC, вписанного
в окружность с диаметром а. В этом треугольнике
/. DAC = /_ DAB — /_ CAB = /_ СВА — /_ CAB.
Но так как треугольник АСВ — прямоугольный, то ^СВА=*
»90°—1_САВ* Следовательно,
£ DAC = 90° — 2 £ CAB = 90° — 2а,
и мы имеем
Ь = a sin (90° — 2а) = а cos 2а.
Наконец, находим
CW == h = AC sin а = a cos а sin а.
Теперь получаем
Ve|.-^±^-hH= 1 д2(1 -f cos2а)cos a sin atf =
= i.45tga2cos2acosasinaV5ctga^^i^l/r5Sctga.
Грань ABE образует с плоскостью ABCD прямой угол.
Для определения угла 9i» образуемого гранью ADE с пло-
скостью ABCD, опустим перпендикуляр из О на AD (он
изображается прямой ОК> параллельной диагонали BD, так
как последняя перпендикулярна к AD; диагональ BD на
чертеже не изображена; ^ЕКО^^). В треугольнике АОК
угол OAK равен £ ABC = 90° — ^ СуШ = 90° — а. Поэтому
ОА:== ЛО • sin (90° —а) = -J cos а
и
И 2Н _ 2И _ 1
Ч??1 — Q# д cos а 2// tg a COS a slna*
Для определения угла 921 образуемого гранью DCE с пло-
скостью ABCD, проводим OIJ_DC; ££Z.O = cp2, Так как
OL = NC = k, то
/У _ И 1
Ч£ ?2 —- Л й; COS a Sin a 2 Sln2 a •
Ome.
<pt = arc tg (cosec a); cp2 = arc tg (-j cosec2 aV
677
гл. 9# МНОГОГРАННИКИ
391
676. Нужно определить (черт. 153) сумму площадей тре-
угольников ЛВС, ABD и ACD. Площадь Sx треугольника
ABC равна
Черт. 153.
Площадь 52 треугольника ABD
равна
S.=i AB-DE = ЛяД—=—;
г 2 2 COS ер COS ер'
площадь 5S треугольника ACD равна
Sb=>±AC-CD=:
=jAB. CD=jAB • С£ • tg<f=*Sx tg?.
Следовательно,
^goK = ^1 + ^a + ^s= 4CQS3y (1+cos? +sin?).
Выражение в скобках преобразуется, как указано в зада-
че 673, и будет равно 2 Y~2 cos у cos ^45°—-|V Если в фор-
муле для 5бок в знаменателе cos?
представить как sin (90° — ф), то
выражение для 5бок можно будет
сократить на
■(»-*)•
д2 УТГ cos -|-
COS
Oftie. StfOK :
4 sin
(«ч)'
677. Так как плоскость осно-
вания ABC (черт. 154) проходит
через прямую АС, а плоскость се-
Черт. 154. чения AtBCt — через прямую AxClt
параллельную АС, то ребрэ ММ
двугранного угла (3 параллельно прямым АС и ALCV Поэтому
для построения линейного угла проводим BD _]_АС и
BDlmLAlC1 (точки D и Dt будут серединами АС и A\CJ.
392
ОТВЕТЫ И РЕШЕНИЯ
673
Имеем
5вок = (2ЛВ-МО • DDt = (2ЛВ + AC) • BD . tgp =
= 2a2(l-J-cosa)sin atgfi.
Объём V\ четырёхугольной пирамиды БЛСС1Д равен
■я- объёма V призмы (см. задачу 673) и, следовательно.
Vx = 4rS.DDv
где
S = -jfl2sin(180°—2a) = 1 я2 sin 2a.
Oma. *Sfl0K = 4a2 cos2 у sin a tg £; Vt = ^ sin 2a sin a tg p.
678. Как в вадаче 630, докажем, что грань ОСЕ (черт. 155)
наклонена к плоскости основания ABCD под углом a = ^ADE,
а грань ВСЕ — под равным ему углом а = ^АВЕ; обе эти
^ ^ грани — прямоугольные треуголь-
ники (£CDE = £СВЕ = 90°).
Площадь St треугольника ADE
(а также равная ей площадь тре-
угольника ABE) равна Sx =
» — АВ • АЕ, Из треугольника
ABE, где ££ = 2/?, находим
АВ == 2/? cos a,
АЕ = 2/? sin a,
так что St = 2/?2 sin a cos a.
Площадь S3 треугольника СОБ (а также треугольника
СВЕ) равна
52=-iBC.^£==Y>lB.B^=2/?2cosa.
Имеем
5Д = 5+ 25t + 252 = 4/?2(cos2 a + cos a sin a -J- cos a) =
= 4/?2 cos a (cos a -j- sin a + 1).
Выражение в скобках преобразуется, как указано в за-
даче 673.
Отв. 5Д = 8/2 Яа cos a cos -J cos (45° — -J).
679 гл. 9. многогранники 393
679. Плоскость сечения ECD (черт. 156), параллельного
гипотенузе АВ% пересекает плоскость грани АВВ^А{ по пря-
мой ED, параллельной АВ. Опустив перпендикуляры СМ и
CF на прямые АВ и ED, получим прямоугольный треуголь-
ник CMFt где /_ CFM = р (доказать!). Следовательно,
/\CMF = &CMB
(у них общий катет МС и
/_СВМ = Ж — а,
а по условию
р = 90° — а).
Требуется найти объём V пирамиды CABDEt у которой
основание ABDE—прямоугольник, а высота равна СМ =
>=• a sin {} = a cos а.
Черт. 156.
Имеем
К = -i.. АВ . Л//7. СМ = 1. АВ • MB • СМ ==
= у • ВС2 • СЛ/ = j а3 cos а
(катет ВС есть средняя пропорциональная между АВ и MB).
Далее имеем
S6os = (BC + AB + AC)H = aH(\+^±ctga);
здесь д# есть площадь грани СВВгСи которая по условию
394 ОТВЕТЫ И РЕШЕНИЯ 630
равна площади 5евч треугольника CDE. Следовательно,
Значит,
5^ = ж(1+^ + С^а)=2|[^(51пв+1+С05а)-
Выражение в скобках преобразуется, как в задаче 673.
Чтобы плоскость CDE пересекала грань ABBtAv отрезок
MF— MB— asina должен быть меньше, чем отрезок MN =
= Н=тг1— • я = к—;—. Из неравенства a sin а < х—— нахо-
2 sin а 2 sin а г ^2 sin а
1 Y2
дим sin2 а < у, т. е. sina<-~. Значит, угол а должен
быть меньше 45°.
Ф cos a VTa2 cos \ cos [& - t)
a < 45°.
680 (черт. 157), Боковая поверхность пирамиды будет
<j _/frctga , //*CtgP ,
^бов 2 1 2 г"
■ //»ctgP . IPctga
* 2 sin a "i" 2sinp Г
Отсюда получим
5б-=2Ш^ПГР(созаз1пР +
-j- sin a cos p + cos P + cos <*)•
Выражение в скобках можно привести к виду, удобному для
логарифмирования, учитывая, что cos a sin р + s*n a cos P =
чим
3i L еле S_
= sin(a-[-P) и cosp+cos a = 2 cos-^cos —2-^.Полу
sin(a + p)+2cos^cos^===2sin^.cos^ +
+ 2cos^cos^^2cos4l(sm^+cos^).
681
ГЛ. 9, МНОГОГРАННИКИ
395
Заменив cos^-тр- через sin (90°— "Ц"^) и преобразовав вы-
ражение в скобках как сумму синусов, получим
4 cos i±S cos (45° — |) cos (45° — |).
2Я2 cos i+l cos ^45° - -J) cos (45° -1)
OfllB» Sgob ■
sin a sin p
681. Пусть r = ON—радиус круга, вписанного в осно-
вание пирамиды1). Из треугольника DON (черт. 158) имеем
DO = //=г tg а. Так как центр О вписанной окружности лежит
на пересечении биссектрис углов А и Л, то /^ОАМ = -«
£ОЯЛГ = 90°~а = 45°— | .
Так как угол С прямой, то четы-
рёхугольник MCNO — квадрат,
так что MC = CN=r. Следова-
тельно,
АС = Ь = АМ + МС =
= r(ctg|+ 1)
и
CB = a = r[ctg(45° — j)-j- l].
Выражения в скобках преобразуются, как в задаче 662, после
чего получаем
flu
/1! \
ill \\
I ! \
■'О \^>
Vooh = -я- flft — 9
j /JJrcoe-j У2r sin(45° +-J)
-=r>ctg-§-cfc(4F — J.).
sin T
i) См. на стр. 342 предварительное замечание к задаче 617*
ОТВЕТЫ И РЕШЕНИЯ
396
Следовательно,
Это выражение можно упростить, если заметить, что
682
sin а
& та et
sin а
2 sin -к* cos -^
COSa sin(90°-a) ^^^„^.-y
Боковую и полную поверхность можно найти по формулам
о 250flHcos2--
S°CH • с оои 2
оов cos a п cos a
J).
Ош?. Г =
r3 COS2 -s-
ОЛПЕ ея
3sin2(45° — jY
^ctg-y
2sin2
(»-i)'
'2ctg_-cos2_-
Черт. 159.
sin2
(«■-*)
682. Плоскость отсекает от призмы пирамиду ВХАВС
(черт. 159), высота которой проходит через центр О окруж-
ности, вписанной в основание пирамиды; поэтому все боко-
вые грани её образуют с плоскостью основания равные
углы а; следовательно,
2SOCHcos*2-
С ±14
Находим
DC • AD.
Из Д OCD, где OD = г и £, OCD = |-, находим DC = r ctg-|.
J) См. на стр. 342 и 344 замечание к задачам 617 и 618.
083 гл. 9. многогранники 397
Из /\ADC находим AD=DC-tg <x=r ctg-^- tg а. Следовательно,
2/«ctg3itgacos3y
5OCH = r2ctg2ytga и 5П
cos a
б виде
sin a
Полученные выражения можно упростить, представив tg a
2 sin -g- cos -j
cos a cos a
Объём призмы
V = 500а • Я,
где
tf = rtga
(из ДВ^Я).
Отв.
4r3 cos*-j ctg |-
S„:
cos2 a
a
l/ = r3ctg2-^tg2a,
683. Из ДВМС (черт. 160), где ^MCB^ 45°, а
£ Л*ВС « 180° — (45° + a) — 45° ==: 90° — a, по теореме
синусов имеем sfa| (ff+a) = ^о^ау Отсюда
ВС = а-.
fflsin(45° + «)
cos a
Из Д ЛВС находим
|Л 1 . m sin (45° +a)
ь sin a
Из Д DCM находим
tf =mtga.
Линейными углами для двугранных DACB и DBCA бу-
дут l^DNNl и ^D/CAf; эти углы равны, так как равны
39S
ОТВЕТЫ И РЕШЕНИЯ
684
треугольники МКС и MNC (по гипотенузе и острому углу) и
треугольники DMK и DNM (по гипотенузе и катету). Обо-
значим их величину через ср; тогда tg ср = тг^, где MN = -—.
Oms. V=*rm*^+*-t т д arctg(/2tg«).
684. Пусть ЛВЯ (черт. 161, а) — первая, a ADE—вторая
боковая грань. По условию они наклонены к основанию под
одним и тем же углом а.
Отсюда следует, что точ-
ка О, через которую про-
ходит высота, лежиг на
диагонали АС. Действи-
тельно, если из точки О
(черт. 161, б) опустить
перпендикуляры ОМ и
ON1) на стороны АВ
и AD, то £_ОМЕ=<*
и £. ONE = а (доказать!);
следовательно,
OM = Hctg<*
и
ON=Hc\ga*
т. е. ОМ = ON Значит,
точка О лежит на бис-
сектрисе угла BAD, т. е.
на диагонали АС ромба
ABCD.
Но тогда также имеем
ОМх = ONt (ОМх и
ONt — продолжения ОМ
и ON), откуда следует
равенство треугольников ОМгЕ и ONtE и, значит, ^ONtE =
= LPMxEy что и требовалось доказать.
1) На пространственном чертеже (черт. 161, а) один из этих
перпендикуляров, например Ом, можно изобразить произвольной
прямой, но после этого второй строится вполне определённым об-
разом, так как прямая MN должна быть параллельна диагонали BD.
Это легко доказать на плоском чертеже (черт. 161, б).
dJL
685
ГЛ. 9. МНОГОГРАННИКИ
399
Из треугольника О ME находим OAf = tfctga, а из тре-
угольника ОМхЕ имеем OMx = Hctg$. Следовательно, вы-
сота h ромба равна A==MAf1 = #(ctga4-ctgP).
Значит,
V = 150СНЯ = ~ ahH = I аН* (ctg a + ctg р),
3
где МЕ =
Тогда
осн
и
Я
• аф + МЕ+^Е),
sin a * J sin p
— -tJ/'i + cosa i l+cosP\
~ ar4~^s7n~^ I sTnTT
a В
Выразив числители и знаменатели через -*■ и -й- и сократив
дроби, получим
S„ = a//(ctg| + ctg-|).
Отв.
V = la№(ctga+ctgp) =
1 ^sin(a + P).
— 3 sin a sin p ■
Sn = atf(ctgJ + ctgi) =
e/Zsin-^ .
1 I
l sin -£ sin £
685. Пусть £A (черт. 162) — острый угол ромба, так что
АС — большая диагональ и /_ ОАО = у. Проведём MKJL.AC
и MNJ^BD1). Пусть <р есть угол, под которым плоскость
ЕАС наклонена к плоскости основания. Тогда ^МКЕ — у
и £mMNE = ty* Для определения Н выразим МК и MN
*) На черт. 162 следует провести MK\\BD и MN\\AC? так как
диагонали ромба взаимно перпендикулярны (ср. предыдущую сноску).
400
ОТВЕТЫ И РЕШЕНИЯ
-через Я; получим MK = Hcigy и MN = Hctgty эти выра*
-жения подставим в соотношение
МК , MN
a = AD = AM + MD = -
sin2" C0S"2
Получим
Отв. Vt
Vsln-| cosi/
Ф sin а Ф sin2 a
,/cttl + ia±\ 6(cosJctg9+sln°ctg*y
\sin2 C0S-2/
где двугранный угол cp имеет ребром ббльшую диагональ
ромба, а угол ф — меньшую.
686. На черт. 163 отрезок АВ изображает гипотенузу
основания. Для построения линейного угла а нужно пересечь
ребро ВВХ плоскостью,
перпендикулярной к это-
му ребру. В данном слу-
ЪД] чае такую плоскость
можно провести через
катет ЛС. Чтобы дока-
зать это, нужно дока-
зать, что ACJ_BBt.
По условию верши-
на В1 проектируется в
точку D (середина ВС),
лежащую на катете ВС.
Следовательно, если про-
вести через В прямую KL9
перпендикулярную к ВС, то KL будет перпендикулярна
также и к ВВХ (теорема о трёх перпендикулярах). А так как
AC\\KLf то АС±ВВи что и требовалось доказать.
Проведём через АС плоскость АЕС, перпендикулярную
к BBV Боковая поверхность призмы равна периметру
СЕ~\- АС-\- АЕ перпендикулярного сечения, умноженному
на ребро BBV. Из прямоугольного треугольника ВСЕ%
где /_СВЕ=$ (доказать!) и ВС = а, находим СЕ я a sin р.
Черт. 163.
637
ГЛ. 9. МНОГОГРАННИКИ
401
Прямая KL, а значит, и параллельная ей прямая АС, перпен-
дикулярна к грани BBxCfi. Поэтому треугольник АСЕ—пря-
CF
моугольный при вершине С. Значит, АС = СЕ tg а и АЕ = —- ,
так что
Ребро BBV находим из треугольника BDBi9 где £D = -g-«
Получаем BBt = а *t так что
Преобразуем выражение в скобках, как указано в за-
даче 673, и cos а, как
указано в задаче 68 К
Отв.
fl?tgpcos.L
°бов —■ т XT •
V2sln(45°-|)
687. Как в предыду-
щей задаче, докажем,
что ребро AAXJ_BC
(черт. 164), а следова-
тельно, и BBt J_ ВС и
грань ВВХСХС— прямо-
угольник. /_ АХАС =»
= £ AVAB = 2а (доказа-
тельство см. в задаче
669) и, следовательно,
грань ААХСХС = ААХВХВ> Точка Е—середина стороны АВ
и EOJ_AB (точка О — центр окружности, описанной около
Д ABC); тогда AXEJ_AB (по теореме о трёх перпендикуля-
рах). По теореме синусов имеем
Черт. 164.
тогда
АВ = 2/? sin (90° — а) = 2/? cos а;
50сн = у АВ* • sin 2а = 2/?2 cos* а sin 2а.
402 ОТВЕТЫ И РЕШЕНИЯ 688
Из треугольника АЛХЕ имеем
лл « АЕ АВ ffcosa
ААг — 1— cos2o —2cos2a— COs2a *
Из ДААгО найдём
Н=УР — R2=~2rVcos^<x — cos22a.
(Подкоренное выражение преобразуем, как указано в за-
даче 6560 Сторона ВС = 2BD = 2 • АВ • sin afr Следовательно,
V=* Soon • Я= 2/?2cos2a sin 2a cQ*2a /cos2a — cos22a =
= 2/?3 cos2 a tg 2a |/*cos2a — cos2 2a
и
S6oB = 25ллав + Sbb&c^ 21* AB* sin 2a + 2/ • AS • sin a =
= 2/. Л5 (sin 2a ~j- sin a).
Ome. V = 2/?3 cos2 a tg 2a У sin 3a sin a;
8/?3 cos2 a sin -„- cos -y
S<J0B =* Eol2S •
688. Проводим высоту ОЖ треугольника ОСЕ (черт. 165);
тогда £mBMD = § (доказать!). Обозначим ОС = ОВ через х
и найдём х из формулы ОС* =
Е = СЕ*СМ, где С£ = / и СЖ=:
я j/*9—ОМ2. Из треугольни-
ка ОМВ находим
аА/ так что
1"'т-$^^ СЛ = * |Л — ctg2-|.
Подставляя в формулу ОС% =*
— СЕ'СМ, получаем уравнение
x* = lx}f\— ctg2|.
ответствует у
Корень х = 0, очевидно, не соответствует условию, так что
имеем
ГЛ. 9. МНОГОГРАННИКИ
Следовательно,
н=ус&—oc*=Vp—*а=
Теперь находим
403
tctg-
Р
Замечание. Величина cosp отрицательна, так как -L>45P
/ В он ОС*
(ибо Ч^^ту***1*Ш/Г* но наклонная ОС больше перпендику-
ляра ОМ, следовательно, tgi>lj.
Отв. ^ = |/3ctg|(l—ctg^|)==-|-P
ctg^-cos?
*4
./^
689. Из треугольника Л^Е (черт. 166), где ^Л1/Г£=а,
находим ^Е = tfctgo^ana: треугольника АгСЕ, где AxC — d%
находим EC — Yd*— Н3 и,
следовательно,
ЕК = ~-■
V2
Теперь находим стороны осно-
ваний
АВ = а = ЕК+ЕР
и
AXBY ==EG = b = EK— GK=*
= EK—EFt
так что для величины
входящей в формулу объёма усечённой пирамиды, получаем
выражение
{EK+EFp + iEK + EFtfK—EF) + (EK— EFf^
= 3EK*+EF*.
Отв. V = »-(3 . £/С2 + Я/72)= ^-[3(tf9— tf2) + 2tf*ctg2a].
Черт. 166.
404
ОТВЕТЫ И РЕШЕНИЯ
690
690. Можно использовать тот же черт. 166, что и в пре-
дыдущей задаче, введя обозначения АЛг = / и ^ ЛгАС = р.
Из прямоугольного треугольника АЛгС находим ^c = ^sT>
так что a = FK = т^1—-. Из треугольника ААХЕ нахо-
/cosp
сле-
V2 cos р
дим Я— /sin р и ^£ = /cosp, так что FE = -~^-
довательно,
l,==EG=FK — 2FE=-rd (1—2cos2p) = /'_s2P .
1^2 cos pv r 1^2 cos p"
Теперь получим
V = ^(a* + ab + b^ = -?^{l-cos2?+cos*2$).
Если числитель и знаменатель помножить на (1 —|— cos 2р)
(применив формулу для суммы кубов), то получим несколько
более простое выражение.
Замечание. Угол р должен
быть больше 45°, так как F/C > 2 • FE.
Поэтому cos2£<0.
Отвш
_ /aSinp(l + cos32p)
12 cos* р
691. Из треугольников ААХЕ
и ЕАгС (черт. 167)г) имеем
AE = Hc\ga и EC = Hctg$.
Боковая поверхность равна
SooK=4-^±A.^N =
Апофему AXN находим из треугольника AxENt где
г. к т АЕ М . '
EN= —== я -— ctg а;
V2 V2 s
i) Об изображении усечённой пврамиды см. стр. 348.
692 гл. 9. МНОГОГРАННИКИ 405
получаем
A^^H^l+-%■<№ а.
Сумма
а + Ъ = АВ + АХВХ = 2А1В1 + 2AN = 2 • NB =
= £С V2 = H- V^2 ctg p.
Следовательно,
S6ok = 2Н]/ 2 ctg р Я j/"l + -i- ctg2 a.
Ome. SeoK = 2//2 ctg p 1/ 2 -j- ctg2 a.
692. Из треугольника AlEN (тот же черт. 167), где
EN=AN= АВ-А^ =.£/3-1),
находим
N=^£=|-(/3-l)tgT
"i™ 2 cos т *
Теперь получаем
V = ^(3e« + e« + fl2^3) = -f-(K3-l)(4 + /3)tgY
и
S^2(AB + AlB1)AlN=2a(V3 + l)-Z&^ = ^.
Следовательно,
Выражение в скобках можно привести к виду, удобному для
логарифмирования.
Оте. yg*'(3T^-l)tgT^0>7fl8tgT.
-. а* (1+2 «»т) ^ cos (-1+30°) cos (1-30")
On = *■■■ ■ ' ■■■■— ess ————— — ■ ,
cos i cos i
406
ОТВЕТЫ И РЕШЕНИЯ
693
693. Обозначим сторону куба через х (черт. 168). Из
подобия треугольников ЕОхКх и БОС имеем
EOi _ ОхКх
'ЕО~ ОС *
Здесь
EOl = EO — OOi = И—х,
°l/Cl = Yf'
/у^з
в
ЕО = Н,
oc=Vp—h*.
Следовательно,
Черт. 168.
Отв. х
НУ 2(/а — №)
имеем W = -2"Ctga, Следовательно, объём
//+У"2(/* — №)
694. Из треугольника ЯО/7 (черт. 169), где 0/7 = -|-
и £_OEF =
пирамиды
y = ia3tf=I-a3ctga.
Выразим сторону а через ребро
куба х^ММ^ Имеем
= KM-\-2MMl-tg**=
= A:VT + 2jctga.
Следовательно,
*3()T2 + 2tgq)9ctg«
6
Здесь jc3 = V\ есть объём куба.
оОТ8.-£*=(^+2Г)8с*а-
Черт. 169.
695. а) Способ построения. Сначала изобразим то
сечение AlMlBl (черт. 170), где лежит «верхняя» грань куба
KXLXMVNX (это сечение есть прямоугольный треугольник
с прямым углом при вершине Мх). Так как вершины KVLV
695
гл. 9. МНОГОГРАННИКИ
407
MXi Nx лежат на боковых гранях, то они находятся на сто-
ронах треугольника АХМХВХ (Мх совпадает с вершиной пря-
мого угла, прямая МХКХ изо-
бражает биссектрису пря-
мого угла, ибо MlN1=aM1Lx).
Теперь изображаем куб
KLMNKXLXMXNV Внутри че-
тырёхугольника KxL\MlNl
берём произвольную точку
Ох, изображающую пересе-
чение высоты DO с гранью
KiLxM1Nx и соединяем её с
точкой О, сходственно рас-
положенной в четырёхуголь-
нике KLMN. Проводим пря-
мые ОхАх, OxBv ОхМх и
прямые ОА, ОВ, ОМ, со-
ответственно им параллель-
ные. В пересечении DAX, DBX и DMX соответственно с ОЛ,
ОВ и ОМ находим точки А> В9 С—вершины основания
пирамиды.
б) Решение. По условию ЛС = 6; #С = 8; 00 = 24*).
Обозначим ребро куба через х. Тогда 00х = х и DOt=24—х.
По свойству сечений, параллельных основанию пирамиды,
имеем ВХМХ : ВС = D0X: DO, т. е. ВХМХ: 8 = (24 — х) : 24,
откуда
о л, _ 8(24 —х) _ 24-л:
Из подобия треугольников KXBXLX и ABC имеем
KXLX:BXLX = 6:S;
Черт. 170.
здесь
KXLX = х и BXLX = ВгМх — MXLX = ^ *
■#==•
24—4л:
Следовательно, л:: g = 6:8, откуда jc = 3.
Отв. 3.
*) На черт. 170 эти соотношения не соблюдены.
408
ОТВЕТЫ И РЕШЕНИЯ
696. Сечение ВССХВХ (черт. 171) есть трапеция (доказать!).
Проведём плоскость MNE (М и N—середины сторон AD
и ВС). Она пересечёт плоскость BCClBi по прямой NK
(К— середина ВХСХ). Имеем £_ NME = £_ MNE = а и
£_ MNK = Р (доказать!). Вы-
сота KN трапеции ВССХВХ нахо-
дится из треугольника KNM9
где MN = a и /. MKN =
= 180°—(а + р). По теореме
KN а
синусов — =
КМ =
sin а
a sin а
Sln(a + B)''T'e*
-. Теперь нахо-
sin(« + P)'
дим верхнее основание ВХСХ
трапеции; из подобия треуголь-
ников ADE и ВХСХЕ имеем
Черт. 171.
КЕ
а-КЕ
NE
Отношение г™- найдём из треугольника KNE, где /_KNE=i
= a — р, а £mNKE=a-\-$ (как внешний для /\KNM).
Получаем
ЛЖ_ sin (а— р) .
следовательно,
Площадь сечения
NE ~ sin (a + р) »
Rr> __ а Sin (a — р) 1
"?"*— sln(a + P) #
a sin (a — р)
Д Sin a
с ^ Sin(a + P)
°свч "" 2 sin (a + Р) e
п с flasinaacosp
Отв. Л0еЧ — sin2(a + P) •
697. а) Способ изображения. Сделав изображение
пирамиды EHPGQ (черт. 172), изображаем прямую MN, по
которой пересекаются плоскости; она параллельна стороне ИР
и пересекает ось ОЕ в точке В. Концы М и N отрезка /ИЛ/
ГЛ. 9. МНОГОГРАННИКИ
409
лежат на апофемах EF и ED. Проведя PN и GNt НМ и
QM, получаем изображение плоскостей, пересекающихся
no MN. Отметим точки At и Ср лежащие на пересечении
АВ и СВ с апофемами ЕА
и ЕС (А и С— середины HP Е
и QG). Угол ABC — линей-
ный угол получившегося
двугранного угла. По усло-
вию /_ ABC з=90°, т. е.
треугольник ABC —- равно-
бедренный прямоугольный и
ВО = АО =
2*
б) Решение. Из подо-
бия треугольников EMN и
EDF, где DF=at имеем
MN = a.~. Угол ОЛ£ //
есть линейный для двугран- Черт. 172.
ного угла а, так что
ЕО = АО* tg а = у tg а. Кроме того, ЕВ = ЕО — ВО
= 2"^ а — *)• Следовательно,
MN = a fg;g7l = a(l-ctga).
Ome. AW == a (1 — ctg a) =
V2asln(a—45°) 1
sin a
698. а) Способ из об pa ж ен и я. Проводим прямую СМ
(черт. 173), изображающую перпендикуляр, опущенный из С
на АЕ. Через точку Ot, где СМ встречает ЕО, прово-
дим КЩВй. Четырёхугольник KCNM изображает сечение.
Доказательство следует из нижеприводимого решения.
б) Решение. Так как плоскость KCNM перпендику-
лярна к ребру АЕ, то стороны МК и MN, а также диаго-
наль СМ сечения KCNM перпендикулярны к АЕ. Так как
диагональ СМ лежит в плоскости равнобедренного треуголь-
ника AECt то она пересекает прямую ЕО, являющуюся
высотой этого треугольника. С другой стороны, диагональ KN,
410
ОТВЕТЫ И РЕШЕНИЯ
698
лежащая в плоскости треугольника BED (и, как сейчас будет
доказано, параллельная основанию BD этого треугольника),
тоже пересекает прямую £0,
являющуюся высотой треуголь-
ника BED, А так как плоскость
KCNM имеет с прямой ОЕ только
одну общую точку 0±, то в
этой точке диагонали KN и МС
пересекаются друг с другом.
Плоскость KCNM перпенди-
ф кулярна к ребру АЕ\ поэтому
углы ЕМК и EMN—прямые.
Прямоугольные треугольники
ЕМК и EMN равны (доказать!);
следовательно, MK=MNn ЕК=*
Черт. 173. =EN. Из последнего равенства
вытекает, что KN\\BD и что
KOt = OtN. Следовательно, диагонали МС и /(TV взаимно
перпендикулярны и, значит, $оеч = -п МС • KN.
Диагональ МС находим из прямоугольного треуголь-
ника АМС, где 21 СЛЖ те <р и ЛС = а |/"2 . Получаем
yWC = a/2"sincp.
Диагональ /(TV находим из равнобедренного треуголь-
ника KEN, где /_EKN=y. Имеем A7V = 2 . Ог£. ctgcp, где
0±Е=ОЕ — 001<( Отрезок 0£ определяется из треуголь-
ника ЛОЕ (или ВОЕ); находим ОЕ
__ а У2
1 tg <р. Отрезок
же 004 определяется из треугольника ОС019 где /тОС01-
= 90°—^.ЖЛС=90° —<р. Находим
V2
ctg?.
001= OCtg(90° — <?) = ■
Теперь получаем
/C^=2.01£.ctg9 = 2(-^^tg?-^|^-ctg?)ctg? =
= а/2 (1— ctg2<p).
Следовательно,
Sw = ^MC.KN=d*(l — ctg2?)sin? =■
аа cos 2<р
sin ф
699
ГЛ. 9. МНОГОГРАННИКИ
411
Замечание. Для того чтобы плоскость KCNM, перпендику-
лярная к АЕ, дала бы сечение пирамиды, нужно, чтобы точка М её
пересечения с прямой АЕ лежала на отрезке АЕ (а не на его про-
должении), а для этого угол АЕС должен быть острым, т. е.
ZAEC=*\SQ0 — 2?<9(У\ Следовательно, <р>45°, а поэтому cos2<p
есть величина отрицательная.
Отв. SQt
a* cos 2у _ a? cos (180° — 2у)
sin 9
sin 9
699. Четырёхугольник AMKN (черт. 174), получающийся
в сечении боковой поверхности призмы, всегда является
параллелограммом (доказать!). Чтобы он был ромбом, должно
Черт. 174.
быть AM = AN, Из равенства треугольников ADN и АВМ
(доказать!) следует, что DN=BM. Значит, прямая MN па-
раллельна прямой BDt а значит, и плоскости ABCD. Следо-
вательно, прямая EFt по которой плоскость AMKN пересе-
кается с плоскостью ABCD, параллельна диагонали ММ
(и диагонали BD)t а значит, перпендикулярна к другой
диагонали ромба АК (и диагонали АС). Отсюда следует,
что ср = £J2AK есть линейный угол искомого двугранного
угла. Прямая OOit соединяющая центр ромба Ох с центром
основания призмы, перпендикулярна к основанию (доказать!).
412
ОТВЕТЫ И РЕШЕНИЯ
700
Из треугольника AOOL находим
АО OB OiM . а
Замечание. Плоскость, проведённая через прямые AM и ANt
пересечёт ребро СС\ лишь в том случае, если СС\^- СК, т. е. если
высота призмы не меньше, чем
дУУу! — cos2y _*V*V 1м*g22"__аУ2Ш~а
г У 2 tg ^
COS ер
lg'
sin-
В противном случае ни через точку А, ни тем более через другую
точку ребра ААХ требуемого сечения провести нельзя.
Отв. ср = arc cos tg-g-. Задача имеет решение только при
„^ а У2 cos а
условии Я]>—- —.
sinT
700 *) (ср. решение предыдущей задачи). Так как
MN=AC (черт. 175) и ВК> BD, а по условию должно
Черт. 175.
быть BK=MN, то АО BDt т. е. АС есть ббльшая
1) Об изображении прямой призмы см. стр. 331 (черт. 83).
ЯР1
ГЛ, 9. МНОГОГРАННИКИ
413
диагональ ромба, так что l^ABC—тупой, a U$AD —
острый.
Угол ср = ^вО£01 — есть линейный угол искомого дву-
ОВ
гранного угла. Из треугольника ООхВ имеем C0S9 = 7nr*
где ОВ = О А • tg -тг . А так как О Л = OtM = ОхВъ то cos 9 =
0ХД
■ — *&■§■• Здесь tg -у < 1, так как а — острый
угол.
Ome, tp = arc cos tg %?; задача имеет решение только при
условии
DDx>BDYYa.
а1а2
701. Cpi предыдущую задачу. Площадь S^, ромба BNKM
(черт. 176) равна
.SCe, = -J-. M/V• ВК = 2 Ж01 • ВОл.
Из треугольника ^OtB, где
/ш.МВОх = ^, находим:
BOl-AfOt.ctg-J-.
Следовательно,
5oe4 = 2.AfO,a.ctg^ =
= 2«/102.ctgj.
<7,
/Г
UZ/
\\
аК
«, !\
it
p47^ty
А
а
£
Черт. 176.
Отрезок АО находим из треугольника AOBt где АВ = а и
^ЛБО = у. Получаем АО = a sin -|-.
Ome. Soe, = 2а2 sin2 j ctg -£.
414 ОТВЕТЫ И РЕШЕНИЯ 702
702 *). Пусть секущая плоскость проводится через сере-
дину М (черт. 177) ребра АВ параллельно рёбрам АС и BD.
Ребро АС лежит в плоскости ABC. Поэтому плоскость, про-
ведённая через М параллельно АС, пересекает грани ABC
по прямой MN, параллельной АС. Значит, MN—средняя
линия треугольника ABC (mN=* ^ АС =2")» т- е- ^ есть
середина ребра ВС. Ребро BD лежит в плоскости BCD,
а плоскость сечения параллельна ребру BD. Поэтому NL\\BD
\NL = -x-BD==~\ и L — середина ребра CD. Так же до-
кажем, что МК —о" и что К—середина ребра AD,
Следовательно,
Ь
КЦАСя KL^^.
Значит, сечение MNLK есть ромб. Но кроме того, угол
NMK—прямой. Действительно, ребро BD лежит в плоскости
BDE (Е—середина АС), а эта плоскость перпендикулярна
к ребру АС. Следовательно, BD±_AC. Но по доказанному
MK\\BD и МЩАС\ значит, MK±_MN. Из этого следует,
что MNLK—квадрат со стороной ■£■•
Отв. See*— "Т.
]) Об изображении правильной треугольной пирамиды см. стр. 330
(черт. 82).
704
ГЛ. 9# МНОГОГРАННИКИ
415
703. Пусть CD (черт. 178) есть боковое ребро, пер-
пендикулярное к плоскости основания. Так как по усло-
вию IJDAC = IPBC^a, то
АС = СВ, т. е. треугольник
ЛВС—равнобедренный при
вершине С и, значит, по усло-
вию 2С = 90°.
Всякое сечение пирамиды,
перпендикулярное к основанию
ЛВС, есть четырёхугольник
NKLM с двумя прямыми углами
(I.NKL и ^KLM). Чтобы
этот четырёхугольник был
квадратом, должно быть /СЛ/ =
= KL = LM ее х. Из равен-
ства треугольников AKN и
BLM (доказать!) следует, что
AK=BL, а значит, KC = CL,
так 4toATC = 4L = -£=. Из
УТ У2
треугольника AKN находим
АК=*К№• ctg а = х ctg а. Так
как
то
Черт.
КС + АК = АС=*а,
получаем уравнение
=+A:ctgoc = a,
(l+l^Ctga)**
704. В сечении полу-
чится трапеция МАЛВ^М
(черт. 179), равная боко-
вой грани DD^Cfi (дока-
зать!). В отсечённой части
A^C^MNCD имеем
AXDX = ВхСг = NC = MD, как отрезки параллельных между
параллельными плоскостями. Полученное тело есть наклонная
призма с основанием CCXDXD. Через апофему FG усечённой
416 ОТВЕТЫ И РЕШЕНИЯ 704
пирамиды и апофему OG основания проведём плоскость FGQQ^
получим ^/7GL = oc (доказать!). Перпендикуляр L/C, опущен-
ный из L на прямую GF, будет высотой призмы (доказать!).
Из треугольника LKG, где LG = QXF = а, имеем LK= a sin а.
Из треугольника FLG находим FG = = ——. Объём
^ J COS a COS а
призмы V вычислим по формуле
у = вхсг + вс ePQ LK
Найдём полную поверхность 5 тела AMAxB^NBy отсе-
чённого плоскостью AXB^NM. Грань ААХВХВ равновелика
сечению MAXBXN (доказать!). Каждая из этих граней имеет
площадь Sx = а g ■ QQl9 где QQX = FG = -^. Каждая из
AM»>4 Р
граней AdjM и £№?t имеет площадь 52 = 2""» где
Л/И = ЛО — ЛШ = За — а = 2а и ДР== FG^ — . Пло-
1 cos а
щадь 53 грани ABNM равна S3 = ЛЖ • Л£ = 2а • За. Имеем
12fl2C0S2-^
0™.^=2a3tga; 5 = ггт^.
Предварительное замечание к задаче 705
и следующим
При решении задачи 705 и трёх следующих мы восполь-
зуемся следующей теоремой.
Если многоугольник ABCDE ..., лежащий в плоскости Р,
проектируется на плоскость Рг (проекция — прямоугольная),
многоугольником Л15ГС101£1..., то площадь S многоуголь-
ника ABCDE... и площадь 5t многоугольника AXBXCVDXEX*. •
связаны соотношением
S^== S cos a,
где a—угол между плоскостями Р и Рх,
На вступительных экзаменах нередко предлагаются задачи,
при решении которых трудно обойтись без этой теоремы !).
*) См., например, задачи 705 и 706.
704
ПК 9. МНОГОГРАННИКИ
417
вг X
а)
Между тем она не содержится в наших учебниках тригоно-
метрии. Поэтому мы даём её доказательство.
Доказательство. Сначала рассмотрим случай, когда про-
ектируемая фигура есть треугольник ABC (черт. 180, я), у которого
одна сторона АВ параллельна плоскости проекций Р}л Проведём через
АВ плоскость Q, параллельную плоскости Рг (Е— точка пересечения
с проектирующей прямой СС|). Получим треугольник ABE, равный
треугольнику AiBid. Проведём высоту CD треугольника АСВ;
прямая ED будет высотой треугольника АЕВ, а угол а = £fiDC
будет линейным для дву-
гранного угла САВЕ, рав- ^*С
ного углу между плоско-
стями Я и Pi. Из треуголь-
ника DCE находим DE =*
=а CD «cos а. Следова-
тельно,
S^^AB-DE =
— Л АВ* DC -cos а »
в 5 cos а.
Затем рассмотрим слу-
чай, • когда проектируе-
мая фигура есть треуголь-
ник LMN (черт. 180, б),
- стороны которого ие
параллельны плоскости
Р\. Такой треугольник
можно разбить на два
треугольника типа, рас-
смотренного выше. Для
этого достаточно через
одну из его вершин М
(не самую близкую и не
самую далёкую от пло-
скости Pi) провести пло-
скость 0, параллельную
Pi; она пересечёт тре-
угольник LMN по прямой КМ, параллельной Рь Если S/ и S"—.
площади треугольников KMN и LMK, a S[ и 5* — площади их про-
екций (треугольников KtMtNi и LtMxKi), то по доказанному
S[ « S' cos а и Si =* S" COS а.
А так как S«S'+S" и St^s[+Sf[f то-
5t — si + si — 5' cos а + $" cos а = (S' + S") cos а ra S cos а.
U4;/Ni
-ч.
6)
Черт. 180.
418
ОТВЕТЫ И РЕШЕНИЯ
705
В случае когда многоугольник имеет более трёх сторон, мы
разобьём его на треугольники и, рассуждая как в предыдущем слу-
чае, докажем общую теорему.
Заметим, что эта теорема справедлива и для площадей криволи-
нейных фигур. Для доказательства нужно вписать в криволинейную
фигуру многоугольник и совершить переход к пределу.
705. Имеем (черт. 181) S^H=2?l2f и H=BBt=BD + DB{.
ЛЬН1
3
Из треугольников BED и BXEXD (Е и Et— середины АС
и i4tCt) имеем
-tgo
в,
я
в
BlD = a-Jf-tg^
Следовательно,
y = SO02./f = 5|!(tga+tgp) =
За? sin (а + р)
И cos a cos р *
Сечение ADC проектируе!
на плоскость нижнего осно-
Черт. 181. вания треугольником ABC*
По доказанному (см. предвари-
тельное замечание) площадь 5 сечения ADC и площадь тре-
угольника АВС% т. е. SoeH, связаны соотношением Sock = S cos a,
о
так что 5==—^. Таким же образом (проектируя сечение
AxDCr на верхнее основание), найдём, что площадь 5' сече-
ния AfiC^ равна S' = ■ °в\-■ Следовательно,
5 + & = 5„0Н [^ + ЕБГр") *
Ome V 3*3sin(g +Pl-
ume, v— 8cosacosp i
706
ГЛ. 9. МНОГОГРАННИКИ
419
706. а) Способ изображения. Соединяем середины
/Си! (черт. 182) сторон АВ и AD. Через точку Е, где KL
пересекает АС, проводим прямую EN (угол NEC изобра-
жает линейный угол двугранного угла а). Через точку 02,
где EN пересекается с ООг (изображение оси), проводим
PM\\BD. Пятиугольник KLMNP изображает сечение. Дока-
зательство вытекает из нижепри-
водимого решения.
б) Решение. Так как KL\\BD,
то плоскость KLMNP (проходя-
щая через KL) пересекается с
диагональной плоскостью DBBtDt
(проходящей через BD) по прямой
РМ, параллельной KL и BD.
Ось призмы OOt лежит в диаго-
нальной плоскости DBBtDx и,
следовательно, пересекается с
прямой РМ. С диагональной пло-
скостью ACCtAt плоскость KLMNP
пересекается по прямой NE
(Е—середина KL); эта прямая
тоже пересекает ось OOt. Но
так как плоскость KLMNP, в
которой лежат прямые РМ и EN, пересекается с осью
ООх только в одной точке 02, то обе прямые EN и MP
проходят через Эту точку, т. е. точка пересечения прямых
РМ и EN лежит на оси OOv Прямые ЕС и EN перпенди-
кулярны к KL (теорема о трёх перпендикулярах); значит,
£CEN=a.
Площадь S пятиугольника KLBCD равна площади квад-
рата ABCD без площади треугольника AKL, так что S =
= &* — -Q- = -q- ЬК Площадь See* пятиугольника KLMNP опре-
доказанной в предварительном замеча-
8 8
деляется по теореме,
нии к задаче 705 (стр. 416). Имеем -^й2 = 5сеч cos а, т. е.
8
Сравнивая треугольники M02N и ВОС (у них ЁО = М02
и MN > ВС), убеждаемся, что 2. MN02 < 2. ВСО; а так как
420
ОТВЕТЫ И РЕШЕНИЯ
707
^ ВСО = 45°, то £_ MNO^ < 45е, и следовательно, угол
9==/. MNP—острый. Остальные углы сечения—тупые (острый
угол ЛШ02 = 90°—^MN02 больше 45°; угол MLK равен
180° — £LM02=s 180° — £ЛШ02). Из треугольника M02N
имеем
М02
ъ$
но
М)0=:
2
ОС
м?2
ов
МО*
2 COS a COS а COS а-
Следовательно,
Огне» «Sceq ==
762
8 cos а '
tg-| = cosa.
9 = 2 arc tg (cos а).
707. a) Способ изображения. Сначала начертим
отдельно основание призмы (черт. 183, а). Затем проведём эл-
липс (черт. 183,6), изобра-
жающий круг, около которого
описано основание х). Проведём
Вг
Черт. 183.
какой-либо диаметр MN эллипса, и через концы его про-
ведём касательные CD и АВ; они изображают прямые, на
которых лежат основания равнобочной трапеции. Проводим
какую-либо прямую KLf параллельную CD и АВ. Через
1) О вычерчивании эллипса см. стр. 339 (черт. 92).
707
ГЛ. 9. МНОГОГРАННИКИ
421
точки К и L, в которых она пересекает эллипс, проводим
касательные к эллипсу (DA и ВС). Четырёхугольник ABCD
изображает равнобочную трапецию, описанную около круга.
Далее строим изображение прямой призмы ABCDA^fifi^
Секущая плоскость, проходящая через боковую сторону AD
и вершину Bi$ пересечёт грань AAtBtB по прямой АВХ,
а параллельную ей грань — по прямой £Ю, параллельной ABV
В сечении получаем четырёхугольник ABXGD. Из точки В
проводим прямую BE, параллельную радиусу ОК, ведущему
в точку касания /С. Эта прямая изображает перпендикуляр,
опущенный из В на AD. Следовательно, угол ВЕВХ есть
изображение линейного угла а.
б) Решение. Из треугольника DFA (черт. 183,6), где
DF=MN=2r и /DAF=a, находим ВС = AD= ~.
*^ Sin at
Обозначим АВ через at CD — через bt AD = BC — через с.
По свойству описанного четырёхугольника
a + d=AB + CD=AD4-BC = 2c=-^-.
1 ' * sin а
Имеем
с _ а + Ъ. 2r 0 4г2
Следовательно (см. предварительное замечание к задаче 705),
с 4г3 8г3
л °ОСН ™ ц/
ееч cos a sin а cos а sin 2а"
Высоту Н = ВВ1 найдём из треугольника BBtE, предва-
рительно определив BE из треугольника ВЕА, где
АВ = а = 2AM = 20М . ctg /. ОЛАГ = 2r ctg у.
Имеем
BE = a sin а и Н=ВЕ -tga.
Следовательно,
#=2rctg £ sin atga.
Теперь находим
S6oK = #(a + * + 2<0 = 4^.
Отв. 5б0В = 16r2 tg a ctg у; S^ == ^j^ •
422
ОТВЕТЫ И РЕШЕНИЯ
708
708. а) Способ изображения. Секущую плоскость Р
можно провести через любую из двух диагоналей грани
ВССгВх (черт. 184). Проведём её через диагональ BCV По
условию РЦЛО. Следовательно, пдоскость Р пересечёт пло-
скость основания ЛВС по прямой ВК, параллельной AD (пря-
мая ВК целиком лежит вне треугольника ABC). Так как грань
ВССХВХ перпендикулярна к ADt то она перпендикулярна и
к прямой ВК\ значит, /_СВСХ есть линейный угол двугран-
ного угла р при ребре ВК.
Черт. 184.
Изобразим теперь треугольник, являющийся сечением
призмы плоскостью Р. Одна сторона этого треугольника {ВСХ)
известна; остаётся найти противоположную вершину, т. е.
пересечение плоскости Р с ребром АА^. Для этого доста-
точно соединить точку Е, в которой прямая ВК пересекает
продолжение ребра АС, с точкой Cv Точка F, где прямая
CjE пересечёт ребро AAV будет искомой вершиной.
Докажем это. Так как точка Е лежит на прямой ВЕУ по
которой пересекаются плоскости Р и ABC, то эта точка при-
надлежит плоскости Р. С другой стороны, точка Е лежит
на прямой АС, по которой пересекаются плоскости АССгАг
и ABC; значит, она принадлежит плоскости АССхАг (она на-
ходится на продолжении грани АССгАг). Следовательно, точ-
ка Е должна принадлежать линии пересечения плоскостей Р
и ACC^AV Точка Сг по условию тоже принадлежит пере-
сечению тех же плоскостей. Следовательно, плоскости Р и
АССгАх пересекаются по прямой СХЕ, т. е. на этой прямой
лежит сторона (CjF) сечения, находящаяся на грани СС^А.
709
ГЛ. 9", МНОГОГРАННИКИ
423
Значит, точка F, где CtE пересекается с ребром AAV есть
искомая вершина.
б) Решение. Так как треугольник ABC есть проекция
треугольника FBCV лежащего в плоскости Р, на плоскость
основания, то
О(№о —-
-£• a2 sin 2а
cos р
cosp
где а = АС—боковая сторона равнобедреннего треуголь-
ника АВСь Выразим а3 через боковую поверхность S.
Имеем
S = (2AC-{-BC)*CCl9
где АС = а, BC = 2acosa и ССХ = ВС • ig£ = 2а cos а tgp.
Следовательно,
5 == 4аа cos а (1 + cos а) tg р — 8а2 cos а cos2 j tgp.
0ш с -3 sia2aCtgp ^2
cos p cos a cosa у
709. a) Способ изображения. Продолжив отрезок
ВС (черт. 185), изображающий катет основания, на расстоя-
Черт. 185.
ние CD = ВС, получаем точку D, которая в натуре симмет-
рична с В относительно катета АС. Возьмём точку М на
424
ОТВЕТЫ И РЕШЕНИЯ
709
середине ребра ААХ й изобразим сечение призмы плоскостью Р,
проходящей через точки Blt М и D. Для этого соединим
точки 5, и D. В пересечении с ребром ССХ найдём точку N.
Треугольник BXNM будет искомым сечением. Действительно,
точка D лежит на прямой ВС и, значит, принадлежит пло-
скости CBBlC1 (D находится на продолжении грани СВВгСг).
Но точка D лежит также и на плоскости Я, поэтому она
находится на линии пересечения плоскости Р с СВВХСХ.
Точно так же и точка Вх находится на этой линии. Зна-
чит, плоскости Р и ВССХВХ пересекаются по прямой BtD.
Точка Л/, где BXD пересекается с ребром CCV есть одна
из вершин сечения, так что сечение призмы есть треуголь-
ник BXNM,
Так как BC=*CD и CN\\BBU tq CN есть средняя ли-
ния треугольника BBtD, т. е. N—середина ребра CCV Сле-
довательно, прямая MN параллельна прямой АС, лежащей
в плоскости основания. Вследствие этого и прямая DE, по
которой плоскость Р пересечёт плоскость основания, парал-
лельна АС и, вначит, перпендикулярна к плоскости грани
BCCXBV Поэтому /^BDBX есть линейный угол двугранного
угла <р при ребре DE.
б) Решение. Имеем (см. решение предыдущей задачи)
(где а=*ВС, Ь = АС)9 а так как b = a\g$, то
с — ^tgp
Найдём яа. По условию £ есть меньший из острых углов
треугольника ABC, так что Ъ < а и площадь ЪН грани АССХАХ
меньше площади аН грани BCCXBV Поэтому разность «S этих
площадей (предполагаем, что она положительна) равна (а—Ь) И.
Из треугольника DBBU где BD = 2ВС = 2ал находим
Н = 2а tg ср. Следовательно,
S = 2aH\ — tgP)tg<p.
Отсюда находим а\
710
гл. 9. МНОГОГРАННИКИ
425
°^ ~ SiflfJ ~ sin ft
710. Угол между непересекающимися диагоналями BAt
и ADX (черт. 186) равен углу у = ^AXBCX межДУ ВАХ и
прямой ВСи параллельной ADX. Имеем ^СВСХ =
= £_ DAD) = а и ^ АВАХ = р. Для определения угла ср
находим ACia сначала из треугольника АХВСХ (по теореме
косинусов), а затем из прямоугольного треугольника АХВ1С1
и приравниваем найденные выражения. Получаем
ВАг* + 5Cj2 — 2 • ВЛг. 5Ct. cos ср = Bt/1 г» + BXCX\
Отсюда
2. ВЛ t. ВСХ • cos ср = (В A t9—Bt Л t2) + (ВСЪ—Bfii2) =2. ВВ^.
В это равенство подставляем
sinf
(из треугольника ВЛ^) и BCts= —i-. Получаем
cos ср = sin a sin fi.
Другой способ. Через ребро ВХСХ проведём пло-
скость ВХСХС2В^ перпендикулярную к ВАХ (это возможно,
так как BxCtJ_BAx). Пусть Е— точка пересечения прямых
ВАХ и ВХВ2. Из прямоугольного треугольника ВСХЕ находим
BE = ВСХ cos ср. а из прямо-
угольного треугольника BBxEt
где ^В1В£=90°— р, имеем
BE = BBt. cos (90° — Р) = £,
= ВВ1 • sin р.
Отрезок ££t выразим через
ВС, из треугольника ВВхСи
где £, 5,5с, = 90°— а. Полу-
чим ВВХ = ВСХ* sin а и, значит,
В2 Л
Черт. 186.
ВЕ=ВСХ* sin a sin р.
Приравнивая два выражения отрезка BE, получаем
BCt • cos ср = BCt • sin a sin p.
О/па. cos cp = sin a siii p.
426
ОТВЕТЫ И РЕШЕНИЯ
711
711. Обозначим двугранные углы при рёбрах SA, SB*
SC (черт. 187) через <рА, срд> ¥#• Проведём через какую-либо
точку F ребра SC плоскость DFE, перпендикулярную к SF*
Тогда Z.bF£ = 9G- Определяем ED* из треугольника EFD
и из треугольника ESD, а затем приравниваем полученные
выражения. Находим
FE*-\-FD*—2-FE<FD-cos<?G=SE*-t-SD*—2'SE.SD.cos-{.
Отсюда
2-FE-FD- cos <р0= 2 - SE • SD • cos y —
— (S£2 — f£«) — (5£>a — FD\
т. e.
2 • FE • /^D • cos <p0= 2 - S£. SD • cos y — 2 • S/4
В это равенство подставляем
FE = SF-tga;
FD = SF.tgp;
SF
SE=
SD =
COSct
cosp\
Получаем
tg a tgp cos ©0=^
cosy
COS a cos p
ь
откуда
Черт. 187.
Аналогично найдём cos уА и cos <рв.
^ cos а — cos В COS Y
Отв. cos<p, = . ъ . ——-,
т^ sin psin y
COS <5/
cost—cos a cosp
f~~ sin a slag
cos ?B =
COS?^
cos p — cos 7 cos a
sin у siu a '
cos y— cos a cos p
sin a sin p
712. Решается как предыдущая задача.
Отв. cos y = cos a cos p 4" sin a s*n P cos ^-
715
гл. 9, МНОГОГРАННИКИ
427
713. См. задачу 71L
Отв. Искомый угол содержит 90°.
714. Пусть точка М лежит на грани Q (черт. 188). По
условию прямая AM образует с АВ угол а, а прямая MB
перпендикулярна к АВ. Проведём через ВМ плоскость МВ№,
перпендикулярную к ребру, и опустим из точки М на BN
Черт. 188.
перпендикуляр MN. Прямая MN перпендикулярна также и
к AU и /_MAN=$ (доказать!). Имеем также <э = /_NBM.
Угол <р мы найдём из треугольника NBM, где MN = AM- sin р
(из треугольника ANM) и М±= AM -sin а (из треуголь-
ника АМВ). Получаем
MN AM sin р sinj
sin ср — вм — ^Msina —since"
л - sln P
О/ия. sin © = -—£-.
T Sin a
715. На черт. 189 PQ изображает общий перпендикуляр
к скрещивающимся прямым LU н ММ'. Чтобы получить
угол, под которым отрезок PQ виден из точки А, нужно
провести луч АР; тогда /_PAQ=a. Аналогично /_PBQ = $.
Проведём через точку Р прямую РЕ, параллельную ММ!,
Тогда угол между прямыми ММ' и LI/ есть (по определе-
нию) угол <р = /JEPB. Опустим из А перпендикуляр АЕ
на прямую РЕ и проведём АВ (все остальные линии,
дающие изображение параллелепипеда, рёбрами . которого
428
ОТВЕТЫ И РЕШЕНИЯ
716
являются PQ, QA и РВ% проведены лишь для наглядности
чертежа). Из прямоугольного треугольника BPQ находим
PB = PQc\g$ = hctg$.
Аналогично
PE=QA = kctga.
Далее
ВЕ* = РВ*-{-РЕ? — 2-РВ*РЕсоъ® =
= № (ctg2 а + ctg2 р — 2 ctg а ctg р cos <р).
Прямая Л£ перпендикулярна к плоскости ЕРВ, так как она
параллельна прямой PQ, являющейся общим перпендикуля-
л?
м д
>7 //'
Черт. 189.
ром для прямых PS и РЕ. Из прямоугольного треугольни-
ка ЛЕВ находим
АВ* = А £2 + ££3 = А8 + В£2.
О/яв. ЛВ3 = А2 (1 + ctg2 а + ctg2 р — 2 ctg а ctg р cos <р).
716. Чертёж предыдущей задачи (в настоящей задаче
<р = 90°). Имеем
BE = /ЯЁз + ЯЙа === h /ctgaa+ctgap.
Угол между прямыми АВ и PQ равен углу между АВ и пря-
мой АЕУ параллельной PQ. Обозначив его через ft имеем
t(Tnr ._ДД_Л Vctg»g + ctg«p
717
ГЛ. 9. МНОГОГРАННИКИ
429
717. Пусть (черт. 190)
DM__mi _DN_m2 DP _ms
АЛ A я. » \1R я. » PC П» *
MA
л.
NB n2
n$
Найдём сначала отношение объёма Vx пирамиды DMNP
к объёму V пирамиды DABC. Примем грань BDC за осно-
вание пирамиды DABC и грань NPD за основание пирами-
ды DMNP. Пусть ребро DA проектируется на плоскость DBC
отрезком, лежащим на прямой
£>£. Тогда точки А и М про-
ектируются в некоторые точки
К и Lf лежащие на прямой DE.
Следовательно, высоты AK=h
и ML = ht лежат в пло-
скости ADE и треугольники
DML и DAK подобны. Значит,
h\__DM__
h~ DA~
DM
m.
— DM + MA mx + ni *
Площадь S± основания
NDP относится к площади 5
основания BDC, как DN • DP >
к DB • DC (так как треугольники NDP и BDC имеют общий
угол D). Значит,
Si DN л DP то ms
S~ DB* DC~~т2 + п2 ' т3 + /г8*
Следовательно,
V\ ftt S\ т^тогп^
T/ — "ft " ~$ "" (тх + щ) (т2 + По) (тя + л3)#
Vi
Теперь находим отношение -t/_V > в котором делится
объём пирамиды DABC.
Отв Ki — т\т*тпъ ^
* V— Vi (mi+nd(m2 + no)(mz + nz)-~m1mimz
-430
ОТВЕТЫ И РЕШЕНИЯ
718
718. План решения: из подобия треугольников OEL
и МЕК (черт. 191) выразим OL через МК—Ъ и АТ£ = у;
из подобия треугольников ОСЕ и MEN выразим ОС через
MN=h и ME = y* Подставив
найденные выражения в соотно-
шение ОС2 = 2 • OL2, получим
уравнение, из которого найдём //.
Решение. Имеем
OL:H = MK:EK,
%-4-V^-^ т-е- л
откуда
OL* =
4ft2//2
Я3 — 4ft* ■
таким же образом найдём
ОС2 =
mm
Следовательно,
4ft2№
= 2
Я2 —4А2'
4ft2#2
Я2 —4ft2 — " № — № *
Деля на №, получим после преобразований
2ftft
// =
У 2ft* —ft* *
Теперь находим
4ft2№
2ft2£2
О/»*. 1/ =
Я2 —4ft2 — ft2—ft2
F=i(20/,)2-tf.
16ft%3
3(ft2 —ft2)!^* — fta"
724 гл. 10. КРУГЛЫЕ ТЕЛА 431
ГЛАВА 10
КРУГЛЫЕ ТЕЛА
719. Отв. V-^.
720. Отв. V^-^У^Ф — с2.
721. Отв. V = ^.
722. Отв. V = -А •
723. Радиус основания /? = /sin<x (черт. 192)1), высота
конуса H = lcosa. Объём q
¥, %R%H я/з sin2 ct cos ct
г—T- з 1
Полная поверхность
S„ = */?(/ + /?)=*
= те/3 sin а (1-f-sin а).
По условию /+//=/»; сле-
довательно,
т
/=*
т
1 + COS а
2 cos2 у
Отв. V
птв sin2 а cos а
24 cose~
S„ =
Черт. 192.
tw^sinacos*^0 — y)
2cos<f
724 (черт. 193). Плоскости Л^ и А2В% отделили от
конуса АСВ конус А1СВ1 и конус А%СВ2, подобные данному
конусу. Их объёмы (V, Vt и Kg) относятся, как кубы высот
Уг _(Н и У, ,(И
О О вычерчивании эллипса (изображения окружности, лежащей
в основании конуса) см. стр. 339.
432
ОТВЕТЫ И РЕШЕНИЯ
725
Объём Vop средней части АгА^В.гВ{ равна Vx — V2. Вы-
читая из первой пропорции вторую, найдём VGp.
7
Отв. Vcp = 27 V,
Черт. 193.
Черт. 194.
725. Из треугольника АОЕ (черт. 194) находим
OA=*R:
АВ
2 sin/
2 sin ^
l7 —"Т
Из треугольника OBD имеем 7/ = /?ctg£.
24 sfn3 .5.
726. По условию ОС—ОСл = к (черт. 195). Имеем
OC = /?ctg|3
OC,=/?ctg«.
Следовательно,
fl =
" ctg р — ctga*
728
ГЛ. 10. КРУГЛЫЕ ТЕЛА
433
Искомый объём V равен разности объёмов конусов ЛСВ
и АСЛВ. Следовательно,
Owe.
v==
«Jr>
i#
Черт. 193.
3(ctgp — ctga)2
_ icft"sln8asinap
3sin3(a — p) *
727. По условию
it/?/=S,
Площадь основания
Sooh = тсЯа
равна Р—S. Деля по-
членно равенство
rtR*=*P — S
на равенство
1с/?/= 5,
/? Р — S
получаем —""""о—* Обо-
вначим искомый угол че-
рез Р; из треугольни-
ка 03D (см. черт. 194) Д<^
имеем
с а *
sin р = у.
О/ив. р = arc sin—^—.
728, Из равнобедренного треугольника ADAX (черт. 196)
находим AD =
ylD/l^ то
2 sin J
. Если а есть радианная мера угла
АВСАХ = AD . а =
2йп|
434
ОТВЕТЫ И РЕШЕНИЯ
729
До развёртывания боковой поверхности отрезок AD был об-
разующей конуса, так что
l = AD = -
2sin|
дуга ABCAt была окружностью основания, так что
Черт. 197.
2тс/? ==
2sin-
Высота Н конуса равна
= —-—|/"4и2_а2.
4те sin -я-
Отв. к = - 1
192«aSin3|-
где а — радианная мера дан-
ного угла.
729. Угол DOM (черт. 197) равен углу f^^DEO.
Из Д ОШ4 и Д ОЯЛ1 находим
OD = H*
cos ?
0£ =
sin 9*
Из Д ОС£ находим
00 = /? =
05
cos-
Отв. V = -
ял3
3 sin2 <р cos с? cosa ■
ЯК* гл. 10. КРУГЛЫЕ ТЕЛА 435
730. Радиус основания конуса # = ~у= (черт. 198). Из
/\AEF находим АЕ=1 = —-—; из /\АОЕ находим
2 sln.J
2sinT
2sln|
Полная поверхность Sa равна
Черт. 198.
Выражение в скобках можно преобразовать:
1 . . а . .-0 , . а п . 90° +а 90°—а
^=+sin-2=sm45°-f-siti -5- = 2 sin—f-~ cos—-—.
л «г ЯЯ3 У COS в
Owe. V = -
y-g 1 — 2 ~ ™ » 2 4 — 4
12 sin-
Sa
ncP (l + У 2 sin ™) ял»
sin
90° + * 90° —а
cos-
2 У 2 sin £
sin-
436
ОТВЕТЫ И РЕШЕНИЯ
731
731. Из треугольника ААуС(черт. 199) имеем АС = /cos а.
Из треугольника AAVB находим AB = 2R = ——, так что
ЛО==/? = 7Г-1—. Значит,
2 cos а '
АО, = г = ЛО — AC = l(7Tl
11 \2 со
Теперь находим
cos а
■COS
■)•
COS а
Л с л/3 sin2 а Ла
Offte. Обок = = ш2 tg а sin а.
■cos
■)•
Черт. 199.
Черт. 200.
732. Из соотношений V = -g- ir/?2tf и # = #ctg а получим
Пусть требуется разделить пополам боковую поверх-
ность. Так как конусы ABC и AxBfi (черт. 200) подобны,
то их боковые поверхности S и St относятся, как Н2 = ОС2
к Нг2 = О^2. Следовательно,
734
ГЛ. 10. КРУГЛЫЕ ТЕЛА
437
Пусть теперь требуется разделить пополам полную
поверхность. Тогда
■ А/ А/
Подставляя сюда #t = Яг^ а; /1 = ^^ и ^ — ^j» получим
откуда /^=8 Я cos-у.
Огив, Если пополам делится боковая поверхность, то
Я1 = -у=|/ —^—; если полная, то Яг = cos y у —^_ш
733. Обозначим (черт. 201) радиус шара через /?, вы-
соту DC сегментной поверхности АСВ через h и отрезок DA
2
через г. Объём V сектора равен K = -g-ir/?2/&. Из треуголь-
ника ACD, где ^ CAD = ~- (как вписанный, опирающийся на
дугу /fc = yj, находим
h = г tg -г-» Из треугольни-
ка ADO имеем г = /? sin i.
Следовательно,
—|*«■./? sin Jtg-J.
#4
■А ^\
D /^
J*s
О
Черт. 201.
Полная поверхность сектора состоит из поверхности сегмен-
та АСВ, равной 2тг/?/г, и боковой поверхности конуса АОВ, рав-
ной icr/?. Следовательно, Sa = 2ir/?& 4- */"/? = *R (2k+r).
Ome. ^ = ^-/?3sin2j; So = ***sln £(2tg-J+l).
734 (см. черт. 201). При обозначениях предыдущей
задачи имеем S = 2ic/?^ + irr2. Из Д ЛОО имеем Л№ =
=:ЛОа + СЮ2; так как OD = R — h, то R*=*r2-f(R — h)*
и г2 = 2/?/г — #*. Значит, 5 = 4ic/?/i — ък\
438
Отсюда
ОТВЕТЫ И РЕШЕНИЯ
735
Так как А < /?, то знак «плюс» не годится.
Отв. h = 2R — y*
4*»-|.
735. На черт. 202 изображено осевое сечение тела, полу-
ченного при вращении треугольника ABC около стороны АВ.
Это тело состоит из двух конусов. Его объём
V =-U • D& • ЛЯ+4- ic • DC2 ■ D£ =
о о
= | DC2 (AD + D£) = | DC2 • Л£.
Учтём, что DC- AB = 2S и что DC = b sin a.
Л ,. 2те56 sin a
Owe. v = —^—•
Черт. 202.
Черт. 203.
736. Объём тела вращения (см. предыдущую задачу)
будет
V = j it. DA2 • (BD + DC) = Iica . DA*
(черт. 203). Для определения DA поступим так. Из тре-
737
ГЛ. 10, КРУГЛЫЕ ТЕЛА
439
угольника BAD находим BD = DA * ctg Bt а из треуголь-
ника DAC найдём
DC = DA-ctgC.
Следовательно,
а = BD + DC = DА (с tg 5+с tg С).
Отсюда находим DA
Owe. I/=4--
тел3
*я8 sin2 В sin* С
3 (ctg В + ctg С)* 3sina(£ + Q *
737- Объём тела вращения (сечение его изображено на
черт. 204) равен сумме объёмов двух равных усечённых ко-
нусов, полученных от вращения трапеций АМВС и ANDC,
Черт. 204.
без суммы объёмов двух равных конусов, полученных от
вращения треугольников АМВ и AND. Радиус одного осно-
вания усечённого конуса AC = dt а другого MB = -к •
Имеем
Из Д АОВ находим
Oms. V = гг-=~.
440 ОТВЕТЫ И РЕШЕНИЯ 738
738. Объём V (черт. 205) тела вращения равен объёму
усечённого конуса, полученного от вращения трапеции ООхВС>
без объёма двух конусов, полученных от вращения треуголь-
ников ЛОхВ и АОС. Так как по условию £тВА01 = £яшСАО%
то /в^ЛО1 = ^вСЛО=:90о—|-, так что
При обозначениях чертежа 205 имеем # = £siiVyf
R = Ь cos y (из треугольника АОС) и h = с sin -^» г = с cos -т>
(из треугольника АОхВ). Значит,
= -Jsin|-cosa|-[^ + ^(^ + ^ + ^) — **—*BJ.
а
я£с (& -Н с) sin а cos -л*
Отв. V= — -.
739. Поверхность 5 тела вращения (черт. 206) состоит из
суммй боковых поверхностей двух равных конусов с осевым
сечением DADt и СВСХ и боковой поверхности цилиндра с осе-
740
ГЛ. 10. КРУГЛЫЕ ТЕЛА
441
вым сечением CDD^CV При обозначениях чертежа 206 имеем
r = bslna, h = MN=AB — 2АМ = - Ь
COS а
- 2Ь cos а.
Значит,
Se-2*r(* + A)e?!^!Ll(Cosa + l—2cos«a).
cos a
3a
Отв. S = 2ir£2 tg a (cos a + 1 — 2 cos2 a) «*
в 4тг£2 tg a sin у sin у
Черт. 206.
740. Вращая данные плоскости вокруг высоты конуса,
не изменяя углов а и р, можно привести их в положение
(изображённое на черт. 207), чтобы они пересекались друг
с другом по общей образующей BD конуса. Из треуголь-
ников ОВМ и OBN находим
ОВа = /г2 = ^+ СШ2=: ^-{- ON2;
вдесь OM = Hctga и OW = //ctg3. Следовательно,
ь1
4
i?2==^^H2ctg^a и £ + №ctg»a—£ + №ctg*p.
4 ( 6 "4
Из этих уравнений находим Ни/?,
я (У ctg* а - а* ctg-' Р) /5^Р
LHIW. V— 24(ctg*a-Ctg*§)%
442
ОТВЕТЫ И РЕШЕНИЯ
741
741. На черт. 208 изображено осевое сечение конуса.
В пересечении с шаром радиуса г оно даёт окружность ра-
диуса OD = r, вписанную & треугольник ЛВС, Имеем
г = R tg у = / cos a tg у.
4я/8 cos8 а tg3 -j
Отв. V = з ■.
С
Черт. 208. Черт. 209.
742. Через точку М (черт. 209) боковой поверхности
конуса проведена касательная прямая MB, составляющая
с образующей СМ А угол 6 = ^ ВМ А. Известен ещё угол
а = £_ ОАМ\ требуется найти угол % образуемый прямой MB
с плоскостью Р основания конуса.
Прямая MB, касающаяся конуса, пересекает плоскость
в некоторой точке В, лежащей на касательной АВ к окруж-
ности основания1). Опустив из точки М перпендикуляр ММ
на радиус ОА% получим проекцию ВЫ прямой ВМ на пло-
м лг
скость Л Значит, ? = Z. NBM. Из /\AMNимеем AM = ~\
из &МАВ Цеем^^д^! из ДЛЛ»
!) Это можно доказать лишь на основе определения касатель-
ной к боковой поверхности конуса. Но такого определения в эле-
ментарной геометрии не даётся.
743
находим
ГЛ. 10. КРУГЛЫЕ ТЕЛА
sin 9==-^- = sin a cos в.
443
Отв. ? = arc sin (sin а cos 8).
743. Поверхность S тела вращения равна сумме боковых
поверхностей двух конусов с осевыми сечениями ВАВг и
BCBV При обозначениях чертежа 210 имеем S = nRc + vRa.
Из Д СВЕ имеем
h .
а =
sinp *
по теореме синусов имеем sln[180</(a + щ =Ж7'0ТСЮда
,_ asin(g + P)
Из &BCD, где ^5CD = a + p, имеем /? = а sin(a + p).
Значит,
^ __ п№ Sin (a + Р) {Sin (a + Р) + sin а]
"~ sin* p sin a
Выражение в квадратных скобках можно преобразовать по
формуле суммы синусов.
2дЛ2 sin (a + Р) sir/a + Jh cos -|
От. S- sTnasin^ J '
444
ОТВЕТЫ И РЕШЕНИЯ
744
744. На черт. 211 изображено осевое сечение кониче-
ского сосуда; ЛОВ — уровень воды. Треугольник ЛВС —
равносторонний; круг DKL (большой круг шара) вписан
в него. При обозначениях чертежа 211/? = OD • tg 60° = г Уъ
и // = CD = 3r1). Объём V воды в сосуде равен объёму
конуса ЛВС без объёма шара, т. е.
V = j я (Я2Я— 4г3) = -| яг3.
Когда шар будет вынут, вода опустится до некоторого
уровня MN и заполнит конус MNC. Пусть СЕ = К Тогда
МЕ = СЕ. tg30° = —JL-, так что
у з
Получаем уравнение
Oms. h = rV\b.
9 — 3 *Г
1) Радиус круга, вписанного в равносторонний треугольник,
равен одной трети высоты этого треугольника; это следует из того,
что точка пересечений медиан каждого треугольника делит каждую
медиану в отношении 1:2.
745
ГЛ. 10. КРУГЛЫЕ ТЕЛА
445
745- Если радиус Oti4t (черт. 212) обозначить через г,
то высота AtM призмы тоже равна г% а из треугольника АуВхСу>
где AlBl = 2rt имеем
i4lC1 = 2rcosa и 51C1 = 2rsina.
Черт. 2Й.
Величину г найдём из треугольника ААХМ, где AM = /? — г.
Имеем R — г = г ctg -^. Отсюда
1 + ctg-l *
Теперь находим боковую поверхность призмы:
£бов = (2r + 2r cos a + 2r sin a) • r =*
2R*
(.+«8|)'
(1 + cos a + sin a).
Ome.
. 2/?*(l + cos« + sina) У^^Чн.
*W = 7~J -™ = t г— .
(l + ctg|) cos (45° -|)
446 ОТВЕТЫ и РЕШЕНИЯ 74в
746. радиус R = OF (черт, 213) цилиндра равен -gBF1).
Но
BF=BE— FE =
= BE—FE1 • ctga =
аУ~3 a .
""2 2Cf^a =
= |(ctg30°-ctga)=
asin(g —30°)
2sinasjn30°
a sin (a — 30°)
Sin a
Поэтому объём ци-
линдра
Vt = *. О/72 • FEX =
g —300)-]2Д
Гд sin (i
asm (a—30°)
Sin a J 2*
Объём K2 пирами-
ды DAXBXCX равен
и Bfi^B.E,. tg a; ДД-^1/8;
2 "" УЭ ' а"~ ЗУЗ '
Задача возможна при условии, что BE > FE, т. е. при
условии •2-g—>-i£Ciga или ctg30°>ctga; следовательно,
о>30°.
0тв у = itg*slt|2(<» — 30°) . у __fl»sta»(a--30,,)tg«
' l 18sln*« ' 2 3V"3sin«a
1) См. сноску на стр. 444.
748
ГЛ. 10. КРУГЛЫЕ ТЕЛА
447
Предварительное замечание к задаче 747
и следующим
Способы правильного изображения шара с его сечениями,
а также различных тел, вписанных в шар и описанных около
него, сложны. Поэтому составители сочли возможным огра-
ничиться схематическими чертежами, которые по возможности
были бы наглядными и вместе с тем доступными для по-
строения при самостоятельном
выполнении чертежа учащимся.
В тех случаях, когда схема-
тический чертёж не обладает
достаточной наглядностью, даны
параллельные объёмные ри-
сунки.
747. Плоскости оснований
(ВАС и BxAfix на черт. 214)
призмы пересекают шар по
окружностям. Прямоугольные
треугольники ABC и АХВЛСХ
вписаны в эти окружности.
Поэтому гипотенузы АВ и AtBt
являются диаметрами окруж-
ностей. Плоскость АВВхАг про-
ходит через центр шара. Так
как по условию АВВХАХ есть
квадрат, то Я = ААХ = /?|/*2
и A8 = RV2.
Отв. V~*J?**3Lm
748. Плоскость основания
пирамиды пересекает шар по
кругу ABCD (черт. 215), опи-
санному около основания. Вы-
сота пирамиды пройдёт через
центр Ох этого круга (так как
чГпеЛе^тГТпГ °Сп ВаНИЮ П°Д РаВШМИ УГлаМИ>' а *™
~о и вершину £, пересечёт шар по большому
кругу, описанному около диагонального cei SEE
448
ОТВЕТЫ И РЕШЕНИЯ
749
ЛЕС. Из Д АЕС, где угол ЛЕС равен 180° — 2ср, находим
по теореме синусов АС = 2R sin (180°—2?) = 2R sin 2<р;
значит, АОг = Я sin 2ср. Из Д Л£Ог найдём высоту пирамиды
£Ot = Я= ЛОг • tg ср = R sin 2<р tg<р.
2
О/из. К = -g- R? sin3 2<р sin a tg ср.
749- Так как радиус ОЕ (черт. 216) окружности, вписан-
ной в основание, равен /?, то
ЛЯ = 2/?}/"3. Из Д DOE на-
ходим DO = Я = /? ctg j .
О/из. 7=/3/?4tg|-.
750. На черт. 217 изобра-
жено осевое сечение. Имеем
= k*AD-(AM + DN).
Но ЛАГ + ЯЛ^Л^ + Я/^
= AD. Поэтому 5бок = тс • AD2.
Из треугольника AED,
где DE = MN=2r, находим
sin СЕ
Отв. S^ = -^.
751. См. предыдущую зада-
чу. Имеем ^=5^+*^+ф.
Из треугольника ЛОЛ1 (см.
черт. 217) находим
3 АМ = гг =
ОЛЬ ctg-| = г ctg-|.
180° —а
Черт. 216.
D N r2 С
Из треугольника DON, где ^ODN
ZW = ra = rctg(90°—|)=>rtg|
имеем
753
ГЛ. Ю. КРУГЛЫЕ ТЕЛА
449
Вычисления упростятся, если выражение г\-\-г\ преобразо-
вать так; r\-\-r\^{rl-\-r^ — 2r^Y Так как гк-\-гг = 1 я
5<юв = ъР (см. предыдущую задачу) и из прямоугольного тре-
угольника AOD имеем AF • FD = OF* или г^^г2, то
5„ = */2-|-*/9 — г*/-* = 2тг(/а —г2).
2г
Сюда подставим /=-:— -
sin а
О-. 5.-2^(^-1).
752. См. предыдущую задачу. Имеем
^-«•Т^ + ^ + 'Ь-т^^ + ^-гл!-
3
2лл
3
(/2 — г%
Сюда подставляем / =
2г
sin а
Отз.
' 3 Vsin2« /•
753. Обозначим длину равных хорд DA, DBt ОС(черт. 218)
через /. Из равнобедренного
треугольника DBC находим
SC = 2/sin
Так же най-
дём, что A3 = АС = 2/ sin ja
Следовательно, треугольник
ABC — равносторонний.
Опустив перпендикуляр DOx
па плоскость ABC и устано-
вив равенство треугольников
DOxA% DOxB9 DOxCt докажем,
что AOx^BOi = COv т. е.
что 0{ есть центр основания
(так что пирамида DABC —
правильная). Так как точки
А, В, С лежат на поверхности
шара, то О А = О В = ОС (О — центр шара). Опустив перпен-
дикуляр из О на плоскость АВСУ докажем, что основание
перпендикуляра есть центр треугольника АВС$ т. е. совпа-
дает с точкой О,. Следовательно, ООх (и значит, DO[) лежи г
450 ОТВЕТЫ И РЕШЕНИЯ 7М
на диаметре шара (DF на черт. 218). Из прямоугольного тре-
угольника DAF, где DF«=* 2#, находим Р — DA*— 2R . DOim
Отрезок DOx можно связать с / ещё одним соотношением.
Именно, ___
DOt*=VAD*—АОг\
где
а
AD=*lf a АОх*=-^=
вс ^"Т
Значит,
у? ут •
>t_y,
4SID« £
3
Подставляем это выражение в равенство Р = 2/? • D0i9 Найдйм
i = 2RV 1.
4 sin* -j
Преобразуем это выражение к виду, удобному для логариф-
мирования. Имеем
/ = 2/?]/"l-.^(1-cosa)g-^/l-|-2cos«B3
УЗ
^1/"coS(30» + |)coS(30--f).
— -р=- К 2 (cos 60°+ cos в)
l=a2RV 1
4sln*.|
^/coS(30'4-|)cos(30^|).
754. Равнобочная трапеция ABCD (черт. 219) изобра»
жает осевое сечение усечённого конуса. По условию
L ЛОВ = а и /_ DOC =* 0. Поэтому
755 ГЛ. Ю. КРУГЛЫЕ ТЕЛА 451
Угол AOD равен .360°-С+?). = 180°_£+1. Поэтому
l=sAD = 2Rcos2d±. Имеем
4
S*0B = ™/(/?i + Я9) = 2тг/?2 cos -!±£ (sin -J + sln-t).
755. Высота пирамиды (черт. 220) ЕО = Н — т sin <р. Из
треугольника Е/Ю находим
ЛО = R = Я ctg а = /и sin 9 ctg а
Sltl а Sin а
Получаем
5n==^/?(/ + /?)==^/»sincpctga(-^-p~-+/w sin <р ctg aj.
Полученную формулу можно упростить, применив формулу
1+COSa _ a
' Sin a -CtS-2'
О/из. Sn = тст2 ctg a ctg ~ sin2 <p.
452
ОТВЕТЫ И РЕШЕНИЯ
756
756. Из /\ASB (черт. 221) находим АВ = 21 sin ^-; сле-
довательно, R = О А = Л£ == 2/ sin -к-. Из Д Л50 находим
SO=:/y==//2_/?2==s/|/"l_4sin2-J.
Получаем
Подкоренное выражение можно преобразовать к виду, удоб-
ному для логарифмирования, как в задаче 753; получим
1 — 4 sins ^ = 4 5Цз0о + -|) sin (30е—J).
Отв. V = ^ъР sin*^^ яп(ж + ^} s\n(SQ° — |).
Черт. 221.
Черт. 222.
757. Из Д/ШУИ (черт. 222) находим AM = / sin |-. Из
Д ЛЛЮ находим
г = ОУИ = ЛУИ • tg30° = /sin - . —Lr
2/3
/? = ЛО=-
ИЛ1
xos 30°
2/ sin -|
758
ГЛ. 10. КРУГЛЫЕ ТЕЛА
453
Из ДЛОО находим
Объём V конуса равен
-/?*:
-ikv^
Уз
4sfn»-|.
/2 Sin* -^ . г
■ 4 sin3-.
2
3 " " 3 3 /3
Выражение под корнем можно преобразовать, как в задаче 753*
Отв. V= т^-У 3 —'
.4sin2-:
9/3
2л/3 sln>y.y cos (30° + у) cos (30° — |-)
= ^lYJ '
758. При обозначениях черт. 223 объём шара равен
■о-7г/?3( а объём конуса ЛСВ равен -^ тгг2 • СОх = -7гпг2Н.
По условию
т, е. г2Я=/?3. Ещё одну зави-
симость между г и /? мы по-
лучим из прямоугольного тре-
угольника CAD; именно, АОг2=
=COrDOu т. е. r*=H(2R-H).
Подставляя это выражение в
предыдущее равенство, полу-
чим R*-2fiPR-)-H* = Q. Хотя
это уравнение третьей сте-
пени относительно неизвест-
ного /?, но одно его решение
R = Я сразу усматривается
(его можно было угадать и не-
посредственно по условию, так как конус, у которого радиус
основания и высота равны радиусу шара, составляет по
объёму — шара). Следовательно (по теореме Безу), левую
часть можно разложить на множители, один из которых
равен R — Я. Для этого достаточно разделить /?з — 2fPR -J- Я3
454
ОТВЕТЫ И РЕШЕНИЯ
759
т R— Н или применить такое преобразование:
R* — 2tr*R-ir№ = (R* — H*R) — (№R — H*) =
^R(R-H) (/?+//)_ Я* (R—H)=(R—H)(Rz+RH—H*>=0.
Уравнение /?a-{-/?tf—tf9 = 0 имеет один положительный
корень /?==-—^~—-^- (отрицательный корень R= *' + '
не годится). Геометрически это означает, что радиус шара
равен большей части высоты конуса, разделённой в крайнем
и среднем отношении.
Ошв, Задача имеет два решения:
759. Высота призмы равна диаметру 2R вписанного шара.
Если через центр О шара провести плоскость, параллельную
N
Черт. 224а.
основаниям призмы, то в сечении призмы получим равносто-
ронний треугольник KLM (черт. 224) *)» равный основанию
призмы, а в сечении шара — большой круг /WQ, вписанный
в треугольник KLM. Из треугольника LON, где ON=R и
l_ NLO = 30°, найдём LN = R V3. Следовательно, LM = а =
») Для наглядности рядом с черт. 224 помещаем рисунок 224а —
наглядное изображение рассматриваемого тела. Такие «параллельные»
рисунки будут даны и в некоторых следующих задачах. Выполнение
их учащимися не обязательно, хотя и очень полезно.
760 ГЛ. 10. КРУГЛЫЕ ТЕЛА 455
= 2/? |^3. Боковая поверхность Se0(t призмы равна $6oK=3atf=
= \2R*V3. Площадь основания S03B===^-|—=::==3/?2Vr3. Сле-
довательно,
S„ = 12/?з V 3 + 6Я* / 3 = 18/?* / 3.
Поверхность же шара равна 4я/?а.
О/яз. Искомое отношение равно ■ ' «
^ 9*^3
760. а) Способ изображения. Центр Ох шара, впи-
санного в пирамиду (если в эту пирамиду можно вписать шар),
должен отстоять на равных расстояниях от боковой грани ВЕС
Черт. 223.
и от основания ABCD (черт. 225). Поэтому он должен лежать
на бнесекторной плоскости двугранного угла о прн ребре ВС.
Точно так же Ot лежит на биссекторных плоскостях двугран-
ных углов о при рёбрах АВ, AD9 DC. Значит, все боковые
грани пирамиды OxABCD (не изображённой на чертеже)
наклонены к плоскости основания под одним и тем же углом у.
Следовательно, высота ОхО пирамиды OxABCD проходит
через центр О окружности, вписанной в ромб ABCD (сч. на
стр. 342 замечание к задаче 617). Через тот же центр прэ-
ходит высота ЕО данной пирамиды. Значит, центр Ог шара
лежит на высоте ЕО.
456
ОТВЕТЫ И РЕШЕНИЯ
760
Точка касания тара с плоскостью грани ВЕС есть основа-
ние L перпендикуляра, опущенного из центра Ох шара на пло-
скость ВЕС. Отсюда следует, что плоскость OyEL перпен-
дикулярна к грани ВЕС (доказать!). Вместе с тем плоскость
О,El перпендикулярна к плоскости основания ABCD (так как
проходит через высоту ЕО). Следовательно, плоскость
OxEL перпендикулярна к ребру ВС. Значит, прямая MN% по
которой пересекаются плоскости OxEL и ABCD, есть высота
ромба (проведённая через его центр О). То же имеет место для
остальных трёх точек касания с боковыми гранями (/С, Q и Я).
Отсюда вытекает следующее построение. Изображаем вы-
соту NOM ромба ABCD (желательно, чтобы она была горизон-
тальной), строим сеченне NEM (равнобедренный треуголь-
ник) и изображаем окружность, вписанную в треугольник A/EAf.
Точки L и Q, в которых эта окружность коснётся сторон
ME и Л/£, будут точками касания шара с гранями ВЕС
и AED. Чтобы изобразить точку К, проведём MS\\AC. Тогда
прямая OS (не показанная на чертеже) изображает другую
высоту ромба (доказать!). Проводим прямую ES и через точку
L проводим (не изображённую) прямую LK\\MS. Четвёртая
точка Р строится аналогично. Из этого построения сле-
дует, что шар с центром Ол и радиусом R = OlL действи-
тельно вписан в пирамиду.
б) Решение. Из треугольника М00х находим
OM = OOtctg% = Rctg±,
так что
Н=ОЕ*=*ОМ. tg9 = Rctg % tg<p.
Далее из треугольника BUA (где ВЩМЫ), находим
sin a sin а sin а *
Значит,
Soo„ в a2 sin а
4*»ctg«£
sin а
761
ГЛ. 10. КРУГЛЫЕ ТЕЛА
457
761. а) Способ изображения
полушара (т. е. кру-
га, ограничивающего $
полушар; черт. 226) *)
лежит на высоте SOx
пирамиды. Так как
то точка М лежит на
биссектрисе 0}М угла
ООгМг. Отметив точ-
ку М как пересе-
чение ОгМ с SF,
изображаем сечение
KLMN, параллельное
основанию. Середины
К, L% М, N сторон се-
чения являются точка-
ми касания экватора
с боковыми гранями.
Полукруг КОгМ есть
сечение полушара пло-
скостью ESF.
б) Решение.
Сторона основания а
равна
a-*EFm*2.0yF=m
- 2 (ОгМг + М,П.
Но ОхМг = ОМ^г%
a M1F^MM1-ctga =
= rctga. Значит,
a = 2r(l+ctga).
Имеем
2Srt
Центр О экватора
Черт. 226.
'Оов cos2 J.
cos a
Черт. 226а.
1) См. сноску ыа стр. 454.
458 ОТВЕТЫ И РЕШЕНИЯ 702
(см. указание к задаче 619). Здесь S0CE = а2 = 4/-2(1 +ctg а)2.
8*(l+-ctg»)W| 4^51пЧ45° + а)
Отв. Sn = — = ——.
cos а sin2-^-
762. Плоскость ESF (черт. 227)а) даёт в пересечении
с полушаром полукруг NPM, касающийся апофем пирамиды
(в точках Q и G). Если обозначим сторону основания пира-
миды через а, а радиус полушара — через г9 то полная по-
верхность полушара S1 будет
а полная поверхность пирамиды
2fl2 COS2 ^
5о = - 2
COS а
(см. указание к задаче 619); их отношение
Зпг2 COS а
£ =
2a2cos2 —
Из Д 0G/7 имеем 0G = OF • sin а, т. е. г *= -j sin а. Это вы-
ражение подставим в предыдущее равенство.
Для вычисления объёма полушара V найдём г из условия
а — 2г = /я и ранее найденного равенства r = ^-sina. По-
лучим
т sin о т sin a
2<1-slna> 4sln«(45-—|)'
^ Зл . 0 a т/ ram3 sin1* о
O/ras. ? = -o- sin 2a tg -s-; K =
96 sine
(<"-*)'
*) См. сноску на стр. 454.
762
ГЛ. 10. КРУГЛЫЕ ТЕЛА
459
Mf
Черт. 227а.
460
ОТВЕТЫ И РЕШЕНИЯ
763
763. На черт. 228 изображено осевое сечение конуса и
вписанного в него шара. Искомый объём V получается вычи-
танием объёма шарового сегмента
MEN из объёма конуса MCN.
Следовательно,
V = ^-MK*- КС —
где г есть радиус шара. Из тре-
угольника AOD находим
r = OD = AD-tg
_/?tg(45e—J).
JDAC
Теперь из треугольника ОМК, где
/_ОМК=а. (стороны углов ОМК и МСК взаимно перпен-
дикулярны) имеем
МК я ОМ • cos а = г cos а и ОК — г sin а.
Значит, КЕ=ОЕ—0/С=л(1 — sin а). Наконец,
КС = МК • ctg а = л cos а ctg а.
Следовательно,
V=-Jr3Cos3actga — да*(1 — slna)»[r — lil^l^ 1 ^
Это выражение можно упростить. Вынесем за скобки
(1—sin а)2, предварительно преобразовав cos4 а; именно.
cos* а = (1 — sin2 а)2 = (1 — sin а)2 (1 + sin а)\
Теперь имеем
V = Kr4l*nT ")2 К1 + *° «Р-(2 + sin «) sin а].
Выражение в квадратных скобках равно единице. Получаем
V =
гсга (1 — sin a)d
3sina
7Ь4 ГЛ. Ю. КРУГЛЫЕ ТЕЛА 461
Сюда подставляем найденное выражение
г —/?tg(45"—J).
Кроме того, можно использовать формулу 1 — sin а =
= 2sin2(45° — j).
4п/?з tg3^45° — -jj sin4 ^45° — jj
Отв. 1/:
3slnc
764. При обозначениях черт. 229 условие задачи выра-
жается равенством ir/? (/ 4- R) = п • 4тсл2. Из треугольника
ОВОл находим r = Rtg^r, а из треугольника ВОС имеем
ВС = /= —^- . Предыдущее равенство по сокращении на
COS О
ir/?3 примет вид
Н—L- = 4fttg2^
' cos о & 2
Применим формулу
l_tg2-
cos а == ■
Будем иметь уравнение
—4=4«tg^.
Положив tg-|-=^, получим1)
г4_г2_^
2и
'0.
откуда
1=1-+- т/1—L
2 — К 4 2я "
Отсюда видно, что при я < 2 задача не имеет решения (под
корнем отрицательное число). При л>-2 оба значения
*) Освобождаясь от знаменателя, мы могли бы внести лишнее
решение ng2-^-= lV но такого решения мы не получаем; оно не
удовлетворяет исходному уравнению.
l№ ОТВЕТЫ И РЕШЕНИЙ 7<>5
величины г3 положительны (ибо у -^ — 2«^КТ,Т' е*
у -£- — ой" < "о )" Так как величина {S Т яолжиа быть
положительной, то можем иметь только два решения:
и
*-*7- + /t-/t==S-
Так как угол у меньше 45°, то ig 4 должен быть меньше
единицы; зиачит, должно быть -гг2<1. Но это неравенство
всегда соблюдено, ибо
И
I — l/"1 Г<Г !
Отв. Задача имеет решение только при я>-2. При я > 2
имеем два решения:
при я = 2 оба решения совпадают уёъ=у -у)*
765. При обозначениях чертежа 229 имеем
Подставляя сюда
I^H^n.i^
' — fltg-J и /y=/?tga,
получим уравнение
766 ГЛ. 10. КРУГЛЫЕ ТЕЛА 463
Применив формулу
tgflf:
и обозначив tg-^- через г% получим уравнение
*(r=F-2«')-0-
Оно распадается на два, но одно из них {г = 0) не согла-
суется с условием (угол а не может равняться нулю). Дру-
гое уравнение приводится к виду г^ — z2-^^-=-0t т. е. сов-
падает с уравнением предыдущей задачи. Получаем два
решения:
При п = 4 одно решение будет
*т- /т+/т-/т+т/т-
= y^l + cos45" = cos 22о30, ^0(92^у.
другое даёт
tcr_
tg£ — sin 22°30'та 0,3827
(отсюда о^тевб^в' и as«41°53/).
0/Л5. Тот же, что в предыдущей задаче.
При п = 4 имеем Oj = 2 arc tg (cos 22°30') (« вб^в*),
а2 = 2 arc tg (sin 22°30') (та 41 °53').
766. Площадь осевого сечения есть RH. Полная поверх-
ность те/?/-|-я/?а. По условию * Т, «== д. Если р — угол
между осью и образующей, то /? = / sin р и # = /cosp. Под-
ставляя эти выражения, получим
1 + sin ft а
cos р it ^
464
ОТВЕТЫ И РЕШЕНИЯ
766
Это уравнение можно решить различными способами; короче
1 -f COS а . а
всего применить формулу —l_—=ctg-g-; мы получим
1 + sin р 1 + cos (90" - р) /45. j\
cosp в sin (90°-Р) *=ctS[^ ~ 2>
Следовательно,
*(«г-4)-*:
и
Отсюда можно определить угол 45°—-|-, а затем и угол 0.
Однако не при всяком п вадача имеет решения. Действи-
тельно, угол |5 заключён в границах от 0 до 90°; значит,
в
угол 45°—у заключён между 0 и 45°, т. е. величина
— = ctg-f 45° —~j непременно должна быть больше еди-
ницы, т. е. должно быть п > те. При л = 1, 2, 3 задача не
имеет решения.
Замечание. Уравнение
1 + Sltl Р £
cos ji «
можно решить ещё так. Представим его в виде — cosfJ — 1 «sing,
к
возведём в квадрат обе части равенства и заменим sin» р через
1 —соз2р. Получим два решения: одно из них, cos£«0, будет по-
сторонним (оно является решением уравнения — cos р — 1 « — sin р);
п
другое решение
совпадает с предыдущим.
Однако теперь легко притти к ошибочному выводу, что задача
имеет решение также и при я =* \, 2, 3. Ведь при любом положи-
тельном значении п величина -=—:—а заключена между 0 и 1 (мы имеем
гс*-4- па
1-д2-Л ~ ^Т Ji > О)» Поэтому в пределах от 0 до 90й всегда
2лл
найдётся угод, гсосинус которого равен -j-t—$•
7W
ГЛ. Ю. КРУГЛЫЕ ТЕЛА
465
Ошибка этого рассуждения состоит в следующем. Из соотношения
cos р « "h'-iln> и энного уравнения следует, что sin Р « лаТда. От-
сюда видно, что должно быть п > я (в противном случае угол р будет
отрицательны^ что невозможно).
О/ив. Бели я < it, то задача не имеет решения. Если
Л>1С, то
Р^ЭО0—2arcctg-
или
P = arccos__fi
i arc sin
я» —*а
767. При обозначениях черт. 230 имеем
/?(/ + *) 13
2гз "* 5 #
Находим (из треугольника AOD)
r = R cos 21 AOD = R cos £ ЛСО = /? cos -|
и (из треугольника АОС) /= 1
sin —
Черт. 230.
Предыдущее равенство принимает вид
l + sm^
2 sin-j cosa^-
18
5 '
1 + sln
т. е.
7
2imj(l-aw>|J
18
5-'
466 ОТВЕТЫ И РЕШЕНИЯ 7&*
Сокращаем дробь на 1 -f-sin-j (эта величина не равна нулю).
Уравнение приводится к виду
Sln^_sin| + | = 0.
Отв. а, = 2 arc sin | (» 112°53')
и
aa==2arcs1nl(«190U').
768. При обозначениях предыдущей задачи имеем соот-
_ 4 2
ношение -г^Нда-г^иг3, Обозначим искомый угол через J3
(на черт. 230 ? = |-). Тогда r = /?cosJ3 и W = /?ctgj9. Из
предыдущего соотношения получим 3 ctg J3 — 8 cos8 (3 = 0.
Ломножио обе части этого уравнения на tgp (эта величина
по смыслу задачи не может равняться нулю), получим урав-
нение
3 — 8 sin? cos? ? = 0,
откуда
8 sin3? — 8slnp + 3=*0.
Лля решения этого кубического уравнения придётся применить
какой-либо искусственный приём. Так, левую часть удаётся
р^ложить на множители:
^sin4р —-8sinР-И = (8 sin*jJ— 1) — (8 sin? — 4)=»
= 1(2 sin J3)3— 1] — 4(2 sin j3— I)ш
= (2sinj3 — l)[(2sin^ + 2sin? + l — 4].
Следовательно, найденное уравнение распадается на два.
Из первого находим sin р =» -л-» а из второго sin £ ез у ~" .
(Другое решение квадратного уравнения не годится.) Про-
верка показывает, что оба найденных решения годны.
Отв. р, = 30°; pflS»arcs)n ^ i .
769» По условию боковая поверхность конуса MCN
^черт. 231) должна составлять половину боковой поверхности
770
ГЛ. 10. КРУГЛЫЕ ТЕЛА
467
конуса АСВ. Но боковые поверхности этих конусов отно-
сятся, как квадраты образующих, т. е. £g} —у* А так как
то
т. е.
Отв. а = 45°.
CN=CO,
/СО\* __ J_
\СВ) ~ 2»
cos^a=-j.
770. По условию задачи объём V шарового сектора
CMKN (черт. 232) должен составлять половину объёма ко-
нуса АСВ. Обозначим отрезок KL через к, а высоту конуса СО
2 о
через Н. Тогда V=-^izr2h. Получаем равенство -jizr2h =
= 1 * Тк/?2Я' т' е" *r*h = R*H или 4r2/* = tf3tg2a. Ве-
личину к выразим через л Имеем
h = LK — СК—CL = г — г cos a ;
Получаем уравнение
8r3sin2|- = tfstg2a.
2rsin2-|.
Отв. г
-21/ -п.*'
463
ОТВЕТЫ И РЕШЕНИЯ
771
771. На черт. 233 осевое сечение той части шара, объём
которой требуется определить, обозначено штриховкой.
Этот объём V получается вычитанием объёма Vx конуса MCN
из объёма V9 шарового сегмента CEMKNF. Введём обо-
значения: МК*=г и КС —к. Так как радиус шара равен ОС=*
Сюда нужно подставить выражения h = МС • cos а=Н cos9 а
и г = МС ' sin а = И cos а sin а (вычисление упростится,
если предварительно заменить
Черт. 233. Черт. 234.
772. При обозначениях черт. 234 имеем: S6oR = n(r-\-rx)L
Провелём ралиусы OM = R и OxMx = Rx в точки касания и
прямую ОхК, перпендикулярную к ОМ. Получим треуголь-
ники ОхМхЕи ОМЕ и ОхКО% которые подобны друг другу
(как прямоугольные, имеющие по равному углу а). В Д 0{КО
имеем
(^О — Я + Кр OK = R — Rx; ОхК = ММх = 1.
773
ГЛ. 10. КРУГЛЫВ ТЕЛА
469
Следовательно,
/ = /(/? + /?г)9 — (/? — /?г)2 = 2 УЩ
отсюда
г = -
//?
Из подобных треугольников ОМЕ и Ot/CO имеем ~7арГо »
сюда rt
tt + /?i ~~ ~Й+~ЯГв
Из треугольников Ot^ft£t и ОхКО имеем ^
* + *,'
от-
773. На плоскости Р (черт. 235) 1) лежат четыре шара
радиуса г; Ж, JV, /С и L — точки их касания с плоскостью Р.
Черт. 235.
Черт. 235а.
Их центры Ov 02, 03, 04 удалены от плоскости на расстоя-
ния ОхМ = 02/V== 03/С = 04L = г. Расстояние между цен-
трами двух касающихся друг друга шаров равно 2г, т. е.
ОхО% = 0203 = 0304 — Ofix = 2г. Пятый шар касается каж-
дого из четырёх первых; следовательно, центр его 06 уда-
лён от центров Ov 0о, Оз» ^* также на расстояние 2г,
т. е. ОхОъ — 0206 =s ОаОб = 0405 = 2г. Поэтому фигурi
ОьОгО^Оь04 будет правильная четырёхугольная пирамила,
у которой все рёбра равны (как при основании, так и
1) См. сноску на стр. 454.
470.
ОТВЕТЫ И РЕШЕНИЯ
774
боковые). Центр пятого шара будет удалён от плоскости Р
на расстояние, равное ООъ-\-ОАх = 006-f-r. Верхняя точ-
ка А пятого шара будет находиться на продолжении перпенди-
куляра АхОъ на расстоянии 05А — г от центра 06. Таким
образом, расстояние ААХ от верхней точки пятого шара до
плоскости Р равно 2г-]-ООь. Отрезок 006 находим из пря-
моугольного треугольника OfiO§t где
ОА-2Г » «>,-$-£.
Отв. ААх=*г(2 + У2)я
774. Центры Ои Оа, 03, 04 четырёх шаров должны на-
ходиться на расстоянии 2г друг от друга (см. предыдущую
задачу). Значит, фигура ОхО^ОйОА— правильный тетраэдр
с ребром 2г. Конус АСЕ (черт. 236)*), описанный около че-
тырёх шаров, касается одного из них 04 по окружности NT,
а каждого из трёх остальных (например шара Ot) в двух
точках: одна из них, К* лежит на основании, другая, М — на
боковой поверхности. Ось конуса совпадает с высотой 040
тетраэдра. Центр Ot лежит в плоскости осевого сечения ACD,
проходящего через точку касания М (ибо прямая ОхМ пер-
пендикулярна к общей касательной плоскости конуса и шара,
а плоскость осевого сечения ACD перпендикулярна к этой
касательной плоскости). Значит, плоскость ACD пересекает
шар Ох по большому кругу; шар 04 она пересекает тоже
по большому кругу, и образующая АС есть общая каса-
тельная этих больших кругов. Следовательно, АС\\ОгОА и
2lOt040= £_ACD = -j (а — искомый угол при вершине С
осевого сечения). Значит, sin ~ = „ * ■. Но ОлО± = 2гу а от-
резок ООх (радиус круга, описанного около треугольника,
ОхО^О^) равен —LJe ——. Получаем sin — = —■=. Отсюда
можно найти cos а = cos3 -к—sin2-^ = -о-«
Отв. а =5 2 arc sin -= = arc cos — •
Уъ 3
0 См. сноску на стр. 454.
774
ГЛ. 10. КРУГЛЫЕ ТЕЛА
471
Черт. 236.
Черт. 236а.
472
ОТВЕТЫ И РЕШЕНИЯ
775
775. Плоскость, делящая пополам двугранный угол при
ребре ДЛд (черт. 237)1) усечённой пирамиды, проходит
через высоту 0,02 и перпендикулярна к грани ВхСхСф^ (до-
казать!). Аналогично для двух других боковых рёбер. Поэтому
центр шара, касающегося граней пирамиды, лежит на высоте
(а именно, на середине высоты, так как шар касается и осно-
ваний), а точка К касания шара с гранью ВхСгС%В^ лежит
на апофеме D^D^ этой грани. Аналогично для других боко-
вых граней. Имеем
(al=-BlC1 и Og = i52C2 — стороны оснований и I=D{Dq —
апофема боковой грани). Если гх = ОгОг и r^ = O^D^ — ра-
диусы кругов, вписанных в основания, то ах = 2rx Yz и
л2 = 2rQ 1^3. Поэтому
Sn = 3K3(r? + ^ + 3/3(r1 + r,)/.
Как в задаче 751, найдём что гг-\-Гъ = 1 и ri + '"2 = /2 — 2г2.
Тогда получим
5а « б/3(/*—Ъ = б КЗ (^ - i*).
Л о с 2ге Sin- а
3^(4 —sin* в)
А) См. сноску к стр 464.
777
ГЛ. Ю. КРУГЛЫЕ ТЕЛА
47d
776. Обозначим радиус OL цилиндра (черт. 238) через х,
а радиус ОБ основания конуса через /?. Так как по условию
ML = /?, то полная поверхность q
цилиндра SD = 2ял;2 + 2tzxR. По
условию 2ял;2 -{- 2tcxR = -я- те/?9
или х2 -f- /?д; — -J /?2 =» 0, откуда
jt = у (отрицательное решение
3
лг = — — /? не годится). Из тре-
угольника LMB находим
LB /? — х \
i
L
й
L
к о
0, \
г+Х —
J4
L
U—/f—*j
\в
Отв. 9 = arctg-j
Черт. 238.
777. Центр О вписанного шара (черт. 239) лежгт на вы-
t
соте пирамиды, а точки касания К, L, М, N шара с боко-
выми гранями лежат на апофемах ЕКХ, ELX, EMU ENX
474
ОТВЕТЫ И РЕШЕНИЯ
773
(ср. задачу 775). Четырёхугольник KLMN— квадрат, явля-
ющийся основанием пирамиды, объём которой требуется
определить.
Проведём через радиусы ОМ и ON плоскость NOM.
Она будет перпендикулярна к грани ВЕС (так как проходит
через прямую ОМ, перпендикулярную к плоскости ВЕС),
а также к грани DEC (так как проходит через ON). Следо-
вательно, плоскость NOM перпендикулярна к ребру ЕС.
Пусть Р — точка пересечения плоскости NOM с ребром
ЕС. Тогда угол NPM есть линейный угол двугранного
угла а. В четырёхугольнике OMPN два угла (при верши-
нах М и N) прямые. Следовательно, ^М1Ш=180о—а.
Значит,
а = NM = 2 • ОМ • sin 180°2~~а = 2r cos -J.
Из треугольника OOtMy где ОхМ= -у=, находим
с h = OOx = Vom^ — o^ =
= rj/"l — 2cos2|.
Отя.
У=-1 rs cos* J- j/*l—2 cos2- =*
= -g- /-3 cos2 у }/" — cos a.
778. Можно провести две
плоскости, перпендикулярные к
данной образующей конуса (СЛ
на черт. 240) и касающиеся
вписанного шара; их точки ка-
сания (N и Nt) лежат на диа-
метре NNU параллельном С/4.
Положим сначала, что берётся плоскость ND, касающаяся
шара в точке N. Четырёхугольник ONDK (К — точка касания
образующей СЛ с шаром) — квадрат, так что D/C = OA/= г.
По условию CD = dt Следовательно, CK = d-\-r* Из тре-
угольника КОС находим
779 гл. 10. КРУГЛЫЕ ТЕЛА 475
Следовательно,
H=CF=OF-\-OC = r-\-Y(d-\-r)*-\-r*.
Из подобия треугольников AFC и КОС находим
AF:H=OK:KCt
откуда
р лв — ОК-Н _rlr+Y(d + r}* + f*]
* — АГ — ~~КС~ J+7 •
Если взять плоскость NXDV то d = CDv и мы таким же
образом получим
Отв.
*r*[r+ Y (d + r)*+r*\3 „_пгг[г+У(<1-г)* + г*\3
779. Центр О шара (черт. 241) *) лежит на диагонали АВ.
Действительно, точка О одинаково удалена от граней AAtNxN
Черт. 241. Черт. 241а.
и AAXQXQ. Значит, она лежит на плоскости, делящей попо-
лам двугранный угол при ребре AAV Таким же образом
точка О должна лежать на плоскости, делящей пополам
') См. сноску на стр 454.
476
ОТВЕТЫ И РЕШЕНИЯ
78Э
двугранный угол при ребре AN. А эти две плоскости пере-
секаются по диагонали АВ.
Пусть С и D — точки касания шара с гранями ANUQ и
ААХЫХМ9 а г — радиус шара. Тогда OC=OD = r9 и пло-
скость ODGC перпендикулярна к ребру AN, а* также
к ребру BQV
Так как ребро BQX по условию касается шара, то пло-
скость ODGC пересечёт ребро в точке Е его касания с ша-
ром; следовательно, ОЕ = г. С другой стороны, точка Е есть
вершина квадрата FGKE, получаемого в сечении куба пло-
скостью ODGC\ значит, четырёхугольник MOLE (OL и ОМ—
продолжения прямых ОС и OD)— квадрат. Следовательно,
ОМ = -£=. Так как OM + OD=*MD = at то ~-Ur==a,
откуда г = (2 — У2) а.
Часть поверхности сферы, лежащая вне куба, состоит из
трёх равных сегментов, один из которых есть EZTL. По-
верхность этого сегмента равна
2кг . LZ = 2кг (CZ — CL) = 2кг (2г — а).
Отз. r = (2— V2)a; S = 6ice*(10 — 7 j/*2).
780. Центр шара, касающегося рёбер тетраэдра ABCD
(черт. 242 и 242а)1), совпадает с центром тетраэдра (т. е.
с точкой О, равноотстоящей от вершин А, Ву С, D), а точки
касания шара с рёбрами суть середины рёбер. Например,
точка касания N есть середина ребра AD. Действительно,
все шесть равнобедренных треугольников АОВ, ВОС, СОА,
BOD, COD* и AOD (начерчен только треугольник AOD)
равны друг другу (по трём сторонам). Следовательно, их
высоты ОМ, ON и т. д. равны. Поэтому, если описать шар
радиусом ON=r, то он пройдёт через середины L, М, N,
Q, К, R рёбер и там коснётся их (так как ON _L ^D
и т. д.).
Проведём через высоту тетраэдра DG и ребро AD пло-
скость ADG. Она будет перпендикулярна к ребру ВС (дока-
зательство дано в задаче 652) и пересечёт это ребро в его
середине М. В сечении получим равнобедренный треуголь-
ник AMD (AM = MD). Проведём высоту MN этого
О См. сноску на стр 454,
ГЛ, 10. КРУГЛЫЕ ТЕЛА
477
Черт. 242.
Черт. 242а.
476 ОТВЕТЫ И РЕШЕНИЯ Я*0
треугольника (N—серслина AD). Центр О лежит па MN(так
как он равноудалён от А и D). Следовательно, MO = NO.
Значит, г = -=-. Высота MN определяется из треугольника
ANMt где AN=£ и АМ= а \. (как апофема равносто*
роинего треугольника ABC). Имеем
Следовательно,
„_MN_ а _аУЪ
Часть шара, расположенная вне тетраэдра, состоит из
четырёх раиных сегментов, отсекаемых от шара гранями тетра-
эдра. Рассмотрим одну из граней В DC. Круг LMK, лежащий
в основании сегмента, вписан в равносторонний треуголь-
ник BDC (ибо стороны треугольника касаются шара; значит,
они касаются и малого круга LMK, лежащего в плоскости BDC).
Радиус этого круга FM = ^ . Следовательно,
OF= VOM*—FM* = Vr^ — FM*^
Значит, высота сегмента
h=*FE = OE—OF=*-
-.££0-У!>
2 VI 2 /ti
Объём V„ одного сегмента равен
Vu-icA«(r —4) —
лд»УТ(9 —4 УЗ)
в 432 ;
искомый объём
V = 4l/e.
ГО ML 11* ТРИГОНОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ 479
Замечание Круг LKMt вписанный в треугольник BCD, изо-
бражается эллипсом, который легко будет начертить от руки, если
кроме точек К, Lf М предварительно отметить еще трн точки, со-
ответственно симметричные с ними относительно Р (точка t* есть
точка пересечения медиан треугольника BDC),
ГЛАВА 11
ТРИГОНОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ
781. Выразим секансы через косинусы; получим в левой
части
I
C0s(7 + e)c0S(j-e)
Так как
cc($ + .)-*[*-(J+«)]--b(t—)'
то левая часть равна
2 2 2 „ 0
^n(i-.)cos(i-.) s.n(i-2«)
782. Приводим левую часть к общему знаменателю и
преобразуем 2 sin a cos О + Р) к виду
sin |а+(а-)-Р)Л-sin [а—(а + p)J« sin (2а-)-р) + ЙП (—Й-
783* Левая часть равна
2(1 +COS 2а) 2.2cos*a 9
Sin 2а в 2 sin а COS а e Z Ct8 а#
Чтобы перейти к углу -£-, используем формулу ctg2<p =
«^JjT (угол -J принимается за <р). Получаем
2ctga«2 —i-—.ctg^-rgi.
480 ОТВЕТЫ И РЕШЕНИЯ 784
784. Имеем
cos а -{" sin а = s*n ("5" — а J -f- s!n а =
= 2sin^cos(j — <xW j/2cos(-j — «)•
Таким же образом найдём
cos a — sin a я j/^2 sin f^- — a).
Следовательно, левая часть равна
с«*({-.)-*1т-(7-«)1 = *(т+.0-
785. Умножим числитель и знаменатель левой части на
упростиз, по
I . sin 2a
. . 1 + Sin 2a
cos a + sin a и, упростиз, получим —!—*— или
COS 2aT COS 2a
= sec 2a -J- tg2a.
о 1 — cos 2ф
786. Так как sin*<p = rj——, то левую часть пред-
ставим так:
l-cos(j + 2a)-l+cos(|--2tt)
COS f -i — 2a J — COS f-j. -|- 2a J
2
"" 2
Применив формулу разности косинусов (или раскрыв вы-
ражения cosf-£—2a j и cos(-r-~f-^a) п0 формулам коси-
нуса суммы и разкости), получим
2 sin-г sin^a . ,,
4 sin 2a
787, Числитель равен cos 2a; знаменатель преобразуется
к виду
»*(*-.)*■[$-($-.)]-
-2*(т—")со,,{т—«)-
791 ГЛ. 11. ТРИГОНОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ 481
С помощью формулы
Sin [-г —а)
*т-°=-к-т
c0S(__aJ
получим
2 sin (~ — а\ cos (~ — а\ = sin ^ — 2aj;
это выражение равно cos 2а, так что левая часть равна 1.
788. Имеем
Рассматривая угол -j- — а как половину угла у — 2а и
применяя формулы для синуса и косинуса половинного угла,
получаем
I — COS (тг—2а) , , _
' I+COS^ — 2а j ^
789. Выразив тангенс и котангенс через синусы и коси-
нусы, получим
. о , о COS 2a
Ctg2tt-tgg«=smaacos;,a.
Подставим полученное выражение в знаменатель левой части;
тогда в левой части получим
. «, 9 4 Sin2a COS3a 1 . ОЛ
sin2 a cos2 a = ^ в -r sin2 2a.
4 4
790. Заменим sin a через cos 1 -j — a j и cos a через
sin (у— a J и применим формулы суммы косинусов и раз-
ности синусов.
791. Заменим в числителе единицу на sin2 a + cos2 а, а
sin 2a на 2 sin a cos a, В числителе получим (sin a-f- cos a)2;
знаменатель же равен
cos2 a — sin2 a = (cos a 4- sin a) (cos a — sin a).
482 ОТВЕТЫ И РЕШЕНИЯ 792
~ - , COS а 4- Sin ее 0
Сократив дробь на cos а 4-sin а, получим ~-—. Раз-
l + tg*
делив числитель и знаменатель на cos а, найдем л ' * .
1—tga
В задаче 784 показано, что это выражение преобразуется
к виду ^(-J+ <*)•]
792. Как в задаче 790* преобразуем левую часть к виду
dg(j — y)* Теперь применим формулу ctg~ = +^s а
(приняв -у—у за y)* Получим
l + cos(|--2y)^1 + sln23>
, / я п \ cos 2у •
SIn(2— 2у)
793. Выразив левую часть данного тождества через си-
нус и косинус, произведя вычитание полученных дробей и
применив формулу разности квадратов^ получим левую часть
в виде
(sin д cos ft — sin ft cos a) (sin a cos р 4* s*n Р CQS а)
а это выражение сразу дает правую часть.
794. Применим формулу
tg
ер Sincp
~2 1 4- COS ср
(приняв -?■ — y за -|Л. Получим
, (п_ а\ \2 / COS а
1 + COS^-a)
после чего левая часть преобразуется в правую.
795. Решается как предыдущая задача.
796. Заменим 2 cos2 а через l-}-cos2a; тогда числитель
примет вид: 2 (sin 2a -f- cos 2a). Члены знаменателя сгруппи-
руем так: (cos a — cos 3a) -f- (sin 3a — sin a) и применим фор-
801 ГЛ. 11. ТРИГОНОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ 483
мулы для разности косинусов и синусов. Вынося 2 sin а за
скобки, получим 2 sin a(sin 2a+cos 2a). После сокращения
на 2 (sin 2a -f- cos 2a) получим правую часть.
797. Преобразуем числитель дроби, стоящей в левой
части тождества:
sin a -f- sin 5a — sin 3a = 2 sin 3a cos 2a — sin 3a =
= sin 3a (2 cos 2a — 1).
Произведя аналогичные преобразования в знаменателе дроби,
получим cos За (2 cos 2а—1).
798. Преобразуем сумму первых двух членов левой части
тождества по формуле суммы синусов, а третье слагаемое
sin(d — с) будем рассматривать как синус двойного угла.
Получим
Л . 2а — Ъ — с Ь—с , Л . Ь — с Ь — с
2 sin 5 cos—g }-2sin —2"— cos—£— =
Лл6—сГ. 2a — 6— с , . &— cl
= 2 cos —s— sin ^ r sin —g— J •
К выражению в скобках применим формулу суммы си*
нусов.
799. Рассматривая выражение sineJt-|-coseA: как сумму
кубов, разложим его на множители и учтем, что sin2x-)-
+ cos2 х = 1. Тогда левая часть равенства преобразуется
к виду
— sin* л: — 2 sin2 х cos2 х— cos4*-)- 1 =
= 1 —(sin2 х 4-cos2a:)2 = q.
800. Сумму двух последних членов преобразуем как сумму
синусов. Получим
sin (a+^Wsinfa + yJ===2sin(it-i-a)cosy==
— — 2 • у sin a = — sin a.
Следовательно, левая часть равна нулю.
801. Применим формулу sin21- = Lzi2L2 к первому н ко
второму слагаемым (приняв за |- один раз 45°+а, а дру-
484
ОТВЕТЫ И РЕШЕНИЯ
802
гой раз 30° — а). Будем иметь
Третий член преобразуем по формуле
sin a cos Л — у (sin (я -f- Ь) + sin(n — ft)|.
Тогда левая часть примет вид
1+ sln2a _ ' — sin (30° 4- 2а) __ sin (30° + 2i) + ЯН (—2а)
"2 " " " 2 2
После приведения подобных членов получаем sin 2а.
802. Числитель левой части представим в виде
(sin2 о -4- cos2 в) — 2 cos2 ср = sin2 ср — cos2 ср.
803. В правой части заменим sin 2а на 2 sin a cos а. Со-
кратив дробь ил 2sina( получим в правой части выражение
1 — COS a 4 9 а
^ , равное tfrf-g-.
804. Объединив второй и третий члены, вынесем за
скобки cos(a-j-f) --cosacos<p — sinasincp. Левая часть при-
мет вид
cos2 -? — (cos a cos ср — sin a sin <p) (cos a cos ? -4- sin a sin <p).
Преобразовав произведение суммы на разность, найдем:
cos2 ср — cos^ a cos2 9 ■+- sin2 a sin2 <p -=
= cos2 о (I — cos2 a) + sin2 a sin2 cp ==
= cos2 cp sin2 a -f- sin2 a sin2 cp,
а это выражение дае! sin2 a.
805. Раскрыв выражение cos(a-f-P)» получим:
sin2 a -r sin2 p + 2 sin a sin p cos a cos p — 2 sin2 a sin2 p.
Оставим без изменения третий член, а остальные сгруппируем
и преобразуем следующим образом:
(sin2 a — sin2 a sin2 p) + (sin2 p — sin2 a sin2 JJ) =
= sin2 a cos2 p -j- cos2 a sin2 p.
ВОТ ГЛ. II. ТРИГОНОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ 485
Теперь данное выражение принимает вид
(sin a cos Р)2 + (cos a sin р)2 -+- 2 sin а sin р cos а cos р =
= (sin а cos р -+-cos а sin Р)2 — sin2 (а + Р)-
Ome. sin2(a-f-P).
806. Преобразуем сначала выражение —2 cos a cos {J cos if •
Применив формулу
cosacosp =i[cos(a —P) + cos(a + P)l,
получим
— 2 cos a cos p cos f =— [cos (a — P) cos-f -|-cos(a + P)coSf].
К каждому из слагаемых применим то же преобразование.
Получим
— 2 cos a cos р cos f =
= — 2-lcos(a—p — T)-f-cos(a — P+f) +
-f-cos(a + p—T)+cos(a + P+T)b
Теперь учтем, что по условию a + P+T=TC- Тогда будем
иметь
cos (a — р — ?) = cos (Р -f- т — a) = cos (a -f- р + f — 2a) =
= cos (тс — 2a) — — cos 2a.
Выполнив аналогичные преобразования, найдем, что
— 2 cos a cos p cos т = -к- (cos 2a + cos 2p + cos 2f -f-1).
Теперь применим формулу cos 2a =1—2 sin2 a и две анало-
гичные формулы для cos2P и cos2f. Тогда данное выраже-
ние преобразуется к виду
sin2 a + sin2 р + sin2 Т + ~ (4 — 2 sin2 a — 2*in2 p — 2 sin2 T),
а это выражение равно 2.
807. Представим левую часть в виде
ctg A ctg В -f- (ctg A -f- ctg В) ctg С.
Выражение в скобках равно ?|5il±Sf а сомножитель ctg С.
если заменить С равным выражением тс — (А-{-В), примет
486 ОТВЕТЫ И РЕШЕНИЯ 80S
вид —ctg(A-{-B). Следовательно, данное выражение равно
civ Л etc В С05(л+Б>
Применив формулу косинуса суммы, преобразуем его к виду
/cos Л cos В sin Л sin В \
ctgActgB — ^
sin A sin В sin A sin В )
= ctgActgB — (ctgActgB—l)=lm
808. Заменим множители cos -^ и cos-=- выражениями
2я 4тс
sin -F- sin ~^-
и п—. Тогда левая часть преобразуется к виду
2sin~ 2з1п4^
о о
. 4тс
о
левая часть обратится в -j
. . тс л . 4гс ./ it\ .тс
4sm-^-. А так как sin -^-=5ifliit ^-j^= sin-^-, то
809. Преобразуем левую часть по формуле суммы коси-
нусов. Получим 2cos-g~ cos-jr-. Дальше — как в предыдущей
задаче.
810. Так как 1 -f-cosa=2cos2-~* то данное выражение
примет вид 2cos2y + cos^ или 2cos~/cos-i + -9"7e ^т
пишем cos 60° вместо -о-» получим 2 cos4-lcos4-+^os60°j.
Отв. 4 cos-J cos (-J +30°) cos (-^ — 30°).
811. Преобразовав данное выражение, как в предыдущей
( V~2\ V~2
задаче, получим 2 cos a (cos а — ^q-j - Вместо ^~— напи-
шем cos 45°.
. 45° + « . 45° — а
Отв. 4 cos a sin—~—sin—*—.
8$5 ГЛ. 11. ТРИГОНОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ 487
812. Запишем данное выражение в виде oos2(a-)-p) —
— sin2(a—р), последнее выражение приводится к виду, удоб-
ному для логарифмирования, как в задаче 65&.
Отв. cos 2a cos 2{L
813. Сгруппируем члены таким образом:
(l+cosa) + (tga + sina),
и вынесем за скобки во второй группе tga. Получим
(1 -j-cosa) • (1 +tga). Вместо 1-f-tga напишем
tg45 +tga—cos45ocosa.
2 }^ cos*— sin (45° + a)
Отв.
COS а
814. Применив формулы 1—cosa = 2sin2-|- и sina =
=2 sin y cos у, в числителе получим 2sin2~-f-2sin-|-cos-^ =
= 2sin-ifsin-2 -|-cos~j. Выражение в скобках равно
sin Пользуясь формулой суммы синусов,
приведем его к виду У 2 cos f 45° — ~\,
Отв. 2 У2 cos (45° — ~\.
815. Данное выражение равно cos а—sing + 1^ Числи-
COS a
тель преобразуется к виду 2yr2cos-| sin f 45° — —} (см. пре-
дыдущую задачу). Дробь еще упростим, представив знамена-
тель в виде
sfn(90° —a) = 2sin(45°—|)cos(45°—-J).
Y~2 cos —
Отв. — — .
C0S(45O"t)
488 ОТВЕТЫ И РЕШЕНИЯ 816
816. Так как cos а — cos За = 2 sin 2а sin а, то
2 sin 2а sin а + sin 2а = 2sin 2a(sin а -+- 77) =
= 2 sin 2а (sin а + sin 30°).
Отв. 4sin2asin(-j+15°)cos(-|— 15°).
817. Данное выражение равно
tg<»+l , tg«— t 4tga о 2tga
l — tge"1"! +!ga"* 1 — tg*a* T' *' * 1— tg*a '
Owe. 2tg2a.
818. Заменив sin 2(3 па 2 sin p cos (3 и сократив на 2 sin p,
1 — cos В
получим YjT—rji применив формулу
p , ,/~l — cos?
в
получим (g2-|.
Отв. tg2-|.
819. Преобразовав сумму cos a -j- sin a в числителе
У~2—• (cosa+sina) и разность sin a — cos a в знаменателе,
как в задаче 814, получим
/2(1—cos(a — 45°)l=:: Ш 2
lT2s1n(a-45*) 2slnlZLl51c0S 1=™L '
r> * a —45°
Owe. tg—^—.
820. Преобразуем сумму двух последних членов:
ь * Sin 2a 2 sin a COS о 6
Отв. 2ctga.
821. Заменим cos 2a на cos2 a — sin2 af a sin 2a — на
2 sin a cos a.
Owe. 1.
825 ГЛ. 11. ТРИГОНОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ 489
822. Заменим 2sin2а—1 на —cos2а и представим дан-
ное выражение в виде 2 f^- sin 2а—yCOs2aj. Напишем
cos 30° вместо -Ц- и sin 30° вместо -^.
Отв. 2 sin (2a— 30°).
823. Числитель равен
cos 2a cos а -|- sin 2д sin a cos (2д — a) 1
" cos 2a cos a cos 2a cos a cos 2a *
Знаменатель равен
sin3 a-}- cos3 a 1
Sin a cos a 1 . о "
■я- Sin 2a
2
Отв. ytg2a.
824. Данное выражение равно (см. предыдущую задачу)
с , 2 2
(1 + sin 4а).
' sin 4а sin 4а
Выражение в скобках равно
l+cos(90° — 4a) = 2cos2 w^4a .
4 со» (46--2.)
sin 4a
825. Последнее слагаемое равно cos2*, так что данное
выражение представляется в виде (tg х —l)(l—sirix)-|~cos2x.
Заменив cos2x на 1 — sin2x, вынесем за скобки 1—sin х.
Получим
(1 —sin х) [(tg х — 1) + 1 + sin х] = (1 — sin х) (tg х + sin х) ==
= (1—sin x)tgx (1 + cosx).
Первый сомножитель преобразуется, как в предыдущей за-
даче.
Отв. 4 tg л; cos2 ^ sin2 (45° — ~V
490
ОТВЕТЫ И РЕШЕНИЯ
826
826. Числитель и знаменатель дроби соответственно равны:
(1 +cos2a)-|~(cosa + cos3a) = 2cos2a-|~2cos2acosa
и
cos a -f- cos 2a.
Отв. 2 cos a.
827. Данное выражение равно
(1 —sin2P)—sin2acos2a — cos4a =
= cos2 f) — cos2 a (sin2 a -(- cos2 a).
Получаем выражение cos2{)—cos2 a, которое преобразуется,
как в решении задачи 656.
Отв. sin (a + Р) sin (a—{)).
828. Приведём данное выражение к общему знаменателю
cos л: cos у cos z. Числитель будет
sin х cos у cos z -f- sin у cos z cos x -f- sin z cos x cos ^y —
Последний член равен —sin (x + у) cos z — cos(x-j-y)s\nz.
Сумма первых двух членов взаимно уничтожается с членом
— $\п(х-\- y)coszt и числитель принимает вид
sin z cos х cos у — cos (х -f- у) sin z =
= sin 2 [cos x cos _y — cos (x -f- _y)].
Раскрывая выражение cos(x-f~.y)> получаем в числителе
sin z sin x sin у.
Отв. tgxtg ytgz>
829. Данное выражение равно 2 sin ^jp- cos tt T p -f- sin -y.
Но по условию f = 180°— (a —j— P); следовательно, получаем
n . a + 8 a —8 . . . a + 8 a + 8
2 sin -—|-i cos —jp- -+ 2 sin -~~- cos —p.
Выносим за скобки 2 sin ^tl f или, что то же, 2 sin —q—^ =
= 2 cos -X) • В скобках получаем выражение cos ?-—■ -+ cos^p-,
которое преобразуется по формуле суммы косинусов.
Отв. 4cos~cos-|cos-j*
832 гл. 12. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ 491
ГЛАВА 12
ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ
830. Произведя упрощения, получим sin5x — sui3a; = 0.
Применив формулу разности синусов, имеем 2 sin х cos Ах = О,
и уравнение распадается на два: sinx = 0 и cos Ах — 0. Из
первого имеем х = тгй (л— любое целое число), из второго
4х = 2™±~ = ~(4я± 1), т. е.
" х = ~(Ап± 1).
Выражение An ± 1 содержит в себе все нечётные числа
(числа —3, 1, 5, 9, 13 и т. д. получаются из выражения
4/г+1; числа —1, 3, 7, 11, 15 и т. д. — из выражения
4л—1). Поэтому вместо An ± 1 можно написать 2л+1
(или 2л—1), где л — любое целое число.
Отв. х=ъп; х = -|-(2я-|-1)| где л — любое целое число.
831. Преобразуем левую часть уравнения следующим
образом:
sin х -(- sin 2х + sin 3jc + sin Ах =
= (sin x + sin 3x) + (sin 2x + sin Ax) =
= 2 sin 2x cos x -f- 2 sinSx cos x = ,
= 2 cos x {sin 2x + sin 3x) =M sin -^ cos -^ tos a:.
Уравнение принимает вид
* Ъх х л (i
an -н-cos yCOS X — 0 V
и распадается на три уравнения:
sin -^ = 0; cos4 =0; cosa; = 0.
Отз. х = 72°п> д:=180°(2л+1); * = 90°<2я+1),
832. Выполним преобразования
cos (х + 60°) = cos [90° — (30° — jc)] = sin (30° — x)
и
1+cos2jc = 2cos2at.
492
ОТВЕТЫ И РЕШЕНИЯ
833
Уравнение примет вид
sin (х + 30°) + sin (30° — х) = 2 cos2 х.
Применим формулу суммы синусов; получим
sin 30° cos л: — cos2x =0 или cosx( ^— cosx) = 0.
Отв. х = 90°(2л+1); x=60°(6/z± I).
833. Перенесем все члены уравнения в левую часть и
сгруппируем следующим образом:
(sin л: + sin Зх) — (cos х + cos Зх) -+- (sin 2х — cos 2х) = 0.
П^образуя выражения в первых двух группах, получим
2 sm 2х со$^-— % соаЗх cds^c -f- (sin 2х — cos 2х) = 0
или
(2 cos х + 1) (sin 2х — cos 2х) = 0,
Это уравнение распадается на два:
2 cos х + 1 — 0 и sin 2х — cos 2х = 0.
1 2
Первое дает: cosx = — -^; х = 2тгл ± -g-тг. Разделив вто-
рое уравнение почленно на cos2x, получим tg2x=l, от-
куда 2х = тгл + -у •
Отв. х = ~(3п ± 1); х = ~(4л+1).
834. Произведем следующую группировку:
(cos 2х + cos 6jc) — (1 + cos 8#) = 0.
Применив формулу 2cos2-2 = 1 + cos а и преобразовав сумму
косинусов, получим
2 cos 4^cos 2х —12 cos2 4х 4= 0.
Вынесем 2cos£x за скобки и претшразуем разность косину-
сов cos2x-rcos4x. Получим уравнение
cos 4х sin Зх sin х ±= 0.
Оно распадается на три:
1) cos 4x^=0; 2) sin3x = 0; 3) sinx = 0.
837 гл. 12. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ 493
Но третье уравнение можно не рассматривать: все его реше-
ния содержатся в числе решений уравнения sin Зх = 0. Действи-
тельно, если sinx = 0, то и sin3x = 3sinx— 4 sin3 л; = 0.
Отв. х = ~(2п-{-1); х = ^-.
4-Х? 3jc
835. В правой части напишем 2sin-2-cos-^- вместо sin Зх.
Уравнение примет вид
п . Зх s х 0 . Зх _ Зх
2 sin ~2" sin y = 2 sin-g-cos-т^-
или
. Зх ( . х Зх\ Л
sin ~y \sm 2"— COS ~2/ =
Выражение в скобках запишем в виде
cos (1 ~ т) - cos-r=2 sin (т+т)sln (* - т) •
Следовательно, данное уравнение распадается на три:
l)sin^ = 0; 2) sin(|+|) = 0; 3) sin(x — ») = 0.
Owe. * = ^; х = |-(4л—1); x=-J(4n+l).
836. Правая часть равна
sin [90° — (х + 30°)] = sin (60° — х) = — sin (х — 60°).
Уравнение принимает вид
sin(x — 60°)== — sin(x —60°) или sin(x — 60°) = 0,
откуда х —60°= 180°я.
Отв. * = 606(Зл-}-1).
837. Заменив 2sin2x на 1—cos2x, приведем уравнение
к виду 2 sin Зх cos 2х — cos 2х = 0. Это уравнение распа-
дается на два; 1) cos2x = 0; 2) этЗх^г-^. Так как -^ есть
sin 30°, то второе уравнение дает
Зх=:180ол + (— 1)*30°.
Отв. х = 45°(2л+1); х = 60°л +(— \)п 10°.
494 ОТВЕТЫ И РЕШЕНИЯ 838
838. Правую часть напишем так: 3 (sin л; cos л:—sin2 jc—f—1 )==
= 3 (sin jc cos x -[- cos2 x) = 3 cos2 x (tg x -|» 1). Данное урав-
нение распадается на два; 1) tg х -f- 1=0; 2) sin2 jc—3 cos2 x=0.
Из второго получим tgx^ + V^-
Отв. jc=^(4fl— 1); jc = -J(3a± 1).
839. Имеем уравнение
cos 4jc -J- 2 cos2 jc = 0.
Так как 2cos2jc= 1-j-cos2jc, to левая часть равна
(1 4- cos 4*) + cos 2jc = 2 cos2 2jc 4- cos 2jc.
Получаем уравнение
cos 2jc (2 cos^x 4- 1) = 0,
распадающееся на два:
1) cos2x = 0 и 2) 2cos2x4-l=0.
Второе дает 2jc = 360°rt± 120°.
Отв. х = 180°л ± 45°; х = 180°л ± 60°.
840. Помножим обе части уравнения на sin jc и, заменив
в правой части единицу на sin2 jc4-cos2jc, получим уравне-
ние sin jc cos jc = cos2 x.
Замечание. Умножая обе частя уравнения на siajc, мы не
получаем посторонних решений, так как sin х ии при одном из най-
денных значении х не Обращается в нуль.
Отв. дг1==|-(2л+1); *2 = j(4w4-1).
841. Запишем уравнение так:
sin3jc — sin (^— 2jcJ = 0.
Оно распадается на два:
l)cos(|4-j) = 0 п 2) «ki(4f-■£) = <>.
Первое дает ^+^- —•£ (2^4-*). откуда х = ~(4п~\-1).
Второе дает jc = ^(4л4-1).
Отв. л; = -^(4л4-0; * = хд(4л+1).
846 гл. 12. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ 4&5
X X
842. Прибавим к обеим частям уравнения по 2 sin2 у cos!2 -g-,
после чего в левой части получим
Si^ -J + 2 Sin2 * COS2 J + COS4 у = (sin2 ^ + COS2 -J)" = 1.
и уравнение примет вид
1 = |- +2 sin2 -J cos2 £ или 2sin2~cos2|-==|-.
Умножим обе части уравнения на 2 и применим формулу
*2х 3
для синуса двойного угла. Получим sin2 -^ = -j- f откуда
,2* , Уз"
Отв. лг = ^(3я± 1).
843. Представим уравнение в виде 3 tg;2 дг—(1 -f-tg2jc) = 1,
откуда tg х = ± 1.
О/и*. je = 45D(2rt-f-l).
844. Заменим 1+cos4jc на 2cos22jt.
ome. х = т4-^; дг==т+(—1)^24-
845. Прибавив к обеим частям уравнения по 2 sin2 jccos2x,
получим (sin2 х -f- cos2 xf — cos 4лг -+-2 sin2 x cos2 x или
1 — cos 4x = -^ sin2 2дг.
О/яв. X—-^ д.
846. Заменим sin2x на 2 sin jc cgs л: и разделим все члены
уравнения на cos2*. Заранее видно, что потери корней не
будет. Действительно, если cosa: = 0, то sin х == ± 1, а эти
значения не удовлетворяют данному уравнению. Получим
3 — tg2JC — 2tgx = 0.
Отсюда находим
tg*=l и tgx =— 3.
Отв. лг = тсл-[—^.; х = кп— arc tg3.
496
ОТВЕТЫ И РЕШЕНИЯ
847
847. Напишем sin2 х -|- cos2 х вместо единицы и, разделив
обе части на cos2 х (см. решение предыдущей задачи), получим
tg2* + /3tgA; = 0,
откуда
tgjc==0 и tgjc ——1/*3.
Отв. х = гсл; лг = ^(3я—1).
848. Представим 2 как 2 sin2 лг-^соэ2.*:, после чего
уравнение решается как предыдущее.
Отв. х = тел + -г- J лг == тел — arc tg -^ ,
п 3
849. О/яя. х = — (4л+1); дг == тел + arc tg-^.
860. Заменим У~3 на ctgjiO0 (вводим «вспомогательный
угол» 30°). Данное уравнение запишется так:
. cos3(P ,
51П^+ЖЖС08Л==1'
или
sin х sin 30° + cos x cos 30° — sin 30°
или еще так:
cos(jc —30°) = ^-.
Отсюда x — 30° — 360°л ± 60°.
Отв. дг = 360°/г + 90° = 90°(4л+1); х = 360°/i—30° =
= 30°(12я — 1).
851. Левую часть можно представить в виде произведе-
ния Vr2cos(jc—45°). Получим уравнение cos {х — 45°) = -^=-;
оно дает х — 45° = 360°/г — 45° и х — 45° = 360°/г-[-45о,
то есть *:=360оя и л; = 360°/г + 90° или л; = 90°. 4л и
лг = 90°(4/г+1).
Другой способ. Возведя обе части уравнения в квад-
рат, получим
sin2 х + 2 sin х cos х -\- cos2 дг = 1
853 ГЛ. 12. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ 497
или sin 2л; = 0. Это уравнение имеет решения х = 90°л, но
среди них имеются посторонние (сравнить с предыдущим ре-
зультатом).
Появление лишних решений обусловлено тем, что
мы возводили обе части уравнения в квадрат; тем самым
мы, кроме данного уравнения, привлекли еще уравнение
sin х4-cos х =—-1 (из него получим тоже sin 2х = 0). Чтобы от-
бросить лишние корни, выполним проверку. При /г = 0 имеем
л: — 0°, и данное уравнение удовлетворяется. Оно удовле-
творяется и при п = 4, 8, 12 и вообще при /z = 4ft (т. е. при
х = 90° • 4ft = 360%). При п = 1 имеем х = 90°; данное урав-
нение снова удовлетворяется. Оно удовлетворяется также
при п = 5, 9, 13 и вообще при ik-\-\ (т. е. при
х= 90° (4ft+1) = 90° + 360%). Но при п = 2, 6, 10 (вообще
при п = 4/2 + 2) и при /г = 3, 7, 11 (вообще при /i=4ft + 3)
данное уравнение не удовлетворяется (вместо него удовле-
творяется уравнение sin jc + cosjc=^=—1).
Отв. дг = 90°.4/г; jc = 90°(4i^+- 1).
852. Преобразуем правую часть:
1 +sin 2*=rsiffr*--r-cos2 -jr + 2 sin x cos*=(sin.* -|-cosjc)2,
после чего уравнение примет вид
sin х -f- cos x = (sin x + cos jc)2
или
(sin x -\- cos jc)(sin x -f- cos x — 1) = 0.
Последнее уравнение распадается на два:
1) sinjc + cos:c = 0;
2) sin х-\- cos х—1=0.
Решая первое, найдем дг = —(4/г—1). Второе решено в пре-
дыдущей задаче.
Отв. х = £(4я—1); *=-J(4n-|-l); x=^.ln.
853. Решается как задача 851.
Отв. х= 15°(8и+1).
498 ответы и решения 854
864. Применив формулу
sin ос sin р = -^ [cos (а—р)—cos(oc + p)]f
получим
~2 [cos (х — 7х) — cos (х -\- 7х)] =
= -i [cos(3*— 5х)— cos(3jc + 5jc)]
или, после упрощений, cos6jc — cos2jc = 0. Это уравнение
распадается на два: sin4jc = 0; sin 2дг = 0, причем все корни
второго уравнения входят в число корней первого.
Отв. дг= —,
855. Применим к левой и правой частям уравнения формулу
sin a cos р = -g- [ sin (a + P) + sin (a — P)].
Отв. x=*^-; jc = -J(2rt+l).
856. Имеем
4 sin x sin 2x sin Ъх = sin 2 (2x)
или
sin 2x (2 sin x sin Зл: — cos 2x) = 0.
Заменяем 2 sin # sin Зх на cos 2x — cos4x (см. задачу 854);
получим уравнение
sin 2х (cos 2х — cos 4х — cos 2х) = 0 или sin 2х cos 4дг = 0.
Отв. *=™; * = £(2л+1).
857. Заменим sin2 дг на 1 — cos2 дг; получим
5 cos2 х + 4 cos х — 3 = 0,
лГ 19 2
откуда найдем cos х == -—? . Другое значение cos х =
т/*19 + 2
— — "—-!— не годится, так как его абсолютная величина
5
больше единицы.
т/"У9 2
Отв. х = 2тс/г ± arc cos ——= .
Ш гл. 12. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ 499
858. Применив формулу cos 2а и выразив косинус через
синус, получим 10 sin2 х + 4 sin х— 5 = 0.
2 ± l/"54
Отв. л: = тс/г + (—l)warcsin г^р—-
859. Применив формулу тангенса суммы, получим
и приведем данное уравнение1) к виду tg2 х — 4tg*~b 1 =0.
Отв. x = ic/z-|-arcig(2 ± УЗ).
860. Так как ^~ = ^^ и вес*--^
то
имеем уравнение
8 (1 — cos х) - . 1
1 -f cos х "•" cos х '
оно приводится к виду
9cos2jc — 6cosjc+1=0 или (Зсоэдг— 1)2 = 0.
Отв. х — 2тс/г ± arc cos у.
861. Левая часть равна
(п \ п , X X
-2~х)_ sin* = 2»штсо«т ^
1 + cos х 1 4- cos х п „ х * 2 "
~ 1 2 cos^-g-
X X
Правая часть равна sec2 -^ — ln=tg2-^-. Получаем
tgf = tg2f
Отв. jc=2it/z; * = -£(4л+1).
1) При освобождении от знаменателя можно получить посто-
ронние решения, но в ближайших трех задачах (в них посторонних
решений нет) исследования мы не проводим. Начиная с задачи 865,
этому исследованию уделяется большое внимание. См. также за-
дачу 867.
500 ОТВЕТЫ И РЕШЕНИЯ 862
862. Так как
cos (тс — х) = — cos х и sin -^t— = cos —,
то имеем
l+cpsje + cos-j=0 или 2cos2^ + c°s -| =0.
Отв. х = 1с(2я+1); х = -у(3я±1).
863. Применив формулы приведения
sia{^—x) = -cosx и tg(£—J) = ctgf,
получим уравнение
2(l+cos*) —V3ctg|=0.
Воспользуемся формулой
х_ 1 -f cos Jg .
ctg 2 — si5T~'
тогда уравнение распадется на два:
1) 1+cosjc = 0 и 2)sin* = ^.
Отв. дг = тс(2/г+1); * = ™ + (—lf-J.
-8G4. Заменив cos2* на 1—sin2 дт, после упрощений по-
лучим 3sin jc + cosjc = 0 или tgx = — -j.
Отв. дг = тс/г — arctg-g.
865. Левая часть равна
cos л: . sin л: cos х -\- cos^ х -\- sin* х 1 -|~ cos х
sin л: "~ 1 + cos х sin х (1 + cos л:) sin х(\ ~\- cos х) '
Сократим дробь на l-j-cos*. при этом предполагается, что
l-f-cosje=£0 (так что если потом получили бы такое ре-'
шение, для которого cos.x: = —1, то оно не годилось бы).
1 1
Получим уравнение ^-^ = 2, т. е. sin х = -g- (при этом зна-
чении sinjc величина cosjc не равна —1).
Отв. дг = тс/г + (— О"-?.
867 гл. 12. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ 501
866. По формулам приведения
ctg (X — It) = — ctg (1С — X) = ctg дг.
Данное уравнение можно записать в виде
2 ctg* — (cos*-4-sin*)/'-7! тггт) = 4.
& ' ' \sln х cos дг/
После приведения левой части к общему знаменателю это
уравнение примет вид
1 4.
sin х cos х
откуда sin л: cos JC = — или sin 2* = -5-•
Отв. x=sjn+ (— 1)"*yj.
867. Правая часть равна
1
— cos ж ., . ,
cos* 1 — COS* Л sinjjc
2 sin х 2 sin x cos л 2 sin x cos x *
Сократим дробь на sin x. При этом предполагается, что
*\пхфО, так что если получится такое решение, для кото-
рого sin jr = 0, то оно не будет годиться. Данное уравнение
'к левой его части применим формулы приведения) примет вид
sin х + tg х = -к- tg х или sin х + -j tg х = 0,
cJto уравнение можно представить в виде
slnjcfl + tjJ ) —0.
\ ' 2 cos х /
и оно распадётся на два уравнения
sin х = 0 и I + -^ = 0.
1 2 cos х
Но первое уравнение даёт посторонние решения, ибо прежде
мы сокращали дробь на sin х. Чтобы лучше уяснить суть дела,
подставим в правую часть sin# = 0; тогда вместо cos х при-*-
дётся подставить 1 или — 1. В обоих случаях получим
неопределённое выражение -д-.
502 ОТВЕТЫ и решения 863
868. Левая часть равна
i-fr-ar ^т('-^т)
1-—т '-tgT
Сокращая на 1 — tg -g- (при этом предполагается, что
1—tg-£^0, см. решение предыдущей задачи), получаем
— tg-i и уравнение принимает вид
— tg-J==2suiY или sin -J- (sec-f 4-2) = 0.
Оно распадается на два:
l)sini«0 и 2)cos-jr ——-у.
Из второго уравнения находим ~ =з360° л d= 120° и полу-
чаем решение х = 720°л=!=240о» Первое же уравнение даст
только посторонние решения (* = 360°'л), хотя и по иной
причине, чем в предыдущей задаче. Именно, в данное урав-
х
нение входит величина ctg-g-, которая теряет смысл («обра-
щается в бесконечность») при дг = 360°л; значит, вся левая
часть уравнения не имеет (прямого) смысла.
Замечание. Девой части можно приписать расширенный смысл
следующим образом. Если угол х мы будем неограниченно прибли-
жать к 360° я (к 0°, 360°, 720° и т. д.), то левая часть будет неогра-
ниченно приближаться к нулю. Величину нуль (предел левой части)
естественно считать значением левой части (в расширенном смысле),
i J3 таком случае корень х = 360° п не будет посторонним. Но в элемен-
тарной математике такое расширение смысла выражений не принято,
Otne. x = 240°(3/?ztl).
869. Применив формулы приведения, получим уравнение
sin х — tg х = sec*—cos л; или sin х———=>- cos*.
ь COS X COS X
Помножим обе части уравнения на cos х (или, что то же,
приведём к общему знаменателю и отбросим его). При этом
предполагается, что cosjc^O, ибо если cos х = 0, то выра-
871 гл. 12. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ 503
жения ^-j: и теряют смысл («обращаются в бесконеч-
ность»). Получаем уравнение
cosx sin л— sin* = sin3*.
Оно распадается на два:
I) sinx = 0; 2) cos л; — sinx=l.
Второе уравнение можно представить в виде \^2 • cos (45°+*)= 1
(ср. задачу 851), откуда х=360°л и * = 360°п — 90°. Ре-
шение * = 360°л входит в число решений первого уравнения
(*=180оя), а решение * = 360°л— 90° является посторон-
ним, так как имеем cos (360° п — 90°) = 0.
Отв. * = 180° п.
870. Применим формулы: sec3* — tg3*=l и cos 2* =
= cos2*—sin3*. Получим уравнение
, , COS2 х — sin- X
1 tg * = .
& COS-* *
которое приводится к виду tg3*— tg * = 0.
Отв. х = м; дг = -|-(4л4-!)•
871. Запишем уравнение в виде
sin» * (sin * +cos*) , cos"* (sin * +cos*) _ _ ^
sin* ~ cos*
Предполагая, что sin*=£0 и cos*^=0, сократим дроби, пе-
ренесем все члечы в левую часть и вынесем ва скобку
sin* + cos*. Получим
(sin * -}- cos *)(sin3 * 4- cos3 * — cos * + ^п *) = 0.
Заменим sin2*-}-cos3* на 1. Уравнение распадается на два:
1) sin*4-cos* = 0 и 2) cos* — sin*=l.
Первое уравнение даёт * = -^(4и—1); второе уравнение
(см. задачу 869) имеет решения * = 2тсд и * = -у (4л— I).
Оба они — посторонние, ибо при * = 2тш имеем sin* = 0,
а при*=-|-(4я—1) имеем cos* = 0.
Отв. * = -|-(4/*— 1).
604 ОТВЕТЫ и РЕШЕНИЯ 872
872. Применим формулы тройных углов:
sin Зх = 3 sin х — 4 sin8 х, cos Здг = 4 cosb х — 3 cos х *).
Левая часть преобразуется к виду
3 3
3 sin х cos х (cos2 х — sin2 x) = — sin 2x cos 2x « — sin 4jc,
и данное уравнение примет вид sin 4jc = -j.
Owa. jce —+ (— О -34.
873. Запишем уравнение следующим образом:
tg3AT — (tg2* + tgAr)=0.
Представим левую часть в виде произведения нескольких
простейших тригонометрических функций. Имеем
tg 2л- I tg л* = Si" дХ = tg °* C0S 3*
й ~Г & cos х cos 2^- Cos х cos 2лг'
так что левая часть равна
, о fi cos Зл; 1 , о Г- cos*cos2jc — slnjtsln2jf"|
l?3* i1 - cosmos 2х\=^Ъх | * cos x cos 2x ('
Выражение в скобках равно tg jf tg 2лг, так что получаем
уравнение tg 3* tg 2х tg х = 0. Рассмотрим по отдельности
три уравнения:
1) tgЗд: = 0; 2) tg2дг = 0; 3) tg* = 0.
Решение первого есть # = -£-. 1ретье уравнение не даёт
ничего нового, так как все его решения (х=пт) входят
в число решений первого (при п = 3т имеем ~=ntnt).
Второе уравнение даёт jc = -y. При чётном а эти решения
опять не дают ничего нового (при п = 2k имеем iSeirftj;
при нечётном же п (п = 2п' -|- 1) они вовсе не являются реше-
ниями данного уравнения. Действительно, величины tg х и tg Зх,
*) Если они не известны читателю, то он ножет их без труда
вывести самостоятельно, применив формулу синуса и косинуса
суммы двух углов: 2а и а и затем формулы синуса и косинуса от 2а.
*75 гл. 12. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ 505
входящие в уравнение, при лг = -2*(2л'+1) теряют смысл
(«обращаются в бесконечность»). Поэтому второе уравнение
необходимо отбросить.
Отв. *-™.
874. Применив формулу косинуса разности, приведём
правую часть к виду J^2 (cos 4- + sin —)• Поэтому и левую
часть выразим через аргумент -у. Имеем
X XX
(1 -j-cosx)-f-sinx = 2cos2-£- + 2 sin -^ cos -ту ==*
= 2 cos-у f cos -^- + sin-yj.
Перенеся все члены в левую часть, получим уравнение
(cos -£ + sin -£) (2 cos у — / 2) = 0f
распадающееся на два: одно даёт x = 3Q0°n— 90°, другое
х = 720°я rt: 90э. В последнем выражении можно двойной
знак заменить знаком плюс, потому что все величины
720°я — 90° содержатся среди величин 360°я— 9(Г (если
в выражении 360°я— 90° брагь только четные я, т. е, по-
ложить я=з2я'р то мы получим 720V — 90°).
Отв. х = 360°л — 90°; х = 720°л + 90°,
875. Перепишем данное уравнение в виде sin2 2х =
е= sin Зх 4- sin х; отсюда sin2 2х = 2 sin 2х cos х. Перенеся
все члены в левую часть, получим
sin2x(sin2x— 2cosx) = 0 или 2 sin 2х cosjc (sinx— 1) = 0.
Уравнение распадается на три:
I) sin2x = 0; 2) cosx = 0; 3) sinx=l.
Два последних можно не рассматривать, так как все их ре-
шения входят в число решений первого. (Имеем sin 2х =а
= 2 sin х cos х = 2 sin x\f 1 — sin2 xt так что, если cos x = 0
или если sinx=l, то sin2x = 0.)
Отв. x = 90°/i.
506
ОТВЕТЫ И РЕШЕНИЯ
876
876. Левая часть равна 2 cos2 л:—3cosx. Правая теряет
смысл при дг = ^-л, ибо ctg2x «обращается в бесконеч-
ность». Поэтому будем считать, что хФ -я- я. Знаменатель пра-
вой части равен
cos 2* cos х (2cos2jc— I) — 2 cos* л- — 1
sin 2x sin x 2 sin x • со* x 2 sin x • cos x *
так что правая часть равна
— cosec(* — х) • 2 sin х» cos х = — 2cosecjc • sinjc • cosx.
Произведение cosecjc • sin л:(т. е. ~-\ можно заменить еди-
\ sin х/ sln х
ницей, так как те значения х, при которых дробь -— при-
л sin X
нимала бы неопределенный вид -т-, мы исключили. Получаем
уравнение
2 cos2 л:— 3cosa: = — 2 cos* или cosjc(cosjc—^Л = 0.
откуда cosjc —0 или cos# = -$. В первом случае получаем
значения х = ^(2k-\~ 0» которые мы выше исключили.
Отв. а: = ^(6л±:1).
Замечание. Значениях = 4 (2* +1) также будут реше-
ниями, если правую часть уравнения понимать в расширенном
смысле, как указано в замечании к решению задачи 868 (стр. 502).
877. Левая часть равна
(cos х + sin xf + 1 — 2 + 2 cos x sin *,
2 sin* x n о
правая часть равна ——^-j— = 2 cos2 л:; при этом предпола-
гается, что sin х Ф0. Уравнение принимает вид
2(1—cos2Ar)4-2cosxsinx = 0 или sin2x + sina:cosx = 0.
Оно распадается iia два уравнения: sin х + cos х = 0
н sinjc = 0, но при sinjc = 0 правая часть не имеет (прямого)
смысла.
Отв. х = —j + яя.
878. Правая часть равна
2sin(-J + дг)со5(| + л:) = 51п(| + 2л:) =
« cos 2х = cos2 х — sin2 х.
879 гл. 12. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ 507
879. Левая часть равна 2 — sin За:, правая равна
1-,2c0!(i_^sln(i-f)=l-sl„(i_3,) =
= 1 — cos Зх.
Уравнение принимает вид
cos Зх — sin 3-v-j- 1 = 0.
Решим его по (первому) способу задачи 851, преобразовав
cos3x—sin3x к виду l/^sinf-^ Зх). Получим
dn(i-3x) ^, т. е. ^(ax-i)-^.
Следовательно,
3*--J—(-lf-L + w. т.е. 3*-i[l+(-l)nl+«ii.
При чётном п выражение в квадратных скобках равно 2,
а при нечётном оно равно нулю. Поэтому, если положить
п = 2я' (я'— целое число), то получим Зх =-^- + 2пя', а
если положить я =в 2/14-1, то получим 3x = «r(2n'-f- О-
Другое решение. Помимо второго способа, указан-
ного в задаче 851 (он вводит лишние корни), можно приме-
нить здесь (а также и в задаче 851) следующий способ. По-
лучив, как выше, уравнение cos Зх—sin Зх -|- 1 = 0, при-
меним формулы
14-cos3x=*2cos2y и sin3x=:2sin^cos^.
Получим уравнение, которое распадается на два. Одно
(cos^=0) дастч^ —-£(2л+1), т. е. Зх = 1г(2л + I).
Другое уравнение (cos у — sin -у = о) даст Щ — тт + *п9
т. е. Злг = -^- + 21г/2.
От. х = £(2п + 1); * = -£(4л + 1).
503 ОТВЕТЫ н решения 880
880. Представим 1 -f- sin 2х в виде
(cos2 х 4- sin2 jc) + 2 sin x cos x = f cos x -f- sfn jc)9
и заменим tgx на ^j-j» Затем приведём все члены к обшему
знаменателю (cos х) и отбросим его, предполагая, что cos хФО.
Получим уравнение
(cos х — sin л:) (cos х -f- sin jc)2—(cos x -f- sin x) = 0.
Оно распадается на два: первое
cosx-f- sin jc = 0
имеет решение
второе
или
имеет решение
ГС
* = т(4л—1),
cos2jc— sin2*— 1 = 0,
cos2jc — 1 = 0,
:ТГЛ,
О/из, х=а~{4п—1); л: = теп.
881, Представим 1 — sin 2х в виде (cos х — sin jc)2,
a cos 2х в виде (cos х + sin jc) (cos х — sin jc). Сократим дробь
на cos *— sin jc, предполагая, что эта величина не равна нулю.
Получим уравнение
cos jc Ч- sin jc = -1—;—.
cos x— sin x
Освободившись от знаменателя (в том же предположении),
получим
(cos jc-)- sin jc)(cos jc— sin jc) — (cos jc-|-sin jc) = 0
или
(cos jc— sin x — l)(cos jc+sin jc)=*0.
Решив уравнение cos x 4- sin x = 0, находим jc = nn — -£.«
Уравнение cosx—sinx—1 = 0 можно решить так (ср. за-
дачу 879). Представим его в виде ]/2 • sin (~ — х) = 1 , т. е.
ап(*~у)--7Г 0тсюда *~т=^-1)П(-т)+я"-
884 гл. 12. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ 609
При чётном п ( = 2/я) имеем х — кп = 2я/м. При нечётном п
( = 2/и—1) имеем #=у+тся =-у (4wt— *)•
Применить другой способ задачи 879.
Отв. * = -1(4л— I); jc = 2im; х = -|-(4л—I).
882. Правая часть равна cos 2х, а левая
(cos jc -|- sin xf (cos х— sin x) =
= (cos x + sin jc)(cos2x — sin3 *) = (cos x + sin x) cos 2x.
Отв. х = -|-(2п+1); jc = 2im; x — у (4л-J- I).
883. Левая часть равна
1 _4sJn!£co!^==al_sinajc
4 4соз^^ 4
(в предположении, что cosjc=£0). К правой части применим
формулу sin a si«p = -j[cos(a — Р)—cos(a-|-(3)|. Получим
| (cos 60° — cos 2х) = I [1 - (1 — 2 sin**)] = Zll±i»!££.
Теперь уравне-ние примет вид
I-sin2A: = -(|-sin3x)>
откуда sin2 jc =-г-, т. е- sin jc = -j или sinjc = — -о-- Два
решения лг=180°я + (—l)n30° и дг= 180°я — (— 1),ь30°
можно записать одной формулой: jc = 180°л:±:30о.
Отв. дг = 30°(6л±:1).
884. Левая часть равна sin 60° cos х; правая равна
tg х cos4 х -f- ctg jc sin4 jc = sin jc cos3 x -J- cos jc sin3 jc
(при последнем преобразовании предполагается, что cosjc=£0
и sin jc^O). Это выражение равно
sin х cos х (cos2 х -|- sin2 х) = sin х cos jc.
Уравнение приводится к виду cos х (sin 60° — sin х) = 0.
Оно распадается на два, одно из которых (cos х — 0) даёт
постороннее решение.
Отв. х= 180°л-К— 1)п60°.
510 ОТВЕТЫ и решения 885
X \ —— COS X
885. Применив формулу tg -^- = s]n —, получим в ле-
вой части sec2 л:—l = tg2jc (сокращая на sin jc, мы предпо-
лагаем, что siruc=£0). Левая часть равна
sin (х — 30°) + sin {х + 30°) _ 2sinхcos30° = ,/-g-
COS Ж COS JT Г 6 •
Уравнение приводится к виду tg#(tg#—1^3) = 0 и распа-
дается на два, одно из которых, именно tgjc = 0, даёт по-
сторонние решения (ибо если tgjc = 0, то и sin jc = 0).
Отв. лг=60°(Зя4-1).
X X
886. Выражение tg -g- -\~ ctg -^ преобразуется к виду
, X X ь\х\х*
sin ~y cos y
Получим уравнение
Отв. л: = — (2я -j- 1).
V2 sin лг=—J ,
У 2 sin x
'о V2,
887. Левая часть равна 2}/2 • -^—(sin jc + cos л:); пра-
2cos3jr 2(1— sin2 х) 0/1 . ч п
вая — равна l + s]QX = i + sinлг =*2(l~sin*)• Получаем
уравнение
2(sinJC + cos jc) = 2(1 — sin л:) или (1 — cosjc) — 2sin*=0
или
2sin^-|- —4 sin ^ cos ^ = 0.
Отв. лг — 2ял; х = 2 (пп 4- arc tg 2).
888* Дробь в левой части равна
-±~(sin 2jc — cos2jctgJc) cos2jc =
yd
2 2
= —= (sin 2л: cos x — cos 2x sin x) cos x = —r= sin x cos jc.
899 ГЛш 12. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ1 511
Правая часть равна
(cos3 х -f- sin2 х) (cos2 х — sin2 л:) = cosa x — sin2 x
(переходить к двойным углам здесь нерационально). Уравне-
ние запишем в виде:
2
(1 — cos2 х) + sin2 х j= sin x cos x = 0
или
2
2 sin2 x ?= sin x cos x = 0.
^3
От*, дг = 180°л; x = 180°л -j- 30°.
889. Левая часть равна 3 sin x — 4 sin3 x, а правая
4sinjc(l—2sln2Jc). Получаем уравнение
sin jc(4 sin2jc— 1) = 0.
Отв. дг=180°л; дг= 180°л±30°.
890. Правая часть равна
X X
sin х sin -н- + COS JT cos —
sin x 4- cos jc ctg ^- s=s ■
sinT
Числитель этого выражения равен cos (х — —J = cos ~ ,
так что в правой части получаем ctg -»* Левая часть равна
1 , 2 cos2 тг
l + cos х 2_
cos х cos х *
Уравнение принимает вид
2cos2^.
Вынося за скобку ctg-^, получаем
/2 cos | sm £ \
\Г~5Гг 7 = °' т- е- clgf <tg*_l) = 0.
Ctg ту
512 ОТВЕТЫ И РЕШЕНИЯ 891
891. Знаменатель дроби равен
sin 2х cos х — cos 2х sin х sin х lg х
cos х cos 2х """" cos х cos 2x cos 2x "
Вся дробь равна sin 2x. Уравнение принимает вид
sin 2jc — 2 sin (45° -J- jc) cos (45° + x) = 0
или
sin 2jc—cos2jc = 0,
откуда tg 2jc = 1.
Отв. x = 90° л -f-22°30'.
892. Имеем
tg (jc — 45°) tg (x + 45°) = tg (jc — 45°) ctg (45° — дг) = — 1;
при этом предполагается, что х ф 45° (2л 4- 1), ибо тогда
один из сомножителей обращается в нуль, а другой — в беско-
нечность. Знаменатель правой части преобразуется к виду
cos х 2 cos л:
. х х sin л:
sin j cos —
■ = —2ctgjc;
при этом предполагается, что х ф 180° л, ибо тогда либо
X X
tg-o > либо ctg-s- теряет смысл (обращается в бесконечность).
Получаем уравнение
4 cos2 х
— tg*=> — 2ctgJ|. ,
которое (в предположении, что хф 180°я) приводится к виду
tg х cos 2х = 0, Последнее уравнение имеет решения лг = 180°л
и х = 45°(2л-|- 1), но они не соответствуют сделанным пред-
положениям.
Отв. Уравнение не имеет решений.
893. Правая часть равна — tg jc (см. предыдущую задачу).
Левую же часть представим в виде
1 Ito (Х + 45°) - cte (х 4- 4541 - з1п2(* + 45°)-со5Ч*+45Ч
= —Ctg(2x-f90°).
Получим уравнение
tg 2jc = — tg*.
896 гл. 12. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ 513
Его можно написать в виде
tg 2а: = tg (— х)\
отсюда заключаем, что углы 2х и —х разнятся на 180° п
и из уравнения 2х — — х+ 180° л находим лг = 60°/*.
Отв. jc = 60° я.
894. Левая часть равна
sin 2х sin 2jf
cos (* + a) cos (х-«) ^(cos2a + cOS2*)*
Получаем уравнение
2 sin 2л;
cos 2a -|- cos 2x
=» 2 ctg AT.
COS Jf
Применив формулы sin 2* = 2 sin x cos л: и ctg x = ~— , при-
ведём уравнение к виду
cos х (2 sin2 jc — cos 2x — cos 2a) = 0.
Уравнение
2 sin2 x — cos 2x — cos 2a = 0,
если в нём написать 1 — cos2jc вместо 2sin2x, даёт
2 cos 2х = 1 — cos 2a,
откуда
cos 2x = sin2 a.
Owtff. x = y(2rt-f- 1); x = ir«^=-^arccos(sin2a).
895. Левая часть равна 1 —sin jc; знаменатель правой части
равен
2
Это выражение приводится к виду —г-г—- - Получаем уравне-
ние 1 — sin х = sin jc.
Отв. л:=180оя + (— 1)*30°.
896. Левая часть равна tgjc. Правая (ср. задачу 894)
равна I4-2tg*.
Отз. лг = 45°(4я — 1).
514 ОТВЕТЫ И РЕШЕНИЯ 897
897. Имеем
аналогично,
sin*
(,+V)-['Z=^±i)]'_(Ltnr.
Уравнение принимает вид 1—cos 2х + sin 2х = 0, или
2 sin2 х -+- 2 sin л: cos л: = 0.
Owe. лг = яи; лг = *«— -^.
897а. Уравнение представим (см. предыдущую задачу)
d виде
/1 — cos 2л: \* . / 1 4- sin 2л: \« . / 1 _ sin 2л: \* 9
I 2 ] +1 2 ) + ( 2 J =6-
После алгебраических преобразований получим
3 —2 cos 2л: + cos2 2л:+ 2 sin2 2л: = -|.
Заменив sin2 2л: на 1—сов^л:, получим уравнение
cos2 2л: + 2 cos 2л: — 1 = 0.
Оно дает cos 2лг = — 1 + ■— (значение cos 2л: = — 1 — —
отбрасываем, ибо его абсолютная величина больше, чем 1).
Отв. лг = 1гл ± -п-arccosf— 1Н-^")*
898. Левую часть первого уравнения представим в виде
т; (cos х -\- cos у). Решив систему, найдем cos х = -п ;
Отв. х = 2тМ±^; y = 2ict±l.
о о
W гл. 12. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ-
899. Так как
sin ^ sin j; = cos (" -^ 7 C°S (" +-У> -
то второе уравнение можно записать так:
cos (л: —у) — cos (л: -f-у) = 2т.
Но x-j-y = a; следовательно,
cos (jc —у) = 2т + cos а,
откуда
х—у as 2яи ±: arc cos (2m -J- cos a),
и данная система распадается на две:
( х+у^а,
\ х —у = 2т -f- arc cos (2т -f- cos a)
515
Отв.
x—у == 2яд — arc cos (2т + cos а).
xt = ял -f- -x -f- -o arc cos (2m + cos a),
j;t = — дй -|- * — — arc cos (2m + cos a);
"2" "2
2 ~ 2"
л:а = Ttn + 4 — -9 arc cos (2m -|- cos a),
j>2 === — «и -{- -g- -f- -^ arc cos (2m + cos a).
900. Применив формулу tga + tgp = ■i^+s^> запишем
второе уравнение так: ■ " =m. Заменив cos* cos у на
^Uj л COS У
cos (д: + у) + cos (х — v) f
—-—' •" A и xJty на a» получим
2 sin с
или
cosa + cos(jc—у)
2 Sin a
= m
C0S(X JfJ:
m
■cos at.
516
ОТВЕТЫ И РЕШЕНИЯ
901
Это уравнение распадается на два;
, /2 sin в
х —у в» 2im + arc cos (—
х—у ssx 2icrt — arc cosf-
sin з
cos a
m
► cos a
)•
Присоединяем к каждому из них уракнение х+у*=&, полу-
чаем две системы уравнений (см. предыдущую вала чу).
, a . I /2stna
jct=* ил + -j "Г 7 агс cos \
Отв.
, а I /2 Sill a
, « —КЛ4-Т—2 arccos("17~
. а | /2 Sin а
«л + -j — -j arc cos^—-—
. а . I /2 Sin а
y9«> —м 4.^4..are cos(~—
л:,
► cos к),
► cos a),
► cos a
► cos а ]
о-
о-
901. Решается как предыдущая задача.
Onus: х% a» j (4л -f l)t >i ™ —■*л;
АГ2 — ил, y9 в —- j (4л — 1).
902. 1ак как 1ш2°и 4в1бг, то данную систему можно
ааписать так:
isln х + cos у ■= 0,
sln^jc-fcos^y— i,
откуда получим
I) sinxea-jf cosy» — -у и 2) sin л: «в — ^р со$у=*-г.
Отв. х, — 180°п + (— 1)»30\ Ух _ 360°п + 120°;
х,в180°л — (—1)»30°, уо«360°л:Е Ы)в.
903. Второе уравнение можно представить в виде
sin х sin у
cos г cos у
где в силу первого уравнения sin х sin у е»
I
АУГ
003 ГЛ. 12. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ 517
Получаем систему уравнений:
cosjrcosy = ^f sin*slny = —.
Складывая и вычитая их почленно, получим
cos(x— У) = у$ и C08^+Jr>™27f'
откуда
jf4-v = 2icm zfcarccos—=. я—у = 2itfc =£ —,
• -^ 2y2p 4
где m и fe —произвольные целые числа. В каждом ив этих
уравнений можно взять любой из внаков dz.
Замечание. Числа m + k и т —-k тоже целые, но не
вполне произвольные (если одно из них чётное, то и другое чётное,
а если одно из них нечётное, то н другое нечётное)»
Отв. 1) х = wi+ — arccos—= + —,
' 2 2-|/2 8
y = it/-|- — arc cos—=——;
' П 2 2УТ 8
2) Jt = iui-4—arc cos—7= ,
^ 2 2/7 8'
у = */-+- —arc cos—-7= + —:
3) л*— ил —— arc cos
I
к
2 гут^в'
1 l a
не/ — — arc cos-
2 2УТ 8'
4) x =» ил — — arc cos —^ ——f
2 2^2 8f
у a «f_—arc COS —= -f. — -
где «=m + *i / = m—fc (in и ft —любые целые числа).
518 ОТВЕТЫ И РЕШЕНИЯ 904
904. Возведём в квадрат обе части каждого из данных
уравнений и сложим почленно. Получим
1 = 4 sin*у + j cos*у или 1 = 4(1 — cos2 у) + 4- cos3 j\
откуда cos2y = -r- и sin2^ = —. В каждом из выражений
2 I
cos^y —— —т=- и sin у =а z*z -7=" можно взять любой знак
У 5 у 5
(так что в пределах от 0 до 360° угол у может иметь че-
тыре значения). Подставляя эти значения в данные уравнения,
находим, что углы х и у удовлетворяют одному из следую-
щих четырёх соотношений:
1 2*2 1
i)cos, = _ -х-^. «о.,-^. -шу-уу;
2)cosx=jf sta*=-7f'C0S^7r' siay~~7f;
12 2 1
3)cos*=.-_,sta* = _, cos,— ^.sln,-—;
4, cos* ^ -n* —^. cosy -^, sin, J=J
Рассмотрим первое из них. Если взять отдельно равен*
ство cos х = —т=г. то оно даёт х =а 2яя ztr arc cos -7=- •
Но (по определению главного значения арккосинуса) угол
<р = arc cos -у=т принадлежит первой или второй четверти,
где функция синус всегда положительна. Значит, нужно
сохранить только знак плюс. Действительно, из равенства
2
х = 2яд ± <р следует, что sin х = ± sin 9 = — —-р=-.
2
Между тем во взятом нами первом соотношении sinjc = —р=
(а не у=\щ То же имеет место для угла у, так что в случае
соотношения 1) мы получим
1 2
^s^iwt-j-arccos-rn, у = 2Tta1+arccos-?=f
Yo < Yb
90S гл. 13. ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ 519
где а и пг — любые целые числа. Рассуждая так же, най-
дём, что в случае второго соотношения
1 2
х — 2ш — arccos-7=, у = 2шх — arc cos -=.
и аналогично для третьего и четвёртого соотношений.
Отв. х = 2w zt= arc cos fdz -j=. J,
у == 2ялг ±: arc cos Л±: -у=Л,
где знаки в скобках одни и те же для х и для у и знаки
перед аркусами также одинаковы.
ГЛАВА 13
ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
905. Имеем
arc sin (— ¥~) = — -jj-, arc ctg (— 1) =
arc cos -7= = — , arc cos (—l) = ic.
/2 4 J
3n
4
Отв, -тг«
о
906, Угол © = arc cos л: заключён между 0 и 180° (по
определению главного значения арккосинуса). Значит, sin о
полежителен (или равен нулю). Имеем cos <р = xt откуда
sin <p = -|-Vrl—х2 (перед радикалом берётся только внак
плюс). Следовательно,
tg<p= ~* , т. е. ig(ш cosх) = ¥—-??-,
что и требуется доказать.
907, См. решение предыдущей ,вадачи.
908, Положим arc ctgf—— W<p, так что ctg<p = —4-
Угол <? заключён между 90° и 180° (ибо главное'значение
520 ОТВЕТЫ И РЕШЕНИЯ 9°9
арккотангенса заключено между 0 и 180°). Требуется найти
sin-^. Применим формулу
где из двух знаков ± нужно взять только внак -{- (ибо
угол -— принадлежит первой четверти). Предварительно нужно
найти cos<p по формуле
Ctga
cos а ?== -—
=fc Vi+Ctgaa '
получаем
COS Ср =
У1 + ш
(перед радикалом берём только знак плюс, так как <р при-
надлежит второй четверти). Теперь находим
sin-?
/" 1 — cos у 1 / 1 + 5 2
2~ V 2 — V 2 —/5"
0me- sin[^arcctg(_T)]=^-
909. Положим arc sin Г ~-1 = <р, так что sin ?=а
2VT
—, L— # угол « заключён в пределах между —90° и 0°
о
(так как главное значение арксинуса заключено между —90°
и +90°). Требуется найти sin-|-. Эта величина — отрица-
1ельная. Поэтому в формулЬ
■т-*/1
sin- — а-соза
2
нужно удержать только знак минус. Получаем
W3 ГЛ. 13. ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ 521
где
(перед радикалом берём только внак плюс!).
910. Угол cp==arccosf — у] заключён между 90° и 180°
(см. решения двух предыдущих задач). Значит, ctg-|- поло-
жителен, так что
Clg 2 К 1 —cos?
(перед радикалом берётся только внак плюс). Сюда подста-
4
вляем соз <р = — у.
Отв. ctg[~-arccos(— у)] = "тх^
911. Так как
* У"3 it . УЗ" тс
то имеем
«(••т-т-т)-*т—'•
Отв. —1.
912. Имеем
arc tg УЗ = i и arc cos -^ = -j •
Дальше — как в предыдущей задаче.
Отв. —-чр.
913. Отв. ~.
522
ОТВЕТЫ Н РЕШЕНИЯ
914
914. Положим
arctg(3 + 2 /2) = а, (1)
arctg^ = p. (2)
Требуется доказать, что
e-p-i. (3)
Найдём tg(a — р):
gK ?) 1 + tgatgP»
с прмощью (1) и (2) получим
tg(«-P) = IT^T^1' №
l + (3 + 2^2)il£
С другой стороны, из (1) и (2) видно, что каждый из углов
аир содержится между 0 и ■£■ t причём a > Р (ибо
3 -\- 2 Y2 > -^- J; следовательно, угол a — р заведомо лежит
между 0 и -j> так что из (4) получаем a — Р = х> что
я требовалось доказать.
Замечание. Для доказательства того, что угол a — р равен
именно —, т. е. 45° (а не 225° и не —135° и т. д.), можно было бы,
пользуясь таблицами, непосредственно найти углы а и р. При этом
можво ограничиться грубыми приближениями (например, учитывать
только градусы). Так, положив |/Тяь 1,4, найдём a^arctg5,S, что
составляет около 80° (погрешность заведомо не превышает -^ ).
Точно так же найдём P^arctg0,7, что составляет около 35° (погреш-
1°\
ность тоже заведомо меньше чем -^ ). Следовательно, а —р не от-
личается от 45° более чем на 1°, а значит, в точности равеи 45°.
913 гл. 13. ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ 523
915. Положим
arc cos у j = a, arc cos g^=- = 3 !).
так что cos a =a у у и cos?« * _Г . Каждый из углов
аир принадлежит первой2) четверти. Требуется доказать,
что а — ? = £.
Найдём sin (а — £), для чего предварительно вычислим
sin а а 1^1 — cos3а и sin р = }Л— cos2?
(перед каждым из радикалов берём только знак плюс, тач
как а и Р принадлежат первой четверти). Находим sin a =s —-
и sin?«=j/ Ь~х1 , так что
Докажем, что найденное иррациональное выражение
равно -о". Для этого преобразуем «двойную иррациональность»
V Ъ — 2УЪ = У 5—V^24. Преобразование можно выпол-
нить по формуле
(при Л = 5, 5 = 24); мы получим
-а
j) Можно обойтись и без введения вспомогательных величин
а н р и решить задачу таким способом, который приведён в заме-
чании к задаче 914.
») Главное значение арккосинуса лежит между Они/
524 ОТВЕТЫ И РЕШЕНИЯ 916
Но проще представить подкоренное выражение 5 — 2 J/15
в виде 3 + 2 — 2 /2 . /3~= (V$ — V%)а. и T0™a имеем
Кб —21/"б = К(/3—1/*2)2=/3 —/2 1),
Поскольку каждый из углов а и Р лежит в пределах от О
до у» угол а — Э заведомо лежит в пределах от — -я-
яо +-?>-, а тогда из равенства sin (а—Р) = тг следУет
а — Р = тг» что и требовалось доказать2).
916. Пусть (см. две предыдущие эадачи)
А=р, arcsir.-^
.4 . 5 0 .16
arc sin -jr- s= a, arc sin -^ = p, arc sin -r^- = f.
Тогда
4 3 . D 5 a 12
sin a = -, cos a = ^; sin P = -yg-, cos p = -^j
16 63
sinn-—, cosT = -g5-.
Отсюда
i / ] оч 4 12 , 3 5 (53 / , оч 16
sta(a + 3)-7-ir + -g-.1a-^ и cosCe + p)-^
Оба угла аир принадлежат первой четверти; поэтому угол
ot-J-P заключён между 0° и 180°, а так как косинус угла
а + Р положителен, то а + Р принадлежит первой четверти.
Кроме того, cos(a-j-P)== sin 7 и sin(a-f-P) = sin (~—-*п.
Поэтому a + Р и "о" — Ч могут отличаться только на 2ъп,
а так как -=- — f тоже принадлежит первой четверти, то п = 0.
Следовательно, а + Р^-о—К* т* е- а + Р"ГК==2'» что
и требовалось доказать.
J) Число УТ— 1^2 положительно.
а) Если бы вместо sin (a — (J) мы вычислили cos (a — р), то
нашли бы cos (a — Р) =» -*-*—; между — -*• и 4- -к- мы имели бы ава
значения а— р. именно —•£■ и + -г*; поэтому пришлось бы пред-
варительно установить что а>р, т. е. что cos а < cos р.
91? ГЛ. 13. ОБРАТНЫЙ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ 525
917. Имеем arccos-^ = у; обозначим arc cos (—у) че-
рез £, так что cos ? = — у. Угол Р содержится между ^- и я
(см. три предыдущие задачи). Поэтому
sinfie + |A-(i)a [а не -|Л-(7/].
т. е.
sin ? = 11/3.
Находим
cos(j + p)= cos J cos p — sin -J sin 3='
1 / i \ /3" 4,д 13
Чтобы доказать справедливость данного тождества, нужно
ещё убедиться в том, что угол -т + Р принадлежит второй
четверти ибо угол arc cos f 777 в правой части равенства
лежит во второй четверти . Угол (3^= arc cos f — у J заключён
между -J и ff; следовательно, угол 4- + Р содержится между
~ и -—. Из этой оценки, однако, ещё не следует, что угол
-5--+-Р принадлежит второй четзерти (ведь угол -g- находится
уже в третьей четверти). Но если учесть, что —у>—-л-
и что, следовательно, arc cos (— у J < arc cos (— у J, т. е.
arc cos f — у J <"g-f то отсюда следует, что -g- -f-
+ arc cos f — у J < те. А так как по предыдущему этот угол
больше, чем -g-, то он лежит во второй четверти. Этим
данное тождество доказано.
526
ОТВЕТЫ И РЕШЕНИЯ
№
Замечание. Принадлежность угла -к- + Р второй (а ие третьей)
четверти можно доказать еще" следующим образом: имеем
sin (^r -f р J =» sin ^- cos р + cos ~ sin р =■
Так как это число положительно, то угол -q- + P принадлежит вто-
рой четверти.
918. Положим arctg—= а и arctg — = ?, откуда
tga = -g- и tg р = —. Вычислим
Предварительно находим
2.-1
tg2a = . 5 5
i
-{if
12
а затем
tg(2a + P)" 5 %
12 + 4 32^
43
l^T2 "Т
Углы a = arctg-j и |3 = arctg-j принадлежат первой чет-
верти, но из этого ещё не следует, что угол 2а + р при-
надлежит первой (а не третьей) четверти. Но если учесть,
что каждый из углов аи^ меньше, чем — (так как их тан-
генсы меньше чем 1), то отсюда следует, что 2а + S меньше
чем -р, а так как сверх тога tg (2а-|-(3) = -^- положителен,
то 2а 4-Р лежит в первой четверти, т. е. 2a-|-{il = arctg£5f
что и требовалось доказать»
Замечание. Вместо того, чтобы доказывать, что угол 2a-f-{J
не выходит за пределы первой четверти, можно найти этот угол
(хотя бы очень грубо) с помощью таблиц (см. замечание к задаче 914).
Получим: а = arc tg -g-« 11% р = arc tg у ^ 14°, та*, что 2а + р«36%
921 ГЛ. 13. ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ. ФУНКЦИИ 527
919. Положим
. 1
arc tg j:
=:а, arctgy = p,
и найдём сначала
затем
и, наконец,
lS V* ~Г Yt —
1 -
tgl(« + P) + Tl =
tg[(a + ? + ^) + S]
. 1
arc tg у = iT-
+ "5 4
1 1 — 7 '
■3-5
1 + 1
7+7 7
; 4 r^ 9
l-yy
1+1
9 + 8
-- 7 Г" =
arctg-»-
1.
= 8
Как в предыдущей задаче, докажем, что угол <x + {3 + 1f + 21
лежит в первой четверти. Следовательно, а-|-{3-{-К+8 = -т«
920. Имеем arctg(xa— Ъх—3) = -|-, откуда х* — Зл;—
— 3 = tg — , т. е. л:2— Ъх — 3 = 1. Отсюда находим хг = 4;
х2 = — 1.
Отв. *! аяя 4; ха = —: 1.
Замечание. Если бы вместо уравнения arc tg (л:3—Зл:—3)=-£
q
мы имели уравнение arctg(A;2 — За: — 3) = — — , то такое уравне-
ние не имело бы решений, так как главное значение арктангенса не
может равняться —-j-. Если ие обратить внимания на это обстоя-
тельство, можно получить то же уравнение х2 — Зл: — 3 = 1, но
кории последнего уравнения не годятся.
921. Имеем
arc sin (*2 — 6л: -f 8,5) = Jj.,
откуда x2 — 6x-j-8,5 = 0,5.
Отв. х. = 4; х2 = 2ш
528 ОТВЕТЫ И РЕШЕНИЯ 922
922. Взяв тангенсы обеих частей уравнения и учитывая,
что tg (arc tg а) = а, получим
(х + 2)-(х+\) _.
l + (* + 2)(.v+l)—1*
откуда хх = — 1; х2 = — 2. Проверяем эти корни. Если
X = — 1, то
arctg(x-f-2) = arctg 1 = -^- и arctg(x+ l) = arctgO = 0#
гак что данное уравнение удовлетворяется. Так же докажем,
что н второй корень годится.
Отв. хх = — 1; х$ = — 2.
Замечание. Почему проверка необходима, видно из следую-
щего примера. Рассмотрим уравнение
arctg(A: + 2) — arcig(* + l)«-|?,
отличающееся от данного только значением свободного члена. За-
ранее нельзя сказать, что оно не имеет решений (ср. задачу 920).
Пели бы, скажем, arc tg (х + 2) равнялся — •?, a arc tg (jc -f- О был pa-
o
oeii jx к (эти значения могут быть главными значениями арктангенса).
го левая часть равнялась бы——. Взяв тангенсы обеих частей
рассматриваемого уравнения, мы снова получим уравнение
(л:+ 2) — (JC+ 1)
. * j_«>\/y!i_ i\e *■ н0 теперь ни один из корней jct = —1,
1 "Г \х ~Т~ *М-* "т~ 1)
xj =—2 не годится.
См. ещё замечание к задаче 925.
923. Берём тангенс обеих частей уравнения. Предвари-
тельно находим (см. предыдущую задачу):
1 \t* J
«(*■"**)-Г=Щ
4
и тогда получаем т-я1, Корень этого уравнения есть
,+i
* = •=-; его нужно проверить (см. замечание к предыдущей
задаче). Подставляя в левую часть уравнения * = у, полу*
924 гл. 13. ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ Б29
чаем 2arctg-^— arctgy. Угол a = arctg-g- заключён в пре-
делах между 0 и j (так как tga = -g-<l). В тех"1ке
пределах лежит угол р = arc tg у „ Угол 2<х принадлежит пер-
вой четверти, а угол 2а — р лежит между —-у и у. Но
tg(2a — P)=U так что 2а — (3 = и:л-|--^. Но только при
и = 0 угол 2а — Э попадает внутрь найденных нами границ.
Следовательно, данное уравнение удовлетворится.
Отв. х = у.
924, Возьмём синусы от обеих частей равенства. Можно
положить 2
arcsin—— = а и arcsin|/4—л; = (3
Ъух
(см. решение задачи 915); но можно обойтись без них, вос-
пользовавшись формулой sin (arc sin х) = х (она непосред-
ственно вытекает из определения арксинуса) и формулой
cos (arc sin jc) = ^1—x*\ Следовательно, синус левой ча-
сти равен
и данное уравнение принимает вид
зуи v зт^ v х з-
2
Решив его, находим х«у. Этот корень нужно прове-
рить (см. замечание к задаче 922), т. е. нужно доказать
тождество _
arc sin у -g- — arc sin у -g- = arc sin -j.
Доказательство ведётся, как в гадаче 917.
Ошв, л; = -77.
L) Эта формула выводится следующим образом. Положим
aicslnAr = o, Тогда s\nv = x и cosa= У"1 — х\ Перед радикалом
Осрётся только знак плюс, так как угол a = arc sin х лежит в гра-
ницах от —90 до +90° (главное значение арксинуса!). Подставляя
вместо а выражение arc sin л:, получаем* требуемую формулу.
530 ОТВЕТЫ Й РЕШЕНИИ 925
925. Взяв тангенсы обеих частей уравнения, получим
а а — Ь
Т~7+Ъ _
l+a а
Ь а + Ь
откуда х=1.
Это значение надо проверить (см. замечание к задаче 922).
Подставляя х=1 в данное уравнение, получаем
arctgj-arCtgJ=|«=45e. (1)
Введём обозначение
arc\gj = <p. (2)
Здесь угол fy (главное значение арктангенса) заключён в гра-
ницах
— 90°<<р<90°. (3)
При этом обозначении имеем
arc tg Ц={ = arc tg *-|^| = arc tg tg (? - 45°), (4)
так что надо проверить равенство
9 — arc tg tg (<p — 45°) = 45°. (5)
Это равенство будет верным в том и только в том случае,
когда
arc tg tg (ф — 45°) = 9 — 45°. (6)
Равенство же (6) имеет место, когда угол 9 — 45° (главное
значение арктангенса) заключён в границах
— 90° < 9 — 45°<90°( (7)
т. е. когда
— 45°<9<135°, (8)
Учитывая неравенство (3), получаем для угла 9 более
тесные пределы
— 45°<9<90°. (9)
Из (2) и (9) находим
y = tg9>tg(-45°)f
т. е.
Т>-1. (Ю)
927 ГЛ. 13. ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ 531
Обратно, при -г- > — 1 угол ср удовлетворяет неравен-
ству (9).
Следовательно, данное уравнение имеет решение (лг=1)
при-т-> — 1. При у <—1 решений нет.
Например, при а==—Y%* b=l имеем
arc tg £ = arc tg (- /з) = - 60°;
агс «к J^jrJ=агс ^^fl^f да arc tg 3'732=75°*
так что левая часть данного уравнения равна -^135°, а пра-
вая часть при jc=1 равна 45°»
Отв. jc== 1 при -г > —1 ; уравнение не имеет решения
при у <—1.
926. Возьмем косинусы обеих частей уравнения. Получим
(см. задачу 924) "^1—9х2 = 4#. Это уравнение имеет един-
ственный корень х = -г. Проверим его. Угол а = arc sin 3jc =
3
= arc sin -г принадлежит первой четверти; угол р = arc cos Ах =
4
= arc cos-?- принадлежит тоже первой четверти. При этом
о
sina = -?-; следовательно, cos a =-г-. С другой стороны,
4
cosp = -c-; следовательно, а = р.
Отв. х = ■=■,
о
927, Возьмем синусы обеих частей уравнения. Получим
Ох
13 '
й. Лз- — уд' п"Лов"Яй" *-*
"1з*
(см. задачу 924) 2^У*1 — -^^fT' откуда ^^ = 0,
.12 12 „
х2 = +?з' *з —— Ту- Проверяем эти корни
Отв. x = Q; jc = dt!2
532
ОТВЕТЫ И РЕШЕНИЯ
923
928. Из первого уравнения находим
т. е.
Принимая во внимание второе уравнение, получим
Из системы уравнений
tgл:-f-tgj/ = 2а, \gx\gy-a*
находим \gx = a\ tgy — a. Отсюда следует, что х =
= 180°# + arctga, 3/ = 180°/n + arctga, где я и т — целые
числа. Но лишь одно из них можно взять произвольным,
так как согласно первому уравнению величина х-\-у, как
главное значение арктангенса, должна содержаться между
— 90° и + 90°.
Чтобы выделить годные значения п и т, подставим най-
денные выражения в первое уравнение. Получим
180°(w + m) + 2arctga = arctgy^~. (А)
Так как согласно условию |а|<1, то угол arctga
содержится между —45° и +45°, т. е. 2 arc tg а содер-
жатся между —90° и +90°. В тех же пределах содер-
жится угол arctg а (главное значение арктангенса). Сле-
довательно, эти два угла разнятся менее, чем на 180°. По-
этому равенство (А) возможно лишь при w+w = 0-
* Отв. х= 180°/z + arctga, у = — 180°>t + arctga.