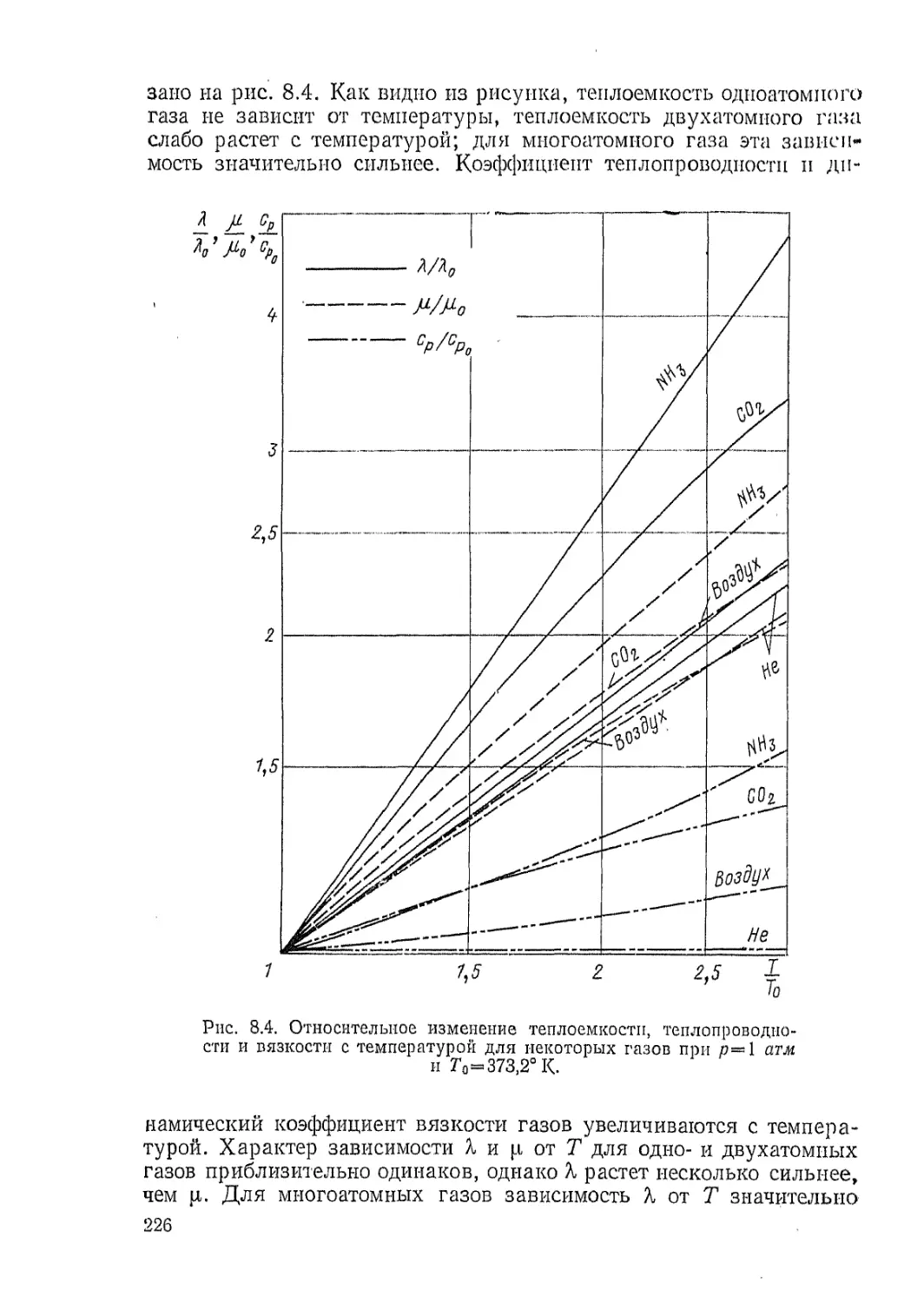
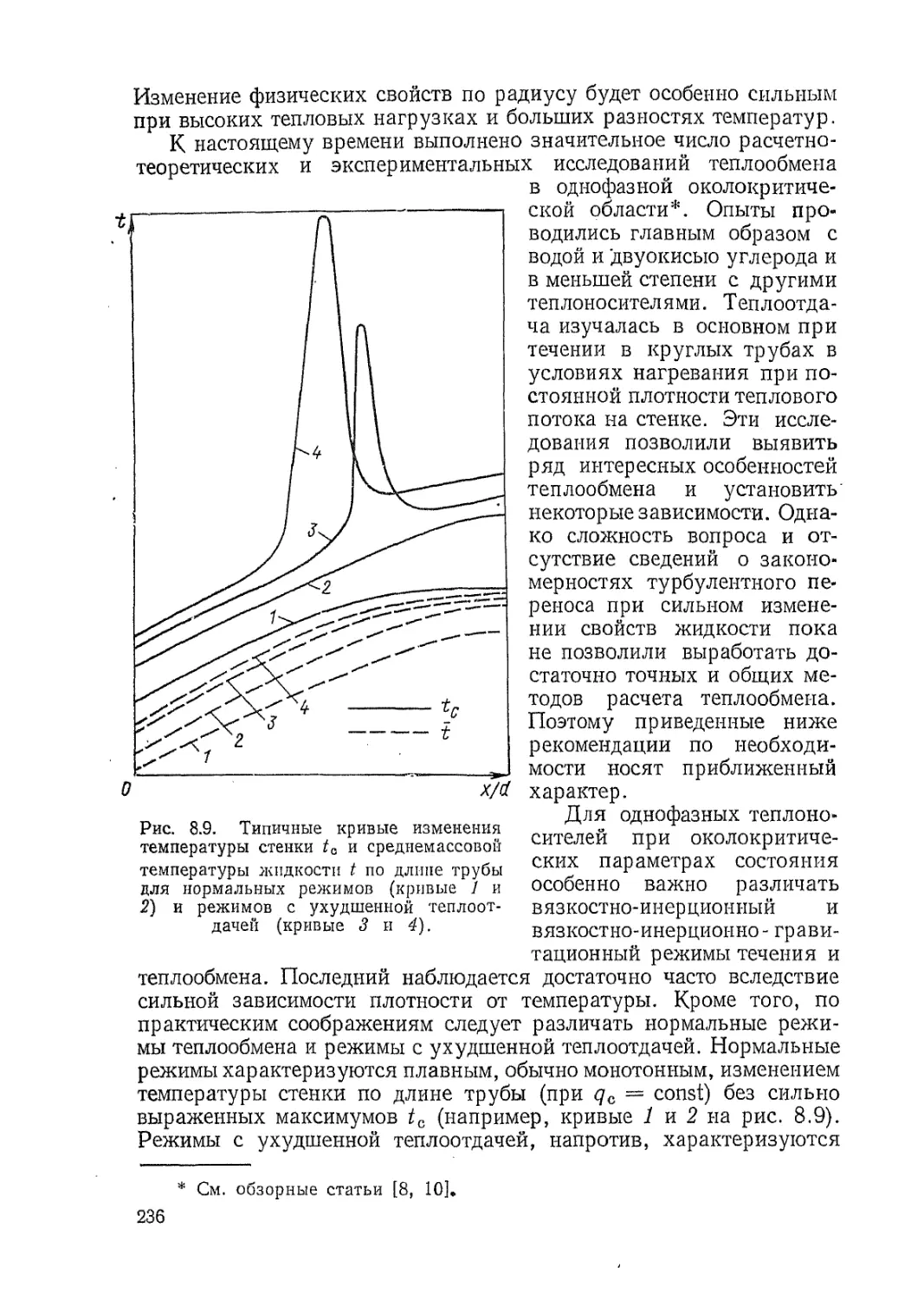
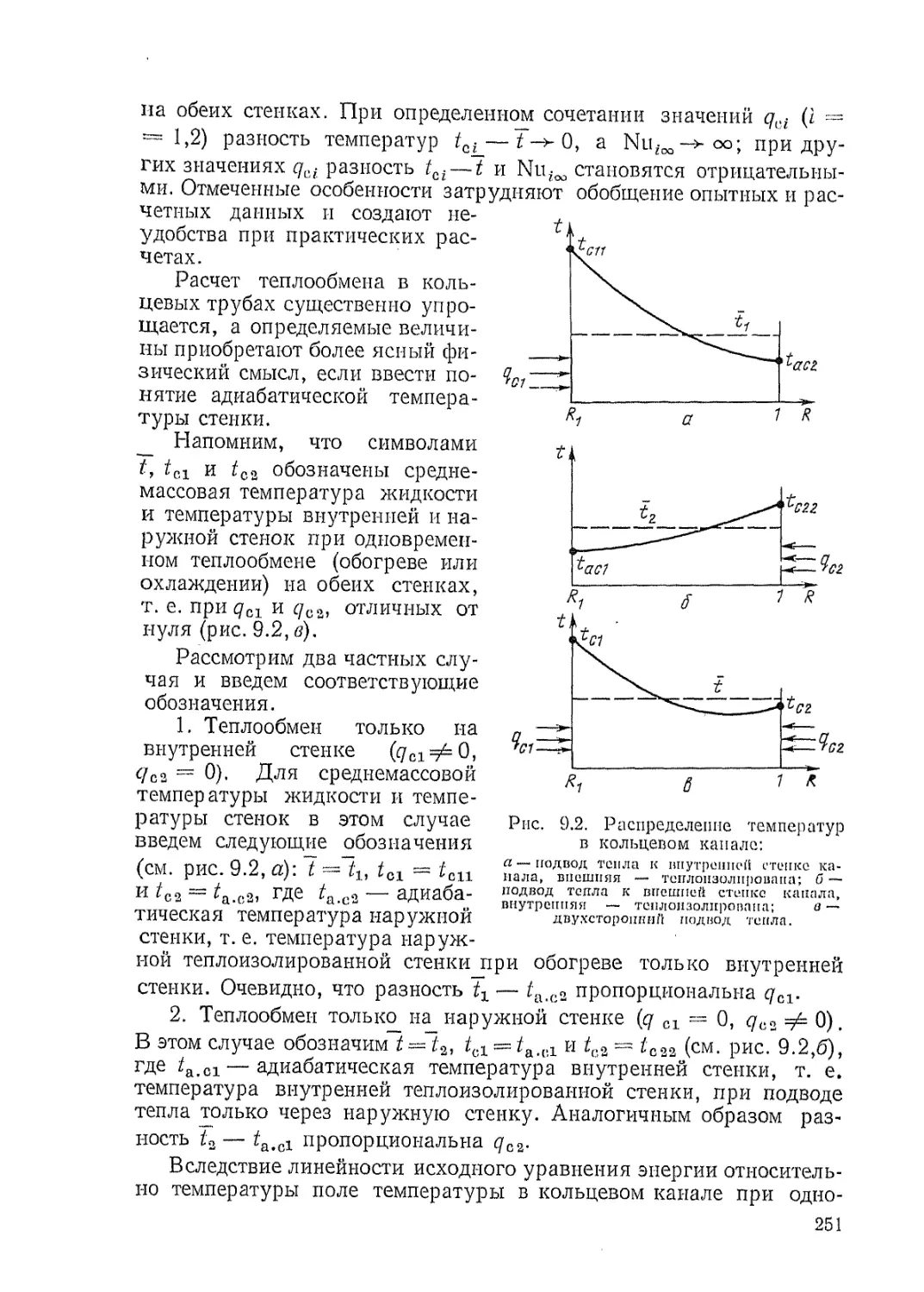
Автор: Петухов Б.С. Генин Л.Г. Ковалев С.А.
Теги: общее машиностроение технология машиностроения энергетика теплопередача гидродинамика
Год: 1974
Текст
Б, С. ПЕТУХОВ, Л. Г. ГЕНИН, С. А. КОВАЛЕВ
ТЕПЛООБМЕН
в ЯДЕРНЫХ
ЭНЕРГЕТИЧЕСКИХ
УСТАНОВКАХ
Под редакцией доктора технических наук
профессора Б. С. ПЕТУХОВА
Допущено Министерством высшего и среднего
специального образования СССР в качестве учебного пособия
для студентов высших учебных заведений
МОСКВА АТОМИЗДАТ 1974
УДК 621.039.553.4(07)
Петухов Б. С., Ген и и Л. Г., Ков а-
л е в С. А. Теплообмен в ядерных энергетических
установках. Под род. Б. С. Петухова. Учебное пособие
для вузов. М., Атомиздат, 1974. 408 с.
В книге изложены основы теории и методы расче-
та процессов теплообмена в ядерных энергетиче-
ских установках. Рассмотрены процессы тепло-
проводности с внутренними источниками тепла; осве-
щены вопросы конвективного теплообмена и гидро-
динамики при движении в трубах (круглого и некруг-
лого сечения) однофазных теплоносителей с постоян-
ными и переменными физическими свойствами. Значи-
тельное внимание уделено особенностям теплообмена
в системах с газообразными и жидкометаллпческпмп
теплоносителями. Рассмотрены механизм п закономер-
ности теплообмена при кипении жидкости в большом
объеме и в трубах, а также элементы гидродинами-
ки двухфазного потока.
Изложение материала рассчитано на читателя,
знакомого с основами теплопередачи.
Рецензе и т ы: Кафедра теплофизики МИФИ;
кандидат технических наук
В. С. Осмачкин.
30315—010
П 034(01)—74 10—74
© Атомиздат, 1974
ПРЕДИСЛОВИЕ
Молодая, быстро развивающаяся область техники — ядерная
энергетика — предъявляет высокие требования к инженерам, заня-
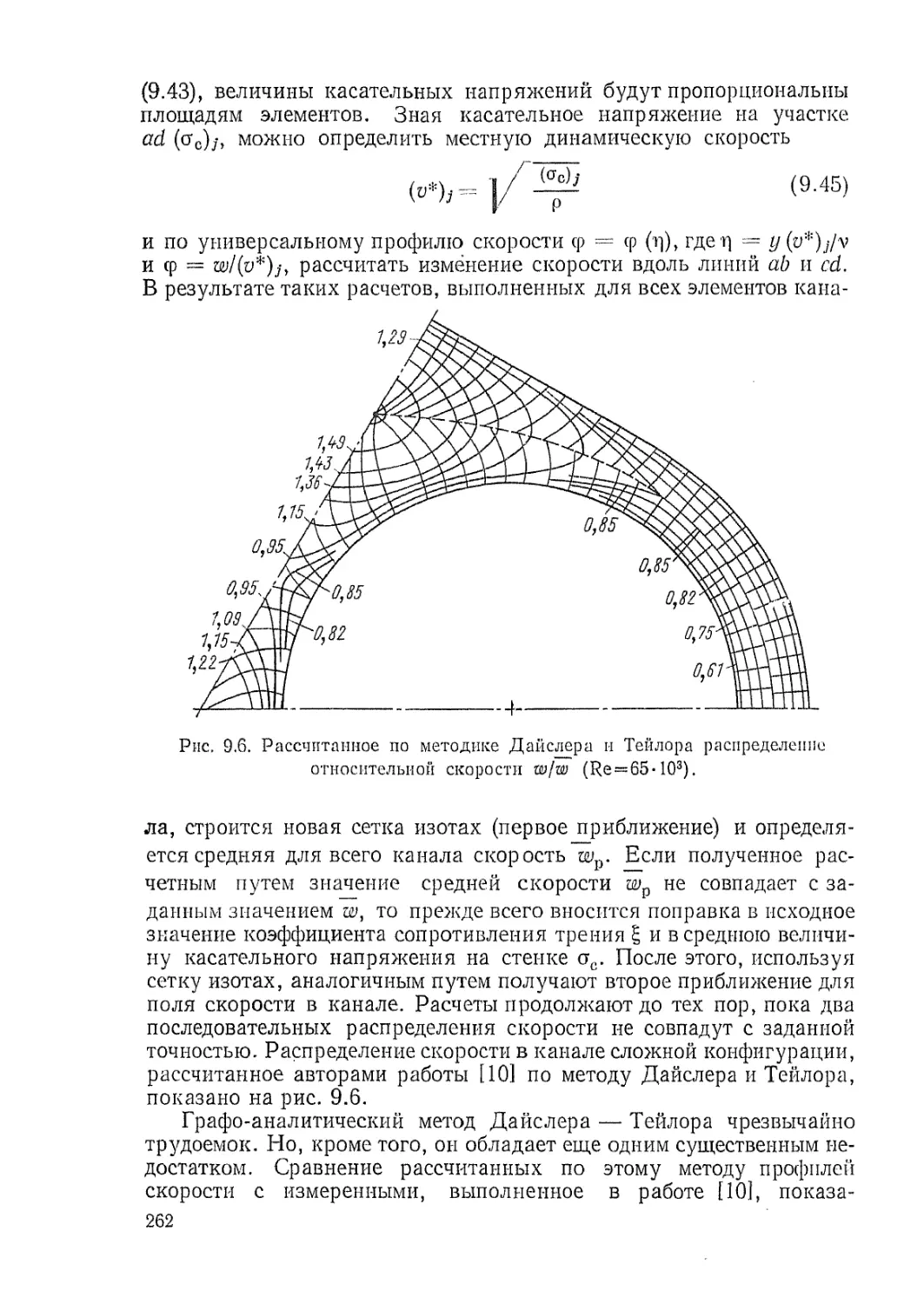
тым разработкой, проектированием и эксплуатацией ядерных энер-
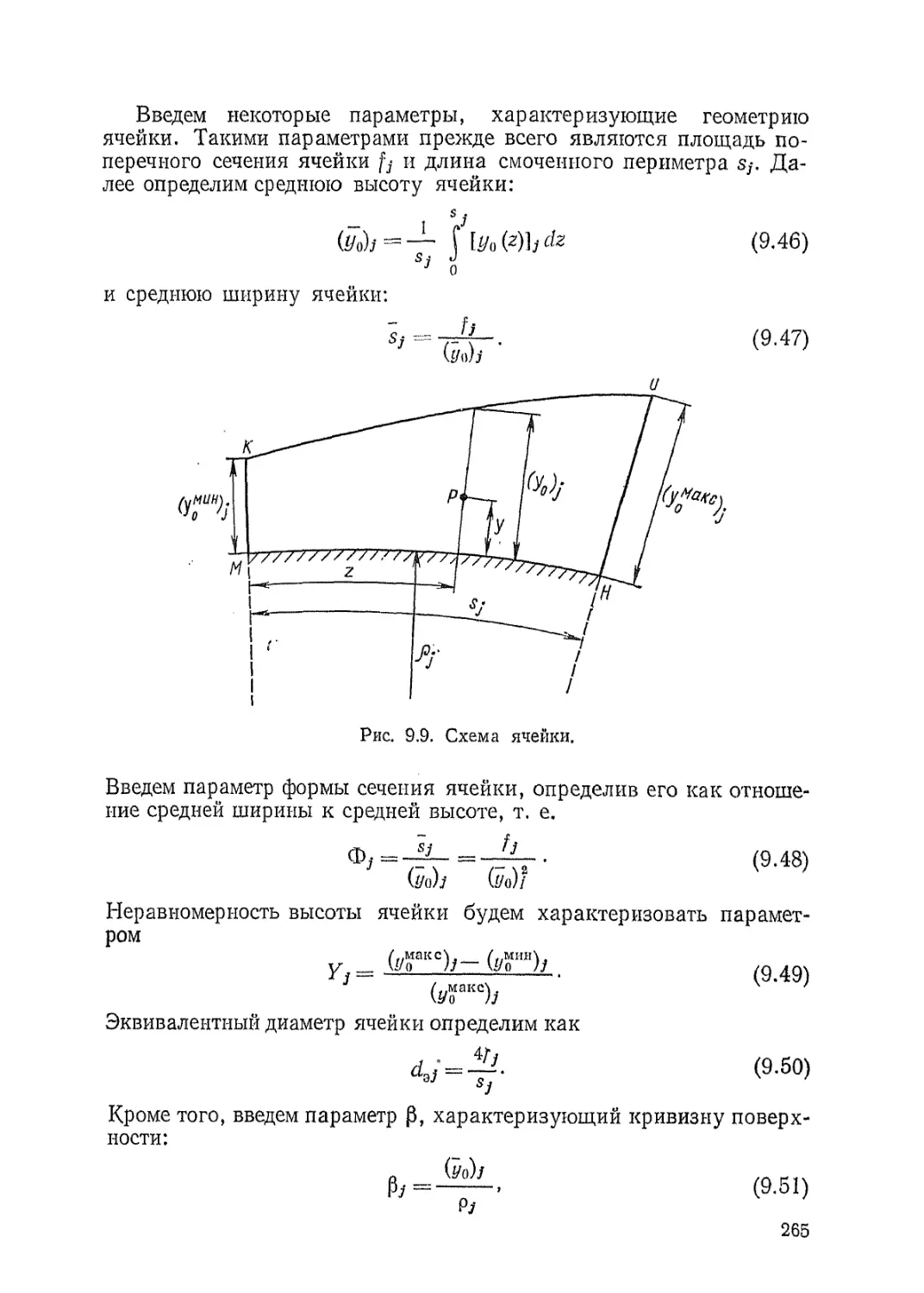
гетических установок. Среди научно-технических дисциплин, фор-
мирующих будущего специалиста, одно из первых мест принадлежит
теории теплообмена. Глубокие познания в теории теплообмена —
необходимое условие плодотворной инженерной деятельности в ядер-
ной энергетике.
Подготовка инженеров-специалистов по ядериой энергетике в
области теории теплообмена обычно осуществляется в два этапа:
посредством изучения общего курса теплопередачи и специального
курса — «Процессы теплообмена в ядерных энергетических уста-
новках». В общем курсе теплопередачи, так же как и в существу-
ющих учебниках по этому курсу, излагаются основы теории тепло-
обмена безотносительно к будущей сфере деятельности инженера.
В специальном курсе более полно и углубленно изучается ряд об-
щих вопросов теории теплообмена, составляющих научную базу
для анализа и расчета процессов теплообмена в ядерных энерге-
тических установках, а также рассматривается ряд специальных
вопросов теплообмена, характерных для ядерных энергетических
установок (главным образом для ядерных реакторов).
Предлагаемая вниманию читателей книга предназначается в ка-
честве учебного пособия по курсу «Процессы теплообмена в ядерных
энергетических установках». Она написана на основе курса того
же названия, который в течение ряда лет читается в Московском
энергетическом институте, и соответствует его программе. Разумеет-
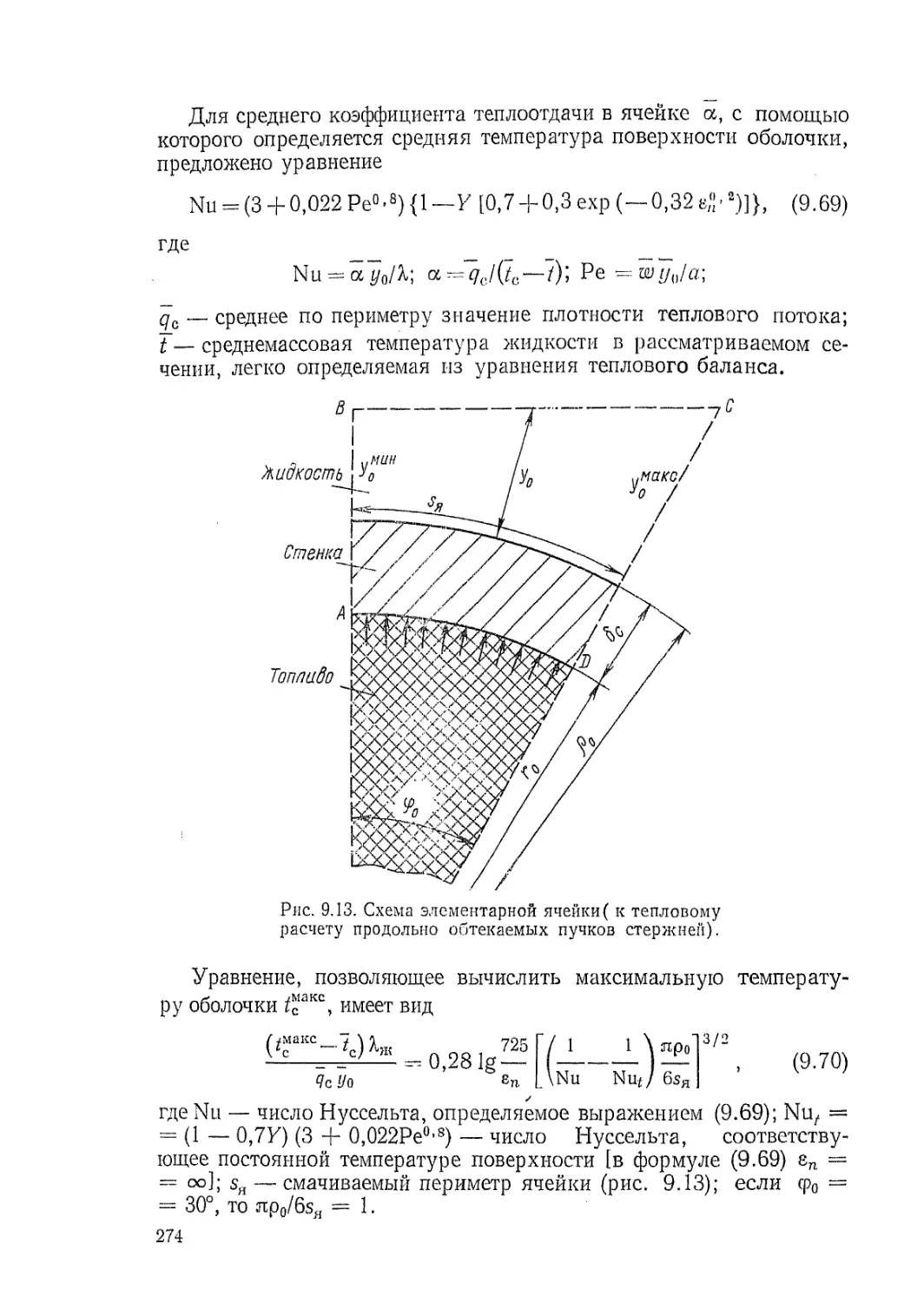
ся, в процессе работы над книгой ряд разделов был переработан и
дополнен, некоторые вопросы уточнены.
Объем и характер книги, как и соответствующего учебного
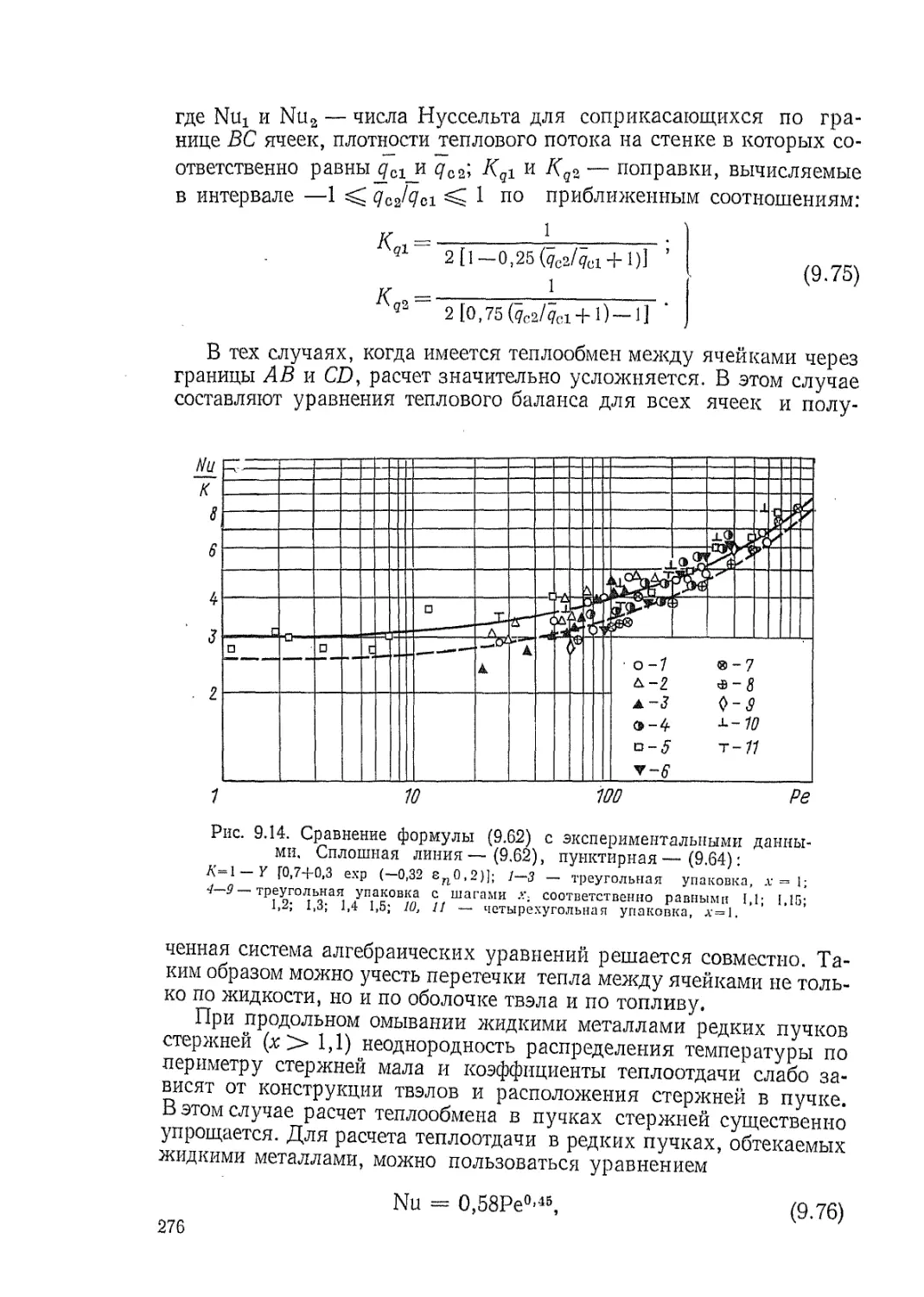
курса, естественно, не позволили рассмотреть все вопросы тепло-
обмена, возникающие при расчете ядерных реакторов разных типов
и назначения. Из широкого круга задач теплообмена, характерных
для этой области техники, выбраны лишь основные, чаще всего
возникающие при разработке современных либо перспективных
реакторов. Рассмотренные в книге задачи составляют основу тепло-
вого расчета реактора. Однако тепловой расчет нельзя проводить
3
вне связи с физическим расчетом, конструкцией реактора, проблемой
надежности и другими важными вопросами, далеко выходящими
за рамки теории теплообмена. Поэтому тепловой расчет как система
вычислений и оценок, на основе которых принимаются технические
решения, в книге не рассматривается.
Книга написана в предположении, что читатель уже знаком с ос-
новами теории теплообмена. Однако в интересах методической це-
лостности и систематичности в изложении материала мы считали
правильным в тех случаях, когда это необходимо, кратко напоминать
положения или результаты, известные из общего курса теплопе-
редачи.
Хотя книга написана в качестве учебного пособия для студентов,
однако мы надеемся, что она будет полезна также аспирантам и ин-
женерам, работающим в области атомной энергетики.
Введение, гл. 4, 5, 7, 8 и §§ 9.1 и 9.2 написаны Б. С. Петухо-
вым; гл. 1, 2, 3, 6, 10, 11 и §§ 9.3, 9.4 и 9.5 — Л. Г. Гениным;
гл. 12, 13 и 14—С. А. Ковалевым.
Авторы признательны В. И. Петровичеву и В. С. Осмачкину,
взявшим на себя труд прочесть рукопись и высказавшим полезные
замечания и советы. Мы будем также благодарны всем, кто сочтет
необходимым направить нам свои замечания и предложения.
АВТОРЫ
ВВЕДЕНИЕ
Ядерный реактор, как и ядерную энергетическую установку
в целом, можно рассматривать как сложную теплообменную
систему.
В активной зоне реактора находится делящееся вещество, чаще
всего смесь изотопов 285U и 238U либо их окислов или карбидов,
и созданы условия, в которых осуществляется цепная реакция деле-
ния ядер. Высвобождающаяся при этом энергия в основном пре-
вращается в тепло вблизи места деления и может рассматриваться
как внутренние источники тепла. Цепная реакция, как известно,
поддерживается нейтронами, выделяющимися в каждом акте деле-
ния. В реакторах на быстрых нейтронах реакция происходит под
действием нейтронов, непосредственно испускаемых при делении
ядер и обладающих большими энергиями. В реакторах на тепловых
нейтронах испускаемые нейтроны предварительно замедляются
путем многократного столкновения с ядрами замедлителя, и деле-
ние ядер происходит под действием медленных, так называемых
тепловых нейтронов. В настоящее время реакторы на быстрых ней-
тронах находятся в стадии разработки и освоения и для энергети-
ческих целей используются реакторы на тепловых нейтронах.
Ядерное топливо может быть твердым, жидким или газообраз-
ным. В случае жидкого или газообразного топлива его обычно сме-
шивают с теплоносителем или замедлителем (если он есть), или
с тем и другим одновременно (гомогенные реакторы, газофазные
реакторы).
В современных ядерных энергетических установках исполь -
зуются гетерогенные реакторы. В активной зоне таких реакторов
твердое ядерное топливо распределено не равномерно, а сконцент-
рировано в тепловыделяющих элементах (твэлах). Последние пред-
ставляют собой пластины, цилиндры или шары из делящегося ве-
щества, заключенные в оболочки и размещенные на определенном
расстоянии друг от друга в активной зоне реактора. В реакторах
на тепловых нейтронах в активной зоне содержится еще один важ-
ный компонент — замедлитель (например, графит, обычная или
тяжелая вода).
Тепло, выделяемое в твэлах, переносится теплопроводностью
к их поверхности и воспринимается омывающим твэлы теплоносите-
5
лем. Нагретый в реакторе теплоноситель поступает в парогенератор,
здесь охлаждается и снова возвращается в реактор. Пар, получен-
ный в парогенераторе, используется в паросиловом цикле.
Существуют различные типы ядерных реакторов и энергетиче-
ских установок. Гетерогенные реакторы на тепловых нейтронах от-
личаются друг от друга видом топлива и степенью его обогащения
делящимися изотопами, материалом, используемым в качестве за-
медлителя, типом теплоносителя. В Советском Союзе получили рас-
пространение водо-водяные реакторы (ВВЭР) и водо-графитовые
Питательная
Вода
г
I
I
1
I
I
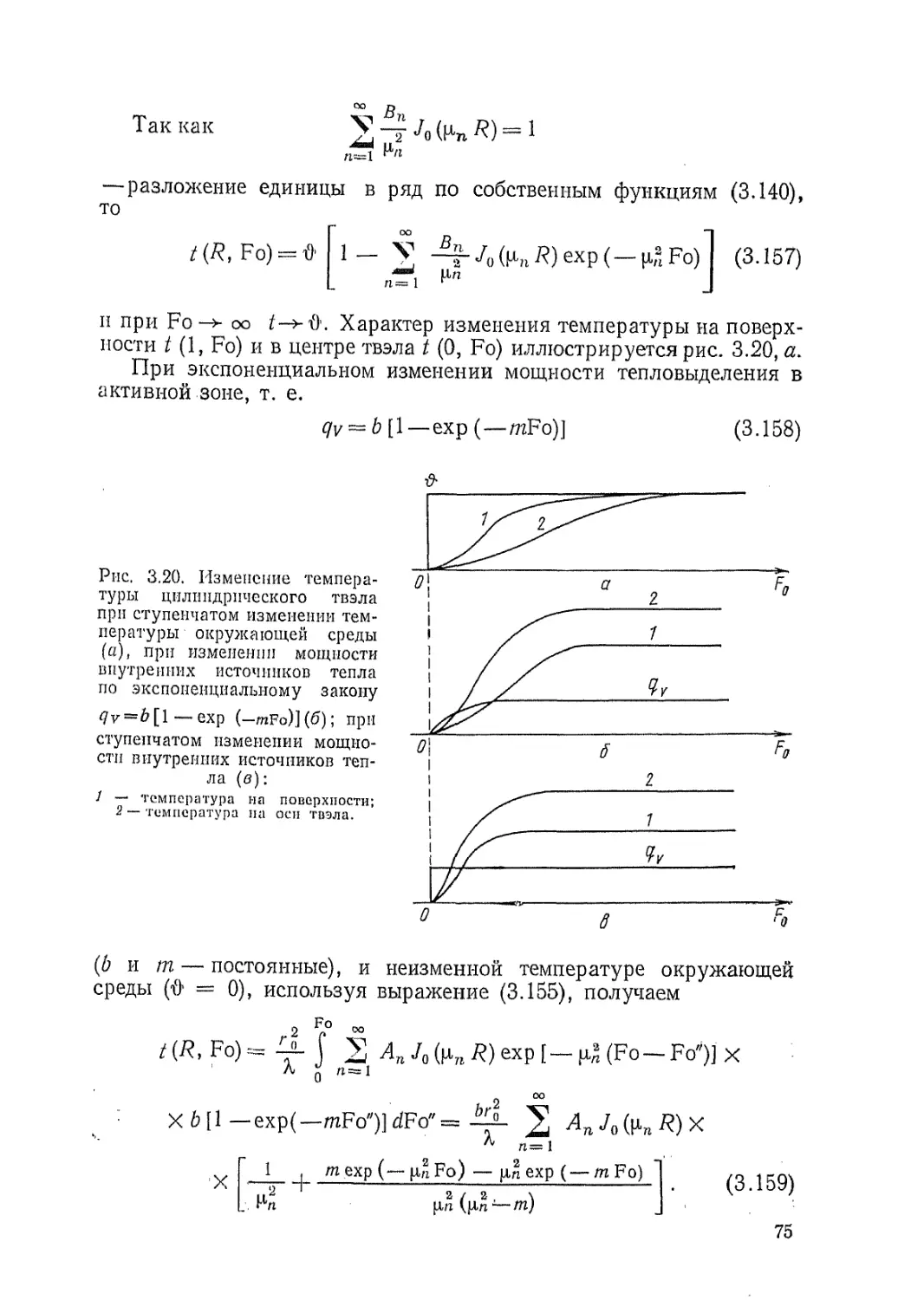
I
I
I
I
I
I
।
I
I
I
I
I
I
I
I
I
I
1
I
I
I
I
I
I.
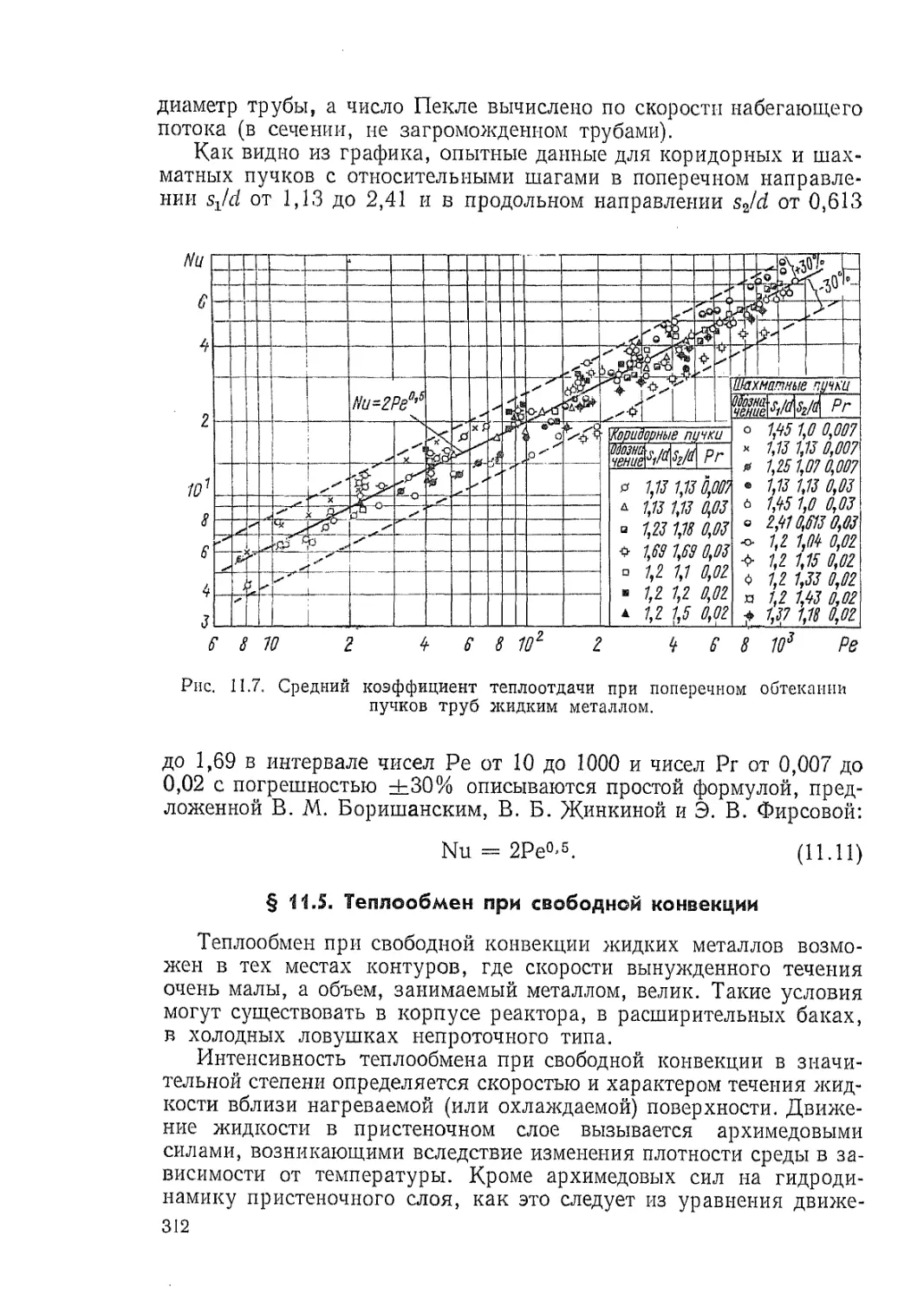
Рис. В.1. Схема отвода тепла из реактора
ВВЭР:
/ — биологическая защита; 2 — корпус реактора;
3 — кассеты с тепловыделяющими элементами;
'/ — регулирующий стержень; 5 — расширитель-
ный резервуар; 6 — парогенератор; 7 — цирку-
ляционный насос.
реакторы. В реакторах первого типа обычная (легкая) вода служит
одновременно замедлителем и теплоносителем. При этом вода нагре-
вается в активной зоне без кипения. Схема отвода тепла из реак-
тора ВВЭР показана на рис. В.1. В реакторах второго типа замедли-
телем служит графит, а теплоносителем — кипящая вода. В США
в основном используются реакторы того же типа, что и в СССР.
В Англии получили распространение уран-графитовые реакторы,
в которых замедлителем служит графит, а теплоносителем — газ
(двуокись углерода). В ЧССР работает реактор с тяжелой водой
в качестве замедлителя, охлаждаемый двуокисью углерода. Более
подробное рассмотрение типов ядерных энергетических установок
не входит в нашу задачу.
Основная цель теплового расчета реактора — определение тем-
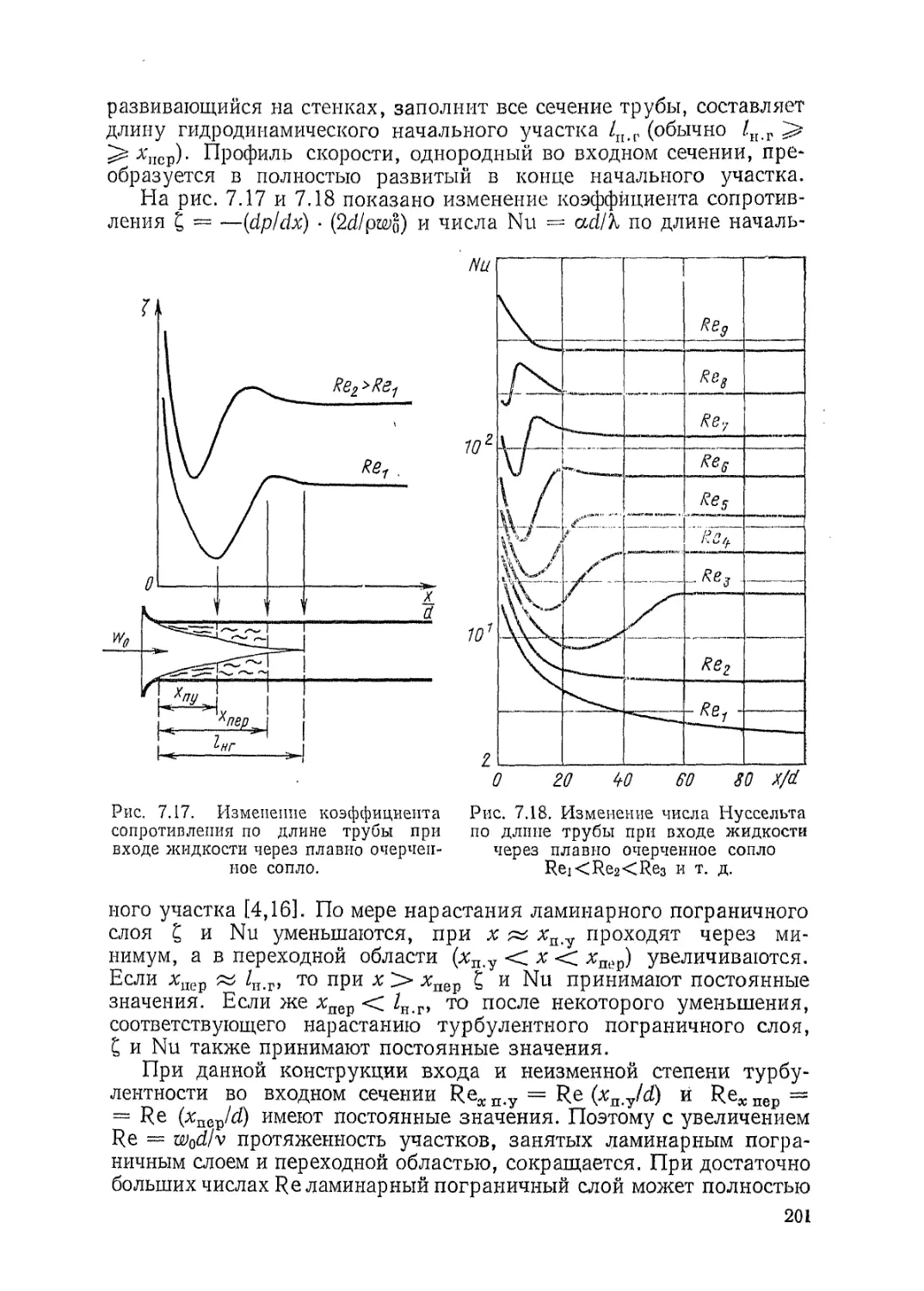
пературных полей в элементах его конструкции при нормальных,
переходных и аварийных режимах. Разумеется, тепловой расчет
тесно связан с физическим расчетом, поскольку ядерно-физическпе
характеристики реактора, например его реактивность, зависят от
6
'Температуры, плотности теплоносителя и других тепловых харак-
теристик. Однако вопросы теплообмена, составляющие содержание
этой книги, не зависят от физики реактора и могут рассматривать-
ея без непосредственной связи с ней.
Одна из основных задач расчета реактора — определение полей
'температуры в твэлах. Твэлы работают в очень напряженных усло-
виях: высокие температуры, большие мощности тепловыделения,
высокий уровень излучения нередко сочетаются с химически аг-
рессивными теплоносителями, омывающими поверхность твэлов.
13 месте с тем к твэлам предъявляются очень высокие требования
15 отношении их надежности, так как выход из строя нескольких
'гвэлов, а в реакторе их тысячи, может привести к аварийной ситуа-
ции. Надежность работы твэла в значительной степени зависит от
правильного выбора его температурного режима, так как от тем-
пературы сильно зависят прочностные свойства делящихся и кон-
еггрукционных материалов, интенсивность протекающих в топливе
радиационно-химических превращений. Например, повышение мощ-
ности тепловыделения сверх допустимых пределов может вызвать
плавление топлива в твэле, что повлечет за собой увеличение его
оОъема, усиление газообразования и, как следствие, нарушение це-
лостности оболочки твэла.
Из сказанного очевидно, насколько важен расчет температурных
полей в твэлах для правильного выбора их конструкции, опти-
мальных размеров и допустимых мощностей тепловыделения.
Перенос тепла в твэлах осуществляется главным образом теп-
лопроводностью, поэтому расчет температурных полей в твэлах
еостоит в решении задач теплопроводности при наличии внутрен-
них источников тепла. К решению таких же задач сводится и расчет
полей температуры в замедлителе, отражателе, корпусе реактора и
других его элементах, расположенных как внутри, так и вне актив-
ной зоны. Тепловыделение в этих элементах хотя и невелико по
сравнению с тепловыделением в твэлах, однако при недостаточном
охлаждении оно может привести к недопустимому повышению тем-
пературы, возникновению температурных напряжений и другим от-
рицательным последствиям.
Лишь немногие задачи теплопроводности в элементах конструк-
ции реактора допускают аналитическое решение. Некоторые из них
рассмотрены в гл. 3. Сложная геометрия конструктивных элементов
реактора, неоднородные граничные условия, зависимость мощности
'гепловыделеиия от координат и времени (для нестационарных за-
дач), необходимость во многих случаях учитывать зависимость
физических свойств материала от температуры — все это затрудняет
либо делает невозможным использование аналитических (точных
II приближенных) методов расчета. Поэтому расчет температурных
полей в элементах реактора обычно проводится численными метода-
ми с использованием ЭВМ. Нередко для этой цели применяют и ме-
'год электроаналогии (модели на электропроводящей бумаге, сеточ-
ные модели, электролитические ванны).
7
Сам по себе расчет температурных полей в элементах реактора не
представляет принципиальных трудностей. Однако для этого необ-
ходимо располагать граничными условиями, которые в основном
определяются конвективным теплообменом между поверхностью
элемента (например, твэла) и потоком теплоносителя.
Процессы конвективного теплообмена играют большую роль
в ядерных реакторах, парогенераторах и других элементах ядерных
энергетических установок. От величины коэффициента теплоотдачи
между поверхностью твэлов и потоком теплоносителя в большой
мере зависит допустимая мощность тепловыделения при безопасном
уровне температуры твэлов, а следовательно, и размеры активной
зоны реактора (если мощность его задана). Поэтому очень важно
изыскание методов интенсификации конвективного теплообмена в ак-
тивных зонах реакторов. Эта задача становится особенно актуальной
в связи с ростом единичных мощностей реакторов. По этим причинам
изучению конвективного теплообмена и тесно связанным с ним
вопросам гидродинамики уделяется большое внимание.
В ядерных энергетических установках наряду с однофазными
теплоносителями, такими, как вода, органические теплоносители,
газы, жидкие металлы, используются двухфазные теплоносители,
например кипящая вода. Могут найти применение диссоциирующие
жидкости и газы, теплоносители типа газовзвесь (газ, несущий
твердые частицы) и др.
Каждый из теплоносителей обладает своими достоинствами и не-
достатками, которые определяются его физическими свойствами,
особенностями теплообмена, технологией применения. Например,
для газов характерны сравнительно низкие значения коэффициен-
тов теплоотдачи, поэтому их использование возможно только при
разработке специальных методов интенсификации теплообмена.
Для воды (в особенности кипящей) и жидких металлов коэффициенты
теплоотдачи гораздо выше. Однако вода может быть нагрета до вы-
сокой температуры, желательной с точки зрения экономичности
паросилового цикла, лишь при высоком давлении, что усложняет
конструкцию реактора. Кроме того, вода замедляет нейтроны и по-
этому не может быть использована в реакторах на быстрых нейтро-
нах. Жидкие металлы лишены этих недостатков, но им свойственны
некоторые другие.
Большое разнообразие конструктивных форм твэлов и необхо-
димость их компактного размещения в активной зоне реактора при-
водят к различным, нередко сложным формам каналов, по которым
движется теплоноситель. Используются . каналы круглого, чаще
кольцевого сечения, однако типичны каналы призматической формы
и в особенности каналы, образованные зазорами между цилиндри-
ческими топливными стержнями (при их продольном обтекании).
В реакторах с газовым охлаждением поверхности твэлов, образу-
ющие каналы для теплоносителя, в целях повышения коэффициен-
та теплоотдачи и увеличения поверхности теплообмена обычно
снабжаются ребрами.
8
Для ядерных реакторов, при нормальных режимах работы ха-
рактерен стационарный конвективный теплообмен* при турбулент-
ном течении теплоносителя. При некоторых аварийных режимах
течение в каналах активной зоны может стать ламинарным. Поэто-
му при тепловом расчете реактора возникают задачи теплообмена
не только при турбулентном, но и при ламинарном течении.
Вопросы гидродинамики и теплообмена при ламинарном течении
однофазных теплоносителей в каналах сложной формы сравни-
тельно хорошо исследованы, а в случае турбулентного течения—
недостаточно. Здесь, несмотря на достигнутые успехи, необходимы
дальнейшие углубленные исследования.
Плотности теплового потока на поверхности твэлов, омываемых
теплоносителем, могут достигать больших значений (до нескольких
миллионов ватт на метр квадратный). В таких условиях физические
свойства жидкости и газа существенно изменяются по сечению, а
иногда и вдоль потока. Изменение свойств, особенно сильное для
теплоносителей при околокритических параметрах состояния, может
оказывать большое влияние на теплоотдачу и сопротивление и долж-
но учитываться при расчетах. Вопросы гидродинамики и тепло-
обмена при переменных физических свойствах теплоносителей еще
недостаточно изучены. В этой области в настоящее время ведется
большая исследовательская работа.
При переходных режимах и в аварийных ситуациях конвектив-
ный теплообмен в каналах реактора протекает в нестационарных
условиях. Нестационарность может быть вызвана изменением во
времени мощности тепловыделения, расхода теплоносителя и его
температуры на входе или всех этих параметров одновременно.
При сильном изменении параметров процесса во времени наблюдает-
ся существенное различие в закономерностях конвективного тепло-
обмена для стационарных и нестационарных режимов. Поэтому
расчеты нестационарной теплоотдачи, выполняемые в предположе-
нии, что эти закономерности одинаковы (так называемое квазиста-
ционарное приближение), в ряде случаев могут привести к сущест-
венным ошибкам. Пока этот вопрос еще мало исследован.
Для реакторов, охлаждаемых кипящей водой, на первое место
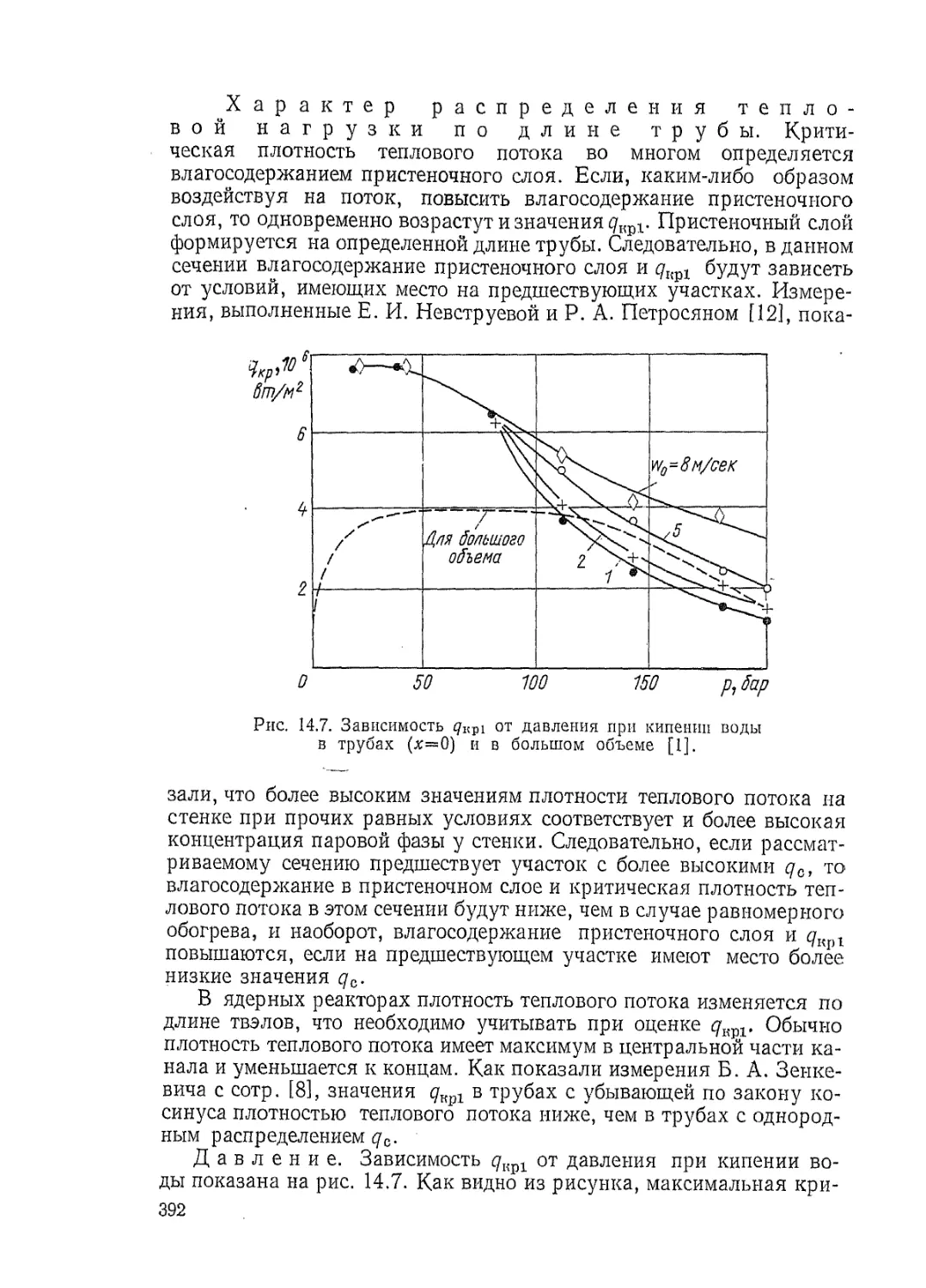
выдвигаются вопросы теплообмена при кипении и гидродинамики
двухфазного потока. В основе расчета кипящих систем лежат дан-
ные о структуре двухфазного потока и закономерности теплообмена
и сопротивления при течении паро-водяной смеси в обогреваемых
каналах. Определение максимальной мощности реактора и обеспе-
чение безопасных условий работы активной зоны требуют достовер-
ных сведений о критических плотностях теплового потока. Методы
расчета теплоотдачи и критических плотностей теплового потока
при движении кипящей жидкости в трубах и в особенности в кана-
* Стационарный в том смысле, что осредненные параметры потока (тем-
пература, скорость и др.) не изменяются во времени.
9
лах сложной формы (например, в пучках стержней) пока еще не-
совершенны. Поэтому в СССР и в других технически развитых стра-
нах в этой области проводятся широкие исследования.
Вопросы теплообмена при кипении и гидродинамики двухфаз-
ного потока важны не только для расчета кипящих систем, но
и для анализа переходных и аварийных режимов работы реакторов,
охлаждаемых однофазными теплоносителями (вода под давлением,
натрий). Например, при сокращении расхода воды через реактор
ВВЭР вследствие выхода из строя одного или нескольких насосов
может возникнуть кипение воды в наиболее напряженных кассетах.
Если интенсивность кипения невелика, то это не должно повлечь за
собой отрицательных последствий. В случае интенсивного кипения
может произойти нарушение гидродинамической устойчивости
параллельно работающих каналов и резкое сокращение расхода воды
в отдельных кассетах. При этом весьма вероятно возникновение кри-
зиса кипения, снижение коэффициента теплоотдачи и недопустимое
повышение температуры твэлов, что может вызвать их повреждение
или даже расплавление.
Высокие требования к безопасности работы реактора делают
необходимым тщательный теплотехнический анализ возможных
аварийных режимов для предотвращения или ослабления их от-
рицательных последствий. Чтобы продемонстрировать возникающие
при этом проблемы, рассмотрим еще один пример. Представим
себе хотя и маловероятную, но в принципе возможную аварию —
разрыв циркуляционного контура реактора ВВЭР. Вследствие
потери теплоносителя давление в корпусе реактора и циркуляцион-
ном контуре быстро понизится и часть теплоносителя испарится.
Активная зона реактора на короткий промежуток времени (до
включения аварийной системы охлаждения) окажется заполненной
паро-водяной смесью или паром низкого давления. Хотя цепная
реакция к этому времени будет прекращена, однако из-за остаточ-
ного тепловыделения и ухудшения теплоотдачи температура твэлов
может превзойти допустимый уровень с вытекающими отсюда тяже-
лыми последствиями. Процесс истечения паро-водяной смеси в рас-
сматриваемых условиях носит нестационарный и притом неравно-
весный характер. При истечении возможно образование и распро-
странение ударных воли.
Для анализа аварийных ситуаций необходимо уметь рассчиты-
вать нестационарные и неравновесные двухфазные течения, вклю-
чая сверхзвуковые, располагать данными о теплоотдаче и крити-
ческих тепловых нагрузках при кипении в нестационарных
условиях. Изучение этих сложных вопросов встречает большие
трудности и пока находится в начальной стадии.
Наряду с реактором в состав ядерной энергетической установки
обычно входят парогенератор и другие теплообменные аппараты.
При всем разнообразии конструктивных форм эти аппараты пред-
ставляют собой систему труб и каналов, гладких или оребренных,
по которым движется один из теплоносителей и которые омываются
10
другим теплоносителем. При расчете теплообменных аппаратов воз-
никают в значительной мере те же проблемы, что и при расчете
реакторов. Однако требования к точности расчета тёплообменных
аппаратов менее жесткие.
Сказанное дает представление об основных вопросах теплообмена
и гидродинамики, которые приходится решать в процессе разработ-
ки ядерных энергетических установок. При создании новых уста-
новок далеко не всегда можно провести достоверный расчет на ос-
нове уже известных данных и рекомендаций. Для получения необ-
ходимых данных обычно требуются специальные исследования про-
цессов теплообмена, особенно экспериментальные. Проведение та-
ких исследований требует глубокого понимания процессов тепло-
обмена и освоения методов их анализа.
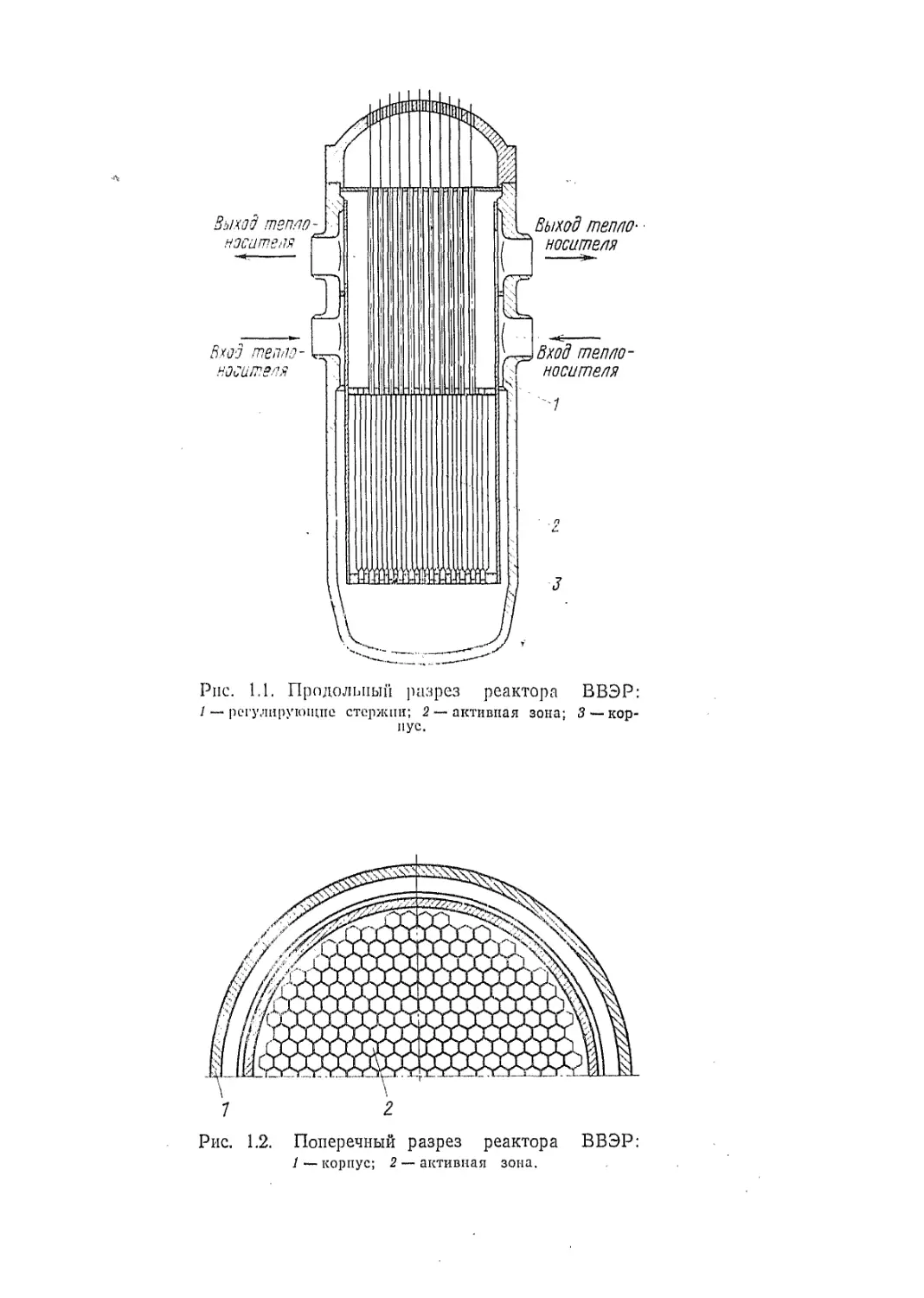
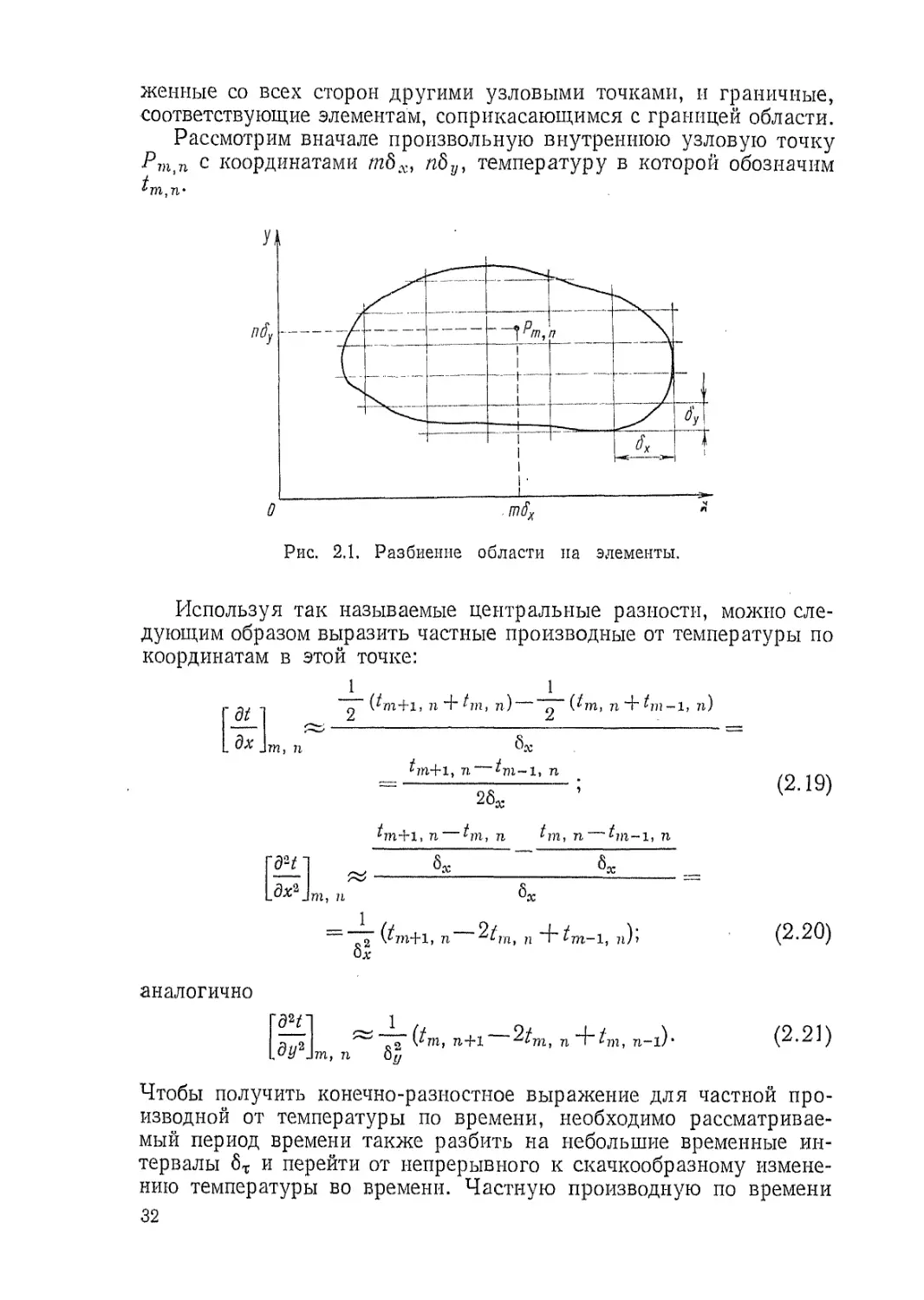
ГЛАВА 1
ТЕПЛОВЫДЕЛЕНИЕ В АКТИВНОЙ ЗОНЕ РЕАКТОРА
И ОТВОД ТЕПЛА ИЗ НЕЕ
§ 1.1. Источники тепла в активной зоне
Для дальнейшего изложения необходимо иметь представление
о конструктивной схеме реактора. Рассмотрим типичный водо-
водяной реактор, продольный и поперечный разрезы которого пока-
заны на рис. 1.1 и 1.2. Активная зона такого реактора собирается
из большого числа топливных кассет. Кассеты представляют собой
шестигранные кожухи, в которых размещены тепловыделяющие
элементы. Продольный и поперечный разрезы типичной топливной
кассеты показаны на рис. 1.3 и 1.4. Твэлы обычно собираются из
топливных таблеток, помещаемых в тонкостенную металлическую
защитную оболочку. В зазорах между твэлами течет вода, выполня-
ющая одновременно функции замедлителя и теплоносителя. Вода,
окружающая со всех сторон активную зону, служит также отража-
телем. Специальная система регулирующих и аварийных стержней,
изготовленных из материалов, сильно поглощающих нейтроны, обес-
печивает надежное и безопасное управление ядерным реактором.
Корпус ядерного реактора представляет собой толстостенный сосуд
высокого давления, рассчитанный на давление теплоносителя. Сна-
ружи корпус реактора окружается биологической защитой (на схе-
ме не показана).
Хотя основная доля тепла в ядерных реакторах выделяется
в твэлах, значительное его количество может выделяться в замедли-
теле, регулирующих стержнях, отражателе, теплоносителе, корпусе
реактора и других элементах. Очевидно, что при тепловых расчетах
тех или иных элементов ядерного реактора необходимо прежде
всего знать выделяемое в них количество тепла.
Источником тепла в реакторах является энергия, высвобож-
дающаяся при делении ядер. При делении одного ядра 236 U выде-
ляется около 200 Мэе*, при делении ядра 239Ри — около 220 Мэв.
Выделяющаяся при делении ядра 235U энергия распределяется
примерно следующим образом [1, 2]:
Кинетическая энергия осколков деления...............166 Мэв
Энергия нейтронов деления............................. 5 Мэв
Энергия у-излучения при делении ...................... 8 Мэв
Энергия p-излучения продуктов деления ................ 7 Мэв
Энергия у-излучения продуктов деления................ 7 Мэв
Энергия нейтрино.....................................11 Мэв
* 1 Мэв = 1,6-10~1в кдж ~ 3,83-10“17 ккал.
12
Рис. 1.1. Продольный разрез реактора ВВЭР:
/ — регулирующие стержни; 2 — активная зона; 3 —кор-
пус.
Рис. 1.2. Поперечный разрез реактора ВВЭР:
/ — корпус; 2 — активная зона.
Так как нейтрино свободно проходят
через большие толщины материалов, то при-
ходящаяся на их долю энергия бесполезно
уносится из реактора в окружающее про-
странство. Таким образом, при расчетах реак-
торов можно считать, что на один акт деле-
ния ядра a36U фактически выделяется около
190 Мэв.
Чтобы рассчитать мощность, выделяемую
в единице объема делящегося материала,
необходимо знать число ядер, подвергаю-
щихся делению в единицу времени в единице
объема. Число делящихся ядер пропорцио-
нально плотности нейтронного потока Ф в
рассматриваемой точке реактора и макроско-
пическому сечению деления ядер Зу.
Плотность нейтронного потока Ф равна
числу нейтронов, проходящих через единич-
ную площадку в единицу времени; его раз-
мерность Плотность нейтронного
потока, как показано ниже, существенно изме-
няется по объему активной зоны, а среднее
для активной зоны ее значение определяется
Рис. 1.3. Продольный раз-
рез топливной кассеты.
14
Рис. 1.4. Поперечный разрез топливной кас-
сеты.
особенностями и типом конкретного реактора. Для энергетических
реакторов средняя плотность нейтронного потока равна 1013 —
10й нейтрон/^слг • сек). Макроскопическим сечением деления Sy
называют величину, характеризующую вероятность захвата нейт-
рона ядрами горючего, заключенными в единице объема, с после-
дующим их делением. Так как эта величина есть произведение
числа атомов в 1 см!! вещества на сечение одного ядра [сжа], то ее
размерность равна кж-1]. Sy зависит от рода делящегося веще-
ства, его состава и энергии нейтронов.
Таким образом, мощность, выделяемая в единице объема в рас-
сматриваемом месте активной зоны, равна
где с — число делений в 1 сек на 1 кет. (величина, обратная энергии,
выделяемой на один акт деления). Считая, что в среднем на каждый
акт деления ядер 235U выделяется 190 Мэе — 3,16 • 10~иквт • сек,
получаем
с, -----!---3,26-1О13 —J.
3,16-1()~14 кет-сек
Как показано выше, основная доля высвобождаемой при делении
ядра энергии приходится на кинетическую энергию осколков деле-
ния. Так как длина свободного пробега осколков деления не
превышает нескольких микрон, то их энергия превращается в
тепло вблизи того места, где происходит реакция деления ядра.
То же самое можно сказать и об энергии ^-излучения. Следователь-
но, около 90% энергии, высвобождаемой в результате реакции
деления ядра, превращается в тепло непосредственно вблизи места
деления ядра. Поэтому при тепловых расчетах реакторов можно
считать, что все тепловыделение сосредоточено в твэлах.
Большая часть энергии у-излученпя, а также энергии, выделя-
емой при замедлении нейтронов, превращается в тепло за предела-
ми твэлов, т. е. в замедлителе, отражателе, конструкционных мате-
риалах, теплоносителе и корпусе реактора. Хотя доля этой энергии
невелика (~ 10%), необходимо предусматривать системы охлаждения
соответствующих элементов реактора. Кроме того, с выделением
этой энергии связаны такие существенные для работы реактора яв-
ления, как термические напряжения, радиационное повреждение
материалов, накопление энергии (эффект Вигнера) в графитовых
замедлителях и т. п.
§ 1.2. Распределение тепловыделения в активной зоне
Количество тепла, выделяемого в рассматриваемой точке про-
странства в единице объема в единицу времени qv 1вт • ж-3], на-
зывают мощностью внутренних источников тепла или мощностью
тепловыделения. Как следует из краткого обзора, приведенного
15
в § 1.1, тепловыделение в топливе и в конструктивных элементах
реактора обусловлено различными физическими процессами, поэто-
му и методика расчета мощности тепловыделения в разных частях
реактора различна. Учитывая, что более 90% тепла выделяется
в твэлах, рассмотрим главным образом способы расчета мощности
внутренних источников тепла в твэлах.
Тепловыделение в твэлах, как это следует из выражения (1.1),
пропорционально плотности нейтронного потока и макроскопичес-
кому сечению деления. В связи с тем, что распределение плотности
нейтронного потока неравномерно по объему активной зоны, а в
некоторых случаях и макроскопическое сечение деления в разных
частях активной зоны различно, тепловыделение в твэлах обычно
существенно изменяется как по высоте, так и по радиусу активной
зоны.
Распределение плотности нейтронного потока определяется в ре-
зультате физического расчета реактора, который, как правило,
предшествует тепловому. Не останавливаясь подробно на физи-
ческих аспектах рассматриваемой проблемы, напомним кратко ос-
новные сведения, касающиеся распределения плотности нейтрон-
ного потока в активной зоне реактора. Оно зависит от того, каким
образом распределены по объему активной зоны топливо, замедли-
тель, поглощающие материалы. Наиболее просто рассчитывается
распределение плотности нейтронного потока в идеализированной
гомогенной активной зоне, в которой топливо, замедлитель и по-
глощающие материалы равномерно перемешаны по объему активной
зоны. В действительности активные зоны не являются гомогенными,
так как в реальных реакторах в активной зоне имеются различ-
ные конструктивные элементы, охлаждающие каналы, по которым
течет теплоноситель, регулирующие органы и т. д. Поэтому все
активные зоны являются гетерогенными. Но так как длина сво-
бодного пробега тепловых нейтронов составляет несколько санти-
метров, что существенно превышает размеры основных «неоднород-
ностей» активной зоны, то в первом приближении активную
зону реакторов на тепловых нейтронах можно считать гомогенной и
распределение плотности нейтронного потока в ней рассчитывать
по соотношению для гомогенных активных зон.
Распределение плотности нейтронного потока в гомогенной среде
описывается уравнением диффузии. В бесконечном однородном
массиве стационарное распределение было бы равномерным и плот-
ность нейтронного потока определялась бы условием равновесия
между процессами выделения и поглощения нейтронов.
В любом конечном объеме вследствие утечки нейтронов через его
поверхность плотность нейтронного потока убывает по направлению
к периферии. Если провести линейную экстраполяцию профиля ней-
тронного потока за пределы активной зоны, то нейтронный поток
обратится в нуль на определенном расстоянии от поверхности б,
называемом эффективной добавкой (см. рис. 1.5). Величина эффек-
тивной добавки определяется длиной среднего свободного пробега
16
нейтрона п может быть рассчитана заранее. Поэтому при решении
уравнения диффузии удобно вместо действительной активной зоны
рассматривать некоторую условную, линейные размеры которой,
называемые обычно экстраполированными, отличаются от действи-
тельных размеров активной зоны на величину эффективной добавки.
Нейтронный поток на поверхности условной зоны можно принять
равным нулю.
Для активных зон простейшей геометрии расчет дает следу-
ющее распределение плотности нейтронного потока по объему ак-
тивной зоны. Для активной зоны в форме прямоугольного парал-
лелепипеда, экстраполированные размеры ребер которого равны
а, b и с,
Фо cos — cos — cos — , (1.2)
a b с
где Фо — плотность нейтронного потока в центре активной зоны;
х, у, z — координаты, отсчитываемые от центра параллелепипеда.
Для цилиндрической активной зоны
Ф = Ф0 jJ 2,405 — cos— , (1.3)
\ До ' н
где Jtt — функция Бесселя 1-го рода нулевого порядка; Д() —
экстраполированный радиус; И — экстраполированная высота ак-
тивной зоны; Д и z — координаты, отсчитываемые от середины
цилиндра.
Для сферической активной зоны
лД
sin —-
(Г) ,ф0-----------------------
nR
Ro
(1.4)
где До — экстраполированный радиус активной зоны; Д — коорди-
ната рассматриваемой точки.
Среднее значение плотности нейтронного потока нетрудно полу-
чить путем интегрирования. Например, для цилиндрической ак-
тивной зоны
Фср=^йнФ0. (1-5)
Если при осреднении для простоты воспользуемся не действитель-
ными, а экстраполированными размерами, то
— f д [ 2,405 — 2лДЛД^ 0,433;
nRo J \ До /
н
2
/гя —— С cos— dz — — «0,637.
Н . Н л
17
Коэффициенты kR и kH характеризуют неравномерность распреде-
ления плотности нейтронного потока соответственно по радиусу и
высоте активной зоны. Величина
k~kRkH (1.6)
называется коэффициентом осреднения нейтронного потока по реак-
тору и характеризует неравномерность распределения плотности
нейтронного потока по объему активной зоны. На практике для
характеристики неравномерности тепловыделения в активной зоне
чаще используют величины, обратные коэффициентам осреднения,
называемые коэффициентами неравномерности: коэффициенты не-
равномерности тепловыделения по радиусу активной зоны к« =
= 1//г^, по высоте кн — 1//?н и объемный коэффициент неравно-
мерности тепловыделения ку = 1//г.
Во всех трех рассмотренных выше случаях распределение плот-
ности нейтронного потока является очень неравномерным (для
цилиндрической зоны k = 0,433 • 0,637 « 0,276), что невыгодно
с практической точки зрения, так как приводит к неравномерному
тепловыделению в объеме активной зоны и снижению общей мощ-
ности реактора.
Для выравнивания плотности нейтронного потока и тепловыде-
ления по объему активной зоны используются различные способы:
установка отражателя, регулирование распределения потока нейт-
ронов с помощью поглощающих присадок, применение переменной
по сечению реактора степени обогащения топлива и др. Типичное
распределение плотности нейтронного потока по радиусу цилинд-
рической активной зоны с отражателем показано кривой 2 на
рис. 1.5. Такой же характер имеет распределение плотности ней-
тронного потока и по высоте активной зоны при наличии торцевых
отражателей. Отражатель уменьшает утечку нейтронов из активной
зоны, вследствие этого повышается нейтронный поток как на по-
верхности активной зоны, так и по всему ее объему. Наличие макси-
мума нейтронного потока в отражателе вблизи границы с активной
зоной объясняется торможением быстрых нейтронов, попадающих
в отражатель, и их более слабым поглощением в нем. Для большей
простоты при тепловом расчете активной зоны с отражателем поль-
зуются также уравнениями (1.2) — (1.4), рассматривая вместо дей-
ствительной некоторую условную активную зону без отражателя.
Распределение плотности нейтронного потока для такой активной
зоны показано на рис. 1.5 штрих-пунктиром (Ro = R + 6' — экс-
траполированный радиус активной зоны с отражателем). Анало-
гичным образом вводится понятие экстраполированной высоты
активной зоны с отражателем Я'.
Действительное распределение плотности нейтронного потока
в активной зоне гетерогенных реакторов значительно сложнее.
Если распределение плотности нейтронного потока в целом по ак-
18
тивной зоне, как об этом говорилось выше, незначительно отличает-
ся от распределения в гомогенной активной зоне, то распределение
нейтронного потока по поперечному сечению отдельной кассеты
существенно неравномерно. Дело в том, что топливо поглощает
нейтроны значительно сильнее, чем замедлитель, поэтому плотность
нейтронного потока в твэле ниже, чем в окружающем его замедли-
теле. Характер распределения плотности нейтронного потока по се-
чению топливной кассеты показан на рис. 1.6. По сравнению с аб-
солютными значениями нейтронного потока эти местные изменения
Ф невелики, поэтому в расчете тепловой мощности реактора ими, как
правило, пренебрегают. При расчете отдельных твэлов в кассете
необходимо учитывать неравномерность Ф, а следовательно, и
qv и вводить коэффициент неравномерности тепловыделения по
кассете кк.
Наличие конструкционных материалов, теплоносителя, регу-
лирующих и аварийных стержней еще более искажает распределение
плотности нейтронного потока в активной зоне. Все эти особенности
реактора учитываются в процессе физического расчета.
Зная распределение плотности нейтронного потока, нетрудно
рассчитать распределение тепловыделения в активной зоне реактора
и его тепловую мощность. Если делящийся материал равномерно
распределен в активной зоне объемом V, то тепловая мощность
реактора
лг Фо2/у И
N =------—кет. (1.7)
Ку с
19
Так как величина
М°> 0) =
Фо 2/
с
(1.8)
в соответствии с (1.1) есть мощность внутренних источников тепла
в центре активной зоны, то
(1-9)
Если тепловая мощность и геометрия реактора заданы, то, поль-
зуясь соотношением (1.9), можно определить мощность тепловыде-
ления в центре активной зоны. В том случае, когда распределение
Рис, 1.6. Распределение плотности нейтронного по-
тока в топливной кассете.
плотности нейтронного потока в активной зоне описывается урав-
нением (1.2), (1.3) или (1.4), нетрудно определить мощность тепло-
выделения в любом месте активной зоны. Например, для цилинд-
рической активной зоны мощность внутренних источников тепла
в середине рабочего канала, удаленного на расстояние от оси
активной зоны, равна
qv(R, 0) = 9„(0, 0)/0/2,405 41 • (1.Ю)
\ /
Изменение же мощности тепловыделения по высоте твэла описы-
вается зависимостью
М7?’ г) = ^(7?, °)cos^ •
(1-И)
20
В тех случаях, когда принимаются специальные меры по выравни-
ванию тепловыделения в активной зоне или когда регулирующие
стержни искажают распределение плотности нейтронного потока,
расчет распределения тепловыделения в активной зоне более
сложен.
Как уже указывалось выше, не вся энергия распада выделяется
в виде тепла в твэлах; заметная доля тепла выделяется в таких эле-
ментах ядериого реактора, как замедлитель, отражатель, биологи-
ческая защита, а также в теплоносителе и конструкционных мате-
риалах. Точный расчет тепловыделения в этих элементах весьма
сложен. Однако с достаточной для практики точностью при расчете
систем охлаждения можно ограничиться приближенными оценками.
Выделение тепла в замедлителе связано главным образом с замедле-
нием нейтронов и поглощением некоторой части у-изл учения и со-
ставляет примерно 5% общей мощности реактора. Тепловыделение
в отражателе и биологической защите в основном обусловлено по-
глощением у-излучения, причем в отражателе выделяется примерно
2—3%, в защитной оболочке 1—2% общей мощности реактора.
§ 1.3. Отвод тепла из активной зоны
Выделяющееся в ядерном реакторе тепло отводится из него
теплоносителем. Расход теплоносителя, скорости его движения по
различным охлаждающим каналам реактора должны быть выбраны
таким образом, чтобы обеспечить нормальную безаварийную работу
всех элементов реактора. Применительно к твэлам это прежде всего
означает, что максимальная температура оболочки твэлов и топ-
лива ни в одном канале активной зоны не должна превышать
предельно допустимые значения. Несмотря на принимаемые меры
по выравниванию тепловыделения по сечению активной зоны, вы-
деляемая в различных рабочих каналах мощность не одинакова.
Поэтому для обеспечения одинаковой температуры теплоносителя
на выходе из всех рабочих каналов необходимо распределять
расходы теплоносителя пропорционально выделяемым в рабочих
каналах тепловым мощностям.
Очевидно, что в различных рабочих каналах активной зоны и
выделяемая мощность, и скорости движения теплоносителя могут
существенно различаться. Но это не означает, что необходимо прово-
дить тепловой расчет всех рабочих каналов активной зоны. Обычно
тепловой расчет выполняется для наиболее теплонапряженных твэ-
лов, а также твэлов, находящихся в наиболее неблагоприятных
в отношении охлаждения условиях.
При тепловом расчете твэла прежде всего определяется измене-
ние температуры теплоносителя по высоте рассматриваемого рабо-
чего канала. Если закон изменения мощности тепловыделения по
высоте твэла qy (z) известен, то среднемассовая температура 7 (г)
теплоносителя на расстоянии z от входа в рабочий канал легко опре-
21
деляется из уравнения теплового баланса*:
/ I’ (2) ^2
/ —• (М2)
Gcp
Здесь \ — температура теплоносителя на входе в рабочий канал;
f — площадь поперечного сечения топливного стержня; G — мас-
совый расход теплоносителя через канал; — удельная тепло-
емкость теплоносителя.
Затем рассчитывается изменение по высоте канала температуры
поверхности оболочки твэла:
/е(г) = Нг)+—* , (1.13)
ОС
где <7с (г) — плотность теплового потока на поверхности твэла
(стенки канала); а — коэффициент теплоотдачи от поверхности
твэла к теплоносителю. Величина qG (г) легко определяется по из-
вестной плотности тепловыделения:
7с(2) = ^(2) — ’ (1Л4)
s
где s — периметр оболочки.
Коэффициент теплоотдачи а зависит от рода теплоносителя, ско-
рости его движения и многих других факторов. Методам опреде-
ления коэффициента теплоотдачи посвящена большая часть после-
дующих глав книги.
После того как рассчитана температура поверхности оболочки
твэла, можно найти поле температур в твэле, максимальную темпе-
ратуру топлива и определить термические напряжения.
Тепловой расчет рабочих каналов активной зоны достаточно
сложен. Чтобы получить самые общие представления о характере
изменения температуры теплоносителя, оболочки топлива по длине
рабочего канала, примем некоторые допущения, существенно упро-
щающие расчеты. Рассмотрим в качестве примера рабочий канал,
изображенный на рис. 1.7. Примем следующие упрощающие допуще-
ния. Распределение мощности внутренних источников тепла как по
сечению кассеты, так и по сечению каждого твэла будем считать рав-
номерным, а по высоте — меняющимся в соответствии с выражением
(1.11). Коэффициент теплоотдачи будем считать постоянным по
периметру и высоте твэла.
Поместив начало координат на входе в кассету, как это показано
на рис, 1.7, и выразив мощность внутренних источников тепла через
* В выражении (1.12) не учитывается перенос тепла вдоль оси канала
за счет осевой теплопроводности. ,0 влиянии осевой теплопроводности на
среднемассовую температуру теплоносителя см. в § 11.2.
22
суммарное тепловыделение в рассматривае-
мой кассете Q, получим
4V(?) (1.15)
k2nLro L
где п — число твэлов в рассматриваемой
кассете; г0 — радиус тепловыделяющего
стержня.
Подставив уравнение (1.15) в (1.12), опре-
делим изменение среднемассовой температуры
теплоносителя по высоте рабочего канала: ;
о г Q nz
ппгг} \------Г s'-11 —
l (z) - h +-----------2—------------------=
OCp
i Q / 1 5X2? \ / i 1 л* \
= J —cos------1 (1.16)
Gcp \ L J
Очевидно, что температура теплоносителя
увеличивается по высоте (см. рис. 1.8) и
максимальна иа выходе из рабочего канала
(z = L):
7-7+-^-. (1-17)
Gcp
Плотность теплового потока на поверхно-
сти твэла 6/с (г) в соответствии с выражением
(1.14) равна
*»
Vc(^) -М2)-1’ (1Л8)
2/-J.
где гг — наружный радиус оболочки твэла.
Подставляя (1.15) и (1.18) в (1.13), по-
лучаем закон изменения температуры обо-
лочки по высоте твэла:
Рис. 1.7. Схема ра-
бочего капала.
(2)
—-— sin
4a/iLri
nz
L
(1.19)
Изменение температуры наружной поверхности твэла, рассчи-
танное по уравнению (1.19), показано иа рис. 1.8. Из рисунка вид-
но, что максимум температуры оболочки достигается не на конце
твэла, а на некотором удалении от него. Координату максимума
температуры стенки, а затем и значение максимальной температуры
(/0)макс нетрудно получить, продифференцировав уравнение (1.19)
по z и приравняв производную нулю (аналогично тому, как это сдела-
но ниже при нахождении максимальной температуры топлива).
23
И, наконец, температура топлива на оси твэла t0 (z) определяется
выражением
/o«=?(2)+-2-sin^-S^. (1.20)
2Ln L
В этом выражении ^-sin представляет собой местную плотность
теплового потока на единицу длины твэла. Множитель
2а/\
есть сумма термического сопротивления на границе жидкость —
стенка, термического сопротивления оболочки и термического сопро-
тивления тепловыделяющего стержня. Температура топлива на оси
Рис. 1.8. Распределение по высоте рабочего ка-
нала мощности тепловыделения qv, средне-
массовой температуры теплоносителя t, тем-
пературы наружной поверхности оболочки t0
и температуры топлива на оси твэла to.
твэла, так же как и температура оболочки, вначале растет, а затем,
достигнув максимума, уменьшается (см. рис. 1.8), что объясняется
уменьшением плотности теплового потока в верхней половине
твэла.
Чтобы определить положение точки zMaKC, в которой достигается
максимальная температура топлива (^0)макс> подставим в выраже-
24
ние (1.20) значение t (z) в соответствии с (1.16):
/о(2)-7х + —/'1—cos —^+-^-sin —2Ж-, (1.21)
26ср V L J 2Ln L 1
продифференцируем (1.21) по z и, приравняв производную нулю,
найдем
L
^макс aictgl
л \ nL ,
(1.22)
Знак минус в этом выражении означает, что
Л - . / 0Ср2-^г \ -
— <Г. arctg I----------л,
2 \ nL
т. е. что максимальная температура топлива достигается в верхней
половине твэла.
Подставляя полученное значение zMaKC в выражение (1.21),
находим максимальную температуру топлива:
«ма.,0 + (1 - cos’ll 4-5- sin 2^ =
2Gcp \ L / 2Ln L
= 44----—( 1— sec"^»'| . (1.23)
1 2Gcp ( LI ' '
Если максимальная температура топлива (/0)макс задана, то вы-
ражение (1.23) позволяет определить предельно допустимую мощ-
ность кассеты:
п 2[(^о)ма1{С—7Х) Gcp
^макс — ~ • \ 1.24)
Рассмотренная выше схема расчета является чрезвычайно упро-
щенной. В действительности тепловой расчет рабочих каналов ак-
тивной зоны реактора гораздо сложнее. Обычно мощность внутрен-
них источников тепла изменяется по высоте твэлов по закону более
сложному, чем (1.11). При расчете температурных полей в твэлах
во многих случаях необходимо учитывать зависимость физических
свойств топлива от температуры, наличие термического сопротивле-
ния между топливом и оболочкой, неоднородность тепловыделения
по сечению твэла. Не менее сложной оказывается задача по определе-
нию коэффициента теплоотдачи, характера его изменения по высоте
твэла. Более того, нередко плотность теплового потока и коэф-
фициент теплоотдачи оказываются переменными и по периметру
твэлов.
СПИСОК ЛИТЕРАТУРЫ
1. Крамеров А. Я., Шевелев Я. В. Инженерные расчеты ядерных реакторов.
М., Атомиздат, 1964.
2. Климов А. Н. Ядерная физика и ядерные реакторы. М., Атомиздат, 1971.
25
ГЛАВА 2
УРАВНЕНИЕ ТЕПЛОПРОВОДНОСТИ И МЕТОДЫ ЕГО РЕШЕНИЯ
§ 2.1. Уравнение теплопроводности
Перенос тепла посредством теплопроводности играет в ядерных
реакторах большую роль. Теплопроводностью осуществляется пере-
нос тепла в твэлах, замедлителе, защитной оболочке, корпусе реак-
тора. Основная цель расчета процессов теплопроводности — опре-
делить температурные поля в указанных элементах реактора. Такие
расчеты позволяют правильно выбрать мощности тепловыделения
в твэлах и их основные размеры (так , чтобы температуры деляще-
гося материала и оболочки не превышали допустимых значений),
найти величину и характер температурных напряжений и деформа-
ций в элементах реактора. '
Наличие внутренних источников тепла в элементах реактора
усложняет как уравнение теплопроводности, так и методы его реше-
ния. Особенно существенна роль внутренних источников тепла
в твэлах, однако ими нельзя пренебрегать и в замедлителе, а часто и
в корпусе реактора.
Поле температур в твердом теле описывается уравнением тепло-
проводности. В основе вывода этого уравнения лежит закон со-
хранения энергии, записанный применительно к бесконечно малому
элементу тела: изменение внутренней энергии рассматриваемого
элемента pc dt равно количеству тепла, вносимому через поверх-
ность элемента вектором плотности теплового потока div q-с/т, плюс
тепло, выделяющееся внутри элемента qvd%. В результате имеем
pc— divq + 7y. (2.1)
от
По закону Фурье вектор плотности теплового потока в любой
точке изотропного тела пропорционален градиенту температуры и
направлен в сторону, противоположную вектору градиента темпе-
ратуры:
q=z—?vgrad/. (2.2)
Подставив это выражение в (2.1), получим уравнение теплопровод-
ности, содержащее только неизвестную температуру:
pCy- = div(Xgrad/) + ^v. (2.3)
26
Входящие в уравнение теплопроводности физические свойства мате-
риала . плотность р удельная теплоемкость с [дж/(кг'град)]
и коырфнциеит теплопроводности А |ь7п/(щ ♦ град) 1 — являются
заданными функциями температуры (а иногда п координат).
Мощность внутренних источников тепла i/у представляет собой
заданную функцию координат п времени.
Уравнение теплопроводности является нелинейным, неоднород-
ным дифференциальным уравнением второго порядка в частных про-
изводных. Его решение обычно сопряжено с большими трудностями.
Однако применительно ко многим конкретным задачам уравнение,
теплопроводности существенно упрощается.
Если коэффициент теплопроводности материала в рассматри-
ваемом интервале температур можно считать постоянной величиной,
то, выпоен ого из-под знака дивергенции и деля уравнение на рс,
получаем:
А а ytt , (2.4)
От рс
где а А/(рс) л/2,ч коэффициент температуропроводности; V2 —
оператор Лапласа.
В случае стационарных процессов температура тела по зависит
от времени, п уравнение теплопроводности (2.3) принимает вид
div (A ^гас! /) I • q\- ; 0. (2.5)
Как видно из этого уравнения, стационарное поле температур не
зависит от плотности и теплоемкости среды.
§ 2,2. Начальные и граничные условия для процессов
теплопроводности
Дифференциальное уравнение теплопроводности описывает са-
мые разнообразные задачи теплопроводности и имеет бесчисленное
множество решении. Для того чтобы из всего многообразия решений
выделить конкретное решение, интересующей пас задачи, к дифферен-
циальному уравнению теплопроводности необходимо присоединить
условия однозначности, а именно начальное н граничные условия
задачи.
Начал иное условие состоит в задании распределения температуры
в рассматриваемой области в начальный момент времени:
t (х, у, 2,0) / (х, I/, z). (2.6)
Если процесс теплопроводности стационарен, то задавать началь-
ное условие не требуется.
Граничные условия сводятся к заданию геометрической формы
рассматриваемой области и условий ее теплового взаимодействия
с окружающими телами пли средой. В самом общем случае эти ус-
27
ловия требуют равенства температур и тепловых потоков по обе
стороны от границы раздела (если на границе раздела не происхо-
дит каких-либо процессов с выделением или поглощением тепла):
С^Г’ Гг» ^Т’ ~ Уг>
zt, Т);'
(2.7)
где и t2, Хг и %2 — соответственно температуры и коэффициенты
теплопроводности соприкасающихся сред; хг, уг, zr — координаты
поверхности раздела.
Задание граничных условий в виде (2.7) требует одновременного
отыскания полей температуры как в интересующей нас области,
так и в окружающей ее среде, т. е. подразумевает решение так назы-
ваемой сопряженной задачи. Многие практические задачи допускают
значительно более простую формулировку граничных условий, при
которых устраняется необходимость отыскания температурных по-
лей в окружающей среде. В зависимости от характера взаимодейст-
вия рассматриваемой области с окружающей средой различают гра-
ничные условия трех родов.
В случае граничных условий первого рода задается распределе-
ние температуры иа границе области (поверхности тела):
i г ф (^ г>
Z г,
т).
(2.8)
У
В стационарных задачах эта температура не зависит от времени,
а в простейшем случае не зависит и от координат, т. е. /г = const.
В случае граничных условий второго рода задается распреде-
ление плотности теплового потока (либо производной от температу-
ры) на поверхности тела:
/ а/ \
А, —= ф(хг, уг, гг, т). (2.9)
\ дп /г
Так как при граничном условии (2.9) температурное поле опреде-
ляется с точностью до постоянного значения, то необходимо еще
задать температуру в какой-либо точке области. В стационарных
условиях qr не зависит от времени, а в простейшем случае
qr = const.
Граничные условия третьего рода заключаются в задании тем-
пературы окружающей тело среды /}К и закона теплообмена между
телом и средой. В качестве такого закона обычно используют закон
конвективного теплообмена Ньютона — Рихмана:
qr=—М — =oc(Zr—ZH!)j (2.10)
у uft / ji
согласно которому плотность теплового потока на поверхности тела
пропорциональна разности температур поверхности и окружающей
жидкости. В общем случае коэффициент пропорциональности, назы-
28
Пг1емь1Й коэффициентом теплоотдачи а [вт/ (мР-град)], и температу-
ра Жидкости /ж могут зависеть от координат и времени, причем
£*ти зависимости должны быть заданы. Во многих задачах с достаточ-
ной дЛя практики точностью можно считать коэффициент теплоотда-
чи и температуру жидкости постоянными.
В тех случаях, когда наряду с конвективным теплообменом су-
щественную роль играет и лучистый теплообмен, граничные условия
Задаются следующим соотношением:
7 Л(А'| =а(Тг-Тя)+8 <T0(T*r-TU (2.11)
где су0 — постоянная Стефана — Больцмана; епр — приведенная
степень черноты системы. Второе слагаемое в правой части уравне-
ния (2.11), учитывающее теплообмен излучением, записано в пред-
положении, что тела, окружающие излучающее тело, имеют постоян-
ную температуру Тот и образуют замкнутую систему, а окружаю-
щая среда практически прозрачна для излучения. Эта запись будет
приближенно верной и в том случае, когда окружающая среда яв-
ляется оптически плотной, если принять Тот Тт.
§ 2.3. Некоторые преобразования уравнения теплопроводности
Вследствие нелинейности и неоднородности уравнения тепло-
проводности его решение обычно сопряжено с большими трудностя-
ми. Однако в некоторых случаях можно устранить нелинейность
или неоднородность уравнения.
Если коэффициент теплопроводности явно не зависит от коорди-
нат, а зависит только от температуры, т. е. % = % (Z), введением
повой переменной можно существенно упростить уравнение тепло-
проводности. Для этой цели используется так называемая перемен-
ная Кирхгофа:
(2.12)
Она представляет собой некоторую фиктивную температуру, от-
считываемую от более или менее произвольной температуры t0, при-
чем вид функции 0 (0 определяется характером зависимости к (/).
Дифференцирование переменной Кирхгофа приводит к следую-
щим соотношениям:
50' к di
дт %0 5т
к
grad й’ = — grad t.
к()
(2.13)
29
Подставляя эти выражения в уравнение теплопроводности (2.3),
получаем
1 о /о 1 л \
у-.}} _к_д.---------(2.14)
а дх-------------------------------%() v 7
Очевидно, что соответствующим образом необходимо преобразовать
начальные и граничные условия задачи, однако это не всегда воз-
можно.
уравнение (2.14), строго говоря, не является линейным, так как
коэффициент температуропроводности а зависит от температуры.
Однако оно значительно проще, чем уравнение (2.3). Кроме того,
обычно коэффициент температуропроводности а слабее зависит от
температуры, чем коэффициент теплопроводности и теплоемкость.
В случае стационарных задач полученное уравнение строго ли-
нейное.
Обратный переход от найденного распределения й (х, у, z, т)
к температурному полю обычно осуществляется по известному графи-
ку зависимости й* = й1 (/), который нетрудно построить с помощью
уравнения (2.12).
Устранить неоднородность в уравнении теплопроводности можно
в тех случаях, когда мощность внутренних источников тепла яв-
ляется постоянной величиной, т. е. qv = const.
Любая из следующих подстановок:
’I’ = t +тг +</“ + ?2);
(2.15)
(А'2 + 4
(2.16)
(2.17)
приводит уравнение теплопроводности (2.4) к однородному урав-
нению
(2.18)
дх
В зависимости от вида выбранной подстановки могут в большей
или меныпей степени усложняться граничные условия для новой
переменной ф. Например, в случае двумерного температурного поля,
если граница области представляет собой окружность, более удоб-
ной является зависимость (2.16), а для прямоугольных областей —
зависимость (2.17).
§ 2.4. Методы решения уравнения теплопроводности
Методы решения уравнения теплопроводности весьма разнооб-
разны [1—5]. Точные аналитические методы решения уравнения
теплопроводности (метод разделения переменных, операционный
30
метод, методы интегральных преобразований, метод функций Грина,
метод тепловых потенциалов и др.) позволяют решать только срав-
нительно простые задачи теплопроводности. Для решения более
сложных задач используются приближенные аналитические мето-
ды, когда отыскивается распределение температур, лишь при-
ближенно удовлетворяющее уравнению теплопроводности или крае-
вым условиям. К ним прежде всего следует отнести интегральный
метод [7 J, а также вариационные методы [6].
Существенный недостаток как точных, так и приближенных
аналитических методов состоит в том, что с их помощью практически
можно решать задачи только для тел сравнительно простой гео-
метрии и при не очень сложных граничных условиях.
В тех случаях, когда невозможно получить аналитическое реше-
ние задачи или когда аналитическое решение очень сложно и неудоб-
но для практического применения, используют численные методы
решения уравнения теплопроводности, или методы аналогий. Чис-
ленные методы 11, 5.1 позволяют получить приближенное решение
практически любых задач. Эти методы требуют большой вычисли-
тельной работы, что длительное время тормозило их использование.
Однако развитие вычислительной техники сделало этот недостаток
несущественным. Сегодня численные методы решения задач нахо-
дят все более широкое применение во всех областях человеческой
деятельности, в том числе и при расчетах ядерных реакторов.
Учитывая большое значение численных методов для расчета
температурных полей в элементах ядерных энергетических уста-
новок, рассмотрим, каким образом из уравнения теплопроводности
получают систему конечно-разностных уравнений, лежащую в ос-
нове численных методов расчета полей температуры.
При расчете температурного поля численным методом рассмат-
риваемая область разбивается па небольшие элементы и примени-
тельно к каждому элементу входящие в дифференциальное уравне-
ние теплопроводности частные производные приближенно заме-
няются конечно-разностными выражениями. В результате такой
операции дифференциальное уравнение теплопроводности заме-
няется системой алгебраических уравнений, решение которой не
вызывает принципиальных трудностей. Очевидно, что чем меньше
размеры элементов, тем меньше погрешность, связанная с заменой
производных их конечно-разностным выражением, но и тем больше
объем вычислительной работы.
Методику получения системы конечно-разностных уравнений
рассмотрим на следующем примере. Пусть требуется рассчитать
нестационарное температурное поле в двумерной области, показан-
ной на рис. 2.1, при заданных начальных и граничных условиях.
Разобьем эту область прямоугольной сеткой на элементы с раз-
мерами бх и б?/. Будем считать, что теплоемкость каждого элемента
ребабу 1 сосредоточена в соответствующей узловой точке (центре
элемента). Все узловые точки можно разделить на внутренние, окру-
31
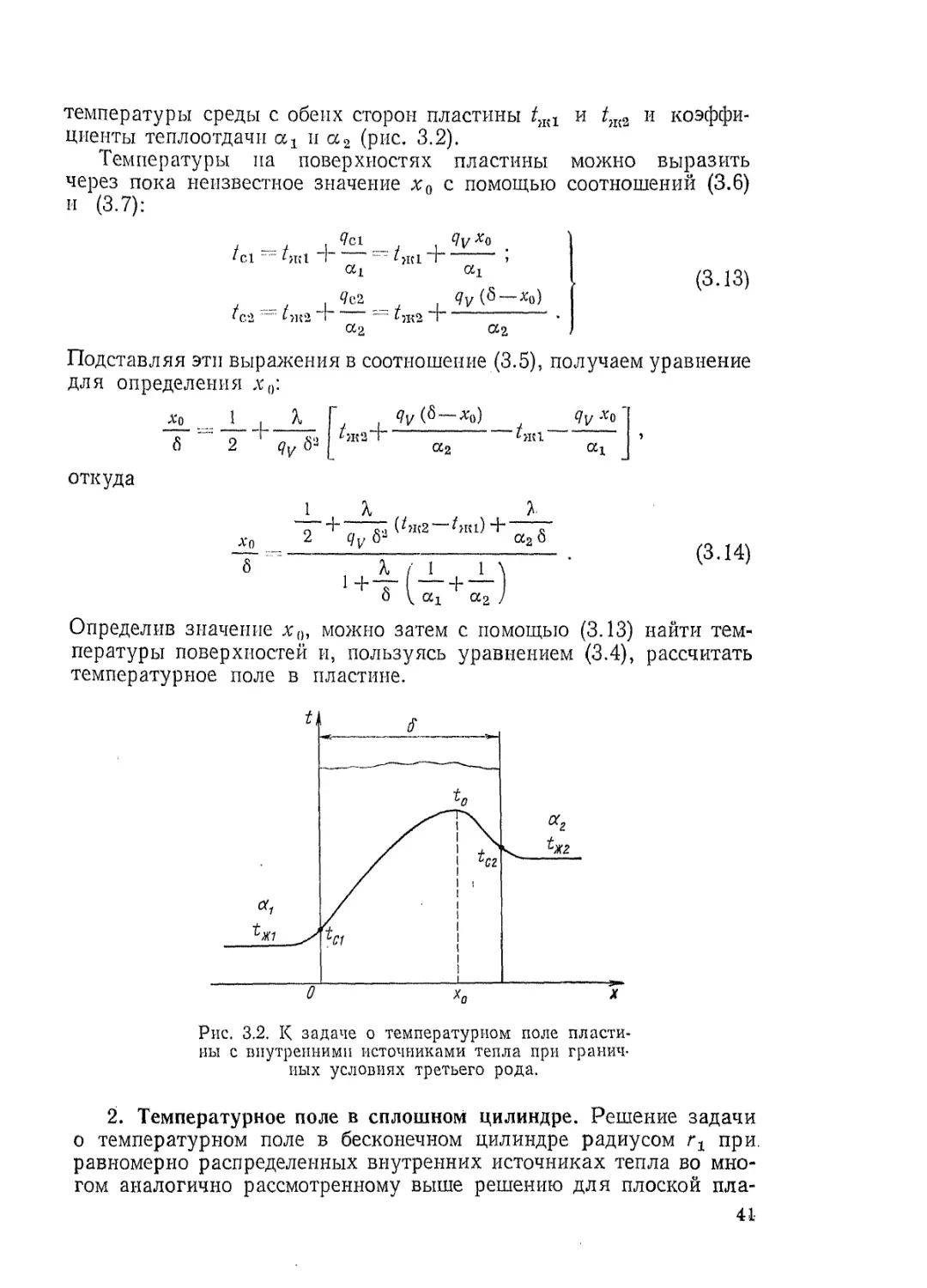
женные со всех сторон другими узловыми точками, и граничные,
соответствующие элементам, соприкасающимся с границей области.
Рассмотрим вначале произвольную внутреннюю узловую точку
Рт,п с координатами т8х, п8у, температуру в которой обозначим
Ап,п*
Используя так называемые центральные разности, можно сле-
дующим образом выразить частные производные от температуры по
координатам в этой точке:
1 1
2 №т+1, n + 6n, 7i) g (6п, п +би-l, п)
дх
Jm, п
‘тп-1, п
26^
6п+1, п 6п, и
т, п чп-1, п
Гд2* 1
'х
Зя2
т,
71
бд;
X
(2.19)
т, п 1 ьт-
(2.20)
аналогично
'd2t~
.дУ“лп, п
n+1 ^т, п tm, п-1)'
(2.21)
Чтобы получить конечно-разностное выражение для частной про-
изводной от температуры по времени, необходимо рассматривае-
мый период времени также разбить на небольшие временные ин-
тервалы и перейти от непрерывного к скачкообразному измене-
нию температуры во времени. Частную производную по времени
32
в точке Рт,п в /г-й момент времени (rZt = /гбг) приближенно можно
выразить, например, через значение температуры в этой точке в на-
стоящий k-ii момент времени 1^г> п и значение температуры в после-
дующий k + 1-й момент времени /JfJ:
(2.22)
Этот способ выражения производной по времени приводит к так
называемой явной схеме разностных уравнений теплопроводности.
Подставив уравнения (2.20) — (2.22) в (2.4), получим:
ДИ- •____fk
tn, п иг, п__
6т
__ /1 , п , п ~Ь ^т— 1 , п . $т, 1 ^т, п + ^т, п — 1 \ (<77)т, п
Л б!- 6“ / рс
(2.23)
Очевидно, что уравнение (2.23) может быть записано для каждой
внутренней узловой точки Рт<п, т. е. число таких уравнений в точ-
ности равно числу внутренних узловых точек. Если интервалы раз-
биения по вертикали и по горизонтали выбраны одинаковыми, т. е.
6,v == 6П = 6 и qv — 0, уравнение (2.23) существенно упрощается:
/т/г ~ FО (Ozi-|- 1 , п "Е tin — 1 , п~[~ tm, zi-|- 1 ~f~ tm, n—-1) (4FО 1) tm, n ’
(2.24)
где Fo = a8x/№ — число Фурье для элемента.
Это уравнение позволяет вычислить температуру в любой внут-
ренней узловой точке в «последующий», /г + 1-й момент времени,
если известно распределение температур в окрестности этой точки
в «настоящий», /г-й момент времени.
В случае стационарного температурного поля температура в лю-
бой узловой точке не зависит от времени, следовательно, if г! =
= t'in, п = tm>n, и из уравнения (2.24) получаем
t ____trn+l, п "Hm-i, n+l~Fm, п-1 ^2 25)
4
Анализ уравнения (2.24) показывает, что для получения устой-
чивого решения! (решения, при котором в процессе решения
ошибка не возрастает) должно выполняться условие Fo^ 1/4. Если
принять Fo — 1/4, то уравнение (2.24) примет наиболее простой вид:
/k I I /fe | //i
,k~l- 1 _ Ltn-\- 1 , n "i" 1 , и ~r n-f- 1 ~r m, n — 1 /9 9fi\
ttn,n— ~
33
2 Зак. 79 2
Хотя явная схема конечно-разностных уравнений (2.26) чрез-
вычайно проста, так как входящие в нее уравнения независимы друг
от друга, ограничения, накладываемые на Fo, связывающие между
собой пространственные и временные интервалы разбиения, часто
оказываются неудобными при расчетах. Этот недостаток явной схе-
мы конечно-разностных уравнений становится особенно сущест-
венным, когда рассматриваемая область состоит из нескольких зон
с различными коэффициентами температуропроводности. Поэтому
при решении задач на ЭВМ чаще используется неявная схема конеч-
но-разностных уравнений. По этой схеме производная по времени
в точке Ртп в k-й момент времени выражается через значения тем-
пературы в’точке Ртп в настоящий, k-й момент времени и в пред-
шествующий, k—1-й момент:
' dt р
. ЙТ _ tn , п
fk ______
п ‘‘т, п
6т
(2.27}
Получаемая при этом неявная система конечно-разностных уравне-
ний при = 6 имеет следующий вид:
1 \ ,k ,k _________________fk ,k
~z~ ]ltn , n 1 , n Lm~ 1, n tm, n-\-1
ro J
k _ 1 ,/e-l
m, n — 1 — ~ Im, n •
Fo
(2.28}
Эта система уравнений значительно сложнее системы (2.26), так
как в каждое уравнение входит по пять неизвестных, но зато ее ре-
шение устойчиво при любых Fo. Так как разработаны эффективные
методы решения неявных схем конечно-разностных уравнений на
ЭВМ, например метод прогонки, сложность системы уравнений не
вызывает каких-либо принципиальных трудностей при решении.
До сих пор не рассматривались граничные условия задачи. Оче-
видно, что эти условия должны войти в конечно-разностные уравне-
ния для граничных узловых точек.
В случае граничных условий первого рода целесообразно раз-
бить область на элементы таким образом, чтобы граничные узловые'
точки расположились на границе рассматриваемой области. При
этом значения температур в граничных узловых точках являются за-
данными и никаких дополнительных уравнений для них соста-
влять не нужно.
При граничных условиях второго или третьего рода температуры
в граничных узловых точках неизвестны, и для этих точек необхо-
димо также составлять конечно-разностные уравнения. Для состав-
ления таких уравнений удобно пользоваться уравнением теплового
баланса. При этом более или менее безразлично, лежат узловые
точки на границе рассматриваемой области или нет.
Например, при граничных условиях второго рода в случае, когда
узловые точки отстоят от границы на половину шага разбиения
34
(рис. 2.2), можно составить следующий баланс тепла для граничной
узловой ТОЧКИ Рт,п-
/k + 1 /А /Л ___/к
о с т, п ьт, п l'm + I , п ьт, п ,
рс Од, Оу с-------------
т тп+1
jk __fk j/c _Jt/г
+ ----^.+ П_. 1,'.^ (2.29)
Рп-1, п Рт—1,т
Термические сопротивления между узловыми точками (Рт, т + ъ
Rn _ Х1 п и Rm _ lt m) пропорциональны расстоянию между ними, об-
Рис. 2.2. 1\ составлению уравнения при граничных усло-
виях второго рода.
ратно пропорциональны площади поперечного сечения, через кото-
рую элементы обмениваются теплом, и коэффициенту теплопровод-
ности среды:
= (2.30)
Йели 8Х = 8У = 6,
Rm, m+1 Rn-1, п Rm~l, т ~ i
и из соотношения (2.29) получаем
= » + i. П-1 + Л-!, ,>+^1-(3Fo-1)4 „• (2.31)
Для стационарных задач ij'i = tm, п = tm, п и> следовательно,
?с 6
В случае граничных условий третьего рода рассмотрим такое раз-
биение, когда узловые точки лежат на границе области (рис. 2.3).
2* 35
(2.32)
^т, п о ( ^пг+1, n + ^m, П--1 ~Ь 6п-1,
и \
Составив баланс тепла для граничной узловой точки Р7)1Л, получим:
я Лг-|-1__у/г у/г ___у/г
X V 1'1П' п Ьт> п 1 , п ьпг, п ।
Р-J Ь С* /у, ——* |
2 6’ Pm,m+1
//г __jk jk __у/г
I m,n~l tm,n , Lm — 1 , n n Ji \
r- । [_ aO^ t m, n J,
Kn-i, n m
где
n _______ n ________ fix . n __________^?/
•r'm, zn+l — ^m-l, m я ’ n ГТ- ‘
- by №>x
Л —
2
Если 6Ж = ду — 6, имеем
tm\ n = Fo 1, n —2ttn, n— 1 “Ь tm— 1 , n 4"
+ 2В i t J ~ (4Fo + 2Fo В i -1) i, n,
где Bi = a6/% — число Био для элемента.
Для стационарных задач это уравнение имеет вид
/ — п ~Ь2^т, п-1 Ч~ 1, и 4~2Bi
(2.33)
(2.34)
(2.35)
Очевидно, что число дополнительных уравнений типа (2.29)
или (2.33) в точности соответствует числу граничных узловых точек.
Таким образом, при использовании метода конечных разностей всег-
Рис. 2.3. К составлению уравнения при граничных условиях
третьего рода.
да можно составить столько уравнений, сколько неизвестных зна-
чений температур в узловых точках появляется при разбиении рас-
сматриваемой области на элементы. Иными словами, получаемая
при этом система алгебраических уравнений всегда является замкну-
той. Последующее решение этой системы на ЭВМ позволяет опреде-
лить температуры во всех узловых точках и тем самым получить
температурное поле в рассматриваемой области.
36
СПИСОК ЛИТЕРАТУРЫ
1. Карслоу Г., Егер Д. Теплопроводность твердых тел. Пер. с англ. М., «Нау-
ка», 1964.
2. Лыков А. В. Теория теплопроводности. М., «Высшая школа», 1967.
3. Лыков А. В. «Некоторые аналитические методы решения задач нестацио-
нарной теплопроводности». — «Изв. АН СССР. Сер. Энергетика и транс-
порт», 1969, № 2, с. 3.
4. Мучник Г. Ф., Рубашов И. Б. Методы теории теплообмена. М., «Высшая
школа», 1970.
5. Шнейдер П. Инженерные проблемы теплопроводности. М., Изд-во иностр,
лит., 1960.
6. Эльсгольц Л. Э. Дифференциальные уравнения и вариационное исчисле-
ние. М., «Наука», 1969.
7. Goodman Т. R. Application of Integral Methods to Transient Nonlinear
Heat Transfer. — «Advances in Heat Transfer», 1964, v. 1, p. 3.
ГЛАВА 3
РАСЧЕТ ТЕМПЕРАТУРНЫХ ПОЛЕЙ
§ 3.1. Одномерные стационарные задачи теплопроводности
Одномерные задачи теплопроводности с внутренними источни-
ками тепла возникают при расчете температурных полей в твэлах,
в корпусе и других элементах ядерных установок. В конструктив-
ном отношении топливные кассеты отличаются разнообразием, но
в большинстве случаев они собираются из элементов, имеющих
форму пластин, полых или сплошных цилиндрических стержней.
Поэтому наибольший интерес представляет решение задач тепло-
проводности для плоской пластины, сплошного и полого цилиндров.
Температура в твэлах изменяется не только в поперечном направ-
лении, ио и вдоль оси. В принципе это двумерное поле можно рас-
считать, используя, например, численные методы. Практически же,
учитывая, что градиенты температуры и тепловые потоки вдоль
оси твэла значительно меньше градиентов и потоков в поперечном
направлении, расчет температурного поля проводят следующим
образом. Вначале находят наиболее опасное в тепловом отношении
сечение твэла с учетом неоднородного тепловыделения по длине,
а затем в этом сечении рассчитывают распределение температуры по
сечению, полагая температурное поле одномерным.
Рассмотрим простейшие одномерные стационарные задачи теп-
лопроводности с внутренними источниками тепла.
1. Температурное поле в пластине. Пусть в неограниченной
пластине толщиной б действуют равномерно распределенные внут-
ренние источники тепла мощностью qv. Сначала решим эту задачу
при граничных условиях первого рода, полагая заданными темпе-
ратуры на обеих поверхностях пластины /С1 и tc2. Дифференциаль-
ное уравнение, описывающее распределение температуры в пласти-
не, имеет вид
rf2/ , о
dx2 к
(3-1)
Если начало координат поместить на левой поверхности пластины,
как это показано на рис. 3.1, то граничные условия задачи запишут-
ся так:
i(0)=u i (6) =
(3.2)
38
Дважды интегрируя уравнение (3.1), получаем
(3.3)
Определив постоянные Сх и С2 из граничных условий (3.2), найдем
распределение температуры в пластине:
Чу 8*
X
1
/ /сХ
\
J 'Н(^С2 ^С1)
X
б"
(3.4)
Первое слагаемое правой части этого уравнения описывает распре-
деление температуры в пластине, создаваемое внутренними источ-
никами тепла при симметричных граничных условиях, т. е. при
/С1 = ^с2- Второе слагаемое описывает распределение температуры
в пластине при отсутствии внутренних источников тепла, т. е. при
qv = 0. Таким образом, полученное распределение температуры
можно рассматривать как суперпозицию двух решений: линей-
ного профиля температуры без внутренних источников теп-
ла и параболического, описы-
вающего распределение темпе-
ратуры при наличии внутренних
источников тепла и Zcx = Zc2.
При заданных значениях /С1
и /С2 уравнение (3.4) дает семей-
ство кривых, каждая из кото-
рых соответствует определенно-
му значению qv (см. рис. 3.1).
При относительно больших зна-
чениях qv кривые имеют макси-
мум, лежащий внутри пласти-
ны. Координата точки макси-
мума х0 определяется из урав-
нения
ЧуЬ qvxQ ^2—^,1
21 Z. 6
откуда
V = (3'5’
о 2 с/у о-
Рис. 3.1. Распределение температуры
в пластине при различной мощности
внутренних источников тепла:
<7у62
1 ~ Qv = 2^^c2-zci)=0: 2-Qv==1;
3-Qv=2.
Таким образом, точка максимума на температурной кривой лежит
внутри пластины, если
2 '
39
Тепловая мощность, выделяемая в расположенной слева от макси-
мума части пластины, отводится через левую поверхность, и, сле-
довательно, плотность теплового потока на ней равна
7ci = Qv хо- (3-6)
Аналогично вся мощность, выделяемая в правой от максимума
части пластины, отводится через правую поверхность, и плотность
теплового потока на ней равна
= *о)« (3.7)
Если максимум температуры расположен на левой поверхности пла-
стины (х0/6 = 0), то qcl = 0, вся мощность отводится через ее
правую поверхность и qG2 = qv8. При х0/д = 1, наоборот, вся
мощность, выделяемая в пластине, отводится через левую по-
верхность.
Если х0/6<0 или л:0/6>> 1, то максимум на температурной
кривой находится вне пределов пластины. Физически это означает,
что происходит не только передача тепла, выделяемого в пластине
одной из охлаждающих жидкостей, но и дополнительная передача
тепла через пластину от одной из жидкостей к другой: в первом
случае от левой поверхности к правой, во втором —- от правой
к левой.
Максимальное значение температуры t0 можно найти, подставив
выражение (3.5) в (3.4):
/о-/а = ^- + ,-Д7(/о3-иа+4(/«-/и)- (3.8)
О/С AtCJ у О At
Если температуры на поверхностях пластины одинаковы
(/С2 = /01 = /с), то температурное поле в пластине симметрично,
х0/6 == 1/2 и
= (3-9)
Расчет температурного поля удобно начинать с определения
х0 по уравнению (3.5). Пользуясь значением х0, уравнениям, описы-
вающим распределение температуры, можно придать более простой
вид:
б/г/ X
= (3.10)
= (3.11)
i»-fC2 = ^(6-Xo)2. . (3.12)
Решение (3.4) для граничных условий первого рода нетрудно
обобщить на случай граничных условий третьего рода. В этом случае
температуры на поверхностях пластины /С1 и /с2 неизвестны. Заданы
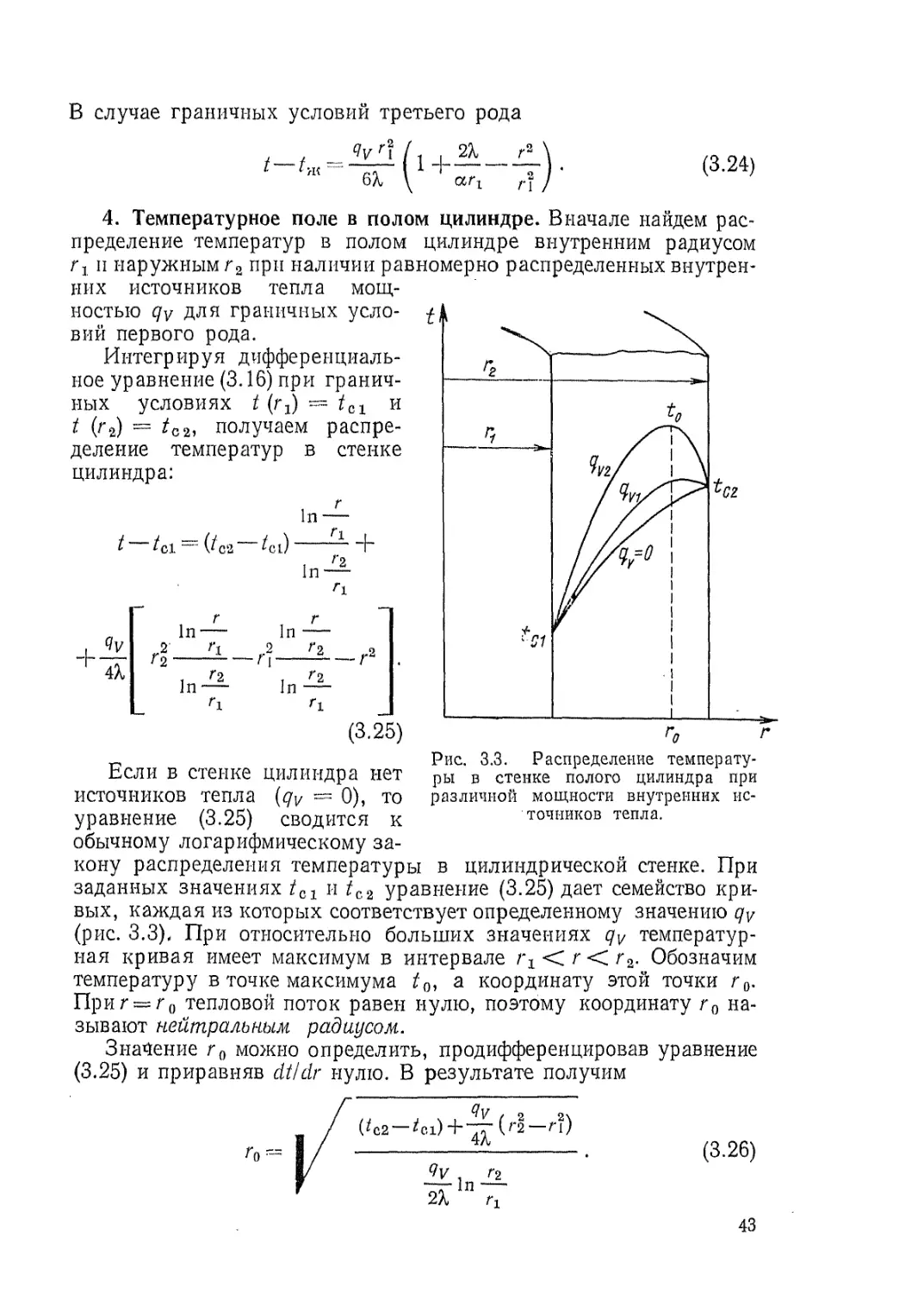
40
температуры среды с обеих сторон пластины /?к1 и /?к3 и коэффи-
циенты теплоотдачи ах и а2 (рис. 3.2).
Температуры па поверхностях пластины можно выразить
через пока неизвестное значение х0 с помощью соотношений (3.6)
и (3.7):
'cl ”.Ок1 I Чк1 ~1 >
CQ CZj ZQ 1 П,
а2
Подставляя эти выражения в соотношение (3.5), получаем уравнение
для определения ,г0:
Х()
б
, Мб~хо)
жзт 'на
а2
QV х0
«1
2
Qv й2
откуда
Хо
б
1 , Л..................X
о Т с.> Ря(2 ^К1)+ о
2 qv о- а2 о
(3.14)
1 «2
Определив значение х0, можно затем с помощью (3.13) найти тем-
пературы поверхностей и, пользуясь уравнением (3.4), рассчитать
температурное поле в пластине.
Рис. 3.2. К задаче о температурном поле пласти-
ны с внутренними источниками тепла при гранич-
ных условиях третьего рода.
2. Температурное поле в сплошном цилиндре. Решение задачи
о температурном поле в бесконечном цилиндре радиусом гх при.
равномерно распределенных внутренних источниках тепла во мно-
гом аналогично рассмотренному выше решению для плоской пла-
41-
стины. В этом случае дифференциальное уравнение теплопроводно-
сти удобно записать в цилиндрических координатах:
с!2/ . 1 dt . Qv
dr2 г dr %
(3.15)
или
1__£
г dr
^ = 0.
к
(3.16)
Решение этого уравнения при симметричных граничных условиях
= f(0) = 0 (3.17)
имеет вид:
, ... QVrl
'с“ а
(3.18)
Таким образом, при наличии равномерно распределенных внутрен-
них источников тепла температурное поле в сплошном цилиндре
описывается параболической зависимостью, при этом максимальная
температура на оси цилиндра равна
io —
4%
(3.19)
При граничных условиях третьего рода распределение температуры
в цилиндре описывается уравнением
^^<=^0+- ...
4Л у агх г\ /
где — температура охлаждающей жидкости; а — коэффициент
теплоотдачи.
3. Температурное поле в шаре. Для определения стационарного
температурного поля в шаре радиусом гг при однородном распреде-
лении внутренних источников тепла необходимо проинтегрировать
следующее дифференциальное уравнение:
dH ( 2 dt , Qy
dr2
Г"
(3.20)
/•
(3.21)
или
1 d ( 2
r2 dr I
^ = 0.
г 2
dr 1 X
о
С учетом того, что t (гг) = tQ и f (0) = 0 (граничные условия перво-
го рода), получим
t— to —
6А,
г2
2
(3.23)
42
В случае граничных условий третьего рода
ж
бх
Як
агг
2
п
(3.24)
4. Температурное поле в полом цилиндре. Вначале найдем рас-
пределение температур в полом цилиндре внутренним радиусом
гг п наружным г2 при наличии равномерно распределенных внутрен-
них источников тепла мощ-
ностью qv для граничных усло-
вий первого рода.
Интегрируя дифференциаль-
ное уравнение (3.16) при гранич-
ных условиях /(п) = /С1 и
Z (г2) = /с2, получаем распре-
деление температур в стенке
цилиндра:
In——
i 41 = (4*2 41) ' “Ь
. Г2
(3.25)
Рис. 3.3. Распределение температу-
ры в стенке полого цилиндра при
различной мощности внутренних ис-
точников тепла.
Если в стенке цилиндра нет
источников тепла (qv = 0), то
уравнение (3.25) сводится к
обычному логарифмическому за-
кону распределения температуры в цилиндрической стенке. При
заданных значениях icl и tc2 уравнение (3.25) дает семейство кри-
вых, каждая из которых соответствует определенному значению qy
(рис. 3.3). При относительно больших значениях qv температур-
ная кривая имеет максимум в интервале rx<Z.r < г2. Обозначим
температуру в точке максимума t0, а координату этой точки г0.
При г = г () тепловой поток равен нулю, поэтому координату г0 на-
зывают нейтральным радиусом.
Значение г0 можно определить, продифференцировав уравнение
(3.25) и приравняв dt/dr нулю. В результате получим
(3.26)
43
Уравнение (3.25) можно представить в более удобном виде, вос-
пользовавшись выражением (3.26) для нейтрального радиуса:
In —— (г2 —г?)
(3.27)
Максимальную температуру найдем, положив в этом уравнении
г = г0. Тогда
to—= 1п — — (/'о —Г?)
(3.28)
Выражения для / — Д2 и /() — /с2 совершенно аналогичны уравне-
ниям (3.27) и (3.28), только в них следует заменить г2.
Во многих практических случаях все выделяемое в полом ци-
линдре тепло отводится только через одну из его поверхностей,
например когда теплоноситель течет только по внутреннему каналу
или внешнему зазору. Расчетные уравнения для этах условий мож-
но получить как частные случаи уравнения (3.27).
Используя прием, который был применен для плоской пластины,
можно найти выражение для нейтрального радиуса при граничных
условиях третьего рода:
.. / Ч , qv Г Г1 > Г2 , 1 / 2 24
Ржа —Gki)+~ --+---+ 77- (/'2 —п)
Г0 =
(3.29)
После этого нетрудно определить плотности теплового потока на
внутренней и наружной поверхностях цилиндра:
п ..._^n(rQ~ri) ^г1/го Л.
С1 2nQ 2 \ г 1 /
\ 1 7 (3.30)
Чу Г2 / 1 Гб \
7с2 о | ч
2 \ Г2 /
и температуры поверхностей цилиндра:
— / •
ci ~ >
«1
। 7с2
(3.31)
С2 fHt2 Г
Далее, воспользовавшись выражениями (3.27) и (3.28), можно рас-
считать распределение температур в цилиндрической стенке и,
в частности, определить максимальную температуру в ней.
5. Температурное поле в пластине и цилиндре с неоднородным
распределением источников тепла. До сих пор рассматривались
одномерные температурные поля при равномерном распределении
44 .
внутренних источников тепла. Однако в действительности тепловы-
деление в' твэлах распределено неоднородно, и в некоторых случаях
при расчете температурных полей эту неоднородность необходимо
учитывать. Полагая qv — qv (х) для пластины и <7у = <7v(r) Для
цилиндра и интегрируя уравнения (3.1) и (3.16), получаем следую-
щие выражения:
для пластины
tx = - f dt, f A) + С, x + C2; (3.32)
J ,1 A,
о 0
для цилиндра
/(r)^ —+ + (3.33)
J £ J л
о о
Постоянные в этих выражениях определяются, как обычно, из гра-
ничных условий. Так как температура на оси цилиндра ограничена,
то, очевидно, С3 = 0.
Рассмотрим в качестве примера задачу о температурном поле
в цилиндрическом твэле радиусом гх, на поверхности которого зада-
на температура /(..
Тепловыделение пропорционально потоку нейтронов, а распре-
деление тепловых нейтронов в цилиндрическом твэле в первом
приближении описывается модифицированной функцией Бесселя,
поэтому интересно рассмотреть случай, когда распределение тепло-
выделения в твэле задано в виде
Qv (г) - Л/0 (%ог), (3.34)
где Л — постоянная, значение которой определено ниже; х0 —
величина, обратная длине диффузии тепловых нейтронов (для естест-
венного урана и о 0,7 слг1).
Подставляя уравнение (3.34) в (3.33) и выполняя интегрирова-
ние, получаем:
® (г) = t — 7„ (х0 г) + с. (3.35)
ы
Постоянная С определяется из условия (гг) = 0, и тогда
')’(О-Л(«О'-)]- (3-36)
Хид
Постоянную А можно определить, например, если известна мощ-
ность, выделяемая в единице длины цилиндрического твэла qL.
Так как эту величину можно выразить через мощность внутрен-
них источников тепла в твэле:
Г1
= $ qv(r)2nrdr,
о
45
то, подставляя сюда значение qv (г) из (3.34) й интегрируя, полу-
чаем
qt = 2лЛ rlo (х0 г) dr = 2nAri 7Х (х0 гг),
о
откуда
Л = . (3.37)
Подставляя выражение (3.37) в (3.36), находим искомое распределе-
ние температуры в цилиндрическом твэле:
О' (г) = (3 38)
2лХ иоГ1А(хоГ1)
Максимальная температура в центре твэла, в частности, равна
, _ , । <4 h (х0 fl) —1
10 *0 I n п г/ % '
2пЛ (х0 /и)
(3.39)
При 1» используя разложение бесселевых функций в сте-
пенной ряд и отбрасывая члены порядка (и0гх)6 и выше, получаем
1-4 г У + (ХоГ1)71—
q, \ Г1 / 16 I Л
тч-п v 1
16
(Ио Г1)а
8
(3.40)
6. Контактное сопротивление. При расчете температурных по-
лей в системе, состоящей из двух или нескольких тел, обычно пред-
полагается, что на границах их соприкосновения выполняется ра-
венство тепловых потоков и температур соприкасающихся тел
[см. условие (2.7)]. Такое предположение оправдано, если поверх-
ности соприкасающихся тел идеально гладкие и термический кон-
такт между ними осуществляется по всей поверхности.
В действительности поверхности отдельных элементов, состав-
ляющих ту или другую конструкцию, никогда не бывают абсолют-
но гладкими. Поэтому термический контакт между ними осущест-
вляется не по всей поверхности, а только в отдельных точках (пят-
нах) или группах точек. Многочисленные исследования показы-
вают, что площадь действительного контакта составляет незначи-
тельную долю номинальной площади соприкосновения. На большей
же части поверхности контактирующие тела (элементы конструк-
ции) разделены зазорами, заполненными воздухом или иной средой.
Если рассматривается тепловой контакт тел, имеющих большую
теплопроводность, например металлических, то наличие плохо
проводящих зазоров вызывает стягивание линий теплового тока
к местам фактического контакта (рис. 3.4). При этом плотность
46
илового потока, проходящего через плохо проводящие зазоры,
Уменьшается. Соответственно меняется и распределение температур
вблизи поверхностей контакта. Так, если линия 0 — 0 соответст-
вует распределению температуры вдоль линий тока при идеальном
Контакте, то распределение температур вдоль линий тока, проходя-
*Цих через контактное пятно и зазор, будет характеризоваться со-
ответственно кривыми I — I и II — II. Таким образом, температу-
Ра в различных точках поверхностей будет различна.
Рис. 3.4. Распределение температуры (сплошные ли-
нии — изотермы) и тепловых потоков (пунктирные
линии) и области контактного пятна (а) и измене-
ние температуры вдоль линий тока /—/ и II—II (б).
Однако при инженерных расчетах нет необходимости рассматри-
вать сложные температурные поля вблизи поверхности контакта.
Для этой цели достаточно определить дополнительный перепад
(скачок) температуры AZ, обусловленный наличием плохо проводя-
щих прослоек и стягиванием линий теплового тока. Скачок темпе-
ратуры пропорционален плотности теплового потока q:
М = RKq, (3.41)
Коэффициент пропорциональности 7?к, смысл которого очевиден,
называется коэффициентом термического сопротивления контакта.
47
При сравнительно небольших плотностях теплового потока скачок
температуры можно не учитывать и считать, что температуры сопри-
касающихся поверхностей одинаковы. Однако в ядерных установ-
ках, где плотности тепловых потоков достигают нескольких мил-
лионов ватт на квадратный метр, неучет контактного сопротивле-
ния может привести к существенным ошибкам.
Величина контактного сопротивления зависит от многих фак-
торов. К их числу прежде всего относятся микро- и макрошерохо-
ватость* соприкасающихся поверхностей, физические свойства со-
прикасающихся материалов, теплопроводность вещества, запол-
няющего зазоры, величина сжимающего усилия, характеризуемая
величиной контактного давления. Учет всех факторов, влияющих
на контактное сопротивление, весьма затруднителен, поэтому
сегодня можно говорить лишь о приближенном расчетном опре-
делении величины термического контакта. Для этой цели можно
рекомендовать формулу, полученную Ю. П. Шлыковым и Е. А. Га-
ниным [9] на основе обобщения обширного экспериментального
материала:
1 2ХС , 9 , Мм
^срх + ^срг Зав SH
Ю-4 . ,
м2-град
(3.42)
где Аср1 и Лср2 — средняя высота выступов микрошероховатости
соприкасающихся поверхностей, определяемая по профилограммам
или в зависимости от способа обработки поверхности (например, по
классу чистоты); %с — коэффициент теплопроводности вещества,
заполняющего зазоры, вт/ (м • град); N — нормальная нагрузка,
н; SH — номинальная (геометрическая) площадь контакта, м2;
ав — временное сопротивление разрыву или предел прочности
менее пластического материала, н/мм2; Хм = -тДгтт > и
%2 — коэффициенты теплопроводности контактирующих материа-
лов, вт/ (м • град). Первое слагаемое в выражении (3.42) харак-
теризует проводимость зазоров, второе — проводимость мест фак-
тического контакта.
Расчет по формуле (3.47) дает минимальное термическое сопро-
тивление контакта, обусловленное только микрошероховатостыо.
Наличие волнистости может привести к существенному увеличению
контактного сопротивления. Формула (3.47) не учитывает также
лучистого теплообмена между поверхностями, но, как показывают
оценки, его вклад в суммарный тепловой поток при температурах
до 560° С не превышает 2%. Необходимо также помнить, что вслед-
ствие ряда причин, в первую очередь вследствие пластичности ма-
териалов, контактное сопротивление может с течением времени
меняться.
* Микрошероховатость характеризует высоту выступов и впадин по-
верхности в пределах небольших участков; макрошероховатость характери-
зует неровность поверхности в пределах сравнительно больших площадей,
ее часто называют волнистостью.
48
Одним из наиболее характерных для ядерных реакторов мест,
где термическое сопротивление контакта играет важную, если не
решающую роль, является контакт оболочки и топлива в твэлах.
При конструировании твэлов принимаются различные меры для
снижения контактного сопротивления между топливом и оболочкой
п обеспечения стабильности контакта. Для этой цели иногда при-
меняют совместную протяжку топлива в оболочке, стремясь осу-
ществить взаимную диффузию материалов. В некоторых случаях
зазор между топливом и оболочкой заполняют веществом, обла-
дающим высокой теплопроводностью, например гелием или жидким
натрием.
7. Температурное поле в плоском и цилиндрическом твэлах,
защищенных оболочкой. В рассмотренных выше задачах поверх-
ности тел, в которых происходит выделение тепла, непосредственно
омывались теплоносителем. В реальных условиях по ряду сообра-
жений (защита от коррозии, улавливание радиоактивных продуктов
распада) тепловыделяющие пластины или цилиндры помещают в за-
щитные оболочки. Оболочки сами по себе обладают термическим
сопротивлением 6 (Д0, которое необходимо учитывать при расчете
поля температуры. Поскольку речь идет о таких теплонапряженных
элементах, как твэлы, где плотность теплового потока имеет поря-
док 103 квт/м1, то необходимо также учитывать и термическое со-
противление контакта или сопротивление зазора 63/Х3, если
топливо и оболочка не соприкасаются друг с другом.
Если пренебречь тепловыделением в оболочке и ввести понятие
эффективного коэффициента теплоотдачи аоф, учитывающего до-
полнительные термические сопротивления, то расчет температурных
полей можно проводить по приведенным выше соотношениям, заме-
нив в них коэффициент теплоотдачи а на аоф. Температурные поля
в плоских твэлах рассчитываются по формулам (3.10)— (3.14).
Эффективный коэффициент теплоотдачи для этого случая опреде-
ляется по формуле
_L__L (3.43)
ССдф Ct А*0
При наличии термического сопротивления контакта jR = jRK,
а при наличии зазора между оболочкой и топливом jR = б3/Х3.
Распределение температуры в цилиндрических твэлах рассчиты-
вается по формулам (3.27) — (3.31) с использованием следующих
эффективных значений коэффициентов теплоотдачи:
+4-1п-+^;
аэфх О. ccj Гю Ао /"ю
(3.44)
ааф2^2 <^2г20 ^0 <723
49
При наличии контактного сопротивления jRx = =
— Т?к/г2, а ПРИ наличии зазора между оболочкой и топливом
__ Г1 — Г13 п Г23 —
1 ?V3 ’ %з
Рис. 3.5. Схема полого цилиндри-
ческого твэла в защитной обо-
лочке:
1 — оболочка; 2 — зазор; 3 — топ-
ливо.
Обозначение геометрических разме-
ров в соотношениях (3.44) пока-
зано на рис. 3.5.
В тех случаях, когда толщина
оболочки 8 о невелика по сравне-
нию с радиусом, вместо формул
(3.44) можно пользоваться более
простыми соотношениями (3.43).
Если 6о/гх<0,1, то связанная
с таким упрощением погрешность
не превышает 5%.
В качестве примера приведем
некоторые сведения о твэлах,
использованных в отечественных
реакторах ВВЭР. Твэлы представ-
ляют собой цилиндрическую обо-
лочку из циркониевого сплава на-
ружным диаметром 10,2 мм с тол-
щиной стенки 0,6 мм (в последних
вариантах диаметр стержней умень-
шен до 9,1 мм), внутрь которой
помещается топливо в виде спе-
ценной окиси урана (UO2), обога-
щенного 236U до 2%. При тепло-
вых расчетах твэлов предполагают,
что между топливом и оболочкой
может образоваться зазор тол-
щиной 0,05 мм. Исходя из условия, что в процессе работы макси-
мальная температура топлива на оси твэла не должна превышать
2800° С (температура плавления UO2), по соответствующим форму-
лам, приведенным в настоящем разделе, нетрудно рассчитать пре-
дельно допустимую мощность тепловыделения на единицу длины
твэла, которая оказывается равной 475 вт!см.
§ 3.2. Теплопроводность через ребра и оребренную стенку
Если интенсивность теплоотдачи (т. е. значение а) между по-
верхностью твэла и теплоносителем относительно мала, например
при охлаждении реактора газом, эффективным средством сниже-
ния температуры твэла (при заданном тепловыделении) может ока-
заться его оребрение. Выгодно также оребрение стенок труб паро-
генераторов, обогреваемых газом. В этом случае оребрение стенки
со стороны газа позволяет увеличить тепловые потоки при одних и
тех же температурах и расходах теплоносителей.
50
Увеличение поверхности плоской стенки путем ее оребрения
приводит к снижению термического сопротивления между стенкой и
теплоносителем и в некоторых случаях может дать значительный
выигрыш в передаваемом через стенку тепловом потоке. Так, если
коэффициент теплоотдачи от стенки к жидкости» мал, а коэффициент
теплопроводности материала ребра X велик (точнее, если число
Био Bi = абр/А, << 1, где бр — толщина ребра), то оребрение по-
верхности приводит к увеличению передаваемого через стенку теп-
лового потока. Если же коэффициент теплоотдачи велик, а ребро'
выполнено из материала с низкой теплопроводностью (Bi 1),
то оребрение может привести к уменьшению количества тепла, пере-
даваемого через оребренную стей-
ку. Но и при значениях Bi < 1
оребрение приносит пользу только
Рпс. 3.6. Схема элемента ребра.
в том случае, если доля «внеш-
него» термического сопротивле-
ния 1/а составляет существенную
часть общего термического сопро-
тивления стенки.
На практике делают ребра раз-
личной формы. Применительно
к интересующему нас случаю —
оребрению цилиндрических по-
верхностей — чаще всего используются продольные, кольцевые
пли спиральные ребра (подробнее о форме оребрения см. гл. 10).
Чтобы определить эффективность оребрения, необходимо рас-
считать температурное поле в оребренной стенке. Точное определе-
ние температурных полей в оребренной стенке — сложная задача.
Так как тепло распространяется вдоль ребра и отдается омывающей
его с боковых поверхностей жидкости, то температурное поле в ребре
должно быть, по крайней мере, двумерным. Однако в тех случаях,
когда число Био ребра мало (Bi < 1), а именно в этих случаях ребра
являются эффективными, температура по толщине ребра меняется
незначительно. При этом с большой степенью точности можно счи-
тать, что температура изменяется только вдоль ребра или, другими
словами, что температурное поле в самом ребре одномерно. При
таком подходе решение задачи существенно упрощается. Используя
допущение об одномерности, рассмотрим задачу о температурных
полях в прямых и кольцевых ребрах.
1. Дифференциальное уравнение, описывающее распределение
температуры по высоте ребра переменного сечения, можно получить,
рассматривая тепловой баланс участка ребра, изображенного на
рис. 3.6. Обозначим / (х) — площадь поперечного сечения ребра;
р (х) — его периметр; t (х) — температуру в сечении х; а—коэф-
фициент теплоотдачи; tm — температуру окружающей жидкости.
Изменение теплового потока вдоль ребра на участке длиной dx
должно быть равно (если тепловыделение в самом ребре отсутст-
вует) теплу, отдаваемому поверхностью элемента окружающей
51
жидкости:
(3.45)
dx \ dx / '
Вводя новую переменную Ф = t — tn{, имеющую смысл темпера-
туры ребра, отсчитываемой от температуры окружающей среды,
окончательно получаем
_£ арЙ = 0. (3.46)
dx \ dx1
Применяя уравнение (3.46) к участку прямого ребра переменного
сечения длиной 1 м (рис. 3.7) и учитывая, что в этом случае f (х) =
= 6 (х) 1 м2 и р (х) = 2 ж, на-
ходим
Рис. 3.7. Схема прямого ребра.
а
dx
^-й = 0. (3.47)
л
В общем виде это уравнение не
решается. Для ребер треуголь-
ного и параболического профи-
лей оно преобразуется соответст-
венно в обобщенное уравнение
Бесселя и уравнение Эйлера
НО].
2. Ребро постоянного поперечного сечения. Уравнение (3.47)
решается наиболее просто в случае ребра постоянного поперечного
сечения б = бр = const. Тогда
dx2
т2 й
О,
(3.48)
где
Г Irx
т= 1 / —
/2Bi
бР
(3.49)
Считая, что температура в основании ребра известна и равна
й0, и учитывая теплообмен на торце ребра, имеем следующие гра-
ничные условия:
й(0) = йо, — Ж (Я)-ай(77). (3.50)
Решив уравнение (3.48) при граничных условиях (3.50), получим
распределение температуры по высоте ребра:
ехР (”**) — ° ехр[—/га(х—2#)],
0 1—о ехр (2тЯ)
(3.51)
где
g —
а—тк.'
52
Зная распределение температуры, нетрудно определить тепловую
мощность, рассеиваемую единицей длины ребра:
а
—г + th mH
= 6 --------
р ОС
x==0 1+-Т th mH
тк
(3.52)
Выражения (3.51) и (3.52) неудобны для расчетов. На практике
обычно пользуются более простыми уравнениями, которые можно
получить, если пренебречь теплоотдачей с торца ребра, т. е. решить
задачу при граничных условиях
й(0)-йо и Й'(Я)-О. (3.53)
В этом случае распределение температуры по высоте ребра выра-
жается зависимостью
(з.54)
Тепловая мощность, рассеиваема^ единицей длины ребра,' равна
Q = бгЛ/71й'() th tn И. ; (3.55)
Если ребра имеют большую относительную высоту И > 6Р,
то пренебрежение теплоотдачей с торца ребра не приводит к зна-
чительным ошибкам. Однако в реакторостроеиии ребра, как пра-
вило, имеют небольшую относительную высоту, и теплоотдачей
с торца пренебрегать нельзя. Чтобы приближенно учесть тепло-
отдачу с торца при использовании простых расчетных соотноше-
ний (3.54), (3.55), в них вместо действительной высоты ребра под-
ставляется фиктивная высота Н’ = Н -|- 6р/2. Если Bi 1/4, то
рассчитанная таким образом тепловая мощность, рассеиваемая
ребром, отличается от результатов расчета по точному выраже-
нию (3.52) не более чем на 7,6% [10].
Введем коэффициент эффективности ребра Е, показывающий,
во сколько раз ребро увеличивает (или уменьшает) теплоотдачу
•с рассматриваемого участка плоской неоребренной поверхности
(площадью 6Р• 1 м*). Тогда тепловую мощность, рассеиваемую реб-
ром, можно выразить следующим образом:
Qp =ай'0арЕ. (3.56)
Полагая, что коэффициенты теплоотдачи на плоской поверх-
ности и на поверхности ребра одинаковы, в соответствии с (3.52)
получаем выражение для коэффициента эффективности прямого
ребра постоянного сечения:
1 — th mH 1 + 1/ ~ th mH
Е =------------------------------------ (3.57)
1 + -2- th mH 1 + Т/— th mH
кт Г 2
53
При Bi 1/4 его с достаточной степенью точности можно заме-
нить более простым приближенным выражением:
E = thm (Н+ — . (3.58)
В практических расчетах обычно используют коэффициент эф-
фективности ребра rip, определенный иначе: показывает, во
сколько раз действительно рассеиваемая ребром тепловая мощность
меньше мощности, которая рассеивалась бы идеальным бесконечно
проводящим ребром тех же размеров,
температура всей поверхно-
сти которого равна й(). Так
как тепловая мощность,
рассеиваемая идеальным
ребром, равна аО'о2/7, а
реальным
Qp =аО02Ят]р, (3.59)
то из уравнений (3.56) и
(3.59) следует, что коэффи-
циенты эффективности Е
и т)р связаны между собой
соотношением
Рис. 3.8. Схема кольцевого ребра.
Up Хи 1|р.
Очевидно, что коэффициент Е может быть и больше, и меньше еди-
ницы, a rip всегда меньше единицы.
3. Кольцевое ребро. Рассмотрим теперь кольцевое ребро, схема
которого показана на рис. 3.8. Применяя к нему уравнение (3.46),
с учетом того, что f (г) = 6 (г) 2 лг, а р (г) = 4 яг, получаем
А Ыг — — 2аг6’ = 0. (3.61)
dr \ dr } \ >
В случае ребра постоянной толщины 6 = = const, и при по-
стоянном коэффициенте теплопроводности уравнение (3.61) упро-
щается и принимает вид
±.[г — \~т2гЬ = ^, (3.62)
dr \ dr J
„ /"2а“
где m=Vwf
Если задана температура в основании ребра и не учитывается тепло-
обмен на его торце, то, приняв во внимание граничные условия
О’ (rj) = Ф 0 и тЭ1' (г2) = 0, найдем распределение температуры в ребре:
ф лл __ ф ;о El (fn/'z) 4~ It (rnrj) Eq (inr)
0 Io (mrj) Ki (mr2) + (tnrz) Ko (тгр ’ ' '
и тепловая мощность, рассеиваемая ребром,
54
Q =; 2nr, S„ Xfl„ m K, (mrj, (3 64)
Л) (.nifi) 7<! (mr2) -I- It (mr2) /<() (//z/'i)
где /(), Д и Л'1, /<2 ~~ модифицированные функции Бесселя.
Чтобы приближенно учесть теплоотдачу с торца ребра, как и ранее,
вместо действительного значения наружного радиуса ребра г2 в вы-
ражения (3.63) и (3.64) подставляется значение г2 = г2 -|- 6р/2.
4. Оребренная стенка. Полученные выше уравнения позволяют
рассчитать тепловую мощность, рассеиваемую ребром. Воспользо-
вавшись этими уравнениями, можно также приближенно определить
тепловую мощность, передаваемую через оребренную стенку. Про-
в оребренной стенке.
иллюстрируем метод расчета и принимаемые допущения на примере
плоской оребренной стенки, схема которой показана на рис. 3.9.
Пусть заданы граничные условия третьего рода: температуры
жидкостей, омывающих стенку с обеих сторон /ж1 и /ш2, и соот-
ветствующие коэффициенты теплоотдачи аг и а2. Для простоты
будем считать, что коэффициенты теплоотдачи постоянны. Полагаем
также, что температурное поле не только в ребре, но и в стенке
одномерное и температура в основании ребра равна температуре по-
верхности пеоребренпой стенки. Последние допущения далеки от
действительности, так как в тех случаях, когда ребра улучшают
теплоотдачу, они сильно искажают температурное поле в стенке и
снижают температуру стенки вблизи основания ребра (рис. 3.10).
Однако более точное решение задачи с учетом двумерности темпера-
турного поля в стенке аналитическим путем получить трудно.
Тепловая мощность, рассеиваемая участком иеоребреш-юй стен-
ки площадью (6Р -|- с) • 1 (см. рис. 3.9), равна
<?.,=(вр-I- а , = («р + , (3.65)
55
где О1 = t — /ж2 — температура, отсчитываемая от /ж3. Темпе-
ратура поверхности стенки со стороны жидкости, имеющей темпе-
ратуру /ж2, равна
Тогда тепловая мощность, рассеиваемая ребром,
Qn = а3 дсз 2Ж1р = 2Ят)р —:-------------— • (3-67)
Л 1 1 ос 1
— _|_ —
cq Л «2
Мощность, приходящаяся на межреберный простенок, равна
---— • (3.68}
1 О Q 1
' — I . — - I ..
Г л Г
ах Л а2
Суммарная тепловая мощность, рассеиваемая оребренной стен-
кой на участке длиной 6р + с, есть
Зор = <ЭР + <3е= —--------------- (2№lp + с). (3.69)
1 ос 1
_|_
cq-----------%-а2
Таким образом, тепловую мощность, рассеиваемую оребренной
стенкой Qop, можно определить по мощности для неоребренной
стенки Qn, умножив эту величину на коэффициент, эффективно-
сти оребрения стенки'.
О0п 1
(3.70)
Формулу (3.70) нетрудно обобщить и на более сложные формы
оребренных поверхностей. Для этого введем следующие обозначе-
ния. Пусть FH — площадь неоребренной поверхности; Рр пло-
щадь поверхности ребер; Fop — полная площадь оребренной по-
верхности. В рассмотренном случае для плоской поверхности и
прямых ребер Fn = 6Р + с; Fp = 2 Н\ FGJ> = 2Н + с. Путем со-
ответствующих подстановок формула (3.70) легко преобразуется
в более общее соотношение, позволяющее определить коэффициент
эффективности оребрения стенки по заданной геометрии оребрения
и коэффициенту эффективности ребра:
Г
йоР= 1 + -“-Опр—1)
С ор
(3.71)
56
Рассмотренные выше соотношения для тепловых расчетов
ореоренпых поверхностей являются весьма приближенными, так
как получены с использованием ряда не всегда выполняющихся до-
пущений. При необходимости проведения более точных расчетов
обычно используют аналоговые методы (особенно часто электротеп-
ловую аналогию) 12]. Следует также помнить, что при любом способе
расчета надо знать коэффициент теплоотдачи и его распреде-
ление на оребренной поверхности. Чаще всего для простоты пола-
гают, что коэффициент теплоотдачи по высоте ребра постоянен.
В действительности же коэффициент теплоотдачи может очень силь-
но изменяться, особенно если межребериые зазоры невелики. Поэто-
му при изучении теплоотдачи через оребренные стенки большую
роль играют экспериментальные методы исследования.
§ 3.3. Двумерные стационарные задачи теплопроводности
В ряде практически важных случаев температурное поле нельзя
даже приближенно считать одномерным, и возникает необходимость
в расчете двумерных температурных полой. Так, существенно дву-
мерны температурные поля в замедлителе, в некоторых типах твэ-
лов и, в частности, в твэлах с повреждениями, в результате которых
нарушается осевая симметрия. Двумерны также температурные
поля в оребренных оболочках н трубах.
Принципиальная трудность при переходе к аналитическому ре-
шению двумерных задач связана с тем, что в этом случае необходимо
решать дифференциальное уравнение в частных производных.
Как указывалось в гл. 2, при расчете двумерных температурных по-
лей в телах достаточной простой конфигурации при не очень слож-
ных граничных условиях можно использовать точные и прибли-
женные аналитические методы. При более сложной геометрии, а во
многих практических задачах приходится иметь дело именно со
сложной геометрией, получить точные и даже приближенные ана-
литические решения невозможно. В этом случае расчет двумерных
температурных нолей удобнее всего осуществлять либо численным
методом, либо методами электротешювой аналогии.
Рассмотрим несколько задач, представляющих интерес для
анализа температурных полей в активной зоне реактора.
1. Температурное поле в тепловыделяющем массиве, пронизан-
ном охлаждающими трубами. Таким массивом является замедли-
тель реактора па тепловых нейтронах. В замедлителе выделяется
заметное количество тепла, отводимое к стенкам рабочих каналов,
пронизывающих замедлитель. На рис. 3.11 показаны схемы распо-
ложения рабочих каналов в замедлителе по углам прямоугольника
и углам равностороннего треугольника. Предполагается, что в на-
правлении нормали к плоскости чертежа температура не изменяется.
Вследствие симметрии температурного поля относительно осей
О А, ОС и АС при решении задачи достаточно рассмотреть треуголь-
ную область ОЛС, заштрихованную иа рисунке; эта область в более
57
Рис. 3.11. Расположение рабочих каналов в активной зоне реактора:
а —по углам прямоугольника (коридорное); б — по углам равностороннего треуголь-
ника (шахматное).
крупном масштабе показана на рис. 3.12. Будем считать, что мощ-
ность внутренних источников тепла распределена равномерно, т. е.
qv = const, температура охлаждаемой поверхности BD постоянна
и равна Тр Граничные условия вдоль линий ОЛ, ОВ и AD очевид-
ны, так как эти поверхности являются адиабатическими. Таким об-
разом, расчет температурного поля в области OBDA сводится к ре“
шению дифференциального уравнения
54 дЧ qv
дх2 "I" ду~ I" Л
(3.72)
при следующих граничных условиях:
на границе BD t = zfx;
на границе OB, DA, О А = О,
где п — направление нормали к границе.
Рис. 3.12. Элементарная ячейка массива.
58
Точное аналитическое решение такой задачи затруднительно.
Поэтому приходится решать ее численным методом [8] либо ис-
пользовать приближенные аналитические методы [10, 12]. При
практических расчетах удобно пользоваться номограммами безраз-
мерной температуры, полученными в работе [12] и приведенными
па рис. 3.13. На этих номограммах построены линии постоянной
безразмерной температуры Т, отсчитанной от произвольно взятого
в точке О значения Тя == 10, для двух случаев: расположение труб
Рис. 3.13. Распределение безразмерной температуры в тепловыделя-
ющем массиве:
а—шахматное (а=л/3); б — квадратное (а=л/4) расположение охлажда-
ющих труб.
по углам квадрата (а = л/4) и по углам равностороннего треуголь-
ника (а ~ л/З). Безразмерная температура в любой точке массива
определена с помощью соотношения:
где Тя = 10.
Достоинством этих графиков является их универсальность по от-
ношению к диаметру рабочих каналов.
В качестве примера определим по этим графикам максимальную
температуру (температура t3 в точке О) для случая расположения
рабочих каналов по углам равностороннего треугольника (а = л/3)
при следующих заданных параметрах (обозначения даны в соот-
ветствии с рис. 3.12):
г0 = 10 мм\ s2 = 50 мм; t-i = 200° С;
Я — 50 вт! (ж граду, qv — 106 вт!м\
59
Прежде всего на графике вдоль линии СА откладывается отре-
зок, соответствующий безразмерному радиусу рабочего канала:
CD~r0 —.
«2
Проходящая через точку D изотерма определяет безразмерную
температуру на поверхности рабочих каналов. В рассматриваемом
с А
случае CD = 10 = 0,2 СА и 7\ = 7,5. Таким образом, без-
размерная разность температур между точками О и D равна
Т3 — 7\ = 10—7,5 = 2,5.
Безразмерная разность температур по соотношению (3.73) легко'
пересчитывается на размерную разность температур:
qvs~> ~ 10(3-0,052 Q1or,
t3—tr--= (Т3—TJ = 2,5------— = 31 °C
3 1 К 3 17 4Л 4-50
и, наконец,
t3 = 200 + 31 = 231° С.
Простой приближенный способ оценки максимальной темпера-
туры массива (температуры t3 в точке 0) предложен в работе [8].
Этот способ применим как к шахматному, так и к коридорному рас-
положению труб в массиве.
Учитывая, что распределение температуры вдоль оси симметрии
ОА близко к распределению температуры в сплошном цилиндре,
в соответствии с уравнением (3.19) можно написать:
= (3.74).
где /2 — температура в точке А.
Распределение температуры вдоль линии AD не сильно отли-
чается от распределения температуры в полом цилиндре, и в со-
ответствии с формулой (3.28)
/a-/i=4r(2siln— ~si + а°ь <3-75>
4л \ а I
Сложив выражения (3.74) и (3.75), получим уравнение для при-
ближенного расчета максимальной температуры массива:
4 %
2In
(3.76)
или в безразмерном виде
Т3 — 7\ = ~ = 2 In —
31 Яу°1 а
(3.77)
60
Расчет по уравнению (3.76) температуры /3 для рассмотренного вы-
ше примера дает значение /3 = 227° С, что немногим отличается от
значения, полученного по номограмме.
2. Температурное поле в твэле при неоднородных граничных
условиях. В качестве второго примера рассмотрим двумерное
температурное поле в поперечном сечении твэла при неоднородных
граничных условиях на его поверхности. Тепловыделяющие сборки
часто выполняются в виде пучка цилиндрических твэлов, в зазорах
между которыми параллельно оси течет теплоноситель (рис. 3.14).
При достаточно тесном расположении твэлов в пучке коэффициент
теплоотдачи оказывается непостоянным
по окружности тепловыделяющих стерж-
ней и зависит от угла ср.
В тех точках поверхности, где за-
зор между твэлами наименьший, коэф-
фициент теплоотдачи имеет минималь-
ное значение (а < а). Там, где зазор
наибольший, коэффициент теплоотдачи
максимален (а > ос). Вследствие зави-
симости а (ср) температурное поле в
твэле будет функцией не только радиу-
са, но и угловой координаты (р. В част-
ности, и температура поверхности обо-
лочки /с, и плотность теплового потока
на поверхности qG будут меняться по
периметру твэла. Очевидно, что там,
где коэффициент теплоотдачи максимален, плотность теплового
потока также максимальна, а температура поверхности минимальна.
И наоборот, там, где коэффициент теплоотдачи минимален, плот-
ность теплового потока минимальна, а температура поверхности
максимальна.
Распределение температуры и плотности теплового потока по
поверхности твэла в общем случае можно записать в виде перио-
дических функций*:
Рис. 3.14. Схема тепловы-
деляющей сборки с пучками
стерж н ей, р асп ол ожеппы м 11
в вершинах правильного,
треугольника.
00
/с = /с 2 ak cos /гф; (3.78)
k
00
qG = <70+ 2 bh cos /гср, (3.79)
k
причем периодичность этих функций определяется геометрией пуч-
ка — числом твэлов, окружающих рассматриваемый твэл. Для
треугольной решетки, изображенной на рис. 3.14,/г = 6, 12, 18,...,
для квадратной решетки k = 4, 8, 12, ...
* Распределение температур и тепловых потоков в твэлах, находящихся
на периферии пучка (в соседстве с оболочкой), более сложно.
61
При экспериментальном исследовании теплоотдачи в продоль-
но обтекаемых пучках прежде всего_получают зависимости для
среднего коэффициента теплоотдачи а, позволяющие определить
среднюю температуру поверхности твэла в рассматриваемом сече-
нии:
(3.80)
Кроме того, измеряется распределение температуры на поверх-
ности твэла и полученные данные обычно обрабатываются в виде
зависимости безразмерной темпера-
туры
= (3.81)
Че. гиар
сс,
Рис. 3.15. Схема тепловыделя-
ющего стержня в оболочке.
от угла ф.
По распределению температуры на
поверхности стержня можно, как это
показано ниже, рассчитать темпера-
турное поле и определить значения
локальных тепловых потоков и ло-
кальных коэффициентов теплоотдачи
на его поверхности. Для этого необ-
ходимо решить задачу о распределе-
нии температуры в твэле при неоднородных граничных условиях,
заданных в виде периодической функции (3.78).
Итак, рассмотрим тепловыделяющий стержень в оболочке, по-
казанный на рис. 3.15*. Радиус тепловыделяющего стержня обо-
значим г15 его температуру tr (г, ср), коэффициент теплопроводности
Хх, мощность внутренних источников тепла qv. Соответственно на-
ружный радиус оболочки г2, ее температура /2 (г, ср), коэффициент
теплопроводности тепловыделение в оболочке отсутствует.
Введем безразмерные величины: текущий радиус R = г/г3,
радиус топливного стержня = гх/г2 и температуру Т = t^xlq^r^
Принятая здесь в качестве масштаба средняя плотность теплового
потока qc, в отличие от местной плотности q0, легко находится из
уравнения теплового баланса:
— f2
<7с= qv-~
2г2
(3.82)
* Решение этой задачи и более сложной (с учетом трех оболочек) полу-
чено П. А. Ушаковым [7].
62
Распределение температуры в тепловыделяющем стержне и оболоч-
ке описывается следующими дифференциальными уравнениями:
J_ д7\ 1 д*7\______2_. п
dR2 R dR 1" R2 дф2 Rl ’ ' ' '
+ + (3.84)
dR2 R OR R2 дф2 V f
которые дблжны быть решены при таких граничных условиях:
dR J7? = o
<Р) = Т2(^, ф);
(3.85)
= А,„
(3.86)
(3.87)
т2 (1, ф) = тс 2 ckcos k(p-
(3.88)
Решение уравнений (3.83) и (3.84) при граничных условиях (3.85) —
(3.88) будем искать в виде суммы:
Т (R, ф) = @ (/?) +ф (Р, ф).
(3.89)
Здесь 0 (R) — решение задачи для случая, когда в тепловыделя-
ющем стержне действуют источники тепла qv, а распределение тем-
пературы на поверхности однородно. Это слагаемое не зависит от ф
и должно удовлетворять следующим уравнениям:
d20t 1 _____2_.
dR2 R dR R%’
d2 €>2 ] 1 402 q
(3.90)
dR2 R dR
(3.91)
при граничных условиях:
©;(0) = 0;
<S>3(1) = TC.
(3.92)
(3.93)
(3.94)
(3.95)
Функцииф (R, ф) —- решение задачи для случая, когда внутренние
источники отсутствуют, а на поверхности твэла задана переменная
температура. Они должны удовлетворять уравнениям
д2Ф1 । 1 ЗФ1 । 1
ад+
д2 42 . 1 дфг I J_ д2 ф2 „ о
dR2 ~ R dR Г R2 <Эф2
(3.96)
(3.97)
63
при таких граничных условиях:
фНЫ^в ф);
00
1р2 (1 > ф) -- 3 Ck C0S ^ф.
k
(3.98)
(3.99)
(3.100)
(3.101)
Решив уравнение (3.90) и (3.91) при граничных условиях (3.92) —
(3.95), получим следующие выражения для и 02;
(3.102)
"X ' 1 / ^2
e2(«)=-T-lnJ? + f«- (З.ЮЗ)
Л-2
Уравнения (3.96) и (3.97) можно решить методом разделения пере-
менных. Полагая
4’ (Я, Ф) = U (R) V (ср),
(3.104)
подставляем это выражение в уравнения (3.96) и (3.97) и, разде-
лив переменные, получаем:
d* U . |__L^_£y=0; (3.105)
dR2 R dR 7?2
^I + p^V^o. dcp2 (3.106)
Решения этих уравнений имеют вид:
(3.107)
V = C sin pep 4- D cos |3cp. (3.108)
Учитывая, что распределение температуры в твэле в соответствии
с граничными условиями должно быть четной функцией ср, при-
нимаем С = 0.
Из условия (3.101) нетрудно получить, что $—k. Поэтому ре-
шение для ф ищем в виде:
оо
Ф1= ^^lkRk + B1}iR~k)cos /гср;
k
оо
= 2 (+ вы R ~,г) cos /гср.
k
(3.109)
(3.110)
64
Постоянные Д1Л, Blh, A2!{, B2k определяются из граничных усло-
вий (3.98) — (3.101):
Ikch
_2___
Мн-о
M /
ik ~~ 0;
= c* T+ntfl“ '
mR
1 + mRi1*
’ — 1 til
Bzk — ck
где т = (%2 — \) /(Х2 + М
Таким образом,
00
сл
2Rk
cos Zxp;
ОС)
У
k
Rk+ mR~k R~k .
Сь----------Цуг-----cos /г ср.
11 1 _1_ /мО-гЯ 1
(3.112)
k
1
Окончательно распределение температуры в тепловыделяющем
стержне и оболочке при неоднородных граничных условиях пер-
вого рода описывается следующими выражениями:
--У -------------cos/ecp; (3.113)
а I 1 + "г- I О + mRi 9
\ М J
оо
Т-2 = In R + 2 cos 1гч>, (3.114)
где ck — коэффициенты в граничном условии (3.88), определяемые
по найденному из эксперимента распределению tc. В частности,
для стержня без оболочки (%х = Х2, т = О, — 1) имеем
__ 1 оо
П = Т„ + 4-(l -R2) + 3 Clt RI‘ cos hf. (3.115)
2 /г
Максимальная температура твэла — температура на его оси (R — 0),
как видно из выражения (3.113), не зависит от коэффициентов ck
и равна температуре в центре такого же твэла, на поверхности ко-
торого температура постоянна и равна Тс.
3 Зак. 792 65
Зная распределение температур в стержне и оболочке, легко
найти плотность теплового потока в любой интересующей нас точке
твэла. В частности, на поверхности оболочки имеем
(3.116)
или в безразмерном виде
7с __ _ \
7с \ dR = i
(3.117)
' дТ \
Вычислив производную I —- и подставив ее в (3.117), получим
\ dR Ji
ОО
7с
7с
1— mRlk <
cos /гср
(3.118)
А
или, обозначив
^2
ek ~ Т~
l—tnRlk
l-\-mRlk
(3.119)
получим окончательно
оо
= 1 — J1 ск k&h cos /гср.
7с
(3.120)
/г
Таким образом, если распределение температуры на поверх-
ности твэла известно, т. е. известны значения коэффициентов ск
в уравнении (3.88), то по уравнению (3.120) можно рассчитать рас-
пределение плотности теплового потока. Параметр еь зависящий
от геометрии стержня и коэффициентов теплопроводности стержня
и оболочки, является заданной величиной.
В качестве примера приведем распределение температуры на
поверхности стержней в плотных пучках, полученное в работе [6],
и рассчитанное по нему распределение плотности теплового потока
(рис. 3.16). Очевидно, что в плотных пучках в тех точках, где
стержни соприкасаются (ср = 0), тепловой поток должен быть
равен' нулю.
3. Температурное поле в поврежденном твэле. В процессе ра-
боты реактора возможны различные повреждения твэлов, в част-
ности нарушение теплового контакта между топливом и оболочкой
на некотором участке поверхности, образование трещин в топлив-
ном стержне. В результате таких повреждений температура твэла
может превысить допустимые для топлива значения, что приведет
к аварийной ситуации. Так как форма и размеры повреждений и их
положение в твэле являются случайными, то для анализа возмож-
ных последствий таких повреждений приходится применять ста-
66
Рис. 3.16. Распределение температуры и плотности
теплового потока на поверхности твэла в продольно
обтекаемом пучке (плотная упаковка).
Рис. 3.17. Схема поперечного разреза
поврежденного твэла с секторным
отслоением оболочки:
2 —топливо; 2 — оболочка; 3 — контактный
слой; 4 — газовая прослойка.
З*
Рис. 3.18. Зависимость безразмерной
максимальной температуры 7Макс и
ее координаты Хмако от угла повре-
ждения ср.
67
тистические методы. Качественное представление об изменении тем-
пературных полей при повреждении твэлов можно получить, рассчи-
тывая некоторые идеализированные схемы.
В качестве примера рассмотрим результаты решения задачи о ци-
линдрическом твэле, по всей длине которого в пределах угла 2q>
произошло отслоение оболочки *. Схема рассматриваемой задачи
показана на рис. 3.17. Твэл состоит из топливного стержня 1, за-
щитной оболочки 2 и контактного слоя легкоплавкого металла 3.
Если в таком твэле возникает повреждение в виде газовой прослой-
ки 4, вытеснившей контактный слой в пределах угла 2 ср по всей
длине твэла, то максимальная температура увеличивается, а коор-
дината максимума температуры смещается в сторону повреждения.
Качественно влияние газовой прослойки на температурное поле
в топливном стержне иллюстрируется рис. 3.18, на котором
показан характер изменения безразмерной максимальной темпе-
ратуры Тмакс = (/макс — /гк) h/(qvr‘o) и безразмерной координаты
Хмакс ~ л'манс/го> где эта температура наблюдается, в зависимости
от угла повреждения ср. Очевидно, что степень повышения темпе-
ратуры и асимметрия температурного поля зависят от многих фак-,
торов и прежде всего от теплопроводности контактного слоя и га-
зовой прослойки.
§ 3.4. Нестационарные задачи теплопроводности
При пуске или остановке ядерного реактора, при переходных
режимах и аварийных ситуациях температурные поля во всех эле-
ментах реактора меняются во времени. Для многих практических
задач, например для оценки термических напряжений, необходи-
мы подробные сведения о переменных во времени температурных
полях в твэлах, замедлителе, корпусе, биологической защите.
Определение нестационарных температурных полей в телах
сложной геометрической формы возможно только с помощью ко-
нечно-разностных методов. Для одномерных температурных полей
иногда можно получить аналитическое решение задачи.
1. Нестационарное температурное поле в плоской пластине.
При переходных режимах плотность нейтронного потока в активной
зоне в течение некоторого периода изменяется во времени по экспо-
ненциальному закону; по такому же закону изменяется и мощность
тепловыделения во всех элементах реактора. Поэтому представляет
интерес рассмотреть температурное поле в каком-либо элементе
реактора, например в твэле, при изменении мощности внутренних
источников тепла во времени по экспоненте.
Рассмотрим простую задачу: в тонкой неограниченной пластине
толщиной 2 6 действуют постоянные внутренние источники тепла
мощностью qvn, а на поверхности пластины заданы граничные
условия третьего рода. В пластине установилось стационарное рас-
,|! Задача решена Е. С. Турилиной и К. Д. Воскресенским [5].
68
пределение температуры, описываемое параболической зависимостью
в соответствии с уравнением (3.4). В момент времени, который будем
считать за начало отсчета т = 0, мощность внутренних источников
тепла начинает меняться по экспоненциальному закону:
qv (т) = ехр (/гт),
(3.121)
оставаясь постоянной по толщине пластины* .
Если ввести температуру, отсчитываемую от температуры ок-
ружающей среды й (х, т) = t (х, т) — i}K, то нестационарное темпе-
ратурное поле в пластине описывается уравнением теплопровод-
ности:
№ qV{]
-----ехр(Лт)
ОТ ОХ- ср
(3.122)
при следующих граничных условиях (учитывая симметрию темпе-
ратурного поля):
(3.123)
В начальный период времени температура в различных точках
пластины меняется с разной скоростью и происходит перестройка
профиля температуры. Но со временем устанавливается так назы-
ваемое асимптотическое распределение температуры, не зависящее
от начальных условий, и скорость ее изменения во всех точках
становится одинаковой. Для простоты ограничимся вычислением
лишь этого асимптотического распределения температуры.
Решение задачи будем искать в виде
Ю1 (х, т) = ср (х) ехр (/гт). (3.124)
рс
Подставляя выражение (3.124) в уравнение (3.122), получаем для
функции ф (х), характеризующей асимптотическое распределение
температуры в пластине, следующее дифференциальное уравне-
ние:
ф" — 1Ф4-1 = О. (3.125)
а а
Решение этого уравнения имеет вид
x+C2sh/4x + 4. (3.126)
* Аналогичным образом можно получить решение задачи для тепловыде-
ления, изменяющегося во времени по закону q^ (т) — qVQ [1 — ехр (—Ат)].
69
Подставив выражение (3.126) в (3.124) и определив из граничных
условий постоянные, получим
4уо й (х, т) = —— ехр (/гт) ! ch/4x ch VJL 8 + Al/Ashl/Afi Та ага Та
(3.127)
Рис. 3.19. Изменение температуры па
оси плоского уранового твэла и
на его поверхности при экспонен-
циальном изменении мощности внут-
ренних источников тепла.
На рис. 3.19 показано изменение температуры поверхности
6'с = Ю1 (6, т) и температуры в середине пластины т0*о =f)’ (0, т),
рассчитанное по (3.127). Рассматривался плоский твэл из естест-
венного урана толщиной 2 6 =
— 4 мм. Наличие оболочки не
учитывалось. Физические свой-
ства естественного урана при
средней температуре около 500° С
соответственно равны: р =
= 18500 /<гЛи3; с = 167 дою/(кг х
X граду, % = 36 вт/(м • граду,
а — 42 • 10~3 мЧч. Начальная
мощность внутренних источни-
ков тепла принята равной qVo =
= 5,8 • 108 вт/м3, коэффициент
теплоотдачи 5800 втЦм2, • град).
Период реактора — время, в
течение которого нейтронный
поток изменяется в е раз, принят
равным т = 33 сек, что соответ-
ствует k = 1/т0 = 0,03 1/сек.
Если считать = 0, то,
как это следует из графика, уже
через 50 сек топливо в центре
твэла расплавится (/пл 1133°С).
Начальные значения темпера-
тур на рисунке тЭс (0) и f>0 (0) соответствуют начальному стацио-
нарному распределению температуры в пластине.
2. Нестационарное температурное поле в цилиндрическом твэ-
ле. Рассмотрим метод расчета нестационарного температурного
поля применительно к цилиндрическому твэлу без оболочки. Ре-
шение более сложной задачи с учетом термических сопротивлений
оболочки и контактного слоя приведено в работе [4].
В цилиндрическом бесконечно длинном твэле радиусом г0 при
т < 0 действуют внутренние источники тепла мощностью qvi (/'),
на поверхности твэла заданы граничные условия третьего рода:
известны коэффициент теплоотдачи а и температура окружающей
жидкости tna. Начиная с момента т = 0 мощность тепловыде-
ления qV2 и температура окружающей жидкости начинают
70
меняться во времени, причем рассматривается только тот случай,
когда тепловыделение меняется на одну и ту же величину во всех
точках твэла.
Обозначим (г) — стационарное температурное поле в твэле
при т < 0, а Л2 (г, т) — нестационарное температурное поле при
т >- 0. Введем также следующие обозначения:
qV2 (г, т) = qvl (г) qv (т); '
/2(г, т)---/1(г) + /(г, т),
(3.128)
где qv (?), 0 (т) и t (г, т) — отклонение соответствующих величин
от начального значения.
Для (г) справедливо следующее уравнение:
а ((3.129)
\ dr2 г dr J рс
при граничных условиях:
ЁЫа = 0; (3.130)
Для f2 (г, т) справедливо уравнение
^ар+-^+^. (3.131)
<3т \ dr2 г dr 1 рс
начальное условие
Ъ (г, 0) = (г) (3.132)
и граничные условия
-0; -%^’т^а[/2(г0, т)-/ж2]. (3.133)
Вычитая из уравнения (3.131) уравнение (3.129), а из граничных
условий (3.133) — условия (3.130), учитывая (3.128), а также вводя
безразмерную переменную jR = rlr0, получаем уравнение, начальное
и граничные условия для «избыточной» температуры t (R, т):
di d21 1 dt Л — = —_] 1- qv^-- (3.134)
dFo dR2 R dR X
t(R, 0) = 0; (3.135)
(°. t) =0- dR (3.136)
_ «lM = Biu(bT)_{).Wb (3.137)
dR
где Fo = ат/го, Bi = аг0/% — соответственно числа Фурье и Био.
Решим эту задачу, пользуясь операционным методом.
Рассматривая температуру t как функцию двух переменных R
и Fo, применим преобразование Лапласа относительно числа Фурье.
71
Тогда изображение температуры / (R, Fo) определяется следующим
соотношением:
оо
L[t(R, Fo)] = T(R, s)= J l(R, Fo)exp(—sFo)dFo. (3.138)
о
Применяя преобразование Лапласа к уравнению (3.134) и учитывая
(3.135), получаем
+ (3-139)
dR2 R dR
где Qv(s) = L —— •
\ A J
Уравнение (3.139) представляет собой уравнение в полных произ-
водных, и его удобнее записать в следующем виде, введя р? = —s:
z/2 Т 1 ИТ
—^L^.u2T==__q (3.140)
dR2 R dR r v 1
Граничные условия для T (R, р.) получим, применив операционное
преобразование к выражениям (3.136) и (3.137):
S1 = о- (3.141)
dR v ’
s). = Bi[T(1, $) — 0], (3.142)
dR
где 0 (s) есть изображение -О- (т), т. е. © (s) = L [О' (т)].
Решением уравнения (3.140) является следующая функция:
т (R, |Х) = М (|*Я) + BYa (ИЯ) - , (3.143)
где Jo иУ0— функции Бесселя соответственно первого и второго
рода нулевого порядка.
Учитывая ограниченность температуры на оси цилиндра, а так-
же то, что У о (0) — °°, получаем В — 0 и, следовательно,
T(R, p.) = /4(^)-iy. (3.144)
ц2
Постоянную А определим из условия (3.142):
(3.145)
где Л (г) = — Jo (z) — функция Бесселя первого рода первого
порядка. Отсюда для А получаем
72
А (ц) — — цД (р.)
(3.146)
И окончательно изображение «избыточной» температуры
где
т (R, р) = 0 4- 'AML—1
ф(и) р
ф(р)=/0(р)—i /Др).
Bi
(3.147)
(3.148)
соответ-
(3.151)
(3.152)
(3.153)
(3.154)
Множители Jo (pR)_______________1_ __ . (3 149)
|Л2Ф(|Л) и2 1 • 7
(3.150)
ф (р.)
обычно называются передаточными функциями. Они характеризуют
реакцию температурного поля твэла на единичное изменение соот-
ветственно мощности тепловыделения или температуры окружаю-
щей жидкости. Оригиналы этих передаточных функций
ственно равны:
оо
R<M = 2 Ап J0(pnR)exp( — Fo);
п — 1
Ro, t = 2 вп (pn R) exp (—щ3г Fo),
n=l
где
4 , 2В i 2,/х (p-n) .
P*n [(1 4-Bi) Д (p,n)+p,n</i (p,n)] P-n IVo (P-n) (P-n)l
q ___Bi 2p,n<7 i (pn)
(1 + Bi) Д (p,n) 4*Pn 71 (P-n)l (P-n) + (P-n)
pn — корни уравнения Ф (p) =0 или Д (ИиУЛ (lb) — M-n/Bi.
Значения шести первых корней этого уравнения приведены
в табл. 3.1.
Чтобы получить решение задачи, необходимо по изображению
Т (R, р) [уравнение (3.147)] найти оригинал. Для этого, восполь-
зовавшись теоремой умножения изображений, получим:
t (R, Fo) = [ Re, t (Fo — Fo')«(Fo') d Fo' -|-
0
2 F°
+ 4 J > (Fo-Fo") (Fo')dFo'.. (3.155)
0
73
Таблица 3.1
Корни уравнения Jo (|л/Л (|i) = p/Bi
Bi p-1 Из 1.1.1 Ив Цо
0,0 0,0000 3,8317 7,0156 10,1735 13,3237 16,4706
0,01 0,1412 3,8343 7,0170 10,1745 13,3244 16,4712
0,02 0,1995 3,8369 7,0184 19,1754 13,3252 16,4718
0,04 0,2814 3,8421 7,0213 10,1774 13,3267 16,4731
0,06 0,3438 3,8473 7,0241 10,1794 13,3282 16,4743
0,08 0,3960 3,8525 7,0270 10,1813 13,3297 16,4755
0,10 0,4417 3,8577 7,0298 10,1833 13,3312 16,4767
0,20 0,6170 3,8835 7,0440 10,1931 13,3387 16,4828
0,30 0,7465 3,9091 7,0582 10,2029 13,3462 16,4888
0,40 0,8516 3,9344 7,0723 10,2127 13,3537 16,4949
0,50 0,9408 3,9594 7,0864 10,2225 13,3611 16,5010
0,60 1,0184 3,9841 7,1004 10,2322 13,3686 16,5070
0,70 1,0873 4,0085 7,1143 10,2419 13,3761 16,5131
0,80 1,1490 4,0325 7,1282 10,2519 13,3835 16,5191
0,90 1,2048 4,0562 7,1421 10,2613 13,3910 16,5251
1,0 1,2558 4,0795 7,1558 10,2710 13,3984 16,5312
2,0 1,5994 4,2910 7,2884 10,3658 13,4719 16,5910
3,0 1,7887 4,4634 7,4103 10,4566 13,5434 16,6499
4,0 1,9081 4,6018 7,5201 10,5423 13,6125 16,7073
5,0 1,9898 4,7131 7,6177 10,6223 13,6786 16,7630
6,0 2,0490 4,8033 7,7039 10,6964 13,7414 16,8168
7,0 2,0937 4,8772 7,7797 10,7646 13,8008 16,8684
8,0 2,1286 4,9384 7,8464 10,8271 13,8566 16,9179
9,0 2,1566 4,9897 7,9051 10,8842 13,9090 16,9650
10,0 2,1795 5,0332 7,9569 10,9363 13,9580 17,0099
20,0 2,2880 5,2568 8,2534 11,2677 14,2983 17,3442
30,0 2,3261 5,3410 8,3771 11,4221 14,4748 17,5348
40,0 2,3455 5,3846 8,4432 11,5081 14,5774 17,6508
50,0 2,3572 5,4112 8,4840 11,5621 14,6433 17,7272
60,0 2,3651 5,4291 8,5116 11,5990 14,6889 17,7807
80,0 2,3750 5,4516 8,5466 11,6461 14,7475 17,8502
100,0 2,3809 5,4652 8,5678 11,6747 14,7834 17,8931
oo 2,4048 5,5201 8,6537 11,7915 14,9309 18,0711
Рассмотрим некоторые частные случаи..Так, если температура ок-
ружающей жидкости в момент т = О меняется скачком на неко-
торую величину О (О = const), а мощность внутренних источников
тепла не меняется (qv — 0), то
t (R, Fo) = # j 2 Вп J„ (ц„ R) exp [—p* (Fo— Fo')] dFo' =
о n= I
0° 1
= '6' 2j — [1—exp(-^Fo)].
n = 1 Hn
(3.156)
74
Так как
ZJ 71
4 /0(Ип/?)=1
Р/г
— разложение единицы в ряд
то
по собственным функциям (3.140),
ЦП, Fo) = fl’
~ Л) (Ип R) ехр (— р,ад Fo)
(3.157)
н при Fo —> оо Характер изменения температуры на поверх-
ности t (1, Fo) и в центре твэла t (0, Fo) иллюстрируется рис. 3.20, а.
При экспоненциальном изменении мощности тепловыделения в
активной зоне, т. е.
qv = b[l—ехр (—mFo)] (3.158)
Рис. 3.20. Изменение темпера-
туры цилиндрического твэла
при ступенчатом изменении тем-
пературы окружающей среды
(а), при изменении мощности
внутренних источников тепла
по экспоненциальному закону
<7н=&[1—ехр (-mFo)] (б); при
ступенчатом изменении мощно-
сти внутренних источников теп-
ла (е):
1 — температура на поверхности;
2 — температура на осп твэла.
(6 и т — постоянные), и неизменной температуре окружающей
среды (й1 = 0), используя выражение (3.155), получаем
2 Fe° 00
t (R, Fo) = Ls- ( 2 4 4 (H„ R) exp [-^ (Fo- Fo")] x
A 5
2 °°
X 6 [1 — exp(—mFo")] ^Fo"= 4~ 2 VoM)X
Л n— 1
X * | OTexP(~ ЦпРо) ~ Цп exp ( — mFo) 159)
..Рл [^(цп—m) 1
75
При Fo -> оо в цилиндре должно установиться стационарное
распределение температуры, соответствующее мощности тепло-
выделения Ь, описываемое уравнением (3.20), и, очевидно,
2
+ (ЗЛ60)
4Л \ Joi )
Подставляя уравнение (3.160) в (3.159), окончательно получаем
Fo) = -^- + +
Л 4 \ ш /
оо
п= 1
т ехр (— p,n Fo) — рЛ ехр (— т Fo)
|1/г (ц/г — /п)
(3.161)
Изменение температур в твэле в этом случае иллюстрирует
рис. 3.20, б.
Положив в выражении (3.161) иг = оо, получим формулу, опи-
сывающую нестационарное температурное поле в цилиндре при сту-
пенчатом изменении мощности внутренних источников тепла qv =
= b (см. рис. 3.20, в).
Таким образом, пользуясь уравнением (3.155) или соответствую-
щими уравнениями для частных случаев, можно, рассчитать откло-
нение температуры твэла t (г, т) от начального значения (г), а за-
Рис. 3.21. Распределение температуры
в прогреваемом с поверхности полу-
бесконечном массиве.
тем наити температуру твэла в
произвольной точке стержня в
любой момент времени:
/2 (г, т) = (/-) -|- t (г, т).
2. Нестационарное темпера-
турное поле в полубесконечном
массиве. В, качестве другого
примера нестационарного темпе-
ратурного поля рассмотрим за-
дачу о прогреве полубеско-
нечного массива, результаты ре-
шения которой можно использо-
вать для расчета температурных
полей в массивных оболочках,
например корпусе реактора.
Хотя внутренние источники теп-
ла в этой задаче отсутствуют,
их нетрудно учесть, используя
метод суперпозиции температур-
ных полей.
Рассмотрим область оо. При т<С 0 температура во всей
области постоянна и равна tQ. В начальный момент времени т = 0
к поверхности области (х = 0) начинает подводиться переменный
по времени тепловой поток, плотность которого q (т). В результате
76'
в массиве возникает нестационарное поле температуры (рис. 3.21).
Для получения точного аналитического решения этой задачи не-
обходимо решить уравнение теплопроводности
dt a21
----- Q ----
5т дх2
при следующих граничных условиях:
ах
/(оо) = /0-
(3.162)
(3.163)
(3.164)
В случае постоянной плотности теплового потока решение этой
задачи несложно и его можно найти в работе 131. При изменении
теплового потока во, времени по произвольному закону точное
решение получить не удается. Поэтому воспользуемся приближен-
ным интегральным методом [1, И]. Выделим в массиве прогретый
слой, толщину которого обозначим 6 (т) (см. рис. 3.21), и запишем
для него уравнение теплового баланса:
d© л / dt \ /о . рг.
ре—=—X —- , (3.165)
dx \ дх ’х—о
6 (т)
где рс0=*рс f |/(х)— /0] dx
о
представляет собой тепло, затраченное на изменение температуры
прогретого слоя от /0 до t (х).
Выражение (3.165) можно получить интегрированием урав-
нения теплопроводности, однако физический смысл его столь оче-
виден, что проще записать его без вывода. А именно изменение
внутренней энергии прогретого слоя в единицу времени [левая часть
выражения (3.165)1 равно подводимому к слою в единицу времени
количеству тепла [правая часть выражения (3.165)1.
Чтобы решить уравнение (3.165), необходимо задаться некото-
рым распределением температуры в прогретом слое. Применитель-
но к плоским задачам удобнее всего распределение температуры
п
задавать в виде полинома Р (х) = >] ahxk; для задач, характеризую-
щее)
щихся осевой симметрией (цилиндра), — в виде Р (г) In г и для сфе-
рической симметрии—в виде — Р (г).
В рассматриваемом случае зададим температурный профиль
в виде полинома второй степени:
t (х) — а0 -|- аух + а%хг, (3.166)
где ah — коэффициенты, зависящие от времени.
77
Учитывая в выражении (3.166) граничные условия
dt (0, т) __ д (т) .
dx X ’
, ,о ч dt (6, т) п
£(6,tWo и —------------= 0
С/ Л
и определяя коэффициенты п0, ах и а2, получаем
t = /0+
2А.6
(6-х)2.
(3.167)
В этом выражении неизвестна толщина прогретого слоя 6. Под-
ставляя выражение (3.167) в уравнение (3.165), находим следующее
дифференциальное уравнение для определения 6 (т):
4" ~ [S2 q (т)] = aq (т). (3.168)
6 dx
Интегрируя это уравнение и учитывая, что 6 (0) = 0, получаем:
6 (т) = 6а
Если q (т) ~ const, то это выражение упрощается:
6 (т) = У бот.
(3.169)
(3.170)
Зная 6 (т), с помощью уравнения (3.167) можно рассчитать поле тем-
пературы в прогретом слое и, в частности, вычислить температуру
на поверхности массива. В случае q (т) = const температура на
поверхности массива
= (3.171)
Эта величина отличается от значения, полученного при точном ре-
шении задачи
^o^)=^+]/v£F- <з-172>
всего на 9%.
При описании профиля температуры полиномом третьей степени
погрешность в расчете температуры поверхности уменьшается до
2%. Однако не всегда увеличение числа членов в полиноме, опи-
сывающем распределение температуры в прогретом слое, приводит
к уменьшению погрешности приближенного решения.
Таким образом, как об этом свидетельствуют рассмотренные
выше задачи, аналитические методы расчета применимы к доста-
точно широкому кругу проблем. Более сложные задачи следует ре-
шать численными методами на ЭВМ. Численные методы позволяют
рассчитывать как двумерные, так и трехмерные температурные
78
поля, при этом можно учесть зависимость физических свойств от
температуры, изменения тепловыделения и граничных условий.
Численным методом можно, например, с необходимой степенью
точности рассчитать температурное поле в оребренной оболочке,
в поврежденном твэле. Этот метод используется для решения и бо-
лее сложных сопряженных задач, например совместного решения
уравнения теплопроводности для твердого тела и уравнения дви-
жения и энергии для движущейся среды.
В заключение следует отметить, что температурные поля в твер-
дых телах в большой степени определяются влиянием окружающей
тело среды. Чаще всего это влияние характеризуется коэффициен-
том теплоотдачи. В предшествующих разделах коэффициент тепло-
отдачи считался величиной известной (заданной). В действительности
при проведении тепловых расчетов теплообменных устройств коэф-
фициент теплоотдачи необходимо вычислять. Он зависит от физиче-
ской природы процесса теплообмена и определяется большим чис-
лом параметров, характеризующих этот процесс. Рассмотрению
процессов теплообмена между поверхностью твердого тела и окру-
жающей средой и методов расчета коэффициентов теплоотдачи
посвящены последующие главы.
СПИСОК ЛИТЕРАТУРЫ
1. Вейник А. И. Приближенный расчет процессов теплопроводности. М.—Л.,
Госэи ер го издат, 19 59.
2. Гентштовт М. А., Бережинский Р. А. Эмпирические зависимости для рас-
чета теплопередачи через оребренную стенку. — «Теплоэнергетика»,
1968, № 1, с. 73.
3. Лыков А. В. Теория теплопроводности. М., «Высшая школа», 1967.
4. Технические проблемы реакторов па быстрых нейтронах. Под ред.
10. Е. Багдасарова. М., Атомиздат, 1969.
5. Турилина Е. С., Воскресенский К. Д. О влиянии некоторых повреждений
тепловыделяющих элементов па поле температур в них.— В сб.: Вопросы
теплофизики ядерных реакторов. М., Атомиздат, 1968, с. 3.
6. Ушаков П. А. и др. Теплопередача и гидравлическое сопротивление в плот-
поупакованных коридорных пучках стержней. — «Атомная энергия»,
1962, т. 13, с. 162.
7. Ушаков П. А. Приближенное тепловое моделирование цилиндрических
тепловых элементов. — В сб.: Жидкие металлы. М., Атомиздат, 1967,
с. 137.
8. Фогель В. О. Температурные поля в межтрубных пространствах при на-
личии внутренних источников тепла. — «Ж- техн, физики», 1953, т. 23,
№2, с. 301.
9. Шлыков К). П., Ганин Н. А. Контактный теплообмен. М., Госэнергоиздат,
1963.
10. Шнейдер П. Инженерные проблемы теплопроводности. Пер. с англ. М.,
Изд-во, иностр, лит., 1960.
11. Goodman Т. R. Application of Integral Methods to Transient Nonlinear
Heat Transfer. — «Advances in Heat Transfer», 1964, v. 1, p. 3.
12. Shih F. S. The Temperature Field surrounding coolant Holes in a heat-
generating Solid. Heat Transfer, 1970. Preprint of papers, presented at the
4-th Internal. Heat Transfer Conf. Paris, Versailles, 1970, v. 1, ch. 1.5.
ГЛАВА 4
(4.1)
ОСНОВНЫЕ УРАВНЕНИЯ КОНВЕКТИВНОГО ТЕПЛООБМЕНА
§ 4.1. Уравнения энергии, движения и неразрывности
1. Предварительные замечания. В теории теплообмена и в
динамике жидкость и газ рассматривают как сплошную среду- №
таком подходе состояние потока однофазной химически однор0^’1
жидкости (или газа) характеризуется макроскопическими пар£1Ме"г"
рами — температурой, давлением и скоростью, значения коТ^Р1*1^
должны быть заданы в каждой точке потока в каждый момент ВР(3"
мени. При этом предполагается, что физические свойства жиД*сОСТ1'*
(плотность, теплоемкость, коэффициенты вязкости и теплопрсход-
ности), зависящие в общем случае от температуры и давления, Из-
вестны. Поэтому состояние потока жидкости полностью опреДеле-
но, если известны поля температуры Т, давления р и скорое'!'11 w>
т. е. зависимости:
Т = Т (х, у, z, т);
Р = Р (х, у, z, т);
w = w(x, у, z, т), ,
где х, у, z — координаты; т — время.
Поля температуры, давления и скорости могут быть нестацио-
нарными, если Т, р и w зависят от времени в соответствии с (4.1)*
или стационарными, если Т, р и w не изменяются во времени. В по-
следнем случае в уравнениях (4.1) время т должно быть опугцсно.
Теоретическое изучение теплообмена и движения жидкости сво-
дится в первую очередь к определению зависимостей (4.1). Зная поля
Т, р и w, а также физические свойства жидкости, можно определить
все величины, характеризующие теплообмен и движение жидко-
сти,— тепловые потоки, гидравлические сопротивления и т. д.
Модель сплошной среды можно использовать не всегда; -так,
например, она непригодна для описания течений сильно разрежен-
ного газа. Однако для задач, рассмотренных в этой книге, модель
сплошной среды полностью применима.
Для определения трех неизвестных (Т, р и w) необходимо иметь
три уравнения. Такие уравнения получаются из основных законов
физики—закона сохранения массы, закона сохранения количества
движения и закона сохранения энергии, записанных применительно
к движущейся жидкости. Однако указанных основных законов
80
недостаточно для определения полей температуры, давления и ско-
рости. Формально это проявляется в том, что число неизвестных
в основных уравнениях оказывается больше трех. Такое несоответ-
ствие объясняется тем, что распределение 7", р и w в потоке реаль-
ной жидкости в значительной мере определяется такими ее свой-
ствами, как способность оказывать сопротивление деформации сдви-
га (внутреннее трение или вязкость) и способность проводить тепло
(теплопроводность). Между тем основные законы никак не отражают
этих свойств жидкости. Поэтому к трем указанным основным зако-
нам физики необходимо добавить специальные законы, характери-
зующие внутреннее трение и теплопроводность в жидкости. Такими
специальными законами являются закон трения Ньютона и закон
теплопроводности Фурье.
Законы сохранения массы, количества движения и энергии,
записанные в дифференциальной форме применительно к движущей-
ся вязкой теплопроводной жидкости, т. е. с учетом законов Нью-
тона и Фурье, называются соответственно уравнениями неразрыв-
ности, движения и энергии.
Уравнения неразрывности, движения и энергии, дополненные
зависимостями физических свойств жидкости от температуры и дав-
ления, составляют замкнутую систему уравнений, описывающую
процессы движения жидкости и конвективного теплообмена. Ре-
шение этой системы при заданных краевых условиях приводит к
определению зависимостей (4.1).
Следует, однако, отметить, что такой подход в чистом виде в ос-
новном применим к ламинарным течениям. Для анализа турбулент-
ных течений, когда мгновенные значения параметров потока (w, Т, р)
изменяются случайным образом, необходимо привлекать закономер-
ности (вообще говоря, статистического характера), отображающие
механизм переноса тепла и количества движения в таких пото-
ках (см. гл. 6).
Ниже приведены без вывода уравнения неразрывности, движе-
ния и энергии для однофазной химически однородной жидкости.
Вывод этих уравнений можно найти, например, в работе [1]. Как
это принято в гидродинамике, под словом «жидкость» будем в даль-
нейшем понимать не только несжимаемую (капельную) жидкость,
но и газ.
2. Уравнение неразрывности, выражающее закон сохранения
массы применительно к движущейся жидкости, в общем случае
имеет вид
— div (pw) =•• 0, (4.2)
дх
или в декартовых координатах
fyi d(pwx) . d(pwy) . d(pm>z) (4 2а)
5т дх ду дг ’
81
где wx, wy и wz — проекции вектора скорости на оси прямоуголь-
ной системы координат; р — плотность жидкости, зависящая от Т
и р.
При стационарном движении др/дт = 0, и уравнение неразрыв-
ности принимает вид
д Gw) , д (pwy) , д (pa>z) 0 ,4
дх ~ дуГ дх ' k '
Если плотность жидкости постоянна (р = const), уравнение
неразрывности записывается в виде
ж ж. = о (4 4)
дх ду дг ‘
3. Уравнение движения. Применив к элементу движущейся
жидкости основной закон механики: масса, умноженная па ускоре-
ние, равна сумме всех сил, действующих на рассматриваемую мас-
су, можно получить уравнение движения в напряжениях. Это
уравнение, записанное в проекциях на оси прямоугольной системы
координат, имеет вид
dwx , . р । 1 7 дохх । до ух । \.
dx х р \ дх ду дг / ’
(4-5)
где
Fx, Fy и Fz — проекции вектора напряжения массовых сил на оси
координат; ахх, ауу, azz— нормальные напряжения, а огж?/,
o!/z, ... — касательные напряжения, приложенные к соответствую-
щим площадкам. Первый индекс у составляющих напряжений
указывает ориентацию площадки и обозначает ось координат,
с направлением которой совпадает нормаль к рассматриваемой
площадке; второй индекс обозначает ось координат, вдоль которой
действует рассматриваемое нормальное или касательное напря-
жения.
В соответствии с теоремой о взаимности касательных напряже-
ний, известной из гидродинамики,
&Ху @ух, ®xz ^zx> ®yz
В динамике вязкой жидкости предполагается, что среднее ариф-
метическое из нормальных напряжений, приложенных к взаимно
перпендикулярным площадкам, взятое с обратным знаком, есть дав-
ление в жидкости:
" (®ХХ ®уу 4- ^zz) Р‘
82
Система из трех уравнений (4.5) и уравнения неразрывности
не замкнута, так как она содержит девять неизвестных (три проек-
ции скорости и шесть напряжений). Чтобы замкнуть систему, не-
обходимо установить связь между напряжениями и составляющими
вектора скорости. Эта связь определяется обобщенным законом
Ньютона. Если принять во внимание два последних соотношения,
то обобщенный закон Ньютона можно записать в виде
, / п dwx 2 ,. \ 1
avv = — р — р 2 —---------div w । ;
хх r V дх 3 I
, /' п диь, 2 ,. \
ап = — Р + |1 2-у--------divw ;
I ( Ci $wz . \
= — р + М 2 —---------div w ;
22 Н dz 3 Г
( dwx , dwn \
^г/= = И I ;
J J \ ду дх /
(4.6)
где р—динамический коэффициент вязкости.
Подставив в уравнения (4.5) выражения для напряжений (4.6),
получим:
(4.7)
Дифференциальные уравнения (4.7) называются уравнениями
движения вязкой ньютоновской жидкости*, или уравнениями На-
вье — Стокса. Левые части уравнений движения представляют со-
* Ньютоновскими называются жидкости, для которых выполняется закон
вязкого трения Ньютона. Существуют и неныотоновские жидкости, для ко-
торых этот закон не выполняется (смолы, коллоидные растворы и др.).
83
бой проекции сил энерции на оси координат. В правой части урав-
нений первые два члена— проекции массовых сил и сил давления,
а последние три слагаемых—проекции сил трения на оси коор-
динат. Все члены имеют размерность силы, отнесенной к единице
объема.
Если р и ц — постоянные величины (заметим, что при р =
— const, div w — 0), то уравнения (4.7) упрощаются и прини-
мают вид:
+ (w grad) wx - Fx--------- -I- vV2 wx\
dx p dx
+ (w grad) wy = F-------J- + vV2 юг/;
dx p dy
^ + (wgrad).ayz = Fz---------- Д-1-vV2^,
dr p dz
(4-8)
где V2 — (d2/dx2) + (дНду2) + (52/dz2) обозначает оператор Лап-
ласа; v = р/р — кинематический коэффициент вязкости.
Уравнения (4.8) и уравнение неразрывности (4.4) содержат че-
тыре неизвестных (wx, wu, wx и р) и образуют замкнутую систему.
Чаще всего единственной массовой силой, действующей в пото-
ке жидкости, является сила тяжести. В этом случае вектор F равен
вектору ускорения силы тяжести g. Сила тяжести оказывает влия-
ние на движение жидкости только при наличии в потоке свободных
поверхностей или неоднородном распределении плотности. При
напорном течении (т. е. при отсутствии свободных поверхностей)
и однородном распределении плотности сила тяжести, действующая
на элемент жидкости, уравновешивается силой гидростатического
давления. В этом случае поле скорости не будет зависеть от силы
тяжести, а поле давления, естественно, будет от нее зависеть.
При неоднородном распределении плотности в напорном потоке
жидкости сила тяжести не уравновешивается силой гидростати-
ческого давления. Чтобы ввести в уравнения движения результи-
рующую этих двух сил — архимедову силу, преобразуем первые
два члена правой части этих уравнений. Учитывая, что в данном
случае F = g, имеем в проекции на ось х
(Р~ Po)gK“ ( Д—роД,
dx \ дх /
где р0 — плотность при постоянной температуре То в какой-либо
фиксированной точке потока.
Считая изменения р и Т малыми по сравнению с их абсолютными
значениями, можно принять
р—р0 = —Рр (Т—То), (4.9)
где |3 ——— коэффициент термического расширения жид-
кости.
84
Величину р0£х можно представить так: p(}^x = др01дх (и анало-
гично pog’w и potfj, где р0 — гидростатическое давление, рассчитан-
ное в предположении, что плотность жидкости всюду равна р0.
Обозначив р — р0 = pt и приняв во внимание сказанное, уравне-
ния движения (4.8) можно записать в виде:
дт -H (w grad) шл. - - g:r ₽ (T-T„) - 1 (> dpi dx 4- vv‘X’> i
0wy di + (w grad) w,, - gi/ P (7 — ? o) — 1 p dpt dy Ф vy'X; (4.10)
dwz di -I- (wgrad) w2--= -^P(T-T0)~ 1 p dpi dz 4- v .
Первые члены правой части уравнений (4.10) представляют со-
бой проекции архимедовой силы g|3 (Т — 70) (отнесенной к еди-
нице массы) на оси произвольно ориентированной прямоугольной
системы координат.
4. Уравнение энергии. Температурное поле в потоке жидкости
описывается уравнением энергии. Это уравнение выводится из рас-
смотрения баланса энергии элемента объема жидкости: изменение
во времени полной энергии (внутренней и кинетической) элемента
жидкости обусловлено притоком тепла извне через его поверхность,
действием источников тепла, заключенных внутри элемента, и рабо-
той поверхностных и объемных сил, приложенных к элементу.
Приток тепла через поверхность элемента, движущегося вместе
с жидкостью, обусловлен теплопроводностью и потому опреде-
ляется по закону Фурье.
Для однофазной химически однородной и изотропной жидкости
с произвольной зависимостью физических свойств от температуры
и давления, но при отсутствии в потоке переноса тепла излучением
уравнение энергии имеет вид
р-у’ div (X grad 7) + 4-цФ, (4.11)
di dr
или в другой форме
рср — = div(^grad Z*)-!- qv + [37-^-4-цФ, (4.12)
di di
где h —энтальпия; T — температура; с}) — изобарная теплоемкость;
% — коэффициент теплопроводности жидкости; qv — мощность
внутренних источников тепла; [3 — коэффициент термического рас-
ширения; рФ — диссипативная функция;
(4.13)
clhldx, dTIdx, dp/dx — субстанциональные производные.
85
Первый член в правой части уравнений (4.11) и (4.12) выражает
тепло, подведенное к рассматриваемому элементу жидкости через
его поверхность вследствие теплопроводности, а второй — тепло,
выделившееся внутри элемента за счет действия внутренних источ-
ников тепла. Диссипативная функция рФ учитывает тепловыде-
ление в потоке, обусловленное диссипацией (рассеянием) кинети-
ческой энергии вследствие действия сил вязкости (эта энергия
превращается в тепло).
В зависимости от физических свойств жидкости и условий
движения и теплообмена возможны различные упрощения урав-
нения энергии. Рассмотрим уравнение энергии для двух обычно
используемых при теоретическом анализе моделей текущей среды:
капельной жидкости и идеального газа.
Плотность капельной жидкости очень слабо зависит от дав-
ления и температуры. Поэтому капельные жидкости можно считать
практически несжимаемыми, и, следовательно, в выражении (4.12)
можно принять |ЗТ (dpldx) « Ои divw = 0. Таким образом, урав-
нение энергии для капельных жидкостей принимает вид
рср -^=div(AgradT) + ^ + |iO0, (4.14)
ах
где Фо — значение Ф [см. (4.13)] при div w = 0.
Для идеального газа [3 = 1/Т и (dpldx) = dpldx. При ско-
рости газа, не превышающей 1/4 скорости звука, члены dpldx и цФ
малы по сравнению с другими членами уравнения (4.12), поэтому
можно принять dpldx + цФ = 0.
Таким образом, уравнение энергии для идеального газа, движу-
щегося с малой скоростью, имеет такой же вид, как и уравнение
для капельной жидкости, записанное для часто встречающегося
случая |хФ0 = 0.
5. Система уравнений, описывающих движение жидкости и теп-
лообмен. Для определения полей трех зависимых переменных (Т,
р, w) мы располагаем тремя основными уравнениями: уравнением
энергии, уравнением движения и уравнением неразрывности. Од-
нако в эти уравнения помимо Т, р и w входят физические свойства
р, ср, ц и %, которые в общем случае зависят от Т и р и поэтому мо-
гут изменяться в пространстве и времени. Кроме того, в уравнение
энергии входит мощность внутренних источников тепла qv, также
зависящая в общем случае от координат и времени. Следовательно,
чтобы замкнуть систему уравнений, к трем основным уравнениям
необходимо добавить зависимости физических свойств жидкости
(р, ср, р и %) от Т и р* и зависимость qv от координат и времени.
Из сказанного видно, что система уравнений, описывающая
процесс теплообмена в потоке вязкой жидкости с переменными фи-
зическими свойствами, очень сложна, и ее решение в общем виде
* В большинстве случаев ср, р и к очень слабо зависят от давления. При
расчете теплообмена этой зависимостью обычно пренебрегают.
86
связано с большими трудностями. Эти трудности вызваны нелиней-
ностью уравнений движения и энергии, обусловленной наличием
конвективных членов в их левой части, и зависимостью физических
свойств жидкости от температуры. Вследствие зависимости р и р
от Т поля скорости и температуры оказываются взаимно связанными.
Поэтому уравнения движения и неразрывности нельзя решать не-
зависимо от уравнения энергии.
Задача существенно упрощается, если предположить, что р
и р постоянны. В этом случае уравнения движения и неразрывности
становятся независимыми от уравнения энергии и поле температу-
ры не оказывает никакого влияния на поле скорости. Последнее
можно определить, решив уравнения движения и неразрывности
(как и в случае изотермического движения). Подставив найденное
распределение скорости в уравнение энергии, можно вычислить
поле температуры.
При постоянстве всех физических свойств система уравнений,
описывающих процесс теплообмена в потоке жидкости, имеет вид:
л/ , и 1
—— + (w grad) l = aVL / -----1---Фо;
от рср рс}1
+ (w grad) wxFx-------- -I- V V2
ди p дх
^ + (wgrad)ny?y = Ft/------ -^--1-vV2^;’ (4-15)*
dx p dy
+ (w grad) wz = F, — -b + vV2 w,;
dx v J 2 z pdz 2
div w = 0;
qv==qv(x, x, у, г),
где a = X/(pcp) — коэффициент температуропроводности жидкости.
Предположение о постоянстве физических свойств существенно
упрощает систему уравнений, благодаря чему становится возмож-
ным решение многих задач конвективного теплообмена. Вместе
с тем это предположение ограничивает область применения полу-
чаемых результатов такими реальными процессами, в которых фи-
зические свойства жидкости изменяются незначительно. Тем не
менее задачи о теплообмене при постоянных физических свойствах
представляют большой интерес, так как позволяют выявить основ-
ные закономерности, присущие различным процессам теплооб-
мена.
В дальнейшем нам понадобятся уравнения энергии, движения
и неразрывности, записанные в цилиндрических координатах. Для
* Здесь температура обозначена символом I, который обычно применяется,
если температура измеряется в °C. Если же температура измеряется в °К,
что удобно, например, в случае теплообмена при движении газа с переменны-
ми физическими свойствами, то, как правило, используется символ Т.
87
двумерного осесимметричного движения вязкой несжимаемой жид-
кости с постоянными физическими свойствами эта система урав-
нений имеет вид:
dt
dx
dwx
dx
dwr
dx
dwx
/ a21 . d2t
a I-----------
\ dx2 dr2
—£-4- V
dx
dp . i d2w
dr ( dx2
Щ +^ + ^Ф„;
dr ) pep
« I da
""г- д),2
PCp
dr
dwr w?
dr r
(4.16)
Р
Р
dwr ,
Wr 0;
г
дх дг
qv = qv (х, г, т),
где
d д д . d
~ U I- ££) ----------•
dx------------------------------------------дх-dx dr
x и r — осевая и радиальная координаты, а и wr — составля-
ющие скорости в направлении этих координат.
Приведенные в этой главе уравнения энергии, движения и не-
разрывности для нестационарных полей температуры, скорости
и давления справедливы как при ламинарном, так и при турбулент-
ном движении. Стационарные процессы движения и теплообмена,
при которых действительные значения зависимых переменных
(Т, w и р) в каждой точке потока не изменяются во времени, возмож-
ны только при ламинарных течениях. В турбулентном потоке значе-
ния скорости, температуры, давления непрерывно изменяются во
времени.
Если в уравнениях (4.15) и (4.16) положить д/дх = 0, то полу-
чим соответствующие системы уравнений для стационарных про-
цессов конвективного теплообмена и движения жидкости, справед-
ливые только для ламинарных потоков.
§ 4.2. Начальные и граничные условия
При выводе уравнений энергии, движения и неразрывности от-
влекаются от конкретных условий, в которых осуществляется дви-
жение жидкости и процесс теплообмена. Между тем формирование
полей температуры, скорости и давления существенно зависит от
конкретных условий, в которых эти процессы протекают. Поэтому
для решения задач о движении жидкости и теплообмене к основным
уравнениям необходимо присоединить ряд условий, конкретизирую-
щих задачу. Эти условия подразделяются на начальные и гранич-
ные.
Начальные условия состоят в задании полей скорости, темпе-
ратуры и давления во всем объеме рассматриваемой области (в том
числе и на ее границах) в начальный момент времени. Если процес-
88
сы движения и теплообмена стационарны, то надобность в зада-
нии начальных условий отпадает.
Граничные условия сводятся к заданию геометрической формы
рассматриваемой области н условий движения жидкости и теплооб-
мена на ее границах. Границы области могут быть как твердыми
(поверхности твердых тел, омываемых жидкостью), так и жидкими
(например, входное сечение трубы).
Граничные условия для скорости на твердой непроницаемой
поверхности задаются, исходя из положения о прилипании вязкой
жидкости к этой поверхности; поэтому скорость жидкости на поверх-
ности неподвижного непроницаемого твердого тела равна нулю.
Граничные условия для температуры на поверхности непрони-
цаемого твердого тела формулируются, исходя из положения о
непрерывности поля температуры на границе жидкость — твердое
тело (стенка), которое можно записать следующим образом:
=== /(. |/z=—о, (4.17)
где t — температура жидкости; tc—температура стенки; н — нор-
маль к границе раздела жидкость — стенка, направленная в сторону
жидкости (/I > 0 — область жидкости, n<Z 0 — область стенки).
Если на границе раздела жидкость—стейка не выделяется и не
поглощается тепло, то по закону сохранения энергии плотность
теплового потока в стейке па границе раздела должна быть равна
плотности теплового потока в жидкости на той же границе. По-
скольку жидкость на границе неподвижна, то перенос тепла в жид-
кости на этой границе осуществляется только теплопроводностью.
Поэтому согласно закону Фурье
t (4.18)
\ дп /о \ дп J ц~-\-о
где qc — плотность теплового потока па границе жидкость — стен-
ка; X и Хо — коэффициенты теплопроводности жидкости и стенки.
Уравнения (4.17) и (4.18) называются условиями сопряжения
температурных полей в жидкости и стенке.
Положения об отсутствии проскальзывания жидкости на поверх-
ности твердого тела и о непрерывности температурного поля на
границе жидкость — твердое тело хорошо подтверждаются опытом
для различных жидкостей и газов (исключение составляют сильно
разреженные газы).
Граничные условия для поля температуры в потоке жидкости
могут быть заданы различным образом. Чаще всего встречаются гра-
ничные условия первого и второго рода.
Граничные условия первого рода состоят в задании распределе-
ния температуры на омываемой жидкостью поверхности твердого
тела (стенки) и ее изменения во времени:
/с = ic (xc, ус, zc, т), (4.19)
где хс, ус и zc — координаты точек на поверхности стенки.
89
В простейшем случае не зависит от времени и постоянна по
поверхности, т. е. tc = const.
Граничные условия второго рода заключаются в задании рас-
пределения по поверхности и изменения во времени плотности теп-
лового потока qc. Из второго условия сопряжения (4.18) следует,
что граничные условия второго рода можно записать в виде
(4.20)
\ дп //г=-|-о
Таким образом, задание плотности теплового потока эквивалент-
но заданию производной от температуры жидкости по нормали к
поверхности стенки, взятой на границе раздела.
В простейшем случае qc может быть постоянной по поверхности
и во времени, т. е. qc = const.
В сложных случаях поля температуры в стенке и потоке жидко-
сти существенно зависят друг от друга. При этом заранее неизве-
стны ни распределение температуры, ни распределение плотности
теплового потока на стенке. В таких случаях приходится одновре-
менно решать задачу о температурном поле в потоке жидкости и в
стейке. Для этого к системе уравнений, описывающих температур-
ное поле в потоке, присоединяется уравнение теплопроводности,
описывающее температурное поле в стенке, а на границе жидкость—
стенка задаются условия сопряжения этих полей. Последние сво-
дятся к равенствам (4.17) и (4.18). Поэтому такие задачи называют-
ся сопряженными.
В случае движения в трубах жидкими границами потока яв-
ляются входное и выходное сечения трубы. Во входном сечении в об-
щем случае задается распределение скорости, давления и темпера-
туры по сечению и их изменение во времени. Обычно распределение
продольной составляющей скорости, температуры и давления по
сечению принимается однородным, а поперечная составляющая
скорости принимается равной нулю. Для упрощения задачи пред-
полагается, что труба является полуограничеииой, т. е. прости-
рается в направлении потока в бесконечность. В этом случае необ-
ходимость в задании граничных условий в выходном сечении трубы
отпадает.
Совокупность основных уравнений, начальных и граничных ус-
ловий составляет математическое описание рассматриваемого про-
цесса конвективного теплообмена и движения жидкости.
§ 4.3. Анализ конвективного теплообмена
и движения жидкости методом подобия
1. Метод подобия. При изучении процессов теплообмена и дви-
жения жидкости обычно большую пользу приносит использование
методов подобия и размерностей. В основе анализа процесса методом
подобия лежит приведение его математического описания к без-
размерному виду. Смысл этой операции состоит в том, что вместо
90
размерных переменных и постоянных вводят новые, безразмерные
переменные и постоянные. Число последних в безразмерном мате-
матическом описании оказывается меньше числа размерных величии
в исходном математическом описании, что даст значительные пре-
имущества при экспериментальном, а нередко и теоретическом изу-
чении вопроса. В случае экспериментального исследования приме-
нение метода подобия или метода размерности позволяет свести
к минимуму число величин, которые необходимо варьировать в
опытах, и указывает рациональный способ обобщения опытных
данных. При теоретических исследованиях с помощью метода подо-
бия пли метода размерностей иногда оказывается возможным путем
соответствующей комбинации независимых переменных уменьшить
их число па единицу (например, свести задачу об отыскании функции
двух переменных к задаче, содержащей! одну независимую перемен-
ную) или даже найти функцию с точностью до численного значения
постоянной. Пользуясь методом подобия, удобно также анализи-
ровать предельные случаи и обобщать результаты численных ре-
шений.
Для приведен ня математического описания процесса к безраз-
мерному виду можно воспользоваться методом масштабных преобра-
зований. Этот метод сводится к выполнению следующих простых
операций.
а. Все величины, входящие в математическое описание процесса,
подразделяются на группы однородных величин, т. е. величии,
имеющих одинаковый физический смысл и одинаковую размерность.
В каждую такую группу могут входить как переменные, так и по-
стоянные величины. Например, группа координат и линейных раз-
меров включает х, у, г, /0, Zj и т. д.; группа скоростей содержит w.v,
Жц, и скорость па входе в трубу &y0.
б. Для каждой группы величин, в составе которой! имеются по-
стоявшие, отличные от пуля и бесконечности, выбирают одну из этих
постоянных I! качестве масштаба (например, го() п т. д.). Для осталь-
ных групп величин масштабы по выбираются.
в. Деленном величин данной группы па их масштабы приводят
эти величины к безразмерному виду (например, x7Z0 ' X, уН(}
- У, wx/w„ Wx н т. д.). Величины, для которых масштабы не
выбраны, пока остаются размерными.
г. В математическое описание вместо размерных величии, для
которых выбраны масштабы, подставляют производен ня из безраз-
мерных величин па их масштабы (например, х Xl0, wx : :
и т. д.),
д. Оставшиеся в математическом описании размерные величины
н появившиеся в них масштабы группируют в безразмерные
комплексы так, чтобы эти комплексы можно было рассматривать
как новые безразмерные переменные и постоянные.
В результате этих операций дифференциальные уравнения, на-
чальные п граничные условия будут записаны в безразмерной фор-
ме. Полученное таким образом безразмерное математическое опн-
91
саиие позволяет установить совокупность безразмерных величин
(безразмерных чисел), характерных для изучаемой задачи. Число
этих величин, как уже отмечалось, будет меньше числа размерных
величин, существенных для этой задачи.
Более полные сведения о методах подобия можно почерпнуть
в работах [2—4].
2. Анализ задачи о движении и теплообмене методом подобия.
Проанализируем с помощью метода подобия задачу о движении
и теплообмене несжимаемой жидкости в круглой гладкой трубе диа-
метром d = 2г0. Пусть во входном сечении трубы скорость жидкости
(направленная вдоль оси) wQ и температура t0 постоянны по сече-
нию и не изменяются во времени. В момент времени, предшествую-
щий начальному (т < 0), температуры жидкости и стенки всюду
одинаковы и равны tQ, т. е. теплообмен отсутствует, и в трубе осу-
ществляется изотермическое течение. В начальный момент времени
(т = 0) температура стенки или плотность теплового потока на
стенке мгновенно изменяется и принимает постоянное во времени
и по поверхности значение tc или q0. При этих условиях в течение
некоторого промежутка времени в трубе будет протекать нестацио-
нарный переходный процесс, а затем (при т -> оо) наступит ста-
ционарное состояние.
Для простоты будем считать физические свойства жидкости,
кроме плотности, постоянными. Зависимость р от t будем учитывать
лишь в члене уравнения движения, выражающем архимедову силу.
Примем эту зависимость линейной:
— = 1 — Рр(/—/о). (4.21)
Ро
где ро — значение р при температуре на входе £0; |3Р — постоянная,
зависящая от рода жидкости и интервала температуры.
В других членах уравнения движения и в уравнениях энергии
и неразрывности плотность, так же как и другие свойства, будем
считать постоянной.
Движение жидкости и теплообмен в рассмотренных условиях
описываются уравнениями (4.15), которые в данном случае целесо-
образно записать в цилиндрических координатах (х, г, ср). Полагая,
что в потоке отсутствуют внутренние источники тепла, а диссипация
энергии пренебрежимо мала, примем в (4.15) qy = 0 и цфо — 0.
С учетом сказанного имеем следующую систему уравнений:
-----j-w grad t — aV2 /;
p / w gra(j w \ _
\ dx "I
= —Po (i — i'o) cos ф — + pV2
dx
(4.22)
div w — 0,
29
где рп — гидростатическое давление, рассчитанное в предположе-
нии, что плотность жидкости всюду равна р0; ф — угол между осью
х, совпадающей с осью трубы, и вектором силы тяжести (gy =
== g соэф).
В (4.22) опущены уравнения для проекции скорости и
в целях сокращения записи. В уравнении для шх сохранен член
dwx/dx, так как вследствие зависимости р от t течение в период пе-
реходного процесса будет нестационарным, хотя по условию ю0 =
= const.
Начальные условия можно записать так:
при т < 0, х 0 и 0 г < г0
/ = ?> — )> (" ==*.'). (4.23)
Щ) \ d d v I
где Fn — заданные функции.
Граничные условия имеют вид:
при т^О х 0, О^СгСГо
tey wQ, wr - ю(р = 0; I /();
при т>0, х>0, /- /•„ (4 24)
= wr Юф 0, t = /с
л dt
или л —q...
дг
а. Проанализируем вначале задачу в случае, когда задана тем-
пература стенки ta.
Для приведения математического описания (4.22), (4.23) и (4.24)
к безразмерному виду введем переменную Ф = / — t0 и выберем сле-
дующие масштабы: для координат и линейных размеров — d, для
скоростей — ау0 и для температур — йс = ta—10. Пользуясь этими
масштабами, введем безразмерные величины:
d d
6 = Оо (n = ^,r,cp). tc—to ^0
Подставим в (4.22) — (4.24) вместо размерных величин, для ко-
торых выбраны масштабы, произведения из безразмерных величин
на их масштабы. Уравнение энергии, например, примет вид:
— + W grad 0 = — V2 0.
дх d d2
Умножив это уравнение на <F/a и выполнив аналогичные подста-
новки и преобразования для остальных уравнений, начальных
93
и граничных условий, получим математическое описание процесса
в безразмерной форме:
— 4-Ре (Wgrad 0) = V20;
д Fo
+ Re (Wgrad =
d Zh
= —© cos ф —- (Eu Re) + V2
Re dX
div W = 0.
При Fo<0, X>0 и y
0 = 0, Wn=Fn(X,R,RQ), (n^x,r).
При Fo>0, X=0 и 0<R<-|-
1, Wr - IF(P = 0, 0 = 0.
При Fo^O, X^O и R= —
2
rx = rr==W\p = 0, 0 = 1.
Полученное безразмерное математическое описание содержит
следующие безразмерные числа:
Fo =
ат
~d^
число Фурье;
Zh=—-----число Жуковского;
d?
ре——число Пекле;
а
Ре — —число Рейнольдса;
V
gpn 0'
Gr =——-------число Грасгофа;
V3
Еи=-——число Эйлера.
Ро 4
Из системы уравнений (4.25) и (4.26) следует, что безразмерные
температура, составляющие скорости и давление (число Ен) явля-
ются функциями таких безразмерных величии:
0 = 0 (Fo, X, R, ср, Ре, Re, Gr, ф); (4.27)
Wn = Wn (Fo, X, R, Ф, Pe, Re, Gr, ф) (n = x, r, <p); (4.28)
Eu = Eu (Fo, X, R, cp, Pe, Re, Gr, ф). (4.29)
94
Число Zh не вошло в уравнения (4.27) — (4.29), так как его мож-
но выразить через другие безразмерные числа: Zh = Ре Fo Re-1.
Вместо Fo в уравнения (4.27) — (4.29) можно ввести число Zh,
а вместо Ре или Re—число Прандтля Рг — PeRe-1 = ц ср/%.
Теперь нетрудно получить систему безразмерных чисел для теп-
лоотдачи и гидравлического сопротивления.
Введем местный коэффициент теплоотдачи как отношение ме-
стной плотности теплового потока на стенке к разности температур
на входе в трубу:
а ---
7с
G ---^0
X
t С — А)
(4.30)
После приведения к безразмерному виду имеем:
Nu —
(4-31)
где Nu = adl'k — местное (т. е. в данной точке поверхности стенки)
число Нуссельта. Подставив (4.27) в (4.31), получим
Nu=Nu (Fo, X, ср, Ре, Re, Gr,ip). (4.32)
Среднее по окружности число Нуссельта в данном сечении
__ 2л ___
Nu —— (J Nudcp = Nu(Fo,X, Ре, Re, Gr,ip). (4.33)
2n0.)
Если в (4.31) вместо Zc — tQ использовать местный температур-
ный напор tG — t (где t — среднемассовая температура жидкости
в данном сечении), то числа Nu и Nu будут зависеть от тех же без-
размерных величин, только характер зависимостей будет иным.
Безразмерное гидравлическое сопротивление принято выражать
посредством коэффициента сопротивления. Под местным коэффи-
циентом сопротивления понимается безразмерный градиент сред-
него (по сечению) давления, взятый с обратным знаком:
r^-d / р—ро \ = _2(4.34)
dX 1 -о dX ’
\ J
где
“ _ 2л 1/2
Ей — — t Eli RdR
эт J <'
о о
(заметим, что в данном случае w = w0). Подставляя значение Ей
из (4.29), находим:
С = С (Fo, X, Ре, Re, Gr,< (4.35)
95
Полученные системы безразмерных чисел справедливы как для не-
стационарного переходного процесса, так и для стационарного со-
стояния, которое наступает при Fo —оо . В последнем случае число
Fo в правой части уравнений подобия должно быть опущено.
б. Рассмотрим теперь ту же задачу, но для случая, когда на внут-
ренней поверхности стенки трубы задана постоянная плотность
теплового потока qc. Таким образом, вместо условия t = tc при
г = г0 имеем условие
(4.36)
При анализе этой задачи можно использовать те же масштабы,
что и в предыдущем случае, за исключением масштаба для темпе-
ратуры. Этот масштаб нельзя выбрать в виде разности tc — t0,
так как температура стенки tc в данном случае неизвестна. Мас-
штаб для температуры можно установить из граничного условия
(4.36), записав его в безразмерной форме:
= 1. (4.37)
dR 7с d
L \ а, /йЧ
Отсюда видно, что в качестве масштаба для температуры целесооб-
разно выбрать величину Ф = qc d/h, имеющую размерность тем-
пературы.
Если ввести безразмерную температуру
fl’g qcd
%
(4.38)
и вместо масштаба -в’о = tc — t0 пользоваться масштабом 0^, то
безразмерное математическое описание (4.25) и (4.26) останется
в силе и в данном случае, за исключением последнего из условий
(4.26), которое должно быть заменено условием (4.37). Поэтому
для задачи о движении жидкости и теплообмене при постоянной
плотности теплового потока на стенке система безразмерных чисел
остается такой же, как в предыдущей задаче, с той разницей, что 0
определяется в соответствии с (4.38), а число Gr принимает вид
Безразмерная температура стенки
tc---^0
7с d
к
(4.40)
96
в рассматриваемой задаче является искомой величиной, обратной
числу Нуссельта (Nu = 0~J). Как 0С, так и Nu зависят от тех
же безразмерных величин, что и в уравнении (4.32), лишь число
Gr надо заменить на GrQ. То же самое относится и к коэффициенту
сопротивления
3. Основные режимы течения и теплообмена. В общем случае
силы вязкости, силы инерции и силы тяжести в потоке жидкости
соизмеримы. Поэтому такое течение можно называть вязкостно-
инерционно-гравитационным. При его анализе необходимо учи-
тывать все члены в уравнении движения, как это было сделано
в п. 2. Этому случаю соответствуют системы безразмерных чисел
для теплоотдачи и сопротивления (4.32) и (4.35), которые мы здесь
перепишем:
Nu = Nu (Fo, X, ср, Ре, Re, Gr, ф); (4.32)
£ = £ (Fo, X, Ре, Re, Gr, ф). (4.35)
Теперь рассмотрим некоторые предельные случаи течения и теп-
лообмена.
Вязкостно- и и е р ц и о н ное т е ч е н и е соответ-
ствует пренебрежимо малому влиянию сил тяжести (архимедовых
сил) по сравнению с силами вязкости и инерции. В этом случае
при анализе задачи первые члены в правой части уравнений дви-
жения систем (4.22) и (4.25) можно опустить. Кроме того, учиты-
вая, что при отсутствии архимедовых сил поле скорости не зависит
от поля температуры и течение становится стационарным* и сим-
метричным относительно оси, получаем для этого случая следующую
систему безразмерных чисел:
Nu = Nu (Fo, X, Ре, Re); (4.41)
С = С (X, Re). (4.42)
Вязкостно-гравитационное течение соот-
ветствует пренебрежимо малому влиянию сил инерции по срав-
нению с силами вязкости и силами тяжести. Опуская второй член
в левой части в уравнениях движения, находим:
Nu = Nu (Fo, X, ф, Ре, Gr-Pr, ф), (4.43)
£Re = f (Fo, X, Ре, Gr-Pr, ф). (4.44)
Здесь комплекс Gr/Re из правой части уравнения движения (4.25)
заменен комплексом Gr • Re-1 Ре = Gr • Рг. Таким образом, чис-
ла Gr и Рг при вязкостно-гравитационном течении входят в урав-
нения подобия для теплоотдачи и сопротивления в виде произве-
* В задаче, рассмотренной в п. 2, нестационарность течения обусловлена
лишь изменением архимедовой силы при изменении tQ или дй во времени. Если
свойства постоянны и, следовательно, архимедова сила отсутствует, то изме-
нение /0 или 7с не приводит к нарушению стационарного характера течения
4 Зак. 792 97
дения. Так как в данном случае числа Ен и Re входят в уравнения
движения только в виде произведения, то в левой части (4.44) по-
лучается комплекс £Re и, следовательно, 1/Re.
Вязкостное т е ч е н и е соответствует пренебрежимо
малому влиянию сил инерции и сил тяжести но сравнению с. силами
вязкости. Силы инерции оказываются несущественными по срав-
нению с силами вязкости в том случае, когда Wr 0, и, следо-
вательно, dWJdX = 0. Такое гидродинамически стабилизован-
ное течение наблюдается вдали от входа в трубу. В этом случае
в уравнении движения можно опустить левую часть и первый член
правой части (т. е. архимедову силу), а в уравнении энергии -...
члены, содержащие Wr и U7cp. Тогда, приняв во внимание, что
при постоянных свойствах поле скорости не зависит от поля тем-
пературы, получим:
Nu - Nn (Fo, X, Ре), (4.45)
(4.4G)
Це
Если, кроме того, предположить, что изменение плотности теп-
лового потока вследствие теплопроводности вдоль осп мало по
сравнению с ее изменением по радиусу, т. с. д~(»)/()Хй '
« (1/R) (д/dR) (RdQ/dR), то в уравнении энергии X и Ре будут со-
держаться в виде X/Ре, и вместо (4.45) получим:
[Nli-Nli (' Ео,х1Л . (4.47)
\ Ре /
После наступления стационарного состояния число Fo из всех
приведенных здесь уравнений исчезает.
Вязкостное и вязкостно-гравитационное течения возможны
лишь при ламинарном движении жидкости, т. с. при значе-
ниях числа Re меньших критического. Вязкостпо-инерциоппое
и вязкостно-ниерционио-гравитациониое течения наблюдаются как
при ламинарном, так и при турбулентном движении. Влияние
свободной конвекции на вынужденное течение отражает число Схг
(или Gr • Рг). Если оно мало, то течение будет вязкостным или
вязкостно-инерционным. При достаточно больших значениях чис-
ла Gr наблюдается переход к вязкостно-гравитационному или вяз-
костно-ииерциоино-гравитациоиному течению.
СПИСОК ЛИТЕРАТУРЫ
1. Лойцянский Л. Г. Механика жидкости и газа. М., «Паука», 1970.
2. Новиков И. И., Воскресенский К- Д. Прикладная термодинамика и тепло-
передача. М., Госатомиздат, 1961.
3. Петухов .Б. С. Опытное изучение процессов теплопередачи. М., Госэперго-
издат, 1952.
4. Седов Л. И. Методы подобия и размерности в механике. М., Гостсхпздат,
1957.
ГЛАВА 5
ТЕПЛООБМЕН ПРИ ЛАМИНАРНОМ ТЕЧЕНИИ ЖИДКОСТИ
В ТРУБАХ
§ 5.1. Теплообмен в круглой и плоской трубах
при граничных условиях первого рода
В каналах активной зоны реактора и других элементах ядер-
ной энергетической установки для достижения высокой интен-
сивности теплоотдачи обычно осуществляется турбулентное те-
чение теплоносителя. Однако при некоторых режимах работы ре-
актора (например, при аварийных режимах) скорость теплоноси-
теля может снизиться и течение перейти в ламинарное. При лами-
нарном течении жидкости в достаточно узких каналах коэффициен-
ты теплоотдачи достигают высоких значений. Поэтому не исклю-
чена возможность создания реактора с ламинарным движением
теплоносителя в системе охлаждения. Изучение теплообмена
при ламинарном течении важно не только с практической точки
зрения. Задачи о теплообмене при ламинарном течении жидкости
относительно просты, могут быть решены с помощью чисто мате-
матических методов и поэтому позволяют наиболее наглядно
и отчетливо проанализировать основные закономерности процес-
сов теплообмена.
В этой главе рассмотрим лишь немногие основные задачи о теп-
лообмене при ламинарном течении в трубах. Более подробные све-
дения можно почерпнуть в работе [6].
1. Теплообмен в круглой трубе при стабилизованном течении.
Рассмотрим задачу о теплообмене при ламинарном (вязкостном)
течении жидкости в круглой трубе в случае постоянной темпера-
туры стенки. Последнее условие часто реализуется на практике,
например при конденсации пара или кипении жидкости на внеш-
ней поверхности трубы. Примем следующие условия:
1) течение и теплообмен стационарны;
2) жидкость несжимаема; ее физические свойства постоянны (т. е.
не зависят от температуры);
3) течение жидкости гидродинамически стабилизовано, т. е.
профиль скорости не изменяется по длине (это означает, что участку
трубы, на котором происходит теплообмен, предшествует необо-
греваемый успокоительный участок). Расход жидкости задан или,
что то же самое, известна средняя по сечению скорость жидкости ш;
4) во входном сечении теплообменного участка температура
жидкости постоянна по сечению и равна t0-,
4* 99
5) температура внутренней поверхности стенки трубы на уча-
стке теплообмена постоянна и равна tc, причем tc /0;
6) в потоке отсутствуют внутренние источники тепла, а теплота
трения пренебрежимо мала;
7) изменение плотности теплового потока в осевом направ-
лении за счет теплопроводности мало по сравнению с изменением
плотности теплового потока вдоль оси, обусловленного конвек-
цией.
Рассмотрим решение этой задачи, известной как задача Грет-
ца — Нуссельта.
Запишем уравнение энергии для несжимаемой жидкости с по-
стоянными физическими свойствами при отсутствии в потоке внут-
ренних источников тепла и диссипации энергии. В цилиндрической
системе координат с учетом того обстоятельства, что поле темпе-
ратуры симметрично относительно оси, это уравнение имеет вид
dt . dt ( d2 t . 1 dt . d21 \ /к n
Ю,.----------------------1-------1----• (5.1)
dx T dr \ dx2 r dr dr2 I
Учитывая принятые условия, уравнение (5.1) можно сущест-
венно упростить.
При постоянных физических свойствах жидкости процесс теп-
лообмена не оказывает никакого влияния на течение жидкости.
Поэтому распределение скорости будет таким же, как если бы те-
чение было изотермическим:
- / ^2 \
wx = 2 w 1------; wr = 0.
к ''о /
Условие 7 означает, что
и, следовательно, первый член в правой части можно опустить.
Указанное неравенство приближенно выполняется при значениях
xld > 1/Ре, где Ре = wd/a. Таким образом, если Ре > 100, то
допущение 7 выполняется практически по всей длине трубы (во-
всяком случае для xld 1). Так как Pe = RePr, то для газов
(Рг « 1) и неметаллических жидкостей (Рг 1 4- 1000) это условие
почти всегда выполняется. Для жидких металлов (Рг « 0,005 4-
4- 0,05) оно может и не выполняться. В последнем случае в урав-
нении (5.1) нельзя пренебрегать членом дЧ1дх2, учитывающим из-
менение теплового потока за счет теплопроводности вдоль оси.
Приняв во внимание сказанное, приведем уравнение (5.1) к без-
размерному виду. Для этого введем безразмерные переменные:
г\ t — tc гл г
0 = ----С_ и R .
to ts Го
100
После преобразований получим
I’d3 ® . I_1 д®_/1 г>2\ ^0 /к о\
1 R (5,2)
где
________________________ я х 2 х
2wro r0 Ре d
Безразмерная координата X, или, точнее, величина j, назы-
вается приведенной длиной трубы.
Граничные условия, отвечающие рассматриваемой задаче, за-
пишутся так:
при X = 0 и 0 < 7? < 1 0=1;
при Х^О и 7? = 0
при Х^ 0 и 7?= 1
(5.3)
(5-4)
д® _ (
~dR ~
0 = 0.
Будем искать решение дифференциального уравнения (5.2) ме-
тодом разделения переменных. Для этого представим безразмер-
ную температуру 0 (X, 7?) в виде произведения двух функций, одна
из которых зависит только от X, а другая — только от R:
0(Х, 7?) - Ф (Х)ф (7?). (5.5)
Подставив выражение (5.5) в (5.2), получим
фф" 4- ~~ Фф' = (1 — 7?2) фф'.
Чтобы разделить переменные, разделим это уравнение на фф (1 —7?2).
Тогда уравнение примет вид
—— =----------- = 8 .
Ф [ф(1—R2)
Так как левая часть этого уравнения зависит только от X, а пра-
вая — только от jR, то равенство возможно лишь в том случае, если
левая и правая части уравнения равны постоянной величине, ко-
торую мы обозначили 82. Таким образом, имеем два обыкновенных
дифференциальных уравнения:
82ф; (5.6)
4-82(1_^2)ф = о. (5.7)
dR2 R dR v '
Решение первого уравнения есть
Ф = А ехр (—82Х), (5.8)
где А — постоянная интегрирования.
101
Для решения второго уравнения удобно перейти от переменной
Я к переменной еЯ- Тогда
d2 ф . 1 Щ|)
d(eR)^lRd(eR)
(eRy 1 „I
s2
(5.9)
r~ ф = 0.
>‘V >. \
Решение уравнения (5.9) должно удовлетворять следующим гра-
ничным условиям:
' при Я = 0 — О;
dR
(5.9a)
при Я — 1 ф — 0. J
Решение дифференциального уравнения (5.9) можно представить
в виде степенного ряда
ОО
ч>(^)= у ьг„(8«)2". (зло:
п —О
Подставляя это выражение в (5.9), находим коэффициенты ряда
60 = 1, п = 0;
2” 4 ’
, 1 ( 1 /
2n “ (2/г)21 82 2/г~4
Постоянная е определяется с помощью второго из граничных
Рис. 5.1. Собственные функ-
ции задачи о теплообмене
в круглой трубе при
fc = const.
условий (5.9а). Применив это условие к
(5.10), получим
-0.
Это уравнение имеет бесконечное мно-
жество корней &п, называемых собствен-
ными значениями задачи. Каждому зна-
чению соответствует собственная функ-
ция ф(епЯ, еп) =фп (Я). Первые три
функции фп (Я) для п = 0,1 и 2 пред-
ставлены на рис. 5.1.
Таким образом, частное решение диф-
ференциального уравнения (5.2), удо-
влетворяющее граничному условию па
стенке, можно записать в виде
0n = Ап exp (—е2Х)фп (Я).
102
Общее решение есть сумма всех частных решений:
оо / 1 Л* \
(н) • фп (7?) ехр (—28,“г ———J . (5.11)
п о к Ре d /
В уравнении (5.11) неизвестны лишь коэффициенты Ап. Они
находятся из граничного условия на входе ( 5.3). Подставляя это
условие в (5.11), имеем
оо
1 Д,Ж (R).
п-1)
Пользуясь свойством ортогональности собственных функций,
получаем
1
(/?) R^—R^dR
А -2____________________
Z1n 1
о
Первые десять значений еп и Ап приведены в табл. 5.1.
Таблица 5.1
Собственные значения и постоянные задачи о теплообмене
в круглой трубе при = const
а «в р2 Ъ Л Ai Вп
0 2,7044 7,3136 -1-1,47644 0,74877
1 6,6790 44,609 —0,80612 0,54383
2 10,673 113,92 4-0,58876 0,46286
3 14,671 215,24 —0,47585 0,41542
4 18,670 348,56 -1-0,40592 0,38292
5 22,670 513,89 —0,35576 0,35869
6 26,669 711,22 -1-0,31917 0,33962
7 30,668 940,55 —0,29074 0,32406
8 34,668 1201,90 -1-0,26789 0,31101
9 38,668 1495,20 —0,24906 0,29984
Распределение температуры в потоке жидкости, вычисленное
по уравнению (5.11), показано на рис. 5.2. При малых значениях
приведенной длины ~ < 0,05 j температура жидкости вблизи
оси слабо изменяется,до радиусу и длине трубы. Лишь вблизи стенки
наблюдаются большие изменения температуры как по так и по X.
Область малых значений приведенной длины характерна тем,
что здесь происходит нарастание толщины слоя прогретой жидко-
сти—теплового пограничного слоя, в пределах которого и изменяет-
ся температура. Распределение температуры в ядре потока, сечение
103
которого сокращается с увеличением X, остается почти однородным,
и температура в нем приблизительно равна температуре на входе.
На достаточном удалении от входа тепловой пограничный слой
смыкается и теплообмен охватывает все сечение трубы. Начиная
с некоторого значения приведенной длины профили температуры
становятся подобными, т. е. температура в разных сечениях отли-
чается лишь по абсолютной величине, а закон изменения темпера-
туры по радиусу остается одинаковым. Такой характер температур-
ного поля отражает решение (5.11). При малых приведенных длинах
распределение температуры описывается с помощью ряда. С увели-
чением X влияние последующих членов ряда по сравнению с пре-
Рис. 5.2. Распределение температуры в потоке жидкости в круглой тру-
бе при t0=const.
дыдущими быстро уменьшается. При достаточно большой приве-
денной длине всеми членами ряда, кроме первого, можно прене-
бречь. В этом случае
9=ЛЛ0(Я)ехр[-2в§-1- -М. (5.12)
у Ре а /
Таким образом, при больших значениях X изменение темпера-
туры по радиусу описывается одной и той же функцией ф0 CR)»
а изменение по длине при всех значениях R следует экспоненциаль-
ному закону.
Определим среднемассовую температуру жидкости в произволь-
ном сечении трубы. При постоянных свойствах жидкости
- 1
t = —— \ twv 2nrdr.
nr^w J
(5.13)
Запишем это уравнение в безразмерной форме. Учитывая, что в на-
шем случае wxtw = 2 (1 — #2), получим
— /_i 1
0 = 2_2с_==4 С 0(1— R^RdR.
io ic X
(5.13а)
104
Подставив в это выражение значение © из (5.11), после интегри-
рования имеем
(5.14)
где
я,. = -Г Л 8?. j 1|>„ (Я) (1 - R2) RdR.
О
Первые десять значений Вп приведены в табл. 5.1.
Определим теперь местный коэффициент теплоотдачи, отнеся
его к разности между температурой стенки и среднемассовой тем-
пературой жидкости:
___ 9с---\ dr Jr^ra
(Л — ----— — ~---------
/с — t t'—/с
где 7С — плотность теплового потока на стенке; Z — коэффициент
теплопроводности жидкости, или в безразмерной форме
Nu
ad
т
Подставив в это уравнение производную, найденную из (5.11),
и значение 0 из (5.14), получим выражение для местного числа
Нуссельта:
ОО Г)
/ П 2 1 х
—Г ехр — 2еп--------—
&п \ Ре d f
п=0 4
(5.15)
Зависимость Nu от приведенной длины у показана на рис. 5.3.
При X -> О, т. е. во входном сечении обогреваемого участка,
Nu оо. Это объясняется тем, что производная от температуры
на стенке (д£/дг)г=Г(| во входном сечении принимает бесконечно
большое значение, а температурный напор конечен. В действитель-
ности, вследствие переноса тепла в стенке и жидкости за счет тепло-
проводности в осевом направлении производная (dt/df)r=r0,.
а следовательно, и число Nu будут иметь при X = 0 хотя и большое,
но конечное значение.
С увеличением X число Nu уменьшается, асимптотически при-
ближаясь к постоянному значению. Это происходит потому, что
начиная с некоторого значения X профили температуры в разных
селениях становятся подобными. При этом (t — — tc)t и число
105.
Nu перестают изменяться по длине. Это постоянное значение числа
Nu называется предельным и обозначается Nu^.
Устремляя X в (5.15) к бесконечности и учитывая только первые
члены рядов в числителе и знаменателе, находим
р2
NUoo = -^- ^3,66. (5.16)
2
Отсюда следует, что предельный коэффициент теплоотдачи
СХоо ~ 3,66 —.
d
Таким образом, зависит только от коэффициента теплопровод-
ности и диаметра трубы.
Из сказанного видно, что всю длину обогреваемой (охлаждае-
мой) трубы можно разделить на два участка. На первом участке
происходит формирование профиля температуры и число Nu убы-
вает по длине. На втором участке закон распределения температу-
ры по радиусу не изменяется по длине (хотя абсолютные значения
температуры меняются) и число Nu сохраняет постоянное значение.
Первый участок называется термическим начальным участком,
Рис. 5.3. Изменение местного (Nu) и среднего (Nu)
чисел Нуссельта по длине круглой трубы при tc = const.
Длину термического начального участка /нт можно определить
как такое расстояние от начала обогреваемого участка, на кото-
ром число Nu с заданной точностью принимает постоянное
(предельное) значение. Определив приведенную длину термиче-
ского начального участка из условия Nux==i = 1,01 Nu^, по-
лучим
-.-^- = 0,055. (5.17)
Ре d v 1
Следовательно, относительная длина
— = 0,055 Ре = 0,055 Re Рг.
(5.17а)
106
При заданном значении числа Re длина термического началь-
ного участка определяется числом Рг. Поэтому для жидкометалли-
ческих теплоносителей, у которых числа Рг да 0,005 4- 0,05, /нт
не превышает нескольких диаметров. Для газов, у которых число
Рг да 1, /пт^ 100 d. Для неметаллических капельных жидкостей
(вода, минеральные масла и др.) с числом Рг от 1 до 100 и выше /пт
может изменяться от нескольких сотен до нескольких тысяч и даже
десятков тысяч диаметров, т. е. охватывает всю длину трубы.
Для практического расчета теплоотдачи вблизи входа в трубу
использование уравнения (5.15) неудобно, так как приходится вы-
числять большое число членов ряда. При значениях приведенной
1 X
длины 0,01 можно пользоваться интерполяционным урав-
нением
Nu= — = 1,03 f— —'I 1/3
Z \Pe d .1
(5.18)
которое с погрешностью около ±3% описывает точное решение и
хорошо согласуется с опытными данными.
В инженерных расчетах часто достаточно знать средний коэффи-
циент теплоотдачи а на участке трубы длиной I (от х = 0 до х ~ /).
Его можно определять различными способами. Найдем выражение
для среднего интегрального коэффициента теплоотдачи:
- 1 с
а ==. — \
1 о
(5.19)
Из уравнения теплового баланса для элемента трубы длиной dx
а 0-2 л r0 dx — — л Го рср wd®,
где находим
adx = — . (5.20)
Следовательно,
-=P£p®d Г <№_ = _ pCptvd ь ,52П
4/ J О' 41 О о
И
= =----Г ре A in 0W,. (5.22)
Подставив сюда 0ж=;=г из (5.14), получим окончательно
Nti= — _Lpe_±in 8 У exp f —-2e„-Y- J-Y . (5.23)
4 / &п k Ре d /
107
При значениях —-j- 0,05 вместо (5.23) с погрешностью около
+3% можно пользоваться интерполяционным уравнением
Nu = = 1,55 (— (5.24)
X (Ре d /
На входе в обогреваемый участок Ыи,так же как и Nu, стремит
ся к бесконечности. Вдали от входа, при ~—>- оо, Nu прини-
мает постоянное значение, равное NuM = 3,66 (см. рис. 5.3). Однако
расстояние от входа, на котором число Nu с погрешностью 1 % ста-
новится постоянным, существенно больше, чем для местного числа
Nu. Это расстояние, называемое длиной термического начального
участка для средней теплоотдачи, равно примерно 25 /пт.
Выражение (5.21) нетрудно привести к виду
Qc = wpc-p (б’о—'0'х==г) = a Az ttdl, (5.25)
где
Отсюда видно, что при вычислении теплового потока средний коэф-
фициент теплоотдачи а, рассчитанный по уравнениям (5.23) и (5.24),
следует умножать на средний логарифмический температурный
напор At
2. Теплообмен в плоской трубе при стабилизованном течении. За-
дачу о теплообмене в плоской трубе (т. е. при движении жидкости
между двумя неограниченными пластинами) при постоянной и оди-
наковой на обеих поверхностях температуре стенки можно решить
тем же методом, что и задачу о теплообмене в круглой трубе. Ре-
зультаты решения этих задач также близки. Для плоской трубы
ah
Nuoo- -^— = 3,770, (5.27)
Л
а
-^- = 0,055 Ре, (5.28)
где Ре = wh!a-, h — ширина трубы.
3. Теплообмен в гидродинамическом начальном участке круглой
трубы. Если жидкость поступает в трубу из достаточно большого
резервуара и кромки трубы хорошо скруглены, то распределение
скорости во входном сечении будет равномерным. По мере удаления
от входа в результате прилипания жидкости к стенке и действия сил
108
вязкости у стенок образуется гидродинамический пограничный слой,
толщина которого нарастает по длине трубы. При этом профиль
скорости изменяется по длине трубы, постепенно преобразуясь
из однородного в параболический; последний уже не изменяется
по длине. Участок трубы вблизи от входа, на протяжении которого
происходит развитие профиля скорости, называется гидродинами-
ческим начальным участком. При однородном распределении ско-
рости на входе безразмерная продольная составляющая скорости
в гидродинамическом начальном участке зависит не только от R,
ио и от приведенной (гидродинамической) длины -j, т. е.
^ = 11^ [ R.M ; (5.29)
\ Re a J
поперечная составляющая скорости Wr при этом отлична от нуля,
что видно из уравнения неразрывности.
При достаточно больших значениях -j- влияние приведенной
длины вырождается, и в потоке устанавливается параболический
профиль скорости: = 2 (1 — R2), Wr — 0. Расстояние от
входа в трубу, на котором скорость жидкости на оси отличается
не более чем на 1 % от осевой скорости развитого течения, называется
длиной гидродинамического начального участка. Эта длина опреде-
ляется из соотношения
^- = 0,065 Re,
d ’
(5.30)
где Re — w — средняя скорость жидкости,
Во многих теплообменных устройствах вход жидкости в трубу
совпадает с началом теплообменного участка. В этом случае разви-
тие профиля температуры и профиля скорости по длине трубы
протекает одновременно. Если при стабилизованном течении в
круглой трубе число Nu = Nu то в гидродинамическом
начальном участке, с учетом (5.29),
Nu = Nuf —
\Ре
или
(5.31)
Nu —Nu (— Рг\
\Ре d )
Число Nu в гидродинамическом начальном участке выше, чем
при стабилизованном течении. Это объясняется более высокими зна-
чениями скорости вблизи стенки и наличием радиальных состав-
ляющих скорости в гидродинамическом начальном участке. Сред-
нее по длине число Nu в гидродинамическом начальном участке
109
круглой трубы при tG = const можно определить с помощью сле-
дующего приближенного уравнения [6]:
= 0,60 l'——V1/7 (1+2,5-Т-Ц, (5.32)
NuCTg \Re d J \ Re d J
которое справедливо при значениях у 0,1; при у >
> 0,1 число Nu ж NiieT6. Здесь Nuct6 — среднее по длине число
Нуссельта при стабилизованном течении, которое рассчитывается
по уравнениям, приведенным в п. 1. Уравнение (5.32) описывает
результаты теоретического расчета с погрешностью 5% и хорошо
согласуется с опытными данными.
Как видно из (5.17) и (5.30), приведенные длины термического
и гидродинамического начальных участков приблизительно оди-
наковы. Отсюда следует приближенное соотношение /пт « /ш,Рг.
Поэтому если число Рг > 1, то ZIrr < ZHT и напротив, если Рг <
< 1, то > /пг; при значении Рг « 1 /пг ж /ит.
§ 5.2. Теплообмен в круглой и плоской трубах
при граничных условиях второго рода
При расчете системы охлаждения реактора обычно известна
плотность теплового потока на поверхности твэла, а температуру
твэла надо определить. Поэтому для расчета реакторов характерны
задачи о теплообмене при граничных условиях второго рода.
1. Теплообмен в круглой трубе при постоянной плотности теп-
лового потока на стенке. При решении этой задачи примем те
же условия, что и в задаче о теплообмене при tc = const
(см. §5.1, п. 1), с той разницей, что в данном случае на внутренней
поверхности стенки задана постоянная плотность теплового по-
тока qc.
Как вытекает из условий задачи, среднемассовая температура
жидкости изменяется линейно по длине трубы. Действительно, из
уравнения теплового баланса находим
7 д । 24с х
t = Zo Н---=— ,
рср w r0
или в безразмерной форме
- 7 —/0 __ 4 х
qGd "Ре d ’ (5.33)
К
г-» wd ,
где Ре =-у; г0 — постоянная температура жидкости на входе.
Таким образом,, среднемассовая температура жидкости в данном
случае задана, тогда как температуру стенки и коэффициент теп-
лоотдачи надо определить. .. .
по
Сформулированной задаче отвечает уравнение энергии, анало-
гичное (5.2), ио безразмерная температура 0 в этом уравнении оп-
ределяется иначе:
^<3> । /1
dR* R i)R ' дХ '
(5.34)
Граничные условия имеют вид:
где
при X 0, 0< R< C 1 0 0;
при X ^5 0, R = 0 =0; dR
при Х>0, R — 1 d@ dR _ 1 2 ’ >
О =. t-ty. qc.d R^- r /'о X . 2 x ~ Pe d
(5.35)
а. Рассмотрим вначале решение этой задачи для области, уда-
ленной от входа в трубу, где влияние заданного распределения тем-
пературы во входном сечении становится несущественным. Можно
предположить, что в этом случае температура 0 при любом значе-
нии R изменяется по длине так же, как 0. Поэтому решение можно
представить в виде
0 - ЛХ + f (R),
(5.36)
где А — постоянная, a f (R) — неизвестная функция.
Подставив выражение для 0 в (5.34), получим:
dR \ dR ) v 1
Интегрируя это уравнение от 0 до R и учитывая, что f (0) = 0,
имеем
-У- ,=; JL С (1 _ R2) RdR _ А (Л—}
dR R J V \ 2 4 J
о
С помощью третьего из граничных условий (5.35) находим, что
Вторичное интегрирование дает
где С — постоянная интегрирования.
111
Подставив выражение для f (R) в (5.36), получим
© = 2Х 4-51 —
2 8
(5.37)
Вычислив среднемассовую температуру по уравнению
__ 1
0 = 4^©(1 — Д2) RdR
о
и сопоставив полученный результат с (5.33), найдем С = — 7/48.
Итак, температурное поле вдали от входа в трубу описывается
уравнением
= 4__L R*____________1
qcd Ре d 2 8 48 ‘
К
(5.38)
Температура стенки
© =0^! =_L _^_4_Л , (5.39)
с Л Ре d 48 V '
Предельное число Нуссельта
^и“":(д/дг=:(0и^§г'^4г~4'36- (5-40)
Полученные результаты соответствуют области, удаленной от на-
чала обогреваемого участка. Эта область характеризуется одинако-
вым законом распределения температуры по радиусу в различных
сечениях трубы, линейным изменением температуры по длине и по-
стоянством числа Nu. Выражение (5.38) является, таким образом,
частным решением уравнения (5.34) для области стабилизованного
теплообмена.
б. Рассмотрим теперь решение задачи о теплообмене в термиче-
ском начальном участке. Для этого необходимо найти общее реше-
ние уравнения (5.34), удовлетворяющее не только граничному ус-
ловию на стенке, но и граничному условию в начальном сечении обо-
греваемого участка трубы.
Перейдем в уравнении (5.34) и граничных условиях (5.35) от
температуры 0 к температуре
01==© —0:i!> (5.41)
где © ;|: — известное частное решение (5.34) для области стабили-
зованного теплообмена:.
©. = 2X4- —Д2-------
2 . 8 48
112
Тогда математическое описание процесса имеет вид:
д* ®i _]_L d®i = ™ .
dR- R dR Д' дХ ’
(5.42)
Х-0, 0<7?<1 01==_ *---
2 8
при Х^ О, R = О
^-•^0
при Х^ 0, jR = 1
dR
^ 0
(5.43)
Решение этой задачи с однородным граничным условием на
стенке можно получить тем же методом, что и задачи, рассмотренной
в § 5.1, п. 1.
Общее решение для имеет вид
®1=S Дик (^) ехр (—е„Х),
(5.44)
где еп (п — 1, 2, 3, ...) — собственные значения; фп (R) — собст-
венные функции; Ап — постоянные коэффициенты.
Таким образом, окончательное уравнение для температурного
поля, справедливое в любой точке потока, записывается следующим
образом:
00 / 1 X
+ 3 Ап фп (7?) ехр — 2е£—- —
/г=1 \ Ре d
(5.45)
Положив в уравнении (5.45) R = l, получим выражение для
температуры стенки:
+ 3 Фп (1) ехР ( —2е^----—
П=1 \ Ре d
(5.46)
Значения 8,% (1) и Ап приведены в табл. 5.2. График распре-
деления температуры в потоке жидкости показан на рис. 5.4. При
малых значениях приведенной длины температура жидкости вблизи
оси мало изменяется по радиусу и длине трубы. Начиная с некоторо-
го значения приведенной длины профили температуры становятся
одинаковыми, т. е. температура в разных сечениях отличается лишь
по абсолютной величине, а характер распределения температуры
по радиусу не изменяется.
113
Таблица 5.2
Собственные значения и постоянные задачи о теплообмене
в круглой трубе при r/c=const
п 4’/г ( 1 ) Ап
1 25,680 —0,49252 + 0,20174
2 83,862 +0,39551 —0,087555
3 174,17 —0,34587 +0,052797
4 296,54 +0,31405 —0,036640
5 450,95 —0,29125 +0,027518
6 637,39 + 0,27381 —0,021742
7 855,85 —0,25985 +0,017799
Определив местное число Нуссельта из соотношения
Nu = , ‘к* Ще.-ё)-1,
получим с помощью (5.46)
Nu ------------------i. (5.47)
П “ / i х \
--+ 2 Ап 'Ь (П ехР —2е«-------
48 \ Ре d /
Характер зависимости Nu от приведенной длины тот же, что и
в случае tc = const (см. рис. 5.3), только кривая лежит несколько
выше.
При достаточно больших значениях приведенной длины сумма
членов рядов (5.45) — (5.47) стремится к нулю, и уравнения пере-
ходят в найденные ранее соотношения для области стабилизован-
ного теплообмена. Таким образом, при значениях X, больших оп-
Рис. 5.4. Распределение температуры в потоке жидкости по
радиусу и длине трубы при <7o=const.
114
(5.48)
сю
(5.49)
ределеииой величины, значения 0, 0 и 0е изменяются линейно по
длине трубы, а число Нуссельта остается постоянным и равным
Nlim- 4,36.
Определив длину термического начального участка из условия
Жг«==/пт = 1>01 NuA), получим
У),07 Ре.
d
Таким образом, значения Nu^ и lmJd при qG const выше,
чем при = const (см. § 5.1).
При малых значениях приведенной длины вместо уравнения
(5.47) удобнее пользоваться интерполяционным уравнением 161:
Nu - 1,31 f— — V1/3 (1 -1-2 — —
\Ре d J \ 1 Ре d
Этим уравнением с погрешностью ±4% можно пользоваться при
1 V 1 V
значениях 0,04. При ~ > 0,04 с погрешностью около
5% можно принять Nu ~~ Nu^., = 4,36.
Приведенные в этом параграфе результаты относятся к тепло-
обмену при стабилизованном течении. Если вход жидкости в трубу
совпадает с начальным сечением обогреваемого участка и профиль
скорости па входе однородный, то для расчета теплоотдачи в гидро-
динамическом начальном участке можно воспользоваться урав-
нением 16]:
Nu О 45 f ' х S
\Re d ?
1/0 Г1 +2,85f-A- _£?
L \Rc cl j
где Nuct6 — местное число Нуссельта при стабилизованном тече-
нии, которое можно вычислить по уравнению (5.47) или (5.49). Урав-
пение (5.50) справедливо в пределах 10~4 < ~ < 0,064 и
0,7 Рг 10:!. При значениях у >0,064 профиль скорости
становится параболическим и, следовательно, Nu ж Nu(.T0.
2. Теплообмен в круглой трубе при переменной по длине плот-
ности теплового потока на стенке. Эта задача характерна для реак-
торов, так как тепловыделение, а следовательно, и плотность тепло-
вого потока на стенке могут существенно изменяться вдоль канала
реактора (т. е. по высоте активной зоны; см. § 1.2).
Пусть плотность теплового потока на стенке круглой трубы
произвольно изменяется по длине, т. е. qG (х)
функцией х. Все остальные условия те же, что
выше задаче о теплообмене при qG = const.
Так как уравнение энергии (5.34) линейно,
о теплообмене при qG ~ <
°’42] (5.50)
N Ист б
является заданной
и в рассмотренной
Так как уравнение энергии (5.34) линейно, то решение задачи
~ const можно обобщить иа случай qG (х)
с помощью метода суперпозиции. Поясним суть этого метода. Кри-
вую qG (х) приближенно можно представить как результат сумми-
115
рования единичных конечных возмущений плотности теплового
потока 7с0, Д?с1, Д(7С2, ..., постоянных по длине трубы, но сдвинутых
друг относительно друга на некоторый конечный интервал Д£
вдоль оси X (рис. 5.5). Каждое единичное возмущение, действуя в от-
сутствие других на соответствующем участке трубы, приводит
к возникновению в потоке жидкости температурного поля, которое
описывается уравнением (5.45), полученным в результате решения
задачи о теплообмене при qc = const.
тока на стенке:
а—кривая ^с(х) как результат суммирования единичных возмущений; б —измене-
ние температуры по длине трубы при Z! = const в случае действия единичного воз-
мущения qco (/); Д^с1 (2); Д<?с2 (3) и т, д_; Л — при одновременном действии воз-
мущений рсо, qci, qa и т. д.
Возмущение дс0 в начальном сечении трубы (т. е. при £ = 0),
действующее по всей ее длине, приводит к возникновению темпе-
ратурного поля:
O. = J^.0+(^>X),
л
где О’ ~ t — t0', t — температура в произвольной точке потока при
действии возмущения дс0; tQ — температура жидкости в начальном
сечении трубы; 0'1’ — решение задачи о теплообмене при qc =
= const. В соответствии с (5.45)
оо
+ 3 Л^п(^)ехР(~
п—1
а значение 0+ при R = 1, т. е.
И
0+= 2Х4- 2 Аг%(1)ехр(--8ДХ),
48 ft==i
116
Любое другое возмущение At/,.z, сдвинутое относительно начала
координат на расстояние £(- /А£, возбуждает температурное поле:
а ннл’,.\-..........у.
/•«
Так как уравнение (5.3-1) линейно относительно температуры,
то температурное поле в потоке при одновременном действии всех
возмущений можно представить как сумму температурных полей,
обусловленных отдельными возмущениями:
-l> . J1 ; "V —^1— (“) 1‘ (/\\ X-'
Л IAj
Заменив конечное приращение Ар,., бесконечно малым и перей-
дя от суммы к интегралу, получим уравнение для температурного
ноля при переменной с/,. по длине:
х
1*)’ «*’ (А\ А) | н г (А>, X’...........А)
о
Разделив это уравнение на среднюю по длине трубы плотность теп-
лового потока
7r 7с (X) ^А,
о
а также па d/k, получим окончательно
х ...
Н р(Ч,Н‘ (A, A) A f !•(£>, х-..............(5.51)
,1
о
где
(Ц , * </{!<) , у tyt’ , Г d I
(led ’ r/c. ’ ' ’ Ре d '
К
Итак, если известно температурное поле 6+ при постоянной плот-
ности теплового потока па стенке, то температурное поле W при пе-
ременной по длине плотности теплового потока qc. U) определяется
выражением (5.51). Это положение известно как теорема Дюамеля,
часто используемая в теории теплопроводности при решении задач
с переменными во времени граничными условиями.
117
Положив в выражении (5.51) 7? = 1, получим аналогичное вы-
ражение для температуры стенки при qc (х):
(5.52)
С /си V . J
О
Из уравнения теплового баланса для участка трубы длиной X
находим выражение для среднемассовой температуры жидкости:
Яс^
к
(5.53)
о
После того как найдены 0С и 0,
число Нуссельта:
легко определяется и местное
Nu=-._2^ — 4е 4
Л,
Яс
(5.54)
Gc-/) % 0с-0‘
Однако в задачах рассмотренного типа наибольший интерес пред-
ставляет безразмерная температура стенки, а не число Нуссельта.
Рассмотрим в качестве примера изменение 0С и Nu по длине тру-
бы при синусоидальном распределении qc по длине:
~ л . л£
qc — — sin —
ZG 2 L
Такой закон распределения qc характерен для реакторов без тор-
цевых отражателей. В данном случае
(5.55)
[?со = О, а
Подставляя эти значения в
для имеем
ГЛ л3 Г 11
0с = — 2(Х — £)-|------
2L J v 7 48
о L
(5.52)
__ л2 _л£
2L L
и используя уравнение (5.46)
оо
L
Выполнив интегрирование, получим
лХ X . 11 . лХ
cos---- -4-----л sin —
L J 1 96 L
2 г г
8/Z L
оо
п~1
лХ
sin------
______L________л £
/ 2 г
I &п L
\ л
лХ , 2 ч
cos —— — ехр (— 8П X)
2
. (5.56)
П = 1
С
£18
Среднемассовая температура жидкости
X t
sin —
1 пХ
1 — cos---
L
(5.57)
о
Вычислив 0(. и 0, с помощью уравнения (5.54) легко определить чис-
ло Нуссельта. Результаты расчета представлены на рис. 5.6 и 5.7.
Распределение 0, 0(. и Nu по длине трубы получается в виде семей-
Рис. 5.6. Зависимость 0 (сплошные линии) и 0С (пунктир) от
х/l при различных значениях L.
ства кривых, каждая из которых соответствует определенному зна-
чению приведенной длины L = -j. Чем больше L, тем выше 0
и 0С, причем 0С проходит через максимум.
На участке трубы, где qc (х) растет, число Нуссельта выше,
а на участке, где qa(x) падает, — ниже, чем в случае qc ~ const.
С увеличением L число Nu в средней части трубы приближается
к предельному значению, характерному для случая qG = const (Nuoo=
= 4,36). На конце трубы Nu быстро падает и при х — I обращается
в нуль, так как здесь qG == 0, а 0С — О конечно.
119
Из рассмотренного примера видно, что при переменной плот-
ности теплового потока на стенке число Нуссельта существенно
зависит от закона изменения qc по длине трубы. Анализ показывает,
что в случае увеличения qG по длине число Nu выше (или равно),
а в случае уменьшения — ниже (или равно), чем при qG — const.
Рис. 5.7. Зависимость числа Nu от х/l при различных значениях
— лх
L; qc ~ sin — (сплошные линии) и <7c=const (пунктир).
Как показал В. Д. Виленский [1], поведение числа Nu при х ->• оо
определяется пределом логарифмической производной от qc (х)
при х -> оо , т. е. величиной
К— lim ----------
Х->оо L Яс
dqc (*)
dx
(5.58)
Если К имеет конечное значение, отличное от нуля, то число Nu
стремится к некоторому предельному (постоянному) значению,
отличному от NuM при qc = const. Если К = О, то число Nu
стремится к NuOT при qc = const. Если же К = ± оо (т. е.
предела не существует), то число Nu неограниченно увеличивается
или уменьшается по длине трубы. Например, если qc (х) ~ ехр (тх),
где т = const, то К = т и Nu-> NuM > NuM при qc = const.
3. Теплообмен в плоской трубе при постоянной плотности
теплового потока на стенках. Рассмотрим задачу о теплообмене
при течении жидкости в плоской трубе (т. е. между параллельными
пластинками), на стенках которой поддерживаются постоянные зна-
чения плотности теплового потока qcl и qG2, причем qal qG^
120
Остальные условия те же, что и в задаче, рассмотренной в § 5.1,
п. 1.
Решение этой задачи можно получить тем же методом, что и за-
дачи о теплообмене в круглой трубе при qG — const (см. § 5.2, п. 1).
Приведем некоторые результаты расчета. Температура первой стен-
ки трубы вдали от входа и число Nu]oo для этой стенки вычисля-
ются по уравнению
Рис. 5.8. Изменение ----—г— по
vci п
длине плоской трубы при различных
значениях АсгЛ/сь
(°!__£ —__L_ 26_________9 —
Qci -^uioo 70 \ qCi /
(5.59)
где
7 = /о + (7с1+7с2)-^Ц-, (5.60)
pCp wn
h — ширина трубы.
Подобные же выражения для
Z'c2 и Nu2oo (вторая стенка) по-
лучаются заменой в выражении
(5.59) индекса cl индексом с2 и
наоборот.
Общее решение задачи, справедливое не только вдали от входа,
по и в термическом начальном участке, приведено в работе [6]. Не
выписывая соответствующих уравнений, покажем, как изменяется
температура стенки (Zcl —0^/ci 1/Nux по всей длине трубы
при различных значениях qai/qoi. Эта зависимость изображена на
рис. 5.8. Кривые для различных значений qGJgai соответствуют сле-
дующим условиям: qGz/qG1 = — 1 — количество тепла, подведен-
ное от первой стенки, равно количеству тепла, отведенному ко вто-
рой стенке (в этом случае t не изменяется по длине трубы); gc2/gcl =
— () — тепло подводится только через первую стенку, вторая стен-
ка теплоизолирована; qGilqGr = 1 — подвод (или отвод) тепла
через обе стенки одинаков и т. д. Таким образом, предельные числа
Нуссельта и длина термического начального участка в данном слу-
чае зависят от отношения плотностей теплового потока на стен-
ках. В частности, длина термического начального участка будет
минимальной при qG1 = qG2.
§ 5.3. Теплообмен и сопротивление в прямоугольных трубах
и продольно обтекаемых пучках стержней
Систему охлаждения активной зоны реактора часто образуют
трубы (каналы) разной формы поперечного сечения: прямоуголь-
ные, кольцевые, продольно обтекаемые пучки стержней и др. Поля
скорости и температуры в таких системах (исключая кольцевые тру-
бы), как правило, трехмерные. Расчет трехмерных полей обычно
проводится приближенными методами (численными или аналити-
121
ческими). Некоторые относительно простые задачи, например,
в случае полностью развитых полей скорости и температуры, до-
пускают точное решение* .
Рассмотрим особенности движения и теплообмена в трубах пря-
моугольного сечения и продольно обтекаемых пучках стержней.
На рис. 5.9 показаны изотахи, т. е. линии равной скорости,
при стабилизованном движении жидкости в трубе прямоугольного
сечения. Как и следовало ожидать, в середине трубы скорость мак-
симальна, а на стенке равна нулю. Однако, в отличие от круглой
и плоской труб, градиент скорости на стенке (dwx/dfi)n==0, где и —
Рис. 5.9. Изотахи в прямоугольной трубе при^ стабилизованном движении
(п/& = 2; Wx=wx/w).
нормаль к поверхности стенки, направленная в сторону жидкости,
изменяется по периметру. В середине граней он имеет наибольшие
значения, а в углах — наименьшие (стремится к нулю). Такой харак-
тер распределения скорости вблизи стенки приводит к соответствую-
щему изменению коэффициента теплоотдачи а по периметру трубы.
На рис. 5.10 показан характерный график изменения предель-
ного коэффициента теплоотдачи на одной из граней квадратной
трубы. Данные, приведенные на рисунке, относятся к случаю,
когда температура стенки постоянна по периметру, а средняя по
периметру плотность теплового потока на стенке qc постоянна по
длине. Такие граничные условия реализуются на практике, напри-
мер при постоянном тепловыделении в стенке, обладающей высокой
теплопроводностью. На рис. 5.10 видно, что местный коэффициент
теплоотдачи в середине грани приблизительно в 1,5 раза выше
среднего по периметру (а^). По мере приближения к углам па-
дает, а в углах становится равным нулю.
* См., например, работы [2, 6].
122
Поля скорости и температуры, а следователы-ю, местные (NtQ
и средние по периметру (NufO) числа Нуссельта в прямоугольных
трубах зависят от отношения сторон поперечного сечения у — h/b.
-0,5-0,0-0,3-0,2-0,1 0 0,1 0,2 0,3 Л
Рис. 5.10. Распределение местного коэф-
фициента теплоотдачи по грани квадрат-
поп трупы.
На рис. 5.11 показана зави-
симость Nu^ = (здесь
d0 = 4/7s — эквивалентный
диаметр) от у для двух типов
граничных условий на стен-
ке: при /с = const по пери-
метру и qc — const по длине
и при /с = const по перимет-
ру и длине. Случай у = 0 со-
ответствует плоской трубе, а
случай у = 1 — квадратной
трубе. С увеличением у = hlb
возрастает доля поверхности
трубы, приходящаяся на уг-
ловые зоны с более низкой
теплоотдачей, поэтому с уве-
личением у число Nli^ умень-
шается. Таким образом, число Nu^, вычисленное по эквивалентно-
му диаметру, существенно зависит от геометрии трубы и совсем
не соответствует значению Nu^ для
круглой трубы.
Если на внутренней поверхности
трубы поддерживается постоянная
(по периметру и длине) плотность
теплового потока qc, то температура
стенки трубы будет изменяться по
периметру, так как коэффициент теп-
лоотдачи в различных точках пери-
метра неодинаков. На рис. 5.12 пока-
зано распределение безразмерной тем-
пературы Стенки Рис. 5.11. Зависимость среднего
по периметру числа Нуссельта
(/с—7)% NUpo от у для прямоугольной
"" ..7с s.. 4 трубы:
при oi-const ио периметру и
<7c=const по длине; 2 — при Д =
[.S = 2 (ll + 6)] по периметру пря- = const по периметру и длине,
моугольной трубы с различным отно-
шением сторон на участке стабилизованного теплообмена, где
не изменяется по длине. Максимальная температура стенки
(в случае нагревания жидкости) наблюдается в углах, где скорость
жидкости минимальна. По мере удаления от углов температура
стенки снижается и в середине каждой из сторон имеет минималь-
ное значение в соответствии с характером профиля скорости. В сред-
ней части граней 0е может принимать отрицательные значения. Это
123
объясняется тем, что в данной точке периметра tG < t, хотя при этом
тепловой поток направлен от стенки к жидкости.
Рассмотрим особенности теплообмена при стабилизованном дви-
жении жидкости вдоль неограниченного пучка круглых стержней,
расположенных по углам равносторонних треугольников параллель-
но друг другу. На рис. 5.13 показано распределение по окружности
стержня местного предельного коэффициента теплоотдачи для
Рис. 5.12. Распределение температуры стенки по
периметру прямоугольной трубы при qc = const.
случая, когда температура стержня постоянна по окружности,
а плотность теплового потока qG на поверхности стержня постоянна
по длине [9]. При относительном шаге стержней b/d > 1,5 теплоот-
дача практически равномерна по окружности » 1); при
b/d < 1,5 наблюдается значительная неравномерность, связанная
с неравномерностью профиля скорости по углу, обусловленной вли-
янием близлежащих стержней.
Зависимость среднего по окружности предельного числа Нус-
сельта от b/d показана на рис. 5.14. Здесь
124
6 f д_\2
Т )
dQ = 4f/s — эквивалентный диаметр проходного сечения пучка.
В данном случае
jg = (1.
. л рЗ
Таким образом, и в случае продольного обтекания стержней
число Ni^, вычисленное по dQ, существенно зависит от b/d.
При стабилизованном течении жидкости в призматических тру-
бах, в частности прямоугольных трубах и продольно обтекаемых
пучках, градиент скорости и касательное напряжение с»с иа стенке
Рис. 5.13. Распределение аю/а«, по
окружности стержня в пучке.
Рис. 5.14. Зависимость числа Nu»
для пучка продольно обтекаемых
стержней от относительного шага b/d.
изменяются по периметру. В этом случае коэффициент сопротив-
ления трения определяется по среднему значению касательного
напряжения:
или
(5.61)
где
= Re-^2, TV——.
w v da
Из (5.61) видно, что при движении в прямоугольной трубе £Re
зависит только от у —h/b. Вычисления дают следующие значения
£Re:
У 0 0,1 0,20 0,25 0,33 0,50 0,66 0,80 1,0
£Ре 96,00 84,61 76,29 72,90 68,35 62,14 58,82 57,47 56,90
125
В случае продольного обтекания пучка стержней £Re зависит
только от bld. При расположении стержней по углам равносторон-
них' треугольников и Ш>1,5 эту зависимость можно выразить
следующим уравнением [3]:
п.
2 УЗ
I ь /
(5.62)
(5.63)
Зная нетрудно определить падение давления па участке тру-
бы длиною I:
§ 5.4. Теплообмен и сопротивление при переменных свойствах
жидкости
1. Предварительные замечания. Физические свойства жидкости
(р, ср, ц, К) зависят от температуры. Поэтому в потоках с неоднород-
ным полем температуры физические свойства также изменяются
в пространстве в соответствии с изменением температуры. При ма-
лых разностях температур в потоке или слабой зависимости свойств
от температуры эти изменения невелики. В таких условиях справед-
ливы результаты, полученные в предположении о постоянстве фи-
зических свойств. При интенсивном теплообмене, когда разности
температур в потоке велики, изменение физических свойств
с температурой оказывает существенное влияние па поля скорости
и температуры, а следовательно, на теплоотдачу и сопротивление.
При переменных свойствах жидкости взаимно связанные поля
скорости и температуры описываются системой нелинейных урав-
нений неразрывности, движения и энергии, которые необходимо
решать совместно. Возникающие при этом математические труд-
ности, за немногими исключениями, не позволяют получить анали-
тическое решение задачи. Поэтому в настоящее время такие задачи
решаются в основном численными методами с использованием ЭВМ.
Значительную роль в изучении этих вопросов играет эксперимент.
Характер изменения физических свойств в зависимости от тем-
пературы для капельных жидкостей (т. е. конденсированных сред)
и газов различен. У капельных жидкостей наиболее сильно изме-
няется с температурой динамический коэффициент вязкости, а дру-
гие свойства сравнительно слабо зависят от температуры. Поэтому
в случае вязкостного или вязкостно-инерционного течения капель-
ных жидкостей можно ограничиться специальным учетом изменения
одной лишь вязкости-, полагая другие свойства постоянными и рав-
ными их значениям при некоторой средней температуре. У газов су-
щественно изменяются с температурой плотность р, коэффициент вяз-
126
кости р и коэффициент теплопроводности X; теплоемкость ср меняется
сравнительно слабо. Поэтому в случае течения газа при достаточно
больших температурных напорах необходимо учитывать зависимость
от температуры р, р и X, а иногда п с/м
При неоднородном распределении плотности в потоке жидкости
в определенных условиях существенную роль начинают играть тер-
мо-гравитационные (архимедовы) силы, что приводит к возникнове-
нию вязкостно-гравитационного или вязкостпо-иперциошю-гравпта-
ционного режима течения. Закономерности движения и теплообме-
на, характерные для этих режимов, существенно отличаются от за-
кономерностей, свойственных вязкостному п вязкостно-инерцион-
ному течениям.
2. Вязкостное течение капельной жидкости с переменной вяз-
костью. Рассмотрим основные закономерности движения и теплообме-
на, характерные для вязкостного течения капельной жидкости, вяз-
кость которой зависит от температуры. Такие течения реализуются
при значениях Re, меныпих критического, и достаточно малых зна-
чениях числа Gr • Рг. Обычно эти условия выполняются при дви-
жении вязких жидкостей, для которых характерны большие зна-
чения чисел Рг. В этом случае, как показано выше, вся или большая
часть длины трубы находится в области термического начального
участка. Поэтому теоретические, и экспериментальные исследования,
относящиеся к обсуждаемому вопросу, проведены в основном для
термического начального участка.
На рис. 5.15 изображены профили скорости в термическом на-
чальном участке круглой трубы по данным теоретического расчета
Б. С. Петухова 161. Вычисления проведены для случая однородного
распределения температуры н параболического распределения ско-
рости в начальном сечении трубы и постоянной температуры стенки.
Зависимость вязкости от температуры описывалась уравнением
..= Но -|- I щ 1“ -|-... .
Р
Остальные физические свойства считались постоянными.
Если (/о—/(.)->-О, т. е. при изотермическом течении, вязкость,
как и другие свойства, постоянна во всей области течения. В этом
случае профиль скорости по всей длине трубы остается таким же,
как в начальном сечении, т. е. параболическим. При конечном значе-
нии как видно из рис. 5.15, профили скорости при нагревании
и охлаждении жидкости различны. В случае нагревания вязкость
жидкости вблизи стенки меньше, чем в ядре. Поэтому скорость вбли-
зи стенки увеличивается, а в ядре уменьшается по сравнению с со-
ответствующими значениями скорости при изотермическом течении
(предполагается, что средняя скорость в обоих случаях одинакова).
В результате профиль скорости при нагревании жидкости становит-
ся более заполненным (см. рис. 5.15, п). При охлаждении жидкости
наблюдается обратный эффект. Так как вязкость вблизи стенки
127
больше, чем в ядре, то скорость в пристеночной области становится
ниже, а в ядре выше, чем при изотермическом течении. В результате
профиль скорости приобретает характерный вытянутый вид (см.
рис. 5.15, б). Как при нагревании, так и при охлаждении жидкости
профили скорости изменяются по длине, что связано с соответствую-
щим изменением поля температуры, а следовательно, и поля вязкости.
Таким образом, при течении жидкости с переменной вязкостью
Рис. 5.15. Профили скорости
в круглой трубе в случае на-
гревания жидкости при
Цс/Но~О,О8 (а) и в случае ох-
лаждения жидкости при
|ЛС/Цо~58 (б).
dwxldx 0, а следовательно, и wr 0, что видно из уравнения не-
разрывности. Такое течение, строго говоря, является вязкостно-инер-
ционным. Однако роль сил инерции при ламинарном течении в тру-
бах обычно невелика. Поэтому такое течение практически можно
считать вязкостным.
Теоретические и экспериментальные исследования показывают,
1 X
что характер зависимости числа Nu от у при переменной вяз-
кости практически тот же, что и при постоянных свойствах. Поэто-
му отношение Nu/Nu0 (гдеЫи0 — число Нуссельта при постоян-
ных свойствах жидкости) зависит только от характера распределения
вязкости в потоке. Последнее можно учесть с помощью отношения
динамического коэффициента вязкости при температуре стенки
к его значению при среднемассовой температуре жидкости в дан-
ном сечении потока Зависимость Nu/Nu0 от jxc/jiJK для тер-
128
мического начального участка круглой трубы при const, по
опытным данным [51, показана па рис. 5.16.
Из рисунка видно, что при нагревании жидкости (це/щк < 1)
теплоотдача выше, а при охлаждении (цс/щк> 1) ниже, чем при изо-
термическом движении (т. е. при рс/рш = 1). Это объясняется тем,
что скорость жидкости в пристеночном слое в первом случае выше, а
во втором ниже, чем при ц — const.
Рис. 5.16. Зависимость Nu/Nu0 от ц0/|л)К при движении жидкости
в круглой трубе в случае Z0=const.
Экспериментальные и теоретические исследования показывают,
что зависимость Nu/Nu0 от |Лс/р}К можно представить в виде
= f ±£_Vl, (5.64)
N Ll() \ fljic /
где n — постоянное число.
Для термического начального участка круглой трубы при Zc а;
аз const значение п = 0,14 (см. рис. 5.16); число Nu0 можно выра-
зить с помощью уравнения (5.18). В результате получим уравнение
для местной теплоотдачи в рассматриваемых условиях:
Nu 1,03 f— _LY~1/3 mV0*14 . (5.65)
\Ре d J \p)K J
В уравнении (5.65) местный коэффициент теплоотдачи отнесен
к местному температурному напору t0 — t. Физические свойства,
входящие в выражения для чисел Nu и Ре, выбираются при темпе-
ратуре t = — (/с + t). Уравнение (5.65) справедливо при значениях
р-е У с 0,01 и 0,07 < цс/щк < 1500.
Соответствующее уравнение для среднего по длине числа
Нуссельта имеет вид:
NL „ 1,55 [ -L -Ь'г'/3 (JM-0’14 . (5.66)
\Ре d J \Иж /
В этом уравнении коэффициент а отнесен к среднему логарифми-
ческому температурному напору А£л. Однако в термическом началь-
ном участке 1 слабо изменяется по длине, поэтому обычно мож-
5 Зак. 792 129
но заменить средним арифметическим_температурным напором. Фи-
зические свойства в выражениях для Nu и Ре выбираются при темпе-
ратуре t' — tc ± (1/2)(знак «+» соответствует охлаждению
жидкости, знак «—» нагреванию»). Уравнение справедливо при
— 0,05 и в том же диапазоне рс/рЯ{, что и (5.65).
Для термического начального участка круглой трубы при с/(. -
— const значение п = 1/6, а число Nu0 можно выразить с помощью
(5.49). Тогда имеем
Nu = 1,31 |'-L 1_]_2— — f J^VI/G . (5.67)
\ Pe d J \ Pe d J \ p!K J
В этом уравнении а отнесен к tc — Z, а физические свойства в вы-
ражениях для Nu и Ре выбираются при температуре / (1/2) (Z(. I
+ 7). Уравнение справедливо при значениях у ~ С- 0,04 и
0,04 рс/Рщ 1.
Для области стабилизованного теплообмена в круглой трубе при
<7с = const по данным теоретического расчета в уравнении (5.64)
можно принять Nu0 = Nu^ = 4,36 и п = 0,14.
Коэффициент сопротивления трения веще большей степени, чем
число Nu, зависит от распределения скорости в потоке, а последнее
при переменной вязкости, как видно из рис. 5.15, в свою очередь,
зависит от Рс/Нж и у- Поэтому средний по длине коэффициент
сопротивления трения £ зависит не только от Re, ио и от р(./рж и
Ре da/l. Анализ опытных данных [5] показывает, что для труб раз-
ной формы (круглых, прямоугольных) при /с ;=» const эту зависи-
мость можно выразить уравнением
-i-AvA. шы
So \ Цо /
где £0 -уу — коэффициент сопротивления трепня при изотер-
мическом течении, вычисленный при температуре жидкости иа вхо-
де в трубу Zo; ср — постоянная, зависящая от формы поперечного
сечения трубы (для круглой трубы ср = 1, для квадратной ср
= 0,889, для плоской ср = 1,50); р.() — динамический коэффициент
вязкости, взятый при температуре /0.
Показатель степени п в формуле (5.68) определяется из уравпе-
ния
п =-- С ( Ре — У" (0,002, (Г>.(>9)
\. I ) \ Ро /
где при Ре у < 1500 С = 2,30, т = — 0,3;
при Ре у > 1500 С = 0,535, т - — 0,1.
130
* Числа Re и Ре в (5.68) и (5.69) вычисляются по эквивалентному
диаметру d.t и значениям физических свойств при температуре /0.
Уравнение (5.68) справедливо для капельных жидкостей в обла-
сти значений Re< 2300; 0,08< р.с/р() С 1200; 60 < Ре ^<3-104.
Заметим, что коэффициент |, вычисленный по этому уравнению,
учитывает затрату энергии не только на трение, но и па перестрой-
ку профиля скорости, обусловленную переменной вязкостью.
Зная нетрудно рассчитать перепад давлений в трубе длиной /:
(5.70)
где —постоянная или средняя но сечению скорость жидкости
в начальном сечении трубы; р0 — плотность жидкости при темпе-
ратуре /о’> k — поправка на гидродинамический начальный участок.
При развитом профиле скорости в начальном сечении /г == 0, при
однородном профиле скорости /г ==1,12 для круглой трубы и k = -
"• 0,62 для плоской.
Важно отметить, что все зависимости, рассмотренные до сих пор
в этой главе, справедливы только для вязкостного течения, когда
влияние свободной конвекции па гидродинамику и теплообмен еще
не существенно. Это условие приближенно выполняется, если
Gr-Pr 8-Ю5. Здесь Gr — где А/ =- (/с — L) — на-
ибольшая разность температур между стенкой и жидкостью в од-
ном и том же сечении потока (если tG = const, t — /о); физические
свойства жидкости в выражении Gr • Рг выбираются при темпе-
ратуре t == (1/2) (/0 /).
3. Вязкостно-гравитационное движение жидкости. При одно-
родном распределении плотности в напорном* потоке жидкости си-
лы тяжести, действующие па частицы жидкости, уравновешиваются
силами гидростатического давления. Поэтому жидкость движется
так, как если бы опа была невесомой, или, точнее говоря, поле ско-
рости в потоке не зависит от силы тяжести. Если же распределение
плотности в потоке неоднородно, то указанное равновесие нарушает-
ся. При этом па каждую частицу жидкости действует некоторая ре-
зультирующая, так называемая архимедова, сила, направленная
вверх, если плотность частицы меньше плотности окружающей жид-
кости, и вниз — в противном случае. Поэтому в вынужденном пото-
ке жидкости с неоднородным полем плотности па основное тече-
ние, обусловленное перепадом давления, накладывается свободно-
конвективное движение, возникающее под действием архимедо-
вых сил.
Течение жидкости, при котором архимедовы силы соизмеримы
с силами вязкости и инерции, называется вязкостно-инерционно-гра-
витационным. Однако при ламинарном течении силы инерции обыч-
* Напорными называются потоки жидкости, в которых отсутствуют сво-
б од и ы е п о в ер х 11 о ст 11.
5* 131
но достаточно малы по сравнению с архимедовыми силами и сила-
ми вязкости. Такое течение называется вязкостно-гравитационным.
Система безразмерных чисел для вязкостно-гравитационного те-
чения приведена в § 4.3, п. 3. Из нее видно, что влияние свободной
конвекции проявляется в существовании зависимости нолей скоро-
сти и температуры, а также теплоотдачи и сопротивления от произ-
ведения чисел Gr • Рг, которое называется числом Рэлея (Ra),
и ориентации системы в поле силы тяжести. Последняя определяет-
ся величиной угла ф между направлениями вектора скорости па
входе в трубу (или осью трубы) и вектора силы тяжести.
При совместном действии вынужденной и свободной конвекции
результирующее течение характеризуется взаимным направлением
сил давления, под действием которых осуществляется вынужденное
течение, и архимедовых сил, вызывающих свободную конвекцию.
С этой точки зрения можно выделить три характерных случая:
а) течение в вертикальной трубе снизу вверх при нагревании жид-
кости и сверху вниз при охлаждении;
б) течение в вертикальной трубе сверху вниз при нагревании
жидкости и снизу вверх при охлаждении;
в) течение в горизонтальной трубе при нагревании и охлажде-
нии жидкости.
Рассмотрим последовательно эти случаи.
а. При нагревании жидкости плотность вблизи стенки меньше
плотности в ядре потока. Поэтому действующие на частицы жидко;
сти архимедовы силы направлены вблизи стенки вверх, а в ядре по-
тока — вниз. Если движение жидкости, обусловленное перепадом
давления, осуществляется снизу вверх, то под действием архимедо-
вых сил скорости жидкости вблизи стенки возрастут, а в ядре пото-
ка уменьшатся по сравнению со значениями скорости при изотер-
мическом движении. То же самое произойдет и при охлаждении жид-
кости, движущейся сверху вниз, — скорости вблизи стенки увели-
чатся, а в ядре потока уменьшатся.
Точное решение рассматриваемой задачи для области, удаленной
от входа в трубу (т. е. при стабилизованном течении и теплообме-
не), при постоянной плотности теплового потока па стенке получено
Г. А. Остроумовым [4.1*. Свойства жидкости принимались постоян-
ными, кроме плотности в выражении для архимедовой силы; плот-
ность считалась линейной функцией температуры. На рис. 5.17 изо-
бражены полученные в результате расчета профили скорости и тем-
пературы. При значении Ra = О (изотермическое течение) профиль
скорости параболический. С увеличением числа Ra скорость вблизи
стенки увеличивается, а в ядре потока уменьшается. При некотором
значении Ra на оси трубы возникает минимум, а между осью и стен-
кой — максимум скорости. Точка максимума с увеличением числа
Ra приближается к стенке. При значении Ra st 630 скорость па
* Холлменом [10] это решение обобщено на случай наличия в потоке
внутренних источников тепла.
132
оси обращается в нуль, а при дальнейшем увеличении Ra в ядре
возникает течение, направленное в сторону, противоположную тече-
нию в пристеночной области.
Изменение предельного числа Нуссельта NulM в зависимости от
числа Ra, по данным теоретического расчета [4, 101, показано на
рис. 5.18 (верхняя кривая). С увеличением значения Ra скорость
вблизи стенки увеличивается, поэтому увеличивается и число Nu^.
При Ra —> 0 число Nu^., приближается к постоянному значению,
Рис. 5.17. Распределение скорости (а) и температуры (б) при подъем-
ном движении в обогреваемой трубе.
характерному для чисто вынужденной конвекции (Nu^ = 4,36).
Как видно из рис. 5.18, результаты теоретического расчета хорошо
согласуются с опытными данными.
Теплообмен во всей области течения в круглой трубе, включая
термический и гидродинамический начальные участки, эксперимен-
тально исследован в работе [7]. Опыты проводились с водой, движу-
щейся снизу вверх в обогреваемой трубе при с[с — const. Резуль-
таты этих измерений показывают, что Nu увеличивается с ростом Ra
тем сильнее, чем больше приведенная длина X. При достаточно боль-
ших X число Nu достигает предельного значения; Nu*, изменяется
в зависимости от Ra так же, как на рис. 5.18. На основе этих дан-
ных, в работе [7] предложено следующее уравнение для расчета
теплоотдачи:
Nu
Nuo
Ra \ 0.27
В /
(5.71)
Здесь Nu0 — число Нуссельта для случая вязкостного течения жид-
кости с постоянными свойствами; при параболическом профиле в иа-
133
чальном сечении Nu0 вычисляется по уравнению (5.47), при одно-
родном профиле — по уравнению (5.50). Число Рэлея
Ra = Gr.Pr = ^^
v2
v __А
а 1 &уа ’
где А — аксиальный градиент среднемассовой температуры.
При 7с = const
А
dx pep wd
Параметр В зависит от X и определяется из соотношений:
В ^L^-pySX1/4, X < 0,07;
X
В -60, X > 0,07,
где
"Ре d ’ а
Все физические свойства жидкости_в уравнении (5.71) выбира-
ются при среднемассовой температуре t в данном сечении трубы.
Рис. 5.18. Предельное число Нуссельта, по данным теоретического рас-
чета (кривые) п опыта (точки), при подъемном (/) п опускном (2) те-
чении в обогреваемой трубе.
Уравнение (5.71) справедливо при значениях 250 Ra 8 х
X Ю5, Re Reup и 3 10~4 =< X < Хкр в случае совпадения вы-
нужденной и свободной конвекции у стенки при qG — const. Ono
проверено экспериментально при значениях 4 < Рг 6.
Характер профилей скорости (см. рис. 5.17) позволяет предпо-
ложить, что не при всех значениях числа Ra (в случае Re< ReKp)
вязкостно-гравитационное течение является устойчивым. Наличие
в профилях скорости точек перегиба и в особенности появление
в ядре возвратного течения стимулирует нарушение устойчивости,
возникновение вихрей и переход к вязкостно-ииерционио-гравита-
134
циошюму (турбулентному) течению. Наблюдения показывают, что
при небольших значениях Ra течение по всей длине трубы вязко-
стно-гравитационное (нижняя кривая на рис. 5.19). При более вы-
соких числах Ra па участке трубы от входа до некоторого сечения
течение остается вязкостно-гравитационным, а затем наступает пе-
реход к вязкостпо-иперцгюипо-гравптационному течению (сред-
няя и верхняя кривые на рис. 5.19), для которого характерны более
высокие значения чисел Nu. Приведенная длина, па которой вязко-
стно-гравитационное течение теряет устойчивость, может быть па-
Рпс. 5.19. Изменение числа Nit по длине трубы при
Re;=55() п различных значениях Ra (подъемное течение
в обогреваемой трубе).
звана длиной потери устойчивости Хц,у. Величина Хп>у уменьшается
с ростом Ra и, по данным работы [7.1, описывается эмпирическим
уравнением
Хп#у--4,25 СRa~0-8, (5.72)
где С=1 при параболическом профиле скорости и С 1 -]10 х
Хехр(—0,0025 Re) при однородном профиле скорости в начальном
сечении обогреваемого участка. Переход к вязкостпо-инерционно-
гравитациогшому (турбулентному) течению наступает при несколько
большем значении X Хкр « 1,3 Хп>у.
б. При нагревании жидкости, движущейся сверху вниз, и охла-
ждении жидкости, движущейся снизу вверх в вертикальной трубе,
скорости жидкости у стенки уменьшаются под действием архимедо-
вых сил, а в ядре потока увеличиваются. Профили скорости и тем-
пературы вдали от входа в трубу, характерные для этого случая,
изображены на рис. 5.20 [10]. При числе Ra = 0 профиль скорости
параболический. С увеличением числа Ra течение вблизи стенки бы-
стро тормозится, а в ядре потока ускоряется. Уже при Ra 100
градиент скорости у стенки обращается в нуль, а при несколько боль-
шем значении Ra вблизи стенки возникает обратное течение. Вяз-
костно-гравитационное течение с таким профилем скорости крайне
неустойчиво и может существовать лишь при малых значениях
135
Ra. Наблюдения показывают, что уже при Ra 170 происходит
нарушение устойчивости, в пристеночной области возникают вихри,
а затем при несколько больших числах Ra течение становится тур-
булентным.
Предельное число Нуссельта NuTO при малых Ra, когда еще су-
ществует вязкостно-гравитационное течение, убывает с ростом Ra
(см. рис. 5.18, нижняя кривая). Последнее связано с соответствую-
щим уменьшением скорости вблизи стенки. При более высоких чис-
лах Ra вязкостно-гравитационное течение в рассматриваемых усло-
виях, как уже отмечалось, не существует.
Рис. 5.20, Распределение скорости (а) и температуры (б) при подъемном
движении в охлаждаемой трубе.
в. В случае нагревания или охлаждения жидкости, движущейся
в горизонтальной трубе, частицы жидкости под действием архиме-
довых сил движутся в плоскости, перпендикулярной оси трубы, а
под действием перепада давления эти же частицы движутся вдоль оси.
При нагревании жидкости плотность у стенки меньше, чем в ядре
потока, поэтому у стенки возникают восходящие токи жидкости,
а в ядре — нисходящие (рис. 5.21, а). При охлаждении жидкости
движение носит обратный характер. В результате взаимодействия
этих свободно-конвективных течений с вынужденным течением вдоль
оси возникает сложное течение, которое схематически можно пред-
ставить как бы происходящим по двум винтовым линиям, причем по
одной из них вращение происходит по часовой стрелке, а по другой —
против часовой стрелки.
При таком течении поле температуры, как и поле скорости, уже
не является осесимметричным. Максимум продольной составляющей
скорости в случае нагревания жидкости (см. рис. 5.21, а) сдвинут
136
55
Рис. 5.21. Течение нагреваемой жидкости в горизонтальной трубе:
а -- свободпо-копвективпые токи в поперечном сечепнп трубы и профиль продольной
составляющей скорости; б — изотермы в поперечном сечении трубы.
вниз. Особенно сильно деформируется поле температуры. Это хо-
рошо видно из рис. 5.21, б, где изображены полученные эксперимен-
тально изотермы в сечении трубы при qa const [81 (в случае р =
const изотермы представляли бы собой концентрические окруж-
ности). В соответствии с характером температурного поля безраз-
мерная температура стенки и число Нуссельта
1
Nu
(/с — /) %
qG d
изменяются не только по длине, ио и по
Рис. 5.22. Зависимость безразмерной темпера-
туры в горизонтальной обогреваемой трубе
от приведенной длины.
Рис. 5.23. Распределение ме-
стного числа Nu по перимет-
ру горизонтальной обогре-
ваемой трубы при различ-
ных значениях X.
137
Изменение 0С на верхней и нижней образующих в зависимости от
X показано на рис. 5.22, а изменение числа Nu по окружности —
на рис. 5.23 [8]. При достаточно больших числах Ra значения ©с
вблизи нижней образующей значительно меньше, a Nu значитель-
но больше, чем при вязкостном течении, т. е. при Ra = 0 (пунктир-
ная линия на рис. 5.22); вблизи верхней образующей напротив, ©с
больше, а число Nu меньше, чем при Ra — 0. С увеличением приве-
денной длины неоднородность в распределении 0С и Nu по окружно-
сти возрастает. Так, при X > 10~2 число Nu на верхней образу-
ющей приблизительно в 10 раз меньше, чем на нижней. Такой ха-
рактер изменения 0С и Nu обусловлен специфическим движением
жидкости. Интенсивность свободно-конвективных токов возрастает
по длине, причем особенно сильно в пристеночной области ниж-
ней части трубы. Это приводит к значительному увеличению теп-
лоотдачи и соответствующему снижению температуры стенки в ниж-
ней части трубы. Уменьшение теплоотдачи в верхней части трубы
связано с тем, что здесь концентрируется сравнительно горячая
жидкость (см. рис. 5.21, б), в которую токи свободной конвекции
почти не проникают.
Более подробные сведения и расчетные рекомендации можно
найти в указанных ниже работах.
СПИСОК ЛИТЕРАТУРЫ
1. Виленский В. Д. Общие закономерности стабилизации коэффициента
теплоотдачи при течении жидкости в канале. «Теплофизика высоких
температур», 1966, т. 4, № 5, с. 675.
2. Минашин В. Е., Шолохов А. А., Грибанов Ю. И. Теплофизика ядерных
реакторов с жидкометаллическим охлаждением. М., Атомиздат, 1971.
3. Осмачкин В. С. Особенности теплообмена в ядерных реакторах, охлажда-
емых несжимаемыми иекипящими жидкостями. Доклад Р/326, пред-
ставленный на Третью международ, конф, по мирному использованию
атомной энергии. Женева, 1964.
4. Остроумов Г. А. Свободная конвекция в условиях внутренней задачи.
М., Гостехтеориздат, 1952.
5. Петухов Б. С., Краснощеков Е. А., Нольде Л. Д. Теплообмен при вяз-
костном движении жидкости в трубах и каналах. — «Теплоэнергетика»,
1956, № 12, с. 41.
6. Петухов Б. С. Теплообмен и сопротивление при ламинарном течении
жидкости в трубах. М., «Энергия», 1967.
7. Петухов Б. С., Поляков А. Ф., Стригин Б. К- Исследование теплообмена
в трубах при вязкостно-гравитационном течении. — В сб.: Тепло- и мас-
соперенос. Т. 1. М., «Энергия», 1968, с. 607.
8. Петухов Б. С., Поляков А. Ф. Течение и теплообмен в горизонтальных
трубах при совместном действии вынужденной и свободной конвекции.
Доклад на IV Междунар. конф, по теплообмену. Версаль, сентябрь 1970г.
9. Спэрроу, Лоффлер, Хаббард. Теплообмен при продольном обтекании ци-
линдров ламинарным потоком.—«Теплопередача», 1961, №4, с. 31.
10. Hallman Т. М. Combined forced and free-laminar heat transfer in verti-
cal tubes with uniform internal heat generation. — «Trans. ASME», 1956,
v. 78, p. 1831.
ГЛАВА 6
ОСНОВЫ ПОЛУЭМПИРИЧЕСКОЙ ТЕОРИИ ТУРБУЛЕНТНОСТИ
§ 6.1. Краткие сведения о механизме турбулентности
Турбулентные течения широко распространены в природе и
технике. Как показано ниже, турбулентные потоки характеризуются
гораздо более интенсивным переносом тепла, вещества и количества
движения по сравнению с ламинарными, что, в свою очередь, свя-
зано с более интенсивным перемешиванием жидкости. Поэтому
в большинстве технических устройств выгодно иметь турбулентный
режим течения.
Турбулентность — очень сложное физическое явление, и, не-
смотря иа большое число теоретических и экспериментальных работ,
посвященных исследованию турбулентности, достаточно полный об-
зор которых можно найти в монографиях [2, 4—- 6], эта проблема
еще мало изучена. Даже определение самого понятия турбулент-
ность вызывает некоторые затруднения. Обычно, определяя поня-
тие турбулентного движения жидкости, говорят, что это такое дви-
жение, при котором в потоке существуют нерегулярные пульсации
скорости и давления, перемешивающие поток и обусловливающие
молярный механизм взаимодействия между ее элементами, т. е.,
в отличие от ламинарного режима течения, подчеркивается неупо-
рядоченный характер изменения параметров потока. Однако если
бы турбулентное течение было полностью неупорядоченным, то оно
не поддавалось бы математическому анализу. На самом деле неупо-
рядоченность турбулентного движения относительна и связана с вли-
янием на поток некоторых не поддающихся точному учету факторов.
Поэтому реализация того или иного значения параметра в турбулент-
ном потоке носит вероятностный характер. С использованием зако-
нов и методов теории вероятностей построена статистическая теория
турбулентности [4, 5].
Все параметры турбулентного потока — скорость, температура,
давление и т. д. — меняются во времени. Типичный характер из-
менения какого-либо параметра ср в произвольной точке потока по-
казан на рис. 6.1. Если проводить многократное измерение мгновен-
ного значения этого параметра ср, то получится целый набор зна-
чений — срх, ср2, ср3, ..., причем вероятность появления того или
иного значения будет характеризоваться соответствующей плот-
ностью вероятности р (ср). Зная распределение плотности вероятно-
сти, нетрудно определить ряд статистических параметров, характери-
139
зующих величину ср, в частности, ее осредненное значение ср. Для
математического описания процесса полезно выделить из рассмат-
риваемой величины ее осредненное значение. Иными словами, можно
представить мгновенное значение действительной величины ср (на-
зываемое также актуальным) в любой момент времени как сумму
осредненного значения ср и ее отклонения от этой величины:
ср — ср ср'. (6.1)
Величины ср' называются пульсационными составляющими или
пульсациями физической величины. Например, если рассматривают-
Рис. 6.1. Изменение во време-
ни параметров турбулентного
потока (скорости, давления,
температуры и т. д.).
ся компоненты вектора скорости, то
w'x, w'y и w'z представляют собой пуль-
сации скорости (или скорости пуль-
сационного движения) вдоль соответ-
ствующих осей координат. Мгновен-
ные значения параметров турбулент-
ного потока меняются в известной
мере хаотически, чего ни в коем слу-
чае нельзя сказать о осредиеииых зна-
чениях параметров. Поэтому, опре-
деляя турбулентное течение, следует
наряду с неупорядоченностью под-
черкнуть, как это делает Хинце 151,
статистическую однозначность пара-
метров турбулентного потока: «Турбулентное движение жидкости
предполагает наличие неупорядоченности течения, в котором раз-
личные величины претерпевают хаотическое изменение по вре-
мени и пространственным координатам и при этом могут' быть вы-
делены статистически точные их осредненные значения».
Хаотический характер изменения параметров турбулентного по-
тока делает невозможным, да и нецелесообразным получение зако-
номерностей, описывающих изменение действительных мгновенных
(актуальных) значений параметров. С практической точки зрения
наибольший интерес представляют осредненные значения параметров
турбулентного потока. Поэтому в последующих разделах мы прежде
всего выясним, каким образом существующие полуэмпирические
теории турбулентности позволяют рассчитывать осредненные значе-
ния скорости и температуры в произвольно выбранной точке пото-
ка. При этом будем рассматривать только так называемый квазиста-
ционариый режим течения, когда осредненные параметры потока не
меняются во времени. Стремление получить некоторые соотноше-
ния для осредненных значений параметров не означает, что можно
при этом отвлечься от пульсационного характера турбулентного
движения. Наоборот, как показано ниже, распределение осредиеп-
ных параметров потока в большой мере определяется его пульса-
ционными характеристиками. Поэтому все существующие полуэм-
пирические теории турбулентности базируются на рассмотрении
той или иной физической модели пульсационного процесса.
140
§ 6.2. Осредненные уравнения неразрывности, движения
и энергии для турбулентных потоков
Мгновенные (или актуальные) значения параметров в произволь-
ной точке турбулентного потока связаны между собой дифферен-
циальными уравнениями неразрывности, движения и энергии, рас-
смотренными в гл. 4. В случае течения несжимаемой жидкости
при условии, что вязкая диссипация энергии пренебрежимо мала,
эти уравнения имеют следующий вид:
Здесь вместо ранее принятых обозначений декартовых осей коорди-
нат (х, у, г) введены обозначения х,, х2, х;!, что позволяет записать
уравнения более компактно. Для получения из этой системы уравне-
ний зависимостей, описывающих изменение осредиенных параметров
потока, нужно заменить в них каждую актуальную величину сум-
мой осредпенного и пульсационного значений в соответствии с (6.1),
а затем провести осреднение. Такой вывод, а также соответствую-
щие правила осреднения впервые были предложены основоположни-
ком теории турбулентности О. Рейнольдсом.
Прежде всего определим понятие осредненной величины. На
практике обычно измеряют параметры в некоторых точках потока
в функции от времени. Поэтому удобнее всего проводить осреднение
пульсирующих величин <р (х, у, z, т) по времени. Тогда осреднеш-юе
за промежуток времени т0 значение пульсирующей величины равно
Т-|-Тц/2
<[) (х, у, г, т) ----- — ср (х, у, г, т) dx.
То J
Г—То/2
(6.5)
При выполнении некоторых условий полученная таким образом ве-
личина совпадает со средней статистической.
Естественно возникает вопрос, каким образом следует выбирать
период осреднения т0. Очевидно, что т0 должно быть достаточно ве-
лико по сравнению с периодом пульсаций и вместе с тем достаточно
мало по сравнению с промежутком времени, в течение которого су-
щественно изменяется осредненное значение параметра.
141
Правила осреднения Рейнольдса различных комбинаций акту-
альных величин срх и ф2 в несколько измененном виде 141 сводятся
к следующим пяти соотношениям:
<5ср ds Ф1 + ф2=-Ф1-Ьф2; (6.6) сир —аср, если а = const, (6.7) а~а\ (6.8) = —, s — это х, г/, z или т; (6.9) ds сР1 сРа (рг ф2. (6.10)
Первые 4 соотношения (6.6) — (6.9) вытекают из определения
операции осреднения (6.5) и вполне очевидны, а именно: осреднеипое
значение суммы двух (или нескольких) пульсирующих значений рав-
но сумме их осредиениых значений [см. (6.6)]. Умножение актуаль-
ной величины на постоянную а увеличивает ее осреднеипое значение
в а раз [формула (6.7)]. Осреднеипое значение постоянной равно
самой постоянной [см. (6.8)]. Соотношение (6.9), означающее, что
осреднениое значение производной равно производной по тому же
параметру от осредненной величины, менее очевидно, но также
следует из (6.5). Выражение (6.10) в случае квазистациопарного
течения, когда осреднеииые параметры не изменяются во времени,
ничем не отличается от выражения (6.7), так как в этом случае (pi
const. Если же турбулентное течение не квазистацпопарпо, то соот-
ношение (6.10), строго говоря, выполняется не во всех случаях, п
его приходится постулировать.
Из соотношений (6.6) — (6.10) можно получить некоторые допол-
нительные полезные сведения. Полагая в (6.10) ср2 == 1, имеем
= (6.11)
т. е. повторное осреднение не меняет среднего значения. Воспользо-
вавшись (6.6) и (6.1), получим также:
ср'=Ф—.ср ф — ср —0. (6.12)
Таким образом, осреднеипое значение любой пульсационной вели-
чины равно нулю.
Итак, рассмотрим, какие результаты дает осреднение уравнений
(6.2) — (6.4). Осреднение уравнения неразрывности (6.2) с учетом
правил осреднения приводит к следующему уравнению:
(6.13)
142
Вычитая из (6.2) уравнение (6.13), получаем уравнение неразрыв-
ности для пульсационных компонент скорости:
У ^=0. (6.14)
/ = 1 dxJ
Пренебрегая массовой силой при осреднении уравнения движения
(6.3), находим
dwj''
дхи
(6.15)
OW j
Прибавив к левой части этого уравнения слагаемое Ъ
i дх j
в соответствии с уравнением неразрывности равное нулю, получим
(6.16)
Осреднение конвективных слагаемых в левой части уравнения (6.16)
дает
Перенеся второе слагаемое этого выражения в правую часть урав-
нения (6.16), объединив его с силой вязкости, окончательно получим
— dwi
Wi —1
dxj
з
dp j. d
dxt dxj
dw; —j—t
—L —pWi'W]
dxj
Аналогичные преобразования уравнения (6.4) дают
рею/ f ]~\~qv.
(6.18)
143
Итак, для осредненных параметров турбулентного течения полу-
чена следующая система уравнений:
4
dxi
/= 1 dxj \ dxj
г=1, 2, 3;
Уравнения (6.19) и (6.20), описывающие турбулентное течение вяз-
кой несжимаемой жидкости, называются уравнениями Рейнольдса.
Сопоставляя эту систему уравнений для осредненных величин
с исходной системой уравнений для актуальных величии, видим, что
в осредненных уравнениях движения и энергии появились дополни-
тельные слагаемые. Слагаемые—pw[wj в правой части уравнения
движения можно интерпретировать как некоторые дополнительные
напряжения [они складываются с вязкими напряжениями р(^/</лу)|,
возникающие в турбулентном потоке вследствие пульсаций скоро-
сти и соответствующего переноса количества движения. Эти допол-
нительные члены в уравнении движения называются турбулентны-
ми напряжениями или напряжениями Рейнольдса.
Причину возникновения дополнительных турбулентных напря-
жений можно пояснить следующим образом. Мысленно выделим в по-
токе жидкости некоторую площадку, и пусть в направлении норма-
ли к этой площадке имеется градиент осреднениой скорости. В слу-
чае ламинарного течения на рассматриваемой площадке возникает
напряжение, обусловленное силами вязкости. Но так можно гово-
рить, если не учитывать микроструктуру вещества и рассматривать
жидкость как сплошную среду. На самом же деле вязкие напряжения
являются результирующим эффектом, связанным с переносом коли-
чества движения отдельными молекулами.
Аналогичный подход можно применить и для объяснения физи-
ческой природы турбулентного переноса. В случае турбулентного
течения в направлении нормали к выделенной площадке помимо пе-
реноса количества движения отдельными молекулами происходит
перенос количества движения вследствие пульсации скорости, свя-
занный с движением некоторых макроскопических объемов жидко-
сти. Именно движение этих объемов, обычно называемых молями,
обусловливает молярный перенос количества движения. При рас-
смотрении жидкости как сплошной среды молярному переносу со-
144
ответствуют дополнительные турбулентные напряжения, выражае-
мые в уравнении движения членами —pw'i w'j.
Таким же образом члены в правой части уравнения энергии
—pcw'jt' можно рассматривать как дополнительные плотности тепло-
вого потока, обусловленные турбулентным переносом [они склады-
ваются с плотностями теплового потока за счет молекулярной теп-
лопроводности к (dt/dxfi. Эти дополнительные плотности теплового
потока называются турбулентными. Таким образом, в турбулентном
потоке наряду с вязкими напряжениями и плотностями теплового'
потока, обусловленными молекулярной теплопроводностью, сущест-
вуют турбулентные напряжения и турбулентные плотности тепло-
вого потока.
Уравнения (6.19) — (6.21) в сочетании с соответствующими на-
чальными и граничными условиями описывают осредненпые пара-
метры турбулентного течения. Однако простейший анализ показы-
вает, что система уравнений (6.19) — (6.21) не замкнута, так как
число неизвестных, входящих в эту систему, превышает число урав-
нений. Причем «лишними» неизвестными, для определения кото-
рых не хватает уравнений, являются дополнительные члены, обус-
ловленные турбулентным переносом. Отсюда следует, что без ка-
ких-либо дополнительных соображений, с помощью которых мож-
но было бы определить осреднеииые произведения из пульсаций ско-
рости и пульсаций скорости и температуры, решение системы урав-
нений (6.19) — (6.21) невозможно. Очевидно, что эти величины мо-
гут зависеть от координат, от времени, от таких осредненных пара-
метров потока, как скорость и температура, от физических свойств
жидкости. Определение зависимостей для осредненных произведе-
ний из пульсаций скорости и температуры, т. е. турбулентных на-
пряжений и турбулентных плотностей теплового потока, составляет
главную цель теории турбулентности.
Для исследования этих зависимостей пользуются различными
методами. Во-первых, применяют теоретические методы статисти-
ческой механики, лежащие в основе статистической теории турбу-
лентности, во-вторых, —различные полуэмпирические теории, осно-
ванные на определенных моделях турбулентного переноса, такие,
как теория переноса количества движения Прандтля, теория пере-
носа завихренности Тейлора. И, наконец, используют эмпирические
методы, когда члены, учитывающие турбулентный перенос, опреде-
ляются экспериментально.
Система уравнений (6.19) — (6.21) записана для общего случая
трехмерного течения жидкости; она может быть существенно упро-
щена в случае двумерных течений, когда осредненная скорость по-
тока вдоль одной из координат равна нулю и все осреднеииые пара-
метры потока не меняются вдоль этой координаты. В частности, тур-
булентное течение несжимаемой жидкости в круглой трубе при сим-
метричных относительно оси полях скорости и температуры описы-
145
вается следующей системой уравнений:
——— (rwr) -|- — 0;
г дг дх
(6.22)
dwv . — дтЛ
. .. „ ££ I I -
дх dr J
/ дюх —7—Д
г |1—-—pwv ад,- ;
дг /
. — dwr\
-се', -- -2
' дг
J
dwp ~} /То \
—' —Р(шг“ ;
dr I
Д <Э/ -V77
Г Л-----QCWr t
\ дг
f dwv . -
О ------ 4- £2
у <9т
_ с)р , 1 д
дх г дг
/дцу, . — дш,
п I -1— ЦИ
Г \ ЙТ А дх
_ др . 1 д
дг г дг
/ д! , — dl dt\
рС _|_цуя (..да
\ дх дх дг
дг
В этой системе уравнений вследствие осевой симметрии потока от-
сутствует компонента скорости и>ф, а также все производные д/дср.
В уравнениях (6.23) — (6.25) опущены также слагаемые, учиты-
вающие изменение напряжений и плотности теплового потока в осе-
вом направлении:
так как при течении в трубах эти производные обычно малы по срыв
нению с производными в радиальном направлении.
§ 6.3. Коэффициенты турбулентного переноса
количества движения и тепла
Как уже отмечалось выше, для того чтобы с помощью осредпеп -
пых уравнений можно было бы решать конкретные задачи, необходи-
мо располагать дополнительными сведениями о слагаемых, описы-
вающих турбулентный перенос количества движения и тепла. lit*
останавливаясь на методах статистической теории турбулентности,
рассмотрим некоторые результаты, полученные при эксперимента л ь-
ном исследовании турбулентных потоков в трубах, а затем основ-
ные полуэмпирические теории турбулентности.
Прежде всего введем некоторые важные понятия, широко исполь-
зуемые для количественного описания турбулентного переноса.
146
Выражение в круглых скобках в правой части уравнения (6.23}
Представляет собой полное касательное напряжение, приложенное
К площадке, нормаль к которой совпадает с направлением радиуса:
(J == стм + отС
Лщ —-----7
Ц —- — pWxWr
дг
(6.26)
Первое слагаемое ом = ц (dwx/dr) в (6.26)—это вязкое напряже-
ние, обусловленное действием молекулярной вязкости; второе
ст.гС = —pWxWr — турбулентное напряжение, связанное с перено-
сом количества движения пульсациями скорости.
Как уже указывалось выше, для замыкания системы уравнений
Необходимо ввести дополнительные гипотезы относительно турбу-
лентного переноса количества движения и тепла. Чаще всего такие
гипотезы позволяют выразить слагаемые, описывающие турбулент-
ный обмен, через осредненные параметры потока.
Для описания турбулентного напряжения обычно вводится по-
нятие кинематического коэффициента турбулентного переноса ко-
л нчества движения (кинематического коэффициента турбулентной
1л яз кости):
ay л- аУг
(6.27)
дг
или динамического коэффициента турбулентного переноса количества
движения (турбулентной вязкости) Л(У =- peff. С помощью коэффици-
ента еа турбулентные напряжения можно выразить следующим об-
р азом:
—т—i dwx
атб = —pwxw* р^-^ •
(6,28)
Уравнение (6.28) базируется на допущении о градиентном характе-
ре турбулентного переноса (локальное турбулентное напряжение
пропорционально градиенту осреднениой скорости в рассматривае-
мой точке потока), и коэффициент р8а формально аналогичен коэф-
фициенту молекулярной вязкости. Однако эта аналогия чисто вне-
шняя, так как коэффициент турбулентного переноса не является
физическим свойством жидкости, а зависит от поля скоростей, и
следовательно, от координаты точки и числа Рейнольдса. В частно-
сти, так как турбулентные напряжения приблизительно пропорцио-
нальны квадрату производной от осреднениой скорости, то коэф-
фициент турбулентного переноса примерно пропорционален пер-
вой степени градиента скорости.
Введение коэффициента турбулентного переноса никоим обра-
зом не решает проблемы замыкания системы уравнений. Если ранее
неопределенной пока величиной, требующей для своего описания
дополнительных гипотез, было турбулентное напряжение сгтб, то
147
теперь такой величиной стал коэффициент турбулентного переноса
еа. Введение коэффициента турбулентного переноса оправдано тем,
что эта величина более консервативна (не так сильно зависит от ос-
редненных параметров потока), чем турбулентное напряжение, и по-
зволяет в более простой форме записать выражение (6.26) для пол-
ного касательного напряжения:
+ (6.29)
дг
Аналогичным образом величина %(д/7дг)—pc w'rt' в уравнении
энергии (6.25) представляет собой полную плотность теплового по-
тока q в направлении радиуса, взятую с обратным знаком. Таким
образом,
7 7м ~Т 7 т о
й7 ——.
л------рсоуг t
дг
(6.30)
Первое слагаемое в этом выражении qM = —Kdt/dr описывает перенос
тепла за счет молекулярной теплопроводности; второе слагаемое
7тб --pcw'rt' —турбулентный или молярный перенос тепла. По ана-
логии с коэффициентом турбулентного переноса количества движе-
ния обычно вводят кинематический коэффициент турбулентного пе-
реноса тепла — коэффициент турбулентной температуропроводно-
сти:
di
дг
или же динамический коэффициент турбулентного переноса те-
пла — коэффициент турбулентной теплопроводности — А(1 ~ рс’е(/.
С помощью коэффициента &q турбулентную плотность теплового по-
тока можно записать следующим образом:
qTG^pcWrt' ~—рсе(/“ > (6.32)
а выражение для полной плотности теплового потока (6.30) предста-
вить так:
7 = — (^ + реву) ~~ •
1 дг
(6.33)
Формула (6.33) позволяет легко найти соотношение между плотно-
стями теплового потока, обусловленными турбулентным и моле-
кулярным переносом тепла:
pcEg Sq _ pr 8(Т
<7м % е.а v у
(6.34)
148
Последний сомножитель в выражении (6.34), как это следует из
(6.29), равен отношению турбулентного касательного напряжения
агС к напряжению за счет молекулярной вязкости ом:
_ г;,г: _2 (Т t (6.35)
Им Р V
Таким образом, соотношение (6.34) можно переписать в следующем
виде:
— . (6.36)
7 м 8(т О’м
Отношение входящее в уравнения (6.34) и (6.36), называется
турбулентным числом Прандтля:
Ргтб = -^. (6.37)
8 7
Следует помнить, что Ргтб, в отличие от молекулярного числа Прапд-
тля, не является физическим свойством среды. Число Ргт(5 изменяет-
ся по сечению потока, а также зависит от числа Рейнольдса и моле-
кулярного числа Прандтля. Исследованию турбулентного числа
Прандтля посвящено большое число экспериментальных работ, со-
гласно которым Ргтб не очень сильно отличается от единицы, По-
этому при теоретических расчетах в качестве первого приближения
можно пользоваться гипотезой Рейнольдса, согласно которой ко-
эффициенты турбулентного переноса тепла и количества движения
одинаковы.
Из соотношения (6.36) следует одно весьма важное обстоятель-
ство: при заданном отношении o',f0/crM отношение q,xG/qM тем больше,
чем больше число Прандтля. Так как о,гб/сум зависит от координаты
точки и числа Рейнольдса и нс зависит от рода жидкости, то это
означает, что роль турбулентного переноса тепла особенно сущест-
венна в жидкостях с большим числом Прандтля. Например, при
о'тб/о'м 1 и значениях Рг -- 0,01; 1 и 100 отношение qTn/qM со-
ответственно равно 0,01, 1 и 100. Как мы увидим в дальнейшем, с уве-
личением числа Прандтля профиль температуры в ядре потока стано-
вится все более равномерным и большая часть температурного пере-
пада между стенкой и жидкостью происходит в пристеночных слоях
жидкости. Поэтому при больших числах Прандтля для правильного
расчета теплообмена очень важно точное описание законов тур-
булентного переноса вблизи стенки, хотя в этой области отношение
сгтС/сгП1 и невелико.
Возвращаясь к системе уравнений, описывающих турбулентное
течение несжимаемой жидкости в круглой трубе (6.22) (6.25),
учтем, что в дальнейшем в основном будут рассматриваться
квазистациоиарные стабилизованные турбулентные течения. Это
позволяет опустить в уравнениях производные по времени, а так-
149
же предположить, что изменение аксиальной компоненты скорости
вдоль оси х невелико, т. е. dwJdx^-О (для жидкости с постоянными
физическими свойствами в случае стабилизованного течения
dwJdx^O), В этом случае из уравнения неразрывности (6.22) следует,
что wr ~ 0, а из уравнения (6.24) — что dpldr = 0, т. е. давление
в любом поперечном сечении канала постоянно и зависит только
от х. Таким образом, квазистационарное стабилизованное течение
О 0,10,10,30,00,50,80,70,8 &
П О
Рис. 6.2. Относительная интенсивность компонент турбулентных пуль-
( wod \
сацип скорости при течении воздуха в трубе (Re=—— ==5-105).
несжимаемой жидкости в круглой трубе описывается двумя уравне-
ниями, которые с учетом выражений (6.29) и (6.33) можно пред-
ставить в следующем виде:
(6.38)
г дг
Г(п+87)
1 д
Турбулентный перенос количества движения и тепла определяет-
ся в первую очередь величиной турбулентных пульсаций скорости.
Некоторое представление о величине пульсаций скорости дает
рис. 6.2, иа котором приведены экспериментальные данные Лауфера,
полученные при течении воздуха в круглой трубе. По оси ординат
на этом рисунке отложены относительные интенсивности компонент
пульсаций скорости, т. е. отношения среднеквадратических значе-
ний пульсаций скорости У(ш/)2, к скорости на оси трубы w*—
пульсации скорости вдоль оси трубы; — пульсации в азиму-
тальном направлении; w’r — пульсации вдоль радиуса.
Из рис. 6.2, а видно, что в центре трубы турбулентность изотроп-
на, т. е. пульсации скорости одинаковы по всем направлениям,
150
а их интенсивность составляет примерно 3% скорости потока па
осп трубы. У стенки турбулентность становится существенно ани-
зотропной, интенсивность всех компонент пульсаций скорости уве-
личивается, особенно сильно увеличивается интенсивность продоль-
ных пульсаций скорости, которая возрастает до 8%. Это обстоятель-
ство связано с тем, что подвод энергии от осредиенного движения
к пульсационному осуществляется главным образом вблизи стенки,
где велики градиенты осреднешюй скорости. В непосредственной
близости от стенки пульсации ско-
рости уменьшаются, а на самой стен-
ке обращаются в пуль (см. рис. 6.2, б).
Однако данные по интенсивности
турбулентных пульсаций скорости не
и оз вол яют оп р еде л ить ту р б у л ei ггн ы й
перенос количества движения. Для
этого необходимо экспериментально
измерить величину w'v w'r, называе-
мую корреляцией между продольной
и поперечной компонентами пульса-
ций скорости. Результаты таких из-
мерений по данным Лауфера приве-
дены на рис. 6.3. На этом рисунке
показано распределение по радиусу
трубы турбулентного касательного
напряжения рау.Ж, отнесенного к ка-
сательному напряжению на стейке ас.
Распределение турбулентных ка-
сательных напряжений в круглой или
плоской трубе можно определить и
другим путем. Полное касательное
напряжение, как это показано ниже,
изменяется в такой трубе по линей-
Рис. 6.3. Распределение турбу-
лентных касательных напряже-
ний при течении в круглой тру-
( Wit d \
бе (,Re== —— 5-!()’ ) по всему
сечению трубы (п) п вблизи
стопки (б).
пому закону от ас на стенке до нуля на оси трубы. Распределение
вязких напряжений можно рассчитать по измеренному профилю ско-
рости. Разность между этими двумя величинами дает турбулент-
ное касательное напряжение. Из рис. 6.3 видно, что вязкие напря-
жения играют важную роль только в области, непосредственно
примыкающей к стенке, а в области, удаленной от стенки, т. е.
в ядре потока, полное напряжение практически равно турбулент-
ному касательному напряжению.
Экспериментально турбулентная плотность теплового потока
определяется аналогичными способами — путем непосредственного
измерения корреляции w'rt'.
В круглой или плоской трубе распределение полной плотности
теплового потока можно рассчитать по распределению скорости,
а распределение плотности теплового потока за счет молекулярной
теплопроводности можно найти по распределению температуры. Раз-
151
ность этих величин даст плотность теплового потока, обусловленную
турбулентным переносом.
Обычно коэффициент турбулентного переноса тепла выражают
через коэффициент турбулентного переноса количества движения.
Используя выражения (6.33), (6.34) и (6.37), плотность теплового
потока записывают в виде:
Как уже говорилось выше, имеющиеся в настоящее время экспе-
риментальные данные о турбулентном числе Прандтля Ргтб(г/г0,
Re, Рг) и характере его изменения очень противоречивы. Одна-
ко все без исключения исследователи сходятся в том, что его значе-
ние не сильно отличается от единицы. Поэтому при теоретических
расчетах большинство авторов полагают Ргтб = 1. Так как для про-
стых случаев турбулентного течения величина sa/v сравнительно
хорошо изучена и может быть рассчитана с помощью полуэмпириче-
ских теорий, то такое допущение позволяет замкнуть систему урав-
нений. Теоретические расчеты коэффициентов теплоотдачи, выпол-
ненные с использованием этого допущения, во многих случаях удов-
летворительно согласуются с экспериментальными результатами.
§ 6.4. Теория пути перемешивания
Рассмотрим теперь некоторые полуэмпирические теории турбу-
лентности. Одна из первых теорий—-теория пути перемешивания —
была предложена Прандтлем. Несмотря на свою простоту и прибли-
женный характер, эта теория позво-
ляет во многих случаях получить
результаты, хорошо согласующиеся
с экспериментом.
Рис. 6.4. Схема, иллюстриру-
ющая модель пути перемеши-
вания.
Удобнее всего теорию пути пере-
мешивания рассмотреть на примере
плоскопараллельного квазистацио-
нар него потока, когда осреднен-
ная скорость направлена вдоль оси х
и меняется только в направлении
оси у:
wx = wx-\-w'x\ Wy = w'y и wz^--w',
так как ~wz — Q.
Выделим в этом потоке два слоя
жидкости на расстоянии Г друг
от друга (рис. 6.4). В первом слое скорость жидкости равна
wx (у), во втором слое — wx (у-\-Г). Рассмотрим некоторую частицу
жидкости (турбулентный моль), которая движется вместе с потоком
в первом слое и имеет осредненую скорость wx («/). В какой-то мо-
152
мент времени под действием поперечной пульсации скорости
эта частица переносится на расстояние Г и попадает во второй слой.
(Очевидно, что Г — случайная величина). Предполагается, что па
пути движения из первого слоя во второй масса частицы и ее ско-
рость, а следовательно, и количество движения не изменяются.
Перемещение частицы из одного слоя в другой связано с переносом
некоторого избытка (пли недостатка) количества движения, поэто-
му в результате такого перемещения во втором слое возникает
пульсация скорости:
= wx (у Ч- /') — wx (у). (6.41)
Если функцию (// + /') разложить в ряд Тейлора в окрестно-
сти точки у и, полагая, что значение Г невелико, отбросить все сла-
гаемые, содержащие вторую и более высокие степени то получим
. (6.42)
с///
Подставляя (6.42) в (6.28), находим, что турбулентное напряжение
отб ;v: —: ' —(»/' wi/ • (6.43)
dy
В модели Прандтля легко усмотреть аналогию между процессом тур-
булентного (молярного) переноса и молекулярного переноса. Не
случайно поэтому, что выражение (6.43) аналогично ньютоновскому
выражению для вязкого напряжения. Более того, из кинетической
теории газов следует, что кинематический коэффициент вязкости
равен произведению среднеквадратичной скорости молекул и сред-
ней длины свободного пробега. Из выражения (6.43) следует, что
коэффициент турбулентного переноса количества движения (коэф-
фициент турбулентной вязкости)
I'w'y, (6.44)
т. е. равен осреднеш-юму значению произведения пути перемеши-
вания и пульсационной скорости моля.
Полагая, что поперечные пульсации скорости пропорциональны
продольным:
находим
// dwx
£ ——
dy
°тб — Р^ а
dwx dwx
dy dy
(6.45)
(6.46)
Wy ~
Здесь коэффициент пропорциональности /ст примерно равен сред-
нему пути, на котором моли сохраняют свою индивидуальность
(/<7 « (О2), и называется длиной пути перемешивания в процессе
153
переноса количества движения. Величина 1а характеризует локаль-
ные свойства турбулентного потока и может рассматриваться как
локальный масштаб турбулентности. Выражение (6.46) называется
формулой Прандтля для турбулентного напряжения. Из нее нетруд-
но получить коэффициент турбулентного переноса количества дви-
жения:
„ °тб /2
£0 — — —
dwx
(6.47)
Однако пока неизвестна длина пути перемешивания, выражения
(6.46) и (6.47) не могут быть использованы для практических
расчетов. Прандтль предположил, что длина пути перемешивания
возрастает линейно по мере удаления от стенки:
1а = иу. • (6.48)
Экспериментальное определение длины пути перемешивания при
течении жидкости в трубе было выполнено Никурадзе. Он измерял
касательное напряжение на стенке и профиль скорости, что позволя-
ло определить производную dwxldy и турбулентное напряжение отб,
а затем вычислить /0. Резуль-
таты его измерений, по казанные
на рис. 6.5, описываются урав-
нением:
Рис. 6.5. Изменение длины пути пере-
мешивания 1й по радиусу трубы
(Re= 1,1 • 105Ч-3,2-106);
/ — опытные данные; 2 — /ff = 0,4 у.
— = 0,14 — 0,08 f 1—у-\2 —
го \ /'о /
— 0,06 (1—Ц4. (6.49)
\ Го J
На малых расстояниях от
стенки, где ylr0 < 1, в формуле
(6.49) можно отбросить все слага-
емые более высокого порядка по
сравнению с у/г0. В результате
получаем
/о = 0,4 у.
Следовательно, вблизи стенки предположение Прандтля подтвержда-
ется экспериментом. Величина х в уравнении (6.48), по данным из-
мерений Никурадзе равная 0,4, называется константой турбулент-
ности. Таким образом, для коэффициента турбулентного переноса
количества движения можно записать следующее выражение:
8СТ -- И^у2
dwx
dy
(6.50)
причем х — 0,4.
154
С несколько иных позиций к проблеме пути перемешивания по-
дошел Карман. Согласно теории Кармана длина пути перемешива-
ния, а следовательно, и 80- в некоторой точке потока определяются
местными условиями течения и могут быть выражены через местные
осреднспные параметры потока. Такими параметрами являются раз-
личные производные от осреднениой скорости. В частности, можно
предположить, что длина пути перемешивания пропорциональна
некоторому характерному масштабу длины;
= kL,
(6.51)
а этот характерный масштаб длины определить как отношение двух
последовательных производных от осреднениой скорости:
r/te’.v
dy
(6.52)
с///'2
Если допустить, как это сделал Карман, что поле скорости обла-
дает геометрическим подобием и величина /г постоянна для всего
поля течения, то для коэффициента турбулентного переноса количе-
ства! движения получим следующее выражение:
clwx
dwx
2 dy
(6.53)
\ dy* /
Расчеты 8CT по формулам Прандтля и Кармана дают близкие
результаты.
Заметим попутно, что Тейлор гораздо раньше Прандтля раз-
работал теорию, подобную теории пути перемешивания, но при
этом в качестве «транспортабельной субстанции» рассматривал
не количество движения, а завихренность ф = rot w.
За первыми работами Тейлора, Прандтля и Кармана, в которых
было сформулировано понятие пути перемешивания, появилось боль-
шее число исследований, посвященных дальнейшему развитию этой
идеи. Отсылая поэтому вопросу читателя к специальной литературе,
назовем лишь работы Ван-Дрийста [101, IT. И. Булеева [1.1,
М. Д. Миллионщикова [3].
Полуэмпирические теории в сочетании с некоторыми физическими
соображениями позволяют выразить турбулентные напряжения
через осредпеиные параметры потока, или, как говорят, замкнуть
уравнения Рейнольдса на уровне первых моментов (первыми момен-
тами называют значения осредненных скоростей).
В последние годы получило развитие другое направление полу-
эмпирич еской теории турбулентности. Наряду с уравнениями
Рейнольдса рассматриваются также уравнения для вторых момен-
тов, т. е. уравнения, описывающие изменение рейнольдсовых на-
пряжений w'i w'j. Уравнения для вторых моментов также явля-
ются незамкнутыми, и для их замыкания необходимы некоторые
гипотезы. Подробно эти вопросы рассматриваются в специальной
литературе [4, 5].
§ 6.5. Универсальный профиль скорости
Используем полученные с помощью теории пути перемешивания
соотношения для расчета распределения скорости при течении жид-
кости в круглой трубе.
Обычно при выводе полуэмпирических зависимостей для профи-
ля скорости при течении жидкости в трубах и каналах принимают
следующую схему потока (рис. 6.6). Весь поток разбивают на две
области — пристеночную область и ядро потока. В пристеночной
области, в свою очередь, условно можно выделить прилегающий
к стенке вязкий подслой, в котором доминирующую роль играют вяз-
кие напряжения, и турбулентную зону, в которой, наоборот, основ-
ную роль играют турбулентные напряжения, а вязкими напряже-
ниями можно пренебречь. Область потока, включающую ядро пото-
ка и турбулентную зону, обычно называют турбулентным ядром.
Целесообразность введения такой схемы подтверждается многочис-
Ядро
потока
> Турбулентное
ядро
{Пристеночная ^УР^ентная J
[область \вязкий подслой
Рис. 6.6. Схема потока при турбулентном течении
в трубе.
ленными экспериментальными исследованиями. Так как течение
в пристеночно?1 области почти не зависит от условий течения вдали
от стенки, то, как показывает эксперимент, закономерности течения
в пристеночной области оказываются одинаковыми для труб разной
формы (круглая, плоская и некоторые другие) и даже для простей-
ших случаев внешнего обтекания тел (продольно обтекаемая пла-
стина).
Чтобы рассчитать профиль скорости в потоке, необходимо знать
распределение полного касательного напряжения по сечению трубы.
Это распределение можно найти из уравнения движения (6.23), ко-
156
торое в случае квазистационар кого стабилизованного течения жид-
кости с постоянными физическими свойствами в круглой трубе
упрощается и принимает вид:
4" 77= ’ (6.54)
I dwx —-—т \
где о = сгм отС •= I р, ----pwxwr/) — полное касательное на-
пряжение в произвольной точке потока. (Здесь и далее мы опускаем
знаки осреднения над осреднеиными по времени величинами).
Интегрируя выражение (6.54) с учетом того, что на оси трубы ка-
сательное напряжение равно нулю, и обозначая касательное напря-
жение на стейке ое, получаем
су -- сг0 ~ сгс f 1-, (6.55)
Го \ Го !
т. е. касательное напряжение в круглой трубе (так же как и в пло-
ской) распределено по линейному закону, уменьшаясь от максималь-
ного значения ст(. на стенке до нуля па оси трубы.
Теперь применим теорию пути перемешивания Прандтля к рас-
смотренной выше схеме турбулентного потока. Так как теория
пути перемешивания оказывается справедливой только в отно-
сительно узкой пристеночной области потока, будем для про-
стоты считать в этой области суммарное касательное напряжение
постоянным (т. е. не зависящим от радиуса) и равным касательному
напряжению на стейке.
В вязком подслое по определению доминирующую роль играют
силы молекулярной вязкости, поэтому, пренебрегая здесь рейнольд-
совыми напряжениями, получаем
(6.56)
dy
В турбулентной зоне пристеночной области, наоборот, силами
молекулярной вязкости можно пренебречь по сравнению с турбу-
лентными напряжениями, и, следовательно,
сге crTG.-. — (6.57)
Или, используя формулу Прандтля (6.46) и выражение (6.48),
получаем:
ac-pxV (6.58)
\ dy I
Распределение скорости в вязком подслое находится простым ин-
тегрированием выражения (6.56):
— (6.59)
Р р v
157
Величина г сгс/р имеет размерность скорости, обозначается сим-
волом v* и называется динамической скоростью. Динамическую ско-
рость нетрудно связать с коэффициентом сопротивления трения.
Из рассмотрения баланса сил, действующих в круглой трубе па
элемент жидкости длиной Дх,
2лг0Дхос = зтгоДр
следует, что
„ &Р го
оР = ——. —
с Дх 2
(6.60)
С другой стороны, по определению, коэффициент сопротивления
трения равен
рш2 Р W2
где w — средняя по сечению трубы скорость жидкости. Откуда по-
лучаем
Коэффициент сопротивления трения для гладких круглых труб при
стабилизованном течении однозначно определяется числом Рей-
нольдса Re — wd/v и может быть рассчитан, например, по фор-
муле Г. К- Филоненко:
£ =-----------!-------- . (6.62)
(1,82 lg Re-1,64)а
Используя понятие динамической скорости, можно распределение
скорости в вязком подслое (6.59) записать в безразмерном виде:
(6.63)
Вводя так называемые универсальные координаты: безразмерную
скорость ср = wx!v* и безразмерное расстояние от стенки ц == o.(.z//v,
находим, что в вязком подслое независимо от числа Re безразмерная
скорость равна безразмерной координате:
ср = т]. (6.64)
Чтобы получить распределение скорости в турбулентной зоне,
выразим из соотношения (6.58) производную скорости
__ .. °C 1 _ U:j: 1
——— I/ . — . рЭ.ОО/
ау Р ИУ К У
и, проинтегрировав, получим:
= -L\ny + C. (6.66)
t>.|. X
158
Вводя в это выражение вместо у безразмерную координату т], имеем
окончательно выражение для распределения скорости в турбулент-
ной зоне:
Ф — _1_ ]п -|_ Л. (6.67)
х
Очевидно, что постоянные % и А в этом выражении должны опре-
деляться по экспериментальным данным. Эти постоянные впервые
были найдены на основе опытов Никурадзе, который измерил про-
фили скорости в круглой трубе в диапазоне чисел Re от 4 • 10:{ до
3,2 • 10°. Оказалось, что х = 0,4
пределение скорости в турбулент-
ной зоне описывается следующей
логарифмической зависимостью:
Ф — 2,51п 7] -|- 5,5. (6.68)
Если нужно проследить харак-
тер изменения скорости вблизи
стенки, что важно, например, при
расчете теплоотдачи, распределе-
ние скорости обычно строят в по-
лулогарифмических координатах,
которые позволяют существенно
растянуть пристеночную область
потока. В таких координатах на
рис. 6.7 представлены зависимо-
сти (6.64) и (6.68).
Точка, соответствующая пересечению кривых, определяет тол-
щину вязкого подслоя: т]1( = 11,7. Используя очевидное соотноше-
ние
)Ь1 :Ц,7, (6.(.9>
v
нетрудно определить размерную толщину ламинарного подслоя ylf,
соответствующую данному значению числа Рейнольдса. Например,
при Re = 105 коэффициент сопротивления трения равен £ == 0,0179,
vjw = 0,047 и, следовательно,
и А = 5,5. Следовательно, рас-
Рис. 6.7. Универсальный профиль
скорости.
Построенный на рис. 6.7 профиль скорости обычно называется
универсальным. Его универсальность обусловлена прежде всего
тем обстоятельством, что в координатах ср = ср (т]) профиль скоро-
сти перестает зависеть от числа Рейнольдса. Кроме того, как уже
указывалось выше, зависимости (6.64) и (6.68) справедливы для
пристеночной области не только при течении в круглых трубах,
но и в плоских, а также для пристеночной области при внешнем об-
текании пластины.
159
Сравнение универсального профиля скорости, т. е. уравнений
(6.64) и (6.68), с опытными данными показано на рис. 6.8 [следует
помнить, что постоянные % и А в уравнении (6.68) определены по
опытным данным].
Из рис. 6.8 видно, что теоретический профиль существенно от-
клоняется от действительного на границе между вязким подслоем и
турбулентной зоной. И это неудивительно. Теоретический профиль
Рис. 6.8. Сравнение универсального профиля скорости с опытными дан-
ными. Пунктиром показано распределение скорости в буферном слое
по Карману [см. уравнение (6.71)].
получен на основе очень упрощенной схематизации потока. Напри-
мер, было принято, что турбулентный перенос в вязком подслое
отсутствует. В результате этого получился резкий излом профиля
(разрыв производной) на границе между вязким подслоем и турбу-
лентной зоной. На самом же деле резкой границы между вязким
подслоем и турбулентной зоной не существует, поскольку турбулент-
ные напряжения постепенно возрастают по мере удаления от стенки.
Экспериментальные данные хорошо согласуются с логарифми-
ческим профилем скорости при ц > 30. Однако при достаточно высо-
ких значениях ц наблюдается отклонение от этой зависимости.
Особенно наглядно это видно на графике безразмерной избыточной :
скорости (избыточной скоростью называют разность между скоростью
на оси потока w0 и скоростью в рассматриваемой точке потока шх),
160 ‘
показанном на рис. 6.9. Пунктир-
ная прямая на этом графике со-
ответствует выражению
Wo~Wx- —2,5 In -У- +0,8. (6 70)
Щ /'о
Из этого рисунка хорошо видно,
что отклонение действительного
распределения скорости от лога-
рифмического закона становится
заметным при z///-0>0,15. Таким
образом, можно считать, что гра-
Рис. 6.9. Распределение избыточ-
ной скорости при течении в трубе.
ница между пристеночным слоем и ядром потока лежит в районе
у!г. 0,15.
Из рис. 6.9 также следует, что отклонение профиля скорости
в ядре потока от зависимости (6.68) невелико. Поэтому очень часто
логарифмический закон (6.68) используется для описания профиля
скорости как в турбулентной зоне, так и в ядре потока, т. е. во всем
турбулентном ядре.
§ 6.6. Полуэмпирические уравнения для профиля скорости
и коэффициента турбулентного переноса
количества движения
Как уже указывалось выше, при расчетах теплоотдачи особенно
важно правильно описать изменение скорости и коэффициент турбу-
лентного переноса количества движения вблизи стенки. Между тем
двухслойная схема потока, введенная Прандтлем, не позволяет это-
го сделать. Карман [8] предпринял попытку улучшить схему
Прандтля, введя понятие промежуточного, или буферного, слоя
между вязким подслоем и турбулентной зоной. Оставив для вязкого
подслоя и турбулентной зоны прежние выражения для профиля ско-
рости [уравнения (6.64) и (6.68)1, он в интервале значений 7] от
5 до 30 провел сглаживающую прямую (см. рис. 6.8) и подобрал
для нее уравнение. В соответствии с трехслойной моделью Кармана
схема деления потока и распределение скорости в соответствующих
областях таковы:
вязкий подслой О^М] <15, ср -= т|;
промежуточный подслой 5 г] 30, ср == 5 f 1 + In — )
\ 5
турбулентное ядро т]>>30, ср = 2,5 In т] + 5,5.
(6.71)
Расчеты теплообмена с применением соотношений (6.71) приво-
дят к несколько лучшим результатам, чем при использовании двух-
слойной схемы, однако при больших числах Прандтля (Рг > 20)
и трехслойная схема потока становится неудовлетворительной.
6 Зак. 792 161
В последние годы проведено много экспериментальных работ по
исследованию полей скорости в турбулентных потоках жидкостей
и газов. На основании этих исследований предложен ряд эмпири-
ческих и полуэмпирических формул для профиля скорости и коэф-
фициентов турбулентного переноса количества движения.
Наиболее часто используются формулы Рейхардта и Дайслера-
Формула Рейхардта [9] для профиля скорости в круглой трубе
имеет вид
ср = 2,5 In (1-4-О,4т])
1,5(14-/?)'
1+27?2
4-7,8 1— ехр f уГехР(“0,33т]) ,
(6.72)’
где R = г/г0 — безразмерный радиус, а т] = v*y!v— безразмер-
ная универсальная координата. Эта формула описывает единой за-
висимостью весь профиль скорости от стенки до оси потока. Для.
коэффициента турбулентного переноса количества движения Рей-
хардт предложил следующие зависимости:
при т]<50 — = 0,4 fт]—-11 th —) ; (6.73)
v \ 11 /
при п>50 — = 0,133ц (0,5 H-R2)( 14-^)- (6.74)
V
Дайслер [7] разбивает поток на две области и для каждой из-
них рекомендует следующие выражения:
при ц <z 26
=--------:----!-----------; (6.75).
dr) 14 п2срт) [ 1 —ехр (—п2срц)]
-X = 4\pT| [1— ехр(—-/г3срт))], (6.76)-
где п — 0,124;
при г] > 26
Ф = ——— 1п —4 12,85; (6.77).
0,36 26 V
— = 0,36 fl—ri—l. (6.78)
Т \ Г)о /
Рассчитанное по формулам (6.75) — (6.77) распределение скоро-
сти приведено в табл. 6.1.
На рис. 6.10 сопоставлены коэффициенты турбулентного пере-
носа количества движения, рассчитанные по формулам Прандтля,
Рейхардта и Дайслера при Re = 105. На рис. 6.11 расчетные форму-
лы сопоставляются в наиболее важной пристеночной области. Из.
162
Табл и ц а 6.1
Универсальный профиль скорости по Дайслеру
Т) Ф Т) Ф Ч Ф
0,0000 0,0 5,5257 5,0 15,0847 10,0
0,5005 0,5 6,2088 5,5 16,0000 10,318
1,0040 1.0 6,9333 6,0 18,206 10,964
1,5134 1,5 7,7051 6,5 28,045 12,702
2,0320 2,0 8,5306 7,0 48,760 14,536
2,5628 2,5 9,4171 7,5 91,189 16,417
3,1093 3,0 10,3726 8,0 177,03 18,320
3,6749 3,5 11,4062 8,5 349,67 20,234
4,2634 4,0 12,5281 9,0 695,93 22,154
4,8789 4,5 13,7499 9,5 1389,4 24,076
этих рисунков следует, что в большей части потока турбулентный
перенос намного больше молекулярного переноса (вязкости). Кри-
вые, соответствующие двухслойной схеме Прандтля и трехслой-
Рис. 6.10. Распределение коэффициента тур-
булентного переноса количества движения по
радиусу трубы:
/ — по Рейхардту [см. формулы (6.73), (6.74)]; 2 — по
Дайслеру [уравнения (6.75), (6.76)]; 3 — по Прандтлю
и Карману.
ной схеме Кармана, свидетельствуют о том, что эти схемы дают гру-
бую аппроксимацию действительных зависимостей. Формулы Рей-
хардта и Дайслера в большей части потока дают достаточно близкие
результаты. Однако в непосредственной близости от стенки между
•6* 163
формулами Рейхардта и Дайел ер а наблюдается принципиальное
различие: по формуле (6.73) при ц 0 величина sG/v пропорциональ-
на т]3, а по формуле (6.76) — ц4.
Итак, несмотря на то что природа турбулентности изучена еще
недостаточно, существующие полуэмпирические теории позволяют
с достаточной для практики точностью рассчитывать профили ско-
Рис. 6.11. Распределение коэффициента турбулент-
ного переноса количества движения в пристеночной
области:
1 — по двухслойной модели Прандтля; 2 — по трехслойпой
модели Кармана; 3 — по Дайслеру [формула (6.75)]; 4— по
Рейхардту [формула (6.73)].
рости и температуры, а следовательно, и коэффициенты сопротивле-
ния и теплоотдачи при течении жидкости с постоянными физиче-
скими свойствами в каналах простой геометрической формы (круг-
лые, плоские, кольцевые трубы).
СПИСОК ЛИТЕРАТУРЫ
1. Булеев Н. И. Теоретическая модель механизма турбулентного обмена
в потоках жидкости. — В сб.: Теплопередача. М., Изд-во АН СССР,
1962, с. 64.
2. Лойцянский Л. Г. Механика жидкости и газа. М., «Наука», 1970.
3. Миллионщиков М. Д. Турбулентные течения в пограничном слое и
в трубах. М., «Наука», 1969.
4. Монин А. С., Яглом А. М. Статистическая гидромеханика. Ч. 1. М.,
«Наука», 1967.
5. Хинце И. О. Турбулентность. М., Физматгиз, 1963.
6. Шлихтинг Г. Теория пограничного слоя. М., «Наука», 1969.
7. Deissler R. G. Analytical and experimental investigation of adiabatic tur-
bulent flow in smooth tubes. NACA Tech. Note, 2138, 1950.
8. Karman Th. «Trans. Amer. Soc. Meeh. Engng»., 1939, v. 61.
9. Reichardt H. Zeitschr. f. angew. Math. u. Meeh., 1951, No. 7, S. 132.
10. Van-Driest E. «J. Aeron. Sci.,» 1956, v. 23, p. 11.
164
ГЛАВА 7
ТЕПЛООБМЕН В КРУГЛЫХ ТРУБАХ ПРИ ТУРБУЛЕНТНОМ ТЕЧЕНИИ
ЖИДКОСТИ С ПОСТОЯННЫМИ ФИЗИЧЕСКИМИ СВОЙСТВАМИ
§ 7.1. Стабилизованный теплообмен при постоянной
плотности теплового потока на стенке. Методы
теоретического расчета
Вопросы теплообмена и сопротивления при турбулентном дви-
жении жидкости в трубах очень важны для техники ядерных реак-
торов и ядерных энергетических установок в целом, поэтому они из-
ложены более подробно в этой и двух последующих главах.
Рассмотрим один из основных вопросов теории теплообмена при
турбулентном течении жидкости — стабилизованный теплообмен
в круглых гладких трубах при постоянной плотности теплового пото-
ка иа стенке. Примем предварительно следующие условия:
1) течение и теплообмен квазистационарны, т. е. осредненные
характеристики течения не изменяются во времени (в частности
dttdx= 0);
2) жидкость несжимаема, а ее физические свойства постоянны;
3) течение гидродинамически стабилизовано, т. е. wx = wx (г),
dwjdx — 0, и в соответствии с уравнением неразрывности wr = 0;
4) изменение плотности теплового потока вдоль оси, обусловлен-
ное теплопроводностью и турбулентным переносом, мало по срав-
нению с его изменением по радиусу, т. е.
5 /„ dt —г-7 \ у, 1 д Г /« dt 7,'ТУ \ 1
" । л----PC-п / j ~~ — г I л--------РСт, wj г t 11 ;
dx \ dx f 1 Г г Зг Ц dr р ) ] ’
5) в потоке отсутствуют внутренние источники тепла (е/у == 0),
а выделение тепла, вызванное диссипацией кинетической энергии,
пренебрежимо мало (это условие выполняется при скорости дви-
жения жидкости, много меньшей скорости звука);
6) рассматривается область течения, удаленная от начального
сечения обогреваемого участка, где поле температуры не зависит от
заданного распределения температуры в начальном сечении;
7) на внутренней поверхности стенки трубы поддерживается по-
стоянная по поверхности плотность теплового потока (qc = const).
Учитывая условия 1) — 5), уравнение энергии для сформулиро-
ванной задачи записывается так:
рср — = — -т- И), (7.1)
dx г дг
где
q^pcp(a-}-z)~- . (7.2)
дг
165
В данном случае изменение среднемассовой температуры жидко-
сти по длине трубы легко определяется из теплового баланса:
pep wrQ
dt _ 2qc
dx pcp wro
Решение уравнения (7.1) будем искать в виде
t (х, г) = Ч (х) + h (/')•
(7.3)
(7-4)
(7.5)
Подставляя (7.5) в уравнение (7.1), получаем
54 __ 1 (_1_ 5
дх wx 1 г дг
/'(«+%) —
1 dr J J
Так как левая часть этого уравнения зависит только от х, а пра-
вая— только от г, то очевидно, что они равны постоянному числу,
т. е.
54 dt >
—i = — = const.
дх дх
Очевидно также, что значение этой постоянной в соответствии с (7.4)
равно 2qc/^cpwr0). Следовательно, из выражения (7.5) находим
dt
дх
dtc _ di 2q0
dx dx pCp wrg
(7-6)
Таким образом, при стабилизованном теплообмене в случае qc =
— const температура в любой точке потока, в том числе и на стенке,
изменяется линейно по длине трубы. С такой же закономерностью
в случае ламинарного течения мы уже встречались ранее (см. § 5.2).
После подстановки значения дНдх из (7.6) в уравнение (7.1) по-
следнее становится обыкновенным дифференциальным уравнением:
2 R____ & (R
w dR \ qc J
(7-7)
Интегрируя это уравнение по R в пределах от 0 до 7? и учитывая
симметрию температурного поля, из которой следует, что q = О
при 7? == О, находим распределение плотности теплового потока
по радиусу:
R
= t^RdR.
Qc R J ®
o
(7.8)
166
Решая совместно уравнения (7.2) и (7.8), имеем:
С wx.
^—RdR
— = 12- ° W______ (7 9)
dR К / е„\ ’ к '
| 1 +-| R
\ а /
Проинтегрировав (7.9) в пределах от R до 1, получим уравнение
для распределения температуры:
р -Z7 R dR
Ц;----------— dR, (7.10)
ЛА/ Рг \
J I 1 + Ц )
R \ Ргтб V /
в котором eq/a заменено следующим соотношением:
Рг ±1
а Ргтб т ’
где Ргтб = еи/е^ — турбулентное число Прандтля.
Если определить коэффициент теплоотдачи как отношение =
== qj(tc— ^r==o), где/д==о—температура на оситрубы, то, положив
в (7.10) Я = 0, сразу получим выражение для соответствующего
числа Нуссельта:
1
%
сУ?.
Nlloo ССоо d \ / Рг ^'(Г \
J 1 + л R
о \ РгТб V /
(7.11)
Однако такое определение коэффициента теплоотдачи неудобно,
так как при инженерных расчетах температура на оси трубы /д=о
обычно неизвестна. Гораздо удобнее определять коэффициент тепло-
отдачи как отношение ато = q J(tc— t), где t — среднемассовая тем-
пература жидкости в данном сечении трубы. По определению
(см. § 5.1)
1
О w
(7.12)
Подставив в (7.12) выражение для (tc — t) из (7.10), получим
1
/с —(7.12а)
о
167
где
д
1 с
J0 ш
------------------
/ Рг sg\
Н у +Ргтб v J
Д
do = -^7 R dR и v = f ~
w J w
о
Интегрируя (7.12 а) по частям, имеем:
2?с d
К
1
о
v du
(7.126)
В этом выражении [ццЦ = 0, так как и (1) = 0 и и (0) = О.
Подставив в (7.12 б) значения v и du, получаем
Разделив это уравнение на qcd!X, получим выражение для числа
Нуссельта:
/д \ 2
1 / Г* Wr 1
р \ -ZT я dR
1 I \ n w /
—Ь_ = 2 I ----------------'—dR, (7.13)
Nu“
О \ РГтб V /
Уравнение (7.13) было получено Лайоном [33], и поэтому его ча-
сто называют интегралом Лайона.
Пользуясь уравнениями (7.8), (7.10) и (7.13), можно рассчитать
распределение плотности теплового потока, распределение темпе-
ратуры и теплоотдачу, если известны профиль скорости, коэффици-
ент турбулентного переноса количества движения и турбулентное
число Прандтля. Для этой цели можно воспользоваться данными о
wxlw, ea/v и Ргтб, приведенными в гл. 6.
Распределение скорости можно также вычислить по заданному
распределению e0/v.
168
Как было показано выше, при стабилизованном движении жид-
кости касательное напряжение о линейно изменяется по радиусу,
поэтому можно записать:
8 \ dwx г
— = о'с — •
v dr г0
(7.14)
Отсюда находим
dwx _о'с г0
н 1+—
\ v /
Интегрируя это выражение от R до 1, имеем
(7Л5)
Определив среднюю по
найдем выражение для
сечению скорость с помощью соотношения
1
w ^=2^wx R dR,
b
безразмерной скорости:
С RdR
J
7? 1 —
V
™х
w С / [' RdR \
2 —----- 1
J J
О \Я V /
(7.16)
Полученные выше уравнения для расчета теплообмена в рамках
принятых допущений являются точными. Заметим попутно, что они
справедливы не только при турбулентном, но и при ламинарном
течении. В последнем случае надо положить е<у = ед = 0. Тогда,
например, из уравнения (7.16) находим хорошо известное выраже-
ние wx/w = 2 (1—R2). Подставив это выражение в (7.13), получим
Nu^ = 4,36. Такое же значение Nu^ было получено_ранее другим
методом (см. § 5.2). В другом предельном случае wx!w ~ 1 (модель
стержневого течения, приближенно соответствующая Re оо) и
= ед — 0 имеем Nu^, = 8.
Наряду с приведенными выше точными уравнениями для расче-
та теплообмена нередко используются более простые приближенные
уравнения. Однако точность расчета с помощью точных или прибли-
169
женных уравнений определяется главным образом тем, насколько
правильно описываются закономерности турбулентного переноса во
всей области течения и в особенности вблизи стенки. Это находит
выражение в используемых для расчета теплообмена зависимостях
для 8а и или Ргтб. Развитие теоретических методов расчета тепло-
обмена и сводилось главным образом к совершенствованию упомя-
нутых зависимостей по мере накопления опытных данных.
Первая попытка теоретически рассмотреть вопрос о теплообме-
не при турбулентном движении жидкости принадлежит Рейнольдсу.
Тейлор и Прандтль усовершенствовали анализ Рейнольдса. Они
приближенно учли влияние на теплообмен особенностей движения
жидкости у стенки, рассматривая поток, состоящий из турбулент-
ного ядра и вязкого (ламинарного) подслоя. Чтобы уяснить особен-
ности теплообмена при турбулентном течении, полезно рассмотреть
расчет теплоотдачи на основе двухслойной модели потока. Введем
следующие предположения:
1) поток состоит из вязкого подслоя толщиной цв = адв/у и тур-
булентного ядра, причем цв — величина малая по сравнению
с "По = v*rQlv,
2) в вязком подслое турбулентный перенос отсутствует, т. е.
8(Г = ед = о при 0 < ц < Т]в;
3) в турбулентном ядре молекулярный перенос импульса и теп-
ла пренебрежимо мал по сравнению с турбулентным переносом,
т. е. v « 80- и п < 8д при лв < Ц < По, а Ргтб = 1;
4) распределение скорости описывается универсальной зависи-
мостью ф = f (ц), причем в вязком подслое ф = т).
По заданному распределению скорости wx/v;i. = f (я), исполь-
зуя уравнение (7.14), можно определить 8ff в турбулентном ядре.
Из (7.14) следует, что
v dwx
dy
Переходя к универсальным координатам и учитывая, что
= dwx. = р, / ч
dy d^ dy v
находим
Условие 3 позволяет пренебречь единицей в правой части урав-
нения (7.17) и принять
1—2.
so~ _ Цо
V f (ц)
(7.17а)
170
Используем для расчета теплоотдачи уравнение (7.11), приняв
в числителе подынтегрального выражения wx/w & 1 и положив
Ргтб = 1. Тогда уравнение (7.11) примет вид
1
Nlloo
1
1 Г RdR
О 1+РГ“
V
Переходя в этом уравнении от переменной 7^ к переменной ц с по-
мощью соотношения 7? — 1 — ц/г]0, получаем
л о
. 2. Г J -
Nu2 2-n„ Рг \
ь ц+v
(7.18)
Разбив интеграл в правой части (7.18) на два интеграла с преде-
лами от 0 до г]в и от т|п до т]0 и использовав принятые допущения
и соотношение (7.17 а), находим
Nth» 2llo Рг
"’Ib По
Jj PrdY]-|~^ f'('Yl)^'rl
-'° Пп
Интегрирование дает
1
Nlloo
“7 [Рг-Пв-Н ы — 7 (Пп)]-
2т)0 Рг
Подставив в это уравнение значения:
'По
Пт|в)==^ = т1в,
ч:1!
где йУдо — скорость на оси трубы и <^ЖГ! — скорость на границе между
вязким подслоем и турбулентным ядром, получим
—- Re Рг
Nu^ =--------------
1+Пв|/ “(Рг-1)
(7.19)
171
Это известная формула Прандтля для теплоотдачи при турбу-
лентном течении в трубах. ПоПрандтлю т|в=11,7 (см. § 6.5). Коэф-
фициент сопротивления £ может быть рассчитан по уравнению,
приведенному в § 6.5. Величину т]в]/£/8 в (7.19) можно заменить от-
ношением wxJw.
При Рг = 1, как видно из выражения (7.19),
Nui = iRe. (7.20)
8
Это соотношение, связывающее теплоотдачу (Nu') и коэффициент
сопротивления трения (|), известно как аналогия Рейнольдса.
Сравнение уравнения (7.19) с опытными данными обнаруживает,
что оно приближенно справедливо в диапазоне чисел Рг от ~1 до 10.
Это ограничение связано с двумя обстоятельствами. При больших
числах Рг изменение температуры жидкости от tG до 6?=о почти пол-
ностью происходит в вязком подслое, а в ядре потока температурное
поле практически однородно (см. приведенный ниже рис. 7.2). В этих
условиях интенсивность теплообмена в основном определяется
термическим сопротивлением вязкого подслоя. Поэтому, прене-
брегая турбулентным переносом в вязком подслое, мы существен-
но завышаем его термическое сопротивление, или, что то же, зани-
жаем число Nu(X). Совершаемая, при этом ошибка будет тем боль-
ше, чем больше число Рг, что хорошо видно из соотношения (6.36),
приведенного в § 6.3. В случае малых чисел Прандтля (Рг < 1),
характерных для жидких металлов, основное изменение температуры
происходит в турбулентном ядре. В соответствии с этим термическое
сопротивление ядра потока составляет основную часть общего тер-
мического сопротивления. Поэтому пренебрежение в турбулентном
ядре'молекулярной теплопроводностью, которая при малых числах
Рг соизмерима с турбулентным переносом, в свою очередь, приводит
к большим ошибкам.
Карман усовершенствовал двухслойную модель, введя дополни-
тельно промежуточный слой между вязким подслоем и турбулент-
ным ядром и полагая, что в промежуточном слое молекулярный и
турбулентный перенос тепла соизмеримы. Однако уравнение, пред-
ложенное Карманом, хотя и справедливо в более широком диапазо-
не чисел Рг (~от 1 до 20), но по существу обладает теми же недостат-
ками, что и уравнение (7.19).
Дальнейшее развитие теоретических методов расчета теплообме-
на при турбулентном течении в трубах жидкости с постоянными свой-
ствами было достигнуто за счет отказа от упомянутых выше допуще-
ний^ использования более точных зависимостей для коэффициентов
турбулентного переноса [17, 21, 30, 31, 34]. Последнее обстоятельство
затруднило аналитическое решение задачи и заставило перейти к чис-
ленным методам расчета. Результаты этих расчетов, как правило,
находятся в хорошем согласии с опытными данными.
172
§ 7.2. Стабилизованный теплообмен при постоянной
плотности теплового потока на стенке. Результаты расчета
и опытные данные
Рассмотрим последовательно результаты расчета поля плотно-
сти теплового потока, поля температуры и теплоотдачи. Расчет про-
водится по уравнениям (7.8), (7.10), (7.13) и (7.16), в_которых пред-
варительно следует перейти от переменных R и wx/w к переменным
Рис. 7.1. Распределение плотности теплового по-
тока по радиусу трубы.
т| = v.^tjh и (р = wjv*. Коэффициент турбулентного переноса еа/т
определяется по уравнениям Рейхардта (6.73) и (6.74), а турбулент-
ное число Прандтля Ргтб — eal&q принимается равным единице.
Вначале вычисляется поле скорости по уравнению (7.16), а затем
рассчитываются q/qG по уравнению (7.8), (tc— t)/(qGd/K) по уравнению
(7.10) и Nu^ по уравнению (7.13).
На рис. 7.1 показано распределение q/qc_po радиусу трубы. При
однородном профиле скорости, т. е. при wjw = 1, что соответствует
значениям чисел Re—>- оо, как видно из (7.8), qlqa — R. С уменьше-
нием числа Re наблюдается тем большее отклонение от линейного
закона, чем меньше число Re. При небольших числах Re возникает
173
максимум в распределении q/qc, который особенно значителен в слу-
чае ламинарного движения жидкости (см. рис. 7.1). Появление мак-
симума объясняется тем, что увеличение q с уменьшением R (в слу-
чае, если бы жидкость была неподвижна) превышает уменьшение
q вследствие уноса тепла из пристеночного слоя движущейся жид-
костью. На некотором удалении от стенки, где скорость жидкости
достаточно велика, всегда превалирует второй фактор и q умень-
шается с уменьшением R.
Рис. 7.2. Распределение температуры по радиусу
трубы при Re=106 и различных значениях числа Рг.
Распределение температуры жидкости по радиусу трубы при
различных значениях чисел Рг и Re = 106 изображено на рис. 7.2.
При других значениях числа Re характер распределения температу-
ры остается качественно таким же. При малых значениях числа Рг,
свойственных жидким металлам (Рг « 0,001 4- 0,1), температурное
поле неоднородно во всей области течения — от стенки до оси трубы.
По мере роста числа Рг изменение температуры все более сосредото-
чивается: в пристеночной области, а в ядре потока температура из-
меняется слабо. Такое различие в температурном поле при разных
числах Рг становится понятным, если учесть, что температурное
возмущение, вносимое в турбулентный поток нагретой стенкой,
распространяется тем дальше от стенки, чем больше коэффициент
теплопроводности жидкости А и чем меньше ее удельная теплоемкость
ср и вязкость ц, т. е. чем меньше число Рг =
Расчет теплоотдачи, проведенный Б. С. Петуховым совместно
с В. В. Кирилловым [17] и В. Н. Поповым [21] рассмотренным выше
174
методом, охватывает диапазон значений чисел Re от 104 до 5 • 10е и
Рг от 0 до 2000. Его результаты показаны на рис. 7.3. Из рисунка
видно, что характер зависимости Nu^ от чисел Re и Рг в различ-
ных диапазонах изменения этих параметров различен. С уменьше-
нием числа Рг, в особенности при значениях 0< Рг< 1, зависи-
мость Nu от Re становится более слабой, что связано с уменьшением
Рис. 7.3. Предельное число Nu« при течении в круглой трубе
в зависимости от Re и Рг в случае <7o=const.
относительного вклада турбулентного переноса и увеличением вклада
молекулярной теплопроводности и теплообмена между стенкой
и потоком жидкости. В предельном случае при числе Рг = 0 тепло-
обмен осуществляется посредством молекулярной теплопроводности
в потоке с турбулентным профилем скорости. В этом случае зави-
симость Nu^ от Re, изображенная на рис. 7.4, связана лишь с из-
менением профиля скорости в зависимости от Re. Характер зави-
симости Nu от Рг также весьма различен. При Рг « 1 число
Nu,» - Pro-е, а при Рг > 100 NUoo - Рг1/3.
Результаты теоретического расчета теплоотдачи в указанном
выше диапазоне значений чисел Re и Рг можно было бы описать еди-
ной зависимостью. Однако такая зависимость оказалась бы сложной
и неудобной для практического применения. Потому целесообразно
всю область значений числа Рг разбить на две более узкие области:
1) Рг > 0,5, что соответствует газам и капельным (неметалличе-
ским) жидкостям, и 2) Рг < 0,1, что соответствует жидким металлам.
175
Для каждой из этих областей можно получить относительно простые
интерполяционные уравнения.
Результаты расчета теплоотдачи в области значений чисел Re от
Ю4 до 5 • 10s и Рг от 0,5 до 2000 описываются уравнением [171
— РеРг
Nuoo-----------, (7.21)
+ ^2 “g" (Рг^3—1)
где
£ = (1,82 IgRe—-1,64)-2;
1,07 и Л?2= 12,7. (7.22)
Отклонение расчетных значений NuM от уравнения (7.21) не
превышает 6—8%. Если в выражении (7.21) принять
/ех = 1 3,4£;
Аг=11,7+1,8Рг-1/з,
(7-23)
то, как показано в работе [21], это уравнение будет описывать ре-
зультаты теоретического расчета с погрешностью 1—2%. Однако это,
разумеется, не означает, что уравнение (7.21) в сочетании с (7.22)
Рис, 7.4. Предельное число NUoo при течении в круглой трубе
при числе Рг=0.
или с (7.23) с такой же погрешностью описывает действительную за-
висимость NuM от Re и Рг. Ответ на этот вопрос можно получить,,
лишь сравнив уравнение с данными эксперимента.
Для сравнения были привлечены наиболее надежные опытные
данные по тепло- и массообмену*, полученные в широком диапазоне
значений Re (от 4 • 103 до 6 • 10б) и Рг или PrD) (от ~ 0,7 до
5 • 105). Сравнение показывает, что во всей области значений Re
и Рг уравнение (7.21) при kr = 1,07 и /г2 = 12,7 хорошо согласуется
* Опытные данные по массообмену получены в условиях, когда аналогия
между процессами тепло- и массообмена хорошо выполняется. При рассмотре-
нии процессов массообмена вместо чисел Nu и Рг используются их диффузи-
онные аналоги Nu^ и Рг^.
176
с результатами эксперимента; лишь при Re< 2 • 10а и 0,7< Рг<
< 1 наблюдается небольшое систематическое отклонение (до 6—
8%). Этот недостаток можно устранить, несколько скорректировав
значениепо опытным данным. В результате были получены сле-
дующие значения/гг и/г 2 [23]:
/г,= 12,7.
(7.24)
На рис. 7.5 уравнение (7.21) в сочетании с уравнением (7.24) со-
поставлено с экспериментальными данными по теплоотдаче к газам
(0,7 гС Рг 1), а на рис. 7.6 — с опытными данными по теплоотдаче
и массоотдаче к капельным жидкостям. Среднее квадратичное от-
клонение экспериментальных значений чисел Нуссельта (Nu«) от
рассчитанных по уравнению (NuJ составляет ±(4 — 5)%, что
соответствует погрешности, с которой получены опытные данные,
Таким образом, уравнение (7.21) в сочетании с (7.24) можно ре-
комендовать для практических расчетов теплоотдачи (а также массо-
отдачи) в диапазоне значений 0,5 < Рг (Рго) <5-10б и 4 • 103
Re 5 • 10°. Разумеется, оно справедливо для полностью
развитых профилей скорости и температуры, т. е. для стабилизован-
ных течения и теплообмена, которые наблюдаются за пределами ги-
дродинамического и термического начальных участков (см. § 7.3—
7.5).
В предельном случае при Рг -> оо уравнение (7.21) принимает
более простой вид:
Nlloo-0,079 р/" -l-RePr'/a. (7.25)
Этим уравнением можно пользоваться для расчета тепло- и массо-
отдачи при значениях Рг (Ргд) > 103.
Уравнение (7.25) можно также получить в результате аналити-
ческого интегрирования выражения (7.13) при Рг -> оо. В этом слу-
чае подынтегральная функция (7.13) быстро уменьшается с увели-
чением расстояния от стенки и уже при малых г] становится прене-
брежимо малой. Примем, как и прежде, Ргт£5 — 1, а для определе-
ния ест/т воспользуемся уравнением (6.73):
—— = 0,40 ( т[— 11 th —- .
v \ и У
Разлагая th (т]/11) в ряд и используя первые два члена, находим,
что при малых -q ea/v = С-ц3, где С — постоянная. Подставляя это
выражение в (7.13), полагая в подынтегральном выражении R «
177
Nut Nux V 1,0 0,9 0,8 о о D о о р
+57 дД Д_ _д_ I |Ч> I >Р> । I I (Р1— 1_ ’ Л ’ о о t>° н 4° 4. О+ _р+ •о-о—-4 о° С С 0 О& 0 0 о 1 | О 0 < 1° с °0?ОО|§эо°& 0 1 1 1 1 '-о 1 1 ° 1 о < 1ч
£ v i ' □ л > > + 0 ++<^р - <73 о <Ъ <0^
-57, А i Zi д Г >в ? а □ ? □ >ь> I * J д г с £° оД 8Д °о __о □ □ д Д ** ft. +ft-++_ 0 > 7 л 1О 1<£ 8 j ®w <> ' v 0 фА* 0 А —
7 а □
□ □ п ++♦ h О
> в 8 10* Z 0- 6 8 10s 2. . Re
Рис. 7.5. Сравнение уравнений (7.21), (7.24) с опытными данными по теплоотдаче к газам
ь 5? К: о 8 8
. V w— д Л Л й _Ja ~^г~ ОС о
. z\
\ V
0,8 / 0
4 <5* Ь 101 i а Z 6 8 РГ
Nu; Лоо о Л
1,0 0,9 0,8 0,7
Q с о о © © у G& ’ё’ ©
60 S в® ? О о oec$s о о 0® ©
© t ФСОЭС о ® б © €
-
6 8 102 2. 4 в 8 10^ 2 4 6 8 105 2 4 Рг^
5
Рис. 7.6. Сравнение уравнений (7.21), (7.24) с опытными данными по теплоотдаче (а) и массоотдаче (б) к ка-
пельным жидкостям.
ж 1 и переходя от переменной R к переменной т], получаем
Чо
1 __ 1 Г di]
Nu^^rioJ 1-j-CPri]3 ’
о
где
Выполнив интегрирование, приходим к уравнению (7.25) при
несколько ином значении постоянной (0,0855 вместо 0,079).
Примечательно, что при больших значениях Рг число Nu^, ~
~ Рг1/", где п — показатель степени в соотношении eo/v т]".
В данном случае п = 3. Очень хорошее согласие уравнения (7.25)
с опытными данными по массообмену при больших значениях Рго
может, таким образом, служить косвенным подтверждением того,
что вблизи стенки sa/v ~ т]3. Следует, однако, заметить, что по
вопросу о характере зависимости so/v от т] вблизи стенки нет еди-
ной точки зрения. Некоторые авторы полагают п = 4 [12]. Для
однозначного решения этого важного вопроса пока не достает
прямых и надежных измерений коэффициента турбулентного
переноса вблизи стенки.
На практике для расчета теплоотдачи часто пользуются эмпири-
ческими зависимостями вида
NuTO = CRe'"Pr", (7.26)
где С, т и п — постоянные. Например, по данным Диттуса и
Белтера, С = 0,023, т = 0,8 и п = 0,4; по данным М. А. Михеева,
С = 0,021, т = 0,8 и п = 0,43.
Результаты теоретического расчета и экспериментальные данные
показывают, что значения С, т и п в выражении (7.26) можно с из-
вестным приближением принять постоянными лишь в ограничен-
ном диапазоне чисел Re и Рг. При изменении Re в пределах от 104
до 10s и Рг (или Ргд) от 0,5 до 103 т изменяется от 0,79 до 0,92, а
п от 0,6 до 0,33. Поэтому использование зависимостей типа (7.26)
при постоянных С, т и «может привести к значительным ошибкам.
О величине возможных ошибок дает представление рис. 7.7. На нем
показано отношение числа NuTO, рассчитанного по уравнению (7.26)
при С = 0,023, т = 0,8 и п = 0,4, к числу ЫиюЭ, рассчитанному
по уравнениям (7.21) и (7.24), в зависимости от числа Рг.
Рассмотрим теперь основные закономерности теплоотдачи для
жидкостей с числами Рг < 1, т. е. для жидких металлов. Как было
отмечено ранее, перенос тепла в этом случае определяется в основ-
ном термическим сопротивлением турбулентного ядра (поскольку
перепад температур в вязком подслое мал по сравнению с перепадом
температур в ядре). В турбулентном ядре доминируют силы инер-
ции, а силы вязкости не играют существенной роли. Поэтому тепло-
обмен в жидкостях с числами Рг 1 в первом приближении не дол-
180
жен зависеть от коэффициента вязкости ц. Отсюда следует, что
числа Re и Рг должны входить в уравнение Nu = f (Re, Рг) в такой
комбинации, которая не содержит р. Такой единственной комбина-
цией является число Ре = Re • Рг = wdla. Эти соображения, вы-
сказанные К- Д. Воскресенским [15], приводят к заключению, что
при Рг « 1 число Nu^ с известным приближением зависит толь-
ко от числа Ре.
Рис. 7.7. Сравнение чисел Nu^, вычисленных по урав-
нениям (7.26) и (7.21).
Действительно, результаты численного расчета [17, 21], приведен-
ные на рис. 7.3, при значениях Рг < 0,1 и 10а Re 5 • 10°
с погрешностью ±10% описываются зависимостью
Nu^ = 7 ± 0,025 Ре0’8, (7.27)
ранее полученной Лайоном [33].
Уравнения типа (7.27) или несколько иного типа предложены во
многих работах советских и зарубежных исследователей. Напри-
мер, С. С. Кутателадзе [9], положив в основу расчета двухслойную
модель потока (ламинарный подслой и турбулентное ядро), нашел
уравнение, близкое к (7.27).
Опытные данные по теплоотдаче к жидким металлам вследствие
трудностей эксперимента имеют небольшую точность. Если исклю-
чить данные, полученные с недостаточно чистым металлом* или
при наличии тех или иных методических недостатков, то даже в этом
случае между данными различных исследователей наблюдается зна-
чительная разница. Имеются опытные данные, хорошо согласующие-
ся с уравнением (7.27). Однако большинство данных, полученных
* Наличие в металле нерастворенных окислов, концентрирующихся
вблизи стенки, приводит к значительному снижению теплоотдачи (см. § 11.3).
181
в последние годы, в среднем лежат ниже уравнения (7.27). Это
различие проявляется главным образом при небольших значениях
числа Ре; по мере роста числа Ре оно постепенно уменьшается и ис-
чезает (рис. 7.8). Причина такого несоответствия, возможно,
заключается в неоправданное™ некоторых предпосылок теорети-
ческого расчета, например предположения о том, что Ргтб = 1 и что
универсальный профиль скорости справедлив во всей области
значений Re. Результаты некоторых измерений показывают, что
Рис. 7.8. Зависимость числа Nu от числа Ре для жидких металлов:
I — Nu-7+0,025 Ре°>8: II — Nu=5+0,025 ре 0,827; ///_ Nu=4,82+0,0185 Ре0’8:
□ —опыты ФЭИ с ртутью [24]; Д — опыты ФЭИ; с NaK [24]; О — опыты
французских исследователей NaK [37].
Ргтб для жидких металлов может быть и больше единицы, а профиль,
скорости при Re< 2 • 104 заметно отличается от универсального.
Уравнение (7.27), как видно из (7.13), можно записать в более-
общей форме:
Nt^ = 7,0 + 0,025 (Р Ре)0-8, (7.28)
где р — некоторое эффективное (осредненное по сечению) значе-
ние 1/Ргтб. _
К- Д. Воскресенский [14] получил выражение для р в уравнении
типа (7.28), исходя из предположения, что энтальпия «турбулентного'
моля» на пути перемешивания изменяется за счет теплообмена с окру-
жающим его жидким металлом. Дуайер [3], руководствуясь неко-
торыми физическими соображениями, но главным образом, опира-
ясь на опытные данные по теплоотдаче, подобрал такие значения р,
182
чтобы уравнение (7.28) наилучшим образом описывало опытные дан-
ные. Исходя из этого им получено следующее выражение для [3:
1,82
М1'4
v /
/ макс
где (e0/v)MaKC — максимальное (в данном сечении трубы) значение
коэффициента турбулентного переноса количества движения, отне-
сенное к кинематическому коэффициенту вязкости. Величина
'(eo/v)M;lI.(. в зависимости от Re
представлена па рис. 7.9.
Уравнение (7.28) справед-
ливо при значениях Ре от 102
до 104 и Рг от 0,005 до 0,03
Это уравнение лучше согласу-
ется с экспериментальными дан-
Re для круглой трубы.
ными, чем уравнение (7.27). Од-
нако оно не имеет существенных
преимуществ перед более про-
стым уравнением, рекомендуемым
В. И. Субботиным с сотр. [251
для области значений 102
<Ре<104 и 104<Re<5-105:
Nuw =5,0 + 0,025 Ре0-8. (7.29)
Послсдиее уравнение, как видно из рис. 7.8, находится в удов-
летворительном согласии с новейшими опытными данными (данные
ФЭИ по ртути и сплаву NaK и данные французских исследователей
по сплаву NaK) [24, 37]. На том же рисунке представлено урав-
нение
Nu*, = 4,82 + 0,0185 Ре0-827,
(7.30)
полученное французскими исследователями на основе опытов, про-
веденных с NaK [37]. Оно справедливо в тех же пределах изменения
определяющих параметров, что и уравнение (7.29).
Теплоотдача к жидкому металлу (ртути) при значениях числа Re,
соответствующих области перехода от ламинарного течения к турбу-
лентному, экспериментально исследована в работе [19]. Результаты
измерений, представленные на рис. 7.ГО, показывают, что для жид-
кого металла (в отличие от жидкостей с числами Рг 1) не наблю-
дается резкого возрастания теплоотдачи при переходе от ламинарного
течения к турбулентному. Это объясняется тем, что при турбулент-
ном течении жидкого металла, в особенности при малых числах Ре,
преобладающую роль играет молекулярный перенос тепла по сравне-
183
Рис. 7.10. Зависимость числа NuM от числа Ре для ртути, по дан-
ным работы [19].
нию с турбулентным. Поэтому возникновение турбулентного пере-
носа при Re > ReKp приводит лишь к слабому увеличению тепло-
отдачи. Для расчета теплоотдачи в рассматриваемых условиях ре-
комендуется следующее уравнение [19]:
NuOT = 4,36 + 0,0053 Ре. (7.31>
Оно справедливо при 15 Ре 600 и 2300 < Re < 23 500.
§ 7.3. Влияние шероховатости на сопротивление и теплоотдачу
Выше шла речь о теплообмене и сопротивлении при течении в.
гладких трубах. Теперь следует кратко рассмотреть, какое влияние-
оказывает шероховатость трубы на сопротивление н теплоотдачу.
При ламинарном течении гидравлическое, сопротивление и тепло-
отдача практически не зависят от шероховатости. В случае тур-
булентного течения, особенно при больших Re, наличие шерохо-
ватости может привести к существенному увеличению не только
сопротивления, но и теплоотдачи.
Под шероховатостью обычно понимают малые (по сравнению с ра-
диусом трубы) отклонения рельефа реальной поверхности от идеаль-
но гладкой. Высота этих отклонений (элементов шероховатости)
обычно соизмерима с толщиной вязкого подслоя или вязкого подслоя
и промежуточного слоя. Поэтому непосредственное воздействие ше-
роховатости на поток сосредоточено в сравнительно тонком присте-
ночном слое и не приводит к возникновению в потоке вторичных те-
чений, что характерно для так называемых «турбулизаторов» (спи-
ральные ребра, вставки типа закрученной ленты или шнека), кото-
рые здесь не рассматриваются.
Шероховатость поверхности, как естественная, обусловленная
технологией производства и условиями эксплуатации труб, так и
искусственная, т. е. специально нанесенная на поверхность трубы
(резьба, поперечные выступы и канавки, бугорки ит. п.), отличает-
184
ся большим разнообразием. В общем случае шероховатость поверх-
ности характеризуется высотой и формой элементов шероховатости,
их числом на единицу поверхности п взаимным расположением. Од-
нако эти характеристики часто можно заменить одной характеристи-
кой — высотой эквивалентной шероховатости /г.,. Прежде чем разъ-
яснить это понятие рассмотрим зависимость коэффициента сопротив-
ления трения % от Re и kjd (d — 2/-0 — диаметр трубы) для труб с
естественной шероховатостью (рис. 7.11). На рис. 7.11 можно вы-
делить три характерные области.
Рис. 7.11. Коэффициент сопротивления трепня труб с естественной
шероховатостью:
/ — гидраплпчеекая гладкая труба.
1. Область гидравлически гладких труб, соответствующая неболь-
шим значениям Re (тем меньшим, чем больше kQld). В этой области
вязкий подслой имеет значительную толщину, элементы шерохова-
тости находятся внутри него и обтекаются без отрыва потока. Поэ-
тому шероховатость нс оказывает влияния на сопротивление и за-
висимость £ — £ (Re) для шероховатых труб совпадает с зави-
симостью для гладких.
2. Переходная область соответствует более высоким числам Re.
Так как с увеличением Re толщина вязкого подслоя уменьшается,
то все большая часть элементов шероховатости полностью или ча-
стично оказывается за пределами вязкого подслоя. Их обтекание
происходит с отрывом потока, что приводит к возникновению допол-
нительного напряжения (наряду с вязкостным и турбулентным на-
пряжениями), обусловленного сопротивлением давления элементов
шероховатости. Поэтому в переходной области коэффициент сопро-
тивления трения шероховатой трубы зависит не только от Re, но и
от kjd, тем сильнее отклоняясь от закона сопротивления для гладкой
трубы, чем больше k.Jd.
3. Область полностью шероховатых труб, или автомодельная
область, соответствует еще более высоким значениям числа Re,
185
при которых вязкий подслой становится тонким и элементы шерохо"
ватости выступают за его пределы. Поэтому доминирующую роль в
формировании касательного напряжения на стенке играет сопротив-
ление давления элементов шероховатости. По этой причине коэффи-
циент сопротивления трения шероховатой трубы перестает зависеть
от числа Re и полностью определяется значением kjd (так называе-
мый квадратичный закон сопротивления, Др ~ w2). Граница наступ-
ления такого режима обозначена пунктиром на рис. 7.11.
Зависимость £ = £ (Re, kQ/d) для искусственной шероховатости
подобна изображенной на рис. 7.11, за исключением переходной
области; здесь характер зависимости будет иным и притом неоди-
наковым для шероховатостей разного типа.
Для автомодельного режима £ можно вычислить по уравнению,
предложенному Никурадзе:
Е = (2 1g У- + 1,74'|~2. (7.32}
Это уравнение было получено для искусственной, так называе-
мой песочной шероховатости (зерна песка одинакового размера,
наклеенные вплотную друг к другу на поверхность трубы), которую-
можно охарактеризовать одной величиной — высотой элемента ше-
роховатости k. Для песочной шероховатости в уравнении (7.32}
/га = /г. Однако уравнением (7.32) можно пользоваться и при дру-
гих типах шероховатости, если для них известны значения /гэ. Под.
/гэ понимается такая высота элемента песочной шероховатости,
при которой труба с этой шероховатостью имеет то же значение
что и труба с данным видом шероховатости. Значение /гэ для данного
вида шероховатости определяется экспериментально [измерив.
по формуле (7.32) можно вычислить /гэ]. Для некоторых видов;
шероховатости значения /гэ приведены в табл. 7.1.
Многочисленные исследования показывают, что нанесение на
поверхность трубы искусственной шероховатости позволяет увели-
чить коэффициент теплоотдачи и тем самым снизить температуру
стенки (при заданном значении qc). Поэтому создание искусственной
шероховатости — один из способов интенсификации теплообмена,
что очень важно для техники ядерных реакторов*.
Увеличение теплоотдачи на шероховатой поверхности связано-
с возрастанием интенсивности турбулентного переноса в пристеноч-
ном слое, что стимулируется образованием вихрей в зонах отрыва
за элементами шероховатости. Одновременно с ростом теплоотдачи,
и нередко более сильно, растет и гидравлическое сопротивление.
Для характеристики относительного увеличения теплоотдачи (на
шероховатой поверхности относительно гладкой) по сравнению с от-
* Другие способы интенсификации теплообмена применительно к систе-
мам с газообразными теплоносителями рассмотрены в гл. 10
186
Таблица 7.1
Значения k0 для некоторых типов шероховатости
Тип шероховатости k, мм s/k k.,, мм о
S $ 0,2 3,5 0,412
0,2 5,3 0,373
0,3 2,33 0,455
0,5 1,6 0,326
\/'// / / //../'//.л 1,0 1,6 1,00
1,5 1,6 1,70
с г 0,107 2,22 0,035
0,165 1,45 0,25
JZ1 I7/L, Г/^L, к 0,240 2,08 0,182
0,50 1,60 0,326
V////////////J 1,00 1,60 1,00
1,50 1,60 1,70
ДД к 0,8 12,5 4,2
0,8 20,0 1,62
Естественная шероховатость:
цельнотянутые стальные трубы 1 — 0,0015
цельнотянутые трубы из латуни, меди и свинца — 1 1 1 0,0015—0,01
оцинкованные стальные трубы — 0,15
чугунные трубы —— -— 0,26
иосительным увеличением гидравлического сопротивления поль-
зуются коэффициентом эффективности-.
г, == Nuni/Nur
£ш/£г
где Num и Nur, и £г — числа Нуссельта и коэффициенты сопро-
тивления трения для труб с шероховатой и гладкой поверхностью
при одних и тех же значениях чисел Re и Рг.
Приближенный анализ и опытные данные показывают, что для
шероховатости различного типа (по крайней мере для типов, пред-
ставленных в табл. 7.1) в круглых трубах и кольцевых щелях коэф-
фициент эффективности г) зависит от числа Рг и параметра шерохо-
ватости
ki = М>иЩе./к,
v у 8
где Re = wd9/v; d3 = 4f/s — эквивалентный диаметр (для круглой
трубы d3 — d).
187
Зависимость т] от kt и Рг, найденная Бурком [29] путем обоб-
щения ряда опытных данных, представлена на рис. 7.12. Эти данные
относятся к шероховатости, находящейся в хорошем термическом
контакте со стенкой, и не справедливы для так называемой нало-
женной шероховатости, когда такой контакт отсутствует (например,
помещенная на стенку проволочная спираль, не припаянная к ней).
Коэффициент теплоотдачи в шероховатой трубе, найденный с по-
мощью рис. 7.12, отнесен к гладкой поверхности (т. е. к поверхности
трубы, вычисленной без учета поверхности элементов шерохова-
тости) .
Рис. 7.12. Зависимость коэффициента эффективности шерохова-
тых труб от kt при различных значениях Рг.
Как видно из рис. 7.12, коэффициент эффективности может быть
как больше, так и меньше единицы, или, другими словами, увели-
чение теплоотдачи в шероховатой трубе по сравнению с гладкой мо-
жет быть больше или меньше увеличения коэффициента сопротив-
ления трения. С ростом /?э Num/Nur стремится к постоянному
значению, а |ш/|г растет, поэтому 1] уменьшается. Увеличение числа
Рг приводит к росту NUjjj/NUr, а значит, и -q, так как при этом воз-
растает вклад турбулентного переноса тепла в пристеночном слое.
Приведенные выше данные позволят рассчитать теплоотдачу
в шероховатой трубе (Num), если известна теплоотдача в гладкой
трубе (Nur) и гидродинамические характеристики гладкой и шеро-
ховатой труб: |г, и /?3. Для автомодельной области можно вы-
числить по уравнению (7.32), а для переходной области необходимо',
располагать опытными значениями для труб с шероховатостью
данного типа. Оценим для примера влияние естественной шерохо-
ватости на теплоотдачу в стальной трубе диаметром d = 5 мм при
значениях чисел Re = 106 и Рг = 0,7. В этом случае /?э = 0,0015 мм
(см. табл. 7.1), a kjd = 3 • 10~4. По рис. 7.11 находим = 0,012
и = 0,016. Следовательно, kt = 3 • 10~4 - 106У 0,016/8 = 13,4.
Как видно из рис. 7.12, q=0,9. Отсюда Num/Nur=0,9(0,016/0,012) =
188
— 1,2. Таким образом, в данном случае теплоотдача в шероховатой
трубе на 20% выше, чем в гладкой. Естественно, что в трубе больше-
го диаметра или при меньших Re это различие будет много меньше.
Более подробные сведения о течении и теплообмене в шерохо-
ватых трубах можно почерпнуть в известной монографии Г. Шлих-
тинга [28.1, в работах М. Д. Миллионщикова [11, 131, а также в ра-
боте Э. К- Калинина, Г. А. Дрейцера и С. А. Ярхо [5]. В последней
дан обзор и ранее опубликованных работ.
§ 7.4. Влияние нестационарности на теплоотдачу
При переходных режимах и аварийных ситуациях тепловыде-
ление в активной зоне реактора, расход теплоносителя или то и дру-
гое одновременно изменяются во времени. В таких условиях процесс
теплопроводности в твэлах и процесс конвективного теплообмена
в потоке теплоносителя становятся нестационарными. Расчет тем-
пературных полей в этом случае, строго говоря, требует совместного
решения уравнения теплопроводности для твэлов и уравнения энер-
гии для потока теплоносителя, т. е. рассмотрения сопряженной за-
дачи (см. § 4.2). Однако такой метод расчета сложен и не всегда оп-
равдан. Поэтому на практике предпочитают пользоваться другим,
более простым, хотя и приближенным методом. Введением местно-
го коэффициента теплоотдачи, зависящего от времени и координат,
задачу разделяют на две: 1) задачу о нестационарной теплопровод-
ности в твэле при переменных во времени граничных условиях тре-
тьего рода и 2) задачу о нестационарном конвективном теплообмене
в потоке теплоносителя, решение которой позволяет определить
коэффициент теплоотдачи.
Изучение нестационарного конвективного теплообмена при тур-
булентном движении жидкости находится в начальной стадии. Прак-
тически отсутствуют данные о закономерностях турбулентного пере-
носа при переменных во времени полях осредненных величин. По-
этому теоретические расчеты базируются, как правило, на законо-
мерностях турбулентного переноса, полученных в стационарных
условиях. Для проверки их результатов пока не достает надежных
опытных данных.
Во многих практически важных случаях параметры процесса
(qc, w, t) сравнительно медленно изменяются во времени. В таких
случаях коэффициент теплоотдачи в нестационарных условиях мож-
но вычислять по уравнениям для стационарной теплоотдачи, под-
ставляя в них мгновенные значения изменяющихся во времени пара-
метров (так называемое квазистационарное приближение). Пара-
метры qG (т), w (т) обычно являются заданными функциями, a t (т)
находится из одномерного уравнения теплового баланса, записан-
ного с учетом нестационарности. Найденный таким способом коэф-
фициент теплоотдачи, естественно, будет изменяться во времени
в связи с изменением параметров процесса.
189
При быстром изменении во времени параметров процесса квази-
стационарный подход не позволяет провести расчет с приемлемой
точностью. Это объясняется тем, что при сильно выраженной не-
стационарности поле температуры в потоке существенно отличается
Рис. 7.13. Зависимость коэффици-
ента теплоотдачи от числа Fo при
изменении q0 во времени.
от стационарного. Поэтому дейст-
вительные значения коэффициентов
теплоотдачи а уже не будут соот-
ветствовать их квазистационарным
значениям акс. Это хорошо видно
на рис. 7.13, где приведено отно-
шение а/акс в зависимости от числа
Fo — ax/d? по опытным данным [7]
для случая турбулентного течения
жидкости в круглой трубе вдали
от входа при w = const. Нестацио-
нарность вызвана изменением во
времени плотности теплового по-
тока на стенке; характер измене-
ния q'c — 7c/(7c)fo=o показан на
том же рисунке. При Fo =
= 1,2- 10~3 (что в случае течения
воды в трубе d « 7 мм соответ-
ствует т « 0,5 сек) действительный
коэффициент теплоотдачи почти в два раза выше квазистационар-
ного. Однако с ростом числа Fo эта разница уменьшается и при
Fo = 5 • 10~3 (что соответствует х 1,5 сек) составляет около 10% .
Вопросам нестационарного конвективного теплообмена при
турбулентном течении жидкости в трубах посвящен ряд расчетных
и экспериментальных работ [2, 7, 81.
§ 7.5. Теплообмен в термическом начальном участке
при постоянной плотности теплового потока на стенке
В предыдущих параграфах мы изучили стабилизованный
теплообмен в круглой трубе при qc = const. Такой процесс тепло-
обмена реализуется вдали от начала обогреваемого участка. Здесь
мы рассмотрим теплообмен во всей области течения в трубе — от на-
чала обогреваемого участка и далее вниз по потоку. Другими слова-
ми, будем изучать не только область стабилизованного теплообме-
на, но и термический начальный участок.
В качестве основного условия примем, что распределение тем-
пературы в начальном сечении обогреваемого участка является од-
нородным. Все остальные условия, сформулированные в начале
§ 7.1 (кроме условия 6), остаются в силе и в данном случае.
В частности, профиль скорости по всей длине трубы предполагается
развитым и, следовательно, неизменным по длине, а плотность теп-
лового потока на стенке — постоянной (qc = const).
190
Уравнение энергии и граничные условия, отвечающие рассматри-
ваемой задаче, имеют вид:
1 д ’ < I ч dt 1
— V г ”1" Т~
г дг |_ 4 дг .
dt 1 д
х дх г дг
(7.33)
где t0 — постоянная температура в начальном сечении обогревае-
мого участка; г0 — радиус трубы.
Полагая Ргтб = sa/sq = 1 и переходя в (7.33) к безразмерным
величинам, получаем:
Эта задача решена несколькими исследователями и, в частности,
Спэрроу, Холлменом и Сайгелом [38]. В последней работе скорость
Ф (т|) и коэффициент турбулентного переноса — (г], ср) (здесь т] =
= /'о — г+) вычислялись по уравнениям Дайслера (6.75)—(6.78).
Задача решается тем же методом, что и рассмотренная ранее задача
о теплообмене при ламинарном течении жидкости (см. §5.2, п. 1).
Решение представляется в виде суммы
0 = 0! + 02,
где ©j — решение задачи для стабилизованного теплообмена;
следовательно, ©х = lim 0; ©2 — дополнительная функция, учи-
Я-Э-00
тывающая развитие температурного профиля в термическом началь-
ном участке; ©2~->0 при х-+-оо.
Уравнение (7.33а) линейно относительно 0, поэтому такие же
уравнения можно записать для 0Х и ©2.
В уравнении для ©j при qc = const 501/5x-=4/(RePr)=const,
и его решение можно представить в виде
01 = _J-r + G(r+).
Re Рг
191
Уравнение для 02 решается обычным методом разделения пере-
менных. Представив 02 в виде 02 = %(х)ф (г+), для % (%) получим
экспоненту, а отыскание^ (г+) сводится к решению задачи Штур-
ма—Лиувилля о собственных функциях. В результате имеем
00 / 1 — \
2 сп фп (г+) ехр ( — 4РЛ — X ) ,
и—о \ Re /
гдефп—собственные функции, а |3Л — собственные значения задачи;
Re = wd/v.
Общее решение задачи, справедливое как для области стабили-
зованного теплообмена, так и для термического начального участка,
имеет вид:
л ~ 00 / 4В2
0 = ——- х +G (г+) ф 2 Сп (г+) ехр —х I .
Re Рг п — о \ ке /
(7.34)
•Функции G (г+), фп (г+) и постоянные Сп и находились числен-
ным решением соответствующих уравнений с помощью ЭВМ.
Определив местный коэффициент теплоотдачи в виде а =
= qc/(tc— f), для местного числа Нуссельта имеем выражение
Nu = —= ..=____Ц_.
Ъ №-() ®о-в
Значение 0С получается из уравнения (7.34) при г+ = го, а 0
находится из выражения для теплового баланса:
0 ==---2 =----X.
qa d Re Рг
V
В результате получим уравнение для числа Нуссельта:
Nu —------------i------------
G(ro )+ 2j CH’nWjexp — — х
п = 0 \ /
(7.35)
Полагая в этом выражении х~>~ оо, находим предельное число
Нуссельта:
Nu„ = —!— . (7.36)
Запишем отношение местного числа Нуссельта к предельному:
— =------------------1---------------s (7.37)
Ntlco “ / л.9 1 X \
1 + 2.1 Ап ехр — 4р“ ---—
п=1 \ ке а /
где
Л = Сп'Фп(/'Л/^(^0+).
192
Рис. 7.14. Зависимость числа Нус-
сельта от x/d в термическом на-
чальном участке круглой трубы
Постоянные А1Ь и собственные значения |3П для нескольких зна-
чений чисел Re и Рг по данным [36, 38] приведены в табл. 7.2 [за-
метим, что при Ло = 0 и ро = 0, поэтому вычисление суммы в зна-
менателе (7.37) начинается с
п = 1].
Зависимость Nu/Nu^ от x/d для
нескольких значений Re и Рг по-
казана на рис. 7.14 и 7.15* . С уве-
личением x/d отношение Nu/Nu^,
убывает, стремясь к единице. Для
чисел Рг < 1 (см. рис. 7.14) число
Нуссельта в термическом начальном
участке значительно отличается от
Nu^, причем это различие увели-
чивается с ростом числа Re. С уве-
личением числа Рг число Nu в тер-
мическом начальном участке умень-
шается и при Рг > 1 мало отли-
чается от NuM (см. рис. 7.15) При
Рг =т 0,7 отношение Nu/Nu^ слабо
зависит от числа Re.
Если определить длину термического начального участка из
Рис. 7.15. Зависимость числа Нуссельта от x/d в термиче-
ском начальном участке круглой трубы при значениях
Re = 105 (сплошные линии) и Re=104 (пунктир).
Таким образом, длина термического начального участка при
турбулентном течении жидкости сравнительно невелика и притом
быстро уменьшается с ростом числа Рг.
Приведенные здесь результаты теоретического расчета тепло-
отдачи в термическом начальном участке хорошо согласуются
* Рис. 7.14 и кривая для Рг = 0,01 на рис. 7.15 построены по данным
работы [6]; остальные кривые на рис. 7.15 рассчитаны по уравнению (7.37).
7 Зак. 792 193
Собственные значения и постоянные в задаче о теплообмене в круглой трубе
при полностью развитом турбулентном течении и #e=const
Таблица 7.2
Рг= 0,7 Рг= 1,0 Рг= 10 Pr= = 100
Re п Раи Ап Р2/г Ап РЛг An An
101,7 125,2 Nu^ 381,8 Nu = oo =834,0
1 1387 0,1785 1380 0,1568 1366 0,05055 1364 0,01150
5-Ю4 2 3730 0,09402 3705 0,08401 3651 0,02945 3645 0,007287
3 7040 0,06502 6981 0,05938 6850 0,02311 6835 0,00633
4 ИЗЗО 0,05008 11220 0,04682 10960 0,02106 10930 0,00675
5 16600 0,04177 16410 0,04012 15950 0,02113 15830 0,00821
Nu = ОО 173,4 213,2 NuM= 688,1 Nu = oo = 1535
1 2545 0,1669 2538 0,1466 2524 0,04876 2522 0,01112
105 2 6822 0,08858 6796 0,07862 6742 0,02726 6737 0,006479
3 12850 0,06093 12790 0,05475 12660 0,02013 12640 0,00487
4 20630 0,04633 20520 0,04224 20270 0,01669 20240 0,00505
5 30190 0,03770 30000 0,03493 29560 0,01506 29510 0,00446
598,8 NuOT= =743,1 NUoo= =2703 Nu = OO =6324
1 10680 0,1435 10670 0,1244 10660 0,04612 10660 0,01080
5-Ю5 2 28520 0,07764 28490 0,06755 28440 0,02531 28430 0,005962
3 53560 0,05386 53490 0,04700 53360 0,01786 53350 0,004232
4 85810 0,04121 85690 0,03610 85440 0,01393 85410 0,03328
5 125300 0,03341 125100 0,02933 124700 0,01154 124600 0,002783
Таблиц а 7.3
Значения 1т/d в задаче о теплообмене при ^c=const
Рг Re=10‘ Re=5-101 Re= 10» Re=5-10°
0,01 - 18 28
0,7 11 12 13 14
10 4 4 4
100 — <1 <1 <1
с опытными данными, по крайней мере для газов [10]. Эти данные
также обнаруживают слабую зависимость Nu/Nu^ от Re, за исклю-
чением области малых значений x/d (меньших ~1), где эта зависи-
мость становится заметной.
Наряду с уравнением (7.37) для расчета теплоотдачи в терми-
ческом начальном участке при движении газа можно рекомендовать
уравнение, полученное В. А. Кургановым:
— = 14-0,48 (—') 4 NUoo hi / / 3b00 \ I p. « r-j Л \ /н QO\ /1+ —-\ exp 1—0,17 —- . (7.38) \ Re |/ 4Г /
Это уравнение обобщает результаты теоретических расчетов и из-
мерений в диапазоне 4 • 103 Re С 5 • 10Г), 0,7 Рг 1 и
x/d 0,06.
При значениях 5 Рг 10, 5 • 103 Re 5 • Ю4 и x/d > 1
можно пользоваться приближенным уравнением:
Nu
1-1-0,5
(7.39)
полученным в Энергетическом институте им. Г. М. Кржижановского
(ЭНИН) [27] в результате опытов, проведенных с водой.
Предельное число Нуссельта Nu^ в уравнениях (7.37)—(7.39)
вычисляется по уравнениям (7.21) и (7.24).
§ 7.6. Теплообмен при постоянной температуре стенки
Исследуем теплообмен при стабилизованном течении жидкости
в круглой трубе при однородном распределении температуры на
входе в обогреваемый участок и постоянной температуре на внут-
ренней поверхности стенки (tG = const). Все остальные условия те
же, что и в §7.1 (см. условия 1—5 на стр. 165). Если положить
Ргтб = 1 и ввести безразмерные величины
7*
195
то уравнение энергии и граничные условия можно записать в виде:
д& г(+ д Г , / 1 . fc'a \ дО
Qx /’+ Рг V у дг+
9(0, r+) = l; 0(х,Щ = О; u =0.
\ дг+ / г + = о
Так как физические свойства жидкости считаются постоянными,
то <р и 8o/v не зависят от поля температуры и могут быть рассчитаны
заранее по данным, приведенным в гл. 6. В данном случае они вы-
числяются по методу Дайслера (см. §6.6).
Задача о теплообмене при турбулентном течении и tc — const,
решение которой получено в работе [36], вполне аналогична задаче
о теплообмене при ламинарном течении жидкости в случае tc —
= const (см. § 5.1) и может быть решена тем же методом. Разница
заключается лишь в том, что в данном случае собственные значения
и постоянные будут иметь другие численные значения, зависящие
от чисел Re и Рг. Решение имеет обычный для таких задач вид:
00 1 \
® = 2 СиМг+)ехР (— ,
n==o \ Re а )
где рп ифп — собственные значения и собственные функции задачи;
Сп — постоянные.
По определению местное число Нуссельта
Nu — а2г° 2г0 _________2гр~ / д& \
К ® 1л+Л+=го+ ‘
Вычислив с помощью (7.41) среднемассовую температуру жид-
кости
0=±1^1===_2_.Г ®Wxr+dr+
^0— tc rf 2 J
0
и производную (д@/дг+) г+=г+,’ получим выражение] для числа
Нуссельта:
Рг У, СпЩгЛехр f — «р,® )
-----RejU . (7Л2)
ЧГЗ бп . ' t 4-4 / 1 х \
Значения Сп,фп (/Д) и [З2 при Рг = 0,7 и Re = 104 и 5 • 104 при-
ведены в табл. 7.4.
При x/d -> оо существенны только первые члены рядов в числи-
теле и знаменателе (7.42), поэтому предельное число Нуссельта
Nu^ = Рг£В. (7.43)
196
Таблица 7.4
Собственные значения и постоянные задачи о теплообмене
при турбулентном течении в круглой трубе в случае const, Рг=0,7
tl
Сп
0 44,371 —0,036269 1,2664
1 454,26 0,022654 — 1,49152
2 1137,4 —0,018059 1,43507
3 2106,2 0,016892 — 1,41660
4 3346,0 —0,016687 1,41254
5 4864,0 0,017637 — 1,41692
6 6617,8 —0,018532 ‘ 1,4912
Re—5-Ю4
0 141,36 —0,030622 1,2267
1 1676,2 0,017838 —1,42513
2 4184,6 —0,013381 1,39001
3 7679,4 0,011209 — 1,37987
4 12167,0 —0,0098511 1,37320
5 17667,0 0,0090539 — 1,36768
6 24167,0 —0,0085049 1,36286
Вычисления показывают, что зависимость местного числа Nu
от чисел Re и Рг, а также его изменение по длине трубы в случае
/с =- const качественно остаются такими же, как и при qQ = const
(см. § 7.5). Более того, при значениях Рг >0,7 наблюдается близкое
количественное соответствие результатов расчета для обоих слу-
чаев. На рис. 7.16 показано отношение предельных чисел Нуссель-
та при 1С --= const (Nu^f) и при <7С — const (Nu^J в зависимости
от чисел Re и Рг. Как видно из рисунка, при значениях Рг < 1, т. е.
для жидких металлов, Nu^ при tc — const на 15—25% ниже, чем
при г/с — const. Однако с увеличением Re и особенно Рг разница
сокращается и при Рг 0,7 и Re 4 • 103 не превышает 5%. При
более высоких значениях Рг различие практически исчезает.
Опираясь на результаты теоретического анализа, которые также
подтверждаются опытными данными, для расчета предельных чисел
Нуссельта при значениях Рг >• 0,7 в случае ta « const можно
пользоваться уравнениями (7.21) и (7.24) , полученными в § 7.2 для
случая г/с — const.
Разница местных значений чисел Нуссельта в термическом на-
чальном участке при tc = const и qG = const несколько больше,
чем разница предельных значений. Однако при Рг > 0,7, как вид-
но из табл. 7.5, эта разница также невелика (не более 9%). Поэтому
для приближенного расчета теплоотдачи в термическом начальном
участке при Рг 0,7 в случае tG = const можно пользоваться ре-
комендациями, приведенными в § 7.5 для случая qQ = const.
197
Табл и ц а 7.5
Числа Нуссельта для термического начального участка
круглой трубы при (?c=const (Nug) и £c=const (Nuf)
Л* d Pr=0,7; Re=104 Pr=0,7; Re=10“
Nui^ NUf Разница, % Nui Разница, %
2 42,83 39,28 9,0 131,6 125,3 5,1
5 36,90 34,68 6,4 116,7 111,9 4,2
10 34,15 32,44 5,3 108,7 104,8 3,7
20 32,72 31,32 4,5 103,8 100,5 3,3
30 32,42 31,11 4,2 102,4 99,40 3,0
СЮ 32,32 31,06 4,1 101,8 98,95 2,8
Предельные числа Нуссельта NuOT для жидких металлов (Pr< 1)
в случае постоянной температуры стенки получены Себаном и Ши-
мазаки [35]. Вычисления проведены с использованием трехслойной
модели потока (ламинарный подслой при т) 5, промежуточный слой
и турбулентное ядро) в предположении, что РгтС = 1. Результаты
их расчета в диапазоне чисел 0,001 Рг 0,1 и 104 Re 106
с погрешностью ±6% описываются уравнением
Nu^ = 5 + 0,025Ре°>8.
(7.44)
198
Отсутствие надежных опытных данных по местной теплоотдаче
к жидким металлам в случае tG = const пока не позволяет проверить
уравнение (7.44)* . Однако до получения таких данных им, по-ви-
димому, можно пользоваться для практических расчетов.
В случае, когда задана постоянная температура стенки, наи-
больший интерес представляет средний по длине трубы (или участка
трубы) коэффициент теплоотдачи. Как показано в §5.1, средний
коэффициент теплоотдачи на участке трубы от х — 6 до х = I
adx
ndlAt
где Qc — количество тепла, подведенное к жидкости (или отведен-
ное) на участке длиной /; AZ — средний логарифмический темпера-
турный напор, определяемый по уравнению (5.26).
Значения а, найденные в результате теоретического расчета и по-
лученные экспериментально при Рг — 0,7, находятся в хорошем
согласии. В. М. Легкий и А. С. Макаров [10], обработав результаты
собственных измерений и опытные данные других авторов, предло-
жили интерполяционное уравнение для средней теплоотдачи в тер-
мическом начальном участке при течении газа:
Nu —— 0,08-10nRe0*7 ( —0,22
(7.45)
где
п = 0,1
d /
Уравнение справедливо при значениях 0,06 < l/d <60, 3 • 10;i <
< Re < 105 и Рг = 0,7. При l/d > 60 значение Nu = Nu^. По-
следнее рассчитывается по уравнениям (7.21) и (7.24).
Таблица 7.6
Отношение Nu/Nuoo в случае £c=const
0,05 0, 1 0,5 1,0 2,0 5,0 10 15 20 30 40 50 60
104 5,10 4,10 2,48 2,02 1,67 1,39 1,26 1,19 1,15 1,09 1,05 1,02 1,0
5- Ю4 3,73 3,01 1,92 1,69 1,53 1,36 1,25 1,19 1,14 1,09 1,05 1,02 1.0
106 3,26 2,65 1,83 1,66 1,51 1,34 1,24 1,18 1,13 1,08 1,05 1,02 1,0
В табл. 7.6 приведено отношение Nu/NuM при различных зна-
чениях l/d и Re. Уравнением (7.45) и табл. 7.6, по-видимому, мож-
но пользоваться и при значениях Рг несколько больших единицы
(например, для воды).
* Совпадение эмпирического уравнения (7.29), полученного при qc •=
= const, с расчетно-теоретическим уравнением (7.44) для случая /е — const
носит случайный характер и не может рассматриваться как эксперименталь-
ное подтверждение уравнения (7.44).
199
Влияние термического начального участка на среднюю тепло-
отдачу для жидких металлов можно приближенно учесть с помощью
соотношения
= 1,72 —) , (7.46)
NUqo U I { J
полученного в работе [14] и справедливого при 5 < lid < 30 и Ре >
> 50. Значение Nu^ вычисляется по уравнению (7.44).
§ Т.7. Теплообмен в гидродинамическом начальном участке
Выше был рассмотрен теплообмен при полностью развитом (ста-
билизованном) течении жидкости по всей длине обогреваемого участ-
ка трубы. Такое течение реализуется при наличии перед обогревае-
мым участком успокоительного (необогреваемого) участка. Однако
в практических условиях успокоительный участок обычно отсутст-
вует и вход жидкости в обогреваемую трубу осуществляется непо-
средственно из достаточно большого резервуара (входной камеры,
коллектора и т. п.). В таких случаях развитие процесса теплообмена
по длине трубы происходит одновременно с развитием течения и в ре-
шающей степени определяется последним; другими словами, терми-
ческий и гидродинамический начальные участки частично или пол-
ностью совпадают.
Характер течения в гидродинамическом начальном участке
существенно зависит от условий на входе — конструкции входного
устройства, числа Рейнольдса и степени турбулентности потока во
входном сечении. В дальнейшем рассмотрим два характерных типа
входного устройства: 1) вход в трубу из резервуара при постепен-
ном уменьшении входного сечения, т. е. через плавно очерченное
сопло, и 2) вход при скачкообразном уменьшении сечения, т. е.
непосредственно через входное отверстие трубы с острыми кромками.
1. Вход через плавно очерченное сопло. При входе турбулент-
ного потока жидкости в трубу через плавно очерченное сопло поле
скорости во входном сечении трубы будет практически однородным.
При не слишком больших значениях числа Re на стенках трубы
вблизи от входа возникает ламинарный пограничный слой (рис.7.17).
Его толщина по мере удаления от входа увеличивается и на расстоя-
нии от входа хп.у достигает значения, при котором ламинарное те-
чение теряет устойчивость и наступает переход к турбулентному те-
чению. Расстояние хп.у определяется значением числа Рейнольдса
потери устойчивости Rex п.у = WqX^^/v, где г^0 — скорость жи-
дкости во входном сечении. На участке от хп у до хпер наблюдается
постепенный переход от ламинарного течения в пограничном слое
к развитому турбулентному. Последнее наступает при некотором
постоянном значении числа Рейнольдса перехода Rexnep =
= ayoxnep/v. При х > хпер течение в пограничном слое остается
турбулентным. Расстояние от входа, на котором пограничный слой,
200
развивающийся на стейках, заполнит все сечение трубы, составляет
длину гидродинамического начального участка /1ЬГ (обычно /Н.Р
>х'пср). Профиль скорости, однородный во входном сечении, пре-
образуется в полностью развитый в конце начального участка.
На рис. 7.17 и 7.18 показано изменение коэффициента сопротив-
ления £ ~ —(dp/dx) • (2d/proo) и числа Nu = ad/K по длине началь-
Рис. 7.17. Изменение коэффициента
сопротивления по длине трубы при
входе жидкости через плавно очерчен-
ное сопло.
Рис. 7.18. Изменение числа Нуссельта
по длине трубы при входе жидкости
через плавно очерченное сопло
Rei<Re2<Re3 и т. д.
иого участка [4,16]. По мере нарастания ламинарного пограничного
слоя £ и Nu уменьшаются, при х & хп.у проходят через ми-
нимум, а в переходной области (хп>у < х <Z хпер) увеличиваются.
Если хцер « /н.г, то при х > jcnep £ и Nu принимают постоянные
значения. Если же хлер < ZH-r, то после некоторого уменьшения,
соответствующего нарастанию турбулентного пограничного слоя,
£ и Nu также принимают постоянные значения.
При данной конструкции входа и неизменной степени турбу-
лентности во входном сечении Цеж п>у = Re (xn,y/d) й Rex пер =
= Re (xnep/d) имеют постоянные значения. Поэтому с увеличением
Re = wQdh протяженность участков, занятых ламинарным погра-
ничным слоем и переходной областью, сокращается. При достаточно
больших числах Re ламинарный пограничный слой может полностью
201
отсутствовать; при этом в самом начале трубы возникает переходная
область. При еще более высоких числах Re исчезает и переходная
область. В этом случае в самом начале трубы возникает турбулент-
ный пограничный слой, для которого характерно уменьшение t
и Nu по длине начального участка.
Критические числа Рейнольдса Rexn.y и Rexnep зависят от кон-
струкции входного устройства (степени сужения и профиля сопла,
наличия и типа решеток во входной камере) и степени турбулент-
ности потока* во входном сечении. По данным А. С. Сукомела и др.
[26], при входе жидкости в трубу из входной камеры, в которой от-
сутствуют специальные турбулизирующие устройства, через плавно
очерченное сопло Rexn.y изменяется в пределах от 4 • 104 до 2 * 10б,
a Rexnep от 2 10бдо ~7 • 106. Значения Rexn,y = 4 • 104 и Rexncp =
= 2 • 105 по данным [26] соответствуют степени турбулентности
во входном сечении е « 0,6%. Более высокие значения ReXJI.y и
Rexnep, по-видимому, соответствуют более низким значениям е.
При наличии перед входом в трубу специальных устройств, турбу-
лизирующих поток, значения е могут достигать нескольких процен-
тов и даже десятков процентов. В этом случае значения Rexn.y и
Rexncp будут ниже приведенных ранее значений.
Длины гидродинамического и термического начальных участ-
ков, насколько можно судить по данным работы [27] и некоторым
другим, приблизительно одинаковы (по крайней мере при Рг «
0,7 ~ 10) и в диапазоне значений Re от 104 до 1,2 • 105 могут
быть оценены по приближенным уравнениям, предложенным
С. С. Филимоновым и Б. А. Хрусталевым [27]:
/н.г 4,5-105
d ~ Re ’
^£«0,6Re‘/4,
Re<5-104;
Re>5-104.
Наблюдения показывают, что степень турбулентности во внешнем
потоке (во всяком случае при небольших значениях 8) почти не
оказывает влияния на закономерности теплообмена при ламинарном
и турбулентном пограничных слоях. Что же касается переходной
области, то здесь теплоотдача, естественно, зависит от степени тур-
булентности, поскольку от нее зависят значения Rexn-y и Rexnep.
В случае qc — const местные коэффициенты теплоотдачи в на-
чальном участке можно рассчитать:
а) при Rex Rexnep по уравнению (5.50) для теплоотдачи в гид-
родинамическом начальном участке при ламинарном течении жид-
кости;
* Степенью турбулентности называется отношение средней квадратич-
ной величины пульсаций составляющих вектора скорости (оф, w'y, w'z) в дан-
ной точке турбулентного потока к осредненному значению скорости
(w ~ ш0)
202
б) при Rexn>y< Rex< Rexncp по уравнению
Nux==CRe“Pr0’4; (7.47)
в) при Rex Rexn(,p по уравнению [22, 26]
Nux. = 0,029ReJ'8Pr°’'1. (7.48)
В формулах (7.47) и (7.48) Nux = ах/Х; а = qa /(ta — /0); Rex =
= wox/v, x — расстояние от входного сечения трубы до рассматри-
ваемого сечения; tc — температура стенки в этом сечении; t0 и ау0 —
температура и скорость жидкости во входном сечении.
Чтобы определить постоянные С и п в уравнении (7.47) , предва-
рительно находят значение Миж при х = хп.у по уравнению (5.50)
и значение Nux при х = хпер по уравнению (7.48). Подставив эти
значения в уравнение (7.47), получим два уравнения, совместное
решение которых позволяет определить значение С и п. Например,
при Rexn.y = 4 • 10% Rex пер = 2 • 105, Re = 2 • 104 и Рг = 0,71
получим С = 0,0021 и п = 1,01.
Заметим, что уравнение (7.48) справедливо при значениях x/d
30 и Re 104. Пользуясь уравнениями (5.50), (7.47) и (7.48),
можно рассчитать а и изменение температуры стенки по длине на-
чального участка при заданном значении qc.
Если задана постоянная температура стенки (£с = const), то
целью расчета обычно является определение среднего коэффициента
теплоотдачи на начальном участке. Последний можно вычислить
с помощью очевидного уравнения
_> р —— •— >. 10 “ t Q
_ &лХа.у4- 1апер (Xrtep Хп.у) 4“ атб Rii.t -Хаср)]--т-т
а =-------------------------------------------—, (7.49)
41. т
где ал, апер, атб — среднеинтегральные значения коэффициентов
теплоотдачи на участках трубы, занятых ламинарным пограничным
слоем, областью перехода и турбулентным пограничным слоем;
ZH.-r /пл. — длина термического начального участка; AZ --сред-
ний логарифмический температурный напор. Коэффициент ал вы-
числяется по уравнению (5.32), а коэффициенты апер и атб—по
уравнениям, которые можно получить в результате интегрирования
(7.47) и (7.48) по длине соответствующих участков.
2. Вход с острой кромкой. В этом случае за острой кромкой об-
разуется система вихрей, оттесняющих на некотором участке трубы
поток от стенки (рис. 7.19). Ламинарный пограничный слой вблизи
от входа в данном случае не возникает. В вихревой области, через
которую жидкость не протекает, наблюдается пониженная теплоот-
дача. Однако по мере удаления от входа теплоотдача быстро растет
и, достигнув максимума, который можно интерпретировать как воз-
никновение развитого турбулентного пограничного слоя, снова
уменьшается, стремясь к постоянному предельному значению (кри-
203
вая 1 на рис. 7.19). При значениях Re > 8 • 103 почти в самом на-
чале трубы возникает развитый турбулентный пограничный слой
с характерным для него уменьшением теплоотдачи (кривая 2 на
рис. 7.19).
Длина термического начального участка при входе с острой
кромкой приблизительно совпадает с длиной гидродинамического
участка (при Рг & 0,7 4- 10). По данным работы [27], при значении
Re 4 • 103 /гьт « 20Д а в диапазоне чисел Re от 10'1 до 8 • 104
длина термического начального участка изменяется в пределах от
10d до 15Д
Рис. 7.19. Зависимость отношения числа Нуссельта к его
предельному значению от x/d в случае входа с острой
кромкой.
Относительная теплоотдача в термическом начальном участке
Nu/NuTO зависит от x/d, а также от Re и Рг. Теплоотдачу на участке
трубы, занятом турбулентным пограничным слоем (т. е. при х <
Д.т)> можно рассчитать по уравнению (7.48), что подтверждено
экспериментально при 8 • 103 Re 2 • 105 в работе [26]. Для
приближенного расчета теплоотдачи можно также воспользоваться
уравнением, предложенным в работе [27]:
(7-50)
где Nu^ вычисляется по уравнениям (7.21) и (7.24). Кривая 2 на
рис. 7.19 соответствует уравнению (7.50). Уравнениями (7.48) и (7.50)
можно пользоваться для расчета теплоотдачи как при qc — const,
та к и при /с = const.
204
§ 7.8. Теплообмен при переменной по длине плотности
теплового потока на стенке
Рассмотрим задачу о теплообмене в круглой трубе, полагая те-
чение гидродинамически стабилизованным, температурное поле на
входе в обогреваемый участок однородным, а плотность теплового
потока на стенке qc (х) заданной функцией расстояния от входа.
Для случая ламинарного течения жидкости такая задача была
рассмотрена в § 5.2, п. 2. Использованный там метод суперпозиции,
а следовательно, и уравнения (5.51) и (5.52) можно применить и к
случаю турбулентного стабилизованного течения жидкости с по-
стоянными физическими свойствами*.
При заданном распределении плотности теплового потока (х)
задача сводится к отысканию распределения температуры стенки
или числа Нуссельта по длине трубы. Безразмерная температура
стенки при переменном значении qa (х) в соответствии с (5.52) оп-
ределяется из уравнения
АГ
в,. ;~q,.a в’ (х) + С ДД 6с (x-g) dl, (7.51)
о
где в* — безразмерная температура стенки в задаче о теплообмене
при qc = const. Решение этой задачи приведено в § 7.5. Положив
в уравнении (7.34) = /Д, получим
в' = -Дг 5 + G < Д + 2 С„ Н) ехр ( х). (7.52)
RePr м = о \ Re J
В уравнениях (7.51) и (7.52) в отличие от уравнения (5.52) ис-
пользуются несколько другие безразмерные величины. Здесь
@с = (tG — Тео = 7соЧ-.м; 7с 7с/7с.м; = х^;
<7со — значение qc при 1' = £ = О, т. е. при входе в обогреваемый
участок; дс.м— масштаб для плотности теплового потока на стенке.
В зависимости от конкретного вида функции qc (х) = qG (£•) в ка-
честве масштаба удобно выбрать либо значение q(. в какой-либо фик-
сированной точке (например, б/с0), либо среднее по длине значение
7с (7с.м = 7с), либо положить qCtM = 1.
Таким образом, с помощью уравнения (7.51), если известно
@с(х), можно вычислить ©с для заданного распределения qc (х).
Определив затем
@ Г ~ ф (7.53)
<7с.м d RePr J \ /
А, °
* Заметим, что уравнение энергии для осреднеиного турбулентного дви-
жения, содержащее коэффициент турбулентного переноса тепла, не является
точным. Поэтому результаты такого расчета нуждаются в экспериментальном
подтверждении.
205
можно найти число Нуссельта:
Nu=^M. (7.54)
0С—0
В тех случаях, когда зависимость 0* (х) не известна, но извест-
на зависимость Nu* (х) при qc = const, уравнение (7.51) можно
Рис. 7.20. Отношение местного числа Нуссельта при
qc ~ехр (0,150 х) (кривая /); ехр (0,074 х) (кри-
вая 2) и <7с = const (кривая 3) к предельному числу Нус-
сельта при <7c = eonst в зависимости от x/d. Re=105
Рг=0,7. Точки — опытные данные.
привести к виду, позволяющему непосредственно определить число
Nu (х) при переменной плотности теплового потока на стенке:
7с0 । С dqc (£)
Nu(x) Nu* (х) J Nu* (x—£)
ИЛИ
Nu(x) _____________7c (x)___________
Nu* ~ ' (7.55)
°° ?co , ? dqc (g) dl,
S*(7) < 8*(7-g)
где e* = Nu*/Nu«, т. e. отношение местного числа Нуссельта
к предельному в случае qc — const. Это отношение можно рассчи-
тать по уравнению (7.37) или (7.38) (при 0,7 Рг < 1), a Nu^ —
по уравнениям (7.21) и (7.24).
Результаты некоторых вычислений для чисел Re = 105 и Рг =
= 0,7 в сопоставлении с опытными данными представлены на
рис. 7.20 и 7.21 [32]. Первый из них относится к случаю экспонен-
20 6
циалы-юго увеличения плотности теплового потока на стенке, вто-
рой — к синусоидальному распределению qc (х). Как видим, ре-
зультаты расчета хорошо согласуются с экспериментальными дан-
ными (некоторый разброс экспериментальных точек при малых х
на рис. 7.21 связан с трудностями измерения малых разностей тем-
ператур). Характер изме-
нения числа Нуссельта по
длине трубы для данного
распределения е/с (х) в слу-
чае турбулентного течения
качественно тот же, что и
при ламинарном. Напри-
мер, при экспоненциаль-
ном увеличении qc (см.
рис. 7.20), в соответствии
с тем, что было сказано в
§ 5.2, п. 2, число Нуссель-
та выше, чем при qG ==
— const, и при х —*-оо,
стремится к предельному
значению. При синусои-
дальном распределении qG
(см. рис. 7.21) также на-
блюдается качественное со-
ответствие в характере рас-
пределения чисел Нуссель-
та при ламинарном и тур-
булентном течениях (см.
рис. 5.7 и 7.21)* .
Влияние на теплообмен
аксиального изменения
плотности теплового пото-
Рис, 7.21. Отношение местного числа Нус-
сельта при ~ sin(nx/21) (кривая /) п
<7c=const (кривая 2) к предельному числу
Нуссельта при qu = const в зависимости от
x/d. Re=l()5, Рг = О,7. Точки — опытные дан-
ка зависит от числа
Прандтля. При значениях
Рг 1 оно невелико, и часто его можно не принимать во внима-
ние** .
При малых значениях Рг, характерных для жидких метал-
лов, это влияние может быть весьма существенным и должно
учитываться при расчете. Известное представление о роли числа
Прандтля может дать рис. 7.16, на котором приведено отношение
Nu^i/Nu^..
* Данные, приведенные на рис. 7.21, соответствуют значению l/d — 28.
В реальных ядерных реакторах l/d гораздо больше, а разница в значениях Nu
при синусоидальном и однородном распределении qc соответственно значи-
тельно меньше.
** Это верно только при постоянных физических свойствах жидкости
(газа). В случае переменных свойств это влияние может быть значительным.
207
Отметим в заключение, что задачи о теплообмене при переменной
плотности теплового потока можно решать, не прибегая к методу
суперпозиции, а используя численные методы. Так, в работе [1]
приведены результаты численного расчета теплоотдачи для различ-
ных законов изменения qc по длине трубы.
§ 7.9. Теплообмен при наличии в потоке внутренних
источников тепла
Этот вопрос особенно важен для гомогенных ядерных реакто-
ров. В таких системах практически все тепло выделяется в потоке
теплоносителя, который одновременно служит и ядерным топливом* .
Однако и в гетерогенных реакторах вследствие поглощения нейтро-
нов и наведенной радиоактивности в потоке теплоносителя также
могут возникнуть внутренние источники тепла.
Рассмотрим стабилизованный теплообмен в круглой трубе при
полностью развитом течении жидкости. Мощность внутренних ис-
точников тепла будем считать постоянной (qv ~ const). Примем
также постоянной плотность теплового потока на стенке (q0 = const).
Все остальные условия те же, что в § 7.1 (см. стр. 165).
Изменение среднемассовой температуры жидкости по длине
трубы легко определяется из теплового баланса
~t - tQ + ..5?r°±?-7c х, (7.56)
pcpWo
где t0 — температура жидкости на входе в обогреваемый участок,
qv — мощность внутренних источников тепла.
Рассматриваемая задача сводится к решению уравнения энергии
(7.57)
при граничных условиях
\ дг /г = о
dt \ qc
дг /г=|г0
(7.58)
Так как теплообмен стабилизован, a qv и qG постоянны, то вы-
полняется условие (см. §7.1)
д‘ = dt<==di = Чуг„+2дс . (7 59)
дх dx dx pep wr0
* Реакторы такого типа неоднократно описывались в литературе, хотя
и не получили пока практического применения.
208
dt
Подставив в уравнение (7.57) значение из (7.59), после иеко-
и X
торых преобразований получим
# (1 _i М
dR L \, a j dR
Qv г2 2<7с гр
JL 9. (Ц7 _ n_L_Z12
X k х 4 г X
где R^r/rn, Wx = wx/w.
Интегрируя это уравнение дважды по 7?, найдем
температуры по радиусу:
Wx , (7.60)
распределение
/ С t 1
2<7сТо J
% «
J?
J‘ WxRdR
.Jo----------dR, (7.61)
( 1 4-JJ) R
\ a 7
где f/y = qvrj2qc — относительная мощность внутренних источни-
ков тепла.
Из уравнения (7.61) видно, что поле температуры в потоке мож-
но рассматривать как сумму двух полей, из которых одно обусловле-
но действием внутренних источников тепла, а другое — теплооб-
меном через стенку. Это результат линейности дифференциального
уравнения энергии и граничных условий относительно темпера-
туры.
Источники тепла оказывают тем большее влияние на поле тем-
пературы и на теплоотдачу, чем больше по абсолютной величине
параметр qv и разность Wx — 1. Если при однородном распределе-
нии внутренних источников профиль скорости также однороден,
т. е. Wx = 1, то изменение температуры, вызванное действием источ-
ников, в каждой точке потока будет одним и тем же. Поэтому про-
филь температуры и коэффициент теплоотдачи не изменяются. Дей-
ствительно, из (7.61) видно, что при qy = 0 или ИД = 1 это уравне-
ние переходит в ранее полученное уравнение (7.10) для поля темпе-
ратуры без источников тепла.
Характер влияния внутренних источников тепла на профиль
температуры проще всего проследить на примере ламинарного те-
чения. Положив в (7.61) &q — 0 и Wx = 2(1 — R2), получим
или
= Т(1 — Я2)2 + (1 — #2)(3 — Я2)
7с г0
AzJ_ = (1 —R^d- — (1 — 7?2) (3 — 7?2).
8А,
(7.62)
209
Профили температуры, рассчитанные по этим уравнениям для
различных значений qv, представлены на рис. 7.22, а (при фикси-
рованном значении qc) и рис. 7.22, б (при фиксированном значении
qv). При qv = 1 тепловая мощность, подводимая (либо отводимая)
к потоку через стенку, равна тепловой мощности, выделяемой (или
поглощаемой) источниками. Если qv ~ —1, эти мощности равны
О 0,2 0,0 0,6 0,8 6 0 0,2 0,0 0,6 0,8 6
а д
Рис. 7.22. Профили температуры при ламинарном
течении жидкости с источниками тепла в потоке
при фиксированном значении qa (а) и при фикси-
рованном значении qv (б).
по абсолютной величине, но противоположны по знаку. В последнем
случае, как видно из выражения (7.59), температура в любой точке
потока не изменяется по длине, а распределение температуры по
радиусу становится подобным распределению скорости. При
qv < —2 на профиле температуры появляется вторая экстремаль-
ная точка (кроме точки на оси трубы).
Чтобы рассчитать теплоотдачу, вычислим предварительно раз-
ность между температурой стенки и среднемассовой температурой
210
жидкости. По определению
1
/,.-/==2 WxRdR.
О
После интегрирования по частям получим
Подставив в это выражение значение dt из (7.61), имеем
/ д \ д
о * f WxRdR f (Гх-1) W
-------Ь------------dR +
1 (l+-h
\ a I
1 / R \ 2
p J RdR
I -lb-------dR. (7.63)
x J (l + ^>
0 \ a /
Уравнение (7.63) позволяет определить температуру стенки при
заданных конечных значениях q0 и qv. Обозначим -f)’o — tc — t эту
температуру, отсчитанную от t. Теперь предположим, что плотность
теплового потока на стенке qa = 0 или, другими словами, что стен-
ка трубы теплоизолирована. Температуру стенки в этом случае бу-
дем называть адиабатической температурой стенки и введем для
нее обозначение Фа.о ~ ^а.о — ^с=о» где = осреднемассовая
температура жидкости при qc = 0.
Из формулы (7.63) следует, что
Последнее уравнение показывает, что при наличии в потоке внутрен-
них источников тепла qc пропорционально разности Оу — д'а_с (а не
разности tc — t). Поэтому коэффициент теплоотдачи и число Нус-
211
сельта целесообразно определять следующим образом:
Тогда из (7.65) находим
1 / R \2
Р f RdR
—= 2 I -Ao----------------L dR.
Nu- J fi + AlU
0 \ a I
Это выражение полностью совпадает с ранее полученным выраже-
нием (7.13) для числа Нуссельта при отсутствии внутренних источ-
ников тепла.
Таким образом, если коэффициент теплоотдачи отнесен к раз-
ности между температурой стенки и адиабатической температурой
стенки (йс — йа.с), то число Нуссельта при наличии в потоке внут-
ренних источников тепла имеет то же значение, что и при отсутст-
вии источников тепла [18]. Поэтому Nu^ можно вычислять по урав-
нениям для теплоотдачи без источников тепла. Например, при ла-
минарном течении NuX, = 4,36, а при турбулентном течении газов
и неметаллических жидкостей число Nul вычисляется по уравне-
нию (7.21). Температура стенки при заданных значениях qc и qv
определяется с помощью очевидного соотношения, вытекающего из
принятого способа определения коэффициента теплоотдачи:
9с 4
~1Г
—г + qv ©аД.
Nuoo
(7.66)
Если qv — 0 или 0а.с = 0, то соотношение (7.66) выражает обычный
способ определения коэффициента теплоотдачи или числа Нуссель-
та (а = qc/(tG — ty.
Итак, для расчета температуры стенки необходимо предваритель-
но определить 0а.с.
Прежде чем перейти к определению ©а.с, отметим, что сформули-
рованные выше положения справедливы не только при однородном,
но и при произвольном распределении источников тепла по радиусу
трубы. В этом случае для адиабатической температуры стенки по-
лучается выражение
1 [R \ R
Р j* WxRdR\ J (№X-Qy) RdR
0а.с = ЁщдА = 2 I -А----------2_о_--------------dR, (7.67)
rQ J
0 \ a I
212
где
2 ( qv(R) RdR;
О
Чу (Я)
Qv
Чу
При qy const уравнение (7.67) переходит в (7.64). Из выраже-
ния (7.67) следует более обшиб вывод (по сравнению с ранее сформу-
лированным): если распределение внутренних источников тепла
подобно профилю скорости, т. е. Qy Ф'Л. (R), то 6)а 0 и внут-
ренние источники тепла не оказывают никакого влияния на профиль
температуры и теплоотдачу. Напри-
мер, если тепловыделение в потоке
однородно, а профиль скорости неод-
нороден, то слои жидкости, близ-
кие к стенке, нагреваются сильнее,
чем слои, находящиеся вдали от нее,
так как первые движутся медленнее,
чем вторые. В результате в сечении
трубы (при (/(. - 0) установится не-
однородное распределение температу-
ры и ёа<(. будет отлична от пуля.
Если же распределение qy подобно
распределению то все слои нагре-
ваются одинаково, температура (при
q(. — 0) будет постоянна по сечению,
а 0а>с — 0. В этом случае и при
qc 0 источники тепла не влияют на
профиль температуры и теплоотдачу.
В случае ламинарного течения жид-
кости при qv — const безразмерная
адиабатическая температура стенки
легко определяется из (7.64), если
положить == 2(1 -— R2) и вд — 0.
В результате получим
0-...,=—. (7.68)
Рис. 7.23. Зависимость адиаба-
тической температуры стенки от
чисел Re и Рг при турбулент-
ном течении жидкости с источ-
пиком тепла в потоке.
В случае турбулентного течения
Температура 0а.(. вычислена в не-
скольких работах. Наиболее полные вычисления при qy = const
проведены Л. Г. Гениным и Б. С. Петуховым [20]. В этой работе
скорость жидкости и коэффициент турбулентного переноса, входя-
щие в уравнение (7.64), рассчитывались по уравнениям Рейхардта
(6.72)— (6.74), а турбулентное число Прандтля sCT/eq принималось
равным единице. Расчет проводился численным методом в диапазоне
значений Re от 104 до 106 и Рг от 0 до 100. Результаты теоретического
расчета представлены на рис. 7.23. Как видно из рисунка, ©а.с
213
уменьшается с увеличением Re и Рг. В интервале чисел Ре от 10 до
108 результаты теоретического расчета с погрешностью ±5% опи-
сываются интерполяционным уравнением
A-I-B Ре'1’
(7.69)
где А, В и п зависят от числа Рг и определяются из следующих соот-
ношений:
при значениях Рг от 0,001 до 1:
А = 31 + Рг-0-4;
В = 0,0066 4- 0,0154 Рг-°’79;
п = (0,82 + 0,08 Pr-o.35)-i;
при значениях Рг от 1 до 100:
А = 250 — 380 Рг°>74;
В = (14,5 + 8,8 Рг1’05)"1;
п = 1,06 Рг°>036.
Измерения адиабатической температуры стенки при однородном
джоулевом тепловыделении в потоке ртути (Рг« 0,02), проведен-
ные в работе [20], подтверждают результаты теоретического расчета.
СПИСОК ЛИТЕРАТУРЫ
1. Достов А. И., Кузнецов Ю. Н. Анализ влияния переменности тепловой
нагрузки на конвективный теплообмен при турбулентном течении на
- основе численного решения задачи. — «Теплофизика высоких темпера-
тур», 1971, т. 9, № 5, с. 948.
2. Дрейцер Г. А., Изосимов В. Г., Калинин Э. К-Обобщение опытных дан-
ных по нестационарному конвективному теплообмену при изменении теп-
лового потока. — «Теплофизика высоких температур», 1969, т. 7, № 6,
с. 1222.
3. Дуайер О. Э., Лайон Р. Н. О теплопередаче жидких металлов. Доклад
№ 225 (США), представленный на Третью междунар. конф, по мирному
использованию атомной энергии. Женева, 1964.
4. Дыбан Е. П., Эпик Э. Я. Теплообмен в начальном участке трубы при
естественной турбулизации потока. — «Инж.-физ. ж.», 1968, т. 14, № 2,
с. 248.
5. Калинин Э. К-, Дрейцер Г. А., Ярхо С. А. Интенсификация теплообмена
в каналах. М., «Машиностроение», 1972.
6. Кейс В. М. Конвективный тепло- и массообмен. Пер. с англ. М.,
«Энергия», 1972.
7. Коченов И. С., Никитин Ю. М. О нестационарном конвективном тепло-
обмене в трубах. — «Теплофизика высоких температур», 1970, т. 8, №2,
с. 346.
8. Кузнецов Ю. Н., Белоусов В. П. Построение расчетных формул для не-
стационарного конвективного теплообмена при турбулентном течении
в трубе в случае произвольного закона изменения тепловой нагрузки во.
времени. — «Теплофизика высоких температур», 1972, т. 10, № 1, с. 207.
9. Кутателадзе С. С. Основы теории теплообмена. М., Машгиз, 1962.
214
10. Легкий В. М., Макаров А. С. Теплообмен в термическом начальном участ-
ке при стабилизированном турбулентном течении воздуха в трубах и пря-
моугольных каналах. — «Инж.-физ. ж.», 1971, т. 20, № 2, с. 215.
11. Миллионщиков М. Д. Турбулентное течение в пристенном слое и в тру-
бах. — «Атомная энергия», 1970, т. 28, № 3, с. 207.
12. Миллионщиков М. Д. О турбулентном тепло- и массообмене. — «Атомная
энергия», 1970, т. 29, № 6, с. 411.
13. Миллионщиков М. Д. Турбулентный тепло- и массообмен в трубах с глад-
кими и шероховатыми стенками.—«Атомная энергия», 1971, т. 31, № 3,
с. 199.
14. Михеев М. А. и др. Теплоотдача расплавленных металлов. —В сб
Реакторостроепне п теория реакторов. М., Изд-во АН СССР, 1955, с. 139.
15. Новиков И. И., Воскресенский К. Д. Прикладная термодинамика и тепло-
передача. М., Госатомиздат, 1953.
16. Петухов Б. С., Краснощеков Е. А. О теплообмене в начальном участке
трубы при смешанном пограничном слое. — В сб.: Теплопередача и теп-
ловое моделирование. М., Изд-во АН СССР, 1953, с. 187.
17. Петухов Б. С., Кириллов В. В. К вопросу о теплообмене при турбулент-
ном течении жидкости в трубах. — «Теплоэнергетика», 1958, № 4, с. 63.
18. Петухов Б. С., Генин Л. Г., Мальтер В. Л. Теплообмен в трубах при
наличии в потоке жидкости внутренних источников тепла. — «Инж.-физ.
ж.», 1960, т. 3, № 9, с. 3.
19. Петухов Б. С., Юшпн А. Я. О теплообмене при течении жидкого металла
в ламинарной и переходной области. — «Докл. АН СССР», 1961, т. 136,
№ 6, с. 1321.
20. Петухов Б. С., Генин Л. Г. Теплообмен в трубах с внутренними источни-
ками тепла в потоке жидкости. — «Инж.-физ. ж.», 1963, т. 6, № 4, с. 3.
21. Петухов Б. С., Попов В. Н. Теоретический расчет теплообмена и сопро-
тивления трения при турбулентном течении в трубах несжимаемой
жидкости с переменными физическими свойствами. — «Теплофизика вы-
соких температур», 1963, т. 1, № 1, с. 85.
22. Петухов Б. С., Мухин В. А. Экспериментальное исследование теплоотдачи
при сверхзвуковом течении газа в круглой трубе. — «Теплофизика вы-
соких температур», 1966, т. 4, № 2, с. 228.
23. Петухов Б. С., Курганов В. А., Гладунцов А. И. Теплообмен в трубах при
турбулентном течении газов с переменными свойствами. — В сб.: Тепло-
и массоперенос, 1972, т. 1, ч. 2, с. 117.
24. Субботин В. И. и др. Теплообмен при течении жидких металлов в круглых
трубах. — «Инж.-физ. ж.», 1963, т. 6, № 4, с. 16.
25. Субботин В. И., Ибрагимов М. X., Номофилов Е. В. Обобщающая зави-
симость коэффициента переноса тепла в потоке жидкости. —«Теплофи-
зика высоких температур», 1965, т. 3, № 3, с. 42.
26. Сукомел А. С. и др. Экспериментальное исследование локальной тепло-
отдачи на начальном участке круглой трубы в случае переходного тече-
ния в пограничном слое и различном уровне турбулентности на входе.
Тр. МЭИ. Вып. 81. Теплообмен и гидродинамика одно- и двухфазных теп-
лоносителей, 1971.
27. Филимонов С. С., Хрусталев Б. А. Расчет теплообмена и гидравлического
сопротивления при турбулентном движении воды в трубах с различными
условиями на входе.—В сб.: Теплопередача. М., Изд-во АН СССР,
1962, с. 43.
28. Шлихтинг Г. Теория пограничного слоя. М., «Наука», 1969.
29. Burck Е. Der Einfluss der Prandtlzah 1 auf den Warmeubergang und Druck-
verlust kunstlich aufgerauhter Stromungskanale. — «Warme- und Stof-
fiibertragung», 1969, Bd. 2, S. 87.
30. Deissler R. G. Investigation of turbulent flow and heat transfer in smooth
tubes, including the effects of variable fluid properties.—«Trans. ASME»,
1951, v. 73, No. 2, p. 101.
215
31. Deissler R. G. Analysis of turbulent heat transfer, mass transfer and fric-
tion in smooth tubes at high Prandtle and Smidt number, NACA Tech.
Report, 1210 (1955).
32. Hall W. B., Price P. H. Effect of heat flux variation along a tube on turbu-
lent flow tube heat transfer, papers presented at the 1961. Intern. Heat
Transfer Conference.
33. Lyon R. N. Liquid metal heat-transfer coefficients. — «Chem. Engng.
Progress», 1951, v. 47, No. 2, p. 87.
34. Reichardt H. Die Grundlagen des turbulenten Warmeiibergangs. —
«Arch. Ges. Warmetechnik», 1951, H. 6/7, S. 129.
35. Seban R. A., Shimazaki T. T. Heat transfer to a fluid flowing turbulently
in a smooth pipe with walls at constant temperature. —«Trans. ASME»,
1951, v. 73, p. 803.
36. Siegel R., Sparrow E. M. Comparison of turbulent heat transfer results
for uniform wall heat flux and inform wall temperature. — «J. Heat Trans-
fer» (Trans. ASME, Ser. C), 1960, v. 82, N 2, p. 152.
37. Skupinski E., Tortel J., Vantrey L. Determination des coefficients de con-
vection d’un alliage sodium—potassium dansun tube circulate. — «Int.
J. Heat. Mass. Transfer», 1965, v. 8, No. 6, p. 937.
38. Sparrow E. M., Hollman T. M., Siegel R. Turbulent heat transfer in the
thermal entrance region of pipe with uniform heat flux. —- «Appl. Sci.
Res.», 1957, Ser. A, v. 7, p. 37.
ГЛАВА 8
ТЕПЛООБМЕН И СОПРОТИВЛЕНИЕ ПРИ ТУРБУЛЕНТНОМ ТЕЧЕНИИ
В ТРУБАХ ЖИДКОСТИ С ПЕРЕМЕННЫМИ ФИЗИЧЕСКИМИ СВОЙСТВАМИ
§ 8.1. Предварительные замечания
Закономерности теплообмена при постоянных свойствах жидкости,
рассмотренные в предыдущей главе, справедливы при условии, что
свойства жидкости мало изменяются в интервале температур, ха-
рактерном для рассматриваемой задачи. Такие условия реализуются
на практике либо при малых разностях температур в потоке, либо
при слабой зависимости физических свойств от температуры. В этих
случаях, выбирая физические свойства при некоторой средней тем-
пературе жидкости (например, при среднемассовой температуре
в данном сечении трубы), можно пользоваться уравнениями для
постоянных свойств, не внося при этом большой ошибки.
Однако в теплообменных системах часто реализуются большие
температурные напоры и высокие плотности теплового потока. На-
пример, в ядерных реакторах плотности теплового потока достигают
нескольких миллионов ватт иа квадратный метр. В качестве тепло-
носителей нередко используются жидкости и газы, физические
свойства которых сильно изменяются в зависимости от температуры.
Примером может служить однофазная среда при околокритических
параметрах состояния. В этих случаях уже нельзя пользоваться
уравнениями для теплоотдачи и сопротивления при постоянных
свойствах. Анализ движения жидкости и теплообмена в таких усло-
виях необходимо проводить с учетом зависимости физ ических
свойств жидкости от температуры.
При неоднородном распределении плотности в потоке жидкости
не только при ламинарном (см. § 5.4), но и при турбулентном дви-
жении следует различать два возможных режима течения: вязкост-
но-инерционный и вязкостно-инерционно-гравитациопиый. Первый
из них характеризуется пренебрежимо малым влиянием термогра-
витационных сил иа вынужденное течение и теплообмен и наблю-
дается при относительно малых значениях числа Грасгофа; второй
характеризуется существенным влиянием термогравитационных
сил и наблюдается при достаточно больших числах Грасгофа. При
одном и том же значении числа Gr влияние термогравитационных
сил проявляется тем сильнее, чем меньше число Re. На рис. 8.1 для
случая подъемного течения в вертикальной обогреваемой трубе
(вдали от входа при qc = const) показаны предельные кривые, соот-
ветствующие отклонению числа Нуссельта под действием термогра-
217
витационных сил на 1 % от его значения при вязкостно-инерционном
течении. Кривые вычислены А. Ф. Поляковым [13] исходя из урав-
нения баланса пульсационной энергии; они находятся в хорошем
согласии с результатами измерений, приведенными в работе [9].
Область, лежащая выше данной кривой, соответствует вязкостно-
инерционному течению, область, лежащая ниже, — вязкостно-
инерционно-гравитационному течению.
Закономерности течения и теплообмена в первой области в слу-
чае постоянных физических свойств изложены в гл. 7, а при пере-
менных свойствах будут рассмотрены в следующих параграфах этой
Рис. 8.1. Границы влияния термогравитацпонных сил на
теплоотдачу при подъемном турбулентном течении в вер-
тикальной обогреваемой трубе.
главы. Характеристики течения и теплообмена во второй области,
т. е. при существенном влиянии термогравитационных сил, зависят
не только от чисел Re и Рг, но и от Gr, а также от взаимного направ-
ления вектора скорости вынужденного течения и вектора термогра-
витационных сил. Последнее обстоятельство приводит, например,
к существенному различию в закономерностях течения и теплооб-
мена в обогреваемых трубах при подъемном и опускном движении
[9].
Для разных веществ и для одного и того же вещества в разных
областях параметров состояния характер изменения физических
свойств с температурой различен. Пока не представляется возмож-
ным с помощью единых зависимостей описать закономерности дви-
жения жидкости и теплообмена при любом характере изменения фи-
зических свойств. Вследствие этого задача о движении жидкости и
теплообмена при переменных свойствах распадается на ряд задач,
каждая из которых соответствует определенному типу зависимости
физических свойств от температуры. С этой точки зрения следует
различать капельную жидкость (конденсированную среду) с пере-
менной вязкостью, газ с переменными свойствами, однофазную среду
при околокритических параметрах состояния.
218
§ 8.2. Метод теоретического расчета
Рассмотрим квазистационарное турбулентное движение жидкости
и теплообмен в круглой трубе вдали от входа (т. е. в той области, где
тепловой и гидродинамический пограничные слои сомкнулись), по-
лагая жидкость несжимаемой, а ее физические свойства произволь-
но зависящими от температуры. Анализ такой задачи в настоящее
время можно провести лишь приближенно, ценой ряда упрощений.
Введем следующие допущения:
1) скорость жидкости невелика, так что диссипацией энергии
можно пренебречь;
2) влияние массовых сил мало по сравнению с силами вязкости
и инерции;
3) физические свойства жидкости в пределах пульсаций темпе-
ратуры изменяются слабо, так что их значения в данной точке можно
принять постоянными и равными значениям физических свойств при
осреднением значении температуры в этой точке;
4) изменение плотности теплового потока вдоль оси, обусловлен-
ное теплопроводностью и турбулентным переносом, мало по сравне-
нию с изменением вдоль радиуса;
5) изменение нормальных напряжений (вязких и турбулентных)
вдоль координатных осей мало по сравнению с изменением каса-
тельных напряжений. Изменением касательных напряжений вдоль
оси трубы, в свою очередь, можно пренебречь;
6) осевая составляющая массовой скорости мало изменяется
вдоль оси трубы, т. е. д (ращ.)/дх 0.
Из принятых допущений, в частности, вытекает, что составля-
ющая скорости вдоль радиуса wr & 0, а давление р постоянно по
сечению (др/дг « 0).
Если учесть перечисленные допущения, то уравнения энергии
и движения при турбулентном течении жидкости с переменными
свойствами можно записать в виде:
д/i 1 д - ч /о
Р^а,- — —-(/'<?); (° - И
дх г дг
— (р рШх) =----------—• (го), (8.2)
дх г дг
где
. Ч дТ
q ~ eQ) —.
dr
cr=-- — (и-фреа)-^,
dr
а р, ср, % и р — заданные функции температуры.
Чтобы выражения (8.1) и (8.2) превратить в обыкновенные диф-
ференциальные уравнения, введем дополнительное предположение
о постоянстве по сечению трубы производных по х, содержащихся
219
в левых частях уравнений (8.1) и (8.2), т. е. примем
=/1«
дх
Заметим, что первое из допущений (8.3) является менее жестким,
особенно при переменной теплоемкости, чем обычно принимаемые
допущения о линейном изменении q по радиусу или о постоянстве по
сечению продольного градиента температуры. Что же касается вто-
рого допущения, то для капельной жидкости и газа, движущегося
с малой дозвуковой скоростью, оно также должно выполняться, по-
скольку в этих случаях ~ < у, а давление в соответствии
с ранее принятыми условиями постоянно по сечению.
Полагая плотность теплового потока на стенке постоянной (qc —
= const) и интегрируя уравнения (8.1) и (8.2) с учетом условий
(8.3), Б. С. Петухов и В. Н. Попов [7] получили аналитические вы-
ражения, описывающие распределение температуры и скорости по
радиусу, а затем нашли выражения для числа Нуссельта и коэффи-
циента сопротивления трения. Эти выражения имеют вид:
1
Nuc
(8.4)
Я ~~RdR
№
% I 1 Рг 1-0 \
%с \ РгТб v /
(8.7)
В уравнениях (8.4) — (8.7)
ad __ _ qccpd . t _ 8стсРс .
A . _ч > Ьс ___ ч О ’
Ло (То-Т)^ (Ло-Л)Л^ (pmj-
220
р, Ср, X, [1 — значения соответствующих физических свойств при
текущей температуре Т; рс, ср , Ас, рс —то же при температуре
стенки Тс; ср— средняя удельная теплоемкость жидкости в ин-
тервале температур от Т до Тс:
hG и h — энтальпия жидкости при температуре стенки и среднемас-
совая энтальпия жидкости.
Если физические свойства постоянны, то уравнения (8.4) — (8.7)
сводятся к соответствующим уравнениям для постоянных свойств,
полученным в § 7.1.
Пользуясь уравнениями (8.4)—(8.7) и применяя метод последо-
вательных приближений, можно рассчитать поля скорости и темпе-
ратуры, число Нуссельта и коэффициент сопротивления при пере-
менных свойствах жидкости. Для удобства вычислений в уравнениях
следует перейти от координаты Д к универсальной координате т]с
с помощью соотношения
R 1-------,
Нос
где
Расчет проводится в такой последовательности.
1. Задают значения т]ос, qc d, Тс и р.
2. Выбрав те или иные зависимости для so/v и Ргтб, по уравне-
ниям (8.5) и (8.4) рассчитывают в первом приближении поля ско-
рости и температуры, полагая свойства жидкости постоянными
и равными их значениям при температуре стенки.
3. По найденному в первом приближении полю температуры рас-
считывают распределение физических свойств по радиусу. Затем
с помощью тех же уравнений определяют ea/v, РгтС, поле скорости
и поле температуры во втором приближении с учетом изменения фи-
зических свойств. Точно так же рассчитывают поле температуры
в третьем и последующих приближениях. Расчет проводится до тех
пор, пока различие в распределении температуры в двух последо-
вательных приближениях не станет меньше некоторого заданного
значения, в пределах которого изменением свойств можно прене-
бречь.
4. По найденному в последнем приближении распределению фи-
зических свойств рассчитывают e0/v, РгтС и распределение скорости.
Затем по уравнению (8.6) находят численное значение отношения
Nuc qc d
Ср (hc — й) А?с
221
Поскольку qcd и Тс заданы, то отсюда находят h и соответствующую
ей среднемассовую температуру Т. После чего определяют Nuc =
= qcd!(Tc - Т)кс.
Пользуясь уравнением (8.7), вычисляют коэффициент |с. Такие
вычисления, естественно, требуют использования ЭВМ.
Точность расчета теплообмена и сопротивления при переменных
свойствах в основном определяется используемыми при расчете за-
висимостями для коэффициентов турбулентного переноса. Законо-
мерности турбулентного переноса при переменных свойствах могут
существенно отличаться от соответствующих закономерностей при
постоянных свойствах, рассмотренных в гл. 6. Однако вопрос о ко-
личественном учете этого различия мало исследован. Его решение
обычно основывается на некоторых предположениях, нуждающихся
в экспериментальной проверке. Например, Голдман Г16], опираясь
на некоторые физические соображения, предложил определять
при переменных свойствах с помощью тех же уравнений, что
и при постоянных свойствах (например, уравнений Дайслера и Рей-
хардта, см. § 6.6), подставляя в правую часть этих уравнений вместо
переменных ср и ц обобщенные переменные:
где р и v — текущие значения плотности и кинематической вязко-
сти. Если р и v — постоянные величины, то ср+ = ср = wx/v* и
т]+ = 1] = v,vtjlv. Следует, однако, иметь в виду, что такой способ
учета влияния переменных свойств на турбулентный перенос, как
и другие способы, далеко не всегда приводит к правильным резуль-
татам. Поэтому результаты вычислений должны контролироваться
посредством сравнения с опытными данными.
В § 8.4 и 8.5 приведены результаты некоторых вычислений тепло-
отдачи и сопротивления, выполненные на основе изложенного здесь
метода.
§ 8.3. Теплообмен и сопротивление при течении
жидкости с переменной вязкостью
Физические свойства неметаллических капельных жидкостей
(конденсированных сред), исключая вязкость, слабо изменяются
с температурой. Вязкость капельной жидкости, напротив, очень
сильно убывает с ростом температуры и нередко изменяется по сече-
нию потока в десятки раз. Поэтому при анализе вязкостно-инер-
ционного течения и теплообмена для таких жидкостей можно огра-
ничиться специальным учетом изменения одной лишь вязкости,
полагая другие физические свойства (р, ср, %) постоянными и рав-
222
ними их значениям при некоторой средней температуре (например,
при среднемассовой температуре в данном сечении трубы).
Теоретический анализ и экспериментальные данные показывают,
что зависимость NuTO от Re и Рг при переменной вязкости сохра-
няется приблизительно такой же, как и при постоянных свойствах.
Поэтому отношение NuJNu^o практически не зависит от Re и Рг
(здесь Nu^ — число Нуссельта при переменной вязкости, найденное
из эксперимента; Nu^o— число Нуссельта при постоянных свой-
ствах, вычисленное при тех же значениях Re и Рг, что и Nu^). Влия-
ние же переменной вязкости можно учесть, поставив отношение
Nli^/Nu^o в зависимость от одного лишь параметра р,с/цж, т. е. от
Рис. 8.2. Влияние переменной вязкости па теплоотдачу при турбулентном
течении жидкости.
(8.9)
отношения динамических коэффициентов вязкости при температуре
стенки tc и среднемассовой температуре жидкости t. Результаты
обработки опытных данных, представленные на рис. 8.2, подтверж-
дают высказанные соображения. Экспериментальные точки хорошо
группируются около кривой (сплошная линия на рис. 8.2), которой
соответствует уравнение, полученное Б. С. Петуховым [10],
NUqo 1 (
NttooO ' В’К '
где п — постоянная. При нагревании жидкости (т. е. при |хс/р.ш
< 1) и — —0,11; при охлаждении жидкости (цс/рж > 1) п =
— —0,25. Nu^o (Re, Рг) вычисляется по уравнению (7.21). Физи-
ческие свойства жидкости (кроме цс) в уравнении (8.9) выбираются
при среднемассовой температуре в данном сечении трубы, а |1с —
при температуре стенки в том же сечении.
Уравнение (8.9) справедливо в пределах изменения отношения
рс/цж от 0,08 до 40, Re от 104 до 1,25 • 10б и Рг от 2 до 140.
Как видно из рис. 8.2, теплоотдача к жидкости, вязкость которой
зависит от температуры, в случае нагревания выше, а в случае ох-
лаждения ниже, чем при постоянной вязкости (т. е. при р-с/Иж =
= 1). Это объясняется тем, что при нагревании жидкости вязкость
в пристеночном слое меньше, а скорость больше, чем при изотерми-
ческом течении; при охлаждении жидкости наблюдается обратный
эффект.
223
Влияние переменной вязкости на коэффициент сопротивления
трения можно видеть на рис. 8.3, где представлены результаты из-
мерений Лафея [17]. Опыты проводились при движении воды в круг-
лой практически гладкой трубе вдали от входа при постоянной
плотности теплового потока на стенке. Они показали, что отноше-
ние коэффициентов сопротивления трения при перетлей ной и по-
стоянной вязкости £/Ej0 зависит не только от р-/р?к, ио и от Re и
практически не зависит от Рг (при его изменении от 2 до 6). Как видно
Рис. 8.3. Влияние переменной вязкости на сопротивле-
ние трения при турбулентном течении воды в обогревае-
мой трубе.
из рис. 8.3, отношение тем сильнее зависит от числа Re, чем
больше цс/ц,ж отличается от единицы. С увеличением [лс/щк отно-
шение увеличивается и, следовательно, при охлаждении жидко-
сти £ должно быть больше, чем при нагревании. Такое изменение £
легко объяснить. Дело в том, что по мере увеличения yiG градиент
скорости настенке уменьшается, однако его уменьшение происходит
медленнее, чем рост цс, поэтому касательное напряжение на стенке
°с = М-с (dwx/dyjg^o и коэффициент сопротивления трения £ --
— 8сгс/рйу2 увеличиваются.
Свои опытные данные и данные других авторов, относящиеся
к случаю нагревания жидкости, Лафей [17] описал эмпирическим
уравнением
t 1
= 1 __ _L_ (1 lg (14-А1), (8.10)
so
224
где
/dM0-17;
к Нс / к Цс /
п — 0,17 —- 2 • 10“6 Re -|-
Re
Для случая охлаждения жидкости в круглой гладкой трубе вда-
ли от входа можно рекомендовать уравнение [10]
-М-’-Г4- (8.11)
ёо к Нж '
Коэффициент сопротивления трения при изотермическом течении
жидкости £0 (Re) вычисляется по уравнению (6.62). Физические свой-
ства жидкости кроме цс, выбираются в уравнениях (8.10) и (8.11) при
среднемассовой температуре в рассматриваемом сечении, а рс —
при температуре стенки в том же сечении.
Уравнения (8.10) и (8.11) справедливы в диапазоне значений Re
от 101 до 3 • 105, Рг от 1,3 до 10 и цс/Щк от 0,3 до 1 [уравнение (8.10)]
и от 1 до 2 [уравнение (8.11)].
Приведенные выше сведения относятся к неметаллическим жид-
костям. Для жидких металлов, вследствие их высокой теплопровод-
ности, перепады температуры в потоке tc — t и в особенности гра-
диенты температуры по радиусу невелики. Физические свойства
жидких металлов в рабочем интервале температур сравнительно
слабо зависят от температуры. В таких условиях изменение физи-
ческих свойств жидких металлов не оказывает существенного влия-
ния на теплообмен и сопротивление. Поэтому все расчеты можно про-
водить, полагая свойства постоянными и выбирая их значения при
среднемассовой температуре жидкости в данном сечении трубы.
§ 8.4. Теплообмен и сопротивление при течении
газа с переменными свойствами
При изучении течений газа и теплообмена в области параметров
состояния, удаленной от кривой насыщения, газ можно рассматри-
вать как идеальный. Плотность такого газа в зависимости от дав-
ления и температуры определяется, как известно, уравнением Кла-
пейрона — Менделеева:
Р = ^. (8-12)
где R — газовая постоянная.
Другие физические свойства газа: удельная теплоемкость, коэф-
фициент теплопроводности и динамический коэффициент вязкости —
практически не зависят от давления и могут рассматриваться лишь
как функции температуры. Относительное изменение ср, Хирс тем-
пературой для некоторых одно-, двух - и многоатомных газов пока-
8 Зак. 792 225
зано на рис. 8.4. Как видно из рисунка, теплоемкость одноатомного
газа не зависит от температуры, теплоемкость двухатомного газа
слабо растет с температурой; для многоатомного газа эта записи*
мость значительно сильнее. Коэффициент теплопроводности и ди»
Рис. 8.4. Относительное изменение теплоемкости, теплопроводно-
сти и вязкости с температурой для некоторых газов при р=1 атм
и 7’0=373,2о К.
намический коэффициент вязкости газов увеличиваются с темпера-
турой. Характер зависимости % и ц от Т для одно- и двухатомных
газов приблизительно одинаков, однако К растет несколько сильнее,
чем р. Для многоатомных газов зависимость К от Т значительно
226
сильнее, чем зависимость ц от Т. Число Прандтля для газов (Рг =
= р,ср/%) слабо изменяется с температурой.
Физические свойства газа в зависимости от температуры можно
выразить с помощью приближенных степенных соотношений, точ-
ность которых обычно достаточна для целей расчета течения и теп-
лообмена:
JL— f Г Vu. f ZQ 194
UI ’ r(, / ’ % I To ? ’ }
где A,o, Цо и CPO — значения %, ц и ср при некоторой фиксированной
температуре То; п^, и пс — постоянные, зависящие от природы
газа и интервала температур.
Пользуясь методом подобия или методом размерностей, нетрудно
получить систему безразмерных чисел, характерных для задачи
о теплообмене и сопротивлении при течении газа с переменными свой-
ствами. Рассмотрим стационарное движение газа в круглой гладкой
трубе при следующих условиях: а) скорость газа мала по сравнению
со скоростью звука, поэтому сжимаемостью газа (зависимостью р
от р) и диссипацией энергии можно пренебречь; б) физические свой-
ства газа изменяются в зависимости от температуры в соответствии
с уравнениями (8.12) и (8.13); в) влияние массовых сил пренебрежи-
мо мало; г) профили скорости и температуры на входе в трубу од-
нородны по сечению; д) на стенке трубы поддерживается постоянная
температура (Тс = const) или постоянная плотность теплового по-
тока (рс — const).
В случае, когда задана температура стенки Тс = const, число
Nu и коэффициент £ зависят от следующих безразмерных чисел:
Nu,^ = Fz Re, Рг, <ЭС, п^, /щ, п^, (8-14)
где I = Nu, £:f!.
В случае задания qc = const безразмерная температура стенки
(а также число Nu) и В определяются системой чисел
®с. £ = ре’ Рг’ (8Л5)
В формулах (8.14) и (8.15) <ЭС = Тс/Т0 — безразмерная темпе-
ратура стенки или так называемый температурный фактор; Qc =
~ qc — безразмерная плотность теплового потока; То —
температура газа на входе. В задаче о теплообмене при Тс — const
'0С — заданная постоянная величина, а в задаче о теплообмене при
7с = const как ®0, так и число Nu,—искомые переменные вели-
чины (функции x/d).
* Функции rNu и jpg описывают соответственно изменение Nu и
8* 227
Безразмерные числа Nu, В, Re и Рг в уравнениях (8.14) и (8.15)
определены по заданным параметрам потока на входе, а <ЭС и Qc
содержат в качестве масштаба То.
Опыт показывает, что такое представление безразмерных чисел
удобно при анализе и обобщении опытных данных (или результатов
численного расчета), относящихся к термическому и гидродинами-
ческому начальным участкам. Вдали от входа в трубу, где влияние
условий во входном сечении уже не существенно, лучшие результаты
и более простые соотношения дает обобщение опытных данных по
местным параметрам потока, например по среднемассовой температу-
ре в данном сечении Т. В этом случае безразмерные числа в (8.14)
и (8.15) определяются следующим образом:
ocd d в о. Sctq Рж.
А-Ж (ТС (ри^х)2
(8.16)
Рг = Рг,„; 0O = -S; Qo=-M-,
1 *
где стс—касательное напряжение настенке; —средняя массовая
скорость; индекс «ж» означает, что соответствующие свойства вы-
бираются при среднемассовой температуре жидкости Т в данном
сечении трубы.
Заметим, что применительно к задаче о теплообмене при qc =
= const использование безразмерных чисел (8.16) вполне коррект-
но, в этом случае Т по существу задана (легко определяется из теп-
лового баланса). В задаче о теплообмене при Тс = const использо-
вание чисел (8.16) некорректно, так как здесь Т — неизвестная
(искомая) величина. Однако на практике для обобщения опытных
данных как при Тс — const, так и при qc~ const нередко пользуются
одной и той же системой безразмерных чисел (8.14), определенных
в соответствии с (8.16). Такой чисто эмпирический прием можно
оправдать лишь неполнотой наших знаний, пока не позволяющих
провести четкую грань между различными задачами.
Таким образом, при переменных физических свойствах газа
в уравнениях подобия появляются четыре новых параметра <ЭС
или Qc, «х., и пс, учитывающих влияния переменных свойств на
гидродинамику и теплообмен. Первые два из них, каждый в своем
случае, характеризуют относительное изменение температуры в по-
токе, а остальные отражают влияние температурной зависимости
%, р и ср, специфической для каждого газа.
Теоретический расчет теплообмена и сопротивления при турбу-
лентном течении газа с переменными свойствами проводился мно-
гими исследователями. Рассмотрим результаты расчета для воздуха
и водорода, движущихся с малой дозвуковой скоростью вдали от
входа в трубу при постоянной плотности теплового потока на стен-
228
ке. Расчет проведен Б. С. Петуховым и В. Н. Поповым [7] по мето-
ду, изложенному в § 8.2. Коэффициент турбулентного переноса ко-
личества движения определялся по уравнениям (6.73) и (6.74) с ис-
пользованием второй из обобщенных переменных (8.8). Турбулент-
ное число Прандтля принималось равным единице.
Рис. 8.5. Распределение по радиусу безразмерных параметров потока
при переменных (сплошные линии) и постоянных (пунктир) свойст-
вах воздуха для значений Rec=43-103 и Рг=0,7:
1 _ Tc=1000° К; 2>=0=1И° К; Гс/Т-ЗЛ;
2—Тс=ЗООК; о =902° К; 7с/Т=0,38.
На рис. 8.5 показано распределение по радиусу безразмерных
параметров потока: температуры, скорости, массовой скорости
и коэффициента турбулентного переноса количества движения.
Кривые 1 и 2 соответствуют случаям нагревания и охлаждения воз-
духа при переменных свойствах (<ЭС = 3,1 и 0,38 соответственно);
229
пунктиром проведены кривые для постоянных свойств. Как видно из
рисунка, изменение физических свойств слабо влияет на профиль
скорости и весьма сильно на профиль массовой скорости. Изменение
массовой скорости рвуж связано в основном с неоднородным распре-
делением плотности по радиусу. При нагревании газа р убывает по
направлению от оси к стенке, а при охлаждении растет, поэтому
в первом случае профиль массовой скорости оказывается менее за-
полненным, а во втором более заполненным, чем при постоянных
свойствах. Изменяется и распределение коэффициента турбулент-
ного переноса. При нагревании sCT/v в пристеночной области стано-
Рис. 8.6. Зависимость теплоотдачи при течении газа с пере-
менными свойствами от температурного фактора по дан-
ным теоретических расчетов:
/—для воздуха и водорода [7]; 2— по уравнению (8.18).
вится меньше, чем при постоянных свойствах, а при охлаждении
остается приблизительно таким же (в ядре потока ситуация иная .
Изменение свойств и связанное с ними изменение гидродинамических
характеристик приводят к изменению профилей температуры. При
нагревании профиль температуры менее заполнен и градиент темпе-
ратуры на стенке меньше, чем при охлаждении.
Результаты теоретического расчета теплоотдачи для воздуха
и водорода представлены на рис. 8.6, кривая 1. Число Nu^ при
переменных свойствах, отнесенное к числу Num0 при постоянных
свойствах [оба значения определены в соответствии с (8.16)], убы-
вает с ростом температурного фактора &С = ТС/Т. Различие в зна-
чениях чисел Нуссельта для воздуха и водорода незначительно,
поэтому результаты расчета для обоих газов изображены одной кри-
вой 1, что вполне естественно, так как температурные зависимости
свойств воздуха и водорода очень близки. Вычисления показыва-
ют, что Nu^/Nu^o практически не зависит от Re, хотя последнее
изменялось при расчете на два порядка. Это означает, что зави-
симость числа NUoo от числа Re при переменных свойствах прибли-
зительно та же, что и при постоянных. Таким образом, для газов
230
с одинаковым характером зависимости свойств от температуры
(т. е. при одних и тех же значениях /гс, и /гц) отношение предель-
ных чисел Нуссельта Nlito/Nlito0 определяется только температур-
ным фактором 0С. Для воздуха и водорода, а также других «подоб-
ных» газов это отношение убывает с ростом 0С. Следовательно, при
нагревании газа (0С >> 1) число Nu^ меньше, чем при охлаждении
(0С< 1). Такой характер зависимости легко объяснить. Как видно
из рис. 8.5, массовая скорость у стенки и градиент температуры на
стенке при нагревании газа меньше, чем при охлаждении, а следо-
вательно, и число Nu^ должно быть меньше.
Результаты расчета теплоотдачи для воздуха и водорода (кривая
1 на рис. 8.6) с погрешностью ±4% описываются интерполяционным
уравнением [10]
Nu
—(8.17)
NUoo0
где п — —{a 1g 0С + 0,36). В случае охлаждения газа а = 0 и,
следовательно, п = —0,36. При нагревании газа а = 0,3 и п убы-
вает с ростом 0С. Если для простоты считать п постоянным и при
нагревании газа, то можно принять п ж 0,5. Уравнение описывает
результаты расчета в пределах значений 0,4 0С С 4 и 104
С Re С 5 • 10°.
Относительный коэффициент сопротивления трения по
данным теоретического расчета приблизительно так же зависит от
0С, как и NuJNu^o.
С.С. Кутателадзе и А. И. Леонтьев [4] получили аналитическое
выражение, описывающее влияние переменных свойств газа на
теплоотдачу и сопротивление при Re -> оо. Приняв ряд допущений* ,
они пришли к зависимости
Nu^o ^оо0
Так как NipjNii^o очень слабо зависит от Re, то авторы рекомен-
дуют эту зависимость и для конечных значений Re. Уравнение (8.18)
(кривая 2 на рис. 8.6) дает более крутую зависимость Nu^/Nu^ 0
от 0С по сравнению с уравнением (8.17) (кривая /), однако разница
между ними не превышает 10%.
Известны многочисленные экспериментальные работы по тепло-
обмену между стенкой трубы и потоком газа при больших темпера-
турных напорах, когда свойства газа значительно изменяются по се-
чению потока. Обзор этих работ можно найти, например, в [10].
Экспериментальные данные, опубликованные в последние годы,
например в работе [Г], показывают, что при охлаждении двухатом-
ных газов (воздух, азот) отношение Nu/Nu0 в пределах погрешности
* Основные из них: ст и q изменяются по радиусу одинаковым образом
в случае постоянных и переменных свойств газа, поля скорости и темпера-
туры, подобны; ср = const.
.........] . (8.18)
1/©с + 1/
231
измерений (±10—15%) не зависит от 0С и равно примерно 1, если
физические свойства выбираются при среднемассовой температуре
газа. К такому же результату приводят и измерения коэффициента
сопротивления. Таким образом, в случае охлаждения газа (т. е.
при 0С < 1) имеется несоответствие между результатами теорети-
ческого расчета (см. рис. 8.6) и эксперимента. Выяснение причин
этого несоответствия — предмет дальнейших исследований.
Из сказанного следует, что для практического расчета тепло-
отдачи и сопротивления при охлаждении газа с переменными свой-
ствами можно пользоваться обычными соотношениями для тепло-
отдачи и сопротивления при постоянных свойствах, полученными
в гл. 7, выбирая свойства при среднемассовой температуре газа.
В случае нагревания газа (т. е. при 0С > 1) опытные данные по
теплоотдаче находятся в удовлетворительном соответствии с резуль-
татами теоретического расчета. Поэтому уравнением (8.17) при
0С > 1 можно пользоваться для практического расчета теплоотда-
чи к двухатомным газам вдали от входа в трубу. Вместе с тем изме-
рения теплоотдачи при нагревании газа в условиях qc == const
показывают, что характер зависимости Nu/Nu0 от 0С изменяется по
мере удаления от входа в трубу. Если для данного газа принять
Nu/Nu0 — 0с, то п изменяется приблизительно от—0,2 при x/d «
10 до—(0,5 — 0,7) при x/d 100, а затем принимает постоянное
значение. Естественно, что результаты теоретического расчета,
проведенного для области, удаленной от входа в трубу, не учиты-
вают отмеченной особенности.
В. А. Курганов и Б. С. Петухов [31 обработали опытные данные
по теплоотдаче при нагревании ряда газов (Аг, N2, Н2, воздух, СО2,
NH3), используя систему безразмерных чисел (8.15), определенных
согласно (8.16). В результате было получено уравнение, обобщающее
опытные данные по теплоотдаче к газам со средней квадратичной
погрешностью ±6% при x/d >25 и ±10% при xld < 25. Это
уравнение, справедливое в случае постоянной плотности теплового
потока на стенке (qc = const), имеет вид:
•^=ехр{ — /С[<(£)± «ц/'2(х)К]) (8.19а)
или
0с=1±Дехр {К + Д']), (8.196)
где
Д' — = qcd
Nuo ’
а =—0,53 пр-----J-rtx--jL пс (здесь пр = —1);
о 4
Л(х) = 1—ехр(— 0,1х), x = x/d‘,
f _ 1,25(0,01 х)2.
1+ (o,oi7)2 ’
232
Nu0 — Nu0 (x, Re, Pr) — число Нуссельта при постоянных свойст-
вах, вычисляемое по уравнениям (7.38) и (7.39), т. е. с учетом по-
правки на термический начальный участок. При вычислении Nu
и_ Nu0 свойства выбираются при среднемассовой температуре газа
Т в данном сечении трубы.
В табл. 8.1 приведены значения а и пц для некоторых газов в диа-
пазоне температур от 300 до 1200° К. Этими данными можно поль-
зоваться для приближенных расчетов. При более точных расчетах
и в другом диапазоне температур значения а и следует определять
по опытным данным.
Таблица 8.1
Значения а и для некоторых газов в диапазоне температур
от 300 до 1200° К
Газ а Газ а
Одноатомный Двухатомный Двуокись углерода 0,3 0,26 0,09 0,67 0,70 0,77 Водяной пар Аммиак Метан 0,013 —0,04 —0,097 1,18 0,92 0,71
Уравнения (8.19а) и (8.196) справедливы при значениях х >= 1,
Re 7 103 и 0,65 Рг 1,2. Они подтверждены опытными дан-
ными в случае нагревания газа при t/c — const в диапазоне значе-
ний 0 < Qc/(RePr) •< 0,01 и 1<0С<6. Однако при Re>
< 5 < 104 их, по-видимому, можно экстраполировать иа более вы-
сокие значения Qc/(RePr). Уравнения (8.19а) и (8.196) учитывают
различия в характере зависимостей свойств газов от температуры
и удовлетворяют требованиям предельного перехода: при Д —> 0
Nu/Nuo->1 и 0с->1.
На рис. 8.7 показана зависимость Nu/Nu0 от Д по уравнению
(8.19а) при xld — 60 для некоторых применяемых в технике газов.
На том же рисунке приведены кривые (пунктир), соответствующие
постоянным значениям 0С, рассчитанные по уравнению (8.196).
Кривые для многоатомных газов при Д 0 или 0G > 1 располо-
жены выше, чем для одно- и двухатомных. Это объясняется главным
образом тем, что коэффициент теплопроводности многоатомных га-
зов гораздо сильнее увеличивается с температурой, чем одно- и
двухатомных. Интересно отметить, что экстраполяция уравнений
(8.19) иа область охлаждения газа (Д < 0 и 0С < 1) не противоречит
опытным данным. Действительно, опытные данные по теплоотдаче
при охлаждении двухатомных газов в согласии с уравнениями (8.19)
показывают, что в пределах погрешности измерений (± 10%)
Nu/Nuo лИ. В случае охлаждения многоатомных газов уравнения
(8.19) предсказывают рост Nu/Nu0 с увеличением К или 0С. Однако
эта закономерность нуждается в экспериментальном подтверждении.
233
Сопротивление при течении газа с переменными свойствами ме-
нее исследовано, чем теплоотдача. Для расчета местного коэффи-
циента сопротивления трения £ в случае нагревания двухатомных
газов можно воспользоваться формулой, рекомендуемой В. Л. Лель-
чуком и Б. В. Дедякиным [5]:
-1=0
п
С 5
(8.20)
где £0 — коэффициент сопротивления трения при постоянных свой-
ствах, а п зависит от x!d и находится из следующей таблицы:
x/d 10 20 30 40 50 60 70 >80
п 0,16 0,08 0 —0,05 —0,10 —0,13 —0,15 —0,16
При вычислении £ и физические свойства выбираются при средне-
массовой температуре газа в данном сечении трубы.
Рис. 8.7. Зависимость теплоотдачи при течении
газов с переменными свойствами от парамет-
ра К (расчет по уравнениям (8.19) при
x/d=60).
Уравнение (8.20) описывает данные, полученные в опытах с воз-
духом с разбросом ±10% в диапазоне значений 105 < Re < 6,5 • 10б
и 1 <0С <2,5.
Сопоставляя уравнение (8.20) с результатами теоретического
расчета, легко заметить, что эксперимент дает гораздо более слабую
зависимость £ от 0С.
234
§ 8.5. Теплообмен в однофазной околокритической области
Говоря о теплообмене в однофазной околокритической области,
мы имеем в виду процессы теплообмена, протекающие при давле-
ниях выше критического и температурах, близких к критической
или псевдо критической (т. е. температуре, соответствующей точке
максимума теплоемкости при постоянном давлении). Интерес к этой
проблеме в энергетике связан с разработкой ядерных реакторов
и созданием котлоагрегатов, в которых теплоносителем служит вода
сверхкритических параметров.
Рис. 8.8. Зависимость физических свойств двуокиси углерода от темпе-
ратуры при давлении 100 бар.
Специфика теплообмена в однофазной околокритической области
состоит в том, что физические свойства вещества в этой области очень
сильно и своеобразно изменяются в зависимости от температуры
и существенно зависят от давления. Представление о характере из-
менения физических свойств в зависимости от температуры дает
рис. 8.8, на котором приведены данные для двуокиси углерода при
р — 100 бар*. На рисунке можно видеть, что удельная теплоемкость
и число Рг имеют сильно выраженные максимумы; коэффициен-
ты теплопроводности и вязкости проходят через точки минимума;
очень сильно изменяется плотность, а коэффициент объемного тер-
мического расширения (3 = — -(— имеет максимум. Поэтому даже
Р\дТ ! р
при относительно небольших разностях температур в потоке физи-
ческие свойства будут сильно изменяться. Например, если Т <
< Тт < Тс (здесь Тт — псевдокритическая температура), то по
мере удаления от стенки ср будет быстро расти, пройдет через мак-
симум, а затем начнет убывать. Плотность в случае нагревания
жидкости будет быстро расти по направлению от стенки к оси трубы.
* Для СО2 рир = 71,49 бар, 71ф - 304,2° К.
235
Изменение физических свойств по радиусу будет особенно сильным
при высоких тепловых нагрузках и больших разностях температур.
К настоящему времени выполнено значительное число расчетно-
теоретических и экспериментальных исследований теплообмена
в однофазной околокритиче-
ской области*. Опыты про-
водились главным образом с
водой и двуокисью углерода и
в меньшей степени с другими
теплоносителями. Теплоотда-
ча изучалась в основном при
течении в круглых трубах в
условиях нагревания при по-
стоянной плотности теплового
потока на стенке. Эти иссле-
дования позволили выявить
ряд интересных особенностей
теплообмена и установить
некоторые зависимости. Одна-
ко сложность вопроса и от-
сутствие сведений о законо-
мерностях турбулентного пе-
реноса при сильном измене-
нии свойств жидкости пока
не позволили выработать до-
статочно точных и общих ме-
тодов расчета теплообмена.
Поэтому приведенные ниже
рекомендации по необходи-
мости носят приближенный
О x/d характер.
Рис. 8.9. Типичные кривые изменения
температуры стенки t0 и среднемассовой
температуры жидкости t по длине трубы
для нормальных режимов (кривые 1 и
2) и режимов с ухудшенной теплоот-
дачей (кривые 3 и 4).
Для однофазных теплоно-
сителей при околокритиче-
ских параметрах состояния
особенно важно различать
вязкостно-инерционный и
вязкостно-инерционно - грави-
тационный режимы течения и
теплообмена. Последний наблюдается достаточно часто вследствие
сильной зависимости плотности от температуры. Кроме того, по
практическим соображениям следует различать нормальные режи-
мы теплообмена и режимы с ухудшенной теплоотдачей. Нормальные
режимы характеризуются плавным, обычно монотонным, изменением
температуры стенки по длине трубы (при qc — const) без сильно
выраженных максимумов tc (например, кривые 1 и 2 на рис. 8.9).
Режимы с ухудшенной теплоотдачей, напротив, характеризуются
* См. обзорные статьи [8, 10].
236
наличием сильно выраженных максимумов (пиков) в распределении
температуры стенки по длине трубы (кривые 3 и 4). Нормальные
режимы и режимы с ухудшенной теплоотдачей наблюдаются как
при вязкостно-пперциониом, так и при вязкостно-ииерционно-гра-
витациошюм течении жидкости.
Относительно полнее исследован теплообмен при нормальных
режимах в случае вязкостно-инерционного течения. Рассмотрим
некоторые результаты, относящиеся к таким режимам течения и
теплообмена.
Рис. 8.10. Коэффициент теплоотдачи при нагревании и ох-
лаждении двуокиси углерода при р/р^р«1,1; =
== 500 кг/(лР• сек); d=l() мм и различных значениях (р-.
На рис. 8.10 показана зависимость коэффициента теплоотдачи
а от i при разных значениях с/(. в случае нагревания и охлаждения
двуокиси углерода по данным теоретического расчета японских
авторов 118]. Кривые а ~ f (/) имеют характерные максимумы вбли-
зи значения i ж /т, связанные с высокими значениями числа Рг
вблизи псевдокритическои температуры (см. рис. 8.8). Максимальные
значения а в случае охлаждения жидкости (qc < 0) больше, чем
в случае нагревания (с/(. >0). Это объясняется тем, что коэффициент
теплопроводности жидкости в вязком подслое в случае охлаждения
почти в два раза больше, чем при нагревании. Коэффициент тепло-
отдачи при нагревании жидкости уменьшается с ростом q0. Такой
характер изменения а становится попятным, если учесть, что с рос-
том qc увеличивается температура стенки, а следовательно, сни-
жаются плотность р и массовая скорость pwx в пристеночной об-
ласти, уменьшается и коэффициент теплопроводности жидкости
вблизи стенки. Все это ведет к снижению а.
Изменение теплоотдачи с ростом температуры стенки хорошо
прослеживается на рис. 8.11, где приведены результаты теоретиче-
237
ского расчета В. Н. Попова [14]* и опытные данные для двуокиси
углерода при р/р^ ж 1,4- Точка, в которой TjTm — Т1Тт = 0,95,
соответствует случаю постоянных свойств. В этой точке, как и сле-
довало ожидать, Nu/Nu0 = 1. С увеличением TJTm (при неизмен-
ном значении 71) отношение Nu/Nu0 растет до тех пор, пока Тс не
достигнет псевдокритической температуры (TJTm = 1). Этот рост
в основном связан с увеличением числа Рг в пристеночной области
Рис. 8.11. Зависимость теплоотдачи при нагрева-
нии двуокиси углерода от Тс[Тт при р/ркрл;1,4
(fm = 44°C), * = 30°С, рш - 212,0 /сг/(м2-сек),
d — 4,1 мм:
/ — теоретический расчет [14]; 2 — эмпирическое уравне-
ние (8.21); точки — опытные данные.
по мере приближения к псевдокритической температуре. При
TJTm > 1 отношение Nu/Nu0 быстро уменьшается с ростом ТС/Т7П,
что объясняется уменьшением р и X в пристеночном слое по мере
удаления от псевдокритической температуры (см. рис. 8.8).
Для случая, приведенного на рис. 8.11, наблюдается удовлетво-
рительное соответствие результатов расчета и эксперимента. К со-
жалению, такое соответствие наблюдается далеко не всегда. Обычно
оно имеет место лишь при сравнительно слабом изменении свойств
по сечению потока. Поэтому практические расчеты теплоотдачи в
* Расчет проведен по методу, изложенному в § 8.2. Значения е0 вычисле-
ны по уравнениям (6.73) и (6.74) с использованием переменной (8.8), Ргтб= 1.
238
Рис. 8.12. Показатель степени п в уравне-
нии (8.21).
воды при 1,02 < р/р..п < 1,45 показа-
однофазной околокритической области следует проводить, опи-
раясь на результаты экспериментальных исследований.
Для расчета теплоотдачи при вязкостно-инерционном течении
однофазных теплоносителей околокритических параметров предло-
жено несколько эмпирических формул. Лишь немногие из них удов-
летворяют минимальным требованиям точности и то лишь для нор-
мальных режимов теплообмена. Некоторыми преимуществами об-
ладает формула Е. А. Краснощекова и В. С. Протопопова [2], полу-
ченная на основе обработки опытных данных для воды и двуокиси
углерода и позволяющая проводить расчет с погрешностью пример-
но ±20%. Эта формула
имеет вид:
/л \ т / 7 \ ч
Nu = Nu0[ —) ,
\ Рж ' \ сРж/
(8.21)
где Nu0 — число Нуссель-
та при постоянных свойст-
вах, вычисляемое по урав-
нению (7.21), ср = (Ас —
— ОСГс — Т) — средняя
интегральная теплоемкость
жидкости в интервале тем-
ператур от Т до Тс. Для
тель т === 0,3; для двуокиси углерода при * 1,02 < р/ркр <
<5,3 т=~ 0,35— 0,05 р/р1ЦГ Показатель степени п зависит от
Тс!Тт и Т1Тт. Эта зависимость изображена на рис. 8.12. При вы-
числении Nu и Nu0 физические свойства выбираются при средне-
массовой температуре в рассматриваемом сечении трубы.
Уравнение (8.21) справедливо для нормальных режимов тепло-
обмена в случае нагревания жидкости при qc — const в пределах
значений 2 • 101 < Re < 8 • 10б; 0,85 < Рг < 55; 0,09 < рс/рж
< 1, 0,02 < CpfCpni
Теплообмен при вязкостно-инерционпо-гравитациониом тече-
нии пока мало исследован. Некоторое представление о влиянии
термогравитационных сил иа теплообмен дает рис. 8.13, на котором
приведены результаты измерений теплоотдачи при подъемном те-
чении двуокиси углерода, воды и азота в вертикальной обогревае-
мой трубе. На рисунке измеренное число Нуссельта отнесено к рас-
считанному по уравнению (8.21) и представлено в зависимости от
Gr/Re3 (здесь Gr — g (1 — Рс/Рж)^3^^)- При значениях Gr/Re2 <
< 0,6 термогравитационные силы практически не влияют на теп-
лообмен*, а при больших значениях этого параметра теплоотдача
* Точнее говоря, не приводят к росту теплоотдачи; что касается возмож-
ного уменьшения теплоотдачи под действием термогравитационных сил, то
этот вопрос еще недостаточно изучен.
239
растет с увеличением Gr/Re2. Существенное увеличение теплоотда-
чи наблюдается даже при сравнительно больших значениях Re.
Так, при Re 105 теплоотдача увеличивается в два раза, а при
Re « 6 • 104 — в три раза по сравнению с вязкостно-инерционным
течением. Качественно такая же картина наблюдается и при опуск-
ном течении в обогреваемых трубах.
Ранее было отмечено, что режимы с ухудшенной теплоотдачей
наблюдаются как при вязкостно-инерционном, так и при вязкост-
но-инерционно-гравитационном течении. В первом случае они
Рис. 8.13. Влияние термогравитационных сил на теплоотдачу при подъемном
течении СО2, Н2О и N2 в вертикальной обогреваемой трубе.
могут возникнуть при любой ориентации трубы в поле силы тяже-
сти. Во втором случае режимы с ухудшенной теплоотдачей возни-
кают при подъемном течении в вертикальных обогреваемых трубах,
слабо выражены при течении в горизонтальных трубах и отсутст-
вуют при опускном течении в вертикальных обогреватемых тру-
бах. Во всех упомянутых случаях режимы с ухудшенной теплоот-
дачей возникают лишь при определенном сочетании средней массо-
вой скорости и тепловой нагрузки и обычно тогда, когда темпера-
тура жидкости в данном сечении t < tm, а температура стенки
в том же сечении > tm, где tm — псевдокритическая температура
при данном давлении [15].
В теплообменных системах с заданной плотностью теплового
потока на стенке, например в твэлах ядерных реакторов или экран-
ных трубах котлоагрегатов, режимы с ухудшенной теплоотдачей
крайне нежелательны, так как при этом появляется опасность не-
допустимого повышения температуры стенки. Поэтому важно оп-
ределить условия, в которых режимы с ухудшенной теплоотдачей
не возникают. На рис. 8.14 показаны предельные значения тепло-
вой нагрузки 7сР, при которых возникает ухудшение теплоотда-
240
чи, в зависимости от среднемассовой энтальпии в том сечении по-
тока, начиная с которого (если двигаться от входа) наблюдается
быстрый рост температуры стенки. Каждому значению средней
массовой скорости соответствует своя прямая, иначе говоря, за-
висимость б/сР от h приближенно можно считать линейной. Область,
лежащая ниже прямых на рис. 8.14, соответствует нормальным ре-
Рис. 8.14. Предельная тепловая нагрузка при подъем-
ном течении воды в обогреваемой трубе d — 8 мм при
различных значениях
жимам теплоотдачи (от начала обогреваемого участка до рассмат-
риваемого сечения, которое, естественно, может быть и выходным),
область, лежащая выше, — режимам с ухудшенной теплоотдачей.
При заданных значениях qc, pwx и р можно определить то зна-
чение среднемассовой энтальпии Лпр или то расстояние от начала
обогреваемого участка хпр, при котором наступает снижение тепло-
отдачи или быстрый рост температуры стенки (при qQ = const).
В результате обработки опытных данных по теплоотдаче к воде
241
и двуокиси углерода в обогреваемых трубах и кольцевых щелях
в работе [12] получено следующее уравнение для хпр:
*лр Sq (hm — й0) 900 ( Pm Г ёУт
f Яс, \ .тсрдаж
3/2
(8.22)
где f — площадь поперечного сечения трубы; sq и s0- — обогревае-
мый и смоченный периметры трубы (для круглой трубы f/sq — d/4,
sG/sq = 1); hm, pm, vm — энтальпия, плотность и кинематическая
вязкость при псевдокритической температуре tm, зависящие от
давления р; hQ — энтальпия на входе в обогреваемый участок трубы;
ршх — средняя массовая скорость; п = р/рнр— приведенное дав-
ление; Re0 и Рг0 — значения Re и Рг на входе в трубу.
Уравнение (8.22) справедливо при подъемном течении в верти-
кальных трубах и при течении в горизонтальных трубах в пределах
значений л от 1,01 до 1,6; Re от 101 до106; Gr/Re2 < 0,6 и q0 от
0,1 до 10 мет!At2.
В трубе длиной I < хпр ухудшения теплоотдачи не будет; если
/ > хпр, то на расстоянии х = хпр от входа в обогреваемый участок
начинается ухудшение теплоотдачи.
Возникновение режимов с ухудшенной теплоотдачей связано
с изменением гидродинамики потока и, в частности, процессов тур-
булентного переноса вследствие сильного изменения физических
свойств теплоносителя по сечению потока. При этом существенное
влияние на характер течения могут оказать архимедовы силы и
ускорение потока, связанные с изменением плотности вдоль трубы.
§ 8.6. Теплообмен при течении диссоциирующего газа
В последнее время диссоциирующие газы привлекают внимание
как возможные теплоносители и рабочие тела для ядерных энергети-
ческих установок, в особенности с реакторами на быстрых нейтро-
нах. Один из таких теплоносителей — газообразная четырехокись
азота (азотный тетраксид) N2O4:,:. Реакция диссоциации в этой си-
стеме обратима и протекает в две стадии по схеме
N2O4+=±2NO3 —624 /<d.w7Ka^±2NO + O2- 1227 кдж/кг. (8.23)
Температурный диапазон реакции 300—1200° К при р = 1 бар и
450—1500° К при р = 100 бар.
В потоке диссоциирующего газа наряду с полями скорости и тем-
пературы существуют поля концентраций различных компонентов
смеси (N2O4, NO2, NO, О2 в случае азотного тетраксида). Наличие
полей концентраций приводит к возникновению диффузионных по-
* В жидкой фазе четырехокись азота — легкокипящая жидкость; тем-
пература насыщения Ts = 294,5° К при р = 1 атм.
242
токов массы различных компонентов смеси. Поэтому перенос тепла
в диссоциирующем газе осуществляется двумя путями: 1) посред-
ством молекулярной теплопроводности и турбулентного переноса
тепла, как в обычном газе, и 2) вследствие переноса энтальпии по-
токами массы; последние в свою очередь вызываются молекулярной
диффузией п турбулентным переносом массы. Сравнительно боль-
шие теплоты реакций диссоциации N3O4 и NOa приводят к значи-
тельному увеличению теплоотдачи за счет переноса тепла диффу-
зионными потоками массы. Оценки показывают, что коэффициенты
теплоотдачи к диссоциирующему азотному тетраксиду от 1,5 —
2 до 8 раз выше, чем к инертному газу.
Состав диссоциирующего газа (содержание отдельных компо-
нентов в смеси) в какой-либо точке потока определяется скоростью
химической реакции образования компонентов смеси (зависящей от
Т и р) и скоростью уноса этих компонентов из рассматриваемой точ-
ки диффузионным и конвективным потоками. Течение, при кото-
ром эти скорости соизмеримы, называется неравновесным. Если
скорость реакции диссоциации много больше скорости уиоса соот-
ветствующих компонентов диффузионным и конвективным потока-
ми, то такое течение называется равновесным. В этом случае состав
смеси в каждой точке потока определяется только температурой
и давлением в этой точке. В другом предельном случае, когда ско-
рость реакции много меньше скорости уиоса массы диффузионным
и конвективным потоками, течение называется замороженным.
В последнем случае (если одновременно отсутствуют химические
реакции на поверхности стенки) газ ведет себя, как смесь химически
инертных газов, в которой отсутствуют химические реакции.
Первая стадия реакции диссоциации азотного тетраксида N3O4
2NO2 при р >• 1 бар характеризуется высокой скоростью, по-
этому в диапазоне температур, соответствующем этой реакции (от
295 до 460° К при р ж 1 бар) течение будет равновесным. Вторая
стадия реакции диссоциации 2NO3 2NO -|- О2 при р от 1 до
100 бар протекает с конечной скоростью, меняющейся в широких
пределах. Поэтому в диапазоне температур, соответствующем этой
реакции (от 420 до 1200° К при р « 1 бар), течение в общем случае
неравновесное, а в предельных случаях может быть равновесным или
замороженным.
При замороженном течении и отсутствии химических реакций
на поверхности стенки полностью справедливы полученные ранее
уравнения для теплоотдачи к потоку газа с переменными физическими
свойствами (см. § 8.4).
В случае равновесного течения диссоциирующей бинарной смеси
(в частности, NaO4 7~* 2NO2) расчет теплоотдачи можно проводить
по уравнению (7.21) для жидкости с постоянными свойствами, если
коэффициент теплоотдачи определить как отношение
hQ—h'
(8.24)
243
где /гс и h — энтальпия газа на стенке и среднемассовая энтальпия
газа с учетом их химических составляющих, а удельную тепло-
емкость и коэффициент теплопроводности рассматривать как эф-
фективные физические свойства равновесно диссоциирующего газа.
Под эффективными значениями ср эф и Хэф понимаются значения
этих свойств, вычисленные с учетом их химических составляющих,
обусловленных тепловым эффектом реакции и переносом энталь-
пии вследствие молекулярной диффузии. Заметим, что срэф и %эф
сильно зависят от Т и р и могут иметь гораздо более высокие зна-
чения, чем ср и X, найденные для смеси газов при отсутствии хими-
ческих реакций (так называемые замороженные свойства)*.
С учетом сказанного уравнение (7.21) применительно к расчету
теплоотдачи при равновесном течении диссоциирующего газа удобно
записать в виде
------------, (8.25)
рЕ0л: /гх + 12,7 |/1-(Рг2/3 — 1)
где /?!, (Re) и £ (Re) вычисляются по уравнениям (7.24) и (6.62);
Re = pwrf/ц; Рг = цсрэф/Хоф.
Чтобы приближенно учесть влияние на теплообмен зависимости
физических свойств от температуры, значения ц, сРоф и Хоф в урав-
нении (8.25) следует выбирать при температуре стенки в случае на-
гревания газа и при среднемассовой температуре в случае охлаж-
дения.
В случае неравновесного течения азотного тетраксида, наблю-
даемого во второй стадии реакции диссоциации, т. е. при диссоциа-
ции двуокиси азота (2NO2 7^ 2NO + О2), для расчета теплоотдачи
в условиях нагревания можно воспользоваться уравнением, полу-
ченным в работе [11]:
Nu' / 1 +2,05-10~3 К1, 17 \0> 15 ,о псч
--- — ------------------ . (о. 2 о)
Nu0 \ 1 + 3,5 • 10“6 №17 J
Здесь Nu' = a'dIK = gc/[X (Тс — То)] — число Нуссельта при не-
равновесном течении N2O4, в котором коэффициент теплоотдачи
а' отнесен к разности температур Тс — То, где Тс — местное зна-
чение температуры стенки, а То — температура начала реакции
диссоциации двуокиси азота. Значение То приблизительно соот-
ветствует точке минимума кривой сРэф (Т), рассчитанной в пред-
положении равновесного протекания как первой, так и второй реак-
ции диссоциации N2O4; Nuo (Re, Рг, x/d) — число Нуссельта, рас-
считанное по уравнению (7.21) в предположении замороженного те-
* Данные по свойствам диссоциирующих газов см. в работе [6].
244
чеиия газа; если это уравнение пересчитать, отнеся коэффициент
теплоотдачи к разности Тс — То, то оно примет вид
-JL це рг
Nli'^= ------------? (8.27)
/Ci+12,7 -|/ JL (Рг2/3 — 1)+JL . JL
/8 2d
К = k^xQp/qa — параметр, учитывающий неравиовесиость те-
чения, где kf — константа скорости реакции диссоциации NO2,
Q — теплота этой реакции; х — расстояние от сечения, соответст-
вующего началу реакции диссоциации NO2 (в котором Т = То), до
рассматриваемого сечения.
мости от параметра Л'.
В уравнение (8.26) входят замороженные значения физических
свойств, взятые при температуре стенки. Уравнение (8.26) подтверж-
дено экспериментально для двуокиси азота в пределах 2 • 104 -С
< Re < 2 • 10б и К < 6,4 • 104 (2 < р 45 бар), 490 <
< 880° К и 540 < Тс < 900° К.
На рис. 8.15 показана зависимость Nu7Nu6 от /< по уравнению
(8.26) в сопоставлении с опытными данными. При К < 25 отношение
Nu7Nuo « 1 и диссоциация ЫО2 не оказывает влияния на теплоотда-
чу (течение практически заморожено). При > 25 теплоотдача
растет с увеличением /<, что соответствует неравновесному течению.
При достаточно больших К отношение Nu7Nu6 изменяется в соответ-
ствии с закономерностями, характерными для равновесного тече-
ния газа.
245
СПИСОК ЛИТЕРАТУРЫ
1. Амбразявичус А. Б., Жукаускас А. А., Валаткявичус П. Ю. Исследова-
ние влияния температурного фактора на теплообмен при турбулентном
течении газа в трубах.—В сб.: Тепло-и массоперенос. Т. I, ч. 1. Минск,
1972, с. 121.
2. Краснощеков Е. А., Протопопов В. С. Экспериментальное исследование
теплообмена двуокиси углерода в сверхкритической области при боль-
ших температурных напорах. — «Теплофизика высоких температур»,
1966, т. 4, № 3, с. 389.
3. Курганов В. А., Петухов Б. С. Анализ и общение опытных данных по
теплоотдаче в трубах при турбулентном течении газа с переменными физи-
ческими свойствами. — «Теплофизика высоких температур», 1974, т. 12,
№ 2, с. 304.
4. Кутателадзе С. С., Леонтьев А. И. Турбулентный пограничный слой сжи-
маемого газа. Изд. СО АН СССР, 1962.
5. Лельчук В. Л., Дедякин Б. В. Теплоотдача от стенки к турбулентному по-
току воздуха внутри трубы и гидравлическое сопротивление при боль-
ших температурных напорах. —В сб.: Вопросы теплообмена. М., Изд-
во АН СССР, 1959, с. 123.
6. Нестеренко В. Б. Физико-технические основы применения диссоцииру-
ющих газов как теплоносителей и рабочих тел атомных электростанций.
Минск, «Наука и техника», 1971.
7. Петухов Б. С., Попов В. Н. Теоретический расчет теплообмена и сопро-
тивления трения при турбулентном течении в трубах несжимаемой жидко-
сти с переменными физическими свойствами. —«Теплофизика высоких
температур», 1963, т. 1, № 1, с. 85.
8. Петухов Б. С. Теплообмен в однофазной среде при околокритических па-
раметрах состояния. —«Теплофизика высоких температур», 1968, т. 6,
№ 4, с. 732.
9. Петухов Б. С., Стригин Б. К- Экспериментальное исследование теплооб-
мена при вязкостно-инерционно-гравитационном течении жидкости
в вертикальных трубах. — «Теплофизика высоких температур», 1968,
т. 6, № 5, с. 933.
10. Петухов Б. С. Теплообмен и сопротивление при турбулентном течении
в трубах жидкости и газа с переменными физическими свойствами. —
В сб.: Advances in heat transfer. V. 6, Academic Press, N. Y., 1970, p. 503.
11. Петухов Б. С., Майданик В. H., Новиков Г. А. Экспериментальное ис-
следование теплоотдачи при турбулентном течении в круглой трубе
неравновесно диссоциирующего газа.—«Теплофизика высоких темпе-
ратур», 1971, т. 9, № 2, с. 316.
12. Петухов Б. С., Поляков А. Ф. Границы режимов с «ухудшенной» тепло-
отдачей при сверхкритическом давлении теплоносителя. •— «Теплофизика
высоких температур», 1974, т. 12, № 1, с. 221.
13. Поляков А. Ф. Границы и характер влияния термогравитационных сил
на турбулентное течение и теплообмен в вертикальных трубах. — «Теп-
лофизика высоких температур», 1973, № 1, с. 106.
14. Попов В. Н. Теоретический расчет теплоотдачи и сопротивления трения
для двуокиси углерода в сверхкритической области. — В сб.: Тепло-
и массоперенос. Минск, «Наука и техника», 1965, с. 50.
15. Шицман М. Е. Ухудшенные режимы теплоотдачи при закритических дав-
лениях. •—«Теплофизика высоких температур», 1963, т. 1, №2, с. 267.
16. Goldman К- Heat transfer to supercritical water and other fluids with tem-
perature — dependent properties. •— Chem. Engng. Progr., Simp. Ser.,
Nucl. Eng., Part III, 1954, v. 50, No. 11, p. 105.
17. Lafay J.Mesure du coefficient frottement avec transfer! du chaleur en con-
vection forcee dans un canal circulaire, Centr d’Etudes, Necleaires de Gre-
noble, Report CEA-R-3896, 1970. ।
18. Tanaka H. e. a. Turbulent heat transfer to supercritical carbon dioxide.—
«Proc. JSME», 1967, Semi-Intern. Symposium, t. 11, Tokyo, 1967, p. 127.,
ГЛАВА 9
ГИДРОДИНАМИКА И ТЕПЛООБМЕН ПРИ ТУРБУЛЕНТНОМ
ТЕЧЕНИИ ЖИДКОСТИ В КАНАЛАХ
НЕКРУГЛОГО СЕЧЕНИЯ
§ 9.1. Предварительные замечания
Вследствие конструктивного разнообразия твэлов, используемых
в реакторостроении, каналы, по которым течет теплоноситель, мо-
гут иметь разную форму поперечного сечения. Так, если твэлы
выполнены в виде набора плоских пластин или коаксиальных ци-
линдрических оболочек, то каналы имеют форму плоских или коль-
цевых щелей. Чаще всего твэлы выполняются в виде сборки боль-
шого числа топливных цилиндрических стержней, вдоль которых
в зазорах между стержнями течет теплоноситель.
В отличие от круглых и плоских труб, поле скорости в призма-
тических трубах (треугольных, четырехугольных и других форм
поперечного сечения) и в каналах, образованных стержнями топ-
ливных сборок, даже вдали от входа является двумерным, а каса-
тельное напряжение на стенке неоднородно по периметру.
Поле температуры в таких системах при однородных (а тем
более неоднородных) по периметру граничных условиях будет трех-
мерным. При этом коэффициент теплоотдачи изменяется не только по
длине, ио и по периметру канала. При расчете теплообмена в каналах
сложной формы нередко оказывается невозможным задать тепло-
вые граничные условия иа стенке (например, распределение qa
по периметру канала заранее неизвестно). В таких случаях прихо-
дится решать сопряженную задачу, рассматривая одновременно
поля температуры в твэле и в потоке теплоносителя.
Из сказанного очевидно, что расчет течения и теплообмена в ка-
налах сложной формы — трудная задача. Для ее успешного реше-
ния нужны специальные методы (см. § 9.3—9.5). Учитывая большое
разнообразие форм поперечного сечения каналов, используемых
в реакторостроении, эти методы должны быть достаточно универ-
сальными, т. е. применимыми к каналам разной формы.
§ 9.2. Теплообмен и сопротивление в кольцевых
и плоских трубах
1. Метод расчета теплообмена. Каналы ядерных реакторов и по-
верхности нагрева теплообменных аппаратов нередко выполняются
в виде системы труб кольцевого сечения (рис. 9.1). Теплообмен
247
в кольцевой трубе может осуществляться через одну или обе стенки.
Плоскую трубу можно рассматривать как предельный случай коль-
цевой трубы, соответствующей значению r-Jr^ -+ 1, где /д и г2 —
радиусы внутренней и наружной труб.
Теоретический расчет теплообмена в трубах кольцевого сечения
в принципе можно провести тем же методом, что и в круглых. Од-
нако задача о теплообмене в кольцевых трубах сложнее, чем задача
о теплообмене в круглых. Это свя-
зано с наличием дополнительного
параметра неодинаковым рас-
п р едел ен и ем скор ости вблизи
внутренней и наружной стенок
кольцевой трубы и, наконец, воз-
можным различием в тепловых
граничных условиях на стенках.
Рассмотрим стабилизованный
теплообмен в кольцевой трубе при
полностью развитом (стабилизо-
ванном) течении жидкости. Пусть
на внутренней и наружной стен-
ках трубы заданы постоянные зна-
чения плотности теплового потока
Рис. 9.1. Схема канала кольцево- qcl и qa2. Все остальные условия
го сечения. те же, чт0 и обычно. Эта задача
рассмотрена в работе [18].
_ Среднемассовая температура жидкости в данном сечении трубы
t (х) легко определяется из теплового баланса
—, . 2 (дс1/д-j-дс2 г2) х -
Н*)=--------—--------— -Но.
pep w — г{)
(9.1)
где tQ — среднемассовая температура жидкости на входе в трубу
(т. е. х = 0).
Так как процесс теплообмена стабилизован, a qcl и qc2 постоян-
ны, то выполняется условие (см. § 7.1):
dt ___ diet _ 2 (gcl + gc2 r2)
dx dx dx pCp щ (r2—rj)
(9-2)
(Z = 1 соответствует внутренней стенке, i = 2 — наружной стенке
трубы).
Учитывая сказанное, уравнение энергии можно записать в виде
d Г / 8„\ dt
CW R— — R {1 + |3 Рг --) —
dR \ v / dR
(9.3)
248
где
2 (<7ci Н + ?с2 >'2) Га
I G1 - Г?)
Граничные условия имеют вид*
?С1 Г1
X
7с2 1'2
К
(9.4)
Значения e0/v, и [3 в уравнении (9.3) должны быть заданы. Обыч-
но для &a/v — f (гр R) используются те же зависимости, что и для
круглой трубы, скорректированные так, чтобы распределения е0А>,
записанные для областей потока, прилегающих к внутренней и на-
ружной стенкам, согласовывались бы друг с другом в окрестности
максимума скорости. Положение линии максимума скорости яв-
ляется важной характеристикой течения в кольцевой трубе. Мак-
симум скорости расположен тем ближе к внутренней стейке, чем
меньше гг!г^. Для определения координаты максимума скорости
гт используются эмпирические или полуэмпирические зависимости
[22, 28]. Зная гт, можно рассчитать значения касательных напряже-
ний на внутренней и наружной стенках ас1 и ос2, которые входят
в выражения для ea/v. Профиль скорости определяется по най-
денным значениям 8a/v или описывается полуэмпирнческими зави-
симостями, подобными зависимостям для круглых труб. Значение
[3 (или Ргт0) обычно.принимают равным единице или выбирают по
эмпирическим или полуэмпирическим данным.
Интегрируя (9.3) по радиусу и учитывая условия (9.4), получаем
... г я
=!---------------- с f Wx RdR + (— I)' -Др-
aR R[I + РРГ.М L k "
\ V /
где
R^ rR f2> R2 ~ 1.
1,2), (9.5)
Интегрируя выражение (9.5) еще раз и выбирая начало отсчета
на внутренней стенке (Z = 1), получаем уравнение, описывающее
распределение температуры по радиусу:
R л р
р WxRdR-P
4^r1+qwr2 J (i+pprVb
Д1 \ V J
(9-6)
* Плотность теплового потока считается положительной, если тепло
подводится от стенки к потоку, и отрицательной — в противном случае.
249
где
Р == ffd''!
<7ci Г1 “F 7c2 r2
Чтобы рассчитать температуры внутренней и наружной стенок
и коэффициенты теплоотдачи на этих стенках, рассмотрим выраже-
ние для среднемассовой температуры жидкости:
Г 2 1
t =------------ f twx2nrdr =------- f tWxRdR.
^rl-r^w J X 1--Rl J
Г1 Я1
Интегрируя это выражение по частям и учитывая, что
st WxRdR — 1, находим
'1 J
/?1
Подставляя в это соотношение dt из (9.5) для соответствующих зна-
чений I, получаем уравнения для температур внутренней и наруж-
ной стенок трубы:
По определению, числа Нуссельта на внутренней и наружной стен-
ках
Nu1M = и Nu2o<,= (9.9)
(/Gi—/) К —dj'k
Пользуясь уравнениями (9.7) и (9.8), нетрудно записать соответст-
вующие выражения для предельных значений чисел Нуссельта
Nuloo и Nu2oo.
Как видно из формул (9.7)—(9.9), температура каждой из сте-
нок кольцевой трубы (fcl или /с2), а также числа Нуссельта на этих
стенках (Nuloo или Nu2oo) зависят от плотности теплового потока
250
на обеих стейках. При определенном сочетании значений qci (2 =
= 1,2) разность температур —t 0, a Nu^—>оо; при дру-
гих значениях qci разность tci— t и Nuioo становятся отрицательны-
ми. Отмеченные особенности затрудняют обобщение опытных и рас-
четных данных и создают не-
удобства при практических рас-
четах.
Расчет теплообмена в коль-
цевых трубах существенно упро-
щается, а определяемые величи-
ны приобретают более ясный фи-
зический смысл, если ввести по-
нятие адиабатической темпера-
туры стенки.
__ Напомним, что символами
t, /С1 и fca обозначены средне-
массовая температура жидкости
и температуры внутренней и на-
ружной стенок при одновремен-
ном теплообмене (обогреве или
охлаждении) на обеих стенках,
т. е. при qcl и qc%, отличных от
нуля (рис. 9.2, в).
Рассмотрим два частных слу-
чая и введем соответствующие
обозначения.
1. Теплообмен только на
внутренней стенке (д-с1:/=0,
qcа — 0). Для среднемассовой
температуры жидкости и темпе-
ратуры стенок в этом случае
введем следующие обозначения
(см. рис. 9.2, a): 1 t01 = fcll
И Zc2 = ^а.с2, где zfa.C2 — адиаба-
тическая температура наружной
в кольцевом канале:
а — подвод тепла к внутренней стенке ка-
нала, внешняя — теплоизолирована; б —
подвод тепла к внешней стенке канала,
внутренняя — теплоизолирована; в —•
двухсторонний подвод тепла.
стенки, т. е. температура наруж-
ной теплоизолированной стенки при обогреве только внутренней
стенки. Очевидно, что разность — /а.с2 пропорциональна qcl.
2. Теплообмен только на наружной стенке (<у С1 = 0, qc2 =^= 0).
В этом случае обозначим t = /2, /с1 = /а.с1 и £с2 = £с22 (см. рис. 9.2,6),
где 2а-01 — адиабатическая температура внутренней стенки, т. е.
температура внутренней теплоизолированной стенки, при подводе
тепла только через наружную стенку. Аналогичным образом раз-
ность /2 — £а<с1 пропорциональна qc%.
Вследствие линейности исходного уравнения энергии относитель-
но температуры поле температуры в кольцевом канале при одно-
251
временном теплообмене на обеих стенках (см. рис. 9.2, в) можно пред-
ставить в виде суммы (суперпозиции) двух температурных полей:
температурного поля, соответствующего теплоподводу на внутренней
стенке и теплоизолированной внешней стенке (см. рис. 9.2, а), и тем-
пературного поля, соответствующего подводу тепла через наружную
стенку и теплоизолированной внутренней стенке (см. рис. 9.2, б).
Отсюда следует, что*
41 I ~~ Gcll О) +va.cl ^2); (9.10)
4 г
Разделив первое
[где d3 = 2 (.
трубы], получим
/ — (/С22 4) -|- (^а.С2 4
из этих соотношений на
2 — /'1)] — эквивалентный
А — А I а ^с2 -
- - ueli f-ua.cl ,
)• (9.П)
qcldj'h> а второе на
диаметр кольцевой
(9.12)
। —, а к. а / ci
С2 V/C22 г vja«c2 ’
7С2
где
гх ___ (4.1 4 А) .
ucl ~ з >
7ел 64
й — ^са 4 .
7с2 ^3
/а ____ (4п— Л) . а,
v411 ~ , > '~'а.с1
<7ci “о
А — (4*д2 4) 4 /а
МС22— , > va.c2
<?С2 “э
(Qi. ci— 4) .
7с2 4)
(4. С2---о)
7ci 4
Как следует из (9.12), чтобы определить температуры стенок в
рассматриваемом сечении кольцевого канала при заданных тепловых
потоках qcl и qc2, необходимо знать 0с11, 0О22, 0а>о1 и 0а.с2. При
стабилизованном теплообмене эти величины определяются из урав-
нений (9.7) и (9.8):
’ 1 \ 2
[ WxRdR]
R '
J (1 + рРг-М/?
«1 \ V J
(9.13)
1 /7 V
р I Wx RdR
I --------_2—dR-
J ( 1 +|ЗРг_^
Дх \ v ;
(9.14)
* Очевидно, что соотношения (9.10) и (9.11), а также вытекающие из
них уравнения (9.12), (9.19) и (9.20) справедливы не только для стабилизован-
ного теплообмена, но и для термического начального участка.
252
(®a.cl)°o
(1-7??) (1 -/?!)
/ 1 \ 2 1
2 / с \ Г
-----2 WxRdR - WxRdR
1 —1\Т \ •' / *'
1 \Д_______/ Д________
f 1 -J- |3Pr —'j 7?
\ V /
dR;
1 27? t с V
Р ----4 WxRdR -7? Л WxRdR
_______1______ 1 ул_______________[_____д,_______
(1-7??) (1 - 7?х) J / 1> + ррг-Му?
Дх к V /
Из (9.15) и (9.16) с учетом очевидного тождества
д 1 0
Гг. RdR + f RdR ——gi.
Дх д z
следует простая зависимость между (0а.с1)оо и (©а.с2)сУ
(9.15)
(9.16)
(9Л7)
(9.18)
(®а-с2)оо — (©а.с1)“ ^1-
Переходя от безразмерных температур к числам Нуссельта, урав-
нения (9.12) можно переписать так:
Nun
Nui=---------
1 + NUji ®a.ci
7ci
Nua =
Nu2a
1 + Nu22 ©a.c2
7c2
(9.19)
(9.20)
где Ntij = ©у/ и Nu3 — ©eV — числа Нуссельта на внутренней
и наружной стенках при их одновременном обогреве; Nun — ©И1!
и Nu22 = ©J22 — то же при обогреве только внутренней и только
наружной стенки.
Как следует из (9.13) и (9.14), (©сп)^, (©022)00. а следовательно,
и (NunL и (Nu^X, всегда положительны; (©a.ci)TO и (©а.02)00, напро-
тив, всегда отрицательны [так как /2> и £а<С2 (см- рис. 9.2)].
Между тем (Nu!)^ и (Nila)» могут быть как положительными, так и
отрицательными и даже обращаться в бесконечность. Например,
для изображенного на рис. 9.2, в распределения температуры fcl
> I, а /02 < t и, следовательно, (Nu!)^ > 0, a (Nu3)oo < О-
В случае плоской трубы по условиям симметрии Nuu = Nli22 и
© — ©
'-'a.cl ^а.с2*
Итак, для определения температуры стенок кольцевого канала
или чисел Нуссельта на них при произвольных значениях qcl и qG2
253
достаточно иметь данные о Nuu, Nu22 и 0а.(11 (или 0а.с2). Эти вели-
чины можно рассчитать по соответствующим уравнениям [для стаби-
лизованного теплообмена по уравнениям (9.13)—(9.16)1 либо опре-
делить экспериментально.
2. Результаты расчета теплоотдачи и опытные данные. Для пол-
ностью развитого (стабилизованного) течения и теплообмена при гра-
ничных условиях второго рода значения (Nuu)^, (Nu22)oo> (®a.ci)~
и (<Эа.с2)оо вычислены в [30, 31] и некоторых других работах. Экспе-
риментальные данные получены в работах [1, 19, 31], а также в ряде
Других.
Основываясь на результатах теоретического расчета и наиболее
надежных опытных данных, Б. С. Петухов и Л. И. Ройзен предло-
жили интерполяционные уравнения, охватывающие диапазон зна-
чений 7?! = cZj/^2 от 0,03 до 1, Рг от 0,7 до 100 и Re от 104 до 10°. Эти
уравнения имеют вид:
(9.21)
(9.22)
(9.23)
где Nu^ — предельное число Нуссельта для круглой трубы, вычис-
ляемое по уравнению (7.21); /г = 0,16Рг~0,15; £ — поправочный ко-
эффициент, учитывающий, что для кольцевых труб с djd2 < 0,2
число (Nun)^ слабее зависит от Re, чем для круглой трубы:
о, 6
(9.24)
(при dx/d2 0,2 значение £ — 1).
При значениях Рг ж 0,7 уравнения (9.21)—(9.24) совпадают с
уравнениями, полученными в работе [19] на основе обработки опыт-
ных данных по теплоотдаче к воздуху.
Результаты измерений и расчетов показывают, что зависимость
числа Нуссельта от числа Рейнольдса для труб кольцевого сечения
остается такой же, как и для круглых труб (лишь на внутренней стен-
ке при (Д/с[2<: 0,2 эта зависимость несколько слабее). Зависимость
теплоотдачи от числа Прандтля для труб кольцевого сечения отли-
чается от аналогичной зависимости для круглых труб. Однако это
различие невелико и проявляется главным образом при небольших
значениях Рг (см., например/табл. 9.1). Адиабатическая температура
стенок кольцевых труб сильно зависит от чисел Re и Рг, уменьшаясь
с ростом последних.
Уравнение (9.22) справедливо при 0
254
Предельные числа Нуссельта и адиабатические температуры сте-
нок в зависимости от djd^ при одностороннем обогреве показаны
на рис. 9.3 и 9.4. Более высокая теплоотдача на внутренней стенке
по сравнению с наружной объясняется тем, что градиент скорости,
а следовательно, и само значение скорости, вблизи внутренней стенки
выше, чем вблизи наружной. С увеличением отношения djd^, эта
разница исчезает.
Рис. 9.3. Зависимость чисел Нуссельта в кольце-
вой трубе при одностороннем обогреве от d^jd^
Приведенные выше уравнения справедливы и для плоской тру-
бы, т. е. при dx/d2 = 1. В случае плоской трубы при одностороннем
обогреве
(NuuL = (Nu22)oo - (9.25)
где /<од — поправочный коэффициент, практически не зависящий
от Re и слабо зависящий от Рг. Например, при Рг « 0,7, как вид-
но из уравнений (9.21) или (9.22),
Лои = 0,86.
В такой же форме можно пред-
ставить число 1~1уссельта для плос-
кой трубы и в случае симметрич-
ного обогрева (т. е. при <ус1 = с/с2):
(NuO^ == (Nu2)to = NuJ<CHM. (9.26)
Значения /<од и Лсим, вычислен-
ные по данным 'работы [301, при-
ведены в табл. 9.1.
Теплообмен при течении жидких
металлов в трубах кольцевого
сечения исследован еще не полно.
Основываясь на результатах тео-
ретического расчета, проведенного
Бейли [25], Лайон [32] рекомен-
Рис. 9.4. Зависимость адиабатиче-
ских температур стенок кольце-
вой трубы от c/i/f/2.
дует следующее уравнение для предельного числа Нуссельта при
обогреве только внутренней стенки (т. е. при qa2 = 0):
(Nun)oo - (5,2+ 0,019 Ре°«8) (
(9.27)
255
Таблица 9.1
Значения Лсд и Х^им Для плоских труб с односторонним и симметричным
обогревом
Re Pr=0,7 Рг— 1,0 Pr=10 Рг=100
КОД ^сим ;<од •^СИМ ;<од ^сим ;<од ^сим
5-103 0,803 1,061 0,850 1,045 0,982 1,005 1,00 1,00
104 0,822 1,055 0,860 1,039 0,982 1,004 1,00 1,00
5-104 0,851 1,048 0,880 1,032 0,983 1,004 1,00 1,00
105 0,860 1,039 0,885 1,028 0,983 1,003 1,00 1,00
5-105 0,880 1,035 0,900 1,025 0,983 1,00 1,00 1,00
Это уравнение справедливо в диапазоне значений dvld% = 0,04 4-1,
Re = 104 -г- 10G и Ре = 5-1024-104. Опытные данные [24] по
теплоотдаче к сплаву натрия с калием подтверждают уравнение
(9.28). Однако экспериментальные результаты работы [17] по тепло-
отдаче к ртути на 15% ниже значений, рассчитанных по этому урав-
нению. ":
Н. И. Булеев с соавторами [7] на основе проведенных ими'рас-
четов получили уравнение для теплоотдачи на наружной стенке
кольцевой трубы при теплоизоляции внутренней (qcl = 0):
- (Nu22)TO = 5 + 0,020Ре°’8. ) (9.28)
Это уравнение справедливо при djd^ = 0,5 -4-1; Re = 1044-5 х
X 10б и Ре = 102 4-5 103. Оно хорошо подтверждается экспери-
ментальными данными по теплоотдаче к ртути [21]. При djd^ = 1,
т. е. для плоской трубы с односторонним обогревом, уравнения (9.27)
и (9.28), как и надлежит, дают практически совпадающие резуль-
таты. При двухстороннем симметричном обогреве плоской трубы
(т. е. при qcl = 7С2) можно пользоваться уравнением
(Nu^ = (Nu^ = 8,6 + 0,029Ре°’8. <(9.29)
Это уравнение, составленное на основе расчетов, проведенных
Н. И. Булеевым, хорошо согласуется с опытными данными [21].
Уравнение (9.29) справедливо в диапазоне значений Re = 104 4- 4 X
X 105, Ре = 102 4- 4 • 10s (Рг = 0,001 4- 0,05).
Теплообмен в термическом начальном участке кольцевых труб
при полностью развитом (стабилизованном) течении воздуха экспе-
риментально исследован в работе [20]. Для расчета местной тепло-
отдачи на внутренней стенке (при теплоизоляции наружной) и на
наружной стенке (при теплоизоляции внутренней) рекомендуются
уравнения:
0,86 + 0,8 0,4; (9.30)
^^Иоо \ d% J \ dg /
=0,86 + 0,54Г1 +0,48 f—V0’4, (9.31)
iNU22oo L \ dz J ]\d3J *
256
где Nulloo, Nu22oo — предельные числа Нуссельта, вычисляемые по
ранее приведенным уравнениям.
Уравнение для Nuu справедливо при 0,14 ^/^2 1, а для
Nu22 — при 0 < cZi/ds < 1. Этими уравнениями можно пользо-
ваться для расчета теплоотдачи к газам (Рг = 0,7 ч- 1) при значениях
Re = 104 ч- 3 • 105 и 1 x/d3 /H.T/da- Если длину термического
начального участка Zn.T определить из условия NuZz- = l,03NuHoo
при х = /и.т, то для внутренней стенки
-А— 40 fAV’43; (9.32)
d \ с?2 /
для наружной стенки
16 f 1 + 1,5 А\
к 4 /
йг.т
d
(9.33)
Температуры теплоизолированных стенок /а.с1 и г?а.с2 в термичес-
ком начальном участке приближенно можно считать постоянными
и равными температуре газа на входе: г?а.с1 « г?а.с2 t0. В области
стабилизованного теплообмена г?а.с1 и ia.c2 будут линейно изме-
няться по длине.
Практический расчет теплообмена в трубах кольцевого сечения
при заданных значениях плотностей теплового потока на стенках сво-
дится к определению температуры внутренней и наружной стенок
в различных точках по длине трубы. Удобные для расчета уравнения
легко получить из уравнений (9.12), прибавив к первому из них ве-
личину (t—t0)h/qclda, а ко второму величину (/— t^k/q^d^ опреде-
лив их предварительно из уравнения (9.1). В результате получим
(^ci — 4) А, _ 1
<7ci NUn
^£20 I
ua.ci И
7ci
л I ।
4 ---- + ~
\ Я С1“2 / . X .
/ di \
Re Рг i 1 + — I 8
\ ^2 /
Rc2 ^о) 1
qC2da Nu22
0 4.
va.c2
“702
4 f — • ~ + 1 'l
\ ffca Д2________/ . х
RePr ( 1 + A'l d°
\ + J
(9.35)
Пользуясь этими уравнениями, легко записать соответствующие
уравнения для различных частных случаев. Например, при qai = О
имеем
Ra.ci— + А. гч , 4 х .
..= °а-ы + peD -4--
• U« о л LJ * I J „L ———• | и
\ d2 /
(9.36)
Rc22— ^0)
Qc2 da
1
Nu22
4 x
/ di\ ’ d»'
Re Pr 1 + А йэ
\ d2 J
(9.37)
9 Зак. 792
257
Таблица 9.2
Отношение коэффициентов сопротивления трения в кольцевой и круглой
трубах ?/5тр по данным работы [28]
Re £/£Тр при di/d.
0,01 0,02 0,03 0,05 0,07 о, 1 0,2 0,3 0,5 0,7 1 , о
10'1 1,004 1,006 1,007 1,010 1,011 1,014 1,018 1,020 1,024 1,025 1,025
108 1,009 1,012 1,015 1,020 1,024 1 ,027 1,037 1,044 1,050 1,053 1,054
При значениях 0 в уравнения (9.34)—(9.37) подстав-
ляют значения Nun, Nu33, 0а.с1 и 0а.(,2 Для термического начально-
го участка; при х > /п.т — значения (Nun)^, (Nn™)^ (0a.ciK и
(0а.с2)« Для области стабилизованного теплообмена.
3. Сопротивление трения. Как показывают расчетно-теоретиче-
ские и экспериментальные исследования, коэффициент сопротивления
трения при стабилизованном течении жидкости в трубах кольцевого
сечения мало отличается от коэффициента сопротивления трения,
вычисленного по уравнениям для круглых труб, если в качестве
характерного размера пользоваться эквивалентным диаметром. От-
ношение коэффициентов сопротивления трения в кольцевой и круг-
лой трубах £/£тр в зависимости от dj/d2 для двух крайних значе-
ний Re приведено в табл. 9.2 [28]. Пользуясь этой таблицей и вы-
числив £тр по одной из формул для круглых труб при значении
d = d0, можно определить коэффициент сопротивления трения для
кольцевой трубы. Перепад давления на участке трубы длиной I
при стабилизованном течении находится с помощью обычного со-
отношения
(9.38)
§ 9.3. Распределение скорости в призматических трубах
и продольно обтекаемых пучках стержней
Если говорить о техническом аспекте проблемы, то поля ско-
рости в каналах сложной формы нужны для определения коэффици-
ентов гидравлического сопротивления и расчета полей температуры,
в свою очередь, необходимых для расчета теплообмена.
При аналитическом подходе к решению задачи о нахождении
профилей скорости в каналах сложной формы приходится совместно
решать уравнение движения (6.20) и уравнение неразрывности
(6.19). Однако при решении этой системы возникают две принципи-
альные трудности. Во-первых, как об этом уже говорилось выше,
система уравнений является незамкнутой и для ее решения требу-
ются дополнительные сведения или гипотезы о коэффициенте турбу-
лентного переноса количества движения eff.
258
Во-вторых, точное аналитическое решение дифференциальных
уравнений в областях со сложной геометрией (даже если система
является замкнутой) чаще всего оказывается невозможным. Поэ-
тому при расчете распределения скорости в каналах сложной гео-
метрии прибегают к приближенным или численным методам реше-
ния дифференциальных уравнений либо вообще отказываются от
решения уравнения движения и применяют более простые полуэм-
пирические методы расчета.
Экспериментальное определение коэффициентов турбулентного
переноса количества движения в каналах сложной формы — труд-
ная задача. Для их расчета по профилям скорости необходимо знать
распределение касательных напряжений, непосредственное измере-
ние которых связано с чрезвычайно большими трудностями. По-
этому при экспериментальном определении еа в каналах сложной
формы чаще всего непосредственно измеряют корреляцию пульсаций
скорости w'xw'r. К настоящему времени имеется очень мало данных
о коэффициентах турбулентного переноса количества движения
в каналах сложной формы.
В. П. Бобков и М. X. Ибрагимов [2] получили выражение для
ьд иным путем. Применив к турбулентным течениям в каналах не-
которые соотношения, строго справедливые только для однородной
турбулентности, введя дополнительные гипотезы и воспользовав-
шись экспериментальными данными для интенсивности и других
статистических характеристик турбулентности при течении в кана-
лах, они получили следующую формулу:
8 / W \ 5 / ~ \ 3, 5 / пй \ 2
-0,11 Re — —) /1 _ ехр (—-1,54Г). (9.39)
V \ W / \ ^0 / \ /
Здесь w — локальное значение, скорости в рассматриваемой точке
потока; w — средняя скорость; — максимальное значение скоро-
ти; У = y/y^LiKC — безразмерное расстояние рассматриваемой точ-
ки от стенки канала (подробнее см. обозначения па рис. 9.9). Оче-
видно, что эта формула нуждается в тщательной экспериментальной
проверке.
К настоящему времени разработано несколько методов прибли-
женного расчета полей скорости в каналах сложной формы. Под-
робный обзор современного состояния этого вопроса приведен
в работе Ниязинга и Эйфлера [34]. Кратко рассмотрим некоторые
из них.
Н. И. Булеев [6], развивая идею метода пути перемешивания,
предложил пространственную модель турбулентного обмена.
При расчете коэффициентов турбулентного переноса количества дви-
жения и тепла в произвольной точке потока учитываются моли, по-
падающие в рассматриваемую точку из всех окружающих точек.
Полученные Н. И. Булеевым выражения для коэффициентов турбу-
лентного переноса количества движения и тепла содержат ряд по-
стоянных, которые определяются по экспериментальным данным для
9* 259
крулгых труб. Хотя правомерность переноса закономерностей, полу-
ченных в круглых трубах, на каналы сложной формы поперечного се-
чения не является очевидной, многие расчеты, выполненные по ме-
тодике [6], находятся в удовлетворительном соответствии с опытными
данными.
В связи с тем что определение коэффициентов турбулентного
переноса в каналах сложной формы чрезвычайно сложно, большин-
ство авторов при практических расчетах полей скорости в каналах
сложной формы стараются обойтись без
использования данных о коэффициентах
турбулентного переноса количества дви-
жения. Имеющиеся опытные данные о
профилях скорости в каналах сложной
формы [10,15, 27] свидетельствуют о том,
что в большей части канала распределе-
ние скорости вдоль нормалей к поверх-
ности канала, построенное в универсаль-
ных координатах, с достаточной для
практики точностью совпадает с распре-
делением скорости в круглой трубе. При
этом динамическая скорость рассчиты-
вается по местному значению касатель-
ного напряжения, т. е. напряжению у
основания нормали. Иными словами, ско-
рость в любой точке канала сложной
формы может быть рассчитана по фор-
мулам, приведенным в § 6.6 для круглых
труб, если известно распределение каса-
тельных напряжений по периметру ка-
нала. Поэтому обычно при расчете про-
филей скорости в каналах сложной формы вместо того, чтобы ре-
шать уравнения движения и неразрывности с использованием дан
ных о распределении коэффициента турбулентного переноса коли-
чества движения, тем или иным путем находят распределение ка-
сательных напряжений по периметру канала.
При таком подходе основная проблема состоит в определении
закона изменения касательного напряжения по периметру канала.
Впервые метод расчета полей скорости в каналах сложной формы
поперечного сечения был разработан Дайслером и Тейлором [26].
Основные идеи этого метода рассмотрим на примере канала, часть
которого ABCD изображена на рис. 9.5. Будем считать, что течение
в этом канале стабилизовано, т. е. профиль скорости по длине канале
не меняется, а расход жидкости или средняя скорость w заданы.
Требуется рассчитать распределение скорости в этом канале.
Расчет начинают с определения средней дла канала величины ка-
сательного напряжения. Необходимый для этого коэффициент
сопротивления трения в качестве первого приближения рассчиты-
260
вается по какой-либо достаточно простой формуле, например по фор-
муле Блазиуса:
0,3164
Re0'25 '
(9.40)
Здесь Re = wdjv— число Рейнольдса, определяемое по экви-
валентному диаметру канала = 4f/s, где f— площадь попереч-
ного сечения канала; s — смоченный периметр канала.
По коэффициенту сопротивления трения определяются продоль-
ный градиент давления в канале
dp
dx
2d3
(9.41)
и средняя величина касательного напряжения на стенке
На схеме канала ориентировочно в качестве нулевого приближения
наносят линии постоянной скорости — изотахи (пунктирные ли-
нии на рис. 9.5). После этого строятся линии максимальной скорости
EF и линиями ab, cd и т. д., перпендикулярными к изотахам, канал
разбивается иа отдельные элементы abed.
Составляя баланс сил, действующих на произвольный элемент
канала abed, размер которого в направлении, перпендикулярном
плоскости чертежа, равен dx, Дайслер и Тейлор полагали, что вза-
имодействие рассматриваемого элемента с соседними вдоль границ
ab, be и cd отсутствует, так как градиент скорости на этих границах
равен нулю. В этом случае на элемент действуют только две силы:
сила, обусловленная продольным градиентом давления и равная
| dp/dx | dxfj, и сила трения вдоль границы ad, равная (cQjdxsj, где fj
и Sj — соответственно площадь поперечного сечения и участок пери-
метра элемента. Так как градиент давления для всех элементов оди-
наков и определяется выражением (9.41), то из баланса рассматри-
ваемых сил нетрудно определить величину касательного напряже-
ния на участке ad:
(°c)j =
(9.43)
4 ’
где daj — эквивалентный диаметр /-го элемента. Сопоставляя выра-
жения (9.42) и (9.43), легко получить следующее соотношение:
К)/ = <Го-^. (9.44)
Выражения (9.42) и (9.44) позволяют рассчитать распределение ка-
сательных напряжений по всему периметру канала. Если все интер-
валы разбиения sj выбрать одинаковыми, то, как следует из формулы
261
(9.43), величины касательных напряжений будут пропорциональны
площадям элементов. Зная касательное напряжение на участке
ad (<гсД, можно определить местную динамическую скорость
]/? (9Л5)
и по универсальному профилю скорости ср = ср (т|), гдет] =
и ср = ш/(и*);, рассчитать изменение скорости вдоль линий ab и cd.
В результате таких расчетов, выполненных для всех элементов каиа-
Рис. 9.6. Рассчитанное по методике Дайслера н Тейлора распределение
относительной скорости wfw (Re=65-103).
ла, строится новая сетка изотах (первое приближение) и определя-
ется средняя для всего канала скорость шр. Если полученное рас-
четным путем значение средней скорости оур не совпадает с за-
данным значением w, то прежде всего вносится поправка в исходное
значение коэффициента сопротивления трения g и в среднюю величи-
ну касательного напряжения на стенке стс. После этого, используя
сетку изотах, аналогичным путем получают второе приближение для
поля скорости в канале. Расчеты продолжают до тех пор, пока два
последовательных распределения скорости не совпадут с заданной
точностью. Распределение скорости в канале сложной конфигурации,
рассчитанное авторами работы [10] по методу Дайслера и Тейлора,
показано на рис. 9.6.
Графо-аналитический метод Дайслера — Тейлора чрезвычайно
трудоемок. Но, кроме того, он обладает еще одним существенным не-
достатком. Сравнение рассчитанных по этому методу профилей
скорости с измеренными, выполненное в работе [10], показа-
262
н 1 ейлора оо отсут
соседними элементами сечения,
Рис. 9.7. Схема вторичных течений
в канале треугольного сечения.
ло, что, хотя расчет дает качественно правильную картину, в ко-
личественном отношении наблюдается различие в локальных зна-
чениях скорости до 25%, а в локальных значениях касательных на-
пряжений до 55%. При этом расчетные значения скоростей оказались
завышенными относительно измеренных значений в широких час-
тях сечения и заниженными в узких.
Такое расхождение расчета с экспериментом объясняется неспра-
ведливостью допущения Дайслера “
на количеством движения между
особенно через участки границы
ab и cd (см. рис. 9.5). На самом
деле, как показывают экспери-
менты, при турбулентном тече-
нии в каналах сложной формы
происходит интенсивный перенос
количества движения через боко-
вые границы элементов. Одни
авторы связывают этот перенос
в поперечном сечении канала в
на п р а влей и и, пар а л л ел ыюм
стенкам, с крупномасштабной
турбулентностью 19, 10], дру-
гие — с наличием вторичных те-
чений [14, 34]. Так как недавно
полученные экспериментальные
данные (см. работу [34]) показы-
вают, что вторичные течения
генерируются в результате интенсивного выброса вихрей из при-
стеночных в центральные области потока, то, по-видимому, воз-
можна любая из этих трактовок. Наиболее интенсивный выброс
вихрей наблюдается в зонах с наибольшими значениями касатель-
ных напряжений. В этих местах возникает течение жидкости от сте-
нок в центральную область канала. Из центральной области течение
поворачивает в углы канала и оттуда вдоль стенки возвращается в
зоны максимальных напряжений. В результате в канале образует-
ся несколько поперечных замкнутых течений, называемых вторич-
ными течениями (рис. 9.7).
Таким образом, очевидно, что дальнейшее уточнение расчетных
методов определения полей скорости в каналах сложного сечения
связано с учетом переноса количества движения в поперечном се-
чении канала в направлении, параллельном стейкам. В настоящее
время создание таких усовершенствованных методов расчета раз-
вивается по двум направлениям.
Ряд авторов — Ниязинг, Гаргантини и Эйфлер [33], Л. С. Коко-
рев, А. С. Корсун и В. И. Петровичев [13], Фишер [29], П. А. Уша-
ков [23] и др. — используют для этой цели уравнение, получаемое
в результате интегрирования уравнения движения вдоль нормали к
стенке канала. Получаемое таким образом интегральное уравнение
263
связывает распределение касательных напряжений по периметру
канала с формой канала и переносом количества движения в попереч-
ном сечении канала в направлении, параллельном стенке. Для реше-
ния этого уравнения помимо допущения об универсальности профи-
ля скорости вдоль нормали необходимы некоторые допущения и до-
полнительные данные о коэффициентах турбулентного переноса ко-
личества движения в направлении, параллельном стенке канала.
Авторы, придерживающиеся второго направления, вообще отка-
зываются от решения уравнения движения и для расчета распределе-
ния по периметру касательных напряжений используют некоторые
физические соображения в сочетании с уравнениями баланса сил.
Рис. 9.8. Схема разбиения канала сложной формы на
ячейки (ЛМС — линия максимальной скорости).
Наиболее полно и последовательно этот метод разработан сотрудни-
ками Физико-энергетического института М. X. Ибрагимовым,
И. А. Исуповым, Л. Л. Кобзарем и В. И. Субботиным [9, 10].
Учитывая, что метод ФЭИ разработан более полно, а получаемые
с его помощью результаты не уступают по точности другим ме-
тодам, ознакомимся с ним более подробно.
Рассмотрим канал произвольного сечения или его часть ABCD,
изображенную на рис. 9.8. Прежде всего поперечное сечение канала
разбивается на отдельные ячейки. Для этого на эскизе поперечного
сечения канала наносятся линии максимальной скорости — ЕО,
ОВ и ОС. В качестве таких линий принимаются геометрические мес-
та точек, равноудаленные от стенок канала. Кроме того, проводятся
нормали OF, OG, ОН, KL и КМ таким образом, чтобы в пределах
каждой ячейки высота (y0)j менялась бы монотонно.
Рассмотрим одну из получившихся ячеек, например, ячейку
КОНМ, показанную в более крупном масштабе на рис. 9.9. Коорди-
наты произвольной точки Р внутри ячейки у и z будем отсчитывать
вдоль нормали от поверхности канала (#) и в перпендикулярном на-
правлении от одной из границ ячейки (г). Расстояние до линии
максимальной скорости обозначим (г/0)/-
264
Введем некоторые параметры, характеризующие геометрию
ячейки. Такими параметрами прежде всего являются площадь по-
перечного сечения ячейки fj и длина смоченного периметра Sj. Да-
лее определим среднюю высоту ячейки:
1 S?j
(Уо)з ~— f (9.46)
и среднюю ширину ячейки:
(9.47)
Введем параметр формы сечения ячейки, определив его как отноше-
ние средней ширины к средней высоте, т. е.
sj Л
(уо); (у о)?
(9.48)
Неравномерность высоты ячейки будем характеризовать парамет-
ром
( .макс\ _ Л мин\.
у —Д—^.0 Д. (9Л9)
(уГкс)/
Эквивалентный диаметр ячейки определим как
d3; = —< (9-50)
J si
Кроме того, введем параметр характеризующий кривизну поверх-
ности:
|37=——, (9.
Pj
265
где pj — радиус кривизны поверхности. Для плоской поверхности
5 = 0, для круглой трубы [3 = —1, для выпуклых поверхностей
5 > 0.
Итак, переходя к методу расчета распределения скорости в рас-
сматриваемой ячейке, авторы работы [9] прежде всего формулируют
гипотезу, позволяющую учесть перенос количества движения в по-
перечном сечении канала в направлении, параллельном стенке. По-
видимому, этот перенос прежде всего связан с изменением высоты
ячейки z/o (г), так как при постоянной высоте отсутствие переноса
вдоль стенки следует из соображений симметрии. Можно предполо-
жить, что в те места ячейки, где у0 мало, крупные вихри прони-
кают с трудом, их влияние на распределение касательного напряже-
ния на стенке несущественно и касательное напряжение на стенке
в этих зонах, как следует из соотношения (9. 43), пропорционально
у0. Иными словами, при малых у0
(9.52)
fe); (Го);
i р
где (ос); = — \ (пс); dz — среднее для всей ячейки касательное на-
sj о
пряжение на стенке. С увеличениему0 роль крупномасштабного пере-
носа вдоль стенки должна возрастать, ос при этом должно меняться
слабее и в пределе при оо можно предположить, что d (о'с/о,с)->-
-> 0. Такому характеру изменения сгс удовлетворяет следующая
функция:
(^с); Г , <^о) j 1 dpj^j
-z—- = ^ехр -Ь3- ---—(9.53)
(ас); L J Ы;
где су и bj — постоянные для рассматриваемой ячейки коэффициен-
ты, определяемые ниже. Если выражение (9.53) проинтегрировать
и учесть, что ос = 0 при у0 = 0, то получим
(ffc) j (.
-—= Cj 1 — ехр
(ffc); I
(9.54)
j (yJj.
Постоянная ty = ty/bt легко определяется путем интегрирования
выражения (9.54) по ширине ячейки:
(9.55)
В выражении (9.54) необходимо также определить постоянную bj,
характеризующую интенсивность крупномасштабного переноса
параллельно стенке канала. Предположив, что интенсивность круп-
номасштабного переноса в первом приближении определяется со-
266
отношением высоты и ширины ячейки, т. е. параметром Ф;, и обра-
ботав имеющиеся опытные данные по распределению касательных
напряжений, авторы работы [9] получили, что
(9.56)
Таким образом, распределение касательных напряжений по пе-
риметру каждой ячейки рассчитывается по формуле*
foe);
1 — exp
7,7
(9.57)
exp
7,7 (j/o)y
Рассчитанные таким образом напряжения не будут терпеть раз-
рыва в месте соприкосновения соседних ячеек только в том случае,
если граница между ячейками является осью симметрии рассматри-
ваемого сечения. Если же граница между соседними ячейками не яв-
ляется осью симметрии, как, например, линия ОН на рис. 9.8,то
рассчитанные по формуле (9.57) касательные напряжения в точке
Н терпят разрыв. Это связано не только с приближенностью рассмат-
риваемого метода, но и с тем обстоятельством, что формула (9.57)
не учитывает переноса количества движения из одной ячейки в дру-
гую. Совершенно очевидно, что перенос количества движения в на-
правлении, параллельном стенке канала, необходимо учитывать не
только в пределах каждой ячейки, но и между соседними ячейками.
Если граница между ячейками является линией симметрии, то
обмен между ячейками отсутствует, ячейки в этом случае называются
изолированными и в расчет по формуле (9.58) не надо вносить ника-
ких поправок.
Если же граница между соседними m-й и /г-й ячейками не явля-
ется линией симметрии, то необходимо учитывать взаимное влияние
этих ячеек друг на друга, обусловленное переносом количества дви-
жения через границу. Это влияние предлагается учитывать с по-
мощью соответствующих функций влияния:
(°c)m ~
(°c)n “ (°c)/i tyrn -> п
(9.58)
(9.59)
* Для получения этой формулы соображения о крупномасштабном тур-
булентном переносе, вообще говоря, не являются необходимыми. Можно
априори принять экспоненциальную зависимость касательных напряжений
(ос);- от (г/0)j и определить коэффициент в показателе экспоненты по экспе-
риментальным данным. Тем самым будет учтен перенос количества движения
параллельно стенке канала независимо от того, связывать ли его с крупно-
масштабной турбулентностью или со вторичными течениями.
267
Здесь (ac)m и (ас)«3—касательные напряжения для изолированных
ячеек, рассчитанные по формуле (9.57); ф71^.то— функция влия-
ния n-й ячейки на m-ю, а — функция влияния /тг-й ячейки
на п-ю.
Для построения функций влияния используются следующие со-
ображения. Очевидно, что влияние, например, ячейки т на касатель-
ное напряжение в точке Л ячейки п должно уменьшаться с увеличе-
нием расстояния sn этой точки от границы раздела (рис. 9.10). Счи-
тая закон убывания экспонен-
циал ьным, можно записать
фт^п = 1 + «п. ехр
(9.60)
где ап — некоторый коэффи-
циент; ss — суммарная длина
периметров взаимодействую-
щих ячеек.
Аналогичным образом
функцию влияния n-й ячейки
иа т-ю можно записать в
виде
Рис. 9.10. Схема взаимодействия сосед-
них ячеек.
фп->т = 1 +«техр
__ sm \
s2 / ’
(9.61)
Таким образом, распределение касательных напряжений в неизо-
лированных ячейках определяется следующим образом:
(^с)т (.°с)1П
Юп = Юп3
1-Итеехр ( —
\ s2
1 + ссп ехр ( —
\ s2
(9.62)
Коэффициенты ат иап, входящие в эти выражения, определяют-
ся из условий сшивки и нормировки.
Условие сшивки означает, что в месте соприкосновения ячеек
(точка С, рис. 9.10) касательные напряжения не должны терпеть
разрыва, т. е.
(сс)т (1 +«m) = (ac)n3 (1 +ап). (9.63)
Условие нормировки означает, что с учетом взаимного влияния
ячеек друг на друга суммарное для двух ячеек значение касательного
напряжения должно остаться неизменным:
I'm Ln
J (<Ус)/п^+ J (<JcMz = j (orX3dz+ j (0c)n3dz.
ООО о
268
Отсюда следует
г \
ат I* (ас)ш ехР ( ап (“ (ас)“э ехр ( — — ~ 0. (9.64)
О о 4
Если в сечении имеется несколько взаимодействующих между
собой ячеек, то вначале производится сшивка касательных напряже-
ний для двух любых соседних ячеек. Затем эти две ячейки рассмат-
Рис. 9.11. Сравнение расчетного распределения скоро-
стей с экспериментальными данными для каналов раз-
личной формы:
1-----расчет и О — эксперимент по линиям максимальной
скорости; ----расчет и • — эксперимент по нормалям
к стенке.
269
риваются как единая ячейка, осуществляется сшивка с третьей
ячейкой и т. д.
После того как найдено распределение касательных напряжений
по периметру канала, с помощью универсального профиля скорости
нетрудно рассчитать распределение скорости вдоль любой нормали
и тем самым построить поле скоростей в рассматриваемом канале.
Затем по точкам стыковки кривых распределения скорости, рассчи-
танных от противоположных стенок канала, проверяется правиль-
ность выбранных линий максимальной скорости, а полученная рас-
четным путем средняя скорость сравнивается с заданной ско-
ростью w. При значительном расхождении этих величин корректи-
руются исходное значение коэффициента сопротивления и положе-
ние линий максимальной скорости и расчет повторяется.
Для проверки предложенной методики в работе [9] были рас-
считаны распределения скоростей в различных каналах сложной фор-
мы и проведено сравнение с экспериментальными данными. Рассмат-
ривались каналы, имеющие поперечное сечение в форме квадрата,
прямоугольника с отношением сторон 1 : 3, равнобедренного тре-
угольника, прямоугольного треугольника, а также круглая труба
с продольным выступом, эксцентричный кольцевой зазор, плот-
ный пучок стержней и три стержня в обечайке. На рис. 9.11 в ка-
честве примера показано сравнение результатов расчета с эксперимен-
тальными данными для квадратного канала, треугольного канала и
трех стержней в обечайке. Для всех рассмотренных каналов полу-
чено хорошее соответствие расчетных и экспериментальных значе-
ний скорости (максимальное расхождение не превышает 10%).
Рассмотренная выше методика позволяет одновременно с рас-
четом поля скоростей определить и коэффициент сопротивления тре-
ния в канале сложного сечения. Однако для расчета сопротивления
трения нет необходимости определять поля скорости. Поэтому та-
кая методика расчета коэффициента сопротивления трения неоправ-
данно сложна. Для этой цели лучше пользоваться упрощенным
методом, описанным в § 9.5.
§ 9.4. Теплообмен в призматических трубах
и продольно обтекаемых пучках стержней
Для определения тепловых потоков от стенок канала к теплоно-
сителю или температуры стенок (если тепловые потоки заданы)
необходимо предварительно рассчитать поле температуры в потоке
теплоносителя, т. е. проинтегрировать уравнение энергии:
‘ ду J dz [ 7
(9.65)
Здесь ось х направлена вдоль оси потока, а оси у иг расположены
в поперечном сечении канала, причем ось у перпендикулярна, а ось
z параллельна стенке канала. При интегрировании этого уравнения
270
применительно к каналам сложной формы возникают значительные
трудности. Во-первых, предварительно необходимо провести доволь-
но трудоемкий расчет распределения скорости в рассматриваемом
канале wx (у, z) (см. § 9.3). Во-вторых, необходимо располагать дан-
ными о коэффициентах турбулентного переноса тепла по двум взаим-
но ортогональным направлениям и uqz. В-третьих, обычно не
удается сформулировать простые граничные условия на границе
стенка — жидкость, поэтому приходится решать сопряженную зада-
чу, т. е. интегрировать уравнение энергии (9.65) совместно с уравне-
нием теплопроводности для стенок капала. В-четвертых, сложная
форма канала и сопряженный характер задачи не позволяют пост-
роить аналитическое решение, поэтому приходится прибегать к чис-
ленным методам расчета.
При использовании численных методов расчета поперечное
сечение канала разбивается на небольшие элементы, и с помощью
метода конечных разностей дифференциальное уравнение энергии
(9.65) и уравнение теплопроводности для стенок канала заменяются
системой алгебраических уравнений. Локальные значения скорости
для каждого элемента находят рассмотренным выше способом. Для
определения коэффициентов турбулентного переноса можно вос-
пользоваться выражениями, полученными в работах [3, 4]:
коэффициент турбулентного переноса тепла в направлении, нор-
мальном к стенке канала:
- 0,16 Re Рг 1.1 —ехр (— 0,62.10"1 Re Рг1 /3)| к
а
/ w w уч / w \ ~
X Ь=- — 1-----ехр( — 1,54У); (9.66)
\W/ \ W() ] , 1 V ’ 7 ’ 4 7
коэффициент турбулентного переноса тепла в тангенциальном
направлении:
.. 0,36 Re Рг [ 1 —охр (—0,62.10-1 ReРг1 /3)| х
а
(9.67)
где У — у/у^'- Re — wd,/v; w — локальное значение скорости;
w и ау0 — среднее и максимальное значения скорости; показатель
степени «1 зависит от кривизны ячейки [3: — 4прир — —1—0,05;
/гх = 4 ехр 1—0,69 ([3 — 0,05)] при |3 > 0,05; показатель — 1.
Если для коэффициента турбулентного переноса количества дви-
жения воспользоваться выражением (9.39), то нетрудно получить
выражение для турбулентного числа Прандтля в направлении нор-
мали к стенке [2]:
_J_ _ Ди 13.5 (ДЦ°’5 [1 —ехр ( —0,62 - lO^RePr1^)]. (9.68)
Ргтб ьа \ Wo )
271
Формула (9.68) дает приближенное представление о турбулентном
числе Прандтля в диапазоне чисел Рг от 0,01 до 10 и чисел Re от
от 104 до 106 и, как и формулы (9.39), (9.66), (9.67), нуждается в экс-
периментальной проверке. Зависимость РгтС от чисел Re и Рг для
центральной части потока, где отношение w/wQ « 1, показана на
рис. 9.12.
Система конечно-разностных уравнений, полученная рассмотрен-
ным способом, решается с помощью ЭВМ. В результате находят тем-
пературы всех элементов, т. е. температурные поля в жидкости
и стенках канала. После этого рассчитывается количество тепла, пе-
Рис. 9.12. Зависимость турбулентного числа
Прандтля от чисел Re и Рг для центральной
часта потока.
редаваемого жидкости в пределах рассматриваемой ячейки, и сред-
няя для ячейки плотность теплового потока^. Зная распределение
температуры на границе стенка — жидкость, нетрудно также
определить среднюю температуру поверхности ячейки (Qj и не-
однородность температуры поверхности в пределах ячейки, ха-
рактеризуемую разностью максимальной и средней температуры:
(Гкс).7- - (7с)у-
Такой метод расчета сложен и требует больших затрат машинного
времени. Поэтому для часто используемой в реакторах геометрии
каналов — продольно обтекаемых пучков стержней — оправда-
на разработка более простых расчетных методов и соотношений.
Рассмотрим несколько подробнее особенности гидродинамики
и теплообмена при течении жидкости в пучках стержней. Геометрия
пучка обычно характеризуется схемой расположения стержней (тре-
угольная, квадратная, прямоугольная и т. д.) и относительным ша-
гом х = b/d — отношением расстояния между центрами соседних
стержней b к диаметру стержня d. В зависимости от относительного
шага различают плотные пучки, у которых х = 1, т. е. соседние
стержни соприкасаются друг с другом, а теплоноситель течет по изо-
272
лированным каналам; тесные пучки— 1,0 <х< 1,1; редкие пуч-
ки — х > 1,1.
Для плотных и тесных пучков, продольно обтекаемых теплоно-
сителем, характерна периодичность изменения касательного напря-
жения и коэффициента теплоотдачи по периметру стержней. Изме-
нение пси а по периметру стержней определяется особенностями те-
чения в зазорах между стержнями. В тех местах, где зазор наимень-
ший, скорость жидкости минимальна и стс и а невелики. В широких
же сечениях зазора скорости жидкости максимальны и <тс и а до-
стигают максимальных значений. Неравномерность теплоотдачи
в пучках приводит к неравномерному распределению по периметру
стержней температуры стенки и плотности теплового потока. Степень
этой неравномерности зависит не только от относительного ша-
га х, но и от толщины оболочки, от соотношения коэффициентов
теплопроводности топлива, оболочки и теплоносителя.
Неоднородность распределения температуры по периметру
стержней следует учитывать при проведении приближенных теп-
ловых расчетов топливных сборок. Такие расчеты обычно прово-
дят, пользуясь средними по периметру значениями коэффициента
теплоотдачи, в результате чего определяют среднюю, а не макси-
мальную температуру оболочки в данном сечении. Для определе-
ния максимальной температуры необходимо дополнительно рассчи-
тать степень неоднородности распределения температуры по пери-
метру стержней, т. е. разность между максимальной и средней
температурами наружной поверхности оболочки Zc“KC— Z(r
Очевидно, что неоднородность распределения касательных на-
пряжений, теплоотдачи и температуры стенки должна уменьшаться
с увеличением расстояния между стержнями. Как показывают экспе-
рименты, в редких пучках эта неоднородность становится малосу-
щественной, а при х > 1,2 практически исчезает.
Переходя к рассмотрению соотношений для расчета теплообмена
в продольно омываемых пучках стержней, обратимся прежде всего
к работе В. П. Бобкова, М. X. Ибрагимова и В. И. Субботина [4].
В этой работе по изложенной выше методике приведен расчет более
1000 вариантов ячеек и в результате обобщения полученных данных
предложены простые зависимости для расчета средней температуры
и неоднородности температуры поверхности твэлов в пучке при про-
дольном омывании жидкометаллическими теплоносителями.
В основу расчетов положена ячейка, показанная на рис. 9.13.
На границе AD задавалась постоянная плотность теплового потока,
границы АВ, ВС и CD считались адиабатическими. Расчеты про-
ведены для жидких металлов в широких диапазонах изменения опре-
деляющих параметров. Число Рг менялось от 0,01 до 0,04; число
Ре = wdja — от 10 до 2000; относительный шаг решетки х =
— b/d— от 1 до 3; относительная толщина оболочки 6с/г0 — от 0,005
до 0,5; угол ср0 — от 15 до 45°; коэффициент теплопроводности мате-
риала стенки — от 0,1 до 1000 вт1(м • град).
27S
Для среднего коэффициента теплоотдачи в ячейке а, с помощью
которого определяется средняя температура поверхности оболочки,
предложено уравнение
Nu = (3 + 0,022 Ре0-8) {1 — Y [0,7+ 0,3 ехр (-0,32 «+№)]}, (9.69)
где __ _ _ _ __ _
Nu = ay0/%; a = gc/(7c —/); Ре = ю//0/щ
qQ — среднее по периметру значение плотности теплового потока;
Г— среднемассовая температура жидкости в рассматриваемом се-
чении, легко определяемая из уравнения теплового баланса.
Рис. 9.13. Схема элементарной ячейки ( к тепловому
расчету продольно обтекаемых пучков стержней).
Уравнение, позволяющее вычислить максимальную температу-
ру оболочки /“акс, имеет вид
(/макс / \л
Ус ~~+)+к
7с Уо
1
Nut
про
6зя
3/2
(9.70)
meNu — число Нуссельта, определяемое выражением (9.69); Nuz =
= (1 — 0,7У) (3 + 0,022Ре0,8) — число Нуссельта, соответству-
ющее постоянной температуре поверхности [в формуле (9.69) —
= оо]; s„— смачиваемый периметр ячейки (рис. 9.13); если ср0 =
= 30°, то np0/6sH = 1.
274
Влияние геометрии ячейки и материала стенки иа неоднородность
температурного поля и на средний коэффициент теплоотдачи учиты-
вается с помощью двух величин: параметра
характеризующего, как об этом говорилось выше, неравномерность
высоты ячейки, и параметра
характеризующего неоднородность температурного поля в твэле
[см. выражение (3.119)1. Здесь
Лс Ч-Л/’г
(9.73)
%, %с и Л,,. — соответственно коэффициенты теплопроводности жид-
кости, оболочки и топлива; 7^~го/Ро— относительный радиус топ-
ливного стержня.
Приведенные выше формулы позволяют рассчитать теплоотда-
чу и температурную неоднородность в изолированных ячейках [не
обменивающихся теплом с соседними ячейками через границы /4В,
ВС и CD (см. рис. 9.13)] со средней квадратичной погрешностью не
более ±10% п максимальной погрешностью ±25%. Они применимы
в следующих диапазонах изменения определяющих параметров,
практически охватывающих все случаи, встречающиеся в совре-
менном реакторостроении: Re(Z = = wcLjv > 2300; Ре = 1 ± 1000;
Рг - 0,01 ± 0,04; Y - 0 ± 1; - 0,1-4-500; [3 = — 1 ± 1.
На рис. 9.14 формула (9.69) сопоставляется с экспериментальными
данными ФЭИ для треугольных (х 1 4-1,5) п четырехугольных
(х = 1) пучков нержавеющих и медных стержней, полученными
при течении Na, Na — К и ртути.
Следует отметить, что формула (9.69) удовлетворительно описы-
вает и экспериментальные данные для круглых труб.
Как указывалось выше, формула (9.69) применима только к изо-
лированным ячейкам, т. е. ячейкам, не обменивающимся теп-
лом через границы А В, ВС и CD (см. рис. 9.13) с соседними ячейка-
ми. Ячейки можно считать изолированными только при полной сим-
метрии рассматриваемой задачи, что характерно для пучков с беско-
нечно большим числом стержней или практически для центральной,
удаленной от обечайки, части пучка. При несимметричном обогре-
ве капала, когда тепловые потоки иа противоположных сторонах
каналов qttl и qQ% неодинаковы и наблюдается теплообмен между ячей-
ками через границу ВС, в работе [4] предполагается вводить в форму-
лу (9.69) поправки, приближенно учитывающие этот теплообмен:
NU1 = NuKf±
Nu2 = NuKg2,
(9.74)
275
где NUi и Nu2 — числа Нуссельта для соприкасающихся по гра-
нице ВС ячеек, плотности теплового потока на стенке в которых со-
ответственно равны 7с1_и 7с2; Kqi и Кд2 — поправки, вычисляемые
в интервале —1 < <7C2/<7ci 1 по приближенным соотношениям:
ql 2[1-0,25(Ы<7с1 + 1)] ’
к _______________1__________
53 2[0,75(<7C2/?ci + 1)-1] ‘
В тех случаях, когда имеется теплообмен между ячейками через
границы АВ и CD, расчет значительно усложняется. В этом случае
составляют уравнения теплового баланса для всех ячеек и полу-
Рис. 9.14. Сравнение формулы (9.62) с экспериментальными данны-
ми. Сплошная линия—(9.62), пунктирная — (9.64):
Л'=1 —У [0,7+0,3 ехр (—0,32 еп0,2)]; 1—3 — треугольная упаковка, х = 1;
треугольная упаковка с шагами х; соответственно равными 1,1; 1,15;
1,2; 1,3; 1,4 1,5; 10, 11 — четырехугольная упаковка, х=1.
ченная система алгебраических уравнений решается совместно. Та-
ким образом можно учесть перетечки тепла между ячейками не толь-
ко по жидкости, но и по оболочке твэла и по топливу.
При продольном омывании жидкими металлами редких пучков
стержней (х > 1,1) неоднородность распределения температуры по
периметру стержней мала и коэффициенты теплоотдачи слабо за-
висят от конструкции твэлов и расположения стержней в пучке.
В этом случае расчет теплообмена в пучках стержней существенно
упрощается. Для расчета теплоотдачи в редких пучках, обтекаемых
жидкими металлами, можно пользоваться уравнением
Nu = О,58Ре°145,
(9.76)
276
полученным в работе [8] путем обобщения опытных данных для пуч-
ков с 1,1 х < 1,5 в интервале чисел Ре от 400 до 6000.
Для тех же целей можно пользоваться формулой [5]
Nu - 6 + 0,006Ре, (9.77)
которая дает результаты, близкие к (9.76) и справедлива при 1,2 <С
< х <Z 1,75, 30 < Ре < 4000 (Re 7> 10‘1). В обеих формулах в качест-
ве характерного размера использован диаметр стержней d.
Для расчета теплоотдачи в редких пучках с шахматным располо-
жением твэлов, продольно омываемых жидкостями с более высокими
числами Прандтля, можно рекомендовать формулу [351
Nu - (0,0122 + 0,00245x)Re0>8BPr0>\ (9.78)
описывающую опытные данные, полученные при течении воды и сме-
си воды с этиленгликолем (Рг от 2,3 до 18) в интервале чисел Re от
104 до 2 • 10б при х от 1,25 до 1,6 с погрешностью -I- 4%. Примерно
аналогичная зависимость получена в работе [12] в результате обоб-
щения имеющихся экспериментальных данных для пучков, продоль-
но омываемых водой в интервале 1,1 х 1,5 и Re 2 • 104:
Nu = (0,032 х — 0,0144) Re°’8PrP3. (9.79)
В качестве характерного размера в уравнениях (9.78) и (9.79) при-
нят эквивалентный диаметр пучка с бесконечно большим числом
стержней dnoo = (1,102ха — l)d.
Прием, удобный для практических расчетов теплоотдачи в ред-
ких пучках, предложил В. С. Осмачкин [16]. Он показал, что если
в качестве характерного геометрического размера в числах Nu,
Re и Ре использовать эффективный диаметр
где е — плотность решетки, равная отношению площади попереч-
ного сечения, занятого стержнями, к полной площади поперечного
сечения решетки; —эквивалентный диаметр пучка, то расчет теп-
лоотдачи с достаточной для практики точностью можно произво-
дить по соответствующим формулам для круглых труб.
§ 9.5. Сопротивление в призматических трубах
и продольно обтекаемых пучках стержней
В тех случаях, когда нет необходимости определять поля скорос-
ти, а требуется рассчитать только коэффициент сопротивления,
можно рекомендовать упрощенный метод расчета, разработанный
М. X. Ибрагимовым и др. [11]. В предложенном ими методе ко-
эффициент сопротивления канала со сложной формой поперечного
сечения выражается через коэффициенты сопротивления образующих
277
его ячеек, а коэффициенты сопротивления ячеек определяются основ-
ными параметрами, характеризующими их геометрию (о разбиении
поперечного сечения канала на ячейки и параметрах ячеек см. §9.3).
Связь между коэффициентом сопротивления трения канала и
коэффициентами сопротивления трения образующих его ячеек уста-
навливается следующим образом. Поделив коэффициент сопротив-
ления трения /-й ячейки
ар | 2daj
dx | р (wj)2
(9.81)
на коэффициент сопротивления трения для этой ячейки, рассчи-
танный по формуле Блазиуса
0,3164
Re0.25
(9.82)
получаем
t- d5/4
Jv_ — л 91
ё/вл (^-)7/4 ’
(9.83)
г
Ь/ Ьл
dp~ l/(0,3164pv1/4) — постоянная, одинаковая для всех
dx
где А = 2
ячеек канала; Wj—средняя скорость жидкости в ;-й ячейке. Оче-
видно такое же соотношение можно получить и для канала в целом:
!=К
, Бл
^/4
(9.84)
где — средняя скорость жидкости для канала в целом. Выражая
из (9.83) и (9.84) значения wj и и пользуясь уравнением баланса
расхода
(9.85)
/
получаем уравнение, выражающее коэффициент сопротивления тре-
ния канала через коэффициенты сопротивления трения отдельных
ячеек:
= (9.86)
\Ьк,Бл / /к \ dg.K/ /
Обобщив результаты многочисленных расчетов коэффициентов
сопротивления трения для ячеек различной конфигурации, авторы
работы [И] получили следующую формулу:
Ji-= [0,58 + 0,42ехр ( — 0.021Л?)] [1+0,1 (₽; + !)</’], (9.87)
Л/,Бл
где Kj = У7-Ф">25—так называемый параметр неравномерности ячей-
ки. Параметры
278
it p ...
J Ж«)? ' |,J p, ’ 1 ' Ы1
[здесь в знаменателе в отличие от выражения (9.49) стоит не (/AJ:,KC)j,
a (//o)i7-J уже рассматривались в § 9.3.
Рассчитанные таким образом значения коэффициентов сопро-
тивления трепня для различных каналов сложной формы отличают-
ся от экспериментально полученных значений на более чем па 10%.
Для расчета коэффициентов сопротивления трения в пучках
стержней можно использовать формулы, полученные П. А. Ушако-
вым [23] на основе обобщения имеющегося расчетного и эксперимен-
тального материала в правильных решетках стержней с 1 <
< 10 при 2 104< Re< 5 • 10б.
Для треугольной решетки
X - 0,57 + 0,18 (х— 1) + 0,53 [1 — ехр ( — а)]; (9.88)
£тр
а~- 0,58 {1 —ехр [ — 70 (х— 1)]} + 9,2 (х — 1), х< 1,02;
а— 0,58+9,2 (х— 1), л* > 1,02.
Для квадратной решетки
Л - 0,59 + 0,19 (х— 1) + 0,52 {1 —ехр [—10 (х— 1)]}, (9.89)
1тр
где £тр — коэффициент сопротивления трепня для круглой трубы
при том же значении числа Рейнольдса.
Как следует из (9.88) и (9.89), коэффициенты сопротивления тре-
ния в треугольных и квадратных решетках стержней не сильно раз-
личаются между собой, особенно при больших шагах стержней.
Как и при расчете теплоотдачи [16], если в качестве характерного
размера в числе Рейнольдса использовать эффективный диаметр
(9.80), то коэффициент сопротивления трения редких пучков можно
вычислить по формуле для круглой трубы.
В заключение следует кратко сказать о проблеме межканального
перемешивания теплоносителя в активной зоне реактора. В плот-
ных пучках, в которых соседние стержни соприкасаются между
собой, возможность межканального перемешивания теплоносителя
практически исключена. Но в тесных и тем более редких пучках на-
блюдается поперечный турбулентный обмен количеством движения
между соседними каналами. Если бы распределение температуры во
всех каналах было одинаковым, то такой поперечный обмен не приво-
дил бы к направленному переносу тепла и его можно было бы не учи-
тывать. Но в действительности не удается добиться одинакового
нагрева теплоносителя во всех каналах и поперечный турбулентный
обмен между соседними каналами приводит к переносу тепла из
более горячих каналов в более холодные. Межканальное перемеши-
вание имеет большое значение и в различных аварийных ситуациях.
279
Так, при повреждении оболочки одного из стержней радиоактивные
продукты могут распространиться в соседние каналы, затрудняя
обнаружение поврежденного твэла.
Процесс межканального перемешивания сложен, зависит от боль-
шого числа факторов и в сильной степени от конструкции дистанци-
онирующих стержни элементов. В последние годы изучению этой
проблемы уделяется большое внимание, но пока получены лишь
немногие предварительные результаты.
СПИСОК ЛИТЕРАТУРЫ
1. Аверин Е. К. и др. Теплоотдача при движении жидкости в кольцевых и
щелевых каналах. — В сб.: Теплопередача и тепловое моделирование.
М., Изд-во АН СССР, 1959, с. 138.
2. Бобков В. П., Ибрагимов М. X. Применение модели однородной диффу-
зии к расчету касательных напряжений и поля скорости в турбулентном
потоке жидкости. — «Теплофизика высоких температур», 1970, т. 8, № 2,
с. 326.
3. Бобков В. П., Ибрагимов М. X., Субботин В. И. Метод расчета коэффи-
циентов турбулентного переноса тепла в каналах сложной формы —
В сб.: Моделирование термодинамических явлений в активной зоне быст-
рых реакторов. Конф. 23—26 февраля 1970 г., Бабилон, ЧССР, с. 8.
4. Бобков В. П., Ибрагимов М. X., Субботин В. И. Обобщающие зависи-
мости для теплообмена в топливных сборках реакторов с жидкометалли-
ческим охлаждением. — «Теплофизика высоких температур», 1972, т. 10,
№ 4, с. 795.
5. Боришанский В. М., Фирсова Э. В. Теплоотдача при продольном обтека-
нии пучка труб металлическим натрием. — «Атомная энергия», 1963,
т. 14, с. 584.
6. Булеев Н. И. Теоретическая модель механизма турбулентного обмена
в потоках жидкости. — В сб.: Теплопередача. М., Изд-во АН СССР,
1962, с. 64.
7. Булеев Н. И., Мосолова В. А., Ельцова Л. Д. Теплоотдача в турбулент-
ных потоках жидкости в кольцевых и плоских зазорах. — В сб.: Жидкие
металлы. М., Атомиздат, 1967, с. 123.
8. Жуков А. В., Субботин В. И., Ушаков П. А. Теплообмен при продоль-
ном обтекании жидким металлом раздвинутых пучков стержней. — В сб.:
Жидкие металлы. М., Атомиздат, 1967, с. 149.
9. Ибрагимов М. X. и др. Расчет касательных напряжений на стенке канала
и распределения скоростей при турбулентном течении жидкости.—«Атом-
ная энергия», 1966, т. 21, с. 101.
10. Ибрагимов М. X., Исупов И. А., Субботин В. И. Расчет и эксперимен-
тальное исследование полей скорости в канале сложной формы. — В сб.:
Жидкие металлы. М., Атомиздат, 1967, с. 234.
11. Ибрагимов М. X. и др. Расчет коэффициента гидравлического сопротив-
ления при турбулентном течении жидкости в каналах некруглого попе-
речного сечения. —«Атомная энергия», 1967, т. 23, с. 300.
12. Калинин Э. К-, Дрейцер Г. А., Козлов А. К- Теплообмен в продольно
омываемых шахматных пучках труб с различными относительными шага-
ми. — «Инж.-физ. ж.», 1969, т. 16, № 1, с. 47.
13. Кокорев Л. С., Корсун А. С., Петровичев В. И. Расчет распределения
скорости и гидравлического сопротивления в пучках стержней, ограни-
ченных обечайкой. — В сб.: Вопросы теплофизики ядерных реакторов.
М., Атомиздат, 1968, с. 20.
14. Кокорев Л. С. и др. Влияние вторичных течений на распределение ско-
ростей и гидравлическое сопротивление турбулентных потоков жидкости
в некруглых каналах. — В сб.: Вопросы теплофизики ядерных реакто-
ров. Вып. 2. М., Атомиздат, 1969, с. 85.
280
15. Левченко Ю. Д., Субботин В. И., Ушаков П. А. Распределение ско-
ростей теплоносителя и напряжения на стенке плотпоупакованных стерж-
ней. — «Атомная энергия», 1967, т. 22, с. 218.
16. Осмачкин В. С. Особенности теплообмена в ядерных реакторах, охлаждае-
мых несжимаемыми пекипящими жидкостями. Доклад Р/326 (СССР),
представленный на Третью междунар. конф, по мирному использованию
атомной энергии. Женева, 1964.
17. Петровичев В. И. Экспериментальные исследования теплообмена при
турбулентном течении ртути в кольцевом канале. — В сб.: Жидкие ме-
таллы. М., Госатомиздат, 1962, с. 139.
18. Петухов Б. С., Ройзеи Л. И. Теплообмен в трубах кольцевого сечения. —
«Инж.-физ. ж.», 1963, т. 6, № 3, с. 3.
19. Петухов Б. С., Ройзеи Л. И. Обобщенные зависимости для теплоотдачи
при турбулентном течении газа в трубах кольцевого сечения. — «Тепло-
физика высоких температур», 1964, т. 2, № 1, с. 78.
20. Петухов Б. С., Ройзеи Л. И. Теплоотдача при турбулентном течении газа
в трубах кольцевого сечения. — «Изв. АН СССР. Сер. энергетика и
транспорт», 1967, № 1, с. 103.
21. Субботин В. И., Ушаков П. А., Свириденко И. П. Исследование тепло-
обмена при турбулентном течении ртути в кольцевом зазоре. — «Атомная
энергия», 1960, т. 9, № 4, с. 310.
22, Субботин В. И., Ушаков П. А. Приближенный расчет гидродинамических
характеристик турбулентного потока жидкости в кольцевых каналах
«Теплофизика высоких температур», 1972, т. 10, № 5, с. 1025.
23, Ушаков П. А. Расчет гидродинамических характеристик при продоль-
ном обтекании жидкостью правильных решеток стержневых твэлов. —
«Теплофизика высоких температур». 1974, т. 12, № 1, с. 103.
24. Хабахпашева Е. М., Ильин Ю. М. Теплоотдача к сплаву натрия с калием
в кольцевых зазорах. — «Атомная энергия», 1960, т. 9, № 6, с. 494.
25. Baily R. Heat Transfer to liquid metals in concentric annuli. U. S. Atomic
Energy Comm., ORNL-521, 1950.
26. Deissler R., Taylor M. NACA, TN-4384, 1958.
27, Eifler W., Nijsing R. Experimental investigation of velocity distribution
and flow resistance in a triangular arroy of parallel rods. — «Nucl. Engng.
Design», 1967, v. 5, No. 1, p. 22.
28. Eifler W. Berechnung der turbulenten Geschwindigkeitsverteilung und
der Wandereibung in konzentrischen Ringsplatten.—«Warme- und Stof-
fubertragung», 1969, Bd. 2, No. 1, S. 36.
29. Fischer M., Shimamune H. Temperature distribution and thermal stabili-
ty in asymmetrical triangular rod—clusters. KFK — Bericht, 724, 1969.
SO. Grdber H. Der warmeilbergang in glatten rohren zwischcn parallclen Plat-
ten in Ringsplatten und Rohrbiindeln beiexponentieller. Warmeflussver-
tcilungen inerzwungener laminarer oder turbulenter Stromung. — «Inter-
nal. J. Heat Mass. Transfer», 1970, v. 13, No. 11, p. 1645.
31. Kays W. M., Leung E. V. Heat transfer in annular passages. Hydrodynami"
caly developed turbulent flow with arbitraly prescribed heat flux. —
«Internal. J. Heat Mass Transfer», 1963, v. 6, No. 7, p. 537.
32. Lyon R. N., Poppendieck N- F. Liquid-metal heat transfer. — Liquid
Metals Handbook, 1952, v. 2.
33. Nijsing R., Gargantini I., Eifler W. Analisis of fluid flow and heat trans-
fer in a triangular array of parallel heat generating rods. — «.Nucl. Engng.
Design», 1966, v. 6, p. 375.
34. Nijsing R., Eifler W. Temperature Fields in Liquid — Metal cooled Rod
Assemblies. Int. Seminar on Heat Transfer in Liquid Metals, Trogir, Yugo-
clavia, 1971.
35. Reiger M. Experimentalle Untersuchung des Warmeubergangs in parallel
durchstromten Rohrbiindeln bei konstanter Warrnestromdichte im Bereich
mittlerer Prandtle zahlen. — «Internal. J. Heat Mass. Transfer», 1969,
v. 12, r. 1421.
ГЛАВА 10
ГИДРОДИНАМИКА И ТЕПЛООБМЕН В СИСТЕМАХ
С ГАЗООБРАЗНЫМИ ТЕПЛОНОСИТЕЛЯМИ
§ 10.1. Особенности газообразных теплоносителей.
Методы интенсификации теплообмена
Такие газы, как гелий, двуокись углерода и некоторые другие,
обладают рядом ценных свойств, что позволяет использовать их
в качестве теплоносителей в ядерных реакторах. Например, в Англии
построено несколько атомных электростанций с газоохлаждаемы-
ми реакторами, такие же реакторы работают во Франции и других
странах.
Достоинства газообразных теплоносителей в основном сводятся
к следующему. Газообразные теплоносители позволяют достигать
высоких температур при низких давлениях, обладают малыми
сечениями захвата и рассеяния нейтронов, что дает возможность
применять их в ядерных реакторах не только на тепловых, ио
и на быстрых нейтронах. Очень важно, что степень активации
большинства газов в реакторе невелика, а некоторые, как, например,
гелий, не активируются совсем. Тем самым упрощается решение мно-
гих проблем, связанных с радиационной защитой оборудования АЭС.
Как правило, газообразные теплоносители слабо реагируют с мате-
риалами активной зоны реактора.
Однако наряду с отмеченными достоинствами газообразные тепло-
носители обладают и рядом недостатков, связанных главным
образом с малой плотностью, невысокой теплоемкостью и очень
низким коэффициентом теплопроводности. Из-за малой плотности и
невысокой теплоемкости необходимо прокачивать большие объемы
газа через активную зону реактора, что связано с большими затра-
тами энергии на перекачку и снижением экономичности АЭС. Не
случаен поэтому интерес к диссоциирующим газообразным теплоно-
сителям. За счет теплоты диссоциации можно существенно увели-
чить эффективную теплоемкость теплоносителя и уменьшить его
расход.
При соблюдении определенных условий можно также повысить
интенсивность теплоотдачи от стенки к диссоциирующему газу
(см. § 8.6).
Низкий коэффициент теплопроводности газообразных теплоно-
сителей обусловливает небольшие коэффициенты теплоотдачи, при-
близительно на порядок меньше, чем для воды или жидких металлов.
Это в свою очередь ограничивает удельную мощность, снимаемую
282
с единицы объема активной зоны. Поэтому в газоохлаждаемых реак-
торах приходится идти на увеличение размеров активной зоны и ре-
актора в целом. Вместе с тем, небольшие коэффициенты теплоотдачи
приводят к значительным температурным перепадам между охлаж-
даемой поверхностью и теплоносителем, а следовательно, и к невысо-
ким температурам теплоносителя на выходе из реактора (при задан-
ной максимально допустимой температуре топлива). Неслучайно при
разработке высокотемпературных газоохлаждаемых реакторов
обычно ориентируются на применение гелия в качестве теплоноси-
теля. Помимо высокой химической инертности гелий обладает тепло-
проводностью, в 5—6 раз превышающей теплопроводность большин-
ства остальных газов, а следовательно, и коэффициенты теплоотдачи
к гелию при одинаковых числах Рейнольдса в 5—6 раз выше, чем
к другим газам.
Однако даже при использовании гелия реализуемые коэффициен-
ты теплоотдачи сравнительно невысоки. Поэтому для реакторов с га-
зообразным теплоносителем необходимы специальные меры по ин-
тенсификации теплообмена.
В ядерных реакторах часто необходимо уменьшить температурный
перепад между теплоносителем и стенкой при заданной тепловой
мощности. Этого можно достигнуть, увеличив либо коэффициент теп-
лоотдачи, либо поверхность, через которую осуществляется тепло-
обмен.
Известны разные способы интенсификации теплообмена. /Для
интенсификации теплообмена при течении в трубах и каналах
применяют, например, винтовые вставки или делают поперечные
накатки на трубе. Интенсификация теплообмена на внешней поверх-
ности чаще всего обеспечивается ее оребрением. В ядерных установ-
ках оребряются поверхности оболочек твэлов и наружные поверх-
ности труб парогенераторов. Возможны и другие способы интенсифи-
кации теплообмена в активной зоне реактора, например, выполне-
ние активной зоны в виде насадки из шаровых твэлов, продуваемой
газообразным теплоносителем, или в виде псевдоожиженного слоя.
Эти способы более подробно рассмотрены в последующих пара-
графах этой главы.
§ 10.2. Перепад давления в системах
с газообразным теплоносителем
Этот вопрос требует специального рассмотрения по двум причи-
нам. Во-первых, на перекачку газообразных теплоносителей затра-
чивается большое количество энергии. Эти затраты существе пно вли-
яют на экономичность АЭС с газоохлаждаемыми реакторами . Поэто-
му при конструировании теплообменных поверхностей и при выбо-
ре метода интенсификации теплообмена важно правильно оценить
не только интенсивность теплоотдачи, но и перепад давлен ия, а сле-
довательно, и мощность, требуемую для перекачки теплоносителя.
283
Это тем более необходимо, что увеличению теплоотдачи, достигаемому
с помощью тех или иных мер, обычно сопутствует увеличение по-
требляемой на перекачку мощности. Поэтому возникает задача оты-
скания оптимального решения.
Во-вторых, при движении газа через теплообменную систему
его температура и давление меняются, а следовательно, меняется
и удельный объем. Вследствие этого меняется скорость потока, и
при расчете перепада давления необходимо учитывать энергию, за-
трачиваемую на изменение кинетической энергии потока.
Определение перепада давления при течении газа через теплооб-
менную систему* рассмотрим на примере канала постоянного по-
перечного сечения. Течение газа будем считать одномерным, полагая
параметры потока постоянными по сечению и меняющимися только
по длине. Обозначим скорость, давление, плотность и температуру
газа на входе в канал ръ р:(, и 7\, а иа выходе из канала соответ-
ственно ш2, р2, р2 и 72. Закон сохранения количества движения для
произвольного элемента потока на участке канала длиной dx имеет
следующий вид:
—dp = dpTp + pwdw, (10.1)
где dp — полное изменение давления на участке канала длиной dx;
dp^ — перепад давления, обусловленный трением и другими необ-
ратимыми потерями (например, сопротивлением формы) на стенках
канала и на поверхностях различных элементов, если таковые име-
ются в канале; pwdw — изменение количества движения газа иа
длине dx.
Перепад давления, обусловленный трением и другими потерями,
можно выразить через коэффициент сопротивления трения:
dAp = g^-.-y., (10.2)
2
где d3 — эквивалентный диаметр канала, обычно определяемый как
учетверенная площадь поперечного (проходного) сечения канала,
деленная на периметр.
Подставляя уравнение (10.2) в (10.1), получаем
— dp~^ ———-------рршс/йу. (10.3)
Р
Так как в канале постоянного сечения массовая скорость по длине
канала не изменяется, т. е. pay = const, то, полагая постоянным ко-
эффициент сопротивления трения и интегрируя выражение (10.3) по
длине канала в пределах от 0 до /, имеем
Pi—J -у + рш^—Ш!). (10.4)
о
* Под теплообменной системой здесь понимается либо рабочий канал
реактора, либо вся активная зона реактора, если она выполнена, например,
в виде насадки шаровых твэлов, либо секция парогенератора.
284
Если определить среднюю по длине плотность газа, воспользовав-
шись интегралом, входящим в выражение (10.4):
i
1 __ 1 Г dx
р I J Р
о
(10.5)
и учесть, что = р2ю2 = рда, то окончательно получим
^Р ' Pl— Pi r:= ~ ..£ ~7~ + f-------------—P • (10.6)
P \ Pa px /
Первое слагаемое в правой части (10.6) означает потери давления
на трение, а второе — потери давления на ускорение потока.
Несколько иное по форме выражение для расчета Др можно полу-
чить, если уравнение (10.3) домножить на р и проинтегрировать по
длине канала:
z I
= f^-tte + (p®)2j>d(—)• (10.7)
9 о о Р
Считая газ идеальным, для интеграла в первом слагаемом получим
i i
^-^-dx = R^ Tdx = RTl,
J Р J
о о
1 (
где Т==— | Tdx — средняя по длине канала температура. При-
Z о __
ближенно в расчетах можно принимать Т = (7\ + Т2)/2.
Интеграл во втором слагаемом (10.7) возьмем по частям:
[rT~ ^R(To-~7\) — RT
J Р Pi
о
Здесь Т —некоторое постоянное по длине канала значение Т, вы-
несенное из-под интеграла.
Подставляя полученные выражения для_интегралов в соотношение
(10.7) и приближенно считая, что Т = Т, получаем
W+(pw)2 •
2 |_ Pi -
Поделив это выражение на р — (Pi + Рг)/2 и обозначив р = p/RT,
найдем:
Ap=ft_pa=(migA+’k^+in-iyi. (Ю.8)
Р L 2 “Э 1 Р2 J
285
Так как перепад давления Др обычно намного меньше абсолютного
давления р2, то
/’2 \ Рз / Р2 Р
Таким образом, обозначив AT = Т2 — 7\, окончательно имеем
АГ
Т
(10.9)
Полученные в результате ряда упрощений соотношения (10.6) и
(10.9) приближенно верны при скоростях потока, не превышающих
~3/4 скорости звука. Очевидно, что при использовании уравнений
(10.6) и (10.9) расчет приходится проводить методом последователь-
ных приближений, так как давление р2 (или перепад Ар) и плот-
ность р2 заранее неизвестны. Соотношения (10.6) и (10.9) позволяют
легко показать, что повышение давления газообразного теплоноси-
теля выгодно, так как при этом уменьшаются расходы энергии на
перекачку. Мощность, необходимая для прокачки G = (рад)^
1ягАж] газа при перепаде давления Ар [Н/м2], равна
Ap/w kpf (pw) kpG
-------—r. --------=----- — 5/7/?
T) Т|р т|р
(10.10)
где f — площадь поперечного сечения газового тракта; р — к. п. д.
газодувки; ад—средняя по длине скорость.
Так как в соответствии с отношениями (10.6) и (10.9) перепад
давления обратно пропорционален средней плотности (Ар ~ 1/р), то
из (10.10) следует, что N ~ 1/р2. Таким образом, повышение
давления газообразного теплоносителя в контуре реактора увели-
чивает его плотность и тем самым снижает расход энергии на
перекачку. Не случайно по мере развития газоохлаждаемых
реакторов давление газа неуклонно повышается. Если в первом
английском реакторе «Колдер-Холл» давление двуокиси углерода
составляло всего 6,8 атм, то на следующих АЭС оно доведено
до 18 атм, а в чехословацком реакторе достигает 65 атм. Следует,
конечно, иметь в виду, что повышение давления связано с боль-
шими технологическими трудностями. Чем выше давление, тем
сложнее создавать корпуса реакторов и парогенераторов, диаметры
которых достигают нескольких метров.
§ 10.3. Теплообмен и сопротивление в ребристых системах
Для увеличения эффективного коэффициента теплопередачи
в технике широко используется оребрение теплопередающих поверх-
ностей. Форма оребрения весьма разнообразна. Применяют продоль-
ные, поперечные, спиральные ребра, ребра в виде шипов и т. д.
Подробные сведения о различных способах оребрения и технологии
изготовления ребристых поверхностей, а также рекомендации по
286
гидродинамическому и тепловому расчету можно найти в работах
[1, 2, 7, 8].
Мы же рассмотрим только те формы, которые чаще всего исполь-
зуются для оребрения оболочек твэлов ядерных реакторов и наруж-
ных поверхностей труб парогенераторов.
Оребрение не только увеличивает поверхность теплообмена с той
стороны, где коэффициент теплоотдачи имеет низкое значение, но и
оказывает большое влияние иа гидродинамику потока, а тем самым
и на коэффициент теплоотдачи. Очевидно, что чем лучше перемеши-
вается газ в основном потоке и в межреберных зазорах, тем выше ко-
эффициент теплоотдачи. Одновременно с увеличением коэффициента
Рис, 10.1. Конструкция оребренных шинами труб, ис-
пользуемых в парогенераторах английских АЭС.
теплоотдачи растет и гидравлическое сопротивление оребренных
элементов. Поэтому при конструировании оребрения стремятся най-
ти такую геометрию, которая дала бы существенный выигрыш в теп-
лоотдаче при не очень сильном увеличении гидравлического сопро-
тивления.
Так как характер обтекания твэлов и труб парогенераторов раз-
личен (твэлы обтекаются газом в продольном направлении, а труб-
ные пучки парогенератора в основном в поперечном направлении),
то и геометрия их оребрения различна.
Для оребрения труб парогенераторов чаще всего используют
широкие шипы (рис. 10.1) или близкие к ним по своим гидродинами-
ческим и теплообменным характеристикам кольцевые и спиральные
ребра. Постепенное усовершенствование шипового оребрения и улуч-
шение компоновки труб в пучках позволили повысить паропроиз-
водителыюсть парогенераторов АЭС «Хинкли-Пойнт» в три раза
по сравнению с производительностью парогенераторов АЭС «Колдер-
Холл» при увеличении диаметра корпуса всего на 25%, а длины на
20%. Коэффициент заполнения поперечного сечения парогенератора
при этом увеличивается до 80% по сравнению с 50% на АЭС «Кол-
дер-Холл».
Сложнее обстояло дело с выбором оребрения для оболочек твэлов.
Вначале казалось, что наиболее выгодными должны быть продоль-
287
ные ребра. Они первые и были экспериментально изучены. Оказа-
лось, что при такой конструкции оребрения (рис. 10.2, а) наблюда-
ется плохое перемешивание газа: внешний поток в зазоре между вер-
шинами ребер и наружной стенкой канала остается относительно
холодным, а в межреберных зазорах сильно перегревается. Поэ-
тому теплосъем при продольном оребрении оказался сравнительно
низким.
После этого были исследованы трубы с поперечными кольцевыми
ребрами (рис. 10.2, б). Можно было ожидать, что при продольном
Рис. 10.2. Схема продольного (а) и поперечного (б) ореб-
рения оболочек твэлов.
обтекании таких труб в межреберных зазорах будут образовываться
застойные зоны. На самом деле оказалось, что в этих зазорах возни-
кает циркуляционное течение в виде вихрей, хорошо перемешиваю-
щее газ. Поэтому на первых английских газоохлаждаемых реакторах
для оребрения оболочек твэлов были использованы кольцевые по-
перечные ребра.
В дальнейшем были разработаны более выгодные формы оребре-
ния оболочек твэлов, так называемое шевронное и полизональное,
схематично показанные на рис. 10.3.
В обоих случаях оребрение выполняется в виде многозаходной
спирали с большим шагом. При шевронном оребрении вся поверх-
ность оболочки делится на четыре, шесть или восемь секторов, и на
соседних секторах спирали расположены симметрично относительно
продольной оси. При полигональном оребрении многозаходная спи-
раль делается общей для всей поверхности цилиндра и в нескольких
288
местах ее пересекают продольные перегородки, высота которых боль-
ше высоты ребер; между наружными кромками перегородок и по-
верхностью канала остаются небольшие зазоры.
Эффективность шевронного и полизонального оребрения опреде-
ляется характером движения газа в канале. Как и ранее, поток га-
за, протекающего в кольцевом зазоре между поверхностью твэла
и наружной трубой рабочего канала, можно условно разбить на
две области: внешнюю — течение над вершинами ребер; и внут-
реннюю — течение в межреберных зазорах.
Рис. 10.3. Схема шевронного (а) и полизонального (б) ореб-
рения оболочек твэлов.
Газ поступает в межреберпый зазор из внешней области. Про-
ходя по зазору, он нагревается и, натолкнувшись на перегородку
(в полизоналыюм оребрении) или на поперечно стоящий зуб (в шев-
ронном оребрении), выбрасывается во внешнюю область потока.
Очевидно, что при этом обеспечивается интенсивное перемешивание
газа и в межреберные зазоры все время поступает хорошо перемешан-
ный, сравнительно холодный газ. Тем самым обеспечиваются высо-
кие коффициепты теплоотдачи от оребренной поверхности к потоку
теплоносителя.
Из приведенного выше краткого описания видно, что харак-
тер течения газа в оребренных элементах чрезвычайно сложен и
зависит от большого числа факторов. Получить обобщенные зависи-
мости для расчета теплообмена и гидравлического сопротивления
оребренных поверхностей в широком диапазоне изменения опреде-
ляющих параметров затруднительно. Поэтому предварительно па-
раметры оребрения обычно выбирают с помощью зависимостей,
полученных для аналогичных или похожих форм оребрения. Окон-
10 Зак. 792 289
нательная же отработка оптимальной формы оребрения осуществля-
ется экспериментально путем изучения различных вариантов моде-
лей твэлов.
В настоящее время в результате многочисленных экспериментов,
проведенных с оребренными поверхностями, предложено много раз-
личных методов и формул для расчета теплоотдачи и гидравличес-
кого сопротивления ребристых элементов. В дальнейшем приведем
только простейшие из них.
Как сказано выше, характер обтекания и форма оребрения обо-
лочек твэлов и трубных пучков парогенераторов различны, поэтому
рекомендации для их расчета рассмотрим отдельно.
В экспериментах с полизоналы-ю оребренными трубами исследо-
валось влияние различных параметров оребрения на теплоотдачу
и гидравлическое сопротивление. Оказалось, что с уменьшением диа-
метра внешней трубы (диаметра рабочих каналов активной зоны)
быстро возрастает гидравлическое сопротивление. Поэтому целесо-
образно принимать наибольший допустимый диаметр этих каналов.
Выгодно увеличение числа ребер, что связано с увеличением тепло-
отдающей поверхности и интенсификацией теплоотдачи. Уменьше-
ние шага винтовой спирали (увеличение угла ребер по отношению к
оси трубы) приводит к возрастанию сопротивления, опережающему
рост теплоотдачи. Поэтому не рекомендуется выбирать шаг винтовой
спирали меньше 300—400 мм. С другой стороны, с увеличением шага
спирали возрастает длина ребер между продольными перегородками,
а тем самым и длина межреберных каналов. При очень больших дли-
нах этих каналов ухудшается перемешивание газа в полигональном
оребрении и теплоотдача снижается. Поэтому не рекомендуется
длину межреберных каналов делать более 50 эквивалентных диамет-
ров этого канала. Увеличение толщины ребер повышает их эффектив-
ность и поэтому в известных пределах является выгодным. С увели-
чением высоты ребер растет поверхность оребрения и по вышается
коэффициент теплоотдачи. Однако при значительном увеличении вы-
соты эффективность оребрения падает, а гидродинамическоесопротив-
ление начинает расти быстрее теплоотдачи. Оптимальная высота ре-
бер зависит от материала оболочки, от величины коэффициента теп-
лоотдачи. Для ребер из магниевого сплава с коэффициентом тепло-
проводности % — 140 втЦм • град) оптимальная высота ребра
равна 8—10 его толщинам.
Местная плотность теплового потока на внутренней поверхности
оребренной цилиндрической оболочки qc связана с температурой на
этой поверхности icl и температурой жидкости (газа), омывающей
снаружи оребренную поверхность, следующим соотношением:
7с = /г (tcl — /ж). (10.11)
Обычно плотность теплового потока qc в данном сечении твэла
известна, а искомой величиной является температура на внутренней
поверхности оболочки (или в другой точке сечения твэла), которая
290
и находится из соотношения (10.11):
Коэффициент теплопередачи k равен
1 1
/С -
Ф , ^2 Ф
--- J ц -- -----------
2Х dx а2>усл^2
(10.12)
Здесь dx и d2 — внутренний и наружный диаметры оболочки; %—ко-
эффициент теплопроводности материала оболочки; а2)УСП — услов-
ный коэффициент теплоотдачи, отнесенный к поверхности неореб-
ренной трубы.
Условный коэффициент теплоотдачи а2,усл связан с коэффициен-
том теплоотдачи, отнесенным к полной поверхности оребрения, а2
следующим соотношением [см. уравнение (3.71)]:
“=,уЫ. = 1 + 4е- (’ll. - >)] -7й ’ <10'13>
г op J Лп
где Fop — полная площадь оребренной поверхности; Fp— площадь
поверхности ребер; Fn — площадь поверхности неоребренной тру-
бы; т]р — коэффициент эффективности ребра.
Коэффициент теплоотдачи а2 со стороны оребрения (отнесенный
к его полной поверхности) по данным Ритца [12], исследовавшего
53 различные конфигурации полизонального оребрения в интервале
чисел Рейнольдса от 2000 до 80 000, описывается уравнением
Nu = l,86Re°-70Pr0-4^— ( —) —) . (10.14)
2О,(И, \ D } \ D' ) v 7
Здесь Nu — a2da/X; Re = wdjv; da — эквивалентный диаметр
равный учетверенной площади свободного сечения канала, деленный
на периметр канала, который в свою очередь равен сумме периметров
оребренного стержня и внешней трубы; w — скорость в полном сво-
бодном (без ребер) сечении канала.
В опытах Ритца диаметр внешней трубы (рабочего канала) D
изменялся от 89 до 108 мм; шаг винтовой линии t от 305 до 610 мм;
диаметр трубки (оболочки), несущей оребрение, d от 33 до 41,7 мм;
наружный диаметр ребер d' от 44,5 до 54 мм. Испытывались полиго-
нальные оребрения с числом ребер (числом заходов) г = 18; 24; 32
и 36 и числом продольных перегородок п ~ 0; 2; 3; 4. Наружный
диаметр перегородок D' был меньше диаметра внешней трубы
на 0—38 мм.
Перепад давления в полизональных твэлах можно определять
по уравнениям (10.6) и (10.9). При этом коэффициент сопротивления
10* 291
для приведенных выше условий с погрешностью ±20% можно рас-
считывать с помощью следующего соотношения [11]:
£ __ Р>е-0,137 Л
\ tz
-F 0,0504^ .
(10.15)
Обозначения здесь те же, что и в уравнении (10.14).
Основные результаты, характеризующие влияние конструктив-
ных параметров оребренных пучков труб, обычно применяемых
в парогенераторах, на их теплоотдачу и сопротивление, при попереч-
ном обтекании сводятся к следующему [2, 8]: коэффициент теплоот-
дача слабо зависит от толщины ребер, а также от расстояния-между
трубами в пучке. Поэтому рекомендуется делать пучки по возмож-
ности более компактными, толщину ребер небольшой, расстояние
между ребрами минимальным. Выгодно уменьшение диаметра труб,
несущих оребрение. Для поперечных ребер также существует оп-
тимальная высота оребрения, составляющая примерно 35% диа-
метра трубы, несущей оребрение.
Расчет парогенераторов, обогреваемых газом, обычно проводится
по отдельным секциям или газоходам. Количество тепла, переда-
ваемое в рассматриваемой секции от греющей среды к нагреваемой
Q = kKiF вт, (10.16)
где k — коэффициент теплопередачи, вт!(л1~ • град), отнесенный
к единице поверхности неоребренных труб; &t — средний темпера-
турный напор между греющей и нагреваемой средами; F — поверх-
ность нагрева секции (т. е. поверхность неоребренных труб).
Коэффициент теплопередачи рассчитывается по известному урав-
нению:
^2 , ^2 , ^2 1
--- 1д ------
ttidi 2Л cli а2,усп
(10.17)
Здесь dt и d%—внутренний и наружный диаметры трубы; X— коэф-
фициент теплопроводности материала трубы; ах — коэффициент
теплоотдачи на внутренней поверхности трубы; а21УСП — условный
коэффициент теплоотдачи на наружной поверхности трубы, отне-
сенный к неоребренной поверхности.
Условный коэффициент теплоотдачи вычисляется по формуле
а2,уСл = <*2 [1-К-/11- (Пр—
L -Гор J Ът
(10.18)
которая отличается от формулы (10.13) только наличием коэффициен-
та ф, учитывающего неоднородность распределения коэффициента
теплоотдачи по поверхности ребра. Для поперечных ребер на круг-
лых трубах при поперечном обтекании пучков можно принимать
ф « 0,85 [6].
292
Для расчета коэффициента теплоотдачи а2 на наружной поверх-
ности поперечно обтекаемого пучка труб с круглыми ребрами в ин-
тервале чисел Рейнольдса от 3000 до 25 000 можно воспользоваться
эмпирическими уравнениями, полученными Э. С. Карасиной [61:
для шахматных пучков
Nu-0,223 Re0-(>5 ( —Y 0,54(А>| °'14
\ t \ t ,1
(10.19)
и для коридорных пучков
Nu-0,104Re0-72 (-уГ'54^)“0,14 , (10.20)
где Nu — сД/%, Re = wt/v, w — скорость в минимальном сечении
пучка; d — наружный диаметр трубы, несущей оребрение;
h — высота ребер; t— шаг ребер. Физические свойства газа в урав-
нениях (10.19) и (10.20) выбираются по средней температуре потока.
Подробные рекомендации по расчету теплоотдачи на ошипован-
ных трубах приведены в работе [Г].
Средний температурный напор между греющим и нагреваемым
теплоносителями А/ [см. уравнение (10.16)1 зависит от взаимного
направления движения теплоносителей и некоторых других особен-
ностей теплообменника. Для противоточного или прямоточного дви-
жения теплоносителей, а также в том случае, когда температура одно-
го из теплоносителей не изменяется вдоль поверхности нагрева,
А/ определяется по уравнению
(10.21)
In —--
А/м
где А/б и AfM — большая и меньшая из разностей температур теп-
лоносителей со стороны входа и со стороны выхода из аппарата или
его секции. Способ определения А/ для некоторых более сложных
схем движения теплоносителей приведен в работе [10].
Перепад давления при течении газа в оребренных трубных пучках
парогенераторов можно рассчитывать по формулам (10.6) и (10.9).
Только в этом случае при определении потерь на трение (первое сла-
гаемое) вместо отношения //d0 обычно подставляют F/4fMmi, где F —
полная поверхность теплообменника (или его секции); fMIin—мини-
нимальное поперечное свободное сечение.
По данным многочисленных экспериментов, определенный таким
образом [т. е. при использовании в уравнениях (10.6) и (10.9) па-
раметра F/4fMH[t] коэффициент сопротивления сильно зависит от гео-
метрии оребренного пучка. Ориентировочно коэффициент сопротив-
ления изменяется от 0,204-0,24 при Re = 5 • ГО3 до 0,08 4- 0,12
при Re — 104. Более подробные сведения можно найти в рабо-
тах [1,2].
293
§ 10.4. Гидродинамика и теплообмен в насадках
В высокотемпературных газоохлаждаемых реакторах в качестве
топлива используют не металлический уран, а керамические топли-
ва — окислы или карбиды урана или плутония. Эти материалы об-
ладают невысоким коэффициентом теплопроводности, поэтому для
уменьшения температурных перепадов в топливе приходится умень-
шать размеры тепловыделяющих объемов. Например, разрабатывает-
ся высокотемпературный газоохлаждаемый реактор с твэлами, изго-
товленными следующим образом. На сферические топливные части-
цы диаметром около миллиметра наносится защитная оболочка,
основное назначение которой — удержать газообразные продукты
распада, образующиеся в процессе работы реактора, и не допустить
их попадания в теплоноситель. Защитная оболочка имеет толщину
0,1—0,2 мм и обычно выполняется многослойной. Первый слой из
пористого пирографита предназначен для поглощения продуктов рас-
пада.
Один или два следующих слоя изготавливаются из плотного
пирографита или карбида кремния и предназначены для удержания
продуктов радиоактивного распада. Наносимый обычно снаружи еще
один слой пористого пирографита обеспечивает механическую проч-
ность частиц. Покрытые защитной оболочкой частицы смешиваются
с графитовой смолой. Из этой смеси прессуются топливные таблетки,
которые после выжига связки представляют собой графитовую мат-
рицу с диспергированными в ней топливными частицами. Готовые
топливные таблетки набираются в графитовую полую цилиндричес-
кую оболочку, герметизируемую по концам.
Однако может оказаться перспективной и другая конструкция
высокотемпературного газоохлаждаемого реактора, когда актив-
ная зона выполняется в виде насадки. В этом случае слой топ-
ливных частиц, смешанных с замедлителем, загружается иа решет-
ку и снизу через этот слой продувается теплоноситель. Такая
конструкция обеспечивает очень большую поверхность теплообмена,
а следовательно, невысокие перепады температуры между топливом
и теплоносителем. Кроме того, упрощается процесс перегрузки топ-
лива в реакторе и может быть увеличена глубина его выгорания.
Теплообмен и гидродинамика в насадках имеют свои особенности,
связанные с характером движения газа в зазорах между частицами.
Форма частиц, если речь идет об активной зоне ядерных реакторов,
близка к сферической.
Малый размер зазоров между частицами, многократное сужение
и расширение газовых струй, их взаимное перемешивание, с одной
стороны, обеспечивают высокие коэффициенты теплоотдачи, а с дру-
гой, — требуют больших перепадов давления и, следовательно,
больших мощностей на перекачку теплоносителя.
Рассмотрим некоторые параметры, характеризующие течение в
насадках. На рис. 10.4 показан канал поперечным сечением S, в ко-
тором на опорной (дутьевой) решетке расположена насадка — слой
294
частиц высотой Н. В зависимости от формы частиц и их взаимного
расположения может изменяться доля объема, занимаемая пустота-
ми. Объемная доля пустот в насадке, называется пористостью (или
порозностыо) слоя и обычно обозначается т. Эта величина равна от-
ношению средней площади свободного сечения слоя (пустот) к пол-
ному сечению капала S.
Если рассматривать слой из сферических частиц одинакового
размера, то при наиболее плотной упорядоченной ромбоидальной
упаковке пористость слоя т равна 0,26;
при кубической укладке сферических
частиц т = 0,47. В случае произволь-
ной беспорядочной засыпки в канал
большого поперечного сечения пори-
стость слоя т •== 0,36-4-0,40.
Средняя скорость газа под решеткой,
или, что то же самое, скорость в иеза-
громождепном сечении капала, назы-
вается скоростью фильтрации. Очевидно,
что средняя скорость газа в зазорах
между частицами
будет выше за счет загромождения попе-
Рпс. 10.4. Схема течения га-
за через насадку.
речного сечения капала.
Как и при движении жидкостей в
каналах других конфигураций, при те-
чеиии в насадках возможны ламинар-
ный, переходной и турбулентный режимы течения. Границы этих
режимов удобнее всего проследить по графику зависимости коэффи-
циента сопротивления от числа Re.
В случае течения через насадки обычно пользуются эффективным
коэффициентом £оф, определяемым через эффективный гидравличе-
ский диаметр каналов и среднюю скорость течения в зазорах w\
&р Ф)ф
" 1} * ' 5
2pteC И
(10.22)
где Ар — перепад давления в слое насадки высотой Н без учета по-
терь на расширение; с/оф = (2/3)/[m/(m—l)Kpida—эффективный гид-
равлический диаметр каналов, образованных частицами; da — диа-
метр шара, эквивалентного частице по объему; <рх == )/0,205F/y2/3 —
коэффициент формы частиц, для шара равный единице; F — поверх-
ность; v — объем частицы.
Зависимость эффективного коэффициента сопротивления от числа
Рейнольдса Rea({) = zM^/v показана на рис. 10.5.
295
При значениях Ие9ф 4 наблюдается чисто ламинарное течение
газа через насадку, и коэффициент сопротивления равен [41:
<10-23)
РеЭф
В интервале 4 < Кеэф < 7000 происходит постепенный переход
к турбулентному режиму течения. В этой области коэффициент соп-
Рис. 10.5. Зависимость коэффициента сопротивления на-
садки от числа Рейнольдса.
положения в насадке. В области значений Иеэф от 2 до 800 коэф-
фициент сопротивления можно определять по формуле [4]
I *
+0,8.
Re эф
(10.24)
При Веэф^ 7000 роль вязких сил становится пренебрежимо ма"
лой и наступает так называемый автомодельный режим. Коэффици-
ент сопротивления определяется геометрией насадки и не зависит
от числа Рейнольдса, а закон сопротивления становится квадра-
тичным (Ар ~ ю2).
Некоторые авторы предпочитают пользоваться более простым
определением коэффициента сопротивления слоя:
__ Д/? d
“ 2ри>2 ‘ ~Н ‘
относя его к диаметру частиц d* и скорости фильтрации йу0.
* Средний диаметр частиц обычно определяется таким образом: d =
= hXidt, где Xi — весовая доля частиц узкой фракции с диаметром di,
причем этот диаметр определяется как среднее арифметическое или среднее
геометрическое размеров отверстий смежных по номерам сит.
296
Для определения коэффициента сопротивления слоя в интервале
чисел Рейнольдса Re — wod/v от 5 • 10:i до 5 • 104 при т 0,4
можно пользоваться следующей формулой [31:
/ 97В \
ГТ)’ (10<26)
Таким образом, перепад давления в слое насадки легко опреде-
ляется из уравнения (10.22) или (10.25). Однако этими уравнениями
можно пользоваться лишь в том случае, если давление и температу-
ра (а следовательно, и плотность газа) в слое насадки изменяются
незначительно. В противном случае нужно пользоваться уравнением
(10.6) или (10.9), подставляя в них вместо (1/2)£(ШЭ) величину
2Ц (ЖФ) или 2£сл (ЯЦ.
Исследованию теплообмена при течении газа через насадки по-
священо большое число работ. Следует прежде всего отметить слож-
ность рассматриваемого процесса. Для единичной частицы коэф-
фициент теплоотдачи и его распределение по поверхности час-
тицы зависят от формы частицы и взаимного расположения частиц
в слое. Для слоя в целом коэффициент теплоотдачи может изменяться
по высоте насадки и по ее сечению в связи с изменением пористости,
(например, пористость насадки у стенок обычно выше, чем в ее цен-
тральной части). Учесть влияние всех отмеченных факторов затруд-
нительно.
Расчетные рекомендации в основном опираются на опытные
данные о средних коэффициентах теплоотдачи от частиц к газу для
слоя в целом. Так, по данным работы [91:
в интервале чисел Re от 20 до 200
Nu- 0,106Re; (10.27)
в интервале чисел Re от 200 до 2000
Nu - 0,61Re°-G7. (10.28)
По другим данным [12], в интервале чисел Re от 500 до 50 000 и
т да 0,4
Nu = 0,57 Re° »7 Рг°>3, (10.29)
где Re = wQdlv; Nu ~ ad/h; wQ — скорость фильтрации; d — диа-
метр частиц. Свойства газа выбираются по средней температуре газа
в насадке.
Для расчета теплоотдачи в слое сферических частиц можно ре-
комендовать также зависимость, полученную в работе [13], которая
удовлетворительно описывает данные различных авторов в диапазо-
не чисел Re от 7500 до 40 000:
Nli= 0,87
md
т
0,19 Re0-625.
(10.30)
297
Здесь md = 0,48 — пористость слоя с кубической укладкой час-
тиц; т — пористость рассчитываемого слоя. Эта формула хорошо
обобщает опытные данные, полученные при значениях т = 0,48;
0,63; 0,73; и 0,84, и даже данные для единичной сферы для кото-
рой т = 1.
§ 10.5. Гидродинамика и теплообмен в псевдоожиженном слое
С уменьшением размеров топливных частиц и увеличением ско-
рости теплоносителя возрастают эффективная поверхность теплообме-
на и коэффициенты теплоотдачи. При этом может наступить такое
состояние, когда топливные частицы приобретают подвижность,
а весь слой частиц начинает вести себя подобно жидкости — насту-
пает так называемое состояние псевдоожижения. Малые размеры час-
тиц и интенсивное перемешивание слоя позволяют значительно ин-
тенсифицировать процессы тепло- и массообмена, поэтому псевдоожи-
женный слой широко исполь-
зуется во многих областях
техники. По тем же причинам
очень заманчиво создание ак-
тивной зоны высокотемпера-
турного газоохлаждаемого
реактора в виде псевдоожи-
женного слоя.
Изучению гидродинамики
и теплообмена псевдоожижен-
ных слоев посвящено большое
количество исследований.
Подробный обзор и анализ
современного состояния вопро-
са дан С. С. Забродским [5].
Рассмотрим, как ведет себя
Рис. 10.6. Зависимость перепада давле- СЛОЙ мелких частиц, располо-
ния Др и высоты слоя Н от скорости женный на решетке в верти-
фильтрации. калькой трубе (см. рис. 10.4)
и продуваемый снизу вверх,
по мере увеличения скорости газа (скорости фильтрации w0).
На первой стадии, пока скорость wQ сравнительно мала, слой час-
тиц неподвижно лежит на решетке, его объем и высота Яо, также как
и пористость т0, практически не изменяются, а перепад давления
Ар увеличивается с ростом скорости (рис. 10.6).
При достижении некоторой скорости перепад давления в слое
становится равным весу частиц, приходящихся на единицу попереч-
ного сечения канала. Эту скорость называют минимальной скоростью
псевдоожижения или скоростью потери устойчивости слоя г^п.у.
Начиная с этого момента в слое возникает режим псевдоожижения.
При увеличении скорости ш0 перепад давления в слое остается
298
неизменным, а среднее расстояние между частицами увеличивается,
что приводит к увеличению пористости т и высоты слоя Н.
При дальнейшем увеличении скорости до некоторого значения
&»к через слой начинают прорываться порции чистого газа. Слой ста-
новится неоднородным, физическая картина слоя во многом напоми-
нает кипящую жидкость, поэтому такой режим называют кипящим
слоем. При еще большем увеличении скорости фильтрации наступает
момент, когда скорость движения газа становится равной скорости
витания (падения) частицы в неподвижном газе, и весь слой, если
он состоит из частиц одинакового размера, уносится потоком газа.
На первой стадии процесса, когда частицы неподвижны, теплооб-
мен и сопротивление в слое рассчитываются по уравнениям, приведен-
ным в предыдущем параграфе.
Для получения режима псевдоожижения необходимо прежде все-
го превзойти скорость потери устойчивости слоя. Эта скорость за-
висит от многих факторов, не поддающихся точному учету (конструк-
ция дутьевой решетки, степень неравномерности слоя частиц и др.),
поэтому имеющиеся теоретические и экспериментальные рекоменда-
ции не всегда хорошо согласуются друг с другом. Следуя работе [5],
для расчета шп>у можно рекомендовать зависимость, предложенную
О. М. Тодесом й др. Для частиц, форма которых близка к сферичес-
кой, и при пористости слоя т ж 0,4 эта зависимость имеет вид
Здесь Ren,y —• оуп.у d0/v — число Рейнольдса, соответствующее по-
тере устойчивости слоя; Ar ~ z/pv2 — число Архимеда; z =
— dig (Рм—Р) — кажущийся вес слоя (за вычетом архимедовой силы),
рм и р — плотности частиц (материала) и газа; v — кинематический
коэффициент вязкости газа.
Так как в режиме псевдоожижения перепад давления в слое
Ар постоянен и определяется весом частиц на единицу поперечного
сечения, то без учета трения на стенках канала
Ар ZsPirac^O»
(10.32)
где £рпао — насыпная масса материала, равная массе материала
в слое, деленной на его объем в неподвижном состоянии.
Как указывалось выше, с ростом скорости фильтрации увеличи-
ваются пористость псевдоожиженного слоя т и его высота Н. Эти
параметры в режиме псевдоожижения приближенно можно рассчи-
тывать по следующим формулам [5]:
18 Re + 0,36 Re2 \ о, 21
Аг /
(10.33)
299
Н 1 — Шд
1—/?Г’
(10.34)
где т0 и Но — начальная пористость и высота слоя.
Экспериментальные данные по теплоотдаче в псевдоожиженном
слое, полученные разными авторами на различных материалах и раз-
личных по конструкции установках, характеризуются большим
разбросом. Однако важно отметить следующее. Изменение темпе-
ратуры газа по высоте псевдокипящего слоя легко определяется из
уравнения теплового баланса, если известно распределение тепло-
выделения по высоте. Расчет же температуры топливных частиц, для
которого, собственно, и необходимо знать коэффициент теплоотда-
чи, в псевдоожиженных слоях не играет большой роли, так как пере-
пад температур между поверхностью частиц и газом очень мал.
Для ориентировочного расчета коэффициента теплоотдачи в псев-
доожиженном слое С. С. Забродский [5] рекомендует следующие
соотношения:
Nu - 2 + 0,16Re0’67 при Re < 150; (10.35)
Nu = 0,62Re0’5 при 150 < Re < 30 000, (10.36)
где Re = wQdlv, Nu = ad/K.
Перепад температур между поверхностью частиц и газом опреде-
ляется по формуле
aF
(10.37)
где q — количество тепла, выделяющееся (и отдаваемое газу) в еди-
ницу времени в единице объема; F — полная геометрическая поверх-
ность частиц в единице объема, приближенно равная 6 (1 — m^ld.
СПИСОК ЛИТЕРАТУРЫ
1. Андреев П. А. и др. Теплообменные аппараты ядерных энергетических
установок. Изд. 2-е, перераб. Под ред. Н. М. Синева. Л., «Судостроение»,
1969.
2. Антуфьев В. М. Эффективность различных форм конвективных поверх-
ностей нагрева. М., «Энергия», 1966.
3. Denton W. Н., Robinson С. Н., Tibbs R. S. The heat transfer and pressure
loss in fluid flow through randomly packed spheres. Res. Group UK.
Atomic Energy Author. 1963, NAER — R, p. 51.
4. Жаворонков H. M., Фурмер И. Э. Гидравлическое сопротивление зер-
нистого слоя при малых скоростях газового потока. — Тр. МХТИ им.
Менделеева, 1952, вып. 12.
5. Забродский С. С. Гидродинамика и теплообмен в псевдоожиженном слое.
М.-Л., Госэнергоиздат, 1963.
6. Карасина Э. С. «Изв. Всесоюз. теплотехническ. ин-та им. Ф. Э. Дзер-
жинского», 1952, № 12, с. 12.
300
7. Кэйс В. М., Лондон А. Л. Контактные теплообменники. Изд. 2-е, пе-
рераб. Пер. с англ. М., «Энергия», 1967.
8. Петровский Ю. В., Фастовский В. Г. Современные эффективные тепло-
обменники. М.—Л., Госэнергоиздат, 1962.
9. Тимофеев В. Н. Теплообмен в слое. —«Пзв. Всесоюз. теплотехническ.
ин-та им. Ф. Э. Дзержинского», 1949, № 2, с. 12.
10. Якоб М. Вопросы теплопередачи. Пер. с англ. Под род. В. П. Мотулсви-
ча. М., Изд-во иностр, лит., I960.
И. Хьюз Д., Слэк М. Расчет теплопередачи оребренных тепловыделяющих
элементов реакторов, использующих в качестве теплоносителя СО2.
В сб.: Ядерная энергетика. (Сборник докладов 2-й Женевской конферен-
ции по некоторым вопросам ядерной энергетики. Под ред. М А. Стыри-
ковича). М., Изд-во иностр, лит., 1959, с. 118.
12. Ритц X. Тепловыделяющие элементы со спиральными ребрами. В сб.:
Ядерная энергетика. (Сборник докладов 2-й Женевской конференции по
некоторым вопросам ядерной энергетики. Под ред. М. А. Стыриковича).
М., Изд-во иностр, лит., 1959, с. 102.
13. Zhitkevich L. К., Zabrodsky S. S. Proc, of Third Internal. Heat Trans-
fer Conf., 7—12 August, 1966, Chicago, 1966, v. 4, p. 302.
ГЛАВА 11
ОСОБЕННОСТИ ТЕПЛООБМЕНА В СИСТЕМАХ
С ЖИДКОМЕТАЛЛИЧЕСКИМИ ТЕПЛОНОСИТЕЛЯМИ
§ 11.1. Жидкие металлы как теплоносители
Хотя мысль об использовании жидких металлов в качестве тепло-
носителей возникла давно, их всестороннее изучение и практическое
применение связано с разработкой и созданием ядерных реакторов.
В ряде случаев жидкие металлы как теплоносители для ядерных
реакторов обладают существенными преимуществами несмотря на
некоторые неудобства и усложнение технологии, связанные с их
применением.
Ценное свойство жидких металлов, выгодно отличающее их от
воды, — высокая температура кипения. Благодаря этому жидкоме-
таллические теплоносители можно нагревать до 500—700° С при ат-
мосферном давлении и тем самым получать водяной пар высоких па-
раметров во вторичном контуре (и следовательно, перед турбиной)
при низких давлениях в корпусе реактора и первичном контуре. Оче-
видно, что снижение давления теплоносителя в реакторе позволя-
ет значительно уменьшить толщину стенок, упростить конструкцию
и снизить стоимость корпуса — одной из самых сложных в изготовле-
нии и дорогих частей ядерного реактора.
Другое ценное свойство жидких металлов, важное при их исполь-
зовании в реакторах на быстрых нейтронах, — это слабое замедление
нейтронов. Для охлаждения реакторов этого типа нельзя применять
воду, широко используемую в реакторах на тепловых нейтронах,
а также органические теплоносители, так как они сильно замедляют
нейтроны. В качестве теплоносителей для реакторов на быстрых
нейтронах могут рассматриваться только жидкие металлы, газы и
водяной пар.
Кроме уже отмеченных достоинств жидкометаллические теплоно-
сители обладают еще одним — высокой теплопроводностью, обеспе-
чивающей большие значения коэффициентов теплоотдачи (обычно
несколько выше, чем для воды), что также весьма существенно для
теплоносителей ядерных реакторов.
В принципе любой металл можно расплавить и использовать в ка-
честве теплоносителя. Однако обычно рассматриваются такие срав-
нительно низкоплавкие и доступные в больших количествах металлы,
как натрий, калий, ртуть, литий, олово, цезий, свинец, висмут, гал-
лий, а также натрий-калиевый и свинцово-висмутовый сплавы.
Как хорошо видно из табл. 11.1, составленной на основании работ
[1, 3], свойства жидкометаллических теплоносителей чрезвычайно
302
Т а б л и ц а 11.1
Свойства жидкометаллических теплоносителей
Металл Атомный но- мер Атомная масса Температура плавления, °C Температура кипения при р=1 бар, °C Коэффициент теплопро- водности при 400° С, eml(м град) Теплоемкость при 400° С дж)(кг град) Плотность при 400° С, кг/м3 J Число Прандтля при 400° С
Литий Li 3 6,940 180,5 1327 49,0 4,20 495 0,0372
Натрий Na и 22,997 97,8 883 71,5 1,26 854 0,0052
Калий К 19 39,096 63,7 760 39,0 0,765 750 0,0043
Галлий Ga 31 69,72 29,8 1983 29,30 0,343 5845 -0,0104
Олово Sn 50 118,70 231,9 2270 33,6 0,255 6865 0,0105
Цезий Cs 55 132,905 28,5 670 14,0 0,227 1620 0,013
Ртуть Hg 80 200,61 —38,0 357 12,6 0,138 12700 0,0091
Свинец РЬ 82 207,21 327,4 1740 15,1 0,147 10592 0,0217
Висмут Bi 83 209,00 271 1490 15,6 0,150 9910 0,0136
Эвтектический нат- рий-калиевый сплав (23 % Na— —77% К) — 12,3 784 26,0 0,88 778 0,0081
Эвтектический свиицово-висму- товый сплав (44,5 % РЬ— 55,5 % Bi) — — 123,5 1670 13,7 0,146 10242 0,0172
разнообразны. Поэтому не все жидкие металлы равноценны с точки
зрения их использования в реакторах и особенно в реакторах на быст-
рых нейтронах.
Для тяжелых металлов в жидком состоянии (свинца, олова, вис-
мута, ртути) характерны более низкие по сравнению с другими метал-
лами коэффициенты теплоотдачи и относительно более высокие за-
траты энергии на перекачку. Большинство из них обладает значитель-
ной коррозионной активностью по отношению к конструкционным ма-
териалам. Пары этих металлов в большей или меньшей степени ядови-
ты. Литий хотя и имеет высокую теплоемкость, но более сильно за-
медляет нейтроны, коррозиошю активен и сравнительно дорог, осо-
бенно в связи с необходимостью очистки от изотопа GLi, сильно пог-
лощающего нейтроны.
В итоге многолетних экспериментальных исследований теплофизи-
ческих, коррозионных, технологических и других проблем, связан-
ных с применением жидких металлов в ядерных реакторах, установле-
но, что натрий является лучшим из жидкометаллических теплоносите-
лей для реакторов на быстрых нейтронах [41. Он слабо поглощает и
замедляет нейтроны, сравнительно низкоплавок, позволяет получать
высокие коэффициенты теплоотдачи, не вызывает коррозии боль-
шинства конструкционных материалов. Основной недостаток нат-
рия — высокая окисляемость на воздухе и бурная реакция с водой,
сопровождающаяся выделением большого количества тепла и нередко
303
взрывом образующейся гремучей смеси. Однако современная техно-
логия позволяет обеспечить безопасную работу с натрием.
Гидродинамика жидких металлов ничем не отличается от гидро-
динамики обычных ньютоновских жидкостей. Для расчета коэффици-
ентов турбулентного переноса количества движения, профилей ско-
рости и коэффициентов сопротивления при течении жидких металлов
применяются те же зависимости, что и при течении неметаллических
теплоносителей.
Основная особенность жидких металлов с точки зрения теплооб-
мена определяется их высокой теплопроводностью. Благодаря вы-
сокой теплопроводности жидких металлов существенно снижается
термическое сопротивление вязкого подслоя, представляющее обыч-
но для неметаллических жидкостей основную долю полного терми-
ческого сопротивления между стенкой и жидкостью. Значительно
большую роль в потоках жидких металлов играет перенос тепла за
счет теплопроводности и в турбулентном ядре. Поэтому при исполь-
зовании жидкометаллических теплоносителей значения коэффициен-
тов теплоотдачи достаточно высоки.
В гл. 5—9 подробно рассмотрены вопросы гидродинамики и теп-
лообмена при течении жидкостей, в том числе и жидких металлов,
в трубах. Там же приведены соотношения, необходимые для расчета
коэффициентов теплоотдачи при течении жидких металлов в круглых
трубах и каналах сложной формы. Однако в этих соотношениях
не учитывается ряд факторов, которые могут оказать влияние либо
на теплоотдачу, либо на температуру жидкости и тем самым привес-
ти к отклонению действительной температуры стенки в рассматри-
ваемом сечении от расчетной. В случае жидкометаллических тепло-
носителей к таким факторам следует прежде всего отнести продоль-
ную теплопроводность и контактное термическое сопротивление, обу-
словленное наличием окислов в жидком металле.
§ 11.2. Влияние осевой теплопроводности
на среднемассовую температуру жидкости
При граничных условиях второго рода, когда задано распреде-
ление плотности теплового потока на стенке qG (х), температуру жид-
кости в какой-либо точке сечения канала, в том числе и темпера-
туру стенки, удобно отсчитывать от среднемассовой температуры
в этом сечении канала t (х). Последняя легко определяется из уравне-
ния теплового баланса:
X
s qc (х) dx
i« = 4 + -A7--------, (ИЛ)
Gcp
где t0 — среднемассовая температура жидкости на входе в обогрева-
емый участок; qG (х) — распределение по длине канала средней по пе-
риметру плотности теплового потока на стенке; s— периметр попереч-
304
ного сечения канала; G — массовый расход теплоносителя через
канал; ср — удельная теплоемкость теплоносителя.
Однако в соотношении (11.1) не учитывается тепло, подводимое
к рассматриваемому участку (от 0 до х) через торцевые сечения вслед-
ствие осевой теплопроводности, обусловленной наличием продоль-
ного градиента температуры. Очевидно, что при dt/dx 0 происхо-
дит перенос тепла в осевом направлении как по самой жидкости, так
и по стенкам канала.
Если канал нагревается, градиент температуры положителен и
тепло передается навстречу потоку теплоносителя. В случае охлажде-
ния канала осевая теплопроводность приводит к переносу тепла вниз
по потоку теплоносителя. Несложный анализ уравнения энергии
показывает, что относительный вклад осевой теплопроводности в теп-
ловой баланс определяется числом Пекле. При достаточно больших
значениях числа Ре влияние осевой теплопроводности не существен-
но и среднемассовую температуру жидкости можно определять по
уравнению (11.1). При небольших значениях числа Пекле (Ре < 100)
неучет осевой теплопроводности при расчете среднемассовой темпе-
ратуры жидкости может привести к ошибкам, тем большим,
чем меньше число Ре.
В случае обычных жидкостей и газов, у которых Рг 1, значе-
ние Ре < 100 соответствует Re < 100. Такие низкие значения чисел
Рейнольдса редко встречаются в технических устройствах, и поэто-
му при расчете теплообмена для обычных жидкостей осевой теплопро-
водностью, как правило, пренебрегают. При течении жидких металлов
картина будет иная, например в случае течения натрия (Рг « 0,005)
числу Ре = 100 будет соответствовать Re — 20 000. Иными словами,
для жидких металлов влияние осевой теплопроводности проявляется
при значительно более высоких числах Рейнольдса.
Проанализируем влияние осевой теплопроводности на средне-
массовую температуру жидкости в том случае, когда задана и постоян-
на по длине канала плотность теплового потока на внешней поверх-
ности канала с/с.п = const. Если не учитывать осевую теплопровод-
ность и считать теплоемкость постоянной, то среднемассовая темпе-
ратура жидкости будет изменяться по длине канала линейно:
(11-2)
Gcp
(как это показано пунктирной линией 1 на рис. 11.1). В действитель-
ности же вследствие осевой теплопроводности по самой жидкости и
по стенкам канала некоторое количество тепла передается от более
нагретого участка канала к менее нагретому. Благодаря этому повы-
шается среднемассовая температура на входе в обогреваемый учас-
ток и по всей длине канала. Кривая 2 на рис. 11.1 соответствует дей-
ствительному изменению среднемассовой температуры жидкости по
длине канала с учетом осевой теплопроводности.
305
Повышение температуры жидкости, обусловленное осевой тепло-
проводностью St (см. рис. 11.1) нетрудно определить в сечениях,
удаленных от концов обогреваемого участка, т. е. там, где про-
дольный градиент температуры dtldx постоянен. Из элементарного
баланса тепла следует, что
(^с /с + X/) -
=------------—. (11.3)
Gcp
Выражение в числителе представляет собой количество тепла, пере-
носимое в осевом направлении по стенкам канала и по жидкости.
Здесь Хс, fc и X, f — соответственно коэффициенты теплопроводности
Рис. 11.1. Изменение среднемассовой_температуры жидкости по
длине канала при qc = const:
1— без учета осевой теплопроводности; 2—с учетом осевой тепло-
проводности; 3 — температура стенки.
и площади поперечного сечения стенок канала и потока теплоносите-
ля. Если выразить продольный градиент температуры через плот-
ность теплового потока и расход теплоносителя:
dt <?c.nS aAzfs
дх Gcp Gcp
(И-4)
то выражение (11.3) можно записать в более компактном виде:
4Nu(l±T) П5
где = tQ — t — —температурный напор между стенкой и
жидкостью, постоянный в удаленной от концов части канала, где
коэффициент теплоотдачи а не изменяется подлине (см. рис. 11.1).
В качестве определяющего размера в числах Нуссельта и Пекле,
как обычно, принят эквивалентный диаметр d3 = 4f/s. Параметр
Ф = Kfe/M
характеризует отношение тепловых потоков в осевом направле-
нии по стенкам канала и по жидкости. Из выражения (11.5) хорошо
видно, что величина St быстро падает с ростом числа Ре.
306
§ 11.3. Контактное термическое сопротивление
Полученные в первых экспериментальных работах по теплооб-
мену при течении жидких металлов в трубах значения коэффици-
ентов теплоотдачи оказались значительно более низкими, чем рас-
считанные теоретически (см. гл. 7).
Это расхождение пытались объяснить с помощью различных
гипотез: плохим смачиванием металлом стенки, наличием газовой
прослойки между металлом и стенкой, несправедливостью допуще-
ния о том, что турбулентное
число Прандтля равно единице,
и т. д. Только тщательное изу-
чение причин этого явления по-
казало, что расхождение резуль-
татов теоретического анализа и
эксперимента объясняется в
большинстве случаев наличием
так называемого контактного
термического сопротивления.
Контактное сопротивление,
представляющее собой дополни-
тельное термическое сопротивле-
ние переносу тепла между стен-
кой и жидким металлом, обязано
своим происхождением наличию
нерастворимых примесей в ме-
талле. При течении чистых ме-
0,07
0,06
0,05
0,00
0,03
0,02
0,01
О
100 200 300 000 t,°0
Рис. 11.2. Растворимость окисла NaaO
(в пересчете па кислород) в натрии
талов контактное сопротивление в зависимости от температуры,
отсутствует [1—3].
Чаще всего примесями, снижающими теплоотдачу, являются
окислы металлов. Жидкие металлы, особенно щелочные, активно
соединяются с кислородом, образуя различные окислы. Окислы
могут попадать в контур вместе с металлом при его загрузке либо
образовываться в самом контуре за счет соединения металла
с кислородом, содержащимся в инертном газе или конструкцион-
ных материалах. Окислы частично растворяются в жидком метал-
ле, причем количество растворенных окислов зависит от температу-
ры жидкого металла. На рис. 11.2 в качестве примера показана кри-
вая растворимости окислов натрия (в пересчете на кислород) в рас-
плавленном натрии. Если содержание кислорода превышает предел
растворимости, то излишек окислов находится в потоке металла
в нерастворенном виде. Нераствореииые окислы концентрируются
преимущественно вблизи твердых поверхностей, в области вязкого
подслоя.
Поскольку теплопроводность окислов намного меньше тепло-
проводности металла, то наличие даже небольших количеств
окислов вблизи поверхности теплообмена приводит к снижению
коэффициента теплоотдачи.
07
Процесс диффузии окислов в пристеночный слой протекает по-
разному в обогреваемых и охлаждаемых каналах. В охлаждаемых
каналах наиболее холодными являются пристеночные слои жид-
кости. Так как с понижением температуры растворимость окислов
уменьшается, то в пристеночных слоях жидкости происходит до-
пол пительное выпадение окислов и осаждение их на стенках канала.
Если контур герметичен и исключено дальнейшее попадание окис-
лов в жидкии металл, то все нерастворенные окислы выпадают на
охлаждаемых стенках, образуя слой, толщина которого опреде-
ляется исходным содержанием окислов в металле. При этом коэф-
Рис. 11.3. Схема распределения взве-
шенных примесей вблизи стенки.
фициеит теплоотдачи стабили-
зируется во времени на каком-то
более низком, чем для чистого
металла, уровне. По такому
принципу работают холодные
ловушки окислов. Если же су-
ществует какой-либо источник
окислов, например вследствие
попадания в контур атмосфер-
ного кислорода, то толщина
слоя окислов все время увели-
чивается, коэффициент теплоот-
дачи уменьшается и может насту-
пить полная закупорка канала.
В случае изотермического те-
чения или течения в обогревае-
мой трубе дополнительного выпа-
дения окислов на стенке не про-
исходит. Частицы окислов собираются вблизи стенки и образуют при-
стеночный слой с повышенным (по сравнению с чистым металлом)
термическим сопротивлением. Процесс концентрации окислов в вяз-
ком подслое в соответствии с представлениями, изложенными в моно-
графии В. И. Субботина, М. Н. Ивановского и М. Н. Арнольдова
[3], происходит следующим образом. Мелкие частицы окислов,
попав в вязкий подслой и двигаясь в основном вдоль стенки, дого-
няют частицы, расположенные ближе к стенке и имеющие меньшую
скорость. Сталкивающиеся частицы слипаются за счет вандерва-
альсовых сил и образуют более крупные частицы. Эти связи между
частицами не могут быть разрушены за счет броуновского движе-
ния, а турбулентность в вязком подслое относительно невелика.
Подвижность частиц после их слипания значительно уменьшается.
Таким образом, вязкий подслой становится своеобразной ловушкой
окислов. Вероятная схема распределения концентрации взвешен-
ных примесей вблизи стенки канала показана на рис. 11.3.
Согласно этой схеме примеси образуют вблизи стенки слой тол-
щиной 6К, концентрация окислов в котором Сс, по-видимому,
в десятки тысяч раз может превышать концентрацию окислов
в турбулентном ядре потока Сж.
308
Как показывают оценки, проведенные в той же монографии [3]
толщина слоя окислов 6К не зависит от концентрации окислов
в турбулентном ядре потока (если содержание окислов значительно
превышает предел растворимости) и уменьшается с ростом числа
Рейнольдса. Эти выводы, как будет видно из дальнейшего, хорошо
подтверждаются эксперимен-
тальными исследованиями коп-
та ктпого сон ротявления.
Чтобы обнаружить контакт-
ное сопротивление в загрязнен-
ном окпсламп металле проводят-
ся измерение температуры стен-
ки трубы (с помощью заложен-
ных в нее термопар) и измере-
ние профиля температуры в по-
токе жидкого металла (с по-
мощью подвижного термопар-
ного зонда). Результаты таких
измерений схематично показаны
на рис. 11.4.
В случае чистого, не загряз-
ненного окисламн металла тем-
пература па поверхности стенки,
получаемая экстраполяцией из-
меренного профиля температуры
в потоке*, совпадает с темпера-
турой поверхности стенки, рас-
считанной ио показаниям зало-
женных в пей термопар. Иначе
обстоит дело в случае содержа-
ния в металле больших коли-
Рпс. 11.4. Распределение температуры
в потоке жидкого металла:
1 — чистый металл; 2 — при наличии окис-
лов.
честв окислов. Тогда температура поверхности стенки, получен-
ная экстраполяцией профиля температуры в потоке, tcl
(см. рис. 11.4) не будет совпадать с температурой поверхности
стенки Zc2, измеренной термопарами, заложенными в стенку.
Слой окислов, схематично изображенный на рис. 11.4 пунктирной
линией, приводит к дополнительному перепаду температур tc2 —
/(!1, величина которого и характеризует контактное термическое
сопротивление:
Сг—^С1
Яс
(11.6)
Как показывают опыты, коэффициенты теплоотдачи, рассчиты-
ваемые по измеренным в потоке жидкости профилям температуры
а0 = —%-, (11.7)
гс1 ?}К
* Вследствие конечных размеров королька измерительной термопары
профиль температуры в потоке не может быть измерен до самой стенки.
309
хорошо согласуются с формулой (7.29), полученной в опытах
с чистыми металлами.
Очевидно, что коэффициент теплоотдачи, рассчитанный для
загрязненного металла по температуре £с2,
будет меньше, чем а0:
а =----^-=—
%2 ^Ж
(11.8)
(Н.9)
Многочисленные эксперименты, выполненные на натрии, свиде-
тельствуют о том, что при содержании окислов в натрии не более
0,02 вес. % экспериментальные значения коэффициентов теплоот-
дачи хорошо согласуются с формулой (7.29). Это означает, что
~ 0. При более высоком содержании окислов контактное сопротив-
ление достигает заметных величин, увеличиваясь с увеличением
концентрации окислов и убывая с ростом числа Рейнольдса. При
Рис. 11.5. Опытные данные по теплоотдаче к загрязнен-
ным теплоносителям:
• — литий в стальной трубе; Я — литий в молибденовой тру-
бе; ® — сплав Na — К в медной трубе; □ — сплав Na — К
в молибденовой трубе; О — сплав Na — К в молибденовой
трубе в условиях частичной очистки; 1 — зависимость Nu=5+
+0,025 Ре018; 2 —Nu=3+0,014 Ре0-8.
увеличении содержания окислов до —0,1 вес. % контактное терми-
ческое сопротивление достигает предельного значения и перестает
увеличиваться при дальнейшем загрязнении металла. Коэффи-
циенты теплоотдачи при этом снижаются примерно на 30% и, как
это видно из рис. 11.5, хорошо описываются формулой
Nu = 3 + 0,014Ре°>8. (11.10)
Таким образом, для получения высоких коэффициентов тепло-
отдачи при использовании жидкометаллических теплоносителей
необходимо поддерживать чистоту металла в контуре на достаточ-
310
но высоком уровне. Для этой цели прежде всего тщательно фильт-
руют металл от окислов при его загрузке в контур. Кроме того,
жидкометаллнческие контуры оборудуются специальными ловушка-
ми для улавливания окислов.
§ 11.4. Теплообмен при поперечном обтекании пучков труб
Промежуточные теплообменники и парогенераторы ядерных
энергетических установок чаще всего представляют собой кожу-
хотрубные теплообменники, поверхности нагрева которых выпол-
няются в виде трубных пучков. Нередко трубные пучки омываются
снаружи жидким металлом в поперечном направлении. Для рас-
чета! таких теплообменников
необходимы данные о теплоот-
даче при поперечном обтекании
жидким металлом трубных пуч-
ков.
Если рассматривать попе-
речное обтекание, жидким ме-
таллом единичной трубы, то
можно заметить существенное
различие в распределении коэф-
фициента теплоотдачи по пери-
метру трубы по сравнению с не-
металлическими жидкостями
Рис. 11.6. Распределение коэффици-
ента теплоотдачи по периметру оди-
ночной трубы, поперечно обтекаемой
воздухом (/) и жидким металлом (2).
(рис. 11.6). В случае неметаллических теплоносителей максималь-
ное значение теплоотдачи достигается на лобовой образующей
трубы (ср ™ 0). С увеличением угла ср коэффициент теплоотдачи
вначале уменьшается, а в кормовой области вследствие образова-
ния вихрей, перемешивающих поток, вновь увеличивается (кри-
вая /).
При обтекании единичной трубы жидким металлом коэффициент
теплоотдачи на лобовой образующей также имеет максимальное
значение, а с увеличением угла ср уменьшается. Однако в этом случае
вследствие высокой теплопроводности жидкого металла перемеши-
вание в кормовой области не играет решающей роли. Поэтому
коэффициент теплоотдачи монотонно уменьшается и достигает ми-
нимума при ср -= 180° (кривая 2 на рис. 11.6).
Примерно также распределяется коэффициент теплоотдачи и по
периметру труб в пучке при поперечном обтекании. Правда, в слу-
чае коридорных пучков вследствие аэродинамического затенения
впереди стоящими трубами на лобовых образующих наблюдается
некоторое снижение теплоотдачи.
В настоящее время получен значительный экспериментальный
материал по теплоотдаче при поперечном омывании жидкими ме-
таллами коридорных и шахматных пучков. На рис. 11.7, заимст-
вованном из работы [1], эти данные представлены в координатах
Nu = f (Ре). В качестве характерного размера здесь использован
311
диаметр трубы, а число Пекле вычислено по скорости набегающего
потока (в сечении, не загроможденном трубами).
Как видно из графика, опытные данные для коридорных и шах-
матных пучков с относительными шагами в поперечном направле-
нии sx/d от 1,13 до 2,41 и в продольном направлении s2/d от 0,613
Nu
я
G
4
Nu=2P8
2
6
101
8
Ф
п
I чение
о
х
м
•
6
о ,
Шахматные пучки
Рг
1,95 1,0 0,007
1,13 1,13 0,007
1,251,07 0,007
1,13 1,13 0,03
1,951,0 0,03
2,910,013 0,03
1,2 1,09 0,02
1,2 1,15 0,02
1,2 1,33 0,02
1,2 1,93 0,02
1,37 1,18 0,02
О 8 10 2 9 6 8 102 2 9 6 8 1Q3 Ре
Рис. П.7. Средний коэффициент теплоотдачи при поперечном обтекании
пучков труб жидким металлом.
Коридорные пучки
Оеозна чение S./0 Рг
1,13 1,13 0,001
1,13 1,13 0,03
1,23 1,18 0,03
1,69 1,69 0,03
1,2 1,1 0,02
1,2 1,2 0,02
1,2 1,5 0,02 $
до 1,69 в интервале чисел Ре от 10 до 1000 и чисел Рг от 0,007 до
0,02 с погрешностью ±30% описываются простой формулой, пред-
ложенной В. М. Боришанским, В. Б. Жинкиной и Э. В. Фирсовой:
Nu = 2Ре0'5. (11.11)
§ 11.5. Теплообмен при свободной конвекции
Теплообмен при свободной конвекции жидких металлов возмо-
жен в тех местах контуров, где скорости вынужденного течения
очень малы, а объем, занимаемый металлом, велик. Такие условия
могут существовать в корпусе реактора, в расширительных баках,
в холодных ловушках непроточного типа.
Интенсивность теплообмена при свободной конвекции в значи-
тельной степени определяется скоростью и характером течения жид-
кости вблизи нагреваемой (или охлаждаемой) поверхности. Движе-
ние жидкости в пристеночном слое вызывается архимедовыми
силами, возникающими вследствие изменения плотности среды в за-
висимости от температуры. Кроме архимедовых сил на гидроди-
намику пристеночного слоя, как это следует из уравнения движе-
312
пня, могут оказывать влияние также силы вязкости и силы инер-
ции.
На примере плоской вертикальной пластины рассмотрим ха-
рактерные для жидких металлов особенности свободной конвекции.
Хорошо известно, что толщина пристеночного слоя и скорость дви-
жения жидкости в нем изменяются по высоте обогреваемой поверх-
ности. Поэтому и коэффициент теплоотдачи также меняется по вы-
соте. Из анализа уравнений движения и энергии следует, что ло-
кальное число Нуссельта Nu.v = axfk должно зависеть от двух без-
размерных параметров: числа Грасгофа Grx = g|Wx3/v2 и числа
Прандтля Рг — v/a, где х — расстояние, измеряемое при нагрева-
нии от нижней, а при охлаждении от верхней кромки пластины.
Очевидно, что среднее для пластины число Нуссельта Nuz =
а/./К определяется средним числом Грасгофа Grz = gfiMl3/v2
и числом Рг, где I — высота пластины. Однако в случае жидких
металлов, для которых v (Рг < 1), из-за высокой тепло-
проводности будет прогреваться и участвовать в движении большой
слой жидкости, прилегающей к стенке. Благодаря этому градиенты
скорости в пристеночном слое должны быть невелики, и можно ожи-
дать, что силы вязкости оказывают малое влияние на теплообмен
при свободной конвекции жидких металлов. В таком случае число
Нуссельта должно зависеть только от одного критерия подобия:
Gr,Pr8 — g|iA<i3 ,
а2
в который не входит вязкость жидкости. Это предположение под-
тверждается экспериментально. Так, опытные данные по средней
теплоотдаче хорошо обобщаются зависимостью вида Nuz =
- / (GiyPr2).
Число Грасгофа пропорционально кубу характерного размера
и поэтому быстро возрастает с увеличением размеров тела. Увели-
чение числа Грасгофа приводит к увеличению архимедовой силы, и
скорость движения жидкости в пристеночном слое также увеличи-
вается. При некотором значении числа Грасгофа ламинарный ха-
рактер движения жидкости в верхней части пристеночного слоя при
нагревании жидкости (в нижней — при охлаждении) сменяется тур-
булентным. По мере увеличения числа Грасгофа турбулентный ре-
жим охватывает все большую часть пристеночного слоя, и при доста-
точно больших значениях числа Gr почти по всей поверхности тела
режим течения становится турбулентным. Исследования многих
авторов показали, что в этом отношении жидкие металлы ничем не
отличаются от других жидкостей и переход от ламинарного тече-
ния к турбулентному происходит при значениях числа Grz« 108.
Имеющиеся экспериментальные данные свидетельствуют о том,
что теплоотдача при свободной конвекции жидких металлов слабо
зависит от формы и ориентации обогреваемой поверхности. Опытные
данные, полученные на горизонтальных цилиндрах и вертикальных
313
пластинах, удовлетворительно обобщаются одними и теми же за-
висимостями 111:
при 102 < Grz <Z 108 (ламинарный режим течения)
Nuz = 0,67 (Vм ; (11.12)
\ 1+Pr / v '
при Grz Z> 108 (турбулентный режим течения)
кт n ou t Grz Pr2 \ U3
Nu, = 0,35 —-— . (11.13)
1 \ 1+Pr J V '
Следует отметить, что для жидких металлов Рг < 1 ив выраже-
ниях (11.12) и (11.13) знаменатель мало отличается от единицы.
Кроме того, при турбулентном режиме течения, согласно выра-
жению (ПЛЗ), NuzGr//3, характерный размер тела сокращает-
ся и, следовательно, коэффициент теплоотдачи вообще не зависит
от размеров тела.
СПИСОК ЛИТЕРАТУРЫ
1. Боришапский В. М. и др. Жидкометаллические теплоносители. Изд. 2-е.
М., Атомиздат, 1967.
2. Кириллов П. Л. Теплообмен жидких металлов в трубах. Докт. дис. Об-
нинск, 1968.
3. Субботин В. И., Ивановский М. И., Арнольдов М. Н. Физико-химические
основы применения жидкометаллических теплоносителей. М., Атомиздат,
1970.
4. Технические проблемы реакторов на быстрых нейтронах. Под ред.
10. Е. Багдасарова. М., Атомиздат, 1969.
ГЛАВА 12
ТЕПЛООБМЕН ПРИ КИПЕНИИ В БОЛЬШОМ ОБЪЕМЕ
§ 12.1. Основные понятия
Высокая интенсивность теплоотдачи, возможность отводить
большие тепловые потоки при малых температурных напорах прак-
тически без затрат или при сравнительно небольших затратах
механической энергии па перекачивание жидкости позволяют рас-
сматривать процесс кипения как весьма перспективный для отво-
да тепла из активной зоны энергетических ядерных реакторов.
Кипением называется процесс парообразования, характеризу-
ющийся возникновением свободных поверхностей раздела жидкой
и паровой фаз внутри жидкости, нагретой выше температуры на-
сыщения. Поскольку парообразование связано с затратой энергии,
то для поддержания стационарного режима кипения требуется не-
прерывный подвод тепла. Тепло к кипящей жидкости может под-
водиться от поверхности нагретого твердого тела или выделяться
непосредственно в объеме жидкости, как, например, в некоторых
типах гомогенных ядерных реакторов. В первом случае пузыри
пара возникают па поверхности нагрева, во втором — в объеме
самой жидкости. Под действием гравитации вследствие различной
плотности жидкой и паровой фаз в объеме жидкости возникает
свободное движение. Если при этом размеры объема, в котором за-
ключена жидкость, велики по сравнению с размерами пузырей,
отрывающихся от поверхности нагрева, то говорят о кипении
в большом объеме.
Проследим изменение режимов кипения на поверхности твер-
дого тела в условиях свободного движения. Пусть в большом объе-
ме жидкости с температурой насыщения ts находится обогреваемое
твердое тело (например, горизонтальная пластинка), на поверхно-
сти которого поддерживается температура tc > ts. Будем посте-
пенно увеличивать температуру поверхности нагрева и проследим,
как при этом изменится плотность теплового потока на этой по-
верхности c/с (рис. 12.1).
При очень малых температурных напорах О’ = t0 — ts парооб-
разования на поверхности либо вообще не происходит, либо число
пузырей столь незначительно, что в процессе переноса тепла они
не играют существенной роли. Теплообмен в этих условиях близок
к режиму свободной конвекции однофазной жидкости, поэтому
плотность теплового потока qc — tW3 (линия А А' на рис. 12.1).
315
Пузыри пара образуются в определенных точках поверхности
нагрева — центрах парообразования. Начиная с некоторого зна-
чения пЭ' = Фи.к дальнейшее увеличение температурного напора
сопровождается быстрым ростом числа действующих центров па-
рообразования, что свидетельствует о начале пузырькового режима
кипения.
Процесс генерации пара при кипении оказывает существенное
влияние на теплоотдачу. Если число действующих на поверхности
центров парообразования мало и работа их нестабильна, то на-
Рис. 12.1. Кривая кипения. Режимы теплоотдачи в условиях свобод-
ной конвекции (ДДЛ); неразвитого пузырькового (ВВ'), развитого пу-
зырькового (CD), переходного (DE) и пленочного (EF) кипения.
блюдаются неупорядоченные пульсации температуры поверхности
нагрева. Такой режим принято называть неустойчивым или нераз-
витым пузырьковым кипением. Обычно подобный режим наблю-
дается при давлениях ниже атмосферного и при малых плотностях
теплового потока (линия ВВ' на рис. 12.1). В случае достаточно
большого числа действующих центров и устойчивой их работы
наблюдаются высокие стабильные значения коэффициента тепло-
отдачи и режим кипения называется стабильным или развитым
пузырьковым кипением (линия CD). При таком режиме плотность
теплового потока возрастает приблизительно пропорционально
'д’3’3.
При больших температурных напорах начинается слияние пу-
зырьков в большие паровые образования (большие пузыри), ко-
торые затрудняют поступление жидкости к поверхности. Если про-
должать увеличивать температурный напор, то плотность теплового
316
потока, достигнув максимума, начинает быстро падать, что свиде-
тельствует о наступлении переходного режима кипения. При пере-
ходном режиме (линия DE) одиночные пузыри на поверхности
нагрева отсутствуют, жидкость, периодически попадая на поверх-
ность, «взрывообразно» вскипает. С ростом температурного напора
контакт жидкости с поверхностью становится менее продолжи-
тельным и в момент перехода к пленочному кипению (точка Е)
прекращается полностью. При пленочном кипении (линия EF)
иа поверхности нагрева образуется сплошная пленка пара. Тепло
передается от поверхности нагрева к жидкости через паровую
пленку. Этот режим кипения характеризуется низким значением
коэффициента теплоотдачи и приблизительно линейной зависи-
мостью г/с от -О’. При высоких температурах поверхности зависимость
t/c от й' становится несколько сильнее линейной, что связано с уве-
личением коэффициента теплоотдачи за счет ’возрастания доли
тепла, передаваемой от поверхности нагрева излучением.
Зависимость плотности теплового потока от температурного на-
пора, изображенная на рис. 12.1, тесно связана со спецификой
каждого режима. Кривая qG — f (ф), фиксирующая эту связь, на-
зывается кривой кипения. На ней отчетливо видны границы су-
ществования различных режимов. Так, границей между пузырь-
ковым и переходным режимами является точка максимума на кри-
вой кипения (точка D), границей между переходным и пленочным
кипением — точка минимума (точка Е). Максимальная и минималь-
ная плотности теплового потока, соответствующие этим точкам,
называются первой ф/крг) и второй (71!р2) критическими тепловыми
нагрузками или критическими плотностями теплового потока.
Последовательность смены режимов и характер кривой кипения
в целом аналогичны для подавляющего числа веществ; однако плот-
ность теплового потока (при фиксированных значениях й) зависит
от физических свойств жидкости и поверхности нагрева. Для каж-
дой пары жидкость — поверхность нагрева кривая кипения будет
меняться в зависимости от давления насыщения.
Воспользуемся кривой кипения, чтобы обсудить вопрос о влия-
нии граничных условий на устойчивость кипения. Обычно для
реализации граничного условия первого рода, используется обогрев
стопки теплоносителем, имеющим постоянную температуру. Если
термическое сопротивление стенки мало, а коэффициент теплоотда-
чи от теплоносителя к стенке велик, то можно считать, что темпе-
ратура стенки со стороны кипящей жидкости приблизительно равна
температуре теплоносителя. Постепенно меняя температуру стенки
посредством изменения температуры теплоносителя, можно вос-
произвести всю кривую кипения. В этом случае кипение будет
устойчивым в любой точке кривой кипения, включая и переходную
область.
В случае граничного условия второго рода на поверхности
стеики со стороны кипящей жидкости задается плотность теплово-
го потока qG. Обогрев стенки происходит за счет действия внутрен-
317
них источников тепла, заключенных в самой стенке (например,
твэлы ядерных реакторов), или за счет теплового излучения.
Постепенно увеличивая qQ, можно получить левую ветвь кривой
кипения (линия ABCD на рис. 12.1). Поскольку при пузырьковом
кипении r/с не может превысить 7кр1, то, как только будет достиг-
нута точка D, соответствующая первому кризису, дальнейшее не-
значительное увеличение тепловой нагрузки вызовет снижение
интенсивности теплоотдачи и быстрый рост температуры стенки.
В результате произойдет переход в направлении ДР на правую ветвь
кривой кипения в точку (F), т. е. режим кипения станет пленочным.
Снижая тепловую нагрузку, можно получить правую ветвь кривой
кипения (линия ЕР). Однако как только qG снизится до значения
<7кр2> произойдет переход от пленочного режима кипения к пу-
зырьковому (в направлении EG), потому что пленочное кипение
не может существовать при значениях qc <Z qKTl2. Из сказанного
видно, что при граничных условиях второго рода переходный ре-
жим кипения не реализуется.
В связи с тем что переход к пленочному режиму кипения
сопровождается значительным снижением коэффициента теплоот-
дачи и соответствующим ростом температуры стенки, возможно
расплавление твэла и выход его из строя. Поэтому для практи-
ческих целей очень важно наряду с коэффициентом теплоотдачи
знать точное значение первой критической тепловой нагрузки.
§ 12.2. Механизм парообразования при пузырьковом кипении
1. Перенос тепла при пузырьковом кипении. В переносе тепла от
поверхности нагрева участвуют как паровая, так и жидкая фазы.
Поэтому плотность теплового потока на стенке можно представить
в виде суммы
7с ' 7коп> (12.1)
где 7„ и 7К0П — плотности теплового потока, обусловленные пере-
носом тепла паром и конвекцией однофазной жидкости.
Пар, находящийся в пузырьках, имеет температуру, близкую
к температуре насыщения, поэтому каждый пузырек представляет
собой своеобразный тепловой сток — он интенсивно отводит тепло
от окружающей его перегретой жидкости. Достигнув определенно-
го размера, пузырек пара отрывается от стенки и уносится в объем
жидкости. Плотность теплового потока, обусловленного переносом
тепла паром, можно выразить через осредненные во времени вели-
чины:
7Г1 == vp"Nfr. (12.2)
Здесь v — средний объем пузырька в момент отрыва от поверх-
ности нагрева; р" — плотность пара; W — число действующих
центров парообразования на единице поверхности нагрева; f —
318
средняя частота отрыва пузырьков, \!сек\ г — теплота парооб-
разования, дж!кг.
При малых значениях qc, когда число пузырьков, образующихся
на поверхности, невелико, перенос тепла осуществляется в основ-
ном за счет конвекции жидкой фазы. С ростом тепловой нагрузки
число пузырьков, образующихся на поверхности, увеличивается.
Соответственно увеличивается и доля тепла, переносимая паром.
Это хорошо видно на рис. 12.2, где изображена зависимость
qjqc от 7с при кипении воды в большом объеме (р = 1 бару При
плотности потока, близкой к критической (Qnplлз 10° вт/я?),
Рис. 12.2. Доля теплового потока, переносимая па-
ром z/n [24].
составляющая qu становится основной. Из сказанного следует, что
для понимания закономерностей теплообмена при кипении необ-
ходимо знать внутренние характеристики механизма кипения:
скорость роста, частоту образования и размеры пузырьков, а также
число действующих на поверхности центров парообразования.
2. Возникновение паровой фазы. При кипении слой жидкости,
соприкасающийся с поверхностью нагрева, значительно перегрет,
> is- Жидкость, нагретая выше температуры насыщения, на-
ходится в неустойчивом (метастабилыюм) состоянии. Однако не-
устойчивость данной фазы может проявиться только при наличии кон-
такта с конкурирующей фазой. Например, перегретая жидкая фаза
может существовать длительное время, если она не соприкасается
с паровой. Поэтому переход перегретой жидкости в пар становится
возможным только после возникновения зародышей новой фазы —
пузырьков пара.
Образование в перегретой жидкости пузырьков пара сопровож-
дается изменением полного термодинамического потенциала:
Дф = (ф" — ф') М" -|- 4л/?2о-, (12.3>
319
где ср и ср" — химические потенциалы жидкости и пара; М" =
(4/3) лЛ3р" — масса пара в пузырьке; R — радиус пузырь-
ка; 4ат7^3сг — работа, затраченная на образование поверхности
раздела фаз; ст — коэффициент поверхностного натяжения.
Радиус пузырька, находящегося в равновесии с окружающей
жидкостью, называется критическим и обозначается 7?кр. Посколь-
ку пузырек пара радиусом /?кр находится в равновесии, то термо-
динамический потенциал должен иметь экстремум. Взяв производ-
Рис. 12.3. Зависимость прираще-
ния термодинамического потенциа-
ла от радиуса пузырька и темпе-
ратуры жидкости. Стрелками
обозначены: *— — конденсация и
н---неограниченный рост пу-
зырька.
ную от ДФ по R и приравняв ее
нулю, получим
> (12.4)
Кир Р
Подставив (12.4) в (12.3), найдем
ДФ = 4п/?2су j' 1-• (12.5)
Нетрудно убедиться, что выраже-
ние (12.5) имеет максимум для
пузырька с критическим радиусом
— U2-6)
3
Связь приращения термодинами-
ческого потенциала и радиуса пу-
зырька показана на рис. 12.3 для трех значений температуры жид-
кости. /ж и /}К = причем С <б
Поскольку система стремится к уменьшению термодинамического
потенциала, то пузырьки в зависимости от своего размера будут:
конденсироваться (jR -> 0 при R < jRKp), неограниченно расти
(jR —оо при R > 7?кр) или находиться в состоянии неустойчивого
равновесия (при R = Лкр)- Приращение термодинамического по-
тенциала, необходимое для образования в перегретой жидкости
пузырька критического размера, называют потенциальным барье-
ром (ДФмакс), преодолев который, система начинает переход из
метастабильного состояния в стабильное.
Если система жидкость — пузырек пара радиусом Лкр нахо-
дится в равновесии, то температуры жидкости и пара будут одина-
ковы, а давление в пузырьке р" выше, чем давление в окружающей
его жидкости р'. Избыточное давление в пузырьке связано с нали-
чием силы поверхностного натяжения <з и определяется по форму-
ле Лапласа
р"-р' = ^-. (12.7)
А’кр
Чтобы определить критический радиус, воспользуемся уравне-
нием Клапейрона—Клаузиуса. Связь между параметрами системы
пар—жидкость, находящейся в равновесии, в случае неодинаково-
320
го давления фаз, будет следующей:
^^-Т^р’-р'. (12.8)
1 S
Здесь Г,к и Ts — абсолютные температуры жидкой и паровой
фаз; р" — р' — избыточное давление в пузырьке. Подставив зна-
чение р" — р' в уравнение (12.7), получим условия равновесия
пузырька в перегретой жидкости:
где А/ = Тт — Ts — перегрев жидкости.
Из формулы (12.9) следует, что с ростом перегрева жидкости
вскипание облегчается, так как уменьшается критический радиус,
а следовательно [см. формулу (12.6)], уменьшается и величина
потенциального барьера. Например, для воды при атмосферном дав-
лении и температуре 300° С критический радиус составляет всего
1,5 • 10~8 см. Пузырьки пара столь малого размера могут возни-
кать в объеме жидкости в результате флуктуаций плотности, свя-
занных с тепловым движением молекул. Для оценки возможности
вскипания перегретой жидкости вводится понятие частоты образо-
вания зародышей J (т. е. число зародышей, образующихся в 1 см3
в 1 сек). Фольмером для частоты образования зародышей пара в ре-
зультате флуктуаций плотности в перегретой жидкости получено
уравнение
J = N]/ -',7 м е*р ехр (- Афма1|с//гг), (12.10)
F л/прь—о)
где ./V — число молекул жидкости в 1 см3\ b = 1 — р'/р"; m —
масса молекулы; I — теплота парообразования в пересчете на одну
молекулу; /г — постоянная Больцмана.
Принимается, что необходимый перегрев для вскипания будет
достигнут при J 1. Как следует из формулы Фольмера, частота
образования зародышей увеличивается с ростом числа частиц А/,
температуры системы Т и уменьшается с увеличением теплоты па-
рообразования и потенциального барьера ДФмаК0.
Расчеты по этой формуле показывают, что вероятность обра-
зования зародышей при малых перегревах жидкости ничтожна
« 0), ио начиная с определенных значений перегревов J воз-
растает настолько, что происходит самопроизвольное вскипание и
дальнейший перегрев становится невозможным. На рис. 12.4
•приведены результаты измерений предельного достижимого перегре-
ва, выполненные В. П. Скриповым. Видно, что при атмосферном дав-
лении температура самопроизвольного вскипания воды составляет
~300°С. Поскольку при поверхностном пузырьковом кипении*
* Пузырьковое кипение называется поверхностным, если пузырьки
пара возникают на поверхности нагрева.
11 Зак. 792 321
воды перегрев жидкости у стенки не превосходит 25—30° С, то от-
сюда ясно, что в этих условиях образование пузырьков в объеме
жидкости практически исключено.
Величина перегрева, необходимого для вскипания, существен-
ным образом зависит от свойств поверхности нагрева. Рассмотрим
взаимодействие жидкости с твердой поверхностью. Прочность связи
(адгезия) между поверхностными слоями двух разнородных тел
Рис. 12.4. Температура
предельного перегрева
воды [15]:
1 расчет по формуле
Фольмера; 2 — температу-
ра насыщения; точки —
опытные данные.
характеризуется работой, которую необ-
ходимо затратить, чтобы разъединить со-
прикасающиеся поверхности. В случае от-
рыва жидкости от твердого тела простран-
ство между образующимися поверхностя-
ми твердого тела и жидкости заполняет газ.
Работу адгезии, отнесенную к единице по-
верхности раздела, выражают с помощью
коэффициентов поверхностного натяжения:
1^А ' ' О'Т1Г —I- ®"ж-г ^т./К‘ (12.11)
Коэффициенты поверхностного натяжения
представляют собой работу, затрачивае-
мую на образование единицы площади по-
верхности раздела двух разнородных тел:
твердого тела и газа от.г, жидкости и
газа ож.г и твердого тела и жидкости от.?к.
Коэффициенты от-г и от.и{ нельзя опреде-
лить экспериментально, но соотношение
между от.г, ож г и от<ж можно установить из условия равенства
сил, действующих вдоль поверхности твердого тела (рис. 12.5):
ож.г COS 0,
(12.12)
где 0 — краевой угол. Краевым углом или углом смачивания на-
зывается угол, образованный плоской поверхностью твердого те-
ла и плоскостью, касательной к поверхности жидкости, грани-
чащей с телом
Подставив (12.12) в (12.11), для работы адгезии получим выра-
жение
WA = аж.г (1 + cos 0).
(12.13)
°т.г °т.ж
Если 0-> 180°, то жидкость не смачивает поверхность и ->0;
если 0 -> 0, то ТГд -> 2ож.г, т. е. работа, необходимая для отделе-
ния жидкости от поверхности твердого тела, практически соответ-
ствует разрыву жидкости. Обычно краевой угол лежит в пределах
0 < 0 < 90°.
Работа, необходимая для образования поверхности пузырька,,
растущего на твердой стенке, равна
Ц7 ^К.П^Ж.П “Ь (^т-п
(12.14)
322
где F?K>n и FT<n—поверхности контакта жидкости и стенки с па-
ровой фазой (рис. 12.6, а)-, индекс «г» (газ) заменен индексом «п»
(пар).
Рис. 12.5. Силы, действующие на липни кон-
такта трех фаз.
Воспользовавшись формулой (12.12),
(12.14):
перепишем уравнение
w = <НД„.„ + fT.„cos0). (12.15)
Рис. 12.6. Возникновение зародышей паровой фазы па
плоской поверхности (а) и в углублениях стенки (б).
Так как при любом краевом угле 0 < 0 < 180° (см, рис. 12.6, а)
о (^к.п Н" Л'.п cos ®) < сг4<гт/?2, то работа, необходимая для об-
разования пузырька на твердой плоской поверхности, меньше, чем
для образования пузырька в жидкости. Чем больше 0, тем меньшую
работу должна совершить система для образования зародыша и тем
меньший требуется перегрев жидкости. Необходимый перегрев
11* 323
существенно снижается, если зародыш образуется не на плоской
поверхности, а в углублении (см. рис. 12.6, б). В достаточно уз-
ких трещинах, поверхность которых плохо смачивается жидкостью
(0 & 90°), может быть столь мала, что образование зародышей
пара становится возможным сразу же после достижения температу-
ры насыщения. Поэтому центрами парообразования, как правило,,
служат углубления в обогреваемой стенке — различные трещины и
царапины. Образование пузырьков в микроуглублениях сущест-
венно облегчается тем, что после отрыва от поверхности нагрева
очередного пузырька в углублении остается небольшое количество-
пара.
Рис. 12.7. Поверхность раздела фаз в осесимметричных углубле-
ниях:
а —центр парообразования с плохо смачиваемым участком поверхности
АОВ; б — углубление «резервуарного» типа.
Устойчивость работы центров парообразования повышается,,
если внутри углубления имеются участки с плохой смачиваемостью'
(загрязнения поверхности) или микротрещина расширяется к ос-
нованию (впадина резервуарного типа). Кривизна мениска внутри
таких углублений будет отрицательной, т. е. мениск обращен вы-
пуклостью в сторону пара, как это видно из рис. 12.7. В соответ-
ствии с формулой (12.9) равновесие пара и жидкости в этом случае
возможно при температурах, меньших ta. Паровая фаза в таких
углублениях будет сохраняться и в том случае, если в результате
временного отключения обогрева температура жидкости станет
ниже ts. После включения обогрева кипение начнется по дости-
жении определенного перегрева, который необходим для выхода
пузырей из впадин. Как видно из рис. 12.7, б, минимальное поло-
жительное значение радиуса кривизны 7?мии близко к характерно-
му размеру впадины 7?у— радиусу устья. В условиях поверх-
ностного кипения можно принять, что температура жидкости в уг-
лублении равна температуре стенки. Тогда перегрев, необходимый
324
для начала кипения •& = tQ — ta, определяется согласно формуле.
(12.9) условием
2aTs
(12.16)
Из этого условия также следует, что с ростом температуры стенки
более мелкие впадины будут включаться в число действующих
центров парообразования. Следовательно, число действующих
центров с ростом температуры стенки увеличивается.
3. Скорость роста пузырьков. Пусть пузырек пара находится в
неограниченном объеме неподвижной перегретой жидкости; если его
радиус превышает критическое значение, то пузырек растет. Рост
пузырька происходит под действием разности давлений пара в пу-
зырьке р" и в окружающей его жидкости р'. Избыточное давление
пара в пузырьке должно преодолеть противодействие сил: поверх-
ностного натяжения 2сг/7^, инерции жидкости р'^(с/27?/б/т2) -|-
-|- (3/2)р' (d^/dr)2 и трения жидкости иа стенке пузырька
4(р'/l^dlR/dx;. Рост пузырька сопровождается испарением жидкости
с его поверхности. Тепло, необходимое для испарения, подводится
теплопроводностью к поверхности пузырька из окружающей его
перегретой жидкости. Следовательно, скорость роста зависит йот
плотности теплового потока на поверхности пузырька. Необходимо
учесть, что интенсивное испарение жидкости, согласно представле-
ниям молекулярной физики, возможно в том случае, если на
границе жидкости и пара существует некоторый скачок темпера-
туры. Этот скачок обычно очень мал, но его следует учитывать при
низких давлениях. Приняв во внимание все сказанное, можно
получить уравнение для скорости роста пузырька [7], описывающее
изменение радиуса пузырька во времени. Это уравнение имеет
следующий вид:
dx (гр")2 (/?3-/?;!р)
R dx
— 2—[3 dR
(12.17)
Здесь — температура жидкости вдали от пузырька, °К; Т8 —
температура насыщения при давлении р', °К; "О' = Т'^ — Ts —
перегрев жидкости; R — газовая постоянная; |3 — коэффициент
конденсации (испарения), равный отношению числа молекул пара,
захватываемых конденсированной фазой, к общему числу молекул
пара, достигающих ее поверхности; физические свойства жид-
кости и пара взяты иа линии насыщения.
Слагаемые в квадратных скобках уравнения (12.17) отражают
соответственно влияние иа скорость роста сил поверхностного
натяжения, инерции жидкости, трения на поверхности пузыря и
неравновесности процесса испарения. По мере охлаждения слоя
жидкости, окружающего пузырек, скорость роста понижается.
Уменьшение скорости роста и увеличение радиуса пузырька приве-
дут к тому, что довольно быстро наступит момент, когда величина
всех членов, заключенных в уравнении (12.7) в квадратные скобки,
окажется пренебрежимо малой. Скорость роста в этом случае це-
ликом определяется условиями подвода тепла. Температура пара
в пузырьке будет при этом асимптотически стремиться к темпера-
туре насыщения. При кипении жидкости асимптотическая стадия
Рис. 12.8. Подвод тепла к растущему пузырю по всей поверхности пузы-
ря (а), через слой жидкости в основании (б) и через микрослой (в).
роста наиболее продолжительная, и именно на ее долю приходится
основное увеличение объема пузырька. Из уравнения (12.17) для
асимптотической стадии роста, если принять R > ^кр и пренеб-
речь скачком температуры на границе раздела фаз, нетрудно полу-
чить выражение
/?==25а]/от, (12.18)
где Ja = р/г) —< число Якоба; а = %7(р'Ср).
Уравнения (12.17) и (12.18) получены для случая, когда пузы-
рек пара растет в неограниченном объеме перегретой жидкости.
При кипении на твердой поверхности задача усложняется, так как
пузырек пара находится в пограничном слое жидкости, имеющем
переменную по толщине температуру. В зависимости от распреде-
ления температуры по толщине пограничного слоя подвод тепла
к пузырьку, а следовательно, и испарение жидкости в пузырек
могут происходить или по всей поверхности, или через испаря-
ющийся клиновидный слой жидкости (рис. 12.8, а, б).
Форма пузырька, растущего на твердой поверхности, зависит
от соотношения между силами поверхностного натяжения, инерции
и вязкости. В случае преобладания силы поверхностного натяжения
пузырек имеет сферическую форму. Если скорости роста велики
(кипение под вакуумом), то преобладают инерционные силы, рост
пузырька происходит взрывообразно, и его форма напоминает полу-
сферу (рис. 12.8, в). Как показывает киносъемка, значительная
часть полусферического пузыря отделена от стенки тончайшим
326
слоем жидкости — микрослоем и только в центре имеется неболь-
шое «сухое пятно». Во время роста пузырька микрослой интенсив-
но испаряется. Суммарная площадь проекции всех пузырьков при
атмосферном давлении и нагрузках, близких к критическим, по-
крывает почти 100% поверхности нагрева. Общая же площадь сухих
пятен не превышает 10%, т. е. на долю микрослоя приходится почти
90% поверхности.
Рис. 12.9. Зависимость отношения R/ "]/ ах от числа Якоба [20]:
/•—расчет по формуле (12.18); 2 — расчет по формуле (12.19).
Радиус пузырька согласно (12.18) увеличивается пропорцио-
нально ]/ ах. Поэтому рост пузырька удобно анализировать в коор-
динатах Riyах — Ja. Если форма пузырька отличается от сфери-
ческой, то в качестве его радиуса принимается радиус сферы рав-
ного объема. Как видно на рис. 12.9, опытные данные, характери-
зующие изменение радиуса пузырька во времени, хорошо описы-
ваются эмпирическим соотношением
-^=vJa+i vB.Ja2 +12 Ja, (12.19)
у ах
где у = sin2 0 1(1 cos О)2 (2 — cos О)]-1, и существенно откло-
няются от зависимости (12.18).
4. Отрывные диаметры пузырьков. Пузырек пара, находящий-
ся на твердой поверхности, испытывает действие подъемной силы
V (р' — р") g и удерживающей его силы поверхностного натяже-
ния oSsin О (S — периметр контакта пузырька с твердой поверх-
327
ностью). Из баланса сил можно определить объем или диаметр рас-
тущего на стенке пузырька, при котором нарушается равновесие
и происходит его отрыв. Из этих соображений В. Фритц получил
формулу для диаметра пузырька в момент отрыва:
Dq —
ст
£(Р'—Р")
(12.20)
Рис. 12.10. Распределение раз-
меров отрывных диаметров пу-
зырей при кипении воды,
р=1 бар [18].
Здесь 0 — краевой угол, град.
При развитом пузырьковом кипении пузырьки, растущие иа
поверхности нагрева, испытывают воздействие большого числа
трудноподдающихся учету факторов.
Таких, например, как пульсации тем-
пературы стеики и конвективные токи
жидкости, возникающие при работе
соседних центров парообразования.
Оказывают влияние на процесс роста
и небольшие отклонения в режиме
работы установки. Это приводит к
тому, что отрывные диаметры пузырь-
ков, образовавшихся даже на одном
и том же центре, оказываются неоди-
наковыми. На рис. 12.10 показано
найденное в опытах распределение
пузырьков по отрывным диаметрам
при кипении воды. Видно, что рас-
пределение близко к нормальному.
При выводе формулы (12.20)
не учитывались силы инерции жид-
вычисленные по формуле Фритца,
кости. Отрывные диаметры,
близки к средним измеренным значениям только при давлениях,
близких к атмосферному. При давлениях ниже атмосферного
формула (12.20) дает существенно заниженные значения Do, а при
высоких давлениях — завышенные. В случае кипения воды при
давлении в интервале 1—100 бар отрывной диаметр обратно про-
порционален давлению [22]:
Do ~ ~р~
(12.21)
Здесь Dop и Do — отрывные диаметры пузырьков при давлении р
и атмосферном давлении р0.
5. Частота отрыва пузырьков. Если просмотреть снятую на кино-
ленту работу одного центра парообразования, то можно заметить,
что пузырьки отрываются от поверхности нагрева через относитель-
но равные промежутки времени. Рост пузыря на стенке сопровож-
дается понижением температуры окружающей его жидкости. После
отрыва пузырька и до появления на поверхности следующего необ-
ходимо некоторое время, в течение которого происходит прогрев
328
пристеночного слоя жидкости. Это время называется временем
ожидания т(). Промежуток времени с момента появления на по-
верхности видимого пузырька и до момента его отрыва называется
временем роста тр. Таким образом, частота отрыва пузырьков
гО + Тр
При малой плотности теплового потока время ожидания и время
роста пузырька примерно одинаковы. С увеличением плотности
теплового потока время ожидания падает почти до нуля и при до-
статочно интенсивном кипении можно считать, что частота отрыва
определяется только временем роста пузырька, т. е. f = х.
При исследовании процесса кипения иногда пользуются произ-
ведением fD(), которое имеет размерность скорости и по существу
может рассматриваться как средняя скорость роста пузырька. Было
отмечено, что средняя скорость роста пузырька остается постоян-
ной в довольно широком диапазоне тепловых нагрузок. С ростом
давления, по данным В. И. Толубииского и др. [19], средняя ско-
рость роста пузырька уменьшается и может быть описана прибли-
женным эмпирическим уравнением
(/Do)z, /_P1V,3+O,51grt
(/Do)p0 \ Р/> '
(12.22)
Здесь индексы рО и р означают, что символы относятся к атмосфер-
ному и искомому давлениям; л = p0/pHp; Ркр — критическое дав-
ление для данного вещества.
Формула (12.22) получена в результате обработки опытных дан-
ных для воды [(РоК 0.155 м/сек], этанола (0,119), метанола
(0,124), бензола (0,1), бутанола (0,111), фреона-12 (0,064) и спра-
ведлива для давлений от'атмосферного до близкого к критическому.
6. Число действующих центров парообразования. С ростом темпе-
ратуры стенки число действующих центров увеличивается за счет
включения все более мелких впадин. Измерения Якоба при кипе-
нии воды в области низких плотностей теплового потока (qc
< 50000 вт/м*) показывают, что число действующих центров воз-
растает примерно пропорционально плотности теплового потока.
При высоких плотностях теплового потока эта зависимость изме-
няется. Так, по данным Р. Гартнера и Д. Вествотера [8], получен-
ным при кипении водного раствора никелевой соли в интервале
от 0,5 до 1,0, число центров на единицу поверхности нагрева
с ростом плотности теплового потока изменяется следующим
образом:
;V-7c2*12. (12.23)
329
§ 12.3. Теплоотдача при кипении
1. Обобщенные зависимости для коэффициента теплоотдачи при
пузырьковом кипении. В силу сложности и малой изученности ме-
ханизма переноса тепла при пузырьковом кипении практические
расчеты теплоотдачи базируются на экспериментальных данных,
обработанных в соответствии с методами подобия и размерностей.
Использование этих методов осложняется тем, что задача пока не
имеет достаточно строгой математической формулировки. Тем не
менее с помощью теории подобия и размерностей удается получить
полезные соотношения.
Работы по обобщению опытных данных по теплоотдаче были
проведены многими авторами: Н. Г. Кружилиным, С. С. Кута-
теладзе, В. И. Толубинским, В. М. Боришанским, Д. А. Лабунцо-
вым и др. В этих работах с помощью методов подобия или размер-
ностей анализировалась система уравнений, включающая уравнения
энергии, движения, неразрывности для жидкой, а иногда и паровой
фаз, уравнения роста и движения пузырька, термодинамические
уравнения (Клапейрона—Клаузиуса, Клапейрона—Менделеева);
учитывались также условия на границе раздела фаз и на поверх-
ности нагрева. В процессе анализа иногда привлекались те или иные
физические соображения, основанные на экспериментальных фак-
тах. Поскольку не существует четкой математической формули-
ровки задачи, то системы уравнений и граничные условия у разных
авторов несколько различаются. Поэтому отличаются и системы
безразмерных чисел, полученных разными авторами. Можно ука-
зать следующие, чаще всего используемые безразмерные числа:
Рг- — ; =
V а' rp"v' (12.24)
К = —==£2^=-; £ =
Уа(р'—р")£ I*
Здесь в качестве характерных линейных размеров приняты следу-
ющие:
величина, пропорциональная отрывному диаметру пузырька
(постоянная Лапласа):
<12-25>
и величина, имеющая размерность длины:
I — с'р р' aTs
* (ф")3
(12.26)
С помощью безразмерных чисел (12.24) проведена обработка
большого числа опытных данных, полученных при кипении воды,
а также некоторых органических жидкостей. Обобщенная зависи-
мость Н. Г. Кружилина [табл. 12.1, уравнение (12.27)] удовлетво-
эзо
Таблица 12.1
Автор У равнение
Е. К. Аверин, Н. Г. Кружил ин [1] ^=о,о82(^ДУ'’р1Г'7АГ а” X \ гр v / \ a ' J \ 1* / (12.27)
С. С. Кутателадзе [10] ^=8,7.10- X \гр V / / -у' \ 0 , 3 6 / п \ 0 , "< XI , I (12.28) \а' ) \ З/сЦр —Р )g )
В. И. Толубииский [19] а/0 „ qc \ ° •7 / v' \“0’2 v -75 П<шп х , ’ (12-29) X' \гр (/£>оЫ \« 1 где (/£)0)р определяется по (12.22)
В. М. Боришаискип и ДР- И] /JKP ( р мм а =405 : г X Мкр / г . 0X1,161 X 1+4,64 М— <7q/3, (12.30) L \ Ркр / J где р и рПр — измеряются в барах, Ткр—-в °К, qG — в 6/п/лс2
Д. А. Лабунцов [11] ДДДГДУ. 1П-Ч fl L Г* £PyL\ /10ОП *10 (1+б го ) (12-31)
рительно согласуется с опытными данными, полученными при
кипении воды, бензола, н-пентана, гептана при давлениях
р<0,3 ркр и дает заниженные значения а при более высоких
давлениях.
Уравнение С. С. Кутателадзе (12.28) (для этих же веществ)
удовлетворительно отражает зависимость коэффициента теплоот-
дачи от давления. Отклонение рассчитанных значений а от опыт-
ных точек не превосходит 30—40% [4].
При построении некоторых обобщенных эмпирических зависи-
мостей используются отдельные характеристики механизма пузырь-
кового кипения. В качестве примера рассмотрим соображения, ле-
жащие в основе зависимости, предложенной В. И. Толубинским
[19]. Воспользовавшись уравнениями (12.1) и (12.2), получим
= + W4 (12.32)
О
где е — поправка, учитывающая долю тепла, переносимого конвек-
тивными токами жидкости. Соотношение (12.32) перепишем в виде
331
Левую часть равенства можно рассматривать как отношение средней
скорости парообразования (qjrp" [W«?k]) к средней скорости роста
пузырька ND о -—величина, пропорциональная поверхно-
сти, занятой пузырьками, отрывающимися с действующих центров
парообразования. Безразмерное число в левой части уравнения
(12.33) пропорционально числу действующих центров парообразо-
вания. Так как последнее оказывает решающее влияние на теплоот-
дачу, то предполагается, что комплекс qc (rp,'fD0)~1 является од-
ним из определяющих критериев. В качестве второго определя-
ющего критерия используется число Прандтля. Обработав опыт-
ные данные по теплоотдаче для воды, спиртов, фреона-12,
В. И. Толубинский получил обобщенную зависимость (12.29).
Уравнение (12.29) удовлетворительно согласуется с опытом,
однако им можно пользоваться, если для данного вещества извест-
но значение (fD^p или опытным путем подтверждена справедливость
зависимости (12.22). Для криогенных жидкостей систематические
данные по (fD0)p отсутствуют. Для этих жидкостей В. И. Толубин-
ский в интервале давлений 0,01 < р/ркр < 0,4 рекомендует при-
ближенное соотношение
{fD„)p = 3,6-10-‘ -М
\ Ркр /
Существует и другой подход, основанный на эксперименталь-
ном факте: коэффициент теплоотдачи зависит от тепловой нагруз-
ки и физических свойств жидкости и может быть представлен в виде
произведения степенных функций
(12.34)
где xlf хг, ...—физические свойства, существенные для тепло-
обмена при кипении; А, п, пъ п2, ... -—постоянные, определяемые
по опытным данным. Предполагается, что изменения любого физи-
ческого свойства данного вещества вдоль линии насыщения мож-
но выразить в виде произведения двух функций: одна из них срг
отражает специфику вещества, а другая фг — изменение рассмат-
риваемого свойства хг- в зависимости от давления:
хг- = (М, Ткр, ркр) f —'j i = 1,2, ....
\ Ркр /
где ркр, Ткр — критические давление и температура вещества,
М — его молекулярный вес.
Уравнение (12.34) можно представить в виде
а = МФ(Л4, T^p^W-M , (12.35)
\ Ркр /
где Ф = ср"1 ср"«...;
Для термодинамически подобных веществ функции срг, как и фг,
одинаковы. Следовательно, одинаковыми будут и функции Ф и
332
Согласно (12.35), коэффициент теплоотдачи можно описать как
функцию qc, М, Ткр, ркр и отношения р/рнр. В. М. Боришанский
с помощью этих величин подобрал по экспериментальным данным
зависимость для коэффициента теплоотдачи. Оказалось, что для
ряда жидкостей (воды, спиртов, аммиака, фреона-12, гептана, пен-
тана, бензола), которые в строгом смысле не являются термодина-
мически подобными, коэффициент теплоотдачи с удовлетво-
рительной точностью описывается единой зависимостью (12.30).
При выводе обобщенной зависимости (12.31) было учтено, что
тепло от стенки частично идет на испарение жидкости в пузырьки,
Рис. 12.11. Изменение коэффициента теплоотдачи с давлением
при пузырьковом кипении воды по данным работ [4, 9].
растущие на стейке, частично передается в объем жидкости тепло-
проводностью через пристеночный перегретый слой. Было принято
также, что число действующих центров парообразования пропор-
ционально j/ tc — ls, рост пузырька происходит в результате под-
вода тепла к его основанию. Количественная оценка отмеченных
эффектов позволила получить численные значения постоянных
в уравнении (12.31). Формула Д. А. Лабунцова может быть исполь-
зована для расчета коэффициента теплоотдачи при кипении воды,
бензола, гептана, кислорода.
Согласно рассмотренным эмпирическим уравнениям, коэф-
фициент теплоотдачи при пузырьковом кипении зависит от теп-
ловой нагрузки (причем а ~ qn, где п « 0,7) и физических свойств
жидкости и пара на кривой насыщения. Так как последние в
свою очередь зависят от давления, то и коэффициент теплоотдачи
меняется с изменением давления. Как видно из рис. 12.11, на
котором приведены опытные данные для воды, а растет с уве-
личением давления тем сильнее, чем больше р. В области
низких давлений а ~ р'1, где п = 0,15-4-0,20.
Важной характеристикой процесса кипения является угол
смачивания жидкостью поверхности нагрева. Однако его влияние
333
изучено пока недостаточно. Можно считать, что изменение крае-
вого угла в пределах 10—45° не оказывает существенного влияния
на теплоотдачу.
Коэффициент теплоотдачи при кипении зависит от шероховато-
сти (способа обработки) поверхности нагрева. Приведенные на
рис. 12.12 данные свидетельствуют о том, что более высокому клас-
су чистоты обработки поверхности соответствуют более высокие
температурные напоры (при одних и тех же значениях <?с). Объяс-
няется это тем, что на шерохова-
той поверхности больше крупных
царапин и углублений, поэтому
работа центров парообразования
возможна при меньших перегре-
вах стенки [21].
Коэффициент теплоотдачи мо-
жет изменяться во времени. Это
особенно заметно в случае кипе-
ния на новой, неработавшей по-
верхности. Обычно в начальный
период работы а несколько умень-
шается, а затем принимает ста-
бильное значение. Связано это с
постепенным удалением адсорби-
рованных поверхностью нагрева
Рис. 12.12. Влияние шероховато-
сти поверхности на кривую кипе-
ния при обработке медной по-
верхности грубой наждачной
шкуркой (/), мелкой наждачной
шкуркой (2), шлифовкой (3)
и полировкой (4).
газов, некоторым окислением ме-
таллической поверхности, отло-
жением на поверхности нагрева
накипи или продуктов разложения
рабочего вещества. В результате
появления окисных пленок на
поверхности нагрева и различ-
ных отложений влияние первона-
чальной обработки поверхности нагрева и теплофизических свойств
материала стенки на теплоотдачу становится несущественным.
При эксплуатации тепловых и атомных электростанций прини-
маются меры по очистке питательной воды и ведется достаточно
строгий контроль за состоянием поверхностей нагрева. Поэтому
наблюдаемый на практике разброс значений коэффициента тепло-
отдачи в стабильных условиях обычно не превосходит 20—30%.
2. Теплоотдача при кипении щелочных металлов. Интерес к во-
просам теплообмена при кипении щелочных металлов вызван пер-
спективой их использования в качестве теплоносителей в ядерных
реакторах на быстрых нейтронах, в космических энергетических
установках и жидкометаллических МГД-генераторах.
Вследствие высокой температуры насыщения кипящие щелоч-
ные металлы используются в технических устройствах при давле-
ниях, близких к атмосферному или ниже. При давлениях ниже
атмосферного вследствие больших значений 7?кр обычно наблю-
334
дается неустойчивый режим кипения, для которого характерны
сравнительно небольшое число действующих центров парообра-
зования и нестабильность их работы. Для возникновения кипения
при низких давлениях обычно требуются значительные перегревы
поверхности. Эти особенности кипения при низких давлениях
в случае щелочных металлов усугубляются их высокой теплопро-
водностью. Действительно, жидкость в объеме интенсивно переме-
шивается мощными конвективными токами. Более холодная жи-
дкость, находящаяся в объеме при температуре, близкой к темпера-
туре насыщения, периодически попадает на стенку. Поскольку
коэффициенты теплопроводности жидкого металла и стенки прибли-
зительно одинаковы, то происходит резкое понижение температуры
поверхности нагрева, что вызывает отключение действующих
центров парообразования. Вследствие прекращения кипения
ухудшается теплоотдача, возрастает температура стенки и присте-
ночного слоя жидкости. Спустя некоторое время отключившиеся
центры восстанавливают свою деятельность. Поскольку жидкость
перегрета, то вскипание происходит весьма бурно, сопровождает-
ся гидравлическими ударами и значительным шумом. Температура
поверхности в момент вскипания понижается, и процесс кипения
продолжается до следующего случайного отключения центров.
Нестабильной работе центров парообразования при кипении ще-
лочных металлов способствует также и хорошая смачиваемость жи-
дкостью конструкционных материалов. Малый угол смачивания
позволяет жидкости легко заполнять микротрещины поверхности,
что существенно затрудняет вскипание. Неустойчивость кипения
приводит к тому, что амплитуды пульсаций температуры стенки
при кипении щелочных металлов значительно больше, чем при ки-
пении неметаллических жидкостей (рис. 12.13). Так же, как и при
кипении неметаллических жидкостей, с ростом давления процесс
кипения становится более устойчивым (рис. 12.13, в и г), чаще
наблюдается развитый режим кипения.
Коэффициенты теплоотдачи при неустойчивом (неразвитом)
режиме кипения зависят от трудно поддающихся учету факторов.
Неразвитый режим кипения может самопроизвольно переходить
в развитый или вырождаться в режим свободной конвекции [17].
В первом случае наблюдается рост коэффициента теплоотдачи, во
втором случае — его снижение до уровня, характерного для сво-
бодной конвекции жидкости без кипения.
Существующие опытные данные говорят о том, что перегревы,
необходимые для вскипания, колеблются в очень широких преде-
лах: от нескольких градусов до десятков и даже сотен градусов.
Если учесть высокие температуры насыщения щелочных металлов,
то становится понятным, что столь высокие перегревы весьма опас-
ны, так как могут привести к пережогу поверхности нагрева еще
до вскипания жидкости.
Стабильность кипения и величина коэффициента теплоотдачи
во многом определяются свойствами поверхности нагрева. Важное
335
значение имеют размеры и геометрия впадин на греющей стенке,
так как от этого во многом зависит возможность для жидкости про-
никнуть во впадину. Можно считать, что чем глубже впадина, тем
стабильнее будет ее работа как центра парообразования. Особенно
устойчиво функционируют впадины резервуарного типа (рис. 12.7,6).
Чтобы поверхность р аздела
0
фаз проникла глубже вход-
ного отверстия такой впади-
ны, радиус кривизны должен
получить отрицательное зна-
чение, что возможно только
при /ж < ts.
> Устойчивые центры паро-
образования формируются
также на пористой поверх-
ности. Марто и Розенау 113]
исследовали процесс кипения
на поверхности с искусственно
созданными центрами парооб-
разования резервуарного ти-
па, на поверхности с пори-
стым покрытием* и на зер-
кально полированной. Пред-
ставлен ные н а р и с. 12.14 дан-
ные { показывают, что мини-
мальная -температура стенки
наблюдается при наличии ре-
зервуарных впадин, а макси-
мальная — на полированной
поверхности.
Свойства материала по-
верхности у нагрева (опыты
проводились с нержавеющей
сталью, никелем, хромом и
молибденом) не оказывают за-
метного влияния на теплоот-
дачу. Не обнаружено также
влияния окислов, содержа-
щихся в металле (в преде-
лах от 0,001 до 0,1 вес. %),
на теплоотдачу при кипении
натрия. В работе В. И. Суб-
ботина с сотр. [17] было отме-
чено стабилизирующее влия-
7, MUH * в целях увеличения шеро-
Рис. 12.13. Пульсации температуры стен-
ки при кипении натрия [23].
ховатости поверхности на стенку
наносились пористые сварные
швы.
335
ние инертного газа (аргона), присутствующего в паровом объеме,
на процесс кипения натрия и соответствующее увеличение коэффи-
циента теплоотдачи.
Для расчета коэффициентов теплоотдачи при развитом кипении
щелочных металлов можно воспользоваться следующими эмпири-
ческими зависимостями.
При кипении натрия на горизонтальной трубке в интервале-
0,01 < ps < 1 бар и qc <Z 1,6 X
X10° вт!м\ по данным работы [23],
a = 4,0-?|!'7'!s, (12.36)
где р — давление насыщения, бар.
При кипении натрия, калия и це-
зия на горизонтальной плоской
поверхности при q0 < дкр1, по дан-
ным работы [17],
2/3 / Х'гр' X1/3
Рис. 12.14. Влияние шероховатости
поверхности па величину перегре-
ва стенки при кипении натрия [13]:
1 — поверхность с углублениями «ре-
зервуарного» типа; 2 — пористая; 3 —
«зеркальная».
Дд V
I J
Ркр /
(12.37)
где с = 1,06 н и = 0,45 при
Рз/РкП 4 • 10“5—• 10“3; с = 0,13 и
0,15 при р8/ркр— 10~3-?-2-10"2.
3. Теплоотдача при пленочном
режиме кипения. Пленочный режим
кипения в условиях свободной
конвекции в большом объеме ис-
аП
пользуется в ряде отраслей техники: при закалке стальных
изделий, при работе с криогенными жидкостями и в других слу-
чаях. Поскольку коэффициенты теплоотдачи при пленочном режиме
кипения невелики, то в энергетических парогенерирующих устрой-
ствах его избегают. Тем не менее в реакторах возможно существо-
вание местных очагов пленочного кипения на поверхности твэ-
лов сложной формы; пленочный режим кипения может возникнуть,
также при аварийных режимах.
При пленочном режиме кипения жидкость отделена от поверх-
ности нагрева пленкой пара. Теплоотдача существенно зависит
от режима течения пара в пленке. Последний определяется размера-
ми и формой поверхности нагрева, ее ориентацией в поле силы тя-
жести. На поверхностях нагрева, имеющих небольшую протяжен-
ность по высоте, наблюдается ламинарное движение пара в пленке.
В этом случае перенос тепла от стенки к жидкости через пленку
пара осуществляется в основном теплопроводностью. Механизм
передачи тепла в этих условиях такой же, как и при пленочной
конденсации. Используя это обстоятельство, можно рассчи-
тать коэффициент теплоотдачи при пленочном кипении по методу
Нуссельта, разработанному для случая пленочной конденсации.
337'
Приведем полученную таким образом формулу С. С. Кута-
теладзе [10] для среднего по высоте коэффициента теплоотдачи при
пленочном кипении на вертикальной пластине высотой h:
(12.з8)
где 0,65 гС Р 1,0; ср = 1 + (£с — Zs)/2r. При кипении на по
верхности горизонтального цилиндра (в этом случае вместо h сле-
дует подставлять диаметр цилиндра) коэффициент теплоотдачи
примерно на 20% ниже рассчитанного по уравнению (12.38).
В случае турбулентного режима течения пара в пленке ее тол-
щина не оказывает существенного.влияния на теплоотдачу. Интен-
сивность свободного движения в пленке в основном определяется
разностью плотностей фаз и плотностью теплового потока.
Как показали исследования В. М. Боришанского и Б. С. Фо-
кина, проведенные с вертикальной трубой при турбулентном дви-
жении пленки пара, коэффициент теплоотдачи не зависит от линей-
ных размеров поверхности. Опытные данные обобщены с помощью
такого уравнения [6]:
— ~с . (12.39)
X" \ v"2 Р" /
где L=261/'-J?^=5C=0,28, «=1/3 при 2- 1О‘< <
< 1,4-10°; С — 0,01, п==0,57 при 1,4И06 < < 1,5-107.
Уравнение (12.39) описывает экспериментальные данные по
теплоотдаче на вертикальных поверхностях при пленочном кипе-
нии воды, этанола, метанола, этилового эфира и н-гексана с погреш-
ностью ±30%.
§ 12.4. Критическая плотность теплового потока
Рассмотрим, как протекает кризис пузырькового кипения на не-
ограниченной горизонтальной пластине, обращенной теплоотдающей
поверхностью вверх. С увеличением температурного напора ta —
— ts растут число действующих центров парообразования и частота
отрыва пузырей. Увеличение частоты приводит к слиянию пузы-
рей, образующихся на одном центре, в столбики пара, а увели-
чение числа центров вызывает слияние пузырей, возникающих
на соседних центрах, и способствует образованию на поверхности
нагрева нестабильной паровой пленки. При плотностях теплового
потока с/о > 0,7дкр1 вместо одиночных пузырей от поверхности
нагрева движутся непрерывные струи пара, а в промежутках между
струями навстречу им движется жидкость. При этом образующий-
ся пар затрудняет доступ жидкости к поверхности нагрева. Когда
плотность теплового потока достигает критического значения,
338
устойчивость встречных потоков пара и жидкости нарушается, что
ведет к нарушению структуры пристеночного слоя, уменьшению
времени и поверхности контакта между жидкостью и стенкой.
Поэтому дальнейший рост температуры стенки сопровождается
резким снижением коэффициента теплоотдачи.
Опираясь на описанную схему процесса, С. С. Кутателадзе
[10] предположил, что кризис кипения имеет чисто гидродинами-
ческую природу и в соответствии с этим определяется совместным
действием сил инерции, термогравитационных сил и сил поверх-
ностного натяжения. Влияние сил вязкости считается несущест-
венным вследствие чрезвычайно сильного перемешивания жидкости
и пара, а значит, и высокой степени турбулентности в пристеноч-
ном слое вблизи кризиса. Силы инерции, термогравитационные
силы и силы поверхностного натяжения, как это следует из уравнения
движения и граничных условий, соответственно пропорциональны
p'W'2/Z, g (pz— р") и cr/Z2. Из этих параметров можно получить
два безразмерных числа
р4"2 _ а
g(p'—P")Z ’ £(р' —Р") Z3 ’
При кипении на неограниченной (достаточно протяженной)
поверхности критическая плотность теплового потока не должна
зависеть от линейного размера системы I. Скомбинировав безраз-
мерные числа таким образом, чтобы исключить линейный размер,
и приняв вместо действительной скорости пара ш" среднюю скорость
парообразования qjrp", С. С. Кутателадзе получил уравнение
----—............... = k = con s t. (12.40)
r V p"- у о (p' — p")g
Сопоставление этого уравнения с опытными данными показывает,
что /г — действительно практически постоянная величина, равная
0,13-4-0,15 (если говорить точнее, то /г слабо зависит от физи-
ческих свойств жидкости).
Несмотря на внешнюю неупорядоченность процесса кипения,
при нагрузках, близких к критическим, существуют вполне опреде-
ленные внутренние закономерности, управляющие движением масс
жидкости и пара. Один из интересных подходов к проблеме изу-
чения кризиса кипения — это попытка связать его возникновение
с нарушением устойчивости движения капиллярных волн, возника-
ющих на границе раздела фаз. Такая модель кризиса предложена
Н. Зубером [25], рассмотревшим кипение жидкости на неограни-
ченной горизонтальной пластине. Как отмечалось выше, при на-
грузках, близких к критической, пузырьки пара на поверхности
нагрева сливаются в сплошные неустойчивые пленки, которые
разрушаются, и пар поднимается вверх в виде отдельных струек.
Пусть поверхность нагрева отделена от жидкости сплошной пленкой
пара (рис. 12.15, п). Положение фаз (жидкость сверху — пар сни-
339
зу) неустойчиво. Как доказывается в гидродинамике, стабиль-
ность такой системы может поддерживаться за счет капиллярных
волн, образующихся на границе раздела фаз. Длина капиллярных
волн не должна превышать критического значения (А,<%кр), ко-
торое определяется соотношением сил поверхностного натяжения
и тяжести:
Л = А । ?---
р |/ £(Р'~Р")
(12.41)
Здесь коэффициент А ограничен пределами 2л; Л 2л]/3. Пред-
полагается, что в пучностях волн, отстоящих друг от друга на рас-
стоянии Хкр, происходят разрывы пленки и здесь поднимаются
струйки пара (см. рис. 12.15, б). Тогда
выражение для плотности теплового
потока можно записать в виде
I/ ц Л7^'“
7кр = Ф ® , (12.42)
Лкр
Рис. 12.15. Схема волнового
где w" — скорость пара в струе; R —
радиус струи; %2кр—площадь элемен-
та поверхности нагрева, приходяще-
гося на одну струйку пара. Как
показано в работе [25], максималь-
ная скорость пара, поднимающегося
от поверхности нагрева в виде струй-
ки, связана с длиной капиллярных
волн, образующихся на поверхности
струйки Хс, соотношением
2лр- р'
W" Р'+Р"
движения: над плоской изо-
термической поверхностью (а) В соответствии с теорией Рэлея ra-
il при кипении 7с==7кР1 (б). зовая струя в жидкости становится
неустойчивой, если длина капилляр-
ной волны равна периметру струи, т. е. Хс.макс = 2л/?. Приняв
радиус струи пара R = Хкр/4, можно определить максимальную
скорость пара в струе:
(12.43)
Из соотношений (12.41)—(12.43) нетрудно получить уравнение для
критической плотности теплового потока:
7кР = сг Ур" Yog (р' — р") 1/_£—
|/ р'+р"
(12.44)
.340
Здесь коэффициент с в зависимости от способа выбора А в уравне-
нии (12.41) лежит в пределах 0,12—0,157.
Формула Н. Зубера (12.44) практически совпадает с формулой,
предложенной С. С. Кутателадзе (12.40), так как член ]/р7(р' + р")
при низких давлениях близок к единице и только при давлениях»
близких к критическим, р7(р' + р") ~ 0,7.
Рис. 12.16. Зависимость первой критической плотности теплового по-
тока от давления [5]:
О — иода; • — этиловый спирт; Д— бензол; о — гептан; V —метиловый
спирт; — пропиловый СНПрТ.
Наряду с формулами (12.40) и (12.44) для расчета ркр1 можно
пользоваться эмпирической формулой, предложенной Л. С. Стер-
маном [16]:
(12.45)
Формула (12.45) описывает опытные данные по критическим плот-
ностям теплового потока в интервале давлений от атмосферного
до (0,8-т-0,9) ркр при кипении воды, органических и криогенных
жидкостей с погрешностью ±30%.
На рис. 12.16 показана зависимость критической плотности
теплового потока от давления для воды и органических жидкостей.
По оси абсцисс отложено отношение р/ркр, а по оси ординат отно-
шение критических тепловых потоков при данном давлении и при
некотором реперном р* = 0,03ркр. Хорошо видно, что характер
изменения ркр в зависимости от р/ркр для разных жидкостей оди-
наков. В области малых давлений (р < 0,2ркр) наблюдается до-
вольно быстрый рост критической нагрузки, здесь ркр1 ~ р°>3.
При давлении, равном примерно 1/Зркр, она проходит через макси-
мум, а с приближением к рир быстро уменьшается.
341
При давлениях ниже атмосферного дкр1 зависит от режима ки-
пения. Объясняется это тем, что с понижением давления увеличи-
вается область температурных напоров, при которых наблюдается
неразвитый режим кипения. При абсолютных давлениях, измеря-
емых десятками миллиметров ртутного столба, неразвитый режим
кипения может существовать вплоть до критических тепловых на-
грузок. Если кризис возникает при неразвитом пузырьковом кипе-
нии, то критические плотности теплового потока оказываются
несколько ниже, чем в случае возникновения кризиса при разви-
том кипении.
Свойства материала поверхности нагрева, а также способ ее об-
работки оказывают существенное влияние на образование пузырь-
ков и несомненно должны сказываться на величине ^кр1. Изучая
этот вопрос, И. Т. Аладьев и В. И. Яшнов [2] пришли к выводу,
что наиболее существенно на критическую плотность теплового
потока влияет краевой угол смачивания, с увеличением которого.
7КР] уменьшается. При кипении воды (р = 1 бар) в интервале
краевых углов 0^0^ 82°, по данным названных авторов,
7кР1 (®) = 7кр1 (0) (1 - 0,00780), (12.46}
где 7кр1(0) — значение 7кр1 при 0 = 0.
При кипении щелочных металлов критическая плотность теп-
лового потока в значительной мере зависит от режима кипения. Как
правило, для неустойчивого режима кипения критическая плот-
ность теплового потока ниже, чем для развитого. По абсолютной
величине (?кр1 несколько выше, чем дает расчет по формуле (12.40).
Для натрия, калия и цезия, кипящих на горизонтальной пластине
в условиях большого объема, В. И. Субботин с сотр. [17] пред-
ложили эмпирическую обобщенную зависимость
<;кр1 = 0,163[Зг |/ р7 frog (р' — р"), (12.47)
где |3 = 1 + (с/рК]?) • (р/Ркр)"0,4- Для неустойчивого кипения
с — 17,6, для развитого — с — 44,2, р измеряется в барах.
§ 12.5. Теплообмен при кипении жидкости
на оребренной поверхности
Эффективным способом увеличения теплоотдачи в системах
с кипящим теплоносителем может служить оребрение поверхности
со стороны кипящей жидкости. Как показывает опыт, на таких
поверхностях средние плотности теплового потока, отнесенные
к единице площади базовой поверхности (поверхности, несущей
ребра), могут превышать критические значения при одновременном
отсутствии опасности чрезмерного повышения температуры стенки.
Процесс кипения на оребренной поверхности имеет специфи-
ческие особенности, связанные с тем, что кипение на поверхности
ребра происходит при наличии значительных градиентов темпера-
342
туры по длине. Поэтому на соседних участках поверхности могут
одновременно существовать различные режимы кипения. Напри-
мер, если температура от основания ребра к его вершине значи-
тельно понижается, то в основании ребра будет пленочное кипение
в центральной части — переходное, а у вершины — пузырьковое
Рассмотрим влияние неизотермичности иа теплоотдачу. Зави-
симость коэффициента теплоотдачи от температурного напора при
кипении иа неизотермической поверхности с неоднородным распре-
Рис. 12.17. Зависимость местной плотности теплового потока от местного
температурного напора при кипении фреопа-113:
О — опытные данные для изотермической поверхности; 9— для непзотермнчеекой.
делением температуры, в данном случае иа ребре, отличается от
соответствующей зависимости для изотермической поверхности.
Об этом дает представление рис. 12.17, на котором сравниваются обе
эти зависимости, полученные при кипении фреона-113 при атмо-
сферном давлении. Измерения на неизотермической поверхности
были проведены при градиентах температуры до 100 град!см [14].
Поскольку разница в значениях qG, а следовательно, и а при кипе-
нии на изотермической и неизотермической поверхностях сравни-
тельно невелика, а систематические данные по теплоотдаче во вто-
ром случае пока отсутствуют, то при расчете теплообмена прихо-
дится использовать данные, полученные для изотермической по-
верхности.
Рассмотрим метод расчета теплообмена при кипении жидкости
на поверхности одиночного цилиндрического ребра. Тепло подво-
дится к основанию ребра (рис. 12.18). Боковая поверхность и то_
343
(12.48}
где Z — длина ребра,
различных значениях
рец ребра омываются жидкостью, находящейся при температуре
насыщения. С целью упрощения расчета можно принять, что тем-
пература в теле ребра меняется только вдоль его оси. В этом случае'
распределение температуры по длине ребра описывается уравнением
М лг “(#) #s-
где s, f0— длина периметра и площадь поперечного сечения ребра;
~ /ЛЛ —............— теплоотдачи к кипящей жидкости, б’ =
условие зададим в виде
X
dz z = i
и проведем расчет распределения б(г) при
температуры
a (б1) — коэффициент
= tc — ts. Граничное
= а (тЭ1) б1,
(12.49}
в основании ребра б’о.
Так как a (б) — сложная
функция (кривая кипения),
то задача решается числен-
ным методом с использова-
нием ЭВМ. На рис. 12.18 по-
казано распределение б по>
длине медного ребра круглого'
поперечного сечения (d
= 6 мм, I = 30 мм) в случае
кипения на его поверхности
фреона-113 (р = 1 бар). Тем-
пература ребра понижается
к свободному концу. Посколь-
ку режим кипения зависит от
температурного напора, то,,
имея распределение темпера-
туры по длине ребра, можно-
судить о режимах кипения на
его поверхности. По мере
возрастания температуры в.
корне ребра наблюдаются
следующие характерные кри-
вые распределения темпера-
туры вдоль ребра (см.,
кипения на его поверхности:
Рис. 12.18. Распределения температуры
по длине ребра, рассчитанные по урав-
нению (12.48) для трех значений До;
Дкрь Д1!Р2 — температурные напоры
в точках первого и второго кризиса.
рис. 12.18) и отвечающие им режимы кипения на его поверхности:
1— в основании1’ребра — пузырьковый режим, на свободном
конце — естественная конвекция однофазной жидкости 6(z) < бкр1;,
2 — в основании ребра — переходный, иа свободном конце —
пузырьковое кипение, б- (г) < бкр2;
3 — на ребре существуют пленочный, переходный и пузырько-
вый режимы одновременно;
4 — вся поверхность ребра занята пленочным кипением,
'б (2) Г>
344
Режимы кипения на поверхности ребра определяют количество
тепла, рассеиваемое им. На рис. 12.19 приведена зависимость плот-
ности теплового потока q0 от температурного напора для корня
ребра (г = 0). Точками 1—4 отмечены режимы теплообмена, отве-
чающие соответствующим профилям температуры на рис. 12.18.
Как видно из рисунка, с ростом 1% плотность теплового потока
сначала резко увеличивается (участок ЛВ), затем по мере распрост-
ранения пленочного кипения
по поверхности ребра падает
(участок ВС) и, после того
как пленочный режим занял
всю поверхность, медленно
возрастает (участок CD).
Согласно данным, приведен-
ным на рис. 12.19, макси-
мальная плотность теплового
потока в основании ребра в
7—8 раз превышает <7кр1.
Среднюю плотность тепло-
вого потока, отнесенную к
базовой поверхности (т. е. к
поверхности стенки, несущую
ребра), можно найти по фор-
муле
Рис. 12.19. Зависимость плотности теп-
лового потока 7о от температурного на-
пора О’о в корне ребра.
.f (12.50)
/о + In
где 7о — плотность теплового потока в основании ребра, опреде-
ляемая при решении уравнения (12.48); qn— плотность тепло-
вого потока на участке поверхности в промежутке между ребрами
qa = ом%; 'б’о — температурный напор в основании ребра; [п — пло-
щадь поверхности промежутка между ребрами.
Эффективность работы оребренной поверхности во многом опре-
деляется рациональным выбором размеров ребер и величины зазо-
ра между ними. С целью повышения эффективности теплообмена
ребра целесообразно располагать на небольшом расстоянии друг от
друга. Однако слишком тесное расположение ребер имеет и отри-
цательные последствия, так как затрудняет приток жидкости к по-
верхности ребер и удаление образующегося на них пара.
При кипении воды (р = 1 бар), по данным работы [3], ширину
зазора между ребрами следует выбирать около 2 мм, а длину ребер
в 3—12 раз больше ширины зазора. Следует учесть: чем больше
высота ребра, тем выше плотность теплового потока, отводимого
ребром, но одновременно выше и температура в корне ребра. Ореб-
ренные поверхности при охлаждении водой (при р = 1 бар) позво-
ляют снимать плотности теплового потока в пересчете на несущую
ребра поверхность до 5 - 106 вт1м\ что почти в 5 раз превышает
9кр1
345
СПИСОК ЛИТЕРАТУРЫ
1. Аверин Е. К., Кружилин Г. Н. Влияние поверхностного натяжения
и вязкости на условия теплообмена при кипении воды. — «Изв. АН СССР.
ОТН», 1955, № 10, с. 131.
2. Аладьев И. Т., Яшнов В. И. Влияние смачиваемости на кризис кипе-
ния. — В сб.: Конвективная теплопередача в двухфазном и однофазном
потоках. М.—Л., «Энергия», 1964, с. 249.
3. Вертере Ш. А. Теплообмен при комплексном испарении жидкости в слу-
чае контакта с неизотермической поверхностью. — В сб.: Тепло-
и массоперенос. Минск, «Наука и техника», 1968, 9, с. 190.
4. Боришанский В. М., Козырев А. П., Светлова Л. С. Изучение тепло-
обмена при пузырьковом кипении жидкостей.—В сб.: Конвективная теп-
лопередача в двухфазном и однофазном потоках. М.—Л., «Энергия»,
1964, с. 71.
5. Боришанский В. М., В сб.: Вопросы теплоотдачи и гидравлики двух-
фазных сред. М.—Л., Госэнергоиздат, 1961, с. 18.
6. Боришанский В. М., Фокин Б. С. «Инж.-физ. ж.», 1965, т. 8, № 3, с. 197.
7. Борнхорст В., Хэтсопулос Ж- Определение скорости роста пузырей. —
«Прикладная механика», М., «Мир», 1967, № 4, с. 125.
8. Гартнер Р., Вествотер Д. Плотность центров парообразования в процес-
се теплоотдачи при пузырьковом кипении. — В сб.: Вопросы физики ки-
пения. Под ред. И. Т. Аладьева. М., «Мир», 1964, с. 301.
9. Головин В. С., Кольчугин Б. А., Лабунцов Д. А. «Инж.-физ. ж.»,
1967, т. 6, № 2, с. 3.
10. Кутателадзе С. С. Теплопередача при конденсации и кипении. М., Маш-
гиз, 1952.
11. Лабунцов Д. А. Приближенная теория теплообмена при развитом пузырь-
ковом кипении. — «Изв. АН СССР, ОТН, Сер. Энергетика и транспорт»,
1963, № 1, с. 58.
12. Лабунцов Д. А. Об одном новом направлении в теории кризиса кипения —
«Теплоэнергетика», 1961, №8, с. 81.
13. Марто П., Розенау В. Нестабильность пузырькового кипения щелочных
металлов. — «Теплопередача», Сер. С.», М., «Мио», 1966, т. 88, № 2,
с. 38.
14. Петухов Б. С. и др. «Теплофизика высоких температур», 1971, т. 9, №6,
с. 1260.
15. Скрипов В. П. Метастабильная жидкость. М., «Наука», 1972.
16. Стерман Л. С. К теории теплоотдачи при кипении жидкости. — «Ж. техн,
физики», 1953, т. 23, с. 341.
17. Субботин В. И. и др. Теплообмен при кипении металлов в условиях
естественной конвекции. М., «Наука», 1969.
18. Толубинский В. И. Скорость роста паровых пузырей при кипении
жидкости. — «Изв. вузов. Энергетика», 1963, № 16, с. 77.
19. Толубинский В. И. и др. Обобщение данных по теплоотдаче при кипении
жидкостей на основе внутренних характеристик процесса. — В сб.:
Теплофизика и теплотехника. Киев. «Наукова думка», 1973, № 23, с. 85.
20. Ягов В. В. Исследование кипения жидкостей в области низких давлений.
Автореферат кандидатской диссертации. Москва, МЭИ. 1971.
21. Berenson Р. J. Experiments on Pool—Boiling Heat Transfer. —«Inter-
nal J. Heat—Mass. Transfer», 1962, v. 5, October, p. 985.
22. Cole R., Shulman H. Chem. Engng Progr. Sympos. Series, 1966, v. 62,
No. 64, p. 6.
23. Petukhov B. S., Kovalev S. A., Zhukov V. W. Study of Sodium Boiling
Heat Transfer. — Proc. 3rd. Internal. Heat Transfer Conf. Chicago, Aug.,
1966, v. 5.
24. Rallis C. J., Jawurek H. H. Latent heat transport in saturated Nucleate
boiling. —«Internal. J. Heat Mass. Transfer», 1964, v. 7, No. 10, p. 1051.
25. Zuber N. Hidrodinamic aspects of boiling heat transfer (thesis). United Sta-
tes Atomic Energy Commision, AECU-4489, 1959.
ГЛАВА 13
ЭЛЕМЕНТЫ ГИДРОДИНАМИКИ ДВУХФАЗНОГО ПОТОКА
§ 13.1. Параметры двухфазного потока
Для количественного описания двухфазного потока необходи-
мо ввести ряд новых понятий: расходы жидкой и паровой фаз, их
средние скорости, плотность смеси и др. Если предположить, что
фазы находятся в термодинамическом равновесии, а их средние
скорости одинаковы, то, зная расход каждой фазы на входе в ка-
нал, геометрию канала и плотность теплового потока на стенке, из
уравнений материального и теплового баланса можно найти изме-
нение расхода и средней скорости каждой фазы, а также плотность
смеси по длине канала. Найденные при таких допущениях парамет-
ры потока называются расходными. Поскольку жидкость в потоке
может быть перегрета или иедогрета по отношению к температуре
насыщения, а средние скорости фаз могут не совпадать, то в этих
случаях расходные параметры не отражают состояния потока. По-
этому наряду с расходными вводятся истинные параметры, описы-
вающие действительное состояние потока. В настоящем параграфе
рассмотрены основные расходные и истинные параметры, применя-
ющиеся для описания двухфазных стационарных потоков.
Массовый расход смеси в двухфазном потоке складывается из
массовых расходов жидкой и паровой фаз:
G = G' -I- G" кг/сек. (13.1)
Если фазы находятся в термодинамическом равновесии, то массо-
вый расход пара можно определить из соотношения
G" J1™-11'. G, (13.2)
г
Здесь /гсм и h! — энтальпия смеси и энтальпия жидкости на линии
насыщения, дж!кг\ г — теплота пароообразования, дж!кг.
Расходное массовое паросодержание характеризует долю пара
в массовом расходе смеси:
х^, (13.3)
расходное массовое содержание жидкости-.
1— х=— . (13.4)
G
347
Для равновесного двухфазного парожидкостного потока имеем
(13.5)
г
Для потока жидкости при температуре насыщения расходное мас-
совое паросодержание равно нулю, для потока насыщенного пара
х — 1.
Если равновесие в потоке между фазами отсутствует, то паросо-
держание, рассчитанное по энтальпии смеси, не отражает ее дей-
ствительного состава. Например, для однофазного потока перегре-
той жидкости х будет больше нуля, а для двухфазного потока, со-
стоящего из холодной жидкости и не успевших сконденсироваться
в ней пузырьков пара, — меньше нуля.
Наряду с расходным массовым паросодержанием используются:
расходное объемное паросодержание
где о' и v" — объемные расходы соответственно жидкой и паровой
фаз; v' = G'/p'; v" = G"/p", м3/сек, и истинное объемное паросо-
держание, равное отношению площади поперечного сечения, зани-
маемой паровой фазой, к полной площади поперечного сечения
парожидкостного потока:
ср = - . (13.7)
/
Обычно в двухфазном адиабатном потоке пар движется быстрее
жидкости, поэтому истинное паросодержание оказывается ниже
расходного:
(13.8)
Зная объемное паросодержание (расходное или истинное),
можно определить расходную плотность потока
рр = р"|3 + р' (1 - Р) (13.9)
и истинную плотность потока
Р<р = р"<р + р' (1 — ср).
(13.10)
Удобной характеристикой потока является средняя массовая
скорость, равная массовому расходу смеси через единицу поверх-
ности поперечного сечения канала:
— G
pw —— кг/(м?* сек).
(13.11)
348
Средняя массовая скорость не зависит от плотности смеси и потому
при стационарном течении в каналах постоянного сечения как при
наличии, так и при отсутствии фазовых превращений в потоке ос-
тается неизменной по длине. Кроме средней массовой скорости для
описания двухфазного потока используются следующие характер-
ные скорости:
скорость циркуляции — скорость, которую имел бы поток, если
бы его плотность была равна плотности жидкости при температуре
насыщения:
(13.12)
приведенные скорости жидкой и паровой фаз — скорости, которые
имели бы соответственно жидкость или пар, если бы только жид-
кость или только пар занимали все сечение канала:
(13.13)
(13.14)
истинные скорости жидкой и газообразной фаз:
(13.15)
(13.16)
истинная средняя скорость потока:
/рф <РР" + (1 —<Р)Р'
(13.17)
и расходная средняя скорость потока:
Zpp
(13.18)
Обычно истинные скорости фаз не равны между собой. Их разность
называется относительной скоростью фаз:
ауотп=Ши—Wn м/сек.
(13.19)
Располагая данными об истинных скоростях фаз, с помощью соот-
ношений (13.15) и (13.16) нетрудно определить истинное объемное
паросодержание потока. Связь между истинным объемным паросо-
34»
держанием и расходным массовым паросодержанием можно выра-
зить через отношение истинных скоростей фаз:
Ф =-----Луг?- <13-20)
1 р" Ши 1 —х
Р' Ши х
Связь объемного и массового расходных паросодержаний можно
получить, если воспользоваться соотношениями (13.3), (13.4) и
(13.6):
р-------J----. (13.21)
р' X
Важной характеристикой двухфазного потока с подводом тепла
является также плотность теплового потока на стенке qc.
§ 13.2. Режимы течения
Режимы течения двухфазных потоков отличаются большим раз-
нообразием. Тот или иной режим течения характеризуется опре-
деленным распределением фаз и скоростей в двухфазном потоке.
Изучение взаимосвязи этих характеристик (даже осредненных во
времени) с законами сопротивления трения и теплоотдачи связано
с большими экспериментальными трудностями. Пока еще не уста-
новлены достаточно строгие количественные связи режимов течения
с местными параметрами потока. Поэтому классификация режимов
течения построена в основном на результатах визуального изу-
чения картин течения.
На основе наблюдений газо-жидкостных и паро-жидкостных
потоков, движущихся в вертикальных трубах снизу вверх, можно
выделить шесть основных режимов течения (рис. 13.1).
а. Пузырьковый — такой режим течения, при котором паровая
фаза распределена в жидкости в виде небольших пузырьков, раз-
меры которых малы по сравнению с характерным размером попе-
речного сечения канала. С увеличением расхода пара количество и
размеры пузырьков возрастают.
б. Снарядный — это режим течения, при котором паровая фаза
движется в виде крупных пузырей*, поперечные размеры которых
соизмеримы с характерным размером поперечного сечения канала,
а длина может достигать нескольких характерных размеров. От
стенки пузыри отделены тонким слоем жидкости, а друг от друга —
жидкостными пробками.
в. Эмульсионный — это режим течения, при котором паровая
фаза распределена в потоке в виде небольших объемов, разделенных
жидкими пленками.
* Передняя часть пузырей скруглена и они напоминают по форме артил-
лерийские снаряды.
350
г. Дисперсно-кольцевой — такой режим течения, при котором
паровая фаза образует ядро потока, а жидкая фаза движется
в виде пленки по поверхности трубы и в виде мелких капель, распре-
деленных в газообразном ядре. Различают два предельных случая
исперсио-кольцевого режима:
о~
•о
"О
о
’ о
_ о
" о
о а
о о
о
°
Л ° с
<? э
О ° "
О 0
° и О
»о 3
°
э
г
о
“О
0°
’0 е
О
о п
О
о
о"
ц
»о
’() Оо
о °
о
о
О
Q
О
о О
О о
е
0
о
6
о
Рис. 13.1. Режимы течения двухфазного потока в вертикальной трубе:
а — пузырьковый; б — епг^лдпый; в — эмульсионный; г — дисперсно-кольцевой;
с — кольцевой; е — дисперсный.
д. Стержневой (кольцевой) режим течения, когда вся жидкость
движется в виде пленки.
е. Дисперсный режим течения, когда вся жидкость движется
в виде мелких капель, распределенных в потоке пара.
Установление четких границ существования режимов течения
встречает определенные затруднения. Во-первых, смена одного
режима течения другим происходит постепенно, без резких гра-
ниц. Во-вторых, устойчивость режима течения зависит от многих
трудно поддающихся учету факторов и граница существования
того или иного режима может смещаться. Наконец, разработанные
методы фиксации режимов течения еще недостаточно надежны.
Поэтому условия, в которых реализуются те или иные режимы и,
следовательно, границы их существования, можно указать лишь
весьма приближенно и в значительной мере качественно.
Области реализации режимов течения принято изображать с по-
мощью диаграмм. В настоящее время предложено несколько типов
диаграмм, но все они не свободны от серьезных недостатков. Области
351
существования различных режимов можно наглядно изобразить
в координатах рш— х. Такие диаграммы для пароводяной смеси
приведены на рис. 13.2 и 13.3.
На рис. 13.2 сплошными линиями показаны границы режи-
мов при движении двухфазного потока в вертикальной обогрева-
емой трубе при давлении 36 бар. При малом паросодержания
(х<2%) наблюдается пузырьковый режим течения (область I).
С ростом паросодержания мелкие пузырьки сливаются в более круп-
ные и при небольших значениях pw пузырьковый режим переходит
Рис. 13.2. Диаграмма режимов течения при кипе-
нии воды в вертикальной трубе при подъемном
течении [3]:
/—область существования пузырькового режима; 2 —
снарядного; 3 — эмульсионного; 4 — дисперсно-кольце-
вого; сплошные линии —р=36 бар, пунктирные — р =
=70 бар.
в снарядный (область 2). В случае высоких массовых скоростей
благодаря сильному перемешиванию в потоке снаряды не образу-
ются и пузырьковый режим с ростом х переходит в эмульсионный
(область 3). С ростом расходного массового паросодержания (в дан-
ном случае при х > 104-15%) отдельные пузыри сливаются, в по-
токе формируется паровое ядро с каплями жидкости, т. е. устанав-
ливается дисперсно-кольцевое течение (область 4). Как видно из
рис. 13.2, наиболее значительный диапазон массовых расходных
паросодержаний занимает дисперсно-кольцевой режим течения
(х> 15%).
С ростом давления до 70 бар (пунктирные линии на рис. 13.2)
границы всех режимов смещаются в область больших значений х.
На положение границ режимов течения существенно влияет
плотность теплового потока на стенке. В дальнейшем основное вни-
мание будет уделено двухфазным потокам, движущимся в обогре-
ваемых трубах, поэтому следует рассмотреть, как влияет обогрев
352
иа гидродинамику двухфазного потока. Пусть в достаточно длин-
ную обогреваемую трубу поступает жидкость, недогретая до тем-
пературы насыщения, а покидает ее перегретый пар. Если плот-
ность теплового потока постоянна по длине трубы, а давление ме-
няется незначительно, то расходное массовое паросодержание бу-
дет изменяться по длине трубы ли-
нейно:
Дх == д/
rG
(13.22)
где Дх — приращение паросодержания
на участке трубы А/.
Гидродинамические характеристики тес-
но связаны с-теплоотдачей. Поэтому при
изучении режимов течения удобно одно-
временно рассмотреть и изменение тем-
пературного режима стенки трубы.
На рис. 13.4 показана зависимость от
расходного массового паросодержания
(или, что то же самое, изменение по
длине трубы) истинного объемного паро-
содержания, температуры стенки tc и
средней температуры потока. Последняя
определяется из уравнения баланса
тепла:
~ , qc л zd Л 1
/ = /вх-рс f.., х<0;
GcP (13.23)
t-=t8 0 < х < 1J
Рис. 13.3. Диаграмма ре-
жимов течения при кипении
воды в вертикальной трубе
при подъемном движении,
р=7 бар [4]:
1 — область существования пу-
зырькового режима; 2 —-сна-
рядного; 3 — дисперсно-кольце-
вого.
где /вх — температура жидкости на входе в обогреваемую трубу.
На этом же рисунке для сопоставления приведено изменение истин-
ного объемного' паросодержания для адиабатного потока.
До тех пор, пока температура стенки ниже температуры насы-
щения t8, в потоке будет только жидкая фаза. После того как темпе-
ратура стенки превысит температуру насыщения (точка А), на по-
верхности трубы начнут возникать пузырьки пара. В случае высо-
ких плотностей теплового потока пристеночный слой жидкости
даже при х О может быть сравнительно сильно перегрет и коли-
чество паровой фазы, находящейся в потоке, будет значительным.
Пузырьки пара могут из пристеночного слоя попадать в холодное
ядро жидкости. Поскольку вместе с пузырьками от стенки в поток
уносится и окружающий их перегретый слой жидкости, то кон-
денсация пара в пузырях происходит сравнительно медленно и они
могут некоторое время двигаться в потоке холодной жидкости.
Потоки, в которых одновременно существуют пар и недогретая до
ts жидкость, называют неравновесными. Как видно из рисунка, ис-
тинные объемные паросодержания ср у неравновесного потока су-
12 |3ак. 792 353
щественно больше нуля при х < 0. В интервале 0 х С 1 темпе-
ратура жидкости в ядре потока остается равной температуре насы-
щения, а истинное объемное паросодержание монотонно растет.
Резкий рост температуры стенки в точке D свидетельствует о воз-
никновении кризиса теплоотдачи. В этой точке наблюдается переход
к дисперсному режиму течения.
Наличие в потоке недогретой жидкости, движущейся в обогре-
ваемом канале, конденсирующихся пузырьков, означает, что пу-
зырьковое течение можно наблюдать не только при положительных,
Рис. 13.4. Изменение ср, t0 и t в зависимости от х
(или по длине обогреваемой трубы); пунктир —
зависимость ф от х для адиабатного потока. Точ-
ками обозначены:
Л —появление паровой фазы; В —начало кипения; CD —
квазнравновесное течение; D — переход к дисперсному
режиму.
но и при отрицательных расходных массовых паросодержаниях.
Поскольку обогрев увеличивает число пузырьков, находящихся
в потоке, и тем самым облегчается их слияние, то переход к снаряд-
ному режиму в случае высокой плотности теплового потока стано-
вится возможным и при малых положительных и даже при отри-
цательных значениях х. Эти соображения подтверждаются дан-
ными, приведенными на рис. 13.3.
Таким образом, наличие обогрева приводит к смещению границ
пузырькового и снарядного режимов в область более низких рас-
ходных массовых паросодержаний.
Тепло, идущее на испарение капель, в дисперсном потоке сна-
чала от стенки передается соприкасающемуся с ней пару и затем от
354
перегретого пара к каплям жидкости. Следовательно, для подвода
тепла от стенки к капле требуется некоторое время. Поэтому в обо-
греваемой трубе при х = 1 и даже при х несколько больших 1 в пе-
регретом паровом ядре могут находиться испаряющиеся капли
жидкости, т. е. возможно существование дисперсного режима.
Если учесть, что область существования двухфазного адиабатного
потока ограничена интервалом 0<х<1, то, как видно из
рис. 13.4, обогрев значительно увеличивает диапазон расходных
массовых паросодержаний, при которых существуют двухфазные
паро-жидкостные потоки.
§ 13.3. Сведения о структуре двухфазных потоков
1. Пленка жидкости. В случае кольцевого режима течения ско-
рость пара превышает скорость жидкости в пристеночной пленке. Под
действием относительной скорости пара и жидкости на поверхности
раздела фаз возникает волновое движение. При малых скоростях
пара поверхность пленки покрывают небольшие волны (рябь).
С ростом скорости пара характер движения меняется. По поверх-
ности пленки, покрытой рябыо, проходят крупные волны, полу-
чившие название скатывающихся. Эти волны характеризуются вы-
сокими амплитудами, крутым фронтом и большими расстояниями
между гребнями. При высокой относительной скорости' пар сры-
вает с гребней скатывающихся воли капли жидкости и они уносятся
в ядро потока. Величина уноса капель жидкости характеризуется
отношением
G ’
где Q' — массовый расход жидкости в потоке; (?пЛ — массовый рас-
ход жидкости в пленке.
Согласно имеющимся опытным данным, на величину уноса
капель кроме относительной скорости оказывают влияние поверх-
ностное натяжение и вязкость пара. В качестве параметра, опре-
деляющего величину уноса капель, используется безразмерная
скорость [15]
~=л£|£|/ЛЕ. (13.24)
На рис. 13.5 приведена кривая уноса, построенная по данным
И. И. Палеева и Б. С. Филипповича. Эта кривая удовлетворитель-
но согласуется с опытными данными в случае достаточно толстых
пленок. Для очень тонких пленок жидкости величина уноса будет
несколько меньше.
При движении двухфазного потока с подводом тепла паросо-
держание по длине трубы увеличивается, следовательно, увеличи-
вается и приведенная скорость пара. В соответствии с кривой
12* 355
уноса жидкости с ростом w'o возрастает доля жидкости, находя-
щейся в ядре потока, и уменьшается расход жидкости в пленке.
Уменьшается также и толщина пленки, так как с ростом w'q воз-
растает скорость движения жидкости. Эти обстоятельства, как
показано в гл. 14, существенным обра-
зом влияют на условия теплообмена.
По данным детальных исследований,
при движении в необогреваемых трубах
даже при очень больших скоростях пара
на стенке всегда имеется очень тонкая
пленка жидкости. В случае движения
потока в обогреваемой трубе тонкая
пленка легко испаряется и дисперсно-
кольцевой режим переходит в дисперс-
ный.
Капли жидкости, находящиеся в по-
токе, выпадают обратно на поверхность
Рис. 13.5. Зависимость ве- пленки. Таким образом, в случае дис-
личины уноса жидкости _от персно-кольцевого течения происходит
безразмерной скорости w. непрерывный обмен жидкостью между
пленкой и ядром потока.
2. Дисперсность жидкости. Разрушение крупных капель в потоке
происходит под действием разности скоростей пара и капли, назы-
ваемой относительной скоростью капли иуотп. Устойчивость капли
определяется значением числа Вебера
_ Рк. ^оти Р"
а
(13.25)
где DK — диаметр капли; о — коэффициент поверхностного натя-
жения.
Капля разрушается, если число We превышает критическое
значение, которое по данным разных исследователей лежит в пре-
делах от 13 до 22. Отсюда, в частности, следует, что максимальный
размер капель, которые еще могут существовать в потоке, обратно
пропорционален оу§Тн-
Наблюдеиия за поведением двухфазных потоков в трубах свиде-
тельствуют о том, что капли образуются в результате срыва жид-
кости с гребней волн. Разность скоростей гребней волн и ядра по-
тока, или, другими словами, относительная скорость гребней волн
и пара, во многом определяет размеры уносимых капель. Посколь-
ку скорость пара по сечению непостоянна и понижается от оси тру-
бы к стенке, то для пленок жидкости разной толщины относительная
скорость гребней волн и пара будет различной. Можно предполо-
жить, что чем толще пленка жидкости, тем дальше гребни волн бу-
дут проникать в ядро потока и тем выше будет относительная ско-
рость. На рис. 13.6 приведены результаты измерений максималь-
ного диаметра капель в зависимости от истинной скорости газооб-
356
разной фазы шп. Как видно из рисунка, максимальные размеры
капель уменьшаются с ростом и лежат в области, ограниченной
линиями А и В. Эти линии соответствуют числу We = 18, рассчи-
танному соответственно по относительной скорости, равной ш,"
и w'h/2. Случай А наблюдается для толстых пленок жидкости, когда
гребень волны глубоко проникает в ядро потока и относительная
скорость близка к истинной скорости газообразной фазы. Случай
В характерен для тонких пленок, когда гребни волн соприкасаются
с периферийными слоями пото-
ка, имеющими низкие скорости,
и относительные скорости близки
к ws"/2.
Число мелких капель в по-
токе значительно превышает
число крупных. Однако основ-
ная масса жидкости переносится
сравнительно крупными кап-
лями. Это видно из рис. 13.7,
где представлена функция рас-
пределения расхода жидкости,
транспортируемой каплями по
размерам капель [G'(£>) — рас-
ход жидкости, транспортируе-
мой каплями, диаметры кото-
Рпс. 13.6. Зависимость максимальпо-
го диаметра капель от истинной ско-
рости газа [5]. Массовый расход
жидкости:
О — G'=0,063 кг/сек-, Д — G'=0,126 кг/сек-,
V — G'=0,2 кг!сек.\ X — G'^0,316 кг/сек.
рых лежат в интервале от нуля
до О, G' — суммарный расход
жидкой фазы]. Видно, что при
скорости газа 37,5 м/сек в кап-
лях диаметром до 0,1 мм сосре-
доточено менее 10% жидкости. Размеры капель с ростом скорости
газа уменьшаются.
3. Распределение скорости в двухфазном потоке. Если измерить
профиль скорости в турбулентном паровом ядре при дисперсно-коль-
цевом течении, то можно обнаружить различие в распределении ско-
ростей для однофазного и двухфазного потоков. Присутствие капель
жидкости в ядре потока приводит к тому, что профиль скорости вы-
тягивается и отношение максимальной скорости иа оси трубы к сред-
ней скорости потока возрастает до 1,4 — 1,5 вместо 1,18 — 1,2 для
однофазного турбулентного потока (рис. 13.8). Другими словами,
поток как бы приближается к ламинарному (говорят, что происхо-
дит ламинаризация потока). Если распределение скорости в паровом
ядре представить в виде
= in + А,
V„. % V"
(13.26)
где v* = ]/ Оу/р"; v" — кинематический коэффициент вязкости
пара; у — расстояние от стенки, а касательное напряжение на по-
12В Зак. 792 357
верхности пленки толщиной 6 рассчитать по формуле
+ pCMgsin «
где со — угол наклона оси трубы к горизонту; г — продольная
координата, то константа турбулентности % окажется рав-
ной 0,1 — 0,2 вместо 0,4, как это наблюдается для однофазного
турбулентного потока [14].
Рис. 13.7. Интегральная кривая
расхода жидкости, транспортируе-
мой каплями различных диамет-
ров [5].
Рис. 13.8. Профили скорости в
ядре турбулентного потока:
1 — дисперсный поток; 2 — однофаз-
ный поток.
Исследования распределения скорости в пристеночной пленке
жидкости показали, что и здесь происходит ламинаризация потока.
Так, в пристеночном слое жидкости, содержащем пузырьки пара, по-
стоянная х равна 0,1 — 0,3.
Деформацию профиля скорости и уменьшение константы турбу-
лентности можно рассматривать как результат уменьшения турбу-
лентной вязкости. Связано это, вероятно, с тем, что многочисленные
мелкие капли жидкости в потоке пара или пузырьки пара в потоке
жидкости затрудняют распространение турбулентных вихрей и тем
самым ослабляют обмен количеством движения между слоями
потока.
4. Истинное объемное паросодержание. В адиабатном потоке ис-
тинное объемное и расходное объемное паросодержания потока,
как видно из (13.20) и (13.21), связаны соотношением
ф = —;-----!------
1-^4-
Uhi \ Uhi
(13.27)
358
Из формулы (13.27) следует, что ср и |3 совпадают в том случае, если
равны истинные скорости фаз. Чем выше относительная скорость па-
ровой фазы, т. е. разность скоростей пара и жидкости [см.
13.19)], тем меньше площадь поперечного сечения, занимаемая
паром, и тем значительнее отклонение ср от р.
Рассмотрим, как изменяется относительная скорость фаз при дви-
жении адиабатного потока в вертикальной трубе. При пузырьковом
режиме течения (малые х) относительная скорость зависит от pw.
Например, в случае больших средних массовых скоростей пузырь-
ки пара равномерно распределены в объеме жидкости и относитель-
ная скорость невелика. При малых расходах в восходящем потоке
Рис. 13.9. Зависимость относительной скорости фаз от истинного
объемного содержания жидкости при движении воздухо-водяной
смеси в вертикальной трубе [2]:
О — ау0-1,5 м/сек- Д — юи=О,52 м/сек-, □ — = 0,26 м/сек-, V — дао=О, 1 м/сек.
пузырьки пара всплывают под действием архимедовой силы и отно-
сительные скорости велики (1 — ср > 0,9, рис. 13.9). Переход к
снарядному течению сопровождается снижением относительной
скорости шОТ11/(йУо + г^о) ~ 0,2. Это связано с тем, что скорости про-
бок жидкости и «снарядов» пара близки между собой. С пере-
ходом к дисперсно-кольцевому режиму относительная скорость
возрастает, а затем с ростом паросодержания и с уменьшением
количества жидкости, текущей в пленке, снижается.
Картина течения существенно изменяется при движении двухфаз-
ного потока в обогреваемой трубе. Вернемся к рассмотренному
в § 13.2 примеру: кипение жидкости в трубе (см. рис. 13.4). В случае
значительных иедогревов образующиеся пузыри пара скользят по
стенке, оставаясь все время в пристеночном слое. После того как
недогрев на некотором расстоянии от входа уменьшится, пузырьки
начинают отрываться от стенки, двухфазный слой утолщается и
истинное объемное паросодержание быстро возрастает (см. рис. 13.4,
точка В). Если в равновесном адиабатном потоке ср = 0 при х ^0,
то в неравновесном потоке при нулевых значениях х истинное объем-
ное паросодержание всегда несколько выше нуля. По мере роста х
это различие сглаживается, и при достаточно больших х На неко-
12В* 359
тором участке CD (см. рис. 13.4) значения (р для обогреваемых труб
и адиабатного течения практически совпадают, а поток можно счи-
тать квазиравновесным. После перехода к дисперсному режиму
(точка D) с горячей стенкой соприкасается только паровая фаза
и тепло, идущее на парообразование, подводится к каплям от пере-
гретого пара. Истинное объемное паросодержание в этом случае
может быть ниже, чем в равновесном адиабатном потоке.
В настоящее время имеется значительное число теоретических и
экспериментальных исследований истинного объемного паросодер-
жания двухфазных потоков в обогреваемых и необогреваемых тру-
бах. В теоретических работах при составлении расчетной модели
рассматривается баланс сил, действующих на пузырек, используют-
ся принципы минимального прироста энтропии или минимума при-
ращения кинетической энергии. Последний принцип применен, на-
пример, в работе Поломика [И], рассмотревшего стационарный од-
номерный (с постоянными параметрами по сечению) кипящий поток.
Уравнение энергетического баланса для двухфазного потока состав-
лено с учетом прироста энтальпии за счет обогрева стенки. Предпола-
гается, что жидкость и пар находятся при температуре насыщения,
а плотность фаз по длине трубы не меняется. Определив условия,
при которых кинетическая энергия двухфазного потока будет мини-
мальна, Поломик получил соотношение для истинного объемного
паросодержания:
ср ---------J--------. (13.28)
1-х у/_р" у
х у \ Р /
Сопоставление формулы (13.28) с опытными данными показало,
что в диапазоне 8 < р 70 бар, 200 < pay < 500 кгЦмР-сек) и
0,05 0,3 расчетные значения ср оказываются приблизительно
на 30% ниже действительных.
Тонг и Ларсен [7] разработали полуэмпирический метод опреде-
ления ср при кипении недогретой жидкости. Предполагается, что пу-
зырьки пара сосредоточены в кольцевом слое у стенки трубы и нахо-
дятся в термическом равновесии с окружающей жидкостью, а цен-
тральная часть потока занята турбулентным ядром холодной жидко-
сти. В ядре потока считается справедливой аналогия между перено-
сом тепла и количества движения. Такой подход позволяет соста-
вить уравнение сохранения массы и энергии для двухфазного слоя.
В результате их численного решения определяется количество тепла,
идущее на увеличение толщины двухфазного слоя, что позволяет
найти изменение истинного объемного паросодержания по длине
трубы.
Многочисленные опытные данные о величине истинного объем-
ного паросодержания получены в результате исследования плот-
ности двухфазных потоков с использованием у-излучения. По этим
данным составлены эмпирические зависимости, позволяющие полу-
360
чить достоверные значения истинного объемного паросодержания.
Истинное объемное паросодержание можно рассчитать с помощью
соотношения (13.20) или (13.27), если известно отношение истинных
скоростей фаз Для определения w"Jw'n в случае адиабат-
ного пароводяного потока в интервале 10<р< 180 бар, 100 «С рш
3000 кг/{м2-сек), 0 •< х •< 1 3. Л. Миропольский с сотр. [9] ре-
комендуют следующую эмпирическую зависимость:
где
н
Юи
Юц
13,5 (1 — р/рКр)
Fr5/12Rel/6 ’
(13.29)
Fr
ML; Re
gp'2 L
ст
£(P' —P")
ст
ст
---------- при d > 22 । ----------,
£(Р' —Р")-I-' £(Р' — Р")
d — диаметр трубы.
Для труб малого диаметра [d < 7 ]/a/g (р' — р") предлагается
зависимость
Юн _ f /?
Wil \ Ркр
— 0,38
(13.30)
Истинное объемное паросодержание в обогреваемых трубах при
х 0 в интервале 5 р 100 бар, 100 рш 3600 кг/(м*-сек),
2-Ю5 qc 2<10свтЛи2 и 11 d 34 мм. 3. Л. Мирополь-
ский предлагает определять с помощью соотношения
_£_у-35
хв J
(13.31)
где ср0 — истинное объемное паросодержание прих=0, ф0 = 0,43 х
xKe^36 Re70’I5(p/piy~°’225; хв— расходное массовое паросодер-
жание в точке В (см. рис. 13.4), в которой начинается интенсивный
рост ср.
хв = —0,49 Де3-7 ^е~°-3 (-ДЛ°’16 ;
кРкр/
1^ = — |/--------; Reo = 1 /-----,
И' У £(Р'~Р") “ у g(p'—p")
ст — коэффициент поверхностного натяжения.
361
Ф = Фо | 1
р'
Квазиравновесное течение, т. е. течение, при котором ср
в обогреваемой и необогреваемой трубах совпадают (участок CD на
рис. 13.4), наблюдается при х хс:
С
’ 22\*1 1
р_ (1 _ 0,3/^ )
Р" \ \ Яс / /
(13.32)
Истинное объемное паросодержание в интервале хс < х 1 с до-
статочной для практических целей точностью можно определить с
помощью формул (13.29) и (13.30). В переходной области 0 < х < хс
можно воспользоваться линейной интерполяцией
ср =_ сРо -|—- (срс ср0).
хс
(13.33)
Для обогреваемых труб диаметром от 5 до 20 мм в интервале
давлений от 30 до 150 бар, средних массовых скоростей от 500 до
4000 кг!(м2-сек) и плотностей теплового потока от нуля до критиче-
ских значений при кипении недогретой воды и пароводяной смеси
В. С. Осмачкин [18] рекомендует истинное объемное паросодержание
рассчитывать по формуле
1 । . Р"
Ши Р' %
ср =
(13.34)
0,6-Ы,5Р
Здесь—т- = 1 Н-----*7=— (1 — р/ркп); Р — расходное объемное
(«и ]/ Fr 1
паросодержание; Fr = w^/gd; w0 — скорость циркуляции; % — ис-
тинное массовое паросодержание потока, равное отношению
истинного массового расхода пара к общему массовому расходу смеси.
Для определения % предлагается эмпирическое соотношение
/ /I—hB
/^'+(/1 + ^-2/^) ехр — 2————
О '
G / h—-hn
r + (h+h' -2/zB) ехр / - 2 -——
\ /1
(13.35)
где /г и У — энтальпия потока и энтальпия насыщенной жидкости;
hn — энтальпия потока в точке начала интенсивного роста ср опре-
деляется по формуле
Л' hB — / q (i \ о,О8 / ау0 0,2
-------р^ = 7,5 —------------- -----
<7с VP" v' / \ v' У
(13.36)
Для равновесного и квазиравновесного двухфазных потоков, т. е.
при низкой плотности теплового потока на стенке или при высокой
энтальпии потока, истинное массовое паросодержание совпадает с
расходным (% -> х).
362
§ 13.4. Перепад давления в двухфазном потоке
При движении парожидкостного потока в обогреваемой трубе
вследствие парообразования происходит перераспределение массо-
вых расходов жидкости и пара, изменяются плотность смеси и ско-
рости фаз. Количество движения на входе в трубу и на выходе из
нее неодинаково. Поэтому при вычислении перепада давления в двух-
фазном потоке наряду с потерями иа трение Дртр и подъем смеси в
поле силы гравитации Дрг.с необходимо также учитывать и затраты
энергии на ее ускорение Друск. С учетом сказанного перепад
давления можно представить как сумму трех составляющих:
Др - Дртр + Дрг.с -|- Друск. (13.37)
Перепад давления, связанный с перемещением потока в вертикальной
плоскости, равен гидростатическому давлению столба смеси:
/
Дрг. С-="^рф/sin w = g sin (0 jj[p' (1— cp) + p"(p]dz, (13.38)
b
где co — угол наклона трубы к горизонту; z — координата; I —
длина трубы.
Ускорение потока в трубе постоянного сечения, связанное с из-
менением плотности .среды, приводит к изменению количества дви-
жения. Перепад давления, обусловленный ускорением потока, мож-
но выразить уравнением
Ар,«К = у + GXM. (13.39)
Индексы 0 и I относятся соответственно к началу и концу трубы. Ес-
ли воспользоваться уравнениями (13.13) — (13.16), то перепад дав-
ления, обусловленный ускорением потока, можно представить
в виде
^Руск
(1—х)а 1 __Г£
(1— ф)Р'л 1фр"
(1-О3 '
(1—ф) Р']о
(13.40)
С ростом давления различие плотностей жидкой и паровой фаз умень-
шается и соответственно снижается перепад давления, связанный с
ускорением потока.
Потери давления на трение зависят от средней массовой скорости
потока, режима течения, истинного объемного паросодержания, от-
ношения плотностей фаз, вязкости жидкости и пара, шероховатости
стенки и, наконец, от плотности теплового потока на стенке. Совмест-
ное воздействие перечисленных факторов на сопротивление трения
в настоящее время изучено еще недостаточно полно. Несмотря на
определенные успехи теоретических исследований, посвященных это-
му вопросу (см. монографию С. С. Кутателадзе и М. А. Стыриковича
[6]), потери на трение обычно рассчитываются с помощью эмпири-
ческих зависимостей и номограмм, построенных по опытным данным.
363
В ряде случаев, например для пузырькового режима течения,
наблюдается сравнительно равномерное распределение обеих фаз
по сечению трубы. Практически одинаковы или близки и скорости
фаз. В таких условиях для определения Артр можно воспользовать-
ся гомогенной моделью течения, согласно которой, вместо действи-
тельного двухфазного потока рассматривается однофазный с соот-
ветствующим образом осредненными параметрами. Перепад давле-
ния, обусловленный трением, можно представить в виде
Ар,гв = ^»р-П = ?®![1+4-^-1РЛ_, (13.41)
^Тр 2 1 d ъ 2р' [ \ р" ,/J d v '
где £—коэффициент сопротивления трения; —расходная средняя
скорость потока [см. формулу (13.18)]; I, d — длина и диаметр тру-
бы. Коэффициент £ определяется по уравнениям для турбулентно-
го изотермического движения однофазной жидкости, зависит от
числа Рейнольдса и относительной шероховатости стенки трубы.
Число Рейнольдса определяется по формуле
Re = -^, (13.42)
Рем
где
1
Рем .
X I * —х
Для технических шероховатых труб можно принять, что £ не за-
висит от числа Рейнольдса. Тогда из формулы (13.41) следует, что
с ростом х от 0 до 1 потери на трение возрастают линейно. Расчет
с использованием гомогенной модели течения дает удовлетворитель-
ные результаты при пузырьковом режиме течения, а также в случае
дисперсного течения при х близких к 1. При расчете потерь на тре-
ние в случае расходных массовых паросодержаний, существенно
отличающихся от 0 и 1, в формулу (13.41) вводится поправочный
эмпирический коэффициент ф:
ДртяМ'р—[1+4——И]—• <13лз>
нтр ъ г 2р/ [ 1 р" J d
По методике, разработанной В. С. Осмачкиным с сотр. [18], коэф-
фициент сопротивления трения В в (13.43) следует рассчитывать
по значению числа 1^е, в которое вместо рсм входит вязкость жидкой
фазы р/, а для поправочного коэффициента ф рекомендуется урав-
нение
ф
1 + 4 — -1]] °’2Х [1 -+ 0,57%0• (1-Х)2 X
k р" /J [
(13.44)
364
Здесь Fr = w^/gd-, wa — скорость циркуляции; % находится по фор-
муле (13.35). Расчет по формуле (13.44) дает удовлетворитель-
ное согласие с данными опытов в интервале давлений от 30 до
150 бар и средних массовых скоростей от.500 до 4000 кг/(м?-сек) при
кипении недогретой воды и пароводяной смеси.
Эмпирические соотношения для поправочного коэффициента ф
не имеют особых преимуществ перед методом использования номог-
рамм. Поэтому для определения ф широко используются номограм-
мы, построенные по опытным данным. Например, для пароводя-
ного потока в книге М. А. Стыриковича, О. И. Мартыновой и
3. Л. Миропольского [12] изложена обстоятельная методика рас-
чета сопротивления трения с помощью номограммы.
Для расчета потерь давления иа трение часто пользуются мето-
дом Мартинелли — Локкарта [17]. Этот метод разработан на ба-
зе опытных данных, полученных при течении двухфазных двух-
компонентных смесей воздуха с водой, бензином, керосином и раз-
личными маслами. Авторы рассмотрели стабилизованный адиа-
батный двухфазный поток с заданными расходами жидкости G'
и газа (пара) G". Физические свойства фаз по длине приняты посто-
янными. Градиент давления по длине трубы не меняется. Предпола-
гается, что жидкость и газ в трубе движутся раздельно, как, напри-
мер, в случае кольцевого режима течения, и вводятся следующие па-
раметры:
(13.46)
Здесь I—длина трубы; ApJlt/1 и &pYH—условные градиенты давле-
ния, которые имеют место при движении по трубе только жидкос-
ти (с расходом G') или только газа ((?"). Они определяются по фор-
мулам для однофазного потока: в случае ламинарного течения —
закон Пуазейля, в случае турбулентного — Блазиуса или Нику-
радзе.
Предполагается, что могут существовать следующие сочетания
режимов течения жидкой и газообразной фаз (соответственно)*:
1) турбулентный — турбулентный
2) вязкостный — турбулентный
3) турбулентный — вязкостный
4) вязкостный — вязкостный
Естественно, что добавление газа к потоку жидкости или жидкос-
ти к потоку газа изменяет критическое значение числа Re. Однако
* Сочетание режимов течения отмечается индексом при соответствующем
параметре -^т.т, Ф?к.т,т» -^в.т н г. д.
365
точные данные по этому вопросу пока отсутствуют. Принимается,
что турбулентный режим существует при числах Re.I; или Rer, боль-
ших 2000, а ламинарный — при ReH< или Rer, меньших 1000,
где Кеж == wod/v'; Rer = w'od/v"-, Wq, w'q — приведенные скорости
жидкости и пара; d — диаметр трубы.
Опытным путем установлено, что в случае кольцевого течения
Фж и Фг являются однозначными функциями параметра X. Эмпири-
ческие зависимости Фш и Фг от параметра X для всех четырех соче-
таний режимов течения жидкости и газа приведены на рис. 13.10.
Расчет перепада давления на трение по методу Мартинелли—
Локкарта проводится следующим образом. Вычисляют &рт/1,
крг11 и параметр X, азатем, определив ReH< и Rer, по рис. 13.10
с учетом режима течения фаз находят Фя{ или Фг. Наконец, по
одной из формул (13.45) вычисляют Др /1.
Одним из достоинств метода Мартинелли—Локкарта является то,
что при его использовании не требуется знать каких-либо трудно-
определяемых характеристик потока. Расчеты удовлетворительно
согласуются с опытом при движении двухфазных потоков различ-
ных составов: вода-—пар, вода —различные газы, смеси органиче-
ских жидкостей с воздухом или газом. Имеющиеся эксперименталь-
ные данные по двухфазным потокам жидких металлов подтверждают,
что метод Мартинелли — Локкарта применим и к этим системам.
Например, выполненное И. Т. Аладьевым с сотр. 11] исследование
сопротивления трения при движении паро-жидкостного потока ка-
366
лия (р = 1 -г 1,5 бар) показало, что расчет по методу Марти-
нелли — Локкарта удовлетворительно согласуется с результатами
измерений.
Сопоставление результатов расчета по гомогенной модели и по
методу Мартинелли — Локкарта позволяет сделать следующий вы-
вод. Расчет по гомогенной модели дает положительные результаты
при дисперсном течении, по методу Мартинелли — Локкарта —
при кольцевом. Для дисперсно-кольцевого течения опытные данные
располагаются в интервале значений, рассчитанных по этим методам.
По оценкам Уоллиса [15], опытные данные тем лучше согласуются
с расчетом по методу Мартинелли — Локкарта, чем больше жидко-
сти находится в пленке.
Метод Мартинелли — Локкарта разработан для адиабатных
потоков, имеющих постоянное значение х по длине канала. Рас-
смотрим, как можно распространить этот метод на случай кипя-
щей жидкости. Составляющие полного перепада давления [см. урав-
нение (13.37)]: Артр, АруСк и Арг.с зависят от паросодержания
потока и будут изменяться по длине трубы. Считая, что в трубу
поступает насыщенная жидкость, с учетом зависимостей (13.38) и
(13.40) для полного перепада давлений можно записать
Ар = — Артр Аруск | Арг, с
b dz
Р' 1
|- g sin со § Гр' (1 — ср) -|- р" ср] dz.
о
(13.47)
Последовательно проследим, как вычисляются составляющие
полного перепада давления. Обозначим Чг отношение градиента
давления, обусловленного трением двухфазного потока, к градиенту
давления, создаваемому жидкостью с расходом, равным расходу
смеси:
Падение давления на трение в двухфазном потоке с учетом (13.48)
можно записать следующим образом:
(13.49)
где — коэффициент сопротивления трения, рассчитываемый по
скорости циркуляции.
367
В случае постоянной плотности теплового потока для прираще-
ния паросодержания на длине dz из теплового баланса получим
dx = dz.
dpwr
Тогда, перейдя от z к переменной х, для падения давления на трение
в канале, в который поступает насыщенная жидкость, а покидает
Р_ис. 13.11. Зависимость параметра
Чг=Дртр/Др/’ от давления и расходного
массового паросодержания па выходе из
капала.
поток с паросодержанием х,
получим
•о
(13.50)
Предположив, что при
кипении режим течения обеих
фаз турболентный, можно ис-
пользовать приведенную ра-
нее зависимость Ф от X для
вычисления Т. На рис. 13.11
приведена зависимость [17]
= Стд-, (13.
Др' х J
о
от р И X. С помощью рис.
13.11 для заданного р и па-
___ росодержания на выходе из
трубы находится Т и по рассчитанному Др' определяется Дртр.
Для расчета Друси приращение объема смеси, наблюдаемое в
результате роста паросодержания от 0 до х
Аусм — (^см)х (исм)о — Н р, • (13.52)
можно определить по рис. 13.12.
Наконец, Дрг.с нетрудно рассчитать, если построить распреде-
ление ср по длине трубы, используя график на рис. 13.10.
Рассмотрим, как влияет обогрев на сопротивление трения. На
рис. 13.13 дано отношение Дртр/Др' при движении двухфазного
потока в обогреваемой и необогреваемой трубах [13]. В интервале
паросодержания от 0 до яДр (см. р = 49 бар) потери на трение
в обогреваемой трубе оказываются более высокими, чем при адиа-
батном течении. Связано это с тем, что образующиеся пузырьки,
интенсивно перемешивая жидкость в пристеночной пленке, вносят
368
дополнительное возмущение и тем самым увеличивают Дртр. При
высоких х на сопротивление трения существенным образом влияет
волновое движение на поверхности пленки. При хДр пленка
становится настолько тонкой, что волновое движение на ее поверх-
ности прекращается и Дртр уменьшается. Это явление получило
название кризиса сопротивления.
Рис. 13.12. Зависимость приращения объема
смеси от давления и от расходного массового
паросодержания иа выходе из канала.
Увеличение сопротивления, вызванное наличием обогрева при
движении воды, нагретой до температуры насыщения в области
давлений от 50 до 200 бар и х<хАр можно учесть с помощью
уравнения, предложенного Н. В. Тарасовой и А. И. Леонтьевым [13]:
1+0,0044 . (13.53)
(й!ртр/^г)о \ pay /
Здесь (dpTp/dz)0, (d'p^ldz)q — соответственно градиенты сопротивле-
ния при адиабатном течении и при течении в обогреваемой трубе;
qa измеряется в вт1м*\ рш — в кгЦм^сек'),
369
Рис. 13.13. Зависимость Дртр/Др' от х при движении
двухфазного потока в обогреваемой (черные точки) и
необогреваемой (светлые точки) трубе. Штрих-пунк-
тир— расчет по гомогенной модели:
(. ,®~р-49 бар; д — р=98 бар; □,В»р == 147 бар;
V.T —р=196 бар-, рш=2000 кг/(л12-ее/с).
370
Тепловая нагрузка оказывает влияние на сопротивление трения
и при кипении недогретой жидкости. В интервале давлений от 1 до
180 бар и плотности теплового потока от 5- 10б до 5-10° вт!мг потери
на трение можно рассчитать по уравнению, предложенному
П. Г. Полетавкиным [10]:
Яе
7 n0,1 5
Г
1,5-10»
(dpTp/dz)u
Re1 ’8 А/3,63
Re < 4,5 • 104;
(13.54)
(4pTp/dz)g
(б/ртр/С?2)о
„0,7 0,15
0,56—----------
(ReAOi)0,63
Re > 4,5 101.
циркуляции. Если
— 0,5 RBX -|- ^вых)’
Здесь А/п = ts — — недогрев жидкости; Re — w()dofv'—число
Рейнольдса; v' — кинематический коэффициент вязкости жидкости,
определяемый по среднемассовой температуре потока /ср = 0,5 X
X (Ат находят по формуле (13.23); L т{ температу-
ра потока в точке начала развитого кипения:
л/А16
—Zn. к == 1,1-10-® ----
<7С измеряется в вт/м*, р— в бар-, да() — скорость
кипение имеет место по всей длине трубы, то £(.р — VBX -г <.вых/,
4jX, Азых — температуры потока на входе в канал и на выходе из него.
Формула (13.54) подтверждена опытными данными в интервале
чисел Рейнольдса от 101 до 7,7- 10г’; А/п от 6 до 150° С для труб и ка-
налов с эквивалентным диаметром от 5,35 до 7,5 мм и l/da
от 20 до 100.
Некоторые дополнительные сведения по методике расчета паде-
ния давления в парогенерирующих каналах можно найти в моно-
гр афи и Л. То и г а [ 141.
§ 13.5. Критическое истечение двухфазного потока
Расход газа, вытекающего через сопло или цилиндрический на-
садок из сосуда, в котором поддерживается постоянное давление,
будет возрастать, если давление в окружающей среде уменьшается.
После достижения определенного перепада давлений скорость ис-
течения в горловине сопла или на выходе из насадка достигает ско-
рости звука. Дальнейшее снижение противодавления не изменяет рас-
хода. Такой режим истечения называется критическим. Расход и от-
ношение давлений в окружающей среде и в сосуде, при котором до-
стигаются условия критического истечения, также называют кри-
тическими. Критическое истечение наблюдается и в случае сжима-
емой двухфазной среды.
Вопрос о критическом истечении представляет интерес с точки
зрения анализа возможных аварийных ситуаций на АЭС. Такое ис-
371
течение возникает, например, при частичном или полном разрыве
трубопровода системы циркуляции теплоносителя. Если даже си-
стема заполнена водой под давлением (как в случае реактора ВВЭР),
то из-за резкого падения давления часть теплоносителя испарится
и поток при истечении будет двухфазным. Чтобы заблаговременно
принять необходимые меры защиты, нужно уметь рассчитывать
время опорожнения, которое определяется величиной критиче-
ского расхода через поврежденный трубопровод.
Критический расход легко определить, если известна скорость
звука с. В случае однофазных потоков обычно режим течения при-
нимается изоэнтропийным и скорость звука определяется с помощью
соотношения Лапласа:
с2 = (<%.'j , /13.55)
\ dv Js
где v — удельный объем газа (индекс s означает постоянство энтро-
пии). Однако в случае двухфазного адиабатного потока течение не
всегда можно принять изоэнтропийным. Действительно, течение
в канале сопровождается уменьшением давления и соответствующим
снижением температуры насыщения. Если температура на поверх-
ности капель или пленки жидкости, текущей на стенке, при измене-
нии давления в потоке меняется достаточно быстро и практически
совпадает с температурой пара (температурой насыщения), то для
охлаждения массы жидкости, сосредоточенной внутри капель или
в пленке, требуется определенное время. Следовательно, в двухфаз-
ном адиабатном потоке температура жидкости может отличаться от
температуры пара.
В случае ускоренного движения потока из-за различной
плотности фаз ускорение капель и пара будет различным. Для вос-
становления механического равновесия в потоке требуется опреде-
ленное время. Процессы выравнивания температур и скоростей фаз
вследствие конечных отклонений протекают необратимым образом
и сопровождаются ростом энтропии.
Следует иметь в виду, что в каналах различной геометрической
формы и длины при одинаковых параметрах потока возможны раз-
личные режимы течения, для которых критический расход и крити-
ческое отношение давлений будут неодинаковы.
Для расчета критических условий в каждом конкретном
случае необходимо знать, каков режим течения двухфазного
потока, так как для разных режимов математические модели про-
цессов будут различными. В настоящем параграфе рассмотрено
критическое истечение двухфазного потока в случае кольцевого
и дисперсного режимов течения.
Как показывает опыт, истечение при разрыве длинных трубо-
проводов небольшого диаметра можно рассматривать как квази-
равновесное. Для этого случая можно воспользоваться методикой
расчета, разработанной Леви [8].
372
Рассмотрим адиабатный поток, в котором жидкая и паровая фа-
зы находятся в термодинамическом равновесии. Если пренебречь
трением, то при кольцевом режиме течения в горизонтальной трубе
для жидкости и пара можно записать уравнения сохранения коли-
чества движения:
dp'4-р'Ши^и = 0; (13.56).
dp" + у [d (G" а»,") + ®,; <Ю'] = 0. (13.57)
Здесь dp' и dp" — падение статического давления в жидкости
и в паре; ay„, — истинные скорости фаз; G' — f (1 — х) рш,
G" = fxpw; p'wndwa и d (G"w„) — изменение количества движения
жидкости и пара; w^dG'— приращение количества движения паро-
вой фазы вследствие присоединения к ней испарившейся жидкости.
Предположим, что изменение паросодержания потока сопровож-
дается обменом количества движения между жидкостью и паром, и
в результате для каждой фазы изменение статического давления оди-
наково, т. е. dp' = dp" — dp. Если уравнения (13.56) и (13.57) ум-
ножить соответственно на f' и f" и сложить, то получим
dpf + d Н G') + d (to" G") = 0.
. Проведя замену WnG' — , и W'^G" = , получим
йр-НЙ)Ч4^7 + -Т-1 = 0- <13'58)
Lp'(1—-<p) _p"<pJ
Выражение в квадратных скобках можно рассматривать как сред*
ний удельный объем двухфазной смеси [см. уравнение (13.40)1:
(1—х)а . х2
У = ----->.-------
р'(1-~ф) Р"Ф
(13.59)
Поскольку мы рассматриваем адиабатный поток без трения, в кото-
ром процессы межфазного обмена протекают обратимым образом, то
течение принимается изоэнтропийиым (S = const) и формулу (13.58)
можно переписать так:
= • (13.60)
\доем / s
Это отношение описывает критическое истечение двухфазного
потока. Такой вывод можно сделать, если учесть, что, согласно со-
отношению Лапласа (13.55),
f др \
\ д^см / 8
са
373
Следовательно, чтобы с помощью соотношения (13.60) определить
среднюю массовую скорость критического истечения двухфазного
изоэнтропийного потока, необходимо определить {dp/duCM)a.
Для полного дифференциала удельного объема смеси имеем
^см —+ dx
\ др Jx \ дх Jp
или
Энтропию двухфазного потока определим по уравнению
S = S'(l-x)4-S"x, (13.62)
где S' и S"— энтропия жидкости и пара.
Изменение энтропии парожидкостного потока можно записать
так:
dS=l — dp+(~'I dx.
\др /х \ дх 1Р
В изоэнтропийном потоке имеем
Отсюда, используя формулу (13.62), получим
/(£"—S'). (13.63)
Частные производные )_ и находятся дифференциро-
\ ил / Р \ О р J
ванием уравнения (13.59), при этом считается, что р' и р" пос-
тоянны, а ф = f(x). Установим связь между х и ф. Если (13.56)
умножить и разделить на G'2, а затем вычесть из (13.58), то
получим
(ри/)2 Г(1 — х)а р'х*1 (1-х)а
р' 1 — ср р"ср 2 (1 — <р)2
Приняв ф = 0 прих = 0, проинтегрируем (13.64) и решим
тичное уравнение:
(13.64)
квадра-
(13.65)
374
Дифференцируя (13.59), с учетом выражения (13.65) нетрудно
получить зависимости для (dv^/dx^p и (dvCM/dp)x от ср, которые
здесь не приводятся ввиду их громоздкости.
Таким образом, для заданных на входе в трубу р и х можно опре-
делить производные (d,v/dp)s, (dvCM/dp)Xi (dvCM/dx)p и с помощью
уравнения (13.60) рассчитать среднюю массовую скорость критиче-
ского истечения. Результаты расчета по методу Леви в виде графи-
Рис. 13.14. Зависимость средней массовой скорости критиче-
ского изоэитропийного истечения от х при различных р.
ков (pto)s=f(x, р) приведены на рис. 13.14. Пользуясь рис. 13.14 для
заданных р и х> можно определить (pw)s и найти искомый крити-
ческий расход. • 1
Метод Леви позволяет определять критический расход для длин-
ных труб (отношение длины к диаметру более 10),. В этом случае
расхождение с опытом не превышает 10%.
Критическое истечение через короткие трубы, диафрагмы и соп-
ла происходит при больших градиентах давления (больших ускоре-
ниях паровой фазы). Пленка жидкости на стенке разрушается, и ос-
новная масса жидкости (95 — 98%) движется в виде капель, взве-
шенных в паровом потоке. Отношение истинных скоростей фаз w^/w'^
вблизи критического сечения при низких давлениях равно 0,25 —
0,4; перегрев капель в этих условиях может достигать несколь-
ких десятков градусов. Следовательно, поток характеризуется зна-
чительной неравновесностью, течение нельзя считать изоэнтропий-
ным, и метод Леви для этого случая неприменим.
В работе Г. В. Циклаури, В. С. Данилина и Л. С. Селезнева [16]
рассмотрен вопрос о критическом, истечении. дисперсного потока.
Вводятся следующие упрощающие предпосылки: капли жидкости
375
равномерно распределены в объеме паровой фазы; смесь монодис-
персная (содержащая капли одного размера); двухфазный поток —
одномерный; трение пара на стенках не учитывается; пар имеет тем-
пературу насыщения, капли жидкости могут быть перегреты.
Система, состоящая из уравнений сохранения массы, импульса и
энергии, записанных отдельно для жидкости и пара, решается чис-
ленно. Результаты расчета [16] удовлетворительно согласуются с
экспериментальными данными.
СПИСОК ЛИТЕРАТУРЫ
1. Аладьев И. Т. и др. Расчет теплообмена при кипении калия в трубах.—
В сб.: Теплообмен, гидродинамика и теплофизические свойства веществ.
М., «Наука», 1968, с. 18.
2. Арманд А. А. Исследование механизма движения двухфазной смеси в вер-
тикальной трубе. — В сб.: Гидродинамика и теплообмен при кипении
в котлах высокого давления. Под ред. М. А. Стыриковича. М., Изд-во
АН СССР, 1955, с. 21.
3. Берглес А., Сю М. Исследование режимов течения кипящей воды. —
В сб.: Достижения в области теплообмена. Под ред. В. М. Боришаиского.
М., «Мир», 1970, с. 30.
4. Берглес А., Лопина Р., Фиори М. Исследование критических тепловых
потоков и режимов течения пароводяной смеси в трубах. — «Теплопере-
дача. Сер. С.», М., «Мир», 1967, № 1, с. 82.
5. Викс М., Даклер А. Новый метод измерения распределения размеров ка-
пель в двухфазном потоке. — В сб.: Достижения в области теплообмена.
Под ред. В. М. Боришанского. М., «Мир», 1970, с. 170.
6. Кутателадзе С. С., Стырикович М. А. Гидравлика газо-жидкостных систем
М., Госэнергоиздат, 1958.
7. Ларсен П., Тонг Л. Паросодержание при кипении недогретого потока. —
«Теплопередача. Сер. С. М., «Мир», 1969, № 4, с. 7.
8. Леви С. Расчет двухфазного критического расхода. — «Теплопередача.
Сер. С.» М., «Мир», 1965, № 1, с. 64.
9. Миропольский 3. Л., Шнеерова Р. И., Карамышева А. И. Паросодержание
при напорном движении пароводяной смеси с подводом тепла и в адиа-
батических условиях.—«Теплоэнергетика», 1971, №5, с. 60.
10. Полетавкин П. Г. Гидравлическое сопротивление при поверхностном
кипении воды. — «Теплоэнергетика», 1959, № 12, с. 13.
11. Поломик Р. Применение метода баланса полной энергии к анализу ско-
ростей фаз в системах с кипящим потоком. — «Теплопередача. Сер. С.»,
М., «Мир», 1966, № 1, с. 8.
12. Стырикович М. А., Мартынова О. И., Миропольский 3. Л. Процессы
генерации пара на электростанциях. М., «Энергия», 1969.
13. Тарасова Н. В., Леонтьев А. И. Гидравлическое сопротивление при те-
чении пароводяной смеси в обогреваемой вертикальной трубе. — «Теп-
лофизика высоких температур», 1965, т. 3, № 1, с. 115.
14. Тонг Л. Теплоотдача при кипении и двухфазное течение. М., «Мир», 1969.
15. Уоллис Г. Одномерные двухфазные течения. М., «Мир», 1972.
16. Циклаури Г. В., Данилин В. С., Селезнев Л. И. Адиабатные двухфазные
течения. М., Атомиздат, 1973.
17. Lockhart R. W., Martinelli R. С. Proposed Correlation of Data for
Isothermal Iwo-Phase Two-Component Flow in Pipes. — «Chem. Engng
Progr.,» 1949, v. 45, p. 39.
18. Osmachkin V. S., Borisov V. D. Pressure drop and heat transfer for flow
of boiling water in vertical rod bundles, B. 4.9. 4-th Internal. Heat Trans-
fer Conf., Paris—Versailles, 1970.
ГЛАВА 14
ТЕПЛООБМЕН ПРИ КИПЕНИИ В ТРУБАХ
§ 14.1. Особенности теплообмена при кипении жидкости
в трубах
Закономерности теплообмена при кипении в условиях вынуж-
денного движения можно проследить, рассматривая изменение тем-
пературы жидкости и температуры стенки по длине обогреваемой
трубы. Пусть плотность теплового потока qG постоянна по поверх-
ности, в трубу поступает недогретая до ts жидкость, а покидает ее
перегретый пар. На рис. 14.1 показано распределение темпе-
ратуры потока t и температуры стенки /с1, /,,2 и tc3 для трех значе-
ний плотности теплового потока qP1 <Z qc2 <Z qc3 в зависимости от мас-
сового расходного паросодержания, которое линейно связано с дли-
ной трубы (см. § 13.2). Температура потока начиная от входного се-
чения линейно возрастает до тех пор, пока не достигнет температуры
насыщения (при х = 0), а затем остается постоянной и равной tSi
пока не испарится вся жидкость (х = 1). Дальнейший рост темпе-
ратуры потока (прих > 1) связан с перегревом пара.
Проследим изменение режимов теплообмена для случая qc = qcl
и соответственно tc = tcl. Вблизи от входа в трубу темпера-
тура теплоносителя и температура стенки ниже ts, поток здесь од-
нофазный и, значит, теплоотдача определяется по соответствующим
уравнениям для однофазного конвективного теплообмена.
В обогреваемой трубе температура жидкости у стенки выше,
чем температура в ядре потока. Поэтому нетрудно представить себе
случай, когда вся жидкость еще недогрета до температуры насыще-
ния, а иа стейке имеет место кипение. Для этого необходимо только,
чтобы температура стенки несколько превышала температуру насы-
щения. Такой процесс кипения называется кипением недогретой
жидкости или кипением с недогревом. Зона кипения недогретой
жидкости находится между сечением, в котором tG — ts и х — хил.
(начало кипения), и сечением, в котором i= t8 и х = 0. После того
как температура потока достигает температуры насыщения (х—0),
начинается пузырьковое кипение насыщенной жидкости. Эта зона
характеризуется меньшими температурными напорами и, следова-
тельно, более высокими коэффициентами теплоотдачи. По мере про-
движения теплоносителя в область высоких паросодержаиий коли-
чество влаги, находящейся в потоке, уменьшается и устойчивость
пузырькового кипения понижается.
13 Зак. 792 377
При некотором паросодержания х = хкр наступает кризис те-
плоотдачи: контакт жидкости с поверхностью нагрева прекращает-
ся и наблюдается рост температуры стенки. Кризис теплоотдачи при
кипении парожидкостной смеси (т. е. при х> 0), а также при неболь-
ших недогревах представляют собой переход от дисперсно-кольце-
вого режима течения к дисперсному; при значительных недогревах
холодная жидкость, сосредоточенная в ядре потока, отделяется от
стенки пленкой пара. Обычно по аналогии с большим объемом, не
Рис. 14.1, Изменение температуры потока и темпе-
ратуры стенки в зависимости от расходного паро-
содержания х (или, что то же, по длине трубы /)
для трех значений /7с(4с1<9с2<<7сз).
вдаваясь в детали гидродинамики, режим кипения при х > хКр на-
зывают пленочным. Механизм кризиса теплоотдачи в условиях вы-
нужденного движения более подробно рассмотрен в § 14.5.
Переход от пузырькового кипения к пленочному происходит на
участке трубы длиной в несколько миллиметров. Так как при пле-
ночном кипении коэффициент теплоотдачи значительно меньше,
чем при пузырьковом, то в зоне перехода от пузырькового кипения
к пленочному имеет место резкий рост температуры стенки. В обла-
сти пленочного кипения (т. е. в интервале от х = х1ф до х = 1)
наблюдается понижение температуры стенки. Связано это с тем,
что коэффициент теплоотдачи несколько возрастает с ростом расход-
ной средней скорости потока. После полного испарения жидкости,
т. е. при х > 1, разность /с— t определяется закономерностями
теплообмена при однофазном течении.
Как видно на рис. 14.1, с ростом тепловой нагрузки хкр умень-
шается, а максимум температуры стенки увеличивается. Подъем тем-
пературы стенки в районе кризиса зависит от давления насыщения,
378
плотности теплового потока, средней массовой скорости и лежит в
пределах от нескольких градусов до 1000° С и более. Таким образом,
кризис теплообмена может привести к недопустимому повышению
температуры твэлов.
§ 14.2. Механизм образования пузырьков
Процессы кипения жидкости при вынужденном движении и при
свободной конвекции в большом объеме имеют много общего. Кипе-
ние начинается после того, как температура поверхности нагрева
превысит температуру насыщения. Зарождение пузырьков происхо-
дит в определенных точках поверхности — центрах парообразова-
ния, представляющих собой небольшие углубления. Число центров
возрастает с ростом перегрева поверхности. Термодинамические со-
отношения, полученные в § 12.2 для критического радиуса пузырь-
ка, остаются справедливыми и в случае вынужденного движения.
Скорость роста пузырьков, так же как при кипении в большом объе-
ме, уменьшается с ростом давления.
Образовавшиеся на стенке трубы пузырьки после их выхода из
углублений попадают в движущийся пристеночный слой жидкости
и начинают перемещаться вдоль стенки. Скорость движения мелких
и крупных пузырей, находящихся на поверхности нагрева, пример-
но одинакова и составляет около 80% средней скорости потока. По-
скольку пузырек имеет контакт с горячей стенкой и окружен пере-
гретой жидкостью, то его рост продолжается. Достигнув определен-
ного размера, он отрывается от стенки и уносится в ядро потока.
При кипении в большом объеме вся жидкость имеет температуру,
несколько превышающую температуру насыщения, в случае вы-
нужденного движения жидкость в ядре потока может быть недог-
рета.
При кипении недогретой жидкости паровая фаза в пузырьках,
после того как они отрываются от стенки и попадают в холодные
слои жидкости, начинает конденсироваться. Визуальные исследова-
ния механизма кипения недогретой жидкости, выполненные Г. Г. Тре-
щевым, показали, что при низких давлениях (до 4 бар) пузырь-
ки растут очень быстро — взрывообразно, скорость роста достигает
12 м!сек\ форма пузырька близка к полусфере. Пузырьки, достигнув
определенного (максимального) размера, сравнительно медленно
уменьшаются и исчезают. При этом значительная часть пузырьков
исчезает, так и не оторвавшись от поверхности нагрева. Отмеченные
особенности поведения пузырьков нетрудно объяснить. В начальной
стадии растущий пузырь выталкивает из пристеночного слоя пере-
гретую жидкость. Поскольку пузырек оказывается окруженным пе-
регретой жидкостью, то скорость его роста велика. В процессе рос-
та пузырек частично проникает в холодные слои жидкости, и на его
вершине начинается интенсивная конденсация пара. Наблюдаемое
при этом неустойчивое равновесие — испарение жидкости в основа-
нии пузыря и конденсация пара у его вершины — довольно быстро
13* 379
нарушается, размеры пузырька начинают уменьшаться, и он исче-
зает.
При давлениях выше 4 бар в связи с более высокой плотностью
пара рост пузырьков происходит сравнительно медленно, скорость
роста составляет около 0,2 м/сек. Достигнув максимального
размера, пузырьки быстро уменьшаются. В связи с медленным
ростом гидродинамические силы, действующие на пузырек, невели-
ки и его форма близка к сфере. Отрыв пузырька происходит в тот
момент, когда его размер близок к
w
Рис. 14.2. Обтекание потоком жид-
кости пузырька пара, находящего-
ся на плоской поверхности.
максимальному.
Рассматривая силы, действую-
щие на пузырек пара, находящий-
ся на поверхности нагрева, следует
помнить, что он располагается
в вязком подслое и омывается пото-
ком жидкости, имеющим градиент
скорости. Обтекание такого пу-
зырька пара можно рассматривать
как обтекание сферы, касающейся
ПЛОСКОСТИ, потоком жидкости с
градиентом скорости (рис. 14.2).
Распределение давления по по-
верхности сферы дает результи-
рующую силу, направленную в сто-
рону большей скорости. В работе И. Г. Друкера [7] показано, что
гидродинамическая сила, действующая на неподвижную сферу и пы-
тающаяся оторвать ее от поверхности, определяется соотношением
(14.1)
где о0 — объем сферы; р' — плотность жидкости; со — градиент
скорости; — скорость набегающего потока в плоскости,
соответствующей центру сферы. Коэффициент пропорциональности
k по приближенным оценкам лежит в пределах 0,1 -4- 0,3.
Пузырек удерживается на стенке силой поверхностного натяже-
ния:
Fff-C(0)Do, (14.2)
где С(0) — коэффициент, зависящий от краевого угла; D — диа-
метр пузырька; о — коэффициент поверхностного натяжения.
Если пренебречь архимедовой силой*, то диаметр пузырька, от-
рывающегося от поверхности нагрева, можно определить из усло-
вия равенства сил:
С(0)оПо = ^Р'^=оСо —.
6
* Расчеты, проведенные И. Г. Друкером, показали, что гидродинамиче-
ская подъемная сила, действующая на пузырек, находящийся на стенке,
в десятки раз превосходит архимедову силу.
380
Приняв — coDq/2, для отрывного диаметра пузырька получим
выражение [7]
3 /~"~сГ
D0^Ci/~, (14.3)
у со2р'
где С — коэффициент, зависящий от краевого угла.
Гидродинамическая сила пропорциональна разности скоростей
жидкости и пузырьков. После отрыва пузырька от стенки он увле-
кается потоком и его относительная скорость резко снижается. Поэ-
тому гидродинамическая сила уменьшается и одновременно уменьша-
ется скорость движения пузырька от поверхности нагрева. Оценки
показывают: чем меньше отношение отрывного диаметра к толщине
вязкого подслоя, тем быстрее снижается скорость поперечного дви-
жения пузырька.
Снижение поперечной скорости движения пузырьков в направ-
лении нормали от стенки должно приводить к росту истинного объем-
ного паросодержания иа границе вязкого подслоя. Из сказанного
следует, что рост скорости потока способствует уменьшению Do и,
как следствие, повышению объемного паросодержания в вязком под-
слое.
§ 14.3. Теплоотдача при кипении насыщенной жидкости
1. Теплоотдача при пузырьковом кипении. В случае кипения жид-
кости в условиях вынужденного движения перенос тепла от поверх-
ности нагрева в ядро осуществляется пузырьками пара, образовав-
шимися на стенке, и конвекцией жидкости. Количество тепла, пере-
носимого паром, зависит в основном от плотности теплового потока
на стенке. Количество тепла, переносимого путем конвекции жид-
кости в случае малых паросодержаний (сначала рассмотрим кипе-
ние при х & 0), определяется скоростью циркуляции. Из сказанно-
го следует, что при кипении в условиях вынужденного движения иа
коэффициент теплоотдачи наряду с плотностью теплового потока
оказывает влияние и скорость циркуляции.
В зависимости от соотношения плотности теплового потока и ско-
рости циркуляции вклад кипения (т. е. переноса тепла пузырьками
пара) и конвективного переноса в процесс теплоотдачи будет неоди-
наковым. Как видно из рис. 14.3, при малых скоростях циркуляции
коэффициент теплоотдачи практически не зависит от скорости (ли-
нии 1 и 2), определяется в основном процессом кипения и с увеличе-
нием плотности теплового потока возрастает. По мере увеличения
скорости циркуляции зависимость а от qc постепенно становится не-
существенной (линии 1 и 2 сходятся) и начинает проявляться зависи-
мость а от ау0 (линия 3). Приведенный пример показывает, что можно
выделить три характерные области: в первой коэффициент теплоот-
дачи зависит в основном от плотности теплового потока [а = f(qa}\,
во второй области коэффициент телоотдачи зависит в основном от
381
скорости [а = /(w0)l, и в третьей — коэффициент теплоотдачи за-
висит как от скорости, так и от плотности теплового потока [а =
= f Иь 7с)]-
В первой области коэффициенты теплоотдачи при кипении в тру-
бах обычно несколько ниже, чем при пузырьковом кипении в боль-
шом объеме:
aKim'-M0,7 4- l,0)a6jO, (14.4)
где аб-0 — коээффициент теплоотдачи при кипении в большом объе-
ме. В случае кипения воды для определения коэффициента теплоот-
Рис. 14.3. Теплоотдача при кипении воды в усло-
виях вынужденного движения [18]:
1 — <7с=8,1 • 105 вт/м2; 2 — <7с=2,3 • 105 вт/м2; 3—-расчет по
уравнению для вынужденного движения жидкости (без
кипения).
дачи в этой области можно воспользоваться зависимостями, пред-
ложенными Н. Г. Рассохиным с сотр. [16]:
оскип = 3,lp°-25 q^3 при l^.p^8Q6ap;
aKira = 0,027р1 *33 q-J3 при 80 200 бар, (14.5)
где qc измерено в em/ж2, ар — в бар.
Во второй области коэффициент теплоотдачи акоп определяется
по уравнениям для однофазного конвективного теплообмена в пред-
положении, что жидкость имеет температуру насыщения и движется
со скоростью циркуляции ®0-
Третью область можно рассматривать как переходную из первой
области во вторую. Для вычисления коэффициента теплоотдачи в
третьей области можно воспользоваться интерполяционной фор-
мулой С. С. Кутателадзе [101
% = “„Ок1/1 + (—У <14-6)
|/ \акон/
где акип определяется по формуле (14.5).
382
Чтобы рассчитать теплоотдачу применительно к конкретным
условиям, следует предварительно рассчитать и сопоставить коэф-
фициенты теплоотдачи акип и акоп. Если один из коэффициентов
окажется пренебрежимо малым по сравнению с другим, то искомый
коэффициент теплоотдачи принимается равным либо акои, либо
аиип. Если коэффициенты теплоотдачи соизмеримы, то расчет сле-
дует проводить по формуле (14.6).
В приведенном методе расчета не учитывалось влияние паросо-
держания потока иа теплоотдачу. Однако с ростом паросодержа-
ния плотность двухфазной среды уменьшается, а скорость жидкос-
ти, текущей у стенки, увеличивается, что способствует некоторому
росту коэффициента теплоотдачи.
При кипении воды в интервале давлений от 2 до 170 бар и плот-
ностей теплового потока от 8-104 до 6-10° emlM? влияние паросодер-
жания иа коэффициент теплоотдачи можно учесть с помощью форму-
лы, предложенной В. М. Боришанским [5]:
—= 1/ 1 + 7-10-9 (14.7)
ап И \ qc / к ап J
где ап определяется по формуле (14.6); а1ШП = (0,7 -т-1)аб>0; =
= wQ [х + (1 — х)] — расходная средняя скорость потока.
На коэффициент теплоотдачи при кипении жидкости в трубах,
как и при кипении в большом объеме, могут оказывать влияние и та-
кие факторы, как материал поверхности нагрева, способ ее обработ-
ки, степень коррозии поверхности, толщина покрывающих ее загряз-
нений, а также краевой угол смачивания. Приведенные выше зави-
симости не учитывают влияния отмеченных факторов. Как показы-
вает опыт, благодаря мерам, принимаемым на тепловых и атомных
электростанциях по очистке питательной воды и предотвращению
загрязнения поверхностей нагрева, отклонения действительных зна-
чений коэффициента теплоотдачи от значений, рассчитанных по фор-
мулам, обычно не превосходят ± 30%. В практических инженер-
ных расчетах необходимость знания коэффициентов теплоотдачи при
кипении в трубах с более высокой точностью возникает сравнитель-
но редко. Действительно, благодаря высоким коэффициентам тепло-
отдачи при развитом пузырьковом кипении разность температур
между стенкой и жидкостью редко превосходит (25 4- 30)° С. Поэ-
тому если по условиям работы системы задана плотность теплового
потока на стенке qc, то погрешность в коэффициенте теплоотдачи в
Ч- 30% приведет к ошибке в температуре стенки не более 10° С,
что в большинстве случаев несущественно.
Если тепло к кипящей жидкости подводится через стенку от гре-
ющего теплоносителя, имеющего заданную температуру, то неточ-
ность в знании коэффициента теплоотдачи приведет к ошибке в рас-
383
чете величины поверхности нагрева. Оценки [16] показывают, что
для промышленных теплообменных аппаратов обычно отношение
ЯкиЖ + Яс + Яок) менее 0,5 (здесь #х, Ro, Яок, Якип — терми-
ческие сопротивления переходу тепла от греющего теплоносителя к
стенке, самой стенки, оксидной пленки и от стенки к кипящей жид-
кости) и погрешность в определении а со стороны кипящей жидкос-
ти, равная ± 30%, приводит к погрешности в величине поверх-
ности нагрева менее 15%.
2. Режим испарения с поверхности пленки. В случае кольцевого
и дисперсно-кольцевого режимов течения перенос тепла через плен-
ку жидкости осуществляется пузырьками пара и конвекцией жид-
кой фазы. При высоких паросодержаниях, а следовательно, боль-
ших расходных средних скоростях потока конвективный перенос
тепла в пленке жидкости становится настолько интенсивным, что
существенно снижается перегрев стенки. Образование пузырей за-
трудняется, и кипение в пленке либо совсем прекращается, либо ста-
новится столь незначительным, что не вносит заметного вклада в пе-
ренос тепла. В этом случае тепло в основном расходуется иа испа-
рение жидкости с поверхности пленки. Изменение механизма пере-
носа тепла, естественно, сказывается на закономерностях тепло-
отдачи. Основным фактором, влияющим иа теплоотдачу, будет уже
не тепловой поток, а скорость двухфазной смеси. Для режима с
испарением пленки коэффициент теплоотдачи можно определить по
формуле Денглера и Аддомса [23]:
= (14.8)
акон "|/Хт. т
где акон — коэффициент теплоотдачи, определяемый по формулам
для однофазного конвективного теплообмена при турбулентном те-
чении жидкости в трубах (рассчитывается по приведенной скорости
жидкости ; свойства жидкости находятся по температуре насы-
щения); Хт.т — параметр Мартинелли — Локкарта (см. § 13.4).
3. Теплоотдача при пленочном (дисперсном) режиме течения. В
случае высоких массовых расходных паросодержаний критические
плотности теплового потока невелики, кризис пузырькового кипения
не вызывает опасного роста температуры стенки и работа поверх-
ности нагрева становится возможной в условиях дисперсного тече-
ния. Поэтому практически важно уметь рассчитать коэффициенты
теплоотдачи при дисперсном течении теплоносителя. В этом случае
поверхность трубы омывается паром. Естественно предположить,
что закономерности теплоотдачи в этой области близки к законо-
мерностям однофазного течения пара. На базе уравнения для од-
нофазного конвективного теплообмена 3. Л. Миропольским [11]
предложено уравнение для расчета коэффициента теплоотдачи на
384
участках трубы с дисперсным режимом течения:
г/ л / \ 0 ’ ^ / riroiri \ О > 8 Г п» "10,8
^- = 0,023 у, (14.9)
\ а'с / \ P' / L Р' J
где У = 1 — 0,1 (^—I)0-4 (1—л:)0-4; Vc, а"с— кинематическая
вязкость и температуропроводность пара при температуре стенки.
Все остальные свойства пара и жидкости выбираются по тем-
пературе насыщения.
Уравнение (14.9) удовлетворительно согласуется с опытными дан-
ными для воды (отклонения не более ± 25%) в интервале давлений
от40 до 220 бар и массовых скоростей от 1000 до 2000 кг/(м?-сек). Для
массовых скоростей от 350 до 700 кг/(ж2 •сек') имеются расчетные реко-
мендации в работе [21].
4. Теплоотдача при кипении щелочных металлов. Как отмечено в
гл. 12, кипение щелочных металлов характеризуется неустойчи-
востью и большими перегревами, необходимыми для возникновения
кипения. Имеющиеся опытные данные свидетельствуют о том, что
перегревы жидкости могут составлять десятки и даже сотни граду-
сов. Вследствие высокой температуры насыщения щелочных метал-
лов* даже сравнительно небольшие перегревы стенки могут привес-
ти к ее расплавлению. Поэтому наряду с изучением теплоотда-
чи большое внимание уделяется разработке методов получения ус-
тойчивого режима кипения щелочных металлов при небольших пе-
регревах стенки.
Теплоотдача при кипении щелочных металлов, так же как и при
кипении воды, зависит от режима течения, средней массовой скорос-
ти, плотности теплового потока, давления, условий на поверхности
нагрева.
В настоящее время режимы течения щелочных металлов изу-
чены недостаточно. Опираясь на опытные данные для неметалли-
ческих двухфазных потоков, можно предположить, что для щелоч-
ных металлов при низких давлениях в широком диапазоне расход-
ных массовых паросодержаний [х Ту (2 4- 3)%] характерны коль-
цевой и дисперсно-кольцевой режимы течения.
Кипение недогретого жидкого металла практически исключено.
Объясняется это тем, что для вскипания металла необходимы боль-
шие перегревы. Поэтому после вскипания щелочных металлов доволь-
но быстро устанавливается кольцевой или дисперсно-кольцевой ре-
жим течения. В пленке жидкости, текущей по стенке, возможно ки-
пение.
По данным работ [2,4], коэффициент теплоотдачи при кипении
калия в трубах диаметром 4—10 мм в диапазоне р от 0,2 до 4 бар,
х от 0,04 до 0,8, pay от 22 до 1490 кг/(.м2-сек), qc от 10б до 1,4-1015впг!м*
Для калия ls ~= 756,9° С, для натрия ts = 881,7° С.
385
близок к значениям а при кипении воды в условиях большого объе-
ма и описывается следующим выражением:
а — cqcQ>7-р0А5 вт/(м2-град), (14.10)
где с = 3 4- 3,2; qc измеряется в вт1л?\ р — давление насыщения,
бар. Однако по некоторым опытным данным [14] показатель степени
п в соотношении ос — qn отклоняется от значения 0,7, характерно-
го для неметаллических жидкостей.
При кипении металлов, как и обычных жидкостей, возможен ре-
жим испарения с поверхности пленки. В этом случае коэффициент
теплоотдачи не зависит от плотности теплового потока. Вследствие
малого термического сопротивления жидкометаллической пленки
коэффициент теплоотдачи оказывается достаточно высоким.
Хак уже отмечалось, кипение щелочных металлов обычно неус-
тойчиво и сопровождается пульсациями температуры стеики. Для
облегчения вскипания щелочных металлов при вынужденном дви-
жении можно воспользоваться теми же методами, что и при кипении
в большом объеме (см. §12.5), например созданием искусственных
центров парообразования, выполненных в виде впадин резервуар-
ного типа, или нанесением на поверхность нагрева пористых покры-
тий. Процесс кипения существенно стабилизируется, если на входе
в канал поступает двухфазная смесь. В работе [24] для стабилизации
кипения на входе в трубу было установлено сопло. За счет резкого
расширения в сопле паросодержание на входе достигало 0,5%, что
позволило исключить пульсации температуры стенки. Стой же целью
в работе [14] в однофазный поток жидкого натрия на входе в обогре-
ваемую трубу подавался в небольших количествах инертный газ
(аргон). В этом случае практически сразу после того, как темпера-
тура жидкости превышала температуру насыщения, начиналось ин-
тенсивное испарение жидкости в пузырьки и в результате пузырь-
ковое течение сменялось дисперсно-кольцевым. Режим теплооб-
мена при этом был достаточно устойчивым, и температура стенки
не испытывала существенных колебаний.
§ 14.4. Теплоотдача при кипении недогретой жидкости
Кипение с недогревом, т. е. кипение при значениях темпера-
туры стенки и средней температуры потока, отвечающих условиям
tc — С>0 и ts — t > 0, в отличие от кипения насыщенной жид-
кости характеризуется более высокой составляющей теплового пото-
ка, передаваемого от стенки конвекцией жидкости. Связано это с тем,
что наблюдающаяся при кипении с недогревом частичная или пол-
ная конденсация пузырьков, находящихся на стенке, приводит к
уменьшению количества тепла, переносимого с пузырьками пара от
стенки в ядро потока. С другой стороны, высокие разности между
температурой стенки и среднемассовой температурой потока способ-
ствуют увеличению конвективного переноса тепла жидкостью.
386
На рис. 14.4 показано изменение плотности теплового потока в
зависимости от температуры стенки при заданной температуре пото-
ка. Пока температура стенки остается ниже температуры насыще-
ния (линия 00'), теплоотдача определяется закономерностями одно-
фазного теплообмена и плотность теплового потока пропорциональ-
на температурному напору tc — t. После того как температура стен-
ки превысит температуру насыщения, дальнейший рост плотности
теплового потока будет связан с кипением в пристеночном слое, т. е.
будет зависеть от разности температур tc — ts. Поэтому для анали-
Рис. 14.4. Зависимость плотности теплового по-
тока от температуры стенки при кипении жид-
кости, недогретой до температуры насыщения:
ОО' — однофазное течение; О'АВ — неразвитое кипе-
ние; ВС — развитое кипение; O'DC—расчет по урав-
нению (14.11); 'tJ'i — расчет но уравнению (14.12).
за теплоотдачи в области кипения с недогревом удобно [15] перейти
к новой системе координат А<7С, <1 с началом координат в точке 0'
(см. рис. 14.4). Здесь О' = tc — ta; = qc — qn.^ qw.K = aKOU
(t8 — if); aIiOn—коэффициент теплоотдачи к однофазному потоку жид-
кости.
При малых значениях О наблюдается режим неразвитого кипения
—теплоотдача в основном определяется закономерностями однофаз-
ного теплообмена. При больших значениях -О’ имеет место развитое
кипение.
В случае развитого кипения недогретой жидкости коэффициент
теплоотдачи (т. е. отношение &qG/$) можно рассчитать с помощью
соотношений, справедливых при кипении насыщенной жидкости
(14.5), подставляя в них Aqc вместо qc, или воспользоваться эмпири-
ческой зависимостью [15]:
«р = 77й8!аГЛ36А1°'18Д?с°'звехр (~5>6^) (14-И>
387
Здесь thp—/с—ts— перегрев стенки в случае развитого кипения;
Ткр, ркр--температура, °Д, и давление, н/м\ в критической точке.
М •— молекулярная масса теплоносителя; A^c измеряется в вт!мг\
При неразвитом кипении температуру поверхности нагрева мож-
но определить с помощью интерполяционной формулы, пред-
ложенной Ю. Е. Похваловым с сотр. [15]:
6'
'б'р
От
А<7с/акои
(14.12)
Здесь акоп рассчитывается по скорости циркуляции.
1
0,8
0,6
0,6
0,2
0,1
0,08
0,06
0,0k
Рис. 14.5. Изменение относительной температуры стеики при ки-
пении воды, недогретой до температуры насыщения [15].
Формула (14.12) обеспечивает плавный переход от закономернос-
тей однофазного конвективного теплообмена к закономерностям раз-
витого кипения. Действительно, при акои имеем Ф А^с/акон—
конвективный теплообмен; при акон < Д^с/А’р А « т0р — раз-
витое кипение. Формулы (14.11) и (14.12) подтверждены опыт-
ными данными, полученными при кипении воды и этилового спирта
в интервале давлений от 1,5 до 90 бар, недогревов от 1 до 260° С, плот-
ностей теплового потока от 0,23-106 до 24-10° вт!м- и скоростей цир-
куляции от 1 до 23 м!сек. На рис. 14.5 приведены опытные данные
по теплоотдаче при кипении недогретой воды. Видно, что при
А7с/акоиАр > 3 имеет место развитый режим кипения, и можно
принять 0' = Ар.
§ 14.5. Кризис теплоотдачи при кипении в трубах
1. Механизм кризиса теплоотдачи. При вынужденном движении
скорости переноса паровой фазы от поверхности нагрева в ядро пото-
ка и жидкости к стенке определяются режимом течения, мас-
388
совой скоростью и паросодержанием потока. Эти характеристики
оказывают существенное влияние как на механизм кризиса, так и на
величину критической плотности теплового потока. Проследим из-
менение механизма кризиса кипения в зависимости от паросодержа-
иия потока.
Пусть на вход в достаточно длинную трубу поступает недогретая
жидкость. На стенке трубы задана постоянная плотность теплового
потока 7с. Разобьем услов-
но весь диапазон возмож-
ных паросодержаний на че-
тыре области. На рис. 14.6
для каждой области схема-
тически показано измене-
ние режимов течения, об-
условленное кризисом.
Рассмотрим последова-
тельно эти схемы в порядке
повышения паросодержа-
иия.
В потоках с расходным
массовым паросодержа-
нием, существенно мень-
шим нуля*, паровая фаза
сосредоточена вблизи обо-
греваемой стенки (см.
рис. 14.6, а). Кризис возни-
кает в результате слияния
пузырьков и образования
сплошной пленки пара,
отделяющей стенку трубы
от ядра потока, состояще-
го, из недогретой жидкости
Рпс. 14.6. Смена режимов течения в момент
кризиса при разных паросодержапиях по-
тока :
и конденсирующихся в ней
пузырьков пара. Коэффи-
циент теплоотдачи при этом
резко снижается.
При х 0 пар сосре-
доточен в ядре потока, а
АВ—кризис первого рода; ВС — кризис второго
рода; CD — высыхание пленки; 1—-Г — кризис
теплоотдачи.
жидкость в виде пленки у стенки (см. рис. 14.6, б). Вследствие
больших градиентов скорости в пленке, отрывные диаметры пу-
зырьков будут малыми [см-, уравнение (14.3)]. Поэтому, несмотря
на сравнительно небольшую толщину пленки, в ней вполне воз-
можно пузырьковое кипение жидкости. Кризис теплоотдачи при
таких режимах означает прекращение контакта жидкости со стен-
* Как отмечено в § 13.2 для высоких плотностей теплового потока истин-
ное объемное паросодержание может быть значительным при массовых рас-
ходных паросодержаниях, меньших нуля.
389
кой трубы и переход к дисперсному течению. Механизм кризиса
кипения как в первой, так и во второй области имеет много об-
щего с кризисом кипения в большом объеме.
По длине обогреваемой трубы количество жидкости в пленке
уменьшается за счет испарения и срыва капель с гребней волн пото-
ком пара. Хотя убыль жидкости в пленке частично восполняется
выпадающими на стенку из ядра потока каплями, толщина пленки
с ростом паросодержания уменьшается. С уменьшением толщины
пленки волновое движение на ее поверхности затухает. При некото-
ром значении расходного массового паросодержания хАр
(см. рис. 14.6, в) волны иа поверхности пленки исчезают и срыв
капель прекращается. Такой режим течения можно зафиксировать
по резкому падению сопротивления трения (о кризисе сопротивления
см. §13.4). При определенных сочетаниях qG и pay незначительна
также и подпитка пленки за счет попадающих на ее поверхность
капель. Объясняется это тем, что капли, движущиеся из ядра потока
к стенке, отбрасываются обратно встречным потоком пара. Поэтому
количество влаги на стенке непрерывно уменьшается и кризис насту-
пает в результате полного высыхания пленки (см. 14.6, в). Количество
тепла, необходимое для испарения жидкости, текущей в пленке:
<2 = г(?пл, (14.13)
где бпл — расход жидкости в пленке в сечении х=хДр.
Паросодержание потока хгр0, при котором пленка высыхает, свя-
зано с кризисом сопротивления соотношением
। $
А'грО — -Г ~ •
Поскольку Хдр и расход жидкости в пленке бпЛ, согласно данным
опыта, практически не зависят от плотности теплового потока иа
стенке, то и хгр0 также не зависит от qc.
Этот вид ухудшения теплоотдачи существенно отличается от опи-
санных ранее, наблюдающихся при более низких х. Чтобы подчер-
кнуть качественные различия в механизме, кризис, связанный с вы-
сыханием пленки, называют кризисом второго рода [6]. Все точки,
отвечающие кризису второго рода, в плоскости б/кр1, х располагают-
ся на вертикальной прямой, имеющей абсциссу х = хгр0. Как вид-
но из рис. 14.6, паросодержание хгр0 (линия ВС) ограничивает спра-
ва область существования кризиса первого рода.
Область высоких паросодержаний (линия CD на рис. 14.6, а) в
настоящее время изучена недостаточно. При малых тепловых пото-
ках здесь возможно существование на стенке трубы очень тонкой
пленки жидкости. При более высоких тепловых нагрузках пленка
отсутствует и охлаждение осуществляется потоком пара, содержа-
щим капельки тумана. Поскольку плотности тепловых потоков здесь
невелики, то малы и скачки температуры в момент кризиса; они не-
редко составляют всего несколько градусов. Поэтому четко зафик-
сировать величину критической нагрузки часто не удается.
390
Как видно из рис. 14.6, рост паросодержания потока сопровож-
дается уменьшением 7 п. Такая зависимость 71{р1 от х легко объяс-
нима. Например, при кипении недогретой жидкости чем меньше х,
а следовательно, выше недогрев, тем интенсивнее конденсация паро-
вой фазы в пристеночном слое, что способствует росту 7кр1. В случае
кипения насыщенной жидкости увеличению х сопутствует увеличе-
ние скорости в пристеночной жидкой пленке и градиента скорости
в вязком подслое. При этом в соответствии с (14.3) отрывные диамет-
ры пузырьков уменьшаются, удаление пара из вязкого подслоя за-
трудняется и кризис наступает при меныпих значениях цкрг. Посколь-
ку паросодержание увеличивается по длине обогреваемой трубы, то
кризис теплоотдачи наблюдается обычно на выходе из трубы. Этот
вывод имеет важное практическое значение, так как позволяет
сосредоточить внимание на наиболее опасных участках канала.
2. Факторы, влияющие на величину 7кр1. Кроме паросодержания
7кр1 зависит от размеров трубы, характера распределения qc по дли-
не трубы, давления, расхода теплоносителя, пульсаций расхода и
состояния поверхности.
Диаметр и д л и и а труб ы. Критическая плот-
ность теплового потока уменьшается с ростом диаметра трубы. В об-
ласти положительных х влияние диаметра на7Х!р1 более сильное, чем
при кипении недогретой жидкости. Зависимость 7кр1 от диаметра
при кипении пароводяной смеси (х > 0) В. Е. Дорощук [6] предла-
гает учитывать с помощью формулы
4кр1 __ 1 А / ~ у одж
ф<р 1 </кр1 \ I cl
(14.14)
где <7кр1 и 7кР1 —критические тепловые нагрузки для труб диамет-
ром d, м, и диаметром 8 мм, вт1мл, а коэффициент А имеет следу-
ющие значения:
р, бар 49 78
98 137 167
Л-10-0 8,20 7,58
7,29 6,71 6,28
При кипении воды, недогретой до температуры насыщения в интер-
вале давлений от 50 до 140 бар и массовых скоростей от 1000 до
7000 кг/(м* - сек), предлагается зависимость [6]
<7кр1 (^1)
4кр1 Иг)
(14.15)
где 7кр1 (^1)» — критические нагрузки для труб диаметром
d1 и cL. Формулы (14.14) и (14.15) справедливы для труб диаметром
от 2 до 13 мм.
Длина трубы слабо влияет иа 7кр1. Если l/d >• 20, то можно счи-
тать, что длина трубы не влияет иа 7кр1. В случае коротких труб
(lid <Z 20) 71ф1 увеличивается с уменьшением длины.
391
Характер распределения тепло-
вой нагрузки по длине трубы. Крити-
ческая плотность теплового потока во многом определяется
влагосодержанием пристеночного слоя. Если, каким-либо образом
воздействуя на поток, повысить влагосодержание пристеночного
слоя, то одновременно возрастут и значения QKpl. Пристеночный слой
формируется на определенной длине трубы. Следовательно, в данном
сечении влагосодержание пристеночного слоя и ^кр1 будут зависеть
от условий, имеющих место на предшествующих участках. Измере-
ния, выполненные Е. И. Невструевой и Р. А. Петросяном [12], пока-
Рис. 14.7. Зависимость г/кр1 от давления при кипении воды
в трубах (х=0) и в большом объеме [1].
зали, что более высоким значениям плотности теплового потока на
стенке при прочих равных условиях соответствует и более высокая
концентрация паровой фазы у стенки. Следовательно, если рассмат-
риваемому сечению предшествует участок с более высокими qc, то
влагосодержание в пристеночном слое и критическая плотность теп-
лового потока в этом сечении будут ниже, чем в случае равномерного
обогрева, и наоборот, влагосодержание пристеночного слоя и qKpl
повышаются, если на предшествующем участке имеют место более
низкие значения qc.
В ядерных реакторах плотность теплового потока изменяется по
длине твэлов, что необходимо учитывать при оценке ^кр1. Обычно
плотность теплового потока имеет максимум в центральной части ка-
нала и уменьшается к концам. Как показали измерения Б. А. Зенке-
вича с сотр. [8], значения дкр1 в трубах с убывающей по закону ко-
синуса плотностью теплового потока ниже, чем в трубах с однород-
ным распределением qc.
Давление. Зависимость </кр1 от давления при кипении во-
ды показана на рис. 14.7. Как видно из рисунка, максимальная кри-
392
тическая плотность теплового потока наблюдается при давлении
30—40 бар (напомним, что при кипении воды в условиях свобод-
ной конвекции в большом объеме максимум <71ф1 соответствует дав-
лению 70—80 бар). В интервале значений 40—200 бар ql(1)1 умень-
шается с ростом давления.
Массовая скорость оказывает неоднозначное
влияние на критическую плотность теплового потока. В случае кипе-
ния недогретой жидкости (х < 0) с увеличением pw увеличивается
приток холодной жидкости в пристеночный слой, и в результате (?кр1
увеличивается (рис. 14.8). При положительных х, напротив, увели-
Рис. 14.8. Влияние массовой скорости и паросодержапия пото-
ка на 7кр1 при давлении р=49 бар [6].
чение массовой скорости парожидкостного потока приводит к сни-
жению Объясняется это тем, что с увеличением рю увеличива-
ется градиент скорости в пристеночной пленке, тем самым уменьша-
ются отрывные диаметры пузырей и ухудшается отвод пара от поверх-
ности нагрева (см. § 14.2). В интервале значений х от 0 до 0,1 с?кр1
практически не зависит от pay.
Пульсации расхода и дав лен и я. Гидравличес-
кая система, состоящая из двух (или более) параллельных каналов,
соединенных на входе коллектором, может оказаться неустойчи-
вой, если в каналы поступает недогретая жидкость. В такой системе
возможно появление на входе и выходе из каналов пульсаций рас-
хода, причем увеличение расхода на входе в одном (или нескольких)
канале совпадает по времени со снижением расхода на входе
в остальные.
Поскольку тепловыделение в каждом канале остается постоян-
ным, то изменение расхода жидкости на входе сопровождается изме-
нением координаты точки начала кипения. Смещение точки начала
кипения изменяет длину участка, на котором происходит парообра-
зование.
393
Увеличение длины кипящего участка сопряжено с ростом количест-
ва пара, образующегося в канале, что приводит к дополнительному
ускорению смеси, и в результате давление внутри канала повышает-
ся. Рост давления приводит к снижению расхода жидкости на входе
в канал (в случае резкого роста паропроизводительности канала воз-
можно возникновение обратного течения жидкости из канала в кол-
лектор). Однако снижение расхода — явление временное. Как толь-
Рис. 14.9. Влияние пульсаций
расхода на 7кР1, [20] (р =
= 100 бар, рw=400 кг/(м2-сек),
d—8 мм):
(—течение без пульсаций; 2 — те-
чение с пульсациями.
ко длина участка кипения достигнет
максимального значения и ее рост
прекратится, давление в канале па-
дает и расход жидкости, поступаю-
щей в канал, начинает увеличивать-
ся. На практике такой пульсирую-
щий режим может продолжаться
сколь угодно долго.
Исследования М. А. Стыриковича
с сотр. [20] свидетельствуют о том,
что при одних и тех же средних во
времени значениях массовой скорости
и расходного массового паросодержа-
ния критическая плотность теплового
потока для режима с пульсациями
расхода оказывается много меньше,
чем для беспульсационного (рис. 14.9).
Например, при х ж 0 наличие пуль-
саций расхода приводит к снижению
qKр1 приблизительно в пять раз. Столь
сильное снижение (/кр1 объясняется
следующим. Измеренные в опытах
значения (?кр1 относятся к осреднен-
ной по времени величине х. В дейст-
вительности пульсация расхода со-
провождается пульсациями х и кризис происходит не при сред-
нем, найденном по тепловому балансу значении расходного массо-
вого паросодержания, а при некотором максимальном значении.
Пульсации расхода сопровождаются низкочастотными пульса-
циями давления. Так как падение давления вызывает вскипание
жидкости, то пульсации давления также способствуют снижению
величины (?кр1.
Пульсации расхода в контуре весьма опасны, так как вы-
зывают значительное снижение 7кр1. Для предотвращения пуль-
саций на входе в каждый из параллельно включенных каналов
устанавливается дроссельное устройство (шайба). Благодаря допол-
нительному гидравлическому сопротивлению, создаваемому шайбой,
давление в коллекторе повышается и небольшие колебания давле-
ния в каналах, связанные с перемещением точки начала кипения, не
могут повлиять на расход жидкости через канал. Работа гидравли-
ческой системы становится устойчивой. Шайбование приводит к
394
некоторым дополнительным потерям давления, но зато позволяет
избежать опасных пульсаций расхода.
Состояние поверхности наг р е в а.
При эксплуатации парогенераторов тепловых и атомных электро-
станций уделяется большое внимание очистке питательной воды и
борьбе с отложениями солей на поверхности нагрева. Имеющие мес-
то на практике небольшие отложения солей на стенке или ее окис-
ление не сказываются заметным образом на величине ^кр1. Также
незначительно влияние на теплофизических свойств материалов,
используемых в котельной и реакторной технике для изготовления
поверхностей нагрева, и способов обработки поверхности [61.
3. Расчетные рекомендации по </кр1. В настоящее время имеется
большое число экспериментальных данных по критическим плот-
ностям теплового потока при кипении воды в трубах. Однако данные
разных авторов не всегда хорошо согласуются между собой, что
объясняется отчасти несовершенством и недостаточной согласован-
ностью методов исследования, отчасти сложностью самого явления
кризиса теплообмена, его зависимостью от большого числа парамет-
ров. Интерпретацию и обобщение опытных данных по критическим
плотностям теплового потока затрудняет также и то обстоятельство,
что измерения как правило, не сопровождаются изучением
режимов течения и механизма кризиса.
Из большого числа имеющихся в литературе опытных данных
В. Е. Дорощук [6] отобрал данные по 7кр1 для воды, полученные в
опытах без пульсаций расхода и давления с равномерно обогревае-
мыми трубами диаметром от 2 до 13 мм и lid > 15. Критические на-
грузки для труб различного диаметра были пересчитаны по форму-
лам (14.14) и (14.15) и приведены к одному диаметру d= 8 мм. По-
лученные значения для каждого р, х и pw были осреднеиы и
сведены в табл. 14.1. Этой таблицей (или построенными с ее помощью
графиками) в сочетании с формулами (14.14) н (14.15) для пересчета
на другие диаметры можно пользоваться для практических оце-
нок (/кр1.
Для расчета кризиса теплообмена при кипении жидкости в усло-
виях вынужденного движения предложено большое число эмпири-
ческих зависимостей. Как и другие эмпирические формулы, их мож-
но использовать лишь в том интервале параметров, в котором они
подтверждены опытными данными. В качестве примера приведем
уравнения, предложенные В. И. Субботиным с сотр. [3]. Эти уравне-
ния охватывают широкий диапазон параметров.
Для воды, недогретой до температуры насыщения (х < 0):
1 /V'0S (1,1—2,4х)[Т0-3~|---------------------] . (14.16)
Г |/ рта \pU 'L (7,4-lOWj
Здесь </кр1 измеряется в вт!л?\ г — теплота парообразования,
дж!кг\ v' — кинематический коэффициент вязкости жидкости, мЧсек.',
395
СО
со
СТ)
Таблица 14.1
Значения ^Kpfl0“6 вт/л? в трубе с внутренним диаметром d=8 мм, охлаждаемой водой
м 1 я 1 Q. S р=4 9 бар р=69 бар р=98 бар
X X X
— 0,2 -0,1 1 0 1 0,1 0,2 — 0,2 —о,1 0 0,1 0,2 0,3 0,4 0,5 — 0,2 — 0,1 0 0,1 0,2 0,3 0,4 0,5
750 1000 1500 2000 2500 3000 4000 5000 9,02 9,32 9,54 9,73 9,93 10,11 10,61 8,18 8,43 8,61 8,78 8,80 8,84 8,86 9,20 7,56 7,73 7,50 7,21 7,21 6,75 6,80 6,25 5,34 5,11 4,76 3,83 3,60 3,36 8,01 3,13 8,34 8,42 8,62 8,56 9,16 7,23 7,25 7,26 7,27 7,42 7,26 8,25 8,28 6,28 6,28 5,92 5,69 5,70 5,23 5,00 5,23 4,94 4,50 4,14 3,81 3,53 3,25 4,41 4,23 3,72 3,25 2,90 2,73 2,32 3,83 3,68 2,90 2,56 2,32 2,09 1,63 3,37 3,11 2,62 2,09 3,02 2,73 5,75 6,00 6,48 6,66 7,05 7,54 8,52 5,07 5,14 5,49 5,49 5,77 5,90 6,52 7,02 4,42 4,48 4,45 4,58 4,19 4,30 4,58 3,84 3,68 3,56 3,06 2,84 2,60 2,32 2,15 3,31 3,07 2,73 2,21 1,93 1,63 1,51 2,84 2,44 1,85 1,51 1,28 1,11 0,80 2,46 1,92 1,29 1,03 2,00 1,35
р W, кг/(м2- • сек) р=137 бар р = 167 бар р=196 бар
X X X
— 0,2 — 0,1 0 0,1 0,2 0,3 0,4 — 0,2 — 0,1 0 0,1 0,2 — 0,2 — 0,1 0 0,1 0,2
750 1000 1500 2000 2500 3000 4000 5000 3,31 3,65 3,92 4,48 4,94 5,37 6,37 6,61 3,15 3,43 3,63 4,14 4,54 4,92 5,75 6,12 2,56 2,56 2,67 2,81 3,26 3,02 3,61 3,73 2,21 2,03 1,96 2,04 2,09 2,11 2,21 1,90 1,65 1,39 1,28 1,21 1,21 1,28 1,44 1,23 0,95 1,04 0,87 2,49 2,76 3,31 3,65 4,13 4,65 5,50 6,78 2,26 2,43 2,94 3,16 3,58 4,04 4,81 5,78 1,69 1,80 2,04 2,29 2,51 2,74 3,26 3,77 1,34 1,41 1,67 1,79 1,94 2,04 2,49 2,62 0,76 0,90 1,16 1,26 1,29 1,35 1,43 1,49 1,70 2,02 2,29 2,56 2,79 2,34 1,43 1,62 1,90 2,13 2,36 2,58 2,93 1,27 1,36 1,52 1,66 1,78 1,88 1,95 1,25 1,35 1,45 1,53 1,72 0,93 1,04 1,10 1,23 1,42
pw—средняя массовая скорость, кг/(м2-сек); в — коэффициент по-
верхностного натяжения, н/ж; р", р'— плотности пара и жидкости,
кг/м3; X'—расходное массовое паросодержание на выходе из трубы;
ау0 — скорость циркуляции, м/сек; п = 1,1 2р7р' — 0,3 х.
Физические свойства определяются по температуре насыщения.
Формула подтверждена экспериментальными данными в интер-
вале давлений от 40 до 205 бар, скоростей циркуляции от 0,5 до
14 м/сек, для труб диаметром от 8 до 10 мм. Недогрев жидкости до
температуры насыщения менялся от 2 до 200° С.
Для пароводяного потока (х > 0):
а) область давлений от 39 до 98 бар
7кр1 — [1,46-Ю^г1172 (1-~х)"г—-418,7ptw] Л0-48. (14.17)
Здесь т = 3,48 — 0,129-10~г7", L = 0,008/d; d — внутренний диа-
метр трубы, м; остальные обозначения см. в формуле (14.16).
Пределы изменения параметров: 550 < pay <7 5000 кг/(м2-сек),
0 С х < 0,4; I > 0,2 м; d = 4 -j- 12 мм;
б) область давлений от 98 до 196 бар:
__ / п / \ 9 2
<7крх 46,5 (ЗбООрау)" (1 ~-х)"1 ’
8-10»
(3600рш)/е
L0-48. (14.18)
Здесь и 0,56 — 0,0189р7р"; т - 0,7р7р" — 0,4; k - 1,13 +
-|- 3,6р7р' — 0,45х; L = 0,008/d, d — внутренний диаметр трубы, м;
остальные обозначения см. в формуле (14.16).
Пределы изменения параметров: 1100 < pay < 5000 кг//лб-сек);
0 < х < 0,4; I > 0,2 м; d = 4 4- 12 мм.
Формулы (14.16)—(14.18) удовлетворительно согласуются с
данными табл. 14.1, хотя при некоторых сочетаниях режимных
параметров различие достигает 50 %.
4. Кризис теплоотдачи второго рода. Область существования
кризиса второго рода иа плоскости 7кр1, х изображается верти-
кальной линией ВС (рис. 14.6). Это означает, что кризису второго
рода соответствует определенный интервал плотностей теплового
потока. Поэтому в качестве параметра, ограничивающего безопас-
ную для работы область, удобно пользоваться не <7кр1, а массовым
расходным паросодержанием хгр0. В. Е. Дорощук [6] получил для
граничного паросодержания соотношения:
хгр0=-7,35р0’15 (р£о)~-°>42, р "5 4-50 бар;
= р^ЪО + Шбар, ' (Ш9)
|/ prov' —Р"
где k — слабо зависящая от диаметра трубы величина (для труб
диаметром 8 мм k = 0,056). Формулы (14.19) справедливы в диапа-
зоне pw от 500 до 2000 кг/(м2-сек).
397
Прекращение обмена жидкостью между ядром потока и плен-
кой, характерное для кризиса второго рода, наблюдается только при
определенных сочетаниях режимных параметров. Например, в слу-
чае малых <7С скорость пара, движущегося от стенки навстречу кап-
лям, становится недостаточной, чтобы помещать их выпадению на
стенку. Расход жидкости в пленке увеличивается, ее высыхание
происходит при х > хгр0 и, как видно на рис. 14.6, при малых qG
график отклоняется от вертикали (кривая CD).
Существенно облегчается выпадение капель с ростом средней
массовой скорости. Снабжение пленки жидкостью становится воз-
можным при более высоких qG, и величина вертикального участка
с ростом pw уменьшается.
При высоких давлениях благодаря высокой плотности паровой
фазы и малому поверхностному натяжению облегчается срыв жид-
кости с поверхности пленки (см. § 13.3). Поскольку при давлениях
выше 170 бар практически всегда наблюдается срыв жидкости с по-
верхности пленки, то можно считать, что кризис второго рода при
р > 170 бар не имеет места. Вопрос о границах существования кри-
зиса второго рода еще не вполне ясен. В этом направлении в насто-
ящее время проводятся исследования. Некоторые дополнительные
данные по этому вопросу можно найти в монографии [6].
§ 14.6. Кризис теплоотдачи при кипении воды
в продольно омываемых пучках стержней
Топливные кассеты ядерных реакторов часто выполняются в ви-
де пучков цилиндрических стержней, продольно омываемых
теплоносителем. Положение стержней в пучке фиксируется с по-
мощью дистанционирующих решеток. Кроме рассмотренных в § 14.5
факторов на условия возникновения кризиса в пучке влияют кон-
структивные особенности (условия входа теплоносителя в пучок,
расположение стержней друг относительно друга и относительно
обечайки, способ их дистаиционирования), а также распределение
мощности тепловыделения по сечению и длине пучка. Небольшие
неточности в сборке или нарушение геометрии пучка во время рабо-
ты (особенно в случае тесного расположения стержней) могут при-
вести к неодинаковым расходам теплоносителя через параллель-
ные ячейки, а следовательно, и к неоднородному распределению па-
росодержания по ячейкам. Если учесть, что в плотных пучках пере-
мешивание между параллельными ячейками недостаточно для вы-
равнивания паросодержания, то неоднородность в распределении
х приведет к снижению критической тепловой нагрузки (кризис воз-
никает в ячейках с максимальным паросодержанием и, следователь-
но, при меньших значениях qG). Перемешиванию потока способству-
ют дистанционирующие решетки; при этом неравномерность паро-
содержания по сечению пучка снижается, что ведет к увеличению
7крг
398
Экспериментально установлено, что изменение в определенных
пределах диамшра стержней и расстояния между ними существен*
по не сказывается на величине 7кр1. Слабо зависит критическая
плотность теплового потока также от числа стержней в пучке и от
геометрии ячейки. Отмеченные обстоятельства облегчают задачу
обобщения опытных данных.
На основании данных собственных исследований, выполненных
па семпстсржневом вертикальном пучке круглых цилиндрических
стержней, а также литературных данных по девяти-и девятнадцати-
стержневым пучкам В. Н. Смолин и В. К. Поляков [17] рекомен-
дуют следующую зависимость для критической плотности тепло-
вого потока:
f/upi —0,845-10°фон)0-2 (1 —-3,35-10’3р)(1—х)1 >2, (14.20)
Здесь щ.р1 измеряется в вт/м2-, pw — средняя массовая скорость,
да/(лг • сек); х — расходное массовое паросодержание на выходе из пуч-
ка; р — давление, бар.
Формула (14.20) получена на основе опытных данных, охватываю-
щих диапазон изменения р от 30 до 100 бар-, pw от 380 до
4000 • ш<); х от —0,2 до 0,25. Зазор между стержнями ме-
нялся от 1,7 до 4,6 мм, длина стержней составляла ~ 500 мм.
Для интервала давлений от 100 до 200 бар В. И. Толубинский
ссотр. [22] предложили формулу
Л 11LV1252,15-10“5 (pw)1-б (0,2 — х) 1/% (14.21)
Vk]h б-о \ Р / гр'
Здесь 7,.р1 — критическая плотность теплового потока при ки-
пении в большом объеме, определяемая по формуле (12.40);
pw — средняя массовая скорость, кг/(м2-сек); паросодержание х бе-
рется на выходе из пучка.
Формула (14.21) обобщает данные, полученные на трех- и семи-
стержневых пучках с диаметром стержней 9 мм. Зазор между стерж-
нями равен 3 мм, длина стержней менялась от 100 до 600 мм. Диапа-
зон исследованных параметров: 250 < pw < 1000 кг/(м2-сек)-,
--0,5 < х < 0,2.
Формулы (14.20) и (14.21) справедливы только для воды.
Они показывают, что критическая плотность теплового потока
при кипении в продольно омываемых пучках стержней в ис-
следованном диапазоне параметров возрастает с ростом средней мас-
совой скорости и уменьшается с ростом расходного массового паро-
содержания.
Отдельные экспериментальные данные говорят о том, что при срав-
нительно высоких расходных массовых паросодержаниях (х= 0,3 -г
-г 0,4) критическая плотность теплового потока для пучков длиной
свыше 3,5 м несколько ниже, чем для коротких. В. С. Осмачкин и
399
Н. Н. Лысцова [13] предлагают следующее выражение для пкп1
учитывающее влияние длины пучка:
—П4 22.
ре1/5рг1/з 320 (1 + //3,54) ’ k J
где
?„р1=-------------
Гр' Ыт(£Я')1/3]1/3
•—* безразмерная критическая плотность теплового потока; Re =
у- poydT/pi'; Рг = v'ja'; dT = 4f/sq — тепловой диаметр пучка:
/ — площадь проходного сечения пучка; sq — обогреваемый пе-
риметр; Z—длина пучка, м; X = х [((Ж^Дсгр')]1/5 — обобщен-
ное расходное паросодержание.
Формула (14.22) удовлетворительно (с погрешностью + 20%) сог-
ласуется с опытными данными в следующих пределах изменения ос-
новных параметров: 40 р 180 бар] 500 pta 5000
—0,5 X3,0; 4 dT +/ 20 мм и 0,4 I 7 м.
Предложены и другие эмпирические уравнения для критических
тепловых нагрузок в пучках труб [23]. Однако все известные зави-
симости носят частный характер, справедливы только в диапазоне
исследованных параметров и для пучков определенной геометрии.
Поэтому если возникает необходимость определить 7кр1 для сборки
стержней несколько иной конструкции или в другом диапазоне па-
раметров, то приходится проводить новые экспериментальные ис-
следования в условиях, возможно более близких к натурным.
§ 14.7. Определение номинальной тепловой нагрузки
Безаварийная работа активной зоны возможна в том случае, ес-
ли плотность теплового потока на стенке для любого кипящего ка-
нала во всех расчетных режимах будет оставаться ниже критичес-
кого значения. Разумно выбранная при проектировании реактора
номинальная плотность теплового потока позволяет разработать на-
дежную и экономичную конструкцию. Выбор номинальной тепло-
вой нагрузки осложняется тем обстоятельством, что существующие
эмпирические расчетные зависимости для критической плотности
теплового потока получены в результате осреднения опытных дан-
ных, в то время как действительные значения 7кр1 могут существен-
но отклоняться от средних значений. Между тем для расчета актив-
ной зоны основной интерес представляют не средние значения кри-
тической плотности теплового потока (?кр1, а минимальные значе-
ния, возможные в данных условиях. Поэтому важно проанализиро-
вать причины и закономерности разброса опытных данных.
Критическая плотность теплового потока является функцией
режимных параметров: давления, средней массовой скорости, расход-
ного массового паросодержания. Во время опытов эти параметры
400
поддерживаются в рабочем участке на заданном уровне. В силу не-
совершенства регулирующих органов и неточности измерительных
приборов кризис теплоотдачи происходит не при заданных значениях
параметров, к которым относятся результаты измерений, а при нес-
колько отличных: р ± Др, pay ± Д(рау), х ± Дх. Неточность в из-
мерении электрической мощности, подводимой к рабочему участку,
и колебания напряжения в электрической сети приводят к погреш-
ности в определении плотности теплового потока на стенке qc ± &q(..
Критическая плотность теплового потока зависит также от клас-
са чистоты обработки поверхности нагрева, степени ее загрязнения,
наличия примесей в жидкости. При составлении расчетных урав-
нений эти факторы, как правило, не учитываются. Можно предпо-
ложить, что отклонения перечисленных факторов от заданного зна-
чения от опыта к опыту носят случайный характер и играют роль
некоторых независимых возмущений, вносимых в процесс. Во вре-
мя опытов различные возмущения могут накладываться друг на дру-
га таким образом, что будут воздействовать на величину 71ф1 одно-
временно в одну сторону, увеличивая или уменьшая ее, и, следова-
тельно, разброс опытных данных относительно среднего значения
может быть значительным. Поскольку установить связь отклонений
qKр1 со всеми вызывающими их возмущениями не представляется
возможным, то целесообразно принять, что величина (?1ф1 имеет ве-
роятностный характер и может быть охарактеризована средним зна-
чением и некоторым вероятностным распределением. Полное описа-
ние условий возникновения кризиса кроме средней критической
плотности теплового потока должно включать закон отклонения
gIipl от среднего значения. Имеющиеся литературные данные свиде-
тельствуют о том, что отклонения <7кр1 от среднего подчиняются нор-
мальному распределению. В силу характера нормального распреде-
ления приходится предполагать, что возможны большие отклонения
^кр1 от среднего значения, хотя вероятность их ничтожна.
Обычно в инженерной практике принимают, что отклонения от
среднего для величин, подчиняющихся нормальному распределе-
нию, не выходят из интервала ± Зег (сг — среднее квадратичное
отклонение). С учетом сказанного допустимая плотность теплового
потока для поверхности, охлаждаемой кипящей жидкостью:
qo ~ 7кр1 — За, (14.23)
где 7крг — среднее значение критической плотности теплового
потока.
Вероятность возникновения кризиса при тепловой нагрузке q$
составляет 0,0014.
К сожалению, результаты измерений ^кр1 обычно не обрабаты-
ваются вероятностно-статистическими методами и характеристики
распределения остаются неизвестными. В этом случае выявляется
интервал, в котором располагаются опытные данные:
<7кр1~-&7 макс макс >
401
где <укр1 — среднее значение, найденное по данным измерений>
6gMaKG — максимальное отклонение от среднего значения.
Затем определяется допустимая тепловая нагрузка:
(14.24)
где k = 1 — 5<7маКс/<7кр1> обычно принимают k = 0,6 — 0,8.
При эксплуатации ядерного реактора возможны периодические
отклонения параметров в отдельных каналах от номинальных зна-
Рис. 14.10. к определению номи-
нальной тепловой нагрузки твэла
в случае тепловыделения по
длине; Xi, х2, — паросодержа-
ние потока на входе в канал, на
выходе и в наиболее опасном се-
чении.
чений. Эти отклонения могут быть
вызваны различными причинами.
Например, колебания расхода мо-
гут произойти в результате пере-
мещения регулирующих и ком-
пенсирующих органов реактора,
колебания мощности — вследствие
установки свежих твэлов вместо
выгоревших. Поэтому плотность
теплового потока, лежащая в ос-
нове расчета реактора при нор-
мальном режиме работы, т. е. но-
минальная плотность теплового
потока должна выбираться ниже
допустимой:
=-К (14.25)
%
где х — коэффициент запаса, к > 1.
При выборе коэффициента запаса руководствуются соображе*
ниями надежности и экономичности. Чем выше х, тем надежнее ра-
бота реактора. Однако увеличение х приводит к уменьшению мощ-
ности тепловыделения, увеличению объема активной зоны и росту
капитальных затрат*.
Определение qH не представляет особых затруднений, если при-
нять, что тепловыделение подлине канала однородно. В этом случае
определяют параметры потока на выходе из канала, затем по опыт-
ным данным находят ^кр1 и с учетом разброса опытных данных и
необходимого коэффициента запаса выбирают qiv
Если мощность тепловыделения по длине канала неоднородна,
то часто оперируют не с плотностью теплового потока, а с тепловой
мощностью канала
i
N = S <7с (2) dz,
о
* Подробности см. в работе [9].
где S, I — обогреваемый периметр и длина канала; (z) —- мест-
ная плотность теплового потока; z — продольная координата.
В координатах q, х в соответствии с опытными данными строится
график qt) — f (х) и для заданного М наносится расчетная кривая
qc ~[(х) (рис. 14.10). Сечение, в котором наиболее близко сходят-
ся t/(. и q(), следует признать наиболее опасным. В зависимости от
характера распределения q{. по длине канала наиболее опасное се-
чение может быть смещено к центру или к выходу из канала. В
наиболее опасном сечении величина должна соответствовать тре-
бованиям надежности, т. е. здесь должно выполняться условие
(14.25).
СПИСОК ЛИТЕРАТУРЫ
1. Аладьев И. Т. и др. Кризисы кипения в трубах.— Веб.: Теплопередача.
М., Изд-во АН СССР, 1962.
2. Аладьев И. Т. и др. Теплообмен при кипении калия в трубах. — В сб.:
Теплообмен, гидродинамика и теплофизические свойства веществ. М.,
«Наука», 1968, с. 18.
3. Алексеев Г. В. и др. Критические тепловые потоки при вынужденном те-
чении воды. Докл. № 327-а, представленный иа Третью междупар. конф,
по мирному использованию атомной энергии. Женева, 1964.
4. Боришанский В. М. и др. Теплоотдача при кипении калия в области уме-
ренного паросодержания.—«Атомная энергия», 1966, т. 21, вып. 1,
с. 58.
5. Боришанский В. М. Теоретическое обоснование теплового расчета
парогенератора в докризисном режиме. —«Тр. ЦКТИ» Вып. 108, 1971,
с. 25.
6. Дорощук В. Е. Кризисы теплообмена при кипении воды в трубах. М.,
«Энергия», 1970.
7. Друкер И. Г. О кризисе кипения при течении пароводяной смеси в тру-
бах. — «Теплоэнергетика», 1967, № 4, с. 76.
8. Зенкевич Б. А. и др. Анализ и обобщение опытных данных по кризису
теплоотдачи при вынужденном течении кипящей воды в трубах. М.,
Атомиздат, 1969.
9. Клемии А. И. Инженерные вероятностные расчеты при проектировании
ядерных реакторов. М., Атомиздат, 1973.
10. Кутателадзе С. С. Влияние скорости циркуляции на коэффициент
теплоотдачи при кипении в трубах.—«Энергомашиностроение», 1961,
№ 1, с. 12.
11. Миропольский 3. Л. Теплоотдача при пленочном кипении пароводяной
смеси. — «Теплоэнергетика», 1963, № 5, с. 49.
12. Невструева Е. И., Петросян Р. А. Исследование локальных паросодер-
жапий пристенного слоя при кипении воды. — В сб.: Конвективная теп-
лопередача в двухфазном и однофазном потоках. М.—Л., «Энергия»,
1964, с. 104.
13. Осмачкин В. С., Лысцова Н. Н. О расчете критических тепловых нагрузок
в пучках стержней. Препринт ИАЭ-2204-, 1972.
14. Петухов Б. С., Зейгарник Ю. А. Кипение жидких щелочных металлов
в трубах. — «Теплофизика высоких температур», 1970, т.8, № 2, с. 309.
15. Похвалов Ю. Е., Кронин И. В., Курганов И. В. Обобщение данных по
теплоотдаче при кипении недогретых жидкостей. — «Теплоэнергетика»,
1966, № 5, с. 63.
16. Рассохин Н. Г., Швецов Р. С., Кузьмин А- В. Расчет теплоотдачи при
кипении. — «Теплоэнергетика», 1970, № 9, с. 58.
17. Смолин В. Н., Поляков В. К. Критический тепловой поток при продоль-
ном обтекании пучка стержней. — «Теплоэнергетика», 1967, № 4, с. 54.
403
18. Стерман Л. С. Исследование теплообмена при кипении жидкости в тру-
бах. — «Ж- техн, физики», 1954, т. XXIV, вып. 11, с. 2046.
19. Стырикович М. А., Мартынова О. И., Миропольский 3. Л. Процессы
генерации пара на электростанциях. М. «Энергия», 1969.
20. Стырикович М. А. и др. Влияние предвключенных элементов иа возникно-
вение кризиса кипения. — «Теплоэнергетика», 1960, № 5, с. 81.
21. Субботин В. И., Ремизов О. В., Воробьев В. А. Теплоотдача в области
ухудшенного режима теплообмена. «Теплофизика высоких темпера-
тур», 1973, т.11, № 6, с. 12.
22. Толубинский В. И., Кичигин А. М., Васильев А. А. Кризис теплоотдачи
при кипении воды в продольно омываемых пучках стержней. — «Тепло-
энергетика», 1971, № 3, с. 51.
23. Тонг Л. Теплоотдача при кипении и двухфазное течение. Пер. с англ.
М., «Мир», 1969.
24. Hoffman Н. W., Krakowiak А. Т. Convective Boiling with Luquid Potas-
sium. Proceedings of the 1964 Heat Transfer and Fluid Mechanics Institute,
Berkeley, Stanford, Calif., 1964.
ОГЛАВЛЕНИЕ
Стр.
Предисловие..................................................... 3
Введение......................................................... 5
Глава 1. Тепловыделение в активной зоне реактора и отвод теп-
ла из нее..........................................12
§ 1.1. Источники тепла в активной зоне...............12
§ 1.2. Распределение тепловыделения в активной зоне 15
§ 1.3. Отвод тепла из активной зоны..................21
Список литературы................................................25
Глава 2. Уравнение теплопроводности и методы его решения . 26
§ 2.1. Уравнение теплопроводности....................26
§ 2.2. Начальные и граничные условия для процессов
теплопроводности ................................... 27
§ 2.3. Некоторые преобразования уравнения теплопро-
водности ............................................29
§ 2.4. Методы решения уравнения теплопроводности 30
Список литературы ............................................. 37
Г л а в а 3. Расчет температурных полей.........................38
§ 3.1. Одномерные стационарные задачи теплопро-
водности ............................................38
§ 3.2. Теплопроводность через ребра и оребренную
стенку...........................................50
§ 3.3. Двумерные стационарные задачи теплопровод-
ности ...............................................57
§ 3.4. Нестационарные задачи теплопроводности ... 68
Список литературы 79
Глава 4. Основные уравнения конвективного теплообмена . . 80
§ 4.1. Уравнения энергии, движения и неразрывности 80
§ 4.2. Начальные и граничные условия.......88
§ 4.3. Анализ конвективного теплообмена и движения
жидкости методом подобия............................90
Список литературы................................................98
Г л а в а 5. Теплообмен при ламинарном течении жидкости в тру-
бах .............................................................99
§ 5.1. Теплообмен в круглой и плоской трубах при гра-
ничных условиях первого рода.........................99
§ 5.2. Теплообмен в круглой и плоской трубах при гра-
ничных условиях второго рода.........................НО
§ 5.3. Теплообмен и сопротивление в прямоугольных
трубах и продольно обтекаемых пучках стержней . . . 121
§ 5.4. Теплообмен и сопротивление при переменных
свойствах жидкости ................................ 126
Список литературы 138
405
Стр.
Глава 6. Основы полуэмпирической теории турбулентности . . 139
§ 6.1. Краткие сведения о механизме турбулентности 139
§ 6.2. Осредненные уравнения неразрывности, движения
и энергии для турбулентных потоков.................141
§ 6.3. Коэффициенты турбулентного переноса коли-
чества движения и тепла............................146
§ 6.4. Теория пути перемешивания...................152
§ 6.5. Универсальный профиль скорости..............156
§ 6.6. Полуэмпирические уравнения для профиля ско-
рости и коэффициента турбулентного переноса количества
движения...........................................161
Список литературы...............................................164
Глава 7. Теплообмен в круглых трубах при турбулентном тече-
нии жидкости с постоянными физическими свойствами 165
§ 7.1. Стабилизованный теплообмен при постоянной
плотности теплового потока иа стенке. Методы теоре-
тического расчета .................................165
§ 7.2. Стабилизованный теплообмен при постоянной
плотности теплового потока на стенке. Результаты рас-
чета и опытные данные ............................ 173
§ 7.3 Влияние шероховатости на сопротивление и тепло-
отдачу ............................................184
§ 7.4. Влияние нестационаркости на теплоотдачу ..... 189
§ 7.5. Теплообмен в термическом начальном участке при
постоянной плотности теплового потока на стенке . . 190
§ 7.6. Теплообмен при постоянной температуре стенки 195
§ 7.7. Теплообмен в гидродинамическом начальном
участке............................................200
§ 7.8. Теплообмен при переменной по длине плотности
теплового потока на стенке ....................... 205
§ 7.9. Теплообмен при наличии в потоке внутренних ис-
точников тепла.....................................208
Список литературы...............................................214
Г л а в а 8. Теплообмен и сопротивление при турбулентном течении
в трубах жидкости с переменными физическими свойст-
вами ......................................................... 217
§ 8.1. Предварительные замечания...................217
§ 8.2. Метод теоретического расчета................219
§ 8.3. Теплообмен и сопротивление при течении жидкости
с переменной вязкостью.............................222
§ 8.4. Теплообмен и сопротивление при течении газа
с переменными свойствами...........................225
§ 8.5. Теплообмен в однофазной околокритичсской
области........................................... 235
§ 8.6. Теплообмен при течении диссоциирующего газа 242
Список литературы.............................................. 246
Глава 9. Гидродинамика и теплообмен при турбулентном течении
жидкости в каналах некруглого сечения ....................... . 247
§ 9.1. Предварительные замечания...................247
-а' § 9.2. Теплообмен и сопротивление в кольцевых и плос-
ких трубах.......................................247
§ 9.3. Распределение скорости в призматических трубах
и продольно обтекаемых пучках стержней.............258
406
Стр,
§ 9.4. Теплообмен в призматических трубах и продольно
обтекаемых пучках стержней...........................270
§ 9.5. Сопротивление в призматических трубах и про-
дольно обтекаемых пучках стержней....................277
Список литературы............................................... 280
I л а и а 10. Гидродинамика и теплообмен в системах с газообраз-
ными теплоносителями...........................................282
§ 10.1. Особенности газообразных теплоносителей. Ме-
тоды интенсификации теплообмена......................282
§ 10.2. Перепад давления в системах с газообразным
теплоносителем.......................................283
§ 10.3. Теплообмен и сопротивление в ребристых систе-
мах 286
§ 10.4. Гидродинамика и теплообмен в насадках ... . 294
§ 10.5. Гидродинамика и теплообмен в псевдоожижен-
ном слое.............................................298
Список литературы.................................................300
Гл а в а И. Особенности теплообмена в системах с жидкометалли-
ческими теплоносителями........................................ 302 .
§ 11.1. Жидкие металлы как теплоносители............302
§ 11.2. Влияние осевой теплопроводности на среднемас-
совую температуру жидкости...........................304
§ 11.3. Контактное термическое сопротивление . . . 307
§ 11.4. Теплообмен при поперечном обтекании пучков
труб 311
§ 11.5. Теплообмен при свободной конвекции...........312
Список литературы 314
Г л а в а 12. Теплообмен при кипении в большом объеме........315
§ 12.1. Основные понятия.............................315
§ 12.2. Механизм парообразования при пузырьковом ки-
пении ..............................................318
§ 12.3. Теплоотдача при кипении......................330
§ 12.4. Критическая плотность теплового потока , . 338
§ 12.5. Теплообмен при кипении жидкости на оребрен-
ной поверхности...................................342
Список литературы.............................................346
Г л а в а 13. Элементы гидродинамики двухфазного потока 1 . . . 347
§ 13.1. Параметры двухфазного потока..............347
§ 13.2. Режимы течения............................350
§ 13.3. Сведения о структуре двухфазных потоков . 355
§ 13.4. Перепад давления в двухфазном потоке . . . 363
§ 13.5. Критическое истечение двухфазного потока . 371
Список литературы.................................................376
Г л а в а 14. Теплообмен при кипении в трубах.....................377
§ 14.1. Особенности теплообмена при кипении жидкости
в трубах...........................................377
§ 14.2. Механизм образования пузырьков...............379
§ 14.3. Теплоотдача при кипении насыщенной жидкости 381
§ 14.4. Теплоотдача при кипении недогретой жидкости 386
§ 14.5. Кризис теплоотдачи при кипении в трубах . . 388
§ 14.6. Кризис теплоотдачи при киипении воды в про-
дольно омываемых пучках стержней.....................398
§ 14.7. Определение номинальной тепловой нагрузки 400
Список литературы.................................................403
Борис Сергеевич Петухов,
Леонид Григорьевич Генин,
Сергей Алексеевич Ковалев
ТЕПЛООБМЕН В ЯДЕРНЫХ
ЭНЕРГЕТИЧЕСКИХ УСТАНОВКАХ
Редактор О. М. Малявина
Художественный редактор А. Т. Кирьянов
Переплет художника А. И. Шавард
Технический редактор Н. А. Власова
Корректор Е. Д. Рагулина
Сдано в набор 28/Ш-1974 г. Подписано к печати 4/Х-1974 г.
Т-13585 Формат 60X90/16 Бумага типографская № 2
Усл. печ. л. 25,5 Уч.-изд. л. 24,84 Тираж 3230 экз.
Цена 1 р. 10 к. Зак. изд. 69092 Зак. тип. 792
Атомиздат, 103031, Москва, К-31, ул. Жданова, 5.
Московская типография № 4 Союзполнграфпрома
при Государственном комитете Совета Министров СССР
по делам издательств, полиграфии и книжной торговли.
г. Москва, И-41, Б. Переяславская ул., дом 46